МАТЕМАТИКА
АЛГЕБРА. НАЧАЛА
МАТЕМАТИЧЕСКОГО АНАЛИЗА
1.ИН0М
М. И. Шабунин, А. А. Прокофьев
МАТЕМАТИКА
Алгебра.
Начала математического анализа
ПРОФИЛЬНЫЙ УРОВЕНЬ
Учебник для 11 класса

Москва
БИНОМ. Лаборатория знаний
2008
УДК 373.167.1:51(075.3)
ББК 22.1я721.6
Ш12
Шабунин М. И.
Ш12 Математика. Алгебра. Начала математического анализа.
Профильный уровень : учебник для 11 класса / М. И. Шабу-
нин, А. А. Прокофьев. — М. : БИНОМ. Лаборатория знаний,
2008.-384 с. : ил.
ISBN 978-5-94774-453-8
Учебник для 11 класса является частью учебно-методического комплекта
для старших классов школ с углубленным изучением математики. Представле-
ны разделы: тригонометрические, показательная и логарифмическая функции,
производная и ее применение, элементы комбинаторики и теории вероятностей.
Каждый параграф учебника содержит теоретический материал, примеры
с решениями и упражнения для самостоятельной работы.
Для учащихся классов физико-математического и естественно-научных
профилей.
УДК 373.167.1:51(075.3)
ББК 22.1я721.6
Учебное издание
Шабунин Михаил Иванович
Прокофьев Александр Александрович
МАТЕМАТИКА. АЛГЕБРА. НАЧАЛА МАТЕМАТИЧЕСКОГО
АНАЛИЗА. ПРОФИЛЬНЫЙ УРОВЕНЬ
Учебник для 11 класса
Научный редактор И. Маховая
Ведущий редактор М. Стригунова
Методист О. С. Медведева
Художественный редактор С. Инфантэ
Технический редактор О. Лапко
Корректор Е. Клитина
Оригинал-макет подготовлен О. Лапко в пакете ЕТеХ2с
Подписано в печать 11.03.08. Формат 60x90/16.
Гарнитура Литературная. Печать офсетная. Бумага офсетная.
Усл. печ. л. 24. Тираж 5000 экз. Заказ 3022.
«БИНОМ Лаборатория знаний» 125167, Москва, проезд Аэропорта, д. 3
Телефон: (499) 157-5272, e-mail: Lbz@aha.ru, http://www.Lbz.ru
Отпечатано в производственной фирме «Полиграфист»
160001, г. Вологда, ул. Челюскинцев, 3
ISBN 978-5-94774-453-8	© Шабунин М. И.,
Прокофьев А. А., 2008
© БИНОМ. Лаборатория знаний,
2008
ПРЕДИСЛОВИЕ
Данный учебник является второй частью курса «Математика.
Алгебра. Начала математического анализа. Профильный уровень»,
предназначенной для преподавания в 11-х классах в объеме 6 часов
в неделю. Полный комплект материалов по данному курсу включает
учебники для 10-го и 11-го классов, методические пособия и дидак-
тические материалы, соответствующие каждому учебнику, а также
задачник для 10-11 классов.
В главе «Тригонометрические и обратные тригонометрические
функции» изучаются свойства тригонометрических и обратных три-
юнометрических функций, их графики. Содержание главы опирается
на материал глав «Тригонометрические формулы» и «Функции»
учебника для 10-го класса, и готовит основу для следующей главы
настоящего учебника.
В главе «Тригонометрические и уравнения и неравенства» рассмат-
риваются различные типы тригонометрических уравнений (сводящи-
еся к алгебраическим, линейные и однородные, содержащие знаки
модуля и корня, а также параметр) и методы их решений (замены
неизвестных, разложения на множители, метод оценки правой и левой
частей уравнения). Также в этой главе рассмотрены методы реше-
ния простейших тригонометрических неравенств. Особое внимание
уделено отбору корней тригонометрических уравнений. Всего в этой
। лаве разобрано 70 примеров. Такое внимание объясняется тем, что
тригонометрия занимает важное место в школьном курсе математики
и широко представлена в материалах итоговой аттестации (ЕГЭ,
вступительные экзамены в вузы).
В главах «Производная и дифференциал», «Применение произ-
водной» и «Первообразная и интеграл» формулируются правила
дифференцирования, интегрирования и использования элементов
математического анализа для исследования функций и решения
прикладных задач. Все основные утверждения и теоремы этих глав
либо сформулированы (условия интегрируемости функции, формула
Ньютона—Лейбница и др.), либо доказаны (правила дифференциро-
вания, основные формулы для производных элементарных функций,
теорема о дифференцировании сложной функции и др.).
Глава «Дифференциальные уравнения», имеющая прикладную
направленность, знакомит учащихся с общими и частными случаями
решения дифференциальных уравнений первого порядка. Здесь
учащиеся могут ознакомиться с линейными уравнениями второго
порядка с постоянными коэффициентами и способами их решения.
11рикладная направленность этой темы проиллюстрирована рассмот-
рением дифференциальных уравнений гармонических колебаний.
В главе «Системы уравнений и неравенств различных типов»
рассмотрены показательные и логарифмические уравнения, содер-
4
Предисловие
жащие показательные и логарифмические функции с переменным
или зависящим от параметра основанием, сводящиеся, как правило,
к совокупностям и системам уравнений и неравенств. Также в этой
главе рассмотрены методы решений систем уравнений и неравенств
(показательных, логарифмических, тригонометрических, смешанных)
различной степени сложности.
В главе «Уравнения и неравенства с двумя переменными» активно
используется метод графической интерпретации на координатной
плоскости уравнений и неравенств с двумя переменными. При изло-
жении материала рассмотрены различные типы задач от простейших,
связанных с решением линейных уравнений и их систем с двумя
неизвестными, до уравнений нелинейных или содержащих параметр.
В главе «Делимость чисел, целочисленные решения уравнений»
изучаются вопросы делимости целых чисел, методы решения в целых
числах линейных уравнений и сравнений. Приведены и рассмот-
рены примеры нелинейных уравнений. Последний параграф главы
посвящен методам решения текстовых задач, часто встречающихся
в вариантах вступительных экзаменов и основанных на том, что
переменные принимают целочисленные значения.
Главы «Комбинаторика» и «Элементы теории вероятностей» явля-
ются заключительными. Для изучения последней необходимо знание
основных правил и формул комбинаторики, а также методов решения
комбинаторных задач.
В каждой главе учебника представлено достаточное количество
разобранных примеров, помогающих учащимся лучше усвоить теоре-
тический материал и познакомиться с различными методами решений
и доказательств. Кроме этого в каждом параграфе дается необхо-
димое количество задач для самостоятельного решения в порядке
повышения их сложности. Часть примеров и задач взята из вариантов
выпускных экзаменов для классов с углубленным изучением предмета
и вариантов вступительных испытаний в вузы, предъявляющих
повышенные требования к математической подготовке поступающих
(МФТИ, МГУ, СПГУ, НГУ, МВТУ, МИЭТ и др.). Задачи на
повторение, а также вопросы и задания для самоконтроля учащихся,
структурированные по главам, приведены в задачнике.
Начало решения примеров отмечено знаком А, окончание —
знаком ▲, начало доказательства обозначается О, окончание —
знаком •. К задачам, номера которых помечены звездочкой (*),
в ответах даются указания к решению. Начало и конец материала,
носящего факультативный характер, отмечены знаком *. Такой
материал можно использовать в классах, где количество часов,
отведенных на изучение предмета в неделю, больше шести.
М. И. Шабунин,
А. А. Прокофьев.
Глава XI
ТРИГОНОМЕТРИЧЕСКИЕ
И ОБРАТНЫЕ
ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ
Числовые функции, заданные формулами у = sinx, у = cos %,
у = tgx, у = ctgx, где % —величина угла в радианах, называют
соответственно синусом, косинусом, тангенсом и котангенсом.
Под аргументом тригонометрических функций понимается угол,
измеряемый в радианах, или просто число. Обычно для обозначения
угла используется буква /, для числа —буква х.
В гл. V, § 3 были отмечены свойства синуса, косинуса, тангенса
и котангенса угла. Соответственно, отметим, что для тригономет-
рических функций справедливы все выведенные ранее формулы,
и сформулируем основные свойства этих функций.
§1. ФУНКЦИИ СИНУС И КОСИНУС
1.	Функция синус и ее свойства
Областью определения функции синус является множество R всех
действительных чисел . Множеством ее значений является отрезок
| 1; 1], поскольку ординаты точек тригонометрической окружности
принимают все значения от —1 до 1.
Периодичность. Ранее было показано, что числам t и / + 2тг на
тригонометрической окружности соответствует одна и та же точка,
поэтому справедливо равенство sin t — sin(/ + 2тт). Следовательно,
можно утверждать, что число 2тг—один из периодов функции синус.
Теорема. Число 2тг — главный период функции sin/.
О Покажем, что не существует такого положительного числа Т,
меньшего 2тг, что для любого / е К. выполняется равенство
sin/ = sin(Z + Г).	(1)
Предположим противное. Тогда существует такое число Г,
0< Т<2тг, что для любого /eR справедливо равенство (1). Отсюда
для всех действительных чисел t получаем
sin (/ + Г) — sin t = 0 или 2 sin • cos — 0.
6
Глава XI. Тригонометрические функции
(т \	т
- + t\ ^0 для любого t eR, то sin - = 0. Это возможно,
т
если - = тип, п е Z, или Т = 2m, neZ, что не может выполняться
ни для какого Т, 0 < Г < 2тг. Полученное противоречие доказывает,
что 2тг —главный период функции sin Л	•
Отсюда следует, что вычисление значений синуса для любого
аргумента можно свести к вычислению его значений для аргумента,
принадлежащего какому-нибудь отрезку длиной 2тг, например отрезку
[—л; тс]. Кроме того, использование формул приведения позволяет
свести подсчет значений этой функции для любого аргумента^
к вычислению значений синуса на отрезке [0;
Нечетность. Ранее было получено соотношение между синусами
углов t и —t. Считая, что t — число, равное значению угла в радианах,
получаем формулу:
sin(—t) = — sin t для любого feR.
Отсюда следует, что функция sin t — нечетная.
Промежутки монотонности. Докажем, что функция sin t воз-
растает на отрезке [—тртр-
О Пусть t\, принадлежат отрезку [—|] и t\ >t^ Нужно доказать,
что sin >sinf2- Рассмотрим разность sin /i — sin/2 и покажем, что она
положительна. Используя формулу преобразования разности синусов
в произведение, получим
sin t\ — sin t<2 — 2 sin - * ~ *2 • cos *1+ .	(2)
Так как 0 < ~ *2 < и —	< ^, то оба множителя в правой
части равенства (2) положительны и поэтому sin t\ > sin Z2-	•
В силу периодичности можно сделать вывод, что функция sin t яв-
ляется возрастающей на любом промежутке вида [— ^ + 2тш; ? + 2т],
neZ. Аналогично доказывается, что функция sin / убывает на любом
промежутке вида [| + 2т; ~+2т], п е Z.
Непрерывность функции sint Покажем, что функция sinf
непрерывна на всей области определения.
Для этого рассмотрим на тригонометрической окружности две
точки Pt и Pt । /z, полученные из точки Pq поворотом вдоль окружности
hi углы I и I + h соответственно (рис. 1). Из рис. 1 видно,
§ 1. Функции синус и косинус
7
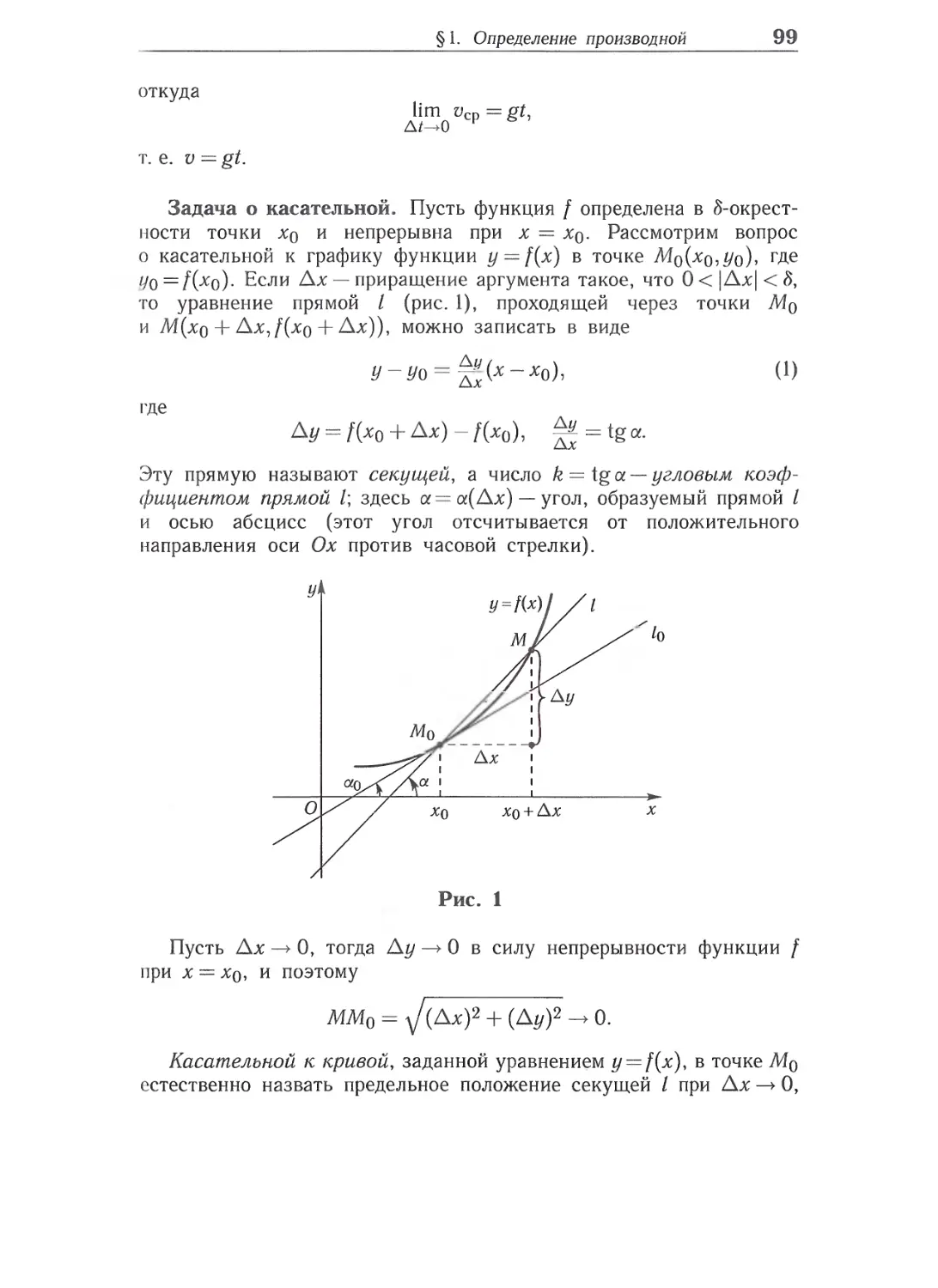
что |sin(/-|-ft) — sin/| — длина катета прямоуголь-
ного треугольника PtKPt+h. Заметим, что
|sin(/ + ti) - sin t\ = KPt+h PtPt+h PtPt+h = \h\-
Отсюда следует, что разность sin(7 + h) — sin t
бесконечно мала при h—>0. Тем самым доказана
непрерывность функции sin/ при любом значе-
нии t.
Отсюда следует, что
lim sin t = sin to при любом /о е R.
t—
Замечание. Проведенные рассуждения дают наглядное представление
о непрерывности синуса. Более строгое доказательство будет приведено в § 4
настоящей главы.
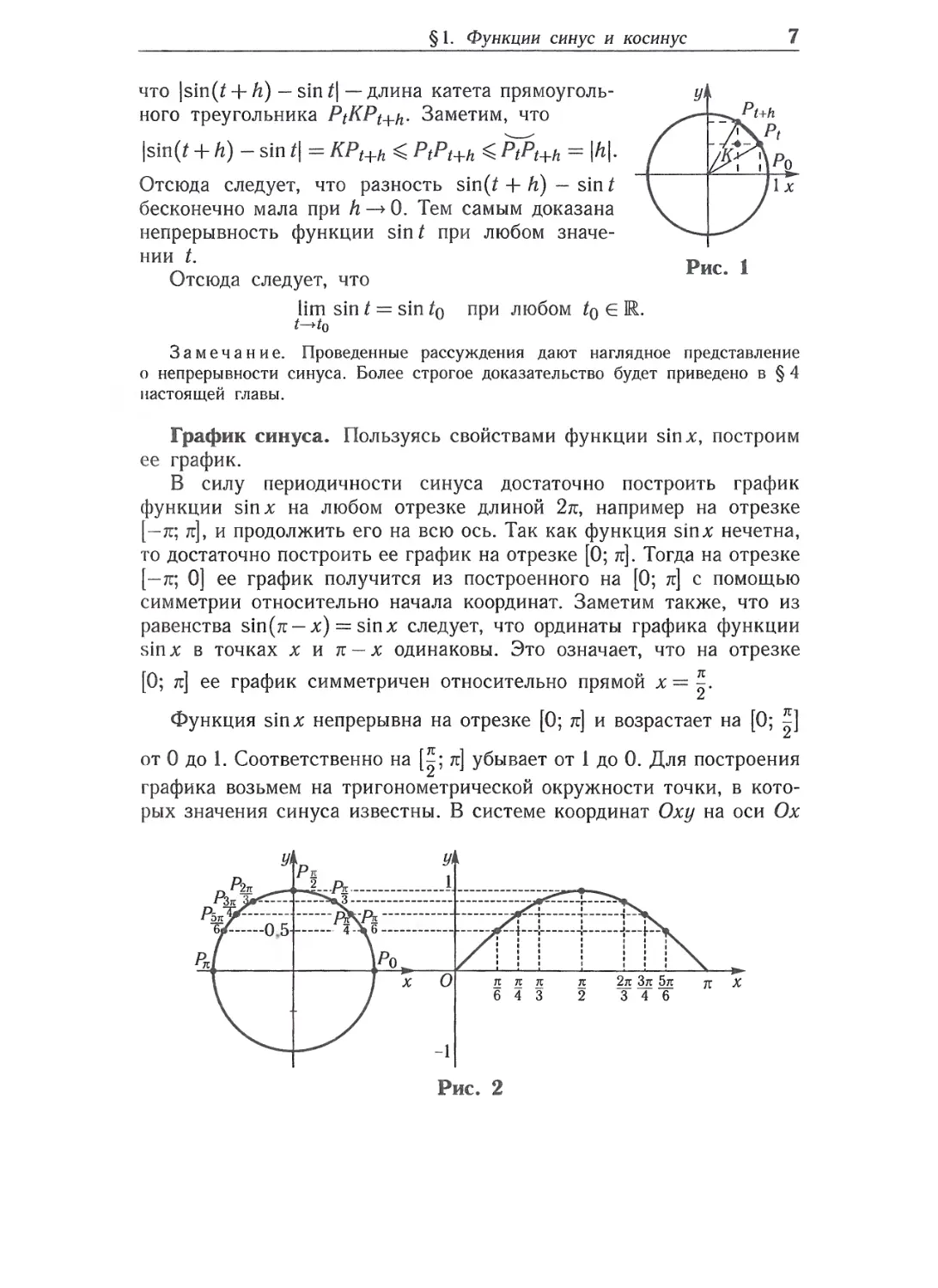
График синуса. Пользуясь свойствами функции sin %, построим
ее график.
В силу периодичности синуса достаточно построить график
функции sinx на любом отрезке длиной 2я, например на отрезке
[—я; я], и продолжить его на всю ось. Так как функция sinx нечетна,
то достаточно построить ее график на отрезке [0; я]. Тогда на отрезке
[—я; 0] ее график получится из построенного на [0; я] с помощью
симметрии относительно начала координат. Заметим также, что из
равенства sin(rc — х) = sinx следует, что ординаты графика функции
sinx в точках х и я —х одинаковы. Это означает, что на отрезке
[0; я] ее график симметричен относительно прямой х=^-
Функция sinx непрерывна на отрезке [0; я] и возрастает на [0;
от 0 до 1. Соответственно на [^; я] убывает от 1 до 0. Для построения
графика возьмем на тригонометрической окружности точки, в кото-
рых значения синуса известны. В системе координат Оху на оси Ох
н
Глава XL Тригонометрические функции
Рис. 3
Рис. 4
на отрезке [0; я] отметим числовые значения соответствующих углов
и на прямых, параллельных оси Оу, отметим точки, ординаты которых
равны значениям синуса (рис. 2). Непрерывная линия, проходящая
через полученные точки, даст эскиз графика функции sinx на [0; я].
В следующей главе будет показано, что полученная кривая образует
в начале координат угол с положительным направлением оси
абсцисс.
Применяя к полученной линии симметрию относительно начала
координат (рис. 3), а затем, продолжая полученный график с перио-
дом 2тг на всю ось, получим график функции z/ = sinx, называемый
синусоидой (рис. 4).
Основные свойства функции у = sin х.
Область определения: множество R всех действительных чисел.
Множество значений: отрезок [—1; 1].
Четность, нечетность: функция является нечетной, т. е. для
любого хе! справедливо равенство sin(—х) = — sinx.
Периодичность: функция периодическая с периодом 2я, т. е. для
любого х е R справедливо равенство sin (% + 2л) = sin х.
Нули: sinx = 0 при х = лп, п G Z.
Промежутки знакопостоянства: sinx>0 при хе(2тт; я+2лп),
/iGZ; sinx < 0 при х е (—л + 2лщ 2пп), я GZ.
Промежутки монотонности: функция у = sin х
возрастает на отрезках [—^4-2лп; ^ + 2лп], п€%;
убывает на отрезках [^+2лп; у + 2яп], п е Z.
Непрерывность: функция z/ = sinx является непрерывной на R.
Экстремумы: функция у = sinx принимает:
наименьшее значение, равное —1, при х=—| + 2тш, п е Z;
наибольшее значение, равное 1, при х=^-\-2пп, п е Z.
Пример 1. Найти область определения и множество значений
функции:
1	// \2	~
1) у = _L-;	2) л/= sin \/(% ) — х2.
7 sinх	7	у \6/
§ 1. Функции синус и косинус
9
I)	Областью определения D(y) функции у= будут все такие
х G R, для которых sinx 0, т. е. х ф тт, n€Z. Так как
—1 sinx 1, то множество значений Е(у) функции у — —~
есть объединение (—ос; —1] U [1; +оо).
2) Областью определения функции у = sin
2
2	2 х
— х2 будут все
такие xeR, для которых
К Y < 71
6	6’
Обозначим t —
2
— х2. При — | < х < ~ получаем
О t При 0 t | функция у — sin/ принимает все
значения из промежутка [0; 0,5], т. е. Е(у) = [0; 0,5].	▲
Пример 2. Исследовать функцию на четность и нечетность:
1)	у = sin (х2 — 2х) ;	2) у = sin (х2 — 2|х|);
3) у = Sin (х3 - 2х);	4) у = sin •
А 1) Для данной функции D(y) = К. Функция у = sin (х2 — 2х) не
является ни четной, ни нечетной, т. е. является функцией
общего вида, так как, например, для х=1 и х = — 1 получаем
//(—1) = sin ((—I)2 — 2(—1)) = sin 3 и
£/(1) = sin (12 — 2^ = sin(—1) = — sin 1,
т. е. £/(—1)	£/(1) и £/( —1)	-£/(1).
2)	В данном случае D(y)—R и для любого xeZ>(£/) справедливо
равенство
£/(—х) = sin ((—х)2 — 2| — х|)) = sin(x2 — 2|х|) = £/(х).
Следовательно, рассматриваемая функция является четной.
3)	Для данной функции D(y) = R и для любого х е D(y)
справедливо равенство
£/(—х) = sin ((—х)3 — 2(—х)) = sin (х3 — 2х)) =
= - sin (х3 — 2х^ =
Следовательно, рассматриваемая функция является нечетной.
10
Глава XL Тригонометрические функции
4)	Заметим, что z/ = sin-—~ — sin х^х- 2^- — sinx при всех х^2,
X £	X £
т. е. D(y) = (—00; 2) U (2; +оо). Так как множество D(y)
не является симметричным относительно начала координат
(x = 2^£)(z/), а х~— 2e£)(z/)), то данная функция не будет ни
четной, ни нечетной, т. е. является функцией общего вида. А
Пример 3. Исследовать функции на периодичность:
1) z/ = sin vCv; 2) у=
А 1) Данная функция не является периодической, так как
£>(z/) = [0; Н-оо). Действительно, если она имеет период
Т ф 0, то для любого х е D(y) должно выполняться условие
х + пТ eD(y\ где neZ. Рассмотрим xq = 0 е D(y), но тогда
и xq — Т= — Т а это неверно, поскольку (—Г) < 0.
2) D(z/)=R. Функция у~ sinx является периодической с главным
периодом Т = 2тг. Следовательно, по свойствам периодической
функции у— sin ~^= также является периодической и ее главный
период равен 2^/2тт.	▲
Замечание. В общем случае, если главный период периодической функции
f(x) равен То, то при а > 0 функция f(ax) будет также периодической с главным
'Г Л)
периодом -у.
Пример 4. Построить графики функций:
1)	у — sin2x; 2) г/= 1,5 sin 2а:;	3) у = 1,5 sin (2х —	.
А 1) График функции у = sin 2х получается из графика функции
z/ = sinx сжатием в два раза вдоль оси Ох (рис. 5).
2)	График функции у— l,5sin2x получается из графика функции
у = sin 2х растяжением в 1,5 раза вдоль оси Оу (рис. 5).
3)	Перепишем исходную функцию в виде
У= 1,5Sin
Ее график получается из графика функции у = sinx по
следующей схеме:
sin х 1—> sin 2х н-> 1,5 sin 2х н-> 1,5 sin

На последнем шаге для графика функции у = 1,5 sin 2х
выполняется сдвиг вправо на расстояние, равное вдоль
о
оси Ох (рис. 5).	▲
§1. Функции синус и косинус
11
Рис. 5
2. Функция косинус и ее свойства
Функция у = cosx определена на всей числовой прямой, яв-
ляется четной и периодической с периодом 2ти. Ее график можно
построить таким же способом, каким был построен график функ-
ции у = sinx. Однако достаточно вспомнить формулу приведения
cosx = sin (х + 0, из которой следует, что график косинуса полу-
чается из графика синуса параллельным переносом влево вдоль оси
Ох на расстояние, равное Поэтому график функции z/ = cosx
(рис. 6) также является синусоидой.
Рис. 6
12
Глава XL Тригонометрические функции
Основные свойства функции у = cos х.
Область определения: множество R всех действительных чисел.
Множество значений: отрезок [—1; 1].
Четность, нечетность: функция у = cosx является четной, т. е.
для любого xeR справедливо равенство cos(—х) = cosx.
Периодичность: функция периодическая с периодом 2ти, т. е. для
любого xeR справедливо равенство cos(x + 2л) — cosx.
Нули: cosx = 0 при х = | + лп, п е Z.
Промежутки знакопостоянства:
cosx > 0 при х €	+ 2лп\ + 2лп^, п eZ;
cosx < 0 при х е Q + 2лп; у + 2лп^, п eZ.
Промежутки монотонности: функция у = cos х
возрастает на отрезках [— л + 2лщ 2лп], и G Z;
убывает на отрезках [2лл; л + 2лп], nEl.
Непрерывность: функция у — cosx является непрерывной на R.
Экстремумы: функция у = cos х принимает:
наименьшее значение, равное —1, при х — л + 2лп, nel]
наибольшее значение, равное 1, при х = 2лп, п е Z.
Пример 5. Найти область определения функции:
1) У = Vcosx-l; 2) у = -—1
2 cosz х — 1
А 1) Выражение у/cosx — 1 имеет смысл для таких значений х,
при которых справедливо неравенство cosx — 1^0. Так как
—1 cosx 1, то неравенство cosx —1^0 равносильно
равенству cosx = l, верному при х = 2лл, neZ. Следовательно,
Z)(z/) — {2лп, п G Z}.
2) Так как 2cos2x — 1 = cos2x, то функция у — -----------
2 cos2 х — 1
определена при всех таких значениях х, что cos 2x^0. Решая
уравнение cos2x = 0, находим + nGZ. Следовательно,
областью определения данной функции являются все значения
+ па.	▲
Пример 6. Найти наибольшее и наименьшее значения функции:
1) у = 6cosx + cos2x; 2) у = cos6х + sin6х.
§1. Функции синус и косинус
13
Л 1) Данная функция определена при всех xeR. По формуле коси-
нуса двойного угла имеем z/ = 6cosx + 2cos2x—1. Используя
замену / = cosx, получаем y = 2t2 + 6t— 1. Так как —
то задача сводится к нахождению наибольшего и наименьшего
значений квадратичной функции f(f) = 2/2 + 6/ — 1 на отрезке
[—1; 1]. Так как абсцисса вершины /в = — | не принадлежит
отрезку [—1; 1], то наибольшее и наименьшее значения дости-
гаются на концах этого отрезка. Имеем /(—1) = 2 — 6— 1 = — 5,
/(1) = 2 + 6 — 1 = 7. Следовательно, унаиб = 7, г/наим = -5.
2)	Данная функция определена при всех х е R. Заметим, что
у = (cos2 х)3 + (sin2 х)3 =
= (cos2 х + sin2 x)(cos4 х — cos2 x sin2 x + sin4 x) =
4	, . 4	2-2
= cos x + sin x — COS X sin X =
— (cos2 x + sin2 x)2 — 3 cos2 x sin2 x — 1 — | sin2 2x.
Так как —1 < sin2x < 1, то 0 < sin22x < 1, а значит,
|	1 - | sin2 2x < 1. Следовательно, //иаим = г/Наиб = 1-	±
Пример 7. Исследовать функцию у — cos х cos (х\/3) на перио-
дичность.
Д £>(у) = R. Допустим, что данная функция имеет период Т ф 0.
Тогда для хо = 0 е /)(z/) и Xq + Т = Т € £>(z/) должно выполняться
условие z/(x0) = z/(T) = 1, т. е.
cos Тcos (тТз) = 1.	(3)
Гак как —1 < cos Т 1 и —1 cos (7\/3) < 1, то равенство (3)
возможно, если
( cos Т = 1,	fcosT=-l,
<А) ( cos (7\/3) = 1 ИЛИ ( cos (Тч/з) = -1.
В случае (А) получаем
J Т = 2тги, п G Z,
[ 7\/3 = 2тг/г, k е Z,
т. е. k = n\/3, и поэтому \/3 = но \/3 — иррациональное число.
В случае (Б) имеем
Г Т = + 2лтг, п Е Z,
[ Тд/З = 71 + 2тг/г, k Е Z,
14
Глава XL Тригонометрические функции
т. е. д/З — •* е Q. Опять получили противоречие. Следовательно,
функция у — cos х cos (хд/З) — непериодическая.	▲
Пример 8. Доказать, что функция у — sin3 х + —
COS2 X COS'5 X
возрастает на интервале (0; ^).
А На интервале (0; р функции sinx и 1 — cosx положительны
и возрастают, а функция cosx положительна и убывает. Следова-
тельно, функции sin3x, —и	положительны и возрастают.
COS2 X COS'5 X
Поэтому возрастает и их сумма, т. е. данная в условии функция. ▲
3. Тригонометрический двучлен a cos х + Ь sin х
В гл. V, § 10 было показано, как, используя метод вспомога-
тельного угла, преобразовать выражение a cosx+ 6 sinx, называемое
тригонометрическим двучленом, к следующему виду:
acosx + ft sin х = \/а2 + b2 sin(x + <j>),
или	_______
a cosx + ftsinx — v a2 + b2 cos(x — epi),
где ср и связаны соотношением cp = — еру При a, b > 0 угол ср
находят из формул:
ср = arcsin = arccos г.......L_„_ = arctg
Пример 9. Найти наибольшее и наименьшее значения функции
z/ = acosx + Z>sinx, если хотя бы одно из чисел а, b не равно нулю.
Л Поскольку
a cos х + b sin х = \/а2 + b2 sin (х + ср),
а — 1 sin (х + ср) 1, то отсюда следует, что наибольшее значение
функции у — acosx + bsinх равно \/а2 + Ь2 и достигается при
значениях х = | — ср + 2тгп, п G Z, а наименьшее значение равно
— \/а2 + Ь2 и достигается при значениях х = — | — ср + 2тт, neZ. ▲
Замечание. Тригонометрические функции широко применяются в ма-
тематике, физике и технике. Например, многие процессы, такие как коле-
бания струны, колебания маятника, напряжение в цепи переменного тока
и т. д., описываются функцией, которая задается формулой у = A sin(wx + ср).
§ 1. Функции синус и косинус
15
I п<ие процессы называют гармоническими колебаниями, а описывающие их
функции — гармониками (от греч. harmonikos — соразмерный). График функции
// -A sin (сох 4- (р) получается из синусоиды у = sin х сжатием или растяжением
се вдоль координатных осей и сдвигом вдоль оси Ох. Обычно гармоническое
колебание у = A sin(cox 4- (р) является функцией времени, где А — амплитуда
колебания, со —частота, <р —начальная фаза, — — период колебания.
(0
Рассмотренный выше пример 9 позволяет сделать вывод о том, что
тригонометрический двучлен у = acosx 4- 6sinx = \/а? -\-№ sin (х 4- <р) задает
некоторое гармоническое колебание с амплитудой \А2 4- Ь2 и начальной фазой (р.
Пример 10. Найти наибольшее и наименьшее значения функции:
1) у = 3cos5х — sin 5х;	2) у = |4cosx + 5sinx|;
3) у — 3sin2x + 4sinxcosx — 2cos2x.
Л 1) Так как a — 3, b= — 1, to c? A-b2 — л/Тб. Следовательно,
у = 3 cos 5x — sin 5x = \/16 cos(5x + <?>), где ср = arccos -y=.
Отсюда получаем, что —л/Ю 3cos5x — sin5x д/ГО, причем
(/наиб
/  1	о	9тгл
уЮ и достигается при х = —arccos -%= 4- п е Z;
5	л/ю	5
//найм = — д/10 и достигается при х = £
| arccos	n G Z.
5 д/io 5
1) Аналогично предыдущему получаем —л/41 4cosx + 5sinx
д/41. Следовательно, наименьшее значение функции
|4cosx 4- 5sinx| равно 0, а наибольшее значение равно %/4Т.
2) По формулам понижения степени и синуса двойного угла
получим:
^ = 3.b^+4.iSin2x-2-l+^ = l-^cos2x + 2sin2x.
Так как \ (—|) + 22 = ^^, to —	cos 2x + 2 sin 2x
у \ X /	£	£	£
< yp-. Отсюда следует, что —уЛ у 1 +	A
Пример 11. При всех значениях параметра р исследовать на
четность и нечетность функцию
у = рcosx4- (1 — р)sinx.
Л Так как D(y) = (—оо; +оо), то для любого xeD(y) в силу четности
косинуса и нечетности синуса имеем
у(—х) = pcos(—х) + (1 — р) sin(—х) =pcosx + (р — 1) sinx.
16
Глава XL Тригонометрические функции
Пусть рассматриваемая функция является четной, т. е. у(—%) = у(х)
для любого х G D(y). Тогда при всех х е R должно выполняться
равенство (1—р) sinx = (р —1) sinx или 2(р — 1)sinx = 0. Последнее
равенство справедливо для всех xeD(y) при р — 1.
Пусть теперь рассматриваемая функция является нечетной, т. е.
р(—х) = — р(х) для любого хеД(р). Тогда при всех ХЕЙ должно
выполняться равенство pcosx = — pcosx, откуда р = 0.
Следовательно, при р = 1 рассматриваемая функция является
четной, при р = 0 — нечетной, при других р — функцией общего
вида.	▲
Задачи
1.	Указать область определения функции:				
	1)	и =	2	•	2)	</ = sin——;	3) X + 71	1! 	 Cin Л/1 	 v2 •	
		1 — sin 2х ’		у — Olli	
	4)	и —	%	5)	у — cos ——;	6) *	х-я	и=Л	x sinx
		cos 0,5х’		cos	
	7)	_ l + sin2x .	у — cos \/sinx; 9)	У = igi	/1 — cosx
		У	? sinx — COSX			V 1 + sinx
Найти		множество значений	функции (2-4):		
2.	1)	у = 4 — 2 sinx;	2) у = 5sin2 | -4;	3)	t,_	3	.
					4 + 3sinx’
	4)	у = sin2 х — 2 sinx;	5) у = sin x + \/— sin2 2x.		
3.	1)	у = 2 4- 3 cosx;	2) у —	2	•	3)	у = 4 cos2 x + 4 cos x;
			3 — 2 cos x ’		
	4)	у — cosx — cos -; 2’	5) у = cos x + \ / — cos2 . V		
4.	1)	4	• 4 у = cos х — sin x;	2) у = cos4 x 4- sin4	x; 3)	у — 3 sin x 4- 4 cos x;
	4)	у — 3 sinx + 2 cosx;	5) у = 3cos2x — 2cosxsinx — sin2x.		
Найти наибольшее и наименьшее значения функции (5-6):
5.	1) у = sin ( 2x4-	) — sin (2х +	;
у 10 у \	5/
2)	у = cos ^4х +	4- cos ^4х +	;
6.	1) у = 2 sin х 4- 3 cos2 х; 2) у =------х— ---------;
.	.	2 sin2 х + sinx 4-1
sin4x + cos4x
О	A	p? •
sin0 x 4- cos0 x
Исследовать функцию на четность и нечетность (7-8):
7. 1) у = sin(x + х3);
4)	у — sin(sinx);
2) г/ = x/sinx;
x + sinx
5)	у =------—;
х — sinx
3) у — |1 + sin х|;
6)	у = sinx +psin2 х, р G Ж.
§ 1. Функции синус и косинус
17
8. 1) у = cos(x4-1);
1 —cosx
4)	у= --------;
1 + cosx
х2 + X
2)	у = cos-------;
* х + 1
5)	у — cos х + sin х;
3) у — cos(sinx);
6)	у — cosx + pcos2x, р е Ж.
9.
Найти точки разрыва и
1) z/ = sin -;
л\	4х2 — 1
4) у — cos———;
7 У 2х+1
2)
5)
промежутки непрерывности
1
у — —;
cosx
_ cos Зх 4- cos 5х.
V sin Зх 4- sin 5х ’
3) У —
6) у =
функции:
1 - - cos х
sin Зх ’
’4	-4
cos*x — sin1 х
10. Вычислить следующие пределы:
1) lim
V__. 7Г
х/2 — 3 cos х
sin Зх ’
2) lim
г_^2тг
3cos4 х 4- sin4 x
3)
lim
• x о
sin-----cos 2x
2__________.
sin 3x 4- cos 6x ’
4) lim .sin2x+cos.2z
x—cos'5 x 4-Ssin*5 x
v_____. 7Г
И. Для каждой из следующих функций указать главный период, если он
существует, или доказать ее непериодичность:
1) у = sin 6х;	2) z/ = sin|;
5
4) ^cos-Ц; 5)f/=-^-;
2х — 1	1 — cos 2х
7) у = cos (х\/3) 4- cos (хх/2) ;
9) у = cos4 х — sin4 х;
их	Зх , п . 9х , 6х	1ОЛ
11) у = cos — 4-2 sin — 4- cos —;	12)
Z	1U	Э
3) у = cos(2x — 1);
6) y — s*n + sin 5x t
cos 3x 4- cos 5x ’
8) у = sin x • sin (x\/2) ;
10) у — cos4 x 4- sin4 x;
2x n . 4x , 6x
z/= cos — — 3sin — + cos —;
13)
. 9
r/ = sin
(<+?)
4- sin2 (x —	4- cos(xx/2).
Построить графики функций
12. 1) у — sinx;
4) У = sin (х - i) ;
7) у = —2 sin тех 4- 2.
13. 1) у = COSX]
4) // — cos ^2x4-	;
14. 1) у = | sin (2x + ^) | i
(12-15):
2)	г/= sin | x |;	3)	у	—	| sinx — 0,51;
5)	у = sin (o,5x 4-;	6)	у	=	sin | x 4-	|;
2)	у = | cosx 4-	0,5	|;	3)	у	=	cos | x 4-	|;
5)	у = 2 cos ^x	— у	—	2.
3) z/ = sin|2x4-
2) у = sin (2|x| + |)
-1
зГ
15. 1)
у = 2 cos \ nx — j 4-1;
2) 1/= 31 cos +x) |
2.
Построить графики функций, предварительно заменив их тождественно равными
(16-17):
16.	1) i/ = cos2^; 2) у = 2 — sin22x; 3) у = sin2 (—!—) 4- cos2 ( —L-
2	\ sinx 7	\sinx>
17.	1) у = cosx4-sinx; 2) у — cosx — \/3sinx.
18
Глава XI. Тригонометрические функции
Построить графики функций (18-20):
18.	2)^=1^;	3)//=Д^.
|cosx|	sinx	sin |х|
19.	1)	у =	cos(—кх) 4- cos 1тех |;	2) у— | sinx — |	sinx 11;
3)	у =	л/1 4- sin 2х;	4) у = у/1 cosx|	—	1;	5)	у =	-yigsinx.
20.	1)	у —	[sin х], где [/] —целая	часть t,	2)	z/ = [cosx].
3)	у =	{sinx}, где {/} —дробная часть	4)	у = {cosx}
Ответы
1.	1) D(y) = К\ {£ + от} 2) D(y) = (-00; -л)и(-л; +оо); 3) D(y) =
= [— 1; 1]; 4) D(y) = Ж\{тс4- 2тсп}, п GZ; 5) D(y) = (—оо; тс) U (тс; 4~оо); 6) D(y) =
=	nGZ; 7) D(y) = R\U +тсп|, п е Z; 8) D(y) = (J Ртгп; тс4-2тш];
9)	D(y) =R\ {-| + 2m, 2тг/е} , n,keZ. 2. 1) Е(у) = [2; 6]; 2) £(z/) = [-4; 1];
3) £(f/) = [|; 3]; 4) E(y) = [-1; 3]; 5) E(y) = {-1, 0, 1}. 3. 1) £(f/) = [-1; 5];
2) E(y) = [0,4; 2]; 3) E(y) = [-1; 8]; 4) E(y) = [~|; 2] ; 5) E(y) = {0}.
4. 1) £(#) = [—1; 1]; 2) £(</) = [0,5; 1]; 3) £(//) = [-5; 5]; 4) E(y) = [-л/13; д/13];
5) E(y) = [1 --\/5; 1 +-\/5] . 5. 1) y/2 и —л/2; 2) 1 и -1.	6. 1) и
8	1
—2; 2) у и -; 3) 2 и 1. 7. 1) Нечетная; 2) общего вида; 3) общего вида;
4) нечетная; 5) четная; 6) функция нечетная при р — 0; общего вида при
р 0. 8. 1) Общего вида; 2) общего вида; 3) четная; 4) четная; 5) общего
вида; 6) четная при всех значениях р. 9. 1) Точка разрыва х = 0; промежутки
непрерывности (—оо; 0) и (0; 4-оо); 2) точки разрыва х — | 4- тсп, п Е Z;
промежутки непрерывности у2—;	+2п^) , п е Z; 3) точки разрыва
х — /г G Z; промежутки непрерывности	 О Y n G Z; 4) точка
3	\ 3	3	/
разрыва х = — промежутки непрерывности (—оо; —0,5) и (—0,5; 4-оо);
5) точки разрыва х= ^4- — и х = 4- ля, n 6 Z; промежутки непрерывности
(—^4-тсп;	4-тспУ (^4-тсп;	4- tc/iY (^4-тсп;	4-тс/?) , f^4-/m;	4-tc/?Y
(уу 4- тсп; уу 4- пп) , п G Z; 6) точки разрыва х = ~ + n EZ; промежутки
непрерывности +	^-%+1)), п G Z. 10. 1) -1; 2) |; 3) 1; 4)
И. 1)	2) Юте; 3) тс; 4) функция непериодическая; 5) тс; 6) тг; 7) функция
о
непериодическая; 8) функция непериодическая; 9) тс; 10) И) 12) 105тс;
13) 7cV2.	16. 1) у= 1 + c°sx;2) // — 3	—-; 3) функция не определена при
х = тсп, n Е Z, и у = 1 при всех остальных х. 17. 1) у = \/2sin(x 4- ^);
2) // = 2cos(x4- 5).
О
§2. Функции тангенс и котангенс
19
§2. ФУНКЦИИ ТАНГЕНС И КОТАНГЕНС
1.	Функция тангенс и ее свойства
Областью определения функции z/ = tgx является множество всех
чисел %, для которых cosx О, т. е. все числа, не равные + от,
п е Z.
Множеством значений функции тангенс является множество R
всех действительных чисел. Докажем это
О Пусть a — произвольное действительное число. Рассмотрим на оси
тангенсов точку Г, которая в системе координат Оху имеет коорди-
наты (1;а), см. рис. 7. В гл. V, §3, п. 1 было показано, что тангенс
угла TOPq равен а. Следовательно, для любого действительного
числа а найдется число t такое, что a = tg/.	•
Докажем, что функция тангенс — нечетная.
О Действительно, ее область определения симметрична относи-
тельно начала координат и для любого t из области определения
справедливо равенство
'	cos(—/)	cos£ 6
Для функции тангенс для любого t из области определения
справедливы равенства:
tg (t + 7Г) = sin(/ + *) =	= tg t.
& v 7 cos(^+tt) — cost &
Отсюда следует, что л—-один из периодов функции тангенс.
Теорема. Число тг — главный период функции tg t.
О Допустим противное, т. е. предположим, что существует такое
положительное число Г, 0 < Т < я, что для любого действительного
числа Л не равного | + от, п е Z, выполняется равенство
tg/ = tg (t+T).
20
Глава XI. Тригонометрические функции
Рассмотрим, например, число t = 0. Тогда из предполагаемого
равенства tgO = tg(O + T) получаем, что tg Т = 0. Это возможно,
если Т = яп, и е Z. Последнее соотношение не может выполняться
ни для какого Т, 0 < Т < л, поэтому л —главный период функции
tg /.	•
Функция tg t непрерывна для всех значений аргумента из области
определения, т. е. функция tg t имеет разрывы только в точках вида
4- яп, п е Z.
О Действительно, так как tg t = а функции sin/ и cos/
непрерывны для всех значений / G R, то функция tg / непрерывна
для всех значений /, при которых cos/y^O, т. е. при всех t^^ + яп,
п G	•
Докажем, что функция у = tg х возрастает на полуинтервале
[°’ 0 '
О Пусть 0 Х[ < %2 < Тогда
О Sin Х[ < sin%2? cosxi > cosx2 > 0.
Следовательно,
tg*l = Вт < S < В? = tg%2’ Т-е-	•
СОо | CC-Jo JO J COS
График тангенса. Функция у = tg х имеет период я и нечетна.
Построение ее графика на интервале	аналогично постро-
ению, описанному в случае синуса. Для определения значений
тангенса в каждой фиксированной точке используется ось тангенсов
(рис. 8).
Отметим, что если х стремится к то sinx стремится к 1, cosx
стремится к 0 и принимает положительные значения, т. е. tgx=
неограниченно возрастает. Аналогично при х, стремящемся к —
tg х неограниченно убывает.
Вследствие тождества
tg х — tg (яп + х), п G Z,
график тангенса на всей области определения получается из графика
на интервале	параллельным переносом вдоль оси Ох (вправо
и влево) на расстояния я. 2я, Зл и т. д. График функции tg х (рис. 9)
называется тангенсоидой.
§2. Функции тангенс и котангенс
21
Основные свойства функции у = tg х.
Область определения', функция у = tg х определена при всех
X 7^ —	Л72, п (Е
Множество значений', множество R всех действительных чисел.
Четность, нечетность', функция г/ —tgx является нечетной, т. е.
для любого х е D(y) справедливо равенство tg (—х) = — tg х.
Периодичность', функция у = tg х периодическая с периодом л,
т. е. для любого х G D(y) справедливо равенство tg (х + л) = tg х.
Нули: tg х = 0 при х — т, п е Z.
Промежутки знакопостоянства: tg х > 0 при х Е (т;	,
neZ; tg х < 0 при х 6	+ т, nnj , и G Z.
22
Глава XL Тригонометрические функции
Промежутки монотонности: функция у = tg х возрастает на
любом промежутке + т; + пи') , neZ.
Непрерывность: функция у = tg х является непрерывной на
промежутках (—^ + тсп; ^ + яп), п е Z.
Экстремумы: нет.
2. Функция котангенс и ее свойства
Областью определения функции у — ctg х является множество
всех чисел х, для которых sinx 0, т. е. все числа %, не равные
та, п е Z. Используя формулу ctgx = — tg Q + х), легко можно
построить график котангенса (рис. 10).
Основные свойства функции у — ctg х.
Область определения: функция у — ctg х определена при всех
х та, п е Z.
Множество значений: множество Е всех действительных чисел.
Четность, нечетность: функция является нечетной, т. е. для
любого х е D{y) справедливо равенство ctg (—х) = — ctg х.
Периодичность: функция периодическая с периодом я, т. е. для
любого х е D(y) справедливо равенство ctg (х + л:) = ctg х.
Нули: ctg х = 0 при х == | + та, п € Z.
Промежутки знакопостоянства: ctg х > 0 при х е (та; + та),
п е Z; ctg х < 0 при хе Q + та; я + та), п е Z.
Промежутки монотонности: функция у = ctg х убывает на
любом промежутке (та; тг+та), п е Z.
Непрерывность: функция у = ctg х является непрерывной на
промежутках (та; лг+та), п е Z.
Экстремумы: нет.
§2. Функции тангенс и котангенс
23
Пример 1. Найти область определения и множество значений
функции:
Ц = tg х 4-ctg х’	2) y=VW^+V^-
Л 1) Заметим, что при всех х^у, п е Z, верно равенство
1	_ 1  sinxcosx _ sin2x
tgx + ctgx	sinx  cosx	sin2 x 4-cos2 x	2
cosx sinx
Следовательно, областью определения функции у =  -----—
tg х 4~ ctg х
будут все х у, п Е Z. Так как данная функция непре-
рывна на каждом промежутке вида	+ у) > п G Z,
0sin2x 1	1 sin2x
< 2 при п четном, и —	- <0 при п нечетном,
то ВД = [-1; о) U (0; 1] .
2) Областью определения функции у = 0g х +- ^/ctg х будут
все такие х € R, для которых tg х 0 и ctg х 0, т. е.
х е (лт?; + лт?), п е Z. Заметим также, что
У =	+ \/ctgx = v/tgx + -Х=.
V 1ь *
Используя замену t = 0g х, получаем у = t + j. Так как
при хе (лл; + лт?), п е Z, множество значений функции
tgx есть (0; +оо), то t также принимает все значения из
(0; 4-оо). В этом случае	как сумма двух взаимно
обратных положительных величин и Е(у) = [2; +оо).	▲
Пример 2. Исследовать на четность и нечетность функцию
Д При всеххеИ справедливо неравенство х2 + 2х + 2 = (х + 1)2 + 10
и, следовательно, 0 < -х— -тс. Заметим, что -х— -----= тс только
х2 4- 2х 4- 2	х2 4- 2х 4- 2
при х = — 1. Поэтому D(y) = (—оо; —1)и(—1; +оо).
В таком случае рассматриваемая функция будет являться функ-
цией общего вида, так как ее область определения не симметрична
относительно начала координат.	▲
24
Глава XL Тригонометрические функции
Пример 3. Найти главный период функции у = ctg х — tg х.
Л Заметим, что при всех х^7^, nel, верно равенство
= ctg х - tg х =	= cos2 * - sin2 х =	= 2 ctg 2х.
sin % cosx sinx cosx sinzx
Учитывая, что главный период функции ctg2x равен заключаем,
что главный период данной в условии функции также равен ▲
Пример 4. Построить график функции у = tg х • | cosx|.
Л Заметим, что при всех х е ^ + 2лл; + п е Z,
|cosx| = cosx и, следовательно, y — tgx-| cosx| = tg х • cosx = sinx. Со-
ответственно, при всех х е Q + 2лл; у + 2тт^, п еZ, | cosx| = — cosx
и, следовательно, у — tg х • | cosx| = — sinx.
На рис. И изображен эскиз графика рассматриваемой функции.
Задачи
1. Указать область определения функции:
1) //= tg 4х;	2) # = tg	;	3) у = ctg(x-1);
xz + 2х + 10
4) у = tg х• ctg 2х;	5) у = lg| tg х - ctg х|.
2, Найти множество значений функции:
1) f/ = tgx+ctgx; 2) y = tg 2 * , ;
xz + 2х + 5
3)	у = 3 tg Зх • ctg Зх;	4)	у =	tg	|х + | - ctg |х - |;
5)	у = tg 2х • ctg х;	6)	у =	tg	4х + 3 ctg 4х.
3.	Исследовать функцию на четность и нечетность:
1)	у = tg(х + 1);	2)	у	= sinx • ctg х;
3)	у = cos х • ctg х;	4)	у	= ctg х + tg х;
(/-------------\ 2
tgxVl + tg2 х \	I	/	-л I
—у,	;	6) j/ = ig ctg (x + -j .
i-0+tg2x;	1	к	471
§2. Функции тангенс и котангенс
25
4.	Вычислить следующие пределы:
2)
3)
.. tg2x + tgx + 2
х^ J 2 + ctg2 х
4)
lim
„ ' я
1>6
lim
tg2 х + 2 .
1 + ctg2 X ’
tg2 X - 2
1 + ctg x + ctg2 X
з
— 3 ctg х ) ;
5.	Для каждой из следующих функций указать главный период, если он
существует, или доказать ее непериодичность:
1) z/ = tg2x;	2)4/ = ctgb	3)}/=-^-;
5	1 - tg2 х
4)l/ = 5tg^-?;	5) У =7^*;	6) у = ctg |х|;
7)	У = 1g | ctg (* +	| •
Построить графики функций (6-8):
6.	1) y = tgx; 2)z/ = tg|3x|;	3)i/ = -tg^;
4)	I/ = tgf|-^.
\ Z О J
7.	1) у = ctg x; 2) у = | ctg x | + 3;	3) у = | ctg x + л/3|;
л\ . Зх+л
4)	}/ = Ctg—.
о
8.	1) t/ = 2-tg(O,5x-^);	2) {/ = 3ctgf3x-^Vl.
\	о/	у 4 /
9.	Построить графики функций, предварительно заменив их тождественно
равными:
1)	У = tg X  ctg х; 2) «/= tg(—х) • ctgx; 3) у = ctg х - tg х;
10.	Построить графики функций:
1)	</= ctg х • | sinx|;	2) z/=^£A;
3)	У = | tgx - 11 - | tgx |;	4) у = tg Q - | 2x - I)
Ответы
1.	1) D(y) = K\{^ + ^}, П e Z; 2) D(y) = (-oo;-4) U (-4;2) U (2;+oo);
3) D(z/)=R\{1 + тел}, neZ; 4) D(z/)=R\{^|, neZ; 5) Z>(f/)=R\{^ ,nezj.
2.	1) E(y) = (-oo; -2] U [2; +oo); 2) E(y) = (0; 1]; 3) E(y) = {3}; 4) E(z/) =
= {-1; 1}; 5) E(y) = (-oo; 0) U (2; +oo); 6) E(y) = (-oo; —2д/3] U [2д/3; +oo) .
3. 1) Общего вида; 2) четная; 3) нечетная; 4) нечетная; 5) четная; 6) нечетная.
4.	1) --L-, 2) 1; 3)	4) -1. 5. 1) f; 2) 5к; 3)	4) 4л; 5) я; 6) функция
V о 1Z О	Z	Z
26
Глава XL Тригонометрические функции
не является периодической; 7) к. 9. 1) Функция не определена при х=~~,
nel, и у — 1 при всех остальных х; 2) функция не определена при х=~,
и z/ = —1 при всех остальных х; 3) z/= 2ctg 2х, х/геZ; 4) z/ = cos2x,
х / + тт, п е Z.
§3. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
1. Функция арксинус
Функция у = sinx является периодической и немонотонной даже
на одном своем периоде (рис. 12). Поэтому при введении обратной для
нее функции следует выделить участок монотонности. Для этой цели
наиболее удобным является отрезок	, на котором функция
у=sinx является возрастающей и устанавливает взаимно однозначное
соответствие между множеством чисел отрезка [ —	оси Ох
и множеством чисел отрезка [—1; 1] оси Оу. Следовательно, функция
у = sinx на отрезке [— является обратимой. Так как отношения
у ~ arcsinx, — 1 х < 1,
и
sin у = х,
тс
2’
к
2

следуют одно из другого, функция у — arcsinx является обратной
к функции z/ = sinx при —
Определение. Арксинусом называется функция у — arcsinх,
определенная на отрезке [—1; 1], обратная функции у = sinx,
;;G fl-
Из данного определения и свойств взаимно обратных функций
(см. § 4, гл. III) следует, что
sin (arcsin х) = х, если |х|	1;	(1)
arcsin (sinх) = х, если — х	(2)
График функции у = arcsinx получается из графика функции
у — sinx с помощью осевой симметрии относительно прямой у — х
(рис. 13).
Свойства функции у — arcsin х.
Область определения: отрезок [—1; 1].
Множество значений: отрезок —
§3. Обратные тригонометрические функции
27
Четность, нечетность', функция у = arcsinx является нечет-
ной, так как область определения симметрична относительно на-
чала координат и для любого х е D(y) справедливо равенство
arcsin(—х) = — arcsinx.
Нули'. arcsinx = О при х = 0.
Промежутки знакопостоянства: arcsinx > 0 при х G (0; 1];
arcsinx<0 при х е [— 1; 0).
Промежутки монотонности', функция z/ = arcsinx возрастает на
всей области определения.
Непрерывность', функция у = arcsinx является непрерывной на
отрезке [—1; 1].
Экстремумы: нет.
Пример 1. Доказать, что функция z/ = arcsinx является нечетной.
Л Область определения функции D(y) = [—1; 1] симметрична отно-
сительно начала координат. Покажем, что
arcsin(-x) = —arcsinx при всех х G [— 1; 1].	(3)
Пусть arcsin(—х) = а. Тогда по определению —	и sina=—х.
Отсюда x = sin(—а). Но |а| = | — а| и, следовательно,
Тогда по определению арксинуса получаем —а = arcsinx, т. е.
а =— arcsinx. С учетом того, что а = arcsin(—х), получаем до-
казываемое равенство (3).	▲
Пример 2. Доказать, что для х е [^; верно равенство
arcsin(sin х) = к — х.
Л Из определения следует, что arcsin (sin х) = х
ТС / к
при
т. е. —| arcsin(sinx)
28
Глава XL Тригонометрические функции
Из неравенства
того, для всех х е
отрезке [^; у
| < х < у следует, что — | < п — х < . Кроме
R справедливо равенство sin(^ — х) — sinx. На
] синус монотонен. Значит,
arcsin(sin х) = arcsin(sin(^ - х)) = л — х.	А
Пример 3. Построить график функции у = sin (arcsinx).
Д Область определения данной функции D(y) — [—1; 1]. В силу
тождества (1) получаем, что на области определения справедливо
равенство
у — sin (arcsinx) = х.
Поэтому графиком данной функции является отрезок прямой у = х
при хе[-1;1] (рис. 14).	▲
Пример 4. Построить график функции у = arcsin (sinx).
Д Функция z/ —arcsin (sin х) — периодическая с периодом 2д. Сле-
довательно, можно сначала построить ее график на каком-нибудь
промежутке длины 2 я, а затем, сдвигая полученную кривую вдоль
оси Ох на 2m (neZ), построить график на всей числовой прямой.
Возьмем отрезок [—у у] . Если хе у
arcsin (sinx) = х.
Если же хе ^у yj , то (см. пример 3)
arcsin(sinx) = л — х.
Учитывая периодичность функции у, строим ее график (рис. 15). ▲
Пример 5. Найти функцию, обратную функции у = /(х) — sin Зх,
я^ х у.
6
Д Имеем Зх е |3я; Зя+|] , откуда Зх —
у = sin Зх = — sin(3x — Зя) = sin(3^ — Зх). Так как Зя — Зх е I —
, то
Далее,
§3. Обратные тригонометрические функции	29
то Зя — Зх = arcsin у. Отсюда х = к — | arcsin у. Это и есть формула
для обратной функции. Таким образом, /-1(х) = л — i arcsin %. А
О
2.	Функция арккосинус
Функция у = cosx на отрезке [0; л] является убывающей (рис. 16) и
устанавливает взаимно однозначное соответствие между множеством
чисел отрезка [0; л] оси Ох и множеством чисел отрезка [— 1; 1]
оси Оу. Следовательно, функция у = cosx на отрезке [0; л] является
обратимой. Так как отношения
у = arccosx, —1 х 1,
и
cos у = х, 0 у л,
следуют одно из другого, то функция у = arccosx является обратной
к функции z/ = cosx при 0 х л.
Определение. Арккосинусом называется функция у — arccosx,
определенная на отрезке [—1; 1], обратная функции у — cosx, хе [0; л].
Из данного определения и свойств взаимно обратных функций
следует, что
cos (arccosx) = х, если |х|	1;	(4)
arccos (cosx) = х, если 0 х л.	(5)
График функции у = arccosx получается из графика функции у = cosx
с помощью осевой симметрии относительно прямой у = х (рис. 17).
Свойства функции у = arccos х.
Область определения*, отрезок [—1;1].
Множество значений*, отрезок [0; л].
Четность, нечетность: у = arccosx — функция общего вида.
30
Глава XL Тригонометрические функции
Нули: arccosx —О при х = 1.
Промежутки знакопостоянства: arccosx > О при х е [— 1; 1).
Промежутки монотонности: функция z/ = arccosx убывает на
всей области определения.
Непрерывность: функция г/= arccosx является непрерывной на
отрезке [—1; 1].
Экстремумы: нет.
Пример 6. Доказать тождество
arcsinx+ arccosx = *, х е [— 1; 1].	(6)
А Докажем тождество, равносильное исходному, а именно:
arcsin х = | — arccos х, х е [— 1; 1].
По определению арккосинуса 0 arccos х я при х е [—1; 1].
Следовательно,
—	arccosx < при х е [—1; 1].
Значит, левая и правая части доказываемого равенства при всех
хе [—1; 1] принадлежат отрезку	. Вычислив синус от обеих
его частей, получим
sin (arcsin х) — х и sin Q — arccos х) = cos (arccos х) = х.
На отрезке	синус — возрастающая функция, т. е. каждое
свое значение принимает ровно в одной точке. Поэтому из последних
соотношений заключаем, что arcsin х = | — arccosx, х е [— 1; 1]. А
Пример 7. Доказать, что функция у = arccosx не является ни
четной, ни нечетной, и что для любого хе [—1; 1] справедливо
равенство
arccos(—х) = я — arccosx.	(7)
А Из тождеств (6) и (3), верных при всех х е [—1; 1], получаем
arccos(—х) = | — arcsin(—х) = | + arcsin х =
—	1 Q — arccosx) = я — arccosx
или
arccos(—х) = я — arccosx.
Это означает, что функция арккосинус — функция общего вида. А
§3. Обратные тригонометрические функции
31
Пример 8. Решить уравнение arccos (	) — 4 л: —2лх.
А В соответствии с определением арккосинуса запишем ограниче-
ния, которым должен удовлетворять х. Имеем следующую систему
неравенств:
' 0 4л: — 2лх тг,
4x4-7
Г 1,5	2,
|-1,1	1,5
<=> х ~ 1,5.
Получили единственное значение х — 1,5. Подставив это значение
в данное уравнение, проверим является ли оно его решением.
Получаем
arccos (	= 4л: - 2тг • 1,5
\ 4 -1,5 4-7 /
или arccos(—1) = л:— верно.
Следовательно, данное уравнение имеет единственное решение
х = 1,5.	А
3.	Функция арктангенс
Функция у = tg х на интервале	является возрастающей
(рис. 18) и устанавливает взаимно однозначное соответствие между
множеством чисел интервала (—^5 0 оси Ох и множеством чисел
оси Оу. Следовательно, функция у = tg х на интервале 0
является обратимой. Так как отношения
у = arctgx, xgR,
и
* = tg у.
следуют одно из другого, то функция у = arctg х является обратной
к функции у = tg х при < х <
Определение. Арктангенсом называется функция у = arctgх,
определенная на множестве R, обратная функции у = tg х,
V 2’ 2/
Из данного определения и свойств взаимно обратных функций
следует, что
tg (arctg х)= х для любого х е К;	(8)
arctg (tg х) = х, если - < х <	(9)
32
Глава XL Тригонометрические функции
Рис. 19
График функции у = arctg х получается из графика функции
у = tg х с помощью осевой симметрии относительно прямой у — х
(рис. 19).
Свойства функции у = arctg х.
Область определения: множество Ж всех действительных чисел.
Множество значений: интервал	•
Четность, нечетность: функция у = arctg х является нечетной,
так как ее область определения симметрична относительно начала
координат и для любого х € R справедливо равенство
arctg (—х) = — arctg х.	(10)
Нули: arctg х = 0 при х — 0.
Промежутки знакопостоянства:
arctg х > 0 при х € (0; +оо);
arctg х < 0 при х е (—оо; 0).
Промежутки монотонности: функция у — arctg х возрастает на
множестве R.
Непрерывность: функция у = arctg х является непрерывной на R.
Экстремумы: нет.
4.	Функция арккотангенс
Функция у = ctg х на интервале (0; я) является убывающей
(рис. 20) и устанавливает взаимно однозначное соответствие между
множеством чисел в интервале (0; я) оси Ох и множеством чисел оси
Оу. Следовательно, функция у = ctg х на интервале (0; я) является
обратимой. Так как отношения
у — arcctg х, х е R,
и
х = ctg //, 0 < у < я,
§3. Обратные тригонометрические функции
33
следуют одно из другого, то функция у = arctg х является обратной
К функции у = ctg X При 0 < X < 7Г.
Определение. Арккотангенсом называется функция у =
= arcctg х, определенная на множестве R, обратная функции у = ctg х,
х G (0; тг).
Из данного определения и свойств взаимно обратных функций
следует, что
ctg (arcctg %) = х для любого х е R;	(11)
arcctg(ctg %) = х, если 0<х<ти.	(12)
График функции у = arcctg х получается из графика функции
у = ctg х с помощью осевой симметрии относительно прямой у = х
(рис. 21).
Свойства функции у = arcctg х.
Область определения: множество R всех действительных чисел.
Множество значений: интервал (0; тг).
Четность, нечетность: функция не является ни четной, ни
нечетной, и для любого х € R справедливо соотношение
arcctg (—х) = л: — arcctg х.	(13)
Нули: нет.
Промежутки знакопостоянства:
arcctg х > 0 при х е R.
Промежутки монотонности: функция убывает на всей области
определения.
Непрерывность: функция у = arcctg х является непрерывной на R.
Экстремумы: нет.
Легко доказать, что функции arctg х и arcctg х связаны формулой
arctg х + arcctg х = | при всех х е R.	(14)
2—3022
34
Глава XL Тригонометрические функции
Функции у = arcsinx, у = arccosх, у = arctg х, у — arcctg х
называются обратными тригонометрическими функциями или
аркфункциями.
Пример 9. Решить уравнение
arccosх — arcsinx = | (arctg х2 + arcctg х2) .
Л Используя тождество arctg х2 + arcctg х2 = верное при всех
xeR, а также тождество arcsinx + arccosх = справедливое при
х € [—1; 1], получим
arccos х — ( £ — arccos х) = или arccos х =
\2	/	6	3
Отсюда х = cos $ = L	А
О Z
Пример 10. Доказать, что
arcsin х + arcsin у = arccos ^д/1 — х2^/1 — z/2 — ху^ ,
О х 1, 0 у < 1.
А Так как 0 arcsinx и 0^ arcsin у то значения левой
2	J 2
части доказываемого равенства принадлежат отрезку [0; я]. Значения
правой части доказываемого равенства также принадлежат отрезку
[0; я].
Вычислим значение функции косинус, монотонной на [0; я], от
левой и правой частей равенства:
cos (arcsin х + arcsin у) — cos(arcsin х) cos(arcsin у) —
— sin(arcsin х) sin(arcsin у) — \/1 — х2^/'1 ~ У2 ~ ХУ-
Соответственно,
cos ^arccos ^а/1 ~х2^/1 — z/2 — xy^j = \/1 — х2— г/2 — ху.
Получили, что эти значения равны. В силу монотонности косинуса
получаем, что доказываемая формула верна.	▲
*5. Соотношения между аркфункциями
Ранее (см. пп.2, 4) были доказаны тождества (6) и (13),
связывающие между собой arcsinx и arccosх, а также arctg х и
§3. Обратные тригонометрические функции
35
iicctgx. В §11, гл. V с использованием метода вспомогательного
। реугольника были получены следующие цепочки формул:
arcsin х = arccos \/1 — я2 = arctg ?	= arcctg ^~Х ,	(15)
VxG (0; 1);
arctg х = arcctg - = arcsin.= arccos . 1 . ,	(16)
*	a/1+x2	х/йх2’
Vx G (0; +oo).
Используя эти формулы, легко, например, доказать, что
{arccos - я2, * 6 [0; 1],
Л-----9	г 1 Л1	(17)
— arccos V1 — %2, хе | — 1; 0];
f arcsin д/1 — *2, х е [0: 1L	, ч
arccosx =< _	,----- г п	(18)
4-	arccos \/1 — х2, хе [-1; 0].
Задачи
1.	Найти область определения функции:
1)	у = arcsin(3 — х2);	2) у = arcsin(0,5х — 1) 4- arccos(l — 0,5х);
/тг	л/9 — х2
3)	у = \ 7 ~ arctg 2х’ У = arcctg -== ;	5) у = arcsin (tgx).
V 4	у х2 — 4
2.	Определить, какие из функций являются четными, какие нечетными и какие
являются функциями общего вида:
1)	г/= arcsinx2;	2) у = 4arccos(-x);	3) у = arccos(cosx);
4)	у = cos(arccosx);	5) у = arccos |х|;	6) у = | arctg х|.
Решить уравнения (3-5):
л2
3.	1)	а)	2 arcsin2 х — 7 arcsin х 4-3 = 0;	б)	2 arcsin2 х — лarcsin х+	—	= 0;
2)	a)	arcsin(x2 — 4х + 2) = — |;	б)	arcsin(x2 — Зх + 0,5)	=
3)	a)	arccos2х — — arccosх+ = 0;	б)	2arccosx = J 4--—--;
4	8	3	9 arccosx
4)	а)	3 arccos(x2 4- 4х — 1) = л;	б)	arccos ~ — 2;
5)	a)	arctg2 (Зх 4- 2) + 2 arctg (Зх 4- 2) =	0;
б)	arcctg2 х 4- arcctg х -	— 0;
6)	а)	4 arctg (х2 - Зх - з") = л;	б)	arcctg * + 3
\	/	Зх — 1 о
4. 1)
arcsin
Зх +11 \
х + 5 )
лх
--7Г-у
। Зх 4“ 4 \	г.
2) arccos -----— Н= лх 4- 6л
\ 1 — 2х /
36
Глава XL Тригонометрические функции
5.
1)
2)
3)
4)
arccos (2х3 + Зх2 — 2) = arccos (2х2 + х — 2
arcsin (Зх3 — х2 +	= arcsin ^2х 4-
/ 9	1
arccos х + х + -7=
к	у/2
( 9	1
= arcsin х 4x4—т=
\	>/2
arccosx — arcsinx = arccos —

6.	Построить графики функций:
1)	у = arccos(cosx);	2) у — cos(arccosx);	3) у — arctg(tg х);
4)	у — tg(arctg х);	5) у = arcctg(ctg х);	6) у = ctg(arcctg х).
7.	Доказать равенства:
1)	arcsin х — arcsin у = arcsin (х\/1 — у2 — уу/\ — х2), O^x^l, 0 у 1;
2)	arccosх 4- arccosу = arccos (xz/ — \/1 — *2 д/1 ~У2^у O^x^l, 0^//^1;
3)	arccosx — arccos//= arcsin ^г/л/1 — *2 — хд/1 — //2), O^x^l, O^z/^1;
4)	arctg x + arctg y = arctg , x>0, //>0;
5)	arcctg x4- arcctg y = arcctg——x>0, //>0.
8.	Решить уравнения:
1)	arcsin 6x 4- arcsin 6\/3x =
3)	arcsin x 4- arccos(x — 1) = .
5)	arcsin x = arccos — x2;
7)	arcsin (sinx) = 5л: — x.
9.	Найти обратные функции к
1)	у — 1 + sinx, х е — J
2 2
Г з
3) у = sinx + cosx, х Е —
10? Построить графики функций:
1) у = cos(2 arccos х);
3) у = arcctg х 4- arcctg i;
5) у = arccos(cosх) 4- arcsin(sinх);
1-х2
7) у — arcsin----
14-х2
11. Решить неравенства:
1) arcsinx ^5;	2) arctg2
3) arcsinx arccosx;	4) tg2 (ar
5) arcsinx < arccos2x.
2) 2arctg(2x4-1) = arccosx;
:;	4) arcsin2x = 3arcsinx;
6) 2 arctgx = arcsin 9;
1 + x2
заданным и построить их графики:
2) у — arcsin л/1 — х2, хЕ [-1; 0];
2) // = tg(2 arctg х);
4) у = arccos(cosx) — х;
1-х2
6) у = arccos-----;
1 4-
— 4 arctg х 4- 3 > 0;
>inx) 1;
§4. Первый замечательный предел
37
Ответы
I 1) D(y) = [-2; -у/2] и [л/2; 2] ; 2) £>((/) = [0; 4]; 3) £>(#) = (-оо; 0,5];
I) D(y) = [-3; —2) U (2; 3]; 5) D(y) = U [-£ + тот; £ + тот|. 2. 1) Четная;
пег 14	4 j
’) общего вида; 3) четная; 4) нечетная; 5) четная; 6) четная. 3. 1) a) sin i;
>) ‘ и 2) а) 1 и 3; б) 0 и 3; 3) а) 0 и б) 0,5; 4) а)	б)
5)	а) б) 1; 6) а) -1 и 4; б) 5^3±6. 4. 1) -3; 2) -5. 5. 1) -1 и 0,5;
2) и 0; 3) -1 и 0; 4) 0,5. 8. 1)	2) 0; 3) 0; 1; 4) 0;	5) O^x^l;
6)	-1 < х < 1; 7) |тг < х < утг. 9. 1) у = arcsin(x - 1), х е [0; 2]; 2) у =
— cosx, хе ^0;	; 3) у = arcsin “ р х^ 1~^; л/2]. Ю- 0 Указание.
// 2х2 — 1,х€[— 1; 1]; 2) Указание. 2х 2, х^±1; 3) Указание. у=^,х>
0; у=^,х<0- 4) Указание у =
х < (2/г 4- 1)тс,
—2% 4- 2/гтг, (2/г 4- 1) лг < х (2Z? 4- 2) зт,
/• € Z; 5) Указание. Период функции равен 2тс. На отрезке [—я; я] получим
—2х — тс, —тс С х
О, -^х<0,
2х, 0О< тр
6) Указание, у = 2arctg|x|; 7) Указа-
и ие. у =	— 2arctg|x|. 11. 1) — 1	х 1; 2) х < tg 1; 3) — 1 х
§4. ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
Целью настоящего параграфа является
установление равенства lim = Для этого
х—>о х
сформулируем и докажем несколько утвержде-
ний.
Утверждение 1. Если хе	и
х ф 0, то
COSX < —— < 1.	(1)
О Рассмотрим на координатной плоскости
круг единичного радиуса с центром в точке О
(рис. 22). Пусть АЛОВ = х, где 0 < х <
Пусть С —про-
екция точки В на ось Ox, D — точка пересечения луча ОВ
38
Глава XI. Тригонометрические функции
и прямой, проведенной через точку А перпендикулярно оси
Ох. Тогда ВС = sinx, DA = tgx. Пусть Si, S2, S3 — площади
треугольника АОВ, сектора АОВ и треугольника AOD соответ-
ственно. Тогда
= ~(ОА)% sinx = i sinx,
S3=i-OA.DA=1-tgx.
Так как Si < S2 < S3, то
i sinx < хХ < х tgx.
2	2	2 s
Если xG (О; to sinx>0, и поэтому неравенство (2) равносильно
неравенству
(2)
1 < х < *
sinx cosx’
выполняется неравенство (1). Так
откуда следует, что при х
как и cosx —четные функции, то неравенство (1) справедливо
и при х е о).	•
Утверждение 2. Для всех х е R справедливо неравенство
| sin х| < |х|.	(3)
О Неравенство (3) выполняется при х = 0. Пусть ху^О. Тогда если
х е
то из (1) следует неравенство < 1? равносильное
неравенству (3). Так как — четная функция, то неравенство (3)
справедливо и при хЕ рО)- Итак, неравенство (3) выполняется,
если |х| < Пусть |х| тогда неравенство (3) справедливо, так
как | sin х| 1, а > 1.	•
Утверждение 3. Функции у = sinx и у = cosx непрерывны
на множестве R.
О Пусть xq — произвольная точка множества R. Тогда
. х — х0 х + х0
Sin X — Sin Xq = 2 Sin —-— COS
_	X - Xq
Так как sin —-—
2 '
в силу неравенства (3), a cos ——
то | sinx — sinхо|	|х — Xq|, откуда следует, что функция у = sinx
непрерывна в точке xq.
X — Xq
2
1,
§4. Первый замечательный предел
39
Аналогично, имеем
0 х + Xq . Xq X
COS X — COS Xq = 2 sin —-— sin —-—,
откуда |cosx —cosxq| |x —xq| и поэтому функция cosx непрерывна
в точке xq.	•
Из непрерывности синуса и косинуса следует, что функция
Igx = непрерывна, если cosx 0, т. е. х - + m (n е Z),
COS JC	2
а функция ctgx=|^ непрерывна, если хфт (n € Z).
Утверждение 4. Если х —> 0. mo —-	1, т. е.
X
lim = 1.	(4)
%->о *
О Воспользуемся неравенством (1). В силу непрерывности косинуса
lim cosx = cos0 — 1.
х—>0
Переходя в соотношении (1) к пределу при х •—> 0, получаем
равенство (4).	•
Предел lim = 1 принято называть первым замечательным
х—>0 х
пределом.
Замечание 1.	Пусть а/З^О, тогда
lim ™	«	(5)
х->0 sin/Зх	р
О Так	как	= sina*	•	то из	(4) следует равенство (5).	•
sin/k ax	sin рх p	J r
Замечание 2. При доказательстве утверждения (5) была использована
теорема о замене переменной при вычислении предела (гл. IX, § 3, теорема 4).
Пример 1. Вычислить пределы:
1) |.m COSX-COS3X; 2) lim tgx-sinx
%—>0 1 — cos 6х	х—>0 sin0 4х
А
1) Так как cosх ~ cos%х — % s*n ' s*n% — s*n2x sinx
1 — cos 6x
формулу (5), находим,
2) Из равенства
--------------------Т0, используя
2 sin* 1 2 Зх sin Зх sin Зх
2
что искомый предел равен -
tgx — sinx _ sinx
sin3 2x sin3 2x
2 sinx • sin2 (0
cos x • sin3 2x
/	• x \ 2
Л / .	\	/ sin - \
2 f sinx \ /	2	i
cosx \sin2x/ I sin2x /
40	Глава XL Тригонометрические функции
применив формулу (5) и используя непрерывность косинуса
(lim cosx = l), находим, что искомый предел равен
х—>0
Задачи
1.	Доказать, что tgx>x при хе
х2
2.	Доказать, что для всех xeR справедливо неравенство 1 —cosx^ —.
3.	Вычислить пределы:
1)	hm 1-см4х	2) |im cos3x-cos5x
х—>0 sin25x	х—0 cosx-cos3x
3)	lim	4) lim 1-COSXCOS3X
x—>o 1 + sin 2x — cos 2x	x—>0	1 —cosx
Ответы
3. 1) A; 2) 2; 3) 1; 4) 10.
Глава XII
ТРИГОНОМЕТРИЧЕСКИЕ
УРАВНЕНИЯ И НЕРАВЕНСТВА
§ 1. ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
1. Уравнение sinx = а
Рассмотрим уравнение
sinx = &.	(1)
Гак как множество значений синуса — отрезок [—1; 1], то уравнение (1)
имеет корни только при — 1 а 1.
Приведем сначала формулы корней уравнения (1) при а = 0, а = 1
и а — —1.
Таблица 1
sinx = 0	х = тт, n G Z
sinx = 1	x — | + 2лп, n G Z
sinx = —1	x = — | + 2лгс, n G Z
Пусть ае(—1; 1) и а^О. Тогда на отрезке	уравнение (1)
имеет единственный корень
xi = arcsin а (гл.У, § 11).
Замечание. Напомним, что арксинусом числа а (обозначается arcsinа),
те |а|	1, называется такое число ае
, синус которого равен а, т. е.
71	.	^71
- < arcsin а <
2	2
sin(arcsina) = а.
Так как график функции у = sinx симметричен относительно
прямой х=| (см. рис. 1), то на отрезке [тру] уравнение sinx = а
также имеет только один корень х% = л — xi = к — arcsin а.
На рис. 1 рассматривается случай, когда 0 < а < 1.
Таким образом, на отрезке у] длиной 2л уравнение sinx = а,
где |а|	1, имеет два корня х — arcsin я и х = тс — arcsin я (при а — 1
они совпадают).
Так как функция sin х — периодическая с периодом 2л, то все
корни уравнения sin х = а получаются прибавлением к найденным
42
Глава XII. Тригонометрические уравнения и неравенства
значениям и х% чисел 2л, —2л, 4л, —4л и т. д. (см. рис. 1), т. е.
все корни уравнения (1) находятся по формулам: х = arcsin a + 2л&,
х = л — arcsin a + 2л&, k е Z.
Эти две формулы можно объединить в одну:
х = (—1)п arcsin бг + tczz, п е Z.	(2)
О В самом деле, если п — четное число, т.е. n = 2k, то из формулы (2)
получаем arcsinя+ 2л&, а если /г —нечетное число, т.е. п = 2/г + 1,
то из формулы (2) имеем
— arcsin a + (2k + 1) л = л — arcsin a + 2nk.	•
Отметим, что, в частности, из формулы (2) при a = 0, a = 1,
a — — 1 получаются формулы предыдущей таблицы. Так как эти случаи
часто встречаются при решении задач, то полезно помнить формулы
приведенной выше табл. 1 и пользоваться ими, а не формулой (2).
Пример 1. Решить уравнение:
1) sinx=|;	2) sinx = —	3) sinx — v^+-1;
z	z	о
4)	sinx — v^+1;	5) sin2x = —1;	6) cos24x=l.
A 1) По формуле (2) получаем
x = (—1)” arcsin + nn = (—1)"| + im, neZ.
2) Так как arcsin (—= —arcsin	to
\ Z / x = (-1)"	+nn 3) Заметим, что 0 <	< - находим корни уравнения: х ~ (—1)п arcsin 4) Так как \/Гб > 3, то	—1 7	4 имеет корней.	Z	о = (-l)"+1£ + wi, neZ. О = 1. Поэтому по формуле (2) □ ^|+1 + пп, пе Z. э > 1. В этом случае уравнение не
§ 1. Простейшие тригонометрические уравнения
43
5)	По табл. 1 находим корни:
2х = — | + 2тилг, откуда х = — ~ 4- тт, и € Z.
6)	Уравнение cos2 4х = 1 равносильно уравнению sin 4х = 0. По
табл 1 находим корни этого уравнения:
4х = ли, х=^, neZ.	А
4
2. Уравнение cosx = я
Рассмотрим уравнение
cosx = a.
(3)
Как и уравнение (1), уравнение (3) имеет корни в том и только
в том случае, когда |а|	1.
В приведенной ниже таблице содержатся корни уравнения (3)
при a = 0, a = 1 и a = — 1.
Таблица 2
cos я = 0	х = | 4- Tin, n ez
cosx = 1	x = 2тт, nel
cosx = —1	x = я+2яп, n E Z
Пусть « — любое число такое, что — 1 < а < 1 и а ф 0. Тогда на
отрезке О^х^л уравнение (3) имеет единственный корень
Xi = arccos а.
Замечание. Понятие арккосинуса числа было введено в гл. V, §11.
Арккосинусом числа а, где |а|	1 (обозначается arccos а), называется такое
число из отрезка [0, л], косинус которого равен а, т. е.
0 arccos а тс, cos(arccosa) = а.
Так как функция у = cosx — четная, то ее график симметричен
относительно оси ординат. Поэтому уравнение cosx = «, где — 1 <а< 1
и на отрезке [—ти;0] также имеет только один корень Х2 такой,
что Х2 = —Xi = — arccos а.
На рис. 2 представлен случай, когда 0 < а < 1.
Таким образом, на отрезке [—тг; тг] длиной 2тг уравнение cosx = я,
где |«|	1, имеет два корня (при а = 1 они совпадают): х\ =arccos«
и Х2 = - arccos а.
Так как функция cosx — периодическая с периодом 2 л, то все
корни уравнения cosx = «, где |«| ^ 1, получаются прибавлением
к найденным значениям х\ и х<2 чисел 2л, —2л, 4л, —4л и т. д. (см.
44
Глава XII. Тригонометрические уравнения и неравенства
рис. 2), т. е. все корни находятся по формулам х\ = arccos а + 2m,
%2 — — arccosa + 2m, nel
Эти две формулы можно объединить в одну:
х = ± arccos а + 2m, neL	(4)
Пример 2. Решить уравнение:
1) cosx = ^;	2) cosx = —3) cosx=^±-^;
4) cosx =	5) cos4x = —1;	6) cos42x — sin42x = 1.
A 1) Применяя формулу (4), получаем
x = ± arccos + 2m =	+ 2zm, n e Z.
2	6
2)	Так как arccos 0 = у, то по формуле (4) находим корни
уравнения:
х = ±у + 2ял, п G Z.
3)	Уравнение не имеет корней, так как > 1.
4)	Поскольку 0 <	< ц уравнение имеет корни, определя-
емые формулой (4):
х = ± arccos + 2тггг, п е Z.
5)	По табл. 2 находим корни уравнения:
4% = 7г+ 2m, х = ^-\-^, п G Z.
4	2
6)	Так как cos42x — sin42x = cos22x — sin22x = cos4x, то исходное
уравнение равносильно уравнению cos4x = l, откуда, используя
табл. 2, находим его корни:
4х = 2m, х=™, neZ.	А
§1. Простейшие тригонометрические уравнения
45
3	. Уравнения tgx = a и ctgx = a
Рассмотрим уравнение
tgx = a.	(5)
При любом действительном значении а это уравнение на интер-
вале 0 имеет единственный действительный корень Х[ — arctga
(гл. V, §11)
Так как функция tgx — периодическая с периодом я, то все корни
уравнения (5) находятся по формуле
х = arctgа + лтг, п е Z.	(6)
Рассмотрим уравнение
ctgx = a.	(7)
11ри любом действительном значении а это уравнение на интервале
(0; тг) имеет единственный действительный корень %i = arcctga (гл. V,
§П).
Так как функция ctgх — периодическая с периодом я, то все
корни уравнения (7) находятся по формуле
х = arcctg a + лпч nel	(8)
При a = 0 корни уравнения (7) имеют вид %	| 4- ям; п е Z.
Если а ф 0, то уравнение (7) равносильно уравнению tgx = ~,
и поэтому корнями уравнения (7) при а 0 являются числа
х — arctg 4- ям, и е Z.
Пример 3. Решить уравнение:
1)	tgx = l; 2) tgx = —5;	3) ctgx = --J=;
4)	(tgx + 2)(ctgx — \/3) = 0.
A 1) Так как arctg 1 = ^, то по формуле (6) находим корни уравнения:
х — + яп, nd
4
2)	Применяя формулу (6), получаем
х = arctg(—5) 4- ям, где arctg(—5) = — arctg 5.
Следовательно, х = — arctg 5 4- ям, п е Z.
3)	Так как ctgx^O, то исходное уравнение равносильно урав-
нению tgx = —д/З, откуда
х — arctg(—л/3) 4- кп — — arctg д/З + m = — | + ям, п е Z.
46	Глава XII. Тригонометрические уравнения и неравенства
4)	Решив уравнения tgx = — 2 и ctg% = х/З, найдем их корни
х = — arctg 2 + лл, х = | + пп, п е Z. Найденные значения х
являются корнями исходного уравнения, так как левая часть
уравнения определена при этих значениях х и обращается
в нуль. В этом случае исходное уравнение равносильно
совокупности уравнений tgx = — 2 и tgx=-L.	▲
v 3
Задачи
Решить уравнение (1-3):
1.
2.
3.
1) sin3x = —1;
4) 16sin4x=l;
1) cos3x = -1;
4) 4 cos4 2% = 1;
6) 2 sin 5xsin 3% = 1
2) sin2x-sin4x = O;
5) sin x sin 2x cos x = |.
2) 1 — 2 sin2 2x = 2 cos 4%;
5) 1 + 3 cos 2x = 2 sin2 x\
2	cos 5x • cos 3x.
3)	sin 2% = 2 sin2 2x;
3)	2 cos4 x = 2sin4x — 1;
1) tg3x = 3tgx; 2) 16tg4x=l;	3) 8tg3x + l = O;
4)	27 tg3 x — 8 = 0.
Ответы
1.	1) x = -% + 2тт, n 6 Z; 2) x = ф, n 6 Z; 3) x = x = (-1)"£ 4-
n 6 Z; 4) x = ±J + zm, n 6 Z; 5) x = ±^ + ^, nGZ. 2. 1) x — 7г4-2тш, n€Z;
b	12 Z
2)	x=g + -^, zzGZ; 3) x = ±£ + ™, zzeZ; 4) x=£ + ^, neZ; 5) x=£ + ^,
о 4	о	о 4	4	2
rc€Z; 6) x = ±-j^ + ^, zzeZ. 3. 1) x=-^, neZ; 2) x = ± arctg + zm, zzGZ;
1	2
3)	x = — arctg+ zrn, n e Z; 4) x = arctg ~ + nn, nel.
Z	о
§2. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ,
СВОДЯЩИЕСЯ К АЛГЕБРАИЧЕСКИМ. ОДНОРОДНЫЕ
И ЛИНЕЙНЫЕ УРАВНЕНИЯ
1. Уравнения, сводящиеся к алгебраическим
Рассмотрим уравнения вида
a sin2x + 6 sinx + с — 0, a / 0.	(1)
Полагая sinx = /, перепишем уравнение (1) в виде
at2 + bt + c = 0.	(2)
Пусть D — b2 — 4ас<0, тогда уравнение (2) не имеет действительных
корней, и поэтому уравнение (1) не имеет корней.
§2. Уравнения, сводящиеся к алгебраическим
47
Пусть D 0, тогда уравнение (2) имеет корни
=	2а”’’ t2 = Ta ; tl = t2 ПРИ D = °’
Уравнение (1), равносильное совокупности уравнений
sinx = ^i, sinx = /2,
имеет корни тогда и только тогда, когда D^Q и по крайней мере одно
из чисел /1, по абсолютной величине не превосходит единицы.
К квадратному уравнению относительно sinx можно свести
уравнение a cos2 х + b sin х + с — 0, а Ф 0, если заменить cos2 х на
1 -sin2x.
Аналогично уравнения вида
a cos2 к + b cosx + с — 0, a sin2 х + b cosx + с = 0, а О,
также приводятся к квадратным уравнениям.
Пример 1. Решить уравнение sin2 х — sin х — 2 — 0.
Д Это уравнение является квадратным относительно sinx. Обозна-
чив sinx = /, получим уравнение t2 — t — 2 = 0. Его корни t\ = — 1, /2 —2-
Гаким образом, решение исходного уравнения свелось к решению
простейших уравнений sinx ——1 и sinx = 2.
Уравнение sinx = —1 имеет корни х = —^ + 2m, neZ; уравнение
sinx = 2 не имеет корней.
Ответ. х = — | + 2лл, nEZ.	▲
Пример 2. Решить уравнение 2sin2x — cosx — 1 = 0.
Д Используя формулу sin2x = 1 — cos2x и полагая cosx = Z, получаем
2(1 — /2) — / — 1 = 0, или 2t2 + t — 1 = 0.
Это уравнение имеет корни t\ = — 1,
Если t = —1, т. е. cosx = —1, то х = л+ 2тш, п е Z.
Если Z = cosx = |, то х = ±arccos| + 2т =	+ 2т, neL
Ответ, х = л + 2т, х = ±| + 2тги, п е Z.	А
Пример 3. Решить уравнение tgx — 2 ctgx — 1 = 0.
Д Заметим, что значения х, при которых tgx = 0, не являются
корнями уравнения, а при tgx^O уравнение равносильно каждому
из уравнений
tgx —	— 1 = 0, tg2 х — tgx — 2 = 0.
48
Глава XII. Тригонометрические уравнения и неравенства
Полагая tgx = /, получаем уравнение t2 — t — 2 = 0, имеющее корни
t\ = —1, /2 — 2.
Если ^ = tgx = —1, то х = —| + яп, neZ, а если Z = tgx = 2, то
х = arctg 2 + ли, п е Z.
Ответ. х = — х = arctg2 + m, neL	А
Пример 4. Решить уравнение 4 cos3 х + 4 sin2 х = 1 + 3 cos х.
А Полагая cosx = t, преобразуем уравнение к виду
4/3 — 4£2 — 3t + 3 = 0. Разложив левую часть полученного уравнения
на множители, приходим к уравнению (t — 1)(4/2 — 3) = 0. Если
t = 1, то cosx = 1, откуда х = 2ж. Если 4£2 = 3, то 4cos2x = 3,
2(1 + cos2x) = 3, cos2x = i, откуда х = ±| + тш.
Ответ, х = 2лл, х = ±£ + лтг, п е Z.	А
6
Пример 5. Решить уравнение ctg4 2х + —]— = 25.
sirr 2%
А Полагая ctg2 2х = t и используя формулу —= 1 + ctg2 а,
sirr а
преобразуем уравнение к виду t2 + (1 + t)2 = 25, или t2 + t — 12 = 0,
откуда t\ — — 4, t% = 3. Так как />0, то ctg22x = 3, откуда tg2x = ±-L,
V 3
2х =	+ тт, neZ; х =	+ ^, п е Z.
о	12	2
Ответ, х =	+ у, п е Z.	А
Пример 6. Решить уравнение sin4x + cos4 х = cos2x.
А Преобразуем левую часть уравнения:
sin4 х + cos4 х = (sin2 х + cos2 х)2 — 2 sin2 х cos2 х = 1 — | sin2 2х. (3)
Полагая cos2x = £, запишем исходное уравнение в виде 1 —1(1 —/2) = /,
или t2 — 2t + 1 = 0, откуда t — 1, т. е. cos2x = 1, х = тт, neZ.
Ответ, х = тт, п е Z.	А
Пример 7. Решить уравнение 16cos4x + sin2x=
Л Используя формулы 2cos2x= 1 + cos2x, sin2x=^—и полагая
cos2x = /, получаем уравнение 4(1 + 02+	= которое преобразу-
ется к виду 16/2 + 30t + 11 = 0, откуда находим /1>2= ~15±^225~
t -	11 t -	1
^-“8’ t2~—r
§2. Уравнения, сводящиеся к алгебраическим
49
Так как t\ < —1, то исходное уравнение равносильно уравнению
cos2x = — откуда х =	+ п е Z.
Z	и
Ответ. х = ±^ + лп, п & Z.	А
и
Пример 8. Решить уравнение cos8x — sin8 % = cos2 2х.
А Используя равенства
cos8 х — sin8 х — (cos4 х — sin4 %) (cos4 x + sin4 x),
cos4 x — sin4 x — (cos2 x — sin2 x) (cos2 x + sin2 %) = cos 2x,
а также формулу (3), преобразуем уравнение к виду
cos2x (1 — |(1 — cos2 2х)) = cos2 2% или
cos 2x(cos2 2x — 2 cos 2x + 1) = 0.
Исходное уравнение равносильно совокупности двух уравнений
cos2x = 0 и cos2x = l.
Ответ, х = j х — т, п е Z.	А
4	2
Пример 9. Решить уравнение
• 6	.	6	13 . о
sinu х + cos х = — sin 2х.
о
А Так как sin6х + cos6 х — (sin2 х + cos2 х) (sin4 х + cos4 х — sin2 х cos2 х),
то, используя формулу (3), получаем
sin6 х + cos6 х = 1 — | sin2 2x.	(4)
Полагая sin 2x — t, запишем исходное уравнение в виде
= или 6/2 + 13/ - 8 = 0,
4	8
откуда
t _ —13 ± л/169 4-192	, _ 8	1 cin9v_l
------12-----’	sm2^-2‘
Ответ, x — (—l)n+ y» я e Z.	▲
Пример 10. Решить уравнение
cos8 x + sin8 x — | sin4 2x — 2 cos 2x — 1.
8
50
Глава XII. Тригонометрические уравнения и неравенства
Л Используя формулу (3), преобразуем левую часть уравнения:
cos8 х + sin8 х — (cos4 х + sin4 %)2 — 2 cos4 x sin4 x —
— (1 — | sin2 2x^ — ± sin4 2x =
= 1 — sin2 2x + | sin4 2x = cos2 2x + | sin4 2x. (5)
О	о
Следовательно, исходное уравнение можно записать в виде
cos2 2х + 2cos2x + 1 — О или cos2x = —1.
Ответ. х | п	▲
2. Однородные уравнения
Рассмотрим уравнения вида
a sin х + b cos x = 0,	(6)
asin2x + b sinx cosx + ccos2x — 0,	(7)
предполагая, что в уравнении (6) хотя бы одно из чисел a, b не
равно нулю, а в уравнении (7) хотя бы одно из чисел а, Ь, с отлично
от нуля.
В каждом слагаемом левых частей этих уравнений сумма степеней
синуса и косинуса одна и та же (в уравнении (6) она равна 1,
а в уравнении (7) равна 2). Такие уравнения называют однородными
относительно sinx и cosx.
Пусть в уравнении (6) а / 0, тогда значения х, при которых
cosx = 0, не удовлетворяют уравнению (6). В самом деле, если
cosx = 0, то из (6) следует, что sinx = 0 (по условию	Но
равенства sinx = 0 и cosx —0 не могут выполняться одновременно,
так как sin2x + cos2x= 1.
Итак, если а ф 0, то cosx / 0. Поэтому, разделив обе части
уравнения (6) на cosx, получим равносильное ему уравнение
atgx + b = 0. Аналогично, если в уравнении (7) коэффициент а^0,
то, разделив обе части уравнения (7) на cos2x, получим равносильное
ему уравнение aig2 х + btgx с = 0,
Пример 11. Решить уравнение 3sinx + 4cosx = 0.
А Разделив обе части уравнения на cosx^O, получим равносильное
уравнение 3tgx + 4 —0, откуда tgx = —х = —arctg| +	пей. ▲
О	о
§2. Уравнения, сводящиеся к алгебраическим
51
Пример 12. Решить уравнение 3 sin2 x + 5sinx cosx — 2cos2x = 0.
А Разделив обе части уравнения на cos2x^0, получим равносильное
уравнение 3tg2x + 5 tgx — 2 — 0, откуда tgx = —2 и tgх = |, /iGZ.
о
Ответ, х = — arctg2 + тт, х = arctg| + т, и G Z.	А
о
Замечание. К уравнению вида (7) можно свести уравнение
a sin2 х + b sin x cos x + c cos2 x = d,
используя тождество d — d(sin2 x + cos2 x).
Пример 13. Решить уравнение 4sin2x + sinxcosx — cos2x = 2.
А Это уравнение равносильно каждому из следующих уравнений:
4 sin2 х + sin х cos х — cos2 х = 2(sin2 х + cos2 х),
2 sin2 х + sin х cos x — 3 cos2 x = 0, 2 tg2 x + tgx — 3 = 0.
3
Отсюда находим tgx=l и tgx = — -.
Ответ, x — у + ял, х = — arctg 1 + яп, п е Z.	▲
4	& 2
Пример 14. Решить уравнение
sin3 * * х + sin2 х cos х + 4 cos3 х = 2 cos х.
А Правую часть уравнения запишем в виде 2cosx(cos2x + sin2x).
Тогда уравнение примет вид sin3x — sin2xcosx + 2cos3x = 0. Разделив
обе части этого уравнения на cos3x и полагая tgx =/, получим
уравнение tg3 х — tg2 х + 2 — 0, которое можно записать в виде
(tgx + 1)(tg2 х - 2 tgx + 2) = 0,
откуда tgx = — 1.
Ответ, х — — £ + тт, п G Z.	▲
4
3. Линейные уравнения
Рассмотрим уравнение вида
a sin х + b cos x = c.	(8)
Если <2 = 0 или fe = 0, то уравнение является простейшим уравнением
вида sinx = р или cosx = q, а если с = 0, то (8) — однородное
уравнение. Поэтому будем считать, что числа а, Ь, с в уравнении (8)
отличны от нуля, т. е. abc / 0.
52
Глава XIL Тригонометрические уравнения и неравенства
Тогда a2 + b2 >0 и, разделив обе части уравнения (8) на у/ а2 + Ь\
получим равносильное ему уравнение
~у=....- Sin X +	.COS X = —=£====.
у/а2 -\-b2	у/а2 + Ь2	у/а2 + Ь2
(9)
Заметим, что | ; а
Кл/^О2
[ка f.............b .Л
\ \/а2 4- b2 %/а2 + Ь2 /
2	/	\ 2
+ I b ) = 1} откуда следует, что
\ у а2 + Ь2 /
лежит на единичной окружности. Поэтому
существует такой угол ср, что
. а = cos ср,	— sin ср.
л/tz2 + 62	\/й2 +
Следовательно, уравнение (9) можно записать в виде
sin(x + (р) =
с
у/ а2 4- Ь2
(И)
Уравнение (11), а вместе с ним и уравнение (8), имеет решение
в том и только в том случае, когда
с
у/а2 -У Ь2
1 или с2 а2 + 62.
(12)
Если условие (12) выполнено, то уравнение (8) имеет следующие
решения: х ——у+(—l)narcsin	с = + пп, neZ, где определяется
V а2 + Ь2
формулами (10).
Если условие (12) не выполнено, т. е. |с| > у/ а? + Ь2, или
с2>а2 + Ь2, то уравнение (6) не имеет решений.
Изложенный метод преобразования линейного уравнения (8)
к виду (11) называют методом введения вспомогательного угла.
Пример 15. Решить уравнение 3 sin х + 4 cos х = 5.
Д Разделив обе части данного уравнения на д/42 + З2 = 5, получим
равносильное данному уравнение | sinx + cosx = 1.
D	D
Пусть ср — такой угол, что coscp = |, sin<p = В ка-
о	D
3
честве ср можно взять угол arccos-, а исходное уравнение
□
записать в виде sin(x + <р) = 1, откуда х + (р =	+ 2т,
п G Z; х = £ — arccos | + 2т = arcsin + 2т, п Е Z, так как
2	э	э
arcsin а + arccos а —
3
Ответ, х — arcsin - + 2тт, п е Z.
э
§3. Метод замены и метод разложения на множители
53
Задачи
Решить уравнение (1-8):
3 cos2 x — sin x — 1 — 0;	2)
4 sin2 x cos x — 5 cos x — 4 sin2 x 4- 5 —
2 cos2 x sin x — 3 sin x — 2 cos2 x 4- 3 =
1.	D
2.	1)
2)
3.	1) 3 cosx 4- 5sinx = 0;
4.	1) 4sin2x + sin2x — 3 = 0;
5.	1) sin Зх 4- cos Зх = \/2;
6.	1) 4 sin4 x 4- | cos2x —
7.	1) sin3 x 4- sin2xcosx = 2cos3x;
8.	1) sin6 x + cos6 x = |;
2 sin2 x 4-3 cosx = 0.
0;
0.
2) 4sinx — 3cosx = 0.
2) 5cos2x + 3sinxcosx— 1 = 0,
2) sin 2x — cos 2x = д/2.
2) cos4x + sin2 x = 1.
2) sin3x + 2cos3x = sin2xcosx.
2) sin8 x + cos8 x = cos2 2x.
Ответы
1. 1) x = — + 2zm, x = (—l)n arcsin | 4- тш, n 6 Z; 2) x =	4- 2тш, n G Z.
Zoo
2. 1) x = 2лтг, n G Z; 2) x = £ 4- 2тт, n G Z. 3. 1) x = — arctg | 4- nn, n G Z;
Z	и
2) x = arctg | 4- Tin, n e Z. 4. 1) x = ^ + тип, x = — arctg 3 + тип, n G Z; 2) x =
= —^ + zm, x = arctg 4 + m, nGZ. 5. 1) x—у|4~|тш, n G Z; 2) х=^+тгп,
n £ Z. 6. 1) x =	4- ля, n G Z; 2) x = n £ Z. 7. 1) x = у 4- лп, n G Z;
6	2	'4
2) x =	4- Tin, n G Z. 8. 1) x = £ + n G Z; 2) x = n G Z.
4	4	2	'2
§3. МЕТОД ЗАМЕНЫ НЕИЗВЕСТНОГО И МЕТОД
РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ
1. Метод замены неизвестного (метод подстановки)
При решении уравнений вида
a(sinx + cosx)+ 6sin2x + c = 0,	(1)
удобно ввести новое неизвестное t = sinx + cosx, что позволяет
свести уравнение (1) к квадратному в силу того, что
t2 _ sin2 х + 2 sin х cos x 4- cos2 x = 1 + sin 2x.
Аналогично, при решении уравнений вида
a (sin х — cos x) + b sin 2x + c — 0, a Ф 0,
используется подстановка t = sinx — cosx.
54
Глава XII. Тригонометрические уравнения и неравенства
При решении уравнений вида
a cos 2х + b cos2k х + с sin2™ х = 0, где k е N, m е N,
можно применить подстановку ^ = cos2x.
Пример 1. Решить уравнение
sin 2х + 5(sin х + cos х + 1) = 0.
А Пусть sinx + cosx — t, тогда l + sin2x = /2, откуда sin2x = /2 — 1.
Исходное уравнение сводится к квадратному /2 + 5/ + 4 = 0, откуда
h = -4, =
Уравнение sinx + cosx =—4 не имеет решений, а уравнение
sinx + cosx = — 1 можно записать в виде
2 (sin | + cos cos | = 0.
Если cos | — 0, то х = тг + 2тгп, п е Z, а если sin | + cos | = 0, то
tg| = —1, откуда х =	+ 2m, neZ.
Ответ, х = я + 2m, x = —^ + 2m, n€Z.	▲
Пример 2. Решить уравнение
cos 2х + 4 sin4 х = 8 cos6 х.
А Используя формулы
2 sin2 х = 1 — cos 2х, 2 cos2 х = 1 + cos 2х
и полагая cos2x = r, запишем уравнение в виде t + (1 — /)2 = (1 + /)3
или t(t2 + 2t + 4) = 0, откуда / = 0, т.е. cos2x = 0.
Ответ. x = y-h^, neZ.	А
4	2
Пример 3. Решить уравнение
• 9	1	.	17
SIH X + -о— = Sin X —	+ -.
sin2x	Sinx 4
Л Пусть sin х — -1— — t, тогда /2 = sin2 х + —-----2, и данное
sinx	sin2x
уравнение можно записать в виде t2 + 2 = t+^ или (f — 0 = О,
т. е. sinx — —или 2sin2x — sinx — 2 = 0, откуда sinx= 1
Ответ, х = (—l)n+1 arcsin 1 + m, nel.	▲
§3. Метод замены и метод разложения на множители
55
При решении тригонометрических уравнений вида F(x) = 0, где
С(х)’
а Р(х) и Q(x) — некоторые многочлены относительно
sinx и cosx, можно применить подстановку tg = Д учитывая, что
sinx =
2t
1 + /2’
I — /2
cosx =----X-.
1 +t2
Следует иметь в виду, что применение этой подстановки может
привести к трудностям, связанным с нахождением корней многочлена.
Поэтому эту подстановку применяют лишь в случаях, когда не видно
других путей решения уравнения. Кроме того, надо учитывать, что
tg| теряет смысл, если cos^=0 (х = л + 2т, п G Z). Поэтому,
применяя эту подстановку, следует выяснить, не являются ли
значения x = n + 2itnf корнями исходного уравнения.
Пример 4. Решить уравнение sin х +ctg ^ — 2.
Л Значения х = п + 2пп, neZ, не являются корнями уравнения.
Поэтому можно применить подстановку tg | = t. Тогда уравнение
можно последовательно преобразовать так:
-^ + 1=2, 2/3 —3/2 + 2/ —1 =0, (7 — 1)(2/2 — Z + 1) = 0.
Уравнение 2t2 — t + 1 = 0 не имеет действительных корней. Следо-
вательно, /= 1, т. е. tg| = 1, откуда
х = | + 2т, n е Z.
Ответ. х = ?+2т, neZ.
2. Метод разложения на множители
Пример 5. Решить уравнение
2 sin 2х • cos х — 1 + 2 sin 2х — cos х = 0.
Д Запишем уравнение в виде
2 sin 2x(cos х + 1) — (cos х + 1) = 0.
Исходное уравнение равносильно совокупности уравнений
cosx + 1 = 0 и 2sin2x — 1 = 0, имеющих корни х = я + 2т
и х = (—1)пу| + ^, п Е соответственно.
Ответ. х = я + 2т, х = (—1)^ + у, п G Z.	к
56
Глава XIL Тригонометрические уравнения и неравенства
Пример 6. Решить уравнение cos3 х + sin3 х = cos 2х.
Л Так как cos3x + sin3x = (cosx + sinx)(l — cosxsinx),
cos 2x = (cos x + sin x) (cos x — sin x),
то исходное уравнение можно записать в виде
(cosx + sinx)(l — cosxsinx — (cosx — sinx)) = 0.
Полученное уравнение равносильно совокупности уравнений
cos х + sin х — 0, 1 — cos х sin х — (cos x — sin x) = 0.
Первое из этих уравнений имеет корни х=— + тш, п е Z. Второе
заменой cosx — sinx = t сводится к уравнению
1 — 1 ~ - — t — 0 или /2 — 2t + 1 = О,
откуда t — cosx — sinx = 1 или cos (х+	х + ~ =	+ 2m,
fl G Z.
Ответ, х ——у + лл, x = 2m, х = — £ + 2т, nel	▲
4	2
Пример 7. Решить уравнение sin 2х cos 4х = sin 6х cos 8х
Д Преобразуя произведение тригонометрических функций в сумму
(разность), запишем уравнение в виде
|(sin6x — sin2x) = |(sin 14х — sin2x),
откуда получаем
sin 14х — sin 6х = 0 или 2sin4xcosl0x = 0.
Исходное уравнение равносильно совокупности двух уравнений
sin4x = 0, coslOx = 0, а также совокупности трех уравнений
cos2x = 0, sin2x —0, cosl0x = 0. Заметим, что все корни первого
из этих уравнений содержатся среди корней третьего уравнения.
Действительно, если cos2x = 0, то 2x = ^ + mt neZ, 10х = у + 5лл,
п 6 Z, и cos 10х = 0.
Задача сводится к решению уравнений sin 2х = 0, cosl0x = 0.
О7Г/1	ТС . 7Г/1	_ Г77	А
твет. х=-, х=- + -, па.	К
Пример 8. Решить уравнение sin2 х + sin2 2х = sin2 Зх.
Д Это уравнение равносильно каждому из следующих уравнений:
1 — cos2x	,	1 — cos4x _i	. 2	_	cos2x + cos4x
~	I ~	— sin	oxJ	sin ox —	~	?
cos2 3x = cos 3x cos x, cos 3x(cos x — cos 3x) = 0,
cos 3x sin x sin 2x = 0, cos 3x sin2 x cos x = 0.
§3. Метод замены и метод разложения на множители
57
Так как все корни уравнения cosx = 0 являются корнями урав-
нения cos3x = 0, то исходное уравнение равносильно совокупности
уравнений sin х = 0, cos Зх = 0.
Ответ, х = тт, х = £ + п е Z.	▲
о 3
Пример 9. Решить уравнение sin Зх + cos 5х = 0.
А Так как sin a = cos Q — а), то уравнение можно записать в виде
cos 5х + cos Q — 3xj = 0 или 2 cos Q + х) cos ^4х — = 0, откуда
+ X — — + 7Ш, 4х — j = — + 7TZ7, И 6 Z.
4	2	4	2
Ответ, х = £ + тт, х = — + 7Г-, п е Z.	▲
4	16	4
Задачи
Решить уравнение (1-10):
2) sinхcosx = 6(sinx — cosx — 1)
2) cos4 x + sin6 x = 1.
1.	1) sinx4-cosx = 1 4-sin2x;
2.	1) sin4x 4-cos6x = 1;
3.	1) sinx4---— =sin2x4-----i
sinx	sin2 x
1
4.	1) cos3 x + sin3 x + sin (x 4-	= 0;	2) cos 2x = cos3 x — sin3 x
5.	1) cos7xcos 13x = cosxcos 19x;	2) sinxsin5x = sin2xsin4x
6.	1) sinx + sin2x4-sin3x = 0;	2) sinx — sin3x = sin4x — sin2x
7.	1) cos2 x 4- cos2 2x 4- cos2 3x = |;
2)	cos2 2x 4- cos2 3x 4- cos2 4x 4- cos2 5x = 2.
8.	1) sin6xcosx4-cos6xsinx = sin2x;
2)	sin7 x cos3 x — cos7 x sin3 x = cos2x.
9.	1) sinx 4-sin2x 4-sin3x —cosx 4-cos2x 4-cos3 x;
2)	1 4-2cosx(l 4- sin2x) = sin2x — cos2x.
10.	1) 2 4- cos 4x = 5 cos 2x 4- 8 sin6 x; 2) 4 4- cos 2x 4- 3 cos 4x = 8 cos6 x.
Ответы
1. 1) x = 2nn, x — — 4- 2/m, x = 4- 2лтг, n G Z; 2) x — it 4- 2лтг, x = 4- 2itn,
nGZ. 2. 1) x=y, nGZ; 2) x=y, nGZ. 3. 1) x = 4-2zm, azgZ; 2) x = im,
n G Z. 4. 1) x = — 4- дуг, n G Z; 2) x = 4- тш, x — 4- 2тш, x = 2тгп, n 6 Z.
58
Глава XII. Тригонометрические уравнения и неравенства
5. 1) х = п е Z; 2) х = у, п С Z. 6. 1) х = у, х =	+ 2тш, п е Z;
2) х = тгп, х=^ + |тгп, neZ. 7. 1) х=~ + ~,х = ±^+тгя, weZ;2) х = ^ + у,
+ neZ. 8. 1) х=™, n<=Z; 2) х=^ + у, n€Z. 9. l)x=y + wz,
п £ Z; 2) х = g ~Г тг/2, х ~ /г Ч- 2тг/2, п G Z. 10. 1) х = 4—g-, х = g 4- кп, п G Z;
2) Х=7ГП. Х = ^ + у, nez.
§4. МЕТОД ОЦЕНКИ ЛЕВОЙ И ПРАВОЙ ЧАСТЕЙ
УРАВНЕНИЯ
Пример 1. Решить уравнение
sin8 х + cos10 х — 1.	(1)
А Заметим, что если 0 < a < 1, то ak < а для любого k е N, k 2,
а равенство ak = а справедливо только при a = 1 и a = 0. Полагая
sin2 х = a, k = 4, получаем неравенство
sin8 х < sin2 х,	(2)
причем равенство sin8 х = sin2 х является верным только в случаях
sin2 х — 0 и sin2x — 1, т. е. тогда, когда либо sinx = 0, либо | sinх| = 1.
Аналогично, для любого х G R справедливо неравенство
cos10x cos2x,	(3)
10	2
а равенство coslvx — coszx является верным только в случаях, когда
либо cosx = 0, либо |cosx| = 1. Складывая неравенства (2) и (3),
получаем неравенство
sin8х + cos10х 1, х ей,
а равенство (1) является верным только тогда, когда либо sinx —О
(| cosx| = 1), либо cosx = 0 (| sinx| = 1), т. е. когда sin2x = 0, откуда
х- у, HGZ.
Ответ, х = у, я е Z.	▲
Пример 2. Решить уравнение sinxsin5хsin 9х = 1.
А Так как | sin ах| < 1 при любых а и х, то уравнение может иметь
решения только в двух случаях: sinx = l, sinx = — 1.
Если sinx = 1, то х = £ + 2тим, 5х — ^ + 2лг(5п + 1),
9х = + 2тг(9п + 2), п е Z, откуда следует, что sin 5х = sin 9х = 1,
и поэтому числа х = | + 2m. и е Z, — корни исходного уравнения.
§4. Метод оценки левой и правой частей уравнения
59
Если sinx = —1, то х = — | + 2лтг, 5х = —| + 2тгт, 9х =
m е Z, k e Z, откуда следует, что sinx sin 5x sin 9x = — 1, и поэтому
значения x = — + 2лтг, n e Z, не являются корнями исходного
уравнения.
Ответ. х = |-Ь2тгп, n € Z.	А
Пример 3. Решить уравнение sin Зх cos 4% = 1.
Л Уравнение равносильно совокупности двух систем
Г sin Зх = 1,
\cos4x = 1;
{sin3x = —1,
cos4x = — 1.
а)	Решим первую систему.
Если sin3x = l, то х = ~ k G Z. При этих значе-
6	3
ниях х равенство cos4x = cos (у +	= 1 справедливо тогда
и только тогда, когда 27Г +	= 2дт, т. е. 1 + 4k = 3m или
1 + /г —Згг, riGZ, откуда k — Зп — 1, х = ^ + |д(3м —1) = — £ + 2тгп,
О о	Л
1Т G Z.
Итак, решениями
х = — + 2m, n е Z.
б)	Рассмотрим вторую
х =	k е Z,
О о
Л	/ 2л . 8тг/г .	,
cos4x = cos ( — у + — I = — 1 является верным тогда и только
тогда, когда — у + ^у = (2m + 1)ти, т. е. 8k — 2 = (2m + 1)3.
Это равенство не выполняется ни при каких целых /гит,
так как в его левой части — четное, а в правой — нечетное
число.
первой системы являются числа
систему. Если sin3x = —1, то
и при этих значениях х равенство
Ответ. х = —^+2тгп, n е Z.	А
Замечание Приведем другое решение. Так как уравнение cosЗх• sin4х = О
является следствием исходного уравнения, то и уравнение
cos3x • sin4x — sin Зх • cos4x — —1,
которое можно записать в виде
sin(4x — Зх) = sinx = — 1,
60
Глава XII. Тригонометрические уравнения и неравенства
также является следствием исходного уравнения. Проверка показывает, что все
корни уравнения sinx = —1, т.е. числа х — — ^ + 2тт, п € Z, удовлетворяют
исходному уравнению.
Пример 4. Решить уравнение
cos2 2х + 4 sin2 4х + 1 = sin 4х cos 2х + sin2 х.
4
Д Запишем данное уравнение в виде
cos2 2х — cos 2х sin 4х + 4 sin2 4х + cos2 х = О
4
или
/	।	\ 2
(cos2х — - sin4хj + cos х = 0.
Полученное уравнение равносильно системе
cos 2х = ~ sin 4х,
<	2
cosx = 0.
Уравнение cosx = 0 имеет решения x = ^ + m, neZ, но эти значения х
не удовлетворяют первому уравнению системы. Следовательно,
исходное уравнение не имеет решений.
Ответ. Нет решений.	▲
Пример 5. Решить уравнение
(3 sin х + 4 cos х) (20 + 12 sin х + 5 cos 2х) — 143.
Д Так как 3sinx + 4cosx = 5 Q sinx + | cosx) = 5cos(x — ср), где
<p = arcsin|, a 20 + 12sinx + 5cos2x = 5(1 — 2sin2x) + 12sinx + 20 =
о
= —10 (sin2x — | sinx +	+ 25 +	— 10(sinx — f)2, to
\	5	25/	55	\	5/
уравнение равносильно следующему:
eos(x-rt(j-lo(si„x-|)2)=l«
Левая часть полученного уравнения совпадает с правой тогда
и только тогда, когда выполняются равенства
cos(x — ср) = 1, sinx — |,
□
з
т. е. при х = (р + 2kn = arcsin - + 2kn, k el
Э
о
Ответ, x = arcsin F + 2kn, k eZ.	▲
5
§4. Метод оценки левой и правой частей уравнения
61
Пример 6. Решить уравнение
(cos 2х — cos 4х)2 = 4 + cos2 Зх.
Д Левая часть уравнения не превосходит четырех, так как
| cos2x - cos4x| 2, и равна четырем в следующих случаях:
cos2x=l и cos4x = — 1,
cos2x ——1 и cos4x = l.
Правая часть не меньше четырех и
Следовательно, исходное уравнение
равна четырем, если cos3x = 0.
равносильно совокупности двух
систем:
cos2x = 1,
cos4x = — 1,
cos Зх = 0;
'cos 2х = —1,
< cos4x = 1,
4cos Зх = 0.
а)	Рассмотрим первую систему. Если cos2x = l, то х = nk, ke’Z,
cos4x = cos4ti/? = 1. Эта система не имеет решений.
б)	Решим вторую систему. Если cos2x = —1, то х = | + rck, keZ,
cos 4х = cos(2tt + 4д/г) = 1,
cos Зх = cos (у + 3nk^ = 0.
Эта система имеет следующие решения: х = | + д/г, k е Z.
Ответ, х — + k е Z.	▲
Пример 7. Решить уравнение
sin2 4х + cos2 х = 2 sin 4х cos4 х.	(4)
Д Первый способ. Запишем уравнение (4) в виде
sin2 4х — 2 sin 4х cos4 х = — cos2 х	(5)
и прибавим к обеим частям уравнения (5) cos8x. Полученное при
этом уравнение запишем в виде
(sin 4х — cos4 х)2 + cos2 х(1 — cos6 х) = 0.	(6)
Так как оба слагаемых в левой части уравнения (6) неотрицательны,
то равенство (6) справедливо тогда и только тогда, когда верны
равенства
{sin 4х — cos4 х = 0,
cos2 х(1 — cos6 х) — 0.
62
Глава XII. Тригонометрические уравнения и неравенства
Система (7) равносильна совокупности двух систем:
sin 4х — cos4 х = О,
cosx = 0;
sin 4х — cos4 х = 0,
| cosx| = 1.
(8)
(9)
Если cosx = 0, то sin4x = 0 и система (8) имеет решения x=^ + nk,
которые являются решениями уравнения (4).
Система (9) не имеет решений, так как из равенства |cosx| —1
следует, что sinx = 0 и sin4x = 0, что противоречит первому
уравнению системы.
Второй способ. Решая уравнение (4) как квадратное отно-
сительно sin4x, получаем
sin 4х = cos4 х ± ^/cos2x(cos6x — 1).	(10)
Из (10) следует, что уравнение (4) может иметь решение лишь
тогда, когда cos2x(cos6x — 1)	0, т. е. при условии, что хотя бы
одно из равенств cosx = 0, |cosx| = 1 является верным.
Если cosx = 0, то из (10) получаем sin4x = 0. Числа x=^ + nk,
keZ, являются решениями уравнения (4). Если |cosx| = 1, то sinx —0
и sin4x = 0, но из (10) следует, что sin4x —1.
О т в е т. х = k е Z.	▲
Задачи
Решить уравнение (1-9):
1.	1)	3 sin3 х 4-4 cos6 2х = 7;	2)	5 cos4 2х — 4sin5x = 9.
2.	1)	sin4 2х 4- cos8 2х = I;	2)	sin6 2x 4- cos4 2x = 1.
3.	1)	sin2 2x 4- 1 = cos2 3x;	2)	8 cos4 3x — 3 sin x 4- 4 — 0
4.	1)	sin5xsinlx = 1;	2)	sinxsin(\/2x) = 1.
5.	1)	sinxcos4x = — 1;	2)	sin5xcos6x = 1.
6.	1)	(cos6x — cos4x)2 =	5 — sin3x; 2) (cos 4x — cos 2x)2 =	4 4- cos2 x.
7.	1)	sinxsin9xsin I3x =	1; 2) cosxcos 2xcos3x = I.
8.	1) (5 sinx 4- I2cosx)(1004-48cosx — I3cos2x) = 1757;
2)	(8 sin x 4- 15 cos x) (53 4- 32 sin x 4- 17 cos 2x) — 1318.
9.	1)	cos2 3x 4-| cos2 x =	cos 3x cos4 x; 2) sin2 4x 4- cos2 x =	2 sin 4x cos4 x
§5. Отбор корней уравнений
63
Ответы
1. 1) х=^+2тт, neZ; 2) х=~+2т, neZ. 2. 1) х = neZ; 2) х=
rceZ. 3. 1) х = тсп, nGZ; 2) нет решений. 4. 1) Нет решений; 2) нет решений.
5. 1) х = — ^ + 2тт, neZ; 2) х = —^ + 2тт, п G Z. 6. 1) х = — + 2тш, п е Z;
2) х = | 4- т, /7. е Z. 7. 1) х = ~ + 2тт, п е Z; 2) х — пп, п е Z. 8. 1) х =
= arcsin+ 2тт, п G Z; 2) х = arcsin-^ + 2тш, п е Z. 9. 1) х = £ + пп, п G Z;
1и	1 /	Z
2) х = ~ + Tin, п G Z.
§5. ОТБОР КОРНЕЙ УРАВНЕНИЙ.
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, СОДЕРЖАЩИЕ
ЗНАКИ МОДУЛЯ И КОРНЯ
Пример 1. Решить уравнение
cos3x _ cos5x
sin 2х sin 2х ’
Д Уравнение можно записать в виде
cos Зх — cos 5х п	„	2 sin 4х sin х п
sin 2х	sin 2х
Уравнение теряет смысл, если sin 2% = 0, а при выполнении условия
sin 2x^0	(1)
оно равносильно уравнению
4 sin % cos 2х — 0.
Если sinx = О, то sin2x = 0 и поэтому корни уравнения sinx = О
не удовлетворяют условию (1), а корни уравнения cos2x = О
удовлетворяют условию (1) и являются корнями исходного уравнения.
Ответ. х = 7 + п е Z.	▲
4	2
Пример 2. Решить уравнение
с.°13_^71 _ sin2xcos2x — 2 sin2 х) — 1.
cosx v	7
Д Пусть cosx ф 0, тогда исходное уравнение равносильно каждому
из уравнений
cos--x-(eos 2х — cos2xsin2x) = 1,
cosx 4	7
cos Зх cos 2х cos2 х _ ।
cosx
cos x cos 2x cos 3x = 1.
(2)
64
Глава XII. Тригонометрические уравнения и неравенства
Уравнение (2) может иметь решения только в том случае, когда
| cosx| = | cos2x| = | cos3x| = 1.
а)	Если cosx = 1, то x = 2im, cos 2x = cos Зх = 1.
б)	Если cosx ——1, to x = n+2nnt cos2x = l, cos3x = —1.
Таким образом, исходное уравнение равносильно совокупности
уравнений cosx=l и cosx ——1, а числа х = пп, п е Z, и только
эти числа —корни исходного уравнения.
Ответ, х = л:/?, п е Z.	▲
Пример 3. Решить уравнение
cos Зх — sin х __ ।
cos 5х — sin Зх
Л Уравнение равносильно каждому из уравнений
sin (4х ~ j + sin — 2xj = 0, sinхcos уЗх — j = О,
если выполняется условие
cos Q — х) sin — 4х) ф 0.
Корни каждого из уравнений
sinx = 0 и cos (Зх — т)—О
\	4/
удовлетворяют этому условию и являются корнями исходного урав-
нения.
Ответ, х = т, х = п е Z.	▲
4 о
Пример 4. Решить уравнение
cos xsin3x sjn2 x cos 3% — 6 cos 2x cos2 x.
sinx
Л Из формул для cos3x и sin3x (см. гл. V, § 7, формулы (5) и (6))
следует, что
cos3x = | (cos Зх + З cosx), sin3x = |(3sinx — sin Зх).
Поэтому
cos3 x sin Зх + sin3 x cos 3x = | (sin 3x cos x + sin x cos 3x) =
= ~ sin 4x = 3 sin x cos x cos 2x,
4
§5. Отбор корней уравнений
65
и исходное уравнение при условии sin х ф 0 равносильно каждому
из уравнений
3 sin х cos х cos 2х = 6 sin х cos2 х cos 2х,
cos х cos 2x (cos x — 0 = 0.
Ответ. x — ^-\-m, x —	* = ±^ + 2ot, n e Z.	▲
Пример 5. Решить уравнение
sin3x _ cos3x _	2
sin 2x cos 2x cos 3x ’
Д Исходное уравнение равносильно уравнению
sinx _	1	/о\
sin 4х	cos Зх ’
а допустимые значения х для уравнения (3) определяются условием
sin4xcos3x ф 0.	(4)
При выполнении условия (4) уравнение
sinx cos Зх — sin4x
является следствием уравнения (3) и в силу тождества
sin4x = sin(3x + x) = sin Зх cos х +cos Зх sinx
равносильно уравнению
sin3xcosx = 0.	(5)
Корнями уравнения (3) являются все те и только те корни
уравнения (5), которые удовлетворяют условиям (4).
Так как (см. гл. V, § 7, формула (5))
sin Зх = sin х(3 — 4 sin2 х) = sin х(1 + 2 cos 2х),
a sinxcosx^O в силу условия (4), то из уравнения (5) следует,
что
cos2x = — |.	(6)
Корни уравнения (6) удовлетворяют условиям (4) и являются
корнями исходного уравнения.
Ответ, х = ±^ + от, п е Z.	▲
Пример 6. Решить уравнение
—.........+ _ _|iH£	= Sin4x - tg2x.
cos 2х cos Зх cos Зх cos 4х
3—3022
66
Глава XII. Тригонометрические уравнения и неравенства
Л Используя формулу
sin(.a ~ Р) — tg a — tgfl,
cos a cos p	1
преобразуем исходное уравнение к виду
tgЗх - tg2x + tg4x — tg3x = sin4x — tg2x.	(7)
Область допустимых значений x для уравнения (7) определяется
условиями
cos 2х Ф 0, cos Зх 0, cos 4х 0,	(8)
а при выполнении условий (8) исходное уравнение равносильно
уравнению
tg4x = sin4x.	(9)
Уравнение (9) равносильно совокупности уравнений
sin4x = 0,	(10)
cos4x = l,	(И)
причем все корни уравнения (11) содержатся среди корней уравне-
ния (10). Из уравнения (10) следует, что либо sinx = 0 (и тогда
х = лп, rzeZ), либо cosx = 0 (и тогда cos3x = 0), либо cos2x —0.
Ответ. х = яи, п € Z.	А
Пример 7. Решить уравнение tgx + tg3x = 4| sin х|.
Д Допустимые значения х определяются условием
cos 3x^0,	(12)
так как все корни уравнения cosx = 0 являются корнями уравнения
cos Зх = 0. Чтобы избавиться от модуля в правой части исходного
уравнения, заметим следующее. Функции tgx, tg3x и |sinx| —
периодические с периодом тг, и поэтому достаточно найти решения
исходного уравнения на промежутке [0; л), где |sinx| = sinx.
Если 0^х<л и выполняется условие (12), то исходное уравнение
равносильно каждому из уравнений
sinx + sin3x =4sin	sin4x =4sinx
COS Л	cos3x	cosx cos Зх
4sinxcosxcos2x=4sin sin x(cos 2x - cos 3x) = 0,
cosx cos 3x	4	7
sin x sin | sin у = 0.	(13)
Все корни уравнения sin|=0 удовлетворяют уравнению sinx = 0,
а решения уравнения (13) задаются формулами
x = nk, х = ke%.	(14)
§5. Отбор корней уравнений
67
Из множества чисел (14) промежутку [0; тг) принадлежат числа О,
и у. Поэтому множество решений исходного уравнения задается
формулами
2ти ,	4ти .	Гт?
х = кп, х = — Т та, х = — + та, п 6 Z.
5	5
0	2ти ।	4ти ।	_г~п	▲
твет. х — т, х = — + та, х = — + та, n G Z.	А
э	э
Пример 8. Решить уравнение
2 + х/З sin 2х — | cos 2х| = 4 sin2 .
Л а) Пусть cos2x 0, тогда уравнение можно последовательно
преобразовать так:
2 + х/3 sin 2х — cos 2х = 2 - 2 cos х,
у sin 2х — i cos 2х — — cos х,
cos ^2х +	— cosx = О,
2sin(^ + =)sinf^ + ^ = 0,
\ о/ \Z о/
откуда получаем две серии корней
х = _л_|_2т1 х = -^ + 2тгп, neZ.
У о	о
Выясним, какие корни первой серии удовлетворяют усло-
вию cos2x^0. Заметим, что любое neZ можно записать в
виде n = 3k+p, где feeZ, а р может принимать значения 0,
1, 2. Тогда
2х = 2(-! + ^) = ^ + ^(3*! + Р) = Ш + к(4!-|).
Если р — 0, то
cos2x = cos у) > 0;
если р — 1, то
cos 2х = cos f |	= cos < 0;
если р = 2, то
cos 2х = cos (I — л = cos Г| — тг = cos > 0.
\ о У /	\ о У /	У
68
Глава XII. Тригонометрические уравнения и неравенства
Таким образом, корни первой серии при п — 3k + 1 не
удовлетворяют условию cos2x 0 и удовлетворяют этому
условию при n = 3k и п — 3k + 2, k G Z.
Для корней второй серии условие cos2x^0 не выполняется,
б) Пусть cos2x<0, тогда уравнение можно записать в виде
cos (2х — £ ) + cos х — О,
\	О /
МИНИН’
откуда
4ти . 2тш	4ти . о	_ гт7
х= —+ —, х— — 4-2т, nel.
У о	о
Корни первой из этих двух серий удовлетворяют усло-
вию cos 2% < 0 только при п = 3k, а корни второй серии
удовлетворяют условию cos 2х < 0.
Ответ. х = — ^ + 2пп, х— + 2т, х = у +2яи, х = ~ + 2тт,
п G Z.	А
тт	Гк г*	2sin3x I cos 6х|
Пример 9. Решить уравнение ----— JL.
д	sin х	cos 2х
Л Воспользуемся формулами
sin Зх = sin х(3 — 4 sin2 х) = sin х(2 cos 2х + 1),
cos 6х = cos 2х(4 cos2 2х — 3),	(15)
и рассмотрим два возможных случая: cos 6x^0, cos6x<0, учитывая
при этом, что
cos 2x^0, sinx^O.	(16)
а) В первом случае нужно решить уравнение
2(2 cos 2х + 1) = 4 cos2 2х — 3	(17)
при условии
cos6x^0.	(18)
Положим cos2x = t, тогда уравнение (17) примет вид
4/2 — 4t — 5 = 0. Это уравнение имеет корни
,	l-\/6	.	1 -ьл/6	,
^1 = -^- и f2 = —2—>1.
1 л/б
Итак, cos 2х = ~2 ° < 0, откуда
х = ±| arccos —+ mi, пе Z.	(19)
§5. Отбор корней уравнений
69
Из равенства (15) следует, что
cos 6% =	— 3),
где	о	г- О	/-
4zf — 3 = (1 — л/6)2 -3 = 4- 2^6 < 0.
Поэтому cos 6% > 0, если cos2x = t\ = —где t\ < 0. Итак,
условие (18) выполняется и значения х, определяемые формулой (19),
•шляются корнями исходного уравнения.
б) Во втором случае (cos6x<0) нужно решить уравнение
4£2 + 4/ — 1 = 0, t = cos 2х.
Это уравнение имеет корни
= —у- >0 и t2 = —< -1.
Проверим выполнение условия
cos 6х < 0,
используя формулу (15). Получим
cos 6% = ^i(4^2 — 3),
4/f - 3 = (V2 - I)2 - 3 = -2V2 < 0.
Так как t\ > 0, то cos6x < 0 и поэтому корни уравнения
о х/2 — 1
cos2x =—-—, т.е. числа
1	л/2 — 1
х = ±- arccos —-— + от, п е Z,
удовлетворяют условиям (16) и являются корнями исходного урав-
нения.
Ответ. х = ±| arccos 1	+ от, х —arccos +от, nGZ.
▲
Пример 10. Решить уравнение
sin х + л/3 cos х = ^2 + cos 2х + л/3 sin 2х.	(20)
Д Так как правая часть уравнения (20) неотрицательна, то уравнение
может иметь решения только в том случае, когда
70
Глава XII. Тригонометрические уравнения и неравенства
Если освободиться от радикала путем возведения в квадрат обеих
частей уравнения (20), то получится уравнение
sin2 х + 3 cos2 х + 2х/3 sin х cos х = 2 + cos 2х + х/З sin 2х,
которое после упрощения примет вид
cos 2х = cos 2х.
(22)
Уравнение (22) является тождеством. Это не означает, однако,
что уравнению (20) удовлетворяют все значения х, так как
уравнение (22) —лишь следствие уравнения (20). Уравнения (20)
и (22) равносильны при выполнении условия (21). Таким образом,
решением уравнения (20) являются все значения х, удовлетворяющие
неравенству (21), и только эти значения.
Решая неравенство (21), получаем — £ + 2m х ~ + 2m.
о	о
Ответ. Объединение всех отрезков вида [—- + 2лл; +2тш|,
L о	о	J
п G Z.	▲
Замечание. Так как
2	+ cos 2х + х/З sin 2х — 2 ^1 + | cos 2х + sin 2х^ =
= 2 (1 + cos ^2х ~	= 4 cos2 (х -	,
то уравнение (20) равносильно уравнению
2cos (х-	= 2 |cos	>
решениями которого являются те и только те значения х, которые удовлетворяют
неравенству cos (х - £ )	0.
Пример 11. Решить уравнение
sin Зх^/ctg — х^ — cos (2х —	— cos ^4х +	.
Д Преобразуем правую часть уравнения:
cos (2х— —cos ^4х +	= 2sin3xsin (х +	= 2sin3xcos(j — х^ .
Исходное уравнение равносильно совокупности двух уравнений
sin Зх = 0 и ^/ctg - х) = 2 cos Q — х} при условии, что
§5. Отбор корней уравнений
71
Первое из этих уравнений имеет корни х = п G Z. Если
n = 3k, keZ, то х = jik и ctg Q — Tik^ = ctg > 0. Если n = 3k ± 1,
го X = Jik ± j и ctg - nk =F = ctg T f) < 0.
Второе уравнение равносильно уравнению
ctg Q — x^ = 4 cos2 Q — x) , если cos Q — x) > 0.
Полученное уравнение равносильно совокупности двух уравнений
cos Q — х) = 0 и
4 sin (— х^ cos (7 - х^ = 2 sin (£ — 2х^ — 2 cos 2х = 1.
\4	/	\4	/	\2	/
Если cos ( 7 — х ) = 0, то х = —7 + Tin, neZ. Эти значения х являются
\4	/	4
корнями исходного уравнения.
Уравнение 2 cos 2х = 1 имеет корни х = ±| + т.
Если n — 2k, то х = ±7 + 2iik и cos ( 7	7 ) > 0, а если п = 2k + 1,
6	\4	6/
го х = ±7 + 7i + 2nk и cos =F < 0.
6	\ 4	6/
Таким образом, уравнение имеет три серии корней: х = Tik,
х—— 7 + Х = ±7+2лД k G Z.
4	6
Ответ. x = nk, х = —7 + Tik, x = ±£+2Tik, keZ.	A
4	6
Задачи
Решить уравнение (1-28):
1.
3.
4.
5.
6.
7.
8.
p sin3x _ Q. 2) cosx
sin x ’ cos 3x
1) (1 + cosx)ctgx = sin2x;
1) sinxtgx = cosx + tgx;
1)
1)
8(ctgx~tgx) =2c0S4x + 5.
ctgx-h tgx
sin3x _j_ cos 3x _	2	.
cos 2x	sin 2x sin 3x'
sin X	COS X
2) (1 — sinx)tgx = sin2x.
2) ctgx (ctgx+ -J—) = 1.
2\ ctgx _ 1 _ sin2 2x
ctgx + tgx 2	3
2) _S2^L_£2^+2cos2x = 0
cos 3x COS X
n ( . 4	, o x , л cosbx + cosdx
1) (sin x + cos2x) ctg4x = ——----------
16sin4x
2) tgx + tg2x + tg3x + tg4x = 0.
1)
____cos3x____= tgx;
sin 3x —2 sinx
2)
sin3x
cos 3x + 2 cos x
= ctgx.
72
9.
10.
И.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
Глава XII. Тригонометрические уравнения и неравенства
sin3x__sinx =2cos2%.
sinx sin3x
cos 2x 4- cos x , o
------------tg2x;
sin2x — tgx
3 4- cos 4x — 8 sin4 x _ 1
4(sinx4-cosx)	cosx’
. 9	, . 9 n 1 cos 3x
sm x + sm 2x = l-------—
cos 2x
2)
2)
2)
2)
2)
1)
1)
1)
1)
1)
1)
2)
1)
1)
2)
1)
1)
2)
1)
2)
1)
2)
1)
2)
О
2)
1)
1)
1)
1)
sin3x	cos3x _	2
sin 2x	cos 2x cos 3x
2 cosx 4-sin* 2 * x , n
-------------- = tg 2x
ctgx — sin2x
3 4-4 cos 2x — 8 cos4 x _
sin 2x — cos 2x	sin 2x ’
cos2 x 4- cos2 2x = 1 4- ctg 3x.
cos 5x 4- sin Зх _ j
cos 3x 4- sinx
sin 3x — cos x _ ।
cos 3x — sin 5x
cos5x/n 9	-2 n i\ i
-----(2 cos x — sin xcos2x - 1) = 1;
cosx
cos 3x 9	-2 n i \	1
-----(2 cos x — sin xcos2x — 1) — 1.
cosx
sin25x	, cos25x
—= 24 cos 2x 4----------n—
sinz x	cosz x
sin 3x .	sin 3x
2)
sin2 3x o „ cos2 3x
---y— = 8 cos4x 4-	n—
sinz x	cosz x
r ।	=sin8x— tg2x;
cos 2x cos 5x	cos 5x cos 8x
sinx . sinx -
	1	= sin _ |g frX.
cos 6x cos 7x-cos 7x cos 8x
ctgx 4- ctg3x =^/14- ctg2 x;	2) ctgx 4- ctg3x = 4| cosx|.
\/l — 4\/2sinx = 2 cos x — \/2 tg x;
a/12 — 6^2 tgx = 3 sin x —.
v	°	cos x
- + cosx cos 2x = sin
2
л/1 4- 2 sinx
= cos x + -;
— sinx.
cos Зх
cos Зх
/5	. 9
\-----sin x +cos
V 4
\	— cos2 x 4-cos
V 4
y/4 4- 3cosx — cos2x = sinx;
\/4sinx 4- cos 2x 4- 5 — 2\/2 cos x.
2)
| cos x| — cos 3x = sin 2x
cos3x । 2| cosx| __
cos x cos 3x
cosx 4- | sin x| 4- cos 2x = sin 4x.
sin 3x — | sin x| — sin 2x;
sin3x 3|sinx| _ o
—-----1—r~5— — — A	£)
sinx sin3x
sinx + | cosx| — sin 4x + cos2x;	2)
cos 3x + cos 2x = 3| cos x| — cos 4x;
§5. Отбор корней уравнений
73
2) sin Зх — cos2x = 3| sinx| — cos 4%.
27.
28.
1)
2)
1)
cos 3x sin 5x + | cos 5x sin 3x|
cos 2x
cos 3x cos 5x + | sin 5x sin 3x|
= 2 sin 2%;
2 sin Зх
sin 2x
cos 6x
— 2 cos 2%.
| sinx] cos2x’
2)
sin 6x _ cos 3x
sin4x |cosx|'
Ответы
1.	1) x = ±| 4- im, nEZ; 2) нет решений. 2. 1) x= 4-яп, nEZ; 2) х = ±^4-яп,
n E Z. 3. 1) x = | 4- тип, x —± j + 2/m, n E Z; 2) x — тсп, x = (—l)n+1 g 4- nn, nd.
4. 1) x — (-1)"+11 + Tin, nd; 2) x =	+ 2тсп, nel. 5. 1) x =	+ jin,
n E Z; 2) х = ±^4-яп, n E Z. 6. 1) х = ±^4-яп, n E Z; 2) x = 4-n E Z.
7. 1) x=g+x = ±^+2m,neZ; 2) x=^,arccos+ tot, n&Z.
8. 1) x= £ + ф, n6Z; 2) x=f + ^, neZ. 9. 1) x = * + n & Z; 2) x =
±^+m, neZ. 10. 1) x = ±arccos|+2tot, nGZ; 2) x = ±arccosi + (2n+l)n:,
mGZ. 11. 1) x = nn, ntl; 2) x= 2 + y, n&Z. 12. 1) x = | x = 2m,
//( Z; 2) x=^ + ^, neZ. 13. 1) x=^+nn, x=-? + m, х = (-1)п^ +
n G Z; 2) x = тт, x =	+ тот, x = (-l)"i + ~, n G Z. 14. 1) x = m, n G Z;
2) x = m, n&Z. 15. 1) x = 5 + ^, n G Z; 2) x = ^, n / 3k, n G Z, k G Z.
16.	1) x=^, п^2 + 4й, n^4 + 8k, keZ, n&Z; 2) x=^, п^2 + 4й, «/4 + 86,
О	о
A* E Z, n E Z. 17. 1) x = у 4~ кп, x = ——h тип, x — ——|- тш, ti E Z; 2) x = 4- тш,
18. 1) x — — 4-7cn, /?EZ; 2) x = arccos -U 4- кп,
о	v3
v = — jg 4- кп, x = ~ 4- тип, n E Z.
v — arccos -Ц 4- (2n 4-1)зт, n E Z.
v3
19. 1) x= 7 4-7ГП, x= 4-2tt/?, /?eZ; 2) x = nn,
4	b
v =	4” 2тш, n E Z. 20. 1) x — —— 4" 2тш, n E Zj 2) x = —~ 4~ 2тш, n E Z.
b	bo
21.	1) х = я4-2тгп, x = arccos I + 2лл, nEZ; 2) x = — |+2ж, x = arcsin g 4-2лтг,
n E Z. 22. 1) x =	4- тип, x =	4- nn, x = —	4- 2nn, x = —^ + 2лп, n E Z;
z	4	о	о
2)	x = 4- яп, x = 4- яп, x=^4- 2тси, x — ^ + 2тсп, и E Z. 23. 1) x = nn,
v = — J 4- 2яп, x = — 4- яп, п E Z; 2) x = J 4- яп, x = 2яп, x = J 4- яп, и E Z.
2	3	2	b
24.	1) x — — 4-2яп, x = —	4-2яп, п E Z; 2) x =	4-2яп, x = я4-2яп, и E Z.
25.	1) x =	4- 2тгп, x = 4г + 2яп, x = nn, x = 4- 2тгп, x = — 4- 2яп, и E Z;
4	2	6	4
2)	x = j + 2яп, x = я 4- 2яп, х=^4-яп, х — — | 4- 2тгп, х = — ~ 4- 2яп, и Е Z.
26.	1) х = 2яп, х = 4- яп, и Е Z; 2) х = яп, х =	4- 2яп, и Е Z. 27. 1) х =	,
74
Глава XII. Тригонометрические уравнения и неравенства
х=% + ™’	2) * = ±+м, х=^ + кп, х = |5 +
1Z, Z,	U	1Z	Z
п G Z. 28. 1) х = arccos 1 +пп, х = (~1) + arccos * + кп, пе Z;
2) х =	+ от, х = ±i arccos + я(2п + 1), п Е Z.
§6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
РАЗЛИЧНЫХ ВИДОВ.
УРАВНЕНИЯ, СОДЕРЖАЩИЕ ПАРАМЕТРЫ
Пример 1. Решить уравнение
1 2х - 1 .	.	7U
arctg-----+ arcsinx = -.
х	2
А Данное уравнение равносильно уравнению arctg u = arccos х при
условии |х|^1, ху^О, где и — %х~ 1. Тогда cos(arccosx) — cos(arctgu),
откуда х = JE *_____,
х2 + (2х — I)2 = 1, 5х2 — 4х = О,
откуда так как х^О.
4
Проверка показывает, что число х = - — корень исходного урав-
нения.
Ответ, х = р.	▲
э
Пример 2. Решить уравнение
sin Зх sin3 х + cos Зх cos3 х = |.	(1)
о
А Так как
sin Зх — 3 sin х — 4 sin3 х, cos Зх = 4 cos3 х — 3 cos х,
eir)3 V — 3sinx-sin3x з v _ 3 cos х + cos Зх	/9х
о 111 А* —	"	• V (J о Л —	~	•	I 2S 1
4	4
Применяя формулы (2), преобразуем левую часть уравнения (1):
(3sinх — sinЗх) -I- c°s3--(3cosх + cosЗх) =
= | (cos2 Зх — sin2 Зх) + | (cos Зх cos x + sin 3x sin x) =
= | (cos 6x + 3 cos 2x) = cos3 2x.
§6. Тригонометрические уравнения различных видов
75
Таким образом,
sin Зх sin3 х + cos Зх cos3 х — cos3 2х,
и уравнение (1) примет вид
cos3 2х = |, откуда cos 2х = |.
Ответ, х = ±5 + пп, п е Z.	▲
6
Пример 3. Решить уравнение
90 ЛХ 2л:Х 4тГ% 87UX 16ТСХ !
32 COS — COS — COS —— COS —- COS —- = 1.
ol	ol	Ol	<ji	ol
Д Умножим обе части уравнения на sin и, используя пять раз
формулу 2 sin a cos a — sin 2a, приведем уравнение к виду
Sin ^ = sin	(3)
ol	ol
Преобразовав разность синусов в произведение, получим
о • пх ЗЗтгх п
2sinTcos^r = 0-
Следовательно, уравнение (3) равносильно совокупности уравне-
ний
• _ кх п ______ 33 тих	Л
sin — = 0, cos = О,
из которых находим х = 2п, х = ||(2п + 1), и е Z.
В процессе решения обе части исходного уравнения умножались
иа функцию sin которая обращается в нуль при х = 31k.
k е Z. Легко видеть, что при этих значениях х левая часть
исходного уравнения не равна единице. Поэтому если среди корней
уравнения (3) есть числа вида 31 k, keZ, то такие корни являются
посторонними, их необходимо обнаружить и устранить.
Для этого нужно решить в целых числах уравнения
2п = 31£, ||(2п + 1) = 316.
ии
Первое уравнение имеет решения (и; £) = (31р; 2р), р е Z. Сле-
довательно, из серии х = 2п нужно удалить корни х = 62р. Второе
уравнение
2п + 1 - 33k
при четном k не имеет решений, а при нечетном k решениями
являются все пары (n; k) = (ЗЗр + 16; 21 + 1), р е Z, /eZ.
76
Глава XII. Тригонометрические уравнения и неравенства
Поэтому из серии х = ||(2п + 1) следует удалить корни, полу-
чающиеся при п = ЗЗр + 16, р € Z.
Ответ. х = 2п, n^31fe; х = ||(2п +1), п^33р +16, neZ, feeZ,
р G Z.	А
Пример 4. Решить уравнение
tgx + 2 tg2x + 3 ctg3x + 4 ctg4x = 0.	(4)
А Допустимые значения x определяются условиями
cosx ф 0, cos2x^0, sin Зх 7^ 0, sin4x^0.	(5)
Но если sin 4х 7^ 0, то sin 2x^0, cosx 7^ О, cos2x^0.
Поэтому условия (5) выполняются, если
sin 3x^0, sin 4x^0.	(6)
Естественно попытаться сгруппировать слагаемые в левой части урав-
нения (4). Преобразуем последовательно сумму второго и четвертого
слагаемых:
2Sin2x | 4COS4X __ 9Sin22x + cos4х _ 2cos22х _ 22х
cos 2%	sin 4%	cos 2% sin 2% cos2xsin2x °
Итак,
2(tg2x + 2ctg4x) = 2ctg2x.	(7)
Отметим, что из соотношения (7) следует равенство
tg a + 2 ctg 2а = ctg a.	(8)
Используя равенство (7), запишем уравнение (4) в виде
tgx + 2ctg2x + 3ctg3x = 0.	(9)
Применив формулу (8), последовательно преобразуем уравне-
ние (9):
ctgx + 3ctg3x = 0,
COSX | gCOs3x _ Q
sinx sin3x ’
sin 3x cos x + 3 sin x cos 3x = 0,
| (sin 4x + sin 2x) + | (sin 4x — sin 2x) = 0,
2 sin 4x — sin 2x = 0,
sin 2x(4 cos 2x - 1) = 0.	(10)
При переходе от уравнения (4) к уравнению (10) были использо-
ваны равенства, справедливые при всех значениях х, удовлетворяю-
щих условиям (6). Поэтому этот переход не мог привести к потере
корней. Так как sin 2x^0 в силу условий (6), то задача сводится
§6. Тригонометрические уравнения различных видов
77
к решению уравнения cos2x=|, корни которого удовлетворяют
условиям (6).
Ответ, х = arccos | + тт, nel.	А
2	4
Пример 5. Решить уравнение
tgf^cos22x) = tg(2n:cos2x).	(11)
Л Из уравнения (11) следует, что
~ cos2 2х = 2л cos2 х + nk, keZ.	(12)
Zu
Пусть Z = cos2x, тогда 2cos2x = / + l и уравнение (12) примет
вид	9
6/2 - 25t - 25(6 + 1) = 0.	(13)
Задача сводится к нахождению значений k е Z, при которых
уравнение (13) имеет действительные корни
,	25 ± 5 VI - 24/г
о — ------------.
из которых один можно отбросить сразу, так как он больше единицы.
Итак,
t = 5(5 - ^ - 24fe) ^ k е	(14)
и нужно найти значения k е Z такие, что 1 — 24/г 0 (и тогда k 0)
и при этом учесть, что |/|	1.
Пусть k^— 3, тогда \/1 — 246 >8 и t<— 1. Поэтому уравнение (12)
может иметь решения лишь при k = 0, k=— 1, и k = — 2.
Если k = 0, то из (14) следует, что Z>1.
Если k — — 1, то t — Q, т. е. cos2x = 0, откуда
+ nez.
4	2
Если
k — — 2, то t = — f, х = arccos
о	2
4" 7Ш, п G Z.
Ответ, х = у + ^, х — arccos f—+ тгя, n e Z.
42	2	\ 6/
Пример 6. Найти общие корни уравнений
2 cos + 4 cos лх + 1 = 0,	(15)
2 cos — + 2 sin 7ix — 2 cos jtx — 1 = 0.	(16)
78
Глава XII. Тригонометрические уравнения и неравенства
Л Пусть х — общий корень уравнений (15) и (16). Тогда (15) и (16) —
верные равенства. Будем исключать из этих равенств слагаемые,
содержащие их первые члены, используя формулу
cos 2/ — 2 cos2 t - 1.
Из уравнения (16) следует, что
2
2cos—=2(2cos2--l) = (2cos-) -2 =
= (1 + 2(cos тех — sin тгх))2 — 2 —
= 3 + 4(cos тех — sin тех) — 8 sin тех cos тех, (17)
а из равенств (15) и (17) находим
4 + 8 cos тех — 4 sin тех — 8 sin тех cos тех — О
или
(1 — sin тех) (1 + 2 cos тех) = 0.	(18)
Из равенства (18) получаем, что либо sin тех = 1 и тогда
x=± + 2k, ke%,	(19)
либо cosffic = — | и тогда
х = ±| + 2k, ke%.	(20)
О
Таким образом, если уравнения (15) и (16) имеют общий корень,
то он является числом вида (19) или (20). Выясним, какие из чисел
вида (19) и (20) являются общими корнями уравнений (15) и (16).
а)	Подставляя значения %, записываемые формулой (19), в урав-
нения (15) и (16), получаем
cos тех = 0, sin тех = 1,
2cos 77^7 = “h 2cos 77^7 = “h
4£ + 1	’	46-1-1	’
откуда
4^1 = 4+-’ 4ГИ = ±1+/’	™
Нетрудно проверить, что равенства (21) являются верными
только при k = — 1 и k = — 4 и поэтому числа Xi = — -
15
и %2 — “тр определяемые формулой (19), являются общими
корнями уравнений (15) и (16).
§6. Тригонометрические уравнения различных видов
79
б)	Рассмотрим числа вида (20). В этом случае равенство (15)
примет вид 2cos^ = l, где х выражается формулой (20).
Отсюда получаем
---------= ±| + 2m, me Z,
±l+2k----3
О
или
45 = (6m±l)(3£±l).	(22)
Равенство (22) не является верным ни при каких целых m и k,
так как его левая часть делится на 3, а правая не делится.
Следовательно, ни одно из чисел вида (20) не является общим
корнем уравнений (15) и (16).
3	15	А
Ответ. —.	▲
Пример 7. Найти все решения уравнения
cos 2х =	2 tg2 х — cos2 х,	(23)
удовлетворяющие неравенству
sinx	cosx.	(24)
Д Так как cos2x — 2cos2x — 1, tg2x = —~ — 1, то, полагая cos2x = Z,
C0S2X
запишем уравнение (23) в виде
2/ — 1 = | — 2 — t или 3t2 +1 — 2 = 0.
Заметим, что /	0 (при t = cosx = 0 исходное уравнение теряет
смысл) и / = cos2x>0. Уравнение 31? +1 — 2 = 0 имеет единственный
положительный корень t = Задача сводится к нахождению
решении уравнения coszx = - или sinzx = удовлетворяющих
неравенству (24).
Если sinx = Д=, то
л
х = (—1)" arcsin + яп, n&Z,	(25)
v3
а если sinx = —то
V3
х = (—l)n+1 arcsin + m, neZ.	(26)
v3
80
Глава XII. Тригонометрические уравнения и неравенства
Если в формуле (25) /г —нечетное число (n = 2k + 1), то
х = — arcsin + (2k + 1)л, k G Z,
и cosx<0. В этом случае выполняется условие (24).
При четном п (п~ 2k) из (25) следует, что
(27)
х = arcsin -4= + 2nk, keZ, cosx—
v3	V
и условие (24) не выполняется.
Аналогично, решения уравнения sinx = —удовлетворяющие
условию (24), определяются формулой (26) при п = 2&4-1, т. е.
х = arcsin + (2k + 1)тг, k G Z.
Ответ. х = ±arcsin + (2k + 1)л, k G Z.
Пример 8. Решить уравнение
14-7rcosx .	14-nrsinx тг
arcsin ——2--+ arccos —
Л Перенесем второе слагаемое левой части в правую часть:
arr«in 1 2 + ЛС05Х — к ягеегк 1 + KSinx
aicsiii-----— — — di ссиь---—---•
Приравняем синусы левой и правой частей:
.	14-71 COSX .	/ 7Г	14-7rsinx
sin arcsin ——---= sin I - - arccos-----
Воспользуемся формулами
sin arcsin a = a, cos arccos a = a, |a|	1
и упростим уравнение. Получим
14-7tcosx _ 14-7tsinx
2
(28)
(29)
2
или cos % = sin %. Следовательно, х = + лтг, п G Z.
Переход от уравнения (28) к уравнению (29) мог привести к по-
явлению посторонних корней. Сделаем проверку. Корни х = ^ + 2лй,
k е Z, не входят в область допустимых значений, так как
1 4- 7TC0S ( т + 2^k
\4
~ 2~~
1 + + 1
2	2V2	2	2
§6. Тригонометрические уравнения различных видов
81
Подставляя х =	4- n(2k + 1) =	+ 2л/г, k G Z, в исходное
уравнение, получаем верное числовое равенство
arcsin |(1- -4=) + arccos | (1 - -4=) = 4
2 V у/27	2 \	у/2/	2
Ответ, х — ~+2nk, keZ.	▲
4
Пример 9. Найти все пары чисел (х;г/), удовлетворяющие
уравнению
12д/6х — х2 — 5 cos2 х ~ 2j/ + 4 sin2(x — 2у) — 8 cos(x — 2у) = 17.
А Левая часть уравнения имеет смысл тогда и только тогда, когда
6х — х2 — 5^0, т.е. когда хе[1;5]. Выразим все тригонометрические
функции, входящие в уравнение, через Z = cos2^-^4 Получим
cos(x — 2у) = 2 cos2 Х~^У — 1 = 2t — 1,
sin2(x — 2у) — 1 — cos2(x — 2у) = 1 — (2t — I)2 = 4t — 4/2.
Следовательно, исходное уравнение можно записать в виде
12а/6х- х2- 5 • t + 4(4/ - 4/2) - 8(2/ - 1) = 17,
или
12д/бх —х2 —5 • / - 16/2 + 9, \/бх- х2- 5 =	/ + 0.
Но у +	2, следовательно,
\/бх — х2 — 5 2.
Решая полученное неравенство, находим
6х — х2 - 5 4, х2 — 6х + 9 0,
(х - З)2 0, х - 3.
Зная х, определяем /, а затем и у.
у + ^=2. '=!• ^¥4 М29-3) = 1,
2у — 3 =	+ 2m, у = ±+ m, nEl.
и	Л О
Ответ. (3; | ± + яп), п е Z.	А
82
Глава XII. Тригонометрические уравнения и неравенства
Пример 10. Решить уравнение
sin4 х — 2 cos2 х + a2 — 0, a G R.
cos2x = i±^
или t2 — 6/ + 4a2 — 3 = 0.
А Так как
Sin2x = b^,
то, положив t — cos 2x, получим
(W-2t+“2=»
Это квадратное уравнение имеет корни /12 = 3 ± 2д/з — а2 при
\а\ Vi.
Условию И 1 удовлетворяет только корень 12 = 3 — 2а/3 — а2
и только при |а|	д/2.
Уравнение cos2x = /2 при |а|	\/2 имеет решения
х = кп ± | arccos(3 — 2\/3 — а2), п е Z,
при |а| > \/2 оно не имеет решений.
Ответ, х = яп ± | arccos(3 — 2д/З — а2), п G Z, если |а|	д/2;
если |а| > д/2, то решений нет.	▲
Пример 11. При каких значениях а уравнение
sin2 х - sin х cos х — 2 cos2 х = а	(30)
имеет решения? Найти эти решения.
А Уравнение (30) согласно замечанию к примеру 12 в § 2 равно-
сильно уравнению
(1 — a) sin2 х — sin х cosx — (а + 2) cos2 х = 0.	(31)
а)	Пусть а уИ. Тогда из (31) следует, что cosx V 0 (в против-
ном случае sinx = cosx = 0). Поэтому, разделив обе части
уравнения (31) на cos2x и положив Z = tgx, получим уравнение
(1 —а)/2 -/-(а + 2) = 0,	(32)
равносильное уравнению (31).
Уравнение (30) при а V 1 имеет решения в том и только
в том случае, когда дискриминант квадратного уравнения (32)
неотрицателен, т. е.
D = -4а2 - 4а + 9 0.	(33)
Решая неравенство (33), получаем
2
2
(34)
§6. Тригонометрические уравнения различных видов
83
Если /1, ^2 — корни уравнения (32), то решения уравнения (30)
имеют вид
xi = arctg t\ + m, %2 = arctg^2 +
б)	Пусть a = l. Тогда уравнение (31) можно записать в виде
cos x(sin х + 3 cos х) = 0,
откуда
х = | + тгп, х = — arctg 3 + тт, и е Z.
Ответ. Уравнение имеет решения при atE,
где Е — [ —	1;	» если a G Е и a ф 1, то
х = arctg t\ + тип, х = arctg 1% + тги,
где /12 = lzt=	’ п если a = 1’ то
х = | + тш, х = — arctg 3 + кп, п G Z.	А
Пример 12. Найти все значения параметра а, при которых
уравнение
2 cos 2х + 2а sin х + а — 1
имеет единственное решение на интервале
А Воспользуемся формулой
cos 2х = 1 — 2 sin2 х
и запишем уравнение в виде
2 — 4 sin2 х + 2а sin х + а — 1 = 0.
Положив Z = sinx, получим квадратное уравнение
4/2 — 2at — а —1 = 0.
Его корни /1 =	/2 = -у--
Таким образом, исходное уравнение равносильно совокупности
уравнений:
1	. а +1
sinx = — sinx = —Т—.
Первое уравнение не содержит параметра а и на заданном
интервале	имеет одно решение х = —
84
Глава XII. Тригонометрические уравнения и неравенства
Второе уравнение при а — — 2 совпадает с первым и, следовательно,
при а = — 2 исходное уравнение на интервале	имеет
единственное решение.
Если а / —2, то уравнение
• а -|- 1
sinx = —~~
на интервале (“трО) не должно иметь решений Это условие
выполняется в случае, когда	— 1, а также в случае, когда
0. Отсюда получаем, что а — 3 и а — 1.
Ответ, а < — 3, а = — 2, а^— 1.	▲
Пример 13. Найти все значения а, при которых уравнение
sin10 х + cos10 х — а	(35)
имеет решения, и найти эти решения.
Л Преобразуем левую часть уравнения. Рассмотрим тождество:
sin8 х + cos8 х = (sin8 х + cos8 x)(sin2 x + cos2 x) =
= sin10 x + cos10 x 4- sin2 x cos2 x(sin6 x + cos6 x),
откуда
sin10 + cos10 x = sin8 x + cos8 x — | sin2 2x(sin6 x + cos6 x).	(36)
В § 2 (примеры 9 и 10, формулы (4) и (5)) получены равенства
sin6 х -Ь cos6 х = 1 — sin2 2х,
4
sin8 х + cos8 х — cos2 2х + | sin4 2x.
о
Преобразуем эти равенства:
sin6x + cos6x = 1 — | ^'1~c°s4x^ = | (5 + 3cos4x),	(37)
sin8 x + cos8 x = - + c°s — + ±(1 — cos4x)2 = X(cos2 4x + 14cos4x +17).
Z oZ	3Z
(38)
Из соотношений (36)-(38) следует, что
sin10x + cos10x =
= j^(cos24-': + 14cos4x +17) — X(1 — cos4x)(5 + 3cos4x),
откуда находим
sin10 x + cos10 x = X (5 cos2 4x + 30 cos 4x + 29).	(39)
§6. Тригонометрические уравнения различных видов
85
Обозначим t = cos4x, тогда, используя формулу (39), запишем
уравнение (35) в виде
5Z2 + 30/+ 29 — 64а = 0.	(40)
Уравнение (35) будет иметь решения при тех и только тех
значениях а, при которых корни уравнения (40) действительны и по
крайней мере один из них по абсолютной величине не превосходит
единицы.
Уравнение (40) имеет действительные корни t\ и тогда
и только тогда, когда 152 — 5(29 — 64а) 0, т. е. при а Решая
уравнение (40), находим
/1 = -3- |у/5(4а + 1), /2 = 1^5(40+ 1)-3.
Так как t\ < — 1, то этот корень следует отбросить. Неравенство
|^|	1 равносильно каждому из следующих двойных неравенств:
10 4^5(4а + 1) «С 20,
5^4(4а+1) ^20, ±^а^1.	(41)
Итак, уравнение (35) имеет решения тогда и только тогда, когда
выполняется условие (41).
Решив уравнение cos4x = ^2> получаем
х = ±7 arccos	kel.
4 у у 5 у 2
Ответ. х = ±| arccos (4а 1 —3]+^,6eZ, если а е 1];
4 у у 5 у 2	L16’ J
решений нет, если a < ~ или a > 1.	А
Задачи
Решить уравнение (1-15):
о	о
1. sin3xsin x+cos3xcos x = cos2x. 2. tg2xd--------= ctgx4-----—
sin x	sin ox
3. ctg2x + 3tg3x = 2tgx+ —4. tg3x = tgxtg(x + ^).
5.	tgx-tg3x + tgxtg2xtg3x = 0.
6.	4 tg 4x - 4 tg 3x - tg 2x = tg 2x tg 3x tg 4x
7.	——I--------------1--— =------——.	8. arctg i-- + arcsin 3x —
sinx cos2xsin3x cosx	sinx cos 2x	3x	2
Л sin29x	o m । cos29x
9. —7— = 16 ctg 2x sin 10x4-----7—.
sin2 x	cos2 x
86
Глава XII. Тригонометрические уравнения и неравенства
IQ sin 4х 4- sin Зх — sin 2х — sin х
cos х + cos 2х + cos Зх 4- cos 4х
| cos 2x|
sinxsin (x +
11. tg(x+£)ctg(3x-£)=7.
13.	sin10 х + cos*°x = cos4 2х.
16
12. tg ( cos2 2x j = tg(27rsin2 x).
14.	3 sin 3x = cos 4x — sin 9x — cos lOx.
15.	2 tg 6x 4- 4 tg 12x 4- 8 ctg 24x 4- tg 3x = tg 2x.
16.
17.
Найти все решения уравнения 4 sin4 х 4- sin2 2х = 2 tg2 х, удовлетворяющие
неравенству sinx 2cosx.
2	4	1
Найти все решения уравнения tg тех 4- - cos 4лх 4- - = 0, удовлетворяющие
 
2	/
18.
неравенству log i log3 ( х2—— х4-34
3	2 \	2
Найти все общие корни уравнений
sin — — cos — — 2 sin 5лх = О,
х х
л/3 sin Ютих — 3 cos Ютгх — sin — = 0.
X
19.	Найти все значения а, при которых уравнение (arcsinх)3 + (arccosx)3 = а
имеет единственное решение.
20.	Найти все значения а, при которых уравнение cos3x = acosxcos2х имеет
0; - I.
21.	Найти все значения а, при которых уравнение sin8 х 4- cos8 х = а имеет
решения.
22.	Найти все значения а, при которых уравнение 4 cos2x4-(2 — 4а) sinx = а 4-3
имеет единственный корень на интервале ^;0^.
Ответы
1. х=^, nez. 2.	+ ^, х=1 + ^ (2Й + 1/9/П), nez, keZ, mez.
3. х = arccos | — 4 ) 4- nn, n e Z. 4. x = nn, x = — J 4- пп, x = -y nn, nel.
2	\ 4/	3	12
5. x = тт, n e Z. 6. x = nn, x = ± arctg 4- nn, n e Z. 7. x =	4-
n^3m, n e Z, m e Z. 8. x = |.	9. x = ? 4- n G Z; x = k / 5p, k G Z,
7	5	4	2	10
p e Z. 10. x — i arctg 2 4- nn, n e Z.	11. x = arcsin | 4- n G Z.
12. x=^4-^, x = arccos | + nn, n<E%. 13. x = 4- n eZ. 14. x = ^,
4	2	2/	о 4	о
х = -?+2тт, neZ. 15. x=A + ^, n^5k + 2, k,neZ. 16. x= ±^+2m,
n EZ. 17. X]	= 5^ Xo =	5-^, X3 = 6^, %4	= 6^.	18. x = —i 19. a =
6	2	4 й 6	4	6	32
20.	a < 1,	a > 3.	21.	| a 1.	22. a 1,	a = a	3.
о	о	о	2
§ 7. Тригонометрические неравенства
87
§7. ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА
Неравенства
sinx > a, cosx > а, tgx>a,
sinx < а, cosx < а, tgx<a, a е R,
будем называть простейшими строгими тригонометрическими
неравенствами. К простейшим неравенствам относятся также со-
ответствующие нестрогие неравенства. При решении тригономет-
рических неравенств используются свойства тригонометрических
функций и, в первую очередь, их периодичность и монотонность на
соответствующих промежутках.
Рассмотрим неравенство
sinx>a,	(1)
Так как |sinx| ^1, то при а> 1 неравенство (1) не имеет решений,
а при а<— 1 его решениями будут все действительные числа. Пусть
ае[— 1; 1]. Поскольку синус — периодическая функция с периодом 2к,
достаточно найти решения неравенства на любом отрезке длины 2тг.
Возьмем отрезок	и построим графики функций у = sinx,
хе |—yj и у— а (см. рис. 3). Решениями неравенства (1) являются
те значения х из этого отрезка, для которых соответствующие
точки графика функции у = sin х лежат выше прямой у = а. Из
рисунка, где — 1 < а < 0, видно, что искомые решения принадлежат
интервалу (xi,X2), где xj и Х2 — корни уравнения sinx = a, лежащие
на рассматриваемом отрезке, т. е. xj = arcsin a, Х2 = я — arcsin а. Таким
образом, множеством решений неравенства на отрезке [~ру]
является интервал (arcsin а; л — arcsin а). В силу периодичности
синуса множество решений неравенства состоит из всех интервалов
вида
(2лл + arcsin а; 2т + тг — arcsin а), и 6 Z.	(2)
Этим же методом можно находить решения неравенств вида
sinx < a, cosx < а, cosx > а, где |а|	1, а также соответствующих
нестрогих неравенств.
Рис. 3
88
Глава XII. Тригонометрические уравнения и неравенства
Пример 1. Решить неравенство sinx<-^.
Л Построим графики функций у = sinx и у — —= (см. рис. 4).
Найдем все решения неравенства sinx < принадлежащие
отрезку |j; yj длиной 2л. На этом отрезке уравнение sinx = -~
имеет два корня: = ~ и х=~. Из рис. 4 видно, что решениями
неравенства sinx <	на отрезке у] являются все числа
7 Зя 9тг \
интервала I —;—j.
Так как функция sin х — периодическая с периодом 2 л, все
решения неравенства sinx < у= — это числа х из интервалов
f + 2лп; + 2т\, и Е X
\ 4	4	7
Ответ. (+ 2т;	+ 2т\ и е Z.	А
\ 4	4	7
Замечание. Вместо отрезка
длиной 2п (Рис-4)-
л. бтс]
2’TJ
можно было рассматривать отрезок
Пример 2. Решить неравенство cosx^-^-
Д Так как косинус — периодическая функция с периодом 2тг, то
достаточно найти решения неравенства на отрезке длиной 2л.
В качестве такого отрезка возьмем отрезок [0;2л]. Рассмотрим
на отрезке [0;2л] график функции у = cosx и проведем прямую
У = ^- (Рис-5)-
Нужно найти все те значения х из отрезка [0; 2л], для которых
соответствующие точки графика функции у = cosx лежат ниже
\/3
прямой у = — и на этой прямой.
§7. Тригонометрические неравенства
89
Рис. 6
/о
Прямая у— пересекает при хе [О;2тг] график функции у — cosx
л/З
в точках А и В, абсциссы которых суть корни уравнения cosx = — на
отрезке [О;2тг]. Одно из решений этого уравнения X] = arccos =
другое: х% =	— х\ = Если хе [|;^]> то cosx<^~L
Следовательно, на отрезке [0; 2тг] все решения неравенства
cosx определяются условием | < х
Ответ. £ + 2тг& х + 2л&, k е Z.	А
6	6
Пример 3. Решить неравенство sin2x<^.
А Это неравенство равносильно неравенству |sinx|<-^=
Построим графики функций у — |sinx| и у— -~
Функция у = | sin х| — периодическая с периодом
[ТС тс1	«	I • I 1
— длиной ти уравнение |sinx| = —г имеет два
2 Z J	V 2
(рис. 6).
тг. На отрезке
корня: х = —
и х=^. Из рис. 6 видно, что решениями неравенства |sinx| < -~=
на отрезке	являются все числа х из интервала ^5^-
90
Глава XII. Тригонометрические уравнения и неравенства
Следовательно, все решения неравенства | sinx| <	— это числа х
'У п е Z (см. рис. 6).
пщ + пп
из интервалов
все решения
4	’	’
Обратимся к простейшим тригонометри-
ческим неравенствам вида tgx<a, tgx^a,
tgx>a, tgx>a. Такие неравенства имеют
решения при всех a е R, так как тангенс
принимает все значения из множества R.
Рассмотрим нестрогое неравенство
tgx^a, aeR.	(3)
Поскольку тангенс — периодическая
функция и ее период равен тг, найдем
этого неравенства на интервале	Построим
и у — а (см. рис. 7).
Функция у — tgx на интервале	строго возрастает
и при любом а пересекает прямую у = а в одной точке, абсцисса
которой равна х\= arctgа. Множеством решений неравенства будет
промежуток
расположена не выше прямой у — а. Учитывая периодичность
тангенса, делаем вывод, что множеством решений неравенства (3)
является объединение всех промежутков вида
(—^ + пп, arctg a + nnj , neZ.	(4)
Проведенное рассуждение одновременно показывает, что множе-
ство решений неравенства
tgx а, а е R,
есть объединение всех промежутков вида
jarctga + пп, ~ + пп) , neZ.
Пример 4. Решить неравенство tgx > 1.
А Построим графики функций у = tgx и у — 1 (см. рис. 8). На
интервале	длиной п уравнение tgx—1 имеет один корень
х = Из рис. 8 видно, что решениями неравенства tgx > 1 на
графики функций y = tgx, хе
= (“5’агс^а]» на котором тангенсоида у — tgx
(5)
(6)
интервале
являются все числа х интервала
§7. Тригонометрические неравенства
91
Так как функция tgx — периодическая с периодом тс, то все реше-
ния неравенства tgx> 1 — это числа х из интервалов Q + от; | + от),
п е Z (см. рис. 8).
Ответ, у-h от < х < ^ + от, n Е Z.	А
4	2
Пример 5. Решить неравенство 4sin2x — 8sinx + 3 0.
Л Обозначая sinx = t, получаем квадратное неравенство
4/2 - 8t + 3	0. Разложив квадратный трехчлен 4/2 — 8^ + 3 на
множители, запишем неравенство в виде 4^—|)(^~|)	0.
Заменяя t на sinx, получаем неравенство (sinx — I) (sinx-0^0.
Последнее неравенство равносильно каждому из неравенств
(| — sinx) (sinx — 0 0, sinx^j,
так как - — sin х > 0 при всех х е R.
Решениями неравенства sin х | являются числа х из отрезков
Г£ + 2пп- 5 + 2кп], ntZ.
Lb	b	J
Ответ. £ + 2от x + 2от, n G Z.	A
6	b
Пример 6. Решить неравенство sin x > cos 2x.
Л Так как cos2x = 1 — 2sin2x, то, положив £ = sinx, получаем
1 -2t2,
откуда 2/2 + t — 1	0. Корни уравнения 2t2 + t — 1 = 0 равны
t\ = — 1, ^2 —I» и, следовательно, решениями квадратного неравенства
являются промежутки — 1 и
Первое неравенство равносильно уравнению sinx = — 1, и поэтому
его решения х = 2от —пей. Решения второго неравенства находим
92
Глава XII. Тригонометрические уравнения и неравенства
по формуле (2) при а — заменяя в ней интервалы отрезками, так
как в данном случае неравенство нестрогое.
Ответ. x = 2m—£, 2m + £ х 2m + п е Z.	А
2	6	6
Пример 7. Решить неравенство tgx 2 cos 2х + sin 2х.
Л Воспользуемся формулами
cos 2х = —sin 2х = 2 tg* -
1 + tg2 х	1 + tg2 X
и введем новую переменную / = tgx. Тогда неравенство примет вид
/ <-' о 1 ~	।	2/
" ТТ? *"Гн2’
т. е. сводится к рациональному неравенству.
Решая его, например, методом интервалов, получаем
t+t3 ^2-2t2 + 2t,
t3 + 2t2 -t-2^0,
откуда t < —2, —1	1.
Возвращаясь к старой переменной, имеем
tgx ^-2, <! ё
откуда согласно формулам (3)-(6) следует, что множество реше-
ний исходного неравенства представляет собой объединение всех
множеств вида
( —+ тгп; — arctg2 + m\ и
Ответ. — + m < х — arctg2 + тот, + кп
nel
7 + кп’
4
Пример 8. Решить неравенство sin4 х + cos4 х > |.
О
А Воспользуемся тождеством
sin4 х + cos4 х = 1 — i sin2 2x = у + | cos 4x,
2	4	4
первое равенство в котором было получено в примере 6, § 2. Тогда
исходное неравенство можно записать так:
cos4x > —i.
§ 7. Тригонометрические неравенства
93
Положив t — 4х, получим простейшее неравенство cost> —
Это неравенство достаточно рассмотреть на отрезке [0; тс], поскольку
у — cos t — четная и периодическая с периодом 2л функция. Построив
графики функций (см. рис. 9) у = cost, t е [0;л] и у = —
видим, что точки графика первой функции лежат выше точек
графика второй функции на промежутке [0;£i), где /j—абсцисса
точки пересечения графиков, т.е. корень уравнения cost = —
принадлежащий отрезку [0;л].
Так как = arccos (—0 — у, то на отрезке [0;л] неравенству
удовлетворяют все значения te [О; у). Учитывая четность косинуса,
заключаем, что на отрезке [—л; тс] неравенству удовлетворяют все
значения
с периодом 2л
принадлежащее
п е Z, является
tE f—Принимая
\ о о /
во внимание периодичность
функции cosZ, получаем, что каждое значение t,
какому-либо из интервалов
(2лп- ^;2лп + ^Y
\ о	о /
решением неравенства. Возвращаясь к переменной
х=“, получаем окончательный результат.
ОТШ 7Г . „	. 7СП , 7Г _ ГП
твет. —-^<х< — + -, neZ.
zb	zb
Пример 9. Решить неравенство Vsinх + у/cosх < у/2.
Л Так как sinx и cosx — периодические функции с периодом 2 л,
будем искать решения неравенства на промежутке [0; 2 л). Левая
часть неравенства имеет смысл тогда и только тогда, когда sinx^O
и cosx 0, т.е. при хЕ гДе °бе части неравенства положи-
тельны, и поэтому данное неравенство равносильно неравенству
sin х + cos х + 2%/sinxcosx < 2.
94
Глава XII. Тригонометрические уравнения и неравенства
t2 - 1
Положим / = sinx + cosx, тогда sinxcosx — —-—, и неравенство
принимает вид	/----
р 1
t + 2y~lT <2’
Так как область допустимых значений неравенства |£|	1, a
то при t 1 получаем ,----------
/t2 1
2V
2t2— 2<4 — 4t + t2,
t2 + 4t - 6 < О,
1 < t< x^0-2.
Следовательно, исходное неравенство равносильно системе
1 sin х 4- cos х < vT6 — 2,
Решая эту систему, находим два полуинтервала ее решений:
| < х + | < arcsin(\/5 — л/2) и
тг — arcsin(д/5 — л/2) < х +	я —
откуда
О < х < агсзт(л/5 — л/2) - и — arcsin(\/5 — д/2) < х <
Таким образом, на отрезке |0; множеством решений исходного
неравенства является объединение двух промежутков:
О < х < arcsin(x/5 — \/2) — р
Y - arcsin(\/5 - л/2) < х <
Учитывая периодичность синуса и косинуса, получаем оконча-
тельный результат.
Ответ. 2zm<x< arcsin (\/5-\/2) — ^+2тт,	—arcsin(\/5 —\/2) +
+ 2яп < х + 2яп, п е Z.	А
Пример 10. Найти на отрезке [0; л] все решения неравенства
| — cos2х > sinx - cosx.
Д Левая часть неравенства имеет смысл тогда и только тогда, когда
cos2x^i. На заданном отрезке [0; я] это неравенство верно при
§ 7. Тригонометрические неравенства
95
хе	Ограничимся рассмотрением только этого отрезка. Те
его точки, для которых sinx<cosx, являются решениями исходного
неравенства, так как правая часть его отрицательна, тогда как левая
положительна. Неравенство sinx <cosx на отрезке [0;тг] справедливо
при хе [О; поэтому множество решений исходного неравенства
содержит промежуток
Пусть теперь хе [р^], т°гда обе части неравенства неотрица-
тельны и, следовательно, оно равносильно неравенству
| — cos 2х > 1 — sin 2х,
решая которое, находим
sin2x — cos2x >
sin 2x • cos 7 — cos 2x • sin -л >
4	4	2x/2
sin (2x - 7) > —
\	4/	2V2
arcsin —^= < 2x — 7 < 71— arcsin
2x/2	4	2x/2
к + 7 arcsin —< x <	— 1 arcsin —
8 2	2V2	8	2	2V2
Из найденных значений x надо отобрать те, которые принадлежат
[к 5тг\
5’ ~б /
Так как
i + larcsin^<i
^-larcsin
то множество решений исходного неравенства содержит еще и про-
межуток	arcsin^).
Объединение этого промежутка и найденного ранее |j; дает
искомое множество решений.
Ответ. х < — -7 arcsin—^=.	▲
6	8	2	2\/2
96
Глава XII. Тригонометрические уравнения и неравенства
Пример 11. Решить неравенство 3sin2х + cosxsinx > 2.
Л Это неравенство равносильно каждому из следующих неравенств:
|(1 -cos2x) + sin2x > 2, sin2x - 3cos2x > 1,
-4= sin 2x — cos2x > sin(2x — cp) > -4=,
x^O	716	x/I6 v	x/lo’
где cp = arcsin -|= = arccos -4=. Отсюда находим
г	x/10	716
arcsin —4= + 2m <2x — cp<it — arcsin —J= + 2ot, n e Z,
x/16	r	x/I6
x ( arccos 4- + arcsin -4= ) + m < x <
2 V 716	x/16/
< к + I (arccos —4= — arcsin -4= I + от, n e Z.
2	2 \	x/16	x/16/
Учитывая, что arccos-4= + arcsin—4= = запишем множество
x/16	x/10	2
решений неравенства.
Ответ. 5 + от<х<? + arccos —4= + от, п е Z.	А
4	4	71о
Пример 12. Решить неравенство
Л Найдем решения неравенства на отрезке тру] длиной 2тг.
Если хе(0;тг), то sinx > 0 и поэтому правая часть неравенства
отрицательна, а левая положительна. Поэтому значения х е (0; я) —
решения данного неравенства.
Пусть sinx0, тогда исходное неравенство равносильно каждому
из неравенств
5	c°s.4_x. > Sjn4 х. 5 + 3 cos4х > 2(1 — 2 cos 2х + cos2 2х),
cos2x(l + cos2x) > 0, cos2x>0, sin2 x < |sinx| < -^=.
Так как sinx 0, то	0» откуда — ~ <x^0, it^x<^-.
Итак, на отрезке [— тру] решениями исходного неравенства явля-
ются все числа из интервала
Ответ. — у + 2m < х <	+2т,	А
4	4
§7. Тригонометрические неравенства
97
Задачи
Решить неравенство (1-9):
1.	1) cosx <
7 \ 2»
2.	1) sinx < -;
7	2
3.	1) cos2 х >
4.	1) 4sin2x — 8sinx+ 3	0;
5.	1) sin + cos > 0;
« .. sin 2х — cos 2х + 1 п
6» 1)	Г О)
sin 2х + cos 2х — 1
7. 1) \/5 — 2sinx 6sinx — 1;
v3
2) cosx > —
2) sin 2х > -.
7	2
2) sin2x <
2) 2cos2—3cosx — 2 > 0
2) cos2x + cosx^0
2)	1 ~ 4 sin2 х < 2
cos x + cos 2x
2) 1 + 6cosx < 2\/2 + 4cosx.
8.	cos3 x cos 3x — sin3 x sin 3x > |.
8
л 4/7 — cos4x o
9.	\ ---------> —2cosx.
V 2
10.	Найти все решения неравенства sinxsin2x<sin3xsin4x на интервале ( 0;
11. Доказать, что если
О
то справедливо неравенство
_______cosx______
sin2 x(cosx — sinx)
>8.
12. Доказать, что если Л, В, С — углы треугольника, то справедливо неравенство
. А	. В .	С	.	1
sin —	sin — sin	—	<	-
2	2	2	8
Ответы
1. 1) %+2m^xs^+2m, neZ; 2) -^+2m<x<^+2m, neZ. 2. 1) ^+2wi<
О	О	о	о	о
<х<^+2тгп, MEZ; 2) ^ + тт<х< ~ + тш, MEZ. 3. 1) — ~ + тот<х<+ тгм,
6	12	12	6	6
п 6 Z; 2) — ^ + тт < х < ^ + тип, п Е Z. 4. 1)	+ 2тт х 5? + 2тт, п Е Z;
о	о	о	о
2) ^+2тт<х<^+2тт, neZ 5. 1) -£ + 1^<х<£ + ^, meZ; 2) х=тг+2тш,
О	О	О О	Z О
— ^+2лт1^х^ ^ + 2тш, nEZ. 6. 1) —у + т^х<тги, 2) — ^ + 2лтг<х< ^ + 2тт,
о	о	4	о	о
^+27г/2^х<7г+2тгм, 7г+27гм<х^^+2тгп, meZ. 7.1) ^+2тт^х^^+2тш, nEZ;
О	ООО
2) £+27rn^x^+2wi, ^+2т^х^+2т, n&Z. 8. -^ + — <х<^ + ^,
О	О	О	О	i.Zf Л	1Z Z
riGZ. 9. -^+27г/г<х<^+2тги, neZ. 10. 0<х<	<х< £.
4	4	5	5	2
4—3022
Глава XIII
ПРОИЗВОДНАЯ
И ДИФФЕРЕНЦИАЛ
§ 1. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ.
производные функций х", sinx, cosx
1. Задачи, приводящие к понятию производной
Задача о скорости. Пусть материальная точка М движется вдоль
оси Os, где О—положение материальной точки в момент времени
t = 0. Если в момент времени t координата материальной точки
равна S, где S = S(t), то функцию S(t) называют законом движения
точки М.
При неравномерном движении материальная точка за равные по
длительности промежутки времени может совершать перемещения,
разные не только по величине, но и по направлению.
Средняя скорость движения материальной точки за промежуток
времени от t до t + &t определяется формулой
WcP------AZ----•
Если рассматриваемое движение не является равномерным, то иср
при фиксированном t будет меняться при изменении Д/, и чем
меньше Д/, тем лучше иСр будет характеризовать движение точки
в момент t.
Скоростью точки в момент t (мгновенной скоростью) называют
предел, к которому стремится средняя скорость, когда Д^—>0, т. е.
скорость v в момент t определяется равенством
„= |im +
ДГ->0
Таким образом, скорость движения в момент t — предел отношения
приращения координаты Д£=£(£+Д£) — S(Z) за промежуток времени
от t до f + Д/ к приращению времени Д^, когда Д£—>0, если этот
предел существует.
Например, если материальная точка движется по закону S=~-
(закон свободного падения), то
Pcp=S(, + A,)-S(,) = &((, + A()2-f2)|
или
fcp =gt+^t,
§1. Определение производной
99
откуда
т. е. v — gt.
lim уср = gt,
Д/->0 н
Задача о касательной. Пусть функция / определена в 5-окрест-
ности точки хд и непрерывна при х = Xq. Рассмотрим вопрос
о касательной к графику функции y — f^x) в точке Alo(^o,Vo)> гДе
Vo— Дхо). Если Дх — приращение аргумента такое, что 0< |Дх| < 5,
то уравнение прямой I (рис. 1), проходящей через точки 7Ид
и 7И(хд + Дх,[(хо + Дх)), можно записать в виде
У - Уо =	-х0),
(1)
где
Ау = /(%о + Д-0 - Я*о), Ху = tg а.
Эту прямую называют секущей, а число k = tg а — угловым коэф-
фициентом прямой /; здесь а= а(Дх) — угол, образуемый прямой I
и осью абсцисс (этот угол отсчитывается от положительного
направления оси Ох против часовой стрелки).
Пусть Дх —> 0, тогда Д// —> 0 в силу непрерывности функции f
при х = х0, и поэтому
ЛШ0 = ^(Дх)2 + (Ду)2 О-
Касательной к кривой, заданной уравнением y = f(x), в точке ТИд
естественно назвать предельное положение секущей / при Дх —> О,
100
Глава XIIL Производная и дифференциал
т. е. прямую, уравнение которой получается заменой отношения
его пределом при Дх —> 0. Если существует
lim =	= k0,	(2)
Дх->0 Ах и’	V
то существует предельное положение секущей. Таким образом, если
предел (2) существует, то прямая с угловым коэффициентом
проходящая через точку TWq, является касательной к графику
функции у — f(x) в точке Mq.
Рассмотренные задачи, в которых речь идет о пределе отношения
приращения функции к приращению аргумента, исторически привели
к появлению понятия производной — одного из важнейших понятий
математического анализа.
2.	Определение производной
Определение. Пусть функция y — f^x) определена в некоторой
окрестности точки Xq и пусть существует конечный предел отношения
/(х0 4- Ах) - /(х0)
Ах
при Дх —> 0. Тогда этот предел называется производной функции f
в точке %о и обозначается /'(хо), т- е-
f(x0) = lim +	•	(3)
Дх—>0	дхх
Согласно определению производная функции у = /(х) в точке х$
есть предел отношения приращения функции Ду = /(хр + Дх) — /(хо)
к приращению аргумента Дх при условии, что Дх —* 0, т. е.
/(х0)= lim	(4)
Дх—>0 ^хх
Из равенства (4) следует, что
- Л*о) = г(Дх),
где е( Дх) —> 0 при Дх —> 0, откуда получаем
Ду = /'(хр) Дх + Дх • е(Дх).	(5)
Если Дх —> 0, то Ду —> 0, и поэтому из существования производной
/'(хо) в точке Хр следует непрерывность функции /(х) в точке х$.
Операция вычисления производной называется дифференцирова-
нием.
Заметим, что если функция /(х) имеет производную /'(х) в каждой
точке некоторого промежутка, то /'(х) является функцией от х на
этом промежутке.
§ 1. Определение производной
101
3.	Производные степенной и тригонометрических функций
Пример 1. Найти производную функции y~f(x), если:
О /W — Q 2) /(х) = х\ 3) /(х) =х2.
Л 1) Если у — f(x) = С, т. е. функция /(х) принимает при всех х
одно и то же значение, равное С, то
Дг/ = /(х + Дх)-/(х) = С-С, =
lim = О, т. е. (С)' = 0.
Дх^оДх	v ’
Итак, производная постоянной равна нулю.
2) Если у = /(х) = х, то Дг/ = (х + Дх) — х = Дх, = 1 (при
Дху^О), откуда следует, что
lim = 1,
Дх—>0 Дх
т. е.
(х)' = 1.
3) Если г/ = /(х) = х2, то
Ду = (х + Дх)2 — х2 = 2х • Дх + (Дх)2,
= 2х + Дх,
Дх
откуда получаем, что
lim = 2х, т. е. (х2)' = 2х.	▲
Дх—>0 A*	v
Пример 2. Найти производные функций z/ = sinx и z/ = cosx.
А При выводе формул для производных синуса и косинуса исполь-
зуем первый замечательный предел (гл. XI, § 4):
lim = i
х-^о *
а также непрерывность функций sinx и cosx.
1) Если z/ = sinx, то
Az/ = sin(x + Ах) — sinx = 2cos (х + sin
откуда
2
102
Глава ХШ. Производная и дифференциал
Так как
cos (х +	—> cos х при Дх —> О
в силу непрерывности функции cosx, а 1 при t —> О,
то > cos х при Дх —> 0, т. е.
(sinx)' = cosx.
2) Если у = cosx, то
Ду = cos(x + Дх) — cosx — —2sin (х + sin
откуда
lim — sinx, т. е. (cosx)' = — sinx. ▲
х—>0 Ах	V '
Пример 3. Найти производные функций и
Д 1) Пусть
у = 1	Д/j — —!— — - = ————
х	х 4- Дх х х(х 4- Дх)
где х ф 0, х + Дх ф 0. Тогда
A# ______1
Дх х(х 4- Дх) *
Если Дх —> 0, то х + Дх —> х и по свойствам пределов
существует
lim	т. е.
Дх—>0 Ах	%2
£
и2-
2) Пусть у = у/х, где х > 0, и пусть х + Дх > 0, тогда
Ду = л/х + Дх — у/х
(у/х + Дх — у/х)(\/х 4- Дх 4- у/х)
у/х 4" Дх 4- у/х
__ ____Ах_____
•\/х 4~ Дх 4" у/х
откуда при Дх 0 получаем
Ау =
Ах у/х 4- Дх 4- у/х
Если Ах—> 0, то у/х + Дх у/х (гл. IX, §3, пример 4).
Отсюда по свойствам пределов получаем, что
lim = -Т=, т. е. (у/х/ = тД=.
Ах—,0Дх	2^/х	k 7 2у/х
§2. Производные показательной и логарифмической функций	103
Пример 4. Доказать, что
(хпУ = пхп~\ пеН.	(6)
Д При п = 1 и п = 2 формула (6) была доказана в примере 1. Докажем
ее для любого n € N. Используя формулу бинома Ньютона, получаем
Ду = (х + Дх)” - х” = х” + их”-’Дх + С2х”-2(Дх)2 +... +
+ (Дх)” — х” = их”-1 Дх + Дх • ег(Дх),
где е(Дх) 0 при Дх —> 0. Отсюда следует, что
= пх”-1 + ег(Дх), е(Дх) —» 0 при Дх—>0.
Поэтому
> их"-1 при Дх—>0, т.е. (х”)' = мх”_|.	▲
§2. ПРОИЗВОДНЫЕ ПОКАЗАТЕЛЬНОЙ
И ЛОГАРИФМИЧЕСКОЙ ФУНКЦИЙ
*1. Второй замечательный предел
Теорема. Функция
(l + -)
\ X/
имеет при % оо предел, равный е, т. е.
Нт (1 + ±Т = е.	(1)
х—>ОО \	X/
О Докажем утверждение (1). Сначала рассмотрим случай, когда
х —> +оо.
В гл. IX, § 2, п. 5 было доказано, что
/	1 \ п
lim (1 + - ) = е.
AZ—>ОО \	П/
Обозначим
/	.\П	/	1\н+1	/	< \П
ап=\1 + п) ’ //”=(1 + п) ’ 2”=(1 + ^м) ’
тогда	_j
Уп = ап (1 +	, z„ = a„+i (1 + -О
Так как ап е при я —> оо, то уп-^ е и zn —> е при п оо. По
определению предела для любого с>0 найдем номер Ne такой, что
для всех n^Ne выполняются условия
уп е (4(e), zn е (7е(е),	(2)
где Ue(e) = (е — е, е + е).
104
Глава XIII. Производная и дифференциал
Пусть х — произвольное действительное число такое, что х Ne,
и пусть п = [х]. Тогда
Ne^n^x <п + \^	(3)
откуда по свойствам числовых неравенств следует, что
1 < 1 < 1
П + 1 X п '
(4)
Из соотношений (3) и (4), используя монотонность показательной
и степенной функций, получаем неравенство
Из условий (2) и (5) следует, что для любого е > 0 найдется номер
Ne такой, что для всех х Ne выполняется условие
(1 + i)' е
Это означает, что	z ч х
lim (1 + -)	—	е.	(6)
х->4-оо X х/
Докажем, что	z
lim (1 + -)	=	е.	(7)
х—>—сх) X х/
Пусть х — — 1 — t, тогда t —> +оо при х —> —оо и
(1 + х) = (1-Гн)	= (1 + ?) (1 + ?)-	(8)
Из соотношений (6) и (8) следует, что справедливо утверждение (7),
а из равенств (6) и (7) следует утверждение (1).	•*
Предел	х
lim (1 + -) = е
х—>оо \	X/
называют вторым замечательным пределом.
2. Некоторые важные пределы
Используя второй замечательный предел, докажем два утвер-
ждения, которые будут использованы при выводе формул для
производных показательной и логарифмической функций.
Утверждение 1. Если а> 0 и а ф 1, то
Нт	— log е = _L_.	(9)
х—>0	*	In a	v 2 * * * * 7
§2. Производные показательной и логарифмической функций
105
О Рассмотрим функцию
Ях) = /(1+х)х’
Функция /(х) определена в окрестности точки х = О,
lim(l+x)* = lim fl + -^ = е
х—>0	х—>оо \ xj
по доказанной теореме, т. е.
limi/(x) = /(0) = е.
х—>0
Поэтому функция /(х) непрерывна в точке х = 0, а функция loga/(x)
непрерывна в точке х = 0 как суперпозиция непрерывных функций
logaf и t — f{x). Следовательно,
Ит l°gafW = loga(lim(l + *)*) = 10ga£?.	(10)
х—>0	х—>0
Гак как	,	.	.
l°ga f(x) = °ga Х + Х пРи х / О,
го из соотношения (10) следует, что справедливо утверждение (9).
Из равенства (9) при a = е получаем
lim |п(1+х) = 1.	(П)
х-+0 *	ф
Утверждение 2. Если а> 0 и a 1, то
lim = In <2-	(12)
х->0	*
О Функция у = ах — 1 непрерывна и строго монотонна на множестве R
(возрастает при а > 1 и убывает при 0 < а < 1). На промежутке
(-1, +оо) существует обратная к ней функция х — loga(l + у),
непрерывная и строго монотонная. Учитывая, что у 0 при х —> О,
и используя формулу (9), получаем
Отметим важный частный случай формулы (12):
lim = 1.	(13)
х—>0 х	А
106
Глава ХШ. Производная и дифференциал
3. Формулы для производных функций ах и logflx
Найдем производные функций ах и loga х.
1) Если у = ах, то
Ду = ах+Лх _ах _ ахгаЛх _П Лу _ аха * - 1
v 7’ Дх Дх ’
откуда
—> ах In а при Дх —> О,
так как
а ~ 1 —> In а при t —* 0 (утверждение 2).
Таким образом, если а > 0, а 1, то
(аху — ах Ina.	(14)
Из формулы (14) при а — е получаем
(еху = ех.	(15)
2) Если у = logtt %, то
= >oga(* + Дх) - loga X = loga (1 +	,
log fl 4- —
Д г/ _	Ч 4 1
Дх	Дх х ’
откуда
lim = —,
дх_>0	х In a
так как
l°gaU 4-1)	t -^0 (утверждение 1).
Итак, если а > 0, а 1, х > 0, то
(logzzX)' =	.
v &а ' xln а
Из формулы (16) при а = е получаем
(1пх)' = ^.
Формулы (16) и (17) верны при к > О
(16)
(17)
§3. Правила дифференцирования. Дифференциал
107
§3. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ.
ДИФФЕРЕНЦИАЛ
1.	Дифференцирование суммы, произведения и частного
Теорема 1. Если функции fug дифференцируемы в точке х,
то в этой точке дифференцируемы функции f + g, fg, £ (при
условии, что g(x) ^0) и при этом
(ZW+gW)/ = /W+gzW,	U)
(/(Ж*))' = f WgW +	(2)
О Обозначим
Д/ = f(x + Дх) - /(x) и Д£ = £(х +Дх)-g(x).
при Дх —»0, так как существуют /'(х) и g'(x). Кроме того,
/(х + Дх) = /(х) + Д/, g(x + Дх) = g(x) + Д§,
где Д/—>0, Ag—>0, так как функции f и g непрерывны в точке х.
1) Если у — /(х) +£(*), то
Дг/ = /(х + Дх) + g(x + Дх) - /(х) - g(x) = Д/ + Д£,
откуда
Ау = А/ + Ag
Ах Ах Ах ’
Правая часть этой формулы имеет при Дх —> 0 предел,
равный /,(x)+g'(x). Поэтому существует предел левой части,
который по определению равен (/(х) + g(x))z. Формула (1)
доказана.
2)	Если у = /(x)g(x), то
дУ = Кх + Дх)§(х + Дх) - /(x)g(x) =
= (Дх) + Д/Ж*) + Д&) - f(x)g(x) =
= ZW Д&+g(x) д/+д/д§,
= /(х)^ +g(x')-jr~ + •^Д^-
Ах 1 v 7 Ах 6 v 7 Ах Ах 6
Отсюда следует формула (2), так как
Д§^° при Д*^о.
108	Глава XIII. Производная и дифференциал
3)	Если у = то
. = /(х + Дх) _ /(х) = /(х) + Д/ _ Дх).
у g(x + Дх) g(x) g(x) + Ag g(x) ’
ИЛИ	Д/j = (A/)g(x) - (Д^)/(х)
У £(х)£(х + Дх) ’
откуда
— (^L0(r\ _	_______!__
Дх \ Дх^к 7 Дх7 k ч g(x + Дх)£(х) ’
Переходя к пределу в этом равенстве и учитывая, что
g(x + Дх) —> g(x) при Дх —> 0, где g(x) / 0, получаем
формулу (3).	•
Следствие 1. Если функция f дифференцируема в точке х и С —
постоянная, то
(Q(x))' = Q'(x),
т. е, постоянный множитель можно выносить из-под знака
дифференцирования.
Следствие 2. Если функции Д(х),... ,fn(x) дифференцируемы
в точке х, а ... ,Сп — постоянные, то
Ш) + ... + CnfnW = С1Д (х) +... + Cnf'n (х).
Пример 1. Найти производную функции /(х), если:
1)	/(х) = х3 + 2х2 — х;	2) /(х) = 2-^/х + Т
3) /(х) = Зе* — 4 In х;	3) /(х) =41og3x —2х.
Л 1) Используя формулу (х”)' = пх"-1 и теорему 1, находим
/(х) = Зх2 + 4х — 1.
2)	Так как
(V^)/=2?T’ Q)
ТО
№» = ?;-?
3)	Используя формулы
(е*)' = ех, (1пх)' = 1,
получаем
/'(х) = 3^-4.
§3. Правила дифференцирования. Дифференциал
109
4)	Так как
0оё«х)' = Ж’ (O' = a%lna,
то
/'(х) = пЦ-2%1п2.	А
1	7 xln3
Пример 2. Найти /'(х), если:
=	2) /(х) = х2sinx;
з
3) ^) = ^Г7;	4> /W = (3x-21og5x)(x4 + 2).
xz 4- 4
А 1) Используя правило дифференцирования частного (фор-
мула (3)), получаем
г// \ _ (х - 2)'(х 4- 2) - (х - 2)(х + 2)' _ х 4- 2 - (х - 2) __	4
1 k '	(х + 2)2	(х + 2)2 (х + 2)2*
2) По формуле (2) находим
/'(х) = 2х sinx 4-х2 cosx.
о\ ff( \ _ Зх2(х2 4- 4) — х3 • 2х _ х4 + 12х2
’ 1	~	(х2 + 4)“2	“ (х2 + 4)2’
4) /'(х) = (з* In 3 -	(х4 + 2) + (3* - 2 log5 х)4х3.	А
Пример 3. Доказать, что:
(tgx)'= —X7^+k7t, keZ,	(4)
(ctgx)' = ——keZ.	(5)
sirrx
A 1) Так как (sinx)'— cosx, (cosx)' = — sinx, то, применяя i
вило (3) дифференцирования частного, получаем
/. у____ ZsinxV _ (sinx)zcosx — (cosx)'sinx _ cos2x4-sin2x
Zos2x~
откуда следует формула (4).
2) Аналогично,
/ , у _ (cosx)'sinx — (sinx)'cosx _ sin2x4-cos2x
(CtgX) — ———7-n	— ———r	5
sin X	sinz X
npa-
откуда получаем формулу (5).
по
Глава XIII. Производная и дифференциал
2. Дифференцирование сложной функции
Теорема 2. Если функции у = (р(х) и z — f(y) дифференцируемы
соответственно в точках xq и у о, где у о = <р(хо), то сложная
функция 2 = /(^(х)) дифференцируема в точке Xq, причем
z'(xo) = Л//о)</(* *о) = f (<Х*о))</(*о)-	(6)
*ОИз существования производных </(%о) и ЛО/о) следует (§ 1, п. 2),
что функции у — ф(х) и z = f{y) непрерывны соответственно в точках
х0 И f/о, где //о = <Х-*о)-
Тогда сложная функция z = /(<?(*)) определена в некоторой
окрестности точки xq и непрерывна в этой точке (гл. IX, § 4, п. 3).
Так как функции z — f(y) и у = ср(х) дифференцируемы в точках
Уо и Xq, то из определения производной (§ 1, п. 2) следует, что их
приращения представимы в виде
=/0/о)д*/+ е(ду) • Д/Л	е(Д«/)->0	при	Дг/—>0,	(7)
Дг/ = </(хо)Дх + Е1(дх) • Дх, £|(Дх)—>0 при	Дх—>0.	(8)
Функция г(Д//) не определена при Д// = 0. Доопределим эту
функцию в точке 0, положив s(0) = 0. Тогда равенство (7) окажется
верным и при Д// = 0.
Считая, что в равенстве (8) приращение Д// определяется прира-
щением Дх, выразим Дг через Дх, подставляя Д// из равенства (8)
в равенство (7).
Тогда
д2 = №о)(</(хо)Дх + Е1(Д*) • Д*) + е(Д//) • Д/Л
ИЛИ
д2 = №оМ*о)д* + Л//оЫд*) • Дх + е(Д//) • Д/л (9)
Поделив обе части равенства (9) на Дх, где Дх / 0, получим
=/'(//о)'?'(^о)+//(г/о) + г1(дл:) + Е(д'/)х7-	(10)
Так как £1(Дх)—>0 при Дх—>0, Дг/—>0 при Дх—>0 (равенство (8)),
а ></(хо), т0> переходя к пределу в равенстве (10) при Дх—>0,
получаем формулу (6).	•*
Замечание 1. Условие е(0) = 0 связано с тем, что Дг/ может оказаться
равным нулю при Дх 0.
Замечание 2. Согласно теореме 2 для нахождения производной сложной
функции z = f(y) = /(<^(х)) в точке х нужно перемножить производные f(y)
и yf — ср'(х), заменив у на </>(х).
Правило дифференцирования сложной функции можно записать
так:	, _ , ,
•	гх 2у ‘ Ух-
§3. Правила дифференцирования Дифференциал
111
Пример 4. Найти производную функции Дх), если:
1) /(х) = sin 2х;	2) Дх) = е*3;
3) Дх) = cos2x; 4) Дх) = In
Д 1) Данная функция — суперпозиция функций г — sin у и у — 2%.
Так как (sin //)' = cos у, yf = 2, то
f'(x) = cos у • 2 — 2 cos 2х.
2)	Пусть z = еу, у — х3, тогда
^У = еУ, (х3)'= Зх2, /'(x) = 3xV.
3)	/'(%) = 2 cosx(cosх/ = 2 cosх • (— sin х) = — sin 2х.
4)	Пусть
z= in г/, г/=ГГ2-
Тогда
(In#)' = у' = , Д.2 (пример 2 (1)),
У	(х + 2)2
Пример 5. Доказать, что
(1п|х|)' = 1, х^О.	(11)
Д В § 2 (п. 3, формула (17)) было доказано, что
(1пх)' = р х>0.	(12)
Пусть х < 0, тогда In |х| = 1п(—х). Используя формулу (12)
и правило дифференцирования сложной функции, получаем
(1п(-х))' = -X • (-х)' = 1.
Таким образом, при любом х^О верна формула (11).	А
Пример 6. Найти /'(х), если:
1) Дх) = ecos2 5%;	2)	Дх) = 2е2 sin3 Зх;
3) f(x) = \/х2 + 1 ctg4x;	4)	Дх) = 1п(х + л/1 +х2).
А 1) /Дх) = ecos2 5% • (cos2 5х)' =	ecos2 5х • 2 cos 5x(cos 5х)'	=
_ ecos2 5х _ 2 cos 5х	•	(—	sin 5х) • (5х)' = — 5ecos2	sin Юх.
112
Глава XIII. Производная и дифференциал
2)	f(x) = 2 sin3 Зх-h £2 -3sin23x-cos3x-3 =
= е* sin3 Зх + 18^2 sin2 Зх cos Зх.
3)	f (х) =	— ctg 4х + \/х2 + 1	1
2\/х2 + 1
=______Л_cte4x - 4x/%2 + 1
ё sin24x ’
14---2х
4)	/-(*) =----—
х4- \/1 4-Х2 уЛ+х2
sin2 4х
* Пример 7. Доказать формулы
(shx)' = chx,
(chx)' = shx,
(thx)/ = —X—,
ch x
(cthx)'= —-4—.
sh x
(13)
(14)
А Гиперболические функции были определены в гл. X, § 2 следу-
ющими формулами:
shx=^^, Chx = ^±^, thx=^, cthx=^.
2	2	chx	thx
1) Применяя теоремы 1 и 2, получаем
(shx)' = ^(ех - е“х(-1)) = chx.
Аналогично доказывается, что (chx)' —shx.
2) Используя правило дифференцирования частного, получаем
/.с \/_ (shx)'chx — shx(chx)' _ ch2x —sh2x
ch2 x	ch2 x ’
откуда следует равенство (13), так как ch2x — sh2x = l (см.
гл. X, § 2, пример 1). Аналогично доказывается формула (14).
А*
Пример 8. Пусть функция / дифференцируема в каждой точке
интервала (—а, а). Доказать, что если Дх) — четная функция, то
ее производная /'(х) — нечетная функция, а если /(х) — нечетная
функция, то /'(х) — четная функция.
А Пусть /—четная функция; тогда
Д-х) = Дх), х е (-а, а).
§3 Правила дифференцирования. Дифференциал
113
Дифференцируя это тождество, получаем
—/'(—х) = {'(х), х е (—а, а).
Это означает, что /'(х) — нечетная функция. Аналогично рассматри-
вается случай, когда /(х) — нечетная функция.	▲
Пример 9. Доказать, что
(/*)' = са06"1, «ей, х>$.	(15)
А В §1 формула (15) была доказана для а е N, а—— 1 (х^О),
(х>0). Функция ха при х > 0, aER определяется формулой
ха _ еа\пх
Применяя правило дифференцирования сложной функции, получаем
(Х«)' = е«1п^(а1пх)' = ^“1пх = ^ = ах“-1. А
3. Дифференцирование обратной функции
Теорема 3. Пусть у — /(х) — непрерывная, возрастающая или
убывающая на интервале (а,Ь) функция; a = f(a), (3 = f(b). Пусть
х — g(y), где а < у < /3, — обратная к f(x) функция (гл. IX, § 4,
теорема 4).
Если функция f(x) дифференцируема в каждой точке интервала
(а,Ь) и /'(%) ^0, то функция x = g(y) дифференцируема в каждой
точке интервала (щ(3), причем
= ж-	<|6>
О Докажем формулу (16), предполагая, что g(y) — дифференциру-
емая функция. Из определения взаимно обратных функций (гл. III,
§ 4) следует, что
Ш)=У. УСЫ.	(17)
Дифференцируя тождество (17) и используя правило дифференци-
рования сложной функции, получаем
f (gQ/Bg'G/) = U
откуда следует, что
= —-— = —-—
Заменяя в этом равенстве у на х, а х на у, получаем
= Ш = №))'	(1ф
114
Глава XIII. Производная и дифференциал
Пример 10. Доказать формулы
(arcsin х)' =	1	М < 1,	(19)
	\/1 — %2 ’		
(arccos х)' =			1	И < 1,	(20)
	\/1 — X2		
(arctgx)'=	14-х2’	х е R,	(21)
(arcctgx)' =			1 14-х2’	х е R.	(22)
то обратная функция
А 1) Если у — g(x) = arcsinx, где |х| < 1
х— /(//) = sin//, где |#| < £. По формуле (18) находим
(arcsin х)' =
1 = 1
(sin y)f cost/’
Так как sinr/ —х и у е	то cosz/ = л/1 - %2. Следова-
тельно, справедлива формула (19).
2) Если у — arctgx, где хей, то x = tgz/, где |z/| < Применяя
формулу (18), получаем
(arctgx)' =	= cos2 у,
где
cos2 у = —Ц- = —Цт.
1 + tg2 у 14-х2
Формула (21) доказана.
3) Аналогично доказываются формулы (20) и (22). Впрочем, эти
формулы легко получить, используя равенства
arcsin х 4- arccos х = arctg х + arcctg х =
и формулы (19) и (21).
§3. Правила дифференцирования. Дифференциал
115
4. Таблица производных
/W	Г(Х)	/to	rw
с	0	sinx, xeR	cosx
хп, neN, xeR	пхп~[	cosx, xeR	— sinx
ха, aeR, х>0	аха~{	tgx, х^^+тг/г, aeZ	1 9 COSZ X
ах, а>0, a^l, xeR	ах Ina		
		ctgx, x^jzn, neZ	__J_ 9 sinz X
ех, xeR	ех		
logGx, а>0, а/1, х>0	1 х In a	arcsin x, |x| < 1	1 \/l ~X2
logG |х|, а>0, а^1, х^О	i xlna	arccosx, |x| < 1	1 \/l —X2
1пх, х>0	1 X	arctgx, xeR	1 _ 1+x2
In |х|, х^О	1 X	arcctgx, xgR		1 1+x2
5. Дифференциал
Если функция /(х) имеет производную в точке xq, то приращение
функции в этой точке (§ 1, п. 2) представляется в виде
Ду = Д/ = /'(хо) Дх + с(Дх) - Дх,	(23)
где е(Дх) —> 0 при Дх —> 0.
Пусть //(хо)^О, тогда первое слагаемое /'(хо)Дх в формуле (23)
является линейной функцией от Дх, бесконечно малой при Дх —»0
и отличной от нуля при Дх^О. Второе слагаемое е(Дх)-Дх в этой
формуле также является бесконечно малой при Дх —> 0 функцией
такой, что отношение второго слагаемого к первому стремится к нулю
при Дх —» 0.
Поэтому первое слагаемое в формуле (23) при /'(хо)^О называют
главной частью приращения функции в точке х$.
Определение. Если функция /(х) имеет в точке xq производ-
ную /'(xq), то произведение /'(хо)Дх называется дифференциалом
функции f(x) в точке Xq и обозначается df(xo) (или df).
Итак, по определению
#(х0) =/'(хо)Дх.
Если функция /(х) имеет производную в каждой точке интервала
(а; Ь), то ее дифференциал
df(x) = f(x)Ax,
где Дх — приращение аргумента.
116
Глава XIII. Производная и дифференциал
Если /(х)=х, то df = dx = (х)'Дх = Дх. Поэтому дифференциал
независимой переменной определяют как ее приращение (dx —Дх),
а выражение для дифференциала функции /(х) записывают в виде
df = f'(x) dx.
Из этой формулы следует, что
т. е. обозначение для /'(х) можно понимать как дробь, в числи-
теле которой стоит дифференциал функции /(х), а в знаменателе —
дифференциал аргумента.
Обратимся к формуле (23). Если отбросить второе слагаемое в ее
правой части, получится приближенное равенство
/(х>/(хоШ'(хо)Дх,	(24)
где Дх — х — Xq, с помощью которого можно находить значения
функции в точке х, близкой к точке xq, зная /(хц) и /'(хц).
Пример 11. Найти с помощью формулы (24) приближенное
значение функции у = tfx при х = 90.
Д Полагая в формуле (24)
/(х) = ^, Xq — 81, Дх = 9
и учитывая, что
/(х0) = ^81 = 3,	=
получаем
у/90«3 + -Ц-9 = 3 + Т т. е. ^90 и 3,083.	▲
4-33	12
Задачи
1.	Найти производную функции /(х), если:
1)	Дх) = 2х2 - 3 In х; 2) /(х) = 2у/х-~;
3)	/(х) = 3sinx — 2tgx; 4) /(х) = ех + 4ctgx;
г3
5)	/(х) = 5х — cos х;	6) /(х) = log3 х + у.
2.	Найти производную функции /(х), если:
1)	/(x)=x3cosx;	2) /(x)=xlnx;	3) f(x) = \/xigx;
4)	Дх) = 2*sinx;	5) Дх) =	6) Дх) = ^±1;
7)/w=Stt; 8)^)=й¥-
§3. Правила дифференцирования. Дифференциал
117
3.	Найти производную функции /(х), если:
1)	/(х)	= е2х sin2 %;	2)	/(х) = xln(x2 + 1);
3)	Дх)	= \/4х2 + з tg2х;	4)	Дх) = (2х + I)3 log3(x3	+ 1);
5)	Дх)	= ^х+-‘4;	6)	Дх) = - ;
'	(2х + 3)2	4 + cos3x
7)	f(x\ _____ th5x_______.. g\ f(x) =_________cll2ji:____
v	arctg 2x + arctg 3x ’	sh 3x + arcsin 2x
4.	Найти /'(xg), если:
1)	Дх)	= ex In X, x0 = 1;	2)	Дх) =	, x0 = 0;
3)	Дх)	= (x — l)2(x + 2), x0 =	—2;	4)	Дх) =	sin2 xx  (x — 1), x0	= 1;
5)	= 7-4^2 ’ XO = 6;	6>	X° = 11
(x - 2)z	(x - 7)z
5.	Решить уравнение /х(х) = 0, если:
1)	/(х) = 2у/х — 31п(х + 2);	2) /(x)=xlnx;
3)	/(х) = х3 - 6х2 + 9х + 5;	4) Дх) = * + *~6
(х-5)2
6.	Пусть /(х) = х3 + Зх2 + ах. Найти все значения а, при которых /'(х) ^0
для всех х G R.
7.	Найти все значения а, при которых уравнение f\x) — Q не имеет действи-
тельных корней, если:
1) /(х) = ах ч- i;	2) /(х) = х3 + 6х2 + ах.
Ответы
1. 1) /'(х) = 4х - 5; 2) Д(х) = 4= + 4; 3) Г(х) = Зсозх - 2 ; 4) Д(х) =
Л	л	COS X
= ех--------1—; 5) /'(х) = 5х In5 4- sinx; 6) /'(х) =	+ х2. 2. 1) f(x) =
sinzx	xln 6
= 3x2cosx — x3sinx; 2) f'(x) = Inx + 1;	3) /'(x) — —^=tgx +	;
X	COS X
4) f(x) = V In 2  sinx + 2х cosx; 5) f'(x) = cosx(3x2 + l)--sinx.6x.
(3x +1)
6)Г(х) =
22x
(2x2 + 1)2 ’
= 2e2xsin2x
].(3x+2) 3(lnx+l)	_ 6x(2x2 + 1)-4x(3x2-4)
(3x + 2)2	’ )tW ~	(2x2 + l)2
(3х +4X) - 2 log3 x(3x in 3+4х in 4)
S) Д(х) =	--------—------------------. 3. I) /U) =
(3X + 4X)Z
+ e2x • 2sinxcosx = 2sinx  e2x(sinx + cosx); 2) f'(x) =
= l"<? +" +	3>	- ^T3,e2‘ +	4)/,w =
=6(2x+1)2 log3(x3 + l)+3x2(2x+l)3	1	;
IX "i 1 J 1П о
118
Глава XIII. Производная и дифференциал
n f>( _ 3(x + 1)2(2x+3)2-(x+1)3-4(2x+3) _ (x+l)2(2x+5).
07 'W-	(2x + 3)4	“	(2x+3)3	’
ex . (—(4-|-cos3x) + ex -3sin3x
6)	=--------------------о---------
(4 +cos 3x)2
—5— (arctg 2x+arctg 3x) — th 5x (
7)	f(x) = ch 5x	'
2	3 \
l + 4x2 l + 9x2/
(arctg 2x + arctg 3x)2
9
3ch 3x4—7----=
\/l —4x2
2 ch х sh x(sh Зх 4- arcsin
8)	/'W =-----------------
(sh 3x4-arcsin 2x)2
4.	1) e; 2)	3) 9; 4) 0; 5) 0; 6) 0 5. 1) xi = l, x2 = 4; 2) x=e-1; 3) xj = l,
x2 = 3; 4) x=yp 6. a^3.	7. 1) a^O; 2) a >12.
§4. ГЕОМЕТРИЧЕСКИЙ И ФИЗИЧЕСКИЙ СМЫСЛЫ
ПРОИЗВОДНОЙ И ДИФФЕРЕНЦИАЛА
1. Касательная к графику функции. Скорость движения
В § 1 было введено понятие касательной к графику функции
y = f(x) в точке 7Ио(хо;/(хо))-
Если функция у = f(x) имеет производную в точке xq, т. е.
существует конечный предел
Л	(1)
то существует предельное положение секущей I (см. рис. 1), заданной
уравнением
У~Уо = ^(х-х°).	(2)
Это означает, что в точке Л4о(хо5/(хо)) существует касательная /о
к графику функции y — f^x), причем, согласно формуле (1) &о~
где k$ — угловой коэффициент прямой 1$. Так как Ло = tgag, где
«0 — угол, образуемый касательной с положительным направлением
оси абсцисс, то
f (xO) = tgao-
Таким образом, геометрический смысл производной состоит в том,
что производная функции в данной точке Xq равна угловому
коэффициенту касательной к графику функции в точке 7Ио(%о5/(хо))-
Уравнение касательной к графику функции у — f(x) в точке
Мо(хо;/(%о))> получаемое из уравнения (2) заменой на
имеет вид	z ,
У = Л*о) + f Оо)(* ~ *о)-	(3)
§4. Геометрический и физический смыслы производной
119
Пример 1. Записать уравнение касательной к графику функции
у = е*, параллельной прямой у = х — 1.
А Так как угловой коэффициент касательной по условию равен
угловому коэффициенту прямой у — х — 1, т. е. равен единице, то из
уравнения
/ (х) = ех = 1
получаем хо = 0, а по формуле (3) при = 0, уо = 1, f'(xo) — 1
находим уравнение касательной
у = х + 1.	▲
Углом между кривыми, пересекающимися в точке ТИо, называют
угол между касательными к этим кривым в точке Мд. В частности,
угол между графиком функции y = f(x), пересекающим ось Ох в
точке Л4о(хд; 0) — это угол между касательной к этому графику в
точке Л40 и осью Ох.
Пример 2. Под каким углом график функции у = sinx пересекает
ось Ох?
А Синусоида пересекает ось абсцисс в точках Xk = kn (kEZ). Пусть
ak ~~ угол между осью Ох и графиком функции в точке с абсциссой Х/г.
Для функции /(х) —sinx найдем значения ее производной в этих
точках:	,	.
f (xk) = cos&Tt = (-1/ = tgak.
Следовательно, в точках х^ = 2/гти (&eZ) синусоида пересекает ось Ох
под углом р а в точках Х/г = (2k + 1)тг (k Е Z) — под углом
Пример 3. Показать, что касательная, проведенная к параболе
у = х2 в точке с абсциссой х$ Ф 0, пересекает ось Ох в точке
с абсциссой
А Пусть /(х)=х2, тогда
f(x) = 2x, Дхо)=*о и //(хо) = 2хо.
120
Глава XIII. Производная и дифференциал
По формуле (3) находим уравнение касательной:
У — %о + 2%о(х — %о) = 2%дх — х£.
Найдем абсциссу точки пересечения этой касательной с осью абсцисс.
Из равенства 2х$х — х^ = 0 с учетом х$ О находим
х = ^	▲
2 ’
Отсюда следует простой геометрический способ построения
касательной к параболе у = х2 в точке А с абсциссой 0:
прямая, проходящая через точку А, и точку оси абсцисс, касается
параболы в точке А (рис. 3).
Фокусом параболы называют точку, в которую нужно поместить
источник света, чтобы все лучи, отраженные от параболического
зеркала, были параллельны оси симметрии параболы. Построив
касательную к параболе, можно построить ее фокус F. Для этого
нужно построить прямую АВ, параллельную оси Оу, и прямую AF,
образующую с касательной такой же угол, как и прямая АВ (рис. 4).
В § 1 (п. 1) был выяснен физический смысл производной. Было
установлено, что если S(f) — координата движущейся материальной
точки в момент времени t от момента начала движения и £(/) —
дифференцируемая функция, то
где v(f) — скорость движения в момент времени t.
2.	Геометрический и физический смыслы дифференциала
Если функция y=f(x) дифференцируема при х=х$, то существует
касательная Iq (рис. 5) к графику этой функции в точке 7Ио(хо;/(%о))’
задаваемая уравнением (3). Пусть Л4(%о + Дх;/(%о + Дх)) — точка
графика функции / с абсциссой х$ + Дх, Е и F — точки пересечения
прямой х =	+ Дх с касательной Iq и прямой у = у$ = /(%о)
§4. Геометрический и физический смыслы производной
121
соответственно. Тогда F(xq + Дх, z/0), E(xq + ^^Уо + f'(xo)Ax),
так как ордината точки Е равна значению у в уравнении (3) при
х = Xq + Ах. Разность ординат точек Е и F равна /'(хо)Дх, т. е.
равна дифференциалу dy функции f при x — xq.
Таким образом, дифференциал функции y = f(x) при х = х0 равен
приращению ординаты касательной к графику этой функции в точке
с абсциссой %о ПРИ изменении аргумента от хо до xq + Дх. Таков
геометрический смысл дифференциала.
Так как
MF = Ay, EF — dy,
ME = MF - EF = Ay - dy.
Из равенства (23) § 3 следует, что
ME = е(Дх) • Дх при Ах —> 0.
Выясним физический смысл дифференциала.
Пусть S(t) — координата движущейся материальной точки в
момент времени t от момента начала движения (см. § 1, п. 1). Тогда
S'(i) = lim
— мгновенная скорость v точки в момент времени t, т. е.
v = S'(f).
По определению дифференциала
dS = vAt.
Поэтому дифференциал функции S(t) равен расстоянию, которое
прошла бы точка за промежуток времени от t до t+At, если бы она
двигалась со скоростью, равной мгновенной скорости точки в момент
времени t. Таков физический смысл дифференциала.
122
Глава XIII. Производная и дифференциал
3.	Геометрическая и физическая интерпретации теоремы
о производной обратной функции
Если рассматривать
Если существует /'(xq)	0, то в точке
ЛТо(хо; Дх0)) существует касательная Iq
к графику функции у = /(х), угловой ко-
эффициент которой равен tg a = /'(хо), где
а —угол, образуемый касательной с положи-
тельным направлением оси Ох. Касательная
не параллельна координатным осям, так как
производная /'(xq) конечна и отлична от
нуля. Пусть для определенности /'(%о) > О,
тогда 0 < a < (рис. 6).
у как независимую переменную, а х — как
функцию, то кривая, заданная уравнением у — [(х), будет графиком
функции х — ф(у). Пусть /3 —угол, образованный касательной Iq
с положительным направлением оси Оу (рис. 6), тогда
tgp = /(f/o)-
Так как а + /3=^, то tg/3 = ctga= т. е.
Z	1g ос
=жг
(4)
Дадим физическую интерпретацию формулы (4). Так как ср'(уо)
есть скорость изменения переменной х по отношению к изменению
переменной у, а /'(х0) — скорость изменения у по отношению к х, то
формула (4) выражает тот факт, что указанные скорости являются
взаимно обратными.
4.	Односторонние и бесконечные производные
Если функция у — Дх) непрерывна слева в точке хо и существует
лНт лй’ ГДе = ДХ0 + Дх) ~ ^Х°)’
то этот предел называют левой производной функции f в точке х0
и обозначают Д_(хо). Аналогично, если функция y — f^x) непрерывна
справа в точке хп, то
lim
Дх—>+о
называют правой производной функции f в точке хо и обозна-
чают /+(х0)-
Прямые, проходящие через точку Afo(xo;/(xo)) с угловыми
коэффициентами /L(xq) и /^(xq), называют соответственно левой
и правой касательными к графику функции y — f{x} в точке Л40.
§4. Геометрический и физический смыслы производной
123
правой
поэтому
= lim ^ = -1,
Дх—0 Ах
= 1.
(6)
Из существования производной /'(х0) следует существование двух
односторонних производных /L(xg) и Д.(хо) и равенство
/Цхо) = 4(*о)=/'(хо)-	(5)
В этом случае левая и правая касательные к графику функции
у = f(x) в точке 714g совпадают с касательной в точке М$.
Обратно: если существуют левая и правая производные функции f
в точке х0 и выполняется условие /L(%g) = /^(х0), то существует
производная /'(xg) и справедливо равенство (5).
Пример 4. Найти левую и правую произ-
водные функции /(х) = |х| в точке Xg = 0.
А Здесь Д// = |Дх|, и
Л(хд)= lim
1 v д^-дДх
Л(х0) = lim
/ + v и' д%^+оЛх
Прямые у = —х и у = х являются соответственно левой и
касательными к графику функции у = |х| в точке О (рис. 7).	▲
Замечание. Так как fL(xg) (xg) для функции /(х) = |х|, то непрерывная
в точке xg = 0 функция |х| не имеет в этой точке производной Этот
пример показывает, что из непрерывности функции f в точке Xg не следует
существование ее производной в данной точке.
Обратимся теперь к понятию бесконечной производной. Пусть
функция у = /(х) непрерывна в точке xg и пусть
lim Т = lim Лхо + Дх)-Лхо)=оо
Дх^О Дх Дх^о
Тогда прямую х = xg называют касательной к графику функции
y = f(x} в точке Afg(xg;/(xg)). Эту прямую можно рассматривать как
предельное положение (при Дх —> 0) секущей /, если уравнение (2)
записать в виде
и воспользоваться тем, что
в силу условия (6).
Если
при Дх —> О
lim
Дх—>0
то говорят, что функция имеет в точке xg производную, рав-
ную -Too, и пишут
Дх
124
Глава ХШ. Производная и дифференциал
Рис. 8
В этом случае односторонние пределы
lim и lim
Дх^-0	Дх—>+0
называют соответственно левой и правой про-
изводными функции y = f(x) в точке Хд и обо-
значают /L(%o) и /+(хо)« Таким образом, если
/'(хо) = +оо, то /1(х0) = +оо и /^(х0) = +оо.
Например, если /(х) = tyx, то /'(0) = +оо, так как
lim
Дх—>о
Дх
lim ......1...=	+оо.
Дх->0 3/(Дх)2
В точке (0,0) касательной к графику функции у = tyx является
прямая x = Q (рис. 8).
Аналогично, если
lim —
Дх-^0 Д*
то говорят, что функция у — f(x) имеет в точке х$ производную,
равную —оо, и пишут /'(х0) — —оо.
В случае когда /'(xq) — +оо или /'(хд) = —оо, говорят, что
функция у = Дх) имеет в точке Хд бесконечную производную
(иногда добавляют: определенного знака).
Обратимся теперь к случаю, когда
lim = оо,
Дх—>0
но не выполняется ни одно из условий /'(хд) = 4-оо или Д(хд) ——оо.
В этом случае говорят, что
lim
Дх-Ю Ах
Рис. 9
не является бесконечностью определенного
знака. Например, эта ситуация имеет место,
если
lim — +оо, a lim	= —оо.
Дх—>+0 Ах	Дх—>—0 Ах
Этим свойством обладает, например, функция
y = V\A (рис. 9).
§4. Геометрический и физический смыслы производной
125
Задачи
1. Составить уравнение касательной к графику функции у = Дх) в точке
с абсциссой %о, если
1) Дх) = х2 + Зх, %о = 2;	2)	/(х) = 2х3 — 5, xq = —2;
3) /(x)=2sin|,	=	4)	Дх)=х + 1пх, х0 = е;
5) ZW — sin(7rx2), %о — 1;	6)	7W — cosx, Х0 = 7.
6
2. Найти точки графика функции у = Дх), в которых касательная к этому
графику параллельна прямой у — kx, если:
1) /(х)=х(х + 1), fe = 3;	2) /(х) = |х3+х2-2х, k=l.
3. Записать уравнение той касательной к графику функции y = f(x), которая
параллельна прямой у = kx 4- b, если:
1) /(%) = х2 — 2х 4- 3, у = — | 4-1;	2) Дх) = —х2 + Зх + 4, у = 5х 4- 3.
4.
5.
6.
7.
8.
На параболе г/ = х2 — 4х 4- 2 найти такие точки, в которых касательные,
проведенные к параболе, проходят через точку (4; 1).
Пусть задана точка Л(0;3), В и С —точки, в которых прямые, проведенные
х2
через точку А, касаются параболы у = ——х + 5. Найти площадь £\АВС.
Касательная к графику функции у = ^х4 — образует с осью абсцисс
угол, равный arctg-, и пересекает в точках А и В окружность с центром
24
в начале координат. Найти радиус этой окружности, если АВ = —
5
Найти точки с одинаковыми абсциссами, в которых касательные к графикам
функций у = х^— х + 1 и у = Зх2 — 4х 4-1 параллельны друг другу. Записать
уравнения этих касательных.
Найти левую и правую производные функции у = f(x) в точке xq, если
1) Дх) = |х2 - 5х + 6|, х0 = 2;	2) Дх) = 12х - 2|, х0 = 1.
Ответы
1. 1) г/= 7х — 4; 2) // = 24х + 27; 3) y = -JL + V2+^ 4) г/ = (1 + е-1)х;
5) у=-2лх + 2к, 6) (/ = -lx+f^ + i).	2. 1) (1;2); 2)	(-3;6).
3. 1) у = -* + ™; 2) у = 5х + 5. 4. (5;7), (3;-1). 5. 8. 6.	7. (1;~1),
z/ = 2x—1; (1;0), у = 2х - 2.	8. 1) 4(2) = -1, 4(2) = 1; 2) 4(1) = - In4,
4(1)= In 4.
Глава XIV
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
К ИССЛЕДОВАНИЮ ФУНКЦИЙ
§ 1. ОСНОВНЫЕ ТЕОРЕМЫ ДЛЯ ДИФФЕРЕНЦИРУЕМЫХ
ФУНКЦИЙ
1. Локальный экстремум и теорема Ферма
Понятие экстремума было введено в § 3 гл. III. Напомним это
определение.
Пусть функция Дх) определена в 3-окрестности точки xq, т. е.
на множестве U^Xq) = (xg — 3;xq + 3), и пусть для всех xeU^Xq),
x^xq, т. е. для всех xeU^Xq), выполняется неравенство
f(x)<f(x0).	(1)
Тогда говорят, что функция имеет в точке %о локальный максимум.
Аналогично, если для всех х G ЦДхо) выполняется неравенство
Дх)>/(х0),	(2)
то говорят, что функция Дх) имеет в точке xq локальный минимум.
Локальный максимум и локальный минимум объединяются общим
термином «локальный экстремум», причем слово «локальный» часто
опускают.
Функция Дх), график которой изображен на рис. 1, имеет
экстремумы в точках Xi = 1, х% = 3, Х3 = 4, а именно, минимумы
при х — 1 и х = 4 и максимум при х = 3.
Теорема 1 (Ферма). Если функция Дх) имеет
в точке xq и дифференцируема в этой точке, то
Г(хо) = О.
экстремум
(3)
О Пусть, например, функция Дх) имеет минимум в точке xq. Тогда
для всех х G (xq — 3;хо + 3), х ф Xq4 т. е. на множестве U$(xq)4
выполняется неравенство
Дх) >/(х0).
(4)
§1. Основные теоремы для дифференцируемых функций
127
Если xg(xq —5;х0), то x — Xq<0 и из условия (4) следует, что
- Д*о) < 0	(5)
х — Xq
а если хе(%о;хо + ^)> т0 выполняется неравенство
/(%) - f(x0) > q	/04
X — Xq	V 7
Так как функция f дифференцируема в точке х$, то существует предел
при x-^Xq — О в левой части неравенства (5), равный /L(xo) —
По свойствам пределов из неравенства (5) следует, что
Ж) < 0.	(7)
Аналогично, переходя к пределу при х —> х0 4- 0 в неравенстве
(6), получаем
f (х0) > 0.	(8)
Из неравенств (7) и (8) следует, что /'(хо) — 0.	•
Замечание Теорема Ферма имеет простой геометрический смысл: если
в точке %о функция /(х) имеет экстремум, то касательная к графику функции
у = f(x) в точке (хо;/(хд)) параллельна оси абсцисс (рис. 2).
2. Теорема Ролля о нулях производной
Теорема 2 (Ролля). Пусть функция f(x)
непрерывна на отрезке [а;Ь], принимает в кон- ---------------
цах этого отрезка равные значения, т. е.
/(«)=/(&),	(9)	J___I_____L
и дифференцируема на интервале	Тогда	а	с	Ьх
существует точка с е (а; Ь) такая, что	Рис. 3
m-о.	(ю)
О Обозначим
М — sup /(х),	inf /(х).
а^х^Ь	а^х^ь
По теореме Вейерштрасса (гл. IX, § 4, теорема 1) на отрезке [о; Ь]
существуют такие точки Q и с%, что f(cy) = m, /(с2)=М.
Если т = М, то / (х) = const, и в качестве с можно взять любую
точку интервала (о;&).
Если т=£М, то т<М, и поэтому /(cj </(с2). В силу условия (9)
по крайней мере одна из точек ci,c2 является внутренней точкой
отрезка [а; 6]. Пусть, например, ще(сц1}). Тогда существует число
5>0 такое, что £7g(ci)c(a;&). Так как для всех хе Us(ci) выполняется
условие /(х) > /(^i) =	то по теореме Ферма f(c\) = 0, т. е.
условие (10) выполняется при с — ср Аналогично рассматривается
случай, когда с2б(а;&).	•
128
Глава XIV. Применение производной к исследованию функций
Теорему Ролля можно кратко сформулировать так:
Между двумя точками, в которых дифференцируемая функция
принимает равные значения, найдется хотя бы один нуль производной
этой функции. Для случая f(a) = [(b) — 0 теорема формулируется
еще короче: между двумя нулями дифференцируемой функции лежит
хотя бы один нуль ее производной.
Например, если /(х) = 2 + 2х — %2 * 4 * *, то /(—1) = /(3) = — 1, и на
интервале (—1; 3) существует точка xq = 1 такая, что f'(xo) = O.
Замечание. Геометрический смысл теоремы Ролля: при условиях тео-
ремы 2 существует значение се (а; 6) такое, что касательная к графику функции
у = f(x) в точке (с;/(c)) параллельна оси Ох (рис. 3).
3. Формула конечных приращений Лагранжа
Теорема 3. Если функция f(x) непрерывна на отрезке [а,Ь\
и дифференцируема на интервале (сцЬ), то в этом интервале
найдется хотя бы одна точка с такая, что
КЬ)-Да)=['(с)(Ь-а).	(11)
О Рассмотрим функцию
<р(х) = /(х) + tx,
где число t выберем таким, чтобы выполнялось условие (р{а) — (р{1)),
т. е. f(a) +ta = f(b) + tb.
Отсюда находим
Так как функция <р(х) непрерывна на отрезке [а;&], дифференцируема
на интервале (сцЬ) и принимает равные значения в концах этого
интервала, то по теореме Ролля существует точка с Е (а\Ь) такая, что
<р'(с)=/,(с) + / = О. Отсюда в силу условия (12) получаем равенство
/'(с) =	(13)
4 7 b — а
равносильное равенству (11).	•
Замечание 1. Точку с, о которой идет речь в
теореме 3, можно представить в виде с — а + tb, где
о<г<1.
Замечание 2. Правая часть формулы (13) равна
угловому коэффициенту секущей, которая проходит
через точки Д(а;/(а)) и B(b\f(b)) графика функции
у = f(x). Левая часть этой формулы равна угловому
коэффициенту касательной к графику в точке (с;/(c)).
§ 1. Основные теоремы для дифференцируемых функций
129
Поэтому теорема Лагранжа имеет следующую геометрическую интерпретацию:
существует значение сЕ(аф) такое, что касательная к графику функции y = f(x)
в точке (с;/(c)) параллельна секущей (рис. 4), соединяющей точки Д(а;/(а))
и Ж/W)-
Пример 1. Доказать, что
In(1 + х) < х при х > 0,	(14)
| arctg Х2 — arctg xj |х2—xi|, xjGR, *2 £ I®-	(15)
А 1) Применяя теорему Лагранжа к функции f(t) = 1п(1 + /) на
отрезке [0;х], где х > 0, получаем
ln(l+x) = j-L-X,
откуда следует неравенство (14), так как 0<с<х.
2) По теореме Лагранжа для функции f(f) — arctg t на отрезке
с концами Х| и Х2 имеем
arctg х2 - arctgxi = *2 ~,
1 + cz
откуда получаем
| arctgх2 - arctgxi | =	< |х2 -Xi|,
1 4- cz
так как
Полагая в соотношении (15) х% — х, xi — 0, получаем
| arctgx| |х|, хей,	(16)
и в частности
О С arctgx С х, х > 0.	(17)
4. Некоторые следствия из теоремы Лагранжа
Следствие 1. Если функция /(х) дифференцируема на интер-
вале (а\Ь) и /'(х) = 0 для всех хе(а]Ь), то
f(c) = С = const, х е (а; Ь).
О Пусть хц — фиксированная точка интервала (а; 6), х — любая точка
этого интервала. Применяя теорему Лагранжа к функции /(£) на
отрезке с концами хц и х, получаем
Дх) -Дх0) = (х-хо)Д(с),
где с е (а; д), Д(с) = 0, откуда Дх) = Дх0) = С.	•
5—3022
130
Глава XIV. Применение производной к исследованию функций
Следствие 2. Если функция /(х) непрерывна на отрезке [а- Ь],
дифференцируема на интервале (сцЬ) и для всех х е (сцЬ)
выполняется равенство f(x) = k, где k — постоянная, то
f(x) = kx + B, хе [а;Ь],
т. е. f — линейная функция.
О Применяя теорему Лагранжа к функции f на отрезке [а;х],
где а х Ь, получаем /(х) — /(а) = k(x — а), откуда следует, что
/(х) = kx + В, где В = f(a) — ka.	•
Следствие 3. Пусть функция /(х) дифференцируема на интер-
вале (сцЬ), за исключением, быть может, точки х$е(а,Ь). Тогда,
если существует конечный или бесконечный
lim /'(х)=Л,	(18)
х—
то в точке xq существует правая производная, причем
=	(19)
Аналогично, если существует
lim f\x) = В,	(20)
X—>Xq— 0
то
f-(x0)=B.	(21)
О Ограничимся доказательством равенства (19). Пусть Дх > 0
и точка хо + Дх принадлежит интервалу (а;Ь). По теореме 3
/(х0 + Дх) — /(х0) — /Х(хо + /Дх) • Дх, 0 < t < 1,	(22)
так как Хо <хо + /Дх<хо +Дх при t е (0; 1). Запишем равенство (22)
в виде
Л*о + Д*)-Л*о) = /' (х0 + /Ах), 0 < t < 1.	(23)
Если существует предел (18), то правая часть соотношения (23)
имеет предел, равный А, так как
lim /'(х) = lim /'(х0 + А*) — А-
Дх—»+0
Поэтому существует предел в левой части соотношения (23), который
по определению равен /^(хо), и справедливо равенство (18).	•
Пример 2. Найти /1(0) и /^(0), если:
1) /(х) = |х2 — х|;	2) /(х) — (х2 - 4)е|х|.
Д 1) Функция /(х) непрерывна на R и дифференцируема при всех
xeR, кроме х = 0 и х — 1.
§1 Основные теоремы для дифференцируемых функций
131
Если х < 0, то /(х) = /Дх) = х2 — х, /Дх) — 2х — 1, а если
О < х < 1, то /(х) = /2 W — х — х2, /Дх) = 1 ~ 2х. Так как
/1_(0) = lim /Дх) = —1 (следствие 3), а /^(0) = lim /Дх) = 1,
х—>—0	х—>+0
то Л(0) = -1, /4.(0) = 1.
2) Функция /(х) непрерывна на R и дифференцируема при всех
х е R, кроме х = 0.
Если х < О, то
/(х) =/i(x) = (х2 — 4)е х,
f[(х) = 2хе~х — (х2 — 4)е~х = (2х + 4 - х2)е-%.
Если х > 0, то
/(х) = /гСО — (%2 — 4)e*, f^x) = (х2 + 2х — 4)ех.
Следовательно,
4(0) = lim /{(х) = 4, 4(0) = lim /2(х) = —4.	А
х—>—0	х—»+0
Пример 3. Пусть функции /(х) и g(x) дифференцируемы при
X > Xq и удовлетворяют условиям /(Xq) = g(xo), /Z(x)>g'(x) ПРИ
X > Xq. Тогда /(х) > g(x) При X > Xq.
Д Применим теорему Лагранжа к функции h(t) = f(t) — g(t) на
отрезке [х0;х], где х>х0, и учитывая, что /z(xq) = O, получим
/Дх) = Л'(с)(х — х0), где с>х0,
/г'(с) = /'(с) -g'(c) >0.
Следовательно, /г(х)>0, при x>xq, т. е. /(x)>g(x) при x>xq. ▲
Пример 4. Доказать, что если х > 0, то
1п(1 + х)>х-^.	(24)
v2
А Пусть /(х) = ln(l+x), g(x) = х — Тогда
/(0) = g(0), /'(х) =	g'(x) = 1 - х,
и при х > 0 справедливо неравенство
7^— > 1 - х,
1 -Ух
равносильное при х>0 неравенству 1>1—х2. Используя результат
примера 3, получаем неравенство (24).	▲
132	Глава XIV. Применение производной к исследованию функций
5. Формула Коши
Теорема 4. Пусть функции f(x) и g(x) непрерывны на отрезке
[а\ Ь], дифференцируемы на интервале (cz; ti), причем g'(x) Ф 0 во
всех точках этого интервала. Тогда найдется хотя бы одна
точка с е (а; Ь) такая, что
_ Г (с)
g(b)-g(a) gf(cY
(25)
О Рассмотрим функцию
(р(х) =f(x) + t-g(x),
где число t выберем таким, чтобы выполнялось равенство <р(«) = <р(Ь),
которое равносильно следующему:
f(0 - /(а) + f(g(&) - g(a)) = 0.	(26)
Заметим, что g(b) ^(tz), так как в противном случае согласно
теореме Ролля существовала бы точка ае(а;6) такая, что g'(oi) = O
вопреки условиям теоремы 4. Итак, g(b)—g(a)^0, и из равенства (26)
следует, что
/ОТ-/ОТ
g(b)-g(a)
(27)
Так как функция ср при любом t непрерывна на отрезке [а; 6],
дифференцируема на интервале (а; 6), а при значении /, определяемом
формулой (27), принимает равные значения в точках а и Ь, то по
теореме Ролля существует точка се(а;6) такая, что </(с) = 0, т. е.
/'(с) + t • g\c) — 0, откуда
ё'(с)
Из этого равенства и формулы (27) следует утверждение (25). •
Замечание. Теорема Лагранжа — частный случай теоремы Коши
(gW = х).
Пример 5. Пусть функция /(х) непрерывна на отрезке [а; Ь]
и дифференцируема на интервале (а; 6), где а > 0. Доказать, что
существует точка с G (a; b) такая, что
(28)
Д Применяя теорему 4 к функциям <j>(x) = ^^ и /г(х) = Т, получаем
cf(c) - /(с)
- y(g) = </(с) т е Ь °	_ с2
h(b) — h(a) h'(c) ’	j j	1
b ~ a
откуда следует равенство (28).
§2. Возрастание и убывание функции
133
Задачи
1.	На интервале (0; 1) найти такую точку с, что касательная к графику функции
у — х^ в точке (с; с3) будет параллельна хорде графика, соединяющей точки
(0;0) и
2.	Пользуясь теоремой Лагранжа, доказать неравенства:
1)	| sin a — sin b\ \a — b\, a e R, b e R;
2)	| cos a — cosb| \a — b\, a e R, b e R; 3) ln(l + x) > при x > 0;
4)	ex 1 + x при x 6 R;	5) ex > ex при x > 1;
6)	(b - a)an~l <bn -an < n(b - a)n~[ при 0 < a < b, n e N;
7)	cosx > 1 — при 0 < x < ^;	8) sinx > x — при 0 < x <
2	2	6	2
3.	Доказать, что если функция Дх) удовлетворяет условиям теоремы Ролля на
отрезке [a;Z?] и не является постоянной, то на этом отрезке найдутся такие
точки ci и с2, что	< 0.
4.	Доказать, что если функция /(х) непрерывна на отрезке [a;b], дифферен-
цируема на интервале (а; Ь) и не является линейной, то существует такая
точка ce(a;b), что
|/'(с)| >
W~/(a)
b~ a
5.	Доказать, что если функция /(х) дифференцируема на отрезке [1;2], то
существует точка с 6 (1; 2) такая, что
г2 ,
Ответы
1,с~7з
§2. ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ
Напомним, что функция /(х) называется возрастающей (гл. III,
§ 3, п. 3) на некотором промежутке (гл. II, § 1, п. 1), если большему
значению аргумента соответствует большее значение функции, т. е.
для любых точек Х[ и х2 из этого промежутка таких, что х2 >*ь
выполняется неравенство
f(x2) >/(Х1).
Если для любых точек Х[ и х2 из данного промежутка таких, что
х2 > %1, выполняется неравенство
/(х2) < Kxi),
то функция /(х) называется убывающей на этом промежутке.
134
Глава XIV. Применение производной к исследованию функций
С помощью производной можно находить промежутки монотон-
ности, т. е. промежутки возрастания и убывания функции.
Теорема 1. Пусть функция f(x) непрерывна на отрезке [а*, Ь]
и дифференцируема на интервале (сцЬ). Тогда если /Дх) >0 для
всех х G (а; Ь), то функция Дх) возрастает на отрезке [а; Ь\,
а если /Дх) < 0л то она убывает на этом промежутке.
О Воспользуемся теоремой Лагранжа (§ 1, формула (11)). Пусть xi
и Х2 — произвольные точки отрезка [а, Ь\ такие, что xi < %2- Тогда
/(х2) — f(>i) =/'(с)(х2 — лл), с €(«;£>)•	(1)
Так как х% — Х[ > 0, то в случае, когда /Дх) > 0 на интервале
(а;Ь), из равенства (1) следует, что Дх2) > /(*1)- Это означает, что
функция Дх) возрастает на отрезке [а;Ь]. Аналогично из условия
/Дх) < 0 на интервале (а; Ь) следует, что функция Дх) убывает на
отрезке [а; 6].	•
Пример 1. Найти промежутки возрастания и убывания функ-
ции Дх), если:
1)	Дх) = х3 — 6х2 — 15х + 4;
2)	Дх) = 12х5 + 15х4 - 140х3 - ЗОх2 + ЗбОх + 7;
3)	f(x) = |х2 - х|;	4) Дх) = (х - 1)2(х + I)3;
5) /(х) =	6>	= sin х + |sin 2х-
А 1) Функция Дх) дифференцируема на Ж и
/Дх) = Зх2 — 12х — 15 = 3(х + 1)(х — 5).
Так как /Дх) >0 при х< -1 и х>5, а /Дх) <0 при хе(—1;5), то
функция Дх) возрастает на промежутках (—оо;—1] и [5;+оо),
а на отрезке [—1; 5] эта функция убывает (теорема 1).
2) /Дх) = 60х4 + 60х3 - 420х2 - 60х+360 = 60 (х4 + х3 - 7х2 - х + 6).
Многочлен
/Дх) = х4 + х3 — 7х2 - х + 6
имеет корни Х[ = -1, Х2 = 1. Разделив /Дх) на х2 — 1, получим
многочлен
х2 + х — 6 — (х + 3)(х — 2).
Следовательно, уравнение /Дх) — 0 имеет корни
xi = —1, Х2 = 1, х3 — — 3, Х4 = 2.
Применив метод интервалов, найдем, что
/Дх) > 0 на промежутках х < —3, — 1<х<1, х>2
и /Дх) < 0 на промежутках — 3<х<—1, 1 < х < 2.
§2. Возрастание и убывание функции
135
Следовательно, функция /(х) возрастает на промежутках
х -3, — l^x^l, х^2
и убывает на промежутках
—3	х — 1 и
3)	Функция /(х) непрерывна при
всех х е R и дифференцируема
во всех точках х е R, кроме то-
чек = 0 и х2 = 1 (§ 1, при-
мер 2). Если х < 0 или х > 1,
то /'(х) — 2х — 1, откуда следует,
что /'(х) < 0 при х < 0 и /'(х) > О
при х > 1.
1 < х < 2.
Если 0 < х < 1, то /'(х) = 1 — 2х, откуда следует, что /'(х) > О
при 0<х<| и /'(х)<0 при хе 1). Следовательно, функция
/(х) возрастает на промежутках 0 х и х 1 и убывает
на промежутках х < О и | х 1. График функции у = |х2 — х|
изображен на рис. 5.
4)	Функция f(х) непрерывна и дифференцируема при всех х € R.
Так как
/'(х) — 2(х - 1)(х +1)3 + 3(х - 1)2(х +1)2 — (х - 1)(х + 1)2(5х -1),
то
/7(х) = 0 при Х1 = —1, х2 = | и х3 = 1.
о
Методом интервалов получаем, что /'(х) > 0 при х < —1,
при — 1 < х < | и при х > 1; /'(х) < О при ? < х < 1. Так как
функция /(х) непрерывна при х = — I, при х=| и при х = 1, то
о
функция /(х) возрастает на промежутках оо; I] и [1;+оо)
и убывает на отрезке
5)	Функция /(х) определена при всех х G R, кроме х = 5,
и дифференцируема в области определения, причем
f(Y\ _ 3(х - 1)2(х - 5)2 - 2(х - 1)3(х - 5) _ (х - 1)2(х - 13)
М ’	(х-5)4	“	(х-5)3	’
Так как /'(х) > 0 при х G (—оо;1), при х G (1;5) и при
х€(13;+оо), а f'(x) < 0 при х G (5; 13), и кроме того, /(х)
136
Глава XIV. Применение производной к исследованию функций
непрерывна при х= 1 и при х = 13, то функция f(x) возрастает
на промежутках (—оо;5) и [13;+оо) и убывает на промежутке
(5; 13].
6)	Функция /(х) дифференцируема на R, является периодической
с периодом 2л и
f(x) = cosx + cos2x = 2cos2x + cosx — 1 — (2 cosx — l)(cosx+1)
Уравнение /'(x) = 0 имеет корни
x — ±^+2лп, х = л + 2ли, n € Z,
О
из которых отрезку [0; 2тг] принадлежат точки
*1 = f,	*2 = ТС, Х3 = у.
Неравенству /'(х)>0 удовлетворяют значения х из интервалов
(0; ) и (у; 2л), а неравенство /'(х) < 0 выполняется на
интервалах ^|;л^ и
Отсюда следует, что функция /(х) возрастает на отрезках
[в; и [у; 2л], а также на отрезках, получаемых сдвигом
этих отрезков на 2лп, n G Z.
На отрезке Д =	а также на отрезках, получаемых
L о о J
сдвигом отрезка Д на 2лп, n е Z, функция /(х) убывает. ▲
Пример 2. Доказать, что если 0 < х < ^, то справедливы
неравенства
tgx > х,	(2)
sinx>-x.	(3)
7Г
Д 1) Рассмотрим функцию f(x) = tgx —х. Эта функция дифферен-
цируема на интервале	причем
/'W = — - 1 > 0 при х € (О; У
cosz X	\	^ /
так как
0<cos2x<l при 0<х<|.
Кроме того, функция /(х) непрерывна при х = 0. По теореме 1
эта функция возрастает на промежутке [б; 0. Так как f(0) = 0,
§2. Возрастание и убывание функции
137
то /(х) > 0 при х € ^0; т. е. tgx — х > 0, откуда следует
неравенство (2).
2) Рассмотрим функцию /(х) =	. Эта функция дифференци-
руема на интервале	Так как
lim = 1,
х-*0 *
то, полагая /(0) = 1, доопределим эту функцию по непрерыв-
ности в точке х = 0.
Найдем ее производную:
/'(х) = xcosx-sinx = cjx(% _
Учитывая, что cosx > 0 и х — tgx<0 (неравенство (2)), отсюда
находим, что /'(х) < О на интервале	Функция /(х)
непрерывна на отрезке |0; и убывает. Поэтому
« /ЙН-
sinx ^2	/гч лЛ
т. е. ---> - при хе (0; - ,
X 7Г г	\	2/ ’
откуда следует неравенство (3).
Это неравенство выражает тот
факт, что на интервале ^0; 0 график
функции у = sinx лежит выше прямой
(рис. 6), соединяющей точки (0; 0)
и f?;lY	А
Найти интервалы возрастания и
1. f(x) = 2х3 + Зх2 - 36х + 10.
3. Дх) = Зх5 - 25х3 + 60х + 7.
5. Дх) = (х — 1)2(х + 2)3.
7. Дх) = \/2х3 + 9х2.
9. Дх) =
(% + 2)2
11. /(х) = sinx — cos2х — 1.
Задачи
убывания функции /(х) (1-12):
2. /(х) — х4 — 2х2 + 3.
4. /(х) = х5 — 5х4 + 5х3 — 9.
6. /(х) = (х - 1)2е2\
8. Дх) = АЗХ + 2-
х2 — Зх + 2
10. Дх) = |х2 — 2х — 3|.
12. Дх) = (х2-1)еЧ
138
Глава XIV. Применение производной к исследованию функций
Ответы
1. Возрастает при х < — 3 и при х > 2, убывает при — 3 < х < 2.	2. Возрастает
при — 1<х<0 и при х> 1, убывает при х<— 1 и при 0<х<1.	3. Возрастает
при х < —2, при —1 < х < 1 и при х > 2, убывает при — 2 < х < — 1 и при 1 < х < 2.
4. Возрастает при х < 1 и при х > 3, убывает при 1 < х < 3.	5. Возрастает при
х < — i и при х > 1, убывает при — | < х < 1.	6. Возрастает при х < 0 и при
О	о
о
х > 1, убывает при 0 < х < 1.	7. Возрастает при - < х < — 3 и при х > О,
убывает при — 3 < х < 0.	8. Возрастает при —\/2 < х < 1 и при >/2 < х < 2,
убывает при х < —\/2, 1 < х < л/2 и при х > 2. 9. Возрастает при х < — 2 и при
х > 2, убывает при — 2 < х < 2.	10. Возрастает при — 1 < х < 1 и при х > 3,
убывает при х < — 1 и при 1 < х < 3.	11. Возрастает при — 4- 2тт < х < | 4- 2тт
и при 4- 2яп < х < ^ + 2тш, и е Z; убывает при 4- 2тш < х <	4- 2тш и
при 4- 2тт < х <	4- 2лтг, n е Z. 12. Возрастает при 1 — л/2 < х < 0 и при
х > \[2 — 1, убывает при х < 1 — у/2 и при 0 < х < >/2 — 1.
§3. ЭКСТРЕМУМЫ ФУНКЦИИ
1. Необходимое условие экстремума
Понятие локального экстремума было рассмотрено в § 1. Необ-
ходимые условия экстремума легко получить из теоремы Ферма.
Согласно этой теореме точки локального экстремума функции f(x)
следует искать среди тех точек области ее определения, в которых
производная этой функции либо равна нулю, либо не существует.
В дальнейшем будем часто опускать слово «локальный» при
формулировке утверждений, связанных с понятием локального экс-
тремума.
Точки, в которых производная данной функции равна нулю, на-
зывают стационарными точками этой функции, а точки, в которых
функция непрерывна, а ее производная либо равна нулю, либо
не существует, — ее критическими точками. Поэтому все точки
экстремума функции содержатся среди ее критических точек.
Точка х = 0 является критической точкой для каждой из функций
у—х2, у=х3 (рис. 7), у = |х| (рис. 8), у = |х|2 (рис. 9), у — \/х (рис. 10).
Причем для функций у — х2, у = |х|, у — |х|г точка х — 0 — точка
экстремума, а для функции у = х °, у = хз эта точка не является
точкой экстремума.
Таким образом, не всякая критическая точка является точкой
экстремума функции.
§3. Экстремумы функции
139
Пример 1. Найти стационарные точки функции /(х), если
1) Дх) = х4 - 8х2 + 5;	2) Дх) = Зх5 - 50х3 + 135х + 4;
3) Дх)=х2е-Х;	4) Дх) = |х — cosx + ~ sin 2х.
Д 1) Стационарные точки функции /(х) — корни уравнения
/'(х) = 4х3 — 16х = 4х(х2 — 4) = О,
т. е. точки Х[ = 0ч %2 — 2, х% = —2.
2) Найдем производную данной функции:
f (х) = 15х4 - 150х2 + 135 = 15(х4 - 10х2 + 9) =
= 15(х2 — 1)(х2 — 9).
Следовательно, стационарными являются точки -3,-1,1,3.
3) Так как
/'(х) = 2хе~х — х2е~х = хе~х(2 — %),
то функция /(х) имеет две стационарные точки Х[ =0, х% — 2.
4) Найдем производную данной функции:
/'(х) = | + sin х + | cos 2х — 2 + sin х — sin2 х =
= (2 - sin x)(sin x + 1).
Уравнение (x) = 0 равносильно уравнению sinx = —1. Отсюда
следует, что стационарными являются точки хп — — ^+2л71,
/2 G 2л.	Ж
Пример 2. Найти критические точки функции /(х), если
1) /(х) = |х2 — х|;	2) /(х) = (х2 — 4)еМ.
Д 1) Критические точки непрерывной функции f(х) — это все ее
стационарные точки (корни уравнения /,(х) = 0), а также точки,
в которых функция не имеет производной.
Функция |х2 — х| дифференцируема при всех xgR, кроме
х = 0 и х —1 (§1, пример 2; §2, пример 1(3)), и непрерывна
140
Глава XIV. Применение производной к исследованию функций
на множестве R, а уравнение /'(х) = 0 имеет единственный
корень х=^ Следовательно, критическими являются точки
0,1,1.
2) Если х > 0, то
/(х) = (х2 — 4)ех, /'(х) = 2хе% + (х2 — 4)ех = ех(х2 + 2х - 4).
Уравнение /'(х) = 0 имеет единственный положительный корень
х\ = д/5 — 1.
Так как /(х) — четная функция, то х2 = 1 — V5 также
является корнем уравнения /'(х) = 0 (при х < 0).
В § 1 (пример 2) было показано, что функция /(х) не имеет
производной в точке х = 0, так как /1(0) =4, а /^(0) = — 4.
Следовательно, критическими для функции /(х) являются
точки 1 — д/5, 0 и д/5 —1.	А
Пример 3. Найти все значения а, при которых функция
/(х) = х3 — Зах2 + 27х - 7
имеет единственную стационарную точку.
А Так как
/'(х) = Зх2 — бах + 27 = 3[(х — а)2 + 9 — а2],
то уравнение /'(х) = 0 имеет единственный корень, а функция /(х)
имеет единственную стационарную точку, тогда и только тогда, когда
9 — а2 = 0, т. е. при а = — 3 и а = 3.	А
2. Достаточные условия экстремума
Для формулировки достаточного условия экстремума ведем по-
нятие смены знака функции.
Пусть функция g’(x) определена в проколотой 8-окрестности
точки xq, т. е. на множестве (xq — 8,xq) U (xq,xq + 8). И пусть
для всех xe(xQ-3,xo) выполняется неравенство g’(x) < 0, а для
всех х е (xq,xq + 8) ~ неравенство g’(x) > 0. В этом случае говорят,
что функция g(x) меняет знак с минуса на плюс при переходе
через точку х0.
Аналогично вводится понятие смены знака с плюса на минус
при переходе через точку xq.
Теорема 1. Пусть функция /(х) дифференцируема в некоторой
окрестности точки xq, кроме, может быть, самой точки xq,
и непрерывна в точке xq.
§3. Экстремумы функции
141
Xq — 8 ^0 Xq + 8 X
Рис. 12
Тогда
а)	если производная f(x) меняет знак с минуса на плюс при
переходе через точку xq, т. е. существует 8 > О такое,
f'M<0 при xe(x0-S,x0),
f(x) > О при X е (х0,Х0 + S),
то xq —точка минимума функции f (рис. 11);
б)	если ff(x) меняет знак с плюса на минус при переходе через
точку xq, то хо ~ точка максимума функции f (рис. 12).
О Пусть функция /Дх) меняет знак с минуса на плюс при переходе
через точку xq, тогда выполняются условия (1).
Если х — произвольная точка интервала (хо~ 8,хо), то функция f
дифференцируема на интервале (х,хо) и непрерывна на отрезке [х,х0].
По теореме Лагранжа
/(х) -/(х0) = /'(с)(х-х0),	(2)
где f(c) < 0, так как с е (хо — 8,хо), и х — хо < О, так как х < xq.
Тогда правая часть равенства (2) положительна и поэтому
f(x) > f(xo) при х е (х0 - 8, х0) •
Аналогично, применяя теорему Лагранжа к функции f(x) на отрезке
[хо;х], где xq < х < xq + 8, получаем, что
f(x) > f(xo) при X е (х0; *о + 5).
Таким образом, для всех х е (хо — 8;хо + 8), х xq, выполняется
неравенство	.
/(х) >Дх0).
Это означает, что xq — точка минимума функции Дх).
Тем же способом рассматривается случай максимума. •
Пример 4. Найти точки экстремума функции Дх), если
1)	Дх) = х3 + 6х2 - 15х + 7;	2) f(x) = х5 + 5х4 + 5х3 + 8;
3) Дх) = (х + 2)2(х - З)3;	4) Дх) =
(х - 1/
5) Дх) = |х — 5|(х — З)3;	6) /(х) = (х2 — 4)е1х1.
142
Глава XIV. Применение производной к исследованию функций
А 1) Так как
/'(х) = Зх2 + 12х — 15 = 3(х + 5)(х — 1),
то Х[ = — 5 и Х2 = 1 — стационарные точки функции /(х). При
переходе через точку X] производная меняет знак с плюса на
минус, а при переходе через точку Х2 — с минуса на плюс.
Следовательно, Xi = — 5 — точка максимума, а х% = 1 — точка
минимума функции /(х).
2)	Уравнение
f(x) = 5х4 + 20х3 + 15х2 = 5х2(х + 3)(х 4-1) = О
имеет корни Xj=O, Х2 = —3, Хз = —1. Точка xi = 0 не является
точкой экстремума, так как функция /(х) возрастает на про-
межутках (—1; 0] и [0;+оо). При переходе через точку х^ — — 3
производная меняет знак с плюса на минус, а при переходе
через точку хз = — 1 — с минуса на плюс. Поэтому xj = — 3 —
точка максимума, а Х3 — 1 — точка минимума функции /(х).
3)	Уравнение
/'(х) = 2(х + 2) (х — З)3 + 3(х + 2)2 (х — З)2 = 5х(х + 2) (х — З)2 = 0
имеет корни xj — —2, Х2 — 0, Х3 = 3. Точка Х3 = 3 не является
точкой экстремума, так как функция /(х) возрастает на
интервале (0;+оо): ее производная положительна при хе(0;3)
и при х е (3; +оо).
Производная меняет знак с плюса на минус при переходе
через точку Х[ = -2 и с минуса на плюс при переходе через
точку Х2 = 0. Следовательно, xi = — 2 — точка максимума,
а Х2 = 0 —точка минимума функции /(х).
4)	Функция /(х) дифференцируема при х / 1, причем
\ _ (Зх2 + 4х)(х — I)2 — (х3 + 2х2)2(х — 1) _ (х + 1)х(х — 4)
1 W	(х-1)3	’
Методом интервалов определяем знаки /'(х) (рис. 13).
Рис. 13
Из рис. 13, используя достаточное условие экстремума,
заключаем, что х = —1 — точка максимума, ах=0их=4—
точки минимума функции /(х).
5)	Функция /(х) непрерывна на R и дифференцируема при всех
х е R, кроме х = 5.
§3. Экстремумы функции
143
Если х > 5, то
/(х) = (х-5)(х-3)3,
/'(х) = (х - З)3 + 3(х - 3)2(х - 5) = (х - 3)2(х - 3 + Зх - 15) =
= 4(х — 3)2(х — 4,5),
а если х < 5, то
/(х) = —4(х — 3)2(х — 4,5).
Отсюда следует, что f'(x)>0 при х>5, при х<3 и 3<х<4,5;
Д(х) < 0 при х е (4,5; 5).
Поэтому х = 4,5 — точка максимума, а х = 5 — точка ми-
нимума функции /(х).
6)	Дх) — четная функция, непрерывная на R и дифференцируемая
при всех xeR, кроме х = 0. В § 1 (пример 2) было установлено,
что если х > 0, то
f'(x) — (х2 + 2х - 4)ех,
а если х < 0, то
/'(х) = (2х + 4 - х2)е-%.
Уравнение х2 + 2х — 4 = 0 имеет один положительный корень
xi = — 1 + д/5, а уравнение 2х + 4 — х2 — 0 имеет один
отрицательный корень х^ = 1 — \/5. Отсюда следует, что Д (х) > О
при x>xi и при хе (х2;0); /'(х) <0 при х<х^ и при хе (0;х[).
При переходе через точки х\ и х% производная меняет
знак с минуса на плюс, а при переходе через точку х = 0 —
с плюса на минус. Следовательно, х\ и х2 — точки минимума,
а х2 — 0 — точка максимума функции /(х).	▲
Задачи
1.	Найти стационарные точки функции /(х), если:
1)	Дх) = 2х3 - Зх2 - 12х + 5;
2)	Дх) = 12х5 - 15х4 - 140х3 + ЗОх2 + ЗбОх + 7.
2.	Найти критические точки функции Дх), если:
1)	Дх) = (х + I)3 — |х|;	2) Дх) = Зе-Х + |3х + х2|.
Найти точки экстремума функции (3-10):
3.	Дх) = Зх5 - 25х3 + 60х + 9.	4. Дх) = (х3 - 10)(х + 5)2.
5. Дх) = (х - 2)2(х + I)3.	6. Дх) =
X I 1
7.	Дх) = ^|§.	8. Дх) = х4^.
(х + З)2
9. /(х) = х|1 — х| — 5х3.	10. f(x) — |х2 — l|e'xL
144	Глава XIV. Применение производной к исследованию функций
11. Найти все значения параметра а, при которых функция f(x) = х^е х имеет
ровно одну точку экстремума на отрезке [а; а 4- 7].
Ответы
1. 1) %i = —1; %2 —2; 2) Х[ = —2; Х2 = — 1; х^ = 1; Х4 = 3. 2. 1) х = 0; 2) xi=0;x2 =
= —3. 3. Х[ = —2; %2 “ 1 ~ точки максимума; х% = — 1; хд — 2 — точки минимума.
4. Х[ — —5 —точка максимума; %2 = 1 — точка минимума. 5. х\ = ^1—точка
максимума; Х2 = 2 — точка минимума. 6. х\ = —3 — точка максимума; Х2 — 1 —
точка минимума. 7. х = —15 —точка максимума. 8. х\ = — л/2, Х2 = v^2 —
точки максимума; х = 0 — точка минимума 9. xj = | — точка максимума;
Х2 = —| — точка минимума. 10. Xi = —1. Х2 = О, Х3 = 1 — точки минимума;
Х4 = 1 — х/2, Х5 — \/2 — 1 — точки максимума. И. —7 а < —1, 0 < а 6.
§4. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ
ФУНКЦИИ
Понятие наибольшего (наименьшего) значения функции было
рассмотрено в гл. III (§ 3, п. 4).
Если функция /(х) непрерывна на отрезке [а;&], то согласно
теореме Вейерштрасса (гл. IX, § 4, п. 4) существует точка Х[ е [а]Ь\
такая, что
f(xi)=7W, где М= sup /(х) = max/(х).
х€[а;6]	хе[аф]
Аналогично, существует точка Х2 6 [а; Ь] такая, что
/(Х2) = т, где т = inf /(х) = min /(х).
х€[а;&]	хб[а;6]
Это означает, что в точке Xi функция /(х) принимает свое наибольшее
значение 7И, а в точке Х2 — свое наименьшее значение т, и для всех
х е [а; Ь] справедливо неравенство
m /(х) М.
Пусть функция /(х) непрерывна на отрезке [&;&], дифференцируема
во всех точках интервала за исключением, быть может, точек
xi,...,x^, и имеет конечное число стационарных точек xi,...,xm
(/'(•^1) = ... =	= 0)- Тогда если М и т — соответственно
наибольшее и наименьшее значения функции /(х) на отрезке
то М — наибольшее из чисел
/(а), ДЬ), Дх0,...,/(хй),/(хО,..., Дхт),
ат — наименьшее из этих чисел.
В прикладных задачах при нахождении наибольшего (наимень-
шего) значения функции на отрезке [а; Ь] или на интервале Ь)
§4. Наибольшее и наименьшее значения функции
145
часто встречается случай, когда f дифференцируема на интервале
и непрерывна на отрезке [а;&], а уравнение /Дх) = 0 имеет
единственный корень хоб(л;&) такой, что /Дх) > О при хе(я;хо)
и /Дх) < 0 при х € (xo;ft) или /Дх) < 0 при х € (а;хо) и /Дх) > О
при х G (хо; Ь).
В этом случае число Дхд) является не только экстремумом
функции /(х), но и наибольшим (наименьшим) значением этой
функции на отрезке [a;b] или на интервале (сцЬ).
Отметим еще, что если на некотором промежутке Д справедливо
неравенство g(x) > 0, то функция g’(x) принимает в точке Е А
наибольшее (наименьшее) значение тогда и только тогда, когда
функция [g(x)]n, где иеК, /0 2, принимает в точке Хд наибольшее
(наименьшее) значение.
Пример 1. Найти наибольшее и наименьшее значения функ-
ции Дх) на множестве Е, если
1)	/(х) = х4 — 8х2 + 3, Е=[—1;2];
2)	/(х) = (х + 2)2(х — З)3, Е=[-3;1];
3)	/(х) = sin х + sin 2х, Е — j(); у];
4)	zw = ?7?
5)	/(х) = |х2 + 2х-3| + ||пх, £= [1;21;
6)	/(х) = |х2-4|е-И, E = R.
А 1) Уравнение
/Дх) — 4х3 - 16х = 4х(х — 2)(х + 2) = О
имеет корни Х1 = — 2, Х2 = 0, хз = 2. Отрезку [—1;2] принадлежат
точки Х2 = 0, хз = 2, при этом
/(-1) = -4, /(0) = 3, /(2) = -13.
Следовательно, наибольшее значение функции /(х) на отрезке
[— 1; 2] равно 3, а наименьшее равно —13.
2)	В § 3 (пример 4(3)) было установлено, что xi = —2 —точка
максимума, а Х2 = 0 — точка минимума функции Дх). Так как
/(-3) = -216, Д-2) - О, ДО) = -108, Д1) = -72,
то наибольшее значение функции Дх) на отрезке [—3; 1]
равно 0, а наименьшее равно —216.
3)	Уравнение
/Дх) = cos х + cos 2х = 2 cos2 х + cos х - 1 = О
146
Глава XIV. Применение производной к исследованию функций
равносильно совокупности уравнений
cosx = —1, cosx=|.
На отрезке у] уравнение cosx = —1 имеет единственный
1
корень = 7г, а уравнение cosx = - имеет единственный корень
Х2 = Найдем значения функции /(х) в точках 0,
Имеем:
/(0) = 0,	=	/(я) = 0,
Следовательно, наибольшее значение функции /(х) на отрезке
Гл 3я1	Зх/З	1
0; у равно -у, а наименьшее равно -1.
4)	Так как
с/z \_4х3(х2 + 1) — 2х(х4 + 1) _ 2х(х4 + 2х2 — 1)
1W (^ЦЛ)2	“	(х2 +1)2	’
то уравнение /'(х) = 0 имеет корни xj = 0, Х2}з = ±л/\/2 — 1;
/(0)=/(1)=/(-1) = 1, /(х2)=Я^) = ^Ц^±1 = 2>/2-2<1.
Наибольшее значение функции равно 1, а наименьшее равно
2V2-2.
5)	Функция/(х) непрерывна на отрезке [i; 2^ и дифференцируема
во всех точках этого отрезка, за исключением точки х — 1.
Если х е 1J, то
/(х) = 3 —2х —х2 + Inx, f (х) = -2 - 2х + ^ = - 4?- ± 4х ~ 3.
1	2	v '	2х	х
Уравнение f(x) = 0 имеет на отрезке единственный
корень Х[=
Если х € (1; 2), то
/(х) = X2 + 2х - 3 + | In х, f(x) = 4*2 + 4* + 3
и уравнение /'(х) = 0 не имеет действительных корней.
Так как
ZG) = ?“Iln2’ Я2) = 5+|1п2,
§4 Наибольшее и наименьшее значения функции
147
а х = 1 — критическая точка функции /(х) и /(1) = 0, где
/(1)</^0, то наибольшее значение функции /(х) равно
о
5 + - In 2, а наименьшее равно О
6)	Функция непрерывна на R, дифференцируема на R, кроме
точек —2,0,2, и является четной. Если х > 0, то
I ПРИ %е(2;+оо),
где g’(x) = (х2 — 4)е~х. Уравнение
g'(x) — (—х2 + 2х + 4)е~х = 0
имеет на промежутке (0; +оо) единственный корень
х( = 1 + д/5 > 2, причем g'(x) = /'(х) при х > 2 и g'(x) меняет
знак с плюса на минус при переходе через точку х\. Поэтому
xj —точка максимума функции /(х), а функция /(х) убывает
При X > Х[.
При переходе через точку Хд = 2 производная /'(х) меняет
знак с минуса на плюс, так как /'(х) = — g'(x) при хе(0;2)
и /'(х) = g,(x) при х > 2. Поэтому х^ — точка минимума
функции /(х).
Учитывая, что функция /(х) строго убывает на интервале
(0;2) и четная, заключаем, что х = 0 — точка максимума
функции /(х).
Используя полученные результаты и четность функции /(х),
получаем, что х = — 2 и х — 2 — точки минимума функции /(х);
х = 0 и х = 1 + х/5 — точки максимума этой функции
Если М и т — соответственно наибольшее и наименьшее
значения функции f(х) на К, то М — наибольшее, а т —
наименьшее из чисел /(0), /(2), /(1 + д/5), где
ДО) = 4, Д2) = 0, Д1 +х/5) = 2(1 + л/5)е-<1+^ < 2,
так как ef > t при t > 0 (а значит, e~l < j при t > 0).
Следовательно, М — 4, т = 0.	А
Пример 2. Доказать, что при х G |^0;	справедливо неравенство
0 sin3xcosx <	(1)
1о
А Обозначим <р(х) = sin3хcosx, тогда
<р(х) — | sin 2х(1 — cos 2х) = i sin 2х — sin 4х,
148
Глава XIV. Применение производной к исследованию функций
откуда
q/(x) = |(cos2x — cos4x) = sinx sin Зх.
Уравнение <j/(x) = 0 имеет единственный корень х — Хд = на
О
интервале	причем <р'(х) > О при х G (О; и </(х) < 0 при

Следовательно, хд — точка максимума функции ср(х)
и
max ф(х) = 9?(х0) =
хб[0;|]
зУз
16 
Правое неравенство (1) доказано. Левое неравенство, очевидно,
выполняется, так как sinx 0 и cosx 0 при х С [О;	.	▲
Пример 3. Среди всех равнобедренных треуголь-
ников, вписанных в данный круг, найти треугольник
с наибольшим периметром.
А Пусть треугольник АВС вписан в круг радиуса 7?,
причем АВ —ВС (рис. 14). Обозначим ABAC — а. По
теореме синусов
АВ = ВС — 2R sin а, АС = 2R sin(тг — 2а) = 2R sin 2а.
Пусть Р(а)периметр треугольника АВС, тогда
Р(а) = 27? (2 sin а -F sin 2а).
где 0 < а< Отсюда находим
Р'(а) — 4/?(cos 2а + cos а) = 47?(2 cos2 а + cos а — 1) =
= 47?(2 cos а — l)(cosa+ 1).
единственное
Уравнение Pr(a) — 0 имеет на интервале (О; 0
решение a = ?, причем /у(а) > 0 при а е (0; *) и P'(oi) < О
О	\ О /
при	Следовательно, число Р(?) является наибольшим
значением функции Р(а) на интервале ^0; 0
. Но если АВАС = а—^,
о
то АВСА = | и, значит, ААВС = |, т. е. АВС — равносторонний
треугольник. Итак, среди всех равнобедренных треугольников, впи-
санных в данный круг, наибольший периметр имеет равносторонний
треугольник.	▲
§4 Наибольшее и наименьшее значения функции
149
Пример 4. Определить отношение радиуса основания к высоте
цилиндра, если при данном объеме цилиндра площадь его полной
поверхности является наименьшей.
Д Пусть х,h,v,S — соответственно радиус основания, высота, объем
и площадь полной поверхности цилиндра. Тогда
S = 2лхИ + 2тгх2, v = юс2И,
откуда
h — при х > О,
лх2
и поэтому
S = S(x) = 2 Q + лх2) , S'(x) = 2 (27ГХ -
Уравнение S' = 0 имеет единственный корень
%о = VT,
V 2л
причем S'(x)<0 при xe(0;xq) и S'(x)>0 при x>xq. Следовательно,
Xq — точка минимума функции S(x), и наименьшее значение этой
функции равно S(xq), т. е. площадь полной поверхности цилиндра
является наименьшей, если его радиус равен Xq. Но тогда
h =	= 2х0,
т. е. цилиндр при заданном объеме имеет наименьшую площадь
полной поверхности, если его высота в 2 раза больше радиуса, т. е.
в случае, когда осевое сечение цилиндра — квадрат.	▲
Пример 5. Определить размеры закрытой коробки объема v
с квадратным основанием, на изготовление которой расходуется
наименьшее количество материала.
Д Пусть х —сторона основания коробки, h — высота коробки, S —
ее полная поверхность. Тогда
S = 2х2 + 4хй, v = x2h,
откуда
S(x) = 2x2+4^
и, следовательно,
S'(x) = 4 Гх — Л) .
Уравнение S'(x) = 0 при х>0 имеет единственное решение XQ = ffi,
причем при переходе через точку xq функция S'(%) меняет знак с
минуса на плюс. Следовательно, Xq —точка минимума функции S(x),
150
Глава XIV. Применение производной к исследованию функций
а число 5(%о) является наименьшим значением этой функции при
х>0. Из формулы v = x2h следует, что если x = tyv, то h = tyv. Таким
образом, высота коробки должна быть равна стороне основания, т. е.
коробка должна быть кубом с ребром J/v.	▲
в.	Пример 6. Найти радиус основания цилиндра
\ наибольшего объема, вписанного в шар радиуса R.
I А Пусть г и h — соответственно радиус основания
J и высота цилиндра, вписанного в шар радиуса /?,
V — объем цилиндра (рис. 15). Тогда
Рис- 15	9,	(h\2 , 9 п9
v = nrh,	(-1
откуда
v = 2кг2 \/r2 — г2, где 0 < г < R.
Обозначим t = г2, тогда
v = 2 W#2 -t, 0<t<R2.
Рассмотрим функцию
и2 — 47г2/2 (Я2 - /).
Так как v 0, то функция v(t) имеет на интервале (О;/?2) те же
точки экстремума, что и функция
= -() = №).
Найдем критические точки функции /(/), решая уравнение
= 2tR2 - 3t2 = 0.
Это уравнение имеет на интервале (О;/?2) единственное решение
.	2Л2
to = ~'
причем точка является точкой максимума функции, а число
/(^-наибольшим значением функции /(/) на интервале (О;/?2).
Следовательно, при
г=^=Л\/1
функция v принимает наибольшее значение, т. е. радиус основания
цилиндра, вписанного в шар радиуса R и имеющего наибольший
объем, равен 7?л/|.	А
§4. Наибольшее и наименьшее значения функции
151
Рис. 16
Пример 7. Найти высоту конуса, имеющего
наибольший объем среди всех конусов, вписанных
в шар радиуса R.
Д В сечении сферы (границы шара) плоскостью,
проходящей через ось конуса, образуется окруж-
ность радиуса /?, а в сечении конуса — равнобед-
ренный треугольник АВС (АВ = ВС), вписанный
в эту окружность с центром О (рис. 16).
Пусть D — центр основания конуса, х — его вы-
сота, г —радиус основания. Тогда BD — x, AD —г,
до пересечения с окружностью в точке Е. Так как ЛВАЕ — прямой,
то по свойству перпендикуляра, опущенного из вершины прямого
угла на гипотенузу треугольника АВЕ, имеем
AEP — ED-DB, где ED = BE - BD = 2R - х.
Следовательно, г2 = (2R — х)х.
Пусть V — объем конуса, тогда
V(x) — | кг^х — ^k(2Rx2 — х3),
О	о
Продолжим BD
откуда
V'(x) = |я(4/?х — Зх2) = inx(4/? — Зх).
О	О
Так как G <х <2R, а на интервале (0; 2R) уравнение И(х) = 0
имеет единственный корень х= —, причем V (х) >0 при 0<х< —
О	О
и 7'(х)<0 при <х <2/?, то значение функции V(x) при * —-у
является наибольшим значением этой функции.
Ответ.
О
Пример 8. На координатной плоскости Оху
дана точка 7И(2;4). Рассматриваются треуголь-
ники, у которых две вершины, симметричные
относительно оси Оу, лежат на дуге параболы
у = Зх2, — 1 < х 1,
а точка М является серединой одной из сторон
каждого треугольника. Среди этих треугольников
выбран тот, который имеет наибольшую площадь.
Найти эту площадь.
Д Пусть 0 х 1, Д(—х;3х2), В(х; Зх2) — вершины одного из
рассматриваемых треугольников (рис. 17)
Q 6*2
0
Рис. 17
х
152
Глава XIV. Применение производной к исследованию функций
Третья вершина С определяется неоднозначно, так как точка М
может быть либо серединой стороны ВС, либо серединой стороны
АС (на рис. 17 это точки Q и С2).
Площади треугольников АС[В и АС^В равны, так как у них
общее основание АВ и равные высоты hi и й2, где = ^2 — Л,
причем h равняется удвоенной разности ординат точек М и А, т. е.
h = 2(4 - Зх2).
Пусть S = S(x) — площадь треугольника АВС, тогда
S(x) = ^АВ • h = xh = 8х — 6х3.
Так как уравнение 5'(х) = 8 — 18х2 = 0 имеет на отрезке [0; 1]
единственный корень xq = |, причем S'(x) > 0 при 0 х < | и S'(x) < 0
о	«5
при | <х С 1, то значение
О
S(x0) = s(|)=3|
является наибольшим значением функции S(x) на отрезке [0; 1].
Ответ. 3|.	▲
Задачи
Найти наибольшее М и наименьшее т значения функции Дх) на множестве Е
(1-Ю):
1.	Дх) = х3 - 6х2 + 9, £ = [—1;2].	2. Дх)	=х5	-	5х4+5х3 + 1, £=[-1;2].
3.	Дх) = |х2 — Зх+ 2|, £ = [—10:10].	4.	Дх)	=	1~Л + * £= [0;1].
1+ X — XZ
5.	Дх) = х - 2Inx, Е = [|; е].	6.	Дх)	=	(х - 2)2(х + I)3, Е = [0;3].
7.	Дх) = 5х3 — х|х+1|, £=[—2;0].	8.	Дх)	=	(х — 3)е|х+11, £ = [-2;4].
9. Дх) = 2 sin 2х + cos 4х, £=[0;^].	10. Дх) = (х - 3)3е|х+11, £=[-2; 4].
11.	Определить углы треугольника АВС с наибольшей площадью, если задана
длина его основания ВС и известно, что угол ВАС равен а.
12.	Среди всех прямоугольников, имеющих данную площадь S, найти прямо-
угольник:
1)	с наименьшим периметром; 2) с наименьшей диагональю.
13.	Найти наибольшую площадь прямоугольника, вписанного в круг радиуса R.
14. Найти наибольшую площадь прямоугольника, две вершины которого лежат
на осях Ох и Оу прямоугольной системы координат, третья — в точке (0;0),
а четвертая — на параболе у = 3 — х2.
15.	Найти угловой коэффициент прямой, проходящей через точку Л(1;2)
и отсекающей от первого координатного угла треугольник наименьшей
площади.
§4. Наибольшее и наименьшее значения функции
153
16.	Найти длину боковой стороны трапеции, имеющей наименьший периметр
среди всех равнобедренных трапеций с заданной площадью S и углом а
между боковой стороной и нижним основанием.
17.	Через точку А ^2; проводятся прямые, пересекающие положительные
полуоси в точках В и С. Найти уравнение той прямой, для которой отрезок
ВС имеет наименьшую длину.
18.	Лист картона имеет форму прямоугольника со сторонами а и b Вырезая
по углам этого прямоугольника квадраты и сгибая выступающие части
крестообразной фигуры, получим открытую сверху коробку, высота которой
равна стороне квадрата. Какой должна быть сторона квадрата, чтобы объем
коробки был наибольшим?
19.	Из трех досок одинаковой ширины нужно сколотить желоб. При каком
угле наклона боковых стенок площадь поперечного сечения желоба будет
наибольшей?
20.	Найти высоту правильной треугольной призмы наибольшего объема, впи-
санной в шар радиуса R.
21.	Найти высоту конуса наименьшего объема, описанного около шара ради-
уса R.
22.	В конус, радиус основания которого равен R, а высота Н, вписан цилиндр
наибольшего объема. Найти радиус основания и высоту этого цилиндра.
23.	Из круглого листа жести вырезают сектор и свертывают его в коническую
воронку. Каким должен быть угол сектора, чтобы воронка имела наибольший
объем?
24.	Найти наименьшую площадь боковой поверхности конуса, имеющего
объем V.
25.	На координатной плоскости дана точка /C(3;6). Рассматриваются треуголь-
ники, у которых две вершины симметричны относительно оси Оу и лежат
на дуге параболы у = 4х2, заданной на отрезке [— 1; 1], а точка К является
серединой одной из сторон. Среди этих треугольников выбран тот, который
имеет наибольшую площадь. Найти эту площадь.
Ответы
1. 9 и—7. 2. 2 и-10. 3. 132 и 0. 4. 1 и 5. е-2 и 2-21п2. 6.64
и 0. 7.^ и-38. 8. е5 и —е3. 9. % и 1. 10. е5 и-125е. 11.^,^.
12. 1) Квадрат со стороной \/S; 2) квадрат со стороной y/S. 13. 2R2.
14. 2.	15. -2.	16. ,/Д^.	17. 2х + 4у = 5. 18. a + fc~ ~cd + ^.
у sin а	6
19.	20.	21. 4R. 22. Радиус основания высота 23.	№.
о уЗ	о	о	У о
X 1
7 /	9 \ 3
24. ЗЕ 1^-1 . 25. 4ч/2.
154
Глава XIV. Применение производной к исследованию функций
§5. ПРОИЗВОДНЫЕ ВТОРОГО ПОРЯДКА.
ВЫПУКЛОСТЬ И ТОЧКИ ПЕРЕГИБА
1. Производные второго порядка
Пусть функция /(х) дифференцируема на интервале («;&). Про-
изводную /'(х) этой функции называют первой производной или
производной первого порядка функции /(х).
Если функция /'(%) дифференцируема на интервале (а\Ь), то
ее производную называют второй производной или производной
второго порядка функции /(х) и обозначают /"(х), т. е.
Г(х) = (/'(%))'.
Пример 1. Найти /"(х), если:
О Дх) = 2х4 — Зх2 + 5х + 1; 2) /(x) = sin22x;
3) Дх) = еЛ	4) /(х) = 1п^|.
Д 1) f (х) = 8х3 - 6х + 5, /"(х) = 24х2 - 6.
2)	f'(x) = 4sin2xcos2x = 2sin4x, /"(х) = 8cos4x.
3)	/Дх) = Зх2^3, f"(x) = бхе*3 + 9х4ех3 = Зх(2 + Зх3)ех3
4)	Г(х) = х-±1 •	/"(%) =	А
х—1	(x4-l)z xz — 1	(xz — l)z
Выясним физический смысл второй производной.
Пусть закон движения материальной точки вдоль прямой задается
формулой
где S —координата движущейся материальной точки (гл. XIII, § 1,
п. 1) в момент времени t. Тогда мгновенная скорость движения и(/)
в момент времени t определяется формулой
Скорость характеризует быстроту (темп) изменения координаты со
временем.
Для описания быстроты изменения самой скорости вводят уско-
рение a(t) по формуле
a(t) =
Согласно определению производной второго порядка
т. е. вторая производная функции S(t) по времени есть ускорение.
В этом состоит физический смысл второй производной.
§5. Производные второго порядка
155
В §§ 2-4 было показано, как с помощью первой производной
можно находить промежутки возрастания и убывания функции,
а также точки экстремума.
Рассмотрим свойства функции, которые устанавливаются с по-
мощью второй производной.
2.	Выпуклость функции
На рис. 18-20 изображены графики функций, имеющих на интер-
вале (a;fe) первую и вторую производные. Выясним, в чем состоит
различие в поведении этих функций и какими общими свойствами
они обладают. На рис. 19 изображен график убывающей функции,
а на рис. 18 — возрастающей функции; функция, график которой
представлен на рис. 20, не является монотонной.
Рис. 18
Рис. 19
Рис. 20
Однако все кривые, изображенные на рис. 18-20, обладают общим
свойством: для любой точки е (а; 6) график функции у = /(%)
лежит ниже касательной к этому графику в точке (%o;/(xo)) ПРИ всех
хе(а;Ь) и x^xq. Поэтому функции, графики которых представлены
на этих рисунках, называют выпуклыми вверх.
Сформулируем определение выпуклости вверх (вниз), предпола-
гая, что функция /(%) имеет первую и вторую производные на
интервале (а;&).
Функция /(х) называется выпуклой вверх на интервале (п;д),
если ее производная f(x) — убывающая функция на этом интервале.
Теперь рассмотрим функции, имеющие первую и вторую производ-
ные на интервале (а;£), графики которых изображены на рис. 21-23.
Рис. 21
156
Глава XIV. Применение производной к исследованию функций
Функции на рис. 21-22 монотонны на интервале (а; Ь); первая
возрастает, вторая убывает; на рис. 23 изображена функция, которая
не является монотонной на этом интервале. Однако все кривые —
графики функций (рис. 21-23) обладают общим свойством. Каждая
из этих кривых лежит выше касательной к этой кривой в любой
точке с абсциссой xq этого интервала. Такие функции (и их графики)
называют выпуклыми вниз.
Рис. 24
(а;&), а это означает, что
Установим связь между выпуклостью
функции и второй производной этой
функции. Для этого сначала рассмотрим
поведение первой производной выпуклой
функции (рис. 24).
Так как первая производная равна тан-
генсу угла между осью Ох и касательной
к графику функции, то из рис. 24 видно,
что для выпуклой вверх функции ее
первая производная убывает на интервале
ее вторая производная отрицательна.
Аналогично можно показать, что для выпуклой вниз функции ее
вторая производная положительна.
Справедливо и обратное утверждение: если функция f{x) имеет
на интервале (а; Ь) вторую производную /"(х) и /''(%)< 0, то функция
/(х) выпукла вверх, а если f'(x) > 0, то выпукла вниз.
Интервалы, на которых функция выпукла вверх или вниз,
называют интервалами выпуклости этой функции.
Пример 2. Найти интервалы выпуклости вверх и выпуклости
вниз функции /(х), если:
1)	/(х) = х3;	2) /(x) = sinx; 3) /(x) = arctgx.
Л 1) Так как f"(x) = 6х, то /"(х) < 0 при х < 0 и /"(х) > 0 при х > 0.
Поэтому функция у = х3 выпукла вверх при х<0 и выпукла
вниз при х > 0 (рис. 25).
2)	Так как у = sin х — периодическая функция с периодом 2л
(рис. 26), то будем ее рассматривать на интервале (—л; л)
Если z/ = sinx, то f"(x) = —sinx, откуда следует, что/"(х)>0
при х е (—л; 0) и f(x)<0 при хе(0;л). Поэтому функция
y = f{x) выпукла вниз на интервале (—л;0) и выпукла вверх
на интервале (0;л).
3)	Если /(х) = arctgх, то
1
1 + х2’
Г(х) = -
2х
(1 +х2)2 ’
§5. Производные второго порядка
157
откуда следует, что /"(х) >0
Рис. 27
при х < 0 и f'(x) < 0 при х > 0.
Поэтому функция у — arctgx выпукла вниз при х<0 и выпукла
вверх при х>0 (рис. 27).	▲
3.	Точки перегиба
Точка %о дифференцируемой функции /(х) называется точкой
перегиба этой функции, а точка (xq;/(xq))—точкой перегиба
графика функции /(х), если xq является одновременно концом
интервала выпуклости вверх и концом интервала выпуклости вниз
для функции /(х).
Иначе говоря, в точке перегиба дифференцируемая функция
меняет направление выпуклости.
Например, для функций х3, sinx, arctgx (пример 2, рис. 25-27)
точка хд = 0 является точкой перегиба.
Пусть функция /(х) имеет вторую производную на интервале
(a;Z>) и х€(а;6). Тогда если /"(х) меняет знак при переходе через
точку Xq, то Xq — точка перегиба функции /(х).
Пример 3. Найти точки перегиба функции /(х), если:
1)	/(х) = хе2х\ 2) f(x) = х4 - 6х2 + 5х 4- 4;
з
3) /(х) =х21пх;	4) /(х) =	*
(х — 2)z
Д 1)	f'(x) = е2х+ 2хе2х = е2х(1+ 2х),
f"(x) — 2е2х(1 + 2х) + 2е2х — 4е2х(1 + х).
Так как /"(х) меняет знак при переходе через точку xq = - 1,
то Xq = —1 — точка перегиба функции /(х).
2)	/'(х) = 4х3 - 12х + 5, /"(х) = 12х2 — 12 = 12(х2 - 1).
Функция /"(х) меняет знак при переходе через точки xj = —1
и х2 = 1, которые являются точками перегиба функции /(х).
3)	/(х) = 2х1пх + х, /"(х) = 2 In х + 3.
158	Глава XIV. Применение производной к исследованию функций
Функция /"(х) меняет знак при переходе через точку
Xq —	— корень уравнения 21пх + 3 = 0. Эта точка есть
точка перегиба функции /(х).
г// х _ Зх2(х — 2)2 — 2х3(х - 2) _ х2(х — 6)
1 W	(х-2)3 ’
pf( и _ (Зх2 - 12х)(х - 2)3 - (х3 - 6х2)3(х - 2)2 _	24х
(х-2)6	~ (х - 2)4 ’
Отсюда следует, что х = 0 — точка перегиба функции /(х). ▲
Задачи
1.	Найти /"(х), если:
1)	/(х) = 2х5 + Зх4 + 2х2 + Зх; 2) Ях) = —Ц;	3) Ях) = хе?;
1 4-х2
4)	Дх) = cos2 Зх;	5) Дх) = х 1п(1 + х2);	6) /(х) = —-—г
(х+1)2
2.	Найти интервалы выпуклости вверх и интервалы выпуклости вниз функ-
ции Дх), если:
1)	Дх) = 2х4 — Зх2 + 5х — 4;	2) Дх) = х5 — 10х2 4-4х;	3) Дх)=ех;
4) /W =	5>	о; 6>	=х3 - 6х 1П Х-
х2 4-12	х64-2
3.	Найти точки перегиба функции Дх), если:
1)	Дх) = собх, —тс^х^к;	2) Дх) = х4 — 12х3 4-48х2 4-Зх + 4;
3)	Дх) = х3е-4х;	4) Дх) = е*;	5) Дх) = х2 1пх; 6) Дх) =	;
х2 — 3
7) /(х) =	8) /(х) =
х6 - 1	(х 4-1)2
Ответы
1. 1) /"(х) = 40х3 + 36х2 + 4; 2) /"(х) = У 3) /"(х) = Чх(? (2х2 + 3);
(14-х)
4) Г(х) = —18cos6x; 5) f(x) = t3)i 6) f"(x) =	. 2. 1) Вы-
(1 4" x )	(1 4- X)
пукла вверх на интервале (— выпукла вниз на интервалах (—оо;~
и Q;+oo); 2) выпукла вверх на интервале (—оо;1), выпукла вниз на интервале
(1;4-оо); 3) выпукла вверх на интервале (—оо; — выпукла вниз на интервалах
и (0;4-оо); 4) выпукла вверх на интервалах (—6; 0) и (6;4-оо),
выпукла вниз на интервалах (—оо:— 6) и (0;6); 5) выпукла вверх на интервалах
§6. Построение графиков функций
159
оо; —и (#4; Too), выпукла вниз на интервале у — v^2; v^); 6) выпукла
вверх на интервале (0; 1), выпукла вниз на интервале (1;Тоо). 3. 1) х\——
х2 =	2) X! = 2, х2 = 4; 3) X] = 0, х2 = ЦТ х3 = ЦТ 4) х = Ц
5) х = е“2; 6) х = 0; 7) х = --^2: 8) х =
§6. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
1. Асимптоты
Термин «вертикальная асимптота» был использован в гл. Ill (§ 1,
п. 3) при исследовании дробно-линейной функции
= ax + b ad_bc^Q C^Q_
и cx + d'	~
Если выполнено хотя бы одно из условий
lim /(х) — оо, lim Дх) = оо,
X—>%о — 0	X—*Xq +0
то прямую х = хо называют вертикальной асимптотой графика
функции У = /(х).
Например, прямая х = 0 — вертикальная асимптота графиков
функций У=±> У~ 4р // = 1пх, а прямые х =—1 и х = 2 — вертикальные
асимптоты графика функции
У = (х+1)(х-2) •
Рассмотрим понятие наклонной асимптоты.
Назовем прямую y = kx + b асимптотой (невертикальной асимп-
тотой) графика функции y = f(x) при х—>Тоо, если разность ординат
графиков функции /(х) и прямой у = kx + b стремится к нулю при
х —> Too т. е.
lim (/(х) — (kx + ft)) = 0.	(1)
х—>4-сю
Если k 0, то асимптоту называют наклонной, а если k = 0, то
асимптоту у — Ь называют горизонтальной.
Теорема. Для того чтобы прямая y = kx + b была асимптотой
графика функции у = /(х) при х —> Too, необходимо и достаточно,
чтобы существовали конечные пределы
lim = k,	(2)
х—>4-оо х
lim (f(x) — kx) — ft.	(3)
x—>4-oo
160
Глава XIV. Применение производной к исследованию функций
О 1) Пусть прямая y = kx + b — асимптота графика функции y = f[x)
при х—*+оо. Тогда выполняется условие (1) или равносильное
ему условие
/(х) = kx + /? + «(%), а(х) —> О при х—>+оо. (4)
Разделив обе части равенства (4) на %, получим
/U)
X	X X ’
откуда следует, что существует предел (2). Из равенства (4)
получаем
f[x) — kx = b + а(х), а(х) —> 0 при х —>+оо,
откуда следует, что существует предел (3)
2) Пусть существуют конечные пределы (2) и (3). тогда
/(х) — [kx + b) = а(х), где а(х) —> 0 при х —> +оо,
т. е. выполняется условие (4) и равносильное ему условие (1).
Это означает, что прямая у = kx + b — асимптота графика
функции у — f[x).	•
Аналогично вводится понятие асимптоты при х —> —оо. В этом
случае должно выполняться условие
lim (/(%)- [kx + bYj = 0.	(5)
х—>—оо
Если выполняются условия (1) и (5), т. е.
lim (/(%) - [kx + ft)) = О,
то говорят, что прямая у = kx + b — асимптота графика функции
у — f[x) при х —> оо.
Пример 1. Найти асимптоты графика функции у = /(х) при
х —> +оо и при х —> —оо, если:
о /М = ттт; 2) /М = У*2 + 4х-5;
q	ч
з) =	4) Ях) =
xz + х + 1	(х — 2)z
Л 1) Так как
Дх) = 2(х~1) + 5 = 2 + -Ц,
v 7 х — Ь	х — Г
и -0 при X оо, то прямая у = 2 — асимптота графика
функции /(х) при х —> +оо и при х —> —оо.
§6. Построение графиков функций
161
2)	Найдем сначала асимптоту при х —> 4-оо.
Если х > 0, то
Vx2 = %, \/х2 + 4х — 5 = х л /1 + - — Л,
V х х2
/W = . /ц-1 - А
х \ X X2
и по формуле (2) находим
k = lim й^ = 1.
х—*4-оо х
Тогда
х) — kx = \/х2 + 4х — 5 — х — —г_-х~ =—
Vх2 + 4х — 5 4- х
откуда следует, что
b = lim (Дх) — kx) = 2,
и поэтому прямая у = х + 2 — асимптота графика функции Дх)
при х 4-оо.
Аналогично находим асимптоту при х —> —оо, пользуясь
тем, что
х/х2 == —х при х < О,
х/х2 4- 4х - 5 = -хл/1 4- - -
V х х2
откуда следует, что
k — lim — —1,
х—>—со х
f(x) + х = а/х2 + 4х — 5 + х —	= ~ 5—— =
\/х2 4- 4х 4- 5 — х
4х — 5
Поэтому
b = lim (Дх) — kx) = -2,
х^—оо
6—3022
162
Глава XIV. Применение производной к исследованию функций
Рис. 28
а прямая у — —х — 2 является асимптотой графика функции
у — Vx2 + 4х — 5 при х —> —оо.
Замечание Нахождение асимптот при х —> 4-оо и при х —> — оо
можно упростить, используя равенство
- |х + 2| = Ух2 + 4х-5- |х + 2| =	(6)
ух2 + 4х + 5 + |х + 2|
откуда следует, что
/(х) — |х 4- 2| —* О при х —> оо,
а прямые у = х 4- 2 и у = — х — 2 являются асимптотами графика функции
у = \/х2 4- 4х — 5 при х —> 4-оо и х —> —оо соответственно.
Из равенства (6) следует, что график функции у = f(x)
лежит ниже асимптот (рис. 28).
3) Так как
то прямая у = х - 1 — асимптота графика функции y = f(x) при
х —> 4-оо и х —> —оо.
4) Для нахождения асимптот можно вычислить пределы (2) и (3).
Мы, однако, применим другой подход и найдем асимптоты,
разделив многочлен х3 на многочлен (х —2)2.
Используя равенство
х3 = [(х - 2) + 2]3
и формулу куба суммы, получаем
х3 = (х - 2)3 + 6(х - 2)2 + 12(х - 2) + 8,
откуда
Лх)=х-2 + 6 + -^-+	8 т.е.
х — 2	(х — 2)£
/W = x + 4+^ + ^=x + 4 + l^>.	(7)
§6. Построение графиков функций
163
Следовательно, прямая у = х + 4 — асимптота графика функции
у = /(х) при х —> -Too и при х —> —оо.
Из равенства (7) следует, что при х < график функции
о
z/ = /(x) лежит ниже асимптоты, а при х> | — выше асимптоты,
о
2.	Графики функций
При построении графика функции y = f(x) можно придерживаться
следующего плана.
1)	Найти область определения функции. Выяснить, является ли
функция четной (нечетной), периодической
2)	Найти точки пересечения графика с осями координат и про-
межутки, на которых /(х) > 0 и /(х) < 0.
3)	Найти асимптоты графика функции.
4)	Вычислить /'(х), найти экстремумы и промежутки возрастания
(убывания) функции.
5)	Вычислить /"(х), найти точки перегиба и промежутки выпук-
лости вверх (вниз) функции.
6)	Нарисовать график функции.
Пример 2. Построить график функции
А Так как
х2 — 4х + 3 = (х — 1)(х - 3),
то
2(х-2)
У	(х—1)(х —3)’
Функция определена при всех х G I, кроме х = 1 и х = 3.
График пересекает ось Ох в точке (2;0), а ось Оу — в точке
(О;— Используя метод интервалов, получаем:
у > 0 при 1 < х < 2 и при х > 3,
у < 0 при х < 1 и при 2 < х < 3.
Прямые х — 1 и х = 3 — вертикальные асимптоты графика функции,
а прямая у = 0 — асимптота при х —> оо.
Найдем f\x), записав /(х) в виде
Я*) = гл + гл-
164
Глава XIV. Применение производной к исследованию функций
Отсюда получаем
и поэтому/'(%)< 0 при xeR, х^1 их/3. Следовательно, y = f(x) —
убывающая функция на промежутках х < 1, 1<х<3 и х>3.
Найдем вторую производную:
Решим неравенство //7(х) > 0. Это неравенство при х^1 и х 3
равносильно каждому из неравенств
1	\	1	1^1	х-2 q
(х-1)3	(х-З)3’	х~1	х-3’ (х —1)(х —3)
Решив полученное неравенство методом интервалов, находим, что
множество решений этого неравенства — совокупность промежутков
1<х<2 и х > 3.
Аналогично получаем, что множество решений неравенства
/"(х) < 0 — совокупность промежутков х < 1 и 2<х<3.
Следовательно, функция /(х) выпукла вверх на промежутках х< 1,
2 < х < 3 и выпукла вниз на промежутках 1 < х < 2, х > 3.
В точках х = 1, х = 2 и х = 3 меняется направление выпуклости
функции. Но при х=1 и х = 3 функция /(х) не определена, поэтому
х = 2 — единственная точка перегиба этой функции.
Используя результат исследования, строим график функции
(рис. 29).	А
Пример 3. Построить график функции
X3
А Функция определена при х ф 2; у > 0 при х > 0 и у < 0 при х < 0,
график проходит через точку (0; 0), а прямая х = 2 — вертикальная
асимптота графика этой функции.
Прямая //=х-Т4 является наклонной асимптотой графика функции
при х —> оо (пример 1(4)).
Найдем yf и у". Имеем:
/ _ Зх2(х — 2)2 — 2х3(х — 2) _ х2(х — 6)
У ~	(х-2)4	(х - 2)3 ’
Так как у1 > 0 на промежутках х<0, 0<х<2 и х > 6, a у' <0
при 2 < х < 6, то функция возрастает на промежутках х < 2 и х > 6
и убывает при 2 < х < 6.
§6. Построение графиков функций
165
При переходе через точку х = 6 производная меняет знак с минуса
на плюс. Поэтому х = 6 — точка минимума функции и z/(6) = у.
Находим вторую производную:
// = (Зх2 - 12х)(х - 2)3 - (х3 - 6х2)3(х - 2)2 =	24х
У	(х - 2)6	(х - 2)4 ’
При х = 0 вторая производная меняет знак, следовательно, х = 0 —
точка перегиба функции.
Используя полученные результаты, строим график функции
(рис. 30).	▲
Задачи
1. Найти асимптоты графика функции г/ = /(х), если:
D	2) f(x) = \/х2—4х—12;	3) /(х) =	%3
4) f(x) =	5) /(х) =	6) /(х) =
xz — 1	3xz - 5	1 - хч
2. Построить график функции Дх), если:
1) Дх)=х+^	2) /(х)=х-?;	3) /(х) = ^±^; 4) /(х) = -^;
X	х	(x-l)Z	(х-1)°
5) Л*) = ПГ7; 6) f(x) = ^g; 7) f(x) = ^g;	8) f(x) = ^-.
xz-l	(x-2)z	(x — 6)z	x°-l
Ответы
1	2
1. I) x = —-,r/ = -;2) y = x — 2 при x—>+oo, y — 2 — x при x—»— oo; 3) ^ = x+l;
О	о
4) x = -1, x = 1, у = x — 1; 5) x = х = у = |х - 2; 6) х = -1,
х = 1, у — —х.	2. 1) Функция нечетная, определена при х 0; график не
166
Глава XIV. Применение производной к исследованию функций
пересекает координатные оси; прямые х = 0 и у = х — ее асимптоты; х = — 2 —
точка максимума, у{—2) = — 4; х = 2 —точка минимума, у(2) = 4; функция
возрастает на промежутках х < —2 и х > 2, убывает при —2 < х < 0 и при
О < х < 2; при х < 0 функция выпукла вверх, а при х > 0 функция выпукла
вниз. 2) Функция нечетная, определена при х / 0; (—3;0) и (3;0) —точки
пересечения графика с осью Ох; экстремумов нет; х = 0 и у — х — асимптоты
/ _____________________________________ 1	\	/	__ 1	\
3) Функция определена при х?М; I —-----;0 1, (	—;0) и (0;—1)—точки
пересечения графика с осями координат; асимптоты х = 1 и у=Л\ х=^—точка
минимума, у Q) =— |; (0; —1) — точка перегиба графика функции. 4) Функция
определена при х/1; пересекает оси координат в точке (0;0); х=1 и // = 0 —
асимптоты; х = 0 —точка максимума, г/(0) =0; х = —2 — точка минимума, у(—2) =
80	г~	г~
= — — \ xj = —2—v3 и Х2 = —24-v3 — точки перегиба. 5) Функция нечетная,
определена при х0±1; пересекает координатные оси в точке (0;0); асимптоты
х — —1, х = 1, у — х\ х = \/3 — точка минимума, г/(л/3) = х — —\/3 — точка
максимума, z/(—\/3) = —^^; (0;0)— точка перегиба. 6) Функция определена
при х 2; (1;0) и	точки пересечения графика с координатными
27
осями; х = 2 и у = х + 1 —асимптоты; х = 4 —точка минимума, //(4) = —;
(1;0) —точка перегиба графика функции. 7) Функция определена при х / 6;
(2;0) и (О;—I)— точки пересечения графика с координатными осями; х = 6
и у = х 4- 6 — асимптоты;
, = (х —2)2(х —14)	„ = 96(х —2).
У (х - 6)2	’ У (х - 6)4 ’
х = 14 — точка минимума, z/(14) = 27; (2; 0) —точка перегиба графика функ-
ции. 8) Функция определена при х Ф 1; (0; 0) — точка пересечения графика
с координатными осями; х = 1 и у = Зх — асимптоты;
/ Зх3(х3 - 4)
У (х3 - I)2
и _ 18х2(х3 4-2)
У ~ (х3-1)2 ’
х = 0 — точка максимума, г/(0) = 0; x = v^4 —точка минимума, у(^4) = 4-^4;
(—	— 2-^2) — точка перегиба графика функции.
Глава XV
ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ
§ 1. ПЕРВООБРАЗНАЯ ФУНКЦИИ
1.	Основные понятия
Действие, обратное дифференцированию, называется интегриро-
ванием (от лат. integrare — восстанавливать). Его цель состоит в
том, чтобы найти все такие функции F(x), производная каждой из
которых равна данной функции Дх).
Определение. Пусть функции Дх) и F(x) определены на
интервале (а; Ь), Если функция /Дх) имеет производную на интервале
(а; Ь) и если для всех х е (а; 6) выполняется равенство
^(х) = /(%),
то F(x) называют первообразной функции Дх) на интервале (a; 6).
Замечание. Понятие первообразной можно ввести и для других промежут-
ков (полуинтервала — конечного или бесконечного, отрезка). Дадим определение
первообразной на отрезке.
Если функции /(х) и F(x) определены на отрезке [а; 6], причем
функция F(x) дифференцируема на интервале (a; 6), непрерывна на
отрезке [а; Ь] и для всех хе (а; 6) выполняется равенство Д'(х) = Дх),
то функцию F(x) назовем первообразной функции f(x) на отрезке
[а; 6].
Пример 1. Найти какую-либо первообразную функции
Дх) = 3 cos 2х.
А Функция /Дх) = | sin 2х является первообразной функции
/(x) = 3cos2x на всей числовой прямой, так как для любого хбК
F'(x)=(|sin2x) — | (sin2x)' — 3cos2x = Дх). ▲
Нетрудно заметить, что первообразная | sin 2х не является
единственной первообразной функции f(x) = 3cos2x. Вообще, любая
функция вида -sin2x + C, где С е R — произвольная постоянная
является первообразной для функции 3cos2x.
Задача интегрирования состоит в нахождении всех первообразных
функции Дх). Если при нахождении первообразной функции Дх) не
168
Глава XV. Первообразная и интеграл
указывается промежуток, на котором она задана, то считается, что
первообразная находится на всей области определения функции /(%).
Докажем теорему, выражающую основное свойство первообраз-
ных.
Теорема (основное свойство первообразных). 'Если F\(x)
и F2(x) — dee первообразные функции f(x) на интервале (а\ &),
то для всех х С (а; Ь) выполняется равенство
F1(x)-F2(x) = C,	(1)
где С — постоянная.
О Обозначим Ф(х) = F\(x) — F2(x). Так как по определению перво-
образной для всех х е (а\ Ь) выполняются равенства
то функция Ф(х) дифференцируема на интервале (а; Ь) и для всех
х е (а; Ь) выполняется равенство
Ф7(х) = 0.
Докажем, что в этом случае Ф(х) = С для всех хе (а; Ь). Для этого
возьмем произвольные х\,х2е(а-, Ь), гд$х\<х2. По теореме Лагранжа
найдется такое c€(xi; х2), что будет выполняться равенство
Ф(х2) - Ф(*1) = Ф'(с)(х2 - *1).
Но по условию Ф'(с) = 0. Следовательно, Ф(х]):=Ф(х2), т. е. функция
Ф(х) постоянна, и значит, справедливо равенство (1).	•
Таким образом, все первообразные функции f(x) имеют вид
F(x) + С, где F(x) — одна из первообразных. Поэтому задача о на-
хождении всех первообразных решается нахождением какой-нибудь
одной из них, из которой любая другая первообразная получается
прибавлением некоторой постоянной.
Выражение F(x) + С, где С Е R - произвольная постоянная,
называют общим видом первообразных функции /(%).
Пример 2. Найти все первообразные функ-
х^——ции /(х) — ^3-
4
Х"*^ О	—х' А Так как (%4)' — 4х3, то ^- — °Дна из пеР"
X^L —вообразных. Следовательно, все первообразные
*-----	х4
Рис. 1 имеют вид F(x) = — + С.	▲
Геометрический смысл основного свойства первообразных со-
стоит в том, что графики любых двух первообразных функции f(x)
получаются друг из друга параллельным переносом вдоль оси Оу
(рис. 1).
§1. Первообразная функции
169
Пример 3. Для функции f(x)=x2 найти первообразную, график
которой проходит через точку (1;2).
Л Общий вид первообразных для функции /(%) = х2 имеет вид
/'(х) = у+ С. Найдем постоянную С из условия 7^(1) = 2: из равенства
2 -F(l) = — + С получаем С = Следовательно, F(x) = — + ^ А
О	О	О о
Таблица 1
Таблица первообразных
Функция /(х)	Общий вид первообразных F(x)
k G К	kx + C
Хр (рек,	1)	~ + c p + 1
1 (х/0)	In |x| + C
COSX	sinx + C
sinx	— cosx + C
COS2X	tg x + C
1 . 9 sirr X	ctg x 4- C
<?x	ex + C
a*	„X ±- + c Ina
1 \/l — X2	arcsinx 4- C
1 x/1 — x2	arccosx 4- C
1 1 +x2	arctg x 4- C
1 +x2	arcctg x 4- C
Для каждой строки этой таблицы равенство F'(x) = /(%) выпол-
няется на любом промежутке, на котором имеют смысл ее левая
и правая части.
Пример 4. Доказать, что функция In |х| — первообразная функ-
ции
170
Глава XV. Первообразная и интеграл
А Функции 1п|х| и определены при всех хе(-оо; 0)и(0; +оо).
При х<0 имеем 1п|х| — 1п(—х) и (1п|х|)/ = (1п(—х)), = -^(—x)z = i.
Следовательно, на этом промежутке функция 1п|х| = 1п(—%) явля-
ется первообразной функции При х>0 функция In |х| = In х
также является первообразной функции р так как In |х| = In х
и (1п|х|)' = (1пх)' = Г	▲
2.	Простейшие правила нахождения первообразных
1.	Если F(x) есть первообразная функции /(х), a G(x) — первооб-
разная функции g(x), то F(x) + G(x) есть первообразная для
f(x)+g(x).
2.	Если F(x) есть первообразная для функции /(х), ай — постоянная,
то йР(х) есть первообразная функции й/(х).
3.	Если F(x) есть первообразная функции /(х), a k и Ь — постоянные,
причем й^О, то ^(йх + й) есть первообразная функции /(йх + й).
Пример 5. Найти все первообразные функции /(х) = \/Зх — 5.
А Первообразная функции /(х) = х^ имеет вид F(x) — |xL Со-
О
гласно правилу 3 первообразную функции /(Зх — 5) = \/Зх — 5
можно получить, умножив F(x) на | и заменив х на Зх - 5.
Отсюда следует, что одной из первообразных данной функции будет
|F(3x —5) = | • |(3х —5)2, а все первообразные задаются формулой
О	О О
|(Зх-5)1+С.	▲
Пример 6. Найти все первообразные функции /(х) = sin 5х • cos Зх.
А Заметим, что (гл. V, § 9, ф-ла (3))
/(х) — sin 5х • cos Зх = sin.8-J^sin2x. — 1 sin 8х + | sin 2х.
Все первообразные функции вида й(х) = sin йх при й 0 имеют
вид Я(х) = — |со5Йх + С. Следовательно, функция F[ (х) = — cos 8х
является одной из первообразных функции Д(х) = | sin 8х, а функ-
ция F2W —“|c°s2x является одной из первообразных функции
/2(x) = |sin2x. Тогда Л(*)+^2(х) — одна из первообразных функции
§1. Первообразная функции
171
/W — fi(x)+/2(x)i а все первообразные функции, данной в условии
задачи, имеют вид
F(x) = — -Г cos8x - | cos 2x4- С.	▲
' '	16	4
Пример 7. Найти все первообразные функции
f(Y\ _ х3 + 2х2 — 6х + 2
Д Выделяя у дроби -	целую часть, получим
х3 + 2х2 - 6х + 2 _ д , 9х + 38
(х + З)2	х2 + 6х + 9
Числитель полученной дроби представим в виде 9x4-38 — 9(х+3)4-11.
Отсюда
/(х) = х - 4 4-
9(х4-3) + 11
~ (хЧ-3)2
_ 11
(Х4-3)2’
9
х + 3
Используя таблицу первообразных и правила нахождения первооб-
разных, получаем
2
F(x) = i--4x + 9ln|x + 3|-4k+C-	А
х	х “г* о
1,
Рассмотрим функцию signx = О,
I -1,
если х > О,
если х — О,
если х < 0.
Заметим, что xsignx = |x|. Кроме того, так как производная
функции |х| равна 1 при х>0 и —1 при х < 0, то |х|' = signx при
х/0. При х = 0 производная функции |х| не существует.
Далее, (|х|3) = 3x2signx = Зх|х| уже при всех х, включая х = 0.
*Пример 8. Найти все первообразные функции:
1) /(х) = x2signх; 2) /(х) = |sinx|.
А 1) Так как /(х) = х2 при х > 0, то /?(х) = ?- + С при х > 0.
О
Соответственно, /(х) = —х2 при х<0 и F(x) =—у+ С при х<0.
Следовательно, все первообразные функции будут задаваться
формулой
3	2
F(x) = sign х 4- С =	• х sign х 4- С = |х2|х| 4- С,
о	и	<5
справедливой и при х = 0.
172
Глава XV. Первообразная и интеграл
2) В данном случае /(х) = | sinх| = sinx • sign (sinx); так как
(—cos х/= sinx, то первообразной для /(х) будет функция
f'(x) = — cosx • sign (sinx) + С = — ctg x | sinx| + C. A*
Задачи
1. Найти множество всех первообразных функции Дх):
1) Дх)=х —cosx; 2) Дх) — Зх2------;	3) /(х) = 2х+-, х > 0;
cos2 х	х
4) Дх) = 2х — е~х\ 5) Дх) — 4х3 — 2х2;	6) Дх) = sin 2х — е5х
2. Найти первообразную функции Дх), график которой проходит через точку
Uo; УоУ
1) Дх) = 2х - 6, xq — 2, уо — —3;	2) Дх) = 8х3 — 5, xq = 1, уо = 4;
3) Дх) = 4х3 — 9х2 + 4х — 5, xq = 2, t/0 = —8;
4) Дх) = —, х0 = у0 = 4;	5) Дх) = (х - 1)-2,х0 = 2, у0 = 1;
9 Г	Z
cos2 2
6) Дх) = Юх^/х, х0 = 1, у0 = 5;	7) Дх) =	^~3, х0 = -1, у0 - 5.
3.	Найти первообразную функции Дх), график которой проходит через точку
М, если:
1)	Дх) = sinx + 5x4, 7И = (0; 3);	2) Дх) = Зх2 - 2 cosx; М = (^; -2) ;
3)	Дх) =sinx — М = (^; — е-?) ;
4)	Дх) = 2х2 - Зу/х + 4, М = (4; -3);
5)	Дх) = Зх2 + 3(3х + 1)“°>5, М = (5; 130);	6) Дх) = ех - х2, М = (1; е).
4.	Доказать, что функция F(x) = 2009 + In х + 4\/2х + 1 является одной из
2jc + 1 I 4jc \/2jc i"" 1
первообразных функции Дх) =-------—---------- на промежутке (0; +оо).
х(2/Х Ч* 1)
5.	Найти множество всех первообразных функции Дх):
г/ \	8х3 —6х2 + 4х —5	z
1)	Дх) =-------------- на промежутке (—оо; 0);
2) Дх) = Зх2 — 2х + 3 — д/х; 3) Дх) = Зх-4+—1—+ •-------!— 
х	Зх —4	(Зх-4)2
и \ f ( А — Зх^ — 12х3 + 12х2 + х — 4
}	~	(Г^)2	’
6. Найти ту первообразную функции /(х) = е2х —cosx, график которой проходит
через начало координат.
7. Для функции Дх) = 2х — 6 найти ту первообразную, график которой
пересекает ось Ох в точке с абсциссой 4.
§2. Неопределенный интеграл
173
8.	Найти первообразную функции Дх) = Зх2 — 4х 4- 5 — i, график которой
проходит через точку пересечения прямых у — 2х 4- 1 и у — — х + 4.
9.	График первообразной для функции Дх) — 6х + 5 пересекает ось абсцисс
в точках, расстояние между которыми равно 3. В какой точке график
первообразной пересекает ось ординат?
10.	Для функции Дх) = sin2xsin6x найти нули первообразной, если известно,
7 л:
что один из них равен — —.
11.	Найти ту первообразную функции Дх) — 2х 4- 4, график которой касается
прямой у = 6x4- 3.
12.	Для функции Дх) = 5(х 4- 3) найти все первообразные, графики которых
имеют с осью абсцисс единственную общую точку.
13.	Доказать, что функция F(x) = (1 — х2)sinx2 — cosx2 является одной из
первообразных функции Дх) = 2(х — х3) cosx2. Найти ту первообразную
функции Дх), наибольшее значение которой на отрезке [0; 3] равно О
14.	Найти все первообразные функции:
1)/(х)=|х|3;	2) /(х)=х3|х|.
Ответы
1.	1) — sinx 4- С; 2) х3 — 2 tg х 4- С; 3) х2 4- 1пх 4- С; 4) х2 4- е х 4- С;
5) х4 - |х3 + С: 6) —со-®2^ -	+ С. 2. 1) х2 - 6х + 5; 2) 2х4 - 5х + 7;
3) х4 - Зх3 + 2х2 - 5х + 2; 4) 6 tg - 2; 5)	+ 2; 6) 4x2 + 1;
7) 2х2 — 3 1п(—х) + 3.	3. 1) —cosx + х5 + 4; 2) х3 — 2sinx — у;
3) — cosx + 2е-2 — Зе-?; 4) |х3 - 2х^/х + 4х -	5) х3 + 2(3х + I)0-5 - 3;
6) ex-4 + i 5. 1) ix3-^x2 + 2x-51n(-x) + C;2) х3-х2 + Зх-^х^+С;
3) {3x^4f + ln|3x —4| _ -1	+ с. 4) х3 + In |х - 2| + -^2 + С.
6. у- — sinx — у 7. х2 — 6х + 8.	8. х3 — 2х2 + 5х — Inx — 1.
9. (0; -у) .	10. n € Z. 11. х2 + 4х + 4. 12. 2,5х2 + 15х + 22,5.
13. (1-х2) sinx2-cosx2-у + 1	14. 1) f(x) = ^ + С;2) /(х) = ^+С.
§2. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Совокупность всех первообразных функции /(х) на некотором
промежутке / называют неопределенным интегралом от функции
f(x) на этом промежутке, обозначают символом \f{x)dx и пишут
f{x) dx — F{x) + С.
(1)
174
Глава XV. Первообразная и интеграл
Здесь F(x) — какая-нибудь из первообразных функции /(х) на проме-
жутке /, С — произвольная постоянная. В равенстве (1) /(х) называют
подынтегральной функцией, выражение /(х) dx — подынтеграль-
ным выражением, переменную х — переменной интегрирования,
а слагаемое С —постоянной интегрирования.
Из определения неопределенного интеграла следует основное
равенство	f
( f(x)dx\ = /(х),
т. е. производная любой первообразной подынтегральной функции
равна этой функции.
1.	Свойства неопределенного интеграла
Свойство I.
d I /(х) dx
= /(х) dx.
(2)
О Из равенства (1) следует, что
d ( f (х) dx I = d (F(x) + C) — dF(x) = F'(x) dx = /(x) dx,
так как dC = 0.
Свойство 2.
dF(x) = F(x) + C.
(3)
О Равенство (3) следует из равенств (1) и (2).
Свойство 3. Если функции /(х) и g(x) имеют на некотором
промежутке первообразные, то для любых а е R, /3 G R функция
ft(x) = af(x)+/3g(x) также имеет первообразную на этом промежутке,
причем
(а/(х)+/3g(x))dx = a f/(x)dx + p g(x)dx. (4)
Свойство 3 называют свойством линейности неопределенного ин-
теграла: интеграл от линейной комбинации функций равен соот-
ветствующей линейной комбинации интегралов от рассматриваемых
функций.
Из свойства 3 получаем, что:
1)	интеграл от суммы функций равен сумме интегралов слагае-
мых,
(Дх) +£W)	= /(x)dx+ g(x)dx; (5)
§2. Неопределенный интеграл
175
2)	постоянный множитель можно выносить за знак интеграла, т. е.
kf(x) dx — k /(х) dx, k 7^ 0.	(6)
Пример 1. Найти:
1) J (5х + 3 sin х) dx; 2) J sin(2x + 3)dx;
3)	J ^-2cosx+dx; *4) Jchxdx;	5) Jshxdx.*
A 1) Используя формулы (5), (6) и таблицу первообразных, полу-
чаем
(5х + 3 sin х) dx = 5xdx + 3sinxdx =
xdx + 3
5 9
sin xdx = -x
— 3 cos x + C.
2) Так как функция —cosx является одной из первообразных
функции sinx, то по правилам нахождения первообразных
| cos(2x + 3)) = sin(2x + 3). Следовательно,
sin(2x + 3)dx = — | cos(2x + 3) + C.
3) Так как cosx = (sinx)', -J 2 = (arctgx)', to
(—2cosx + —dx = —2 I cosxdx+ 2
J \	1 + x2 /	J	J 1 + x2
= —2 sinx + 2 arctgx T C.
*4) Так как chx = —, to
ch x dx =
ex + e x
~~T~
dx =
| exdx + 1 e Xdx —	~	+ C — sh x + C.
6х — e~x
5) Так как shx = —-—, то
sh x dx = -——dx =
1 6х dx — | e Xdx = у 4-	4- C = chx + C. A*
176
Глава XV. Первообразная и интеграл
2. Методы вычисления неопределенных интегралов
Непосредственное интегрирование. Этот метод вычисления
неопределенных интегралов заключается в непосредственном исполь-
зовании таблицы первообразных и правил вычисления первообраз-
ных, поскольку из всякой формулы dF(x)=f(x)dx дифференциаль-
ного исчисления и свойства (2) неопределенного интеграла следует
соответствующая формула интегрального исчисления
/(х) dx = F(x) + С.
(7)
Пример 2. Вычислить интеграл
А Имеем
Значит,
х dx — 2 dx +
2
1 dx — 2x + In Ix| + C.
x 2	11
Замечание. Иногда искомый интеграл путем преобразования подынте-
гральной функции удается свести к уже известным. В частности, для нахождения
интегралов от функций вида sinmxcosnx, cos/nxcosnx и sin/пх sin ях удобно
преобразовать произведение тригонометрических функций в сумму.
Пример 3. Найти:
dx .
1) sin2xdx;
2) sin2xcos3xdx; *3)
J	J ch2x
dx *
sh2 x
J	J2 J2 J2 24
2) Так как sin2xcos3x = i (sin5x — sinx), to
sin 2x cos 3xdx = ±
sin 5x dx -
sin x dx =
( — | cos5x) — 5 (— cosx) + C =
\ O	/ z
= | cos x — cos 5x + C.
*3) Так как thx = a (shx)' = chx, (chx)' = shx
2	2
и (th xY = -h x ~	, то, используя формулу ch2x —sh2x = l,
chzx
§2. Неопределенный интеграл
L77
получаем (thx)' = —. Следовательно,
ctrx
4)
Аналогично
dx
sh2x
dx
ch2x
(th x)fdx = thx + C.
(cthx)'dx= — cthx+C.
предыдущему
A*
Следующие методы позволят свести искомый интеграл к уже
известным. Это поможет расширить множество функций, интегралы
от которых выражаются через элементарные функции
Метод замены переменной (метод подстановки). В основе
этого метода лежит формула дифференцирования сложной функ-
ции. Пусть функция t — <р(х) определена и дифференцируема на
промежутке I и пусть промежуток — (р(Г) — множество значений
функции ср на /.
Если функция (7(f) определена и дифференцируема на проме-
жутке 7i, причем
=	(8)
то на промежутке I определена и дифференцируема сложная функция
F(x) = U(cp(x)) и
Г(х) = (£%(х)))' = и (<р(х)) /(х).	(9)
Из равенств (8) и (9) следует, что если (/(/) —первообразная для
функции и(0, то (7(<р(х)) — первообразная для функции w(<p(x) )</(%).
Отсюда следует, что если
	J u(t)dt =	+ С	(10)
TO	p	u (<p(x)) <p'(x) dx = U (^(x)) + C,	(H)
или	u (<p(x)) d<p(x) = U (<p(x)) + C.	(12)
Формулу (12) (или формулу (11)) называют формулой интегриро-
вания методом замены переменной. Она получается из формулы
(10), если вместо t подставить дифференцируемую функцию t=(.p(x).
Замечание. Формула (12) дает возможность найти интеграл J/(%)dx,
если функция f(x) представляется в виде f(x) = и (<р(х)) и если известна
первообразная функции u(t), т. е. известен интеграл (10).
Пример 4. Вычислить интеграл:
1)	J esinx cosxdx] 2) J xcosx2dx; 3)
dx
2 + y/x'
178
Глава XV. Первообразная и интеграл
А 1) Имеем
esinxcosxdx = esinx (sinx)/dx =
_ । eSin Xrf sin x __ et^ = et C — gSin X _]_ Q
Здесь произведена замена / = sinx.
2)	Имеем
xcosx2dx =
cos x2d(x2) =
cos t dt= | sin t+ C= | sinx2 + C.
Здесь произведена замена t — x2.
3)	Пусть t = y/x, тогда x = t2 и dx = 2tdt, Отсюда
' dx	2tdt _ a f 2 4-^ — 2
2 + \/x	2 4" t J 2 4- t
(1 - 2 4 dt = 2 | dt - 4
\	2 + tJ J
— 2/ — 4 In [2 + /| + C — 2\fx — 4 ln(2 4- \/x) 4- C.
Формулу (11) иначе можно назвать формулой подведения под
знак дифференциала, так как J и (<р(х)) <f>'(x) dx — J и (<р(х)) dcp(x).
При использовании метода подстановки полезно помнить равен-
fx2\
ства, связанные с дифференциалами. Так, например, xdx — d{ —
cosxdx = d(sinx), sinxdx = — d(cosx), ~=d\x\x при x>0, ^ — 2dy/x,
exdx = dex и т. д.
Отметим важные частные случаи формулы (12).
а)	Пусть F(x) — первообразная функции /(х), т. е. справедливо
равенство J* /(х) dx = f’(x) 4- С.
Тогда
/(ах 4- b)dx = ^(ах + Ь) + С, а^О.
Здесь <р(х) = ax + b, f(ax 4- b)dx =	+ b)d(ax 4- b).
б)	Используя равенство у = In |/| 4- С, получаем
(13)
У	= 1п |л?(х)| 4-С, если <р(х)	0.	(14)
<?>(Х) J (р(х)	ITK/I	Т\7/
§2. Неопределенный интеграл
179
в)	Так как J tadt —	+ С, а / —1, t > 0, то
<ра(х)</(х) dx = [ <ра(х) dcp^x) =	+ С, (15)
где а / -1, (р(х) > О.
Приведем примеры применения формул (13)—(15).
Пример 5. Вычислить интеграл:
1) J (5х + З)8 dx-
2)
dx
(х + а)А
xdx .
x2 + a ’
5) f ctgxdx;
6) -/ где а > 0;
J Vfl — *
7) 2rix ,, где a 0;
J a£ + xz
8)	где а/0.
J cr — xz
A 1) J(5x + 3)8Jx = | J (5x + 3)8 (5x + 3) = 1 <5x + 3Л + C =
_ (5x + 3)9 i
2)
3)
4)
5)
6)
7)
8)
dx_____
(x + a)*
xdx _
x2 + a 2
xdx
'ln|x + a| + C, k = l,
‘	+ C, k^i.
’^±^ = Ип|х2 + а| + С.
J x2 + a
d(x? + a) _ ,/7 i.„ i r
. 2\/x2 + a
Г ctgx dx = [ ^^-dx — rf(sin x) = In | sin x| + C
J	J sinx J sinx
In |x — a|
2^
In |x + a|
2a
180
Глава XV. Первообразная и интеграл
Пример 6. Доказать формулу
-7—— - = In |х + \/а2 +х2| + С, а ф 0.
J v с2 + х2
Д Пусть х + \/а2 + х2 = £(х). Тогда
di — tf(x) dx —
откуда -  dx-— = Поэтому
v^2 4- х2 К*)	у
dx
у/о2 + х2
= In И(х)I + С - In |х + \42 + х2| + С. А
Как показывает следующий пример, иногда для вычисления
интеграла J/(x) dx бывает удобнее положить х = cp(t), где (p(t) —
дифференцируемая функция, имеющая обратную функцию /=^(х).
Вычислив полученный интеграл по t, в найденном результате нужно
заменить t на /=<^(х).
Пример 7. Вычислить интеграл J \/a2 — x2dx, а > 0.
Д Подынтегральная функция определена на отрезке [—а; а]. По-
ложим х — (p(f) = а-sin /, t е	. Тогда t — ср(х) = arcsin и
подынтегральная функция примет вид \J а2 — x2 — yja2 cos2 t — a cos
так как t е ^], а > 0. При этом dx = cpf (t)dt = a cos tdt.
Следовательно,
V a2 — x2dx = a cos t a cos t dt =
(1 + cos2t)dt =
Так как
sin/=^, cos^A/l-4-
a	V a2 a
TO	_____
~ sin 2t = sin t cos t = xy^a ~ x .
a2
Поэтому
\/a2 — x2dx =	arcsin - + —+ C.
2 a 2
§2. Неопределенный интеграл
181
Используя таблицу первообразных (табл. 1), определение неопре-
деленного интеграла и интегралы, найденные в примерах, составим
таблицу основных интегралов (табл. 2).
Таблица 2
va4-l 1. Jxa6/x=^-y4-C (aeR, a/-l)		2	у = ln|x| + C
3. [axdx——+C J	In a		4. Jexdx — ex 4-C	
5. J cosxdx = sinx4-C		6. Jsinxdx = — cosx4-C	
7.	-4-=tgx+C COSZ X	8.	-^- = -ctgx + C sinz x
9. Jchxdx = shx4-C		10. J sh x dx = ch x 4- C	
11 c	Г dx _ arcsin X + c \ x/a2 —x2	a z>0	12 c	[^^l.arctgi+C, | a2 + x2 a	a Z0O
4 c	~2^4 = ?-'ln	+C> | x2 - a2 2a	x 4- a z/0	14. i	1	 = In |x + \/x2 + a| + C. 1 vx24-a z/0
При вычислении интегралов вида
fx+P—dx и [ -rax + P =dx, где аа ф О,
t + h + c J у/ах2 + bx + c
полезно преобразовать числитель подынтегральной функции, выделив
в нем производную от знаменателя, т.е. воспользовавшись равенством
оа+£=£(2ах + Ь)+р-%.	(16)
Проиллюстрируем сказанное следующим примером.
Пример 8. Вычислить интеграл:
1)	93х + 4 dx-, 2)	^-~5..Jx;	3) Г ;-^-+2 =dx.
J x2 + 3x + 5	J 7% -x2	J л/х2 + х + 3
A 1) Так как Зх + 4 = |(2x + 3) + 4 — | = |(2x + 3) — to
3x + 4 dx =	2-^-+3 dx - 1 f -----------------
x2 4- 3x 4- 5	2 J x2 4- 3x 4- 5	2 J x2 4- 3x 4- 5
3 d(x2 4- 3x 4- 5) _ J. dx
2 x2 4- 3x 4- 5	2 x2 4- 3x 4- 5
182
Глава XV. Первообразная и интеграл
Далее выделим полный квадрат в знаменателе:
х2 + Зх + 5 =
з л/ГГ
где t = х 4- a = Поэтому, используя формулу
~ * arctg + С, где а 0, получим
Следовательно, 7 = | ln(x2 -I- Зх + 5) — -^== • arctg 4- С.
2)
dx - f 2(1 2x) 3 dx = -2
yx-x2 J yx-x2
-ЬВ^х-з[^= =
yx-x2 J yx-x2
d (x—x2)
\/x —x2
dx
y/x—x^
Следовательно, J = —4y/x^ ~£- — 3 arcsin(2x — 1) + C.
f 2(2x + 1)+L_v = 1 (2x + l)dx ,
J V^+x’+S	2 J yx2 + x + 3 +
rf(x2 + x + 3) + 3	dx Так KaK
V x2 4x4-3 2J vx2 4 x 4 3
x2+x + 3=(x+1)2+(^I)2
—2== — In |Z 4" \/fl a\ + C,
yf24a
И
§2. Неопределенный интеграл
183
где а Ф 0, то
dx
Vx2 4- х + 3
= In |х + | + л/х2 + х + з| + С
Следовательно,
J = \/х2 + х + 3 + | In |х + | + л/х2 + х + з| + С. ▲
Z | Z
*Метод интегрирования по частям. Пусть w(x) и v(x) —
дифференцируемые функции от х, определенные на одном и том
же промежутке. Тогда
d(uv) = udv + vdu.
Так как J d(uv) — uv + C, то из этой формулы вытекает, что
udv+ vdu — d(uv) = uv + C,
и поэтому справедлива формула, называемая формулой интегриро-
вания по частям. Эту формулу можно записать в виде
udv = uv — vdu.	(17)
Пример 9. Вычислить интеграл:
1) Jlnxdx; 2) Jxcosxdx.
A 1) Обозначим w(x) = lnx и u(x)=x. Используя то, что d\nx = ^dx,
и формулу (17), получим
In х dx — In x • x —
xdlnx = xlnx —
x-dx = х Inх — х + С.
X
2) Обозначим u(x) = х и d(x) = sinx Используя то, что
dsinx = cosxdx, и формулу (17), получим
х cos х dx = х sin х — sin х dx — х sin х + cos х + С.
Пример 10. Вычислить интеграл J \/х2 + a dx.
/\ Обозначим и(х) — \/х2 + а и у(х)=х. По формуле (17) находим
J— у/х2 + a dx = х\/х2 + а — xdyfx2 + а = х\/х2 + а~
X2
\/х2 4-а
dx.
Имеем:
/2 dx = [ x2.+ a~adx = J - а
\/х2 + a J V 4-
dx
\/х2 + а
184
Глава XV. Первообразная и интеграл
Отсюда получаем уравнение относительно /:
J = х\/х2 + a - J + a
dx
\/х2 + a
Выражая J и используя таблицу интегралов, находим
/ = | \/х2 + а + “ In |х + >/х2 + а| + С.	к*
Замечание. Существуют интегралы, которые нельзя выразить через
элементарные функции. К числу таких интегралов, например, относятся:
2
a)	J ех dx — интеграл Пуассона\
dx
б)	:----интегральный логарифм-,
J 1пх
ч f sinx , Г cosx ,
в)	-----dx и - —dx — интегральные синус и косинус соответственно;
г)	Jsinx2Jx и J cos x2dx — интегралы Френеля.
При этом сложность подынтегральной функции не имеет решающего
значения. Так, например, интеграл Jхех dx, который на вид сложнее, чем
2	2	1	2	1	2
J ех dx, легко вычисляется: Jхех dx = - J* ех d(x2) = ^ех 4- С
Задачи
Используя таблицу интегралов, вычислить интегралы (1-2):
1. 1) Jx 6dx;
5) J2"^x;
2)	j
6) 1
dx
\/16 — X2
dx
\/16 4-x2
3)	1
7) I
dx
x2 - 25 ’
dx
x2 + 25’
4)	[ x4 y/xdx\
8) J e2xdx.
2. 1) J(x 2 —4cosx)dx;
4) [ 3dx
J \/5 - 4x2 ’
7\ f (1 ~ \fitfdx >
J 2x
i f dx
2)
5)
8)
H)
J (x2 4- kx 4- b)dx-,
f 12х + 15х ,
J tg2 x dx-,
f 2x2 + x — 1 ,
--------5------dx.
3)
6)
9)
—I-----dx\
J 16x2 + 5
x2dx
< 1+x2’
J cos x sin 3x dx-,
3. Вычислить интегралы,
1) J(5x-3)6dx;
dx
J \Z6x — 4x2
7) J\/3x + 2dx;
используя линейную
o\ Г dx
} J Ж+1’
5)	;
J x2 —8x4-17
8) J cos 3x dx-,
замену:
dx
9)
x/11 — 12x — 4x2
dx
x2 — 5x
dx
sin2(3x — 2) ’
12) J* 32x”3dx.
________dx________ф
(sin 3x 4- cos 3x)2
dx
cos2 4x
§2. Неопределенный интеграл
185
4. Вычислить интегралы, используя подходящую замену:
1) 4) 7) 10)	J x(2x2 — l)6dx; f (2x + 3)dx	2) 5) 8) ID 1ЛЛ	Г v2. /Qv3 1 O^/v.		3) ] 6) J 9) j 12)	xdx
			1 Л V	|	5 Jxcos(l — x2)dx; J cos3 xsin2 xdx; f tg3xdt.			\/2х2-Г Psin(lnx)rfx. 1 X Г sin y/xdx
	J >/x2 4- 3x 4- 2 f x3dx					
	J v/l-x4? J sin3 x cos4 x dx; f (3 — 21n2x)^ Inxdx					\fx ’ Г 2х dx
			2	’ J cosz X 9 J (1 - 2x)e~x +xdx. ) частям: arctg xdx; x3 In x dx; xdx sin2 2x			1 V2^ + r
J	x 5. Вычислить интегрированием	п( 1)	$xexdx;	2)	f 4)	J (2x - 1) sin 3x dx;	5)	J 7)	J*xsinxdx;	8)	J				3) 6) 9)	J2x(2x -l)dx; J x Igxdx; Jx arctgxdx;	
10)	J \/9 — x2dx;	11) J x/11 4- 4x - x2dx				
6. Вычислить интегралы:
__Л_2__dx-
х2_2х_3 ’
2)	3) (—
J х2 — 5x4-6	J х(х4-1)2
7. Вычислить интеграл:
О [-^7^;
J X — 1
2) |
dx
у/х(х - 4) ’
Ответы
1. 1) ~^ + C; 2) arcslni+C; 3) X.ln|g| +С; 4) ^+С-, 5) -g+C;
6) ln|x+Vx2 + 16| + C; 7) |arctg£+C; 8)	+ C. 2. 1) -l-4sinx + C;
2) ^+bx+C; 3) ^-arctg^+C; 4) jarcsin^+C; 5) ^ + g+C;
6) x-arctgx+C; 7) 1 ln|x|-377+|x-^+C; 8) tgx-x+C; 9) _£2^x_£°s2x+c;
z	z о	о	i
10) 1 ((х+2)1-(х-2)П+С; Ч) §£l + 3x3 _Зхз+c 3 j) 1 (5x_3)7 + c.
2) |(4x+l)3+C; 3) 5 arcsin Щ^+С; 4) | arcsin (|*-1UC; 5) arctg(x-4)+C;
6) ^Inll—-l+C; 7) A(3x + 2)5+C; 8) |sin3x + C; 9)	‘ ctg(3x-2) + C;
□	| X |	IO	о	*J
10) - ' ctg (Зх+5) + C; 11) Itg4x + C; 12)	+ C. 4. 1)	+ C;
OX4!/	x	ZlUu	zo
2)	(Зх3+2)2 +C; 3)	4) 2a/x2+3x+2+C; 5) _sin(l-x2)+(?.
186
Глава XV. Первообразная и интеграл
6) -cos(lnx) + C; 7) -|(1-х4)3+С; 8)	+ С; 9) -2coSx/x + C;
Ю) _£о|х + со^х+С; П) 1^х+С; 12) ®+С; 13) _^3^п^ +
d- С; 14) е~х +х + С. 5. 1) ех(х — 1) + С; 2) х • arctg х — 1п(х2 4- 1) 4- С;
3) 1Ш2%-1~йУ+С;4) -|((2x+1)cos3x-|sin3x)+C;5) ±(x4lnx-^-)+
+С; 6) in (*2 1пх— ]+С; 7) — xcosx+sinx+C; 8) — ^-ctg2x+|In|sin2x|+C;
9) ^arctgx-x+ar£tKx+c. ю)	+1 arcsin £+ C; Ц) £=2 x/ll+4x-x2 +
+1* arcsin ^2+C. 6. 1) 'iL^.+U3.^-^)J.+C; 2) x+3ln|^4|+C; 3) Inl-Z-k
A v 15	4	I x—z |	I x-H I
+ -U+C. 7. 1) 2vT+ln|^||+C; 2) ln|^=||+C.
x+l	v I x/x+11	I x/x+21
§3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1.	Задачи, приводящие к понятию определенного интеграла
Площадь криволинейной трапеции. Пусть на отрезке [а; &]
задана непрерывная функция	где /(х)^0 при всех х€[а;6].
Рассмотрим фигуру, ограниченную графиком функции y — f{x\ двумя
вертикальными прямыми х=аих=Ьн осью Ох. Такая фигура
называется криволинейной трапецией (рис. 2). Пусть требуется
найти площадь этой фигуры.
Поставленную задачу можно решить так:
1)	разобьем отрезок \сц 6] на п равных частей и обозначим
последовательно точки деления через %о,	xn_i, хп
(рис. 3), причем а = xq < Х[ < ... < хп_[ < хп = b;
2)	обозначим длину отрезка [х^_]; х^\ через Дх/г, т. е.
=	—х^-1, и пусть Q,—-середина отрезка [х^_где
k — 1, 2,..., и;
Рис. 2
Рис. 3
§3. Определенный интеграл
187
3)	значение f(ck) функции /(х) в точке q умножим на Ах^ для
всех k = 1, 2,..., п, получим /(q) • Ах^. Геометрически каждое
такое произведение численно равно площади прямоугольника
со сторонами /(q) и Ах^. Составим сумму всех таких
произведений /(^) • Ах^ (k = 1, 2,..., п)
п
On = ДС1) • ДХ1 +/(с2) • Д*2 + • • • +Ксп)  Ь.ХП = £/(Cfe) • Дх*.
k=\
При п —> оо длины Ахп —> 0 и сумма численно равная
площади ступенчатой фигуры, составленной из п прямоуголь-
ников, стремится к значению площади S данной криволинейной
трапеции
Пример 1. Вычислить площадь криво-
линейной трапеции, ограниченной графиком
функции у = х2, вертикальными прямыми
х = 0 и х = 1 и осью Ох.
А Разобьем отрезок [0; 1] на п равных
частей, тогда Дх/г = ~ и х^ = (см. рис. 4).
Положим q = Xk = k — \b 2,..., п (т. e. q совпадает с правым
• 2
концом отрезка [х^-ьхП). Тогда /(q) = Составляя сумму
/г
получим
✓г — V^2 1 — I2 + 22 + • • • + к2
П rfi п
k=[
, то, подставляя в сумму,
п—>оо 3
Так как 12+22 + ... + и2 = "(” + 1)(2" + 1)
О
получим
’” = s(1 + ;) (2 + ;)
Поэтому искомая площадь равна S=|.	▲
О
Замечание. Используя предельный переход, еще Архимед получил, что
площадь фигуры, ограниченной графиком функции // = х2, отрезками прямых
а3
х = 0 и х = а, где а > 0, и осью Ох, равна —.
о
Работа переменной силы. Пусть материальная точка движется
вдоль числовой прямой Ох под действием переменной силы Р,
направление действия которой совпадает с направлением движе-
ния материальной точки. Предположим, что сила Р задана как
непрерывная функция от координаты х этой точки, т. е. Р = Р(х).
188
Глава XV. Первообразная и интеграл
Найдем работу силы Р при перемещении материальной точки
из положения х = а в положение х = Ь. Разобьем отрезок [а; 6],
как и в задаче о площади криволинейной трапеции, точками
xi,..., хп и выберем q е	где k — 1, 2,..., п.
Тогда работа переменной силы Р на отрезке xk] приближенно
равна	а на отрезке [a\b] работу этой силы можно считать
приближенно равной сумме
п
k=l
Предел этой суммы (при тех же условиях, что и в задаче о площади)
естественно назвать работой переменной силы при перемещении
материальной точки из точки а в точку Ь.
В рассмотренных задачах речь идет о нахождении предела сумм
п
вида ^2 /(q) ' которые называют интегральными суммами.
k=\
К вычислению предела таких сумм сводится решение многих важных
задач из геометрии, физики, техники и других дисциплин.
2.	Понятие определенного интеграла
Пусть функция /(х) определена на отрезке [я;Ь], и пусть задано
разбиение отрезка [а; произвольным образом на п частей так, что
а = х0 < %! < ... < хп_\ <хп = Ь.
Назовем совокупность точек xq, xi,..., xrt_ i, хп разбиением отрезка
[а; Ь] и обозначим Т = {х^ k = 0, 1,..., и}, а отрезки А^ = [x^-i; х^],
где £ = щ назовем отрезками разбиения Т.
Пусть Ах/j = х^ — X£-i —длина £-го отрезка разбиения Т. Тогда
число /(Т) = max{Axi, , Axrt} назовем мелкостью разбиения Т
(или диаметром этого разбиения). Если с^ е [х&_i; х^], то сово-
купность точек с^ (k— 1,..., п) назовем выборкой и обозначим {q,}
(k = 1, ... , п).
Составим сумму всех произведений /(q) • Ах^ (k = 1, ..., и),
которую обозначим а(Т, {q}) и назовем интегральной суммой
функции /(х) для данного разбиения Т и фиксированной выборки
{сЦ (k = 1, ... , п), т. е.
п
<Т, {^}) = £/(q)-Axa.	(1)
k=l
§ 3. Определенный интеграл
189
Определение. Число J называется определенным интегралом
ь
от функции f на отрезке [а; Ь] и обозначается J f(x)dx, если для
а
любого е > 0 существует такое число 3 = 5(e) > 0, что для любого
разбиения Т, мелкость которого /(Т)<3, и для любой выборки {q}
(6=1, ... , п) выполняется неравенство
п
22/(q)- &xk-J
k--A
(2)
Иногда это определение записывают в виде сг(Т, {q}) —> / при
/(7)—>0 или ^Игп^а(Т, {q})=/, имея в виду, что этот предел не
зависит от выбора точек q (& = 1, ... , п).
ь
Функция /(х), для которой существует интеграл Jf(x)dx, называ-
а
ется интегрируемой на отрезке [а; &], числа а и Ь — соответственно
нижним и верхним пределами интегрирования.
п
Геометрический смысл определенного интеграла. Заметим,
что для неотрицательной, непрерывной на [а; Ь] функции /(х)
геометрически сумма
п
S = /(ci) • Д%1 + /(с2) • Дх2 +  • • + Дсп) • Дх„ =	• Axk
k=\
численно равна площади ступенчатой фигуры, составленной из п
прямоугольников, и при /(7)—>0 стремится к площади криволинейной
трапеции, т. е.
ь
q) • ДхЛ = f(x)dx.
а
Следовательно, определенный интеграл от неотрицательной непре-
рывной функции /(х) на отрезке [а; Ь] численно равен площади
криволинейной трапеции с основанием [а;6], ограниченной сверху
графиком функции у — f(x). В этом заключается геометрический
смысл определенного интеграла.
Выясним условия интегрируемости функции /(х).
Теорема 1 (необходимое условие интегрируемости). Если
функция /(х) интегрируема на отрезке [а;Ь], то она ограничена
на этом отрезке.
190
Глава XV. Первообразная и интеграл
*ОПусть функция /(х) не ограничена на отрезке [а; Ь]. Покажем,
что в этом случае за счет выбора точек ci, eg, ..., сп можно сделать
интегральную сумму сколь угодно большой при любом разбиении
отрезка [а; 6]. Зафиксируем некоторое разбиение Т отрезка [а;Ь].
В этом случае функция Дх) не ограничена по крайней мере на
одном отрезке Ах- = [х/_ i; х,] разбиения Т. Будем для определенности
считать, что Дх) не ограничена на отрезке на Ai = [x0; xj. Выберем
на остальных отрезках точки С2, ..., сп и обозначим
*=2
Так как Дх) не ограничена на отрезке Aj = [xq; xi], то найдется
точка ci G [хо; xj такая, что
Well >
где М — любое наперед заданное число. Тогда
|/(с1)|.Ах1>Л+М,
п
YJ(ck)-bxk
k=\
= |ДС1). АХ! + А I > \Kci) I • Axi - И | > м,
т. е. интегральная сумма будет больше любого наперед заданного
числа. Отсюда следует, что интегральные суммы ^2 Kck) * ^xk не
6=1
могут стремиться ни к какому конечному пределу при /(Г) —> 0.
Теорема доказана.	• *
Следующий пример показывает, что условие ограниченности не
является достаточным, т. е. существуют функции, ограниченные, но
не интегрируемые на заданном отрезке.
Пример 2. Доказать, что функция Дирихле не интегрируема ни
на каком отрезке.
А гн	п	£/ \ Г 1,	если X G Q,
А Функция	Дирихле	Дх)	= < g х Q	ограничена на всей
числовой прямой. Покажем, что она не интегрируема ни на каком
отрезке
Зафиксируем произвольное разбиение Т = {х^, k — 0, 1,..п}
отрезка Если выбирать все точки qg[x^_i;x^], где £ = п,
рациональными, то /(q) = 1 и v
п	п
&xk = '^&xk = b- а.
k- i	k=i
§3. Определенный интеграл
191
Если же выбирать точки q иррациональными, то /(q) = 0 и
п
52 Лс*)- Дха = о.
fe=l
Следовательно, интегральные суммы не стремятся ни к какому
пределу при ЦТ) —> 0.	▲
3. Достаточные условия интегрируемости функции
Теорема 2. Всякая функция, непрерывная на отрезке [а; 6],
интегрируема на этом отрезке.
Замечание Имеет место общая теорема: если функция /(х) ограничена
на отрезке [а; Ь] и непрерывна на нем всюду, кроме конечного числа точек, то
она интегрируема на этом отрезке.
Теорема 3. Всякая функция, монотонная на отрезке [а; 6],
интегрируема на этом отрезке.
4. Свойства определенного интеграла
ь
1.	Если k — константа, то ^kdx-k{b — а),
а
2.	Если функции /(х) и g(x) интегрируемы на отрезке [а; 6],
то функции /(x)±g(x) также интегрируемы на отрезке [а;Ь\
и выполняется равенство
ь	ь	ь
j (/(x) ±g(x)) dx = /(x)dx± g(x)dx.	(3)
a	a	a
Это значит, что интеграл от алгебраической суммы интегри-
руемых функций равен алгебраической сумме их интегралов.
3.	Если функция /(х) интегрируема на отрезке [а;&], a k —
константа, то функция kf(x) также интегрируема на отрезке
[а; Ь] и выполняется равенство
ь	ь
kf(x)dx = k f(x)dx.	(4)
а	а
Это значит, что постоянный множитель можно выносить за
знак определенного интеграла.
192
Глава XV. Первообразная и интеграл
Совокупность свойств 2 и 3 называется линейностью определен-
ного интеграла.
4.	Если функция /(х) интегрируема на отрезке [а; Ь] и /(х) > О,
то
ь
f(x)dx 0.
a
Замечание. Если f(x) непрерывна на отрезке [а;6], Дх) О на [а;Ь]
ь
и Дх) > 0 хотя бы в одной точке этого отрезка, то J f(x)dx > О
a
5.	Если функции /(х) и g(x) интегрируемы на отрезке [a-,b\
и /(х) g(x) для всех точек этого отрезка, то
ь ь
f(x)dx g(x)dx.	(5)
6.	Если функция Дх) интегрируема на отрезке [а;&], то функция
|/(х)| также интегрируема на этом отрезке и выполняется
неравенство
f(x)dx | /(х) | dx.	(6)
a	a
7.	Если функция Дх) интегрируема на отрезке [щ с] и на отрезке
[с; 6], причем a < с < то эта функция интегрируема также
на отрезке [а; Ь] и выполняется равенство
ь	с	ь
f(x)dx = f(x)dx + j f(x)dx.	(7)
a	a	с
Это означает, что определенный интеграл по всему отрезку
равен сумме интегралов по его частям.
Формула Ньютона—Лейбница. Пусть функция /(х) непрерывна
х
на отрезке Можно показать, что функция Ф(х) = Jf(f)dt
a
является первообразной для Дх) на отрезке [а; 6]. Используя этот
факт, докажем формулу Ньютона—Лейбница'.
ь
f{t)dt — F(b} — F(a\	(8)
а
§3. Определенный интеграл
193
где F(x)—любая первообразная функции f(x). Действительно, так
как Ф(х) и Л(х) — первообразные функции /(х), то F(x) = Ф(х) + С,
где С—постоянная. Имеем:
F(6) - F(a) = (Ф(6) + С) - (Ф(а) + С) = Ф(Ь) - Ф(а) =
b	a	b	b
f(f)dt-O= f(t)dt.
a	a
a
= р(/)Л- f(f)dt =
a	a
Формула Ньютона—Лейбница осуществляет связь между перво-
образной данной функции и определенным интегралом. Правую часть
формулы часто записывают в виде F(x) |£. Тогда формула принимает
вид	ь
f(t)dt=F(x)\ba.	(9)
a
Пример 3. Вычислить интеграл:
1
1) J x2dx,
О
з	о	ь	з	/	ч
2) ]’(2х2 — Зх) dx; 3) Jcosxdx; 4) J cos (2x— dx.
1	a	о	v
Д 1) Одной из первообразных функции /(х) = х2 является функция
= поэтому p2dx=^|‘=^-^ = l.
2)	Одной из	первообразных	функции /(х) = 2х2 — Зх является
ч	о г3	о у2
функция	F(x)	= —-----—	. Поэтому
О	Z
3Г	Т
j(^-3x)^= (¥-¥)!,=
1
= f2 •33 _	_ (2‘13 _ ЗИ2\ = 51
\ 3	2 /	\ 3	2/	3*
3)	Одной из первообразных функции f(x) = cosx является функ-
ь
ция F(x)==sinx. Поэтому J cos xdx = sinx|* = sin b — sin a.
1Z
3	K
4)	jcos (2x - j) dx= I sin (2x - |) j’ = 1 (sin - sin (-|)) =
0
7—3022
194
Глава XV. Первообразная и интеграл
6
Пример 4. Вычислить интеграл J f(x)dx, если
0
, \ _ / х + 1 ПРИ х < 2’
/ (х) “ | х2 ПрИ х 2.
А Используя свойство 7 определенного интеграла, получаем:
6	2	6	2	6
: (х + l)Jx + x2dx =
0	2
-3|6	, .	1
f(x)dx =
о о
- (*L
к 2
6
x)dx 4- f(x)dx =
2
А 1)
Пример 5. Вычислить интеграл:
6	2
1)	J|5-2x|dx;	2) J |2x-|x-l||dx.
-1	—2
Раскрывая модуль, получаем
 г 9 । f 5 — 2х при х 2,5,
|й - zx| -	2% _ 5 при х > 2д
Для вычисления интеграла воспользуемся формулой (7):
6
j |5 — 2x|dx =
-1
2,5	6
(5 — 2x)dx +	(2х — 5)dx =
-1	2,5
Х‘
2)
к 71-1 к 712,5
- (7,5 - 6,25) - (-5 - 1) + (36 - 30) - (6,25 - 7,5) = 14,5.
Раскрывая модули, начиная с внутреннего, получаем
I9r_lr_lll-J |2х+(х—1)1 прих<1, _
|3х — 1| при х < 1,
|х + 1| при х 1
1 — Зх при х <
О
з
§ 3. Определенный интеграл
195
Далее, используя формулу (7), имеем
Способы вычисления определенного интеграла. Для вычис-
ления определенных интегралов так же, как и для неопределенных,
часто используется замена переменной
Р	ь
f (<?(*)) <pf(t)dt — f(x)dx,
a	a
(10)
где функция cp(t) имеет непрерывную производную на отрезке [а; /3],
(р(а) = а, <р(/3) = /?, /(х) непрерывна, и множество значений функции
(p(t) на отрезке [а; /3] содержится в области определения функции /(%).
4	.
Пример 6. Вычислить интеграл J ——
о 1 +v*
А Обозначим y/x=-t. Тогда x — t2 и dx = 2tdt. Так как х изменяется
от 0 до 4, то te [0; 2], поэтому
2	2
J 1-М	J V	l + f J
0	0
dt = (2t - 2 In 11 + ф = 4 - 2 In 3.
Замечание. При вычислении определенного интеграла не нужно возвра-
щаться к исходной переменной.
196
Глава XV. Первообразная и интеграл
*Еще одним методом вычисления определенных интегралов служит
метод интегрирования по частям:
ь	ь
j u(x) dv(x) = (w(x)u(x))|a — v(x) du(x).
a	a
e
Пример 7. Вычислить интеграл J In xdx.
1
А Используя формулу интегрирования по частям, получим
е	ее
In xdx = xlnx|i — xdlnx = e — dx = e — e+1 = 1 A*
1	1 1
Для непрерывной на отрезке [—a\ a\ функции /(x) справедливы
равенства:
a	a
| /(x)dx = 2 j/(x)dx, если /(x) четная,	(11)
-a	о
И
a
j /(x)dx = 0, если /(x) нечетная.	(12)
•a
Пример 8. Вычислить интеграл:
1	я
1)	J (6x5 — tyx — х2 +х) dx; 2) J sin3 x cos4 x dx.
-1	-я
A 1) Используя свойства линейности определенного интеграла, по-
лучаем
1
1
-1
1	I
6х5 — tyx — x2 +х) dx= | 6х5 dx- |
-1	-1
tyxdx—
x2dx+
xdx.
Так как функции 6х5, у/х и х —нечетные, то соответству-
ющие интегралы на [—1; 1] от этих функций равны нулю.
Следовательно,
1	1 1 1
(бх5 — у/х — х2+х^) dx=— I x2dx=—2 x2dx——2-^1 =—
J \	/ J	J	3 io 3
-1	-1	0
§3. Определенный интеграл
197
2	) Так как функция sin3хcos4х является нечетной, то интеграл на
[—л; л| от нее равен нулю. Следовательно, J sin3xcos4xdx = 0.
—тс
Пример 9. Найти все положительные значения параметра а, для
которых выполняется неравенство
а
(l-x)dx<*±?
о
значения а удовлетворяют системе неравенств
= а — у. Таким образом, искомые
Решениями системы являются а Е (0; 0,5] U [1; +оо).
Пример 10. Найти все положительные значения параметра а,
для которых
(а2 — (4 — 4а)х + 4x3)dx 12.
1
Д Имеем
2
(а2 — (4 — 4а)х + 4x3)dx —
1
2	2	2
= a2 dx—(4 — 4d) xdx + 4 x^dx —
1	1	1
= а2х| j — (4 “4а)у | + 4у| = а2 +6а + 9 = (а 4-3)2.
Таким образом, искомые значения а удовлетворяют системе нера-
венств
(а > О,
{(а + 3)2^12.
Откуда следует, что а е (0; 2\/3 —3].
198
Глава XV. Первообразная и интеграл
Задачи
I. Вычислить интеграл:
1)	2 f (2x - 3)7 dx- 1	2)	0 J (3 + 5x)2 dx; -1	3)	0 p	dx Д x2 + 2x + 2’
4)	2	< p dx о X2 + 4 ’	5)	Jsin2x cos 5xdx; 0	6)	0 J cos5xcos4xdx; —Л
7)	Г	dx • 0,5 \/2x-x2 ’	8)	!•	dx	. 0 \/3 + 4л - 4x2	9)	f ^dx; sin3 43x
10)	5	- X Ъ Sin - f — 2 dx; 0 cos4 - 2	11)	П J cos’5 x dx; n 6	12)	?	3	. j sin xdx;
13)	1 j x(3x — 2)12 dx; i 3	14)	2 J x(x — 2)9 dx; 0	15)	2 J xexdx; 0
16)	0 J (x + l)e~2xdx. -1				
5
2.	Зная, что Jf(x)dx = 4, найти значение интеграла.
2
1	-1	у/7
1)	J/(2x)rfx; 2) J /(l-4x)dx;	3) J xftx2 -2)dx.
1	-0,25	2
3.	1) Дана функция
( 2x, если x О,
' X [ x2, если x > 0.
Вычислить
-0,5	1
a) J f(x)dx;	6) j f(x)dx.
—2	—2
2)	Дана функция
J если x
/(x) — | 4%з, если x > ।
3
Вычислить Jf(x)dx.
о
4.	Вычислить интеграл:
2
1)	J |x - 3|dx;
-1
3) J (|x|4-|x-2|)rfx;
-2
2
2)	J |2x+l|dx;
-1
5
4)	J (|x| + |x — 3|) dx.
-1
§4. Применение определенного интеграла для вычисления площадей 199
5.	Вычислить интеграл, пользуясь четностью или нечетностью функции,
стоящей под знаком интеграла:
2 /у6	„3 оу2	f .--------
В J (б4-32 + V ~ dx; 2) Wl~cos2j,:rf-+
?	5 ______________
3) / (tg3x — 7x1 dx\	4) J \/cos x — cos3 x dx
К '	'	П
“I	“2
6. Найти все числа a и b, при которых функция f(x) удовлетворяет заданным
условиям:
2
1) f(x) = a-3x + b, /'(0) = 2 и Jf(x)dx = 12;
1
2
2) /(х) = a sin их 4- b, /'(!) = 2 и §f(x)dx = 4.
0
7. Найти все положительные значения параметра а, для которых выполняется
неравенство:
1) J (2 - 4х + 3x2)dx О; 2) -L Л 1 ~ 4= Их < 4-
л	V । \ 2	\/х j
Ответы
1. 1) 0; 2) Г 3) 2; 4) £; 5) 0; 6) 2: 7) £; 8)	9)	10) 4V^~2;
о 4 О	О О	У	о
11) А; 12)	13)	14)	15) е2 + 1; 16) -е2. 3. 2. 1) 2; 2) -1; 3) 2.
Z4 О	11/	ОО	4
3. 1) а) -3,75; б) -Н; 2) ^9+80. 4. 1)	2)	3) 20; 4) 23. 5. 1) 4^;
О	Z III Z	Z	Z	9
2) 2; 3) 0; 4)	6. 1) а = Д, 6=12-4?-; 2) а = -~, Ь = 2. 7. 1) а = 1;
3	In3’	In2 3	л
2) а 6(0; 4).
§4. ПРИМЕНЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
ДЛЯ ВЫЧИСЛЕНИЯ ПЛОЩАДЕЙ
Напомним, что площадь криволинейной трапеции, ограниченной
графиком непрерывной неотрицательной на отрезке [я; 6] функции
/(%), прямыми х — а, х = Ь и осью Ох, равна определенному интегралу
'Ь
/(х) dx.
Ja
Рассмотрим фигуру, ограниченную графиком непрерывной функ-
ции /(х) на отрезке [а; 6], принимающей только неположительные
200
Глава XV. Первообразная и интеграл
значения, двумя вертикальными прямыми х = аих = Ь(а<Ь)и осью
Ох (см, рис. 5) Составим интегральную сумму
п
'n=№k)^k.
k=l
В приведенной сумме k-e слагаемое
/(с/г) • Дх^ по модулю равно площади
прямоугольника с основанием Дх^
и высотой k=l,,..,n. Поэтому
интегральная сумма <тп, взятая со
знаком минус, численно равна пло-
щади соответствующей ступенчатой
ь
фигуры, т. е. число, равное — J/(x)dx,
а
совпадает с площадью рассматриваемой фигуры. Следовательно, если
ь
/(х) 0 для всех хе [а;6], то число, равное J f(x)dx, представляет
а
собой величину площади S между графиком функции у = f(x) на
ь
отрезке и осью Ох, взятую со знаком минус, т. е. J/(x)rfx = —S.
а
Рассмотрим теперь фигуру, ограничен-
ную на отрезке [a; Z?] осью Ох и графиком
непрерывной функции y = f{x\ принима-
ющей как положительные, так и отрица-
тельные значения (рис. 6), Тогда число,
ь
равное J/(x)dx, совпадает с величиной,
а
равной сумме площадей фигур между
графиком функции у = /(х), х € [а;Ь], и осью Ох, лежащих выше
оси Ох, минус сумма площадей фигур между графиком функции
У —/(х), xe[a;Z>], и осью Ох, лежащих ниже оси Ох. Например,
для функции y — f{x\ непрерывной на отрезке [а;Ь], график которой
изображен на рис. 6, имеем
ь
f(x}dx = (S] + S3) — (S2 + S4).
а
§4. Применение определенного интеграла для вычисления площадей 201
Рис. 8
Пример 1. Используя геометрический смысл определенного инте-
грала, найти такие числа а и Ь, при которых выполняются равенства:
I)	J (ах + &)</* = 0;	2) J(2x-4)dx = 0;	3) f (|х| - 4)dx = 0.
-1	О	—4
Л 1) Линейная функция f(x) = ax + b на своей области определения
меняет знак не более одного раза (если функция — константа,
то она не меняет знака). Из геометрического смысла опреде-
ленного интеграла для функции, меняющей знак, следует, что
должны быть равны площади фигур, ограниченных частями
графика функции (Si и S2), отрезками оси Ох и вертикальными
прямыми х = — 1 и х = 1 (рис. 7). Это возможно в том
случае, если график линейной функции проходит через начало
координат, т. е. при Ь = 0 и a е R.
2)	Функция f(%) = 2% — 4 пересекает ось Ох в точке х = 2. По
аналогии с решением предыдущего пункта задачи, получаем,
что равенство нулю интеграла возможно при Si = 82 (рис. 8).
Последнее равенство возможно только в случае равенства
соответствующих треугольников, т. е. при a = 4,
3)	На промежутке (—4; 4) функция /(%) = |х| — 4 отрицательна,
при х > 4 положительна. Следовательно, необходимо найти
такое значение параметра а, при котором равны площади
Si и S2 фигур (треугольников) АВС и CDE (рис. 9). Так
как Si = 16, то площадь прямоугольного равнобедренного
треугольника CDE тоже должна равняться 16. Это возможно,
если АВ — СЕ = 4л/2, значит, а — 4 + 4л/2.	▲
Рассмотрим фигуру, ограниченную отрезками прямых х = а и х = Ь
(а < Ь) и графиками неотрицательных и непрерывных на [а; Ь]
202
Глава XV. Первообразная и интеграл
функций А(х) и /зОО? причем	(рис. 10,а). Площадь
данной фигуры равна разности площадей двух криволинейных
трапеций aA^B^b и aA\B{b, т. е.
ь	ь	ь
S =	- h(x)dx = (/2(х) - AW) dx. (1)
a	a	a
Докажем утверждение, справедливое в общем случае (функции А(х)
и /2W не обязательно неотрицательны).
Площадь S фигуры, координаты точек которой удовлетво-
ряют неравенствам a^x^b, /1(х) < у г^е AW и /2W “
заданные непрерывные функции, вычисляется по формуле
ь
S = j(/2«-/i(x))rf%.
а
(2)
О Действительно, пусть т — наименьшее значение функции А(х)
на [а\Ь] (см. рис. 10,6). Тогда /2 W ~ /i W — w О для любого
хе [а;Ь]. Фигура, координаты которой удовлетворяют неравенствам
а х < 6, А(х) — т у < /2(х) — т>
§4. Применение определенного интеграла для вычисления площадей 203
получается из данной параллельным переносом вдоль оси Оу.
Следовательно, их площади равны, и поэтому (см. формулу (1))
ь	ь
S = (/2ОО — m — /i(x) + in)dx — (/2W ~/1 W) dx. •
a	a
Площадь фигуры, ограниченной графиками функций # = /i(x),
У = /2(х) и прямыми х = а, х = Ь (здесь неравенство f\(x) fz(x)
ь
может не выполняться), выражается формулой 5 = J| /2W - /1W I dx.
а
Пример 2. Найти площадь фигуры, ограниченной линиями
у = —х2 + 10х — 16 и у —х + 2.
Д Построим эскизы графиков заданных функций (рис. 11). Найдем
абсциссы точек пересечения графиков функций у = — х2 + 10х — 16
и у = х + 2 из уравнения —х2 + 10% — 16 = х + 2. Из квадратного
уравнения х2 — 9х + 18 = 0 находим Х\ — 3 и %2 — 6. Так как для
всех х е [3; 6] выполняется неравенство х + 2 < — х2 + 10% — 16, то,
используя формулу (2), получаем:
6
S = (-х2 + 10% - 16 - (х + 2)) dx =
з
= (-х2 + 9х - 18) dx =	+ ^ - 18х) I =
V	/	\ 3	2	/1з
3
=	(б3 - з3) + | (б2 - З2) - 18(6 - 3) =
= -63 + 121,5 - 54 = 4,5 (кв. ед.).
Пример 3. Пусть а^х^Ь, /(х) и g(x) — заданные непрерывные
функции. Написать формулы, по которым можно вычислить площади
заштрихованных на рис. 12 фигур.
204
Глава XV. Первообразная и интеграл
b
Л a) S = J ffx^dx-,
a
с	b
б) S = J f(x)dx— J f(x}dx\
a	с
в) 5 = J(/(x)-g(x))dx.
a
b	b	c	b
r) S = J /(x)dx — J’g(x)dx или S = jf(x)dx + J (/(x) — g(x)) dx-,
a	c	a	c
b
Д) 5 = J|/(x)-g(x)|dx;
a
c	b
e) s = J7(x)dx + Jg(x)dx.	J
a	c
Пример 4. Найти все значения а (а>0), для которых площадь
фигуры, ограниченной линиями у~ех, у = 0, х = —а, х — а, больше 1,5.
Л Криволинейная трапеция ABCD ограничена линиями у = ех,
г/ = 0, х = -а и х = а (рис. 13). Согласно геометрическому смыслу
определенного интеграла, ее площадь S можно найти по формуле
§4. Применение определенного интеграла для вычисления площадей 205
a	a
S = J e*dx. Так как J exdx = ex\a_a = ea — e~a, то заданное условие
—a	—a
равносильно неравенству ea — e_£Z > 1,5. Полагая t = ea, где t > 0,
приходим к неравенству t— | > |, которое на промежутке (0; +оо)
равносильно неравенству t>2 или еа>2, следовательно, a > In 2. ▲
Пример 5. При каком значении а прямая у = а делит площадь
фигуры, ограниченной линиями у = 0, у=2+х— %2, пополам?
Л Парабола у — 2+х —х2 = — (х — 0,5)2 + 2,25 получается из параболы
у = —х2 + 2,25 сдвигом вдоль оси Ох (рис. 14), поэтому искомая
прямая у = а разделит пополам площади под обеими параболами.
Вычислим площадь S под графиком функции у = — х2 4-2,25, учитывая
четность функции под знаком интеграла:
1,5
-1,5
^9
0	2’
Теперь определим, при каком значении b площадь под графиком
параболы у — —х2 4- b равна | = 2,25. Тогда искомое число а будет
равно 2,25 — Ъ.
Находим
V?	V?	з
(6 — х2) dx = 2 (Ь — х2) dx = 2 (^bx — у) |	= ^bVb.
-у/ь	о
Таким образом,	— |,
9 _ 9 = 9 Л _ 1 А
4	4 3^	4 V З/j/
если b = —. Отсюда получим
4(74
Пример 6. Найти все положительные значения параметра 6,
при которых площадь фигуры, ограниченной параболами у — 1 - х2
и у = Ьх2, равна а. При каких значениях а задача имеет решение?
Д Абсциссы точек пересечения парабол у = 1 — х2 и у — Ьх2
(рис. 15) найдем, решив уравнение 1 — х2 = Ьх2. Его корнями
являются числа xi = —— и хо =	. Вычислим площадь S
х/5ТТ z x/F+T
206
Глава XV. Первообразная и интеграл
фигуры, ограниченной параболами, учитывая симметричность фигуры
относительно оси Оу:
Решив уравнение = а, получим b~^ — 1. Из условий а>0,
b > 0 следует, что решение задачи существует при а е (0; |. ▲
Задачи
1. Исходя из геометрического смысла определенного интеграла, найти такие
числа а и Ь, при которых выполняются равенства:
1	a	О
1) f(2x + 6)dx = 0;	2) J (2 - \x\)dx = 0;	3) J (х - a)3dx = 0;
-1	-4	-2
a+b
7) J* sinxdx = 0.
a
§4. Применение определенного интеграла для вычисления площадей 207
2. Используя геометрический смысл определенного интеграла, вычислить:
1
1)	j kxdx\
- 1
2 у__________
3) J* \/2х — x2dx\
0,5
a __________
2) J \/cfl — x2dx, a > 0;
a
0 t_________
4) J \/25 —x2dx.
-5
Найти площадь фигуры, ограниченной линиями (3-8):
3.	1) у — 2х2 и г/= 1;	2) у = 2х2 и у = 4х;
3)	у = х2 - 4х - 4 и у = -х;	4) у = —х2 4- 4х 4- 3 и у ~ х2 - 2х 4- 3.
4.	Графиками функции f(x) = 2x — 2 и ее первообразной F(x), если /ДО) = 1.
5.	Графиками функций f(x) = х3 4- 2х2 — 2х 4- 11 и g(x) = х2 4- 8х 4- 3,
6.	1) у = у и у = \/2х;	2) у = л/х, у = i и у = 2;
3)	у = у/х 4-1 4- 2, у — —- у  и у = 1 - х;
4)	у = 4 4- л/х 4- 2, у — —0,6х 4-2,8 и х = >/10 - у.
7.	1) у = у = 2х и х = 3;	2) у = х2, у = - и х = 0,5;
3)	У=^5—"------ и У =
х2 4-2x4-!	4х + 7
8.	1) у = 3 — х2 и #=14-|х|;	2) х-|г/| = 2, х=1, х = 3;
3)	осью абсцисс и графиком функции /(х) = (х — 1) • |х|;
V) У = Г7Т7Т и У = 3 “ I3 “ х1>	5) |^| = х2 — 4|х| + 4.
|Х “1“ 11
9.	Найти площадь фигуры, ограниченной графиком функции / = sinx, опре-
деленной на отрезке [0; л], и прямой, проходящей через точки М—
и АГ = (л:; 0).
10.	Найти площадь фигуры, ограниченной линиями у = х2 — 1 и у = cos .
11.	Найти площадь криволинейной трапеции, ограниченной графиком функции
у — 3cos2х4-3sinЗх4-8, осью абсцисс и прямыми х = —их=у.
12.	Найти наибольшее значение площади фигуры, ограниченной линиями
i/ = 2 4-cosx, r/ = sin2x — 2, x = a и х = а4-я.
13.	Найти площадь фигуры, ограниченной линиями z/=44-sinx, у — sin2x4-cosx,
X = О И X = Л.
14.	Найти все первообразные F(x) функции Дх) = cos 2х, для которых выпол-
няются два условия: на промежутке
графики функций Дх) и F(x)
не имеют общих точек; площадь фигуры, ограниченной этими графиками
л	Зл	о
и прямыми х = 2 и х = равна 3.
208
Глава XV. Первообразная и интеграл
15.	При каких положительных значениях р площадь криволинейной трапеции,
ограниченной графиком функции у = х-е~2х и прямыми х = р, х=р4-О,5,
наибольшая?
16.	Найти наименьшую площадь криволинейной трапеции, ограниченной гра-
фиком функции у = ех + е2~х и двумя прямыми, параллельными оси Оу,
расстояние между которыми равно 2.
17.	Фигура ограничена линиями у = 0 и у = —х2 4- 2х 4- 3. Найти отношение
площадей фигур, на которые данная фигура делится графиком функции
У= (х+ I)2-
18.	Найти площадь фигуры, ограниченной графиком функции у — х2 — 2х + 3,
касательной к графику функции в его точке с абсциссой 2 и прямой х = — 1.
19.	Найти площадь фигуры, ограниченной графиком функции у =
= —х3 — 2х2 — х4-3 и касательной к нему, проведенной в точке с абсциссой
х0 = “1-
20.	Найти все такие точки М графика функции у = х2 — 4х, что площадь
фигуры, ограниченной этим графиком, касательной к графику, проходящей
через точку М, и осью ординат, равна 72.
21.	Найти площадь фигуры, ограниченной гиперболой у = — касательной
к этой кривой, проведенной в точке с абсциссой х = 1, и прямой х = 2.
22.	Найти площадь фигуры, ограниченной графиками функций f(x) = 2-х,
g(x) = 0,5-\/* и касательной к графику функции g(x) в точке с абсциссой 16.
23.	Доказать, что площади фигур, каждая из которых ограничена графиком
функции у = х3 — 6х2 4- 1 и одной из касательных к этому графику,
параллельных оси абсцисс, равны.
х2
24.	Фигура ограничена линиями у — — и у=х. Отрезок наибольшей длины,
заключенный внутри этой фигуры и принадлежащий прямой х = а, делит
фигуру на две равные части. Доказать что площади этих частей равны.
25? а) Найти значения параметра а, при которых площадь фигуры, ограничен-
ной кривой f/ = sin2x, прямыми х= |, х — а и осью абсцисс, равна 0,5;
б) найти значения параметра а, при которых площадь фигуры, ограни-
ченной кривой p = cos5x, прямыми х = х = а и осью абсцисс,
равна 0,2.
26. а) Найти все такие а, чтобы площадь фигуры, ограниченной линиями
у . х2 = 4, х = 2, х = а, у — 0, была вдвое больше площади фигуры,
ограниченной линиями р-х2=4, х = 2, х = 3, р = 0;
б) найти все такие а, чтобы площадь фигуры, ограниченной линиями
у . у/х = 2, х = 1, х — а, у = 0, была вдвое меньше площади фигуры,
ограниченной линиями у-у/х = 2, х = 1, х = 4, у = 0.
27. Найти площадь фигуры, ограниченной параболой у = х2 4- Ьх + с и каса-
тельными у —Ах — 13, z/ = —4x4-3, проведенными к этой параболе.
28? Дана криволинейная трапеция, ограниченная линиями у = 0, х = а (а>0)
и р = х3. Какую часть площади трапеции составляет площадь треугольника,
§4. Применение определенного интеграла для вычисления площадей 209
..	о	з
отсекаемого от данной трапеции касательной к линии у = х в точке
с абсциссой х = —?
29.	Найти все значения параметра a (a 1), при которых:
а)	площадь фигуры, ограниченной прямыми у = 1, у — 2 и параболами
у —ах2, у = 0,5ах2, будет наибольшей;
б)	площадь криволинейной трапеции, ограниченной графиком функции
у = хе~2х и прямыми х = а, х = а 4- 0,5 и у = 0, будет наибольшей
30.	а) Найти наибольшее значение площади фигуры, ограниченной линиями
у — 2 + cos х, у = sin |, х = а. х = а 4- я;
б)	найти наименьшее значение площади фигуры, ограниченной линиями
у = cosx, z/ = sin2x —2, х = а, х = а4-у
31.	Найти значения параметра а, при которых будет наименьшей площадь
фигуры, ограниченной:
а)	прямыми у = 0, х = О, х = 1 и параболой у — а2х2 — ах 4-1;
9
б)	графиком кривой (/ = — — ах 4-а; прямыми х = 0, х = 2и осью абсцисс.
32.	Найти значение параметра а, при котором прямая у — а делит фигуру,
ограниченную линиями у — х2 4-1 и у = 5, на две равновеликие части.
33.	Через данную точку с координатами (а; Ь), лежащую внутри параболы
у = х2, провести прямую, отсекающую от внутренней области параболы
сегмент наименьшей площади Найти значение этой площади.
34.	Найти наименьшее положительное число Ь, при котором для любого дей-
ствительного а площадь фигуры, ограниченной линиями z/ = 0,x = a,x = a4-l
и z/ = — х2, не больше площади фигуры, ограниченной линиями z/ = 0, х — а,
х = а 4-1 и у = 2(х — I)2 4- Ь.
35.	При каком значении t площадь фигуры, ограниченной графиком функции
^ = х44-2х2, касательной к нему, проведенной в точке графика с абсциссой t,
и прямой x = t — 1, наименьшая?
Ответы
1.	1) 6 = 0; 2) «1 = 0 и б?2 = =Ь4; 3) а = — 1; 4) а = ±2;5) если а —3, то значений
Ь, удовлетворяющих условию задачи, не существует; если а<— 3, то Ь — — 6 — а;
6) a = -^+2nk, keZ-, 7) aeR, b = 2nk, keZ. 2. 1) 0; 2) Указание.
Интеграл дает значение площади полукруга радиуса а; 3)	4- 5 кв ед.;
4)	кв. ед. 3. 1) ур кв. ед., 2) 2 j кв. ед.; 3) 20g кв. ед.; 4) 9 кв. ед.
4. кв. ед.	5.	73| кв. ед.	6. 1) | кв. ед.; 2) | - In2 кв. ед.; 3)	у кв. ед.;
4)	12,5 кв. ед.	7.	1) 8 — 2 In 3	кв. ед.; 2) In 2 — кв. ед.; 3) |	In 3 кв. ед.
8.	1) кв. ед.;	2)	4 In 3 кв. ед.;	3) g кв. ед.; 4) 6,5 — 6 In2 кв. ед.; 5)	ю| кв. ед.
9.	1 - £ кв. ед.	10. 4 (| 4-	кв. ед. И. 16я кв. ед. 12. 4л: 4- 2 кв. ед.
4	\3 л/
210
Глава XV. Первообразная и интеграл
13. 4л+2 кв. ед. 14. Г(х) = 5sin2x-—, F(x) = |sin2x+—.	15.	‘ ...
4	2	л v '	2	л	2(е — 1)
16. 2(е2 - е) кв. ед. 17. 1 : 3 (или 3 : 1).	18. 9 кв. ед. 19. у2 кв- еД-
20. (-6; 60) и (6; 12). 21. In 2-1 кв. ед. 22. 3- у.1 кв. ед. 25. а) щ 1
X	Z 111 Z	о
и а2 = 5; б)	и а2 =	26. а) а = 6 и а = б) а = | и а =
z 3	30 z 6	'	5	4	4
27. b= — 4,с = 3, 5 = 5^ кв. ед. 28. Указание. Уравнение касательной
имеет вид у = а2х — ^а3. Абсцисса точки пересечения касательной с осью
О	Z /
Ох равна ~а. Площадь треугольника ^п4.	29. а) а = 1; б) а =
2(е-1)’
30. а) 2я+ 2,5 кв. ед.; б) у - кв. ед. 31. а) а = б) а = |. 32. а =
— 1 4- \/16.	33. Smjn = (b — а2)2 кв. ед. Уравнение прямой у = 2ах 4- b — 2а2.
34. 6min =	35. 0,25.
§ 5. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
К ФИЗИЧЕСКИМ ЗАДАЧАМ
Определенный интеграл широко применяется при решении физи-
ческих задач. Рассмотрим несколько задач из различных разделов фи-
зики, иллюстрирующих физический смысл определенного интеграла.
Такими являются задачи, в которых требуется найти закон изменения
некоторой величины у(х) или ее приращение при заданном изменении
независимой переменной х, если г/(х) удовлетворяет уравнению
/=/(*)•
В частности, величина у(х) может быть перемещением, работой,
массой, электрическим зарядом, давлением, теплотой. Функция /(х)
в этих случаях задает скорость изменения у(х). Переменная х
в конкретной задаче есть время или координата. Соответственно,
функция /(х) — скорость движения, мощность или переменная сила,
плотность, сила тока, теплоемкость.	'
Предполагается, что функция /(х) определена и непрерывна
в некотором интервале (а; &). Задача определения величины у(х)
сводится к нахождению множества всех первообразных для функ-
ции /(х). Искомым является множество всех функций
х
у(х) = dt + С,
хо
где Xq — любая внутренняя точка интервала (a; &), а С — произ-
вольная постоянная. При x = Xq получим у(хо) = С. Первообразной,
§5. Приложения определенного интеграла к физическим задачам
211
являющейся решением и принимающей при x=xq значение у(%о)— Уо,
х
будет функция у(х) = уо + J /(/) dt. Равенство у(*о) = Уо называют
х0
начальным условием.
Изменение величины у(х) при переходе аргумента от значения
*2
jq к значению х2 равно интегралу J /(х) dx.
Х1
Пример 1. Точка движется по прямой, и в момент времени t
ее мгновенная скорость равна v(t). Определить закон изменения ее
координаты, если в момент времени / = координата равна х$.
Найти x(t) и путь S, пройденный точкой за промежуток времени
от до t2.
А Задача отыскания закона движения x(f) по известной скорости
v(f) сводится к решению уравнения xf(t) = v(t). Следовательно, зави-
t
симость координаты x(t) от времени имеет вид x(t) =х$ + J* v(t) dr.
to
Вычисление пути S сводится к нахождению разности значений
первообразных для у(/), т. е.
to
S — x(t2) — x(t\) — v(t)dt.	A
to
Пример 2. Тело движется прямолинейно со скоростью
v(t) — (2 + 3/2) м/с. Найти путь, пройденный телом за первые 5 с.
А Используя приведенную выше формулу, получим
5
S = j (2 + 3t2)dt = (2t +| o = 10 + 125 = 135 (m). A
о
Пример 3. Материальная точка под действием переменной
силы Р(х) перемещается вдоль оси Ох. Вычислить работу, про-
изведенную этой силой на отрезке от х = а до х = Ь.
Л Будем считать, что при прохождении точкой малого отрезка пути
[х; х +Дх] сила на этом участке изменяется незначительно, поэтому
ее можно приближенно считать равной значению силы в начальной
точке участка, т. е. Р(х). Тогда работа ДД на отрезке [х; х + Дх]
выражается приближенно формулой ДД Р(х) Дх или
Совершая предельный переход при Дх —> 0, получаем Д' = Р(х).
ь
Интегрируя, имеем А = J P(x)dx.	А
212
Глава XV. Первообразная и интеграл
Замечание В§3 настоящей главы было показано, что работа переменной
силы Р(х) при перемещении материальной точки из точки а в точку b есть
п	b
предел интегральных сумм А = lim V P(q) • Дх^, т. е. А = ГP(x)dx.
п—oofe=1	a
Пример 4. Вычислить работу, затрачиваемую на растяжение на
4 см пружины, находящейся в состоянии равновесия, если известно,
что действующая сила пропорциональна растяжению пружины, а для
растяжения на 1 см необходима сила ЗН.
Л По закону Гука для растяжения пружины на величину х требуется
сила, равная F — kx. Следовательно, 3 — /г-0,04, или k = 300. Значит,
0,04
f	/	I0’04
А = 300xdx = ( 150а:2 )	= 0,24 Дж.	А
J	\	7 1о
0
Рис. 16
Пример 5. Вычислить работу, которую необ-
ходимо затратить, чтобы выкачать воду из вер-
тикально стоящей цилиндрической цистерны,
радиус основания которой равен /?, а высота И.
А Разобьем цистерну на «элементарные ци-
линдры» плоскостями, параллельными плоскости
основания (рис. 16). Рассмотрим один из полу-
чившихся цилиндров, высеченный плоскостями,
находящимися на расстояниях х и х + Ах от
плоскости верхнего основания цистерны. Его
объем равен я/?2 Дх, а масса — тг/?2рДх, где р — плотность воды.
Обозначим через ДД работу, требуемую для подъема рассматривае-
мого цилиндра на высоту х. Тогда АД ^xR2pgx Дх, или ^^7iR2pgx.
Переходя к пределу, получим Д' = xR2pgx. Тогда
н
Л = j itR2pgxdx = |nR2pg x2 | o = ^nR2pgH2.
0
Пример 6. В неоднородном стержне длиной L функция р(х)
выражает линейную плотность стержня в точке с координатой х
(один из концов стержня принимается за начало отсчета). Найти
массу стержня.
А Рассмотрим часть стержня между точками, расположенными
соответственно на расстоянии х и х + Дх от фиксированного конца
Пусть Дт — масса этой части стержня. Тогда — средняя линейная
§5. Приложения определенного интеграла к физическим задачам
213
плотность стержня на рассматриваемом участке. Переходя к пределу,
L
получим т'(х)=р(х). Следовательно, М = Jp(x)dx.	▲
о
Замечание. При нахождении координаты центра масс стержня исполь-
зуется формула Хц.
1
м. = ду / xp(x)dx.
Задачи
1. Материальная точка массой в 1 г движется прямолинейно под действием
силы, прямо пропорциональной времени, отсчитываемому от момента t — 0,
и обратно пропорциональной скорости движения точки. В момент t = 10 с
скорость равнялась 50 см/с, а сила — 4 дин. Какова будет скорость спустя
минуту после начала движения?
2. Пуля входит в доску толщиной h = 10 см со скоростью vq — 200 м/с,
а вылетает из доски, пробив ее, со скоростью V[—8Q м/с. Считая, что сила
3.
4.
5.
6.
сопротивления доски движению пули пропорциональна квадрату скорости
движения, найти время движения пули через доску
Корабль замедляет свое движение под действием силы сопротивления воды,
которая пропорциональна скорости корабля. Начальная скорость корабля
10 м/с, скорость его через 5 с станет 8 м/с. Когда скорость уменьшится до
1 м/с?
По закону Ньютона, скорость охлаждения какого-либо тела в воздухе
пропорциональна разности между температурой Т тела и температурой
воздуха То. Если температура воздуха равна 20° С и тело в течение 20 мин
охлаждается от 100° С до 60° С, то через сколько времени его температура
понизится до 30° С?
Определить путь S, пройденный телом за время t, если его скорость
пропорциональна проходимому пути и если тело проходит 100 м в 10 секунд
и 200 м в 15 секунд.
Дно резервуара, вместимость которого 300 л, покрыто солью. Допуская, что
скорость растворения соли пропорциональна разности между концентрацией
в данный момент и концентрацией насыщенного раствора (1 кг соли на 3 л
воды) и что данное количество чистой воды растворяет | кг соли в одну
минуту, найти, сколько соли будет содержать раствор по истечении одного
часа.
7. Некоторое количество нерастворимого вещества содержит в своих порах
10 кг соли. Подвергая его действию 90 л воды, нашли, что в течение
одного часа растворилась половина содержавшейся в нем соли. Сколько
соли растворилось бы в течение того же времени, если бы количество
воды было удвоено? Скорость растворения пропорциональна количеству
нерастворенной соли и разности между концентрацией раствора в данный
момент и концентрацией насыщенного раствора (1 кг на 3 л).
8? Некоторое количество вещества, содержащее 3 кг влаги, было помещено
в комнате вместимостью 100 м\ воздух которой первоначально имел
влажность 25%. Насыщенный воздух при той же температуре содержит
0,12 кг влаги на 1 jw3. Если в течение первых суток вещество потеряло
214
Глава XV. Первообразная и интеграл
половину своей влаги, то сколько влаги в нем останется по истечении
вторых суток?
9. Некоторое количество нерастворимого вещества, содержащее в своих порах
2 кг соли, подвергается действию 30 л воды. Через 5 мин 1 кг соли
растворяется. Через сколько времени растворится 99% первоначального
количества соли?
10? Кирпичная стена имеет 30 см толщины. Найти зависимость температуры
от расстояния точки от наружного края стены, если температура равна
20° С на внутренней и 0° С на внешней поверхности стены. Найти также
количество тепла, которое стена (на 1 ж2) отдает наружу в течение суток.
Ответы
I. ^=20'; v =107725^/6.	2. m ^ = kv\ t =	с.
dt v	'	dt	у у ]п £1	40 In 2,5
и0
3. m^=-kv; t = -^^ с. 4.	= k(T-To); 7 = 20 +80(0,5) S> =60мин.
dt	In 0,8	dt v	3 4 5 *	7 * 9
5.	= kS, S = 25 25.	6. 18,1 кг; = k	, где fe-коэффи-
циент пропорциональности 7. 5,2 кг, = kx (x —	.	8. 0,82 кг;
ds
— =^s(s4-6). Указание. Влага, содержащаяся в пористом веществе,
испаряется в окружающее пространство со скоростью, пропорциональной
количеству влаги в данном веществе, а также пропорциональной разности
между влажностью окружающего воздуха и влажностью воздуха насыщенного.
9. 32,2мин. 10. Т =	864000 кал; = — -Д-, где Q = const. Указание.
3	dx kA
В силу закона Ньютона скорость Q, с которой теплота распространяется через
площадку Л, перпендикулярную оси Ох, равна Q=—kS^, где & —коэффициент
теплопроводности данного вещества, Г —температура, / — время, S —площадь
площадки A; (k = 0,0015).
Глава XVI
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
§1. ОСНОВНЫЕ ПОНЯТИЯ
1. Задачи, приводящие к дифференциальным уравнениям
С помощью производной можно исследовать свойства данной
функции — определять промежутки ее возрастания и убывания, ско-
рость роста, точки максимума и минимума, направление выпуклости
и точки перегиба ее графика и пр. Часто приходится решать обратную
задачу нахождения неизвестной функции по заданным ее свойствам.
В простейших случаях эта задача сводится к нахождению первооб-
разной. В других случаях для нахождения неизвестной функции
по данным ее свойствам составляют соотношение, связывающее
неизвестную функцию и ее производные. Это соотношение называют
дифференциальным уравнением.
В качестве примеров рассмотрим несколько задач, приводящих
к дифференциальным уравнениям.
Радиоактивный распад. Из эксперимента известно, что скорость
распада радиоактивного вещества пропорциональна имеющемуся
количеству вещества.
Обозначим через х = %(7) массу вещества, еще не распавше-
гося к моменту времени t. Тогда ~ — скорость распада вещества
удовлетворяет уравнению
§ = -kx,	(1)
где k — некоторая положительная постоянная, являющаяся коэффи-
циентом пропорциональности.
В уравнении (1) перед k поставлен знак минус, так как %(/) > О,
а — < 0.
dt
Уравнение (1) называется дифференциальным уравнением радио-
активного распада.
216
Глава XVI. Дифференциальные уравнения
Падение тела в воздушной среде. Пусть в некоторый момент
времени на землю сброшено тело массы т. Если v(t) — скорость
падения, то согласно второму закону Ньютона
(2)
где ~^ = а есть ускорение движения тела (производная от скорости v
по времени t), a F— результирующая сила, действующая на тело
в процессе движения. В данном случае
У7 = mg — Fсопр. >	(3)
где mg —сила тяжести, а Есопр. —• сила сопротивления со стороны
воздуха. Как известно, при обтекаемой форме тела и не слиш-
ком больших скоростях движения сила сопротивления воздуха
пропорциональна скорости движущегося тела, т. е. Есопр. = kv,
где k — коэффициент пропорциональности. Подставив равенство (3)
в формулу (2), получим
m^ = mg — kv или ^=g— — v.	(4)
dt	dt tn
Уравнение (4) описывает падение тела в воздушной среде.
1АЛЛЛМЖ
О т
Рис. 1
Колебания груза под действием упругой
силы. Рассмотрим прямолинейное колебание
груза массы т под действием упругой силы F,
с которой на тело действует пружина с коэффи-
циентом упругости k > 0, как показано на рис. 1.
Для составления уравнения движения груза на прямой линии вве-
дем координату л, изменяющуюся со временем /, приняв за начало О
положение равновесия груза, а за положительное направление —
направление слева направо. Тогда в силу второго закона Ньютона
уравнение движения имеет вид
mx"(t)=F.	(5)
По закону Гука для не слишком больших растяжений (сжатий)
упругая сила F, действующая со стороны пружины на груз, будет
прямо пропорциональна отклонению груза от положения равновесия
и направлена против движения, т. е.
F = -kx.
(6)
Подставляя равенство (6) в формулу (5), получим
mx"(f) = — kx или х"(1) = —^х.	(7)
Уравнение (7) называется дифференциальным уравнением коле-
баний груза под действием упругой силы
§1. Основные понятия
217
2.	Основные определения
Дифференциальным уравнением называется уравнение, которое
содержит неизвестную функцию и ее производные. Общий вид такого
уравнения:
F(x, у, у', ... , yw) = 0.
(8)
Число п, показывающее порядок старшей производной неизвестной
функции, входящей в уравнение (8), называют порядком дифферен-
циального уравнения. Решением дифференциального уравнения (8)
называют дифференцируемую функцию у — ср^х), удовлетворяющую
этому уравнению, т. е. обращающую его в тождество (по крайней
мере, в некотором промежутке изменения х).
Обыкновенным дифференциальным уравнением l-го порядка
называется соотношение, связывающее независимую переменную,
неизвестную функцию этой переменной и ее производную Общий
вид такого уравнения:
F(x, z/, i/)=0.	(9)
Решением дифференциального уравнения (9) называют дифферен-
цируемую функцию у = <р(х), обращающую его в тождество (по
крайней мере, в некотором промежутке изменения х), так что
F(x, <р(х), </(х)) = 0.
Так, например, одним из решений дифференциального уравнения
xyf + у — 0 является функция у = i (х / 0); одним из решений
уравнения у1 — у/1-у2 служит функция у = sinx | х 0 .
Пример 1. Показать, что функция z/(x) является решением
данного дифференциального уравнения:
1)	у' — х-\-у, у(х) = ех-х-1-
2)	у” + у — sinх, z/(x) = sinx + cosx — 0,5xcosx.
A 1) z/(x) = ex — x — 1, y'(x) = ex — 1. Подставляя z/(x) и z/'(x)
в уравнение, получаем, что для любого хеК верно равенство
х + у — х + (ех — х — 1) = ех — 1 — уг. Следовательно, уг = х + у.
2)	yf = cos х — sin х — 0,5 cos x + 0,5x sin x,
y" = — sin x — cos x + 0,5 sin x + 0,5 sin x + 0,5x cos x =
= — cosx + 0,5x cosx;
y"+y = — cosx + 0,5x cos x + sin x + cos x — 0,5x cosx = sinx. ▲
Уравнение (9), разрешенное относительно производной, имеет
ВИД	у' = К*, у).	(10)
218
Глава XVI. Дифференциальные уравнения
Его частным случаем является уравнение вида
у1 ~ где Дх) - заданная функция	(11)
Легко видеть, что задача нахождения решения этого уравнения
сводится к нахождению первообразных функции /, т. е. к вычислению
интеграла J/(x)dx. Таким образом, решение уравнения (11) имеет
ВИД	у(х) = J
Если F(x)— некоторая первообразная для функции /, то семейство
первообразных для этой функции есть J f(x)dx = F(x) + С, где С—
произвольная постоянная. Следовательно, можем записать
у(х)=Г(х) + С.	(12)
Таким образом, дифференциальное уравнение (11) имеет бесконечно
много решений, каждое из которых получается из формулы (12) при
фиксированном С. Функция, заданная формулой (12), называется
общим решением уравнения (11).
Вернемся к общему случаю дифференциального уравнения (10).
Функция
у — ф(х, С), где С — произвольная постоянная, (13)
которая при каждом фиксированном значении С как функция
независимой переменной х является решением уравнения (10),
называется общим решением дифференциального уравнения (10).
Каждое решение уравнения (10), которое получается из общего
решения (13) при конкретном значении постоянной С, называется
частным решением.
Рис. 2
Геометрический смысл решения диффе-
ренциального уравнения. Общее решение
у = (р(х, С) дифференциального уравнения с гео-
метрической точки зрения представляет собой
семейство кривых на плоскости (зависящее от
одного параметра С); их называют интеграль-
ными кривыми дифференциального уравнения.
Интегральная кривая — это график его решения
(или интеграла).
Например, общее решение дифференциаль-
ного уравнения у' = 2х задается формулой
у=х^ + Су где С — произвольная постоянная. Семейство интегральных
кривых данного уравнения — семейство парабол, получаемое из
параболы у — х2 параллельным переносом вдоль оси Оу (рис. 2).
Не существует каких-либо общих правил для составления диф-
ференциальных уравнений по условиям конкретной задачи. Условия
§2 Уравнения с разделяющимися переменными
219
задачи должны быть такими, чтобы они позволяли составить
соотношение, связывающее независимую переменную, функцию и ее
производную (или производные).
Задача Коши. Задача нахождения решения у(х) дифференци-
ального уравнения у1— fix, у), удовлетворяющего условию
У(хо)=Уо,	(14)
где %о, уо — заданные числа, называется задачей Коши дифферен-
циального уравнения первого порядка. Условие (14) носит название
начального условия. Решение, удовлетворяющее начальному усло-
вию (14), называется решением задачи Коши (10), (14).
Решение задачи Коши имеет простой геометрический смысл.
Решить задачу Коши (10), (14) означает найти ту интегральную
кривую уравнения (10), которая проходит через заданную точку
М0(*0, //о)-
Задача отыскания решения уравнения F(x, z/, у\ ytr) = 0, удовле-
творяющего начальным условиям
у(*о) = Уо, у'(хо) = У1,	(15)
называется задачей Коши дифференциального уравнения второго
порядка.
Решение задачи Коши называют частным решением, а сово-
купность частных решений — общим решением дифференциального
уравнения. Так, решением задачи Коши
у'(х) = 2, i/(0) = 1
является функция у(х) = 2х + 1. А общее решение дифференциального
уравнения у'(х) — 2 имеет вид у(х) = 2х + С.
§2. УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ
ПЕРЕМЕННЫМИ
Напомним, что производную у'(х) функции у(х) можно выразить
через отношение дифференциалов, т. е. у' = Поэтому диффе-
ренциальное уравнение 1-го порядка, разрешенное относительно
производной, записывается в следующем общем виде:
(')
Рассмотрим некоторые типы уравнений вида (1).
Уравнение (1) называется уравнением с разделяющимися пере-
менными, если функция /(х, у) представляет собой произведение
функции переменной х и функции переменной у:
Й=/«-Л)-	(2)
220
Глава XVI. Дифференциальные уравнения
Если функции /(х) и непрерывны в промежутках (с; 6) и (с; d)
соответственно и ср(у) 0 в (с; d), то уравнение (2) можно записать
в виде
^у=/и)Л-	(3)
Так как функции -~у и /(х) непрерывны, то они имеют первооб-
разные Ф(//) и F(x). Поэтому уравнение (3) может быть переписано
в виде
б?Ф(//) = ^(х).	(4)
Из равенства дифференциалов двух функций (здесь у рассматрива-
ется как функция от х, определяемая дифференциальным уравне-
нием) заключаем, что сами функции отличаются на постоянную:
Ф(у) = F(x) 4-С,	(5)
или

f(x)dx + С.
(6)
Пример 1. Решить уравнение у' = ху2.
Л Очевидно, что у— 0 является решением данного уравнения. Пусть
теперь у ф 0. Тогда
= х dx,
Г
и, следовательно,
-1 = Ь2 + С.
У 2
Таким образом, общее решение данного уравнения имеет вид
где С — произвольная постоянная.
Заметим, что у = 0 не получается из общего решения ни при
каком значении постоянной С.
Ответ. у = —, где Се R; у = 0.	А
х2 + С	*
Пример 2. Найти решение уравнения ху/1 + г/2 +у\/1 + х2^ = О»
удовлетворяющее начальному условию //(0) — 1.
А хУ1+^ + ух/Г+^^=0 ^-^= + -Ж= = 04Ф
dx vTW 7‘ + г/2
о = _ [_^=+C^vTW + л/1 + г/2 = С
J +х2 J х/1+у1	V
§2. Уравнения с разделяющимися переменными
221
Подставив в общий интеграл начальные условия х = 0 и у — 1,
получим \/1 + 02 +\/Ц-12 = С, т. е. С = 1 + V2.
Ответ. \/1 +х2 + \/1 + z/2 =	+ 1.	А
Пример 3. Решить уравнение у1 = у.
Данное уравнение = у при условии, что у ф 0, преобразуем
к виду = dx. Интегрируя левую и правую части полученного
уравнения, имеем In |z/| = х + С. Отсюда следует, что
\у\ = ех+с = есех, где С G R,
или	г
|у| = С\ех, где Ci=e, т. е. С\ > 0.
Освобождаясь от модуля, получим у = ±Qex или у = С2вх. где
С2 = R\{0}.
Проверкой убеждаемся, что у = 0 также является решением.
Следовательно, решением уравнения являются функции у =
где С2 = К\{0}, и у — 0.
Заметим, что у = 0 получается из формулы общего решения, если
снять ограничение С2^0. Значит, решением данного уравнения будут
все функции вида у = где С е R.
Ответ, у = Сех, С 6R.	▲
* Найдем решения задач радиоактивного распада и падения тела
в воздушной среде, которые были сформулированы в § 1, п. 1.
Пример 4. Найти решение дифференциального уравнения ра-
диоактивного распада — = —kx(f), удовлетворяющее начальному
условию x(t$)=x$.
Д Так как (иначе решение отсутствовало бы), то
— = -kdt.
X
Интегрируя обе части уравнения, находим
In |х| = -kt + In С
(здесь произвольную постоянную лучше взять в виде In С, где С>0).
Или имеем	.
^ = e-kt+,nC = C-e~kt.
Таким образом, общее решение имеет вид x(t) = С  e~kt, где С>0.
Из условия х(/о) = хо получаем, что C = Xoekt°- Следовательно,
функция
х(/) = Хое~к^~^	(7)
222
Глава XVI. Дифференциальные уравнения
является решением дифференциального уравнения радиоактивного
распада, удовлетворяющим данному начальному условию. ▲
Замечание. На практике скорость распада радиоактивного вещества
характеризуется периодом полураспада, т. е. промежутком времени, в течение
которого распадается половина исходного вещества. Так, если Т — период
полураспада, то из решения (7) при t = /q + Т находим = XQe~kT, откуда
/ 7"	1	IП
efil = -, kT = In2, k = Отсюда, подставляя в формулу (7), получаем
x(t) =	,п 2 = х02—т~^.
Пример 5. Найти закон изменения скорости от времени v(f) при
падении тела в воздухе при условии, что сопротивление воздуха
пропорционально квадрату скорости.
Д В соответствии с условием получаем, что действующая на
падающее тело сила задается формулой
F = mg - Fconp., или F = mg — av2,
где a — коэффициент пропорциональности (считаем положительным
направление движения вниз). В итоге
mvf = mg — av2 или v* — g — kv2, где	~ •
Решим полученное уравнение. Так как в начале движения v = О
и g — kv2 > 0, то получаем
dv о = dt.
g — kv2
Интегрируя обе части уравнения, находим
dv
g — kv2
1 = 1 = 1 / 1 ___________________________1
g~k°2	(v®2-(Vto)2 2Vg\Vg+>/kv y/g-
Заметим, что
Тогда
dv __ ________ _________
с g-kv2 к \^^yg + y/kv
dv
j-— ] dv =
dv
1 г 1
i
2^
1 InV£±v^ + Cb
§2. Уравнения с разделяющимися переменными	223
Подставляя полученное значение в формулу (8), имеем
2 Vg/г y/g - y/kv
Так как С, С\ — произвольные постоянные, то можем записать
1 ,nvl±^=f+c.
(9)
Из условия а(0) — 0 следует 0 = 0 4- С, т. е. С = 0. Тогда, выражая
v из равенства
имеем
Замечание. Из
растет неограниченно,
1 in^±Vto = /i
2Vg* y/g-Vkv
ijekt _ [
Л^' + l’
формулы (9) следует, что при t —> оо скорость и(/) не
а стремится к значению

Экспериментально
оПр = 50 м/с.
ynp = (hm vW = Vr
известно, что при падении человека (без парашюта)
Задачи
Решить уравнения (1-11):
1. i//cosx=^ у(0) = 1.
3. (1 + x2)dy 4- ydx = 0, у(1) = 1.
5. e'+^tgydx- ~^dy = Q, у(1) =
7. у' + cos(x 4- 2у) = cos(x - 2у), у(0) =
9. г/4-sin(x 4-г/) = sin(x- у).
2. / = tgx-tgi/.
4. У£ +еУ = 0,^(1) = 0.
6. (1 4- e2x)y2dy = exdx,y(0) — О
8. ^ = lni/, t/(2) = 1.
10. у! = ех^У-^ех~У
Ответы
1. iln2y = lntg|^ + j|. 2. sin у cosx = С. 3. у = е* arctg *. 4. 2е У(у +1) =
= х24-1.	5. 2 In | sinу\ = Л*-1) _ р 6. arctg ех —	4-	7. in | tg г/| =
= 4(1 - cosx). 8. 2(х - 2) = In2у. 9. 2sinx + In |tg || = С, у = д/г, k е Z.
10. у — In tg (ех 4- С). И. у — a sin (arcsin 4- Cj, у = ±а.
224
Глава XVI. Дифференциальные уравнения
§3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ПЕРВОГО И ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ
1.	Линейные дифференциальные уравнения первого порядка
Дифференциальное уравнение вида
У' + ay = f(x),	(1)
где а —число, а Дх)—заданная функция, называют линейным
дифференциальным уравнением первого порядка с постоянным
коэффициентом. Если f(x) = 0, то это уравнение называют одно-
родным-.
у'+ ау = 0.	(2)
Уравнение (2) является уравнением с разделяющимися перемен-
ными. Его общее решение имеет вид у = Се~ах, где С G R.
Пусть z/q(x) — некоторое решение неоднородного уравнения
i/ + ay = f(x).	(3)
Такое решение называют частным решением уравнения (3). Можно
показать, что любое решение уравнения (3) имеет вид
у = Се^ + Уо{х),	(4)
где С —некоторая постоянная.
Задачу нахождения решения уравнения (3), удовлетворяющего
условию
И*о) = */о,	(5)
где %о, z/q —заданные числа, называют задачей Коши, а условие (5)
носит название начального условия.
Пример 1. Решить задачу Коши для дифференциального урав-
нения:
1)	у'-у=\, f/(0) = l;	2)у' + 2у = х, г/(0) = 2;
3)	у' + у = sinx, #(0) = -1;	4) у'-Зу = е21С, у(0) = 2.
А 1) Однородное уравнение имеет решения вида у = Сех, а в каче-
стве частного решения неоднородного уравнения можно взять
Уо = — 1. Тогда любое решение исходного уравнения имеет вид
у = Сех - 1.
По условию //(0) = 1, тогда 1 = С — 1, откуда С = 2,
а у — 2ех — 1 — решение .задачи Коши.
2)	Здесь у = Се~2х — общее решение однородного уравнения,
а частное решение у$ неоднородного уравнения будем искать
в виде уо = ах + Ь. Тогда, подставляя его в уравнение, получим
§3. Линейные уравнения с постоянными коэффициентами	225
a + 2(ах + Ь) = х, откуда 2a = 1, a + 2b — 0. Следовательно,
Любое решение исходного уравнения имеет вид
у = Се~2х + %-±.
Так как z/(0) = 2, то 2 = С — отсюда С = Поэтому
у = ^е~2х + | — | — решение задачи Коши.
3)	Частное решение у$ неоднородного уравнения будем искать
в виде уо = a sinx+ 6 cosx. Тогда, подставляя его в уравнение,
получим
a cos х — b sin x + a sin x + b cos x = sin x.
Приравнивая коэффициенты при cosx и sinx, получим a + b=O,
a — b = 1, откуда a — b = — Поэтому любое решение
неоднородного уравнения имеет вид
у — Се~х 4- sinx~cosx
По условию z/(0) — —1, т. е. — 1 = С — откуда С = —
а у — —л +--------------— решение задачи Коши.
4)	Частное решение у$ неоднородного уравнения будем искать
в виде у$ = ае2х. Тогда, подставляя его в уравнение, получим
2ае2х - Зае2х = е2х, откуда а = — 1, а у — Се3х — Зе2х — любое
решение неоднородного уравнения.
Так как z/(0) = 2, то 2 = С-3, откуда С=5, а у = 5е3х —Зе2х —
решение задачи Коши.	▲
2.	Линейные дифференциальные уравнения второго порядка
Дифференциальное уравнение вида
у" + ay' + Ьу = /(х)	(6)
называют линейным уравнением второго порядка с постоянными
коэффициентами, а уравнение
/ + аУ + ^ = 0	(7)
называют линейным однородным уравнением второго порядка (а
и b — действительные числа).
Пример 2. Найти все решения уравнения
/-</ = 0.	(8)
8 3022
226
Глава XVI. Дифференциальные уравнения
Д Функции у — ехиу — е х являются решениями этого уравнения
Действительно, так как (ех)„ = ех и = е~х, то у" — у = 0.
Отсюда следует, что при любых постоянных С\ и С2 функция
// = Ciex + C2e"x	(9)
также является решением уравнения (8). Можно показать, что всякое
решение уравнения (8) определяется формулой (9).
Если для уравнения (8) поставлена задача Коши, т. е. заданы z/o
и th такие, что
0	yW = yo,y'W = y'o,
то из равенства (9) следует
f f/o = + С2,
I Уо = — С2.
(Ю)
~	п Уо+Уп п Уо~Уо
Эта система имеет единственное решение Gj — —С2 —
Следовательно, функция
У =	е~х
является решением задачи Коши (8), (10).	▲
Пример 3. Найти все решения уравнения
У' - 4г/'4-Зг/ = 0.	(11)
Д Будем искать решение этого уравнения в виде у — еХх, где 2 —
неизвестное число. Подставив эту функцию в уравнение, получим
у11 - 4yf + 3у = (eAx)/Z - 4 (eAx)Z + ЗеАх =
= 22еАх - 42еАх + ЗеАх = еАх(22 - 42 + 3) = 0.
Следовательно, функция у = еХх удовлетворяет уравнению (11) тогда
и только тогда, когда Л — корень уравнения 22 — 42 + 3 = 0.
Этому уравнению удовлетворяют числа 2=1 или 2 = 3, и поэтому
функции ех и е^х являются решениями уравнения (11).
Рассуждая так же, как это было сделано в предыдущем при-
мере, можно доказать, что общее решение уравнения (11) задается
формулой
у = С^ + С2е\
где Ci и С2 •— произвольные постоянные.	▲
Как и в примерах 2 и 3, решения линейного однородного
уравнения (7) можно искать в виде у = еХх. Действительно, подставив
функцию у = еХх в уравнение (7), получим:
у" + ay1 + by = (eAx),Z + a (eAx)Z + beXx =
= 22eAx + aXeXx + beXx = eAx(22 + aX + &) = 0.
§3. Линейные уравнения с постоянными коэффициентами
227
Из последнего равенства видно, что функция = будет являться
решением уравнения (7), т. е. равенство (7) обратится в тождество
при любом х, тогда и только тогда, когда Л будет корнем уравнения
Л2 + аЛ + 6 = 0.	(12)
Уравнение (12) называется характеристическим уравнением диф-
ференциального уравнения (7). Для получения характеристического
уравнения надо в соотношении (7) заменить у” на Л2, у1 на Л и у на 1.
Случай различных действительных корней характеристиче-
ского уравнения. Рассмотрим случай, когда характеристическое
уравнение (12) имеет два различных действительных корня Ai и Ад,
Ai ф Аг. В этом случае общее решение уравнения (7) задается
формулой
у =	+	(13)
где Q и С% — произвольные постоянные. Тот факт, что функция (13)
является решением уравнения (7), проверяется непосредственной под-
становкой, а то, что других решений нет, примем без доказательства
Итак, чтобы найти решение дифференциального уравнения
у" + ay' + by = О,
следует:
1)	составить характеристическое уравнение
А2 -Г аХ 4- Ъ — О,
соответствующее данному дифференциальному уравнению;
2)	найти корни Ai и А2 характеристического уравнения;
3)	в случае если уравнение имеет два различных действительных
корня Ai А2, записать общее решение данного дифференци-
ального уравнения в виде у(х) = C\e*xX + С^е^х. Сд и —
произвольные постоянные.
Пример 4. Найти общее решение уравнения
у” -у' - 2г/ = О,
а также частное решение, удовлетворяющее начальным условиям
г/(0) = 1, У(0)=3.
Д Составим характеристическое уравнение: А2 —А —2 = 0. Его корни:
Ai = — 1, А2 = 2. Следовательно, общее решение данного уравнения
имеет вид
у(х) = С\е~х + С2е2х,
где С[ и С2 — произвольные постоянные.
228
Глава XVI. Дифференциальные уравнения
Для получения частного решения найдем Ci и С2 из начальных
условий. Так как у'(х) — — Cie~x + 2С2е2х, то
(//(0) = Q 4- С2 = 1,
|/(0) = -С! Т2С2 = 3,
откуда С1 = — | и С2 = ^. Таким образом, искомое частное решение
есть у(х) =	+ |е2х.	▲
Случай, когда характеристическое уравнение имеет один
корень. Пусть характеристическое уравнение Л2 + 6zA + b — О,
соответствующее дифференциальному уравнению у" + ayf + by = О,
имеет один корень кратности два, т. е. Л] = Л2 = а. В этом случае
дифференциальное уравнение имеет вид
у" - 2ау' + а2у = 0.	(14)
Непосредственной проверкой убеждаемся, что функция у = еах —
его решение. Покажем что функция у = хеах также является его
решением. Так как у = хеах, yf — еах + ахеах, у” — 2аеах 4- о?хеах, то
у" — 2ayf 4- о? у = 2аеах 4- о?хеах — 2а (еах 4- ахеах} + с?хеах =
= 2аеах + о?хеах - 2аеах - 2a2xeQfX + оРхе™ = 0.
Следовательно, функция у = хеах — также решение. Так как функция
у = еах и функция у — хеах суть решения дифференциального
уравнения (14), то и любая функция вида
у = С[еах + С2хеах,	(15)
где Ci и С2 — произвольные постоянные, также является его реше-
нием. Тот факт, что функция (15) является решением уравнения (14),
проверяется непосредственной подстановкой, а то, что других реше-
ний нет, примем без доказательства.
Пример 5. Найти общее решение уравнения:
1) Ъу"-6у' + у = 0;
2) у" — 2у1 4- у = 0, а также частное решение, удовлетворяющее
начальным условиям у(0) = 1, у1 (0) — 2.
А 1) Соответствующее характеристическое уравнение 9Л2 — 6Л + 1 =
= 0 имеет корни	Следовательно, по формуле (15)
записываем общее решение данного уравнения:
у(х) = С\е% 4- С2хе%<
где Ci и С2 — произвольные постоянные.
§3. Линейные уравнения с постоянными коэффициентами
229
2) Составим характеристическое уравнение: Л2 — 2Л + 1 = 0 Его
корни: Л1}2 = 1. Общее решение уравнения: г/Общ — С\ех + С2хех.
Для получения частного решения найдем С] и из
начальных условий. Так как yf — С\ех + С2вх + С2хех, то
£/(0) = +0 = 1,
У(0) = С1 + С2 = 2,
откуда С|=С2 = 1. Следовательно, искомое частное решение
имеет вид у = ех + хех.	к
Случай, когда характеристическое уравнение имеет комплекс-
ные корни. Пусть характеристическое уравнение Л2 + aX + b = О,
соответствующее дифференциальному уравнению у" + ayf + by = О,
/2
о	-п	i	a i и <
не имеет действительных корней. В этом случае a12 = —-iy - —b,
n2
где b — — > 0.
2
Обозначим о2 — b —	Характеристическое уравнение
имеет два комплексно-сопряженных корня X = a + io и Л — a — io.
Замечание. Кроме рассмотренных в гл. VI алгебраической и тригономет-
рической форм комплексного числа z в математике используется показательная
форма z = r-elif\ где г— |z|, (p — avgz, которая получается из тригонометрической
с использованием формулы Эйлера:
et(p — cos 9? 4- i sin ср.
Тогда еЛх = eaxeuox = еах (cos ox 4- i sin = еах cos ox + ieax sin ox.
Рассмотрим функции eaxcoscox и eaxsino>x. Непосредственной
проверкой можно убедиться в том, что эти функции являются
решениями дифференциального уравнения //" 4- ау( 4- by = 0.
Так как функция r/ = eaxcos6ix и функция у = еах sin ох суть
решения дифференциального уравнения (7), то и любая функция
вида
у — С\еах cos ох + С2вах sin ох,	(16)
где С] и С2 — произвольные постоянные, также является его реше-
нием. Тот факт, что функция (16) является решением уравнения
у” + ау' + Ьу = О, проверяется непосредственной подстановкой, а то,
что других решений нет, примем без доказательства
Пример 6. Найти общее решение уравнения:
1) //" + 2У + 5//-0;
2) у" + 4у = 0, а также частное решение, удовлетворяющее
начальным условиям t/(0) = 0, У(0) = —1.
230
Глава XVL Дифференциальные уравнения
А 1) Составим характеристическое уравнение: Л2 + 2Л + 5 = 0. Его
корни: Л = —1 + 2/ и Л = —1 — 2/.
Тогда согласно формуле (16) общее решение данного
дифференциального уравнения имеет вид
у(х) = С\е~х cos2x + С2^"х sin 2х,
где Ci и С2 — произвольные постоянные
2) Соответствующее характеристическое уравнение Л2 + 4 = О
имеет корни Л — ±2/. Поэтому общее решение уравнения
записывается в виде у = Ci cos2x + С2 sin 2х.
Для получения частного решения найдем С\ и из
начальных условий. Так как yf — 2С% cos 2% — 2Q sin 2х, то
Г z/(0) = С] = О,
1У(0) = 2С2 = - 1,
Таким образом, Ci = О, С2 — — Значит, искомое частное
решение имеет вид у = — ^sin2x.	▲
3. Уравнение гармонических колебаний
Рассмотрим уравнение
х" + б)2х = 0,	(17)
где 6) —некоторое положительное число, а х(/) —искомая функция.
Уравнение (17) относится к уравнениям рассмотренного в преды-
дущем пункте вида. Корни соответствующего характеристического
уравнения суть Л = i(d и Л = —i(d. Поэтому общее решение имеет
вид
x(t) — Ci cos (dt + C2 sin (dt,	(18)
где Ci и C2 — произвольные постоянные
Выражение Ci cos (dt + C2 sin (dt можно привести к виду
A cos ((dt + а), где числа А и а выражаются через Cj и С2.
Соответственно функция
x(f) =А cos (б)£+ а),	(19)
где А и а—произвольные постоянные, представляет собой общее
решение уравнения (17).
Формулы (18) и (19) получаются одна из другой следующим
образом:
A cos ((dt + a) = A cos a cos (dt -r- A sin a sin (dt — Q cos (dt + C2 sin
где Ci = A cos a, C2 = — A sin a.
Функция (19) при любых значениях A,(d и а описывает гармо-
нический колебательный процесс. Число |Л| называют амплитудой,
§3. Линейные уравнения с постоянными коэффициентами
231
а число а — начальной фазой или просто фазой колебания, задан-
ного уравнением (17). Уравнение (17) называется уравнением гармо-
нических колебаний. Положительное число й) называют частотой
колебания.
Общее решение (19) уравнения (17) содержит две произвольные
постоянные: амплитуду |Л| и начальную фазу а. Для их определения
нужно
задачи
задать два условия, например можно задать два условия
Коши:
x(to) = хо,
(20)
Тогда для определения постоянных А и а получаем систему
уравнений:
Г Л cos (б>^о + а)
[ — Д easin (б)£0 + а) = 0Q-	'
Из нее следует, что A2 cos2 (б^о + а) + A2 sin2 (w/g + а) =
си
Г~ I?
Откуда, считая, что А > 0, получаем А = \/%п + -4. Далее из
V U б/
системы (21) находится начальная фаза а.
Пример 7. Решить задачу Коши для уравнения (17) с начальными
условиями х(0) = Xq, х'(0) = Vq.
Д В этом случае удобнее использовать для записи общего решения
формулу (18):	.
Х(г) = Cl COS G)t + С2 Sin 6)t.
Из начальных условий получаем систему уравнений
( х(0) = Ci cos 0 + С2 sin 0 = х0,	( Q — х0)
| х'(0) = —(46)sin 0 + C26>cos0 = Ц) ИЛИ I Со = —.
k	I 2 со ’
Таким образом, функция
х(£) = xq cos ot +	sin cot	(22)
о
является решением задачи Коши для уравнения (17) с начальными
условиями x(0)=xq, х'(0)=Ц), и Других решений задача не имеет.
Пример 8. Найти решение дифференциального уравнения коле-
баний груза под действием упругой силы
mxff + kx — 0.	(23)
Д Данное уравнение является уравнением гармонических колебаний
с частотой 6) = Поэтому его общее решение можно записать
в виде x(t) = A cos	или *(0 = Ci cos \J~^t + С% sin
232
Глава XVI. Дифференциальные уравнения
Если заданы начальные условия х(0)=Хд, х'(0) = ид, то общее
решение будет иметь вид
х(0 = ЛО cos ^0-y/jsin
Амплитуда этого гармонического колебания вычисляется по формуле
Рассмотрим несколько частных случаев решения задачи Коши
для уравнения (23).
1. Пусть х(0) = xg > 0, х'(0) =	— 0- Тогда x(f) = х0 cos
т. е. А = xq и a = 0. Эта функция описывает гармонические
колебания груза массой т, который в начальный момент
времени fg = 0 начал двигаться из точки с координатой xq > 0
с нулевой начальной скоростью
2 Пусть х(0)	= 0, х'(0) = у0 > 0. Тогда x(t) = VQyJ~^sin
и, следовательно, А	и Эта ФУНКЦ™ описывает
гармонические колебания груза массой т, который в началь-
ный момент времени /0 = 0 начал двигаться из положения
равновесия со скоростью Уд > 0.
Уравнение (23) описывает многие колебательные процессы в фи-
зике. Так, например, движение маятника с длиной нити L характе-
ризуется уравнением
La” = — gsin а,
где а —угол отклонения нити от положения равновесия. Уравнение
малых колебаний (т. е. считаем |а| < 1) получится, если применить
приближенную формулу sin a « a:
La" = —ga.
Изменение напряжения на катушке в электрической цепи, со-
стоящей из соединенных последовательно конденсатора емкостью С
и катушки индуктивностью Л, описывается уравнением
и" = -с^и-
*4. Неоднородные линейные уравнения
В общем случае при решении неоднородного линейного диффе-
ренциального уравнения у" + ayf + by = /(х) используется следующая
теорема.
§3. Линейные уравнения с постоянными коэффициентами
233
Теорема 1. Всякое решение неоднородного уравнения
у” + ayf + by = /(х) является суммой какого-либо (частного)
решения этого уравнения и общего решения соответствующего
однородного уравнения уи + ayf + Ьу = 0.
Символическая запись этой теоремы имеет следующий вид:
//общ. неоднор. — //част. неоднор. + //общ. однор. •	(24)
Рассмотрим несколько примеров в случае, когда /(х) ~ некоторый
многочлен. В этом случае, если характеристическое уравнение
имеет отличные от нуля решения, частное решение неоднородного
уравнения есть некоторый многочлен той же степени, что и правая
часть.
Пример 9. Найти общее решение дифференциального уравнения
1)	у" + 2f/' - 8у = 3;	2) у" - 3yf 4- 2у = 2х 4- 1; 3) у" + у' = 2х.
А 1) Сначала решим соответствующее однородное уравнение
у" 4- 2yf — 8у = 0. Его характеристическое уравнение имеет
вид А2 4- 2А — 8 = 0. Числа Aj = 2 и А2 = -4 являются его
корнями, поэтому уОбщ. однор. = Ci^2x + С2е“4х, где Ci, С2 € R.
Частное решение неоднородного уравнения следует искать
в виде у = А, где А — неизвестное число. Подставим эту
функцию в исходное уравнение: 0 + 0 — 8/1 = 16. Отсюда А = —2.
Таким образом, частное решение неоднородного уравнения
равно //части. = —2. Прибавив к этому решению общее решение
однородного уравнения, получим ответ:
//общ. неодн. — Cje 4- С^е 2, где С4, С2 Е К.
2)	Сначала решим соответствующее однородное уравнение
уи — 3yf + 2у = 0. Его характеристическое уравнение имеет вид
А2 — ЗА 4-2 — 0. Числа Aj = 1 и А2 = 2 являются его корнями,
поэтому //общ. однор. =:Ciex4-C2e2x, где Q, C2eR. Частное реше-
ние неоднородного уравнения следует искать в виде у—Ах+В.
Продифференцируем эту функцию: у1 =А, у" = 0. Подставим
в исходное уравнение: 0 —ЗЛ 4-2(Дх4-В) = 2x4-1. Приравняв
коэффициенты при х и свободные члены в левой и правой
частях равенства, получим: — ЗА 4- 2В — 1, 2А — 2. Отсюда
А = 1, В —2. Таким образом, частное решение неоднородного
уравнения равно учаСтн. = х 4- 2. Прибавив к этому решению
общее решение однородного уравнения, получим ответ:
//общ. неодн. — х 4~ 2 4~	4~ С2е , где Cj, С2 Е М.
234
Глава XVI. Дифференциальные уравнения
3)	Характеристическое уравнение имеет вид Л2 + Л = 0. Числа
Л1 = 0 и Л2 = —1 являются его корнями, поэтому
//общ. однор. — Ci + С2в , где Сь С2 G IR.
В этом случае частное решение неоднородного уравнения
следует искать в виде у = х(Ах + В), так как правая часть
уравнения есть многочлен первой степени и, кроме того, нуль
совпадает с одним из корней характеристического уравнения.
Продифференцируем эту функцию: у1 = 2Ах + В, у" = 271.
Подставим в исходное уравнение: 2А+2Ах + В = 2х. Приравняв
коэффициенты при х и свободные члены в левой и правой
частях равенства, получим: 2А = 2, 271 4- В — 0. Отсюда
71 = 1, В — — 2. Таким образом, частное решение неоднородного
уравнения равно участн< =х2 — 2%. Прибавив к этому решению
общее решение однородного уравнения, получим ответ:
//общ. неодн. — % ~ 2х + С1 + С2в , где бц, С2 G К. А*
Задачи
1.	Найти все решения уравнения:
1)	у”	+ 2у' - 8у = 0;	2)	у" - Sy' + 15^ =	0;	3)	у"	- Sy' 4- 16у = 0;
4)	у”	- 6/ + 13г/ = 0;	5)	4х"4-х = 0;	6)	х"	4-2х'+ Юх = 0;
7)	у"	— у = 2\	8)	х" + 2х' = 2.
2.	Найти решение уравнения, удовлетворяющее заданному начальному условию:
1) у" -Чу' + у = 0; г/(2) = 1, у'(Ч) = -2;
2)	у" + Чу' + 5у = 0; г/(0) = у'(0) = 1;
3)	у" -у' -6у = 0; //(0) = 1, /(0) = 0.
3.	Какая из функций описывает гармонический колебательный процесс:
1) х(/) = sin t 4- cos /;	2) x(t) = t sin t\	3) x(/) = sin 2t 4- cos
4) x(£) = sin/-h 1;	5) x(/) = 3cos(2£ + 1)?
4.	Найдите уравнение гармонических колебаний, которому удовлетворяет функ-
ция:
1)	х(/) = sin t + cos t; 2) x(/) = sin 2/4- cos2Z.
Ответы
1.	1) C\e2x 4- 6?2e’4x; 2) Cie3x 4- C2e5x; 3) (Q + C2x) e4x; 4) Cie3xcos2x 4-
4- C2e3xsin2x; 5) C\ cos | 4- C2 sin |: 6) е~1(С\ cos St 4- C% sin 3/); 7) C\e~x 4-
4-C2ex — 2; 8) Ci 4- C2e-2r 4-t. 2. 1) у = (7 - 3x)ex~2; 2) e-x(cos 2x 4- sin 2x);
3) ^e~2x + Ae3x-3. x(/)=sin/4-cos^ и x(/)=3cos(2/4-l). 4. 1) x// + x =
= 0;2)«"Лх = 0
Глава XVII
СИСТЕМЫ УРАВНЕНИЙ
И НЕРАВЕНСТВ РАЗЛИЧНЫХ
ТИПОВ
§1. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ
УРАВНЕНИЯ С ПАРАМЕТРОМ
Основные методы решения показательных и логарифмических
уравнений были рассмотрены в §§ 4, 5 гл. X. Здесь мы применим
их для исследования соответствующих задач, содержащих параметр.
Пример I. Для каждого значения параметра а решить уравнение
3  4х-2 4- 27 = а + а • 4Х“2.
А Произведя замену 4х-2=у, где у > 0, получим линейное уравнение
Зу + 27 = а(1+у) или (а —3)у = 27 —а.
При а = 3 это уравнение не имеет решений. Если а ф 3, то
у—-----—. Из условия y>v следует неравенство --->0, которое
а — о	и — о
справедливо при а е (3; 27). При этих значениях а из уравнения
4Х~2 _ 27— а находим х — ]Og4 27..тс -|-2.
CL — о	CL о
Ответ. Если ае(3;27), то х = log4 2J+ 2; при других а
решений нет.	▲
Пример 2. Для каждого значения параметра а решить уравнение
log^ - log 1 X = 0.
v	u	а
А Находим ОДЗ: а > 0, а 7^ 1, 2а — х>0 и х > 0
Приведем уравнение к виду 2 logfl + logfl х = 0 или
loga(2a — х) — 2 + logax = 0 <=> loga(2ax — х2) = 2 2ах — х2 = а2.
Из последнего уравнения получаем (% — а)2 = 0 или х — а
Ответ. Если а^О или а = 1, то решений нет; если а>0,
то х = а.	▲
Пример 3. Для каждого значения параметра а решить уравнение
loga х + 1оё«2 х + logfl3 х = 11.
236
Глава XVII. Системы уравнений и неравенств различных типов
Д Учтем, что а > 0, и х > 0. Переходя в данном уравнении
к одному основанию а, получим logax + logflx + | logax = 11 или
Л	О
^logaX= 11.
Из уравнения Iogax — 6 получаем x = cfi. С учетом ограничений
на а, запишем ответ.
Ответ. Если или а=1, то решений нет; если a>0,
то х = а6.	▲
Отметим, что при решении показательных уравнений с пара-
метром необходимо учитывать случай, когда основание равно 1.
Случай, когда основание отрицательно, хотя выражение имеет
смысл, если f(x) — целое число, рассматривать не следует, исходя
из определения показательной функции. Проиллюстрируем сказанное
следующим примером.
Пример 4. Для каждого значения параметра а решить уравнение
a2x-3 _ а2х-2 +а2х = 1
Д Имеем а2х~3 — а2х~2 + а2х = 1 о a2x~3(a3 — a + 1) = 1 Если
а — 1, то х может принимать любое действительное значение. Пусть
а > 0, а 7^ 1. Покажем, что в этом случае а3 — а + 1 > 0, и поэтому
уравнение
„2х—3 _	1
a3-a + l
имеет решение. Действительно, при 0 < а < 1 слагаемое а3 поло-
жительно и — а + 1 > 0, а при а > 1 имеем а3 > а. Итак, решением
п /1	3 — logrt(a3 — а 4-1)
исходного уравнения при a>0,	1 является х—-----
Ответ. Если а = 1, то х G R; если а > 0, а 1, то
3 - loga(a3 -й + 1)	.
2	*
Пример 5. Для каждого значения параметра а решить уравнение
(3log0 х - 2) log^ а = log^ X - 3.
Д Учтем, что a> 0, а^ \ и х>0,х/1. Приведем уравнение к виду
(31ogttx — 2)-—у- = 21ogflx — 3.
Положим logflx = у. Тогда уравнение примет вид (Зу — 2)-^- = 2у — 3
У
или 2у3 — Зу2 — Зу + 2 = 0. Последнее уравнение раскладывается на
§1. Уравнения с параметром
237
множители {у + 1) (2г/2 — 5у + 2) = 0 и имеет корни у\ = —1, у% = 2,
г/з — 0,5. Откуда х\ =	%2 — &2> %з = у/а.
Ответ. При а < 0 и a — 1 решений нет; если a > 0, a 1, то
12	г-	▲
Х\ =	%2 — a , х3 = Na-	*
Пример 6. Найти все значения параметра а, для которых
уравнение log2 х + loga х + log4 х = 1 имеет решение.
Д ОДЗ уравнения: х>0, а>0, а/1. Перейдем в данном уравнении
к одному основанию 2. Имеем:
logo х +	| log? х — 1
log2a 2
или
(1 + г — +	• log2X = 1 <=>	/'3Jo^2«-+2\ ,]Og х= 1.
\ log2 a	\ 21og2a J £
При 3 а + 2 О получим log? х = 2 log2 а . При любом значе-
r 21og2a	J	31og2a + 2 г
нии правой части найдется значение х, при котором выполняется
равенство. Если же 3^-2 = 0, то 31og2a + 2 = 0, т.е. а = 2~з.
Следовательно, исходное уравнение не имеет решения при а < О,
а = 1 и а = 2~з.
Ответ, a G (0; 2”з) и (2~з; 1) и (1; +оо).	А
Пример 7. Найти все значения а, при которых уравнение
logax + 1°£\/х а * \а + 1°£а%1 — al°gxa имеет решение, и найти это
решение.
Д Находим ОДЗ уравнения: х > 0, х 1 и а > 0, а^\.
Перейдем в уравнении к основанию а :
logfl % +	• | а + loga х | = —
а ^gax 1	1 logcx
При замене logax = y получим уравнение у+^-\а+у] = или
у2 + 2|а + у\ - а = 0.
Последнее уравнение равносильно совокупности двух систем:
(a + f/^O,	fa + y<0,
[ у2 + 2у + а = 0, И | у2 - 2у - За = 0.
г-'	/ * ч	Г log. х —а,
В случае (А) получаем | [Og х	Эта система имеет
решение при выполнении условий 1>а>0 и —1 — уЛ — а — а или
238
Глава XVII. Системы уравнений и неравенств различных типов
— 1 + \/1 — а —а. При 1 > а > 0 неравенство —1 — д/1 — а > —а не
выполняется, а неравенство — 1 +л/1 — а^—а или \/1 — а>1 — а явля-
ется справедливым. Следовательно, решением исходного уравнения
является х = а-1+х/1-ав
/т^ч	flOg„X<—а,	гч
В случае (Б) получаем |	% — 1 ± УГ+За ^та система имеет
решение при выполнении условий а > 0 и 1 — л/1 + За < —а или
1 + \/1 + За < —а. При а > 0 неравенство 1 + д/1 + За < —а или
\/1 + За < — 1 — а не выполняется, а неравенство 1 — \/1 + За < —а
или V1 + За> 1 4-а справедливо только при 0<а<1. Следовательно,
х = дД-х/НЗа — решение исходного уравнения.
Ответ. Уравнение имеет решения xj = fl-i4-Vl-a и Х2 — a1-vZl+3a
при 0 < a < 1.	▲
Задачи
1.	Найти все значения параметра р, при которых имеет хотя бы одно решение
уравнение:
1)	(р 4-1) • 4х 4-4 • 2х 4-р — 2 = 0;	2) (р - 1) • 4х - 4 • 6х 4- (р + 2) • 9х = 0.
2.	Найти все значения параметра р, при которых не имеет решений уравнение:
1) (р-4)-9х + (р+1)’Зх + 2р-1=0;
2)	(10 — р) • 52х+* — 2-5х+1+6 — р = 0.
3.	При каких значениях параметра а имеет хотя бы одно решение уравнение:
1) 2х + 22“х = а;	2) 4х 4- а • 2х = 1;
3)	х2 - 2х - log, а2 = 0; 4) х2 - (2а - 1)х - 3(4“-* - 2°~2) = О?
4.	Определить, при каких значениях параметра а уравнение:
I)	log3(9x 4-9a3) = х имеет два решения;
2)	logx_|_a(x — 2) = 2 имеет единственное решение;
3)	lg(x2 + 2ах) = lg(8x — 6a — 3) имеет единственное решение.
5.	В зависимости от значений параметра а определить число решений
уравнения:
1)	2xlgx = 3 — algx; 2) ^х + a 4- log5(x — 5a) = 0.
При всех допустимых значениях параметра а решить уравнения 6-9 :
6.	1) loga(x2-3a) = loga(a2-3x); 2) log^/jr^x + а) = log^^rj(V2 - х)4;
3)	lo£a2_x2 [(a-*)2 - 1] = 1.
7.	1) а2 - 9Х+1 - 8 • 3х • а = 0;	2) 144^ - 2 • 12*х1 +а = 0;
3)	3  4*~2 + 27 = а + а  4х"2.
§ 1. Уравнения с параметром
239
8.	1) logax + loga(x-1) = 2;	2) logo2 х + logx2 a = 1;
3)	2 logx a + logox a + 3 loga2jc a = 0.
9.	1) xloga x = a2x;	2) alog« x + xlog« x = 2a
ЮТ Найти все значения x, удовлетворяющие уравнению
logx+a2+1 (a2x + 2) = 2 log7+2x(5 - \/б - 2x)
при любом значении параметра a.
11. Определить, при каких значениях параметра а данное уравнение имеет не
менее двух корней:
1) loga+p + l°gx(19-8a) = 2;	2) logax + logx(17-10a) = 2
Ответы
1. 1) —2	р < 2; 2) —2 < р 2.	2. 1) р е (-оо;	U [4; +оо);
2) р € (-оо; 5) U [10; +оо). 3. 1) a > 4; 2) a е R; 3) а е [-75; 0) U (0; 75];
4) ae(-oo;-2]U[0;+oo). 4. 1) 0<а<^=;2) а€(-оо;-2)и{~}; 3) а=1
1	3
и--^а^-—. 5. 1) Если а 0, то одно решение; если a < 0, то два
решения; 2) если a < — g, то решений нет; если а то одно решение.
6. 1) Если a е (0; 1) U (1; 3], то х = — a — 3; если a > 3, то х = — a — 3 и х = а;
2) если a G (—8; —3) U (—3; +оо), то х = 4 — х/12 + а; 3) если 0 < a 1 или
a = л/2, то решений нет; если 1 < a < \/2 или a > \/2, то х = — 1 и х = 1.
7. 1) Если а = 0, то решений нет; если a < 0, то x = log3(—а), если a > 0, то
х = log3 a — 2; 2) если a 0, то х^ — ± l°gi20 + л/1 — аУ> если 0 < а < 1, то
xli2 = ± logl2(1 + л/1 — я)» *3,4 = ± log12(l “ х/1 — а); если а = Ь то х = 0, если
а > 1, то решений нет; 3) если а Е (—оо; 3]и[27;+оо), то решений нет; если
3 < а < 27, то х = 2 4- log4 ~.27. 8. 1) Если а 0 и а = 1, то решений нет;
О — Q.
если а > О и а 1, то х— 1±а/Г±4^£-
нет; если а > 0 и а / 1, то х = а\ 3)
а > 0 и а / 1, то = -у= и х2 — а 3 5
2) если а 0 и а — 1, то решений
если а 0, то решений нет; если
если а — 1, то хе (0; 1) U (1; 4-оо).
9. 1) Если а 0 и а = 1, то решений нет; если a е (0; 1) U (1; +оо), то х\ = а2
и Х2 = 2) если а 0 и а = 1, то решений нет; если а е (0; 1) U (1;+оо),
то xi = а и Х2 =-. 10. х = 1. Указание. Решите уравнение при а = 1.
11. 1) а е (-1; 0)и (2; U (»; £); 2) а « (0; 1) U (£; |) U (|; И) .
240
Глава XVII. Системы уравнений и неравенств различных типов
§2. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ
НЕРАВЕНСТВА С ПАРАМЕТРОМ
Многие из изученных ранее методов решения неравенств (разло-
жение на множители, замена переменной и т. д.) применяются также
к логарифмическим и показательным неравенствам
Пример 1. Для каждого значения параметра а решить неравен-
ство ах ~х < 1.
А Исходя из определения показательной функции, рассматриваем
только значения а > 0. При а = 1 решений нет. Из неравенства
ах ~х < а® при а > 1 получаем х2 — х < 0 или х е (0; 1), а при
О < а < 1 получаем х2 — х > 0 или х € (—оо; 0) U (1; +оо).
Ответ. При а < 0, а = 1 решений нет; если 0 < а < 1, то
х е (-оо; 0) U (1; +оо); если а > 1, то х 6 (0; 1).	▲
Пример 2. Для каждого значения параметра а решить неравен-
ство
logc(x2 + 2x) <0.
А Находим ОДЗ: а > 0, а/1; х2 + 2х>0. На ОДЗ имеем:
loga(x2+ 2х) < О <4> loga(x2+2х) < loga 1.
Последнее неравенство равносильно совокупности двух систем нера-
венств
fl>x2 + 2x>0, /iz\ Гх2 + 2х>1,
<АЦО>1 " (Б) (0<й< I.
Решая систему (А), получаем, что х е (—1 - \/2; —2) U (0; —1 + л/2)
при а > 1.
Решая (Б), получаем х е (—оо; —1 — х/2) U (—1 + х/2; +оо) при
О < a < 1.
Ответ. При а 0 или а = 1 решений нет; если 0 < а < 1,
то х е (—оо; —1 — \/2) U (—1 + \/2; Ч-оо); если а > 1, то
х е ( -1 - %/2; -2) U (0; -1 + Л).	А
★Пример 3. Для каждого значения параметра а решить неравен-
ство
logx2(x + a) < 1.
А Находим ОДЗ: х + а > 0, х ±1, х =4 0. На ОДЗ неравенство
l°gx2(x + a) < 1 равносильно совокупности двух систем:
/л\ fx2>x + a>0,	fx + a>x2,
(A) S 2	1	И n / 2 / 1
I х£ > 1	I 0 < xz < 1.
§2. Показательные и логарифмические неравенства с параметром
241
Числа xi = —	+ 4а и %2 — ~+ 4а~ ~ КОРНИ уравнения
х2 — х — а = 0 при а > —При а < — | неравенство х2 — х + а > О
справедливо при всех х.
Решая систему (А), получаем
х2 — х + а
х + а > О,
|х|>1
О,
или
' х > —а,
< х е (—oo;xi) U (х2;+оо),
< х € (—оо; - 1) U (1; +оо).
Убеждаемся, что на числовой оси Ох значение х = — а для всех
а 7^ 0 расположено левее, чем xj; при а > 0 значение х% больше
х = 1; при а>2 значение х\ меньше х = — 1. Запишем решение
первой системы: если а < — то решений нет; если — | а < О,
то х Е (1; +оо); если 0 < а < 1, то хе (хг; +оо); если 1 а < 2,
х е (—а; —1) U (х2; +оо), если а 2, то хе (-а; xi) U (Х2; +оо).
Решая систему (Б), получаем
r0< |х| < 1,
< х2 — х — а < О,
х + а > 0;
или
гхе (-1; O)U(O; 1),
< Xi < X < Х2,
. х > —а.
Получаем, что решений нет при а < — если — | а < 0, то
х е (—оо; xi) U (х2; +оо), если 0 а < 2, то хе (xj; 1); если а 2,
то х е (—1; 0) U (0; 1).
Ответ исходного неравенства является объединением ответов
систем (А) и (Б).
Ответ. Если а < —то решений нет; если — < а < О,
то х е (1 ~ +4~? 1 + ^2+4g~) и (1;+°°); если о а < 1, то
X е (-оо;	и (L+Vj+4a;+oo). если 1 а < 2, то
х G (—а;—1) U	и (1+^±^;+оо); если а 2, то
хе (-Щ 1-vJTn°)u(-l:l)u(1 + ^+^;+OO).	Л*
Пример 4. Для каждого значения параметра а решить неравен-
ство
xog°x<a.
Д Найдем ОДЗ: а > 0, а 1; х > 0. Воспользуемся основным
логарифмическим тождеством x = alog«\ Тогда неравенство примет
242
Глава XVII. Системы уравнений и неравенств различных типов
вид (aloSax)log“x < а или
alog“х < a
0<a< 1,
log^x> 1,
a > 1,
log2%<l;
!0 < a < 1,
|logax| > 1,
a > 1,
|10gcx| < 1;
Ответ.
Если 0 < a < 1, то x € (0; d) U
; если a > 1, то
если a < 0 или a = 1, то решений нет.
Пример 5. Найти все действительные значения параметра а,
при которых неравенство loga4_x |х(а — х)| < logfl+xx имеет хотя бы
одно решение.
Д Находим ОДЗ:
' х(а — х) ф О,
а + х > О,
а + х^ 1,
. х > О
' х а,
х > —а,
х 1 — а,
< х > 0.
На ОДЗ преобразуем исходное неравенство:
1оёа+х к(а - х) I < loga+x X О
1о£а+хх + 1о£а+х1а-*1 <loga+xx
& ]°ёа+х \а - х\ < ° &
{а + х> 1,
О < \а — х| < 1,
О < а + х < 1,
|а — х\ > 1
х > 1 — а,
О < |а — х| < 1,
—а < х < 1 — а,
|а — х| > 1.
Рассмотрим первую систему неравенств полученной совокупности:
{х > 1 — а,
О < \а — х| < 1
' х > 1 — а,
< х^ а,
а — 1 < х < а + 1.
§2. Показательные и логарифмические неравенства с параметром
243
Система имеет хотя бы одно решение, если a + 1 > 1 — а, т. е. при
a > 0.
Рассмотрим вторую систему неравенств совокупности:
( —а < х < 1 — а,
[ \а — х| > 1
—а < х < 1 — а,
а — х > 1,
а — х < -1
' — а < х < 1 — а,
< х < а — 1,
х > а + 1.
Система имеет хотя бы одно решение, если имеет решение совокуп-
ность
а - 1 > -а,
а + 1 < 1 - а
а > 0,5,
а < 0,
т.е. при ае(—оо;0)и(0,5;+оо).
При а = 0 неравенство приводится к виду logxx2 < logx% или
2 < 1, т. е. не имеет решения.
Ответ, а ^0.	▲
Пример 6. Найти все действительные значения параметра а, при
которых неравенство 1 + log2(2x2 + 2х + 3,5) > log2(ax2 + а) имеет
хотя бы одно решение.
А Находим ОДЗ:
Г 2х2 + 2х + 3,5 > 0, f (2х +1)2 + 6 > О,
•So	9	'	=> а > 0.
(ах2 + а>0	(а(х2 + 1)>0
Преобразуем исходное неравенство:
1 +log2(2x2 + 2х + 3,5) > log2(ax2 + а) <=>
<=> log2(4x2 + 4х + 7) > log2(ax2 + а).
Потенцируя (с учетом ОДЗ), получаем двойное неравенство
4х2 + 4х + 7 ах2 + а > 0.
Решим неравенство
4х2 + 4х + 7 > ах2 + а или (4 - а)х2 + 4х + 7 - а > 0.
Дискриминант квадратного трехчлена (4 — а)х2 + 4х + 7 - а равен
D = —4a2 + 44a — 96 = —4(a — 3)(a — 8). Квадратичное неравенство
имеет хотя бы одно решение в случае выполнения условий
"4 —а>0,
J 4 - а < 0,
.4 —а = 0
'а < 4,
( а > 4,
[3;8],
.а = 4
"а < 4,
а = 4,
_4<а^8.
Учитывая ОДЗ, получаем а е (0; 8].
Ответ, a G (0; 8].
244	Глава XVII. Системы уравнений и неравенств различных типов
Пример 7. Найти все значения параметра а, при которых
неравенство а • 9х + 4(а — 1)3* + а > 1 справедливо для всех х € R.
А Сделаем замену t = 3х, где t > 0. Тогда получим неравенство
а • t2 + 4(а - V)t + а > 1. Исходное неравенство будет справед-
ливо при всех х е R, если полученное неравенство выполняется
при всех t > 0. Это возможно, если для квадратного трехчлена
= а • t2 + 4(а — 1)/ + а — 1 будут выполняться условия:
’ ( D<0,
| а > О,
{а > О,
/(0) = о - 1 > 0,
где /о — абсцисса вершины параболы.
Решением последней совокупности является а 1.
Ответ, а 1.	▲
Как показывает следующий пример, иногда для решения нера-
венств с параметром удобно воспользоваться графическим методом
Пример 8. Для каждого возможного значения параметра а
решить неравенство
logx2(a + х) 1.
А Перепишем неравенство в виде
logx2(a + x)^logx2|x|.
Последнее неравенство равносильно совокупности двух систем:
(А)
а + х > 0,
0 < |х| < 1,
а + х < |х|
и (Б)
|х| > 1,
а + х |х|.
В случае (А) получаем
			(х>— а,	1		г х>—а.				
<	o' V + V <3 о к	 _	<		г( Г-1<х<0, [а+х^—х,	<=> J		(1)<	-1 х	<х < _ а о }	:0,
	_ а+х^ |х|			(п) 1 Lv ' ( а+х^х,	|		(И)	г 0< [ a s	Z ; х < :0.	:1,
Аналогично в		. случае (Б) получаем							
	Г М > 1, [ а + х >	|х|		'Oinfexs-x;	( (	III) < IV) <	Б \V V W Л	рг- 1	1 ND|й	
§2 Показательные и логарифмические неравенства с параметром
245
Рис. 1
Все решения исходного неравенства выделены на координатной
плоскости Оах (рис. 1). Используя рисунок, запишем ответ.
Ответ Если -1 < а < 0, то х е (—а; 1); если а = 0, то
х е (0: 1) U (1;+оо); если 0 < а < 1, то хе (-а; -|] U (1; +оо);
если 1 < а < 2, то х е (—1; — |] U (1; +оо); если а = 2. то хе (1; +оо);
если а > 2, то хе [—|; —1) U (1; +оо).	▲
Для решения некоторых неравенств с параметром применяют
метод разложения на множители. Приведем пример.
Пример 9. При каждом значении параметра а решить неравен-
ство	.	о
24х + (х — 4 - а)22х + (5tz + х — 5 — ах) < 0.
Л Разложим левую часть неравенства на множители. Сделаем
замену 4х = t, где t > 0, и рассмотрим левую часть неравенства
как квадратный трехчлен относительно переменной t:
P(t) = t2 + (х — 4 — а) • t + (а — 1)(5 — х) —
— t2 — ((а — 1) + (5 — х)) • t + (а - 1)(5 - х).
Корнями P(t) являются числа ^=5 —х, tz — a — l. Следовательно,
Р(/) = (/-(5-х)).(^(а-1)).
Сделаем обратную замену и запишем неравенство в виде
(4х - (5 - х))(4х - {а - 1)) 0.
Это неравенство равносильно совокупности систем:
Г 4х —(5—х)^0,	, . Г 4х-(5-х)>0,
(AJ | 4х - (а - 1) > 0;	| 4х -(а -1)^0.
Рассмотрим функцию /(х) = 4х + х — 5. Заметим, что /(1) — 0.
Кроме того, функция /(х) монотонно возрастает на всей числовой оси.
Поэтому Дх)^/(1), или 4х+ х — 5<0 для любого х^1 и Дх)^/(1),
246
Глава XVII. Системы уравнений и неравенств различных типов
или 4х+х-5<?0 для любого х 1. Следовательно, совокупность
систем А и Б равносильна совокупности систем
( X 1,	( X 1,
| аг$4х + 1; и а^4х + 1.
На плоскости Оху изобразим множе-
ство точек (рис. 2), координаты которых
удовлетворяют полученной совокупности.
На рисунке это множество заштриховано.
Точки 1 и 5 разбили ось Оу на три
участка, на каждом из которых легче вы-
писывается решение данного неравенства.
Для этого на соответствующем участке
проводим горизонтальную прямую у — a
и находим значения, соответствующие кон-
цам участков этой прямой, принадлежащих
заштрихованной области. Абсциссу точки
пересечения прямой у = а и графика функции у = 4х + 1 находим,
решив уравнение a = 4х -Ь 1. Получаем x = log4(a —1).
Ответ. Если а е (—оо; 1], то х е (—оо; 1]; если a е (1; 5), то
% е [log4(a — 1); 1]; если a = 5, то х — 1; если a 6 (5;+оо), то
хе [1; log4(a — 1)].	▲
Задачи
Найти все значения параметра а, при которых имеет решение неравенство (1-2):
1. 1) а2 -2-4х+1 -а-2х+1 > 0;	2) ах2~2х 4- а2х~х2 4.
2.	1) IogG(l+x) >loga2(l+x); 2) loga(x2 + 2х +2) < 0.
Определить, при каких значениях параметра а неравенство выполняется при
любом значении х (3-4):
3.	1) а-9* + 4(а-1)3*+а>1;	2) 4*2 + 2(2а + 1)2*2 + 4а2 - 3 > 0.
4.	1) loga(x2 + 2) > 1;	2) loga(a+1)(|x|+4) > 1;
3)	>oga2_6 [(а2 - 1)х2 + 4ах + б] <1.
Для каждого значения параметра а решить неравенство (5-7):
5.	1) а*2~*>1;	2) loga(l+x) > 1;	3) loga(x2 + 2х) < 1
6.	1) a2 - 9x+1 - 8а • 3х > 0;	2) |3* - 3~*| < 3“ - 3~°;
3)	|0,Гх - 0,1х| < 0,1“ - 0,Га.
7.	1) 34х + (х - 8 - а)32х + (10а + 2х - 20 - ах) 0;
2)	1 - (5 + а + 2х)22* + 24х(6а - 2х - 6 + 2ах) > 0.
§2 Показательные и логарифмические неравенства с параметром
247
8.	Для каждого значения параметра a > 0 решить неравенство:
1)	ах+2 + 8йх-' - 4а-1 > a - 2;	2) —!— >-------!—
сг — 1	1 — ax~l
Для всех значений параметра a
решить неравенство (9-10):
9. 1)
10. 1)
3)
1 + logfl X v
1	+ loga X
logx(x — a) > 2;
a log3 x + log3jc 3 + a 0;
2	) $	-^4-6 > ।
2 + log2 x
2) loga x + logx a 3;
4) 2 log4(x — a 4- 1) + log| (x — 3 — 2a)	2.
Ответы
1. 1) a G (-oo;0) U (0;4-oo); 2) a > 0. 2. 1) a € (0; 1) U (l;4-oo);
2) 0 < a < I. 3. 1) a > 1; 2) a G (-oo;-l) U (0;+oo). 4. 1) 1 <
< « < 2;	2)« 6	и (rl+vl; ^±v2Z) ;
3) « e (--v^) U (V6; \/4T\/5). 5.1) Если a<0 или a = 1, to
решений нет; если 0 < a < 1, то х G (0; 1); если a > 1, то х G (—оо;0) U (1; 4-оо);
2) если а 0 или a — 1, то решений нет; если 0 < a < 1, то х G (—1; a — 1);
если a > 1, то х > a — 1; 3) если а 0 или a = 1, то решений нет; если
О < a < 1, то х G ( —оо; —1 — л/1 4-a) U (—1 4- \/1 4-а; 4-оо); если a > 1, то
х G (—1 — \/1 4- а\ —2) U (0; —1 4- \/1 4-а). 6. 1) Если а = 0, то решений
нет; если а > 0, то х < —2 4- log3a; если а < 0, то х < log3(—а); 2) если
а 0,	то решений нет; если а > 0, то х G (—а; а); 3)	если	а > 0,	то
х G R;	если а	0, то х G (—оо;	a] U [—а;4-оо). 7. 1) Если a	G (—оо;	2],
то х G	(-оо; 1];	если a G (2; 11),	то х G [log9(a - 2); 1];	если	а — И,	то
х = 1;	если a G	(11;4-оо), то х G	[1; log9(a — 2)]; 2) если	a G	(—оо; 1],	то
х G (—оо; -1]; если a G (1; 5), то х G (-оо; —1] U [- log4(a - 1); +оо); если а = 5,
то х G R; если a G (5; 4-оо), то х G (-оо; - log4(a — 1)] U [—1; 4-оо). 8. 1) Если
О < а < 1, то х G (—оо; — logc(a 4- 2)); если а = 1, то х G R; если а > 1, то
х G (— loga(а 4- 2); 4-оо); 2) если а = 1, то решений нет; если 0 < а < 1, то
х G (-оо; 0) U (loga	; если а > 1, то х G (б; loga U (1;4-оо)
9. 1) Если 0 < а < 1, то х G (0; a) U (1; i); если а > 1, то х G (^; 1) U (а; +оо);
а 0 или а = 1, то решений нет; 2) если 0 < а < 1, то х G (a4;	; если
а > 1, то х G Q; а4) ; если а 0 или а = I, то решений нет. 10. 1) Если
а < 0, то х G (1; 1	4—) ; если а = 0, то решений нет; если 0 < а то
xG (а; -—U +	; 1) ; если | < а < 1, то х G (а; 1); если а 1,
то решений нет; 2) если а 0 или а = 1, то решений нет; если 0 < а < 1,
" З+л/5	3—\ ~
то х G а 2 ; а 2
Г З-х/5
U (1; 4-оо); если а > 1, то х G (0; 1) U а 2 ; а
3)
если а < 0, то х G
-1-л/СТ
0; 3 V °
если а 0, то
248
Глава XVII. Системы уравнений и неравенств различных типов
х >	4) если a < 0, то решений нет; если a = О, то х > 0; если a > О, то
х € (0; a) U (16а; +оо).
§ 3.	СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ
И ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ
Системы, содержащие показательные и логарифмические урав-
нения, обычно решаются сведением тем или иным способом
к алгебраической системе или к уравнению с одной переменной.
Основные методы решения систем алгебраических уравнений были
представлены в гл. VIII.
Сначала рассмотрим несколько примеров, в которых выполняются
стандартные замены для систем показательных и логарифмических
уравнений.
Пример 1. Решить систему уравнений
/ 5х + У = 3,
| Ьх+у = 2.
Д Обозначим 5х = и > 0, 5^ = v > 0. Тогда получим систему
( и + v — 3,
( uv = 2,
решением которой являются пары чисел (iq; uj) = (1; 2)
и (и2; ^2) — (2; 1).
Выполняя обратную замену, для первой пары получим систему
Г 5х = 1, /х = 0,
| & = 2	( у = log5 2;
для второй —
/5х = 2, Г х = log5 2,
[5^ = 1 ^\у = 0.
Ответ. (0; log52), (log52; 0).	▲
Пример 2. Решить систему уравнений
< G) + logs г/= 504,
4% _ 2-*-1 log^ у + log2 у = 84.
Д Перепишем систему, переходя в логарифмах к основанию 3,
а в степенях — к основанию 2:
f 23х + logs I/= 504,
I 22х - 2х log3 У + 1оёз У = 84-
§3. Системы логарифмических и показательных уравнений
249
Пусть 2 х = и > 0, v — log3 у. Тогда получим систему
Г и3 + у3 = 504,	f u + v = 6,
( н2 — uv + у2 = 84	( u2 — uv + у2 = 84.
Выражая v = 6 — и из первого уравнения и подставляя во второе,
получим 3z/2 — 18zz — 48 = 0. Откуда и — 8 или и = - 2. Но и > 0,
поэтому и — 2х = 8, т. е. х = 3, и v = 6 — и = —2, т. е. v = log3 у = — 2
или у = З-2.
Ответ. (3; *).	▲
у
Далее рассмотрим несколько более сложных примеров, в кото-
рых приходится выполнять различные преобразования уравнений,
входящих в систему.
Пример 3. Решить систему уравнений
13 • log5(x 4-г/) — х — у.
Д Из первого уравнения системы получаем
х + у = |.з^ = 5-Зх-^-з.	(1)
Подставляя во второе уравнение, имеем
3 • log5(5 • Зх-г/-3) = х — у & 3 (1 +(% - г/— 3) log5 3) = х — у 4»
& 3(1 — 31og53) = (1 — 31og53) (х —у).
Поскольку 1 —31og53^0, то х — у = 3. Подставляя в уравнение (1),
получим х + у = 5. Из системы
{х + у — 5,
x-z/ = 3
следует, что х = 4, у = 1.
Ответ. (4; 1).	▲
Пример 4. Решить систему уравнений
' 10g2	+ W) - log 1 (I + i) = 4,
I	I	2	4
Д Первое уравнение системы можно записать в виде
log2 \ху(х + 2#)] + log2 х = 4,
Л1/
а множество допустимых значений х и у определяется условием
ху(х + 2у) > 0.	(2)
250
Глава XVII. Системы уравнений и неравенств различных типов
При выполнении условия (2) исходная система равносильна системе
x + 2i/)2 = 16,
?!='
а система (2)-(3) равносильна совокупности двух систем
х + 2у = 4,
хг/ = 6,
(3)
(4)
И	х	~	.
\ х + 2у = —4,
\ху = -6.
Исключая х из системы (4), получаем уравнение у2 — 2у + 3 = О,
не имеющее действительных корней. Поэтому система (4) не имеет
действительных решений.
Из системы (5) получаем уравнение у2 + 2у — 3 = 0, имеющее
корни у[ =— 3, у2 = 1. Поэтому исходная система имеет два решения
(2; -3) и (-6; 1).
Ответ. (2; —3), (—6; 1).	▲
Пример 5. Найти решения системы уравнений
( log3(5f/ - х - 2) - >og9(x - г/)2 = 1,
( 1о£з “ -у - 4х) “ 1о&9 х2 =
удовлетворяющие неравенству х — у < 0.
А Запишем исходную систему в виде
' >og3(5«/ - х - 2) = log3 3|х - у\,
\1оёз	= 1о£з3М-
Потенцируя в каждом уравнении и учитывая данное условие,
получаем систему
Г 5у-х-2 = 3\х-у\,	,
[z/-2-4xt/ = 3z/|x|,	1 j
являющуюся следствием данной.
а)	Пусть х>0, тогда |х|=х и с учетом условия х<у из первого
уравнения системы (6) получаем х — 1 — у.
Тогда второе уравнение этой системы преобразуется к виду
7 2 е о л	З + д/23	3-У23	4 — л/23
7у - бу - 2 = 0, откуда ух = - 7 у2 = —у—, %1 = —7—,
_ 4 + V23
Х2 7	•
Здесь для Х[ не выполняется условие х > 0, а для пары
(%25 Уъ) не выполняется условие х < у.
§3. Системы логарифмических и показательных уравнений
251
б)	Пусть х < 0, тогда из системы (6) с учетом условия х < у
получаем x—i — y^ а из второго уравнения системы следует,
что у2 = 2, откуда у$ = — \/2, у^ — л/2, х3 = 1 + х/2, х4 = 1 — х/2,
Пара чисел (х3; z/3) не удовлетворяет условию х < О,
а пара чисел (х4; z/4) удовлетворяет этому условию и исходной
системе.
Ответ. (1 — \/2; д/2).	А
Пример 6. Решить систему уравнений
Зх+г/+1 + 7.3^-2 = 8,
\Л + */2 = х + у.
А Возведя в квадрат обе части второго уравнения системы, получаем
х+у2 =х2 + 2ху + у2 или
х(х + 2у - 1) = 0,	(7)
откуда следует, что либо х = 0, либо х = 1 — 2у,
Уравнение (7) равносильно второму уравнению исходной системы,
если
x + z/^O.	(8)
а)	Пусть х = О, тогда из первого уравнения получаем 3^ =
откуда у = log3 Пара числе (О; log3 удовлетворяет
условию (8) и является решением исходной системы.
б)	Пусть х = 1 — 2у, тогда из первого уравнения получаем
32—_|_ 7.3^-2 — g или / _(_ Z — 87 где t — 32~у. Уравнение
t2 — 8t + 7 = 0 имеет корни t\ = 1,	= 7.
Если Z=l, то 32—= 1, откуда у = 2, х=— 3. Однако пара чисел
(—3; 2) не удовлетворяет условию (8).
Если t = 7, то 32“^ = 7, 3^ = ®, z/ = log3y, х = 1-21og31 = log3
Пара чисел (log3 log3 у) удовлетворяет условию (8)
Ответ. (0; log3|y), (iog3^; log30 .	А
Пример 7. Решить систему уравнений
log5(5x -3^-1) _ log2(5 + 4у - Зх) - 1
log5(2i/ - х + 3)	log2(3x-y + l) ’
2х2 + у2 — Зху — х — 1 — 0.
252
Глава XVII. Системы уравнений и неравенств различных типов
Л Разложив левую часть второго уравнения системы на множители,
запишем его в виде (2х — у + 1)(х — у — 1) = 0. Поэтому второе
уравнение равносильно совокупности двух уравнений:
у = 2% + 1 и у — х-\.
а)	Если г/ — 2а: + 1, то 5х - Зу — 1 = — х — 4, Зх — у + 1=х.
Так как неравенства — х — 4 > 0 и % > О несовместны, то
в этом случае система не имеет решений (левая и правая части
первого уравнения не имеют общей области определения).
б)	Если у — х — 1, то первое уравнение системы примет вид
logs2 + logs(x + О __ l°g2(x + 1)~1
logS^+O log2(x+l) + l’
откуда
1 I i _ l°g2(% +0 + 1-2
log2(x+l)	log2(x+l) + l ’
1	=_______2______
log2(x+l) log2(* + 0 + 17
3 log2(x 4-1) = —1,
X = - 1 I- у — x — 1 = —24 L
v2	V2
Ответ. ( -1 4- -J-; -2 4- 4- ) .
\ v2	V2/
Пример 8. Решить систему уравнений
' (х-2)(х + 3) = z/(z/-5),
1оёх(2-</) =
Д Первое уравнение системы можно записать в виде %2 — z/2 + х +
4-5// —6 = 0 или (х + у — 2)(х — //4-3) = 0. откуда
х = у-3	(9)
или
х = 2 — у.	(10)
Из второго уравнения следует, что
2>у, у^0, х > 0, х^1.	(11)
а)	Если справедливо равенство (10), то из второго уравнения
системы находим х = //2, откуда, используя равенство (10),
получаем
2-i/ = у2 или (у- l)(z/ + 2) = 0.
Если //=1, то х = 1 и не выполняется условие (11).
Если у = —2, то х = 4 и пара чисел (4; —2) — решение
данной системы.
§3. Системы логарифмических и показательных уравнений	253
б)	Если справедливо равенство (9) и условия (11), то у>3 и у<2,
что невозможно.
Ответ. (4; —2).	▲
Пример 9. Решить систему уравнений
' 2 log2(x + 2у) = log! (х + 2у)  log, (х - у) + log|(x -«/),
<	3	3
х2 4- ху - 2у2 - 9.
Л Исходную систему запишем в виде
'(l°g3(x - у) - log3(x + 2z/)) (log3(x -у)+2 log3(x + 2у)) = 0, (12)
\х-у)(х + 2у)=Ъ.	(13)
Из уравнения (12) следует, что либо
х — у = х + 2у,	(14)
либо	о
(х —z/)(x + 2t/)2 = 1.	(15)
Если выполнены условия
х — у> 0, х + 2у > 0,	(16)
то система (12)—(13) равносильна совокупности систем (14), (13)
и (15), (13). Первая из этих систем имеет единственное решение
(3; 0), удовлетворяющее условиям (16), а вторая система равносильна
системе
Гх + 2г/=
1 х — у = 81,
для которой выполняются условия (16); она имеет решение
/1459.	728 \
К 27 ’	27 /
/о (1459	728 \	*
Ответ. (3; 0),	J .	▲
Пример 10. Решить систему неравенств
Г х2 + 2г/+2 г/4 — 4х + 13,
[ х2 — у2 < 4 — 2у+1.
Д Перепишем систему неравенств в виде
(у4-4х + 13-х2-2У+2 ^0,
( —г/2 + х2 — 4 + 2^+1 5^0.
Умножая второе неравенство на 2 и складывая с первым, получаем
следствие
у4 - 2г/2 + х2 - 4х + 5 О,
254
Глава XVII. Системы уравнений и неравенств различных типов
которое перепишем, выделяя полные квадраты:
(г/2 - I)2 + (х - 2)2 < 0.
Отсюда получаем систему уравнений
х — 2 = 0,
У2 - 1 = о,
которая имеет две пары решений (2; 1) и (2; -1).
Мы получили необходимые, но не достаточные условия на
решение задачи. Выполняя проверку, убеждаемся, что для пары
(2; 1) второе неравенство исходной системы не выполняется, а пара
(2; —1) является решением.
Ответ. (2; -1).	▲
Задачи
Решить системы уравнений (1-13).
.	. /2х+ 2‘-У = 12,
Ь 4 [х —у = 5;
Г 3х - 2^ = 77,
о) \	о
( (л/3)х - (л/2)^ =7;
9 П i ^gty + log х = 2,5,
2' [ху = 27;
3 в /	+у2) = 5>
12 log4 х + log2 у = 4.
4. I) /№-,,) 2'^-1
( 4 log3(3x - у) = 2у - х.
3х -3^ = 1,
Зх+// = 6:
31gx I 61gу = 0,
9 Igx — 61g у = 24
пч (х‘^ = 2,
’ [ху = 20.
2Ч / 3 l°g27 х + 2 logg у = 3 log3 2,
’ { х2 + у2 = 20.
2) ( (2х - у)  2х+2у = 14,
I log7(2x-y)=x + 2y.
5.
7*
9.
Г log3x - 2У + у = 3,
I у2у + 2У  log3 х = 4.
bxlog«x = x2’5,
(Jog3y • log^(y — 2х) = 1.
6* ( 6х2 + 17ху + 7у2 = 16,
I log2x+i/(3x + 7У) = 3-
( log2 х + log4 у + log4 z = 2,
8. < log3 у + logg z + log9 X = 2,
I log4 z + log16 x + log16 у = 2.
11.
12.
= X,
Zy = y,
yy =x.
1)
' l°g2 (б5 — 22+у>) = 4 — у,
10g2 у-*& + 6 = 10g2 (X ~	“ 10g2 (2 “	’
' 2х + 2y + 2Z = 7,
2-x 4-2_y + 2-z = -,
4
ч x + y + z = 3.
2)
' 2xy - 2 • 4хг + 64 = 0,
< 2^<x+z) + 2 • 2x^+z> - 20 • 2xy = 0.
ч 2^ + 2г<х+«) - 24  2yz = 0
/(I) 1,5* + >og^=702,
9X-3X-1 log3^y+lo^y=117.
13.
< log3(^-+x)+logi
, log2|x+i/| = l-
Zu2 \
(—+«/) =2,
\ X /
§3. Системы логарифмических и показательных уравнений
255
14. Найти решения системы уравнений
' log2 (Зг/ - Зх + 1) - log4(x - Зу)2 = 1,
l°g2 ~ ~ -	~ 10g4 X2 = 1’
удовлетворяющие неравенству х — Зу < 0.
Решить систему уравнений (15-19):
С ох+jr+l , ]fi оу—3 = ,n	log2(-X + 2y-5) = log3(2x —у) - 1
15.	дг—4	,	16. { log2(3x-2y + l) log3(2x + y-4)’
lv2x + y2 = x + y.	( у2+xy + 1 = 2x2+2y + x.
( (x-4)(x+l)=y(y + 5),
17	I logx-2(2 + //) = ^.
1	у
18	(lod(x +У) + *ogj (x + y)- bgi (x - 2y) = 2 log|(x - 2y),
[ x2 - xy - 2y2 = 4.
19.	/ log3(xz/) xy
I Iog3(3 + ХУ) “ 21о&9 У = IoS3 (У “ 0 •
20.	Найти все значения параметра а, при которых система уравнений не имеет
решений:
1)	( (15-а2) •3i/-5-log4x = 4a + 5,	~ Г (а2 + з)-2x-3-log5y = 5a-6,
[ 2-3^4-log4x = 3;	[ 4-2х — 3 = log5у.
21.	Найти все значения параметра а, при которых система уравнений
г ^х+у _|_ з*+31/ _ з
» | Зу + 3-Зх-Зй = за’-2х имеет решение;
{2*4-// _ 22х~у = 1 — 2а
24х _ 2х+Зу+1 = з. 2а+2у _ 22у+2 имеет единственное решение.
22.	Найти все значения параметра а, при которых данная система уравнений
имеет ровно два решения:
n f log2(3 - X + у) + 3 = log2(25 - 6х + 7у),
[ у + 2 = (х — 2а)2 +а + 2х;
2)	Г log3(2 - х - у) + 2 = log3 (17 - 8х - 10г/),
( (х — a)2 + x = z/ + a + 6.
23.	Определить, при каком значении параметра а имеет единственное решение
система неравенств:
Г^-б-^+^+ЧО,	2) (эх-у-Зх+а + 9а>0,
I l°g2(% + я) 2;	log j (х + а) О,
3
24? Решить систему неравенств
Г 2х2 - log2(z/x/2 + 6)3 - 16	z/4 - Зх - у2,
1 х2 -у2	log2(уу/2 + 6) 4-х + 1.
256
Глава XVII. Системы уравнений и неравенств различных типов
Ответы
1. 1) (3;-2),(2;-3);2) (l;log32);3) (4;->/2); (4;V2); 4) (100;0,1). 2. 1) (3;9),
(9; 3); 2) (2; 10), (10; 2). 3. 1) (4,4); 2) (2; 4), (4; 2). 4. 1) (2; 3); 2) (3;-1).
5. (81, 0).	6-(п;1т)- Указание- 6х2 + 17хг/ + 7«/2 = (2х + </)(Зх + 7^).
7. (3; 9). Указание. Прологарифмировать первое уравнение по основа-
НИЮ х. 8.	у) .	9. (1; 1; 1), (4; 2; д/2).	10. х Е (1; 2) при
у = -2; (1,5; 4). И. 1) (0; 1; 2), (1; 0; 2), (1; 2; 0),(2; 1; 0),(0; 2; 1),(2; 0; 1);
2) (3;2;1),(-3;-2;-1). 12. (2;1). 13. (|; 1) , (-3; 1). 14. (1-л/З; -^) .
15. (0; log3 . (21og38—4; 3—log38).	16.	+	17. (6; 2).
18- (т; т)’(2;°). 19-	20. 1) а>5; 2) а^-З. 21. 1) а>-1;
2) а = 0 и 1 ^a<log2(5 + V5)-l. 22. 1) аё(-1;3); 2) а&(-5;	
23* 1) а = 2; 2) а = 0. 24. (3; х/2). Указание Умножить на —3 второе
неравенство и сложить с первым.
§4. СИСТЕМЫ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
И НЕРАВЕНСТВ
Системами тригонометрических уравнений называют системы
уравнений, содержащие либо только тригонометрические уравнения,
либо тригонометрические и алгебраические уравнения (смешанные
системы).
К системам тригонометрических уравнений, а также к смешанным
системам применимы общие методы решения систем. Разберем
некоторые приемы решения.
Иногда в случае решения систем уравнений смешанного типа
удается выразить одно неизвестное через другое и свести задачу
к решению одного тригонометрического уравнения
Пример 1. Решить систему уравнений
cos х + cos у = х/3,
х+У=1
А Из второго уравнения у = — х. Подставим в первое уравнение:
О
cosx + cos — х) = л/3. Получили тригонометрическое уравнение
относительно х. Для его решения преобразуем сумму косинусов
в произведение:
2 cos £ cos (х —	= х/3 О cosfx —^ = 1 о х — ^=2т, nch.
6	\	6/	х 6/	6
§4. Системы тригонометрических уравнений и неравенств	257
Отсюда х = | + 2m, у — - 2m, neZ.
Ответ. (^ + 2m:> %—2m\ n^Z.	▲
\6	6	/
Следует обратить внимание на одну особенность тригонометри-
ческих систем, связанную с появлением в их решении параметров.
В рассмотренном примере все решения записаны с помощью одного
параметра п е Z. Обычно при решении систем тригонометрических
уравнений с двумя переменными для записи решений требуется два
целочисленных параметра.
Пример 2. Решить систему уравнений
sin (х + у) = О,
sin (х — у) = 0.
Д Из первого уравнения системы получаем
х + у = лп, n е Z,
а из второго следует
х — у = nk, keZ,
Следовательно, исходная система равносильна совокупности систем
вида
{х + у = т,
х — у = тгй,
, п. k е Z.
где п и k — произвольные целые числа, т. е. и, k е Z.
Решая полученную систему, находим х =	у =
п, й е Z.
г\	( л(п 4- k)
Ответ.
Замечание. Было бы ошибкой рассматривать вместо второго уравнения
исходной системы уравнение х — у = кп, п eZ, так как в этом случае получилась
бы система
х + г/ _ im, решения такой системы имеют вид (тип; 0),nGZ,
и не исчерпывают всех решений исходной системы. Так, например, пара чисел
(2щ тс) является ее решением, но не представляется в виде (тглг; 0),neZ.
Дело в том, что параметры п и k появляются при решении разных уравнений
системы, независимо друг от друга, и поэтому должны обозначаться разными
символами.
Иногда удается систему тригонометрических уравнений свести
к системе алгебраических уравнений. Например, если систему
удается свести к системе уравнений, содержащих только две
тригонометрические функции или комбинации тригонометрических
функций, то можно применить метод введения новых неизвестных.
9—3022
258
Глава XVII. Системы уравнений и неравенств различных типов
Пример 3. Решить систему уравнений
' COS X, + cos у — 1,
cos + cos |	- 1.
Л Для решения данной системы воспользуемся формулами
cosx = 2cos2 | - 1, cosy = 2cos2 | — 1. Перепишем систему в виде
2 cos2 + 2 cos2 | = 3,
cos^ + cos| = ^-l.
Используя замену tz = cos|, u = cos|, получим систему алгебраи-
ческих уравнений
ы2 +v2 = 3
Л + о = 2Г-1’
имеющую две пары решений (и; у):	—А и (—1;
Выполняя обратную замену, в первом случае получаем
V5
2 ’
cos | =
cos | — -1.
Откуда следует х =	+ 4m. у = 2 л + 4л&, n. k е Z.
Во втором случае:
cos| = -1,
2	./о
т. е. х — 2л + 4m. у —	+ 4л&, n. k € Z.
Ответ. + 4m; 2л + 4л&) , ^2л + 4т;	+ 4л&), n. k € Z.
Пример 4. Решить систему уравнений
( cos х — sin х = 1 + cos у — sin у,
[ 3 sin 2х — 2 sin 2у = 0,75.
Д Воспользуемся тождеством (cosx — sinx)2 = 1 — sin2х и обозначим
cos х — sin х — щ cos у — sin у = v.
§4. Системы тригонометрических уравнений и неравенств
259
Тогда sin2x = l —u2, sin 2г/ = 1 — и2, и исходная система сводится
к виду
( U = I + v,
| Зы2 - 2у2 = 0,25.
Решая эту систему уравнений методом подстановки, получаем два
решения (ад uj) = (—4,5; -5,5) и (ад — (0,5; —0,5).
Возвращаясь к исходным переменным, заметим, что для первой
пары чисел (щ; гц) = (—4,5; —5,5) система уравнений
( cos х — sin х = —4,5,
( cos у — sin у = —5,5
не имеет решений, так как справедливы неравенства
—д/2 cosx — sinx < х/2 и — л/2 < cosy — sin у < \/2.
Для второй пары чисел (ад V2) = (0,5; —0,5) получаем
{cosx — sinx = 0,5,
cosy — sin у = —0,5.
Используя метод введения дополнительного угла, приведем получен-
ную систему уравнений к виду
,'c°s(x+?) = t-
,C0S(s + j) = _t-
Отсюда
х + 7 = ± arccos + 2тгп, п е Z,
4	4
а
у + 7 = ± arccos + 2я£, k е Z.
4	\	4 )	’
Запишем окончательный ответ.
Ответ. f—7 ± arccos^ 4- 2лтг; + arccos^ 4- 2тг&У
\ 4	4	’4	4	/
(— 7 ± arccos 4- 2тгп; —— arccos 4- 2^, n, k е Z.	▲
\ 4	4	4	4	/	’
В некоторых случаях с помощью преобразований уравнений
системы удается получить уравнения, содержащие только одну
переменную или одну комбинацию неизвестных.
Пример 5. Решить систему уравнений
( sinxsinz/ = 0,75,
1 tg x tg у = 3.
260
Глава XVII. Системы уравнений и неравенств различных типов
А Отметим, что cosх cosy ф 0, и перепишем систему в виде
sinx sin у — 0,75,
sin х sin у = 3 cos х cos у.
Отсюда получаем
sinx sin у = 0,75,
cosx cos у — 0,25.
Складывая уравнения системы и вычитая из второго уравнения
первое, получим
( cos(x — у) = 1,
( cos(x + у) = —0,5.
Ответ. (±^ + тг(п + Л);
\ о	<5
Следовательно, х — у — 2тт, х + у =	+ 2nk, n, k Е 1 Снова
складывая и вычитая эти равенства, получим окончательный ответ.
+ 7t(k — л)), n, k е Z.	▲
В ряде случаев тригонометрические системы с помощью почлен-
ного сложения, вычитания, умножения, деления удается свести к
более простым системам. Однако некоторые преобразования могут
приводить к потере решений или к появлению посторонних значений
переменных.
Например, в некоторых случаях систему можно привести к виду:
Г sin х =/(</),	l'tgx = №),
(cosx=gQ/)	(ctgx = g(i/).
Тогда в случае (1) из основного тригонометрического тождества
sin1 2х + cos2х = 1 получаем уравнение f2(y) + g2(y) = 1, содержащее
только переменную у, В случае (2) из равенства tg х • ctg х = 1
следует соотношение f(y) -g(y) = 1.
При таких способах решений необходимо следить за тем, чтобы
не потерять и не приобрести посторонних решений.
Пример 6. Решить систему уравнений
Г 4 sinx — 2 sin у = 3,
[ 2cosx — cosy = 0.
А Приведем систему к виду
< .	4	1.
sin X = j + sin I/,
1
k COSX - - cosy.
§4. Системы тригонометрических уравнений и неравенств
261
Возводя левые и правые части уравнений полученной системы
в квадрат и почленно складывая, получим уравнение, являющееся
следствием исходной системы:
О Q	19	19	1
l = -^ + Jsini/4-^sinzz/4-lcos2i/ sin^=_.
Отсюда у = (—1)"arcsin | + тт, nel.
Тогда из первого уравнения исходной системы с учетом получен-
ного решения находим sinx = |, откуда х = (—1)^ arcsin | + тг£, k EZ.
Поскольку при использовании операции возведения в квадрат
левых и правых частей исходной системы могли появиться посто-
ронние корни, необходимо произвести отбор, подставив найденные
решения в исходную систему уравнений.
Заметим, что из уравнения cosx = cos у следует, что cosx
и cosy принимают значения одного знака, т. е. при четных п и k
положительны, а при нечетных п и k отрицательны. Кроме того, из
7-1	II Л ' 2 '
равенств sinx=^ и siny=- следует, что |cosx| = V1 — sinzх =
о	4	о
и |cosy| = -—.
С учетом этих замечаний получаем две серии решений
Ответ, (arcsin + 2тгЛг; arcsin | + 2тт^ ,
(— arcsin | + (2k + 1)тг; — arcsin | + (2п + 1)тг), п, k С. Z.	А
Иногда при решении систем тригонометрических уравнений можно
использовать метод оценки.
Пример 7. Решить систему уравнений
( cosx — arccosy = 1,
[ cos(Tuy) - arcsinx = —1.
А Приведем первое уравнение к виду cosx = 1 + arccosy.
Так как 0 С arccosу С к, то последнее равенство возможно только
в случае cosx=l, arccosy = 0, т. е. при х = 2тгя, п е Z, у=1.
Из полученных значений для переменной х только значение х = 0
входит в область определения функции arcsinx Далее убеждаемся,
что пара х = 0, у = 1 удовлетворяет и второму уравнению системы.
Ответ. (0; 1).	А
Пример 8. Решить систему неравенств
( sin х — cos у > х/2,
( sin у + cosx < —д/2.
262
Глава XVII. Системы уравнений и неравенств различных типов
А Вычтем из первого неравенства второе:
(sin х — cosx) — (cosу + sin у) 2\/2.
Преобразуем это неравенство:
2 cos
—2.
<=> cos (х + у ) + cos
к 4/
Такое неравенство возможно в том и только в том случае, если
cos
Отсюда		получаем х =	+ 2тш, у —		+ 2nk, где n, k e Z.	
	Ответ. х = ^+2тгп, 4		y=^ + 2nk,	( /2, k C. zZ.	
			Задачи		
Решить		систему уравнений (1-	-19):		
1.	1) -	(	5л 1 х — у = —, *	3 ’ ( sinx = 2sinу\	2) J	f X-y= ( sinx • cosy = 0,5.	
2.	1) <	[ cos(x-«/)= ( cos(x 4- у) = 0;	2)	[ sin (2x4- 3r/) = 0, [ cos(3x — 2y) = 1;	
	3) <	( sin(2x 4- у} = 0, [ cos(x 4- у) = 1,	—7t	X Л, -	-2tu у —7Г.	
3.	1) <	[ sinxcosz/ = 0,25, 1 sin у cosx = 0,75;	2) <	( .	V3 sinxsin у =	, 4’ V3 cosx cos у =	.	
4.	1) <	f 3x4-4sini/ = —11, 1 -2x4- 5 sin у = 3,5;	2) ]	f sin(2x + sin2#) = L x — sin2 у = 3.	o,
5.	1) <	f sinx — sin у = 0,5, \/3 ( cosx 4- cosy = —;	2) <	2 sin x 4- 3 cos у = 2 cosx 4- 3 sin у =	5 x/2’ 5
	( х+у х—у 1 1 РАС	- Г*ПС 	_				
6.	<	2	2	2				
4 cosx cosy = 1.
7.
6 sinх cos г/4-2 cosx sin^/ = —3,
5 sinx cost/ — 3cosxsinr/ = l;	'
9 cos x cos у — 5 sin x sin у — —6,
7 cosx cos у — 3 sinx sin у = —4.
§4. Системы тригонометрических уравнений и неравенств
263
8 Г 2 sinx sin у 4-3 cos 2х = 1,
t tgx ctg//=-1.
10? Itef+tef = 2’
[ ctg x 4-ctg// = -1,8.
11* 1) f 8cosx — 2sin//= 9,
' [ 4 sinx 4- cos у = 0;
{sinx — arcsin// = — 1 —
2’
cos — arcsin - = J;
2	7C 6
9.
sin 2x sin у 4- sin x cos у = ,
cos 2x sin//4-cosx cos// = -~
( 6 cos x 4- 4 cos у = 5,
[ 3sinx 4-2sin// = 0.
cosx 4- arccos// =	— 1,
. щ	, x	1
sin -4	4- arccos -	=	- .
6	л	2
13Г
arccos 2y 4- arcsin 3x = ^,
arcsin 2y • arccos 3x =	.
*	64
14Г 1)
15? 1)
{2 sin(2x 4- y) sin у — cos 2x,
sin 2x — sin 2y = \/2;
I sin ^3x4-j = sin// — cos//,
sin 2//4-2 sin 2= 14-sin3 2x;
Г 3 cos 3x = sin(x 4- 2//),
' [ 3 sin(2x 4- y) = - cos 3//
( | cos 3x | = sin у 4- cos y,
[ 2 sin2 2x cos 2x 4- - = — sin 2y,
16.
sinx __________1
cos(x-|-//)	x/2’
COS// _ _1
k cos(x4-//)	V2‘
17? 1) f3ctgx = tg3^
7 [ cos x = sin 2//;
2)
ctg4 2x 4- 32 sin2 у = 55,
—1— —4 cos у = 5.
sinz 2x
{i/13cosx4-98sin у — a/13cosx4-28 sin// = 4,
2^/13 cosx 4-28 sin// - -/70 sin//4-8 = 2.
19.
1)
' 3 tg x 4- 40 log3 //2 = 163,
^2
cosx
< l°g^9
Г 2*2-2х1/4-1—
I cos(5rcz) = — 1,
где x, у e Z.
20. Найти все значения параметра а, при которых имеет решения система
уравнений
(4л 4~ х)2 4" у^ 4" 3 = 2&,
Y/log2(l 4-c°sx) - 1 4- //x/З = a.
Найти эти решения.
264
Глава XVII. Системы уравнений и неравенств различных типов
Решить системы неравенств (21-23):
21 (sinx + cosO'/2, 22 l'^/3sinx>2sinf/-cosx,
( sin у 4- cos х д/2.	’	— х =
* ( 6 д/З cos 4х — 3 cos 8х > 41 -5~^ - 25~у + 39,5,
| 7f(vz2 + \/3)_4y +	+ 2 + 101og2(cos8x)+4v/2sin4x>{/+3.
24? При каких значениях параметра р система
Г х2 4- 2рх + Зр2 + Зр 4- 3	3 sin у — 4 cos р,
I 0 у 2л
имеет единственное решение?
Ответы
1. 1) (|(2*4-3); -| + ^), k е Z; 2) (g + я*; nk), + g + J^) ,
keZ. 2.1) (| + |(2n+A); | + ^-2n)), (| + |(2n+A); 5 + 5(Л-2л)),
n, k e Z; 2) (А(2й+6л); ^(Зй-4п)), n, k € Z; 3) (-Щ -n),
(0; -2k), (щ -k).	3. 1) (|-(-l)*A +2*+даг; 5 + (-l)^-y+ ™).
s, «ez. 2) («(|+«+l); ,(^«+A)). („(t+„+!);
k, n € Z. 4. 1) x = -3, у = (-l)n+1g + wi, n e Z; 2) x = у =
= ±1 arccos + m, n e Z. 5. 1) (|+2roi; |+2лй), (-|+2лп;
-5+2zrfe), fe.neZ; 2) (|+2wi; |+2nfe), ft, nGZ. 6. (±|+2лэт; ±|+2яб),
k, neZ. 7.1) (-5 + (-l)*A + ^ + wz; -2I-(-l)*A - f + w), k, n G Z.
2) (^+я(/г+/г); | + л(Л-/1)),	(| + я(п+й); ^-7г(/г-л)), k, n 6 Z.
8. (zrfeig; 2яй-лпт|). (^±|; 2тЛ-кпт^), k, n e Z. 9. (§ + y;
| + к(2л-й)}, (l + nk; (-1)*+1^+л(2п-й)), (д + я/г; л(2п-Й)), k, n 6 Z.
10. (2arctg2,5+2Trn; —2 arctg 0,54-2^)	(—2 arctg 0,54-2?rn; 2arctg2,54-2rc/e),
k, n € Z. Указание. Воспользоваться тем, что ctg 2<р = *~.
Б r 2tg<p
И. 1) ((-l)n+I arccos ^4-2л£; (-1)л+1 arcsin 4- ля), k, n€Z. Указа-
т,	f 8cosx = 2sinp4-9,
ние. Из системы получаем < 8sinx — — 2cosp Отсюда следует, что
(2sinp 4- 9)2 4- (—2cosp)2 = 64. Обратить внимание на то, что sinx
и cosy должны быть разных знаков. 2) (arccos 14-2л/г; — arccos 4-2лп),
(-arccos 14-2я/г; arccos 14-2ля), k, я е Z. 12. 1)	1) ; 2) (л; 1).
13. (— У^2~^j ^2~# Указание. Воспользоваться тождеством
§4. Системы тригонометрических уравнений и неравенств
265
arccosa=£ —arcsina. 14. 1)	+	— 5+	+ zm; -^ + zr/eY/г, neZ.
z	\o	o/\o	о /
Указание. Первое уравнение преобразовать к виду sin2xsin2r/=cos2xcos2z/.
2) arctg| + ^4-y-Нтт; | arctg^ + y) ,/г, neZ. Указание. Перемножить
уравнения системы «крест-накрест» и преобразовать полученные в обеих
частях равенства в сумму и разность косинусов. 15. 1) ((—+ у J
+ (— 1/^4-тт/г) , /г, п е Z. Указание. Перемножить уравнения системы
«крест-накрест» и преобразовать полученные в обеих частях равенства в сумму
и разность косинусов. 2) (db^+zu/г; —	l)^4-zu/?),/г, nGZ. 16. ^4-2zrn;
^+2тг*г), (-^ + 2да; ^ + 2^), k,neZ. 17. 1) (^ + л/г; тот), ((-1)^ + тг/г;
(—, k, п € Z. Указание. Составить уравнение относительно
cos2</. 2)	±i arctgл/5; 2nA±arccos |), k, п € Z. 18. (±arccos |+2тгй;
(-1)" arcsin 1+mY k,neZ. 19. 1) x=^+m, neZ, y=9; 2)
20. a = 3, x = -4n, y=Jb. 21. (J+2tot; ^+2тй), k, neZ. 22. (a;a+|),
где aeR. 23. y= — 1, x=^ + y’ n€Z. Указание. Максимальное значение
выражения 6\/3cos4x—3cos8x совпадает с минимальным значением выражения
41,5“^_25~^+39,5. 24. р—-2,р— i. Указание. Убедиться, что 3sinу-4cosy
равно 5 или —5 (иначе не будет единственности решения).
Глава XVIII
УРАВНЕНИЯ И НЕРАВЕНСТВА
С ДВУМЯ ПЕРЕМЕННЫМИ
§ 1. ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА С ДВУМЯ
ПЕРЕМЕННЫМИ
1. Линейные уравнения с двумя переменными
Пусть на плоскости дана прямоугольная система координат Оху.
Тогда уравнение
у — tixb	(1)
определяет прямую I (рис. 1), пересекающую ось Оу в точке 714(0; 6)
и образующую угол а с положительным направлением оси Ох, где
tg а = k — угловой коэффициент прямой I.
Чтобы построить прямую /, заданную уравнением (1), достаточно
найти две точки этой прямой. На рис. 2 изображены прямые 1[ и 1%,
заданные соответственно уравнениями
у— |х + 2 и у — ~ х-1.
Рассмотрим уравнение
Ах + By + С =	(2)
предполагая, что хотя бы одно из чисел А, В отлично от нуля
(А2 + В2>0).
Пусть В 0, тогда уравнение (2) можно записать в виде
и = -^х-^
у в в'
§1. Линейные уравнения и неравенства с двумя переменными
267
т. е. в виде (1), где
»=-£, b=~l-
Если В — 0 и А ф О, то уравнение (2), которое можно записать
в виде х = — j, есть уравнение прямой, параллельной оси Оу.
Таким образом, при любых А, В, С таких, что Д2 + В2 > О,
уравнение (2) является уравнением некоторой прямой.
2. Линейные неравенства с двумя переменными
Пример 1. Дать геометрическое опи-
сание множества точек координатной
плоскости, удовлетворяющих неравенству
Зу — 2х — 6 < 0.
А Уравнением Зу — 2х — 6 = 0 задается
прямая (рис. 3), проходящая через точки
(—3; 0) и (0;2). Пусть Ali(xi;yi) — точка,
расположенная ниже прямой /, а М2(х\\у2) — точка с абсциссой х\
и ординатой у2, лежащая на прямой Z. Тогда
2у2 — Зх] — 6 = 0, 2z/i — 3%1 — 6 < 0,
так как у\ < у2-
Аналогично, в любой точке 7И(х;у), лежащей ниже прямой /,
выполняется неравенство 2у — Зх — 6 < 0, а в любой точке 7W(x;y),
лежащей выше прямой /, справедливо неравенство 2у — Зх — 6>0. ▲
Рассмотрим неравенство
Ах -|- By + С < 0,	(3)
считая, что А2 + В2 > 0.
Как и в примере 1, возьмем точки (они лежат на прямой,
параллельной оси Оу) Ali(xj; yi) и M2(xi;y2) такие, что Afi лежит
ниже прямой /, заданной уравнением (2), а М2 — на этой прямой,
тогда yi < у2.
Если В > 0, то Ву\ < Ву2 и поэтому
Ах[ + Ву\ + С < 0,
т. е. координата точки Afi удовлетворяет неравенству (3). Этому
неравенству удовлетворяют координаты любой точки, расположенной
ниже прямой /, если В > 0.
Если В < 0, то неравенству (3) удовлетворяют координаты любой
точки, лежащей выше прямой I.
Если В — 0 (Д ф 0), то неравенство (3) примет вид
Дх + С < 0.
268
Глава XVIII Уравнения и неравенства с двумя переменными
Это неравенство равносильно неравенству
х < — j при А > О
и неравенству
х > — при А < 0.
Например, неравенство Зх + 4<0, равносильное неравенству х<—
О
4
выполняется во всех точках, лежащих слева от прямой х — — -.
Таким образом, прямая, заданная уравнением (2), разбивает
плоскость на две полуплоскости такие, что во всех точках одной
из этих полуплоскостей выполняется неравенство (3), а в другой —
неравенство
Ах 4" By 4- С > 0.	(4)
Чтобы решить неравенство (3) или нера-
венство (4), т. е. чтобы определить, в какой
из полуплоскостей оно справедливо, доста-
точно определить знак левой части этого
неравенства в какой-либо точке одной из
полуплоскостей.
Если С 7^ 0 (прямая не проходит через
начало координат), то в качестве такой точки
удобно взять точку (0;0).
Например, неравенство
5% - Зу - 15 < 0
при х — у — 0 является верным. Поэтому
оно выполняется во всех точках той из
полуплоскостей (их общая граница — прямая 5х — Зу —15 = 0), которая
содержит точку (0;0). Эта полуплоскость отмечена серым цветом
на рис. 4.
3. Системы линейных неравенств с двумя переменными
Рассмотрим систему неравенств
( А[Х 4- В\у 4- Ci >0,
I /12^ + &2У 4- ^2 > 0,
предполагая, что А^ + В^ >0, А% + В%>0. Тогда первому неравенству
системы (5) удовлетворяют точки множества Afj, лежащие по одну
сторону от прямой /[, заданной уравнением AfX 4- В\у 4-	= 0.
Аналогично второе неравенство системы (5) является верным
на множестве М2 — одной из полуплоскостей, на которые разби-
вается координатная плоскость прямой I2, заданной уравнением
А2Х 4- В2У 4- С2 = 0.
§ 1. Линейные уравнения и неравенства с двумя переменными
269
Множество решений системы (5) — пересечение множеств THj
и М2.
Если прямые 1\ и I2 пересекаются в точке А, то множество решений
системы (5) — множество точек, расположенных внутри одного из
четырех вертикальных углов с вершиной в точке А.
Пример 2. Решить систему неравенств
Г 2х — Зу + 6 > О,
1 х + у + 1 < 0.
(6)
Л Найдем точку А, в которой пересекаются
прямые /] и /2, заданные соответственно урав-
нениями
2х — Зу + 6 = О,
х + у + 1 = 0.
Решив систему (7), найдем, что прямые 1\
и I2 пересекаются в точке А	Так
(7)
Рис. 5
как координаты точки 0(0; 0) удовлетворяют
первому неравенству системы (6) и не удовлетворяют второму
неравенству, то системе (6) удовлетворяют координаты тех и только
тех точек, которые лежат ниже прямой 1\ и ниже прямой /2, т. е.
точки угла с вершиной Л, содержащего точку (—2;0), см. рис. 5. А
Рассмотрим неравенство вида
(Л]Х + В\у + С1)(Д2х + ^2У + О>) > 0,	(8)
предполагая, что прямые 1\ и /2, заданные соответственно уравне-
ниями
А[Х + В\у + 6*1 — 0,	(9)
Л2х + В2У + С2 = О,	(Ю)
пересекаются в точке А.
Покажем, что множество решений неравенства (8) является либо
объединением вертикальных углов Mi и Л12 с вершиной А (рис. 6),
либо объединением двух других вертикальных углов Ni и N2 с той
же вершиной.
В самом деле, во всех точках каждого из множеств М\, N\, М2,
N2 левая часть неравенства (8) принимает либо положительные,
либо отрицательные значения, а при переходе от одного из всех
этих множеств к соседним (через одну из прямых 1\, /2) знак левой
части этого неравенства меняется на противоположный.
270
Глава XVIII. Уравнения и неравенства с двумя переменными
Рис. 6
Рис. 7
Если, например, на множестве М\ левая часть неравенства (8)
положительна, то на множествах и N2 она будет отрицательной,
а на ~ положительной.
Чтобы определить, на каком из двух множеств М\ U М2 или
TViUA^ справедливо неравенство (8), достаточно определить знак
левой части этого неравенства в какой-либо точке одного из множеств
Л11, М2, Л/i, Л^2-
Пример 3. Решить неравенство
(г/-х-2)(Зх + г/-6)>0.	(11)
Д Прямые у — х — 2 = 0 и Зх + у — 6 = 0 пересекаются в точке А (1; 3).
Первая из этих прямых проходит через точки С(—2;0) и £>(0;2),
вторая —через точки Е(2; 0) и F(0;6).
На рис. 7 угол Afi (содержит точку О) и угол М2 составляют одну
пару вертикальных углов с вершиной А\ N\ и —другую пару.
В точке ОеЛ41 левая часть неравенства (11) положительна, и поэтому
множество решений неравенства (11) — объединение множеств М\
и М2.	А
Пример 4. Найти площадь фигуры Ф, координаты точек которой
удовлетворяют системе неравенств
' х О,
<	(12)
х — у+ 2 О,
< Зх + у — 6 0.
Д Первым двум неравенствам системы удовлетворяют все точки
первого квадранта (включая его границу), третьему— точки, лежа-
щие ниже прямой 1\ и на этой прямой (рис. 7), а четвертому— точки,
лежащие ниже прямой /2 и на этой прямой (рис. 7).
§1. Линейные уравнения и неравенства с двумя переменными
271
Следовательно, множество решений системы (12) (фигура Ф) —
четырехугольник OEAD.
Пусть Si, S2 и S — площади треугольников OEF, DAF и фигуры Ф
соответственно.
Тогда
$1=6, $2 = 1dF-1 = 2, S = S,-S2 = 4.	▲
Пример 5. Пусть Ф — множество точек плоскости с координатами
(х;у) таких, что числа Зх, 2у и 9 — у являются длинами сторон
некоторого треугольника. Найти площадь фигуры Ф.
А По свойству длин сторон треугольника справедливы неравенства,
образующие систему неравенств
' 0 < Зх < 2у + 9 - у,
< 0 < 2у < Зх + 9 - у,
. О < 9 — у < Зх + 2у.
Эта система равносильна системе неравенств
г у — Зх + 9 > О,
у - х - 3 < О,
х + у — 3 > О,
< х > 0, у > 0, у < 9.
Пусть /1, /2 и /з~пРямые (рис. 8),
заданные соответственно уравнениями
у — Зх + 9 — 0, у — х — 3 = 0, х+у —3 = 0.
Прямые 1\ и /2 пересекаются в точке
А (6; 9), прямые /2 и /3 пересекаются в точке
В(0;3), а прямые /3 и — в точке С(3;0).
Системе неравенств (13) удовлетворяют
точки, расположенные внутри треуголь-
ника АВС.
Пусть D и Е — проекции точки А на
оси Ох и Оу соответственно, тогда £>(6;0), £(0; 9). Если S —
площадь фигуры Ф, Si, S2, S3 —площади треугольников ОВС, ACD
и ВАЕ соответственно, a S4 — площадь прямоугольника ODAE, то
S = S4 — (Si + S2 + S3). Так как
S4 = 9.6 = 54, $i = l-32 = |, $2 = 1.3-9 = ^, $з = 1-62 = 18,
то S = 18. Итак, искомая площадь равна 18	▲
272
Глава XVIII. Уравнения и неравенства с двумя переменными
Пример 6. Найти все пары целых чисел х,у, удовлетворяющих
системе неравенств
г Зу — 2х < 45,
< х + у > 24,	(14)
. Зх — у < 3.
Л ’Эту задачу можно решить, изобразив фигуру Ф, координаты точек
которой удовлетворяют системе неравенств (14), а затем найти точки
с целыми координатами, принадлежащие фигуре Ф.
Рассмотрим другой способ решения
Умножая третье неравенство на 3 и складывая с первым, получаем
7х < 54, откуда
'<4
Умножая второе неравенство на —3 и складывая с первым, находим
—5% < —27, откуда
х 5—.
5
Итак, из условия целочисленности переменной х вытекает, что
6 < х < 7, т. е. х = 6 или х = 7.
При х = 6 из первых двух неравенств системы (14) получаем
18 < у < 19, что не выполняется ни при каком целом у. При х = 1
получим у = 19. Следовательно, система (14) имеет единственное
целочисленное решение (7; 19).	к
Задачи
1.	Найти множество точек (х;у) координатной плоскости, удовлетворяющих
неравенству:
1) Зх - 2у 4- 6 > 0;	2) Зх - 4у - 12 < 0.
2.	Решить систему неравенств:
х + у — 4 < 0,
Зх — 4у - 12 < 0;
х + у 2,
2)
2у - х - 1 < 0,
2-х-у > 0;
4)
х — Зу + 2 0;
' х + 6 — 2у 0,
< 2х — у + 2 0,
3.	Найти все пары натуральных чисел х,у, удовлетворяющие системе неравенств:
f х + 2у > 9,
< х — у < 2,
k 2у — х < 3;
2)
г х + у — 8 < О,
< х - 2у + 4 > О,
ч х + Зу — 11 > 0.
4.	Решить неравенство:
1) (х + у — 4)(3х —4у — 12) > 0;
3) х2 +ху — 2у2	0;
2) (х + у- 1)(х —у + 3) О,
4) Зх2 + 5ху — 2у2 > О
§2. Нелинейные уравнения и неравенства с двумя переменными
273
5.	Найти все пары натуральных чисел х,г/, удовлетворяющие системе неравенств:
!3у — 5х — 16 > О,
Зу- х — 44 < О,
Зх — у — 1 > 0;
f х 4- у - 26 > О,
2) < Зу — х — 5 < О,
к Зх — 2у — 46 < О
6.	Пусть Ф — множество точек с координатами (х; у) таких, что числа х, у
и 6 —2х являются длинами сторон некоторого треугольника Найти площадь
фигуры Ф.
7.	Пусть Ф — множество точек с координатами (х;у) таких, что числа 2х, у
и 3 — х являются длинами сторон некоторого треугольника Найти площадь
фигуры Ф.
Ответы
1. 1) Множество точек, расположенных ниже прямой, проходящей через точки
(—2;0) и (0;3); 2) множество точек, расположенных выше прямой, проходящей
через точки (4;0) и (0;—3). 2. 1) Угол с вершиной (4;0), образованный
Q
прямыми у = 4 — х и у=-х — 3, содержащий точку (0; 0), без границы; 2) угол
с вершиной (1;1), образованный прямыми 2у — х — 1 = 0 и у —2 — х, содержащий
точку (0;0), без границы; 3) треугольник с вершинами (1; 1), (4; 2) и (2; 0);
4) треугольник с вершинами (—6;0), Qly) и (—1;0)« 3. 1) (4;3); 2) (4;3).
4. 1) Два вертикальных угла без границы с вершиной (4;0), образованных
прямыми х + у — 4 = 0 и Зх — 4у — 12 = 0; один из этих углов содержит точку
(0; 0); 2) два вертикальных угла с вершиной (—1;2), образованных прямыми
у—1 — х и у — х-у 3; один из этих углов содержит точку (0;0); 3) два
вертикальных угла с вершиной (0;0), образованных прямыми у — х и г/ = —
один из этих углов содержит точку (0;1); 4) два вертикальных угла без границы
с вершиной (0;0), образованных прямыми у = 3х и # = — один из этих углов
содержит точку (1;0). 5. 1) х = 6, у = 16; 2) х = 20, у = 8. 6. 6.	7. 6.
§2. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
С ДВУМЯ ПЕРЕМЕННЫМИ
1. Нелинейные уравнения с двумя переменными
Пример 1. Найти множество точек координатной плоскости,
удовлетворяющих уравнению:
1) у2 - 4х2 = 0;	2) 6х2 + ху - у2 = 0;
3) 4х2 — 4 — 4//— г/2 = 0;	4) 2х2 + Зг/2 - 8х + 18г/+ 35 = 0.
А 1) Запишем уравнение в виде
(у - 2х)(у + 2х) = 0.
Множество точек, удовлетворяющих этому уравнению, — со-
вокупность прямых
у = 2% и у = —2х.
274
Глава XVIII. Уравнения и неравенства с двумя переменными
2)	Разложим левую часть уравнения на множители-
9х2 - у2 - Зх2+ху—(Зх+у) (Зх - у) - х (Зх - у) = (Зх - у) (2х+у).
Искомое множество —совокупность прямых
Зх - у — 0 и 2х + у — 0.
3)	Запишем уравнение в виде
4х2 - {у + 2)2 = 0.
Этому уравнению удовлетворяют точки, лежащие на прямых
у + 2х + 2 = 0 и у — 2х + 2 = 0.
4)	Преобразуем левую часть уравнения, используя метод выде-
ления полного квадрата:
2(х2 - 4х + 4) + 3(у2 + бу + 9) = 0.
Тогда уравнение можно записать в виде
2(х - 2)2 + 3(г/ + З)2 = 0.
Это уравнение имеет единственное решение (2;—3).	▲
Пусть на координатной плоскости Оху выбрана точка A(a-,b),
Л4(х; у) — произвольная точка этой же плоскости, R — расстояние от
точки М до точки А. Тогда
(х - а)2 + (у - Ь)2 = R2.
Если задано число R > 0, то данное уравнение — это уравнение
окружности С радиуса R с центром в точке А (а; 6).
Пример 2. Найти множество точек координатной плоскости,
удовлетворяющих уравнению:
1) х2 + у2 — 4х + бу — 3 = 0;	2) х3у = 8у4.
А 1) Применяя метод выделения полного квадрата, получаем
х2 + у2 — 4х + бу — 3 = (х - 2)2 + (у + З)2 — 16 = 0,
или (х - 2)2 + (у + З)2 = 16.
Следовательно, множество решений данного уравнения —
окружность радиуса 4с центром в точке /4(2;—3).
2) Преобразуем уравнение:
х3у - 8у4 = у(х3 - 8г/3) = 0,
у(х - 2у)(х2 + 2ху + 4у2) = 0,
у(х - 2у)((х 4- у)2 + Зу2) = 0.
§2. Нелинейные уравнения и неравенства с двумя переменными
275
Так как равенство
(х + yf + 3у2 -О
выполняется только при х = 0 и у = 0, то множество решений
исходного уравнения — совокупность прямых у=Оих- 2у — 0.
Рассмотрим примеры уравнений с двумя переменными, содержа-
щих знак модуля.
Пример 3. Найти множество точек координатной плоскости,
удовлетворяющих уравнению:
1)	х-М=0;	2) И + Ы = 2;	3) \х\ + 2\у\ + \2у-3х\ = 12.
Л 1) Уравнение равносильно совокупности двух систем:
х — у — 0, С х + у = О,
у^О, t У < °-
Первой системе удовлетворяют точки, принадлежащие
биссектрисе I координатного угла, второй системе —точки,
принадлежащие биссектрисе IV координатного угла (рис. 9).
2)	Если х 0, у 0, то уравнение можно записать в виде
х + у —2. Множество решений этого уравнения — отрезок АВ,
где /1(2; 0), В(0; 2).
Так как | — х| = |х|, | - у\ = |у|, то множество решений
исходного уравнения — граница квадрата ABCD (рис. 10), где
С(—2;0), 0(0;-2).
Замечание. Для нахождения координат вершин квадрата нужно
в уравнении |х| + |i/| = 2 положить х = 0 (и тогда |г/| — 2, т. е. у = ±2),
а затем положить # = 0 (тогда х = ±2) Это связано с тем, что в точке, где
выражение под знаком модуля обращается в нуль, происходит «излом»
кривой.
3)	Множество решений уравнения — граница многоугольника.
Чтобы найти его вершины, нужно решить (см. замечание)
276
Глава XVIII. Уравнения и неравенства с двумя переменными
исходное уравнение, полагая в нем последовательно х = О,
у — 0, 2у — Зх = 0. Если х = 0, то из данного уравнения
следует, что |у| = 3, т. е. у — ±3.
Если у = 0, то |х| = 3; если у — |х, то |х| = 3, |у| —
Многоугольник А\С\В\А<2С%В<2, где
А1 (-3; 0), Л2(3;0),В,(0; -3),В2(0; 3), С, (-3; -|) , С2 (3; |) ,
изображен на рис. 11.	А
2. Нелинейные неравенства с двумя переменными
Если А (а; 6) —точка координатной плоскости, /? > 0, то неравен-
СТВУ	(x-a)2 * * * * * * + (i/-fe)2</?2
удовлетворяют все те точки, которые находятся от точки А на
расстоянии, меньшем /?, т. е. все точки (и только они), расположенные
внутри окружности С радиуса R с центром в точке A(a;b).
Аналогично множество решений неравенства
(х - a)2 + (у- b)2 > R2
есть множество точек, лежащих вне окружности С.
Пример 4. Найти множество точек координатной плоскости,
удовлетворяющих неравенству:
1)	2х2 + 2у2 + 2х - Ьу - 13 < 0;
2)	9х2 + 9г/2 - 6х + 12у - 76 0.
Д 1) Преобразуем неравенство, выделяя полный квадрат:
2(х2 + х + |) +2(/-Зг/ + |) — 13 — 5 < О
Множество решений этого неравенства — множество точек,
лежащих внутри окружности радиуса 3 с центром ( — х5х)-
2) 9х2 + 9у2-6х + 12у- 76 = 9 (х2 —	+	+9 (у2 + +	-81,
\ о У /	\ о У /
/	] \ 2	/ п \ 2
(х-з) + и+1) ^9-
Искомое множество решений неравенства — множество то-
чек, лежащих на окружности радиуса 3 с центром
и вне этой окружности.	А
§2. Нелинейные уравнения и неравенства с двумя переменными
277
Пример 5. Найти множество точек координатной плоскости,
удовлетворяющих неравенству:
1)	|х| + М 2;	2) х2 + у2 < 4Ы;	3) ,
А 1) Пусть х О, у 0, тогда неравенство
примет вид х + у 2.
Этому неравенству удовлетворяют
точки первого квадранта, лежащие
выше прямой х 4- у = 2 (рис. 12) и на
этой прямой (вне треугольника АОВ,
где А(2;0), В(0;2)).
Так как | -х| = |х|, | - у\ = |у|, то
множество решений исходного неравен-
ства — множество точек, лежащих на
сторонах квадрата ABCD, где С(—2; 0), В(0; — 2), и вне этого
квадрата.
2)	Если у 0, то неравенство можно записать в виде
(у — 2)2 + х2 4.
Полученному неравенству удовлетворяют точки множества Е\,
лежащие на окружности радиуса 2 с центром (0;2) и внутри
этой окружности.
Аналогично если у < 0, то исходное неравенство можно
записать в виде
(f/ + 2)2 + x2^4,
а множество £2 решений этого неравенства — множество точек,
лежащих на окружности радиуса 2 с центром (0; —2) и внутри
этой окружности. Следовательно, множество £ решений ис-
ходного неравенства — объединение множеств Е\ и £2, т.е.
£ = £1 U £2.
Данное неравенство, равносильное
неравенству
(х - 13)2 +j/2 - 144 <0
х2 + У2 — 625	’
является верным в тех и только
в тех точках плоскости Оху, кото-
рые лежат вне окружности радиуса
12 с центром (13; 0) и внутри окруж-
ности радиуса 25 с центром в точке О
(рис. 13).
278
Глава XVIII. Уравнения и неравенства с двумя переменными
3.	Системы нелинейных уравнений с двумя переменными
Решение системы уравнений
Г F(x;z/) = O,
I G(x;z/) = 0
(1)
(2)
с двумя неизвестными х и у геометрически можно истолковать
как поиск координат точек пересечения линий Г1 и Г2, заданных
уравнениями (1) и (2).
Построив эти линии на клетчатой бумаге и найдя координаты
точек пересечения линий Г1 и Г2, можно найти приближенные
решения системы.
Пример 6. Решить систему уравнений
х2 — 2х — у + 1 = 0,
х2 4- у2 + 2х — бу + 5 = 0.
Д Первое уравнение системы, записанное в виде
z/=(x-l)2, задает параболу. Второе уравнение
системы, записанное в виде (х+1)2 + (у — 3)2 = 5,
задает окружность радиуса а/5 с центром (—1;3).
Окружность и парабола, изображенные на
рис. 14, имеют две общие точки >4(0; 1) и B(x2;z/2)>
где Х2 ~ —1,3, У2& 5,3.
Ответ. Х[ = 0, у\ = 1; х^ж—1,3, у% ~ 5,3.
4.	Системы нелинейных неравенств с двумя переменными
Пример 7. Решить систему неравенств
Г 9х2 + у2 — 18х 0,
t 2у + 3 — 2ху 0.
Д Складывая первое неравенство со вторым, умноженным на 3,
находим
9х2 - бху -\-у2 + 6(у — Зх) + 9^0 или (у — Зх + З)2 0,
откуда у — Зх + 3 = 0. Подставляя у ь= Зх — 3 в исходную систему,
получаем систему неравенств
( 9х2 - 18х + 9 + 9х2 — 18х 0,
t 6х — 6 + 3 — 2(3х — 3)х 0,
которую можно записать в виде
( 2х2 - 4х + 1 0,
1 2х2 - 4х + 1 > 0,
§2. Нелинейные уравнения и неравенства с двумя переменными
279
откуда следует, что 2х2 — 4х + 1 = 0. Решив систему уравнений
( г/ = Зх — 3,
t 2х2 - 4х + 1 = 0,
найдем два ее решения, которые являются решениями исходной
системы неравенств.
Ответ. ("1 + Д=;Д=\	А
\	х/2 \/2/ X л/2	у/2/
Пример 8. Найти все такие пары целых чисел х,г/, которые
удовлетворяют системе неравенств
< у - |х2 - 2х| + ± > 0,
. у+ |х — 1| <2.
Д Запишем данную систему так:
Г у+ | > |х2 — 2х|,	(3)
(t/<2 —|х —1|.	(4)
Так как |х2 - 2х| > 0, |х —1|>0, то из неравенств полученной системы
следует, что
-|<У<2.	(5)
Целыми числами, удовлетворяющими неравенству (5), являются
лишь 0 и 1, поэтому система (3), (4) может иметь целые решения
только при у = 0 и у = 1.
а)	Если у —0, то система (3), (4) примет вид
' |х2 — 2х| <
Jx —1|<2.
Второму из этих неравенств удовлетворяют целые числа
0, 1 и 2. Проверка показывает, что первому неравенству
удовлетворяют лишь 0 и 2. Следовательно, пары чисел и х\ = 0,
У\ =0 и %2 — 2, z/2 — 0 образуют решения исходной системы
неравенств.
б)	Если у — 1, то система (3), (4) приводится к виду
Г |х2-2х| < |,
||х-1|<1.
Второму неравенству этой системы удовлетворяет единственное
целое число х — 1, которое является также и решением первого
неравенства.
Ответ, xi =0, z/i = 0; х2 = 2, у2 = 0; х3 = 1, г/3 = 1.	▲
280	Глава XVIII. Уравнения и неравенства с двумя переменными
Пример 9. Изобразить на координатной плоскости Оху фигуру Ф,
заданную системой неравенств, и найти площадь S этой фигуры:
1)
' х2 + у2 < 4,
<
х — 3z/ + 2 < 0;
х2 + у2 < 4,
(х 4-1)2 4-г/2 >
1.
А 1) Неравенство х2 4- у2 < 4 задает множество точек, лежащих
внутри окружности с центром в начале координат и радиусом 2,
а неравенство х — Зу + 2<0 — множество точек, расположенных
выше прямой % —3z/ + 2 = 0. Эта прямая пересекает окружность
в точках Д(—2;0) и	а фигура Ф представляет собой
сегмент (рис. 15). Искомая площадь S равна разности площадей
51 — ^2, где Si — площадь сектора с углом л—arcsin | (рис. 15),
S2 — площадь треугольника АОВ. Так как
Я-arcsin |	.
Si =----------— • 4л = 2 ( к — arcsin ,
2л	\	57
а
S2 = |О4 • ОВ  sin (л — arcsin
Z	\	и /	10
ТО
5 = 2 Гл — arcsin
\	5/	10
2) Фигура Ф — это множество точек, лежащих внутри окружности
с центром в точке 0(0; 0) и радиусом 2, но вне окружности
с центром в точке (—1;0) и радиусом 1 (рис. 16). Значит,
площадь фигуры Ф равна S = 4л - я = Зл.	▲
Ответ. 1) 2 (л-arcsin	2) S = Зл
*Пример 10. Найти площадь фигуры Ф, которая задается на
координатной плоскости системой неравенств
' х2 + у2 10,
< Зх24-4х- 32 < О,
. (Зх + 2г/) (Зг/ + х 4-10) < 0.
А Первое неравенство системы определяет множество точек, лежа-
щих вне и на границе круга с центром в точке 0(0; 0) и радиусом
х/Ю (рис. 17).
§2. Нелинейные уравнения и неравенства с двумя переменными
281
Рис. 16
Решив второе неравенство, полу-
чим —4^х^|. Поэтому второе нера-
венство системы задает вертикаль-
ную полосу, лежащую между прямыми
х = — 4 и х = | (включая и точки этих
прямых).
Наконец, третьему неравенству си-
стемы удовлетворяют точки множества
7И, которое состоит из двух острых
вертикальных углов, образованных
прямыми 3% + 2у = 0 и Зу + х +10 = 0
(включая и точки этих прямых), так
как в точке (—4; 0), принадлежащей
множеству Л/, левая часть этого нера-
венства отрицательна.
Множество М изображено на
рис. 17, где указанные прямые обозна-
чены 1[ и 1%.
g
Прямая /j пересекается с прямыми х = - и х = —4 в точках
о
в точках
и В{—4; 6), а прямая /2 пересекается с теми же прямыми
8. _38\
3’	9 /
и С(—4;—2). Далее, прямая /2 касается
окружности х2+у2 = 10 в точке £(—1;—3), так как система уравнений
х2 + у2 = 10,
Зу + х + 10 — 0
282
Глава XVIII. Уравнения и неравенства с двумя переменными
имеет единственное решение (—1;—3). И наконец, прямая 1[ проходит
через центр этой окружности.
Итак, фигура Ф — это трапеция ABCD, из которой удален полукруг
радиуса \/10 с центром в точке О. Искомая площадь
5=(ЛД + ВС)>._5ж
где AD= 1 ВС = 8, Л=?.
У	3
Ответ. 5тг.
Задачи
1. Найти множество точек координатной плоскости, удовлетворяющих уравне-
нию:
1)	4х2	- 9//2 = 0;	2)	2х2 + Зу2 +4х- 12// +	14 = 0;
3)	Зх2	+ 3у2 + 6х	— 12//	+	Ю = 0;	4)	ху + х — у — 1 = 0;
5)	f/ +	|f/|=x;	6)	у = х\у\.
2.	Найти	множество	точек	координатной	плоскости, удовлетворяющих уравне-
1)	|x-l| + |j/ + 2| = l; 2) 3|x| + |//| + |3x + 2//| = 30.
3.	Найти множество точек координатной плоскости, удовлетворяющих неравен-
ству:
+	2) +	+ l <о
х 4- # — 169
4.	Решить систему неравенств:
Г 4х2 +//2 + 8х < 0,	2) Г у2 + Зху + 1 О,
Iху + // + 1 < 0;	[ 9х2 - 12х - 8у 0.
5.	Найти площадь фигуры, заданной на координатной плоскости системой
неравенств:
1)	+ +	2’ 2) 1х2+^2^4х’
[(х + 2)2 + //2 < 1;	1|//|^|2-х|.
6. Найти все пары целых чисел х.у, удовлетворяющих системе неравенств
Г 2х2 4- 2#2 — 12х 4- 20# 4- 65 < О,
t 4х 4- 2# — 3 > 0.
7. Дана система неравенств
г х2 4- #2	4|х|,
< И + Ы > 2,
х2 — #2 4-16 4- 8х 0.
Найти площадь фигуры, координаты точек которой удовлетворяют:
а) первому неравенству системы;
§3. Уравнения и неравенства, содержащие параметры
283
б)	первым двум неравенствам системы;
в) всем трем неравенствам системы.
8. Дана система неравенств
<.х2+у2^3(2у-2х-3),
,(2х + у- 3)(х 4- 5// + 3)	0.
Найти площадь фигуры, координаты точек которой удовлетворяют:
а) первому неравенству системы;
б)	первым двум неравенствам системы;
в)	всем трем неравенствам системы.
Ответы
1. 1) Совокупность прямых 2х + Зг/ = 0 и 2х - Зу = 0; 2) точка (—1; 2);
3) окружность радиуса с центром (—1;2); 4) совокупность прямых х=1
и у = —1; 5) лучи у = у 0 и х = 0, у < 0; 6) ось Ох, лучи х = 1, у > 0
и х = —1, у<0. 2. 1) Граница квадрата с вершинами (0;—2), (2;—2), (1; —1),
(1;—3); 2) граница шестиугольника с вершинами (0;—10), (0; 10), (—5;0), (5;0),
^;io),	К)). 3. 1) Объединение двух кругов радиуса 1 (включая их
границы) с центрами (1; 0) и (—1; 0); 2) множество точек, расположенных внутри
круга радиуса 13 с центром (0; 0) и вне круга радиуса 2 с центром (—1;2).
4. 1)	+	2) (^;1-V2);	1 +	.
5. 1) 1 + |; 2) 2л. 6. (3;-4), (4;-5).	7. а) 8л; б) 6л; в) 4л+ 4. 8. а) 18;
б) |(10-л); в) |(6-я).
§3. УРАВНЕНИЯ И НЕРАВЕНСТВА С ДВУМЯ
ПЕРЕМЕННЫМИ, СОДЕРЖАЩИЕ ПАРАМЕТРЫ
1. Уравнения с параметрами
Пример 1. Найти все значения параметра а, при которых суще-
ствует ровно одна пара действительных чисел (x;z/), удовлетворяющая
уравнению
2х2 — 4х + 2у2 + 8у + 10 — а = 0.
А Запишем уравнение в виде
2(х - I)2 + 2(z/ + 2)2 = а,
откуда следует, что исходное уравнение имеет единственное решение
(1; -2) при а = 0.	к
284
Глава XVIII. Уравнения и неравенства с двумя переменными
Пример 2. Найти все значения параметра а, при которых вершина
параболы
у = х2 — (2х/б cos a — 3)х — у cos 4а
лежит на прямой у = Зх, а парабола пересекает ось Оу в точке
с отрицательной ординатой.
Д Вершиной параболы является точка (%о?Уо)» где
%0 = v 5 cos а — z/o = — (5 cos а — 3v5cosa + - ) — — cos 4а,
Так как точка (xqjz/q) принадлежит прямой у — Зх, то
~ cos 4а + 5 cos2 a — — О
4	4
или 50 cos2 2а + 10 cos 2а — 24 — 0,
откуда
cos 2а = — cos 2а = |.
о	э
По условию
//(0) = “7 cos 4а < 0,
откуда
cos4а > 0 или cos22a>|.
Этому неравенству удовлетворяют значения а такие, что cos2a=—
Ответ, a = ±| arccos (-4) + nn, n G Z.	▲
2	\ □ /
Пример 3. Найти все значения параметра а, при которых
найдется хотя бы одна пара действительных чисел (х;г/), удовле-
творяющая уравнению
х2 — 5ху + bay2 + ^2a — у) у + 2х + 2 = 0.	(1)
Д Будем рассматривать уравнение (1) как квадратное относи-
тельно х. Найдем дискриминант этого уравнения:
D(y, a) = (2 - 5yf - 4 (5a#2 + Чау - у# + 2) =
= 5(5 - 4a)#2 + 2(5 - 4a)# - 4.
Хотя бы одна пара действительных чисел (%;у), удовлетворяющая
уравнению (1), существует тогда и только тогда, когда имеет решение
неравенство D(y; а) 0, т. е. неравенство
5(5-4a)#2+?(5-4a)#-4^0.	(2)
Возможны три случая:
1) а = |;	2) а<5--,	3) а>
'	4’	'	4	7	4
§3 Уравнения и неравенства, содержащие параметры
285
В первом случае неравенство (2) не является верным. Во втором
случае это неравенство имеет решения, так как у параболы
z = ay2 +{3у + х, где a = 5(5 — 4а) > О,
имеются точки, расположенные выше оси Оу (ветви параболы
направлены вверх). Наконец, в третьем случае, т. е. при a > |,
неравенство (2) имеет решения тогда и только тогда, когда дискри-
минант D\ квадратного трехчлена, стоящего в левой части этого
неравенства, неотрицателен:
£>1(а) = 4(5 - 4а)2 + 80(5 - 4а) = 4(5 - 4а) (5 - 4а + 20) =
= м(а-|)
откуда
64 (“Ч) О’-?)» °’	<3>
Действительно, если a < 0, то ветви параболы г = ay2 + [Зу + у
направлены вниз и хотя бы одна точка параболы лежит выше оси
Оу (или на этой оси) тогда и только тогда, когда
D[ — /З2 — 4ау 0.
При a > | решениями неравенства (3) являются значения а такие,
\ 25
что a > —.
4
~	К ^25	А
Ответ. а< А, .	▲
4	4
2. Системы уравнений с параметрами
Пример 4. Найти все значения параметра а, при которых система
УР”Й	Г|х|+2|,| + |2,-Зх| = 12,
[х2 + у2 = а
имеет ровно два действительных решения.
Д Множество решений первого уравнения данной системы, получен-
ное при решении примера 3 (3) из § 2, — граница шестиугольника,
изображенного на рис. 11. Множество решений второго уравнения
системы — окружность радиуса у/a с центром 0(0; 0).
Данная система имеет ровно два решения в следующих случаях:
1) радиус окружности равен расстоянию от точки О до границы
многоугольника; это имеет место в случае, когда окружность
__________________________________________ о	g
касается отрезков Д1В2 и тогда у/а — —^
\/2 л
286
Глава XVII1. Уравнения и неравенства с двумя переменными
2) радиус окружности равен расстоянию от точки О до точек Q
и С2, тогда
“ = з2 + © =Т-
Ответ, a =	▲
2	4
Пример 5. Найти все значения параметра а, при которых система
уравнении Г log5(# + 3) - 2 log25x = О,
( (х + а)2 - 2(у + 6) - 9а = О
имеет хотя бы одно решение.
Д Данная система равносильна системе
{х > О,
// = х-3,
(х + а)2 — 2(х + 3) — 9а — О,
откуда	х2 + 2(а — 1)х + а2 — 9а - 6 = 0.	(4)
Уравнение (4) имеет действительные корни xi и Х2 тогда и только
тогда, когда его дискриминант неотрицателен:
D = 4((а - I)2 - (а2 - 9а - 6)) = 28(а + 1)^0,
т.е. при а^—1, причем
xi = 1 - а - yjlici + 1), Х2 = 1 - а + ^/?(а + 1).
Данная система и равносильная ей имеют хотя бы одно решение,
если уравнение (4) имеет хотя бы один положительный корень,
а это условие равносильно тому, что наибольший из корней этого
уравнения Х2 > 0.
Таким образом, задача свелась к решению нера-
венства
У?(а + 1) > а - 1,
для решения которого построим графики функ-
ций у = у/7(а + 1) и у — а — 1 (рис. 18). Из
рисунка видно, что решения этого неравенства
образуют промежуток [—1;а0), где ад —положи-
тельный корень уравнения
У?(а + 1) = а - 1.
§3. Уравнения и неравенства содержащие параметры
287
Отсюда получаем
7{a + 1) = (а- I)2, а2-9а-6 = О, а0 = 9 + ^.
z-x	<	9 4~ \/105	а
Ответ. — 1 С а <-------.	▲
Пример 6. Найти все значения параметра при которых система
уравнений
' (х — 1 - 4f)2 + (у — 1 — З?)2 = 9/2,
\(x-5)2 + Q/-3)2 = 4
имеет единственное решение.
Д Первое уравнение системы задает множество окружностей Ct
с центрами 0/(1 +4f; 1 + 3Z) и радиусами Rt — 3|f|. Если у = 1, то
из уравнения следует, что х = 1 + 4Л Это означает, что каждая
такая окружность имеет с прямой у = 1 единственную общую точку
Л/(1 + 4£; 1), т. е. касается прямой z/=l в точке Л/.
Второе уравнение системы задает окружность С радиуса R — 2
с центром 0(5; 3), которая также касается прямой у = 1 в точке
Л(5; 1).
Система имеет единственное решение тогда и только тогда, когда
окружности Ct и С касаются.
Заметим, что касание возможно лишь при t > 0, так как при
t < 0 окружности Ct и С лежат по разные стороны от прямой у = 1
и At ф Д.
При t > 0 возможны два случая. В первом случае касание
происходит по прямой £/ = 1, т. е. Д/=Д, и тогда t=l. Во втором
случае условие касания определяется уравнением
|осм2 = (/?, +/?)2,
откуда
(4 - 4/)2 + (2 - З/)2 = (3/ + 2)2,
т. е.	_
2t2 — 7/ + 2 = 0, t= 7±/+
4
Ответ. t= 1,	7±V?3.	▲
4
Пример 7. Найти все значения параметра а, при которых система
уравнений
' +2 + г/2 + 64 + 16х + +2 + / + 36 - 12^ = 10.
. X2 + у2 = а2
имеет единственное решение.
288
Глава XVIII. Уравнения и неравенства с двумя переменными
А Запишем первое уравнение системы в виде
У(х + 8)* 1 2 * * * + у2 + i/x2 + (r/-6)2 = 10.
Ему удовлетворяют координаты точки М(х\у) такой, что сумма
расстояний от точки М до точек Mf(—8;0) и ^(О; 6) равна 10 Так
как расстояние М]М2 равно 10, то точка М должна принадлежать
отрезку М1М2 (в противном случае сумма указанных расстояний
была бы больше 10 согласно свойству сторон треугольника).
ук	Если точка М лежит вне отрезка М1М2 на
прямой, проходящей через точки Mi и М2, то
сумма расстояний от точки М до точек Mi
\	и М2 больше 10.
__________\_____Итак, первому уравнению системы удо-
М\________Оа влетворяют координаты точек отрезка М1М2,
и только эти точки (рис. 19).
Второму уравнению системы удовлетворяют
координаты точек окружности радиуса |а| с центром 0(0; 0). Эта
окружность имеет с отрезком М1М2 единственную общую точку
в следующих случаях:
1) окружность касается отрезка М1М2; в этом случае |а| = ОД —
высота в треугольнике М1ОМ2,
ОА = 0М{ ’0М2 = 6 *’8 = 24-
714^2 Ю 5 ’
2) окружность пересекает отрезок М1М2 в одной точке; в этом
случае ее радиус должен быть больше катета ОМ2, но не
превышать катета OMi прямоугольного треугольника ОМ1М2,
т. е. 6 < |а| 8.
Ответ. — 8 a < — 6, a = —	a=~, 6 < a < 8.	▲
*Пример 8. Найти все значения параметра а, при которых
существуют ровно две пары действительных чисел (x;z/), удовле-
творяющих системе уравнений
/ (х + У2 - l)(i/ — \/б|х|) = О,
_ 2ay + х = 1 +а2.
Д Пусть П —парабола у2 = 1 — х, L — ломаная у = >/б|х|, образован-
ная лучами 1\ и /г> которые задаются соответственно уравнениями
У = — >/бх, у 0 и у - \/бх, у 0;
/ — прямая Чау + х = 1 + а2 (рис. 20).
§3. Уравнения и неравенства, содержащие параметры
289
Общие точки прямой I и параболы П найдем, решая систему
уравнений
Г г/2 = 1 — х,
[ 2ay — а2 = 1 — х.
Из этой системы следует, что
у2 - Чау + а2 = (у- а)2 = О,
откуда
у = а, х — 1 — а2,
т. е. выписанная система имеет единственное решение при любом
а е К. Это означает, что прямая / касается параболы П в точке
С(1 - а2; а).
Рассмотрим три возможных случая: а = 0, а > 0, а < 0.
а)	Если а — 0, то прямая I задается уравнением х = 1. Эта прямая
касается параболы П в точке (1; 0), пересекает луч но не
пересекает луч 1\, Поэтому при а —0 исходная система имеет
ровно два решения.
б)	Если а > 0, то прямая I пересекает ось Оу в точке Е
«	о 1 4-
с положительной ординатой , а также пересекает лучи
/1 и /2-
Найдем сначала значения а > 0, при которых прямая /
проходит через одну из точек А и В, являющихся точками
пересечения лучей 1\ и 1% с параболой П (рис. 20). Координаты
10 3022
290	Глава XVIII. Уравнения и неравенства с двумя переменными
точек А и В найдем, решив систему уравнений
Г г/2 = 1 - х,
= х/б|х|.
Из этой системы получаем уравнение 6х2 = 1 — х, имеющее
корни xj = —^ %2 — I- Числа Х\ и Х2 —абсциссы точек А
Z	о
и В.
Значения а, при которых прямая / проходит через точки
А и В, принадлежащие параболе П, найдем из уравнений
1_а2=	1	1_а2=1
Z	о
Так как а > 0, то
= а2 = у/1-
I пересекает ломаную L ровно
При а — а\ и а = а% прямая
в двух точках (одна из них — общая для L и П) и поэтому
при а = а\ и при а — система имеет ровно два решения.
Если
или а
то прямая I не проходит через точки Л и В и пересекает L
в двух различных точках. В этом случае исходная система
уравнений имеет ровно три различных решения (одно из
решений — координаты точки касания прямой / с параболой П).
Пусть k.k\ и ^2 — угловые коэффициенты прямой I и лучей
1\ и /2 соответственно. Тогда
k = -± (Й/О), ^ = -7б, k2 = а/6.
Если 0<й<у|, то прямая I пересекает 12 и не будет
пересекать 1\ только в том случае, когда k = k\, т. е.
откуда о=^=.
Следовательно, при а — исходная система имеет ровно
два решения.
§3 Уравнения и неравенства, содержащие параметры
291
Если
аЕ (2^’ ^/1) ’
то прямая I пересекает ломаную L ровно в двух точках,
не лежащих на П. В этом случае система имеет ровно три
различных решения.
Пусть
О < а < —тогда ~ > \/б,	< — \/б,
2\/б	2а ’ 2а	’
т.е. k<k\, и поэтому прямая I не пересекает /1, но пересекает
/2. В этом случае система имеет ровно два различных решения.
в)	Пусть а < 0, тогда прямая I пересекает ось Оу в точке
с отрицательной ординатой.
Если
~2\/б <6Z<0’ т’ е’ ~^а < то ^<^2 и k>k\ (£>0,&i <0).
В этом случае прямая I пересекает луч /2 и не пересекает
луч /ь и поэтому система имеет ровно два решения.
Наконец, если
а ----1~7- >
2 ч/б
то прямая / не пересекается с ломаной L.
Итак, исходная система уравнений имеет ровно два решения
в следующих случаях:
а=л/|,	А*
V 3 V 2 2ч/б 2ч/б
3. Неравенства и системы неравенств с параметрами
Пример 9. Найти все значения параметра а, при которых
существует хотя бы одна пара действительных чисел (х; у), удо-
влетворяющая неравенству
х2 + 6х + у2 - 4у а.
А Исходное неравенство, равносильное неравенству
(х + З)2 + {у — 2)2 cl + 13,
имеет хотя бы одно решение тогда и только тогда, когда а + 13 > О,
т. е. при а —13.	А
Пример 10. Пусть G — треугольник, образуемый при пересечении
прямых /1, /2, /3, заданных соответственно уравнениями
у — Зх + 9 — 0, х + у — 3 = 0, у — х — 3 = 0,
292
Глава XVIII. Уравнения и неравенства с двумя переменными
а фигура Ф состоит из точек множества G таких, что неравенство
t2 + 2t(x — 2)+ 7 — у> О
выполняется при всех значениях параметра t. Найти площадь
фигуры Ф.
Д В примере 5, § 1 было установлено, что прямые 1\ и 1% пересекаются
в точке С(3;0), прямые 1% и /3 — в точке Л(0;3), прямые 1\ и /3 — в
точке /3(6; 9), а площадь треугольника АВС равна 18. Неравенство
t2 + 2f(x — 2)+ 7 — у> О
является верным при всех t € R тогда и только тогда, когда
дискриминант квадратного трехчлена в его левой части отрицателен:
(х-2)2-(7-у)<0,
т. е.
у <7- (х-2)2.
(5)
Условию (5) удовлетворяют все точки, лежащие под параболой
у —7 — (х — 2)2 с вершиной 23(2; 7), а фигура Ф —множество точек,
указанных серым цветом на рис. 21, где F(4;3) — точка пересечения
Рис. 21
параболы с прямой /1, /f(3; 6) — точка пересечения параболы с
прямой /3.
Если а—площадь фигуры Ф, то о = oi + о2 +	где <?1 ~
площадь треугольника ACF, — площадь треугольника АКМ, где
М(3; 3) — точка пересечения AF и КС, 03 — площадь криволинейного
треугольника KMF.
§3. Уравнения и неравенства, содержащие параметры
293
Так как
Ст1 = 14-3 = 6, 0-2 = 1,
f4
(“%2 + 4х) dx =
3

то
73
°	6 
О	/О	А
твет. —.	▲
о
Пример 11. Найти все значения параметра при которых
множество решений системы неравенств
х2 + х + {у — а)2 < 11,
х + а + у2 О
содержит отрезок / с концами в точках Л(1;0) и 23(1; 1).
Л Пусть точка М(х,у) принадлежит отрезку /, тогда х = 1, 0 <у < 1.
Поэтому задача сводится к нахождению значений а, при которых
система неравенств
(6)
полученная из данной системы при х = 1, имеет решения при любом
у е [0; 1]. Система (6) равносильна системе
у -3^a^z/ + 3,
а^-у2- 1.
Если z/= 1, то система (7) примет вид
Г - 2^а^4,
[ а < -2,
(8)
откуда следует, что а = —2.
Если у € [0; 1], то из системы (7) получаем
Г -З^а <4,
( а —1,
откуда следует, что —З^а^—1.
Так как —2 е [—3; — 1], то при а = — 2 (и только при этом значении а)
система (7) и равносильная ей система (6) имеют решение при всех
У€[0;1].
Ответ, а = —2.	▲
294
Глава XVIII. Уравнения и неравенства с двумя переменными
Пример 12. Найти все значения параметра а, при которых
множество решений системы неравенств
( х2 — (а — 2)х — 2 — г/ < О,
[ 2х + // — а О
содержит отрезок [— 1; 0] оси Ох.
Д Подставив в данную систему у — 0, получим
Г х2 - {а - 2)х - 2 < О,
I 2х — а 0.
(9)
(Ю)
Множество решений неравенства (10)—луч х а отрезок
Д = [—1; 0] принадлежит этому лучу тогда и только тогда, когда
т. е. при а^0.
Множество решений неравенства (9) —отрезок Д1 = |xj;Х2], где
и Х2 — абсциссы точек пересечения параболы
/(х) = х2 — (а — 2)х — 2
с осью Ох. Если ДсДь то
/(-1)^0, /(0)^0,	(11)
так как /(х) 0 для всех х € Др Обратно, если выполняются
условия (11), то —1 е Д1 и 0е Дь откуда следует, что Д С Дь
Таким образом, условиям задачи удовлетворяют те и только те
значения а 0, для которых выполняются неравенства (11), т.е.
/(-1) = 1 +(а-2) - 2 0, /(0) = —2 0,
откуда находим 0 < а < 3.
Ответ.	▲
Задачи
1.	Найти все значения параметра а, при которых найдется хотя бы одна пара
действительных чисел (x;z/), удовлетворяющая уравнению
5х2 + аху + у2 4- 8ах + 8у 4- 20 = 0.
2.	Найти все значения параметра а, при которых нет ни одной пары
действительных чисел (х;у), удовлетворяющей уравнению
2х2 — 4х 4- 2у2 + 8у 4- 10 — а = 0.
3.	Найти все значения параметра а, при которых парабола
у = х2 — 8х ctg а 4- 5 cos 2а
касается прямой у = —7, а абсцисса точки касания отрицательна
§3. Уравнения и неравенства, содержащие параметры
295
4.	Найти все значения параметра а, при которых вершина параболы
у = х2 4- (2 sin a — \/3)х 4- cos 4a
лежит на прямой у = —х/Зх, а парабола пересекает ось Оу в точке
с положительной ординатой.
5.	Найти все значения параметра а, при которых система уравнений
Г x + y/у = 1,
| а-I - 3 - y/у =Д(а - х)2
имеет единственное решение.
6.	Найти все значения параметра а, при которых система уравнений
{у = х2 — 2х,
х2 + у2 + а2 = 2х + 2ау
имеет хотя бы одно решение.
7.	Найти все значения параметра а, при которых система уравнений
j 2|х| + |г/| + |3х — 4г/| = 10,
12	2
+ у =а
имеет ровно два действительных решения
8.	Найти все значения параметра а, при которых система уравнений
Г log3(2 - х - «/) + 2 = log3( 17 - 8х - Юг/),
t (х — а)2+х = # + гЦ-6
имеет ровно два решения.
9.	Найти все значения параметра а, при которых система уравнений
fx2+/=l,
\г/- |х| — а
имеет два решения.
10.	Найти все значения параметра а, при которых система уравнений
( ^/х2 4- #2 4- 64 — 16х 4- ^/х2 4- г/2 4- 36 4- 12г/ = 10,
I 2 , 2	2
XX 4~ у — а,
имеет единственное решение.
11.	Найти все значения параметра t, при которых система уравнений
Г (х + 1 - 2/)2 + (г/ - 1 + Ы? = 4/2,
| (х + 2)2 + (г/ - 6)2 = 1
имеет единственное решение.
12.	Найти все значения параметра а, при которых система уравнений
Г (г/ + 8 -х2)(2х+ |г/|) = О,
1 2ах — у = 8 + а2
имеет ровно два решения.
296
Глава XVIII. Уравнения и неравенства с двумя переменными
13.	Найти все значения параметра а, при которых система уравнений
у Vi — х2 — х2 = 2a — 1,
у2 + у \/i — х2 = 2a — с?
1)	не имеет решений;
2)	имеет конечное множество решений;
3)	имеет бесконечное множество решений.
В случаях (2), (3) найти все решения.
14.	Найти все значения параметра а, при которых нет ни одной пары
действительных чисел (х\у), удовлетворяющей неравенству
х2 4- 6х 4- у2 — Ay а.
15.	Вершины B,C,D параллелограмма ABCD имеют соответственно координаты
(—3;2), (2;3), (3; —4). Найти все значения параметра а. для которых
координаты вершины А являются решением системы неравенств
2х — у — 2а < О,
2х 4- бу 4- 5а 0.
16.	Пусть G — множество точек плоскости с координатами (х; z/) таких, что
числа х, у и 6 — 2х являются длинами сторон некоторого треугольника
Найти площадь фигуры G.
Фигура Ф состоит из точек множества G таких, что неравенство
t2 4- 2tx 4- 4х — у > О
выполняется при всех значениях параметра t. Найти площадь фигуры Ф.
17.	Найти все значения параметра а, при которых система неравенств
2 о 7 2	14-а
< X -2ху-7у > —,
t Зх2 - 10х«/ — 5у2 С —2
имеет решение.
18.	Найти все значения параметра а, при которых множество решений системы
неравенств
{х2 4- (а 4- 4)х 4- 4а у,
Зх 4- у - (2а 4- 4) О
содержит отрезок АВ, где Д(—2;0), В(—1;0).
19.	Найти все значения параметра а, при которых система неравенств
х2 4- 2а	у,
у2 4- 2а	х
имеет единственное решение.
20.	Найти все значения параметра а, при которых множество решений системы
неравенств
{(х — а) 4“ х 4~ у 3,
х — а 4- у2 С О
содержит отрезок с концами в точках (1; 0) и
§3. Уравнения и неравенства, содержащие параметры	297
Ответы
1. а —2, а 2.	2. a < 0.	3. а = — arctg2 4- тт, n е Z. 4. а =
= ±| arccos (— 4-тгп, neZ. 5. a = — 7, -1 <а^5. 6. —2^а^|. 7. а = 2,
2	\ 4/	4	4
а=^5Р 8. -5<а<2-^. 9. а =-Л, -1 <а< 1. 10. -8 a < -6,
a = ~, a =	6<а^8. 11. /=-1, /= =29±6V^	12. а =-4, а =-2,
5	5	25
—1 a < 1.	13. 1) Если — 2 — 2л/2<а<0 или а>2\/2 —2, то решений нет;
2) если а — 2 — 2д/2 или 0 < a 2\/2 — 2, то система имеет два решения
Uo;//o) и (-xoi'/o). rnex0 = J—»4q~4, Уо = (2-fl2) .,/ ° о! 3) если a = 0, то
у a — 4	у 4 — a
система имеет бесконечное множество решений (%о; — ^/1 ~ хо)’ где ~
14. а <-13.	15.	16. 6 и 17. а > 1.	18.
Л	о	о	Л
19. а=|. 20. а = 2.
О
Глава XIX
ДЕЛИМОСТЬ ЦЕЛЫХ ЧИСЕЛ.
ЦЕЛОЧИСЛЕННЫЕ РЕШЕНИЯ
УРАВНЕНИЙ
§ 1.	ДЕЛИМОСТЬ ЧИСЕЛ
Пусть а — целое число (aeZ), т — натуральное число (т е N).
Говорят, что а делится на т, если существует целое число р (р е Z)
такое, что
а = тр.
Число т называется делителем числа а, р — частным от деления а
на т.
Два натуральных числа тип называют взаимно простыми
и пишут (т, п) = 1, если единственным общим натуральным
делителем этих чисел является число единица.
Например, числа 12 и 35 взаимно просты, так как натуральными
делителями числа 12 являются числа 1, 2, 3, 4, 6, а натуральными
делителями числа 35 являются числа 1, 5, 7.
Наибольшее натуральное число, являющееся натуральными дели-
телем каждого из натуральных чисел тип, называют наибольшим
общим делителем этих чисел и обозначают НОД(т, п) или просто
(т, п).
Например, если т = 36 и п — 84, то НОД(36, 84) = 12.
Перечислим свойства делимости суммы (разности) и произведения
чисел, считая, что aeZ, b е Z, т е N, п G N.
1.	Если а делится на т и b делится на т, то числа а + b и а — Ь
также делятся на т.
2.	Если а и Ь делятся на т, то при любых целых числах k и I
число ak + bl также делится на т.
3.	Если а делится на m, а Ь не делится на т, то числа а + Ь
и а — Ь также не делятся на т,
4.	Если а делится на т, а т делится на k е N, то число а также
делится на k.
5.	Если а делится на m, а Ь не делится на т, то число ab
делится на т.
6.	Если а делится на каждое из чисел тип, причем (т, h) — 1,
то а делится на произведение тп.
7.	Если а делится на т, то ak делится на mk при любом k е N.
§1. Делимость чисел
299
8.	Если ab делится на m и b взаимно просто с то а делится
на т.
Ограничимся доказательством свойства 1.
О Если целые числа а и b делятся на /п, то существуют числа
р е Z и q е Z такие, что а = тр, b = qm. Отсюда следует, что
а + b — pm + qm — (р + q)m, а — b = pm — qm = (р — q)m. Так как
числа p + q и p — q — целые, то числа а + b и а — Ь делятся на т. •
Пример 1. Известно, что натуральные числа Зи + 2 и 8п 4- 3
делятся на натуральное число р^1. Найти р.
Д Так как числа 3/г + 2 и 8п + 3 делятся р, то и число
8 • (Зп + 2) — 3 • (8и + 3) = 7 должно делиться на р. Но единственное
натуральное число р ф 1, на которое делится 7, равно 7. Значит
р = 7.	А
Целое число, делящееся на 2, называют четным, а целое число,
не делящееся на 2, называют нечетным. Четное число а можно
представить в виде a = 2k, а нечетное число а —в виде а = 2/г Н- 1,
где k — некоторое целое число.
Пример 2. Доказать, что квадрат четного числа делится на 4,
а квадрат нечетного числа имеет вид 4р+ 1, где р е Z.
Д а) Пусть а —четное число, тогда а — 26, откуда находим
a2 = 2k-2k = 4k2, где &2 — натуральное число. Следовательно,
а2 делится на 4.
б) Пусть а —нечетное число, тогда a = 2k + l, откуда следует,
что а2 = (2k + 1) • (2k + 1) = 4k2 + 4k + 1 = 4(k2 + k) + 1, где
k2 + k = p — целое число, т. e. a2 = 4p + 1.	▲
Простые и составные числа. Натуральное число р называется
простым, если р > 1 и р не имеет натуральных делителей, отличных
от 1 и р.
Из определений легко следует, что если р и р\ — простые числа
и р делит pi, то р = Кроме того, для любого натурального числа
его наименьший отличный от единицы положительный делитель
является простым числом.
Натуральное число п > 1 называется составным, если п имеет
по крайней мере один натуральный делитель, отличный от 1 и п.
Число 1 не считается ни простым, ни составным.
Пример 3. Доказать, что число а = 4- 1612 _ 240 делится на 33
А Так как 4 • 1612 = 22 • 248 = 250, то
а = 250 - 240 = 240(210 - 1) = 240(25 - 1)(25 4-1) = 240 • 31 • 33,
откуда следует, что а делится на 33.	▲
300
Глава XIX. Делимость целых чисел
Пример 4. Доказать, что число а является составным при любом
натуральном п :
1) а = 8п2 + 10и + 3;	2) а = 4 • 16" + 3 • 9".
Л 1) Число а является составным при любом натуральном и,
поскольку 8п2 + 10гг 4- 3 = (2п + 1)(4п + 3), где числа 2п + 1
и 4п + 3 — натуральные, большие единицы.
2) Так как (см. пример 14 в §5 гл. II)
а = 4 • 42л + 3 • З2" = 42гнЧ + 32n+1 =
2л+1
= (4 + 3)- 52 (42"+1-<3fc-1
k=\
то число а является составным, так как оно делится на 7. А
Теорема 1 (Евклида). Множество простых чисел бесконечно.
О Предположим, что множество простых чисел конечно и состоит
из чисел рь рг, - • •, Р«- Рассмотрим число а — р\ . -рп + 1. Тогда
либо натуральное число а, большее единицы, само является простым,
либо оно разложимо в произведение положительных простых чисел
и поэтому обладает хотя бы одним простым делителем р. По
предположению а не может быть простым, так как оно не совпадает
ни с одним из чисел pi, р2,..., Рп- Если же а разложимо, то его
делитель р должен быть отличен от чисел pi, р2,..., Рл, так как
в противном случае р делит pi • р2  ...  рп и а, а значит, делит
и разность а — р\  р% ... -рп = 1, а это невозможно. Следовательно,
множество простых чисел бесконечно.	•
Простые числа, хотя их и бесконечно много, составляют неболь-
шую часть всех натуральных чисел, что выражается следующей
теоремой.
Теорема 2. Для любого целого числа k 1 в натуральном ряду
можно найти k составных чисел, непосредственно следующих
друг за другом.
О Возьмем число а = (k + 1)! и рассмотрим k следующих друг
за другом чисел а\ = а + 2, а% = а + 3, ..., а^ = а + (г + I), ...,
а^ = а + (k + 1). Каждое число в этом списке является составным,
так как ai делится на 2, а% — на 3, а% — на 4, ..., а^ — на fed-1. •
Теорема 3. Если произведение нескольких натуральных чисел
делится на простое число, то на него делится хотя бы один из
сомножителей.
Представление натурального числа п в виде произведения двух
натуральных чисел ab называется разложением на множители.
§1. Делимость чисел
301
Представление числа в виде произведения простых чисел называется
разложением на простые множители. Считается, что если п —
простое число, то оно имеет разложение на простые множители,
состоящее из одного числа п. Два разложения на множители
называются одинаковыми, если они отличаются только порядком
множителей. Например, разложения 70 = 2-5-7 и 70 = 7- 5- 2
считаются одинаковыми.
Теорема 4 (основная теорема арифметики). Для каждого
натурального числа п > 1 существует единственное разложение
на простые множители.
Это значит, что для любого натурального числа два разложения
на простые множители могут отличаться только порядком этих
множителей.
Каноническим разложением натурального числа п > 1 называ-
ется представление п в виде
n=pf‘.p**.....ph
где	, Ps — попарно различные простые числа, a k\, ^2,..., ks —
натуральные числа. Для отрицательных целых чисел п < — 1
каноническим разложением считается представление в виде
ri = ~Pl' -Р2 •••• -PsS-
Теорема 5. Пусть п — натуральное число и п=р\' • р^2 •    -pss —
его каноническое разложение на простые множители Тогда
каждый натуральный делитель d числа п может быть записан
в виде d=р™' • р™2 •. . • pTs , где пц — целые числа, удовлетворяющие
условиям 0 < т\ fei, ... , 0 < ms < ks.
О Пусть d — какой-либо делитель натурального числа п. Так как
каждый простой делитель числа d является делителем числа п, то
в разложении d на простые множители могут встречаться только
числа из множества {/?i, Р2>--ч Ps}- Поэтому число d представимо
в виде d = p™' -р™2	-p™s.	•
Наибольшим общим делителем (НОД) чисел а\, а<2, ... , ап
называется наибольшее натуральное число, на которое делятся
данные числа. Наименьшим общим кратным (НОК) — наименьшее
натуральное число, делящееся на каждое из этих чисел. Наибольший
общий делитель чисел а^ а^ ... , ап обозначают (ai, а%,... , ап\
а наименьшее общее кратное — [ai, а^ ... , ап\. В частности, (а, Ь) —
НОД чисел а и Ь, а [а, Ь] — НОК этих чисел
Числа а[, а2-> ..., ап называются взаимно простыми, если
(а^ &2, ••• > ап) — 1, и попарно взаимно простыми, если любые
два из них взаимно просты, т. е. (а/, aj) = 1 при i j. Попарно
302
Глава XIX. Делимость целых чисел
взаимно простые числа являются взаимно простыми (простыми
в совокупности). Обратное неверно, как показывает следующий
пример: п — 3, а\ — 2 • 3,	= 2 • 5, а% = 5 • 3.
Теорема 6. Пусть даны два натуральных числа а и Ь,
а Р\'Р2> • • - ips — простые числа, входящие в канонические раз-
ложения а и Ь. Представим числа а и b в виде а — р^ • pk^ • •.. • pkss
и b = р™' • р™2 •... • pTs. где гщ О, kt 0 — целые числа. Тогда
iA — min(mi,/<|)	min(/n2^2) min(wsA)
{U. и) — p^	' P<2	’ • • * Ps	j
Al _ max(mbA!i) тах(т2Л2) max(msA)
[u, t/j p^	’ P2	* • • • ’ Ps
Например, пусть g = 23-32-7, 6 = 24 • 3  52 -11. Запишем их в виде
а = 23  З2 • 5° • 71 • 11°, b = 24 • 3* • 52 • 7° • II1. Тогда
(a, b) = 23 • З1 = 24, [а, Ь] = 24 • З2 • 52 • 7* 11* = 277 200.
Пример 5. Найти (5160,16920) и [5160,16 920].
Д Напишем канонические разложения чисел 5160 и 16 920:
129
5160 = 2^5,-2 • 2 • 3~^43 = 23 • 3 • 5 • 43,
10	516
423
16 920 = 2 Ji - 2 >2 ♦ З^ЗЛ7 = 23 • З2 • 5 • 47.
10	1692
Тогда
(5160, 16 920) = 23 • З1 • 51 • 43° • 47° = 120,
[5160, 16 920] = 23 • З2 • 51 • 431  471 = 727 560.	▲
Существует еще один способ нахождения НОД двух чисел,
называемый алгоритмом Евклида. Он использует деление чисел
с остатком.
Деление с остатком. Не всякое целое число а делится (нацело)
на данное натуральное число т.
Деление числа а на число b с остатком есть отыскание наиболь-
шего натурального числа q, которое в произведении с делителем
дает число, не превышающее делимого: а = bq + г, 0 < г < Ь.
Искомое число q называется неполным частным. Разность г между
делимым и произведением делителя на неполное частное называется
§1. Делимость чисел
303
остатком. Если остаток равен нулю, то говорят, что а делится на
b (без остатка) (или что число Ь —делитель числа а).
Теорема 7 (о делении с остатком). Для любого целого а
и целого b > 0 существуют и притом единственные целые q
и г такие, что
а = bq + г и 0 г < Ь.
О Рассмотрим рациональное (не обязательно целое) число
Если а—целое, то возьмем q = a. Если же а не целое, то найдутся
два соседних целых числа, в промежуток между которыми попадает
а. Меньшее из них обозначим q. Тогда q <a<q+l, т. е. q<^<q + \.
Умножив все три части этого двойного неравенства на b (Ь > 0 по
условию), получим
bq < а < bq + Ь,
откуда 0 < а — bq < Ь. Положим r — a — bq. Число г—целое. Тем
самым существование q и г доказано.
Докажем единственность такого представления. Пусть a — bq-Yr
и а ~ bq\ + г\ — два таких представления и q q\. Тогда
bq + r = bqi+ri, b(q - 41) = (п - г). Так как q^q\, то |4“<71|^1-
Тогда — (?1| > &, и значит, |rj — r\ b. Но так как 0 < г < b
и 0^Г1 <&, то |п — r| ^b— 1, что противоречит ранее установленному
условию. Следовательно, q = q\, но тогда и г — г\. А это значит, что
представления а = bq + г и а = bq\ + Г\ совпадают.
Теорема доказана.	•
_ 3 — (п3 - п)(п2
и + 3
то
Пример 6. Найти все целые и, при которых дробь а —	+
целое число.
А Так как гг5 -
й = фЦ = „з_„ +
п2 ч- 1	п2 + 1
Поскольку п3 — п — целое число, то а — целое число тогда и только
тогда, когда ” + 3 — целое число. Поиск значений и, для которых
п2 +1
дробь — целое число, можно упростить, сведя его к перебору
п2 +1
значений щ являющихся решениями совокупности
\п + 3| п2 + 1,
п Т 3 — О,
т. е. п е {—3, —1, 0, 1, 2}.
304
Глава XIX. Делимость целых чисел
Убеждаемся, что при всех этих значениях дробь — целое
гг +1
число. Следовательно, при п е {—3, —1, 0, 1, 2} дробь а — целое
число.	▲
Алгоритм Евклида. Для нахождения НОД двух чисел делят
большее число на меньшее, и если получается ненулевой остаток, то
делят меньшее число на остаток; если снова получается ненулевой
остаток, то делят первый остаток на второй. Так продолжают делить
до тех пор, пока в остатке не получится нуль. Последний делитель
и есть НОД данных чисел:
b — ащ + г\ (О О1 < я),
a = r1u2 + ''2 (0 С г2 < и),
................................... (1)
= rnun+l + г„+1 (0 rn+i < гп),
Гп — ^п+1^72+2’
Число является НОД чисел а и Ь.
Замечание. Для доказательства того, что гп+\ является НОД чисел а
и 6, нужно, поднимаясь по равенствам (1) снизу вверх, убедиться, что rn_|_i
является делителем чисел а и Ь, а затем, взяв любой общий делитель d чисел
а и Ь, опускаясь вниз по равенствам (1), убедиться, что d является делителем
Gz+1-
Пример 7. Используя алгоритм Евклида, найти (5160,16 920).
А Используя алгоритм Евклида, получаем:
16 920 = 3- 5160 + 1440,
5160 = 3-1440 + 840,
1440 = 1  840 + 600.
840 = 1•600 + 240,
600 = 2 • 240 + 120,
240 = 2 • 120.
Следовательно, (5160, 16 920) = 120 (см. пример 5)	▲
Использование алгоритма Евклида бывает удобнее метода разло-
жения на простые множители в тех случаях, когда трудно получить
канонические разложения чисел.
Пример 8. Известно, что дробь | несократима (a, b е N).
Доказать, что дробь также несократима.
оа + о о
§ 1. Делимость чисел
305
А Так как дробь | несократима, то (а, &) = 1. Найдем наибольший
делитель d чисел 5а + 3b и 2а + Ь. Используя алгоритм Евклида,
получаем:
5а + ЗЬ — 2 • (2а + &) + а + Ь,
2а + b = 1 • (а + Ь) + а,
а + b = 1 • а + Ь.
Отсюда получаем, что d — (5а + ЗЬ, 2а + 6) = (2а + Ь, а + Ь) = (а + Ь, а).
Далее по алгоритму Евклида задача сводится к нахождению
наибольшего делителя чисел а и Ь, но по условию (a, b) = 1. Отсюда
следует, что d=(a, b) = 1. В таком случае дробь -2-6Z-t6 несократима.
uG “I- ЗО
▲
Пример 9. Найти наибольший общий делитель d чисел 27 и 96
и представить его в виде d = 27х + 96у, где х и у — целые.
А Используя алгоритм Евклида, найдем наибольший делитель d
чисел 27 и 96:
96 = 3-27+ 15,
27 = 1-15 + 12,	(2)
15 = 1-12 + 3,
12 = 4-3.
Отсюда получаем, что d = (27, 96) = 3.
Начиная с первого равенства алгоритма Евклида, спускаясь до
предпоследнего, получаем:
15 = 96 - 3  27,
12 = 27 — 1 • 15 = 27 — 1 • (96 — 3 - 27) = 4 • 27 — 1 - 96,
3 = 15 - 1 -12 = (96 - 3 • 27) - 1 • (4 • 27 - 1 • 96) = -7 • 27 + 2	-	96.
Это и есть искомое представление 3 = —7 • 27 + 2 • 96,	т.	е.	х	= —7,
У = 2.	▲
Замечание. Отметим, что найденное представление не является един-
ственным (см. ниже теорему 1 в § 3 настоящей главы).
Задачи
1.	Доказать, что число а является составным:
1)	а = 6я + 3я + 2”+1 + 2 при любом натуральном и;
2)	а — 25п4 + 9лг2 f 1 при любом натуральном tv,
3)	а — пА 4-4 при любом натуральном п> 1.
2.	Доказать, что число 555777 + 777555 делится на 37.
306
Глава XIX. Делимость целых чисел
3.	Доказать, что
1)	г? — п делится на 3;	2) и3 4- 5и делится на 3;
3)	п5 — п делится на 5;	4) я4 4-6п3 4-11п3 4-6п делится на 4.
4.	Доказать, что:
1)	не существует простого числа, которое можно представить в виде суммы
нескольких последовательных положительных нечетных чисел;
2)	если к произведению четырех последовательных натуральных чисел
прибавить единицу, то получится число, равное квадрату некоторого
натурального числа.
5.	Доказать, что
1)	число 1620 4- 276 делится на 17;
2)	число 163 4- 314 — 2 делится на 15;
3)	число 10ю 4- 283 — 2 делится на 9;
4)	число З63 4-193 — 16 делится на 17.
6.	Найти наибольший общий делитель чисел:
1)	6787 и 7194;	2) 2691 и 40572;	3) 10™ - 1 и 10" - 1.
7.	Найти наименьшее общее кратное чисел:
1)	420, 312 и 333333;	2) 1403, 1058 и 3266.
8.	Найти наибольший общий делитель d чисел а и b и представить его в виде
d = ах 4- by, где х и у — целые:
1)	21 и 17;	2) 321 и 843;	3) 23520 и 75222.
9.	Найти натуральные числа а и Ь, если (а, Ь) = 6, [а, Ь] = 90
10.	Известно, что дробь несократима (a, b G N).
b
1)	Доказать, что дробь —также несократима.
а 4- b
2)	На какие числа может сокращаться дробь: a) ; б) 0 а + Ь—
а + 4о ст — ab 4- tr
И. Доказать, что несократима дробь:
1) ~х~—г ПРИ всех а 2)	ПрИ всех а € N.
7 2а 4-1 Н	а2 + 2а -
-отто	Л п4 +3л2 4-7 .
12. Наити все целые п, при которых дробь а =---~-----будет целым числом.
гг 4-1
Ответы
6. 1) 11; 2) 207; 3) 10d - 1, где d =	7. 1) 23 • З2 • 5 • 7 • И • 13 • 37;
2) 2 • 232 • 61 - 71. 8. 1) d = 1 = 5  17 - 4 • 21; 2) d = 3 = 8  843 - 21  321;
3) d = 42 = 111 -75222 -355 -23520. 9. 30 и 18 или 6 и 90. 10. 2) а) Дробь
может быть сокращена на 2 или 5, или 10, если на эти числа делится а 4- 46.
Указание. (За4-26, а4-46) = (—106, а4-46), а (6, а4-46) = 1. б) Сокращение
возможно лишь на 3, если а 4- 6 делится на 3.	12. —2; 0; 2.
§ 2. Сравнения
307
§2. СРАВНЕНИЯ
Пусть т — произвольное натуральное число, т>1. Каждое целое
число при делении на т дает некоторый остаток, причем разных
остатков ровно т. Это могут быть числа 0, 1, 2, ... , т — 1.
Если числа а и b при делении на натуральное число т дают
равные остатки, то говорят, что эти числа сравнимы по модулю т,
и пишут
а = b (modm).
Иначе говоря, запись а = b (mod tri) означает, что разность чисел
а — b делится на т. Например, 7 = 27 (mod 5), 40 = 14 (mod 13),
10 = —4 (mod 7).
Сравнения были введены в XIX в. немецким математиком К. Гаус-
сом. Они обладают многими из тех свойств, которые справедливы
для равенств.
Перечислим основные свойства сравнений.
1)	Если a = /?(modm) и b = с (modm), то а = с (modm).
2)	Если a = b (mod m) и c = d(modm), то
а + с = b + d (mod m), а — с = b — d (mod m),
ас = bd (mod m), ak = bk (mod m), где k e N,
т.е. сравнения можно складывать, вычитать и перемножать, как
и верные равенства. В частности, можно обе части сравнения
умножать на одно и тоже число.
3)	Если a + b = c (modm), то а = с — 6 (modm).
4)	Если ak = bk (modm), а числа k и т взаимно просты, то
a = b(modm), т.е. обе части сравнения можно сокращать
на общий множитель, если этот множитель и модуль т —
взаимно простые числа.
5)	Если а = Ь (уаоЛт) и d — делитель числа т, то a = 6(modd).
Ограничимся доказательством свойств 4 и 5.
О 1) По условию число ak — bk — k(a - b) делится на m. Так как
k не делится на m (fe и т — взаимно простые числа и 1),
то число а — Ь делится на т, т.е. a = 6(modm).
2)	Так как a = 6(modm), то число а — Ь должно делиться на т,
а значит, и на любой делитель d числа т, т.е. a = 6(modd). •
Пример 1. Найти остаток от деления числа а на т, если:
1) а = 2636, т = 7;	2) а = 2OO72009, т = 13;
3)	а = 2425 • 3611 • 4915, т = 11.
А 1) Так как 26 = 5 (mod 7), то по свойству сравнений 2636 =
= 536 (mod 7). Учитывая то, что 536 = (52)18 = 2518, а 25 =
308
Глава XIX. Делимость целых чисел
= 4 (mod 7), получаем 536 = 418 (mod 7). Заметим теперь, что
418 = (43)6 = 646, а 64 = 1 (mod 7), значит, 418 = I6 (mod 7).
Так как I6 = 1, получаем, что остаток равен 1. Проведенные
рассуждения можно представить в виде цепочки сравнений
2636 = 536 = 2518 = 418 = 646 = I6 = 1 (mod 7).
2) Запишем цепочку сравнений:
2OO72009 = 52009 = 5 • 52008 = 5 • (25)1004 =
= 5 • (-1)1004 = 5 • I502 = 5 (mod 13).
Следовательно, остаток от деления числа 2OO72009 на 13
равен 5.
3) Числа 24, 36 и 49 не делятся на И, поэтому
2425 = 225 = (25)5 = (-1)5 (mod 11),
3611 = З11 = З2 • (З3)3 = 9  53 = 9-4 = 3 (mod И),
4915 = 515 = (53)5 = 45 = 4 • (16)2 = 4 • 25 = 4 • 3 = 1 (mod 11).
Следовательно, по свойствам сравнений 2425 • 3611 • 4915 =
= (—1) - 3 1 = — 3 = 8 (mod 11), т. е. остаток от деления числа
а на 11 равен 8.	А
Пример 2. Доказать, что число а делится на т, если
1) а = 9619 + 3213 - 8 • 7316, zn = 10;
2) а = (1715 + 1517)1517, m = 32.
Д 1) Пользуясь тем, что 96 = 6 (mod 10), и учитывая то, что при
возведении числа 6 в любую степень получается число,
оканчивающееся цифрой 6, имеем по свойству сравнений
9619 = 619 = 6 (mod 10). Так как
3213 = 213 = 2 • (26)2 = 2-42 = 2- 6 = 2 (mod 10),
7316 = З16 = (З2)8 = (-1)8 = 1 (mod 10),
то а^6 + 2- 8 = 0 (mod 10), т. е. число а делится на 10.
2) Найдем сначала остаток от деления на 32 числа 1715 +1517.
Так как
1715 = 17-1714 = 17- (172)7 = 17- (289)7 = 17- (I)7 = 17 (mod 32);
1517 = 15• 1516 = 15- (152)8 = 15• (225)8 = 15- (I)8 = 15 (mod 32).
Следовательно, 1715 + 1517 = 17 + 15 = 32 = 0 (mod 32), т. е.
число 1715 +1517 делится на 32, а значит, и число а делится
на 32.	▲
§ 2. Сравнения
309
Пример 3. Доказать, что если целое число а не делится на 5,
то число a4 — 1 делится на 5.
А Пусть г —остаток от деления а на 5, тогда a = 5k + r, где keZ,
г —одно из чисел 1, 2, 3, 4, так как а не делится на 5 По свойству
сравнений, если а = г (mod 5), то а4 = г4 (mod 5). Учитывая, что
I4 = 24 = З4 = 44 = 1 (mod 5), т. е. г4 = 1 (mod 5) при г = 1, 2, 3, 4,
получаем а4 = 1 (mod 5).
Это означает, что число а4 — 1 делится на 5.	А
Данный пример является частным случаем малой теоремы Ферма,
которая формулируется следующим образом.
Теорема (малая теорема Ферма). Если р — простое число
и число а не делится на р, то ар~х — 1 делится на р (или
ар~[ = 1 (modp)).
О Поскольку а взаимно просто с р, то остатки от деления па р
чисел а,2а,3а,..., (р-1)а — это с точностью до перестановки числа
1,2,... ,р — 1, т. е.
а  2а • За •... • (р — 1)а = 1 • 2 • 3 •... • (р — 1) (modp).
Отсюда	аР~1(р- 1)! = (р- 1)! (modp).
Сократив обе части сравнения на (р — 1)!, получим
ар~{ = 1 (modp).
Теорема доказана.	•
Замечание Теорему Ферма часто записывают в форме, равносильной
приведенной выше, ap=a(modp). В этой записи предположение о том, что а
не делится на р, становится излишним.
Докажем признак делимости на 11. Пусть натуральное число а
имеет вид
а — апап~\... дздао =	+• • • + Ю2а2 + 10ai + «о- (О
Пример 4. Доказать, что натуральное число а, записанное
в виде (1), делится на 11 тогда и только тогда, когда делится
на 11 сумма а^ — а^ + а% — ... + (- 1)пап.
А Так как 10 =—1 (mod 11), то
102 = 104 = ... = 102^ = 1 (mod 11) при любом k е N,
10 = 103 = ... = 10wl = —1 (mod 11) при любом k € N.
По свойству сравнений получаем
10пап +... + 102Я2 + Юсц + п0 = а0 “ °Л + а^ - ... + (-l)nart(mod 11),
т. е. число а делится на 11 тогда и только тогда, когда на 11 делится
сумма его цифр, взятая с чередующимися знаками.	А
310
Глава XIX. Делимость целых чисел
Пример 5. Найти остаток от деления числа а = (987654321)4
на И.
Д Пусть Ь — основание данной степени, тогда а = 64. Сумма
1 — 2 + 3 — 4 + 5 — 6 + 7 — 8 + 9, составленная из цифр числа b
(с чередующимися знаками), равна 5. Поэтому fe = 5(modll), откуда
следует, что а = Ь4 = 54 = (52)2 = 9 (mod 11). Следовательно, искомый
остаток равен 9.	▲
Аналогично признаку делимости на И можно доказать следующий
общий признак делимости чисел-, для того чтобы число N делилось
на d, необходимо и достаточно, чтобы сумма произведений цифр этого
числа на остатки, получаемые от деления на d соответствующих
степеней числа 10, делилась на d.
Действительно, пусть а — \Qnan + ... + Ю2^ + lOai +
и 10п = dqn + гп, ..., 102 = dq% + г*}, 10 = dq\ + г\. Тогда N делится
на d в том и только том случае, если на d делится сумма
М = апГп + ап-\гп-\ +... + а{г{ + ац.
Решение сравнений. Рассмотрим сравнения вида
ах = 6 (mod т),	(2)
где числа a, fe, т известны, ах — неизвестное целое число.
Возможны два случая.
1) Пусть (а, т) — 1, тогда найдутся такие числа Х\ и у\
(см. пример 9 из § 1), что l = ax\ + myi, откуда ах\ — —ту\ + \.
Ясно, что числа xj и т взаимно просты, так как иначе их
общий делитель являлся бы и делителем числа 1. Тогда
ах = 6 (mod т) о ах\х = bxi(mod т).
Но axi = l(modm), поэтому множество решений сравнения (2)
запишется в виде
х = bx](mod т).
2) Пусть (а, т) = d > 1. Тогда, чтобы существовало решение
сравнения (2), необходимо, чтобы b делилось на d (см. свой-
ство 5 для сравнений), иначе сравнение (2) невозможно ни
при каком целом х. Положим в этом случае a = da\, b = db\,
m = dm\. Тогда после сокращения на d исходное сравнение
будет равносильно сравнению
а\х =7?i(mod mi),
в котором уже (ai, mi) = l, и потому оно будет иметь решение
по модулю /щ.
§ 2. Сравнения
311
Пусть X] — наименьший неотрицательный вычет этого ре-
шения по модулю т\. Тогда все числа х, образующие это
решение, найдутся в форме
х =xi(modmi).	(3)
По модулю же т числа (3) образуют не одно решение,
а столько решений, сколько чисел (3) найдется в множестве
{О, 1, 2, ... , т — 1}. Сюда попадет всего d чисел
хь Х[ + mi, Х[ -|- 2mj, ... , х\ + (d — l)mi,
т. е. сравнение (2) будет иметь d решений:
x = xi, x = xi + mi, x = xi +2mi, ... , x = xi + (d — l)mi (modm).
Пример 6. Решить сравнение:
1) 3x = 6(mod7);	2) 3x = 6(mod9).
A 1) Так как (3, 7) = 1, то найдем такие целые числа Х[ и у\,
что 1 = 3%1 + 7у\, В данном случае х\ = —2, у\ = 1. Отсюда
3-(_2) = 1 — 7 -1.
Умножая обе части решаемого сравнения на —2, получим
3 • (—2)х = 6 • (-2) (mod 7) о х = 2 (mod 7).
2) Так как (3, 9) — 3, то после сокращения на 3 исходное сравнение
будет равносильно сравнению
х = 2 (mod3).
Пусть Х[ = 2 наименьший неотрицательный вычет этого
решения по модулю 3. Тогда получаем три числа
Х[ = 2, Х[ + 3 = 5, Xi + 2 • 3 = 8, которые дают три решения
исходного сравнения:
х = 2, х = 5, х = 8 (mod9).	А
Существует еще один способ, который можно применять для
рассмотренных и более сложных сравнений.
Пример 7. Решить сравнение:
1) 3x = 5(mod8);	2) х2 — 2х+ 4 = 0 (mod 7);
3) х3 + х2 + х = 4 (mod 5).
А 1) Построим таблицу остатков, которые дают целые числа при
делении на 8 (в таблице keZ).
Число X вида	8k	86+1	86 + 2	8Лг 4-3	86 + 4	86 + 5	86 + 6	86 + 7
Остатки от деления на 8								
X	0	1	2	3	4	5	6	7
Зх	0	3	6	1	4	7	2	5
312
Глава XIX. Делимость целых чисел
Следовательно, решением данного сравнения будут числа
вида х = 7 по модулю 8.
2) Исходное сравнение сводится к сравнению (х — l)2 = 4(mod7).
Положим у — х — 1 и решим сравнение у2 = 4 (mod 7). Из
таблицы остатков, которые дают целые числа при делении на
7 (в таблице £eZ), имеем:
Число у вида		| 7k + l |	| Ik + 2 | 7k + 3		| 7£ + 4 |	| 7* + 5 |	| 7/? + 6
Остатки от деления на 7							
у2	0	1	4	2	2	4	1
Решением сравнения у2 = 4 (mod 7) будут числа вида у = 2
и у = 5 по модулю 7. Следовательно, решением исходного
сравнения будут числа вида х = 3их~6по модулю 7.
3) Построим таблицу остатков, которые дают целые числа при
делении на 5 (в таблице keZ).
Число х вида	5А	5Й+1 |	| 5А + 2 |	| 5/г + З |	| 56 + 4
Остатки от деления на 5					
х2	0	1	4	4	1
X3	4	0	1	3	2	4
х3 4- х2 + х	0	3	4	4	4
Следовательно, решением данного сравнения будут числа
вида х = 2, х = 3 и % = 4 по модулю 5.	А
Задачи
1.	Найти остаток от деления числа а на т, если:
1)	а = 14256, т = 17;	2) а = 6592, т = 11;	3) а = 21993, т = 33;
4)	а = З333, m = 5;	5) а = (116 + 1717) , т = 8.
2.	Доказать, что число 22 225555 + 55 552222 делится на 7.
3.	Доказать признаки делимости.
1)	Натуральное число а делится на 9 тогда и только тогда, когда сумма
его цифр ад + С1 + а2 + •. • + ап делится на 9.
2)	Пусть натуральное число а = алал-1. •. а2а\ао = ЮООЛ -Ь В, где
А = апап_[... аз, В = а2а1ао* Число а делится на 7 (или на 11, или
на 13) тогда и только тогда, когда А = В (mod 7) (соответственно mod 11
или mod 13).
4.	Доказать, что а не может быть четвертой степенью натурального числа,
если а — 5 делится на 9
§3. Решение уравнений в целых числах
313
5.	Доказать, что числа следующего вида не могут быть квадратами целых
чисел:
1)	12п + 5, где п G Z; 2) 7п + 3, где п 6 Z.
6.	Найти наименьшее натуральное число, большее 1 и дающее при делении
на 2, 3, 4, 5, 6 остаток, равный 1.
7.	Доказать, что
1)	квадрат простого числа, большего 3, дает остаток 1 при делении на 24;
2)	квадрат простого числа, большего 5, при делении на 30 дает в остатке 1
или 19.
8.	Доказать, что любое натуральное число, десятичная запись которого состоит
из 5/7 единиц, делится на 41.
9.	Доказать, что ни при каком натуральном п число 1 + 2 +... + п не может
оканчиваться ни одной из цифр 2, 4, 7, 9.
10.	Доказать, что число п7 — п делится на 42 при любом п 6 Z.
11.	Решить сравнения*
1)	2х + 3 = 0 (mod 6);	2)	Зх + 5 = 0 (mod 7);
3)	х2 + х + 3 = 0 (mod5);	4)	х2 + 1 = 0 (mod 13).
Ответы
1. 1) 1;	2) 3; 3) 8; 4) 3; 5) 5.	6.	61. 11. 1) Решений	нет;	2) x = 3(mod7);
3) х =	1 (mod 5) или х = 3 (mod 5);	4) х = 5 (mod 13) или	х =	8 (mod 13).
§3. РЕШЕНИЕ УРАВНЕНИЙ В ЦЕЛЫХ ЧИСЛАХ
Любое уравнение, которое требуется решить в целых числах,
называют диофантовым уравнением. Простейшими из них являются
линейные диофантовы уравнения вида ах + Ьу — с, где a, b, ceZ. Его
решение (х, у) — пара целых чисел. При решении этого уравнения
используется следующая теорема.
Теорема 1. Линейное диофантово уравнение ах + by = с, где
а, Ь, с 6Z, имеет решение тогда и только тогда, когда с делится
на НОД чисел а и Ь. Если б? = НОД(а, Ь), а — а\ф Ъ — b\d, c = c\d
и (xo,f/o) — некоторое решение уравнения ах -Р by = с, то все
решения задаются формулами
х = х0 + М, */ = #0-^1*,	(О
где t — произвольное целое число.
О Пусть й = НОД(а, £>), т.е. существуют такие числа а\ и что
а = a\d, b = b\d. Тогда уравнение преобразуется к виду
а\d- х + bid -у— с или d (сцх + Ь\у) = с.
Отсюда следует, что уравнение имеет решение в целых числах
тогда и только тогда, когда с делится на d, т.е. c = c\d. Переписывая
уравнения в виде	z	.
d (а\х + Ь\у) —
314
Глава XIX. Делимость целых чисел
и сокращая на d, получим уравнение
ар; + b[y = ci,	(2)
где («1, b\) = 1, т. е. числа щ и Ь\ взаимно просты.
Пусть теперь (xq,z/q) — некоторое решение этого уравнения.
Рассмотрим пару чисел, заданных формулами (1), и покажем,
что эта пара также является решением уравнения (2). Подставив
их в уравнение (2), получим ai(%o + М) + ^1(Уо —	= е1 или
aiXQ + b[t/o + aibit — biait = ci, т.е. равенство верно при любом t.
—с\	=-0
Пусть (х*, z/*) — также решение уравнения а\х + Ъ\у = с\, т.е.
оцх* + Ь\у* — с\. Вычитая из левой и правой частей этого равенства
соответственно левую и правую части равенства ai*o +
получим
О1 (х* - Хо) + ь\ (у* - Уо) = О-
Заметим, что при ау, Ь\ ^0, если х* ^xq, то и у* ^уо, и наоборот.
Так как («1, Ь\) — 1, то
х* — xq = kb\ и у* — уо = tai,	(3)
где k, t е Z. Тогда имеем
kbiai + taibi — aibi(k + Z) = О,
т.е. k = — t. Отсюда из (3) получаем формулы (1).
Теорема доказана.	•
Замечание. Теорема 1 утверждает, что если линейное диофантово
уравнение имеет решения, то их все можно представить в виде (1), однако
для этого нужно знать некоторое решение (хо,г/о)- Как правило, оно находится
подбором.
Линейное диофантово уравнение ах + by = с, где a, b, с е Z
и с 7^ 0, назовем неоднородным, а соответствующее ему уравне-
ние ах + by — 0 — однородным. Пусть (х0, Уо) — частное решение
неоднородного уравнения, a (bt, —at), где teZ, — общее решение
однородного уравнения.
Так же, как и при решении линейных дифференциальных
уравнений, в случае (a, b) = 1 справедливо утверждение: общее
решение линейного неоднородного диофантова уравнения равно
сумме частного решения неоднородного уравнения и общего решения
соответствующего ему однородного уравнения.
Пример 1. Решить уравнение 5х — 8у — 4 = 0.
Д Первый способ. НОД(5, 8) = 1. Найдем какое-нибудь решение
(хО'Уо) данного уравнения 5х — 8у — 4 — 0. Выразим переменную, име-
§3. Решение уравнений в целых числах
315
ющую наименьший по модулю коэффициент: х = 8j/+ 4 = у +1 + ~1 .
Достаточно взять уц = 2, тогда xq = 4. Запишем ответ:
х = 4 - 8t, у = 2 - 5/, t € Z.	(4)
Второй способ. Выразим х: х = 8j/4~4 = у + 1 + 3j/~ *. Целые
решения существуют, если Зу — 1 = 5п (п. е Z).
Аналогично у =	1 = п + 2п + т. е. 2п + 1 — Зр (р G Z).
О	О
Отсюда п=	=p + £zl. Последнее равенство в целых числах
возможно, если р — 2t +1 (t G Z). Выражая х и у через /, получим
х — 4 + Sty у — 2 + 5/, t G Z.
Отметим, что полученный ответ совпадает с ответом (4), так как
/ — любое целое число.	▲
Пример 2. Найти все целые решения системы уравнений
( 2x + Sy + 4z = ly
[ Зх + 2у + 3z = 2.
Л Преобразуем уравнения системы, умножив первое на 3, второе
на 2:
Г 6х + 9у + 12г = 3,
[ 6х + 4у + 6z = 4.
Вычитая второе уравнение из первого, получим линейное дио-
фантово уравнение Зу + 6z = — 1, решением которого будут пары
целых чисел вида (//, г), где у = 1 + 6/, г — —1—5/ (/GZ).
Подставляя полученные числа в первое уравнение исходной
системы, найдем
2х = 1 - Зу - 4г - 1 _ 3(1 + 6/) - 4(—1 - 5/) = 2 + 2/ (/ G Z).
Отсюда х = 1 + t (/ G Z). Следовательно, решением данной в
условии системы уравнений будут тройки целых чисел вида (х, г/, г),
где х = 1 + /, у = 1 + 6/, z = -1 - 5/ (/ g Z).	▲
Диофантовы уравнения более высоких степеней. Рассмотрим
на примере разные приемы решения уравнений в целых числах,
степень которых превышает 1.
Пример 3. Решить уравнение Зху — 6х2 = у — 2х + 4.
А Первый способ (разложение на множители). Перепишем
уравнение в виде
Зх(у - 2х) - (у -2х) — 4 о (у — 2х)(3х - 1) = 4.
316
Глава XIX. Делимость целых чисел
Так как xeZ и у € Z, то (у — 2х) е Z и (Зх —l)eZ. Поэтому для
решения задачи достаточно рассмотреть все возможные варианты
разложения числа 4 в произведение двух целых множителей. Всего
существует четыре случая:
4 - 2-2 = (-2)* (-2) = 1-4 = ( 1) - (—4).
Соответственно, далее остается решить шесть систем линейных
уравнений:
1)
4)
f у — 2х = 2,
( Зх — 1 = 2;
( у — 2х = 4,
(Зх — 1 = 1;
у — 2х = —2,
Зх - 1 = -2;
у — 2х — — 1,
Зх - 1 = —4;
( у — 2х = 1,
( Зх - 1 = 4;
(у — 2х = —4,
(Зх —1 = —1.
Вторая, третья и четвертая системы не имеют решений в целых
числах. Из первой получаем х = 1, у = 4. Из пятой х = — 1, у = — 3
и из шестой х = 0, у = —4.
Второй способ (выражение одной неизвестной через дру-
гую). Заметим, что неизвестная у входит в уравнение в первой
степени. Выразим ее через х:
Зху - у = 6х2 - 2х + 4 о у = 6х2-2х + 4 =2х	4.
v J	v Зх -1	Зх - 1
Решение в целых числах возможно только в случае, если число
Зх — 1 является делителем 4. Существует шесть вариантов:
1) Зх — 1 = 2;	2) Зх - 1 - -2;	3) Зх — 1 = 4;
4) Зх — 1 = 1;	5) Зх-1 = -4;	6) Зх — 1 = — 1.
Второе, третье и четвертое уравнения не имеют решений в целых
числах. Из остальных получаем х = 1, или х — —1, или х = 0.
Подставляя их в выражение для у, получаем целые решения
исходного уравнения, т. е. (1; 4), (—1; —3), (0; —4).
Третий способ (решение уравнения как квадратного от-
носительно одной из неизвестных). Перепишем уравнение в виде
6х2 — (2 + Зу)х + (у + 4) = 0. Решим его относительно х:
(2 + 3z/) ± 7(2 + Зг/)2 — 24(г/+ 4)	(2 + 3//) ± 7(3г/- 2)2 - 96
^1,2 = ------------------------- =--------+-----------•	(5)
Для существования целых решений необходимо, чтобы дискриминант
уравнения был квадратом целого числа, т. е. (Зу — 2)2 — 96 = /г2,
где k € Z. Получаем (Зу — 2)2 — Л2 — 96. Следовательно,
k = П\.
ь _ где П[ и П2 — два
(Зу — 2 — k)(3y — 2 + &) = 96 или f
I о// — z —
§3. Решение уравнений в целых числах
317
целых числа таких, что п\  п% — 96. Сложив уравнения системы,
получим бу — 4 = щ + П2 или
у=21±^±1.	(6)
Поскольку — 96 < /11, /12 < 96, п\ и /22 одного знака, то возможны
варианты
96 = 1 • 96 - 2 • 48 = 3 • 32 = 4 • 24 = 6 • 16 = 8 • 12
Аналогично,
96 = (-1). (-96) = (-2) • (-48) = (-3)  (-32) =
= (-4) • (-24) = (-6) • (-16) = (-8) • (-12).
Отсюда, учитывая условие (6), получаем возможные значения у:
У = 9, у = 4, у = —4 и у = -3.
Подставляя полученные значения в (5), убеждаемся, что при
у = 9 значение х не является целым. Для остальных случаев
получаем следующие решения в целых числах исходного уравнения
(1; 4), (0; -4), (-1; -3).
Ответ. (1; 4), (0; -4), (-1; -3).	▲
Великая теорема Ферма. Примерно в 1630 г. Пьером Ферма
была сформулирована следующая теорема.
Теорема 2 (Ферма). Всякое уравнение хп +уп — zn при п>2
не имеет решений в области натуральных чисел.
Доказательство этой теоремы состоит в большой серии утвержде-
ний, полученных многими математиками XVII-XX вв., завершение
доказательства получено Эндрю Уайлсом лишь в 1994 г.
Пифагоровы тройки. При /2 = 2 уравнение хп -\-уп = zn принимает
вид	x2 + y2 = z2.	(7)
Оно имеет бесконечно много решений. Тройки целых чисел (х, у, г),
удовлетворяющие этому уравнению, называют пифагоровыми трой-
ками.
Теорема 3. Пифагоровы тройки образуют числа следующего
вида:		^2	yyfl. । „2 x = t-—, y = tmn, z — t	£—,	(8)
а также	_ „2	w2 i „2 x = tmn, y = t		—, z = t	g—,	(9)
где тип — нечетные взаимно простые натуральные числа (т>п),
a t — произвольное натуральное число. Наоборот, любая тройка
318
Глава XIX. Делимость целых чисел
чисел (х, у, г), удовлетворяющая формулам (8) или (9), является
решением уравнения (7).
Например, при t = 1 из формул (8) получаем такие решения:
n = l,m = 3 => х = 3, у —A, z = 5;
п = 1,	т = 5	=>	х = 5, у = 12,	z = 13;
п = 1,	т = 7	=>	х = 7, у = 24,	z = 25;
п = 3,	т = 5	=>	х = 15, у = 8,	z = 17;
/г = 3,	т = 7	=>	% = 21, у = 20, z = 29; и т. д.
Задачи
1. Найти все целые решения уравнений:
1) 6x4- 9у = 2;	2) 5x4-9г/= 2;	3) 15х 4- 78у = 12;
4)	13x4-9z/ = 1;	5) 7x4-17г/= 5.
2* Пусть А — множество целых чисел, имеющих при делении на 5 остаток 3.
а В —множество целых чисел, имеющих при делении на 8 остаток 7 Найти
все числа, которые входят одновременно в оба множества
3.	Найти все целые решения систем уравнений:
. Г Зх 4-Зг/4-5z = 1,	( 2х 4- Зу 4- 5z = 8,
[ 4х 4-5у — 2z = 4;	( 5х - бу 4- 8z = 9.
Решить уравнения в целых числах (4-6):
4.	1) 2ху — 6х2 = 9х — Зу 4- 6;	2)	Зху — 9х2 = у — Зх 4- 8.
5.	х2 4- (х 4~ l)^ 4- (х 4- 2)2 4- (х 4- З)2 = 10z/.
6.	1) х2 - 6xz/ 4- 13z/2 = 100,	2)	2x2z/2	4- z/2 — 6x2 — 12 = 0;
3) 2xy 4- x 4- у — 83.
7? Доказать, что следующие уравнения не имеют решений в целых числах:
1)	х2 4-г/2 = 1971;	2) 19х3 - 17z/3 = 50;	3) 2x2-5z/2 = z2.
8? Найти все рациональные решения уравнения: х2 4- Зу2, = 1.
Ответы
1.	1) Нет решений; 2) х = 44-9/, у = — 2 — 5/, /EZ; 3) х = —204-26/, z/ = 4 —5/,
t € Z; 4) х = 2 4- 9/, у = -3 - 13/, t е Z; 5) х = 25 4- 17/, у = -10 - 7/, / е Z.
2. Числа вида 234-40/, / G Z. Указание. Решить в целых числах уравнение
5х 4- 3 = 8у 4- 7. 3. 1) х = -85 - 31/, у = 72 4- 26/, z = 8 4- 3/, / € Z; 2) нет
решений. 4. 1) (-2; -12), (-1; 3), (-3; -11), (0; 2); 2) (3; 10), (1; 7), (0; -8),
(-1; -5). 5. х = 5п + 1, г/= 10/г2 + 10п + 3 (ngZ). 6. 1) (1, 3), (-1, -3),
(17, 3), (-17, -3), (-6, -4), (6, 4). (—18, -4), (18, 4); 2) (2, 2), (-2, -2),
(-2, 2), (2, -2); 3) (0, 83), (83, 0), (-1, -84), (-84, -1). 7. 1) Указание.
Рассмотреть остатки суммы квадратов х и у при делении на 3. 2) Указание.
Рассмотреть остатки левой и правой частей уравнения при делении на 9.
§4. Текстовые задачи с целочисленными неизвестными
319
3) Указание. Рассмотреть остатки левой и правой частей уравнения при
3^2 _ 1
делении на 5. 8. х = ^2	, у = -fe2 € Q); х — 1, // = 0. Указание.
Положить у = k(x — 1)
§4. ТЕКСТОВЫЕ ЗАДАЧИ С ЦЕЛОЧИСЛЕННЫМИ
НЕИЗВЕСТНЫМИ
Пример 1. Даны два двузначных числа. Если большее число
написать впереди меньшего и полученное четырехзначное число
разделить на меньшее, то в частном получится 247, а в остатке 10.
Если же меньшее число написать впереди большего и разделить
полученное число на большее, то в частном получится 41, а в остатке
20. Найти сумму данных двузначных чисел.
А Запишем меньшее число в виде ху, большее —в виде
zt. Тогда, написав большее впереди меньшего, получим
ztxy = 1000г + 100/ + Юх + у. Запишем тот факт, что при делении
полученного числа на ху = Юх + у в частном получится 247,
а в остатке 10:
1000г + 100/ + 10% + у = 247 (1 Ох + у) + 10.
Аналогично во втором случае:
ЮООх + 100// + Юг + / = 41 (Юг + /) + 20.
Обозначив s = zt — Юг + /, и = ху = Юх + у, получим систему
уравнений
( 100s + и — 247и + 10,
( lOOu -Т s — 41s -р 20,
из которой получаем s = 37, и = 15.
Ответ. 37 и 15.
Пример 2. Техническая реконструкция предприятия была прове-
дена в четыре этапа. Каждый из этапов продолжался целое число ме-
сяцев и сопровождался падением производства. Ежемесячное падение
производства составило на первом этапе 4%, на втором —12,5%, на
третьем — и на четвертом — у%. По окончании реконструкции
первоначальный объем производства на предприятии сократился на
64%. Определить продолжительность периода реконструкции.
А Пусть х, у, г и / — продолжительности соответственно первого,
второго, третьего и четвертого этапов (в месяцах), где х, у, z и / —
натуральные числа. Если первоначально объем производства был
равен V, то после реконструкции он будет равен
у. fl _ _4_V. fl _ _25_y.fi -	. fl - _50_V= v-fl - 61Y
V 100 J v 2-100/ \	7-100/ v 3-100/	\	100/
320
Глава XIX. Делимость целых чисел
Сократив на I/, получим
24 V /б\2 /<5У — _9.
25/ ’ \8/ ’ \7/ ’ \6/ ” 25’
/23-З\х /7_У (L1V ( 5 У - 32
\ 52 /	\23/ Ч 7 )	\2-3/	52
23х-Зу+z—t gx+z—t g—2х+/ . yy—z — 2^ • 3^ • g—2 . yO
Так как x, у, z и t — натуральные числа, a 2, 3, 5 и 7 —простые
числа, то в силу единственности разложения натурального числа на
простые множители получаем систему линейных уравнений
f Зх — Зу + z — t — О,
x + z — t = 2,
< -2х +1 - -2,
<y-z = O.
Решая ее, получаем х = 2, у = 2, z — 2 и / = 2. Следовательно, весь
период реконструкции длился 8 месяцев.
Ответ. 8 месяцев.	▲
Иногда при решении задач на целые числа количества получаю-
щихся уравнений недостаточно для выбора однозначного ответа. По-
этому на одном из этапов решения приходится использовать перебор
получающихся вариантов, чтобы отобрать решение, удовлетворяющее
всем условиям задачи.
Пример 3. В финальном забеге соревнований по кроссу ока-
залось, что число спортсменов, выполнивших мастерский норматив,
меньше но больше от общего количества спортсменов,
закончивших дистанцию. Какое минимальное число спортсменов
закончило дистанцию?
Л Пусть 7V — число спортсменов, закончивших дистанцию, а п —
число спортсменов, выполнивших мастерский норматив. Тогда, со-
гласно условию, N и п удовлетворяют неравенству	< —
или ^ > — > ^ о > N > Подберем такое наименьшее
7 п 6	7	6	г
значение п, чтобы в интервале у и) содержалось хотя бы одно
целое число N. Перебором, начиная с и = 1, получим, что при п = 4
такое N, удовлетворяющее неравенству 9^ > N > 8^, существует
h7V = 9.
Ответ. 9 спортсменов.	▲
Пример 4. Квартал застроен пятиэтажными и девятиэтажными
домами, причем девятиэтажных домов меньше, чем пятиэтажных
§4 Текстовые задачи с целочисленными неизвестными
321
Если число девятиэтажных домов увеличить вдвое, то общее число
домов станет более 24, а если увеличить вдвое число пятиэтажных
домов, то общее число домов станет менее 27. Сколько построено
пяти- и девятиэтажных домов?
А Пусть построено х девятиэтажных и у пятиэтажных домов Из
условия задачи получаем систему неравенств
{%<#,
2х + у > 24,
х + 2у < 27.
Из второго неравенства имеем х > 24-^из третьего х < 27 — 2у.
Отсюда	Л О/1
( 24 — у
J 2 Х	(1)
\^<х<27-2у
V 2
или, освобождаясь от %,
( 24 — у .
I —2"^ < У,
1	< 27 - 2у.
Следовательно, у удовлетворяет неравенствам
Г8<г/,
[//<10.
Поскольку r/eZ, то у = 9. Тогда из первого неравенства системы (1)
имеем 7,5 < х < 9, т. е. х — 8.
Ответ. 9 пятиэтажных и 8 девятиэтажных домов	▲
Задачи
1.	Найти двузначное число, которое меньше суммы квадратов цифр, состав-
ляющих его, на 11, и больше их удвоенного произведения на 5.
2.	Сумма цифр двузначного числа равна 12 Если к искомому числу прибавить
36, то получится число, записанное теми же цифрами, но в обратном порядке.
Найти это число.
3.	Результат деления двузначного числа на произведение его цифр равен 2.
Найти это число.
4. На складе имелось несколько одинаковых ящиков, в каждом из которых
было равное количество одинаковых заготовок. Заготовки используются
следующим образом: сначала со склада в цех берут один ящик, заготовки
из которого последовательно поступают в производство, а пустой ящик
возвращается обратно на склад и берется следующий ящик и т. д. После
того как было израсходовано ровно — всех заготовок, оказалось, что на
складе имеется ровно 7 пустых ящиков. Сколько ящиков с заготовками
было первоначально на складе?
11—3022
322
Глава XIX. Делимость целых чисел
5.	Если двузначное число разделить на сумму его цифр, то получится
в частном 4, а в остатке 3. Если же разделить его на произведение цифр,
то получится в частном 3, а в остатке 5. Найти это число.
6.	В первый день Маша собрала на 25% грибов меньше, чем Вася, а во второй
день — на 20% больше, чем Вася. За два дня Маша собрала грибов на 10%
больше, чем Вася. Какое наименьшее количество грибов они могли собрать
вместе?
7.	Сумма цифр искомого четного трехзначного числа равна 11 Если к искомому
числу прибавить 594, то получится число, записанное теми цифрами, но
в обратном порядке. Найти это число.
8.	Если двузначное число разделить на произведение его цифр, то в частном
получится 1, а в остатке 16. Найти это число.
9.	Произведение двузначного числа на число, записанное теми же цифрами,
но в обратном порядке, равно 1008. Найдите это двузначное число.
10.	На стоянке находятся машины марок «Москвич» и «Волга». Общее число их
менее 30. Если число «Волг» увеличить вдвое, а число «Москвичей» — на 27,
то «Волг» станет больше. Если, не изменяя число «Волг», увеличить вдвое
число «Москвичей», то «Москвичей» станет больше. Сколько «Москвичей»
и сколько «Волг» находятся на стоянке?
11.	Квартал застроен пятиэтажными и девятиэтажными домами, причем девя-
тиэтажных домов больше, чем пятиэтажных. Если число девятиэтажных
домов увеличить вдвое, то общее число домов станет менее 32, а если
увеличить вдвое число пятиэтажных домов, то общее число домов станет
более 28. Сколько построено пятиэтажных и девятиэтажных домов?
12.	При подведении итогов шахматного турнира оказалось, что на первое
место претендуют сразу несколько спортсменов Их количество оказалось
7	5
больше —, но меньше — от общего числа участников соревнований. Какое
минимальное количество шахматистов принимало участие в турнире?
13.	После сдачи студентами факультета сессии оказалось, что количество
4	5
отличников меньше —, но больше — от общего числа студентов факультета.
Какое наименьшее число студентов может быть на факультете?
14.	Все члены семьи выпили по чашке кофе с молоком, причем Катя выпила
четвертую часть всего кофе и шестую часть всего молока Сколько человек
в семье?
15.	Химический завод имеет цеха трех типов. В каждом цехе первого, второго
и третьего типов работает соответственно 350, 80 и 30 рабочих, а также
91, 19 и 8 технологов. Всего в цехах завода работают 980 рабочих
и 252 технолога. Найти число цехов каждого типа, если известно, что
общее количество цехов не превосходит 15.
16.	На какое целое положительное число надо разделить 180, чтобы остаток
составлял 25% от частного?
17.	Техническая реконструкция предприятия была проведена в четыре этапа
Каждый из этапов продолжался целое число месяцев и сопровождался
падением производства. Ежемесячное падение производства составило на
50
первом этапе 4%, на втором —10%, на третьем ——% и на четвертом —
65%. По окончании реконструкции первоначальный объем производства на
§4. Текстовые задачи с целочисленными неизвестными
323
предприятии сократился на 93%. Определить продолжительность третьего
этапа реконструкции.
Ответы
1. 15 и 95. 2. 48. 3. 36. 4. 10 ящиков. 5. 23. 6. 189. 7. 218. 8. 37,
48 или 79. 9. 24 или 42. 10. 19 «Волг» и 10 «Москвичей». 11. 9 пятиэтажных,
11 девятиэтажных. 12. 45 первого и 20 второго. 13. 25.	14. 5.	15. Цехов
1-го и 2-го типов по 2, третьего 4. 16. 11. 17. 7 месяцев.
Глава XX
КОМБИНАТОРИКА
§1. ОСНОВНЫЕ ЗАКОНЫ КОМБИНАТОРИКИ
На практике часто приходится выбирать из данного множества
объектов подмножества элементов, обладающих некоторыми свой-
ствами, располагать элементы одного или нескольких множеств
в определенном порядке и т. д. Поскольку в этих задачах речь идет
о тех или иных комбинациях элементов, их называют комбинатор-
ными задачами. Область математики, изучающая комбинаторные
задачи, называют комбинаторикой. Она является частью теории
конечных множеств —любую комбинаторную задачу можно свести
к задаче о конечных множествах.
Различают несколько уровней решения комбинаторных задач.
Начальным является поиск хотя бы одного расположения объек-
тов, обладающего заданными свойствами (например, расположения
восьми ферзей на шахматной доске, не бьющих друг друга). Если
комбинаторная задача имеет несколько решений, то возникает вопрос
о подсчете числа таких решений, об описании всех решений задачи. И
наконец, может возникнуть проблема поиска оптимального варианта
решения в случае, если различные решения комбинаторной задачи от-
личаются друг от друга некоторыми параметрами. Для подсчета числа
решений комбинаторных задач используются формулы, основанные
на двух простых правилах, называемых правилами произведения
и суммы.
Правилом суммы называют следующее утверждение. Если
множества Х], Л2, . попарно не имеют общих элементов,
т. е Xi П Xj = 0 при i ], то число элементов в их объ-
единении равно сумме чисел элементов в каждом из множеств
|X( UX? U ... UXn| = |АД + |%2| + • • - + IM
При п = 2 правило суммы можно сформулировать так:
Если элемент х можно выбрать k способами, а элемент у можно
выбрать т способами, причем любой выбор элемента х отличен
от любого выбора элемента у, то выбор х или у можно сделать
k + m способами.
Правилом произведения называют следующее утверждение. Если
даны два множества X и У, состоящие соответственно из k и т
§ 1. Основные законы комбинаторики
325
элементов, то пару (%, у) такую, что хеХ.уе У, можно составить
km способами. Правило произведения можно переформулировать так:
Если элемент х можно выбрать k способами, а элемент у можно
выбрать m способами, то пару (х, у) можно выбрать km способами.
Замечание. Правило обобщается на случай, когда выбирается не пара,
а тройка, четверка элементов и т. д.: если элемент х\ можно выбрать k[
способами, элемент х% можно выбрать k% способами, .., элемент хт можно
выбрать km способами, то набор (%ь• • •,хт) можно выбрать й| х^х... хkm
способами.
Пример 1. Бросают две игральные кости (с шестью
гранями каждая) (рис. 1). Сколькими способами они могут
упасть так, что либо на каждой кости выпадет четное
число, либо на каждой кости выпадет нечетное очков?
А Пусть k — число способов выпадения на каждой кости
четного числа очков, т — число способов выпадения на каждой кости
нечетного числа очков. Тогда по правилу суммы искомое число равно
k + m.
Пусть k\ — число способов выпадения четного числа очков на
первой кости, а &2~число способов выпадения четного числа очков
на второй кости. Тогда k\ ~ k<2 — 3 и по правилу произведения
k — k\ • feg — 9. Аналогично получаем, что т — 9. Следовательно,
искомое число способов равно k + т — ^ + — 18.	▲
Упорядоченный набор (xi, х^ ... , хт\ где xt € X/, называ-
ется кортежем длины т, составленным из элементов множеств
Хь Х2, Хт, и является элементом декартова произведения
Xi х Х2 х ... х Хт. Элемент хг(1 < I < т) называют i-й компонентой
или f-й координатой кортежа (xi, Х2, ... , хт). Если все множества
Xi равны X, то (xi, Х2, ... , хт) называется кортежем длины т,
составленным из элементов множества X.
Два кортежа (xi, Х2, ..., хп) и (f/i, у%,..., yk) считаются равными,
если длина их одинакова, а их компоненты, имеющие одинаковые
номера, равны.
Например, равны кортежи а= (2, х/9, З2) и /3 = (х/4-, 3, 9), так
как 2 = \/4, л/9 = 3, 32 = 9, и неравны кортежи (а, Ь, с) и (6, а, с),
так как порядок их компонент различен.
Пример 2. Сколько различных кортежей длины k можно соста-
вить из элементов множества Х= {xi, Х2,..., хп}, если это множество
не содержит одинаковых элементов?
А Используя правило равенства кортежей, получаем, что два кор-
тежа одинаковой длины различны, если они различаются порядком
326
Глава XX. Комбинаторика
следования элементов, Будем из элементов хь %2, •хп составлять
различные кортежи
Так на первую позицию можно поместить любой из п эле-
ментов Xi, %2, хп на вторую уже любой из л-1 элементов,
а различных способов для заполнения первых двух позиций по
правилу произведения получается п(п — 1). Далее аналогично, на
третью — любой из п — 2 элементов, а различных способов для
заполнения первых трех позиций получается п(п — 1)(я — 2), и т. д.
Окончательно получаем, что общее число кортежей длины k,
формируемых из различных элементов п-элементного множества,
равно п+1) =	▲
Пример 3. Сколько различных кортежей длины k можно со-
ставить из элементов множества X = XiUX2U... где каждое
множество Xi состоит из k или более одинаковых элементов X/,
причем все элементы х^ Х2, .хп различны?
Д По аналогии с предыдущим примером будем из элементов
Xi, Х2, хп составлять различные кортежи. Так как на первую
позицию можно поместить любой из п элементов Xj, Х2, .хп
и на вторую также любой из п элементов, то различных способов
для заполнения первых двух позиций по правилу произведения
получается п • п = г?. Далее аналогично, на третью —любой из
п элементов, а различных способов для заполнения первых трех
позиций получается и3, и т. д. Окончательно получаем, что общее
число кортежей длины k в этой задаче равно п-п*... -n = nk. ▲
k раз
Задачи
1.	Сколькими способами можно расставить на книжной полке подряд друг за
другом книги десятитомного собрания сочинений?
2.	В подземную пещеру ведут 6 путей. Сколько туристических маршрутов
посещения можно составить, чтобы спуск и подъем происходили по
различным путям?
3.	1) Сколькими способами можно сделать трехцветный флаг с вертикальными
полосами одинаковой ширины и различных цветов, если имеется материя
7 различных цветов?
2)	Сколькими способами можно сделать флаг, содержащий 7 вертикальных
полос одинаковой ширины красного, белого и синего цвета, причем любые
две соседние полосы должны быть разных цветов?
4.	В некотором государстве нет двух жителей с одинаковым набором зубов.
Какова может быть наибольшая численность этого государства? Напомним,
что у человека может быть не более 32 зубов.
§2. Основные формулы комбинаторики
327
5.	1) Сколько пятизначных чисел можно составить из цифр 1, 3, 4, 6, 7, 9,
чтобы каждая цифра входила в число не более одного раза? Найти
сумму всех этих чисел.
2)	Сколько четырехзначных чисел можно составить из цифр 0, 2, 3, 4,
8, 9, если каждая цифра, входящая в число, может повторяться? Найти
сумму всех этих чисел.
6.	Сколько существует четырехзначных чисел, в которых две единицы стоят
рядом, а остальные цифры различны и не равны 1? А пятизначных?
7.	1) Сколькими способами можно на шахматной доске расставить 8 ладей,
чтобы они не били друг друга, если: а) ладьи неразличимы; б) ладьи
различимы (например, пронумерованы)?
2)	Сколькими способами можно на шахматной доске расставить 7 ладей,
чтобы они не били друг друга, если: а) ладьи неразличимы; б) ладьи
различимы (например, пронумерованы)?
8.	Сколько существует пятизначных чисел, которые одинаково читаются слева
направо и справа налево? А шестизначных?
9.	Пусть рь Р2,-’ч pfe — различные простые числа Сколько делителей имеет
число а = р”1 -р^ •.. • *Р^? гДе гц, > nk ~~ некоторые натуральные числа,
включая 1 и само число а?
10.	Сколько диагоналей имеет выпуклый п-угольник?
Ответы
1. 10!	2. 30.	3. 1) 210; 2) 3 • 26 = 192.	4. 232 .	5. 1) 720;
39 999 600; 2) 1080; 6135480.	6.200; 1848.	7. 1) а) 8! = 40 320;
б) (8!)2; 2) а) 8! • 8=322 560; б) (7!) • 8! • 8= (8!)2.	8. 900; 900.
9. (л, + 1)(л2 +1)...(л* + 1).	10.
§2. ОСНОВНЫЕ ФОРМУЛЫ КОМБИНАТОРИКИ
1.	Размещения с повторениями
Кортежи длины k, составленные из элементов п-элементного
множества X, называют также размещениями с повторениями из
п элементов по k. Их общее число обозначают Д^ (Д — первая
буква франц, arrangement — размещение). Из примера 3 предыдущего
параграфа следует, что
4 = л*.	(1)
Пример 1. Имеется 5 различных стульев и 7 рулонов обивочной
ткани различных цветов. Сколькими способами можно выполнить
обивку стульев?
Д Так как стулья различны, то их можно расположить в опреде-
ленном порядке, и каждому способу обивки будет соответствовать
кортеж длины 5, составленный из данного 7-элементного множества
цветов ткани. Их число найдем по формуле (1): Д? = 75 = 16807. ▲
328
Глава XX. Комбинаторика
Пусть есть ^-элементное множество X и n-элементное множество
Y. Для подсчета числа отображений f множества X в множество Y
(f:X-+Y) используется формула числа размещений с повторениями
из п элементов по k элементов. Число отображений k-элементного
множества в п-элементное множество равно А„ = nk.
Этот результат позволяет найти число подмножеств п-элемент-
ного множества X. Для этого возьмем числа 0 и 1. Каждому под-
множеству А множества X соответствует отображение ср множества
X в множество {0: Ц, при котором элементы из А отображаются в 1,
а остальные — в 0. Число таких отображений равно 2", где п — число
элементов множества X. Значит, число подмножеств п-элементного
множества X равно 2Л.
Пример 2. Сколько существует способов размещения п различ-
ных предметов по т различным ящикам?
Д Каждый предмет может быть помещен в любой из т ящиков.
Тогда по правилу произведения число размещений п различных
предметов по т различным ящикам равно
т • т . - гп = тп = Апт.	А
п
2.	Размещения без повторений
Во многих случаях возникает задача нахождения числа кортежей
длины k из элементов данного ^-элементного множества, в которых
нет повторяющихся элементов. Образование таких кортежей можно
наглядно представить следующим образом.
Элементы множества X, помещенные в мешок, извлекаются из
него один за другим без возвращения назад и записываются. После k
извлечений запись представляет собой кортеж длины k, состоящий
из элементов множества X (точнее говоря, из их названий), без
повторов. Кортеж состоит из k различных элементов, расположенных
в определенном порядке. Такие кортежи называют упорядоченными
множествами. Их отличие от произвольного кортежа состоит в том,
что в них нет двух одинаковых элементов.
Одно и то же множество можно упорядочить различными
способами (например, множество школьников данного класса можно
упорядочить по возрасту, росту, весу, алфавиту).
Если задано n-элементное множество X и k < п, то можно соста-
вить различные упорядоченные fe-элементные множества, в которые
входят лишь элементы множества X. Например, для множества
{а, Ь, с. d} можно составить 12 упорядоченных подмножеств по два
элемента в каждом: (а, Ь), (Ь, а}, (а, с), (с, а), (а, d), (d,a), (6, с),
(с, &), (ft, d), (d, &), (с, d), (d, с).
§2. Основные формулы комбинаторики
329
Упорядоченные ^-элементные подмножества данного множества X,
содержащего п элементов, называют размещениями без повторений
из п элементов по k. Их число обозначают А^- Из примера 2
предыдущего параграфа следует, что
А^ = п • (л - 1) •... • (и - k + 1).	(2)
Формулу (2) можно записать в виде
Пример 3. Сколькими способами из 40 учеников класса можно
выделить актив в следующем составе: староста, физорг и редактор
стенгазеты?
Л Требуется выделить упорядоченные трехэлементные подмноже-
ства множества, содержащего 40 элементов, т. е. найти число
размещений без повторений из 40 элементов по 3. По формуле (2)
находим	= 40 х 39 х 38 = 59 280.	А
3.	Перестановки без повторений
Пусть множество X содержит п элементов. Рассмотрим его
различные упорядочивания Получаемые при этом упорядоченные
множества (кортежи) отличаются друг от друга лишь порядком
входящих в них элементов и называются перестановками без
повторений из п элементов. Число перестановок без повторений
обозначается Рп (от фран. permutation — перестановка) или Р(п).
Например, Р% = 6, так как из элементов а, Ь, с можно составить
шесть перестановок: (а, Ь, с), (а, с, 6), (/?, а, с), (/?, с, а), (с,	а),
(с, а, 6).
Чтобы найти выражение для Рп, заметим, что перестановка без
повторений из п элементов — это то же самое, что размещение без
повторений из п элементов по п. Поэтому для отыскания Рп по
формуле (2) положим k = п:
рп = п • (и - 1) • (п - 2).... . 2 • 1 = п\	(4)
Пример 4. Сколько существует пятизначных чисел, не кратных
пяти и не содержащих одинаковых цифр, составленных из цифр 1,
2, 3, 4, 5?
А Из пяти различных цифр можно составить Р§ пятизначных чисел.
Эти числа не должны быть кратны 5, т. е. не могут оканчиваться
цифрой 5. Если же цифру 5 поставить на последнее место, то осталь-
ные могут распределиться по разрядам числа Р$ способами. Поэтому
условию задачи удовлетворяет Р$ — Р^ = 5! — 4! = 120 — 24 = 96
чисел.	▲
330
Глава XX. Комбинаторика
4.	Сочетания без повторений
Неупорядоченные подмножества, содержащие k элементов из
данного n-элементного множества, называют сочетаниями без по-
вторений из п элементов по й, а их число обозначают С% (от
франц, combination — сочетание). Отметим, что — 1, т.е. каждое
множество X имеет лишь одно подмножество, не содержащее эле-
ментов (пустое множество). Количества сочетаний С„ и размещений
А„ связаны соотношением A^ — kl -Сп, так как упорядочить каждое
сочетание (получив при этом размещение) можно k\ способами.
ь
Отсюда С„ = Используя формулу (3), получим
п	(п - k)\kl ’
(5)
Пример 5. Сколькими способами можно расставить на 32 черных
полях шахматной доски 12 белых и 12 черных шашек?
А Поля для белых шашек можно выбрать способами. После
этого остается 20 полей, на которых можно способами выбрать
поля для черных шашек. Следовательно, искомое количество способов
равно ^32*^20-
Пример 6. На плоскости проведены п прямых, среди которых
нет ни одной пары параллельных прямых и ни одной тройки прямых,
пересекающихся в одной точке. Найти:
1)	число точек пересечения этих прямых;
2)	число треугольников, образованных этими прямыми;
3)	число треугольников, которые можно построить, взяв в каче-
стве вершин точки пересечения этих прямых.
Д 1) Число точек пересечения прямых равно числу способов выбора
неупорядоченной пары прямых, т. е. С„.
2)	Аналогично, каждый треугольник определяется тройкой пря-
мых, поэтому общее число треугольников равно С„.
3)	При пересечении указанных п прямых образуется С2п точек.
Выбрав три точки из этого множества, треугольник можно
построить в случае, если эти точки не лежат на одной прямой.
Каждую из п прямых остальные прямые пересекают в п — 1
точке. Соответственно, на каждой прямой можно выбрать
неупорядоченных троек точек, построение треугольника по
которым невозможно.
Всего способов выбора трех точек из множества, содержа-
щего точек, имеется С;* где т = С%. Исключая отсюда число
ft-	tiir*	f L
§2. Основные формулы комбинаторики
331
выборов троек точек, лежащих на одной прямой, получаем,
что искомое число равно
С^-п-С^, где т = С2п.	А
Пример 7 (задача о книжной полке). На книжной полке стоят
п книг Сколькими способами можно выбрать из них k книг так,
чтобы в их число не попали никакие две стоящие рядом?
А Рассмотрим последовательности из k единиц и т = п — k нулей.
Посчитаем количество таких последовательностей, в которых никакие
две 1 не стоят рядом. Отметим, что каждой такой последовательности
соответствует способ выбора книг на полке.
Для подсчета запишем сначала т нулей. Тогда у единиц
получается т + 1 место, из которых два по краям и т — 1 мест
в промежутках между нулями. На любое из них можно поставить
одну из k единиц. Следовательно, это число способов равно
G/n+l — сп-АН-Г
Значит, выбрать k книг так, чтобы в их число не попали никакие
две стоящие рядом, можно Ckn_k^x способами. Заметим, что задача
разрешима, если 2k п + 1.
Так, например, для десятитомного издания, тома которого стоят
в некотором фиксированном порядке, извлечь 4 книги так, чтобы
в число извлеченных не попали никакие две стоящие рядом, можно
Сц)_4+1 = С? = 35 способами.	▲
Пример 8 (задача о рыцарях). За круглым столом сидят п
рыцарей. Сколькими способами можно из них отобрать k рыцарей,
чтобы в их число не попали никакие два сидящих рядом?
А Выберем произвольным образом какого-нибудь рыцаря. Тогда
остается п — 3 рыцарей, из которых нужно отобрать k — 1. Можно
считать теперь, что п — 3 рыцаря сидят в один ряд и из них нужно
отобрать k — 1 рыцаря так, чтобы в их число не попали никакие
два сидящих рядом. Используя результат примера 7, получаем, что
это число равно C(„_3)_(ft_1)+1 = Cn_k_{.
Мы получили количество вариантов, в которых участвует вы-
бранный в начале рыцарь. Теперь посчитаем количество вариантов
выбора k рыцарей, в которых он не участвует. Считая, что оставшиеся
рыцари сидят в один ряд, получаем, что это число равно Ckn_k.
Отсюда получаем окончательный ответ. Искомое число способов
равно
1	। pk	д
^п-k-l ф	А
332
Глава XX. Комбинаторика
5.	Перестановки с повторениям
Перестановками с повторениями называют различные составы
кортежей длины k, образованные из т групп неразличимых внутри
каждой группы элементов, а их число обозначают Р(п\, п^ пт\
где п\+ п% +  • • + nm = k. Для подсчета их общего числа поступим
следующим образом.
Пусть дан кортеж а длины k, составленный из элементов
множества Х=Х[ UX2U. • • где каждое множество X/ состоит из
k или более неразличимых элементов х£-, причем все xj, х2, • • •, хт
различны. Каждому числу г, 1 i т, поставим в соответствие
число п/, показывающее, сколько раз элемент xt встречается среди
компонент кортежа а Выписывая по порядку эти числа, получаем
новый кортеж (пь п2^..., nm), где п\ + п2 + ... 4- пт называемый
составом кортежа а.
Например, если
X = XiUX2UX3UX4,
а
а= {Х1, Х2»	х2, *3» *4, х2, х3},
то кортеж а имеет состав (2, 3, 2, 1).
Кортежи, имеющие один и тот же состав и отличающиеся друг
от друга лишь порядком компонент, называются перестановками
с повторениями данного состава. Их общее число обозначают
Р(М1, ПЪ Пт).
Чтобы найти число п^ .пт), заметим, что каждый
рассматриваемый кортеж а имеет длину k. Из элементов а
можно составить k\ — (п\ + п2 + ... + пт)\ кортежей, переставляя
элементы. Однако среди этих k\ кортежей имеются одинаковые.
В п\ позициях находятся элементы xj (считая первоначально их
элементами хц, х}2,..., xinp их можно переставить щ\ способами),
в п<2 позициях — элементы х2 (их можно переставить между собой п2!
способами) и т. д. Поскольку, в действительности, отмеченные внутри
каждой указанной группы элементы неразличимы, то получается, что
для нахождения Р(п\, п^, .п^) общее число кортежей k\ должно
быть разделено на nJ • п2! • ... • пт\. В итоге получаем формулу
для подсчета числа перестановок с повторениями, имеющих состав
(«1, п2,..., Пт) :
Р(т, П2,..., Пт) =	+п4!.	(6)
v и 25	’ mf п{1'П2Ь... -nml	v 7
Пример 9. Сколькими способами можно расставить белые фи-
гуры: 2 коня, 2 слона, 2 ладьи, 1 ферзя и 1 короля на первой линии
шахматной доски?
§2. Основные формулы комбинаторики
333
Д Для решения задачи надо найти число кортежей длины 8,
имеющих заданный состав (2, 2, 2, 1, 1). Число таких кортежей,
т. е. перестановок с повторениями, равно
2’ 2- ' 1)=2Г2Г1ЬГЙ=5040-
6.	Сочетания с повторениями
Сочетанием с повторениями из п элементов по k называют
различные составы кортежей длины п, образованные из k групп
неразличимых внутри каждой группы элементов. Для подсчета их
общего числа поступим следующим образом.
Обозначим число элементов каждой группы, участвующих в обра-
зовании кортежа длины п, через п^..., где п\ + п^ + -. . + п^ = п.
Общее число таких кортежей длины п равно количеству способов
представления числа п в виде суммы целых неотрицательных
слагаемых rzi, ^2,..., п^.
Представим теперь п как п единиц, разбитых на k групп,
причем группа может и не содержать единиц. Для этого между
группами поставим нули (всего получится k — 1 нулей). Тогда
каждому разложению п в виде суммы слагаемых п\, п^,..., п^
будет соответствовать набор из п единиц и k — 1 нулей, т. е.
О 0' ’'	(и на°б°р°т, каждому такому набору —
П\ п2	nk
разложение). Всего таких наборов
- <24-.-
(7)
Соответственно, общее число сочетаний с повторениями из п
элементов по k обозначают С£:
Спк=Спп+к_г=Р(п,к-1).
Пример 10. Сколькими способами можно составить набор из
8 пирожных, если имеется 4 вида пирожных?
Л Поскольку порядок пирожных не играет роли, то каждый набор
задается кортежем длины 8 из 4 элементов (названий видов
пирожных), причем порядок компонент кортежа не играет роли.
Иными словами, нам надо найти число различных составов таких
кортежей, т. е. число сочетаний с повторениями из 4 элементов по 8.
Имеем
= ^ = STS! =165-	А
334
Глава XX. Комбинаторика
Пример 11. Сколько существует способов размещения п одина-
ковых предметов по m различным ящикам?
Л Будем рассуждать так же, как рассуждали при выводе фор-
мулы (7). Предположим, что п элементов разместились по ящикам
так, что в первый, второй, ..., m-й ящик попало соответственно
/21, П2,..пт предметов. Такому размещению поставим в соответствие
набор из п единиц и m—1 нулей, т. е. О 0 • • • 0 Л
rtl	rim
(и наоборот, каждому такому набору — размещение) Тогда число
таких размещений равно
рп   /-'П	__ f'k—i	Л
Чг — bn+k-l — ьп+/г-Г	ж
Пример 12. Сколько существует способов размещения тр раз-
личных предметов по т группам, содержащих р предметов, при
условии, что порядок групп не учитывается?
Д Число способов разбиения тр различных предметов по т группам
по р предметов равно
Р(п п п} =____________М________=
~’£,> р\ -р\.... -pi (р!)т 
т
Учитывая теперь, что группы неразличимы, полученный результат
нужно разделить на ml —число перестановок групп между собой
Следовательно, окончательный ответ будет
(М!
(pl)m • т\ *
Задачи
1. Решить неравенство:
i\ л+4 < 15	г4 _ 1^3 Рп+5 л
' (п + 2)!^	W 9б >п+3<и-
2. Вычислить:
Л2 Л3 * 5
1) / +	2) Р{а\+Р2а1 + Р3а1+Р4а1-РхР2Р3Р4-
3>
3. 1) Сколькими способами можно расставить 25 учеников в одну шеренгу?
2) Сколькими способами можно рассадить 25 учеников за 15 парт (считая,
что за каждой партой может сидеть не более двух учеников)?
4. В высшей лиге чемпионата России по футболу принимают участие
22 команды. По итогам сезона три команды, занявшие первое, второе
и третье места, объявляются призерами, а две команды, занявшие два
последних места, переходят в первую лигу Сколькими способами могут
распределиться между командами призовой пьедестал и два последних
места при условии, что уровень всех команд одинаковый?
§2. Основные формулы комбинаторики
335
5.	Сколькими способами можно расставить на книжной полке подряд друг
за другом книги десятитомного собрания сочинений так, чтобы:
1)	том 1 и том 2 стояли рядом и в порядке возрастания;
2)	на четных местах стояли тома с четными номерами?
6.	Сколько шестизначных чисел, кратных 5, можно составить из цифр 0, 1,
2, . .,9 при условии, что в записи числа не г одинаковых цифр?
7.	1) Сколько существует натуральных чисел, меньших 105, в десятичной
записи которых соседние цифры различны?
2)	Сколько существует натуральных чисел, меньших 1О72, в десятичной
записи которых соседние цифры различны?
8.	Хоккейная команда состоит из 2 вратарей, 7 защитников и 10 нападаю-
щих Сколькими способами тренер может образовать стартовую шестерку,
состоящую из вратаря, двух защитников и трех нападающих?
9.	Вокруг костра сидят 13 разбойников. Каждый из них смертельно ненавидит
двух ближайших соседей (и только их). Надо выбрать 5 разбойников, чтобы
спрятать награбленное добро. Сколькими способами их можно выбрать,
чтобы между ними не было распрей?
10.	На окружности отмечено 9 точек. Сколько можно построить:
1)	хорд, соединяя любые из них;
2)	различных треугольников с вершинами в этих точках;
3)	выпуклых четырехугольников с вершинами в этих точках?
11.	Сколькими способами можно рассадить 12 человек за круглым столом, если
для каждого человека важно не место, которое он занимает за столом,
а лишь то, кто:
1)	является его соседом слева, и кто является соседом справа;
2)	кто является его соседями (и не важно, кто из них сидит слева, а кто —
справа);
3)	сидит напротив него, т. е. на диаметрально противоположном месте?
12.	Для проведения письменного экзамена по математике надо составить
4 варианта по 7 задач в каждом. Сколькими способами можно разбить
28 задач на 4 варианта?
13.	На линии расположены п стульев. Сколькими способами можно убрать три
стула так, чтобы не были убраны:
1)	три рядом стоящих стула; 2) никакие два рядом стоящих стула?
14? Сколько можно сделать перестановок из п элементов, в которых:
1)	данные два элемента не стоят рядом;
2)	данные три элемента не стоят рядом (в любом порядке);
3)	никакие два из данных трех элементов не стоят рядом?
15.	Сколькими способами могут распределиться 15 пронумерованных бильярд-
ных шаров по 6 лузам?
16.	Три парня и три девушки решили после окончания школы поступить на
работу в своем родном городе. В городе имеются 3 завода, на которые
берут только мужчин, 2 — где нужны женщины и 2 — которые принимают
на работу и мужчин, и женщин. Сколькими способами пять выпускников
могут распределиться по заводам города?
17.	Каждая сторона квадрата разбита на п частей. Сколько можно построить
треугольников, вершинами которых являются точки разбиения (вершины
квадрата такими точками не считать)?
336
Глава XX. Комбинаторика
18.	Сколько натуральных делителей имеет число 2OO72007?
19.	Сколько слов можно получить, переставляя буквы слова:
1)	винегрет; 2) математика?
20.	Сколькими способами можно расставить на шахматной доске трех бело-
польных слонов так, чтобы они не могли бить друг друга?
21.	Из колоды, содержащей 52 карты, вынули 10 карт. Сколько существует
способов вынуть их так, чтобы среди этих карт
1)	был хотя бы один туз;	2) был ровно один туз;
3)	было не менее двух тузов;	4) было ровно два туза?
22.	При игре в преферанс каждому из 3 игроков раздают по 10 карт, 2 карты
кладут на стол в прикуп (игра ведется колодой из 32 карт). Сколько
различных сдач возможно в этой игре?
23.	1) Сколькими способами можно разложить 15 книг по пяти бандеролям
по 3 книги в каждой?
2)	Сколькими способами можно разложить 9 книг по четырем бандеролям
по 2 книги и одной бандероли с 1 книгой?
24.	Бросают п игральных костей. В результате получают п чисел от 1
до 6 Сколько может получиться различных результатов, если результаты,
отличающиеся друг от друга лишь порядком очков, считаются одинаковыми?
25.	Сколько можно построить различных прямоугольных параллелепипедов,
у которых длина каждого ребра является целым числом от 1 до 10?
26.	Сколькими способами можно разделить 12 конфет «Белочка», 15 конфет
«Мишка» и 6 конфет «Гусиные лапки» между 5 ребятами?
27.	Сколькими способами можно разделить П[ предметов первого вида,
предметов второго вида, ..., предметов £-го вида по пг различным
ящикам, считая, что предметы каждого вида неразличимы между собой?
28.	Сколько решений имеет уравнение xi 4-Х2 + • • • +х7 — Ю, где:
1)	xi, Х2,..., Ху — целые неотрицательные числа;
2)	xi, Х2,xy — натуральные числа?
29.	Лифт, в котором находятся девять пассажиров, останавливается на шести
этажах. Пассажиры выходят группами по два, три и четыре человека.
Сколькими способами это может произойти, если на каждом этаже может
выйти только одна группа пассажиров, при этом порядок выхода пассажиров
из лифта не имеет значения?
30.	Сколько цифр потребуется для записи всех чисел от 1 до 10" — 1, если
1)	/г = 3;	2) /2 = 6;	3) n = k?
31.	Сколькими способами можно разместить 5 одинаковых предметов по трем
ящикам, если в каждый ящик можно поместить от нуля до пяти предметов?
32.	Комиссия из 7 человек хранит материалы в сейфе. Сколько замков должно
быть на сейфе и сколько ключей должно быть у каждого члена комиссии
для того, чтобы сейф мог быть открыт, когда соберутся любые четыре члена
комиссии, но не мог бы быть открыт при меньшем количестве членов?
33.	Сколькими способами можно выбрать комиссию в составе tn человек из
группы, состоящей из п мужчин и k женщин, при условии, что m п
и m k?
34? Доказать равенство £2 [Clk - Alm 
§3. Бином Ньютона и полиномиальная формула
337
Ответы
1. 1) {2, 3, 4, 5, 6}; 2) {1, 2, 3}. 2. 1) 46; 2) 2750; 3)	3. 1) 25! 2)	=
= Л|§. 4. А%2. 5. 1) 9!; 2) Р5 • Р5 = (5!)2 = 14400. 6.	+ 8 • А% = 28560.
7.	1) 9 + 92 + 93 + 94 + 95 = 9 •	= 66429; 2)	8. С12 • cf0 =
= 5040. 9. Cg + Cl = 93. 10. 1) 36; 2) 84; 3) 126. 11. 1) 11!; 2) И!;
3>	- 10395. 12. 1  4 - С', - Cl, = ± 
13.	1) С2 - п + 2; 2) С3 - Цп - 2) + 2(п - 3) + (п - 3)(п - 4))	= С3_2.
количество способов убрать какие-то стоящие рядом
14.	1) n! - 2(п - 1)!; 2) л! - 6(п - 2)!; 3) п! - 6(л - 1)! + 6(л - 2)!. Ука-
зание. Использовать формулу включений и исключений. 15. А$5 = 615.
16. 3 • 52 • 43 + 3 • 53 • 42 = 10800. 17.	- 4С3_, = 2(и - 1)2(5л - 8).
18.	2008  5005. 19. 1) 20160; 2) 151200. 20. 1704. 21. 1) С'5% - С^;
2) С\  С98; 3) С'° -	- С\  С948; 4) С24 • С38. 22. Р(10, 10, 10, 2) =
=	—. 23. 1) ‘г-!- . 2) 945. 24. С% = С?. =. 25. С?о = С?2 = 220.
(Ю!)3.2!	(3!)5-5!	п+5	10	12
26.	C^-C^-Cf = С|1|-С;| -С?0. 27. С% (% -... (%. 28. 1) 8008; 2) 84.
k		1
29.25200. 30. 1) 2889; 2) 588889; 3) 9 -£ МО1-1. 31.21.	32. 35; 350.
i=l
m ,	.ч
33.	z (Cn-c”~‘ =c-+ft. 34. Указание. Рассмотреть алфавит из ш «глас-
но v	7
ных» и п «согласных». Тогда r-й член суммы Clk -Alm • А\~' представляет собой
число размещений i «гласных» и k — i «согласных».
§ 3. БИНОМ НЬЮТОНА
И ПОЛИНОМИАЛЬНАЯ ФОРМУЛА
1.	Бином Ньютона
В гл. II, § 5, п. 5 была доказана формула бинома Ньютона,
справедливая при всех n е N:
(<7 + 6)" = ^^-^,	(1)
k=0
а также ряд свойств биномиальных коэффициентов С^:
1)	С° = С" = 1;	2) Ckn = C^
3)	С^-1 + Сд = (свойство Паскаля)}
338
Глава XX. Комбинаторика
4)	Ckn = ф1 •	5) Е Ckn = 2”;
*	k=0
7) Е c2nk =
0sJ2A^n
Е С®Л+* =2«-1.
0<2Л+1^п
6) Е (-1)М = 0;
k=0
2.	Треугольник Паскаля
Свойство Паскаля для биномиальных коэффициентов
С*-1 4-C„ = C^+1 позволяет вычислять биномиальные коэффициенты,
используя только операцию суммирования, записав С„ в приведенной
ниже треугольной таблице, называемой треугольником Паскаля'.
п = 1	11
n=2	1	2	1
п=3	1331
м = 4	14641
п = 5	1	5	10	10	5	1
п = 6	1	6	15	20	15	6	1
п = 7	1	7	21	35	35	21	7	1
п = т
п — т + 1
1...
1	Ck~'[
1 • • Gm+1
/с*+2^... 1
т+1 ‘ ’ 1
В я-й строке треугольника Паскаля стоят коэффициенты разло-
жения бинома (а + Ь)п. Причем каждый коэффициент, кроме крайних
двух, равных 1, получается как сумма соответствующих коэффициен-
тов из предыдущей строки. Число всех членов разложения на единицу
больше показателя степени бинома, т. е. равно п +1, а показатель
степени а и b каждого члена разложения равен показателю степени
бинома, так как (и — Л) + k = п.
Кроме того, что биномиальный коэффициент — число раз-
личных сочетаний из п по k, биномиальные коэффициенты имеют
и комбинаторное применение. Рассмотрим пример, демонстрирующий
применение треугольника Паскаля.
Пример 1. Дана прямоугольная сетка квадратов размером п х т.
Сколько существует различных дорог по этой сетке, ведущих из
левого нижнего угла в правый верхний?
§3. Бином Ньютона и полиномиальная формула
339
Л Пути, по которым можно пройти из левого
нижнего угла в правый верхний, представляют
собой ломаные линии, длина которых равна
n + m, если за единицу брать сторону клетки,
так как они состоят из п горизонтальных и m
вертикальных отрезков (рис. 2). Эти ломаные
линии отличаются порядком чередования гори-
зонтальных и вертикальных отрезков. Но таких
различий, если учесть, что всего отрезков п + ш
и из них m вертикальных, будет С^п = С^+п. Следовательно, всего
способов, которыми можно пройти из левого нижнего угла в правый
верхний, существует С^+п.	▲
Замечание. Если на рис. 2 на каждом перекрестке разрешено движение
вверх или направо, то на перекресток с координатами (г, /), выделенный на
рисунке черным кружком, можно попасть из левого нижнего угла
способами. Если на каждом перекрестке поставить числа, равные количеству
способов попадания на них из левого нижнего угла, то будет видно, что их
заполнение происходит так же, как и в треугольнике Паскаля. Например, на
рис. 2 светлым кружкам соответствуют коэффициенты разложения (а + 6)3.
3.	Наибольший член разложения бинома (a + Ь)п
Нетрудно доказать, что если показатель бинома четный: п = 2/,
то С1П является наибольшим биномиальным коэффициентом и спра-
ведливы неравенства
Если же показатель бинома нечетный: n = 2/+ 1, то имеется два
наибольших биномиальных коэффициента С1П = С1^ и справедливы
неравенства
rl _ сМ u rl _ гМ г1+2	Г2'-1 С21
Напомним, что общий член разложения имеет вид
Т^\ = C^an~kbk. где k = 0,1,2,..., п. Индекс k + 1 внизу у члена
разложения 7^+i означает его порядковый номер, считая слева
направо, в разложении бинома
Задача о нахождении наибольшего члена разложения будет
использоваться в следующей главе.
/ О 1 \ 100
Пример 2. Найти наибольший член разложения I - + - 1
А Рассмотрим отношение членов разложения
т -ck (3\™-k (\\k ~rk З100-*
u+i —	— Чоо -^iocr
340
Глава XX. Комбинаторика
т _гЛ-1/3)100	1 — z"^—lolOl—Лд—100
lk~ с 100 1^4 J	\4;	— С1003	4
В данном случае Л = 1,2,... ,п, поскольку непосредственно исполь-
зуется номер члена разложения. Тогда
Tk+l _ Cf003lo°-*4-100 _ ЮО! (Л-1)! (101-й)! 1_101-Л
Т/г c*-l3101-/i4-100 k\ • (100 - Л)! ’	100!	’3 ЗЛ
100
Если 10^fe > 1, то Tk+l > Tk, а если 101 ~fe < 1, Tk+\ < Tk. Так как
> 1 при k < 25 (члены возрастают), а < 1 при k > 25
оЯ	о Я
(члены убывают), то наибольший член Т25 = C^q03764“100.	▲
4.	Доказательство комбинаторных тождеств методами
математического анализа
В качестве примеров рассмотрим также методы доказательства
комбинаторных тождеств средствами математического анализа, т. е.
с применением дифференциального и интегрального исчисления.
Пример 3. Доказать равенство
пС° + (и - 1)С’ +... + (п - k~)Ckn +... + С"’1 = п • 2"-1.
А Запишем биномиальное разложение для (х+1)Л:
(х + 1)" = С°пхп + Схпхп~х +... + Cknxn~k +... + СГ’х + С".
Дифференцируя по х данное равенство, получим:
[(х + !)"]'= (с°хп + С^х"-1 +... + Cknxn~k +... + Сп-Хх+С")' =
= п(?пхп-х+ (п - 1)С* х"”2 + ... + («-k)Cknxn~k-x +... + С"-1.
С другой стороны, [(1 +х)”]/ = п • (1 + х)"-1. Получаем равенство,
справедливое при всех значениях х:
п • (х 4-1)"-1 = пС^хп~} + (n — 1)С„х"-2 + .
... + (п-й)фп-Л-1 + ... + сг1-
При х =1 получаем доказываемое равенство:
п  2п~х = пС°п + (я -	+ ... + (n - kjC* +... + С"”1.	▲
Пример 4. Доказать равенство ^2 ------f—г =-----т ’ (2” — х).
о п-fc+l п 4- 1 \	2/
А Запишем биномиальное разложение для (1+х)п:
(х + 1)" =	+ С‘хп-‘ + ... + Cknxn~k + ... + спп~1х + С".
§3. Бином Ньютона и полиномиальная формула
341
Обе части равенства представляют собой многочлены от х, поэтому
I	1
(х + 1)" dx= (с%хп + с\хп~х + ... + Cknxn~k + ...+ Cnn-'x + С") dx.
О	о
/	। 1 ч п-{~ 1
Первообразная функции (х + 1)” равна I — + С, где С —
произвольная постоянная Первообразная функции, стоящей в правой
части разложения бинома, равна
Ефп+'~*
п 4-1 — k
k=0
где С — произвольная постоянная.
Используя формулу Ньютона-Лейбница, получаем
Сравнивая правые части в формулах (2) и (3), убеждаемся в спра-
ведливости доказываемого равенства.	▲
5.	Полиномиальная формула
Ответ на вопрос, как раскрывать скобки при вычислении выра-
жения (ai+^2 + ... + дает следующая теорема, которая носит
название полиномиальной теоремы.
Теорема. Справедливо равенство
(0, + 02 + .Е ?	.	щ
Суммирование производится по всем наборам (п^ п%,	п^)
неотрицательных целых чисел таких, что щ + п% + .. + Щ = п.
Коэффициенты —-----р------- называют полиномиальными коэффи-
циентами.
342
Глава XX. Комбинаторика
Замечание 1 Полиномиальные коэффициенты совпадают с числом пере-
становок с повторениями, имеющими состав (гц, г?2,..., п^) :
Р(п\,n2,...,nk) =	+
Замечание 2. Формула бинома Ньютона — частный случай полиномиальной
теоремы при k = 2, так как
= Pin - k, k) и (а, + а2)" = Р(п - k, k) • a'{~kc4
Л-0
О Для доказательства утверждения теоремы для всех натуральных
значений п воспользуемся методом математической индукции.
Положим п — 1. Так как щ +	+ ... +	= 1, то правая
часть полиномиальной формулы представляет сумму k слагаемых,
в которых поочередно одно П[ = 1, а остальные равны 0, т. е.
1!	^1^0	^,0 ।	। U Л0 Л0 1 __________Л 1 z-v ।	। п
иоЕ .ТО’ ’ a[Cl2 • • •	+ • • • h О’бГ.Л! • п2 • • •	+ й2 + • • • + «Л-
Соответственно, и левая часть (aj	. Н-а^)1 — a\ + a% + • • .+ ал-
Следовательно, при п = 1 формула (4) верна.
Предположим, что формула (4) верна при п-m, т.е. имеет место
равенство
(at+a2 + ... + ak)m =	Р(п\, п2,..., nk) 	a!^ ... ankk.
rtl + ...+/?^=/7Z
Докажем теперь, что, что формула (4) верна при n = m + l.
Для этого (ai +^2 +... + представим в виде произведения
(#1 + а<2 + ... + CLk}m^ = (aj + а% + • •. +	. + а^)
и для множителя (сц + «2 + - • - + ak)m воспользуемся предположением
индукции. Тогда получим
(#1 +«2 + - • - +	— (^1 +«2 + - • • + ak)m(а1 + ^2 + ..»+ ^л) —
гдеЛ,= 52	P(«i,«2,••• a";+1... ankk.

§3. Бином Ньютона и полиномиальная формула
343
k
После приведения подобных в получим сумму слагаемых
вида .. .aq^ где q\ + q2 + ... + q^ = w + 1, коэффициенты при
которых — результат суммирования k членов
/’(^l — 1, 92,---, 4k) + P(qi, 92-!>•••, %) + ••• +P(qi>q2,---, 9Л~1) =
_ (<71 -1)! <72! • • • %! + <71 ’(<72 - 1)!  • • Як'- + ’ ' ’ + <71!<?2! • • • (<7fe ~ *)! ~
—____________________________( <?1+<?2+-+<?<Л — Р(д, Пп /7 д')
(<7,-1)!(<72-1)!... (<?*-!)! к <71«72---<7fe /
Следовательно, имеет место равенство
01 + а2 + • • • + ak)m+{ =	Р(?Ь ?2,---> q^-a^af ...aqkk.
q&O1...,qk^
qi+...+qk=m+\
В силу метода математической индукции отсюда вытекает справед-
ливость формулы (4) для всех n е N.
Теорема доказана.	•
Ответим на вопрос о количестве неподобных членов в правой
части формулы (4).
Общее число членов в разложении (ai +	. + а^п равно
количеству способов представления числа п в виде суммы целых
неотрицательных слагаемых П[,	где п\ + п<2 +... +	= я,
т. е. равно P(k - 1, п) =	= С1^ = Ckn~lk_t.
Пример 5. Выписать разложение:
1) (щ + а2 + а3)2;	2) (сц + а2 + а3)3.
Л 1) Разложение (ai+a2 + a3)2 содержит Р(2,2) —	= 6 непо-
добных членов и
(а 1 + а,2 +	— ^(2? 0,0) • + /^(0,2,0) • +
+ Р(0,0,2)  а23 + Р(1,1,0) • atа2 +
+ Р(1,0,1) • а\а3 + Р(0,1,1) • 0203 =
= af + al +	+ 2aia2 + 2ctj а3 + 20203.
344	Глава XX. Комбинаторика
2) Разложение (ai + а2 + аз)3 содержит Р(2,3) =	= 10
неподобных членов и
(ai + а2 + аз)3 =
= Р(3,0,0) • а? + Р(0.3,0) • а| + Р(0,0,3) • 0% +
+ Р(2,1,0) • а2а<2 + Р(2,0,1) • а2а% +
+ Р(1,2,0) • а\а^ + Р(0,2,1) а2а3 + Р(1,0,2) - ща2 +
+ Р(0,1,2) • а2а2 + Р(1,1,1) •	=
= а3 + а3 + а2 + За2а2 + За2аз +	+ 3aia2 + За2а2 +
+ За^аз + 6а1а2аз-
▲
Пример 6. Найти коэффициент при ab2c3 в разложении
(a + 26-Зс)6.
Д Соответствующий член разложения имеет вид
Р(1, 2, 3) • а(26)2(—Зс)3 =	• 4 • (-27) • ab2c3 = -6480 • aft2?.
Следовательно, искомый коэффициент равен —6480.	▲
Пример 7. Найти в разложении (ai + a2 +... + а^)п сумму всех
полиномиальных коэффициентов и количество неподобных членов.
Д Сумма всех полиномиальных коэффициентов может быть выра-
жена формулой
у	—f = (l + l + ... + 1)" = F.
П\\* . . . *П^\	v
ni^-.,^nk=n	£раз
Число неподобных членов разложения совпадает с количеством
способов представления числа п в виде суммы целых неотрица-
тельных слагаемых ai, п2, ..., т. е. +а2 +.. . + п^ = п и равно
рп___рп ______ (и + А? — 1)!	*
п!(А? — 1)! ’	Ж
Задачи
1.	Найти наибольший член разложения:
/л 1 \	/1	1 \	9Л
'> (й+й) ; 21 (Н) ; -3> <v5+v5> 
2.	При каких положительных значениях х наибольшим слагаемым в разложении
(3 + 5х)10 является шестой член разложения?
§3. Бином Ньютона и полиномиальная формула
345
3.	Доказать, что нечетное число предметов можно выбрать из п предметов 2П~|
способами Сколькими способами можно выбрать четное число предметов?
4.	Исходя из комбинаторных соображений доказать, что для любых
/?1,	, km, где k\ 4- k2 4-. . • + km = и, справедливо равенство
&  c^_k)  С^_А2 .. •	= P(kt, k2,..., km).
5* Исходя из комбинаторных соображений, найти сумму
(с°)2 + (с’)2 + .-. +(с^)2.
6.	Доказать равенство:
1)	n(n - 1)С° + (я - 1)(я - 2)С„ + ... + (я - k)(n - k - 1)С* + ... + 2С”-2 =
= я(я — 1)-2"-2;
2)	"Ё’(-1)*(я-й)С* = 0.
k—0
7.	Найти коэффициент при х19 в разложении (1+х5 4-х9)30.
8.	Найти сумму всех коэффициентов многочлена (1 4-х — х2)2007.
Ответы
1.	1) Гц = С'8о •	2) Т5| =	3) Т9 = 314925 • 105. 2. х е (0,5; 0,72).
3. 2Л-1.	5. (?2n. Указание. Использовать результат примера 1, взяв
сетку пхни рассмотрев перекрестки с координатами (/, /), где 0 i п.
7. Р(27, 2, 1) = 12180.	8. 1.
Глава XXI
ЭЛЕМЕНТЫ ТЕОРИИ
ВЕРОЯТНОСТЕЙ
§1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
1.	Случайные события
Практикой установлено, что в часто происходящих случайных
событиях (явлениях) существуют определенные закономерности.
Задача теории вероятностей — установление и математическое иссле-
дование закономерностей массовых случайных явлений. Предметом
теории вероятностей являются модели экспериментов со случайными
исходами. Любой наблюдаемый результат интерпретируется как
случайный исход опыта (случайное событие).
Рассмотрим несколько примеров испытаний со случайными ис-
ходами.
1)	При одном бросании правильной шестигранной игральной
кости опыт состоит в наблюдении числа выпавших очков. При
проведении опыта возможны следующие результаты (исходы):
на верхней грани может оказаться одно из чисел 1, 2, 3, 4,
5, 6.
2)	Пусть, например, в урне находятся шары белого, красного
и черного цвета, а опыт заключается в извлечении шара из
урны. В результате однократного извлечения шара возможны
три исхода: «извлечен белый шар», «извлечен красный шар»
и «извлечен черный шар».
3)	При однократном подбрасывании монеты возможны два исхода:
монета упала гербом вверх (выпал «орел») или гербом вниз
(выпала «решка»).
Каждый исход приведенных в этих примерах испытаний является
случайным, так как он может произойти, а может не произойти.
Далее будем считать, что в результате проведения опыта с п
возможными исходами наступает один и только один из исходов. То
есть в результате опыта наступает один из исходов и никакие два
исхода не могут произойти одновременно. Каждый такой исход назы-
вают элементарным событием. Все элементарные события образуют
множество элементарных событий. Произвольное подмножество
множества элементарных событий называется событием. Случайные
события обычно обозначают буквами А, В, С и т. д.
§1. Основные понятия теории вероятностей
347
Например, при одном бросании правильной шестигранной играль-
ной кости: элементарный исход (событие) = {выпало i очков};
неэлементарное событие, например событие А — {выпало четное
число} = {б)2,6)4, 6)g}; множество элементарных событий этого
опыта Q — {й>1, о>2, 6)3, 6)4,6)5, б)^} состоит из шести элементов, т. е.
W(Q) = 6.
Некоторое событие называют случайным по отношению к дан-
ному опыту (испытанию), если при осуществлении этого опыта оно
либо происходит, либо не происходит. Считается, что событие А
произошло (наступило), если результатом случайного опыта явился
какой-либо из элементарных исходов, входящих в подмножество
события А с Q.
Достоверное событие U —- событие, которое обязательно насту-
пает в результате данного опыта (t/ = Q).
Невозможное событие 0 — событие, которое заведомо не может
произойти в результате данного опыта.
Пусть, например, в урне находятся только черные шары, а опыт
заключается в извлечении шара из урны. Тогда событие «извлечен
черный шар» является достоверным, а событие «извлечен белый
шар» — невозможным.
При одном бросании игральной кости тот факт, что выпадает
одно из чисел 1, 2, 3, 4, 5, 6, — достоверное событие, так как при
бросании кости оно обязательно произойдет, а выпадение, например,
числа 7 является невозможным _событием.
Противоположное событие А (по отношению к событию Л) —
событие, которое наступает тогда и только тогда, когда А не насту-
пает. Противоположному событию благоприятствуют элементарные
исходы, которые не входят в А,
В примере с игральной костью события «выпало четное число»
и «выпало нечетное число» являются противоположными. При одном
подбрасывании монеты события «выпал орел» или «выпала решки»
являются противоположными.
Говорят, что событие А влечет событие В (обозначается Л СВ),
если В всегда наступает, когда наступило Л. Пусть опыт заключается
в том, что из колоды игровых карт вынимается наудачу одна карта,
и пусть рассматриваются следующие события: Л ={вынута карта
пиковой масти}, В ^{вынута карта черной масти}. В этом случае
событие А влечет событие В.
2.	Операции над событиями. Алгебра событий
Суммой (объединением) случайных событий Л и В называется
событие, которое наступает тогда и только тогда, когда наступает
348
Глава XXI. Элементы теории вероятностей
хотя бы одно из событий А, В. Сумму событий А и В обозначают А +В
(или ЛиВ). Событие А +В состоит из исходов, благоприятствующих
хотя бы одному из событий А или В.
Произведением (пересечением) случайных событий А и В на-
зывается событие, которое наступает в том и только том случае,
когда наступают оба события А и В. Произведение событий А и В
обозначают А В или просто АВ (или АпВ). Событие АВ состоит
из исходов, благоприятствующих как событию А, так и событию В.
События А и В несовместны, если АВ = 0. В противном случае
события А и В называют совместными. Например, если в опыте
с бросанием кости А = {oj, В = {<z>2, то АВ = 0.
Через А\В обозначают событие, состоящее из исходов, благопри-
ятствующих А, но не благоприятствующих В.
Рассмотрим примеры с конкретными событиями А и В.
1)	Пусть в опыте с бросанием игральной кости события А
и В определяются так: А —{выпало число очков, кратное 3},
В={выпало четное число очков}. Тогда событие А + В означает,
что выпало одно из чисел 2, 3, 4, 6; событие АВ — выпало
число 6, А\В —выпало число 3.
2)	Пусть в опыте с извлечением наудачу одной карты из колоды
игровых карт событие А ={вынута дама}, В ={вынута карта
бубновой масти}. Тогда событие А+В означает, что вынута
дама или карта бубновой масти; событие АВ — вынута дама
бубен, А\В —вынута дама пиковой, крестовой или червовой
масти.
Говорят, что система всевозможных подмножеств множества эле-
ментарных исходов Q = {б>1, б>2, •• • , Ып} образует алгебру событий,
поскольку в результате применения любой из введенных выше
операций к любым подмножествам этой системы опять получается
элемент этой системы, т. е. подмножество множества Q.
3.	Свойства операций над событиями
•	А+В = В + А, (А+В) + С = А + (В + С), А+А=А;
•	АВ = ВА, (АВ)С = А(ВС), АА=А;
•	А+0 = A, A + Q = Q, А-0 = 0, A-Q = A;
•	А(В + С)=АВ+АС, А + ВС=(А+В)(А + С);
•	АВ-А + В, А+В —А-В.
Замечание. Для доказательства указанных свойств достаточно воспользо-
ваться определением операций и показать, что множества элементарных исходов,
благоприятствующих событиям в левой и правой частях равенств, совпадают.
§1. Основные понятия теории вероятностей
349
Пример 1. Пусть Д, В, С —три произвольных события Записать
с помощью введенных операций следующие события:
1)	— все три события произошли;
2)	А<^ — ни одно из событий не произошло;
3)	Дз — произошло только событие В;
4)	А4 — произошло, по крайней мере, одно из событий Д, В, С;
5)	Д5 — произошло одно и только одно из этих событий;
6)	Дб — произошло, по крайней мере, два из этих событий.
А 1)Д1=ДВС;	2)Д2=Д-В.С;	3)Д3=Д-В.С;
4) А4=А+В + С; 5) Д5=Д-В-С + Д-В-С + Д-В С;
6) А6=А.В-С + А-В-С + А>В-С + А-В-С.	д
Пример 2. Доказать, что (Д\В)+В = Д+В.
Д Сначала докажем, что Д\В — АВ. Действительно, пусть исход
б>еД\В. Это значит, что о)ЕА и 6)^В, т.е. &>еВ. Следовательно,
—общий исход событий Д и В, т.е. д>еДВ. Пусть теперь о>еДВ.
Это значит, что б)бД и оеВ, т.е. д>^В. Следовательно, д>еД\В.
Тогда (Д\В) + В = АВ + В. Используя свойство
А +ВС= (Д +В)(Д + С), получаем
(Д\В) + В = ДВ + В = (Д + В) (В + В) = (Д + В)П = Д +В. ▲
4. Вероятность события
Классическое определение вероятности. Предположим, что до-
стоверное событие Q состоит из элементарных событий о>1, о>2, • •<*>п
(элементарных исходов), которые по условиям опыта можно считать
равновозможными. В этом случае Q = {йц,	**>«}, и его назы-
вают пространством элементарных событий. Каждое событие А
является подмножеством множества Q, т.е. А =	6)ik}.
Опыт, удовлетворяющий условиям: а) пространство его эле-
ментарных событий конечно; б) элементарные исходы равновоз-
можны,называют классической схемой.
Определение. Вероятностью Р(А) события А в классической
схеме называется отношение числа исходов, благоприятствующих
событию Д, к числу всех исходов.
Если 7V(Q) = п — общее число элементарных исходов пространства
элементарных событий, N(A) = k — число элементарных исходов,
образующих событие Д, то
=W = ;	(1)
350
Глава XXL Элементы теории вероятностей
Заметим, что вероятность каждого элементарного события в опыте
с равновозможными исходами равна
Из формулы (1) легко выводятся свойства классической вероят-
ности:
1) 0 В(Д) 1 для всех Л; 2) B(Q) = 1; В(0) = 0;
3)	В(Д)^В(В), если ДСВ.
Пример 3. Из 27 вопросов экзамена ученик выучил 24. С какой
вероятностью при случайном выборе вопроса он получит вопрос,
который он выучил?
Д В данном примере N(Q) = 27, a N(A) = 24. Следовательно,
Р(А\ = в = = 8	▲
/V(Q)	27	9’	А
Пример 4. Монета бросается дважды Найти вероятность со-
бытия А ={хотя бы один раз выпадает орел}.
Д Пусть О—появление орла, В—появление решки. Тогда резуль-
татом двух бросаний будет появление одного из равновозможных
исходов ОО, ОВ, ВО, ВВ. Событию А благоприятствуют три исхода,
поэтому Р(Л) = да = 3.	А
Пример 5. Бросают одновременно две кости. Найти вероятности
следующих событий:
1)	А ={сумма выпавших очков равна 8};
2)	В ={произведение выпавших очков равно 8};
3)	С ={сумма выпавших очков больше, чем их произведение}.
Д Будем считать, что в данном примере кости различимы. Предста-
вим множество элементарных исходов данного опыта в таблице, где
(/, /) означает, что на первой кости выпала цифра г, а на второй —
цифра /.
(1.1)	(1. 2)	(1. 3)	(1, 4)	(1, 5)	(1, 6)
(2, 1)	(2. 2)	(2, 3)	(2, 4)	(2, 5)	(2. 6)
(3, 1)	(3, 2)	(3, 3)	(3, 4)	(3, 5)	(3, 6)
(4. 1)	(4. 2)	(4, 3)	(4, 4)	(4, 5)	(4, 6)
(5, 1)	(5, 2)	(5, 3)	(5, 4)	(5, 5)	(5, 6)
(6. 1)	(6, 2)	(6, 3)	(6, 4)	(6, 5)	(6, 6)
Получаем, что Af(Q) = 36.
Число 8 как сумма выпавших очков может быть получено в данном
случае следующим образом: 8 = 2 + 6 = 6 + 2 = 3 + 5 = 5 + 3 = 44-4,
§ 1. Основные понятия теории вероятностей
351
т. е. при пяти различных исходах. Следовательно, вероятность этого
события равна Р(Л) = Д.
Число 8 как произведение выпавших очков получается при двух
исходах 8 — 2х4 = 4х2. Следовательно, вероятность этого события
равна Р(В) = | = ±.
Событию, состоящему в том, что сумма выпавших очков меньше
их произведения, соответствуют исходы первой строки и первого
столбца таблицы, т. е. И исходов. Поэтому вероятность этого события
равна Р(С) =	▲
Пример 6. В урне лежат десять одинаковых на ощупь шаров,
из которых 3 белых и 7 черных. Наугад вынимаются два. Найти
вероятности событий:
1)	А ={оба вынутых шара черного цвета};
2)	В ={вынуты шары одного цвета}.
3)	С ={вынуты шары разного цвета}
А 1) Общее число возможных исходов равно числу сочетаний из 10
п	10!	10-9
элементов по 2, т. е. Стп = ——— = —= 45, а число исходов,
2! • о! 2
благоприятствующих событию Л, равно С? =	=21.
Поэтому Р(А) =$. = £ = 1.
2) Число исходов, благоприятствующих тому, что будут вынуты
два белых шара, равно	= 3, а тому, что будут
вынуты два черных шара, равно С? = 21. Следовательно, число
исходов, благоприятствующих событию В, равно 21 + 3 = 24.
Тогда Р(В) =	= g = Д.
4 7 cfo 45	15
3) Так как любой из трех белых шаров можно комбинировать
с любым из семи черных шаров, то по правилу произведения
имеется 3’7 = 21 исходов, благоприятствующих событию С.
Поэтому Р(С) = |- = g = 1.	А
Определение. Вероятностным пространством называется
конечное множество Q = {o>i,	ып}, каждому элементу
со, которого поставлено в соответствие неотрицательное число pi
(вероятность), где	п
=	(2)
/=1
352
Глава XXL Элементы теории вероятностей
Вероятностное пространство можно обозначать
(б>ь й>2, • ••« pi, Рч, •••, рп)
или (Q, Р), где Q = {&>], 6)2,	6)„},P = {pi, р2, Рп}-
Пример 7. Игральная кость налита свинцом, в результате чего
вероятность выпадения каждого числа очков пропорциональна этому
числу. Найдите указанные вероятности и вероятностное простран-
ство.
Л Пространство событий Q состоит из шести исходов где
& = 1, 2, 3, 4, 5, 6, и ^{выпало k очков}. Пусть р^ — вероятность
исхода о/г. По условию задачи = Xk. Используя формулу (2),
получим
6	6	6
]Грй = 1, т.е. 22а/> = Л]Г£ = Л(1 + 2 + 3 + 4 + 5 + 6) = 21Л=1.
k=\	k=l	k=\
Отсюда Л = и Pk = Следовательно,
(Я, Л) =(1.2, 3, 4, 5, 6; 1 А А А А А
Статистическое определение вероятности. Это определение
является рабочим для практических применений, но не строгим
математическим определением. Предположим, что производится боль-
шое число N испытаний, в каждом из которых событие А может
наступить или не наступить. Если А наступает в m испытаниях, то
число называется частотой появления события А. Вероятность
Р(А) события А — это число, которое при больших А можно
приблизительно считать равным частоте Р(А) « Как правило,
разница между числами Р(А) и тем меньше, чем больше число N.
Геометрическая вероятность. В этом случае пространство
элементарных событий Q представляет собой множество, на котором
задана мера (например, длина, площадь, объем). Элементарные
события, число которых бесконечно, считаются равномерно рас-
пределенными в этом множестве. Алгебру событий составляют
измеримые подмножества множества элементарных событий Q. Если
по условиям опыта элементарные события, имеющие равные меры,
равноправны между собой, т. е. равновозможны, то вероятность
события А полагается равной v
Р(Л) = ^1,
4 7 tnes(&)
где /nes — мера (длина /, площадь S, объем V).
§1. Основные понятия теории вероятностей
353
Пример 8. Результат точного измерения физической величины
округляют до ближайшего целого числа Найти вероятность того,
что абсолютная величина ошибки округления не превысит 0,1.
Д При округлении точного значения до ближайшего целого возни-
кает случайная ошибка измерения -0,5 < х < 0,5. Таким образом
опыт состоит в случайном выборе числа х из промежутка (—0,5; 0,5].
Соответствующий элементарный исход опыта &) = х, пространство
элементарных исходов Q = (—0,5; 0,5] С R.
Интересующее нас по условию задачи событие — это множество
А = {х| - 0,1 х 0,1} = [-0,1; 0,1].
—6—
-0,5
-4-
0,5
Рис. 1
Пространство Q и множество А представлены на рис. I. В данной
задаче мерой множества является его длина, поэтому
р(л) = яй=¥=0’2-
I I G U J	1
Пример 9. Пусть круглая мишень радиуса R разделена концен-
i R
трическими окружностями с радиусами г/ = —, i = 0,1, 2,..., 9, на 10
колец (внутренний круг радиуса г\ также назовем кольцом). Будем
считать, что стрелок выбил k очков, если он попал в кольцо между
окружностями радиусов гщ-й и Эксперимент состоит в том,
что плохо стреляющий стрелок (у него точка попадания равномерно
распределена по кругу) делает один выстрел по мишени. Вычислить
вероятность события А^ ={стрелок выбил k очков} и построить
вероятностное пространство эксперимента.
Д Множество элементарных исходов задачи есть =	Л2,.. .,Лю}.
Используя геометрическое определение вероятности, получаем
Wk)
5(G)
/W =
, где S(Ak) — площадь кольца между окружностями
радиусов гщ-й и гц-fe, S(Q) = xR2. Отсюда


kR2
10-й\2
ю )
21 — 2k
100 ’
k = 1, 2, ... , 10.
12—3022
354	Глава XXI. Элементы теории вероятностей
Получаем таблицу значений вероятностей событий Ak.
	1	2	3	4	5	6	7	8	9	10
p(At)	0,19	0,17	0,15	0,13	0,11	0,09	0,07	0,05	0,03	0,01
Вероятностное пространство данной задачи имеет вид (Q, Р),
где П = {ДЬЛ2, ...,Л10}, Р = {Р(Аг), РЦЬ), ...,Р(ЛЮ)}. А
Задачи
1.	Каким событием (достоверным, невозможным или случайным) является
следующее событие:
1)	при одновременном бросании шести игральных костей сумма выпавших
очков будет меньше 6;
2)	при одновременном бросании двух костей черного и белого цвета число
выпавших очков на черной кости будет больше, чем на белой;
3)	на 33 карточках написали все буквы русского алфавита (по одной букве
на каждой карточке) и после перемешивания из 5 лежащих сверху
карточек сложили слово «МОРОЗ»;
4)	наугад названное натуральное число будет положительно?
2.	Для случайных опытов 1)-5): а) указать элементарные исходы; б) приве-
сти пример случайного события, не являющегося элементарным; в) описать
множество элементарных событий и в случае, если оно конечно, указать
число его элементов М(П).
1)	Опыт состоит в подбрасывании двух одинаковых игральных костей
и фиксировании выпавших очков. По условиям опыта кости неразличимы.
2)	Опыт состоит в подбрасывании двух игральных костей и фиксировании
выпавших очков. По условиям опыта кости различимы.
3)	Цифры 1, 2, 3, 4, 5 написаны на пяти карточках. Опыт состоит
в последовательном выборе 3 карточек и фиксировании полученного
трехзначного числа.
4)	На шахматную доску ставят случайным образом две ладьи —белую
и черную и наблюдают полученную расстановку этих фигур.
5)	На шахматную доску ставят случайным образом две белые ладьи
и наблюдают полученную расстановку этих фигур. По условиям опыта
ладьи неразличимы.
3.	Мишень состоит из 10 кругов, ограниченных концентрическими окружно-
стями с радиусами п, i — 1, 2, ... , 10, причем г\ < г2 < ... < По- Событие
At ^{попадание в круг радиуса г/}. Что означают события:
6	ю	_
I)	Д = ЕЛ; 2) в = п А; 3) с = д2д3?
/=1	/=5
4. Доказать равенства:
1) Д(В + С)=ДВ+ДС;
3) АВ = А+В,
5) ДВС = Д + В + С;
2) А + ВС = (А + В)(А + С)
4) ДТВ = Д-В;
6) Д + В + С-Д-В-С
5.	Доказать, что если А с В, то (Д\В) + В = В.
§1. Основные понятия теории вероятностей
355
6.	Для некоторого эксперимента множество Q содержит ровно п элементарных
исходов. Определить число наблюдаемых событий данного эксперимента,
если:
1)	п = 2;	2) п = 3;	3) п = 6;	4) n = k.
7.	Игральная кость налита свинцом, в результате чего вероятность выпадения
каждого числа очков обратно пропорциональна этому числу. Найдите
вероятностное пространство и указанные вероятности.
8.	Среди 100 электроламп 5 испорченных. Какова вероятность того, что
выбранные наудачу 3 лампы окажутся исправными?
9.	Набирая семизначный номер телефона, абонент не смог вспомнить две
последние цифры и, помня лишь, что они четные и различны, набрал их
наудачу. Какова вероятность того, что номер был набран правильно?
10.	Бросаются две игральные кости. Какова вероятность того, что на первой
кости число очков будет больше, чем на второй?
И. Десятитомное собрание сочинений в случайном порядке, но подряд уста-
новлено на полке. Найти вероятность события:
1)	тома установлены в порядке возрастания;
2)	первый и второй тома стоят рядом и в порядке возрастания;
3)	на четных местах стоят тома с четными номерами;
4)	том 2 стоит раньше томов 5 и 8
12.	На отрезок длиной L наудачу бросают точку. Найти вероятность того, что
она упадет не дальше, чем на расстоянии I от середины этого отрезка.
13.	На отрезке АВ случайным образом выбирают две точки М и N. Найти
вероятность того, что из трех отрезков, на которые точки и 7V разбивают
отрезок АВ, можно построить треугольник.
14* К причалу для высадки пассажиров в течение часа в случайные моменты
времени должны подойти два катера Одновременное причаливание катеров
невозможно. Время высадки пассажиров с первого катера составляет 10 мин,
а со второго — 20 мин. Найти вероятность того, что одному из катеров
придется ожидать освобождения причала.
15.	Найти вероятность того, что три точки, случайно выбранные на окружности,
являются вершинами треугольника: 1) остроугольного; 2) прямоугольного.
Ответы
1. 1) Невозможным; 2) случайным; 3) невозможным; 4) достоверным.
2. 1) W(Q) = 21; 2) A/(Q) = 36; 3) JV(Q) = 60; 4) 7V(Q) = 64 х 63 =
= 4032;	5)	= 64 * 63 = 2016.	3. 1) Л6;	2) А5;	3) попада-
ние в кольцо радиуса г, где г% < г г3.	6. 1) 4; 2) 8; 3) 64;
д\ ok 7 (л о л с с. 60	30	20	15	12	10 \	© £95	_
4) 2 .	7. ^1, 2, 3, 4, 5, 6,	—, —, — ,	.	8’	“
= fra> «> о* 9 °-05 ‘°- гг “ о вг 2>	3> & з-
12. если	1, если 1>	13. 0,25.	14.	» 0,43. Указание.
Пусть А ={одному из катеров придется ожидать освобождения причала}. Пусть
х — время прихода первого катера, у — второго. Тогда элементарные исходы
имеют вид б) = (х,#), Q={(x, г/)|0^х^60,0^z/^60} — квадрат со стороной 60
на плоскости Оху, А = {(х, г/)|0 у — х 10, 0 х — у 20}, Р(Д) =
15. 1) 0,25; 2) 0.
356
Глава XXI. Элементы теории вероятностей
§2. СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ
1. Теорема сложения вероятностей для несовместных событий
Теорема 1. Вероятность суммы двух несовместных событий А
и В равна сумме вероятностей этих событий, т. е.
Р(Л+В) = Р(Л) + Р(В).	(1)
О Пусть событиям А и В благоприятствуют соответственно k и т
исходов, а всего имеется п равновозможных исходов. Так как события
А и В несовместны, то АВ — 0, т. е. среди п исходов нет таких,
которые благоприятствовали бы как событию Д, так и событию
В. Поэтому событию А + В благоприятствуют k + т исходов. По
определению вероятности события
Р(Л) = £, Р(В) = ^, Р(Л+В) = Ц^ = ^ + ^=Р(Л) + Р(В),
т. е. равенство (1) верно.	•
Следствие. Сумма вероятностей противоположных событий
равна единице, т. е.
Р(Д) + Р(Д) = 1.	(2)
О События А и А несовместны, поэтому по теореме 1 имеем
Р(А 4-Д) = Р(Д) + Р(Д). Но А 4-Д = J2 — достоверное событие, и по-
этому Р(А +A)=P(ty = 1, т. е. Р(А +Д)=Р(А)+Р(А) =P(Q) = 1. •
Замечание. Терема 1 верна для любого конечного числа событий Если
события Дь Д2,	> Ап попарно несовместны, т.е. А^Ащ = 0 при то
Р(Дj 4- А2 + ... + Ап) = Р(АО 4- Р(Д2) 4-... 4- Р(Ап).
Пример 1. Пусть в урне лежат 12 шаров: 3 белых, 4 черных
и 5 красных. Наугад вынимают один шар. Какова вероятность того,
что этот шар окажется не белым?
Д Первый способ. Пусть событие А ={вынут черный шар},
В={вынут красный шар}, тогда А +В={вынут черный или красный
шар}. Так как события А и В несовместны и Р(Д) = тн — I? В(В) — tL
то по теореме 1 имеем Р(А +В) = | 4- А =
Второй способ. Пусть событие С ={вынут белый шар}
и Р(С) = Тогда появление небелого шара С = А 4-В ={вынут
черный или красный шар}. Следовательно, по формуле (2)
Р(А + В) = Р(С) = 1 -Р(С) = 1 - |	А
§ 2. Сложение вероятностей
357
Пример 2. В партии из 100 деталей 3 оказались бракованными.
Какова вероятность того, что среди случайно отобранных 25 деталей
будет хотя бы одна бракованная?
Д Пусть событие А ={среди случайно отобранных 25 деталей будет
хотя бы одна бракованная}, тогда А ={среди случайно отобранных
25 деталей нет ни одной бракованной} Событие А представляет
собой сумму событий /1=Д1+Л2+^з? гДе А; ={среди случайно
отобранных 25 деталей будет ровно I бракованных}, поэтому легче
вычислить вероятность события А.
Число способов выбора 25 деталей из 100 деталей равно С^о.
Число не бракованных деталей равно 100 — 3 = 97. Тогда число
способов выбора 25 не бракованных деталей из 97 деталей равно
Найдем вероятность того, что среди случайно отобранных 25
деталей нет ни одной бракованной:
97’
Р(А\ =	= 25ПТ2! = 73-74-75 = 2701
v 7	С&) ЮО! 98-99-100	6468'
25! -75!
Отсюда находим Р(Д) = 1 - Р(Л) = 1 -	и 0,582.	▲
4 7	к	6468	6468
2. Теорема сложения вероятностей для произвольных событий
Теорема 2. Вероятность суммы двух произвольных событий
А и В равна сумме вероятностей этих событий за вычетом
вероятности их произведения, т. е.
Р(А + В) - Р(Д) + Р(В) - Р(АВ).	(3)
О Пусть событиям А и В благоприятствуют соответственно k и т
равновозможных исходов, а совместному осуществлению событий А
и В, т. е. событию АВ, благоприятствует г исходов Если число всех
равновозможных исходов равно п, то Р(А) — Р(В) — Р(АВ) = Q.
Так как событию А + В благоприятствует (fe — г) + (т — г) + г =
= k + т — г исходов, то
Р(А + В) = +	= £ +	= Р(А) + Р(В) -Р(ДВ),
т. е. равенство (3) верно	•
Следствие. Для произвольных событий Д1, А2, ... , Ап веро-
ятность события Д1+Д2 + ••• + Дп вычисляется по формуле
Р(Д1+Д2 + ... +Лп) = ^(-1)*+1Р(А1Д/-2...ЛД	(4)
358
Глава XXI Элементы теории вероятностей
где суммирование распространено на все возможные комбинации
событий Ль Л2,..., по одному, по два, по три и т. д. В частности,
при п — 3 имеем:
Р(А + В + С) = Р(Л)+Р(В)+Р(С) -Р(ЛВ) —Р(АС) - Р(ВС) +Р(ЛВС).
Замечание. Формула (4) аналогична формуле включений и исключений
для подсчета количества элементов объединения п множеств.
Пример 3. Из 99 карточек, на каждой из которых написано
натуральное число п, где 1 ^п^99, наудачу вынимают одну карточку.
Какова вероятность того, что число, написанное на вынутой карточке,
делится на 3 или на 11?
Л Пусть событие А ={число, написанное на карточке, делится на
3}, В={число, написанное на карточке, делится на 11}. Нужно найти
вероятность события Д+В={число, написанное на карточке, делится
на 3 или на 11}. События А и В не являются несовместными, поэтому
для нахождения вероятности события А + В воспользуемся форму-
лой (3). Так как А = {п\п — 3k. 1 < k < 33}, В — {п\п = 116, 1 < k < 9},
ЛВ = {ф = ЗЗМ<*<3},где*€К, то Р(Л) = || = * Р(В) = = 1
УУ О	УУ 11
= -з-.
Из формулы (3) получаем
Р(Л+В) = Р(Л)+Р(В)-Р(Дв) = 1 + 1-±=*Ц|^ = |. ▲
Пример 4 (задача о рассеянной секретарше). Имелось п писем,
предназначенных разным адресатам, и п конвертов. Рассеянная
секретарша разложила письма по конвертам и запечатала их, а после
этого наудачу написала адреса Какова вероятность того, что хотя
бы на одном письме адрес будет написан правильно?
А Перенумеруем письма от 1 до п. Пусть событие А^ ={k-e
письмо подписано правильно}, k = 1, ... , п. Тогда событие В =
— А\ 4- А2 + ... +Л/2={хотя бы одно письма подписано правильно}.
Вероятность события В вычисляется по формуле (4):
Р(Л1+Л2 + - • • +^п) — ^(^1)+P(^2) + ...
... +Р(Ап) — (Р(Л1Д2) + .. ^4-Р(Лп 1Лп)) 4-
все пары (Д/Д/), 1^Хл,
+ (^ИИ2^з) + - • - + Р(4-24-А)) + -• • 4~(—1)'г“1Р(Л1Л2 . . . Ап).
все тройки (Л/ЛуЛ^),
§ 2. Сложение вероятностей
359
Учитывая, что
Р(Д1) = Р(Д2> ,= Р(Л„) ==
CJt вариантов
/W2) = Р(лиз>... = Р(л„и„) =
С% вариантов
Р(Л1Д2Л3) = = р^Лп-М =	;
С% вариантов
р(ли2;..л>1.
Q вариантов
Следовательно,
Р(В) = с* - с2^1 + С3 -... + (- 1)П+1С"1 =
==1-^ + ^----+(-0"+1^
Задачи
1.	Каждое из четырех несовместных событий может произойти соответственно
с вероятностью 0,012, 0,01, 0,005 и 0,003. Определить вероятность того,
что в результате опыта:
1)	произойдет хотя бы одно из этих событий;
2)	не произойдет ни одно из этих событий.
2.	Из колоды в 36 карт наудачу вынимается одна карта. Какова вероятность,
что будет вынута карта пиковой масти или дама?
3.	Две монеты радиусов г\ и г% расположены внутри круга радиуса /?, в который
наудачу бросают точку. Определить вероятность того, что эта точка упадет
на одну из монет, если монеты не перекрываются
4.	Вероятность поражения мишени при первом выстреле равна 0,7. Вероятность
поражения мишени при втором выстреле равна 0,8. Вероятность поражения
мишени при первом и при втором выстрелах равна 0,56. Найти вероятность
того, что:
1)	мишень будет поражена хотя бы одним выстрелом;
2)	мишень не будет поражена ни одним выстрелом.
5.	Имеются две урны: первая содержит 1 белый, 3 черных и 4 красных шара,
вторая — 3 белых, 2 черных и 3 красных шара. Из каждой урны наудачу
извлекают по одному шару. Найти вероятность того, что цвета вынутых
шаров совпадут.
6.	В копилке лежат 8 монет достоинством в 1 рубль, 10 монет достоинством
в 2 рубля и 4 пятирублевых монет. Найти вероятность того, что 5 взятых
наугад монет в сумме составят не более 15 рублей.
360
Глава XXL Элементы теории вероятностей
7.	Из урны, в которой лежит k белых и / черных шаров, наудачу вынимают
два Шара Найти вероятность того, что они окажутся:
1)	разного цвета; 2) белого цвета; 3) черного цвета.
8.	Из урны, в которой лежит k белых и / черных шаров, наудачу вынимают без
возвращения один за другим все шары, кроме одного. Найти вероятность
того, что шар, оставшийся в урне, будет белым.
9? Элементы а\,	, ап случайным образом переставили (все п\ перестановок
равновероятны). Какова вероятность того, что хотя бы один элемент окажется
на своем прежнем месте?
Ответы
1. 1) 1-0,988-0,99-0,995-0,997^0,03; 2) 0,97. 2. |. 3.	4. 1) 0,94;
2) 0 06 5 —	6 1 -	(С‘° + Cs) + С4 (С?о + С!о ' С8 + С1) + с4 ' сю ~ q 949
64 ’	с®	’	'
7 |) __________-	2) _	3) _1-^Л_	8
7 (й + /)(А + /-1)’	’ (k + l){k + l-1)’	’ (k + l)(k + l-iy k + Г
9. 1 —	... +(—Указание. Смотри пример 4 (задача
«о рассеянной секретарше»).
§3. УСЛОВНАЯ ВЕРОЯТНОСТЬ.
НЕЗАВИСИМОСТЬ СОБЫТИЙ
1.	Условная вероятность
Пусть при проведении некоторого опыта с числом п равновозмож-
ных элементарных исходов имеется дополнительная информация или
условие, позволяющее рассматривать не все множество элементарных
исходов Q, а лишь некоторое его подмножество Н, которому
благоприятствует k элементарных исходов В этом случае, если
исход 6) не принадлежит И, то его вероятность полагается равной
нулю, если же он принадлежит Н, то его вероятность увеличивается.
При этом ясно, что вероятность таких исходов увеличивается в одно
и то же число раз, поскольку отношения их вероятностей не зависят
от получения дополнительной информации.
Обозначим исходы, благоприятствующие событию Н, через
tai, • • • j ^k-> а их вероятности до получения дополнительной инфор-
мации— черезрьр2, •. • ,Ра- Соответственно, Р(Н)— Р1+Р2 + - • • +Р&-
Тогда после получения этой информации вероятности исходов
6)1, 6)2,	, 6)^ станут равны числам Api, Ар2, ... , Ар&. Из условия
Api + Ар2 + ... + Apfe = 1 или А(р! + р2 + ... + pk) = 1 следует, что
А = 1
PW'
§3. Условная вероятность. Независимость событий
361
Таким образом, новые вероятности исходов 6>i, 6)2, • • • ,
становятся равны JL, JL, , А.
Рассмотрим теперь событие А. Ему благоприятствуют исходы
двух видов: благоприятствующие Н и не благоприятствующие Н
Если известно, что произошло событие Н, то вероятности исходов
первого типа умножаются на
типа полагаются равными 0. А
, а вероятности исходов второго
так как исходы первого типа
составляют событие Р(АЯ), то мы можем сформулировать следующее
утверждение: если известно, что произошло событие Н, то
вероятность любого события А принимает новое значение, равное
Р(АН)
Р(Н) ‘
Замечание. Проводимые выше рассуждения имели место в случае
конечного множества О. Однако сформулированное утверждение справедливо
и в случае бесконечного множества Q.
Пусть А и Я —события и Р(Я) 0.
Определение. Число, выражающее вероятность события А при
условии наступления события Я, называется условной вероятностью
события А относительно события Я и обозначается Р(А|Я).
Проведенные выше рассуждения показывают, что

(1)
Из формулы (1) вытекает равенство
Р(АЯ) = Р(Я).Р(А|Я),	(2)
называемое формулой умножения.
Таким образом, может быть сформулирована следующая теорема,
называемая теоремой умножения вероятностей.
Теорема 1. Вероятность совместного наступления двух собы-
тий равна вероятности одного из них, умноженной на условную
вероятность другого при условии, что первое наступило:
Р(АВ) = Р(А) • Р(В\А) или Р(АВ) = Р(В) • Р(А\В).
Пусть в некотором опыте с числом п равновозможных элементар-
ных исходов событию Я благоприятствует k элементарных исходов
(6^0), а событию АН благоприятствует г элементарных исходов.
Тогда Р(Я) = ^, Р(ЛЯ) = Т. Согласно формуле (1) имеем
Р{А\Н) =	= г- : = г~.
4 1 7 Р{Н) п п k
362
Глава XXI. Элементы теории вероятностей
Пример 1. Какова вероятность того, что кость, вынутая наугад
из полного набора домино, окажется «дублем», если известно, что
сумма очков на ней меньше, чем 6?
Л В наборе домино 28 костей, из них 7 «дублей». На 12 костях
сумма очков меньше, чем 6:
0-0,0-1,0-2,0-3,0-4,0-5,1-1,1-2,1-3,1-4,2-2,2-3.
Пусть событие А ={вынутая кость — «дубль» }, В ={сумма очков
на вынутой кости меньше 6}, тогда событие АВ ={вынутая кость —
«дубль» с суммой очков меньше 6}. Событию АВ благоприятствуют
три исхода: 0-0, 1-1, 2-2. Вычислим вероятность
3
р(А\В\ =	= 28 - А = 1	а
р(в) 22	12	4*	А
28
2.	Независимость событий
Определение. События А и В называются независимыми,
если
Р(АВ)=Р(Л)-Р(В).	(3)
Если равенство (3) не выполняется, то события А и В называются
зависимыми.
Наверняка можно говорить о независимости событий, если они
появляются в независимых испытаниях. Например, при стрельбе
по мишени несколькими стрелками независимо друг от друга
вероятность поражения мишени каждым стрелком не зависит от
вероятности поражения ее другими стрелками.
Когда же независимость испытаний неочевидна, то независимость
событий А и В проверяется с помощью формулы (3).
Пример 2. Выяснить, являются ли события А и В независимыми,
если:
1)	Р(Д) = 0,4, Р(В) = 0,3, Р(АВ) = 0,12;
2)	Р(Л) = 1, Р(В) = |, Р(ЛВ) = ^;
3)	при бросании кости А ^{выпало четное число}, В ={выпало
простое число}.
Д 1) Так как Р(Д) • Р(В) = 0,4 • 0,3 = 0,12 = Р(АВ), то события А
и В независимы.
2)	Так как Р(А) • Р(В) =	| =	Р(ДВ), то делаем вывод,
что события А и В зависимы.
§3. Условная вероятность. Независимость событий
363
3)	Р(Л) = | = Р(В) = | = Так как АВ ={выпало число 2},
Р(АВ) = 1 и Р(Л) • Р(В) = 1.1 = 1/! = Р(ДВ), то делаем
вывод, что события А и В зависимы.	▲
События Л], Л2, • - • , Лл называются независимыми в совокупно-
сти (или просто независимыми), если для любых k из них (k п)
выполняется соотношение
Р(А^ ...Aik} = P(Aix) • Р(Д,2).....
Если это соотношение выполняется при k = 2, то события
Ль Л2, ... , Ап называются попарно независимыми.
Замечание. Из попарной независимости событий Ль Л2,	, Л« не
следует их независимость в совокупности.
В качестве примера рассмотрим следующий опыт. Пусть на плоскость
бросается правильный тетраэдр, три грани которого окрашены соответственно
в белый, красный и черный цвет, а на четвертую нанесены все три цвета. Событие
Б = {тетраэдр упал на плоскость гранью, содержащей белый цвет}, К = {тетраэдр
упал на плоскость гранью, содержащей красный цвет}, Ч = {тетраэдр упал на
плоскость гранью, содержащей черный цвет}. Так как каждый цвет содержится
на двух гранях, то Р(Б) = Р(К) = Р(Ч) = |. Вероятность пересечения любой
пары этих событий равна | | так как любая пара цветов присутствует
только на одной грани. Это означает их попарную независимость, но
Р(БКЧ) = 1/Р(Б) • Р(К)-Р(Ч) = 1.
4	о
Пример 3. Бросили монету и игральную кость. Определить,
зависимы или независимы события: А ={выпал орел}, В ={выпало
нечетное число очков}.
Д В данном в условии опыте все множество элементарных исходов
Q содержит 12 элементов
Q = {01, 02, 03, 04, 05, 06, Pl, Р2, РЗ, Р4, Р5, Р6},
где О —выпадение орла, Р— выпадение решки, 1, 2, 3, 4, 5, 6 —
числа очков, выпадающих на игральной кости. Будем считать, что
каждый исход равновозможен, т. е. Р(01) = Р(02) = ... = Р(Р6) =
Событие ДВ = {01, 03, 05} состоит из трех элементарных исходов,
следовательно, Р(АВ) = А — 1. Так как Р(Л) = а Р(В) = |
IX *	х	ох
то получаем, что Р(Л)Р(В) = 1 • ~ — ± = Р(АВ), т. е. по определению
события А и В независимы.	▲
364
Глава XXL Элементы теории вероятностей
Пример 4. Доказать, что если события А и В независимы, то
события А и В также независимы.
А Событие А можно представить как сумму непересекающихся со-
бытий АВ и АВ, поэтому Р(А) =Р(АВ) + Р(АВ) = Р(А)Р(В) +Р(АВ).
Отсюда
Р(АВ) = Р(Д) - Р(А)Р(В) = Р(А) (1 - Р(В)) = Р(А)Р(В),
т. е. события А и В также независимы.	А
Пример 5. Доказать, что если события А и В независимы, то
Р(А + В) = I — Р(А)  Р(В).
А Используя теорему сложения вероятностей для произвольных
событий, запишем:
Р(А +В) = Р(А)+Р(В) - Р(АВ) =
=Р(А)+Р(В) -Р(А)- Р(В) =Р(А)+Р(В) -
- (1 -Р(Д)) • (1 -Р(В)) =Р(Д)+Р(В) -1 +Р(В)+Р(А) -Р(Д)Р(В) -
=Р(А) 4- Р(А) + Р(В)+Р(В) -1 - Р(А)Р(В) = 1 - Р(А )Р(В),
=1 =1
т. е. равенство верно.	А
Замечание Для независимых событий Ai, А2,	, Ап имеет место
формула
P(Ai + А2 +... + Ап) = 1 - Р(А{) • Р(А2) ...  Р(Ап).
3.	Формула полной вероятности и формула Байеса
Пусть события Н\, Н2, .Нп таковы, что Hi'Hj = 0 при i^j
и Н[ + Н2 +... +Нп = Q. В этом случае говорят, что Нх, Н2, ..Нп
составляют полную группу событий.
Теорема 2. Пусть вероятностное пространство Q представ-
лено в виде суммы попарно независимых событий Нх, Н2, Нп:
+	+	=	(4)
где Н[ • Hj = 0 при i j. Тогда вероятность любого события А
может быть вычислена по формуле
п
Р(Л)-£Р(Яг)Р(Л|//().	(5)
О Используя свойства операций над событиями и равенство (4),
можем записать следующую цепочку равенств
А =А -П=А .(Я1+Я2 + ... +Нп)=А -Нх+А*Н2 + ... +А-Нп.
§3. Условная вероятность. Независимость событий
365
По условию Hi • Hj — 0 при i ф j. В этом случае события А • Н[
и А • Hj будут также попарно независимы, так как
(A.Hi)-(A-Hj)=A-Hi-Hj = 0 при
Следовательно, событие А представляется в виде суммы попарно
независимых событий A - //j, А , А-Нп и поэтому вероятность
Р(А) по теореме сложения равна
Р(Д) - Р(А • Н{) +Р(А • Я2) + ... + Р(А • Нп}.
Заменяя в полученном равенстве Р(А • Hi) по формуле (2) на
P(Hi) • P(A\Hi), получаем доказываемое равенство
п
Р(А) = P(H[)P(A\Hi) +... +Р(Нп)Р(А\Нп) = Y,P(Hi)P(A\Hi),
называемое формула полной вероятности.	•
Замечание Эта формула справедлива и в более общей ситуации Условие
Н\ + Я2 + • • • +	= Q может быть заменено условием А С Н\ + Л/2 + • • • + Яп •
Одной из форм формулы полной вероятности является равенство
р(Н h\A} =__________________P(Hk)P(A\Hk)_______	,б)
P(H{)P(A\Hi) + ... + Р(Нп)Р(А\Нпу	W
Для доказательства равенства (5) достаточно заметить, что
Р(А  Нк) = Р(Нк)Р(А\Нк) = Р(А)Р(Н.\А).
П°ЭТ0МУ	P(HkW = Ж®.	(7)
Если Н\,	Нп — попарно независимые события, составляющие
полную группу событий, то, заменив в (7) Р[А) по формуле полной
вероятности, получаем формулу (6).
Равенство (6) называют формулой Байеса. Она истолковыва-
ется следующим образом. Если существуют попарно исключаю-
щие друг друга события (гипотезы) H\t Н}, ..., Нп такие, что
Я1 + Я2 +... +Нп = £1, и если известны вероятности события А при
условии справедливости каждой из этих гипотез, то по формуле (6)
можно найти вероятность справедливости гипотезы Hk при условии,
что произошло событие А.
Если Я2, .. .^Нп — полная группа событий и Р(Я1), Р(Я2), ...,
Р(Нп) — их вероятности, то эти вероятности называются апри-
орными (доопытными) вероятностями. Если произошло событие
А, то мы получаем апостериорные (послеопытные) вероятности
Р(Я1|/1), Р(Я2|Д), ...,	вычисляемые по формуле (7).
Пример 6. При выборах в районный совет голосование прово-
дилось на трех избирательных участках. На первом участке прого-
лосовало 25%, на втором 35% и на третьем 40% всех избирателей.
366
Глава XXL Элементы теории вероятностей
За депутата Иванова проголосовало соответственно 20, 30 и 12%
избирателей от числа голосовавших на этих участках.
1) Какова вероятность того, что случайно выбранный избиратель
проголосовал за Иванова?
2) Оказалось, что случайно выбранный избиратель проголосовал
за Иванова. Какова вероятность того, что он голосовал: а) на
первом избирательном участке; б) на втором; в) на тре-
тьем?
А Пусть событие А ^{случайно выбранный избиратель проголосовал
за Иванова}. Рассмотрим гипотезы: Н\ ^{избиратель голосовал на
первом участке}, Н2 ^{избиратель голосовал на втором участке},
Я.З ={избиратель голосовал на третьем участке}. Априорные (доопыт-
ные) вероятности этих гипотез равны Р(Н[) = 0,25,	— 0,35,
Р(Я3) = 0,4. Соответственно, Р(А|Я1) = 0,2, Р(А\Н2) = 0,3,
Р(А\Н3) = 0,12.
Тогда по формуле полной вероятности
Р(Д) = Р(Н1)Р(А\Н{) + Р(Н2)Р(А\Н2) + Р(Я3)Р(А|//3) =
= 0,25 0,2 + 0,35 • 0,3 + 0,4 • 0,12 - 0,203.
Найдем по формуле (7) апостериорные (послеопытные) вероятно-
сти Р(Нк\А), где k = 1, 2, 3. Вероятность того, что случайно
выбранный избиратель проголосовал за Иванова, голосуя на первом
участке, равна Р(//1|Л) =	= °’2^0з’2 = Соответ-
ственно, вероятность того, что он голосовал на втором участке,
равна Р(Н2\А) =	и того, что он голосовал на третьем
участке, равна Р(Я3|Л) = °q2q’12 = ^.	А
Задачи
1.	Три стрелка независимо друг от друга стреляют по мишени по одному
разу. Вероятности попадания в мишень для них равны соответственно 0,7,
0,8 и 0,9. Найти вероятность того, что:
1)	все стрелки попадут в мишень;
2)	хотя бы один стрелок попадет в мишень.
2.	Бросили игральную кость. Какова вероятность того, что выпало простое
число очков, если известно, что число выпавших очков нечетно?
3.	В изготовленной партии деталей вероятность появления бракованной равна
0,008. В 75% всех деталей стоят медные вставки, а на остальных цинковые,
что никоим образом не влияет на их качество. Какова вероятность того, что
произвольно выбранная деталь будет с цинковой вставкой и небракованной?
4.	Монета последовательно бросается три раза. Определить, зависимы ли
события: А ={при первом бросании выпал орел}, В ={решка выпала хотя
бы один раз}.
§3 Условная вероятность Независимость событий
367
5.	1) Доказать, что если события_ А и В независимы, то независимыми
являются также события: а) А и В\ б) А и В.
2)	Доказать, что если события Xj, Х2, >Ап независимы, то события
Л1, Х2, ••• , также независимы.
6.	Из урны, в которой лежит k белых и / черных шаров, наудачу вынимают
один шар, записывают его цвет и возвращают обратно Затем вынимают
следующий шар. Найти вероятность того, что оба шара окажутся:
1) белого цвета; 2) черного цвета.
7.	Из урны, содержащей 12 белых, 8 красных и 10 синих шаров, наудачу
извлекают два шара. Найти вероятность того, что вынуты шары разного
цвета, если известно, что не вынут синий шар.
8.	Из урны, содержащей 4 белых и 5 красных шаров, последовательно
извлекают без возвращения два шара Найти вероятность того, что:
1)	вторым оказался красный шар при условии, что и первый был красным;
2)	оба раза извлекались красные шары
9.	Из колоды в 36 карт последовательно наугад вынимаются без возвращения
2 карты. Найти вероятность того, что:
1)	оба раза извлекались карты красной масти;
2)	первой была вынута карта красной масти, а второй — черной масти;
3)	второй была вынута карта черной масти при условии, что первой была
извлечена карта красной масти.
10.	Два стрелка независимо друг от друга стреляют по одной мишени, делая
каждый по одному выстрелу. Вероятность попадания в мишень для первого
стрелка равна 0,8, для второго — 0,4. После стрельбы в мишени обнаружена
ровно одна пробоина. Найти вероятность того, что в мишень попал первый
стрелок.
11* При помещении в урну тщательно перемешанных п шаров, из которых m
белых и п — m черных, один шар неизвестного цвета выпал и закатился.
Из оставшихся в урне п — 1 шаров наудачу вынимают один шар. Найти
вероятность того, что этот шар будет белым
12Т Имеются две урны: в первой 3 белых шара и 2 черных; во второй 4 белых
и 4 черных. Из первой урны во вторую перекладывают, не глядя, два шара.
После этого из второй урны берут один шар Найти вероятность того, что
этот шар будет черным.
13. В цеху, изготовляющем микросхемы, первый станок производит 20%, второй
35% и третий 45% всей продукции. В их продукции брак составляет
соответственно 0,05, 0,15 и 0,18%.
1) Какова вероятность того, что случайно выбранная из партии готовой
продукции микросхема окажется бракованной?
2) Случайно выбранная микросхема оказалась бракованной. Какова веро-
ятность того, что она была произведена: а) на первом станке; б) на
втором; в) на третьем?
Ответы
1.	1) 0,504; 2) 0,994. 2.	3. 0,248.	4. Зависимы. 6. 1)	*2, 
О	(k + /)
о\	7 (12 • 8) .	_ 48 ~ q 505	8 П • 9)	9 1)	. 2)	.
2)	7-	• ct~95~°’5U5-	° 2’ 2} 18-
х	'	uU	OV
368	Глава XXL Элементы теории вероятностей
3)	10.	11. —. Указание. Событие А = {появление белого шара}.
35	7 п	1	r J
Гипотезы: Н\ — {утерянный шар был белым}, Н% = {утерянный шар был черным}.
12. 0,48. Указание. Событие А = {из второй урны вынут черный шар}.
Гипотезы: Н\ = {из первой урны во вторую положены два черных шара}, //2 = {из
первой урны во вторую положены два белых шара}, //3 = {из первой урны
во вторую положены один белый шар и один черный} 13. 1) 0,001435;
2) а) ^0.07; б) ^0,37; в) ^0,56.
§4. ФОРМУЛА БЕРНУЛЛИ
Пример 1. Стрелок поражает мишень при каждом выстреле
с вероятностью 0,7. Стрелок сделал 3 выстрела. Какова вероятность
того, что мишень была поражена:
1) только одним выстрелом; 2) только двумя выстрелами;
3) всеми тремя выстрелами?
А Пусть событие А ^{попадание стрелком в мишень при одном
выстреле}, тогда А ={промах при одном выстреле}. По условию задачи
Р(А) = 0,7, значит, Р(А) = 0,3. Событие Bi = AAA + ААА + AAA
означает, что мишень была поражена одним выстрелом из трех. Его
вероятность равна
Р(В1) = Р(А) • Р(А) • Р(А) + Р(А) • Р(А) • Р(А) + Р(А) • Р(А) • Р(А) =
= ЗР(Д) • (Р(Д))2 = 3  0,7 • 0,32 = 0,189.
Событие В2 = AAA + AAA -F ААА означает, что мишень была
поражена двумя выстрелами. Его вероятность равна
Р(В2) = з  (Р(Д))2 Р(Д) = 3 • 0,72 • 0,3 = 0,441.
Поражению мишени тремя выстрелами соответствует событие
В$ = ААА. Его вероятность равна Р(Вз) = (Р(А))3 = 0,73 = 0,343. ▲
Рассмотрим теперь общую задачу.
Задача. Вычислить вероятность события В, заключающегося
в том, что при испытаниях событие А произойдет ровно k раз,
считая, что при каждом испытании происходит событие А или А.
Рассмотрим событие состоящее в том, что в первых k испы-
таниях наступило событие А, а в следующих (п — /г) испытаниях —
событие А, т. е.
В{ — А-А •... -А- А-А -... -А .
k множителей п—k множителей
§4. Формула Бернулли
369
События Л и Л, одно из которых наступало в каждом из испыта-
ний, — независимые в совокупности события Согласно утверждению
о вероятности произведения независимых событий
= Р(А) • Р(Л) •... • Р(Д) • Р(А) • Р(А) •... • Р(Д) =
k множителей	п—k множителей
= р-р-... -р-(1-р)-(1-р)---- -(1-р) = рй(1 -p)n~k- (1)
k множителей	п—k множителей
Рассмотрим теперь событие В/, в котором событие А происходит k
раз в различных последовательностях. Тем не менее, вероятность
события Bi, являющегося произведением k событий А и (п — &)
событий А, будет также равна рА(1 ~p)n~k.
Число способов записи произведений k событий А и (п — й)
событий А, отличающихся друг от друга порядком расположения
в них множителей А и А, равно числу перестановок с повторениями
\n-k = Ckn.	(2)
Событие В, состоящее в том, что в испытаниях событие А наступит
k раз и не наступит (n-ti) раз, очевидно, равно сумме несовместных
событий Bi, отличающихся друг от друга порядком расположения
в них k множителей А и (n — k) множителей А. Число таких событий
согласно формуле (2) равно С„ :
В = Bi + В% + ... + В/ + ... .
С* слагаемых
По теореме I о вероятности суммы несовместных событий имеем
Р(В) = Р(В1) + Р(В2) + ... +Р(В,) + ... =
слагаемых
=р*(1 - ру-ь+pfe(l - p)n-fe +    +pfe(l - pf~fe +   =
С* слагаемых
= CknP\l-Py-k.
Вероятность события В принято обозначать Pn(k), подчеркивая тем
самым, что рассматривается вероятность события, наступившего
ровно k раз в серии из п однотипных испытаний. По доказанному
выше
/>„(£) = С*р*(1-р)л k,
(3)
где р = Р(Л).
370
Глава XXL Элементы теории вероятностей
Формулу (3) называют формулой Бернулли в честь швейцарского
математика Якоба Бернулли, изучавшего в начале XVIII в. испытания
с двумя возможными исходами, а само испытание такого типа —
схемой Бернулли.
Схема Бернулли. Схемой Бернулли называют случайный опыт,
состоящий в повторных испытаниях, удовлетворяющий следующим
условиям:
1)	в каждом испытании возможны только два исхода: появле-
ние определенного события А (успех) или противоположного
события А (неудача);
2)	испытания являются независимыми, т. е. вероятность успеха
в каждом испытании не зависит от исходов в других испы-
таниях;
3)	вероятности событий А и А остаются неизменными во всех
испытаниях: Р(А) = р и Р(Д) = 1 — р = q.
Пусть производится серия из п независимых испытаний, в каждом
из которых событие А может наступить с вероятностью р, и k —
количество наступлений события А в этой серии. Тогда
Pn(k) = Cknpkqn~k,	где q=\—p, k = O,l,...,n.
Приведем примеры случайных опытов, проходящих по схеме
Бернулли.
1) Последовательное подбрасывание правильной монеты п раз
и наблюдение выпадающих сторон монеты. При каждом
подбрасывании возможен один из двух исходов, являющихся
противоположными. Если, например, событие А ={выпал орел},
то А ={выпала решка}. В данном опыте Р(А) = Р(А) =
2) Последовательное подбрасывание п раз игральной кости и на-
блюдение выпадающих сторон кости. Если событие А ={выпало
число 3}, то А ={не выпало число 3}. В данном опыте при
каждом подбрасывании Р(А) — |, Р(А) =
Пример 2. Монету бросают 10 раз. Какова вероятность того,
что орел появится при этом ровно: 1) 4 раза; 2) 5 раз?
А Пусть событие А ={появился орел}, тогда А ^{появилась решка}.
Вероятность Р(Д) = Р(Л) = По формуле (3) находим:
1) p.o(4) = Cjo(l)4(l)6=J^.A = ^;
2) P.»(S) = Cfo(j)5G)S = S-	*
§4. Формула Бернулли
371
Пример 3. Процент выпуска бракованной детали составляет
5%. Для продажи взяли партию из 200 деталей. Найти наиболее
вероятное число бракованных деталей в этой партии.
А Вероятность того, что выбранная наугад из партии деталь
окажется бракованной, равна р = 0,05, а того, что она окажется
исправной, равна q = 1 — р = 0,95.
Пусть событие А ={в партии оказалось k бракованных деталей}.
Тогда вероятность
рщ=р200 m =	=с20о
200-k
_ rk 5ft95200-ft
С200 10q200 ’
Заметим, что
(P + <7)200 =	C200PV°° k = 22 p2oo(fe)-
6=0	6=0
Найдем наибольший член разложения бинома (р + ^)200.
Для этого решим неравенство	^2оо(^ + 0 или
°™ -У—	 '9 « 1
или k 9.
Следовательно,
^2Оо(О) ^2оо(0	^2Оо(10) ^2Оо(И)	^2Оо(2ОО).
Таким образом, наиболее вероятное число бракованных деталей
в этой партии равно 10.	▲
Пример 4. Пусть вероятность выигрыша при покупке одного
лотерейного билета равна р = 0,01. Сколько билетов нужно купить
для того, чтобы вероятность хотя бы одного выигрыша была не
меньше, чем 0,75?
А Предположим, что куплено п билетов. Введем событие А ={среди
купленных билетов оказался хотя бы один выигрышный}, тогда
А ^{выигрышных билетов нет}. По формуле (3) имеем P(A) = C®p°qn,
а вероятность Р(А) равна
Р(Д) = 1 - Р(Д) = 1 -	= 1 - (1 - р)п 0,75.
Требуется найти такие значения и, при которых Р(А) 0,75. Для
этого решим неравенство
1 - (1 - р)п 0,75 или (1 - р)п 0,25.
372	Глава XXL Элементы теории вероятностей
Отсюда и1п(1 — р) In 0,25 или, с учетом того, что 1п(1 — р) < 0,
получаем п ^ь-р) “ Гп~о''9'1 ~ 137,9. Следовательно, нужно купить
не менее 138 билетов.	▲
Вообще, при большом числе испытаний относительная частота
появления события, как правило, мало отличается от вероятности
этого события Математическую формулировку этого утверждения
дает принадлежащий Я. Бернулли закон больших чисел, который
в уточненной форме гласит следующее.
Теорема. Пусть вероятность события А в некотором испы-
тании равна ру и пусть проводятся серии, состоящие из п
независимых повторений этого испытания. Через т обозначим
число испытаний, в которых происходило событие А. Тогда для
любого положительного числа а выполняется неравенство

р(1 -р)
а?п
(4)
Смысл этого неравенства состоит в следующем. Выражение ™
равно относительной частоте события А в серии опытов, а |	— Р | “
отклонению этой относительной частоты от теоретического значе-
ния р. Неравенство |	— р | > а означает, что отклонение оказалось
больше а. Но при постоянном значении а с ростом п правая часть
неравенства (4) стремится к нулю. Это означает, что серии, в которых
отклонение экспериментальной частоты от теоретической велико,
составляют малую долю всех возможных серий испытаний.
Задачи
1.	Из урны, содержащей 4 белых и 5 красных шаров, последовательно 10 раз
извлекают один шар, записывают его цвет и возвращают обратно в урну.
Найти вероятность того, что 4 раза вынимался красный шар
2.	Что вероятнее выиграть у равносильного противника (ничейный исход партии
исключен): три партии из четырех или пять из восьми?
3.	Вероятность попадания в цель при каждом выстреле из орудия равна
0,8. Сколько нужно произвести выстрелов, чтобы наивероятнейшее число
попаданий было равно 20?
4.	Для п испытаний по схеме Бернулли с вероятностью р успеха в одном
испытании найти вероятности событий:
1)	А —{не появилось ни одного успеха};
2)	В ={появился хотя бы один успех};
3)	С = {успех появился не менее k\ и не более &2 раз}.
5.	Игральный кубик бросают четыре раза. Какова вероятность того, что 5 очков
в этой серии испытаний появятся не менее трех раз?
§5. Числовые характеристики случайных величин
373
6.	В приборе стоят 6 одинаковых предохранителей Для каждого из них
вероятность испортиться после 1000 часов работы равна 0,4. Если испор-
тилось не менее двух предохранителей, то прибор требует ремонта. Найти
вероятность того, что прибор потребует ремонта после 1000 часов работы,
если предохранители портятся независимо друг от друга.
7.	Вероятность рождения мальчика равна 0,515, девочки — 0,485. В некоторой
семье шестеро детей. Найти вероятность того, что среди них не больше
двух девочек.
8.	Вероятность того, что насекомое определенного вида будет жить более
100 дней, равна 0,5. Найти вероятность того, что среди выбранных для
наблюдения 10 насекомых этого вида не менее 8 экземпляров будут жить
более 100 дней.
9.	Пусть производится серия из п независимых испытаний, в каждом из
которых событие/1 может наступить с вероятностью р, и Pn(k) — вероятность
того, что событие А произойдет k раз. Вывести рекуррентную формулу,
связывающую значения вероятностей Pn(k + V) и Pn(k)-
10? (Задача Банаха.) Некий курящий математик носит с собой две коробки
спичек. Каждый раз, когда он хочет закурить, он выбирает наугад одну
из коробок. Найти вероятность того, что когда математик вынет в первый
раз пустую коробку, в другой коробке окажется г спичек (г = 1, 2, ... , п;
п — число спичек, бывших первоначально в каждой из коробок)
Ответы
LCio©4(§)6^ 0’1542-
рех. 3. 24 или 25.	4.
= 1 - (1 - р)л; 3) Р(С) = k^(^npkqn-k.
kkx
8.
2. Вероятнее выиграть три партии из четы-
1) Р(А) = qn = (1 - р)п- 2) Р(В) = 1 - qn =
5. Л-.	6. 1 - 3 • 0,65 « 0.77.
432
7. Р6(0) + Р6(1) +^(2)^0,3723.	8.
10.	Указание. Спички брались 2п — г раз, причем п раз из
коробки, оказавшейся пустой. Это соответствует п успехам в 2п — г испытаниях.
§5. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ
ВЕЛИЧИН
Случайная величина £—это числовая величина, принимающая
различные значения случайным образом. В данном параграфе мы
рассмотрим лишь дискретные случайные величины т. е. слу-
чайные величины £ принимающие конечное множество значений
%1,	• • •, Ял-
Замечание. В теории вероятностей рассматриваются также дискретные
случайные величины, принимающие значения из счетного множества значений,
а также непрерывные случайные величины, принимающие значения, заполня-
ющие отрезок, интервал, полупрямую или всю числовую прямую.
374
Глава XXI. Элементы теории вероятностей
Пусть P(£=Xi)=pi — вероятность того, что случайная величина £
примет значение, равное X/. Законом распределения дискретной
случайной величины называют соответствие между возможными
значениями и их вероятностями; его можно задать таблично,
аналитически в виде формулы и графически.
Рассмотрим матрицу	, в первой строке ко-
торой перечисляются все возможные значения случайной величины,
а во второй строке указываются соответствующие вероятности их
реализации. Такая матрица называется таблицей распределения
случайной величины %. Сумма чисел второй строки таблицы равна
единице: р\ +р2 + ... +рп = 1-
Пример 1. Игральная кость брошена 3 раза. Написать закон
распределения появления числа три.
Д Пусть событие А ={при одном бросании выпала тройка},
Р(Д) = |, Р(Л) = |. Тогда случайная величина %— число выпадений
тройки при трех бросаниях кости. Она может принимать значения
О, 1, 2 и 3. Тогда
Л(^=0) = Л>(ЛЛЛ)= (I) = g|,
Р« = 1) =Р(ДЛЛ +АА А +Л А А) = 3-1 • (|)2 =
Р^=2) = Р(ААА +ААА +ААА ) = 3-1	= А
Р({=3) = Р(ЛЛЛ) = (1)3 = Х
Закон распределения имеет вид
/ О	I	2	3 \
( 125	75	15	1	) • ,	А
416	216	216	216'
Функция распределения Ff(x) случайной величины £ определя-
ется формулой
F&) = P{Z<x}= £ P{f = x*}.	(1)
k: хь<х
Пример 2. Построить функцию распределения для случайной
величины из примера 1.
§5. Числовые характеристики случайных величин
375
Д Подставляя в формулу (1) найденные выше вероятности, получим
р{е<о},х^о
Р{£=0},0<х^1
125 о
216’
200 .
216’
215 9
216’ Z
1,еслих>3.	(1,х>3. А
Функция распределения обладает свойством монотонности, т. е.
Ff(xi) ^/ч(х2) при Xi 02-
1. Математическое ожидание дискретной случайной величины
Математическое ожидание (или среднее значение) А4(£) дис-
кретной случайной величины принимающей конечное множество
значений, определяется следующим образом:
п
М(^) =Х1Р1+Х2Р2 + --- + XnPn = '^XiPi-	(2)
1=1
Замечание. Из определения следует, что математическое ожидание
дискретной случайной величины с не является случайной величиной.
Пример 3. Пусть случайная величина £ задана законом распре-
деления
/X] х2	*п\
\ - - 1 ) •
' п п ’ ” п '
Найти математическое ожидание 7И(£).
Д По формуле (2) находим
М(0=Х11+х2- + ... +х/ = Х1+Х2 + ---^.	▲
v 7 п п	п	п
Видим, что в случае р\ = р% = ... = рп = - математическое
ожидание — среднее арифметическое значений xi, Х2, .хп.
Замечание. Математическое ожидание /И(<*) является средним значением
случайной величины f по распределению, поэтому его часто называют «центром
распределения».
Перечислим свойства математического ожидания.
Свойство 1. Математическое ожидание постоянной величины
равно самой постоянной: М(а)=а.
п
О Это свойство следует из условия J2 Pi — 1-	•
/=1
376
Глава XXL Элементы теории вероятностей
Свойство 2. Постоянный множитель можно выносить за знак
математического ожидания: М(а£) = а • Л4(?) (здесь а — постоянная
неслучайная величина)
О Пусть случайная величина £ задана законом распределения
Х2	•••	хп\
\Р1	Р2	•••	Рп)
Тогда закон распределения случайной величины имеет вид
(aXj	UX2	. . .
Pl	Р2		Рп)'
Отсюда
п
М(а£) = axipi + ах2Р2 + • • • + ахпрп — а ^iPi-a-M^. (3)
/=1 •
Суммой случайных величин £ и ту с таблицами распределения
*2	•••	Х/Л	и fpi	У2	•••	УпЛ
Р2	• •	Рп)	\Q\	Q2	• • •	Яш)
называется случайная величина	а	(обозначается а = f +	ту),
принимающая пт значений	+	уь xi -I- у2,..., xj +	У™,
Х2 + Уь Х2 + У2, . . . , %2 + Ут,-	*п	+ У1, Хп + у2, . . . , Хп +	ут,
С вероятностями Рп, . . . , р1т, р21,	• • • , Р2т, • , РпЬ Рпт^- • , Рпт,	Где
Ру — вероятность того, что £ принимает значение х/, а ту принимает
значение уу
Для ру справедливы равенства
т	п
7Уч=р^ Еа = */-
/=1	Z=1
Свойство 3. Математическое ожидание суммы двух случайных
величин равно сумме их математических ожиданий:
Ж+т^ад+Лфу).	(4)
Случайные величины £ и зу называют независимыми, если они
являются численными характеристиками независимых случайных
событий. Если и ту независимы, то Рц^ргЦу Ру — вероятность
совместного появления событий £ = х, и ту = у у pi — вероятность
события £ = Xi, qj — вероятность события ту = z/y.
Произведением независимых случайных величин £ и ту называется
случайная величина /3 (обозначается /3=^ту), принимающая пт значе-
ний Х1У1, Х]У2, • • •, Х1У/П, Х2У1, Х2У2, • • •, %2У/и, • • • * ХлуЬ ХпуЪ . . ., Хпут,
с вероятностями pxq^ , Piqm, Р2Я\> • • • Р2Ут, • • • , РпУЬ • • • , РпЯт-
§5. Числовые характеристики случайных величин
377
Свойство 4. Математическое ожидание произведения двух
независимых случайных величин равно произведению их матема-
тических ожиданий:
(5)
2.	Дисперсия дискретной случайной величины
Рассмотрим две случайные величины £ и т? с таблицами распре-
деления
(-8	-6	—4	-2	0	3	4	7	8 А
^0.1	0.08	0.12	0.12	0.2	0,18	0.04	0,06	0.1 )
и (-2 \0,2	-1 0,13	-0,5 0,2	-0,2 0,05	0 0,03	0,5 0,2	1,5 0,04	2 0,1	4 А 0,05 )
Эти две случайные величины имеют разные но их математические ожидания совпадают:						законы МЮ =	распределения M(tj) = -0,08.	
				М(х)	/-Ч	Z4			
	-8	-6	-4	-2	0	3 4	7 8	X	
				М(г))				
			-2	kJ UJtkJ kJ 0	2	4		Г)	
Рис. 2
На рис. 1 значения случайных величин £ и т?, а также их
математические ожидания нанесены на числовую прямую. Видно,
что эти случайные величины имеют различный разброс около их
математического ожидания.
Для измерения разброса возможных значений случайной вели-
чины используют математическое ожидание случайной величины,
представляющей квадрат отклонения £ —7И(£), т. е.
вд = м((£-А1(<0)2).	(6)
Такую меру называют дисперсией случайной величины. Дисперсия
показывает «степень разброса» значений случайной величины около
ее математического ожидания.
Пусть случайная величина £ задана таблицей распределения
Xf х2 ... хп
Р\ Р2 ••• Рп
и пусть
Af(f) = xipi + х2р2 +  •  + хпрп = а.
378
Глава XXI. Элементы теории вероятностей
Тогда таблица распределения случайной величины (£ — а)2 имеет
ВИД	/22	2\
/ (%1 - а)	(х2-а)	 	(хп - а) \
\ Pl Р2	 Рп J
Дисперсия случайной величины £ вычисляется по формуле
п
D(&=52 (Xi ~ a^pi-
i=l
n
Преобразуя эту формулу и подставляя а = xiPh получим
/=1
п
D{^=^^xi~a^pi=
/=1
п	п	п	/ п	\ 2 п
=52 x^pi ~2 52Xipi' 52XiPi+(52xipi) 52pi=
Z=1	Z=1	i=l	\Z=1	/ i=l
n	( n	\ 2
i=l	\i=l	/
так как pi = 1.
/=1
Получили, что для вычисления дисперсии также можно исполь-
зовать формулу
л	/ п	\ 2
d{^}=J2x2ipi ~ (52XiPi) •
i=\	\f=l	/
Отсюда следует, что
ад = м((?-Ж))2) =Ж2)-м2(П-	(8)
Перечислим свойства дисперсии.
1)	D(a} = 0, если а — неслучайная величина.
О По формуле (8) получаем D(a) =М(а2) -М2(а) = а2 — а2 = 0. •
2)	D(a£) = £2D(£), если а — неслучайная величина
О По формуле (8) имеем
D(a<) = Л4((а^)2) -M2(af) = й27И(£2) - а2М2(О =
= а2 (М(^) - М2(С)} = a2D(f).	•
§5. Числовые характеристики случайных величин
379
3)	£>(£ + zj) =	+ D(ri), если f и z? независимы.
О Пусть случайные величины £ и z? независимы По формуле (5)
имеем
По формуле (8) получаем
D(£+ rj) =М(^+ 7))2) -М2(е+ zj) =
=М(£2+2£z?+ zj2) - (7И(0+M(zj))2 =
=М«2)+2M(£)M(z7) +M(zj2)-M2(f) - 2M«)M(z})-M2 (zj) =
= (м(^) -ТИ2(О) + (m(zj)2 -M2(zj)) =ОД +£>(zj).	•
3.	Два закона распределения дискретной случайной величины
Рассмотрим два закона распределения дискретной случайной
величины.
Равномерное распределение. Дискретная случайна величина %
называется равномерно распределенной, если она задается следую-
2
щей таблицей распределения: I i ]	” * i j.
'л п	п'
Распределение случайной величины задается значением п.
Легко посчитать, что	/)(£) — П '
Биномиальное распределение. Дискретная случайная ве-
личина называется распределенной по биномиальному за-
кону, если она задается следующей таблицей распределения:
(О 1	... k ... П	Ь п__ь
, где рь = C„pKqn .
Ро Р\ ••• Pk ••• Рп) ™	4
Распределение задается значениями n.p.q (здесь q = \ — р).
Пример 4. Найти математическое ожидание дискретной случай-
ной величины %, подчиненной биномиальному закону распределения
P{£=k} = CknPkqn~k.
А По формуле (2) имеем
п	п	п
м(с=52 kCnPk(in~k=52 kCnpk(in~k = пр^ ^cknpk-iqn~k.
6=0	6=1	6=1
Заметим, что -С„ = - •	... = С*-!.
п п п 6!-(п-6)!	(6 - 1)! • (п - 6)!	”-1
380
Глава XXI. Элементы теории вероятностей
Следовательно,
п	п
Ж) = «Р ^Cknpk~xqn~k = пр^ Ckn~\pk-'qn~k =
k=l	k=\
~	— пр(р + ?)п-1*
k=[
Отсюда получаем, что
Ж) - пр,	(9)
так как р + q = 1.	▲
Пример 5. Найти дисперсию дискретной случайной величины
подчиненной биномиальному закону распределения Р{£ = k} =
= Cknpkqn~k.
Л Предварительно найдем ЛЦ^2):
М(£2) = k2CnPkqn~k = У2 k2Cknpkqn~k —
/г^о	£=1
k—i
п
= np^2^n-\pk^ q(n~^~(k~l) =
k=l
= прУ~У&-1)С„1{рй~1д(';~1)-(*:~1> +
*=1
п
+ пр	C„~\pk~lqtn~v)~(k~i}.
k=l
l
Заметим, что (k — l)C^~\pk^q^n~^~^k~^ является математиче-
k=\
ским ожиданием случайной величины подчиненной биномиальному
закону распределения Р{£ = k — 1} =	поэтому
ее сумма равна (п — 1)р (см. предыдущий пример). Сумма же
£ CknZ.\pk~{q{n~|)-(А“° = (р + ?)"-1 = 1-
k=-\
Отсюда следует, что 7И(^) = пр(п — 1)р + пр = п2р2 — пр2 + пр.
§5. Числовые характеристики случайных величин	381
Так как D(g) = М(?) - (М(£))2 , то
£>(£) = п2р2 — пр2 + пр — п2р2 — пр — пр2 — пр{\ — р) = npq.	(10)
Пример 6. Вероятность попадания стрелком в мишень равна
0,75. Стрелком сделано 20 выстрелов. Случайная величина £ —
количество попаданий в мишень. Найти математическое ожидание
и дисперсию случайной величины %.
Л Как уже известно, в данном случае случайная величина £
подчинена биномиальному закону распределения P{^=k} = C^pkqn~k.
По формулам (9) и (10) имеем
М(?) = пр = 20 • 0,75 = 15, £>(£) = npq = 20 • 0,75 > 0,25 = 3,75. ▲
Задачи
1.	Устройство состоит из трех независимо работающих элементов Вероятность
отказа каждого элемента равна 0,1. Составить закон распределения числа
отказавших элементов в данном опыте и найти функцию распределения
полученной случайной величины
2.	Построить закон распределения и функцию распределения случайного числа
попаданий баскетболистом мячом в корзину при четырех бросках, если
вероятность попадания при одном броске равна 0,4.
3.	Пусть случайная величина £ задана законом распределения
—5 -3-10	1
11111
.8	8	8	8	8
Найти математическое ожидание Л4(£) и
4. Независимые случайные величины £ и у
5
0,6
2
ОД
4 А
о,з;
2	3	4А
1	1	1 I
8	8	8/
дисперсию D(f).
заданы законами распределения
( 7	8 А
\0,2	0,8 J
соответственно. Построить закон распределения случайной величины и
найти ее математическое ожидание.
5.	Найти математическое ожидание суммы числа очков, которые могут выпасть
при бросании двух игральных костей.
6.	Пусть случайная величина £ задана законом распределения
%2	• • • хп
Р\ Р2 Рп
Доказать, что математическое ожидание случайной величины /? = <; —Л4({),
называемой отклонением, равно нулю, т.е. что 714(<; — М(£)) = 0.
7.	Сравнить математические ожидания и дисперсии случайных величин с и т),
заданных следующими законами распределения:
/ -1	1	2 ЗА ( -1	1	2	ЗА
\0,48	0,01	0,09	0,42J	и 1^0,19	0,51	0,25	0,05)	’
382
Глава XXI. Элементы теории вероятностей
Ответы
/О 1	2	3 \	( О 1	2	3	4 \
*• \0,729 0,243 0,027 0,001/	^0,1296 0,3456 0,3456 0,1536 0,0256J
О	А ЮК п/п 519 q7	л ( 14	16	28	32	35	40 \
3.	Af(<)	- 0,125, D(<)	- 64	- 8Й.	4. ^0)02	0 08	0 06 0,24 0)12 0 48 J	;
М(£• 7]) = М(£) • М(т)) = 4,4 • 7,8 = 34,32. 5. Ж + >?) = Mtf) + М(>?) = \ \ = 7,
где и г/— случайные величины числа выпавших очков на одной и другой
костях. 7. М(0 = M(rj) = 0,97, D^) « 3,69 > D(j]) » 1,21.
ОГЛАВЛЕНИЕ
Предисловие ..	............................ 3
Глава XI. Тригонометрические и обратные тригонометри-
ческие функции ....	5
§1	. Функции синус и косинус. . .	5
§2	. Функции тангенс и котангенс ...	...	...	19
§3	. Обратные тригонометрические функции.	...... ........... 26
§4	. Первый замечательный предел .................................... 37
Глава XII. Тригонометрические уравнения и неравенства. 41
§1	. Простейшие тригонометрические уравнения......................... 41
§2	. Тригонометрические уравнения, сводящиеся к алгебраическим. Однород-
ные и линейные уравнения .	.......................... 46
§3	. Метод замены неизвестного и метод разложения на множители. . .	53
§4	. Метод оценки левой и правой частей уравнения ................... 58
§5	. Отбор корней уравнений. Тригонометрические уравнения, содержащие
знаки модуля и корня. .	.................................... 63
§6	. Тригонометрические уравнения различных видов. Уравнения, содержащие
параметры......................... . .	...	74
§7	. Тригонометрические неравенства.............................. ...	87
Глава XIII. Производная и дифференциал ..	...	98
§1	. Определение производной. Производные функций хп, sinx,	cosx	....	98
§2	. Производные показательной и логарифмической функций	103
§3	. Правила дифференцирования. Дифференциал........................ 107
§4	. Геометрический и физический смыслы производной и дифференциала .	118
Глава XIV. Применение производной к исследованию
функций....................................................... 126
§1	. Основные теоремы для дифференцируемых	функций.................. 126
§2	. Возрастание и убывание функции...............................   133
§3	. Экстремумы функции...........................................   138
§4	. Наибольшее и наименьшее значения функции....................... 144
§5	. Производные второго порядка. Выпуклость	и точки перегиба....... 154
§6	. Построение графиков функций.................. ....	...	159
Глава XV. Первообразная и интеграл..................................... 167
§1	. Первообразная функции . .	..... 167
§2	. Неопределенный интеграл .	173
§3	. Определенный интеграл............... .................. 186
§4	. Применение определенного	интеграла	для	вычисления	площадей .	199
§5	. Приложения определенного	интеграла	к	физическим	задачам........ 210
384
Оглавление
Глава XVI. Дифференциальные уравнения.	215
§1	. Основные понятия................ ...	215
§2	. Уравнения с разделяющимися переменными..................... 219
§3	. Линейные дифференциальные уравнения первого и второго порядка с по-
стоянными коэффициентами .....	224
Глава XVII. Системы уравнений и неравенств различных
типов........................................................   235
§1	. Показательные и логарифмические уравнения с параметром..	235
§2	. Показательные и логарифмические неравенства с параметром.	240
§3	. Системы логарифмических и показательных уравнений. .	248
§4	. Системы тригонометрических уравнений и неравенств.......... 256
Глава XVIII. Уравнения и неравенства с двумя перемен-
ными .	  266
§1	. Линейные уравнения и неравенства с двумя переменными....... 266
§2	. Нелинейные уравнения и неравенства с двумя переменными ....	273
§3	. Уравнения и неравенства с двумя переменными, содержащие параметры 283
Глава XIX. Делимость целых чисел. Целочисленные реше-
ния уравнений .	...	298
§1	. Делимость чисел. .	...	298
§2	. Сравнения................. ..	307
§3	. Решение уравнений в целых числах........................... 313
§4	. Текстовые задачи с целочисленными неизвестными.	319
Глава XX. Комбинаторика.	324
§1	. Основные законы комбинаторики. .	324
§2	. Основные формулы комбинаторики...........................   327
§3	. Бином Ньютона и полиномиальная формула....	337
Глава XXI. Элементы теории вероятностей	....... 346
§1	. Основные понятия теории вероятностей	346
§2	. Сложение вероятностей...................................... 356
§3	. Условная вероятность. Независимость событий ....	...	360
§4	. Формула Бернулли........... .	. . .	368
§5	. Числовые характеристики случайных величин.................. 373

'тот \че< ник является частью уче но-методическото комплекта
для преподавания математики в старших классах
физико-математического и естественно-научных профилей.
Комплект включает в себя:
•	учебник для 10 класса
•	учебник для 11 класса
•	методическое пособие и дидактические материалы для 10 класса
•	методическое пособие и дидактические материалы для 11 класса
•	задачник для 10-11 классов
Шабунин Михаил Иванович —
доктор педагогических наук, профессор кафедры
высшей математики МФТИ, автор свыше двухсот
научных и учебно-методических работ, один
из авторов учебников алгебры для 7-11 классов
средней школы, учебников и сборников задач
по математическому анализу и теории функций
комплексного переменного для студентов вузов,
автор многих пособий для абитуриентов.
Заслуженный работник высшей школы РФ,
лауреат премии Правительства Российской Федерации в области
образования за 2002 год, член Научно-методического Совета по
математике Министерства образования и науки РФ, заслуженный
профессор МФТИ.
Прокофьев Александр Александрович —
доктор педагогических наук, доцент, профессор
кафедры высшей математики МИЭТ. преподаватель
математики Физико-математического лицея №1557
Зеленоградского округа г. Москвы, учитель высшей
категории
Автор более 40 книг, в том числе монографий,
учебных и методических пособий по математике для
школьников и студентов. Область научных
интересов связана с разноуровневыми
и вариативными моделями математического образования
в средней и высшей школе