Author: Шабунин М.И. Прокофьев А.А. Олейник Т.А. Соколова Т.В.
Tags: общее школьное образование общеобразовательная школа математика учебные пособия и учебники по математике алгебра
ISBN: 978-5-94774-456-9
Year: 2009
10-11
М. И. Шабунин А. А. Прокофьев Т. А. Олейник Т. В. Соколова
МАТЕМАТИКА
Алгебра
Начала математического анализа
ЗАДАЧНИК
М. И. Шабунин, А. А. Прокофьев Т. А. Олейник, Т. В. Соколова
МАТЕМАТИКА
Алгебра Начала математического анализа
ПРОФИЛЬНЫЙ УРОВЕНЬ
Задачник для 10-11 классов
Москва
БИНОМ. Лаборатория знаний
2009
УДК 373.167.1:51(076)
ББК 22.1я721.6
Ш12
Шабунин М. И.
Ш12 Математика. Алгебра. Начала математического анализа. Профильный уровень : задачник для 10-11 классов / М. И. Шабунин, А. А. Прокофьев, Т. А. Олейник, Т. В. Соколова. — М. : БИНОМ. Лаборатория знаний, 2009. — 477 с. : ил.
ISBN 978-5-94774-456-9
Задачник для 10-11 классов является частью учебно-методического комплекта для старших классов школ с углубленным изучением математики. Главы задачника соответствуют главам учебников для 10 и 11 классов. Задачи по каждой теме расположены в порядке возрастания трудности (три уровня).
В книгу включены задачи из вариантов выпускных экзаменов и ЕГЭ, а также варианты вступительных письменных экзаменов в вузы, предъявляющие повышенные требования к математической подготовке абитуриентов.
Для учащихся классов физико-математического и естественно-научных профилей, учителей средних школ.
УДК 373.167.1:51(076)
ББК 22.1я721.6
По вопросам приобретения обращаться: «БИНОМ. «Лаборатория знаний» Телефон: (499)157-5272 e-mail: binom@Lbz.ru, http://www.Lbz.ru
ISBN 978-5-94774-456-9
© БИНОМ. Лаборатория знаний, 2009
ПРЕДИСЛОВИЕ
Сборник задач по курсу «Математика. Алгебра. Начала математического анализа. Профильный уровень» предназначен для изучения профильного курса алгебры и начал математического анализа в 10-м и 11-м классах школ с углубленным изучением математики в объеме 6-8 часов в неделю. Задачник является составной частью учебно-методического комплекта (УМК) «Математика. Алгебра. Начала математического анализа. Профильный уровень», в который входят также учебники для 10-го и 11-го классов (авторы Шабунин М. И., Прокофьев А. А.) и методические пособия для учителей к соответствующим учебникам (авторы Шабунин М. И., Прокофьев А. А., Олейник Т. А., Соколова Т. В.).
Задачник состоит из 23 глав и приложения с образцами вариантов ЕГЭ 2005-2008 гг. Главы 1-21 и порядок их следования соответствуют главам и их расположению, принятому в учебниках для 10-го и 11-го классов. Так, в учебниках представлены следующие разделы курса.
Десятый класс: «Элементы математической логики», «Числовые множества», «Функции», «Алгебраические уравнения и неравенства» и «Системы алгебраических уравнений», «Тригонометрические формулы», «Комплексные числа», «Многочлены от одной переменной», «Предел и непрерывность функции», а также «Степенная, показательная и логарифмическая функции».
Одиннадцатый класс: «Тригонометрические и обратные тригонометрические функции» и «Тригонометрические и уравнения и неравенства», «Производная и ее геометрический смысл» и «Применение производной», «Первообразная и интеграл» и «Дифференциальные уравнения», «Системы уравнений и неравенств различных типов», «Уравнения и неравенства с двумя переменными», «Делимость чисел, целочисленные решения уравнений», а также «Комбинаторика» и «Элементы теории вероятностей».
4
Предисловие
Дополнительные 22-я и 23-я главы содержат задачи обобщающего характера (в частности, задачи с параметрами, текстовые задачи и др.) и будут полезны для подготовки к вступительным испытаниям в вузы, предъявляющие повышенные требования к математической подготовке абитуриентов. Непосредственно 23-я глава предназначена для подготовки к выпускной аттестации в виде ЕГЭ на этапе итогового повторения и содержит избранные задачи уровней В и С из вариантов прошлых лет.
Внутри каждой из гл. 1-21 тематика задач соответствует параграфам учебников, а задачи разбиваются на три уровня сложности. В учебниках и задачнике нет совпадающих задач. В каждой главе учебников для 10-го и 11-го классов представлено большое количество разобранных примеров, помогающих учащимся усвоить теоретический материал и познакомиться с различными методами решений и доказательств, а также задачи для самостоятельного решения. Авторы считают, что количество задач, содержащихся в учебниках для 10-го и 11-го классов, является вполне достаточным для изучения курса в рамках профильного образования по математике. Однако использование в процессе преподавания только учебников предполагает достаточно однородный уровень подготовки учащихся класса. Наличие задачника позволит учителю организовать индивидуальные и дифференцированные формы работы.
Несмотря на то, что данный задачник адресован учащимся классов с углубленным изучением математики, авторы считают, что его можно успешно использовать и в общеобразовательных школах и классах (в частности, задачи первого уровня сложности), а также для дифференцированной работы на уроках и занятиях кружков.
Авторы выражают благодарность Царьковой Галине Георгиевне, оказавшей большую помощь в подготовке рукописи.
Глава I
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
§1. ВЫСКАЗЫВАНИЯ И ОПЕРАЦИИ НАД НИМИ Первый уровень
1.1. Установить, являются ли истинными или ложными следующие высказывания:
1) А = {Число 54 делится на 2 или на 3};
2) В = {Число 54 делится на 2 и на з};
3) С = {Число 27 делится на 2 или на 3{;
4) D = {Число 27 делится на 2 и на з}.
1.2. Даны высказывания А и В. Определить, является истинным или ложным высказывание С={Д=>В}, если:
1) А = {5 > 3}, В = {6 >4};
2) А = {5<3}, В = {6 < 4};
3) А = {5<3}, В = {6 > 4};
4) А = {5>3{, В = {6 < 4}.
L3. С помощью таблицы истинности и диаграмм Эйлера—Венна доказать следующие свойства операций над высказываниями: 1) Д Л (В Л С) = (Д Л В) Л С;
2) Д У(ВУС) = (Д VB)vC;
3) А Л (В V С) = (Д Л В) V (Д Л С);
4) А V (В Л С) = (Д V В) Л (Д V С);
5) А V В = А Л В;
6) A f\B = AvB.
1.4. Выяснить смысл высказывания А, если:
1) А = {Число 377175 делится на 7 и на 3};
2) А = {Число 377175 делится на 7 или на 3};
3) Д = {Если 377175 делится на 49, то оно делится на 7}.
6
Глава I. Элементы математической логики
Второй уровень
1.5. Даны два высказывания:
А = {Число 2222 — 1 делится на 15},
В = {Число 2222 — 1 делится на 3}.
Является ли истинным высказывание С = {Д => В}?
1.6. Даны два высказывания:
А = {Число 24100 — 1 делится на 93},
В = {Число 24100 — 1 делится на 31}.
Является ли истинным высказывание С = {Д => В}?
1.7. Истинно ли высказывание Д = {Если число 19171941 делится на 19412, то оно делится на 1941}? Выяснить смысл высказывания А.
1.8. Истинно ли высказывание А = {Если 19211925 > 19251921, то 19211925 + 1 > 19251921 + 1}? Выяснить смысл высказывания Д.
1.9. С помощью таблицы истинности проверить, верны ли равенства:
1) {Д => (В V С)} = {(Д => В) V (Д => С)};
2) {(Д=>С)л(В^С)} = {(ДВ)^С}.
1.10. Построить отрицания и упростить полученные формулы:
1) АВ=> (Av (В^А)); 2) А => BV (В ~ A)V ВА.
1.11. На столе в приемной комиссии института перед абитуриентом стоят две коробки. В каждой их них лежит либо табличка «Принят», либо табличка «Не принят». На крышках коробок написано: «В обеих коробках лежит по табличке „Принят*1». Известно, что если в первой коробке находится табличка «Принят», то надпись на коробке истинна, если же там находится табличка «Не принят», то надпись на коробке ложна. Что касается второй коробки, то там все наоборот: если в ней находится табличка «Принят», то надпись на коробке ложна, если же там табличка «Не принят», то надпись на коробке истинна. Какие таблички находятся в коробках?
1.12. На столе в приемной комиссии института перед абитуриентом стоят две коробки. В каждой их них лежит либо табличка «Принят», либо табличка «Не принят». На крышке первой
§2. Неопределенные высказывания
7
коробки написано: «В этой коробке лежит табличка „Не принят14 или в другой коробке лежит табличка „Принят44», на крышке второй: «В другой коробке находится табличка „Принят44». Известно, что надписи либо одновременно истинны, либо одновременно ложны. Какие таблички находятся в коробках?
§2. НЕОПРЕДЕЛЕННЫЕ ВЫСКАЗЫВАНИЯ. ЗНАКИ ОБЩНОСТИ И СУЩЕСТВОВАНИЯ
Первый уровень
L13. Записать с помощью кванторов следующие высказывания и установить, истинны они или ложны:
1) если некоторое число делится на 6, то оно делится на 3;
2) существует число большее 10, и меньшее 9.
L14. Выяснить, истинны или ложны следующие высказывания:
1) \/х (х > 2 V х < 2);
2) Вх (х < 10 Ах > 9).
1.15. Построить отрицания следующих высказываний, выяснить истинны они или ложны:
1) \/х (х > 2 V х < 3); 2) 3% (х>10Ах<9).
Второй уровень
1.16. Пусть /(х) и g(x) — некоторые функции, заданные на множестве X С R,
А(х) = {|/(х)| > g(x)}, В(х) ее {/(%) > g(x)}, С(х) = {/(х) < g(x)} — неопределенные высказывания, заданные на множестве X. Доказать истинность высказывания
\/х е X (А(х) ~ {В{х) V С(х))).
1.17. Пусть f(%) и g(x) — некоторые функции, заданные на множестве X С R, А(х) = {\f(x)| g(x)}, В(х) = {f(x) g(x)}, С(х) = {f(x) — g(x)} — неопределенные высказывания, заданные на множестве X. Доказать истинность высказывания МхеХ (А(х)-(В(х)лС(х))).
8
Глава I. Элементы математической логики
1.18. Выяснить смысл приведенных высказываний и установить, истинны они или ложны:
1) Vx Зу (х + у = 3); 2) Зу \/х (х + у = 3);
3) Vx (х 1 => х2 х);
4) Va, b, с (Зх (ах2 + Ьх + с = 0) <=> b2 — 4ас 0);
5) Va, b, с (а 0 Л Зх (ах2 + Ьх + с = 0) <=> Ь2 - 4ас 0).
1.19. Выяснить смысл приведенных высказываний и установить, истинны они или ложны:
1) Зх,у (х + у = 3); 2) Vx, у (х + у = 3);
3) Vx, у (х < у ~ Зг (х < у < г));
4) Vx(x2 > 1 ~ (х > 1 V х > 0);
5) Va, b, с (Vx (ax2 + bx + с 0) ~ b2 - 4ас < 0).
1.20. Натуральное число п является составным тогда и только тогда, когда оно имеет делители, отличные от 1 и самого себя. Записать символически с помощью кванторов это определение
1.21. Записать с помощью кванторов неопределенное высказывание А(т, п), заданное на множестве натуральных чисел: А (т, п) = {Числа т и п не имеют общих делителей, отличных от 1}.
1.22. Натуральное число называется простым, если оно имеет ровно два различных делителя. Записать символически с помощью кванторов определение простого числа.
1.23. Записать символически с помощью кванторов высказывание, заданное на множестве целых чисел: А(г) = {Для всякого натурального числа b найдутся целые числа q и г такие, что 0 г < b и z = bq + г}.
§3. НЕКОТОРЫЕ ПРИЕМЫ ДОКАЗАТЕЛЬСТВА Первый уровень
1.24. Определить, верны ли следующие теоремы:
1) Т\ ={Для того чтобы произведение двух чисел было положительным, необходимо, чтобы оба числа были положительны};
§3. Некоторые приемы доказательства 9
2) ={Для того чтобы произведение двух чисел было положительным, достаточно, чтобы оба числа были положительны};
3) 7з ={Для того чтобы через две прямые в пространстве можно было провести плоскость, необходимо, чтобы прямые пересекались};
4) Т4 ={Для того чтобы через две прямые в пространстве можно было провести плоскость, достаточно, чтобы прямые пересекались};
5) 7g ={Для того чтобы через две прямые в пространстве можно было провести плоскость, необходимо, чтобы прямые пересекались или были параллельны}.
1.25. Сформулировать следующие теоремы в виде В необходимо для А и А достаточно для В:
Т[ = {Если треугольник равносторонний, то он равнобедренный}; Т% = {Если все углы треугольника равны между собой, то треугольник равносторонний}.
1.26. Сформулировать отрицание следующих теорем:
1) если некоторое число не делится на 7, то оно не делится на 21;
2) найдется квадрат, который не является параллелограммом.
Второй уровень
1.27. Сформулировать символически с помощью кванторов теорему: Если суммы противоположных внутренних углов четырехугольника равны между собой, то около него можно описать окружность. Сформулировать (не в символическом виде) для нее обратную, противоположную, противоположную обратной теоремы.
1.28. Сформулировать символически с помощью кванторов следующие теоремы, а также сформулировать для них не в символическом виде теоремы — обратную, противоположную, противоположную обратной, отрицание:
1) всякое простое число, не равное 2, нечетно;
2) если квадрат натурального числа, делится на некоторое простое число, то и само число делится на это простое число;
10
Глава I. Элементы математической логики
3) в параллелограмме диагонали делятся точкой пересечения пополам;
4) через две пересекающиеся прямые проходит плоскость и притом только одна.
§4. МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ Первый уровень
1.29. Доказать равенства:
п у 1 - п . V (Ь - 1U = ^п~ 1)/2(/г + 1)
/г+г 3
1.30. При всех натуральных значениях п доказать делимость:
1) (22п+1 + 1) 5 3; 2) (72п — 1) ! 48.
Второй уровень
1.31. Доказать равенства:
1)
у 1 __ п .
(4^-3)(4^+ 1) “ 4n + 1 ’
2) Е + l)(fe + 2) = п(,г + 1)(/г + 2)(” + 3); k=\ 4
D\ у _______fe2_____ _ n(jl + 1) .
1) • (26 + 1) 2(2/г+1)’
л \ у*______1 + 2___ _____ п(п -f- 5) .
f i(i + l)(i + 3)(i + 4) 8(п + 1)(л + 4) ’
(п \ 3 п п
=з-Е<5+Е?.
z=l / i=l i=l
1.32. Доказать равенства:
п
|) Е
fe-(fc + l)! _ (« + 2)!
2^ 2п
2) ^2 /г • /г! = (гг + 1)! — 1.
k=\
1.33. Доказать равенства:
1) П (1-
А=1 \
1
(6 + 1)2
п + 2 . 2/г + 2’
Ответы к главе I 11
1.34.
1 — 2п' значениях п доказать делимость:
2) (7 52“ + 12 • 6") 1 19;
(22""' + Зя + 4) 1 9.
1.35.
2) ft (1------—5 ) =
4=Д (24-I)2/
При всех натуральных
1)
3)
5)
6)
При всех натуральных значениях п доказать делимость:
1) (23" + 1) : 3n+1; 2) (пр — п) р, где р — простое число.
ОТВЕТЫ К ГЛАВЕ I
1.1. 1) Истинно; 2) истинно; 3) истинно; 4) ложно. 1.2. 1) Истинно; 2) истинно; 3) истинно; 4) ложно. 1.4. 1) А = {Число 377175 не делится на 7 или не делится на 3}; 2) А = {Число 377175 не делится на 7 и не делится на 3}; 3) А = {Число 377175 делится на 7 и не делится на 3}. 1.5. Да. 1.6. Да. 1.7. Истинно, А = {Число 19171941 делится на 19412 и не делится на 1941}. 1.8. Истинно, А = { 19211925 > 19251921 и 19211925 + 1 19251921 + 1}. 1.9. 1) Равенство верно; 2) равенство неверно. I.1O. 1) J; 2) L. 1.11. В первой коробке находится табличка «Не принят», во второй коробке — табличка «Принят». 1.12. В обеих коробках лежат таблички «Принят». 1.13. 1) Vx(x : 6 => х : 3) — истинно; 2) Зх(х > 10 А х < 9) — ложно. 1.14. 1) Ложно; 2) истинно. 1.15. 1) Зх(х 2 А х 3) — ложно; 2) Vx(x 10 V х 9) — истинно. 1.18. 1) Истинно; 2) ложно; 3) ложно; 4) ложно; 5) истинно. 1.19. 1) Истинно; 2) ложно; 3) истинно; 4) ложно; 5) ложно. Указание: при а = О, b = 0, с^О высказывание Vx(ах24-Ьх + с^О) — истинно, b2 — 4ас<0 — ложно. 1.20. VnGN(^(n) = {а — составное число} ~ (Вт G N3& € N((/n ^lAm^n)An = km))). 1.21. А(т,п) = {Va G N [(3b G N (m = ab)) A (3c G N (n = ac))] => (a = 1)}. 1.22. Зададим на множестве натуральных чисел неопределенное высказывание Д(х), означающее, что х g N — простое число: Р(х) — {3a G N Bb G N((x : а Ах : Ь) /\а^ b) A (Vc G N(x : c=>(c = aVc = b))))}. 1.23. A(z) = {Vb G N3<? G Z 3r G Z(0 r < b A z — bq + r)}. 1.24. 1) Неверно; 2) верно; 3) неверно; 4) верно; 5) верно. 1.25. 1) Т\ = {Для того чтобы треугольник был равносторонним, необходимо, чтобы он был равнобедренным} = {Для того чтобы треугольник был равнобедренным, достаточно, чтобы он был равносторонним}; 2) Тз = {Для того чтобы все углы треугольника были равны между собой, необходимо, чтобы треугольник был равносторонним} = {Для того, чтобы треугольник был равносторонним, достаточно, чтобы все его углы были равны между собой}. 1.26. 1) Каждое число не делится на 7 и делится 21. 2) Каждый квадрат является
параллелограммом. 1.27. Пусть М4 — множество четырехугольников,
12
Глава I. Элементы математической логики
m Е /И4; А(т) = {противоположные внутренние углы т равны между собой}, В(т) = {около т можно описать окружность}. Тогда теорему можно записать в виде: Ут {Д(/и) => В(т)}. Обратная теорема: если около четырехугольника можно описать окружность, то его противоположные внутренние углы равны между собой. Противоположная теорема: если противоположные внутренние углы четырехугольника не равны между собой, то около него нельзя описать окружность. Теорема, противоположная обратной: если около четырехугольника нельзя описать окружность, то его противоположные внутренние углы не равны между собой. 1.28. 1) Пусть Р— множество простых чисел, ^—множество нечетных чисел. Тогда теорему можно записать в виде: VxeN{xe/)Ax^2=>xeW|}. Обратная теорема: всякое нечетное число является простым и не равным 2. Противоположная — если число не является простым или равно 2, то оно четное. Противоположная обратной: всякое четное число либо не простое, либо равно 2. Отрицание: существует натуральное число, не являющееся простым или равным 2, являющееся четным. 2) Пусть Р— множество простых чисел. Тогда теорему можно записать в виде: VxeN УаЕР {х2 : a => х : а}. Обратная теорема: если натуральное число делится на некоторое простое число, то и его квадрат делится на это число. Противоположная: если квадрат натурального числа не делится на некоторое простое число, то и оно само не делится на это число. Противоположная обратной: если натуральное число не делится на некоторое простое число, то и его квадрат не делится на это число. Отрицание: найдется такое натуральное число, что его квадрат делится на некоторое простое число, а оно само — не делится. 3) Пусть /И4 — множество четырехугольников, Р — множество параллелограммов, Д(р), р ЕМ^, — неопределенное высказывание, заданное на множестве четырехугольников, Д(р) = {В четырехугольнике р диагонали делятся точкой пересечения пополам}. Тогда теорему можно записать в виде: Ур Е Мц{р Е Р => Д(р)}. Обратная теорема: если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм. Противоположная — если четырехугольник — не параллелограмм, то диагонали в нем не делятся точкой пересечения пополам. Противоположная обратной — если в четырехугольнике диагонали точкой пересечения не делятся пополам, то этот четырехугольник — не параллелограмм. Отрицание — найдется параллелограмм, у которого диагонали точкой пересечения не делятся пополам. 4) Пусть Р— множество плоскостей в пространстве, L — множество прямых, S(a, b) — неопределенное высказывание, заданное на множестве пар (а, Ь)у где а и Ь— прямые в пространстве, S(a, b) = {Прямые а и b пересекающиеся}. Тогда теорему можно записать в виде: Уа Е L УЬеВ {5(а,&) => (За Е Р(а с а/\Ь с а Л (V/3(a с/Злй С/3=> а = /3))))}. Обратная теорема: если через две прямые можно провести плоскость и притом только одну, то эти две прямые пересекаются. Противоположная: если две прямые не пересекаются, то через них нельзя провести плоскость, или можно, но не одну. Противоположная обратной: если через две прямые в пространстве нельзя провести плоскость или можно, но не одну, то прямые не пересекаются. Отрицание: найдутся две пересекающиеся прямые, через которые нельзя провести плоскость, или можно, но не одну.
Глава II
МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИ
§1. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Первый уровень
II.1. Выяснить, верны ли следующие утверждения:
1) 2 е {х |х3 - Ъ? - 4х + 3 = 0}; 2) 2е > 0};
3) 1 С {1,2,3}; 4) {1} С {1,2,3}.
IL2. Выписать все подмножества множества М:
1) М = 2) М = {а,Ь,с}.
II.3. Заданы множества А = [— 1; 5) и В = (—2; 3]. Найти множества Ди В, ДпВ, Д\В, В\Д.
II.4. Заданы множества А = (—сю; 2] и В = (—2;+сю). Найти множества Ди В, ДПВ, Д\В, В\А.
Второй уровень
II.5. Выяснить, верны ли следующие утверждения:
1) Зе {х|зпеН;х = 2) {0}с0;
3) 0€{0}; 4) {l,2,3}eZ;
5) {1,2,3} CZ; 6) {х |х2 - 5х + 6 < 0} С {х |х2 - 9 0}.
II.6. Изобразить с помощью диаграмм Эйлера—Венна множества Д, В, С, удовлетворяющие следующим условиям:
1) АсВ и ДсС; 2) ДсВ, ВсС и Д\В^0;
3) ДсВ, ВсС и С = ДПВ; 4) ДсВ, ВсС и ДпС = 0.
II.7. Функции /(х) и g’(x) определены на множестве R. Пусть А = {2; 5; 7} — множество решений уравнения /(х) = 0, В = {—2; —5; 2} — множество решений уравнения g(x) = 0. Найти множество С решений уравнения = 0.
II.8. Функции /(х) и g(x) определены на множестве R. Пусть А = {3; 9; 10} — множество решений уравнения /(х) = 0, В = {—2; 3; 10} — множество решений уравнения g(x) = 0. Найти множество С решений уравнения f(x)g(x) = 0.
14
Глава II. Множества и операции над ними
II.9. Пусть А — множество натуральных чисел, кратных 12, В — множество натуральных чисел, кратных 15. Что из себя представляет множество А П В?
II.1O. Пусть А — множество натуральных чисел, кратных 21, В — множество натуральных чисел, кратных 28. Что из себя представляет множество ДпВ?
11.11. Пусть R— множество всех ромбов, Р— множество всех прямоугольников. Что из себя представляет множество ЯПР?
11.12. Пусть А — множество четырехугольников, которые имеют хотя бы пару параллельных сторон, В — множество параллелограммов. Выяснить, что из себя представляет множество А \В.
11.13. Пусть А — множество равнобедренных треугольников, В — множество треугольников, у которых хотя бы один из углов равен Выяснить, что из себя представляет множество АпВ.
11.14. Пусть А — множество простых чисел, В — множество составных чисел Выяснить, что из себя представляет множество A U В.
11.15. Доказать следующие равенства с помощью диаграмм Эйлера—Венна, таблиц истинности и преобразований множеств:
1) А\(А\В) = А И В; 2) А П (Д UB) = A U (Д П В)
3) Д\Вп(ДиВ)=Д; 4) (Д\С)\(В\С)сД\В.
11.16. Найти количество трехзначных чисел:
1) кратных по крайней мере одному из чисел 3 или 4;
2) кратных 4, но не кратных 3.
11.17. Найти количество трехзначных чисел:
1) кратных 4 или 6;
2) кратных 4, но не кратных 6;
3) кратных 6, но не кратных 4;
4) кратных 4 или 6, но не кратных 9.
§2. Целые, рациональные и иррациональные числа 15
§2. ЦЕЛЫЕ, РАЦИОНАЛЬНЫЕ И ИРРАЦИОНАЛЬНЫЕ ЧИСЛА
Первый уровень
II.18. Представить периодическую десятичную дробь в виде обыкновенной дроби:
1) 1,2(7); 2) 2,13(8); 3) 1,3(48); 4) 0,(09).
11.19. Представить рациональное число в виде периодической десятичной дроби:
1) 211 2) — 3) — • 4) 117-
, 180’ 72’ 44’ ' 7 '
27. 29. 133. П
^13’ 14’ 65’ 120’
11.20. Вычислить значение выражения, ответ представить в виде периодической десятичной дроби:
1) 1,0(16) : 11,1(7); 2) 0,6(461538) • 1,0(6).
II.21. Доказать, что число является иррациональным:
1) х/З; 2) х/7; 3) х/5; 4) х/10; 5) </б; 6) У2.
11.22. Сравнить числа:
1) a = v^5 и b = х/З; 2) а = — у/4 и Ь = — х/3;
3) а = 2х/б - 1 и Ь = 4; 4) а = 4х/2 + 3 и b = 5х/3;
5) а = 6х/2-5 и b = 2\/3; 6) а = х/7 и 6 = 4х/2-3.
II.23. Записать выражение без знака модуля:
1) 1 - |1 - х/2|; 2) |х/5 - х/3- 1 ;
3) |х/3 4-х/2 - 4| — |—4|; 4) |х/5 - х/2 — 1 + |1 - У2|.
11.24. Записать выражение без знака модуля:
1) |1 - 2х|; 2) |х2 - 4|; 3) 4 + Зх - х21;
4) |х| • |2 — х|; 5) |х-1| + |6 + 2х|; 6) 1 + 2х| - |4х - 2|
II.25. Записать числа без использования символов целой и дробной частей:
1) 3], {3}, [-5], {-5}, [3,9], {3,9}, [-5,2], {-5,2}, [-0,4], {-0,4};
16
Глава II. Множества и операции над ними
П.26. Записать числа без использования символов целой и дробной частей:
1) [72], {72}, [77], {77}, [-72]. {-72}, [-75],
1-4]' {-4}'
2) [1 + 75], {1 + 72}, [-1-75], {-1-72}. [1-72], {1-75}, [4-715], {4-715}.
П.27. Решить уравнение:
1) [4х] = 3; 2) [5х] = —2;
3) [5х + 1] = 6; 4) [х + 1] + [% + 2] = 7;
5) [2х + 3] + [2х-2] + [2х + 4] = 17; 6) 3 [Зх] - [Зх- 3] = 11.
П.28. Решить уравнение:
1) {% + 1} = 0,2; 2) {х +0,5} = 0,8;
3) {2х} = 0,4; 4) {х + 1} + {х - 2} + {х + 3} = 2;
5) {Зх + 7} = 0,5; 6) 3 {5х + 1} + {5х - 4} = 1.
Второй уровень
П.29. Представить периодическую десятичную дробь в виде обыкновенной дроби:
1) 1,(153846); 2) 2,2(285714);
3) 2,0(923076); 4) 1,9(076923).
П.30. Не выполняя деления, выяснить, в виде какой десятичной дроби представимо данное рациональное число: конечной или периодической. Если в виде конечной десятичной дроби, то сколько знаков после запятой она имеет; если в виде периодической, то сколько знаков после запятой не входят в период?
n 57 • О'! 343- §943. 4ч 2831. 291 . 133
' 800’ ’ 320’ ’ 1250’ ’ 1500’ ’ 550’ ' 144'
II.31. Доказать, что число является иррациональным:
1) х/3 + УП; 2) \/5 + а/7.
II.32. Доказать, что число является иррациональным;
1) ^5 + ^3; 2) </б-2>УЗ.
§3. Степени и корни 17
11.33. Доказать, что число является иррациональным:
1) ^5 + \/2; 2)
3) Зх/2 + 2х/3-а/6; 4) х/2+х/3 + \/5.
11.34. Выяснить, является ли рациональным число:
1) 2\/3 + 2х/5 — д/9 4- 4х/5; 2) \/14 4-6\/5 — х/29 — 12\/5;
3) л/4-Ь \/7-Ь л/8 — Зл/7; 4) \/14 + 5\/3 +\/б-ЗУЗ.
11.35. Сравнить числа:
1) а = у/2 — и /?=\/3 —2;
2) <т = \/б —2 и Ь = \П— у/5;
3) а = л/7-4л/5 и Ь = х/З —8;
4) £z = x/TT —2х/3 и b = \/6-V7.
11.36. Выяснить, при каком натуральном п выполняется неравенство:
1) 5n<ll<5 + 5n; 2) -n<30<j + 5n;
3) 2«<52<2 + 2n; 4) -2 + 2n<26<2”-
11.37. Упростить выражение:
1) Ц47Г2 - 41| + 7С2 - 12|; 2) 1|78 - 8тс2| + бти2 - 61|.
11.38. Решить уравнение:
D 2)
3) И = ^; 4)
4х- 281 _ _ 2х + 13 17 J 7 ’
11.39. Решить уравнение:
1) {Зх} = х - 0,5; 2) {4х — 1} = 2х + 0,3;
□ к Г х — 21 _ 7x4-6 /2х — 31 .5x4-17 _ Л
' l^7j+—56
§3. СТЕПЕНИ И КОРНИ
Первый уровень
11.40. Найти числовое значение выражения:
3) </(—2)8 (—2)12; 4) ^3242-^Г27.
18
Глава II. Множества и операции над ними
11.41. Найти числовое значение выражения:
1) х/Ж’.УТЖ 2) (л/З2-^2)6;^2.
11.42. Избавиться от иррациональности в знаменателе:
11.43. Упростить выражение при заданных значениях х:
1) \/(х — I)12 при х > 1,5; 2) у/(Зх - I)6 при х<|.
11.44. Внести множитель под знак корня:
1) х^/х; 2) Хд/—3) х3 • tyx;
4) (х-2)</2^х; 5) Ху/у; 6) (х-1)^.
11.45. Упростить выражение:
О 2) у* у/у^\ 3) (</16х~12)3; 4) Ух4\/?.
11.46. Сократить дробь:
п а + 2х/а + 1. y/a + Vb . о\ y/a-y/b. дч by/b-a?
' а-1 ’ } ay/E + bVb' ' fa+Vb’ ’ Vb-a
П.47. Упростить выражение:
11.48. Упростить выражение:
11.49. Вычислить:
1) 8Й-ЗУЗ-35; 2) (2-52)2-^Т25;
3) 325 - (4v^)2; 4) Зх/2 • 20’5 — </16.
II.5O. Вычислить:
1) (16-°>25 - (2х/2) 3(16"°’25 + (2\/2) *
2) (з"1’5-(ЛvY f3-i’5 + f—
\ КУЗ/ J \ \л/3/ )
§3. Степени и корни 19
11.51.
11.52.
11.53.
11.54.
Найти 11.55.
11.56.
11.57.
11.58.
Упростить и вычислить при указанном значении х:
30 24
/ 2 1 \ 29 / 2 \ 17
1) I -—I при % = 64; 2) I % *3 I при х = д/3
\ X? / \ х< /
Упростить выражение:
Вычислить: п 4а2,5 -25а3’5 5
' 2 + 5а°’5 а"3’
п. 121а2’5-4а1’5 П
J На0-5-2 а-2’
если а - 9;
если £2 = 36.
Найти числовое значение выражения:
1\-1 v-i 1
1) \ —т) , если --;——г=6
' \x-lJ 2х~1+у~1
/ _i\ -1 _1 _1
о\ I х 1 \ 4х 1 + у 1 Q-1
2) , если ——j—тгг = 3 .
\У J х -у
Второй уровень
числовое значение выражения (И.55-11.58).
1) У4 - У37 • У16 + 4У37 + У372;
2) УЗ + У37-У9-ЗУ37 + У372.
(5ч/3 + \/50) (5-V24) .
^/75-5^2
2' /Зч/3-2У2 _ 1 \ ч/2 . 4
' \ 5 + \/б УЗ-У2/ у/З + ч/2 \/3 + \/2’
1) У11-4\/7 + х/23-8х/7;
2) (У123-55\/5-2,5У10) • \/2;
3) У5-2х/б: ((УЗ + У2)-(УЗ-У2));
4) л/11 -6х/2: ((УЗ + У2)-(УЗ-У2)).
1) У9 + 4У5-\/9-4х/5;
2) У15-4У14-\/15 + 4У14.
20 Глава II. Множества и операции над ними
Упростить
11.59. 1)
11.60. 1)
3)
11.61. 1)
2)
3)
4)
11.62. 1)
2)
3)
4)
выражение (II.59-11.62).
fyab — \Ab . fyab tyR-fyb ‘ fa’
: (\/2а + л/3^);
(д/а2/? - Vх 16а/?2 + л/Ч/?3) : (\/а - ^2/?);
(bx/$b — a^/a): (2b + V2ab + a).
ay/a by/b . \/a — b _|_ Д3 — 63 .
^(a^-abf-x^2 ' ay/E-bVb b — a ’ (у/a- y/b)3 + by/b + 2a2 : у/a 3\/д6- 36.
a.y/a + by/b a — b
11.63. Доказать тождество:
o\ /7 /Г a + V a2 — b a — x/a2 — b n n
2) v a — \/b = у ——-----------у------—— при a > 0, b > 0,
a2 -b>0.
11.64. Сравнить числа А и В, если:
1) Д = х/7-2х/10 и В = \/3- 2;
2) А = \/98-40Уб и В = 5УЗ-3\/2-4.
11.65. Избавиться от иррациональности в знаменателе:
1) Зл/3 2) 14л/5
' V2 + V3 + V5' V2 + V5-V7'
§4. Логарифмы 21
11.66. Решить уравнение:
1) у/к2 • — у/ Ху/х — 56;
2) />=240'
Упростить выражение (II.67-11.69).
11.67. 1) а6 - у/а12-4^4 + 4а-12^8;
2) \/4с16 - 4б/6 + c~16d12 - 2с8.
11.68. 1)
2)
х-25х~‘ _ 2х + 7 + 5х 1 . X0,5 — 5х-0,5 х0,5+х~0’5
(\ 2
4х-9х-1 , х-4 + Зх-1 |
1 _ 1 "I I _ 1 I
2х 2 — Зх 2 х2 — х 2 /
тт еп 1\ „2 a —a 2 . 1 —а 2 . 2 .
11.69. 1) а-у-—г + —-----—+ Т»
а'2 —а 5 а2 +а 5 а2
iiii 11
J-2 .u1 -I- Y1 -LT2 Л
q\ х — у * х У 'х У х -у
3 1 1 11 '1 111
х5 — х2-у? х2+У2 х2+2х^у^+у2
х(х2 —а2) 2 + 1 . а2(х + а)2 1
'J/ _ 1 1 • | “г 2
а(х — а) 2+(х —а)2 х—(х2 —а2)2 х ах
1
2У12+ ^32z'
§4. ЛОГАРИФМЫ Первый уровень
Вычислить (II.70-11.72).
11.70.1)108^27; 2) log 8; 3) log2^ 1;
4) 10g3V5jL; 5) log^ А; 6) 10g^21
11.71. 1) log^2 (logI I); 2) log9 (log4 \/4).
22 Глава II. Множества и операции над ними
11.72. 1) log9 3 - 3 • logyg 0,2; 2) log25 0,2 +0,5 • log^ 6;
3) log^ 8 — 2 log| 9; 4) 2 log^ 27 - 41g д/П).
11.73. Решить уравнение:
1) log. (2% + 1) = — 3; 2) log2 (x2 — 3x — 6) = 2;
3) 10gXjL=4; 4) 10g,l = -3; 5) log,.) 625 = 4;
6) 2х-3 = 7; 7) 82*-1 =5; 8) 5x+1 = 1 - V2;
9) 91"x = 4.
11.74. Зная, что log3a = 2, log3b = 6, найти:
0 i°g3 (Л); 2) log3-^-.
9 vo
Найти числовое значение выражения (II.75-11.82).
11.75. 1)
2)
3)
4)
11.76. 1)
3)
11.77. 1)
3)
11.78. 1)
11.79. 1)
2)
II.8O. 1)
2)
11.81. 1)
log3 3,6 — log3 1,4 + log3 1|;
log20,8 —log2 1| + log2 22,5;
2 log i 0,4 — logi 28 + ^ log i \/49; 5 5^5
| log ^-31og2 3+| 10g2 36.
<5 § 3-^3
2)^(4^);
log Д Ж; 4) log ,
V 3 > ut
log25 64 + logs 2) 3 log27 8 — | log9 64 — log3 18;
8-2 log i 9; 4) log25 0,2 + 0,5 • log^ 6.
log3 9</5 - log9 27\/5; 2) log8 64>/3 - log2 2^3.
(3 logl Упб - logl : log^ \ 2 ’ IZo 4 OZ/ V
log9 Уз^зТз- log9
(2 log5 3 - log5 36): (log5 4 + log5 8); (log3 200 - 3 log3 2): (log3 5 + log3 125). logo,75 logi25 6 25 ; 2) log125 log243 81.
11.82. 1) log1)227:loglj29; 2) log310-lg27.
11.83. Зная, что log2 = 9, log2n = 2, найти:
1) logn(mn3); 2) logm гг
Вычислить (II.84-11.87).
П.84. 1) log, 12-^;
3) 1о^У15 3 - |Og3 225
П.85. 1) !°^-log23;
7 log634 52
2) log749 + log214-^;
4) l°g18 3 + j + lo^ 9.
2\ lpg5 10-Hog2 10
log5 10-log2 10 '
11.86. 1) (4loSi 2) 3|0^4; 3) 27I(,S32;
4) 4~ log25; 5) 49l-l°g72 —5~ l()g54;
6) 0,8-(l + 9loS38)lo&655.
I 4 Igl2 —Ig3
11.87. 1) 3‘°kii3; 2) 10,OKi3100; 3) 6 ;
1+ig 6
4) 7lg28-lg4
11.88. Показать, что при всех допустимых значениях а справед-
ливо равенство:
!) log3x/3^a-logo27=|; 2) log 2\/24og8 а = 4.
11.89. 1) Чему равен log9 8, если log2 3 = а?
2) Чему равен log8 0,04, если log52 = b?
II.9O . Выяснить, при каких значениях х имеет смысл выражение:
1) log7 (х2 —8x4-7); 2) logi (8х — х2 —15);
3) log9 (2х —х2 -1); 4) logi (х2-4x4-4).
11.91 . Записать выражение в виде суммы или разности логариф-
1) ”og2((-7)-(-5)); 2) log, ((-2)3 (-7));
3) log,-=8.; 4) lg<-3>2'<-6).
b (-3)5 (-7)
Второй уровень
11.92 . Выяснить, при каких значениях х имеет смысл выражение:
1) Зх); 2) logx(7-4x);
3) 1о£х-з(5-*)2; 4) 1о£|х-2| (*-*)•
24 Глава II. Множества и операции над ними
11.93 . Выяснить, при каких значениях а и b справедливо равенство:
О l°ga(^—1)2~2-loga(l —6); 2) log2-a610 = 2-log2_a (-65);
3) loga2 6=0,51og_a 6; 4) loga6(6+2)=0,5-loga3(6+2).
11.94. Записать выражение в виде суммы или разности логарифмов:
1) log2 (ху), если х<0, у<(У,
2) (—*2*/), если *>0, г/< 0;
3) logs %2Z/3)> если х<0, г/<0; ..2
4) 1g если %<0, г/<0.
Вычислить (И.95-11.98).
11.95. 1) 1^2.19—4log 1 5; 2) log^O-1^^;
log187 ё2 ё2 log52
3) j2S3_l|-iOg 2-log3 162; 4) log5 4-log5 100— log5 2^;
log,83 £3 S3 - / K5 £5 iog20 5’
5) 31og336-6) l£giJ8_ log2_9
53 log72 5 I°g36 2 log722
11.96. 1) 7^2-2^7; 2) 21^6-6^2-1S6.
11.97. 1) log3ll logn 19-log1927; 2) log2 3-log3 4-log4 5-...-log15 16.
11.98. 1) 26 log2V2 (5~+8 * loSo,25('/S-У2) .
2) 6lo^3 + log/3-7Л^ + 1о&1 — &V3 Уб + ч/2 з 7 + 2У10
11.99. Сравнить:
1) log0 3 5 и log0,2 5; 2) log8 5 и log6 5.
II.100. Выразить через заданные величины а и b следующие логарифмы:
1) log15 49, если a = log7 9, 6 = log745;
2) lg 15, если a = lg2, 6 = lg3;
3) logi2 90, если a = log24 3, 6 = log24 5;
4) log350 140, если a = log52, 6 = log75.
II.101. 1) Чему равен logy г/, если logxy (x2i/) = a?
2) Чему равен log^^y^), если logxy2x = a?
§5. Суммирование 25
11.102. Найти:
1) loga b, если log^ (W)=4;
2) logfea, если log^ (a3b&) = 9;
3) loga&2(ab), если logafe (ab3) = 5;
4) [°Sab^ab)’ если 1о£а&-1о£/>а = 1,5.
§5. СУММИРОВАНИЕ
Первый уровень
II.103. Сумма трех чисел, являющихся последовательными членами арифметической прогрессии, равна 2, а сумма их 14 тт ~ квадратов равна —. Наити эти числа.
11.104. Третий член возрастающей арифметической прогрессии равен 4, а произведение второго и шестого членов на 5 больше произведения первого и седьмого членов. Найти седьмой член прогрессии.
3 7
11.105. В арифметической прогрессии а§ = и = Найти сумму первых шести членов прогрессии.
11.106. Сумма третьего и шестого членов арифметической прогрессии равна 5, а их произведение равно 6. Найти сумму первых десяти членов этой прогрессии.
II.107. Произведение третьего и девятого членов геометрической прогрессии равно 16. Найти шестой член прогрессии.
11.108. Найти знаменатель геометрической прогрессии с положительными членами, если разность третьего и второго членов прогрессии составляет 231% от ее первого члена.
II.109. Сумма двух первых членов геометрической прогрессии равна (—1), а сумма следующих двух членов равна (—4). Найти сумму первых шести членов этой прогрессии.
11.110. Разность четвертого и первого членов возрастающей
26 геометрической прогрессии равна -у, а разность третьего
и первого членов равна -. Наити сумму первых пяти членов этой прогрессии.
26 Глава II. Множества и операции над ними
Второй уровень
11.111. 1) Первый член арифметической прогрессии равен 111, а разность прогрессии равна (—6). Какое наименьшее число последовательных членов этой прогрессии, начиная с первого, надо взять, чтобы их сумма была отрицательной?
2) Первый член арифметической прогрессии равен (—100), а разность прогрессии равна 8. Какое наименьшее число последовательных членов этой прогрессии, начиная с первого, надо взять, чтобы их сумма была положительной?
11.112. Сумма первых п членов некоторой последовательности
11^_5^2
{an}, neN, при любом п выражается формулой Sn = —-—. Найти сумму первых пятидесяти четных членов этой последовательности.
11.113. Арифметическая прогрессия состоит из 105 членов. Сумма членов с нечетными номерами на 1 больше суммы остальных членов. Найти 53-й член прогрессии.
11.114.
II.115.
11.116.
Чему равно п, если имеет место равенство 1+7 + 13 + ... + (6я + 1) = 280?
Решить уравнение 52-54-56•...-52x = 0,04 -28.
1) При каких значениях х числа |, х +3 и являются последовательными членами арифметической
прогрессии?
о । о
2) При каких значениях х числа ;--- и -—
х х(1— х) 1— х
являются последовательными членами арифметической
прогрессии?
11.117. Найти число членов геометрической прогрессии {6П}, если <7=|> 64=^, а сумма членов прогрессии равна
11.118. Найти число членов возрастающей геометрической прогрессии {bn}, начиная с первого, если известно, что Ь\ = 5, 65 = 405, а сумма членов прогрессии равна 1820.
11.119. Найти сумму шести чисел, расположенных между и 4,5, из которых вместе с числами и 4,5 можно составить геометрическую прогрессию.
§5. Суммирование 27
11.120. Сумма первых четырех членов геометрической прогрессии равна 3, а сумма членов с пятого по восьмой равна 12. Вычислить сумму членов с девятого по двенадцатый.
11.121. Геометрическая прогрессия состоит из 2003 членов. Произведение членов с нечетными номерами в 3 раза больше произведения членов с четными номерами. Найти 1002-й член прогрессии.
11.122. Арифметическая прогрессия состоит из четырех различных чисел. Известно, что если заменить в ней третье число на единицу, то получится геометрическая прогрессия. Найти исходную прогрессию.
11.123. Три числа являются последовательными членами возрастающей геометрической прогрессии. Если первый член прогрессии умножить на (—3), то новые числа в том же порядке составят арифметическую прогрессию. Найти знаменатель геометрической прогрессии.
II.124. Найти первый член и знаменатель бесконечно убывающей геометрической прогрессии, если ее сумма равна 4, а сумма кубов ее членов равна 192.
11.125. Первый член бесконечно убывающей геометрической прогрессии равен 3, а сумма всех членов равна 10. Найти сумму квадратов членов этой прогрессии.
11.126. Сумма бесконечно убывающей геометрической прогрессии равна S. После того, как из этой прогрессии вычеркнули каждый пятый член, начиная с третьего (3-й, 8-й, 13-й, . . . ), сумма стала равна ^S. Найти первый член и знаменатель прогрессии.
11.127. Найти сумму членов бесконечно убывающей геометрической прогрессии, если сумма всех ее членов, стоящих на четных местах, в три раза меньше суммы всех ее членов, стоящих на нечетных местах, и сумма первых пяти членов этой прогрессии равна 484.
11.128. Доказать, что если Sn обозначает сумму первых п членов арифметической прогрессии {ап}, то — 35п_|_2 Н- 35п_|_ 1 — Sn = 0.
11.129. Доказать, что если при некотором значении п для сумм первых п и 2п членов арифметической прогрессии
28 Глава II. Множества и операции над ними
{ап},пбМ, выполняется условие S2n = 4-Sn, то при любых i am 2m— 1
m и k справедливо равенство ~ = —i’-
ll.130. Доказать, что если при некотором значении п для сумм первых п и 2« членов арифметической прогрессии {ап},пбМ, выполняется условие 3Sn = > то при любом
п справедливо равенство a^n_\ — ?>-an.
11.131. Сократить дробь:
х1 —128 х5 —1 32х5 + 1 х14 + 2х7 + 1
' } j ~2l+r; ' (х+1)2
11.132. Избавиться от иррациональности в знаменателе дроби:
1) -Д-; 2) .
<УЗ-1 </2 + 1
11.133.
Найти пятый член разложения
если отношение
коэффициента 3-го члена к коэффициенту 2-го равно 5,5.
11.134. В разложении бинома —>/1 — а)” коэффициент
третьего члена разложения равен 28. Найти средний член
разложения.
11.135. Найти сумму коэффициентов разложения (a-\-b)n, если известно, что наибольший коэффициент имеют пятый
и шестой члены разложения.
/ 1 \ 12
В разложении бинома щий х.
11.136.
11.137.
найти член, не содержа-
/ 3/_ \ п
В разложении бинома | Д—+ -Д— | найти член, не \ Ь 15/^28 /
содержащий а, если сумма биномиальных коэффициентов
трех первых членов разложения равна 79.
11.138. Найти члены разложения (х/З + ^УЗ) , не содержащие иррациональностей.
11.139. Найти член разложения ('УЗ+-х/2) , не содержащий иррациональностей.
11.140. Сколько рациональных членов содержится в разложении (^3 + \/2)10°?
11.141. При каком значении п коэффициенты 2-го, 3-го и 4-го членов разложения бинома (а + Ь}п составляют арифмети-
ческую прогрессию?
§6. Числовые неравенства 29
§6. ЧИСЛОВЫЕ НЕРАВЕНСТВА Первый уровень
11.142. Доказать, что для любых действительных чисел а и b верно неравенство:
1) а2— 8а+ 62— 26 4-20 >0; 2) а2 +4622а-1.
11.143. 1) Доказать, что для любых действительных положительных чисел а выполняется неравенство а+|^2, причем равенство имеет место тогда и только тогда, когда а — 1.
2) Доказать, что для любых действительных отрицательных чисел а выполняется неравенство а+^^—2, причем равенство имеет место тогда и только тогда, когда а = — 1.
II.144. Доказать, что для любых действительных чисел а и b выполняется неравенство:
1) a24-ab + b2 >0; 2) а2-аЬЧ-Ь2>®.
11.145. Доказать, что для любых действительных чисел а и b выполняется неравенство:
1) а2+962-4а6^0; 2) а2-За6+З62 +1 >0;
3) a2—2а6+62+4(а-6+1)^О; 4) a24-b2+2ab—2a-2b-\-2>Q.
Доказать (II.146-11.149),
11.146. а3 + 27За2 + 9а, если а>0.
П.147. 4 + ?^ + -, если а>0.
а2 4 2 а
11.148. если а>0, Ь>0.
11.149. 4 + -4>- + L если а + 6>0, а=£Ь, а^О.
Ь2 а2 а ь
11.150. Пусть где 6>0, d>0. Доказать, что < < J-
11.151. Сумма квадратов положительных чисел а и b равна единице. Доказать, что а10 + 610<1.
30 Глава II. Множества и операции над ними
Второй уровень
11.152. Доказать, что для любых действительных чисел а и b выполняется неравенство:
1) я2 —2я6 + 262 + 2я+3>0;
2) а2 + 562 + 4а6-2а-66 + 3>0.
Доказать (II.153-IL156).
П.153. (1 — я)(1 — 6)(1 — с) >8abc, где a + b + c=l, a>0, b>0, с>0.
11.154. a + b+c>y/^+x/bc+>/ac, где a^O, b^O, c^O.
11.155. где я>0, x>0.
11.156. где я>0, 6>0, nGN.
Доказать (II.157-11.164)
11.157. 2n>n2 при всех wgN, «^5.
11.158. 2">п3 при всех пбН, п^Ю.
П.159. 1+> + 1 4-...+ при всех neN.
11.160. JL- + -L- + -L-... + -L>g при всех neN, n^2. «+1 n+2 n+3 2n 48 r
11.161. l + x + l+- • • + -->-^T при всех neN, n^2. 2 3 n n +1
n.162. !• !•!•...J—при всех neN.
2 4 6 2n У3й+Т H
11.163. ^<14-' 4-1+... + -1 =£„ при всех леН. 2 23 2—1
П.164. 1+ ' + >+...+ >>-^т при всех пбН, п^2.
22 З2 п2 2«+1
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ II
II.165. Найти количество трехзначных чисел, кратных
1) 21, 77 и 33; 2) 8, 12 и 18.
П.166. На выпускных экзаменах по алгебре, геометрии и физике каждый выпускник получил оценку «5» или «4», причем оценку «4» каждый получил не более одного раза. Оценку «5» по алгебре и геометрии получили 55% выпускников, по геометрии и физике — 30%, по физике и алгебре — 45%. Сколько процентов выпускников получили оценку «5» по всем предметам?
Задачи повышенной сложности к главе II 31
11.167. Решить уравнение:
d М=М; 2) [^]=М-
11.168. Решить уравнение:
1) {Зх —0,7} = 5 {х} + 0,3; 2) {5х + 0,6} = 2 {х}-0,4;
3) {5х + 0,3} = 9 {х} - 3,2; 4) {9х+0,9} = 3 {х}-Ц.
11.169. Доказать равенство [\/И] =
11.170. Упростить выражение:
I) /х2+2х+1 — /х2 — 2х +1. 2) - 2/а — 1 + \/a+2\/a — 1
/х2 + 2х+1 + /х2—2х + 1 а2 - 4а + 4
11.171. Сократить дробь
11.172. Найти значение выражения:
। \ 2 + /3 । 2 — /3 . Q \ ___\/2 -4~ /3 + /4
/2 + /2 + /3 /2-/2-/з’ /2 + /3 + /б+/8 + /1б‘
11.173. Освободиться от иррациональности в знаменателе:
11.174. Доказать, что является иррациональным число: 1) ^3 + ^9; 2) л/2 + ^4.
11.175. Доказать, что является рациональным число:
11.176. Найти значение выражения:
/5-2/б-(5 + 2/б)-(49-20/б) ' ^7-3/18 + 3/12-/8
11.177. Упростить выражение:
32
Глава II. Множества и операции над ними
11.178. Вычислить:
П finer Q\2 i 1о^6 324 . log224 log2 192
11.179. Сравнить числа:
1) log34 и log5 6; 2) log135675 и log45 75.
11.180. Сравнить числа log9 32 + log4 27 и 4.
11.181.
11.182.
11.183.
Доказать, что lg = Oga + lg^)> если a2 -\-b2 = 7ab.
(\ 2 / \2 / \2
х+-) +(^2 + Л) +...+ (х8 + -4 ) , где
X/ \ X2 / \ X8/
1) Шестой член и разность арифметической прогрессии удовлетворяют неравенствам 1<Яб<3, l<t/<4. Найти
все возможные значения, которые может принимать сумма первых восьми членов прогрессии.
2) Первый и пятый члены арифметической прогрессии удовлетворяют неравенствам 0<aj<2, 3<а$<4. Найти все возможные значения, которые может принимать сумма первых семи членов прогрессии.
11.184. Второй и четырнадцатый члены арифметической прогрессии — целые положительные числа. Вычислить сумму
первых девяти членов прогрессии, если известно, что она удовлетворяет неравенству 12,5 <S9< 14.
11.185. 1) Последовательность {Ьп} такова, что разности соседних членов bn+\—bn образуют арифметическую прогрессию. Найти £>201’ если &i = 2, £>2 = 5, &з = 10.
2) Последовательность {Ьп} такова, что разности соседних членов bn+[ — bn образуют арифметическую прогрессию. Найти &204» если £>i = 86, b2 = 88, Ь3 = 93.
11.186. Из пункта А в пункт В с интервалом в 4 минуты вышли 22 спортсмена, каждый из которых затратил на весь путь 1,5 часа. Одновременно с ними из пункта В в пункт А выезжали велосипедисты, каждый из которых затратил на весь путь одинаковое время. В пути произошло 439 встреч (без учета встреч в пунктах А и В). Какие значения может принимать время нахождения в пути каждого велосипедиста?
11.187. Найти первый член целочисленной арифметической прогрессии, у которой сумма первых шести членов отличается
Ответы к главе II 33
от суммы следующих шести членов менее, чем на 450, а сумма первых пяти членов превышает более, чем на пять, сумму любого другого набора различных членов этой прогрессии.
п
11.188. Вычислить сумму S=52&3-
Л=1
11.189. Пусть а^0,6^0,с^0. Доказать неравенство
3 (а3 + 63 + с3) (а + 6 + с) (a2 + b2 + c2^ .
II.19O. Пусть а>0,6>0,с>0. Показать, что при любом neN выполняется неравенство
/ a. + b \ । / о + с \ _|_ / & + с \ > 3 • 2”
\с/ \ b / \ a )
11.191. Доказать неравенство
(х2 + х + 2^ (х2 + х + 1) > (з - х2^ (х2 + х + 1) - 1.
11.192. Доказать неравенство (2х2 + 5х — 2) (х2 + х + 2) + 16 0.
11.193. Применяя неравенство Коши—Буняковского, доказать, что при a G [1; 7,5] выполняется неравенство
Va- 1 + 2V3a - 1 + ЗУЗО - 4а < 14л/2.
При каких значениях а достигается равенство?
11.194. Найти наибольшее значение выражения a — 3b — 2с, если 5a2 + b2 + 2с2 = 70. При каких значениях a, b и с оно достигается?
11.195. Найти наименьшее значение выражения А — 2а2 + 6b2 — Aab + Зс2 — 6с,
если 4а — 26 + Зс = 43. При каких значениях а, b и с оно достигается?
11.196. Доказать неравенство (1 + 2а2 + 2а)3 24а2 + 24а — 4. При каких значениях а выполняется равенство?
ОТВЕТЫ К ГЛАВЕ II
II.1. 1) Неверно; 2) верно; 3) неверно; 4) верно. II.2. 1) 0, {1}, {а}, {1,а}; 2) 0, {а}, {Ь}, {с}, {а,Ь}, {а,с}- {6,с}, {a,b,c}. И.З. ДиВ = (-2;5), Д ПВ= [—1;3], Д\В= (3;5), В\Д = (—2;—1). II.4. 1) A UB = R, А ПВ = (2;2], А \ В = (-оо; —2], В \ А = (2;+ос)- П-5. 1) Неверно; 2) неверно;
3) верно; 4) неверно; 5) верно; 6) верно. II.7. С = Д\В = {5;7}.
2—5682
34 Глава II. Множества и операции над ними
И.8. С = А UB = {— 2,3,9.10}. И.9. А Г)В — множество натуральных чисел, кратных 60. 11.10. А П В — множество натуральных чисел, кратных
84. 11.11. В П В—множество квадратов. 11.12. А \ В —множество
трапеций. 11.13. А П В —множество равносторонних треугольников. 11.14. ДиВ = М\{1}. 11.16. 1) 450; 2) 150. 11.17. 1) 300; 2) 150; 3) 75; 4) 475. 11.18. 1) 2) g; 3) ||; 4) 1. 11.19. 1) 1,17(2); 2) 1,069(4);
3) 2,02(27); 4) 16,(714285); 5) 2,(076923); 6) 2,0(714285); 7) 2,0(461538); 8) 0,091(6). 11.20. 1) 0,(09); 2) 0,68(923076). 11.22. 1) a < 6; 2) a > 6; 3) a<b; 4) a <b\ 5) a>b\ 6) a < b. 11.23. 1) 2 — v<2; 2) 1 + a/3-\/5; 3) -л/З-уИ?; 4) 2\/2-\/5. 11.24. 1) I - 2x, если x G (-oo; 0,5); 2x — 1, если xG[0,5;+oo); 2) x2 — 4, если x G (—oo; — 2] U [2; +oo); 4 —x2, если xg(—2;2); 3) x2 — 3x — 4, если x G (—oo; — 1] U [4;+oo); 4 + 3x — x2, если x G ( —1;4); 4) x2 — 2x, если x G (—oo; 0] U [2; +oo); 2x — x2, если xg(0;2); 5) —3x — 5, если xG(-oo;-3]; x + 7, если x G (—3; 1]; Зх + 5, если xG(l;+oo); 6) 2x — 3, если x G (-oo; —0,5]; 6x - 1, если x G (—0,5; 2]; 3 — 2x, если xG(2;+oo).
11.25. 1) 3; 0; -5; 0; 3; 0,9; -6; 0,8; -1: 0,6; 2) 1; |; -3; J; 3; |; -4; f; -1; j.
i 9 4 ob
11.26. 1) 1; У2 - 1; 2; v/7 - 2; -2; 2 - ч/2; -3; 3 - У5; -1; 1 -
2) 2; \/2 - 1; -3; 2 - ^2; -1; 2 - v^; 0; 4 - У15. 11.27. 1) [0,75; 1);
2) [-0,4;-0,2); 3) [1; 1,2); 4) [2;3); 5) [2,2,5); 6) [^;|).
11.28. 1) n. — 0,8, n. G Z; 2) rt + 0,3, n. G Z; 3) + |. rt G Z; 4) n + rt G Z; 5)^ + 1, hgZ; 6)bl,«GZ. 11.29. 1) 2)^; 3)^; 4)^.
о o □ 2U 13 ob ob ob
11.30. 1) Конечная, 5 знаков; 2) конечная, 6 знаков; 3) конечная, 4 знака; 4) периодическая, 3 знака; 5) периодическая, 2 знака; 6) периодическая, 4 знака. 11.32. 1) Решение. Пусть у^5 + уИЗ = a G Q,
(y/5+у^з) — З’УТб = | G Q, y^l5 G Q. Далее доказать, что это неверно. 11.33. 4) Указание. Предположить, что \[2 + \/3 + \/5 = a G Q, перенести л/5 в правую часть, возвести в квадрат и показать, что тогда \/6 + a\/5GQ, далее доказать, что это неверно. 11.34. 1) Да; 2) нет; 3) нет; 4) да. 11.35. 1) a < b; 2) a > Ь] 3) a < b; 4) a > b. 11.36. 1) 7; 2) 19; 3) 33; 4) 17. 11.37. 1) Зт^-29; 2) 139 - 14тЛ 11.38. 1) -2; 2) -1; 3) -|; 4) 1. 11.39. 1) |, |; 2) 0,15; 3) -1; 4) -13,-у,-у,-5. 11.40. 1) 5; 2) 0,16; 3) 32; 4) 12. 11.41. 1) |; 2) 162. 11.42. 1) \/8+\/7; 2) 4 + У15; 3)^9+^4+^6; 4) 1,6+ 0,8-Й +0,4-^9. 11.43. 1) х - 1; 2) 1 - Зх. 11.44. 1) х/х$; 2) — \/—х3; 3) vG^; 4) — у/(2 - х)5; 5) \/х2г/ при
х 0, — у/х^у при х < 0; 6) >/(х — 1)2у при х 1, — \/(х — 1)2у при х < 1. 11.45. 1) у, 2) |</|; 3) 8|х|-9; 4) |х|. 11.46. 1) 2) -----
ya - 1 a — y/a\/b + b
Ответы к главе II 35
3) ^a--^b; 4) b + a^b + a2. 11.47. 1) х; 2) 11.48. 1) 2) 2a.
11.49. 1) -6; 2) 15; 3) -30; 4) 4. 11.50. 1) -1,75; 2) 11.51. 1) 8;
2) 3. 11.52. 1) л/2; 2) 11.53. 1) 486; 2) 432. 11.54. 1) 2)
11.55. 1) 3; 2) 4. 11.56. 1) 1; 2) 0. 11.57. 1) 2; 2) -И; 3) 1; 4) 1.
11.58. 1) 4; 2) -2^7. 11.59. 1) х; 2) х. 11.60. 1) а; 2) а2; 3) Ущ 4) a2. 11.61. 1) J-; 2) - Ш; 3) tyab - 4) \/2Ь - у/а.
уа
11.62. 1) 0; 2) 3; 3) -</&; 4) v^. 11.64. 1) А > В; 2) А < В.
11.65. 1) 1(1+ ~ ^)-; 2) LL2+V^+1^) п.66. 1) 1024; 2) ±8.
11.67. 1) 264а-6, если |6| < Ш; 2а6-264а~6, если |6| > Ш; 2) -rf6c“8, v2 v 2
если |d|^ №с2; если |d|> ^2с2. 11.68. 1) —х0’5; 2) 9х. 11.69. 1) 0; 2) х1; 3) ^2-2--2-; 4) 4. 11.70. 1) 6; 2) 9; 3) -2; 4) -2; 5) -6; 6) -4. 11.71. 1) 2; 2) 11.72. 1) 6,5; 2) 0,5; 3) 10; 4) 10. 11.73. 1) 13;
2) 5, —2; 3) 0,5; 4) 2; 5) 6; 6) 3 + log2 7; 7) 1о^2+1; 8) нет корней; 9) 1 _ ]Og9 4. 11.74. 1) 10; 2) 0,5. 11.75. 1) 1; 2) 4; 3) 2; 4) 2.
11 .76. 1) 1,5; 2) |; 3) -|; 4) -4. 11.77. 1) 3; 2) -2; 3) 10; 4) 0,5. 11.78. 1) 0,5; 2) 1. 11.79. 1) 1; 2) -1. 11.80. 1) —0,4; 2) 0,5.
11 .81. 1) -1; 2) -1. 11.82. 1) 1,5; 2) 3. 11.83. 1) 7,5; 2)
11 .84. 1) 1; 2) 3; 3) 0; 4) 1. 11.85. 1) 1; 2) 1. 11.86. 1) 5;
2) 2; 3) 8; 4) 0,04; 5) 12; 6) 4. 11.87. 1) 11; 2) 169; 3) 4;
4) 60. 11.89. 1) 2) -Д-. 11.90. 1) х < 1,х > 7; 2) 3 < х < 5;
2а За
3) таких значений х не существует; 4) х 2. 11.91. 1) Например,
3) например, log5 8 — log5 243;
log2 7 + log2 5; 2) например, log3 8 + log3 7;
4) например, Ig9 + lg6-lg7. 11.92. 1) (0; 1)U(1; 1|); 2) (-1|;-1) U(-l;0); 3) (3;4) U (4; 5) U (5;+oo); 4) (1; 2) U (2; 3) U (3;+oo). 11.93. 1) a > 0, a 1, b < 1; 2) a < 2, a 1, b < 0; 3) a < 0, a —1, b > 0;
4) a > 0, a 1, b > -2. 11.94. 1) Например, log2(-x) + log2(-y);
2) например, 2log3x + log3(-z/); 3) например, 21og5(-x) + 3log5(-y);
4) например, 2 lg(—y) — lg3 — lg(—x). 11.95. 1) 6; 2) 4; 3) 4; 4) —1;
5) 2; 6) 2. 11.96. 1) 0; 2) 0. 11.97. 1) 3; 2) 4. 11.98. 1) 25;
2) 11. 11.99. 1) log0)35 < log0,2 5; 2) log8 5 < log6 5. 11.100. 1)
a r, i i + 3& + 1. 2ab + b + 1 ТТ1Л1 i \ 2 — a n\ 3a + 1
2)6-^ + !, 3) a + 2 , 4) ab + 2b + l. И.1О1.1)з-^, 2)—.
11.102. 1) -1,25; 2) -2,5; 3) 4) |. 11.103. |,^,1 или 1,
О Э о о ОО
11.104. 8 11.105. И.Ю6. 281 или 21| 11.107. ±4 11.108. 2,1
11.109. -21 11.110. 11.111. 1) 39, 2) 27 11.112. -12350 11.113. 1
36 Глава II. Множества и операции над ними
11.114. 9. 11.115. 7. 11.116. 1) 1; 2) (—оо; 0) U (0; 1) U (1;-|-оо). 11.117. 5.
11.118. 6 11.119. 8|у. 11.120. 48 11.121. 3 11.122. |, --1, -2.
11.123. 3. 11.124. bi = 6,q = -0,5. 11.125. 11.126. b{ = 1,55 л =
= -0,5. 11.127. 486. 11.131. 1) х6 + 2х5 + 4х4 + 8х3 + 16х2 + 32х + 64;
2) х4 + х3 + х2 + х + 1; 3) 16х4 — 8х3 + 4х2 -2x4-1;
4) (х6 - х5 + х4 - х3 + х2 - х +1)2. 11.132. 1) Ж + Ж + Ж + Ж + 1;
2) У16 - Ж + Ж - Ж + 1. 11.133. 40095х“2. 11.134. 70 (1 - а2} .
11.135. 512. 11.136. 11.137. 792b7. 11.138. 3672
16
и 55080. 11.139. 60. 11.140. 26 членов. 11.141. п = 7.
11.165. 1) 73; 2) 175. 11.166. 15. 11.167. 1) [1; 2) U [3;7) U [8; 9);
2) [—22; —21)U[—19; —17)U[—13; —10)О[—9; —7)U[—5; —4). 11.168. 1) ^,fcGZ;
2) | + k, k G Z; | + k, k G Z; 3) j + k, k € Z; 4) | + k, k G Z; О 3 O i _____
+k, ke Z. 11.170. 1) если |x| 1; x, если |x| < 1; 2) 2^- -1,
42 x । । a — 2
если a > 2; , 2 , если 1 C a < 2. 11.171. + 5 + Ж — 2,
2 — a
если a 2; V—a — 5 + л/2 — а, если a —5. 11.172. 1) Ж;
2) Ж - 1. 11.173. 1) 0,5 (Ж- 1) (ЖТ+2Ж + 4); 2) 7^~23^~3-
11.176. 1) -Ж; 2) 1. 11.177. 1) Ж; 2) Ж. 11.178. 1) 4; 2) 3.
11.179. 1) log34>log56; 2) log135 6 75 > log45 75. 11.180. log9 32 + log4 27 < 4. 11.182. ----4- у ----Ж 16. 11.183. 1) (-40; 12); 2) (15,75; 24,5).
11.184. 13,5. 11.185. 1) 40 402; 2) 62 001. 11.186. (48; 52] мин.
11.187. 54. 11.188. 5= Ж+.А. П.193. а = 3. 11.194. Наибольшее
4
значение выражения равно 28 и достигается при а = 0,5, 6 = —7,5, с ——2,5. 11.195. Наименьшее значение выражения равно 77 и достигается при а = 7, b = -3, с = 3. 11.196. а = -1± А
Глава III
ФУНКЦИИ
§1. ЛИНЕЙНАЯ, КВАДРАТИЧНАЯ И ДРОБНОЛИНЕЙНАЯ ФУНКЦИИ
Первый уровень
III.1. Выяснить взаимное расположение прямых:
1) у = 2х + 3 и у = 4х - 5;
2) у = — Зх + 6 и z/ = -3x + 7;
3) 2\/3z/ + 2х — 2 д/2 — 0 и \/бг/ + \/2х — 2 = 0;
4) 2г/ + х = 3 и у = —2х + 4.
III.2. Написать уравнение прямой, если эта прямая:
1) пересекает координатные оси в точках (2;0) и (0;—12);
2) проходит через точки (1; 1) и (—2; 10).
Ш.З. 1) Найти площадь треугольника, образованного осями координат и прямой у = — 2х + 4.
2) Найти площадь треугольника, образованного осью абсцисс и прямыми у = —Зх — 10 и у = 0,5х — 3.
III.4. 1) Написать уравнение прямой /1, которая проходит через точку А(1;2) перпендикулярно прямой 1%, задаваемой уравнением у = — 2х + 3.
2) Написать уравнение прямой /1, которая проходит через точку А(—1;3) перпендикулярно прямой /2, задаваемой уравнением г/= Зх — 1.
III.5. 1) Написать уравнение прямой /1, проходящей через точку А(—2; 3) параллельно прямой /2, проходящей через точки 5(2; 2,5) и <7(1; 3).
2) Написать уравнение прямой /[, проходящей через точку /4(1; — 2) параллельно прямой /2, проходящей через точки 5(—1; 3) и С(2;9).
III.6. Построить график функции y = f(x). Указать область ее определения, множество значений, наибольшее и наименьшее значения (если они существуют), промежутки монотонности:
1) /(х) = х2 + 4х + 1; 2) /(х) =-х2 + 6х + 1.
38 Глава III. Функции
Ш.7. 1) Найти уравнение параболы с вершиной в точке (1;—8), проходящей через точку (2;—12).
2) Найти уравнение параболы с вершиной в точке (—3;1), пересекающей ось ординат в точке (0;—8).
III.8. 1) Построить график функции у — —х2 — 6х + а, если известно, что ее наибольшее значение равно 4.
2) Построить график функции у = х2 — 2ах — За, если известно, что ее наименьшее значение равно 2.
IIL9. Найти значения параметра а, при которых парабола у = ах2 — 4х + а + 3 расположена:
1) выше оси абсцисс;
2) ниже оси абсцисс;
3) пересекает ось абсцисс в двух точках;
4) касается оси абсцисс.
ШЛО. Построить график функции у = [(х). Указать область ее определения, множество значений, промежутки монотонности:
Второй уровень
III.11. 1) Написать уравнение прямой 1\, проходящей через начало координат и пересекающей прямую /2, заданную уравнением у — — Зх + 2, под углом (р = 30 °.
2) Написать уравнение прямой /1, проходящей через начало координат и пересекающей прямую /2, заданную уравнением у = 2х + 1, под углом <£> = 45°.
III.12. Выяснить взаимное расположение прямых:
1) у — а2х — 1 и у = (2а + 3)х + а\
2) у = (а2 — 3) х + 2 и у = (а — 1)х + а.
III.13. 1) При каких значениях параметра а функция
у = ах2 + 4х + 2 возрастает на промежутке [2; 4]?
2) При каких значениях параметра а функция
у = ах2 — 6х + 2 убывает на промежутке [—1:2]?
III.14. 1) При каких значениях параметра а график функции у = х2 + ах — 2а + 10 пересекает ось Ох в двух
§2. Основные понятия, относящиеся к числовым функциям 39
точках, расположенных по разные стороны от начала координат?
2) При каких значениях параметра а график функции у = ах2 + х — 2а пересекает ось Ох в двух точках, расположенных по разные стороны от точки (1;0)?
X I 1
III.15. 1) При каких значениях параметра с функция у = сх^~2 убывает на промежутке [—0,5; 1)?
2) При каких значениях параметра с функция У — возрастает на промежутке [—1; 1)?
§2. ОСНОВНЫЕ ПОНЯТИЯ, ОТНОСЯЩИЕСЯ К ЧИСЛОВЫМ ФУНКЦИЯМ
Первый уровень
III.16. Пусть множество значений функции у = [(х) есть отрезок [—6;2]. Найти множество значений функции:
1) у = 2/(х) - 7; 2) </= 3 — 8/(х); 3) {/ = у?(х) + 7;
4) У = (/(х))2; 5) у = (/(х) + 7)2; 6) у = (/(х) - 4)2;
7) У = |/(х)|; 8) у = |/(х) + 8[; 9) у = |/(х) - 3|.
III.17. Найти множество значений функции:
1) /(х) = \х + 4| - 3; 2) f(x) = 5 — |х — 21;
3) f(x) = \2х - 6| +1; 4) /(%) = 3 - |6х + 3|.
III.18. Найти множество значений функции:
1) /(х) = |х - 1| - |х - 2|; 2) /(х) = |х + 1| + |х - 2|.
III.19. 1) Каким выражением задается функция y = f(x'), если /(лУх)=х + 3 при любом неотрицательном значении х?
2) Каким выражением задается функция у = f(x), если / (2 + х) = 8 — 4х — х2 при любом действительном значении х?
III.20. Решить уравнение:
1) / (*2) = Кх), если Кх) — +1;
2) / (х + 6) = / (х2), если /(х) = 3 —х.
40 Глава III. Функции
III.21. Найти f(g(x)) и g(/(x)), если:
1) ZW = 2x4-1, g(x) = |x|;
2) /(x) = x2, g(x) = x4-3.
III.22. Найти функцию /(/(x)), если:
1) /(x) = 2x4-1; 2) /(x) = — 3x4-1.
III.23. Найти функцию /(/(x)), если:
1)/W = £±A; 2)/W = ^L.
III.24. 1) Найти /(/(1)), если f(x) = { -f’ x^2
2) Найти /(/(6)), если f(x) = {
III.25. 1) Найти множество значений функции /(х)—х+^.
2) Найти множество значений функции /(х) = х —
Второй уровень
Найти область определения и множество значений функции (III.26-III.29).
III.26. 1) /(х) = л/х2 - 2х - 3; 2) /(х) = \/-х2+х + 2.
9 9
III.27. 1) = 2) /(х) = ^.
III.28. 1) /(х) =х + л/х^Л; 2) /(х) = Д~Дс - 2х.
III.29. 1) /(х) = х 4- 4хД+1 + 5; 2) /(х) =--х + 2^/х + 1.
§3. СВОЙСТВА ФУНКЦИЙ
Первый уровень
Ш.ЗО. Найти точки, в которых непрерывна функция:
1) /(*)= {
х О, х > 0;
X 1,
2) = {
I 1 “1“ Л 5
§3. Свойства функций 41
III.31. Исследовать на четность и нечетность функцию:
1) /(х) = х4 + х2 + И + 3. 2) f(x) = /’ + 2х3;
3) Дх) = -х5+х3 + 1; 4)/(x) = iil.
III.32. Пусть наименьшее и наибольшее значения функции у = [(х) равны соответственно А и В. Найти наибольшее и наименьшее значения функции:
1) </ = 3/(х) + 4; 2) y = -f(x\
3) у = 6-2[(х)-, 4) у = —2 — 5[(х).
III.33. Найти наименьшее и наибольшее значения функции на указанном отрезке:
1) [(х) = \х — 3\, [2; 5]; 2) /(х) = |1-3х|, [1;5];
3) = |х2-4|, [-1;3]; 4) /(х) = |х(6 - х)|, [7;9].
III.34. Найти наименьшее и наибольшее значения функции на указанном отрезке:
1)/(х)=х2 + 4х-12, [-3;!]; 2) /(х) = -х2+6х+1, [-2; 4].
III.35. 1) Функция /(х) определена на всей числовой прямой, периодическая с периодом Т = 2 и на отрезке [0; 2] задается формулой /(х) = х2 — 2х. Построить график функции /(х) на отрезке [—4; 4].
2) Функция /(х) определена на всей числовой прямой за исключением х Е Z, периодическая с периодом Т = 1 и на промежутке (1;2) задается формулой /(х)=х2. Построить график функции /(х) на отрезке [—4; 5].
III.36. 1) Функция /(х) нечетная и периодическая с периодом Т = 10. Найти значение /(1004), если /(—4) = 1,5.
2) Функция /(х) четная и периодическая с периодом Т — 40. Найти значение /(1604), если /(—4) = —4,5.
Второй уровень
III.37. Исследовать на четность и нечетность функцию:
1) /(х) = \/5 — х2 — 4х — \/5 — х2 + 4х;
2) /W = \/*3 — 1 - "Ух3 + 1;
3) /(•*) = у/х — 1 - \/х + 1;
4) /(х) = |х - 1| - |х + 1|.
42 Глава III. Функции
III.38. 1) При каких значениях параметра а функция /(х) = = оаХ + ч является нечетной?
az — а + х6
2) При каких значениях параметра а функция /(х) = ах — 2 о
= -s------ является нечетной?
az + а + х
III.39. 1) Вычислить /(—3), если известно, что функция g’(x) =/(х) + х2 четная и /(3) = 4.
2) Вычислить /(5), если известно, что функция &(х) =/(х) + х2 нечетная и /(—5) = 1.
111.4 0. Найти промежутки монотонности функции:
1) /(х) - \/б — х2 — х; 2) /(х) = у*х2 — х.
III.4 1. На йти наименьшее и наибольшее значения функции на указанном отрезке:
= [-1;2]; 2) /(х) = -^£—. [-3;0];
3) /и = [-5; 1]; 4) /(х) = [1;4].
III.42. 1) Привести пример двух функций, наибольшее значение суммы которых не равно сумме их наибольших значений.
2) Привести пример двух функций, наибольшее значение суммы которых равно сумме их наибольших значений.
3) Привести пример двух функций, наибольшее значение произведения которых не равно произведению их наибольших значений.
4) Привести пример двух функций, наибольшее значение произведения которых равно произведению их наибольших значений.
III.43. 1) При вести пример функции /(х), наибольшее значение модуля которой не равно модулю наибольшего значения самой функции.
2) Привести пример функции /(х), наибольшее значение модуля которой равно модулю наибольшего значения самой функции.
3) Привести пример функции /(х), квадрат наибольшего значения которой не совпадает с наибольшим значением функции /2(х).
§3. Свойства функций 43
4) Привести пример функции /(х), квадрат наибольшего значения которой совпадает с наибольшим значением функции /2(х).
Ш.44. Найти наименьшее и наибольшее значения функции у = f(x) на указанном промежутке:
1) /(х) = х4 - х2 - 2, [—3; 2];
2) /(х) = х4 + х2 + 1, [2;+оо);
3) /(х) = х-6^ + 3, [4;25];
4) f(x) = 8y/x — х, [9;+оо).
III.45. 1) Для каждого действительного числа х обозначим через f(x) наибольшее из чисел х2 +1, х + 3 и 11 —Зх. Найти наименьшее значение функции /(х).
2) Для каждого действительного числа х обозначим через /(х) наименьшее из чисел —х2, х —2 и 2 — Зх. Найти наибольшее значение функции /(х).
III.46. Найти основной период функции:
l)f(x) = {2x}; 2)/(х) = {|};
3) «х) = {4х} + 1; =
Ш.47. Найти один из периодов функции:
1) f(x) = {8х} + {6х}; 2) /(х) = {^} + {Д
3) /W = {2х} 4) /(х) = {15х} + {6х}.
III.48. 1) Функция /(х) периодическая с периодом 3. Зная, что [ (х2) = х6 - Зх4 при х е [0; л/3], найти /(—1).
2) Функция /(х) периодическая с периодом 4. Зная, что f (х2) = х8 — 4х6 при хе[0;2], найти /(—3).
Ш.49. 1) Известно, что /(х) — нечетная периодическая функция с периодом 4 и /(х)=х4 —2х3 при х 6 [0;2]. Вычислить сумму /(1) + /(2) + ... + /(150).
2) Известно, что /(х) — нечетная периодическая функция с периодом 6 и /(х) = 3х —х2 при хе[0;3]. Вычислить сумму /(1) + /(2) + ... + /(100).
44 Глава III. Функции
§4. ГРАФИКИ ФУНКЦИЙ Первый уровень
Ш.50. На рисунке изображен график функции y = f(x).
Построить графики функций:
1) y = f(x-2); 2) y = f(x) + 4;
3) y = f(-0,5x); 4) y = 3f(x);
5) y = O,5f(x); 6) y = -f(x);
7) y = f(2x + 3); S)y = f(4-x).
III.51. Построить график функции
Г1, если X £ $-з,
f(x\ = J -^-2, если если -3< 0< Z х 0, Z х 2,
(2, если х ' >2.
Путем элементарных преобразований графика функции построить графики следующих функций:
1) У = /(Зх); 2) у = f(2x - 4); 3) у = /(1 - х);
4) У = 2/(х); 5) у = -/(х); 6) у = /(х + 1) - 2;
7) у = /(|х-2|); 8) г/—/(|х| — 2); 9) у = 3- |/(х)|.
С помощью элементарных преобразований построить графики функций. Для каждой функции указать область определения, множество значений, промежутки монотонности (III.52-III.58).
Ш.52. 1) 4) 9 У = х , у = О,5х2; 2) 5) у = х2 - 4; 3) 6) У = У = (х — З)2; - (х + 3)2 + 9
У = (О,5х)2;
Ш.53. 1) 2) У = 1 +х. X 3) У = X ’
4) 7) и=^ У ~ 4х + 3 ’ 5) 8) У = У = 1 И’ 1 |х-2Г 6) У = 3 . х + 1’
§4. Графики функций 45
III.54. 1) у=— х2 + 4х + 5; 2) у = — х2 + 4|х| + 5;
3) у = | - %2 + 4х + 5|; 4) у = | - х2 + 4|х| + 5|.
III.55. //=(~3(Х + 2)2-1’ e“H
4х, если
III.5 6. *+!’
если х < 1;
если х > 1.
III.5 7. 1) // = ^/х;
III.5 8.
4) у = х/^х;
1) У = х3-,
3) у= |х - 2|3;
2) у = х/х - 2;
5) у - — 3;
8) у= |Vx + 4.
2) z/ = (2х)3;
4) у = (|х| - 2)3
3) у = -у/х\
6) у =
к — 2х + 2,
На координатной плоскости построить множество точек, координаты (х, £/) которых удовлетворяют указанному условию (III.59-III.63).
III.59. 1) 3) (х - 3)(z/ + 1) = 0; х2 — 2ху — Зу2 = 0; 2) 4) 4у2 — 9х2 - 0; 2х2 - 7ху - 4у2 = 0.
III.60. 1) (х - 4)2 + (у + 2)2 = 25; 2) X2 + у2 = 4х;
3) х2 + 4х + у2 + 6 г/ = 3; 4) х2 + у2 - 8х + 2у + 8 = 0
III.61. 1) х + 2у — 3 > 0; 2) 2у — Зх + 6 0.
III.62. 1) у + 4 > х2 — Зх; 2) у - 6х + 9 < —х2.
III.63. 1) х2 + у2 < 9//; 2) х2 + z/2 > 2х - 4у.
Второй уровень
Построить график функции. Для каждой функции указать область определения, множество значений, промежутки монотонности (III.64-III.72)
III.64. 1) у = |||х|-3| - 2|; 2) у = |2 - |4 - |х + 3|||.
III.65. у = —!— + 3. III.66. у =
2х - 1 у х - 2
III.67. y^^zl. III.68. y=^di. Ш.69. у = 3,^~2.
у х + 1 2х — 4 |х| — 1
III.70. у = 1 - 3V^x. III.71. у = х/5 + 2х - 3.
III.72. 1) г/ = х/9 — Зх — 2; 2) г/ = д/9 - 3 |х| - 2;
46 Глава III. Функции
3) 1/ = У|9 - Зх| - 2; 4) ;/= 1^/9 - 3|х| - 2|.
Построить график функции, предварительно заменив ее тожде-
ственно равной (Ш.73-Ш.83)
III.73. z/= У(2х-3)2.
ттт -те 5+Х —4х2
III.75. у=-^------.
2х2 + х- 1
III.77. \/х2 + 2х+1 — л/х2 — 2х+1.
III.79. (Vx2 — 6х)2 — х/(36 —6х)2.
III.81. y=-^t
|х-4| + 2
III.83. у—тх—-Ц-— |2х + 5| — 12х — 5|
III.84. Построить график функции
/(х) =
III.74. у = V2y + l8Z.
V3x + 2
III.76. у= |х +1| - |х| + 3.
III.78. г/ = х2 — |х +1| — 1.
III.80. у= |х + 2|-|х2-1|.
III.82. у= .
У = l/(/W) I + 2> где
Построить график функции (Ш.85-Ш.86).
III.85. 1) г/ = [х]; 2) z/ = [x + 2];
3) у = [2х — 2]; 4) у = [3-х].
III.86. 1) у = {х}; 2) у = {х- 1,5};
3) z/ = 2{x}-3; 4) у = {0,5х} + 1.
На координатной плоскости построить геометрическое место точек, координаты (х, £/) которых удовлетворяют указанному условию
(III.87-III.91)
III.87. \у + 1| = х - 2.
III.89. 1) |z/ + x| = у,
III.90. 1) (х + 3)(z/ - 1) > 0;
III.91. 1) |z/-2| |х + 3|;
III.88. |z/ + 2| - |х| = 4.
2) |х — у\ = х — 2.
2) у2 - 5х2 - 4ху < 0.
2) \у\ <]х + 1| - 1.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ III
III.92. 1) При каких значениях параметра а площадь треугольника, ограниченного прямыми у = х, у = ах + 2х + 4а + 4 и осью Ох, равна 2?
2) При каких значениях параметра а площадь треугольника, ограниченного прямыми у = х + 1, у = ах + а и осью Оу, равна 1?
Задачи повышенной сложности к главе III 47
III.93. При каких значениях параметра а уравнение %2 — (2a — 1)х — 8 = 0 не имеет решений на промежутке (2;3]?
III.94. При каких значениях параметра а каждое число из промежутка [5; 7] является решением неравенства ах2 + 2(5а - 1)х - 75а + 4^0?
III.95. 1) Функция /(х) для каждого х равна наименьшему значению квадратного трехчлена g(t) = t2 — 6t + 8 на отрезке [х + 1;х + 2]. Построить график функции /(х).
2) Функция /(х) для каждого х равна наибольшему значению квадратного трехчлена g(t) = — t2 + 10^ — 16 на отрезке [х + 1;х + 3]. Построить график функции /«•
III.96. 1) Найти наименьшее значение функции
/(х) = (4 - х)(1 - х)(х + 4)(х + 7).
2) Найти наибольшее значение функции
/(х) = (5 - х)(х — 3)(х + 2)(х + 4).
III.97. 1) При каком значении параметра а наибольшее на промежутке [1;2] значение функции f(x) — | —2х2 + 7х — а — б| является наименьшим из всех возможных?
2) При каком значении параметра а наибольшее на промежутке [0,5; 1] значение функции /(х) = = | — 8х2 + 10х + 2а — 3| является наименьшим из всех возможных?
III.98.
2)
Функция /(х), определенная при всех значениях х и не равная 0 ни при каком значении х, удовлетворяет равенству f(x + 3) = — 1 • Найти /(1996), если
/(10) = 3.
Функция /(х), определенная при всех значениях х и не равная —1 ни при каком значении х, удовлетворяет равенству /(х + 7) = 1 — - • Найти /(1992), если
/(И) = 4-
III.99. Дана функция
1, ХЕ (—оо; —6] U [2; +оо), X + 7, хе (-6; -2], 3-х, хе (—2;2).
48 Глава III. Функции
Построить графики функций:
1) у= |/(2х + 1)— 4|; 2) У = /(||х-1|-2|-3).
Построить график функции (III.100-III.105).
III.100. П р-3|х|-10|. |х2 - 9|х| + 20| ’ 2) |х2-8|х|+12| |х2 - 5|х[ + 6|
III.101. 1) У= [х2]; 2) У= [(х-2)2].
III.102. 1) У= {х2}; 2) у = {4х2}.
III.103. 1) У — h/х]; 2) у= [У0,5|х|].
III.104. 1) у = {\/х}; 2) у = {70,51x1}.
III.105. 1) £/ = [х2 + 4х + 3]; 2) у = {х2 +4х + 3}.
III.106. Построить график функции /(/(х)), если:
. f х + 2, х? U, > 1 г/ ч f 2 - х, х 2,
1) /(х) = 5 с 9 '4 ' 1 5 - 2х, х ; 2) = { 2х - 4, х > 2.
III.107. Графики функций /(х) = и g(x) симметричны относительно прямой у = х — 1. Найти функцию g(x) и построить ее график.
III.108. Найти площадь фигуры, ограниченной графиками функций /(х) = - |х - 3| + 3 и g(x) — 2 — у/6х - х2 - 8.
III.109. На координатной плоскости построить геометрическое место точек, координаты (х;у) которых удовлетворяют условию %2 + 10 |х| + у2 + 10 |z/| < 119.
III.110. Построить график уравнения ||z/| — 2| + 2 |х| — 1 = 2.
III.111. В зависимости от значения параметра а найти количество точек пересечения графиков функций /(х) = 2 ||х| — 2| и g’(x) — ах — 2а + 1.
III.112. В зависимости от значения параметра b > 0 найти количество точек пересечения графиков уравнений |х| + |z/| = b и I ,.2 — 1 И X
ОТВЕТЫ К ГЛАВЕ III
III.1. 1) Пересекаются; 2) параллельны; 3) совпадают; 4) пересека-
ются. III.2. 1) у = 6% — 12; 2)
III.4. 1) у = 0,5х + 1,5; 2) У=^^-
III.6. 1) £>(/) = К, E{f) = [—3;+оо),
у = 4 - Зх. Ш.З. 1) 4; 2) 1в|.
III.5. 1) у = -0,5х + 2; 2) у = 2х-4. /"найм = -3, на (—оо;—2] функция
Ответы к главе III 49
убывает, на [—2;+оо) функция возрастает; 2) £>(/) = К, Е(/) = (—оо; 10], [наиб = Ю. на (~оо; 3] функция возрастает, на [3; +оо) функция убывает. III.7. 1) у — 2х2 — 4х — 6; 2) у = —х2 — 6х — 8. III.8. 1) Парабола
у = —х2 — 6х — 5; 2) параболы у = х2 + 4х + 6 и у = х2 + 2х + 3.
III.9. 1) (1;+оо); 2) (-оо;-4); 3) (-4; 1); 4) -4; 1. III.1O. 1) £>(/) = = (—оо; 3) U (3;+оо), E(f) = ( — оо; 0) U (0; +оо), на ( — оо; 3) и на (3; +оо) функция возрастает; 2) £>(/) — (—оо; 2) U (2; +оо), Е(/) = (—оо; 1) U (1; +оо), на (—оо;2) и на (2; +оо) функция убывает. III.11. 1) у = (2+^у^) х
Л 5х/з\ и у= I 2-----I х;
2) у = — Зх и у=^. III.12. 1) При a —-1 прямые
совпадают, при a = 3 параллельны, в остальных случаях пересекаются;
2) при a = 2 прямые совпадают, при a = — 1 параллельны, в остальных случаях пересекаются. III.13. 1) a 6 [—0,5; +оо); 2) a G [— 3; 1,5]. III.14. 1) a 6 (5;+оо); 2) a 6 (-оо;0) U (1;+оо). III.15. 1) с G (2; 4);
2) с€(-3;3). III.16. 1) [—19; -3]; 2) [—13;51]; 3) [1;3]; 4) [0; 36]; 5) [1; 81]; 6) [4; 100]; 7) [0,6]; 8) [2; 10]; 9)[1;9]. III.17. 1) Е(/) = = [-3; +оо); 2) Е(/) = (-оо;5]; 3) Е(/) = [1;+оо); 4) Е(/) = (-оо;3]. III.18. 1) £(/) = [-1; 1]; 2) £(/) = [1; +оо). III.19. 1) /(х) = х4 + 3, х 0;
2) /(х) = 12 - х2. III.20. 1) 0;±1; 2) 3;-2. III.21. 1) /(g(x)) =
= 2 |х| + 1, £(/(х)) = |2х + 1|; 2) /fe(x)) - (х + З)2, ^(/(х)) = х2 + 3.
III.22. 1) /(/(х)) = 4х + 3; 2) /(/(х)) = 9х - 2. III.23. 1) /(/(х)) - х
при х / 1; 2) /(/(х)) = при х / -0,5 их/ 0,25. III.24. 1) 9;
2) -9. III.25. 1) £(/) = (—оо; —2] U [2;+оо); 2) £(/) = К. III.26. 1) £)(/) = = (—оо; —1] U [3;+оо), £(/) = [0;+оо); 2) />(/) = [-1;2], £(/) = [0; 1,5].
III.27. 1) £>(/) = (-оо;-3) U (3;+оо), £(/) = (—оо; 7 — 4л/3] U [7 + 4-/3;+оо); 2) £)(/) = (—оо;—2) U (-2;+оо), £(/) = (-оо;-5 - 2ч/б] U [-5 + 2ч/б; +оо). III.28. 1) £>(/) = [1; +оо), £(/) = [1; +оо); 2) D(/) = (-оо; 1], £(/) = [-2; +оо). III.29. 1) D(/)-[-l;+oo), £(/) = [4;+оо); 2) £>(/) = [0;+оо), Е([) = (-оо;2]. III.30. 1) Непрерывна во всех точках х € К; 2) непрерывна при х / 1. III.31. 1) Четная; 2) нечетная; 3) общего вида; 4) общего вида. III.32. 1) /найм ~ ЗД + 4, /наиб = ЗВ + 4; 2) /найм = —В, /наиб = ~Д;
3) /найм = 6 — 2В, /наиб = 6 — 2Д; 4) /найм — — 2 — 5В, /наиб = _2 — 5Д.
III.33. 1) /найм = 0, /наиб = 2; 2) /найм = 2, /наиб = 14; 3) /найм — 0,
/наиб = 5; 4) /найм = 7, /наиб ~ 27. III.34. 1) /найм ~~ /( —2) = —16,
/наиб = /(1) = -7; 2) /найм = /(-2) = -15, /наиб = /(3) = 10. III.36. 1) -1,5; 2) —4,5. III.37. 1) Нечетная; 2) четная; 3) общего вида; 4) нечетная. III.38. 1) а = 0; 2) a = 0. III.39. 1) 4; 2) -51. III.40. 1) Возрастает на промежутке [—3;—0,5] и убывает на промежутке [—0,5;2]; 2) убывает на промежутке (—оо;0] и возрастает на промежутке [1;+оо). III.41. 1) /найм = = «2) = /н.нб = /(0) = 2) /наии = /(-3) = 1, /наи6 = Л-1) = 1;
50 Глава III. Функции
3) /найм — /(1) — уд, /наиб — /(“4) — 4) /найм — /(2) — ту, /наиб — /(4) — 1.
IIL44. 1) /найм = —1|, /наиб = 70; 2) /найм = 21, наибольшего значения
не существует; 3) /Наим = -7, /наиб = -2; 4) /наиб = 16, наименьшего
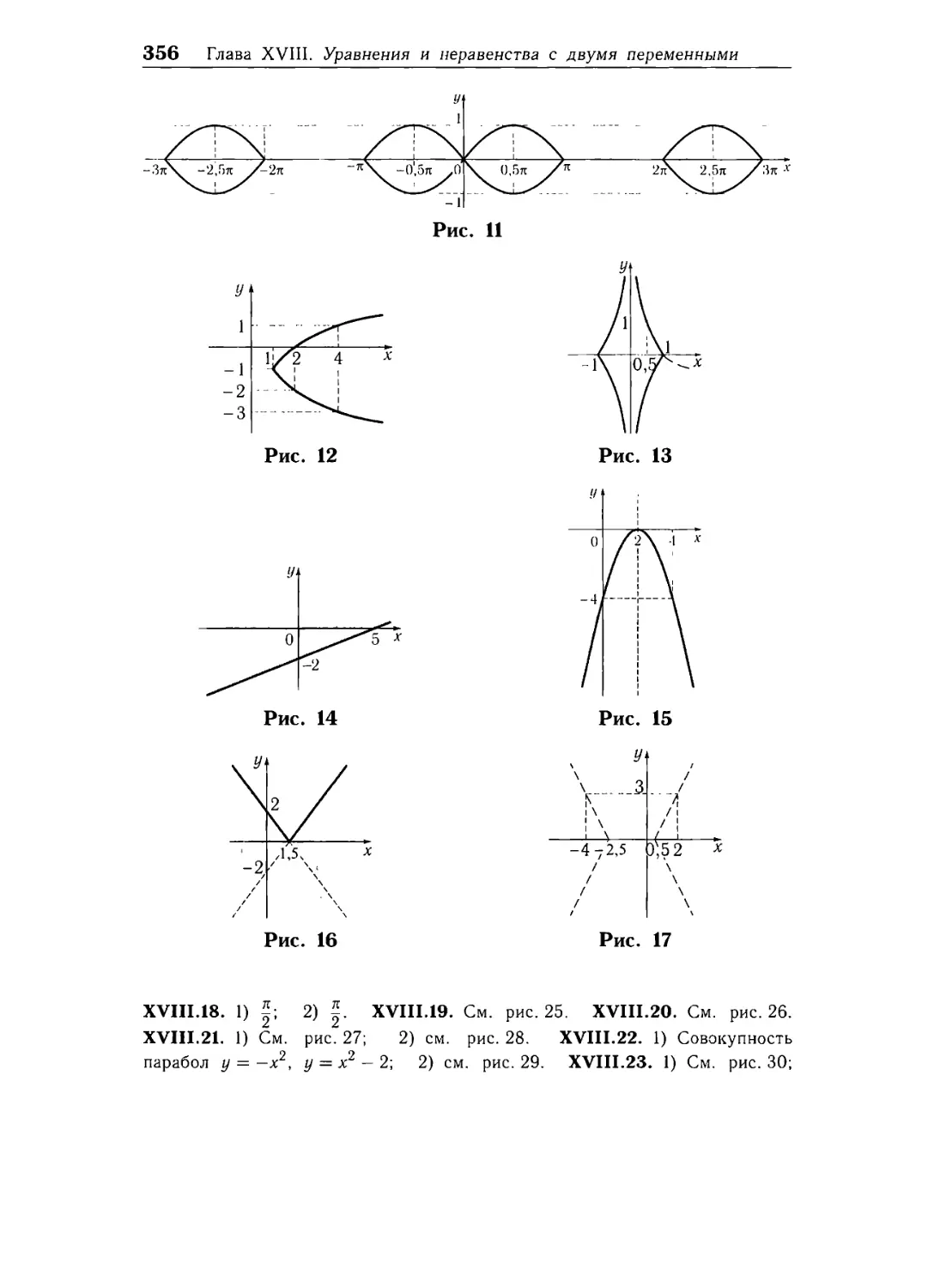
значения не существует. IIL45. 1) 5; 2) —1. III.46. 1) Т = 0,5; 2) 7 = 3; 3) 7=|; 4) 7 = 5. III.47. 1) 7 = 0,5; 2) 7=12; 3) 7 = 3; 4) 7=|. III.48. 1) —4; 2) -3. IIL49. 1) -1; 2) 2. IIL5O. 1) Рис. 1; 2) рис. 2; 3) рис. 3; 4) рис. 4; 5) рис. 5; 6) рис. 6; 7) рис. 7;
8) рис. 8. III.52. рис. 9. III.53. 6) Рис. 10; 7) рис. 11; 8) рис. 12.
III.54. 1) Рис. 13; 2) рис. 14; 3) рис. 15; 4) рис. 16. III.56. рис. 17.
III.57. 8) рис. 18. III.59. 1) Пара прямых х = 3 и у = —1; 2) пара
прямых у = 1,5х и у—— 1,5х; 3) пара прямых у = — 2х и у = 0,25х; 4) пара
прямых у — — 2х и у = 0,25х. III.60. 1) Окружность с центром в точке (4;—2) и радиусом 5; 2) окружность с центром в точке (2; 0) и радиусом 2; 3) окружность с центром в точке (—2; —3) и радиусом 4; 4) окружность
с центром в точке (4;—1) и радиусом 3. III.61. 1) Полуплоскость, лежащая
над прямой у = 1,5 — 0,5х (прямая не включается); 2) полуплоскость,
лежащая под прямой у=1,5х —3 (включая саму прямую). III.62. 1) Часть
плоскости, лежащая над параболой у = х2 — Зх — 4 (включая параболу);
2) Часть плоскости, лежащая под параболой у = —х2 + 6х — 9 (парабола не
включается). III.63. 1) Круг с центром в точке (0;3) и радиусом 3;
2) часть плоскости, лежащая вне круга с центром в точке (1;—2)
и радиусом х/5 (включая границу круга). III.69. Рис. 19. III.71. Рис. 20. III.72. 2) Рис. 21. III.73. График функции у = |2х — 3|. III.74. Рис. 22.
III.75. Рис. 23. III.76. Рис. 24. III.77. Рис. 25. III.79. Рис. 26.
III.80. Рис. 27. III.81. Рис. 28. III.82. Рис. 29. III.83. Рис. 30.
III.84. График функции у = |х| + 2, из которого выколота точка (1; 3).
III.85. 3) Рис. 31. III.86. 3) Рис. 32. III.92. 1) а = -? и а = -f;
3 5
2) а = — 1 и а = 3. III.93. а € (—оо; — 0,5] U +оо). III.94.
III.95. 1) /(х) =х2 — 2х, если х 1; /(х) = — 1, если 1 < х < 2; /(х) =х2 — 4х + 3,
если х 2; 2) /(х) = —х2 + 4х + 5, если х 2; /(х) = 9, если 2 < х 4; /(х) = —х2 + 8х — 7, если х > 4. III.96. 1) -144; 2) 49. III.97. 1) а = -^; 2)а=^. III.98. 1) 2) Ш.ЮО. 1) Рис. 33; 2) рис. 34.
х + 4,
х — 1;
III.106. 1) График функции у = <
1 -2х,
4х — 5,
W —2х,
— 1 < х 1;
1 <х 2;
х > 2.
2) График функции
Ответы к главе III 51
52 Глава III. Функции
Ответы к главе III 53
54 Глава III. Функции
Ответы к главе III 55
*/
-4-3-2-1 ; 1 1 i-1,
0 12 3 4
х
I I I 1 1111
WW/h
-3
Рис. 32
— 2х, х 0;
У =
0 <х 2;
—2х + 6,
III.107. g(x} = —2 + III.108. | + 1.
Ux - 12,
х > 3.
III.111. При a < — 2 и a 2 одна, при — 2 < a < —1,5 и 0,25 < a < 2 две, при
a =—1,5 и a = 0,25 три, при —1,5 <a< 0,25 четыре. III.112. При 0<Ь<1 и b > \/2 общих точек нет, при b = 1 и b = ^2 четыре, при 1 < b <
восемь.
Глава IV
АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
§1. РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Первый уровень
IV.1. Определить графически число корней уравнения:
1) х2 + 1 = Ь 2) (х4-1)3 = |;
3) 4-х2 = —Ц-; 4) х3 =---.
х 4- 1 х 4-1
IV.2. Определить графически число корней уравнения:
1) /(х) = х+1, если /(х) = <
2) /(х) — 4 — х, если /(х) = <
х2, х О,
—Ц-, х > 0;
х + 1 ’ ’
х2 + 4х + 4, х < 1,
х 1.
х
Решить
IV.3.
IV.4.
IV.5.
IV.6.
IV.7.
IV.8.
IV.9.
уравнение (IV.3-IV.9),
1) 1^-х-2 = 0;
х — 1
1) /~4 = 0;
х3 — 5х 4- 2
1) 2 + Зх 2 + х 0,75 Н- х _ 0,25-х’
1) 1 — X 1 2 =4
X
1) х+1 I 2 _ 2 .
2+х х2 4-6x4-8 х4-4 ’
х —1 . 1 = 9 .
х+2 х—1 х2+х — 2’
1) (х + 2)(х + 5)у/^ + 3 = 0;
3) (х2 —7х+12) \/4 — х2 = 0;
1) (х2 - 9) \/х2 4- 5х — 14 =
2) ^-±1 = 2-2х.
’ 2х+1
v2 1
2) / --1-- =0.
х3 + 6х —7
1 — Зх _ 0,25 — х
1 + х 1,25 — х '
2) —-- = 1£.
3-1
х
2) 1 2х _ 48 .
х + 4 х2 —4x4-16 х3 + 64’
8 _224-х । 2
х2+2х + 4 8 —х3 х~ 2
2^ (х2- 16)(х2-9) q.
V3 — х
4) (х2 -25) (4-х2) = 0
\/х2 — 4х — 12
(23 — х2) у/х2 + 5х — 14;
2) (х3 + 2х) • -\/2х + 5 • Vx + 3 = (х2 + 8) • х/Чх2 + Их + 15.
§1. Рациональные уравнения 57
Решить уравнение методом замены переменной (IV.10-IV.13).
IV.10. 1) х6 = 7х3 + 8; 2) х6 + 27 = 28х3.
IV.11. 1) 1 _ 1 = X- х2 — 2х х2 — 2х + 1 12’ 2) -s—— = 6 + х2 — 4х. х2 — 4х + 10
IV.12. 1) х + -+ v = 2,5; х X2 + 1 2) Зх + - = + 8. X х2 + 2
IV.13. 1) (х + 2) (х — 2)х(х — 4) = 20; 2) (х + 1)х(х — 1)(х — 2) = 15.
IV.14. Решить при каждом значении параметра а уравнение: 1) а(х — 1) = а2 + 2(х — 3); 2) 2 (4 - а2) х = а + 2.
IV.15. 1) Найти наименьшее целое число а, при котором
уравнение Зх2 —9х + а2 = 0 имеет хотя бы одно решение.
2) Найти наименьшее целое число а, при котором уравнение Зх2 — ах + 4 = 0 не имеет решений.
IV.16. 1) Определить, сколько общих точек имеют графики функций у = х2 2х и у = х + а в зависимости от значений параметра а.
2) Определить, сколько общих точек имеют графики функций у = ах2 — 3 и у = 2ах — 1 в зависимости от значений параметра а.
IV.17. 1) Найти все значения параметра а, при которых графики функций у = х2 — ах — а и у = (1 + а)х2 + 2х имеют не более одной общей точки.
2) Найти все значения параметра а, при которых графики функций i/ = x2 + ax + a + 2 и у = (1 — а)х2 — 2х имеют не более одной общей точки.
IV.18. 1) При каких значениях параметра а уравнение х2 + Зх + а = 0 имеет хотя бы один общий корень с уравнением х2 + х — 1 = О?
2) При каких значениях параметра а уравнение х2 + 4х + а = 0 имеет хотя бы один общий корень с уравнением х2 + 2х — 2 = О?
IV.19. Пусть Xi, Х2 — корни уравнения Зх2 — 4х — 1 = 0. Используя теорему Виета, найти:
1) Х1+Х2; 2) Xj-x2; 3) —+ —; 4) x^+XoXj;
Х1 %2
5) х2 + 2xjx2 + х^; 6) Xj + Зх2х2 + 3xix| + х^.
58 Глава IV. Алгебраические уравнения и неравенства
IV.20. 1) Вычислить значение выражения , где Х1.Х2 —
-Ч-2 -^1
корни квадратного уравнения %2 — V%x — 7 = 0.
2) Вычислить значение выражения Л* ~ —}•, где
%2 + 1 Х1 + I
%1,%2 ~ корни квадратного уравнения х2 — \/2х — \/2 = 0.
IV.21. 1) Найти все значения параметра а, при которых сумма корней уравнения 4х2 + 4(а+1)х + 1 = 0 отрицательна.
2) Найти все значения параметра а, при которых сумма корней уравнения х2 — 3(2 — а)х + 1 = 0 положительна.
IV.22. 1) Найти все значения параметра а, при которых произведение корней уравнения (а + 1)х + а — 2 - х2 = 0 неотрицательно.
2) Найти все значения параметра а, при которых произведение корней уравнения 4х2 — 4(4 — а)х — 25а = 0 положительно.
IV.23. 1) Определить, при каком значении параметра а справедливо равенство Xj=2x2, где xj, Х2 — корни уравнения х2 - (а + 2)х + 2а = 0.
2) Определить, при каком положительном значении р корни уравнения 2х2 — (р + 2)х + 7 = р2 обратны друг другу по абсолютной величине и противоположны по знаку.
Второй уровень
IV.24. Определить графически число корней уравнения:
1) {%} = -0,25х + 0,5; 2) [х] = ^--.
IV.25. Используя графический подход, решить уравнение:
1) х4(х - 1) = 16; 2) х3(2х + 5) + 8 = 0.
Решить уравнение (IV.26-IV.31).
IV.26. 1) х4 + 10х3 + 24х2 - 6х - 9 = 0;
2) х4 - 8х3 + 15х2 + 14х, - 49 = 0.
IV.27. 1) (х2 + 6х + 5) (х2+ 14х + 45) = -39;
2) (х2 - 9) (8х - 7 - х2) = 23.
§1. Рациональные уравнения 59
IV. 28. 1)
2)
IV. 29. 1)
2)
3)
4)
IV.3O. 1)
2)
3)
4)
IV.31. 1)
(х2 + х + 2)2 - 6% (%2 + х + 2) + 8х2 = 0;
14х2 - 5х(х2 - 4х - 5) - (х2 - 4х - 5)2 = 0.
х4 + 5х3 + 2х2 + 5х + 1 = 0;
2х4 + Зх3 - 4х2 - Зх + 2 = 0;
2х4 - Зх3 — Зх2 + Зх + 2 = 0;
х4 + 12х3 + 24х2 - 72х + 36 = 0.
4х।5х ____________ _3.
х2 4- х 4- 3 х2 — 5х 4- 3 2 ’
4х।Зх _
4х2 - 8х + 7 4х2 - 10х 4- 7
2х 7х _ р
Зх2 — х 4- 2 Зх2 4- 5х 4- 2
6х _ 15х2 — 20х 4- 4 15х2 — 16x4-4 15х2 — 12x4-4
(5 - х)4 + (х - 2)4 = 17; 2) (х + 4)4 + (х + З)4 - 97.
IV.32. При каждом значении параметра а решить уравнение:
х 4- За _ 1 _ 2а _____q. 2х 4-1 2х _ ах — 2 _q
х 4- а х-а х2-а2 ’ х-а а а2- ах
IV.33. 1) Пусть Xi, Х2 — корни уравнения 2х2 — 7х — 13 = 0, а у\, z/2 — корни уравнения у2, + ау + b = 0. Найти а и Ь, если г/! = J- -|- -L, а г/2 = л| %2 Xj “г %2
2) Пусть Xi, Х2 — корни уравнения 2х2 — 4х + 1 = 0, а yi, У2 — корни уравнения у2 + ау + b = 0. Найти а и Ь, Xi 4-1 Хо 4- 1
если у1 = -L—, а //2 = -•
Х2 Х1
IV.34. Пусть Х[, Х2 — корни квадратного уравнения 2х2 + 4х — 1 = 0. Не вычисляя их, найти:
1) х?+х%; 2) Xi — Х2; 3) xf + x^; 4)
z х2
IV.35. 1) Найти а, если известно, что + -L = 2, где Xj, Х2— %1 х2 корни уравнения 2х2 — (6 + а)х — а = 0.
2) Найти все значения а, при которых сумма корней уравнения Зх2 — (3 + а)х + а = 0 равна сумме квадратов корней.
IV.36. Пусть Xi, Х2 — корни уравнения х2 — ах + а = 0. При каком а выражение x24-x^ принимает наименьшее значение?
60 Глава IV. Алгебраические уравнения и неравенства
IV.37. 1) Найти все значения параметра а, при которых уравнение -4 — (а + 7) • + 9а — 18 = 0 имеет ровно два корня.
х4 х2
2) Найти все значения параметра а, при которых уравнение х8 — (а + 8)х4 + 16а — 128 = 0 имеет ровно два корня.
IV.38. 1) Найти все значения параметра а, при которых уравнение ах2 + 2(а — 1)х + (а — 3) = О имеет два различных отрицательных корня.
2) Найти все значения параметра а, при которых уравнение (1 — а)х2 + 2(а — 3)х + (4 — а) = О имеет два различных положительных корня.
IV.39. Найти все значения параметра а, при которых уравнение (4 + а) х2 — 2ах + 2а + 6 = 0 имеет корни, и определить знаки корней в зависимости от значения параметра.
IV.40. 1) Определить все значения параметра р, при которых корни уравнения 2х2+х — р = 0 меньше 1.
2) Определить все значения параметра а, при которых уравнение х2 + х + а = 0 имеет два различных корня, значение каждого из которых больше а.
IV.41. Дано квадратное уравнение х2 — х + а = 0. Найти все значения параметра а, при которых уравнение: 1) не имеет корней на отрезке [—2,1];
2) имеет два различных корня на отрезке [—2,1];
3) имеет ровно один корень на отрезке [—2,1];
4) имеет хотя бы один корень на отрезке [—2,1];
5) не имеет корней, меньших —2.
IV.42. Дано квадратное уравнение — х2+4х — За = 0. Найти все значения параметра а, при которых уравнение: 1) не имеет корней на промежутке [—1,4);
2) имеет два различных корня на промежутке [—1,4);
3) имеет ровно один корень на промежутке [—1,4);
4) имеет хотя бы один корень промежутке [—1,4);
5) не имеет корней, больших 4.
IV.43. 1) Найти все значения параметра а, при каждом из которых ровно один корень уравнения х2 + 2(а — 3)х + 9 — 2а = 0 удовлетворяет неравенству х < 2.
§2. Рациональные неравенства 61
2) Найти все значения параметра а, при каждом из которых ровно один корень уравнения х2 + 2(а — 2)х + 4 - За = О удовлетворяет неравенству х > 1.
IV.44. 1) При каких значениях параметра а корни уравнения ах2 + (2а — 1) х + 1 = 0 различны и содержатся в интервале (—1; 1)?
2) Определить значения параметра а, при которых корни уравнения х2 — ах + 2 = 0 принадлежат интервалу (0;3).
§2. РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
Первый уровень
IV.45. Используя графический подход, решить неравенство:
1) х — 3 > 2) _2_>х2_2х+1.
х 2 — х
IV.46. Используя графический подход, решить неравенство:
1 X с — х 1 .
—Ц, х> -1 х + 1
{х + 1, х < 1,
х2 - 2х - 1, 1 < х 3,
2, х > 3
и g(x) = х.
IV.47. Решить неравенство:
1) Уб(х + 3) - Зх - 6 0; 2) (х — 3)д/2 - Зх + 2 0.
IV.48. Решить неравенство:
1) (2х — I)2 3(2х - 1); 2) (1 - Зх)2 -3(1 - Зх).
IV.49. Найти область определения функции:
( \ _ / 2х — 1 । 1 q\ /1 4х 3
)У=уТ+2"+’ 2)i/=V
IV.5O. Найти область определения функции:
П — /*2 - 6х + 8 . _ / 7 х — х2 -10
У у 6 — Зх’ у 5х —10 ’
62 Глава IV. Алгебраические уравнения и неравенства
Решить неравенство методом интервалов (IV.51-IV.57).
IV.51. 1) (х+ 1)(х — З)2 > Q. х + 4 2) (± - 1) (1-2х) >0;
3) (?-4) G+Ф гО; 4) (-L - 1) (х + I)5 > 0. \ х° /
IV.52. 1) X3 — X2 + X — 1 > Q. —х — 8 2) —х4 + Зх3 — 2х2 > Q х2 — х + 30
IV.53. 1) 3 1. 2) 1 2
Зх — 1 х ’ х 2х + Г
IV.54. 1) х -f- 2 2) ——7 > х~2. 2х — 1
IV.55. 1) 1 < Зх + 1 6Х’ 2) х + 2 2х - 3
IV.56. 1) „2 2) 4 — х2 < р
х2 + Зх — 4 5 + 4х — х2
3) < 4 5; X 4) i 1 ± > 0. 3x3
IV.57. 1) 2 - Х~* п. 1 о Z> 2) 2 + х 1 Q Е 1
х 1 — 3 5 — х 1
IV.58. 1) Найти наибольшее целое ; число, удовлетворяющее
2 неравенству у-у-у . > X + 3.
2) Найти наименьшее целое число, удовлетворяющее
9 неравенству -—- > 4 — х.
IV.59. Решить систему неравенств:
Гх2Я, Ux-х3 > О,
[ (х - 2) (х + З)3 < 0; ( х2 - 8х + 7 > 0.
IV.6O. Решить совокупность неравенств:
х2 — Зх - 4 > О, Ц - 2 > О,
1) 9 2) х
_х2 - 16 < 0; |_х3 + 1^0.
IV.61. Решить неравенство:
1) Зх"1 < х6; 2) 7х“3 >х2.
Решить неравенство методом замены переменной (IV.62-IV.65), IV.62. 1) х9 10 - 31х5 - 32 0; 2) х6 + 26х3 - 27 0;
3) (х — 4)6 — 7(х — 4)3 —. 8 > 0;
4) 8(х — I)6 — 7(1 — х)3 - 1 < 0.
IV.63. 1) х2 (13 - х2) > 36; 2) х2 (101 - 4х2) < 25.
§2. Рациональные неравенства 63
IV.64. 1) 1 1 - 12 > 0; 2) - 1 < 0.
х^ ХЛ х° хч
IV.65. 1) х15 - Зх8 > 4х; 2) х11 + 2х6 < Зх.
IV.66. При каждом значении параметра а решить неравенство: 1) (х + 3)(х - а) < 0; 2) х2 + ах - 2х — 2а 0.
IV.67. При каждом значении параметра а решить неравенство: (л~ ~ 4)(х + 1) q. 2) ~ а)(х + 2) > Q
х — 2а ’ х — а — 1
IV.68. При каждом значении параметра а решить систему неравенств:
1) Р2-4<0, 2) f*2^i> [ х я; [ х + я < 0.
IV.69. При каждом значении параметра а решить совокупность неравенств:
х + 4<0, х2 + Зх + 2 О, а - х > 0; [х - а < 0.
IV.7O. 1) Найти все значения параметра а, при каждом из которых неравенство (я — 3) х2 + 2(я + 1)х + 1 + 6я О выполняется для всех действительных чисел х.
2) Найти все значения параметра я, при каждом из которых неравенство (я2 — 1) х2 + 2(я — 1)х + 1 > О выполняется для всех действительных чисел х.
Второй уровень
Решить неравенство (IV.71-IV.77).
IV.72. 1) х3 - х2 - 8х + 12 0; 2) 4х3 + 7х2 + 7х + 3 < 0.
IV.73. 1) /(х)</(х-2), если /(х) =
2) /(2х) </(3 + 2х), если /(х) =
IV.74. 1) 2 —5х^—; 2) 2х - 1 -Д-.
' 4х + 1 ' 5 - 2х
IV.75. 1) (х2 + 2х)2 - 3 (х + I)2 + 5 < 0;
2) (х2-4х)2 — (х —2)2 + 2<0.
IV.76. 1) (х4-х2 + 1) (-х2 + 4х + 5) >0; 2) —> 0.
' 4х4 — Зх2 — 1
64 Глава IV. Алгебраические уравнения и неравенства
IV.77. 1) (1 + х)3 + (1 + х)2(2 + 3х) — 2(2 + Зх)3 > 0;
2) (6 — х)(х — 2)(х + 3)(х + 9) > 24х2.
IV.78. При каждом значении параметра а решить неравенство:
1) (х + а)(х + 1) < Q. 2) (х-а)(* + 3) g х — a ’ х + a
IV.79. 1) При каждом значении параметра а решить неравенство а — х2 — 1 < q а + 2х — 4
2) При каждом значении параметра а решить неравенство
IV.8O. 1) Найти все значения параметра а, при каждом из кото-ах2 + 2(а + 1)х + 9а + 4
рых неравенство -----1-------------- < 0 выполняется
для всех действительных чисел х.
2) Найти все значения параметра а, при каждом из х2 — 2х -4- 2
которых неравенство —3 3 > а выполняется для
всех действительных чисел х.
§3. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Первый уровень
IV.81. Используя графический не имеет корней:
1) х/х = —х2 + 6х - 8;
подход, показать, что уравнение
2) Vx — 2 — 1 — у/х.
IV.82. Определить графически число корней уравнения:
1) \/х + 3 = —4 — х; 2) х/12 — х = 8 — х;
3) 2\/х - 3 - - х - 3; 4) л/х+~4 ='х - 8.
IV.83. Решить уравнение аналитически и дать графическую интерпретацию полученного решения:
1) д/7 — 2х + 2 = х; 2) 2>/1 — х - 7 = х.
Решить уравнение (IV.84-IV.86).
IV.84. 1) Зл/5^х + 1=х; 2) х = л/Зх + 7- 1.
IV.85. 1) л/х + 8 - х + 2 = 0; 2) 7Ю-х + 9 = х.
IV.86. 1) WTZx = v/r=Fi; 2) У26 - х2 = $х=1.
§3. Иррациональные уравнения 65
IV.87. 1) При каких значениях b число 1 является корнем уравнения \/7х — 2b = b — 2х?
2) При каких значениях а число 2 является корнем уравнения х/2х — 3tz = a + х?
IV.88. Найти абсциссы точек пересечения графиков функций:
1) у = х + 1 и у — \/9 - х2 -Ь 2х;
2) у — х/22 — 4х — х2 + 2 и у = х.
Решить уравнение (IV.89-IV.91),
IV.89. 1) х + Vx4 - 20 = 0;
IV.90. 1) yiO + у/х2 -5 = 3;
IV.91. 1) ^Е + х/Т^х =
V1 — х у 1 — х
2) х + х/х4 - 2х — 19 = 1.
2) У\/7ТТ - 16 = -2.
2) х/3 + х + х/6 + х —
v 3 +
IV.92. Решить уравнение и дать графическую интерпретацию
полученного решения:
1) 7х +VT^X= 1; 2)
у/х + х/4 — х = 2>/2.
IV.93. Решить уравнение и дать графическую интерпретацию
полученного решения:
1) д/2х - 6 + ^/х + 4 = 5; 2) V3x 6 = 5 х/Г^Т.
Решить уравнение (IV.94-IV.101).
IV.94. 1) 2-^х + ^х = 10;
IV.95. 1) 9</7^5 + 5 = 2x/F75;
IV.96. 1) х-9^/^ +20 = 0;
2) З дД-5-д/х = 2.
2) 2^Т+9-7^ГГ9 = 4.
2) Хх/~х + 3х +\/—х +3 = 0.
IV.97. 1)
2)
Зх±6 _2 = 0
IV.98.
IV.99.
IV.1OO.
IV.101.
1) х/х + 4 = 2х-7;
1) х2 + Ух2+ 20 = 22;
2) —^== + 2х/ГП = 5.
1 + ух+ 1
2) х/* — 5 = х — 11.
2) х2 + \/х2 + 2х + 8 = 12 — 2х.
IV.1O2.
3—5682
При каждом значении 1) х/%^3 = а-1; 2)
2) ^ = да-1.
Vх +1
параметра а решить уравнение: (я+ l)y/x + a = a2 - 1.
66 Глава IV. Алгебраические уравнения и неравенства
IV.103. При каждом значении параметра а решить уравнение: 1) у/х — 1 = \/а — 2х; 2) у/х — а = ау/х.
Второй уровень
Решить уравнение (IV.104-IV.114),
IV.104. 1) Vx + З + \/2х^1 = 4; 2) у/х±4 + 2 = у/4^х.
IV.105. 1) у/х + у/х^З = у/2х + 1\ 2) /Ю^х- у/х = \/х-5;
3) у/2х = у/2х — 4 + 2\/Зх — 3;
4) л/12 — х = \/х — 2 + у/2х + 6.
IV.106. 1) y/x(x + 2) + (x + 2)J^=x + 4\
IV.107. 1) \/хП- = у/х1 - 1;
2) 2Х1 — Зхл/З + х = 2(3 + х).
IV.108. 1) у/х3 - 4х + 24 = 4х - х3 - 12;
2) у/—х3 + 5х +13 = 2х3 - 10х - 23.
IV.109. 1) </х + 9- УГЛ0 = 1; 2) s/x + 50 - </7^48 = 2.
IV.110. 1) ^2l+3 + ^xTT=l; 2) ^2x^T+s/x^T=l.
IV.lll. 1) ^+T+^T2 + ^+3 = 0;
2) ^+#21^3= s/12(x- 1);
3) ^x + #5x + 3 = Ж + 3;
4) Ж +a/6x^5 = ^32x - 5.
IV.112. 1) #24 + x + 712^7 = 6; 2) y/2^x = 1 - 7x^1-
IV.113. 1) y/x + y/2^x + \/x2 - 3x = y/2\ ,
2) \/4x — x2 — 3 + -\A2 ~ 5x + 6 = л/бх — x2 — 8.
IV.114. 1) Vx=-— -3y ; 2) -L-6v/x = V12x-2.
v бхД + УбТ^З 7 y/x v
IV.115. При каждом значении параметра а решить уравнение у/х2 — а —2 — х — а.
IV.116. Определить, при каких значениях параметра а уравнение \/я + 13х = — 1 — Зх не имеет корней.
§4. Уравнения с модулем 67
§4. УРАВНЕНИЯ С МОДУЛЕМ
Первый уровень
IV.117. Определить графически число корней уравнения: 1) х + 2 |х + 1| - 2 = 0; 2) (х - 2)2 = 1 - |х|.
IV.118. Определить графически число корней уравнения: 1) |х + 3| - |х + 1| = 2; 2) |х - 4| + |х — 1| — 6.
Решить уравнение (IV.119-IV.132).
IV.119. 1) |2х — 1|=х;
IV.12O. 1) |3х —5| = 5 —Зх;
IV.121. 1) |2- х| + к + 3| = 6;
IV.122. 1) |2 + х| = 8- |х —6|;
IV.123. 1) |х2 + 5х + 4| =х + 1;
IV. 124. 1) к±3|-1=4;
IV.125. 1) |-х2- 4| =5х;
3) |х + 4-Ух + 4| = 1+4-Ух;
IV.126. 1) |2х2 — 43| = 7;
3) |х2 + 2х - 8| = 7;
IV.127. 1) |х- 1| = -х4;
3) |х + 1| = —х2 — 4;
IV.128. 1) |х + 1| = 2|х-1|;
IV.129. 1) 0,125-|1-х|-|х —3| = 1;
IV.13O. 1) х - 1| = |х2 - Зх + 2|;
IV.131. 1) х2-х —3 =-1-х;
IV.132. 1) х7-х-1 = х —1;
2) |3х-2|==2х.
2) 7 + 4х = ]—4х — 7|.
2) |5 - х| + |х - 2| = 5.
2) |х + 3| = 2 + |х + 5|.
2) |х2 - 9| 4- (х - 2)(х + 2) = 5.
__74- Зх ___I
' |х+1|-6 — ’
2) |х — 2\fx + 11 — \[х 4- 1;
4) |-9 - у/х\ = у/х + х2.
2) |27 — х| = л/6 - 3;
4) |х 4~ 11 — л/7 — л/З — 1.
2) х - х3| + |х2 + х - 2| = 0;
4) х2+х|+х/хТТ=0.
2) 4|х-6| = |х + 9|.
2) 0.25 • |1+х| • |2 - х| = 1.
2) х24-6х4-3| = |х2 + 4х + 5|.
2) х2 + 2х - 4| + 2х + 6 = 0.
2) х4 — х + 1| = 1 - х4.
IV.133.
Найти абсциссы точек пересечения графиков функций: 1) у = |2х + 6| 4- |2х — 6| и у = х + 12;
2) у = |х — 1| + |х 4- 1| и у —2.x2.
Решить уравнение (IV.134-IV.137).
IV.134. 1) х • |х + 1| + |х| • (х + 1) = 4;
2) х • |х 4- 3| 4- |х| • (х4- 3) = — 8.
IV.135. 1) |х3 - 2| = |х3 -х + 2|; 2)
IV.136. 1) |3 —|5 —х|| = 3; 2)
IV.137. 1) |4Vx - 2| =х + 1; 2)
8х + ^-4| = |8х-^-4|. X хА I I X Xs I
|3х 4-2| — 1| = 3.
71^1+ 1| + |л/ГЛ- 1| -4.
68 Глава IV. Алгебраические уравнения и неравенства
IV.138. Решить уравнение:
1) х2 - 6 |х| - 7 = 0; 2) (х + I)2 + 2 |х + 1| = 3.
IV.139. Реш ить уравнение:
1) х2 — 2х + |х — 1| = 1; 2) х2 - 3 |х - - 2| = 4х.
IV.140. Решить при каждом значении параметра а уравнение:
1) (a— 1) • ]х| = 1; 2) я-|х| = я2 — а.
IV.141. Реш ить при каждом значении параметра а уравнение:
1) |х — tz| — 2х; 2) |ах| = х.
IV.142. При каждом значении параметра а определить число корней уравнения:
1) |х| — |х — 2| = а; 2) |х| + |х + 3| = а.
Второй уровень
Решить уравнение (IV.143-IV.150).
IV.143. 1) х2 - 4 |х + 1| + 5х + 3 = 0; 2) х2 - 6 |х - 2| - 8х + 11 = 0.
IV.144. 1) |х-3| = Ух2 + 4х + 4 + 5;
2) \А2 + 2х + 1 + \/4 — 4х + х2 = 4.
IV.145. 1) |х2 — 1| + |х2-4| = 3; 2) |х2 - 9| + |х + 3| = х.
IV.146. 1) |х2 + 3х- 10| + |х2-25| = 55;
2) х2 + 5х - 6| - Vx4 - 2х2 + 1 = 10.
IV.147. 1) х2 - 6х - 1б| + |2х + 4| = 13;
2) х2 + 3х — 10| +2\/*2 —4х + 4= 10.
IV.148. 1) 4х3 — 4х — \/2 =4х3 + \/2;
2) 9х3 — 6х — х/З = 9х3 + \/3.
IV.149. 1) л/2х^7 + 22 = -х + |2х+1|;
2) 3-x/F+l= v/(2x-2)2.
IV. 150. 1) ^4 — х + 4у/=3: = 4 — \/4 — х — 4\Л^х;
2) \/х + 6\/х — 9 + \/х — 6\/х — 9 = 6.
IV.151. При каждом значении параметра а решить уравнение:
1) |х —я|=2х + 1; 2) |х— 1|=ях.
IV.152. 1) Найти значения параметра а, при которых уравнение
—р---:— = я — 2х имеет бесконечно много корней.
§5. Иррациональные неравенства 69
2) Найти значения параметра а, при которых уравнение х + 5% 6 — 2а2 — 15 не имеет корней.
|х-1|
IV.153. Определить, при каких значениях параметра а имеет ровно три корня уравнение:
1) (|х —2| -а-4) (а4-6 + х2-4х) =0;
2) (а 4- |х — 4| - 2) (16 - а-\-х2 — 8х) = 0.
IV.154. 1) При каких значениях параметра а уравнение 3|х —а| + + 2я — 3-|-х = 0 имеет корни и все корни удовлетворяют неравенству —2^х^5?
2) При каких значениях параметра а уравнение 3|х-я|4-+ а + 2 — 2х = 0 имеет корни и все корни удовлетворяют неравенству — 1 х 4?
IV.155. Для каждого значения параметра а определить число корней уравнения:
1) |х2 —2х —3|=а; 2) ^/2 |х| — х2 = а.
IV.156. 1) Найти все значения параметра а, при которых уравнение |х + 3| — а |х — 1| = 4 имеет ровно два корня.
2) Найти все значения параметра а, при которых уравнение |х — 2| + а |х + 3| = 5 имеет бесконечно много корней.
§5. ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
Первый уровень
IV.157. Используя графический подход, решить неравенство:
1) \/6 — х < —х; 2) у/х — 5 х — 11;
3) \/1 — л: — 1; 4) \/х 4- 1 < —х - 2.
IV.158. Используя графический подход, решить неравенство:
1) у/3 + х>-\ 2) у/2х^1^-^—.
X 1 —X
Решить неравенство (IV.159-IV.163).
IV.159. 1) \/5-х2^-1; 2) ^/х(х4-3) > 2;
3) \/5 - 9х2 > 2 - д/5; 4) \/х3 - 11 > 4.
IV.160. 1) у/х2 -4x^1-V2; 2) \/Зх^2<2;
3) \/-х2- 10х<4; 4) \ДТЮ<-?-1.
70 Глава IV. Алгебраические уравнения и неравенства
IV.161. 1) у/х-у/5-х<2; 2) \/Зх + 2 • л/% + 1 < 2.
IV.162. 1) у/5х2 + 6х + 5,4 > \/х2 + 5х + 4;
2) у/Зх — 1 • \/х + 2 > 2 у/х;
3) \/х3 — 1 < у/х^; 4) \/х2 — 4 — д/х2 + Зх + 2.
IV.163. 1) х/ТТх^УГП^х; 2) </2 + х • </2 - х <
IV.164. Найти область определения функции:
1) £/=\/1-л/2х^Т; 2) у= \/1-у/5^4х.
Решить неравенство (IV.165-IV.172),
IV.165. 1) \/2 + х>х—10; 2) \/7 — х^х— 1;
3) 3\/2 — х>х — 4; 4) \/6 —5х^х —2.
IV.166. 1) у/х2 + 2х — 8 > х — 1; 2) \/2х2 — 18х + 40 — х + 1 0
3) у/х2 + х — 2>х; 4) \/5х2 — 20х+15 — х 2.
IV.167. 1) \/2х + 9^3 —х; 2) х — 1>\/5 — 2х;
3) \/2х—1 — х + 2^ 0; 4) у/х + 7 — х^1.
IV.168. 1) \/Зх —х2<4 —х; 2) >/2х2 — Зх — 5 < х — 1;
3) \/3 + 2х — х2 4 - 2х; 4) >/2х2+ 5х —3 < х +1.
IV.169. 1) у/х 2 ~Ь у/х +1^0; 2) у/х -|- 6 -|- у/2 — х -|- 4 0.
IV. 170. 1) у/2 +х +у/2 —х>2; 2) д/1 + х 1 - у/\ - х.
IV.171. 1) (х-2)-л/х + 1^0; 2) (1-х2)-х/2х-1^0;
3) у/х — 2 • л/4 + х • (х2 — 9) 0;
4) у/\ — х-у/х + З-у/х + 2- (4 — х2) С 0.
IV.172. 1) (10 - х2) • у/х - 3 > 0; 2) ^1^0;
3) ^х + 3 V5-x-(х2-1) >0; 4) ^_zl°^t|L>0.
Решить неравенство (IV.173-IV.176),
IV.173. 1) х + 2д/х— 15 >0; 2) х — у/Г^х + 6<0.
IV. 174. 1) ^-^>3; 2) —= СЗ, 2 — у/х. 1 — 2^/х
IV.175. 1) ~^=-у/2-х<2-, 2) -^=-4Vx + l<l.
IV.176. 1) Ху/х-\-Х2 >Q. 2) — X -j- х2 — 2х ~i~ 1 >Q х — 3 х 4-1
IV.177. При каждом значении параметра а решить неравенство: 1) у/2 + x^a; 2) у/х + 3 4 — а.
§5. Иррациональные неравенства 71
IV.178. При каждом значении параметра а решить неравенство:
1) \/2а + х \/2 — х; 2) %/2х — а у/х + 4.
Второй уровень
Решить неравенство (IV.179-IV.197),
IV.179. 1) \/х -|- 3 <с — \/х', 2)
IV.180. 1) \/-х2-4х+х-Н >0; 2)
IV.181. 1) \/х3+х2 — 2х +1 х; 2)
IV.182. 1) /2~х> £• ух+3 2’ 2)
IV.183. 1) у 1 + 2х 2)
IV.184. 1) \/Зх - х2^х3-28; 2)
IV.185. 1) 1 1 . \/3—х х — 2 ’ 2)
IV.186. 1) -4=Х<7+\/5-х; ух — 2 2)
IV.187. 1) х2 — \/ х2 — 2х < 2х +12; 2 2)
IV.188. 1) —.х-— — 4 \/5х — 6 + Зх < у/5х — 6 :0;
IV.189. 1) \/1-х2 + 1<\/3—х2; 2)
\/1-х> -д/х2 —1.
1 —\/13 —Зх2>2х.
\/х2 + 34х + 64 х2 — 2х — 8.
\/2х —х2 >х3- 10.
1
-/1 +х 2 — х
уХ-<4+УЗ-х.
л/Х — 1
2\/х2+х — х>х2 — 8.
2) ^L-2y/3^x-3x^0. у/З — Х
2—\/1-х2> \/4 — х2.
IV.190. 1)
IV.191. 1)
IV.192. 1)
IV.193. 1)
IV.194. 1)
3)
4)
IV.195. 1)
3)
IV.196. 1)
IV.197. 1)
\/5х+7—л/Зх+1>\/х+3; 2) х/х+2 —\/х—2 —\/х —5>0.
\/10—2х+\/3—х^\/1+^; 2) \/4х —8+\/х-1^\/3—х. \/х2-2х-\/х2-х—2<1; 2) \/х2-4х+3-\/х2-5х+4<1.
5х+л/4—х2<\/5х+2; 2) 4х+-\/25-х2<\/4х+5.
(х-1)-\/х2—х — 2^0; 2) х-у/х2+х- 2 3 л/х2 +х—2;
(2х2 — Зх - 4) • \/ х3 —2х2—2х+4 0;
(х2 -9) • \/х2-4х-12^ (41 —х2) • \/х2—4х—12.
(х —3)\/х2+4^х2—9;
(х + 1) Зх>х2—х—2;
2) ^2х~5>-1 4—х
-\/5х Ч~ 11 ।
X -|- 1
,4х~5 <5; \/х2 — 1 — 1 Зу<х-5 <5. \/х —1 —1
2)
2)
^3. \/х2—2 —1 7у/х — 9
\/х—2—1
72 Глава IV. Алгебраические уравнения и неравенства
IV.198. Решить неравенство:
1) х3+y/x^8+V%', 2) \/х — 4+у/х>6—х;
3) v^+v^+3+x/*+8< р 4) х2+2х+\А+2^3+\/3.
IV.199. При каждом значении параметра а решить неравенство: 1) у/Ъх+а^х-, 2) у/а—х>Чх.
IV.2OO. При каждом значении параметра а решить неравенство: i\ (х-1)-х/а^х<0. 2) (х—а)-\/х2 —a2
} х—2 ’ 7 х+3 ’
§6. НЕРАВЕНСТВА С МОДУЛЕМ
Первый уровень
IV.201. Используя графический подход, решить неравенство:
1) 2 |х—2|<х+1; 2) |х-3|>|х+2|-5.
IV.2O2. Используя графический подход, решить неравенство:
1) |х| + |х+2|<2х+6; 2) |х+3| — |х—3|^2х.
Решить неравенство (IV.203-IV.205).
IV.203. 1) |3-6х|^4-2х; 2) |х+2|^7+0,5х.
IV.204. 1) |х- 1|+|х-2|^3; 2) |х+3|^2-х-|х+5|;
3) х-1|+4^2 |х|; 4) |х-2| + |х|^7-|х+4|.
IV.205. 1) 2 |х| — |х2 — 4х|>х; 2) |х2-Зх+2|-12-х|^4.
IV.206. 1) При каких значениях х график функции г/=|2х+2| лежит выше графика функции г/=3+|х-2|?
2) При каких значениях х график функции г/=|х+1| лежит ниже графика функции у=7— |2х—5|?
IV.207. Решить неравенство:
1) |4-5х|^-3; 2) |4—х|>0;
3) |3+х|<1-л/2; 4) |9-х2|^0.
IV.208. Решить неравенство:
1) х2—Зх —1|>3; 2) х2—х —1|^1;
3) х2-х —4|^2; 4) х2-2х-1|<2.
IV.209. Найти область определения функции:
2> *=\/1нН-
§6. Неравенства с модулем 73
IV.210. Решить неравенство:
1) |13—2х|^|4х—9|; 2) |х2-3х-3|>|х2+7х-13|;
3) 3 |х+1|^|х+5|; 4) |х-3|-|х—2|<|х2—Зх—1б|.
IV.211. Решить неравенство:
1) х2<2 |х+1|; 2) |Зх+5|<х2+1.
IV.212. Решить систему неравенств:
Г |х+4|М, ( |х+3|^4,
' ( |х+3|^5; > | |х+1|^6.
IV.213. Решить систему неравенств:
Г |2х—0,8| <0,75, Г |4х—0,5| <0,8,
' | Зх+7^5(2-х); } | 6(1-х)^5-2х.
IV.214. Решить систему неравенств:
( х2-4х|<5, Г |х2+5х|<6, ' \ х+1|<3; ' | |х+1|^1.
Решить неравенство (IV.215-IV.220).
IV.215. 1) 2|х+1|Мх+2;
3) 3 |х+11 ^х+5;
IV.216. 1) х2-х— 1|<х+2;
3) х—3|-|х+1|<3х—3;
2)
4)
2)
4)
х2-3х—3| >3x4-4; х3—х2 — 11 >х2 — 1. х2—4х—4 ^х2-4; х3-2х-4 ^2х-4.
IV.217. 1) (|х—1|+2) (|х|—3)<0;
IV.218. 1) (х- 1)-|х—3|>|3—х|;
IV.219. 1) (|х| —1)2>2;
IV.220. 1) |\/х+5—1|<3;
2) (|х2 —3| —1) (л/х+7)>0.
2) |х—2|-(х2 —9)^0.
2) (|х+1|-2)2^4.
2) |\/х+7—2|<5.
IV.221. Решить неравенство:
1) 3 |х —1|>(х-1)2+2; 2) (х-2)2-4 |х-2|>5.
IV.222. При каждом значении параметра 1) |х—2|^а-1; 2) |х+о:|<2а:—3. а решить неравенство:
IV.223. При каждом значении параметра 1) |х+1|>2—а\ 2) |х-а|1+3а. а решить неравенство:
IV.224. При каждом значении параметра 1) а|х+1|^3; 2) (а-1) |х+3|^1. а решить неравенство:
74
Глава IV. Алгебраические уравнения и неравенства
Второй уровень
IV.225. Используя графический подход, решить неравенство:
1) 2) ^-1>|х-1|.
Решить неравенство (IV.226-IV.231)
IV.226. 1) - ^1; 2х-1| 2) 1 >5 3-2л-|
IV.227. 1) |2х+4|-2| <3; 2) |2х+4|—2|>3.
IV.228. 1) 1 < - 2) _2_ л-
х-9| 4х-11 х—6 х+2
IV.229. 1) x-_2H.t+2| (): х — 1 2)
3) л-2|-2|х+1| <0; 4) ! <2.
X х 31 — | х—21
IV.23O. 1) х2 —8х—9 +4х>3; 2) х2+Зх-10|+7>5х.
IV.231. 1) 6\/4 — 2х—81^5—2х; 2) 16л/2^х-25 ^11-2х.
IV.232. Пр л каждом значении параметра а решить неравенство
1) |2х—4|^3х+2а; 2) |5х+3|^2х—За.
IV.233. При каждом значении параметра а решить неравенство: 1) |х+а| + |х—а|<4; 2) |х—3а| + |х+3а|^5.
IV.234. 1) Определить, при каких значениях х оба неравенства |х+у|^1, |х—Зу|^2 выполняются хотя бы для одного значения у.
2) Определить, при каких значениях х оба неравенства |2х+3у|6, |х—2у|^5 выполняются хотя бы для одного значения у.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ IV
Решить уравнение (IV.235-IV.238).
IV.235. 1) </ГЙ5=4-У97^х; 2) ’ </х^2+</19-х=3.
IV.236. v/F:3+\/5zx=x2-8x+18.
IV.237. УЗх+5-273х+4+У4х+5+47х+Т=57^+Т.
IV.238. 5^/1 + |х2-1|=3+|5х+3|.
IV.239. Доказать, что не имеет корней уравнение:
1) \/3—х+х—А=\/х—2\ 2) V*+4+\/3—х=х2—8х+21.
Задачи повышенной сложности к главе IV 75
IV.240. Решить неравенство:
1) (x+3)2^4(x+l)X+2; 2) 2(х+1 )2+(2х+1)\/4х+3.
IV.241.
1) Пусть /(х) = х 14л+3~» g(x) = v^- Решить неравенство /feMW(4)- %
2) Пусть [(х) = \/2х—7, g(x) = 3х^~22х+^35 Решить неравенство f(4)^g(f(x+3)).
Решить неравенство (IV.242-IV.252).
IV.242.
IV.243.
IV.244.
IV.245.
IV.246.
IV.248.
IV.249.
1) ^6%+12,5+3,5>х;
1) 06-У132-И^<4-х;
\/2х3 27х2+90х~> г-2х-15 ’
1) ^4х3~12х+8 ^747+7;
2) л/х/16х+"36+6 х.
2) 0-2 \/19+81х3<3+Зх.
2)
у/х3 — Зх+2 х+0,5
+ л/х+Т.
\Z243'tx+32X->9~l%l- IV*247*
1) к2-5х+В| + |9-2х|-5 <Q \/19х2—4х3—4х+19
1) у/(х —3) (—х+5)> — \/х—3 — 1 + V—*+5;
______\/—х2—2х+3________ |х2+2х—3| — |х2+6х+5| |х2-2х+0,75| + |2х+2|-5
\/2х3 -4-2,5х2+2х-|-2,5
2) vX-7-l< vXX5+\/(x+7)(-x-5).
IV.25O. 1) ----J.____2) ------------------- *______<
6— ух2-2х—8 vx2+32 4—\/х2—2х—15 ух2+7
IV.251. 1) Х +-------5 . > 1 .
х-! 6—3\/б+х—х2 1 + к~1|
2) J-+_______5 >___L_
х+! 6—За/4 —Зх—х2 1 + |*+1| ’
IV.252.
IV.253. При всех допустимых значениях параметра а определить количество корней уравнения
х4+2ах2+х+а2+а=О
и найти их.
IV.254. Найти все значения параметра а, при каждом из которых из неравенства (а2+а—2) х2 — (а+5)х-2^0 следует неравенство
76 Глава IV. Алгебраические уравнения и неравенства
IV.255. При всех допустимых значениях параметра а определить количество корней уравнения
х/х—4а + 16=2 \/х—2а+4—>/х
и найти их.
IV.256. Найти все значения параметра а, при каждом из которых имеет единственное решение уравнение:
1) х/х - 9 = ах + 7 а — 3; 2) х/х — 8 = ах — За — 2.
IV.257. При каждом значении параметра а решить неравенство:
1) 3(2х — а) + 5а\/2х — а — 2а2 > 0;
2) 2(а — х) — а^/а — х — а2 > 0.
ОТВЕТЫ К ГЛАВЕ IV
IV.1. 1) Один; 2) два; 3) три; 4) корней нет. IV.2. 1) Один; 2) три.
IV.3. 1) -1; 2) 0,5. IV.4. 1) -2; 2) -1. IV.5. 1) -0,5; 2) 0,5.
IV.6. 1) -3; 1,6; 2) 4; IV.7. 1) -1; 2) -8; 3) 3; 4) 0,5.
IV.8. 1) — 3; —2; 2) -4;-3; 3) -2; 2; 4) -5. IV.9. 1) -7; 2; 4; 2) -2,5; 2. IV.1O. 1) -1; 2; 2) 1; 3. IV.11. 1) -1; 3; 2) 1; 3. IV.12. 1) 1; 2) 1;
2. IV.13. 1) 1 ± х/П; 2) IV.14. 1) Если а = 2, то х-любое
действительное число; если а / 2, то х = а + 3; 2) если а = 2, то корней нет; если а = — 2, то х — любое действительное число; если а ± ±2, то х= . .
4 — 2а
IV.15. 1) —2, 2) —6. IV.16. 1) При а < —0,25 общих точек нет, при
а — —0,25 одна общая точка, при а > —0,25 две общие точки; 2) при—2<а^0 общих точек нет, при а = —2 одна общая точка, при а<— 2 и а>0 две общие точки. IV. 17. 1) ( —оо; — | j U {0} U [2; +оо); 2) ( — оо; — 2] U {0} U [|; +оо). IV.18. 1) ±х/5, 2) ±273. IV.19. 1) 2) 3) -4; 4)
5) 6) IV.2O. 1) -^; 2) 2^2. IV.21. 1) [0;+оо); 2) (-оо;|].
IV.22. 1) (-оо;-7] U [1; 2]; 2) (—оо; —16] U [—1: 0). IV.23. 1) 1 и 4; 2) 3. IV.24. 1) Пять; 2) одно. IV.25. 1) 2; 2) -2. IV.26. 1) -2 ± у/7, -3±х/б; 2) 1,5±0,5\/37. IV.27. 1) -5±\/3, -5±У13; 2) 2±х/2, 2±2х/б. IV.28. 1) 1; 2; 2) 3 ± У14; IV.29. 1) -2,5 ± 0,5х/21; 2) ±1;
—2; 0,5; 3) 0,5±0,5х/5, 0,25± 0,25\/17; 4) -3± х/15. IV.30. 1) ~5±
2) 3,5; 0,5; 3) 4) И-^2-^. IV.31. 1) 3; 4; 2) -1; -6.
IV.32. 1) Если а 0 и а —0,5, „то уравнение имеет корни xj = —За, х2 = а + 1 (при а — — | они совпадают); если а — 0, то х = 1; если 2
а = —0,5, то х = 1,5; 2) если а ± —1, а ± 0 и а то уравнение
Ответы к главе IV 77
имеет корни х\ = —1, х% = 1 — 0,5а (при a = 4 они совпадают); если 2
a — — 1, то х = 1,5; если a = то х = — 1; если a = 0, то корней нет.
IV.33. 1) а = -^, 6=--Ь 2) а = -10, b = 7. IV.34. 1) 5; 2) ±\/б;
3) 24,5; 4) -5 ± 2\/б. IV.35. 1) -2; 18; 2) О; 3. IV.36. a = 0.
IV.37. 1) (-оо; 2] U {11}; 2) a < 8; а = 24. IV.38. 1) а G (—1; 0) U (3; 4-оо);
2) а G (—оо; 1) U (4; 5). IV.39. Уравнение имеет корни при а Е [-12;— 2];
при а G [—12;— 4] корни положительны (при a = — 4 корень один); при a G (—4; —3) корни разных знаков; при a = — 3 один из корней равен нулю, а другой отрицателен; при а G (—3; —2] корни отрицательны. IV.40. 1) ре [-1;3); 2) aG(-oo;-2). IV.41. 1) a G (-ос; -6) U +ос) ;
2) a G [0; 1) ; 3) a G [-6; 0) U {; 4) а G [-6; |] ; 5) a G [-6;+оо).
IV.42. 1) aG (-oo;-g)u(g;+oo); 2) а G (О; g) ; 3) a G [-g; о] U {g } ;
4) a e [~|; g] ; 5) a G [0; +oo). IV.43. 1) а < -0,5, а = 4; 2) а > 1,
а = 0. IV.44. 1) ^^<a<2; 2) [2\/2;у). IV.45. 1) [—1; 0) U [4; 4-оо); 2) [0;2). IV.46. 1) (—оо; —1) U (—1;0); 2) (-оо; 1]. IV.47. 1) (—оо; \/б]; 2) (—оо; — \/2]. IV.48. 1) (-ею; 0,5] U [2;+оо); 2) (-сю; 1] U [|; +оо).
IV.49. 1) (—оо; —2) U [—|;+оо); 2) (—0,5;2]. IV.5O. 1) (-ос;2) и (2;4];
2) (-сю; 2) U (2; 5]. IV.51. 1) (—оо; —4) U ( —1; 3) U (3; 4-оо); 2) (0; 0,5] U
U[l;+oo); 3) {-0,5} U (0; 0,5]; 4) (—оо; — 1) U (0; 1). IV.52. 1) (-8;!];
2) [1;2] U {0}. IV.53. 1) 2) (-оо;-0,5) U (0;оо).
IV.54. 1) (-4;-2)U(3;+oo); 2) (-oo;-l,5)U(0,5;4). IV.55. 1) (-|;+оо); 2) (1,5; +oo). IV.56. 1) (-4;—1) U [| ;+оо); 2) ( —сю;—1) U
U (-0,25; 5); 3) (—оо;0) U (0,25; 2); 4) [-2; 0) U [6;+оо).
IV.57. 1) (—оо;0) U (0;|) U [g;+oo); 2) (-оо;0) U (0;0,2) U [^;+оо).
IV.58. 1) —4; 2) 5. IV.59. 1) (—3;—1] U [1;2); 2) (-оо;-2) U
U (0; 1). IV.60. 1) (—оо;4) U (4; +оо); 2) (—оо;—1) U (0; 0,5).
IV.61. 1) (—oo;0)U (^3;+оо); 2) (О; </?]. IV.62. 1) (—оо; — 1] U [2;+оо); 2) [-3;!]; 3) ( —оо; 3) U (6;+оо); 4) (0; 1,5). IV.63. 1) [-3; -2] U [2; 3];
2) (-оо;-5] U [-0,5; 0,5] U [5;+оо). IV.64. 1) [-0,5; 0) U (0;0,5];
2) (-oo;-2)u(2;+oo). IV.65. 1) (—l;0)U (^4; +оо); 2) ( — оо; — ^з)и(0; 1). IV.66. 1) Если a < —3, то х G (а; —3); если a = —3, то решений нет; если a > —3, то х G (—3; а); 2) если a < —2, то х G (—оо; 2] U [—а;+оо); если а = —2, то х G (—оо;+оо); если а > —2, то х G (—оо; — а] U [2; +оо). IV. 67. 1) Если a < —0,5, то х G (2а;—1] U [4; +оо); если а = —0,5, то xg[4;+oo); если —0,5 < а < 2, то х G [—1; 2а) U [4; 4-оо); если а = 2, то х G [—1; 4) U (4;+оо); если а > 2, то х G [— 1; 4] U (2а; +оо); 2) если а < —3, то х G (а; а + 1) U (—2;+оо); если а = —3, то х G ( — 3; — 2) U (-2; +оо); если
78 Глава IV. Алгебраические уравнения и неравенства
—3 < a < —2, то хе (а; —2) U (а 4- 1; +оо); если a = —2, то хе ( — 1; +оо); если
a > —2, то х е (—2; а) U (а + 1; +оо). IV.68. 1) Если а У —2, то х е (—2; 2);
если —2 < а < 2, то хе [а; 2); если а 2, то решений нет; 2) если a < — 1, то х е (—оо; — 1] U [1; — а); если — 1 У a < 1, то х е ( —оо; — 1]; если а 1, то хе (—ос; — а]. IV.69. 1) Если a < —4, то хе (—оо;—4); если
а —4, то х е (—оо;а]; 2) если а У —2, то х е (—ос;—2] U [—1;+оо); если -2 < a < -1, то хе (—оо; а) U [-1;+оо); если a —1, то
х е (-оо;+оо). IV.7O. 1) (-оо;-0,2]; 2) [1;+оо). IV.71. 1) (-оо; 1) U
U (1; 2) U {3} U [4; 5); 2) [0; 1) U (1; 2) U {3} U [4; +оо). IV.72. 1) (-оо;-3]и
U {2};
IV.74. 1)
2) (-оо;-0,75). IV.73. 1) (1,5;3,5); 2) (-оо;-1) U (0,5;оо).
— оо;
3- У89. 3+ \/89
40 ’ 40
2)
3- УЗ. 3+ Уз
2 ’ 2
U (2,5; +оо).
2) (2 — Уб; 2 - Уз) U
IV.75. 1) (-1-УЗ;—1 - У2) U (-1 + У2;-1 + Уз);
U (2+УЗ;2+Уб). IV.76. 1) (—1;5); 2) (-оо; — 1) U (—1; 1) U (1;Ч-оо).
IV.77. 1) (—оо;—0,5); 2) (-6; U (з; IV,78. Если
a < — 1, то х е (—оо; а) U (—1; —а); если a = ±1, то х е ( —оо; — 1) U ( —1; 1); если — 1 < a < 0, то х е ( —оо; — 1) U (а; —а); если a — 0, то х е (—оо; —1); если 0 < а < 1, то х е (—оо; — 1) U (—а; а); если a > 1, то х е (—оо; —а) U (—1; а); 2) если
a < —3, то х е (—оо; а] U [—3; —а); если a = —3, то х е (—оо;3); если —3 < а < 0, то х е ( —оо; —3] U [а; —а); если a = 0, то х е ( — оо; — 3]; если 0 < а У 3, то х е (—оо;-3] U (-а; а]; если a > 3, то х е (—оо; — a) U [—3; а]. IV.79. 1) Если а < 1, то хе (4 ~ а; +оо); если а = 1, то х е {0} U (4 ~ а; +оо); если 1 < а < 2, то х е [—Уа — I; Уа — 1] U ( 4 ~ ; +оо); если а — 2, то х е [—Уа — 1; +оо); если 2 < а < 10, то хе [—Уа — 1; 4 ~ U [Уа — 1; +оо); если а = 10, то х е [Уа — 1; +оо); если а > 10, то хе (4 ~ —Уа — lj U [Уа — 1; +оо); 2) если а < —0,5, то х е (—оо; 2а — 3] U — 2; —2^; если а = —0,5, то х е (—оо; —2); если —0,5 < а < 0, то х е оо; — 2^ U [2а — 3; —2); если а — 0, то х е [2а — 3; —2); если 0 < а < 0,5, то х е [2а — 3; —2) U — 2; +оо); если а = 0,5, то хе — 2; +оо); если 0,5 < а < 1, то хе (—2; 2а — 3] U — 2; +оо); если а = 1, то хе (—2; +оо); если а > 1, то хе ^—2; — 2^ U [2а — 3; +оо). IV.80. 1) а у -0,5; 2) а у |. IV.82. 1) Корней нет; 2) один; 3) два; 4) один. IV.83. 1) 3; 2) -3. IV.84. 1) 4; 2) 3. IV.85. 1) 5+/4Т;
2) 17 +A IV.86. 1) 2; 2) 5. IV.87. 1) 3; 2) 0. IV.88. 1) 2; 2) 3. IV.89. 1) -Уб; 2) -Уб. IV.90. 1) ±2; 2) 3. IV.91. 1) Нет корней; 2) —2. IV.92. 1) 0; 1; 2) 2. IV.93. 1) 5; 2) 5. IV.94. 1) 64; 2) 16. IV.95. 1) 630; 2) 4087. IV.96. 1) -2; 2) -1. IV.97. 1) 0,5; 2) -3.
Ответы к главе IV 79
IV.98. 1) 9; 2) 3. IV.99. 1) 5; 2) 14. IV.100. 1) ±4; 2) -4; 2.
IV.101. 1) 64; 2) 0; 1. IV.1O2. 1) Если a < 1, то корней нет; если a 1, то х-а2 — 2а + 4; 2) если а G (-ос; — 1) U ( — 1; 1), то корней нет; если а — — 1,
то х G [1; -1-ос); если а 1, то х — а2 — За + 1. IV.103. 1) Если а < 2, то корней нет; если а 2, то х = а- + 1; 2) если а G (—ос; 0) U {!}, то корней нет; если а = [0; 1) U (1; +ос), то х = — -Ц,IV.104. 1) 52 — 8х/39; 2) —2\/3.
1 - а
IV.105. 1) 4; 2) 5; 3) 2; 4) 2. IV.106.
IV.1O7. 1) 2) -0,75; 6. IV.108. 1) -3;
2) -77; 75. IV.110. 1) -1; 2) 1. IV.111. 1)
4) 0; 1; Д. IV.112. 1) -24; 3; -88; 2) 1; 2; 10.
1) -4;-^; 2) -4;ДД-.
2) 3. IV.109. 1) -17; 18;
— 2; 2) 1; 3; 3) 0; 1; - ~;
IV.113. 1) 0; 2) корней нет
IV.114. 1) Ь 2) 1 IV.115. Если аЕ (-ос; -1] U (0; 2], то х = а-
2 6 2а
если а е (—1; 0] U (2; +оо), то корней нет. IV.116. ti<y. IV.117. 1) Два корня; 2) корней нет. IV.118. 1) Бесконечно много; 2) два. IV.119. 1) 1;
|; 2) 2; 0,4. IV.12O. 1) (—ос; |]; 2) [-^;+оо). IV.121. 1) -3,5; 2,5;
2) 1; 6. IV.122. 1) [-2;6]; 2) (-сю;-5]. IV.123. 1) -1; 2) [-3;3]. IV.124. 1) 2; 2) -0,5. IV.125. 1) 1; 4; 2) 0; 9; 3) корней нет; 4) 3.
IV.126. 1) ±3\/2, ±5; 2) корней нет; 3) —5; 3; — 1 ± \/2; 4) корней нет.
IV.127. 1) Корней нет; 2) 1; 3) корней нет; 4) —1. IV.128. 1) 3;
2) 3; 11. IV.129. 1) -1; 5; 2) -2; 3. IV.130. 1) 1; 3; 2) -4; -1; 1.
IV.131. 1) 1-х/5, -\/2; 2) -2-^2, -Ую. IV.132. 1) ^2; 2) 0;
IV.133. 1) 0; 4; 2) -1; 1. IV.134. 1) 1; 2) -4. IV.135. 1) 4,--^-,
0; 2) -1, 1. IV.136. 1) -1; 5; И; 2) -2; |. IV.137. 1) 9 - 4\/5;
1; 9; 2) 5. IV.138. 1) ±7; 2) 0; -2. IV.139. 1) 0; 2; 2) -2; 6. IV.140. 1) Если а 1, то корней нет; если а > 1, то х = ± 1 j-; 2) если
а е ( — ос; 0) U (0; 1), то корней нет; если
а — 0, то х — любое действительное
число; если а> 1, то х = ±(а— 1); если а= 1, то х = 0. IV.141. 1)Еслиа^0,
то х = если а < 0, то х = — а; 2) если а = ±1, то х 0; если а / ±1, то х = 0.
IV.142. 1) Если а е (—ос; —2) U (2;+оо), то корней нет; если а = ±2, то корней бесконечно много; если а G (—2; 2), то корень один; 2) если а С (—оо;3), то корней нет; если а = — 3, то корней бесконечно много;
о fir < л *> 1 \ —14- —9 — \/53 7 -|- \/26
если а > 3, то два корня. IV.143. 1) -------------------2---- ---------2--’
IV.144. 1) (—оо;—2]; 2) -1,5; 2,5. IV.145. 1) [—2; — 1]U[1;2]; 2) корней нет. IV.146. 1) -7,5; 6; 2) -1,5; -1; 3. IV.147. 1) -3; 4-^23; 2) 3; 5 .
IV.148. 1) -Д=, Д=, 0; 2) ±^, 0. IV.149. 1) 28; 2) 21 ~ ; 0.
у/2 V2 3 7 ’ 8
80 Глава IV. Алгебраические уравнения и неравенства
IV.150. 1) [—4;0]; 2) [9; 18]. IV.151. 1) Если а —0,5, то х = — a — 1; если a > —0,5, то х = а Г ; 2) если a < — 1, то х = —?—; если —1 a < 0, то корней 3 1 -|“ CL
нет; если a — 0, то х = 1; если 0 < а < 1, то xi = , х? = ’> если а > 1, то
1 1 + а z 1 - a
х=р-^. IV.152. 1) -3; 2) [—2;2]. IV.153. 1) a = -4, a = -2; 2) 0; 2. IV.154. 1) [—0,2;!]; 2) [2;3]. IV.155. 1) При а<0 корней нет; при а = 0 и а >4 два корня; при 0<а<4 четыре корня; при a = 4 три корня; 2) при а < 0 и а > 1 нет корней; при a = 0 три корня; при 0 < а < 1 четыре корня; при а = 1 два корня. IV.156. 1) — 1 < а < 1; 2) a — ±1. IV.157. 1) (—оо; — 3); 2) [5; 14]; 3) {1}; 4) решений нет. IV.158. 1) [—3; 0) U (1; +оо); 2) (1;+оо).
IV.159. 1) [—ч/5;\/5]; 2)
(—оо; —4) U (1;+оо); 3)
IV.160. 1) Нет решений; 2) [|;2) 3) [—10; —8) U (—2; 0]; 4) нет решений. IV.161. 1) [0; 1) U (4;5]; 2) [-|;|). IV.162. 1) (-оо;-4] U [-1;+оо);
2) [|; +оо); 3) [1;+оо); 4) -2. IV.163. 1) [-1;2]; 2) [-2;-%/2).
IV.164. 1) [0,5; 1]; 2) [1; 1,25]. IV.165. 1) [-2; 14); 2) (—оо;3]; 3) (-оо;2]; 4) (—оо; 1,2]. IV.166. 1) (—оо;—4] U (|;+оо); 2) (-оо;3] U [13;+оо);
3) (—оо; —2] U (2;+оо); 4) (-оо;0,5] U [5,5;+оо). IV.167. 1) [-4,5; 0];
2) (2; 2,5]; 3) [5;+оо); 4) [2;+оо). IV.168. 1) [0;3]; 2) [2,5; 3);
3) [—1; 1]; 4) [0,5; 1). IV.169. 1) [0; +оо); 2) [-6;2]. IV.17O. 1) (—2;2); 2) [—1; 1]. IV.171. 1) {-1} U [2;+оо); 2) [1;+оо) U {0,5}; 3) [2;3];
4) {—2; 1}. IV.172. 1) (3;УЮ); 2) (-3;-2] U [2;+оо); 3) (-3; -1) U U (1;5); 4) (-6;-5) U (-5;+оо). IV.173. 1) (9;+оо); 2) (-оо;-4).
IV .174. 1) 2^;4); 2) [О; 1] U (|;+оо) . IV.175. 1) (-оо; 1); 2)(0;+оо). IV.176. 1) {0}и(3;+оо); 2) (-1;1). IV.177. 1) Если a < 0, то решений нет; если a = 0, то х = — 2; если a > 0, то хЕ — 2; а2 — 2 ; 2) если a > 4,
то х Е [-3;+оо); если а 4, то х Е [а2 — 8а + 13;+оо). IV.178. 1) Если
а < —1, то решений нет; если a — — 1, то х = 2; если а > —1, то х Е [1 — а; 2]; 2) если а —8, то х Е [а + 4;+оо); если а < —8, то х Е [—4;+оо). IV.179. 1) Нет решений; 2) (-оо;-1]. IV.180. 1) f ~3~ ^;0 ;
Г /13 2 — У88\
2) Гуз'1-~)'
2) (1;2]. IV.183.
IV.181. 1) 1; 2) [-2;3 + х/10]. IV.182. 1) (-3;1);
1) ( —оо;—1] и [—0,2;0]; 2) U [|; +оо).
L О 10 J /
IV.184. 1) Нет решений; 2) [0;2]. IV.185. 1) (-оо;2) U
2) (-1; U IV.18.6. 1) [0;4) U (4; 5); 2) [0; 1) U (1;3).
IV.187. 1) (1- х/17;0] U [2; 1 + д/17); 2) f-1+<^;-l
U О;^-1).
Ответы к главе IV
81
IV.188. 1) (2; 3); 2) (—оо; — 1] U [2; 3). IV.189. 1)
'с Г>.| 2У37\
5’—з— )
2) (—оо; 1] U
IV.191. 1) 3;
U (^;1 . IV.190. 1) 2)
2) 2. IV.192. 1) (-оо; 1~^5) U[2;+oo):
IV.193. 1)
-До)и(О;2];
IV.194. 1) {-1} и [2;+оо); 2) {-2; 1} U [3;+оо);
2) [-4=;0) U (0;5].
L VI/ /
и Г2. З + х/41'
□ {-V2}; 4) [-5;-2] U {6}.
IV.195. 1) (—оо; — |] U [3;+оо);
. , (8 + 2^ , \
U I 3 - ; +оо I.
4
2) [2,5; 4) U (7; +оо); 3) (-1; 0] U (4;+оо); 4) [-2,2;-1) U (5;+оо).
IV.196. 1) (-оо;-У2) U [1;У2) U [|; +оо); 2) (-оо;-л/3) U [У2; 1,5) U
U [л/3;+оо). IV.197. 1) [1; g] U (2;+оо); 2) [2; 3) U [Ц;+оо).
IV.198. 1) [0;2]; 2) [4; +оо); 3) (0; 1); 4) [1;+оо). IV.199. 1) Если
a < — 1, то решений нет; если — 1 а 0, то х G [1 — -/1 + а; 1 + \/1 + а]; если
a > 0, то хе [—0,5а; 1 + \/1 + а]; 2) если а < 0, то х G (—оо;а]; если а 0,
то \ —оо; + д6д — ). IV.200. 1) Если a 1, то х = а; если 1 < а < 2, то
хе [1;а]; если а = 2, то хе[1;2); если а > 2, то хе[1;2)и{а}; 2) если а < —3, то х е (—оо; а] U [—а;+оо); если a = — 3, то х е (—оо; —3) U [3;+оо); если — 3 < а С 0, то хе (—оо;-3) U [—а;+оо); если 0 < а 3, то хе(-оо;-3)и[а;+оо); если а>3, то хе(-оо;-а]и[а;+оо). IV.201. 1) (1;5);
2) (-оо;3). IV.2O2. 1) (-2;+оо); 2) (-оо;3]. IV.203. 1)
2) [-4|; К)]. IV.204. 1) [0;3]; 2) [-10;-2]; 3) [-3; 5]; 4) [-1; 1].
IV.2O5. 1) (3;5); 2) ( —оо;1 — \/5] U[4;4-oo). IV.206. 1) ( — оо; — 7) U (1; +оо); 2) IV.2O7. 1) (-оо;+оо); 2) (—оо;4) U (4;+оо); 3) нет
решений; 4) ±3. IV.208. 1) (—оо; —1) U (1; 2) U (4;+оо); 2) [-1; 0] U [1; 2]; 3) (—оо; —2] U [—1; 2] U [3;+оо); 4) (-1; 1) U (1; 3). IV.2O9. 1) [2,4; 3,6];
2) (-оо;2|] U [5^;+оо). IV.21O. 1) [-2; Н]; 2) (-оо;-4) U (1;2);
3) (-оо;-2] U [1;+оо); 4) (-1; 5) U (11;+оо). IV.211. 1) (1 — л/3; 1 + %/3);
2) (—оо;—1) U (4;+оо). IV.212. 1) {-8} U [0;2]; 2) {-7} U [1;5].
IV.213. I) [|;|1); 2) [1; g). IV.214. 1) (-1;2); 2) (-2;0].
IV.215. 1) ( — оо;0]; 2) (—оо;—1) U (7;+оо); 3) (—оо; —2] U [1; +оо);
4) (-оо; ^2) U (2;+оо). IV.216. 1) (—1;3); 2) [1 + \/5; +оо); 3) (2; 5);
4) 2. IV.217. 1) (—3;3); 2) [0; У2) U (2;+оо). IV.218. 1) (2; 3) U (3; +оо); 2) (-оо;-3] U {2} U [3;+оо). IV.219. 1) (-оо;-1-д/2) U (1 + У2; +оо);
2) (—оо; —5] U {-1} U [3;+оо). IV.22O. 1) [-5; 11); 2) [-7;42).
82 Глава IV. Алгебраические уравнения и неравенства
IV.221. 1) ( —1; 0) U (2; 3); 2) (—оо; —3) U (7;+оо). IV.222. 1) Если a < 1, то решений нет; если a = 1, то х — 2; если a > 1, то х е [3 — a;a + 1];
2) если a > 1,5, то х G (3 — 3a;a — 3); если а 1,5, то решений нет.
IV.223. 1) Если а < 2, то х
то х — любое действительное
действительное число; если а
IV.224. 1) Если а > 0, то а 0, то решений нет;
1 / 2 — 3а1 . .
а > 1, то х G ( —ос:-------- U
\ а - 1 J
2) (-1; 0) U (0; 1). IV.226. 1) [—1.5; 0,5) U (0,5; 2,5];
IV.227. 1) (-4,5; 0,5); 2) (—оо; —4,5) U (0,5; 4-оо).
е ( —оо;а — 3) U (1 — а; 4-ос); если а 2, число; 2) если а — |, то х — любое > — то х G ( — ос; —2а — 1] U [4а + 1; 4-ос).
/ 3 1 Г 3 \
х е -оо;—-- —1 U-----------1;+ос ; если
\ ' a J La /
2) если а 1, то решений нет; если IV.225. 1) [0; 1) U (1; 4-оо);
2) [1.4; 1,5) U (1,5; 1.6].
IV.228. 1) (-оо; U \ 4 /
U{4}U [8 + У26;+оо); 2) (-оо;-2)U{2}U [4 4-2л/5;+оо). IV.229. 1) (0;1);
2) (—оо; —2) U (—1; 1) U (д/2; 4-ос); 3) (-4; 0) U (0;+оо); 4) (-ос;-0,5) U
U (-0,25; +оо). IV.23O. 1) (-оо;-2) U (6 - х/42;+оо); 2) (—оо; —4 4-\/33) U U(3;+oo). IV.231. 1) {—2,5} U [1,5;2]; 2) {-14} U[l;2], IV.232. 1) Если а 6 (—оо; -3], то х е [—4 — 2а; 4-ос), если а <Е (—3; 4-оо), то х G [0,8 — 0,4а; 4-ос);
2) если a е (—оо;—0,4), то х G (—ос; j U [—а — 1; +оо), если а 6 [—0,4;+оо), то х G 1R. IV.233. 1) При |а| 2 решений нет,
при |а| < 2 х Е (-2,2); 2) при |а| - х — любое действительное
число, при |а| < -, х <Е ( —оо; —2,5] U [2,5;+оо).
IV.234. 1) [-1,25; 1,25];
2> [-
IV.238. ( —оо; —1] U {0,2}. IV.240. 1) 1 + 2\/2; 2) . Указание: если
все выражения перенести в левую часть, то левую часть можно будет представить как квадрат некоторого выражения. IV.241. 1) [9:18)U(18;25];
2) [8,5; 13) U (13;+оо). IV.242. 1) [-у;3]; 2) [-2,25; 4].
у; у . IV.235. 1) 16; 96;
2) 3; 18.
IV.236. 4. IV.237.
О
IV.243. I) [-^;V5); 2) Д
IV.244. [0; 5] U {6} U (7,5; 9].
IV. 245.
IV.246.
IV.248.
1) [-1|;-1) и - 1;+оо);
(-ос;-9) U (-1,5; 0) U (4,5; 13,5).
2)
2) [—l;0,5)U Зч/^6~17;+оо).
IV.247. [—3; — 2) U (-2 + У3;1].
IV.249. 1) (4— \/4%/5 —8;5];
2) [-7;-6+ 74^5-8). IV.25O. 1) (-оо; 1-Зл/5) U {-2} и (1 + Зл/5;+оо);
2) (-оо; 1 -4>/2) U{-3}U (1+ 4V2; +оо). IV.251. 1) [-2; -1) U (1; 1,2) U (2; 3];
2) 1-4;-3) и (—1: -0,8) U (0:1]. IV.252. [-^о) и (2; |) U (|;1|).
L 1U / \ ч / \ Ч 1о /
IV.253. Если а < —0,75, то уравнение имеет четыре корня Хц2 =
Ответы к главе IV 83
= —0,5 ± 0,5\/1 — 4a, х3<4 — 0,5 ± 0,5л/— 3 — 4a; если a = -0,75, то уравнение имеет два корня х\ = —0,5 + 0,5/1 — 4a и %2 = 0,5; если —0,75 < a < 0,25, то уравнение имеет два корня х^2 = —0,5 ± 0,5/1 — 4a; если a = 0,25, то уравнение имеет один корень х=— 0,5; если a > 0,25, то уравнение не имеет
корней. IV.254. — IV.255. Если a Е (—оо;0] U [8; +оо), то х = ~;
если аб(0;8), то уравнение не имеет корней. Указание: избавиться от иррациональности, дважды возведя уравнение в квадрат; затем сделать проверку, подставив полученное значение переменной х в исходное уравнение. / з \ ] ----
IV.256. 1) я 6 0; — , а = Указание: после замены /х — 9 = t задача \ 16/ 4
сводится к исследованию квадратного уравнения (случай а = 0 следует
/ 2 \ 1
рассмотреть отдельно); 2) аЕ 10; ^1, а = IV.257. 1) Если а < 0, то
х G ^2а2 + +оо); если а ( 2 \ х G 1 —оо; а — ~ 1; если а > \ 4 / 0, то х G Г ; +оо ); 2) если а < 0, то \1о 2 / : 0, то х 6 оо; а — а2) .
Глава V
ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ
§1. ТРИГОНОМЕТРИЧЕСКАЯ ОКРУЖНОСТЬ
Первый уровень
1. Градусная и радианная меры угла
V.I. Найти радианную меру угла, равного:
1) 1°; 2) 15°; 3) 18°; 4) 75°; 5) 105°; 6) 270°
V.2. Найти градусную меру угла, равного:
1) 0 радиан; 2) 1 радиан; 3) радиан;
4) 2 радиана; 5) л: радиан; 6) 2д радиан.
V .3. Заполнить таблицу:
Радианы л 6 л 3 л 2 Зл т 5л т Зл Т
Градусы 45° 120° 180° 360°
2. Точки тригонометрической окружности, соответствующие заданным числам, их декартовы координаты
V .4. Отметить на тригонометрической окружности точки, соответствующие числам:
q л л л л 2тг Зл 5 тг 7л 5л 4л Зл 5л 7л Пл
’ 6’ 4’ 3’ 2’ У’ Т’ Т’ 7Г’ Т’ Т’ Т’ Т’ Т’ Т’ “б"'
V .5. Отметить на тригонометрической окружности точки, соответствующие числам (задача будет считаться выполненной, если точки правильно помещены в координатную четверть и верно расположены друг относительно друга):
1) 0; 2) 1; 3) 1,57; 4) 1,58; 5) 2; 6) 3; 7) 3,14; 8) 3,15;
9) 4; 10) 4,71; 11) 4,74; 12) 5; 13) 6; 14) 6,28; 15) 6,30; 16) 7.
V.6. Отметить на тригонометрической окружности точки, соответствующие числам:
1) 2л-п, ц е Z; 2) л-п, п е Z; 3) • п, п G Z;
4) у • п, п е Z; 5) — £ + 2тпг, п с Z; 6) — лп, п е Z;
4 2 2
§1. Тригонометрическая окружность 85
7) -ЗД + 2тш, neZ; 8) + neZ.
4 4 2
V.7. Отметить на тригонометрической окружности точки, соответствующие числам:
1) n€Z; 2) nGZ; 3) п Е Z; J J ь
л \ IZfT — гт? гт \ ТГ । 2 7Г/2 _ Гт? /2 \ ТГ . ТГИ гт?
4) neZ; 5) -+ •, neZ; 6) - + /iGZ;
1 £ О О
7) тг+^, rceZ; 8) 7Г+?, neZ.
5 5
V.8. Отметить на одной тригонометрической окружности точки, соответствующие данным числам, и указать на координатных осях их декартовы координаты:
л л. . Зл. л. 2л. 4л. 5тг. л. Зл. 5л. 7л. я. 5л. 7л. Пл
и,2,7Г’Т’ з’Т’Т’Т’ 4’Т’Т’Т’ 6’ Т’ Т’ "б
Отметить на тригонометрической окружности точки с заданными координатами и указать, каким числам они соответствуют (V.9-V.12).
V.9.1)(l;0); 2) (0; 1); 3) (-1;0); 4)(0;-1).
V.1O.1)(^);
V.13. Отметить на тригонометрической окружности точки с заданными ординатами и указать все числа из отрезка [—2тг,2тг], которым эти точки соответствуют:
1) 1; 2) -1; 3) 4)
V.14. Отметить на тригонометрической окружности точки с заданными абсциссами и указать все числа из отрезка [—2д, 2тс], которым эти точки соответствуют:
1) -1; 2) 1; 3) 2^; 4)
86 Глава V. Тригонометрические формулы
3. Пересечение и объединение числовых множеств, соответствующих точкам тригонометрической окружности
V.15. Задать формулой пересечение множеств:
1) гДе 2) — £ + я/г, где
2 2 4 2
3 ) где 4) , £+2л:£, где n,ke%.
оо о 2
V.16. Задать формулой пересечение множеств:
1) + тот, ±^ + 2тс^, где n,k€%;
2) J + тг/г, где n,ke%. О □
V.17. Задать одной формулой объединение множеств:
1) кп, ~ + nk, где 2) + у, где
3) л:+^, где 4) ^ + тот, у + тс/г, где n,ke
4. Аналитическое задание дуг тригонометрической окружности
V.18. 1) Выделить на тригонометрической окружности дугу, ординаты точек которой положительны, и задать аналитически множество соответствующих ей чисел.
2) Выделить на тригонометрической окружности дугу, абсциссы точек которой неотрицательны, и задать аналитически множество соответствующих ей чисел.
3) Выделить на тригонометрической окружности дугу, ординаты точек которой отрицательны, и задать аналитически множество соответствующих ей чисел.
4) Выделить на тригонометрической окружности дугу, абсциссы точек которой отрицательны, и задать аналитически множество соответствующих ей чисел.
V.19. 1) Выделить на тригонометрической окружности дугу, абсциссы и ординаты точек которой неотрицательны, и задать аналитически множество соответствующих ей чисел.
2) Выделить на тригонометрической окружности дугу, абсциссы которых отрицательны, а ординаты положительны, и задать аналитически множество соответствующих ей чисел.
§1. Тригонометрическая окружность 87
3) Выделить на тригонометрической окружности дугу, абсциссы и ординаты точек которой отрицательны, и задать аналитически множество соответствующих ей чисел.
4) Выделить на тригонометрической окружности дугу, абсциссы которых положительны, а ординаты отрицательны, и задать аналитически множество соответствующих ей чисел.
V.20. 1) Выделить на тригонометрической окружности дугу, ор-динаты точек которой больше и задать аналитически множество соответствующих ей чисел.
2) Выделить на тригонометрической окружности дугу, абс-
циссы точек которой меньше и задать аналитически множество соответствующих ей чисел.
3) Выделить на тригонометрической окружности дугу, ор-
4)
V.21. 1)
динаты точек которой меньше и задать аналитически множество соответствующих ей чисел.
Выделить на тригонометрической окружности дугу, абс-„ . У2
циссы точек которой больше — —и задать аналитически множество соответствующих ей чисел.
Задать аналитически лежащую в правой полуплоскости дугу тригонометрической окружности, концами которой (л/2 х/2 \
—: --- I.
2) Задать аналитически лежащую в верхней полуплоскости дугу тригонометрической окружности, концами которой являются точки с координатами Q; и (—1;0).
3) Задать аналитически лежащую в нижней полуплоскости дугу тригонометрической окружности, концами которой являются точки с координатами 0 и (0;1).
4) Задать аналитически лежащую в левой полуплоскости дугу тригонометрической окружности, концами которой являются точки с координатами и (О;-О-
88 Глава V. Тригонометрические формулы
Второй уровень
V.22. Найти пересечение множеств:
О Л/? л/? 1 гп ТГ/? Л& 1 гп
~г, n,keZ; 2) —, —, rz,Ai€Z; и 4 3 4
о \ Л । КЛ Kk i гр л \ । Л/? Л& 1 гп
3) о + ^Г- ~л' 4) 71+—, —, tl,k(E%.
Z 3 4 3 6
V.23. Найти пересечение множеств:
1 \ ТГ I ТГ/? ТГ . Ttk 1 ryi 0 \ ТГ । ТГ/? /Г । Ttk < 171
2б+Ю' 4+У n’*£Z’ 2) * 2б+ 10’ 12 + ТГ "-AeZ’
3> 18 + Т’ 12 + Т' MeZ’ 4) ~I8 + V “9+Т’ n'k^
§2. СИНУС, КОСИНУС ТАНГЕНС И КОТАНГЕНС
Первый уровень
1. Вычисление значений синусов, косинусов, тангенсов и котангенсов углов
V.24. Отметить на одной тригонометрической окружности точки, соответствующие указанным углам, и указать их координаты на линиях тангенсов и котангенсов:
л. к. Зтг. тг. 2тг. 4тг. 5л. л. Зл. 5л. 7л. л. 5л. 7л. Пл и’2;7Г’Т; з’Т’Т’Т’ 4’Т’Т’Т’ 6’Т’T’"б"’
V.25. Опираясь на рисунки, выполненные при решении задач V.8 и V.24, заполнить таблицу (если значение не определено — поставить прочерк):
t 0 £ |CO 1 л 2 2л T Зл Т 5л Т 4л Т 7л т 8л -т Зл Т 13л Т _3л 2 11л V
sin t
cos t
ctgf
V.26. Найти а, если:
1) sin а = - | и
3) sinot=^ и
у <а<-д;
2) cosa= —и —жа<—
4) cosa=| и — 2тг<а<-у.
§2. Синус, косинус тангенс и котангенс 89
V.27. Найти а, если:
1) tgа = 1 и — /г < а < —
2) о V в V к |см 1 S (со 1 II йо "о
3) tg а = — и — ~ < ct < —тс, 6 Уз 2
4) ctga=l и —2тг<а<—у.
V.28. 1) Найти числовое значение выражения sin a —cos а, если известно, что sin и 8тг < а < 9тг. 4 2
2) Найти числовое значение выражения \/2-(sin ^ — 2cos . a , 5л 7л если известно, что sin - = — 1 и — <а<-у
Решить уравнение, используя модель тригонометрической окруж-
ности (V.29-V.32).
V.29. 1) sin t=0; 2) sin/=l; 3) sin Z = — 1;
4) sin^=^~; 5) sin£= — 6) sin2t=~-,
7) = 8) sin^ = |; 9) sin (&+ \ О / £ £ \ и /
V.30. 1) cos/ = 0; 2) cos/=l; 3) cos/= —1;
4) cos£=^; 5) cos/=|; 6) cos(—=
7) о о C/5 tOl ~ 1 to 1 W1 00 о о C/5 + w| Я II 1 toi —
9) А л\ У2 cos АГ“Т'
V.31. 1) tg^ = O; 2) tgf=l; 3) tgf = -1;
4) tg^x/3; 5) tg/ = —\/3; 6) tg(2/) = -^=;
7) <rq Уч'Г' T 05 1 Я II 1 SA
V.32. 1) ctg£ = O; 2) ctgf=l; 3) ctg/=—1;
4) ctg^ = x/3; 5) ctg^-x/3; 6) ctg(/-^ = -^;
7) ct&l = -"7=< 6 3 ^3
90 Глава V. Тригонометрические формулы
Найти наименьшее и наибольшее значения выражения (V.33-V.35).
V.33. 1) cosa-1; 2) 1 — sin а; 3) 1 —3cosa; 4) 2-3sina.
V.34. 1) l + 4sina, если ^а^; 2)3 — 2cosa, если О^а^;
о 2 3
3) 1 —2tga, если — ^^а^ — р 4) 3 + 5ctga, если
V.35. l)2+sina, если 2)cosa—2, если —
4 3 о 3
3) 2 —8 sin а, если — ^^а^ 4) 2 — 3 cos а, если — ^а^
6 4 6 3
2. Определение знаков синусов, косинусов, тангенсов и котангенсов углов
Определить знак выражения (V.36-V.38),
V.36. 1) sin 158°-cos (-222°)-tg(— 144°)-ctg92°;
2) cos 134 ° - sin 272 ° • tg 95 ° • ctg(-27 °).
V.37. 1) sin 0,4л?cos 0,9л:-tg ^--ctg
2) cos0,6tt-sin (—1,2л:)-ctg -tg
V.38. 1) sin 1-cos (—1,5)-tg4-ctg6,2;
2) ctgl,7-sin (—2)-cos6-tg2,5.
V.39. Сравнить:
1) tgl,2jr и cos 1,4л:; 2) cos 4 и sin 7.
V.40. Определить знак выражения:
D (tg3 — ctg7)-cos2-sin 4; 2) (sin6 —cos6)-tg4-ctg2.
V.41. Решить неравенство:
1) |x|-ctg9>cos9; 2) |x|-tg3> — sin3.
V.42. Решить неравенство:
1) (д/х —2 — 1) - cos 2 > 0; 2) sin 3-\/1 — х —tg3- \/1 — х> 0.
V.43. Определить знак выражения:
1) cos2a, если ^<a<-^;
2) tg3a, если ^<а<^; 3) sin если 2д<а<3л:;
о 3 2
о а 2л „
4) ctg-, если — <а<д.
§ 2. Синус, косинус тангенс и котангенс 91
3. Сравнение и оценка значений синусов, косинусов, тангенсов и котангенсов углов
Не пользуясь калькулятором, сравнить значения выражений (V.44-
V.46)
V.44. 1) sin у и sin 2) cos у и cos у;
3) tgy и tg|; 4) ctg у и ctg у.
V.45. 1) sin 2 и sin 3; 2) cos 2 и cos3;
3) tg2 и tg3; 4) ctg2 и ctg3.
V.46. 1) tgl500° или tg 1501 °; 2) sin 1300° или sin 1301 °;
3) cos 1700° или cos 1699°; 4) ctg 1750° или ctg 1751 °.
V.47. He пользуясь калькулятором, определить наибольшее
и наименьшее из чисел:
1) cos 1000°, sin 1000°, tglOOO0;
2) cos2900 °, sin 2900 °, ctg2900°.
V.48. He пользуясь калькулятором, определить знак выражения:
1 /о" о\ * 17тг . \/3
1) 2) sin — +
>/2 21л7 . 19тг . ,
3) -Y~cos“iy; 4) ctg Tf + L
4. Формулы приведения
Упростить выражение, , используя свойства синуса, косинуса,
тангенса и котангенса (V.49-V.54).
V.49. 1) sin (а+6д); 2) зш(а-4д); 3) зш(3а+д);
4) sin (—а— д); 5) 51п(а+3д); 6) sin (5д—2а).
V.50. 1) sin (77 +а); 2) sin (-у - а); л \ • [ 3 тс । of \ 3) sm(y + ^;
4) sin (а— 0; 5) sin (—а — ; 6) sin (у—4а).
V.51. 1) cos (а + 8д); 2) соз(бд-а); 3) соз(7а + д);
4) cos ( — а— д); 5) со5(а+5д); 6) cos (Зд— у).
V.52. 1) cos (д+ 2) cos у — а); о \ ( 3 тг об \ 3) C0S\'F~5/’
92 Глава V. Тригонометрические формулы
4) cos (а— ^);
V.53. 1) tg(a+3;c);
4)
V.54. 1) ctg(5n:+a);
4) ctg(a+^);
V.55. Вычислить:
5) cos (—а — ^);
2) tg(a—2л:);
5) tg(a+y);
2) ctg(—2л:—а);
5) ctg(-a+y);
6) cos — 3a).
3) tg(—2а-л:);
j /5л a\
6) tg(y-2).
3) ctg (g —3л;);
6) ctg (-у-2a).
1) sin960°-cos495°-tg(-840°);
2) sin585°-cos (—930°)-ctg510°;
3) sin (-570°)-cos870°-tg945°;
4) sin 1020 ° • cos 675 ° • ctg (-1050 °).
V.56. Вычислить:
.4 2cos196 ° + 12 cos 164 °
’ cos 16 °
ox 2 sin 204 ° — 10 sin 156 °
~ sin(—24°)
5 cos 70 ° — 2 sin 160 ° . cos 110 °
sin 20 ° — 3 cos 110 °
sin 160 °
Второй уровень
Решить неравенство (V.57-V.60).
V.57.1)sin^0; 2)sin/^^; 3)sin2^|;
V.58.1) cos ^0; 2)cos/< —3)cosj^ —
V.59. l)tg/>0; 2)tg^V3; 3) tg3/^-1;
V.60.1) ctg/^O; 2)ctg^l; 3)ctg^>--^;
V.61. Найти a, если:
1) sin a = cos 1812° и 90°<a<270°;
2) ctga=tg988° и 180°<a<360°.
V.62. Сравнить:
1) sin2 и sin8; 2) cosI'h cos7;
3) tg3 и tg 12; 4) ctg(-l) и ctg6.
• (j. k\ \/2 4)sm
4)cos(2«-f)<^.
4М3Ч>7у
4)ctg
§3. Тригонометрические формулы 93
V.63. Сравнить:
1) sin 2 и sin 0,5; 2) cos 2 и cos 4,5;
3) sin 4 и sin 5,5; 4) cos 5 и cos 7,5.
V.64. Извлечь квадратный корень:
1) у0^25 —sin 1 + sin2 1; 2) \/ 4 cos2 3 + 4 cos 3 +1.
V.65. 1) В каких четвертях расположен график функции y = tg5-x — cos 8?
2) В какой полуплоскости расположен график функции у~х2 sin 4 —cos 6?
V.66. 1) Найти все решения неравенства %2+ 2% + cos 5 < 0, лежащие в промежутке — 2 + % + —
2) Найти все решения неравенства tg^+бх —%2>0, лежащие в промежутке
§3. ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ
1. Зависимости между синусом, косинусом, тангенсом и котангенсом одного угла
Упростить выражение (V.67-V.70),
V 67 1) sin cy+tgcy . l+ctgc*. 2) cosac~ctg°f 1 — tgсу 1+cosa 1 + tga’ 1 — sin a 1—ctga'
V.68. 1) 1-sin4a + ctg (у-4«У cos4a;
2) cos (-2a)+ctg (—7i-2a) -cos (y +2a).
v 69 1) tg3cy 1 —ctg2 3a. 2) ctg(270°-2a) ctg2 (360°-2a)+ 1
7 tg23a—1 ctg3a ’ 7 1 + tg2 (2a—180°) ctg(180° +2a)
V.7O. 1) sin2 a-ctg2 a + sin2 a—1; 2) ctg2 a + sin2 a-ctg2 a-cos2 a;
3) cos2 (n:-a) + cos2 (y — a);
4) ctg2 (y - a) -cos2 (тс+a) +sin2 +
V.71. Вычислить:
1) cos2 10°-sin2 100°; 2) cos220°+ cos2 110°.
94 Глава V. Тригонометрические формулы
V.72. Вычислить:
1) sin2 13° + sin2 77°-tg2 225°;
2) cos2 21 ° 4-cos2 69 °-ctg 135 °.
V.73. Извлечь квадратный корень:
1) \/l —cos2 4; 2) у/ 1 + tg2 2; 3) \/1 —sin2 5; 4) 14-ctg2 6.
V.74. 1) Найти tga, если cosa = — | и ^<а<д.
2) Найти ctga, если sina=-^ и ^<а<д. v5 I
3 T7”
V.75. 1) Найти sin a, если tga = 3 и л:<а<^.
3 7Г
2) Найти cos а, если ctga=2 и д<а<у.
V.76. 1) Найти значение выражения —, если tga=—2. sin a—cos a
2) Найти значение выражения-----, если ctga=2.
sina+3cosa
w, -- i\ тт - sin2a+6cos2a . o
V.77. 1) Наити значение выражения —ъ, если tga=3. sin2 a—4 cos2 a
2) Найти значение выражения 2si'1 если cfga=4.
sin2 a+3 cos2 a
V.78. 1) Найти значение выражения tg2a + ctg2a, если
tga+ctga = 2.
2) Найти значение выражения tg2a + ctg2a, если
tga-ctga = 3.
2. Формулы сложения
Вычислить (V.79-V.82).
V.79. 1) sin25° cos350 + cos25° sin350;
2) sin -sin 50 ° — cos -cos 50 °;
18 18
3) sin £-cos65° — cos ^sin65°; 9 У
. 4л . 5л , 4л 5л
4) Siny sin^+cosy cos^.
V 80 1) 10 ° + tg20 ° .
" ’ 1 —tg 10 ° tg 20 ° ’
3) tg70 ° — ctg 50 ° .
’ l + ctg20°-ctg50° ’
2x tg50o + ctg80° .
’ 1 —tg50°-tg 10° ’
4) tg 155 ° +tg 160 ° ’ 1 + ctg 115°-tg20° '
§3. Тригонометрические формулы 95
V .81. 1) sin 15°; 2)sin75°; 3)sinl05°; 4)cos^;
5)cos^; 6)cos^; 7)tgl5°; 8)ctg^; 9)tglO5°.
V .82. 1) tg 1065 °; 2) sin (-1335°).
V .83. Доказать тождества:
1) tga+tg/3=sln; 2) tga-tgfi= —
& cos a cos/3 & cos a cos/5
V.84. Вычислить:
1) sin740-ctg53°+cos74°; 2) cos78°-ctg6°-sin 78°.
Упростить (V.85-V.88).
V.85. 1) (cos3a—cos a)2 3 + (sin 3a—sin a)2 + 2cos2a;
2) (cos a—sin 5a)2 + (sin a+cos 5a)2+2 sin 4a.
V.86. 1) sin4a-ctg2a—cos4a;
2) cos2a+sin 2a-tga.
V.87. 1) sin a+sin fa+ —'j +sin fa— ^Y,
2) cos | a+^ )-cos | a-^ )-\/2cosa. \ 4 / \ 4 /
К „Д • Л, лД у-a -sin a-- ; o / \ О /
2) cos2 3a+cos f^+3aYsin f3a+^Y \ о / \ 3 /
V.89. Вычислить:
1) sin ( ) +sin ( a+^Y если sina= —Y
\ 3 / \ 3 / 5
2) cos fa+^Y —sin fa—^Y если sina=YY \ 3 / \ 6/ 5
V.9O. Вычислить:
1) cos (a+P)+2cos -sin a, если a—/3=^;
2) 2sin —a)-sin/3—sin (a+/3), если a—/3= —
V.91. Используя метод введения вспомогательного угла, представить выражение как косинус и как синус некоторого угла:
1) Y^-cosa+Y^-sina; 2) Y^-cos a+^-sin a;
3) Y^-cos a—YYsin a; 4) YYsin a—|-cos a.
V.88. 1) sin2 a—cos
96 Глава V. Тригонометрические формулы
V.92. Преобразовать, используя метод введения вспомогательного
угла:
1) -cos a—sin а; 2) cos а—sin а;
3) \/3-sin а — cos а; 4) ч/б-cos а—\/2-sin а.
V.93. Найти наименьшее и наибольшее значения выражения:
1) 2cosa+2sina; 2) sin a—cos a;
3) ч/3-sin a+cos a; 4) — sin a—ч/3-cos a.
3. Формулы кратных u половинных углов
V.94. Вычислить:
1) cos2 75° —sin2 75°; 2) 2sin 15°-cos 15°;
2 бтг 2 77T л\ 7n 7Г
3) sin2 — -cos2 —; 4) sin—-cos-.
1Z 1Z 0 0
V.95. Вычислить:
n 2tg75°________. 2tgl65°
' 1 —tg75°-ctgl5° ’ tgl5°-ctglO5° + l ’
V.96. 1) Найти cos2a, если cosa=|.
2) Найти cos2a, если cos^ — a
V.97. 1) Найти sin 2a, если cosa=| и — ^<a<0.
2) Найти sin 2a, если sina=| и ^<а<д.
V.98. 1) Найти tg4a, если tg2a=3.
2) Найти ctg p если tg^ = —
V.99. Вычислить:
sin2 70 °-sin2 20° sin 25 °-cos 25 °
sin 84 ° cos 84 °
,4 sin2 5 °—cos2 5 ° .
sin 40 ° cos 40 °
V.100. Вычислить:
n sin 54 ° _ cos 54 ° .
* ) 1 r\ n _ 1 r\ n ’
V.101. Доказать тождество:
1) (cos a+sin a)2 = l+sin 2a;
/ a a\ 2
2) (cos--sin-I =1 — sin a.
V.1O2. Найти sin 2a, если:
1) sin a-cos a=0,3; 2) sin a+cos a=l,3.
§3. Тригонометрические формулы 97
V.103. Доказать тождество:
1) tga+ctga=~72^; 2) ctga-tga=2ctg2a.
V.104. 1) Найти значение выражения sin3 a cos a—sin a cos3 а при __25_ 24
2) Найти значение выражения cos4 a—sin4 a при a=^. О
V.1O5. Вычислить:
» cos£-sin£ cosiTcosrsinJ;
2) 8 sinA cos£.(cos2A-sin2A);
3) 8 cosA-sini cos| sin| cosi;
4) 4.sin2A.ctgA.(sin2A_Cos2i).
V.106. Упростить:
1) +c,s2« ,t . 2) 2c_os2a-l. 2a
7 sin (zr— 2a) & sin 2a &
V.1O7. Доказать тождество и указать значения а, при которых
оно справедливо:
в tg2-^1"00^- 2) ctg-=1+cosa
' g 2 1 + cosa’ ? g2 sina ’
V.1O8. Вычислить:
1) 1 — 2sin2 22,5°; 2) 3-4cos21j.
V.109. 1) Вычислить \/2sin (n:-|-a)-sin (a—y)~0,5cos9«
при
12
2) Вычислить sin2 ^5a—^)+0,5cos(2a—тс) при
V.11O.
V.lll.
V.112.
Извлечь квадратный корень:
1) Vl + cos8; 2)
' у 1-cos 6
1) Найти cos a и sina, если cos2a= —^<а<д.
8 2
2) Найти cos a и sina, если cos2a=|, ^<а<2д.
5 2
1) Найти cos и sin^, если cosa=|, ^<а<д. 2 2 8 2
a • а Зя,,
2) Наити cos- и sin-, если sina=-, -<а<д.
Z Z □ Z
4—5682
98 Глава V. Тригонометрические формулы
V.113. Найти наименьшее и наибольшее значения выражения:
1) 3 — 2 sin2 а; 2) sina-cosa;
3) 1 —(sin За—cos3a)2; 4) sin2 —cos2
4. Формулы преобразования суммы в произведение и произведения в сумму
V.114. Упростить:
cos 2/3 —cos 6/3 sin 2/3+sin 6/3 ’
V.115. Вычислить:
1) s'n 3 ° - cos 3 ° sin 54 ° —sin 66 0
V.116. Вычисл ить:
px sin a-sin 5a cos a+cos 5a
2\ cos 74 ° +cos 46 0 cos2 7 ° —sin2 173 °
1) 2cos20°-cos40° — cos20°; 2) 2sin 10° cos20° —cos 100°.
V.117. Определить знак выражения:
1) sin2+sin5; 2) cos4-|-cos7.
V.118. Определить, что больше:
1) sin 13 или sin 12; 2) sin 12 или cos 10.
§4. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
Первый уровень
Вычислить (V.119-V.121),
V.119. 1) sin 142°+tg26°’Sin 52°;
3) cos 106°—tg37°-cos 16°;
V 120 1) sin68°'Sin22° .
1-2cos2 23° ’
yr 121 1) 1 —2 cos2 55 0
2 tg 10 0-sin2 100 0 ’
2) cos438°-ctg 186°+sin 618°;
4) sin 602°-ctg211 ° —cos242°.
рч cos2 24 ° —cos2 66 0
2 sin2 66 0 — 1
p\ _____2sin2 25° —1____
ctg 70 °-cos 160 0-sin 110 0 ’
Доказать тождество (V.122-V.128), 2 2
V 122 Slfl cos a_sina—c°s a l+sin2a cosa+sina’
V 124 sin4a-cos2a = fp a
‘ (1+cos 4a) (1+cos 2a) ё
V.123.
V.125.
cos3 a-sin3 a л
-—o - =cos a-sin a. 1+0,5 sin 2a
1-cos 2a+sin 2a , „ =tg a.
1+cos 2a+sin 2a
§4. Преобразование тригонометрических выражений 99
V.126. sin2 (y+aj-sin2 ^y-aj=0,5sin2a.
V.127. 1) cos2 За+cos2 2a=cos5a-cos a+1;
2) sin a-sin 3a=sin2 2a-sin2 a.
V.128. (1—sin (3n:-a)+cos (Зтс+a)) (1-sin (y — a)+cos (y-a)) = — sin 2a.
Упростить (V.129-V.133)
V.129. ( (cos a-cos /3)2 + (
:2 sin2 —
V.130.
4 (cos2 a—sin2 a)
—---------s—- + COS2 2a.
ctg2 a—tg2 a
V.131.
4/
V.132.
V.133.
_______2 cos2 a— 1_______
. , ( 7Г \ 2 ( \
4 tg - — a sin - + a
\4 ) \4 J
32cosa-sin a-cos2a-cos4a-cos8a
V.134.
V.135.
sin 16a ’
n\ cos 3a-cos 6a-cos 12a-cos24a
sin 48a
Вычислить:
1) sin2 ( a+^ )—sin2 ( a—j, если sin2a=— \ 8/ \ 8/ 2У2
2) cos2 ( a—-^ ) —sin2 ( a+-^ ), если cos2a=-^. \ l^/ \ 12/ v3
Найти наименьшее и наибольшее значения выражения:
sin2 (у+a)—sin2 а, если ^а^у
• тг . 2тт 5тг
sin acos-—cos asm —, если — — ^a^O;
3 3 б
sin a-cos y+cos a-sin у если
2)
3)
4) (sin 2a—cos 2a)2 —1, если — ^a^O.
V.136. Определить, при каких значениях а хотя бы для одного значения а выполняется равенство: 1) cos2 a=a; 2) 1—4sin2a=a.
V.137. Определить, при каких значениях а хотя бы для одного значения а выполняется 1) х/3 cos a+3 sin a=a;
равенство:
2) \/6cosa—\/2sin a=a.
100 Глава V. Тригонометрические формулы
V.138. Найти наименьшее и наибольшее значения выражения:
1) 1-2|cos/|; 2) |4cos£—1|;
3) |cosZ—3|; 4) |sin t—0,7|.
V.139. Найти наименьшее и наибольшее значения выражения:
1) cos2 t—4 cos t-h4; 2) 4 sin2 t+4 sin /-3;
3) — l+2sin Z-sin2 t\ 4) cos2 t—cos H-l.
Второй уровень
V.140. Вычислить:
1) sin2 40 °+sin2 20 °+sin2 50 °+sin2 70 °;
2 3л . . 2 5л . 2 7л
2) sin2-H-cos —+sinz — H-cos —. о о о о
V.141. 1) Найти значение выражения sin/~5co^ , если tgt=—3. sind t—cosJ t т т ° 3 sin cos t j j r*
2) Наити значение выражения —=--------г-, если ctgr=0,5.
sind Z+cosJ t
V.142. Доказать справедливость неравенства при всех допустимых значениях t\
1) |tg Z+ctg Z|^2; 2) tg2 Z+ctg2 Z^2.
Вычислить (V. 143-V. 146).
V.143. 1) 2\/2sin ^+a/3; 2) 2\/6 cos ^-а/З.
V 144 sin 35 °-sin 84 °+cos 145 °-sin 6 ° .
cos50° sin 21 °—cos40°-sin 111 ° ’
sin 22 °'Cos 8 °+cos 158 °-cos 98 °
sin 23 °-cos 7 °+cos 157 °-cos 97 ° ’
V.145. 1) sin 40 °+2 sin 20 °-д/З cos 40 °;
2) cos 50 ° —\/3 sin 50 °+2 sin 20 °.
V 146 11 "^/3 cos 8 °+sin 188 ° . cos4°+x/3sin 176°
‘ cos7°+sin7° ’ ' cos 11 ° —cos 79 ° '
V.147. 1) Какие значения может принимать выражение sin а— —2 cos а, если углы а удовлетворяют условию sin а+ 4-cos а=1?
2) Какие значения может принимать выражение sin2 а— 2
—cos а, если углы а удовлетворяют условию cos а— — \/3 sin а=1?
§4. Преобразование тригонометрических выражений 101
V.148. Найти:
1) sin 2а, если tga=3; 2) sin 2a, если ctga=—2.
V.149. Найти:
1) tg2a, если cos (а— 0=—| и у<а<2я;
2) ctg2a, если cos(a+y:) — | и ^<а<я.
V.150. Найти cos а и sina, если:
1) sin2a=--|, -^<а<-^; 5 2 4
2) sin2a=—^<а<я. 5 4
V.151. 1) Найти значение выражения sin > если известно, что sin a=—0,6 и ^<а<2тг.
2) Найти значение выражения cos , если известно, что cos a=—0,8 и rc<a<y.
V.152. Вычислить:
^СО5ТГСО5^ 1 2> ctg^cos^.cos^sin-".
V.153. 1) Найти значение выражения 4+^in2o?) если tga=—0,5. cos2 a+4
2) Найти значение выражения если ctga=0,5.
V.154. 1) Найти значение выражения cos a+sin_a_—1 если
г cos a—sina cos 2а
tg2a=5.
2) Найти значение выражения ^sina~sin2ot если tg^= 2.
' r 2sina+sin2a ь2
V.155. Упростить:
1) c°s3a-sin3a _lsin2a; 2) c°s3 a+sl"3 « + 1 sin 2a.
r~ i 7Г \ 2 /— I tC\ 2
v2cos a+- v2sin a+-
\ 4/ \ 4/
V.156. Найти значение выражения:
1) sin jy (1—2 sin2 20 —sin l^-cos
2) 2cos ^-(2cos2 ^L-lWcos
1 / \ / 1 /
102 Глава V. Тригонометрические формулы
V.157. Доказать тождество:
1) 8 cos4 а=3+4 cos 2a+cos 4а;
2) 8 sin4 а=3 —4 cos 2a+cos 4а.
V.158. Доказать тождество и указать значения а, при которых оно имеет место:
1) tgg= sinQf • 2) tg1~cos“
7 ё2 1+cosa’ 7 ё2 sin a ‘
V.159. Доказать тождество и указать значения а, при которых оно имеет место:
2tg — 1-tg2 “
1) sin a= -——2—; 2) cos a= —----.
. x 9 a , , о a
1+tg^2 1+tg 2
V.160. Извлечь квадратный корень:
1) 2) i/r+i
у 1 — sin 2
V.161. Определить знак выражения:
1) tg2+ctg4; 2) tg3—ctg7.
V.162. 1) Для каких углов а из промежутка [(J; выполняется равенство л/1 —sin 2a=sin a—cos a?
2) Для каких углов а из промежутка я] выполняется равенство д/1+sin 2a=sin a+cos a?
V.163. 1) Для каких углов а из промежутка выполняется
неравенство sina^sin2a?
2) Для каких углов а из промежутка [0; я] выполняется неравенство cosa^sin2a?
V.164. 1) Найти все значения а из промежутка при
которых выражения tga и cos 2a— -—имеют разные знаки.
2) Найти все значения а из промежутка при
которых выражения ctg а и -^^—2 cos 2a имеют разные
знаки.
§4. Преобразование тригонометрических выражений 103
V.165. Доказать тождество:
1) sin 2a+sin 4а—sin 6а=4 sin а-sin 2a-sin За;
2)
3)
sin 4a+sin 5a+sin 6a _± r .
cos4a+cos5a+cos6a &
sin a+sin За+sin 5a+sin 7a=4 cos a-cos 2a-sin 4a;
4)
_sin a—sin 3a—sin 5a+sin 7a __ ± a cos a—cos За+cos 5a—cos 7a s
V.166. В ычислить:
0 ^-“s20°; 1 2>
-—^—— + 2 sin 10°. 2 sin 50 °
V.167. Вычислить:
1) (sin 160 °+sin 40 °)-(sin 140 °+sin 20 °) + (sin 50 °-sin 70 °) x x(sin 130°—sin 110°);
2) cos 70 °-sin 110 ° —cos76°-sin 64 °+cos 174 °-sin 6°.
V.168. 1) Найти значение выражения cos a+sin a, если известно, 2
что sin2a=7 и д<а<2д.
2) Найти значение выражения cos a+sin а, если известно, что cos a—sin а=^ и 0<а<^.
4 2
V.169. Доказать тождество:
1) i±sis2a=t /-5+a\; 2) ;~sin2a!=tg2(;-aY
cos2a s \4 / l+sin2a 5 \4 /
V.17O. Доказать тождество:
1) cos4 a+sin4 a=l—0,5 sin2 2a; 2) sin6 a+cos6 a=l — |-sin2 2a.
V.171. i) Найти значение выражения sin3 a—cos3 a, если sin a—cos a=a.
2) Найти значение выражения sin3 a+cos3 a, если
sin a+cos a—a.
V.172. i) Найти значение выражения cos4 a+sin4 a, если
sin a—cos a=0,5.
2) Найти значение выражения cos8a—sin8a, если cos2a=|.
V.173. Вычислить:
1) cos3 2a-sin3 2a при a=^;
2) sin6 2a—cos6 2a при a=2^.
V.174. Выч ислить:
4 Зтг . . 4 29тг . 4 5тг . . 4 17л
1) cos4 -+sin4 2) sin4 -+sm4 —.
104 Глава V. Тригонометрические формулы
3 1
V.175. 1) Найти sin а, если sin2a^~, tga^.
2) Найти sin если cos2a^ — cosa^ —-.
2 8 4
V.176. 1) Найти sin a-(1+tg a-tg , если tga=2;
2) Найти 4-(—L+ctg2a), если ctg^ = l.
Упростить (V.177-V.179).
V .177. sin* 2 a+sin (60 °+a)-sin (60 ° —a).
V .178. 1-sin 4a+ctg 2a)-cos 4a.
V .179. tg3 * a+tg2 a+tg a+1 --sin ot .
cos5 a
V .180. Выч ислить:
1) cos 73 °-cos 47 °+cos2 47 °+cos2 73 °;
2) 2 sin 20 °-sin 40 ° sin 30 °+sin2 20 °+sin2 40 °.
Доказать тождество (V.181-V.188).
V.181. ctg a—tga—2 tg 2a—4 ctg 4a.
V.182.
sin oH-cos (2/3-a) = f / n _ „\ cos a—sin (2/3—a) ° \4 ’
V.183. tg (?+^)-tga=—
6 \4 2/ 6 cos a
Vl+cos cos a
VH-cos a—+1—cos a
V.184.
V.185.
V.186.
=ctg(^ + v), если д<а<2д. ° \2 4/
+H-sin a++l—sin a
VH-sin a—+1—sin a
, ОС
~ g 2
если ^<a<7C.
a/-^——2sin f J—a^ cos f ^ + a^ + 1=- cos a-sin a, у 2 \ 6 / \6 /
5л . 7tu если —<a< —.
4 4
V.187. у cos ^2a+y)—2tga-(l+tg2 a) sin(^-a), если J<a<^.
2 4
V.188. cos a-cos 2a-cos 4a-... -cos 2fea— sj,n,+—.
2*+1 sin a
§4. Преобразование тригонометрических выражений 105
Найти наименьшее и наибольшее значения выражения (V.189-
V.193)
V.189. 1) 2 cos2 /+cos2/; 2) sin2/+3 cos 2/;
3) (cos/+sin/)2—4 sin 2/; 4) cos4 t—sin4 t+2 cos2 t.
V.190. 1) 4—|2sinZ—1|; 2) 3—5-13 cos11.
V.191. 1) sin2/-cos/; 2) 6cos/+cos2/;
3) 5sin/+cos2/; 4) cos/-sin
V.192. 1) sin2 a-|cos a|; 2) 6 |cos a|-cos2 a+4.
V.193. 1) 2 sin2 2/-4cos2 /+1; 2) sin2 4/-4 cos2 2/+2.
V.194. Найти наибольшее значение выражения и указать значе-
ния а, при которых оно достигается:
1) ______!_____; 2) _________5______.
2 sin2 а—2 sin а+1 ’ 7—4 sin2 а—4 cos а
V.195. Найти наибольшее значение выражения:
1) 1________; 2) _______1______.
4 sin4 a—sin2 а+1 9 cos4 а—2 sin2 а+4
V.196. Найти наименьшее значение выражения и указать значения а, при которых оно достигается: 1) tg2a+ —-—1-0,5; 2) ctg2 а+^^+4.
° cos а /о sina
V.197. Найти наибольшее и наименьшее значения выражения:
1) 3 sin а—4 cos а+2; 2) —6 sin а—8 cos а+1.
V.198. Найти наименьшее и наибольшее значения выражения:
1) sin4 0,5/+cos4 0,5H-cos2 t\ 2) sin6 /+cos6 t.
V.199. 1) Какие значения может принимать выражение sina—3cos/3, если ^а^^Д, — £^/3^7? 1 4 6 6'3
2) Какие значения может принимать выражение 2 cos a—3 sin/3, если — ^a^^,
V.200. 1) Какие значения может принимать выражение sina-cos/3, тг 5 тг тг 5 тг если 7^а^ — ;
4 6 3'6
2) Какие значения может принимать выражение sina-cosj3, если
6 4 3'6
106 Глава V. Тригонометрические формулы
V.201. 1) Какие значения может принимать выражение sin a-|cos а|, если 6 3
2) Какие значения может принимать выражение cosa-|sin а|, 7Г 7 ТС
если ——?
6 12
V.202. Найти наибольшее значение выражения sin18 a+cos12 а.
2) Найти наименьшее значение выражения — sin8 a—cos22 а.
V .203. Найти решение неравенства |х—cos2 a|<sin2a в зависимости от значения параметра а.
V .204. Указать значения параметра а из промежутка при которых уравнение
|x-2|=\/2cos ^2а-|)
не имеет решений.
V .205. При каких значениях параметра а наибольшее значение выражения a sin 2% + 4 sin2 х + 3 не превышает 8?
§5. АРКСИНУС, АРККОСИНУС, АРКТАНГЕНС И АРККОТАНГЕНС
Первый уровень
V.206. Заполнить таблицу и для каждого найденного значения дать геометрическое толкование:
V.2O7. Вычислить:
1) cos (з arcsin | — arctg (—1))
2) sin (arccos( — 1) + arctg \/3);
§5. Арксинус, арккосинус, арктангенс и арккотангенс 107
3) tg (arcsin (- —-) + 2 arcctg;
4) ctg (arccos | - 3 arcctg (-x/3)).
V.208. Указать значения с, при которых имеет смысл выражение: 1) arcsin a = с — я; 2) arccosя = 2с — 0,5тс;
3) arctga=^-4c; 4) arcctgя = Зс —
V.209. Указать значения а, при которых имеет смысл выражение: 1) arcsin (За — 5); 2) arccos (2 — 5я);
3) arcsin (8 — я2); 4) arccos (я2 — 3).
V.210. Сравнить:
1) arcsinO,25 и arcsin0,7; 2) arccos0,3 и arccos0,6;
3) arcsin (—0,1) и arcsin 0,2; 4) arccosO,9 и arccos (—0,3).
V.211. Определить знак выражения:
1) arctg3 — arctg 4; 3) arctg (-0,5) + arctg0,7; 2) arcctgO,5 — arcctg 1,5; 4) arcctg(-5) - arcctg(-3)
Вычислить (V.212-V.215)
V.212. 1) arcsin (sin у j; 2) arcsin (sin (_0);
3) ( 7тг\ arcsin sin — ; \ 3 ) 4) arcsin ( — sin ^ ); \ 8 /
5) . ( 12tt\ arcsin sin ; \ 5 / 6) arcsin (sin (~~^))•
V.213. 1) / 2л?\ arccos 1 cos — ); \ У / 2) ( ПтгЧ arccos 1 cos — J;
3) arccos (cos (— 4) ( 117г\ arccos cos —- ; \ 6 )
5) ( 14tt\ arccos cos —— ; \ 5 / 6) ( /2бтг\\ arccos 1 — cos I — ) )•
V.214. 1) arctg (tg|); 2) arctg (tg (~y));
3) arctg (tgy); 4) arctg (- tg^);
5) arctg (tg^); 6) arctg (tg (-
V.215. 1) arcctg (ctg^); 2) arcctg (ctgy);
108 Глава V. Тригонометрические формулы
3) arcctg (ctg 5) arcctg (ctg^); 4) arcctg (-ctg j); 6) arcctg (ctg (-у
Вычислить (V.216-V.218).
V.216. 1) cos (arccos 0,1); 2) sin (arcsin (—0,2));
3) tg(arctg4); 4) ctg(arcctg(-0,6)).
V.217. 1) tg (arcsin 0,2); 2) tg (arccos (-|));
3) ctg (arcsin 0,6); 4) ctg (arccos (—|)) •
V.218. 1) sin (arctg 2) sin (arcctg (~|));
3) cos (arctg2); 4) cos (arcctg (-|))-
Второй уровень
V.219. Преобразовать выражение, используя метод введения вспомогательного угла:
1) 3 cos а + 4 • sin а; 2) 6 cos а —8 sin а;
3) 5 cos а — 2 sin а; 4) 4 • sin а — 2 cos а.
V.220. Указать все значения х, при каждом из которых справедливо равенство:
1) arcsin (sin х) = х; 2) arccos (cosx) = x;
3) arctg(tgx) = x\ 4) arcctg (ctgx) = x.
V.221. Указать все значения x, при каждом из которых справедливо равенство:
1) sin (arcsin х) = %; 2) cos (arccosx) = х;
3) tg(arctgx) = х; 4) ctg (arcctg x) = x.
Вычислить (V.222-V.231), V.222. 1) arcsin (sin 2);
3) arcsin (sin 8);
V.223. 1) arccos (cos 3);
3) arccos (cos 5);
V.224. 1) arctg(tg 1,8);
3) arctg(tg3,5);
2) arcsin (cos 6);
4) arcsin (cos4).
2) arccos (sin 7);
4) arccos (sin 4).
1 2) arctg (ctg5);
4) arctg(ctg(-ll)).
§5. Арксинус, арккосинус, арктангенс и арккотангенс 109
V.225. 1) 3) arcctg (ctg4); arcctg (ctg 9); 2) 4) arcctg (tg (-6)); arcctg (tg 10).
V.226. 1) sin (2 arccos 0; 2) sin (2 arcsin 0,6);
3) cos (2 arccos 0,6); 4) cos (2 arcsin — 1.
V.227. 1) sin (2 arctg 0; 2) cos (2 arcctg3);
3) sin (2arcctg5); 4) cos (2 arctg2).
V.228. 1) sin (arccos 0,6 4- arcsin • 1 \ 3/’
2) cos (arcctg (—3) + arccos | J >
3) sin (arctg (—2) + arcsin 0,2);
4) cos (arccos0,8 + arcsin
V.229. 1) tg f arcsin + arccos 0,5); \ □ / (/3 \ arccos (—0,6) — arccos -y-
V.230. 1) cos f| arcsin 2) sin farcsin
\ 2 □/ \ 2 5/
3) cos (| arccos (—|)); 4) cos Q arcsin0,6^.
V.231. 1) tgQ arcsin^); 2) ctg (| arccos 0.
V.232. Доказать справедливость равенства:
1) arcsin = arccos 2) д — arcsin = arccos
8 \
17/
V.233. Вычислить:
1) arcsin 0,6 + arcsin 0,8; 2) arcsin j| — arccos (—
V.234. Доказать справедливость равенства:
1) arcsin j = arctg |; 2) arcsin = arctg
□ т ZD Z4
V.235. Доказать справедливость равенства:
1) arctg | + arctg | 2) arcctg | + arcctg | = y.
u D i Zj От
V.236. Вычислить:
1) arctg + arctg |; 2) arccos-L - arctg
2 3 x/5 3
по Глава V. Тригонометрические формулы
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ V
V.237. Не пользуясь калькулятором, доказать справедливость неравенства:
1) log2 7 + (з + cos у) log7 2 < 4;
2) log2 31 + (14 + sin 91 °) • log31 2 < 8.
V.238. Вычислить:
1) cos 36 °; 2) sin 18 ° • sin 54 °.
V.239. Вычислить: tg81 ° - tg27° + tg9° - tg63°.
V.240. Доказать тождество:
1) sin a • sin (60 ° + a) • sin (60 ° — a) = 0,25 • sin 3a;
2) cos a • cos (60 ° + a) cos (60 ° — a) = 0,25 • cos 3a;
3) tg a • tg (60 ° + a) tg (60 ° — a) = tg 3a;
4) ctg a • ctg (60 ° + a) • ctg (60 ° - a) = ctg 3a.
V.241. Вычислить:
1) 8\/3-cos 10° cos50° • cos70°;
2) 8 • sin 10 ° • sin 50 ° • sin 70 °;
3) 8-cos 260 °-sin 130 °-cos 160 °;
4) tg20° • tg40° • tg60° • tg80°.
V.242. Доказать, что при всех значениях а справедливо неравенство:
1) |sin s: 3 |sin f |; 2) |sin y| 5 |sin 2|.
V.243. Сравнить:
1) arcctg0,4 и arccos^; 2) arccos^ и arcctgO,7; 8 7
3) arcctgO,5 и arccos0,4; 4) arccos'0,7 и arcctgO,9.
V.244. Доказать справедливость равенства:
1) 2 arctg | + arctg
2) 2 arctg V2 — arcsin | = у
оч -7,1 7 3
3) arcsin — + - arccos — = arccos -;
25 2 25 • 5
4) 2 arctg | + arctg | = arctg .
Ответы к главе V 111
V.245. Доказать, что при любом действительном значении a справедливо равенство:
1) cos (arctg а) = -Д==; 2) sin (arcctg а) = -Д=. V 1 + az V 1 + а2
V.246. Доказать, что если |а| < 1, то справедливо равенство:
1) tg (arcsin а) = —; 2) ctg (arccos а) =
V.247. Доказать, что если |а| 4 1, то справедливо равенство:
1) sin (2 arcsin a} = 1ayJ\ — a2\
2) tg f arcsin a ) =--~^=.
J i + /i-a2
Доказать тождество (V.248-V.253).
. . П “h 1
sin nasin —-a V.248. sin a + sin 2a + sin 3a + ... + sin na = ---------------—.
. a Sin 2 n + 1 sin nacos —=—a
V .249. cos a + cos 2a + cos 3a + ... + cos na =--------------—.
a
Sin 2
V .25O. cos2 a 4-cos2 2a + cos2 3a + ... + cos2 na = ~ + sin ragcos(” + 906 2 2 sin a
чг -2 । • 2n । • 2o । i-2 n sin nacosin + l)a
V .251. sinz a + sinz 2a + sinz 3a + ... + sinz na = - -------—-----—
2 2 sin a
. 2
V.252. sin a + sin 3a + sin 5a + ... + sin(2n — l)a = sin n—. ' ' sin a
V.253. cos a + cos 3a + cos 5a + ... + cos(2rc — l)a = s*n .
4 7 2 sin a
ОТВЕТЫ К ГЛАВЕ V
v-t Пф; 2)i; 3)i; 4)§;°5)g; 6)^. V.2. 1) 0»;
2) ~ 57 3°; 3) 90°; 4) f — V « 114,6°; 5) 180°; 6) 360°.
\ 7Г / \ 7Г /
V.8. (l;0); (0;l); (-l;0); (0;-l); (1; (-^Y
(^г;-0- v-9' *> 2m< 2) f + 2™, «ez;
3) к + 2тш, n G Z; 4) — ^ + 2лп, n G Z. V.1O. 1) + 2лп, n G Z;
2) у + 2кп, n G Z; 3) + 2?rn, n g Z; 4) + 2m, n G Z.
112 Глава V. Тригонометрические формулы
V.11. 1)^+ 2тт, п 6 Z; 2) + 2тм, п 6 Z; 3) -у + 2тш, п 6 Z;
4) + 2яп, п G Z. V.12. 1) £ + 2тс/1, п G Z; 2) у + 2™> п £ z'-
3) + 2яп, и G Z; 4) -J + 2яп, п 6 Z. V.13. 1) 2)-^,
о о 2 2 о
тг 7я Итг 4тг 5тг я 2я 7я 5тг я Зтг V1«
-6’ У У 3) -у -у з’ У 4) -у “У 4- У V-14- ° -* гс; 2) ±2, ±^2; 3) ±2, ±-Ц2; 4) ±52, ±52. V.15. 1) 2 I лМг е Z; 3 3 6 6 4 4 2
2) + 7Tfe, feeZ; 3) neZ; 4) |+2л/г, k 6 Z. V.16. 1) ^ + 2тг/г,/г е Z;
2) у + 2тг/г, k G Z. V.17. 1) me Z; 2) те Z; 3)
т е Z; 4) + у, т е Z. V.18. 1) (2яп,я + 2яп^, пе%\ 2) |+2л/г,
+ 2лт1], и е Z; 3) (—к + 2яп, 2яп^, п е Z; 4) + 2яп, у + 2яп^, п е Z.
V.19. 1) ^2ti/i , ^ + 2ti/i] , п е Z; 2) + 2яп, я + 2яп), nEl\ 3) + 2тт/1,
~ +271/1), /1GZ; 4) (-J + 271/1, 2тш), /1GZ. V.2O. 1) (% + 2яп, + 2яп},
/1GZ; 2) (^ + 271/1,^+271/1), /1GZ; 3) (-^ + 2тш, J + 2ti/i), п е Z;
4) (-^ + 27i/i,^+27i/i), и е Z. V.21. 1) Г—^ + 2тг/1, ? + 2ттп1, п е Z;
2) |у + 2тш, тс + 2тш], п е Z; 3) [— у + 2яп, 2тт/1], п е Z; 4) [у + 2тг/1, у +2л/1], /I G Z. V.22. 1) ф, т е Z; 2) лт, т G Z; 3) + лт, т G Z; 4) пт, т G Z. V.23. 1) р е Z; 2) U peZ;
3) 0; 4) р G Z. V.26. 1) -Ь, 2) 3) 4)
1о О о о о о
V.27. 1) 2) 3) 4) V.28. 1) Д±-1; 2) 3.
4 6 6 4 2
V.29. 1) тс/i, п е Z; 2) у + 2tt/i, п е Z; 3) — у + 2тт/1, п е Z; 4) + 2тт,
+ 2тс/1, п е Z; 5) —у+2лп, — ^ + 2tc/i, п е Z; 6) ^+тг/1, + лп, пе%\
4 4 4 6 3
7) 2лп, - J + 271/1, п е Z; 8) J + 4тс/1, + 4ti/i, п е Z; 9) - J
, п е Z. V.30. 1) | + яп, пе Z; 2) 2яп, п е ъ, 3) я + 2яп, п G Z; 4) + 2яп, п е%', 5) + 2яп, п 6Z; 6) + 2яп, п 6 Z;
4 3b
7) ±у +4тт/1, п GZ; 8) — тс + 2яп, + 2яп, п е Z; 9) я+2яп, — +2яп, пе%.
V.31. 1) яп, nel; 2) + яп, пе^', 3) — у + тт/i, п е Z; 4) + яп, пеЯг,
5) +71/1, и е Z; 6) ^ + ^, /1GZ; 7) /1 G Z. V.32. 1) + яп,
nel; 2) + яп, п е Z; 3) — у + тс/i, п е Z; 4) + яп, п е Z; 5) - + яп, пеТг, 6) уу + тг/1, п е Z; 7) —тс + Зтг/i, п е Z. V.33. 1) —2 —найм., О — наиб.; 2) 0 —найм., 2 —наиб.; 3) —2 —найм., 4 —наиб.; 4) —1 —найм., 5 —наиб. V.34. 1) 3 — найм., 5 —наиб.; 2) 1 —найм., 2 —наиб.; 3) 3 —
Ответы к главе V 113
найм., 1 + 2\/3 — наиб.; 4) 3——найм., 8 — наиб. ¥.35. 1) 2+^ — найм., 3 —наиб.; 2) —1,5 —найм., —1 —наиб.; 3) 2 — 4\/2 — найм., 10 — наиб.; 4) —1 —найм., 0,5 — наиб. ¥.36. 1) «+»; 2) «+». ¥.37. 1) «+»;
2) «+». ¥.38. 1) «—»; 2) «—». ¥.39. 1) tg 1,2л > cos 1,4я; 2) cos4<sin7. ¥.40. 1) « —»; 2) «+». ¥.41. 1) (—sin9,sin9); 2) (cos3, — cos3).
¥.42. 1) [2; 3); 2) (-oo, 1). ¥.43. 1) «-»; 2) «-»; 3) «-»; 4) «+».
¥.44. 1) sin у < sin у; 2) cos у > cos 3) tg у < tg 4) ctg у > ctg ¥.45. 1) sin 2 > sin 3; 2) cos 2 > cos3; 3) tg2 < tg3; 4) ctg 2 > ctg3.
¥.46. 1) tgl500° <tg!501°; 2) sin 1300° >sin 1301°; 3) cos 1700° >cos 1699°;
ctg 1750° > ctg 1751 °. ¥.47. 1) cos 1000° — наиб., tg 1000° — найм.;
4)
2)
4)
6)
5)
5)
4)
4)
4)
4) n
n
n
n
n
4)
2)
ctg2900° — наиб., sin2900° — найм. ¥.48. 1) «+»; 2) « —»; 3) «+»;
«+». ¥.49. 1) sina; 2) sina; 3) —sin3a; 4) sina;
sin 2a. ¥.50. 1) cos a; 2) —cos a; 3) — cos (y);
-cos a; 6) cos 4a. ¥.51. 1) cos a; 2) cos a; 3) —cos 7a;
— cosa; 6) — cos (y). ¥.52. 1) —sina; 2) —sina; 3)
5) — sin a;
4) - cos a;
4) — cos a;
6) —sin3a. ¥.53. 1) tga; 2) tga; 3) — tg2a;
6) ctg^. ¥.54. 1) ctga; 2) —ctga; 3) ctg
6) tg2a. ¥.55. 1) ^2; 2) -^; 3) -^;
5) sin a;
5) -ctga;
5) tga;
sin a;
ctg a;
- tg a;
3v/2
4 ’
G Z;
G Z;
G Z;
G Z;
G Z;
¥.56. 1) -14; 2) -3; 3) 12;
2) [j + 27r«, у+2тш], n G
4) [2тсл, у + 2яп], n G Z.
2) + 2яп, + 2яп), n G
\ 4 4 )
4) ( F + ЯП, Л + ЯП ), n G \ b /
2) у 4" ян, — + тш], n G Z;
4) 4. ¥.57. 1) [-Я + 2яп, 2яп],
Z; 3) [-yf + m, £ + „],
V.58. I) [-| + 2wi, I + 2m ,
Z; 3) [—2я + бяп, 2я + &яп],
Z. ¥.59. 1) (яп, у + яп^, оч \яп к к . яп\ г»
3> 1Т-12’6+Т> " 5 г-
v + 5-тг + т)- " е Z- V.60. 1) [г + т.л+да], п е Z;
о У У D / L Z J
? + яп,я+яп), neZ; 3) (2яп,^+2яп), 4) [^ + Т’Т + т)’
n G Z. ¥.61. 1) 102°; 2) 182°. ¥.62. 1) sin2 < sin8; 2) cosl<cos7;
3) tg3>tgl2; 4) ctg(—1) > ctg6. ¥.63. 1) sin2>sinO,5; 2) cos2<cos4,5; 3) sin 4 < sin 5,5; 4) cos5<cos7,5. ¥.64. 1) sin 1 — 0,5; 2) —2 cos 3 — 1. ¥.65. 1) Прямая расположена во второй, третьей и четвертой четвертях; 2) парабола расположена в нижней полуплоскости. ¥.66. 1) (-1-Vх!-cos5;-|]; 2) [0,25; 3 + у'Э + tg2,5). ¥.67. 1) 1; 2) 1. ¥.68. 1) 1; 2) 0. ¥.69. 1) 1; 2) 1. ¥.70. 1) 0; 2) 1; 3) 1; 4) 1.
¥.71. 1) 0; 2) 1. ¥.72. 1) 1; 2) 1. ¥.73. 1) — sin4; 2)-Ц; 3) cos5;
cos 2
4) —Д-,. ¥.74. 1) 2) -2. ¥.75. 1) —£=; 2) -4=- ¥.76. 1) |;
sin о 3 уЮ v5 3
114 Глава V. Тригонометрические формулы
2) |. V.77. 1) 3; 2) V.78. 1) 2; 2) 11. V.79. 1) 2) -1;
3) 4) V.80. 1) -Ь 2) УЗ; 3) -Ь 4) -1. V.81. 1)
Уб + У2. gx Уб + У2 . Уб + У2 . Уб — У2, g\ У2 — Уб , 4 ' ' 4 ’ 7 4 ’ 7 4 ' 4 ’
7) 2-УЗ;
8) 2-УЗ; 9) -2-/3. V.82. 1) УЗ-2; 2) + V.84. D h 2) 1-
V.85. 1) 2; 2) 2. V.86. 1) 1; 2) 1. V.87. 1) 0; 2) 0. V.88. 1) 2) |.
V.89. 1) 2) -0,6. V.90. 1) 2) V.91. 1) cos(a-~),
sin (а+ 2) cos (а— ^), sin (а + ; 3) cosfa+^j, sin (у —а);
\ 4/ \ 6/ \ 3/ \ 4/ \4 /
4) cos (а-у), sin(a- g). V.92. 1) У2cos (а- ~; 2) x/2cos(a+j);
3) 2sin ( а — 4) 2\/2cos (а+ ). V.93. 1) — 2\/2 — найм., 2\/2 —наиб.;
\ о / \ о /
2) — У2 — найм., У2 — наиб.; 3) —2 — найм., 2 — наиб.; 4) —2 —найм., 2 — наиб. V.94. I) 2) 1; 3) 4) V.95. I) --1-; 2) --С.
V .96. I) -1; 2) V.97. 1) -4-А 2) -||. V.98. 1) 2)
V .99. 1) —2; 2) 2. V.1OO. 1) -2; 2) -2. V.102. 1) 0,91; 2) 0,69.
V .104. 1) 2) V.105. 1) 1; 2) 1; 3) 4)
V .106. 1) 1; 2)1. V. 107. 1) а к + 2яп, а е Z; 2) а У тш, a G Z.
V .108. 1) 2) 1 - УЗ. V.109. 1) 0; 2) 0,5. V.110. 1) -\/2cos4;
2) -ctg3. V.lll. 1) cosa=—|, sina=y^; 2) cosa=y-, sina=-yy. V.112. 1) cos£ = 5, sin£ = 2) cos £ = -1=, sin £ = -^L. V.113. 1) 1 -
’ 2 4’ 2 4 7 2 710 2 710
найм., 3 —наиб.; 2) —0,5 —найм., 0,5—наиб.; 3) —1 —найм., 1 —наиб.; 4) -1-наим., 1-наиб. V.114. 1) ig2p; 2) -tg2a. V.115. 1) -0,5; 2) 1. V.116. 1) Ь 2) 1. V.117. 1) «-»; 2) «+». V.118. 1) sin 13 > sin 12; 2) sin 12 >coslO. V.119. 1) 1; 2) 1; 3) -1; 4) -1. V.120. 1) -0,5; 2) 1. V.121. 1) 1; 2) 2. V.129. 2. V.130. 1. V.131. 2tg2a. V.132. 1.
V.133. 1) 2; 2) 1 o . V.134. 1) 0,25; 2) 0,5. V.135. 1) 0,5-
16sin3a
\f^2t
найм., у--------наиб.; 2) —1 —найм., 0,5 —наиб.; 3) —0,5 —найм.,
^у- наиб.; 4) -^у-найм., 1 - наиб. V.136. 1) [0; 1]; 2) [—3,1].
V.137. 1) [-2УЗ;2УЗ]; 2) [-2У2;2У2]. V.138. 1) -1-наим., 1-наиб.; 2) 0 — найм., 5 — наиб.; 3) 2 — найм., 4 — наиб.; 4) 0,3 — найм., 1,7 — наиб.
V.139. 1) 1 —найм., 9 —наиб.; 2) —4 —найм., 5 —наиб.; 3) —4 —найм., 0 —наиб.; 4) 0,75 —найм., 3 — наиб. V.140. 1) 2; 2) 2. V.141. 1) 2у 2) 4у V.143. 1) 1; 2) -3. V.144. 1) -1; 2) 1. V.145. 1) 0; 2) 0.
Ответы к главе V 115
V.146. 1) \/2; 2) \/2. V.147. 1) -2; 1; 2) -1; 0,5. V.148. 1) 0,6;
2) -0,8. V.149. 1) —4\/5; 2) V.15O. 1) cosa = sina=-~;
2) cos«=-A, 5ina=^. V.15L 1) 2) V.152. » 1; 2) 1.
V.153. 1) 2) |. V.154. 1) 5; 2) 4. V.155. 1) 1; 2) 1. V.156. 1) 0;
2) 1. V.158. 1) a^7i + 27in, п G Z; 2) а 7^ лп, ntZ. V.159. 1) а /
= тс + 2яп, п G Z; 2) а л + 2тш, п G Z. V.160. 1) л/2 sin ^2 — или sin2 — cos2; 2) — tgfl + y) или bj 21+cosl у jg| р « —»;
2) «-». V.162. 1) 2) V.163. 1) [-|;0] U [5; ?];
2) [О; £1 и [2; ^1. V.164. 1) (2; 2); 2) (- J;-2). V.166. 1) 0.5;
2) 1. V.167. 1) 1; 2) 0. V.168. 1) 2) V.171. 1)
2) За^-. V.172. 1) 2) А. V.173. 1) -ф; 2) -15-^.
V. 174. 1) 2) V.175. 1) ±J^; 2) ±,/|. V.176. 1) 2;
о б у 10 у о
2) -3. V.177. 0,75. V.178. 0. V.179. —L-. V.180. 1) 0,75; 2) 0,75. cosz а
V.189. 1) —1 —найм., 3 —наиб.; 2) —2—найм., 3 —наиб.; 3) —2 — найм., 4 —наиб.; 4) —1 —найм., 3 — наиб. V.190. 1) 1—найм., 4 —наиб.; 2) —17 —найм., 3 — наиб. V.191. 1) —1 —найм., 1,25 —наиб.; 2) —5— д
найм., 7 —наиб.; 3) —5 —найм., 5 —наиб.; 4) —2 —найм., — наиб. V.192. 1) —1 —найм., 1 — наиб.; 2) 4 —найм., 9 — наиб. V.193. 1) —3 — найм., 1,5 —наиб.; 2) —2 —найм., 2 — наиб. V.194. 1) 2 при а=^4-2яп, nGZ, и а=^г+2тш, neZ; 2) при а=^+2яп, nGZ, и а= — +2лп, n€Z. V.195. 1) 2) 0,5. V.196. 1) —0,5 при а = я + 2ял, п G Z; 2) —1 при
а= —+2тш, nGZ, и а= —4-2тсп,/1GZ. V.197. 1) —3 — найм., 7 — наиб.; 2) —9 —найм., 11 —наиб. V.198. 1) 0,5 —найм., 2 —наиб.; 2) 0,25 — найм., 1-наиб. V.199. 1) [-2,5;-0,5]; 2) [-4; 3,5]. V.200. 1) ;
2) [-1;1]. V.201. 1) [0;1]; 2) [-|;^]. V.2O2. 1) 1; 2) -1.
V.203. Если a = лп, то решений нет; если а лп, то (cos2a: 1). V.2O4. V.2O5. [-х/5;\/5]. V.207. 1) 2) 3) УЗ;
4)-V3. V.2O8. 1) 2) [^]; 3)(-A;g); 4) (£;%).
V.2O9. 1) [1|;2]; 2) [|;|]; 3) [-3;-х/7] U [л/7; 3]; 4) [-2;-\/2] U [\/2; 2]. V.21O. 1) arcsin0,25 < arcsin0,7; 2) arccos0,3 > arccos0,6; 3) arcsin(—0,1) < <arcsin0,2; 4) arccos0,9 < arccos(—0,3). V.211. 1) « —»; 2) «+»; 3) «+»;
116 Глава V. Тригонометрические формулы
4) «+».
V.213. 1)
2)
4)
V.217. 1)
V.212. 1) Ь 2) -j; 3) 4) -%; 5) 6)
2) 1^; 3) 4) 5) 6) V.214. 1)
У 12 И о Э { У
3) 5; 4) 2; 5) 6) 2 V.215. 1) 2) 3) 2;
т О / / IV / О
5) 6) ¥• V.216. 1) 0,1; 2) -0,2; 3) 4; 4) -0,6.
10 о
2) -2Л; 3) 4) -А. V.218. 1) 2)
3) -Д=; 4) —i=. V.219. 1) 5 sin (а + arcsin 0,6); 2) 10 cos (а + arccos 0,6); х/5 v37
3) x/29 cos (а + arccos—)=); 4) 2x/5-sin (a — arcsinV.22O. 1) [—
2) [0;ж]; 3) (-|;|); 4) (0; it). V.221. I) |-l;l]; 2) [-!;!]; 3) x -
любое действительное число; 4) x — любое действительное число.
V.222. 1) л - 2; 2) 6 - 1,5щ 3) Зд - 8; 4) 4 - 1,5л:. V.223. 1) 3; 2) 2,5д — 7; 3) 2л - 5; 4) 4 — 0,5л:. V.224. 1) 1,8 - д; 2) 1,5л: — 5; 3) 3,5 -к; 4) 11 - 3,5 д. V.225. 1) 4 - д; 2) 6 - 1,5д; 3) 9 - 2д;
4) 3,5д-1О. V.226. 1) 2) 0,96; 3) -0,28; 4) V.227. 1) 0,8;
У 1ЬУ
2) 0,8; 3) 4) -0,6. V.228. 1) + 0,2; 2)
\/5 — 4хХЗО, д, х/15 3 ут ллл i\ 48 -|~ 25х/3. п\ 48 — 25х/3
25 ’ 5 20’ v-zzy- 39 > 39 ’
V .23O. 1) 4=; 2) -U; 3) 4=; 4) —1=. V.231. 1) 0,5. 2) х/2.
х/5 х/Ю х/3 х/Ю
V .233. 1) 2) V.236. 1) 2) V.238. 1) 2) 0,25.
V .239. 4. V.241. 1) 3; 2) 1; 3) 1; 4) 3. V.243. 1) arcctg0,4 > arccos |;
О
2 ) arccos у > arcctgO,7; 3) arcctgO,5 < arccos0,4; 4) arccos0,7 < arcctgO,9. V.248. Указание. Умножить и разделить левую часть равенства на 2sin^,
затем применить формулу sinmasin ka = 0,5 (cos(/n — k}a — cos(/n + k)a).
Глава VI
КОМПЛЕКСНЫЕ ЧИСЛА
§1. ОПРЕДЕЛЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ. ОПЕРАЦИИ СЛОЖЕНИЯ И УМНОЖЕНИЯ
VI.1. Выполнить действия:
1) (2; —1) + (3; 1); 2) (2;-1) • (3; 1);
3) (4; —1) + (2; 3) • (—1;0); 4) (2; 0) • (3; 0) + (0; 2) (0; 3).
VI.2. Найти комплексное число (а; Ь), удовлетворяющее условию:
1) (3; 4) + (а; &) = (7; 8); 2) (3; 4) (а; Ь) = (25; 0).
V I.3. Найти комплексное число г, удовлетворяющее условию:
1) г-(-1;-1) = (1;0) (1; -5);
2) (—1;0) (-5; 10) =г- (2;-1);
3) (2; 3) г = (4; 1) (0; 1);
4) г-(3;-4) = (0;-1) • (-2; 11).
V I.4. Показать, что операции сложения и умножения комплексных чисел коммутативны.
V I.5. Выполнить действия:
1) (1 + 0+ (2 + 30; 2) 2(3 + 4/);
3) (3 + 0(4 + 50; 4) (1 + 30(2 + 0+4(1 + 0(1+0;
5) (2 + 0(2-0* + (1-40(2 +30;
6) (2 + 30(1 + 0(1 - 0 + (1 - 20(1 + 20-
VI.6. Выполнить действия:
1) (1 + 2г)2(1 + I')2; 2) (2 + 31)3;
3) (3 - 2i)3; 4) (1 - i)4.
VI.7. Решить уравнение:
1) Re г = iz + 1 + 2 Im г;
2) 5 Im г + 4z Re z — (4 — 20^ + 2/.
118 Глава VI. Комплексные числа
VI.8. Найти действительные числа х и у из равенства:
1) (2 + 41}х + (5 - 4i)y = 16 + 4z;
2) (-3 + i)x + (3 - 4i)y = 18 - 18/.
VI.9. Какие значения может принимать irL при различных натуральных значениях и?
§2. КОМПЛЕКСНО-СОПРЯЖЕННЫЕ ЧИСЛА. МОДУЛЬ КОМПЛЕКСНОГО ЧИСЛА. ОПЕРАЦИИ ВЫЧИТАНИЯ И ДЕЛЕНИЯ КОМПЛЕКСНЫХ ЧИСЕЛ
Первый уровень
VI.10. Выяснить, при каких действительных значениях х и у числа z\ и Z2 являются комплексно сопряженными:
1) Z\ = х + 6/ — 2xi + 2, Z2 = у3 + 4zx;
2) z\ — z/4 + \fx I, Z2 = x(4 — i) + 2z.
VI.И. Показать, что если z = z, то z — действительное число.
VI.12. Решить уравнение:
1) z2 + 2z + 6 = 0; 2) z2 — 4z + 13 = 0.
VI.13. Найти комплексные числа z и ш, для которых одновременно выполняются равенства:
1) 3z + w=l, z + iw = 4l; 2) 2z — w = — 1, 3z — w — — i.
VI.14. Найти модуль комплексного числа:
1) 5 — 3z; 2) 5z; 3) (3 - z) (4 + 2z); 4) (-2-5z)2.
VI.15. Решить уравнение:
1) 2z = — | z | + 2 z; 2) 3z \z\ + 5z = 20;
3) |z| - z = 1 + 2z; 4) z + |z + 1| i = 0.
VI.16. Решить систему уравнений:
Г |z —2z| = |z|, Г |z+l- 2z| = 1,
VI.17. Выполнить действия:
1) (1 + 2z) - (2 + 3z); 2) (2 - z)(2 + 3z) - (1 - 3z);
3) (5 + z)z-(2 + 2z)(3-z); 4) (2 - z)2 - 2(z - 2)z - 1.
§2. Комплексно-сопряженные числа. Модуль комплексного числа 119
VI.18. Вычислить:
1) (1-z) (l-z2)-(l + z3) (1 + Z4); 2) (3z4-z7)2-(z6-2z3)3.
VI.19. Вычислить:
1) J.+ 3L- 2) __-__•
J -н-2/’ (1 + 02’
ох 5_____. 5 . 6 + 2/ _ 3 - 5Z
) 1 + 2/ 2 — 1' 7 1 — 3z 2 + 2Z ’
VI.20. Вычислить;
3) (4 — 2/)2 / 2 + i 3 + i \ f 1 _ 1 A 10 + 5Z
(1+03 2-i)' \(1 +2/)2 (1 — 2i)2/
VI.21. Найти действительные значения х и у, при которых справедливо равенство:
1) (£^4_W£_+l)i = 2 - 5г 2) =4-3z.
7 1 + i 7 2-i
VI.22. Решить уравнение:
1) (г + 1)(1 - 3z) + (2 + гг)(2 - 4z) = 16 - 8z;
2) (2 - z>)(4 + 3z) + (z - г)(2 + 3z) = 22 - llz.
VI.23. Найти пару комплексных чисел (z,w), для которых одновременно выполняются равенства:
1) Зг — 2iw = 14 + Зг, 2гг — w = —9;
2) iz + (1 + t)w = 4z — 1, (1 — i}z — 3iw = 7 — 3z.
VI.24. Показать, что:
1)Кег = ф; 2)Imz=^.
Второй уровень
VI.25. 1) Вычислить г10, если число z удовлетворяет условию z — 2г + 1 + Зг = 0.
2) Вычислить г15, если число г удовлетворяет условию г - (1 — i)z = -1 - z.
VI.26. Доказать, что для любых z\ е С и z^ G С справедливы равенства:
1) 21 + г2 = г1 + г2; 2) z\ • г2 = z\ • г2;
3) 21- z2 = zi- г2; 4) (г2 0).
Vz2/ z2
120 Глава VI. Комплексные числа
VI.27. Найти действительные значения х, удовлетворяющие неравенству:
1) |2 + 4г + а/ТТ^| < 5; 2) |4 + 6г + Ух2-9| 10.
VI.28. Решить уравнение:
1 \ 1 . 2 3 — i . л \ 2 4- г . 2 2 -Г i
’ z + Зг 5 “ 6 + 2Г ' г — 3 ' 2 + Зг — 3 — 2г ’
VI.29. Решить уравнение:
1) г = г3; 2) г3 = -22.
VI.30. Доказать, что для любых z\ Е С, 22 G С справедливы равенства:
О 1г1г2 + 1|2 + 1г1 _гг|2 — (|г1|2 + 1) (j^2|2 +
2) |2122 - 1|2 - |zi -г2|2 = (jzil2 - 1) (|г2|2 - 1).
§3 . ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Первый уровень
VI.31. Изобразить точкой комплексной плоскости число:
1) —2; 2) 6г; 3) 3 + 2г; 4) -2-1.
VI.32. Изобразить множество точек комплексной плоскости, удовлетворяющих условию:
1) 1гп2 = -3; 2) Rez = 4;
3) Re 2 = Im г; 4) Re2 + 2Im2 = 4.
VI.33. Изобразить множество точек комплексной плоскости, удовлетворяющих условию:
1) 1т2^-1; 2) Re2<3;
3) Re 2 ^—2 Im 2; 4) Im 2 > Re 2+ 2.
VI.34. Описать геометрически множество точек комплексной плоскости, удовлетворяющих условию:
1) Im (2 - 2 + 0 = —2; 2) Re(2 + 3 + 4г) > 1.
VI.35. Описать геометрически множество точек комплексной плоскости, удовлетворяющих условию:
1) |2 —2-Ь/| = 2; 2) 1<|2 + г|^3.
§3. Геометрическое изображение комплексных чисел 121
VI.36. Пусть 2\ = 2 — 3/, 22 = 1 + 2z. Используя изображение комплексных чисел векторами, выполнить на комплексной плоскости следующие действия:
1) zi+z2; 2) 21- 3z2; 3) (21 +22) -2; 4) 22] - 322.
VI.37. 1) При повороте на угол против хода часовой стрелки и удлинении в два раза вектор z\ = i переходит в вектор 22. Найти комплексное число, соответствующее вектору 22.
2) При повороте на угол по ходу часовой стрелки и сокращении по длине в два раза вектор Z\ =6 + 8/ переходит в вектор 22. Найти комплексное число, соответствующее вектору 22.
VI.38. 1) При повороте на угол против хода часовой стрелки и удлинении в три раза вектор Z\ переходит в вектор 22 = —3 + 3z. Найти комплексное число, соответствующее вектору Z\.
2) При сокращении по длине в три раза и повороте на угол против хода часовой стрелки вектор Z\ переходит в вектор 22 = 1 — 3z. Найти комплексное число, соответствующее вектору Z\.
Второй уровень
VI.39. 1) Среди комплексных чисел, удовлетворяющих условию
—— ------ = 1, найти наименьшее по модулю.
I z-3-4i I
2) Среди комплексных чисел, удовлетворяющих условию | (2 — 8) (2 — 8) | = 12 Im 2, найти наибольшее по модулю.
VI.40. 1) Среди комплексных чисел, удовлетворяющих условию |2 — 2 — 2z| |1 + z|, найти наибольшее по модулю.
2) Среди комплексных чисел, удовлетворяющих условию |z - 5i(l +1)| s: |4 + г/21|, найти наименьшее по модулю.
VI.41. Среди комплексных чисел, удовлетворяющих указанному условию, найти наименьшее по модулю:
1) Re Q) = Jz + Im 2) Im (2(г-3))^1т (г(2-/))-6.
122 Глава VI. Комплексные числа
VI.42. Среди комплексных чисел, удовлетворяющих указанному условию, найти наименьшее по модулю:
1) \z + i\ = \z - 3z|; 2) \z - 2z| = \z + 4 + 2z|.
VI.43. Изобразить множество точек комплексной плоскости, удовлетворяющих условию:
1) \z + 1 + i\ < \z — 1 — z|; 2) \z — 3z| \z — 3|.
VL44. Изобразить множество точек комплексной плоскости, удовлетворяющих условию:
1) |г + 3|<72-|2-1|; 2) |f-~| > 2.
VI.45. Изобразить множество точек комплексной плоскости, удовлетворяющих условию:
1) Re (= 0; 2) Re (= -1.
\z — 1 / \ Z )
VI.46. Изобразить множество точек комплексной плоскости, удовлетворяющих условию:
1) Re (1; 2) Re f—-Л < -1. \z — I/ \ z J
VI.47. Изобразить множество точек комплексной плоскости, удовлетворяющих условию:
1) Rep- Л 1; 2) Rep + lVs. \Z Z J \ Z)
VI.48. Изобразить множество точек комплексной плоскости, удовлетворяющих условию:
1) |z|^l —Imz; 2) \z + z| > 1 + Re (iz).
VL49. Изобразить множество точек комплексной плоскости, удовлетворяющих условию:
D 2) |1-2«K|^ + ^|s:|3 + 4<|.
VI.5O. Найти действительное число а из условия, что точки 21,22,23 лежат на одной прямой:
1) Z\ — 1-|- 2z, 22 — —2 4- 3z, 23 — а -Г z;
2) Z[ = — 4 4- ai, 22 = 2 + z, 23 = 5 + 5z.
VI.51. Задать равенством геометрическое место точек комплексной плоскости, лежащих" на биссектрисе угла z\Oz^, если: 1) 2] = 12 — 5z, Z2 = 3 + 4i; 2) z\ = 2z, 22 = 4 — 3/.
§4. Тригонометрическая форма комплексного числа 123
§4. ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА
Первый уровень
VI.52. Найти аргументы комплексного числа:
1) z = — 2; 2) 2 = —/; 3) z — 2 — /; 4) z=— 3 + 4/.
VI.53. Описать геометрически множество на комплексной плоскости, состоящее из точек, для которых выполняется условие:
1) argz= 2) - argz| +
VI.54. Записать в тригонометрической форме комплексное число:
1) z — —3; 2) 2 = 4/; 3) z — — 1 — /; 4) 2 = —1 + 2/.
VI.55. Записать в тригонометрической форме комплексное число:
ТС • • ТС • 7Г । • ТС
1) 2 = — cos - — I sin2) 2 = sin - + i cos F. 9 9 5 5
VI.56. Найти модуль и аргументы комплексного числа 2, не вычисляя его:
VI.57. Записать комплексное число в алгебраической форме:
1) (V3 + i)10; 2) (l-VSi)'1;
3) (1 + i)12; 4) (V3-i)8.
VI.58. Представить комплексное число в тригонометрической форме:
(у'з-О7. (1 + О12
(‘-О9’
VI.59. Изобразить на комплексной плоскости множество точек, удовлетворяющих условию:
1) |(1+/)2 + 2/| ^4х/2; 2) 5 < |(3 + 4i)z - (10 + 5/)| < 10.
124 Глава VI. Комплексные числа
Второй уровень
VI.60. Записать в тригонометрической форме комплексное число:
1) г = 1 + cos у + isin у; 2) 2 = sin у + i (cos у ~ 1) •
VI.61. Записать в тригонометрической форме комплексное число:
1) z = sin а - i cos а; 2) z = 1 — cos а + i sin а (у<а<я).
VI.62. Найти модуль и аргумент комплексного числа:
_ 1 + cos а + isin а. %) z — sin a + *(cos a ~ 0
1 + cos а — zsin a’ sin a + i(l — cos a) ’
VI.63. Записать в тригонометрической форме комплексное число:
1)2= (/ - VS) (cos - i sin ;
f cos 77 - i sin (1 + \/3z)7
_ . \ О О /
2) 2 = —---------------------- •
VI.64. Вычислить: и , люо / & \12
’ (]_096_z(1 + /)98’ '
VI.65. Записать в тригонометрической форме комплексное число:
1) г = (-3 + 4/)3; 2) г = (2/ - I)6.
VI.66. Выразить через cos а и sina:
1) cos 3a; 2) sin 3a.
VI.67. Выразить через cos a и sin a:
1) cos 4a; 2) sin 4a.
§5. ИЗВЛЕЧЕНИЕ КОРНЯ ИЗ КОМПЛЕКСНОГО ЧИСЛА
Первый уровень
VI.68. Используя определение корня степени п из комплексного числа, найти:
1) V-S + 12/; 2) \/ЗТ4/;
3) V7 - 24/; 4) х/—21 - 20/.
VI.69. Используя определение корня степени и из комплексного числа, найти:
1) \/—а2, где a — действительное число;
2) ч/а2, где a — действительное число.
§6. Алгебраические уравнения 125
VI.70. Используя формулу Муавра, найти все значения корня и отметить на комплексной плоскости точки, соответствующие найденным значениям:
1) + y/3i- 2) >/4- 3) \/4л/3 4- 4г; 4)
VI.71. Найти все значения корня и отметить на комплексной плоскости точки, соответствующие найденным значениям:
1) VT; 2) \/1; 3) 4) У1.
VI.72. Найти все значения корня и отметить на комплексной плоскости точки, соответствующие найденным значениям:
1) 2) 8; 3) У^4;
4)
У^27.
VI.73. Найти все значения корня и отметить на комплексной плоскости точки, соответствующие найденным значениям:
1) 2) Vi\ 3) 4) Vi.
VI.74. Найти числа 2, удовлетворяющие условию:
7- I .
3 - 41 ’
1) г2 =
2) =
у/3 + i
§6. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ Первый уровень
VI.75. Решить уравнение:
1) 22 + 9 = 0; 2) 25г2+ 16 = 0.
VI.76. Решить уравнение:
1) г2 + 4г+ 5 = 0; 2) 2z2 + 2z + 3 = 0;
3) z2 + 2z + 10 = 0; 4) 2z2 + 3z + 9 = 0.
VI.77. Решить уравнение, разложив его левую часть на линейные множители:
1) 9z2 + 1 = 0; 2) г2 + 4г + 8 = 0;
3) г2 + 6г + 10 = 0; 4) 4г2 - 4г + 26 = 0.
VI.78. Составить квадратное уравнение с действительными коэффициентами, которое имело бы корень, равный:
1) 6г; 2) 2-3Z.
126 Глава VI. Комплексные числа
VI.79. Найти действительные значения а, при которых корни квадратного уравнения будут комплексными:
1) (5 - a)z2 + 2az - а - 1 = 0; 2) (а + 5)г2 - 4г - а = 0.
VI.80. Решить уравнение, разложив его левую часть на линейные множители:
1) z2 - 2/z -1 = 0; 2) 4z2 + 12/z -9 = 0.
VI.81. Найти, при каком значении параметра а корни квадратного уравнения будут равными:
1) z2- + 2(3 + i)z + а = 0; 2) г2 — (6 + 2t)z — (1 + i)a = 0.
VI.82. Решить уравнение:
1) г2 + 6г - 40/ = 0; 2) z2 - Зг - 10/ = 0.
VI.83. Разложить на линейные множители выражение:
1) 16z4- 1; 2) г3+ 8;
3) г4 - 2г3 - 8г 4- 16; 4) г4 - 4г2 + 4.
VI.84. Решить уравнение:
1) 16г4 + г2 = 0; 2) г4 + 8г2 + 16 = 0;
3) (г2 + 2г)2-16 = 0; 4) (г2-г)2-9 = 0.
Второй уровень
VI.85. Решить уравнение:
1) (2 + /)г2 — (5 — /)г + 2 - 2/ = 0;
2) (1 — /)г2 + (/ — 5)г + 10 = 0.
VI.86. Решить уравнение:
1) г4-6г2+ 25 = 0; 2) г4 + 10г2+'169 = 0.
VI.87. Составить биквадратное уравнение с действительными коэффициентами, если известны два его корня: 1) \/3 и 4/; 2) 5 и —2/.
VI.88. Составить уравнение наименьшей степени с действительными коэффициентами, имеющее корни:
1) /, 2, 3; 2) 1 + / и —/.
Задачи повышенной сложности к главе VI 127
VI.89. Решить уравнение:
2
1)г3 = 1±Ь 2) (г-<)4 = 25-(|^) .
VI.90. Решить уравнение:
1) z4+ 8z3 + 9z2+ 8z +1 = 0; 2) 2г4 + z3 + 3z2 + z + 2 = 0.
VI.91. Составить биквадратное уравнение с действительными коэффициентами, имеющее корень, равный:
1) 5 —2г; 2) 3 + 5/.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ VI
V I.92. Пусть ц6С, Imц> 0, Л = |^“ | (га). Доказать, что если Imz<0, то А > 1, а если Imz>0, то Л<1.
V I.93. Пусть (ZGR, cgR, be С, а>0, ac<\b\2. Доказать, что уравнение а |z|2 + bz + bz + c = O является уравнением окружности, а также найти центр этой окружности и ее
радиус.
VI.94. Вычислить
1+( т9)’п>1-
V I.95. Доказать, что
/-l + tV3\" /-1-гУз\” = (2, п = 3/г,
V 2 ) 2 ) [-1, n = 3k + 1, и = 3/г + 2,
(/г = 0,1,2,3,...).
V I.96. 1) Решить уравнение z5 + 25z3 - 8z2 + k = 0, зная, что один из его корней равен 5г.
2) Решить уравнение z5 — z4 + 4z3 — 22z2 + k = 0, зная, что один из его корней равен —2/.
VI.97. Доказать, что при любом положительном действительном а, а / 1, уравнение ||—= а> где г1£(^ Z2 € С, Z[ Z2, является уравнением окружности, а также найти центр и радиус этой окружности.
VI.98. Доказать, что три попарно различные точки zj, Z2, Z3 лежат на одной прямой тогда и только тогда, когда ——— —действительное число.
г2 ~z\
128 Глава VI. Комплексные числа
VI.99. Пусть Д1 — треугольник с вершинами zj, 22, Z3, а Д2-треугольник с вершинами W\, ®2> w3- Доказать,
что треугольник Ai подобен треугольнику А2, если + ~*\ _ w^-w\ z^ — z\ а?2 — аУ|
VI.100. Пусть точки Zi, 22, Z3 лежат на окружности с центром в точке z = 0. Доказать, что треугольник с вершинами в точках Zi, 22, 23 является равносторонним в том и только в том случае, когда 21+22 + 23 = 0.
VI.101. Доказать, что точки zj, 22, Z3, Z4, лежащие на одной окружности, являются вершинами прямоугольника в том и только в том случае, когда 21+23 = 22 + 24 (точки занумерованы в порядке следования при обходе окружности).
ОТВЕТЫ К ГЛАВЕ VI
VI.1. 1) (5;0); 2) (7;-1); 3) (2;-4); 4) (6;-6). VI.2. 1) (4;4); 2) (3;-4). VI.3. 1) (2;3); 2) (4;-3); 3) (|2; А|); 4) (1;2). VI.5. 1) 3 + 4/; 2) 6 + 8/; 3) 7+19/; 4) -1 + 15/; 5) 14; 6) 9 + 6/. VI.6. 1) -8-6/; 2) -46 + 9/;
3) -9 - 46/; 4) -4. VI.7. 1) -/; 2) 3 + 4/. VI.8. 1) х = 3, у = 2;
2) х = —2, у — 4. VI.9. 1 при n = 4k, / при n = 4 k + 1, —1 при n = 4k + 2, —/ при n = 4k + 3, где k G N U {0}. VI.10. 1) х = — 3, у = —1; 2) х = 4, у = ±2. VI.12. 1) 1 + 3/; 2) -2 ± 5/. VI.13. 1) z = - ^/,
' -j 7 10 10
а,= |1-А/; 2) Z = l + i, w = 3 — 2i. VI.14. 1) У34; 2) 5; 3) 10%/2; 4) 29. VI.15. 1) --^ + /; 2) 4 + 3/; 3) 1,5-2/; 4) -1 -/. VI.16. 1) 1 +/;
2) —2 + 2/, -1 + /. VI.17. 1) -1 - /; 2) 6 + 7/; 3) -9 + /; 4) 4.
VI.18. 1) 0; 2) -3 + 8/. VI.19. 1) 1 - /; 2) -0,5/; 3) 3 - /;
4) 0,5 + 4/. VI.2O. 1) /; 2) -24 + 24/; 3) 4 + 3/; 4) 2,4 - 0,8/.
VI.21. 1) х = 11, у = 2; 2) х = 3, у = 6. VI.22. 1)2 + /; 2) 3 + 2/.
VI.23. 1) 2 = 2 + 3/, ^ = 3 + 4/; 2) z = 2-z, w = 2i. VI.25. 1) 32/; 2) 128. VI.27. 1) [—1; 0); 2) [—5; —3] U [3; 5]. Замечанйе. Выражения у/Г+х
и л/х2 ~ 9 понимаются как арифметический корень из неотрицательного числа. VI.28. 1) |/; 2) 4-2/. VI.29. 1) 0; ±1; +/; 2) 0; 1 ±/; -1 ± /. VI.34. 1) Прямая у=—3; 2) точки плоскости Оху, лежащие правее прямой х = — 2 (сама прямая в множество не входит). VI.35. 1) Окружность радиуса 2 с центром в точке (2,-1); 2) кольцо, заключенное между
окружностями радиусов 1 и Зс центром в точке (0,-1) (включая внешнюю границу). VI.37. 1) — а/2. + /%/2; 2) 4 — 3/. VI.38. 1) 1 +/;
2) 9 + 3/. VI.39. 1) 1,8 - 2,4/; 2) 12.8 + 9,6/. VI.40. 1) 3 + 3/;
2) -2 + 2/. VI.41. 1) 0,8+1,6/; 2) -0,6+1,8/. VI.42. 1) /; 2) -1 -/. VI.43. 1) Часть комплексной плоскости, лежащая ниже прямой у — —х;
Ответы к главе VI 129
2) прямая х = у и часть комплексной плоскости, лежащая над ней. VI.44. 1) Область, лежащая вне окружности с центром (5; 0) радиусом 4\/2; 2) область, лежащая внутри окружности с центром (—6;0) радиусом 6, из которой выколота точка (—3;0). VI.45. 1) Окружность радиуса 1 с центром в точке (0;0), из которой выколота точка (1; 0); 2) парабола у — — х2, из которой выколота точка (0;0). VI.46. 1) Часть плоскости, лежащая выше параболы z/ = x2 +1, включая саму параболу, за исключением точки (0;1); 2) часть плоскости, лежащая между прямыми х = 0 и х = 0,5 (прямые не включены). VI.47. 1) Круг с центром в точке (0,5; 0) радиусом 0,5 с выколотой точкой (0;0); 2) круг с центром в точке (—1;0) радиусом 1 с выколотой точкой (0;0). VI.48. 1) Парабола у = 0,5 — 0,5х2 и область, лежащая под ней; 2) область, лежащая над параболой у = — 0,25х2. VI.49. 1) Кольцо, заключенное между двумя окружностями с центром в точке (1; 1), радиусами 1 и 2 (сами окружности в искомое множество не входят); 2) кольцо, заключенное между двумя окружностями с центром в точке (1;—2) и радиусами \/5 и 5 (включая сами окружности). VI.5O. 1) 4; 2) —7. VI.51. 1) 27Rez = 991mz; 2) Rez = 21mz.
VI.52. 1) 7г + 2тгп, n G Z; 2) — + 2тгп, n G Z; 3) — arccos-Д= + 2тгп, n G Z;
£ v 5
3
4) 7Г—arccos 5 + 2тгп, nGZ. VI.53. 1) Луч, выходящий из начала координат
и образующий угол с положительным направлением оси Ох; 2) раствор угла между биссектрисами 1-го и 2-го координатных углов, исключая начало координат. VI.54. 1) 3(cos тг + i sin тг); 2) 4 (cos + i sin 3) \/2-(cos (— у) + £ sin (— у)); 4) \/5-(cos (тг — arctg2) + i sin (тг — arctg2)). VI.55. 1) 1 (cos^ + isin^); 2) 1 • (cos + i sin VI.56. 1) |z| = - \/2, argz = + 2nk, k G Z; 2) |z| = 1, argz = —+ 2n£, k € Z.
VI.57. 1) 512 — 512%/3e; 2) 1024 + 1024^3i; 3) -256; 4) — 128z + 128%/Зг. VI.58. 1) 4\/2 (cos + z sin ; 2) 0,25 (cos + i sin VI.59. 1) Область вне окружности с центром в точке (—1; —1) радиусом
4 и сама эта окружность; 2) кольцо, заключенное между
окружностями с общим центром (2;—1) и радиусами 1 и 2
(окружности в область не входят). VI.60. 1) 2cos^(cos-^ +
-Hsin^); 2) 2sin (cos (-|) + zsin (-^)). VI.61. 1) 1 • (cos (а- +
+ tsin (а-2) 2sin«. (cos (| - |) + zsin (^ - |)). VI.62. 1) |z| = = 1, argz = а + 2m, п G Z; 2) |z| — 1, argz = —а + 2m,
п G Z; VI.63. 1) 2 • (cos-у + zsin 2) 128 (cos у + z sin
VI.64. 1) — 2) 4096. VI.65. 1) 125 (cos3<^+ tsin3<ya), ср = л — arctg
2) 125 (cos 6<p + z sin 6<p), cp = —arctg 2. VI.66. 1) cos За = cos3 а —
— 3cosasin2a; 2) sin 3a = 3cos2asina — sin3 a. VI.67. 1) cos4a =
5—5682
130 Глава VI. Комплексные числа
Л 0 0 Л ч
= cos а — 6cos asin а + sin а; 2) sin4а = 4cos asin а — 4cosasin a.
VI.68. 1) 2 + 3/, —2 — 3/; 2) 2 + z, -2 - i; 3) 4 — 3/, —4 + 3/; 4) 2 — 5/, —2 + 5z. VI.69. 1) ±z|a|; 2) ±|a|. VI.70. 1) ^2 (cos | + z sin ,
V2 (^cos у+zsin yj, v2 ^cos-y +/sin-g-j; 2) у - -y + (y; о \ г) ( 7Г * 7Г \ о ( 13 7U . 13 7Г \ n ( 25 7Г I 2o 71 \
3) 2 lC0S 18 + ZS'n 18?’ 2V T8 /’ 2VOS“18’+ ПЧГ/:
4/o ( Зтг . . . Зтг\ 4/5 ( Utt , . . 11тг\ 4/5 ( 19тг , . 19тг\
4) v2 cos + i sin , v2 cos —+ (sin -— , V2 cos + t sin —, \ lb lb / \ lb lb / \ lb lb /
У2 (cos 2/ -+ z’sin VI.71. 1) ±1; 2) 1, -1 ± 3) ±1, ±z;
4) ±1, 4 1 VI-72. 1) ±2i; 2) -1, ± i^; 3) 1 ± i;
-l±i; 4) ±| + ^<. ±/3<. VI.73. I) ~+'^,
2) ±^ + i. -i; 3) ±(yl+3+;v5H^y
,, , /х/2 + ^з , , Z/2-^3 , ./г + 'ЛА , /V2 ,.^2\
4) ±( 2"-+'—2~)’ d+—2~ + ~)' U- 2~/
VI.74. I) v^ficos £±tsin^); 2) cos - z sin cos у + zsiny,
cos у + zsiny. VI.75. 1) ±3z; 2) ±0,8/. VI.76. 1) -2 ± i;
2) -1 ± y/5i; 3) -1 ± 3z; 4) ± ^z. VI.77. 1) ±|z;
2) —2 ± 2z; 3) -3 ± z; 4) 0,5 ± 2,5i. VI.78. 1) z2 + 36 = 0;
2) z2 - 4z + 13 = 0. VI.79. 1) a < -1,25; 2) -4 < a < -1.
VI.80. 1) z; 2) —1,5/. VI.81. 1) 8 + 6z; 2) -7 + i. VI.82. 1) 2 + 4z,
-8 - 4z; 2) 4 + 2z, -1 - 2z. VI.83. 1) (2z - l)(2z + l)(2z + z)(2z - z);
2) (z + 2) (z - 1 + л/3«) (z - 1 - V3z); 3) (z - 2)2 (z + 1 + v^z) (z + 1 - x/3/);
4) (z-\/2z)2 (z-У2«)2- VI.84. 1) 0, ±0,25z; 2) ±2z; 3) -1 ± z\/3,
-l±\/5; 4) VI.85. 1) 1 - i, 0,8-0,4z; 2) 14-3/, 2 - z.
VI.86. 1) 2±z, —2 ± /; 2) 2 ± 3z, -2 ± 3z. VI.87. 1) z4 + 13z2 - 48 = 0; 2) z4 - 21z2 - 100 = 0. VI.88. 1) z4 - 5z3 + 7z2 - 5z + 6 - 0;
2) z4 - 2z3 + 3z2 - 2z + 2 = 0. VI.89. 1) -z, ±2)2, -2 + 2z,
1 + 2/, —1—2/. VI.9O. 1) -l±^z, ~7±23v^; 2) -1 ± | ± ^yz.
VI.91. 1) z4 - 42z2 + 841 = 0; 2) z4 + 32z2 + 1156 = 0. VI.93. Центр
окружности в точке(““) радиус равен Q~- VI.94. (1 — уг) (1 + z).
VI.96. 1) 2, — 1 ± \/3z, ±5z; 2) 3, — l±\/5z, ±2z. VI.97. Центр окружности z\ — a Izi — zol
в точке-1---5^, радиус равен —
1 — az 1 — иг
Глава VII
МНОГОЧЛЕНЫ ОТ одной ПЕРЕМЕННОЙ
§1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Первый уровень
VII.1. На йти коэффициенты многочлена Р(х), если:
1) Р(х) = Зх4-ах2 + Зх + Ь, Р(0)~4; Р(1) = 2;
2) Р(х) = ах3 + Ьх2 + 2х + с, Р(0) = 5; Р(1) = 6, P(-V) = -2.
VII.2. Найти свободный член многочлена:
1) Р(х) = (х24-х- 1)(х4-3)5;
2) Р(х)=(2х2-5х + 6) (4х4 —Зх3-2)5.
VII.3. Записать в каноническом виде многочлен:
1) /}(х) = (х-|-4) (2х2 — х + 3);
2) Р(х) = (х —1) (х —2) (х —3)(х —4);
3) Р(х) = (х-1)3(х + 1)3;
4) Р(х) = (х —2)2 (х2 + 2х + 4).
VII.4. 1) Найти коэффициент при х3 многочлена
Р(х) = (Зх2-4х + 5) (х3-2х24-Зх — 1).
2) Найти коэффициент при х4 многочлена
Р(х) = (х — 1)2(х34-Зх2-х4-3).
VII.5. Найти числа а, Ь, с, при которых равны многочлены Р(х) и Q(x):
1) /}(х) = 2х44-Зх3 —5х —2, Q(x) = (ах + 3) (х3 - Ь) - Зх 4- с;
2) Р(х) = Зх4 + 7х3 + Зх2 + х + 2,
Q(x) = (x4-1) (ах3 + Ьх2 — х + с).
VII.6. Используя метод неопределенных коэффициентов, найти частное Q(x) и остаток R(x) при делении многочлена Р(х) на Т(х\.
1) Р(х) = 2х2 + 3х-3, Г(х) = 2х-1;
132 Глава VII. Многочлены от одной переменной
2) Р(х) = х3 — 2х2 -х-2, 7\х) = х2 + х + 2;
3) Р(х) = х3 — 5х2 +15х —6, Т(х)=х-3;
4) Р(х)=х5-1, Г(х)=х2 + 2х-1.
VII.7. Используя способ деления «уголком», найти частное Q(x) и остаток R(x') при делении многочлена Р(х) на Т’(х): 1) Р(х) = х3 —2х2-5х-7, Т(х) = х-4’, 2) Р(х) =х4 — Зх3 — х2 +10х —3, Т(х) =х2 — Зх + 1;
3) Р(х) = 2х4 + х3-х2-Зх- 1, Г(х) = х2 + 2х + 2;
4) Р(х) = 8х4-4х3 — 16х2-4х + 9, Т(х) = 2х2-х-1.
VII.8. Выяснить, при каких целых значениях х принимает целые значения выражение:
«х 2х2 —7х+4. х3 —Зх + 6.
2^ ’ х + 2 ’
ох х4 + Зх3 + 2х2+х + 2. дх 2х4-Зх2+4 / 9 i ’ ' 9 1
х2+х + 1 х—1
Второй уровень
VII.9. На йти значение многочлена Р(х) при x = xq, если: 1) Р(х)=х3 + 9х2+27х + 29, х0 = -3-\/2;
2) Р(х)=х4 — 8х2 + 20, хо = 1 + \/3.
VII.10. На йти сумму коэффициентов многочлена Р(х), если:
1) Р(х) = (х- 1)4(х + 3)3;
2) Л*(х)- (1 + 2х —4х2)248 (1 — 5х + Зх2)75.
VII.И. Найти а и Ь, при которых многочлен Р(х) делится на многочлен Г(х) без остатка:
1) Р(х)=х3 + ах2 — х + b, Г(х) =х2 + 2х + 5;
2) Р(х)=х4 + ах3 — 2х2 + Ьх + 4, Г(х) — х3 — 2х +1.
VII.12. 1) При делении многочлена Р(х) на двучлен х —4 получается остаток 6, а при делении на двучлен х + 3 получается остаток 27. Найти остаток от деления многочлена Р(х) на многочлен (х — 4)(х + 3).
2) Остатки от деления многочлена Р(х) на х + 1, х —2, х —3 равны соответственно 3, 1, —1. Найти остаток от деления многочлена Р(х) на многочлен Т’(х) = (х + 1) (х — 2) (х - 3).
§2. Схема Горнера 133
V II.13. При делении многочлена Р(х) на многочлен (х + 1)(х —2) получается остаток 2х+1, а при делении на многочлен х —1 получается остаток 5. Найти остаток от деления многочлена Р(х) на многочлен (х + 1)(х —2)(х —1).
V II.14. Не проводя деления, найти остаток от деления многочлена Р(х) = х20 +х15 + 4 на многочлен Г(х) = х2 —1.
V II.15. Решить уравнение:
I) х4 + 2х3 + Зх2 + 2х + 9_g. х4 — 2х3 —Зх2+4х —10 g _ q
х2+х + 1 ’ х2—х —2
VII.16. 1) Доказать, что при любых пбН, mEN многочлен
Р(х) =хп+т — хп — хт +1 делится на (х—I)2.
2) Доказать, что при любых пбН, meN многочлен
Р(х) = x2m+n+1 хп — x2m+1 — 1 делится на х2 —1.
3) Доказать, что при любом пбН многочлен Р(х) =хп+2 — 2xn+1 -\-хп-х2 + 2х — 1 делится на (х —I)3.
4) Доказать, что при любых пбН, mEN многочлен Р(х) =хт+п+х-хт+п-xm+l -хп+[ +хп + хт +х- 1 делится на (х —I)3.
VII.17. Найти наибольший общий делитель и наименьшее общее кратное многочленов Р(х) и Г(х):
1) Р(х) = 3х4 - 12х2, Г(х)=х4 —16;
2) Р(х) = х4 + х3 + 2х2 + х + 1, Т(х) =х4 — Зх2-4.
VII.18. Используя алгоритм Евклида, найти наибольший общий делитель многочленов Р(х) и Т’(х):
1) Р(х) = Зх3 + 4х2 + 7х + 2, Г(х) = Зх4 —8х3 + 12х2 —13х-6; 2) Р(х)=х4+х3 + Зх2-|-х-|-2, Т(х) = х5-2х4 — Зх3 — 4х + 2.
§2. СХЕМА ГОРНЕРА
Первый уровень
VII.19. Используя схему Горнера, найти частное и остаток при делении многочлена Р(х) на двучлен Т’(х):
1) Р(х) = х4 + 2х3 —Зх2 —4х-15, Т(х) = х — 2;
2) Р(х) = х3—Зх + 2, 7\х) = х + 2;
3) Р(х) =х4-ЗОх3 + 81х2- 10x4-271, Г(х) = х-27;
4) Р(х) = х3 — 2х2 — 5х + 6, 7’(х)=х —1.
134 Глава VII. Многочлены от одной переменной
VII.20. Проверить, что многочлен Р(х) делится на двучлен Т(х) без остатка, и найти частное от деления:
1) Р(х) = х3 — х2 — 8x4-12, Т(х) = х — 2;
2) Р(х) = 2х4 4-Зх3 4-х — 6, Г(х)=х4-2;
3) Р(х) =х4 — 6х2-5х —12, Т(х) = 3 — х;
4) Р(х) = 3х5- х4-83х3- 17х2 — 8x4-10, Г(х) = х + 5.
VII.21. Используя схему Горнера, найти частное Q(x) и остаток R(x) при делении многочлена Р(х) на Т(х):
1) Р(х) = х3 - 1,5х2 + 1, 7’(х) = 2х + 1;
2) /Дх) = 6х3 4-5х2 — 4х — 4, Г(х) = 2x4-3;
3) Р(х) = 6х3-4х2 + 12х, Г(х) = Зх-2;
4) Р(х) = 4х4 + 2х3 + ||х2 + х, 7’(х) = 7х4-3.
Второй уровень
VII.22. Доказать, что многочлен Р(х) делится на многочлен Т(х) и найти частное от деления:
1) Р(х)=х44-4х3 —Зх2 — 10х + 8, Т(х) = (х —I)2;
2) Р(х) = х4 — 5х3 4-5х2 — х — 12, Т(х) = (х — 4)(х-Н 1);
3) Р(х) = 2х5 — х34-х2 — х —1, Г(х)=х2 —1;
4) Р(х) — х6 -Зх5 -х4 + 13х3 -54х2 + 140х- 120, Г(х) = (х-2)3(х + 3).
VII.23. Применяя схему Горнера, доказать что многочлен Р(х) делится на квадратный трехчлен Т’(х):
1) Р(х) = х4 4-4х3 — х2 4-4х —2, Г(х) = х24-4х —2;
2) Р(х) = х7 4-2х6 — х5 4-х3 — 5x4-2, Г(х) = х24-2х —1.
VII.24. Применяя схему Горнера, доказать 'что многочлен Р(х) делится на квадратный трехчлен Т(х):
1) Р(х)=х4-2х3 + 12х2 — 18x4-27, Г(х)=х2 + 9;
2) Р(х) = 2х64-3х54-8х4 —6х3—х2 — 3x4-5, Т(х) =х2 + 2х + 5.
VII.25. 1) Найти а и Ь, если известно, что многочлен х34-ах24-6х —20 делится на х2-4.
2) Найти а и Ь, если известно, что многочлен ах4 4-Ьх3 4-1 делится на (х—I)2.
§3. Теорема Безу. Корни многочлена 135
VIL26. Разложить многочлен Р(х) по степеням двучлена x — Xq:
1) Р(х) = х3 - 7х2 +18х - 32, Хо = 3;
2) Р(х) = 2х3-15х2 + 31х-26, х0 = 2;
3) Р(х) = 2х4 + 9х3 + 5х2-|-2Ох-|-1, xq = —1;
4) Р(х) = х4-7х3 + 18х2-20х, х0 = -2.
§3. ТЕОРЕМА БЕЗУ. КОРНИ МНОГОЧЛЕНА Первый уровень
VII.27. Не выполняя деления, найти остаток от деления многочлена Р(х) на двучлен Т'(х):
1) Р(х) = 4х3-Зх2 + 5х-6, 7(х)=х-2;
2) Р(х) = (х3-2х2 + 5)3 (2х + 1)5, Т(х)=х+1.
VII.28. Используя схему Горнера, доказать, что числа
—2 и —| являются корнями многочлена Р(х) = Зх6 + 7х5 + 2х4 + Зх3 +1 Ох2 + 9х + 2.
VII.29. Определить кратность корня Xq многочлена Р(х):
1) Р(х) =х3+х2- 10х + 8, Хо = 2;
2) Р(х)=х4 + 7х3 + 13х2-Зх-18, х0 = -3;
3) Р(х) = 4х4 + 4х3 + 5х2 + 4х + 1, xq = -0,5;
4) Р(х) = х5 + 4х4 + 2х3-8х2 — Их-4, хо = -1.
VII.30. 1) Записать в канонической форме многочлен Р(х) 3-й степени со старшим коэффициентом 2, имеющий простой корень —5 и двукратный корень 1.
2) Записать в канонической форме многочлен Р(х) 4-й степени со старшим коэффициентом 4, имеющий двукратный корень —0,5 и двукратный корень 3.
VII.31. Разложить многочлен Р(х) на линейные множители, выписать его корни и указать их кратность: 1) Р(х)=х4-18х2 + 81; 2) Р(х) = х5-Зх4 + Зх3-х2;
3) Р(х)=х3-х2-х + 1; 4) Р(х) = х4 + 2х3-2х-1.
VII.32. Представить многочлен Р(х) в виде произведения квадратных трехчленов:
1) Р(х)=х4 + 6х2 + 8; 2) Р(х) = 2х4 + 7х2 + 3.
136 Глава VII. Многочлены от одной переменной
VII.33. Разложить многочлен Р(х) на линейные множители:
1) Р(х) =х4 +13х2 + 36; 2) Р(х) = х4 + 4х3-х-4;
3) Р(х) = х4 + 2х2 + 1; 4) Р(х)=х6-х4-х2 + 1.
Второй уровень
VII.34. Найти остаток от деления многочлена Р(х') на двучлен Т’(х), не выполняя деления:
1) Р(х) = 8х3 + 2х2 + Зх-1, Г(х) = 2х + 1;
2) Р(х) = 3х2о+х19-7х+1, 7’(х) = Зх + 1;
3) Р(х) = (х2-х-6)2(х-3) + 2, Г(х) = -х + 3;
4) Р(х) = х6-12х4 + 48х2 + 64, Т’(х) = (1 — х/З)х + 2.
VII.35. 1) Н айти многочлен наименьшей степени с действительными коэффициентами, имеющий корень 3 кратности 2 и корень 1 — 2/ кратности 1.
2) Найти многочлен наименьшей степени с действительными коэффициентами, имеющий корень 1 кратности 3 и корень 14-i кратности 1.
VII.36. Представить многочлен Р(х) в виде произведения квадратных трехчленов:
1) Р(х) = х4 + 64; 2) Р(х) = х4 + х2 + 1;
3) Р(х) = х4 + 2х2 + 9; 4) Р(х) = 4х4 + 8х2 + 9,
VII.37. Решить уравнение:
1) 1___+_______!_____=______!____•
х4+5х2 + 9 х4+2х3+х2 — 9 х4 —х2+6х —9
2) ____1___+_________2-______=__________±_______
х4+9х2 + 18 х4- Зх3+7х2-9х + 12 х4-Зх3 + 6х2 - 14х+24
VII.38. 1) Разложить на линейные множители многочлен
/’(х) = х4Н-х3-|-2х2Ч-4х — 8, если известно, что один из
его корней равен —2/.
2) Разложить на линейные множители многочлен
Р(х) = х4 - 4х3 + 14х2 — 4х +13, если известно, что один из его корней равен 2 + 3/.
VII.39. Разложить на множители с действительными коэффициентами методом неопределенных коэффициентов многочлен: 1) Р(х) = х4 + 5х3 + 5х2-4х-2;
2) Р(х) = х4 + х3 + Зх2 + 32х-10;
§4. Алгебраические уравнения 137
3) Р(х)=х4 —2х3 + 2х2 —11х + 4;
4) Р(х) = х4 —Зх3 —7х2 —8х + 2.
VII.40. Разложить на множители многочлен Р(х,у\.
1) Р(х, у)—ух2 + 3ух + х-4у-1;
2) Р(х)=хг/2 + 5хг/ + 6х-г/-2;
3) Р(х,у') = хА-2ух2-х+у2-у\
4) Р(х, у) = х4+х3 + 2ух2 + ху+у2.
V II.41. При каких значениях параметра а уравнение Зх2+ Зях + 4а + 9 = 0 имеет два различных действительных корня, удовлетворяющих условию -^f+^2 —36?
V II.42. Доказать, что между корнями xi,x2,x3 многочлена ax3 + bx2 + сх + d и его коэффициентами существует следующая зависимость:
Х1+Х2+Х3 = -^, Х1Х2+Х1Хз+Х2Хз = ^, xix2x3 = -^.
V II.43. 1) Пусть х2> хз ~ корни многочлена х3-2х2+х + 1. Составить новый многочлен, корнями которого были бы числа у1=х2-Х3, У2=ХЗ'Х1’ УЗ=ХГХ2-
2) Пусть Х[, х2, х3 — корни многочлена х3 — х2 — 1. Составить новый многочлен, корнями которого были бы числа У1=х2 + х3, у2 — х3 + xi, Уз = Х[ + х2.
§4. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
Первый уровень
VII.44. Решить уравнение:
1) х3 - 2х2 - х + 2 = 0; 2) х3 + 2х2 — Зх - 6 = 0.
VII.45. Найти действительные корни уравнения:
1) х3 — Зх2 — 4х + 12 = 0;
2) х3 - 2х2 - 9 = 0;
3) х4 — 5х3 — х2 + 23х — 6 = 0;
4) х4 — х3 — 5х2 + Зх + 2 = 0;
5) х4 + Зх3 - 12х2 - 20х + 48 = 0;
6) х4 + 2х3 + 2х2 + х - 6 = 0.
138 Глава VII. Многочлены от одной переменной
VII.46. На йти все корни уравнения:
1) х3 + 5х + 6 = 0;
2) х4 + 5х3 + 7х2 + 5х + 6 = 0.
VII.47. Найти все корни многочлена:
1) Р(х) = х4 + х3 + 2х2 + 4х - 8;
2) Р(х) = х4 - 4х3 - 17х2 - 26х - 14.
VII.48. Разложить многочлен на множители:
1) Р(х) = х4 + Зх3 - Зх2 — Их — 6;
2) Р(х) = х5 + х4 - 5х3 - х2 + 8х — 4.
VII.49. Один из корней уравнения х3 — 6х2 + ах — 6 = 0 равен 2. Найти а и два других корня этого уравнения.
VII.50. 1) Уравнение ах3 - 2х2 — 5х + b = 0 имеет корни Х[ — 1, Х2 = —2. Найти а, b и третий корень этого уравнения.
2) Уравнение 2х3 + тх2 + пх + 12 = 0 имеет корни х\ = 1, Х2 = 2. Найти m, п и третий корень этого уравнения.
Второй уровень
VII.51. Найти рациональные корни многочлена:
1) Р(х) = 2х5 - х4 + 4х - 2;
2) Р(х) = Зх7 + 2х6 - 5х5 + Зх3 — х2 - 7х + 5.
VII.52. Реш ить уравнение:
1) Зх3 + 5х2 + 16х — 6 = 0;
2) 6х4 + х3 + 5х2 + х - 1 = 0;
3) Зх4 + 2х3 - Зх2 + 16х + 12 = 0;
4) 2х5 + 4х4 - 9х3 - 17х2 + 8х + 12 = 0.
VII.53. 1) Известно, что один из корней уравнения х4 - 2х3 + Зх2 - 2х + 2 = 0 равен i. Найти остальные корни.
2) Известно, что один из корней уравнения х5 + 25х3 - 8х2 + k = 0 равен 5г. Найти остальные корни.
Задачи повышенной сложности к главе VII 139
V II.54. Найти все значения Л, при которых два уравнения Лх3 — х2 — х - (Л + 1) = 0, Лх2 — х - (Л + 1) = О имеют общий корень, и найти этот корень.
V II.55. Доказать, что корни уравнения
х3 - (a + b + с)х2 + (ab + ас + bc)x - abc = О равны а, b и с.
V II.56. Решить систему уравнений:
fx + y + z — 9, Гх + // + г = — 1,
1) < ХУ + xz + У2 — 26, 2) < ХУ + xz + yz = —13,
I xyz = 24; I xz/z = 21.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ VII
VII.57. Сократить дробь:
i\ х5 + х4 + х3 + 5х2 — 2х + 6 . 2) 2х5 — 2х4 + Зх3 — 5х2 + х — 2
' 2х5 + 2х4 - х3 + 7х2 - х + 3 ’ ' Зх5 - Зх4 + 4х3 - 7х2 + х - 2 '
VII.58. 1) Число 1 + \/3 является корнем уравнения х4 + ах3 + Ьх2 + 6х + 2 = 0. Найти остальные корни уравнения, если известно, что а и Ь — рациональные числа.
2) Число 1 + х/2 является корнем уравнения х5 + ах3 + Ьх2 + 5х + 2 — 0. Найти остальные корни уравнения, если известно, что а и Ь — рациональные числа.
V II.59. Пусть Xi, х2, хз — корни уравнения х3 + рх + q = 0. Доказать, что х3 + х^ + х| = Зх]Х2хз.
V II.60. Пусть известно, что все корни некоторого уравнения х3 +рх2 + qx + г = 0 положительны. Какому дополнительному условию должны удовлетворять его коэффициенты p,q,r для того, чтобы из отрезков, длины которых равны этим корням, можно было составить треугольник?
V II.61. Решить кубическое уравнение х3 + ах2 + Ьх + с = 0 (а 7^0), если его корни образуют убывающую арифметическую прогрессию.
140 Глава VII. Многочлены от одной переменной
VII.62. Пусть х\, %2> *3» %4 — корни уравнения
4х4 — х3 — 12х2 + 2% + 5 = 0. Найти значение выражения -*1-*2хЗ -*1Х2Х4 X 1*3*4 *2*3*4
*4 *3 *2 *1
VII.63. Дано биквадратное уравнение ах4 + Ьх2 + с = О (а / 0). Найти:
1) сумму его корней;
2) сумму квадратов корней;
3) сумму кубов корней;
4) сумму четвертых степеней корней.
V II.64. При каком условии многочлен Р(х) = х3 + рх + q имеет два равных корня?
V II.65. Доказать, что если действительные коэффициенты уравне-/ ч2 / чЗ ния х3+рх + <? = 0 удовлетворяют условию +(3) то уравнение имеет ровно один действительный корень.
V II.66. Доказать, что при любом действительном с уравнение х3 — х2 + х + с = О имеет только один действительный корень.
VII.67. Используя формулу Кардано, найти действительные корни уравнения:
1) х3 - Зх2 - 12х -16 = 0; 2) Зх3 + 18х2 + 45х + 50 = 0;
3) х3 - 6х2 + 6х - 2 = 0; 4) 4х3 - 12х2 -9 = 0.
VII.68. Доказать, что иррационально число:
1) W31-2-W5T + 2; 2) | - {А/Ж + Г
у V 2У1о о у V 2У1о о
VII.69. Доказать, что рационально число:
1) ^2 + У5+\/2-75; 2) У7 + 5\/2 -- 1 -- .
^7 + 5^2
ОТВЕТЫ К ГЛАВЕ VII
VII.1. 1) а = 8, 6 = 4; 2) а = 2, Ь = -3, с = 5. VII.2. 1) -243; 2) -192. VII.3. 1) Р(х) = 2х3 + 7х2 - X + 12; 2) Р(х) = х4 - 10*3 + 35х2 - 50* + 24; 3) Р(х) = х6 - 0 х5 - Зх4 + 0 • х3 + 3 • х2 + 0 • х - 1; 4) Р(х) =
= х4 — 2 • х3 + 0 • х2 — 8 • х + 16. VII.4. 1) 22; 2)1. VII.5. 1) а = 2, b = 1, с=1; 2) а = 3, 6 = 4, с = 2. VII.6. 1) Q(x) =х + 2, Я(х) = -1; 2) Q(x) = x-3,
Ответы к главе VII 141
/?(х) = 4; 3) Q(x) = %2 — 2х + 9, Я(х) — 21; 4) Q(x) = х3 — 2х2 4- 5х — 12,
Я(х) = 29х - 13. VII.7. 1) Q(x) = х2 + 2х + 3, Я(х) = 5; 2) Q(x) = х2 - 2, /?(х) = 4х — 1; 3) Q(x) = 2х2 - Зх 4- 1, /?(х) = х — 3; 4) Q(x) = 4х2 — 6,
/?(х) = -10х + 3. VII.8. 1) 0; 1; 3; 4; 2) 2; 0; -1; -3; -4; -6; 3) 0; ±1; -2;
4) 0; ±2. VII.9. 1) 0; 2) 16. VII.1O. 1) 0; 2) -1. VII.11. 1) а = -1, Ь = —15; 2) а = 4, b = -7. VII.12. 1) -Зх + 18; 2) -|х2 - ^х + 3.
VII.13. -х2 + Зх + 3. VII.14. х + 5. VII.15. 1) -1±2^;
2) • VII.17. 1) НОД(Р(х),<2(х))=х2-4, HOK(P(x),Q(x)) = 3x6-48x2;
2) НОД(Р(х),<?(х)) = х2 4-1, HOK(P(x),Q(x)) = x6 + x5 —2х4 —Зх3 —7х2 —4х —4. VII.18. 1) НОД(Р(х), Q(x)) = Зх + 1; 2) НОД(Р(х), Q(x)) = х2 4- 1.
VII.19. 1) Частное х3 4-4х2 4-5х 4-6, остаток —3; 2) частное х2 — 2х 4-1,
остаток 0; 3) частное х3 — Зх2 — 10, остаток 1; 4) частное
х2 — х — 6, остаток 0. VII.20. 1) х2 + х - 6; 2) 2х3 - х2 + 2х - 3;
3) -х3 - Зх2 - Зх - 4; 4) Зх4 - 16х3 - Зх2 - 2х + 2. VII.21. 1) Q(x) =
= О,5х2 — х 4- 0,5, Я(х) = 0,5; 2) Q(x) = Зх2 — 2х 4- 1, /?(х) = —7;
3) Q(x) = 2х2 + 4, Я(х) = 8; 4) <?(х) = |л3 + + |х + Я(х) =
VII.22. 1) х2 4- 6х + 8; 2) х2 - 2х 4- 3; 3) 2х3 4- х 4- 1; 4) х2 4- 5.
VII.25. 1) а = 5, b = —4; 2) а = 3, b = -4. VII.26. 1) Р(х) =
= (х - З)3 4- 2(х - З)2 4- 3(х - 3) - 14; 2) Р(х) = 2(х - 2)3 - 3(х - 2)2 - 5(х - 2) - 8; 3) Р(х) = 2(х 4- I)4 4- (х 4- I)3 - Ю(х 4- I)2 4- 29(х 4- 1) - 21; 4) Р(х) =
= (х + 2)4 — 15(х 4-2)3 + 84(х + 2)2 — 208(х 4-2) 4-184. VII.27. 1) 24; 2) -8. VII.29. 1) 1; 2) 2; 3) 2; 4) 3. VII.3O. 1) Р(х) = 2х3 4-6х2 - 18х + 10;
2) Р(х) = 4х4 - 20х3 4- 13х2 4- ЗОх 4- 9. VII.31. 1) (х - З)2 (х 4- З)2, корень 3 кратности 2 и корень —3 кратности 2; 2) х2 (х — I)3, корень О
кратности 2 и корень 1 кратности 3; 3) (х 4-1) (х — I)2, корень -1
кратности 1 и корень 1 кратности 2; 4) (х — 1) (х 4-1)3, корень 1
кратности 1 и корень —1 кратности 3. VII.32. 1) (х2 4-2^ (х2 + 4^;
2) (2х24-1) (х24-з). VII.33. 1) (х - 2i) (х + 2i) (х - 3i) (х 4-3i); 2) (х-1)х х(х+4) (x-~1+2tV5) + з) (*-02(* + 02; 4) (х — i)2x
х (х 4-1)2 (х — i) (х + О- VII.34. 1) -3; 2) у; 3) 2; 4) 128 + 24ч/3. VII.35. 1) Р(х) = адх4 ~ 8аох3 4- 26адх2 — 48адх + 45ад, где а$
0; 2) Р(х) = адх5 — 5адх4 + llagx3 — 13адх2 + 8agx — 2а0, где
ад / О- VII.36. 1) (х2 —4x4-в) (х24-4x4-8^; 2) (х2 — х + 1)х
х (х2 + х-Ь1); 3) (х2 — 2x4-3^ (х2 4- 2х4-3); 4) ^2х2 — 2х4-3) ^2х2 + 2х4-з). VII.37. 1) -±2^; 2) 1; —4. VII.38. 1) Р(х) = (х - 2i)(x + 2i)(x + 2)(х - 1);
142 Глава VII. Многочлены от одной переменной
2) Р(х) = (х - 2 - Зг)(х - 2 4- 3i)(x - i)(x 4- г). VII.39. 1) Р(х) =
— (х2 4- 2х — 2^ (х2 + Зх + 1); 2) Р(х) = (х2 4- Зх — 1) (х2 - 2х 4- К)};
3) Р(х) = (х2 + х + 4) (х2 - Зх + 1); 4) Р(х) = (х2 — 5х -Ь 1) (х2 + 2х + 2).
VII.40. 1) Р(х,г/) = (х — 1) (хг/4-4г/4-1); 2) Р(х,г/) = (г/+ 2) (хг/+ Зх - 1);
3) Р(х,у) = (х2 - х - yj (х2 + х - у + 1); 4) Р(х, г/) = (х2 + х+у) (х2 4- у^.
VII.41. а = -3. VII.43. 1) г/3 - у2 - 2г/ - 1; 2) г/3 - 2у2 + у + 1.
VII.44. 1) 1; -1; 2; 2) -2; ±\/3. VII.45. 1) -2; 2; 3; 2) 3;
3) 3; —2; 2 ± г/3; 4) 1; -2; 1 ± л/2; 5) -3; -4; 2; 6) 1; -2.
VII.46. 1) -1; 2) —2; -3; ±г. VII.47. 1) 1; -2; ±2г;
2) 7; —1; —1 ± г. VII.48. 1) (х + I)2 (х - 2) (х + 3); 2) (х - I)3 (х + 2)2.
VII.49. а =11, х2 = 1, х3 = 3. VII.50. 1) а = 1, b = 6, х3 = 3; 2) m = О,
п = —14,х3 = -3. VII.51. 1) 1; 2) 1; VII.52. 1) -1 ± г/5г;
2) -Ь ±г; 3) -2; 1 ± Лг; 4) 1; -2; VII.53. 1) х1?2 = ±г,
хз 4 = 1 ± г; 2) Х[ 2 = ±5/, х3 4 = —1 ± л/Зг, Х5 = 2. VII.54. Л = = ’±1. VII.56. 1) (2;3;4), (2;4;3), (3;2;4), (3;4;2), (4;2;3), (4; 3; 2);
2) (-3; 1 4-2\/2; 1 - 2х/2), (-3; 1 - 2\/2; 1 + 2^2), (1 + 2л/2;-3; 1 - 2у/2),
(1 — 2л/2; —3; 1-Ь 2л/2), (1 + 2л/2; 1 — 2У2; —3), (1 — 2л/2; 1 4-2л/2; —3).
VII.57. 1) 2) VII.58. 1) 1 — л/З, 1 — л/2, 1-Ь л/2; 2) 1 - л/2,
2xz 4-1 3xz + 1
±1, —2. VII.60. р3 — 4pq 4- 8r > 0. Указание. Рассмотреть выражение (xi 4- х2 — х3) (х2 4- х3 — Х[) (х3 4- Х[ — х2). VII.61. Х[ = + -
х2 = х3 = ~g2 ~ VII.62. 6,2. VII.63. 1) 0; 2) - —;
z 3 J За ’ ’ a
3) 0; 4) ~22ac) . VII.64. 4p3 4- 27г/2 = 0. VII.67. 1) 1 + ^5 + Ж;
2)4= -^3-2; 3)2+ ^2+^4; 4) 1 + 4= + ^4-
^3 fa
Глава VIII
СИСТЕМЫ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Первый уровень
Решить систему уравнений (VIII.1-VIII.32)
VIII.1. J х2 + у2 — 74, х + у = 12. VIII.2. ( х2 - у2 = 16, [ х — у = 1.
VIII.3. J х + у = 8, ху = 15. VIII.4. Г ху-2(х + у) = 2, ( ху + х + у = 29.
VIII.5. х2 + у2 = 10, ху = 3. VIII.6. ( х2 + 4хг/ + у2 = 94, [ ху = 15.
VIII.7. < ' х2 — 2ху + 4у2 = 7, к х3 + 8г/3 = 35. VIII.8. ( х2 - ху + у2 = 19, [ х2 + ху + у2 = 49.
VIII.9. х2 + Зху = 54, к 4г/2 + ху = 115. VIII.10. Г (х - 1)(У - 1) = 3, 1 (х + 2)(е/ + 2) = 24.
VIII.И. < х + У = 1, х3 + у3 = 19. VIII.12. ( х2 + у2 = х + г/, - \{х + у}2.
VIII.13. < VIII.14. < ' ХУ + х + 2У - 2. х + 2у ху ’ ху х-2у = < х — 2у ‘ ху х2 - ху + |г/2 + х - х-у |х2 + ху + у2 + 2у + х = 2, = 3.
VIII.15. < \х — 1| — Зу = 2х - 8, кх + 2|г/| = 6. VIII.16. ( 2% — у = 2|г/ + 1| + 2 | 2|х| - Зу = 4% + 12.
VIII.17. < 5(х + I)2 + у2 = 21, , х.у + у = 2. VIII.18. ( 2х2 + (г/ + 4)2 = 6, [ 4х + ху = 2.
144 Глава VIII. Системы алгебраических уравнений
' 2% + У. + 6 = —
VIII.19. < У х ху
6у । 4% _ 1 _ 45
X У ху
х~У ^х + у _ X + у х — у ’
ху = -2.
VIII.21.
VIII.23.
VIII.25.
VIII.27.
VIII.29.
VIII.31.
V х у
( х2 — у2 — 3, [%2 + ху + у2 — 7.
( у2 - х2 = 4х + 4, [ х2 + у2 ~ 4 — Зху.
2х + у = Зх2, х + 2у = Зу.
х — ху3 = 7,
ху — ху = 3.
f 2х2 + ху + Зу2 = 11,
VIII.20. । п о
[ л - Зху + 4у2 = 2.
VIII.22.
VIII.24.
VIII.26.
VIII.28.
VIII.30.
VIII.32.
' х + У ХУ = 2 ху X + у ’
х — у । ху _ 5 ху х — у 2 ’
ху + х — у = 3, х2у — ху2 = 2.
(х-!)({/-!) =-8, (х + 2)(у + 2)=7.
у2 — 1 = 4х2 + 4х, 4х2 + у2 = 1 + Зху.
| х2 — ху — 6,
[ ху + у2 = 4.
( 2у2 — 4ху + Зх2 = 17,
| ,,2 „2 ___ if?
I у — X = 10.
Найти действительные решения VIII.43). системы
VIII.33. ' (х24-х + 1)(у2+у4-\) = 1 (х-1)0/-1) = 6. г 1 1 1 з,
VIII.34. < X у 6 ’ 2 2 л 1 ху —х у = Ь. VIII.35.
VIII.36. < х + у + ху = 5, х2 +ху + у2 = 7- VIII.37.
VIII.38. < ' х + у = 3, х5 +у5 = 33. VIIL39.
VIII.40. < х2 — 7х — г/+11 = 0, у2 — Зх — // + 15 = 0. VIII.41.
уравнений (VIII.33-
х3 + %//2 = 10, 3 2 с
[yd4-x2y = 3.
Г х3 + у3 + х3у3 = 17, [ ху + х + у = 5-( х2 — 4х — 2у — 1 = О, [ у2 — 2х + Зу +14 = 0. Г х2 = 3% + 4г/, 1 у2 =4% + 3//.
Глава VIII. Системы алгебраических уравнений 145
VIII.42. /(*2 + Л(*~!/) = 13, [ху(х-у) = 6.
VIII.43.
(х3 + 1)(г/3 + 1) = 18, ху + х + у = 5.
Найти действительные решения
VIII.52).
системы
VIII.44. < __-___
I V*+//~4= Vx+#-
VIII.50. Г +
^=2,
VIII.46.
VIII.48.
VIII.49.
= 78.
(Зх —2z/=5.
(х J~x — хГх=у Ju + 8 xfy, VIII.51. VIII.52.
(х=у+5.
VIIL45.
VIII.47.
уравнений (VIII.44-
(хн/)^=^>
(%+г/)у/х = Зг/р.
'Ух/у+х/У=5 х/х - х х/х, x=z/+3.
Решить систему уравнений (VIIL53-VIII.56).
{xz/=6, г/г = 15, гх = 10.
VIII.55.
' x2+xy+xz — х=2,
< у2 +xy+yz-y=-2, к z2+xz+yz — г=6.
' x+y+z=2,
VIII.54. х+2г/+3г=5,
к х2+//2+г2=6.
{x+y=xyz, y+z=xyz, z+x=xyz.
Второй уровень
Решить систему уравнений (VIII.57-VIII.71).
VIII.57. ^3-У3=61(х-^), ц%+1)(//+1) —12.
^4-^ = 2
У X 2’
1.1 = 3
х^у 2‘
VIII.58.
146 Глава VIII. Системы алгебраических уравнений
vni.59. F‘+y4=17a+^ VIII.60. < z о 9 х +у — х—у. /+/ = ^(*-//)2-
рсу=2(х-\-у).
VIII.61. < х2(1+г/+г/2+у3) = 160, 52(1-г/+г/2-г/3) = -80. VIII.62. < 2х2у2 — Зг/2+5ху—6=0, Зх2 у2 - 4 г/2+Зху — 2=0.
VIII.63. < х3у+хг/3 = ^(х+г/)2, A/ + x/ = |(x + #)3. VIII.64. < rx(t/2 + l)_3 х2 + г/2 5’ У(£2 -0 _ 4 < х2+г/2 5’
VIII.65. < х2+ху — 2z/2 + 8x+10y+12=0,
х2 + Зху + 2 г/2—х+у — 6= :0.
VIII.66. < ^{3 + 2х) = 3у—х. VIII.67. < — + — = 12, х у
г/2 4-2хг/=Зх2 — 2г/. У з
VIII.68. < х4+х2г/2 + г/4 = 91, 2 ,2-7 х -ху+у =7. VIII.69. < х3 —г/3 = 19(х —г/), х3 + г/3 = 7(х+г/).
VIII.70. < ху+х+3у=\, х2у+Зху2 + Зх+9у=4. VIII.71. < 2хг/+4х+Зг/=2, 4х2г/+Зхг/2+12х+9г/=8
Найти действительные решения системы уравнений (VIII.72-
VIII.83)
х3 + г/3 = 1, Зх2у — Зх4 = 4,
VIII.72. < 9 9' VIII.73.
xzy+2xyz+у=2. 8г/3-Зх2у2 = 2.
' Зх2 = г/4 + г/. } . 9 д 1 ^у =Х +х,
VIII.74. < о VIII.75. <
5%=^ + г/2. х J Юг/=^-х2.
VIII.76. < (х+г/)(х2-г/2) = 9, м ’ VIII.77. ' (%2 + 1)(г/2 +1) = 10,
ч (х-г/)(х2+/) = 5. 1 (х+г/)(хг/-1) = 3.
( / 2 , 2\Х с +у )- = 6, (х-г/)(х2 —г/2) = 7,
VIII.78. < у VIII.79.
. (^2-г/2)^ = 1- ч (х+г/)(х2 + г/2) = 175.
х3+4г/ = г/3 +16%, х3 + г/3+х2 у+ху2 = 5,
VIII.80. < _ _ VIII.81.
ч 5(1 +х2) = 1 + г/2. х4г/2 + г/4х2 = 20.
Глава VIII. Системы алгебраических уравнений 147
VIII.82.
Х~\~ , ~ X У~\~ 21
х у ху VIII.83. <
-+%3у3 + 1Оу2 = О.
у14-2z/6+3х2=О,
4 х3 х2
У
У* У
Найти действительные решения системы уравнений (VIII.84-
VIII.97).
V III.84.
V III.86.
V III.88.
VIII.90.
VIII.91.
VIII.93.
VIII.94.
VIII.96.
VIII.97.
х/7%+у + х/х+г/=6, у/х+у-у+х=2.
У + 19=20(х+//), у/х у/ х+2у — а/2 .
y/lix-у-/y-X=i, 7у/у — х+6у — 26х=\.
'1 + У2х-у=^-£
< I---
VIII.85.
VIII.87.
VIII.89.
ху
ХУ ^2х-у'
J-=4-3v^^.
2х - у v J
х2у3 = 2(х2+у2), VIII.92.
х , 2
&У 3
_ У_ 2х'
x+J— = — , у х-у х-у
ху — 4х=9.
VIII.95.
(^-2\/х2-1+у2 = 3,
) уЛ
|3(%-//) + ^L+3y2 = 0.
V ухЛ — {—х
'4+2Ух2 + 1+1/2 = 3,
< V
х+ у--—+у2 = 0.
\/Зу—~х-\-х-\-у—2, \/8y-x+x=2.
3+21х= у +4^/^/ —Зх, X
у - \^у-Зх=у-\-7х-2.
Г1+ху = ^2- + 2^, 2х-у ху
^у/2^=4-Зху.
ху
'у+
у х+у х+у, кху-у=\е>.
148 Глава VIII. Системы алгебраических уравнений
Решить систему уравнений (VIIL98-VIIL114).
'(4х+//)(з+1)+4г=0, '3xz+l=4x+3z,
VIII.98. < ху+у—х= —1, VIII.99. < pcy-yz+2z=i+x. '3x—y—5z—'2,yz=0, 4xy—3xz=4y — 3z+9, ^xy—2x=y—1. '3x+y+2z—x2=0,
VIII.100. < VIII.102. < x-5y-z-2z2=0, VIII.101. < л+9у-Зг+2хг=0. '(у+х)2=3+4г2, (2z-y)2 —4+х2, VIII.103. < <(2г-х)2=2+у2. 'х+у+ху=7, 10%—3y—3z+%2=0, Дбх—y+z—xy=O. r(3y-x)2=2+z2, (3y+z)2^3+x2, Jz-x)2=4+9y2. <x+y _ 7 xyz 12’
VIII.104. < VIII.106. < VIII.107. < y+z+yz=—3, VIII.105. < jz+x+zx= —5. '24 (%+//-г) =%//£, 24(y4-z—x)=5xyz, j$(x+z—y)=xyz. fx2+5y2 +4z2 +4xy+4уг=125, х2+3у2-4г2+4ху-4уг=75, yc+y+z=8. 'x+y—z=\, y+z _ 5 yz 12’ z+x _ 1 xyz 3 ’ И . 1—6 x y+z 5’
VIII.108. < x2+y2-z2 = -3, VIII.109. < x5+y5 — z3 = -29. f<2x+y+z=0, ><; n i— i — + + + II +-+I-1 N 1 II II Wltsj 45. | W
VIII.110. < VIII.112. yz+zx+xy—y2=O, VIII.111. < [xy+z2=Q. / 9 \x y=x-\-y-z, xz2=x-y+z, VIII.113. < tz/ z = z/ —x + z. у2+г2=13х2, k2(x3+z3)=7z/3. f3xy-^ = -5, xz xz+ —=4, yz
ху
Задачи повышенной сложности к главе VIII 149
{2х2 + Зу2=8х+6г/+8г+П,
г/2—г2=2г/+г+1,
2х2 — 4у 2+2z2=8%—8 у+z — 1.
Найти действительные решения системы уравнений (VIII.115-
VIII.121) 'xy+xz+yz=\l, ' x2+xy-\-4xz—4z2=0,
VIII.115. < x2+j/2+z2=14, VIII.116. < y2+xy+4yz—8z2=0,
xyz=6. <xyz=8.
'2хг/+| + 3=0, 2xz+-+3=0, у
VIII.117. < xz+4—2=0, VIII.118. < У ^+1-2=0,
<i/z+|+2=0. r2x3 —y3 — 2z3+x£/z+5=0, jcy-\-2+2=0.
VIII.119. < £/3+2z3—x3 — 2xyz—2=0, jc3—y3—z3+xi/z+4=0. f3x3 — 3y3+z3—xyz—3=0,
VIII.120. < Зу3—x3—z3—%£/z+5=0, <x3-y34-z3-xyz—2=Q. '4xy+y 2 + 2z2 =—3,
VIII.121. < 4xz+x2 + 2z2 = 1, <8yz+y24-2z2 = \.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ VIII
Решить систему уравнений (VIII.122-VIII.147).
{х — 2г/+3г=9, х2+4г/2 + 9г2 = 189, Зхг=4г/2.
{х2 —у2 = 2х+4у—3z, y2-z2=x-3y+4z, z2 —x2 = — Зх+y—5z.
<2x2 = £/z + 2x,
'xyz+xz2 = 2,
VIII.124. <2y2=xz+2y,
VIII.125. <xy+2xz=-z,
<2z2=xy+2z.
<x2yz= —15.
150 Глава VIII. Системы алгебраических уравнений
VIII.126.
'(x+y)(x+z)=x, < (г/+2Г) (г/+%) = £/, ,(2+х)(2+г/)=2.
VIII.127.
'(x4-2r/)(x-|-2z)=x, < (г/+2х)(г/+22) = г/, ,(2+2х)(2+2у) = 2.
'ху=х + у — 2, 1 Г(Х+//)(Х + 2)=Х,
VIII.128. <] х2 = 2(х-г/+2), VIII.129. < (у+2)(г/+х) = 2гл
,г/2=3(г/-х+2). <(2+х)(2+г/) = 32.
'2(х2 +y2)=xyz, '6х(г/2 + 22) = 13г/2,
VIII.130. < 10(г/24-22) = 29хг/2, VIII.131. < Зг/(х2+22) = 5х2,
,5(224-х2) = 13хг/2. fiz(x2 +у2') = 5ху.
'2 (х2 у2 + у2 z2 + z2 х2)+9xyz=0,
VIII.132. < 2у(х2 — z2) + 3x2=0,
<22 (х2 — у2) + Зхг/=0.
'Х2+у2-22 _ 3 ху z' fi+г+^-З у z х 2
VIII.133. < у2+г2-х2 = 3 VIII.134. < yz х г+г.^= з х у z 2
y2—x2—z2 _ 21 кхг/+ух+2х=-3.
' xz у
px2+y2 + z2 = 9-hyz, fx2—yz=3,
VIII.135. < Х2+2у2+22=6 + Х2, VIII.136. < у2 -Х2=5,
[х2+у2 + 2z2 = 3+ху. <22-Х£/= —1.
Гх2+хг/ + г/2 = 7, rx2 + z/2=42,
VIII.137. < у2 + 1/г+г2 = 3, VIII.138. < у2+х2=42,
1,22+Х2 + Х2 = 1. <22 4-х у=50.
VIII.139.
Найти все решения системы уравнений
'yz-x2 —xz-xy=2, < у2 +xy+zy — zx=3, jz2+zy+xz — xy = 6,
удовлетворяющие условию х 0, у 0, 2^0.
Задачи повышенной сложности к главе VIII 151
\y + 2yz2-4z3 = 0, (xy-xz + 3y + 6z = 0,
VIII.140. < y-yz-xz — Q. VIII.141. < у2-z/2 + 4x-42 = 0. jj2 -4xz2 - 13z3 = 0. лу-z2 -2x — у = 0. 'xz2-\-2x^yz — 3y2, (2x2y — xy^z = z2,
VIIL142. < yz + 3x2y2 = 4x3r/2, VIII.143. < xz + 3f/4z2 = 10x3r/5, Jx:2y - 6>x4y2z = z2. l5z/4 + 3xy^z2 = 2x2. 'x2 + 6z/ — z2 = —6,
VIII.144. < r/2+ 4x + z =-4, Jx - 11г/ + 2г(г +1) = 4. x — y2 — 5z = 5,
VIII.145. < x2 -8y — z2 = 8, ,x(5x — 1) — 4z;2 — 35z/ = 35. '2z2 — xz + 5xr/2 = 0,
VIII.146. < xz — z2 + 3x2y = 9x2 r/3, <z2 — 2x2 - 5z/2z = 18x2y. '2x2 + z/z+ 10x2r/ = 0,
VIII.147. < yz + z2 + 9x3 y2 = 3xy2, ^y2 + \3xy2 -z2 = 10x2z.
Найти действительные решения системы уравнений (VIIL148-
VIII.156). '4zx2 — yz2 + 2xy2 = 3xyz,
VIII.148. < zy2 + 2xz2 — 4yx2=3xyz, 2xy — 2xz+yz = 3. r2r/22 — 4xr/2 + zx2 = 3xr/z,
VIII.149. < 2z;x2 + 4zy2 — xz2 = 3xz/2, ^2xy + xz — 2yz = 3.
152 Глава VIII. Системы алгебраических уравнений
VIII.150.
x£z£
Х+У
2 2 ху
VIII.151.
'x(l + 2yz2)=y, r/(l-zx2) = z(l+x2z/), .z(l +xy2) — X.
1х3 + //3 = 19xr/ + 7xz+ llr/z, х3 +z3 — 26(xf/+xz + f/z), r/3 + z3 = 47xr/4-35xz + 39r/z.
I3x — 6y — 8z = xyz2, 2x — 5y — 7z = —x2yz, 3x — 9y — 13z = — xy2z.
VIII.154.
у 9 9 9
у -xy + x =z ,
VIII.155. < x2 — xz-+z2=y2,
VIII.156.
.z3 — z/3 = x2 -+y2 + z2.
'x2-y2 +z = —, xy
< y2-Z2+-X——, У*
z2 -X2+ у = — .
3 zx '2xz-+y-4xy— 1, < 4xz2 + 4z/2 — 16xz/2 = 5, k2xz3 + 4z/3 - 16xz/3 = 7.
ОТВЕТЫ К ГЛАВЕ VIII
VIII.l. (5; 7), (7; 5). VIII.2. (6; 2). VIII.3. (3;5), (5;3). VIII.4. (4; 5), (5;4). VIII.5. (3; 1), (1;3), (-3; — 1), (—1; —3). VIII.6. (3; 5), (5;3), (—3; -5), (-5;—3). VIIL7. (3; 1), (2;|). VIII.8. (3;5), (5; 3),
(-3;-5), (—5; —3). VIII.9. (3;5), (-3;-5), (36;-^), (-36;^). VIII.10. (4; 2), (2; 4). VIII.ll. (-2;3), (3;-2). VIIL12. (0;0), (1; 1). VIII.13. (^2 + 2x/3;l+-A=), (% - 2\/3; 1 - ' VIII.14.
I), VIII.15. (4;1), (0;3). VIII.16. (3;-6).
VIII.17. (-3;-l), (1;1), (-1 - -A=;-2л/5), (-1+ ^;2л/5). VIII.18. (l;-2), (—1;—6), (x/2;-4 + x/2). (-x/2;-4 - x/2). VIII.19. (-3; 1), (3;-1), VIII.20. (-2;-i), (2;1), (-!;-!), (1; 1). VIII.21. ч/б; (2;-l), (—2; 1). VIII.22. (-2;|),
(4-1). VIII.23. (Ц). VIII.24. (1 - x/2;-l - x/2),
\ О / \ О / \ О /
Ответы к главе VIII 153
(1 + х/2; — 1 Н-х/2), (1 + х/3; х/3 - 1), (1 - 73;-73 - 1). VIII.25. (2; 1),
(-2;-1), ( & ® ; * Y VIII.26. (5;-1), (-1;5). VIII.27. (0;2),
\уЗ уЗ/ \ у3 уЗ/
(-2;0), (0; —2). VIII.28. (0; 1), (0,-1), VIII.29. (0;0), (1;1),
1 + ч/5. 1 - ч/5\ Л
6 ’ 6 М
VIII.30. (3; 1), (-3;-1), (х/2; — 2х/2),
(~72;272). VIII.31. (|;-з), (y;-g)- VIII.32. (-3;—5), (3; 5),
(fiy)- VIII.33. (-1;-2), (—2;—1). VIII.34. (2; 3), (—3; —2). VIII.35. (2; 1). VIII.36. (1;2), (2;1). VIII.37. (2; 1),
(1;2). VIII.38. (2; 1), (1;2). VIII.39. (3; —2). VIII.40. (5; 1).
VIII.41. (0;0), (7; 7). VIII.42. (3;2), (-2;-3). VIII.43. (2; I), (1;2). VIII.44. (4;4), (|; 0. VIII.45. (-5;-3), (3; 1), -1
f-710- 1;-^-+5У VIII.46. (Ц;|\ \ □ J \ 12 3 /
VIII.47. (3;-1), (5;1),
(4 - 710;-3 - 7Ю), (4 + 7Ю;7Ю - 3). VIII.48. (4; 9), (9;4), (-4;-9), (-9;-4). VIII.49. (0; 0), ^72; VIII.50. (3; 2),
VIIL5L (9;4)‘ VI1152- (4;0- VIII.53. (2;3;5), (—2;—3;—5).
VIII.54. (1;-1;2), (-|; Ц). VIII.55. (1;-1;3), (-|;|;-2).
VIII.56. (0;0;0), (72; 72; 72), (—у/2; — х/2; — v/2). VIII.57. (-4;-5), (-5;-4), (-1 + 2ч/3;-1 + 2ч/3), (-1 - 273;-1 - 2ТЗ), (4 + 713; 4 - 713),
VIII.58. (2; 1), (1;2),
(3;6), (-2;1), (1;-2).
(4 - 713; 4 + 713).
VIII.59. (0; 0), (6;3),
VIII.61. (2;3), (—2; 3).
ч/б7). VIII.63. (0;0),
(—1;—2). VIII.64. (3; 1), (^-1)- VIII.65.
VIII.66. VIII.67. (6;6),
\ Л <4 / \ OD OD /
VIII.62. (1;2), (—1; —2), (2;1), (-2;-1), (1;2), (-2,0), (-3;3), (-4; 2).
VIII.68. (3,1), (—3;-1), (1;3), (-1;-3).
VIII.69. (0;0), (V7-,V7).
(-2;-3), (3;2), (-3;-2).
3. _2\
2’ ЗЛ
VIII.72. (^;^\
(_У7;_У7)> (х/19;-У'Ю), (-719; х/19), (2;3),
VIII.70. (—1; 1), VIII.71. (-^2),
VIII.73. (72; 1), (-72; 1)
154 Глава VIII. Системы алгебраических уравнений
VIII.74.
VIII.76. (2; 1),
(—1;3). VIII.81.
VIII.75. (3 3;-3 Л. 3\
\ у \ 2 о /
(-1;-2). VIII.77. (2; 1), (1;2), (-3:0), (0;-3),
VIII.78. (У8; №), (-Ж-^2),
VIII.79. (4;3), (3;4). VIII.80. (0;2), (0:—2), (1;-3),
(2;—1), (-1;2). VIII.82. (-2;|). VIII.83. (-125;-5).
(9\/3; — 3), (—9\/3; —3). VIII.84. (2:2). VIII.85. (-1; 1). VIII.86. (0;1), (2;—1). VIII.87. ---7—У VIII.88.
V III.89. (1:1), (-1;-2). VIII.90. (1; 1), (-*; -2). VIII.91. (0;0),
(-2; 4), (2; 4). VIII.92. (0;0), (4:2), (4;-2) VIII.93. (б; |),
(- 3;-Л. VIII.94. (9;5), (2 - Уб2; ALz_9A1 ). VIII.95. (5;4),
\ 2 / \ Ьо у
/41-8УГЗЗ 1 + VT33\ vninc /5 9 + \/21\ /б 9-->/21\
I,—зз—) vni96 б-/ ;•
V III.97. (0;—1). VIII.98. (о, -1; |), (-2;3; — 5). VIII.99.
(g;3;2). VIII.100. (0:0:0),
V III.101. (0;0;0), (4; 12;-4), (1;6: -4). VIII.102. Q; Z;-1),
VIII.103. f-l; A; JY VIII.104. (—5; —3; 0),
(3; 1; — 2). VIII.105. (3;4;1), (—3;—4;—1). VIII.106. (0;0;0), (2;3;4),
( —2;—3;—4). VIII.107. (4;3;1), (A-*;-?), j),
VIII.108. (2;3;4), (3; 2; 4). VIII.109. (1;2:3). VIII.110. (0;0;0).
VIII.111. (c;2c;3c), где с —любое число. VIII.112. (0;0;0), (0;ч/2;ч/2), (0;-\/2;-\/2), (\/2; 0; x/2), (-v/2; 0; — x/2), (ч/2;ч/2;0),
(-х/2;-ч/2;0), (1;1;1), (-1; -1;-1). VIII.113. x/2; 2x/2^,
^-^;-V2--2>/2y ^-2; 1;—4), (2;-l;4). VIII.114. (5;3;1), (5;-1:1), (-1;3;1), (-1;-1;1), (4:1 + \/2:-1), (4; 1 - x/2;-l), (0; 1 + v/2; —1),
(0:1 - ч/2;-1). VIII.115. (1;2;3), (2; 1:3), (3:1;2), (3;2; 1), (1;3;2),
(2;3;1). VIII.116. (-2:-4; 1), ^9; | >/9;
VIII.118. (-1; 3;2). VIII.119. (-^9;-v/3;-2),
vin.120. (-^;-^-3/3). (_y|;_y|;y|) (-1; l;0). VIII.122. (3;3;4), (12:3; 1).
VIII.117. (2;—1;3).
VIII.120. (1;—1;0),
VIII.123. (0;0;0),
Ответы к главе VIII 155
п 9 п /17-У37. 1 + У37. 1 + л/37\ /У37 +17. У37-1. У37-1\
6 3 ’ 6 )' 6 ’ 3 ’ 6 /
VIII.124. (0;0;0), (1;0;0), (0;1;0), (0;0;1), (2;2;2);
VIII.125. f-3;|;-lY (- ; 2^1
12х/2. _2ч/2^. VIII.126. (0;0;0), (0; 0; 1), (1;0;0), (0;1;0),
VIII.127. (0;0;0), (0; 0; 1), (0;1;0), (1;0;0), (Ц;|),
VIII.128. (0;0;0). (2;2;0),
(4;0;4), (0;6;6), VIII.129. (0;0;0), (0;0;3), (0;2;0),
(1;0;0), VIII.130. (0; 0; 0), (1;2;5), (1; -2; -5).
(-1;2; —5), (-1;-2; 5). VIII.131. (а; 0; 0), (0;д;0), (0;0;с), где
а, Ь, с — любые числа.
VIII.132. (а-, 0; 0), (0;Ь;0), (Ь;0;с), где а, ЬЛ с — любые числа, (2; 1; — 1),
(2;—1: I), (-2; 1; 1), (-2;-1;-1). VIII.133. (1;3; 1), (-1;—3;1), (-1;3;-1), (1;—3;—1). VIII.134. (1; 1;—2), (—1;—1;2), (1;-2; 1). (-1;2;-1),
(—2;1; 1), (2;—1;—1). VIII.135. (2;1;0), (-2;-1:0). VIII.136. (1;2;-1),
( —1;—2:1). VIII.137. (1;2:-|), (-1;-2;|), ( 3 . 5 1 \
I УГ У7’У7Г (—ЗУ2; —3\/2; —4У2),
VIII.138. (7;7;—1), (—7;—7; 1), (Зх/2; Зх/2: 4х/2),
У46 + УЗО У46 — УЗО /ттЛ (У46 — УЗО ----2-----; -----2------------------------2----'
У46 + УЗО . -У46 + УЗО . -У46 - УЗО . V/4Q—У46 — УЗО .
~У46 + У30._у4бу VIII.139. (0;1:2). VIII.140. (2;—1;—1), (с;0;0), где с —любое число. VIII.141. (0;0;0),
VIII.142. (1:1:1), (2“ *; - - ?Y
\ О О / \ о J \ /
(а;0;0), где а € R — любое число. VIII.143. (1;1;-2), |;И0,
Q1; 15-и;5 - 15-g J, (^5; 15”У 25 15~5 J, (0;а;0), где а е К - любое число. VIII.144. 1), ^-2 + ^; 5 ~2ч/П;-5 +
(-2--^Д±У11;5-VIII.145. (6-У2;3-У2;-2 + У2),
(6 + У2;3 + У2;-2 - У2). VIII.146. (-1;-1:1), (0;а:0), где а е К -
любое число. VIII.147. (—1;—1;—2), (а:0;0), где а е К — любое число.
156 Глава VIII. Системы алгебраических уравнений
VIII.148. (1;2; 1), (-‘;-2;-1), (1;1;-1), (|;-1; -2). (-1; 1; 2).
VIII.149. (2;1; 1), -1), (1;-1;2), (-1; (1; 1;-1),
(—1;—1;1). VIII.150. Нет действительных решений. VIII.151. (0;0;0),
| )• VIII.152. (0;0;0), (-1;2;3). VIII.153. (0;0;0),
\2v3 v3 2v3/
(2;2;2)’ (2;-2;2)'
(—2;2;—2), (-2;—2;2). VIII.155. (0;0;0), (O;-l;l). VIII.156. f|; \ о 2 /
fl-1-зА
Глава IX
ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ
§1. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ИХ СВОЙСТВА
Первый уровень
1. Способы задания числовых последовательностей
IX.1. Выписать шесть первых членов последовательности {xrt}:
1) хп = COS у; 2) хп = [у/п ];
3) хп = [^4^1; 4) = Е (^ - О-
L 13 J А=1
IX.2. Написать формулу общего члена последовательности {хп}:
1) {3,7,11,15,19,...}; 2) {1,-1,1,-1,1,...};
3) {3,6,12,24,48,...}; 4) {-2, ... }.
IX.3. 1) Задать формулу общего члена последовательности натуральных чисел, дающих при делении на 4 в остатке 3.
2) Задать формулу общего члена последовательности натуральных чисел, дающих при делении на 5 в остатке 2.
IX.4. Выписать первые шесть членов последовательности {хп}, заданной рекуррентно:
1) = 2хп — 3, Х[ = 2;
2) хп+2 = 2хп - xn+i; Х[ = 0, х2 = -1;
3) х^+2 — хп • xn+i, X} = 1, %2 ~ 3;
4) хп+1 = Х[ +%2 + • • • +хп, Х[ = 2.
IX.5. Выписать первые пять членов последовательности {хп} с указанным общим членом, а также задать последовательность рекуррентно:
1) х„ = 3(п-1) + 2; 2)х„ = 2'1+1;
3) х„ = 7 - 6п; 4) хп = (-1)" г2*-4.
158 Глава IX. Предел и непрерывность функции
2. Исследование числовых последовательностей на монотонность
IX.6. 1) Доказать, что последовательность с общим членом хп = п2 + п — 4 является возрастающей. Дать геометрическую иллюстрацию.
2) Доказать, что последовательность с общим членом хп = 6 — п2 — является убывающей. Дать геометрическую иллюстрацию.
IX.7. 1) Доказать, что последовательность с общим членом хп = Л является убывающей. Дать геометрическую п"
иллюстрацию.
2) Доказать, что последовательность с общим членом хп = ——-—а- является возрастающей. Дать геометри-(и + I)2
ческую иллюстрацию.
IX.8. Исследовать на монотонность последовательность с указанным общим членом. Дать геометрическую иллюстрацию.
1) хп = cos (тш); 2) хп =-----;
3)z/„ = td^; 4)л„ = ^.
п п
IX.9. 1) Привести примеры двух немонотонных последовательностей {х„}, {уп}, произведение {хп •уп} которых является последовательностью монотонной.
2) Привести примеры двух немонотонных последовательностей {хп}, {уп}> частное { —} которых является последовательностью монотонной.
IX.10. Привести пример двух последовательностей и {уп}, одна из которых убывающая, а другая возрастающая, таких что:
1) {хп + Уп} является возрастающей последовательностью;
2) {хп-\-уп} является убывающей последовательностью.
IX.11. Привести пример двух последовательностей {хп} и {уп}, одна из которых убывающая, а другая возрастающая, таких что:
1) {хп—уп} является возрастающей последовательностью;
2) {хп—уп} является убывающей последовательностью.
§1. Числовые последовательности и их свойства 159
3. Исследование числовых последовательностей на ограниченность
IX.12. Доказать, что последовательность {%„} ограничена сверху:
1) хп — 4 — {п — З)2; 2) хп = 8 — 4п2 — 4п.
IX.13. Доказать, что последовательность {хп} ограничена снизу: 1) хп = 2гс2 — 12гс — 7; 2) хп = (п — 2)(п — 6).
IX.14. 1) Доказать, что последовательность с общим членом хп = —2п2 + 9/7—4 ограничена сверху, дать геометрическую иллюстрацию. Найти наибольший член последовательности.
2) Доказать, что последовательность с общим членом хп = 2п2 — 13п + 12 ограничена снизу, дать геометрическую иллюстрацию. Найти наименьший член последовательности.
Доказать, что последовательность {%„} ограничена, дать геометрическую иллюстрацию этого факта, указать наибольший и наименьший члены этой последовательности (если они существуют) (IX.15-IX.17)
IX.15. 1) хп = 0,5п“2 + 2; 2) хл = 1-3"-1.
IX.16. 1) Хп = 2)
IX.17. 1) хп = sin (+ лп} + 2; 2) хп = 3 - \/2sin (+ лп\.
\ о / \ 4 /
IX.18. Доказать, что последовательность {хл} ограничена: 1)х„ = 1 + 2-4; 2)х„ = 3 + ^Ц-3;
П tl
r\ Sinn • I
5) хп = —о) хп = sin п + cos п. 3+
IX.19. Доказать, что последовательность {яп} не является ограниченной:
1) хп — у/п\ 2) хп = 10 - ^п.
160 Глава IX. Предел и непрерывность функции
Второй уровень
IX.20. Написать формулу общего члена последовательности {%„}: {4’7’10’13’16’”'}’ {0,1,0,-1,0,1,..
3) {1, 1, 1, g’ 2’ 2’ 2’ 2’ 3’ 3’ ’ ’ ’ }’ {2’ 6’ 12’20’30’ ” * }
IX.21. Задать рекуррентно последовательность {хп}:
1) хп = и2; 2) xn = sin
3) хп = п2 — 2п + 3; 4) хп = 4 cos2 .
IX.22. Доказать, что последовательность {%„} является возрастающей:
= 2) = 2" + 2~";
3) хп = п - у/п\ 4) хп =
IX.23. Доказать, что последовательность {хп} является убывающей:
1) хп = Юн — 4П; 2) хп — п2 — п^;
3)х„ = ^±Л; 4)х„ = £.
IX.24. Исследовать на монотонность последовательность {%„}:
1) хп = -0,5"+2; 2)х„ = ^;
3) xn = yjn + 1; 4) хп — х/п + 2 - у/п + 5.
IX.25. 1) Доказать, что сумма двух последовательностей, одна из которых возрастающая, а другая неубывающая, есть возрастающая последовательность.
2) Доказать, что сумма двух последовательностей, одна из которых убывающая, а другая невозрастающая, есть убывающая последовательность.
Доказать, что последовательность {хп} является ограниченной (IX.26-IX.28)
IX.26. 1) хп = у/п + 3 — у/п\ IX.27. 1) х„ = п1 + 6 IX.28. 1) х„ = 2) хп = \/п2- + 4 — п. _ sin кп + Зп 1 " +5Л + 10' 2 ) х„ = (-!)" + 4^
§2. Предел последовательности 161
Указать наибольший и наименьший члены последовательности (если они существуют) (IX.29-IX.32), 1 \ * (7Г । 2/Гга \ (ТГ । ТГга \
IX.29. 1) xn = sin - + — ; 2) xn = cos - + — .
\ о о/ \ 3 4 /
IX.30. 1) 2)
IX.31. 1) хп = \/п2 + 8 - и; 2) хп = \/п2 — Ьп + 8.
IX.32. 1) = 2) =
п га
§2. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ Первый уровень
1. Определение предела последовательности
IX.33. Пусть хп — 3 + п 2' Д^я числа £ указать наименьшее число Ne такое, что \хп — 3| <£ при каждом n>N£, если: 1) £ = 0,2; 2) £ = 0,02.
о
IX.34. Пусть хп — Для числа £ указать число Ne такое, что \хп — 0| < £ при каждом п > Ne, если: 1) £ = 0,1; 2) £=0,001.
IX.35. Используя определение предела последовательности, показать, что:
1) число 2 является пределом последовательности с общим 2га + 1 членом хп =-------;
га
2) число 3 не является пределом последовательности < 2га + 1
с общим членом хп = !—. га
IX.36. Используя определение предела последовательности, показать, что:
1) число 4 является пределом последовательности с общим 4га-3 членом хп =-------—;
п га + 2 ’
2) число 1 не является пределом последовательности g, 4га — 3
с общим членом хп =-----—.
6—5682
162 Глава IX. Предел и непрерывность функции
IX.37. Привести пример двух различных последовательностей, каждая из которых имеет своим пределом число:
1) 3; 2) —2; 3) 0; 4) -1,5.
IX.38. 1) Доказать, что если предел последовательности {х/г} равен 2, то, начиная с некоторого номера, каждый ее член меньше 2,1.
2) Доказать, что если предел последовательности {хл} равен 1, то, начиная с некоторого номера, каждый ее член больше 0,8.
IX.39. 1) Опираясь на определение предела последовательности, показать, что —1 не является пределом последовательности с общим членом хп = (—1),г.
2) Опираясь на определение предела последовательности, показать, что 2 не является пределом последовательности с общим членом = 1 — ( —1)".
IX.40. 1) Известно, что каждый член некоторой последовательности положителен. Может ли предел такой последовательности быть равен 0?
2) Известно, что каждый член некоторой последовательности меньше 3. Может ли предел такой последовательности быть равен 3?
IX.41. Известно, что предел последовательности равен нулю. Могут ли в этой последовательности:
1) все члены быть отрицательными;
2) бесконечное число членов быть больше 0,01?
IX.42. Привести пример ограниченной последовательности {хл} такой, что:
1) {хп} не имеет предела;
2) {хл} имеет предел. '
IX.43. Привести пример знакопеременной последовательности {хл} такой, что:
1) {хл} не имеет предела;
2) {хл} имеет предел.
IX.44. Привести пример возрастающей последовательности {хл} такой, что:
1) {хл} не имеет предела;
2) {хп} имеет предел.
§2. Предел последовательности 163
IX.45. Привести пример убывающей последовательности {хл} такой, что:
1) {хл} не имеет предела;
2) {хп} имеет предел.
IX.46. Привести пример последовательностей {ап} и {Ьп}, каждая из которых не имеет предела, но:
1) сумма {an + bn} которых имеет предел;
2) разность {an — bn} которых имеет предел;
3) произведение {an bn} которых имеет предел;
4) частное } которых имеет предел.
IX.47. Привести пример ограниченных последовательностей {tz„} и {Ь„}, каждая из которых не имеет предела, но: 1) сумма {an + bn} которых имеет предел;
2) разность {an — bn} которых имеет предел;
3) произведение {an-bn} которых имеет предел;
4) частное которых имеет предел.
2. Вычисление предела последовательности
IX.48. Известно, что lim ап = 2, lim bn = 3. Применяя свойства п—>оо п—>оо
сходящихся последовательностей, найти:
1) lim (an + 3b„); 2) lim (а2-2ал&„);
п—>оо п—>оо 4 7
3) lim ап~^-; 4) lim
п—>оо ап + 2Ьп п-ч-оо
IX.49. Известно, что lim ап = 3, ап 3. Применяя свойства п—>оо
сходящихся последовательностей, найти:
1- — 9 а? — 5ап + 6
1) lim 2) lim -------V—•
п—>оо ап — 3 п-^-оо ап — 3
Вычислить (IX.50-IX.57),
IX.50. 1) lim п—>оо п + 7 . 2п — 3 ’ 2) lim п—>ос Згс2 + 1 . п2
3) lim п—>ос Зп3 — 2п + 3 . 2гс3 + гс2 4) lim п—>оо (гс —3)(5 —бгс) 2п2 + 5
IX.51. 1) lim п—>ос п + 2 . п2 - 6 ’ 2) lim п—»оо 2 + гс - 4п2 гс3 + 1
3) lim п—>оо (п + 2)2. п3 + 1 4) lim п—>оо гс + 100 (гс + 1)3’
164 Глава IX. Предел и непрерывность функции
IX 52 1) 3) 1) 3) 1) 1) 3) f п — 2 г? — 3 \. lim Л «2 . га2 \.
IX.53. IX.54. IX.55. п—>оо lim п—>ОО lim п—>оо lim п—>оо lim п—>оо lim п—>оо lim п—>00 \2га + 2 5 + 2га — га2 / ’ (1 + га)(1 — 2га)(1 + Зга) га3 \/га . га + 1 ’ у/га - 2. га + 3 1 \/га + 2 + 3 ’ 1 . 3" + 4’ 3w+1 - 1. 3«-’+1’ ’ П-^OQ к 2га2 + 1 1-4га27’ 4) lim f 2 ~ ) . га—>оо \ Зга + 1) 2) Ит ч/¥ + 2; га—>оо i/ra + 3 4) lim га—>оо 4 — v 5га 2) lim —. 2 —-. и—2 \/ и -|- 1 -|- 3-^/7? 2) lim -2 -Ь -; га—>оо 2 +1 4) lim 22;„+' + 2. 7 га—>оо 4П — 3 / „ , , \ га— 1
IX.56. 1) 3) lim га—>оо lim п—>оо (1 + 0 ; \ п) очг 2) lim (—-) га—>оо \ га / 4) Um га—>оо \ га / >
IX.57. 1) lim | п—>оо а + ± + ... + _ly <з з2 злг7 ’ 2) lim Q - -4 + • • • га—>оо \2 22 1 (-1П 2П / ’
IX.58. 1) При каком значении бесконечно убывающей а предел суммы членов геометрической прогрессии
а-? + 1т_Л+-” равен 16?
4 16 64 г
2) При каком значении а предел суммы членов бесконечно убывающей геометрической прогрессии 2а + а\/2 + а + ... равен 8?
IX.59. 1) Найти знаменатель бесконечно убывающей геометрической прогрессии, первый член которой равен 3, а сумма членов равна 3,5.
2) Найти знаменатель бесконечно убывающей геометрической прогрессии, первый член которой равен 66, а сумма членов равна ПО.
IX.60. 1) Найти бесконечно убывающую геометрическую прогрессию, первый член которой в 10 раз больше суммы всех членов, следующих за ним.
2) Найти бесконечно убывающую геометрическую прогрессию, сумма первых шести членов которой состав-
7
ляет - суммы всех членов последовательности. О
§2. Предел последовательности 165
Второй уровень
IX.61. Используя определение предела последовательности, до-
казать справедливость
1) lim
= д.
ЛТ п
равенства:
2)
lim
IX.62.
IX.63.
IX.64.
IX.65.
IX.66.
3)
5)
lim
lim
n 2y/n sin n + cos n ___p
-'Lt-1- =0;
и1’ _1_ Q
cos n _q.
у/n
1 + Ц2 = 0;
2n -p \/П
-^-±1- = 0;
n4 + 3n
4)
6)
lim
lim
lim п—>оо Используя определение предела последовательности, доказать справедливость равенства:
1)
7)
8)
lim n—>oo
n2 + 1 - n
n—>oo n—>oo \ /
Опираясь на определение предела последовательности, показать, что 0,5 не является пределом последовательности с общим членом xn — sin ( + лп 1.
\ 6 /
Опираясь на определение предела последовательности, показать, что 1 не является пределом последователь-ности с общим членом = cos
Пусть {Ьп} — некоторая последовательность. Можно ли утверждать, что lim (anbn) = 0, если lim an = 0? Ответ п—>оо п—>оо
обосновать.
Известно, что в любой окрестности точки 2 находится бесконечно много членов последовательности {хп}. Следует ли
1)
2)
2)
2)
отсюда, что: lim xn — 2;
последовательность {xn} ограничена?
Пусть lim IxJ = Ы. Следует ли отсюда, что lim xn = a? n^tx> n—too
Пусть lim |xn| = a. Следует ли отсюда, что {xn} n—>oo
СХОДИТСЯ?
IX.67. Известно, что lim an = (l. Применяя свойства сходящихся n—>oo
последовательностей, найти:
1) lim (2ал+2+an+i+ 3); п—>оо
3) lim
n^><x> an + 3
2)
4)
lim —L;
n—>oo 2ап_|_з + an g
ljm (.an+a +3)
n^°° 2an+2
166 Глава IX. Предел и непрерывность функции
IX.68. Известно, что lim an = 2, lim bn = 3. Применяя свойства п—>ос п—>оо
сходящихся последовательностей, найти:
1) Пт 2) lim
n—>оо bn + 2.П п-^-ао 2.П • bn + an
3) lim ((3an — 2bn+i) • sin n);
n—>oo
4) lim ((a„ • b„+2 — 6) • cos(n + 1)).
П—¥(*V'
Вычислить (IX.69-IX.76).
IX.69.
IX.7O.
IX.71.
IX.72.
IX.73.
IX.74.
IX.75.
IX.76.
1)
3)
5)
1)
3)
1)
3)
1)
3)
1)
3)
5)
1)
1)
2)
1)
2)
lim
n—>oo
lim
n—><X)
lim
n—>OG
lim
n—>oo
lim n—>oo
n + 2^/ra . y/n — 3n ’ __y/ii — y/n 4y/n - tyn + Г y/2n + 4 .
y/n + \/4ra + 5 ’ 3" + 4.
6" + 1 ’ 6"-l + 2“".
lim
n—>oo
lim
n—>OG
lim
n—>oo
lim
n—>oo
lim
n—>OC'
lim
n—>oo
lim
n—>oo
lim n—>oo
lim
n—>oo
lim
n—>oo
lim
n—>oo
lim n—>oo
3й + 6"
2ra+4
\ n +17 n + (-l)n.
n + 2 ’ Зга + 2 cos ra .
ra + 2
(\/3n + 6 — \/ЗЙ);
(\/4n2 + n — 2n y/n + 4 — y/n .
y/n — x/п + 5 ’ (\/n - 1 - y/n);
2) lim
ra—>oo
4) lim
ra—>oo
6) lim
ra—>oo
2) lim
ra—>oc
4) lim
ra—>oo
2) lim
ra—>oo
4) lim
ra—>oo
2) lim
ra—>oo
4) lim
ra—>oo
2) lim
ra—>oo
4) lim
ra—>oo
n2y/n — 2ra ra3+l~;
2\/fi ~l~ 1 Я- л/ii ~l~~2,
\/ra + 1
\/7i + v^8ra + 5
^T^ra
3" + 4" .
2" + 5” ’
6» + 3 • 2n
5n+1 + Tl '
/n + l\2-3ra
\ ra. 7
/Зга + 1\[~n
\ Зга /
2 + sin ra .
ra
sin y/n — ra
y/n + 2ra
(\/n2 + 3-n);
(\/2n2 + 6n — л/2п2 — 1);
6) lim (y/rt + y/n — y/n).
2) lim (n- \/n3 + 8Y ra—>oo \ /
ra \. ra2 7 ’ 2ra — 1 \
ra2 /
_______i______Y
2ra • (2ra + 2) J
+_____________!__________Y
(2ra — 1) • (2ra + 1)7’
§3. Предел функции 167
3) ,г'Д5с <2 ’5 + 5 • 8 + ' ‘ ’ + (Зя - 1) • (Зя + 2) ) ’
4) lim ( 1 + + ... + —- 1 ——г-).
п—>ос\4-11 11-18 (7я — 3) • (7я + 4) /
IX.77. Найти lim хп, если:
1) х„=О,П_^; 2) хп = 0,3333... 33.
хг1 2я
IX.78. Задать формулой общего члена бесконечно убывающую геометрическую прогрессию, второй член которой равен 6, а сумма членов равна -I суммы квадратов членов.
8
IX.79. Обратить бесконечную десятичную периодическую дробь в обыкновенную:
1) 0,373737...; 2) 0,23(345).
IX.80. Сумма членов бесконечно убывающей геометрической прогрессии равна 4, а сумма кубов ее членов равна 192. Найти первый член и знаменатель прогрессии.
IX.81. В равносторонний треугольник со стороной 2 вписан посредством соединения середин его сторон новый треугольник. В этот треугольник тем же самым образом вписан новый треугольник и так далее до бесконечности. Чему равна сумма периметров этих треугольников?
IX.82. В квадрат со стороной 4 вписан посредством соединения середин его сторон новый квадрат. В этот квадрат тем же самым образом вписан новый квадрат и так далее до бесконечности. Чему равна сумма периметров этих квадратов?
§3. ПРЕДЕЛ ФУНКЦИИ
Первый уровень
1. Определение предела функции на бесконечности
IX.83. Дана функция /(х) = 3 — —.
1) Построить график /(х). Какие выводы, опираясь на график, можно сделать относительно пределов этой функции при стремлении х к +оо и —ос?
2) Обосновать, опираясь на определение предела, предположение о поведении функции /(х) при х —> +оо.
168 Глава IX. Предел и непрерывность функции
IX.84. Дана функция f(x) = —у.
1) Построить график f(x\ Какие выводы, опираясь на график, можно сделать относительно пределов этой функции при стремлении х к +оо и —оо?
2) Обосновать, опираясь на определение предела, предположение о поведении функции /(х) при х —> +оо.
IX.85. Нарисовать эскиз графика функции /(х), определенной на всей числовой прямой и удовлетворяющей следующим условиям:
1) lim /(х) = —3, lim Дх) = 2; х—>+оо х—>—оо
2) lim f(x) = 4, /(2) = -1, Д-З) = 5.
Используя определение предела функции, доказать справедливость
равенства (IX.86-IX.90).
IX.86. 1) lim Зг = 0;
X—>ОО х4
IX.87. 1) lim = 1;
х->оо 4х - 1 4
IX.88. 1) lim —=0;
X—>-|-ОО у/х 1
IX.89. 1) lim -U = 0;
х—>—оо у—х
IX.90. 1) lim х2 ~ +оо;
х—>оо
2) lim = -з.
х—>оо х + 4
2) lim J_________= 0.
х->+оо у/%3 _|_ 1
2) lim --1— = 0. х->-оо У2 — Зх
2) lim (х + З)4 = +эо.
X—ОО
2.
Вычисление пределов функции на бесконечности
IX.91. Вычислить:
1) Jim ((х - 2)2 - (х - 4)2 - 4х); 2) Jim ^±^+2.
3) lim 4) lim ,(|~х)2
х—>—оо X4 — 1 ' х—>+оо xJ — Зх + 1
IX.92. Вычислить:
1) Нт 7х-2^ + 5.
X—У-|-ОО х 1
3) lim
X —-|- ОО у/X 1
2) lim ^Д1;
X —— ОО □ у/ X
4) Um x + x^-J
х—>—оо 3\/—х — 5х ух
§3. Предел функции 169
Рис. 5
3. Определение предела функции в точке
IX.93. Среди функций, графики которых приведены на рис. 1-6, указать функции, имеющие предел в точке х = 2.
IX.94. Нарисовать эскиз графика функции /(х), определенной на всей числовой прямой и удовлетворяющей следующим условиям:
1) lim/(x)=3, limf(x) = l, lim /(х)=4, /(1) = 3, /(3) = 0; х—Я х->3 х-Ц-оо
2) lim /(х) = 0, lim/(x) = —3, lim /(х) = 2, /(4) = -3. х—>—2 х->4 х->—оо
170 Глава IX. Предел и непрерывность функции
IX.95. Построить график функции \ (2х — 1, х<2,
(0,5х + 2, х>2.
Для £=1 и £=0,5 отметить на оси Ох проколотые 5-окрестности точки х = 2, для точек которых график функции y = f(x) лежит внутри полосы 3 — £<у < 3 + £. Доказать, что lim/(x) = 3, указав правило выбора 5 по £. х—>2
IX.96. Построить график функции
х<3, (2х-4, х>3.
Для £= 1 и £=0,5 отметить на оси Ох проколотые 5-окрестности точки х = 3, для точек которых график функции y = f[x) лежит внутри полосы 2 — £< л/< 2-f-£. Доказать, что lim/(x) = 2, указав правило выбора 5 по £. х—>3
IX.97. Используя определение предела функции в точке, доказать справедливость равенства:
1)
3)
lim (4х — 2) = 10;
х—>3
lim х->1
х2 -1 х — 1
= 2;
2)
4)
lim (4- Зх) = —2; х—>2
х2-4
lim 1 = -4.
4. Вычисление предела функции в точке
IX.98. Известно, что lim/(x) = 3, limg(x) = -l. Используя свойства пределов функций, найти:
!) Jim (4ftx)-g(x)f(x)); 2) Jim (/2(х)-5g(x)/(x));
3) lim (/(х) — 2) (g(x)+4); 4) lim ;
5) lim 6) lim ( —-j—- + -?— ----\
x->a /(x)-3 x-»a \g(x) + l g2(x)+g(x) /
IX.99. Вычислить:
1) lim x—>3 3x2 +1 . 2 —x 2) lim x—>2 x2 + x — 6 x2-4
3) lim x—1 2 —x + x2 . 1 -|- X 4) lim x2 —25. 5 * + 5
5) lim X—>1 2x2 — 3x +1. x — 1 6) lim x—>3 x3 —27 x2 — 9
§3. Предел функции 171
IX.100.
IX.101.
IX.102.
Вычислить:
1) lim -4^;
х—>4 х/*^ 2
3) lim х~4^4; х—>4 2 — у/х.
2) lim
х—>8 *-8
4) |im 1+^
5. Различные типы пределов
Указать, чему равны односторонние пределы функций, графики которых приведены на рис. 1-6, в точке х~2.
1) Построить график функции
/«=
Что можно сказать о значениях односторонних пределов этой функции при стремлении х к 2, —1, 5?
2) Построить график функции (4, х<—2,
10,5x4-2, х>4.
Что можно сказать о значениях односторонних пределов этой функции при стремлении х к —2, 4, 6?
IX.103. Дана функция /(х) = 2
|х 11
1) Построить график /(х). Какие выводы, опираясь на график, можно сделать относительно пределов этой функции при стремлении х к 1, 3, 4-оо, —оо?
2) Обосновать, опираясь на определение одностороннего предела, предположение о поведении функции /(х) при
IX.104. Нарисовать эскиз графика на всей числовой прямой и условиям: 1) lim /(х)=2, х—>+оо
lim /(х) = -4; х—>2—О
2) lim /(х) = 0, х—>оо
lim /(х) = -2, /(4) = 1.
lim
функции f(x), определенной удовлетворяющей следующим
lim /(х) = 5, х->2+0
lim /(х) = 2,
lim /(х) = 3, х->—34-0
172 Глава IX. Предел и непрерывность функции
Второй уровень
IX.105. Вычислить:
1) lim f\/x2 + 3 —х); х—>оо \ /
3) lim (\А2 + 9х —х X—>4-00 \
2) lim f >/х2 +1 + х);
х—> —оо \ /
4) lim f2x + \/ 4х2 + х х—>—оо \
IX.106. Найти р и q, если:
1)
2)
lim х—>оо
lim х—>оо
/?х2 +1 qx + 2 2х2 — 1
X -|-1
-Н х — 2^ — — 1; +px + q) = 1.
IX.107. Используя определение предела функции в точке, доказать справедливость равенства:
1) limx2 = 9; 2) limx3 = 8.
х—>3 х—>2
IX.108. Используя определение предела функции в точке, доказать справедливость равенства:
1) lim (х2 — 8х) = -16; 2) lim (4х2-4х) = -1.
х—>4 х—>0,5
IX.109. Используя определение предела функции в точке, доказать справедливость равенства:
1) lim x/x = v3; 2)
х->3
lim x/* + 6 = 3. х->3
Вычислить
IX.110. 1)
3)
5)
IX.lll. 1)
IX.112. 1)
IX.113. 1)
(IX.110-IX.113).
2)
4)
6)
2)
2)
2)
< x3 —2x2—x + 2 lim ------к----;
x—>2 7x —Зх2 —2
lim
x—>—3 x3 + 3x2+x + 3
§ 3. Предел функции 173
IX.114. Известно, что lim/(x) = 0, limg(x) = 0. Привести примеры х—>3 х—>-3
таких функций /(х) и g(x), для которых справедливо равенство:
1) lim Д4 = 2; 2) lim =
х->3 gW х->3 g(*)
3) lim Д^ = +оо; 4) lim &\- = — оо. х->3 g(*) х^З g(x)
IX.115. Известно, что lim/(х) =+ос, limg(x) = +oo. Привести X—И X—>1
примеры таких функций /(х) и g(x), для которых справедливо равенство:
1) ПгпД^-=4; 2) lim44 = +°°;
х—>1 g(x) xW g(x)
3) lim (/(x)-g(x)) = 0; 4) lim (/(x)-g(x)) = +oo.
x—>1 x—>1
IX.116. Найти значение а, при котором существует конечный предел функции /(х) в точке Xq, если:
» /«=(7ТТ)-^Т- "0=-^
2> х»=1 2-
IX.117. Используя определение одностороннего предела, доказать
справедливость равенства: lim (у/х — 2) = - 2;
х->0+0
2) lim (х/х^Т + 3) = 4. х->2+0
IX.118. Найти односторонние пределы функции /(х) в точке Xq и выяснить, существует ли конечный предел функции в этой точке, если:
i\ \ Г2х^+3x4-2, х<1, .
/« = 1зх + 4, х>1, х“ = 1;
2) = х°=3;
3) хо = 2;
4) = *о = 1.
|Л 1 |
IX.119. Найти односторонние пределы функции /(х) в точке Xq,
1) f(x) = [x], х0 = -2; 2) f(x) = {x}, х0 = -4;
3) /(х) = [х +1], Xq = 3; 4) /(х) = {х-3}, х0 = 5.
174 Глава IX. Предел и непрерывность функции
IX.120. Найти значение а, при котором существует конечный /(х) в каждой точке ее области
предел функции определения, если:
*> ^) = {йз|8’
2) /^) = UX7a„2(Xt^)’ Х^3’
§4. НЕПРЕРЫВНОСТЬ ФУНКЦИИ Первый уровень
IX.121. Какие из функций, графики которых приведены на рис. 1-6, непрерывны в точке % = 2?
IX.122. Я вляется ли функция /(х) непрерывной в точке xq, если:
1) /(х) = (х-3)3, х0 = 3;
2) f(x) = |хН-2| х0 = -2;
3) /(х) = </х + 4, *о = О;
4) /(*) =
*0 = 0;
[9-х2 /3
5) f(x} = < ”3^7 ’ [б, х = 3,
6) = %о = -4;
( г2 _ д
7) /(х) = < Т+Т’ %^-2’
2, х = — 2, ' х2 — 8х — 9 г
*о = 3;
*о — 2,
*р = 9?
— 10, х = 9,
IX.123. Имеет ли точки разрыва функция:
1) /(х) = х |х-1|; 2) /(x)=x+\/j?
IX.124. Найти точки разрыва функции:
1) = 2) ^W=k^r-2'
4) /(х) = .
л/бх — 1 — 9х2
х + 2
§4. Непрерывность функции 175
IX.125. J) Имеет ли уравнение х5 — Зх3+х —9 = 0 корни на отрезке [0:2]?
2) Имеет ли уравнение х3 — 4х2 — 4х +16 = 0 корни на отрезке [1;3]?
IX.126. Доказать, что уравнение имеет хотя бы один действительный корень:
1) х3 — Зх2 + 6х-7 = 0; 2) х8-х2-9 = 0;
3) х5 + х + 8 = 0; 4) х6 —Зх3 —х-27 = 0.
Второй уровень
IX.127. При каком значении b функция /(х) будет непрерывной в точке xq, если:
1) х2_41 х>31 ^0-3,
{|х —Ь|, х^З, V^+7-4 о *0 = 3?
х —3 ’ Х> ’
IX.128. Можно ли доопределить функцию /(х) до непрерывной в точке Xq, если:
1) f(x) = 2x-^~, х0 = 0;
2) %0 = 1?
\х£ -х| — х+ 1
IX.129. Найти точки разрыва функции:
'* =7|7-4гтт'• 2) № = 2 Л172
х|х —3| —|х| —4х + |х —3| + 3
IX.13O. Найти точки разрыва функции:
1) /(х) = {х + 3}; 2) /(х) = [х]-х.
IX.131. Доказать, что уравнение на указанном отрезке имеет хотя бы один действительный корень:
1) х3-9х2 + 24х- 17 = 0, [3;5];
2) 12х4- 16х3 + 1 = 0, [0; 1,5].
IX.132. Решить неравенство, используя обобщенный метод интервалов:
1) (х-1) (^25-х2 -4) ^0;
176 Глава IX. Предел и непрерывность функции
2) (4-л/х + З) (>/Г+2+1)^0;
3) (х + 4) (У25-х2-з) ^0;
4) (х2-9) (х/х+ТЗ-4)<0.
IX.133. Решить неравенство, используя обобщенный метод интервалов:
1) (х3-1) (|х + 1|-2)^0;
2) (з-л/х2-1б) (|х + 4|-9)^0;
3) (|х —3| — |2х —1|) (Зх2—х —4)^0;
4) (|х| + 2х) х/36-х2^0.
§5 . ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
Первый уровень
Вычислить (IX.134-IX.137).
IX.134. 1) lim 2)
3) lim 4)
х—>1 хл/2 —х
IX.135. 1) lim г/7+1~3; 2)
х >5 х-5
3) lim S5+*-2. 4)
х—> —1 х2 + 5х + 4
IX.136. 1) lim -ч-3~х 2)
х->3 ух —2 — 1
IX.137. 1) lim 2)
X—— ОО %т4
lim \/2 + Зх4; х^О
lim \/>/Ю + Зх + 5.
х->2
lim
х->2 х2 —4
Второй уровень
Вычислить
IX.138. 1)
3)
IX.139. 1)
IX.140. 1)
3)
(IX.138-IX.143)
lim '/з±?~2х-;
х—>1 1~*
lim
X—) — 1
\/2х + 3 — 1, х/5 + х — 2
lim Зх + 5\/—х+2. х->—4 х + 4
lim /* + 7 -3: х—>2 v+ 4- 6 - 2
2)
4)
2)
lim v^+-xA2+x-3.
х—>2 х2 — 4
lim х->3
-/З + х — x/9 —x x3 —4x —15
lim 3 —2x —7V— x—>—9 x + 2\/—x + 3
lim x->2
lim X—1
x3-x2-x-2.
v/x2+4- 2
Зх2 — 2x — 1 ^2x^3- fyx^2'
Задачи повышенной сложности к главе IX 177
IX.141. 1) lim (у/х+4-у/х);
х—>4-оо
IX.142. 1) lim х—>—оо X
3) lim (х + \/х2 —4х х—>—оо \
IX.143. 1) lim GA+Ocosx. х—>4-оо х-|-4
2) lim (\/х2+4х— \/х2 + 5х х—^Н“ОО \
2) lim
X—> —оо
4) lim
х—>—оо
2) lim
х —-j-oo
\/х2 4- 2х — 3 .
2^х ’
\/х2 4-2 4- у/8х3 4- 3
\/х4 4-1
7Г
(1 — у/х — х) sin(x-|- -)
--------х^+2-------~
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ IX
IX.144. Используя определение предела последовательности, доказать равенство:
1) lim 2) lim 2”2 + 1 =2.
n-ioo 2n2 — 9n 2 n->oo n2-|-6n — 2
IX.145. Доказать, что отбросив, добавив или заменив конечное число членов сходящейся последовательности, получим последовательность, имеющую тот же предел.
IX.146. Доказать, что отбросив, добавив или заменив конечное число членов расходящейся последовательности, получим последовательность, которая также является расходящейся.
IX.147. 1) Пусть lima„=a. Доказать, что Пта2й=а и Iima2/e4-l=a-П—k—>оо k—>оо
2) Пусть последовательность {ап} такова, что lim a^k—a k—>oo
и lim Я2й4-1=а- Доказать, что lim an=a. k—>OO rt—>oo
IX.148. Пусть последовательность {ап} такова, что lim Я2/г = а k—>оо
и lim a2k+[ = b, причем a^b. Доказать, что последова-k—>оо
тельность {an} расходится.
IX.149. Используя определение предела последовательности, доказать, что если lim an=a, то lim 1яп| = |а|.
п—>оо п—>оо
IX.150. Доказать, что последовательность {ап}, где a = 1 + 1 + + 1
у/ 4п2 4-1 у/ 4п2 4-2 у/ 4п2 4-п4-1
сходится, и найти ее предел.
IX.151. Доказать, что последовательность {x^}, где хп =--------------------------%----------, a > О,
(1+а)(1+а2)... (1 + а") ’
178 Глава IX. Предел и непрерывность функции
IX.152.
IX.153.
сходится, и найти ее предел.
Доказать, что последовательность {ал}, где ап =
п\
(2/1 + 1)!!’
сходится, и найти ее предел (здесь (2n + 1)!! — произведе-
ние всех нечетных чисел от 1 до 2п + 1 включительно). Доказать, что последовательность {ал}, где = сходится, и найти ее предел (здесь (2/? — 1)!! — произве-
дение всех нечетных чисел от 1 до 2п — 1 включительно,
(2я)!! — произведение всех четных чисел от 1 до 2п включительно).
IX.154. Используя определение предела функции в точке, доказать:
1) lim (х2 — 4) = —3; 2) lim (2х2 — 1) = 3.
х—>1 х—>2
IX.155. Используя определение предела функции в точке, доказать:
О
lim - = х^2 X
L
2’
2) lim --4 - 1. х->3 х “ 2
IX.156. Пусть функции /(х) и g(x) определены в некоторой окрестности точки х = а, причем функция /(х) ограничена в этой окрестности, a g(x) при х —> а имеет предел, равный 0. Доказать, что lim |/(x)g(x)| = 0.
IX.157. Пусть функции /(х) и g(x) определены в некоторой окрестности точки х = а, причем в этой окрестности функция g(x) совпадает с функцией /(х) всюду за исключением конечного числа точек, а функция /(х) при х а имеет предел, равный А. Доказать, что функция g(x) при х -+ а также имеет предел, равный А.
ОТВЕТЫ К ГЛАВЕ IX
IX.1. 1) 1, -±, -1, -1, 1; 2) 1, 1, 1, 2, 2, 2; 3) -3, -2, -1, -1, 0, 1; 4) О, 1,3,6,10,15. IX.2. 1) хп = 3 + 4(п — 1); 2) xn = (-1)п+1; 3) хп = 3 • 2"-*; 4) х„ = 2-|=^". IX.3. 1) хп = 4(п- 1)4-3; 2) xn = 5(и- 1) + 2. IX.4. 1) 2, 1, -1, -5, -13, -29; 2) 0, -1, 1. -3, 5, -И; 3) -1, 3, -3, -9, 27, -243; 4) 2, 4, 6, 12, 24, 48. IX.5. 1) 2, 5, 8, 11, 14; xi = 2,
хп+\ = Хп + 3; 2) 4, 8, 16, 32, 64; х\ — 4, хп+\ = 2 • хп; 3) 1, -5,
-11, -17, -23; xi = 1, хп+\ = хп - 6; 4) 1, -4, 16, -64; Xi =-|,
хп+1 = (-4) • Хп. IX.8. 1) Последовательность не является монотонной; 2) последовательность убывает; 3) последовательность не является монотонной; 4) последовательность возрастает. IX.14. 1) х2 = 6 — наибольший
Ответы к главе IX 179
член; 2) Х3 = —9 — наименьший член. IX.15. 1) Х[ = 4 — наибольший
член; наименьшего члена нет; 2) Х| = 0 — наибольший член; наименьшего члена нет. IX.16. 1) %2 = — — наименьший, х$ = 1 — наибольший член; 2) %4 =—2 — наименьший, х$ — 2 — наибольший член. IX.17. 1) Х2п = 2,5 — наибольшие, %2п-1 = 1,5 — наименьшие члены (п G N); 2) %2п-1 — 4 —
2п — 1 наибольшие, Х2п = 2 — наименьшие члены (п 6 14). IX.20. 1) хп =
2) например, хп = - cos 3) хп = г4=г: 4) хп — ———г-. IX.21. 1) Х[ = 1, 2 [УА] «(« + 1)
v/2 j—
%2 — 4, xfl^2 — 2хл_|_[ Хп + 2, 2) Х[ — , %2 = 1, хп+2 = *2 хп+1 Хп,
3) х\ = 2, Х2 = 3, х,;+2 = 2х„.|4 — хп + 2; 4) xj = 2 + д/2, х'2 = 2,
х„+2 — \f2-Xn ь 1 — хп — 2\/2 + 4. IX.24. 1) Последовательность возрастающая; 2) последовательность возрастающая; 3) последовательность возрастающая; 4) последовательность возрастающая. IX.29. 1) х-^т = х$т. 2 = 0,5 — наибольшие, а хзт_] =—1 — наименьшие члены последовательности (meN); \/2 + \/fi g- \/2 + \/б
2) xgm-i =----------наибольшие, a xgm-5 =--------------наименьшие члены
последовательности (m 6 N). IX.30. 1) Х3 =—2 — наименьший, Х4 —- 4 — наибольший член последовательности; 2) х\ = 0,5 — наименьший, хз = 5 — наибольший член последовательности. IX.31. 1) Х[ = 2 — наибольший, наименьшего члена нет; 2) Х2 = х% = \/2 — наименьшие члены, наибольшего члена нет. IX.32. 1) Х[ = 2 — наименьший член, наибольшего члена нет;
2
2) хз = 5д — наименьший член, наибольшего члена нет. IX.33. 1) 3; 2) 48. IX.34. 1) Любое натуральное число, не меньшее 4; 2) любое натуральное число, не меньшее 44. IX.40. 1) Да, например хп = 2) да, например
x„ = 3-k IX.41. 1) Да; 2) нет. IX.48. 1) 11; 2) -8; 3) 4) 4.
IX.49. 1)” 6; 2) 1. IX.50. 1) 0,5; 2) 3; 3) 1,5; 4) -3. IX.51. 1) 0;
2) 0; 3) 0; 4) 0. IX.52. 1) 1,5; 2) 3) -6; 4) 1. IX.53. 1) 0;
2) 2; 3) 0; 4) -р=. IX.54. 1) 0; 2) 0. IX.55. 1) 0; 2) 4; 3) 9; 4) 2. IX.56. 1) е; 2) е; 3) Ь 4) е2. IX.57. 1) 0,5; 2) |. IX.58. 1) a = 20;
2) а = 2 (2 — \/2). IX.59. 1) |; 2) 0,4. IX.60. 1) Любая бесконечно
убывающая геометрическая прогрессия со знаменателем q — р; 2) любая g, А V2
бесконечно убывающая геометрическая прогрессия со знаменателем q =
или q — — IX.64. Нельзя. IX.65. 1) Нет; 2) нет. IX.66. 1) Нет; 2) нет. IX.67. 1) 9; 2) |; 3) -1,6; 4) 8. IX.68. 1) 2) 3) 0; 4) 0.
IX.69. 1) 2) 0; 3) |; 4) 3; 5) 1; 6) -3. IX.70. 1) 0; 2) 0;
_ 1^
3) | 4) 0. IX.71. 1) е; 2) е“3; 3) е“2; 4) е 3. IX.72. 1) 1; 2) 0; ь
180 Глава IX, Предел и непрерывность функции
3) 3; 4) —0,5. IX.73. 1) 0; 2) 0; 3) 0,25; 4) 5) -0,8; 6) 0,5.
IX.74. 1) 0; 2) 0. IX.75. 1) 0,5; 2) 1. IX.76. 1) 0,25; 2) 0,5; 3) ь
4) ± IX.77. I) 1; 2) '. IX.78. &„ = 12-0,5-'. IX.79. 1) g; 2) Щ. IX.80. Первый член равен 6, знаменатель равен -0,5. IX.81. 12. IX.82. 16(2 + \/2). IX.91. 1) -12; 2) -0,5; 3) 0; 4) 0. IX.92. 1) 7; 2) —2; 3) 1; 4) —0,2. IX.93. Функции, графики которых изображены на рис. 1, 2, 6. IX.98. 1) 15; 2) 24; 3) 3; 4) -2; 5) 6; 6) -1.
IX.99. 1) —28; 2) 1,25; 3) 1; 4) -10; 5) 0,25; 6) 4,5. IX.100. 1) 4; 2) .4; 3) 0; 4) |. IX.101. Рис. 1: lim /(х) = lim /(х) — -3; рис. 2: 12 3 х->2-0 х—>2+0*'
lim /(х) = lim /(х) = 4; рис. 3: lim /(х) - 4, lim /(х) -- —оо; рис. 4:
х—>2-0 х—>2+0 х—>2-0 х—>2+0
lim f(x) = 5, lim f(x) = 0; рис. 5: lim f(x) = +oo, lim f(x) — —oo;
x—>2—0 x—>2+0 x—>2—0 x—>2+0
рис. 6: lim /(x) = lim /(x) = — 3. IX.102. 1) lim f(x) = 4, lim /(x) = — 3, x—>2—0 x—>2+0 x—>2+0 x—>2 — 0
lim /(x) = lim /(x) = 3, lim /(x) = lim /(x) = 5; 2) lim /(x) = -4, x—>-1-0 x—>—1+0 x—>5 —0 x—>5+0 x—> —2 —0
lim = -2, lim /(x) = lim ftx) = 4; lim /(x) = lim /(x) = = 5. IX.103. 1) lim/(x) =+oo, lim/(x) = 1, lim /(x) = lim /(x) = 0. IX.105. 1) 0; 2) 0; 3) 4,5; 4) -0,25. IX.106. 1) p = -2, q = 2; 2) p = -2; <7 = 3. IX.107. Указание: полезно использовать геометрическую интерпретацию предела функции в точке. IX.110. 1) оо; 2) —0,6; 3) 0,75; 4) 1; 5) оо; 6) -7,2. IX.111. 1) 0,8; 2) IX.112. 1) 3; 2) IX.113. 1) |;
о ЗЬ
2) -7|. IX.116. 1) а = 2; 2) а = 3. IX.118. 1) Существует; 2) не
существует; 3) существует; 4) не существует. IX.119. 1) lim Ях) = -1, х—>— 2—О
lim fix') = —2; 2) lim /(х) = 1, lim /(х) = 0; 3) lim /(х) = 3, х—>—2+0 х—>—4 —О х—> —4+0 х—>3—О
lim Дх) = 4; 4) lim ftx) = 1, lim Дх) = 0. IX.12O. 1) а = 2,5;
х—>3+0 х—>5—0 х—>5+0
2) а = 0 и а = 1. IX.121. Функция, график которой изображен на рис. 1. IX.122. 1) Да; 2) да; 3) нет; 4) да; 5) да; 6) нет; 7) нет; 8) нет. IX.123. 1) Не имеет; 2) не имеет. IX.124. 1) х = —2, х = 3; 2) х = 1, х = 5; 3) х = -2; 4) х=|. IX.125. 1) Да; 2) да. IX.127. 1) 6 = 2; 2) 6 = 2,25, 6 = 3,75. IX.128. 1) Нельзя; 2) нельзя. IX.129. 1) х = 0, х = 2, х = 4; 2) х = 0, х = 2; х = 3. IX.130. 1) х = п, п G Z; 2) х = n, п = ±1, ±2, ±3,.... IX.132. 1) [—3; 1] U [3;5]; 2) [-3; 1] U [13; +оо); 3) {-4} U [4; 5];
4) [-13;-3). IX.133. 1) (—оо; —3) U {!}; 2) (—оо; —13] U [—5; —4] U [4;+оо); 3) {и |-2; -1]; 4) {—6} U [0; 6]. IX.134. 1) 1,5; 2) \/2; 3) 1; 4) 3. IX,135. 1) 1; 2) 3) + 4) X IX.136. 1) -3; 2) 1.
о lb 12 4о 12
IX.137. 1) 0; 2) 0. IX.138. 1) -1,25; 2) --Д=; 3) 4; 4)
8V3 13о
IX.139. 1) Ь 2) -1,25. IX.140. 1) |; 2) 3; 3) 2; 4) 12. IX.141. 1) 0;
Ответы к главе IX 181
2) -0,5. IX.142. 1) -1; 2) -1; 3) 2; 4) -1. IX.143. 1) 0; 2) 0. IX.150. 0,5. Указа ни е: полезно использовать теоремы о пределах последовательностей, связанные с неравенствами. IX.151. 0. IX.152. 0. IX.153. 0. IX.154. Указание: полезно использовать геометрическую интерпретацию предела функции в точке. IX.155. Указание: полезно использовать геометрическую интерпретацию предела функции в точке.
Глава X
СТЕПЕННАЯ, ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
§1. СТЕПЕННАЯ ФУНКЦИЯ
Первый уровень
В одной системе координат построить графики функций (Х.1-Х.5).
Х.1. 1) г/ = х2; 2) t/ = x3; 3) у = х4; 4) у = х\
Х.2. 1) у = х~\ 2) у — %-2; 3) у = х~^\ 4) у — х~4.
Х.З. 1) у = у/х\ 2) г/ = у/~х\ 3) у = у/х\ 4) у = у/~х.
Х.4. 1) у = х*\ 2) у — х^3) у = х*\ 4) у = хъ.
_1 _2 _4 _3
Х.5. 1) у = х з; 2) у = х з; 3) у = х з; 4) у=х 2.
Х.6. Найти область определения функции:
1) у = — 4х + \/2х +~1 + -7Г-— —
V2x - 1
2) у — \/2-у^х+У/3-х--+=;
V2x + 1
3) у = (х - 3)з + —+ (х - 4)5;
4) у = (2х - 1)1 + + (1 - *)“3-
Х.7. Используя свойства степенных функций, сравнить значения выражений:
1) /(13)+/(14) и /(15)+/(16), если /(%) =-L;
2) /(11)—/(10) и /(12)-/(9), если /(х) = х+
Х.8. Используя свойства степенных функций, сравнить значения выражений:
1) 0,3"! и 0,5“ + 2) 4-3-43 и 1-3-6+
Х.9. Найти наименьшее и наибольшее значения функции на указанном промежутке (если они существуют):
1) f(x)=x-3, [8;20); 2) /(х) = -4, Щ2];
3) /(х) = \/2х+Т, (-2; 15]; 4) f(x) = 3 - Т [1;3].
Глава X. Степенная, показательная, логарифмическая функции 183
Построить график функции и с его помощью исследовать функцию (найти ее область определения, множество значений, промежутки возрастания и убывания; выяснить, является ли функция ограниченной, четной (нечетной, общего вида); определить ее наибольшее и наименьшее значения) (X.10-Х.12).
Х.1О. 1) г/= 0,5(2 + х)3; 2) у = (1-х)4.
Х.12. 1) у = \/-х-4; 2) у = \/2х - 4.
Х.13. Построить график функции у = /(х) и с его помощью определить число корней уравнения а=/(х) при указанных значениях параметра а:
1) Кх) = 3 — д/Й; а = —2, а = 3, а = 5;
2) /(х) = |х/х + 3 — 2|; а = — 4, а = 0, а = 2; а = 3.
Х.14. Решить графически уравнение:
1) (3 - х)0’5 = (х - I)3; 2) 4 = (^ - 2)3 + °Д
Х.15. Решить графически неравенство:
1) (х + 7)3 < -2) 2
у с) zV О
Х.16. Оценив значения левой и правой частей уравнения, доказать, что уравнение не имеет корней:
1) \/х +4=1 — у/х; 2) л/х - 1 + у/х =
2+
Второй уровень
Х.17. Используя свойство монотонности функций вида у = хг (г — положительное нецелое рациональное число), доказать, что: 1) функция у = (5 — 2х)з убывает на всей области определения;
2) функция у = (Зх — 7)2 возрастает на всей области определения.
Х.18. Среди функций /(х) = \/Зх + 4, g(x) = \/х + 5,
/г(х) = (3 + 7х)+ р(х) = 1 - х, q(x} = (х — З)2,
w(x) = (2х — 5)3, и(х) = (х — 3)~7, z(x) = (6х + 3)-2 указать те, которые:
1) возрастают на всей своей области определения;
2) убывают на всей своей области определения.
184 Глава X. Степенная, показательная, логарифмическая функции
Х.19. 1) Найти наименьшее и наибольшее значения выражения
—— г/2 + бу, если —1,2 ^х^ 1,8 и у С 5. х-2 3 2
2) Найти наименьшее и наибольшее значения выражения
х2 + 3х + —, если и -l^r/^2,9.
у-3 2
Х.2О. Найти наименьшее и наибольшее значения функции на
указанном отрезке:
1) /(х) = х^ - х3 - 1, [1,8];
2) /(х) = 4 —х^ +4x3, [8,27].
Х.21. Решить уравнение:
1) х2 + х~? = -х2 + 2х + 1;
2) \/х + 2 + —+ х2 + 2х — 1 = 0. ух + 2
Х.22. Построить график функции у — /(х) и с его помощью определить число корней уравнения я = /(х) при указанных значениях параметра а\
1) / (х) — (1 — х)з — 2|; а = — 2, а = 0, а — 2, а — 3;
2) /(х) = \/2х — б| — 4; а — — 6, а = —4, а = 1.
Х.23. Решить уравнение:
1) |х + 4| + |х — 4| =2) |х — 2| + |х + 2| = х
Х.24. Решить неравенство:
1) х? + х§ + хз < - + 2; 2) 4= + - . 1 < Jx + 0,5.
X у/Х у/х + З
Х.25. При каждом значении параметра а определить число корней уравнения:
1) (2 |х| + 1) з = а; 2) ] ^/|х| - 3 - 1| = я.
Х.26. Используя графический подход, определить, при каких значениях параметра а имеет решение неравенство:
1) (х + 1)2<а —х; 2) \/6 — 2х < Зх + а.
§2. Показательная функция 185
§2. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
Первый уровень
Х.27. В одной системе координат построить графики функций:
1) у = 2х- 2) г/= 3х; 3) г/ = 4х;
4),= (1У; 5), = (!)*; 6) у = (1)‘
Х.28. Исследовать на монотонность функцию:
1) у = (8 - 2УП)Х; 2) у = (^6 - Л/.
Х.29. Используя свойства показательной функции, определить знак выражения:
1) 40,7 _ 80,4. 2) 21,1 _ 3~0,1 _ о,5~0’9-h 1;
3) 0,2s1’1-32-°’92; 4) - 3 • 9°’3 - 3~°’001.
Х.ЗО. Исследовать функцию на четность:
1) г/ = 4-2-х+ 2х+2; 2) у = 3х-1 + З1^;
3) у = 2 • 23-И; 4) у = 102х - 0,01х;
5) у = 5lx+3l; 6) у = Ьх + 5“х +2.
Х.31. Найти наименьшее и наибольшее значения функции на указанном промежутке:
1) f(x) = 23-’, [-2;3];
2) /(х) = 3 - 0,12х-3, [—1; 2];
3) /(х) = 2 + 4 О,!2-*, [1;3];
4) /(х) = 4 - З3*+2, [-1; 1].
Построить график функции и с его помощью исследовать функцию (найти ее область определения, множество значений, промежутки возрастания и убывания; выяснить, является ли функция ограниченной, четной (нечетной, общего вида); определить ее наибольшее и наименьшее значения ) (X.32-X.33).
Х.32. 1) у = 3 - (0,5)х; 2) у = 0,5 • Зх+2 - 2;
3) г/ = 22х~2; 4) у = 3°’5х+1 - 5.
Х.ЗЗ. 1) у = О,ЗИ-2; 2) у = |4 — 2Х| - 1;
3) у = 3lx+2l - 3; 4) у = 0,5 • |1 - 3"х|.
Х.34. Построить график функции у = и с его помощью определить число корней уравнения a = f(x) при указанных значениях параметра ст.
186 Глава X. Степенная, показательная, логарифмическая функции
1) /(х) — |2Х — 4| + 1; a - — 3, a = 1, a-- 2, a — 5, a = 6;
2) /(я) = O,5l'Y-2l-2; a = -3, a = -1,5, a = -l, a = 4.
X.35. Решить графически уравнение:
1) 2“x = 2x + 4; 2) 0,5х"1 - 3 = 5 • 5х;
3) 2х - 2х = 1 - х2; 4) 2х + Зх+1 - 1,5 = 0.
Х.36. Решить неравенство:
1) Зх+1 10 - х-, 2) 0,5 х + 1 < Зх+2.
Х.37. Доказать, что не имеет решений неравенство:
1) 5х-1<-0,5х; 2) 3х + 3~х < 1.5.
Х.38. При каждом значении параметра а определить число корней уравнения:
1) 0,5 • 31-х — 4 = а; 2) 52х + 0,2“2х = a - 3.
Второй уровень
Построить график функции и с его помощью исследовать функцию (X.39-Х.40).
Х.39. 1) у = 2lx“2l+lx+1l - 1; 2) у = 2 - 0,5lx43l-2lxl-\
Х.40. 1) у = 5 - 2 • 3l°'5x'-2l; 2) у = 3 - |0,5l2x~4l - 4|.
Х.41. Исследовать на монотонность функцию:
1) у = 0,31х1~4; 2) у = 22-1х-11;
3) у = 22И-1х+31; 4) у = 0,б1х'-2Н-<+1|-\
Х.42. Доказать, что функция ограничена:
1) у = 0,5И - 2; 2) у = 24-(х-3)2;
3) у = 2-И -3-1х+11; 4) у = 0,42х+х2 + 7.
Х.43. Найти наименьшее и наибольшее значения функции на указанном промежутке:
1) /(х) = 0,11-1х-21, [1;5];
2) Дх) = 3 0,521х+31-3, [-2; 2].
Х.44. Найти наименьшее и наибольшее значения функции на указанном промежутке:
1) /(х) = 2х-1 -4 , [2;6>
2) /(х) = 4 - 0,51х |, [—3; 1].
§ 3. Логарифмическая функция 187
Х.45. Найти наименьшее и наибольшее значения функции (если они существуют):
1) /(х) = 31-л2; 2) /(х) = +1;
3) /(х) = 0,5х2-4х+5; 4) Дх) = 5-I*-1!.
Х.46. Найти наименьшее и наибольшее значения функции на указанном промежутке:
1) Дх) = 4 х - 6 • 2 х + 1, [1;3];
2) Дх) = 0,25х-4-0,5х + 3, [-4,-1].
Х.47. Найти наименьшее значение функции у — ах + а~х (а>0,а/1).
Решить уравнение (Х.48-Х.51),
Х.48. 1) (\/3 + 2\^)51ПХ = 3; 2) ( х/эП?!) = 5.
Х.49. 1) 2х2+4х+5 = —х2 — 4х — 2; 2) (|)х4-2х‘2 = х2 - 2х + 4.
Х.50. 1) 4х + 6х = 10; 2) 2х + 5х = 0,7.
Х.51. 1) —Ц = 3Х + 3“Х; 2) ^_ = 10х + 0,1х.
1 + X2 1 + X4
Х.52. Решить неравенство:
1) 3х + 4х + 5х < 3; 2) 3х + 5х > 34.
Х.53. Решить неравенство:
1) 0,5х + 0,5“х > 2 - уД- 2) 0,25х > 40-5-И - 4х.
Х.54. Определить, при каких значениях параметра а функция Дх)= —L является нечетной.
4 ' а — 3А 2
§3. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
Первый уровень
Х.55. В одной системе координат построить графики функций:
1) у = logi х; 2) у = logi х; 3) у = logi х; 4 3 2
4) i/ = log2x; 5) у = log3x; 6) у = log4x.
Х.56. Найти область определения функции:
О У = log2 (9 - х) + log3 (х - 7); 2) у = х log2 (х - х2);
3) У = log2
4) у = log2 (|х + 3| - 4) + log0д(1 - 4х).
188 Глава X. Степенная, показательная, логарифмическая функции
Х.57. Исследовать на монотонность функцию:
1) у — 1°&8—3\/б 2) У = 1014—х/7 х-
Х.58. Исследовать на монотонность функцию:
О */ = log5O + 3); 2) у = log0?2(2x + 1);
3) У = log4(l - х); 4) у = log0 з(1 “ 4%)-
Х.59. Определить, какие значения может принимать а, если известно, что функция убывает на всей области определения: О У = loga(2x + 1); 2) у = log2_a(1 - х).
Х.60. Используя свойства логарифмической функции, сравнить значения выражений:
1) log4 15 и logo 5 0,24; 2) logo i 0,015 и log12 146.
Х.61. Расставить числа в порядке убывания:
1) log5 4, log0 2 10, log25 2; 2) log3 2, log0 3 3, log98.
X.62. Исследовать функцию на четность:
1) J/ = log2(|x|-l); 2) у = log2 |х — 1|;
3) У = log0i5 |х - 1| + log05 |х + 1|; 4) у = logi |^|.
Х.63. Найти наименьшее и наибольшее значения функции на указанном промежутке (если они существуют): 1) /(х) = log2x, [2; 64];
2) /(х) = logi (2х - 3), (2; 14];
3) /(х) = 1 - 2 • log01 (4 - х), [-96; 3];
4) /(х) = -3 • log2 (4% + 12) - 2, [-1;29].
Построить график функции и с его помощью исследовать функцию (найти ее область определения, Множество значений, промежутки возрастания и убывания; выяснить, является ли функция ограниченной, четной (нечетной, общего вида); определить ее наибольшее и наименьшее значения) (X.64-Х.65).
Х.64. 1) у = 1 + log2(x + 3); 2) у = 3 — 2 • log05 х;
3) у = - log3(2x - 4); 4) у = logi (6 - Зх) - 4.
Х.65. 1) у = log2(|x| + 1); '2) у= |logi (2х - 4)|;
3) у = - log05 |х + 3|; 4) у= |log3(2 —х)|.
§3. Логарифмическая функция 189
Х.66. Решить графически уравнение:
1) logsk + 3) — 3 — %; 2) log2 х = |х - 4| — 1;
3) log9 х + 2 = 20 • 0,5х; 4) log3x=-^-j-.
Х.67. Решить уравнение:
1) cos тих - log3 (1 + х2) = 1;
2) (sin х + cos %)2 = log5 (|4x - тг| + 25).
X.68. Решить неравенство:
1) log2 (x — 1) 2x — 15; 2) 3х < 10 - log2 x.
X.69. Построить график функции у = /(х) и с его помощью определить число корней уравнения ц = /(х) при указанных значениях параметра а\
1) /(х) = log3(1 — х) — 2|; а = -3, а = 0, а = 2, а = 5;
2) /(х) — log0 5(2х — 6)| — 4; а = "6, а = — 4, а = 0, а = 1.
Второй уровень
Х.7О. Исследовать на монотонность функцию:
1) у = 2 - log3(4 — 2х); 2) у = 1 - log01(l + Зх).
Х.71. Исследовать на монотонность функцию:
1) У = log3 |2х - 4|; 2) у = log05 (|х| + 1).
Х.72. Используя свойства логарифмической функции, определить знак выражения:
1) log2 3+12В —; 2) log0>2 (log0|20,007 + 2) + 1;
3) logo., (0,5 log2 63 - 2); 4) log2 ‘^o.i 0.0002 + 6
X.73. Построить график функции:
1) У = bg3 (х2 + 6х + 9); 2) у = log0 5 (х2 - 4х + 4).
Х.74. Построить график функции и с его помощью исследовать функцию:
1) У = log2 (к- 31 + к + 3|);
2) У = log0,5 (к + 2| + |х - 1| +х).
Х.75. 1) Построить график функции у = log2 (|3 — 2 |х|| — 3), указать промежутки возрастания и убывания функции. Найти наименьшее и наибольшее значения этой функции на отрезке [5; 7].
190 Глава X. Степенная, показательная, логарифмическая функции
2) Построить график функции у = log4 (8 — |3 |х| — 8|), указать промежутки возрастания и убывания функции. Найти наименьшее и наибольшее значения этой функции на отрезке
Х.76. Найти наименьшее и наибольшее значения функции (если они существуют):
1) У = log2 (|х| + 4); 2) у = log0 2 (4*2 + 4х + 6);
3) г/= log-i (х2 - х + 1) - 4; 4) у = 2 - 3 • log2 (|х + 5| + 8).
Х.77. Найти наименьшее и наибольшее значения функции на указанном промежутке:
1) /(x) = |log2(x + 4)-4|, [0:28];
2) = log0,5 (I*” 11 + 2) - 5. [-29;7].
Х.78. 1) График функции у = 1 — log2 (2х + 3) отразили симметрично относительно прямой у — 4. График какой функции получился?
2) График функции у — logi (1 — 5х) отразили симметрично относительно прямой х = 4. График какой функции получился?
Х.79. Определить число корней уравнения:
1) х2 — 2х — log2 11 — х| = 3; 2) log3 (|х| - 2) + ||х| - 1| = 0.
Х.80. Решить неравенство:
1)5 + sin (1,5тгх) < log5 х • (4 — log5 х);
2) log2 (4 + \/х^2) + 14 + 4х 23+х.
Х.81. Определить, при каких значениях параметра а уравнение 3% 1gх = 1 + a 1gх имеет:
1) один корень; 2) два корня.
§4. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ
Первый уровень
Решить уравнение (X.82-Х.89).
Х.82. 1) 2х-3 = 5;
Х.83. 1) 5х+3 = 0,2х+1;
3) (0,2/2+2х = (0,04)16-л;
2) 5x+1 = log2 0,3.
2) (|)Х = У1Д
4) (—L-) = (0.04)21'-42.
\25-v5/
§4. Показательные уравнения 191
Х.84. 1) 4х + 4х-1 = 4х+1 - 11; 2) 5Х+2 + 0.2-х-1 + 4 • 5x+1 = 2.
Х.85. 1) 7^+6.зх+6 = 21Зл-; 2) 1ОО3х • 56х = 2500;
3) 100х-1-2,71-х = 0,09; 4) 10 х-1 • 0,42-х = 0,08.
Х.86. 1) б2х • 4Х+2 = 16 • 104-2х;
2) 13х+4 • 5х+4 = (О,2)-Зл • 133х;
3) (l)'V ‘2 = 32t-(0,25)--2t;
4) (0,2) 'л' '7 Зл+7 = 53х-1 (I)'’3''.
Х.87. 1) 2-х • 5х+1 - 22-х • 5х-1 = 10,5;
2) 3х”1 • 5 х + Зх“2 • 5|-х = 0,32.
Х.88. 1) 2х + 2х 11 = 3 х — 3 х-2;
2) 2х+3 - 7х-1 = 2х + 7х-2;
3) 2х+4-5х"1 = 2-(5х-2х);
4) 4х — 3х-О’3 = Зх+о,5 _ 22л'-1
Х.89. 1) 2х+3 - 2х = 5Х+2 - 5х+1 + 5х;
2) 7Х+2 + Зх+1 = 3х + 7х+1 + Зх+2.
Решить уравнение (X.90-Х.99).
Х.90. 1) 32х — 8 • 3х — 9 = 0;
3) 9-х - 6 • 3-х = 27;
Х.91. 1) 3-52х-1 -2-5х-1 = 0,2;
3) 0,04 х-1 + 52-х = 6;
Х.93. 1) 5^ -б'^8 =24;
3> (1)3х-(1Г'-128=0;
Х.94. 1) 2х - 6 • л/2* = 16;
Х.95. 1) 2х + 10 = 36 • 22-х;
Х.96. 1) 8х - 4х = 2х;
Х.97. 1) 32х + 2х+4 = 8 • 23х;
Х.98. 1) 3 - 25х Н-2 -15х — 5 - 9х = 0;
3) 36х = 2 • 12х + 3 • 4х;
5) 5-25х —30х —6-36х = 0;
Х.99. 1) 9х + И • 24х = 12х+1;
2) 4х + 3 • 2х = 10;
4) (О,25)х + 2 • (0,5)х = 3.
2) 1 — 3 • 21-х + 23-2х = 0;
4) 0,25х-3 = 9 - 5 • 22-х.
2> ^-4 = 3(0.4)'.
х+7 х_
2) 4 7 4-414 = 68;
1 з+-
4) 64л -2 х +12 = 0.
2) (\/4)х + 4-(^4)х“Ю=20.
2) Ю1+х2-101-х2 = 99.
2) 125 х + 25х = 0,2-х.
2) 27х + Зх+4 = 82 • 9х.
2) 2-9х + 6х = 3-4х;
4) 16х+°-5-20х-б-25х = 0;
6) 32х+4 +45-6х-9-22х+2 = 0.
2) 16х + б2х+1 =6-20х.
192 Глава X. Степенная, показательная, логарифмическая функции
Х.100. Определить, при каких значениях параметра а имеет решение уравнение:
1) 2х = а2 - 4; 2) (а + 1) • 5“х = а2 - 1.
Х.101. Определить, при каких значениях параметра а имеет ровно два корня уравнение:
1) (25х-5) (х2-а2) =0;
2) (4х - 5 • 2х + 4) (х - а) = 0.
Х.1О2. Определить, при каких значениях параметра а имеет ровно один корень уравнение:
1) 4х - (4 + За) • 2х + 12а = 0;
2) 25х - (20 + а) •5х + 25а - 125 = 0.
Х.103. При каждом значении параметра а решить уравнение:
1) 9х - (1 + а)Зх + а = 0; 2) 4х + а • 2х - 2а2 = 0.
Второй уровень
Решить уравнение (Х.104-Х.108).
Х.104. 1) 2х2-х-6 = 3х-3; 2) 25 • 4Х(3~Х> = 16 • 52х;
3) зх'2-3х+2 = 7*-1; 4) 27 • 5х(х“2) = 125 • 3х.
Х.1О5. 1) 18х-9х+1-2х+2 +36 = 0; 2) 12х-4Х+2 - Зх+1+48 = 0.
Х.106. 1) 16х = (6 • 0,8х + 7) • 52х;
2) 2 • (0,5)х • (e^-’ + l) = 7-3х-1.
Х.107. 1) (5 + \/24)" + (5- х/24)" = 10;
2) (\/2 - д/з)Х + (\/2 + д/з)Х = 4.
Х.1О8. 1) 32х2-1 _3(х-1)(*+5) _2-38(х“1) = 0;
2) 42х'2-1 _ 4O+I)2 _ з . |g2(x+l) _ q
Х.1О9. Найти все значения параметра а, при каждом из которых имеет хотя бы один корень уравнение:
1) 25х + а • 5х + а + 3 = 0; 2) 4х + а • 2х + 8 - а = 0.
Х.11О. Найти все значения параметра а, при каждом из которых не имеет корней уравнение:
1) 9х — (6 + 2а) • 3х — а — 1 = 0;
2) 25х + (а + 4) • 5х + 4а + 1 = 0.
§5. Показательные неравенства 193
Х.111. Определить, при каких значениях параметра р имеет ровно один корень уравнение:
1) Зх + З~х=р; 2) Зх+2 + 3~х=р.
Х.112. При каждом значении параметра а решить уравнение:
1) 4х — (1 + а) • 2х + 4а2 = 0;
2) 36х - (4 + 2а) • 6х + а2 + а = 0.
Х.113. При каждом значении параметра а определить число корней уравнения:
1) 0,51х!-1 + 2 = а; 2) 5°’5х + 5~°’5х = 1 - а.
§5. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА
Первый уровень
Решить неравенство (Х.П4-Х.121).
х.114. 1) 2х-1 4-; 2)
V2
3) 2х2-7х+14 < 16; 4)
Х.115. 1) ^+7>^2-Зх+2. 2)
Х.116. 1) (2д/3 — 3)х2“2х < 1; 2)
Х.117. 1) 2^ < 4х; 2)
3) 32+х; 4)
Х.118. 1) (0,16)1+2х • (6,25)х 1; 2)
3) f 27_А <94-2х-81; 4)
\ V3/
Х.119. 1) 5х+2 + 5х+1 ^6; 2)
Х.120. 1) 122х+3 - 144х+0’5 < 1716; 2)
3) 25х+1’5 - 52х+2 > 2500; 4)
Х.121. 1) 9х - 2х+°’5 > 2Х+3’5 - 32х-1;
2) 5х+1 + 2 • 3х Зх+3 — 2 • 5х-1.
0,1]-х < 0,01;
°’2'+х2 > is-
/ j \ х2+2х / । \ 16—х
> \9J
(3 - 2д/2)3х-х2 < 1.
х+2
ас / ос \ 2-4х
52х-5 >0,04- ( ) ;
’ \д/5/
о о / Q9 \
163“2х-0,25^ (^)
3х + Зх+2 90.
5*“х - (0,2)х+1 <4,8;
(0,5)-4х-8 - 16х+1’5 > 768.
7—5682
194 Глава X. Степенная, показательная, логарифмическая функции
Решить Х.122. неравенство (X.122-Х.124). 1) 2Х+4 - 4х < 15; 2) 5х+1 - 25х > 4; 3) 9х + 8 > Зх+2; 4) 4-х+0’5 - 7 2“х - 4 < 0.
Х.123. 1) 5 4х + 2 • 25х > 7 • 10х; 2) 2 • 4х - 5 6х + 3 9х < 0.
Х.124. ') Л,т7 ; > 4-'; 2) 5 х + „ 'Г < 0. 4 ' +1 _ 4 2 — □
Х.125. Найти все значения параметра а, при каждом из которых для любых х выполняется неравенство: 1) а-Зх + а>1; 2) а • 5-х + а > 2.
Х.126. При каждом значении параметра а решить неравенство: 1) {а + 1) • 0,5х > а2 - 1; 2) (а2 - 4) • 2х < а + 2.
Х.127. При каждом значении параметра а решить неравенство: 1) 9х - а • 3х - 2а2 >0; 2) 5 • 16х + а • 4х+1 - а2 0. Второй уровень
Решить неравенство (X.128-Х.135).
Х.128. 1) 2х-2 > 5х2-8x4-12. 2) 7Х—> 3*2+x—зо
Х.129. 1) (10-х/2)х^73*; 2) (4 + у/1)х < 43*.
Х.130. 1) 2х + 4х 6; 2) (0,5)2 + 2 > 3 • (0,5)^.
Х.131. 1) 72х — 33 • (1,4)х — 14 • 51-2х 0; 2) 32х — 35 • (1,5)х — 9 • 41-х < 0.
Х.132. 4 — 7 • 5х <2. 2Х+3 + 11 <3 ' 52*-»-1 - 12 - 5* 4-4 " 3’ 22х+1 + 2х - 15
Х.133. 2) 15-^>1 + (|)7
Х.134. 1) 9^ 6 • 9х - 5 • 3^ • 3х; 2) 25^ 4 • 25х - 3 • 5^ • 5х.
Х.135. 1) (У5 + 2)л+ (J5-2)X <2V5; 2) (\/з + \/8)'' +(У3-78)Г >6.
Х.136. 1) Найти все значения параметра а, при каждом из которых неравенство 4х — а • 2х — а + 3 0 имеет хотя бы одно решение. 2) Найти все значения параметра а, при каждом из которых неравенство а • 9х + 4(tz — 1) • 3х + а > 1 справедливо для любого X.
§ 6. Логарифмические уравнения 195
§6. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
Первый уровень
Решить
Х.137.
Х.138.
Х.139.
Х.140.
Х.141.
уравнение (X.137-Х.145).
1) 3 log3 х — log9 х = 5;
3) log16 х + log4 х + log2 х = 7;
1) logx+12 = 2;
1) logr_3 (4x — 15) = 2;
3) 21ogx_, (x - 3) = 1;
1) 1o£o,25 (5 log3—6) = — 1;
1) logo,7 (x2 -6x + 2) = log0 7
2) log3 - = iOg3 (1 — x);
2) 5 logys x - log5 x = 18;
4) 1.5log4 Ух-0,5log2x= 1.
2) logx_! 3 = 2.
2) logv (3x2 - x — 3) = 2;
4) 2 log8_x (x - 2) = 1.
2) log2 (1 + 31og2x) = 2.
(7 — 2x);
Х.142.
Х.143.
Х.144.
Х.145.
Решить
Х.146.
Х.147.
Х.148.
Х.149.
Х.150.
3) log5 (x - 1) + ^go,2 = °;
4) Юй - log. = 0.
1) log2(3x - 1) = log2 (3 — x) + 1;
2) log4(x + 4) = 2 - log4 (x - 2);
3) log5(x - 9) = log0 5 4 - log5 (x - 5) + 3;
4) log, (x — 1) 4~ log, (x + 1) — logj (7 —x) = l.
2 2
1) 21g(x + 0,5) - lg(x — 1) = lg(x + 2,5) + 1g 2;
2) | log3 x5 + log3 x-±^- = 3 log27 (x + 4) - 3 log3 \/2
1) 2 log2(x + 6) — log2 (x — 4)2 = 2;
2) 2 log3(x + 3) - 2 = log3 (x - 5)2.
1) logx_, 0,001 + log(x_1)2 100 = 0,5;
2) log2_x 27 - log(x_2)4 9 = 0,625.
уравнение (X.146-X.148),
1) lgx-(lgx-2) = 3; 2) log2 x + 3 log2 x —4 = 0.
1) log2x-log2 (4x) — 15 = 0; 2) (log4x)2 +20 = 6 log4 (16x).
1) log, x = 31ogx 1 — 0,5; 2) 2 log4(3x-2) + 2 log3x_2 4 = 5.
9 У
При каждом значении параметра а решить уравнение:
1) (x + 2a)-log5(x + l) = 0; 2) (х — 2a)-log5(x — a) = 0.
При каждом значении параметра а решить уравнение: 1) log3 (2x-4) = log3 (а-Зх);
2) log2 (ax — 4) = log2 (a — x).
196 Глава X. Степенная, показательная, логарифмическая функции
Второй уровень
Решить уравнение (X.151-Х.170).
Х.151. 1) (log9(7 —x) + l)-log3 3 = 1;
2) (log4(2x + 9) + l)-logv4_22=l.
Х.152. 1) log3log2(2x-l) + logi logi ^L = log32;
2) log2log3(2x + 3) + logi logi =
X.153. 1) log16 (x2-2x-3)2-21og16 (x2+x-2) =0,5;
2) 1g (x3 + 27) - 0,5 1g (x2 + 6x + 9) = 3 1g a/7.
X.154. 1) log2x + log3x + log4x = l;
2) log9x —logo x-log9 x-2 logox = 0.
X.155. 1) log2x2_10,2 = -log1._3x5;
2) 0,5-log3x_89 = logx2„3x3.
X.156. 1) log2x-log2(x —3) + l = log2 (x2-3x);
2) lg(x - 10) • lg(x +10) = 1g (x2 - 100) - 1.
X.157. 1) log2 x +(x-1) log2 x = 6 —2x;
2) (x + 1) log2 x + 4xlog3x — 16 = 0.
X.158. 1) lg2(x+1) = lg(x +1) • 1g (x —1)+2 lg2(x—1);
2) lg2(4-x) + lg(4-x)-lg(x + 0,5) = 21g2(x + 0,5).
X.159. 1) log^x + 40^/log^ x-48 = 0;
2) у/4 log4 x — ^/log2 x — 2 = 0.
X.160. 1) ((log2 x)2+ 3^ (3 log8 x —1) = 2 log2 -log2 x2;
2) (log3x)2 (1+2 log9x) = log3 9x-logi
X.161. log2 (x2 + 7) =5 + log2x-----•
log2
X.162. 1) logx2-log2x 2 = log4 2;
2) logx25 + log125x5 = log25x625.
X.163. 1) logx (9x2) • log3 x = 4;
2) 31og3xx = 21og9xx2.
X.164. 1) logx+1(x-0,5) = logx_a5(x + l);
2) logx_! (x2 + x + 1) = logx2+x+1 (x- 1).
X.165. 1) 2log5_x (x+l) = log5_x (6-2x);
§6. Логарифмические уравнения 197
2) 2 logr_2 (х — 1) = log„_2 (5 + х).
Х.166. 1) l + logx(5-x) = log74-logx7;
2) 1+ logx (4-х) = log5 3-logx 5.
X.167. 1) log2v f—-16х^ = —Ц--3;
\ X ) log56 2x
, 2l°gO,25(4-*) = i
' log6(3+x) log2(3+x)
X.168. 1) (x + 5) • log4_x (x2-4) =2x + 10;
2) (1 —4x)-logx+1 (x3 + 3x2) =3-12x.
X.169. 1) log4x_,x = log3_xx;
2) log2xx + log8x2x = 0.
X.170. 1) 2x-x2 = log2 (x2 + l) — log2x;
2) i+x = log2 (x2 + x)+log2
X.171. 1) Найти все значения параметра а, при которых каждое решение неравенства log0 5 х2 log0 5(х + 2) является решением неравенства 49х2 —4а4^0.
2) Найти все значения параметра а, при которых каждое решение неравенства log3(21 — х) ^log3 (2х2) является решением неравенства 9а4 —64х2^0.
Х.172. 1) Найти все значения параметра а, при каждом из которых уравнение
log5x + 4 (1 - а2) log25x 5-2 = 0
имеет два корня, расстояние между которыми 24
больше —.
5
2) Найти все значения параметра а, при каждом из которых расстояние между корнями уравнения 2 loga х + 3 logox2 а + 5 = 0 меньше
Х.173. Найти все значения параметра а, при каждом из которых имеет ровно один корень уравнение:
1) log2 (ах) = 2 log2(2x + 1);
2) 2 1g (х — 2) = 1g ((а — 3)х — а2 — а + 12).
198 Глава X. Степенная, показательная, логарифмическая функции
Х.174. Найти все значения параметра а, при каждом из которых имеет два различных корня уравнение:
1) log3 (3 + х) = log3(а - х) + log3(x - 1);
2) logo,5 (l-x) + log0>5(-l-x) = log3 О(2х — а — 3) — 4х— 1).
Х.175. 1) При каких значениях параметра а все корни уравнения l°g3(x — 2) + (6 — 5а) • log3(x - 2) + 4а2 — 9а + 5 = О больше 11?
2) При каких значениях параметра а хотя бы один корень уравнения log^(х + 3) + (3 — 5а) • log4(x + 3) + 6а2 - 7а + + 2 = 0 меньше 13?
§7. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА
Первый уровень
Решить неравенство (Х.176-Х.179).
Х.176. 1) log0 5 (2х + 6) log0 5 (х + 8);
2) log8 (Зх - 1) - log8 (3 - х) > 0.
Х.177. 1) 1о&^(х2-8) + 1о&Уз(7х);
2) logo,5 (*2 + 4) logo,5 (7х - 8)-
Х.178. 1) log0 5 (27773) > log2 (Зх — 5);
2) log0,36 (Зх + 4) log0)6x.
Х.179. 1) log0 5 (Зх — 4) > — 1;
2) log0,5^.
Х.180. Найти все целые решения неравенства:
1) logo,25 > 0; 2) logo.5 > 0.
Решить неравенство (Х.181-Х.184),
Х.181. 1) log8x- log8 7 -1; 2) log0 5 (х + 2) > log4 Q) + 1;
3) 1 — log-ioo 4 logo 1 (7 —х); 4) log 1 (х + 5) log27 8 - 2.
’ з
Х.182. 1) | log2 (х + I)3 < - log2 -3; 2) 21og0 5 Vx + 1 < - log0 5 5.
X.183. 1) log2 logi (x - 1) 0; 2) log2 log3 (x + 2) > 0.
3 5
§ 7. Логарифмические неравенства 199
Х.184. 1) lgxl6-lgx8 + l ^0; 2) log2 х12 + log2 х4 - 4 > 0.
Х.185. 1) Известно, что неравенство logfl (х2 — Зх) > logfl (4х —х2) выполняется для х = 3|. Найти решение этого неравенства.
2) Известно, что неравенство loga (х2 - х — 2) > > loga (—х2 + 2х + 3) выполняется для х = |. Найти решение этого неравенства.
Решить неравенство (X.186-Х.188).
Х.186. 1) logx+2 (5 -х) < 1; 2) log2x_3x^l.
Х.187. 1) logx_! 9 1; 2) logx._9 2 > log/x7^ 2.
Х.188. 1) 1 -logJ ^2; 2) log6 1 + 4 > --i-
7 logx 2 Б2 x 7 БЬ x logx 6
Решить неравенство (X.189-Х.191).
X.189. 1) log2 x + 3 log2 x 2,5 • Iog4v/2 16;
2) log2 x + 3 log2 x 5 • log2 У16.
X.191. 1) logv 3 + log3 x < 0; 2) log2 x + logx 2 > 2.
X.192. При каждом значении параметра а решить неравенство: 1) (a — 1) • log5(x + a) < 0; 2) (a + 2) • log0 5(x — 4a) 0.
X.193. При каждом значении параметра а решить неравенство: 1) !og3 (* + a)>log3 2) Iog3 (x-2a)^log3 (2x + l).
Второй уровень
X.194. Найти наименьшее целое х, удовлетворяющее неравенству: 0 log3(7|T)^log3(5-x); 2) log6 (4-х)^log, Q+ .
Решить неравенство (X.195-Х.198).
Х.195. 1) 21og;(x —2) —logi (х2-х+2)^1;
2) i-lg(2x-l)>l-lgv^9.
Х.196. 1) (х2 —3)-lgx2^x-lgx4;
2) х(х-2) log0 5 х2+2 log2 х8^0.
200 Глава X. Степенная, показательная, логарифмическая функции
Х.197. 1) x-lgx4 — 3^ 12-lgx —х;
2) log2 (х2-4х+4)+2х>2 — (х+1) logi (2—х).
Х.198. 1) log5 logi (x+1)^0; 2) log2 logs (x+2) ^0.
3 5
X.199. Найти область определения функции:
1) //=log2logi l°g4(x —i); 2) z/=logi log5logi (2-x).
3 2 3
Решить неравенство (X.200-X.207), X.200. 1) log3 (log2 (2 —log4x)~1)<1;
2) log, (4-log5 (l-log0 5x))^-l.
X.201. 1) Iogx^<-1; 2) logx_,|pf>l.
X.202. 1) 2+logx_j lO^log^i (6x2-15);
2) 2н-^2х_! S^log^-! (8x2 —6).
X.203. 1) logx (log2 x) >0;
2) logx (logx \/6-x)>0.
X.204. 1) log2 4+logx 2 —5^0; 2) log2 49-3 logx 7-1 >0.
X.205. 1) 2 log3 x—logx 27<5; 2) log2 x-logx 32<4.
X.206. 1) 3 >1; 2) ‘ 4.
Iog2 (xz —8) log2 (5—xz)
X.207. 1) 1-lg2^ >lg (x4)+5; 2) 1о^х'1о/22х ^l.log4 8x.
Igx-21g2x 7 l°g2 "3 54
X.208. При каждом значении параметра а решить неравенство: n 3logflx+6 , 1 + log^x .
2 + log^x l + l°gflx
X.209. При каждом отрицательном значении параметра b решить неравенство b-log3 x+log3x 3+b^0.
Х.210. 1) Найти все значения параметра с, при каждом из которых неравенство l+log2 (2х2+2х+3,5) ^log2 (сх2 + с) имеет хотя бы одно решение.
2) Найти все значения параметра с, при каждом из которых неравенство,. l + log5 (х2 + 1)^log5 (сх2+4х+с) справедливо при всех х.
§8. Смешанные уравнения и неравенства 201
§8. СМЕШАННЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
Первый уровень
Решить уравнение (Х.211-Х.217),
Х.211. 1) 51’-х1=25; 2) g|3x-i| =38х-2
Х.212. 1) 5-2х-8 = 25^+2; 2) 2'/х+]2 = (0,5)-х.
Х.213. 1) 61О&б(х+3)=0,51оеЯх2+5х+12);
_. nlog I (х+2) log, (2х24-Зх+2)
2) 9 з — / 7х
Х.214. 1) 3-5lo^x + 10 = 5log^x; 2) 22|^х-‘^6-х) = 1.
Х.215. 1) 3^/log^x — log2 8х+1 = 0;
2) 3yiog3 х- log3 Зх —1 = 0.
Х.216. 1) log7 (6+7-х) = 1+х; 2) х-(2—lg25) = lg(2X + 12).
Х.217. 1) 3 log8(x —2) = log2 \/2ГЛ;
2) logi (x-3) + log3 -\/3x+l = 0.
Решить показательно-степенные уравнения (X.218-Х.220).
Х.218. 1) (х2-4)*“2 = 1; 2) (2-х)х2-4 = 1.
Х.219. 1) xlgx = 100x; 2) х'^-^ЮО;
3) 0,lxlgx-2 = 100; 4) = 10^х+1.
Х.220. 1) х1о^7 = 7; 2) х|о^6=6.
Решить неравенство (X.221-Х.223).
Х.221. 1) 2~log°>5X>0;
8 — 5х
Х.222. 1) (2-5х) (7х2-10х+3) <0;
Х.223. 1) (|}Х-(х + 2)2>(2+х)2;
2) 6х~и <$0. 2+log l х
3
2) (3х —2) (5х2+22х —15) >0.
2) log2х-|х —3|>|3—х|.
Х.224. 1) При каких значениях параметра а уравнение |Зх+а| =4 имеет хотя бы один корень?
2) При каких значениях параметра а уравнение |2х + а| = |2а —4| не имеет корней?
202 Глава X. Степенная, показательная, логарифмическая функции
Х.225. При каждом значении параметра а определить число корней уравнения:
1) log3 х = >/а—х; 2) log0 5(х— 1) = л/2х+4а.
Второй уровень
Решить уравнение (Х.226-Х.231).
Х.226. 1) (х2 —0,01х)
2) x'Og2 98 •14|о^-’7 = 1.
Х.227. 1) 1ое3(3+^+3) = Ш..;
2) logx+20 (2х-Ух+20)=0,5.
Х.228. 1) log^ (4х —6) —logy^ (2х —2)=2;
2) log2(9x-5)=2-log05(3x-2).
Х.229. 1) log6 (3-4x + 2-9x)-x = log65;
2) log5 (3-2x+l-2~x-52x+1) —x = log5 13.
X.230. 1) log12 (43x + 3x —9) =3x—x-log12 27;
2) lg(2x+x-l)=x(l-lg5).
X.231. 1) 3-|log2v^(x-l)|=4 log4 (3,5—x);
2) 5-1 log9^ ^x-2| = log3x/3 (3,5-0,75x).
Решить неравенство (X.232-X.248),
X.232. 1) log3 (2^+2)—log9 (2х —12)>1;
2) lOg16(3x-5)-log4(3*+5)^-1.
X.233. 1) 4—x<log2 (6+2x);
2) x+3>log3 (26+3-x).
X.234. 1) log2 (2x + l)-log| (2x+1+2)>—2;
2) log4 (3--l)-log. (^)4.
X.235. 1) log6(x-3x/x+2)<l;
2) log2 (\/7—x+3—x) ^3."
X.236. 1) log9(2x + l) + |log3(2x + l)|-1^0;
2) |logo,2(x-0“11 + 3>2 log0;2(x-!)•
§8. Смешанные уравнения и неравенства 203
Х.237. 1) |x|-log5(2+3x)^x;
3) |log3 х —2|+2x^x-log3 х;
Х.238. 1) |log2^|>|log2x|;
2) |2Х —1|+х^х-2х;
4) 1^Г<1о£0,2*-
2) I |<i
’ |log2x-5| ’
X.239. 1)
2)
X.240. 1)
2)
>ogo,5*-|l°g2x|-2<0;
lg2 x-4 |lgx|+3>0.
g2x-10 —3\/х—2g.v—5 <gl+3\/x—2.
41,5x_|_2x“ \/* <3-21 x-2\/x
X.241.
X.242.
X.243.
X.244.
X.245.
X.246.
0 VioS2x+V{°sx^^
2) y/\og2x+2y/\ogx2^3.
1) yiog3(9x + 18)^log3(x+2);
2) \/21og100x>logi0 y/x.
D ; 1о^5 (y~5“x)>1; 2) llog01(6,5-3-10^)^-l.
logQ 2 x/x + io^p log3(x + 7) >1
1о6о.2(л~2) ’ l°g3 л/7-Зх
1) |logx4-l|^3; 2) |logx9-3|^l.
1) log|2x+i|X2^2; 2) logv2 |3x+l|<0,5.
X.247. 1) (|x|+0,5)3x-1^(|x| + 0,5)2-x; 2) |x|x2-x-2< 1;
3) |x-3|2x2"7x>l; 4) |2+||%|2 + ||25.
X.248. 1) |x + l|2x/xT3<|x + l|1-x; 2) |x-2|2vOT< |x-2|x“3.
X.249. Найти все значения параметра а, при каждом из которых имеет решение уравнение:
1) log3 (х/а+4-х) +logi {x-a~ l)=log9 4;
2) log5 (л/а+3—x) +logi (x—a — 2) = 2 log5 2.
X.250. Найти все значения параметра а, при каждом из которых имеет единственное решение уравнение:
1) log7 (7х —log7 €z) = 2x; 2) log5 (25х —log5 a)=x.
204 Глава X. Степенная, показательная, логарифмическая функции
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ X
Х.251. Сравнить:
1) log5 6 и log67; 2) log7 8 и log8 9.
Х.252. Определить число корней уравнения 3lxl• |2 — |х|| = 1.
Х.253. Решить уравнение:
1) |l°g7 (2* + 3)| = log7 (1 -1% +1|) + log7 (1 + |х+1|);
2) |l°g2 (Зх + 9)| = log2 (1 —|4x+4|) + log2 (1 + |4х4-4|).
Решить неравенство (Х.254-Х.265),
Х.254. \/13х+3->/|13х —4| < 1.
Х.255. 3 х (а/91-х-1 + 1)<3|Зх-1|.
Х.256. у0,5-(15х + 9)ч/15х + 12-д/0,5-(15х-9).
X. 257. log6x+1 (25х) - 2 • 1 og25x (6х -Ы) > 1.
Х.258. logx+1 log2 (4х —48)^1.
Х.259. log|3x_3| (25x-9x)<log|3x_3| (5x + 3x) + log|3x_3| (б-^З^1).
X.260. 16-log7_x (Их-x2 —28) +0,5-logx_4 (x2-14x+49) ^8.
X.261. 4 log2W+1 ^5x + 3-logx/5Fp3 (2 |x| +1) >0.
Iog8 x < log2 v9+2x log2(l + 2x) "" log2 x
(log|x+0,5| (0,25-x)-l) log16 (0,25 —x) >log4 .
1 < 1 llog27x3l'"2"|log3(i)|-l
X.265. Iogx4-log2^p2.
X.266. При каких значениях параметра р имеет решение уравнение 4х_р2х+2+7=р-4~х-2-21-х?
Х.267. При каждом значении параметра а решить неравенство: 1) 24х + (х — 4 — а)22х + (5а + х — 5 — ах) 0;
2) 1 - 32х(х + 2а + П) + 34х(20а + х + 10 + 2ах) 0.
Х.268. Найти все значения параметра а, при каждом из которых имеет решение уравнение:
1) l°g5 (х + Vх2-а) + log02(a - 1 - х) = log25 9;
2) log3 (х + \/5 — а) + logi (а — 2 — х) = log9 4.
Х.262.
Х.263.
Х.264.
Ответы к главе X 205
Х.269. Найти все значения параметра а, при каждом из которых имеет единственное решение уравнение:
1) log4x (1 + ах) = 0,5; 2) logx_j (х - а) = 0,5.
Х.27О. Найти все значения параметра а, при каждом из которых уравнение
logax-6 (4* - *2) = 2 имеет единственное решение.
Х.271. 1) При каких значениях параметра а каждое решение неравенства logx+1 (3 — ах) > 0 удовлетворяет также 2 । 2б1 о 5 ___________________________ z"v
неравенству х + —2--х — > 0?
2) При каких значениях параметра а каждое решение неравенства х2 + (3 — 2а2) х — 2а2 + 2 < 0 удовлетворяет также неравенству logj_av (х 4- 2) < 0?
Х.272. При каких значениях параметра а любое решение 1°ёз (х2 - Зх + 7) .
неравенства —[Og (Зх + 2) < будет также решением
неравенства х2 + (5 — 2а)х 10а?
Х.273. При каждом значении параметра а решить неравенство log„ (1 - 8-а-*) > 2(1 -х).
Х.274. При каких значениях параметра а на отрезке [16; 32] найдется хотя бы одно значение х, удовлетворяющее неравенству 1g (з loga х — log2 х + 4^ > 1g (8 — 2 loga х)?
Х.275. При каждом значении параметра а решить неравенство х1о^х+1 >а2х.
ОТВЕТЫ К ГЛАВЕ X
Х.6. 1) [-0,5; 0,5) U (0,5;+оо); 2) (-0,5; \/2]; 3) (3; +оо); 4) (0,5; 1) U U(l;+oo). Х.7. 1) /(13)+/(14)>/(15) + /(16); 2) /(11) -/(10) </(12) -/(9). _1 1 11
Х.8. 1) 0,3 3 > 0,5 3; 2) 4 - 3 • 43 > 1 - 3 • 63. Х.9. 1) Наименьшего
значения не существует, 0,25 — наибольшее значение; 2) —2 — наименьшее, —0,25 — наибольшее значение; 3) наименьшего значения не существует, 80
6 — наибольшее значение; 4) 2 — наименьшее, 2—— наибольшее значение, о!
Х.1О. 1) D(y) = R, £(у) = R, возрастает на D(y), не ограничена сверху, не ограничена снизу, функция общего вида, наибольшего и наименьшего значений не имеет; 2) £)(y)=R, £(у) = [0; +оо), убывает на (—оо;1], возрастает [1; +оо), ограничена снизу, не ограничена сверху, функция общего вида, наименьшее значение 0. Х.11. 1) D(y') — (—оо;— 1)U(- 1;+ос), £'(у) = (0;+оо),
206 Глава X. Степенная, показательная, логарифмическая функции
возрастает на (—оо; — 1), убывает на (—1;4-оо), ограничена снизу, не ограничена сверху, функция общего вида, наибольшего и наименьшего значений не имеет; 2) D(y) — (—ос; 2) U (2; +оо), Е(у) = (—ос; 0) U (0; +оо), возрастает на промежутках (—ею; 2) и (2;+оо), не ограничена снизу, не ограничена сверху, функция общего вида, наименьшего и наибольшего значений не имеет. Х.12. 1) D(y) = (—оо; -4], Е(у) = [0; 4-эо), убывает на D(y), не ограничена сверху, ограничена снизу, функция общего вида, наименьшее значение 0, наибольшего значения не имеет; 2) D(y) = R, Е(у) = R, возрастает на R, не ограничена снизу, не ограничена сверху, функция общего вида, наименьшего и наибольшего значений не имеет. Х.13. 1) При а = — 2 два корня, при а — 3 один корень, при а = 5 корней нет; 2) при а = — 4 корней нет, при а — 0 один корень, при п = 2 два корня, при а = 3 один корень. Х.14. 1) 2; 2) 2. Х.15. 1) (0,5; 1); 2) (1; 3) U (5; +оо). Х.18. 1) /(х), g(x), Л(х), ш(х); 2) р(х). Х.19. 1) —15 — наименьшее, 7,75 — наибольшее значение; 2) —22 — наименьшее, —1,65 — наибольшее значение. Х.2О. 1) —2 — наименьшее, 0 — наибольшее значение; 2) 64 — наименьшее, 319 — наибольшее значение. Х.21. 1) 1; 2) —1. Х.22. 1) При а = — 2
корней нет, при а = 0 один корень, при а = 2 два корня, при а — 3 один корень; 2) при а = — 6 корней нет, при а = — 4 один корень, при а = 1 два корня. Х.23. 1) X; 2) ^20. Х.24. 1) (0;1]; 2) [1;+ос).
V?
Х.25. 1) При а < 1 корней нет, при а = 1 один корень, при а > 1 два корня; 2) при а < 0 корней нет, при а = 0 два корня, при 0 < а 1
четыре корня; при а>1 два корня. Х.26. 1) (—1;+оо); 2) (—9; 4-ос).
Х.28. 1) Функция возрастает на всей числовой оси; 2) функция возрастает на всей числовой оси. Х.29. 1) Выражение положительное; 2) выражение положительное; 3) выражение положительное; 4) выражение отрицательное. Х.ЗО. 1) Четная; 2) общего вида; 3) четная; 4) нечетная; 5) общего вида; 6) четная. Х.31. 1) 1 — наименьшее, 32 — наибольшее значение; 2) —99997 — наименьшее, 2,9 — наибольшее значение; 3) 2,4 — 2 наименьшее, 42 — наибольшее значение; 4) -239 — наименьшее, 3^ — наибольшее значение. Х.32. 1) D(y) =R, Е(у) = (-оо; 3), возрастает на D(y), ограничена сверху, не ограничена снизу, функция общего вида, наибольшего и наименьшего значений не имеет; 2) D(y) = R, Е(у) — (—2; 4-ос), возрастает на D(y), ограничена снизу, не ограничена сверху, функция общего вида, наибольшего и наименьшего значений не имеет; 3) D(y) =R, Е(у) — (0; 4-00), возрастает на D(y), ограничена снизу, не ограничена сверху, функция общего вида, наибольшего и наименьшего значений не имеет; 4) D(y) = R, £(//) = (—5; 4-оо), возрастает на D^y), ограничена снизу, не ограничена сверху, функция общего вида, наибольшего и наименьшего значений не имеет. Х.ЗЗ. 1) £>(v) = R, Е(у) = (О; yj, возрастает на ( —оо; 0], убывает на [0;4-оо), ограничена, четная, у — наибольшее значение, наименьшего значения нет; 2) D(y) = R, £'(//) = [—1; 4-оо), убывает на (—оо; 2], возрастает на [2;4-оо), ограничена снизу, не ограничена сверху, общего вида, —1 — наименьшее значение, наибольшего значения нет; 3) D(y)=R, Е(у) = [—2;4-оо), убывает на (—сю;—2], возрастает на [—2;4-оо), ограничена снизу, не ограничена
Ответы к главе X 207
сверху, общего вида, 2 — наименьшее значение, наибольшего значения нет; 4) D(y) — R, Е(у) = [0; +ос), убывает на (—оо;0], возрастает на [0;+оо), ограничена снизу, не ограничена сверху, общего вида, 0 —наименьшее значение, наибольшего значения нет. Х.34. 1) При a = — 3 корней нет, при a — 1 один корень, при a = 2 два корня, при a — 5 и a = 6 один корень; 2) при a = — 3 корней нет, при a = —1,5 два корня, при a~ — 1 один корень, при а = 4 корней нет. Х.35. 1) —1 2) —1; 3) 0; 1. 4) —1. Х.36. 1) (—оо; 1]; 2) ( — 1:+оо). Х.38. 1) При а —4 корней нет, при
а > — 4 один корень; 2) при а 3 корней нет, при а > 3 один корень. Х.39. 1) D(y) — IR, £({/) = [7;+ос), убывает на (—оо; — 1], постоянна на [—1;2], возрастает на [2;+оо), ограничена снизу, не ограничена сверху, общего вида, 7 —наименьшее значение, наибольшего значения нет; 2) D(y) = R, 15
Е(у) = ( —оо; у], постоянна на ( —оо; —3], возрастает на [—3;0], убывает 15 на [0;+оо), ограничена сверху, не ограничена снизу, общего вида, у— наибольшее значение, наименьшего значения нет. Х.40. 1) D(y) = R, Е(у) = ( — ос; 3], возрастает на ( — оо;4], убывает на [4; -|-оо), ограничена сверху, не ограничена снизу; 3 — наибольшее значение, наименьшего значения нет, общего вида; 2) Z)(i/)=IR, Е(у) = (—1;0], возрастает на (—оо;2], убывает на [2;+оо), ограничена, общего вида, 0 — наибольшее значение, наименьшего значения нет. Х.41. 1) На ( — оо;0] функция возрастает; на [0; +ос) функция убывает; 2) на (—оо; 1] функция возрастает; на [1;+оо) функция убывает; 3) на ( — оо; 0] функция убывает; на [0; +оо) функция возрастает; 4) возрастает на R. Х.43. 1) 0,1 — наименьшее, 100 — з наибольшее значение; 2) ^-—наименьшее, 6 —наибольшее значение. 128
Х.44. 1) 0 — наименьшее, 28 — наибольшее значение; 2) 0 — наименьшее, 3,875 — наибольшее значение. Х.45. 1) Наименьшего значения не существует, 3 — наибольшее значение; 2) наименьшего значения не
существует, 2 —наибольшее значение; 3) наименьшего значения не
существует, 0,5 — наибольшее значение; 4) наименьшего значения не существует, 1 — наибольшее значение. Х.46. 1) —8 — наименьшее, 17 — наибольшее значение; 2) —1 — наименьшее, 195 — наибольшее значение. Х.47. 2. Х.48. 1) Корней нет; 2) корней нет. Х.49. 1) —2; 2) 1. Х.5О. 1) 1; 2) -1. Х.51. 1) 0; 2) 0. Х.52. 1) (-оо;0); 2) [2; +оо). Х.53. 1) [0;+ос); 2) (-оо;0) U (0;+оо). Х.54. 1. Х.56. 1) (7; 9);
2) (0;1); 3) (2; 5); 4) (—оо;—7). Х.57. 1) Функция убывает на
всей области определения; 2) функция возрастает на всей области определения. Х.58. 1) Функция возрастает на всей области определения; 2) функция убывает на всей области определения; 3) функция убывает на всей области определения; 4) функция возрастает на всей области определения. Х.59. 1) 0 < а < 1; 2) а < 1. Х.6О. 1) log4 15 < log0 5 0,24; 2) log0 1 0,015 < log12 146. Х.61. 1) log5 4; log252; log0 2 10; 2) log9 8, log3 2, logn33. X.62. 1) Четная; 2) общего вида; 3) четная; 4) нечетная. Х.63. 1) 1 — наименьшее, 6 —наибольшее значение; 2) —2 — наименьшее значение, наибольшего значения не существует; 3) 1 — наименьшее, 5 — наибольшее значение; 4) —23 — наименьшее, —11 — наибольшее значение.
208 Глава X. Степенная, показательная, логарифмическая функции
Х.64. 1) D(y) = (—3; +оо), £(t/)=R, возрастает на D(y), не ограничена, общего вида, наибольшего и наименьшего значений не имеет; 2) D(y) = (0; +оо), = R, возрастает на D(y), не ограничена, общего вида, наибольшего и наименьшего значений не имеет; 3) D(y) = (2; +оо), Е(у) = R, убывает на D(y), не ограничена, общего вида, наибольшего и наименьшего значений не имеет; 4) D(y) = (—оо; 2), Е(у) = R, возрастает на D(y), не
ограничена, общего вида, наибольшего и наименьшего значений не имеет. Х.65. 1) D(y) = R, Е(у) = [0;+оо), убывает на (—оо;0], возрастает на [0;+оо), ограничена снизу, не ограничена сверху, четная, наибольшего значения нет, наименьшее значение 0; 2) D(y) = (2; +оо), Е(у) = [0; +оо), убывает на (2;2,5], возрастает на [2,5; +оо), ограничена снизу, не ограничена сверху, общего вида, наибольшего значения нет, наименьшее значение 0; 3) £)([/) —(—оо;-3) U (—3;+оо), Е(у)~№., убывает на (—оо; — 3), возрастает на (—3;+оо), не ограничена, общего вида, наибольшего и наименьшего значения не имеет; 4) D(y) = (—оо;2), Е(у) = [0; +оо), убывает на (—оо; 1], возрастает на [1;2), ограничена снизу, не ограничена сверху, общего вида, наибольшего значения нет, наименьшее значение 0. Х.66. 1) 2; 2) 2; 8; 3) 3; 4) 3.
Х.67. 1) 0; 2) J. Х.68. 1) (1;9]; 2) (0;2). Х.69. 1) При a = -3 корней
нет, при а = 0 один корень, при а = 2 иа = 5 два корня; 2) при а = — 6 корней
нет, при а = — 4 один корень, при а = 0 и а=1 два корня. Х.7О. 1) Функция
возрастает на всей области определения; 2) функция возрастает на всей области определения. Х.71. 1) Функция убывает на (—оо;2), возрастает на (2;+оо); 2) функция возрастает на (—оо;0], убывает на
[0;+оо). Х.72. 1) Положительное; 2) отрицательное; 3) положительное; 4) положительное. Х.74. 1) D(y) — R, Е(у) = [log26;+oo), убывает на (—оо;—3], постоянна на [—3;3], возрастает на [3;+оо), ограничена снизу, не ограничена сверху, четная, наибольшего значения нет, log2 6 — наименьшее значение; 2) D(y) = R, Е(у) = (—оо; 0], возрастает на (—оо;—2], убывает на [—2;+оо), ограничена сверху, не ограничена снизу, общего вида, наименьшего значения нет, 0 — наибольшее значение. Х.75. 1) Функция убывает на
(—оо;—3), возрастает на (3;+оо); 2 — наименьшее, 3 — наибольшее значение;
2) и
функция возрастает на
^2|;5^; 0 — наименьшее, 1,5
— наибольшее значение.
наименьшее значение, наибольшего значения не существует; 2)
убывает
на [-2|;0)
Х.76. 1) 2-наименьшего
значения не существует, —1 — наибольшее значение; > 3) —5 — наименьшее значение, наибольшего значения не существует; 4) наименьшего значения не существует, —7 — наибольшее значение. Х.77. 1) 2 — наибольшее, 0 — наименьшее значение; 2) —6 — наибольшее, —10 — наименьшее значение. Х.78. 1) у = 7 + log2 (2х + 3); 2) у = logi (5х - 39). Х.79. 1) 4; 2)2.
Х.8О. 1) 25; 2) 2. Х.81. 1) (—оо; 0]; 2) (0;+оо). Х.82. 1) log2 5 + 3;
2) корней нет. Х.83. 1) -2; 2) -0,25; 3) -8; 4; 4) 3; 6. Х.84. 1) 1;
2) —2. Х.85. 1) 3; 2) |; 3) 4) 0,5. Х.86. 1) 1; 2) 2; 3) |; 4) 4.
Х.87. 1) 1; 2) 2. Х.88. 1) 3; 2) 3;'' 3) 1; 4) 1,5. Х.89. 1) log0>4 3;
2) log3 6. Х.9О. 1) 2; 2) 1; 3) -2; 4) 0. Х.91. 1) 0; 2) 1; 2; 3) 1;
7
Ответы к главе X 209
4) 2. Х.92. 1) 3; 2) log04 4. Х.93. 1) 8; 2) 14; 3) 4) 3; log6 8.
Х.94. 1) 6; 2) 10. Х.95. 1) 3; 2) ±1. Х.96. 1) log2 (1 + \/5) - 1;
2) log5^=^. Х.97. 1) 1; 2) 0; 4. Х.98. 1) 0; 2) 0; 3) 1; 4) -1; 5) -1;
6) —2. Х.99. 1) 0; log0 75 11; 2) O;log0)85. Х.1ОО. 1) (-oo;-2) U (2; ±oo);
2) { — 1} U (1;±оо). Х.1О1. 1) a = ±0,5 и a = 0; 2) а = 0 и a = 2.
Х.1О2. 1) (—оо;0] U {1|}; 2) (—оо;5] U {30}. Х.1ОЗ. 1) При а 0
и a = 1 х = 0, при а G (0; 1) U (1;±оо) х = 0 и х = log3 a\ 2) при
a < 0 х = log2(—2а), при а = 0 корней нет; при а > 0 х = log2a. Х.104. 1) 3; log2 0,75; 2) 1; 2-log425; 3) 1; log363; 4) 3; log53 —1.
X.1O5. 1) log3 2, log29; 2) log4 3, log3 16. X.1O6. 1) log0 8 7; 2) 0,1.
X.1O7. 1) ±2; 2) ±2. X.108. 1) 1; 3; 2) -1; 3. X.109. 1)’a G (-oo;-2]; 2) a G (—oo; — 8] U (8; ±oo). X.11O. 1) a G ( —oc; — 2); 2) a G (—0,25; ±oo).
X.lll. 1) 2; 2) 6. X.112. 1) При aG (—oo; — U ±oo) корней нет,
12 12
при a = — 5 x — log2 g, при a = - x = log2 при a = 0 x = 0, при
ae u (0; 0 x1>2 = log2 1 + a± 3g)(1 + 5g); 2) при a = 0 x = log6 4; при a = —1 x = log62; при a — — | x = log6 |, при a G (—ос; — корней нет, при a 6 — 1^ U (0;+oo) X[j2 = log6 (2 + a ± \/3a~H^), при a G ( —1;0)
xl 2 = log6 (2 ± a + y/3a + 4). X.113. 1) Если a E ( — oc; 2] l_J (4; ±00), to
корней нет; если 2 < a < 4, то два корпя; если а = 4, то один корень; 2) если a G ( — оо; — 1), то два корня; если a = — 1, то один корень; если a G (—1; ±оо), то корней нет. Х.114. 1) (-оо;|]; 2) (-оо;-1); 3) (2;5); 4) [—1; 1]. Х.115. 1) (-1;5); 2) (-8; 4). Х.116. 1) (—оо; 0) U (2; ±оо);
2) (0;3). Х.117. 1) (—оо;—4) U (0; 4); 2) [|;3); 3) (—оо; 0);
4) (—оо; —4,5] U (2; ±оо). Х.118. 1) (-оо; -1]; 2) (0,75;+ос); 3) (-оо;9); 4) (—оо; 8]. Х.119. 1) [- 1;+оо); 2) [2;±оо). Х.12О. 1) (—оо;0);
2) (0;+ос); 3) (1; ±оо); 4) (0,5; ±оо). Х.121. 1) (|;+оо); 2) (3;±оо).
Х.122. 1) ( —оо; 0) U (log2 15; ±оо); 2) [0;log54]; 3) (-00; 0) U (log3 8; ±оо);
4) (—2;±оо). Х.123. 1) (-оо; 0) U (1;+оо); 2) (-1;0). Х.124. 1) (0; 0,5); 2) (log52;l). Х.125. 1) а 1; 2) а 2. Х.126. 1) При а <-1 решений нет, при — 1 а 1 неравенство выполняется при любом значении х, при a > 1 х G (—00; log0 5 (a - 1)]; 2) при a —2 решений нет,
при — 2 < а 2 неравенство выполняется при любом значении х, при a >2 х G (—00; — log2 (a — 2)). Х.127. 1) При a<0 х G (log3(-a); +00),
при a = 0 неравенство выполняется при любом значении х, при a > 0 х G (log3(2a); +00); 2) при a < 0 х G (—00; log4(—а)], при
a = 0 неравенство не имеет решений, при a > 0 х G oc;log4^j. Х.128. 1) (2; log5 2 ± 6); 2) (log37-6;5). Х.129. 1) [0; +00); 2) (-00; 0). Х.130. 1) (—00; 0) U (1;+00); 2) (0;±оо). Х.131. 1) (—оо;1]; 2) (-оо;2).
210 Глава X. Степенная, показательная, логарифмическая функции
Х.132. 1) (log5 0,4; log^ 0,8] U (logr, 2; 4-ос); 2) ( —оо; log2 2,5) U [log2 3,5; 4-оо). Х.133. 1) ( —оо; 0) U (1; 4-ос); 2) (0; log0 75 0,25). Х.134. 1) [1;+ос) U {0}; 2) [l;4-oo)U{0}. Х.135. 1) (-1;1); 2) (-oo;-3)U(3;+oo). Х.136. 1) а^2; 2) a^l. Х.137. 1) 9; 2) 25; 3) 16; 4) 1. Х.138. 1) -1 + \/2; 2) 1 + у/З.
Х.139. 1) 6; 2) 1,5; 3) 5; 4) 4. Х.140. 1) 9; 2) 2. Х.141. 1) -1; 2) -1;
3) ~2^; 4) 8. Х.142. 1) 1,4; 2) 4; 3) 10; 4) 3. Х.143. 1) 1,5; 2) 2.
Х.144. 1) 14; 2) 9; 3. Х.145. 1) 1,0001; 2) -79. Х.146. 1) 0,1; 1000;
2) 2; 0,5. Х.147. 1) 8; 2) 16; 256. Х.148. 1) -1-; 81; 2) 6;
Х.149. 1) При a < 0,5 х = 0 и х = —2a (при a = 0 корни совпадают); при
а 0,5 х = 0; 2) при а 0 х = a 4-1; при a > 0 х = a 4-1 и х = 2a (при a = 1 корни совпадают). Х.15О. 1) При д^б корней нет, при а >6 х- -У—;
2) при a 6 (-сю; —2] U [—1; 2] корней нет; при a 6 (—2; -1) U (2; 4-оо) х = |.
Х.151. 1) -9;
Д 2> '2-
Х.156. 1) 5; 2)
2) 8. Х.152. 1) 2 + \/2; 2) л/2. Х.153. 1) -2 - Уб,
Х.154. 1) 2loSi<)89; 2) 1; 0,75. Х.155. 1) -2; 2) 4.
20. Х.157. 1) 2; 0,25; 2) 3; 1. Х.158. 1) \/2; 3; 2) 0;
О 1
1,54-Уб. Х.159. 1) 3; 2) 256; 0,5. Х.160. 1) 2; 8; 2) 9; |. Х.161. 1;7.
Х.162. 1) 2; 0,25; 2) 5±2y/5. Х.163. 1) 3; 2) 1; 9. Х.164. 1) 1;
2) У2. Х.165. 1) 1; 2) 4. Х.166. 1) 4; 2) 3. Х.167. 1) 2) 3.
Х.168. 1) 2,5; -5; 2) -|. Х.169. 1) 1; 0,8; 2) 1; -1-. Х.170. 1) 1;
4 3 2-i/2
Х.172. 1) (—оо;—1) U ( — 1;—0,5) U (0,5; 1) U (1; 4-ос); 2) (|; 1) U (1; |) U (|; +оо)
Х.173. 1) a < 0, a = 8; 2) -2 < a < 3. Х.174. 1) a е (6;+оо);
2) де ос; U Ц- —: у У Х.175. 1) (3;+оо); 2) (-оо; 1,5).
Х.176. 1) (—3;2]; 2) (1;3). Х.177. 1) [8;+оо);- 2) (|;3] U[4;+oo).
Х.178. 1) (|;2); 2) [4;+оо). Х.179. 1) (^;2); 2) (1:257].
Х.180. 1) —2; 2) 0;1. Х.181. 1) [Z;4-oo); 2) (-2;-0,5); 3) [6,8; 7);
4) (-5;-0,5]. Х.182.
2) (—1; 1). Х.184. 1)
(-0,8; 4-оо). Х.183. 1) (1; |];
; 2) ( —ос; — V2) U (¥2 ; 4-ос).
1) (-1;-|); 2)
Х.185. 1) (3,5:4); 2) (2; 2,5). Х.186. 1) (-2;-1) U (1,5; 5); 2) (2; 3]
Х.187. 1) (1;2) U [10; 4-ос); 2) (9; 10). Х.188. 1) (0; 1) U (1:2];
2) (0; 1) U (1;36]. Х.189. 1) [±:2]; 2) [1;2]. Х.190. 1) (1;9];
Ответы к главе X 211
2) (0; 0,5) U [1; Ч-оо). Х.191. 1) (0; 1); 2) (1; 2) U (2;+оо). Х.192. 1) При
a < 1 х е (1 — а; +оо), при a = 1 решений нет, при a > 1 х Е (-a; 1 — а); 2) при а < — 2 х Е (4а; 4а + 1), при а = — 2 х Е (—8; +оо), при а> — 2 х Е [1 + 4а; +эо). Х.193. 1) При а — 4 решений нет, при а > — 4 х Е (2 - 0,5а; 4); 2) при а < —0,25 х Е [—2а — 1; +оо), при а -0,25 х Е (2а; +оо). Х.194. 1) 2;
-1. Х.195. 1) (2;6]; 2) (13;+оо). Х.196. 1) ( —оо; 0) U (0; 1] U [3;+ос); ( —оо;—2] U [-1; 0) U (0; 1] U (4;+оо). Х.197. 1) (о;
Х.198. 1) 2) [-1,4;-1). Х.199. 1) (2;5);
) (2~28; 1); 2) (0,5; 16]. Х.2О1. 1) (0,25; 1) U (2,5; 3);
2)
2)
2)
(—оо; —2) U (1; 2).
2)
U [3; +оо);
Х.2О2. 1) (/2,5; 2) U {2,5}; 2)
Х.203. 1) (2;+оо); 2) (2; 5). Х.204. 1) 2 “ 5 ; 1 ) и(1; 2]; 2) [7 4; 1) U(1; 7].
Х.2О5. 1) (О; U(l;27); 2) (0; 0,5) U (1; 32). Х.206. 1) (-4;-3) U (3; 4);
2) [-\/5;-2) U [—1; 1] U (2; х/5]. Х.2О7. 1) (О; U (1; /16); 2) (0;0,25)U н Ь"1-2-
2)
(1,5;2) U (3; 4).
Х.208.
;2
при a
О
и a - 1
1) При 0 < a < 1 х 6 (а4; при a > 1 х 6 ; а4),
решений нет; 2) при 0 < a < 1 х 6 (0;а) U (1; ±),
при a
a
U
(а;+оо). Х.209.
5;3
Х.21О.
Х.212.
Х.215.
2) 8.
0,1;
с 8;
2) 4.
16; 2)
1) 0 <
1) -9;
1) 2;
Х.218. 1) ±У5;
3) 1000; 0,1;
1) (0,25; 1,6); 2)
Х.213. 1) 3;
3;
81.
2) 1; -2.
4) 10;
3 Х.211.
2) -1;2.
Х.216. 1) 0;
Х.221.
2) (-5; 0,6) U (log3 2; +оо). Х.223.
Х.224. 1) (—оо;4); нет; если a нет; если a Х.227. 1) 6; Х.23О. 1) 3; 2) (log35;2],
2) (0; 1] U [2;-ню).
Х.236. 1)
2) \
2) 2.
Х.217. 1) 5;
0,1; 2) 100;
2)6. 1.
-1;
1) 3;
Х.214. 1) 2;
2) 2.
Х.219. 1) 100;
0,0001. Х.22О. 1) 7;
(0;1|] U(9;+oo). Х.222. 1) (|;1о{
1) (-ос;-2) U (-2; 0); 2) (2; 3) U (3;+оо)
Х.225. 1) Если
один; один. 2;
то корень то корень
Х.228. 1)
Х.231. 1) 1,5; 2,25;
2)
2)
> 1.
> -1, 2) 5.
2) 1.
Х.233. 1) (1;+оо);
Х.235. 1) [0; 1) U (4; 16);
2) если a < — 1, Х.226. 1) 1; 100;
1. Х.229. 1) 0;
,,8.22
' 3’ 7 ' (0; +оо).
корней корней 7; 14.
2) -1.
Х.232. 1) (log2 12; 4);
Х.234. 1) (—оо;0);
2) [-2;5±g!ZY
то
то
2) 1;
9’ 2
2) (1,04;+оо).
Х.237. 1) М;-?1 U [0; 1] \ о О J
212 Глава X. Степенная, показательная, логарифмическая функции
2) [—1;1]; 3) [9;+оо); 4) (0,2; 1). Х.238. 1) (0;2);
Х.239. 1) (|;4); 2) (0;0,001) U (0,1; 10) U (1000; +оо). Х.240.
2) [0; 0,25). Х.241. 1) (1; U [8;+оо); 2) (1;2] U
Х.242. 1) [7; +оо); 2) (1; 10000). Х.243. 1) (log5 0,3; - log5 3) U (0; log5 3);
2) (lg U (0; lg6]. X.244. 1) (2; 3) U (6;+oo); 2) [-3;2).
X.245. 1) (0; 0,5] U [\/2;+oo); 2) (0; 1) U (1; ^3] U [3;+oc).
X.246. 1) [—l;o); 2) (—1;—0,5) U ( — 0,25; 0) U (0; 1). X.247. 1) [-05; 0,5] U
U[0,75;+oo); 2) (1;2); 3) (-oc;0)U(2;3,5)U(4;+oo); 4) (-oo;-9]u[-5;-3]U U [5; +oo). X.248.
2) (0-8].
1) [2; 18); [16; +оо).
2)
1) [-3; —2) U (3 - 2л/5; -1) U (-1; 0);
Х.249. 1)
-4;
< log56;
2) -1. X.254.
О < а 1; 2)
log8 9 < log7 8.
2 /
ef. а > I-
/5
Х.252. 4.
2) (1; 2) U (2; 3) U
2) -3;
U (1;+оо).
2 7 Х.251. 1) log67 < Х.253. 1) -1; Х.255. (log32,4; 1].
Х.258. (log448;3].
X.256. [21og153;l]. X.257. U
X.259. (0;|) U (1; X.26O. (4;5)U(6;7). X.261. (—-j
U (0;+oo). X.262. (0; 0,5] U (l;+oo). X.263. (-2;-1,5) U (-0,125; 0).
X.264. (1;1) U [3;9) U (9;+oo). X.265. (^;0,5],
X.267. 1) При a G (—oo; l]x G ( —оо; 1], при a G (1;5) при a — 5 x = 1, при a G (5;+oo)x G [1; log4(a — 1)];
и
Х.266. р 17.
% G [log4(a - 1), 1], 2) при a 6 (—оо; — 0,5] х 6 (-оо; -1], при a 6 (-0,5; 4) х 6 (-оо;-1] U [- log9 (1 + 2а); +оо), при а = 4 х G (— оо;+оо), при a 6 (4; +оо) х 6 ( — оо; — log9 (1 + 2а)] U [— 1; +оо).
Х.268. 1)
2) а > 1, a — 0,75.
;2 ;
2
;5 . X.269. 1) a < 0, a = 1;
X.27O. (6; 14) U (14;+oo). X.271. 1) [-2,5; 0);
1;—X.272. [2,5;+oo). X.273. При a 1 решений нет,
а2 -2
при а > 1 х G
Х.274. (2; 32). Х.275. При
aV2; a-V2 ), при а > 1 х G (0; а-4^ U (а^; Н-оо').
Глава XI
ТРИГОНОМЕТРИЧЕСКИЕ И ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
§1. ФУНКЦИИ СИНУС И КОСИНУС
Первый уровень
XI.1. 1) Построить график функции у = sin х на отрезке [—2тс; 2 тс].
2) Указать промежутки знакопостоянства функции у = sin х на отрезке [—2л; 2л].
3) Указать промежутки монотонности функции у = sin х на отрезке [—2тс;2тг].
4) Найти корни уравнений sinx = -2, sinx = —1, sinx = — sinx = —0,5, sinx = 0, sinx = 0,5, sinx = ^, sinx = l, sinx = 2 на отрезке [—27с;2тг].
XI.2. 1) Построить график функции у = cosx на отрезке [-2л:; 2л].
2) Указать промежутки знакопостоянства функции у = cosx на отрезке [—2л; 2л].
3) Указать промежутки монотонности функции у = cosx на отрезке [—2л;2л].
4) Найти корни уравнений cosx = —2, cosx = —1, >/3 а/З
cosx = ——, cosx = —0,5, cosx = 0, cosx = 0,5, cosx=—, cosx = l, cosx = 2 на отрезке [—2л; 2л].
Построить график и указать основные свойства функции (XI.3-
XI.6)
XI.3. 1) /(x) = 2cosx;
XI.4. 1) /(x) = sin2x;
XI.5. 1) /(х) = |sinx|;
XI.6. 1) /(x) = sin2x;
2) /(х) = cos 0,5х.
2) /(х) = — sin х.
2) /(х) = |cosx|.
2) /(х) = cos2 х.
214 Глава XI. Тригонометрические функции
XI.7. Найти область определения и множество значений функции:
1) f(х) = у/(cosx — 1) (cosx +1); 2) / (х) = %/2sinxcosx- 1.
XI.8. Найти наименьшее и наибольшее значения функции и указать значения х, при которых они достигаются: 1) у = — 3 sin 5х + 2; 2) // = 4-3 cos 0,5х.
XI.9. Найти наименьшее и наибольшее значения функции и указать значения х, при которых они достигаются: 1) // = 3 —5 |sinx|; 2) //= 3 |cosx| — 1.
Найти множество значений функции
XI.10. 1) /(x) = cos2x-A/3sin2x;
XI.11. 1) /(х) = 5+4 cosx —sin2 х;
XI.12. 1) /(х) = 3 —2 sinx —2 cos2 х;
XI.13. 1) /(х) = 2 cosx —sin2 х;
(XI.10-XI.13)
2) /(х) = -cos 5х —sin 5х.
2) /(х) = 10 — 9cos2x — 6sinx.
2) /(х) = 2 cosx + cos 2х.
2) /(x)=2cos2x — 8sinx-5.
Исследовать на четность и нечетность функцию (XI.14-XI.17).
XI.14. 1) /(x) = cosx + sinx; 2) /(х) = —cos2x-sin 6х.
3) /(x) = (cosx+sinx)2-l; 4) /(x)=cosx-sin Зх-sin 5х—2.
Х1-15- /М=2Й'
XI.16. 1) /(х) = Ус05х;
XI.17. 1) /(x) = sin (2 cosx);
2) /W=—;
4) /(*) = — ' cosx
2) /(x) = Vsinx.
2) /(x)=5cos(sinx).
XI.18. 1) Доказать, что число 2д является периодом функции /(x) = sinx + cos7x. Указать несколько других периодов этой функции.
2) Доказать, что число тг является периодом функции /(х) = cos4x + sin2x. Указать несколько других периодов этой функции.
XI.19. Установить, является ли периодической функция:
1) /(x) = cos(Vx); 2) /(х) = sin -J-y.
XI.20. Найти один из периодов .функции:
О /(x) = sin | + cos р 2) /(x) = sin5x + cos!0x.
Глава XI. Тригонометрические функции 215
XI.21. Найти один из периодов функции:
1) /(x) = 4cos2 ^ + sin 2) /(х) = 6sin2 H-sin
о 2 lb Z
XI.22. Найти нули и указать промежутки знакопостоянства функции:
1) /(x) = sin2x; 2) /(x) = cos(x + ^);
3) /(%) = sin (о,5х + 4) /(х) = 1 — cosЗх.
XI.23. Найти нули и указать промежутки знакопостоянства функции:
1) /(х) = д/З sin х-cosx; 2) /(х) = - cosx — д/3 sin х.
XI.24. Построить график функции:
1) f/=(ycosx)4 + (Vsinx)4; 2) у=(у/— cosx)4 + (Vsinx)4
XI.25. 1) Найти все значения х из промежутка [я; 2л:], удовле-п и 2|cosx| творяющие уравнению 2х —11 — •
2) Найти все значения х из промежутка удовле-
творяющие уравнению х2 —6х+9=
XI.26. Указать промежутки монотонности функции:
1) ftx) = cos(x+£); 2) /(x)=sin (о,х— .
Построить график функции (XI.27-XI.30).
XI.27. 1) г/=2 sin (х—; 2) у=1 — cos ^x-t-^.
XI.28. 1) t/=sin (2х+^\ 2) z/=cos (o,5x-.
XI.29. 1) z/=-4cos2y; 2) y=(sinx+cosx)2;
3) w = 3sin2^; 4) t/=l-sin J-cos f.
2 6 6
XI.30. 1) z/=sin|x|; 2) z/=cos|x —я|.
XI.31. Изобразить на плоскости Оху множество точек, коорди-
наты которых удовлетворяют неравенствам: 1) cosx^z/^3cosx; 2) sinx^z/^2sinx.
216 Глава XI. Тригонометрические функции
Второй уровень
Найти область определения и множество значений функции (XI.32-XI.35).
XI.32. 1) /(x) = (sinx+cosx)2 ——cosx;
4 ' ' 2 sin 2х
2)
1+sinx cosx
XI.33. 1) /(x)=cos2 tj + a/~ cos2 3%; 2) /(x)=sin2 ^ + \/— sin2 3%.
XI.34. 1) /(x) = a/1-2cosx; 2) Дх) = д/-1-2 sinx.
XI.35. 1) /(x) = log3 (1+2sinx); 2) /(x) = lg|sin *|.
Найти множество значений функции (XI.36-XI.39),
XI.36. 1) f(x)=cos(3x+^+cos(3x+?Y
2) /(x) = sin (4х+^Д)-sin ^4x + ^.
XI.37. 1) /(x) = sin4 2x+cos4 2x; 2) /(x) = sin6 x+cos6 x.
XI.38. 1) f(x)=-s[nx+n[-y 2) /(x) = -C0SX-+2,.
7 sinx + 2 'v ’ 2cosx + l
XI.39. 1) /(x)=8 sin2 4x+5 sin 8x; 2) /(x)=6cos2 2x+6sin 4x—5.
XI.40. Найти наименьшее и наибольшее значения функции;
О /W=—з—!-----------; 2) /(%)=--------j------.
4 sin2 х + 3 sin х+2 4 — 3sin2 х — cosx
XI.41. Найти наименьшее и наибольшее значения функции:
1) /(x) = sin8 x+cos8 х; 2) /(x) = sin2 x+sin4 x + cos4 x.
Доказать, что функция периодическая, и найти ее основной период (XI.42-XI.45)
XI.42. 1) /(x)=sin^p; 2) /(x) = cos^.
XI.43. 1) /(х)=2 sin2 x + cos2х;
2) /(x)=sin4x+sin2x-cos2x+cos2х.
XI.44. 1) /(x)=2 |sin 6x|; 2) /(x) = |sin4x|;
3) f(x) = |cosO,25x|; 4) /(x) = |cos (x+^) |.
XI.45. 1) /(x)=sin 2x-|cosx|; t2) /(x) = cos2 2x — |sin 2x|.
XI.46. Построить график функции:
1) y=-^L.- 2) z/ = l^L.
|cosx| sinx
Глава XI. Тригонометрические функции 217
Найти промежутки монотонности функции (XI.47-XI.49).
XI.47. 1) /(х) = 3 — 4 cos2 2%; 2) /(x) = (sin Зх + cos Зх)2.
XI.48. 1) /(х) = —\/3sinx-cosx;
2) f(x)=sin f2x+7^+cos f2x — \ 4/ \ 4/
XI.49. 1) /(x) = 2 |cosx| —cosx; 2) /(x) = |sinx|-cosx.
XI.50. Построить график функции:
1) r/ = l,5sin ^2x-^; 2) z/ = 2-cos (Зх-у).
XI.51. Построить график функции:
1) z/ = cos (тгх—4) ; 2) z/=cos (л: |х| — ;
3) у= |cos (лх— |; 4) y = cos тех-~ |).
XI.52. 1) Построить график функции r/=sin |х| — |sinх|. Определить, сколько корней имеет уравнение sin |х| — |sin х| =а на отрезке если а= —3; — 2; — 0,5; 0; 1.
2) Построить график функции y=cos |—х| + |sin (х+ 3-7Г) |. Определить, сколько корней имеет уравнение cos |— x| + |sin (х + ^у) |=а на отрезке [—л; 2,5л] в зависимости от значения параметра а.
XI.53. Изобразить на плоскости Оху множество точек, координаты которых удовлетворяют неравенству:
1) у (z/ —cosx)^0; 2) у (r/4-sinх)0.
XI.54. Изобразить на плоскости Оху множество точек, координаты которых удовлетворяют неравенству:
1) |//+2|^sinх; 2) \у— 3|cosx.
XI.55. Изобразить на плоскости Оху множество точек, координаты которых удовлетворяют неравенствам:
1) sin x^z/^ cosx; 2) cosx^z/^sinx.
Решить уравнение (XI.56-XI.58).
XI.56. 1) 3 cos (2х—4)=х2—4х-|-7;
2) 2 sin лх=-4х2 + 12х-11.
XI.57. 1) |x+||=cosx-\/3sinx — 2;
2) л/Зcosx — sinx — 2 = |x + ^
218 Глава XI. Тригонометрические функции
XI.58. 1) 2rt-cosx=|x|-|х —д|;
2) тг-sin х= |х-| - |х-3~ |.
XI.59. 1) Найти сумму наибольшего и наименьшего корней
уравнения sin2 2х — 2 cos3 х~ — 1, принадлежащих промежутку [-^].
2) Найти сумму наибольшего и наименьшего корней уравнения 4 cos3 Зх —sin2 2х = 3, принадлежащих промежутку [—7г;тг].
XI.60. Решить неравенство:
1) 2+sin ^8х~2 (1-2х“2);
2) 4х2— x4-sin (37tlog2x)^5.
§2. ФУНКЦИИ ТАНГЕНС И КОТАНГЕНС
Первый уровень
XL61. 1) Построить график функции r/ = tgx на отрезке [—2тг;2д].
2) Указать промежутки знакопостоянства функции r/=tgx на отрезке [—2д;2д].
3) Указать промежутки монотонности функции y = tgx на отрезке [—2д;2д].
4) Найти корни уравнений tgx= —1, tgx = O, tgx=~, v3 tgx = \/3 на отрезке [—2д;2д].
XI.62. 1) Построить график функции y = ctgx на отрезке [-2л:; 2д].
2) Указать промежутки знакопостоянства функции y = ctgx на отрезке [—2л;2л].
3) Указать промежутки монотонности функции y=ctgx на отрезке [—2тг;2тг].
4) Найти корни уравнений ctgx = —\/3, ctgx = —1, ctgx=O, ctgx^-^ на отрезке [—2л;
XI.63. Построить график и указать основные свойства функции:
1) f(x) = 2tgx; 2) /(x)i=tgO,5x;
3) f(x) = —ctgx; 4) f(x)=ctg2x.
§2. Функции тангенс и котангенс 219
XI.64. Построить график и указать основные свойства функции:
1) /W = |tgx|; 2) /(x) = |ctgx|.
XI.65. 1) Найти наибольшее отрицательное число, не входящее в область определения функции /(x) = tg3ftx.
2) Найти наименьшее положительное число, не входящее в область определения функции /(x) = ctg (0,5дх).
XI.66. Найти область определения и множество значений функции:
О /(x) = tgx-ctgx;
2)
XI.67. Найти наименьшее и наибольшее значения функции на
указанном отрезке:
1) /«=tg р 2) /«=ctg(x+?£).
XI.68. Найти область определения и множество значений функции:
1) /(x) = |ctgx|-sin2х; 2) /(x) = |tgx|-(1+cos2х).
XI.69. Исследовать на четность и нечетность функцию:
1) /(x) = ctg (х4у); 2) /(x) = tg2x+cos6х.
XI.70. Исследовать на четность и нечетность функцию:
1) /(x) = ctg3x-a/cos х 4-2 • sin х; 2) /(x) = tgx-ctgx;
3) /(x) = tg5x+sin4x; 4) /(x) = tg (x+^)-ctg (x-y).
XI.71. Указать один из периодов функции:
1) /(x) = ctg3x+tg5x; 2) f(x)=cos -tg О о
XI.72. Найти нули и указать промежутки знакопостоянства функции:
1) ftx) = ctgx-tgx; 2) ftx) = -2ctg(x-|).
XI.73. Указать промежутки монотонности функции:
1) f(x) = tg3x; 2) /(х) —ctg (2х+£).
220 Глава XI. Тригонометрические функции
Второй уровень
XI.74. Найти область определения и множество значений функции:
1) /(x) = (tgx —ctgx)-sin 2х; 2) /(x) = tgx + ctgx.
XI.75. Доказать, что функция периодическая, и найти ее основной период:
1) /(х) = 8sinI) 2x-cos2x + tgx;
2) /(х) = 3 tg2x +ctg Зх + cos 5х.
XI.76. Доказать, что функция периодическая, и найти ее основной период:
О Кх) = №х\> 2) ftx) = ]ctg2x|.
XI.77. Построить график функции:
XI.78. Построить график функции:
1) у=sin2 ytgx+cos2 ytgx;
2) у— — sin2 л/ctgx —cos2 x/ctgx.
XI.79. Найти промежутки монотонности функции:
1) /(x) = ctg2x; 2) /(x)=tg2 (х-^У
XI.80. Построить график функции:
1) </ = -2tg(l-2x); 2) j/=l+ctg(| + |).
XI.81. Построить график функции: • (\ 11 (1 ।
sin И+п cos |х[ — —
I) у=—^-.—2) У=— J sinx cosx
XI.82. 1) Построить график функции y = ig . Определить,
сколько корней имеет уравнение tg | — =а на отрезке [—2л:; 2л], если а = — 0,5; 0; 0,5; 1.
2) Построить график функции y = ctg ^2 |х| — Определить, сколько корней имеет уравнение ctg^2|x| — на отрезке [—2я;2я], если а =—2; — \/3; — 1; 1.
§3. Обратные тригонометрические функции 221
XI.83. Изобразить на плоскости Оху множество точек, координаты которых удовлетворяют неравенствам: 1) ctgx^z/^tgx; 2) tgx^y^ctgx.
XI.84. Определить графически число решений уравнения:
1) |tgy|=2-vCt+T; 2) |ctg7гх|=3— v/2 — |х|.
XI.85. Решить неравенство:
1) 2)
§3. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ Первый уровень
Построить график и указать основные свойства функции (XI.86-XI.88).
XI.86. 1) /(х) = arcsin2%; 2) /(x) = arcsin(x+3);
3) /(x) = arccos0,5x; 4) /(x) = arccos(x — 2).
XI.87. 1) /(x) = arctg ; 2) /(x) = arcctg 4x.
XI.88. 1) /(x) = |arcsinx|; 2) /(x) = |arccosx|;
3) /(x)=arcsin |x|; 4) /(x) = arccos |x|.
XI.89. Найти область определения функции:
1) /(x) = arccos(4—х)- \/х2-Зх-4;
2) f, ,arcsin(l+2x)
XI.90. Найти область определения и множество значений функции:
1) /(х)=2 arccos(2 —5х); 2) f(x)=3-arcsin(3+2x).
XI.91. Найти область определения и множество значений функции:
1) /(х) = arcsin (2 —2x)+arccos(2 —2х) +arccos х;
2) /(x) = arcsin(4x+3)+arccos(4x + 3)+4 arcsin х.
XI.92. Указать значения, которые может принимать выражение:
1) arcsin (2х2 + 1); 2) arccos (—Зх4 —1);
3) arcsin (—5х4 —1); 4) arccos (5х4 + 1).
222 Глава XI. Тригонометрические функции
XI.93. Построить график функции и указать ее область определения, множество значений, промежутки возрастания и убывания, наибольшее и наименьшее значения:
1) у=2 arccos (х— 3); 2) z/ = arcsin |4+2х|.
Второй уровень
XI.94. Найти область определения и множество значений функции:
1) /(х) = arcsin2 Зх+arcsin Зх;
2) /(х) = arccos2 (х — 1)+ 2 arcsin (х — 1).
XI.95. Найти область определения и множество значений функции:
1) /(x) = arcctg (х2 + 1);
2) /(х) = arctg (л/3-3+2\/Зх—х2).
XI.96. Исследовать на четность и нечетность функцию:
1) /(x) = arcsin (0,5 sin х)— arccos (sinx);
2) /(x) = sin (2 arcsinx)-f-cos(arccosx).
XL97. Построить график функции:
1) z/=sin(arcsinx); 2) z/=cos (arccos2х).
XI.98. Решить графически уравнение:
1) arccos2х= +arctgх; 2) arcctg(x— l) = arcsinx.
XI.99. Решить графически неравенство:
1) arcsinx<arccosx; 2) arcctgx^arctgx.
XI.100. Решить неравенство:
1) arccos 3x^arccos (1 — 2х);
2) arcsin(l,5—x)^arcsin 0,5х.
§4. ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
Первый уровень
Вычислить (XI.101-XI.104)
XI.101. 1) lim —2) lim
л_>0 sin 0,5л x^.q sin 4х
Задачи повышенной сложности к главе XI 223
XI.102. 1) lim ? ;
х—>0 4х2
XI.103. 1) lim
х->0 tg 5х
3) lim А44-; х->0 tg0,5x
ллт tл л 1 \ 1 * 1 cos 2х
XI.104. 1) lim ------о
X- >0 х2
2)
2)
2)
lim
х_>0 х sin 0,5x
i- sin3x lim -т-s-;
x—>0 tg 2x
lim
x—>0 ctg 6%
lim x—>0
1 —cos6x xsin3x
Второй уровень
Вычислить (XI.105-XI.110).
г sin3x+sin5x
XI.105. 1) lim — ----------;
x—>0 2x
XI. 106. 1) lim v—>0 sinzx
wr w -a 1 • 1 ' COS 4.V
XI. 107. 1) lim -----—
x—>0 l-cos2x
XI.108. 1) lim ;
x->J 2 —ctgx —ctgJ x
XI.109. 1) lim x—>тг cosx+1
XI.110. 1) lim cos2% ;
V v R sin X —COSX
1. cos4x—cos6x
2) lim-------.
x—>0 sin2 5x
1. tg2x —sin2x
2) lim b — -------.
x—>0 sinJ 3x
2) lim -bS??8x, .
X—>0 sin 6x —sin 4x
2) lim s‘n2x+sinx'~2 X^f £ cos2 x
2) lim —1+tg-l_ cos(x-f)
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ XI
XI.111. 1) Показать, что функция /(x)=2sin2x+12sinxcosx + +4 cos2 х —5\/б принимает только отрицательные значения.
2) Показать, что функция /(x) = 3sin2x+16sinxcosx + + cos2 x + 2v^44— 1 может принимать отрицательные значения.
XI.112. Найти наименьшее и наибольшее значения функции:
1) /(x) = sinx+cosx-|-sinx-cosx;
2) /(x)=sinx—cosx+sinx-cosx.
XI.113. Доказать, что функция /(x)=cosx+cos (\/3x)+cos (\/5х) непериодическая.
224 Глава XI. Тригонометрические функции
XI.114. Доказать, что функция не является периодической:
1) /(x)=sin (|х|); 2) /(x) = sin (х2);
3) /(x) = cos(vR); 4) /(x) = cos|.
XI.115. 1) Найти все значения параметра а, при каждом из которых график функции /(х) = а2+а — sin2 х — 2а cosx лежит выше прямой г/=1.
2) Найти все значения параметра а, при каждом из которых график функции /(x) = cos2 х+2а sinx — а2 — а лежит ниже прямой у— — 2.
XI.116. Построить график функции:
1) z/=cos{x}, где {х} — дробная часть х;
2) f/=sin {х}, где {х} — дробная часть х.
XI.117. Построить график функции:
О i/=tg|x|-|ctg(x-^)|; 2) r/=ctg|x| + |tg(x-J)|.
XI.118. 1) Дана функция /(х) = ||х| —|х+2|| —3. Сколько решений имеет уравнение cos/(x) = 0,2?
2) Дана функция /(х) = 1 — ||х—4| — ]х||. Сколько решений имеет уравнение sin/(x) = —0,6?
XI.119. Построить график функции:
1) f/=arcsin(sin 2х);
3) r/=arctg(tg4x);
2) //= | —arcsin (cos 3x);
4) z/=arcctg(ctg5x).
Вычислить (XI.120-XI.122)
XI.120. 1) lim sin(xzf) ;
x—1 —zcosx
XI.121. 1) lim tg3x~3tgX; cos(x+£)
XI.122. 1) lim 2sin2x-3sinx+l
X-K
2)
lim
x—>y
cos (*-g)
1 + 2 cosx
2) lim
x—>£ sin (x + ^j
2)
И 2 cos2 x + cosx —1
з
Ответы к главе XI 225
ОТВЕТЫ К ГЛАВЕ XI
XI.7. 1) D(f) = {nk\kez}, £(/) = {0}; 2) D(/) = { J + Ttk\k E z} , £(/) = {0}.
XI.8. 1) //„аим = -1 при X = + у, k 6 Z; 1/наиб = 5 при х = + у,
k 6 Z; 2) z/наим = 1 при х = 4тг£, k 6 Z; г/наиб = 7 при х = 2тг + 4тг£, k 6 Z. XI.9. 1) г/наим = -2 при х = + яп, п 6 Z, г/наиб = 3 при х = яп,
п G Z; 2) f/наим = -1 при х = | + тг, п G Z, г/11аиб = 2 при х = тг, tiEl. XI.1O. 1) [-2;2]; 2) [-V2-V2]. XI.11. 1) [1;9]; 2) [0; 16].
XI.12. 1) [0,5; 5]; 2) [-1,5; 3]. XI.13. 1) [-2; 2]; 2) [-15; 1]. XI.14. 1) Общего вида; 2) нечетная; 3) нечетная; 4) общего вида. XI.15. 1) Общего вида; 2) нечетная; 3) общего вида; 4) четная. XI.16. 1) Четная; 2) общего вида. XI.17. 1) Четная; 2) четная. XI.18. 1) Все числа вида 2я(г, где k Е N, являются периодами, в том числе 4тг, 6я, 8тг и т. д.; 2) все числа вида Ttk, где k 6 N, являются периодами, в том
числе 2тг, Зтг, 4тг и т. д. XI.19. 1) Нет; 2) нет. XI.20. 1) Например, 24тг; 2) например, XI.21. 1) Например, 8тг; 2) например, 16тг. XI.22. 1) п 6 Z, — нули; /(х) > О на промежутках (тпг; + яп), п G Z; /(х) < 0 на промежутках (— + тг; яп), п е Z; 2) + яп, п Е Z, —
нули; /(х) > 0 на промежутках (— + 2яп; + 2яп), п Е Z; /(х) < О
на промежутках + 2яп; + 2яп), п Е Z; 3) — + 2яп, п Е Z, —
нули; /(х) > 0 на промежутках f—+ 4яп; + 4яп\ п Е Z; /(х) < О
на промежутках (— + 4яп; — + 4тш), п Е Z; 4) рр, гг Е Z, — нули;
/(х) > 0 при всех х^рр, п Е Z. XI.23. 1) + яп, п Е Z, — нули; /(х) > О
на промежутках
+ 2яп; % + 2яп\, nel;
\ о 6 /
f к + 2яп; + 2тт), п Е Z; \ 6 о /
2) + яп,
О
промежутках
(-^+2яп;-1 \ о b
(-£ +2яп; +2яп), n G Z.
\ 6 6 /
+ 2яп}, n G Z;
XI.25. 1) 4,5;
/(х) < 0 на промежутках n Е Z, — нули; /(х) > 0 на /(х) <0 на промежутках 2) 2. XI.26. 1) Функция
возрастает на каждом отрезке
— + 2яп; — + 2яп], n Е Z, и убывает на
каждом отрезке
каждом отрезке
— + 2яп; + 2яп^, n Е Z; 2) функция возрастает на
— ? + тгл; + тгл], и Е Z, и убывает на каждом отрезке
О о J
+ яп;~ + яп], nE^. XI.29. 1) Рис. 1; 2) рис. 2; 3) рис. 3; 4) рис. 4. L о о J
8—5682
226 Глава XI. Тригонометрические функции
У
Зтг 7Г 7Г
7Г 7Г ЗТГ
10 5 10 10 5 10
Рис. 1
У'
Я _7Г _Я 7Г 7Г 7Г X
2 3 6 6 3 2
Рис. 3
XI.32. 1) Функция определена при всех kel; Е(/) = (0; 1) U (1; 2);
2) функция определена при всех х + тг£, k G Z; £(/) = (—оо: — 2] U [2; +оо).
XI.33. 1) Од = {£ + ^}, 6GZ, Е(/) = {0,5±0,25\/3;0,5}; 2) £>(/) = k&Z, £(/) = {0,5±о,25х/3;0;0,25;0,5;0,75; 1}. XI.34. 1) Область определения — объединение промежутков + 2тш; + 2тгтг^, п G Z; множество
Ответы к главе XI 227
значений — [0; \/3]; 2) область определения — объединение промежутков
у + 2ди; — + 2ди], п 6 Z; множество значений — [0; \/3]. XI.35. 1) Область определения — объединение промежутков + 2ди; у + 2ди), и 6 Z; множество значений — (—сю; 1]; 2) область определения — любое значение х, кроме х = 0 и х= у где п = ±1,±2,±3,...; множество значений — (—оо;0]. XI.36. 1) [-У2;72]; 2) [—ч/3;\/3]. XI.37. 1) [0,5; 1]; 2) [0,25; 1].
XI.38. 1) [—1;1]; 2) (—оо; -1] U [1;+оо). XI.39. 1) [4 — ч/41; 4 + ч/41];
2) [-2-Зч/5;-2 + Зч/5]. XI.40. 1) /найм = |, /наиб = 2) /наим = |,
/наиб = jj- XI.41. 1) /найм = 0,125, /наиб = 1; 2) /найм = 0,875, /наиб = 2.
XI.42. 1) 12д; 2) 6д. XI.43. 1) Основного периода нет; 2) основного
периода нет. XI.44. 1) 2) 3) 4д; 4) д. XI.45. 1) д; 2)
XI.47. 1) /(х) убывает на каждом отрезке [— + и возрастает на
каждом отрезке [у;^г + ^]> 6 Z; 2) /(х) убывает на каждом отрезке
\ TZ , пп п , ппЛ Г Д , кп к , тот]
112 + Т’ 4 + T I И В03Растает на каждом отрезке I -+ у; + -у I, п 6 Z. XI.48. 1) /(х) убывает на каждом отрезке у + 2ди-у 4-2ди] и возрастает на каждом отрезке [у 4-2ди; у 4-2ди], п 6 Z; 2) /(х) убывает на каждом отрезке + ди; у + тт^ и возрастает на каждом отрезке [—у 4-ди; 4-ди], п Е Z. XI.49. 1) /(х) убывает на каждом отрезке ^2 ди; + 2ди], [д + 2ди; у + 2ди] и возрастает на каждом отрезке [у + 2ди; д + 2ди], [у 4-2ди; 2д 4-2ди], и 6 Z; 2) /(х) убывает на каждом отрезке 4-2ди; у 4-2ди], [д + 2ди; у 4- 2ди , [у + 2ди; 2д+ 2ди] и возрастает на каждом отрезке |2ди-у-|-2ди , |^у + 2ди; д + 2ди],
[у + 2ди; у + 2ди], и Е Z. XI.52. 1) График представлен на рис. 5; если
228 Глава XI. Тригонометрические функции
а = —3 и а = 1, то корней нет; если а = —2, то 3 корня; если а = —0,5, то 5 корней; если а — 0, то бесконечно много корней. 2) График представлен на рис. 6; если а < 0 и а > 2, то корней нет; если а = 0, то корней бесконечно много; если 0 < а < 2, то 4 корня; если а — 2, то 2 корня. XI.53. 1) Рис. 7. XI.54. 1) Рис. 8. XI.56. 1) 2; 2) 1,5.
XI.57. 1) 2) XI.58. 1) - 2тгЛ,k G N; ±| + 2тгЛ,k G N;
2) (—(k= 1,2,...); (-l)*+1g + 7ik (Л-0,-1,-2,...). XI.59. 1) 0;
Ответы к главе XI 229
2) 0. XI.6O. 1) 2; 2) У2. XI.65. 1) 2) 2. XI.66. 1) Функция
О
определена при всех х 7^ —, и £ Z; £(/) = {1}; 2) функция определена
при всех х ф п Е Z; £(/) = {0}. XI.67. 1) /найм = -1, /наиб = h
2) /найм = -Уз, /наи6 = 1. XI.68. 1) £)(/) = К \ {дп}, «и, £(/) = (-2; 2);
2) /)(/) = R \ |- +дл|, п G Z, £(/) = [—1;1]. XI.69. 1) Функция общего
вида; 2) функция общего вида. XI.70. 1) Четная; 2) нечетная;
3) нечетная; 4) четная. XI.71. 1) Например, д; 2) например, 24д.
"Vж гул 1 \ 7Г I 7T/Z _ гт? г / \ z-v ( ТТЛ 7Г । ТТЛ \
XI.72. 1) х = - + -у, nEZ,- нули; /(х) >0 на промежутках I —; - + -- 1,
п G Z; /(х) < 0 на промежутках - + ф; -у), п £ Z; 2) х = + 7Г/г-
п Е Z, — нули; /(х) > 0 на промежутках ( + яп; -£ + лп), п £ Z; /(х) < О
на промежутках + яп; — + дл), п £ Z. XI.73. 1) /(х) возрастает на — - + g + — 1, п G Z; 2) /(х) убывает на промежутках
(-j +™;у+ у). XI.74. 1) £>(/) = R\nez, ад = (—2:2);
2) D(/) = IR \ п £ Z, £(/) = (-ос;-2] U [2;+оо). XI.75. 1) д;
2) 2д. XI.76. 1) д; 2) XI.79. 1) /(х) убывает на промежутках (дл; + дп| и возрастает на промежутках [^ + дл;дл), п £ Z; 2) /(х) убывает на промежутках ^ + дл:^ + дл] и возрастает на промежутках + дл; + дл), пЕЪ. XI.82. 1) Если a = — 0,5, то уравнение имеет
1 корень; если a = 0, то 2 корня; если a = 0,5, то 3 корня; если a = 1,
то 2 корня; 2) если a — — Уз, то уравнение имеет 9 корней; если
а = — 2;— 1; 1, то уравнение имеет 8 корней. XI.84. 1) Четыре; 2) восемь. XI.85. 1) 1; 2) 0. XI.89. 1) [4:5]; 2) [-1; 0). XI.90. 1) £>(/) = [0,2;0,6], Е(/)=[0;2е|; 2) D(f) = |-2;-1|. E(f) = [з- 5;3 + |]. XI.91. 1) £>(/) = [0,5; 1|, £(/)=[|;у]; 2) W) = H;-0,5], £(/)= XI.92. I) 5; 2) к
3) — ^; 4) 0. XI.93. 1) График представлен на рис. 9; D(y) — [2; 4];
£((/) = [0; 2д]; функция убывает на всей области определения; наибольшее значение функции равно 2д, наименьшее — 0; 2) график представлен на ; функция убывает на отрезке —2;—1,5]; наибольшее значение XI.94. 1) от = [-1;1].
рис. 10; О(у) = [—2,5; —1,5]; £(</)= [О; 2 [—2,5; —2] и возрастает на отрезке функции равно наименьшее равно 0.
230 Глава XI. Тригонометрические функции
-2,5-2-1,5 О
Рис. 10
У‘
1
Рис. 13
Рис. 14
X
+ 2) D(/)=[0;2|, E<J1= [я-I; я2 - я].
XI.95. 1) D(f) = R,
£(/) = (О;^; 2) /)(/) = К, E(f)= • XI.96. 1) Функция общего вида;
2) функция общего вида. XI.97. 1) Рис. 11; 2) рис. 12. XI.98. 1) 0;
2) 1. XI.99. 1) -1;^); 2) [1;+оо). XI.100. 1) [О; ; 2) [1;2].
XI.101. 1) 2; 2) 0,75. XI.102. 1) 2,25; 2) 8. XI.103. 1) 0,8; 2) 1,5;
3) 8; 4) |. XI.104. 1) 2; 2) 6. XI.105. 1) 4; 2) 0,4. XI.106. 1) 1;
2) А. XI.107. 1) 4; 2) 16. XI.108. 1) 0,75; 2) -1,5. XI.109. 1) 8;
2) 9. XI.110. 1) -л/2; 2) 2. XI.112. 1) /|1аим = -1, /наиб = У2 + 0,5;
2) /найм =—"'/2 — 0,5; /наиб = Г XI.113. Указание. Достаточно пока-
зать, что функция /(х) принимает значение 3 только в точке х = 0. vine 1 \ ( 3 + У13\ . ( 1 + \/5 \ г,, ( 3 + \/17\ ./ о \
XI.115. 1) (-оо;----— I U I 2 ; +ос I; 2) I -оо;--------— lU(2;+oo).
XI.116. 1) Рис. 13; 2) рис. 14. XI.117. 1) Рис. 15; 2) рис. 16.
Глава XII
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
§1. ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Первый уровень
XII.1. Реш ить уравнение:
1) sin Зх — 0; 2) cos(x + ^)=-l;
3) sin(x-^) = l; 4) cos5x = 0.
Решить уравнение, записав ответ в виде совокупности двух серий решений (XII.2-XIL4).
XII.2. 1) ( । л\ cos х + - = \ о / / 7Г \ V3. 2 ’ _У2. 2) sin (x — nA 6/ 3 л: _ _ 1. 2’ i x/2
3) sin - — X = \4 / 2 ’ 4) cos (x — T; 1 — 2 ’
ХП.З. 1) sin х = 4; 4 2) cos2x = 1. 3’
3) cosx = — 4) sin 0,5x : 5’
XII.4. 1) sin(2 — х) — V ^3 = 0; 2) cos (x + nA 6/ = - 5’
3) 3 sin (х — 2) - 1; 4) Q f X + 71A 2 cos —— \ 4 > | + i/5 = 0
XII.5. Решить уравнение:
1) tg3x + 5 = 0; 2) 4 - cig (2x+i ) = 0.
XII.6. Найти нули функции:
1) у = \/2 sin (хтс) + 1; 2) z/ = tg3x —д/З;
3) у = л/З cos ^2х — + 1,5; 4) у = 1 + \/3ctg ^2х +
XII.7. Решить уравнение:
1) (1 — ctgx) • cos 0,5х = 0;
2) sinx • cosx • (tg0,5x + 1) = 0;
§1. Простейшие тригонометрические уравнения 233
3) (1 + ctgx) • tg2х = 0;
4) (1 — tgx) • sin 4% • (2 cosx — 1) = 0.
Решить уравнение (XII.8-XII.13).
XII.8. 1)
3)
XII.9. 1)
XII.10. 1)
2)
3)
4)
XII.11. 1)
3)
XII.12. 1)
XII.13. 1)
(п тг \ 11 тг
2х - — = sin —;
1Z / о
tg (4х + = ctg
sin2 | — cos2 | = cos —;
117Г
2) cos ox — - = cos —; \ 6 / 4
4) ctg (Зх + = tg
2) 4 —18 sin 3x cos 3x = cos-y.
4 cos — x) - sin (Зя + x) + 3 = 0; tg(f+ *) - tg (|-x) + 3 = 0;
ctg (j - x) • tg (x + я) - 3 = 0;
2 cos (я - x) • sin (2,5я + x) + 1 = 0.
I . I V3 |sin x| = -2"-.
I— cosxl = -U;
' 1 V2
sin2 x — 3 cos2 x = 1;
(sinx + cosx)2 = 1;
2) |ctgx| = 2;
4) |tg(-x)| =
2) 5 sin2 x + 3 cos2 x = 4.
2) (sin 2x — cos2x)2 = 1.
XII.14. 1) Найти наименьший положительный корень уравнения sin4 х — cos4 х = 1.
2) Найти наибольший отрицательный корень уравнения . 4 / тг \ .4 1
Sin ( 2 — X ) — Sin X = 1.
XII.15. Реш ить уравнение:
1) tg2x + —^- = 7; 2) ctg2 х + —= 5.
cosz х sinz х
v2
ХП.16. 1) Найти корни уравнения sin3x = —, удовлетворяющие условию tg3x < 0.
2) Найти корни уравнения cos2x = —удовлетворяющие условию sin2x < 0.
234 Глава XII. Тригонометрические уравнения и неравенства
XII.17. Воспользовавшись тригонометрической окружностью, найти корни уравнения, принадлежащие указанному промежутку:
l)cosx=|, хе(0;2л); 2)cosx = -^y, хе(-л; л); о\ • __\/3 _ ( 3 тг 7Г \ л \ • _ \^2 ( К 3 71 \
3)smx=—, 4)smx = - —; xe^yj.
XII.18. Воспользовавшись тригонометрической окружностью, найти корни уравнения, принадлежащие указанному промежутку:
1) tgx = v3, хе(0;2л);
3) ctgx = \/3, хе у);
л \ • 1 ( 3 ТС ТС \
2) tgx= -1, ХЕ Q—у; 2/
4) ctgx = --L, хс(—тг; тс).
Найти значения х, удовлетворяющие указанным условиям (XII.19-
XII.23).
XII.19.
XII.20.
XII.21.
XII.22.
XII.23.
1) cos2x = 0, 0<х<л; 2) sin3x = l, — л<х<0;
3) sin2x = 0, 2л<х^3л;
4) cos4x = —1, — 1,5л<х —0,5л.
1) cos (0,5лх) = 1, 2<х^5;
2) ctg(2jrx) = l, — 1<х<—0,5;
3) sin (Зтгх) = —1, —0,5<х^0,5;
4) tg7rx = \/3, 1<х<3.
1) cos fx— 0 и х>л; 2) cos3x=^ и х>0; \ 4/ 2
3) sin ^4х—— 1 и -*<0; 4) sin2x=-| и х<2л.
1\ ( Зтг\ \/2 ГЗтг 11тг1
1) cos^x-TJ=--,
2) sin2x=y хе л);
3) cos3x = -|, хе|у;л|;
4) sin (о,5х-у) =-^у, хе(0;л].
• 71 . . 71 1 Г 371 1
1) sinx-cos - +cosx-sin - = -, — — ;л ; о о 2 L J
7Г , • .71 д/З Г 7Г 97ll
2) cosx-cos-+sinx-sin- = —, .
' 5 5 2 L 4' 4 J
§ 1. Простейшие тригонометрические уравнения 235
XII.24. Решить уравнение:
1) ctgx- \/д2 — х2 = 0; 2) sin х • \/9д2 — 4х2 = 0;
3) tgх • \/25д2 — 4х2 = 0; 4) cos х \/4д2 — х2 = 0.
XII.25. Решить уравнение:
1) \/3sinx + cosx = \/2; 2) sin х + л/З cosx —2 = 0.
XII.26. Найти сумму корней уравнения sin Зх —cos Зх = \/2,
Г д! принадлежащих промежутку — д; - .
2) Найти сумму корней уравнения sin Зх+ cos Зх = \/2, принадлежащих промежутку [т)-;3д].
Решить уравнение, воспользовавшись условиями равенства одноименных функций (XII.27-XII.29).
XII.27. 1) sin 2x = sin 2) cos 3x = cos 5
3) sin 5x = sin 2х; 4) cos4x = cos9x.
XII.28. 1) |OO hfi 7i tbD 4-> 2) ctgO,5x = ctg =
3) tg3x = tg2x; 4) ctg3x = ctg2x.
XII.29. 1) sinx = cos7x; 2) cos x = sin 4x;
3) ( 5 тг\ . / 7Г \ cos x —— =sin - —x : \ 6 / \ 3 / ; 4) • (4тг \ ( 7Г . sin — -x =cos - +x \ 3 / \6
Второй уровень
XII.30. Найти корни уравнения, жутке:
0 1 ( ЗтГ 71 \
sinx = j,
3) cosx=0,2, хе(-д, д);
5) tgx=-4, xe(-f;^);
XII.31. Найти корни уравнения, жутке:
1) tg3x=3, xe[-f;f];
3) sin2x=0>2, xe[o;yj;
лежащие в указанном проме-
• 1 / Д Зд\
2) sinx= —
4) cosx = -0,6,
6) ctgx=—2, хе(0;2д).
лежащие в указанном проме-
2) ctg2x=-2, хе[0;д];
4) cos4x=0,3, хе[0; д].
236 Глава XII. Тригонометрические уравнения и неравенства
Решить уравнение (XII.32-XII.36).
XII.32. 1) sin (x-*W9-x2=0; 2) cos f2х—Y л/2—|х|=0;
\ О / \ т /
3) tg (0,5х)-\/9-4х2=0; 4) ctg (Зх+^) • >/1 - |х|=0.
XII.33. 1) sin (2tccosx) = 1;
3) cos (2rcsinx) = l;
XII.34. 1) sin (кarccosx)=0;
XII.35. 1) cos 2x-arcsin x=0;
3) sin Зх-arccos |=0;
XII.36. 1) 3cosx+4 sinx=2;
3) 7sinx—3cosx=4;
2) tg(ftsin x) = -v3;
4) ctg (7,5 л: cos х) = д/3.
2) cos (2n:arcsin х) = 1.
2) ctgx-arctg (0,5x—Зл:) = О;
4) tg4x-arcctg (Зх+л:)=0.
2) 4 cosx+8 sin x=3;
4) 5cosx—6sinx=3.
Решить уравнение, используя условия равенства одноименных
функций (XII.37-XII.39).
XII.37. 1) 2cos2х— l=cos6; 2) (sinx+cosx)2 = l+cos 10.
XII.38. 1) tgx=tg3x;
3) tgx=tg5x;
2) ctgx=ctg3x;
4) ctgx=ctg5x.
XII.39. 1) tg6x=tg (д-5х); 2) ctg (^-2x)=ctg5x;
3) ctg3x=tg8x;
4) tg4x=ctg5x.
§2. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, СВОДЯЩИЕСЯ К АЛГЕБРАИЧЕСКИМ ПУТЕМ ЗАМЕНЫ
ПЕРЕМЕННОЙ
Первый уровень
XII.40. Решить уравнение:
1) cos2x—2cosx—3=0; 2) sin2 х—5 sin х+4=0.
XII.41. Решить уравнение:
1) cos2x+3sinx—3=0; 2) 3sin2 2х+7cos 2х—3=0;
3) 2 sin2 ^—9 cos ^+3=0; 4) 8 cos2 ^+6 sin ^—3=0.
7 3 3 4 4
XII.42. Найти точки пересечения графиков функций:
1) z/=2tgx и r/=ctgx—1; 2) i/=ctgx и г/=10tgx-3.
§2. Уравнения, сводящиеся к алгебраическим заменой 237
XII.43. Решить уравнение:
1) 4 sin4 х+12 cos2 х=7; 2) 4 sin4 х—4 cos2 х+1=0.
XII.44. Решить уравнение:
1) tg2 х+2 ctg2 х-3=0; 2) ctg2 х4-4 tg2 х-5=0.
XII.45. 1) Найти корни уравнения 2 cos2 х4-5 sin х=4, удовлетворяющие условию cosx^O.
2) Найти корни уравнения 2sin2х—5cosx4-l=0, удовлетворяющие условию ctgx<0.
XII.46. 1) Найти корни уравнения tgx—3ctgx4-2=0, удовлетворяющие условию sin2x<0.
2) Найти корни уравнения tg2 x4-ctg2 х=2, удовлетворяющие условию sin2x>0.
Решить уравнение (XII.47-XII.49).
XII.47. 1) sin х—5 cosx=0;
2) 3 sin 2x4-7 cos 2х=0.
XII.48. 1) cos2 x—3 sin x-cosx4-2 sin2 x=0;
2) sin2x—7sinx-cosx4-12cos2x=0;
3) cos2 x4-3 sin x-cosx—4 sin2 x=0;
4) 2 sin2 x4-3 sin x-cosx4-cos2 x=0.
XII.49. 1) 6 sin2 x—3 sin x cosx—cos2 x=l;
2) 26sinxcosx—2sin2x=6;
3) 7 cos2 2x4-5 sin 2x cos 2x=l;
4) 6 sin2x4-sinx cosx—cos2x=2.
Второй уровень
Решить уравнение (XII.50-XII.55).
XII.50. 1) cos4x—(24-д/З) cos 2x4-14-1/3=0;
2) 2 cos4x4-2 (i/2-l) sin 2х+а/2—2=0.
XII.51. 1) 3 tg2 x-4 cos2 x=8; 2) 2 cos2 x4-3=4 ctg2 x.
XII.52. 1) tgx—15ctgx=2, если xe(—я;я);
2) 20 sin2 x4-tg2 x=20, если хб(0;2д).
XII.53. 1) 84-9 sin 2x=4 cos2 x; 2) 5 sin2 x4-4 sin 2x4-cos2 x=7.
XII.54. 1) 14-2sinxcosx4-2 (sinx4-cosx)=0;
2) 6 sin 2x4-sin x4-cosx=6;
238 Глава XII. Тригонометрические уравнения и неравенства
3) 10 sin 2х+29 sin х—29 cosx=31;
4) 5 sin 2х-12 (sin х—cosx) + 12=0.
XIL55. 1) tg2 x+ctg2 x—3 (tgx+ctgx)+4=0;
2) 2+-^= (tgx-ctgx)=tg2x+ctg2x.
Решить уравнение (XII.56-XII.58).
XIL56. tgx+l=2sin (1,5д+2х).
XII.57. sin x+ctg ^=2.
XII.58. ctgx-l = ^.
6 tgx+1
§3. МЕТОД РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ. ТИПИЧНЫЕ ПРЕОБРАЗОВАНИЯ, ИСПОЛЬЗУЕМЫЕ ДЛЯ УПРОЩЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Первый уровень
Решить уравнение, используя метод разложения на множители
(XII.59-XII.66).
XII.59. 1) 2 cos x cos 2x=cos x; 2) 2 sin 2x cos х=д/3 sin 2x
XII.60. 1) 3 cosx+2 sin 2x=0; 2) sin 2х=д/3 sin x;
3) sinx—\/2cos ^=0; 4) sinx=\/5cos
XII.61. 1) cos 8x-tgx=tgx; 2) sin 3x-ctgx=sin 3x.
XII.62. 1) cosx+ctgx=0; 2) sin x+tgx=0;
3) \/2 cos 5x=— ctg 5x; 4) 2 sin 4x=\/3 tg4x.
ХП.63. 1) _^LL_ = l-cosx; 1+cosx 2) ~^2L = l+sinx. I —sinx
XII.64. sin 2x=sinx-(sinx+cosx)
XIL65. 2 cos3 x-sin x sin 2x=2 cos x.
XII.66. cos2x—sinx+cosx=0.
Решить уравнение, изменив степень входящих в него тригонометрических функций (XIL67-XIL70).
XII.67. 1) cosx-2 sin2 |=0; 2) 2cos2x+cos2x=0.
XII.68. 1) 1-6 sin2 4x=cos 27 д-cos 8%;
2) 6 cos2 Зх+sin 3,5д=—cos 6x.
§3. Метод разложения на множители 239
XII.69. 1) 16sinf- 8cos^+7=0; 2) 8cos £ + 16cos * = -7;
5 5 2 4
3) 2 sin —I-cosx; 4) cos |=2cos | —1.
XII.70. 1) (1—cos3x) ctgx=2 sin2 * l,5x;
2) ctg2x-sin2 4x=^-(l —cos 8x).
XII.71. Решить уравнение, преобразовав произведение в сумму или разность:
1) 2 sin 5x-sin Зх—cos 2х;
2) 2 cos 6x-cos 8x=cos 14x;
3) sinx-cos7x+0,5sin6x=0;
4) 2 cos Зх-sin 4x—sinx=0.
XII.72. Решить уравнения, преобразовав сумму или разность в произведение:
1) sin x+sin 3x=cosx; 2) cosx+cos 5x=cos (д+2х);
3) sin 5x-sin 7x=sinx; 4) cos 2x—cos 3x=2 cos
Решить уравнение (XII.73-XII.76).
XII.73. 1) sin (x-^-cos (x+^ = ^; \ 3 / \ b / 2
2) cos (x-^)-sin (x+i^) = 5 \ О / \ 3/2
XII.74. 1) cos (%—x^-sin (%—x^=cosx;
2) sin ( ^+x) —cos ( ^+x ) = \/3cosx. \ b / \ 3 /
XII.75. 1) 2 sin (2x+y) = \/3cos2x;
2) \/2cos (Зх+^Д^+соь3x=0.
XII.76. 1) cos4 x—sin4 x=2 sin 2x cos 2x;
2) sin4 7—cos4 ^=sinx. 4 4
XII.77. Найти корни уравнения, принадлежащие указанному промежутку:
1) 2cos2i=sinЗх,
2) cos2 2x=sin2 2x+cos2x, (б;
240 Глава XII. Тригонометрические уравнения и неравенства
ХИ.78. Найти корни уравнения, принадлежащие указанному промежутку:
/ х у\2 / rr \
1) 1—sin Зх= ( sin- — cos тг 1;
2) 1 — sin 5x=(sin |+cos
XII.79. Решить уравнение:
1) 2 sin3 х+5 cos2 х+2 sinx—5=0;
2) 2cos3х+3sin2х-2cosx—3=0.
XII.80. 1) Найти все решения уравнения sin2х—cosx+2sinх=1, удовлетворяющие условию 0<х<5.
2) Найти все решения уравнения \/3 sin х+2 cosx=\/3+ +sin2x, удовлетворяющие условию 0<х<2.
XII.81. Решить уравнение: cosx _р 2) sinx_________________।
1+sinx ’ 1—cosx
Второй уровень
Решить уравнение (XII.82-XII.87).
XII.82. 1) cos( —3x)+tgx-cos 3x=0; 2) cos5x=tgx-cos5x.
XII.83. (2 sinx—cosx) (l+cosx)=sin2x.
XII.84. sin x+cos x= ——H——. cosx sinx
XII.85. . . cosx—sinx ctg x—tg x=—————. & 6 0,5 sin 2x
XII.86. XII.87. cos3x—sinx=\/3 (cosx—sin3x). 1 —sin x=cosx-(sin x+cos x).
XII.88. В интервале (О; найти наименьший корень уравнения tg5x+2 sin 10x=5 sin 5x.
XII.89. Найти корни уравнения, принадлежащие указанному промежутку: 1) 2sin2x=sinx—\/3cosx, хе(— 2) а/2cos2x=sinx+cosх, хе(О;тг).
XII.90. Решить уравнение двумя способами (преобразованием к однородному и методом введения вспомогательного аргумента): 1) 10 cos2 х—5 sin 2х=4; 2) 8+9 sin 2х=4 cos2 х.
§3. Метод разложения на множители 241
XIL91. 1) Найти все корни уравнения sin2 х—>/3 sin 2х—cos2 х= =—2, удовлетворяющие условию 0<х<4.
2) Найти все корни уравнения 5cos2x—\/3sin2x+3sin2x= =2, удовлетворяющие условию 0<х<5.
Решить уравнение (XII.92-XII.94).
XII.92. 1) sin3 %—cos3 %—sin % cos jc=1;
2) sin3 x+cos3 x=l+0,5 cos (2х+4,5д).
XIL93. 1) sin4 x+cos4 x=sinx-cosx;
2) sin4 x+cos4 x=sin 2x—0,5.
XII.94. 1) sin6 2x+cos6 2x=^-;
16
2) sin6 2x+cos6 2x—cos2 2x==.
16
Решить уравнение (XII.95-XII.99).
XII.95. 1) sin2 x+sin2 2x=sin2 Зх+sin2 4x;
2) cos2 8x+cos2 4x=cos2 5x+cos2 7x.
XII.96. 1) 4 sin4 x+sin2 2x=l;
2) 8 cos4 x=ll cos2x—1.
XII.97. 1) 4 sin4 2x+16 cos4 2x=5;
2) 4 sin4 x+cos 4x=l + 12 cos4 x.
XII.98. 1) cos 2x+4 sin4 x=8 cos6 x;
2) 2+cos4x=5 cos2x+8 sin6 x.
XII.99. 1) cos 8x=l—2 sin2 2x;
2) cos 10x=l—6 cos2 2,5x.
XII.100. 1) На интервале (О; найти корень уравнения
sin2 2x+sin2 4x=l.
2) На интервале ^0; найти корень уравнения
4 cos2 2x+16 cos2 x—13=0.
XII.1O1. 1) Найти наименьший положительный корень уравнения sin2 x+sin2 2х=1.
2) Найти наибольший отрицательный корень уравнения 4 cos2 6х+16 cos2 3х=13.
242 Глава XII. Тригонометрические уравнения и неравенства
Решить уравнение (XII.102-XII.105).
XII.102. 1) sinx-sin Зх=|;
2) 2 cosx-cos Зх= —1.
XII.103. 1) sinx-cos 5x=sin 9x-cos3x;
2) sin x-sin Зх+sin 4x-sin 8х=0;
3) cos3x-cos6x=cos4x-cos7x;
4) sin 2x-sin 6x=cosx cos 3x.
XII.104. 1) 2sin 5xycosx=cos4x;
2) sin —Зх^-sin4x=sinx.
XII.105. 1) cos Зх+cos 2x=sin 5x+sin 4x;
2) sinx+sin 2x+sin Зх+sin 4x=0.
Решить уравнение (XII.106-XII.118).
XII.106. 1) 4 cos 4x+6 sin2 2x+5 cos 2x=0;
2) 1+2 cos2 x+2\/2 sin x+cos 2x=0.
XII.107. 1) 2-4 sin2x=\/2 (sinx —cosx);
2) 2—4 cos2 x=\/2 (sin x+cosx).
XII.108. 1) sin2 x—cosx-cos 3x=^;
4
2) 12 cos2 |=9—4 cos |-cos у.
XII.109. 1) tg3x-tg4x=l; 2) ctg2x-ctg9x=l;
3) tg5x-tg8x=—1; 4) ctg2x-ctg3x=l.
2 sin2 x+2 cos2 ( x+ j — 1
XII.110. 1) -------------2---<---=0;
\/бх—X2
2д/3cos2x — 2sin2 fx— + l
2) ------------------------=0.
\/7x—x2
XII.lll. tgx+ctgx=-V-Б Б sin4x
XII.112. tgx—tg2x=sinx.
XII.113. sin x-tgx+cosx-ctgx=sin x+cosx.
XII.114. sin3 x-(l+ctgx)+cos3 x-(l+tgx)=cos2x.
XII.115. tgx-(4+3cos2x)=2 (cos2x—1).
§4. Метод оценки левой и правой частей уравнения 243
ХП.116. Snl3x=4cos2x. sin х
XII.117. -L-------1 - ‘ - 1 =-2.
sinzx coszx tg x ctg x
XII.118. sin (тс—x)+ctg (= —-J—--cos (2k—x).
4 7 ° \ 2 / cos (—X) 4 '
XII.119. Найти корни уравнения tgx-ctg(3x—2) = 1, принадлежащие ( Зтг X промежутку I щ _ I
XII.120. Найти тот корень уравнения 4 cos x-sin х) =\/3, для которого выражение 2х2+х—3 принимает наименьшее значение.
§4. МЕТОД ОЦЕНКИ ЛЕВОЙ И ПРАВОЙ ЧАСТЕЙ УРАВНЕНИЯ
Первый уровень
Решить уравнение (XII.121-XII.124).
XII.121. 1) cosx+cos4x=2; 2) cosx—cos4х=2;
3) sinx+cos4x=2; 4) cosx+cos4x=—2.
XII.122. 1) sinx-cos4x=l; 2) sinx-cos4x= —1.
XII.123. 1) sin y=x2-2x+2; 2) cos у = 12x-37-x2.
XII.124. 1) cos 7Сх=>/х+1; 2) 2 cos 2ttx=x+-L
Второй уровень
Решить уравнение (XII.125-XII.131),
XII.125. 1) cos x+cos Зх=—2; 2) cosx—cosЗх=—2.
XII.126. 1) cos 4x+sin у—2\ 2) sin 7x+cos 2x=-2.
XII.127. 1) sin 7x-cos 4x=—1; 2) sin Зх-sin 5x=l;
3) sin 3x-cos4x=—1; 4) sinx-sin Зх-sin 7x=l
XII.128. 1) tgx+ctgx=2 cos 8x;
2) (sinx—cosx) \/2=tgx+ctgx.
XII.129. 1) a/cosx—0,9—л/sinx—0,5=y
2) 1— - t 1 =10
•^sinx—0,9 ^соэх—0,6
244 Глава ХП. Тригонометрические уравнения и неравенства
XII.130. 1) ~^= sin2 (x+^+sin 3x=cos3x—д/2; х/2 \ 12/
2) 3 sin 5х+\/2 sin2 (х+ =3 cos 5х—3\/2.
XII.131. 4 sin2 x+sin2 Зх=4 sin x-sin2 Зх.
§5. ОТБОР КОРНЕЙ УРАВНЕНИЙ. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, СОДЕРЖАЩИЕ ЗНАКИ МОДУЛЯ, КОРНИ И ЛОГАРИФМЫ
Первый уровень
Решить уравнение (ХН.132-ХН.134).
XII.132. 1) | sinx|=sinх+2cosx; 2) |cosx| = — cosx—2\/3sinx.
XII.133. 1) tgx-|cosx| = ^0; 2) ctgx-|sinx|=—
XII.134. 1) |tgx| = -ctgx; 2) |cosx|=-2sinx;
3) |sinx|=cosx; 4) |sinx|=—5cosx.
XII.135. Решить уравнение, сделав подходящую замену переменной:
1) 2cos2x— |cosx|=0; 2) 2cos2х+|—sinх|=2;
3) 6sin2x+|cosx|—5=0; 4) 4—cos2x—5 |sinx|=0.
XII.136. Решить уравнение:
1) (x2—4x+3)-i/cosx—0; 2) (x2— x—2)-\/sinx=0.
XII.137. Реш ить уравнение:
1) ^1+c°s2i=2Z2; 2) \/sinx=\/2cos2 x—1.
XII.138. Решить уравнение, сделав подходящую замену переменной:
1) 8sinx+2\/sinx—1=0; 2) cosx—д/- cosx+2=0.
Второй уровень
Решить уравнение (XII.139-XII.143).
XII.139. 1) (х-3)2=М-; tgx _____________________________
2) (х—2)2-cosx=д/1 — sin2х.
§5. Отбор корней уравнений 245
XII.140. 1)
2)
XII.141. 1)
2)
XII.142. 1)
2)
XII.143. 1)
2)
|sin 2х|=—v3 cos х;
|sin 2x|=\/2 sin %. cosx-|sinx|=0,25;
i i \/3 sin x-|cosx|=- —.
sin 3x+|sin x|=sin 2x; |cosx|-cos3x=sin 2x.
sin 2x—5 |sin x+cosx|+5=0; 6+sinx-cosx=6 |sinx—cosx|.
Решить уравнение (XII.144-XII.148).
XII.144. 1) (x2-4x—21) •x/cosx—sinx=0;
2) (x2—6x—40) • Vcos x-f-sin x=0.
XII.145. 1) \/14 sin2 x+3 sin x—1=2 sin x;
2) x/21 cos2 x—4 cosx—1=3 cosx.
XII.146. 1) A/l + —~=ctgx;
7 V sinx s
2) \A+z£=t^'-
XII.147. 1) A/3+2sin2x=x/6cos^;
2) \/2—cos2 x=\/7 sin
XII.148. 1) 3,5—3 sin2 x=sin x-f-cos x;
2) -\/l,5+cos2x=sinx—cosx.
XII.149. Найти корни уравнения tgx-л/1+cos2x=sin2x, принад-
лежащие промежутку (0;д).
Решить уравнение (XII.150-XII.154).
XII.150. 1) log4 (cos 2х—0,l) + l=log2 tgx;
2) logx/gCtgx=l+log6 (l,5-cos2x).
XII.151. 1) log2 (— sin x) — log4 cosx=-0,5+log4 3;
2) log3 (— cosx)—log9 sin x+0,25=— log9 2.
ХП.152. 1) logyraF7(-4/2cosx)=l;
2) 2 log2sin2 0,5x (-^sin x) =1-
246 Глава XII. Тригонометрические уравнения и неравенства
XII.153.
XII.154.
1) log125 (sin 2x-sinx) + |=log5(—2sinx);
2) log27
sin 2x—| cos x^ = |+log3(— cos x).
1) log3 (sin 3x—sinx)=2 log9(17 sin 2x) — 1;
2) log6 (cosx+cos3jc)=2 log36(sin 2x)-l.
§6. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ С ПАРАМЕТРОМ
Первый уровень
XII.155. Найти все значения параметра а, при каждом из которых имеет решение уравнение:
1) 2sinх+2cosx=a; 2) sinx—>/3cosx=l — 2а.
XII.156. Найти все значения параметра а, при каждом из которых имеет решение уравнение:
1) sin2x=a — 1; 2) cos2 Зх—a=sin2 Зх+2.
XII.157. Найти все значения параметра а, при каждом из которых не имеет корней уравнение:
1) a2-cos2х=1; 2) (а—l)-|sinx|=2.
XII.158. 1) Определить, при каких значениях параметра b
уравнение cos2 х—(2+36) cosx+66=0 не имеет корней.
2) Определить, при каких значениях параметра b
уравнение sin2 2х+(26—4) sin 2х—86=0 имеет корни.
XII.159. 1) Определить, при каких значениях параметра b уравнение cos2 х+(56—3) sin х+156—1=0 не имеет корней.
2) Определить, при каких значениях параметра b уравнение 2 sin2х+(86—3) cosx+126—2=0 имеет корни.
XII.160. 1) Определить, при каких значениях параметра b уравнение cos2 х+(1—26) cosx+62—6=0 не имеет корней.
2) Определить, при каких значениях параметра 6 уравнение cos2 х+26 sin х—62=0 имеет корни.
§6. Тригонометрические уравнения с параметром 247
Второй уровень
XII.161. Определить, при каких значениях параметра а имеет хотя бы один корень уравнение: 1) sinх+2cosx=a; 2) \/3a-cosx—sinx=2.
XII.162. Определить, при каких значениях параметра а имеет хотя бы один корень уравнение:
1) |2 sin х—3 cos =cz; 2) |4cosx+3sinx—а|=2.
XII.163. Определить, при каких значениях параметра а уравнение sin2x+3sinxcosx—2cos2x=a имеет хотя бы один корень.
XII.164. Найти все значения параметра а, при каждом из которых имеет решение уравнение:
1) sin2 х+3 cos х=а\ 2) 4 cos 6х—sin Зх=а+8.
XII.165. Найти все значения параметра а, при каждом из которых имеет решение уравнение:
1) |5sin2x+cosx—7|=а; 2) |8—9sin2х—6cosх|=а.
XII.166. Определить, при каких значениях параметра а уравнение 4 (sin4 x+cos4 х)=а2+а+3 имеет хотя бы один корень.
XII.167. При каждом значении параметра а решить уравнение sin4 x+cos4 x+sin 2х+а=0.
XII.168. Найти все значения параметра а, при каждом из которых уравнение 2sinx-tgx—y/a=y/a-tgx—2sinx имеет единственный корень на отрезке
XII.169. 1) Найти все значения параметра а, при каждом из которых уравнения %/3-sinx—cosx=l и sin имеют хотя бы один общий корень.
2) Найти все значения параметра а, при каждом из которых уравнения %/3-cos x+sin х=у/3 и cos^=a имеют хотя бы один общий корень.
XII.170. Найти все значения параметра а, при каждом из которых уравнение 8а sin | — (а2 —16) cos | = 12а—16 имеет корни.
XII.171. Найти все значения параметра а, при каждом из которых уравнение sin2 х— |sin x-cosx|=a имеет хотя бы один корень.
248 Глава XII. Тригонометрические уравнения и неравенства
§7. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ
Первый уровень
Решить неравенство (ХП.172-ХП.175),
XII.172. 1) sinx^O; 2)
3) cos 2x<0; 4) ctg(x+|^O.
XII.173. XII.174. XII.175. 1) 3) 1) 3) 5) 1) 3) sin 3x^ — 1; cos 4x^1; sin ^ + ~>0; COS \4 / 2 2cos (x—y)+>/3>0; l-tg2x^0; 1 — \/3ctg (x+^)^0; 2) cosx> —1; 4) sinxcl. о \ х । л/2 2) cos- + —>0; • ( 7Г \ - х/з 4) sin Q_—xj< ——; 6) 2sin (Зх-|) —1^0. 2) ctg(x-2)s£\/3; 4) tg(4x)W3sS0.
XII.176. 1) Найти все значения i/=\/2cos 2x^ — 1 x, при которых график функции лежит выше оси абсцисс.
2) Найти все значения х, при которых график функции у=2 sin ( х ) — 1 лежит ниже оси абсцисс. \6 /
XII.177. Решить неравенство:
1) cos1 2 3 2х—sin2 2х^|; 2) sinx-cosx< —
3) sin4 х—cos4 х^^; 4) (sin 7cx-cos 7сх)2^|.
XII.178. 1) Найти все значения х, при которых график функции о 9 X v3 о <
у=2 cos -—— лежит ниже прямой у=1.
2) Найти все значения х, при которых график функции r/=3—4sin23x лежит выше прямой у=—2.
XII.179. Решить неравенство, используя метод введения вспомогательного угла:
1) i/З sin Зх+cos 3x^—2; 2) cos4x—sin4x^\/2;
3) %/3sin2x—3cos2x^2\/3; 4) cos6x—sin 6x^ —\/2.
§ 7. Решение тригонометрических неравенств 249
XII.180. Решить неравенство, используя метод введения вспомогательного угла:
1) \/3cosx+sinx^l; 2) cosx^sinx.
XII.181. Решить неравенство, используя метод оценок:
1) \/3 sin Зх+cos 3x^—2; 2) cos4x—sin 4х^д/2.
XII.182. Найти все значения параметра а, при которых имеет решение неравенство:
1) cos3 х^-8я3; 2) cosx+\/3sin х>а—4.
Второй уровень
Решить неравенство (XII.183-XII.186).
XII.183. 1) 4 cos ( 2x-y)-3^0; 2) 2-3 sin (3x-^0.
XII.184. 1) cosx-Ь smzx ^Q. cosx —2^ 2) 2+sin x+-—7—. ^0 2sin x—4
XII.185. 1) |cosx| < "" 2 ’ 2) |sin 2x|^
3) =\/3; 4) ctgCH)>L
XII.186. 1) |cosx| < 4. "'6’ 2) |sinx|^b
3) |tgx|^3; 4) |ctgx|>4.
Решить неравенство (XII.187-XII.189).
XII.187. 1) cos 5x—cos 3x<0, если - К .11 ~2<X<2'
2) sin x-sin 2x<sin Зх-sin 4x, если 0<x<^.
XII.188. 1) x/3sin x—sin 2x<0; 2) cosx—sin 2x<0.
XII.189. 1) 2 sin2 x+3>7 sin x; 2) 2 cos2 x+3 cosx>2;
3) 3 sin x>2 cos2 x; 4) 2 cos2 x+sin x—1<0
XII.190. Решить неравенство:
1) |cosx|<|sinх|; 2) |sinх|л/3|cosх|.
XII.191. Решить неравенство:
1) |д/Зcosх|^sinх; 2) |cosx|^— sinx.
XII.192. Решить неравенство:
1) д/З—2cos2х<—2cosx; 2) \/5—4sin2х<—4sinx.
250 Глава XII. Тригонометрические уравнения и неравенства
§8. РЕШЕНИЕ УРАВНЕНИЙ И НЕРАВЕНСТВ, СОДЕРЖАЩИХ ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Первый уровень
Решить уравнение (ХП.193-ХП.196).
ХИ.193. 1) arcsin х2=arcsin (7х+8);
2) arccos (x2 —jc)=arccos(3jc2 —8jc+3).
XII.194. 1) arccos £—7=я;
2x-|-o
2) arcsin =
XII.195. 1) arccos2 x—8 arccos jc+15=0;
2) 2arcsin2x—5arcsinjc—12=0;
3) arcsin2 x —2 arcsin x—3=0;
4) arccos2 jc—8 arccosjc4-12=0.
XII.196. 1) arccos (4jc2—jc) — arcsin (4jc2—jc) = =
2) 2 arcsin (x2 —jc+0,5)=arccos (jc2—xH-0,5).
Второй уровень
Решить уравнение (XII.197-XII.201).
XII.197. 1) arcsin Q + ^ cos jc) 4-arccos Q + sin jc)
2) arcsin (1+2 cos jc)+arccos (1+3 tgx)=y
XII.198. 1) arccos jcx/3+arccosjc=^; 2 /
2) arccos jc=arcsin 2x;
3) arccos (jc—l)+arcsin jc=tc;
4) arcsin 6jc+arcsin 6x/3jc=—
XII.199. 1) 2 arccos jc=arcsin у;
2) 2 arcsin 2jc=arccos lx.
XII.200. 1) arctg 3x=arccos8jc;
2) arcsin 5x=arcctg6jc.
Задачи повышенной сложности к главе XII 251
XIL201. 1) arctg ^^-+arcsin х=^;
2) arcctg ^^+arccos 2x=J. ° 2x 2
XII.202. Решить неравенство:
1) arcsin x< ух2-1;
2) arccos x2+x—6.
XII.203. Решить уравнение:
1) arccos f =4д—2дх;
’ \ 4x+7 /
. /3x+ll\ _ nx
2) arcsin ---— =-7r-~~.
' \ x+5 / 2
XII.204. Решить неравенство:
1) arccosx^arcsin Зх; 2) arccosx^arcsin 2x;
3) arcsinx^arccos3x; 4) arcsinx^arccos2x.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ XII
Решить уравнение (XII.205-XII.211).
XII.205. (cosx—sinx) (1+0,5 sin 2x)+sinx=2 cos2x.
XII.206. 2cos2x—1=(2cos2x+l)-tgx.
XII.207. 8 cos 4x-cos 2x-cosx=l.
XII.208. sinx+2sin3x=3cosx.
XH.209. cos4x=cos2 3x.
XII.210. cos4x+5 cos 2x+3=sin 3x.
XII.211. 3 sin 5x=cos 2x—cos 8x—sin 15x.
XII.212. Найти все корни уравнения
sin (4x+^+cos f4x+^^=V2, \ 4/ \ 4 /
удовлетворяющие неравенству - 2 - 2^2'
Решить уравнение (XII.213-XII.219).
XII.213. ctg2x—ctgx=2ctg4x.
XII.214. 2 ctg2x-ctgx=sin2x+3 sinx.
XII.215. -?- +----L—= _L_— 1—
cosx cosx-cos2x sinx cos2x-cos3x
252 Глава XII. Тригонометрические уравнения и неравенства
XII.216.
cos3 x+sin3 х _ sin3 х—cos3 x 1 — 2 cos4 2x m ( лА /К . / лД sin2x
VOSin X-j- — VoSin x — -
\ 4/ \ 4/
XII. 217. tg2x'ctg3x — tg3x-ctg4x tg2x+ctg3x tg3x+ctg4x’
XII.218. 1) tg cosx) — ctg(TTsin x)=0;
2) tg cosx)-ctg sin x) =0.
ХП.219. sinx+cos8x-cosx=\/2.
Решить уравнение (ХП.220-ХП.230).
XII.220. 1) tgx+8 |ctgx|+ctg2x=0;
2) ctgx—ctg2x+18 |tgx|=0.
XII.221. 1) |cosx+2 sin 2x—cos 3x| = 1+2 sin x—cos2x;
2) 11—2 cosx+cos2x|=sin x—2 sin 2x+sin 3x.
XII.222. 2\/3sinx=- ^---УЗ.
2\/sin x— 1
XII.223. cos 2x-\/15 cosx=sin x—sin 3x.
XII.224. 1) \/3sin2x=4-y— sinx-tgx;
2) У 6 sinx-cos2x=y/—7 sin 2x.
XII.225. 1) У5 —cos 2x=cosx—3 cosx;
2) sin2x=3cosx—5sinx.
XII.226. 1) л/З sin 2x-2 cos2 х=2л/2+2 cos 2x;
2) 2tgx-4ctgx=ytg2 ^-2+ctg2
XII.227. 1) tg2 6x+cos2 6х+1 = \/1—2 cos2x—4 cosx;
2) ctg2 Зх+sin2 Зх+1 = \/14-2 cos 2x—4 sin x.
XII.228. л/tgx+sin x+x/tgx-sin x=-^3 tgx. ‘
XII.229. sin x+\/l+sin 2x—cosx=0,5.
XII.230. 1) logyy(sin x—cosx) + l=log7(7+3 cos 4x);
2) logyjjsin (x+^)=logu(6+cos4x)-l.
XII.231. Решить неравенство:
0 10g2sinxcoS^<2; 2) logv^cosxSin%<2-
XII.232. Решить уравнение:
1) arctg ^-^+arcsin Зх=^; 2) arcctg i-+arccosx=^.
Ответы к главе XII 253
XII.233. Решить уравнение:
1) 2,25—5 cos2 дх4-3 sin дх= У5-24х-Збх2;
2) 3,25—7sin2 л:х4-4cos юс=у/ — 15х—9х2—4.
XII.234. Решить неравенство:
1) (х2 4-2x4-2)-cos (х4-1)^2х24-4х4-3;
2) (х2—4x4-5)-cos л:х^2х2—8x4-9.
XII.235. Решить неравенство:
1) бтс2 (cos ^-2cos ~^24дх-2х2-81тс2;
2) 2/г2 f2 sin f-cos f ^28дх-2х2-101д2.
\ 0 3 /
XII.236. Найти все тройки чисел (х,1/, г), удовлетворяющие усло-
вию
3 cos х+4 sin %+5тг-|-5 г , • г
-=arccos |4-arcsin ~.
3 sin i/+4 cos у+5
XII.237. При каждом значении параметра а решить уравнение sin х • tgx 4- 2 cosx = a.
XII.238. При каждом значении параметра а решить уравнение sin Зх 4- sin 2х — a sin х = 0.
XII.239. 1) Найти все значения параметра а, при каждом из которых уравнение (1 — а) • tg2x — 4* 1 4* За = О
имеет более одного корня на интервале (б;
2) Найти все значения параметра а, при каждом из которых уравнение 4 cos 2х — (4а — 2) sin х — а — 3 = О имеет единственное решение на интервале (—^;0).
XII.240. 1) Определить, при каких значениях параметра а равносильны уравнения sinx = 1 4* 2а|х| и 10sinx 4- 4а sinx — cos2х = 11 - 10а.
2) Определить, при каких значениях параметра а равносильны уравнения cosx = 2а ]х| — 1 и 5 4-cos2х 4-8аcosx 4-6 cosx 4-12а = 0.
ОТВЕТЫ К ГЛАВЕ XII
ХИЛ. 1) neZ; 2) ^+2™, neZ; 3) ^+2тш, neZ; 4) £ + neZ. 34 b 10 э
XII.2. 1) — +2тгп, 2тш, neZ; 2) +2ттл, 2тгл, n6Z; 3) + 2тш, яЧ-2тш,
о о Z
254 Глава XII. Тригонометрические уравнения и неравенства
п 6 Z; 4)
п G Z; 2) arccos ( 5 )
^+2m, 2m, nEZ. XII.3. 1) arcsin 4 + 2m, тг — arcsin | + 2m, 2 4 4
| arccos | + яп, — arccos | + тгп, n G Z; 3) n — arccos ( + 2m,
— /г + 2m, neZ; 4) -2 arcsin | + 4m, 2тг — 2 arcsin | + 4тгп, □ □
n 6 Z. XII.4. 1) Корней нет; 2) — arccos 5 + 2тгп, — + arccos | + 2m,
г 6 5 6 5
n G Z; 3) 2 + arcsin | + 2тгп; 2 + тг — arcsin | + 2m, n e Z; 4) корней нет. XII.5. 1) -larctg5+^, n g Z; 2) -j + + 0,5arcctg4, n e Z.
XII.6. 1) —0,25 +2n,—0,75 +2n, nGZ; 2) ^ + j,nEZ; 3) j + тгп,-| + тгп, neZ; 4)-^ + ^, nGZ. XII.7. 1) J + m, n G Z; 2) + m, 2m, n e Z;
3) % + m, neZ; 4) J + y, ±^ + 2тш, m, n G Z. XII.8. 1) + m,
-^ + m, nEl', 2) ±g + A + 2™, n e Z; neZ.
4)§ + ^,/+Z. XII.9. 1) ±£+3™, nGZ; 2) + + neZ.
ob о Z ob о lb о
XII.10. 1) ±5 + m, n G Z; 2) j + m, у + m, neZ; 3) ±| + m,
nEZ; 4) ±^ + m, n g Z. XII.11. 1) ±^ + тгп, n G Z; 2) ± arcctg2 + m,
n G Z; 3) + m, n G Z; 4) ±^ + m, n G Z. XII.12. 1) £ + m, n G Z;
4 6 2
2) J + y,nGZ. XII.13. 1) y.rtGZ; 2) y, nGZ. XII.14. 1) 2) -тг.
XII.15. 1) ±5 + ™, M€Z; 2) ±J + ™, nGZ. XII.16. 1) J + y^, n G Z; 2) + m, nEZ. XII.17. 1) 2) -^, 3) 4) -^,
XII.18. 1) 5, y; 2) -y, -J; 3) |, y; 4) -^, XII.19. 1) у
2) -5; 3) Зтг; 4) -^, -^. XII.20. 1) 4; 2) -I; 3) -1 4) Z.
ХП.21. 1) y+™, neZ, n 1; 2) ^ + ^, nGZ, OO, -A + 2^,
k G Z, k 1; 3) j + y, n G Z, n -1; 4) + m, n G Z, n 2,
g+тг/г, kEl, k^\. XII.22. 1) Ц, 2tt; 2) I 3) 4)
XII.23. 1) A 2) 2L, И., xil.24, 1) -f, 2) 0;±я,
±^; 3) O;±tt, ±2tt; 4) ±y ±у;±2тг. XII.25. 1) +2™, +2™, nGZ;
2) j+2™, nGZ. XII.26. 1) -|; 2) XII.27. 1) + Ttk, у + тг/г,
ftGZ; 2)±5 + ^,AgZ; 3) « e Z; 4) nGZ.
luo о// olo
XII.28. 1) n Z; 2) у+ 2™, nGZ; 3) m, ne.%, 4) корней нет.
XII.29. 1) - + T,-- + _,n6Z; 2),- + —, уди-—. «e2; 3) j + ra, n 6 Z; 4) I + m, XII.30. 1) arcsin^, —л— arcsin 2) — arcsin
Ответы к главе XII 255
тг 4- arcsin 3) arccos0,2, 2тг — arccos 0,2; 4) —тг—arccos0,6, arccos0,6 — тг;
5) — arctg4, тг—arctg4; 6) тг-arcctg2, 2тг-arcctg2. XII.31. 1) |arctg3±^,
|arctg3, 2) —|arcctg2, тг—^arcctg2; 3) 0,5arcsin0,2, тг+0,5 arcsin 0,2,
0,5тг—0,5arcsin0,2, 1,5тг— 0,5arcsin0,2; 4) 0,25arccos0,3, 0,5тг±0,25агссоз0,3,
тг-0,25arccos0,3. XII.32. 1) ±3; 2) ±2’. 3) ±15;
3 3 ooo
0; 4) ±1; i; -J. XII.33. 1) ± arccos | + 2тг/г, ± (тг — arccos + 2тг/г,
12 4 4 \ 4/
fteZ; 2) y, & G Z; 3) (-1)/г+1 arcsin | + nk, (—1 )A arcsin | + тг/г, k 6 Z;
4) ± arccos (1 ) + 2m, n,kEZ и |/г| 7. XII.34. 1) 1; cosl; cos2;
cos3; 2) 0; isinl. XII.35. 1)
±£, 2; 4) n G Z. XII.36. 1)
3 4
3 1
2) (—l)narcsin—7= —arcsin —t= + m, neZ;
4v 5 v 5
, 0; 2) g + тг/г, re E Z;
2 3
± arccos F + arccos F + 2m, о □
3) ( —l)n arcsin -4= + arcsin —+ m, ’ \/58 \/58
3) 0, ti G Z;
XII.37. 1) ±3 + m, neZ;
n GZ; 4) ±arccos —|= — arccos —±= + 2m, neZ. x/61 x/61
2) ±5+ 7 +m, nEZ. XII.38. 1) лги, nGZ; 2) % + m, n G Z; 3)7 + ^, 4 2 4 2
тгтг, n G Z; 4) ? + m, 7 + ^, n 6 Z. XII.39. 1) £ + n G Z; 2) 4 + ^, ' 2 4 2 22 11 14 7
/2 G Z; 3) + nGZ; 4)± + y, nEZ. XII.40. 1) тг + 2тгп, n G Z;
2) £+2тгп, nGZ. XII.41. 1) ^+2m, nEZ; 2) y + v^GZ; 3) ±тг + 6тгп, 2 2 4 2
n G Z; 4) (-l)n+1y + 4m, n G Z. XII.42. 1) -^ + m, arcctg0,5 + m, nEZ; 2) arctgO,5 + m, — arctgO,2 + m, neZ. XII.43. 1) я 6 Z;
2) nEZ. XII.44. 1) ij + тг/г, ±arctgV2 + nk, 2) J +
±arcctg2 + 71k, kEZ. XII.45. 1) + 2m, ne%', 2) — + 2m, n G Z.
XII.46. 1) — arctg3 + тш, n G Z; 2) + m, n G Z. XII.47. 1) arctg5 + Trn;
2) —0,5 arctg + 0,5тгп; n G Z. XII.48. 1) arctg0,5 + m, + m, n G Z;
2) arctg3 + m, arctg4 + m, n G Z; 3) + тглг, — arcctg4 + m, n G Z;
4) + m, -arctgI + m, n G Z. XII.49. 1) + m, -arctg| + m,
nEl-, 2) arctg0,25 + m, arctg3+Trn, n G Z; 3) -J + ^, + ~,
o 2 2 2
n G Z; 4) — + m, arctg^ + Trn, n G Z. XII.50. 1) m; ±-£- + m, n G Z; 4 4 ’ 12
2) (-l)nf+ y! (-l)n+1^ + ^, nGZ. XII.51. 1) ±^ + тш, nGZ; 2) J +
n G Z. XII.52. 1) — arctg3, Tr-arctg3, arctg5, arctg5 — тг; 2) arccos-^, тг — arccos -L, тг + arccos Д=, 2тг — arccos XII.53. 1) — arctg0,25 + m,
v5 v5 v5
— arctg2 + Trn, n G Z; 2) + m, arctg3+Trn, n G Z. XII.54. 1) — + m,
256 Глава XII. Тригонометрические уравнения и неравенства
п G Z; 2) — у + (—l)n arcsin + пп, л G Z; 3) 7 + (—l)n arcsin-4= + ттл, 4 v ' 3 4 v ' 5v2
ле2; 4) 7г + 2ттл, £+2тгл, neZ. XII.55. 1) 7 + Tin, n e Z; 2) £ + 2 4 4 2
7 + ттл, — + Tin, л G Z. XII.56. — + Tin, пЕ%. XII.57. ^+2тгл, n G Z. 3 6 4 2
XII.58. ^ + Tin, na. XII.59. 1) £ + Tik, ±£ + Tik, k G Z; 2) $,±? + 2яй, 4 2 6 2 6
ftGZ. XII.60. 1) % + Tin, (-l)n+1 arcsin 7 + ттл, л e Z; 2) ±£+2тгл, Tin, 2 v 7 4 6
Лбг; 3) тт + 2тгл, 1 )л + 2тгл, л G Z; 4) тг+2тгл, ле2. XII.61. 1) J + y. ТТЛ, neZ; 2) J + Tin, + ТТЛ, лсг. XII.62. 1) | + Tik, keZ; 2) Tik, M; 3) (-l)/i+1^ + ^, A + ZE* fcGZ; 4) ±A + k e Z.
4 7 20 5 10 5 24 2 4
XII.63. 1) ^ + 27гл, 2ттл, raGZ; 2) -^+2тгл, 2тгл, л G Z. XII.64. J + Tin, Tin, л G Z. XII.65. ~, л G Z. XII.66. 7 + Tin, — 7 + 2тгл, 7г+2тгл, л G Z.
2 4 2
XII.67. 1) ±£ + 2тгл, лег; 2) ±£ + Tin, ntZ. XII.68. 1) ±£ + ~, 3 3 24 4
nGZ; 2)±j + ™, ле2. XII.69. 1) (-1)"-5 arcsin +57ГЛ, лег; 2) ±4arccos + 871л, лег; 3) 2ттл, 71 + 4ттл, raeZ; 4) 12ттл, Зтт+бттл, лег. XII.70. 1) J + Tin, ±^+2тт, neZ; 2) ± + + ntZ.
хп.71. 1) + лег; 2)^ + ^, лег; 3) лег; 4)^, лег.
wr т т *7П * \ ТС । / 1 \ fl ТС । ТС АТ — rjj о \ ТС . ТСТТ । 2 ТС . 2 ТСТТ _ г-н
XII.72. 1) 2 + (“О 12 + Т’ 2) 4 + Т’ ±'9_ + Т’ е Z;
3) ттл, ±х + ^т. «eZ; 4) 2ттл, -£ + ^, лег. XII.73. 1) ±^+2тгл,
УЗ э э 4
лег; 2) ±~+2тгл, лег. ХП.74. 1) I + Tin, ПЕ1-, 2) 7 + Tin, nel. 7 6 6 4
хп.75. 1) лег; 2) лег. хп.7б. 1) J +
ne^-, 2) 7Г+27ГЛ, -7+47ГЛ, -^ + 4ттл, лег. XII.77. 1) 2) J.
3 3 о 3
XII.78. 1) ±7,0,^; 2) XII.79. 1) ттл; (-l)n + ттл, n G Z; 2) ^Н-ттл;
4 4 3 6 2
±у+2ттл, лег. XII.80. 1) у, тт; 2) XII.81. 1) 2тгл, л 6 Z;
2) ^ + 2ял, ле2. XII.82. 1) —7 + ттл, + ттл, л GZ; 2) 7 + Tin, ±-^- + Tin, 2 4 6 , 4 10
iy^ + тгл, лег. XII.83. (-1)^ + ттл, 7Г + 27ГЛ, лег. ХП.84. -J + ТГЛ, лег. XII.85. У Л-Tin, nez. XII.86. + Tin, 7 + ^, лег. ХП.87. ТТЛ,
4 12 8 2
£ + 2ттл, лег. XII.88. larccosl. XII.89. 1) 2)
2 5 4 7 9 3 7 12 4
XII.90. 1) arctg0,5 + ттл, — arctg3 + Tin, п е Z; 2) — arctg0,25 + ттл, — arctg2 + ттл, лег. XII.91. 1) у; 2) XII.92. 1) + 2ттл,
тт + 2тш, л G Z; 2) + 2ттл, 2тгл,„ л G Z. XII.93. 1) + Tin, п G Z;
2) + ттл, ле Z. XII.94. 1) ±А + ™, п е Z; 2) ле Z.
Ответы к главе XII 257
XII.95. 1) у, + я/г, /г G Z; 2) у, nGZ. XII.96. 1) ±| + яп,
nGZ; 2) ±| + яп, nGZ. XII.97. 1) j+™, nGZ; 2)±^ + яп, nGZ. XII.98. 1) + у, nGZ; 2) J + ^, | + 7ik, п G Z. XII.99. 1) ™,
±| + у, nGZ; 2) + ±^ + ^, nGZ. XII.100. 1) у|; 2)
XII.101. 1) £; 2) XII.102. 1) ^ + у. ±| + яп, nGZ; 2) + ф,
±| + яп, nGZ. ХИ.ЮЗ. 1) у, nGZ; 2) nGZ; 3) у,
nGZ; 4) £ + + neZ. XII.104. 1) А + ™ „ G Z; 2)
о 6 1U о 12 о о
J + ?, nGZ. XII.105. 1) 7 + яп, Л + ^, nGZ; 2) J + яп, 8 4 4 14 7 5 2
я + 2яп, nGZ. XII.106. 1) + яп, nGZ; 2) (—1)м+1^ + яп, nGZ.
XII.107. 1) + 2я/г, -7 + ^, /г g Z; 2) -^ + 2я/г, 7 + ^, k G Z.
4 4 3 4 4 3
XII.108. 1) ±£ + яп, и G Z; 2) ±£ + 2яп, и G Z. XII.109. 1) £ +
6 3 14 7
и 3 + 7/г, и,/г G Z; 2) и / 5 + 116, и,/г G Z; 3) , и 1 + 3/г,
h,6gZ; 4) + п/2 + 56, n,6GZ. XII.110. 1) £,я,у; 2) ^yiy-y-
XII.111. + ЯП, и G Z. XII.112. ЯП, и G Z. XII.113. 7 + ^, nGZ.
6 4 2
XII.114. -у + яп, nGZ. XII.115. яп, nGZ. XII.116. + яп, и G Z.
XII.117. ±7 +яп, nGZ. XII.118. яп, hgZ. XII.119. я+1. XII.120. J. 4 6
XII.121. 1) 2яп, и G Z; 2) корней нет; 3) + 2яп, и G Z; 4) корней
нет. XII.122. 1) + 2яп, и G Z; 2) + 2яп, и G Z. XII.123. 1) 1;
2) 6. XII.124. 1) 0; 2) 1. XII.125. 1) я+2яп, и G Z; 2) корней нет. XII.126. 1) у-Нбяп, nGZ; 2) j + 2яп, nGZ. XII.127. 1) + 2яп, nGZ;
2) корней нет; 3) + 2яп, nGZ; 4) + 2яп, nGZ. XII.128. 1) + яп,
и G Z; 2) — ^ + 2яп, и G Z. XII.129. 1) Корней нет; 2) корней нет. XII.130. 1) -^ + 2яп, nGZ; 2) -^+2яп, hgZ. XII.131. яп, (-1)л|+ яп, и G Z. XII.132. 1) 7 + 2яп, — 7 + 2яп, nGZ; 2) —^+2яп, я + 2яп, и G Z. 2 4 6
XII.133. 1) 7 + ЯП, и G Z; 2) -^ + яп, и g Z. XII.134. 1) -7 + 3 4 4
и g Z; 2) — arcctg2 + 2яп, я + arcctg2 + 2яп, и G Z; 3) ±^+2яп, и G Z; 4) — arctg5 + 2яп, я + arctg5 + 2яп, nGZ. XII.135. 1) + яп, + яп,
и G Z; 2) + яп, яп, и G Z; 3) + яп, и G Z; 4) + яп, и G Z.
XII.136. 1) 1, 7 + яп, и G Z; 2)2, яп, и G Z. XII.137. 1) ±7 + яп, 2 4
и G Z; 2) (—1)"^ + лп, и G Z. XII.138. 1) (—1)" arcsin^ + яп, и G Z; 2) я + 2яп, nGZ. XII.139. 1) 4; 2) 1, | + яп, nGZ. XII.140. 1) j + яп,
9—5682
258 Глава XII. Тригонометрические уравнения и неравенства
±у±2тш, п 6 Z; 2) яп, (-1)п^±тш, п Е Z. XIL141. 1) ±^ ± 2тш, ±^ + 2тш, п 6 Z; 2) | ± 2тт, у + 2тт, j + 2тш, у + 2тш, п 6 Z. XII.142. 1) яп, £ ± 2тш, ± яп, п 6 Z; 2) 2тт, £ + яп, + яп, п е Z. 2 о 2 b
XII.143. 1) nGZ; 2)^, nez. XII.144. 1) 7, J + яп, пЕ%; 2) -4, —± яп, п е z. XII.145. 1) (—1)" arcsin | + яп, п Е Z; 2) + 2яп,
nEZ. XII.146. 1) — ± 2яп, ± 2яп, п Е Z; 2) я + 2яп, + 2яп,
nEl. XII.147. 1) ±^ ± 4тт, n е Z; 2) у ± 4 дм, + 4дп, п G Z.
XII.148. 1) ^+2яп, я— arctg5 + 27m, neZ; 2) у +2яп, я— arctg3±2rtn, nGZ.
XII.149. у у. XII.150. 1) arctgy/Ofi + яп, пЕ%; 2) arcctg\/5 + яп, n€Z.
XII.151. 1) -£±2дп, neZ; 2) + 2яп, nEl. XII.152. 1) ± 2дм,
3 3 о
п Е Z; 2) + 2дм, п Е Z. XII.153. 1) arccos 0,25 — я + 2дм,
9 1
п Е Z; 2) arcsin^ + я ± 2яп, п е Z. XII.154. 1) arccos — я + 2яп, 3 6
9
п Е Z; 2) arcsin0,75 + я + 2яп, arcsin- + 2яп, п Е Z.
XII.155. 1) 2) [-0,5; 1,5]. XII.156. 1) [1;2]; 2) [-3;—1].
XII.157. 1) (—1; 1); 2) (-оо;3). XII.158. 1) (-оо;-|) U (|;±оо);
2) [-0,5;0,5]. XII.159. 1) (-оо;-0,2) U (0,2; +оо);
XII.160.
2) а
XII.163.
1) (—ос;—1) U (2;±оо); 2) [-2; 2]. XII.161. 1)
1. XII.162. 1) 0 а л/13; 2)
-3V5-1.. 3-/2- 1 XII.164. 1) -3 < а 3; 2)
2) [-0,25; 0,25]. — \/5 а \/5; -7 а 7.
XII.165. 1) g а 8;
2) 0 < а 14.
XII.166.
-1 - V5. —1 + х/5
2 ’ 2
XII.167. При а Е (—ос; —1,5) U (0,5; +оо) корней нет; при а = —1,5 х=^ + тгн;
1 г п г (~1)А arcsin (1 - У2а + 3) + тсА vti ico гот , . ги , \
при -1,5 < а 0,5 х=-—------------------------------. XII.168. {2}U[4;+oo).
XII.169.
XII.171.
1) ±1, ±0,5; 2) ±1, ±Y- XII.170. (-оо;-12] U [0; 4] U [8; ±оо). l^/2;i . XII.172. 1) [2ящя+2яп\, ПЕТ/, 2) [^±7ш;у±7ш),
п Е Z; 3) (j ± яп\ ± тш'), п Е Z; 4) ± яп\ ± , п Е Z.
\4 4 / L3 6 /
XII.173. 1) -I + п Е Z; 2) х — любое действительное число за о 3
исключением я + 2яп, пЕ%\ 3) пЕ %', 4) х — любое действительное число за исключением ^+2яп, nEZ. XII.174. 1) (— у ± 4яп; у ± 4яп^, п Е Z; 2) ±6тш; ±6тт\ п е Z; 3) + 2яп- ± 2яп\,
\ 4 4 7 L 12 12 J
Ответы к главе XII 259
п Е Z;
п G Z;
п Е Z;
4> н п е Z;
п G Z;
п G Z;
п G Z;
4) (тг+2тт; у + 2тт), п G Z; 5) + 2тт; у + 2тт)
6) + + «ez. XII.175. 1) + +
L о о У о J X 4 Z о z J
2) [— + тт; ——h Tinj, n E Z; 3) — + тт; + Tin], n E Z
+ т;-т1 + т]’ n 6 Z- XII.176. 1) (A + 7m;g + 7m)
2) (2яп-^ + 2яп), n G Z. XII.177. 1)
2) + тт; — ^ + zm^ , n E Z; 3) + тт; -у + Tin
4) [-+ n-1 + n], n E Z. XII.178. 1) + 2тт; + 2тт)
2) при любых x. XII.179. 1) -у + n G Z
+ n G Z; 3) + Tin, n E Z; 4) J + ^, n G Z
2 12 ou
XII.180. 1) Г-^ + 2тт;-£+2тт|, n E Z; 2) Г-+ 2тт; 7 + 2тт1, и G Z L 2 b J L 4 4J
ХП.181. 1) + «eZ; 2)-^ + y«GZ. XII.182. 1) (—00;0,5]
2) (—00; 6). XII.183. 1) + 1 arccos I + zm; arccos I +
m n\ ( ti , 1 2 , 2nn 5tc 1 . 2 , 2nn\ 57
n E Z; 2) I — + ^ arcsin arcsin +-z-I, n G Z
\ 12 о □ □ 12 и и о /
XII.184. 1) + 2Т1П-, + 2тт], п G Z; 2) [-J + тт; J + ™
п Е Z. XII.185. 1) [j + тш; y + ™]’ п 6 Z; 2)[-i + T;f + T
п Е Z; 3) + TinU |у + Tin', + Tin'j, п G Z; 4) + Tin
+ лп^ U (тг+ лп\ у + лп^, п Е Z. XII.186. 1) [тг—arccos | + тт arccos | + тт|, п Е Z; 2) [arcsin | + тт; тг — arcsin | + тш], п Е Z
3) [—arctg3 + тт; arctg3 + тт], n GZ; 4) (тт; arctg4 + тт] U [тг—arctg4 + тт тг+тт), n G Z. XII.187. 1) М;0) U (О; j); 2) (О; U
\ 4 / \ 4 / \ D / \DZ/
ХП.188. 1) (2тт; £+2тт^ U (тс+2тт; 4?+2тт\ п е Z; 2)(^+2тт
X 6 / \ b / \о
£ + 2тт^и(^ + 2тт; ^ + 2тт), nGZ. XII.189. 1) (+ 2тт; + 2тт") 2/\Ь 2 / \Ь о/
п G Z; 2) + 2тт; + 2тт), п Е Z; 3)
4) (_^ + 2тт; + 2тт), п Е Z. XII.190.
2) [^ + тт; у+ тт], n G Z. XII.191. 1)
2) +2тг^; у+2тг^], k G Z. XII.192. 1)
2) (_§Е + 2тт; -£+2тт\ пЕ%. XII.193. 1)
+ 2тт; + 2тт\ п G Z
О + ¥ + ™Y п е z
\4 4 /
+2тгй; у+2тг/!г], feGZ (^+2Tin-, ^ + 2тт\ п GZ \ 4 4 J
-1; 2) 0,5. XII.194. 1) -2
0; 2) -4, 2. XII.195. 1) cos3; 2) —sin 1,5; 3) — sinl; 4) cos2
XII.196. 1) —0,25; 0,5; 2) 0; 1. XII.197. 1) -^ + 2тг6, feGZ; 2) ^+2nk
260 Глава XII. Тригонометрические уравнения и неравенства
£ G Z. XII.198. 1) 0,5; 2) 3) 0; 1; 4) -1 XII.199. 1) Нет
V 5 12
корней; 2) |. XII.2OO. 1) -Ь; 2) -L XII.201. 1) 0,8; 2) 0,4.
о 6v2 3v5
XII.202. 1) -1; 2) 2. XII.203. 1) 1,5; 2) -3. XII.204. 1) [-1; -JL];
2> БЯ 3> [w!]• 4> НЯ хп-205- -2 + т- "е г-
XII.206. (-1)"+ тсп, п G Z (другая форма ответа: + у , neZ). XII.207. + nGZ, AjGZ, п^7р, 2k+ 1 ^9m,peZ, meZ.
Указание: преобразовать уравнение к виду sin8x = sinx (учесть, что sinx 7^0). XII.208. + тсп; arcctg + тсп, nEl. Указание: воспользоваться формулой тройного угла. XII.209. тсп ± 2L + nGZ. Указание: воспользоваться формулами понижения степени и тройного угла. XII.210. ^+2дп; ±^ + л:п, nGZ. Указание: воспользоваться формулами sin3x = sinx(l + 2cos2x), cos4x = 2cos2 2x — 1, и преобразовать уравнение к виду (2 cos 2х + 1) (cos 2х — sin х + 2) = 0.
XII.212.
XII.211. ™
у + тсп, п G Z. XII.213. + тсп, п G Z.
XII.215. + тсп, + тсп, п Е Z. XII.216.
±2L + nGZ. XII.218. 1) тсп — arccos 0,6 nGZ;
XII.219. 7 + 2тсп, п G Z. XII.220. 1) - arccos j 4 4
2) —arcsin | + тсп, nEl. XII.221. 1) + 2тсп, + 2тсп, ;
nGZ; 2) ^ + тсп, у +2тсп, 2тсп, -^ + 2тсп, nEZ.
Ц^ + 2тсп, n€Z. XII.223. ±7 + 2дп; — arccos+2дп, nGZ. 18 4 4
д +arcsin |+ 2дп, nGZ; 2) тсп, — arccos | + 2тсп, п G Z.
-у+2тгп, nGZ; 2) ~^+2тсп, + 2тсп, neZ.
п G Z; 2) — + тсп, — — + тсп, п G Z.
2) (-1)"+1д + тгп, nGZ. XII.228. тсп, О
+ 2тсп, тс — arccos 0,25 + 2тсп, п G Z.
тс — arcsin | + 2тсп, п G Z;
nGZ. XII.231. 1) {2тсп ;arccos
п е z.
XII.217.
п е z.
7Г
6
2) % -
8
+ 2тсп, XII.214. ±у . тсп ! + Т’ 2) ±^ + 2тш, + тсп, п G Z;
. у г тсп, -^+2ТСП, XII.222. ^ + 2тт; у+ 2лгп, XII.224. 1) тсп, XII.225. 1) -? + 2тсп, XII.226. 1) Н + тсп, XII.227. О ±у + 2тт, п G Z; + тсп, n^Z. XII.229. arcsin0,25 + 2тт,
П€1.
+ 2тт,
п G Z.
XII.230. 1) ^ + ^ arcsin | +
1 .I|O 1 . 1 ,
- arcsin - + 2тсп, „ arcsin - +
2 4 2 4
h 2icn ) U f + 2тсп;
п
2тсп,
G Z;
2) (2тсп; 7 + 2тсп) U ( arcsin — \ 4 /у 4
2) 0,6. XII.233. 1) 1; 2)
О о
2) 7тс. XII.236. х = 77 — arcsin 2 + 2тсп, п G Z; у = arcsin 2 + 2тск,
2 5 27 5
+ 2дп; ^ + 2дп j , nGZ. XII.232.
XIL234. 1) -1; 2) 2. XII.235.
3 । и. .. 3 , о^.х,
5 5
1)
0,2;
1) 6д;
k G Z,
Ответы к главе XII 261
ге[-3;3] XII.237. При а 6 (-оо;-2) х = ± arccos -+ ~ 4 + 2лп,
п е Z; при a = — 2 х = я+2ягг, п е Z; при а 6 (-2; 2) корней нет; при а _ >/а2 _ 4
a = 2 х = 2лп, п Е Z; при a е (2;+оо) х = ± arccos--------------Н 2лп,
п G Z. XII.238. При a Е ( —оо; —1,25) U (5;+оо) х = Tin, п Е Z;
при a Е [—1,25; 1] х = кп, х = ± arccos ± ^4д_+_5 2т, п Е при
a 6(1; 5] х = Tin, х = ± arccos 1 + ^4а + 2лп, п Е "Ъ. Указание: вос-
пользоваться формулами sin3x — sinx — 4sin3x, sin2x = 2sinxcosx и преобразовать уравнение к виду sinx ^3 — 4sin2х + 2cosx — aj = = 0. XII.239. 1) U Q;l); 2) (-oo;l] U {1,5} U [3;+oo).
XII.240. 1) {0}U (з|;+оо); 2) (-oo;-0,6) U {0}.
Глава XIII
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
§1. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ. ПРОИЗВОДНЫЕ ФУНКЦИЙ XN, SINX, COSX
Первый уровень
Для функции у = Дх) заполнить таблицу, указав для данного приращения аргумента Дх = х — xq соответствующее приращение функции Ду = Дх) - f (х0) (XIII.1-XIII.3).
Д X 0,4 -0,4 0,1 -0,1 0,01 -0,01 0,001 -0,001
М
At/ Дх
XIII.1. 1) у = 4х-6, х0 = 2; 2) у = 3 - х, х0 = 3.
XIII.2. 1) у = 2 — х2, xq — — 1; 2) у = 2х + х2, xq2.
XIIL3. 1) у = х3 - 1, х0 = 1; 2) у = (х - I)3, х0 = -2.
Рассмотреть приращение Ду функции у = [(х) в точке х = xq как функцию от приращения аргумента Дх и построить график функции Ду(Дх) (XIIL4-XIII.5).
XIII.4. 1) у = Зх + 9, х0 = 1; 2) у = 7 —4х, х0 = -2.
XIII.5. 1) у = 2х2-8х, х0 = 3; 2) у = 1 + 4х - х2, х0 = -1.
Пользуясь определением производной, вычислить значение производной функции у = [(х) в указанной точке x = xq (XIII.6-XIIL8).
XIII.6. 1) Дх) = 2х — 4, х0 = 3; 2) Дх) = 2 - 5х, х0 = 1.
XIII.7. 1) Дх) = 1 - х2, х0 = 0; 2) Дх) = Зх - х2, х0 = 4;
3) Дх) = 3х2 — 2х + 2, xq = —2: 4) Дх) = 2(х — З)2, Xq = 1.
XIII.8. 1) Дх) = 2д/х, х0 = 4; 2) Дх) = -у/х, х0 = 9.
Пользуясь определением производной, вычислить значение производной функции у = Дх) в точке х = xq (XIII.9-XIII.10).
XIII.9. 1) Дх) = 2(х - З)2; 2) Дх) = (Зх + I)2 - х.
XIII.10. 1) Дх) = -(х + I)3; 2) Дх) = (2х - 5)3 + 1.
§1. Определение производной. Производные функций xn, sinx, cosx 263
Используя формулы для производных функций xn, sinx, cosx, вычислить значение производной функции у = Дх) в указанной
точке х = хо (XIII.11-XIII.12) ХШ.11. 1) Дх) = х6, х0 = —2;
3) Дх) = х“5, х0 = 2;
5) Дх) = х 2, хо = 0,25;
2) Дх) = х100, х0 = -1;
4) Дх) = х3, х0 = 27;
6) Дх) = х % xq = 32.
XIII.12. 1) /(x) = sinx, xq = ^; 2) /(x) = cosx, xq = ~;
3) Дх) = sin 3xcos2x - cos3xsin2x, хо = — —;
4) /(х) = 2 cos2 | - 1, x0 = y.
Второй уровень
Пользуясь определением производной, вычислить значение производной функции у — Дх) в каждой точке хд ее существования (XIII.13-XIII.17).
XIII.13. 1) 3) К*) К*) = -+4; X = J_. X2 ’ 2) 4) fW K*) _ 1 . x + 3 ’ _ 1 (x + I)3 ’
XIII.14. 1) /W = \/3 — x; 2) zw = 2\/x - 2;
3) 4) K*) = \/2x + 3.
XIII.15. 1) fW = cos2x; 2) zw = 4 sin2 3x.
XIII.16. 1) К*) = sinf; 2) = (sin x + cosx)2
XIII.17. 1) = tgx; 2) f(p = ctgx.
Пользуясь определением производной, выяснить, существует ли производная функции у = Дх) в точке х = 0 (XIII.18-XIII.19).
_. . f х2, х 0, г. . f х3, х 0,
XIII.18. 1) Дх) = < ' 2 х= \ '
к [ х, х < 0; ' [ -xz, х < 0.
XIIL19. 1) Дх) = 2|х| + 1; 2) Дх) = х|х|.
ХШ.20. Пользуясь определением производной, выяснить, существует ли производная функции у = Дх) в точке х = 0:
1) Дх) = |х| • sinх; 2) Дх) = |х| • cosx;
3) Дх) = х| sin 2х|; 4) Дх) = 2х| cosx|.
264 Глава XIII. Производная и дифференциал
XIII.21. Пользуясь определением производной, вычислить значение производной функции у = Дх) в каждой точке ее
существования:
1) Дх) = х |х — 11; 2) Дх) = |х2 - 4|.
XIII.22. Подобрать коэффициенты а и b так, чтобы функция У = Кх) была непрерывной в точке x = xq и имела в этой точке производную:
( х2 х > 1
1) /W = ’ / ’ , х0 = 1;
V ах + о, х < 1,
{х3 х > 2
Л ’ 9 Х0 = 2'
ах + Ь, х < 2,
§2 . ПРОИЗВОДНЫЕ ПОКАЗАТЕЛЬНОЙ И ЛОГАРИФМИЧЕСКОЙ ФУНКЦИЙ
Первый уровень
Пользуясь определением производной, вычислить значение производной функции y = f(x) в указанной точке х = хд (ХШ.23-ХШ.24).
XIII.23. 1) Дх) = 2х, х0 = 1; 2) Дх) = 3х, х0 = 0,5.
XIII.24. 1) /(x) = log2x, х0 = 4; 2) /(x) = log03x, х0 = 5.
Используя формулы для производных показательной и логарифмической функций, вычислить значение производной функции y = f(x) в указанной точке х = Xq (ХШ.25-ХШ.26).
XIII.25. 1) Дх) = 0,5х, х0 = -1; 2) Дх) = 22х, х0 = -3;
3) Дх) = 5-х, х0 = 2; 4) Дх) = 2х • 3х, х0 = 1.
XIII.26. 1) Дх) = log0 5 х, х0 = 2; 2) /(x) = log2x3, х0 = 4;
3) Дх) = 21og9x, х0 = 5;
4) f(x) = 1g (х2 - х) - lg(x - 1), х0 = 3.
Второй уровень
Пользуясь определением производной, вычислить значение производной функции у = Дх) в точке х = хд (ХШ.27-ХШ.28).
XIII.27. 1) Дх) = 10х-2; 2) Дх) = е~х + 3.
XIII.28. 1) Дх) = 21п(х + 5); 2) Дх) = log3(x + 1) - 2.
§3. Правила дифференцирования 265
XIII.29. Пользуясь определением производной, выяснить, существует ли производная функции у = f(x) в точке х = 0:
1) /(х) = ^1; 2) /(х) =
XIII.30. Подобрать коэффициенты а и b так, чтобы функция /у = Дх) была непрерывной в точке x = Xq и имела в этой точке производную:
z . f ех, х О,
О ftx) = s . . . п х0 = 0;
’ 1 v 7 [ ax + о, х < 0, и ’
_ ч ( logo х, х 4,
2) f х = J 62 ’ ’ х0 = 4.
’ 7 [ ax + b, х < 4, и
§ 3. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ Первый уровень
XIII.31. Найти производную функции у = f(x):
1) у = 3 — 2х + х3; 2) у = х5 - 2х2 + 8;
3) У = |х4 + |х3 + lx2 - х - 21;
4) У = А + А + р-х3-2х4.
4.v Зх3
XIII.32. На рис. 1 и 2 изображены график функции /(х) = ах2 + + Ьх + с и четыре прямые. Одна из прямых — график производной данной функции. Указать номер этой прямой: 1) для /(х) на рис. 1; 2) для /(х) на рис. 2.
XIII.33. Найти производную функции у = f(x)\
1) У — %у/х + 2) у = у/х+-^\
3) у =
4) у = 4V6C3 + 3^ - 4 - .
7 3/—9 4л-о
V XZ V х°
XIII.34. Найти значение производной функции y = f(x) в точке Xq: 1) у = 6х7 — 14х3 + 4х — 4, Xq = 1;
2) у = х3 — Зх2 + 2х - 4>/х + 5, xq = 4;
266 Глава XIII. Производная и дифференциал
3) у — у/х, - | + - 5, %о = -1;
4) у = + А. + 3 - 4, х0 = 1.
хЛ
XIII.35. Найти производную функции у = f(x):
1) z/ = xcosx; 2) z/ = x3cosx;
3) у = х2 cosx — 2х sinx; 4) y — xtgx]
5) у = x2 ctgx - 2x tgx; 6) у — (2x - 1) sinx.
XIII.36. Найти значение выражения:
1) /'(2л:) + 2f (0 , где /(х) = (1 - 2х) cosx;
2) /'(д) + к- f (^0 , где /(х) = 3x2sinx.
XIII.37. Найти значение производной функции y = f(x) в точке xq:
1) у = х2(3х — 1)(х + 1), xq — — 1;
2) у = (х — 2)(2х + 3)х2, xq = 2;
3) у = х2(х2 - 1)(х2 + 2), Xq = -1;
4) у = (2х — 2)(3 — х2)(4х3 — 32), х0 = 2.
XIII.38. Найти производную функции у = f(x):
xcosx cosx оч’ х2+2х
О У = ; 2) у = 3) у = ——
SUL# X Z.X — 1
лч ____ X2 + X + 1 . г\ ____ 1 — X2 , z?\ _ 1 + у/х ,
4) У~ x^-x + l’
7) y = ^+lt
' у х2п-1
§4. Производная сложной функции и обратных функций 267
XIIL39. Найти значение выражения:
1) /'(0)-/'(-2), гае =
2) /'(2) -/'(-2), где /(х) = фЦ-
XIII.40. Найти производную функции у = Дх):
1) у = х In х + 2х; 2) у — 3х + 3-х;
3) У = 4) ^ = xl°g2^-7-
XIII.41. Вычислить производную функции у — f(x) в точке xq:
1) У = -*0 = 0; 2) у = (4 + log4 х)(4х - 2), х0 = 1-
XIII.42. На йти значение выражения:
О /'(0) - /'(0, гДе Дх) = х2ех;
2) /'(-!)-/'(1), где /« = |±^;
3) /'(«)- /Д)- где /« = !!^;
4) /,(е)_/'(з)’ г«е /Ц)=х1пх.
XIII.43. Решить данные уравнения и неравенства:
1) f'(x) = g'(x), где f{x) = 3 + 2х2, g(x) = Зх2 -- (5х —3)(2 —х);
2) f'(x) = g'(x), где f(x) = х5 — 4х3, g(x) = уХ3 - 180х;
3) Дх) =/Дх), если Дх) = 2созх;
4) > 0, где Дх) = 4 - 15х2 - 2х3, g(x) = 2х3 + 18х + 1;
5) f'(x)^g'(x), где Дх) = 2, g(x)=x-x3;
6) + g'W < 0, где Дх) = g(x) = —Ц.
Л — О Л О
§4. ПРОИЗВОДНАЯ сложной ФУНКЦИИ И ОБРАТНЫХ ФУНКЦИЙ
Первый уровень
XIII.44. На йти производную сложной функции //= Дах + Ь):
1) у = cos(2x + 13); 2) у = sin(3x — 1);
3) Дх) = cos(l - 2х); 4) у — — Зх)3;
5) г/ = 1п(1 — 5х); 6) г/ = 69х+2.
268 Глава XIII. Производная и дифференциал
XIII.45. Найти производную функции y = f(x)\
1) у = (2х + 1)10; 2) у = sin3 2х; 3) z/ = xcos3x;
4) у = sin3x5; 5) у = sin(4x - I)2; 6) z/ = x2tg2x;
7) у = у/1 - х2; 8) у - \/1 - cosx; 9) у = е-хх2.
Второй уровень
XIII.46. Найти производную функции у = Дх):
1) у = In ctg2x; 2) у = log2(x3 - х2 + 1);
3) г/ = (log5(x2 + l))3;
4) У = tg \/x - (x + 2)e2x + in 4x + 2.
XIII.47. Найти производную функции y = f(x\.
1) у — arcsin2x; 2) у = arcctg(2x + 1);
3) y = arcsin y/x] 4) у = arctg a/x3; 5) y=^^---.
XIII.48. Выразить как функцию от х производную функции, обратной данной:
1) у = х3 + Зх; 2) у = \/х + 2 (х > —2);
3) у = 2х2 — х4 (х > 1); 4) г/ = О,1х —х2 (х > 0,05);
5) у = х2 — х (х < 0,5); 6) у = arccos 4 (х > 1).
§5. ОДНОСТОРОННИЕ И БЕСКОНЕЧНЫЕ ПРОИЗВОДНЫЕ
Второй уровень
XIII.49. Доказать, что функция недифференцируема в указанных
точках: ।
1) Дх) = х + |х - 1|, х0 = 1;
2) Дх) = |х3 — 4х|, xq = — 2, Xi = 0, Х2 = 2;
3) HP = ( f ,ПРИ * < Q' п *0 = 0:
v [ 1 — 2х, при х О,
4) Дх) = л/х2, Xq = 0.
§6. Дифференциал функции 269
XIII.50. Найти точки, в которых производная функции Дх) не существует. Найти в этих точках левую и правую производные:
1) Дх) = |2х - 1|; 2) Дх) = |15 - 8х + х2|;
3) Дх) = У16- 8х + х2; 4) Дх) = \/16-8х2+х4;
5) Дх) = \/1 - cos2х; 6) Дх) = In |х2 — 4х + 3|;
7) Дх) = arcsin(sinx); 8) Дх) = arcsin 2% 9.
1 +
XIII.51. Найти производные данных функций:
1) у = In |х|; 2) у — arcsin Д-.
|х|
§6. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Первый уровень
XIII.52. Обосновать приближенную формулу:
1) </х + Дх « д/х + ; 2) </1 + Дх « 1 + -х.
3 vCc2 п
XIII.53. Используя формулу Дх) « Дхо) + /Дхо)Дх, найти приближенные значения следующих выражений:
1) sin29°; 2) а/34; 3) У120; 4) </100;
5) л/1000; 6) In 1,02; 7) In 0,9; 8) sin 1°;
9) a/25; 10) cos 0,02; 11) arctg0,01; 12) In 0,2.
Второй уровень
XIII.54. Используя понятие дифференциала, найти приближенное значение функции y = f(x) при данном значении х:
0 У= ПРИ X = 0,15;
2) у = \/Зх3 + 2х — 4 при х = 1,001;
3) r/ = xln(x —2) при х = 3,001;
4) у = х5 — 2х4 + Зх3 — 4х2 + 6 при х = 1,001.
XIII.55. Найти дифференциал функции при произвольных значениях аргумента х и при произвольном его приращении Дх - dx :
1) у = ха/а2 - х2 + а2 arcsin — 5;
2) у = sin х — х cosx + 4;
270 Глава XIII. Производная и дифференциал
3) у = х arctg х — In \/1 + х2;
4) у = х 1пх — х + 1.
XIII.56. Ребра куба увеличили на 1 см. При этом дифференциал dV объема V оказался равным 12 сж3. Найти первоначальную длину ребер.
XIII.57. Радиус круга увеличили на 1 см. При этом дифференциал dS площади S оказался равным 6л см2. Найти первоначальный радиус круга.
XIII.58. С какой относительной погрешностью допустимо измерение радиуса R шара, чтобы его объем можно было определить с точностью до одного процента?
§7. ГЕОМЕТРИЧЕСКИЙ И ФИЗИЧЕСКИЙ СМЫСЛЫ ПРОИЗВОДНОЙ
Первый уровень
ХШ.59. Составить уравнение касательной к графику функции у = f(x) в точке графика с абсциссой Xq:
1)V=^2. ^0 = 2; 2) у = ^1, х0 = -1;
3) г/ = | >*0 = 1; 4) у = х • cosx, х0 =
5) у= | sin2 (4х- х0 =
6) у = cos (%х - + 2, xq =
XIII.60. Найти тангенс угла наклона касательной к графику функции у = /(х) в точке графика с абсциссой xq:
1) у = sin х, xq = д; 2) у = 1 — $х, xq = 1;
3) У = ^х~х > хо = О; 4) г/= х3 — 2х — 1, xq = — 1;
5) у = X2 Irfx, Xq = 1; 6) у = 31nx, Xq = 1.
ХШ.61. н айти угловой коэффициент касательной к графику функции у = f(x) в точке графика с абсциссой xq:
1) у = Зх - х3, х0 = -2;. 2) у = sin Зх, х0 =
3) У = хо = 3; 4) г/ = 1пх, х0 = 1.
1П о
§7. Геометрический и физический смыслы производной 271
XIII.62. Найти координаты точек пересечения с осями координат тех касательных к графику функции y = f(x), у которых угловой коэффициент равен k:
1) У=^, 2) у = х4 + 4х3-8х + 3, 6 = 8;
3) у = |х3 — х2 — х-Г 1, 6 = 2; 4) у=(х + 1)х/х, 6 = 2.
XIII.63. Найти координаты всех точек графика функции y — f{x\ в каждой из которых касательная, проведенная к этому графику, образует угол ф с положительным направлением оси Ох:
1) у = хА-4х3-х, ф=135°;
2) у = 2х3 -2х2 + х — 1, ф = arctg 3; r3 с 2
3) у=~з~ т- + 7х~4’ ^ = 45°;
4) у = 1-2sin2x, r)o = arctg2.
XIII.64. Составить уравнение касательной к графику функции y = f{x). параллельной оси абсцисс:
1) у=3х—х2; 2) z/=x2-4x; 3) у=х3 — 2х2 — 4х+2.
XIII.65. Составить уравнение касательной к графику функции _2
г/=5х 5+27 в точке графика с ординатой 32.
XIII.66. На графике функции у=[(х) найти координаты всех его точек, в которых касательная параллельна заданной прямой:
1) у—4х2 — 6х+3, у=2х]
2) z/=y—х2—х+1, у=2х— 1;
3) г/=\/1+х2, z/=0,5x-f-l; 4) у=х3—х, у=х.
XIII.67. Составить уравнение касательной к графику функции y~f{xY параллельной данной прямой:
1) /(х)=2+х—х2, х —z/+7=0;
2) /(х)=х2 —Зх+7, Зх —z/+2 = 0.
XIII.68. Составить уравнение касательной к графику функции y=f(x), перпендикулярной данной прямой:
1) /(х)=х2—х+1, Зх—у+8=0;
2) f(x) = 2x2 + 3x — 7, х+^+8=0.
272 Глава XIII. Производная и дифференциал
XIII.69. Найти координаты точки пересечения двух касательных, проведенных к графику функции у—cosx в точках графика а тг 7тг
с абсциссами х=- и х = — .
6 6
XIII.70. Доказать, что касательные, проведенные к графику функции у=—- в точках его пересечения с осями координат, параллельны между собой.
XIII.71. При каких р касательная, проведенная к графику функции у=х^—рх в точке графика с абсциссой Хд = 1, проходит через точку /И=(2; 3)?
XIII.72. Написать уравнение касательной к графику функции у=[(х) в точке с абсциссой Xq:
1) у=х2-е~\х\, х0=1; 2) z/ = |x2-|х||, х0 =—2.
XIII.73. Закон движения материальной точки по прямой имеет вид ^4 ч о
——4г + 16г. Определить, в какие моменты времени мгновенная скорость точки положительна.
XIII.74. 1) Материальная точка движется прямолинейно по закону х(£) = 3£2+4^+2 (х измеряется в метрах, t — в секундах). Найти путь, пройденный точкой с момента времени t—О к тому моменту времени, когда ее скорость стала равной 16 м/с.
2) Материальная точка движется прямолинейно по закону x(t) = ±t2+4t+2. Найти отношение средней скорости точки за время /=1 к ее мгновенной скорости в момент времени t=2.
XIII.75. Материальная точка движется прямолинейно по закону x(t). Определить с какого момента времени ее скорость будет:
1) больше 2, если x(/) = 3£+e9-z+38;
2) меньше 2, если x(f) = t—е4-*+41.
XIII.76. Тело, выпущенное с поверхности земли вертикально вверх, движется по закону /г(/) = 60/~5/3 (h измеряется в метрах, t— в секундах). Через сколько времени оно достигнет верхней точки своего подъема? Определить высоту, на которую ему удастся подняться.
XIII.77. Два тела совершают прямолинейное движение по законам Х1(^) = |/3 + ^2 + ^£+4 и %2(0~|^* +^£2 +12/+3, где t — О L / Э Z
§7. Геометрический и физический смыслы производной 273
время в секундах, xj(/) и — пути в метрах, пройденные, соответственно, первым и вторым телами.
В какой момент времени, считая от t=0, скорость движения первого тела будет в четыре раза меньше скорости второго тела?
XIII.78. Тело падает по закону h(t)=4+8t—5/2, где /г — высота падения в метрах, / — время в секундах. Найти скорость тела в момент соприкосновения с землей.
XIII.79. Человек, рост которого равен 1,8 м, удаляется от источника света, находящегося на высоте 12 м, со скоростью 50 м/мин. С какой скоростью перемещается тень от его головы?
Второй уровень
XIII.80. Составить уравнение касательной к графику функции y—f{x\ проходящей через заданную точку Л4=(хо;//о), не лежащую на графике:
1) у=х2-4х+4, Л4=(2;-4);
2) у=х2 —8х+12, Л4=(4,5;-4);
3) у=2х2 —4x4-3, Л4=(1,25;-2);
4) у=х2 — 4х, М(2; — 5).
XIII.81. Составьте уравнения всех общих касательных к графикам функций:
1) у=х2+4х+8 и у=х2+8х+4;
2) у=—х2+4х+1 и у=Зх2+4х4-|;
3) z/=x24-l и у=4х2-2;
4) у=х2 — х4-1 и у = 2х2—х4-0,5.
XIII.82. Написать уравнения касательной и нормали к графику функции у=/(х) в его точке с абсциссой хр:
1) г/=(х-1)(х-2)(х-3), хо=О;
2) х0 = л/2; 3) у = у/5-х2, х0=1;
l+xz
4) z/=arctg2x, xp = 0; 5) t/=In х ~2х+~, хр = 0;
х2+х + 1
6) у = е[~х\ х0 = -1.
274 Глава XIII. Производная и дифференциал
XIII.83. Найти уравнение касательной к графику функции y=f(x), образующей с осями координат равнобедренный прямоугольный треугольник:
1) г/=е2х-х+3; 2) y=21n х-х — 1.
XIII .84. Найти углы, под которыми пересекаются следующие кривые:
1) у=х2 и у=х3;
2) у — (х-2)2 и у = 4х-х2+4\
3) r/=sinх и у=с.о5х, хе[0; 2д];
4) х2 +у2 = 8ах и ^2 = 2^7‘
XII I.85. Найти величину угла, под которым парабола у=х2 видна из точки А = (2; — 1).
XI II.86. Найти геометрическое место точек, из которых парабола 2 у=х видна под прямым углом.
XII I.87. Найти все значения параметра а, при которых данная прямая касается графика функции у=[(х):
1) у=ах — 5, f(x) — 3x2 — 4х — 2;
2) у=3х+а, f(x)=2x2 — 5х+1.
XIII.88. Выяснить, является ли данная прямая касательной к графику функции z/=/(x):
1) г/=х4-2, f(x)=2x—Inх\ 2) у=\ — х, f(x)=x+e~2x.
XIII.89. Найти расстояние от начала координат до касательной / к графику функции у=х In х, параллельной оси абсцисс.
XIII.90. Найти расстояние от оси абсцисс до касательной к графику функции у=4 ln(x— 1)— х2, параллельной оси абсцисс.
XIII.91.
При каком значении k касательная к графику функции
y—kx2 образует с осью Ох угол, равный и отсекает
от 4-й четверти треугольник с площадью, равной
8>/Зэ
3 ’
Задачи повышенной сложности к главе ХШ 275
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ XIII
XIII.92. Найти производную функции y=f(x,\.
1) !/=2Kj_____ 2) у=У^}
3) У= x/arcctg^x; 4) </ = л/|о§з |пх; 5)/w=^+lnyrg.
XIII.93. Найти значения параметра а, при которых касательные к данным параболам образуют в точке их пересечения угол ср:
1) z/=x24-3x, z/=x24-x4-a; <р=^ и а> — 1;
2) z/=x24-3x —4, z/=x2—х4-а; <р~~ и а>— 2.
XIII.94. Окружность радиуса 1 с центром на оси Оу (z/>0) касается параболы //=х2. Найти координаты точки касания М и центра окружности С.
XIII.95. В какой точке параболы у—ах^-\-Ьх-\-с (а?^0) нужно провести касательную к ней для того, чтобы касательная проходила через начало координат?
XIII.96. Определить значения коэффициентов р и q, при которых: 1) парабола у=х^ -\-px-\-q касается прямых //=5x4-1 и z/ = -x-2;
2) парабола у=— 3x24-px4-Q касается прямых у=—5x4-4 и //=7x4-4.
v Ч-1
XIII.97. Найти уравнение касательной к кривой у='--, если
известно, что касательная проходит через точку Л4=(а,Ь). Сколько существует решений в зависимости от выбора точки М=(а, Ь)? Найти эти решения.
XIII.98. Две касательные к графику функции у= л/17(х24-1) пересекаются под прямым углом в некоторой точке на оси Оу. Написать их уравнения.
XIII.99. 1) Найти кратчайшее расстояние от параболы у=х2‘ — 8x4-16 до прямой у——2x4-1.
2) Прямая I проходит через точки (3;0), (0;4). Точка А лежит на параболе //=2х—х2. Указать координаты точки А, при которых расстояние от нее до прямой I будет наименьшим.
276 Глава XIII. Производная и дифференциал
XIII.100. В каких пределах изменяется величина х2 — Зу при условии (-^/-2)^1?
х- 2
ОТВЕТЫ К ГЛАВЕ XIII
XIII.4. 1) Ду = ЗДх; 2) Ду = -4Дх. XIII.5. 1) Ду = 2(Дх)2 + 4Дх; 2) Ду = 6Дх - (Дх)2. XIII.6. 1) 2; 2) -5. XIII.7. 1) 0; 2) -5; 3) -14; 4) -8. XIII.8. 1) 0,5; 2) -|. XIII.9. 1) /' (х0) = 4 (х0 - 3); 2) /'(х0) = 18х0 + 5. XIII.1O. 1) /,(х0) = -3(х0 + 1)2; 2) [' (х0) = (2х0 - 5)2. ХШ.И. 1) -192; 2) -100; 3) 4) 4; 5) -4; 6) XIII.12. 1) 0;
64 320
2) -0,5; 3) 4) XIII.13. I) -4,.Хо/О; 2) - 1 х0/-3;
2 2 4 (*о+3)2
3) -4. хо/О; 4) ———-д-. х0 / —1. XIII.14. 1) /<х0) = J ; .
*0 (*о + *) 2уЗ —х0
х0<3; 2) /'(х0)=^Ц,, х0>2; 3) f (х0) = -Д-. х0 # 0; 4) f (х0) = \М0 - 2 3 ЗД2
= —. , xq —1,5. XIII.15. 1) [' (х0) — — 2sin2%о; 2) /(х) = 12sin6x.
3у(2хо + 3)2
XIII.16. 1) /'(x0) = icos^; 2) /'(xo) = 2cos2x0. XIII.17. 1) f'(x0) = —1—, 2 2 cos Xn
x0 + £ + im, neZ-, 2) f (xn) =-------------i—, Xq / лп, n G Z. XIII.18. 1) He
2 sinz Xq
существует; 2) существует и равна 0. XIII.19. 1) Не существует; 2) существует и равна 0. XIII.20. 1) Существует и равна 0; 2) не существует; 3) существует и равна 0; 4) существует и равна 2. XIII.21. 1) [' (х) = < 2^’ * > j.’ в точке х = 1 производная не существует;
2х, х G (—оо; — 2) U (2; +оо), —2х, х € (-2; 2);
в точках х = ±2 производная не
существует. XIII.22. 1) a = 2,b=-l; 2) а=12, Ь = -16. XIII.23. 1) 21п2;
2) х/3 In 3. XIII.24. 1) 2) XIII.25. 1) 2lnO,5; 2) 1Д;
3) O,O4lnO,2; 4) 6ln6. XIII.26. I) 2) 3) Д^; 4)
2 In U,t> 4 In о Dino olnlU
XIII.27? 1) 10x°-2ln 10; 2) -e~xo. XIII.28. 1) —; 2) -----b—.
' ’ x0 + 5’ (x0 + l)ln3
XIII.29. 1) He существует; 2) существует и равна 1. XIII.30. 1) a — 1,
b = 1; 2)а=-пЦ, b = 2 - -b. XIII.31. 1) -2 + Зх2; 2) 5х4 - 4х;
’ 4 In 2 In 2
3)
2)
4)
Зх3 + 2х2 + х2 - 1 + 2-V; xz
№ 1. ХШ.ЗЗ. 1) 4= -
ух
4) - 3 - 2 +х-Зх2-8х3. XIII.32. 1) №3; хэ хч
1. ox J____J_. ох 1_____2_____5_ х/2.
с2’ 2^х vG?’ 3^2 3^5 2VT+ х2’
XIII.34. 1) 4; 2) 25; 3) 4) -18,25.
Ответы к главе ХШ 277
XIII.35. 1) cosx — xsinx;
4) tgx 4---4—; 5) 2xctgx —
cos2 x
XIII.36. 1) 2л. - 4; 2) 0.
XIII.38. 1) £2sxsin*-2E; 2) sin2 x
c\ -2x(l - x3) + 3x2(l - x2) } ’ (1-x3)2 ;
XIII.39. 1) -0,96; 2) -1^.
2) 3x2cosx — x3sinx; 3) —x2sinx — 2sinx;
-------2 tgx ; 6) 2sinx 4- (2x - 1) cosx. sin2x-cos2x
XIII.37. 1) -4; 2) 28; 3) -6; 4) -96.
— sinxx- cosx, q, 2x2 - 2x — 2 . -2x2 4- 2 .
x2 ’ (2x — I)2 ’ (x2—x4-l)2’
m 1 ~ nx2”-1 • (x3ri - 3x” - 2)
x/xO-^/x)2’ (x2" - I)2
XIII.40. 1) 1 4-lnx4-2x ln2; 2) 3х In3-3“xIn3;
(l + 7«ln7)lnx-l(x + 7-) |„x + l
3)--------(777^---------1 4) Til---------
2) ~ 4- 32 In 2. XIII.42. 1) -3e; 2) 0; 3) —2e2; 4)
2) ±2;±3; 3) - J + 7Ш, n G Z; 4) (-5;0);
6) (0;3) U (3;6). XIII.44. I) -2sin(2x + 13);
3) 2sin(l - 2x); 4) 5)
XIII.41. 1) -2;
3. XIII.43. 1)
5) [-1; 0) U (0; 1];
2) 3cos(3x - 1);
6) 9 • 69x+2 • In 6.
XIII.45. 1) 20(2x4-1)6 * * 9; 2) 6sin22x-cos2x = 3sin2x-sin4x; 3) cos3x-3xsin3x;
4) 15x4 sin2x5 cosx5; 5) 8(4x — l)cos(4x — I)2; 6) 2x tg2x 4- —
-5e +'. x
x 3Vx .
J 2(1 4-x3)’
1
4x(l - x2) ’
7)---Д==; 8) n ,,s^ ; 9) e~x(2x - x2). XIII.46. 1) —Д-;
71 - x2 2VI - cosx’ ’ v ! ’ sin4x
9x 3x2 - 2x ox 6x(log5(x2 4- I))2 . 4x 1___________ ’
(x3 — x2 4- 1) In 2 ’ (x2 4-1) In 5 ’ 2 Vx • cos2 Vx
XIIL47' '» утТт 2) 3>
5) X~x7^(yleX- ХШ-48-'>тА1)! 2)^’
4) OjT' 5) 27T; 6) XIII.60. 1) X, = 0,5, /L(x,) = -2,
/V(x1) = 2; 2) x, = 3, /L(xi) = —2, 7(x,) = 2; x2 = 5, /'_(x2) = -2, Д(х2) = 2;
3) X1=4, /1(х,) = -1. /;(x,) = l; 4) X| = —2, /'_(x1) = -4, /'+(x,) = 4; x2 = 2, f_(x2) = -4, /+(x2) = 4; 5) Xn = m, n G Z, f_(xn) =-72, f+(xn) = 72;
6) Xi = 1, x2 = 3 — точки разрыва функции; 7) xn = ^ + лп, nE Z, /L(xn) — 1,
/V(x„) = -1; 8) x, = -1, /L(xO =-1, /V(X!) = 1; x2 = 1, f'_(x2) = l, 4(x2) = -1. XIII.51. 1) 1; 2) —-j . XIII.53. 1) «0,485; 2) «5,833;
3) « 10,955; 4) « 1,938; 5) « 1,995; 6) « 0,02; 7) «-0,1; 8) « 0,0174;
9) 725. « 2,93; 10) « 1; 11) « 0,01; 12) -0,8. XIII.54. 1) « 0,97; 2) «1,0016; 3) «0,003; 4) « 3,98; 5) « 1,995. XIII.55. 1) 27a2 - x2dx-, 2) xsinxrfx; 3) arctgxrfx; 4) Inxdx. XIII.56. 2 см. XIII.57. 3 cm. XIII.58. XIII.59. 1) y = 2x-2\ 2) z/ = x4-l; 3) z/ = 0; 4) z/=^-^x;
5) у = 73x4- | 6) у = -ТЗх 4- 7rv^+3. XIII.60. 1) tg(p = -1;
278 Глава XIII. Производная и дифференциал
2) tg? = 3)tg?=l; 4) tg?=l; 5) tg? = 1; 6) tgtf = 3.
XIII.61. 1) 4 = —9; 2) 4 = 1,5; 3) k = 4) 4 = 1. XIII.62. 1) (-1;0),
(3;0), (0;-3), (0; I); 2) (l;0), (0;-8). (0; 19), (-^;0); 3) (0;-8). (4;0), (fl;?), (-!;<)); 4) (0;0), (0;A), (-A;o) . XIII.63. 1) (0;0), (3;—30); 2) (l;0), 3) (2;|), (3;3,5); 4) (-5 + m; fl), n 6 I.
XIII.64. 1) y= 2,25; 2) (/=-4; 3) у = -6. у-3^. XI11.65. у = -2x + 34. XIII.66. 1) (1;1); 2) (3;-2), (-1; |) ; 3) Ц; ; 4) (±ДЧ\/1)-XIII.67. 1) x - у + 2 = 0; 2) Зх - у - 2 = 0. XIII.68. 1) Зх + 9у - 8 = = 0; 2) 2х - 2у - 15 = 0. XIII.69. ^3^ + 2л._^ XIII.71. При
р = 0,5. XIII.72. 1) у = 2) р = —Зх — 4. XIII.73. t G (0; 4) U (8; +oo).
XIII.74. 1) 20 м. 2) XIII.75. 1) t>9. 2) t > 4. XIII.76. Через 2 c на высоту 80 ж. XIII.77. 2,5c. XIII.78. 12>и/с. XIII.79. m/muh. XIII.80. 1) y= — 4x +4 и у — 4x — 12; 2) у — 2x — 13 и у - — 4; 3) // = —4x4-3 и у = 6x — 9,5; 4) у — —2x — 1 и у = 2х — 9. XIII.81. 1) у = 8х 4- 4;
2) у = 2х + 2, у = 6х + 2; 3) у — 4х — 3 и у = — 4х — 3; 4) у = — Зх и у — х. XIII.82. 1) Касательная у = Их — 6, нормаль у = — у[Х — 6; 2) касательная
2 , 8^2 9 23V2 о
у = --х-\——, нормаль у = -х-----—; 3) касательная у — — Зх, нормаль
У — ^ 4) касательная у — 2х, нормаль у = — ^; 5) касательная у = 2х, нормаль у = — |; 6) касательная у = 2x4-3, нормаль р = — ^ 4-^- XIII.83. 1) у = х4-4; 2) у — х — 3. XIII.84. 1) В точке М[ = (0; 0) угол равен 0 (параболы 18 г~
касаются), в точке М2 = (1; 1) угол равен arctg-; 2) arctg — ; 3) -arctg2v2;
4) | и XIII.85. arctg XIII.86. у = -0,25. XIII.87. 1) a = -10 и a = 2; 2) a = —7. XIII.88. 1) Нет; 2) да. XIII.89. k XIII.90. 4. XIII.91. XIII.92. 1) 2^ - In2- lnx.~ 2) £ • 3^^ • In 3• Tsinx • cosx;
10 lnzx 2
34____________________. 44 _________1__________. x arcsin x
Ay/arcctg^/x- (1 +x)y/x> ' 2 • yiogg Inx • In 3 • lnx-x’ ^(1 - x2)3’
XIII.93. 1) -2+У|; 2) -6 + 2%/7. XIII.94. Два возможных положения окружности: 1) М = (0;0), С = (0; 1); 2)Л4=(±^;|), С = (О; .
XIII.95. При ас > 0 в точках (\/1;2б?+й\/Т)и (~71;2с_&71) ; при с = 0 в точке (0; 0), при ас < 0 решений нет. XIII.96. 1) р = 3, q = 2;
Ответы к главе XIII 279
12 2
2)р=1, <7=1. XIII.97. Одна касательная у = —^х-\----pl, где xq = -—-
Xq xq b - 1
при a = 0 и 6 7 1, xq = | при а 7 О и 6 = 1; х0 = при а^О и b = 1 + 1 , 2 , . -1 ± 71 +а(1 - 6)
две касательные и = —ух Н-----1- 1, где Хп —---\7при а > О,
х£ х0 ’ 1 -ь
6^1, 6 < 1 + и при а < 0, b / 1, b > 1 + |. В остальных случаях (а = О, 6=1, а > О, 6 > 1 + |, а < О, 6 < 1 + ^) искомой касательной не существует. XIII.98. у = х + 4 и у—— х + 4. Указание: поскольку данная функция — четная, искомые касательные к ее графику симметричны относительно оси 6 у?
ординат. XIII.99. 1) ; Указание: провести касательную к параболе,
(5 5 \
3? g ) • XIII.100. [21;+оо).
Глава XIV
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ
§1. ОСНОВНЫЕ ТЕОРЕМЫ ДЛЯ ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ
Первый уровень
XIV.1. Не вычисляя производной, объяснить, почему внутри указанного отрезка функция у = /(х) имеет точку, в которой производная этой функции равна нулю:
1) /(х) = —х2 + 4х + 5, [-4;-2];
2) /(х) = -х3 + Зх, [—1;2];
3) /(х) = х3 + Зх, [0; — 3];
4) f(x) = sinx,
XIV.2. Дана функция y — f(x). Внутри заданного отрезка [а,/?] найти точку с, для которой справедливо равенство
‘ ' Ь — а ’
1) /(х)=х2, а = 1, 6 = 4;
2) Дх)=х3, а = — 2, b = 1;
3) f(x) = у/х, а = 4, 6 = 16;
4) /(х) = tfx, а = —8, 6=1;
5) /(х) = 4х3 — 5х2 + х — 2; а = 0, 6 = 2.
XIV3. Через две точки А и В графика функции /(х) = х2, с абсциссами а и 6 соответственно, проведена секущая АВ. Через точку С с абсциссой сЕ (а, 6) проведена касательная к графику этой функции, параллельная секущей АВ. Доказать, что справедливо равенство _ а + Ь
2 ‘
XIV.4. 1) Доказать, что уравнение: х3 + Зх —6 = 0 имеет только один действительный корень.
2) Доказать, что уравнение: х3 + 9х2 + 2х — 48 = 0 не имеет кратных корней.
§2. Возрастание и убывание функции 281
XIV.5. Можно ли на отрезке [— 1; 1] применить к функции f(x) = 2 - v^2 :
1) теорему Ролля;
2) теорему Лагранжа о конечных приращениях?
Второй уровень
XIV.6. Доказать, что:
1) arcsinх + arccosх =
2) arctg х + arcctg х =
3) arcsin -----
1 + X2
' — 71 — 2 arctg х, если х^—1, < 2arctgx, если — l^x^l, л:—2arctg х, еслих^1;
4) 3 arccosх — arccos(3x — 4х3) = тг (—0,5 < х < 0, 5).
XIV.7. Доказать, что уравнение Зх+2 - 26х = 29 имеет не более двух различных действительных корней.
XIV.8. Доказать, что если число х\ является корнем кратности k для многочлена Р(х), то для производной Р'(х) он будет являться корнем кратности k — 1.
§2. ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ
Первый уровень
Найти промежутки возрастания и убывания функции (XIV.9-
XIV.12) XIV.9. 1) у = х3 — 2х2; 2) у = х3 + х2 — 16х — 2; 3) у = х2(х + 1); 4) у = х3(х —5).
XIV.10. 1) 3>/М = 24з’ 4) /(х) - -JX5 X)
XIV.11. 1) Дх) = х (s/x - 1); 2) Дх) = - tyx.
XIV.12. 1) Дх)=х —21пх; 2) Дх) = х1пх; 3) Дх) = 21п(х — 2) — х2 + 4х + 1; 4) Дх) = -61п х + 2х2 + 5х + 11.
282 Глава XIV. Применение производной к исследованию функций
XIV.13. 1) Доказать, что функция /(x)=2x + sinx возрастает на всей числовой оси;
2) доказать, что функция Дх) = cos2 х — Зх убывает на всей числовой оси.
Второй уровень
Найти промежутки возрастания и убывания функции (XIV.14- XIV.18)
XIV. 14. 1) z/ = x\/l — х2; 2) у = 2$2х-1-х.
XIV.15. О у= Д; J In Л 2) у = Inх — arctgx.
XIV.16. 1) у — х — 2 sin х; 2) у — cos 2х - х.
XIV.17. 1) Дх) = 4х — 5 • 2х + (21п2)х; 2) Дх) = 1, 5 In2 х - In3 х
XIV.18. 1) Дх) = |х4 — 8х|; 2) Дх) = |х-х3|.
XIV.19. 1) Найти все значения параметра а, при которых функция
= ^х3 + (а —1)х2 + 2х + 1 возрастает на всей
числовой оси;
2) найти все значения параметра а, при которых функция
Дх) = (а + 2)х3 — Зах2 + 9ах — 2 убывает на всей
числовой оси.
XIV.20. 1) При каких значениях параметра а функция Дх) = 2 • ех — a • е~х + (1 + 2а)х - 3 возрастает на всей числовой оси?
2) При каких значениях параметра с функция Дх) = (с — 3) • 5х — (Зс + 4) • 5-х + 7 возрастает на всей числовой оси?
§3. ЭКСТРЕМУМЫ ФУНКЦИИ
Первый уровень
XIV.21. Найти критические точки функции:
1) /(х) — х + sin 2х; 2) Дх) =-\/Зх + cos 2х.
XIV.22. Найти экстремумы функции:
1) Дх) = ^—х2; 2) Дх) = х3 + Зх2 — 9х + 1;
3) Дх) = х2 (1 - х); " 4)J/(x) = х3 (1 + ;
5)- Дх) = 2х3 + Зх2 — 12х + 5; 6) Дх) = (х — 4)2х2.
§3. Экстремумы функции 283
Найти точки экстремума функции (XIV.23-XIV.27), XIV.23. 1) Дх) — 2x^7+ 3х - 12^+1; 2) Дх) = - %.
XIV.24. 1) Дх) = ^-^;
XIV.25. 1) Дх) = x + cos %;
XIV.26. 1) у = х-е~3х-, xiv.27. 1) « = Л;
1пх
2) =
' 2). Дх) = 2 — х + sinx.
2) у = (2х-1)-е3+
2) У = +•
Второй уровень
Найти точки экстремума функции (XIV.28-XIV.31).
XIV.28. 1) /(х) = 2 sin'^ + sin х + х + 3;
2) Дх) = (1 + cosx) sinx.
XIV.29. 1) Дх) = \/3 cos | + sin — ^-5-:
2) Дх) = sin 2х + | cos 2х — XIV.30. 1) Дх) = х2 — 1п(1 + 2х);
2) Дх)=21п|+х(0,5х-3).
XIV.31. 1) у = е2х-2+-4х ^2;
2) у = —2 • З"4*2 - 2 • З-3*2 + З"2*2 + 1.
XIV.32. При каждом значении параметра а найти критические точки функции Дх) = (2х — 1) • у/х — а.
XIV.33. При каких значениях параметра b точка xg = b является точкой максимума функции у= |х3 — (Ь — 2)х2 — 46х + 3?
XIV.34. При каких значениях параметра а функция Дх) = х3 + 3(а — 7)х2 + 3 (а2 — 9) х + 1 имеет положительную точку максимума?
XIV.35. Пусть Х[, Х2 — соответственно точка максимума и точка минимума функции Дх) = 2х3 — 9ах2 + 12а2х + 1. Найти о значения параметра а, при которых х^ = х%.
284 Глава XIV. Применение производной к исследованию функций
§4. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ
Первый уровень
Найти наибольшее и наименьшее значения функции на указанном отрезке (XIV.36-XIV.38),
XIV.36. 1) Дх) = х3 - Зх2 + Зх + 2, хе [—2;2];
2) Дх) = Зх4 + 4х3 + 1, хе [-2; -0, 5];
3) /(х) = 4х- X 6 [0,5; 1];
4) Дх) = Зх5 - 5х3 + 1, х G [-2; 2];
5) Дх) = х2 (х2 — 8) — 9, хе [—1;3];
6) Дх) = у+х2 + 1, хе [—3; — 1].
XIV.37. 1) хе [-3; 0] ; 2) г/ = х-рА, хе [_2;—1];
3) у=-Л-. хе[-4;0]; 4) у= 1^, х е [-1;3].
+4 4 + х.
XIV.38.
1)
2)
У = X + COS2 X,
X . .9
У = к + Sirrx, 2
0- -1 •
’ 2] ’ _ я. я' ”2 ’ 2.
X 6
X 6
XIV.39. 1) Число 18 представить в виде суммы двух положи-
тельных слагаемых так, чтобы сумма их квадратов была наименьшей.
2) Число 10 представить в виде суммы двух положительных слагаемых так, чтобы сумма половины квадрата / первого слагаемого и куба второго была наименьшей.
3) Число —10 представить в виде суммы двух слагаемых так, чтобы сумма их кубов была наибольшей.
4) Число 12 представить в виде суммй двух слагаемых так, чтобы сумма их кубов была наименьшей.
XIV.40. 1) Число 180 разбить на три положительных слагаемых так, чтобы два из них относились как 1 : 2, а произведение трех слагаемых было наибольшим.
2) Число 26 представить в виде суммы трех положительных слагаемых так, чтобы сумма их квадратов была наименьшей и чтобы второе слагаемое было втрое больше первого.
§4. Наибольшее и наименьшее значения функции 285
XIV.41. 1) Периметр прямоугольника равен 12 м. Какими должны быть длины сторон, чтобы его площадь была наибольшей?
2) Из всех прямоугольников площади 100 ж2 найти тот, периметр которого наименьший.
XIV.42. В зоопарке куском веревки длиной 100 м огораживают загон для зверей, имеющий форму равнобедренного треугольника, основанием которого служит стена павильона. Каким следует выбрать основание треугольника, чтобы его площадь была наибольшей?
XIV.43. Определить размеры открытого бассейна объемом 32 ж3 с квадратным дном, на облицовку дна и стен которого затрачивается наименьшее количество материала.
XIV.44. Среди всех равнобедренных трапеций с острым углом 45° и суммой длин высоты и большего основания, равной а, найти трапецию наибольшей площади.
XIV.45. Сумма двух сторон треугольника равна а, а угол между ними равен 30°. Каковы должны быть длины сторон этого треугольника, чтобы его площадь была наибольшей?
XIV.46. Найти минимум суммы квадратов длин всех сторон параллелограмма, если известно, что сумма длин диагоналей этого параллелограмма равна 8.
XIV.47. Найти наименьшее значение площади круга, описанного около прямоугольного треугольника площади 10.
XIV.48. В полукруг радиуса 2 вписан прямоугольник наибольшей площади. Найти его площадь.
XIV.49. Найти радиус круга, в который можно вписать прямоугольник наибольшей площади с периметром, равным 56 см.
XIV.50. Найти длину бокового ребра, при котором объем правильной четырехугольной призмы наибольший, если диагональ ее боковой грани равна 6.
XIV.51. 1) Найти наибольшее значение объема цилиндра, площадь полной поверхности которого равна 6л.
2) Требуется изготовить закрытый цилиндрический бак объемом 16тг. Какими должны быть его размеры, чтобы на его изготовление ушло наименьшее количество материала?
286 Глава XIV. Применение производной к исследованию функций
XIV.52. 1) Найти наименьшее значение диагонали осевого сечения цилиндра, площадь боковой поверхности которого равна 50тг.
2) Найти наибольшее значение объема цилиндра, диагональ осевого сечения которого равна л/З-
XIV. 53. 1) Найти наименьшее значение длины образующей конуса, объем которого равен 18тг.
2) Найти наибольший объем конуса, образующая которого имеет длину 3.
XIV.54. По двум взаимно перпендикулярным дорогам к перекрестку движутся две машины со скоростями 40 км/ч и 50 км/ч соответственно. В данный момент они находятся от перекрестка на расстоянии 20 км и 30 км соответственно. Через сколько времени расстояние между машинами будет наименьшим?
XIV.55. Движение первой и второй материальных точек вдоль одной прямой заданы, соответственно, уравнениями $1(£) = t3 — 3t2 + 3t + 2 и S2(t) = - t2, где t —
время в секундах, si(Z) и s<2(t) — пути в метрах. Найти наименьшую скорость первой точки в промежутке убывания скорости второй точки.
Второй уровень
Найти наибольшее и наименьшее значения функции на указанном отрезке (XIV.56-XIV.60),
XIVT56. 1) /(х)=х —21пх, %е[1;е];
2) /(х) = 1п(2х) — х2 + х, хе [0,5; 2].
XIV.57. 1) у = >/хТТ - х е [0; 1];
2) // = х + у/3 — х, х е [—6;3].
XIV.58. 1) /(х) = (Зх2 —'7х + 1)ех, х 6 [О; |] ;
2) Дх) = е2-^1 + 2 • е1-2х + 7х - 3, хе [0,14; 1).
XIV.59. 1) у = 24х — cos 12х — 3 sin 8х, 5
2) у = 18х — sin 9х + 3 sin 6х, хе тн •
J L 18 18.
XIV.60. 1) у = х 1пх — х In 5, х е [1; 5];
2) у — 2х2 — 1пх, х е [1;е].
§4. Наибольшее и наименьшее значения функции 287
Найти наибольшее и наименьшее значения функции на указанном отрезке (XIV.61-XIV.64).
XIV.61. 1) //= 2 • 23х - 9 • 22х + 12 • 2х, х G [—1; 1];
2) у = 2 • З3х - 4 • 32х + 2 3х, х G [—1; 1].
XIV.62. 1) у = In3 х - 6 In2 х — 15 In х, хе[е-2;е3];
2) у = 2 log2 х - 15 log2 х + 36 log2 x, x e [4; 16].
XIV.63. 1) y = 3\/3 • sinx- sin 2x, xG ;
2) у = 2 sin 2x + cos 4x, x G ^0; .
XIV.64. 1) у = (x - 2)2 • Ух2-4х + 6, x g [1; 4];
2) y = (x + 1)2\/x2 + 2x + 3, xG [—3;0].
XIV.65. Найти наибольшее и наименьшее значения функции и указать все значения х, при которых они достигаются: 1) /(х) = 3sin2х — 2cosx + cos2x — 4;
2) /(х) = 3 — 2 sin2 2х — 2 cos 2х.
XIV.66. Найти множество значений функции на указанном отрезке:
1) у = 2cosx - sin2х, х G [— ;
2) у = sin3 х + 2 cos3 х, х G [О; .
XIV.67. Найти множество значений функции:
1) Дх) = sin х • cos 2х;
2) Дх) = cosx • sin 2х.
XIV.68. 1) Найти наименьшее значение функции
у = — 12х3 + 15х2 + 36х — 301 на отрезке [—3;2].
2) Найти наибольшее значение функции
у = |(х + 1) (2х — 5)2| на отрезке [—5;4].
XIV.69. Найти наибольшее и наименьшее значения функции на указанном отрезке:
1) у = 4х3 — х|х — 2|, х G [0: 3];
2) у = 2х|х + 2| — х3, х G [—3;0].
XIV.70. Найти множество значений функции Дх) = |х2 + 2х — 3| + + 1,5-1пх на отрезке [0,5;4].
288 Глава XIV. Применение производной к исследованию функций
Найти наименьшее значение функции на указанном промежутке (XIV.71-XIV.72)
XIV.71. 1) у = 2х3 + Зх2 - 120х + 100, хе (-4;5];
2) У = ’ + х е (0; 1).
XIV.72. 1) у = -№-х, х е [1; +оо);
2) у = --Х, хе[-5;0). + 1
XIV.73. Найти наибольшее и наименьшее значения функции на указанном промежутке (если они существуют): 1) # = 3х —tgx, хе [0;£) ;
2) у = Зх + 2 ctgx, х е (О; .
XIV.74. Определить, в какой точке промежутка (О; функция у = tgx + 0, 75 ctgx принимает наименьшее значение.
XIV.75. Определить, при каком значении параметра а функция у= (\/3ctgx + а2)3 • tgx достигает наименьшего значения на промежутке (б; в точке х =
XIV.76. Доказать справедливость неравенства на указанном промежутке:
1) 2х + 4, > 5, 0 < х < 0, 5; 2) х2 — х3 < |, х 0;
— х2 °
3) х2 — 1^21пх, х > 1; 4) 6х — 41пх^х2, 0 < х 4;
5) 8х — 61пх^х2, 0 < х 4; 6) 1п(1+х)<х, х > 0;
7) 2д/х > 3 — | при х > 1; 8) ех>1+х при х ф 0;
9) 1 — у cosx, х 0; 10) х - у sinx, х 0.
XIV.77. Даны точки А = (0; 3) и В = (4;5). Найти на оси Ох точку М такую, чтобы 5 = ЛМ + Л4Д было наименьшим.
XIV.78. На координатной плоскости даны точки Д = (—2; 0), В = (0; 4) и прямая I: у = х. При каком положении точки М на прямой / периметр треугольника АВМ будет наименьшим?
XIV.79. Корабль стоит на якоре в 9 км от ближайшей точки берега. С корабля можно послать матроса в лагерь, расположенный в 15 км, считая по берегу, от ближайшей к кораблю точки берега (лагерь расположен на берегу).
§4. Наибольшее и наименьшее значения функции 289
XIV.80.
XIV.81.
XIV.82.
XIV.83.
XIV.84.
XIV.85.
XIV.86.
XIV.87.
Если матрос передвигается пешком со скоростью 5 км/ч, а на веслах — 4 км/ч, то в каком пункте берега он должен пристать, чтобы попасть в лагерь в кратчайшее время?
На графике функции у = у/х, х G [1;9], найти такую точку М, для которой имеет наибольшее значение площадь треугольника АМВ, где А и В —точки графика с абсциссами 1 и 9 соответственно.
В равнобедренной трапеции меньшее основание и боковая сторона равны а. Найти большее основание трапеции наибольшей площади.
Длина всей границы кругового сектора равна /. Каким должен быть радиус сектора, чтобы площадь сектора была наибольшей?
Найти косинус угла при вершине равнобедренного треугольника, имеющего наибольшую площадь при данной длине I медианы, проведенной к его боковой стороне.
В равнобедренный треугольник с основанием а и высотой h вписан прямоугольник так, что две его вершины лежат на основании треугольника, а две другие — на боковых сторонах. Какова должна быть высота прямоугольника, чтобы он имел наибольшую площадь? Найти эту площадь.
1) На окружности радиуса 2 дана точка А. Хорда ВС проведена параллельно касательной к окружности в точке А так, что площадь треугольника АВС наибольшая. Найти расстояние от точки А до хорды ВС.
2) Найти угол при вершине равнобедренного треугольника наибольшей площади, вписанного в окружность радиуса R.
Каким должен быть угол при вершине равнобедренного треугольника заданной площади S, чтобы радиус вписанного в этот треугольник круга был наибольшим? В прямоугольный треугольник с гипотенузой 24 см и углом 60° вписан прямоугольник, основание которого лежит на гипотенузе. Каковы должны быть длины сторон прямоугольника, чтобы его площадь была наибольшей?
10—5682
290 Глава XIV. Применение производной к исследованию функций
XIV.88. Найти углы прямоугольного треугольника, в котором отношение радиусов вписанной и описанной окружностей будет наибольшим.
XIV.89. Высота прямоугольного треугольника, опущенная на гипотенузу, равна h. Какую наименьшую длину может иметь медиана, делящая пополам больший катет?
XIV.90. Среди всех конусов, периметр осевого сечения которых равен 8, найти конус с наибольшим объемом и вычислить этот объем.
XIV.91. Определить наибольший объем правильной треугольной пирамиды, у которой апофема равна 2\/3.
XIV.92. Объем прямой треугольной призмы равен V. В основании призмы лежит равносторонний треугольник. Какова должна быть сторона основания, чтобы полная поверхность призмы была наименьшей?
XIV.93. Диагональ прямоугольного параллелепипеда имеет длину d и образует с двумя смежными боковыми гранями равные углы, величина которых равна а. Найти значение а, при котором объем параллелепипеда будет максимальным.
XIV.94. Рассматриваются всевозможные треугольные призмы, у которых все боковые грани имеют периметр, равный а. Найди среди них призму с наибольшим объемом (в ответе указать боковое ребро призмы).
XIV.95. Рассматриваются всевозможные правильные четырехугольные призмы с площадью боковой поверхности а2. Какой наибольший объем может иметь такая призма?
XIV.96. Одно из оснований цилиндра является сечением шара, а другое основание принадлежит большому кругу этого шара. Радиус шара равен R. Какой должна быть высота цилиндра, чтобы его объем был наибольшим?
XIV.97. Прямоугольный параллелепипед вписан в шар радиуса R. Найти площадь поверхности параллелепипеда, если он имеет наибольший возможный объем.
XIV.98. Определить высоту конуса, вписанного в шар радиуса R и имеющего наибольшую площадь боковой поверхности.
XIV.99. Определить высоту конуса, вписанного в шар радиуса R и имеющего наибольшую площадь полной поверхности.
§5. Производные второго порядка 291
XIV.100. Определить высоту конуса, описанного около шара радиуса R и имеющего наименьший объем.
XIV.101. Найти высоту конуса наименьшего объема, описанного около полушара радиуса R = \/3 так, чтобы центр основания конуса лежал в центре шара.
XIV.102. Вокруг шара радиуса г описана правильная треугольная пирамида с высотой Н. При каком значении Н площадь боковой поверхности пирамиды наименьшая? Найти это наименьшее значение.
XIV.103. Все вершины правильной треугольной призмы принадлежат сфере радиуса R. Какой должна быть высота призмы, чтобы ее объем был наибольшим?
XIV.104. Найти высоту треугольной пирамиды наибольшего объема, вписанной в шар радиуса R.
XIV.105. Найти наибольший объем цилиндра, вписанного в конус высотой Н с радиусом основания R.
XIV.106. В правильную четырехугольную пирамиду с высотой Н и стороной основания а вписан прямоугольный параллелепипед, основанием которого является квадрат со стороной Ь, так, что его нижнее основание лежит на основании пирамиды, а вершины верхнего основания лежат на боковых ребрах пирамиды. При каком значении b объем вписанного параллелепипеда будет наибольшим? Найти объем при этом значении Ь.
§5. ПРОИЗВОДНЫЕ ВТОРОГО ПОРЯДКА. ВЫПУКЛОСТЬ И ТОЧКИ ПЕРЕГИБА
Первый уровень
XIV.107. Найти производную второго порядка функции:
1) у = х4 - Зх2 - Зх + 2; 2) у = х^/х + ~^= - %;
3) У ~ 2%+ 4 ’ 4) i/= sin 2х — cos Зх;
5) у = (х + 1) sin 5х; 6) у — е2х + ех + Зе-Х;
7) у = х In (1 - х2) ; 8) у = 1П^’-
XIV.108. Найти вторую производную функции в указанной точке:
1) У = + 4 “ 4’ х = 2; 2) У = ГГТЗ’ х =
292 Глава XIV. Применение производной к исследованию функций
3) z/ = tg2x-x, х =-\ 4) у = (Зх + 4)2Х, х = 0.
О
XIV.109. 1) Точка движется по закону s(/) = t + 3£2 + |^3 (s измеряется в метрах, t— в секундах). Найти ее
ускорение через
2) Точка движется в метрах, t— i ускорения через Найти интервалы выпуклости XIV.111)
XIV.110. 1) z/ = x4 —6х2 + 4;
3) у = 2х-^;
XIV.111. 1) //-sinx;
о с после начала движения.
по закону s(t) = 9\/? (s измеряется секундах). Найти величину ее
9 с после начала движения.
1 точки перегиба функции (XIV.110-
2) у = 2х3 - 9х2 + 8х;
4) г/ = Зх2 - If. xz
2) у = x + cos х.
Второй уровень
Найти интервалы выпуклости и точки перегиба функции (XIV.112-
XIV.114)
XIV.112. 1) y = x2 + vx; 2) У=^-
XIV.113. 1) у = s/(x-2)5 + 4; 2) //= #хТТ - \/х^Т;
3) у =/J/(l-x)2 + \/(1 + х)2; 4) у = У1 + х3.
XIV.114. 1) у = arctg Ь 2) у = earcts\
XIV.115. Найти интервалы выпуклости, точки перегиба и угловые коэффициенты касательных в точках перегиба функции: 1) у = хе2х + 1; 2) у = х31пх + 1.
§6. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
Первый уровень
Найти асимптоты графика функции у = f(x) (XIV.H6-XIV.H7),
XIV.116. 1) У = 4 —Зх. 2) У = 1 + 2х.
х ’ х — 1 ’
3) У = 2х — 1. 4) У = 2, 5 — х.
3 — х ’ 2х-5 ’
5) У = 4 cosx — Зх. 6) У = 4 — Зх cosx.
х ’ X 1
7) У = х3 — Зх: 8) У = —х4 + 5х - 3
§6. Построение графиков функций 293
XIV.117. 1) у = X2 . х —5’ х% T- х T- 3 х Я-1 2) =
3) у = 4) у = ~ с2 + 4х — 1 х — 2
Исследовать XIV.118. 1) 3) XIV.119. 1) 3) 5) XIV.120. 1) функцию и построить ее г/ = Зх3 — х Ч-2; 2) у = -х3 + 4х; 4) у = х4 - 2х2 + 5; 2) //= х4 - уХ3 + 8х2; 4) у = х4 - 8х2 — 9. у=ъ + -х> 2) „_2х2 + 1. график (XIV.118-XIV.121) у = х3 — Зх2 + 2; у = х3 - 9х2 + 24х - 1. у = х4 - 6х2 + 9; у = £ (х - I)2 ; х2 + 2х + 1
XIV.121. 1) У У = 2х ’ х 4- 2) 2 + х х2 + х — 2
% х’ х + 1
Второй уровень
Найти асимптоты графика функции у = /(х) (XIV.122-XIV.123).
XIV.122. 1) у= х2 + л:.+2; 2) (/=^±4;
1 + Х£ 1 + X 1
3) У = ^-, 4)'/ = 1f4;
xz xL — 4
5) У = 2х2 Д-1’ 6) У = х2-Зх + 2’
wr w w г а л |\ sinx о\ cosx
XIV.123. 1) У= —2) //=——;
4х2 + х — 5sin(4x2 + х)
3) у = X + Sin X; 4) у = -----------
Исследовать функцию и построить ее график (XIV.124-XIV.138)
XIV. 124. 1) X2 . 1 + X ’ 2) У = 3 — х2 х + 2
XIV.125. 1) х х2 - 1 ’ 2) У = х — 1
XIV.126. 1) У = 2х2 + Зх — 4 . х2 ’ 2) У = х2 — 2х — 3 (х-1)2
XIV.127. 1) У = + 4; xz 2) У = ^—7 +Х. (х-1)2
294 Глава XIV. Применение производной к исследованию функций
XIV.128. XIV.129. и _ 2х 1+х2’ _ X2 . х2 + 3 ’ 2) 2) У = У = X -I- 1 х2 + х + 1 х2-1 х2 + 4’
1) У У
XIV.130. 1) У х2 — 4 ’ 2) У = х2 — 9 х2 — 4
XIV.131. XIV.132. 1) 1) У У _ X 2) 2) У = У = 3 — х
х2-!’ _ X3 . х2 — 6х + 8 X3
х2 — 4 ’ 2(х+1)2’
XIV.133. 1) У _ х3 + 2. ~ 2х ’ 2) У = (I-*)3 1 — 2х
XIV.134. 1) У = (х - 1)3(х - 2)2; 2) У = |х3(х2 - 5).
XIV.135. 1) У = (3 -x)Vx; 2) У = s/x (4 + х);
3) У 3/ 9 = vx2 — х; 4) У = х\/4 — х2;
5) У _ х 6) У = y/x + l + s/x — 1.
\/1 + X2
XIV.136. 1) У = 2 sin х + sin 2х; 2) У = sinx cos 2х.
3) У = sin3 х + cos3 х; 4) У = sin2 х
2 + sin х ’
XIV.137. J) У = х arctgx; 2) У = 2x + 4 arcctgx.
XIV.138. 1) У _ i = е 2) У = xe~x;
3) У _ g2x-x2. 4) У = ln(x + 1) - x;
5) У = X2 in X.
В зависимости от значений параметра а определить число корней уравнения (XIV.139-XIV.140).
XIV.139. 1) 1 + 4% = а\ 2) i - х = а. X X
XIV.140. 1) х3 - Зх2 - а = 0; 2) 4х3 - 15х2 - 18х - 3 = а.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ XIV
XIV.141. При каких значениях параметра а функция /(х) = (1 + а)х + 2 sin — (8а + 4) sin имеет на
интервале х Е (—5д; 11 д) четыре экстремума?
XIV.142. Доказать, что функция у = Зх4 — 4х3 + 6х2 + ах + b при любых а и b имеет только одну точку экстремума.
Задачи повышенной сложности к главе XIV 295
XIV.143. 1) При каких значениях параметра а функция /(х) = -х-----------------— х + 2% + а имеет на промежутке
(—2; 0) ровно один экстремум?
2) При каких значениях параметра а функция г/ \ аз а + 82 ,4
Дх) = -х°-----— х + a имеет на промежутке
(0; 2) ровно один экстремум?
XIV.144. 1) При каких значениях параметра а функция /(х) = х3 — 1, 5ах2 — 36а2х + а3 является монотонной на отрезке [—1;2]?
2) При каких значениях параметра а функция г/ \ з 3 2 4 2 5
f\jc) = х^ ~ ~ax ~-a x + а не является монотонной на отрезке [—0, 5; 1]?
XIV.145. 1) При каждом значении параметра а (а > 1) найти а2 1 наибольшее значение функции /(х) = —— ——- на отрезке [3;4].
2) При каждом значении параметра а найти наименьшее значение функции /(х) = ----------Ц----~ на отрезке
х4 — 4ах2 + 5а2
1-1; 2).
XIV.146. Доказать справедливость неравенства
In2 х > In (х — 1) 1п(х + 1) при х > 2.
XIV.147. Решить неравенство:
1) \/х + 7 + л/11 — х Зу/х2 - 4х + 20;
2) V30 + 2х + х/42 - 2х > 4 Ух2 - 6х + 90.
XIV.148. 1) В две бочки были налиты различные растворы соли, причем в первую бочку налито 16 кг, а во вторую — 25 кг. Оба раствора разбавили водой так, что процентное содержание соли уменьшилось в п раз в первой бочке и в m раз во второй. О числах п и m известно только, что mn = m + n + 3. Найти наименьшее количество воды, которое могло быть долито в обе бочки вместе.
2) В два сосуда налиты различные растворы соли, причем в первый сосуд налито 25 кг, а во второй — 36 кг.
296 Глава XIV. Применение производной к исследованию функций
При испарении воды процентное содержание соли в первом сосуде увеличилось в т раз, а во втором сосуде — в п раз. О числах т и п известно только, что тп + т = 4. Какое наибольшее количество воды могло испариться из обоих сосудов вместе?
XIV.149. 1) При каких значениях параметра р наименьшее на промежутке [—1;0] значение функции /(%) = х3 — 2рх2 + 1 достигается на правом конце промежутка?
2) При каких значениях параметра р наибольшее на промежутке [0; 1] значение функции /(х) =х3 — 4рх2 — 10р3 достигается на левом конце промежутка?
XIV.150. 1) На координатной плоскости дана точка Л4 = (2;4). Рассматриваются треугольники, у которых две вершины симметричны относительно оси Оу и лежат на дуге параболы у = Зх2, выделяемой условием — 1 х 1, а точка М является серединой одной из сторон. Среди этих треугольников выбран тот, который имеет наибольшую площадь. Найти эту площадь.
2) На координатной плоскости даны точки В = (3; 1) и С= (5; 1). Рассматриваются трапеции, для которых отрезок ВС является одним из оснований, а вершины другого основания лежат на дуге параболы у=(х — I)2, выделяемой условием 0 х 2. Среди этих трапеций выбрана та, которая имеет наибольшую площадь. Найти эту площадь.
XIV.151. 1) На координатной плоскости рассматриваются всевозможные треугольники АВС, у каждого из которых ZACB = 90°, вершина А имеет координаты (1; 0), вершина С лежит на отрезке [0; 1] оси Ох, а вершина В лежит на параболе у — х — х2. Какие координаты должна иметь вершина В, чтобы площадь треугольника АВС была наибольшей?
2) На координатной плоскости рассматриваются прямоугольные треугольники АВС (ЛАСВ — 900), у каждого из которых вершина А имеет координаты (—4;0), вершина С лежит на отрезке [0;4] оси Ох, а вершина В лежит на параболе у = 4х — %2. Какие координаты
Задачи повышенной сложности к главе XIV 297
должна иметь вершина В, чтобы площадь треугольника АВС была наибольшей?
XIV.152. 1) Найти координаты точки, лежащей на графике функции у = 1 + cosx при 0 х д и наименее удаленной от прямой х\/3 + 2у + 4 = 0.
2) Найти координаты точки, лежащей на графике функции у = 1 — sinx при х и наименее удаленной от прямой х — \/2у — 5 = 0.
XIV.153. 1) Криволинейная трапеция ограничена параболой у = х2 + 1 и отрезками прямых у = 0, х = 1, х = 2. Найти координаты точки Л4 на кривой у = х2 + 1, х 6 [1;2], через которую следует провести касательную, отсекающую от данной криволинейной трапеции обычную трапецию наибольшей площади?
2) Найти координаты точки А на кривой у = —х2 + 2х, через которую должна проходить такая касательная к этой кривой, что трапеция, образованная этой касательной и отрезками прямых у = 0, х = 0, х = 1 имела наименьшую площадь?
XIV.154. В сферу вписана правильная четырехугольная пирамида; в пирамиду вписана правильная четырехугольная призма, одно из оснований которой лежит в плоскости основания пирамиды, а вершины другого основания принадлежат боковым ребрам пирамиды. Длина высоты призмы равна Ь, а ребро ее основания имеет длину 2Ь. При какой высоте пирамиды радиус описанной около нее сферы будет наименьшим? Найдите это наименьшее значение радиуса.
XIV.155. В замкнутую фигуру, ограниченную графиком функции у = 27 — 6х — х2 и осью абсцисс, вписан прямоугольник наибольшей площади так, что две вершины прямоугольника лежат на графике функции, а две другие — на оси абсцисс. Найти координаты вершин и площадь прямоугольника.
XIV.156. В фигуру, ограниченную линиями т/ = х2, z/ = 2x2, х = 6, вписан параллелограмм наибольшей площади так, что две его вершины лежат на прямой х = 6, а две другие —
298 Глава XIV. Применение производной к исследованию функций
на параболах у = %2, у = 2х2. Найти значение этой площади.
XIV.157. j) Касательная к графику функции z/ = x-2 такова, что абсцисса с точки касания принадлежит отрезку [5; 9]. При каком значении с площадь треугольника, ограниченного этой касательной, осью Ох и вертикальной прямой х — 4, будет наибольшая и чему равна эта наибольшая площадь?
2) Касательная к графику функции у = УхУ такова, что абсцисса с точки касания принадлежит отрезку [0,5; 1]. При каком значении с площадь треугольника, ограниченного этой касательной, осью Ох и вертикальной прямой х = 2, будет наименьшая и чему равна эта наименьшая площадь?
XIV.158. Определить количество корней уравнения х2 • е2~И = 4а в зависимости от значения параметра а.
XIV.159. 1) Найти все действительные числа х такие, что при всех положительных у выполнено неравенство 5х z/3 — Зх2//.
\ 2) Найти все действительные числа х такие, что
при всех положительных у выполнено неравенство х З//2 — х2//3.
ОТВЕТЫ К ГЛАВЕ XIV
XIV.2. 1) с = 2,5; 2) с = -1; 3) с = 9; 4) с = -1; 5) с=5 + рЛ XIV.5. Нет.
XIV.6. Указание. Используя теорему Лагранжа, можно доказать, что функция [(х), определенная на отрезке [а,Ь], постоянна на этом отрезке тогда и только тогда, когда она дифференцируема на [а, Ь] и ее производная равна нулю при всех хе (a,b). XIV.7. Ук а з а н и е. Применить
теорему Ролля к функции /(х) — Зх+2 — 26х — 29. XIV.9. 1) На (—оо;0]
возрастает, “ [-1=0]
возрастает, на [б; убывает; 2) на на [—1;2] убывает; 3) на °о; — |]
/ 151
убывает; 4) на I — оо; — I убывает, на
(-оо;-|] и [2;+оо) и [0; +оо) возрастает, [^;+оо) возрастает.
XIV.10. 1) На (—оо; —3] и [1;+оо) возрастает, на [—3;—1) и (—!;!] убывает; 2) на [0; 1) возрастает, на (—оо;0] и (1;+оо) убывает; 3) на (-оо; —2] и [— 1;+оо) возрастает, на [—2;—1,5) и (—1,5;—!] убывает;
4) на [—3 — 4\/5; — 3) и (-3; — 3 + 4\/5] возрастает, на (—оо; — 3 - 4\/5]
Ответы к главе XIV 299
возрастает, на
/~~ / 271 Г27 \
и [—3 + 4v5;+оо) убывает. XIV.11. 1) На ( —оо; I убывает, на I +°о)
возрастает; 2) на (—оо; — 1] и [1; +оо) возрастает, на [—1; 1] убывает. XIV. 12. 1) Убывает на (0;2], возрастает на [2;+оо); 2) на (О; убывает, на |^;+оо) возрастает; 3) на (2; 3] возрастает, на [3;+оо) убывает; 4) на ^0; убывает, на [|;+оо) возрастает. XIV.14. 1) На
[—1;—-^] и убывает; 2) на [0,5; 1] возрастает, на [1; +оо) убывает.
XIV.15. 1) Возрастает на [е;+оо), убывает на (0; 1) и (1;е]; 2) возрастает на (0;+оо). XIV.16. 1) Убывает на ^(6/г — 1); ^(6/г + 1)], k 6 й, возрастает на Г^(6/г + 1); ^(6/г + 5)1, k е й; 2) убывает на Г--^ + л/г; + тг/г], /гей, L о о J L 1Z J
возрастает на + л/г; — + л/г^, /г € й. XIV.17. 1) На (—оо; — 1] и [1; +оо)
возрастает, на [— 1; 1] убывает; 2) на [1;е] возрастает, на (0; 1] и на [е; +оо) убывает. XIV.18. 1) На (—оо;0] и [\/2;2] уб ывает, на и [2; +оо) возрастает; 2) на (—оо;
вает; на
XIV.21. 1) %, = ^ + тг/г,
XIV. 22. 1) х = 0 — точка
минимума,
локального
Г—1;—т=], [О; -U1 и [1;+оо) возрастает. XIV.19. 1) ае(-
L v3J L v3J
2) а е (—оо;—3]. XIV.20. 1) О 0; 2) с 3.
х2 = -^ + л/!, /ге2; 2) х = (-1)^+И + ^,/гей.
локального максимума, /(0) = 0; х = ±\/2 —точки локального
/(\/2) =/(—\/2) = — 1; 2) х=—3 —точка локального максимума, /(—3) = 28;
9
х — 1 — точка локального минимума, /(1) = —4; 3) х = - — точка
(2 \ 4
3 ] = —; х — 0 —точка локального минимума, /(0) = 0;
27
4) х = —3 — точка локального минимума, /(—3) = — —; 5) х = — 2 — точка локального максимума, /(—2) = 25; х = 1 — точка локального минимума, /(1) = — 2; 6) х = 2 — точка локального максимума, /(2) = 16; х = 0 и х = 4 — точка локального минимума, /(0) — /(4) = 0.
локального минимума; 2) х = 0 — точка локального минимума, х —
локального максимума. XIV.24. 1) х = —1—точка локального х= 1 — точка локального минимума; 2) х = 5 — точка локального х — —1 —точка локального минимума. XIV.25. 1) Точек нет; 2) точек экстремума нет. XIV.26. 1) х = | — точка
максимума; 2) х=|—точка локального минимума. XIV.27. 1) х = е — точка локального минимума; 2) х — е — точка локального максимума.
XIV.28. 1) л + 2лп, п е й, —точка локального максимума; + 4яп, п е й, —точка локального минимума; 2) х = + 2тт,п е й, —точка
XIV.23. 1) х = 1 — точка
8
— — точка
максимума; максимума; экстремума
локального
300 Глава XIV. Применение производной к исследованию функций
локального максимума, х = — + 2тт, n е. Z, — точка локального минимума. 4 т
XIV.29. 1) х = 4тг/2, ней, —точки локального максимума, х — — — + 4тш, n е й, — точки локального минимума; 2) х — + тт, n е й, — точки
локального максимума, х = — ^ + лп, пей, —точки локального минимума. XIV.30. 1) х = i — точка локального минимума; 2) х= 1 — точка локального максимума; х = 2 — точка локального минимума. XIV.31. 1) х = 1п2 — точка локального минимума; 2) jq 2 = i \/2 log3 2 — точки локального максимума, х = 0 — точка локального минимума. XIV.32. х = 0,8а + 0,1
при a < 0,5; если a > 0,5, критических точек нет. XIV.33. При b <—2. XIV.34. (—оо; —3) U (3; 2-9) . XIV.35. 2. XIV.36. 1) (/|1аиб. = 4, (/наим = —24; 2) 1/иаиб — И, (/наим = 0; 3) (/иаиб — 4g и (/наим — _
7
4) (/наиб = 57 И (/цацм = —55; 5) 1/цаиб = О И (/найм — —25; 6) (/цаиб = g>
1 3
(/наим = 1- XIV.37. 1) (/наиб = h (/наим = — 2) (/наиб = 7, (/наим = —
1 5 я
5) (/наиб — 0, (/наим — — ; 4) (/наиб = Ь (/найм — — • XIV.38. 1) (/наиб = 2’
(/наим = 1; 2) (/наиб = + 1- (/наим = — | • XIV.39. 1) 18 = 9 + 9;
2) 10= | + у! 3) -10= (-5) +(-5); 4) 12 = 6 + 6. XIV.40. 1) 40; 80; 60; 2) 4; 12; 10. XIV.41. 1) По 3 м; 2) квадрат со стороной 10 м.
XIV.42. 50х/2. XIV.43. Дно — квадрат со стороной 4 м, глубина — 2 м.
XIV.44. Большее основание равно 0,75а, высота и меньшее основание —
0,25а.
XIV.49.
XIV.45. ?^2 XIV.46. 32.
R = 7 <1/2. XIV.50. 2^3. XIV.51.
XIV.47. Юл. XIV.48. 4.
XIV.52. 1) 10; 2) XIV.53. 1) 3^3;
XIV.55. 0. XIV.56. 1) 1 и 2(1п2 - 1);
1) 2л; 2)
2) 2УЗл.
2) In 2
R = 2, Н = 4.
XIV.54. ч.
41 и 2(1п 2 - 1).
XIV.57. 1) (/Наиб — 2, (/наим — х/2;
XIV.58. 1) уу'? и 5^ё; 2) е+|+4
— 4л — 1 + 1,5 х/3, (/наим — —1 — 4л — 1,5 х/3;
2) (/наиб — 3,25, (/наим — —3.
10 — 7 In 2 vrv КП 1 \
И - . XIV.59. 1) (/наиб —
2) ^наиб — я I + 1,5х/3,
(/наим — —1 — 7л—1,5х/3. XIV.60. 1) (/наиб — (/наим— J 2) (/наиб — 2в2 — 1, (/наим = 2. XIV.61. 1) 5 и 4; 2) 24 и 0. XIV.62. 1) 8 и -13;
2) 32 и 27. XIV.63. 1) 4 и 0; 2) 1,5 и 1. XIV.64. 1) г/Наиб = 4х/б,
(/наим — 0; 2) (/наиб = 4х/б, (/наим = 0. XIV.65. 1) 1,5 — наибольшее значение, 2тг
достигается при х = ±^± + 2лп, пей; —3 — наименьшее значение, достигается
при х = 2тт, neZ; 2) 5 — наибольшее значение, достигается при % = ^ + лп,
пей; 0,5 — наименьшее значение, достигается при х = + лп, пей.
XIV.66. 1)
о- Зх/3
2) ^;2 .
XIV.67. 1) [—1; 1]; 2)
4у/3. 4у/3
9 ’ 9
Ответы к главе XIV 301
XIV.68. 1) z/наим = -118; 2) //наиб = 900. XIV.69. 1) //„аиб - 105,
//найм = 2) //наиб = 21, z/наим = -у. XIV.70. [0;21 + 3In2].
XIV.71. 1) z/наим = -204; 2) //11аим = 64. XIV.72. 1) г/наиб = -2; 2) //Наиб = = 0,5. XIV.73. 1) z/Iiai16 = 3arccos)-4=) - У2,//||аим не существует; 2) //иаиб
не существует, z/наим = 3arcsin -у + v2. X1V.74. arctg у. X1V.75. ±\/2. XIV.76. Указание. 1) Исследовать поведение функции 2х + Ду на промежутке (0; 0,5) с использованием производной; 3) Исследовать поведение функции /(х) = х2 — 1 — 21пх на промежутке [1;+оо) с использованием производной, от лагеря.
XIV. 84.
и ЗУЗ см.
XIV.77. М = (1,5; 0).
XIV.8O. М = (4; 2). ah 4 ’
XIV.85. 1) 3;
XIV.88.
4 4’2
XIV.78. М = (0;0). XIV.79. В 3 км
XIV.81. 2a. XIV.82. XIV.83. 0,8.
XIV.86. £. XIV.87. 12 см
l,5/i. XIV.90. 64
= arctg/2. XIV.94. 2.
87?2. Указание. Следует
2) ’ 3
XIV.89.
XIV.96. Я = 4=
Уз
XIV.93. а
XIV. 97.
XIV.91. 16 УЗ.
XIV.95.
1 о доказать, что основанием прямоугольного параллелепипеда наибольшего
объема является квадрат. XIV.98. ~R. XIV.99. R- XIV.100. 47?.
XIV.101. 3. XIV.102. Я = (2+У2)г, ЗУЗ(3 + 2У2)г2. XIV.103. Н = 27?УЗ. XIV.104. ^7?. Указание. Следует доказать, что пирамида большего объема — правильная. XIV.105.
XIV.107. 1) у" = 12х2 - 6;
У = —а2Я.
27
3) и" = 40
У (2х — 4)3 ’
6) у" = 4е2х + е
XIV.108. 1)
О
наи-
XIV.106. b = |а, 4 гЗ’
4) у" — — 4sin2x + 9cos3x;
2х ТГ?
+ Зе
П у‘
2)
2) -2^ м/с. XIV.11O. 1) На
выпукла вверх; х = — 1, х = 1 — точки перегиба;
вверх, на (1,5;+оо) выпукла вниз; х = 1,5 — точка перегиба; 3) на (—оо;0) выпукла вниз, на (0; +оо) выпукла вверх, х = 0 —точка перегиба;
( —оо;—2) и (2;+оо) выпукла вверх; на ( —2;0) и (0;2) выпукла вверх;
и х = 2 — точки перегиба. XIV.111. 1) На (2тг/г; тг + 2тг/г) выпукла на (тг + 2тгХг; 2тг + 2тгХг) выпукла вниз, х — л/г, k 6 Z, — точки перегиба;
+ 2л/г; у + 2л/г) выпукла вниз, на (у + 2л/г; + 2л/г) выпукла
х=^ + л/г, feeZ,—точки перегиба. XIV.112. 1) На (0;0,25) выпукла
2>»" = + У;
5) у" = 10cos5x - 25(х + 1) sin5x;
4х о\ // 2 In х - 1
“(Г—?—
3) 16; 4) 6 In 2 + 4 In2 2. XIV.109. 1) 18 м/с\
(—оо; — 1) и (1;+оо) выпукла вниз, на (— 1; 1)
2) на (—оо; 1,5) выпукла
4) на х = — 2 вверх, 2) на
вверх,
вверх,
302 Глава XIV. Применение производной к исследованию функций
на (0,25;+оо) выпукла вниз, х = 0,25 — точка перегиба; 2) на (0;-^= + 1) \ v3 / / 2 \ 2
выпукла вверх, на + 1; +ooj выпукла вниз, х = +1 — точка перегиба.
XIV.113. 1) На (—оо;2) выпукла вверх, на (2; +оо) выпукла вниз, х = 2 — точка перегиба; 2) на (—оо;—1) и (1;+оо) выпукла вниз, на (—1; 1) выпукла вверх, х = — 1 и х = 1 —точки перегиба; 3) выпукла вверх на К. 4) на (—оо;—1) и (0;+оо) выпукла вниз, на (—1;0) выпукла вверх, х = -1 и % = 0 —точки перегиба. XIV.114. 1) На (-оо;0) выпукла вверх, на (0;+оо) выпукла вниз, точек перегиба нет; 2) на (—оо; 0,5) выпукла вниз, на (0,5; +оо) выпукла вверх, х = 0,5 — точка перегиба. XIV.115. 1) На ( —оо;—1) выпукла вверх, на (—1;+оо) выпукла вниз, _ 5
2) на (0; е 5) выпукла вверх, на
5 3
— I " ТОЧКа П С р Г И <7 а, rv — —
х = 0,//=-3; 2) х = \, у = 2\ 3) х = 3, у = — 2; 4) у = — |; 5) х = 0, х — 0; 7) асимптот нет; 8) асимптот нет.
2) х = —2, у = — х + 2; 3) х = — 1, у = х; £>(//) = К. Функция возрастает на (—оо; — х = — | — точка локального максимума, х=^ — точка локального х = 0 —точка перегиба; на (—оо;0) выпукла вверх, (0; +оо) 2) £>(//) = К. Функция возрастает на (—оо;0]
х=—1 — точка перегиба, k = —е 2;
(е +оо) выпукла (вниз, Л4 (е ь;1 — 2 j — точка перегиба, k = —
1
XIV. 116. 1) z/=-3; 6) У = X + 5;
XIV.118. 1)
на
з
2 •
XIV.117. 1) х = 5,
4) х = 2, у = 2х + 8.
минимума;
выпукла вниз; асимптот нет;
и [2;+оо), убывает на [0;2]; х — 0 — точка локального максимума, х = 2— точка локального минимума; х = 1 — точка перегиба; на (—оо; 1) выпукла вверх, (1; 4-оо) выпукла вниз; асимптот нет; 3) £)(//)= К. Функция нечетная (график симметричен относительно начала координат), на (— оо; —
и
убывает, на
возрастает; х
— точка
минимума, х= у-—точка максимума; х = 0 —точка перегиба; на (—оо; 0) выпукла вниз, (0;+оо) выпукла вверх; асимптот нет; 4) £>(//) = К. Функция возрастает на (—оо;2] и [4;+оо), на [2; 4] убывает; х = 2 — точка максимума, х — 4 — точка минимума; х = 3 —точка перегиба; на (—оо;3) выпукла вверх, (3;+оо) выпукла вниз; асимптот нет. XIV.119. 1) D(y) =R. Функция четная; возрастает на [—1;0] и [1;+оо); убывает на (—оо;—1] и [0; 1]; //max = //(0) = 5, z/min =«/(±1) = 4; (±4?; тП-точки перегиба; на (-оо;—М и (-U;+oo) X VO у / х VO/ X V о /
выпукла вниз, (—4=; 4=) выпукла вверх; асимптот нет; 2) £>(//) = К. \ v3 v3/
Функция четная; возрастает на [-УЗ; 0] и [У3;+оо); убывает на (—оо; — д/З] и [0; УЗ]; утах = z/(0) = 9, //min = 1/(±У8) = 0; (±1; 4)—точки перегиба, на (—оо;—1) и (1;+оо) выпукла вниз, (—1; 1) выпукла вверх; асимптот нет; 3) £>(//) = К. Функция возрастает на [0; 1] и [4;+оо); убывает на (—оо;0]
Ответы к главе XIV 303
и [1;4]; //max —//(1) — , //min —//(0) — О И //min — //(4) — — i X- —
абсциссы точек перегиба; асимптот нет; 4) £>(//) = К. Функция возрастает возрастает на [0;0,5] и [1; +оо); убывает на (—оо;0] и [0,5; 1]; //max = //(0,5) = //min = //(0) = о и //min = //(1) = 0; (3±6-^3; 3^) — точки перегиба; асимптот 5) £>(//)= К. Функция четная; точки пересечения с осями координат (±3;0); возрастает на [—2; 0] и [2;+оо); убывает на (—оо;-2] //max = //(0) = —9, //min — //(i2) = —25; у-;
2>/3 2\/з\ / 2х/з\
—I выпукла вверх, на —оо;--------------
О j \ О /
вниз; асимптот нет. XIV.120. 1) у = 2 (д + 1) . £>(//) = 1R \ {0}.
нет;
(0; —9) и
и [0;2];
й ( 2\/3 перегиба; на I----;
выпукла
Функция нечетная; возрастает на (—оо;—4] и [4; 4-оо), убывает на [—4; 0) И (0;4]; //max на (0;+оо) выпукла вниз; асимптоты х = 0 — вертикальная и у =
наклонная; 2) у — х — 1 Н----—- + 1. £>(//) = К \ {1}. Функция возрастает на
точки
= у(—4) = —4, //min — //(4) = 4; на (—оо;0) выпукла вверх, х____________________________________________________________
2
(—оо;0] и [2;+оо), убывает на [0; 1) и (1;2]; //max = //(0) = 1, //min = //(2) = 3; на (—оо; 1) выпукла вверх, на (1;+оо) выпукла вниз; асимптоты х = 1 —
вертикальная и у = х — наклонная;
£>(//) = К \ {0}. Функция возрастает на
3) у = х +
1
2х и
= 1 (У2Х+ 1 Y х/2 \ V2xJ
-g-;+ool, убывает
(—оо; 0) выпукла вверх, на (0;+оо) выпукла вниз; асимптоты х = 0 —
вертикальная и у = х — наклонная; 4) у = (х + 2) + - — 2. D(y) = R\{—2}.
Функция возрастает на (—оо;—3] и [—1;+оо), убывает на [—3;—2) и (—2; — 1]; //max =//(—3) = —4, //min =//(—1) = О’, на (~°о; —2) выпукла вверх, на (—2;+оо) выпукла вниз; асимптоты х — —2 — вертикальная и у — х — наклонная. XIV.121. 1) £>(//) = 1R \ {0}. Функция нечетная, график симметричен относительно начала координат; на (—оо;0) и (0;+оо) возрастает; на (—оо;0) выпукла вниз, (0; +оо) выпукла вверх; х = 0 — вертикальная асимптота у = х — наклонная асимптота; 2) £)(//) = R \ { — 1}. Функция возрастает на (—оо;—1) и (—1;+оо); на (—оо;—1) выпукла вниз, (— 1;+оо) выпукла
вверх; х = —1 — вертикальная асимптота, у — х — наклонная асимптота. XIV.122. 1) //=1; 2) // = 0; 3) х = 0, // = 1; 4) х = ±2,//=-1; 5)х=-1,
х = 0,5, // = 0; 6) х = 1, х = 2, // = 0; 7) х — — 1, // —х; 8) х — —1,у — х — 2.
XIV.123. 1) у = 0; 2) х = 0, у — 0; 3) асимптот нет; 4) у = 4х + 1.
XIV.124. 1) £>(//) = К \ {—1}. Функция возрастает на (—оо;—2] и [0;+ос),
убывает на [—2;—1) и (—1;0]; //min = //(0) = 0, //max =//(-2) = -4; на (—оо;—1) выпукла вверх, (—1;+оо) выпукла вниз; х =—1 — вертикальная асимптота, // = х — 1 — наклонная асимптота; 2) £>(//) = К \ {—2}. Функция убывает на (—оо;—3] и [—1;+оо), возрастает на [—3;—2) и (—2;—!];
304 Глава XIV. Применение производной к исследованию функций
Утт = у(-3) = 6, г/max = t/(—1) = 2; на (—оо; —2) выпукла вниз, (—2;+оо) выпукла вверх; х = —2 — вертикальная асимптота, у = 2 — х наклонная асимптота. XIV.125. 1) £>(//)= К \ {±1}. (0;0) — точка пересечения с осями координат; функция убывает на ( —оо; — 1), ( — 1; 1) и (1;+оо); на (—оо;—1) и [0; 1) выпукла вверх, на (— 1; 0] и (1;+оо) выпукла вниз, (0; 0) — точка перегиба; х = ±1 — вертикальные асимптоты, у — 0 — горизонтальная асимптота; 2) £>(//) = К\ {0}. (1;0) — точка пересечения с осями координат; на (—оо;0) и [2; +оо) убывает, на (0; 2) возрастает, г/max = г/(2) = |; на (—оо;0) и (0; 3] выпукла вверх, на [3; +оо) выпукла вниз, (3; —
точка перегиба; х — 0 — вертикальная асимптота, у = 0 — горизонтальная асимптота. XIV.126. 1) D(y) = R\{0}. Х[^ — ~ точки пересечения
[8 \
3; +оо1 , возрастает на (°;|]; Утах = у на (-оо;0) и (0; 4] выпукла вверх, [4;+оо)
выпукла вниз, (4; 2,5) — точка перегиба; х = 0 — вертикальная асимптота у = 2 — горизонтальная асимптота; 2) D(y) = R\{1}. (—1; 0) и (3; 0) — точки пересечения с осью Ох, (0; —3) — точка пересечения с осью Оу, функция убывает на (—оо; 1), возрастает на (1; +оо); на (—оо; 1) и (1;+оо) выпукла вверх; х = 1 — вертикальная асимптота, у = 1 — горизонтальная асимптота. XIV.127. 1) D(y) = К \ {0}. Функция возрастает на (—оо; 0) и [\/2;+оо), убывает на (О; ; х= х^2 — точка минимума; точек перегиба нет, на (—оо;0)
и (0;+оо) выпукла вниз; х — 0 — вертикальная асимптота; у = х — наклонная асимптота; 2) D(y) =R\{!}; х= — 1 — точка пересечения с осью Ох; на (—оо; 1) и [3; +оо) возрастает, на (1; 3] убывает; t/min = у(3) = 4; на (—оо; 1) и (1;+оо) выпукла вниз; х — 1 — вертикальная асимптота, у — х — наклонная асимптота. XIV.128. 1) D(r/) = ]R. Функция нечетная (график симметричен относительно начала координат), на (—оо;—1] и [1; +оо) убывает, на [— 1; 1] возрастает; х = —I — точка минимума, х = 1— точка максимума; х = ±\/3, х = 0 — точки перегиба (на (—оо; — \/3) и (0; \/3) выпукла вверх, (—л/3; 0) и (У3;+оо) выпукла вниз); у — 0 — горизонтальная асимптота; 2) D(y) — К. Функция убывает на ( —оо;—2] и [0;+оо), на [—2;0] возрастает; r/min — 2) = —
Ушах = У (0) = 1;х = 0 — точка максимума; у = 0 — горизонтальная асимптота. XIV.129. 1) D(y} = R. Функция четная (график симметричен относительно оси ординат); на (—оо; 0] убывает, на [0; +оо) возрастает; t/min = у(0) = 0; на (—оо;—1] и [1; +оо) выпукла вверх, на [— 1; 1] выпукла вниз; (±1;0,25) — точки перегиба; у = 1 — горизонтальная асимптота; 2) D(y) — К. Функция четная (график симметричен относительно оси ординат); на (—оо;0 убывает, на [0;+оо) возрастает; z/min — z/(0) = — 0,25; на (—оо; — -^=] и
Г 2 2 1 / 2 1 \
выпукла вверх, на —=5-7= выпукла вниз; ( ±^=;— точки L v3 v3J \ v3 1о/
у = 1 — горизонтальная асимптота. XIV.130. 1) D(y) = К \ {±2}.
четная (график симметричен относительно оси ординат); (0; 0) — точка
перегиба; Функция
Ответы к главе XIV 305
пересечения с осями координат; возрастает на (—оо; —2) и (—2; 0], убывает на [0; 2) и (2; +оо); Утах = у(0) = 0; на (—оо; — 2) и (2; +ос) выпукла вниз, на (—2; 2) выпукла вверх; х = ±2 — вертикальные асимптоты, у = —1 — горизонтальная асимптота; 2) D(y) = К \ {±2}. Функция четная (график симметричен относительно оси ординат); (—3; 0), (3; 0) — точки пересечения с осью Ох, (0; 2,25) — точка пересечения с осью Оу, убывает на (—оо;—2) и (—2;0], возрастает на [0; 2) и (2;+оо); z/min = у(0) = 2,25; на (—ос;—2) и (2; +оо) выпукла вверх, на (—2; 2) выпукла вниз; точек перегиба нет; х = ±2 — вертикальные асимптоты, у — —1 — горизонтальная асимптота. XIV.131. 1) D(y) = R \ {±1}. Функция нечетная (график симметричен относительно начала координат); (0; 0) — точка пересечения с осями координат; убывает на ( —оо;—1), ( — 1; 1) и (1;+оо); на ( —оо;—1) и [0; 1) и выпукла вверх, на ( —1;0] и (1;+оо) выпукла вниз, (0; 0) — точка перегиба; х = ±2 — вертикальные асимптоты, у = 0 — горизонтальная асимптота; 2) D(y) = К \ {±2}. (3; 0) — точка пересечения с осью Ох, (3 X
0; о — точка пересечения с осью Оу, функция возрастает на (—оо;2) о /
и (2; 4) и (4;+оо); на ( —оо;2) и (3; 4) выпукла вниз, на (2; 3) и (4;+оо) выпукла вверх; (3;0) —точка перегиба; х = 2 и х = 4 — вертикальные асимптоты, у = 0 — горизонтальная асимптота. XIV.132. 1) D(y) = R\{±2}. Функция нечетная (график симметричен относительно начала координат); возрастает на (—оо;—2\/3] и [2\/3;+оо), на [-2^3;-2), (-2; 2) и (2; 2^3] убывает; ymax = г/(—2>/3) = — Зл/З, z/min = у (2\/3) = 3\Л; на (-оо; -2) и [0; 2) выпукла вверх, на (—2; 0] и (2; +оо) выпукла вниз; (0;0) — точка
перегиба; х — ±2 — вертикальные асимптоты, у — х — наклонная асимптота; 2) £>(у) = IR \ { —1}. (0;0) — точка пересечения с осями координат; функция возрастает на (—оо;—3] и (—1;+оо), убывает на (—3; — 1); z/max = у(-3) = — у; на (—оо; —1) и ( —1;0] выпукла вверх, на [0;+оо) выпукла вниз; (0; 0) — точка перегиба; х = — 1 — вертикальная асимптота, у= | — 1 — наклонная асимптота. XIV.133. 1) £)(у) =К\{0}. (—^2,0) — точка пересечения с осью Ох; функция возрастает на [1;+оо), убывает на (—оо;0) и (0; 1], ут;п = у(1) = 1,5; на (—оо; — v2] и (0;+оо) выпукла вниз, на [—v2;0) выпукла вверх; (— v2,0)— точка перегиба; х = 0 — вертикальная асимптота; 2) О(у) = К\ {0,5}. (1,0) — точка пересечения с осью Ох; функция возрастает на [0,25;0,5) и (0,5; +оо), 27
убывает на (—оо;0.25], ymin = у(0,25) — на (-оо;0,5) и [1; +оо) выпукла вниз, на (0,5; 1] выпукла вверх; (1,0) —точка перегиба; х = 0,5 — вертикальная асимптота. XIV.134. 1) О(у) = К. (1;0), (2; 0) и (0;—4) —точки пересечения с осями координат; на (—оо; 1,6] и [2; +оо) возрастает, на [1,6; 2] убывает;
Утах = у(1,6) ‘ 0,03456, х =
——, х = I — абсциссы точек перегиба; на
I. — 1
’ io
выпукла вверх,
и
10
к —, *J 'Ц 10 > ю
выпукла вниз; асимптот нет; 2) О(у) = К. (0; 0) и (±л/5; 0) — точки пересечения с осями координат; углах = у(—\/3) = \/3, z/min = у("/3) = ~\/3;
306 Глава XIV. Применение производной к исследованию функций
(0;0) и
— точки перегиба; асимптот нет, на (—оо; — х/3]
( х/б
и [У3;+оо) возрастает, на [— д/3; >/3] убывает; на I —оо;——
и
/6
2
выпукла вверх. XIV.135. 1) D(y) = [0; +оо);
выпукла вниз, на
(0; 0), (3; 0) — точки пересечения с осями координат; на [0; 1] возрастает, на [1;+оо) убывает; z/max = у(1) = 2; на (0;+оо) выпукла вверх; асимптот нет; 2) £)(//) = R; (0; 0), (—4; 0) — точки пересечения с осями координат; функция убывает на (—оо;—1], на [— 1;+оо) возрастает; ymin = у(—1) = —3; ^2; 6лУ2^ — точка перегиба; на (—оо;2) выпукла вниз, на (2;+ос) выпукла вверх; асимптот нет; 3) D^y) = К; z/(0) = z/(l) — 0; (0; 0), (1; 0) — точки пересечения с осями координат; функция возрастает на [б; и убывает на [—оо;0] и Утах = у t/min = у(0) = 0, асимптот нет;
4) D(y) = [—2;2]; (0; 0), (±2; 0) — точки пересечения с осями координат; на [—2;— л/2] и [\/2;2] убывает, на [— у/2; у/2] возрастает; ymjn = у(—у/2) = -2, Утах = у(\/2) = 2; (0; 0) — точка перегиба, на [—2;0) выпукла вниз; на (0;-2] выпукла вверх; асимптот нет; 5) D(y) = R; (0;0) — точка пересечения с осями координат; функция возрастает на R; (0;0) — точка перегиба; на (—оо;0] выпукла вниз, на [0; +оо) выпукла вверх, у = — 1, у = 1 — асимптоты; 6) D{y} — R; (0; 0) — точка пересечения с осями координат; функция возрастает на R; (0;0) и (±1;±v2) — точки перегиба; на (—оо; — 1] и [0; 1] выпукла вниз, на [— 1;0] и [1; +оо) выпукла вверх; асимптот нет. XIV.136. 1) D(y) = R; имеет период 2л; (тгХг; 0), /з 6 Z, — точки пересечения с осями координат; в пределах отрезка [0;2тг] возрастает на
Г 5тг о ] й Г л 5тг1 /5тг\ 3>/3
и [у;2тг| , убывает на [у у]; Утт = У (yj =--у, Утах = у выпукла вверх на |0; л — arccos и [тг; тг 4- arccos
тг+arccos 2; точки перегиба ^тг— arccos (тг;О) и + arccos |। .
период 2л; (тг/з;О),
arccos л
2 ’ 2
8
лк. т;
координат; в пределах
отрезка
на
л - arccos
arccos
Уггпп
тг + arccos
тг\ = Зу/З, 3/ 2 ’
, выпукла вниз на
ЗУПЛ
' 8 Г
асимптот нет; 2) D(y) = R;
k € Z, — точки пересечения с
[0; 2л] возрастает на
и
2л — arccos
л — arccos 4 / -; л + arccos
и
имеет
осями
0;arccos
убывает
-1, Утт = У я + arccos
у; 2л — arccos у х/б
------у. Утах
Ответы к главе XIV 307
Л . /13 4 /13\
асимптот нет;
3) D(y) = К; имеет период 2д; + д/г; 0^ ,k е Z, — точки пересечения
с осями координат; в пределах отрезка [0;2тг] возрастает на
Г5тг Зтг] Г д д] Г б/гЗ ГЗтг о 1 /5тг\ х/2
и [Т’Т]’ убывает (.4’2.1’ 1’4“] и [т;27ГР Ута* = у 1т/ = ~Т'
Упип — У(я) — У (у) — 1’ ^min — У — ~у > Утах — У (2 ) — У$) ~ У(?я) — Ь х = х = х = ~ arcsin |, х = J - / arcsin |, х = J + / arcsin |, 4 4 £ о £ £ о l £ о
х = у — | arcsin | — абсциссы точки перегиба; асимптот нет; 4) D(y) = К; имеет период 2д; (д/г;0),k 6 Z, — точки пересечения с осями координат; в пределах отрезка [0; 2тг] возрастает на [О; у] и [д;у], убывает на [^;д| и [у; 2д]; //min = //(д/г) = 0, //max = у (J + дй) = |, //тах = у (у + л*) = 1, /г 6 Z; асимптот нет. XIV.137. 1) £>(//) = IR; //mjn = //(0) = 0, у—— у — 1 — левая асимптота; // = у — 1 — правая асимптота; выпукла вниз при всех %еК; 2) D(y) = К; //min = */(1) = 2 + д, //max =//(-1) =-2 + Зд; г/ = 2х + 4д — левая асимптота; у = 2х — правая асимптота; (0;2д)— точка перегиба. XIV.138. 1) D(y) = ( — 00; 0) U (0;+00); у > 0 при всех х 6 £>(//); функция возрастает на (—оо;0) и (0;+оо); на (—оо;0) и (О; выпукла вниз, на [^;4-оо) выпукла вверх; х = 0 — вертикальная асимптота, у —> +<х> при х —> — 0; lim у = 0;у = 1 — горизонтальная асимптота при х —> +оо;
х->+ О
2) D(y) = (-00; 0) U (0;+оо); //max =//(-1) =-е, на (-оо;-1] и (0; +оо) возрастает, на (—1;0) убывает; на (—оо; 0) выпукла вверх, на (0; +оо) выпукла вниз; х = 0 — вертикальная асимптота; 3) D(y)= К; //max = //(1) = е, ( 2 ^2^>е2 ) — точки перегиба; на ( — 00; 1] возрастает, на [1;+ос) убывает; на
выпукла вниз, на
2-х/2. 2 + х/2
2 ’ 2
выпукла
вверх; у = 0 — горизонтальная асимптота; 4) D(y) = (—1;4-00), утах =//(0) = О, х — —1 — вертикальная асимптота; на (—1;0] возрастает, на (0;4-оо) убывает, выпукла вверх при всех хб£>(//); 5) D(y) — (0; +00); (1;0) — точка пересечения с осью Ох; функция на (в; убывает, на [-^;+оо) возрастает; //min = У = — — 2^) — точка перегиба; на (О; выпукла
308 Глава XIV. Применение производной к исследованию функций
вверх, на [-^=;+ос) выпукла вниз; lim ^(х2 Inx) = 0. XIV.139. 1) При
aE (—4;4) нет корней; при а = ±4 — один корень; при аЕ (—оо;—4)и(4;+оо) — два корня; 2) два корня при всех a. XIV.140. 1) При а < — 4 и а > О
один корень; при а — 0 и а = —4 два корня; при — 4 < а < 0 три корня; 2) при а < —84 и а > 1,75 один корень; при а = —84 и а = 1,75 два корня; при —84 < а < 1,75 три корня. XIV.141. а 6 (—оо;—1) U (1;+оо). XIV.143. 1) а^|; 2) «>8,5. XIV.144. 1) a £ (-оо;-|] U {0} U [0,5; +оо);
2) а е (—3; 0) U (0; 1,5). XIV.145. 1)^^ при 1 < а 2, (а~^2 при
2 < а < 3, а< 3 при а 3; 2) —-------------------- при а < 1, -Ц при а 1.
3 5az — 16а +16 5az
XIV.146. Указание.
п 111Л 111 IX
Переписав неравенство в виде 5-------------— > -А—-
r In (х — 1) In х
рассмотреть функцию
^%)“in(x-i)’ хе(2;+ос).
и исследовать ее
поведение с помощью производной. XIV.147. 1) 2. Указание. Можно рассмотреть функцию /(х) — у/х + 7 + >/11 — х и найти ее наибольшее значение на области определения функции; 2) 3. XIV.148. 1) 80 кг\ 2) 24^ кг. XIV.149. 1) (-оо;-0,5]; 2) [0,25;+оо). XIV.150. 1) з|;
2) 1А XIV.151. 1) (Ц); 2) (А;^(УЗ-1)У XIV.152. 1) (0;2);
£1 \ О □ / X V О '
2) f^;l-4=Y XIV.153. 1) 2) XIV.154. Наи-
\ 4 ’ v/2/ \2 4 ) ’ ’ \Т 4/
меньшее значение радиуса равно при высоте 3d. XIV.155. (-3 + 2х/3; 0),
(—3 + 2д/3;24), (—3 —2\/3;О), (—3 — 2д/3; 24); площадь прямоугольника равна 96\/3. XIV.156. 32. XIV.157. 1) Наибольшее значение площади |
__о
получается при с — 8; 2) Наименьшее значение площади 1,92 • ^/1,25 получается при с = 0,8. XIV.158. Один корень при а = 0, два—
при a = 1, четыре — при 0 < a < 1; при a < 0 и при а > 1 корней нет. XIV.159. 1) [— V%5;0]. Указание. Можно рассмотреть функцию /(//) — уЗ — Зх2г/ —5х (х выступает в роли параметра) и переформулировать задачу следующим образом; найти все значения параметра х, при каждом из которых на множестве (0;+оо) функция /(z/) принимает неотрицательные значения; 2) К/4; +оо) .
Глава XV
ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ
§1. ПЕРВООБРАЗНАЯ ФУНКЦИИ
Первый уровень
XV.1. Показать, что функция F(x) является первообразной функции /(х) на всей числовой прямой:
1) F(x) = ~ sin(2x + 3), /(х) = cos(2x + 3);
2) F(x) = cos4x - 2, /(х) = 3 sin 4х;
3) F(x) = |е3х + 8, /(х) = е3х;
4) ш> = г-кз4А- /М = 34";
5) F(x) = 0,2(х + I)5 + 10х2 *, /(х) = (х + I)4 + 20х;
6) Г(х) = 2\/х + 9 + Зх, /(х) = + 3;
7) F(x) = v^+T, /М = -7Т=Г;
8) F(x) — In (х + V1 + х2), /(х) = 1 _.
\ / х/1+х2
Написать общий вид первообразных функции (XV.2-XV.4).
XV.2. 1) /(х) = х2 + 5х4; 2) f(x) =
3) /(х) = + </х; 4) /(х) = -L - '
y/Х X6
XV.3. 1) f(x) = cos(5x-3); 2) /(х) = (2х + З)12 ;
3) /(*) = 3 — 2 sin 4х; 4) /(х) = д/4х + 1.
XV.4. 1) /(х) = (sin + cos J ; 2) /(х) = (sinx - cosx)2 .
Найти первообразную функции /(х), график которой проходит через
точку Мо (XV.5-XV.8).
xv.5. 1) Дх) = Ц-, м0= -1);
COSZ X /
2) /М = Ц-. мо= М;2).
Sin X \ 4 /
310 Глава XV. Первообразная и интеграл
XV.6. 1) /(х) = 4*. Л40 = (log43; А) ;
2) f(x) = 5‘, A70 = (log54;A). xv.7. i) /(х) = -U. м0 = (-V |);
2) /М = гЬ' "о = (А|).
XV.8. 1) /(x) = ^J=, М0 = (Ы;
Второй уровень
Написать общий вид первообразных функции (XV.9-XV.13).
XV.9. D fW = ^; 2) /(x)= 6x — 1 x + 5 ’
XV.10. 2) /(x) = 1_ X2 (1 + X2)
XV.11. 1) f(x) = cos2 2x; 2) /(x) = sin2 5x.
XV. 12. 1) f(x) = sinx • cos3x; 2) /(x) - sin 3x • sin 5x
XV.13. 1) /(x) = (ex + e~x)2; 2) /(x) = (2х - 2'x)3.
§2. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Первый уровень
Используя таблицу интегралов, вычислить интеграл (XV.14-XV.18).
XV.14. 1) J (5x4 + 6x3 — 2x + 6) dx; 3) f(x + dx; 2) J (x — 3)2 x dx-, 4) J
XV. 15. 1) J (^x — Xyfx + 1) dx; 2) J (v^ — 2)2 dx;
3) r (1 + V?)2 d J X 4) Г 1 + x + x2 dx. J Xy/X.
XV.16. D S^dx; n\ r dx } J x2(l + x2) ’
3) J’ ^Tidx’ Л ч r 2x2 — 3 , 4) b+idx-
XV.17. 1) J (sin x + 2 cos x)dx; 2> J (2- dx; \ sin X/
3) J tg2xdx; 4) J ctg2 xdx.
§2. Неопределенный интеграл 311
XV.18. 1) /3х (1 - 3~х) dx;
3) +
2) J(2x-5x)dx;
4) J ^dx.
Вычислить интеграл, используя линейную замену (XV.19-XV.24)
XV.19. 1) J (х - 5)4 dx; 2) J (4 — 3x)5dx;
3) J sin(4x + 3)dx; 4) J гДг dx'
5) Г • \/1 — 4х2 6) Г _ dx J 1 + (2x + 3)2
XV.20. 1) г dx . J 4х2 + 5 ’ 2) r dx . J x2 + 4x + 5 ’
3) Г J 4 + 9х2 ’ 4) r dx J x2 —6x+18'
XV.21. 1) J-t=^==; 2) Г ^x
уб —(х+1)2 \/5 — 4x2
3) J , ; ys-u-x)2 4) J-Г- d* —
yl6— (3x + l)2
XV.22. 1) J cos2 xdx; 2) J sin2 3xdx;
3) J (1 + cosx)2dx; 4) J (1 + sinx)2dx.
XV.23. 1) f dx J 1 + cos 2x ’ 2) Г dx 1 — cos x ’
XV.24. 1) J cos6xcos4xdx; 2) J sin 2x sin 5x dx;
3) J cos 8x sin 5x dx; 4) J* cos x sin x cos 5x dx.
Второй уровень
Вычислить интеграл (XV.25-XV.32).
XV. 25. 1) J* x (x + I)5 dx; 2) J x(2 — x)4 dx.
XV. 26. 1) r dx . J y/l + X — \/x — 1 ’ 2) J"x2x/1 — xdx.
XV. 27. 1) J ?—^dx; 2) [^ЦОх^
3) J J 2x + 1 4) J 3x — 2
XV.28. 1) J , 1 dx; J x(x - 1) 2) J* тт— dx’
3) J 2 1 fidx; x — x — 6 4) J -5—-— x2 — 4x + 3
5) Г —у—! dx; J 2x2 + x - 1 6) J / + 3 dx. J x2 + x-2
312 Глава XV. Первообразная и интеграл
XV.29. 1) f -4 Ц dx; 2) J х4 - 13х2 + 36 Г -d—Ц dx x4 + 2x2 — 3
XV.30. 1) г dx . \/8 — 2х — х2 2) J dx \/22 + 8x - 2x2
XV.31. 1) г cos 2xdx . J . 9 2 ’ sin X cosr X 2) J dx • 2 2 ’ sin X cos^ X
XV.32. 1) J cos4 x dx; 2) sin4 x dx;
3) J* (cos4 2x + sin4 2x) dx;
4) J* (cos6 2x + sin6 2x) dx.
Вычислить интеграл, сделав подходящую замену (XV.33-XV.4O).
XV.33. п р х dx . Ч J 2) J x6 + 4
XV.34. XV.35. 3) Jх3\/1 + х4 dx; 4) J---x-^dx. J \/16- 9x4
о J 'ф <+ 2) I®
о\ р dx ' J x(2 + lnx)’ 4) Г dx J x In x(ln x + 2) ’
1) J 4^ Л;
3) Г-Д-pdx; 4)
XV.36. 1) J cosx\/sinx dx; 3) J 4 + sin2 x 2) J*sinx(cosx + 2)3 dx; 4) J sln2* dx. 1 + cos2 2x
XV. 37. 1) J sin3 xdx; 3) J sin5 xdx; 2) J cos3 xdx; 4) J cos5 xdx.
XV.38. . 9 DTP sm^dx. COS4 X 2) f^dx. sin4 x
XV.39. 1) Jtgxdx; 2) Jctgxdx.
XV.40. i) J—; J sinx 2) f-^. J cosx
Вычислить интеграл, используя метод интегрирования по частям (XV.41-XV.45).
XV.41. 1) J (x + 2)ex dx; 3) J xe2x dx; 2) Jx Inxdx; 4) J x ln(x + 1) dx.
XV.42. 1) Jx Inxdx; 2) ,J x ln(x + 1) dx.
XV.43. 1) J (x — 1) sinx dx; 3) Jxsin2xdx; 2) f x cos 3x dx; 4) fx cos2 xdx.
§3. Определенный интеграл 313
XV.44. 1) J 1п(х + 1) dx; 2) Jarctgxdx;
3) J arcsin x dx; 4) J arccos xdx.
§3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Первый уровень
Используя геометрический смысл определенного интеграла, вычислить интеграл (XV.45-XV.47).
4 1
XV.45. XV.46. 1) J (2 + х) dx; 2) J (1 - x) dx.
1) 1 1 J |x + 3| dx; -4 2) -3 2 J (2-M)dx. —2
XV.47. 1) J \/l — x2 dx; 0 2) 2 J \/2x — x2 dx 0
XV.48. Выяснить, какое из чисел больше: 2 2 1) J (х + 2)dx или J(x + 6)dx; 1 1 6 6 2) J x^dx или J х2 dx; 2 2 1 2 3) $y/x + 3dx или J (1 — х2} dx; 0 1 71 71 4 4 4) J cosxdx или J sinxdx.
О О
XV.49. Вычислить интеграл, используя формулу Ньютона—Лейбница: 3 О
1) J (3x2 -4x —3) dx; 1 5 3) J cos2 £ dx; 0 2 0,5 5) J x/l-2xdx; 0 3 / 7) J </2-idx; -18 ’ 2) J (2\/x —l)dx; -1 6 , 4 d) 9 6) ^+1 dX^ 0,25 2 8) J (i—F)d*; 9>J q X COSr7TX/ |
314 Глава XV. Первообразная и интеграл
Вычислить (XV.50-XV.53)
0 XV.50. 1) Jx(l + x)10dx; -1 2 XV.51. 1) f^dx; 0x+1 4 XV.52. 1) J f(x}dx, где f(x) 0 4 2) J f(x}dx, где /(x) —2 2 XV.53. 1) J|x- l|dx; 0 2) 2) = < 2) ' х(1 + х)5 dx. ’ 2х+ 1 2, 0^х<1, х+1, 1 х 4; ' х, —2 х < 0, 2х, 0 х 1, 3, 1 <х^4. 2 Р |5х — 11 dx. I
XV.54. Найти числа А и В, при которых удовлетворяет заданным условиям: 2 О /(зс) = Л • sin дх + В, /'(1) = 2 и Jf(x)dx 0 2 2) f(x)=A-3x + B, /'(0) = 2 и $ f(x)dx = 1 функция = 4; 12.
XV.55. Найти все числа a > 1) J (2х - V)dx > 12; 2) удовлетворяющие a J xdx a + 4. 0 условию
Второй уровень Вычислить (XV.56-XV.66). 3 , 3 - XV.56. 1) Г ; 2) Г-^—. 2 х2 + Зх — 4 2 ~ Зх — 4 0,5 1 XV.57. 1) Г ; 2) Г . q х2 — х + 1 q 4х2 + 4х + 5 3 2 । о 22_1_о XV.58. 1) f ^—^dx; 2) Г ^bgdx. 7 J2 х + 1 ’ ' J х+1
XV.59. 1) J -2^-; 0 1 1 3 j n\ p xJax 1 4- Y8’ 0 1 +x
§4. Применение интеграла к вычислению площадей 315
XV.60. 1) j (4 sin2 х + cosx^ Д 3 7Г ) dx-, 2) К 2 J (6 cos2 2x + sin 3x) dx Д 6 7Г
XV.61. 1) J (sin4 х + cos2 х) dx-, 2) J (cos4 x + sin2 x) dx. К
2 3 2 4
XV.62. 1) J ||x|-l|dx; 2) J (|x + 2| — |x — 1|) dx.
-0,5 -3
3 jt 4zr
XV.63. 1) J x/1 + cosxdx\ 2) ]' \/l — cosxdx.
0 i 0 2
XV.64. 1) Jx3\A2 + 3dx; 2) fx\/4 - x2 dx.
0 JT 0
XV.65. 1) j sin3 x dx-, 0 2) J cos3 x dx. JT 2
XV.66. 1) Л 2 J sin x sin 2x sin 3x dx\ 2) 7T 3 J cos x sin 2x cos 3x dx.
О О
XV.67. Применяя формулу интегрирования по частям, найти:
2 1) Jlnxdx; 1 2) J xe~2x dx\
1 0 я
7Г 4
3) Jxsinx dx; 0 4) J x arctg x dx 0
§4. ПРИМЕНЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА К ВЫЧИСЛЕНИЮ ПЛОЩАДЕЙ
Первый уровень
Найти площадь фигуры, ограниченной следующими линиями (XV.68-XV.86),
XV.68. 1) у = -х, у = 0, х = 2, х = 4;
2) у = у/х + 1, х 3, у = 0.
XV.69. 1) у = 1 - х2, у = 0;
2) у — 20 - 6х — 2х2, у -- 0.
316 Глава XV. Первообразная и интеграл
XV.70. 1) у = — х2+4х — 4, у = 0, х = — 1, х = 4;
2) у --- — д/2 — х, х = — 7, у = О.
XV.71. 1) у = cos2 х — sin2 х, у = О, х = О, х—
2) у = 1 + sinx, у = О, х = О, х -
XV.72. 1) у = х2 + 2, у = \-х2, х = О, х = 1;
2) у = х/ у = -2х3, х = 2.
XV.73. 1) у = х2, у = 2-х-
2) г/= 5 + Зх — 2х2, у = х-\-\.
XV.74. 1) у = у/х, х - Зг/ + 2 = О;
2) у = х/х+Т, у = + 1.
XV.75. 1) у = х2 - 4, у = 4 - х2;
2) у = х2 - 2х + 2, г/ = 2 + 4х —х2.
XV.76. 1) у= г/= 6 — х;
2) у = х3, у = Ух;
3) у = х2, у = \/х~,
4) у = х2, у = 2У2х.
XV.77. 1) у — ех, у = е~х, х = 1;
2) у = 2х, у = 4х, х = 1.
XV.78. 1) у = 0,5 х, х-2у + 2 = О, х = 2;
2) у - 2-х, у = — х2 + 3,5х + 1, х = 2 (х < 2).
XV.79. 1) у^=х2, у = \-
2) у - 5 -х2, у = 1.
XV.8O. 1) у = у/х, у = 2, х = О;
2) у = у/х + 2, у = 2, х = 7.
XV.81. 1) у = sin х, у = х2 — тгх;
2) у = sin тгх, у = 4 (х2 — х) .
XV.82. 1) у = х, у = у = О, х = е;
2) у = х2, У=-х, У = О, х = 2.
XV.83. 1) у — у/х, у - /8 — х, у = О, х = 1;
2) у — у/х + 2, у — 4 — х, у = 0.
§4. Применение интеграла к вычислению площадей 317
XV.84. 1) у - sin 2х, £/= О, х = 0, х = тс;
2) у = cosЗх, у = 0, х = ~^< х ~ f •
XV.85. 1) у — sinx, у = cosx, у = 0, х = 0,
2) у = sinx, у = cosx, х = 0,
XV.86. 1) у = |х1 2 - 1|, у = 0, х = 0, х = 2;
2) у = |х2 — 4|, £/ = 4,
Второй уровень
Найти площадь фигуры, ограниченной линиями (XV.87-XV.92), XV.87. 1) у = 2 + sin х, у = 1 4- cos2 х, х = 0, х = я;
2) у - sin 2х, у = 1 - sin 2х, х = -£, х=-~. /у у 12- 12
XV.88. 1) г/= sinx, £/ = cosx, х = 0, х = 2тг;
2) у = sin 2х, £/ = cosx, х = 0, х = тг.
XV.89. 1) у=^\, У = 7~\х\;
2) у = 2-|2-х|, у = А
XV.9O. 1) у=±, у = 4-х, х = 1;
2) у = \/х — 3, у - 0,5х — 1, у = 0.
XV.91. 1) у = tg х, у = sinх, х = — j, х=^; 4 и
q \ j ___ 7Г 3 7Г
2) у — ctgx, £/=COSX, Х=Т*
XV.92. 1) г/ = 2х2 + 1, у = х + 2, £/=1,5;
У2
2) ^ = х-у, t/ = 2-x, у = 0,5;
3) г/ = 2-х2, £/ = 0, у=1-
4) у = х2 — 6х + 5, у = 2х — 7, у = 0 (у 0).
XV.93. Вычислить площадь криволинейного треугольника, расположенного в 1-й четверти и ограниченного следующими линиями:
1) у = 12 + 4х — х2, у = Зх, у = 8х;
2) ху = 4, у = х, у = 2х.
318 Глава XV. Первообразная и интеграл
XV.94. Вычислить площадь фигуры, ограниченной графиком функции у = х2 - 2х + 2, касательной к этому графику в точке М = (3; 5) и осью ординат.
XV.95. Вычислить площадь фигуры, ограниченной графиком функции у = 2х2, осью Ох и касательной к графику функции у = 2х2 в точке с абсциссой х — 2.
XV.96. Вычислить площадь фигуры, ограниченной линиями у — - + 1, х = 1 и касательной, проведенной к кривой у = | + 1 в точке с координатами (2; 1,5).
XV.97. Из точки с координатами (1,5;0) к параболе г/ = 2х2 —6x4-9 проведена касательная, образующая острый угол с положительным направлением оси Ох. Определить площадь фигуры, заключенной между параболой, осью Оу, осью Ох и этой касательной.
XV.98. Вычислить площадь фигуры, ограниченной графиком функции у = х^ +1 и касательными, проведенными к этому графику в точках с абсциссами х = 0 и х = 2.
XV.99. 1) Вычислить площадь фигуры, ограниченной графиком функции у = х2 — 4л:+ 5 и касательными, проведенными к этому графику в точках с абсциссами х = 1 и х = 4.
2) Вычислить площадь фигуры, ограниченной графиком функции у = х2 — 2л:+ 2 и касательными, проведенными к этому графику в точках с абсциссами х = 0 и х = 3.
xv.ioo. 1) Вычислить площадь фигуры, ограниченной параболой у = 4х — х2 и касательными к этой параболе, проходящими через точку 7И = (2,5;6).
2) Вычислить площадь фигуры, ограниченной параболой у = 6х — х2 и касательными к э4ой параболе, проходящими через точку М — (2; 12).
XV.101. Вычислить площадь фигуры, заключенной между линиями у -- х3 — Зх, у - х.
XV.102. Вычислить площадь фигуры, заключенной между графиком функции у = х3 — х и касательной к нему в точке с абсциссой х= — 1.
XV.103. Вычислить площадь фигуры, заключенной между линиями у = х4 — 10х2 4-9, у = 0, х = 0.
§ 5. Приложения определенного интеграла к физическим задачам 319
XV.104. Вычислить площадь фигуры, заключенной между графиками функций у - х2, у = У = 0, х = 4.
XV.105. Через три точки А = (0;4), В = (1;9), С = (3; 7) проведена парабола у = ах2 + Ьх + с. Найти уравнение прямой, проходящей через точку А так, что площадь фигуры, g ограниченной этой прямой и параболой, равна
XV.106. 1) Найти все значения параметра Ь (Ь> 0), при каждом из которых площадь фигуры, ограниченной кривыми г/= 1 — х2, у = Ьх\ равна числу с. При каких с задача имеет решение?
2) Найти все значения параметра b (Ь > 0), при каждом из которых площадь фигуры, ограниченной кривыми у — Ьу/х, у — 2 — у/х, и осью Оу, равна числу с. При каких с задача имеет решение?
XV.107. Обозначим через 5(/г) площадь, заключенную между параболой у = х1-\-2х — 3 и прямой y = kx + \- Вычислить наименьшее значение S(k).
§5. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА К ФИЗИЧЕСКИМ ЗАДАЧАМ
Первый уровень
XV.108. Скорость поезда, движущегося под уклон, задана уравнением и(/) = 15 + 0,2Л Вычислить длину уклона, если поезд прошел его за 20 с (путь измеряется в метрах).
XV.109. Скорость автомобиля при торможении выражается формулой v(t) = 18 — 1,2Л Вычислить путь, пройденный автомобилем, если он остановился через 15 с после начала торможения (путь измеряется в метрах).
XV.110. Скорость прямолинейно движущегося тела равна ц(£) = 4t — £2. Вычислить путь, пройденный телом от начала движения до полной остановки (путь измеряется в метрах).
XV.111. Какую работу надо совершить, чтобы растянуть пружину на 0,05 ж, если известно, что для ее растягивания на 0,01 м нужна сила в 1 Я?
320 Глава XV. Первообразная и интеграл
XV.112. Вычислить работу, совершаемую при сжатии пружины на 0,04 м, если для сжатия ее на 0,01 м нужна сила в 10 Н.
XV.113. Для сжатия пружины на 0,03 м необходимо совершить работу 16 Дж. На какую длину можно сжать пружину, совершив работу 144 Дж?
XV. 114. Вычислить массу стержня, длины 6, если его линейная плотность задается формулой р(х) = 2х2 + 3, где х — расстояние от начала стержня.
Второй уровень
XV.115. Вычислить работу, необходимую для запуска ракеты весом Р = 2-104// с поверхности Земли на высоту Л = 1500 Радиус Земли R = 6400 км.
XV.116. Под действием электрического заряда величиной q электрон перемещается по прямой с расстояния а до расстояния Ь. Найти работу силы взаимодействия зарядов в двух случаях:
1) a < b, q < 0; 2) a > b, q > 0.
Считать коэффициент пропорциональности в формуле, выражающей закон Кулона, равным у>0.
XV.117. Треугольная пластина с основанием 0,3 м и высотой 0,6 м погружена вертикально в воду так, что ее вершина лежит на поверхности воды, а основание параллельно \ ей. Вычислить силу давления воды на пластину, приняв плотность воды р = 1000 кг/м.^, а ускорение свободного падения g = 9,807 м/с2.
XV.118. Треугольная пластина с основанием 0,9 м и высотой 0,12 м погружена вертикально в воду так, что ее вершина лежит на 0,03 м ниже поверхности воды, а основание параллельно ей. Вычислить силу давления воды на пластину, приняв плотность воды р = 1000 кг/м\ а ускорение свободного падения g = 9,807 м/с?.
XV.119. Вычислить общую силу давления воды на дно и стенки аквариума, имеющего форму прямоугольного параллелепипеда, если стороны основания равны 0,9 м и 0,6 м, а высота равна 0,4 м. Аквариум доверху наполнен водой.
Задачи повышенной сложности к главе XV 321
XV.120. Вычислить силу давления воды на вертикальную плотину, имеющую форму равнобедренной трапеции, верхнее основание которой 38 м, нижнее 20 ж и высота 12 м. Уровень воды доходит до верха плотины.
XV.121. Цилиндрический бак, высота которого равна 5 м, а радиус основания равен 0,8 м, заполнен водой. Определить, за какое время вытечет вода из бака через круговое отверстие радиуса 0,1 ж в его дне, если скорость вытекания воды v зависит от высоты столба воды h и вычисляется по формуле Бернулли v = 0,5y/2gh, где g = 9,8 м/с1.
XV.122. Жидкость плотности р, подаваемая с плоскости основания в цилиндрический бак через отверстие в дне, заполняет весь бак. Определить затраченную при этом работу, если высота и радиус основания бака равны соответственно h и г.
XV.123. Найти работу против выталкивания при погружении шара радиуса R в жидкость плотности р.
XV.124. Найти координаты центра масс однородной фигуры С, ограниченной линиями у = 2-^/х, у = 0, х = 0, х = 4.
XV.125. Найти координаты центра масс однородной дуги полуокружности х2 + у1 = 25, расположенной над осью Ох.
XV.126. Найти координаты центра масс однородной дуги кривой х/х2-!- х/^2 = (астроиды), лежащей в первой четверти.
XV.127. Найти центр масс однородного прямого кругового конуса.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ XV
Вычислить (XV.128-XV.132),
XV.128. О „ v3 , „7 J 14-х8 2) J \/l-x8
XV.129. 1) J cos5 x sin3 x dx: 2) J cos7 x sin3 x dx
XV. 130. 1) Г X8 j f dx; J 2x2 4-3x 4-2 2) [-7^— dx. J x2 - x 4- 1
XV. 131. 1) J xVx4 + 2dx; 2) J x5\/x2 — 1 dx.
XV.132. н 'sinix + cosix\ dx <cos2x sirrx/
XV.133. При каком значении а прямая у = а делит площадь фигуры, ограниченной линиями у = 0 и у=2+х— х2, пополам?
11—5682
322 Глава XV. Первообразная и интеграл
XV.134. Через начало координат провести прямую, делящую криволинейный треугольник с вершиной в начале координат, ограниченный линиями у = 2х — х2, у — 0, х=1, на две равновеликие части.
XV.135. 1) Найти все значения параметра a (1 а 4), при каждом из которых площадь фигуры, лежащей в полуплоскости х:>0 и ограниченной прямыми z/ = 2, у = 3 и графиками функций у = ах2, у=~ах2, будет наименьшей. Найти эту площадь S.
2) Найти все значения параметра а (а 2), при каждом из которых площадь фигуры, ограниченной прямыми у=1, у = 2 и графиками функций у = у/ах, у = 0,5у/ах, будет наибольшей. Найти эту площадь S.
XV.136. На йти все положительные значения параметра а, при каждом из которых площадь фигуры, ограниченной параболой у = (1 + я2)2х2 и прямой у = а, будет наибольшей.
XV.137. Найти все положительные значения параметра а, при каж-
дом из которых площадь фигуры, ограниченной параболой
у = -4-- - (х2 + 2ах + За2) будет наибольшей.
и прямой у — -4~- - (а2 — ах
ОТВЕТЫ К ГЛАВЕ XV
XV.2. 1) F(x) - |х3 + х5 4- С- 2) F(x) = х + In |х| + С; 3) F(x) = = jXyfi 4- + С- 4) Г(х) = 2/£ 4- 4- С. XV.3. 1) F(x) =
= |sin(5x-3) 4-С; 2) F(x) = ±(2х + З)13 + С; 3) F(x) = Зх 4- | cos 4х 4- С-4) F(x) = |(4х 4- l)V4x+"T 4- С. XVА. 1) F(x) = х - cosx 4- С; 2) F(x) = х + ^cos2x 4- С. XV.5. 1) F(x) = tgx - 2; 2) F(x) =
= ctgx + 1. XV.6. 1) F(x) = Х(4х + 1). 2) F(x) = [^5 (5х-2).
XV. 7. 1) F(x) = arctgx 4- j; 2) F(x) = arctgx - XV.8. 1) F(x) =
= arcsinx 4-^; 2) F(x) = arcsinx + ^. XV.9. 1) F(x) — x — 7In |x + 4| 4- C; 2) F(x) = 6x - 31 In |x 4- 5| 4- C. XNAQ. 1) F(x) = In |x| - In |x 4- 1| 4- C; 2) F(x) = ~-x - arctgx 4- C. XV.ll. 1) F(x) = lx 4- |sin4x 4- C;
2) F(x) — ^x — sin lOx 4- C. XV.12. 1) F(x) = — | cos4x 4- 1 cos2x 4- C;
4 ' 2 20 4 ' 8 4
Ответы к главе XV 323
2) F(x) = | sin4x - 1 sin8x + С. XV.13. 1) F(x) = ±е2х - ±е~2х + 2х + С;
2) F(x) = - 3 • - 3 р + + С. XV.14. 1) S + 1,5/ - ? + 6х + С;
2) 1х4-х3-Лх2 + С; 3) + 2ln|x| - -L + С; 4) - -L + § + 121п |х| - 8х 4- С.
4 £ о оХ 2х х
XV.15. 1) ~.х^х - |х2^ + х 4- С; 2) |х^х2 - Зх^Е 4- 4х 4- С;
3) In |х| + 4>/х + х + С\ 4) --1 + 2^/х + ^ху/х 4- С. XV.16. 1) х-arctgx 4-С; х/Х О
2) — — arctgx 4- С;
3) |х3 - х 4- arctgx 4- С; 4) 2х — 5arctgx 4- С.
XV.17. 1) —cosx 4- 2sinx 4- С; 2) 2х 4- 4ctgx 4- С; 3) -х 4- tgx 4- С;
4) -х - ctgх + С. XV.18. 1) - х 4- С; 2) + С;
3)
In 8
о 2х 3(0,5)х (0,125)'
13 ' In 2 In 2 31n2
4)
XV.19.
1)
4) -f In |1
XV.20. 1)
- 2х| 4- С;
—ly= arctg 2у/Ъ & У5
4) | arctg + с
2) -1(4-Зх)6 4-С; arcsin 2х 4- С;
2) arctg(x 4- 2) -
5» '2
с-,
XV.21.
1) arcsin ^-у=- 4-V б
3) cos(4x 4- 3) 4- С;
6) arctg(2x 4- 3) 4- С. С;
С;
3) | arctg £
2) ^arcsinM
С;
С\
3) arcsin ^4-С; 4) | arcsin ^£±1 + С. XV.22. 1) ^4-^sin2x + C; 2) £-<3 □ х Z 4 Z
— Isin2x4-C; 3) 1,5x4-0,25sin2x4-2sinx4-С; 4) 1,5х — 0,25sin2x — 2cosx4-С.
XV.23. 1) tgx + С; 2) - ctg | 4- С. XV.24. 1) 1 sin 10х 4- | sin 2х 4- С;
2) |sin3x — lsin7x 4- С; 3) — lcosl3x 4- |cos3x 4- С;
4) -lcos7x 4- lcos3x + C. XV.25. 1) |(x 4- I)7 - |(x 4- I)6 4- C;
2) l(x - 2)5 4- |(x - 2)6 4- C. XV.26. 1) |(x 4- 1)2 4- |(x - 1)2 + C;
2) -^(1 - x)3-/l - x 4- |(1 - x)2v4 -x - |(1 - x)>/l -x 4- C.
XV.27. 1) x 4-In |x — 3| 4-C; 2) 2x — | In 11 — 5x| 4-C; 3) 2x - 2 In |2x 4-1| 4-C;
4) 2x-|-|ln|3x-2| + C. XV.28. 1) In |x-1| - In |x| 4-C; 2) In |x| — In |x 4-0,5| 4-C; 3) 0,2 In |x - 3| - 0,2ln|x + 2| 4- C; 4) | In |x - 3| - 1 In |x - 1| 4- C;
5) -1 In |x + 1| + | In |x - 0,5| + C; 6) -1 In |x + 2| + | In |x - 1| 4- C. xv-29. 1) 5^ In I I - 1|n I I + C; 2) 1 In I I - X arctg + C. XV.30. 1) arcsin ^11 4-C; 2) -1 arcsin 4-C. XV.31. 1) -tgx-ctgx4-C;
3 V2 v7
2) tgx - ctgx 4- C. XV.32. 1) у 4- |sin2x 4- 32-sin4* +
2) - 1 sin 2x + 1 sin 4x 4- C; 3) 1 + Isin8x4-C; 4) ^ + Isin8x + C.
o 4 oZ 4 oZ о 04
324 Глава XV. Первообразная и интеграл
XV.33. 1) 0,5 In (х2 + 1) ; 2) | arctg у + С; 3) |(1 4- х4) У1 4-х4 + С;
4) 1 arcsin 4- С. XV.34. 1) 0,25 In4 х 4- С; 2) In |1пх| + С;
3) In |2 4- Inх| 4-С; 4) 0,51п |1пх| - 0,51п |1пх + 2| 4-С. XV.35. 1) 1п(ех 4-2) + С;
2) 2Ч/ГТР7 + С; 3) х - ln(ex + 1) 4- С; 4) ln(ex -- I)2 -- х I С.
XV.36. 1) |sin2x 4- С- 2) -|(cosx 4- 2)4х + С; 3) arctg 4- С;
4) —0,5arctg(cos2x) 4-С. XV.37. 1) - cosх 4- 4- С; 2) sinx-^у^ 4-С;
О О 1 Е О О 1 Е
3) —cosx + у cos х — -cos х -I- С; 4) sinx — - sin х + f sin x + C. 3 5 3 b
XV.38. 1) 4- C; 2) 4- C. XV.39. 1) -ln|cosx| 4- C;
2) ln|sinx| 4- C. XV.40. 1) In |tg|| + C; 2) -ln|tg(^-|)| 4- C.
XV.41. 1) xex + ex 4- C; 2) у (inx- 1) 4- C; 3) ~xe2x - |e2x 4- C;
4) £2MpLl) _ |(X _ 1)2 _ 1 + c XV.42. 1) (inx- 0 + C;
2) x2 Infx+J) _ _ j)2 _ In]^±J1 + c XNA3 1) (1 _ X) cosx + sinx + c.
2) ^xsin3x 4- -cos3x 4- С; 3) у - ~xsin2x — -^cos2x 4- C;
y2 i i
4) — 4- ^xsin2x 4- |cos2x 4- C. XV.44. 1) (1 4- x)ln(x 4- 1) — x 4- C; 2) xarctgx — 0,51n(x2 4- 1) 4- C; 3) xarcsinx 4- \/l ~ *2 4- C;
4) x arccosx - \/l - x2 + C. XV.45. 1) 13,5; 2) 8. XV.46. 1) 8,5; 2) 4. 2 2 6 о 6 о
XV.47. 1) J; 2) у XV.48. 1) J (x + 6) dx > J (x + 2) dx; 2) Jx3t/x> Jx2t/x;
4 2 1 1 2 2
1 ,_____ 2 . . 7 ?
3) J Vx 4- 3 rfx > J fl — x2] dx; 4) J cosx dx > J sinx dx. XNA9. 1) 4; o 1 v 2 о о
2) -0,5; 3) J 4- 1; 4) |; 5) 6) 9; 7) 33,75; 8) -0,75;
9) ^3. XV.50. 1) -jb; 2) 1^. XV.51. 1) 2 - In 3; 2) 2-Ini,4.
XV.52. 1) 12,5; 2) 8. XV.53. 1) 1; 2) 8,2. XV.54. 1) A = В = 2;
2) A = -Д-, B=12 —Д2-. XV.55. 1) [4;+oc); 2) (0;41. XV.56. 1) |ln^; In 3 |nz 3 5 7
2) | in XV.57. 1) 2) ^arctgl XV.58. 1) | + 4In 2) 4-ln3.
XV .59. 1) 2) XV.60. 1) у 4-1; 2) XV.61. 1) 2)
XV. 62. 1) 2b 2) 6. XV.63. 1) 6д/2; 2) 8д/2. XV.64. 1) 6x/|~8; 2) |.
XV.6 5. 1) I. 2) XV.66. 1) b 2) -b XV.67. 1) 2In2 - 1;
2) | - |e-2; 3) л; 4) i + XV.68. 1) 4 In 2: 2)
*1 4 Z OZ о О
Ответы к главе XV 325
XV.69. 1) 2) 114?. XV.7O. 1) 11?; 2) 18. XV.71. 1) 0,5; 2) | + 1.
XV.72. 1) Ф 2) 12. XV.73. 1) 4,4; 2) 9. XV.74. 1) 2) |. Ь о
XV.75. 1) 64. 3 ’’ 2) 9. XV.76. 1) 12 - 51п5; 2) А; 3) А; 4)
XV.77. 1) е + - - 2; 2) -Ц-. XV.78. 1) 3 - 2) 6~ - е ’ ’ 2 In 2 7 41п2’ ’ 3 4 In 2
XV.79. 1) ф 2) 10? XV.8O. 1) 2?; 2) |. XV.81. 1) 2+-^-. 2) - + ^. 3 3 3 ' 6 яЗ
XV.82. 1) 1,5; 2) |+1п2. XV.83. 1) 10?; 2) ??. XV.84. 1) 2; 2)
XV.85. 1) 1; 2) 2^2-2. XV.86. 1) 2; 2) ~(х/2~1). XV.87. 1) ^+2;
2) у/3- Я 3 . XV.88. 1) 4л/2; 2) 2\/3-2. XV.89. 1) 32; 2) 2 -0,5 In 27.
XV.90. 1) 41п2 —2,5; 2) ?. XV.91. 1) |(1п2-1) + ~; 2) | (In 2 - 1)+ у.
XV.92. 1) А?. 2) 3) 8ч/|~4; 4) б|. XV.93. 1) у; 2) 2 In 2.
XV.94. 9. XV.95. |. XV.96. In2 — |. XV.97. 11,25. XV.98. ?.
XV.99. 1) 2,25; 2) 2,25. XV.99. 1) 2,25. 2) 2,25. XV.100. 1) 2,25;
2) у. XV.101. 8. XV.102. у. XV.103. XV.104. 14,5 + In 16.
XV.105. у = Зх + 4 и у = Их + 4. XV.106. 1) 0 < с < b = Д - 1;
3 9с2
2) О < с < ?, b = - 1. XV.1O7. XV.1O8. 340 л*. XV. 109. 405 л*.
3 у Зс 3
XV.110. ю| м. XV.111. 0,125 (Дж). XV.112. 0,8 (Дж). XV.113. 0,09 л*.
XV.114. 162. XV.115. ~ 24,3 • 1010 (Дж). Указание. Сила / притяжения тела Землей есть функция от расстояния х до центра Земли: f(x) = Д, где Л = Р 7?2. XV.116. (1 - IV XV.117. « 353 (Н).
х~ \b a J
Н2
Указание. Р = gp J hf(h)dh, где [(h) — ширина пластины на глубине h.
XV.118. 58,25 (Н). XV.119. « 4472 (Н). XV.12O. « 13 557 197 (Н).
XV.121. 108 с. XV.122. XV.123. ^ri^pg. XV.124. хс = 2,4,
*/t = l,5. XV.125. хс = 0, Ус~~~- XV.126. хс=ус=^- XV.127. Центр масс находится в точке, делящей высоту конуса в отношении 3: 1, считая от вершины. XV.128. 1) 1 In (х8 + 1) + 1 arctgx4 + С; 2) 1 arcsin х4 - 1^1 -х8 + С. XV.129. 1) |cos8x - ?cos6x + С: 2) -l-cos10x - |cos8x + С.
о о 1U о
XV.13O. 1) 1 (х2 - Зх + | In (2х2 + Зх + 2) + arctg + С; 2) +
+ - 1 In (х2 - х + 1) - 4= arctg + С. XV.131. 1) -Пх4 + 2)5 +
Z Z \ /уд у о О \ /
326 Глава XV. Первообразная и интеграл
+ 1 (х4 + 2) 5 + С- 2) 1 (х2 - 1) 5 + | (х2 - 1) 5 + 1 (х2 - 1) 5 + С. XV.132. tgx — ctgx — Зх + С. XV.133. a = | . XV.134. у = |х.
XV.135. 1) a = 4, S = ^-Юх/З. 2) a = 2, S = 3,5. XV.136. a = х/3.
XV. 137. a = ^3.
Глава XVI
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§1. ОСНОВНЫЕ ПОНЯТИЯ
Показать, что функция у[х) является решением дифференциального уравнения (XVI.1-XVI.3)
XVI.1. у' = Зх + у + 5; у(х) = ех - Зх - 8;
XVI.2. у' + 2у = е-х; у(х) = Зе-2х + е~х\
XVI.3. у" + 2/ - 2 = 0; у(х) = 2 + Зе“2х + х.
Показать, что функция у(х) является решением задачи Коши (XVI.4-XVI.6)
XVI.4. х + у — 2 + (1-х)у' = 0, у(2) = 1; у(х) = 1 + (х- 1) ln(x — 1);
XVI.5. х(х —1)у'+у = х2(2х-1), г/(2) = 6; у(х) = +х2;
XVI.6. ху' = у(1пу — Inх), у(-0,5) = — 0,5; у(х) = xe1+2v.
Показать, что при каждом действительном значении параметра С функция у(х) является решением дифференциального уравнения (XVI.7-XVI.9)
XVI.7. ху'+у = у2 Inx; у(х) = -—-1 , у J ’ 1 + Сх + 1пх
XVI.8. xyz —2у = х3 cosx; у(х) = Сх2+х2 sin х;
XVI.9. у' — у cosx = sin 2х; у(х) = Cesinx — 2(1+ sin х).
§2. УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
Найти общее решение дифференциального уравнения, а также указать его частное решение, удовлетворяющее заданному начальному
условию (XVI.10-XVI.14),
XVI.10. у' = 2х, у(1) = 3. XVI.11. у' = 4х —3, у(0) = 0.
XVI.12. у' = £, у(5) = 10. XVI.13. у' = 2(у-3), у(0) = 4.
328 Глава XVI. Дифференциальные уравнения
XVI.14. 1/' = ^. 1/(1) = 0.
14-xz
XVI.15. Найти функцию, удовлетворяющую условию У = Л, гра-У фик которой проходит через точку Л4 = (4;3).
XVI.16. Найти функцию, удовлетворяющую условию ху' = (х +1)//, график которой проходит через точку М= (1; е).
XVI.17. Вывести уравнение кривой, проходящей через точку 7И=( —1;0) и всюду имеющую касательную с угловым коэффициентом 2.
XVI.18. Вывести уравнение кривой, проходящей через точку Л4= (1; 0,5), если угловой коэффициент касательной в любой точке кривой равен квадрату ординаты точки касания.
XVI.19. Вывести уравнение кривой, проходящей через точку М = (0;2), если угловой коэффициент касательной в любой точке кривой равен произведению координат точки касания.
XVI.20. При прямолинейном движении тело удаляется от некоторой фиксированной точки. Скорость тела в любой момент времени численно равна | пройденного пути. Найти путь s (м), скорость v (м/с) и ускорение a (м/с2) как функцию времени t, если в начальный момент скорость равна е м/с.
Найти общее решение дифференциального уравнения (XVI.21-XVI.30)
XVI.21. у+у' (\-у)х = Ъ.
XVI.22. (у2 + \)dy + dx=(2x — x2)dx + <lydy.
XVI.23. ^(ydy-xdx)^ \dy-\dx. У х
XVI.24. у' = ех+У.
XVI.25. (1+х)гд/х-|-(1 — y)xdy = Q.
XVI.26. ydy--^dx = Q.
XVI.27. (ху2+x)dx + (x2y — y)dy = Q).
XVI.28. =
у In у sinx
XVI.29. х(у2 - \)dx+y(x2 - \)dy = Q.
XVI.30. -±Sdi_dx + -&l-dy = Q.
cos2x cos2 у
§ 3. Линейные уравнения с постоянными коэффициентами 329
Найти частное решение дифференциального уравнения, удовлетворяющее заданному начальному условию (XVI.31-XVI.33) XVI.31. [-^dy=-^-, у(0) = 1.
у COSX 4 '
XVI.32. e'-2x+x2(l-x)dx + ctg ydy=O, {/(!) = ?•
XVI.33. y2dy-^ = 0, </(0) = 0.
1
§3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКОВ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Найти общее решение дифференциального уравнения, а также указать его частное решение, удовлетворяющее данному начальному условию (XVI.34-XVI.37),
XVI.34. 1) У = -2^4-4, ^(0) = 5;
2) /-44/ = 8, ^(0) = 4.
XVI.35. 1) у'-у = 2х, 4/(О) = 3;
2) у' + 3у = 1 — 6х, 4/(0) = —2.
XVI.36. 1) у' — 24/ = cosx, 4/(0) = -1;
2) У' -^ = sin 2х, 4/(0) = 0.
XVI.37. 1) у' + у = ех, 4/(О) = 2;
2) у'— Зу = с1е2х, 4/(0) = 1.
Найти общее решение дифференциального уравнения (XVI.38-XVI.40).
XVI.38. 1) у”-б4/' + 84/ = О; 2) у"-4у'-5у = 0.
XVI.39. 1) у" + 4у' + 4у = 0-, 2) у"- 10/ + 254/ = 0.
XVI.40. 1) у"-4у’ + 134/ = О; 2) у” + 6/ + Юг/ = 0.
XVI.41. Найти частное решение, удовлетворяющее указанным начальным условиям:
1) /' + 3/ = 0, 4/(О) = 2, /(0) = 3;
2) 4/'-4/ + 4/ = 0, 4/(0) = 0, /(0) = 2.
XVI.42. Найти общее решение дифференциального уравнения:
1) /'-94/ = 3; 2) у"-7 у' + 124/ = -6.
330 Глава XVI. Дифференциальные уравнения
XVI.43. Найти общее решение дифференциального уравнения:
1) у"-2у'+у = 2х- 2) у"-у'-6у = х + 2.
XVI.44. Найти уравнение гармонических колебаний, которому удовлетворяет функция:
1) x(Z) = 2sin3Z + cos3/; 2) x(7) = 2sin ^2Z + .
XVI.45. Пусть x(f) — решение уравнения х" + 6J2x = 0, причем при некотором t — to выполняется условие x(/q) = x/(Zq) = 0. Доказать, что в этом случае x(t)=O при всех t.
XVI.46. Пусть %1(/) и Xztt) — решения уравнения х" + б)2х = 0, причем при некотором t = to выполняются равенства A?i(Z^o) — х2(^о)> х1(^о) =х2(^о)- Доказать, что в этом случае X1(^ = X2(Z).
XVI.47. Пусть X\{t), x<2[t) — решения уравнения х" + щ2х = 0. Найти 6) (б)>0), амплитуду А и начальную фазу фо решения %1(0 + ^2(0 = А sin(ei)Z + ^0), если:
1) X[(t) = 4 sin 2t, x<2[t) = 3 cos2/;
2) %i(/) = sin X2(0 = s*n
XVI.48. Тело, масса которого равна т, свободно падает с некоторой высоты. Вывести закон, по которому изменяется скорость v = v(t) падения тела, если на него кроме силы тяжести Р действует сила F\ сопротивления воздуха, пропорциональная скорости падения.
XVI.49. Найти зависимость от времени массы колонии бактерий при условии, что скорость размножения бактерий в любой момент времени положительна и пропорциональна их массе.
XVI.50. На материальную точку массой т действует постоянная сила Fi, направленная в сторону движения, и сила F%, пропорциональная скорости и направленная против движения. Вывести закон движения точки.
XVI.51. Найти закон прямолинейного движения материальной точки массой т под действием постоянной силы F.
XVI.52. Найти функцию, график которой обладает тем свойством, что отрезок любой касательной, заключенный между осями координат, делится пополам точкой касания.
Ответы к главе XVI 331
XVI.53. Скорость распада радия пропорциональна наличному его количеству. В течение года из каждого грамма радия распадается 0,44 л«г. Через сколько лет распадается половина имеющегося количества радия?
XVI.54. Материальная точка массой в 1 г движется прямолинейно под действием силы, прямо пропорциональной времени, отсчитываемому от момента t = 0 и обратно пропорциональной скорости движения точки. В момент ^=10 с скорость равнялась 50 см/с, а сила — 4 дин. Какова будет скорость спустя минуту после начала движения?
XVI.55. Корабль замедляет свое движение под действием силы сопротивления воды, которое пропорционально скорости корабля. Начальная скорость корабля 10 м/с, скорость его через 5 с станет 8 м/с. Когда скорость уменьшится до 1 м/с?
XVI.56. По закону Ньютона, скорость охлаждения какого-либо тела в воздухе пропорциональна разности между температурой Т тела и температурой воздуха Tq. Если температура воздуха равна 20°С и тело в течение 20 мин охлаждается от 100°C до 60°C, то через сколько времени его температура понизится до 30 °C?
XVI.57. Скорость истечения воды из сосуда через малое отверстие определяется формулой и = 0,6 \/2^/г, где h — высота уровня воды над отверстием, g —ускорение свободного падения (принять £=10л//с2). За какое время вытечет вся вода из цилиндрического бака диаметром 2R = 1 м и высотой Н=\,Ьм через отверстие в дне диаметром 2г = 0,05щ?
XVI.58. Некоторое количество нерастворимого вещества, содержащее в своих порах 2 кг соли, подвергается действию 30 л воды. Через 5 мин 1 кг соли растворяется. Через сколько времени растворится 99% первоначального количества соли?
ОТВЕТЫ К ГЛАВЕ XVI
XVI.10. у = х2 + С, у = х1 + 2. XVI.11. у = 2х2 - Зх + С, у = 2х2 - Зх.
XVI.12. у = Сх, у = 2х. XVI.13. у = Се2х + 3, у = е2х + 3. XVI.14. arctgz/ = = arctgx + С, arctgу = arctgx — XVI.15. у = S^6x + 3. XVI.16. у =
332 Глава XVI. Дифференциальные уравнения
= хех. XVI.17. у = 2х + 2. XVI.18. у = . XVI.19. у = 2<Л.
3 — х
t i t
XVI.20. s(/) = 3<?1+3 м, и(/) = <?1+з м/с, а(г) = ^<?1+3 м/с2. XVI.21. уг'у =
= £. XVI.22. (у - I)3 + (% - I)3 = С. XVI.23. у2 - х2 + ~ =
= С. XVI.24. ех + е~» = С. XVI.25. ху = Cel/X. XVI.26. у2 = = 1п(1 + е*)2 + С. XVI.27. (1 + г/2)(1 - х2) = С. XVI.28. у = еСЛё 2.
XVI.29. (х2 - l)(z/2 - 1) = С. XVI.30. tg х tg у = С. XVI.31. l- 1п2у =
= ln|tg(g + ^) |. XVI.32. 2 In | sin z/| = e(x-1)2 — 1. XVI.33. arctg ех =
= + J. XVI.34. 1) у = 2 + Се~2х, у = 2 + 3<Г2х; 2) у = Се4х - 2,
у = 6е4х - 2. XVI.35. 1) у = Сех - 2х - 2, у = Ьех - 2х - 2; 2) у =
= Се'3* — 2х + 1, у = — Зе~3х — 2х + 1. XVI.36. 1) у — Се2х — | cosx + | sinx, у = ~|е2л — |cosx + | sin х; 2) у = Сех — |cos2x — |sin2x, у = = ^ех — | cos 2х - | sin 2х. XVI.37. 1) у = Се~х + 0,5ех, у = 1,5е-х + 0,5ех; 2) у = Се3х - 2е2х, у = Зе3х - 2е2х. XVI.38. 1) у = Ср>2х + С2<?4*; 2) у = = С\е~х + C2eSx. XVI.39. 1) z/ = C1e“2x + C2xe-2x; 2) у = С,е5х + С2хе5х. XVI.40. 1) у = е2х (Ci cos Зх + С2 sin Зх); 2) у = е~3х (С) cosx + С2 sinх).
XVI.41. 1) у = 3-е~3х- 2) у = 2хе°'5х. XVI.42. 1) у = Схе3х + С2е~3х -2) у = С\е4х + С2<?3х - 0,5. XVI.43. 1) у = С{ех + С2хех + 2х + 4; 2) у =
= Схе3х + С2е~2х - |х - XVI.44. 1) х" + 9х = 0; 2) х" + 4х = 0.
О оо
XVI.47. 1) о = 2, А = 5, фо = arccos 2) о = 3, А = фо = J-
XVI.48. v — Се~~т + — решение уравнения т^ — mg — kv, где k —
коэффициент пропорциональности в условии F\ = —kv. XVI.49. т = Cekt — решение уравнения — —km. XVI.50. x(f) = С\е т + -±t + С2 — решение уравнения mx"(t) = F\ — kx\f). XVI.51. x(Z) = ^t2 + C\t + C2 — решение уравнения mx''(t) = F. XVI.52. у = ^ — решение уравнения у' =
XVI.53. Через 1575 лет. XVI.54. v = 10л/725 см /с. У к а з а н и е: уравнение имеет вид =20-. XVI.55. t= — с. Указание: уравнение
dt v In 0,8
имеет вид т • = — kv. XVI.56. t = 60 мин. Указание: уравнение
at
имеет вид = k(T - То), Т = 20 + 80(0,5)2° XVI.57. « 365 мин.
Указание: уравнение имеет вид (livQijdt = — S(h')dh, где to—площадь отверстия, u(/z) — скорость истечения воды, h — уровень жидкости, S(Ji) — площадь поперечного сечения сосуда, t — время. XVI.58. 32,2 мин.
Глава XVII
СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ РАЗЛИЧНЫХ ТИПОВ
§1. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ СИСТЕМЫ
Первый уровень
Решить систему уравнений (XVII.1-XVIL10).
ХУПЛ. 1) ] '4х~у = 128, (5х +у = 125, 53x+2i/- з = 1; 2) |4(x-i/)2--1 = j
XVII.2. 1) J 'зх-2^ = 1 (8Х = 32-2У, <у-х = 2; \2х + у = log2 32.
XVII.3. 1) <99 Г 9 9 / 1 \ —64 QXz+t/z _ Q ОХЛ+Ц£ _ 1 1 | г- 7— 2) V " ’ .V x’v У [л/х-л/^ = 4.
XVII.4. 1) J '5х + 2у = 100, Jgx - 1gу = 1g 1,6;
2) '52+iog5(x-у) = 125, Jg (х - у) + lg(x + у) = 2 - 1g 5.
XVII.5. 1) <| 'log2x + log2t/ = 4, 2 Igx - 1gу + 1g 2 = 0;
2) < logs 0°g27 + loS 1 (logi У ) =1> 3 \ 2 / Jog2 x + 2 log2 у = 2.
XVII.6. 1) < log3 x - log9 у = 0, Г log0 5 (-x) - log0 25 у = 0, У-2у + 5О = О; ’ \x2 + y = 8.
XVII.7. 1) 'log2x + log2z/ = 4, pog4x + log4(-t/) = 3, Jog4(x + t/) = 1,5; |log8(x-y) =
XVII.8. 1) J ГЗУ • 9х = 81, ^21g(x + y) - lgx = 21g3;
2) < <3x+l . 93£/-2 = 9 log^_ (y + 7 + 2 log3(1 + x) = 4. v/3 \
334 Глава XVII. Системы уравнений и неравенств различных типов
(х2 + у2 = 50,
XVII.9. 1) \ log! 0,5 llog5 X + 2 log5 y/у = 3 3 ;
2) (log2 (х2 + t/2) = 5, \21og4(-x)-log05z/ = 4.
XVII.10. 1) (2(log^x + logxz/)=5, (log^x + logxz/ = 2, [xz/ = 8; (x2 - 2y = 8.
Решить систему уравнений методом замены переменных (XVII.11-
XVII.18)
xvii.ii. i) (2 х + 2" = 4, (3х-3^ = 1, (2x-y = 3; 2) \3x+^ = 6.
XVII.12. 1) (9х - 25^ = 56, ((2х - 22^) (4х - 24^) = 45, (3х+ 5^ = 14; ' (2х+4^ = 5.
XVII.13. 1) Г32х+1 + 52"+l = 152, (52x+32^+1 =36, (3 х + 5^ = 8; } (5х-3^ = 4.
XVII.14. 1) ГЗХ+4^ = 11, [9х+ 24^ = 3Х+1 -4^ + 31;
2) Г7х + 2^ = 9, (72х +4^ = 2^ 7Х+1 - 45.
XVII.15. 1) (у2 = 4х + 8, р + 2^+1 =3, (2x+l 4-t/+ 1 = 0; ' (4x4-4^ = 32.
XVII.16. 1) (log2 X + log3 у2 = 0, Г 2 log4(-x) + log 1 y3 = -l, |log2 X2 - logi у = 5; |log4x4 - logi у = 5.
XVII.17. 1) flog, 10 + logy 10 = 5, riogx3-log^5 = 2, \lgx + !gz/ = !,25; J l^x^Jog^z^S.
XVII.18. 1) J 2 • 5l-y = log3 (x-2) , pog5^/=-7~x, [5^ + log3x = 4; (7х + log5 у = 6. Второй уровень
Решить систему уравнений (XVH-19-XVII.25).
XVII.19. 1) < -22log2x + 32log3? = 8> ,52log5x _ 4log2i/ = 3; 22'°S2X + 32l<>g3!/ = 0.5; 1252logs+ 24= 17.
§1. Показательные и логарифмические системы 335
XVII.20. 1) < '2х-3^ = 54, ГЗх-5^ = 135, + Зу - 11; [Зх — Ъу = 4. <22 <22 — + — = 28, — + — = 12,
XVII.21. 1) J У х 2) < У х 21og9x - log! t/ = 3; 2~1о^х + 5-log'r’-/ = 1. < з V 3
XVII.22. 1) < <log2t/ = log4(xr/ —2), Jog9 x2 + log3(x-//) = 1;
2) < 'log-2 x + log3(x + ^) = l°gi + < 3 Л
XVII.23. 1) < ^2x^y)-2-^ = H, l'(5x + ;/)-3t+!'=+ Jog7(2x-r/) = x + 2y\ (-log7(5x + r/) = x + r/.
XVII.24. 1) < flog2(x + i/) - log3(x- y) = 1, +2 - У2 = 2;
2) < flog2 xy + 41og4(x - y) = 5, x2 + y2 = 20.
XVII.25. 1) -—2 F logo xy = 3, Iog3 ХУ 3 Jog3(3 + xy) - 2 • log9 у = log3(t/ - 1); +. =5 + l0g2(x)’
2) < 1082 и [21og4(l +{/) + log2z/ = log2 (-2 + ^)
XVII.26. Найти все числа х и у, для которых
1) (2x+l =4z/2 + l, (2x+1-4 = y2, \2x^2y; } [2х-1 ^-y.
XVII.27. Найти все числа х и у, для которых
1) f41og2(—x) + 1 = 21og2y, 2) f log2 x + 1 — log2 t/2, llog2x2 log2y; Uog2x log2(-//).
Решить систему уравнений (XVII.28-XVII.33).
XVII.28. 1) ( I x , u (\ 2 x о I 2 I । 2 I °^4 о 1°ё4 о Jig -=3lg2x + lg2//, 1 —5- = —A < У 2) < 10g4(/ log4x [1g 2Q/-3x) + lgx-lgz/ = 0; lo * = v 54 у log4x
336 Глава XVII. Системы уравнении и неравенств различных типов
log4 ху + 3 • = 0,
XVII.29. 1) < 10g4 у Jog4 - log4 х • log4 у = 0;
2) < 'log8 ху = 3 • log8 х • log8 t/, l ё8 10g8//
XVII.30. 1) < 'log2i>f^ = 2, Jog2^/x-log2(i/+l)2 = |;
2) < finer £ = 20 lpg2 x S2y 31og2//’ 4x5 — y\
XVII.31. 1) < 'log2r/-k)gi 2 = 1- logx2, 2 - log^ x = 1;
2) < flg2-lg(2x) = Ig3-lg(3;/), Ilgxlg3 = lgylg2.
XVII.32. 1) < 'log2(l -x) + log2t/ = 3, jc2 + y2 = 2x + 64;
2) < logs +1о?5(1-^) = 1, чх2 + t/2 = 40 + 2t/. [2 log2(x + y) - log2 x = 2 log4 2 + log2(3t/ - x),
XVII.33. 1) < log2 2 Xy^l . . 2 log4 yx °; k xz — у + 3x + 1 x
2) < рое2(65-2^) = 4-</, l1Og2//-X2t+6 “10g2^ 1Og2(2
XVII.34. Найти все значения параметра а, при каждом из которых имеет единственное решение система:
1) ( (3 - 2V2)y + (3 + 2V2)y - 3a = x2 + 6x + 5, Si/2 — (a2 — 5a + 6) x2 = 0, I — 6 C x 0;
2) ( (2 - V3)x + (2 + V3)x-5 = a-2y + y2, $ x2 + (2 - a — a2) y2 = 0, lo у 2.
§ 2. Тригонометрические системы 337
XVII.35. 1) Найти все значения параметра а, при каждом которых любое решение системы х-а2 log3t/ = 1, х + За log3 у — 1 удовлетворяет неравенству у > 1 — х.
2) Найти все значения параметра а, при каждом которых любое решение системы
|у - a3 log2 х = 3, \у — a log2 х — 3 удовлетворяет неравенству у > 3 — х.
XVII.36. 1) Найти все значения параметра а, при каждом которых система уравнений
1°£з(2х - У) = l + log3x, х(2х + у + 2а) = а - 2 имеет два решения.
2) Найти все значения параметра а, при каждом которых система уравнений
log2(x ~У) = 1 + l°g2X, (х - а)2 + (х + у + а)2 = 1
имеет единственное решение.
XVII.37. Реш ить систему уравнений
l°g%-2 (2х2 -4x + t/ + 1) = 2, х + у — 3 = а — а2.
из
из
из
из
§2. ТРИГОНОМЕТРИЧЕСКИЕ СИСТЕМЫ
Первый уровень
Решить систему уравнений (XVII.38-XVII.42).
XVII.38. 1)
sin(2x + Зу) = О, cos(3x — 2у) — 1;
XVII.39. 1)
XVII.40. 1)
х — у = 2д, cos4x + sin 2у = —2;
5 тс Х"^=Т’ sinx = 2 sin у,
2)
2)
2)
(cos(x — у) = 0,5, \cos(x + у) — -0,5.
J2x + Зу = 1,5л:,
(3 cos 4х + sin Зу = 4 . 7тс
X 4-у = -г, < J 6
2 cosx + sin у = 0.
338 Глава XVII. Системы уравнений и неравенств различных типов
XVII.41. 1) f / 3’ 2) H y 6> (cosz тих — sinz 7iy = 0,5; (sinx • cosy = 0,5. (л/—cos y-cosx = 0, (\/sinx-cosz/ = 0,
XVII.42. 1) J v » 2) < ( cos 2x — 2 cos2 у + 2 = 0; ( 2 sin2 x — cos 2y — 2 = 0.
XVII.43. Решить систему уравнений методом введения новых переменных: (cos х + cos у = 0,5, l+gx + ctgy = 2, (sin2 x + sin2 у = 1,5; (ctgx + tgy = 2.
XVII.44. 1) Найти все решения системы (sin х + cos у = 0, (sin2 х + cos2 у = 0,5, удовлетворяющие условиям 0 < х <71, 0 < у < к. 2) Найти все решения системы (sinx + tgy = 0, (sin2 х + tg2 у = 1, удовлетворяющие условиям 0 < х < 71, 0 < у <71.
XVII.46. 1)
2)
Второй уровень
Решить систему уравнений (XVII.45-XVII.50).
[ х 4-1/ = — [ х + 2у = я.
XVII.45. 1) Iх 2’ 2) < У
3 sin Зх + cos у = —4; (4 cos Зх - cos 2у = -5.
sinx = sin 2у,
2 sin(4x + 8t/) sin(3x + Юу) + cos(7x + 2z/) = 4; cos 3x = cos y,
2 cos(9x + 3t/) + 9 sin(15x — 2y) = 4.
ftgx + tgy = 1,
XVII.47. ।
COSX • COS У - -7=.
I У V2 tg* + tgt/ = 1 -tgx-tgy, sin 2y — \[2 sinx = 1; tg//-tgx= l+tgx-tgz/, cos 2y + x/з cos 2x = — 1.
XVII.48. 1)
2)
§ 2. Тригонометрические системы 339
XVII.49. 1) t71 + sin*-sin</ = cosz, [2sinx • ctgу + 1 = 0;
y/1 + sinx • sin у — cos t/,
(sin х + sin у = sin(x + у),
XVII.50. Л . . , 7
Решить систему уравнений (XVII.51-XVII.54).
XVII.51. 1)< 'cos 2x - 2 tg4 у = -4, sinxd—-9— = 3; * t cos2 у '3 cos 2x - 6 ctg4 2 cos x — —=— = I sin2 у y = -5.
XVII.52. XVII.53. ( cosx — cos у = —1,5, D У _l_ ’ , 2) [cos|+sin- = —-1; (sin x + sin у = sin3 x + sin3 t/, (sin2x + sin2 у — sin4x + sin4 y. 'cosx + cos у = . X . . u sin - + sin -1,5, 2
XVII.54. (cos(x -1/) = 2 cos(x + t/),
19,
(cosx • cost/ = U,75.
Решить систему уравнений (XVII.55-XVII.58).
(2 sinx cost/ = 2ctgx + ctg у,
XVII.55. s
[2 sin у cosx = ctgx + 2ctgt/.
XVII.56. Jcosx,cos^ 4 >
4ctgx • ctg r/ = 3 + 2\/2.
{cos x + 3 sin x = 2 cos y, cos у + 3 sin у = 2 cos x.
{. о / 7f\ 9 / 7г\
x sin2 x - - = у cos2 \y + - ,
> 6\ > 6<
9/ 7Г \ . 9 / yr \
X cos2 x — - = у sin2 \y + - .
\ 6 J \ 6 /
Решить систему уравнений (XVII.59-XVII.62).
"2 sinx — sin у = О,
"2 cosx — \/3 cos у = 0.
(sinу = 3 sin x, (3 cosx + cos у = 2,
XVII.60. 1) 2) < У
(2cosx + cos у = 1; (sin у = 5 sinx.
XVII.59.
340 Глава XVII. Системы уравнений и неравенств различных типов
XVII.61.
XVII.62.
XVII.63.
XVII.64.
XVII.65.
XVII.66.
XVII.67.
XVII.68.
{• 2
sinz X = sin у,
4
COS X = cos у.
{6 cosx — 4 cos у = 5, у
3 sinx + 2 sin у = 0;
{2 sin х + 4 cos 1/ = 3, у
cosx — 2 sin у = 0.
Решить систему уравнений <
tgx + ctgx = 2sin (y - ,
tgi/ + ctgt/ = 2 sin (x + ^) • Решить систему уравнений:
{sinx — arcsin у = —1 —
2
7CU . X X
cos — arcsin - =
2 7Г 6
{sinx + arccost/ = — 1,
xy x i 2л
sin — arccos - = 1 — —.
2 л 3
При каждом значении параметра а решить систему: f sinx • sin у = a, f sin x • cos t/= a,
D 2)
{х-у = Щ [x-t/=-.
При каждом значении параметра а решить систему: (sinx • cos у = a, (2 sinx • cos 2y = (a — I)2,
(cosx • sin у = a — 1; (cosx • sin 2y = a + 0,5.
Определить, при каких значениях параметра а система х2 + ax + 3 = О, sin2 an + cos2 + 2y2 = sin ^x имеет решения, и найти все эти решения.
Определить, при каких целых значениях k система имеет решения, и найти все эти решения:
((arctgx)2 + (arccost/)2 = n2k, (arctgx + arccos у = {arccosx + (arcsinz/)2 = k, ,2 /
(arcsiny) -arccosx=—. v J' 16
.2
Задачи повышенной сложности к главе XVII 341
XVIL69. Определить, при каких значениях параметра а система 9 9
х + у = а, cos(x — у) + ху = 1 имеет единственное решение.
XVIL70. Определить, при каких значениях параметра а система х2 + 2ах + За2 + За + 3 3 sin у — 4 cos у, О г/ 2д имеет единственное решение.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ XVII
Решить систему уравнений (XVIL71-XVII.75).
XVII.71. 1) < '5 + logy X2 - - logy^ £/, Нойх -6-3^-log25</;
2) < pog9(10y-9x)_2 )о^, g _|_ (log3x) ~4 _ ^y-x _|_ |Qg x2 I log3t/ by
XVII.72. 1) < 27 • 32x~y + 3%2 = 4x/3, 1g (t/ - 4x) = 2 lg(2 + 2x - t/) - 1g t/:
2) < '8>2_х-2у+ 2i/2 =3x/2? Jg (x + 4t/) = 2 lg(2 - x - 2t/) - Igx.
XVIL73. 1) < 'logi x + logi у - logi (x + y) = 1, 3 3 3 log3 x • log3 у + log3 (x + y) = 0; 2 2 2
2) * pog|x + 2-log| + y — 3 log3 x • log3 £/, log! X • log, у - 3 logi . x. . logi y. k з 3 з 3X + 41/ 3
XVII.74. 1) < '2 + |о£х/з(2х) = 1о£з<А 2 • log3 (9 + - log3 x2 = 2-log3(x + 2);
2) < ' log3 (y + 3x) - log27 8 = log3 (3 - x), 4 + 1о?3^ = 1ое7з(9х).
342 Глава XVII. Системы уравнений и неравенств различных типов
XVII.75. И 1 + 21о£|х//| 2) • loSx+// \*у\ = [х — у - 2\/3; 2) = ' I21og5|xt/|-log|x//|(x + i/) = l.
XVII.76. Найти все пары чисел (x;t/), удовлетворяющие одновременно двум неравенствам: px+zz-i + з . 42//-1 2, r3x+2i/-l + 2 • З3^1 2, ) [х + 2г/ 2 — log4 3; [х + 5г/2 - log3 2.
Решить систему уравнений (XVIL77-XVIL83).
XVII.77. ( log3(7 - 2х) + log j (5х - 7у) = 0, < 3 [ д/х + г/ + 3 — \/8 — 2х = >/Зх + у - 9.
XVII.78. Г 2х = 2У + (х2 + Зг/2 - 4х£/)2 , (4^ = 4 х + (2х3 - 5 г/3 + 3x2t/)4 ; 2 Г5У = 25х - (ху - 10х2 + 2г/2)4 , [25^ = 625х + (ху2 - 12х3 + у3)2 .
XVII.79. (cos2 у + 3 sin х sin у = 0, [21 cos 2х — cos 2у = 10.
XVII.80. fctgx + sin 2у = sin 2х, [2 sin у • sin(x + у) = cosx; 2) |4tg3x = 3tg2t/, [2 sin x • cos(x — t/) = sin y.
XVII.81. ( sin2 x + sin2 у = 0,5, [cos(x + y) sin2(x — t/) + cos(x - y) siri2(x + y) = 0,75. pgx-tgz = 3,
XVII.82. < tg£/-tgZ = 6, lx + у + Z - 71. f 3 sin x + 15z/ = 5x + 3 sin 3z/,
XVII.83. 1) < 2 [3 х = 5^; Гб sinx — 16t/ = 6 sin 2y — 8x, ^) \ 2 I 7х = 9^.
Ответы к главе XVII 343
XVII.84. Найти все значения параметра а, при каждом из которых система имеет ровно два решения:
п f log2 (5х + 1у + 2) = log2(X + 2t/ + 1) + 2,
I (х + 2а)2 + у = х + а + 0,5;
2) По£з(?х + 4г/ - 11) = log3(2x + у - 3) + 1, [(t/ + a)2 + x + t/ + a = 7.
ОТВЕТЫ К ГЛАВЕ XVII
XVII.1. 1) (2;-1,5); 2) (1;2), (2; 1). XVII.2. 1) (-2; 0); 2) (2; 1).
XVII.3. 1) (-1;-1); 2) (4; 4). XVII.4. 1) (16; 10); 2) (4,5;-0,5).
XVII.5. 1) (2; 8); 2) (64; 0,25). XVII.6. 1) (5x/2;50); 2) (-2;4).
XVII.7. 1) (4; 4); 2) (8;-8). XVII.8. 1) (1;2); 2)
XVII.9. 1) (5; 5); 2) (-4; 4). XVII.10. 1) (2; 4), (4; 2); 2) (4;4).
XVII.11. 1) (log23:0); 2) (l;log32). XVII.12. 1) (2; 1); 2) (2;0),
(0; 1). XVII.13. 1) (Iog3 7; 0); 2) (log5 (ч/б + 3); log3(x/6 - 1)).
XVII.14. 1) (2; 0,5), (log32;log23); 2) (1;1), (log, 2; log2 7).
XVII.15. 1) (0;—3); 2) (-17;log2 10). XVIL16. 1) ^8^2; 2) (-4; 5).
XVII.17. 1) (10,У1б), (Ш,1о); 2) 25), (3; У5). XVII.18. 1) (|;1);
2) (1; j). XVII.19. 1) (2,2); 2) (2,1). XVII.20. 1) (1;3); 2) (3; 1).
XVII.21. 1) (9,3), (3;9); 2) (6;6). XVII.22. 1) (3;2); 2)
XVII.23. 1) (3,-1); 2) (2;-3). XVII.24. 1) (1,5; 0,5); 2) (4,2), (-2;-4),
(2 + V6;-2 +V6), (2-V6;-2-V6). XVII.25. 1) (1;3), (|;4); 2) (4; 1); (16;2). XVII.26. 1) (0; 0,5); 2) (2;-2). XVII.27. 1) (-лЛ;2); 2) (2;-2). XVII.28. 1) (1; 4), (0,5;2); 2) (4;2), (_L^;16x/2). XVII.29. 1) Q;|), (|;64); 2) (8;2\/2), XVII.30. 1) (2;3), (x/2; 15); 2)
XVII.31. 1) 2) Q;|). XVII.32. 1) (0;8), (-7;1); 2) (5;-3),
(4;—4). XVII.33. 1) (1; 1), (c;3c), где с — любое положительное число;
2) (1,5; 4); (с;—2), где с —любое число, удовлетворяющее условию 1 < с < 2. XVII.34. 1) -1; 2; 2) -3; -2. XVII.35. 1) а / -3; 2) а / 1.
XVII.36. 1) (1; 2); 2) U {1}. XVII.37. (а;3-а2), если
a € (2; 3) U (3; +оо); (1 — а; 2 + 2а — а2), если a € (—оо; —2) U (—2; — 1); 0, если а G [-1; 2] U {—2; 3}. XVII.38. 1) (2/г + 6п); ^(3/г - 4п)),
2) ^(6fe + 6n±l);^(2fe-2rt±l)), (J(2£ + 2п ± 1); ^(6/г - 6а ± 1)),
344 Глава XVII. Системы уравнений и неравенств различных типов
k.n&Z. XVII.39. 1) (^ + л/г;-^ + л/г), /ге2; 2) +
k G Z. XVII.40. 1) (^(2/г + 3);-^ +л/г), k G Z; 2) (у + ли; - ли),
n G Z. XVII.41. 1) (|(6/г-1); | (6/г+1)), /г G Z; 2) (J +л/г; л/г), (j + л/г;| + л/г), k G Z. XVII.42. 1) (| + л/г; ±у + 2ли) , /г, n G Z; 2) {(-1)^+ л/гу + ли) , /г,и€2. XVII.43. 1) ((-1)" arcsin 0,75 + л/г; ± arccos 0,25+ 2ли), /г, и € Z; 2) + л/г; ^+ли), /г, и G Z.
XVII.44. 1) (|; у), (^Д); 2) (V л-arctg (Д
л-arctg^^. XVII.45. 1) + 2л/г; л - 2л/г), k G Z; 2) (л + 2л/г;
— л/г), /г € Z. XVII.46. 1) (±£ + + 2л/г; ±А + ^), (5л ^+2л/г;
£ + f). k,neZ-. 2) (<^arc5ml + f;b^arcsinl + = +2^), (- ' arcsin | + у ; -——arcsin | — у + 2л/г^, /г,иЕ2. XVII.47. (л/г;
у + 2ли — л/г), (у + л/г; 2ли — л/г), /г, и € Z. XVII.48. 1) (л/г; + ли),
4 7 \4 J У 4 7
(- у + 2л/г; ли), /г, и G Z; 2) ^-у+л/г; -^ + ли), /г, и G Z.
XVII.49. 1) (±^ + 2л/г; т^+2ли), /г,и С S; 2) (±^+2л/г; т^ + 2ли), /г,иег. XVII.50. (0,5;-0,5), (-0,5; 0,5), (1,0), (-1; 0), (0; 1), (0;-1). XVII.51. 1) ((— 1)”^ + ли; ± arctg \/h5 + л/г), и,/г €Z; 2) (±arccos | + 2ли; ± arcctg + л/г') , и,/г G Z. XVII.52. 1) ((-1)"у + 2ли;
и,/г G Z; 2) ((-1)л у + 2ли;
л+4л/г) , (л + 4ли; (—1)Лу + 2л/г), и,/ге2. XVII.53. (у; у), /г, и G Z. XVII.54. (±^+л(и + /г); ±^ + л(и-/г)), /г,и G Z. XVII.55. (у + ли; f + ^). (д + у; -5-T+27m)’ XVII'56. (±^ + л(6 + и);
± + л(и-/г)), (±^ + л(/г + и) ; ±^ + л(и-/г)), /г,и G Z.
XVII.57. (arcsin у= + л(2и +/г); arcsin-)== +л/г), (у+л(и + 2/г);
-£ + ли), /г,и G Z. XVII.58. (0;0); Гт + ?Л + 2?)- /г е Z.
4 7 v ' \4 2 4 2 7
XVII.59. +2ли; £+ 2л/г), +2ли; +2л/г), (-£+2ли; -?+2л^),
\6 4 / \ 6 4 7 \ 6 4 7
(-у+2ли; -^+2л/г), k,n G Z. XVII.60. 1) (2л/г; л + 2ли), /г, и G Z;
л + 2л/г) , (—л + 4ли; + 4л/г)
2) (2л/г; л + 2ли), k, и € Z.
XVII.61. (л/г;2ли), (у + л/г; | + 2ли),
Ответы к главе XVII 345
k,n G Z. XVII.62. 1) (± arccos 7 + 2тг&; я ± arccos | + 2ти\ k, п G Z;
/1 7 \ ( 1 7 \
2) — arcsin -+ 2rk; arccos „+2тгп , hr + arcsin- +2тг&; л + arccos- +2лт1, X 4 8 ) \ 4 8 )
k,neZ. XVII.63. (^ + 2ттг, + 2jrk), m,keZ. XVII.64. 1) (~^1);
2) (—yl). XVII.65. 1) Если a G (-ос;—1) U (0;+оо), то решений нет; если а € [-1;0], то (( —1)л arcsin -/—а + 7т; (—1)” arcsin -/—а — тг + тт),
((—1)л+1 arcsin 7~a + тт; (—1)л+1 arcsin y/^a — тг 4- гт), п G Z; 2) если a G (—ос; 0) U (1; +оо), то решений нет; если a = 0, то (jm; тт — ^) ,п G Z; если a G (0; 1), то (±(-1)л arcsin y/a + rm; ±(-1)" arcsin у/a - , n g Z;
если a = 1, to + rn; rn^, n G Z. XVII.66. 1) Если a E ( — oc;0)U(l;+oc), то решений нет; если a G [0,1], то x = arcsin(2а—Г) r rm
у = С"1) arcsin(2a ~ Q — ^ + у — тг&, g Z; 2) если a / 0, то решений n n . (2п + /г)тг л . (2n - k)n „ ,
нет; если a = 0, то x = - + У = „ + An,k E
4 2 8 4
XVII.67. Система имеет решения при a = ±4; если a = — 4, то х = 1,у — 0; если a = 4, то х = — 3,у = 0. XVII.68. 1) k — 1; х = tg (л-— у = cos 2) k = 2; х = cos (у), у = ±1. XVII.69. a = 0
XVII.70. —2; 0,5. XVII.71. 1) (5; 0,04), ( \/(log3 6)2; ^log^); 2) (3; 3); (| log4 3; | log4 з). XVII.72. 1) |±Т2); 2) Q =f х/2; ±^).
XVII.73. 1) (1,5; 0,5); (0,5; 1,5); 2) (16; 4); (Ь|). XVII.74. 1) (3; 18),
(1;—6); 2) (1;1); (2;-4). XVII.75. 1) (1,5 + \/3; 1,5 - Уз); 2) (2,5+75; 2,5-75). XVII.76. 1) (l + l|Og23; 1 - 1 lOg2 з); 2) (| + |log32;
1 — llog32). XVII.77. (3;2). XVII.78. 1) (а;п), где a G К;
2 ) (а; 2а), где a G К. XVII.79. ((-1)л^ + тт; (-1)л+1 g + тгб), ((_1)«+^ + ^; (-1)^ + ^), kyn G z. xvii.80. 1) (f + ^;y)> (^± у+л6;+^+ тм), MGZ; 2) (тгб; кп), k.n GZ. XVII.81. (±у+2тш; ±^ + 2тгт),(±^ + 2л7г; ±^ + 2лт), п,т G Z. XVII.82. (д + у;
±arctg2 +дд; у - у+arctg2-лд), k<n G Z. XVII.83. 1) (0;0),
(9 log5 3; 3 log5 3); 2) (0;0), (4 log9 7; 8 log9 7). XVII.84. 1) a G (-2,5;-0,25); 2) ae (1; 5).
Глава XVIII
УРАВНЕНИЯ И НЕРАВЕНСТВА С ДВУМЯ ПЕРЕМЕННЫМИ
§1. ГЕОМЕТРИЧЕСКОЕ ОПИСАНИЕ РЕШЕНИЙ УРАВНЕНИЙ, НЕРАВЕНСТВ И СИСТЕМ С ДВУМЯ ПЕРЕМЕННЫМИ
Первый уровень
Найти на координатной плоскости множество точек, удовлетворяющих уравнению (XVIII.1-XVIII.8)
XVIII.1. 1) 3) у2 — 4х2 = 0; 2х2 - Зхг/ - 2у2 = 0; 2) 4) х2 - 2ху - Зу2 = 0; х2 - 2ху - 4х + Зу = 0.
XVIII.2. 1) х2 + у2 = 2х; 2) х2 + у2 — 6х + 4у = 12.
XVIII.3. 1) sin (г/ — х) = 0; 2) cos(x + у) = -1.
XVIII.4. 1) |t/| - х + 3; 2) |</-3|=:|х + 2|.
XVIII.5. 1) М+# = |х|+х; 2) |t/| - |х| = х + у.
XVIII.6. 1) |t/-2| =4 —х2; 2) Ы=4|х|-х2.
XVIII.7. 1) \у — 1| = 2 cosx; 2) |i/| = sin |х|.
XVIII.8. 1) |t/ + l| = log2x; 2) \У\ = >ogo,5 М-
Найти на координатной плоскости множество точек, удовлетворя-
ющих неравенству (XVIII.9-XVIII.14)
XVIII.9. 1) Зх — 4у + 12 > 0; 2) 2х — Ъу — 10 < 0;
3) у + 3 х2 + 2х; 4) у < -х2 + 4х - 4.
XVIII.10. 1) у^ |3х - 2|; 2) Ы< 2|х+ 1| - 3.
XVIII.il. 1) (х — 1)(г/+ 2) 0; 2) (|х| — 2)(г/+ 1) 0.
XVIII.12. 1) log2(3x - у - 1) 0; 2) log-0,5(2i/ — а;) ^0.
XVIII.13. 1) 4у2 х2 + 4х + 4; 2) 9г/2 х2 — 6х + 9.
XVIII.14. 1) (х + I)2 + [у - З)2 > 4; 2) х2 + у2 4(х - у - 1).
XVIII.15. Найти на координатной плоскости множество точек,
удовлетворяющих системе неравенств:
1) х2 + t/2 1, у —х, у 0;
2) х2 + у2 — 4х 5, у + х 2, у 0.
§1. Геометрическое описание решений уравнений 347
XVIII.16. Найти площадь фигуры, координаты точек которой
удовлетворяют системе неравенств:
к| — 1, у 3 - 2 ]х|;
У 2 |х| + 1, У И + 3.
XVIII.17. Найти площадь фигуры, которая задается на коорди-
натной плоскости неравенством:
О М +1«/1 $ 3;
2) |х - 2| + |j/| sc 5;
3) И + \у + 3| 4;
4) |x + 3| + |z/ —1| sc 2.
XVIII.18. Найти площадь фигуры, которая задается на координатной плоскости системой неравенств:
(х2 - у2 0, (у 2х,
[х2 + г/2 1; 2 |/2 + у2 + 4 2х + 4г/.
Второй уровень
XVIII.19. Дать геометрическое описание множества точек координатной плоскости, удовлетворяющих уравнению у — kx — 3k + 1 = 0 при всевозможных действительных значениях k из отрезка — 1 k 1.
XVIII.20. Дать геометрическое описание множества точек координатной плоскости, удовлетворяющих уравнению х2 + у2 — 2 (х cos a + у sin а) + 0,75 = 0 при всевозможных действительных значениях а.
Найти множество точек координатной плоскости, удовлетворяющих уравнению (XVIII.21-XVIII.24).
XVIII.21. 1) \у + х| = х + 3; 2) |х - у\ + |х + у\ = 2.
XVIII.22. 1) х4 - 2х2 = у2 + 2г/; 2) х2 - 2 |х| = г/4 + 2г/2.
XVIII.23. 1) = 1; 2) У1 4 =
(х + 4)8 ’ (х + 2)4 у1
(.У -х)4 — 1. (у ~ х)4 _ 1
’ х8 ’ ' (х2 — 2)4
XVIII.24. 1) k)g2^^ = -3; 2) log05^=4;
/ toZ 4 |у| 8 \у\
3) log = —2; 4) logo 5 ctg<^5x) = 3.
348 Глава XVIII. Уравнения и неравенства с двумя переменными
XVIII.25. Найти на координатной плоскости множество точек, координаты которых удовлетворяют системе неравенств: 1) ху 1, у х + 2, у х — 2;
2) ху — 2 < 0, у - 2х < 0, 2у — х 0.
XVIII.26. Найти на координатной плоскости множество точек, координаты которых удовлетворяют неравенству: 1) |2Х + i/| < 2х+1; 2) |0,5х - у\ > 0,5х"2;
3) |t/-3x| > 3х"1; 4) 10,5х"1 + у\< 0,5х.
XVIII.27. Найти на координатной плоскости множество точек, координаты которых удовлетворяют неравенству: 1) log1+//(l+ sinx) > 1; 2) log1+{/(l - cosx) 1.
XVIII.28. Найти на координатной плоскости множество точек, координаты которых удовлетворяют неравенству: 1) у У6 Iх + 61 “ (х + б)2;
2) у л/2 |х - 2| — (х - 2)2.
XVIII.29. Построить множество точек, координаты которых удовлетворяют системе неравенств, и найти площадь получившейся фигуры:
р^|х + 2|-1, (у |х + 4| - 2,
[х2 + у2 + 4х + 3 0; [х2 + у2 + 8х + 12 0.
XVIII.30. 1) Построить множество точек, координаты которых удовлетворяют системе неравенств х2 + у2 2х, х^7у — 4, и найти площадь получившейся фигуры.
2) Построить множество точек, координаты которых удовлетворяют системе неравенств х2 + у2 —6х,
у 7х + 6 и найти площадь получившейся фигуры.
XVIII.31. Найти площадь фигуры, которая задается на координатной плоскости неравенством:
1) |3 - |х|| + |5 - |у|| sc 6; 2) ||х| - 4| + 1Ы - 3| «с 5.
XVIII.32. Найти площадь фигуры, координаты точек которой удовлетворяют системе неравенств:
fx2 + 25г/2 Юхг/+ 144. (у2 + 4х2 4ху + 9,
' Чи^Ы-
§1. Геометрическое описание решений уравнений 349
XVIII.33. Найти площадь фигуры, координаты точек которой
удовлетворяют системе неравенств:
ГО-М)2 + (*/-Ы)2^4, [х + у 0;
Г(2 - |х|)2 + (2 — |у|)2 4, 2) |х| s$2,
XVIII.34. 1) Пусть тах(Д,В) = < D’ Вычислить площадь
D А.
фигуры, которая задается на координатной плоскости системой неравенств тах(х, у) 1, х2 + г/2 1, х 0,
У^О.
{А А < В
р р^ д Вычислить площадь фигуры, которая задается на координатной плоскости системой неравенств min(x,у} 1, х2 + у2 + 1 2х + 2у. XVIII.35. 1) Изобразить на координатной плоскости множество точек (х,у), для каждой из которых существует остроугольный треугольник со сторонами 1, 2 + х, \/3 -г/.
2) Изобразить на координатной плоскости множество точек (х,у), для каждой из которых существует остроугольный треугольник со сторонами + у, 2, 1-х.
XVIII.36. 1) При каких значениях х оба неравенства |х + у\ 1 и |х — Зу| 2 выполняются хотя бы для одного значения у?
2) При каких значениях у оба неравенства |3х + 2у| 6 и |2х — у\ 5 выполняются хотя бы для одного значения х?
XVIII.37. Найти все значения переменной х, удовлетворяющие неравенству \у — х2| 2
1) при любом у из отрезка [1; 3];
2) хотя бы при одном значении у из отрезка [1;3].
350 Глава XVIII. Уравнения и неравенства с двумя переменными
XVIII.38. Найти все значения переменной х, удовлетворяющие неравенству |ху —5|^3
1) при любом у из отрезка [1; 2];
2) хотя бы при одном значении у из отрезка [1;2].
XVIII.39. Реш ить систему неравенств:
(х2 + у1 + 4х + 2г/ 20, [х2 + у2 — 8х — 14г/ 40;
(х2 + у2 + 4х - 8г/ 80, [х2 + у2 - 4х — 2г/ 20.
§2. АНАЛИТИЧЕСКИЕ ПРИЕМЫ РЕШЕНИЙ УРАВНЕНИЙ И НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ
Первый уровень
XVIIL40. Найти все пары чисел (х;у), для каждой из которых выполняется равенство:
1) х2 + у2 + 10 = 2х — 6г/;
2) х(х - 2г/) + х(х - 4) + у2 + 4 = 0.
XVIII.41. Найти все пары чисел (х;у), для каждой из которых справедливо равенство:
1) х2 + 1 = 2-^2; 2) у4 — 4у2 — cos2 х + 5 = 0;
3) sin у + УЗ cos у = 4х — 4х2 + 1;
4) =У2-4у + 5.
1 + tgz X
XVIII.42. Решить уравнение:
1) 2х + 2-х = 2 sin у,
2) (cos2 х + cos-2 х) (1 + tg2 2г/) (3 + sin 3z) = 4.
XVIII.43. Решить неравенство:
1) 2^х/г/2-г/ + 0,5^ 1;
2) 6г/-г/2 - 7 |tgх + ctgх|.
§ 3. Использование геометрического подхода 351
Второй уровень
XVIII.44. Найти пары чисел (х;у), удовлетворяющих уравнению: 1) (х2 + -Q (5 — 2sin2(х + //)) = 6 - cos2(x + //); 2) (|у| + (2 + cos2(x -//)) = 10 + 2 sin2(x - у).
XVIII.45. Найти наименьшее значение выражения у2 — 2у + 4х, если пары чисел хну удовлетворяют уравнению (у2 + 2у - 3) у/х = у + 3.
XVIII.46. Для пар чисел (х;у), удовлетворяющих уравнению х2(у — 1) + х(2// — 1) + (2д/ — 1) = 0 найти те, для которых у принимает наибольшее значение.
XVIII.47. 1) Найти наибольшее значение выражения х + Зу, если пары чисел хну удовлетворяют неравенству х2 + ху + 4z/2 + 6.
2) Найти наибольшее значение выражения 2х + у, если пары чисел хну удовлетворяют неравенству х2 + 2ху + Зу2 2.
XVIII.48. Найти все пары чисел (х;//), удовлетворяющие условию: 1) (|х| - 2х) у2 18х (6 — 2у);
2) (|х| + 2х) z/2 ^24х(у-2).
§3. ИСПОЛЬЗОВАНИЕ ГЕОМЕТРИЧЕСКОГО ПОДХОДА ДЛЯ РЕШЕНИЯ УРАВНЕНИЙ, НЕРАВЕНСТВ И СИСТЕМ С ДВУМЯ НЕИЗВЕСТНЫМИ, СОДЕРЖАЩИХ ПАРАМЕТРЫ
Второй уровень
XVIII.49. Найти все значения параметра а, при каждом из которых система уравнений имеет два решения:
|х2 + / = 2(1 + а), (х2 + у2 = 3(2 + а),
( (я + /2 = 14; [ (х - у)2 = За - 14.
XVIII.50. При каких значениях параметра а найдутся числа хну, удовлетворяющие уравнению:
1) у/2ху + а = х + у + 1;
2) у/2ху — 12х — 12// - а = х + у - 4.
352 Глава XVIII. Уравнения и неравенства с двумя переменными
XVIII.51. Найти все значения параметра а, при которых имеет решение система неравенств:
Пх — 1| + 3 |г/| 3, <(х + у)(х-3у) О,
[х2 4- у2 + а 4х — 6г/; [х2 + г/2 - а 2х — 1.
XVIII.52. Найти все значения параметра а, при которых не имеет решений система неравенств:
Лх — 1| + 2 |г/| 2, Г (х + г/)(4х — Зг/) О,
|х2 + у2 + 4х + 2г/ а; |х2 + у2 + 4 а2 + 4г/.
XVIII.53. Определить, при каком значении параметра а система
неравенств имеет
Гг/^х2 + а, П л \ 2 । |^х у + а;
3 Г г/ у/х - а,
' (х \/г/ - а;
единственное решение:
глч [у ^ах — х2 — 3,
2) < , 2 о
(х < ау - у — 3;
2 г/^х^-а,
\ 2
х у — а.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ XVIII
XVIII.54. Найти площадь фигуры, которая задается на координатной плоскости двойным неравенством: 1)4- 12х| 12г/ - 3| У16-4х2;
2) 1 — |х - 3| < \у\ < \/бх — х2 — 8.
XVIII.55. На йти на координатной плоскости множество точек, координаты которых удовлетворяют неравенству: 1) log|r|cosl > logy cos 1; 2) logx у > logy x.
XVIII.56. Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют неравенству:
1) \у + 2| (х2 + Зх + 2) > |х + 1| • |х + 2| • (0,5)Х+Й;
2) \у + 3| • (х2 + х - 12) > |х + 4| • |х - 3| • (0,25)Х~3И.
XVIII.57. 1) Найти наибольшее и наименьшее значения, которые может принимать выражение 2г/ — х, если х и у одновременно удовлетворяют условиям 3 \у\ 8 — 4х
и \у\ -8-4х.
Задачи повышенной сложности к главе XVIII 353
2) Найти наибольшее и наименьшее значения, которые может принимать выражение 2у + 6х, если х и у одновременно удовлетворяют условиям 2 |г/| х + 3 и 2 |//| Зх + 1.
XVIII.58. 1) Найти все значения у, при которых равенство । /2 с । п\ 6х3 + 28х2 + 42х + 20
log5 / - 6// + 9) =
\ / 2xd + 9xz + 13х + 6
выполняется хотя бы при одном значении х.
2) Найти все значения у, при которых равенство
i-™ 2х3 — Зх2 — 8х — 3
logo,25 (У + Юг/ + 25) = - 2—-------
’ \ / 5х'5 - 9xz — 17х — 3
выполняется хотя бы при одном значении х.
XVIII.59. Определить, при каких значениях параметра а равносильны системы уравнений:
{х-\-у = — л, fcos(x + у) — -1,
х2 + у2 -I- 4г/ = а И |х2 + у2 + 4у = а;
{х — у = 0, fcos(x — у) = 1,
9 9 . И \ 9 9 .
х + у — 4х - а \хЛ -V у — 4х = a.
XVIII.60. Найти все значения параметра а, при которых система
уравнений имеет бесконечно много решений:
1)
XVIII.61. 1)
2)
XVIII.62. 1)
г|х + 0,5а + 1| = г/, \у + За - 3| = х;
(|х + а + 11 — у, ) l|^ + 1 + f|=x-
При каких значениях параметра а площадь фигуры, заданной на координатной плоскости Оху условием [2 |г/| х + 8;
S I..I . равна 100?
При каких значениях параметра а площадь фигуры, заданной на координатной плоскости Оху условием (3|г/|^х + 6:
< । । 1П равна Ь4?
При каких значениях параметра а решением системы {2х — у + а < О,
_ п „ будут координаты хотя бы одной
6х + Зу + За О г
точки отрезка АВ, если Л(0,9) и В(3,6)?
12—5682
354 Глава XVIII. Уравнения и неравенства с двумя переменными
2) При каких значениях параметра а решением системы (2х + у — 2a О, < Q _ п будут координаты хотя бы одной I £у OX d и
точки отрезка АВ, если А(2,2) и В(4, 8)?
XVIII.63. 1) Множество М состоит из всех точек плоскости, координаты которых удовлетворяют системе нера-f х1 - (a - 2)х -2 С у, „ венств <_ х _ Определить, при каких
\2х + у — а 0.
значениях параметра а множество М содержит отрезок [— 1; 0] оси Ох.
2) Множество М состоит из всех точек плоскости,
координаты которых удовлетворяют системе нера-f 4х2 + 4(а - 1)х — 2 С у, „
венств V + 2у + (а + 2) > 0. Определить, при каких значениях параметра а множество М содержит отрезок [0:1] оси Ох.
XVIII.64. j) в каких пределах изменяется величина х2 — Зу при условии, что log 2 (—// — 2)^1?
х —2
2) В каких пределах изменяется величина х2 — 8х+9// при условии, что log2_x (Зу — 3) — 1?
XVIII.65. На йти все действительные значения у такие, что при
всех положительных х выполнено неравенство:
1) Зу х3 - Зу2х; 2) у Зх2 — у2х3.
ОТВЕТЫ К ГЛАВЕ XVIII
XVIII.1. 1) Рис. 1; 2) пара прямых: у — —х> и у = |; 3) рис. 2;
4) рис. 3. XVIII.2. 1) Окружность с центром в точке (1;0) радиусом 1. 2) рис. 4. XVIII.3. 1) Совокупность прямых у =
— х + тт, n е Z; 2) совокупность прямых у = — х + д + 2дп, n G Z. XVIII.4. 1) Рис. 5; 2) пара прямых: у = х 4- 5 и у = 1 - х. XVIII.5. 1) См. рис. 6; 2) см. рис. 7. XVIII.6. 1) См. рис. 8; 2) см. рис. 9. XVIII.7. 1) См. рис. 10; 2) см. рис. 11. XVIII.8. 1) См. рис. 12;
2) см. рис. 13. XVIII.9. 2) См. рис. 14; 4) см. рис. 15.
XVIII.10. 1) См. рис. 16; 2) см.„ рис. 17. XVIII.И. 1) См. рис. 18;
2) см. рис. 19. XVIII.12. 1) Прямая у = Зх — 2 и часть плоскости,
расположенная под ней; 2) см. рис. 20. XVIII.13. 1) См. рис. 21;
2) см. рис. 22. XVIII.14. 1) Часть плоскости, лежащая вне круга
Ответы к главе XVIII 355
радиусом 2 с центром в точке (—1; 3); 2) круг радиусом 2 с центром в точке (2;—2). XVIII.15. 1) См. рис. 23; 2) см. рис. 24.
XVIII.16. 1) 5|; 2) 4. XVIII.17. 1) 18; 2) 50; 3) 32; 4) 8.
356 Глава XVIII. Уравнения и неравенства с двумя переменными
Рис. 17
XVIII.18. 1) 2) XVIII.19. См. рис. 25. XVIII.20. См. рис. 26.
XVIII.21. 1) См. рис. 27; 2) см. рис. 28. XVIII.22. 1) Совокупность парабол у = — х2, у = х2 — 2; 2) см. рис. 29. XVIII.23. 1) См. рис. 30;
Ответы к главе XVIII 357
2) см. рис. 31; 3) см. рис. 32; 4) см. рис. 33. XVIII.24. 1) См. рис. 34
2) см. рис. 35; 3) см. рис. 36; 4) см. рис. 37. XVIII.25. 1) См. рис. 38
2) см. рис. 39. XVIII.26. 1) См. рис. 40; 2) см. рис. 41
358 Глава XVIII. Уравнения и неравенства с двумя переменными
У
1
0
-1
Рис. 28
Рис. 32
Рис. 33
Ответы к главе XVIII 359
3) см. рис. 42; 4) см. рис. 43. XVIIL27. 1) См. рис. 44; 2) см. рис. 45.
XVIII.28. 1) См. рис. 46; 2) см. рис. 47. XVIII.29. 1) 1 + |;
2) 2тг + 4. XVIII.30. 1) + Ь 2) 6,75тг + 4,5. XVIIL31. 1) 248;
2) 180. XVIII.32. 1) 12; 2) 6. XVIII.33. 1) 1 + р 2) 16 - 4тг.
360 Глава XVIII. Уравнения и неравенства с двумя переменными
Рис. 41
Рис. 46
Рис. 47
Ответы к главе XVIII 361
XVIII.34. 1) 1 —0,25тг; 2) 0,25тг. XVIII.35. 1) См. рис. 48; 2) см. рис. 49. XVIII.36. 1) [-1,25; 1,25]; 2) [-yi y]- XVIII.37. 1) [-х/3; -1] О [1; УЗ]; 2) [—х/5; х/5]. XVIII.38. 1) [2; 4]; 2) [1;8]. XVIII.39. 1) (1; 3);
2) (6;-2). XVIII.40. 1) (1;-3); 2) (2; 2). XVIII.41. 1) (0;0);
2) neZ; 3) (Ь^+2тш), п G Z; 4) (^ + ™;2),
п G Z. XVIII.42. 1) (0;^+2тш), п G Z; 2) (тт; у;, n,k,m G Z. XVIII.43. 1) (тт; 0,5), n G Z; 2)(^ + y;3), n G Z. XVIII.44. 1) (1;^-1 + тт), (-1; £ + 1 + тт) n G Z; 2) (-3 + ^ + тт;-З) , (3+ | + тт;3) n GZ. XVIII.45. 4. XVIII.46. (-2; 1,5). XVIII.47. 1) 4; 2) 3. XVIII.48. 1) (x;6), где x. < 0; (0;//), где у G R; (x;z/), где x > 0, у G (—oo; 18 — 6\/6] U [18 + 6%/6; +oo); 2) (x; 4), где x > 0; (0; i/), где у G R; (x;z/), где x < 0, у G (-oo; 12 - 4\/б] U [12 + 4^/6; +oo). XVIII.49. 1) 2,5; 2) I. XVIII.50. 1) [-0,5;+oo); 2) (-oo;-40], XVIII.51. 1) [-12;+oo); 2) [0,1;+oo). XVIII.52. 1) (21;+oo); 2) (-oo;l,2). XVIII.53. 1) 0,25;
2) 1 ± 2^3; 3) 0,25; 4) -0,25. XVIII.54. 1) 4л - 8; 2) л - 2.
XVIII.55. 1) См. рис. 50; 2) см. рис. 51. XVIII.56. 1) См. рис. 52;
2) см. рис. 53. XVIII.57. 1) 20; -12; 2) 10; -18. XVIII.58. 1) г//3, у^ ^-2, у/3, г/^3±5х/5, у^-22, у^ 2) у^-5, г/^-5± ^=, у^-5± у^-5±^=. XVIII.59. 1) оо; —+ ~ ; 2) (-оо;2л2 - 4тг- 2).
XVIII.60. 1) 1; 2) -1,5. XVIII.61. 1) 1; 2) -1. XVIII.62. 1) [-7,2;9];
362 Глава XVIII. Уравнения и неравенства с двумя переменными
Рис. 52
ч । ky
V ! ।
2) [-6; 8]. XVIII.63. 1) [0;3]; 2) [-2; 0,5]. XVIII.64. 1) [21,+оо);
2) [8,+оо). XVIII.65. 1) [—а/2Д0]. Указание. Если ввести функцию Дх) =х3 — Зу2х — 5у (у выступает в роли параметра), то можно переформулировать задачу следующим образом: найти все значения параметра у, при каждом из которых на множестве (0;+оо) функция /(х) принимает неотрицательные значения. Для решения задачи в новой формулировке нужно исследовать функцию Дх) на множестве (0;+оо) с помощью производной. 2) v^4; +оо).
Глава XIX
ДЕЛИМОСТЬ ЦЕЛЫХ ЧИСЕЛ. ЦЕЛОЧИСЛЕННЫЕ РЕШЕНИЯ УРАВНЕНИЙ
§1. ДЕЛИМОСТЬ ЧИСЕЛ
Первый уровень
XIX.1. Доказать, что число является составным:
1) 3478 - 2318; 2) 27124 - 5220;
3) 2525 — 3232 ; 4) 2919 - ЗЗ6.
XIX.2. Доказать, что:
1) число 256 + 1615 делится на 17;
2) число 1О10 + 10 делится на 11;
3) число 44488 + 88844 делится на 148;
4) число 2114 — 441 делится на 442.
Доказать, что число является составным при любом натуральном п (XIX.3-XIX.4).
XIX.3. 1) /73 - 243; 2) п4 - 529;
3) п6 + 64; 4) /74 + 8/72 + 15.
XIX.4. 1) 27"+ 1; 2) 7" - 1;
3) 125"+ 8"; 4) 729* -64*.
Доказать, что при любом натуральном значении п (XIX.5-XIX.6):
XIX.5. 1) п? — п делится на 3;
2) /73 — п делится на 6.
XIX.6. 1) /73 + 20/7 + Ю6 + 2 делится на 3;
2) /73 + 11/7 делится на 6;
3) /73 — 25/7 + 28 + 2 делится на 6;
4) /73 + 15/72 + 8/7 + 3 делится на 3.
XIX.7. Написать каноническое разложение числа:
1) 2520; 2) 13 230; 3) 13 200;
4) 52 650; 5) 930 930; 6) 6 019 530.
364 Глава XIX. Делимость целых чисел
XIX.8. 1) Доказать, что если целое число делится на 3 и 40, то оно делится и на 120.
2) Доказать, что если целое число делится на 12 и 90, то оно делится и на 180.
XIX.9. Найти наименьшее общее кратное [а, 6] чисел а и Ь, если:
1) а = 204 и b = 120; 2) а = 240 и b = 1512;
3) а = 420 и b = 650; 4) а = 3675 и 6 = 880.
XIX.10. Найти наибольший общий делитель (а, 6) чисел а и 6, если:
1) а = 165 и b = 1386; 2) а = 600 и b = 1260;
3) а = 6930 и 6=10296; 4) а = 16 170 и 6 = 11781.
XIX.11. Найти все такие натуральные числа а и 6, где а 6, что:
1) а + 6 = 432 и (п,6) = 36; 2) п6 = 864 и (а,6) = 6;
3) [а, 6] = 840 и (а, 6) = 15; 4) а + Ь= 165 и [а, 6] = 420.
Второй уровень
XIX.12. Найти натуральное число d/1, если известно, что оно является делителем следующих натуральных чисел: 1) 5п + 6 и 8п + 7; 2) Зп + 8 и 7п + П.
XIX.13. Указать все натуральные числа, на которые может оказаться сократимой при целом п дробь:
t\ 2п + 9 . /7 + 3 . 4/7 + 7, 5/74-8
’ 1п+2Ь' ’ 2/7 + 7’ ' 3/7 + 4 ’ ' 3/7 + 5’
XIX.14. Доказать, что:
1) число 10020 —50-165 делится на 49;
2) число II10 —1 делится на 100.
3) число 1020 + 373 —2 делится на 9;
4) число 1О8+283 —2 делится на 9;
5) число 163 + 314 —17 делится на 15;
6) число 393 + 774 + 36 делится на 19.
XIX.15. Доказать, что при любом натуральном значении п
1) 16п + 1000л — 2 делится на 6;
2) 400п +256п — 9п — 1 делится на 323.
Глава XIX. Делимость целых чисел 365
XIX.16. Доказать, что при любом натуральном значении п
1) п3 + (n +1)3 + (п + 2)3 делится на 9;
2) 2п3-Зп2 + 7п делится на 6.
Доказать утверждение (XIX.17-XIX.23),
XIX.17. При любых натуральных тип число (5m + 3/? + 7)4(3m + + 5п + 2)5 делится на 16.
XIX.18. Не существует таких целых чисел тип, что т2-п2 = 20790.
XIX.19. Число п5 —5п3 + 4п делится на 120 при любом натуральном значении п.
XIX.20. Если р — любое простое число, большее 3, то р2 — 1 делится на 24.
XIX.21. Число п5-п делится на 5 при любом натуральном
значении п.
XIX.22. Число п1 — п делится на 7 при любом натуральном
значении п.
XIX.23. Если т2 делится на n2 (m, neZ), то т делится на п.
XIX.24. Определить, каким количеством нулей оканчивается десятичная запись числа: 1) 40!; 2) 100!.
XIX.25. Доказать, что:
1) если число п составное, то у него есть делитель, не превосходящий у/п и больший 1;
2) если d — наибольший делитель составного числа п, о п
меньшии п, то число - простое;
3) составное натуральное число п, большее 4, является делителем числа (n —1)!;
4) среди натуральных чисел от 1 до 30m (m= 1,2, 3,...) не более 10m простых чисел.
XIX.26. Привести пример п последовательных составных чисел в натуральном ряду, если: 1) п = 6; 2) п = 9.
XIX.27. Найти все целые п, при которых данное число является целым:
П п4 + 3 . ™ Зп2 + 28. ох 2/?2Н-4 . дх 2/?3 + гг2 + 5п + 6
лг2 Ч-2 ’ 5/72 + 1О’ 6/г2 — 3 ’ я2 + п + 3
366 Глава XIX. Делимость целых чисел
XIX.28. Найти наибольший общий делитель d чисел а и b и представить его в виде d — ax + by, где x,i/EZ: 1) я = 24 и 6 = 378; 2) а = 30 и 6 = 4851;
3) а = 882 и 6 = 528; 4) а = 204 и 6 = 372.
XIX.29. Найти все тройки последовательных нечетных чисел, каждое из которых является простым.
XIX.30. н айти все простые числа р, для которых:
1) число 4р +1 является квадратом некоторого целого
числа;
2) число 4р+ 1 является кубом некоторого целого числа;
3) число 5р+1 является кубом некоторого целого числа;
4) число 7р + 1 является кубом некоторого целого числа.
XIX.31. Найти все простые числа р такие, что следующие числа также являются простыми:
1) р+10 и р + 14; 2) р + 4 и р+14;
3) 4р2 +1 и 6р2 + 1; 4) 8р2 + 1.
§2. СРАВНЕНИЯ
Первый уровень
Найти остаток от деления числа а XIX.32. 1) ц = 2256, т = 10;
3) а = 3124, т = 4;
XIX.33. 1) а = 2-341, т = 10;
3) а = 454 + 2-1328, т = 5;
XIX.34. Решить сравнения:
1) 2х +1 = 0 (mod7);
3) 2х2 + Зх +1 = 0 (mod 5);
5) х3 + 4х2 = — 1 (mod9);
на m (XIX.32-XIX.33).
2) а = 481, т = 7;
4) я = 5128, т = 3.
2) а = 532+416, т = 7;
4) а = 2-618 +3-520, т = 8.
2) 2%+ 3 = 0 (mod 6);
4) 4x2 + 3x = 5 (mod 11);
6) 7х2 — 4х3 = 2 (mod6).
Второй уровень
Найти остаток от деления числа а на tn (XIX.35-XIX.36).
XIX.35. 1) а = 255 + 374 + 757, т = 10;
2) а = 2625-6111 • 1713, т = 3;
§3. Решение уравнений в целых числах 367
3) а —8614 — 225 — 58б, т = 13;
4) п = 2127 + 3519, т —17.
XIX.36. 1) п-52265 + 63241, т = 5;
2) п-92325 + 27135, т-7;
3) а = (51-40)16 + (53-77)13, т-13;
4) а —2-521 + 9-610, т-13.
XIX.37. Реш ить сравнение:
1) 12х = 15 (mod 35);
3) 15х = 21 (mod 18);
2) 21х = 10 (mod25);
4) 18х=12 (mod30).
( х = 2 ( mod 15),
( х~=3 ( mod 8);
( 4% +1 -0 (mod7), [ x = 3 (mod8).
XIX.39.
XIX.40.
XIX.41.
XIX.38. Реш ить систему сравнений:
( х = 3 ( mod 5),
[ х = 1 ( mod 8);
( Зх + 4 = 0 (mod 14), 3) | 2х +1 = 3 (mod 5);
Найти все такие натуральные числа п, что числа п + 1, п + 71, п + 66 — простые.
Доказать, что:
1) числа 2Л — 1 и 2Л +1, где п — натуральное число, большее 2, не могут быть одновременно простыми;
2) если р и 8р—1 —простые числа, то 8р +1 — составное число.
Доказать, что уравнение х3+% +10// —20004 не имеет решений в натуральных числах.
§3. РЕШЕНИЕ УРАВНЕНИЙ В ЦЕЛЫХ ЧИСЛАХ Первый уровень
XIX.42. Доказать, что уравнение не имеет решений в целых числах:
1) 20х —10//—19; 2) 3% + 9//=14;
3) 22х + 6//= 133; 4) 5х + 10// = 21.
XIX.43. Найти все целочисленные решения уравнения:
1) 3% + 8//=1; 2) 4% + 7// = 9; 3) 5% + 4//=И;
4) 11х + 8//=1; 5) 7% + 9//=10; 6) 5% + 7// = 4.
368 Глава XIX. Делимость целых чисел
XIX.44. 1) Пусть А — множество целых чисел, имеющих при делении на 3 остаток 2, а В — множество целых чисел, имеющих при делении на 8 остаток 6. Найти все числа, которые одновременно входят в оба множества.
2) Пусть А — множество целых чисел, имеющих при делении на 7 остаток 3, а В — множество целых чисел, имеющих при делении на 17 остаток 13. Найти все числа, которые одновременно входят в оба множества.
3) Пусть А — множество целых чисел, имеющих при делении на 5 остаток 4, а В — множество целых чисел, имеющих при делении на 7 остаток 1. Найти все числа, которые одновременно входят в оба множества.
4) Пусть А — множество целых чисел, имеющих при делении на 8 остаток 2, а В — множество целых чисел, имеющих при делении на 7 остаток 5. Найти все числа, которые одновременно входят в оба множества. Найти все пары целых чисел х и у, удовлетворяющих уравнению (XIX.45-XIX.51)
XIX.45. 1) х2- z/2 = 1982; 2) x2_^2 + 2z/ = 8.
XIX.46. 1) х2-ху-2у2 = 18; 2) x2 + 3xz/ + 2z/2 = 3.
XIX.47. 1) Ъху—20х2=4у — 16х-|-16; 2) 2ху+ 4х2 = 5у + 10х + 21
XIX.48. 1) х2+ху+у2 = 1; 2) х2 — ху + Зу2 = 5.
XIX.49. 1) 2ху+у — 8х + 2 = 0; 2) Зх — ху-2у = 4\
3) Зху+у — х — 2 = 0; 4) 3ху+у — 2х = 3.
XIX.50. 1) х2 —2ху + 2у2 = 9; 2) 2х2 + 4ху+ 5у2 = 11.
XIX.51. 1) х3—у3 = 19; 2) у3-х3 = 91.
Второй уровень
XIX.52. Найти все пары натуральных чисел х и у, удовлетворяющих уравнению:
1) 2х2 —2ху + х + 3у = 36; 2) 2х2 + 2ху — х+у = 112.
XIX.53. Найти все пары целых чисел х и у, удовлетворяющих уравнению:
1) 6х2у — Зх2-5ху — 2х-Н 1 = 0;
2) Зх2у + 9х2 — 5ху + 6х — 2у + 1 = 0.
§4. Текстовые задачи с целочисленными неизвестными 369
XIX.54. Найти все пары целых чисел х и у, удовлетворяющих системе уравнений:
Г х2+ху-у2 = 4,
[ (х-2)2 + {у-1)2 = 1;
f -Зх2 + ху + у2 = 9,
2) { (х-1)2 + («/+3)2 = 1.
XIX.55. Найти все пары целых чисел х и у, удовлетворяющих системе неравенств:
( х2 + у2 < 12х — 18у- 103,
[ х2 + 10у + у2 <26х- 172;
( х2+у2 < 10х-16у-75,
[ х2 + 8у + у2 <24х-138.
XIX.56. Найти все пары целых чисел х и у, удовлетворяющих условиям:
Зу —х<5, х + у>26, Зх — 2г/< 46.
XIX.57. Найти наименьшее значение переменной х, удовлетворяющей уравнению:
1) Зх2 = 2у4, при условии, что х и у — натуральные числа;
2) 5г2 = 2у3 • (log5x_10y+1 4 + log11+10(y_5x 9) , при условии, что х,у, z — натуральные числа.
§4. ТЕКСТОВЫЕ ЗАДАЧИ С ЦЕЛОЧИСЛЕННЫМИ НЕИЗВЕСТНЫМИ
Первый уровень
XIX.58. Знаменатель несократимой дроби на 2 больше, чем числитель. Если у дроби, обратной данной, уменьшить числитель на 3 и вычесть из полученной дроби данную дробь, то получится Найти эту дробь.
XIX.59. После деления натурального двузначного числа на произведение его цифр в частном получилось 5 и в остатке 2. Найти это двузначное число.
XIX.60. После деления натурального двузначного числа на произведение его цифр в частном получилось 3 и в остатке 8. Найти это двузначное число.
370 Глава XIX. Делимость целых чисел
XIX.61. Ученику дали задание, состоящее из 20 задач. За каждую правильно решенную задачу ему ставят 8 баллов, за каждую неверно решенную — вычитают 5 баллов; если же он задачу не решил, ему ставят 0 баллов. В результате ученик получил 13 баллов. Сколько задач решал ученик?
XIX.62. Партию деталей решили поровну разложить по ящикам. Сначала в каждый ящик положили по 12 деталей, но при этом осталась одна деталь. Тогда из одного ящика вынули все детали, и в оставшиеся ящики удалось разложить все детали поровну. Сколько деталей было в партии, если в каждый ящик помещается не более 20 деталей?
Второй уровень
XIX.63. Поменяв местами две первые цифры натурального четырехзначного числа п, получили четырехзначное число k. Разность п — k оказалась в 100 раз больше суммы цифр числа п. При каком наибольшем п выполнено сказанное?
XIX.64. Поменяв местами первую и последнюю цифры натурального четырехзначного числа п, получили четырехзначное число k. Разность п — k оказалась в 111 раз больше суммы цифр числа п. При каком наименьшем п выполнено сказанное?
XIX.65. Найти все натуральные трехзначные числа, каждое из которых обладает следующими двумя свойствами: (1) первая цифра числа в три раза меньше суммы двух других его цифр; (2) разность между самим числом и числом, получающимся из него перестановкой двух последних его цифр, неотрицательна и делится на 81 без остатка.
XIX.66. На йти все натуральные трехзначные числа, каждое из которых обладает следующими двумя свойствами: (1) первая цифра числа в три раза меньше последней его цифры; (2) сумма самого числа с числом, получающимся из него перестановкой второй и третьей его цифр, делится на 8 без остатка.
XIX.67. Заданы четыре натуральных числа. Сумма первых трех чисел не превосходит трети четвертого числа. Сумма первого числа, умноженного на 7, и третьего числа на 58 меньше четвертого. Если к четвертому числу прибавить 11, то эта сумма будет равна сумме первого, второго и пяти
§4. Текстовые задачи с целочисленными неизвестными 371
третьих чисел. Найти четвертое число, если оно на 52 больше суммы первого, удвоенного второго и третьего.
XIX.68. Компания владеет гостиницами трех типов. В каждой гостинице первого типа работает 114 горничных и 62 рабочих, второго типа — 20 горничных и 28 рабочих, третьего типа —21 горничная и 5 рабочих. Общее число горничных — 537, рабочих —337. Найти количество гостиниц каждого типа, если общее число гостиниц превосходит 11.
XIX.69. В корзине лежало не более 70 грибов. После разбора оказалось, что 52% из них — белые. Если отложить 3 самых мелких гриба, то среди оставшихся будет ровно половина белых. Сколько грибов было в корзине?
XIX.70. В пачке письменных работ абитуриентов — не более 75 работ. Известно, что половина работ в этой пачке имеют оценку отлично. Если убрать три верхние работы, то 48% оставшихся работ будут с оценкой отлично. Сколько работ было в пачке?
XIX.71. Поселок N застроен лишь двухэтажными, трехэтажными и пятиэтажными домами. В каждом двухэтажном доме 3 однокомнатные и 15 двухкомнатных квартир, в пятиэтажном — 29 однокомнатных и 87 двухкомнатных квартир. Общее число однокомнатных квартир равно 244, двухкомнатных — 669. Найти число двухэтажных, трехэтажных и пятиэтажных домов, если их общее число не превышает 13.
XIX.72. Двум рабочим и ученику поручили изготовить некоторое количество деталей. За одну смену они выполнили меньше половины задания. Заканчивать работу пришлось второму рабочему, который затратил на это еще две смены. Если бы им помогал еще один рабочий с той же производительностью, как у первого, то за смену они сделали бы на 23 детали меньше задания. Если бы производительность ученика была вдвое больше, то после одной смены работы им осталось бы сделать 32 детали. Сколько деталей надо было изготовить?
372 Глава XIX. Делимость целых чисел
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ XIX
XIX.73. Доказать, что дробь п +<1п— несократима ни при каком п'Л + Зпг + 1 целом значении п.
XIX.74. Найти различные между собой натуральные числа k, m и п такие, что ? + — + - = -1-. k m п 2
XIX.75. На йти все пары целых чисел х и у, удовлетворяющих уравнению х2 + 19100ху — 91100у2 = 0.
XIX.76. Найти все пары целых чисел х и у, удовлетворяющих уравнению:
1) (х2 + у2) (х + г/-5) = 2хг/; 2) (х2 + у2) (х+у — 3) = 2ху.
XIX.77. Найти все тройки целых чисел x,y,z, удовлетворяющих уравнению 5х2 + у2 + 3z2 - 2yz = 30.
XIX.78. Найти два действительных корня данного уравнения, если известно, что это различные целые числа: 1) х4 — 5х + я = 0; 2) х4 — 41х + а = 0.
XIX.79. Четырехзначное число а оканчивается цифрой 1. Двузначное число, образованное цифрами тысяч и сотен, число десятков и число единиц числа а представляют три последовательных члена арифметической прогрессии. Из всех чисел а, удовлетворяющих указанным условиям, найти то, у которого разность между числом десятков и числом сотен имеет наименьшее возможное значение.
XIX.80. Совокупность А состоит из различных натуральных чисел. Количество чисел в А больше 7. Наименьшее общее кратное всех чисел из А равно 390. Наибольший общий делитель любых двух чисел из А больше единицы. Произведение всех чисел из А не делится на 160 и не является четвертой степенью никакого целого числа. Найти числа, из которых состоит А.
XIX.81. Совокупность А состоит из различных натуральных чисел. Количество чисел в А не меньше 8. Наименьшее общее кратное всех чисел из А равно 330. Никакие два числа из А не являются взаимно простыми. Сумма всех чисел из А равна 755. Произведение всех чисел из А не является четвертой степенью никакого целого числа. Найти числа, из которых состоит А.
Ответы к главе XIX 373
ОТВЕТЫ К ГЛАВЕ XIX
XIX.7. 1) 23 З2 5 • 7; 2) 2 • З3 5 • 72; 3) 24 • 3 • 52 • 11; 4) 2 • З4 52 • 13; 5) 2 3 5 • 7 И 13 • 31; 6) 2 • 3 • 5 И • 17 29 37. XIX.9. 1) 2040;
2) 15 120; 3) 27 300; 4) 646 800. XIX.1O. 1) 33; 2) 60; 3) 198;
4) 231. XIX.11. 1) a = 36 и b = 396 или a = 180 и b = 252; 2) a = 6
и b — 144 или a = 18 и Ь = 48; 3) a = 15 и b - 840 или a = 105
и b = 120; 4) a = 60 и b = 105. XIX.12. 1) d = 13; 2) d = 23.
XIX.13. 1) 13; 2) таких чисел нет; 3) 5; 4) таких чисел нет.
XIX.24. 1) 9; 2) 24. XIX.26. 1) 5042____ 5047; 2) 3 628 802___
3628810. XIX.27. 1) —2;—1;0; 1;2; 2) —3;3; 3) 1;-1; 4) -3; -1;0;2. XIX.28. 1) d = 6 = 24 16 + 378 • (-1); 2) d = 3 = 30 (-485) + 4851 3;
3) d = 6 = 882 3 + 528 • (-5); 4) d = 12 = 204 И + 372 • (-6). XIX.29. 3, 5, 7. XIX.30. 1) p = 2; 2) p = 31; Указание: Если 4p + 1 = a'\ то
4p = (a — l)(a2 + a + 1). Отсюда a — 1 — 4k или p = A(a2 + a + 1); 3) p = 43; 4) p = 73; XIX.31. 1) p = 3. Указание. Рассмотреть числа вида р = 3/г + 1 ир = 3/г + 2; 2) р = 3; 3) р = 5; 4) р = 3. XIX.32. 1) 6; 2) 1; 3) 1; 4) 1. XIX.33. 1) 6; 2) 1; 3) 3; 4) 3. XIX.34. 1) x = 3(mod7); 2) нет решений; 3) х = 2(mod5); 4) х = 5 (modll); 5) х = 7 (mod9); 6) х = 2 (mod6).
XIX.35. 1) 4; 2) 1; 3) 10; 4) 14. XIX.36. 1) 0; 2) 0; 3) 0; 4) 0. XIX.37. 1) x = 10(mod35); 2) x = 10(mod25); 3) х = 5 ( mod 18), х= И ( mod 18) или х = 17 (modl8); 4) х = 4 (mod30), х = 9 (mod30), х = 13 (mod30), х=17 (mod30), х = 21 (mod30), х = 25 (mod30). XIX.38. 1) x = 33(mod40). Указание fX~3 (mod5)’ ~ 18х = 24 (mod40), Q 3 = ,9 ( .4оу
Указание. (mod8), = 5 (mod40). Отсюда 6х - 1У (moc1
2) х= 107 (mod 120); 3) x = 36(mod70); 4) x = 19(mod56). XIX.39. п = 2. Указание. Данные числа сравнимы по модулю Зс числами п+1, п + 2, п соответственно. Следовательно, имеют различные остатки от деления на 3. Но различных остатков при делении на 3 всего три: 0, 1, 2. Значит, одно из чисел делится на 3, а так как это число простое, то оно равно 3. XIX.40. 1) Указание. 2п не делится на 3, следовательно, либо 2” = l(mod3), либо 2” = 2(mod3). В первом случае 2я — 1 = 0( mod 3), во втором 2п + 1 = 0( mod 3). 2) Указание. Если р = 3, то утверждение верно. Если р — простое число, большее 3, то либо р = 1 (mod3), либо p = 2(mod3). В первом случае 8р — 1 = 1 (mod3) и 8р + 1 = О (mod3), т. е. 8р + 1 делится на 3. Во втором случае 8р — 1 = 0 (mod3), что противоречит условию. XIX.41. Указание: Предположим, что найдется пара натуральных чисел (х,у), удовлетворяющих уравнению. Тогда х3 + х + Юр (modlO) = 20004 (mod 10), откуда х3+х (mod 10) = 4 (mod 10). Но нетрудно показать, что для числа х3 + х реализуется один из следующих вариантов: х3 + х (mod 10)= О (modlO), или х3 + х (modlO) = 2 (modlO), х3 + x(modlO) = 8 (modlO).
XIX.43. 1) х = 3 + 8?, y=-l-3t, t(=Z-, 2) x = 4 + 7t, y=-\-4t, teZ-
3) x = 7 + 4t, у = — 6 — 5t, teZ\ 4) x = 3 + 8?, y — — 4— 11?, ?€Z; 5) x = 4 + 9?, у =—2 — 7t, t e Z; 6) x = 5 + 7?, y = -3-5t, teZ. XIX.44. 1) Числа вида
14 + 24?, ?eZ; 2) числа вида 115+119?, ?GZ; 3) числа вида 29 + 35?, ?€Z;
4) числа вида 26 +56?, ?€ Z. XIX.45. 1) Решений нет; 2) (4;—2), (—4;—2),
374 Глава XIX. Делимость целых чисел
(4;4), (—4;4). XIX.46. 1) (4;-1), (-4; 1), (5; 1), (-5;-1); 2) (1;-2), (-5;2), ( —1;2). (5;-2). XIX.47. 1) (4; 17), (1;20), (0; 1); 2) (3; 15), (4;—1), (6;-9), (2;-25), (-8; 15), (1;5), ( —1;—1). XIX.48. 1) (1;0), (—1;0), (0; 1), (0; -1), (1;-1), (-1; 1); 2) (2;1), (-1; 1), (-2;-1), (1;-1). XIX.49. 1) (0;-2), (-1; 10), (1;2), (—2;6); 2) (-1;-7), (-3; 13), (0;-2), (-4;8), (3,1), (-7:5), (8;2), (—12;4); 3) (0;2), (-2;0); 4) (0;3), (2;1). XIX.5O. 1) (3;3), (-3,-3), (—3;0), (3;0); 2) (1; 1), (—1;-1), (3;—1), (—3; 1). XIX.51. 1) (3;2), (—2; —3); 2) (5:6), (-6;-5), (—3; 4), (—4; 3). XIX.52. 1) (9; 9), (1; 33); 2) (1; 37).
XIX.53. 1) (0;—1), (2:1), (1;2), (—1;0); 2) (3; —10), (1;4), (9;-4), (-5;-2). XIX.54. 1) (2;0), (2;2); 2) (1;-4), (0;-3). XIX.55. 1) (9;-7); 2) (8;-6).
XIX.56. (20; 8). XIX.57. 1) 24; 2) 11. XIX.58. XIX.59. 12, 22,
32, 42, 52, 62, 72, 82, 92. XIX.60. 53. XIX.61. 13. XIX.62. 169. XIX.63. 9720. XIX.64. 2061. XIX.65. 233, 390, 466, 699. XIX.66. 153, 226, 379. XIX.67. 90. XIX.68. 2, 6, 9. XIX.69. 25. XIX.7O. 28.
XIX.71. 3, 3, 5. XIX.72. 64, или 71, или 78. XIX.74. С точностью до обозначений имеем 6 троек таких чисел: 1) 3, 9, 18; 2) 3, 8, 24; 3) 3, 10, 15; 4) 3,7,42; 5) 4,6,12; 6) 4,5,20. XIX.75. (0;0). XIX.76. 1) (0;0), (3;3), (5;0), (0;5); 2) (0;0), (2;2), (3;0), (0;3). XIX.77. (1;5;0), (—1;5;0), (1; —5;0), (-1;-5;0). XIX.78. 1) —1;2; 2) -4;5. XIX.79. 1791. XIX.80. А =
= {15,30,39,65,78,130,195,390}. XIX.81. А = {6,15,30,33,66, ПО, 165,330}.
Глава XX
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
§1. ОСНОВНЫЕ СХЕМЫ ПОДСЧЕТА ЭЛЕМЕНТОВ В КОНЕЧНОМ МНОЖЕСТВЕ
Первый уровень
1. Правило произведения
ХХ.1. Семья Ивановых в полном составе (мама, папа и их дети Таня, Оля, Лена, Ваня, Игорь, Боря и Андрей) принимает участие в игре «Дружная семья». Один из конкурсов игры — эстафета, на первом этапе которой соревнуются взрослые, на втором — мальчики, на третьем — девочки. Сколькими способами Ивановы могут сформировать команду для участия в эстафете?
ХХ.2. Из города А в город В ведет шесть дорог, а из города В в город С —три. Сколько путей, проходящих через В, ведет из Л в С?
XX.3. К концу первого года обучения в кулинарном колледже Иван научился готовить четыре первых блюда, пять — вторых и три — третьих. Сколько вариантов комплексных обедов, состоящих из 1-го, 2-го и 3-го блюд, может приготовить Иван?
ХХ.4. Сколько различных двузначных чисел можно получить, выкладывая в ряд две карточки с цифрами от 1 до 9 так, чтобы на первом месте стояли «четные» (2,4,6,8), а на втором — «нечетные» (1,3,5,7,9) цифры?
ХХ.5. Из города А в город В ведут четыре дороги. Сколькими способами можно съездить из А в В и обратно, если: 1) путешествие туда и обратно совершается по разным дорогам?
2) дороги туда и обратно выбираются независимо друг от друга?
ХХ.6. 1) Сколько имеется четырехзначных чисел, составленных из цифр 1,2,3,4,5,6,7,8,9, в десятичной записи которых все цифры различны?
376 Глава XX. Элементы комбинаторики
2) Сколько имеется четных четырехзначных чисел, составленных из цифр 1,2, 3,4, 5, 6,7, 8,9, в десятичной записи которых соседние цифры различны?
XX.7. 1) Сколько имеется шестизначных чисел, составленных из цифр 1,2,3,4,5,6,7,8,9, у которых соседние цифры различны?
2) Сколько имеется нечетных шестизначных чисел, составленных из цифр 1,2,3,4,5, 6,7, 8, 9, у которых все цифры различны?
ХХ.8. У Саши десять марок, а у Вани — двадцать. Сколькими способами можно осуществить обмен одной Сашиной марки на одну Ванину?
XX.9. Сколькими способами можно рассадить за шестью партами 6 девочек и 6 мальчиков так, чтобы за каждой партой слева сидел мальчик, а справа — девочка?
ХХ.10. в классе двадцать человек — десять девочек и десять мальчиков. Сколькими способами можно составить график дежурств по классу на десять дней так, чтобы каждый день дежурил один мальчик и одна девочка, и при этом никто из ребят не дежурил дважды?
2. Правило суммы и формула включений и исключений
ХХ.11. Сколько имеется натуральных чисел, меньших 10 000, в десятичной записгЬ которых все цифры различны?
ХХ.12. Сколько имеется шестизначных чисел, в десятичной записи которых «четные» (0,2, 4,6, 8) и «нечетные» (1,3, 5, 7, 9) цифры чередуются?
ХХ.13. 1) Сколько имеется четырехзначных чисел, в десятичной записи которых встречается цифра 5?
2) Сколько имеется шестизначных чисел, в десятичной записи которых встречается хотя бы одна из цифр 1, 2, 3?
XX.14. Сколько имеется пятизначных чисел, в десятичной записи которых встречаются одинаковые цифры?
XX.15. Сколько имеется шестизначных чисел, в десятичной записи которых хотя бы одна цифра «нечетна»?
§1. Основные схемы подсчета элементов в конечном множестве 377
3. Перестановки
ХХ.16. 1) У Ивана есть десять карточек, на которых записаны цифры от 0 до 9. Сколькими способами он может выложить их на столе в ряд?
2) У Ивана есть десять карточек, на которых записаны цифры от 0 до 9. Сколькими способами он может выложить их на столе в ряд так, чтобы непосредственно за цифрой пять следовала цифра шесть?
ХХ.17. 1) У Ивана есть десять карточек, на которых написаны цифры от 0 до 9. Сколькими способами он может выложить их на столе в ряд так, чтобы карточки, на которых записаны цифры 1,2,3, лежали рядом?
2) У Ивана есть десять карточек, на которых написаны цифры от 0 до 9. Сколькими способами он может выложить их на столе в ряд так, чтобы карточки, на которых записаны цифры 8 и 9, не лежали рядом?
ХХ.18. 1) Сколькими способами на одной полке можно разместить шесть книг по физике и шесть книг по математике так, чтобы книги по физике стояли правее всех книг по математике?
2) Сколькими способами на одной полке можно разместить шесть книг по физике и шесть книг по математике так, чтобы книги по физике чередовались с книгами по математике?
XX.19. Сколько существует перестановок цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, в которых цифра 2 занимает одно из первых четырех мест, а цифра 0 — одно из пяти последних?
ХХ.20. Сколькими способами можно рассадить на стоящих в ряд 12 стульях 4 мальчика и 8 девочек так, чтобы на крайних стульях ряда сидели мальчики?
4. Перестановки с повторениями
ХХ.21. 1) Сколько разных шестибуквенных слов можно получить, переставляя буквы в слове «фартук»?
2) Сколько разных шестибуквенных слов можно получить, переставляя буквы в слове «физика»?
3) Сколько разных восьмибуквенных слов можно получить, переставляя буквы в слове «черчение»?
378 Глава XX. Элементы комбинаторики
4) Сколько разных слов можно получить, переставляя буквы в слове «комбинаторика»?
XX .22. Сколько имеется девятизначных чисел, в десятичной записи которых цифра 4 встречается три раза, цифра 5 — четыре раза, цифра 8 — два раза?
XX. 23. У мамы четыре одинаковых яблока и три одинаковых груши. Каждый день в течение семи дней она выдает сыну по одному фрукту. Сколькими способами она может распределить фрукты по дням?
XX.2 4. Сколько различных семибуквенных слов можно составить, переставляя буквы в слове «потолок», если в полученных словах три буквы «о» не должны стоять рядом?
XX.25 . У Ивана восемь шаров: три синих и пять красных. Сколькими способами он может разложить их по восьми занумерованным коробкам так, чтобы в каждой коробке оказалось ровно по одному шару?
XX.2 6. Мама привезла в дом отдыха кулек, в котором оказалось 24 карамельки, в том числе 7 малиновых, 4 яблочных, 5 лимонных, 6 персиковых и 2 апельсиновых. Каждый день в течение 24-х дневного отпуска она решила давать сыну по одной конфете. Сколькими способами она может это сделать? х
Второй уровень
ХХ. 27. 1) Сколько различных натуральных делителей имеет число 23 • З4 • 52?
2) Сколько различных натуральных делителей имеет число 10!?
ХХ.28. 1) Сколько имеется подмножеств множества {1,2,3,..., п}?
2) Сколько имеется подмножеств множества {1, 2, 3,.... п}, содержащих элемент 1, но не содержащих элемент 2?
3) Сколько имеется непустых подмножеств множества {1,2,3,... ,п}, содержащих только четные числа?
4) Сколько имеется подмножеств множества {1, 2, 3,..., п}, содержащих хотя бы одно четное число?
XX.29. Из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 составляются всевозможные пятизначные числа, не содержащие одинаковых цифр.
§1. Основные схемы подсчета элементов в конечном множестве 379
Сколько среди них чисел, содержащих одновременно три цифры—1, 2, 3?
ХХ.ЗО. Сколько имеется четных четырехзначных чисел, в десятичной записи которых все цифры различны?
XX.31. Сколько существует целых положительных чисел, меньших 10 000 и делящихся на 4, в десятичной записи которых встречаются только цифры 0, 1, 2, 3, 5, причем ни одна цифра не повторяется дважды?
ХХ.32. Сколько существует положительных шестизначных чисел, в десятичной записи которых используются только три цифры, одна из которых повторяется четыре раза?
ХХ.ЗЗ. Из цифр 1, 2, 3, 4, 5, 6 составляются всевозможные числа, десятичная запись которых не содержит одинаковых цифр. Сколько среди них чисел, содержащих цифры 2, 4, 6, одновременно?
ХХ.34. На каждой стороне треугольника АВС отмечено по 7 точек, разбивающих ее на 8 равных частей. Рассмотрим всевозможные треугольники с вершинами в отмеченных точках (по одной на каждой стороне) Сколько среди этих треугольников таких, у которых ни одна из сторон не параллельна стороне треугольника АВС?
ХХ.35. У Ивана есть десять карточек, на которых написаны цифры от 0 до 9. Сколькими способами он может выложить их на столе в ряд так, чтобы карточка с цифрой 0 лежала левее карточки с цифрой 1?
XX.36. Сколькими способами можно рассадить за двенадцатью партами 12 девочек и 12 мальчиков так, чтобы каждый мальчик сидел рядом с девочкой?
ХХ.37. Сколькими способами можно рассадить в два ряда по шесть человек шесть мальчиков и шесть девочек так, чтобы никакие два мальчика не сидели рядом и никакие два мальчика не сидели друг за другом?
ХХ.38. Сколько существует перестановок цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, в которых цифра 2 занимает одно из семи первых мест, а цифра 0 — одно из семи последних?
ХХ.39. Сколько существует перестановок цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, в которых цифра 0 занимает одно из шести первых мест, а цифра 9 — одно из первых восьми и между цифрами 0 и 9 расположены две другие цифры?
380 Глава XX. Элементы комбинаторики
XX.40. Сколько различных каруселей можно сделать, расположив по окружности фигурки десяти зверей (карусели считаются одинаковыми, если фигурки идут друг за другом в одинаковом порядке)?
XX.41. 1) Сколькими способами можно рассадить 12 человек за круглым столом, если для каждого человека учитывать не место, которое он занимает, а то, кто является его соседом справа и кто является его соседом слева.
2) Сколькими способами можно рассадить 12 человек за круглым столом, если для каждого человека учитывать не место, которое он занимает, а лишь то, кто является его соседями (при этом не важно, кто из этих соседей сидит справа, а кто —слева).
§2. СОЧЕТАНИЯ И РАЗМЕЩЕНИЯ
Первый уровень
XX.42. У Ани есть семь цветных карандашей. Мама нарисовала на листке бумаги девочку и предложила Ане раскрасить ее шапочку, платье и туфельки, используя для каждого предмета одежды^один цвет.
1) Сколькими способами Аня сможет раскрасить картинку, если она решила, что шапочка, платье и туфельки должны быть раскрашены в разные цвета?
2) Сколькими способами Аня сможет раскрасить картинку, если она готова раскрашивать шапочку, платья и туфельки как в разные, так и в одинаковые цвета?
XX.43. В магазине продаются воздушные шары семи цветов. Саша решил купить для праздника три шара.
1) Сколькими способами Саша может выбрать шары, если он хочет, чтобы шары отличались по цвету?
2) Сколькими способами Саша может выбрать шары, если ему все равно, будут они отличаться по цвету, или нет?
ХХ.44. 1) Сколькими способами Маша может выбрать два предмета из восьми для сдачи экзамена по выбору?
2) Маша должна сдать два экзамена за восемь дней. Сколькими способами она может составить расписание
§2. Сочетания и размещения 381
экзаменов, если нельзя сдавать больше одного экзамена в день?
XX.45. 1) Сколькими способами можно разместить пять занумерованных шаров по девяти пронумерованным коробкам, если в одну коробку можно положить не более одного шара?
2) Сколько пятибуквенных «слов» можно составить в алфавите из девяти букв, если буквы в «словах» не должны повторяться?
ХХ.46. 1) Сколькими способами можно разместить пять занумерованных шаров по девяти пронумерованным коробкам, если в одну коробку можно положить неограниченное число шаров?
2) Сколько пятибуквенных «слов» можно составить в алфавите из девяти букв, если буквы в словах могут повторяться?
XX.47. Десять различных ящиков нужно доставить на шесть этажей строящегося дома.
1) Сколькими способами можно распределить ящики между этажами?
2) Сколькими способами можно распределить ящики между этажами так, чтобы на шестой этаж попал хотя бы один ящик?
ХХ.48. 1) Сколько различных наборов из восьми пирожных можно составить, имея четыре вида пирожных?
2) Сколько различных букетов из семи гвоздик можно составить, имея в распоряжении гвоздики трех цветов?
ХХ.49. В киоске продаются 10 видов рождественских поздравительных открыток. Тане нужно купить 8 открыток. Сколькими способами Таня сможет это сделать, если: 1) она решила купить открытки только разных видов; 2) она решила купить по две открытки четырех видов; 3) Тане все равно, какие открытки покупать;
4) одна из открыток понравилась Тане больше других, и она решила купить хотя бы одну такую открытку?
XX.50. Сколько различных шестизначных чисел можно получить, выкладывая в ряд карточки с цифрами от 1 до 9 так, чтобы
382 Глава XX. Элементы комбинаторики
на первых трех местах стояли четные, а на последних трех — нечетные цифры?
ХХ.51. В классе учатся 14 девушек и 10 юношей. Сколькими способами можно выбрать состав исполнителей для школьного спектакля, если в сценарии 5 женских и 4 мужские роли?
XX.52. У Саши десять марок, а у Вани — двадцать. Сколькими способами можно осуществить обмен трех Сашиных марок на три Ванины?
ХХ.53. В классе учатся 12 девушек и 10 юношей. Сколькими способами можно сформировать группу из четырех девушек и трех юношей для участия в субботнике?
XX.54. Сколькими способами можно расставить 12 белых и 12 черных шашек на черных полях шахматной доски?
ХХ.55. 1) Собрание из 50 человек выбирает председателя, секретаря и трех членов счетной комиссии. Сколькими способами это можно сделать?
2) Собрание из 30 человек выбирает президиум в составе пяти человек и делегацию в составе 6 человек. Сколькими способами может быть произведен выбор, если в делегацию должны войти два члена президиума? XX.56. Сколькими способами можно выбрать из 10 человек рабочую группу, состоящую из 6 человек, если среди них есть двое, которые не должны работать вместе?
ХХ.57. В классе учатся 20 человек. Сколькими способами можно в течение двух дней выбирать из его учеников группы по 12 человек для дежурства по школе так, чтобы эти группы не полностью совпадали по составу?
Второй уровень
ХХ.58. 1) Сколько имеется пятизначных чисел, в десятичной записи которых цифры расположены в порядке убывания?
2) Сколько имеется пятизначных чисел, в десятичной записи которых каждая следующая цифра меньше либо равна предыдущей?
ХХ.59. 1) Сколько имеется четырехзначных чисел, в десятичной записи которых цифры расположены в порядке возрастания?
§2. Сочетания и размещения 383
2) Сколько имеется четырехзначных чисел, в десятичной записи которых каждая следующая цифра больше либо равна предыдущей?
ХХ.60. На конференции должны выступить 8 человек. Сколькими способами можно расположить их в списке выступающих, если Иванов должен выступать не раньше Петрова?
ХХ.61. В классе учатся 9 девушек и 11 юношей. Сколькими способами можно сформировать команду из 7 человек для участия в спортивном состязании, если в нее должно войти не менее трех юношей?
ХХ.62. 1) В классе учатся 18 человек. Сколькими способами можно составить график дежурств по классу на шесть дней так, чтобы каждый день дежурили по три человека, причем никто не дежурил дважды?
2) В классе учатся 18 человек. Сколькими способами можно разбить его учеников на 6 одинаковых по численности групп?
ХХ.63. 1) Сколькими способами из 5 мужчин и 6 женщин можно составить 4 танцевальные пары?
2) В школьном спортивном празднике принимают участие 7 первоклассников, 8 второклассников, 6 третьеклассников и 5 четвероклассников. Сколькими способами можно составить из них 3 команды по 4 человека в каждой так, чтобы в каждую команду вошло по одному ребенку из каждой параллели?
ХХ.64. Сколько имеется семизначных чисел, в десятичной записи которых цифра 5 встречается трижды, а цифра О — дважды?
ХХ.65. 1) Сколькими способами можно распределить обязанности между 10 туристами, если двое из них должны собирать дрова, трое готовить ужин, а остальные ставить палатки?
2) Сколькими способами можно разместить 10 туристов в трех одинаковых двухместных и одной четырехместной палатке?
ХХ.66. Для 16 мальчиков, занимающихся в спортивной секции, для проезда в лагерь на сборы были забронированы места в четырех купейных вагонах. Сколькими способами тренер
384 Глава XX, Элементы комбинаторики
может разместить в поезде членов секции, если один из мальчиков может ехать только на полке, расположенной по ходу поезда (не важно, верхней или нижней), а еще двое не могут ехать на верхних полках.
XX.67. В классе три ряда парт: в каждом ряду по четыре парты. За каждой партой могут сидеть два человека. Сколькими способами учительница может рассадить девять девочек и девять мальчиков, если мальчики должны сидеть рядом с девочками, Машу нужно обязательно посадить за первую парту, а Ваню нужно разместить за партой в левом ряду?
ХХ.68. 1) Сколькими способами можно разложить 8 одинаковых шаров по трем занумерованным коробкам так, чтобы ни одна из коробок не осталась пустой?
2) Сколькими способами можно разложить 8 одинаковых шаров по трем занумерованным коробкам?
ХХ.69. 1) Сколькими способами можно 12 одинаковых конфет распределить между пятью детьми так, чтобы каждому ребенку досталось хотя бы по одной конфете?
2) Сколькими способами можно 12 одинаковых конфет распределить между пятью детьми (варианты, при которых некоторые дети остаются без конфет, не исключаются)?
XX.70. Двадцать одинаковых банок с красками нужно доставить на пять этажей строящегося дома. Сколькими способами это можно сделать, если на каждый этаж нужно доставить не менее трех банок?
ХХ.71. 1) Иван должен покрасить за 3 дня 24 заборных столба. Сколькими способами он может распределить работу по дням, если он решил красить не менее пяти столбов в день?
2) Иван должен покрасить за 3 дня 24 заборных столба. Сколькими способами он может распределить работу по дням, если максимальное число столбов, которое можно покрасить за один день, равно 20?
§3. Комбинаторные соотношения 385
§3. КОМБИНАТОРНЫЕ СООТНОШЕНИЯ
Первый уровень
Доказать тождество (ХХ.72-ХХ.75).
ХХ.72. 1) Akn = n-Akn~\-, 2) Akn=Ak~l -(n-k + 1);
3) A^+kA^A*.
XX.73. 1) Ci + 6C2 + 6C3 = n3;
2) + 7Cln + 12C^ + 6C3 = (n + I)3.
XX.74. 1) Ckn = Cnn-k\
2) C„ = Cn-\ + CL1 (тождество Паскаля).
XX.75. 1) C^+C^^C^;
2) CJ-C'”_7 = C‘ -C,7;
3) "(q„-Cl) = c2„+1;
4) (cj+i - cj) ck-_\ = k ((cj)2 - cix; ci=!).
Второй уровень
XX.76. Используя тождество Паскаля, доказать тождество:
О С^ = (^ + 2-Ск-_\+Ск„_}-,
2) =CS-?+3 cn-i+з • c‘t;+ci_,.
ХХ.77. Используя бином Ньютона, доказать тождество:
1) 1 + С' +С?, + .. + С^ = 2'1;
2) l-Ci + c2-.. + (-l)»-C» = 0;
3) 1 + 2С‘„ + 22С2 + .. + 2" С” = 3";
4) 1 + 4CJ + 42С2 + .. + 4” Ci = 5".
ХХ.78. Найти такое число k, при котором число сочетаний из п элементов по k наибольшее, если: 1) п — четное натуральное число;
2) п — нечетное натуральное число.
ХХ.79. Доказать, что для любого нечетного п выполняется равенство:
1) £ {-l)fryC* = O; 2) f*C‘ = „-2"-1; /г=0 k=0
13—5682
386 Глава XX. Элементы комбинаторики
п 2п+1 ,
3) £ = 0; 4) S ^=!L = 0.
*=‘ ‘=0 (Ч+|)
XX.80. Доказать тождество:
1 \ rm pm — 1 । pm
'-'n+m ьп+т-1 “Г Ljri+m-l’
2) С“_1 + С1 + ...+С?+„ = С”+т.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ XX
ХХ.81. 1) Сколькими способами можно представить число п в виде упорядоченной суммы k положительных целых чисел?
2) Сколькими способами можно представить число п в виде упорядоченной суммы k неотрицательных чисел? XX.82. Сколько шестизначных чисел имеют в своей десятичной записи точно четыре различные цифры?
ХХ.83. Семь различных ящиков нужно доставить на четыре этажа строящегося дома. Сколькими способами можно распределить ящики между этажами, если на каждый этаж должен попасть хотя бы один ящик?
ХХ.84. По 10 различным урнам распределены 6 белых и 6 черных одинаковых по размеру шаров, причем в каждой урне имеется хотя бы один шар. Сколько существует различных вариантов распределения шаров?
ХХ.85. Доказать, что при любом натуральном п выполняется
равенство:
1) = (с„0)2 + (с),)2 + (с2)2 +... + (cj)2;
2) £ (-1)* (С*)2 &=0
О, п нечетно, (—п четно.
XX.86. Доказать тождество
'О рт । гЧ рт—1 । । pk pm—k I । pm pO ___________pm
'p ' ^n—p ' ‘ L'n—p “Г • • • “Г Ьр • . -f- Cp • ьп_р • .
XX.87. Доказать тождество ^2 & (C^)2 = ^2n’ k=0 2
k . .
XX.88. Доказать равенство £2 (Q’^m ‘ = ^m+n-
i=0
Ответы к главе XX 387
ОТВЕТЫ К ГЛАВЕ XX
ХХ.1. 24. XX.2. 18. ХХ.З. 60. ХХ.4. 20. ХХ.5. 1) 12;
2) 16. ХХ.6. 1) 3024; 2) 2048. ХХ.7. 1) 96; 2) 33600.
ХХ.8. 200. ХХ.9. (6!)2 = 518400. ХХ.1О. (10!)2. ХХ.11. 5274.
ХХ.12. 56 + 4 • 55 = 28125. ХХ.13. 1) 3168; 2) 9 • 105 - 6 • 75 = 799158.
ХХ.14. 9-104-9-9-8-7-6 = 62784. ХХ.15. 9 • 105 - 4 • 55 = 887500.
ХХ.16. 1) 10!; 2) 9!. ХХ.17. 1) 6 8!; 2) 8 • 9!. ХХ.18. 1) (6!)2;
2) 2-(6!)2. ХХ.19. 4-5-8! = 20-8!. ХХ.20. 12-10!. ХХ.21. 1) 6! = 720;
2) = 360; 3) = 3360; 4) Ж. ХХ.22. 1260. ХХ.23. 35.
Z о !Z. (Z!)
ХХ.24. 720. ХХ.25. 56. ХХ.26. 24! с, . ХХ.27. 1) 60; 2) 270.
7! • 4! • 5! • 6! • 2!
XX.28. 1) 2П; 2) 2"-2; 3) 2? —1, если п. — четное; 2~^~ — 1, если п —
нечетное; 4) 2п — 22, если п — четное; 2п — 2 2 , если п — нечетное. ХХ.29. 1800. ХХ.ЗО. 2296. ХХ.31. 31. ХХ.32. 9720. ХХ.ЗЗ. 1158. ХХ.34. 216. ХХ.35. 45-8!. ХХ.36. (12!)2-212. ХХ.37. 2 • 6! 6! = 1036800.
ХХ.38. 45 • 8!. ХХ.39. 8 • 8!. ХХ.40. 9!. ХХ.41. 1) 11!; 2) у.
ХХ.42. 1) 210; 2) 343. ХХ.43. 1) 35; 2) 84. ХХ.44. 1) 28; 2) 56. ХХ.45. 1) 15120; 2) 15120. ХХ.46. 1) 95 ; 2) 95. ХХ.47. 1) 610;
2) 6ю-510. ХХ.48. 1) = 165; 2) С^ = 36. ХХ.49. 1) С?о = 45; 2) С?0 =
= 210; 3) С?о= 24310; 4) С?о - C| = 11440. XX.50. 1440. XX.51. Д14-Д4О. ХХ.52. Cf0 • С|о = 136800. ХХ.53. С?2 С?о = 59400. ХХ.54. Cl322 • С^.
ХХ.55. 1) 42 375 200; 2) С^о • С% • С$5. ХХ.56. Cf0 - Cf = ’40.
ХХ.57. С’2 • (C$-1). ХХ.58. 1) 252; 2) 2001. ХХ.59. 1) = 126;
2) £5 = 495. ХХ.60. 20 160. ХХ.61. 69 630. ХХ.62. 1) 2) ^уу^у-
ХХ.63. 1) 1800; 2) 4 233 600. ХХ.64. 9600. ХХ.65. 1) С?о • С% = 2520;
2) hlQ Ч = 3150. ХХ.66. 392-13!. ХХ.67. 768-8! II!. ХХ.68. 1) 21; 2) 55. ХХ.69. 1) 330; 2) 1820. ХХ.70. 126. ХХ.71. 1) 55; 2) 295.
ХХ.78. 1) Cj; 2) и С^~. ХХ.79. Указание. 1) За-
пишем сумму Sn — ]С(—1)^\/с* двумя способами —в прямом k=0
и обратном порядке:
- Уа + %/с2 - ... + у/ср - у/с% = о
Так как С™ = т, то выражение в каждой скобке равно нулю. Следовательно, 2Sn = 0, откуда Sn = 0. XX.81. 1) С^~\\ 2)
388 Глава XX. Элементы комбинаторики
ХХ.82. 294 840. ХХ.83. 8400. ХХ.84. 23 100. Указание. Возможны
два варианта размещения шаров: либо в какой-то урне 3 шара и в 9 урнах — по 1 шару, либо в каких-то двух урнах —по 2 шара и в 8 урнах — по 1 шару. XX.86. Указание: Каждое сочетание без повторений из п элементов по m можно составить в два этапа: сначала взять некоторое число элементов из каких-то р элементов, а потом недостающие взять из остальных п—р элементов. XX.87. Указание: использовать тот же прием, что и в номере 79, а также воспользоваться тождеством из номера 85 1). XX.88. Указание. Рассмотреть алфавит из m «гласных» и п «согласных». Тогда i-й член С'1г-А‘т -А^~1 суммы из левой части равенства представляет собой число размещений i «гласных» и k — i «согласных».
Глава XXI
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
§1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ Первый уровень
1. Множество элементарных исходов эксперимента
XXI.1. Иван проводит следующий эксперимент: два раза подбрасывает монету и после каждого броска записывает на листе, что выпало — герб или цифра. Описать множество элементарных исходов данного эксперимента.
XXI.2. В урне лежат два белых и два черных шара. Из урны наудачу последовательно и без возвращения извлекаются три шара. Описать множество элементарных исходов данного эксперимента.
XXI.3. Из урны, содержащей три белых и один черный шар, наудачу последовательно и без возвращения извлекается по одному шару до появления черного шара. Описать множество элементарных исходов данного эксперимента.
XXI.4. Саша проводит следующий эксперимент: подбрасывает монету до тех пор, пока не выпадет герб, после каждого броска фиксируя на листе, что выпало — герб или цифра. Описать множество элементарных исходов данного эксперимента.
XXI.5. Маша проводит следующий эксперимент: рисует в тетради отрезок ОА длиной 10 см, произвольно ставит на нем точку В, после чего измеряет длину отрезка ОВ. Описать множество элементарных исходов данного эксперимента.
XXI.6. Оля проводит следующий эксперимент: рисует в тетради отрезок ОА длиной 5 см, произвольно ставит внутри него две точки В и С, после чего строит прямоугольник со сторонами, равными по длине отрезкам ОВ и ОС. Описать множество элементарных исходов данного эксперимента.
XXI.7. В коробке лежат три шара: красный, синий и белый. Рассмотрим четыре эксперимента, состоящие в последовательном извлечении из коробки двух шаров и фиксации
390 Глава XXI. Элементы теории вероятностей
их цветов. Эксперименты различаются по условиям проведения:
1) в эксперименте А шар, извлеченный из коробки первым, откладывается в сторону; порядок, в котором были извлечены шары, фиксируется;
2) в эксперименте Б шар, извлеченный из коробки первым, откладывается в сторону; порядок, в котором были извлечены шары, не фиксируется;
3) в эксперименте В шар, извлеченный из коробки первым, возвращается в коробку перед извлечением второго ш'ара; порядок, в котором были извлечены шары, фиксируется;
4) в эксперименте Г шар, извлеченный из коробки первым, возвращается в коробку перед извлечением второго шара; порядок, в котором были извлечены шары, не фиксируется.
Описать множество элементарных исходов каждого эксперимента.
XXI.8. В городе N проводится следующий опыт: наугад выбирается семья с тремя детьми и выясняется, сколько мальчиков и сколько девочек растет в этой семье. Построить множество элементарных исходов опыта так, чтобы исходы были равновозможными.
XXI.9. В коробке лежат 4 белых и 2 черных шара. Эксперимент состоит в одновременном извлечении пяти шаров и регистрации числа черных шаров среди извлеченных. Построить множество элементарных исходов эксперимента так, чтобы исходы были равновозможными.
XXI.10. Подбрасываются две одинаковые игральные кости и фиксируются очки, выпавшие на этих костях. Построить множество элементарных исходов опыта так, чтобы исходы были равновозможными.
2. События и действия над ними
XXI.11. Каждая из цифр 1, 2, 3 записана на отдельной карточке. Наугад вытягивается одна карточка, на листок записывается находящаяся на ней цифра и карточка возвращается обратно в стопку. Затем вытягивается вторая карточка, и ее цифра записывается справа
§1. Основные понятия теории вероятностей 391
от первой цифры. Наблюдаемый результат — двузначное число. События: А = {число четное}, В = {количество десятков не равно количеству единиц}.
1) Построить множество элементарных исходов эксперимента.
2) Задать перечислением элементов события А, В, А, В, АВ, А+В, АВ.
3) Определить, какие события, упомянутые в пункте 2, попарно несовместны.
XXI.12. Эксперимент состоит в однократном подбрасывании игральной кости. События: А — {число выпавших очков кратно трем}, В = {число выпавших очков нечетно}, С = {число выпавших очков больше 3}, D = {число выпавших очков меньше 7}, Е = {число выпавших очков нецелое}, F = {число выпавших очков меньше 1,5, но больше 0,5}.
1) Описать множество Q элементарных исходов эксперимента.
2) Задать перечислением элементов события В, С, АВ, А + В, AC, E + D, EF.
3) Определить, какие события, упомянутые в пункте 2, попарно несовместны.
XXI.13. На отрезке [2,8] числовой оси наудачу ставятся две точки М и N. Пусть % и у — координаты точек М и N соответственно. Событие А — {точка N ближе расположена к правому концу отрезка, чем точка 7И}, а событие В — {расстояние между точками М и N меньше половины длины отрезка}.
1) Описать множество Q элементарных исходов эксперимента и изобразить его на плоскости Оху.
2) Описать события А, В, А, В, АВ, А + В и изобразить их на плоскости Оху.
XXI.14. Используя свойства операций над событиями, доказать тождество:
1) (Л+В) (Л+В)=Л; 2) (Л + 5) (А+В) (А+В)=АВ;
3) А+В=А+АВ; 4) А + В = АВ+АВ+АВ.
392 Глава XXI. Элементы теории вероятностей
XXI.15. Пусть А и В — события, наблюдаемые в данном эксперименте. Выразить, используя операции над А и В, следующие события:
С={из двух событий не произойдет ни одного}, 2)={из двух событий произойдет ровно одно}, Е={из двух событий произойдет ровно два}, F={vi3 двух событий произойдет хотя бы одно}.
XXI.16. Опыт состоит в трех выстрелах по мишени и фиксации факта попадания (промаха) при каждом из них. Событие Ak = {попадание при /г-м выстреле} (/г= 1,2,3).
1) Построить множество элементарных исходов данного эксперимента и выразить каждый элементарный исход через события А/{.
2) Выразить через А/{ следующие события: А = {ровно три попадания}, В = {не меньше двух попаданий}, С= {промах не раньше, чем при втором выстреле}, £)={хотя бы одно попадание}.
3. Классическое определение вероятности
XXI.17. Один раз бросают игральную кость.
1) Какова вероятность, что выпадет четное число очков?
2) Какова вероятность, что выпадет число очков кратное 3?
XXI.18. Четырехтомное собрание сочинений поставили на полку в случайном порядке.
1) Какова вероятность, что тома будут стоять слева направо в порядке возрастания их номеров?
2) Какова вероятность, что третий и четвертый том окажутся рядом?
XXI.19. Учительница попросила Сашу написать в тетради двузначное число, используя цифры от 1 до 9.
1) С какой вероятностью написанное Сашей число окажется кратным 5?
2) С какой вероятностью в написанном Сашей числе количество десятков будет отличаться от числа единиц?
§1. Основные понятия теории вероятностей 393
XXI.20. Бросают три игральные кости.
1) Найти вероятность того, что на всех гранях выпадет одинаковое число очков.
2) Найти вероятность того, что на всех гранях выпадет четное число очков.
XXI.21. Одновременно бросают две игральные кости. Найти вероятности следующих событий: А = {сумма выпавших очков равна 10}; В = {произведение выпавших очков равно 10}; С = {сумма выпавших очков меньше, чем их произведение}.
XXL 22. 1) Какова вероятность, что шестизначный цифровой пароль состоит из разных цифр?
2) Какова вероятность, что шестизначный цифровой пароль не содержит нулей?
XXI.23. В семье пятеро детей.
1) Какова вероятность того, что среди них три девочки и два мальчика?
2) Какова вероятность того, что среди них есть хотя бы один мальчик?
XXI.24. В лотерее 20 билетов, из которых 5 выигрышных.
1) Какова вероятность выигрыша для того, кто имеет один билет?
2) Какова вероятность выигрыша для того, кто имеет три билета?
XXI.25. Какова вероятность, что хотя бы у одного из 25 учеников класса, рожденных в високосном году, день рождения будет 29 февраля?
XXI.26. Цифры от 1 до 7 написаны на семи карточках. Наугад последовательно вытягиваются три карточки и выкладываются на столе слева направо.
1) Найти вероятность того, что выложенное число будет нечетным.
2) Найти вероятность того, что в записи выложенного числа будет хотя бы одна цифра 5.
XXI.27. На семи карточках написаны числа 4, 5, 6, 8, 7, 13 и 16. Наугад берутся 2 карточки. Определить вероятность того, что дробь, которую можно составить из чисел, записанных на карточках, сокращается.
394 Глава XXI. Элементы теории вероятностей
XXI.28. В спортивной секции занимаются 6 девушек и 10 юношей. Между ними путем жеребьевки разыгрываются 4 путевки в зимний лагерь. Какова вероятность, что три путевки достанутся девушкам, а одна — юноше?
XXI.29. В спортивной секции занимаются 6 девушек и 10 юношей. Между ними путем жеребьевки разыгрывается 1 путевка в лагерь под Москвой и три путевки — в лагерь под Новгородом. Какова вероятность, что путевка в подмосковный лагерь достанется юноше, а остальные путевки достанутся девушкам?
XXI.30. 1) Из колоды в 36 карт наугад выбирают десять карт. Найти вероятность того, что среди них окажутся две дамы, три короля и один валет.
2) Из колоды, состоящей из 36 карт, случайным образом отбирают восемь карт. С какой вероятностью среди отобранных карт окажется ровно три туза и ровно две дамы?
4. Геометрическая вероятность
XXI.31. На участке АВ телефонной линии протяженностью 2 км произошел разрыв.
1) Чему равна вероятность того, что точка разрыва удалена от точки А меньше, чем на 600 м?
2) Чему равна вероятность того, что точка разрыва удалена от точек А и В на одинаковое расстояние?
XXI.32. На отрезке, длина которого равна 6 см, наудачу поставлена точка. Какова вероятность, что расстояние от этой точки до левого конца отрезка будет отличаться от расстояния от нее до правого конца не менее чем на 2 см?
XXI.33. На перекрестке установлен автоматический светофор, на котором одну минуту горит зеленый свет и две минуты — красный, затем вновь одну минуту — зеленый и две минуты — красный и т. д. В случайный момент времени к перекрестку подъезжает автомобиль. Какова вероятность того, что он проедет перекресток без остановки?
§ 1. Основные понятия теории вероятностей 395
XXL34. Луч локатора перемещается в горизонтальной плоскости с постоянной угловой скоростью. Какова вероятность того, < < тг
что цель будет обнаружена в угловом секторе - радиан, если появление цели по любому направлению одинаково возможно?
XXL35. На окружность радиуса 1 случайным образом поставлены две точки. Какова вероятность, что меньшая из дуг, заключенных между ними, не превосходит
XXL36. В круг вписан квадрат. Найти вероятность того, что точка, наудачу поставленная внутри круга, окажется и внутри квадрата.
XXL37. На отрезке [—2; 4] наудачу взяты два числа.
1) Какова вероятность того, что их сумма окажется меньше единицы?
2) Какова вероятность того, что сумма их квадратов окажется больше 4?
XXI.38. На отрезке АВ, длина которого равна 10 см, наудачу поставлены две точки С и D. Какова вероятность, что площадь квадрата, построенного на отрезке CD, не превосходит 36 сж2?
XXI.39. В куб вписан шар. Найти вероятность того, что точка, брошенная наудачу внутрь куба, окажется и внутри шара.
XXI.40. В шар вписан куб. Найти вероятность того, что точка, брошенная наудачу внутрь шара, окажется вне куба.
Второй уровень
XXI.41. У Вани — 15 марок, у Пети —10. Ваня отдал Пете одну из своих марок, а Петя Ване — одну из своих. Спустя некоторое время они вновь осуществили обмен: каждый отдал другому одну из имевшихся у него марок.
1) Какова вероятность, что после второго обмена у каждого мальчика будет исходный состав марок?
2) Какова вероятность, что после второго обмена хотя бы у одного мальчика будет исходный состав марок?
XXI.42. Четыре школьника случайным образом выбираются из группы, состоящей из 4 первоклассников, 3 второкласс
396 Глава XXI. Элементы теории вероятностей
ников и 2 третьеклассника. Найти вероятность того, что
1) среди них окажется ровно^два первоклассника;
2) в выбранную четверку входят школьники каждой параллели.
XXI.43. На батарее сушатся 14 пар варежек. Из них случайным образом отбирают 6 варежек. Какова вероятность, что среди выбранных варежек отсутствуют парные?
XXL44. Из коробки, в которой лежат 2 белых, 3 синих и 5 красных шаров, наугад вынимаются три шара.
1) Найти вероятность того, что среди вынутых шаров хотя бы два будут одного цвета.
2) Найти вероятность того, что среди вынутых шаров хотя бы два будут различаться по цвету.
XXL45. Класс, в котором учатся 12 девочек и 8 мальчиков, разбивается на две группы по 10 человек в каждой. Какова вероятность, что все мальчики окажутся в одной группе?
XXI.46. В розыгрыше первенства по футболу участвуют 18 команд, из которых случайным образом формируется две подгруппы по 9 команд в каждой. Среди участников чемпионата имеются 5 лучших команд прошлогоднего первенства. Какова вероятность, что все они попадут в одну группу?
XXI.47. Карты из колоды, содержащей 36 карт, раздают четырем игрокам, по 9 карт каждому. С какой вероятностью каждому из них достанутся карты одинаковой масти?
XXI.48. Колоду, состоящую из 36 карт, случайным образом делят пополам. С какой вероятностью в каждой половине окажется хотя бы один король?
XXI.49. Десять школьников, среди которых 5 юношей и 5 девушек, случайным образом группируются попарно. Найти вероятность того, что каждая из пяти пар состоит из лиц разного пола.
XXI.50. На отрезок ОА длины 9 см наудачу поставлена точка В. Найти вероятность того, что наименьший из отрезков ОВ и ВА имеет длину, большую, чем 3 см.
§2. Сложение вероятностей 397
XXI.51. На отрезке длиной 6 см наудачу выбраны две точки А и В. Какова вероятность, что расстояние между ними меньше 2?
XXI.52. Две баржи должны подойти к одному и тому же причалу для погрузки. Время прихода каждой из барж равновозможно в течение данных суток. Определить вероятность того, что одной из барж придется ожидать освобождения причала, если время, необходимое для погрузки первой баржи — четыре часа, а второй — шесть часов?
XXI.53. На бесконечную шахматную доску со стороной квадрата 3 см наудачу бросается монета радиуса 1 см. Найти вероятность того, что монета попадет целиком внутрь одного квадрата.
XXI.54. Какова вероятность того, что сумма трех наудачу взятых отрезков, длина каждого из которых не превосходит /, будет меньше /?
XXI.55. На плоскость с нанесенной на ней квадратной сеткой многократно бросается монета диаметром 2 см, в результате чего установлено, что в 25% случаев монета не пересекает ни одной стороны квадрата. Оценить размер сетки.
§2. СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ
XXI.56. Каждое их трех несовместных событий может произойти соответственно с вероятностями 0,05, 0,2 и 0,24. Определить вероятность того, что произойдет хотя бы одно из этих событий.
XXI.57. События А и В могут произойти соответственно с вероятностями 0,7 и 0,4. Кроме того, известно, что вероятность наблюдения хотя бы одного из этих событий равна 0,9. Определить вероятность того, что оба этих события произойдут одновременно.
XXI.58. События А, В и С могут произойти соответственно с вероятностями 0,3, 0,4 и 0,6. Кроме того, известно, что вероятность одновременного наблюдения событий А, В равна 0,15, В и С —0,3, а Л и С —0,2. Все три события можно наблюдать с вероятностью 0,1. Определить
398 Глава XXI. Элементы теории вероятностей
вероятность того, что произойдет хотя бы одно из этих событий.
XXI.59. Статистика, собранная среди студентов одного из вузов, обнаружила следующие факты: 60% всех студентов занимается спортом, 40% участвуют в научной работе на кафедрах и 20% занимаются спортом и участвуют в научной работе на кафедрах. Корреспондент местной газеты подошел к наудачу выбранному студенту. Найти вероятности следующих событий: В = {студент занимается хотя бы одним из двух указанных видов деятельности}, С= {студент занимается только одним видом деятельности}.
XXI.60. Статистика, собранная среди работников фирмы, показала, что 70% из них —мужчины, 80% — имеют машину, 60% — состоят в браке. Помимо этого, выяснилось, что 50% мужчин состоит в браке, 90% из них имеют машину, причем 20% мужчин состоят в браке и имеют машину одновременно. Кроме того, оказалось, что среди сотрудников, состоящих в браке, машину имеют 80%. Найти вероятность того, что случайно выбранный сотрудник фирмы окажется женщиной, не состоящей в браке и не имеющей машины?
XXI.61. Из урны, содержащей 9 красных шаров, 6 белых и 5 синих шаров, извлекают два шара. Какова вероятность, что оба шара одного цвета?
XXI.62. При изучении группы, состоящей из 150 школьников, оказалось, что 70 школьников успешно занимаются по математике, 70 — по литературе, 100 — географии. Кроме того, было обнаружено, что 30 школьников успешно занимаются как по математике, так и по литературе, 40 — как по математике, так и по географии, 50 — как по литературе, так и по географии. И только 20 школьников преуспевают сразу по трем предметам. Из группы в 150 человек случайным образом выбирается школьник.
1) Определить вероятность того, что он успешно занимается ровно по двум предметам.
2) Определить вероятность того, что он успешно занимается более чем по одному предмету.
§3. Условная вероятность. Независимость событий 399
XXI.63. Из ящика, содержащего 6 белых и 8 черных шаров, одновременно вынимают пять шаров. Найти вероятность того, что количество белых и количество черных шаров в выборке различаются не менее чем на два шара.
§3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. НЕЗАВИСИМОСТЬ СОБЫТИЙ
Первый уровень
1. Условная вероятность
XXL64. Маша участвует в розыгрыше призов, который организован следующим образом. Десять карточек, на которых записаны натуральные числа от 1 до 10, сложены в коробку. Ведущий, действуя случайным образом, достает из коробки одну карточку. Чтобы получить приз, Маша должна угадать, какое число, четное или нечетное, записано на карточке. Есть два варианта правил, по которым проводится розыгрыш:
1) при игре по первым правилам ведущий, вытянув карточку, не сообщает игроку никакой информации;
2) при игре по вторым правилам ведущий, вытянув карточку, сообщает игроку кратно или не кратно трем записанное на карточке число.
По каким правилам выгоднее играть Маше?
XXI.65. Один раз подбрасывается игральная кость. События: А = {выпало число очков, большее 2}, В = {выпало четное число очков}. Вычислить: 1) Р(А\В); 2) Р(В\А).
XXI.66. Известно, что при броске двух игральных костей на каждой из костей выпало четное число очков. С какой вероятностью можно утверждать, что сумма выпавших на костях очков равна 8?
XXI.67. Пусть вероятность рождения мальчика равна 0,5. Известно, что в семье двое детей, причем как минимум один ребенок — мальчик. С какой вероятностью можно утверждать, что оба ребенка — мальчики?
XXI.68. Из колоды в 36 карт вытаскивается карта черной масти. Из оставшихся 35 карт случайным образом выбираются
400 Глава XXI. Элементы теории вероятностей
9 карт, причем оказывается, что все они одного цвета. С какой вероятностью можно утверждать, что они красной масти?
2. Формула умножения вероятностей
XXL69. Из коробки, содержащей 6 белых и 4 красных шара, наудачу и последовательно извлекают по одному шару до появления красного шара. Найти вероятность того, что придется производить четвертое извлечение, если каждый извлеченный шар:
1) откладывается в сторону;
2) возвращается обратно в коробку.
XXL70. Школьник подготовил на зачет 10 вопросов из 15. Учитель задает ему последовательно три вопроса. Найти вероятность того, что:
1) он не знает ответ на первый и третий вопрос, но знает ответ на второй;
2) что он знает ответ на один вопрос из трех.
XXI.71. На полке стоят двенадцать книг, из которых три книги по математике, семь — по физике, и две — по химии. Ваня наугад достает с полки три книги подряд. Какова вероятность, что:
1) первые две книги будут по математике, а третья — по физике;
2) книги будут по разным предметам?
3. Независимые события
XXI.72. Из колоды в 36 карт наудачу извлекается одна карта. Наблюдаемые события: А = {вынутая карта — дама}, В = {вынута карта красной масти}, С= {вынутая карта — фигура (т. е. валет, дама, король или туз)}. Установить, зависимы или независимы следующие три пары событий: А и В, А и С, В и С. Выяснить, являются ли события А, В и С независимыми в совокупности.
XXI.73. Статистические исследования, проведенные в городе N, показали, что 80% „детей любят шоколад, 50%— бананы, 60% — йогурт. Кроме того было установлено, что 40% детей любит как шоколад, так и бананы,
§3. Условная вероятность. Независимость событий 401
30% — как бананы, так и йогурт, 48% — как шоколад, так и йогурт. И только 10% любит и шоколад, и бананы, и йогурт. Случайным образом из всех детей города выбирается ребенок и рассматриваются следующие события: А = {ребенок любит шоколад}, В = {ребенок любит бананы}, С = {ребенок любит йогурт}. Установить, зависимы или независимы следующие три пары событий: А и В, А и С, В и С. Выяснить, являются ли события А, В и С независимыми в совокупности.
XXI.74. Три пушки производят по одному выстрелу по мишени. Вероятность попадания для первой пушки равна 0,8, для второй — 0,7, для третьей —0,4. С какой вероятностью в мишени окажется ровно две пробоины?
XXI.75. Три члена команды по очереди пытаются поразить мишень. Первый спортсмен может это сделать с вероятностью 0,8, второй —0,6, третий —0,3. По условиям соревнований второй спортсмен делает свой выстрел только в том случае, если первый промахнулся, а третий стреляет только в случае промаха первых двух спортсменов. Найти вероятность того, что команде удастся поразить мишень.
XXI.76. Над изготовлением изделия работают последовательно трое рабочих. Качество изделия при передаче следующему рабочему не проверяется. Первый рабочий допускает брак с вероятностью 0,1, второй —0,2, третий —0,05. Найти вероятность того, что при изготовлении изделия будет допущен брак.
4. Формула полной вероятности
XXI.77. На складе хранятся 2000 деталей, изготовленных на первом станке и 3000 деталей, изготовленных на втором станке. Известно, что первый станок дает в среднем 0,1% брака, второй —0,2%. На сборку берется одна деталь со склада. Какова вероятность, что она окажется бракованной?
XXI.78. В тире имеются 8 ружей одного типа, 7 ружей второго типа и 5 ружей третьего типа, вероятности попадания из которых в мишень соответственно равны 0,5, 0,7 и 0,8. Определить вероятность того, что, взяв одно из ружей наугад, стрелок попадет в мишень.
402 Глава XXI. Элементы теории вероятностей
XXL79. Три машины производят болты. Первая из них производит 10% всей продукции, вторая — 40%, третья — 50%. Доля брака в продукции первой машины составляет 5%, в продукции второй — 10%, в продукции третьей — 2%. Какова вероятность, что наудачу взятый болт окажется качественным?
XXI.80. На сборку приборов поступили три партии однотипных деталей. В первой партии было 40 деталей, во второй— 60, в третьей —20. Вероятности того, что деталь не проработает расчетное время, для этих партий равны, соответственно, 0,05, 0,1 и 0,2. Найти вероятность того, что выбранная наудачу деталь проработает расчетное время.
Второй уровень
XXI.81. Двадцать учеников класса писали самостоятельную работу по математике, включавшую две задачи. Положительная оценка ставилась, если хотя бы одна задача была решена правильно. После проверки оказалось, что первую задачу правильно решили 70%, вторую — 60%, обе задачи — 40% учеников класса. С какой вероятностью можно утверждать, что ученик правильно решил первую задачу, если известно, что он получил за самостоятельную работу положительную оценку?
XXL82. Известно, что при броске двух игральных костей не выпало ни одной единицы. С какой вероятностью можно утверждать, что хотя бы на одной кости выпала шестерка?
XXI.83. 1) Показать, что если А и В — независимые события и Р(А)^0, Р(В)%0, то Р(А\В) = Р(А), Р(В\А)=Р(В).
2) Показать, что если выполняется одно из равенств Р(А\В)=Р(А) или Р(В\А) = Р(В), то А и В-независимые события.
XXI.84. Проводится эксперимент, состоящий в подбрасывании игральной кости до тех пор, пока на одной из ее граней не выпадет число очков, кратное трем. Какое минимальное число бросков следует запланировать, чтобы с вероятностью большей 0,8 можно было ожидать, что его хватит для завершения эксперимента?
§ 3. Условная вероятность. Независимость событий 403
XXI.85. В ящике лежат 16 теннисных мячей, в том числе 10 новых и 6 играных. Для игры из ящика берут два мяча наугад, а после игры их возвращают обратно в ящик. После этого из ящика вынимают два мяча для следующей игры. Найти вероятность того, что оба меча будут играными.
XXI.86. Программа экзамена содержит 30 различных вопросов, из которых студент Иванов знает только 15. Для успешной сдачи экзамена достаточно ответить на 2 предложенных вопроса или на один из них и дополнительный вопрос. Какова вероятность, что Иванов успешно сдаст экзамен?
XXI.87. Статистические данные показывают, что 95% всех изделий некоторого производства удовлетворяет стандарту. Предлагается упрощенная система контроля качества, которая с вероятностью 0,03 классифицирует стандартное изделие как бракованное и с вероятностью 0,06 расценивает бракованное изделие как стандартное. Какова вероятность, что изделие, прошедшее упрощенный контроль с положительным результатом, удовлетворяет стандарту?
XXI.88. Прибор может работать в двух режимах: стандартном и экстремальном. Нормальный режим наблюдается в 70% всех случаев работы прибора. Вероятность выхода прибора из строя за время Т в условиях нормального режима равна 0,2, а в условиях экстремального — 0,6. Прибор вышел из строя. Найти вероятность того, что при этом он работал в нормальном режиме.
XXI.89. Ученики восьмых и девятых классов поехали на экскурсию. Известно, что 20% из них — восьмиклассники, причем среди учеников восьмых классов девочек и мальчиков поровну, а среди девятиклассников девочек втрое больше мальчиков. Во время посещения музея экскурсовод обратился с вопросом к выбранной наугад девочке. Какова вероятность, что ею оказалась девятиклассница?
XXI.90. На склад поступили изделия от трех поставщиков с процентным содержанием брака 3%, 5% и 6% соответственно, причем от первого поступило в 4 раза больше продукции, чем от второго, а от второго в 2 раза больше, чем от третьего. Наудачу взятое изделие оказалось качественным. С какой вероятностью оно поступило от второго поставщика?
404 Глава XXI. Элементы теории вероятностей
XXI.91. В урне лежал шар неизвестного цвета — с равной вероятностью белый или красный. В урну опустили один белый и один красный шар и после тщательного перемешивания наудачу извлекли из нее один шар. Он оказался белым. Какова вероятность того, что в урне остались шары одного цвета?
§4. ФОРМУЛА БЕРНУЛЛИ
XXI.92. Пара игральных костей бросается 8 раз. Какова вероятность, что ровно пять раз сумма очков, выпавшая на костях, окажется четной?
XXL93. На сборку поступили 12 деталей из партии, в которой 10% всех деталей не удовлетворяет стандарту.
1) Найти вероятность, что в партию попадет меньше двух бракованных деталей.
2) Найти вероятность, что в партию попадет хотя бы одна бракованная деталь.
XXI.94. Монету бросают 6 раз. Какова вероятность, что герб выпадет:
1) четыре раза; 2) менее двух раз;
3) ни одного раза; 4) хотя бы один раз?
XXI.95. Для стрелка, выполняющего упражнения в тире, вероятность попасть в «яблочко» при одном выстреле не зависит от результатов предшествующих выстрелов и равна |. Спортсмен сделал пять выстрелов. Найти вероятности событий: А = {ровно одно попадание}, В — {ровно два попадания}, С={хотя бы одно попадание}, /)={не менее трех попаданий}.
XXI.96. Внутри квадрата со стороной \/5л см нарисован круг радиусом 1 см. Шесть человек по очереди внутри квадрата отмечают точку. Найти вероятности событий: А = {ровно три точки попадут в круг}, В={все точки попадут в круг}, С={в круг попадет нечетное число точек}.
§5. Дискретные случайные величины и их числовые характеристики 405
§5. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
1. Понятие случайной величины
XXI.97. Эксперимент состоит в подбрасывании игральной кости и фиксации выпавшего на верхней грани числа. Задать на множестве элементарных исходов этого эксперимента какие-нибудь две случайные величины. Для каждой из них записать закон распределения.
XXL98. Экспер имент состоит в подбрасывании двух монет и фиксации выпавшей стороны (герба или цифры). Задать на множестве элементарных исходов этого эксперимента какие-нибудь две случайные величины. Для каждой из них записать закон распределения.
2. Функция распределения и числовые характеристики случайной величины
XXL99. Из ящика, содержащего 3 красных и 5 синих шаров, случайным образом и без возвращения отбираются 2 шара. Случайная величина <f—число синих шаров в выборке. 1) Задать таблицей закон распределения 2) Найти Р{£<1} и 1.5}.
3) Найти функцию распределения случайной величины £ и построить ее график.
4) Вычислить математическое ожидание и дисперсию XXL100. Известно, что только один ключ из четырех подходит к данной двери. Последовательно опробуют ключи для открывания замка.
1) Задать таблицей закон распределения случайной величины числа проб, понадобившихся для открывания замка.
2) Найти Р{£<2} и Р{£>3}.
3) Найти функцию распределения случайной величины £ и построить ее график.
4) Вычислить математическое ожидание и дисперсию
XXI.101. Два стрелка независимо друг от друга делают по одному выстрелу в мишень. Вероятность попадания в мишень для первого стрелка равна 0,8, для второго —0,6. Случайная
406 Глава XXI. Элементы теории вероятностей
величина суммарное число попаданий в мишень в данном эксперименте.
1) Задать таблицей закон распределения
2) Найти P{(f<0,5} и Р{£^1}.
3) Найти функцию распределения случайной величины f и построить ее график.
4) Вычислить математическое ожидание и дисперсию %. XXI.102. На полке стоят десять книг, из которых две — книги по геометрии. Ваня наугад снимает с полки две книги. Случайная величина число книг по геометрии, снятых Ваней с полки.
1) Задать таблицей закон распределения f.
2) Найти Р{£<3} и Р{£>2}.
3) Найти функцию распределения случайной величины % и построить ее график.
4) Вычислить математическое ожидание и дисперсию f.
3. Биномиальное распределение
XXI.103. Монету бросают 3 раза. Случайная величина % — число выпадений герба.
1) Задать таблицей закон распределения
2) Найти функцию распределения случайной величины
3) Вычислить математическое ожидание и дисперсию
XXI.104. Четыре игрока по очереди бросают кубик. Случайная величина число игроков, у которых выпадет менее пяти очков.
1) Задать таблицей закон распределения
2) Найти функцию распределения случайной величины
3) Вычислить математическое ожидание и дисперсию
XXI.105. И меется 1000 семей, в каждой из которых два ребенка. Случайная величина число семей, имеющих двух мальчиков. Найти математическое ожидание и дисперсию
XXI.106. В продукции завода брак составляет 5% от общего количества выпускаемых деталей. Для контроля отобрано 20 деталей. Случайная величина число бракованных деталей в партии. Найти математическое ожидание и дисперсию
Задачи повышенной сложности к главе XXI 407
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ К ГЛАВЕ XXI
XXI.107. На окружность единичного радиуса наудачу ставятся три точки А, В и С. Какова вероятность того, что треугольник АВС окажется остроугольным?
XXI.108. Школьник знает 20 из 25 вопросов к зачету по геометрии. Зачет считается сданным, если школьник ответит не менее чем на три из четырех поставленных в билете вопросов. Взглянув на первый вопрос билета, школьник обнаружил, что он его знает. Какова вероятность того, что он сдаст зачет?
XXI.109. В круг вписан квадрат. Какова вероятность того, что из 10 точек, брошенных наудачу независимо одна от другой внутрь круга, четыре попадут в квадрат, три — в один сегмент и по одной — в оставшиеся три сегмента?
XXI.110. в одном из матчей на первенство мира по шахматам ничьи не учитывались, а игра шла до тех пор, пока один из участников не набирал 6 очков (выигрыш — 1 очко, проигрыш или ничья — 0 очков). Считая участников матча одинаковыми по силе, а результаты отдельных игр независимыми, найти вероятность того, что при таких правилах в момент окончания матча проигравший набирает К очков.
XXI.111. Два игрока бросают по очереди монету. Выигравшим считается тот, у кого первого выпадет герб. Найти вероятности выигрыша для каждого из игроков, если игроки договорились, что каждый сделает не более 100 бросков.
XXI.112. Баллотируются два кандидата, причем за первого в урну опущено п бюллетеней, а за второго — m бюллетеней Какова вероятность того, что в ходе подсчета бюллетеней число подсчитанных голосов, поданных за первого, все время будет больше числа голосов, поданных за второго?
XXI.113. За некоторый промежуток времени амеба может погибнуть с вероятностью |, выжить с вероятностью | и разделиться на две с вероятностью |. В следующий такой же промежуток времени с каждой амебой независимо от
408 Глава XXI. Элементы теории вероятностей
ее «происхождения» происходит то же самое. Сколько амеб и с какими вероятностями может существовать к концу второго промежутка времени, если к началу первого промежутка имелась одна амеба?
XXI.114. На шахматную доску ставят двух слонов, белого и черного. Какова вероятность, что слоны побьют друг друга?
ОТВЕТЫ К ГЛАВЕ XXI
XXI.1. $1={гг, гц, цг, цц} (г — выпал герб, ц — выпала цифра). XXI.2. С1={ббч, бчч, бчб, ччб, чбб, чбч} (б —извлечен белый шар, ч — извлечен черный шар). XXI.3. 12 = {ч, бч, ббч,
бббч} (б—извлечен белый шар, ч — извлечен черный шар).
XXI.4. Г2 = {г, цг, ццг, цццг,...}. XXI.5. 12 = {х| х е [0; 10]}.
XXI.6. 12 = {(х,у)|х G (0;5),yG (0;5)}. XXI.7. 1) A: 12А
= {кс, ск, кб, бк, сб, бс}; 2) Б: 12б = {кс> к&> сб}< 3) В: 11в = = {кс, ск, кб, бк, сб, бс, кк, сс, бб}; 4) Г: 12р = {кс, кб, сб, кк, сс, бб]. XXI.8. 12 = {ммм, ммд, мдм, дмм, мдд, дмд, ддм, ддд}. XXI.9. Если пронумеровать все шары числами от 1 до 6, то в качестве элементов множества элементарных исходов можно взять сочетания из 6 по 5 (или размещения из 6 по 5) элементов множества {1,2,3,4,5,6}. XXI.10. Помети м одну из игральных костей. Множество элементарных исходов 12 составим из упорядоченных пар (t,/), где г —число очков выпавших на помеченной кости, а / — число очков выпавших на непомеченной кости. Таким образом, элементами множества 12 являются размещения из 6 по 2. Заметим, что если в качестве элементов 12 взять сочетания из 6 по 2, то получится множество с неравновозможными исходами. XXI.11. 1) 12 = {11,12,13,21,22,23,31,32,33}; 2) А = {12,22,32}, В= {12,13,21,23,31,32}, А = {11,13,21,23,31,33}, В = {11,22,33}, АВ= {12,32}, А + В = {12,13,21,22,23,31,32}, АВ = {22}; 3) А и А, В и В, В и АВ,
А и АВ, А и АВ, В и АВ, АВ и АВ. XXI.12. 1) Q = {1,2,3,4,5,6}; 2) В={2.4,6}, С= {1,2, 3}, АВ = {3}, А +В = {1, 3,5,6}, АС= {3}, E + D = Cl, EF = 0', 3) В и АВ, В и АС, В u_EF, С и EF, _АВ и EF, АС и EF, E + D и EF. XXL15. Например, С = А В, D — AB + AB, Е = АВ, F = A + B или F = АВ + АВ + BA. XXI.16. 1) Обозначим попадание цифрой 1, а промах — цифрой 0, тогда каждому элементарному исходу опыта можно сопоставить упорядоченную тройку этих цифр. Например, запись 011 будет означать, что при первом выстреле имел место промах, а при втором и третьем — попадание. Множество элементарных исходов опыта: 12 = {000,001,010,100,011,101,110,111}. Элементы множества 12 можно представить через события А^ следующим образом: 000 = Ai • А% • A3, 001 = A?jJ7 • А3, 010 = А?_А2 Аз. Ю0 = А] • Аг A3, 011 = А? • А2 • А3, 101 =Ai-А2 А3, 110 = А1-А2-Аз, 111 =А]-А2 • A3. 2) Например, А =Ai-А2-Аз; В = Ai • А2 • A3 + А] А2 • A3 + А] • А2 • A3 + Ai • А2 • A3 = Ai • А2 + Ai A3 + А2 A3;
Ответы к главе XXI 409
С = Д| Д2 • Дз + Л] - Д2 Дз + А\ • Д2 • Д3 + Д1 Д2 • Д3 — ^1; D — А\ А2 Д3 + Д1 • Д2 • Д3 + Д1 • Д2 • Д3 + Д1 • Д2 ^з + • /Г2 • Д3 + А{ Д2 • Д^ + Д1 • Д2 • Дз = А • л? д;. XXI.17. 1) 1;
2) 1. XXI.18. 1) ±; 2) 1. XXI.19. 1) 2) XXI.20. 1) -Ь
2) XXI.21. Р(Д) = 1; Р(В) = 1; Р(С) = XXI.22. 1) 0,1512;
2) 0,96 = 0,531441. XXI.23. 1) Ь 2) XXI.24. 1) 2)
XXI.25. 1 - XXI.26. 1) 2) XXI.27. XXI.28.
\ obb / /7 7 91
г С3 С2 С3 9
XXI.29. XXI.30. 1) « 0,004; 2) — = ~ 0.0036.
182 С°6 561
XXI.31. 1) 0,3; 2) 0. XXI.32. |. XXI.33. |. XXI.34. XXI.35. |.
XXI.36. XXI.37. 1) Ц; 2) 1 - XXI.38. XXI.39. ?
л 72 9 25 6
ХХ1-40-1 - ХХ14* *> iio; 2> А' ХХ142»2> г
хх,.43. < XXI.44. 1) 2) XXI.45. —д. XXI.46.
XXI.47. XXI.48. XXI.49. A. XXI.5O. |. XXI.51. |.
XXI.52. XXI.53. 1. XXI.54. |. XXI.55. 4 см. XXI.56. 0,445
XXI.57. 0,2 XXI.58. 0,75. XXI.59. Р(В) = 0,6, P(Q = 0,6. XXI.60. 0,85. XXI.61. XXI.62. 1) 0,4; 2) A XXI.63. XXI.64. Маше
190 15 143
2 1 1
выгоднее играть по вторым правилам. XXI.65. 1) д', 2) XXI.66. -.
XXI.67. |. XXI.68. |. XXI.69. 1) |; 2) 0,216. XXI.70. 1) -°-;
2) XXI.71. 1) 2) XXI.72. А и В независимые, В и С
независимые, А и С зависимые, Д, В и С не являются независимыми
3, В и С, А и С независимые, Д, в совокупности. XXI.74. 0,488.
XXI.77. 0,0016. XXI.78. 0,645.
7~. XXI.82. XXI.84. Четыре.
9 Ло
XXI.87. и 0,9968. XXI.88.
1Ь
XXI.92. XXI.93. 1) «0,659;
4) XXI.95. /’(Д)«0,3955,
64 7 64 7
0,1035. XXI.96. Р(Д) = 0,08192,
в совокупности. XXI.73. Пары А и j В и С не являются независимыми
XXI.75. 0,944. XXI.76. 0,316.
XXI.79. 0,945. XXI.80. 0,9. XXI.81.
XXI.85. « 0,1906. XXI.86. 0,5.
XXI.89. |. XXI.90. XXI.91. |
7 10b о
2) ^0,7176. XXI.94. 1) 2) 3)
' ’ 7 64 7 64 7
Р(В} 0,2637; Р(С) « 0,7627, P(D} «
Р(В) = 0,000064; Р(С) = 0.476672. XXI.99. 1)
410 Глава XXI. Элементы теории вероятностей
2) Р{4<1} = Ь
Z0
Р{4<1,5} =
2
14’
3) F?(x) = <
О, _3_ 28’ 2 14’
1,
2.
4) Л4(4)=£; 0(4)
= 45
112'
1)
XXI.100.
X/ 1 2 3 4
Pi £ 4 £ 4 £ 4 £ 4
2) Р{4<2} =
о,
1,
4’
4’
Р{?>2} = }
3) ^(х)
4) М(4) = |;
Dtf) =
1} = 0,92.
3)
D(£) = 0,4.
и Р{4>2} = 0.
0,4; 0(4) =
(О, х О,
2) F^x)
1)
2’ 3
4’
ч,
5 XXI.Ю1.
4
х. 0 1 2
Pi 0,08 0,44 0,48
о, ; 0,08,
1,
2)
Р{£< 0,5} = 0,08;
4) М(0 = 1,4;
3)
= <
XXI.102.
1)
1, х > 2.
х. 0 1 2
Pi 28 45 16 45 1 45
2) Р{4< 3} = 1
0,125, 0<х^1,
< 0.5, 1 < х 2, 0,875, 2 < х <$ 3, <1, х > 3.
О, 28 45’ 44 45 1,
1,
4) ЛСД
XXI.103.
1)
Xi 0 1 2 3
Pi 0,125 . 0,375 0,375 0,125
3) Л4(£) = 1,5; Dtf) = 0,75.
Ответы к главе XXI 411
XXI.104. 1)
0 1 2 3 4
Pi “Г-_81_ “8“ _SJL_ ~^Г __ajL_ “ЗТ" 81 _81
О, J_ 81’ 2. 81’ 33 81 ’ 65 81 ’
х О,
О < х 1,
1 <х ^2,
2 < х 3,
3 < х 4,
1, х > 4.
3) М(£) = D(g) = XXI.105. М(£) = 250, £>(£) = 187,5.
XXI.106. Mtf) = 1, D«) = 0,95. XXI.107. 0,25. XXI.108. Щ.
XXI.109. • (-V fl --V. XXI.ПО. cLs • 2“А“5. XXI.111. Ве-
4!3! \тг/ \ тг/ л+&
роятность выигрыша первого игрока равна |(1 —О,5100), второго — | (1 -О,5100). XXI.112. XXI.113. Могут существовать О, 1, 2, 3, 4
л 11 4 9 4 4 5
амебы соответственно с вероятностями =, XXI.114.
Глава XXII
РАЗНЫЕ ЗАДАЧИ
§1. ТЕКСТОВЫЕ ЗАДАЧИ
Первый уровень
XXII.1. Товар продавался в течение двух дней: в первый день по цене 20 руб. за 1 кг, а во второй — 90 руб. за 1 кг. Какая часть общей выручки была получена за товар в первый день, если средняя цена товара оказалась равной 60 руб. за 1 кг?
XXII.2. 16 кг огурцов на 20 руб. дешевле, чем 13 кг помидоров, а 24 кг огурцов на 24 руб. дороже 15 кг помидоров. Определить общую стоимость 6 кг огурцов и 13 кг помидоров.
XXII.3. Если двузначное число разделить на произведение его цифр, то в частном получится 3, а в остатке 9. Если же из квадрата суммы цифр этого числа вычесть произведение его цифр, то получится данное число. Найти это число.
XXII.4. Произведение цифр двузначного числа в 3 раза меньше самого числа. Если к искомому числу прибавить 18, то получится число, записываемое теми же цифрами, но в обратном порядке. Найти это число.
XXII.5. Турист проехал расстояние между городами за 3 дня. В первый день он проехал пятую часть всего пути и еще 60 км, во второй — четвертую часть всего пути и еще 23
20 км, а в третий день — — всего пути и оставшиеся 25 км. Найти расстояние между городами.
XXII.6. Площади трех участков земли относятся как 4:3:5. Урожайность всех трех участков одинакова и составляет 28 центнеров с гектара. Известно, что со второго и третьего участков вместе было собрано на 336 центнеров больше, чем с первого. Определить, какова площадь каждого из участков.
XXII.7. Некоторый сплав состоит из двух металлов, входящих в него в соотношении 1 : 2, а другой содержит те же
§1. Текстовые задачи 413
металлы в отношении 2 : 3. Сколько частей каждого сплава надо взять, чтобы получить третий сплав, содержащий те же металлы в отношении 17 : 27?
XXII.8. Поезд был задержан ввиду неисправности пути на 10 мин, а затем на расстоянии 75 км наверстал потерянное время, развив скорость на 15 км/ч больше предполагаемой по расписанию. Определить скорость поезда, с которой он двигался после задержки.
XXII.9. Поезд должен пройти 54 км. Пройдя 14 км, он был задержан на 10 мин у светофора. Увеличив первоначальную скорость на 10 км/ч, он прибыл на место назначения с опозданием на 2 мин. Определить первоначальную скорость поезда.
XXII.10. Рукопись в 120 стр. отдана двум машинисткам. Если первая машинистка начнет печатать через 1 ч после второй, то каждая из них напечатает по половине рукописи. Если же обе машинистки начнут работать одновременно, то через 4 ч останутся ненапечатанными 32 стр. За какое время может перепечатать рукопись каждая машинистка в отдельности?
XXII.И. Четыре одинаковых насоса, работая вместе, наполнили нефтью первый танкер и треть второго танкера (другого объема) за 11ч. Если бы три насоса наполнили первый танкер, а затем один из них наполнил четверть второго танкера, то работа заняла бы 18 ч. За сколько часов три насоса могут наполнить первый танкер?
XXII.12. Две трубы, работая одновременно, наполняют бассейн за 12 ч. Первая труба наполнит бассейн на 10 ч раньше второй. За сколько часов наполняет бассейн вторая труба?
XXII.13. Начав движение одновременно из пунктов А и В навстречу друг другу, велосипедист и бегун встретились через 30 мин. За какое время бегун преодолеет расстояние между пунктами А и В, если велосипедисту для этого потребовалось 45 мин?
XXII.14. Два каменщика разной квалификации, работая отдельно, могут выложить стену за 4 и 6 ч соответственно. За какое время они выложат ее, работая вместе?
414 Глава XXII. Разные задачи
XXII.15. По реке из пункта А в пункт В выплыл катер. Одновременно из пункта В в пункт А выплыла моторная лодка. Пройдя четверть пути от В к А, лодка встретилась с катером. Катер, достигнув пункта В, повернул обратно и прибыл в пункт А одновременно с лодкой. Во сколько раз скорость катера больше скорости лодки?
XXII.16. Пароход вышел из пункта А в пункт В, расположенный ниже по течению реки, и, дойдя до пункта В, сразу же повернул обратно, затратив на весь путь 5 ч. Сколько времени идет пароход от пункта В до пункта А, если известно, что плоты сплавляются от А до В за 12 ч?
XXII.17. Первую половину пути поезд двигался со скоростью 40 км/ч, а вторую — со скоростью 60 км/ч. Найти среднюю скорость поезда на всем пути.
XXII.18. Расстояние в 160 км между пунктами А и В автомобиль проехал со средней скоростью 40 км/ч. Часть пути по ровной дороге он ехал со скоростью 80 км/ч, а другую часть, по бездорожью — со скоростью 20 км/ч. Какое расстояние автомобиль проехал по ровной дороге?
XXII.19. Из пункта А в В и из пункта В в А вышли одновременно два пешехода. Когда первый прошел половину пути, второму осталось пройти 24 км, а когда второй пешеход прошел половину пути, то первому осталось пройти 15 км. Определить, сколько километров осталось пройти второму пешеходу, когда первый закончил свой путь.
XXII.20. Для рытья котлована выделили два экскаватора. После того, как первый проработал 2 ч, его сменил второй, который за 3 ч закончил работу. Всю работу один второй экскаватор выполнил бы на 4 ч быстрее, чем один первый экскаватор. За какое время выроют котлован оба экскаватора, работая вместе?
XXII.21. Дорога от пункта А до пункта В длиной 11,5 км идет сначала в гору, затем по ровному месту, а далее под гору. Пешеход, идя из пункта А в пункт В, прошел всю дорогу за 2 ч 54 мин, а на обратную дорогу затратил 3 ч 6 мин. Скорость его передвижения составляет при ходьбе в гору 3 км/ч, по ровному месту 4 км/ч и под гору 5 км/ч. На каком протяжении идет дорога по ровному месту?
§1. Текстовые задачи 415
XXIL22. Автомобиль проходит путь с постоянной скоростью. Если бы он увеличил скорость на 6 км/ч, то затратил бы на 4 ч меньше, а если бы уменьшил на 6 км/ч, то затратил бы на 6 ч больше. Найти длину пути.
XXII.23. Располагая некоторой суммой денег, фирма могла купить 44 телевизора равной стоимости. Сколько телевизоров смогла бы купить фирма на эту сумму денег, если бы стоимость телевизоров была снижена на 12%?
XXII.24. Из 50 тонн руды выплавляется 20 тонн металла, содержащего 12% примесей. Каков процент примесей в руде?
XXII.25. Свежие фрукты содержат 78% воды, а сухие — 12% воды. Сколько килограммов сухих фруктов получится из 40 кг свежих фруктов?
XXII.26. Из молока, жирность которого 5%, делают творог жирностью 15,5%, при этом остается сыворотка жирностью 0,5%. Определить, сколько творога получается из 1 tn молока.
XXII.27. В начале года в банк было положено 1000 руб., а в конце года было взято обратно 900 руб. Еще через год на книжке снова оказалось 900 руб. Сколько процентов в год начисляет банк?
XXII.28. В результате реконструкции завода объем его производства в течение года снизился на р%, зато в следующем году вырос на (р + 30)%. Оказалось, что за два года объем производства вырос на 20%. Найти р.
XXII.29. Имелось два водных раствора соляной кислоты, содержащих 800 г и 600 г неразведенной кислоты соответственно. Их смешали и получили 10 кг нового раствора. Определить массы растворов, если известно, что в первом процентное содержание кислоты на 10% выше.
ххп.зо. в связи с неблагоприятными погодными условиями фермер собрал зерна на 10% меньше, чем в предыдущий год. Как изменилась в процентах по сравнению с предыдущим годом его выручка от продажи зерна, если закупочная цена на зерно по сравнению с прошлым годом повысилась на 15%?
416 Глава XXII. Разные задачи
Второй уровень
XXII.31. Из пункта А по одному и тому же маршруту одновременно выехали грузовик и легковой автомобиль. Скорость легкового автомобиля постоянна и составляет | скорости грузовика. Через 30 мин вслед за ними выехал мотоциклист со скоростью 90 км/ч. Найти скорость легкового автомобиля, если известно, что мотоциклист догнал грузовик на 1 ч раньше, чем легковой автомобиль.
XXII.32. Из городов А и В, расстояние между которыми 70 км, навстречу друг другу выехали одновременно автобус и велосипедист и встретились через 1 ч 24 мин. Продолжая движение с той же скоростью, автобус прибыл в город В и через 20 мин после прибытия отправился в обратный рейс. Найти скорости автобуса и велосипедиста, если известно, что автобус обогнал велосипедиста через 2 ч 41 мин после первой встречи.
XXII.33. Три свечи имеют одинаковую длину, но разную толщину. Первая свеча была зажжена на 1 ч раньше других, зажженных одновременно. В некоторый момент горения первая и вторая свечи стали одинаковой длины, а через 2 ч после этого одинаковой длины стали первая и третья. За сколько часов сгорает первая свеча, если вторая сгорает за 8 ч, а третья за 12 ч?
XXII.34. Два велосипедиста выехали одновременно из пунктов А и В навстречу друг другу. Через 4 ч после встречи велосипедист, ехавший из А, прибыл в В, а через 9 ч после встречи другой велосипедист прибыл в А. Сколько часов был в пути каждый велосипедист?
XXII.35. Два пешехода вышли одновременно навстречу друг другу: первый — из пункта А, второй из пункта В. До встречи первый пешеход прошел на 1 км больше, чем второй. Через 45 мин после встречи первый пешеход пришел в В, а второй пешеход прибыл в пункт А через 1 ч 20 мин после встречи. Найти расстояние от А до В.
XXII.36. Часовая и минутная стрелки часов совпадают в 12 ч. Какое время будут показывать часы при следующем совпадении стрелок?
§1. Текстовые задачи 417
XXII.37. Найти угол между часовой и минутной стрелками часов, когда часы показывают 2 ч 20 мин.
XXII.38. Города А и В расположены на берегах реки. Два парохода, имеющие в стоячей воде скорость 21 км/ч, вышли одновременно из городов А и В навстречу друг другу. Каждый из них, достигнув второго города, сразу поворачивал обратно и прибывал в пункт отправления через 18 ч после начала движения. Известно, что вторая встреча пароходов произошла через 13 ч после первой. Найти скорость течения реки.
XXII.39. От пристани А одновременно отправились вниз по течению реки катер и плот. Катер спустился вниз по течению на 96 км, а затем повернул обратно и вернулся в А через 14 ч. Найти скорость катера в стоячей воде и скорость течения реки, если известно, что катер встретил плот на обратном пути на расстоянии 24 км от А.
XXII.40. Пассажирский поезд обгоняет товарный, идущий по параллельному пути. Мимо машиниста товарного поезда пассажирский проходит за 10 с, а мимо машиниста пассажирского поезда товарный проходит за 40 с. Если бы эти поезда двигались навстречу друг другу, то полное время встречи (от встречи локомотивов до расставания хвостовых вагонов) было бы 1б| с. Во сколько раз скорость пассажирского поезда больше скорости товарного?
XXII.41. Два спортсмена бегают по одной замкнутой дорожке стадиона. Скорость каждого постоянна, и на пробег всей дорожки один из них тратит на 5 с меньше другого. Если они начинают бег с общего старта одновременно и в одном направлении, то окажутся рядом через 30 с. Через какое время они встретятся, если побегут одновременно с общей линии старта в противоположных направлениях?
XXII.42. По круговому маршруту из одного и того же места одновременно в разных направлениях выехали велосипедист и мотоциклист. До момента их первой встречи расстояние в 6 км, измеряемое по меньшей из дуг
14—5682
418 Глава XXII. Разные задачи
маршрута, было между ними дважды: в первый раз через 5 мин после старта, когда велосипедист проехал часть маршрута, второй раз, когда мотоциклист проехал 3 тт
- части маршрута. Через какое время после старта расстояние в 6 км было между ними во второй раз?
XXII.43. Два тела движутся равномерно по окружности в одну сторону. Первое тело проходит окружность на 3 с быстрее второго и догоняет второе тело каждые полторы минуты. За какое время каждое тело проходит окружность?
XXII.44. Из точки А, лежащей на окружности, выходят одновременно два тела, движущихся равномерно по этой окружности в противоположных направлениях. Через некоторое время они встретились, и оказалось, что первое тело прошло на 10 см больше второго. После встречи тела продолжили путь, причем первое тело пришло в точку А через 9 с, а второе — через 16 с после встречи. Найти длину окружности, по которой двигались тела.
XXII.45. Двое рабочих выполняют некоторую работу. Если первый рабочий проработает 2 ч, а затем они вместе будут работать 3 ч, то они вместе выполнят 75% всей работы. Какие значения может принимать время выполнения всей работы двумя рабочими вместе?
XXII.46. Два поезда отправляются одновременно навстречу друг другу со станций А и В, расстояние между которыми 600 км. Первый из них приходит на станцию В на 3 ч раньше, чем второй на станцию А. В каких пределах заключено время движения первого поезда, если известно, что скорости поездов отличались более чем на 10 км/ч, а максимальная скорость на перегоне не должна превышать 60 км/ч?
XXII.47. Расстояние между пунктами А и В равно 100 км. Из А в В одновременно отправляются два велосипедиста. Скорость первого на 10 км/ч больше скорости второго. В пути первый велосипедист делает остановку на 50 мин, но в пункт В прибывает первым. В каких пределах заключена скорость второго велосипедиста, если известно, что в дороге он провел меньше 4 ч?
§1. Текстовые задачи 419
XXII.48. Первая и вторая бригады, работая вместе, могут выполнить задание не более чем за 9 дней. Первая и третья бригады, работая вместе, могут выполнить то же задание не менее чем за 18 дней. Первая и третья бригады, работая вместе, могут выполнить то же задание ровно за 12 дней. За какое минимальное количество дней может выполнить это задание одна третья бригада?
XXII.49. Из пункта Л по направлению в сторону пункта В выехали автомобиль и мотоциклист. Одновременно с ними из пункта В в том же направлении выехал велосипедист. Автомобиль догнал велосипедиста и сразу же повернул назад. Проехав четверть своего обратного пути, автомобиль встретил мотоциклиста и вернулся в пункт А в тот момент, когда мотоциклист догнал велосипедиста. Найти отношение скоростей мотоциклиста и велосипедиста.
XXII.50. Автобус и мотоцикл выезжают одновременно навстречу друг другу: автобус — из пункта А в пункт В, мотоцикл — из пункта В в пункт А, и встречаются в 10 ч. Если скорость автобуса увеличить в 2 раза, оставив неизменной скорость мотоцикла, то встреча произойдет в 9 ч 10 мин. Если же увеличить в 2 раза скорость мотоцикла, оставив скорость автобуса прежней, то встреча произойдет в 8 ч 50 мин. Во сколько раз скорость мотоцикла больше скорости автобуса?
XXII.51. Квартал застроен пятиэтажными и девятиэтажными домами, причем девятиэтажных домов меньше, чем пятиэтажных. Если число девятиэтажных домов увеличить вдвое, то общее число домов станет более 24, а если увеличить вдвое число пятиэтажных домов, то общее число домов станет менее 27. Сколько построено пяти-и девятиэтажных домов?
XXII.52. На стоянке находятся машины марок «Москвич» и «Волга». Общее число их менее 30. Если число «Волг» увеличить вдвое, а число «Москвичей» — на 27, то «Волг» станет больше. Если, не изменяя число «Волг», увеличить вдвое число «Москвичей», то «Москвичей» станет больше. Сколько «Москвичей» и сколько «Волг» находятся на стоянке?
420 Глава XXII. Разные задачи
XXII.53. При подведении итогов шахматного турнира оказалось, что на первое место претендуют сразу несколько 7 спортсменов. Их количество оказалось больше —, но 5 меньше — от общего числа участников соревнований. Какое минимальное количество шахматистов принимало участие в турнире?
XXII.54. После сдачи студентами факультета сессии оказалось, 4 5
что количество отличников меньше —, но больше — от 33 42
общего числа студентов факультета. Какое наименьшее число студентов может быть на факультете?
XXII.55. Вся семья выпила по чашке кофе с молоком, причем Катя выпила четвертую часть всего кофе и шестую часть молока. Сколько человек в семье?
XXII.56. Пассажир метро спускается вниз по движущемуся эскалатору за 24 с. Если пассажир идет с той же скоростью, но по неподвижному эскалатору, то он спускается за 42 с. За сколько секунд он спустится, стоя на ступеньке движущегося эскалатора?
XXII.57. Интервалы движения морских катеров по трем маршрутам, начинающимся на общей пристани, составляют 30, 36 и 45 мин соответственно. Сколько раз с 740 до 1730 того же дня на этой пристани одновременно встречаются катера всех трех маршрутов, если одна из таких встреч происходит в ц15?
XXII.58. Для получения смеси было взято 18 г одной жидкости и 30 см другой, в - раза более плотной. Определить плотности этих жидкостей, если известно, что 22,5 г полученного раствора занимают такой же объем, как вся первая жидкость.
XXII.59. Из 2 кг первого металла и 2,4 кг второго изготовили сплав. Найти плотности металлов, если известно, что деталь, изготовленная из полученного сплава, имеет массу 550 <?, а такая же деталь, изготовленная из первого металла, имеет массу 400 <?, и плотность второго металла на 4 г/см? больше плотности первого.
XXII.60. Скорость товарного поезда линейно зависит от числа его вагонов, а скорость состава из 60 вагонов равна
§1. Текстовые задачи 421
9
- скорости состава из 40 вагонов. Паровозная бригада выполняет план перевозок на 100% при наибольшем грузообороте (грузооборот есть произведение числа вагонов на скорость поезда). На сколько процентов выполняет план перевозок паровозная бригада, составляя товарный поезд из 40 вагонов?
XXII.61. Брокерская фирма приобрела два пакета акций, а затем их продала на общую сумму 7 млн 680 тыс руб., получив при этом 28% прибыли. За какую сумму фирма приобрела каждый из пакетов акций, если при продаже первого пакета прибыль составила 40%, а при продаже второго — 20%?
Третий уровень
XXII.62. Три бегуна стартуют одновременно из трех точек круговой беговой дорожки, являющихся вершинами правильного треугольника, и бегут в одном направлении. Первый бегун обгоняет второго, стартовавшего перед ним, через 4 мин после старта, а третьего — через 5 мин после старта. Через какое время после старта второй бегун догонит третьего?
XXII.63. Автомобили марок «Рено» и «Крайслер» движутся по кольцевой дороге, | часть которой проходит по городу. Скорость «Рено» в городе равна 2щ а за пределами города равна —. Скорость «Крайслера» в городе равна и, а за пределами города равна Зу. Автомобили одновременно въезжают в город. Через какое время один из них впервые совершит обгон другого, и какое расстояние он для этого проедет, если длина городского участка кольцевой дороги равна S?
XXII.64. По дороге, имеющей форму окружности, из двух диаметрально противоположных точек А и В выбегают одновременно два спортсмена и бегут с постоянными скоростями навстречу друг другу. Первая их встреча произошла через t с в а м от В, а вторая — в 2a м от А (под расстоянием понимается длина кратчайшего пути по дорожке). Найти скорости спортсменов.
422 Глава XXII. Разные задачи
XXII.65. Пароход по реке и автобус по дороге, идущей вдоль берега реки, отправляются одновременно из пункта А в пункт В и совершают безостановочное движение между А и В. Первая встреча их произошла, когда пароход прошел | всего пути от Л до В, а вторая встреча — когда з пароход после первого захода в В прошел - пути В до 0
А. На путь от А до В и обратно пароход затрачивает g
- ч. Через сколько часов после начала движения автобус и пароход первый раз окажутся одновременно в пункте В, если скорость парохода в неподвижной воде и скорость автобуса постоянны?
XXII.66. Бассейн был наполнен несколькими насосами, которые включались один за другим через некоторые промежутки времени. Большую часть времени насосы работали все вместе и вторую половину бассейна наполнили на t ч быстрее первой. На сколько быстрее будет заполнен бассейн, если промежутки времени между включениями насосов уменьшить в п раз при той же последовательности включения (производительность каждого насоса постоянна)?
XXII.67. Две бригады с одинаковым количеством косцов получили задание скосить траву на двух полях равной площади. На первом поле все косцы бригады начали работу одновременно, а на другом члены второй бригады приступали к работе один за другим через равные промежутки времени, и далее каждый работал до окончания работы. Какая бригада выполнила работу быстрее и во сколько раз, если производительность 4 косцов второй бригады в - раза выше и первый из приступивших к работе членов второй бригады работал в 5 раз дольше последнего?
XXII.68. Из пункта А в пункт В с интервалом 10 мин выехали 24 велосипедиста, каждый из которых затратил на весь путь 5 ч. Одновременно с ними из пункта В в пункт А выехали мотоциклисты, каждый из которых затратил на весь путь одинаковое время. В пути произошло 498 встреч (без учета встреч в пунктах А и В). Какие
§1. Текстовые задачи 423
значения может принимать время нахождения в пути каждого мотоциклиста?
XXII.69. Из пункта А в пункт В с интервалом 2 мин вышли 20 спортсменов, каждый из которых затратил на весь путь 1 ч. Одновременно с ними из пункта В в пункт А выехали велосипедисты, каждый из которых затратил на весь путь одинаковое время. В пути произошло 355 встреч (без учета встреч в пунктах А и В). Какие значения может принимать время нахождения в пути каждого велосипедиста?
XXIL70. Два банка начисляют определенные проценты по вкладам (свои в каждом банке). Причем, первый из них начисляет проценты ежеквартально на всю лежащую на счете сумму, второй — начисляет проценты по вкладу в конце года. Если клиент положит на два года треть имеющейся у него суммы денег в первый банк, а оставшуюся часть — во второй, то его прибыль составит 66% от первоначальной суммы. Если же наоборот, две трети исходной суммы — в первый, а оставшуюся часть — во второй, то через два года прибыль составит 76%. Какую бы сумму получил клиент через два года, если бы положил на этот срок сумму денег в размере 1000 условных единиц в равных долях в оба банка?
XXII.71. Вклад, находящийся в банке в течение года, возрастает на определенный процент, свой для каждого банка.
3
В начале первого года - некоторой суммы положили в первый банк, а оставшуюся часть —во второй. К концу первого года сумма вкладов составила 1140 единиц, а к концу второго— 1302 единицы. Если бы в начале 9 первого года в первый банк положили - исходной суммы, а оставшуюся часть во второй, то в конце первого года сумма вкладов составила бы 1160 единиц. Какова стала бы сумма вкладов к концу второго года?
XXII.72. Вклад, находящийся в банке в течение года, возрастает на определенный процент, свой для каждого банка. В начале первого года треть некоторой суммы положили в первый банк, а оставшуюся часть —во второй банк. К концу первого года сумма вкладов составила
424 Глава XXII. Разные задачи
350 единиц, а к концу второго года — 409 единиц. Если бы в начале первого года в первый банк положили две трети, а во второй банк — треть исходной суммы, то в конце первого года сумма вкладов составила бы 340 единиц. Каким станет вклад в конце второго года, если в начале первого года всю сумму положить
1) во второй банк; 2) в первый банк?
XXII.73. Техническая реконструкция предприятия была проведена в четыре этапа. Каждый из этапов продолжался целое число месяцев и сопровождался падением производства. Ежемесячное падение производства составило на первом этапе 4%, на втором — 12,5%, на третьем — -у- % 50
и на четвертом----у %. По окончании реконструкции
первоначальный объем производства на предприятии сократился на 64%. Определить продолжительность периода реконструкции.
XXII.74. Техническая реконструкция предприятия была проведена в четыре этапа. Каждый из этапов продолжался целое число месяцев и сопровождался падением производства. Ежемесячное падение производства составило на первом 50 этапе 4%, на втором — 10%, на третьем--------------—% и на
четвертом — 65%. По окончании реконструкции первоначальный объем производства на предприятии сократился на 93%. Определить продолжительность третьего этапа реконструкции.
XXII.75. На деньги, размещенные в трех банках, за год начисляется определенный процент, свой для каждого банка. Если пятую часть некоторой суммы положить в первый банк, а оставшуюся часть — во второй банк, то через год сумма вкладов превысит исходную сумму на 106%. Если же четверть суммы положить в первый банк, а остальные деньги — во второй банк, то через год сумма вкладов будет такой же, как и при размещении половины исходной суммы во втором банке, а остальных денег — в третьем банке. Наконец, при размещении всей суммы во втором банке через год вклад станет на 5% больше, чем сумма вкладов в первом, втором и третьем банках,
§1. Текстовые задачи 425
если разместить в них деньги в равных долях. Найти процент, начисляемый на вклады во втором банке.
XXII.76. На деньги, размещенные в трех банках, за год начисляется определенный процент, свой для каждого банка. Если четверть некоторой суммы положить во второй банк, а оставшуюся часть — в третий банк, то через год сумма вкладов превысит исходную сумму на 130%. Если же половину суммы положить в первый банк, а остальные деньги — во второй банк, то через год сумма вкладов будет такой же, как и при размещении трех четвертей исходной суммы во втором банке, а остальных денег —в третьем банке. И, наконец, при размещении долей суммы в первом, втором и третьем банках в отношении 1:1:3 через год сумма вкладов станет на 14% больше, чем стала бы, если бы положили всю сумму во второй банк. Найти процент, начисляемый на вклады в третьем банке.
XXII.77. Два банка начисляют определенные проценты по вкладам (свои в каждом банке). Причем, первый из них начисляет проценты ежеквартально на всю лежащую на счете сумму, второй начисляет проценты по вкладу в конце года. Если клиент положит на два года четверть имеющейся у него суммы денег в первый банк, а оставшуюся часть — во второй, то его прибыль составит 40,08% от первоначальной суммы. Если же наоборот, три четверти исходной суммы — в первый, а оставшуюся часть —во второй, то через два года прибыль составит 70%. Какова будет его прибыль в процентах от первоначальной суммы, если он положит все деньги на один год в первый банк?
XXII.78. Два банка начисляют определенные проценты по вкладам (свои в каждом банке). Причем, первый из них начисляет проценты ежеквартально на всю, лежащую на счете сумму, второй начисляет проценты по вкладу в конце года. Если клиент положит на два года третью часть имеющейся у него суммы денег в первый банк, а оставшуюся часть — во второй, то его прибыль составит 65,04% от первоначальной суммы. Если же наоборот, две третьи исходной суммы — в первый, а оставшуюся
426 Глава XXII. Разные задачи
часть —во второй, то через два года прибыль составит 75%. Какова будет его прибыль в процентах от первоначальной суммы, если он положит все деньги на один год в первый банк?
XXIL79. В соревнованиях по легкой атлетике 82% от числа участников выполнили норматив П-го разряда по прыжкам в высоту, 65% — по прыжкам в длину и 70% — в тройном прыжке. Оказалось, что каждый участник выполнил норматив хотя бы по двум дисциплинам. Выполнившие норматив по всем дисциплинам мечтают стать мастерами спорта, а выполнившие норматив только по прыжкам в высоту и длину мечтают получить П-й разряд в тройном прыжке, остальные собираются остановиться на достигнутых результатах. Какой процент юношей мечтает получить П-й разряд в тройном прыжке, если известно, что 22% юношей и 63% девушек собираются остановиться на достигнутых результатах, а 15% девушек мечтают выполнить норму П-го разряда в тройном прыжке?
XXII.80. На заводе было несколько одинаковых прессов, штампующих детали, и завод выпускал 6480 деталей в день. После реконструкции все прессы заменили на более производительные, но также одинаковые, а их количество увеличилось на 3. Завод стал выпускать 11 200 деталей. Сколько прессов было первоначально?
XXII.81. Сорок девять колхозников, работающих с одинаковой производительностью, были разбиты на две бригады, каждая из которых собрала одинаковое количество картофеля. Первая бригада закончила работу на 1 ч позже второй. Обе бригады работали с перерывами на О отдых, причем вторая бригада отдыхала не менее - ч и не более | ч. Если бы обе бригады работали без перерывов, 7 то первая бригада могла бы собрать картофеля в - раз 5
больше, а вторая — в - раз больше. Сколько колхозников в каждой бригаде?
XXII.82. Из пункта А в пункт В по железной дороге нужно перевезти 20 больших и 250 малых контейнеров. Один
§2. Многочлены от одной переменной 427
вагон вмещает 30 малых контейнеров, вес каждого из которых 2 т. Большой контейнер занимает место 9 малых и весит 30 т. Грузоподъемность вагона 80 т. Найти минимальное число вагонов, достаточное для перевозки всех контейнеров.
XXII.83. Магазин радиотоваров продал в первый рабочий день месяца 29 телевизоров. Каждый следующий рабочий день дневная продажа возрастала на одно и тоже число телевизоров ежедневно, и месячный план продажи — 497 телевизоров был выполнен досрочно, причем за целое число рабочих дней. После этого ежедневно продавался 71 телевизор. На сколько процентов был перевыполнен месячный план продажи телевизоров, если в месяце было 26 рабочих дней?
XXII.84. Девятизначное натуральное число А, записанное в десятичной системе счисления, получается из числа В перестановкой последней цифры на первое место. Известно, что число В взаимно просто с числом 18 и В 222 222 222. Найти наибольшее и наименьшее среди чисел А, удовлетворяющих этим условиям. (Два натуральных числа называются взаимно простыми, если они не имеют общих делителей, отличных от единицы.)
§2. МНОГОЧЛЕНЫ ОТ ОДНОЙ ПЕРЕМЕННОЙ
Второй уровень
XXII.85. Функция у = —7х3 + 18х2 — 12% является суммой кубов двух линейных функций. Найти эти функции.
XXII.86. Фу нкция у = 6х2 + 24х + 26 является суммой кубов двух линейных функций. Найти эти функции.
XXII.87. Все корни многочлена
Р(х) = х3 + рх + q
с действительными коэффициентами и q^O — действительны.
Доказать, что р < 0.
XXII.88. Доказать, что уравнение
х3 + ах2 - b = 0,
428 Глава XXII. Разные задачи
где a G 1R, b 6 1R и b > 0, имеет один и только один положительный корень.
XXII.89. Доказать, что при любом натуральном п справедливо равенство
ф(1 - х)п~1 + 2С2х2(1 - х)Г!~2 + ...
. . . + kCnXk(l - x)n~k + ... + пС”хп = пх.
XXII.90. Показать, что если каждый коэффициент в разложении х(1+х)л разделить на показатель степени х, при которой этот коэффициент стоит, то сумма полученных частных будет равна f
п + 1
XXII.91. Выразить свободный член с кубического уравнения х3 + ах2 + Ьх + с = О
через коэффициенты а и Ь, зная, что корни уравнения образуют арифметическую прогрессию.
Третий уровень
XXII.92. Уравнения
х3 +р[Х + qi = О, х3 + р2х + q2 = О
(Р\ / Р2> 41 / Яъ) имеют общий корень. Найти этот корень, а также остальные корни обоих уравнений.
XXII.93. Найти все значения Л, при которых два уравнения Лх3 — х2 - х — (Л + 1) = О,
Лх2 - х — (Л + 1) = О
имеют общий корень, и найти этот корень.
XXII.94. Пусть известно, что все корни некоторого уравнения х3 + рх2 + qx + г = О
положительны. Какому дополнительному условию должны удовлетворять его коэффициенты р, q, г для того, чтобы из отрезков, длины которых равны этим корням, можно было составить треугольник? Указание: Рассмотреть выражение
(Х1 + Х2 - *з)(*2 + *3 - х1)(х3 + *1 “ *2}-
§3. Графики функций 429
XXII.95. На йти все вещественные значения а и Ь, при которых уравнения
х3 + ах2 4-18 = 0, х3 + Ьх + 12 = 0
имеют два общих корня, и определить эти корни.
XXII.96. Найти общие корни уравнений
х3 4- 2х5 + Зх4 + 2х3 -|- Зх2 + 2х -|- 2 = 0.
х4 + Зх3 + 6х2 + 6х + 4 = 0.
XXII.97. Найти общие корни уравнений
х$ + х3 4- 2х4 4~ х3 4- 2х2 4~ х 4~ 1 — 0, х§ - х5 + 2х4 - х3 + Зх2 - 2х 4- 2 = 0.
§3. ГРАФИКИ ФУНКЦИЙ
Второй уровень
XXII.98. Рассматриваются всевозможные параболы, симметричные относительно прямой х = — 2 и касающиеся прямой у = 1 — 8%; ветви парабол направлены вверх. Найти уравнение той из них, которая пересекает ось Оу в точке с наименьшей ординатой.
XXII.99. В прямоугольном треугольнике АВС точка D — середина гипотенузы АВ, а медианы треугольника пересекаются в точке Е. Треугольник АВС расположен на координатной плоскости Оху так, что точка А лежит на оси Оу, точка D симметрична точке С относительно оси Оу, а точки С, D и Е лежат на графике функции у=(х2 —5)2. Найти уравнение прямой CD и площадь треугольника АВС.
XXII.100. Через точку 7И(5;6) проведена касательная / к параболе у = ^|х2, пересекающая ось абсцисс в точке N, а ось ординат —в точке Р. Найти радиус окружности, вписанной в треугольник N0P (О —начало координат).
XXII.101. Через точку М(2; |) проведена касательная I к гиперболе □
у = -. Найти радиус окружности с центром на оси ординат, касающейся прямой I и оси абсцисс. Найти все решения.
430 Глава XXII. Разные задачи
XXII.102. Две параллельные касательные к графику функции у = х3 + | пересекают оси координат: первая — в точках А и В, вторая — в точках С и D. Найти площадь треугольника АОВ, если известно, что она в 4 раза меньше площади треугольника COD.
XXII.103. Фигура М на плоскости (%, у) ограничена графиками функций у — ^е~ах и у =15 — 4еах и имеет единственную общую точку с прямой у = —18%+ 9. Найти а и площадь фигуры М.
XXII.104. Из точки Л4(1; 1) проведены касательные к двум ветвям гиперболы (&<0), касающиеся этих ветвей в точках А и В, причем треугольник МАВ — правильный. Найти коэффициент k и площадь треугольника МАВ.
X2
XXII.105. К параболе у = — + х + 1 проведены касательные в ее вершине и в двух точках, лежащих по разные стороны от вершины. Треугольник с вершинами в точках пересечения этих касательных является правильным. Найти площадь этого треугольника.
XXII.106. в точке М, принадлежащей параболам у=— х2+2х — 6 и у = х2 + ах + 2 (а < 0), эти параболы имеют общую касательную, которая пересекает ось абсцисс в точке Af. Из точки N проведена еще одна касательная к первой параболе, касающаяся ее в точке Р Найти коэффициент а и расстояние между точками М и Р.
XXII.107. Из точки М проведены касательные к двум ветвям гиперболы У = ~ (Ze > 0), касающиеся этих ветвей в точках А и В, причем АВ= Найти коэффициент k и длину медианы треугольника МАВ, проведенной из вершины М.
XXII.108. Из точки М, расположенной на положительной полуоси ординат, проведены касательные к графику функции Q
у—-^, пересекающие ось абсцисс в точках К и L. Найти радиус окружности, описанной около треугольника MKL, если известно, что угол KML равен 2 arcsin ~.
§3. Графики функций 431
XXII.109. Касательная к графику функции у = -^х4 — образует о с осью абсцисс угол, равный arctg- и пересекает в точках С D окружность с центром в начале координат. Найти радиус этой окружности, если известно, что CD= -2-. 5
Третий уровень
XXII.110. Парабола Щ симметрична параболе П1 у = ax2, a < О, относительно точки /С(6;а62), где Ь>0. Некоторая прямая пересекает каждую из парабол ровно в одной точке: П] в точке В\, Щ — в точке В% так, что угол В\В^К — прямой. Касательная к параболе П1, проведенная в точке /С, пересекает отрезок В\В% в точке L. Определить, в каком отношении точка L делит отрезок В\В<±. Найти значения параметров а и Ь, при которых длина отрезка KL минимальна, если площадь треугольника В\В^К равна
XXII.111. График функции z/=/(x), где /(х) = —2х3 —8ах2 —4а2х4-5, a < 0, и прямая I, заданная уравнением у = 4а2х 4- 5, имеют ровно две общие точки.
1) Найти а, если площадь фигуры, ограниченной
27 графиком функции у = /(х) и прямой /, равна — .
2) Рассматриваются прямые, каждая из которых касается графика функции у = [(х) в точке с положительной абсциссой. Среди этих прямых выбрана та, которая пересекает ось Оу в точке с наименьшей ординатой. Найти эту ординату.
XXII.112. Графи ку функции у = х3 4- ах2 4- Ьх 4- с принадлежат точки А и В, симметричные относительно прямой х = —2. Касательные к этому графику в точках А и В параллельны между собой. Одна из этих касательных проходит через точку (0; 1), а другая — через точку (0;5). Найти значения а, b и с.
XXII.ИЗ. Графику функции у = —х3 4- ах2 4- Ьх 4- с принадлежат точки А и В, симметричные относительно прямой х = —2. Касательные к этому графику в точках А и В параллельны между собой. Одна из этих касательных
432 Глава XXII. Разные задачи
проходит через точку (0;—2), а другая — через точку (0; —6). Найти значения a. b и с.
v2 9
XXIL114. К графику функции у— проведена касательная,
пересекающая график функции z/= | — 2|х + 2| в точках А и В. Найти радиус окружности, описанной около треугольника с вершинами в точках А, В и С 2;
если АСАВ = 2 arccos + АСВА.
V 5
1 17
XXII.115. Графики функций у= — и у= — —2х, рассматриваемые в первой координатной четверти (х > 0, у > 0), пересекаются в точках А и В. Гипотенуза равнобедренного прямоугольного треугольника перпендикулярна оси Ох, две его вершины лежат на первом графике, а третья — на отрезке АВ. Найти длины сторон треугольника.
XXII.116. График функции у = х3 + ах2 + Ьх + с, с < 0, пересекает ось ординат в точке А и имеет ровно две общие точки М и N с осью абсцисс. Прямая, касающаяся этого графика в точке М, проходит через точку А. Найти а, Ь, с, если площадь треугольника AMN равна 1.
XXII.117. График функции у = — х3 + ах2 + Ьх + с, с<0, пересекает ось ординат в точке М и имеет ровно две общие точки А и В с осью абсцисс. Прямая, касающаяся этого графика в точке А, проходит через точку М. Найти я, Ь, с, если площадь треугольника АВМ равна 1.
§4. ЗАДАЧИ НА КООРДИНАТНОЙ ПЛОСКОСТИ
Второй уровень
XXII.118. На координатной плоскости даны трчка А(4:2) и прямая у = — 2х + 5. Найти координаты точек, лежащих на этой прямой и удаленных от точки А на расстояние 5.
XXII.119. На координатной плоскости дан круг радиуса 8 с центром в точке (3;7). Найти все точки этого круга, координаты которых удовлетворяют системе уравнений
1°§Гз + 1°£з(# + 2) = 1,
(х-у)2 = 9.
§4. Задачи на координатной плоскости 433
XXII.120. На координатной плоскости дан круг радиуса х/14 с центром в точке (—1;—1). Найти все точки этого круга, координаты которых удовлетворяют системе уравнений
Г 2х+1 +2у = 10,
I (2% -у)2 = 9.
XXII.121.
XXII.122.
Из точки Е, расположенной на положительной полуоси ординат, проведены касательные к графику функции у — -Д, пересекающие ось абсцисс в точках А и В. Найти радиус окружности, описанной около треугольника ЕАВ, если известно, что угол АЕВ равен 2 arcsin
На координатной плоскости Оху задан треугольник с вершинами /1(0;0), В(0;4), С(2;4). К графику функции у = 2х + |, х > 0, проведена касательная, отсекающая от треугольника АВС четырехугольник, около которого можно описать окружность. Найти координаты центра этой окружности.
XXII.123. На координатной плоскости рассматривается фигура Ф, состоящая из всех точек, координаты (х;#) которых удовлетворяют системе неравенств
logy+x(2xy + 2x) ^2, М + Ы ^2.
Найти площадь фигуры Ф.
Третий уровень
XXII.124. На координатной плоскости рассматривается множество N всех точек, координаты (я; Ь) которых удовлетворяют условиям: a < b, |я| <3, |6| < 3 и таковы, что уравнение
(я3 — 63)х4 + (Зя + Ь)х2 + = О
не имеет корней.
1) Принадлежит ли точка Р(—2;—1) множеству W?
2) Найти площадь многоугольника, внутренней областью которого является множество /V.
434 Глава XXII. Разные задачи
XXII.125. Множество М состоит из точек (я; Ь) координатной плоскости, для которых уравнение
(8a -156 - 135)х4 + (36 - 4я + 27)х2 +162 - 9| + 62 - 9 = 0
имеет ровно одно решение. Доказать, что в многоугольник, которым является множество М, можно вписать окружность, и найти координаты центра этой окружности.
XXII.126. На координатной плоскости изображена фигура М, состоящая из точек, координаты (х',у) которых таковы, что выражение
4 + р2(2у - х2 + 14) - р~2(х2 + 4х + 2у)
неотрицательно при всех р / 0.
Из точки А проведены лучи а\ и Я2, а из точки С —лучи С] и с<2, каждый из которых касается границы множества М. Лучи а\ и cj пересекаются в точке В, а лучи «2 и с2 — в точке D, причем ABCD — прямоугольник, одна из диагоналей которого параллельна оси Ох.
Изобразить на координатной плоскости фигуру М, найти координаты центра прямоугольника ABCD и его площадь.
XXII.127. На координатной плоскости даны две параболы: у -- х2 + 5х + 7 и г/= х2 — х — 5. Найти:
1) значения а и 6, при которых прямая у — ах + 6 касается обеих парабол;
2) координаты точек касания;
3) площадь фигуры, ограниченной этими параболами и касающейся их прямой.
XXII.128. На координатной плоскости рассматривается фигура Ф, состоящая из всех точек, координаты (я; 6) которых таковы, что система уравнений
ах + 4у = 2,
Ьх + ау = — 1,
(6 “Г 3)х “Г (я -|- 8)г/ = —3
имеет решение.
§4. Задачи на координатной плоскости 435
Изобразить фигуру Ф и составить уравнения всех прямых, каждая из которых проходит через точку (—6; 4) и имеет с фигурой Ф единственную общую точку.
XXII.129. На координатной плоскости расположен квадрат ABCD.
Вершины А и В квадрата лежат на графике функции у = х2, а вершины С и D — на графике функции у — х — 4. Определить длину стороны квадрата.
XXII.130. На координатной плоскости даны две прямые: у = — х
и у = 5х — 6. Найти:
1) значения а и Ь, при которых обе данные прямые касаются параболы у = х2 + ах + Ь;
2) координаты точек касания;
3) площадь фигуры, ограниченной найденной параболой и данными прямыми.
XXII.131. Для каждого числа р на координатной плоскости
рассматривается множество М всех точек, координаты (а; 6) которых удовлетворяют условиям: а > О, b > О, а + b < 2, 2Ь > а + Зр и таковы, что система уравнений
п 9 9
х — 2ху + ру^ = а ,
х — 2у = b
имеет два различных решения.
1) Найти площадь многоугольника, внутренней областью которого является множество М, если р = —~^.
2) Найти все действительные р, при которых множество М является внутренней областью многоугольника.
XXII.132. На координатной плоскости рассматривается фигура М,
состоящая из всех точек, координаты (х;у) которых удовлетворяют системе неравенств
У~8 . 2
х2 + у2 — 64 Ю
Найти площадь фигуры М.
436 Глава XXII. Разные задачи
XXII.133. Найти площадь фигуры М, которая задается на координатной плоскости системой неравенств
\/х2 - З//2 + 4х + 4 2х + 1, х2 + у2 4.
§5. ЗАДАЧИ С ПАРАМЕТРАМИ
Второй уровень
XXII.134. Найти все значения а, при которых вершина параболы у = х2 + ах + 1 принадлежит множеству точек на плоскости, заданному неравенством |х — 4//| 1.
XXII.135. Найти все значения параметра а, при которых расстояние между корнями уравнения
2 logfl х + 3 loga%2 а + 5 = О
6 меньше —. 2,и
XXII.136. Найти все значения параметра а, при которых парабола у(х) = х2 — 8 ctg а • х + 5 cos 2а
касается прямой у = —1, причем абсцисса точки касания отрицательна.
XXII.137. На координатной плоскости даны точки А(2; — 3) и В(4;0). При каких значениях параметра р, р > —5, ближайшая к графику функции р = \/х^ + р точка прямой АВ лежит на отрезке АВ?
XXII.138. Найти все значения параметра я, при которых уравнение log9x(l + ах) = ± имеет единственное решение.
XXII.139. Найти все значения параметра а, при которых уравнение Vx — 9 — 3 — ах — 1а
имеет единственное решение.
XXII.140. Найти все значения параметра я, при которых уравнение log2(x + л/3 - я) + log 1 (я + 1 - х) = log4 9
имеет решение.
§5. Задачи с параметрами 437
XXII.141. Найти все значения параметра а, при которых уравнение ах2 + (2а — 5)х + а — 6 = О имеет на отрезке [0; 2] единственный корень.
XXII.142. При каких значениях параметра а уравнение 2х - |х31 + а = 0
имеет единственное решение? Решить это уравнение для всех найденных значений а.
XXII.143. Найти все значения параметра а, при которых уравнение log3(3x + log3 а) = 2х имеет единственное решение.
XXII.144. Найти все значения параметра а, при которых уравнение (а - 2 — \х + 3|)(я + х2 + 6х) = 0 имеет:
1) ровно три корня; 2) ровно два корня.
XXII.145. Найти все значения параметра а, при которых квадратичная функция
2 • . , о . , cos a + sin а
х sin а + 2х cos а -|------
является квадратом линейной функции.
XXII.146. Найти все значения параметра а, при которых квадратичный трехчлен
х2 sin 2a — х(sin2 2a — 4 cos6 a) -I—— ' 7 cos a
имеет два одинаковых по абсолютной величине корня разных знаков.
XXII.147. Найти все значения параметра а, при которых вершина параболы
у = х2 + 2ах + Зя2
принадлежит множеству точек на плоскости, заданному неравенством \у — 2х — 6| > 6.
XXII.148. Найти все значения параметра я, при которых расстояние между вершинами парабол у = 2х2 + Зях + 1 2 , За2 \/5
и у = х + ах — —— меньше —.
и 8 2
438 Глава XXII. Разные задачи
XXII.149. Найти все значения а, при которых уравнение sinx = (2а - 2)2 16(1 - 2а) имеет корни, а числа —4 4 7 являются целыми.
XXII.150. Найти все значения параметра Ь, при которых для любого значения параметра а существует тройка действительных чисел (x,z/,z), удовлетворяющая системе уравнений ах + 4у = z2 + 1, х + ay = z - Ь.
XXII.151. Числа х и у являются решениями системы уравнений ( — х + ау = 2а, [ ах — у = За — 5, где а — параметр. Какое наименьшее значение принимает выражение x2+z/2? При каком а это происходит?
XXII.152. Найти все значения параметра а, при которых система неравенств
Зх2 - 6х + 2а О, < 9
х + 4х - 4а О имеет единственное решение.
Третий уровень
XXII.153. Найти все значения параметра а, при которых уравнение 4 4
4(cosx)3 +(sinx)3 = а
Г л I имеет единственное решение на отрезке -,тг .
XXII.154. Найти все значения параметра а, —тг<а<тг, при которых система уравнений
( (4 - х2 - у2)(у2 -4х + 28) = О, х cos а + у sin а = 2 имеет ровно три решения.
XXII.155. Найти все значения параметра а, при которых наибольшее значение величины х2 +2у на множестве пар действительных чисел (x;z/), удовлетворяющих одновременно двум неравенствам у \/9 — х2 и у + |2х — а\ 3, будет максимально возможным. Найти это максимально возможное значение.
§5. Задачи с параметрами 439
XXII.156. Найти все значения параметра а, при которых уравнения 2х4 — 5х3 — 16ях2 + 25х — 10 = 0 и
2х4 + 2ях3 — Их2 — 5х + 5 = О
имеют общие корни. Найти эти корни.
XXII.157. Найти все значения параметра а, при которых уравнения 22х4 + ЗЗх3 — 1 Ъах2 — Зх + 2 = О и
Их4 + ЗЗх3 + 21х2 - 2ях - 2 = О
имеют общие корни. Найти эти корни.
XXII.158. На координатной плоскости рассматривается фигура Ф, состоящая из всех точек, координаты (я; Ь) которых таковы, что каждое решение неравенства
х2 + (я2 — 362)х - 2я2(я2 + 362) О
является решением неравенства
х2 + (я2 — 262 — 15)х — (а2 + 1)(2Ь2 + 16) 0.
Найти площадь фигуры Ф.
XXII.159. Вершины Д,В,С треугольника имеют соответственно координаты (2; 9), (6;—3), (—2;3). Найти:
1) все значения а, для которых координаты точки пересечения медиан треугольника АВС являются решением системы неравенств
( х — 2у + а 0, ( х + у — а 0;
2) все значения а, для которых координаты хотя бы одной точки отрезка АВ являются решением этой системы.
XXII.160. Найти все такие значения р, чтобы к графику функции у = х4 - 4х/3х2 + р — 53-р
можно было провести касательную, пересекающую ось ординат в точке (0;а), где я^24+р — 5Р.
XXII.161. Для каждого значения параметра а G [- тс; 0] найти максимальное значение g(a) функции
/(х, I/) = х(х + 1) + Г/(с/ — 6)
440 Глава XXII. Разные задачи
на множестве точек (х; //) таких, что х2 + у2 4(х cos a + у sin a).
Найти значения параметра a G [-тс; 0], при которых g(a) принимает наибольшее значение.
XXII.162. Для каждого значения параметра а 6 найти
максимальное значение g(a) функции
/(х, £/) = х(х — 1) +у(у + 2)
на множестве точек (%‘,у) таких, что
9 9
х + у х cos a + у sin a.
Найти значения параметра ае ’ ПРИ КОТОРЫХ принимает наименьшее значение.
XXII.163. Корни уравнения
х3 - (logg р)х2 + 11 log4 р| х - у = О
являются длинами сторон некоторого треугольника, а корни уравнения
%3-1^х2 + т1^^Л4=0
XXII.164.
XXII.165.
— длинами и площадь Найти все значения параметра р, при которых сумма всех корней уравнения
(х - 12р)4 - 6р(р - 1)(х - 12р)2 + р\р + 4) = О
меньше —р2 + 48р + 25.
Числа х О, у > 0 — решения системы уравнений
( 3х2-8ху-3у2=''%-^,
1 У У 4р2 + 9
| х2 - 5ху + бу2 = 10 ~р .
I У 4р2 + 9
высот этого же треугольника. Найти р треугольника.
р — параметр.
При каких р выражение х2 + у2, принимает:
1) наибольшее значение;
2) наименьшее значение? Вычислить эти значения.
Ответы к главе XXII 441
XXII.166. При каких значениях р каждое решение неравенства
х2 + (3 - 2р2)х - 2р2 + 2 < О
удовлетворяет также неравенству + 2) < 0?
ОТВЕТЫ К ГЛАВЕ XXII
XXII.1. у XXII.2. . 207 руб. XXII.3. 63. XXII.4. 24. XXII.5. 400 км.
XXII.6. 12, 9 XXII.9. ЬО км/ч. и 15 га. XXII.7. XXII.1O. 10 ч и 12 ч. 9 : 35. XXII.11 . 8 ч. XXII.8. 90 км/ч. XXII.12. 30 ч.
XXII.13. 90 мин. XXII.14. 2,4 ч. XXII.15. 9 7’ XXII.16. 3 ч.
XXII.17. 4% км/ч. XXII.18. 10б| км. 4 км. XXII.22. 720 i XXII.19. 8 км XXII.20. 2 ч
40 мин. XXII.21. км. XXII.23. 50 телевизоров.
XXII.24. 64,8%. XXII.25. 10 кг. XXII.26. 300 кг. XXII.27. 50%.
XXII.28. 20%. XXII.29. 4 и 6 кг. XXII.30. Возросла на 3,5%.
XXII.31. 72 км/ч. XXII.32. 35 и 15 км/ч. ХХП.ЗЗ. 16 ч. XXII.34. 10 и 15 ч. XXII.35. 7 км. XXII.36. 13 ч 5-jy мин. XXII.37. 50°.
XXII.38. 14 км/ч. XXII.39. 14 км/ч и 2 км/ч. XXII.40. В 2 раза. XXII.41. 6 с. XXII.42. 15 мин или 20 мин. XXII.43. 15 и 18 с. XXII.44. 70 см. XXII.45. 4 < t < б| ч. XXII.46. От 10 до
12 ч. XXII.47. (25; 30) км/ч. XXII.48. 24 дня. XXII.49. 3.
2 Ч- \/39
XXII.50. В — раз. XXII.51. 9 пятиэтажных и 8 девятиэтажных.
XXII.52. 19 «Волг» и 10 «Москвичей». XXII.53. 13. XXIL54. 15.
XXII.55. 5 XXII.56. 56 с. XXII.57. 4 раза (в 815, II15, 1415, 17|э).
XXII.58. 1,8 и 2,4 г/см3. XXII.59. 4 и 8 г/см3. XXII.60. 96%.
XXII.61. 2 млн 400 тыс руб. и 3 млн 600 тыс руб. XXII.62. 6 мин 56 S
40 с. XXII.63. «Рено» обгонит «Крайслер» через проехав 10 полных кругов и еще | S. XXII.64. —, -. XXII.65. О ч. XXII.66. 2Ц.
rJ 3 t t п — 1
XXII.67. Вторая в | раза быстрее. XXII.68. (НО; 120] мин.
XXII.69. (20; 22] мин. XXII.70. 1710 у. е. XXII.71. 1348 единиц.
XXII.72. 1) 432 единицы; 2) 363 единицы. XXII.73. 8 месяцев.
XXII.74. 7 месяцев. XXII.75. 110%. XXII.76. 140%. XXII.77. 36%.
XXII.78. 36%. XXII.79. 76,5%. XXII.80. 5. XXII.81. 21 и 28 человек соответственно в 1-й и 2-й бригадах. XXII.82. 15 вагонов. XXII.83. 342у%, 271 у % или 171 у %. XXII.84. 4min = 122 222 224, Лтах = 999 999 999. XXII.85. у = (-2х + 2)3 + (х - 2)3 XXII.86. у = = (х + З)3 + (-х - I)3. XXII.91. с = -~a3 + ^ab. XXII.92. х,.2 =
442 Глава XXII. Разные задачи
= | l-x0±Jx2 + ^), х34 = 1 {-xq±Jx2 + ^2 ). XXII.93. % = 1 + |.
2 у у U -г0 / ’ 2 у u у и х0 у Л
XXII.94. р3 - 4pq + 8г > 0. XXII.95. jqi2 = 1 ± i\/5. XXII.96. х, = -1 + /, х2 = -1 - i. XXII.97. х, = 1(1 + z\/3), х2 = 1(1 - Д/З). XXII.98. у = = 2(х + 2)2+25. XXII.99. у = 16, S = 18\/3. XXII. 100. 1 XXII. 101.
12. XXII.102. S, = ф (// = 2L + 4, Хо = X); S2 = -8- (у = Зх - 1, х0 = 1). XXII.103. a = 2, S=151n2-9. XXII.104. /г =-1, S = ф. XXII.105. S = ф. XXII.106. a = -6, MP = 6х/17. XXII.107. k = 2; 1\/37. XXII.108. R = XXII.109. R = XXII.110. B\L : B2L - 1 : 1;
3 4 5
a =—3, b=±. XXII.lll. a --|; t/lllin = -11. XXII.112. a = 6; b = -11; c = 6. XXII.113. a = —6; b =-11; c = -6. XXII.114. ф. XXII.115.
ф. XXII.116. a = —4, b = 5, c = —2. XXII.117. a = 4, b = 5,
c = 2. XXII.118. (0;5), (4;-3). XXII.119. (—2;1). XXII. 120. (0; 3).
XXII.121. /?=|. XXII.122. (2г/5 —4:2). XXII.123. |. XXII.124. 1) Да, 2) j. XXII.125. (y;0). XXII.126. Фигура M ограничена
параболами у = ^ — 7 и у = — + 2. Центр прямоугольника —
точка (—1;—| ). XXII.127. 1) а =-2, Ь = -^; 2) (-|J), 9 1 9
3) XXII.128. Фигура Ф — парабола b=—(a —а + 6) с исключенной
/3 9 \ 13 5
точкой I— I. Прямые: a = —6 — параллельная оси, b = — — а — - — 11 5 г~
касательная, Ь= ——а+проходит через искомую точку. XXII.129. 5v2, 3\/2 XXII.130. 1) а = 0, b = 1; 2) (-Ц), (|,у); 3)
XXII.131. 1) S = |у 2) р Е (—оо;0) U (о; 4+g2V7)- XXII.132. S =
= 32 (arctg | + arctgз) - |тг. XXII.133. у/з + у. XXII.134. -2 а
2 а |. XXII.135. | < а < 1, 1 < а < |, а > XXII.136. а =
= — arctg2 + яп, п G Z. XXII.137. -у р 1. XXII.138. а < О, а = -л. XXII.139. О а А, а = -± XXII.140. -3+/17 < а 3.
4 16 16 2
XXII. 141. а 6. XXII.142. а=-|</|, х= ./|. XXII.143. а = J-, 9 „ 3 у 3 у 3
а 1 XXII.144. 1) а = 2, а = 9; 2) а < 2, а > 9, а = 3+У^.
Ответы к главе XXII 443
XXIL145. а = ^ + 2тт, а = л — arctg2 + 2тш, п е Z. XXII.146. а = = (-l)n+1 arcsin 7гп, neZ. XXII.147. ае (-оо;-3)U(-l;0)U(2;+oo).
XXII.148. |а| < 2 XXII.149. |. XXII.150. 6 = 0. XXII.151. 2,
a = 1. XXII.152. a = 0, a = |. XXII.153. 1 a < 4, а = (1 + 26)3.
XXII.154. -я+ arccos | < а < — , - ^ < а < — |< а < ^, < я — arccos |.
XXII.155. 472 - 2 <$ |а| <$ 472 + 2, a = 10. XXII.156. 1) a = х = -2; 2) fl = l, xi = -^ х2,з = ±У5, х4 = Ь, 3)a=^,x=-4. XXII.157. При а=| Xi = -2, х2.з = ±^; при а=1 х4 = ~^ при а = *5 = -|-
XXIL158. 5 = 2715 +32 arcsin XXII. 159. 1) 4 а 5; 2) -12 а 9.
,-----------------. 2
XXII.160. р 2. XXII.161. g(a) = +2 cos а — 12sina-2j -
/ /-------------\2
а = — arctg6. XXII.162. g(a)= ( j|-^ + sina+i) - а = - arctg2. XXII.163. р = 16, S = 1. XXII.164. -5 < р < —4, -1 < р 0, | О < 5. XXII.165. f = х2 + z/2, /max = (при р = 1), /mjn = | (при р = 1). XXII.166. -1^р<--L, о<р<^. 72 72
Глава XXIII
ИЗБРАННЫЕ ЗАДАЧИ ПОВЫШЕННОГО И ВЫСОКОГО УРОВНЕЙ СЛОЖНОСТИ ИЗ ВАРИАНТОВ ЕГЭ
§1. ПРЕОБРАЗОВАНИЕ И ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ВЫРАЖЕНИЙ
Вычислите значение выражения (XXIII.1-XXIIL2).
_ 6.
XXIII.1. 1) (з,4 \/25х/5-И 1.6 л/5\/25) 11;
2)
3) ^/(34 — 24\/2)2 - Зл/2;
4) У |12%/5-29| - \/12\/5 + 29.
XXIII.2. 1) \/зб + 25(1о^8 5)’1 + У(log6 9 + log6 4)3 + 28;
2) (log+ 48-log316)-510^4;
3) (log2 3 + 1 - log2 9) ’ — log2 (12\/2);
4) log2 sin + log2 sin j + log2 sin
Найдите значение выражения (XXIII.3-XXIII.6).
XXIII.3. 1) Ух2 - 14х + 49 + Ух2 + 14% + 49 при х = 0,2007;
2) \/х — 2\/х — 1 + \/х + 2\/х — 1 при х — 1,2007.
XXIII.4. %/25 - 10 • 6х + 36х - 6х - 1,5, если 4х = 13.
XXIII.5. 1) >/19 cos ( — х ), если cosx=-^=, д^х^2л:; \3 / х/19
2) 26sin2x, если sinx = —-^=, при —^<х<—•£.
\/13 2 2
§2. Функции 445
XXIII.6. 1) 5sin (~+arcsin ; 2) 5л/2sin -arctg (—0).
XXIII.7. 1) При каком значении x из множества {1, 2, 3, .. .,98, 99} значение выражения
ближе всего к 73?
2)
При каком целом положительном значении х значение
выражения
/ х — 5
у х + 2
х2 + (2 — х)\/х2 - Зх - 16 - 4
х2 — (х + 5) /х2 — Зх — 10 — 25
ближе всего к —0,7?
fW = {
§2. ФУНКЦИИ
XXIII.8. Найдите значение функции
|cosх — 3|, если \х\^ 1, sin(-x), если |х| < 1
при х=
XXIII.9. Найдите нули функции f(x) = f \ еслих^3, ( sinx + З, если х > 3.
XXIII.10. 1) Укажите наибольшее целое число из области определения функции у = In (35 — |3х — 11|).
2) Укажите сумму всех целых чисел, входящих в область определения функции у — In (х — 2 \х — 3|).
XXIII.11. Найдите наибольшее целое значение функции:
1) у = \/4 cos2 х + 4 cos х + 8;
2) у = Зу/(sinx — cosx)2 + 0,25.
XXIII.12. 1) Нечетная функция у = [(х) определена на всей числовой прямой. Для всякого неотрицательного значения переменной х значение этой функции совпадает со значением функции g(x) = х(2х + 1)(х - 2)(х — 3). Сколько корней имеет уравнение /(х) = 0?
446 Глава XXI11. Избранные задачи из вариантов ЕГЭ
2) Найдите значение функции у = —^g(~)
в точке xq, если известно, что функция y = f(x) четная, а функция у = g(x) нечетная, /(xq) = 5, g(xo) — 1-XXIII.13. Да ны четная функция у = /(х) и нечетная функция у = g(x). Найдите сумму корней уравнения /(<v)=g(x), если для всех действительных значений х выполняется равенство:
1) /(x)+g(x)=x2 —8х —6; 2) /(x)+g(x) = x2 — 9х —4.
XXIII.14. 1) Функция y = f(x) определена на всей числовой прямой и является периодической с периодом 6.
При —2^х<4 она задается формулой /(х) = |х —2| — 3. Найдите значение выражения 4Д11)-2Д-15).
2) Функция z/ = /(x) определена на всей числовой прямой и является периодической с периодом 4. На рис. 1 изображен график этой функции при — 1^х^3. Найдите значение выражения /(—9)-/(2)+/(5).
XXIII.15. Найдите наименьший положительный период функции: 1) /(х) = sin2 4х —cos2 4х;
2) g(x) = 0,2sin Зх cos 6х cos Зх.
XXIII.16. 1) Укажите количество промежутков возрастания функции /(х) = —% > заданной на отрезке [0;2д].
2) Укажите количество промежутков убывания функции /(х) = — 2cos2x — cos2x, заданной на отрезке [0;2д].
XXIII.17. Найдите разность между наибольшим и наименьшим значениями функции:
1) у = ?Лх -1 на отрезке [—3;1];
2) y = V81-x2 на отрезке [—Зл/б;4л/2].
XXIII.18. Найдите наименьшее значение функции:
1) # = (16-х2) на промежутке [0;д/7];
2) z/ = log0 5 (2-х2);
§2. Функции 447
3) z/ = 4\/3sin (х — на промежутке [у? у]’>
4) У = на пР°межУтке [-2;1].
Найдите множество значений функции (XXIII.19-ХХШ.21).
XXIII.19. 1) z/ = sin2x, если xe[arctgO,5; arctg3];
2) z/ = sin2x, если хе [arccos .
VVTIT ПЛ 9 /Зх/2+sin x-cosxX
XXIII.20. I) у— — arccos--------—-=---- ;
’ Ti \ 4\/2 J
2) у— | arccos (^/0,125(cosx —sinx)) .
XXIII.21. 1) i/~log01 (-----Д°—
y &UJ \l + lg(100+x2) J
2) #=у~р+31х1 при x^-1.
XXIII.22. 1) При каком наибольшем отрицательном значении а функция z/ = sin (25х+|^) имеет максимум в точке Xq = 7С?
2) При каком наименьшем положительном значении а функция у = со$ ^24х+ ^0 имеет максимум в точке х0 = д?
XXIII.23. 1) Найдите точки минимума функции z/=(o,6V/°’5“x-2x) (о,6^°’5“х+2х) +2х4- 0,36^°’5“х.
2) Найдите точки максимума функции
у = 48х2 - Зх4 - 9х3 + 0,Г lg(A'3+8).
XXIII.24. Найдите наименьшее значение функции
/(х) = | \/4 — х2 — б| + \/4 - х2 + х4 - 4х3.
^2 1
XXIII.25. Найдите максимум функции у — — у + + 6х — 4-.
XXIII.26. Найдите наибольшее значение функции у — 2,7е3х2_х3-4 на отрезке [1;3].
448 Глава XXIII. Избранные задачи из вариантов ЕГЭ
XXIII.27. Найдите наибольшее значение функции
Дх) = 50 (0,5х - I)2 - (0,5х - I)4 при |х - 3| 3.
XXIII.28. 1) Определите абсциссы точек, в которых угловой коэффициент касательной к графику функции h(x) = = 1 — 2 sin2 х равен 2.
2) Найдите абсциссы точек графика функции у — з 9 — х^
= х + ——касательные в которых параллельны прямой у — 26х или совпадают с ней.
XXIII.29. 1) При каком значении аргумента равны скорости изменения функций Дх) = \/Зх — 10 и g(x) = л/14 + 6х?
2) Найдите наибольшее положительное значение аргумента из промежутка [0;2д], при котором скорость изменения функции Дх) = tgx не меньше скорости изменения функции g(x) = 4х + 23?
XXIII.30. При каком наибольшем значении b функция Дх) = = х3 + Ьх2 + ЗЬх — 1 возрастает на всей числовой оси?
XXIII.31. Найдите длину промежутка возрастания функции
XXIII.32. 1) Вычислите площадь фигуры, ограниченной линиями у = Зл/5 — х и у = - |х + 6.
2) Найдите значение выражения 2S, если S — площадь фигуры, ограниченной линиями z/ = x2 + l и у + х = 3. XXIII.33. Найти все значения параметра а, при каждом из которых не имеет решений неравенство:
1)
(log2 х + Зу/З logv 2 — 6) — а а — (2 sin у/х - 4 — 4)
а — (л'Т + 2\/5 • х — 5)
2) --------------------------------0.
(3 sin у/х — 16 — 4) — а
XXIII.34. Решить уравнение:
1) х8 + 98 cos(4x + 3) = 98 cos х2 + (4х + З)4;
2) х12 — (12 + 8х)6 = 32 sin 112 + 8х| — 32 sin х2.
§2. Функции 449
XXIII.35. 1) Решите уравнение f(g(<v)) + g(3 + /(%)) = 30, если известно, что /(х) = 0,5х4 — 4х + 5 ( 25, если х 4,
И 4Г(х) = { 2.<+ если* <4 к 5 — х
2) Решите уравнение f(g(x)) = g(Kx)), если для каждого действительного числа х известно, что /(х) = |х2 + 2х| + 1 и g(x) равно наименьшему из чисел 1 и 2х + 4х-1 — 2.
XXIII.36. Решите уравнение /(/(х)) = f + 4^ , где г/Г 8 — £ Н-2 ] Z — 4|, если t > 0, ~ [ 4?3 - З/2 + 2Л если t 0.
XXIII.37. 1) Найдите все корни уравнения 10х3 —63х2+48х —9 = 0, при подстановке каждого из которых в уравнение (7х - 1,1) sin // + 3 — 9 = (х + 3,7)z/2 + + а/-^т - ЮОх2 + 160х - 169 • cos 2г/ у х 4- 1
получится уравнение относительно г/, имеющее более одного корня.
2) Найдите все корни уравнения 6х3 + 28х2 + 39х + 15 = 0, при подстановке каждого из которых в уравнение
51ог,0+Зл(</+ 8 + ;) -3 = +
+ У^-Зх(7 + Зх) + 5 • In {у + 5) получается уравнение относительно //, имеющее более одного корня.
XXIII.38. Докажите, что система уравнений не имеет решений: ' Юх3 + 47х2 + 52х + 12 = О,
1) < loS8+5x (// + £ + 6) = +
+ л/^-5х(7 + 5х)+24 • lg(r/ + 1): ч у х
15—5682
450 Глава XXIII. Избранные задачи из вариантов ЕГЭ
Г 6х3 + 22х2 + 21х + 6 = 0,
J sin + cos ((6х + 5)у) = —Ay (z/ + 2 + 4^ +
+ + 8 — Зх(1 + Зх) • cos 2у.
/« =
XXIII.39. 1) Для чисел а\, а2, . . . , £39 верны равенства ап+[ = f(an), п = 1, 2, . . . , 38. Найти а$, если известно, что <239 = 0, а
___8
3х + 5 + 1 — 10, если х —5,
— 5, если х > — 5.
х + 5
2) Для чисел а,[, а2. . . . , 6*28 верны равенства ап+1 = Кап)> п = 1, 2, . . . , 27. Найти zzg + а-? — а§, если известно, что ^28 = 0, а
/(х) = <
Зх — 3 . о
——, если х < 3, X о
rJx-4 !ч1х - 17
ух — 2 у Зх + 7’
если х 3.
§3 . УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ
XXIII.40. 1) Пусть (xq; z/q) — решение системы уравнений
Г у + 2 = х/х + 4, t z/ + |x —5| = 1.
Найдите отношение —.
Уо
2) Пусть (xq; z/o) — решение системы уравнений
Г у = \/х2 + 6х + 9 — 3,
[ Зх — 2у + 3 — 0.
Найдите произведение Xq-z/q.
XXIII.41. Решите уравнение:
1) 2-Зх+х2 =2(х- 1)л/х; 2) 40 —14х+х2 = 2(х-4)л/х.
XXIII.42. Решите уравнение:
1) х2 — 6х + 5= — 3\/х —3; 2) —3\/х— 1 =х2 —2х —3.
§3. Уравнения и системы уравнений 451
XXIIL43. Укажите абсциссы точек пересечения графиков функций:
1) у = х2+х и // = 0,5(6 —х) + \/2х2-|-Зх + 2;
2) // = х2 + 1 и // = 0,5 ^2 + 6х + 4\/2х2 — 6%+ 5^.
XXIII.44. 1) Найдите все значения х, при каждом из которых выражения 4<Ух-9л + 3-3Х и ^/x'3x+4-32x+1 принимают равные значения.
2) Найдите все значения х, при каждом из которых выражения
Зх2 logo (2 + Зх) — 6х log 1 ^2 + Зх — 6х log i s/2 + Зх 3 3
и Зх2 + 2х принимают равные значения.
Решите уравнение (XXIII.45-XXIIL53).
XXIII.45. У49 + 9х|х+4|-2х = 7.
XXIII.46. У1-2х + х2 +у/26 + Зх-5х2=х-1.
XXIII.47. lg(x + l) + Уlg6(4x + 7) = 0.
XXIII.48. 4sin х“0’25 - —1—2sin х -1 = 0.
2 + V2
XXIII.49. 1) 32x+3-33x+1-625x+2 = 600x+7;
2) зх+13.4х+1.53х-7=25.54011-х
XXIII.50. sin = (\/25-х2)2 +х2-25.
XXIII.51. sin J-cos J-\/16-x2 = 0.
2 2 v
XXIII.52. 1) v/16 + (2x-3)2=4-cos2
2) 3(^2-sin 15^)(x/2+sin 15™) = i8 + 30x + 25x2.
XXIII.53. 1) 2x =2sinx — 2; 2) Isinxl-cosx= sinx.
|cosx| 1 ' 2
XXIII.54. Найдите нули функции:
1) // = sin2 дх + ln2 (x2+x+1);
2) у = In2 (x2 — 3x — 9) + \/^3 —8x —8.
452 Глава XXIII. Избранные задачи из вариантов ЕГЭ
XXIII.55. Определите количество корней уравнения:
1) (sinx + cosx)2- \/х-х2 = 0;
2) (1-2sin2 -log2 (4-х2) =0.
XXIII.56. Найдите наименьший корень уравнения
cos (Этих) + tg (5ях) sin (9^x) = cos (4ях) на промежутке (3;4].
XXIII.57. Найдите сумму корней уравнения
sin 4sin27n:x-cos277cx+sin2 f—+ 14тгх>) =----------+cos f — ,
V2 ' V3 67
\ 2 2 J
принадлежащих отрезку [3;5].
XXIII.58. Найдите значения х, при каждом из которых выражения sin2x + 9 и 9cos2 — 6sinxsin (^ принимают равные значения.
Решите уравнение (XXIII.59-ХХШ.66).
XXIII.59. ^/(sin Зх-2)2 - ^9sin2 Зх - 24 sin Зх + 16 = -4.
XXIII.60. sin2 х + 6 sin х sin (^ + 9 = 9 cos2 (^.
XXIII.61. 4 cosx ctgx + 4 ctgx + sinx = 0.
XXIII.62. logsinx (\/3 cosx + 2sinx) = 1.
XXIII.63. --------!-----f | sin 3x.
(sin x + x/3 cos x)
XXIII.64. cosx + cos 16x sinx = \/2.
XXIII.65. 4 log6 (3 + = 3 log6 (2 - -L) + 4.
\ ZA -f U / \ A -I- О /
XXIII.66. logoc nv2 (625 - 81x4) = 2 +---------X-.
625-9x v 7 log3 (25 — 9x2)
XXIII.67. Найдите сумму корней уравнения
g2x2+6x—9 . jgx2+3x—5 _ 2 ^2х"+6х—9
XXIII.68. При каких значениях а выражение 2 + cosx(5 cosx + a sinx) будет равно 1 хотя бы при одном значении х?
XXIII.69. При каких значениях а сумма
loga (cos2 х + 1) + loga (cos2 х + б)
равна 1 хотя бы при одном значении х?
§4. Неравенства 453
XXIII.70.
XXIII.71.
XXIII.72.
XXIII.73.
Найдите все целые значения параметра а, при каждом _____________________________________Зх । 4
из которых среди решений уравнения -------= а есть
х — 2х + 2
целые числа.
Найдите все значения р, при которых уравнение 2cos2x4—£— = —12 имеет решение.
sinx 1
1) Найдите все значения параметра а, для которых при каждом х из промежутка (—3; — 1] значение выражения %4 — 8х2 — 2 не равно значению выражения ах2.
2) Найдите все значения параметра а, для которых при каждом х из промежутка (2; 4] значение Iog2 х + 3 log2 х ~ 7 не равно значению a log2 х-
Найдите количество всех решений системы f //(1-х)2+х3 = О, ( 2% - = 5log32 (°Д25у2) - 7.
выражения выражения
уравнений
§4. НЕРАВЕНСТВА
XXIII.74. 1) Найдите количество целочисленных решений неравенства 6 — 5% — х2 0, удовлетворяющих условию i+tg27> °-
2) Найдите количество целочисленных решений неравенства log2 (х2 4- 5х — 5) О, удовлетворяющих условию 1 4-cos(ttx) > 0.
XXIII.75. На йти все значения х, при каждом из которых произведение выражений \/2х+2 — 4 и 5х2-2х — 5(х-1)"+1 4- 120 положительно.
Решите неравенство (XXIII.76-XXIII.78).
XXIII.76. (х2 - 4,2х + 4,41) • log0 5 (х2 - 4) > 0.
XXIII.77.
!°g6,5-x (log3 Р4) °-
ХХШ.78.
(25х — Зх2 + 18) л/х — 1 > q log4 |х - 7| - 1 ""
454 Глава XXIII. Избранные задачи из вариантов ЕГЭ
XXIII.79. 1) Найдите все значения %, для каждого из которых 4х — 18 • 2х
точка графика функции у = ———-— лежит ниже ZU — ОХ
—32 соответствующей точки графика функции У=-^р.—
2) Найдите все значения %, для каждого из которых
, , log? (23 — 4%)
точка графика функции у= z —-—- лежит выше оХ “|" О
соответствующей точки графика функции у= 11 .
— и — оХ
XXIII.80. 1) Найдите все значения %, при каждом из которых расстояние между соответствующими точками графиков функций /(%) = ~ и g(x) = 1 меньше, чем 0,5.
2) Найдите все значения х, при каждом из которых расстояние между соответствующими точками графиков функций /(%) = log^^Sx 4- 14) и g(x) = 10 меньше, чем 2.
XXIII.81. При каких значениях х соответственные значения функций /(%) = log2* и g(x) = log2(3 — х) будут отличаться меньше, чем на 1?
XXIII.82. 1) Найдите все положительные значения а, при каждом из которых наименьшее из двух чисел b — 6а2 (2а~2 — а) — а6 и с = а-6 — 6а-3 4- 1 не меньше —4.
2) Найдите все значения а, при каждом из которых наибольшее из двух чисел b = 4а 4- 23+а — 3 и с = 23-а — 4~а — 9 меньше 6.
/ 7.V+4 \
XXIII.83. Из области определения функции у = log? ( аа — a -v+4 ) взяли все целые положительные числа и сложили их. Найдите все значения а, при которых такая сумма будет больше 7, но меньше 11.
XXIII.84. Найдите все значения параметра а. при каждом из которых неравенство (х — 2)а2 — (х2 — 2х 4- 8) а 4- 8х О верно хотя бы для одного значения переменной хе [4;6].
XXIII.85. Найдите все значения параметра а, при которых область определения функции
у = 1g (ах+2 X3 |ое« ° + а4 X5 - (^)10+2'l0fc ° - (\/Н)18) содержит ровно одно целое число.
§5. Текстовые задачи 455
XXIII.86. Найдите все значения параметра а, при которых множество решений неравенства а2 + 8а < —---------------х(х — 2а — 4)
содержит какой-нибудь отрезок длиной 2, но не содержит никакого отрезка длиной 3.
XXIII.87. Найдите все значения а, при каждом из которых оба числа а 2й-2 и За • 2й — 4а2 • 4й-3 — 27 являются решениями неравенства l°Sv-5 5 О-
XXIII.88. Шесть чисел образуют возрастающую арифметическую прогрессию. Первый, второй и четвертый члены этой прогрессии являются решениями неравенства l°g0,5.v-l (1о&4 > °, а остальные не являются
решениями этого неравенства. Найдите множество всех возможных значений первого члена такой прогрессии.
§5. ТЕКСТОВЫЕ ЗАДАЧИ
XXIII.89. На рынке костюм, состоящий из пиджака и брюк, на 20% дешевле, чем такой же костюм в магазине, причем брюки стоят на 35% меньше, чем в магазине, а пиджак — на 10%. Сколько процентов стоимости этого костюма в магазине составляет стоимость пиджака?
XXIII.90. Объемы ежегодной добычи нефти первой, второй и третьей скважинами относятся соответственно как 7:6:5. Планируется уменьшить годовую добычу из первой скважины на 4%, а из второй — на 2%. На сколько процентов нужно увеличить годовую добычу нефти из третьей скважины, чтобы суммарный объем добываемой за год нефти не изменился?
XXIII.91. Два фермера, работая вместе, могут вспахать поле за 25 ч. Производительность труда первого и второго фермеров относятся как 2:5. Фермеры планируют работать поочередно. Сколько времени должен проработать второй фермер, чтобы это поле было вспахано за 45,5 ч?
XXIII.92. Найти двузначное число, если количество единиц в нем на 4 больше количества десятков, а произведение искомого числа на сумму его цифр равно 90.
XXIII.93. После двух повышений зарплата увеличилась в 1,43 раза. При этом число процентов, на которое повысилась
456 Глава XXIII. Избранные задачи из вариантов ЕГЭ
зарплата во второй раз, было в 3 раза больше, чем в первый раз. На сколько процентов повысилась зарплата во второй раз?
XXIIL94. Велосипедист каждую минуту проезжает на 800 м меньше, чем мотоциклист, поэтому на путь в 30 км он затратил времени на 2 ч больше, чем мотоциклист. Сколько километров в час проезжает мотоциклист?
XXIIL95. Первый сплав серебра и меди содержит 70 г меди, а второй сплав — 210 г серебра и 90 г меди. Взяли 225 г первого сплава и кусок второго сплава, сплавили их и получили 300 г сплава, который содержит 82% серебра. Сколько граммов серебра содержалось в первом сплаве?
XXIII.96. По пенсионному вкладу банк выплачивает 10% годовых. По истечении каждого года эти проценты капитализируются, т. е. начисленная сумма присоединяется к вкладу. На данный вид вклада был открыт счет в 50 000 руб., который не пополнялся и с которого не снимались деньги в течение 3 лет. Какой доход был получен по истечении этого срока?
XXIII.97. Катер прошел 5 км против течения реки, а затем 21 км по течению, затратив на весь путь 1 ч. Найти собственную скорость катера, если скорость течения реки 4 км/ч.
XXIII.98. Для монтажа оборудования необходима подставка объемом 1296 дм? в форме прямоугольного параллелепипеда. Квадратное основание подставки будет вмонтировано в пол, а ее задняя стенка — в стенку цеха. Для соединения подставки по ребрам, не вмонтированным в пол или в стену, используется сварка. Определите размеры подставки, при которых общая длина сварочного шва будет наименьшей. 1
ОТВЕТЫ К ГЛАВЕ XXIII
XXIII.1. 1) 0,2; 2) 144; 3) -4; 4) -6. XXIII.2. 1) 16; 2) 14;
3) -3,5; 4) -3. ХХШ.З. 1) 14; 2) 2. XXIII.4. -6,5 XXIII.5. 1) 0,5;
2) 24. XXIII.6. 1) 4; 2) 7. XXIII.7. 1) 72; 2) 18. XXIII.8. 3.
XXIII.9. 0. XXIII.10. 1) 15; 2) 12. XXIII.И. 1) 9; 2) 4.
XXIII.12. 1) 5; 2) 1. XXIII.13. 1) -8; 2) -9. XXIII.14. 1) 4; 2) -6.
XXIII.15. 1) 2) g. XXIII.16. 1) 2; 2) 2. XXIII.17. 1) 3,5; 2) 3.
XXIII.18. 1) 2; 2) -1; 3) -6; 4) 8. XXIII.19. 1) [0,6; 1]; 2) [о,5; .
Ответы к главе ХХШ 457
XXIII.20. 1) [0;3]; 2) [1;2]. XXIII.21. 1) [-2;+оо); 2) (-4; -2] U(6; +оо).
XXIII.22. 1) —50; 2) 50. XXIII.23. 1) -1; 2) 2. XXIII.24. -10.
XXIII.25. 9 XXIII.26. 2,7. XXIII.27. 184 XXIII.28. 1) + лп,
4
п е Z; 2) -3. XXIII.29. 1) 9; 2) XXIII.32. 1) 4; 2) 9. ХХШ.ЗЗ. 1) [-2; 2 ХХШ.ЗО. 9 XXIII.31. 2 • </27 — б); 2) [-1; 2- ^20-5).
XXIII.34. 1) 2 ± л/7; -1;-3; 2) 4 ± 2г/7; -2;-6. XXIII.35. 1) -1; 2) log2 (УЗ- 1) + 1. XXIII.36. у; 8. XXIII.37. 1) 0,3; 2) -|. XXIII.39. 1) 16; 2) 2. XXIII.40. 1) 5; 2) 9. XXIII.41. 1) 1; 4 + 2\4; 2) 4; 12 + XXIII.42. 1) 4; 2) 2. XXIII.43. 1) -3,5; 2; 2) -2; 5. XXIII.44. 1) 9; 2) 0: XXIII.45. -1,6; 0. XXIII.46. 2,6. XXIII.47. -0,75. XXIII.48. (-1)"? + тт, п е Z. XXIII.49. 1) 3; 2) 5. XXIII.5O. 0. XXIII.51. -4, -л, 0, л, 4. XXIII.52. 1) 1,5; 2) -0,6. XXIII.53. 1) 4- 2л1г, k е Z; О
2) + 2л(г, -у + 2ти/г, лк, k е Z. XXIII.55. 1) 2; ' 2) 4. XXIII.56. 3,125. п G Z. XXIII.59. + п G о 3 XXIII.54. 1) -1; 0; 2) -2. XXIII.57. 8 XXIII.58. 2лп, Z. XXIII.60. 2тгл7, л G Z.
XXIII.61. ± (я — arccos + 2лк, k G Z. XXIII.62. у + 2тт, п G Z.
XXIII.63. £ + 2тт, л 6 Z. XXIII.64. Н + 2лп. nel. XXIII.65. -2. 6 4
XXIII.66. ±^. XXIII.67. -3. XXIII.68. (—ос; —2\/б] U [2л/б:+оо).
XXIII.69. [5; 12]. XXIII.70. 1; 2. XXIII.71. [-10; 0) U (0; 10].
XXIII.72. 1) (-ос;-9) U [у+ос); 2) (—ос; —3] U (1,5;+оо).
XXIII.73. 2. XXIII.74. 1) 6; 2) 4. XXIII.75. (0; 1 + V2).
XXIII.76. (—х/5; —2) U (2; 2,1) U (2,1; х/5). XXIII.77. (3; 4] U (5.5; 6,5).
XXIII.78. [1;3) и [9; 11). XXIII.79. 1) (1; 4) U (б|;+оо); 2) (-1|;5|).
XXIII.80. 1) (-оо;|) U (4;+оо); 2) (0,4; 10). XXIII.81. (1; 2).
XXIII.82. 1) (0;^= U [1;^]; 2) (-oo;-log25) U (- log23;0).
XXIII.83. (4;4|j. XXIII.83. [2; 6]. XXIII.85. [2; 3) U (5; 6]. XXIII.86. [1;2) U (2; 3]. XXIII.87. 3. XXIII.88. (2; 2,5). XXIII.89. 60%. XXIII.90. На 8%. XXIII.91. 28 ч. XXIII.92. 15. XXIII.93. На 30%.
XXIII.94. 60клс XXIII.95. 430 г. XXIII.96. 16 550 руб.
XXIII.97. 24 км/ч. XXIII.98. 12 дм, 12 дм, 9 дм.
Приложение
МАТЕРИАЛ ДЛЯ ПОДГОТОВКИ К ЕГЭ
§ 1. ЕГЭ 2005 Г.
3
А1. Найдите значение выражения при п = 8. п~ 5
1) 8~^; 2) 64; 3) 16; 4) 8"L
А2. Упростите выражение у/214г?14.
1) 221?21; 2) 27^7; 3) 298?98; 4) 22?2.
АЗ. Вычислите значение выражения log5(5ab), если JoggO) = 0,7.
1) 1,7; 2) 3,5; 3) 5,7; 4) 4.
А4. Упростите выражение sin sin ^ + cos а — cos cos
1) cos а+cos 6а; 2) 0; 3) 2 cos а; 4) cos a —cos 6а.
А5. Найдите производную функции у = — ^х6 + 5х4 — 14.
1) у' = —lx1 + х5 - 14х; 2) //=-|х7 + х5 - 14х;
3) у' = -7х5 + 20х3; 4) у' = — 7х5 + 9х3.
А6. На каком из следующих рисунков функция, заданная графиком, убывает на промежутке [0,3]?
§1. ЕГЭ 2005 г. 459
А7. Найдите множество значений функции у = 7 4- cosx.
1) [6,8]; 2) [7,8]; 3) (-оо,+оо); 4) [-1,1].
А8. Решите уравнение cosx—1 = 0.
1) | + 2тг/г, keZ- 2) l + nk, kE%-
3) д/г, k Е Z; 4) 2д/г, k Е Z.
А9.
Решите неравенство
% +11
(% — 8)(3х + 2)
< 0.
1) [-11,и(8,+оо); 2) (-оо,-11];
3) (-оо,8); 4) (-оо,-11] U (-|, 8).
А10.
Найдите область определения функции /(х) =
11
2 + log3 х ’
1) (0,9)и(9,+оо);
3) (0, 4-оо);
2) (-оо, U (|,+оо);
4) (°’l)UG’+o°)-
В1. Решите уравнение д/2х2 4- 2х — 3 4-1 = — х.
/ 1 \ |я+1
В2. Решите уравнение 1 — 1 =8.
ВЗ. Точка движется по координатной прямой согласно закону х(/) = 74-5/ — e4-z, где х(/) — координата точки в момент времени t. Найдите скорость точки при t = 4.
Часть 2
В4.
В5.
_____ 6.
Вычислите: Ml,2 64\/8 — 3,2 x/Ss/frlJ 11 .
Найдите значение функции у = \/3 sin 2/ 4- sin
. 19тг
в точке t = —.
460 Приложение. Материал для подготовки к ЕГЭ
В6. Функция y = f(x) определена на промежутке (—5,7). График ее производной изображен на рис. 1. Найдите промежутки убывания функции y = f(x). В ответе укажите наибольшую из длин этих промежутков.
В7. Найдите наибольший корень уравнения
(32’5-2*2 _ Уз) lOg5(3 - 10%) = 0.
В8. Найдите значение функции у(х) = 1
в точке %о, если известно, что функция у — — четная,
функция у = g(x) — нечетная, /(%о) = 1, g(%o) = —3.
В9. Двум сотрудникам издательства поручили отредактировать рукопись объемом 560 страниц. Один сотрудник, отдав второму 80 страниц рукописи, взял остальные себе. Второй выполнил свою работу за время, в 8 раз меньшее, чем первый свою. Сколько страниц рукописи первый сотрудник должен был сразу отдать второму (взяв остальное себе), чтобы они, работая с прежней производительностью, выполнили свою работу за одинаковое время?
В1О. Через образующую ВС цилиндра проведено сечение BCDE. Объем цилиндра равен 1440л, BE = 8, тангенс угла между прямой СЕ и плоскостью основания равен 1,25. Найдите площадь осевого сечения.
ВИ. Дан ромб ABCD с острым углом А. Высота ВН, проведенная к стороне CD, пересекает диагональ АС в точке М. Найдите площадь треугольника СМИ, если высота ромба равна 8, а площадь ромба равна 80.
§1. ЕГЭ 2005 г. 461
Cl. Найдите все значения х, для которых точки графика функции logo 2 (20 —5х) у =---------------лежат ниже соответствующих точек графика
функции z/ =
Часть 3
С2. Решите уравнение \/16 — 8х + х2 + \/4х2 — 13х — 17 = х — 4. СЗ. Найдите все значения а, при каждом из которых наибольшее из двух чисел b — 9а + 32+а — 1 и с = 32-а — 9-а — 5 меньше 9.
С4. Отрезок PN, равный 8, — диаметр сферы. Точки М и L лежат на сфере так, что объем пирамиды PNML наибольший. Найдите площадь треугольника KLT, где К и Г —середины ребер РМ и NM соответственно.
С5. Даны два уравнения log7(x(12 + = р(р — 1) — 6х + 3
и 2х — у = ---+ 15 • Значение параметра р выбирается
так, что р 0, р^~ 1 и число различных корней первого уравнения в сумме с числом р + 5 дает число различных корней второго уравнения. Решите первое уравнение при каждом значении параметра, выбранного таким образом.
ОТВЕТЫ
А1 А2 АЗ А4 А5 А6 А7
64 22q2 1,7 cos а — cos 6а -1хъ + 20х3 Рис. 1 [6, 8]
А8 А9 АЮ
2 л/г, k е Z (-оо, -11] и 8) (°, 1) и +оо)
В1 В2 ВЗ В4 В5 В6 В7 В8 В9 В10 В11
-2 -3,5 6 8 2 4 0,2 0,8 320 240 9
С1 С2 СЗ С4 С5
(-00, -21)U(3, 4) 17 4 аб(-оо, - log37)U(- 1о£32, 0) 4д/5 7 2
462 Приложение. Материал для подготовки к ЕГЭ
§ 2. ЕГЭ 2006 Г.
А1.
72,8
Упростите выражение
1) 2,1 2) 72,1 3) 74 4) 4
А2. Найдите значение выражения 121og6(62).
1) 27 * * * * 12 2) 144 3) 24 4) 14
АЗ. Выч ислите л/125 • 0,027
1) 1,5 2) 0,15 3) 15 4) 0,015
А4. На каком из следующих рисунков изображен график функции, возрастающей на промежутке [—1,2]?
7
А5. Найдите множество значений функции у = -cosx.
1) [-1,1] 2) [-Ц] 3) [0,|] 4) (-оо,+оо)
А6. Найдите область определения функции f(x) = —.
4 —
1) [0, 256) U (256,+оо) 2) (-оо,256) U (256, +оо)
3) [0,4) U (4, 4-оо) 4) [0, 4-оо)
А7. На рис. 2 изображены графики функций y = f(x) и y = g(x), заданных на промежутке [—3,6]. Укажите те значения х, для которых выполняется неравенство /(x)^g(x).
1) [-1,1] 2) [-2,2]
3) [-3,-1] U [1,6] 4) [-3,-2] U [2, 6]
§2. ЕГЭ 2006 г. 463
Рис. 2
А8. Найдите производную функции у = ^хб — 5х4 — 17.
6
1) у> = 7х5 - 20х3 2) у' = |х7 - X5 - 17х
3) у' = 7х7 -х5 — 17х 4) / = 7х5-9х3
А9. Решите уравнение tg 4х = — 1.
1) — тг + 4лтг, neZ 2) — + лтг, neZ
3) -£ + ^, neZ 4) -5 + тш, neZ
16 4 4
А1О. Решите неравенство logi (5х — 6) > logi (4х).
1) (-оо,6) 2) (1,2,6) 3) (1,2,+оо) 4) (6,+оо)
В1. Решите уравнение 4л+2 — 11 - 4х = 80.
В2. Решите уравнение 4 • 5logsх = 2х + 3.
ВЗ. Найдите значение выражения 3cos + а) + sin(?r — а), если
sin а = 0,3.
Часть 2
В4. Вычислите 7 log9 з/д(27\/3).
В5. К графику функции у — f(x) в точке с абсциссой Xq = 4 проведена касательная. Найдите ее угловой коэффициент, если на рис. 3 изображен график производной этой функции.
В6. Найдите разность между наибольшим и наименьшим значениями функции у = 2(х-2)2-3 на отрезке [0,3].
В7. Решите уравнение
16х2 - 24х + 12 = (л/3 - sin ^л/З + sin .
В8. Найдите значение функции y = f(x)g(—х) + 2/( — х) в точке Хд, если известно, что функция у = /(х) — четная, функция У = g&) ~ нечетная, /(х0) = 2, g(x0) = -3.
464 Приложение. Материал для подготовки к ЕГЭ
В9. Объемы ежегодной добычи нефти первой, второй и третьей скважинами относятся как 4:5:7. Планируется уменьшить годовую добычу нефти из первой скважины на 7% и из второй — тоже на 7%. На сколько процентов нужно увеличить годовую добычу нефти из третьей скважины, чтобы суммарный объем добываемой за год нефти не изменился?
В10. Основание прямой призмы ABCDA]B]C\D[ — параллелограмм ABCD, в котором АВ = 4, Z.ABC = 30°. Высота призмы равна 3. Найдите тангенс угла между плоскостью основания призмы и плоскостью ADC[.
ВИ. Найдите площадь равнобедренной трапеции, если ее высота равна 8, а синус угла между диагональю и основанием равен — н Из
С1. Решите уравнение sin 0,8% = (\/4 — х2) + х2 —3.
С2. Найдите все значения %, при каждом из которых расстояние между соответствующими точками графиков функций /(x) = log36(9x + 27) и g(x) = 1,25 меньше, чем 0,25.
Часть 3
СЗ. Требуется разметить на земле участок ABCDEFGH площадью 2000 м2, состоящий из трех прямоугольных частей и имеющий форму, изображенную на рис. 4, где FG = BC = 20m, EF = 10 м и CD 15 м. Найдите наименьшее значение периметра такого участка и какие-либо значения длин KL, LH и CD, при которых периметр является наименьшим.
С4. В пирамиде FABC грани ABF и АВС перпендикулярны, FB: FA = 13: 3. Тангенс угла между прямой ВС и плоскостью ABF равен 1,5. Точка М выбрана на ребре ВС так, что
§2. ЕГЭ 2006 г. 465
ВМ :МС = 2:3. Точка Т лежит на прямой AF и равноудалена от точек М и В. Центр сферы, описанной около пирамиды FABC, лежит на ребре АВ, площадь этой сферы равна 4л. Найдите объем пирамиды АСЛ4Т.
С5. Найдите все значения а, при каждом из которых оба числа а • 4а и 4 (а • 4а-0,5 — а2 • 16а-0,5 + 1) являются решениями неравенства logx_0 5 (log4 0.
ОТВЕТЫ
А1 А2 АЗ А4 А5 А6
72,1 24 1,5 Рис 4 Г~- 1 СО г-~ |со 1 [0. 256) U (256, +оо)
А7 А8 А9 А10
[-1,1] 7х5 - 20х3 _ л 1( 1 z— ^77 т + —, п G Z 4 (1,2, 6)
В1 В2 ВЗ В4 В5 В6 В7 В8 В9 В10 В11
2 1,5 -0,6 10 -2 1,875 0,75 10 9 1,5 96
С1 С2 СЗ С4 С5
5тг т (1, 21) 200 м, 50 м, 50 м, 15 м 416 325 4 2
466 Приложение. Материал для подготовки к ЕГЭ
Рис. 5
§ 3. ЕГЭ 2007 Г.
А1. Упростите выражение Ь~3,4 • 5Ь0,2.
1) 5Ь~3,6 2) 50,2 • Ь-3,2 3) 5b-3,2 4) 5°>2 • Ь~3$
ло ^189
А2. Вычислите —=—.
3V7
1) 1 2) 1 3) 9 4) 27
АЗ. Найдите значение выражения 3 • 2log25.
1) log2 15 2) 125 3) 30 4) 15
А4. Функция задана графиком (рис. 5). На каком из указанных промежутков она возрастает?
1) [1,4] 2) [2,5] 3) [0,5] 4) [-2,1]
А5. Найдите производную функции у — 12х3 - ех.
1) у' = 15х2 - хех~1 2) у' = Зх2 —
3) у' - 36х2 — хех~х 4) у' = 36х2 — ех
А6. Найдите множество значений функции у — 3sinx.
1) [-3,3] 2) [0,3] 3) [-1,1] 4) (-оо,+оо)
А7. Функция задана графиком (рис. 6). Укажите промежуток, на котором она принимает только отрицательные значения. 1) (3,6) 2) (3,5) 3) (-2,-1) 4) (-2,0)
А8. Решите неравенство ——уур—— 0.
1) (-00,-5] 2) [-5,4) U (7, +оо)
3) (-оо,7) 4) (-оо,-5] U (4, 7)
§3. ЕГЭ 2007 г. 467
А9. Решите уравнение sinx— — 0.
1) ±| + 2тгА!, /г с Z 2) | + 2nk, ke%
3) + AjgZ 4) (-l)*j + 2nk, keZ
A1O. Решите неравенство 54х+6 125х.
1) (—oo,—6] 2) (—oo,—2] 3) [—2,+oo) 4) [—6, +oo)
Bl. Найдите значение выражения 3sin2a — 5 cos2 а, если cos a = — |.
B2. Решите уравнение Зх+2 + 6 • 3х = 5.
ВЗ. Решите уравнение \/2х2 — х — 6 = —х.
Часть 2
В4. Найдите значение выражения sin г/, если известно, что {7Г
7 cosx — 3 sin у = 9.
В5. Функция у = /(х) определена на промежутке (—6,7). На рис. 7 изображен график производной этой функции. К графику функции провели все касательные, параллельные прямой у = 3 — х (или совпадающие с ней). Укажите количество точек графика функции, в которых проведены эти касательные.
В6. Найдите значение выражения ^/(37 — 20л/3)2 + 2л/3.
В7. Решите уравнение log7(3x + 5) + log4(2х + 5) = 0. (Если уравнение имеет более одного корня, то в бланке ответов запишите произведение всех его корней.)
В8. Функция у — f(x) определена на всей числовой прямой и является периодической с периодом 3. На рис. 8 изображен
468 Приложение. Материал для подготовки к ЕГЭ
Рис. 8
график этой функции при — 2 х 1. Найдите значение выражения /(—5) —/(—1) +/(12).
В9. Две бригады, работая вместе, ремонтировали дорогу в течение 6 дней, а затем одна вторая бригада закончила ремонт еще за 10 дней. За сколько дней могла бы отремонтировать дорогу одна первая бригада, если она может выполнить эту работу на 6 дней быстрее, чем вторая бригада?
В1О. Точки К и М лежат на окружностях двух оснований цилиндра. Синус угла наклона прямой КМ к плоскости оснований цилиндра равен 0,6, КМ = 10, объем цилиндра равен 15071. Найдите площадь осевого сечения цилиндра.
В11. Боковая сторона равнобедренного треугольника АВС равна 15, а его площадь равна 67,5. К основанию АС и стороне ВС проведены высоты BE и АН, пересекающиеся в точке О. Найдите площадь треугольника ВОН.
С1. Найдите точки минимума функции
/(х) = Зх4 + Зх3 - 72х2 + 2" 10Ч(х2+8).
С2. Решите уравнение х2 + х = |(6 — х) + \/2х2 + Зх + 2.
§3. ЕГЭ 2007 г. 469
Часть 3
СЗ. Найдите все значения а, для которых при каждом х из промежутка (-3,-1] значение выражения %4 — 8х2 — 2 не 9 равно значению ах .
С4. В прямоугольном параллелепипеде ABCDA\B\C\D\ с боковыми ребрами Л/li, ВВ\, СС\, DD\ на сторонах AD, AiBi, В\С\ его оснований лежат соответственно точки L, К, М AL 2 А{К 2 В}М 5 D Л
так, что - = - , Во сколько раз объем
LD 5 КВ\ 3 №(?! 2 н
параллелепипеда больше объема пирамиды с вершиной /С и основанием LDMB\?
С5. Докажите, что система уравнений
' 15х3 + 36х2 + 22х + 4 = 0,
< 9 sin |+ cos((5x +1)у) =
— У — + 16 + 5х(1 — 5х) • sin у
не имеет решений.
ОТВЕТЫ
А1 А2 АЗ А4 А5 А6 А7
5Ь~ 3,2 1 15 [2, 5] 36х2 — ех [-3. 3] (з, 5)
А8 А9 А10
(-оо, -5] U (4, 7) (-l)*g-|-rcAi, fceZ (-оо, -6]
Bl B2 ВЗ В4 В5 В6 В7 В8 В9 В10 В11
1 -1 —2 -0,9 3 5 -1,5 —4 18 60 24
С1 С2 СЗ С4
3 -3,5; 2 а 6 (—оо, —9) U +оо) В семь раз
470 Приложение. Материал для подготовки к ЕГЭ
С1.
С2.
СЗ.
С4.
С5.
§4. ЕГЭ 2008 Г.
Найдите наибольшее значение функции
/(х) = 3(2х - 4)4 - (2х - 4)5
при |х — 2| 1.
Найдите все значения х, при каждом из которых выражения 5xlog2(3 — 5х) + 9х2 logi </3 — 5х и 5х — Зх2 принимают 2 равные значения.
Найдите все значения а, при каждом из которых неравенство a- (log3 х + 2>/б logt 3 — 5) л
—/ __——0 не имеет решении.
(3 cos Vx — 9 — 4) — а
Дан конус с вершиной М, радиус основания которого равен
В основание этого конуса вписан четырехугольник ABCD так, что углы ВМА, СМВ, DMC, AMD равны а каждый, причем tg На дуге ВС окружности основания конуса, не содержащей точки А, выбрана точка F так, что объем пирамиды MABFCD наибольший. Найдите расстояние от точки F до плоскости МАВ.
Для чисел а\, а%, .... 023 верны равенства
ап+1 = ffan), и = 1, 2, ..., 22. Найдите 05 + а%, если
{Зх — 6 . о
-----если х < 3, 5/х-4 /18х — 53 >ч
л/---о + V о . о > если х 3.
ух — 2 V 2х + 3
ОТВЕТЫ
С1 С2 СЗ С4 С5
80 0; 0,2 -1 ^a<2v/24-5 11 2,
ОГЛАВЛЕНИЕ
Предисловие.............................................. 3
Глава I. Элементы математической логики.................. 5
§1 . Высказывания и операции над ними................... 5
§2 . Неопределенные высказывания. Знаки общности и существования ......................................... 7
§ 3. Некоторые приемы доказательства.................... 8
§4 . Метод математической индукции.................... 10
Ответы к главе 1........................................ 11
Глава II. Множества и операции над ними................. 13
§1 . Операции над множествами.......................... 13
§2 . Целые, рациональные и иррациональные числа.. 15
§3 . Степени и корни.................................. 17
§4 . Логарифмы........................................ 21
§5 . Суммирование..................................... 25
§6 . Числовые неравенства............................. 29
Задачи повышенной сложности к главе II.................. 30
Ответы к главе II....................................... 33
Глава III. Функции...................................... 37
§1 . Линейная, квадратичная и дробно-линейная функции. 37
§2 . Основные понятия, относящиеся к числовым функциям 39
§3 . Свойства функций................................. 40
§4 . Графики функций.................................. 44
Задачи повышенной сложности к главе III................. 46
Ответы к главе III...................................... 48
Глава IV. Алгебраические уравнения и неравенства .... 56
§1 . Рациональные уравнения............................ 56
§2 . Рациональные неравенства......................... 61
§3 . Иррациональные уравнения......................... 64
§4 . Уравнения с модулем.............................. 67
§5 . Иррациональные неравенства....................... 69
472 Оглавление
§6 . Неравенства с модулем........................... 72
Задачи повышенной сложности к главе IV 74
Ответы к главе IV..................................... 76
Глава V. Тригонометрические формулы 84
§1. Тригонометрическая окружность..................... 84
1. Градусная и радианная меры угла (84); 2. Точки
тригонометрической окружности, соответствующие заданным числам, их декартовы координаты (84); 3. Пе-
ресечение и объединение числовых множеств, соответствующих точкам тригонометрической окружности (86); 4. Аналитическое задание дуг тригономет-
рической окружности (86).
§2. Синус, косинус тангенс и котангенс.................. 88
1. Вычисление значений синусов, косинусов, тангенсов и котангенсов углов (88); 2. Определение знаков
синусов, косинусов, тангенсов и котангенсов углов (90);
3. Сравнение и оценка значений синусов, косинусов, тангенсов и котангенсов углов (91); 4. Формулы
приведения (91).
§ 3. Тригонометрические формулы......................... 93
1. Зависимости между синусом, косинусом, тангенсом и котангенсом одного угла (93); 2. Формулы
сложения (94); 3. Формулы кратных и половинных
углов (96); 4. Формулы преобразования суммы в произведение и произведения в сумму (98).
§4. Преобразование тригонометрических выражений..... 98
§5. Арксинус, арккосинус, арктангенс и арккотангенс .... 106
Задачи повышенной сложности к главе V................. ПО
Ответы к главе V..................................... 111
Глава VI. Комплексные числа......................... 117
§1 . Определение комплексных чисел. Операции сложения и умножения.......................................... 117
§2 . Комплексно-сопряженные числа. Модуль комплексного числа. Операции вычитания и деления комплексных чисел................................................ 118
§3 . Геометрическое изображение комплексных чисел.. 120
§4 . Тригонометрическая форма комплексного числа... 123
§5 . Извлечение корня из комплексного числа......... 124
Оглавление 473
§6 . Алгебраические уравнения...................... 125
Задачи повышенной сложности к главе VI............... 127
Ответы к главе VI.................................... 128
Глава VII. Многочлены от одной переменной............ 131
§1 . Основные определения........................... 131
§2 . Схема Горнера................................. 133
§3 . Теорема Безу. Корни многочлена................ 135
§4 . Алгебраические уравнения...................... 137
Задачи повышенной сложности к главе VII.............. 139
Ответы к главе VII................................... 140
Глава VIII. Системы алгебраических уравнений......... 143
Задачи повышенной сложности к главе VIII............. 149
Ответы к главе VIII.................................. 152
Глава IX. Предел и непрерывность функции............. 157
§1 . Числовые последовательности и их свойства...... 157
1. Способы задания числовых последовательностей (157); 2. Исследование числовых последовательностей на монотонность (158); 3. Исследование
числовых последовательностей на ограниченность (159).
§2 . Предел последовательности...................... 161
1. Определение предела последовательности (161);
2. Вычисление предела последовательности (163).
§3 . Предел функции................................ 167
1. Определение предела функции на бесконечности (167); 2. Вычисление пределов функции на
бесконечности (168); 3. Определение предела функции в точке (169); 4. Вычисление предела функции
в точке (170); 5. Различные типы пределов (171).
§4 . Непрерывность функции......................... 174
§5 . Техника вычисления пределов................... 176
Задачи повышенной сложности к главе IX............... 177
Ответы к главе IX.................................... 178
Глава X. Степенная, показательная и логарифмическая функции........................................... 182
§1 . Степенная функция.............................. 182
§2 . Показательная функция......................... 185
§3 . Логарифмическая функция....................... 187
474 Оглавление
§4 . Показательные уравнения........................ 190
§5 . Показательные неравенства...................... 193
§6 . Логарифмические уравнения...................... 195
§7 . Логарифмические неравенства.................... 198
§8 . Смешанные уравнения и неравенства.............. 201
Задачи повышенной сложности к главе X................ 204
Ответы к главе X..................................... 205
Глава XI. Тригонометрические и обратные тригонометрические функции............................ 213
§1 . Функции синус и косинус........................ 213
§2 . Функции тангенс и котангенс.................... 218
§3 . Обратные тригонометрические функции............ 221
§4 . Первый замечательный предел ................... 222
Задачи повышенной сложности к главе XI............... 223
Ответы к главе XI.................................... 225
Глава XII. Тригонометрические уравнения и неравенства 232
§1 . Простейшие тригонометрические уравнения........ 232
§2 . Тригонометрические уравнения, сводящиеся к алгебраическим путем замены переменной.................... 236
§3 . Метод разложения на множители. Типичные преобразования, используемые для упрощения тригонометрических уравнений .................................... 238
§4 . Метод оценки левой и правой частей уравнения.. 243
§5 . Отбор корней уравнений. Тригонометрические уравнения, содержащие знаки модуля, корни и логарифмы 244
§6 . Решение тригонометрических уравнений с параметром 246
§7 . Решение тригонометрических неравенств.......... 248
§8 . Решение уравнений и неравенств, содержащих обратные тригонометрические функции....................... 250
Задачи повышенной сложности к главе XII.............. 251
Ответы к главе XII................................... 253
Глава XIII. Производная и дифференциал............... 262
§1 . Определение производной. Производные функций хп, sinx, cosx........................................... 262
§2 . Производные показательной и логарифмической функций ................................................. 264
§3 . Правила дифференцирования...................... 265
Оглавление 475
§4 . Производная сложной функции и обратных функций . 267
§5 . Односторонние и бесконечные производные........ 268
§6 . Дифференциал функции........................... 269
§7 . Геометрический и физический смыслы производной... 270
Задачи повышенной сложности к главе XIII............. 275
Ответы к главе XIII.................................. 276
Глава XIV. Применение производной к исследованию функций......................................... 280
§1 . Основные теоремы для дифференцируемых функций . 280
§2 . Возрастание и убывание функции................. 281
§3 . Экстремумы функции............................ 282
§4 . Наибольшее и наименьшее значения функции.... 284
§5 . Производные второго порядка. Выпуклость и точки перегиба........................................... 291
§6 . Построение графиков функций.................... 292
Задачи повышенной сложности к главе XIV.............. 294
Ответы к главе XIV 298
Глава XV. Первообразная и интеграл................... 309
§1 . Первообразная функции.......................... 309
§2 . Неопределенный интеграл........................ 310
§3 . Определенный интеграл.......................... 313
§4 . Применение определенного интеграла к вычислению площадей........................................... 315
§5 . Приложения определенного интеграла к физическим задачам............................................ 319
Задачи повышенной сложности к главе XV............... 321
Ответы к главе XV.................................... 322
Глава XVI. Дифференциальные уравнения................ 327
§1 . Основные понятия............................... 327
§2 . Уравнения с разделяющимися переменными......... 327
§3 . Линейные дифференциальные уравнения первого и второго порядков с постоянными коэффициентами......... 329
Ответы к главе XVI................................... 331
Глава XVII. Системы уравнений и неравенств различных типов........................................... 333
§1 . Показательные и логарифмические системы...... 333
§2 . Тригонометрические системы..................... 337
476 Оглавление
Задачи повышенной сложности к главе XVII............. 341
Ответы к главе XVII.................................. 343
Глава XVIII. Уравнения и неравенства с двумя переменными ............................................ 346
§1 . Геометрическое описание решений уравнений, неравенств и систем с двумя переменными.............. 346
§2 . Аналитические приемы решений уравнений и неравенств с двумя переменными....................... 350
§3 . Использование геометрического подхода для решения уравнений, неравенств и систем с двумя неизвестными, содержащих параметры................................. 351
Задачи повышенной сложности к главе XVIII.......... 352
Ответы к главе XVIII................................. 354
Глава XIX. Делимость целых чисел. Целочисленные решения уравнений................................ 363
§1 . Делимость чисел................................ 363
§2 . Сравнения...................................... 366
§3 . Решение уравнений в целых числах............... 367
§4 . Текстовые задачи с целочисленными неизвестными... 369
Задачи повышенной сложности к главе XIX........ 372
Ответы к главе XIX................................... 373
Глава XX. Элементы комбинаторики..................... 375
§1 . Основные схемы подсчета элементов в конечном множестве............................................ 375
1. Правило произведения (375); 2. Правило суммы
и формула включений и исключений (376); 3. Пере-
становки (377); 4. Перестановки с повторениями (377).
§2 . Сочетания и размещения......................... 380
§3 . Комбинаторные соотношения...................... 385
Задачи повышенной сложности к главе XX............... 386
Ответы к главе XX.................................... 387
Глава XXI. Элементы теории вероятностей.............. 389
§1. Основные понятия теории вероятностей............. 389
1. Множество элементарных исходов эксперимента (389); 2. События и действия над ними (390);
3. Классическое определение вероятности (392);
4. Геометрическая вероятность (394).
Оглавление 477
§2. Сложение вероятностей............................. 397
§3. Условная вероятность. Независимость событий...... 399
1. Условная вероятность (399); 2. Формула умножения вероятностей (400); 3. Независимые события (400);
4. Формула полной вероятности (401).
§4 . Формула Бернулли............................... 404
§5 . Дискретные случайные величины и их числовые характеристики........................................ 405
1. Понятие случайной величины (405); 2. Функция
распределения и числовые характеристики случайной величины (405); 3. Биномиальное распределение (406).
Задачи повышенной сложности к главе XXI............... 407
Ответы к главе XXI.................................... 408
Глава XXII. Разные задачи............................. 412
§1 . Текстовые задачи................................ 412
§2 . Многочлены от одной переменной................. 427
§3 . Графики функций................................ 429
§4 . Задачи на координатной плоскости............... 432
§5 . Задачи с параметрами........................... 436
Ответы к главе XXII................................... 441
Глава XXIII. Избранные задачи повышенного и высокого
уровней сложности из вариантов ЕГЭ............ 444
§1 . Преобразование и вычисление значений выражений... 444
§ 2. Функции......................................... 445
§3 . Уравнения и системы уравнений.................. 450
§4 . Неравенства.................................... 453
§5 . Текстовые задачи............................... 455
Ответы к главе XXIII.................................. 456
Приложение Материал для подготовки к ЕГЭ.............. 458
§ 1. ЕГЭ 2005 г...................................... 458
Часть 2 (459); Часть 3 (461).
§2 . ЕГЭ 2006 г..................................... 462
Часть 2 (463); Часть 3 (464).
§3 . ЕГЭ 2007 г..................................... 466
Часть 2 (467); Часть 3 (469).
§4 . ЕГЭ 2008 г..................................... 470
Учебное издание
Шабунин Михаил Иванович Прокофьев Александр Александрович Олейник Татьяна Анатольевна Соколова Татьяна Владимировна
МАТЕМАТИКА. АЛГЕБРА. НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА. ПРОФИЛЬНЫЙ УРОВЕНЬ
Задачник для 10-11 классов
Ведущий редактор М. С. Стригунова Художник С. Инфантэ Технический редактор Е. В. Денюкова Корректор Е. Н. Клишина
Подписано в печать 27.08.09. Формат 60x90/16.
Усл. печ. л. 30. Тираж 1000 экз. Заказ 5682.
Издательство «БИНОМ. Лаборатория знаний» 125167, Москва, проезд Аэропорта, д. 3 Телефон: (499)157-5272 e-mail: binom@Lbz.ru, http://www.Lbz.ru
Отпечатано в ООО ПФ «Полиграфист», 160001, г. Вологда, ул. Челюскинцев, 3. E-mail: forma@pfpoligrafist.com
ЛИТЕРАТУРА ДЛЯ ШКОЛ
МАТЕМАТИ КА
ИМЕЕТСЯ В ПРОДАЖЕ:
Я
МАТЕМАТИКА
АЛГЕБРА. НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
Шабунин М. И. Математика. Алгебра. Начала математического анализа. Профильный уровень : учебник для 10 класса / М. И. Шабунин, А. А. Прокофьев. — 2-е изд., испр. и доп. — 2009. — 424 с. : ил.
Учебник для 10 класса является частью учебно-методического комплекта для старших классов школ с углубленным изучением математики. Представлены разделы: элементы математической логики, числовые множества, рациональные функции и графики, многочлены и системы уравнений, комплексные числа, степенная, показательная и логарифмическая функции, тригонометрические формулы, предел и непрерывность функции.
Каждый параграф учебника содержит теоретический материал, примеры с решениями и упражнения для самостоятельной работы.
Для учащихся классов физико-математического и естественно-научных профилей.
• ИЗДАТЕЛЬСТВО
«БИНОМ Лаборатория знаний»
125167, Москва, проезд Аэропорта, д. 3
Телефон: (499)157-5272
e-mail: binom@Lbz.ru, http://www.Lbz.ru
Оптовые поставки:
(499)174-7616, 171-1954, 170-6674
ЛИТЕРАТУРА ДЛЯ ШКОЛ
МАТЕМАТИКА
ИМЕЕТСЯ В ПРОДАЖЕ:
Шабунин М. И. Математика. Алгебра. Начала математического анализа. Профильный уровень : учебник для 11 класса / М. И. Шабунин, А. А. Прокофьев. — 2008. — 391 с. : ил.
Учебник для 11 класса является частью учебно-методического комплекта для старших классов школ с углубленным изучением математики. Представлены разделы: тригонометрические, показательная и логарифмическая функции, производная и ее применение, элементы комбинаторики и теории вероятностей.
Каждый параграф учебника содержит теоретический материал, примеры с решениями и упражнения для самостоятельной работы.
Для учащихся классов физико-математического и естественно-научных профилей.
• ИЗДАТЕЛЬСТВО
«БИНОМ Лаборатория знаний»
125167, Москва, проезд Аэропорта, д. 3
Телефон: (499)157-5272
e-mail: binom@Lbz.ru, http://www.Lbz.ru
Оптовые поставки:
(499)174-7616, 171-1954, 170-6674
. гi>ihi- ннЛйсюя частью учабно-меГОДИЧНО। и и
комплекта для преподавания матьмлики в старших классах физико-математического и естественно-научных профилен Комплект включает в себя:
• учебник для 10 класса
• учебник для 11 класса
• методическое пособие и дидактические материалы для 10 класса
• методическое пособие и дидактические материалы для 11 класса
• задачник для 10-11 классов
Шабунин Мих зил и па ню —
доктор педагогических наук, профессор кафедры высшей математики МФТИ. Автор свыше 200 научных и учебно-методических работ, один из авторов учебников алгебры для 7-11 классов средней школы, учебных пособий для студентов.
' ipo-' i -фьеь Александр Алекса! —
доктор педагогических наук, доцент, профессор кафедры высшей математики МИЭТ, преподаватель математики физико-математического лицея №1557 Зеленоградского округа г. Москвы, учитель высшей категории. Автор более 40 книг, в том числе для школьников и студентов.
Олейник Татьяна Анатольевна —
кандидат педагогических наук, доцент кафедры высшей математики МИЭТ. Автор более 20 учебных и методических пособий по математике для старшеклассников, абитуриентов и студентов.
Соколова Татьяна Владимировн —
| кандидат физико-математических наук, доцент,
’ доцент кафедры высшей математики МИЭТ.
Автор более 25 научных статей и методических пособий •7 по математике для старшеклассников и студентов.