Т. Б. Айзенберг,
И. М. Воронков,
В. М. Осецкий
УКОВОДСТВО
К РЕШЕНИЮ ЗАДАЧ
ПО ТЕОРЕТИЧЕСКОЙ
МЕХАНИКЕ
Под редакцией
проф. И. М. Воронкова
ИЗДАНИЕ ШЕСТОЕ,
СТЕРЕОТИПНОЕ
Допущено Министерством высшего и среднего
специального образования СССР в качества
учебного пособия для студентов высших
технических учебных заведений
ИЗДАТЕЛЬСТВО
«ВЫСШАЯ ШКОЛА»
МОСКВА- 1Э08

УДК 531
А —36)
?-. 4— 2
БЗ —39/30 —68

ПРЕДИСЛОВИЕ
Важной задачей при изучении курса теоретической механики
является самосюятельная работа студентов
Особую актуальность она приобретает в последнее время,
в связи с сокращением для ряда специальностей числа ауди-
аудиторных часов отводимых на теоретическую механику Поэтому
возникает потребность в учебных руководствах и пособиях ко-
которые облегчат студентам самостоятельное изучение теоретиче
ских разделов курса и помогут им научиться самостоятельно при-
применять теорию к решению практических задач.
Основная цель настоящего пособия — помочь студенту при
обрести навыки в решении задач по теоретической механике.
Пособие предназначается главным образом для студентов заочных
и вечерних отделений высших технических учебных заведений,
но оно может быть также полезным и для студентов очного
обучения.
Объем и расположение материала в пособии в основном со-
соответствует «Курсу теоретической механики» проф. И. М. Ворон-
кова и «Сборнику задач по' теоретической механике» проф. И. В. Ме-
Мещерского. Для облегчения пользования пособием каждому раз-
разделу предшествуют краткие сведения по теории и основные фор-
формулы, необходимые для решения последующих задач, а также
даются соответствующие методические указания.
Большое внимание уделено подбору задач, их классификации
и методам решения. Разобранные в пособии задачи в подавляю-
подавляющем большинстве составлены специально для данного руковод-
руководства. Они не дублируют задачи из сборника И. В. Мещерского,
но охватывают основные типы задач этого сборника (в соответст-
соответствии с обычными программами по теоретической механике).

При подготовке в печать этого издания учтены замечания
к предыдущим изданиям руководства и внесены следующие ис-
исправления и дополнения: уточнена классификация задач по всем
трем частям курса, в связи с чем увеличено число рассматривае-
рассматриваемых задач; некоторые задачи заменены новыми, введены новые
параграфы (разложение силы на составляющие, аналитические
методы расчета с|ерм), заново написаны § 2 гл. I и § 3 гл. IV
раздела 1, а 1акже § 4 гл. III и гл. V раздела П.

РАЗДЕЛ t
СТАТИКА
Глава I
СХОДЯЩИЕСЯ СИЛЫ
§ 1. СЛОЖЕНИЕ СИЛ, СХОДЯЩИХСЯ В ОДНОЙ ТОЧКЕ
Сложение двух сил, сходящихся в одной точке
Равнодействующая Я двух сил F1 и Fs, приложенных в одной
точке и направленных под углом а друг к другу, равна гео-
геометрической сумме этих сил и изображается диагональю парал-
параллелограмма, построенного на
силах F, и F2 (рис. 1), т. е.
R^F. + F,.	A)
Модуль равнодействующей
определяется по формуле
R =
, B)
Рис. 1
а направление ее определяет-
определяется углами Р и у между силами_
F, и F, и равнодействующей R, которые можно найти по те-
теореме синусов:
F, F,	R
sin
sin у
или
sin В
,sm y
sin A80°—а) '
R
sin а
C)
Если силы F, и F2 и угол a между ними заданы, то сна-
сначала по формуле B) находим модуль равнодействующей, а за<

тем, подставив ее значение в равенства C), найдем sin p и
а следовательно, и углы р* и у.
При графическом_определении равнодействующей двух схо-
сходящихся сил F, и Рг не следует строить весь параллелограмм;
достаточно из конца силы F, провести вектор, параллельный
и равный второй силе Ft. Вектор, соединяющий начальную и
конечную точки полученной ломаной линии, изображает ис-
искомую равнодействующую R двух данных сил F, и Ft.
Вектор ~AC = R называется замыкающей стороной силового
треугольника ABC (рис. 2). _ _
Если две слагаемые силы Ft и Ft равны по модулю, то па-
параллелограмм, построенный на этих силах, является ромбом,
а равнодействующая —диагональю это-
этого ромба. Так как диагонали ромба
взаимно перпендикулярны и в точке их
пересечения делятся пополам,то равно-
равнодействующая, изображаемая вектором
А *?•	=	^-? АС, делит вторую диагональ BD попо-
пополам, перпендикулярна к ней и, кроме
того, сама делится пополам в точке О.
Следовательно, для того чтобы найти
равнодействующую двух равных по модулю сходящихся сил,
достаточно построить вектор АО, соединяющий точку прило-
приложения слагаемых сил с серединой отрезка, соединяющего
концы этих сил, и затем этот вектор удвоить, т. е.
R = 2 АО.	D)
Модуль силы R равен R = 2 F cos ~ ,	E)
где а—угол между силами Ft и Ft (рис.3).
Это свойство дальше будет использоваться при нахождении
равнодействующей двух равных сходящихся сил.
ь
R
Рис. 2
Пример 1. Как относятся модули сил F, и F,, если угол
между ними равен 135°, а равнодействующая равна по модулю
меньшей силе (рис. 4)?

Решение. Пусть векторы АВ и АС изображают искомые
силы "Р, и "F,, причем fs<F, и _</СЛВ= 135°. Тогда диаго-
диагональ ЛЛ7 параллелограмма ABDC, построенного на этих силах,
есть равнодействующая сил F% и Fit т. е.
По условию задачи R = i7,, или AD — DB; следовательно,
треугольник ABD—равнобедренный.
Отсюда следует, что /_BAD — /_ ABD. Но
ZBAC + Z ABD =180°,
откуда
/ ABD -= 180° — / ВАС = 180° —135° = 45°
и, следовательно,
/_ BAD = 45° и ,//ШВ = 90°,
т. е. треугольник ABD—прямоугольный, а потому
F, АВ~ Б1П ^° 2 •
Эту же задачу можно решить, пользуясь формулой B).
Действительно:
\-tFl + 2FxFt cos 135°,
но R — F2, а потому
F\--=F21 + Fl-2FlFi cos45°,
откуда
т. е.
Пример 2. Веревка DABC, перекинутая через блок, закреп-
закреплена одним концом С неподвижно; ко второму концу D этой
веревки подвешен груз М весом Qh. Найти давление, пере-
передаваемое на ось блока, и угол, который сила давления обра-
образует с горизонталью. Угол а между веревкой ВС и горизонталью
задан (рис. 5).
Решение. В точке А к блоку приложена сила Г, натя-
натяжения веревки AD, а в точке В—сила Тг натяжения верев-
веревки ВС, причем эти две силы по величине равны, так как на-
натяжение веревки DABC во всех ее точках одинаково.

Продолжим прямые AD и ВС до Пересечения в точке В И
перенесем силы Т, и Тг по линиям их действия в эту точку Е.
Тогда получим две равные силы Г, и Г2, пересекающиеся под
углом 90° — а в точке Е. Найдем их равно-
равнодействующую, для чего построим на этих
силах параллелограмм. Так как эти силы
Тг	равны, то полученный параллелограмм яв-
является ромбом и равнодействующая направ-
направлена по биссектрисе угла АЕВ, т. е. прохо-
проходит через точку О. Величину этой равно-
равнодействующей найдем по формуле E)
•R = 2 Т1 cos
90° —а
Так как сила натяжения Г, веревки
AD равна весу груза М, то 7\ = Q, а по-
потому
Рис. 5
Сила R и есть искомое давление, передава-
передаваемое на ось вращения блока. Теперь нахо-
находим угол р между силой R и горизонталью:
а
2,
Сложение нескольких сил, сходящихся в одной точке
и лежащих в одной плоскости
Равнодействующую нескольких сил, сходящихся в одной
точке, можно определить способом последовательного сложения.
Равнодействующая такой системы сил
равна геометрической сумме этих сил, т. е.
F)
и выражается по величине и направле-
направлению вектором, замыкающим ломаную
линию, стороны которой параллельны и
равны данным силам. На рис. 6 пока-
зано сложение четырех сил. Многоуголь-
Многоугольник ABCDE называется силовым много-
многоугольником.
Таким образом, применяя правило
силового многоугольника, равнодействующую силу можно най-
найти при помощи геометрического построения (графически).
Равнодействующую системы сходящихся сил можно опреде-
л
Рис. 6
8

лить и аналитическим способом (способом проекций). При этом
пользуются теоремой о проекции равнодействующей силы на
данную ось, согласно которой проекция равнодействующей на
данную ось равна алгебраической сумме проекций слагаемых
сил на ту же ось.
Применяя эту теорему для случая плоской системы сходя-
сходящихся сил, находим проекции равнодействующей этих сил на
две координатные оси х и у:
По этим проекциям определяются модуль и направляющие
косинусы равнодействующей по следующим формулам:
cos (Я, Т) = Щ^; -cos OR, 7) = ^.	(8)
Таким образом, при решении задачи о сложении сходящихся
сил, лежащих в одной плоскости, аналитическим способом
сначала нужно выбрать систему координатных осей х и у, найти
углы каждой силы с координатными осями и вычислить проек-
проекции каждой силы на эти оси.
При вычислении проекции данной силы на ось необходимо
иметь в виду, что абсолютное значение этой проекции равно
произведению модуля силы на косинус острого угла между
силой и осью проекций. При этом если направление этой про-
проекции совпадает с положительным направлением оси, то проек-
проекция положительна; в противном случае проекция отрицательна
(рис. 7).
Иногда бывает удобнее знак проекции определять иначе,
а именно: если направление силы составляет острый угол с по-
положительным направлением данной оси, то проекция силы на
эту ось положительна. Если же направление силы составляет
острый угол с отрицательным направлением данной оси, то
проекция на эту ось отрицательна. Если сила параллельна
оси, то проекция силы на эту ось равна модулю силы, взятому
со знаком плюс или минус в зависимости от того, какой угол
(О ил-и 180) составляет сила с положительным направлением
оси. Если сила перпендикулярна к оси, то проекция силы на эту
ось равна нулю.
Пример 3. Определить модуль и направление равнодействую-
равнодействующей плоской системы сил F,, Fs, Ft,Fx, приложенных в точке А,
если F, = Fi=l00n, Fz = \20h, Fs — 80h и если извеетны углы
между этими силами а = 45°, р=105°, y = 60° (рис. 8, а).
Решение. Решим эту з адачу аналитическим способом. Для
этого построим систему координатных осей Ах и Ау, направив
ось х по линии действия силы /\. Вычислим проекции искомой

равнодействующей на оси х и у по формулам G). Для этого
найдем сначала проекции каждой силы на эти оси. Сила F]
направлена по оси х, а потому FiX = F, = 100; Fiy=*0. Сила Fz
составляет острый угол, равный 45°, с положительным направ-
направлением оси х и такой же угол с положительным направлением
оси у, а потому Ftx = F2 cos 45°, Ftv = Fa cos 45°. Сила Ft состав-
составляет острый угол, равный 180°—(a-fp) = 30°, с положительным
направлением оси i, ас отрицательным направлением оси у эта
сила составляет острый
угол, равный 60°, а по- а)
тому F,x = — F, cos 30°,
Fsy=—ps cos 60". Сила
Ft составляет острый
угол, равный а + р" +
.} у— 180° = 30°, с поло-
У\
Рис. 7
Рис. 8
жительным направлением оси хп острый угол, равный 60°, с по-
положительным направлением оси у, а потому FiX— Ft cos 30°,
Fiy = Ft cos 60°. После того, как проекции всех сил на коорди-
координатные оси найдены, вычислим проекции равнодействующей на
те же оси:
#* = 2 Fx = Fx + р% cos 45°-f/^ cos 30° -\ Ft cos 30° = 100 + 60^2+
+90УЗ~== 340,3;
Ry = 2 Fv= F» cos 45° — F, cos 60°+F4cos60° = 601/2+10 = 94,6.
Теперь находим модуль и направление равнодействующей по
формулам (8):
Я = VR1 + Rl = V C40,3)* + (94,6J ^353,5 н,
cos(R, 0 = ^ = зж1 =

Графическое решение этой задачи показано на рис. 8,6, где
Сложение сходящихся сил, не лежащих в одной плоскости
Равнодействующая пространственной системы сходящихся сил
так же, как и в случае, когда сходящиеся силы лежат в одной
плоскости, равна геометрической сумме слагаемых сил, т. е.
выражается по величине и направлению замыкающей стороной
силового многоугольника, стороны которого равны и парал-
параллельны данным силам. Следовательно, /? = 2^«- В частном слу-
случае, когда число слагаемых сил, не лежащих в одной плоскости,
равно трем, их равнодействующая выражается по величине и
направлению диагональю параллелепипеда, построенного на
этих силах. Силовой многоугольник, построенный для простран-
пространственной системы сходящихся сил, не является плоской фигу-
фигурой. Поэтому при сложении сил, не лежащих в одной плоско-
плоскости, предпочтительнее аналитический способ.
Чтобы найти аналитически величину и направление равно-
равнодействующей пространственной системы сходящихся сил (при-
(применяя теорему о проекции равнодействующей на данную ось),
сначала находят проекции равнодействующей на три коорди-
координатные оси Ox, Oy, Oz:
О)
Определив проекции равнодействующей на координатные оси,
находят затем ее модуль и направляющие косинусы по фор-
формулам:
R =
cos (Я", 0 = ^, cos (R. /) = §j\ cos (Я, ?) = ^. (Ю)
При вычислении проекции данной силы на три взаимно
перпендикулярные координатные оси чаще всего встречаются
следующие два случая:
1.	Углы между силой и координатными осями заданы или
их легко определить, исходя из условия задачи, например из
соответствующего треугольника. В этом случае величина и знак
проекции определяются так же, как и в случае плоской системы
сходящихся сил (см. предыдущий параграф).
2.	Данная сила и координатная ось, на которую нужно
проектировать эту силу, не лежат в одной плоскости и угол
между ними не задан. В этом случае часто бывает целесообразно
сначала спроектировать данную силу на координатную пло-
плоскость, в которой лежит ось проекций, а затем полученную
U

проекцию силы на эту плоскость спроектировать па данную
координатную ось.
При этом необходимо сначала найти угол между данной
силой и координатной плоскостью, на которую проектируют
эту силу, а затем определить угол между проекцией силы на
эту плоскость и данной координатной осью.
Пример 4. К вершине О прямой треугольной призмы при-
приложены пять сил F, Fz, ..., f5, причем сила Ft направлена
по диагонали ОБ грани О ABC, силы Flt Fs, F5 —по ребрам OD,
ОС, О А, а сила Ft лежит в плоскости грани ODC и составляет
с ребром OD угол 30°. Определить модуль и направление равно-
равнодействующей этой системы сил, если Fl — F3— 100«,
Рис. 9
= 200h, F4=1501/r5«, F3 = 250« и если известны углы:
/K = 30°, /®со ж ZCBD 60e OD OA CB
(рис. 9).
Решение. Построим систему координатных осей Ох, Оу
и Ог, направив ось Ох по линии действия силы /\., ось Оу—
параллельно ребру DC призмы, а ось Ог —по ребру DO. Вы-
Вычислим проекции искомой равнодействующей на оси х, у и г
по формулам (9). Для этого найдем сначала проекции каждой
силы на эти оси. Сила Fb направлена по оси х, а потому
Fsy — Fsz = 0, F5X = Fy Сила /\ направлена по оси г, а потому
FiX = Fiy = 0, Flz = — Fv Кроме того, силы Ft и F3 лежат
в плоскости zOy, а потому F1X = FdX = 0.
Так как сила F% образует острый угол, равный 30°, с от-
отрицательным направлением оси у и острый угол, равный 60°,
с отрицательным направлением оси у, то Fsz — —Flcot30°,
Ш

Fsz = — F3 cos 60° Аналогично вычисляем F и FM:
f2y = —F,, cos 60°, Ftz =— F2 cos 30°.
Углы, образованные силой F4 с осями х и г/, нельзя опре-
определить непосредственно из чертежа. Поэтому, чтобы найти
проекции силы Ft на оси хну, спроектируем сначала эту
силу на плоскость хОу и полученную проекцию, которую
обозначим через /*> спроектируем затем на оси х и у. Тогда
/4 cos a =
/4 sin a ==
°s p cosa,
4 cos p sin a,
где p = Z
Кроме того, ^4г= — f4sin p.
Найденные значения проекций всех заданных сил на ко-
координатные оси можно расположить в табл. 1.
Таблица 1
Проекции
РХ
Ру
р*
Силы
0
0
-f,
р.
0
-"¦4
0
*г 2
— /-3-2
Р.
f 4 -J" C0S Р
-f4^-cosp
— f4sinp
P,
0
0
Из прямоугольных треугольников ODB и DSC находим:
• a 0D
OB = /OD2 + DB\
Кроме того, BC = OD, а потому
OS
Отсюда
-i- 4OD', или
= OD /5.

Далее вычислим проекции равнодействующей на оси х, у
и 2 по формулам (9):
/?v=-^-/r3-^-F4^|=-Ю0A+21/3),
Модуль и направление равнодействующей определяем по
формулам A0):
=\ 4002 + Ю02A +2/3J -f 1002C fVSj1». 763,69 «,
cos^' 0-&-0-523,
cobCR.ft)»-^..-0,619.
§ 2 РАЗЛОЖЕНИЕ СИЛЫ НА СОСТАВЛЯЮЩИЕ
Задача о разложении заданной силы на две или несколько
составляющих является обратной по отношению к задаче об
определении равнодействующей сходящихся сил. Рассмотрим
следующие основные случаи решения этой обратной задачи.
1.	Разложение данной силы на две составляющие, лежащие
с ней в одной плоскости, если'
а)	заданы направления составляющих,
б)	заданы модули этих составляющих.
2.	Разложение данной силы на три составляющие, лежащие
с ней в одной плоскости и направленные по трем заданным
непараллельным прямым, не пересекающимся в одной точке.
3.	Разложение данной силы по трем заданным направлениям,
не лежащим в одной плоскости.
Для того чтобы разложить силу F (рис. 10) по двум задан-
заданным направлениям Ах и Ау, достаточно из конца В этой силы
провести две прямые, параллельные прямым Ах и Ау, до их пере-
пересечения с этими прямыми в точках С и D. Тогда векторы АС
и AD являются искомыми составляющими, т. е.
,, Ft, a F=Fl + T,
Пример 5 К узлу В шарнирно-стержневого многоуголь-
многоугольника ABCD, сторона AD которого закреплена неподвижно,
приложена заданная сила F. Найти силы, передающиеся на
стержни АС и DC, если F = 2kh, ,/ABC =120°, /ВСЛ 30°
ZACD90° и ^/и = 60° (рис. 11).
14

Решение. Разложим силу F на две составляющие F, и Ft,
направленные вдоль стержней А В и ВС. Для этого построим па-
раллелограм A1BiClB, в котором сила F является диагональю, т. е.
T — Ft + F^. Так как в треугольнике Л,В,В все углы равны_по
60°, то F, = Fz = F — 2кн. На стержень ВС действует сила Fa;
перенесем эту силу по линии ее действия в точку С и разло-
разложим ее на две составляющие S, и S2, направленные вдоль
Рис. 10
'///77//////////////////////////////////////////''''''
Рис. 11
стержней АС и CD, т. е. построим параллелограмм, в котором
сила Ft является диагональю. Тогда сила S, действует на стер-
стержень CD, а сила S2 — на стержень АС. Таким образом, эти
силы являются искомыми; причем, учитывая направления сил
Sj и S2, видим, что стержень АС испытывает растяжение, а стер-
стержень CD — сжатие. Из прямоугольного силового треугольника
находим:
т. е. St = 1,73 кн, St = lKH
Если требуется разложить данную силу F на две состав-
составляющие, лежащие с ней в одной плоскости, зная модули Ft
и Fz этих составляющих, то задача сводится к построению си-
силового треугольника по трем его сторонам. Для построения
этого треугольника проведем из центров А я В (начала и
конца данной силы F) дуги радиусов r1 = Fl ис, = F2 до их
взаимного пересечения в точке С и дополним полученный тре-
треугольник ABC до параллелограмма АСВЕ, в котором сила"?
является диагональю (рис. 12).*
Если требуется разложить заданную силу F по трем за-
заданным непараллельным направлениям, лежащим с ней в одной
* Задача, очевидно, имеет два решения (почему?) Если же Fl + F1<F,
то задача решений не имеет.
15

плоскости и не пересекающимся в одной точке, то сначала
продолжим эти направления так, чтобы они попарно пересе-
пересекались в трех точках А, В и С, а за!ем перенесем заданную
силу F по линии ее действия в точку пересечения с одним из
трех заданных направ-
направлений, например в точ-
точку В, пересечения ли-
линии действия силы F с
прямой АС (рис. 13).
Точку В, соединим с
F,	В,
Рис 12
Рис 13
точкой В пересечения двух других заданных направлений АВ
и СВ и разложим силу F по направлениям АС и ВВХ. Тог-
\
Рис 14
да
да F^^-f?,.	Сила ?х и есть одна из трех искомых
составляющих	силы F, направленная вдоль АС. Остается
теперь силу Rt	перенести по линии ее действия в точку В и
IS

разложить ее по направлениям А В и СВ Тогда Ri = Fz (- Ft.
Силы F2 и Fs определяют искомые составляющие силы F, нап-
направленные вдоль прямых АВ и ВС.
Пример 6. К горизонтальной балке АВ, подвешенной на трех
канатах AC, ED и ВК, составляющих с прямой ДВ,углы 120°,
90° и 30°, в точке М приложена вертикальная сила F, равная
0,8 кн. Определить усилия, растягивающие канаты, если AM =>
= МЕ = ЕВ=\ м (рис. 14).
Решение. Для определения искомых усилий нужно раз-
разложить силу F на три составляющие, направленные вдоль ка-
канатов AC, ED и ВК. Для этого продолжим линию действия
силы F и прямую АС до их пересечения в точке Av а прямые
ED и ВК—яо их пересечения в точке В,. Соединив точки Л,
и Bv перенесем силу F в точку Аг и разложим ее на две сос-
составляющие S, и 7\, направленные по прямым АХА и /1TSt.
Применяя формулу C) к построенному параллелограмму сил,
получим:
iiM3ra = ^ = sU'где
Отсюда находим:
<, __ F sin 30"
sin C0° + а) '
j, _ F sing
1 ~" sin C0° + a)"
перенесем силу S, в точку 8, и разложим ее на две
составляющие Тг и Tt, направленные вдоль прямых В,? и
BBt. Так как сила Т2 составляет с силами Ть и S1 соответст-
соответственно углы а и 60°, то по формуле C) получим:
s, тх та
sin 60° sin F0° — a) sin a'
откуда
т _ о sin F0°—a)
2~ i sin 60° '
j, _ „ sina
Подставив найденное значение силы S,, получим:
Т — _ 2 F
1 O + ctga '
Г - /-tga f
2. Зак. 23 74	17

где
A,l
Из прямоугольных треугольников ABCt, BEB1} AMAt нахо-
находим:
ВС, = АВ cos 30°,
АСЛ = АВ sin 30°,
а потому
т. е.
откуда
2 '
tg a =
6
Т = — F
Силы Т,, Т2 и Т8 являются искомыми силами, растягива-
растягивающими канаты СА, DE и ВК-
Пример 7. Три невесомых стержня соединены мелаш
собой в точке В. Стержни АВ и ВС лежат в координатой
плоскости zOx и составля-
составляют с осью х углы и и р,
а стержень BD располо-
расположен в плоскости zOy и
составляет с осью Оу угол
у. К узл-у В приложена
сила F, параллельная оси
у. Определить силу S,,
растягивающую стержень
BD, и силы S2 и 5,, сжи-
сжимающие стержни АВ и ВС
(рис. 15).
Решение. Так как
плоскость гОу, в которой
лежат сила F и прямая
BD, пересекается с плос-
плоскостью zOx, в которой рас-
расположены стержни АВ и
рис is	ВС, по прямой Oz, то раз-

ложим снячата силу F на две составляющие S: и Т7, направ-
направленные по прямым BD и ВО. Из построенного прямоугольного
треугольника с углом у находим:
Для определения сил S., и S3, действующих на стержни ВА
и ВС, следует разложить силу Ft по направлениям этих стер-
стержней, построив соответствующий параллелограмм сил. Из этого
параллелограмма, заметив, что углы, образуемые силой F, с
силами S2 и S,, равны соответственно 90° —а и 90° — р\ по
формуле C) находим:
F,	S,	S,
sin[180° —(a + P)] sui(90° —P) sin(90Q —аI
sin (а + C) cos р cos а '
откуда
5 — f'cos Р ~ /г'
2 sin (o + p) sin a-j-cos a tg P
с F, cos a
о. =
* sra(a + P) smp + cosP'tga *
Таким образом,
S =-L
1 cos y '
2 sin a -)- cos a tg P
8 sin p -1- cos p tg a "
§ 3. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
При решении задач по статике, относящихся к равновесию
твердого тела, почти всегда рассматриваемое тело является не-
несвободным. Условия, стесняющие свободу движения рассмат-
рассматриваемого тела, называются в механике связями. В статике
связи осуществляются при помощи твердых или гибких тел,
соединенных с данным твердым телом или касающихся его. Обычно
задача состоит в определении сил взаимодействия между дан-
данным твердым телом и телами, осуществляющими связи, нало-
наложенные на это тело. Сила, с которой связь, препятствующая
перемещению данного твердого тела в каком-нибудь направле-
направлении, действует на это тело, называется реакцией связи. Направ-
Направление реакции связи противоположно тому направлению, в
котором связь препятствует перемещению данного тела.
2*	18

Основные типы связей
Основные типы связей показаны на рис. 16.
1.	Тело опирается на абсолютно твердую гладкую неподвиж-
неподвижную поверхность в точке А. Реакция N такой поверхности
направлена по общей нормали к поверхности данного тела и к
опорной поверхности в точке А соприкосновения тела с опорой.
2.	Тело опирается на неподвижную точку или на неподвижную
линию. Если трением пренебречь, то в этом случае реакция
связи N приложена к телу в точке соприкосновения его с
опорой и направлена по нормали к поверхности тела в этой
точке.
3.	Тело опирается одной точкой на гладкую неподвижную по-
поверхность. Реакция связи N в этом случае приложена в точке
соприкосновения тела с поверхностью и направлена по нормали
к этой поверхности.
4.	Связь осуществляется гибкой, нерастяжимой нитью (це-
(цепью, или канатом). Реакция этой связи приложена в точке
прикрепления нити к телу и направлена вдоль нити. При этом
следует отметить, что нить может быть только растянута. По-
Поэтому реакция нити может быть направлена вдоль нити только
в одну сторону, а именно от точки закрепления нити на данном
теле к другому закрепленному концу нити.
б. Тело опирается на гладкую неподвижную плоскость
катками, которые могут перемещаться по этой плоскости. Реак-
Реакция RA такой опоры направлена перпендикулярно к плоскости,
по которой могут перемещаться катки.
6.	Связь осуществляется при помощи неподвижного цилиндри-
цилиндрического шарнира. В этом случае рассматриваемое тело может
только вращаться вокруг неподвижной оси цилиндрического
шарнира. Если трением в шарнире пренебречь, то реакция не-
неподвижного цилиндрического шарнира направлена по нормали
к его цилиндрической поверхности, т. е. лежит в плоскости,
перпендикулярной к оси шарнира, и пересекает эту ось. Но
направление реакции шарнира в этой плоскости заранее неиз-
неизвестно; это направление приходится определять в каждом от-
отдельном случае, т. е. в каждой конкретной задаче.
7.	Связь осуществляется при помощи невесомого твердого
стержня, шарнирно соединенного концами с данным телом,
равновесие которого мы рассматриваем, и с другим каким-
нибудь телом, например со стойкой, стеной или полом; причем
никакие заданные силы к этому стержню не приложены (его
весом пренебрегаем). Реакция Л?в такого стержня, приложен-
приложенная к данному телу, направлена вдоль стержня. При этом
стержень может подвергаться как сжатию, так и растяже-
растяжению.
90

^> «=
\

8.	а) Связь осуществляется при помощи подпятника. Под-
Подпятник А служит для укрепления пяты стойки и допускает
только одно перемещение рассматриваемого твердого тела, а
именно вращение этого тела вокруг оси стойки. Основание
подпятника препятствует перемещению тела по вертикали вниз
(вдоль оси стойки), а стенки подпятника препятствуют переме-
перемещению тела в плоскости, перпендикулярной к оси стойки. Реак-
Реакция Za ¦основания подпятника направлена по вертикали вверх,
а реакция стенок подпятника лежит в горизонтальной плос-
плоскости, но направление ее в этой плоскости в общем случае не-
неизвестно, поэтому при решении задач се нужно разложить на
две составляющие по направлениям осей х и у, перпендикуляр-
перпендикулярным к оси Аг стойки.
б) Связь осуществляется при помощи неподвижного ци-
цилиндрического подшипника. Подшипник В не препятствует
вращению тела вокруг оси Аг и скольжению вдоль этой оси.
Если трением пренебречь, то реакция Rb подшипника (реакция
цилиндрической поверхности его стенок) пересекает ось враще-
вращения тела и лежит в плоскости, перпендикулярной к этой оси;
так как подшипник не препятствует скольжению тела вдоль оси
вращения, то нет и реакции, направленной вдоль этой оси.
9.	Связь осуществляется при помощи сферического шарнира.
Сферический шарнир не препятствует вращению тела вокруг
любой оси, проходящей через центр О этого шарнира (точку О).
Реакция сферического шарнира проходит через центр шарнира
О, а направление ее заранее указать нельзя. Поэтому при реше-
решении задач эту реакцию приходится разлагать на три составля-
составляющие по направлениям выбранных осей координат.
10.	Если балка АВ, расположенная с приложенными к ней
заданными силами F,, Fit . .. в плоскости хАу, закреплена
концом А жестко, т. е. заделка в точке А препятствует как
поступательному перемещению балки в любом направлении в
плоскости хАу, так и вращательному движению вокруг оси Аг,
перпендикулярной к плоскости хАу, то реакция заделки экви-
эквивалентна силе RA, приложенной в точке А, направление кото-
которой заранее неизвестно, и паре сил с моментом т, причем силу
RA можно разложить на составляющие, направленные по осям х и
у, т. е. RA = ХА +YA.
g 4. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
Для того чтобы система сходящихся сил находилась в рав-
равновесии, необходимо и достаточно равенство нулю равнодейст-
равнодействующей этой системы сил. Это условие можно выразить одним
векторным равенством
22

или тремя скалярными равенствами:
, =0, 2Y, =0, 2fr =0>	A2)
где Xt , Yt , Z,- —проекции силы Ft на координатные оси.
Если уравновешенная система сходящихся сил является
плоской, то вместо трех равенств A2) будем иметь два:
2]Х, =0,
Уравнение A1) выражает условие замкнутости многоуголь-
многоугольника данных сил, т. е. условие равновесия сходящихся сил в
геометрической форме.
Уравнения A2) выражают условия равновесия системы схо-
сходящихся сил в аналитической форме.
Задачи статики, относящиеся к равновесию несвободного
твердого тела, можно классифицировать, во-первых, по распо-
расположению линий действия сил, приложенных к рассматриваемому
телу, и, во-вторых, каждую такую группу задач можно под-
подразделять на отдельные виды по характеру связей, наложенных
на данное тело. В этом параграфе мы рассмотрим равновесие
системы сходящихся сил.
Задачи на равновесие системы сходящихся сил можно раз-
разделить на следующих два типа:
I.	Равновесие плоской системы сходящихся сил.
II.	Равновесие сходящихся сил, не лежащих в одной плос-
плоскости.
Задачи, относящиеся к первому типу, можно подразделить
но характеру связей, наложенных на данное тело, на две
группы:
1.	Задачи, в которых линии действия всех реакций связей,
наложенных на данное тело (равновесие которого рассматри-
рассматривается в задаче), известны.
К таким связям относятся:
а)	невесомый стержень, одним концом шарнирно соединен-
соединенный с данным телом, а другим концом закрепленный при по-
помощи неподвижного шарнира;
б)	неподвижная гладкая поверхность или неподвижная глад-
гладкая линия, на которую опирается данное тело;
в)	гибкая нить (канат, трос);
г)	цилиндрический подшипник, ось которого расположена
в плоскости действия заданных сил.
2.	Задачи, имеющие хотя бы одну связь, наложенную на
данное тело, направление реакции которой заранее неизвестно.
Такими связями являются неподвижный цилиндрический
шарнир и подпятник.
В задачах, относящихся к равновесию несвободного тела
3*

под действием системы сходящихся сил, не лежащих в одной
плоскости, связи, наложенные на это тело, чаще всего осуще-
осуществляются гибкими телами, шарнирно закрепленными стерж-
стержнями и неподвижными опорными плоскостями. В этих случаях
линии действия реакций всех связей известны и, следовательно,
задача сводится только к определению модулей этих реакций.
При решении задач, относящихся к равновесию несвобод-
несвободного твердого тела, надо придерживаться следующего общего
плана.
Необходимо выделить тело, равновесие которого будем рас-
рассматривать в данной задаче, т. е. то тело, к которому прило-
приложены как заданные силы, так и те силы, которые требуется
определить в данной задаче.
Далее необходимо выяснить, какие связи наложены на рас-
рассматриваемое тело, и учесть реакции этих связей.
При этом рекомендуется начертить выделенное тело, изо-
изобразить на чертеже в виде векторов заданные силы и реакции
связей и установить, каким уравнениям равновесия должна
удовлетворять эта система сил, а затем составить и решить
эти уравнения.
Рассмотрим сначала решение таких задач, когда все прило-
приложенные к телу силы, включая и реакции связей, пересекаются
в одной точке и лежат в одной плоскости.
В этом случае задачу можно решить двумя способами: или
геометрическим (графически), или аналитическим (по способу
проекций).
Задачи типа I
Равновесие плоской системы сходящихся сил
Первая группа
Задачи, в которых линии действия реакций всех связей известны
(задачи 17—21, 26—32)*
Пример 8. Плоская ферма, состоящая из невесомых стерж-
стержней, соединенных между собой по концам шарнирно, находится
в равновесии под действием сил F, и Fit причем сила Fl го-
горизонтальна, а сила F2 составляет со стержнем ED угол а =
= 45\ Определить усилия в стержнях /, 2, 3 и 4, если F, =
= 30 кн, Ft = 20 кн (рис. 17).
Решение. Рассмотрим сначала узел D; к этому узлу, на-
находящемуся в равновесии, приложены заданная сила F, и не-
неизвестные реакции стержней / и 2, которые обозначим через
* Здесь и дальше в тексте указаны номера задач из «Сборника задач
по теоретической механике» И. В. Мещерского, изд. 1950 г. и последу-
последующих изданий.
24

S, и S2. Так как весом стержней пренебрегаем, то эти реакции
направлены вдоль соответствующих стержней (см. стр. 20, п. 7).
Таким образом, узел D находится в равновесии под дейст-
действием трех сил Flt S, и S2, поэтому F,-fS,-f-S2 —0. Далее за-
задачу можно решить либо геометрическим способом, либо анали-
аналитическим. Решим сначала эту задачу геометрическим способом.
Построим замкнутый силовой треугольник, начав его построе-
построение с известной силы Ft. Из произвольной точки а проведем
вектор ab, параллельный данной силе Ft, длина которого в
выбранном масштабе изображает модуль этой силы. Через точки
а и b проведем два луча, параллельные силам S, и S2, до
их пересечения в точке с.
Треугольник abc и есть
искомый замкнутый сило-
силовой треугольник. Чтобы
найти направление неиз-
неизвестных сил Sx и S2, нужно
обойти силовой треуголь-
треугольник по его периметру так,
чтобы он замкнулся; на-
направление этого обхода
определяется направлени-
направлением известной силы Ft. Из-
Измерив длину сторон be и .
са силового треугольника
выбранной единицей мас-
масштаба, найдем числовое
значение сил St и S2. Мо-
Модули неизвестных сил S, и S2 можно также найти тригономет-
тригонометрически из треугольника abc, в котором известны сторона ab =
~FX и два угла: /_abc—120° (углы abc и DBA равны как
углы с параллельными сторонами) и /_acb — 30° (см. рис. 17 и
18). Из этого треугольника находим:
а потому
Рис. 17
s,
sin 120°
t i
S2
sin 30°
.» i
F}
Л
sin 30° '
sin 60°
1 sin 30°
или
= F, = 30 кн, S1=
==51,9 кн.
Мы нашли реакции Sx и S2 стержней DE и DK, т. е. те силы,
с которыми эти реакции действуют на узел D. Важно при этом
выяснить, будут ли стержни DE и DK работать на растяжение
25

или на сжатие. Для этого рассмотрим равновесие каждого стержня
отдельно; начнем со стержня DK (рис. 19, а).
Реакция стержня DK, приложенная к узлу D, направлена
от узла D внутрь отрезка DK- Но тогда сила S'2, с которой
шарнир D действует на стержень DK, или иначе—реакция шар-
шарнира D, приложенная к стержню DK, равна по модулю и про-
противоположна по направлению силе S2, т. е. S\ = —S2. Стержень
DK находится в равновесии под действием двух сил: реакции
52 шарнира D и реакции шарнира К, которую обозначим через
S2. Отсюда следует, что силы 52 и S2, направленные по одной
прямой, равны по модулю и противоположны по направлению,
т. е. Sa=—Sj. Силы S2 и S2, приложенные к концам стержня
Рис. 18
Рис. 19
KD, вызывают, очевидно, растяжение этого стержня. Отсюда
заключаем, что если вектор S2, изображающий реакцию стержня
KD на шарнир D и показанный на самом стержне, направлен
от узла D, то стержень растянут. Теперь рассмотрим стержень
DE (рис. 19,6). Реакция St этого стержня на шарнир D, на-
начерченная на самом стержне DE, направлена, как видно, к
шарниру D. Аналогично предыдущему заключаем, что реакция
S[ шарнира D на стержень DE, приложенная к этому стержню,
будет равна по модулю и прямо противоположна по направле-
направлению силе Sx, т. е. S,'=-—S,. Так как стержень DE нахо-
находится в равновесии, то реакция S, шарнира Е, приложенная
к этому стержню, равна по модулю и прямо противоположна
по направлению силе S[, т. е. 5"= —Si. Очевидно, что силы
Si и Si, приложенные к стержню DE, сжимают этот стержень.
Поэтому можно сказать, что если вектор S,, изображающий ре-
реакцию стержня DE на шарнир D и начерченный на самом
стержне, направлен к узлу D, то стержень сжат- Твкцм об-
образом, сформулируем следующее правило:

Если изображенный на самом стержне, вектор силы, с ко-
которой данный стержень действует на шарнир (узел), направ-
направлен от шарнира (от узла), то стержень растянут. Если же
этот вектор направлен к шарниру (к узлу), то стержень сжат.
Рассмотрим далее аналитический способ решения этой за-
задачи. Направим ось Dx по линии действия силы Т7,, а ось Dy пер-
перпендикулярно к ней, как показано на рис. 20, и найдем проекции
всех сил, приложенных к шарниру D на эти оси. Известно,
что абсолютное значение проекции
силы на ось равно произведению
модуля этой силы на косинус ост-
острого угла между направлением
силы и осью проекций. При этом,
если направление силы составля-
составляет острый угол с положительным
направлением оси проекций, то
проекция силы на эту ось поло-
положительна.Если же направление
силы составляет острый угол с
отрицательным направлением оси
проекций, то проекция силы на
эту ось отрицательна.
Сила F, совпадает с отрица-
отрицательным направлением оси Dx,
а потому проекция ее на эту ось равна модулю самой силы,
взятому со знаком минус, а ее проекция на ось Dy равна
нулю. Сила S, составляет острый угол 30° с положительным
направлением оси Dx и острый угол 60° с положительным на-
направлением оси Dy, а потому
SiX = S1 cos 30°, Sly = Si cos 60°.
Сила S8 составляет острый угол 60° с отрицательным на-
направлением оси Dx и острый угол 30° с отрицательным на-
направлением оси Dy, а потому
Рис. 20
= — S2 cos 60е,
= — S2 cos 30°.
При равновесии тела сумма проекций всех приложенных
к телу сил на каждую из координатных осей равна нулю.
Таким образом, получим два следующих уравнения равнове-
равновесия:
1)	— f, -fS.cosSO0- S2 cos 60° = 0,
2)	S, cos 60° — S2 cos 30° = 0,
или
j
27

Решим теперь эту систему уравнений относительно неизвест-
неизвестных S, и Ss:
S2 = /7i = 30kh, S,=S2 J/3 = 51,9 кн.
Чтобы определить усилия в стержнях 3 и 4, рассмотрим узел_ Е,
находящийся в равновесии под действием заданной силы Ft и
трех реакций стержней /, 3, 4, направленных вдоль этих стерж-
стержней. Неизвестные реакции стержней 3 и4обозначим через SinSi,
направив их от рассматриваемого узла Е. Что касается реакции
стержня 1, приложенной к узлу Е, то по закону равенства
действия и противодействия она равна по модулю и противо-
противоположна по направлению силе S, т. е. равна силе St. Следо-
Следовательно, S'i + S, + S4 + fs = 0. Для определения неизвестных
сил применим сначала аналитический способ решения за-
задачи. Для этого выбе-
у(+)	рем оси координат, как
указано на рис. 21, и най-
найдем проекции каждой
силы на эти оси.
Тогда имеем:
Xf+)
Рис. 21
, = — S, cos 30°,
= 0, Ргх = — _F3cos75°;
,= — Si cos 60°,
F*y = — F2 cos 15°;
x = — S4cos30°;
= — S, cos 60°.
Приравнивая нулю сумму проекций всех сил на каждую из
координатных осей Ех и Еу, получим два уравнения равновесия:
—Si cos 30° — Рг cos 75° —S4 cos 30° = 0,
—S5 —Si cos 60° — Ft cos 15° —S4 cos 60° = 0.
Из этих уравнений находим:
S4 = -^
Ss = —Si cos60° —FjCos 15°—S4 cos60°,
cos ^°
ИЛИ
т. e.
5 _ 90 Y<1(\ [ ~\ ¦
>4 — — ги-j-i^i ~Y~
cos 75C
S4= — 57,9 к«, S, = —16,2/cm.
28

Так как после решения уравнений равновесия мы получили
отрицательные значения для неизвестных реакций S3 и S4, то эти
силы имеют направления, противоположные выбранным нами
на рис. 21, т. е. силы S3 nSi направлены к узлу Е и стержни 3 и 4
сжаты. Полученные результаты проверим геометрически, т. е.
рассмотрим геометрический способ
решения этой задачи. Для этого по-
построим замкнутый многоугольник
сил Р„ Su_'Si, S4(pnc. 22). Направ-
Направления сил S, и S4 найдем после то-
того, как обойдем периметр построен-
построенного силового многоугольника dekld,
причем направление этого обхода
определяется направлением извест-
известных сил Ft и S,. Измерив стороны
Id и kt силового многоугольника
выбранной единицей масштаба, най-	Рис. 22
дем модули искомых сил S, и S4.
Так как углы между силами Fs, Slt S, и S4заданы, то можно
найти углы силового многоугольника, а затем вычислить и длины
двух неизвестных его сторон, что и рекомендуется выполнить
студенту самостоятельно.
Чтобы определить, будут ли стержни 3 и 4 растянуты или
сжаты, перенесем векторы S, и S, с силового многоугольника на
стержни ЕС и ЕК, фермы; тогда силы S, и S4 будут направлены
к узлу Е, а потому эти стержни сжаты.
Примечание. При аналитическом способе решения этой задачи зара-
заранее неизвестно, в какую сторону следует направлять реакции стержней.
В таких случаях эти реакции можно направлять по соответствующим стерж-
стержням в ту или другую сторону произвольно. Если в результате решения
уравнений равновесия для этих реакций получим положительные значения,
то реакции были направлены верно Если же для какой-нибудь из этих неиз-
неизвестных сил получим отрицательное значение, то выбранное направление
реакции нужно изменить на противоположное. В дальнейшем условимся
неизвестную реакцию стержня, приложенную к шарниру (к узлу), направ-
направлять по самому стержню от этого узла. Если, решая уравнения равнове-
равновесия, получим для этой реакции положительное значение, то реакция
направлена верной, следовательно, стержень растянут. Если же
для искомой реакции получим отрицательное значение, то это укажет на
то, что в действительности реакция данного стержня имеет направление,
противоположное принятому нами, т. е. она направлена к узлу и, следо-
следовательно, данный стержень сжат.
Таким образом, при указанном условии относительно направления реак-
реакции стержня, по знаку этой реакции можно определить, будет ли данный
стержень растянут или сжат.
Пример 9. Груз весом Р = 60 кн подвешен при помощи каната,
перекинутого через небольшой блок А и идущего к лебед-
лебедке D. Определить усилия в стержнях АС и ВА крана. Углы,
29

определяющие направления стержней и каната, заданы на
рис. 23.
Решение. Рассмотрим равновесие узла А крана, к кото-
которому приложены сила Р, реакции стержней АС и АВ и сила
натяжения каната AD, Обозначим реакцию стержня АВ через S,,
реакцию стержня АС через S2 и
силу натяжения каната AD че-
через Т.
Реакции стержней S, и S% на-
направим вдоль этих стержней от
узла А; сила Т направлена, оче-
очевидно, вдоль каната от А к D, так
как канат растянут. Кроме того,
Т~Р, так как при отсутствии
трения в блоке натяжение кана-
каната, перекинутого через этот блок,
во всех точках одинаково,.
Так как узел А находится в
равновесии под действием сил S,,
S2, P, Т, то можно составить два
уравнения равновесия этой систе-
системы сходящихся сил.
Выберем оси координат, как указано на рис. 23, найдем
проекцию каждой силы на эти оси и составим два уравнения
равновесия, приравнивая нулю сумму проекций всех сил на
каждую из координатных осей:
—S, — S2 cos 60° -f Т cos 60° = 0,
— S2cos30° — Р—ГсозЗО° = 0.
Из второго уравнения находим:
_S2 = ~^4 Т = Р Л -\-у=) = 129,1 кну
St = — 129,1 кн.
Теперь из первого уравнения получаем:
Рис 23
S, =Г cos 60° ~S2 cos 60° =
Р+р(
Гъ)
Так как полученное значение силы S, отрицательно, то си-
сила S2 имеет направление, противоположное направлению, выб-
выбранному на рисунке, т. е. она направлена от С к Л, и, следо-
следовательно, стержень АС сжат.
30

Задачу можно решить изометрически, построив замкнутый
многоугольник сил Т, Р, St, S2 (рис. 24).
Направления сил S, и S2 найдем после того, как обойдем
периметр построенного силового многоугольника, причем направ-
направление этого обхода определяется направ-
направлением известных сил Р и Т.
Измерив стороны cd и da силового много-
многоугольника выбранной единицей масштаба,
найдем величину искомых_сил S, и S2. Так
как углы между силами Р, Т, S,, S2 зада-
заданы, то можно найти углы силового многоу-
многоугольника, а затем вычислить и длины двух
неизвестных его сторон. В самом деле, из
построения силового многоугольника сле-
следует, что
/_dcb = 90°, ^.cda = 60°, /_ bad = 60°,
а потому
/_ аЪс = 360°—(90° + 60° + 60°) = 150°.
Если соединим точки а и с, то треугольник abc будет равно-
равнобедренным, так как Р = Т, а потому
Zbca =
Отсюда следует, что
/_dca = 75°,
и
ас = 2ab cos 16° = 2Р cos 15°.
Применяя теперь к треугольнику adc теорему синусов, получим:
ас _ St _ St
sin 60° ~ sin 75° ~ bin 45" '
откуда
с _ 2Pcos 15° sin 45° Q.
Dl ~ ШГ&У ' ^ У4 KH'
о _ 2P cos 15° sin 75° _ - 9q
^ - iliTeo3	 12y KH-
Чтобы определить, будут ли стержни АВ и АС сжаты или
растянуты (рис. 23), перенесем векторы S, и Sa с силового мно-
многоугольника на стержни АВ и АС, тогда сила S2 будет направ-
направлена к узлу А, а сила Sj будет направлена от узла А, а потому
стержень АС сжат, а стержень АВ растянут.

Вторая группа
Задачи, где имеются связи, направление реакций которых неизвестно
(задачи 36—41, 43)
Пример 10. Жесткая рама закреплена в точке А при помощи
неподвижного цилиндрического шарнира, а в точке В опирается
катками на гладкую наклонную плоскость, составляющую с
горизонтом угол
а = 30°. На гори-
горизонтальном участ-
участке CD рама нахо-
находится под дейст-
действием равномерно
х
Рис. 25
распределенной вертикальной нагрузки интенсивности q = 5KHJM.
Определить реакции опор в точках А и В, если CD = 2а = 1,2 м
и 0/С = ^=о(угЗ-1)(рис. 25).
Решение. Найдем сначала равнодействующую Q системы
параллельных сил, приложенных к раме на участке CD, кото-
которая равна сумме слагаемых сил, т. е. Q=q-2a = 6 кн, и
приложена в середине отрезка CD. Реакцию опоры В обозна-
обозначим через Re. Она направлена перпендикулярно к опорной пло-
плоскости катков. Реакция RA неподвижного шарнира приложена
к раме в точке Л, но направление ее неизвестно. Для определе-
определения линии действия силы RA воспользуемся теоремой о трех
уравновешенных непараллельных силах. Так как рама нахо-
находится в равновесии под действием трех сил Q, RB и RA, то ли-
линии действия этих сил пересекаются в одной точке.
Продолжив линии действия сил Q и RB, найдем точку Е,
через которую должна проходить сила RA, приложенная в точ-
точке А. Следовательно, прямая АЕ является линией действия
силы RA. Теперь задача может быть решена двумя способами:
32

геометрическим (построением замкнутого силового треугольника)
и аналитическим (методом проекций). Построим замкнутый тре-
треугольник аЪс сил Q, RB и RA, в котором ab = Q~, а стороны be
и ас соответственно параллельны прямым BE и АЕ. Тогда
bc=RB и cd — RA (рис. 26). Далее определим углы в построен-
построенном силовом треугольнике: ^/аЬс = а. Из прямоугольного тре-
треугольника КЕВ находим:
КЕ = BE cos 30° = а
а потому ОЕ = КЕ — КО = ау 3 — Ь, или ОЕ — а]
— 1)—а. Отсюда АО=ОЕ и /_АЕО = /_cab=\b°. Втреугольнике abc
проведем прямую се, перпендикулярную к ab, тогда ае = се=-^,
be = be cos 30°, и ab = ае -\-eb =
ас = ае ]/ 2, а потому
кн.
Рассмотрим теперь аналитический способ решения. Начало коор-
координат выберем в точке О, ось у направим по прямой ОЕ, а ось х —
по прямой АО. Проектируя силы Q, RA и RB на оси х и у,
получим следующие два уравнения равновесия:
1)	2^ = ^cos45°— /?B cos60° = 0;
2)	2У = — Q + Ra cos 45° + ^в cos 30° = °-
Из первого уравнения находим
Тогда из второго уравнения имеем
Отсюда
3 Зак. 237,	33

В заключение можно сделать следующие выводы:
1.	Если линии действия всех реакций связей, наложенных
на данное тело, равновесие которого рассматривается в задаче,
известны, то при геометрическом способе решения задачи нужно
построить замкнутый силовой многоугольник, начав построение
его с известных сил. Число неизвестных сил не должно быть
больше двух. В случае, когда число всех приложенных к дан-
данному телу сил, включая и реакции связей, равно трем, задача
сводится к построению силового треугольника по заданной сто-
стороне и заданным направлениям двух других его сторон.
После того как построен замкнутый силовой многоугольник,
две неизвестные силы можно определить либо непосредственным
измерением, либо вычислением.
При тригонометрическом решении силового треугольника
обычно применяется теорема синусов.
Однако иногда бывает удобнее вместо теоремы синусов при-
применить метод подобия, т. е., исходя из условия задачи, найти
такой треугольник с известными сторонами, который был бы
подобен силовому треугольнику. Тогда легко определить неиз-
неизвестные стороны силового" треугольника из условия пропорцио-
пропорциональности соответственных сторон подобных треугольников.
2.	При аналитическом способе решения нужно выбрать си-
систему координатных осей, найти углы, образуемые каждой силой
с этими осями, и определить проекции каждой силы на коорди-
координатные оси; затем нужно составить два уравнения равновесия,
приравнивая нулю сумму проекций всех сил на каждую из
координатных осей, и решить эти уравнения.
Если в результате решения этих уравнений значение какой-
либо неизвестной сил'ы получилось отрицательным, то это значит,
что эта сила имеет направление, противоположное тому, которое
мы выбрали для нее при составлении уравнений равновесия.
Следует иметь в виду, что если число всех сил, приложенных
к данному телу, больше трех, то вычисление величины искомых
в задаче сил тригонометрическим способом становится обычно
громоздким. В этом случае предпочтительней аналитический
способ решения.
3.	Когда линия действия какой-либо реакции неизвестна,
как, например, в случае неподвижного цилиндрического шар-
шарнира или подпятника, а число сил, приложенных к данному
телу, равно трем, то, применяя теорему о пересечении в одной
точке трех непараллельных уравновешенных сил, можно найти
точку, через которую приходит эта неизвестная реакция. Так
как точка приложения неизвестной реакции задана, то тем самым
определяется ее линия действия. Далее задача решается или
геометрическим, или аналитическим способом, как это было ука-
указано в рассмотренных выше примерах.
44

Задачи типа II
Равновесие системы сходящихся сил, не лежащих в одной плоскости
(задачи 212, 213, 215, 217)
В настоящем параграфе рассмотрим равновесие тела, к кото-
которому приложена система сходящихся сил, не лежащих в одной
плоскости.
В общем случае задачи, от/носящиеся к равновесию неплоской
системы сходящихся сил, проще решать аналитическим способом
при помощи трех уравнений
равновесия.
При этом необходимо об-
обратить внимание на нахож-
нахождение проекций сил на коор-
координатные оси.
Следует иметь в виду,
что если имеем систему четы-
четырех уравновешенных сил, не
лежащих в одной плоскости,
то задачу часто можно ре-
решить проще, заменив две за- 1
данные силы их равнодей-
равнодействующей, так как три урав-
уравновешенные силы всегда ле-
лежат в одной плоскости, то
задачу о равновесии четырех
сходящихся сил, не лежа-
лежащих в одной плоскости,
можно свести, таким обра-
образом, к задаче о равновесии
плоской системы трех сил,
решение которой рассмотре-
рассмотрено в предыдущем параграфе.
Пример 11. Груз Р весом
10 кн поддерживается при
помощи каната, перекинутого через блок О и идущего к лебед-
лебедке Е. Определить усилия в стержнях АО, ОВ, ОС крана, если плос-
плоскость ОАВ горизонтальна, AD—DB, OA^OB, /DCO = 60°
/С0? = 30° и /ЛОВ = 90° (рис. 27).
Решение. Рассмотрим равновесие шарнирного болта О,
к которому приложены_реакции стержней SA, SB, Sc и силы на-
натяжения каната Г, и ГЕ. Так как натяжение каната во всех
его точках одинаково, то Т1 = Тг = Р.
Так как стержни закреплены шарнирно и их весом мы пре-
пренебрегаем, то реакции стержней направлены вдоль этих стерж-
стержней. Допустим, что стержни растянуты, т. е. реакции направ-
Рис 27
35

лены от узла О. Силы SA, SB, $c, Г,, Тг не лежат в одной пло-
плоскости.
Составим три уравнения равновесия этих сил, для чего выбе-
выберем сначала систему координатных осей х, у z так, чтобы
силы SA, SB, Sc, Г,, Т2 лежали в координатных плоскостях;
ось Dz направим перпендикулярно к плоскости АОВ; начало
координат выберем в точке D, а оси хну направим соответ-
соответственно по прямым АВ и 0D. Тогда силы SA и SB будут распо-
расположены в плоскости xDy. а силы Sc, Tt, T2 — в вертикальной
плоскости zDy. При тагам выборе координатных осей легко
определить углы каждой силы с координатными осями, а следо-
следовательно, и ее проекции на эти оси. Так как силы SA и SB ле-
лежат в плоскости xDy, то SAz = SBz = 0. Найдем углы, составляе-
составляемые этими силами с осями х и у. По условию задачи АО = ОВ,
а потому треугольник АОВ равнобедренный; кроме того, AD = DB
и /_ АОВ = 90°. Следовательно, прямая OD есть биссектриса
угла АОВ и /_DA0 = /_DBO = \b\
Теперь находим проекции сил SA и SB на координатные оси
хну.
Проекции SBx, SA SBy, очевидно, отрицательны, так как
силы SA и SB образуют острые углы с отрицательным направле-
направлением оси Dy, а сила SB образует острый угол и с отрицатель-
отрицательным направлением оси Dx:
SAx = SA cos 45°, SSx = -SB cos 45°,
Силы Sc, 7\, Тг лежат в плоскости zDy, а потому они пер-
перпендикулярны к оси Dx и, следовательно,
Сила Т2 параллельна оси Dz, а потому Тгу — 0 и Т\z — — Р.
Углы между силой Sc и осями у и z заданы по условию задачи,
а потому находим:
Scz = — Sc cos 60°, SCy = — Sc cos 30°.
Остается найти углы силы Г, с осями у и г. Для этого рас-
рассмотрим треугольник ОСЕ. Угол DC0 — внешний угол этого
треугольника, а потому он равен сумме углов СОЕ и СЕО, т. е.
60° = 30° + /_СЕО, откуда /_СЕО = 30°. Из прямоугольного
треугольника ODE находим, что /_DOE = 60°. Таким образом,
7", образует острый угол в 30° с отрицательным направлением
оси z и острый угол в 60° с отрицательным направлением оси у,
а потому
7'IJ, = -r-7'1cos60o и 7\г = — Г, cos 30°.
36

Указанные значения проекций можно расположить в виде
табл. 2.
Составим теперь три уравнения равновесия, для чего доста-
достаточно приравнять нулю сумму проекций всех сил на каждую
координатную ось:
1)	5Л cos 45°—SBcos45° = 0;
2)	— SA cos 45°—SB cos 45° — Sc cos 30° — Tx cos 60° = 0;
3)	— Tt — 7\cos30° —Sccos60° = 0,
Таблица 2
Острый угол силы
С ОСЬЮ X
Знак проекции си-
силы на ось х
Проекция силы на
ось х
Острый угол силы
с осью у
Знак проекции си-
силы на ось у
Проекция силы на
ось у
Острый угол силы
с осью г
Знак проекции си-
силы на ось г
Проекция силы на
ось г
Силы
45°
+
+ SA cos 45°
45°
—
—SA cos 45°
90°
0
45°
—
—5ясоз45°
45°
—
—Sflcos45°
90"
0
sC
90°
0
30°
—
—Sccos30°
60°
—
—5ccos60°
Г,
90°
0
60°
—
—Г, cos 60°
30°
—
—Т, cos 30°
90°
1
0
90°
0
0"
—
или
УН
— «V

Решая эту систему трех уравнений относительно неизвестных
SA, SB> Sc, получим:
-Sc = 2Р + Р ]/~3 = Р B + /~3) = + 10 (/ + 2),
или
Sc« —10-3,73 = —37,3 кн; SA = SB
= — 10/3-10^-27,3 кн,
или
Так как мы получили отрицательное значение для силы Sc,
то выбранное нами направление этой силы нужно изменить на
противоположное; следовательно, стержень СО не растянут,
как мы предполагали, а сжат.
Пример 12. Невесомые стержни АС, АВ и AD соединены
шарнирно между тобой в точке Лис неподвижными опорами
в точках С, D и В. К узлу А приложена сила F = 8 кн, со-
составляющая с координатными осями хну углы а = р = 60°.
Определить реакции стержней АС, АВ и AD, если 6 = 60°,
Ф = 45° (рис. 28).
Рис 28

Решение. Рассмотрим равновесие узла А, к которому
приложены заданная сила F и реакции Slt St, S, стержней AC,
АВ и AD, направленные вдоль этих стержней. Допустим, что
эти реакции направлены от узла А. Так как линии действия
сил F, S,, S2, S, пересекаются в одной точке А, то имеем че-
четыре уравновешенные сходящиеся силы, не лежащие в одной
плоскости, а потому вычислим проекции этих сил на выбранные
координатные оси и составим три уравнения равновесия.
Силы Si и S2 параллельны соответственно осям х и у, а по-
потому Siy=S,, = 0, Slx = SlirO, Slx = —SltSty = — St. Так как
углы аи^ между силой F и положительными направлениями
осей х и у заданы, то Fx = F cos 60° = 17% Fy = F cos 60° = -i F.
Угол у между силой F и осью г мы найдем из соотношения
cos" а + cos1 р -f cos* у = 1, откуда cos2 y = 1 — cos2 a — cos2 P — -5-
и cos y = ±
Так как сила F составляет острый угол с отрицатель-
ным направлением оси г, то Fz = — ^~ F. Угол б между
силой Sa и положительным направлением оси г задан, а
потому SbZ — S, cos 60° = -у 5,. Углы между силой S, и осями
х и г/ не заданы и их нельзя определить непосредственно из
чертежа, а потому спроектируем эту силу на плоскость хОу и
полученную проекцию, которую обозначим через S,xjt, спроекти-
спроектируем затем на оси х и у. Тогда SSxv = S, sin б, Stx = — S8sin6cos(p,
Sty — — 5, sin б sin ф. Приравнивая нулю сумму проекций всех
сил на оси х, у и г, получим следующие три уравнения рав-
равновесия:
S +
3)
Из третьего уравнения находим: S, = F]^=- 11,28 кн.
Из первых двух уравнений имеем:
Так как мы получили отрицательные значения для сил Sx и S,
то выбранные нами направления для этих сил следует изме-

нить на противоположные; следовательно, стержни АВ и АС
сжаты, а стержень AD растянут, так как реакция этого стержня,
как мы и предполагали, направлена от узла А.
Глава II
ПЛОСКАЯ СИСТЕМА СИЛ
§ 1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
Моментом силы F относительно данной точки О называется
произведение величины силы на ее плечо, т. е. на длину пер-
перпендикуляра, опущенного из точки О на линию действия этой
силы. Если сила F стремится вращать тело вокруг данной
Рис. 29
точки О в направлении, обратном движению часовой стрелки,
то условимся момену силы F относительно точки О считать по-
положительным; если же сила стремится вращать тело вокруг
точки О в направлении, совпадающем с направлением движения
часовой стрелки, то момент силы относительно этой точки
будем считать отрицательным. Следовательно,
mo(F) = -Fh (рис. 29, а)
И	mo{F1)= + F1hi (рис. 29,6).
Если линия действия силы F проходит через данную точку О,
то момент силы F относительно этой точки равен нулю.
Сложение сил, расположенных как угодно на плоскости,
можно выполнить двумя способами:
1)	последовательным сложением;
2)	приведением данной системы сил к произвольно выбранно-
выбранному центру.
Первый способ становится громоздким при большом числе
слагаемых сил и неприменим для пространственной системы
сил, второй же способ является общим, более простым и
удобным. -
Если задана система сил Fv Fs, F3, ..., Fn, расположенных
как угодно в одной плоскости, то, перенося все эти силы в про-

извольпо выбранную в этой плоскости точку О, называемую
центром приведения, получим приложенную в этом центре силу
я=2^	си)
и пару с моментом
2F	A5)
Геометрическая сумма сил данной системы называется рав-
равным вектором этой системы сил.
Алгебраическая сумма моментов сил плоской системы отно-
относительно какой-нибудь точки О плоскости их действия назы-
называется главным моментом этой системы сил относительно этой
точки О.
Главный момент изменяется с изменением центра приведения;
зависимость главного момента от выбора центра приведения
выражается следующей формулой:
где О и О,—два различных центра приведения.
Так как сила R и пара с моментом Мо, получающаяся в ре-
результате приведения данной плоской системы сил к центру О,
лежат в одной плоскости, то их можно привести к одной силе
R* — R, приложенной в некоторой точке О*. Эта сила является
равнодействующей данной плоской системы сил.
Таким образом, если ИфО, Моф0, то система сил приво-
приводится к одной равнодействующей, не проходящей через центр
приведения О. При этом момент равнедействующей относи-
относительно любой точки будет равен алгебраической сумме момен-
моментов всех данных сил относительно той же точки (теорема Ва-
риньона).
Если начало координат выбрано в центре приведения и
известны проекции всех сил на оси координат и координаты
точек приложения этих сил, то момент равнодействующей нахо-
находим по формуле
2	A7)
Если в результате приведения системы сил к данному центру
окажется, что главный вектор этой системы рпвен нулю, а глав-
главный момент ее отличен от нуля, то данная система эквивалентна
паре сил, причем главный момент системы равен моменту этой
пары и не зависит в данном случае от выбора центра при-
ведения. Если Мо = 0, a R ф 0, то система приводится к равно-
равнодействующей, приложенной в центре приведения О.
Если Мо = 0 и R — 0, то система сил находится в равнове-
равновесии. Все случаи, встречающиеся при сложении сил плоской
системы, можно представить в виде табл. 3.
ЗП Зак. 2374	^

R ф 0, Mo = 0
«-0. «„-0
Таблиц
Система приводится к равнодействующей силе /?* =
не проходящей через центр приведения 0
Система приводится к равнодействующей R = ^ ~Fl,
ходящей через центр приведения О
Система приводится к одной паре, момент которой
^]tno(Fj) и не зависит от выбора точки О
Система сил находится в равновесии
а 3
про-
равен
Равновесие плоской системы сил рассмотрим в следующем
параграфе, а теперь перейдем к решению задач на сложение
сил плоской системы.
Пример 13. Дана плоская система четырех сил Р,, Р2, Ра, Р4;
проекции X и Y этих сил на координатные оси, координаты
х, у точек их приложения заданы в табл. 4.
Таблица 4
X
Y
X
У
Силы
1
4
2
1
F,
— 2
1
— 2
— 1
F3
3
	 О
3
	з
	4
— 3
-4
— 6
Привести эту систему к началу координат и затем найти
линию действия равнодействующей.
Решение. Найдем проекции главного вектора заданной
системы сил на координатные оси по формуле A4)
Откуда
l
= 4 + 1-3-3= -1.
42

Главный момент Мо находим по формуле A5)
мо = 2 т0 (F,) = 2 (*У - УХ) =
= 8—2 — 9+12 —A -f 2 —9+24) = 9—18 = —9.
Пусть_Л (л:, у)— точка линии действия искомой равнодействую-
равнодействующей R*. Тогда
но
а потому
С другой стороны, по теореме Вариньона имеем:
Следовательно,
или
2у-х = 9
х—2у+9
Это и есть уравнение линии действия равнодействующей
Пример 14. Найти равнодействующую четырех сил,
вующих по сторонам правильно-
правильного шестиугольника, направление
которых указано на рис. 30,
если Р, = Р3 = 2Р и Р2 = РА = Р.
Решение. Выберем за
центр приведения центр О шес-
шестиугольника и найдем главный
вектор R и главный момент Мо
данной системы сил относитель-
относительно центра О. Так как Р, = —Р,
и Р2 = Р4, то главный вектор R
дейст-
дейст1
в
"¦ \
/г' v
г?
\
Л
/? \
V*
\з, 1
R*
равен 2Р4, а главный момент
Рис. 30
М0 = т0 (PJ + т0 (Ра) + т0 (Рг) Ь т0(Р4).
Для того чтобы найти момент силы Р1 относительно точки О,
опустим перпендикуляр ОА1 из точки О на линию действия
этой силы. Так как сила Рг стремится вращать шестиугольник
вокруг точки О по часовой стрелке, то

где It —длина апофемы ОА1 правильного шестиугольника. Анало-
Аналогично вычислим моменты остальных сил относительно точки О:
Итак, данная система сил эквивалентна силе R — 2Pt, прило-
приложенной в точке О, и паре с моментом Мо — — 4РН.
Одну из сил R' этой пары выберем равной и противопо-
противоположно направленной силе R и приложенной в точке О. Тогда
вторая сила пары R* будет приложена в точке О*, причем
Ш* ±_R. Так как
M0 = m(R*,R),
то
пп* \М0\ 4Ph __ „,
Силы R и R' эквивалентны нулю, а потому данная система сил
приводится к одной силе R*, которая, следовательно, и есть
равнодействующая этой системы сил.
§ 2. РАВНОВЕСИЕ РЫЧАГА
Рычагом называется твердое тело, которое может вращаться
вокруг неподвижной оси под действием сил, лежащих в одной
плоскости, перпендикулярной к этой оси. Точка пересечения
плоскости, в которой лежат все силы, приложенные к рычагу,
с осью вращения называется точкой опоры рычага.
Условием равновесия рычага является равенство нулю алгеб-
алгебраической суммы моментов всех приложенных к нему сил
относительно точки О — опоры рычага, т. е.
2mo(F,) = Q.	A8)
Задачи этого параграфа можно разделить на следующие
две группы:
1)	задачи, относящиеся к равновесию рычага;
2)	задачи, относящиеся к равновесию твердого тела при
возможном его опрокидывании.
44

Первая группа
Равновесие рычага
(задачи 81—84, 112, ИЗ)
Пример 15. Буровая штанга АВ весом Q = 20 кн укреплена при
помощи каната BCD, перекинутого через шкив С и наверну-
навернутого на барабан лебедки D диаметром 25 см. С барабаном
жестко соединен рычаг ОЕ длиной 180 см и весом G = l кн, на
конце которого укреплен противовес Е.
Найти вес Р этого противовеса (рис. 31).
Решение. Так как натяжение каната во всех его точках
одинаково, то реакция каната Т, приложенная к барабану
лебедки, равна весу штанги Q.
Рычаг ОЕ с неподвижной точкой О находится в равновесии;
поэтому алгебраическая сумма моментов всех приложенных
к нему сил относительно этой
точки О равна нулю, т. е.	i^
или
+
откуда
Р —	(
или
р-
., I
1 2
ОЕЛ
р
-G —
Т г
1 ОЕ
0,89
— 77
= —
кн.
= 0,
1+
Пример 16. Однородная бал-
балка АВ весом G = 6 кн, закреп-	ч
ленная в точке А шарнирно, Рис. 31
наклонена к горизонтальной оси
Ах под углом а = 30° и удерживается в равновесии при
помощи прикрепленной к ней в точке В веревки BDE. переки-
перекинутой через неподвижный блок Д к свободному концу которой
подвешен груз Е весом Р. Балка АВ находится под действием
перпендикулярной к ней равномерно распределенной нагрузки
интенсивности q = 2 кн\м и вертикальной силы F=l кн, при-
приложенной в точке С, причем -qq — у- Веревка BD составляет
с вертикалью угол р = 30°. Определить вес груза Р, если
АВ = 3 м (рис. 32).
Решение. Равнодействующая системы равных параллель-
параллельных сил, приложенная в середине С, бачки АВ, равна О =
AB = 2& — 6 кн. Так как натяжение веревки во всех ее
45

точках одинаково, то реакция веревки Т, приложенная к балке
в точке В, равна по модулю весу груза Р. Таким образом,
рычаг АВ с неподвижной точкой Л находится в равновесии
под действием четырех сил F, Q, G и Т; поэтому алгебраиче-
алгебраическая сумма моментов этих сил относительно точки опоры Л
равна нулю, т. е.
mA (F) + <ПаШ)_\ rn_A (G) + mA (T) = 0.	(а)
Так как каждая из сил F, Q, G вращает балку АВ вокруг не-
неподвижной точки Л по часовой стрелке, а сила Т вращает эту
балку вокруг точки Л против часовой стрелки, то тл(Г)>>0,
а моменты остальных сил относительно точки А отрицательны.
Кроме того, А~В J_ Q, а
л# потому
Чтобы вычислить
моменты остальных сил
относительно точки Л,
опустим из этой точки
на линию действия каж-
каждой силы перпендику-
перпендикуляры, тогда
Рис. 32
mA{T)=T-AAx.
Из треугольников ЛСД,
AC^L и АА,В нахо-
находим:
. AL = -у cos а и ААХ = АВ sin у,
АВ
= ^, Y = 90°-a-p\
причем
а потому
AAt = АВ sin [90° —(а + $)] = АВ cos (а + Р).
Подставив эти значения в уравнение (а), имеем-
откуда
46
Т =
— F cos а + -=¦ -\- — cos а
cos(a+P)

или
^ + 6*. 11,63 кн.
Вторая группа
Равновесие тела, которое может опрокидываться
(задачи 94—97)
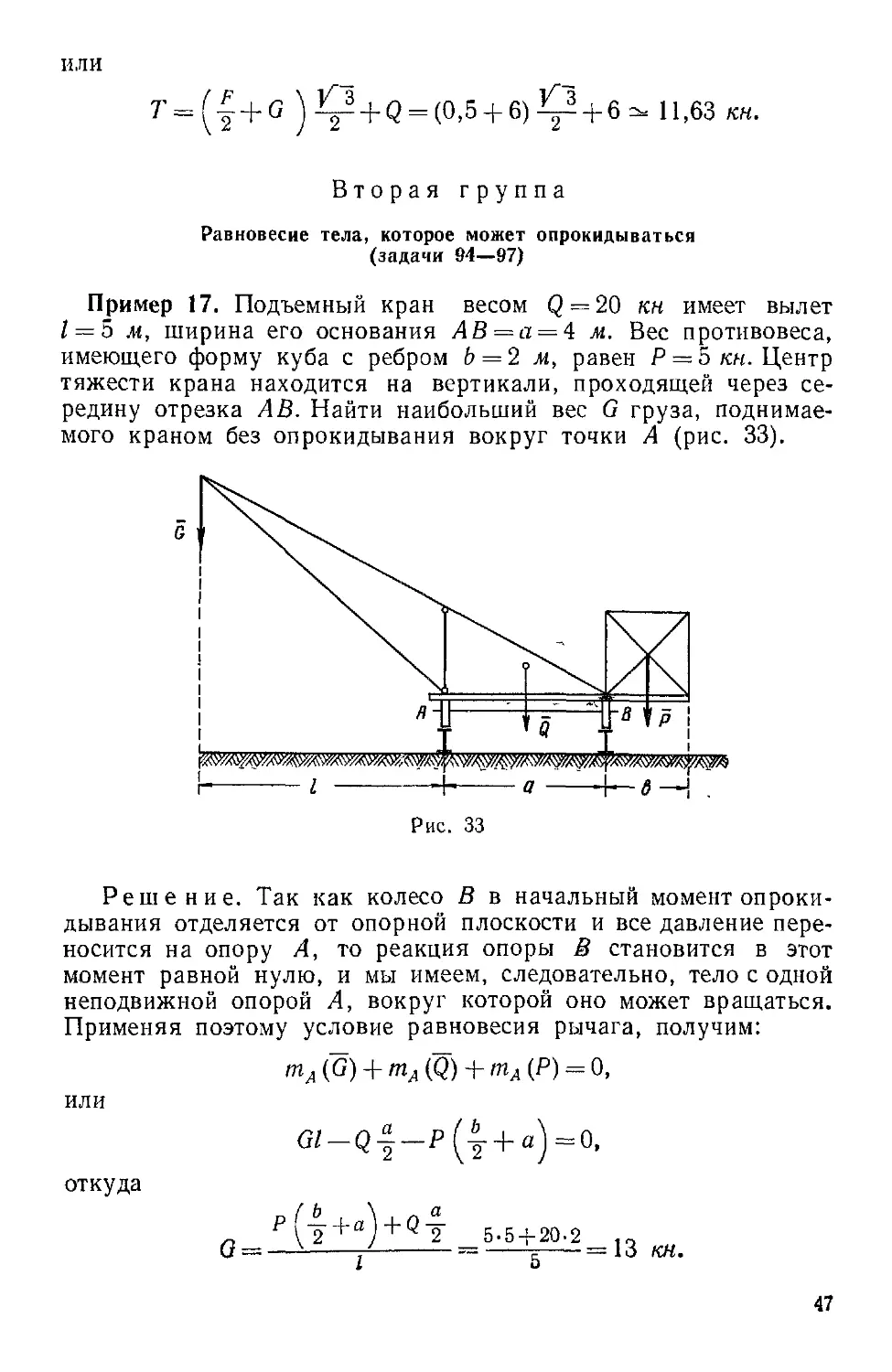
Пример 17. Подъемный кран весом Q = 20 кн имеет вылет
1 = 5 м, ширина его основания АВ=а=А м. Вес противовеса,
имеющего форму куба с ребром b = 2 м, равен Р = 5 кн. Центр
тяжести крана находится на вертикали, проходящей через се-
середину отрезка АВ. Найти наибольший вес G груза, поднимае-
поднимаемого краном без опрокидывания вокруг точки А (рис. 33).
Рис. 33
Решение. Так как колесо В в начальный момент опроки-
опрокидывания отделяется от опорной плоскости и все давление пере-
переносится на опору А, то реакция опоры В становится в этот
момент равной нулю, и мы имеем, следовательно, тело с одной
неподвижной опорой А, вокруг которой оно может вращаться.
Применяя поэтому условие равновесия рычага, получим:
или
откуда
а)=0,
р 4"
47

§ 3. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА ПОД ДЕЙСТВИЕМ ПЛОСКОЙ
СИСТЕМЫ СИЛ
Для равновесия плоской системы сил, приложенных к твер-
твердому телу и не пересекающихся в одной точке, необходимо
и достаточно, чтобы главный вектор R этих сил и их главный
момент Мо относительно произвольной точки О, лежащей в пло-
плоскости действия этих сил, были равны нулю, т. е.
A9)
В координатной форме эти условия выражаются следующими
тремя уравнениями:
.	B0)
= 0. )
Условия равновесия плоской системы сил, расположенных
как угодно на плоскости, можно выразить еще в двух других
видах.
1. Алгебраическая сумма моментов сил относительно трех
произвольных точек А, В, С, не лежащих на одной прямой,
равна нулю, т. е.
2>лE)=°. \
B1)
0F,) = O,
(F,) = 0. J
2. Алгебраическая сумма моментов всех сил относительно
двух произвольных точек А и В равна нулю и сумма проек-
проекций этих сил на какую-либо ось, не перпендикулярную к прямой,
соединяющей точки А и В, равна нулю, т. е.
B2)
В частном случае, если все силы плоской системы парал-
параллельны, то условия равновесия B0) таких сил выражаются не
тремя, а двумя уравнениями:
2*.,=о,
причем ось Ох параллельна данным силам.
48

Условия равновесия плоской системы параллельных сил
можно выразить и в другой форме:
=0,
причем прямая АВ не параллельна данным силам.
Задачи на равновесие плоской системы сил можно разбить
на два основных типа, а именно:
1)	задачи на равновесие плоской системы параллельных сил;
2)	задачи на равновесие плоской системы сил, расположен-
расположенных как угодно.
Задачи второго типа можно еще классифицировать по харак-
характеру связей, наложенных на рассматриваемое тело, подразде-
подразделяя их на следующие две группы:
а)	задачи, в которых линии действия реакций всех связей
известны;
б)	задачи, в которых линия действия реакции одной из свя-
связей неизвестна.
Общие указания, сделанные в § 6. гл. I, о направлении ре-
реакций связей и решении задач на равновесие несвободного
твердого тела, остаются такими же и при решении задач этого
параграфа.
Чтобы задача была статически определима, число неизвест-
неизвестных реакций должно быть не больше трех, так как при равно-
равновесии твердого тела под действием плоской системы сил в общем
случае можно составить три уравнения равновесия [уравнения
B0) или B1), или B2)].
При составлении уравнений равновесия за центр моментов
следует выбирать такую точку, через которую проходят линии дей-
действия двух неизвестных сил, тогда в уравнение моментов отно-
относительно этой точки войдет только одна неизвестная сила и ее
легко будет определить из этого уравнения.
Если данное тело находится в равновесии под действием
плоской системы параллельных сил, то число неизвестных ре-
реакций не должно быть больше двух, так как в этом случае мы
имеем только два уравнения равновесия [уравнения B3) или B4)].
Задачи типа I
Равновесие плоской системы параллельных сил
(задачи 89—94)
Пример 18. Однородная горизонтальная балка АВ — 1,5 м
весом Р = 1500 н, заложенная между двумя опорами С и D, на-
находится в равновесии под действием пары сил (F1, Ft) с мо-
моментом т=1000 н-м. К концу В балки прикреплена веревка,
переброшенная через блоки К и ?, другой конец которой за-
49

ш
1 j
А
Щ
Г
и
л
*.
0
1
р
л
в
креплен неподвижно в точке L. К центру подвижного блока Е
подвешен груз весом Q = 400«. Определить реакции опор С
и D, если АС^- 25 см, CD = 30 см; трением на блоках и в опо-
опорах пренебречь (рис. 34).
Решение. Так как опоры С nD относятся к типу связей,
указанному на рис. 16 B), то реакции этих опор Rc и RD на-
направлены перпендикулярно к балке. Как видно из рисунка,
силы, приложенные к балке, стремятся повернуть балку так,
что давление балки на опо-
опору С направлено по верти-
вертикали вверх, поэтому реак-
реакция Rc направлена по
вертикали вниз; давле-
давление балки на опору D на-
направлено по вертикали
вниз, поэтому реакция RD
опоры D направлена по
вертикали вверх. Реакция
веревки Т, приложенная
к балке в точке В, на-
направлена вдоль веревки,
рис 34	т- е- п0 вертикали вверх.
Так как натяжение ве-
веревки во всех ее точ-
точках одинаково, то сила Т равна натяжению части КЕ ве-
веревки, которое равно, очевидно, у. Следовательно, Т=~ .
Таким образом, балка АВ находится в равновесии под дей-
действием параллельных сил Р, Т, Rc, RD, Fit Ft, причем F2 =
=-_=—Fj, а потому составим два уравнения равновесия B3) для
этой балки. Приравняв нулю алгебраическую сумму сил, при-
приложенных к балке АВ, и сумму их моментов относительно
точки С, получим два уравнения равновесия для определения
двух искомых реакций #с и Rd- При составлении этих урав-
уравнений необходимо учесть, что сумма моментов сил пары отно-
относительно любой точки не зависит от положения этой точки и
равна моменту этой пары, поэтому
пгс G\) + гпс (F2) = m (Fx, Ft) =
= — 1000 н-м.
Этот момент берем со знаком минус, потому что пара стре-
стремится повернуть балку по часовой стрелке. Алгебраическая
сумма сил пары равна нулю, следовательно, имеем:
1)	RD~-Rc-P+T = 0, _
2)	mc(P)^mc{T) \-mc{RD) im(Fl,Fl) = 0.
50

Найдем теперь моменты сил Р, Т, RD относительно точки С:
mc(f)= ТСВ= Г 1,25 ==250 н-м,
= —Р-0,5 = — 750 н-м.
Так как силы Т и Rd стремятся повернуть балку вокруг
точки С против часовой стрелки, то моменты этих сил относи-
относительно точки С положительны, а момент силы Р относительно
точки С отрицателен, так как сила Р стремится повернуть
балку вокруг точки С по часовой стрелке. Подставив все за-
заданные и найденные значения сил и их моментов в уравнения
равновесия, получим:
1)	Rd — Яс=1300;
2)	0,3 Rd — 750 +-250—1000 = 0.
Из второго уравнения находим
п 1500 СГ1ПА
Rd = -Q-3- = 5000 н,
Подставив значение Rd в первое уравнение, получим
tfc==#D_ 1300 = 3700 н.
Задачи типа II
Равновесие плоской системы сил в общем случае
Первая группа
Задачи, в которых линии действия реакций всех связей известны
(задачи 118—125)
Пример 19. Однородная горизонтальная балка А В весом
Р = 120я концом В опирается при помощи катков на гладкую
наклонную плоскость с углом наклона а = 30°, а в точках А
и С балка соединена шарнирно с невесомыми стержнями АК
и CL, шарнирно закрепленными в неподвижных точках К и L.
В точке D под углом р = 45° к балке приложена сила F^=60 н.
Определить реакции в точках А, С и В, если AD = 5DB,
ВС = 2СА, стержень CL вертикален, а стержень АК составляет
с осью балки угол у = 60° (рис. 35).
Решение. Реакция Rg в точке В направлена перпенди-
перпендикулярно к опорной плоскости катков, а реакции RA и Rc не-
невесомых стержней АК и CL направлены вдоль этих стержней
[см. рис. 16 E и 7)]. Так как балка находится в равновесии
51

под действием плоской системы непараллельных сил (F, Р, RA>
Rc, RB), то нужно составить три уравнения равновесия, при-
приравнивая нулю суммы проекций на оси Сх к Су всех сил, при-
приложенных к балке, и сумму моментов этих сил относительно
Рис. 35
точки С Вычисления моментов всех сил относительно точки С
и проекций этих сил на оси Сх и Су расположим в табл. 5.
Составим следующие три уравнения равновесия:
\) — RA cos 60° - RB cos 60° + F cos 45° = 0;
2) - RA cos 30° — P—Rc—F cos 45° -f RB cos 30° = 0;
3) R,
AB f'i
,AB
6
AB
А В f'A
6 ' 6	4 F 'чв з^
Из первого и третьего уравнений имеем:
= 0.
Решая последние два уравнения совместно, находим RB и RA:
RA = F ]/2—#д з* 26,8 «.
Подставив найденные значения RA и RB во второе уравнение
равновесия, найдем:
о	р	F ~\~ (R 	I
52
- г)*- — 135,5 н.

Таблица 5
Сила
Р
F
А
Rb
«с
X
0
F cos 45° =
F 2
2
2
0
у
	р
~ f cos 45° =
- F 2
i?^ cos 30° =
Уз~
«A 2
#B cos 30° =
— ^ 2
-Re
Плечо силы относительно
точки С
„ АВ АВ_АВ
~ 2 3 ~~ fa
СМ = CD sin 45е" =
ХЛВ
CiV = CA sin 60° =
3 2 ЛВ 6
СЕ —С В sm 60° =
~3 Л 2 3
0
Знак момента
относительно
точки С
—
+
тс
— P-Q-
Ra 6
Уз
3
0

Знак минус, полученный для значения силы Rc, указывает,
что эта сила имеет направление, противоположное принятому
на рисунке, т. е. стержень CL не растянут, а сжат.
Вторая группа
Задачи, в которых линия действия реакции одной из связей неизвестна
(задачи 129—135)
Пример 20. Однородная балка АВ весом Р = 40 н концом А
закреплена шарнирно, а промежуточной точкой D опирается
свободно на гладкий неподвижный цилиндр. К концу В балки
прикреплена веревка, перекинутая через неподвижный блок и
несущая на свободном конце груз весом Q1 — 10h. В точке С
к балке подвешен груз весом Q2 = 20 н. Определить реакции опор
RA и RD в точках А и D, если /_ КВА = /_ВАК = 30°, ^ = 4"
AD
и щ = 2 (рис 36).
Решение. Реакция Rd гладкой цилиндрической неподвиж-
неподвижной поверхности направлена по общей нормали к поверхности
цилиндра и балки, а реакция веревки Т направлена вдоль ве-
веревки. Так как натяжение
веревки во всех ее точках
одинаково, то T=Q1 = \0 н.
Реакция неподвижного ци-
цилиндрического шарнира при-
приложена в точке А, а модуль
и направление этой реакции
неизвестны. Поэтому выбе-
выберем оси координат Ах и Ау,
направленные, как указано
на рис. 36, и разложим реак-
реакцию RA на две составляю-
составляющие ХА и Уд, направленные
по этим осям. Следователь-
Следовательно, балка АВ находится в
равновесии под действием
плоской системы непарал-	рис
лельных сил Р, Г, ХА, YА,
Rd, Q2, а потому составим три уравнения равновесия для этой си-
системы сил. Эти уравнения упрощаются, если их составить в форме
B2). При этом за центры моментов следует выбрать такие
точки, в которых пересекаются по две неизвестные силы, т. е.
точку Л и точку Е пересечения линий действия сил Ул и RD.

Составим теперь два уравнения моментов относительно точек Л
и Е и уравнение проекций на ось Ау, не перпендикулярную
к прямой АЕ:
1) S У = У а + Rd cos 60° — Т cos 60° — Qs—Р = 0;
о\ Vm,-	О -°
6) 7,гпд — V2 '
3) 2тя = ХдЛ?— 7-?M-Q2 ^ cos60°-Р ^ cos60° = 0.
Отрезки AAt, АЕ и ЕМ найдем из треугольников АА В,
AED и ЕМК:
ЛЛ1 = ЛВ sin 30°=^,
О 2-2АВ
ЕА =
cos 30°
Так как /?/CL = /_KLE = 60°', то
?M = K?cos30°,
a KE = LE = LK.
Из равнобедренного треугольника Л/(В находим:
^ = ЛК cos 30°,
откуда
/з	з /з у з з
Следовательно,
: У! АВ
ЕМ-
_
3/3" 2 - 6 •
Подставив значения заданных сил и вычисленных плеч, полу-
получим:
2) |^о = -10.1 + 20.1 + 40.|;
3) X^-^-Q.-i—20~ —40-JL = 0.
3 /З '6	6	4
Из третьего уравнения находим Хд:
Из второго уравнения находим
55

Найденные значения ХА и RD подставим в первое уравнение
и найдем УА:
Гл-65-^ = 58,75 н.
Модуль полной реакции RA и ее угол ср с осью Ах определим
по формулам:
ИЛИ
т. е.
= arc tg 3,01,
Ф = 72а.
Пример 21. Однородный стержень АВ весом Q — 20 н в точке
Л закреплен шарнирно, а в точке С свободно опирается на опору
С. На стержень АВ действует пара с моментом М = 5 н-м, а к
концу стержня В привязана
^[	веревка, перекинутая через
блок D, на конце которой
висит груз весом Р =5 j/^fw.
Определить реакции шар-
S нира А и опоры С,
если ЛС = 2ВС = 40 cjm, a
^/ЛВ?, = 45° (рис. 37). _
Решение. Реакция /?с
опоры С направлена перпен-
перпендикулярно к стержню АВ.
Направление реакции /^л
шарнира А неизвестно; по-
поэтому разлагаем эту реакцию
на две составляющие ХА и YА,
направленные по осям ко-
координат, причем ось Ах на-
направлена вдоль стержня АВ, а ось Ау перпендикулярна
к нему. Реакция веревки BD приложена к стержню в точке В
и направлена вдоль веревки. Так как натяжение веревки BLK
во всех ее точках одинаково, то реакция веревки Т равна по
величине весу груза Р, т. е. Т—Р.
Составим три уравнения равновесия, приравнивая нулю
сумму проекций всех сил на координатные оси и сумму момен-
моментов этих сил относительно начала координат:
1)	ХА— Г cos 45° = 0;
2)	YA +tfr-Q-rcos45° = 0,
3)	Rc AC-T y4Bcos45° — Q-AE — /И=0.
Рис 37
56

Из первого уравнения находим:
Из уравнения C), в котором
АС = 40, А
и
находим:
40	Г" Ч*" 40""""
Подставив значение Rc во второе уравнение, получим:
V2 3 V2 D 3 п _М.
или
4
40
Пример 22. Вертикальная ось АВ подъемного крана, вес
которого равен Р = \2кн, может вращаться в подпятнике А
и подшипнике В. Груз весом
Q = 8,4kw поднимается при помо-
помощи веревки, перекинутой через
блок Е и идущей к лебедке D,
закрепленной на оси крана, как
указано на рис. 38. Определить
реакции подшипника В и под-
подпятника А, если центр тяжести С
отстоит от оси вращения на рас-
расстоянии, равном 0,9 м, АВ =12 м
и /С? = 4 м (рис. 38). _
Решение. Реакция RB под-
подшипника В перпендикулярна к
оси вращения А В, а реакция RA
подпятника слагается из двух со-
составляющих ХА и YА, где Хл —
реакция стенок, a YА — реак-
реакция дна подпятника [см. рис.
16 (8)].
Составим три уравнения
равновесия для сил ХА, YA, RB,
Р, Q, приложенных к крану, при-
приравнивая нулю суммы проекций
этих сил на оси х и у и сум-
сумму их моментов относительно	Рис. 38
67
? в

точки А:
2)	YA-P-Q = 0;
3)	— Р-0,9 — Q-4— /?B-12 = 0.
Из третьего уравнения находим /?в:
{\ц==	Го	== >^>' КН.
Подставляя значение RB в первое уравнение, найдем ХА:
Ад = —H.b = q,i /см.
Из второго уравнения находим YА:
Примечание. Уравнения равновесия можно было составить и в
другой форме, приравнивая нулю сумму моментов всех сил, приложенных к
крану относительно точек А и В, и сумму проекций этих сил на ось у:
— RBl2—P0,9—Q-4 = 0,
2—Р0,9—Q-4 = 0,
§ 4. РАВНОВЕСИЕ СИСТЕМЫ,
СОСТОЯЩЕЙ ИЗ НЕСКОЛЬКИХ ТВЕРДЫХ ТЕЛ
В случае системы твердых тел, соединенных между собой,
силы, действующие на эту систему, можно подразделить на две
группы:
1)	внешние силы;
2)	внутренние силы.
Внутренними силами называются силы взаимодействия между
телами, входящими в данную систему. По закону равенства
действия и противодействия внутренние силы всегда попарно
равны по модулю и прямо противо-
противоположны по направлению, но при-
приложены к двум разным взаимодей-
взаимодействующим между собой телам си-
системы.
Внешними силами называются те
силы, с которыми тела, не входя-
входящие в данную систему, действуют на
тела этой системы.
Рассмотрим, например, систему, изображенную на рис. 39.
Балка АВ весом Р, может вращаться вокруг оси А непо-
неподвижного цилиндрического шарнира и концом В опирается сво-
свободно на другую балку CD весом Рг, которая подперта в точке Е
и соединена со стеной шарниром ?>,

В данном случае система состоит из двух тел: балки АВ и
балки CD.
Внутренними силами для дгнюй системы являются силы
взаимодействия между балками, т. е. сила N2 давления балки АВ
на балку CD и сила N}, с которой балка CD действует
на балку АВ. По закону равенства действия и противодействия
силы Ыл и jft равны по модулю и противоположны по направ-
направлению, т. е. Nt = —N2,
Веса Р, и Рг балок представляют собой силы, с которыми
эти балки притягиваются к Земле, и, следовательно, для данной
системы являются силами внешними, так как Земля по отноше-
отношению к этой системе есть внешнее тело. Реакции RA и RD шар-
шарнирных опор А и D, а также реакция RE опоры Е являются
для данной системы тоже внешними силами, так как шарнирные
опоры А и D и опора Е не принадлежат к рассматриваемой
системе, состоящей только из двух балок.
При решении задач на равновесие системы тел необходимо
учесть, что все внешние и внутренние силы, приложенные
к каждому телу в отдельности, уравновешиваются. Следова-
Следовательно, в случае плоской системы сил можно составить по три
уравнения равновесия для каждого из этих тел в отдельности.
Таким образом, для системы, состоящей из п тел, можно
составить всего Ъп уравнений равновесия. Поэтому, если число
неизвестных сил в данной задаче не более Зя, то такая задача
является статически определенной. Если же число неизвестных
в задаче окажется больше Ъп, то такая задача не может быть
разрешена только на основании уравнений статики абсолютно
твердого тела и потому является статически неопределенной.
Так как внутренние силы попарно равны по величине и
направлены по одной прямой в противоположные стороны, то
алгебраическая сумма их моментов относительно любой точки
равна нулю и сумма их проекций на любую ось также равна
нулю. Поэтому, если составим уравнение равновесия (уравне-
(уравнение моментов относительно какой-либо точки, или уравнение
проекций на какую-либо ось) для каждого тела в отдельности
и затем все эти уравнения сложим, то в полученном уравнении
члены, содержащие внутренние силы, попарно уничтожаются
и, следовательно, в это уравнение будут входить только внеш-
внешние силы.
Таким образом, если система тел находится в равновесии, то
внешние силы, приложенные к этой системе, удовлетворяют
тем же трем уравнениям равновесия, что и в случае равновесия
одного абсолютно твердого тела. Эти уравнения представляют
собой условия равновесия внешних сил, действующих на систему.
Из этих уравнений можно найти все внешние реакции, если
число этих внешних реакций не больше трех. Если же число
59

внешних реакций окажется больше трех или если в задаче,
кроме внешних реакций, требуется найти неизвестные внутрен-
внутренние силы, то необходимо применять метод расчленения системы,
т. е. нужно рассматривать равновесие каждого тела системы
в отдельности и для каждого из этих тел составлять уравнения
равновесия, учитывая при этом все силы, приложенные к рас-
рассматриваемому телу. Если система состоит, например, из двух
твердых тел, то, применяя метод расчленения, получим в общем
случае всего шесть уравнений равновесия (по три уравнения
для каждого тела). Для составления шести уравнений равно-
равновесия можно применять еще и другой прием, а именно: соста-
составить сначала три уравнения для всей системы в целом (как
для одного абсолютно твердого тела) и затем к этим трем урав-
уравнениям присоединить три уравнения равновесия, составленные
только для одного из двух тел данной системы. Этот второй
прием нередко предпочтительнее, так как в уравнения равно-
равновесия, составленные для всей системы в целом, входят только
внешние силы и потому эти уравнения обычно оказываются проще.
Задачи, относящиеся к равновесию системы твердых тел,
в зависимости от вида соединения этих тел между собой можно
разделить на следующие четыре типа:
1.	Задачи, где тела, входящие в систему, опираются свободно
друг на друга.
2.	Задачи, где тела, входящие в систему, соединены между
собой гибкой нитью или невесомым стержнем, концы которого
прикреплены к этим телам при помощи шарниров.
3.	Задачи, где тела, входящие в систему, соединены между
собой при помощи шарнира.
4.	Задачи, относящиеся к определению усилий в стержнях
плоской фермы.
Задачи типа I
Тела, входящие в систему, опираются свободно друг на друга
(задачи 108, 109, 164, 166—168)
В задачах этого типа внутренние силы, т. е. силы давления
этих тел друг на друга, направлены по общей нормали к поверх-
поверхности одного из этих тел в точке соприкосновения его с другим
телом.
Пример 23. Однородная горизонтальная балка АВ дли-
длиной 6 м и весом Р, = 2400 н, закрепленная в неподвижной
точке А шарнирно, опирается свободно в точке С на подпор-
подпорную балку CD длиной 5 м и весом Р2 = 3200 н. Балка CD,
составляющая с вертикалью угол а = 60°, закреплена в точке D
при помощи неподвижного цилиндрического шарнира и удержи-
удерживается в равновесии при помощи горизонтальной веревки ЕК
причем DE = 2 ц,
60

В точке В к балке АВ приложена сила Р = 1200 н, наклонен-
наклоненная к балке под углом р = 60°. Определить реакции шарниров А
и D, натяжение веревки и давление балки АВ на балку CD,
если точки А и D лежат на одной вертикали (рис. 40).
У
Рис 40
Решение. Данная система состоит из двух тел: балок АВ
и CD. Внешними силами для этой системы тел являются силы Plt
Pt, F, реакция веревки Т, направленная вдоль веревки, и реак-
реакции RA и RD шарниров А и D.
Разложим каждую из этих реакций на две составляющие:
вертикальные (YA и YD) и горизонтальные (ХА и XD). Для внеш-
внешних сил, приложенных ко всей системе, можно составить только
три уравнения равновесия, а число неизвестных сил равно пяти
(ХА, YA, XD, YD, T), поэтому расчленим систему, т. е. рассмот-
рассмотрим равновесие каждой балки в отдельности. Так как балка АВ
опирается на конец балки CD сво.
бодно, то реакция Rc балки CD,
приложенная к балке АВ, направ-
направлена перпендикулярно к АВ, т. е.
Г 2
Рис 41
Рис 42
по вертикали вверх. Следовательно, балка АВ находится в равно-
равновесии под действием сил Хл, YA, F, Rc, Р, (см. рис. 41).
Составим три уравнения равновесия этих сил, приравняв
нулю алгебраическую сумму их моментов относительно точек А
61

и С и алгебраическую сумму проекций этих сил на ось х:
1)	-Р,^~ F
2)	YAAC-P
3)	ХА—F cos 0=0.
Но
AC = CD sin a = 5 sin 60° =
а потому эти уравнения принимают вид:
б 5^) fi -0
° 2 У 2 ~U>
Из этих уравнений находим:
У • 6 =* 3100.8*.
3
5 /3
з—-^) = (96-36|Лз). 10^337,2 «.
Далее рассмотрим равновесие балки CD под действием сил
XD, YD, Pt, T, Re, где Re — давление балки АВ на балку CD,
причем по закону равенства действия и противодействия
/?с=— Re Составим три уравнения равновесия сил, прило-
приложенных к балке CD, приравнивая нулю алгебраическую сум-
сумму моментов этих сил относительно точки А и алгебраическую
сумму их проекций на оси х и у (см. рис. 42):
4) Хц-Т=0;
б) YD-P2-Rc = 0;
6) — P.^sina—Rc DC sin a +- T-DE = 0.
Из этих уравнений находим:
sma = A600 ^3100,8)^^ = 10,17 кн,
XD=T= 10,17 кн,
Ve=P, + /?c = 6,3 icw.
62

Задачи типа Л
Тела, входящие в систему, соединены между собой гибкой нитью
или невесомым стержнем, концы которого прикреплены
к этим телам при помощи шарниров
(задачи 108, 162, 163)
В задачах этого типа реакции нити или стержня, направлен-
направленные вдоль этой нити или вдоль этого стержня, являются внут-
внутренними силами.
Пример 24. В шестизвенном механизме к кривошипу ОА
приложена пара сил с моментом т, вращающая этот кривошип
против часовой стрелки. Стержень АВ соединен шарнирно с кри-
кривошипом ОА и коромыслом ВС, причем коромысло ВС может
Рис. 43
вращаться вокруг неподвижной точки С. Стержень ED соединен
шарнирно концом Е с серединой звена СВ, а концом D—с пол-
ползуном, который может перемещаться в горизонтальных направ-
направляющих. Определить, какую горизонтальную силу F следует
приложить к ползуну D, чтобы механизм оставался в равнове-
равновесии, а также реакции шарниров О и С и реакцию горизонталь-
горизонтальных направляющих ползуна D, если О А ]_АВ, /_ ABC = 60°,
/_DEC = 90°; кривошип О А вертикален. Весами всех звеньев
механизма пренебрегаем; /п==30 н-м, ОА = 0,5 м (рис. 43).
Решение. Система состоит из трех тел: кривошипа О А,
коромысла С В и ползуна D, соединенных между собой шар-
шарнирно невесомыми стержнями АВ и DE. Поэтому расчленим
систему и рассмотрим равновесие каждого из этих тел в отдель-
отдельности. Реакции S, и S2 невесомого стержня АВ, приложенные
к звеньям ОА и СВ соответственно в точках А а В, направ-
направлены вдоль стержня АВ в противоположные стороны и равны
по модулю, т. е. 5, = —5„. Точно так же реакции Ss и 54
63

невесомого стержня ED, приложенные соответственно в точке ? к
коромыслу СВ и в точке D к ползуну, направлены вдоль стержня
ED в противоположные стороны и по модулю равны, т. е. Ss = — S4
[см. рис. 16G)]. Реакцию каждого из шарниров О и С разло-
разложим на составляющие: вертикальную (Уо и Ус) и горизонталь-
горизонтальную С^о и Хс). Нормальная реакция N горизонтальных
направляющих ползуна вертикальна; предположим, что она
направлена вверх. Для определения всех неизвестных сил
составим уравнения равновесия для каждого из трех указан-
указанных тел: кривошипа ОА, коромысла СВ и ползуна D:
а)	для кривошипа ОА (два уравнения моментов относи-
относительно точек О и Л и уравнение проекций на ось у):
1)	m—SfiA = O,
2)	т + ХоОА=0,
3)	Ко = 0;
б)	для коромысла СВ (два уравнения проекций на оси х
и -у и уравнение моментов относительно точки С):
4)	Хс—S2 +5, cos (90°-60°) = О,
5)	Yc—S, cos 60° = О,
6)	— SfiE + StCB sin 60° = 0;
в) для ползуна (только два уравнения проекций на оси х
и у, так как силы, приложенные к ползуну, пересекаются
в одной точке):
7)	54cos30°— F = 0,
8)	S4cos60° + yV = 0.
Из первого и, шестого уравнений находим:
так как
то
= 60 н и S, = S4 = 601/1 н.
Далее из четвертого и пятого уравнений находим Хс и Ус,
а из седьмого и восьмого уравнений F н N:
= 60-30/3-1/3"= —33 н, F = S4-^ =
Л/ = -|= -30 К~3= —51,9 н.
я,
64

Знаки минус, полученные-для N и Хс, указывают, что направ-
направления этих сил противоположны указанным на рисунке.
Задачи типа III
Тела, входящие в систему, соединены между собой шарнирно
(задачи 110—112, 143, 147—154)
В этом случае внутренняя сила, т. е. сила, с которой одно
тело действует на другое, приложена в центре шарнира, но
направление ее неизвестно.
Поэтому при решении таких задач эту силу разлагают
на две составляющие, направленные по координатным осям.
Из задач этой группы следует особо отметить важный частный
случай, а именно: система состоит из двух тел с тремя шар-
шарнирами, из^которых два являются неподвижными опорными
шарнирами, а третий соединяет эти два тела между собой,
например, в случае трехшарнирной арки (рис. 44). Если трех-
шарнирная арка находится в равновесии
под действием плоской системы сил, то
можно составить всего шесть уравнений
равновесия (по три уравнения для каж-
каждой части АС и ВС арки в отдельно-
отдельности).	44
Так как направление реакции в каж-
каждом из трех шарниров А, В и С неиз-
неизвестно, то при решении задачи о равновесии трехшарнир-
трехшарнирной арки каждую из этих реакций нужно разложить на две
составляющие (по координатным осям х и у). Следователь-
Следовательно, всего будем иметь шесть неизвестных реакций, которые
можно найти из шести уравнений равновесия. Таким образом,
задача о равновесии трехшарнирной арки является статически
определимой.
Пример 25. Две однородные балки АВ — 4ми весом Р, =60 «
и ?С = 3 м и весом Рг = 40 н соединены в точке В шарнирно.
Первая балка горизонтальна и концом А заделана жестко,
а вторая концом С свободно опирается на гладкую наклонную
плоскость с углом наклона а = 30°. Определить реакции в точ-
точках А и С, если /_АВС =120° (рис. 45).
Решение. Данная система состоит из двух тел: балок АВ
и ВС. Реакция Rc наклонной плоскости направлена перпенди-
перпендикулярно к этой плоскости, а реакция заделки эквивалентна
силе RA, приложенной в точке А, направление которой не-
неизвестно, и паре сил с неизвестным моментом т [см. рис. 16A0)].
Обозначая составляющие силы RA по координатным осям
через ХА и YA, составим три уравнения равновесия внешних
сил, приложенных к данной системе: уравнения проекций
4 3«к, 2374	63

на оси х и у и уравнение моментов относительно точки В:
1)	Хл + #ссоз60° = 0,
2)	YA + Rc cos 30°—Р% — Рг = 0,
3)	Pi^_y^B-Ps^cos60° + /?cB/< + m = 01
где B/C_L^c Так как в этих трех уравнениях число неизвест-
неизвестных равно четырем (ХА, У'А, Rc, m), то для решения задачи
необходимо данную систему расчленить в шарнире В и рас-
рассмотреть равновесие одной из балок в отдельности. При этом
достаточно составить только одно уравнение равновесия для
этой балки. В данном случае проще всего составить уравнение
8
Рис 45
моментов относительно точки В для балки ВС, так как неизвест-
неизвестная реакция шарнира В в это уравнение не войдет. Составляя
это уравнение, получим:
4) -Р2^сс
Отрезок ВК найдем из прямоугольного треугольника ВСК,
в котором /_ВСК = 60°; B/C = BC-cos30°, а потому Rc= Pa т§^=-
20
11,52 н. Подставив найденное значение R,
в первые три уравнения, находим:
100—10 = 90
— Рг^ = 240 «-
66

Пример 26. На рис. 46 показана схема копра, состоящего
из двух одинаковых ферм, соединенных между собой шарни-
шарниром В. Веса этих ферм Q, и Qt равны и приложены в точ-
точках D и Е.	__
На левую ферму действует горизонтальная сила Р давления
ветра. Определить реакции в шарнирах А, В, С при указан-
указанных на рисунке размерах.
Решение. Направле-	ivs
ния реакций в шарнирах х» » х«
А ВГС неизвестны, а по-
потому разложим каждую
из них на горизонталь-
горизонтальную и вертикальную со-
составляющие, направив их,
как указано на рисунке.
Пусть Хв, Yв — реакции
левой фермы, приложен-
приложенные к ферме ВС в точке
В, а Х'в, Ув — реакции
правой фермы, приложен-
приложенные в той же точке к фер-
ферме АВ, причем Хв= —X в
и УВ=—7В.
Так как в данной за-
задаче нужно найти 'шесть
неизвестных реакций (ХА,
УА, Хс, Ус, Хв, YB), то нужно составить шесть уравнений
равновесия. Для этого сначала составим три уравнения равно-
равновесия для всей системы в целом (уравнения равновесия внеш-
внешних сил КА, ТА, хс, 7С, р, Qlf qt).
Приравнивая нулю сумму моментов сил относительно каж-
каждой из точек Л и С и сумму проекций этих сил на ось к,
получим:
ОI \J 11 	(л) ~~т- \J CZ	ril	 j дь ^= \Jm
Далее составим три уравнения равновесия для фермы ВС
(уравнения равновесия сил Хс, Yc, XB, YB, Q2, приложенных
к этой ферме). Приравнивая нулю сумму моментов этих сил
относительно точки С и сумму их проекций на оси хну,
получим:
4)	X
5)	У
6)	Qa X h'y l
Рис 46
4»
67

Решим теперь полученную систему шести уравнений.
Из второго и третьего уравнений находим:
Ph _ Qjl-Ph _ р h
Y =¦
Из пятого уравнения находим:
Qtl + Ph_n , Dh
тр-
Из шестого уравнения имеем:
h P и X _
Теперь из четвертого и первого уравнений получаем:
у — у — 2aQ* +hP
лс— — лв— щ
p
ЧН	2Н
ИЛИ
Задачи типа IV
Задачи, относящиеся к определению усилий в стержнях плоской фермы
(задачи 197—207)
Фермой называется геометрически неизменяемая система
прямолинейных стержней, соединенных по концам шарнирами.
В задачах статики рассматриваются только статически опреде-
определимые фермы, т. е. такие фермы, для которых выполняется
соотношение
т = 2п—3,
где т—число стержней,
п —число узлов (шарниров) фермы.
Кроме того, предположим, что внешние силы приложены
только в узлах фермы и трение в шарнирах отсутствует. Тог-
Тогда, если пренебречь весом стержней, их реакции будут направ-
направлены вдоль этих стержней и каждый стержень будет либо сжат,
либо растянут. При решении задач, как правило, направляют
реакцию каждого стержня от соответствующего узла, т. е.
предполагают, что стержень растянут. Будет ли данный стер-
стержень в действительности растянут или сжат определяется по
знаку найденной из уравнений равновесия реакции этого стерж-
стержня: если реакция положительна, то стержень растянут, а если
она отрицательна, то стержень сжат (см. гл. I, § 4).
68

Пример 27. Определить усилия в стержнях плоской фермы,
изображенной на рис. 47, пренебрегая весами стержней, если
силы Fj_ и Fz горизонтальны и каждая из них равна 20 кн,
а сила F, вертикальна и равна 15 кн; АН = #С = CD = h,
AB = a = jh (рис. 47).
Решение. Внешними силами для данной системы являются
заданные силы Fs, Ft, Fz и реакции опор RA и RB в точках А
и В. Усилия в стержнях, соединяю-
соединяющих узлы фермы, являются внутрен-
внутренними силами для этой системы. Для
того чтобы определить внутренние
силы, необходимо систему расчле-
расчленить. Поэтому, чтобы определить
усилия в стержнях 1,2, 3, разре-
разрежем ферму по этим стержням, мыс-
мысленно отбросим нижнюю часть фер-
F,
гу\
Ех
I /
V
с
Рис. 47
Рис. 48
мы и уравновесим оставшуюся верхнюю часть реакциями раз-
разрезанных стержней Slt S2, S3, которые направлены вдоль этих
стержней. Предполагая, что стержни /, 2, 3 растянуты, напра-
ним каждую из сил Sj, S2, S3 от соответствующего узла. Соста-
Составим три уравнения равновесия для верхней части фермы в
виде B2), т. е. два уравнения моментов относительно точки С
пересечения стержней 1 а 2 я относительно точки Е пересече-
пересечения стержней 2 и 3 и одно уравнение проекций на ось х, пер-
перпендикулярную к параллельным стержням / и 3 (рис. 48).
Тогда в каждое уравнение равновесия войдет только одна
неизвестная сила:
63

Из этих уравнений находим:
где
а потому
„.	р 	р =—	416
s -A.
°*~coso '
cos a
Так как S2>0, S3<0, S, = 0, то стержень 2 растянут, 3—сжат,
а / — не работает.
Для определения усилий в стержнях 7, 8, 9 проведем сече-
сечение II —П по этим стержням и рассмотрим равновесие части
фермы HDEK, находящейся под
3	действием сил Fv Ft, F3 и реак-
реакций S,, S6, S9 перерезанных стерж-
стержней 7, 8, 9. Направляя каждую
из сил 5„ 58, S9 от соответствую-
соответствующего узла, составим два уравне-
уравнения моментов относительно то-
х
Рис 49
Рис 50
чек А и К и одно уравнение проекций на ось х^ (рис. 49)
70

Из этих уравнений находим:
кн,
S =M^j = 66,6 кн.
8 cos a
Так как 5, >0, S8>0, a S9<0, то стержни 7 \\ 8 растянуты,
а стержень 0 сжат. Аналогично, проводя разрез /// — ///, най-
найдем усилия в стержнях 4, 5, 6.
Для определения усилия в оставшихся стержнях 10, 11, 12,
13 проще воспользоваться способом выр'езания узлов Вырежем,
например, узел В, к которому приложена неизвестная вертикаль-
вертикальная реакция RB опоры В, неизвестная реакция Slo стержня 10
и реакция Ss стержня 9, равная по модулю и противоположная
по направлению найденной уже реакции S9. Так как стержень 9
сжат, то реакция S9 направлена к узлу В и по модулю равна
|S,|, т. е. |5,1 = |5,| = ^, + (^ + 3^)| (рис. 60).
Для сходящихся сил RB, S,, Sl0 составим два уравнения
равновесия (два уравнения проекций на оси х и у):
откуда S10 = 0, RB = | S9 \ = F3 + (F8+ 3F,)|= 121,6 кн. Анало-
Аналогично, вырезая узлы D, L и Н, найдем реакции Su, Slt и S1S.
Примечание Силу Se можно было бы направить по общему пра-
правилу от узла В, но тогда эту силу нужно считать равной найденному
алгебраическому значению силы S9, т е S9 = — < F% + (F2 + 2F{)—>, урав-
уравнение проекций на ось у при этом будет
откуда
Описанные классификация и типы задач не включают всех
видов задач на равновесие системы тел. Необходимо иметь
в виду, что возможны и такие задачи, в которых два тела,
входящие в данную систему, соединены между собой двумя
внутренними связями того или другого из описанных типов
связей, например при помощи нити и шарнира, как в задаче
71

№ 147 из «Сборника задач» И. В. Мещерского. Кроме того,
возможны задачи на равновесие системы трех тел. Методы ре-
решения всех таких задач остаются такими же, как и в случае
одной внутренней связи, соединяющей два тела системы.
Глава III
РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
Трением скольжения называется сопротивление, возникаю-
возникающее при относительном скольжении двух соприкасающихся тел.
Поэтому сила трения скольжения, приложенная к одному из
трущихся тел, направлена противоположно его скорости отно-
относительно второго тела.
Опытным путем установлено, что величина силы трения
скольжения пропорциональна нормальному давлению одного из
трущихся тел на другое, т. е.
FTV = fN.	B5)
Коэффициент пропорциональности / (отвлеченное число) на-
называется коэффициентом трения скольжения
Как показывает опыт, величина этого коэффициента зависит
от материала трущихся тел, от состояния их поверхностей,
а также от их относительной скорости.
Если трущиеся тела находятся в покое, то в этом случае
трение называется статическим Максимальная величина силы
статического трения, т. е. величина этой силы, соответствующая
моменту начала относительного скольжения трущихся тел, опре-
определяется по той же формуле, что и в случае трения при отно-
относительном движении, т. е
(^тр)И.х = /сЛ	B6)
где /ст — статический коэффициент трения.
Этот коэффициент обычно несколько больше коэффициента
трения при движении. Отсюда следует, что величина силы ста-
статического трения всегда удовлетворяет условию:
F^^fjf.	B6')
Благодаря наличию силы трения между данным телом и опор-
опорной поверхностью полная реакция R этой поверхности есть
равнодействующая двух сил: нормальной реакции N и силы
трения Fn (рис. 51).
72

Угол q> между направлениями нормальной реакции /V и
полной реакции R, соответствующий максимальному значению
силы трения, называется углом трения.
Отсюда следует, что
^4JM-X = /-?#==^-	B7)
Метод решения задач статики при наличии трения остается
таким же, как и в случае отсутствия трения, т. е. сводится
к составлению и решению уравнений равновесия, но только
в эти уравнения, кроме заданных сил, приложенных к данному
телу, и тех реакций, которые рассматривались в предыдущей
главе, войдут еще и силы трения. При
этом следует иметь в виду, что в таких
задачах расчет ведется обычно на макси-
максимальную величину сил трения, а потому
эти силы определяются по формуле
Рассматриваемые ниже задачи, отно-
относящиеся к равновесию тел при наличии
трения, можно разделить, как и в пре-	Рис. 51
дыдущей главе, на два основных типа:
I. Задачи, относящиеся к равновесию одного твердого тела.
П. Задачи, в которых рассматривается равновесие систе-
системы тел.
Задачи, относящиеся к первому типу, можно еще подразде-
подразделить на следующие две группы:
1)	задачи, решаемые при помощи двух уравнений равнове-
равновесия (двух уравнений проекций);
2)	задачи, решаемые при помощи трех уравнений равно-
равновесия.
Задачи типа 1
Первая группа
Задачи, решаемые при помощи двух уравнений равновесия
(задачи 73, 74)
Пример 28 Дробление руды при помощи щековой дробилки
происходит путем раздавливания ее между подвижной щекой ВС
и неподвижной щекой АС.
Найти максимальную величину угла а между щеками, при
котором возможно дробление, для чего руда не должна выдав-
выдавливаться вверх. Угол трения между куском руды и щеками
дробилки равен ср (рис. 52).
4В Зак 2374	„„

Решение. Нормальные реакции щек АС и ВС обозначим
#, и Мг, силы трения —F, и Fs; при этом
F.^/JV, и F^fN,,
где f—коэффициент трения между куском руды и поверхно-
поверхностями щек АС и ВС, f = tg(f, ф — угол трения.
Так как под действием сил А/, и Л/2 кусок руды будет вы-
выдавливаться вверх, то приложенные к нему силы трения F, и
F2 будут направлены вдоль щек
АС и ВС вниз.
Следовательно, кусок раздраб-
ливаемой руды находится в равно-
равновесии под действием сил F,, F2
N,, Ns (весом руды пренебрегаем
ввиду малых размеров куска ру-
руды), а потому сумма проекций
этих сил на любую ось равна
нулю. Если за оси проекций вы-
выберем направления СА и СВ, то
будем иметь:
1)	— F, — F2cosa +
+N2 sin a = О,
2)	— Fi—Flcosa +
-f-^V, sin a = 0,
или
1)
2)
Рис. 52
-)- F2 cos a = N2 sin a,
cos a -(- F2 = Л^г sin a.
Сложив эти уравнения, получим:
(F! + F2) (I + cos a) = (N, + Nt) sin а.
Так как
то
пли
отсюда
или
Но
(H-cosa)(F, -j-Fs)^/(l-
(А\ + Nt) sin a < (/V, + N,) f A + cos a),
sin a s?/(l +cosa),
sin a _ г
1 -f cos a'
sin a = 2 sin -5- cos -^ ,
74

1 Ц- cos a = 2 cos3 -|-,
поэтому
„ . а а
2 sin ^ cos T
а
2cos2 ±
ИЛИ
tg f ^ tg
откуда
или
Следовательно, максимальная величина угла, при котором
руда не будет выдавливаться вверх, равна удвоенному углу
трения.
Приведенное решение этой задачи можно упростить, если за
ось проекций принять биссектрису угла АСВ. Тогда достаточно
составить только одно уравнение проекций на эту ось. В самом
деле, проектируя все силы, приложенные к куску руды, на
направление биссектрисы угла АСВ, получим:
—F, cos ~ - F, cos | + N, sin | + JV2 sin ~ = О,
или
(F, + f.) cos !=(JV, + tf,) sin-J,
откуда
*„ а - F- + Pi
Le 2 -/V,+yV2-
Ho
F, + Ft < / (A/, t /V2) = tg Ф {N, + N2),
поэтому
tg f < tg Ф,
откуда
или
Рассмотрим далее геометрический способ решения	этой
задачи. _
Сначала построим линии действия полных реакций Rt	и R2
щек АС и ВС, приложенных к куску руды в точках Е	и D.
4В*	75

Уюл между полной реакцией и ее нормальной составляющей
не превышает угла трения, поэтому, обозначая уюл между си-
силами /?, и /V, через р и угол между силами R2 и А'г через у,
будем иметь: $ ^ ф и у ^ Ф-
Так как кусок руды находится в равновесии под действием
двух сил Rt и /?8, то линии действия этих сил лежат на пря-
прямой ED. Из треугольника CDE имеем:
а=180° — (90°—р) — (90°—Y) =
Но
Следовательно,
т. е.
Вторая группа
Задачи, решаемые при помощи трех уравнений равновесия
(задачи 175—182)
Пример 29. Вращающийся кулачок / сообщает толкателю 2
поступательное равномерное движение в вертикальных направ-
направляющих (рис. 53). При своем движе-
движении толкатель преодолевает сопротив-
сопротивление Q. Учитывая трение в направ-
направляющих, определить давление кулачка
на толкатель при указанном на рисун-
рисунке положении механизма. Размеры h
и Ь, толщина б толкателя, а также
угол а между осью толкателя и ка-
касательной к профилю кулачка в точ-
точке его касания с острием толкателя
известны, коэффициент трения в на-
направляющих равен f. Трением между
кулачком и толкателем пренебречь.
Какому условию должен удовлетво-
удовлетворять угол а, чтобы не произошло за-
заклинивание механизма? _
Решение. Давление N кулачка
на толкатель направлено перпендику-
перпендикулярно к профилю кулачка. Силу N
	,5 можно разложить на две составляю-
составляющие: JV' = A/sina — вдоль оси толка-
толкателя и N" = N cos a — перпендикулярно
к оси толкателя. Первая из них пере-
перемещает толкатель и преодолевает со-
Рис. 53	противление его движению, вторая
76

изгибает толкатель. Благодаря этим силам толкатель перемеща-
перемещается и прижимается к направляющим в точках В и С, где воз-
возникают нормальные реакции iV, и Nt и силы трения F,=fNx
и Ft~fNz. Так как толкатель движется прямолинейно и
равномерно, то все приложенные к нему силы уравновеши-
уравновешиваются. Поэтому, располагая, как указано на рисунке, оси
координат, получим:
2 X = — Ncosa + N,— tf, = О,
^,Y=Ni\na—fN1—fNt-Q=O,
2>в = Ntb — fNfi — Q 0,55 +- N sin a 0,56 — N cos a-h = 0.
Эти уравнения можно переписать в следующем виде:
Af, —iV2 = ./Vcosa,
N. + N^j-iNsina-Q),
#2 (Й —/б) = 0,56Q + N(h cos a—0,55 sin a).
Из первых двух уравнений находим:
N2 = j}(N sin a — Q)—^ W cos a.
Подставляя это выражение N2 в третье уравнение, имеем:
^=Д (ЛГ sin a — Q)—b-^- Ncosa = 0,5dQ + N(h cos a — 0,56 sin a),
или
F-/6) (N sin a — Q) — / (b—/S) JV cos a =
= /6Q + /V/ BA cos a—5 sin a).
Отсюда получаем:
(ft —/6) (sma—/cos a)—/Bft cos a—6 sin a)
Для того чтобы не произошло заклинивания механизма,
должно соблюдаться условие:
(Ь—/6) (sin a—/cos a)—/B/z cos a—6 sina)>0,
или
(ft-/6) (tga-/) > BA-6 tga)./,
откуда
Задачи типа II
Равновесие системы тел при наличии трения
(задачи 186 — 188)
Пример 30. Два груза А и В, веса которых равны Р и Q,
лежащие на наклонных плоскостях с углами аир, связаны
веревкой, перекинутой через блок 0.

Найти отношение весов -j при равновесии, если угол тре-
трения грузов о плоскость равен ср (рис. 54).
Решение. Найдем наибольшую величину отношения -q- ,
при которой еще возможно равновесие, предполагая, что дадь-
нейшее увеличение этого отноше-
отношения вызовет движение груза А
по наклонной плоскости вниз, а,
следовательно, груз В начнет
двигаться вверх. В этом случае
силы трения F,
прило-
Рис. 54
женные к грузам А и В, будут
направлены вдоль соответствую-
соответствующих наклонных плоскостей, как
указано на рисунке. Нормальные
реакции наклонных плоскостей,
_ _	приложенные к грузам, обозна-
обозначим JV, и Nr Рассмотрим равновесие груза А, к которому при-
приложены силы Р, Nt, F]p, а также сила натяжения Т, веревки.
Проектируя эти силы на направление АО и направление,
перпендикулярное к АО, получим два уравнения равновесия:
2)	Nt— Pcosa = 0.
Аналогично, рассматривая равновесие груза В, к которому
приложены силы Q, Т\р, АГа и сила Tt натяжения веревки, и
проектируя эти силы на направление ОВ и направление,
перпендикулярное к ОВ, получим еще два уравнения равнове-
равновесия:
3)	Flp-72 + <?sinp = 0,
4)	N,—Q cos 0 = 0.
Учитывая, что Г, = Тг, исключим эти две неизвестные силы,
сложив первое уравнение с третьим.
Тогда получим:
2) Л^ = /
3)WS = C
Но
4) Frp =:
а
поэтому
78
F]p i- F? = tg ф (P cos a -I- Q cos

С другой стороны, из первого равнения имеем:
Следовательно,
Р sin а—0 sin p = tgcp (Р cosa+ Q cos Р).
Разделив это уравнение на Q, получим:
Отсюда
Р	IP
-q sin a— sin |3 = tg ф ( -Q- cos а -(- cos
р
-q (sin a—tg ф cos а) = sin р 4- tg ф cos
Р 	sin р -f- tg ф cos р	sin ф cos р + cos ф sin р sin (Р -f- ф)
Q sin a—tg ф cos a sm a cos ф—cos a sin ф sin (a — ф)
Таким образом, мы нашли наибольшее значение отношения
Р
¦q-, при котором еще возможно равновесие, т. е.
Sill ф 4- ф)
mdx~bin (a—ф) "
Найдем теперь наименьшее значение отношения -j-, при ко-
котором существует равновесие, но так, что дальнейшее уменьшение
этого отношения вызовет опускание груза В и поднятие груза А,
В этом случае направления сил трения F]p и F]p будут про-
противоположны направлениям этих сил в предыдущем случае.
Поэтому, чтобы получить наименьшее значение отношения -~- ,
достаточно в первом и третьем уравнениях равновесия изменить
знаки при F]p и FTp на обратные, что равносильно изменению
знака при tg ф в четвертом уравнении.
Следовательно, будем иметь:
_Р_\ _ ипф-ф)
Q /min ^
Таким образом, равновесие данной системы возможно при
условии:
sin(P—ф)^ Р ^s
' Q ~~~ sin (а—ф)
Пример 31. Два клина А и В, коэффициент трения между
которыми / = tg ф, могут двигаться без трения в своих направ-
направляющих. К клину А приложена сила Р.
Какую силу Q нужно приложить к клину В, чтобы клин А
двигался равномерно в направлении действия силы Р, если
углы аир известны? Весом клиньев пренебречь (рис. 55).
79

Решение Обозначим реакцию направляющих, приложен-
приложенную к клину А, через #,, а реакцию направляющих, при-
приложенную к клину В, через /?2. Так как каждый клин может
двигаться в своих направляющих без трения, то реакции /?, и
Rt направлены по нормали к поверхности соответствующего
клина
При равномерном движении клина А в направлении силы
Р клин В будет скользить по клину А вверх а потому сила
трения Рг, приложенная к клину В, будет направлена по пря-
прямой CD вниз, т. е. в сторону, противоположную перемещению
Рис 55
клина В относительно клина А- По закону равенства действия
и противодействия сила трения Fx клина В, приложенная
к клину А, будет равна по величине и направлена противопо-
противоположно силе трения Ft, а нормальная реакция N2 клина Л,
приложенная к клину В, равна по величине и направлена про-
противоположно нормальной реакции Nt клина В, приложенной
к клину А, т. е.
Так как клин А движется равномерно, то силы Р, /?,, JV,
и Z7!, приложенные к этому клину, уравновешиваются. При этом
клин В будет также двигаться равномерно, и, следовательно,
силы Q, Ft, Rt, Nt, приложенные к этому клину, тоже уравнове-
уравновешиваются. Поэтому сумма проекций всех сил, приложенных
к каждому клину, на направление движения этого клина равна
нулю, т. е.
1)	Р — /^cosct—iV, sina = 0,
2)	FjC
Кроме того,
= fNl и /W
80

где /—коэффициент динамического трения. Подставив эти зна
чения сил трения в первое и второе уравнения, будем иметь:
Р == yV, (/ cos a + sin а),
Q = N,(j cos p + smp).
Но
sin ф cos a + cos ф sin a
-sin p sin фcos p + cos фsin p
_ p
(Ф-fa)
поэтому
P 	/ cos a + sin a
Q f cos p + sin p
откуда
Пример 32. Подъемное приспособление состоит из двух жест-
жестких прямоугольных рычагов АСВ и DK.E, скрепленных шар-
нирно с поперечиной СК. Верхние подушки, соединенные с этими
рычагами при помощи шарниров А и D, раздвигаются клином
М, а нижние подушки; вращающиеся на шарнирах В и Е,
зажимают поднимаемый груз весом Р. Определить силу, растя-
растягивающую поперечину СК, и наименьший коэффициент трения /,
нижних подушек о стенки груза, при котором, груз мо-
может быть удержан, если заданы коэффициент трения f между
верхними подушками и клином, углы а и C и длины AC = DK — lv
СВ = КЕ~1г. Весом приспособления пренебречь (рис. 56).
	' -JH-
8]

Решение. Система состоит из трех тел: двух рычагов АСВ
и DKE и поднимаемого груза. Обозначим силы давления рычагов
на груз в точках В и Е, направленные перпендикулярно
к стенкам груза, через Nt и Ns
за, приложенные к рычагам
ВС A H_EKD,-_4ep&3_Nl и %.
Тогда n[ = — Nj и Ж, = — Nt.
Силы трения F, и F2, прило-
приложенные к грузу, направлены
по вертикали вверх, а к подуш-
подушкам рычагов приложены соот-
соответственно силы трения F\ и F2,
причем 7\'= — 7, Hfi = -F!.
В точках А и D к верхним по
а нормальные реакции гру-
1
Рис
р
57
—Я I
Рис. 58
душкам приложены нормальные реакции N3 и yV4 клина, на-
направленные перпендикулярно к его боковым поверхностям, и
силы трения F3 и /?4, направленные перпендикулярно к силам
N, и Af4 вверх. По формулам B5) и B6) имеем:
Из условий равновесия груза под действием веса Р, нормаль-
нормальных реакций Af, и N 2 и сил трения F, и Fs, имеем:
Тогда
N =N
1 а
Л
(с)
Теперь рассмотрим равновесие рычага АСВ под действием сил
К, #i, N,, Fs и реакции S, поперечины СК, направленной вдоль
82

этой поперечины. Приравнивая нулю сумму проекций всех этих
сил на оси х и у и сумму их моментов относительно точки С,
имеем:
Fa cos а—./V, sin а + S,— ЛГ = О,
F, sin а + Nt cos а — F[ = 0,
__ —N'fiCi — F'fiB, + Ffi A, + ^>СС^= 0,_
гдеСС,1^5, ССг\_Ы\, CB, J_Fi, CM.IF,. (рис.58)
Из треугольника САС^, в котором ^/СЛЛ, = а—р, находим:
СС, = AAt = ЛС cos (a —P) = /, cos (а —Р),
CAt = ЛС sin (а — р) ==/, sin (а — р).
Далее, из треугольника СВВг имеем:
СВг = СВ sin p = /2sinp,
ВВ, =-СВ cos p =/2 соь p.
Кроме того, из уравнений (а), (Ь) и (с):
т N' — N = —
где ф—угол трения между верхними подушками и клином.
Уравнения равновесия принимают вид:
Р
Ыг (tg ф cos а — sin а) -f- о, — ^т = О,
Р
yV3 (tg ф sin а 4- cos а) = -~- ,
N3l, [cos (а —Р) + tg ф sin (а —Р)] = Щ- (~^ + sin p).
Так как
,	. sin (ф—а)
tg ф cos а — sin а = ——	¦ ,
& т	cos ф
то окончательно имеем:
п л; sin (ф—а)
Л/
cosq> ' °'~ 2/, '
cos (Ф~а) - р •
cos ф ~ Т '
83

Из уравнения B) находим:
л/ Р cos ф
» ' 2 cos (ф—а) *
Подставив найденное значение N3 в уравнения 1 и 3, находим
из этих уравнений /, и S,:
Р	Р
— tg(cp — a) + S,= 5Г,
il cos(9—Д + P)	L a- ts? R
/acospcos(9—a) Л Р>
откуда
Глава IV
СИСТЕМА СИЛ, РАСПОЛОЖЕННЫХ КАК УГОДНО
В ПРОСТРАНСТВЕ
§ 1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ КАК ВЕКТОР
И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
При изучении системы сил в пространстве момент силы F
относительно точки О изображается вектором, приложенным
в точке О, перпендикулярным к плоскости л, в которой лежат
сила ~F и точка О, и направленным так, чтобы наблюдатель,
смотрящий с конца этого вектора на плоскость я, видел силу
7 направленной по отношению к точке О против часовой
стрелки.
Рис. 59
Рис 60
Модуль этого момента равен произведению силы F на
длину перпендикуляра d, опущенного из точки О на линию
действия этой силы (рис. 59).
Аналогично в виде вектора изображается и момент пары,
а именно: вектор-момент пары перпендикулярен к плоскости этой
84

пары и направлен так, что наблюдатель, смотрящий на пару
с конца этого вектора, видел направление вращения, вызывае-
вызываемого парой, против часовой стрелки.
Абсолютное значение момента пары равно произведению
модуля одной из сил пары на плечо этой пары (рис. 60).
Вектор-момент пары равен вектору-моменту одной из сил пары
относительно точки при-
приложения второй силы этой
пары.
Кроме момента силы
относительно точки, при
изучении системы сил в
пространстве приходится
рассматриватьтакже и мо-
момент силы относительно
той или иной оси.
Моментом силы F от-
относительно данной оси на-
\
\а!М
Рис. 61
зывается алгебраическое
значение момента проек-
проекции этой силы на плос-
кость, перпендикулярную
к этой оси, относительно точки пересечения оси с этой плоскостью.
Следовательно, чтобы найти момент силы F относительно
оси г, нужно спроектировать силу F на плоскость, перпенди-
перпендикулярную к оси z и проведенную через произвольную точку О,
лежащую на этой оси, и затем полученную проекцию / умножить
на длину h перпендикуляра, опущенного из точки О на линию
действия проекции /. При этом произведение fh берется со зна-
знаком плюс или минус (рис. 61).
Таким образом, _
F	№ = ±fh*	B8)
Знак момента силы относительно данной оси выбирается сле-
следующим образом: если наблюдатель, смотрящий с положитель-
положительного конца оси, видит проекцию/ направленной по отношению
к точке О против часовой стрелки, то момент силы F относи-
относительно этой оси считается положительным. В противном случае
этот момент считается отрицательным. Поэтому на рис. 61
момент силы F относительно оси z положителен.
Из формулы B8) следует, что момент силы относительно
оси г равен нулю, если / = 0, или /г = 0, т. е. когда сила F
* Здесь и в дальнейшем под то([) понимается модуль момента вектора /j
относительно точки О.
65

параллельна оси либо когда линия действия этой силы пере-
пересекает данную ось.
Моменты силы F относительно трех координатных осей х,
у и г выражаются следующими формулами:
B9)
где X, Y, Z — проекции силы F на координатные оси, а х, у,
г — координаты точки приложения силы.
Между моментом силы F относительно данной оси и векто-
вектором моментом той же силы относительно какой-нибудь точки,
лежащей на этой оси, существует следующая зависимость: про-
проекция вектора-момента силы F относительно произвольной точки
О на какую-либо ось, проходящую через эту точку, равна мо-
моменту силы F относительно этой оси, т. е.
тг (?) = т0 (F) cos у.
Пример 33. К вершинам Q, В и ?_куба_со стороной а прило-
приложены равные по модулю силы Р, S и Q, направленные соот-
соответственно по стороне
BE и по диагоналям
DA и D/(. Найти мо-
8 менты каждой из этих
сил относительно коор-
координатных осей х, у и г
(рис. 62).
Решение. Первый
способ (геометриче-
у ский). При вычислении
моментов нескольких
сил относительно коор-
координатных осей следует
сначала выделить те
силы, которые пересе-
пересекают одну из коорди-
координатных осей или ей
параллельны, так как
в этих случаях мо-
момент силы относительно оси равен нулю. Сила Р параллель-
параллельна оси х, а сила S пересекает ось г, а потому тх (Р) = 0 и
mz(S) = 0. Далее следует выделить те силы, которые располо-
расположены в плоскости, перпендикулярной к одной из координатных
Рис. 62

осей; в этом случае момент силы относительно такой оси по
абсолютной величине равен моменту силы относительно точки
пересечения этой оси с перпендикулярной к ней плоскостью,
в которой расположена эта сила.
Сила Q лежит в плоскости KEDAt, перпендикулярной к оси
х, причем Л,— точка пересечения оси к с этой плоскостью.
Так как AtE ^ KD, то плечо силы Q относительно точки Л,
равно AtO, — —к— а. Следовательно, m.A,(Q)~^—ciQ. Для на-
наблюдателя, смотрящего с положительного конца оси* на
плоскость Л,?>?¦/(, сила Q стремится вращать куб вокруг оси х
против часовой стрелки, поэтому момент силы Q относительно
оси х положителен, и, следовательно, mx{Q) = mAl (Q) = ^-aQ.
Аналогично вычисляются моменты силы Р относительно осей
у а г, так как сила Р расположена в плоскости EBCD, перпен-
перпендикулярной к оси {/.ив плоскости АВЕК, перпендикулярной
к оси г:
mv (Р) = nicJP) = P-CB = Ра,
тг(Р)= —тА(Р)= - Р-АВ= ~Ра
Теперь переходим л вычислению моментов силы Q относи-
относительно осей у и г и моментов силы S относительно осей х и у.
Чтобы вычислить момент силы Q относительно оси у, сле-
следует сначала эту силу спроектировать на координатную плос-
плоскость гОх. Для этого следует из начала D и конца D, силы Q
провести прямые, параллельные оси у, до пересечения с плос-
плоскостью гОх в точках Л, и d,. Тогда вектор Aidl = Qxz явля-
является проекцией силы Q на плоскость хОг. Плечо гЯ'ОЙ проекции
относительно точки О равно 0Л, =а. Для наблюдателя, смотря-
смотрящего с положительного конца оси у на плоскость гОх,
сила QX2 стремится вращать куб вокруг оси ц по часовой
стрелке, поэтому момент силы Q относительно оси у отрицате-
отрицателен, и, следовательно,
Но	V
Qxz — Q sin 45° =
а потому
Для вычисления момента силы Q относительно оси z спроекти-
спроектируем эту силу на плоскость хОу; для этого ИЗ конца D, силы
87

Q проведем прямую параллельную оси г, jio пересечения с
плоскостью хОу в точке d. Тогда вектор Dd = Qxy является
проекцией силы Q на плоскость хОу. Плечо силы Qxyотноси-
Qxyотносительно точки О равно ОА1 = а. Так как момент силы Q отно-
относительно оси 2 отрицателен, то
mz(Q) = -mo(Qxy) = -QXya.
Но
Q,v = Qcos45°=Q^.
а потому
Чтобы вычислить моменты силы S — DH относительно осей х и у,
находим проекции этой силы Syz = Ch и Sxz = Alhl на коорди-
координатные плоскости уОг и xOz. Так как грани куба являются
квадратами, то OB _\_Ch и OK_\_Atht, а потому
Далее
Sxz = Syz = S cos б;
из прямоуюльного треугольника DAC находим
cos6= = ^=/!-
AD ау з Г 3
Следовательно,
Второй способ (аналитический). Под аналитическим спосо-
способом определения моментов силы относительно координатных
осей понимается вычисление этих моментов по формуле B9).
При этом нужно предварительно найти (если они не заданы)
координаты точки приложения силы и ее проекции на оси коор-
координат. Принимая во внимание, что сила Р параллельна оси х,
сила Q перпендикулярна к этой оси и составляет с осями у и г
углы 45°, получим:
Р„ = Р, Ру = Рг = О, Qx = О, QV = -Qcos45° =
= -^ Q. Q* = Q cos 45° = ^2- Q.
88

Обозначим угол /_DAO через у. Тогда 5j = S cosy. Чтобы вы-
вычислить проекции силы S на оси х и у, спроектируем эту силу
на плоскость хОу, а затем полученную проекцию Sxy, направ-
направленную по прямой DO, спроектируем на оси хну. Тогда
имеем:
S = S sin у, Sx=- Sxy cos 45°,
S S45°
или
= S,, =
у x xy
S =-SxvcoS45°,
xy
sin yS.
Из прямоугольного треугольника О AD находим:
ОА а У~з
OD -, /~ 2
зш у = w = 1/ -3 .
Значения координат точек приложения заданных сил, кото-
которые находим непосредственно из чертежа, и значения моментов
этих сил, вычисляемые по формулам B9), указаны в табл. 6 и 7.
Таблица 6
Точка приложения силы
В
D
Координаты
X
0
а
у
а
а
z
а
0
Сила
Р
Q
S
0
Л
3
Моменты сил относительно координатных
-ZY
aS
m^zX-xZ
Pa
1 ^
3
Таблица 7
осей
— Ра
2 аУ
0
Таким образом, момент силы относительно координатной оси
можно вычислить двумя способами:
1) аналитическим способом, пользуясь формулами B9), выра-
выражающими искомый момент силы через проекции этой силы на
координатные оси и через координаты точки ее приложения;
89

2) геометрическим способом.
При геометрическом способе определения момента силы отно-
относительно координатной оси следует различать три случая:
1)	сила лежит в координатной плоскости, перпендикулярной
к координатной оси, относительно которой вычисляется момент,
тогда момент силы относительно этой оси равен по модулю ее
моменту относительно начала координат;
2)	через линию действия силы можно провести плоскость,
перпендикулярную к одной из координатных осей, тогда момент
силы относительно такой оси равен по модулю моменту силы
относительно точки пересечения этой плоскости с данной коор-
координатной осью;
3)	если сила не лежит в плоскости, перпендикулярной к дан-
данной координатной оси, то следует эту силу спроектировать на
координатную плоскость, перпендикулярную к данной оси,
и вычислить момент полученной проекции относительно начала
координат.
§ 2. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
К ДАННОМУ ЦЕНТРУ
(задачи 232—240)
Если задана система сил Ff (i= I, 2, ..., ri), расположенных
как угодно в пространстве, то эти силы можно привести к про-
произвольно выбранному центру О. В результате такого приведе-
приведения, как и в случае плоской системы сил, получим одну силу
R, приложенную в центре приведения О и равную главному
вектору данной системы сил, и одну пару с вектором-моментом
Мо, равным главному моменту этой системы сил относительно
центра О.
Следовательно, будем иметь:
Аналитически модуль и направление векторов R и Мо опре-
определяются по их проекциям на координатные оси х, у и г,
начало которых находится в центре приведения О, причем
Rx — 2 *i,
RZ =2^!'
Mox = ^ms(F,),	C0)
MOv = 2 mv (Fi)>
90

Отсюда имеем:
cos
C1)
cos (M i) — Ox — *¦* "'* M
cos(Mo, /) = ^ = S^C
C2)
Модуль и направление главного вектора не зависят от вы-
выбора центра приведения. Поэтому главный вектор является
первым инвариантом данной
системы сил. Модуль и направле-
направление главйого момента Мо изменя-
изменяются с изменением центра при-
приведения.
Но скалярное произведение
R-Mo главного вектора и главно-
главного момента не зависит от выбора
центра приведения, т. е. являет-
является вторым инвариантам
данной системы сил. При этом
R-Mo = RMocos ф, где ф—угол
между направлениями главного вектора R и главного момента
Мо. Выражая это скалярное произведение через проекции векто-
векторов R и Мо, имеем:
Рис. 63
R ¦ М 0 = RXM ох + RvMOy + R,MOZ.
C3)
Если второй инвариант данной системы сил не равен нулю,
то эта система приводится к динаме, т. е. к паре и к силе,
перпендикулярной к плоскости этой пары (рис. 63).
Прямая, проходящая через точку О,, по которой направлены
векторы R и Мо,, называется центральной осью данной системы
сил. При этом отрезок 00t перпендикулярен к векторам R
91

Mo, а его длина равна:
00,=
Мо sin ф
R '
При перемещении центра приведения по центральной оси
главный момент данной системы не изменяется, т. е. остается
равным Мо1г причем его модуль является наименьшим по
сравнению с модулем главного момента данной системы сил
относительно всякого другого центра приведения, не лежащего
на центральной оси.
Величина этого наименьшего момента определяется по фор-
формуле
Mmin = /Wocos(p =	^—з- =—^—.	C4)
Аналитически положение центральной оси определяется ее
двумя уравнениями, которые имеют следующий вид:
М0х — {yRz— zRv) Moy—(.zRx—xRz) Moz—(xR,,— yRx)
	1. =	_	=	^	, C5)
Rx	Ry	Rz
где x, у a z—текущие координаты точки, лежащей на централь-
центральной оси.
Может оказаться, что скалярное произведение R-Mo равно
нулю, но каждый из сомножителей отличен от нуля. В этом
случае главный момент перпендикулярен главному вектору,
т. е. сила и пара, получающаяся в результате приведения
данной системы сил к центру О, лежат в одной плоскости.
М,
Рис. 64
Рис. 65
В этом случае, как уже было указано в § 1 гл. II, система
приводится к равнодействующей, R* = R, которая проходит
через точку О,, лежащую на перпендикуляре, к векторам R
и Мо на расстоянии
Мг
(рис. 64). Если Мо =*0 и
то система сил приводится, очевидно, к одной равнодействую-
равнодействующей силе R, проходящей через центр приведения О.
92

Если же R=0, а Моф0, то заданная система сил приво-
приводится к одной паре с моментом /Ио; в этом случае главный
момент системы не изменяется с изменением центра приведения,
т. е. относительно любого центра приведения главный момент
будет равен Мо (рис. 65).
Наконец, если главный вектор R и главный момент Мо
одновременно равны нулю, то данная система находится в рав-
равновесии.
Эти результаты можно расположить в табл. 8.
R-Mq^O
Система
сил приводится
к динаме
Т
а б л и п а 8
R-м0=о
R?.-0
Система
сил приводит-
приводится к равно-
равнодействующей
#* = 2Л- не
проходящей
через центр
приведения О
/?=о
Система сил
приводится к
одной паре, мо-
момент которой
равен ?то(?,.)
и не зависит
от выбора
центра приве-
приведения О
R?=0
Afo = O
Система сил
приводится к
равнодейст-
равнодействующей R —
= 2/?i • "Ро-
ходящей через
центр приве-
приведения О
Afo = 0
Система
сил нахо-
находится в рав-
равновесии
Пример 34. Даны три силы Р, Р2, Рз, приложенные в точ-
точках Л, @; 2; 1), Л2 A; —1; 3), Л8 B; 3; 1)*, и их проекции на
координатные оси (в ньютонах).
Силы
Р~,
Проекции
X
3
о
— 1
У
5
2
—7
z
4
—6
2
Привести эту систему сил к началу координат.
Решение. Определим сначала проекции главного вектора
и главного момента на координатные оси:
Я* = 2*, = 3—2—1=0,
* Координаты заданы в метрах.
93

Для вычисления моментов сил Р,- относительно координат-
координатных осей воспользуемся формулами B9). Тогда имеем:
- гУд = (- 5 ¦ 1 + 4 • 2)
-1(—7)]=3 + 0+13=16,
+ [—2-2 + 1 (-1I = 3 + 0-5 = -2,
= 2(^-УЛ) = @-5-2-3) +11.2-(-1)(- 2)] +
Теперь по найденным проекциям определяем величину глав-
главного вектора и главного момента:
h-m.
Для определения направления главного момента находим
его направляющие косинусы:
cos (Мо, 0 = ^ = ^ = 0,683
^-^
COSi
COS
. = ^ = _"==—0,726.
Mq 23,4
Так как главный вектор данной системы сил раве_н нулю, то
эта система сил приводится к одной паре с моментом Мо, причем
этот момент не изменяется с изменением центра приведения.
Пример 35. По реб-
ребрам призмы действуют,
как указано на рис. 66,
силы Р, = 40, Р2 =
= Р,= 10, Р8=15,
Рл — 5 н. Кроме того,
дано О А = 20/С = 20 см,
а = 30°. Привести эту
у систему сил к простей-
шему виду.
Решение. Выбе-
Выберем систему координат-
координатных осей, как указано
на рисунке, и найдем
проекции главного век-
Рис. 66	тора на координатные

оси:
R,, =- 2 К, = Р, cos a = 40 cos 30° = 20
Я, = ]? 2,-=Р3 + Р4-Р, sin а = 15+5-40-1 = 0.
Отсюда следует, что главный вектор направлен по оси у
и равен 20J/3 н.
Приводя данную систему сил к началу координат, найдем
проекции МОх, МОу, МОг на оси к, у, г главного момента Мо
относительно точки О:
Так как силы Ра> P4, Ps пересекают ось х, а силы Р2 парал-
параллельна этой оси, то моменты этих сил относительно оси х равны
нулю и, следовательно,
МОх = тх(Р1).
Сила Р, лежит в плоскости zOy, причем наблюдатель, смот-
смотрящий с положительного конца этой оси, видит силу Р, на-
направленной относительно точки О по часовой стрелке, поэтому
тх (Р,) = — PfiE = — PfiK cos a = — 3,46 н ¦ м.
Далее
мо, = 2/МЛ).
Силы Р,, Р3, Ps пересекают ось у, поэтому их моменты
относительно этой оси равны нулю.
Следовательно,
Силы Р2 и Р4 лежат в плоскости zx, поэтому
1 н-м
my (Pj = _ Р40Л = — 1 «• л.
Итак,
MOy=*PfiK-~PfiA~ 10-0,1 — 5.0,2 = 0.
Так как силы Р,, Р2, Ра, Р5 пересекают ось г, а сила Р4
параллельна этой оси, а потому момент каждой из этих сил
относительно оси г равен нулю, следовательно,
0,5>
Так как
_ МО;, = МОг = 0,
то главный момент Мо направлен по оси х и
Мо = y^Afo* + МЬУ + Мог = 3,46 я-л.

Таким образом, данная система сил эквивалентна силе R,
приложенной в точке О, и паре с моментом Мо.
Остается теперь выяснить, к какому простейшему виду можно
привести данную систему сил: к одной равнодействующей силе
или к динаме. Так как главный_вектор R перпендикулярен
главному моменту Мо, то сила R и пара (с моментом Мо)
лежат в одной плоскости гОу, поэтому они приводятся к одной
равнодействующей силе R*, равной и параллельной силе R и
приложенной в точке О1. Найдем эту точку О,.
Для этого нужно на прямой, проведенной из точки О и
перпендикулярной к векторам R и Мо, т. е. в данном случае
на оси г, отложить отрезок, равный
г И 20
При этом отрезок ООХ следует отложить на оси_в таком
направлении, чтобы, смотря с конца вектора-момента Мо, можно
было видеть равнодействующую силу R*, приложенную в точ-
точке 0t> направленной по отношению к точке О против часовой стрел-
стрелки. Так как 00, = 10,
то точка О, совпадает
сданной точкой /С.
Точка К и будет точ-
точкой приложения равно-
равнодействующей.Итак, дан-
данная система сил при-
приводится к равнодейст-
равнодействующей силе R*, при-
приложенной в точке К и
'У направленной парал-
параллельно оси у, причем
н.
Рис. 67
Пример 36. Дана
система сил F,, Рг, Ft,
Ft, Fit приложенных в вершинах прямоугольного параллелепи-
параллелепипеда и направленных, как указано на рис. 67, причем
F, = 60, F±=Ft= 10 я,
r5 = zU н,
ОА=ОВ = 20 см, ОС =10 см.
Привести эту систему сил к простейшему виду.
Решение. Координатные оси х, у, z направим, как ука-
96

зано на чертеже, и введем следующие обозначения: угол ODK
обозначим а, угол КОВ — р и угол АОЕ—у.
При вычислении проекций заданных сил на координатные
оси заметим, что проекции силы F, на оси хну нужно нахо-
находить так же, как это было указано в примере № 12, т. е. сна-
сначала силу Z7, следует спроектировать на плоскость хОу и полу-
полученную проекцию ft спроектировать затем на оси х и у.
Значения проекций всех заданных сил и координаты их
точек приложения расположим в виде табл. 9.
Таблица 9
Pi
У,
—f, sin р =
= —F, sin a sin p
F2
0
F4 sin у
0
Y,
—/, cos p =
= — F, sin a cos j}
0
Ft
0
0
Z,
—Fi cos a
0
0
Ftcos у
F>
K,
10
0
10
0
0
У1
20
20
0
0
0
г
20
20
0
0
20
Из прямоугольных треугольников ODK, ОСЕ и ОВК на-
находим:
20
DK
соза = ^- =
sin a = j/l — cos* a =
a SO 20
OSP = W=T
sin p = l/l —
3 '
2
-Ц
-sin1
Теперь вычислим проекции главного вектора на координат-
координатные оси:
Rx = — Ft sin u sin p 4- f, 4- F4sinY =
= —30,
f ^ = —
5 Заказ , 2374
97

Отсюда видим, что главный вектор R направлен по оси у
влево и по величине равен 30 н.
Переходим к вычислению главного момента Мо относительно
центра приведения О.
Сила F2 параллельна оси х, а остальные силы пересекают
эту ось, поэтому момент каждой силы относительно оси х равен
нулю. Следовательно, МОх = 0.
Точно так же момент каждой из сил F,, Ft, Ft, F, относи-
относительно оси у равен нулю, а потому
МОу = mv (Рг) - z2X2—x2Z2 = 20F2 = 200 н-см.
Моменты сил Flt Ft, Fs относительно оси г равны нулю,
так как эти силы пересекают эту ось, следовательно,
Так как МОх = 0, то главный момент Мо лежит в плоскости
гОу и по величине равен
Так как главный вектор и главный момент отличны от нуля,
то необходимо выяснить, приводится ли данная система сил к
динаме или к одной равнодействующей силе. Для этого вы-
вычислим скалярное произведение главного вектора и главного
момента:
# .~М0 <= RxMOx + RyM Oy + R2M0l = (— 30) 200 = — 6000 н ¦ см
Так как это произведение не равно нулю, то векторы R и
Мо не перпендикулярны и, следовательно, данная система сил
приводится к динаме.
Найдем точку, через которую проходит центральная ось
данной системы сил, а также величину главного момента отно-
относительно этой точки.
Для этого построим главный вектор R и главный момент Мо
по их проекциям на координатные оси и разложим главный
момент по правилу параллелограмма на два составляющих мо-
момента М' и М", из которых М' направлен вдоль главного век-
вектора, т. е. по оси у, а М" перпендикулярен к нему, т. е. на-
направлен по оси г.
Следовательно,
М' = [МОу\ = 2 н-м, М" = \МОг\ = \ н-м (рис. 68).
Пара, имеющая момент М", лежит в плоскости хОу, т. е.
в одной плоскости с главным вектором /?, поэтому одну из
98

сил R' этой пары можно выбрать равной по величине силе R
и направленной прямо противоположно этой силе. Тогда вторая
сила этой пары R* будет приложена в точке О*, лежащей на
оси х, причем плечо пары
будет равно	zl
п/1* м' 100 о о
00* = -н- = -^-я» 3,3 см.	!
Система, состоящая из
силы R и пары (R', /?*),
очевидно, эквивалентна
/?
Л?"
0
W
i
одной силе7?*. Таким обра- ,-^ М' №w«™*» «»
зом, заданная система сил *х
эквивалентна силе R* и	Рис 68
паре с моментом ЛГ, при-
причем M'\\R*. Следовательно, заданная система сил приводится
к динаме, а точка О* находится на центральной оси.
М' есть наименьший главный момент данной системы сил, т. е.
т	-см = 2 н-м.
Эту же задачу можно решить другим способом.
После того как определим проекции на координатные оси
главного вектора и главного момента, можно составить уравне-
уравнения центральной оси данной системы сил:
МОх—(yR, — zRy) MOy—(zRx—xRz) _ MOz—(xRy—yRx)
R~x	Rv ~~ Rz
Подставляя сюда значения MOx, МОу, МОг и Rx, Rv, Rz, получим:
г ( — 30) _ 200 _ —100 — [х(— 30)]
0 ~— 30"""	0	'
откуда
2 = 0 и 30jc —100 = 0,
т. е.
Эти равенства показывают, что центральная ось проходит
через точку О* (-j ; 0; 0j и параллельна оси у. Чтобы найти
51*	99

модуль наименьшего главного момента, достаточно скалярное
произведение R- Мо разделить на величину главного вектора, т е.
§ 3. РАВНОВЕСИЕ СИСТЕМЫ СИЛ В ПРОСТРАНСТВЕ
Для равновесия системы сил, приложенных к твердому телу,
в общем случае необходимо и достаточно, чтобы главный век-
вектор R этой системы сил и ее главный момент относительно
произвольно выбранного центра О были равны нулю т. е.
C6)
Учитывая формулы C0), выражающие проекции главного
вектора и проекции главного момента на координатные оси,
заключаем, что предыдущие два векторных равенства эквива-
эквивалентны следующим шести скалярным уравнениям:
C7)
Эти шесть уравнений выражают условия равновесия системы
сил в общем случае. В частных случаях число уравнений рав-
равновесия может оказаться меньше, так как некоторые из шести
уравнений C7) обращаются в тождества.
В настоящем параграфе рассмотрим задачи на равновесие
несвободного твердого тела под действием пространственной
системы сил, не сходящихся в одной точке. По расположению
линий действия всех сил, приложенных к рассматриваемому
телу, включая и реакции связей, такие задачи можно разделить
на четыре типа: 1) задачи на равновесие пространственной си-
системы параллельных сил; 2) задачи на равновесие пространст-
пространственной системы сил, образующих систему непараллельных ком-
компланарных * векторов, 3) задачи на равновесие системы неком-
некомпланарных сил, каждая из которых параллельна одной из
координатных осей; 4) задачи на равновесие системы неком-
некомпланарных сил в общем случае.
* Компланарными называются векторы, параллельные некоторой пло-
плоскости Если такие векторы приложены в одной точке, то получится
система векторов, расположенных в одной плоскости.
100

Задачи типа I
Равновесие пространственной системы параллельных сил
(задачи 246—252)
Если все силы, приложенные к рассматриваемому твердому
телу, параллельны между собой, то, направляя одну из коор-
координатных осей, например ось Ог, параллельно этим силам,
имеем три уравнения равновесия:
C8)
2)	2
3)	2
Остальные уравнения обращаются в тождества. Таким образом,
число неизвестных в задачах этого типа не должно превышать
трех. Оси Ох и Оу, перпендикулярные к направлениям данных
сил, следует выбирать так, чтобы моменты сил относительно
этих осей вычислялись возможно проще.
Рис. 69
Пример 37. Однородная прямоугольная плита весом G = 300 «
подвешена горизонтально на трех вертикальных тросах. К плите
подвешены грузы весом Р = 200 н и Q = 100 н. Определить
реакции тросов. Размеры в сантиметрах указаны на рис. 69.
_ Решение. Изобразим в виде векторов заданные силы W,
Q и G, учитывая что центр тяжести С прямоугольника нахо-
101

дится в точке пересечения его диагоналей, а также реакции
связей Т,, Т2 и Т,, направляя последние вдоль тросов и учи-
учитывая, что тросы могут работать только на растяжение.
Располагаем, как указано на рис. 69, координатные оси и
составляем уравнения равновесия сил (заданных и реакций
связей), действующих на плиту. Так как силы Р, Q, G, 7\, Тг
и Г3 параллельны оси Oz, то следует составить три уравнения
равновесия в форме C8). Проекции сил 7\, Т2, Тг на ось г
положительны, а проекции сил Р, Q и G отрицательны. Кроме
того, силы Т', и Tt пересекают ось х, а сила Q пересекает ось у,
поэтому моменты сил Т, и Г2 относительно оси х и момент
силы Q относительно оси у равны нулю.
Поэтому уравнения равновесия C8) принимают вид:
2)	тх (Р) + тх (G) + тх (Q) + тх {TJ = О,
3)	mv (Р) + mv (G) + mv (Тг) + mv (T,) = 0.
Сила Р лежит в плоскости, перпендикулярной к оси х, а потому
(см. пример 33)
Аналогично силы G и 7j так же как и сила Q, лежат в пло-
плоскости, перпендикулярной к оси х, а потому
Таким же образом вычисляем моменты сил Р, G, Г2 и Та отно-
относительно оси у.
Для вычисления моментов силы относительно координатных
осей можно также воспользоваться аналитическими формула-
формулами B9). В этом случае имеем:
тх (О) = ycGt—zcGy = ycGz,
так как Gv = 0.
Но #с = 0,5 м, Gz-= — G,
следовательно,
mx (G) = — 0.5G, mv (G) = 2CGX—a:cGs = — л:сОг,
но
хс = 0,2 ж, Сг = — G,
102

а потому
mv(G) = —0.2G.
Аналогично можно вычислить моменты всех остальных сил от-
относительно осей х и у.
Таким образом, уравнения равновесия перепишутся так:
— 20-200 — 50-300- 60-100 + 7,100 =
— Г2-40 + Р-40 t-G-20 — 7>20 = 0,
или
1)
2)
3) , \
Из второго уравнения находим
Т3 = 250 н.
Подставив это значение в первое и третье уравнения толучим:
к.
откуда
7г = 225 н и Г, = 125 н.
Задачи типа И
Равновесие сил, образующих систему непараллельных
комп ланарн ых ~ векторов
В рассматриваемом случае одну из трех координатных осей
например, ось х) располагают перпендикулярно к данным силам.
Еумма проекций этих сил на выбранную таким образом ось
тождественно равна нулю Q?X,- = 0), поэтому из шести урав-
уравнений равновесия пространственной системы сил остается только
пять:
= 0
C9)
Следовательно, число неизвестных в задаче на равновесие одного
тела не должно превышать пяти. Обычно в задачах данного
типа приходится рассматривать равновесие тела, имеющего
103

неподвижную ось вращения. Так, например, тело может быть
закреплено на валу, который опирается на два цилиндрических
подшипника (рис. 70), причем на тело действуют силы, пер-
перпендикулярные к оси вращения. Обычно подшипники конструк-
конструктивно оформляются так, что препятствуют осевым перемещениям
вала (рис. 70, а); применяются также упорные подшипники
(рис. 70, 6). Однако, если на тело действуют силы, перпенди-
перпендикулярные к оси вала, то вдоль этой оси никаких реакций не
возникает и реакции подшипников направлены тоже перпенди-
перпендикулярно к оси вала, т. е. опоры, показанные на рис. 70, а
и 70, б, в рассматриваемом частном случае эквивалентны опо-
опорам, изображенным на рис. 70, в, где никаких устройств, фик-
фиксирующих вал в осевом направлении, нет.
Если действующие на тепо силы перпендикулярны к оси дала то опоры
на рисунках а,бив эквивалентны
Рис 70
Ось вала следует принять за одну из координатных осей
например, ось х), тогда две другие оси (у и г) располагаются
перпендикулярно к оси вала и реакция каждого подшипника
разлагается на два компонента вдоль этих двух осей (см.
оис. 70). В некоторых случаях координатные оси можно выбрать
гак, чтобы каждая сила, действующая на тело, была парал-
параллельна одной из координатных осей [см. задачи №254—256, 261].
Пример 38. Груз Q опускается равномерно при помощи
каната, навернутого на барабан радиуса rD. На общем валу
с барабаном заклинено колесо Е и тормозной шкив С радиуса гс.
К колесу Е приложена пара сил, тормозящая вращение вала,
момент которой равен т* (силы, образующие эту пару, на
рисунке не показаны, а направление ее указано круговой стрел-
стрелкой). Ввиду того, что этот момент не обеспечивает равномерного
спуска груза, осуществляется еще притормаживание системы
при помощи колодочного тормоза, причем колодка тормоза при-
* В таких случаях обычно говорят короче, «к колесу Е приложен
тормозящий момент «г».
104

жимается к тормозному шкиву силой Р. Определить эту силу,
а также реакции подшипников, если коэффициент трения между
колодкой и тормозным шкивом равен /. Размеры указаны на
рисунке (рис 71).
Решение. Рассмотрим равновесие вала с закрепленными
на нем телами. На вал, кроме реакций подшипников, дейст-
действуют: вертикальная сила Q натяжения каната, равная весу
груза Q; вертикальная сила Р давления колодки на тормозной
шкив; сила трения F, направленная по касательной к тормоз-
тормозному шкиву (т. е. в данном случае горизонтально), и, наконец,
тормозящий момент т, который можно изобразить в виде век-
вектора, направленного по
оси вала. Рассмотренные
силы образуют систему
вертикальных и горизон-
горизонтальных векторов, перпен-
перпендикулярных к оси вала
(силы, образующие задан-
заданную пару, можно напра-
направить параллельно оси у,
или оси z, так как пару
можно расположить как
угодно в ее плоскости).
Поэтому, принимая точку
А за начало координат,
ось х направим по оси
вала, а две другие оси
располагаем, как указано
на рисунке (горизонталь-
(горизонтально и вертикально). Учи-
Учитывая, что реакции под- /х
шипников направлены
перпендикулярно к оси
вала, разлагаем каждую
из них на два компонента вдоль осей у и г. Таким образом,
получаем систему сил, расположенных параллельно плоско-
плоскости уг, причем каждая из них параллельна одной из коорди-
координатных осей. Поэтому в данной задаче можно составить пять
уравнений равновесия по формулам C9). При этом вычисления
проекции сил на координатные оси не вызывает трудностей.
Остановимся на определении моментов сил относительно этих
осей. Силы ZA, YA, ZB, YB и P пересекают ось х, поэтому их
моменты относительно этой оси равны нулю. Точно так же силы
УА и ZA пересекают каждую из осей у и г, а потому их моменты
относительно этих осей равны нулю. Силы Р, Q, ZB парал-
SB Зак 237/1	105
Рис 71

дельны оси z, а силы F и YB параллельны оси у, поэтому
mz (Р) = тг (Q) = тг (ZB) = 0, ту (?) = ту (Ув) = 0.
Следовательно, уравнения равновесия C9) принимают вид:
2) Z
3)
4)
5)
При составлении этих уравнений учтено, что сумма моментов
сил, образующих пару, относительно какой-либо оси равна про-
проекции вектора-момента пары на эту ось. Поэтому тормозящий
момент т вошел лишь в уравнение C), так как вектор т про-
проектируется на ось х в свою натуральную величину, а на осталь-
остальные две оси его проекции равны нулю.
Найдем теперь моменты сил F и Q относительно оси х; эти
силы расположены в плоскостях, перпендикулярных к оси х,
поэтому
тх (F) = тс (F) = Frc
и
тх (Q) = — mD (Q) = — QrD.
Далее вычислим моменты сил Р, Q и ZB относительно оси у;
силы Р и ZB расположены в плоскости гАх, перпендикулярной
к оси у, поэтому
ту(Р) = тЛ(Р) = Ра;
mv (zb) = — тл (zb) = — ?в (а + b + с).
Чтобы вычислить момент силы Q относительно оси у, доста-
достаточно эту силу спроектировать на плоскость zAx, тогда
ту (Q) = тА (Qxz) = QX2 (a + c) = Q(a + с),
гак как QXZ = Q (проекция силы Q на плоскость гАх показана
пунктиром).
Теперь находим моменты сил F и YB относительно оси г:
m2(F) = — mA (F ) = —
xyl	' xy1*
* Силы, составляющие пару, приложенную к вороту, в первое и вто-
второе уравнения не входят, так как сумма проекций сил пары на любую
ось равна нулю.

так как Fxy*=F (проекция силы F на плоскость ху показана
пунктиром),
fc).
Таким образом, получим следующие пять уравнений равнове-
равновесия рассматриваемой системы сил:
2)
3)	Frc-QrD + m = 0,
4)	Pa + Q(a+c)—ZB
5)	-Fa + YB(a + b + c)~0.
К составленным выше пяти уравнениям равновесия присоеди-
присоединяется еще одно уравнение, выражающее закон Кулона:
6)	F = fP.
Из третьего уравнения находим:
F = ~(QrD-m).
Тогда из шестого уравнения имеем:
P = f = ±(QrD-m).
Из четвертого уравнения:
где
Из пятого уравнения:
После этого из первого и второго уравнений нетрудно найти
YA и ZB:
ZA = P + Q — ZB = {Qr 	m) \ Q .
В ряде случаев координатные оси невозможно выбрать таю,
чтобы каждая из действующих на тело сил была параллельна
одной из осей (см. задачи № 251, 257, 260, 262—264, 266, 276,
279—281). Тогда координатные оси следует выбрать так, чтобы
наибольшее число сил удовлетворяло этому условию.
5В*	1°7

Пример 39. Ворот, при помощи которого поднимается груз О,
удерживается в равновесии вертикальными силами Р я Q, из
которых сила Q известна по модулю. Вес ворота равен Qlt
радиус колеса равен г, остальные размеры указаны на рисунке.
Определить модуль силы Р и реакции подшипников А в В,
если угол а известен (рис. 72).
Решение. Рассматриваем равновесие ворота. За начало
координат принимаем точку А, ось у направим по оси ворота,
а ось z—по вертикали вверх, т. е. параллельно силам Р, Q и й^;
Рис 72
ось х направим, как указано на рис. 72. Канат мысленно раз-
разрежем и заменим его действие на ворот силой F, равной по
модулю весу груза, т. е. F = G. Каждую из реакций в точках
А и В разлагаем на две составляющие, параллельные осям
х и г, т. е.
Вычислим моменты действующих на ворот сил относительно
координатных осей.
юз

Относительно оси х:
(Проекция силы Р на плоскость уг, перпендикулярную к оси х,
показана пунктиром; очевидно, Руг = Р.)
т* (F) = тА (Руг) = Fyza = F cos a • а.
(Проекция силы F на плоскость уг показана на рисунке пунк-
пунктиром; сила F образует с плоскостью уг угол, равный углу а,
а потому FVZ=*F cos а.)
««(G.) =- тл (\) - - б,а; т* (ZB) - тл BВ) - Za (а + Ь);
Относительно оси </:
ту (ХА) = ту (гд) = ту (Хв)~ ту (ZB) =_my (G,) = О,
ту (Р) = тс (Р) = Pk\ my (f) = — т? (F) ^ — Fr,
"tv(Q) = mo(Q) = Q/.
Относительно оси г:
Щ (Р)_= т* &л>» тг AА) - ш, (гд) = т?гг (G.) = тг (Q) = 0;
тг (F) -= тА (^Х)|) = Fxya = i7 cos (90ч —а) а = Z7 sin а а;
«. Л) = - тА &в) = - Хв (а + *)¦
Учитывая, что F — G, составим пять уравнений равновесия рас-
рассматриваемой системы сил:
1)	ХА— Gcos(90°—a) + Xa = 0,
2)	ZA f ZB—P — 0, + Q + Ocosa^O,
3)	P-c + Gcosa-a—G1a
4)	Рй —G/- + Q/
5)	Gsina-a—X
Из пятого уравнения имеем:
Из четвертого уравнения находим:
P = ±(Gr-Ql
Из третьего уравнения:
109

Подставив найденные значения Хв и ZB в первые два урав-
уравнения равновесия, находим из этих уравнений ХА и ZA:
= G sin a-XB = G sin a ( 1 -
= _L G sin a;
Задачи типа III
Равновесие системы некомпланарных сил, каждая из которых параллельна
одной из координатных осей
В задачах этого типа рассматриваются только те случаи,
когда три координатные оси можно выбрать так, чтобы каждая
из сил, приложенных к телу, была параллельна одной из этих
осей. Для системы некомпланарных и не сходящихся в одной
точке сил имеем шесть уравнений равновесия C7). Следова-
Следовательно, число неизвестных в задаче на равновесие одного тела
может быть равно шести.
В задачах этого типа, где рассматривается равновесие тела
с неподвижной осью вращения (практически наиболее часто
встречающийся случай), уже нельзя считать, что цапфа или вал
и подшипник при различных конструктивных его оформлениях
образуют цилиндрическую пару (такое соединение, при котором
возможны и повороты вала в подшипнике, и осевые перемеще-
перемещения), как это показано на рис. 70.
Если на тело действуют силы, не перпендикулярные к оси
вала, то в подшипнике, фиксирующем вал в осевом направле-
направлении, возникает реакция, состоящая из трех компонентов, два
из которых направлены перпендикулярно к оси вала и один —
Рис. 73
ПО

вдоль оси вала, как это показано для упорного подшипника на
рис. 73, а и для подпятника — на рис. 73, б. Поэтому, для обес-
обеспечения равновесия тела, имеющего ось вращения, должны при-
применяться специальные устройства для устранения возможности
осевого перемещения тела (упорные подшипники, подпятники,
стопорные кольца и т. д.).
В ряде случаев возможность поступательного перемещения
тела вдоль трех осей исключается соответствующим расположе-
расположением цилиндрических подшипников, не имеющих фиксирующих
устройств в осевом направлении (рис. 73, е). В зависимости от
характера связей, наложенных на несвободное тело, задачи
третьего типа можно подразделить на две группы.
Первая группа
Задачи о равновесии тела, имеющего неподвижную ось вращения
(задачи 277, 278)
Пример 40. Массивная однородная плита, имеющая форму
прямоугольного параллелепипеда, весом G, может вращаться
вокруг вертикальной оси
АВ. К плите в точке D
прикреплен канат, пере-
переброшенный через непо-
неподвижный блок и несущий
на свободном конце груз
весом Q, а в точке Е при-
приложена сила Р, направ-
направленная вдоль ребра Ь.
Система удерживается в
равновесии при помощи
пары с моментом т, при-
приложенной к диску, закреп-
закрепленному на валу АВ.
Определить величину мо-
момента т, а также реакции
подпятника А и подшип- ^
ника В. Размеры указаны "*~
на рис. 74.
Решение. Рассматри-
Рассматриваем равновесие плиты.
Изобразим в виде векто-
векторов действующие на пли-	рис_ 74
ту силы Р, G и Q (послед-
(последняя направлена вдоль каната). Так как все эти силы взаимно
ортогональны, располагаем оси координат х, у и z так, чтобы
каждая сила была параллельна одной из осей. Момент пары
Ш

изобразим в виде вектора; этот вектор направлен по оси z вниз
(глядя из конца этого вектора на плоскость действия пары, мы
должны видеть пару направленной против часовой стрелки).
Реакцию подпятника разложим на составляющие ХА, Y А и ZA,
направленные по осям х, у и г. Учитывая, что реакция под-
подшипника В направлена перпендикулярно к оси АВ, разлагаем
ее на две составляющие Хв и Y в, направленные вдоль осей
х и у. Следовательно, в случае равновесия тела, закрепленного
при помощи подпятника и подшипника, имеем пять неизвестных
опорных реакций ХА, УА, ZA, XB, YB. Но число уравнений рав-
равновесия, в которые входят эти неизвестные реакции, также равно
пяти, так как в уравнение моментов относительно оси вращения
(оси г) эти реакции не войдут (силы ХА, YA> XB, YB, ZA пере-
пересекают ось 2 и моменты их относительно этой оси равны нулю).
Искомый момент пары найдем из уравнения моментов относи-
относительно оси г. Из рис. 74 легко определяются проекции сил
Р, G и Q, приложенных в точках Е, С и D, на выбранные коор-
координатные оси, а также координаты указанных точек:
xF = — a, yB=b, zp =
c = 0, Ус = 0, Zc = — G, л
a	b	, , с ?
,= — a, yD=b, zD = d. I
Отсюда
m,, (Q) = zdXd—XdZd = — dQ;
mx (RA) = m, (RA) = mz (RA) = 0.
П2

Таким образом, приходим к следующим уравнениям равновесия
рассматриваемой системы сил:
1)	X
2)	Y
3)	Z
5)	hXB —|G-dQ = 0,
6)	— aP + bQ— m = 0.
Из пятого уравнения имеем: ХЛ= -т- (у<5 + dQ ).
Из шестого уравнения находим: m = bQ—aP.
Из четвертого уравнения: Ув =—^- (c + d)P + -|- G\.
Теперь нетрудно из первого, второго и третьего уравнений найти
остальные три неизвестные величины:
+* ZG
Вторая группа
Задачи в равновесии тела, имеющего три цилиндрические опоры
Задачи этой группы тоже имеют большое практическое зна-
значение, так как в технике часто применяется крепление узлов
машины на три точки.
Пример 41. Тело, имеющее форму прямоугольного паралле-
параллелепипеда, опирается на три_цилиндрические опоры А, В я С.
К телу приложены силы Р, Q и О и, кроме того, в плоскостях
трех граней действуют три пары с моментами яг,, т, и лг,
(направления вращения этих пар указаны круговыми стрелками).
Расстояние ОС=*с, остальные размеры указаны на рисунке.
Определить опорные реакции в точках А, В а С (рис. 75).
Решение. Выберем, как указано на рис. 75, систему
координат О хуг. Моменты пар, действующих на тело, изобразим
в виде векторов т,, т, и т,, приложенных в точке О. Реакции
каждого шарнира разлагаем на две составляющие, перпендику-
перпендикулярные к его оси и направленные параллельно двум другим осям:
Ra — Ya + 2д^ Rb = YB + ZB\
Таким образом, в данной задаче имеем шесть неизвестных сил:
YА' 2д, YB, ZB, Xc, Zc.
Так как число уравнений равновесия также равно шести,
то задача является статически определенной. Все еилы, при-
приложенные к телу, параллельны одной из координатных осей
113

и определение проекций этих сил на оси координат не вызы-
вызывает трудностей. При вычислении моментов этих же сил отно-
относительно координатных осей необходимо учесть, что силы ZA,
У А' %в> Ув пересекают ось х, а силы Zc, Xc, P пересекают ось у,
а потому момент каждой из этих сил относительно соответст-
соответствующей оси равен нулю, т. е.
тх (RA) = тх (RB) = ту (Rc) = ту (Р) = 0.
Кроме того, сила Р параллельна оси х, сила Q—оси у, а сила
G параллельна оси г и mx(P)*=my(Q) = mz(G) = 0. Моменты
остальных сил относительно осей х, у и z определяются одним
из указанных выше способов (см. пример 33):
тх (Q) = mD (Q) = Qh, mz (Q) = m0 (Qxy) = Qa,
(проекция Q силы Q на плоскость ху на рисунке не показана,
очевидно, Qxy = Q);
тх (G) = — tnt- (G) = —Gc,; my (G) = — тк (g) = — Gbt;
my{RA) = — ZA a; mz (Jt A) = YAa; my (RB) =ZBb;
mz{RB) = — YBb; mx{Rc) = Zcc; mz(i?c) = — Xcc.
Составляем шесть уравнений равновесия системы сил:
)
2)
3)
Хс-Р =
B
ZB+ZC-G = O,
114

4)	Qh — G
5)	— Gbt
6)	Рс1 + да1
Из первого и четвертого уравнений имеем:
Теперь второе и шестое уравнения можно переписать так:
Рещая совместно эти уравнения, находим:
^ IP (c-c,)-Q (a, + ft)-m,];
Аналогично решаем совместно третье и пятое уравнения и опре-
определяем ZA и ZB:
Таким образом, все шесть неизвестных компонентов опорных
реакций определены.
Задачи типа IV
Равновесие системы некомпланарных сил в общем случае
В задачах этого типа, так же как и в задачах типа III,
имеем шесть уравнений равновесия. Кроме связей, рассмотрен-
рассмотренных в задачах предыдущего типа, здесь находят применение
сферические подшипники (рис.73, г) и опоры в виде стержней,
имеющих на концах сферические шарниры (рис. 73, 3).
Задачи этого типа в зависимости от характера связей, нало-
наложенных на данное тело, можно подразделить на три группы.
Первая группа
Задачи о равновесии тела, имеющего неподвижную ось вращения
(задачи 270, 271, 273, 274)
Пример 42. Груз Q поднимается равномерно при помощи
лебедки (рис. 76). Струна каната в точке Е набегания каната
на барабан составляет с образующей барабана угол 90° —у> пло*
скость, проходящая через ось барабана и точку Е, наклонена
к горизонту под углом р, причем расстояние от точки Е до
плоскости симметрии зубчатого колеса лебедки равно с; радиусы
барабана и зубчатого колеса лебедки соответственно равны г и R,
115

остальные размеры указаны на рисунке. Определить модуль
движущего усилия Р, приложенного в точке D и образующего
с касательной к начальной окружности колеса угол а, а также
реакции подшипников А и В, если силы сопротивления движе-
движению, возникающие в подшипниках, приводятся к одной паре
с моментом т. Вес ворота равен G и центр тяжести его нахо-
находится посредине между опорами А к В (рис. 76).
Решение. Рассмотрим равновесие барабана лебедки вместе
с колесом, которые совместно с валом АВ составляют одно
твердое тело. Показываем на рисунке силы, действующие на
Рис.
это тело: силу Р, приводящую ворот в движение, и силу F натяже-
натяжения каната, которая равна весу груза Q, если пренебречь потерями
в блоке (на трение в подшипниках и на изгиб каната), т. е. F = Q.
Так как ворот, если смотреть от Л к В, вращается по часовой стрел-
стрелке, то пара, препятствующая этому движению, направлена против
часовой стрелки и, следовательно, момент этой пары изобра-
изобразится в виде вектора т, направленного по оси ворота, как
указано на рисунке. Вертикальную силу веса G ворота на ри-
рисунке не показываем, чтобы излишне не загромождать рисунок.
Точку А принимаем за начало координат и координатные оси
располагаем, как указано на рисунке, принимая ось вала за
ось у и направляя ось г по вертикали вверх. Обращаем вни-
внимание на конструкции подшипников Л и В. Так как эти под-
подшипники фиксируют вал лебедки в осевом направлении, то в
них, кроме перпендикулярных к оси вала реакций, могут воз-
возникать также продольные реакции, направленные вдоль оси
вращения. Очевидно, продольная реакция возникает в том под-
подшипнике, который воспринимает давление, направленное вдоль
116

оси вращения и вызываемое действием приложенных к телу
заданных сил. В рассматриваемом случае осевое давление вое*
принимает подшипник А. Поэтому реакция подшипника А со-
состоит из трех компонентов:
Ra — %А + 'А + Z-A'
Реакция подшипника В состоит из двух компонентов:
Rb == % В
Разложив силу F натяжения каната на две составляющие Fx и
Ft, направленные вдоль образующей барабана и перпендику-
перпендикулярно к ней, имеем:
Fr = F sin y = Q sin y; Ft = F cos у «= Q cos y-
После этого легко найти проекции силы ^приложенной в точкеЯ,,
на выбранные координатные оси:
Хв = — Ft cos (90° — р1) = — Q cos y sin §;
У,-—F,- —Qsinv;
ZE = Ft cos p = Q cos y cos p.
Находим координаты точки Е:
P; yE = a—c; zB = rsinp.
Далее находим проекции силы Р и координаты точки ее прило-
приложения:
XD=Pcosa; Уо = 0; ZD = — P sin a;
*о=°; ^o=a; ^о=/г.
Обозначая через С центр тяжести ворота, имеем:
Xc = Yc = 0, ZC = — G, *c=2r =0, i/<c = 4>
где l — a + b.
Моменты всех действующих сил относительно координатных
осей вычислим по формулам B9):
тпх (F) = (а—с) Q cos p cos y + г sin p Q sin y = Q (h cos p cos y +
-f-л snip1 sin y), где h = a—c;
my (F) — — r sin P Q cos y sin p—r cos p Q cos y cos p = — Qr cos y;
(
mx (P) = — P sin a -a; my (P) = PR cos a; mz (p) = — P cos a • a;
x (P) = P sin a -a; my
± 5
y	z
= — G± ; myE) = mz(G) = 0; mx (RA) = /ny
117

Составляем уравнения равновесия рассматриваемой системы
сил:
2)	-Qsi
3)	Qcospcosy—Я sin a—G + ZA+ZB = 0,
4)	Q (ft cos В cos y + r sin p sin y) — Pa sin a—G -^ + ZB/ = 0,
5)	—Qr cos y + P# cos a—m = 0,
6)	Q (h sin P cosy—rcosp sin y)—Pa cos a—XBl =0.
Из второго и пятого уравнений находим YА и Р:
F^ = QsinY;
р 	Qr cos у + пг
R cos a *
Подставив найденное значение силы Р в оставшиеся уравнения,
определяем из них остальные неизвестные реакции.
Из шестого уравнения:
у Q (hsin В cosy— rcosp sin у—-^
Из четвертого уравнения:
После этого из первого и третьего уравнений находим:
Хд = 4 { [Ф +е) «in P--?-/] cos у +r cosp sin Y—J • ~
i Г —(&+c)cospl cosy-H r sinPsi
Втор ая группа
Задачи о равновесии тела, имеющего одну из опор в виде
сферического шарнира
(задачи 265, 267, 275)
Пример 43. Тело, имеющее форму шестигранной призмы
(рис. 77), закреплено в точке А при помощи сферического шар-
шарнира, а в точке В—при помощи цилиндрического подшипника
и, кроме того, шарнирно соединено с прямолинейным невесомым
стержнем СЕ, конец Е которого закреплен шарнирно. Через
блок D перекинут канат. Один конец каната закреплен в не-
неподвижной точке L, а к свободному его концу прикреплен груз
весом Q. В точке К приложена вертикальная сила Р, направ-
118

ленная вверх, и в наклонной грани призмы действует пара сил
с моментом т, направление которой указано круговой стрелкой.
Определить реакции связей при следующих данных: Р = 400«,
Q = 500«, m=1000 н-м, o 80 6 40	d 20
Решение. Показываем силы, действующие на призму: Р,
Q, Т, которая удовлетворяет условию T — Q. Момент пары изо-
изобразим в виде вектора т, приложенного в точке Л; этот вектор
/л
Рис. 77
направлен перпендикулярно к наклонной грани призмы так, что из
его конца видим пару направленной против часовой стрелки. Реак-
Реакция S стержня СЕ направлена вдоль стержня так, что стержень
работает на растяжение. Принимая центр А сферического шар-
шарнира за начало координат, располагаем координатные оси, как
указано на рисунке. Реакцию сферического шарнира разлагаем
на три компонента вдоль выбранных осей:
Реакцию цилиндрического шарнира В разлагаем на две состав-
составляющие, учитывая, что она перпендикулярна к оси цилиндра:
119

Реакцию S стержня, приложенную в точке С и направленную
вдоль стержня СЕ, разлагаем предварительно на горизонталь-
горизонтальную ~S\ и вертикальную S, составляющие, после чего легко на-
находим ее проекции на координатные оси:
Хс *= S, sin р = S cos y sin р = 0,25 S,
Ус = — S, cos p = —S cosy cos р = — 0,433 S,
Zc = 5, =- S sin у =* 0,866 S.
Силы Y и Q заменяем одной равнодействующей /?D = T-f Q, на-
находим проекции этой силы на оси координат:
Хо = 0; VD = Qsin6 = 500 0,866 = 433;
Zo = — Q — Qcos6 = — Q(l+cos6) = — 750.
Далее имеем:
X^ = 0; YK = 0; ZK=P~400.
Теперь вычислим координаты точек приложения всех прило-
приложенных к призме сил и моменты этих сил относительно коор-
координатных осей (см. формулы 29):
yB***b; zB = h—c;
mx (RA) = my (RA) = mz (RA) = 0;
m, (RB) = bZB-(h-c) YB = 0,4ZB-0,69 7B; my (Яв) = -xfiZB =
= — (a + d)ZB = -ZB;m,{RB) = xaYB = (a + d)YB = YB,
mx (S) = ft sin yS + hS cos у cos p = (b sin у + h cos у cos p) S = 0,73 S;
Wji (s) = zcXc = AS cos y sin p - 0,22 S; /иг (S) = — г/сХс =
= — ftScosy sin p = — 0,1 S; mx(P) = mt (P) = 0;
my (P) = — Pa = —320;
mx (RD) = — bQ A + cos 6) — (A—c) Q sin б =
= — (ft A -f cos 6) + (A—c) sin 6] Q = — 600;
"iy Eo) = — xo Zo = -J <? A + cos 6) = 300;
mz(RD) =xDYD =| Q sin б = 173,2.
Наконец, находим проекции вектора-момента пары ~т на коор-
координатные оси:
тх = 0, Шу~т cos a = 866; mz = — m sin a = — 500.
120

Теперь нетрудно составить шесть уравнений равновесия сил,
действующих на призму:
Уд + У*—0,433 S 4 433 = 0,
ZA + ZB + 0,866 S + 400—750 = 0,
0,4 ZB—0,69 YB + 0.73S—600 = 0,
— ZB+0,22S—320 + 300 + 866 = 0,
Кд—0,1 S + 173,2 -500 = 0.
Эти уравнения можно представить проще в таком виде:
Xj4 + 0,25S = 0,	(a)
Уа + Ув — 0,433 S = — 433	(б)
ZA + ZB + 0,866 S = 350,	(в)
0,4Za* —0,69 yB+0,73S = 600,	(г)
- ZB -f- 0,22 S= -846,	(д)
Гв —0,1 S= 326,8.	(e)
Из уравнений (д) и (е) имеем:
ZB = 0,22S + 846 и FB = 0,lS+326,8.
Подставляя эти выражения ZB и У- в уравнение (г), полу-
получим уравнение с одним неизвестным S, из которого получаем:
S = 652h.
После этого находим: ZB = 989«; Ув = 392 н.
Теперь из уравнений (а), (б) и (в) легко определяются величины
ХА, YA и 1А.
Третья группа
Задачи о равновесии тела, закрепленного при помощи шести
стержней, соединенных с телом и опорами шарнирно
(задачи 268, 269)
Пример 44. Однородная плита весом G (рис. 78), имеющая
форму прямоугольного параллелепипеда, опирается на шесть
прямолинейных стержней, соединенных своими концами с плитой
и с неподвижными опорами при помощи сферических шарниров.
На плиту действует, как указано на рисунке, горизонтальная
сила Р и в точке А подвешен груз Q. Найти усилия в стержнях,
пренебрегая их весом. Указанные на рисунке размеры и углы
заданы [эти величины связаны между собой очевидными соот-
соотношениями: h = actga — bctgf} (рис. 78)].
Решение. Рассматриваем равновесие плиты под действием
силы Р, веса G, натяжения Q каната, на котором подвешен
груз, и реакций S1	 S, стержней. Последние направляем
121

так, как будто все стержни работают на растяжение (т. е. от
шарниров А, В, С и D вдоль стержней). Координатные оси
х, у, г располагаем, как указано на рисунке. Чтобы определить
шесть реакций S,,..., S,, неизвестных по модулю, но известных
по направлению, составим шесть уравнений равновесия, при-
приравнивая нулю сумму проекций всех сил на координатные оси
и сумму их моментов относительно тех же осей. Следовательно,
при решении задач о равновесии тела, закрепленного при по-
помощи шести невесомых прямолинейных стержней, не лежащих
Рис. 78
в одной плоскости, получаем шесть неизвестных по модулю, но
известных по направлению реакций стержней, которые опреде-
определяются из шести уравнений равновесия системы; поэтому задача
статически определенная. Для того чтобы составить шесть урав-
уравнений равновесия, определим проекции каждой силы на оси к,
у и г и ее моменты относительно этих осей. Определение проек-
проекций рассмотренных сил на координатные оси не вызывает труд-
трудностей. Остановимся на определении моментов этих сил относи-
относительно осей х, у и г. Силы S, и ,Sa приложены в начале коор-
координат, поэтому моменты этих сил относительно каждой из осей
122

х, у и z равны нулю, т. е.
m, E.) = 0.
Силы Q, Ss, S, пересекают ось х, а сила Р параллельна этой
оси, поэтому mx(Q) = mx (SJ = mx(iSl) = mx(P) = 0.
Точно так же силы S, и S5 пересекают соответственно оси г
а у, а потому mz (SJ = ту E5) = 0.
Силы Q, 54, S5 параллельны оси г, а потому
m2(Q) = m,Ej = m,E5) = 0.
Кроме того,
mx(G) = — m0 (буг) = — G у так как Gvz= G (проекция силы G
на плоскость yz на рисунке не показана);
mv (Ss) = m0 (S^) = S2a sin (90°—a) = S2a cos a;
mv (SJ = ma (S5XZ) =aS, cos pj
b=S, sin p -a;
Теперь можем составить шесть уравнений равновесия рассмат-
рассматриваемой системы сил:
2)	S3sin
3)	—S, — S2 cos a—S, cos p —S4—S, —Se cos p — Q — G = 0,
4)	_S46_55ft_G|- = 0,
5)	aSacosa + aS3cosp4-S4a + Pc + Qa + G-| = 0,
6)	aS3 sin p —6P = 0.
Из первого и шестого уравнений определяем S2 и 5,:
S __Р_ с 6 р
2 ~ sin a' s a ' sin p '
123

Далее, из второго уравнения имеем:
«<г b p
Подставляя найденные значения St, S, и 56 в остальные урав-
уравнения системы и учитывая, что h = actga—b ctgp, определяем
из четвертого и пятого уравнений силы 54 и 55, а затем из
третьего уравнения—силу St:
-Sv-Pctga—(S,4-S.)cosp-Q
откуда
S,=
Знаки минус, полученные для реакций S,, 54 и 5б, указывают
на то, что эти силы имеют направления, противоположные при-
принятым на рисунке, и, следовательно, стержни /, 4 и 6 сжаты.
Следует отметить, что третье и пятое уравнения получились
громоздкими: в первое из них входят все шесть неизвестных,
во второе — три. Эти уравнения можно было бы заменить урав-
уравнениями моментов относительно осей х' и у'. Действительно,
силы S3, S4, -S} и S6 пересекают ось х', следовательно,
тх. (SJ = т* (SJ = т* (S.) = т* (S.) = 0;
тх-(Р) = 0 (сила параллельна оси х'),
т%. (S,) = S,&; т* (S,) = S% cos a • 6;
Таким образом,
? m* = SYb -t- &S2 cos a + Qb + G -| = 0,
т. е. получаем уравнение, в которое входят только две неизвест-
неизвестные величины, одну из них Eг) мы уже определили из первого
уравнения. Поэтому
Аналогично имеем:
m, (SJ = mr (SJ = ти (Ss) = m, (S.) = 0
124

(силы пересекают ось у');
тУ E,) = S, cos р • а; т^ (St) = Sta\
my.(G)^Gj\ ml/.(Q)=Qa.
Следовательно,
"V = aS, cos p + S4a + (/г + с) P + Qa + -J G = 0.
Воспользовавшись выражением Sa, найденным из первого урав-
уравнения, имеем:
или, учитывая, что 6ctgp* = /i; S4 = — (^-^ P + Q4 0,5g] .
Силу S, можно было бы найти непосредственно из уравнения
моментов относительно оси г'. Действительно, моменты всех
сил, за исключением Se и Р, относительно оси г' равны нулю,
так как все эти силы либо пересекают ось г', либо ей парал-
параллельны.
Таким образом,
2тг- = — S6 sin P a—Pb = 0,
откуда
6
sin
Глава V
ЦЕНТР ТЯЖЕСТИ
Задачи, рассматриваемые в этой главе, можно разделить на
следующие четыре группы:
1)	задачи на определение общего центра тяжести нескольких
тел, веса и положения центров тяжести которых известны;
2)	задачи на определение центра тяжести однородного кон-
контура;
3)	задачи на определение центра тяжести площади плоской
фигуры (однородной тонкой плоской пластинки);
4)	задачи на определение центра тяжести объема (однород-
(однородного тела).
125

При решении задач, относящихся ко второй, третьей и чет-
четвертой группам, рассмотрим только те случаи, когда применим
метод разбиения данной линии, плоской фигуры или данного
тела на конечное число простейших по форме частей, центрь
тяжести которых легко определяются.
Если данное тело имеет плоскость или ось, или центр сим-
симметрии, то центр тяжести такого тела лежит соответственнс
в этой плоскости, на этой оси или в этом центре симметрии.
Поэтому для упрощения вычислений при решении задач пло-
плоскость симметрии всегда нужно выбирать за одну из коорди-
координатных плоскостей, а ось симметрии—за одну из координатных
осей.
Первая группа
(задача 298)
Если веса данных тел обозначим Pt, а координаты их цент-
центров тяжести *,-, уо zt, то координаты общего центра тяжести
этих тел определятся по формулам:
Ус
Пример 45. Центры
г„ =
' = !, 2,
я). D0)
Рис 79
тяжести грузов Л,, Л2, Ла, Л4, веса
которых соответственно равны
, — Г8— Ш, Г2 — О, Г4= 10 И,
находятся в вершинах тетраэд-
тетраэдра; высота этого тетраэдра Л4/И
проходит через точку М пересе-
пересечения медиан основания А1А2А>
тетраэдра. Дано: Л,Л2 = 4 см,
Л,Л3 = 8 см, Л4/И = 40 см. Угол
а = 30°. Найти положение цент-
центра тяжести этих грузов (рис. 79).
Решение. Координатные оси
с началом в точке Лг направим,
как указано на рис. 79. Тог-
Тогда координаты центров тяжести
данных грузов Л,, Л2> Л,, Л4
будут соответственно равны:
,=х
М>
х, =0, х2 — 2 см, ха = 0,
у1 — 0, у1 — 2\гЪсм, у, = 8 см, yt — yM,
г1==0, г2 = 0,	г, = 0, г4 = 40сж.
Так как точка М есть точка пересечения медиан треуголь-
треугольника АлАгАг, то, как известно из аналитической геометрии,
=т; ум =
У1 + У2 + У>_2
126

Теперь, применяя формулы D0), находим координаты иско-
искомого центра тяжести:
Хс
PiVi + РгУг '
Pi + Pi
Хс
РЛ + Р1Х, + Р,Х,-
40
5-2
+ Р, + Ра
Pih + P^s + P>zs
Р1_|„р2_(-Рз-
= 0,5 см; ус-
Вто р а
(задачи
+-Р
V
\-р,
= з,
я
286
'х 5'2+15'
40
-3+10-8+15-2
40
\гА 15-40
86 см; zc -
группа
, 299—301)
3
\ J
3
15,
= 15
0 cv
+ 8
о У 3
' 2
ИЛИ
см.
Разбив данный однородный контур на п простейших по форме
линий, обозначим длины этих линий /,-, а координаты их цент-
центров тяжести Xj, i)i, zt. Тогда координаты центра тяжести данного
контура определяются по формулам:
В случае плоского контура, плоскость которого принимаем за
координатную плоскость хОу, будем иметь: г, = 0 (f = l, 2, 3,
4, ..., п) и, следовательно, 2^ = 0.
Пример 46. Определить координаты
центра тяжести С однородного контура
AEBDKA, состоящего из дуги полуокруж-
полуокружности АЕВ, прямолинейного отрезка BD и
дуги окружности DKA с центром в точке
В, если АО = 0В=-г; BD = 2r; /_ ABD = 90°.
Оси координат указаны на рис. 80.
Решение. Заданный контур разобьем
на три части: полуокружность АЕВ, отре-
отрезок BD и четверть окружности DKA. Обо-
Обозначим центры тяжести этих частей соот-
соответственно С,, С2, С3, а их длины /г,
/2, /,. Тогда llF=nr; /2 = 2r; /8 = ш\
Центр тяжести С1 дуги АЕВ лежит на оси у, причем ОСХ —
. я
я
У
2г*
~ТГ'
поэтому
¦«1 =
= 0;
2л
^ = -7Г-
* Расстояние от центра тяжести С дуги окружности радиусом R до
центра О этой окружности определяется по формуле ОС =	. , где а—
половина центрального угла этой дута.
127

Центр тяжести отрезка BD лежит в середине этого отрезка,
а потому
BD
хг = г; t/^ — ^r.
Центр тяжести дуги AKD лежит на отрезке KB, причем
ВС.=
2'sinT
Следовательно,
х, = — (BCtcos 45° — г) = — (™-') ; уш = ВС, cos 45° = ^.
Полученные расчетные данные расположим в табл. 10.
Таблица 10
No частей
1
i
3
'.
nr
fr
nr
*,
0
r
4r
г
Я
V.
1r
It
Ar
я
0
2^
4
ЛГ ( r	j
liU,
r*
2r*
Теперь координаты искомого центра тяжести находим по
формулам D0):
l^Xs + ^x, _ г (я—2) . _ hyi+ityz + lMt _ 2г
Третья группа
(Задачи 287—296)
Разбив данную плоскую фигуру на п простейших по форме
частей, обозначим площади этих частей S,-, а координаты их
центров тяжести xh у{. Тогда координаты центра тяжести дан-
данной фигуры определяются по формулам:
С~
Ус~
D2)
(i=l 2, 3	п).
128

Пример 47. Определить координаты центра тяжести площади,
ограниченной контуром AEBDK.A (рис. 81).
Решение. Разобьем данную плоскую
части: полукруг АЕВ и четверть круга
BAKD. Обозначим центры тяжести
этих частей и их площади соответ-
соответственно Cj, Ct и SJ( S2. Тогда Sl = -~-,
S2 = nr*. Центр тяжести полукруга АЕВ
лежит на оси Оу, причем
2 rSin T
ос, =4-
It
т
4/-*
:Зя~
поэтому а;, =
Зя
Центр тяжести С, кругового сектора ЛВ?)/С.<4 лежит на пря-
прямой В/С. причем
я
т
Зя
, = ВС, sin 45е = ?-.
Координаты искомого центра тяжести данной плоской фигуры
AEBDK.A находим по формулам D1):
Г \Зк Т ) 2 _(-
	я	= ТГ
I-
Аг
8r
4r
2r
Пример 48. Определить положение центра тяжести профиля,
состоящего из прямоугольника и двух уголков, размеры кото-
* Расстояние от центра тяжести С кругового сектора радиусом R до
2JL?, где а—половина
(X
центра круга О определяется по формуле ОС = -^
центрального угла этого сектора.
б Зак. 23741-
129

ft
рых в миллиметрах указаны на рис. 82.
Решение. Выберем систему коорди-
координатных осей, как указано на рис. 82, и
заданный профиль разобьем на шесть
прямоугольников /, //', ,.. , VI. Обозна-
Обозначим центры тяжести этих прямоугольни-
прямоугольников соответственно С\, С2, ... , С„, а их
площади 5„ S2, 5„ ... , 5,.
Тогда S, =200-12 = 2400 мм' = 24 см*;
Sz = 60-10 = 600 мм* = 6 еж2;
S, = Ss = S, = 80-10 = 800 мм* = 8 см2;
S=350-10 = 3500 мм* = 35 аи*.
При вычислении координату, yt, xz,
Рис. 82	yt> ... , хв, yt точек С„ С2, ... , С, следу-
следует учесть, что центр тяжести прямоуголь-
прямоугольника находится в точке пересечения его диагоналей, а поэтому
xt = 100 лш= 10 см;
х% = 200—5 = 195 мм = 19,5 ел;
xt — xt= 10 + 40 = 50 л.м = 5ш; х4== 5 лш = 0,5 cjh;
х8 = 200 —10—40 = 150 jhm = 15 см\
yv= 6 мм = 0,6 еж; «/, = 12 + 30 = 42 мм = 4,2 еж;
у, = 12 + 350—5 = 357 мм = 35,7 ш; у€ = 12 + ^=» 187 лш =
= 18,7 си; {/5= г/, = 12 + б = 17 мм = 1,7 еж.
Полученные данные расположим в виде табл. 11.
Искомые координаты центра тяжести данного профиля нахо-
находим по формулам D2):
v 2.У/ 240+117 + 40+17,5 + 40+120 _574,5_в
V.S, ~ 24 + 6 + 8+35 + 8 + 8 ~~ 89 <
S,y; 14.4 + 25,2 + 285,6 + 654,5+13,6+13,6 1006,9
89
89
= 11,31с*.
Если в данной фигуре имеются вырезы (отверстия), то коор-
координаты центра тяжести такой фигуры определяются тем же спо-
способом, как и в примерах 47 и 48, по тем же формулам D2),
но только площади вырезанных частей (поскольку они отни-
отнимаются) нужно считать отрицательными, т. е. брать со знаком
минус.
130

Ne частей
1
2
3
4
5
6
Si
24
6
8
35
8
8
*i
10
19,5
5
0,5
5
15
0,6
4,2
35,7
18,7
1,7
1.7
S(Xt
240
117
40
17,5
40
120
Та б л и
14,4
25,2
285,6
654,5
13,6
13,6
ца 11
Пример 49. Определить положение центра тяжести фигуры,
представляющей собой круг радиусом R с центром в точке О,
из которого вырезаны три круга с центрами в точках Olt О,, 0„
если расстояния между центрами этих
кругов и их радиусы соответственно
равны:
1 i> *i з	4 2 ' • 4 '
D	D	Р
ООг=1г, г1==|-, г,=4, г, =4,
00, = /,.
Угол а равен 120° (рис. 83).
Решение. Начало координат вы-
выберем в центре О большого круга, а
ось х направим по прямой, соединяю-
соединяющей точки О и О,. Будем рассматри-
рассматривать данную фигуру, как состоящую из кругов радиусов г,, г2,
г, и полного круга радиусом R (без вырезов). Обозначим площа-
площади этих кругов S,, 52, S,, Sv а координаты их центров тяжести
Х1> Уг> Лг. i/s' Ла> i/S' Л4' »4*
Так как центр тяжести каждого круга совпадает с центром
этого круга, то
Рис. 83
R
б*
131

зя
4 '
= /, cos 30° =
= -/, cos 30° ==~
Кроме того, S4 = n/?*. Так как площади вырезанных кругов
отнимаются, то, как было указано выше, их надо считать отри-
отрицательными, т. е.
о, — — яг, =—g^-, -bj —— пгг ——jg-,
Таким образом, получим табл. 12.
Таблица 12
Координаты искомого центра тяжести будут:
_L_±+
192 64 + 48
192 + 64
4J
111
515
Итак, xc = 0, ye^0,02R.
№ частей
1
2
3
4
64
—nR'
16
—п/?!
36
nR'
*i
/?
3
/?
4
— 3/?
4
0
V.
R VI
3
-я Кз
4
0
0
S,xt
-nR>
192
-nR'
64
48
0
Siv,
—nR' VH
192
nR' V~~3
64
0
0
Четвертая группа
Разбив данное тело на п простейших по форме частей, обо-
вначим объемы этих частей V{, а координаты их центров тяже-
тяжести х(, ylt г;. Тогда координаты центра тяжести данного тела
132

определяют по формулам:
Пример 50. На рис. 84 показан разрез тела, состоящего из
цилиндра радиусом г и высоты h и двух
полушаров радиусами Rx, /?„ центры ко-
которых совпадают с центрами нижнего и	/ qi
верхнего оснований цилиндра. Определить т~11
центр тяжести этого тела, если Rl = 2Rl,
Решение. Так как ось г является для
данного тела осью симметрии, то искомый
центр тяжести С этого тела лежит на оси
г, поэтому достаточно вычислить только
одну координату zc.
Обозначим объемы полушаров и цилинд-
цилиндра соответственно V,, Vt, Vt, а их центры	рис 84
тяжести С,, С,, С,. За начало координат
выберем точку С,. Тогда эти объемы и координаты центров тя-
тяжести Сх, С,, С, будут соответственно равны:
г =_fl + -
' \ 2 ~ 8
Искомую координату ге центра тяжести данного тела нахо-
находим по третьей формуле из D2):
33... ,57
144+
174
1413
232 х'
или
Итак,
гс = — 6,09 г.
гс =s —6г.
В некоторых случаях применение метода разбиения тела (или
данной плоской фигуры) на простейшие части связано с особым
приемом, который можно назвать методом дополнения.
* Расстояние от центра тяжести полушара радиусом R до его основа-
ния равно -т- R (см учебник проф. И М. Воронкова, § 56).
о
133

Сущность этого метода состоит й следующем: к данному
телу / присоединяют второе тело // так, чтобы получилось новое
тело /// простой геометрической формы, центр тяжести которого
легко можно определить. Например, продолжив две противо-
противоположные стороны данного четырехугольника до их пересечения,
можно дополнить его до треугольника; усеченный тетраэдр можно
дополнить до четырехгранной пирамиды. Если при этом поло-
положение центра тяжести присоединенного тела // также легко
можно определить, то к телу /// применяем метод разбиения
на простейшие части; это тело можно рассматривать состоящим
из двух частей: данного тела / и добавлен-
добавленного тела //, и, следовательно, можно вос-
воспользоваться формулами D3).
Пример 51. Определить расстояние цент-
центра тяжести усеченного круглого конуса
ADEB от его нижнего основания, если
известны радиусы R и г верхнего и ниж-
нижнего оснований конуса и его высота h
(рис. 85).
Решение. Начало координат выберем
в центре О нижнего основания усеченно-
усеченного конуса, а ось г направим по его высоте.
Так как ось г является осью симметрии усеченного конуса, то
искомый центр тяжести лежит на этой оси в некоторой точке С
с координатой гс, которую и требуется определить. Применяя
метод дополнения, дополним данный усеченный конус до кону-
конуса АВК.
Пусть С, и С2—центры тяжести конусов АКВ и DKE,
К„ Vt — их объемы. Тогда OC1=zl, ОС8 = гг и К, =-• Vt + V,
где V—объем данного усеченного конуса. Рассматривая ко-
конус АКВ, как бы состоящий из двух частей ADEB и DKB и
применяя формулу D3), имеем:
Рис. 85
откуда
или
сс — у
v,-v, '
D4)
Так как объемы двух подобных конусов АКВ и DKE про-
V, R'
порциональны кубам радиусов их основании, то rf—-j и, сле-
следовательно,
zc- к,_гш •
134

Кроме того, расстояние от центра тяжести конуса до его
основания равно -^ высоты этого конуса, а потому
zi— 4' zt —" Г 4 — «i 4—— 4
Учитывая, что -=1- = ^з^, т. е. hl= , получим
Следовательно,
Если данное тело имеет полости (вырезанные части), то
координаты центра тяжести тако-
такого тела определяются по тем же
формулам D3), но только в этих
формулах объемы вырезанных ча-
частей нужно брать со знаком минус.
Пример 52. Из усеченного конуса,
радиусы нижнего и верхнего основа-
оснований которого R и г, а высота h,
вырезан круглый цилиндр радиусом
гх, имеющий с конусом общую ось и
высоту, равную/г, = у Найти расстояние центра тяжести ос-
оставшейся части от нижнего основания конуса (рис. 86).
Решение. Возьмем начало координат в центре нижнего
основания конуса, а ось z направим по его оси симметрии.
Искомый центр тяжести С лежит на оси г. На этой же оси ле-
лежат центр тяжести С, сплошного усеченного конуса (без выреза)
и центр тяжести С, вырезанного цилиндра, причем
Рис 86
* См. предыдущий пример.
135

Объемы сплошного усеченного конуса и вырезанного цилиндра
будут соответственно равны:
(объем У, вырезанного цилиндра счшаем отрицательным).
Применяя теперь третью формулу из D2), получим

СО
Положение центров тяжести некоторых однородных линий, фигур и тел
Таблица 13
Положение центра тяжести
I. Периметр треуголь-
треугольника
Центр тяжести находится в центре круга, вписан-
вписанного в треугольник ВгВ2В„ где В,, Вг, Вг — сере-
середины сторон данного треугольника.
где a,,6j,a,—стороны данного треугольника нЯ,—
высота, соответствующая стороне аг
S
S
X
S
2. Дуга окружности
радиуса R
,slnq
а
<3
I
3. Треугольник
Центр тяжести находится в точке пересечения медиан:
*с=-з"(*1 + *2 + *«).
Ус = -з(У1 + Уг + У»)> где
х$, i/j — координаты вершин треугольника

00
Положение центра тяжести
4 Трапеция
Центр тяжести находится в точке
пересечения прямой АВ и пря-
прямой, соединяющей середины па-
параллельных сторон.
, где Н—высота
а г---—t
а + Ь
трапеции
3
о
с;
С
5 Четырехугольник
Центр тяжести С находится в точке пересече-
пересечения отрезков СхСг и СаС4> где С, — центр тяже-
тяжести треугольника ASASAX, Сг—центр тяжести
треугольника A^AfA^, С,—центр тяжести тре-
треугольника Л,ЛгЛ4 и С4—центр тяжести тре-
треугольника Л^аЛ,

Положение центра тяжести
2
о
6 Круговой сектор
радиусом R
7. Круговой сегмент
радиусом R
Параболический
сегмент
0С--
2

sing
3 2а—sin* a
о

Положение центра тяжесгй
ш
9 Призма или
цилиндр
Центр тяжести С находится в середине отрезка,
соединяющего центры тяжести С, и С. верхнего и
нижнего основании
10 Пирамида или
конус
€tC = -^- ЛС,, где С,—центр тяжести основания,
А — вершина иС — центр тяжести пирамиды или
конуса

Положение центра тяжести
11. Шаровой сектор
радиусом R
Центр тяжести С лежит на оси симметрии, причем ОС = -=- X.
о
XBR—Л), где /i^ высота шарового сегмента
12 Шаровой сегмент
радиусом R
Центр тяжести С лежит на оси симметрии на расстоянии
.„ 3 BR hf
от основания сегмента лС = — •
4
4 CR—А)
13 Параболоид враще-
вращения
Центр тяжести С лежит на оси симметрии на расстоянии от верши-
2
чы параболоида OC = -^-h, где h—высота параболоида
о

РАЗДЕЛ II
КИНЕМАТИКА
Глава I
КИНЕМАТИКА ТОЧКИ
Кинематика изучает движение механической системы, в част-
частности абсолютно твердого тела, независимо от сил, действующих
на эту систему. Так как при движении твердого тела различные
его точки могут двигаться различно, то в кинематике сначала
изучается движение более простого объекта, а именно движение
точки, а затем — движение твердого тела.
Определить движение точки — это значит уметь определить
положение этой точки по отношению к выбранной системе
отсчета в любой момент времени t.
В кинематике применяются три способа, описывающих дви-
движение точки: векторный, координатный и естественный.
При векторном способе определения движения радиус-век-
радиус-вектор г движущейся точки М, проведенный из выбранного непод-
неподвижного центра (начала системы отсчета), выражается как
векторная функция от времени, т. е.
г =7@.	D5)
Координатный способ определения движения точки состоит
в том, что координаты движущейся точки в выбранной системе
координат выражаются как функции времени t.
Уравнения движения точки в декартовых координатах
имеют вид:
I	D6)
= /,(')• J
Если точка движется в плоскости хОу, то будем иметь только
142

два уравнения движения:
У = Ш-
В этом случае можно определить движение точки, применяя
и полярную систему координат; уравнения движения точки
н полярных координатах запишутся так:
ф-?(о." }	D7)
где т и ф—полярные координаты движущейся точки
При естественном, или натуральном, способе движение точки
определяется ее траекторией и уравнением движения по этой
траектории:
s = ^ОМ = f @,	D8)
где О — начало отсчета дуг на траектории, a s—дуговая коор-
координата точки М или взятая с соответствующим знаком длина
дуги, отсчитываемая вдоль траектории от начала отсчета до
точки М (рис. 87).
М
Рис 87
Уравнение D8) называется законом, или уравнением, дви-
движения точки М по ее траектории
Задачи, относящиеся к «Кинематике точки», можно разде-
разделить на следующие основные типы:
I	Задачи, относящиеся к прямолинейному движению
точки. В задачах этого типа требуется определить скорость v и
ускорение до из уравнения прямолинейного движения точки,
причем это уравнение или задано, или его нужно предвари-
предварительно составить, исходя из условия задачи.
II	Задачи, относящиеся к криволинейному движению точки.
Задачи, относящиеся ко второму типу, можно разделить на
четыре группы:
1)	задачи, в которых требуется определить траекторию,
скорость и ускорение точки по заданным уравнениям движения
в декартовых координатах;
2)	задачи, в которых требуется составить уравнения движе-
движения точки в декартовых координатах и определить траекторию
движения точки, а также ее скорость и ускорение;
143

3)	задачи, в которых применяется естественный способ зада-
задания движения точки, т. е. задана траектория движения, а урав-
уравнение движения по этой траектории либо задано, либо его можно
найти из условия задачи;
4)	комбинированные задачи.
§ 1. ЗАДАЧИ ТИПА I
Прямолинейное движение точки
(задачи 322—324, 336—342, 408—411)*
Если точка движется прямолинейно, то в этом случае ско-
скорость v и ускорение w направлены по прямолинейной траекто-
траектории, а модули их равны:
IV =
d's
а?
df
D9)
где s—расстояние движущейся точки, отсчитываемое от некото-
некоторой неподвижной точки О траектории.
Если выбрать прямую, по которой движется точка, за ось Ох,
а расстояние ОМ — s обозначить через х, то проекции векторов
скорости v и ускорения w на направление траектории будут
равны:
v==7t> w = dF>	E0>
где v и w — алгебраические значения скорости и ускорения,
причем знаки ~ и -? указывают, в какую сторону по оси Ох
направлены векторы скорости и уско-
^1	рения.
При составлении уравнения прямо-
прямолинейного движения точки необходимо
рассматривать положение движущейся
точки в произвольный момент време-
времени /, а не ее начальное или конечное
положение и выразить ее расстояние
от начала отсчета как функцию вре-
времени /.
Пример 53. Линейка эллипсогра-
х фа длиной АВ = 1 = \ м скользит сво-
ими концами по осям Ох и Оу. Ко-
Конец А линейки движется по оси Oxt
причем закон этого прямолинейного
движения выражается так: ОА —0,Им. Составить уравнение дви-
движения точки В и определить скорости и ускорения точек А и В
(рис. 88).
* Здесь и дальше номера задач указаны по «Сборнику задач по теоре-
тическбй механике* проф. И. В. Мещерского, изд. 1950 г. и послед, изд.
Рис.
144

Решение. Точка В движется прямолинейно по оси Оу;
расстояние этой точки от неподвижной точки О найдем из пря-
прямоугольного треугольника ОАВ:
ОВ = VAB*—OA2 = /1—0,01 f.
Таким образом, уравнением прямолинейного движения точ-
точки В запишется так: yB~V^—0,0\t*.
Скорости и ускорения точек А и В, которые направлены
соответственно по осям Ох и Оу, найдем по формулам D9):
d0'U = 0,l м\сек,
„ _dxA
JA-~df
dt
|_0,0И2 —О,ОП
dt
dt
f\— O.OH2
м\сек.
dvA
T
—O.Olf
wB=-af-w=-
1—0,0U2
0,01
м сек
Так как |я<0 и ^
A-0.СШ2J
то скорость ползуна В направлена
к точке О и ползун движется ускоренно.
Пример 54. Круглый эксцентрик диаметром 2т вращается
вокруг оси О, отстоящей от геометрической оси С эксцентрика
на расстоянии равном ОС = а =
= -д- ; угол ф изменяется по зако-
я , .
НУ y — 'o't (угол ф измеряется в
радианах, г — в см, а / — в сек).
Найти уравнение прямолинейного
движения точки М стержня ММ,
движущегося в вертикальных на-
направляющих, как указано на
рис. 89, а также скорость и уско-
ускорение этой точки в момент t1 = 3 сек
(рис. 89).
Решение. Стержень MN
движется в вертикальных направ-
направляющих, а потому точка М
стержня движется прямолинейно
по неподвижной прямой, проходящей через точку О и направ-
направленной вдоль стержня MN. Выберем эту прямую за ось Оу,
а начало отсчета —в точке О и выразим расстояние
Рис. 89
145

как функцию времени /; для этого достаточно выразить отре-
отрезок ОМ через угол <р. Проведя из точки С высоту СЕ в тре-
треугольнике МОС, имеем:
HoO? = acoscp, ?C = a sin ф, ЕМ =
а потому
у = ОМ—a cos (f+ V
Подставляя значения угла ср и r
получим закон движения точки М:
sin'tp,
*—a' sin'<p.
= 3a в последнее равенство,
9 — sinfy
Скорость и ускорение точки М найдем по формулам D9):
х
cosf t
па sin —
>-sin'T/
ИЛИ
Кроме того,
j/g-sin'-J
d'y dv
yjt\
SU1T
ТаккаК|=,и,4|
9- sin2 -J-
4' \
2	'
9n cos TT-
146

то
У
9 cos -5-
>-**% if
Таким образом,
В момент f, = 3 сек
w1 = " _ a cMJceK.
Так как и, >¦ 0 и а\ > 0, то скорость и ускорение точки М
направлены от точки О, т. е. по вертикали вверх, и точка М
движется ускоренно.
§ 2. ЗАДАЧИ ТИПА II
Криволинейное движение точки
Пер вая группа
Задачи, в которых требуется определить траекторию, скорость
и ускорение4 точки из уравнений движения в декартовых координатах
(задачи 311, 313—316, 320, 322, 326, 328, 349, 352, 354)
Если движение точки опреде .яется уравнениями в декарто-
декартовых координатах, то, для того чтобы найти траекторию точки,
достаточно из уравнений движения исключить время t. Вектор
скорости и вектор ускорения определяются по их проекциям
на оси декартовых координат, причем
dx
v* = x==Tt'
n -ij-dl
У У~~ dt'
v*-z==di'
• E0)
• _d*y
¦¦ <Рг
г~ dt*
E1)
Отсюда получаем формулы разложения векторов скорости
v и ускорения w по координатным осям:
E2)
E3)
147
zk.

Модули и направляющие косинусы векторов скорости и уско-
ускорения определяются по формулам:
cos (у, i) = -^>
N
cos (v, ~j) = -^-,
v\
cos Co, k) = ^-,
W |
cos (да, i) = =^-,
cos
\w\
cos (да, *)==-^=- .
E4)
E5)
E6)
E7)
Пример 55. По заданным уравнениям движения точки в де-
декартовых координатах найти траекторию, скорость и ускорение
этой точки:
2) х== Rs'm at;
y^=R (I—cos2at);
z — R sin со/.
(Координаты x, у и г заданы в метрах, а /—в сек.)
Решение. 1) Чтобы найти траекторию точки, исключим из
уравнений движения время /; из первого уравнения имеем:
-? = ekt + e~kt, а из второго: if- = ekt — ~ekt. Возведя эти равенства
в квадрат и вычитая второе из первого, получим:
%% <« *)'-(в«-*-"Г = 4, или g-f!=l.
Следовательно, искомая траектория есть гипербола с полуосями
а и Ь. Полагая в начальный момент to — 0, находим: хо — а,
уо = 0, т. е. в начальный момент точка находится в вершине
гиперболы Л0 (а, 0). При дальнейшем возрастании t координаты
х и у точки возрастают, оставаясь положительными. Следова-
Следовательно, точка А движется по правой ветви гиперболы в направ-
148

лении, указанном на рис. 90. Воспользовавшись формулами E0),
E1), найдем проекции скорости и ускорения точки на коор
динатные оси:
bk
v4 — у I
^=1-'
x
Рис 90
Далее по формулам E4) — E6) находим*
Но х* + у* = г*, а потому w = k*r.
Кроме того, w = k*xi + k2yj = k*(xi + yj).
Так как xi + y} = r, то w — k*r, т. е. вектор ускорения на-
направлен по радиусу-вектору движущейся точки.
2) jc = /?sincof,
y = R(\— cos 2 to/).
г = /? sin со/
Чтобы найти уравнение траектории, достаточно из уравнений
движения исключить время t. Из первого и третьего уравне-
уравнений имеем: г = х—это есть уравнение плоскости, проходящей
149

через ось у и биссектрису координатного угла гОх. Далее,
находя из первого уравнения sin at и подставляя это значение
во второе уравнение, имеем: %mat = -^,
# = A — cos 2at) = Я B sin2 at),
или
Это есть уравнение параболического цилиндра с образую-
образующими, параллельными оси г, причем направляющей этого
2
цилиндра является парабола у = -^х, лежащая в плоскости
хОу. Таким образом, траекторией точки является линия пере-
пересечения поверхностей
г = х, )
2 , }
В начальный момент /0 = 0, *0 = 0, */0 = 0, г„ = 0, т. е. Точка
находится в начале координат; так как координаты х и г из-
изменяются периодически в пределах от —R до R, а координата
у—в пределах от 0 до 2R, то точка совершает колебательное
движение по дуге параболы.
По формулам E0) и E1) вычислим проекции скорости и уско-
ускорения на оси х, у и г:
vx = Ra cos at, wx=—Ra*smat,
vy = 2R sin 2at, wy — 4Ra" cos 2wt,
vz = Ra cos at, wz = — Ra* sin at.
Следовательно,
v — Ra cos at i -f 2Rm sin 2atj + Ra cos at Ъ,
w = — /?co* sinco^t-f 4#cuscos2(o//—Ras sin atli,
или
v — Ra (cos©? i-\-2 sin 2at j + cos o>/&),
w = 7?©1 (— sin ati -f- 4cos 2cd// — sin co/&).
Далее находим модули векторов скорости и ускорения по фор-
формулам E4) и E6):
| v \ = RaV2 (cos'oof 4- 2 sin* 2at) = /2/? to cos at-Vl+8 sin* cof,
|ш| = /^со'/г (sin'orf f 8cos'2coO = /2^(ог • ]/sin2 ©/ + 8 cos2 2wt.
150

Вторая группа
Задачи, в которых требуется составить уравнения движения точки
в декартовых координатах и определить траекторию движения, а также
скорость и ускорение точки
(задачи 317, 319, 327, 332—334, 359, 369)
При решении задач этой группы следует сначала составить
уравнения движения точки; для этого нужно рассмотреть поло-
положение движущейся точки в произвольный момент времени,
а не ее начальное или конечное положение, и выразить ее
текущие координаты как функции времени t. Далее следует
придерживаться такого же плана, как и при решении задач
предыдущей группы.
Пример 56. Составить уравнения движения точки М колеса па-
паровоза, отстоящей от оси колеса на расстоянии г, равном 0,8 м,
Рис 91
если паровоз движется равномерно по прямолинейному участку
пути со скоростью ис=16 м/сек, и найти скорость и ускорение
точки М. Колесо катится по рельсу без скольжения, а его
радиус равен R = 1 м. В начальный момент точка М занимает
положение Мо на вертикальном диаметре колеса (рис. 91).
Решение. Ось Ох направим по рельсу, а ось Оу проведем
через точку Мо, принимая за начало координат точку Аа. Рас-
Рассмотрим два положения колеса в начальный момент ? = 0
и в текущий момент времени t. Отметим положение центра С
колеса и его радиуса С А, на котором расположена точка М
в момент t. Так как расстояние от центра колеса до рельса
все время равно радиусу R, то точка С движется по прямой,
параллельной оси Ох, и притом по условию задачи равномерно,
а потому расстояние от этой точки до ее начального положения
равно CcC = vct. Так как CD \\ С0А0, то /_ A CD есть угол пово-
поворота колеса вокруг своей оси за t сек, который обозначим
через «р. Для того чтобы найти уравнения движения точки М,
151

найдем координаты зтой точки:
Но <4,B = i4,D—CE = CtC —СЕ и MB = ME + ЕВ, или
*Л1 = »С* —СЕ, ^, = /? + EM.
Из треугольника МЕС имеем:
ME=r sin (ф—90°) = — г cos q>,
EC = r cos (ф—90°) = r sin ф,
а потому хм = о/—rsir^, yM = R—совф.
Найдем зависимость угла ф от времени /. Так как качение
колеса по рельсу происходит без скольжения, то ~ AD = DA0.
Но
DA0 = СС0 = vc t, ^DA = R<p,
а потому
ф = ^г = 16/.
Таким образом,
хм= 16/ —rsin 16/,
у м = 1 — г cos 16/
г. е. искомой траекторией является укороченная циклоида. Если
точка М находится на ободе колеса, то г = R и мы получаем
следующие уравнения движения циклоиды:
Если же r^>R, например, г =1,2/?, то аналогично можно получить
уравнения движения точки М, описывающей удлиненную цик-
клоиду.
Подставив значение т в уравнения движения точки М, имеем-
хм = 16/ —0,8 sin 16/
ум= 1—0,8 cos 16/.
Для определения проекций векторов скорости и ускорения
на оси хну воспользуемся формулами E0) и E1):
vx= 16— 12,8cos 16/, ш,.=204 8 sin 16/,
tiy = — 12,8 sin 16/. шу=204.8 cos 16/.
152

Таким образом,
F= 16 [7A — 0,8cos 160 — 70,8sin 16/],
w = 204,8 (Г sin 161 + J cos 16*).
Далее вычислим модули векторов скорости о и ускорения w
по формулам E4), E6):
|г| = /A6— 12,8cosl602 + A2,8Jsin46* =
= 16/l 64 + 0,1 cos 161\
Iw\ = /(cos216/-f sin46/)B04,8)a = 204,8 м/сек2.
Пример 57. Линейка эллипсографа АВ — 10 Y% CM концами
А и В скользит по двум прямолинейным направляющим, образую-
образующим между собой угол а = 135*. Найти траекторию, скорость и
ускорение точки М линейки, если ^ = 3 и закон движения пол-
Зуна А выражается уравнением О A = s = 20sin-2-/ (рис. 92).
Решение. Ось Ох направим по прямой ОВ, а ось Оу —
перпендикулярно к ОВ и построим координаты точки М:
Х = ОЕ = ВС—ОС — ВЕ;
у=МЕ.
Далее выразим координаты точки М через заданный отре-
отрезок ОА; для этого опустим перпендикуляр из точки А на ось
Ох. Из подобных треугольников АСВ и МЕВ находим:
Следовательно,
х==* ВС-ОС.
4
153

Так как из прямоугольных треугольников АОС и ABC имеем:
ОС = АС = АО sin a,
АС = АВ sinq>,
ВС = АВ сощ,
то
х = j А В cos ф — А О sin а = -| • 10 /2cos q> — 20 sin -?. *. sin 45°,
или
* = 10/2(|-cosф- sin |
Остается выразить зависимость между ф и t. Из треугольника
ОЛВ по теореме синусов имеем:
АВ _ АО
sin a stn q> '
откуда
АО . . я ,	п .
sin ф =-jn sin а == sin-у г и ф = -2"Г.
Таким образом, уравнения движения точки М имеют вид:
х = ЮУ^Г-!"cos-^-f — sin ~
У = -у- sin-2" t.
Чтобы найти уравнение траектории, достаточно из этих
уравнений исключить t; для этого перепишем уравнения дви-
движения в виде:
. п_, _ у
sin 2 i -
cos тг = (ш% + [F7T V т •
*
Возведя эти уравнения в квадрат и складывая их, получим
уравнение траектории (эллипс):
Теперь вычислим проекции векторов скорости и ускорения
на оси координат по формулам E0) и E1):
154

или
=* — х х>
Отсюда по формулам E2) и E3) находим:
v = ? {-D
где г — радиус-вектор точки М. Таким образом, вектор уско-
ускорения направлен противоположно радиусу-вектору движущейся
точки.
§ 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ
ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
(задачи 323, 324, 336—349)
Если заданы траектория движущейся точки и закон ее
движения по этой траектории s = f(t), то вектор скорости
направлен по касательной к траектории, а его проекция на
направление касательной определяется по формуле
** = §,	E8)
причем абсолютное значение этой проекции равно модулю
скорости, т. е.
ds
т
От =
= V .
Вектор ускорения определяется по его проекциям на естест-
естественные оси (касательную, главную нормаль и бинормаль):
где Q —радиус кривизны траектории в данной точке.
155

Следовательно.
Если плоская траектория задана уравнением y = f(x), то
радиус кривизны траектории вычисляется по формуле
Q = —jTs-j	,	(DJ)
где у' = -~ и у" = -т-|.
Рассмотрим частные случаи:
1.	Если точка движется прямолинейно и неравномерно, то
радиус кривизны траектории q—»-оо и, следовательно, wn — 0.
В этом случае ускорение w направлено по прямолинейной
траектории точки и по модулю равно
^Ь = ^-1	F2)
dt dt* \"	у '
2.	Если точка движется по кривой равномерно, то
от = const и wr = —^ = О,
а потому ускорение до направлено по нормали к траектории и
по модулю равно
w = ш„ = - .	F3)
3.	Если точка движется прямолинейно и равномерно, то
Пример 58. Вагонетка движется равномерно по закруглению
радиусом # = 600 м, причем ускорение ее центра тяжести равно
и» = 0,0026 м}секг. Найти скорость центра тяжести вагонетки.
Решение. Так как центр тяжести вагонетки перемещается
по окружности равномерно, то его ускорение w направлено по
радиусу этой окружности к центру и согласно формуле E9)
по модулю равно
w — wn— ^ .
Но радиус кривизны окружности равен ее радиусу, а потому
откуда
156

v =
= УО.0026 • 600 = V\ ,56 = 1,25 —,-t.
C6K
Пример 59. Точка движется с постоянным тангенциальным
ускорением а по окружности радиуса R без начальной ско*
рости. Через сколько секунд после начала движения касатель-
касательное и нормальное ускорения станут численно равны между
собой?
Решение. Для решения задачи воспользуемся формулами:
га
dv
~ dt
V*
=: — =
е
= а.
_V*
Интегрируя уравнение dv = a dt,имеем:
отсюда, принимая во внимание, что vo = O и а = const, находим
v — at и, следовательно,
аНг
хю„ =¦
R '
В искомый момент времени tt касательное и нормальное
ускорения равны между собой, а потому
откуда
аЧ\
t. = У --
1 г а
Рис. 93
Пример 60. Точка движется по ок-
окружности; в некоторый момент ее ско-
скорость равна v, а ускорение направлено по хорде MN = l.
Зная v и I, найти ускорение точки в этот момент (рис. 93).
Решение. Пусть на рис. 93 векторы МА и MS обозна-
обозначают соответственно ускорения w и wn. Тогда из подобия прямо-
прямоугольных треугольников МАВ и MLN имеем:
w _ ML _2R
wn~ MN ~ I '
отсюда
_?5 —?? v^_2R v^
2v*
157

Пример 61. Машина идет по выпуклому мосту А В. Ее центр
тяжести Л1 описывает при этом параболу у — — 0,005л:г, а рас-
расстояние s — vAM, отсчитываемое от точки А вдоль дуги пара-
болы, изменяется по закону s — -^t'—9t* + f>0t (x, у я s выра-
выражены в метрах, a t—в сек). Определить скорость и ускорение
центра тяжести машины в тот момент, когда он находится в вер-
вершине параболы, если в этот момент скорость машины достигает
минимума (рис. 94).
У\
Рис 94
Решение. Так как траектория и закон движения точки М
по ее траектории заданы, то для решения задачи воспользуемся
формулами E8), E9) и F0). Тогда имеем:
у = ^ = 2^ —18/+60
u2
??>„ = —
" Q
Радиус кривизны траектории определим по формуле F1)-
Следовательно,
где ^
A+0,0001х') '»
0,01
Но в вершине параболы координата х точки М равна нулю,
поэтому q = 100 м.
Остается определить, в какой момент времени машина дости-
достигает вершины параболы; так как скорость ее в этот момент
достигает минимума, то ^ = 0, откуда 4?, —18 = 0 и t1==-^==
= 4,5 сек. Следовательно, ^ = 2^ —18^+60 = 60—81+9-4,5=
¦=19,5 MJceK.
Так как в вершине параболы касательное ускорение ^=~
равяо нулю, то
158
= 3,8 м\секг.

§ 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
(задачи 312, 353, 355—358, 367—369, 371, 373)
К задачам этого типа относятся такие задачи, в которых
требуется, исходя из уравнений движения точки в декартовых
координатах, найти закон движения точки по ее траектории,
т. е. выразить дуговую координату s в функции времени, а также
найти касательное и нормальное ускорения точки и радиус
кривизны траектории.
Чтобы найти закон движения точки по ее траектории, нужно
из заданных уравнений движения определить скорость о и со-
составить уравнение: ds = vdt.
Отсюда, интегрируя, получим:
s0	о
ИЛИ
t
где s0 — значение дуговой координаты s при ^ = 0.
Касательное ускорение определяется по формуле
F4)
после этого нормальное ускорение можно найти из равенства
wn = у w*—w\,	F5)
где
wx = "х%+"уг+"г*.
Определив wn, найдем радиус кривизны по формуле
Q =»-?-.	F6)
Пример 62. Даны уравнения движения точки:
х = akt,
Найти траекторию, закон движения точки по траектории и
радиус кривизны траектории в зависимости от ординаты у.
Решение. Чтобы найти траекторию, достаточно исключить
из уравнений движения время t; для этого найдем значение t
159

из первого уравнения и подставим его во второе. Тогда имеем:
Следовательно, траектория точки есть цепная линия. Далее
находим скорость v:
vx = x = ak.
Предполагая, что so = O, теперь имеем:
Ускорения wx и wn находим по формулам E1), E9) и F5):
wx = х = О,
w, = y = ?Y {ekt + e~h1) = ak' ch {kt),
Теперь по формуле F6) находим радиус кривизны траекто-
траектории:
Но
поэтому
а 4уг
4 " о2
Пример 63. Даны уравнения движения точки:
x = 2t, y = M\ z = 3t*,
причем х, у, г выражены в метрах, а время t — в сек.
Найти радиус кривизны траектории в точке, где скорость v
движущейся точки равна 5 м\сек.
160

Решение. Скорость и ускорение движущейся точки нахо-
находим по формулам E0) и E1):
| v | =
- 25t\
Далее находим
wn и q по формулам F4), F5) и F6):
2-50t _ I00i
dv
W = ¦— =
_ l^LL — H у v> _ 100^" =
20
V
:20
5»
25
: 4 :
=6,25 ж.
Пример 64. Точка описывает плоскую траекторию так, что
проекция ее скорости на ось Ох постоянна и равна с. Доказать,
что в этом случае ускорение
равно
CQ
где и—скорость,
q—радиус кривизны тра-
траектории (рис. 95).
Решение. Так как
vx = c — const, то wx = x—Q,
т. е. вектор ускорения парал-
параллелен оси Оу. Построив
проекцию вектора скорости
v — MA на ось Ох и про-
проекцию вектора ускорения
w = ME на нормаль к траектории, получим два прямоугольных
треугольника МАВ и MED. В этих треугольниках углы ^_АМВ
и /_EMD равны, как углы с перпендикулярными сторонами,
а потому эти треугольники подобны. Отсюда находим:
Рис. 9S
MA ME
MB
Но
следовательно,
MD '
MD = и)„ = —
О 	 WQ
С СJ
7 Зак. 2374
V'
7q~
161

Глава (I
ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Если твердое тело движется так, что две его точки остаются
неподвижными, то такое движение тела называется вращатель-
вращательным движением вокруг неподвижной оси.
Прямая, соединяющая две неподвижные точки тела, назы-
называется осью вращения этого тела.
Если выбраны две плоскости, проходящие через ось вра
щения, причем одна из них неподвижна, а вторая неизмен-
неизменно связана с вращающимся телом,
то угол ф между этими двумя пло-
плоскостями, измеряемый в радианах
и отсчитываемый в направлении, про-
противоположном движению часовой стрел-
стрелки, если смотреть с положительного
конца оси вращения, определяет по-
положение тела в любой момент време-
времени t и является непрерывной одно-
однозначной функцией времени (рис. 96),
т. е.
Ф = /(/)¦	F7)
Равенство F7) называется уравне-
уравнением, или законом, вращательного
движения твердого тела вокруг не-
неподвижной оси. Угол ф —ф0 называ-
называется углом поворота, или угловым
перемещением тела.
Первая и вторая производные по
времени от угла ф называются соот-
соответственно угловой скоростью и угловым ускорением тела и обо-
обозначаются буквами со и е, т. е.
ш — 37 — / w> ь — ~ш — At —/ v)'	v30)
Рис 9S
При этом М-^-1
сек
И
гЕ1 =^i^ = —=ге/с-2
^ •¦ сек* сек*
Если число оборотов в минуту вращающегося тела равно п, то
ЯП
со —
F9)
162

Задачи, относящиеся к вращательному движению твердого
тела вокруг неподвижной оси, можно разделить на три основ-
основных типа:
1)	определение углового перемещения, угловой скорости и
углового ускорения тела,
2)	определение скоростей и ускорений точек вращающегося
тела,
3)	задачи, относящиеся к передаче вращательного движения
от одного тела к другому.
§ 1. ОПРЕДЕЛЕНИЕ УГЛА ПОВОРОТА, УГЛОВОЙ СКОРОСТИ
И УГЛОВОГО УСКОРЕНИЯ ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ
ВОКРУГ НЕПОДВИЖНОЙ ОСИ
(задачи 375—385)
Если со == const и, следовательно, 8 = 0, то вращение тела
называется равномерным, в этом случае
Ф = Фо + со/.	G0)
Если е = const, то вращение тела называется равномерно
переменным; в этом случае
+ ^-.	G1)
Если соо>0, то при е> 0 вращение тела —равноускоренное,
а при е<;0, вращение тела — равнозамедленное.
Пример 65. С момента выключения мотора пропеллер аэро-
аэроплана, вращавшийся с угловой скоростью, соответствующей
л =1200 об\мин, сделал до остановки 80 оборотов.
Найти, сколько времени прошло с момента выключения мо-
мотора до остановки пропеллера, считая его вращение равномерно
замедленным.
Решение Так как вращение пропеллера равномерно за-
замедленное, то по формулам G1), считая <р„ = 0, будем иметь:
Ф =-- aj + g у,
причем
пп лг. 1
ю„ = 5к =» 40я —.
0 30	сек
Так как пропеллер сделал 80 оборотов, то угол поворота
равен ф = 80 2л=160я рид
Так как, кроме того, в момент остановки угловая скорость
пропеллера равна нулю, то со = 0.
7*	163

Таким образом, получаем два уравнения:
40я/ + ^-=160я,
40л -f e/ = 0.
Отсюда находим:
40я
6 = - —
лг, , 40я 1г 1сп
4СЫ	т- у = 160я;
следовательно,
Пример 66. В период разгона маховик вращается вокруг
своей оси по закону
Определить угловую скорость и угловое ускорение маховика
в момент, когда он сделает 27 оборотов.
Решение. По формулам F8) находим:
dcp з .,
Далее находим, в какой момент времени / угол поворота
будет равен 27-2я = 54 л рад:
отсюда
^ = j/54-4 = 6 сек.
Угловая скорость и угловое ускорение в этот момент будут
равны:
т=3 п-62 = 27л —,
4	сек '
3 с п 1
§ 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ ТОЧЕК
ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
(задачи 386—394)
Если твердое тело вращается вокруг неподвижной оси, то
любая его точка, не лежащая на оси вращения, описывает ок-
окружность, плоскость которой перпендикулярна к этой оси, а
164

скорость и ускорение точки определяются по формулам:
v = Ra, wT = Re, wa = Ru>*, w = RVz2 + a>\ G2)
где R — расстояние движущейся точки от оси вращения.
Векторы скорости v и касательного ускорения хюх направлены
по касательной к окружности, описываемой данной точкой тела,
а вектор нормального ускорения wn направлен по радиусу этой
окружности к ее центру.
Если вращение тела ускоренное, то векторы v и wz направ-
направлены в одну и ту же сторону; в случае же замедленного враще-
вращения— в противоположные стороны.
Если тело вращается равномерно, то со = const, следовательно,
в этом случае и = const; е = 0, а>т = 0 и
w = wn,	G3)
т. е. вектор ускорения w совпадает в этом случае с нормаль-
нормальным (центростремительным) ускорением.
Пример 67. Колесо радиуса R = \ м вращается равномерно
вокруг своей оси, делая один оборот за 0,25 сек. Найти ско-
скорость и ускорение точки, лежащей на ободе колеса.
Решение. Так как колесо вращается равномерно, то со-
согласно формуле G0)
Но за время / = 0,25 сек угол поворота колеса равен
ср—сро = 2я рад,
поэтому
2я о 1
Далее по формуле G2) будем иметь:
v = R(a = 1 ¦ 8я MJceK « 25,12 м\сек,
w^wn==R-ai = \ 64л2 = 631,04 м\секг.
Пример 68. Вал начинает вращаться с угловой скоростью
и„==2я —
0 сек
равноускоренно и за 10 сек делает 30 оборотов. Найти ускоре-
ускорение точки, отстоящей от оси вращения вала на расстоянии,
равном 0,5 м, в тот момент, когда скорость этой точки равна
2я м\сек.
Решение. Для определения углового ускорения вала вос-
воспользуемся формулами G1), считая сро^0:'
165

Но при /=10 сек ^гол поворота равен ф = 30 2л = 60л рад,
а потому
2лЮ + 50е = 60л,
откуда
ев=«* о,8*Л.
Далее по формулам G2) находим:
w = R /е2 + со4 = 0,5 |/0,64я2 + ш4 и v = Ra> = 0,5ю.
Б тот момент, когда и = 2л м/сек, имеем:
о) = ^=4л— и ш = 0,5]/0,64л2+ 44я" =
= 4л /4л2+ 0,01 & 8л2 = 79 л/сек2.
Пример 69. Вал вращается в подшипниках вокруг неподвиж-
неподвижной горизонтальной оси по закону ф = ^ sin -^ nt, где ф —угол
поворота вала в радианах. Определить скорость и ускорение
точки М вала, отстоящей от оси вращения на расстоянии
г = 0,8 м в тот момпнт, когд^ угловая скорость вала достигает
наибольшего абсолютного значения.
Решение. Найдем сначала угловую скорость и угловое
ускорение вала по формулам F8):
dtp п 3 3 . Зяг 3 , _,
ю = jf = те • -г- я cos -г- л г = -х-г cos -г- яг сек ,
d/ 16 4	4	Ь4 4	'
da 9я8 . 3 , _2
8 = -гг = — ^rr sin -г- яг сек .
Теперь по формулам G2) получим:
Зя2 3 ,
и = гю = -пГСО5Тл*>
— 9я» . 3 ,
?^ r8''Slnrt*
Угловая скорость ю достигает наибольшего абсолютного значе-
3	3
ния в момент/,, когда cos -j- nt =1, отсюда -j- nt^ = kn, т. е.
4	4 8
tl = -j k, где fc = 0,l, 2,3, ..., следовательно, /, = 0,-^-, -^ .
..., се/с. В эти моменты имеем:
Зяа п о Зя2 0,Зя2 „ „
«Ч, = 0, ш, = шп, = ^ 0,8 = ^ я4 да 10.94 ж/сек2.
166

§ 3. ПЕРЕДАЧА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ОТ ОДНОГО ТЕЛА
К ДРУГОМУ
Пример 70. Шкив / радиусом О1В = г1, вращаясь равномер-
равномерно, делает п оборотов в минуту; он соединен бесконечным
ремнем со шкивом // радиусом ОгС = гг. Определить скорость
и ускорение точки А шкива /// радиу-
радиусом O2A=R, жестко соединенного со
шкивом // (рис. 97).
Решение. Так как все точки ремня
имеют одинаковые скорости, то
или (D1r1 = w2r2, где со, и со2 — угловые
скорости шкивов / и //, или
w, = rj
ша г, '
т. е. угловые скорости шкивов, соеди-
соединенных бесконечным ремнем, обратно
пропорциональны их радиусам. Отсюда
:С0.
или, учитывая формулу F9), со2 ==— ¦ у- =
— const. Так как шкив ///, которому при-	Рис. 97
надлежит точка А, жестко соединен со
шкивом //, то их угловые скорости равны и, следовательно,
скорость точки А равна
Так как со2 = const, то ускорение wA точки А равно нормаль-
нормальному (центростремительному) ускорению этой точки, и, следо-
следовательно,
А	900 rj
Пример 71. Зубчатое колесо / с числом зубьев г, =80 начи-
начинает вращаться равноускоренно из состояния покоя с угловым ус-
ускорением е, = 1 сек~г и приводит в движение находящееся с ним
во внутреннем зацеплении колесо // с числом зубьев za = 20.
Определить угловую скорость колеса // и ускорение точки В,
лежащей на окружности этого колеса через 1 сек после начала
движения, если радиус колеса // равен rt=15 см (рис. 98).
167

Решение. Допустим, что колесо / вращается в направлении,
противоположном движению часовой стрелки; тогда скорость
точки С зацепления колес бу-
будет направлена, как указано на
ve рис. 98, и, следовательно, коле-
колесо // будет вращаться в юм же
направлении, что и колесо /, т. е.
против движения часовой стрел-
С ки. Для скорости точки С, как
принадлежащей одновременно и
колесу //, имеем
Рис 98
Следовательно,
где со, и юг—угловые скорости
колес / и //, а гх и г2 — их
радиусы.
Но
2яг, =
где Л—шаг зацепления*,
отсюда
2nr,
А поэтому
и 2яг2 =
или ^- = ^-.
т. е. угловые скорости находящихся в зацеплении зубчатых
колес обратно пропорциональны числам их зубцов.
Следовательно,
.. г, 80 ..
но, согласно формуле G1), ю1 = е,/ = ;
При t = 1 сек имеем: со = 4я—.
сек
поэтому сог = 4л^-!-
сек
Угловое ускорение колеса // будет равно
dw,
См сноску на стр 222.
F8

Теперь по формуле G2) находим ускорение точки В:
wB = г У е* + со* = 15 /DяJ + Dл*I = 60я /Т
При * = 1 сек
дав = бОя ]/1 + 16яа ж 60я • 4я сж/шс2 « 2,4я'
Направление ускорения аув определяется углом а между ра-
радиусом 0гВ и вектором дов:
Глава III
ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Если при движении твердого тела расстояние от любой его
точки до данной неподвижной плоскости не изменяется, то та-
такое движение тела называется плоскопараллельным.
Изучение плоскопараллельного движения тела сводится к
изучению движения плоской фигуры, движущейся в своей пло-
плоскости (сечения тела плоскостью, параллельной данной непод-
неподвижной плоскости).
Задачи, относящиеся к плоскопараллельному движению тела,
можно разбить на следующие основные типы:
1.	Составление уравнений плоскопараллельного движения
твердого тела (уравнений движения плоской фигуры).
2.	Определение скоростей точек плоской фигуры.
3.	Нахождение подвижной и неподвижной центроид.
4.	Определение ускорений точек плоской фигуры
§ 1. УРАВНЕНИЯ ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
(задачи 492—500)
Положение неизменяемой плоской фигуры в ее плоскости
вполне определяется положением двух произвольных ее точек
А и В.
Следовательно, изучение движения плоской фигуры в ее пло-
плоскости сводится к изучению движения прямолинейного отрезка
АВ, с которым фигура неизменно связана. Но положение от-
7В Зак. 26/4	16Э

резка АВ определяется положением, т. е. двумя координатами
хА и уА, ег* точки А, называемой полюсом, и углом <р, который
образует этот отрезок с некоторой осью неизменного направле-
направления, лежащей в плоскости данной фигуры (рис. 99).
Таким образом, движение плоской фигуры, движущейся в
своей плоскости, можно определить следующими тремя уравне-
уравнениями:
G4)
Уравнения G4) называются уравнениями движения плоской
фигуры, или уравнениями плоскопараллельного движения твер-
твердого тела. Из этих уравнений следует, что движение плоской
фигуры можно разложить на два движения: 1) поступательное
движение, определяемое первыми двумя уравнениями G4), и 2)
вращательное движение вокруг полюса, определяемое третьим
из уравнений G4).
Рис. 99
Пример 72. Линейка АВ эллипсографа приводится в движе-
движение кривошипом ОС, вращающимся равномерно вокруг оси О,
с угловой скоростью со = const. Принимая точку А за полюс,
составить уравнения движения линейки эллипсографа если
(рис. 100)
ОС = ВС=АС = г.
Решение. Так как точка А движется по оси Ох, то уд — 0.
Если угол, образуемый линейкой АВ с осью х, обозначим
<р, то из равнобедренного треугольника АОС будем иметь:
АО = 2ОС coscp, или xA = 2rcosq>.
При равномерном вращении угол АОС поворота кривошипа
за t сек будет равен со^, т. е.
170

Таким образом, уравнения движения линейки АВ имеют вид;
xA = 2r cos (со/),
Ф = со/.
Пример 73. Шестеренка радиуса г, катящаяся внутри не-
неподвижного колеса радиуса R, приводится в движение кри-
кривошипом О А, вращающимся равномерно вокруг оси О этого
колеса, с угловой скоростью со = const.
Составить уравнения движения подвижной шестеренки, при-
принимая ее центр А за полюс (рис. 101).
Решение. Найдем координаты
хА, уА полюса А.
Из треугольника ОАВ имеем:
хА — ОВ = О A cos a,
уА = АВ = О A sin а,
но ОА—ОС — AC = R — гиа = со/, как
угол поворота кривошипа при равно-
равномерном вращении.
Следовательно,
хА ~(R —r) cos со/,
Далее нужно найти угол поворо-
поворота подвижной шестеренки вокруг полюса А. Для этого рас-
рассмотрим радиус AM подвижной шестеренки, который в началь-
начальный момент занимал положение АоМ0.
Тогда угол поворота равен /_ЕАМ — у.
При этом отрезок АЕ параллелен оси х и, следовательно,
/JZAE — a. Так как качение подвижной шестеренки по непод-
неподвижной происходит без скольжения, то
Но
а поэтому
откуда
73*
СМ —г (ф-f а),
г (а + ф) = R а,
-«(¦f-O-Of-O
со/.
171

Таким образом, искомые уравнения движения запишутся так:
xA = (R — r) cos at,
yA = (R—r) sin at,
§ 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ,
ДВИЖУЩЕЙСЯ В СВОЕЙ ПЛОСКОСТИ
(задачи 501 —538)
Движение плоской фигуры в ее плоскости можно разложить
на два движения:
1)	поступательное движение со скоростью, равной скорости
какой-либо точки А тела, принятой за полюс, и
2)	вращательное движение вокруг этого полюса (вокруг оси,
проходящей через полюс и перпендикулярной к плоскости дви-
движущейся фигуры). При этом угловая скорость вращательного
движения не зависит от выбора полюса. Отсюда следует, что
скорость любой точки В плоской фигуры равна геометрической
сумме двух скоростей: скорости полюса иА и скорости vBA точ-
точки В во вращательном движении вокруг полюса, т. е.
oB = vA + vBA,	G5)
причем vBA\^AB и vBA — AB'o.
Отсюда следует теорема о проекциях скоростей точек пло-
плоской фигуры: проекции скоростей двух точек плоской фигуры
на прямую, соединяющую эти точки, равны между собой.
Мгновенным центром скоростей (МЦС) называется такая
точка Р плоской фигуры, скорость которой в данный момент
равна нулю.
Если известны скорость vA какой-либо точки А плоской
фигуры и угловая скорость этой фигуры, то, повернув вектср
vA вокруг точки А на 90° в направлении вращения фигуры и
отложив на этой полупрямой отрезок
ЛР = ^,	G6)
получим точку Р, которая является МЦС (рис. 102).
Если же известны направления скоростей двух точек пло-
плоской фигуры, то МЦС находят как точку пересечения перпен-
перпендикуляров, восставленных в этих точках к направлениям их
скоростей.
Если мгновенный центр скоростей Р найден и если извест-
известна угловая скорость со фигуры, то скорость любой точки В
фигуры определяется как скорость этой точки во вращательном
172

движении вокруг мгновенного центра скоростей, т. е, вектор
vB перпендикулярен к отрезку РВ и по модулю равен произве-
произведению а>РВ.
Отсюда следует, что скорости точек плоской фигуры про-
пропорциональны их расстояниям от мгновенного центра скорос-
скоростей, т. е.
vB
G7)
Таким образом, скорость любой точки движущейся плоской
фигуры можно определить двумя способами:
1)	по формуле G5);
2)	при помощи мгновенного центра скоростей.
Из задач, относящихся к этому параграфу, следует обратить
внимание на такие задачи, в которых имеются плоские меха-
механизмы, состоящие из нескольких
звеньев (например, задачи 517, 533,
536—538). При решении этих задач
рассматривают последовательно движе-
движения отдельных звеньев механизма, на-
начиная с того звена, движение которо-
которого задано, и при переходе от одного
звена к другому определяют скоро-
скорости тех точек, которые являются об-
общими для этих двух звеньев механиз-
механизма. Следует подчеркнуть, что мгновен-
мгновенный центр скоростей можно находить
только для каждого звена в отдельно-
отдельности; то же относится и к угловым скоростям (см. пример 75).
Пример 74. Стержень А В длиной 5 м опирается на непо-
неподвижное ребро С двугранного угла и движется в плоскости
чертежа так, что нижний его конец А скользит по горизонталь-
горизонтальной оси х со скоростью, равной vA = 4 м\сек. Определить угло-
угловую скорость со и скорости точек В и С стержня в момент,
когда угол ф = 30°, если ОС —2 м (рис. 103).
Решение. 1-й способ. Скорость точки А направлена по
прямолинейной траектории этой точки, а скорость точки
С стержня АВ направлена вдоль этого стержня. Принимая точку
А за полюс, по формуле G5) имеем:
причем vCA J_ AC. На основании этого векторного равенства
строим jpeyroflbHHK скоростей. Для этого в точке С строим
вектор vA, из кон а а которого опустим перпендикуляр ас на
прямую АВ, тогда vc = Cc и vCA = ac, причем /_аСс=-у. Из
173

этого треугольника имеем:
Рис 103
Но
откуда
= ^ = 1 = 0,5 {/сек.
¦/////////л
Переходя к определению скорости точки В, имеем:
vB = vA -\-vBA, причем вращательная скорость vBA точки В во-
174

круг полюса А перпендикулярна к АВ и по модулю равна
Ъ 2Ъ Мсек
Аналогично предыдущему строим для точки В треугольник
скоростей, в котором известны по модулю и направлению две
стороны vA и vBA Так как угол в треугольнике скоростей,
лежащий против стороны vB, равен 90° — <р = 60°, то
|-)-2.4.}- 1 = 3,5 м'сек.
2-й способ. Скорости точек С и В и угловую скорость
стержня АВ можно найти и другим способом, построив мгно-
мгновенный центр скоростей стержня АВ, как точку Р пересечения
прямых АР и СР, перпендикулярных к скоростям vA и vc.
Тогда
VA __ ^В _ УС _..
РА~ РВ ~ PC -
Расстояния РА и PC находим из треугольника АРС, а рас-
расстояние РВ — из треугольника В PC.
	а м
PC = AC ctg ф = 4 ctg30° = 4/3 л,
РВ = /ВС2 -f РСа = /ТТ48 = 7 л.
Следовательно,
ж/сек,
Вектор г7в перпендикулярен к отрезку РВ.
Пример 75. Кривошип OtA = 20 см делает 120 оборотов
в минуту и при помощи звена АВ =400 см приводит в движе-
движение стержень O2fi = 60 см, закрепленный шарнирно в точке Ог.
Определить угловую скорость стержня АВ и угловую скорость
стержня ОгВ в момент, когда кривошип OtA займет вертикаль-
вертикальное положение, если известно, что в этот момент звено А В
образует с вертикалью /О,АВ = 60° и /ДВО8 = 30° (рис. 104).
Решение. ! и способ. Данный механизм состоит из трех
звеньев.
175

1) кривошипа 0%А, вращающегося вокруг оси 0^ с угловой
скоростью:
ЯП
2)	стержня ОгВ, вращающегося вокруг оси 02;
3)	стержня АВ, движущегося в плоскости чертежа.
Найдем скорость точки А. Вектор ид перпендикулярен к ра-
радиусу вращения 0хА и по модулю равен
= olm см 'сек.
Далее рассмотрим точку В.
Так как точка В принадлежит звену 02В, вращающемуся
вокруг неподвижной точки Ог, то скорость точки В перпенди-
перпендикулярна к ОгВ. Принимая точ-
точку А за полюс, по формуле G5)
имеем:
vB — vA-\-vBA, причем vBAj_AB
На основании этого векторного
равенства строим треугольник
скоростей. Для этого в точке
В строим вектор Ba = vA и луч,
перпендикулярный к 0гВ, а из
точки а—луч, перпендикуляр-
перпендикулярный к АВ, до их взаимного пе-
пересечения в точке Ь. Тогда
vB — Bb, vBA=ab, причем
Рис 104
Следовательно,
vBA = vA = 80 см 'сек и
vв = 2vA cos 30° = vAVb_=
= 80л/3 см1 сек.
Теперь, зная скорости vB и vBA, находим искомые угловые ско-
скорости ш, и со2 стержней АВ и ОгВ:
З _4к\гЗ 1
vBA
60
80 л
сек
Если бы в данной задаче не требовалось находить угловую
скорость звена АВ, то скорость точки В проще было бы найти
176

по теореме о проекциях скоростей точек Л и В на прямую АВ.
Этой теоремой удобно пользоваться в тех случаях, когда заданы
направления скоростей двух точек плоской фигуры и модуль
одной из этих скоростей.
2-й способ. Находим мгновенный центр вращения Р звена АВ
как точку пересечения прямых О^А и О2В, перпендикулярных
к скоростям vA и vB. Так как скорости точек звена АВ про-
пропорциональны их расстояниям от мгновенного центра вращения
этого звена, то
откуда
vB PB '
— EA
i~VA'PA
45
V///&J t
Рис 105
Из треугольника АВР имеем:
РВ _ sm 120°
FA ~ sin 30°
Следова тел ь н о,
2-1
: = 1/3.
1\сек.
Угловую скорость звена АВ найдем по формуле G6):
со -^L — V-A.~~ — 0 4 1/
Пример 76. Кривошип Ofit вращается вокруг неподвижной
оси Ot с угловой скоростью со0 = 4я \)сек и приводит в движе-
движение колесо // радиуса гг = 10 см, катящееся без скольжения
177

по неподвижному колесу / радиуса г1 = 50 см. С колесом //
в точке А соединен шарнирно стержень ЛВ = 80 см, который
приводит в движение ползун S, перемещающийся по горизон-
горизонтальной направляющей, проходящей через точку О,. Построить
мгновенный центр скоростей звена АВ и найти его угловую
скорость, а также скорость точки В в тот момент, когда криво-
кривошип 0,02 вертикален и 0гА || 0уВ (рис. 105).
Решение. Так как движение кривошипа О,Ог задано, то
этот кривошип является ведущим звеном, поэтому сначала най-
найдем скорость точки Ог. Вектор у0, перпендикулярен к О,Ог и
по модулю равен
Vo2 = a>o0,02 = 4л• 40¦= 160л см',сек.
Далее рассмотрим точку А, которая принадлежит колесу //;
это колесо катится без скольжения по неподвижному колесу /
и поэтому скорость точки С колеса / равна нулю, т. е. точка С
является мгновенным центром скоростей для колеса //, и ско-
скорость vA точки А перпендикулярна к С А. Кроме того, по фор-
формуле G7) имеем:
х>д _ АС
откуда
ол = с;Оз)/2= 160л 1/2 см,'сек.
Перейдем теперь к стержню АВ. Так как ползун В движется
прямолинейно, то скорость vB точки В направлена по прямой
ОХВ. Чтобы построить мгновенный центр скоростей для звена АВ,
достаточно восставить перпендикуляры в точках А и В к на-
направлениям векторов vA и vB до пересечения этих перпендику-
перпендикуляров в точке С,. Тогда ?ВСХА=45°, sin y = ?ф = ^ = 4" .
откуда у = 6и .
По формулам G6) и G7) находим идя и ив:
*в~ AC, ' vA~ACl '
Из треугольника АВС1 имеем:
ВС, _ АС, _ АВ
sin 15° — sin 120 " ~ sin 45° '
ВС, _ sin 15° _ 1
AC, ~ sin 30° ~~ 2 cos 15°
Таким образом, a>AB = — ^-	= —3—\!сек
178

§ 3. ЦЕНТРОИДЫ
(задачи 542, 544—549, 552, 553)
Геометрическое место мгновенных центров вращения на не-
неподвижной плоскости, в которой движется плоская фигура,
называется неподвижной „центроидой, а геометрическое место
мгновенных центров скоростей на плоскости самой движущейся
фигуры называется подвижной центроидой.
В каждый данный момент подвижная и неподвижная центро-
центроиды касаются друг друга, и точка касания этих кривых является
в данный момент мгновенным центром вращения (мгновенным
центром скоростей) движущейся плоской фигуры.
Данное движение плоской фигуры в ее плоскости можно
осуществить, построив подвижную и неподвижную центроиды
и заставив первую катиться без скольжения по второй с соот-
соответствующей угловой скоростью.
Задачи, в которых требуется найти неподвижную и подвиж-
подвижную центроиды, решаются двумя способами: аналитическим
и геометрическим.
При аналитическом способе определения центроид текущие
координаты мгновенного центра вращения в неподвижной системе
координат и текущие координаты того же центра в подвижной
системе координат, неизменно связанной с движущейся фигурой,
нужно выразить как функции времени, или другого перемен-
переменного параметра (например, угла поворота фигуры); исключив
затем этот переменный параметр, получим соответственно урав-
уравнения подвижной и неподвижной центроид (см. задачи 552, 553).
При геометрическом способе определения центроид искомые
центроиды находят, исходя из геометрических соображений.
Например, если расстояние мгновенного центра вращения от
данной неподвижной точки оказывается постоянным, то непод-
неподвижная центроида есть окружность; если сумма расстояний
мгновенного центра вращения от двух данных точек подвижной
плоскости, т. е. плоскости самой движущейся фигуры, есть
величина постоянная, то подвижная центроида есть эллипс,
фокусы которого находятся в этих точках подвижной плоскости,
и т. п. (см. задачи 542, 547, 548).
Пример 77. Стержень АВ — I концами скользит по двум
прямым О А и ОВ, образующим между собой угол а = 45°. Найти
подвижную и неподвижную центроиды (рис. 106).
Решение. 1-й способ (геометрический). Так как скорости
точек А и В направлены соответственно по прямым О А и ОВ,
то мгновенный центр вращения Р стержня АВ находим как
точку пересечения перпендикуляров, восставленных из точек
А а В к прямым О А и OS. Поэтому углы а и АРВ равны как
углы с перпендикулярными сторонами, т. е. /_ АРВ — 45° = const.
Отсюда следует, что подвижная центроида есть геометрическое
179

место таких точек, из которых отрезок АВ виден под одним и
тем же углом, равным 45°. Как известно из геометрии, таким
геометрическим местом является дуга АР В окружности, описан-
описанной около треугольника АРВ; так как сумма углов АРВ и АОВ
равна 180°, то эта окружность проходит и через точку О. Но
сторона треугольника равна диаметру описанного круга, умно-
умноженному на синус угла, противолежащего этой стороне, поэтому,
обозначая радиус подвижной центроиды через R, имеем:
/ = 2R sin 45°,
откУДа	i _\Г21
К 2 sin 45° ~ 2 *
Так как /_ О АР = 90°, то отрезок ОР является диаметром
подвижной центроиды, а потому OP = 2R = 1/2/ = const, т. е.
расстояние мгновенного центра вращения Р от неподвижной точки
О постоянно; отсюда следует, что неподвижная центроида есть
окружность радиуса OP = 2R = V2 I с центром в точке О.
Рис. 103
2-й способ (аналитический). Построим две системы коорди-
координатных осей: неподвижную Оху и подвижную О'х'у', неизменно
связанную со стержнем АВ, как указано на рис. 106; начало
О' подвижной системы возьмем в середине отрезка АВ. Если
обозначим координаты точки Р в неподвижной системе Оху через
х и у, а в подвижной системе О'х'у' — через х' и у', то
х = ОВ, у = ВР, х'^О'С, у' = СР.
Обозначим далее переменный угол ОАВ через ф и выразим
координаты х и у через этот угол. Из треугольников ОАВ и АРВ
по теореме синусов имеем:
х _ l	у _ I
sin <p~sin A80° —а) И sin (90° — ф) ~sina'
180

отсюда находим:
х =	sin ю, « =	cos m.
sin a T> v sin а ^
Чтобы найти геометрическое место точек Р на неподвижной
плоскости, т. е. получить уравнение неподвижной центроиды,
нужно из этих уравнений исключить параметр ср. Для этого
достаточно возвести каждое из этих уравнений в квадрат и затем
их сложить. Тогда получим:
sin2a sin2 45°
или
Отсюда видим, что неподвижная центроида есть окружность
радиуса V21 с центром в начале координат О.
Чтобы выразить теперь через угол <р координаты х' и у' точки
Р в подвижной системе осей, рассмотрим треугольники АСР и
ВСР из которых имеем:
АС = СР tgcp
или
|—х' = у' tg (а —ф) = у' tg D5°-Ф) =.
tg45°-tg9 , = 1 —tg cp ,
~ 1 + tg 45° tg ф У 1 + tg ф У
Освобождаясь во втором уравнении от знаменателя, получим:
j-x' 4-(y-*')tg9 = */'-f/'tg?.
Чтобы найти геометрическое место точек Р на подвижной
плоскости, т. е. найти подвижную центроиду, нужно из этих
двух уравнений исключить tg9- Из первого уравнения имеем:
~°т У '
Подставляя это значение ^ф во второе уравнение, получим:
ИЛИ
181

отсюда видим, что подвижная центроида есть окружность радиуса
i ]/ ,	~ /п I \
гт= = -2-/ с центром в точке 0,@, —J.
Пример 78. Стержень, согнутый в виде прямого угла ABC,
перемещается так, что точка А движется по оси х, а сторона
ВС все время проходит через неподвижную точку D на оси у.
Найти уравнения подвижной и неподвижной центроид, если
AB = 0D = a (рис. 107).
Решение. 1-й способ (геометрический). Скорость точки А
направлена по оси Ох, а скорость точки D—вдоль стержня ВС.
Мгновенный центр вращения Р стержня ABC находится в
точке пересечения перпендикуляров, восставленных из точек А
и D к скоростям этих точек. Так как прямоугольные треуголь-
Рис 107
ники ABE и 0ED, в которых /_ АЕВ = /_ OED и АВ = OD, равны,
то AE = ED, а потому из равенства треугольников АРЕ и DPE
заключаем, что АР —DP. Но, как известно из аналитической
1еометрий, геометрическое место точек, расстояния от которых
до данной неподвижной точки (точки D) и до данной неподвиж-
неподвижной прямой (прямой Ох) равны между собой, есть парабола.
Поэтому неподвижная центроида есть парабола, для которой
прямая Ох является директрисой, а точка D—фокусом. Точно
так же рассматривая геометрическое место точек Р на подвижной
плоскости, связанной со стержнем ABC, из равенства AP = DP
заключаем, что подвижная центроида есть парабола, для которой
директрисой является прямая ВС, а фокусом —точка Л.
182

2-й способ (аналитический). Если построим координату
х и у точки Р в неподвижной системе Оху, то
Из треугольника PDK имеем:
PD* = РК* + DK2 = РК° + (О/С—а)\
или, принимая во внимание, что PD = AP,
уг = хг + {у~а)\ или х2 = 2а(у—|).
Следовательно, неподвижная центроида есть парабола с осью
Оу и с вершиной в точке @, — \.
Построив теперь координаты х' и у' точки Р в подвижной
системе осей Вх'у', неизменно связанных со стержнем ЛВС, имеем:
*' =- PD, у' = BD.
Чтобы найти зависимость между х' и у', проведем отрезок.
AL, параллельный BD.
Тогда
LD = a, AL = BD = y', PL = x'—a
AP2 = PL2 + LA\
или
PD2 = PL* + LA2,
х>* = {х>-аТ + у'\
или
у —г
Следовательно, подвижная центроида есть парабола с осью
Вх' и с вершиной в точке f-^ , Oj.
§ 4. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
(задачи 557—578)
Ускорение любой точки движущейся плоской фигуры можно
определить двумя способами: 1) как геометрическую сумму уско-
ускорений этой точки в поступательном и вращательном движениях
фигуры и 2) как ускорение этой точки во вращательном движе-
движении вокруг мгновенного центра ускорений, причем мгновенным
центром ускорений называется такая точка плоской фигуры,
ускорение которой в данный момент равно нулю.
Если известны ускорение wA некоторой точки А фигуры
(ускорение полюса), а также угловая скорость со и угловое
183

ускорение е фигуры, то ускорение любой ее точки В опреде-
определяется по формуле
= WA + W$3A + WBA-	G8)
Здесь вектор wBA—ускорение точки В во вращательном дви-
движении вокруг полюса A; w(ba и ы>ва — касательная и нормальная
составляющие этого ускорения.
Следовательно,
и#А = ©МВ, шй = еЛВ;	G9)
при этом вектор w{ba направлен вдоль АВ (от точки В к точке А),
а вектор w{ba перпендикулярен к АВ.
Угол а между векторами wBA и В А определяется по формуле
tga = -^L,	(80)
при этом в случае ускоренного вращения фигуры векторы w(ba
и vBA (вращательная скорость точки В вокруг полюса А) лежат
по одну сторону от прямой АВ, в противном случае эти векторы
расположены по разные стороны от этой пр-ямой.
Если угловая скорость фигуры постоянна, т. е. ю = const,
то е = 0, а следовательно, и а = 0, т. е. вектор wBA совпадает
по направлению с вектором ВА. Если же в данный момент ш = 0,
то a = Y и векТ0Р wba перпендикулярен к вектору ВА.
На основании равенства G8) ускорение точки В можно найти
построением многоугольника ускорений и применением затем
метода проекций, спроектировав векторное равенство G8) на
выбранные оси.
Если мгновенный центр ускорений Q принять за полюс, то
для ускорения произвольно выбранной точки М фигуры имеем:
q
но wQ = 0, а потому
wM = ™mq =ЙЙЬ -Н wHSq,	(81)
т. е. ускорение любой точки М плоской фигуры определяется
как ускорение во вращательном движении вокруг мгновенного
центра ускорений (рис. 108).
При этом ускорение w(mq направлено по прямой MQ от точки
М к центру Q, а ускорение w{mq перпендикулярно к MQ и
w№Q=QM<o\ wWQ=QMs.	(82)
Ускорение wM точки М равно по модулю
wM = QM /со1 + е*	(83)
184

и составит с направлением MQ угол
'&¦	(84)
Отсюда следует: 1) угол а для всех точек фигуры имеет в
данный момент одно и то же значение; 2) ускорения точек
плоской фигуры пропорциональны расстояниям этих точек от
мгновенного центра ускорений.
Чтобы определить для данного момента
положение мгновенного центра ускорений
нужно:
1)	найти ускорение wA какой-либо точ-
точки А фигуры [обычно при решении задач
рассматриваемого типа ускорение одной точ-
точки фигуры (механизма) или задается, или
его можно легко найти];
2)	повернуть полупрямую, по которой
направлен вектор wA, вокруг точки А на
I e I	,
острый угол a = arctg ¦*—?- или в направлении вращения фигуры,
если это вращение является ускоренным, или в противополож-
противоположном направлении в противном случае;
3)	на полученной после этого поворота полупрямой отложить
отрезок
AQ^ rWA .	(85)
Отметим два частных случая:
1)	пусть е = 0, тогда tg а —* 2 = 0 и а = 0, следовательно,
ускорение wM любой точки М движущейся фигуры направлено
по MQ, т. е. проходит через центр Q. Поэтому мгновенный
центр ускорений Q в этом случае можно найти как точку пере-
пересечения прямых, по которым направлены ускорения двух каких-
либо точек фигуры;
2)	пусть со = 0, тогда tga = oo и а — 90°; следовательно, уско-
ускорение wM любой точки М фигуры перпендикулярно к MQ.
Поэтому мгновенный центр ускорений Q в этом случае можно
найти как точку пересечения перпендикуляров, восставленных
из двух каких-либо точек движущейся фигуры к ускорениям
этих точек.
Задачи, относящиеся к этому параграфу, можно разделить
на следующие четыре группы:
1) задачи, в которых заданы векторы скорости и ускорения
одной точки и прямолинейная траектория второй точки плоской
фигуры, ускорение которой требуется найти (задачи 566—571,
573—579);
185

2)	задачи, в которых заданы векторы скорости и ускорения
одной точки и криволинейная траектория второй точки плоской
фигуры, ускорение которой требуется найти (задачи 572,
573, 575);
3)	задачи, в которых требуется определить ускорение точки
катящегося без скольжения колеса (задачи 556—563);
4)	задачи, в которых заданы ускорения двух точек плоской
фигуры, а требуется определить ускорение третьей точки этой
фигуры (задачи 564, 574, 576—578).
Первая группа
В задачах первой группы известны ускорение ^ полюса А
и направление искомого ускорения wB точки В плоской фигуры,
так как точка В движется прямолинейно. Для определения
модуля ускорения wB следует найти сначала угловую скорость
фигуры, а затем ускорение w"ba- Далее задача решается по фор-
формуле G8), на основании которой следует построить в выбранном
масштабе многоугольник ускорений, в котором будут известны
направления всех сторон и модули сторон, изображающих уско-
ускорения wA и w"ba- Из построенного многоугольника ускорений
определяются графически ускорение wxBA и искомое ускорение wB.
Ускорения wxba и wb можно определить также без построения
многоугольника ускорений методом проекций, спроектировав
равенство G8) на прямую ВА (для определения wB) и на пря-
прямую, перпендикулярную к векто,ру wB (для определения wxBA).
Из полученных двух уравнений находим wxba и wb.
Пример 79. Кривошип О А = 10 аи нецентрального кривошипно-
шатунного механизма вращается вокруг неподвижной оси О
с угловой скоростью шо= 2 {/сек и угловым ускорением е0=4 1 /сек*
и приводит в движение шатун ЛВ = 550 см, соединенный
с ним шарнирно в точке А. Ползун В перемещается в наклон-
наклонных неподвижных направляющих тп Определить ускорение
ползуна В и угловое ускорение шатуна АВ в тот момент, когда
/ЛВ« = 60° и АВ\_ОА (рис. 109, а).
Решение. Так как движение кривошипа О А задано, то
можно найти скорость и ускорение точки А. Вектор vA перпен-
перпендикулярен к О А и по модулю равен vA = со0 О А = 2-10 = 20 ом/сек.
Вектор ускорения wA слагается из касательного ускорения wA,
направленного перпендикулярно к О Л, и нормального ускорения
Wa, направленного по кривошипу О А от Л к О, т. е. wA —
=¦ wa 4 w\, причем и\ -а>о О А =4-10 = 40 CMJcen*, w\ =
=_ ьоОЛ = 4 10 = 40
186

Так как ползун В движется поступательно и прямолинейно,
то векторы vB и wB направлены по прямой т.п. С другой сто-
стороны, точка В принадлежит шатуну АВ, движущемуся в плос-
плоскости рисунка; принимая в этом движении точку А за полюс,
по формулам G5) и G8) имеем:
vB = vA + vBA,	(a)
		i Я , Т	/^\
причем vBA_\_AB, ^йд J_ ЛВ, вектор Швл направлен вдоль В А п
AD "	Л D	• Л D ел
где со, и е, —угловая скорость и угловое ускорение шатуна АВ.
Для определения вращательной скорости точки В вокруг полюса
Ч)
Рис 109
А построим на основании равенства (а) треугольник скоростей,
в котором
Ва — 1)л ab = vR» Bb = va
Из этого треугольника имеем:
vBa = vA tg60° = ол УЗ = 20 1Л3 = 34,6 см,сек
187

и, следовательно,
"Jg = Ш = 24 см!сек*.
Теперь в векторном равенстве (б) остаются неизвестными
только модули ускорений wB и wxBa\ на основании этого равен-
равенства построим многоугольник ускорений, учитывая, что направ-
направление его замыкающей стороны wB известно. Построение этого
многоугольника следует начать с известных его сторон, т. е.
с ускорений w"a , w\ и wBa- Из точки о проведем вектор оаг =
= wX, из точки at—вектор а2ал — и)А, а из точки о, — вектор
a1bl! = w%A- Далее из точки Ьг проводим прямую, параллельную
вектору Wba, т. е. перпендикулярную к а2а,, а из точки о —
прямую, параллельную вектору wB, т. е. параллельную направ-
направлению тп. Если точку пересечения этих прямых обозначим через
Ьг, то bibJ = WBA и ob,=wB (рис. 109,6). Измерив длины сто-
сторон об, и btbt в выбранном масштабе ускорений, найдем чис-
ленные значения шв, wBa и е, = -^.
Если в построенном многоугольнике ускорений обозначить
точку пересечения сторон оаг и ЬгЪх через сх, то получим пря-
прямоугольный треугольник ос^Ь^, в котором /_cxob% = 60°, а потому
ob, = 2oc1, 6,с, = ос, tg 60°;
кроме того
oct = oat—albt = wA — wBA.
Следовательно,
wB = оЬл ==2 {w\ — wBA) = 2 D0—24) = 32 ЛИ/W;
6,6, = 02c. + cA = wnA + (a»5 — a-вл
= 40+ 16/3 ^ 67,68 сл*/се/сг,
Рассмотрим теперь, как найти численные значения ускорений
дав и wBa методом проекций. Для этого спроектируем векторное
равенство (б) на прямую ВА и на прямую Вр, перпендикуляр-
перпендикулярную к тп:
1)	wBcos60° = wA—wnBA,
2)	0 = (wxA — w'ba) cos 30° + wA cos 60° — wBa oos 60°.
18S

Отсюда
wB*=2(wA — w%a),
x wnA + {w\ — w%a)
Вторая группа
В задачах второй группы известны ускорение wA точки А
и криволинейная траектория точки В, ускорение которой тре-
требуется найти. Поэтому известны радиус кривизны q траектории
и направления векторов vB Wb (по касательной к траектории)
и w% (по нормали траектории), причем
wB — Wb 4- Wb-
Если принять точку А за полюс, то по формуле G8) получим:
WB = WA
следовательно,
Wb + wxb = wa + wba + wIa.	(a)
Определив угловую скорость фигуры со и скорость vB,
найдем ускорения:
Теперь в векторном равенстве (а) остаются неизвестными только
модули ускорений w\ и wBA. На основании этого векторного
равенства следует построить две ломаные линии:
1)	сторонами одной из них являются векторы wnB и wB;
2)	сторонами второй ломаной линии являются векторы wA,
wba и wba- ^3 этих построенных многоугольников графически
определяются неизвестные ускорения wB, wBA и wB. Задача
может быть решена также методом проекций. Для определения
ускорения wB достаточно спроектировать векторное равенство
(а) на прямую АВ, после чего ускорение точки В находим по
формуле
Пример 80. В механизме, изображенном на рис. ПО, а, кри-
кривошип О А = 25 см вращается с постоянной угловой скоростью
@ = 2 \jceK в плоскости рисунка вокруг неподвижной точки 0
и при помощи стержня А В приводит в движение кривошип ВС,
вращающийся в той же плоскости вокруг неподвижной точки С.
Определить скорость и ускорение точки В в тот момент, когда
189

кривошип О А горизонтален, ^/ОЛВ = 60°, /_ ABC = 30°, если
АВ = ВС=* 50 см.
Решение. Найдем сначала скорость vA и ускорение wA
точки А звена О А, движение которого задано. Вектор vA пер-
перпендикулярен к ОА и по модулю равен
vA =
= 2 ¦ 25 = 50 см]сек.
Так как кривошип ОА вращается равномерно, то ускоре-
ускорение wA направлено вдоль АО, причем
wл = сог0 А = 4 ¦ 25 = 100 см1секг.
а)
Рис. ПО
Так как точка В принадлежит звену ВС, вращающемуся
вокруг неподвижной точки С, то траекторией точки В является
дуга окружности с центром в точке С и радиусом СВ. Поэтому
векторы vB и wxB направлены по одной прямой, перпендикуляр-
перпендикулярной к ВС, а вектор w^ направлен вдоль ВС и по модулю
равен Щ*а = §§-- Кроме того,
(а)
С другойiстороны, точка принадлежит звену ВС, движуще-
движущемуся в плоскости рисунка; принимая в этом движении точку Л
190

за полюс, по формулам G5) и G8) имеем:
»в = "л + УвЛ1	(б)
шв=шл + ^«л + ^вл>	(в)
где векторы ивл и йу*л направлены по одной прямой, перпен-
перпендикулярной к АВ, а вектор wBA направлен вдоль В А, причем
w'ba~~ab' ^° того как пеРех°Дить к определению ускорений,
следует найти скорости vB и vBA; для этого построим, согласно
равенству (б), треугольник скоростей В. Тогда
Ba = vA, ab — vBA, Bb~vB,
причем
/_ВЬа = /_АВС = 30°, /_ аВЬ = 90° — / СВО =- 30°.
Отсюда
Ba = ab, т. е. илл = ил = 50 см\сек,
vB = Bb = 2Ba cos 30° = /3 ул = 50 /3 сж/се/с.
Следовательно,
Теперь переходим к определению искомого ускорения wB.
Для этого построим многоугольники ускорений по формулам (а)
и (в), начиная построение с известных векторов wB, wA и wBA .
Из точки о проводим вектор oal = wA, из точки а, — вектор
aicJ = wBA, a из точки с, — прямую ^с, параллельную век-
вектору wBA, т. е. перпендикулярную к а,с. Далее, из точки о
проведем вектор oe1 = wB, а из точки е, — прямую е,е, парал-
параллельную вектору а>?, т. е. перпендикулярную к оег Точку пе-
пересечения прямых схс и е^е обозначим через 6U тогда
elbl = wB, clbl = wxBA и obJ = wB. Измерив выбранной единицей
масштаба длины сторон егЬг, ctbt и obt, найдем модули уско-
ускорений wxB, wxBA и wB.
Так как все углы в многоугольниках ускорений известны
(см. рис. 110,6), а неизвестными остаются только модули двух
сторон, то эти стороны можно вычислить по формулам триго-
тригонометрии. Так как oal=2aicl и ^/moaic1 = &0°, то ^/а1ос1 = 30°,
191

/_Я\С10 — 90° и прямая сгс проходит через точку о, т. е. много-
многоугольник ускорений превращается в два треугольника: Д оахсх
и /Хое^^ в которых 2.б,о6,-60°. Из этих прямоугольных
треугольников имеем:
e,fe1=oe1tg60°I ob, = 2oe и ос, = оа, sin 60°,
откуда
Как было указано выше, численные значения векторов wxB ,
wB, wBA можно найти методом проекций: проектируя вектор-
векторное равенство wB+wB = wA + wBA-{-wBA на прямые В А и ВС,
получим:
1)	wxB cos 60° — wB cos 30° = wA cos 60° — wnBA;
2)	oy?— wA cos 30° + и>?л cos 30° -f wBA cos 60°.
Отсюда
wl = wA — 2wnBA + wb /3 = 150 J/3 c^/ce«:2,
A + 2wnB—w%A /3 = C00 + 50
= 300 см\сек\
Третья группа
Особенностью задач этой группы является то, что угловое
Ж
ускорение е фигуры находится здесь как производная ~ по
времени от угловой скорости, т. е. е = -п-.
Пример 81. Кривошип О А вращается в плоскости рисунка
вокруг неподвижной точки О с угловой скоростью ю = 2 1/дас
и угловым ускорением е = 4 1/сек2 и приводит в движение сво-
свободно насаженную на него в точке А шестерню / радиуса
г1 = 5см, катящуюся без скольжения внутри неподвижного колеса
//радиуса гг=15см. Определить скорость и ускорение точки В
подвижной шестерни, если /_ОАВ = 60° (рис. 111, а).
Решение. Найдем сначала скорость vA точки А и каса-
касательное и нормальное ускорения wA и w"A этой точки: vA — a0A =
— ю(гг—г\)= 20 cMJceK, wA = a'OA = 40 см/сек2, w\ = гОА =
= 40 сн\секг; так как wA = wA, то вектор wA составляет с на-
направлением АО угол 45°, а с направлением АВ — угол, равный
60° —45°= 15°. Качение шестерни / по неподвижному колесу //
192

происходит без скольжения, а потому мгновенный центр ско-
скоростей шестерни / находится в точке касания Р колес и сле-
следовательно, угловая скорость подвижной шестерни / равна:
э' л № ', ^U," /'
отсюда угловое ускорение этой шестерни равно
Далее задача может быть решена двумя способами:
1)	по формуле G8);
2)	при помощи мгновенного центра ускорений по форму-
формулам (83), (84).
Рис. 111
1-й способ. Цыбирая точку А за полюс, имеем:
(а)
причем
WBA =
= е,Л5 = е /^— 1) Л5 = 40 см/се/с1.
Вектор wB есть замыкающая сторона ломаной линии, сторонами
которой являются векторы Ъ\, wA, w^A, wBA, известные как
по модулю, так и по направлению. Таким образом, все сла-
слагаемые в правой части предыдущего векторного равенства
известны и по модулю, и по направлению. Построив много-
Зак. 2374
193

угольник ускорении, в котором
Oc=wA, ca^w
ae=w"BA,
найдем искомое ускорение wB точки В: Ob=wB (рис._ 111,6).
Для определения модуля и направления вектора wB мето-
методом проекций, спроектируем векторное равенство (а) на оси х
и у, направленные по ВА и перпендикулярно к ВА. Тогда
w
Bx
= wba — w"a cos 60° — Дол cos 30°
Отсюда
«= 80 — 20 — 20V3 = F0 — 20 /З) см\сек\
wBy = tsisA — wnA cos 30° + wA cos 60° =
40—201^3 + 2 0 = F0—20 / 3) см\секг.
wb =
= 20 C —1^3) /2 = 35,8 см)сек\
Так как wBx=wBy, то вектор шв образует с направле-
направлением В А угол 45°.
2-й способ. По формулам (84) и (85) находим:
wA
40 V 2
и отложив на
Повернув вектор wA вокруг точки А в направлении вращения
шестерни /, т. е. по часовой стрелке, на угол a = arctg -5-
полученном после этого луче отрезок
AQ = ^Ю^«3,16 см, получим точку
гц Q — мгновенный центр ускорений
(рис. 112). Тогда для ускорения wB
точки В по формуле (83) имеем:
щ,
Рис. 112
= BQ К 82
Расстояние
BQ вычислим из
треугольника ABQ, в котором
/_ Q = a—\5°;BQ* = АВг 4- AQ*—2АВ ¦ AQ cos (а -15°) = 35—
—20 /2 (cos 15° + tg а sin 15°) =« 4,15, т. е. BQ = 2,03 см и, сле-
следовательно, wB = 2,03 8 Vb^ 36 см1секг.
Вектор wB составляет с направлением BQ такой же угол а,
как и вектор wA с направлением AQ,
194

Четверта я группа
Пример 82. Равносторонний треугольник ABC движется
в плоскости хОу так, что его вершины А я В перемещаются
по осям Ох и Оу, причем wA = 20]/3 см\се.кг, а ьу5 = 20 cMJceic'.
Найти ускорение wc вершины С в момент, когда сторона АС
параллельна оси Ох, если АС = 20см (рис. 113, а).
Рис. 113
Решение. 1-й способ. Выберем точку А за полюс, тогда,
согласно формуле G8), имеем:
Векторы wnBA и WqA направлены соответственно по ВА и СА,
а векторы wxBA и wxCA—соответственно перпендикулярны к ВА
и СА, причем
= eCA.
8»
195

Так как ВА = СА, то
На основании равенств (а) и (б) построим многоугольники
ускорений точек В и С. Для_этого из произвольной точки О
проводим векторы Oa = wA и ОЬ — юв. Далее из точки а прово-
проводим прямую, параллельную вектору wBA, т. е. параллель-
параллельную ВА, а из точки Ь — прямую, параллельную wBA, т. е. пер-
перпендикулярную к В А до их взаимного пересечения в точке е.
Тогда
Чтобы построить многоугольник ускорений для точки С,
проведем вектор ad, параллельный вектору Wca, т. е. парал-
параллельный С А и равный по модулю ае (так как ю?л = w?A, то
°^ = wba — wca ~ ае' т- е- а^~ wca)- Затем из точки d проведем
вектор dc, перпендикулярный вектору ad, причем dc=W*,A —
— wba ~ е&- Соединив точки О и с, получим замыкающую сто-
сторону многоугольника Oadc, т. е. Oc = wc (рис. 113,6).
Для решения задачи методом проекций спроектируем равен-
равенство (а) на прямую ВА и прямую, перпендикулярную к ВА,
а равенство (б)—на оси х и у. Тогда имеем:
1)	—wB cos 60э = — wA cos 30° -f- w"BA;
2)	— wB cos 30° = wA cos 60° — u>lA\
3)	wcx = -wnCA;
4)	wey = —
Отсюда
wBA = wA cos 30°—wB cos 60° = 20 /3 ij5—^ = 20 см\секг\
wba = wa cos 60° + wB cos 30° = ^Jp + ?°il? = 201/3 см\сек\
wcx = — К a = — wIa = — 20 см\сек\
Следовательно, ускорение wc точки С равно по модулю
20 cMJceK2 и направлено по оси Ох влево.
2-й способ (при помощи мгновенного центра ускорений).
Так как в данной задаче ускорения wA и wB заданы, то мгно-
мгновенный центр ускорений проще всего можно найти как точку
пересечения двух прямых, проведенных из точек А и В под
196

одним и тем же углом а = агсЧ?^ к ускорениям точек [см.
формулу (84)]. Но угол а равен углу между векторами wBA
и ВА [см. формулу (80)]. Из равенства G8) имеем:
Чтобы построить вектор wBA, т. е. разность wB— wA, про-
проведем из произвольной точки О векторы Oa=wA и Ob — wB и
соединим их концы. Тогда wBA — ab (рис. 113, в). Из прямоуголь-
прямоугольного треугольника Oab находим:
^ = Й = ^ = /3, где ^/_ОЬа,
т. е. у = 60°. Отсюда следует, что вектор wBA, проведенный из
точки В, направлен по стороне ВС треугольника ABC и потому
составляет с направлением В А угол 60° (рис. 113, г). Следова-
Следовательно, а = 60°. Теперь, чтобы построить мгновенный центр
ускорений, достаточно повернуть на угол 60° против часовой
стрелки вектор wA вокруг точки А, а вектор wB вокруг точки В.
Полученные после этого поворота векторы будут направлены
соответственно по биссектрисе угла А треугольника ABC и по
стороне ВС; точка пересечения Q этих прямых является мгно-
мгновенным центром ускорений. Так как, очевидно, QC = QB, то
wc = wB = 20 см/сек* [см. формулу (83)].
Вектор wc составляет с направлением CQ угол а = 60°,
т. е. направлен по стороне С А треугольника ABC (рис. 113, г).
Глава IV
СОСТАВНОЕ ДВИЖЕНИЕ ТОЧКИ
§ 1. УРАВНЕНИЯ ДВИЖЕНИЯ И ТРАЕКТОРИЯ СОСТАВНОГО
ДВИЖЕНИЯ ТОЧКИ
Если мы рассматриваем движение точки по отношению к системе
координат Ox1yiz1, которая в свою очередь движется относительно
системы отсчета Oxyz, принимаемой за неподвижную, то движение
точки М по отношению к подвижным осям Olxly1zl называется
относительным. Движение подвижных осей Olx1yiz1 относительно
неподвижной системы отсчета Oxyz называется переносным, а дви-
движение точки М относительно неподвижных осей называется в этом
случае составным, или абсолютным движением. В связи с этим
197

различают абсолютную (va), относительную (иг) и перенос-
переносную (ve) скорости точки М, а также абсолютное (дао), относи
тельное (wr) и переносное (we) ускорения этой точки При этом
относительной скоростью и относительным ускорением точки
называют ее скорость и ускорение в относительном движении,
абсолютной скоростью и абсолютным ускорением точки назы-
называют ее скорость и ускорение в абсолютном движении. Пере-
Переносной скоростью и переносным ускорением точки называются
соответственно скорость и ускорение той точки, неизменно
связанной с подвижной системой осей, с которой в данный мо-
момент совпадает точка М.	/
Задачи, относящиеся к этому параграфу, можно разбить на
два основных типа:
1)	зная относительное движение точки и переносное движе-
движение, найти уравнения и траекторию абсолютного движения
этой точки (задачи 417, 419—422);
2)	зная абсолютное движение точки и переносное движение,
найти уравнения и траекторию относительного движения точки
(задачи 418, 423, 425).
При решении этих задач следует прежде всего установить
подвижную и неподвижную системы отсчета и выяснить харак-
характер переносного движения, т. е. характер движения того тела,
с которым неизменно связана выбранная подвижная система
осей. После этого следует установить, какое движение рассмат-
рассматриваемой точки является абсолютным движением и какое—от-
какое—относительным.
Пример 83. Движение точки относительно подвижных осей
Оххуг задано уравнениями:
Подвижные оси Ох1у1 вращаются в своей плоскости вокруг
неподвижной точки О по закону ф=-^-?. Составить уравнения
движения точки М относительно осей Оху (уравнения абсолют-
абсолютного движения) (рис. 114).
Решение. Переносным движением в данной задаче является
вращение подвижных осей Ох,г/, вокруг точки О. Чтобы найти
уравнения абсолютного движения точки М, нужно ее коорди-
координаты х и у в неподвижной системе осей выразить в функциях
времени t.
Построив координаты точьи М в подвижных и неподвижных
системах осей, имеем по формулам преобразования координат
195

при повороте осей на угол ср-
Рис 114
или, подставляя значения ж,, у1 и ф, получим искомые урав-
уравнения абсолютного движения точки М:
х = 4 sin -д-1 cos -^ ^ -+- ( 1 — cos -F- м sin -s- ^,
ft	Ы ,\	Я, ..Я,.Я,
у—\\ — cos -н- / cos -тг г — 4 sin тг t sin -д- г,
\	г / г	t г.
или
3 .. , , . я ,
д; = -g- sm лг -f- sin -д- г,
я , , 3 , 5
г/ = cos-д- / + -г, cos я^ — т.
Примечание Исключив / из уравнений относительного движения
точки М, находим ее относительную траекторию:
Это есть эллипс с полуосями о=2, Ь=1 и с центром в точке А @, 1).
Следовательно, абсолютное движение точки М можно представить как
движение по этому эллипсу, который вращается вокруг точки О
Пример 84. Резец совершает прямолинейное возвратно-посту-
возвратно-поступательное движение так, что его конец М движется по непод-
неподвижной оси Ох по закону х = ОМ = a sin at. Составить уравне-
уравнения движения точки М относительно диска, вращающегося
199

равномерно с угловой скоростью ю вокруг точки О, и найти траек-
траекторию этого относительного движения (рис. 115).
Решение. Подвижную систему координатных осей Охгу^
неизменно связанных с диском, выберем так, чтобы в началь-
начальный момент ось Ох% совпадала с неподвижной осью Ох.
Тогда уравнение переносного вращательного движения запи-
запишется так:
Чтобы получить уравнения отно-
относительного движения точки М, нахо-
находим ее координаты в подвижной си-
системе отсчета Ох,ух:
хл=ОВ = ОМ cos ф,
ух = — О А — — ОМ sin ф.
Подставив сюда значения фи
получим:
, , a sin 2mt
х1 = а sin at cos шг =	=— >
у, = — a sin to/ sin at = — a sin2 <
Рис. 115
Это и есть уравнения относительного движения точки М.
Чтобы найти траекторию относительного движения этой
точки, достаточно из последних двух уравнений исключить
время t.
Для этого возведем первое из этих уравнений в квадрат:
х\ = аг sin2 at cos2 at = a2 sin2 at A — sin2 at).
Заменяя a sin2 at через */,, получим:
или
или
или
, + # = О,
Следовательно, искомая траектория есть окружность радиуса
0, —~)
4 с центром в точке
200

§ 2. ТЕОРЕМА СЛОЖЕНИЯ СКОРОСТЕЙ
Если точка М участвует в составном движении, то имеет
место следующая теорема: абсолютная скорость точки равна
геометрической сумме переносной и относительной скоростей
этой точки (рис. 116), т. е.
»в = «в+й,.	(86)
Если угол между векторами ve и vr обозначим а, то модуль
и направление вектора абсолютной скорости определяются по
Рис. 116
формулам (87) и (88):
va = V v\ -f v'j + 2vevr cos a	(87)
И
-^-=-^5 = -^,	(88)
sin a sin p sin y
где р и у — углы, образуемые вектором va с векторами vr и ve.
Задачи, относящиеся к этому параграфу, можно разделить
на четыре основных типа.
Задачи типа I
(задачи 435, 439, 444)
Зная переносную и относительную скорости точки найти ее
абсолютную скорость.
Решение задач этого типа сводится к построению паралле»
лограмма скоростей по двум смежным его сторонам ve и vr.
Пример 85. Круглый цилиндр радиуса г вращается вокруг
своей вертикальной оси Oz с угловой скоростью ш=-д-/8 1/се/с.
По поверхности цилиндра перемещается точка М по винтовому
пазу по закону s = -5-, где s есть длина дуги М0М винтовой
линии.
Касательная к винтовой линии составляет с образующей
цилиндра угол у = 30°. Определить абсолютную скорость точки
М в момент t (t выражено в сек, а s—в м) (рис. 117).
8В Злк. 237 1	201

Решение. Если систему
подвижных осей Oxtytz неизмен-
неизменно свяжем с цилиндром, то пе-
переносное движение будет вра-
вращательным вокруг неподвижной
оси Oz с угловой скоростью а>е —
= %-t2 \\сек. Поэтому перенос-
на я скорость точки М будет
направлена перпендикулярно к
плоскости MOtz и по модулю
равна ve = <d/ ~-^rf. Относи-
Относительным движением точки М
(движением по отношению к
цилиндру) является ее движе-
движение по заданной винтовой ли-
линии по закону s = V- Следова-
Следовательно, относительная скорость
точки М направлена по каса-
касательной к винтовой линии и по
модулю равна
ds , i
о, = -тг = at см сек.
' at	'
Рис. 117
Так как угол между векто-
векторами ve и vr равен 90*—y = 60°, to по формуле (87) абсолютная
скорость точки М будет равна
а * е ' г ' е г
+ Ъагсм\сек.
Задачи типа II
(задачи 433, 441—443)
Зная абсолютную скорость точки и направления переносной
и относительной скоростей этой точки, найти модули этих ско-
скоростей.
Решение задач этого типа сводится к построению парал-
параллелограмма скоростей по данной диагонали и направлениям двух
смежных его сторон.
Пример 86. Механизм состоит из двух параллельных валов
О и О,, кривошипа О А и кулисы О,В; расстояние между осями
валов равно 00,== 30 ел, длина кривошипа О А равна 10 еж.
Кривошип вращается равномерно вокруг оси О с угловой ско-
202

ростьюсо = 4 \'сек. Найти переносную и относительную скорости
точки Л, а также угловую скорость cOj кулисы в момент, ко( да кри-
кривошип О А составляет с вертикалью угол ф = 60° (рис. 118).
Решение. Если за подвиж-
подвижную систему отсчета выберем си-
систему, неизменно связанную с ку-
кулисой 0хВ, то переносное движе-
движение будет вращательным вокруг
оси О, с угловой скоростью со,.
Поэтому переносная скорость точ-
точки Л будет перпендикулярна к
0хА и по модулю равна ие = ОхАсох.
Относительное движение точки Л,
т. е. ее перемещение относительно
кулисы, является прямолинейным
вдоль О,Б. Поэтому вектор относи-
относительной скорости vr этой точки
направлен по прямой О,й. Но точ-
точка А принадлежит одновременно
и кривошипу ОА, вращающемуся
вокруг неподвижной оси О с угло-
угловой скоростью со = 4— , а потому
траекторией абсолютного движе-
движения точки Л, т. е. ее движения
по отношению к неподвижной системе
ся окружность радиуса ОА.
Абсолютная скорость точки Л направлена
к ОА и по модулю равна
va — со О А = 4 • 10 = 40 cMJceK.
Зная модуль и направление вектора vaи направления век-
векторов ve и vr строим параллелограмм скоростей, в котором
вектор va должен быть диагональю. Так как vr J_ ve, то из пря-
прямоугольного треугольника имеем:
j
I
Рис. 118
координат Охху, являет-
перпендикулярно
где у—угол между векторами va и ve, равный углу ОАОг. Для
определения этого угла из треугольника ООХА находим:
ОХА =
cosA80°-cp)
102+2-30-10-cos60o =
__ OtA _ OXA
Ofi __
siny sin A80° — ф) ~ sin ф
SB*
203

Отсюда
зо
27 5
Следовательно,
Из равенства ve — a1 OtA находим
юо ^Д w 0|771/eac.
I 1 о \ А	'
' 13-ю- ухз '3"
Направляющее
колесо
Задачи типа III
(задачи 436, 437, 440)
Зная векторы va и v^ (или векторы v& и уг), найти модуль
и направление вектора vr (или вектора ve).
Решение задач этого типа
сводится к построению паралле-
параллелограмма скоростей по данной
диагонали, одной из его сторон
и углу между ними.
Пример 87. Частица М воды
поступает из направляющего
колеса турбины в рабочее коле-
колесо (рис. 119) со скоростью
о = 7,57 м[сек, которая образу-
образует с направлением касательной
к внутренней окружности на-
направляющего колеса угол
Рабочее а = 40°. Найти скорость части-
колесо	К-
цы относительно рабочего коле-
колеса и угол р, который должны
составлять лопатки рабочего
Рис 119	колеса с направлением каса-
касательной в месте входа воды,
если вода поступает в рабочее колесо без удара, наружный
радиус рабочего колеса R — 225 мм и угловая скорость враще-
вращения турбины равна л = 320 o6jmuh.
204

Решение. Если за переносное движение принять вращение
турбины вокруг оси О с угловой скоростью со =^- = ^~- =
32
— -g-л 1/шс, то переносная скорость частицы М будет направлена
перпендикулярно к радиусу ОМ и по модулю равна ve = u>ex
хОМ = уЯхО,225 = 2,4я ж/се/с.
Заданная скорость, с которой частица вступает в рабочее
колесо, является абсолютной скоростью va. Зная векторы va и
ve, строим параллелограмм скоростей, в котором вектор va яв-
является диагональю, и находим относительную скорость vr ча-
частицы М, направленную по касательной к лопатке рабочего
колеса. Из треугольника скоростей, в котором известны стороны
va, ve и угол а между ними, находим:
о, = \f v\ + о= — 2veva cos a =
= 1/7,57г + B,4яJ —2 • 7,57 • 2,4л cos 40° = 5,16 м[сек.
По формуле (88) имеем:
откуда
. D o.-sioo 7,57-0,643 п ,,,„
sin р = ^— = 5>1'6 = 0,939,
Задачи типа IV
(задачи 430, 434, 438)
Зная вектор v"e (или вектор vr) и направления скоростей va
и vr (или о0 и ое), найти модули этих скоростей.
При решении задач типа IV параллелограмм скоростей сле-
следует строить по заданной его стороне ve (или vr) и известным
направлениям другой его стороны vr (или ve) и диагонали v .
Решение задач этого типа аналогично решению задач типа II.
Пример 88. Параболический кулак, контур которого имеет
форму параболы у1 = 9--хги движется поступательно и прямо-
прямолинейно по неподвижной горизонтальной плоскости по закону
s — 30t и толкает опирающийся на него стержень CD, который
перемещается в вертикальных направляющих. Найти скорость
стержня в зависимости от расстояния конца С стержня от оси
Охх (рис. 120).
205

Решение. Подвижные оси О^г/,, неизменно связанны
с кулаком, направлены, как указано на рис. 120. Переносным
движением является поступательное и прямолинейное движение
кулака со скоростью и, =^| = 30 см\сек. Поэтому переносная
скорость ve точки С независимо от ее положения на параболе
равна поступательной скорости кулака о, = 30 см/сек и направ-
направлена по горизонтали вправо. Так как абсолютное движение
стержня CD есть поступательное движение в вертикальном на-
направлении, то абсолютная скорость точки С направлена по вер-
вертикали. Кроме того, точка С стержня CD перемещается отно-
относительно кулака по заданной параболе, а потому относительная
Рис 120
скорость этой точки направлена по касательной к этой пара-
параболе. Таким образом, нам известны модуль и направление ско-
скорости ve и направления скоростей va и vr Для определения
абсолютной скорости va нужно построить параллелограмм скоро-
скоростей, в котором одной стороной является вектор ve, другая сто-
сторона направлена по касательной к параболе в точке С, а диа-
диагональ направлена по вертикали CD. Так как va J_ ve, то из
прямоугольного треугольника скоростей находим:
Касательная к параболе, по которой направлен вектор vr, со-
составляет с положительным направлением оси Охг угол, рав-
равный 180° — а, а потому
или
206

Следовательно,
или
0в = 6О1/<Г=?.
§ 3. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОМ
ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
В случае составного движения точки, если переносное дви-
движение является поступательным, абсолютное ускорение точки
равно геометрической сумме ее переносного и относительного
ускорений (рис. 121), т. е.
Wa = We + wn	(89)
ИЛИ	_
(90)
Wr
где wlx) и
-касательная и нормальная составляющие пере-
пере[n)
носного ускорения точки, a wy и w\ —касательная и нор-
нормальная составляющие ее относительного ускорения (рис. 122).
Если переносное или отно-
относительное движение является	—ft) a.
прямолинейным, то соответст-	е-
вующее нормальное ускорение
(ад<п> или ш[п)) будет равно ну-
нулю; при криволинейном равно- -,
Рис 122
мерном переносном или относительном движении обращается в
нуль соответствующее касательное ускорение (да(ех) или а>(гт)).
Задачи, относящиеся к этому параграфу, можно решить двумя
способами: геометрическим или аналитическим
Геометрическое решение задачи состоит в построении парал-
параллелограмма или многоугольника ускорений на основании вектор-
векторных равенств (89) или (90)
При аналитическом решении задачи применяется метод
проекций, т. е. искомое ускорение определяется по его проек-
проекциям на выбранные координатные оси При этом следует иметь
в виду, что проекция абсолютного ускорения на какую-либо
207

ось равна алгебраической сумме проекций составляющих уско-
ускорений на ту же ось, проектируя, например, векторные равен-
равенства (89) или (90) на ось х, имеем:
(91)
или
wax = Ч? +4? + Ч* +Ч"'-
(92)
Задачи, относящиеся к этому параграфу (в основном задачи
из сборника И. В. Мещерского), можно разделить на следую-
следующие три основных типа
Задачи типа I
(чадачи 447—450, 455, 457—459)
I. Заданы перекосное и относительное ускорения точки,
т. е. векторы we и wr, или эти ускорения можно непосредст-
непосредственно найти из условий задач, характеризующих относительное
И переносное движения.
Определить абсолютное ускорение wa этой точки.
Пример 89. Кривошип ОгА = 0,5 м шарнирного параллело-
параллелограмма OtABO3 вращается вокруг неподвижной оси О, с угло-
угловой скоростью со, — 2t \\сек.
Вдоль стороны АВ этого параллелограмма перемещается
ползун М по закону AM = s — 5/2 (s выражено в метрах, t—в сек).
Определить абсолютное ускорение ползуна М в момент времени
* = 2сек, если угол <р в этот момент равен 30° (рис. 123).
Решение. Аналитический способ. Движение ползуна М бу-
будем рассматривать как составное, состоящее из двух движений:
1) относительного движения, т. е. движения по отношению
к стержню АВ, и 2) переносного движения вместе с этим стерж-
стержнем. Так как при движении стержень АВ остается параллель-
параллельным неподвижному звену Ofi^, то движение этого стержня яв-
является поступательным. Следовательно, переносное ускорение
точки М равно ускорению точки А, т. е.
208

Но точка А принадлежит кривошипу 0,4, а потому
Чя> = ©1-0,4 = 8 м,сек\
= е, • 0,4 = ^ 0,4 =2 0,5 = 1 м\сек\
При этом вектор о/*> направлен перпендикулярно к 0,4,
а вектор ш^' направлен вдоль ЛО, к центру О,. Так как в от-
относительном движении ползун перемещается вдоль стержня АВ
по закону s = 5t", то его относительное ускорение до<?> направ-
направлено вдоль этого стержня, причем
ш<м) = ^ = Юм1сек\
Абсолютное ускорение и/м точки М определяется по теореме
сложения ускорении при переносном поступательном движении:
Проектируя это равенство на координатные оси хну, по-
получаем
%у(а) = эд(г) + 1л)^ + {д)(п) = w^ + w^ • sin ф —
—wf cosф « 10+ 1 • у — 8^—= 10,5 — 4 /3 = 3,58 л/сек2,
j^f^) === ^(r) _|_ ^(t) + j?i(rt) =	^^^ * cos ф—w^n^ * sin ф :==i	4.
Отсюда
'= /A0,5—4 VW -
= /175 — 801/3 «6,1 mjc
Если угол между ускорением vfff и осью л; обозначим а, то
cos а = —~ = -^-у = 0,586,
откуда
а = 54°6'.
Решим теперь эту задачу геометрическим способом. Для этого
из произвольной точки О (рис. 124) проводим вектор Ou = wi'a\
причем длина этого вектора равна восьми единицам выбранного
масштаба ускорений, затем из точки а проводим вектор ab =
*= Wa\ длина которого равна единице масштаба ускорений.
209

Далее из точки Ь лроводим вектор be причем be = 10 еди-
единицам масштаба. Вектор Ос, замыкающий ломаную линию Oabc,
определит по модулю и направлению искомое абсолютное уско-
ускорение точки М, т. е. w{m =Ос (рис. 124).
Задачи типа II
Заданы векторы wa и we (или wr), либо эти векторы можно
найти непосредственно из условий задачи, характеризующих
абсолютное и переносное (или относительное) движения. Опре-
Определить вектор wr (или we).
Пример 90. Полуцилиндр радиуса г =10 см движется посту-
поступательно и прямолинейно по неподвижной горизонтальной пло-
плоскости с ускорением тл и толкает опирающийся на него стер-
стержень CD, который пе-	т\
ремещается поступа-	х \У, д
тельно в вертикальных I*	N. ™ш
Рис. 124
Рис 125
направляющих с ускорением wt. Определить касательное и нор-
нормальное ускорения точки С в ее движении по отношению к ци-
цилиндру в тот момент, когда ^/СО,*, = а = 60" (рис. 125).
Решение. Переносным движением в данной задаче является
(так же, как и в примере № 88) движение полуцилиндра, а так
как это движение поступательное, то переносное ускорение we
точки С стержня равно да,. Абсолютное ускорение точки С
равно, очевидно, заданному ускорению wt стержня CD, т. е.
wa = wt. В относительном движении (в движении по отноше-
отношению к полуцилиндру) точка С перемещается по полуокруж-
полуокружности радиуса г. Поэтому относительное ускорение равно
wr = w^n) -f ау(гт). причем вектор относительного нормального
ускорения w^ направлен по радиусу СОг, а вектор относи-
относительного касательного ускорения w^ направлен перпендику-
перпендикулярно к Ofi, как указано на рисунке. По формуле (89) имеем:
vr = we \ w(rn) -f w(P,
210

или
w = w -f- wr ' w)- •	(a)
В этом векторном равенстве неизвестны только модули искомых
ускорений w(rn) и w?\ Для определения этих модулей достаточно
спроектировать это векторное равенство на две выбранные оси.
В данном случае, принимая во внимание направления векторов
и/гх) и w^"\ эти оси целесообразно направить по радиусу 0гС и по
касательной Ст. Проектируя равенство (а) на эти оси, получим:
шг cos (90° — а) = да, cos а—w{rn),
w2 cos а = —w1 sin a -f- w™,
откуда
w<P) = w1 cos a—тг sin a,
to(rT> = w2 cos a -f wt sin a,
т. e.
(n) _ w1 — wl V% (t) _ ffii, Y~~
Задачи типа III
(задачи 445, 446)
Известны абсолютное ускорение wa и направления всех
составляющих ускорений w?\ wln), ш(гт), wf1, а также модули
двух из них. Найти модули двух других составляющих уско-
ускорений.
Пример 91. Кривошип ОС —г вращается вокруг неподвижной
оси О с данной угловой скоростью со = const. Соединенный
с ним при помощи шарнира ползун С может перемещаться
вдоль стороны АВ шарнирного параллелограмма OtABO2 с не-
неподвижным звеном ОхОг. Углы аир для данного положения
механизма известны.
Определить относительное ускорение ползуна С и угловое
ускорение кривошипа ОГА. длина которого равна а (рис. 126).
Решение. Движение ползуна С будем рассматривать как
составное, слагающееся из двух движений: 1) относительного
движения по отношению к стержню АВ и 2) переносного дви-
движения вместе с этим стержнем. Так как при движении стер-
стержень АВ остается параллельным неподвижному звену О1О2, то
движение этого стержня, а следовательно, и переносное движе-
движение, будет поступательным.
2П

Поэтому переносная скорость и переносное ускорение точки С
равны соответственно скорости и ускорению точки А, т. е.
= vA и
векторы ЪА и w(T направлены перпендикулярно к кривошипу
0^, а вектор wf — вдоль О,Л к центру О,, причем
ил = асо„
= шв?,
= ае„
где ю, и р, — угловая скорость и угловое ускорение стержня OtA.
Так как относительное движение точки С есть прямолинеи-
о,
Рис 126
ное движение вдоль стержня АВ, то относительная скорость
и относительное ускорение к>с' этой точки направлены вдоль
стержня АВ.
Но точка С принадлежит одновременно и кривошипу ОС,
вращающемуся равномерно вокруг оси О, поэтому абсолютная
скорость ос1 и абсолютное ускорение ©(?' точки С направлены
соответственно по перпендикуляру к ОС и вдоль ОС к центру О,
причем
Зная модуль и направление вектора Ус' и направления
векторов ^'с* и 1>{с, строим параллелограмм скоростей и по тео-
теореме синусов из него находим:
sin (90°— a) sin (90°
212

отсюда
(е) _ (a) COS p _ ПО COS р
bOs a cos а
Но
поэтому
	г cos Й
1 а cos а
и, следовательно,
(я)	 г	Гг(Ог COS2 В
1 a cos2 a'
По теореме сложения ускорений имеем:
(а)	' (г) . ' (е) (г) | (т) i^ (гс)	/ \
В этом векторном равенстве известны теперь направления
всех векторов и модули двух из них: w^ и шл"\ остается няйти
модули векторов wc} и w^- Для этого спроектируем равен-
равенство (а) на оси Axt и Aylt тогда получим
Шс" cos В = w{r) -\ w{a] sin a + w{a] cos а,
Шс' sin В = шдт) cos а—ш^' sin а.
Из этих уравнений находим:
sin |5 -}- Wa ьш а) =	f sin p -1— • —— sin а
= гсо^ (а sin В cos2 a + r sin a cos2 В),
} = да'с0 cos 6—шлт> sin а—w1^ cos а =
= wha) cosB-sinp-sina w(ca)-
^ cos a
wc
cos a	cos a
>- ш(лч cos a -=
= г(й. [а cos (а + 6) cos2 а —г cos2 В],
а cos" а i v i f	г-'
Угловое ускорение е, звена 0,Л находим по формуле:
о|5г = jS^ (a sin P cos2 a +r sin a
Рассмотрим теперь геометрический способ решения этой за-
задачи (рис. 127).
Из произвольной точки О строим в выбранном масштабе
векторы Oa = w(c) и Ob— w{a\ Затем из точек а и Ь проводим
213

прямые, параллельные соответственно	векторам
их пересечения в точке с. Тогда
~<Т) 1Г ""(г) —	Ьс
Wa = ос, We =са и	е = ^—г .
, до
§ 4. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОМ
ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
В случае составного движения точки, если переносное дви-
движение является вращательным, абсолютное ускорение точки
равно геометрической сумме переносного, относительного и
кориолисова или добавочного, ускорений этой точки, т. е.
Wa = We + Wr -f Wk,
ИЛИ
(93)
(94)
Рис. 127
Рис. 128
Кориолисово ускорение wk равно удвоенному векторному
произведению угловой скорости переносного вращения на от-
относительную скорость точки, т. е.
(95)
wk — 2ае х vT.
Следовательно, модуль этого ускорения равен
wk — 2(uevr sin a,
(96)
где а—угол между векторами сог и vr.	_
Чтобы найти направление кориолисова ускорения wk дви-
движущейся точки /И, достаточно в точке М построить векторы сое
и у, и восставить из этой точки перпендикуляр к плоскости,
214

в которой лежат эти векторы о>е и vr. Вектор wk направлен
по этому перпендикуляру так, чтобы наблюдатель, смотрящий
с конца этого вектора, видел поворот вектора сое на угол_а
против часовой стрелки до совмещения его с вектором vr
(рис. 128).
Направление вектора wk можно определить и другим спо-
способом.
Проведем через точку М плоскость л, перпендикулярную
к вектору <ае, и спроектируем относительную скорость vr на эту
плоскость. Если полученную проекцию v'r повернем в плоскости л
на 90° вокруг точки М в направлении переносного вращения
(рис. 128), то получим направление вектора wk.
Если vr _[_ ci>e, т. е. если вектор vr лежит в плоскости я, то
для того, чтобы получить направление кориолисова ускорения,
достаточно повернуть вектор vr в плоскости я на 90° в на-
направлении переносного вращения; в этом случае
а = 90°, sincc=l
и, следовательно,
Если вектор угловой скорости переносного вращения парал-
параллелен относительной скорости vr, то либо а = 0, либо а=180*
и, следовательно, sina = 0, а потому в этом случае wk = Q.
Задачи этого параграфа можно решить двумя способами:
геометрическим и аналитическим.
Геометрическое решение задачи состоит в построении мно-
многоугольника ускорений на основании векторного равенства (93)
или (94).
При аналитическом способе решения применяется метод
проекций, т. е. искомое ускорение определяется по его проек-
проекциям на выбранные координатные оси.
Задачи, относящиеся к этому параграфу, можно разделить
на следующие два основных типа.
Задачи типа 1
(задачи 462—464, 466—468, 470, 476—483, 489, 490)
Требуется найти модуль и направление абсолютного уско-
ускорения.
Пример 92. В примере 85 определить абсолютное ускорение
точки М (рис. 129).
Решение. Переносным движедием в данном примере яв-
является вращение цилиндра вокруг оси г с угловой скоростью
215

o\ = ^y~ сек~1 и угловым ускорением eg =
этому переносное ускорение точки М равно
= -^- = jtf \1сек*- По-
ПоПереносное нормальное ускорение w(en) точки М направлено
по радиусу МОг кругового сечения цилиндра, проходящего
через точку М, причем
We '=0,/И-(Ое =—т-.
Рис 129
Переносное касательное ускорение w^ точки М направлено по
касательной к этому круговому сечению, причем
Относительным движением точки М (движение по отношению
к цилиндру) является ее движение по винтовой линии со ско-
скоростью
ds ,
Поэтому
Относительное касательное ускорение w^ точки М направлено
по касательной к винтовой линии, причем
216

Относительное нормальное ускорение w("] точки М направлено
по главной нормали винтовой линии, т. е. по радиусу М0
причем
«**-¦?-
где q—радиус кривизны винтовой линии определяется по фор-
формуле п = -г^- = 4г *.
v sin2 у
Следовательно,
Остается найти кориолисово ускорение wk, построив предвари-
предварительно вектор переносной угловой скорости сое, направленный
по оси Oz вращения цилиндра. Так как векторы сог и vr не
перпендикулярны, то для того, чтобы найти направление век-
вектора wk, нужно спроектировать вектор vr на плоскость, прохо-
проходящую через точку М и перпендикулярную к вектору сов. и
полученную проекцию, направленную, очевидно, по одной пря-
прямой с вектором w], повернуть на 90° в направлении переносного
вращения; следовательно, вектор wk будет направлен по ради-
радиусу MOlt причем
wk = 2<aevr siny = <uevr = -Y t*-at.
По теореме Кориолиса имеем:
wa == we + ~wr +~wk = win) + w{^ -f ш(гт) + win) + wk.
Проектируя это векторное равенство на три взаимно перпенди-
перпендикулярные оси Мхл, Myiy Mzx, получим:
wax = w[x) cos (90°—y) + ©Г',
ИЛИ
waZl = w^} cosy,
	t^
ay, ~ 4r
a \
"az-, — о
* См «Курс теоретической механики» проф. И М Воронкова, изд.
1962 г., § 70.
217

По найденным проекциям находим модуль абсолютного
ускорения точки М:
л
~ (а
Задачи типа II
(задачи 465, 469, 471—474)
Требуется найти одно или два из составляющих ускорений.
Пример 93. Найти относительное ускорение камня кулисы
(по отношению к кулисе) и угловое ускорение кулисы в при-
примере 86 при условии, что криво-
кривошип О А вращается равномерно,
т. е. со = const (рис. 130).
Решение. Так как абсо-
абсолютное движение точки А есть
равномерное вращение вокруг
неподвижной оси О, то вектор
wa абсолютного ускорения этой
точки направлен вдоль АО к
центру О и по модулю равен
wa^w{a) = ai-АО = 160 см(секг.
Переносное движение, т. е.
движение кулисы является вра-
врай
у
щательным вокруг неподвижной
оси „	ш i) ш(>
ру д
>„ а_потомушг = win) +ш(ет>;
вектор w[n) направлен вдоль
ЛО, к центру О,, а вектор w™
перпендикулярен к О^А, при-
причем wln) = О, А • со? = 21,3 см\сек\
wlx) = O1A- &it где 6j есть угло-
угловое ускорение кулисы.
Относительное движение
камня А есть прямолинейное
Рис 130	движение вдоль прорези кули-
кулисы, поэтому вектор относитель-
относительного ускорения wr направлен вдоль Л0._
Вектор переносной угловой скорости со, направлен по оси
переносного вращения, т. е. перпендикулярно к плоскости
рисунка, а вектор vr относительной скорости лежит в этой
плоскости, следовательно, vr J_ со,. Поэтому чтобы найти на-
направление кориолисова ускорения wk, достаточно вектор vr по-
218

вернуть на 90° в плоскости рисунка в направлении переносного
вращения. Модуль этого ускорения находим по формуле 9
wk = 2ш,vr sin 90° = 2оа, vr = 37,24 см\сек\
По теореме Кориолиса имеем:
Wa = We + Wr + Wk = we™ +• w?m + Wr -f ША.
Проектируя это векторное равенство на оси хх и цл, направ-
направленные, как указано на рис. 130, получим:
Отсюда находим:
Wr = —We +WaCOSy=	в
= _ 21,3 + 160 —|=z. = 89,62 см!сек\
= шо sin у—wft = 160- AJpL-37,24 = 77,88
2. у lo
Геометрический способ решения. В векторном равенстве
направления всех векторов и. модули трех из них (wa, wl"\ до4)
известны. Нужно найти модули ускорений wlT) и wr.
Для этого из произвольной точки а строим в выбранном
масштабе векторы ab = ш(ап> и ас — w?} и из точки с—вектор
cd — wh (рис. 131).
Затем из точек b и d проводим два луча, параллельных
векторам wf и wix), до их пересечения в точке е.
Тогда
~йе = wr, eb = w{,\
eb
8
219

Глава V
СОСТАВНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 1. ОБЩИЕ ЗАМЕЧАНИЯ
Задачи данной главы относятся к составному движению
твердого тела, которое складывается из двух вращательных
движений вокруг параллельных или пересекающихся осей.
Из таких задач особое практическое значение имеют те, в ко-
которых рассматриваются планетарные (задачи 580—584, 593, 613)
и дифференциальные (задачи 588, 589, 615, 622 — 633) механизмы.
Зубчатые механизмы с одной степенью свободы, в числе
звеньев которых имеются колеса с подвижными осями, назы-
называются планетарными, в отличие от обыкновенных зубчатых
передач, у которых геометрические оси колес при работе меха-
механизма остаются неподвижными. Колеса планетарного механизма
с неподвижными осями называются солнечными или централь-
центральными, а с подвижными — планетарными или сателлитами. Звено,
несущее оси сателлитов называется поводком или водилом.
Зубчатый механизм с подвижными осями, число степеней свободы
которого больше единицы, называется дифференциальным. В про-
простейшем случае дифференциальный механизм имеет две степени
свободы, т. е. два звена механизма могут обладать независимыми
друг от друга движениями. При решении задач данной главы
удобно пользоваться понятием передаточного отношения. Пере-
Передаточным отношением i между звеньями ц и y механизма
передачи вращательного движения называется отношение угло-
угловой скорости со^ звена \i к угловой скорости соу звена у:
'.т=^.	<97>
Пусть имеется сложная передача, состоящая из л звеньев. Обоз-
Обозначим через со,, и3, ..., соп их угловые скорости, а через г12,
i23. ¦¦-, in-i,n—передаточные отношения от первого звена
ко второму, от второго к третьему и т. д. Тогда
12~ 0>2' 2S (В, ' "•'
Перемножая эти равенства, имеем:
(98)
т. е. передаточное отношение сложной передачи равно произ-
произведению промежуточных передаточных отношений. Передаточное
отношение (число) может быть выражено через конструктивные
220

параметры механизма передачи. Простейшая зубчатая передача
состоит из двух круглых цилиндрических зубчатых колес, кото-
которые служат для передачи вращения между параллельными
валами (рис. 132). Для обеспечения постоянного передаточного
отношения профили зубьев, находящихся в зацеплении колес,
должны иметь определенные очертания, причем с указанными
колесами можно мысленно связать две взаимно касающиеся
окружности, центры которых совпадают с центрами этих колес
и которые при вращении этих колес катятся одна по другой
без скольжения. Такие окружности называются начальными
Рис. 132
или центроидными окружностями этих колес, а точка Р их ка-
касания— полюсом зацепления. Цилиндры, соответствующие началь-
ным окружностям, называются начальными цилиндрами. Рассмот-
Рассмотрим внешнее зацепление двух круглых цилиндрических колес
с параллельными осями (рис. 132, а). Пусть /?, и ^„—радиусы
начальных окружностей этих колес, а со, и ю2—их угловые
скорости. В данном случае направления вращения ведущего
и ведомого колес противоположны, поэтому угловую скорость
одного колеса можно рассматривать как положительную, а дру-
другого— как отрицательную величину. Так как соприкасающиеся
в данный момент точки начальных окружностей, находящихся
в зацеплении зубчатых колес, должны иметь общую скорость,
то, обозначая величину этой скорости через vp и полагая ю1>0,
со2<!0, имеем:
221

или
где Zj и г2—числа зубьев соответствующих колес; отношение
радиусов начальных окружностей, находящихся в зацеплении
колес, можно заменить отношением чисел их зубьев, потому
что шаг * зацепления у этих колес должен быть одинаков
и, следовательно, радиусы начальных окружностей этих колес
прямо пропорциональны числам их зубьев.
Таким образом, при внешнем зацеплении двух круглых ци-
цилиндрических колес с параллельными осями передаточное отно-
отношение равно обратному отношению радиусов начальных окруж-
окружностей или чисел зубьев этих колес, взятому со знаком минус.
Знак минус показывает, что ведущее и ведомое колеса вращаются
в разные стороны и, следовательно, их угловые скорости имеют
разные знаки. Если нас интересуют только абсолютные значения
угловых скоростей ведущего и ведомого колес, то знак минус
в выражении передаточного отношения следует опустить. В слу-
случае внутреннего зацепления двух круглых цилиндри-
цилиндрических колес с параллельными осями (рис. 132, б) оба колеса
вращаются в одну сторону, поэтому
т. е. в этом случае передаточное отношение равно
обратному отношению радиусов начальных ок-
окружностей или чисел зубьев и всегда является
числом положительным.
Аналогично определяется передаточное отношение между
коническими колесами. Следует иметь в виду, что в тех слу-
случаях, когда оси колес не параллельны, передаточное отношение
является величиной положительной.
§ 2. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА
ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
Если относительное и переносное движения тела являются
вращательными вокруг параллельных осей (рис. 133), то рас-
распределение абсолютных скоростей в теле в каждый данный
момент такое, как при вращательном движении вокруг мгно-
мгновенной оси, которая параллельна осям составляющих вра-
вращений и делит расстояние между ними внутренним образом
(если направления переносного и относительного вращений
* Шагом зацепления называется расстояние между двумя одноименными
точками двух смежных зубьев, измеренное по начальной окружности.
222

совпадают) или внешним образом (если направления этих вра-
вращений противоположны) на части, обратно пропорциональные
относительной и переносной угловым скоростям, т. е.
Ч.	(ion
ООг 0,0
где юг, а>г и (иа—соответственно переносная, относительная и
абсолютная угловые скорости.
а)
Рис 133
Если направления угловых скоростей те и юг совпадают
(рис. 133, а), то абсолютная угловая скорость соа направлена
в ту же сторону и по модулю равна сумме их модулей:
(ов = (ое + шг	A02)
Если же векторы сог и (яг направлены в противоположные
стороны (рис. 133, б), то абсолютная угловая скорость а>а на-
направлена в сторону большего из них и по модулю равна раз-
разности их модулей, т. е.
<ов = ш,—ю„	A03)
если шг>(ов,
и
(ов = н>в—юг,	A04)
если юг > о>г.
Если относительная и переносы ая угловые скорости образуют
пару угловых скоростей, т. е. юг — — ше (рис. 133, в),
223

то распределение абсолютных скоростей в теле такое, как при
поступательном движении, причем абсолютная скорость любой
точки тела в данный момент равна вектору-моменту указанной
пары:
w = m(©e, ©,); о = ©е О1О1 = шг-О,О1.	A05)
При решении задач на сложение вращений вокруг параллельных
осей часто оперируют не с модулями угловых скоростей, а с их
алгебраическими величинами, которые представляют собой про-
проекции угловых скоростей на ось, параллельную осям рассмат-
рассматриваемых вращений. Выбор положительного направления ука-
указанной оси произволен. В этом случае угловые скорости одного
ШхШШ.
Рис. 134
направления являются положительными, а противоположного
направления—отрицательными величинами и абсолютная угло-
угловая скорость выражается в виде алгебраической суммы состав-
составляющих угловых скоростей.
Пример 94. В дифференциальном механизме (рис. 134, а и б)
ведущими звеньями являются колесо 1 и водило Н, несущее
ось двойного сателлита 2—2'. Зная угловые скорости со, и ан
колеса / и водила Н, а также числа зубьев всех колес, найти
угловую скорость w, колеса 3.
Решение. 1-й способ (метод Виллиса). Сущность метода
заключается в сведении задачи анализа планетарных и диффе-
дифференциальных механизмов к анализу обыкновенных зубчатых
механизмов путем перехода от абсолютного движения звеньев
рассматриваемого планетарного механизма к их относительному
движению по отношению к водилу.
Пусть имеем планетарный механизм, оси колес которого
параллельны. Обозначим через со^, со, и шн алгебраические зна-
224

чения абсолютных угловых скоростей соответственно звеньев
\i, v и водила Н. Для перехода к движению относительно
водила сообщим мысленно всей системе вращение вокруг оси
водила с угловой скоростью—сон (т. е. равной угловой скорости
водила, но направленной в прямо противоположную сторону).
Тогда водило остановится, и звенья ц и v, на основании тео-
теоремы сложения вращений, получат угловые скорости со> — юя
и <av—а>и. Так как при неподвижном водиле получаем обыкно-
обыкновенный зубчатый механизм, звенья которого вращаются вокруг
неподвижных осей, то к этому механизму можно применить
формулу (97) для передаточных отношений, что приводит нас
к так называемой формуле Виллиса:
где «jxv—передаточное отношение между звеньями ц и v в их
движении относительно водила Н (о чем говорит верхний индекс).
Это передаточное отношение, как уже указывалось в § 1, можно
выразить через конструктивные и геометрические параметры
механизма (числа зубьев или радиусы начальных окружностей,
находящихся в зацеплении колес).
В нашей задаче применим формулу Виллиса к звеньям 1 и 3:
<0s — ®Н _ АН) _ АН) АН)
~~- ; — 'si ¦— *аа' *2i »
НО	Ml —«я
АН) __ JV_
'"' Ч
(передаточное отношение между колесами 3 и 2' положитель-
положительно, так как колеса имеют внутреннее зацепление);
(здесь передаточное отношение отрицательно, так как колеса 2
и / имеют внешнее зацепление).
Таким образом,
откуда
ан)	(ответ).
Пусть, например, г1 = 60, г2 = 40, г2-=20, г, = 120 и, кроме
того, колесо / и водило Н вращаются в одну сторону с угло-
угловыми скоростями ©j = 140 1/ше и <он = 60 \\сек. В этом случае
о)8 = 60 — х^й(Н0—60) = 60— — 80-40 се/с. Если бы колесо
/ и водило Н вращались в противоположные стороны, то угло-
угловую скорость одного из этих звеньев необходимо было бы счи-
считать величиной положительной, а другого —отрицательной.
9 Зек, 2374	225

В этом случае при тех же абсолютных значениях угловых
скоростей звеньев / и Н мы бы имели:
со, = 140 сек'1; соя= —60 сек'1; со,- -60--^^ A40 +60) =
= — 60-50 = —ПО I/me,
т. е. колесо 3 вращалось бы в ту же сторону, что и водило,
так как знаки их угловых скоростей совпадают.
Если закрепим колесо /, то получим простой планетарный
механизм. Формула Виллиса в этом случае остается в силе,
надо только положить в этой формуле со, = 0, что дает:
2-й способ (метод мгновенных центров скоростей). Так как
звенья планетарного или дифференциального механизма с парал-
параллельными осями совершают плоскопараллельное движение, то
при анализе такого механизма можно применить теорию плос-
плоскопараллельного движения и, в частности, воспользоваться
методом мгновенных центров скоростей. Решение задачи полезно
сопровождать построениями треугольников скоростей, которые
обычно выносят за пределы механизма (рис. 134, в). Радиусы
колес рассматриваемого механизма обозначим через Rit Rz,
R*, R,. Тогда имеем:
vA = Rla>i и vB = aH{Rt+Rt)
на рис. 134, в скорость точки Л касания колес 1 и 2 изображена
в виде вектора Аа, а скорость точки В —в виде вектора ВЬ. Зная
скорости точек А и В, через концы а и b этих скоростей про-
проводим прямую и в пересечении этой прямой с продолжением
прямой АВ в точке Рг получаем мгновенный центр скоростей
сдвоенного колеса 2—2'.Скорость точки С касания колес 2' и 3
изобразится на рисунке вектором Сс. Зная скорость точки С
колеса 3, находим угловую скорость этого колеса:
Построение треугольников скоростей и является геометрическим
решением данной задачи. Для получения аналитического выра-
выражения для со, воспользуемся следующими уравнениями, выте-
вытекающими из наших построений:
vA = /?,©, = со, {P? + Rf +Rt),	(a)
о„ = (/?, +Л,) «о„ = щ,(Р,С+ /?,-).	(б)
ис = а>,РгС,	(в)
где cOj—угловая скорость колеса 2—2' вокруг мгновенного
(гентра скоростей Рх.

Вычитая из равенства (а) равенство (б), получим:
R1wi-{R1+Rt)ioH = a>iRi,
откуда
Поделив эти равенства почленно друг на друга, находим"
»' + R,
или
?,0),-(/?,
откуда
nr RAR, + R,)uH R	..
г*и ~ R^,-(R, + Rt)со„ Кг'-	(.V
Используя равенства (в), (г) и (д), имеем:
Отсюда
Заменив отношения радиусов отношениями чисел зубьев,
получим ранее найденный отве'ь
§ 3. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА
ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
Если относительное и переносное движения тела являются
вращательными вокруг пересекающихся осей (рис. 135), то рас-
распределение абсолютных скоростей в теле в каждый данный момент
такое, как при вращательном движении вокруг мгновенной оси,
проходящей через точку пересечения осей составляющих враще*
ний и направленной по диагонали параллелограмма, построен-
построенного на угловых скоростях этих вращений. Вектор абсолютной
угловой скорости тела равен геометрической сумме векторов его
переносной и относительной угловых скоростей:
па = пе+аг.	A07)
Пример 95. Зная угловую скорость тн водила Н планетарной
конической передачи (рис. 136, а) найти относительную и абсо-
абсолютную угловые скорости колеса /, находящегося в зацеплении
9Р	22?

с неподвижным колесом 2. Даны радиусы i?, и R2 колес*, а
также углы 2а, и 2а2 растворов их начальных конусов.
Решение. Движение колеса / складывается из вращатель-
вращательного движения водила Н вокруг оси 0Аг с угловой скоростью
«я (переносное движение) и вращательного движения вокруг оси
ОАЛ по отношению к водилу Н с некоторой угловой скоростью
ю1Н (относительное движение). При указанном на рис. 136, а
круговой стрелкой направлении вращения водила вектор сон
переносной угловой скорости колеса / направлен по оси ОА2
вниз. Вектор
его относительной угловой скорости направ-
направлен по оси CMj. Мгновенная ось абсолют-
абсолютного движения колеса / совпадает с общей
образующей ОР начальных конусов колес
/ и 2, так как при работе механизма эти
конусы должны катиться один по другому
без скольжения, что обеспечивается
соответствующей формой зубьев находящих-
находящихся в зацеплении конических зубчатых колес.
Таким образом, вектор cotабсолютной угловой
скорости колеса / направлен по линии ОР.
Применяя формулу A07), имеем:
« Здесь и в дальнейшем одной чертой внизу
подчеркнуты векторы, для которых известны
только линии действия, двумя чертами —
векторы, известные и по модулю и по на-
направлению.
Для построения параллелограмма угло-
угловых скоростей, соответствующего этому
векторному равенству, от центра О пере-
пересечения осей рассматриваемых вращений откладываем заданный
вектор От--(аи (рис. 136, а), из конца т этого вектора проводим
прямую, параллельную оси О А, до пересечения в точке п с осью ОР
абсолютного вращения и дополняем полученный треугольник Отп
до параллелограмма, для чего из точки п проводим прямую, парал-
параллельную ОАг, до пересечения в точке е с осью 0Ах. Векторы Ое и
On дают соответственно искомую относительную угловую ско-
скорость (о,н и абсолютную угловую скорость ю, колеса /. Вместо
построения параллелограмма угловых скоростей можно ограни-
ограничиться построением треугольника угловых скоростей, который
лучше вынести за пределы механизма (рис. 136, б). Для этого
Рис
* Радиусами конических колес называют наибольшие радиусы их
начальных конусов.
22S

ОТ произвольного Центра о откладываем заданный вектор
оа2 = соя, а из конца а2 и начала о этого вектора проводим до
взаимного пересечений в точке а, прямые aia1\\(olH (т. е. парал-
параллельно оси ОАг) и оа, || со, (т. е.
параллельно оси ОР). Стороны
полученного треугольника оа2ах
и выражают собой заданную и
искомые угловые скорости, т. е.
оа2 = соя; а2а, = со,я; oat = со,. Из
параллелограмма или треуголь-
треугольника угловых скоростей имеем:
sui a, sin а2 sin а
где а = а, + а2 — межосевои
угол конической передачи.
Отсюда относительная угло-
угловая скорость колеса / по отно-
отношению к водилу Я равна
sin сц R „
" — 2'он = тг-гсо„, так как
\'
sin a, = -^ и
ina2 = -^, где
R = OP. Абсолютная угловая
Рис 136
sma
скорость колеса / равна cOj = -—шн. Модуль абсолютной угловой
скорости можно определить также по теореме косинусов:
со, =
+
cos a
R	р
©я + —f «я + 2юя п^ cos a =
Пример 96. На ведущем валу / планетарной передачи с кони-
коническими колесами (рис. 137, а) заклинено колесо /, находящееся
в зацеплении с колесами 2 двойных сателлитов, свободно сидя-
сидящих на осях водила Н. Колесо 2 находится в зацеплении
с неподвижным колесом 4, а колесо 2'—с колесом 3, заклинен-
заклиненным на ведомом валу //. Определить передаточное отношение
между валами / и //.
Решение. 1-й способ (метод Виллиса). Обозначим через
/?,, Rt, Rt', R, и Rt радиусы колес /, 2, 2', 3, 4. Перейдем
от абсолютного движения звеньев рассматриваемого механизма
к их относительному движению по отношению к водилу Я. Для
229

этого сообщим мысленно всей системе вращение вокруг оси
/ — // с угловой скоростью—сон. Тогда водило, несущее ось
сателлитов, остановится и мы получим обыкновенную кониче-
коническую передачу, колеса которой вращаются вокруг неподвижных
осей с угловыми скоростями со^ — юя, где ц=1, 2, 3, 4. Поль-
Пользуясь методом Виллиса, установим связь между угловыми ско-
рсстями колес /, 3, 4 и водила Н. Так как звенья 1, 3, 4 и
Рис 137
Н имеют общую ось вращения, то угловые скорости этих
звеньев являются параллельными векторами и их можно рас-
рассматривать как алгебраические величины.
Применяя формулу Виллиса к колесам 1 и 4, имеем:
со,—а>я__ ли) _ Rt
где га,— «и и со4—ын—относительные угловые скорости колес
/ и 4 по отношению к водилу Н. Передаточное отношение
230

в данном случае считаем of р и uaf ел ьным, так как колеса
/ и 4 при неподвижном водиле (при неподвижной оси колеса 2)
вращаются в разные стороны (линейные скорости точек А и
В этих колес при неподвижной оси колеса 2 имеют противопо-
противоположные направления). Колесо 2 здесь играет роль паразит-
паразитного колеса, его радиус не влияет на величину передаточного
отношения между колесами 1 а 4. Так как абсолютная угловая
скорость четвертого колеса <о4 = 0, то из последнего уравнения
находим:
/ о \
(а)
Применяя вторично формулу Виллиса, уже теперь к колесам
3 и 4, имеем:
со,—шм _ .(Н)	Rt^ Ri
Передаточное отношение в данном случае равно произведе-
произведению двух передаточных отношений (от колеса 3 к колесу 2' и
от колеса 2 к колесу 4), причем это передаточное отношение
является величиной положительной, так как колеса 3 и 4
при неподвижной оси колес 2 и 2' вращаются в одну сторону
(линейные скорости точек В и С имеют одинаковое направле-
направление). Таким образом,
-.--.(.-%?).
Равенства (а) и (б) выражают абсолютные угловые ско-
скорости колес / и 3 через угловую скорость водила. Разделив
равенство (а) на (б), получим передаточное отношение между
ведущим и ведомым валами рассматриваемой передачи, т. е.
передаточное отношение между колесами / и 3 при неподвиж-
неподвижном колесе 4:
it. ii = »1V =	h^l_ (ответ).
В этой формуле отношения радиусов находящихся в зацепле-
зацеплении колес могут быть заменены отношениями чисел их зубьев.
2-й способ (геометрический). Этот способ основан на постро-
построении векторных треугольников угловых скоростей. При постро-
построении указанных треугольников исходят из векторных уравне-
уравнений, выражающих зависимость между угловыми скоростями
звеньев рассматриваемого механизма.
Принимая движение колеса 2 за переносное движение и при-
применяя формулу A07) к колесу / имеем:
231

где <!*, — абсолютная угловая скорость колеса /, известная по
модулю и направлению (что показывают две черты снизу);
©2— абсолютная угловая скорость колеса 2, которая по
отношению к колесу / является переносной угловой скоростью
и для которой известна линия действия (что показывает одна
черта снизу);
со,,, — относительная угловая скорость колеса / по отношению
к колесу 2, для которой линия действия тоже известна (что
показывает одна черта снизу). Вектор ео2 направлен по мгно-
мгновенной оси вращения колеса 2, которая совпадает с общей
образующей ОБ начальных конусов колеса 2 и неподвижного
колеса 4, а вектор со1г — по общей образующей О А начальных
конусов колес / и 2 (рис. 137, а).
Для построения треугольника угловых скоростей, соответ-
соответствующего последнему векторному уравнению, от произвольного
центра о (рис. 137,6) откладываем заданный вектор оа1 = со,,
а из начала о и конца а, этого вектора проводим до взаимного
пересечения в точке аг прямые оаг |] ОБ и а,а2||0Л. Тогда
имеем:
Определив угловую скорость со2 колеса 2, переходим к опре-
определению угловой скорости со, колеса 3. Принимая опять дви-
движение колеса 2 за переносное, имеем:
Вектор со, направлен по той же оси I—II, что и вектор со,, а век-
вектор ш32 —по общей образующей ОС колес 3 и 2'. Для постро-
построения треугольника угловых скоростей достаточно из точки а2
провести прямую aial \\ ОС до пересечения в точке а, с прямой
oalt что дает:
Угловую скорость соя водила и угловую скорость двойного
сателлита 2—2' по отношению к водилу находим на основании
уравнения
Вектор сон направлен по оси / — //, а вектор со2Н—по оси 0D.
Проведя из конца аг вектора со2 прямую а%ан \\ 0D до пересече-
пересечения в точке ан с прямой oalt имеем:
: соя; анаг = со2Н.
232

Искомое передаточное отношение определяется так:
_ Ml _ 00,
11 ¦ "~щ~оа,
Это передаточное отношение можно выразить также через
углы растворов начальных конусов конических колес. Обозна-
Обозначив половины указанных углов через a1F <ха	из треуголь-
треугольника оахаг имеем:
1 z sui a,
Из треугольника oaiai следует:
,., _,., sin(a8-aa>)
sin a.
(Г)
Поделив эти равенства, получим
sin 2cu • sin a,
ii и 	Л	г
(a2—a2
(ответ).
Выражая функции углов a,, a2, ... через радиусы кони-
конических колес, этот ответ можно привести к виду, найденному
ранее.
Пример 97. В дифференциальном механизме (рис. 138) веду-
ведущими звеньями являются колесо / и водило Я, несущее ось
двойного сателлита 2—2'. Зная угловые скорости со, и шд колеса
/ и водила Н, а также радиусы всех колес, найти угловую
скорость колеса 3. Известно, что w1 <C <ая.
Решение. 1-й способ (метод Виллиса). Сообщим мысленно
всей системе вращение с угловой скоростью — юн. Тогда водило
Н остановится, а к векторам угловых скоростей остальных
звеньев механизма прибавится вектор — сон. Рассматривая угло-
угловые скорости звеньев /, Н и 3, имеющих общую ось вращения,
как алгебраические величины, получаем следующее соотноше-
соотношение между относительными угловыми скоростями колес 1 и 3
по отношению к водилу Н:
ма—со я _ АН)	Я? /^
m1-u>«~tfl R, 'I?,'
Передаточное отношение между колесами 3 и / в их отно-
относительном движении по отношению к водилу Я здесь отрица-
отрицательно потому, что при неподвижном водиле Я эти колеса
вращаются в разные стороны. Отсюда, учитывая, что со, < соя,
имеем:
со, = соя + 5щ-1 (соя—со,) (ответ).
В этой формуле отношения радиусов находящихся в зацеп-
зацеплении колес могут быть заменены отношениями чисел их
9В Зак, 2374	233

зубьев. Если бы колесо / и водило Н вращалось в противопо-
противоположные стороны, то угловую скорость одного из этих звеньев
следовало бы считать положительной, а другую —отрицательной.
Знак в этом случае показывал бы, в сторону какого звена'
(У или Н) вращается колесо 3.
При решении подобных задач необходимо внимательно про-
проследить, какой знак имеет передаточное отношение соосных
звеньев в их движении по отношению к водилу. Так, например,
в механизме, изображенном на рисунке 138 в, колеса / и 3 при
неподвижном водиле Н вращаются в одну сторону, следо-
следовательно, здесь, в отличие от предыдущего, 4f)>0, т. е.
«В. —ШЯ _ АН) __ . /?2' _ Я,
откуда, если, по-прежнему, юя>а>1, то
234

2-й способ (геометрический). Решим эту же задачу при по-
помощи векторных треугольников угловых скоростей. В данном
случае мгновенная ось абсолютного движения двойного сател-
сателлита 2—2' заранее неизвестна, поэтому для определения его абсо-
абсолютной угловой" скорости ш2 воспользуемся двумя векторными
уравнениями, приняв сначала за переносное движение враще-
вращение колеса /, а затем—вращение водила:
со, = ю, + со„; со, = юн + <о_,н.
Вектор со,, относительной угловой скорости сателлита 2—2'
по отношению к колесу / направлен по общей образующей ОА
начальных конусов этих колес, а вектор со2Н относительной уг-
угловой скорости сателлита 2—2' по отношению к водилу Н — по
оси ОВ (рис. 138, а). От произвольного центра о (рис. 138, б)
откладываем заданные векторы oal — (i>i и оан — шя, из концов
а, и ан этих векторов проводим до взаимного пересечения
в точке аг прямые ахаг \\ О А и анаг \\ О В, тогда получим:
Определив вектор ю2, переходим к определению угловой ско-
скорости со, колеса 3, исходя из равенства:
Вектор со, направлен по оси вращения колеса 3, совпадающей
с осями вращения звеньев / и Н, а вектор со„—по общей
образующей ОС начальных конусов колес 2' и 3. Проведя из
начала о и конца аг вектора оа2— ш2 прямые ш81| и>8 и ага3\\шJ
до их взаимного пересечения в точке а3, получаем треуголь-
<ник Оагаг угловых скоростей колеса 3, из которого находим:
Обозначая половины углов раствора начальных конусов кони-
конических колес 1 я 3 соответственно через а1 и а3, имеем (рис.
138, а и б):
откуда окончательно:
со, = сон + («>н— «J tg a, ¦ ctg а, (ответ).
Учитывая, что tgaj^-H-5 и ctga, = -^- (см. рис. 138, а), при-
придем к найденному ранее результату. На рис. 438, г показаны
треугольники угловых скоростей для механизма, изображен-
изображенного на рис. 138, в.
235
6В*

РАЗДЕЛ III
ДИНАМИКА
ДИНАМИКА ТОЧКИ
Глава 1
ДВЕ ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ ТОЧКИ
§ 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
МАТЕРИАЛЬНОЙ ТОЧКИ
В динамике изучается движение механических систем в связи
с действующими на них силами. Простейшим объектом меха-
механики является материальная точка — тело, размерами которого
при решении данной задачи можно пренебречь.
Если на положение материальной точки и на ее движение
не наложены никакие ограничения, то точка называется сво-
свободной, в противном случае имеем движение несвободной точки.
Условия, которые накладывают определенные ограничения на
положения материальной точки и на ее движение, называются
связями, наложенными на эту точку. Материальное тело, при
помощи которого осуществляется связь, наложенная на данную
материальную точку, действует на эту точку с некоторой силой,
называемой реакцией этой связи.
Согласно закону равенства действия и противодействия,
сила, с которой материальная точка действует на тело, осу-
осуществляющее связь, равна по модулю и прямо противоположна
по направлению реакции этой связи.
На основании второго и четвертого законов динамики имеем:
mw^m~=F,	A08)
гдет—масса материальной точки; w—ее ускорение и F—равно-
236

действующая всех сил, приложенных к этой точке, включая
(в случае несвободной точки) и реакции связей.
В Международной системе единиц масса измеряется в кило<
граммах, а сила — в ньютонах (н). Обычно массу тела находят
как отношение его веса Р, выраженного в ньютонах, к ускоре-
ускорению силы тяжести g = 9,81 ju/ce/c2, т. е.
т=~.	A09)
Проектируя векторное равенство A08) на оси той или иной
системы координат, получаем дифференциальные уравнения
движения материальной точки в этой системе.
В прямоугольной системе декартовых координат имеем:
тх=Х; my = Y; mz = Z,	(ПО)
где х, у, z—координаты точки, а X, Y, Z —проекции действую-
действующей силы (равнодействующей) на соответствующие оси. В слу-
случае несвободной точки к этим уравнениям присоединяются
уравнения связей. Если точка движется прямолинейно,
то, принимая эту прямую за ось х, имеем:
тх = Х.	A11)
В системе естественных осей имеем:
d t T> q ni	^'
где
v—скорость точки;
q — радиус кривизны траектории;
Fx, Fn, Fb—проекции действующей силы соответственно на ка-
касательную, главную нормаль и бинормаль траектории.
Уравнения A12) называются эйлеровыми или естественными
уравнениями движения материальной точки.
Пользуясь уравнениями A08) и (ПО), можно решать две
основные задачи динамики точки.
§ 2. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
Эта задача заключается в том, что по заданному движению
и известной массе материальной точки требуется определить
силу, действующую на эту точку, или, если на материальную
точку действует несколько сил, определить одну из них.
Решение этой задачи сводится к определению ускорения
точки, которое в том случае, когда движение точки задано,
нетрудно найти по правилам кинематики.
237

Задачи этого параграфа можно разделить на следующих два
основных типа в зависимости от траектории движущейся точки:
I.	Задачи, относящиеся к прямолинейному движению точки.
II.	Задачи, относящиеся к криволинейному движению точки.
Задачи типа I
Задачи этого типа, в которых рассматривается прямолиней-
прямолинейное движение точки, решаются при помощи уравнения A11);
их можно разделить на две группы.
Первая группа
Задачи, в которых к движущейся материальной точке при-
приложена одна сила. Необходимо определить эту силу.
Пример 98. Материальная точка массой т = 400 г совершает
гармонические колебания по горизонтальной оси Ох по закону
ж = 20sin у/ (х выражено в см, t—в сек). Найти силу, дейст-
действующую на точку в функции от х.
Решение. Находим проекцию ускорения точки на ось Ох:
Далее находим проекцию на ось действующей силы:
X = mwx = — 400 5яг. sin у = —2000яг sin у .
Но siny?= ~ , а потому Х = —100лгл: дин,
Так как проекция силы на ось Ох и координата х движу-
движущейся точки противоположны по знаку, то искомая сила направ-
направлена вдоль оси Ох к началу координат О.
По модулю эта сила равна 986 | х \, т. е. пропорциональна
расстоянию от движущейся точки до начала О.
Вторая группа
Ко второй группе относятся задачи, в которых к движущейся
материальной точке приложено несколько сил, причем требуется
найти одну из них.
К этой группе следует отнести такие задачи, в которых
требуется определить неизвестную реакцию связи, что характерно
для движения несвободной материальной точки.
Пример 99. Клеть весом Р поднимается с помощью каната,
навернутого на барабан радиуса R, вращающийся вокруг непод-
238

вижной горизонтальной оси по закону:
Определить натяжение каната как функцию высоты подъема h
(рис. 139).
Решение. При повороте барабана на угол <р клеть подни-
поднимается на высоту h = Rq>. Силу натяжения каната обозначим
через Т. На клеть действуют две силы: натяжение каната Т
и вес клети Р, причем Т>Р, так как ускорение клети направ-
направлено вверх. Равнодействующая этих сил F = T—Р. Применяя
формулу A08), получим:
mw=T—P,
откуда
77%.
Ускорение w клети найдем по формуле
ИЛИ
Следовательно,
Рис. 139
Задача типа II
Задачи этого типа, в которых рассматривается криволиней-
криволинейное движение материальной точки, можно также разделить на
две группы, как и задачи первого типа.
Первая группа
Задачи, в которых к движущейся материальной точке при-
приложена одна сила; требуется определить эту силу.
Если движение точки задано уравнениями в декартовых коор-
координатах:
*=М0; </ = Ш; г=МО,	(ИЗ)
где
х, у, г — координаты точки;
t — время,
то на основании уравнений A10) находим проекции искомой
силы на три координатные оси:
Х = тх = mf, @; У = Щ = mf\ (t); Z = mx = mf,{t). A14)
239

Затем нужно найти модуль действующей силы F и ее неправ-
ляющие косинусы по формулам:
A15)
X	Y	Z
-p-; cosfi = -7r; cosy = -tt-	A16)
Пример 100. Материальная точка массой т = 0,5 кг совер-
совершает движение согласно уравнениям:
причем координаты точки выражены в метрах, время — в секун-
секундах. Определить величину и направление силы, действующей
на точку, в момент t=\ сек.
Решение. 1. Находим проекции скорости данной точки
иа оси координат:
i = 4f; i/ = 2t; г = 3/2.
2.	Находим проекции ускорения точки на оси координат:
х = 4; у = 2\ z = 6* = 6 (при ^=1).
3.	На основании уравнений A14) находим проекции силы на
оси координат:
Х = тх = 2; Y = ту' = 1; Z = mz = 3.
4.	По формулам A15) и A16) находим модуль силы и на-
направляющие косинусы:
c©sa = g^4 = °>334; cosp = 3-!^ = 0,267;
cosy =3^4 = 0,804,
откуда
a = 57°41; p = 74°30'; y = 36°42'.
Если же движение точки задано естественным способом,
т. е. задана траектория точки и закон ее движения по этой
траектории s = /@, то следует, воспользовавшись уравнениями
A12), найти проекции искомой силы F на естественные оси, а
затем по этим проекциям вычислить ее модуль.
Пример 101. Материальная точка массой т = 2 кг описывает
криволинейную траекторию по закону s = 12 sin -~ (s выражено в м,
t—в сек). В данный момент она занимает положение М и имеет
скорость v—3 м]сек, причем радиус кривизны траектории в точке М
равен 6 м. Найти в этот момент силу, действующую на эту
материальную точку.
240

Решение. Находим скорость точки и проекции ее ускоре-
ускорения на касательную и главную нормаль траектории:
ds
V~dl
Согласно
l
= COS g- ,
условию,
w
в
dv
^~dT~
данный
"q
момент
поэтому 6cos-h-=3, откуда cos-H-=-?r и
Следовательно, в этот момент
имеем
о" = "о
v = 3 л'се/с;
, _ 2я
ИЛИ Г — -^-
9 3
	 ==z
6 2 *
Теперь на основании уравнений A12) находим проекции
искомой силы на касательную и главную нормали:
Отсюда искомая сила
= 6 н.
при-
приВторая группа
Задачи, в которых к движущейся материальной точке
ложено несколько сил и одну из них требуется найти.
В этой группе, так же как и в задачах второй группы типа 1,
часто встречаются такие задачи, где
требуется определить неизвестную
реакцию связи при движении несво-
несвободной материальной точки.
Пример 102. Центробежный регу-
регулятор состоит из двух шаров А и В
весом Р каждый, муфты С весом Q
и четырех одинаковых невесомых
стержней АС = ВС = DA = DB = I,
закрепленных по концам шарнир-
но. Регулятор вращается вокруг
неподвижной вертикальной оси г.
Определить усилия в стержнях и
угловую скорость регулятора, пред-
предполагая, что угол а, образуемый
каждым из стержней с вертикалью,
имеет заданное постоянное значе-
значение а (рис. 140).
Решение. Рассмотрим движе-
движение шара А, принимая его за матери-
материальную точку, которая описывает	Рис. 140
р,
241

окружность, расположенную в горизонтальной плоскости, с
центром в точке О, и радиусом, равным R. К этому шару при-
приложены три силы: вес ~Р и реакции S, и S, стержней AD и АС,
направленные вдоль этих стержней и равные искомым усилиям.
Применяя уравнения движения материальной точки в естествен-
естественной форме, т. е. уравнения A12), и проектируя все силы, при-
приложенные к шару А, на естественные оси т, п и Ь, показанные
на* рис. 140, имеем:
m- = (S1 + St) sin a,
0 = (S2—S,)cosa—P,
или, учитывая, что y=co/? = co/sina, получим:
ml sma~ = 0,
ml sin a®* = E, -f St) sin a,
O = (S,—St)cosa —P.
Следовательно,
, = —/to', (o = const,
S.-S, = P
* ' cos a
Аналогичным соотношением удовлетворяют действующие на
шар В реакции S, и St стержней BD и СВ, причем, очевидно,
5, = S, и S1=Si. Рассмотрим теперь муфту С, к которой прило-
приложены вес Q и реакции Su S[ стержней С А и СВ, равные по мо-
модулю и противоположные по направлению силам 5, и S4. Так
как при a = const муфта С по оси г не перемещается, то сумма
проекций всех приложенных сил на ось г равна нулю, т. е.
Q — (Sl+S't)cosa = Q — (Sl+S1)cosa = 0.
Таким образом, мы получили следующие три уравнения для
определения неизвестных Slt Sx и <d:
3) Q = 2S,cosa.
242

Решая эти уравнения, находим:
с - Q с _Q±2f m«_l Q±I
°>~2cosa' °«~2cosa ' "~ / " />cos<*
Пример 103. Материальная точка массы т движется в пло-
плоскости Оху в сопротивляющейся среде под действием силы при-
притяжения к центру О, равной F — —k'mr, где &»= const, r—ра-
r—радиус-вектор этой точки. Найти силу сопротивления среды Fx
как функцию скорости, если известны уравнения движения точки:
y = be-nt sin
причем
Решение. 1. Находим проекции скорости и ускорения дви-
движущейся точки на ось Ох:
ох = х = ae-nt [kx cos {kj 4 a) — n sin (kj + a)]
wx = x = ae-nt[(nl—k\)s\n (kj+ a)—2nklcos{klt fa)];
так как
пг — # = 2ns — k\
TO
wx = — k*ae-ni sin (kj+ a)—2ane-nt x
у [kx cos(?,rf4-a) — n sin (fe,^ + a)] = — k*x—2nvx.
На основании уравнений (96) имеем:
но
Fx = — kzmrx = — k*mx,
& потому
mwx = — k*mx + FIX,
или
— mk'x—2mnvx = —
откуда
Аналогично находим Fxy = — 2mn vx. Следовательно, искомая
сила Fx — —2mnv, т. е. сила сопротивления среды, пропорцио-
пропорциональна скорости точки и направлена противоположно этой ско-
скорости.
243

Таблица 14
Классификация задач
Группы
1-Я
(к движущейся точке при-
приложена одна сила)
2-я
(к движущейся точке при-
приложено несколько сил)
Типы задач
I
(прямолинейное движение)
Задачи
649—651 *
Задачи
637, 638, 640, 648,
653—655, 658,
659—661, 662
II
(криволинейное движение)
Задачи
652, 672, 673
Задачи
644—646, 656, 663,
667, 669, 670, 671
§ 3. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
Эта задача заключается в том, что по заданным силам, при-
приложенным к движущейся материальной точке, массе этой точки
и начальным условиям ее движения (начальному положению и
начальной скорости), требуется определить движение этой точки.
Для решения этой задачи необходимо:
1)	установить, какие силы действуют на материальную точку;
2)	составить дифференциальные уравнения движения точки
в форме A10) или A12);
3)	проинтегрировать эти уравнения;
4)	определить по начальным условиям движения произволь-
произвольные постоянные, которые войдут в интегралы этих уравнений.
Если интегрирование дифференциальных уравнений движения
точки сводится к квадратурам, как в приводимых ниже приме-
примерах, то будем вычислять эти квадратуры в соответствующих
пределах, т. е. будем вычислять определенные интегралы, причем
нижние пределы интегрирования определяются начальными
условиями движения точки. Тогда отпадает необходимость опре-
определения произвольных постоянных. Заметим, что почти во всех
задачах, помещенных в сборнике И. В. Мещерского и относя-
относящихся ко второй основной задаче динамики точки, имеются два
типа дифференциальных уравнений: или уравнения с разделяю-
разделяющимися переменными, или линейные уравнения второго порядка
с постоянными коэффициентами.
Задачи эюго параграфа можно разделить на следующие три
основных типа.
I. Задачи, относящиеся к прямолинейному движению свобод-
свободной материальной точки.
* Номера задач указаны из сборника И. В. Мещерского изд. 1950 г. и
последующих изданий,
244

II.	Задачи, относящиеся к криволинейному движению сво-
свободной материальной точки.
III.	Задачи, относящиеся к движению несвободной материаль-
материальной точки.
Задачи типа I
Задачи этого типа, в которых рассматривается прямолинейное
движение точки, можно разделить на четыре группы.
Первая группа
Задачи, в которых равнодействующая всех сил, приложенных
к данной материальной точке постоянна.
Если траекторию прямолинейного движения точки принять
за ось х, то дифференциальное уравнение движения точки в этом
случае примет вид
откуда
х ~~ — const.
Так как в случае прямолинейного движения точки ускорение ее
w = x, то w = const, т. е. движение точки является равнопере-
равнопеременным. Поэтому по формуле кинематики для пройденного пуги
при равномерно-переменном движении имеем:
s xx vt +
где у0—начальная скорость точки.
Отсюда
Это уравнение выражает закон прямолинейного движения
точки под действием постоянной силы.
Если в задаче требуется найти скорость и как функцию от
расстояния х, то левую часть уравнения A08) приведем к виду
dv	 dv dx	 dv
тогда уравнение A11) принимает вид
v у- — — = const,
dx in	'
откуда
V	X
\ v dv = \ —dx,
245

или
г. е.
¦¦vl + 2 — (x—xJ.	A18)
Пример 104. Материальная точка массы m = 0,5 кг движется
под действием постоянной силы F= Юн. В начальный момент
скорость точки равна с, = 2 ж/гас. Определить скорость точки
в тот момент, когда она пройдет расстояние s = 5 м.
Решение. Так как скорость точки требуется найти как
функцию расстояния, то по формуле A18) имеем:
т. е.
1Л -5 = 204,
0,5
откуда
о = 14,28 м^сек.
Вторая группа
Задачи, в которых равнодействующая всех сил, приложенных
к одной материальной точке, есть функция времени t.
В этом случае дифференциальное уравнение движения имеет
вид
тх = Х =/(/).
Так как x=vx — v, to получаем дифференциальное уравнение
первого порядка
dv
или
mdv-=f(t)dt.
Интегрируя это уравнение в соответствующих пределах, имеем:
откуда
246

Интегрируя это уравнение первого порядка, получим х как
функцию от /, т. е. найдем искомый закон движения точки.
Пример 105. На материальную точку, совершающую прямо-
прямолинейное движение, действует сила F, равномерно убывающая
с течением времени и по истечении Т сек обращающаяся в нуль.
Какой скорости достигнет точка по истечении Т сек и какой
путь она пройдет за это время, если в начальный момент (t = 0)
скорость точки равна нулю, а ее ускорение равно wa (рис. 141)?
Решение. Так как сила F, действующая на материальную
точку, убывает равномерно с течением времени, то F = Fa—at,
причем а = const.
Рис 141
В начальный момент ускорение точки равно до0, поэтому
FQ = mw0; кроме того, при t = T по условию F = 0, а потому
Fo — аГ = 0; отсюда
mwa p		гаш,
4).
Следовательно, дифференциальное уравнение движения точки
на основании равенств A11) запишегся так:
_y), или dv = wo[l—
Интегрируя это уравнение в пределах от vo = O до v и от 0
до t, имеем:
Так как у = g, > то
dx
откуда
Интегрируя это уравнение в пределах от 0 до л; и от 0 до t,
находим:
247

Чтобы найти скорость vi и пройденный путь хл к моменту
времени Т, достаточно в предыдущих равенствах положить
время t равным Т сек.
Тогда имеем:
т и
Третья группа
Задачи, в которых равнодействующая всех сил, приложенных
к данной материальной точке, есть функция координаты этой
точки. В этом случае дифференциальное уравнение движения
точки имеет вид
или
«37
dv г. .
«37 = /(*)•
Чтобы свести это дифференциальное уравнение к уравнению
с разделяющимися переменными, преобразуем левую часть:
dv dv dx __dv
Тогда
dv	dv ufjc	 dv
Ш^Тх' Tt~Vdx '
mvdv _f, ,
ИЛИ
mvdv = f(x)dx.	A20)
Отсюда, интегрируя это уравнение в соответствующих пределах,
имеем:
2 — mv\ Г
2	J
f(x)dx.	A20')
Из этого равенства находим скорость о как функцию от рас-
расстояния х, т. е. и = -^ = <р(х), или, разделяя переменные —?-r = dt
и проинтегрировав это уравнение первого порядка, найдем зави-
зависимость между х и. t. Если f (x) является линейной функцией
от х, то уравнение A11) будет линейным дифференциальным
уравнением второго порядка с постоянными коэффициентами.
Поэтому для решения этого уравнения можно воспользоваться
общей теорией интегрирования таких дифференциальных уравне-
уравнений, т. е. составить соответствующее характеристическое урав-
уравнение, найти его корни и затем—общее решение данного диффе-
248

ренциального уравнения. Две произвольные постбянные в общем
решении находятся по начальным условиям движения точки.
Пример 106. Материальная точка М массы т движется
прямолинейно по оси Ох. Точка отталкивается от неподвижного
центра О силой F, пропорциональной массе т и расстоянию,
причем коэффициент пропорциональности равен /г = 4. Найти
закон движения точки, если начальное расстояние ее от центра О
равно xQ = 5 м, а начальная скорость va = 2MJceK (рис. 142).
0	F
Рис. 142
Решение. Первый способ. По условию задачи F=kmx,
поэтому дифференциальное уравнение движения имеет вид
mx=r kmx,
или
Так как в данном случае f[x) = 4mx, то по формуле A20) имеем;
vdv = '
откуда
или
т е.
—24
dx
'—24
= 2dt.
Отсюда
т. е.
или
X
I
dx
246

Следовательно,
Из этого соотношения находим:
х2—24 = (бе2'—д;J,
откуда
ИЛИ
Второй способ. Так как в данном случае функция
f(x) — 4tnx является линейной функцией от х, то дифферен-
дифференциальное уравнение A20) является линейным дифференциаль-
дифференциальным уравнением второго порядка с постоянными коэффициен-
коэффициентами.
Для решения этого уравнения воспользуемся теорией инте-
интегрирования линейных дифференциальных уравнений с постоян-
постоянными коэффициентами и составим соответствующее характери-
характеристическое уравнение: иг — 4 = 0. Найдем его корни: ы, = 2
и ы2 = — 2.
Следовательно, общее решение выразится так:
Постоянные С, и Сг находим по начальным условиям дви-
движения. Для этого сначала найдем скорость точки, продиффе-
продифференцировав последнее уравнение по времени t:
v=~ = 2C,elt-2Cie-2t.
at '	г
В начальный момент при t — О согласно условию имеем:
*0 = 5 и о0 = 2.
Следовательно,
2С,-2Са=2,
откуда
С,=3, С2 = 2;
таким образом,
32' 2t
Четвертая группа
Задачи, в которых равнодействующая всех сил, приложен-
приложенных к данной материальной точке, зависит от скорости этой
точки, что имеет место при движении точки в сопротивляю-
сопротивляющейся среде.
250

В этом случае дифференциальное уравнение движения имеет
вид
или, разделяя переменные,
mdv
f(v)
Отсюда
Выполняя здесь интегрирование и разрешая затем получен-
полученное уравнение относительно и, находим скорость точки как
функцию времени, т. е.
dx
Следовательно,
A22)
Это уравнение выражает искомый закон движения точки. Если
в задаче требуется найти скорость v как функцию расстоя-
расстояния х, то левую часть уравнения A08) преобразуем:
dvdv
и
Тогда уравнение A09) принимает вид
или, разделяя переменные,
mv dv .
откуда
Пример 107. Материальная точка массы пг = О, I кг движется
прямолинейно под действием постоянной силы F = 0,3 к. Дви-
Движение происходит в среде, сила сопротивления которой выра-
251

жается линейной функцией скорости
R = 0,2v + 0,l v\
где v—скорость точки. Найти закон движения точки, если
начальная скорость равна нулю (рис. 143).
Решение. Изобразим действующие силы на рисунке.
Сила F направлена в сторону движения, а сила Я —противо-
—противоположно скорости. По формуле A11) дифференциальное урав-
уравнение движения точки имеет вид
0,1* = 0,3—0,2о — 0,lf2.
Так как в данном случае равнодействующая всех приложен-
приложенных сил есть линейная функция от скорости, т. е.
0,3—0,1у2 — 0,2у,
О я М V F
Рис 143
то по формуле A21) имеем:
о
dv
откуда
4 "' 3A — v)'
Из этого уравнения находим v:
Воспользуемся далее уравнением A22) и найдем искомый
закон движения точки:
Чтобы вычислить этот интеграл, сделаем замену переменных
е4' = г;
тогда	dz = 4г dt
252

Следовательно,
Задачи типа II
Задачи этого типа, в которых рассматривается криволиней-
криволинейное движение свободной материальной точки, можно также
разделить на четыре группы.
Первая группа
Задачи, в которых движение материальной точки происхо-
происходит под действием постоянной силы.
Пример 108. Начальная скорость снаряда ио = 490 м[сек-
Под каким углом а к горизонту следует бросить этот снаряд
из начала координат, чтобы он попал в точку с координатами
у = 700 м, 2 = 680 м>
Сопротивлением воздуха пренебрегаем.
Решение. Ось г направим по вертикали вверх, а ось у—
по горизонтали так, чтобы начальная скорость снаряда лежала
в плоскости Ozy.
Тогда, как известно (см., например, курс теоретической
механики И. М. Воронкова, § 100), снаряд будет двигаться
в вертикальной плоскости zOy, причем уравнения его движе-
движения имеют вид
y = vot cos a, z = u^sina—%? ,
Исключая отсюда t, получаем уравнение траектории (параболы):
или, заменяя —-j- на l-ftg2a, получаем:
COS d
Подставляя сюда значения у = 700; г = 680; g = 9,8; yo = 49O,
получаем:
tg2a—70 tg a + 69 = 0.
Решая это квадратное уравнение относительно tg a, находим:
tga, = l; tga, = 69,
253

откуда
а, =45°;
Пример 109. Частица М массы т, несущая заряд отрица-
отрицательного электричества е, вступает в однородное электрическое
поле постоянного напряжения Е, имеющего горизонтальное
направление, с вертикальной скоростью с0.
Определить дальнейшее движе-
движение частицы, зная, что в электри-
электрическом поле на нее действует сила
F = e?, направленная в сторону,
противоположную напряжению по-
поля. При решении задачи учесть дей-
действие силы тяжести Р (рис. 144).
Решение. За начало коорди-
—— нат О возьмем начальное положе-
положение частицы, ось х направим по
горизонтали в сторону, противопо-
противоположную напряжению поля, а ось
у—по вертикали Bjsepx (рис. 144). Тогда проекции равнодей-
равнодействующей сил Р и F на оси к и у будут равны:
Рис 144
X=F = eE = const,
—Р= —mg = const.
Дифференциальные уравнения движения частицы, согласно
уравнениям (ПО), имеют вид:
или
тх =
ту — -
dx
dt =
1t =
dx**—dt;
m
= eE,
— mg;
__eE
~ m '
~-—g-
dy =
Отсюда
Интегрируя эти уравнения в соответствующих пределах,
получаем:
Ho xa = uox = 0 и yu = vQyl = va поэтому
dx eb , du
254

или
dx = — tdt, dti = (va — ut)dt.
Отсюда, интегрируя, находим:
t
от
о
t	1
Так как в начальный момент частица находится в начале
координат, то хй — уй = 0 и, следовательно,
хеЕ f
Х
Эти уравнения определяют	движение частицы М. Предла-
Предлагается читателю доказать, что	проекция скорости частицы на
прямую, перпендикулярную к	равнодействующей сил F и Р,
остается неизменной.
Вто рая группа
Задачи, в которых равнодействующая всех сил, приложен-
приложенных к данной материальной точке, а следовательно, и ее
проекции на координатные оси, являются функциями времени.
В этом случае
* = Л@; г = М0; 2 = МО.
причем функции Д (t); /2 (t), /, (/) известны. Тогда дифферен-
дифференциальные уравнения движения точки имеют вид
Каждое из этих уравнений можно проинтегрировать
в отдельности таким же способом, как и в задачах второй
группы типа I.
Третья группа
Задачи, в которых равнодействующая всех сил, приложен-
приложенных к данной материальной точке, зависит от положения этой
точки, т. е. является функцией ее координат. Такой случай
возможен, например, когда материальная точка притягивается
256

к данному неподвижному центру или отталкивается от него
силой, зависящей от расстояния точки до этого центра.
Пример НО. Материальная точка М массой т отталкивается
от неподвижного центра О силой F = cr, где г —расстояние
точки М от центра О, а с—постоянный коэффициент. В началь-
начальный момент расстояние г0 = ОМ0 = а, а скорость точки v0 — пер-
перпендикулярна к направлению ОМй. Найти движение точки М
и ее траекторию (рис. 145).
Решение. Принимая центр О за начало координат, ось х
направим по ОМ0, как указано на рис. 145.
Так как F = cr, то, проектируя обе части этого векторного
равенства на оси Ох и Оу и учитывая, что гх = х, гу = у, где
х и у—координаты движущей-
движущейся точки, получаем:
рх — сх, Fy = cy.
Дифференциальные уравне-
уравнения движения точки М соглас-
согласно уравнениям (ПО) имеют вид:
tnx == сх у
ту^су,
х
или, полагая — =кг,
Рис 145
Каждое из этих линейных уравнений можно проинтегрировать
отдельно, для этого составим характеристическое уравнение
и2 — ?2 = 0 и найдем его корни:
Следовательно, общее решение дифференциальных уравне-
уравнений движения точки запишется так:
Отсюда
Остается найти постоянные Clt С2, С8, С4. При * = 0 имеем:
Хо = а> #о = °> &о* = °> % = ио-
Подставляя эти значения в предыдущие уравнения, получаем:
256

Отсюда находим:
Следовательно,
У~2Ь\е —е )¦
Эти уравнения определяют движение точки М. Чтобы найти
уравнение траектории в обычном виде, достаточно из них иск л ю-
v" L перепишем предыду-
чить параметр t. Для этого,полагая ~ =
ем+е-ы
щие уравнения в виде:
X
а
У
= sh(kt).
У
Возведя теперь эти уравнения в квадрат и вычитая второе
уравнение из первого, получаем:
х« у* _ .
а* ь2 ~ '¦
Траектория точки М есть гипербола.
Четвертая группа
Задачи, в которых рассматривается движение материальной
точки под действием некоторой заданной силы (постоянной или
переменной) в сопротивляю-
сопротивляющейся среде, причем сила со-
сопротивления среды зависит от
скорости материальной точки.
Пример 111. Точка М мае- VOy
сой т = 0,1 кг движется под
действием силы, которая при-
притягивает ее к неподвижному
центру О и пропорциональна о
расстоянию точки от этого цент-
центра, причем коэффициент про-
пропорциональности с = 0,6 н\см..
Движение происходит в среде,
сопротивление которой пропор-
пропорционально первой степени ско-
скорости, причем коэффициент про-
пропорциональности ц,—-0,5^-^.	Рис' 14
м
Начальные условия: ха — 0, t/0 = 30«, vtx = jc0 = 20 м\сек,
vay==ytl== Юл/сек. Найти кинематические уравнения движения
точки (рис. 146).
10 Зак. 2374
257

Решение. Обозначим F силу, притягивающую точку М
к центру О, и F' силу сопротивления среды, направленную
противоположно скорости v точки М. Тогда
F =— cr и F' = — ц,и.
Обозначая аир углы, соответственно образуемые радиусом-
вектором г точки М и вектором v скорости этой точки с осью х,
составляем дифференциальные уравнения движения точки
в декартовых координатах:
тх = Х — — F cos а—F' cosfi = — cr cos а—\xv cos|J;
ту — Y — — F sin а—F' sin P = — cr sin а—\xv sin p.
Или после подстановки числовых значений
Дальнейшее решение задачи зависит от характера получен-
полученных дифференциальных уравнений. В данном случае получены
независимые друг от друга линейные дифференциальные урав-
уравнения второго порядка, и для решения их можем воспользо-
воспользоваться теорией интегрирования таких уравнений, известной из
курса математики. Составляем характеристическое уравнение,
соответствующее первому уравнению:
«2 + 5ы + 6 =-О,
отсюда
иг = — 2; ыг = — 3.
Следовательно, общее решение данного дифференциального
уравнения выразится так:
Совершенно аналогично для второго дифференциального
уравнения получаем:
Отсюда
х = — 2Cle~tt—3C>-", у = — 2Cse-2t — 3C4e"rt.
Подставляя начальные данные в найденные для х, у,
х и у выражения
имеем:
0 = С,+С2; 20 = —2С, —ЗС„
30 = С8 + С4; 10 = —2С, —ЗС4.
25S

Отсюда
С, = 20; С2 = —20; С, = 100, С4 = — 70.
Таким образом, окончательно получаем следующие кинема-
кинематические уравнения движения точки:
лг = 20(е-2' — е-'*); у= 10A0e~s* — 7е~г*).
Задачи типа III
Задачи этого типа, в которых рассматривается движение
несвободной материальной точки, можно разделить на две
группы.
Первая группа
Задачи, в которых рассматривается движение несвободной
точки по заданной неподвижной линии.
В этом случае, поскольку траектория точки известна, проще
воспользоваться дифференциальными уравнениями движения
Ч\
Рис. 147
Рис. 148
точки в естественной форме A12); при этом необходимо учесть
реакции связей, т. е. нормальную реакцию и силу трения
(если трение учитывается).
Пример 112. Известно, что на прямолинейном участке железно-
железнодорожного пути с углом наклона а вагон, получив некоторую
начальную скорость вниз по уклону, движется затем равномерно.
Считая сопротивление движению пропорциональным нормаль-
нормальному давлению колес на рельсы, определить закон движения
этого вагона, если он будет двигаться вниз без начальной
скорости по прямолинейному участку пути с углом наклона
Р>а (рис. 147 и 148).
Решение. Вагон движется поступательно под действием
iseca P, нормальной реакции N и силы сопротивления F, кото-
которая направлена по наклонной плоскости вверх, противопо-
противоположно движению вагона.
Сначала рассмотрим равномерное движение вагона по пути
с углом наклона а.
Ю*
269

Согласно уравнениям (ПО), имеем:
тх — mg sin a— F,
ту = mg cos a—N.
Так как вагон движется прямолинейно и равномерно, то
д: = 0, г/ = 0; поэтому N = mg cos а и F — mgsma.
Согласно условию,
где /—коэффициент сопротивления. Следовательно,
mg sin a = f mg cos а,
откуда
Теперь рассмотрим второй случай, когда вагон движется
по участку пути с углом наклона р.
Аналогично предыдущему на основании уравнений A10)
имеем (см. рис. 148):
тх = mg sin p — F,
ту = — mg cos p + N = 0.
Так как ускорение w вагона параллельно оси х (рис. 148),
то w —у = 0, поэтому iV = mgcosp и F = fmgcos$, следова-
следовательно, mx = mg sinfi—fmgcosfi, или, подставляя значение f
и сокращая на т, получим:
или
х = —^— • sin (В—a) = const.
cos a vr^ '
Следовательно, вагон движется с постоянным ускорением
w — —— • sin ф — а). Поэтому по формуле для пройденного пути
при равномерно ускоренном движении без начальной скорости
имеем:
2
^ '
Это и есть искомый закон движения вагона.
Пример 113. Материальная точка весом Р = 1,96 «, лежа-
лежащая на горизонтальной поверхности стола, пр-ивязана к непо-
деижной точке О нитью длиной / = 35 см. Точке сообщена
начальная скорость ио = 4,9 м\сек, перпендикулярная к направ-
направлению натянутой нити, вследствие чего точка описывает на
столе окружность (рис. 149). Найти скорость точки и силу
260

натяжения нити через 1 сек после начала движения, если коэф-
коэффициент трения / = 0,25.
Решение. К данной материальной точке приложены силы:
вес Р, нормальная реакция стола N, сила трения FTP=fN и
натяжение Т нитч.
Составляем уравнения
движения точки в фюрме Эй-
Эйлера (в проекциях на каса-
касательную, нормаль и бинор-
бинормаль):
п~—	F -	FN-
•п fa — *тр — /JV,
2
	 ГГ>* Q ___ Д/	р
Q
Из последнего уравнения
N = P = mg; следовательно,
т-гг = — ftng, откуда dv = — fgdt и v = — fgt + C. Так как
v — v0, при ^ = 0, то С = и0; поэтому v = v0—fgt. При t=\ и
при числовых данных задачи имеем: у = 4,9—0,25-9,8 = 2,45 м\сек.
Из второго уравнения Эйлера, учитывая, что q = / = 0,35 м,
находим натяжение нити в момент ?=1 сек:
рис
' — I — gt — 0,35-9,8 -"'*" '-
Вторая группа
Ко второй группе относятся задачи, в которых рассматри-
рассматривается криволинейное движение точки по данной неподвижной
поверхности.
В этих задачах следует составлять дифференциальные урав-
уравнения движения точки в координатной форме, учитывая при
этом, кроме равнодействующей F заданных сил, приложенных
к движущейся точке, нормальную реакцию JV поверхности и силу
трения FTP. Поэтому дифференциальные уравнения движения
точки имеют вид:
A24)
Если к этим уравнениям присоединить уравнение Кулона
где /—коэффициент трения, и уравнение связи (т. е. уравнение
261

поверхности ф(х, у, г) = 0, по которой перемещаете.! точка, то
получим систему пяти уравнений, из которых можно опреде-
определить все пять искомых величин: х, у, г, N и FTp. Если трение
отсутствует, то последние члены в правых частях уравне-
уравнений A24) исчезают.
Пример 114. Материальная точка М движется по гладкой
наклонной плоскости с углом наклона а под действием собст-
собственного веса Р; ее начальная горизонтальная скорость о0 перпен-
перпендикулярна к линии наи-
г\	большего ската этой
плоскости. Определить
\ ___——7 движение этой точки и
ее траекторию, а также
реакцию наклонной
плоскости (рис. 150).
Решение. Начало
координат выберем в
начальном положении
материальной точки, а
оси х и у—лежащими
в наклонной плоскости,
причем ось х—горизон-
х—горизонтальна, а осъ у—парал-
у—параллельна линии наибольшего ската; ось г направим по нормали
к наклонной плоскости. Так как на точку М действуют сила
тяжести Р, направленная по вертикали вниз, и реакция
наклонной плоскости N, перпендикулярная к этой плоскости,
то дифференциальные уравнения движения точки запишутся
так:
тх = Х = 0,
my = Y = — Р sin а = — mg sin a,
mz — Z = N— P cos а.
Так как точка М движется в плоскости хОу, то получим
z = 0 (уравнение связи) и, следовательно, г = г = 0; поэтому
JV—Pcosa = 0, откуда Af = .Pcosa,
Остается проинтегрировать первые два уравнения, которые
перепишем в виде:
?-<>•
Рис. 150
Интегрируя эти уравнения, получим:
х = const = x0> y — yo = —g/sina.
262

Но
а поэтому
dx
Отсюда, интегрируя и принимая во внимание. что
хо~Уо = ®, находим:
x—vj., у — — ^- sin a.
Эти уравнения определяют движение точки М по наклонной
плоскости.
Исключая отсюда параметр t, находим траекторию этой
точки:
у = -
Это — парабола, расположенная под осью Ох.
Посмотрим теперь, как изменится решение этой задачи,
если учесть силу трения между материальной точкой и на-
наклонной плоскостью, равную
FTp=fN,
где /—коэффициент трения.
Третье дифференциальное уравнение движения точки М
(относящееся к оси г) остается, очевидно, без изменения;
поэтому N = Pcosa и, следовательно, FTp =fP cos a = const. Так
как сила трения направлена противоположно скорости о, то
FTP = — fP cos a ~ .
Отсюда
v	у
FTpv = — fP cos a — = —fP cos а — •
V	V
Следовательно, дифференциальные уравнения движения точки М
в плоскости хОу после сокращения на т имеют вид:
х = — fgcosa-, у =— gsina—/gcosa-^.
Интегрирование этих дифференциальных уравнений можно
выполнить, пользуясь приближенными методами.
Пример 115. Тяжелая материальная частица массы т дви-
движется по внутренней поверхности шероховатого круглого
263

цилиндра х* \-y* — R* — O. Коэффициент трения между частицей
и цилиндром равен к. В начальный момент частица находится
на оси Ох и получает скорость и0, перпендикулярную к оси Ох
и составляющую с плоско-
плоскостью хОу угол а. Составить
дифференциальные уравне-
уравнения движения частицы и
определить ее давление на
связь. Проинтегрировать по-
полученные уравнения в слу-
случае гладкой поверхности
(А = 0) (рис. 151).
Решение. Частица
М (х, у, г) движется под_дей-
под_действием трех сил: веса Р, на-
направленного по вертикали
и вниз, нормальной реакции
	 N цилиндра, направленной
по внутренней нормали к
его поверхности, и силы
трения FTp, направленной
противоположно вектору
Рис [5j	скорости и. Найдем проек-
проекции этих сил на каждую из
трех координатных осей:
Pz~ — tng; Nz = 0\ Nx = — Ncos<p; N — — N sin ф,
где ср—угол
точки М на
образуемый с осью Ох проекцией радиуса-вектора
плоскость хОу.
Так
как
СОБф:
X
~W
_Х
R
sin«p = -^-, то
х
R
— Л/ у
, — N T.
Далее имеем:
где	единичный вектор скорости.
Отсюда
V '
261

Следовательно, уравнения A24) принимают вид:
1)	mx' = -N±-kN?-; j
2)	my = -NJr-kN^; \	(a)
3)	mz = — kN ^-—mg. j
Присоединяя к этим уравнениям уравнение связи
х"+уг—R* = Q,	(б)
мы получили систему четырех уравнений с четырьмя неизвест-
неизвестными х, у, г и N. Продифференцируем дважды уравнение
связи:
хх-\-уу = 0.	(в)
х*+хх + у' + уу = 0.	(г)
Умножим первое из уравнений (а) на х, второе—на у
и сложим их почленно:
т(хх +уу) = — NR--^N(xx + yy).	(д)
Учитывая соотношения (в) и (г), получим:
N = — ~(xx +yy),
или
N = %(x> + y>).	(e)
Подставляя найденное значение N в уравнения (а), получим
систему нелинейных дифференциальных уравнений, содержащих
координаты х, у я г, а также первые и вторые производные от
этих координат по времени.
Так как решение этой системы дифференциальных уравне-
уравнений представляет собой сложную математическую задачу, то
рассмотрим частный случай, когда поверхность цилиндра
гладкая.
Тогда система (а) принимает вид:
1)	mi = -N±;
2)	my = -N±; \	(а')
3)	mz = — mg.
Чтобы исключить из первых двух уравнений силу N, поделим
10В Зак. 2374	265

почленно первое уравнение на второе; тогда имеем:
? — Л
У У '
откуда
ху—'у'х = 0.
Но
ху—ху = jf (x'y—'yx) = О,
а поэтому
ху—ух = const.
Так как
x = Rcos({>, y = R sin<p,
то
ху—ух = — R* ф = const.
Следовательно,
Ф = const — Ct.
Постоянную С, находим из начальных условий движения:
,-,	оо cos a
zo = uosina, С1 = ф„=-2-г- .
Отсюда
йш »0cosa p , v0 cos a
ИЛИ
Таким образом,
x = i?cos(-^—П; y = R sin f "^ П.
Интегрируя третье уравнение системы (а') и определяя произ-
произвольную постоянную интегрирования, получим:
г = —^-+у0/ sin a.
266

Подставляя найденные значения х и у в равенство (е), имеем:
. mvl cosa a
Таблица 15
Классификация задач
Груп
па
1-Я
2-я
3-я
4-я
t
1
(прямолинейное
ние материально)
Движение
под действием
цвиже-
точки)
ТОЧКИ
ПОСТО-
янной силы (задачи
674, 675, 678
682, 686)
Движение
под действием
зависящей от
679,
точки
силы,
време-
ни (задачи 694, 698,
701, 702)
Движение
под действием
зависящей от
динаты точки
чи 699, 700)
Движение
под действием
зависящей от
сти (задачи
683—685, 693,
697, 706—708)
точки
силы,
коор-
(зада-
точки
силы,
скоро-
680,
695-
Типы задач
II
(криволинейное движе
ние свободной мате
риальной точки)
Движение точки
под действием посто-
постоянной силы (задачи
709—71Q. 729)
Движение точки
под действием силы,
зависящей от време-
времени (задача 731)
Движение точки
под действием силы,
зависящей от поло-
положения точки (зада-
(задачи 724—728)
Движение точки
в сопротивляющейся
среде (задачи 720—
722, 730)
т
(движение несвобод-
несвободной материальной
точки)
Точка движет-
движется по заданной
линии (задачи 820,
821)
Точка движет-
движется по заданной
поверхности (за-
(задачи 642, 643,
646, 650, 816,
819, 822)
Глава II
КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
Задачи, относящиеся к этой главе, можно разделить на
следующие основные типы:
I. Гармонические свободные колебания.
П. Затухающие колебания.
III. Вынужденные колебания: а) при наличии сопротивле-
сопротивления (задачи 853, 855, 858, 859, 860); б) при отсутствии сопро-
сопротивления (задачи 854, 857, 861).
10В*
267

§ 1. СВОБОДНЫЕ КОЛЕБАНИЯ
(задачи 825—842)
Пусть материальная точка М массы т. движется прямоли-
прямолинейно под действием силы F, притягивающей ее к неподвиж-
неподвижному центру О и пропорциональной расстоянию движущейся
точки от центра О. Следовательно,
F = cOM,
где с—постоянный коэффициент пропорциональности.
Силу F назовем восстанавливающей силой. Если выбрать
за ось х прямолинейную траекторию точки М, поместив начало
О	F м
координат в точке О, то (рис. 162) дифференциальное уравне-
уравнение движения точки М запишется так:
md'x
-fir- — ex,
где х—абсцисса точки, или -гг?-\—х = 0.
Обозначив — через k", получим:
m
A26)
это—линейное однородное дифференциальное уравнение вто-
второго порядка. Так как корни характеристического уравнения
tt*-|-&s = 0 являются мнимыми, то общий интеграл этого диф-
дифференциального уравнения имеет следующий вид:
A26)
где А и В — произвольные постоянные, которые определяются
по начальным условиям движения.
Если при / = 0, х — хл, v — va, то А = хл и В = ~, следова-
следовательно,
х = х„ cos kt + j° sin kt.	A27)
Общий интеграл уравнения A25) можно представить и так:
x = asin{kt + a),	A28)
263

где а и а—постоянные, определяемые по начальным условиям
движения при помощи следующих формул:
х\-\- ~—амплитуда колебаний,
a = arctg — — начальная фаза,
A29)
Уравнение A28) есть уравнение гармонических колебаний
с круговой (циклической) частотой k.
Период этих колебаний Т определяется по формуле
1 —"Г — *п у — •	v1JU)
Пример 116. Груз весом Р = 20н подвешен на пружине,
которая в естественном состоянии
имеет длину /0 = 40сж.
Статическое удлинение пру-
пружины под действием этого груза
равно 4 см. Груз приведен в по-
положение Мй и отпущен без на-
начальной скорости.
Определить период колебаний
груза и наибольшую силу натя-
натяжения пружины, если АМй = 42 см
(рис. 153).
Решение. Ось х направим
по вертикали вниз, а начало ко-
координат О выберем в положении
равновесия груза, т. е. в том по-
лэжениц, где вес груза и реак-
реакция пружины уравновешиваются.
Статическое удлинение пру-
пружины, соответствующее положе-
положению равновесия груза, обозна-
обозначим Яст, а удлинение пружины, соответствующее положению
М груза, обозначим X. Тогда
А Аст f- X.
Так как реакция пружины пропорциональна ее удлинению,
то
р
Рис. 153
где с—постоянный коэффициент пропорциональности, называ-
называемый жесткостью пружины.
В положении равновесия модуль силы F равен весу груза;
поэтому
СКх~ ^чт — Р'
269

откуда
с = г- = т = 5 hjcm.
л,ст ч
Дифференциальное уравнение движения груза имеет следую-
следующий вид:
m^ = P—F или т~-=Р—с(кС1: + х).
(Рх
Ьо Р — сХсг, поэтому т-ш = — с%, или
~.+ k*x = 0, где fe2=-.
Мы получили дифференциальное уравнение A26) гармониче-
гармонических свободных колебаний.
Отсюда следует, что груз, подвешенный на пружине, будет
совершать гармонические колебания около начала координат,
т. е. около равновесного положения. Период этих колебаний
найдем по формуле A30):
р	р
но /п = - и с — т—, поэтому
g
Амплитуду колебаний определяем по формуле A29):
,.8
К
г
По условию задачи хй = — 2 см и t>0 = 0, поэтому а = 2см.
Следовательно,
Fmax = С^шах = 5 • 6 = 30 К.
Пример 117. К свободному концу А упругой горизонтальной
балки, другой конец которой закреплен неподвижно, подвешен
на пружине груз весом Р. Упругая сила балки пропорциональна
стреле прогиба Д а сила натяжения пружины пропорцио-
пропорциональна ее удлинению К, причем жесткость балки равна сх,
а жесткость пружины равна с2. Определить период колебаний
груза, пренебрегая массами балки и пружины (рис. 154).
Решение. Как и в предыдущей задаче, ось х направим по
вертикали вниз, а начало координат О выберем в положении
равновесия груза. Если статический прогиб балки, т. е. ее
прогиб при равновесии груза, обозначим fCT, естественную
270

длину пружины обозначим /„, а ее статическое удлинение А,ст,
то (рис. 154)
V=/CT и ЛО = /„ + >,„.
Прогиб балки в некоторый момент t, когда груз занимает
положение М, обозначим f. Длина пружины в этот момент, как
видно из рис. 154. б, равна
Следовательно, удлинение пружины
К грузу М приложены две силы: вес Р и реакция пружины
F, причем F = ctk Если пренебречь массой пружины, то силы
натяжения пружины на ее концах будут равны; следовательно,
Рис 154
к концу А балки приложена сила, равная сг%. С другой сто-
стороны, если пренебречь массой балки, то приложенная к ней
в точке А реакция пружины будет cj, а потому cj = c2k.
Отсюда / = -f^> и. следовательно,
или
В положении равновесия груза имеем:
откуда
= - и
271

ПОЭТОМУ
отсюда
с, + сг,
,= v _L p I ±
Дифференциальное уравнение движения груза по оси х
имеет вид:
Подставляя значение Я, получим:
.„ d*x с.с.
или
%. + k'x = 0, где k*~
m(Cl+Cl)»
т. е. получаем дифференциальное уравнение A25) гармониче-
гармонических колебаний с частотой k.
Отсюда следует, что искомый период колебаний груза
с, + с2)
или
§ 2. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
(задачи 843—852)
Если материальная точка М массы ш движется по оси Ох
под действием восстанавливающей силы F, притягивающей эту
точку к неподвижному центру О в сопротивляющейся среде, то
на эту точку, кроме силы F, действует еще сила сопротивле-
сопротивления R, пропорциональная скорости v точки М, т. е.
R = — (АО,
где \х — постоянный коэффициент пропорциональности (рис. 155).
Тогда Rx = — №х — — I1 jt и дифференциальное уравнение дви-
движения точки под действием восстанавливающей силы в сопро-
сопротивляющейся среде принимает вид:
d2x _	dx
272

Введем обозначения: — = k* и — = 2п. Тогда имеем
т	т
g + fca* + 2ng = 0.	A31)
Если fe>n, то движение точки является колебательным и
общее решение этого уравнения имеет вид:
x = e~nt(A cos A,/ -ff sinft,*) = e-"'-asin(&1/+a), A32)
где &, = ]/V2
0
Т
i
!
R
Г
Риг-
М V
f
i
155
Постоянные А и В (либо а и а) определяются по начальной
скорости ол и начальной координате х0 следующим образом:
А=х9, B = v-i±
к,
либо
A33)
Уравнение A31) есть уравнение затухающих колебаний.
Период затухающих колебаний определяется по формуле
2я	A34)
Моменты времени, в которые точка получает максимальные
отклонения от начала координат (положения равновесия), обра-
образуют арифметическую прогрессию с разностью, равной полупе-
полупериоду —. Амплитуды затухающих колебаний образуют убыва-
убывающую геометрическую прогрессию, знаменатель которой назы-
называется декрементом затухания и обозначается буквой D, причем
Величина lnZ) называется логарифмическим декрементом^
Пример 118 Материальная точка совершает-прямолинейные
колебания в сопротивляющейся среде под действием силы, про-
пропорциональной расстоянию от этой точки до неподвижного
центра 0. Сила сопротивленчя среды пропорциональна скорости
точки. В начальный момент *0 = 0 и v0 — 1 м.\сек. Зная, что
973

период колебаний Т = 2 сек, а декремент затухания D = y,
найти закон движения точки (рис. 156).
Решение. Выберем начало координат в неподвижном
центре О; ось х направим по прямолинейной траектории точки,
силу притяжения к центру О обозначим F, а силу сопротивле-
сопротивления среды обозначим R. Тогда
х = — ex, Rs = — м- 57 .
где с и \i — постоянные коэффициенты; дифференциальное урав-
уравнение движения точки имеет вид:
g + 2/.g+ *¦*-<>,
где 2n = i^- и k' — ~ , a m—масса точки,
m	tn
U F R MU Л4
Рис 156
Решение этого уравнения найдем по формулам A32) и A33):
х = e~nt ( jc0 coskj: -f- """I""*0 sin k.t),
или, подставив значения хл и va, получим:
x = e~nt т- sinftt?.
Чтобы найти постоянные k и л, 'воспользуемся формулами
A34) и A35):
-—
— Г —— ?> t/civ H LJ — с — ~п ,
К|	Z
отсюда
I
&, = л и е~ =-5", или п = 1п2.
Закон движения точки принимает вид:
_e~l m 2 :
но
поэтому
_ 2-' sin nt
274

§ 3. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
(задачи 853—861)
Если на материальную точку М, движущуюся по оси х,
кроме силы F, пропорциональной расстоянию х, и силы сопро-
сопротивления среды, пропорциональной скорости v, действует еще
некоторая периодически изменяющаяся сила F', которую назо-
назовем возмущающей силой (рис. 156), то дифференциальное урав-
уравнение движения точки запишется так:
dx
Пусть, например, возмущающая сила изменяется по закону
TJ
Тогда, полагая — = h и сохраняя обозначения, принятые в преды-
предыдущем параграфе, получим:
g ^	A36)
При k~>n общее решение этого уравнения имеет вид:
x = ae-ntsm(kJ + a) + bsm(pt + $-Jr у),	A37)
где
„8V Г-*"	рад
Первый член правой части равенства A37) представляет
собой затухающие колебания, а второй—так называемые вы-
вынужденные колебания.
Постоянные а и а определяются по начальным условиям
движения. Если k">2n', то при
p = Vks—2пг	A39)
амплитуда вынужденных колебаний достигает максимума, рав-
равного
<140>
При отсутствии сопротивления R = 0, а следовательно,
и п = 0; дифференциальное уравнение движения точки прини-
принимает вид:
= ft. sin 0=>* + р).	A41)
275

Полагая в равенствах A37), A38) п = 0, имеем его общее
решение:
х = а • sin (kt + a) + b sin (pt + p),
где
b= fe2_^p2 при ?=^p.	A42)
Первый член последнего равенства представляет собой сво-
свободные колебания, второй член — вынужденные.
Если частоты свободных и вынужденных колебаний совпа:
дают, т. е. если р = &, то возникает резонанс, тогда решение
уравнения A41) представляется в виде
х = a sin (kt + а) — у- cos (pt + Р).
A43)
В этом случае амплитуда вынужденных колебаний неогра-
неограниченно возрастает с возрастанием t.
Пример 119. Тело весом Р = 49 н, погруженное в жидкость,
подвешено на пружине, статическое удлинение которой под
действием веса этого тела равно
1 см.
Свободный конец пружины
совершает вертикальные колеба-
колебания около неподвижной точки Ао
по закону уА = А0А = 0,05 sin 5nt,
причем уА выражено в метрах,
t — в секундах.
Сила сопротивления жидкости
при движении груза пропорцио-
пропорциональна его скорости v и при
и = 1 MJceK равна 15,7 н. Найти
амплитуду вынужденных колеба-
колебаний (рис. 157).
Решение. Выберем начало
координат О в положении равно-
равновесия тела, предполагая при этом,
что конец А пружины находится в точке Ло; тогда А0О = 10-\-
+ XCTi где 1й -—длина недеформированной пружины, Яст—ее ста-
статическое удлинение.
Ось у направим по вертикали вниз. В некоторый момент t,
когда тело занимает положение М, длина пружины
а ее удлинение
276

Если жесткость пружины обозначим с, то реакция пружины
F = ск=сксг:+ су—0,05сsin 5nt,
но сХст = Р, поэтому
F = Р + су—0,05 с sin 5nt.
Сила сопротивления жидкости
где ц.— коэффициент пропорциональности, v—скорость тела.
Дифференциальное уравнение движения тела имеет вид:
или
где
Мы получили дифференциальное уравнение A36), в котором
нужно положить р = Ъп и р = 0. Поэтому искомую амплитуду
вынужденных колебаний находим по формуле A38):
,	h	¦ 0,05fea
разделив числитель и знаменатель на kz, получим:
,	0,05
Подставим числовые значения входящих сюда величин:
Следовательно,
о = —-	м да 6,7 см.
А'" A,57J
980
277

Пример 120. Колеблющаяся масса вибрационного грохота,
установленного на наклонной плоскости с углом наклона а
(рис. 158, с), приводится в движение при помощи двух пружин
жесткостью с н\м каждая, соединенных с ползуном В криво-
шипно-шатунного механизма. Длина / шатуна АВ значительно
больше длины г кривошипа О А, так что первой и более высо-
высокими степенями отношения — можно пренебречь, т. е. можно
считать, что ползун В движется по тому же закону, что и про-
проекция А' пальца А кривошипа на ось х. Вес грохота равен
Gh. Определить вынужденные колебания грохота, пренебрегая
потерями на трение, если кривошип вращается по закону
<p = (ot. При каком числе оборотов в минуту кривошипа насту-
наступит резонанс?
a)	6) '
Рис 158
Решение. Обозначим среднее положение ползуна (при
Ф-0) через Вй, а смещение ползуна из этого положения —
через хв тогда имеем:
хй — ВЛВ & О А' —г sin ф = г sinto^.
Смещение х центра тяжести грохота отсчитываем от того
положения So> в котором он находился бы при среднем поло-
положении ползуна, если бы система оставалась в покое. Очевидно,
п о 	1 	Gsin g
о в~ сг ~~ 2с '
т. е. BqSq—статическая деформация пружин привода грохо-
грохота под действием составляющей его веса, направленной вдоль
наклонной плоскости. Отсюда деформация пружин (см. рис.
158, б, где смещения ползуна и грохота показаны в увеличен-
увеличенном масштабе) выразится следующим образом:
Л = Хд X
278

а потому проекция силы упругости пружины на ось х опреде-
определяется так:
Хупр = 2с% = 2с (хв— х— Хст).
Отсюда получаем дифференциальное уравнение движения гро-
грохота:
- X = ХуПр + ХВеса = 2с (Хд—X— !„) +
-f- G sin a = 2схв—1сх = 2cr sin at — 2сх,
или
•• , 2cg 2cg . .
х + ~ х = —¦ г sm (at.
Вводя обозначения ~ = k* и -^$-r = h, имеем:
о	о
х -\- k'x = h sin sit.
Отсюда на основании уравнения A41) получаем:
*Wbsin **	sin @^
Резонанс наступает при © = coKp = ft, откуда
S = 300 /1-424
1
Пример 121. Материальная точка массой т = 50 кг движется
по горизонтальной прямой, притягиваясь к неподвижному
центру О силой F, пропорциональной расстоянию точки от
этого центра, причем коэффициент пропорциональности с==
= 200 н/ж. Кроме того, на точку действует возмущающая сила
л^
F М Г
Рис 159
F' = 2sin2?, выраженная в ньютонах. Найти закон движения
точки если в начальный момент x = x9 = 0, v = vo=l см,\сек
и возмущающая сила F' в начале движения (при ^<С^-) сов-
совпадает по направлению с начальной скоростью (рис. 159).
Решение. Выбирая начало координат в центре О и направ-
направляя ось Ох по траектории точки в сторону ее начальной ско-
скорости, составляем дифференциальное уравнение движения точки:
50л: = — 200а- + 2 sin 2t или х + 4х = 0,04 sin 2t,
279

т. е. получаем уравнение A41), в котором
/гг = 4, /1 = 0,04, р = 2, р=-0.
Так как частоты свободных и вынужденных колебаний
совпадают (k = р = 2), то возникает резонанс и закон движения
точки определяется уравнением A43).
х = a sin (kt + а) — |^ cos (JW -f 0) = a sin B/ + a) —0,01* cos 2t,
откуда
ti = x = 2a cos B* + a) -f- 0,02/ sin It — 0,01 cos 2t.
Пользуясь начальными условиями (/„ = 0, л;0=0; о„ = 1 cMJceK =
= 0,01 м/сек), имеем:
jeo = asina = O; w0 = 2acosa—0,01=001.
Следовательно,
a = 0, a = ^ = 0,01.
Таким образом,
001
Глава III
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ И ПРИНЦИП ДАЛАМБЕРА
ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
§ 1. ТЕОРЕМА О КОЛИЧЕСТВЕ ДВИЖЕНИЯ
Теорему о количестве движения материальной точки можно
выразить в векторной или в скалярной форме.
В векторной форме теорему о количестве движения можно
выразить двумя способами:
а)	дифференциал количества движения материальной точки
равен элементарному импульсу силы, действующей на эту
точку:
d (тЪ) = Fdt = dS;	A44)
б)	изменение количества движения материальной точки за
некоторый конечный промежуток времени t — t0 равно полному
импульсу действующей силы за тот же промежуток времени:
mo —mot = Jw^=»S.	A45)
280

Скалярное выражение теоремы о количестве движения в диф-
дифференциальной или конечной форме получаем, проектируя век-
векторное равенство A44) или векторное равенство A45) на каждую
из трех неподвижных координатных осей:
A46)
mvy—mv^ =
mvz — mvaZ--
A47)
В случае движения материальной точки по прямой линии,
которую примем за ось х, имеем (рис. 160):
d(mv)~=Xdt,
) — mv — [
A48)
A49)
где v—алгебраическое значение скорости, Х= +F или X ==
= —F в зависимости от направления силы, причем F — равно-
равнодействующая всех сил, приложенных к точке. Задачи этого
параграфа можно разделить на три основных типа:
Рис 160
1)	задачи, относящиеся к прямолинейному движению точки,
в которых требуется определить или скорость точки, или время
движения, или действующую силу;
2)	задачи, относящиеся к криволинейному движению точки,
в которых требуется определить ее скорость или время дви-
движения;
3)	задачи, в которых по заданному изменению количества
движения материальной точки требуется определить импульс
действующей на нее силы.

Задачи типа I
Задачи этого типа можно разделить на три группы:
1)	задачи, в которых сила, приложенная к материальной
точке (или равнодействующая всех приложенных сил), постоянна;
2)	задали, в которых сила, приложенная к материальной
точке (или равнодействующая всех приложенных сил), есть
функция времени.
3)	задачи, в которых сила, приложенная к материальной
точке (или равнодействующая всех приложенных сил), есть
функция скорости этой точки.
Пе рвая группа
Движение точки происходит под действием постоянной силы,
т. е. X = ± F — const. В этом случае можно применить теорему
о количестве движения в конечной или интегральной форме
A49), причем отсчет времени здесь можно вести от нуля:
mv—mvo = )Xdt = Xt.	A50)
/0=о
Отсюда нетрудно определить одну из трех величин v. F или
t, если две другие заданы.
Применяя теорему о количестве движения к прямолинейному
движению точки, ось х удобнее всегда направлять в сторону
начальной скорости точки, а если начальная скорость равна
нулю, то в сторону силы, действующей на точку.
Пример 122. Вагонетка, вес которой вместе с полезной на-
нагрузкой Р = 8500 н, при движении по горизонтальному пути
испытывает сопротивление, величина которого составляет 0,01
от всех вертикальных нагрузок. Рабочий толкает вагонетку
с силой F = 170 н (рис. 161).
Через сколько времени рабочий сообщит вагонетке скорость
о = 0,6 MJceK?
Решение. На вагонетку действуют: 1) вертикальная сила
тяжести Р = 8б00 н, 2) нормальная реакция N рельсов, 3) гори-
-	зонтальная сила F=170 н, с
которой рабочий толкает ваго-
вагонетку, 4) горизонтальная сила
сопротивления:
В данной задаче имеется не
материальная точка, а система
тел (кузов вагонетки, полезная
нагрузка, колесные скаты), ко-
которые связаны друг с другом. Пренебрегая вращательным дви-
282

жением скатов, можно считать, что все части рассматриваемой
системы движутся поступательно вместе с кузовом вагонетки.
При этом можно считать, что масса вагонетки сосредоточена в
центре ее тяжести и в центре тяжести приложена равнодействую-
равнодействующая всех сил, действующих на вагонетку (справедливость этих
допущений доказывается в динамике системы).
Таким образом, данная задача о движении системы сводится
к задаче о движении материальной точки (центра тяжести ва-
вагонетки), на которую действует сила
Обозначая проекцию силы R на направление движения ваго-
вагонетки через X, имеем:
X = F — F' = F—0.01P = 170—85 = 85 н = const.
Теперь применяем теорему о количестве движения:
mv — mva = Xt,
р
откуда, учитывая, что в( = 0 и что т — —, находим:
, mi Рг 8500-0,6 - .
Вторая группа
Движение точки происходит под действием силы, которая
является функцией времени, т. е. X = f(t). В этом случае тео-
теорему о количестве движения тоже применяют в конечной форме,
но отсчет времени здесь не всегда можно вести от нуля.
В общем случае имеем:
t
mv — mvo=\f{t)dt = q>(t),	A-51)
и
отсюда находим скорость:
» = », + ^ф@.	A52)
Если в задаче требуется определить время, то это уравне-
уравнение нужно разрешить относительно t. Если же нужно найти
закон движения точки, то это уравнение нужно проинтегри-
проинтегрировать, заменив скорость v на -^.
Пример 123. На тело весом Р = 20 н, находящееся в покое
на горизонтальной плоскости, действует вертикальная сила F,
возрастающая от нуля пропорционально времени, причем коэф-
коэффициент пропорциональности равен 2 н/шс (рис. 162). Через
283

сколько времени после начала действия силы F тело начинает
двигаться? Найти закон этого движения.
Решение. На тело, пока оно находится в покое, действуют
три силы: сила тяжести Р = 20 н, сила F = 1t и нормальная
реакция N плоскости АВ. В момент начала дви-
движения сила N, очевидно, обращается в нуль, и
с этого момента на тело действуют только две
силы: F и Р. Проекция равнодействующей сил,
приложенных к телу с момента начала движе-
движения, на ось л, по которой будет двигаться центр
тяжести тела, выразится так:
X = F — P = 2/ —20 = 2 (/—10).
Это выражение для X справедливо только с
момента /=10 сек, когда движущая сила F ста-
станет равна силе тяжести Р, ибо до этого момен-
момента на тело действует, как мы уже отмечали,
еще третья сила N.
Так как в данном случае X = /(/), то для
решения задачи можно применить теорему о ко-
количестве движения в конечной форме. Учитывая,
Р 20 10
F,
1
'/У//.
Рис. 162
Р 20
что « = _ = _ =
=
и va =
имеем:
— \O)dt=
10	10
откуда
но
следовательно,
(/-10J =(/-10J,
y = 0,49(/—10)a,
X) =r
_
dt
Выбирая начало координат в начальном положении центра
тяжести тела, т. е. полагая #0 = 0, получаем:
х= f 0,49 (f—10)" Л = 0,49-
<*~10)t
=0,163 (/ —
Итак, движение начинается через 10 сек после начала дей-
действия силы F, причем я = 0,163(/—10)*. Заметим, что получен-
полученное уравнение справедливо только с момента /=10 сек.
284

Третья группа
Движение точки происходит под действием силы, зависящей
от скорости, т. е. X=f(v). В этом случае теорему о количестве
движения следует применять в дифференциальной форме A48):
d(mv)=Xdt = f
или
отсюда находим время:
Если в задаче требуется определить скорость, то это урав-
уравнение нужно разрешить относительно v.
Пример 124. В тот момент, когда скорость моторного судна
равна ч0, выключается мотор, и судно движется, испытывая
сопротивление воды, величина которого пропорциональна ско-
скорости, причем коэффициент пропорциональности равен (х: масса
судна равна т. Через какой промежуток времени скорость
судна уменьшится вдвое (рис. 163)?
Решение. Вес судна Р уравновешивается архимедовой
силой А. В горизонтальном направлении действует одна только
сила сопротивления воды R, направленная в сторону, противо-
противоположную скорости судна. Направляя ось х в сторону движе-
движения, имеем:
X = —\iv,
т. е. X является функцией от v. Поэтому применяем теорему
о количестве движения в дифференциальной форме A48):
d(mv) = Xdt = — \xvdt.
Разделяя переменные, получим:
285

Теперь интегрируем в соответствующих пределах:
V	t
откуда
L nV\v0~~ ~~~in '
или
In v — In v. = —^ t,
0	m
ИЛИ
, v 	 \i ,
w0 m
Отсюда находим:
t = -E In -^ = ^ ln-' = ^ In jr?- ==- In 2.
Задачи типа II
Задачи этого типа, в которых рассматривается криволиней-
криволинейное движение точки и требуется найти скорость точки или
время движения, можно разделить на такие же три группы, как
и задачи первого типа:
1)	движение происходит под действием постоянной силы;
2)	движение происходит под действием силы, зависящей от
времени;
3)	движение происходит под действием постоянной силы
в среде, сопротивление которой пропорционально первой сте-
степени скорости.
В этих трех случаях теорема о количестве движения дает
первые интегралы дифференциальных уравнений движения.
В первом и во втором случаях, т. е. когда сила постоянна
или является функцией времени, теорема применяется в ко-
конечной форме, выражаемой уравнениями A47). Из уравнений
A47) по заданным проекциям силы находят проекции скорости
на координатные оси. В третьем случае теорема применяется
в дифференциальной форме.
Перва я группа
Так как в этом случае сила F — const, то и ее проекции на
координатные оси х, у, г постоянны. Поэтому теорему о коли-
количестве движения можно применять в конечной форме A47).
Следовательно, имеем:
286

Из этих уравнений определяются проекции скорости, а затем
и скорость v. Наоборот, зная проекцию скорости на какую-
либо ось, можно найти время.
Пример 125. Определить, пользуясь теоремой о количестве
движения, время, в течение которого тело, брошенное под углом
а0 к горизонту с начальной скоростью у0, достигает максималь-
максимальной высоты (рис. 164).
Решение. Координатные оси располагаем в плоскости
движения тела, причем ось к направляем горизонтально, а ось
М, V,
Рис 164
у—вертикально вверх. Составим уравнение, выражающее изме-
изменение проекции количества движения на ось у:
mv^ — mv^ = Sy = — jj Pdt = — mg \dt= —mgtv
о	о
но w,v = 0 (в наивысшей точке скорость тела горизонтальна),
и v =yosinao, а потому t1 =
ve sin a0
8 "
Вторая группа
В этом случае сила F, а следовательно, и ее проекции на
координатные оси являются известными функциями времени, т. е.
Х=/,@; Y = ft(t); Z = }t{t).
Теорема о количестве движения применяется здесь в конеч-
конечной форме A47).
Выполняя интегрирование, находим_ из этих уравнений
проекции скорости, а затем и скорость ь.
Пример 126. На материальную точку массой т = 2 кг
действует сила, проекции которой на координатные оси равны:
X = 6 cos 2t;
Y = 6 sin It;
Z= — 6sin2*
(сила выражена в н, время t — в сек).
287

Определить скорость vt точки в момент ^ = я = 3,14 сек,
если в момент <, = у тс ее скорость и, равна по модулю
2 м1сек и составляет с координатными осями к, у, г углы,
равные соответственно 30°, 60° и 90°.
Решение. Так как проекции силы на координатные оси
являются функциями времени, то теорему о количестве движе-
движения можно применить в конечной форме A47). Для этого
вычислим сначала проекции на координатные оси импульса
действующей силы за промежуток времени от момента tx до
момента t3:
n
S=\
= 6J cos{2t)dt = 3\ sin2<| =0,
я	—
л
== 6 \ sin B0dt = — 3[ cos2t{" — — 6 «сек.
_л	п_
а	г
Так как Z отличается от Y только знаком, то Sz —
Далее на основании уравнений A47) получаем:
Отсюда при т — 1 находим проекции искомой скорости:
Так как
и,я = о,-cos 30° = ]/^
то
Следовательно,
о, = j^oL+^ + t'L = КГб = 4 ^/сек.
288

Если углы вектора у, с координатными осями обозначим
а, р, у. то
cos а --= ^н = ill = 0,4330,
v2 4
cosp = ^ = —0,5,
cosY = ^ = 0,75.
Отсюда u = 64°30', р* = 120°, у = 48°30'.
Третья группа
В этом случае проекция силы на каждую из трех коорди-
координатных осей является линейной функцией проекции скорости
на ту же ось, и теорему о количестве движения применяют
в форме A46).
М, V,
Рис 165
Прежде чем интегрировать уравнения A46), надо разделить
переменные, для чего достаточно эти уравнения разделить
соответственно на X, Y, Z; последующее решение аналогично
решению в случае прямолинейного движения точки под дейст-
действием силы, зависящей от скорости.
Пример 127. Решить пример 125, учитывая сопротивление
воздуха, величина которого выражается формулой
R=kP-v,
где к — постоянный коэффициент, Р — вес тела, v—его скорость
(рис. 165).
Решение. Координатные оси располагаем так же, как
в примере 125 (см. рис. 164). Так как на тело действует сила,
которая является функцией скорости, то теорему о проекции
количества движения на ось у применяем в дифференциальной
форме
d (mv v) = Y dt\
11 Зак. 2374
289

но
К = — Р—Rs\na = — P A+feu sin a) = — P{\+kvy).
Следовательно,
+kvy)dt,
откуда
Учитывая, что vv изменяется в пределах от uosinao до нуля,
имеем:
dvv
d0 sin a0
kg
in (n-*ig
Задачи типа III
В задачах этого типа известно количество движения точки
в начальный и конечный моменты, а следовательно, и его
проекции на координатные оси. Проекции искомого импульса
силы определяются по формулам A47), т. е.
По этим проекциям находятся модуль и направление им-
импульса S.
Пример 128. Материальная точка М перемещается по шеро-
шероховатому криволинейному желобу, расположенному в. верти-
,	кальной плоскости хОу, под
|	действием собственного веса Р.
Угол трения равен ор. Началь-
Начальная скорость этой точки, ког-
когда она занимает положение А,
составляете вертикальной осью
Оу угол а и по модулю равна
vQ, а ее конечная скорость в
точке В направлена по горизон-
горизонтальной оси Ох и по модулю
равна v. Найти импульс нор-
¦ мальной реакции N желоба за
промежуток времени t, в те-
течение которого точка М пе-
переместилась из Л в В (рис. 166).
Решение. Применим теорему о количестве движения ма-
о\
Рис. 166
290

териальной точки в форме A47):
t
о
t
т(у„ — ?>„„) =
Здесь X и Y — проекции на оси хну равнодействующей всех
сил, приложенных к точке М, т. е. сил Р, N и силы трения
FTP. Поэтому
Кроме того, имеем:
Fw=fN,
где /—коэффициент трения, / = tgcp.
Если угол силы N с осью х обозначим fi, то
Nx = Ncos$, Ny = Nsin$, Fy = — /^-sin p = — fN sin
= — fNy, ^P = /rTP-cosp=/A/cosp
Следовательно, уравнения A47) принимают вид:
t	t
m{v — va sin a) = J Nxdt — f
Xdt — Pt.
о	о
Так как
где Sx, Sy — проекции искомого импульса S силы /V на оси
х и у, то:
Sx—fSy = m {v — o0 sin a),
/Sx + 5у = ти0 cos a + Pt = m (va cos a -fgO-
Из этих уравнений можно найти Sx и Sy и затем по этим
проекциям вычислить импульс 5. Но проще возвести эти урав-
уравнения в квадрат и сложить их. Тогда получим:
Отсюда, замечая, что
11 *	291

находим:
= m coscp /(у—с, sin aJ -+ (gt + w0 cos аJ =
V(v-vt sin аI + (gt + vt cos а)'.
Таблица 16
Классификация задач
Типы
I
Определение
времени или ско-
скорости при прямо-
прямолинейном движе-
движении точки
II
Определение
времени или ско-
скорости при криво-
криволинейном движе-
движении точки
III
Определение
импульса силы по
изменению коли-
количества движения
(задачи 741, 744)
Группы
1 я
Постоянная си-
сила (задачи 733,
734, 737, 743)
Постоянная
сила
2 я
Сила, чавися-
щая от времени
(задачи 694, 698)
Сила, завися-
зависящая от времени
3 я
Сила, завися-
зависящая от скорости
(задачи 687, 691,
696)
Движение
точки в сопротив-
сопротивляющейся среде
§ 2. ТЕОРЕМА О МОМЕНТЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
Момент количества движения материальной точки mv отно-
относительно некоторого центра О равен векторному произведению
радиуса-вектора движущейся точки г на количество движения
mv, т. е.
m,(mti)=rxm9.	A53)
Очевидно, что модуль момента количества движения равен
|	|	A54)
где h—плечо вектора v относительно центра О (рис. 167).
Проектируя векторное равенство A53) на координатные оси,
проходящие через центр О, получаем формулы для моментов
количества движения материальной точки относительно этих
292

осей:
тх{mv) =m(yz—гу); т (mv) = т(?х—хг)\
mz(mv) = xy—ух.	A55)
В векторной форме теорема о моменте количества движения
выражается так: производная по времени от момента количества
движения материальной точки относительно какого-либо непод-
неподвижного центра О равна моменту действующей силы относи-
относительно того же центра, т. е.
d - ,„._- ;~о(р)ш	A55)
Проектируя векторное равенство A56) на какую-либо из
координатных осей, проходящих через центр О, получаем урав-
уравнение, выражающее ту же теорему в скалярной форме:
d	—	—
-л тх (mv) = mx (F),	A57)
т. е. производная по времени от момента количества движения
материальной точки относительно какой-либо неподвижной оси
_ _
' mo(mV)
mV rt M
— Y
Рис 167
равна моменту действующей силы относительно той же оси.
Эта теорема имеет большое значение при решении задач в слу-
случае движения точки под действием центральной силы Цент-
Центральной силой называется такая сила, линия действия которой
все время проходит через одну и ту же точку, называемую
центром этой силы. Если материальная точка движется под
действием центральной силы F с центром в точке О, то
и, следовательно, mo(mv) = const. Таким образом, момент ко-
количества движения в данном случае остается постоянным по
модулю и по направлению. Отсюда следует, что материальная
точка под действием центральной силы описывает плоскую
292

кривую, расположенную в плоскости, проходящей через центр
силы.
Если известна траектория, которую описывает точка под
действием центральной силы, то, пользуясь теоремой о моменте
количества движения, можно найти эту силу как функцию рас-
расстояния г от точки до центра силы.
Действительно, так как момент количества движения отно-
относительно центра силы остается постоянным, то, обозначая h
плечо вектора tnv относительно центра силы, имеем:
vh = const.	A58)
Для определения этой постоянной должна быть известна
скорость точки в каком-либо месте траектории. С другой сто-
стороны, имеем (рис. 168):
где q—радиус кривизны траектории, ф — угол между радиусом-
вектором точки и касательной к траектории в этой точке.
Отсюда
У	F = ^^. A59)
Итак, имеем два уравнения
A58) и A59) с двумя неизвест-
неизвестными v и F; остальные величи-
величины, входящие в эти уравнения,
т. е. h, q и ф, являясь элемен-
элементами заданной траектории, лег-
легко могут быть найдены. Таким
образом, можно найти v и F
как функции г.
описывает эллипс под действием
Рис. 169
Пример 129. Точка М
центральной силы F (рис. 169). Скорость в вершине А равна
v0. Найти скорость v в вершине В, если ОА = а и ОВ = Ь.
Решение. Так как в данном случае
m0 (mv) — const, то mvb = mvlla, откуда v = ^-v0.
Пример 130. Точка М массы т описывает окружность ра-
радиуса а, притягиваясь точкой А этой окружности (рис. 170).
В начальный момент точка находится в положении В и
имеет скорость v0. Определить скорость v точки и силу притя-
притяжения F как функции радиуса-вектора г.
то
Решение. Так как mA(F) =
mA(mv) =- const = тА (tnv0),
294

следовательно,
откуда
mvh =
la
J* h '
Но из рисунка имеем:
г = 2а cos (90°—а)=2а sin a,
откуда sinct= ?¦ , поэтому h = r sin а = ~ и, следовательно,
1а
_ 4аЧ
Рис 170
Силу Z7 находим, пользуясь уравнением A59):
отсюда
г, „ . rnv2 mv*
г„ — F sin а = — = —¦ ,
т 16а9и022а 32ma'v%
	X
а sin а а
§ 3. РАБОТА И МОЩНОСТЬ
Работа dA силы на бесконечно малом перемещении ds, на-
называемая элементарной работой, выражается формулой
dA = F cos a-ds = Ft -ds,	A60)
где ds — MMt, a — угол между силой F и скоростью v точки
ее приложения (рис. 171), или в виде скалярного произведения:
dA^I-dr,	A61)
где dr = vdt—дифференциал радиуса-вектора точки приложения
силы.
295

Выражая это скалярное произведение через проекции век-
векторов F и dr на координатные оси, получаем аналитическое
выражение элементарной работы:
dA^Xdx + Ydy + Zdz,	A62)
где X, Y, Z — проекции силы на координатные оси, dx, dy,
dz—бесконечно малые изменения (дифференциалы) координат
точки приложения силы
при элементарном переме-
перемещении этой точки
Если сила F приложе-
приложена к твердому телу, вра-
вращающемуся вокруг непод-
неподвижной оси z, то
dA = тг (F) dy, A63)
где dtp — элементарный
угол поворота тела во-
вокруг оси.
Если к телу, имеюще-
имеющему неподвижную ось вра-
_	щения Oz приложена пара
сил с моментом /п, то элементарная работа этой пары выра-
выражается следующим образом:
dA = тг d<p,
где тг—проекция вектора — момента пары на ось Oz
Особый интерес представляет случай, когда сила является
функцией координат точки и, кроме того,
._.
ду ~дх ' dz ~~ ду ' dx
dz
В этом случае существует такая функция координат U—
= ?/(*, у, z), частные производные которой по координатам
равны проекциям силы на соответствующие координатные
оси, т. е.
dU_ „ dU _ dU_?	.-,..
Такая функция называется силовой, или потенциальной,
функцией. Таким образом, если существует силовая функция,
то
_
dll
dU
A66)
т. е. элементарная работа силы равна полному дифференциалу
силовой функции. Ограниченная или неограниченная часть про-
296

странства, где проявляется действие силы, имеющей силовую
функцию, называется силовым потенциальным полем. Геометри-
Геометрическое место точек силового потенциального поля, в которых
силовая функция сохраняет постоянное значение, называется
эквипотенциальной поверхностью, или поверхностью уровня.
Работа А силы F на конечном пути определяется как пре-
предел суммы элементарных работ и выражается в виде криво-
криволинейного интеграла, взятого вдоль дуги МаМ траектории от
точки Ма до точки М:
(М)	Ш)	Ш)
Л= \ Fcosads = \ ~F dr = $ (Xdx + Ydy -\-Zdz). A67)
Если произведение Fcosa выражается известной функцией
дуговой координаты s точки приложения силы, то переменной
интегрирования является эта величина s и формула для вы-
вычисления работы принимает вид
А = ^ Fcos a-ds = l Fzds,	A68)
So	So
где s0 и s — значения дуговой координаты, соответствующие
положениям Ма и М точки приложения силы, Fx — проекция
силы на касательную к траектории этой точки.
Если постоянная по модулю сила образует с прямой, по ко-
которой движется ее точка приложения, постоянный угол а, то
А = Fa cos a.	A69)
В частном случае, когда точка М движется по прямой под
действием постоянной силы F, направленной по той же прямой
в сторону движения или против движения, то соответственно
имеем:
A = + Fa, или A= — Fa,	A70)
где а—путь пройденный точкой.
Если при вращательном движении твердого тела вокруг не-
неподвижной оси момент приложенной к нему силы является
функцией угла ф поворота тела, т. е.
то
ф
Л = 5 тг (F) d<p.
Фо
Аналогично определяется работа пары сил:
<р
А = J тг dq>.
Фо
ЦВ Зчк 2374
A71)
A72)
297

Работа силы, имеющей потенциальную функцию, на конечном
перемещении выражается разностью значений этой функции
в конечной и начальной точках пути:
А = J dU~U-U0,	A73)
т. е. в этом случае работа силы не зависит от кривой, по ко-
которой перемещается точка М, а зависит лишь от начального
и конечного ее положений. При изучении движения материаль-
материальной точки в силовом потенциальном поле весьма большое зна-
значение имеет понятие потенциальной энергии. Потенциальная
энергия материальной точки представляет собой особый вид
энергии, которым обладает точка, находящаяся в силовом по-
потенциальном поле. Потенциальная энергия П равна работе,
которую совершила бы сила поля при перемещении точки ее
приложения из данного положения М (х, у, г) в положение
Мт(х{0), у^"\ z@)), принятое за нулевое, т. е.
n = Uw—U,	A74)
откуда
dn = — dU = — dA.	A75)
Работа силы на конечном пути через потенциальную энергию
выражается так:
А=Пй — П	A76)
Если на точку действует несколько сил, то работа равно-
равнодействующей этих сил на каком-либо пути равна сумме работ
составляющих сил на том же пути.
В технической системе единиц работа измеряется в кило-
килограмм-метрах (кГм). В Международной системе единиц еди-
единицей работы является 1 джоуль =1 н. м. =0,102 кГм.
Мощность N характеризует быстроту, с которой совершается
работа, и в общем случае определяется как производная от
работы по времени*
iV==^ = Fcosa-v = F о,	A77)
т. е. мощность равна скалярному произведению вектора силы
на вектор скорости.
Если работа А производится равномерно, то мощность опре-
определяется так:
4
где t—время, в течение которого произведена работа.
Таким образом, в этом частном случае мощность численно
равна работе, производимой в единицу времени.
298

При вращательном движении твердого тела вокруг непод-
неподвижной оси г:
N=*Mz<s>,	A79)
где Mz = y^mz{F)—главный момент приложенных к телу сил
относительно оси вращения, со—угловая скорость тела.
В технической системе единиц мощность измеряется
в кГм/сек или в лошадиных силах, причем
1 л. с. = 75 кГм\сек
В Международной системе единиц единицей мощности яв-
является
1 em=l дж\сек или 1 кет = 1000 вт =102 кГм1сек.
При решении задач на вычисление работы и мощности часто
используют коэффициент полезного действия. Коэффициентом
полезного действия ц называется отношение полезной работы
или мощности * к работе или мощности движущих сил:
Л =?-?*».	A8°)
Так как вследствие вредных сопротивлений АП ^ Ал, то
¦П<1.
При вычислении работы нужно различать следующие случаи.
1.	Прямолинейное движение под действием постоянной по
модулю и направлению силы, в задачах такого типа приме-
применяются формулы A69) и A70) (задачи 756, 762).
2.	Прямолинейное движение под действием силы, проекция
которой на направление прямолинейной траектории является
функцией расстояния точки от некоторого неподвижного центра
на этой прямой (задача № 768), в задачах этого типа приме-
применяется формула A67), которая, если направить ось х по траек-
траектории точки, принимает вид
х
A = \Xdx.	A81)
3.	Криволинейное движение под действием постоянной по
модулю и направлению силы, в этом случав можно использо-
использовать формулу A67).
4.	Криволинейное движение под действием силы, которая
является функцией координат точки приложения силы.
Здесь определение работы сводится к вычислению криво-
криволинейного интеграла по формуле A67). Если в рассматриваемом
случае существует силовая функция, то работу определяют по
формуле A73) или A76).
* Если мощность вычисляется по формуле A78)
ИВ*	299

5. Вращательное движение твердого тела под действием
постоянного момента или момента, являющегося функцией угла
поворота тела; в этом случае для вычисления работы приме-
применяется формула A71).
Для вычисления мощности в зависимости от характера дви-
движения пользуемся формулой A77) при прямолинейном или криво-
криволинейном движении точки приложения силы (задачи 760, 764),
или формулой A79) — в случае вращательного движения твердого
тела (задачи 771, 772, 765). Среднюю мощность можно опреде-
определять по формуле A78).
Пример 131. Вдоль тяги, при помощи которой тянут вагон-
вагончик по горизонтальному пути, действует постоянная сила
/¦ = 250 н (рис. 172). Тяга образует с горизонтом угол а = 32°.
Определить работу, совершенную силой F на пути а = 200 м.
Решение. Здесь работу определяем по формуле A69):
А = Fa cos a = 250 -200 0,848 = 4240 дж.
Пример 132. Тело весом Р = 20 н передвигают по горизон-
горизонтальному полу при помощи горизонтальной силы на расстояние
о = 6м. Определить работу, ко-
которую совершит при этом сила
трения, если коэффициент тре-
трения между поверхностью тела
и полом f = 0,35.
L
'///////////////////////////////, Решение. Согласно зако-
закону Кулона, сила трения
Рис т	FTp=fN, где N — нормальное
давление тела на поверхность
пола, причем в данном случае N = P = 20 н. Так как сила
трения направлена в сторону, противоположную движению, то
работа этой силы отрицательна:
Лтр = — fPa = — 0,35-20-6 = — 42 дж.
Пример 133. Найти работу силы тяжести при перемещении
материальной точки из положения М0(хл, уа, гв) в положение
М (х, у, г), а также вычислить потенциальную энергию точки
в положении М (рис. 173).
Решение. Направляя ось г вертикально вверх, имеем:
Х = 0; У = 0; Z = — P,
где Р—вес тела. Следовательно, по формуле A62)
&А = — Pdz,
откуда	г
A = -Jpd2 = —РB-го)=аРBо-г).	A82)
300

т. е. работа силы тяжести равна произведению веса материаль-
материальной точки на разность ее высот в начальном и конечном поло-
положениях, причем эти высоты отсчитываются от произвольно
выбранной горизонтальной плоскости.
Потенциальную энергию точки определим на основании фор-
формулы A75):
dI7 = — dA=Pdz.	A83)
Отсюда
где С — произвольная постоянная интегрирования *.
Пример 134. Определить работу силы упругости растянутого
стержня, к концу которого подвешен груз
М, при перемещении этого груза из поло-
положения Мо в положение М, если длина
недеформированного стержня равна /0;
вычислить также потенциальную энергию
точки в положении М (рис. 174).
Решение. Обозначив силу упруго-
упругости F и направив ось х по вертикали
вниз, имеем:
	сх
м
Рис
Рис. 174
где х—удлинение стержня, с—его жесткость.
Следовательно,
dA — Xdx — — сх dx,
X
А= — \ сх dx = — -|- (х3 —xl),
"а
dfl — — dA=cx dx,
отсюда
A84)
A85)
* Обычно потенциальная энергия определяется с точностью до произ-
произвольной постоянной, т. е. в выражении потенциальной энергии произволь-
произвольную постоянную отбрасывают, так как при решении задач приходится
иметь дело или с дифференциалами и ^производными от потенциальной
энергии, или с разностью значений потенциальной энергии для двух по-
положений точки или системы.
301

Пример 135. На материальную точку действует сила, проек-
проекции которой на координатные оси выражаются так:
Определить работу этой силы при перемещении точки из по-
положения Л40A; 2; 3) в положение Л4, B, 3, 4), если сила выра-
выражена в «, а координаты—в -см.
Решение. Выясним прежде всего, существует ли в данном
случае силовая функция: для этого находим частные производ-
производные:
ду -1' дх~~ '• dF~/z' ду ~гг'
f = 0; « 0.
дх дг
Отсюда получаем, что
ду ~ dx ' дг ду ' дх~ дг '
т. е. условия A64) выполняются, и силовая функция сущест-
существует. Полный дифференциал этой функции равен элементарной
работе, т. е. dU — dA. Элементарную работу находим по фор-
формуле dA = Xdx-\-Ydy-\-Zdz или, подставляя значения X, Y, Z:
= 2xdx + ydx + xdy + z2dy + 2yzdz + dz.
Это выражение действительно является полным дифферен-
дифференциалом
dA^d (x*)+d (xy)+d (yz*)+d (z)^
Итак,
dU
Отсюда
Значения функции U в точках Мо и М равны:
?/, = 1 + 1-2 + 2 38 + 3 + С=24
3 + 3
Следовательно, искомая работа равна
А = U,— Ua «= 62—24 = 38 « см.
Пример 136. Определить работу центральной силы, модуль
которой является функцией расстояния материальной точки от
центра этой силы, т. е. F — f(r) (рис. 175).
202

Решение. В данном случае единичный вектор силы Т равен
±~ , причем знак (-f-или —) выбирается в зависимости от того,
отталкивается от центра силы или притягивается к нему точка М.
Таким образом, вектор силы F
выразится так:
формулой
Отсюда, пользуясь
A61), имеем:
Но	~ 7= г\
Следовательно,
г dr = r dr,
fj&rir
откуда
dA
Рис 175
±f(r)dr,
т. е. элементарная работа является полным дифференциалом и,
значит, существует силовая функция, причем
отсюда
Итак, в данном случае имеем общую формулу, по которой сразу
можем определить силовую функцию в зависимости от радиуса-
вектора точки приложения силы, а затем вычислить работу
силы при перемещении этой точки из положения Мо (г0) в поло
жение М (г)-
г
A = U — ?/„ = U (г) — U (г0) — \ ± f (r) dr	A86)
Пример 137. Один конец пружины закреплен шарнирно
в точке О, а к другому концу ее прикреплен шарик Длина
нерастянутой пружины — /0, жесткость ее—с. Шарик переме-
перемещают из положения Л4, в положение М2, причем пружина рас-
растянута и не изгибается. Определить работу силы упругости
пружины, если
OMi = r и ОМг = гг
(рис. 176)
Решение. Модуль силы упругости пружины в данном слу-
случае выражается так"
303

Следовательно, можно воспользоваться формулой A86):
А = -
Знак минус перед интегралом стоит потому, что сила при-
притягивает шарик к центру О.
Пример 138. Колесо радиуса R катится без скольжения по
горизонтальному рельсу. Найти работу трения качения при пе-
перемещении центра колеса на расстояние s, если вертикальная
нагрузка на ось колеса равна Р и коэффициент трения качения
/* (рис. 177).
Рис. 176
Решение. Трение качения возникает, как известно, вслед-
вследствие деформаций колеса и рельса. Момент пары трения каче-
качения по закону Кулона будет равен
Так как эта пара стремится повернуть колесо в направлении,
противоположном его вращению, то работа трения качения будет
отрицательна и равна произведению постоянного момента Мк на
угол поворота ср колеса [по формуле A72)]:
При качении колеса без скольжения имеем: s = Rq>. Следова-
Следовательно,
Пример 139. К валу длиною /, один конец которого закре-
закреплен жестко, приложен на свободном конце крутящий момент,
который заставляет вал испытывать деформацию кручения. Оп-
Определить работу возникающих при этом сил упругости, если
суммарный момент упругих сил пропорционален углу закручи-
закручивания, причем коэффициент пропорциональности (коэффициент
304

жесткости вала на кручение) равен с. Определить также потен-
потенциальную энергию этого вала в зависимости от угла закручи-
закручивания (рис. 178).
Решение. Момент сил упругости выражается формулой
Отсюда, на основании формулы A72), имеем:
dA=dU = — ,
Следовательно,
А =
=—4 (ф2—ф»)-
Для потенциальной энергии имеем:
dlJ — — dU = сер dq>,
а потому
Пример 140. Для определения натяжений S, и S2 ветвей
конвейерной ленты привод А конвейера установлен на катки и
включен динамометр D между приво-
приводом и неподвижной стойкой С.
Определить натяжения St и S2,
если показание динамометра равно Р
(в ньютонах), диаметр приводного ба-
барабана d, потребляемая электродвига-
электродвигателем привода мощность равна N и
^ приводной барабан делает п оборотов
в минуту (рис. 179).
Рис 178
Решение. Рассматривал равновесие действующих на привод
сил и пренебрегая трением между катками и опорной плоско-
плоскостью, имеем:
2
ОТКУДЗ
(a)
Так как привод барабана вращается равномерно, то вращаю-
вращающий момент на валу двигателя, очевидно, определится так:
mav~ ^i 2 * 2 ~^ 1 *' 2 '
305

но на основании формулы A79), мощность двигателя
Отсюда
вр п >
п, следовательно,
? о ЮЛ' 2	_
Решая совместно уравнения (а) и (б), находим:
Пример 141. Найти мощность машины, поднимающей 100 раз
в минуту молот весом Р = 9000н на высоту /г = 0,6 ж, если ко-
коэффициент полезного действия т) = 0,8.
Решение. Находим полезную работу за 1 мин:
Ап = Р-h-100 = 9000-100-0,6 = 540 000 дж.
Теперь по формуле A78) находим полезную мощность:
., Ап 540 000 ОЛЛЛ л
Na = -~ = —gg— = 9000 вт = 9 кет.
Далее, пользуясь формулой A80), определяем искомую мощ-
мощность двигателя:
Классификация задач данного параграфа приведена в табл. 17.
§ 4. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ
Кинетическая энергия материальной точки выражается по-
половиной произведения массы этой точки на квадрат ее скорости.
Теорему о кинетической энергии материальной точки можно
выразить в трех видах:
— )=Fcosads = <L4,	A87)
т. е. дифференциал кинетической энергии материальной точки
равен элементарной работе силы, действующей на эту точку;
оч й {mv*\ 4A .,
2)[)N
т. е. производная по времени от кинетической энергии мате-
материальной точки равна мощности силы, действующей на эту
306

точку;
<Л1)
\ F cos a ds,
A89)
Ш.)
т. е. изменение кинетической энергии материальной точки на
конечном пути МаМ равно работе силы, действующей на точку
на том же пути.
Таблица 17
Классификация задач
Группы
Типы
(прямолинейное дви-
движение)
II
(криволинейное
жение)
дви-
III
(вращательное движе-
движение твердого тела во-
вокруг неподвижной
оси)
1-я
2-я
Действующая сила
постоянна (F=const).
Задачи 756—764,
766
Действующая сила
зависит от положения
точки приложения
силы [F=f{x)].
Задачи 768, 790 (вы-
(вычисление потенциаль-
потенциальной энергии), 769, 784
Действующая сила
постоянна (F •= const)
Действующая сила
зависит от координат
точки приложения
силы ]? = Р~(х,!/, г)).
Задачи 770, 788 (вы-
(вычисление работы)
Вращающий момент
постоянный.
Задачи 755, 765,
767, 771, 772
Вращающий момент
зависит от угла по-
поворота тела
Если на точку действует несколько сил, то в правые частя
уравнений A87)—A89) входит работа или мощность равнодей-
равнодействующей этих сил, которая равна сумме работ или мощностей
всех составляющих сил.
В случае прямолинейного движения точки, направляя ось х
по прямой, по которой движется точка, имеем:
d ??) = xdx
A90)
mv*
2
A91)
где X = ± F, так как в этом случае равнодействующая всех
приложенных к точке сил направлена по оси х.
307

Применяя теорему о кинетической энергии в случае несво-
несвободного движения материальной точки, нужно иметь в виду
следующее: если на точку наложена совершенная стационарная
связь (точка движется по абсолютно гладкой неподвижной по-
поверхности или линии), то реакция связи в уравнения не входит,
лбо эта реакция направлена по нормали к траектории точки и,
следовательно, ее работа равна нулю. Если же приходится учи-
учитывать трение, то в уравнение кинетической энергии войдет ра-
работа или мощность силы трения.
Задачи, относящиеся к этому параграфу, можно разделить
на два основных типа.
I.	Задачи на применение теоремы о кинетической энергии
при прямолинейном движении точки.
II.	Задачи на применение теоремы о кинетической энергии
при криволинейном движении точки.
Кроме того, задачи, относящиеся к типу I, можно разделить
на три группы:
1)	сила, действующая на точку (или равнодействующая не-
нескольких сил), постоянна, т. е. X = const, где X— проекция
силы (или равнодействующей) на ось х, направленную по пря-
прямолинейной траектории точки;
2)	сила, действующая на точку (или равнодействующая), яв-
является функцией расстояния (абсциссы этой точки), т. е.
3) сила, действующая на точку (или равнодействующая),
есть функция скорости этой точки, т. е.
X=f(v).
Задачи, относящиеся к типу II, можно разделить на три
группы:
1)	сила, действующая на точку (или равнодействующая),
постоянна и по модулю и по направлению (например, сила веса);
2)	сила, действующая на точку (или равнодействующая), есть
функция положения этой точки (функция координат точки);
3)	движение точки при наличии сил сопротивления.
Задачи типа I
Первая группа
Точка движется прямолинейно под действием постоянной силы
В этом случае F = const, и уравнение кинетической энергии
принимает вид:
где а—путь, пройденный точкой.
308

Из этого уравнения определяется скорость о, если пройден-
пройденный путь известен, или, наоборот, по заданной скорости v оп-
определяется пройденный путь а.
Пример 142. Вагонетка движется самокатом вниз по наклон-
наклонной плоскости, образующей с горизонтом угол а (рис. 180).
Определить скорость вагонетки в конце пути, длина кото-
которого равна /; начальная скорость вагонетки vo = O, коэффициент
общего сопротивления движению f.
Решение. На вагонетку действуют сила тяжести P = mg,
нормальная реакция N наклонной плоскости и сила сопротив-
сопротивления движению F = fN. Применяя теорему о кинетической
энергии на пути длиной I, имеем:
mo» «»,'_	А.
Лр = mgh = mgl sin a,
Для определения нормального	Рис 180
давления вагонетки на наклонную
плоскость вес вагонетки Р разлагаем на две составляющие,
направленные вдоль наклонной плоскости и перпендикулярно
к ней.
Последняя составляющая и определяет нормальное давление
на плоскость, равное нормальной реакции этой плоскости.
Следовательно, N = mg cos а и AF = — fmgcosal. Таким об-
образом, уравнение кинетической энергии принимает вид:
^	in a—/mgl cos а = mgl (sin а—f cos а),
откуда
v = V 2gl (sin a — f cos a).
Следует заметить, что при решении некоторых задач можно
одновременно применять теорему о кинетической энергии и тео-
теорему о количестве движения. Это относится к задачам, в кото-
которых рассматривается движение под действием постоянной силы
(задачи 678, 775, 776, 779) или силы, зависящей от скорости
(задачи 687, 689, 693, 696), причем требуется определить и
время, и путь движения точки. Для определения времени дви-
движения следует применить теорему о количестве движения, а
при определении пути—теорему кинетической энергии.
Пример 143. Телу весом Р, лежащему на горизонтальной
плоскости, сообщают начальную горизонтальную скорость v0.
309

Во сколько времени и на каком расстоянии остановится тело,
если коэффициент трения тела о плоскость равен /?
Решение. Так как в задаче требуется определить время
движения и расстояние, пройденное телом до остановки, то при
решении этой задачи проще всего воспользоваться и теоремой
о количестве движения, и теоремой о кинетической энергии. Так
как скорость тела в момент остановки равна нулю, то, приме-
применяя теорему о количестве движения, имеем:
—/иио = — FTPt,
откуда
По закону Кулона сила трения Fxv = fN, причем в данном слу-
случае N = P. Следовательно, t = ~.
Далее, применяя теорему о кинетической энергии, имеем:
где о—путь, пройденный телом до остановки. Отсюда находим:
Вторая группа
Точка движется прямолинейно под действием силы,
которая является функцией абсциссы этой точки
В этом случае X — f(x), следовательно, по формуле A91)
имеем:
это уравнение, устанавливающее зависимость между v и х, по-
позволяет найти величину х, если скорость v известна, или, на-
наоборот, зная х, определить и.
Пример 144. Клеть весом Р опускается на канате равно-
равномерно со скоростью v0. Внезапно верхний конец каната защем-
защемляется. Определить наибольшее удлинение каната после аащем-
ления, если его статическое удлинение под действием веса клети
равно ксх (рис. 181).
Решение. На клеть действуют две силы: сила веса Р и
сила упругости каната F = cX, где с—жесткость каната, к —
его удлинение. Пока клеть опускается равномерно, удлинение
каната равно статическому удлинению (А, = Я.СХ) и сила Р урав-
310

новвшивается силой упругости каната, т. е.
откуда
и, следовательно,
С= ;
л.ст
Положение центра тяжести клети в момент защемления каната
выбираем за начало координат и ось х направляем по верти-
вертикали вниз. После защемления каната, благодаря его способно-
способности деформироваться, клеть продолжает опускаться. В момент,
когда удлинение каната достигает максимальной величины, ско-
скорость клети обращается в нуль. Обозначая через X проекцию на
ось х равнодействующей сил, приложенных к клети, и учитывая,
что Я, = А,ст -|- х, имеем:	^,
X PFPk P ^
Применяя теорему о кинетической энергии,
имеем:
Но при х = хта% скорость клети v равна нулю;
поэтому
откуда
Чт ~ ~7 « И ^юах — ''
о-к
Ш
Следовательно,
^тах — К
Третья группа
х
Рис. 181
Точка движется прямолинейно под действием силы,
являющейся функцией скорости этой точки
В этом случае X = f (v) и теорему о кинетической энергии
применяют в дифференциальной форме:
311

Прежде чем интегрировать, здесь нужно разделить перемен-
переменные, что даст:
о
v dv , г\	С v dv
тГпТ • Отсюда: т)
Выполнив интегрирование и решив полученное после этого
уравнение относительно v, находим скорость как некоторую
функцию от х, т. е. v = <D(x). Если в задаче требуется найти
закон прямолинейного движения точки, то, заменяя v на -г. ,
получим:
или, разделяя переменные,
dx
отсюда
х„	о
Это уравнение устанавливает зависимость между х и t, т. е.
дает искомый закон движения материальной точки.
В некоторых случаях, когда действующая на материальную
точку сила зависит от скорости этой точки, закон движения точки
можно найти несколько проще, применяя совместно и теорему
о количестве движения и теорему о кинетической энергии.
Если X = f(v), то, применяя теорему о количестве движения
в дифференциальной форме, имеем*:
W)~dL
Отсюда, интегрируя, получаем уравнение вида:
<p{v) = t —10.	(a)
Применяя затем теорему о кинетической энергии, в диффе-
дифференциальной форме, получим:
mv dv	 ,
Отсюда, интегрируя, имеем:
${v) = x—xt.	(б)
Исключая теперь из уравнений (а) и (б) переменную v, нахо-
* См. § 1 настоящей главы.
312

дим зависимость между координатой х и временем t, т. е. нахо-
находим искомый закон движения.
Пример 145. В момент, когда скорость моторного судна
равна у0, выключается мотор. Сила сопротивления воды опре-
определяется по эмпирической формуле:
где а и р — постоянные.'Масса судна равна т. Найти расстоя-
расстояние, которое пройдет судно с момента выключения мотора до
остановки.
Решение. Направляем ось х в сторону движения судна и
выбираем начало координат в той точке, где находился центр
Тяжести судна в момент выключения мотора. Проекция на ось х
силы сопротивления, приложенной к судну, равна
Так как эта сила является функцией скорости, то применяем
теорему о кинетической энергии в дифференциальной форме:
= X dx = — (а + Ру) о dx.
Разделяя переменные, получим:
mdv 	 ,
	1 5 — CIJC •
а+ $i-
Обозначая о путь, пройденный судном, и учитывая, что в на-
начале этого пути скорость судна равна «0, а в конце обращается
в нуль, имеем:
о
откуда
Пример 146. Материальная точка массы т, получив началь-
начальную скорость у0, движется по горизонтальной, абсолютно глад-
гладкой плоскости, испытывая сопротивление среды, определяемое
формулой R = kmVv, где v—скорость точки. Найти закон дви-
движения точки.
Решение. Рассмотрим решение этой задачи при помощи
совместного применения теоремы о количестве движения и тео-
теоремы о кинетической энергии.
313

Принимая начальное положение точки за начало координат
и направляя ось х в сторону движения точки, находим:
Применяя теорему о количестве движения и теорему о кине-
кинетической энергии в дифференциальной форме, имеем:
d (tnv) — Xdt = — km y~vdt
и
d (Щ-) = Xdx = — km Vv dx,
или, разделяя переменные и сокращая их на т:
—?=¦ = —kdt и Vvdv = — kdx.
интегрируя эти уравнения, находим:
dV'v~ J
Отсюда
" -V^a = -~	(a')
v*-va*=	r.	F')
Чтобы найти зависимость между х и /, достаточно из урав-
уравнений (а') и (б') исключить скорость v. Из уравнения (а') имеем:
Подставляя это значение в уравнение (б'), получаем:
Это уравнение, выражающее х как функцию времени t,
и есть искомый закон движения точки.
Из уравнений (а') и (б') можно также найти время Т, в тече-
течение которого двигалась точка до остановки, и пройденный ею
за это время путь а. Полагая в равенствах (а) и (б) и = 0,
имеем:
2	2-2
314

Задачи типа II
Первая группа
Точка движется криволинейно под действием постоянной силы
Такой постоянной силой является обычно сила тяжести, т. е.
вес Р материальной точки. Поэтому работа силы определяется
по формуле А — — Р (г— г0) при условии, что ось г направлена
по вертикали вверх. Следова-
V
тельно, применяя в этом случае
теорему о кинетической энергии,
получаем уравнение:
Пример 147. Определить для
данного момента высоту h подъ-
подъема тела М, брошенного под уг-
углом а к горизонту с начальной
скороетью и0, если в этот момент
известен угол 0, образуемый скоростью v с горизонтальной
осью абсцисс.
Сопротивлением воздуха пренебречь (рис. 182).	__
Решение. Так как действующая на тело сила тяжести Р
вертикальна, то проекция скорости на горизонтальную ось х
остается постоянной и равной своему начальному значению, т. е.
vx = const == и0 cos a.
Рис. 182
С другой стороны,
о.cos а
и V =——Q-.
cos 8
= t)cos9, поэтому
и0соза= и cos 9.
Применяя теорему о кинетической энергии, в конечной форме
на участке пути ОМ имеем:
Отсюда

cos2 а
" cos2 9
Вторая группа
Точка движется криволинейно под действием силы,
зависящей от положения этой точки
В задачах этой группы теорема о кинетической энергии при-
применяется обычно в случае, когда для сил, действующих на мате-
материальную точку, существует силовая функция. Тогда работа
вычисляется по формуле A73).
315

Следовательно, в этом случае имеем:
-2	r-A = U—Ut.
Пример 148. Материальная частица массы т = 90 г, нахо-
находящаяся в поле силы тяжести, отталкивается от неподвижного
центра О силой, сбратно пропорциональной квадрату расстоя-
расстояния частицы от этого центра (рис. 183). В начальный момент
частица находится в положении М0 (х0 =1 см; уй — 2 см; г0 = 2 см)
и имеет скорость ио = 281/5 см/сек, направленную так, что при
дальнейшем движении частица проходит через точку М1(х1=2 см;
?/, = 4 см; гг = 4 еж).
Ar^*
	у
-У
о:
Рис
Определить скорость частицы в точке Aflt если известно,
что величина отталкивающей силы в момент, когда частица нахо-
находится в положении Мо, равна 0,03 н.
Решение. На частицу действуют две силы: сила тяжести
k
Р = mg и отталкивающая сила F — -^, где г—расстояние ОМ.
Определим коэффициент k. В начальный момент по условию
f f 003	1 J ; + + ;9101 \ С
-10
м
Сле-
Слезадачи t = ta = 0,03 н и r* = r\ = .
довательно, k = f/; = 0,03-9• 10 = 27-10"'.
Применяем теорему о кинетической энергии на участке пути
но на основании формул A82) и A84) имеем:
Ар = — P(z,—20) = — OTgr(z1—г.);
316

следовательно,
кроме того
Отсюда
= Vd = 3 см; r1 = /x;
= 6 см.
. 2-27-10"' @,06 — 0,03) „ п.	л/гГгП ni
+ ¦ 0,09.0,03.0,06 -°'01 И ^ = 1/0,01=0,1
Третья группа
Движение точки при наличии сил сопротивления
Пример 149. Автомобиль весом G, обладающий в положении
Л1, скоростью vt (рис. 184), начинает с этого положения дви-
движение самокатом и в положении М2 приобретает скорость v2,
после чего включается двигатель. Определить суммарную работу
сопротивлений движению автомобиля на участке М,М2, а также
среднюю величину приведенной к центру тяжести автомобиля
силы сопротивления движению. Высоты Ну и Н2 даны.
Рис. 184
Решение. Применяя теорему кинетической энергии в конеч-
конечной форме на участке пути М,М2, имеем:
где Ас—абсолютная величина суммарной работы сопротивлений
движению автомобиля. Отсюда
и	G	г г
С	J J g
317

Среднее значение суммарной силы сопротивления движению на
участке MtM2 определится так:
где s — длина участка М,М2.
Таблица 18
Классификация задач
Типы
i
Прямолинейное
движение точки
II
Криволинейное
движение точки
Группы задач
1 я
Постоянная си-
сила (задачи 773,
774, 777—781,
805)
Постоянная си-
сила (задача 783)
2-я
Сила, завися-
зависящая от положения
точки (задачи 699,
785—787, 793—
796)
Сила, завися-
зависящая от положения
точки (задача 788)
3-я
Сила, завися-
зависящая от скорости
(задачи 687, 689,
693, 695, 696, 782)
Движение точки
при наличии сил
сопротивления
§ 5. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
Векторное дифференциальное уравнение движения несвобод-
несвободной точки имеет вид
где F — действующая на точку заданная (активная) сила,
N—реакция связей (рис. 185).
Это уравнение можно переписать так:
F + N + (— mw) = 0.	A92)
Последний член уравнения A92) представляет собой некото-
некоторую силу, по модулю равную произведению массы т точки на
ее ускорение w и направленную
противоположно этому ускоре-
ускорению. Эта сила называется си-
силой инерции и обозначается
F(H\ т. е.
Рис 185
Рис 186
318

Пользуясь этим обозначением, уравнение A92) можно пред-
представить в следующем виде:
7m = 0,	A94)
т. е. заданная сила, действующая на материальную точку, реак-
реакция связей и сила инерции для каждого момента движения урав-
уравновешиваются (принцип Даламбера).
Таким образом, силу инерции можно определить так же, как
такую силу, которая, будучи приложена к материальной точке,
уравновешивает все заданные силы, приложенные к этой точке,
и реакции связей.
Проекции силы инерции на координатные оси на основании
равенства A94) выражаются следующим образом:
Р(У = — тх, F(aJ = — my, F{V = — mz	A95)
При криволинейном движении материальной точки сила инер-
инерции слагается из двух составляющих, из которых одна направ-
направлена по касательной к траектории, а другая — по главной нор-
нормали (рис. 186). Первая составляющая называется касательной,
или тангенциальной, силой инерции и обозначается Fiux\ вторая
составляющая называется нормальной силой инерции, или цент-
центробежной силой, и обозначается Р{„\ причем
F\ = — mw^\ F<^> = —mt?)(").	A96)
Для модулей тангенциальной и нормальной сил инерции
имеем следующие выражения:
i ль., i dv
dt
A97)
Если точка совершает вращательное движение по окружно-
окружности радиуса R с угловой скоростью <л и угловым ускорением е,
то модули тангенциальной и нормальной сил инерции выразятся
следующим образом:
\Fw\ = mR\b\, |7=w| = m?co2	A98)
Тангенциальная и нормальная силы инерции направлены
соответственно противоположно тангенциальному и нормальному
ускорениям точки.
Задачи, относящиеся к этому параграфу, можно разделить
на следующих три типа:
I.	Материальная точка движется прямолинейно.
II.	Материальная точка совершает криволинейное равномер-
равномерное движение.
III.	Материальная точка совершает неравномерное криволи-
криволинейное движение.
319

Задачи типа I
Прямолинейное движение несвободной материальной точки
(задачи 637—640, 647, 648, 649)
В этом случае радиус кривизны траектории q = oo и, следо-
следовательно, /^п^ —= 0, поэтому сила инерции состоит из одной
тангенциальной составляющей, т. е. ЯН| = F^x\
Пример 150. Тело весом Р движется прямолинейно с данным
ускорением w по горизонтальной плоскости под действием неко-
некоторой силы F, образующей с
горизонтом угол а. Определить
модуль этой силы, если коэф-
коэффициент трения между передви-
передвигаемым телом и плоскостью ра-
равен f (рис. 187).
Решение. На рис. 187 по-
показаны действующие на тело
силы: вес Р, сила ~F, нормаль-
нормальная реакция пола N и сила тре-
трения FTp. Если приложить к те-
телу силу инерции /Г(И), направ-
ленную_противоположно уско-
ускорению ш, то располагая коор-
координатные оси, как указано на рисунке, будем иметь два урав-
уравнения равновесия:
2 X = F cos а—fN — F1H> = 0,
2 Y = F sin a—P+N = 0,
p
причем FlH) = mw~— w.
Решая совместно эти уравнения, находим:
г
1 тр
У
р
Рис 1R7
,	г
cos a + f sin а g (cos а -f / sin а)
Задачи типа И
Равномерное криволинейное даижение несвободной материальной точки
(задачи 646, 670)
Если материальная точка движется по некоторой кривой
с постоянной по модулю скоростью (и = const), то тангенциаль-
ное ускорение, точки равно шт = -^ = 0, поэтому сила инерции
состоит из одной только нормальной составляющей, т. в.
320

Пример 151. Полый полушар радиусом R = 2 м равномерно
вращается вокруг своей вертикально расположенной оси сим-
симметрии, делая 30 об[мин. Внутри полушара находится шарик
весом Р = 2 н. Найти высо-
высоту h, соответствующую поло-
положению равновесия шарика от-
относительно полушара и реак-
реакцию полушара N в этом по-
положении (рис. 188).
Решение. Три силы —
вес шарика Р, но_рмальная
реакция полушара N и сила
инерции Fm— уравновешива-
уравновешиваются. Располагая координат-
координатные оси, как указано на ри-
рисунке, и обозначая а угол,
образуемый реакцией N с го-
горизонтом, составляем уравне-
уравнения равновесия:	Рис
^X = Fm—Ncosa^0; ^Y = N sina—P = 0.
Учитывая, что при равномерном вращении полушара Fw =
= /^и) = m AM®2 = mR cos аи2, эти уравнения можно переписать
так:
N cos a — mR cosaco2, JVsina = P.
Из первого уравнения находим:
б
НО
Следовательно,
со = 5q- = я 1 /сек.
Р	2
= — Rn* — ^-^ • 2 • 9,86 ;w 4 н.
Из второго уравнения находим:
.1	р __Я1	е.
9,81
' 2.9,86 ~ 2 '
откуда a = 30°. Далее из треугольника СМ А имеем:
С A — R sin a = 1 м,
и, следовательно,
ОД ОССА = 2—1 = 1 м.
Пример 152. Лента ленточного конвейера наклонена к гори-
горизонту под углом а. Определить минимальную скорость ленты,
12 Зак. 2374
321

при которой несомая лентой частица руды отделяется от поверх-
поверхности ленты в месте набегания ленты на барабан, если радиус
барабана равен R (рис. 189).
Решение. На частицу, находящуюся в данный момент
в точке набегания ленты на барабан, действуют: вес Р, нор-
нормальная реакция барабана
N и сила трения FTp. При-
Прикладываем к частице нор-
нормальную силу инерции F*"'
и составляем уравнение рав-
равновесия полученной после
этого системы сил, проекти-
проектируя эти силы на ось у, на-
направленную по нормали к по-
поверхности ленты:
2 Y =f („и) + N—P cos a=0,
Рис
но
Ри2
= Pcosa	-
8"
=-?-, поэтому /v =
Частица от-
деляется от поверхности
ленты в месте набегания ленты
на барабан, если N = 0. Поэтому минимальная скорость, при ко-
которой происходит отделение частицы от ленты, определяется из
уравнения:
откуда
Задачи типа III
Неравномерное криволинейное движение несвободной материальной точки
(задачи 802, 803, 816—820, 822)
В этом случае при решении задач по принципу Даламбера
к движущейся материальной точке необходимо прикладывать
две силы инерции: тангенциальную F{f и нормальную F{V.
Уравнения равновесия лучше составлять так, чтобы в каждое
уравнение входила только одна из этих сил инерции, для чего
координатные оси следует направлять по касательной и главной
нормали к траектории движущейся точки.
В выражение нормальной силы инерции входит величина vz;
если скорость v в данной задаче неизвестна, то в большинстве
ЗЙ2

случаев для ее нахождения проще всего применить теорему
кинетической энергии материальной точки.
Пример 153. Математический маятник длиной / и весом Р
отвели на угол ф0 от положения равновесия и сообщили ему
начальную скорость v0, направленную перпендикулярно к нити
вверх. Найти натяжение нити маятника в зависимости от угла
Ф нити с вертикалью (рис. 190).
Решение. Четыре силы — вес маятника Р, реакция нити N,
касательная и нормальная силы инерции F1?' и FiaJ, согласно
принципу Даламбера, уравновешиваются. Поэтому, проектируя
эти силы на нормаль траек-
траектории маятника (на направ-
направление радиуса МО), получим
W-Pcoscp—/^> =
Так как
г-(и)	тм	тиг
п ~1> ~Т'
\>
iN
тиг
то из этого уравнения нахо-
находим
/ ^т
т-Рг
-1.Д
Рис

-<
V
i X
190
\MjZ
р
Ч
\ Fm
Чтобы найти скорость v маятника, применим на участке пути
М0М теорему о кинетической энергии:
Ч^-Ч^-А	РА
о	о — Р —' ^^
uo — 2Ph
(——2h) и,
Отсюда
Но А==/со8ф0 — / cos ф = / (cos ф0 — совф), а поэтому
следовательно,
N = Р (з cos ф—2 cos ф„ + ^ .
Пример 154. Материальная частица находится внутри неподвиж-
неподвижного цилиндра радиусом R. В начальный момент частица находится
в положении /Ио и получает вертикальную скорость у0. Коэф-
Коэффициент трения частицы о поверхность цилиндра равен f. Пре-
Пренебрегая действием силы тяжести, найти зависимость между
скоростью v частицы и углом а, определяющим ее положение
внутри цилиндра (рис. 191).
12»
323

Решение. На частицу действуют: нормальная реакция
цилиндра N и сила трения Frp. Применяя принцип Даламбера,
прикладываем к частице тангенциальную F^ и нормальную F(n'
I	силы инерции. Приравнивая
нулю сумму проекций этих
сил на нормаль, получим:
¦fr.M	ИЛИ
Рис 191
Согласно закону Кулона,
р —fM — tilEl
Далее применяем теорему о кинетической энергии в диффе-
дифференциальной форме:
ид"
2
Отсюда, учитывая, что ds = Rda, имеем: tnvdv — — ~/i?du или
dv
Интегрируем
или 1n^- = —/a,
откуда
ДИНАМИКА СИСТЕМЫ
Глава IV
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ СИСТЕМЫ
§ 1. ТЕОРЕМЫ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ СИСТЕМЫ
И О ДВИЖЕНИИ ЦЕНТРА МАСС
Количеством движения системы называется геометрическая
сумма количеств движения всех материальных точек этой
системы, т. е.
K-^mv,	A99)
324

где К—количество движения системы; отсюда получаем проек-
проекции количества движения на координатные оси:
B00)
dz V4
37 = 2jm3-
Теорема о количестве движения системы формулируется так.
Векторная производная по времени от количества движения
системы равна главному вектору всех внешних сил, приложенных
к этой системе, т. е. .-^	__
rl! = №)_y№]	B011
dt	^^ '	^ '
отсюда следует, что производная по времени от проекции коли
чества движения системы на данную неподвижную ось равна про
ёкции главного вектора внешних сил на ту же ось, т. е.
dKx	 г,{е)
ЧГ~Кх z
(е) _ V
y — 2*
M _ V
г - l
B02)
Центром масс системы называется геометрическая точка С,
координаты которой определяются по формулам:
М
м
B03)
где М—масса данной системы, причем М = "?т; х, у, z — коор-
координаты материальных точек этой системы. Из формул 203) сле-
следует, что положения центра масс и центра тяжести твердого
тела сонпадают.
Если данная система состоит из нескольких, например, из
трех тел, то, обозначая массы этих тел Мг, Мг, Л1,, а их центры
масс (центры тяжести) С,, С2, С,, имеем:
а+луСз
М
Ус-
A1,2C,
М
B04)
32а

Если предположить, что в центре масс сосредоточена вся
масса системы, то количество движения системы будет равно
количеству движения ее центра масс (центра тяжести). Следо-
Следовательно, обозначая через vc скорость центра масс системы,
имеем
K=Mvc,	B05)
отсюда:
Kx = Mvc^MxcA
B05')
Учитывая, что ускорение центра масс С равно wc = -~-, из
равенств B01) и B05) имеем
Mwc = R^ = ^F{e),	B06)
отсюда
Mxr = Rie) = ^X^, )
B06')
Уравнения B06') представляют собой дифференциальные
уравнения движения центра масс системы и выражают следую-
следующую теорему о движении этого центра: центр масс системы
движется так же, как материальная точка, в которой сосредо-
сосредоточена масса всей системы и к которой приложены все внешние
силы, действующие на эту систему.
Следствие. Если главный вектор внешних сил или его
проекция на данную неподвижную ось равны нулю, то количество
движения системы или его проекция на эту ось остаются неиз-
неизменными, т. е.
1)	если /r» = 2J?<e) = °>
то	_
/( = 2 mv = Mvc = const;	B07)
2)	если /^' = 2*<е)=0.
то
Kx = 2jmvx = MvCx = const.	B07')
Задачи, относящиеся к этому параграфу, можно разделить
на следующие три основных типа:
I.	Задачи на вычисление количества движения системы (за-
(задачи 966—969).
II.	Задачи, в которых осуществляется сохранение количе-
количества движения системы или его проекции на данную неподвиж-
326

ную ось, т. е. применяются равенства B07) или B07') (Задачи
951—957, 970-974)
III. Задачи на применение теоремы о количестве движения
системы или о движении центра масс к определению реакций
связей (задачи 958—963, 975—980).
Задачи типа I
Задачи этого типа можно решать двумя способами: либо при
помощи формул A99) и B00), либо при помощи формул B05) и B06).
Пример 155. В механизме, изо-
изображенном на рис. 192, кривошип
ОО,= г весом Рх вращается в вер-
вертикальной плоскости вокруг не-
неподвижной оси О с постоянной
угловой скоростью (л и приводит
в движение колесо / радиусом г
и весом Р, которое катится без
скольжения по неподвижному ко-
колесу // радиусом 2г. Центр тяже-
тяжести колеса / находится в точке
О,. Прямолинейный стержень АВ
весом Р2, соединенный шарниром
А с колесом /, движется посту-
поступательно в вертикальных направ-
направляющих.
Найти проекции количества
движения этой системы на коор-
координатные оси х я у (рис. 192).
Решение. Первый способ.
Данная система состоит из трех
тел: кривошипа 00,, подвижного
колеса / и стержня АВ. Поэто-
Поэтому К = К1 + Кг + К„, где /(,, Кг, К, — количества движения
кривошипа, колеса / и стержня АВ.
На основании формулы B05), применяемой к каждому из
этих тел в отдельности имеем
К=^о +-2у + — о
	S	S
где vOt, vCt, vc^—соответственно скорости точек О,, С, (центра
тяжести кривошипа) и С2 (центра тяжести стержня)
Так как точки 0, и С, принадлежат кривошипу вращающе-
вращающемуся вокруг оси О, то векторы vCi и vOi перпендикулярны
к ООг и по модулю равны:
Рис 192
"с, = г" ш
vOi=rw.
327

Так как стержень АВ движется поступательно, то vc^ — vA,
причем вектор vA направлен по АВ.
Чтобы найти скорость точки А, принадлежащей колесу /,
заметим, что мгновенный центр вращения этого колеса нахо-
находится в точке С касания колес / и //.
Следовательно,
va	АС 	2r sin q>	,, .
где ф = и^ — угол поворота кривошипа;
отсюда
vA = 2vOi sin ф = 2rco sin (at).
Теперь из равенства (а) находим искомые проекции количе-
количества движения данной системы:
f "с, sin ф + у vOl sin ф +12 vA = ~i • j со sin at +
+ — ra sin at + —2 ra sin at = m 'in Ш (P, + 2P + 4P2).
ь	б	б
Второй способ. На основании формул B04) имеем:
yCi+yCt + yOi,
где М — масса всей данной системы, состоящей из трех тел;
С—центр масс этой системы.
Из рис. 192 находим:
хСх = — OCt sin ф = — ^ sin at, xC2 = О,
^С)== — ОС, cos ф= —у cosu)i\ г/Са = ЛС2 — О А = 1—2rcosat,
где
I — ЛС2 = const,
xOi — —00', sin ф = —г sin @^,
«/Oi = —ООЛ СОЭф= — Г
Следовательно,
328

= — —' • — coscd/	г
б	5
Отсюда на основании формул B05') получаем:
Задачи типа И
К задачам второго типа относятся задачи, в которых сумма
проекций всех внешних сил на данную неподвижную ось, на-
например, на ось к, равна нулю. В этом случае (см. равен-
равенство 207') имеем
Кх = 2 mvx — const.
Следовательно, если обозначим Ко количество движения системы
в начальный момент (при ^ —0), то КХ = КОХ или
^mvx = ^mvax.	B08)
Если в начальный момент система неподвижна, т. е. началь-
начальные скорости всех ее точек равны нулю, то в этом случае
/СОх = 0 и, следовательно,
%тих = 0.	B09)
Так как K.x — MvCx (см. равенства 205'), то при Кх — const
имеем:
Если в начальный момент скорость центра масс системы
равна нулю, то (vcJ<=o = O и, следовательно, Vcx = 0 илн -^г—0'>
отсюда
хс — const — xca>	B10)
т. е. абсцисса центра масс системы в рассматриваемом случае
постоянна.
Задачи второго типа можно решать двумя способами:
1)	на основании равенств B08) и B09);
2)	с применением равенства B10).
Пример 156. Определить перемещение плавучего крана, под-
поднимающего груз весом Р, =¦ 20 кн, при повороте стрелы крана
на 30° до вертикального положения. Вес крана Р2 = 200км,
длина стрелы ОА — 8 м. Сопротивлением воды пренебречь
(рис. 193).
12В Зак. Я374	аа9

Решение. Первый способ. В данной задаче имеем систему,
состоящую из двух тел: плавучего крана и груза; внешними
силами, приложенными к этой системе, являются вес крана Р2>
вес груза Р, и вертикальное давле-
давление воды, направленное снизу вверх
(архимедова сила). Гак как все эти
внешние силы вертикальны, то сум-
сумма их проекций на горизонтальную
ось х равна нулю.
Кроме того, в начальный момент
система неподвижна, поэтому, при-
применяя равенство B09), получим
й
193
1Х !Х р
абсолютных скоростей груза и пла-
плавучего крана.
Заменяя vJX и игх на
dxx dx2
if И
it
где х, и х,—соответственно
абсциссы груза и центра тяжести крана, получим:
или, интегрируя,
P,a:, 4 Ptxt = const = Р,л:0] + Ргхог,
где х0) и *„,, — абсциссы груза и центра тяжести крана в началь-
начальный момент, причем, как видно из рисунка,
хо1=— О A sin 30°=— 4.
В момент, когда стрела займет вертикальное положение,
абсцисса л:,, груза будет равна перемещению s крана; следова-
следовательно, в этот момент имеем
или
Так
как
то
откуда находим
-ух= -0,36 ж.
Знак минус указывает на то, что кран переместился влево.
Второй способ. Применяя равенС1во B10), имеем
хс — const,
330

где хс — абсцисса центра масс (центра тяжести) данной сисгемы
(груза и крана).
Но
поэтому
^ const.
Таким образом, мы имеем то же уравнение, которое полу-
получили выше, при первом способе решения задачи. Из этого урав-
уравнения так же, как при	yv
первом способе решения,
лаходим искомое переме-
перемещение крана.
Пример 157. На гори-
горизонтальной платформе ве-
весом Р, установлена на-
наклонная плоскость АВ,
образующая с горизон-
горизонтом угол а (рис. 194). По
этой наклонной плоско-
плоскости при помощи лебедки
поднимается груз С весом
Рис. 194
Я2 так, что расстояние АС изменяется по закону s=^~at\
В начальный момент вся система находится в покое
Определить скорость, с которой будет двигаться платформа;
сопротивлением движению платформы пренебрегаем
Решение. Первый способ. В данной задаче мы имеем си-
систему, состоящую из двух тел: платформы и груза С; внешними
силами, приложенными к этой системе, являются вес плат-
платформы Рг1 вес груза Ps и нормальные реакции N. и Ж рельсон
в точках D и Е. Так как все эти силы вертикальны, то сумма
v у?Р°елЦИИ На г°Ризонтальную ось х равна нулю, т. е,
2jA =u; поэтому, учитывая, что в начальный момент система
неподвижна, и применяя равенство B09), как в предыдущей за-
даче, получим	v Ауш,*п
где vlx и vix — проекции на ось л: скоростей платформы и груза
Если поступательное движение платформы принять за пере-
переносное движение, то относительным движением груза будет его
перемещение по наклонной плоскости АВ. Следовательно" вектор
vr относительной скорости груза направлен параллельно АВ и
по модулю равен
i'.'B"
331

Вектор ve переносной скорости груза равен скорости плат-
платформы у1( параллельной оси х, поэтому
По теореме сложения скоростей имеем: vex= vex+ ^r» — vt -\-at cosa.
Поэтому равенство (а) перепишется так:
Отсюда находим
р
vi~ —р -iV g/cos a-
Знак минус указывает на то, что платформа будет перемещаться
влево.
Второй способ. Абсцисса центра масс данной системы равна
где х, и д:2 — абсциссы центров тяжести платформы и груза.
Следовательно, на основании равенства B10) имеем
Р\х\~^ ^Л = const
Но, как видно из рисунка, хг = хх —1-\ scosa, а потому
P,xt + P% (xx — l-\ s cos a) = const.
Дифференцируя это равенство по /, получим:
п dx, . п /их, ds
или
отсюда
dx,
Задачи типа III
Задачи типа III, в которых требуется определить реакции
связей, также можно решать двумя способами:
1)	по теореме о количестве движения системы [по уравне-
уравнениям B02)],
2)	по теореме о движении центра масс [по уравнениям B06')].
Пример 158. Мотор, вес которого равен Р, прикреплен
к фундаменту болтами.
Вес ротора мотора равен Ptl а его центр тяжести С2 смещен
относительно оси вращения на расстояние ОС2 = е. Ротор вра-
вращается по закону ф = -х-. Определить вертикальное давление
мотора на фундамент и горизонтальное усилие, приходящиеся
332

на все болты, в момент (— 1 сек
(рис. 195).
Решение. Первый способ.
В данной задаче мы имеем си-
систему, состоящую из двух тел:
корпуса мотора и ротора.
Внешними силами, прило-
приложенными к этой системе, явля-
являются вес мотора, вес ротора,
реакции в болтах.
Обозначим вертикальные ре-
реакции в точках А ч В через
Yab YB, а горизонтальные ре-
реакции обозначим ХА и Хв.
Если количества движения
мотора и ротора обозначим Кх
и /Са, то количество движения
данной системы будет K = KlJr
+ Кг. Так как мотор неподвижен, то /Сг = 0 и, следовательно,
Количество движения ротора находим по формуле B05)
J
1
%
я
рЧ
77.
(Со
ч /
////////
pt у
V///////
Уа
В
¦Л
X*
.лв
77/
Рис 195
—	~ Р —
где v2—скорость точки С2. Следовательно, K=-rVt. Отсюда
находим проекции количества движения данной системы на
координатные оси: Kx = ~vix, K.y = ~vly.
Применяя теперь теорему о количестве движения системы
[уравнения B02)], получим
dt
dt
или
g dt
(a)
Скорость центра тяжести С2 ротора перпендикулярна к ра-
радиусу ОСг и по модулю равна v% = 0С,ш = е<а, где a — -^- = nt —
угловая скорость ротора.
Следовательно, v2x= v2 cos cp = eco cos ф; vty = — иг sin q> =
= —е» sin <p.
Поэтому уравнения (а) принимают вид:
g
eP, fdiu
-ю sin ф
333

В момент ^=1 сек имеем:
Ф = ^- = ~, sin ф = 1, с
поэтому в этот момент
-л
= я;
Таким образом, полное вертикальное давление на фундамент
р
в момент t—\ сек равно Р, -\- Р2 — ел —, а общзе горизонтальное
еР
усилие, приходящееся на все болты, равно —2зх .
Второй способ. Применяя теорему о движении центра масс
системы [уравнения B06')], имеем
где хс и ус—координаты центра тяжести данной системы, со-
состоящей из корпуса мотора с центром тяжести в точке О и из
ротора с центром тяжести в точке С2. По формулам B04)
находим:
Но xa — y0 =
а потому
Отсюда
= OCS sin ф = е sin qp.
г/с2 = ОС2 cos ф = е cos ф,
р
Мхс= —esin ф, Мус =
Мхс — -^
л^	Р.
Муг= — -2
334

Следовательно,
Мы получили, таким образом, те же уравнения, как и при
первом способе решения. Из этих уравнений так же как ука-
указано выше, получим тот же результат.
§ 2. ТЕОРЕМА О КИНЕТИЧЕСКОМ МОМЕНТЕ СИСТЕМЫ
Главный момент количеств движения всех материальных то-
точек системы относительно данного центра или данной оси назы-
называется кинетическим моментом системы относительно этого
центра или этой оси.
Следовательно, обозначая кинетический момент системы отно-
относительно точки О (начала координат) Lo, а кинетические моменты
системы относительно координатных осей Lx, Lv, Lz, имеем:
L0 = 2m0(mv),	B11)
Lx = 2m, (my) = 2 (ymvz — zmv ) — 2m (yz - zy),
Lz = 2тг (mv) = 2 (xmvv—ymvx) = 2m (xy—yx).
Теорема о кинетическом моменте системы состоит з сле-
следующем:
производная по времени от кинетического момента системы
относительно данного неподвижного центра или данной неподвиж-
неподвижной оси равна главному моменту всех внешних сил, приложенных
к этой системе относительно того же центра или той же
оси, т. е.
= 2mo(Fw).	B13)
dt x	x\i>
B14)
dLz
dt
Следствие. Если главный момент всех внешних сил отно-
относительно неподвижного центра О или данной неподвижной оси г
равен нулю, то кинетический момент системы относительно
этого центра или этой оси остается неизменным, т. е.
1)	если М^=0, то Lo = const,	B15)
2)	если Afi" = O, то Lg = const,	B16)
335

При поступательном движении твердого тела его кине-
кинетический момент относительно любой оси z равен моменту отно-
относительно той же оси количества движения центра масс этого
тела в предположении, что в этом центре сосредоточена вся
масса М тела, т. е.
Lt = mt(Mvc).	B17)
Если твердое тело вращается вокруг оси г с угловой ско-
скоростью со, то его кинетический момент относительно этой оси
равен произведению момента .инерции этого тела относительно
оси вращения на угловую скорость, т. е.
Lt = J,ta.	B18)
При этом моментом инерции тела относительно данной оси г
называется сумма произведений массы каждой элементарной
частицы тела на квадрат ее расстояния до этой оси, т. е.
,/г = 2тЛ	B19)
где т — масса элементарной частицы, а г —ее расстояние до сси г.
Если твердое тело движется параллельно данной неподвиж-
неподвижной плоскости, то его кинетический момент относительно любой
оси г, перпендикулярной к этой плоскости, равен моменту от-
относительно оси г количества движения центра масс С этого
тела в предположении, что в этом центре сосредоточена вся
масса М тела плюс кинетический момент тела относительно
оси Cz' в его вращательном движении, вокруг этой оси, причем
ось Cz' проходит через центр масс тела и параллельна оси г,
т. ,е.
Lz = m,(Mvc) + Jct'«>,	B20)
гед
Jo,,' — момент инерции тела относительно оси Cz',
со—алгебраическое значение угловой скорости тела (поло-
(положительное, если тело вращается вокруг оси Cz' против часовой
стрелки, и отрицательное в противном случае).
Из равенств B14) и B18) получаем дифференциальное урав-
уравнение вращательного движения твердого тела вокруг неподвиж-
неподвижной оси г:
J,% = Zmt(F%	B21)
где jr=8 — угловое ускорение тела.
Задачи, относящиеся к этому параграфу, можно разделить
на следующие пять основных типов:
I.	Задачи на вычисление кинетического момента системы.
II.	Задачи, в которых осуществляется сохранение кинети-
кинетического момента системы относительно неподвижного центра
336

или неподвижной оси, т. е. используются равенства B15) или
B16).
III. Задачи, относящиеся к вращению твердого тела вокруг
неподвижной оси.
IV Задачи, относящиеся к крутильным колебаниям.
V. Задачи на определение гироскопических реакций в слу-
случае гироскопа с двумя степенями свободы.
Задачи типа I
Задачи этого типа можно решать при помощи общих формул
B11) или B12).
Кинетический момент твердого тела следует вычислять в зави-
зависимости от вида движения тела по формулам B17), B18) или B20).
Пример 159. Механизм
эллипсографа состоит из ползу-
ползунов А и В весом Р каждый,
кривошипа ОС весом Р и ли-
линейки АВ весом 2Р. Кривошип
ОС вращается вокруг неподвиж-
неподвижной оси Ог, перпендикулярной
к плоскости чертежа, с угловой
скоростью ю.
Найти кинетический момент
этой системы относительно оси
Oz, рассматривая линейку АВ и
кривошип ОС как однородные
тонкие стержни, а ползуны А и
Б — как материальные точки
если ОС=ЛС = СВ=/(рис. 196).
Решение. Первый спо-
способ. Данный механизм состо-
состоит из четырех тел: кривошипа
ОС, линейки АВ и ползунов
Л и В, а потому искомый
Рис
кинетический момент равен
где L%\ L[i]', ?.?", L^4)—соответственно кинетические моменты
кривошипа, линейки и ползунов А и В относительно оси г.
Кинетический момент кривошипа ОС находим по формуле B18):
где Д" — момент инерции кривошипа относительно оси г, рав-
ный ^ = ||-;
следовательно
337

Так как скорости ползунов А к Б направлены соответственнб
вдоль осей Ох и Оу и, следовательно, пересекают ось Ог, то
l<9) = z44 =o.
Чтобы вычислить кинетический момент L{'} линейки, приме-
применим последнюю из формул B12).
Разобьем стержень А В на бесконечно малые элементы (мате-
(материальные частицы); массу такого элемента обозначим т, а его
координаты обозначим х и у. Тогда
х = B/—s)coscp; y — ssmcp,
где s—расстояние рассматриваемого элемента от точки В. От-
Отсюда
х— —B1—s) sin ф>ф = —B1—s) sin ф-to; y — s coscp-co.
Следовательно, момент количества движения элемента относи-
относительно оси 2 будет
m2(mv) — m(xy—ух)— m[Bl — s)scocos2(p4- B1—s) son sin29] =
= mB/ — s)sro;
а поэтому LBS) = 2m(xy—yx) — ZtnBl — s) sot = m B/2ms—I>mss),
np
но Urns — Mssc~—- lt a l>ms"~момент инерции стержня АВ отно-
относительно точки В, равный М4-^-=я—Г. Следовательно,
Таким образом, искомый кинетический момент механизма
будет
Второй способ. Так как движение стержня АВ является
плоскопараллельньш, то его кинетический момент относительно
оси г можно найти проще, применяя формулу B20),
где ic2> — момент инерции стержня АВ относительно оси, прохо-
проходящей чергз его центр тяжести С и перпендикулярной к пло-
плоскости хОу (относительно точки. С),
со, — угловая скорость вращения стержня вокруг эгой оси
(вокруг точки С).
Следовательно,
Jc =M.-12-- — -
Так как стержень АВ вращается вокруг точки С по часовой
стрелке, го со1=— -^=— со. Так как точка С принадлежит и
338

кривошипу ОС, то ее скорость vc перпендикулярна к ОС и
ус = /(о, поэтому inz{Mtvc) = М2/2ш. Следовательно,
Задачи типа II
К задачам типа II, как было указано выше, относятся такие
задачи, в которых сумма моментов всех внешних сил, дейст-
действующих на систему относительно данной неподвижной оси, напри-
например оси z, равна нулю. В этом случае (см. равенство 216) имеем
L2 — 2 tnz (mv) = const.
Следовательно, если обозначим L{0) кинетический момент системы
относительно оси г в начальный момент при ^ = 0, то в рас-
рассматриваемом случае имеем
Lz = Ll0), или 2тЛт°) =2тг(тио)-	B22)
Если в начальный момент система неподвижна, то начальные ско-
скорости всех ее точек равны нулю, следовательно, L*0) = 0, и
в этом случае	f _vi «,„;*_, 0.	B22')
При решении задач второго типа нужно- составить уравне-
уравнение B22) или уравнение B22') и определить из него ту вели-
величину, которую требуется найти в данной за
даче.
Пример 160. На поверхности круглого
однородного цилиндра радиусом г и массы М,
который может вращаться без трения вокруг
неподвижной вертикальной оси z, имеется ка
нал в форме винтовой линии; в этом канале Т~
находится шарик (материальная точка) массой | т?
т. В некоторый момент, когда система не
подвижна, шарик начинает двигаться по винто
вой линии под действием силы тяжести, а ци
линдр начинает при этом вращаться вокруг
оси z в противоположном направлении. На
какой угол повернется цилиндр за то время, в
течение которого шарик опустится на расстоя-
расстояние, равное шагу h винтовой линии (рис. 197).
Решение. Внешними силами для данной
системы, состоящей из цилиндра и шарика,
являются их веса и реакции закрепленных .то-
.точек, через которые проходит ось вращения рИс. 197
339

цилиндра z. Так как моменты этих сил относительно оси г
равны нулю и в начальный момент система неподвижна, то
применяется уравнение B22'), т. е. Lz — 0, где Lz—кинетиче-
Lz—кинетический момент данной системы относительно оси г. Этим уравне-
уравнением и воспользуемся для решения задачи.
Кинетический момент вращающегося цилиндра относительно
оси вращения г равен iza —	?- со, где со— угловая скорость
цилиндра (знак минус берем потому, что цилиндр вращается по
часовой стрелке, если смотреть с положительного конца оси г).
Если относительную скорость шарика, направленную по
касательной к винтовой линии, обозначим vr, а постоянный
угол скорости с осью г—через у, то горизонтальная составля-
составляющая относительной скорости, направленная по касательной
к цилиндру, по модулю будет равна vr siny- Переносная ско-
скорость ve шарика (скорость во' вращательном движении вокруг
оси г) направлена противоположно горизонтальной составляю-
составляющей относительной скорости и по модулю равна га. Поэтому
горизонтальная составляющая абсолютной скорости шарика равна
vr sin у—га,
а момент количества движения шарика относительно оси г равен
m(vr sin у—га) г,
следовательно,
Lz =	g—\-mr {vrs\ny — ra)\
так как ?г = 0, то
2—\-m(vr sin Y—rco)r = 0
или
(-Y + m) ra —mvr sin у.	(а)
Если угол поворота цилиндра обозначим ср, то
проекция vz абсолютной скорости шарика на ось г, очевидно,
равна —L^cosy, а потому
3 Y = — tg Y з? ¦
Следовательно уравнение (а) принимает вид
340

или
-f tri j rd(f = — tntgyaz.
Интегрируя это уравнение и принимая во внимание, что
в начальный момент ф„ = 0 и го = О, получим
.-f-т \ гц> = — mtgy г.
Полагая по условию задачи г = — h, находим искомый угол
поворота цилиндра
mtgyh
Ф
Так как между углом наклона у винтовой линии и ее шагом
п имеется зависимость tg у = -т— , то (f = -n
Если, например, /И=6/п, то цилиндр повернется на 90°.
Задачи типа III
В зависимости от внешних сил, приложенных к вращающе-
вращающемуся твердому телу, задачи типа III можно разделить на три
группы.
1.	Главный момент приложенных к телу сил относительно
оси вращения есть величина постоянная.
2.	Главный момент приложенных к телу сил относительно
оси вращения зависит от угловой скорости тела. Этот случай
возможен при вращении тела в сопротивляющейся среде.
3.	Главный момент приложенных к телу сил относительно
оси вращения есть функция угла ф поворота тела, как, напри-
например, это бывает в случае движения физического маятника.
Первая группа
Для решения этих задач нужно составить и затем проинтег-
проинтегрировать дифференциальное уравнение вращательного движения
твердого тела [уравнение B21)].
Пример 161. Сплошной цилиндр радиусом г, положенный,
как указано .на рис. 198, на цилиндрические ролики А и В,
вращается с угловой скоростью (о0 вокруг своей горизонтальной
оси О. В некоторый момент ролики затормаживаются. Через
сколько времени после этого цилиндр остановится, если коэф-
коэффициент трения между цилиндром и роликами равен /, а
А АО В =-2а.
341

Решение. Внешними силами, приложенными к вращаю-
вращающемуся цилиндру, являются его вес Р, нормальные реакции
Nt и N2 роликов и силы трения F, и F2 между цилиндром и
роликами, причем F1 =fNx и F2 =/<V2.
Так как моменты сил Р, Nx и Ns
относительно оси вращения О ци-
цилиндра равны нулю, то главный
момент внешних сил относитель-
относительно этой оси /Ио = — F/— F/ =
х — — fr (JV, + Nt), поэтому дифферен-
дифференциальное уравнение вращательного
движения цилиндра имеет вид
Рис 198
Найдем теперь силы Nl и N2;
для этого, применяя теорему о дви-
движении центра масс системы, составим
дифференциальные уравнения дви-
движения центра тяжести О цилиндра:
>= — р + (^i + Л'2)cos a—F*sin а+Fisin а>
) = N\ sin а — Nz sin а—F% cos а — Fl cos а.
Так как точка О неподвижна, то хс — ус = 0, а потому
(Л/, — Л'2) sin a-
(N,+N,)cosai !(N1—N2)sma = P.
Исключая из этих уравнений разность Nt— Nit получим
Л т i A 7	¦*
и, следовательно,
A+И cos a
A+/») cos а ¦
P r2
Но для цилиндра •/„ — -у, а потому
da
гг
/2) г cos a
Интегрируя это уравнение, находим
— const.
- ш°~ (l+Hrcosa
Так как в момент остановки цилиндра
время равно
A + Г) г cos acoo
= 0, то искомое
342

Вторая группа
При интегрировании дифференциального уравнения враща-
вращательного движения твердого тела в этих задачах нужно приме-
применить способ разделения переменных.
Пример 162. Для быстрого торможения больших маховиков
применяется электрический тормоз, состоящий из двух полюсов,
расположенных диаметрально противоположно и несущих на
себе обмотку, питаемую постоянным током. Токи Фуко, инду-
индуцируемые в массе маховика, при его движении около полюсов
создают тормозящий момент М,, пропорциональный скорости v
на ободе маховика: Ml = kv, где k — коэффициент, зависящий
от магнитного потока и размеров маховика. Момент /И2 от
трения в подшипниках можно считать постоянным: радиус ма-
маховика г; момент инерции его относительно оси вращения J.
Найти, через какой промежуток времени остановится маховик,
вращающийся с угловой скоростью ш0.
Решение. Главный момент внешних сил, приложенных
к маховику относительно его оси вращения, равен
М = — (М, + Mt) = — (Ь -f Mt),
поэтому, составляя для маховика уравнение B21),
имеем
или, заменяя v на га,
Разделяя здесь переменные, получим
Jdai
¦= -dt.
Отсюда, интегрируя, находим
J
kr
или
\n{Mt+kri?>)
= —- t
Третья группа
В этих задачах главный момент внешних сил, приложенных
к вращающемуся твердому телу, является функцией угла пово-
поворота ф этого тела, т. е. /И = /(ф) Если в уравнении B21) угло-
bj'uj скорость ш заменить производной ^7 = '+', то это уравнение

принимает вид:
При решении задач третьей группы нужно проинтегрировать
это уравнение.
Пример 163. Однородный круглый диск радиуса т совершает
колебания вокруг неподвижной горизонтальной оси, перпенди-
перпендикулярной к плоскости диска и проходя-
проходящей через точку О, причем расстояние от
точки О до центра тяжести С диска
равно -j .
Найти закон движения диска при ма-
малых колебаниях, а также период этих
колебаний. В начальный момент угол <р
отклонения диска or равновесного поло-
положения равен ср0, а его начальная угло-
угловая скорость равна нулю фис. 199).
Решение. В данной задаче диск
является физическим маятником. Если вес
маятника обозначим Р, а расстояние
ОС обозначим а, то ша (Р) = —aPsincp;
а поэтому дифференциальное уравнение вращательного движе-
движения маятника имеет вид
Уоф = — аР sincp.
При малых колебаниях можно положить sin ср»ф. Тогда
получим дифференциальное уравнение малых колебаний маят-
маятника
Рис 199
или
где
ф'
Мы получили дифференциальное уравнение гармонических
колебаний; его общее решение имеет вид: ф = С, sin (kt) +
-fC8cos(&/) Отсюда <.f = kC1cos(kt) — kCts\nkt.
Так как в начальный момент по. условию задачи ф = ф^
ф = 0, то из этих уравнений, полагая в них ?=0, находим
С? = Ф0, С,=0. Следовательно,
ф = ф0 COSkt.
Это уравнение выражает искомый закон движения маятника
при малых колебаниях. Период этих колебаний равен
344

В данной задаче а = ~ ; момент инерции диска находим по
теореме о моментах инерции относительно параллельных осей:
Поэтому
Сравнивая последнюю из этих формул с периодом колебаний
математического маятника Т = 2п 1/ —, где /—длина нити ма-
6
ятника, видим, что приведенная длина рассматриваемого физи-
физического маятника равна
lr
Задачи типа IV
Задачи этого типа, относящиеся к крутильным колебаниям,
можно разделить на три группы:
1)	свободные крутильные колебания;
2)	затухающие крутильные колебания;
3)	вынужденные крутильные колебания.
При решении всех этих задач следует составить дифферен-
дифференциальное уравнение вращательного движения твердого тела
[уравнение B21)] и затем это уравнение проинтегрировать.
Первая группа
В задачах этой группы приложенный к телу момент про-
пропорционален углу ф, определяющему положение вращающегося
тела, и имеет противоположный знак, т. е. М = — сер, где
с—коэффициент пропорциональности. Следовательно, уравнение
B21) принимает вид
или
Ф+62Ф = 0,
где &г = у; это есть дифференциальное уравнение гармонических
колебаний, решение которого рассмотрено в главе П. По
формулам A27) и A30) находим
-Trsin (fit)
345

или
Период этих гармонических колебаний равен
Вторая группа
В задачах этой группы к вращающемуся телу, кроме мо-
момента М = — сер, приложен еще момент сопротивления, пропор-
пропорциональный угловой скорости тела, т. е. момент М1 = — щр,
где ц— коэффициент пропорциональности.
Поэтому уравнение B21) принимает вид:
J'f = —Сф— Цф
или
или ф -f 2пф + ?2ф = 0, где 2л = у и k" = ~. Мы получили диф-
дифференциальное уравнение затухающих колебаний (при k>n),
решение которого находим по формулам A32) и A33):
Ф=ш?-И' sin ()/V — я2 t )
или
sm\-jjV*Uс—цг t-\-а \.
Период этих затухающих колебаний [см. формулу A34)]:
Т 2я	4л,/
Постоянные а и а определяются по начальным условиям
движения тела (по начальному углу ф0 и начальной угловой
скорости ф0).
Третья группа
В этих задачах, кроме моментов М = —сф и Mt = —цр,
к вращающемуся телу приложен момент М,, выражающийся
периодической функцией времени, т. е. изменяющейся со вре-
временем, например по гармоническому закону (по закону синуса
или косинуса).
34Ь

Если Мг = Н sin (pt), где Я и р — постоянные величины, то
уравнение B21) имеет вид
Уф -f (a f + сф = Я sin (/?/)>
или
ф 4 2пц> + ?2ф = /г sin
где
Здесь мы имеем дифференциальное уравнение 2-го порядка
с правой частью, отличной от нуля. Интегрирование такого
уравнения рассмотрено в § 3 главы II; его общее решение
имеет вид
y = ae-nt sin (//г2—rf t A a) +6 sin (pt f 0),
или
^sin (pt-i P).
Второй член в правой части этого равенства выражает вынуж-
вынужденные крутильные колебания. Амплитуда h и начальная фаза р
этих вынужденных колебаний, согласно сказанному в § 3 главы II,
определяются по формулам:
fc	h	H
н
Л ~-г
Постоянные а и а определяются по начальным условиям
вращательного движения тела.
При p = fe=l/y, т. е. при равенстве частот свободных
гармонических и вынужденных колебаний, имеем явление резо-
резонанса. Амплитуда вынужденных колебаний в этом случае будет
Р«з цр [ife ц
При отсутствии момента сопротивления нужно в уравнениях
и формулах третьей группы задач положить ц = п = 0. Тогда
дифференциальное уравнение крутильных колебаний имеет вид:
) = Н sin (pt), а его общее решение
Ф —asin (fe^4"a)+^sin (pt),
347

или
I -. f с. . \
• sin
<p = asin ( у у t + a )
Амплитуда вынужденных крутильных колебаний будет опре-
деляться по формуле Ь =	г1.
/Т •
При р = у у, т. е. в случае резонанса при отсутствии
сопротивлений общее решение предыдущего дифференциального
уравнения (закон вращательного движения тела) имеет вид
= а sin {kt -\-a) — ^j- t cos(kt),
или
Постоянные а и а определяются, как и в предыдущем случае
(при наличии сопротивления), по начальным условиям движе-
движения тела.
Пример 164. Для определения коэффициента вязкости жидко-
жидкости наблюдают колебания диска, подвешенного на упругой вер-
вертикальной проволоке в жидкости. К диску приложен перемен-
переменный момент, равный М' sin (pt)(M' = const), при котором
наблюдается явление резонанса. Момент сопротивления движению
диска в жидкости равен \x'Sa>, где \i' — коэффициент вязкости
жидкости, S—сумма площадей верхнего и нижнего оснований
диска, со—его угловая скорость.
Определить коэффициент вязкости жидкости \i', если ампли-
амплитуда вынужденных колебаний диска при резонансе равна ср'.
Решение. К диску, вращающемуся вокруг вертикальной
оси, приложен момент М упругих сил, возникающий при закру-
закручивании проволоки на угол ф и пропорциональный этому углу,
момент сопротивления жидкости M,==n'Sco и переменный момент
Мг = М' sin (pt).
Поэтому в данном случае имеем:
Так как по условию задачи при данной частоте р наблю-
наблюдается резонанс, причем амплитуда вынужденных крутильных
колебаний диска равна ф', то по вышеуказанной формуле
^е3 = ~ находим ф' = ^, откуда ц' = ^-
Задачи типа V
Представим себе движущееся твердое тело, одна точка О
которого закреплена неподвижно, например при помощи сфери-
сферического шарнира (рис. 200). Как известно из кинематики, в каж-
548

дый данный момент такое тело вращается вокруг некоторой
определенной мгновенной оси, проходящей через неподвижную
точку О. Вектор мгновенной угловой скорости тела, направ-
направленный по мгновенной оси
вращения, обозначим ю, а
его проекции на коорди-
координатные оси, начало кото-
которых находится в точке О,
обозначим ах, со , сог. Най-
Найдем кинетический момент
этого тела относительно
оси х. Разбивая тело на
Рис 200
элементарные частицы и применяя формулы B12), имеем
Lx = ^mx(mv) = Xtn(yvz—zVy),
где т— масса элементарной частицы, у и г —ее координаты, а
Vy, vz— проекции скорости частицы на оси у и г.
Проекции на координатные оси скорости v точки вращаю-
вращающегося твердого тела определяются по кинематическим формулам
Эйлера *:
Следовательно,
Lx — 2 т (юл#2"
или
Lx =
- - Jx/oy
где Jx — 2 tn (у2 + z2) — момент инерции тела относительно оси х,
Jxy — ^tnxy и JXit = '2im.xz — центробежные моменты инерции
тела.
* Вывод этих формул можно найти, например, в курсе теоретической
механики проф. И М. Воронцова.
349

Если координатные оси х, у, г направим по главным осям инер-
инерции данного тела в точке О, то Jxy = JX!. — Ot а потому в этом
случае LX = JX<?>X.
Аналогично найдем, что при этом условии кинетические
моменты тела относительно осей у и z будут равны
Предположим теперь, что твердое тело, имеющее форму тела
вращения вокруг оси АВ, например колесо или тор, равно-
равномерно вращается вокруг этой оси АВ с угловой скоростью ш^,
в то же время эта горизонтальная ось А В вращается равно-
равномерно вокруг неподвижной вертикальной оси с угловой ско-
скоростью со2. Требуется определить реакции в подшипниках А и В,
перпендикулярные к оси АВ, если вес тела равен Р и АС = 11,
СВ — 1г, y4B = Zj-f lt — l, причем С — центр тяжести данного тела
(рис. 201, а и б). Такое тело представляет собой гироскоп
с двумя степенями свободы.	_
Вращение вокруг оси АВ с угловой скоростью сох называется
собственным вращением гироскопа, а вращение с угловой ско-
скоростью ю2 вокруг оси г называется прецессионным вращением,
или прецессией гироскопа. Неподвижную точку пересечения
осей вращения примем за начало координат О и направим
координатные оси, как указано на рис. 201, а. Горизонтальные
реакции подшипников А и В, параллельные оси х, обозначим
ХА и Кв: вертикальные статические реакции подшипников,
обусловленные только весом Р гироскопа, обозначим Та и Zb,
• PI ' Р
причем очевидно ZA = -f и ZB = -rli, а динамические вертикаль-
вертикальные реакции обозначим Za и Zb-
Найдем кинетический момент Lo гироскопа относительно
неподвижной точки О. Сложив векторы и, и о, получим абсо-
абсолютную мгновенную угловую скорость гироскопа Q [см. равен-
равенство A07)]. Так как гироскоп есть тело вращения вокруг оси г/,
то эта ось и две перпендикулярные к ней оси х и z являются
главными осями инерции гироскопа в точке О, а потому, как
было указано выше, кинетические моменты гироскопа относи-
относительно этих осей равны
или, так как Qx = 0, Qy = coi; йг = <о2, то LX =
Учитывая, что Lx, Ly, Lz являются проекциями вектора Lo на
координатные оси, по найденным проекциям строим вектор
О^ = ГО (рис. 201,6).
350

Применяя теперь теорему о кинетическом моменте системы
относительно неподвижной точки О (см. уравнение 213), имеем
Так как производная -~ есть скорость vK точки К,
то
vK=W.	B23)
Это равенство выражает теорему Резаля, т. е. скорость,
с которой перемещается конец вектора, изображающего кинети-
кинетический момент системы относительно неподвижной точки О,
равна главному моменту внешних сил, действующих на эту
систему, относительно той же точки.
Так как L= const и Lz — const, то вектор OK, описывает
круглый конус, вращаясь вокруг оси г с угловой скоростью
о)г. Отсюда следует, что вращательная скорость vK точки К
направлена параллельно оси х, как показано на рис. 201 б и
по модулю равна
Применяя затем теорему о движении центра тяжести системы
(см. уравнение 206), имеем
где R(e)—главный вектор внешних сил, которыми в данной
задаче являются вес Р и искомые реакции подшипников А и В.
Проектируя это векторное равенство и равенство B23) на оси х
и г и учитывая, что силы Р, ZA и Z'B взаимно уравновешива-
уравновешиваются, получим четыре уравнения:
2)
3)	vKx = M& = -ZAA0- fB0B,
4)	ort=M$ = XAAO—XBOB.
Так как скорость vK параллельна оси х, а центростреми-
центростремительное ускорение точки С направлено по оси у (от С к О),
то vKx — — JyCOjOOj, vKz = 0, wCx=wC!l = 0. Поэтому предыдущие
уравнения принимают вид
Из этих уравнений находим:
ЛА~ ЛВ~- и> ^А=^В——j	¦
331

Так как динамические реакции Z"A и Z"B равны по модулю
и направлены противоположно, то они образуют пару с момен-
моментом, равным УуО^ю.,, называемым гироскопическим моментом.
Следовательно, обозначая этот момент Л1Г, имеем
Л!г = ./,,©,©,.	B24)
Эта пара лежит в плоскости, в которой расположены век-
векторы го, и со2. Учитывая направления векторов vK, ш, и ш3, по-
получаем векторное равенство:
^	ш	B24')
Возникновение реакций Za и Zb> а также гироскопического
момента, обусловленное изменением направления оси АВ соб-
собственного вращения гироскопа, называется гироскопиче-
гироскопическим эффе ктом.
Пример 165. Турбина, вал которой параллелен продольной
оси судна, делает 300 оборотов в минуту: вес вращающихся
частей равен 200 кн, а их радиус инерции относительно оси вра-
вращения турбины равен 1,5 м. Определить гироскопические дав-
давления на подшипники, расстояние между которыми 1=6 м,
если судно поворачивается вокруг вертикальной оси на 15°
в сек.
Решение. Обозначая угловую скорость вращения судна
вокруг вертикальной оси г через сог, а угловую скорость вра-
вращения турбины вокруг горизонтальной оси у через со,, имеем:
л 300 1Г1 . ,	2я 13 л , ,
<»1 — —отг — Ю л \jceK, И2==~збб" =12 *-1сек-
По формуле B24) находим гироскопический момент
но
где Р — вес вращающихся частей турбины и гин — их радиус инер-
,. Р а	200 000 о ос 10 2 O7Cmn
ции; поэтому Мс — — г„н«Iсо2 = —g-g—• 2,25 • ^л =375000« м.
Искомые гироскопические давления образуют пару сил, ле-
лежащую в вертикальной плоскости, причем момент этой пары
равен Мт, а ее плечо равно /, следовательно, вертикальное гироско-
гироскопическое давление на каждый подшипник равно
Л!, = 375000 = 6
{	6
Пример 166. С концом вертикального вала ОО1 шарнирно
соединен горизонтальный стержень ОС, на который свободно
насажен массивный цилиндрический каток (бегун). При враще-
352

нии вала OOt вокруг вертикальной оси г бегун катится без
скольжения по горизонтальной плоскости, на которую закла-
закладывается измельчаемый материал (рис. 202, а и б). Определить
гироскопические реакции в точках О а А, а также усилие в
стержне ОС, если заданы вес 6eryEia Р, длина ОС — 1, радиус
бегуна R и угловая скорость вала to = const.
Решение. Обозначим угловую скорость собственного вра-
вращения бегуна вокруг оси ОС через со,. Так как качение бегуна
по горизонтальной плоскости происходит без скольжения, то
скорость точки А равна нулю; поэтому мгновенная ось враще-
вращения бегуна проходит через точки О и Л, а его абсолютная
угловая скорость п направлена по прямой О А, причем Q =
Построив параллелограмм угловых скоростей, из подобных
треугольников ОАС и Оас имеем:
ш AC R	Iй)
~~~ОС~~Т' 0ТКУда ^i^^W '
Теперь по формуле B24) нахо- 70
дим гироскопический момент
Рассматривая бегун как однород- ю
ный цилиндр, имеем
, PR*
Jy~ 2g
и, следовательно,
.. PR' . I PRaH
Гироскопические реакции Zo и ZA в точках О и А образуют
пару сил, момент которой равен Мг и направлен, согласно фор-
формуле B24'), по оси х, как указано на рис. 202, а. Отсюда сле-
следует, что, во-первых, силы ZA и Zo имеют направления, ука-
указанные на рис. 202, а, и, во-вторых,
Таким образом, полно,е давление бегуна на горизонтальную
плоскость в точке А равно сумме двух сил: веса Р и гироско-
гироскопического давления, равного ZA, т. е.
Центростремительное ускорение центра тяжести С бегуна
направлено вдоль оси у от С к О и по модулю равно wc = lat'.
Поэтому, применяя теорему о движении центра тяжести системы,
13 J<ik. 2374

354

получим:
где Уо — реакция в точке О по направлению оси у.
Отсюда
Растягивающее усилие в стержне ОС, очевидно, равно этой
реакции Yа.
§ 3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
Кинетической энергией, или живой силой системы, называется
сумма живых сил всех материальных точек этой системы, т. е.
Г-Е2?.	B25)
где Т — кинетическая энергия системы, пг и v—масса и скорость
материальной точки, принадлежащей данной системе.
Теорему об изменении кинетической энергии системы можно
выразить в трех видах:
1) dT — ^dA,	B26)
т. е. дифференциал кинетической энергии системы равен сумме
элементарных работ всех внешних и внутренних сил, действую-
действующих на эту систему,
2) Ж = ЕЛ/-	B27)
т. е. производная по времени от кинетической энергии системы
равна мощности всех внешних и внутренних сил, действующих
на эту систему;
3) Т-Т^^А,	B28)
т. е-, при перемещении системы из одного положения в другое,
изменение ее кинетической энергии равно сумме работ на этом
перемещении всех внешних и внутренних сил, действующих на
эту систему.
Равенство B26) выражает теорему об изменении кинетической
энергии системы в дифференциальной форме, а равенство B28) —
ту же теорему в конечной форме. Равенство B27) выражает
теорему о зависимости между кинетической энергией системы и
мощностью действующих на систему сил. Следует иметь в виду,
что только в случае, когда имеется неизменяемая система (абсо-
(абсолютно твердое тело), сумма работ всех внутренних сил на лобом
перемещении системы равна нулю.
13*	865

Поэтому в общем случае при применении теоремы об изменении
кинетической энергии системы внутренние силы учитываются.
В случае стационарных связей без трения реакции таких
связей не производят работы (сумма работ реакций при пере-
перемещении сис1емы равна нулю). Поэтому в этом случае реак-
реакции связей не входят ни в одно из равенств B26) — B28).
При вычислении работы и мощности сил, действующих на
данную систему, следуе1 пользоваться формулами и указани-
указаниями, приведенными в § 3 главы III.
Задачи, относящиеся к этому параграфу, можно разделить
на следующие два основные типа:
I. Задачи на вычисление кинетической энергии системы.
П. Задачи на применение теоремы об изменении кинетиче-
кинетической энергии системы, состоящей из одного тела или из несколь-
нескольких гел.
Задачи типа 1
При решении задач этого типа необходимо иметь в виду
следующее:
а)	если тело, принадлежащее данной системе, движется по-
поступательно то его кинетическая энергия равна
Т = М^,	B29)
где М—масса тела, vc — скорость его центра тяжести (или любой
другой его точки, так как при поступательном движении тела
скорости всех его точек равны);
б)	если тело вращается вокруг данной оси, то его кинети-
кинетическая энергия вычисляется по формуле
T = J~,	B30)
где J—момент инерции тела относительно оси вращения,
со—его угловая скорость;
в)	если тело, входящее в систему, совершает плоскопарал-
плоскопараллельное движение, то в этом случае его кинетическая энергия
вычисляется по формуле
T^M^ + JC^,	B31)
где М—масса тела, vc—скорость центра тяжести тела, со—его
угловая скорость, Jc—моменг инерции тела относительно оси,
проходящей через центр тяжести тела и перпендикулярной к
неподвижной плоскости, параллельно которой перемещается это
тело (задачи 1045, 1046).
356

Пример 167. Вычислить кинетическую энергию механизма
эллипсографа, состоящего из кривошипа ОС весом Р, вращаю-
вращающегося вокруг неподвижной оси О с угловой скоростью со и
приводящего в движение линейку
АВ с ползунами А и В, причем
Вес линейки 2Р, а веса пол-
ползунов А а В равны Qt = Q2 = Q
(рис. 203).
Решение. Так как данная
система состоит из четырех тел,
то ее кинетическая энергия, со-
гласно формуле B25), равна
Рис 203
где Т,— кинетическая энергия
кривошипа, Тг— кинетическая
энергия линейки АВ, Т3 и 7\—соответственно кинетическая
энергия ползунов А и В.
Кинетическую энергию кривошипа находим по формуле B30)
Так как движение линейки АВ является плоскопараллель-
плоскопараллельным, то по формуле B31) имеем:
где
op V%	СО*
T?l	Li 1 Т	1
, , 2PB0f
Чтобы найти угловую скорость «в, линейки, построим ее
мгновенный центр вращения Ои тогда
to
и, следовательно,
ли
2=
4 P/V
Теперь находим скорости точек Л и S:
857

Отсюда по формуле B29) имеем:
Q vi
и, следовательно,
Таким образом,
^g ^ 3,g	g 2g
Пример 168. Планетарный механизм приводится в движение
кривошипом О А, соединяющим оси трех зубчатых колес /, //
и ///. Колесо /, радиус кото-
которого равен rlt неподвижно;
кривошип вращается вокруг не-
неподвижной оси О с угловой ско-
скоростью со. Вес каждого из ко-
колес // и /// равен Р, радиус
каждого из них г, вес криво-
кривошипа Q.
Вычислить кинетическую
энергию механизма, считая ко-
колеса однородными дисками, а
кривошип—однородным тонким
стержнем, если г, = 2г (рис.204),
энергия данной системы равна
Рис 204
Решение. Кинетическая
где 71,, Т„ Та—соответственно кинетическая энергия кривошипа
и колес // и ///. По формуле B30) находим:
Г _-/pf>2_Q QA*tf 25Q . .
1 2 J 3 2~6grM>
6g
Кинетическую энергию колес // и /// вычисляем по фор-
формуле B31):
т =^
2 8 2
1 8 2
где 7Я и JA—моменты инерции колес II и III относительно
осей, проходящих через точки В и А и перпендикулярных к
358

плоскости рисунка, со2 и со,—абсолютные угловые скорости этих
колес.
Так тсак точки А и В принадлежат кривошипу, то
vA — OA о> = 5 гю и vR = OB со — 3 ret».
Кроме того, 1а = 21г* и /я = 2^Л
Так как колесо / неподвижно, то скорость точки С, принад-
принадлежащей колесу //, равна нулю, т. е. точка С является для
колеса // мгновенным центром вращения. Отсюда следует, что
vB = СВ со2 = гсо2 и «, = -^ = — = 3@.
По теореме сложения угловых скоростей в случае паралле-
параллельных осей вращения относительная угловая скорость (по ог-
ношению к кривошипу) колеса II будет равна
©J = сй2—со = Зсо—со = 2со.
Так как колеса // и III имеют равные радиусы и находятся
во внешнем зацеплении, то их относительные угловые скорости
равны по величине и противоположны по знаку, т. е.
(о3 = —и2 = —2со.
Потому по той же теореме абсолютная угловая скорость
колеса /// равна
caa = <й3 -j- <й =• —<а.
Следовательно,
Задачи типа II
Задачи этого типа можно разделить на следующие три группы:
1. Задачи, решаемые при помощи уравнения B28), т. е. на
основании теоремы об изменении кинетической энергии в конеч-
конечной форме.
Уравнение B28) следует применять в тех случаях, когда
действующие на систему заданные сипы или постоянны (и по мо-
модулю, и по направлению), или для них существует силовая
359

функция, а в числе известных и искомых в задаче механических
величин имеются, кроме этих сил, только скорости (линейные
или угловые) и перемещения (поступательные или угловые) тел,
входящих в данную систему
2.	Задачи, решаемые при помощи уравнения B26), т. е. на
основании теоремы об изменении кинетической энергии в диффе-
дифференциальной форме.
Уравнение B26) следует применять в тех случаях, когда
заданные переменные силы (или сила), действующие на систему,
зависят от скорости, а известные и искомые в задаче механи-
механические величины те же, что и в предыдущем случае.
В этом случае при интегрировании уравнения B26) сначала
нужно разделить переменные.
3.	Задачи, решаемые при помощи уравнения B27), т. е. на
основании теоремы о зависимости между кинетической энергией
системы и мощностью действующих на систему сил. Уравнение
B27) следует применять в тех случаях, когда требуется найти
(либо, наоборот, задано) ускорение тела — линейное (при посту-
поступательном движении тела) или угловое (при вращательном дви-
движении).
Первая группа
Пример 169. Груз А весом Р, подвешен к однородному не-
нерастяжимому канату длиной L и весом Q.
Канат переброшен через блок В, вращающийся вокруг оси О,
перпендикулярной к плоскости рисунка. Второй конец каната
прикреплен к оси катка С, катя-
катящегося без скольжения по непо-
неподвижной горизонтальной плоско-
"г сти. Блок В и каток С— одно-
J родные круглые цилиндры радиу-
радиусом г и весом Рг каждый. Коэф-
Коэффициент трения качения катка С
о горизонтальную плоскость ра-
равен fk. В начальный момент, когда
система находилась в покое, с
блока В свешивалась часть кана-
каната длиной /. Определить скорость
груза А в зависимости от его
вертикального перемещения h
(рис. 205).
Решение. Так как в данной задаче известными величинами
являются перемещение h груза и постоянные силы Р1( Рг Q,
а требуется найти скорость v груза, то следует воспользоваться
уравнением B28), выражающим теорему об изменении кинети-
360
Рис. 205

ческой энергии в конечной форме:
Кинетическая энергия данной системы равна
где 7\, Г2, Г,, Tt—соответственно кинетическая энергия груза
А, блока В, катка С и каната. Так как скорость любой точки
каната равна скорости v груза, движущегося поступательно, то
по формуле B29) находим:
т -L*vl т -Я.*
1 g 2 ' 4 g 2 '
Кинетическую энергию вращающегося блока находим по
формуле B30):
(угловая скорость блока); следовательно,
1 . = —г— •
2
Так как движение катка С является плоскопараллельным,
то по формуле B31) имеем:
1 •" g 2 ^JC 2 •
Р гг
где Jc=-k— , и,—угловая скорость катка.
Так как каток катится без скольжения, то скорость точки
касания его с неподвижной плоскостью равна нулю, т. е. эта
точка является мгновенным центром вращения катка.
Отсюда следует, что ис = га1, поэтому
Таким образом,
В начальный момент система находилась в покое, поэтому
Г0 = 0.
Перейдем теперь к вычислению суммы работ всех сил, при-
приложенных к данной системе при перемещении груза А на рас-
расстояние А.
Работа_ силы Р„ очевидно, будет Al = Plh. Работа каждой
из сил Ра равна нулю, так как точка О неподвижна, а точка
13В—1 Зак. 2374	361

С перемещается по горизонтали. Момент пары трения качения
равен }кРг, а работа сил этой пары, согласно § 3 гл. III, будет
равна произведению момента пары на угол ср поворота катка,
взятому со знаком минус, так как направление момента пары
трения качения противоположно направлению угловой скорости
катка; следовательно,
Так как угловая скорость катка о^ равна угловой скорости
со блока В, то угол поворота <р катка равен углу поворота
,	h
блока, т. е. ф = —, поэтому
При качении катка без скольжения, работа силы
трения скольжения F^ будет равна нулю, поскольку равна
нулю скорость точки приложения этой силы.
Так как, согласно § 3 гл. III, работа силы тяжести равна
произведению веса тела на вертикальное перемещение его центра
тяжести, то, сравнивая начальное положение C^EDA^ каната с
его конечным положением CEDA, нетрудно видеть, что работа
Л2 веса каната равна произведению веса его части CaC=^h,
равного -у- /г, на разность высот центров тяжести этой части
С0С и части каната А0А, т. е. на г+1 + -^. Поэтому
¦«.-I
Таким образом,
Подставляя найденные значения суммы работ и кинетической
энергии Т в уравнение B28), находим:
Отсюда находим искомую скорость груза:
V —

Вторая группа
Пример 170 Прямоугольная пластинка ABCD со сторонами
а и b и весом Р вращается вокруг вертикальной оси г с началь-
начальной угловой скоростью ю0. Каждый элемент пластинки испыты-
испытывает при этом сопротивление воздуха, направление которого
перпендикулярно к плоскости пластинки, а величина прямо
пропорциональна площади элемента и квадрату его скорости и;
коэффициент пропорциональносги равен \и. Сколько оборотов
сделает пластинка до того момента, когда ее угловая скорость
станет вдвое меньше начальной (рис. 206)?
Решение. Так как силы сопротивле-
сопротивления, приложенные к пластинке, завися! от
скорости, то для решения задачи следует
воспользоваться уравнением B26)
Так как пластинка вращается вокруг
неподвижной оси, то ее кинетическую энер-
энергию находим по формуле B30):
Г = / -д-, откуда dT = Jz (о da>.
dx
Рис 206
Работа силы тяжести Р, очевидно, равна
нулю, так как высота центра тяжести пластинки не изменяется.
Чтобы вычислить работу сил сопротивления, воспользуемся
формулой для определения работы сил, приложенных к враща-
вращающемуся твердому телу (см. главу III, § 3):
где Mz—сумма моментов всех приложенных к телу сил отно-
относительно оси вращения, йф— элементарный угол поворота тела.
Чтобы вычислить Мг, разобьем пластинку на элементарные
прямоугольники со сторонами b и dx.
Тогда сила сопротивления, приложенная к такому прямо-
прямоугольнику, равна
dF = fxo* bdx — \ab (<ах)г dx
и
tnz (dF) — —xdF = —fxibcoV dx;
следовательно,
a
Mx = '^lmz(dF), т.е. Мг= — fi&u)8] x' dx = — ^цЬа*со2 и ^fiA =
0
= — -r-ц ba*(x>'d(p.
13B—2 Зак. 2374	363

Таким образом, уравнение B26) принимает вид
J za>da = —т- [I ba* a*dq>,
или
JzdQ = —j-ц ba* <odtp.
Разделяя здесь переменные, получим:
отсюда, интегрируя, имеем:
-v или J^Xnb%
С00
откуда находим угол поворота пластинки:
_4JZ In 2
Применяя вышеуказанную разбивку пластинки ABCD на
элементарные прямоугольники, момент инерции Jz пластинки
представим в виде:
/2>!
где /и — масса элементарного (заштрихованного) прямоугольника.
Если массу пластинки обозначим М, то масса, приходящаяся
м
на единицу площади, будет -^, а потому
m = -г fo rfx — — dx
ab	a
3g
Разделив этот угол ср на 2я, получим искомое число оборо-
2Р 1п2
тов пластинки, равное ^-—r-j ¦
Третья группа
Пример 171. Прямоугольная пластинка со сторонами а и 6
может вращаться без трения вокруг вертикальной оси АВ,
проходящей через ее середину и параллельной стороне Ь. На
3R4
п	4 Я In 2
Следовательно, Ф =

конце оси надет шкив С радиусом г, на который намотана
гибкая нерастяжимая нить; другой конец нити перекинут через
блок D, и к нему привязан груз весом Р, приводящий во вра-
вращение пластинку.
Пренебрегая массами шкива и блока, найти ускорение груза,
если вес пласгинки равен Q и никаких сопротивлений движе-
движению нет (рис. 207).
Решение. Так как требуется определить ускорение груза,
то для решения этой задачи воспользуем-
воспользуемся уравнением B27)
dJ — Zi
Кинетическая энергия данной систе-
системы, состоящей из пластинки, вращаю-
вращающейся вокруг неподвижной оси г, и rpy-
за, движущегося поступательно, равна
Т — J —-!- —и2
1 — Jz 2 + 2g '
где Jz—момент инерции пластинки отно-
относительно оси вращения, to — ее угловая
скорость, v—скорость груза.
Так как нить нерастяжима, то скорость груза равна окруж-
окружной скорости шкива, т. е. и = гсо, и, следовательно,
Т— I v"
Зная момент инерции прямоугольной пластинки относительчо
ее стороны, равной Ь, найденный в предыдущем примере, и
применяя теорему о моментах инерции относительно двух па-
параллельных осей, имеем:
откуда
поэтому
и
z~ g 12
g 2ra 12
dt
9^. pV_e.
g V 12/-a ~+"J j dt
При перемещении груза работу будет производить только
сила Р (вес груза), поскольку сопротивлениями пренебрегаем.
13В-2*
365

Так как сила Р и скорость груза v направлены по одной
прямой в одну и ту же сторону, то мощность найдем по фор-
формуле A77) (см. гл. III, § 3) N = Pv. Подставив найденные зна-
чения мощности и производной -п в уравнение B27), получим:
отсюда
dv
41 _. "'г	ст-const
di * Qa* +12 r'pg-conbl-
Следовательно, движение груза является равномерноускорен-
ным.
§ 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
В этих задачах приходится применять совместно две из тех
теорем динамики системы, которые рассмотрены в предыдущих
параграфах; например, теоремы о количе-
количестве движения и о кинетическом моменте
системы или теоремы об изменении кине-
кинетической энергии и о движении цешра
масс системы.
Пример 172. На ступенчатый шкив не-
несом Ра, вращающийся вокруг неподвиж-
	х ной оси О, навернуты канаты, к концам
которых подвешены грузы А и В весом
Р, и Рг. Предполагая, что на эту систему
действуют только силы тяжести, и пре-
пренебрегая сопротивлениями, найти ускоре-
ускорения грузов и реакцию в точке О.
Радиусы R и г и радиус инерции гин
шкива относительно оси О известны (рис.
208).
Решение. Так как в заданной зада-
задаче требуется определить ускорения гру-
грузов, то применим уравнение B27). Сна-
Сначала вычислим по формулам B29) и B30)
кинетическую энергию Т данной системы,
состоящей из двух грузов, движущихся поступательно, и шкива,
вращающегося вокруг неподвижной оси:
Рис
где и, и v2—скорости грузов А и В, Jo—момент инерции шкива
относительно оси вращения, с» — его угловая скорость.
366

Но
поэтому
Т = — Ргь>* -4-— г2 а" 4- — г2 fiJ = — IP /?2 j- Р гг -I P г1 1
2g	2g	2g ин 2g^ ' "is г ' з'ин/'
Отсюда
^Г_/р /j! i p ;-s i p r! ) — е
где е = -^ —угловое ускорение шкива.
Так как груз В поднимается, а груз А опускается, то сумма
мощностей, действующих на систему сил, равна
Следовательно, уравнение B27) имеет вид
откуда
е = -
Искомые ускорения грузов равны:
Для определения реакции в точке О применим теорему о про-
проекции количества движения К системы на неподвижную ось
(см § 1 этой главы). Выбрав координатные оси хну, как ука-
указано на рисунке, на основании этой теоремы имеем:
где Хо, YQ—составляющие искомой реакции по координатным
осям. Учитывая, что скорости грузов А и В параллельны оси у
и что количество движения шкива равно нулю, так как его
центр тяжести лежит на оси вращения, находим:
Из этих уравнений получаем:
367

Угловое ускорение шкива можно найти и по теореме о кине-
кинетическом моменте системы. Применяя эту теорему по отношению
к оси О, имеем:
^ = Smo(F(e') = mo(P1) + mo(Ps) = P1R-P/.	(a)
(Моменты внешней силы Р, и реакции в точке О относительно
оси вращения шкива равны, очевидно, нулю). Кинетический
момент La данной системы относительно оси О равен сумме ки-
кинетических моментов шкива и двух грузов относительно той же
оси. Следовательно,
Поэтому уравнение (а) принимает вид
01 сюда
df~E:
в.
Пример 173. Доска весом Р, лежит на двух цилиндрических
катках радиусом г и весом Рг каждый. Вся система движется
под действием заданной горизонтальной силы F, приложенной
Я,
В,
Рис 209
к доске; при этом предполагается, что катки катятся без сколь-
скольжения и что скорость доски равна скорости катка в точке А.
Найти ускорение доски и общую силу трения в точках А и В
(рис. 209).
Решение. Для определения ускорения ш доски восполь-
вуемся, как и в предыдущей задаче, уравнением B27):
dt
Так как доска движется поступательно, а движение катков
является плоскопараллельным, то кинетическую энергию данной
36§

системы находим пи формулам B2Э) и B31):
где и—скорость доски, vo~скорость центра тяжести катка,
©—угловая скорость катка, Jo—его момент инерции, относи-
относительно оси О, перпендикулярной к плоскости рисунка.
Так как каток катится без скольжения, то точка А^ есть его
мгновенный центр вращения; отсюда следует, что
= лю и vo = ^ = ~
р
Кроме того, Jo~^r%> поэтому
Отсюда
dt "
Так как силы Р\ и Р2 перпендикулярны к скоростям их
точек приложения, а силы трения между катками и опорной
\У
I С t	F
i
f" В
Рис 210
плоскостью приложены в точках Л, и В,, скорости которых
равны нулю, то работа каждой из этих сил равна нулю. Сумма
работ внутренних сил трения между доской и катками, прило-
приложенных в точках А и В, также равна нулю, так как доска не
скользит по каткам.
Поэтому работу производит только сила F, мощность кото-
которой равна N = Fv.
Следовательно, уравнение B27) принимает вид
откуда
W —

Чтобы найти равнодействующую FTp сил трения FTP и FTp,
приложенных к доске в точках А к В, рассмотрим отдельно
движение доски и составим уравнения движения ее центра тя-
тяжести С:
где Nl и N2 — нормальные реакции катков, приложенные к доске
в точках А я В (рис. 210).
Р	АР F
Но wx = w и шу = 0, поэтому FTp = F — -j±w=F — ? j
Если обозначим ^ коэффициент трения между доской и кат-
катками, то FTp&gfN1 и Flp^fN^ Отсюда следует, что
или
3P.F
Р1DР1+ЗР2)'
Такому условию должен удовлетворять коэффициент трения,
чтобы доска не скользила по каткам.
Таблица 20
Классификация задач
Группы
1-Я
2-я
3-я
Типы задач
]
Задачи на вычисление KHHeTBqe-
ской энергии (задачи 1040—1048)
—
11
Задачи на применение теоремы
об изменении кинетической энер-
энергии системы, состоящей из одного
тела или нескольких тел
Задачи, решаемые при помо-
помощи теоремы об изменении ки-
кинетической энергии в конечной
форме (задачи 1053—1074)
Задачи, решаемые при помо-
помощи теоремы об изменении ки-
кинетической энергии в диффе-
дифференциальной форме
Задачи, решаемые при по-
помощи теоремы о зависимости
между кинетической энергией
системы и мощностью дейст-
действующих на систему сил (зада-
(задачи 932—934, 940—942, 1091)
370

Глава V
ПРИНЦИП ДАЛАМБЕРА И ПРИНЦИП ВОЗМОЖНЫХ
ПЕРЕМЕЩЕНИЙ
§ 1. ПРИНЦИП ДАЛАМБЕРА ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
Если к каждой материальной точке движущейся системы
приложить силу инерции этой точки, то все эти силы инерции
будут уравновешиваться заданными силами и реакциями связей,
приложенными к данной системе. В этом и состоит сущность
принципа Даламбера для системы.
Таким образом, если заданную силу, приложенную к fe-той
точке механической системы, состоящей из п материальных точек,
обозначим Fk, реакцию связей, приложенную к той же точке,
обозначим Nk и силу инерции этой точки F{"\ то имеем:
Fk + Nk + FiM) = Q, (k = \, 2	п).	B32)
При этом
—
— —mkwk,	B33)
т. е. сила инерции материальной точки равна по модулю про-
произведению массы этой точки на ее ускорение и направлена про-
противоположно этому ускорению.
Отсюда следует, что система заданных сил, реакций связей
и сил инерции удовлетворяет уравнениям статики, т. е. сумма
проекций всех этих сил на любую ось и сумма их моментов
относительно любой точки или любой оси равна нулю.
Таким образом, принцип Даламбера дает общий прием со-
составления уравнений, необходимых для решения задачи дина-
динамики системы, причем эти уравнения имеют ту же форму, что
и уравнения статики. Этот прием оказывается особенно полезным
при решении тех задач, в которых требуется найти динамические
реакции связей, т. е. реакции, возникающие при движении
системы.
Задачи, относящиеся к этому параграфу, можно разделить
на два основных типа:
I.	Задачи, в которых силы, приложенные к каждому телу
системы (заданные силы и реакции связей), и силы инерции, их
уравновешивающие, лежат в одной плоскости.
II.	Задачи, в которых заданные силы, реакции связей и силы
инерции, их уравновешивающие, образуют пространственную
систему сил.
Задачи типа I
Так как в задачах этого типа рассматривается плоская сис-
система сил (заданные силы, реакции связей и силы инерции), на-
находящихся в равновесии, то применяем три уравнения плос-
37J

кой статики- два уравнения проекций и одно уравнение мо-
моментов.
В частных случаях будем иметь только два из этих уравне-
уравнений: два уравнения проекций (в случае сходящихся сил) или одно
уравнение проекций и одно уравнение моментов (в случае па-
параллельных сил).
Если в задаче имеется система, состоящая из двух или не-
нескольких тел, то приходится, расчленив эту систему, составлять
уравнения равновесия для каждого тела в отдельности, совер-
совершенно так же, как в статике.
Задачи типа I можно разделить на три группы.
Первая группа
К этой группе относятся задачи, в которых тела, входящие
в систему (или одно тело), движутся поступательно.
Решая эти задачи по принципу Даламбера, необходимо к
калсдой материальной частице движущегося тела приложить
силу инерции этой частицы. Так как при поступательном дви-
движении тела все его точки имеют одно и то же ускорение w, то
силы инерции материальных частиц тела будут в этом случае
пропорциональны массам этих частиц, параллельны и направ-
направлены в одну сторону (противоположно ускорению ад), поэтому
все эти силы инерции приводятся к одной равнодействую-
равнодействующей силе, приложенной в центре тяжести тела.
= —Mw,
где М—масса тела.
Игак, сила инерции поступательно движущегося тела равна
по модулю произведению массы этого тела на его ускорение, на-
направлена противоположно этому ускорению и приложена в центре
тяжести тела.
После того как в центре тяжести каждого поступательно
движущегося тела мы приложим силу инерции этого тела, дан-
данная система, согласно принципу Даламбера, будет в равновесии.
Поэтому для этой системы нужно составить уравнения равно-
равновесия и, решив их, найти те неизвестные величины, которые
требуется определить в данной задаче.
Обычно искомыми величинами в этих задачах являются уско-
ускорения тел и реакции связей.
Пример 174. Два груза А я В весом Р и Q, связанные не-
нерастяжимой нитью, перекинутой через невесомый блок, вращаю-
вращающийся вокруг неподвижной оси О, могут скользить по граням
неподвижной призмы, причем коэффициент трения равен /. Найти
ускорение w, с которым будут двигаться грузы, и силу натя-
натяжения нити, если углы аир известны (рис. 211).
§7?

Решение. Каждый из грузов А и В движется поступательно
и прямолинейно. Допустим, что груз А опускается с ускоре-
ускорением wx. Так как грузы А и В связаны нерастяжимой нитью,
то груз В будет подниматься с ускорением ws, равным по мо-
модулю ускорению wl, т.е. wi = wi = w.
Применяя принцип Даламбера, приложим к грузу А силу
р
инерции этого груза, равную по модулю Р[ю = — w и направ-
ленную противоположно ускорению w%, а к грузу В—силу инер-
инерции, равную по модулю F*H) = — w и направленную противопо-
_____	&
ложно ускорению wt. Тогда, по принципу Даламбера, данная
система будет находиться в равновесии.
Рис 211
Расчленив эту систему, т. е. перерезав нить, составим по два
уравнения равновесия для каждого груза в отдельности. Для
этого спроектируем все силы, приложенные к грузу А, т. е. силы
Р, N,, ~FTplJ FiH\ 7\, на оси Ojt, и Оух, а силы, приложенные
к грузу В, т. е. силы Q, Nit F^ 2, F[a\ Ts,— на оси Ох, и Оуг.
Здесь Af, и Nt — нормальные реакции граней призмы, FTPi и
/чР2—силы трения, 7\, Tt — реакции (силы натяжения) нити,
приложенные соответственно к грузам А и В, причем T1 = TZ = T.
Тогда имеем для груза А:
Pslna—FTVl—F[tl)—T = O>
JV, — Р cosa =
для груза В:
,
Из второго и четвертого уравнений находим:
Щ

Следовательно,
F,pi = fNt=fP cosa,
Подставив значения сил трения и сил инерции в первое и
третье уравнения, получим:
— w -\-Т — Р sin а—/ Р cosa = P(sina—/ cos а),
Т — R. w
Отсюда находим:
Т — R. w = Q sin p + fQ cos p = Q (sin p +/ cos p).
_ P (sing— fees a) — Q (sin
P + Q	?
rp_PQ [slna + sinP —f(cosct —cosP)]__ 2PQ . g + p
. a— B
in—gc
Вторая группа
К этой группе относятся задачи, в которых тела, входящие
в систему (или одно тело), имеют вращательное движение вокруг
неподвижной оси.
Ускорение каждой точки такого тела равно геометрической
сумме касательного и нормального (центростремительного) уско-
ускорений. В соответствии с этим, решая задачу по принципу Да-
ламбера, мы должны к каждой материальной частице вращаю-
вращающегося тела приложить две силы инерции частицы: 1) касатель-
касательную силу инерции, равную по модулю произведению массы
частицы на ее касательное ускорение и направленную противо-
противоположно этому ускорению, и 2) нормальную силу инерции (цен-
(центробежную силу), равную по модулю произведению массы
частицы на ее нормальное ускорение и направленную противо-
противоположно этому ускорению.
В остальном метод решения задач этой группы остается та-
таким же, как и в задачах первой группы. Если тело вращается
равномерно, то касательные ускорения, а следовательно, и ка-
касательные силы инерции всех его материальных частиц равны
нулю.
Пример 175. Два однородных стержня О А и ОВ весом Р
каждый прикреплены концами при помощи шарнира О к верти-
вертикальному стержню OD, а их концы А а В привязаны нерастя-
нерастяжимыми горизонтальными нитями к точке D этого стержня.
Треугольник АОВ начинают вращать вокругхоси OD с постоян-
постоянной угловой скоростью ш. Найти натяжения Т нитей и реакцию
374

ф
шарнира 0, приложенную к стержню ОВ, если ОА=ОВ = а и
/_DOB = y (рис, 212).
Решение. К стержню ОВ, вращающемуся равномерно во-
вокруг оси OD, приложены заданная сила Р, реакции Хо> Yo
шарнира О и реакция Т нити.
Применяя принцип Даламбера,
разобьем стержень ОВ на бес-
бесконечно малые элементы и при-
приложим к каждому такому эле-
элементу силу инерции /'"'. направ-
направленную противоположно его
ускорению wk и равную по мо-
модулю fk) = mkwk, где тк—мас-
тк—масса элемента.
Если рассматриваемый эле-
элемент находится на расстоянии
sft от точки О, то wk — rk(if —
— sk sin ф со2, и, следовательно,
Ди1 = mkafsk sin ср.
Согласно принципу Далам-
Даламбера, сила Р, реакции Хо, Yo, T
и силы инерции Ди), приложенные к каждому элементу стержня
ОВ, взаимно уравновешиваются. Поэтому будем иметь три урав-
уравнения равновесия:
уравнение проекций на ось х:
Рис 212
уравнение проекций на ось у:
и уравнение моментов относительно точки О:
— Р j sin ф + Та cos ф — 2/jt,H)sft cos ф = 0.
Вычислим суммы, входящие в эти уравнения:
ЕДИ) == SmftoiJsft sin ф = (о2 sin (p"Zmksk,
ffrSfe cos ф = 2 mka>zsl sin cp cos ф = m2 sin ф cos ф2тfs*.
Но по формуле B03) для координаты центра тяжести С имеем:
-М — — —
у * _ j __Ма"_ Раг
^mksk ~J0- 3 - 3g ,
где JQ—моме}1т инерции стержня ОВ относительно точки О.
»7б

Поэтому уравнения равновесия принимают вид
— Р Y sin
Решая эти уравнения, получаем
Y = Р
	~- sin ф cos ф = 0.
Третья группа
К этой группе относятся такие задачи, в которых некоторые
из гел, входящих в систему, имеют вращательное движение, а
другие движутся поступательно.
Метод решения задач этой группы на
основании принципа Даламбера по существу
ничем не отличается от метода решения за-
дач первых двух групп. Только здесь име-
имеются и тела, поступательно движущиеся, и
гела, вращающиеся.
Пример 176. К шкиву подъемника ради-
радиусом R приложен вращающий момент М;
веса грузов равны Р1 и Рг. Определить
угловое ускорение шкива и натяжения ча-
частей каната АС и BD, считая шкив однород-
однородным круглым цилиндром весом Рь и пре-
пренебрегая сопротивлениями и весом каната
(рис. 213, а и б).
Решение. Решая задачу по принципу
Даламбера, приложим к грузам силы инер-
р	р
ции, равные F(f =—г ш,, F^ = —- w2 и направ-
ленные противоположно ускорениям до, и
ш2 этих грузов, причем wl = wz — w. Кроме
Рис. 213
того, нужно приложить силу инерции к каж-
каждой материальной частице шкива. Так как ускорение такой
частицы слагается из касательного ускорения wx и нормального
ускорения до„, то и сила инерции этой материальной частицы
является равнодействующей двух сил: касательной силы инерции
/t"\ направленной противоположно ускорению wz, и нормальной
376

силы инерции (центробежной силы)пИ\ напрявленной противо-
противоположно ускорению wn. Если массу материальной частицы обо-
обозначить т, а ее расстояние от оси вращения г, то
где в и (в — угловое ускорение и угловая скорость шкива.
После того как мы приложим все эти силы инерции, можно,
согласно принципу Даламбера, рассматривать данную систему,
как находящуюся в равновесии. Следовательно, сумма моментов
всех внешних сил, приложенных к этой системе, и сил инерции
относительно точки О будет равна нулю. Поэтому, учитывая,
что моменты относительно точки О силы Рг, центробежных сил
и реакции в точке О равны нулю, получаем следующее урав-
уравнение:
М -Ь ЯР,-RPt-RF\a) -#/*/" -2г/<и) = О,
или
M R(P P)R(P + P)
Силы натяжения канатов АС и BD в это уравнение не входят,
так как для данной системы эти силы являются внутренними.
Но 2тгге = eSmr2 =У0-е,
где Jo—момент инерции шкива относительно оси О, причем для
однородного круглого цилиндра J0 — ~R*. А потому предыду-
предыдущее уравнение принимает вид
Так как w — Rs, то из этого уравнения находим:
R(Px+P%+0,5Pt)*
w _ M-RjP.-P,)
Для определения натяжения каната BD расчленим систему
и рассмотрим в отдельности правый груз, к которому^ прило-
приложены сила Р„ сила инерции /^и) и реакция каната Tt (рис.
213, б).
Так как эти силы уравновешиваются, то
i)
откуда
T.-P.
р Г. , M
г I f /?(
377

Рассматривая затем равновесие левого груза в отдельности,
найдем натяжение каната АС
т =
+ О.бР.) •
Задачи типа II
К этому типу относятся задачи, в которых заданные силы,
реакции связей и силы инерции образуют пространственную
систему сил. Эти задачи можно разделить на две группы.
Первая группа
К этой группе относятся задачи, в которых требуется опре-
определить реакции двух закрепленных точек оси при вращении
точечных масс вокруг этой оси.
Решение задач этой группы аналогично решению задач вто-
второй группы типа I, только здесь приходится составлять в общем
случае шесть уравнений равновесия пространственной статики.
Вторая группа
К этой группе относятся задачи, в которых требуется опре-
определить реакции двух закрепленных точек твердого тела (двух
подшипников или подшипника и подпятника), возникающие при
вращении твердого тела вокруг неподвижной оси, проходящей
через эти закрепленные точки.
При решении этих задач по принципу Даламбера нужно раз-
разбить вращающееся твердое тело на элементарные материальные
частицы и к каждой такой частице приложить касательную и
нормальную силы инерции этой частицы. Так как, согласно
принципу Даламбера, все эти силы инерции уравновешиваются
заданными силами, приложенными к телу, и реакциями закреп-
закрепленных точек, то в общем случае имеем шесть известных из ста-
статики уравнений равновесия (три уравнения проекций и три
уравнения моментов). В эти уравнения войдут, во-первых, сумма
проекций всех сил инерции на каждую из трех выбранных ко-
координатных осей, или, что то же, проекции главного вектора
сил инерции на каждую из этих осей, и, во-вторых, суммы
моментов всех сил инерции относительно каждой координатной
оси, или, что то же, главные моменты сил инерции относительно
каждой из этих осей. Если ось вращения тела примем за ко-
координатную ось z, то проекции главного вектора сил инерции
на координатные оси будут равны (см., например, «Курс теоре-
теоретической механики» И. М. Воронкова, § 139)
ЯТ = М(хс^+усг), R^^M{ycu*-xcs), tf<"> = 0, B31)
378

а главные моменты сил инерции относительно координатных
осей выразятся так:
, Мв> = -У,е. B35)
В этих формулах М—масса тела, о и е—соответственно
угловая скорость и угловое ускорение тела, хс и ус— коорди-
координаты центра тяжести С тела, Jzx и Jyz—центробежные моменты
инерции тела и Jt—момент инерции тела относительно оси
вращения.
Отметим некоторые частные случаи:
1.	Тело вращается равномерно. Тогда о = const и е = 0.
2.	Центр тяжести тела лежит на оси вращения. Тогда
хс = ус = 0 и, следовательно,
Я<;>=Я<,н> = ^и> = 0.	B36)
В этом случае все силы инерции приводятся к одной
паре, проекции вектора-момента которой на координатные оси
определяются по формулам B35).
3.	Координатная плоскость хОу является плоскостью
симметрии тела. Тогда центр тяжести тела лежит в этой пло-
плоскости, и ось вращения г как ось, перпендикулярная к плоско-
плоскости симметрии, является главной осью инерции тела в точке О,
поэтому Jvz = Jix = O. Если при этом s = 0, то
\ R?} = 0.	B37)
В этом случае все силы инерции приводятся к одной
равнодействующей, равной Rw — Ma)Vc, где гс—радиус-
вектор точки С, т. е. приводятся к одной силе, равной центробеж-
центробежной силе центра тяжести, если предположить, что в этом центре
сосредоточена вся масса тела; при этом линия действия этой
равнодействующей R<a) проходит через центр тяжести тела.
4. Если ось вращения г является главной централь-
центральной осью инерции тела и если при этом тело вращается
равномерно, то е = 0, хс — ус = 0 и Jyz = Jzx — O, а потому
/?<:и) = ^(я> = ^<и>==0 и М? = М? = МР = 0, т. е. система сил
инерции является в этом случае уравновешенной системой. Сле-
Следовательно, в уравнения равновесия, составленные на основании
принципа Даламбера, силы инерции не войдут; эти уравнения
будут совпадать с уравнениями статики, которые используются
при равновесии тела под действием приложенных к нему
заданных сил. Поэтому искомые реакции закрепленных точек
будут в этом случае равны статическим реакциям.
379

При решении задач этой группы по принципу Даламбера
следует иметь в виду, что в уравнение моментов относительно
оси вращения z искомые реакции закрепленных точек не в'ходят,
так как их моменты относительно этой оси равны нулю. Поэтому
эти реакции определяются из остальных пяти уравнений равно-
равновесия. Если в данной задаче, как это нередко бывает, требуется
найти только реакции, перпендикулярные к оси вращения z, то
достаточно составить четыре уравнения равновесия (два уравне-
уравнения проекций на оси к и у
и два уравнения моментов
относительно этих осей).
Пример 177. Однородный
тонкий диск радиусом R и
z весом Р насажен на горизон-
тальный вал под углом а к
оси вала и жестко скреплен
с валом, причем центр тяже-
тяжести О диска лежит на оси
вала.
Определить реакции под-
подшипников А а В, если вал
вращается с постоянной угловой скоростью со и АО~ОВ = а
Весом вала и трением в подшипниках можно пренебречь
(рис.214).
Решение. Реакция каждого из подшипников перпендику-
перпендикулярна к оси вращения вала и равна геометрической сумме двух
сил: статической реакции, вызываемой весом ^ диска, и
инерционной реакции, возникающей при вращении диска и
обусловленной проявлением инерции материальных частиц вра-
вращающегося диска.
Каждая из статических реакций равна, очевидно, -у и на-
направлена по вертикали вверх. Для определения инерционных
реакций применим принцип Даламбера. Составляющие инерцион-
инерционной реакции по координатным осям х и у, приложенные в точке
А, обозначим ХА и Y А, а инерционные реакции, приложенные
в точке В, обозначим Хв и Ув. При этом ось х лежит в одной
плоскости с осью вращения вала и с нормалью On к плоскости
диска, ось у—в плоскости диска; ось z направим по оси вра-
вращения вала« Оси х и у связаны с диском и вращаются вместе
с ним. Диаметр 0zx диска лежит в плоскости xOz и, следова-
следовательно, перпендикулярен к оси у.
Так как сила Р уравновешивается статическими реакциями
подшипников, то, согласно принципу Даламбера, силы инерции
материальных частиц диска_будут уравновешиваться инерцион-
инерционными реакциями ХА, YA, XB, YB.
380

Поэтому имеем следующие четыре уравнения равновесия:
уравнение проекций на ось к
уравнение проекций на ось у
R(ya) + YA+YB = 0
уравнение моментов относительно оси х
MZ'> + aYA-aYB =
уравнение моментов относительно оси у
В этих уравнениях, как было уже указано выше, R("\ R^—
проекции на оси х и у, главного вектора сил инерции матери-
материальных частиц диска, Мх*] и М^ — главные моменты этих сил
относительно тех же осей. Так как в данной задаче центр тя-
тяжести диска лежит на оси вращения г и со = const, то хо=уо~0
и 6 = 0, поэтому из формул B34) и B35) имеем:
р(и) г>(и) о Л.(и)	г г ««(и)	 1 2
Кроме того, так как ось у, направленная по диаметру диска,
есть ось симметрии диска, то она является его главной цент-
центральной осью инерции, а поэтому J =0.
Следовательно, предыдущие уравнения принимают вид:
Из этих уравнений находим:
у 	v 	п У 	 / ю Y 	 7й
Вычислим центробежный момент инерции J2X. Если рассмотрим
материальную частицу диска с массой т, то, как видно из
рис. 215, координаты этой частицы будут равны
x — hsina, z = h cos a,
где h — расстояние этой частицы от оси у. Следовательно,
J2X= V mh2 sin acosa = -2- sin2a V mh", но V^a —
момент инерции диска относительно оси у (относительно диа-
s	„ MR1	, MR2 . о
метра), равный —j— , поэтому Jгх == —^— sin 2a.
381

Таким обрчзом, окончательно получаем:
Отсюда видно, что инерционные реакции подшипников парал-
параллельны оси х; следовательно, эти реакции, сохраняя постоянную
величину, непрерывно изменяют свое направление, так как ось х
вращается вместе с диском. Отри-
Отрицательное значение силы Хв указы-
указывает на то, чго эта сила имеет
направление, противоположное
принятому на рис. 214, а поэтому
реакции X А, Хв образуют пару
сил, лежащую в плоскости, про-
проходящей через ось вращения и
нормаль On к плоскости диска-
Рис 215
Рис 216
Пример 178. С вертикальной осью, укрепленной в подшип-
подшипнике А и подпятнике В, жестко соединены перпендикулярный
к этой оси тонкий стержень DE длиной / и весом Р, и круглый
однородный цилиндр весом Pt. образующие которого паралле-
параллельны оси АВ. При этом цилиндр насажен эксцентрично так, что
его центр тяжести С2 находится от оси АВ на расстоянии
ОСг = а. Цилиндр и стержень вращаются вокруг оси АВ с дан-
данной угловой скоростью со = const. Найти реакции подшипника А
и подпятника В, если ВЕ — 1, ЕО = АО=-^ и 0Ct _L ED (рис. 216).
Решение. Проведем координатные оси, связанные с цилинд-
цилиндром, как указано на рис. 216, т. е. ось z направим по оси
вращения В А, ось у — по прямой ОСг и ось х—параллельно
стержню ED.
Составляющие реакции подшипника А по осям х и у обозна-
обозначим Хд и YА, а составляющие реакции подпятника В по коор-
координатным осям—Ха, YB и ZB.
38^

Применяя принцип Даламбера, разобьем стержень DE на бес-
бесконечно малые элементы и к каждому такому элементу прило-
приложим соответствующую силу инерции.
Так как со = const, то е = 0 и, следовательно, касательные
силы инерции всех элементов стержня будут равны нулю, а их
нормальные силы инерции (центробежные силы) будут направ-
направлены вдоль стержня от оси вращения.
Равнодействующая этих центробежных сил имеет то же на-
направление и по модулю равна
F AИ> = 2 mxuf = со8 2 tnx,
где т—масса элемента, х—расстояние от элемента до оси вра-
щения. Но V тх = Mtxct = — Xct, где Хс, — расстояние центра
тяжести С, стержня от оси АВ, равное у, поэтому F\n) = ~ 1аг.
Так как плоскость хОу является для цилиндра плоскостью
симметрии и цилиндр вращается равномерно, то, как было указано
выше, силы инерции материальных частиц цилиндра приводятся
в этом случае к одной равнодействующей F["\ равной центро-
центробежной силе центра тяжести С2 цилиндра в предположении,
что в этом центре сосредоточена вся масса цилиндра. Следова-
Следовательно, 7*1"' = М2г/с2<в2 = — а<о°; эта сила F^ приложена в точке
Са и направлена по 0С„ т. е. по оси у.
Согласно принципу Даламбера, заданные силы Р,, Р2 реак-
реакции Хв, YB, Zs, XA, YA и силы инерции F\"\ F1^ взаимно
уравновешиваются; поэтому для этой системы сил можно соста-
составить следующие пять уравнений равновесия (три уравнения
проекций на оси х, у, г и два уравнения моментов относительно
осей х и у):
-\ F™ = 0; YA + YB + /f > = 0;
или
383

Из этих уравнений находим
_
а
у _аР,B
Таблица 21
Классификация задач
Ураьнения
1-я группа
Тела, вхо-
входящие в си-
систему (или
одно тело),
движутся
поступатель-
поступательно
Задачи
878—830,
925, 926, 928
Тип 1
лоскля система сил
равновесия. 1) у
2) 2
3) ^
2-я группа
Тела, входя-
входящие в систему
(или одно те-
тело), имеют вра-
щательноедви-
жение
Задачи
891—901, 1101,
1102, 1099
1 х=о,
<
]к=о.
3-я группа
Некоторые
из тел, входя-
входящих в систему,
имеют враща-
тельноедвиже-
ние, а другие
тела движутся
поступательно
Задачи 927,
929, 930
Тип
II
Пространственная система сил
Уравнения ц
равновесия.
2)
3)
4)
5)
6)
1-я группа
Определение
реакций двух
закрепленных
точек оси при
вращении то-
точечных масс
вокруг этой
оси
Задачи 1103,
1104
7 X = 0,
Уг=о,
2-ая группа
Определение
реакций двух
закрепленных
точек оси при
вращении твер-
твердого тела во-
вокруг этой оси
Задачи 1100,
1105—1110
§ 2. ПРИНЦИП ВОЗМОЖНЫХ (ВИРТУАЛЬНЫХ) ПЕРЕМЕЩЕНИЙ
Если на систему материальных точек наложены те или иные
связи, то для такой системы не всякое перемещение оказывается
возможным. Если при этом связи не зависят от времени, т. е.
если в уравнения связей время ? явно не входит, то такие
связи называются стационарными; в противном случае связи
называются нестационарными. В дальнейшем рассматриваются
только стационарные связи.
Возможным (виртуальным) перемещением данной системы
называется совокупность любых бесконечно малых перемещений
материальных точек этой системы, допускаемых в данный мо-
момент наложенными на систему связями.
Проекции на координатные оси возможного перемещения
bsA точки А системы обозначаются SxA, 6yA> 6гА н представляют
384

собой изменения координат этой точки при ее возможном пере-
перемещении, называемые вариациями координат этой точки.
Если на систему, состоящую из п материальных точек,
наложены s стационарных связей вида
/,(*х, у„ 2„ ..., ха, уп, гп) = 0	B38)
(» = 1, 2, ..., s),
то из Зя координат точек системы произвольными являются
только Зп — s, а остальные s координат могут быть выражены
как функции этих произвольных координат из s предыдущих
уравнений. Число
й = 3п—s,	B39)
т. е. число независимых координат точек системы называется
числом степеней свободы этой системы.
Если сумма элементарных работ реакций связей, наложен-
наложенных на систему, при любом возможном перемещении системы
равна нулю, то такие связи называются совершенными (идеаль-
(идеальными). Необходимое и достаточное условие равновесия системы
с совершенными связями дает принцип возможных перемещений,
который формулируется следующим образом: для того чтобы
рассматриваемое положение системы с совершенными связями
являлось положением равновесия этой системы, необходимо и
достаточно, чтобы сумма элементарных работ всех заданных
(активных) сил, действующих на систему, при любом ее возмож-
возможном перемещении из этого положения равнялась нулю.
Следовательно, необходимое и достаточное условие равно-
равновесия системы выражается уравнением
264 = 2Fcosa6s = 0.	B40)
Пользуясь аналитическим выражением элементарной работы,
получим общее уравнение статики в таком виде:
2(Xox + y8t/ + ZSz) = 0.	B41)
Задачи, относящиеся к этому параграфу, можно разделить
на три типа:
I.	Задачи, в которых при заданном положении равновесия
системы требуется определить силы, действующие на систему,
или найти зависимость между этими силами.
II.	Задачи, в которых при заданных силах, действующих
на систему, требуется определить положение равновесия этой
системы.
III.	Задачи на применение принципа возможных перемеще-
перемещений к определению реакций связей.
Следует иметь в виду, что в каждом из этих типов могут
рассматриваться системы с одной или несколькими степенями
свободы.
385

Задачи типа I
(задачи 903—908, 911—921)
Пример 179. Два невесомых стержня АВ и ВС соединены
шарниром В, в котором приложена вертикальная сила Q, на-
направленная вниз. Конец С шар-
нирно прикреплен к стене, а
Т^р^—	 — — -л конец А шарнирно соединен с
J ^J^?5^^*	ползуном, который может без
Я " %:^ ¦	трения скользить по полу. Ка-
Какую горизонтальную силу Р
надо приложить к ползуну,
чтобы система при заданных уг-
углах аир находилась в равно-
равновесии (рис. 217)?
Решение. Если ползун
прижат к полу, то рассматрива-
рассматриваемая система имеет одну степень
свободы, так как на две точки
В {хв, ув) и А (хА, уА), опре-
определяющие положение системы, наложены три связи:
J+ (Ул-УвУ-а* = 0,
Рис
Поэтому число степеней свободы данной системы равно
k = 2n —s = 2-2—3=1.
Применяя принцип возможных перемещений, задачу можно
решить двумя способами.
Первый способ. Сообщаем системе возможное перемещение.
Для точки А возможное перемещение bsA направлено парал-
параллельно оси х, а возможное перемещение 8sB точки В направлено
по касательной к траектории (к окружности с центром в точке С),
которую может описывать точка В, т. е. перпендикулярно
к стержню СВ. Далее, пользуясь основным выражением элемен-
элементарной работы, на основании принципа возможных перемещений
имеем [см. уравнение B40)]
2 6 А = — PbsA -f QSsB cos p = 0.
Отсюда
* Эти уравнения выражают следующие условия: а) расстояние ВС = 6
= const, б) расстояние ЛВ =-а = const и в) расстояние от точки А до оси
т е DC = c — const,
38b

Теперь нужно найти зависимость между 6ss и бял. Так как
расстояние между точками В л А при возможном перемещении
системы остается неизменным, то проекции возможных переме-
перемещений этих точек на прямую ВА, их соединяющую, равны
между собой:
^Рвл \ в)== Рва \ а)*
т. е.
8s3 cos f -к— a -f- p 1 = os,, cos а,
или
6sB sin (а—р) = 6s4 cos а,
откуда
следовательно,
Зависимость между SsA и 6sB можно также найти, построив
мгновенный центр вращения С стержня АВ, который лежит
на пересечении перпендикуляров, восставленных из точек А и В
к векторам 8sA и 6sB (см. рис. 217). Тогда возможные переме-
перемещения точек А и В, так же, как их возможные скорости, про-
пропорциональны расстояниям этих точек от мгновенного центра
вращения звена АВ. Следовательно,
bsB_C'B
bsA~C'A •
Но из треугольника АС'В по теореме синусов имеем
. / п \
_, „ sin —	a )
С В \ 2 / соьа
С A sin (a— p) sin (а—р) •
поэтому
fisq	 cos a
~б$л ~~ sin (а—р) '
Второй способ. Сообщая системе возможное перемещение и
пользуясь аналитическим выражением элементарной работы,
имеем [см. уравнение B41)]
S (Х8х + Yby) = Рх8хд + Ру6уА + QxbxB + Qy8yB =
Q80
Теперь следует найти зависимость между вариациями Ьув и
8хА координат точек Б и Л.
Для этого выражаем координаты ув и хА через углы а и р;
6iP DE + EA —b cos p-J-a cos a. При бесконечно
38?

малом возможном перемещении системы углы аир получат
бесконечно малые приращения 6и и 8C, а координаты хА и ув,
являющиеся функциями этих углов, получают приращения бл^
и 6г/в. Пользуясь тем, что приращение функции при бесконечно
малом приращении аргумента можно заменить ее дифференциа-
дифференциалом, имеем
Ьув = Ь cosf}6P; ЬхА= —b sin р Sp—a sin аба.
Подставляя эти значения ЬхА и &ув в уравнение равновесия
системы, получим
6Р sin р 6р + аР sin а 6а + 6 Q cos рбр = 0.
Таким образом, вариации координат точек А и В мы вы-
выразили через вариации углов аир. Зависимость же между
вариациями 6а и бр легко установить, исходя из того, что
CD = CK + KD = c=; const,
или
b sin р + a sin а = с = const.
Варьируя это уравнение, находим
acosa6a+6cosp6p = 0, откуда 6а = —
Подставляя это значение 6а в уравнение, выражающее усло-
условие равновесия системы, получаем
i Г\ • Д С О Ln Sill Ct COS P С О	/ v"i	о ел /л
ЬР sin р 6р — ЬР	*-брЧ ?>Qcosp6p = 0,
" г	cos a "
или
6 [Р sin (P — a) + Q cos p cos а] бр = 0,
и, следовательно,
Р sin (P—a)+Q cosacosp = 0;
отсюда
рcos a cos p _
Задачи типа П
(задачи 909, 910)
Пример 180. Три стержня одинакового веса Q соединены
между собой шарнирами. Первый стержень может вращаться
вокруг неподвижного шарнира О, а к свободному концу треть-
третьего стержня приложена горизонтальная сила F, которая удер-
удерживает всю систему в вертикальной плоскости в равновесии.
388

При этом стержни образуют с вертикалью углы, соответст-
соответственно равные (р ф, ф3. Определить эти углы, если F—Q
(рис. 218).
Решение. Принимая центр шарнира О за начало коорди-
координат, координатные оси направляем, как указано на рис. 218.
На шесть координат точек А, В и С
рассматриваемой системы наложено
три условия (ОА — const, AB = const,
ВС = const); следовательно, система
имеет k = 2n—s = 2-3 —3 = 3 степе-
степени свободы.
В соошетствии с этим положе-
положение данной системы определяется
тремя независимыми друг от друга
параметрами — тремя углами ф,, фа
и ф,.
Вес каждого стержня можно раз-
разложить на две составляющие, при-
приложенные по его концам; тогда по-
получим систему сил, показанную на
рис. 218. Пользуясь аналитическим
выражением элементарной работы,
условие равновесия этой системы сил можно выразить в следую-
следующем виде:
Q8xA + Q6xB +| Ьхс + Fbyc =» 0.
Учитывая, что по условию задачи F — Q, и производя сокра-
сокращение, имеем
8хА -f 8хв + у 8хс + Ьус = 0.
Вводя обозначения О А—а, АВ = Ъ и ВС = с, выражаем
координаты точек А, В и С через искомые углы фх, ф2, фэ:
д:л = асозф,; хв — a cos ф, + b cos ф2;
хс — a cos ф, + b cos ф2 -f с cos ф,; ус = a sin ц>г + Ь sin ф2 + с sin ф,.
Отсюда находим выражения вариаций координат этих точек
через вариации углов фх, фа, ф,:
Рис 218
14 Зап. 237 4

содержащие бф^ 6ф2 и бф3, получаем
a (v.os ф, — 2,5 8тфг)бф, + Ь (cosq>2—1,5 sin<p2N(p2 +
+ с(созф3 —0,5 sin ф3) бф8 = О.
Это равенство должно выполняться при всяком возможном
перемещении данной системы, т. е. при любых значениях ва-
вариаций бф1( 6ф2 и бЧр3, а так как эти вариации друг от друга
не зависят и каждая из них может иметь произвольное значе-
значение, то это возможно лишь при условии, что коэффициент при
каждой из Э1их вариаций равен нулю, т. е.
соэф, — 2,5 о1Пф1 = 0,
cos ф2 — 1,5 sin ф2 = 0,
cos ф3 — 0,5 sin ф8 = 0,
или tg(p, = 0,4; tgф2 = 0,6667;
Отсюда находим*
Ф1==21°48'; ф2 =
= 64°25'.
Задачи типа III
(задачи 922—924)
Пример 181. Трехшарнирная симметричная арка Hai ружена
силами Р и Q (рис. 219). Найти горизонтальную составляющую
реакции шарнира В при ука-
указанных на рисунке размерах.
Решение. Горизонталь-
Горизонтальную составляющую реакции
шарнира В обозначим X. Что-
Чтобы найти эту реакцию, нужно
шарнирно-неподвижную опору
В заменить опорой на катках
для того, чтобы точка В могла
перемещаться в горизонтальном
направлении Сообщим теперь
этой точке возможное горизон-
горизонтальное перемещение 8sB.
Тогда полуарка О А повер-
повернется вокруг неподвижной точ-
точки А на некоторый злементар-
-•? ный угол бфл. При этом точка
О получит возможное переме-
перемещение 6s0, которое будет на-
Рис 219	правлено по касательной к дуге
окружности, описываемой точ-
точкой О, т. е. перпендикулярно к АО Зная направления возможных
перемещений bs0 и bsB точек 0 и В, находим мгновенный центр

вращения С полу арки ВО как точку пересечения перпендику-
перпендикуляров, восставленных в точках О и В к векторам 6s0 и bsB.
Тогда перемещение полуарки ВО можно представить как пово-
поворот вокруг центра С на некоторый элементарный угол 6фс.
На основании принципа возможных перемещений имеем
Вычисляя работу каждой из сил Р, Q, X как произведение
момента этой силы относительно центра вращения на угол по-
поворота (см. формулу 163), получим
ЬАХ = | тс (X) | бФс = X 2/i бфс>
bAQ=-\mc(Q)\ бФг =¦ — Q BA —й)
Следовательно, получаем уравнение
откуда
v_Q B/t—b)
2/z 2/г б<рс *
Так как точка О принадлежит одновременно обеим полу-
полуаркам О А и ОВ,
то	6s0 — ЛОбфл = ОСбфс.
Но О А —ОС, а потому бфл = бфс> и
§ 3. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
(уравнение Даламбера — Лагранжа)
Применяя совместно принцип Даламбера и принцип возмож-
возможных перемещений к движущейся системе, можно сделать сле-
следующий вывод: при движении системы, на которую наложены
совершенные связи, сумма элементарных работ всех заданных
сил, действующих на систему, и сил инерции материальных
точек системы равна нулю при любом возможном перемещении
системы из занимаемого ею в каждый данный момент положения.
* Работа силы Q отрицательна, так как сила Q направлена относительно
центра С по часовой стрелке, а поворот полуарки ВО вокруг итого центра
происходит против часовой стрелки,
14*	391

Этот результат выражается одним из следующих уравнений:
2G-fF(H)N7 = 0,	B42)
или, так как F(ll)r= — mw,
^(F—mw) 67 = 0,	B43)
или в координатной форме
§) (z-fflg)&]=0. B44)
Уравнение B42), или B43), или B44) называется общим
уравнением динамики (уравнением Даламбера — Лагранжа).
В настоящем параграфе рассмотрим задачи двух типов:
I.	Задачи, в которых требуется установить условия отно-
относительного равновесия системы.
II.	Задачи, в которых требуется определить ускорения точек
системы.
В задачах каждого из этих типов могут рассматриваться
системы с одной или несколькими степенями свободы.
Задачи типа 1
(задачи 925—029, 935—939)
Пример 182. Центробежный регулятор (рис. 220) состоит из
двух шаров А и А' весом Р каждый, размерами которых можно
пренебречь. Шары закреплены
на концах А и А' коленчатых
прямоугольных рычагов, кото-
которые имеют шарнирные опоры С
и С на перекладине С ОС, сое-
соединенной неизменно с осью ре-
регулятора. Муфта D весом Pt
отжимается вниз пружиной, а
с другой стороны поддержива-
поддерживается роликами В и В' рычагов
регулятора. Определить жест-
жесткость с пружины, если при за-
заданной постоянной угловой ско-
скорости ю угол отклонения стерж-
^	ней С А и С А' от вертикали ра-
равен ф. Даны расстояния: ОЕ = I,
Рис 220	ОС^ОС' = е и длина недефор-
мированной пружины /0!>/.
Высота муфты равна h.
Решение. Координсиные оси располагаем, как указано на
рис. 220. Заданными силами, дежпв^ющими на систему, яв-
Щт я
— X
892

ляются веса шаров и муфты, а также сила упругости пру-
пружины Q^cX, где X—деформация (сжатие) пружины. Кроме
того, в точках А и А' приложим центробежные силы
инерции Я">= F[x) = — R®', где R— расстояние от центра каж-
каждого из шаров до оси вращения у.
На основании уравнения Даламбера—Лагранжа сумма
работ всех этих сил при любом возможном перемещении си-
системы равна нулю. Следовательно, пользуясь аналитическим
выражением элементарной работы, имеем
— {PlL -f Q) 6^ = 0.
Но
хд — — хА> = е-> as\nq>, уд = уА> —a cos у и yD= b sin ср + -к->
откуда §хА — — Ьха' =а соэф бф, 6г/л = бг/д< =— автфбф,
6yD= b
Кроме того, R — хА — е-\-а s'mq> и, следовательно, /<w =
= F\и) = — /?©2 = — (е + a sin ф) ш2 .
Таким образом, уравнение Даламбера—Лагранжа прини-
принимает вид
2 — (е + a sin ф) со2 a cos ф -f- 2Pa sin ф — (Р, -+ Q) Ъ cos ф бф ¦= 0.
Отсюда, учитывая, что бф=^О, находим
bQ совф = 2Ра (e + asin(p aJcosф f sin <p) — ЬРг cosф;
следовательно, Q = 2Pj
Определив Q, нетрудно найти жесткость с пружины. Дейст-
Действительно деформация пружины X = l0 — (l—h — b sin ф), поэтому
Q
к /0—l + h + b sincp
Задачи типа II
(задачи 930, 943—948)
Пример 183. Через блоки А н В с неподвижными осями
переброшен шнур, поддерживающий подвижной блок С, части
шнура, не лежащие на блоках, вертикальны. Блок С нагружен
гирей весом Р=~40 н а к концам шнура прикреплены грузы
весом Pj = 20 н и Ps = 30 н. Определить ускорения всех трех

Грузов, пренебрегая массой блока и шнура и трением на осях
(рис 221).
Решение. Располагая координатные оси, как указано на
рис. 221, применяем общее уравнение динамики в форме B44),
которое в данном случае принимает вид
где до, до,, да2 — проекции искомых ускорений грузов на ось х.
Учитывая, что длина шнура постоянна, очевидно, имеем
дс, -f- 2x -f хг = const.
Таким образом, три координаты х, хг и xt, определяющие
положение данной системы (предполагается, что все грузы
перемещаются прямолинейно), связа-
связаны одним условием, следовательно,
¦у данная система имеет две степени сво-
ооды. Варьируя последнее равенство,
находим зависимость между вариаци-
вариациями координат трех грузов:
6 8b
отсюда
Подставляя это значение бх в уравне-
уравнение Даламбера—Лагранжа и вынося
за скобки множители бх, и бхг, полу-
получим
Рис 221
Это уравнение имеет место при любых, независимых друг
от друга значениях вариаций бх, и 6х2, а это возможно лишь
при условии, что коэффициент при каждой из этих вариаций
равен нулю. Следовательно, должно быть:
2g
до
Р,	Р п Р Р2	Р
или, подставляя данные числовые значения весов,
Отсюда
ДО, = U. И Wt =
364

Чтобы получить третье уравнение для определения трех
искомых ускорений, продифференцируем дважды но t уравнение
хх + 2х + хл — const. Тогда имеем
cfa. 9d2x d2xs_()
dt' ^ dt* "¦" dt* ~~ '
ИЛИ
= 0.
Подставляя сюда значения да, и wt, получаем
2
ш + 2w +¦ -j
Отсюда находим
и, следовательно,
Отрицательное значение ускорений да и да, указывает на то,
что их направление совпадает с отрицательным направлением
оси х, т. е. что эти ускорения направлены вверх.
§ 4. УРАВНЕНИЯ ЛАГРАНЖА II РОДА (ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ)
Обобщенными координатами механической системы назы-
называются независимые друг от друга параметры, при помощи
которых можно определить в каждый данный момент положение
этой системы и через которые, следовательно, можно выразить
декартовы координаты всех ее точек.
Таким образом, если обозначим k обобщенных координат
qt, qs, ... , qk, то декартовы координаты каждой материальной
точки Ml (xn yt, 2,) системы можно выразить как функции па-
параметров </,, цг, q3, ..., qk а времени t, т. е.
xl = x,(ql, q%, qt, ... , qk, t), \
yi = y,(Qt Ч„ q,, •••• Я», 0. > (x = 1. 2. ... n). B45)
2«=2> (<?i> qt, qv ••• . <b. 0. J
Если связи, наложенные на систему, являются стационар-
стационарными, то время t в правые части этих уравнений не войдет.
Число k независимых обобщенных координат равно числу
степеней свободы данной системы.
В соответствии с числом независимых вбобщенных коорди-
координат, т. е. с числом степеней свободы данной механической
395

системы, имеем для нее k уравнений Лагранжа II рода:
dt\dq
±(d-L)—d-L = <
dt \dqk) dqk
B46)
-s—; Q, Q2, • • •
— так называемые обобщенны силы, которые определяются
формулами
B47)
(=1
Производные qlt цг, ... ^А от обобщенных координат по вре-
времени называются обобщенными скоростями.
Уравнения Лагранжа II рола представляют собой систему
обыкновенных дифференциальных уравнений второго порядка
относительно неизвестных функций qlt qz, . . qk.
Для того чтобы составить эти уравнения, кинетическую
энергию Т системы необходимо выразить через обобщенные
координаты и обобщенные скорости. Обобщенные силы можно
вычислять одним из следующих способов:
а)	непосредственно по формулам B47),
б)	чтобы найти обобщенную силу Qj, соответствующую обоб-
обобщенной координате q,, нужно данной механической системе
сообщить такое возможное перемещение, при котором изме-
изменяется только одна координата qp а все остальные обобщенные
координаты остаются неизменными; затем составить сумму
элементарных работ
всех заданных сил на этом пере-
мещении и разделить эту сумму на вариацию &qp т. е.
0=1, 2, ... k),
B48)
в) в частном случае если система находится под действием
сил, имеющих потенциал, то обобщенные силы определяются по
396

формулам
где U—силовая функция, П — потенциальная энергия системы,
т. е. обобщенная сила равна частной производной от силовой
функции или взятой с обратным знаком частной производной от
потенциальной энергии системы по соответствующей обобщен-
обобщенной координате.
При вычислении обобщенных сил по формулам B49) необ-
необходимо предварительно силовую функцию или потенциальную
энергию системы выразить через обобщенные координаты этой
системы.
Интегрируя систему уравнений Лагранжа, находим обоб-
обобщенные координаты <7,, q2, ... qk как функции времени t м. 2k
произвольных постоянных Ct, C2, ... C2ft, определяемых на-
начальными условиями движения системы.
Задачи на применение уравнений Лагранжа в большинстве
случаев можно отнести к одному из следующих типов:
I.	Задачи, в которых требуется только составить дифферен-
дифференциальные уравнения движения системы.
II.	Задачи, в которых требуется определить ускорения (ли-
(линейные или угловые).
III.	Задачи, относящиеся к малым колебаниям системы.
Задачи каждого из этих типов можно разделить на две группы
в зависимости от того, рассматривается ли в данной задаче
система с одной степенью свободы или с числом степеней свобо-
свободы, большим единицы.
Задачи типа 1
Первая группа
(задачи 1190, 1193, 1194, 1196, 1197, 1201, 1203—1205)
Пример 184. Кулачок, имеющий форму круглого эксцентрика
радиуса R, вращается вокруг оси О парной сил с моментом М
(рис. 222). Вес кулачка равен Р, и центр тяжести его нахо-
находится в геометрическом центре Clt причем ОС1 = е; радиус
инерции кулачка относительно оси О равен k. Жесткость пру-
пружины, прижимающей тарелку толкателя к кулачку, равна с и
при наинизшем положении толкателя (<р = 0) пружина сжата
на величину Ао. Принимая угол поворота ф кулачка за обоб-
обобщенную координату, составить дифференциальное уравнение
движения системы. Трением пренебречь. Вес толкателя равен Р2.
Решение. Движение системы определяется одним урав-
уравнением
it \ «Эф/ g
W

Кинетическая энергия Т системы слагается из кинетической
энергии Т, кулачка и кинетической энергии Т% ъолкателя,
причем
2 g 2
Кроме того,
Ус, ~ У)~ — ОС, cos ф = — е cos <p
Ус,~ Уг — R—еcosф + const.
Учитывая, что уг = е sin <p • ф, получаем
¦' I
(б)
дТ
4-1?/ sin 2Ф
(в)
1
Переходим к определению обобщенной силы, соответствующей
обобщенной координате ф. Кроме движущего момента М, на
систему действуют веса Р, и Р2 ку-
кулачка и толкателя, а также сила Р
упругости пружины. Последняя на-
направлена вертикально вниз и по мо-
ЛЩ	дулю определяется так:
Р = с()
Варьируем координату ф и опреде-
определяем сумму виртуальных работ дей-
действующих на систему активных сил:
V S А = МЬср—Р ,6ул —Pfiy, — Р8уг.
Но на основании равенств (б) имеем
= е sin
= е ып
Таким образом,
Рис 222
Q = <
— е cos фI е sin фбф.
Отсюда находим обобщенную силу
системы, соответствующую обобщен-
обобщенной координате ф:
ЬР, + с(Ь0Н-е—е cos ф)] е sin ф. (д)
Учитывая равенства (в), (г) и (д), уравнение (а) можно предста-

вить в следующем виде:
(Р^2 +Р2ег sin»'cp 4 0,5P2e2sin 2cp <ps 4-
+ [Р, + Рг + с (Ао + е—е cos q>)J c?g sin ф = Mg.
Вторая группа
(задачи 1210, 1213, 1214, 1218, 1221)
Пример 185. На шкив радиуса г намотана нить, к концу
которой подвешен точечный груз весом P=mg, где т—масса
груза (рис. 223). К шкиву при-
приложен вращающий момент М,
при помощи которого этот груз
поднимается, раскачиваясь в то же
время в вертикальной плоско-
плоскости. Составить дифференциальные <р
уравнения движения системы,
если момент инерции шкива отно-
относительно его оси равен Ja и длина
свисающей части нити при ее
вертикальном положении в на-
начальный момент равна /0.
Решен и е. Система имеет две
степени свободы. В качестве обоб-
обобщенных координат принимаем
угол ф поворота шкива и угол	Рис 223
\(з отклонения нити or вертика-
вертикали. Тогда движение системы определяется уравнениями
d ( дТ \ дТ_
(а)
Расстояние от точки В подвеса грузе до точки А набегания
нити на шкив определяется следующим образом:
/ = ВЛ=/0 — Гф + м|).
Отсюда находим координаты точки В:
х~1 соь ф—г sin \\ — (/0—гф~)-?"ф) cos г|)—г sin if>; )
у = / sin ty f гсоэф = ('0—^ф-)-rip) sin гр-t-r cos г|э. (
Кинетическая энергия системы слагается из кинетических энер-
энергий шкива и груза
399

но на основании равенств (б)
х = — гф cos ij) —• (/„ —
у = — гф sin ij) -} (la — г
Следовательно,
4 rty) sin -ф ij;
-| rty) cos \jp ф.
Производим операции, указанные уравнениями (а):
Уф + тггф (/ t mr2) ф
д'Г
—
о — Гф 4-
(в)
+ 2mr(/0-
—ф) ф;
(r)
Варьируя координаты Ф и if, находим сумму виртуальных работ
сил, действующих на систему:
2] б Л = УИбф -f РЬх,
но на основании уравнений (б) имеем
- д-т- 6\1> =— г соэ^бф— (i0—гф-ргф) sin \fi-6ij>.
Таким образом,
2 б Л = (М —Pr cos г|>) 6>—Р (/0 — лф + пр)
Коэффициенты при вариациях бф и 6i|> обобщенных координат
в выражении виртуальных работ и являются обобщенными си-
силами системы
— М — Pr cos гЬ;
'	(Д)
M — Prcos-ф;	\
Учитывая равенства (в), (г) и (д), уравнения (а) можно пред-
представить в следующем виде:
ф М — Pr cos if;
(J а 4-
4- пег A0—гф 4-
400

Задачи типа IF
Первая группа
(задачи И79, 1180, 1182—1189)
Пример 186. Водило АВ, представляющее собой однородный
тонкий стержень длиной 2/ и массой т, вращается вокруг оси О
неподвижной шестерни / под действием приложенного к нему
момента М и приводит в движе-
движение две одинаковые свободно на-
насаженные на водило шестеренки
2 и 2' радиусом г и массой тг — т
каждая, которые катятся по сцеп-
сцепленной с ними неподвижной ше-
шестерне / и приводят в движение
зубчатое колесо 3, обладающее
5 „
массой m, = -jt m. К. окружности
колеса 3 приложена сила сопро-
сопротивления Р. Определить угловое
ускорение е водила, если шесте-
шестеренки 2 и 2' представляют собой
сплошные однородные диски, а мас-
масса колеса 3 равномерно распреде-
распределена по его окружности (рис. 224).
Решение. Положение данного механизма вполне опреде-
определяется одним параметром—углом ф поворота водила, который
и принимаем за обобщенную координату. В соответствии с этим
в данной задаче имеем одно уравнение Лагранжа:
Рис. 224
Вычисляем кинетическую энергию Т системы, которая сла-
слагается из кинетической энергии Гвод водила, энергии 2Tt двух
бегающих шестеренок и энергии 7\ колеса 3:
т-т
i — i в
"г'
где J и У,—моменты инерции водила и колеса 3 относительно
оси О, a J2 — момент инерции шестеренки 2 относительно оси
вращения А.
Угловые скорости ю2 шестеренки 2 и со3 колеса 3, а также
линейную скорость точки А выражаем через угловую скорость
водила к> = ф, которая в данном случае является обобщенной
скоростью:
х)л = шОА = ю/, ш,=
С А
Ы
г
401

(мгновенный центр вращения шестеренки 2 находится в точке С
зацепления этой шестеренки с неподвижной шестерней /), для
определения ю8 находим скорость точки D зацепления шесте-
шестеренки 2 с колесом 3: vD = 2vA = 2al\ следовательно,
ид2со/
Теперь вычисляем моменты инерции:
. _ п
ml\
ПГ
Таким образом, для кинетической энергии системы получаем
следующее выражение:
rr ml2 z , 2/2 тгг<й4г ,5 .. . ., 4м3/2
— —g—(- тоз / Н—s—f- -5- (aim = 5ш / т = 5/'<рт,
Отсюда находим
10/гт
0/гтф; ±(*L) = Юш/'ф = Ю/п/г8,
Зф	"г \ дер /
где е—угловое ускорение водила;
—- = 0, так как Т не зависит от ф.
Определим теперь обобщенную силу.
При повороте водила на элементарный угол 6<р сумма работ,
действующих на данную систему сил, равна
26Л = Мё(р — Р (I +г) бф3>
где бф, — угол поворота колеса 3. Но зависимость между углами
Ф и ф3, очевидно, такова же, как и между угловыми скоростями
водила и колеса 3. Следовательно,
поэтому
Р(/ + гNф = (
отсюда
Q = ИМ. = М- 2Р1,
402
6ф (Л1 — 2Р/NЧр;

Подставляя найденные значения обобщенной силы и произ-
производных if—} и т~ в уравнение Лагранжа, пол}чаем
"' \ дф / ''Ф
откуда
= М— 2Р1,
8 = -
2Р/
Ют/-8
Вторая группа
(задачи 943—947, 1114, I B0)
Пример 187. Невесомая и нерастяжимая нить, намотанная
на однородный цилиндрический барабан D радиуса R — 10 см
и весом G = 20 н, охватывает подвижный блок С, неподвижный
блок 8 и идет параллельно наклонной плоскости тп, образую-
образующей с горизонтом угол а = 30° (рис. 225) К свободному концу
нити прикреплен груз А весом Р =40 я, который может без трения
Рис 225
перемещаться по плоскости тп, а к подвижному блоку подвешен
груз весом Q — 2Qh Определить ускорения грузов, если к бара-
барабану приложена пара сил с моментом М — 1 н м, направленным,
как указано на рисунке. Массами блоков В и С пренебречь.
Решение. Система имеет две с(епени свободы. В качестве
обобщенных координат системы принимаем расстояния s, и s2
(рис. 225). Тогда движение системы определяется уравнениями
d /дТ \ дТ „
±(*L\_#L = o i	(a)
403

Обозначая угол поворота барабана D через (р, имеем
s,-)-2s2 + #ф = Z. = const.	(б)
Составляем выражение кинетической энергии системы:
' ~ g 2 + ? 2 + 2g 2 •
На основании равенства (б)
7?
Ф = —b(s, + 2s,)-
Следовательно,
Производим операции, указанные уравнениями (а)
as,
Варьируя обобщенные координаты системы, находим сумму вир-
виртуальных работ, действующих на систему сил
SS А = Р sin «6s,
но на основании равенства (б)
следовательно,
у<
in а—о~ j 6s, + ( Q—2 -g-\ 6sr
sin
Отсюда определяем обобщенные силы:
t
П ¦	М
, = P sin а—-?-;
Учитывая равенства (в), (г) и (д), уравнения (а) можно пред-
404

ставить в следующем виде:
(Р + 0,5 G)s1 + Gs2 = (р sin a -
(е)
Подставляя сюда числовые данные, имеем
s'i+3s2 = 0. I
Отсюда
1 Т^ б' 2	"р3 С>'
10	10
Задачи типа III
В задачах этого типа рассматриваются малые колебания
системы с одной (первая группа) или двумя (вторая группа)
степенями свободы около положения устойчивого равновесия.
В этих задачах положение устойчивого равновесия следует при-
принять за начало отсчета обобщенных координат и, далее, пользуясь
уравнениями Лагранжа. составлять дифференциальные уравне-
уравнения движения системы.
Эти уравнения получаются, вообще говоря, нелинейными.
Однако, если заранее известно, что обобщенные координаты
и обобщенные скорости являются малыми величинами, то
полученные уравнения можно линеаризовать. Линеаризованные
уравнения получаются из данных нелинейных уравнений путем
отбрасывания членов, содержащих квадраты и более высокие
степени обобщенных координат и скоростей. Например, при
малых значениях координаты а можно положить sin а яз а;
cosa=^l. Члены, содержащие а2, а2, аа, следует отбросить.
Первая группа
(задачи 1243—1247)
Пример 188. Составить дифференциальное уравнение малых
колебаний системы, показанной на рис. 226, около ее равновес-
равновесного положения и найти период этих колебаний, если известны
массы ш, и т2 грузов AnD, жесткость с пружины BE и длины
стержней OA = lx, OB = 0C = CD = l2. Массами пружины и стер-
стержней, а также размерами груза А можно пренебречь. При го-
горизонтальном положении стержня АВ вес груза А уравновеши-
уравновешивается силой упругости пружины. При малых отклонениях
системы от равновесного положения можно считать, что пружина
остается вертикальной.
15 Зак 2 3 i	405

Решение За обобщенную координату данной системы
с одной степенью свободы принимаем угол а отклонения стержня
АВ от горизонтали, отсчитываемый от
оси х против часовой стрелки, тогда
имеем уравнение Лагранжа:
Вычисляем кинетическую энергию си-
системы:
Т = ¦
m,
где vA и vD— скорости грузов А и D,
но
= lla и vD = yD=~
поэтому
= j {mj) + 4тJl sin8 a) a2.
При малых колебаниях системы можно пренебречь малой
величиной 4-го порядка sin'aa2. Тогда Т = ~11аг.
Вычисляем потенциальную энергию системы:
П = mxg{h—yA) + m2g (h—yD) + ~ =
— ^ sin a) + mtg{h~<ll^ cos a) + -^ ,
Где h—высота точки О над поверхностью земли, К—удлинение
пружины, причем
Я = Хст + /2 sin a,
где Я,Ст—статическое удлинение пружины при равновесном по-
положении системы.
Следовательно,
Л — (m, + ms)gh~m1 gl, sin a—2msgZ2 cos a + \ (^CT + К sin a)'.
Теперь находим
дТ ,f d /дТ \ ,i- дТ
Вычисляем обобщенную силу как взятую с обратным знаком
частную производную от потенциальной энергии по обобщенной
406

координате:
Q = —^ = m,g/, cos a—2m2gZ2 sin а—с (Хст +/2 sin а)/2 cos а.
Так как при равновесном положении системы сумма моментов
относительно точки О сил, приложенных к рычагу АВ (веса
груза А и силы упругости пружины), равна нулю, то m,g/, =>
— clcjs; поэтому
Q = — Bm3g/2 -We/! cos a) sina = — /2 Bm2g + d2 cos a) sin a.
При малых колебаниях системы около положения равновесия
ввиду незначительности угла а можно положить
sina^a и	l
Тогда
Подставляя найденные значения производных -п (~т-), -г- и
at \ да/ аа
обобщенной силы Q в уравнение Лагранжа, получим дифферен-
дифференциальное уравнение малых колебаний данной сиешмы
или
а + /г2а=0,
где
-
Мы получили дифференциальное уравнение гармонических коле-
колебаний с круговой часготой k. Период этих колебаний равен
¦/-=
2д
k
Втора я группа
(задачи 1219, 1301, 1303, 1304)
Пример 189. Два однородных сплошных цилиндра общим
весом Р,, жестко закрепленные на оси, толщиной и массой ко-
которой можно пренебречь, образуют скат, опирающийся на гори-
горизонтальные опоры (рис. 227). На той же оси свободно насажен
тонкий стержень длиной I, несущий на конце' точечный груз А
весом Р2. Определить движение этой системы, пренебрегая массой
стержня и предполагая, что отклонения маятника СА от верти-
вертикали весьма малы; трение в узле С отсутствует и цилиндры
катятся но опорам без скольжения (рис. 227).
15*	407

Решение. В данном случае рассматривается система с двумя
степенями свободы. Координатные оси располагаем так, как ука-
указано на рис. 227. В качестве обобщенных координат выбираем
абсциссу х точки С и угол ф
отклонения стержня СА от
вертикали. В соответствии с
этим в данной ?адаче состав-
составляем дна уравнения Лагран-
жа:
дх
dt I Ox
d_fdj
dt \dcp
Обозначив общую массу
цилиндров через т,, а массу
груза А через т2, вычисляем
кинетическую энергию Т си-
системы, которая слагается из кинетической энергии 7\ цилиндров
и кинетической энергии Т2 груза А, причем
где vc и vA—скорости ючек С и Л, со —угловая скорость
цилиндров, a Jc—момент инерции цилиндров относительно оси
вращения, проходящей через точку С. Следовательно,
Т = Т +Т —¦
I
При этом
и © =
'IT
где R — радиус цилиндров.
Для определения скорости точки А выразим ее декартовы
координаты хА и уА через выбранные обобщенные координаты
хД = x-\-l sin ф, г/^ = /со5ф.
Отсюда
л:л = х + / соь фф, ул = — / sin фф.
Следовательно, v\ = х\ + Ул = (# + ^ соь ффJ +12 sin2 ффг =*
= хг 4- /2 соэ'срф2 + 2хгр / cos ф +12 sin2 фф2 = ха + /2ф2 + 2xipl cos ф.
Теперь получаем
mjx2
403

Отсюда
— = A 5 m i/и)
дх 'i2
- ] — A,5m, i-m2) х-\-тг1 (ф соьф—ц>2 sincp);
-т- = A,5т. I m2)i+m/фсоэф;
дх
ml( /ф+дссозф); ^ (^
Оф	ul ЧОф
ч (ЭТ	, •
— лхр sin ф), ^- = — т2г лгф sm ф.
Обобщенные силы Qx и Q находим по общим формулам B47).
Замечая, что Р1Х=Р2Х = 0, Р,у = Р„ Р,У = Я„
г/с = 0 и г/„ = / cos ф,
на основании этих формул получаем
о =р ^ + р дм^о
Так как в данной задаче система находится под действием
сил тяжести, для которых существует силовая функция, ю
обобщенные силы можно опре 1елить и по формулам B49). Си-
Силовая функция для сил Р1 и Р_, имеет вид
V = P,yc + PtyA = P1
Следовательно,
п ди п г\ ди п , ¦	i ¦
Q* = d7 =¦ °- Qv = ^ = ~" Р>l sin ф = — т* "l sm (Р-
Таким образом, уравнения Лагранжа принимают вид
A,5т, + т2) х + т%1 (фсоэф—ф2 sin ф) = 0,
Так как по условию задачи отклонения маятника С А от вер-
вертикали весьма малы (г. е. координата ф и ее первая производная
по времени являются весьма малыми величинами), то полученные
точные дифференциальные уравнения движения системы можно
заменить более простыми приближенными уравнениями, полагая
эШфраф и соэф«Л. Кроме того, произведение ф2 sin ф является
малой величиной более высокого порядка, чем остальные члены;
поэтому можно положить ф2 БШфя»0; тогда получаем прибли-

женные уравнения Лагранжа:
(а)
(б)
Из уравнения (а) имеем
тЛ
х = —г-=—-,	ф.
1, 5т, + тг т
Первое интегрирование этого уравнения дает
^—	т4
После вторичного интегрирования получаем
Для того чтобы определить функцию ф, из уравнений (а) и
(б) исключаем х:
1,5/и, + тг
ИЛИ
1,5/п,/ф h(l,5
или
Вводя обозначение
имеем
Общее решение этого уравнения будет
Ф = С, cos kt + Ct sin ^i,
откуда
Следовательно,
x = С,* + С, — 15mffl8|OT (С, cos kt -f C4 sin kt).
Полученные уравнения, выражающие координаты х и ф как
функции времени /, и апределяюг движение рассматриваемой
системы. Произвольные постоянные С,, С2> С, и С4 определяются
по начальным условиям движения системы. В начальный момент

при t =0 имеем
cp0
Пусть
X
Тогда
и, следовательно,
где
Пример 190. Крановая тележка (рис. 228) массой т1 = 22000 кг
наезжает со скоростью уо=1 м\сек на упругий буфер, жесткость
которого с = 8700 н\см. В центре тяже-
тяжести А тележки подвешен груз В мас-
массой тг = 20400 кг на каната длиной
1= 14 м Определить движение тележки
и груза после соприкосноЕендя тележ-
тележки с упором, пренебрегая массой ка-
каната.
Решение. В качестве обобщенных
координат данной системы с двумя сте- пв-
пенями свободы принимаем перемеще-
перемещение s тележки с момента соприкоснове-
соприкосновения с упором и угол ф отклонения ка-
каната от вертикали, который в началь-
начальный момент равен нулю. Если рас-
рассматривать груз как материальную точку, то кинетическая энер-
энергия системы равна
Т =
m,
''«"В
где скорость тележки vA = s, а скорость vB груза —геометриче-
—геометрическая сумма переносной скорости, равной vA, и относительной
скорости (по отношению к гележке) и' = /ф и направленной пер-
перпендикулярно к АВ. Поэтому
v%= va i-o' -f- 2vAv' соэф = s2 -f /*ф* +2sl<p
и, следовательно,
1 = (m, f mt) ^ + ~г (iy -t- 2lys созФ).
41»

Так как сжатие пружины равно, очевидно, s, то потенциаль-
потенциальная энергия данной системы равна
2— cos<p).
Отсюда
д-= —m2Z<pssmq), —^ = т2 (/2ср 4 /s cos го),
°Ф	dip
HAdV = m2 (»P + SC0SCP—S(P эшф), g^ = "i2g/sin ф,
¦^- = (m,+m2) s+m8/9 cos ф, -^ = 0,
М (—г- J = (т, + т2) s + та/ cos фф —mjcp2 sin ф,
ал
Составляя теперь для данной системы два уравнения Лаг-
ранжа, получаем
(т, + т2) s + oij/ф coscp + cs — тгЩ 2sin ф;
s cos ф + /ф + g sin ф = 0.
Считая, что в данном случае угловая скорость ф и угол ф
отклонения каната от вертикали при движении остаются неболь-
небольшими, полученные уравнения можно заменить приближенными
уравнениями, полагая sin ф ж ф, cos ф да 1 и пренебрегая членом,
содержащим ф2. Тогда получаем следующую систему двух линей-
линейных дифференциальных уравнений:
ms -f mjy -f cs = 0; ^
0 |
где m = mi +m2.
Частные решения уравнений (а) ищем в виде
s = At sin (kt -(-а) и ф = Л2 sin (kt -\ a).
Подставляя эти выражения и их вторые производные в урав-
уравнения (а) и сокращая эти уравнения на s'm(kt + u), имеем
(с—ткг) Al—mJktA1 = 0; —AM, + (g-/62) Л, = 0,
или
Л2	с—mks	 k2 	,
Отсюда получаем следующее уравнение частот:
(с—mk2)(e-lk2)—m,/&4 = 0.
41S

После упрощении это уравнение принимает вид
или
kl — pk2 4-9=0,
где
^ 40
Решая уравнение частот, находим
и q =^-=27,9,
4 mxl
откуда
ft, да 0,8 сек-1 и &2 ж 6,3 се/с.
Таким образом, для отношения амплитуд получаем два зна-
значения:
c—mk\ k\	c—mkl kl
'к =-	' =	— =0,76 и А2 =	- = —^— = — 0,07.
1 тг1к\ g—lk\	2 mj,k\ g—lk\
Обозначая через А[1} и А[и амплитуды, соответствующие
первой частоте klt а через А\2) и А^ амплитуды, соответствую-
соответствующие второй частоте fe2, имеем
Итак, получаем две системы частных решений уравнений (а).
Первая система:
m(kJ 4-at) и
ФA) = Л'1' sin (Jfe,< +«4) =^И<.1) sin (^
Вторая система:
s<2> = Л12) sin (kj + а„) и фсг> = Л*2) sin (ft.Z+a,) = X,А[2) sin
где а, и а2 — начальные фазы, соответствующие частотам &, и /г2.
Первая система частных решений соответствует так назы-
называемому первому главному колебанию рассматрива-
рассматриваемой механической системы, вторая система частных решений
соответствует в т о р о м у главному колебанию.
В силу линейности исходных дифференциальных уравне-
уравнений (а) общее решение этих уравнений складывается из част-
частных решений, т. е.
(б)
sin (kj + a,) 4- КЖА\*' sin {kj -f a2). '
Ш

В этих уравнениях /41", А\*\ а, и а2 являются произволь-
произвольными постоянными, которые определяются по начальным усло-
условиям движения системы.
Дифференцируя уравнения (б) по времени *, имеем
% cos (*,* +og--Mi1'*, cos (*,/ + <*,); \
Ф = к,Л1,11[k, cos (ft,* + о,) + XtA?% cos (kj + az). ]
В рассматриваемом примере so = O, фо = 0, so = o0, ф0 =0
при /==0,
Подставляя эти значения в уравнения (б) и (в), имеем
0 = А?} sin а, + А[г) sin а8; 0 = ^Л*" sin а, + А.,Л}" sin а4;
Vt=A<?)klcosat + A(,2)fe2cosa2; 0 = Д^'Х.^, cos a, +A^\kt cos a,.
Из этих уравнений находим
Таким образом,
s = 0,11 sin 0,8t -t- 0,14 sin 6,3*;
Ф = 0,08 sin 0,8*—0,01 sin 6,3*.
Рассмотрим еще второй способ решения полученной системы
(а) двух линейных дифференциальных уравнений второго порядка:
s + /ф + gq>
cs = O, \
= 0. |
Путем последовательного дифференцирования каждого из
уравнений этой системы находим
d's . , d'm ds n \
dt* ' Л* +g Л u*
d's , ,dl
d4(P
(Д)
Исключая сначала из этих шести уравнений обобщенную ко-
координату ф и ее производные, а затем координату s и ее производ-
производные, получаем два независимых друг от друга линейных диф-
414

ференциальаых уравнения четвертого порядка:
dS , mg + cl dfs,	_?g.s== q
dt* m,/ dt2	tnj '
<Pq> . mg + cl d*(p	. eg q
dt* mxt dt2 mj. ' '
или, введя опять обозначения —а—j— = р, —, = q,
d*s . d
Составим характеристическое уравнение, соответствующее
каждому из уравнений этой системы.
Корни этого уравнения равны:
Следовательно, решение уравнений (е) имеет вид
sin k.t + C. coskj-{-C.s'm kj; }
Ф = С, cosfe,/-(- C2 sin ftj/ -f C3 cos^^T-Clsin kj, j *¦
где С,, C2, C8, C4, C^, C't, C',, C\ — произвольные постоянные.
Перейдем к определению этих постоянных, для чего восполь-
воспользуемся начальными условиями движения. Полагая в уравнениях
(а) и (г) / = 0 и учитывая, что по условиям задачи se = 9o = 0,
Фо = 0, so = va, имеем
"" "J"""lm ~П '	(а')
Решая каждую из этих систем в отдельности, получим
Теперь определяем постоянные Ct, С,, Ct, Cv Для этого

вычислим из первого из уравнений (ж) производные s, s, s:
s = — С,/г, sin kj +C2k, cos kj — Csk2 sin kj -\-Ctk2 coskj, "j
s = —C^tcosfe,/ — C^sinV — C3klcoskJ—CfitsinkJ, \ (з)
s = C,/feJ sin kJ — CJi\ cos /fe/ + C8/fe23 sin kJ—Cfil cos *аЛ J
Полагая в этих равенствах и в первом из уравнений (ж)
? = 0, получим следующую систему четырех уравнений относи-
относительно неизвестных С,	С4:
s = — С k\ — С k\ = 0,
о	-	СУл
mi
Решая совместно первое и третье уравнения, находим
С, — Ct — Q. Из второго и четвертого уравнений имеем
откуда
Таким образом,
Аналогично, для определения постоянных Си С2, С3, С4
получим следующую систему четырех уравнений:
1 О ^ /ь ^ 1_* згС ;> ~~~ Vj j
Отсюда находим С, — Сэ = О, С2 = ¦
Т > и* следовательно,
i- sin Ai.t—i- sin
^i sin Ai.ti-
Подставляя в полученные уравнения числовые данные, приходим
к прежним результатам.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Н Н. Бухгольц, И М. Воронков, А. П. Минаков Сбор-
Сборник задач по теоретической механике. М., Гостехтеоретиздат, 1949
Н А. Бражниченко, В. Л. Кан, Б Л. Минцберг,
В И. Морозов Л., Сборник задач по теоретической механике. Суд-
промгиз, 1962
И М. Воронков Курс теоретической механики. М., Гостехтеорет-
Гостехтеоретиздат, 1957 и последующие издания.
Л. Г. Л ой ця не кий и А. И, Лурье. К^рс теоретической меха-
механики, ч. I и II М., Гостехтеоретиздат, 1954, 1957 и последующие издания.
Е. Л. Николаи Теоретическая механика, ч. I и II. М., Гостехтео-
Гостехтеоретиздат, 1957 и последующие издания.
В М. Осецкий. Сборник задач по теоретической механике Дина-
Динамика. Под редакцией проф. И. М Воронков а. М., 1962.
В. М. Осецкий Техническая механика. М., Госгортехиздат, 1962.
С М. Т а р г. Краткий курс теоретической механики. М., Физмат-
гиз, 1958.
А А. Яблонский, В. М. Никифорова. Курс теоретической
механики, ч. I. M., Высшая школа, 1962
А А Яблонский. Курс теоретической механики, ч. II, М., Выс-
Высшая школа, 1962.

ОГЛАВЛЕНИЕ
Предисловие 		3
Раздел \ СТАТИКА
Глава 1. Сходящиеся силы		5
$ 1. Сложение сил, сходящихся в одной точке		5
§2. Разложение силы на составляющие		14
§3 Связи и реакции связей 		19
§4. Равновесие системы сходящихся сил		22
Г л d в а II Плоская система сил		40
§1. Приведение плоской системы сил к данному центру		40
§2. Равновесие рычага		44
§3. Равновесие твердого тела под действием плоской системы сил .	48
§4. Равноресие системы, состоящей из нескольких твердых тел . .	58
Глава 111. Равновесие<цри наличии трения		72
Глава IV. Система сил, расположенных как угодно в пространстве . .	84
§ 1. Момент силы относительно точки как вектор и момент силы
относительно оси 	4		84
§ 2. Приведение произвольной системы сил к данному центру . .	90
| 3. Равновесие системы сил в пространстве		100
Глава V Центр тяжести		125
Раздел II. КИНЕМАТИКА
Глава 1. Кинематика точки .		142
J 1. Задачи типа 1		144
§ 2. Задачи типа II		147
§ 3. Определение скорости и ускорения точки при естественном
способе определения движения точки 		155
§ 4. Комбинированные задачи		159
Глава II. Вращение твердого тела вокруг неподвижной оси ....	162
$ 1. Определение угла поворота, угловой скорости и углового уско-
ускорения твердого тела, вращающегося вокруг неподвижной оси	163
§ 2. Определение скоростей и ускорений точек твердого тела,
вращающегося вокруг неподвижной оси		164
§ 3. Передача вра,нательного движения от одного тела к другому	167
416

Глава Ш. Плоскопараллельное движение твердого тела	169
§ 1. Уравнения движения плоской фигуры .	jg9
§ 2. Определение скоростей точек плоской фигуры', 'движущейся
в своей плоскости			172
§ 3 Центроиды	!!!""!."	179
§ 4. Определение ускорений точек плоской фигуры \ [ '. \ [ \ \	183
Глава IV. Составное движение точки	 ^	^ J97
§ 1. Уравнения движения и траектория составного движения точки 197
§ 2 Теорема сложения скоростей	201
§ 3 Теорема сложения ускорений при переносном поступательном
движении 	207
§ 4 Теорема сложения ускорений при переносном вращательном
движении 	214
Глава V. Составное движение твердого тела	220
§ 1 Общие замечания 	220
§ 2 Сложение вращений твердого телз вокруг параллельных осей 222
§ 3. Сложение вращений твердого^ тела вокруг пересекающихся осей 227
Раздел 111. ДИНАМИКА	236
ДИНАМИКА ТОЧКИ 	236
Глава 1 Две основные задачи динамики точки	236
§ 1 Дифференциальные уравнения движения материальной точки 236
§ 2 Первая основная задача динамики точки	237
§ 3. Вторая основная задача динамики точки	244
Глава II. Колебательное движение материальной точки	267
$ 1 Свободные колебания 	268
§ 2 Затухающие колебания 	272
§ 3. Вынужденные колебания	275
Глава Ш Общие теоремы динамики и принцип Даламбера для
материальной точки 	 280
§ 1	Теорема о количестве движения	280
§ 2	Теорема о моменте количества движения 	292
§ 3	Pa6oTJ и мощность 	295
§ 4	Теорема о кинетической энергии материальной точки	306
§ 5	Принцип Даламбера для материальной точки	318
ДИНАМИКА СИСТЕМЫ	324
Глава IV Общие теоремы динамики системы	 324
§ 1. Теоремы о количестве движения системы и о движении центра
масс 	324
§ 2 Теорема о кинетическом моменте системы 	335
§ 3 Теорема об изменении кинетической энергии системы	355
§ 4 Комбинированные задачи 	366
Глава V Принцип" Даламбера и принцип возможных перемещений 371
§ 1. Принцип Даламбера для системы материальных точек	371
§ 2 Принцип возможных (виртуальных) перемещений	384
§ 3 Общее уравнение динамики (уравнение Даламбера—Лагранжа 391
§ 4 Уравнения Лагранжа II рода (дифференциальные уравнения
движения системы в обобщенных координатах)	395
Рекомендуемая литература	417

Айзенберг Татьяна Борисовна
Воронков Иван Михайлович
Осецкий Всеволод Михайлович
РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
Редактор 3. Г. Овсянникова
Технический редактор В А, Зорина
Корректор М И Козлова
Т-02424. Сдано в набор 10/IX 64 р. Подп. к печати 9/VI-65 Формат 60x90Vw.
Объем 26,25 печ. л. Уч.-изд. л. 24,08. Изд. № ОТ-162 Тираж 50 000 экз.
Зак. 2374, Цена 82 коп
Москва, К-51, Неглинная ул., д 29/14.
Издательство «Высшая школа»
БЗ —39/30 от 30/V-68 i.
Отпечатано с матриц Первой Образцовой типографии имени А. А. Жданова
в Московской типографии Л° 4" Главполиграфпрома
Комитета по печати при Совете Министров СССР
Б. Переяславская, 46