Author: Деннис Дж. Шнабель Р.
Tags: вычислительная математика численный анализ математика численные методы
ISBN: 5-03-001102-1
Year: 1988
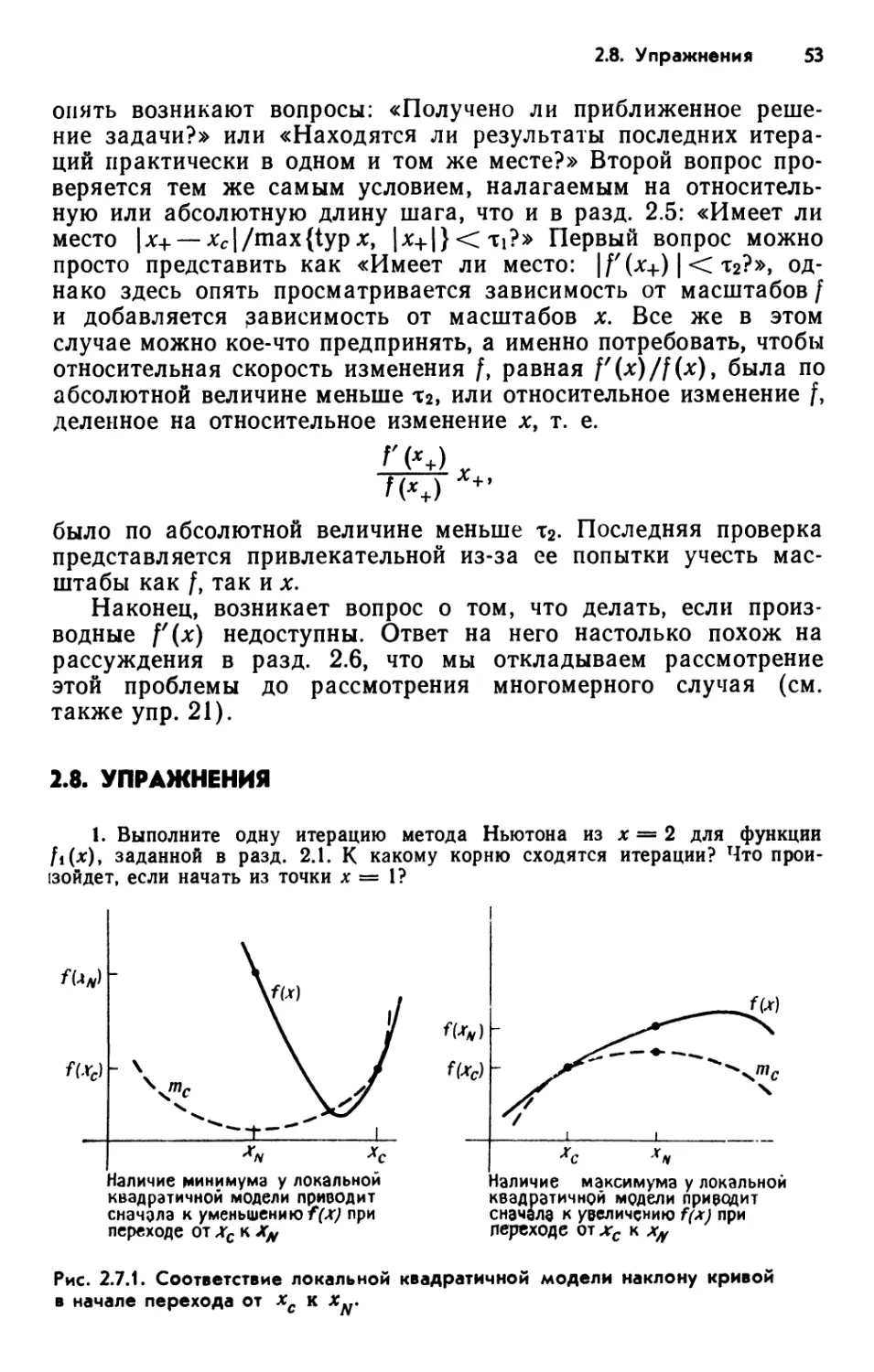
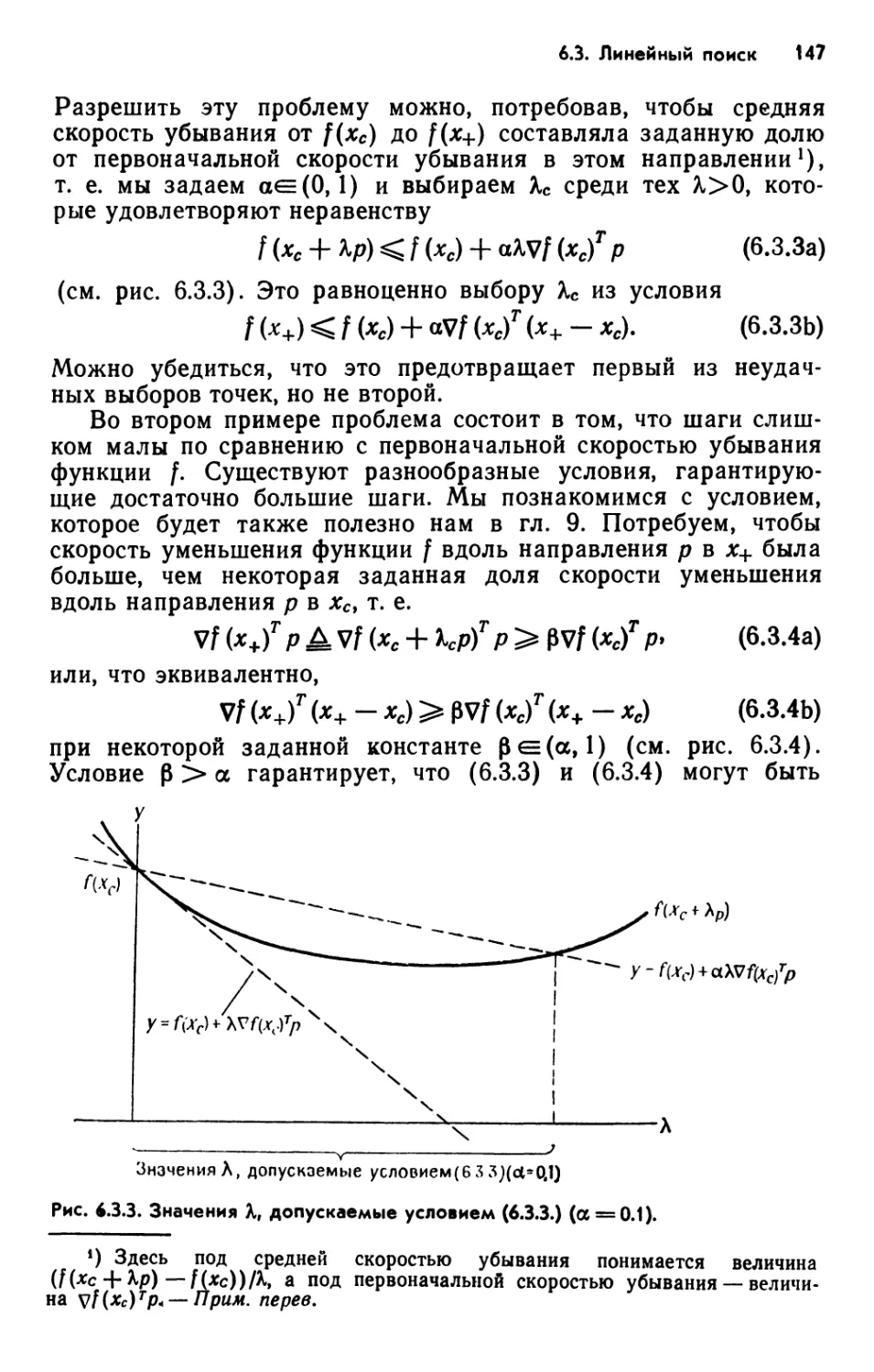
Text
Дж.Дэннис, Р.Шнабель
Численные методы
безусловной оптимизации
и решения нелинейных уравнений
/
Prentice-Hall Series in Computational Mathematics
Numerical Methods for Unconstrained Optimization
and Nonlinear Equations
J. E. Dennis, Jr.
Rice University
R. B. Schnabel
University of Colorado at Boulder
Prentice-Hall, Inc., Englewood Cliffs, New Jersey 07632
Дж. Дэннис, мл., Р. Шнабель
Численные методы
безусловной оптимизации
и решения
нелинейных уравнений
Перевод с английского
О. П. Бурдакова
под редакцией
Ю. Г. Евтушенко
Москва «Мир» 1988
ББК 22.193
Д94
УДК 519.61
Дэннис Дж., мл., Шнабель Р.
Д94 Численные методы безусловной оптимизации и решения
нелинейных уравнений: Пер. с англ. — М.: Мир, 1988. —
440 с, ил.
ISBN 5-03-001102-1
Монография известных американских специалистов, посвященная как теории
численных методов оптимизации, так и вопросам реализации этих методов на
ЭВМ. Особое внимание уделено наиболее эффективным методам ньютоновского
типа. Приведены пакеты программ решения прикладных задач оптимизации.
Для математиков-вычислителей, инженеров-исследователей, аспирантов и
студентов вузов.
Редакция литературы по математическим
наукам
ISBN 5-03-001102-1 (русск.) © 1983 by Prentice-Hall, Inc.
ISBN 0-13-627216-9 (англ.) © пеРевод на РУССКИЙ язйк* с ,оВоТо0р"
w**^ V'UU6 *1UJ \ап f скими исправлениями, «Мир», 19?§
Предисловие редактора перевода
и переводчика
Вниманию читателя предлагается книга американских
специалистов в области численного анализа Джона Дэнниса, мл., и
Роберта Шнабеля. Она посвящена двум важным и тесно
между собой связанным разделам: безусловной минимизации и
решению нелинейных уравнений. Наряду с серьезным
теоретическим материалом, отражающим современное состояние
исследований в рассматриваемой области, в книге большое
внимание уделяется вопросам программной реализации
численных методов и их преподавания в высшей школе.
Авторы сознательно ограничились рассмотрением
численных методов ньютоновского (квазиньютоновского) типа.
Класс этих методов отличает концептуальное единство и
достаточная широта охвата, причем на практике такие
методы—одни из наиболее эффективных. Общая идея методов
такова: на каждой итерации сначала строится модельная
аппроксимация исходной задачи (линейная в случае нелинейных
уравнений и квадратичная для безусловной минимизации), а
затем на основе ее решения находится новое приближение.
По такой же схеме проводится исследование сходимости.
Впервые столь подробно в литературе на русском языке
излагаются метод доверительной области, квазиньютоновские
методы типа секущих и др. Методы, не вошедшие в указанный
класс, в достаточной мере представлены ссылками на
литературу. В связи с тем что в оригинале имеется только одна
ссылка на работу советских авторов, мы решили указать несколько
отечественных монографий, содержащих обширные списки
литературы. Полагаем, что книга вполне пригодна для
формирования у читателя целостного представления о современном
состоянии численных методов минимизации и решения
нелинейных уравнений.
Более четверти книги занимают два приложения,
написанные Робертом Шнабелем. В отличие от несколько
схематичного описания алгоритмов в основной части цнрги, впрлне до-
6 Предисловие редактора перевода и переводчика
статочного для их теоретического рассмотрения, здесь
алгоритмы представлены уже с той степенью детализации,
которая требуется для их непосредственной программной
реализации. Они составляют в приложении А целостную систему
алгоритмов безусловной минимизации и решения нелинейных
уравнений. Эта система основана на модульном принципе,
ориентирована на учет особенностей машинной реализации и
хорошо документирована. При ее написании использован
условный алгоритмический язык, который вполне естественно
реализуется на Фортране, Алголе, Паскале, Си и других
языках программирования. Кстати, некоторые конструкции этого
псевдоязыка, описанного в разд. 1.3 приложения А, иногда
используются и в основной части книги. Приложение В
составляют тестовые задачи безусловной минимизации и
решения нелинейных уравнений. Как отмечали сами авторы,
любая большая система алгоритмов неизбежно содержит
опечатки и некоторые неточности. В этом авторы оказались, к
сожалению, правы. Вероятно, и мы окажемся правы, если
повторим это утверждение.
Несколько глав вводного характера делают книгу
доступной для тех, кто знаком лишь с основами математического
анализа и линейной алгебры. Изложение методически
продумано и сопровождается упражнениями. Имеются подробные
рекомендации по использованию книги в качестве учебного
пособия. При этом следует учитывать, что в США учебный
семестр длится 12—15 недель, а в неделю проводится 3
лекции, каждая около одного часа. Основная часть книги может
быть использована для чтения лекций студентам и
аспирантам, а упражнения — для проведения семинаров. Приложения
могут составить основу учебных проектов. Однако
возможности содержащейся в приложении А модульной системы
алгоритмов гораздо шире и позволяют создавать также пакеты
прикладных программ для решения практических задач.
В процессе работы над переводом возникали
всевозможные вопросы, породившие довольно интенсивную переписку с
авторами. Все исправления в книге сделаны либо с ведома
авторов, либо по их собственной инициативе. Мы выражаем
Дж. Дэннису и Р. Шнабелю глубокую признательность за
внимание к нашему труду.
Русскому изданию авторы предпослали посвящение «То
world peace», что можно перевести как «Делу мира во всем
мире». Они предложили подписаться под ним и нам, также
работавшим над книгой. Мы с радостью подписываем это
посвящение, отражающее искреннее стремление наших народов
к миру.
Ю. Г. Евтушенко
О. П. Бурдаков
Делу мира во всем мире
Дж. Дэннис, мл., Р. Шнабель,
О. Бурдаков, Ю. Евтушенко
Предисловие к русскому изданию
С большим удовольствием мы приветствуем издание этой
книги на русском языке. При ее написании мы стремились
к тому, чтобы она была полезной для студентов, научных
работников, а также для практиков, инженеров и всех тех, кто
использует методы оптимизации. На наш взгляд английский
вариант книги соответствует этим целям, и мы надеемся, что
русское издание окажется столь же полезным.
Хотя прошло уже четыре года со времени выхода в свет
первого издания на английском языке, книга на наш взгляд
практически не устарела. Основной материал книги по
безусловной минимизации и решению нелинейных уравнений, как
мы считали, стабилизировался в своем развитии в период ее
написания, и время, по-видимому, доказало правильность этой
оценки. Хотя исследования в этой области продолжались, мы
считаем, что за прошедшее время не произошло каких-либо
существенных изменений. Вероятно, наиболее важное
продвижение, о котором нам известно, заключалось в разработке
усложненных вариантов алгоритмов и программного
обеспечения для решения задачи «модель — доверительная область»
в случае, когда матрица Гессе не является знакоопределенной
(см., например, работы More, Sorensen [SIAM Journal on
Scientific and Statistical Computing 4, 1983J, Gay [SIAM
Journal on Scientific and Statistical Computing 2, 1981]), и
кроме того в широком развитии теории исследования таких
методов (см. также Shultz, Schnabel, Byrd [SIAM Journal on
Numerical Analysis 22, 1985]). Это привело к появлению
алгоритмов, которые обладают более сильными свойствами
глобальной сходимости по сравнению с приведенными в разд. 6.3.1,
и в которых удается избежать априорного возмущения незна-
коопределенных матриц Гессе в целях получения
положительно определенных матриц, как это делается в разд. 5.6. Еще
одним интересным достижением являются анализ и
вычислительный эксперимент, проведенные в недавних работах Powell
8 Предисловие к русскому изданию
[Mathematical Programming 34, 1986] и Byrd, Nocedal, Yuan
[SIAM Journal on Numerical Analysis, 1987J, которые дают
более удачное объяснение превосходству положительно
определенной формулы секущих (BFGS) над обратной положительно
определенной формулой секущих (DFP) при решении задач
безусловной оптимизации. Были достигнуты успехи также и в
некоторых непосредственно примыкающих областях, включая
глобальную оптимизацию, методы решения задач большой
размерности со специальной структурой и методы для решения
задач безусловной оптимизации и систем нелинейных
уравнений на параллельных ЭВМ.
Приведенное в приложении программное обеспечение
получило широкое распространение и было включено в другие
пакеты программ, книги-и библиотеки математического
программного обеспечения. Мы по-прежнему предоставляем это
программное обеспечение в распоряжение научных работников для
использования в исследовательских целях.
Нам хочется выразить особую благодарность О. Бурдакову
за превосходно выполненную работу по переводу. Стремясь как
можно точнее перевести книгу, он изучил ее столь тщательно,
что выявил большое количество опечаток и неточностей. Мы
признательны ему за этот вклад в укрепление международных
научных связей.
Дж. Дэннис, мл.
Р. Шнабель
Май 1987
Предисловие
Книга представляет собой подробное введение в численное
решение задач безусловной оптимизации и систем нелинейных
уравнений, не требующее от читателя глубоких знаний
математических и вычислительных дисциплин. Работа над книгой
была начата в 1977 г., поскольку мы считали, что к этому
времени алгоритмы и теория решения таких задач малой и
средней размерности достигли зрелого состояния и что был бы
полезен подробный справочный материал. Книгу можно
использовать при подготовке курса лекций для аспирантов или
студентов-старшекурсников, а также ее можно рекомендовать
для самостоятельного изучения научным работникам,
инженерам и всем, кому рассматриваемые задачи интересны с
практической точки зрения.
Минимальная подготовка, необходимая для чтения книги,—
это знание основ математического анализа и линейной алгебры.
Читатель, должно быть, в той или иной мере знаком с
математическим анализом многих переменных, тем не менее в гл. 4
приводится подробный обзор всей необходимой информации.
Несомненную пользу мог бы принести курс
вычислительной линейной алгебры или элементов численных методов;
часть этого материала кратко представлена в разд. 1.3 и
гл. 3.
Все рассматриваемые здесь алгоритмы основываются на
идее метода Ньютона. Они часто называются методами
ньютоновского типа, однако мы предпочитаем термин
квазиньютоновские методы. К сожалению, этот термин используется
специалистами лишь для подкласса методов, представленного
гл. 8 и 9. Поскольку этот подкласс состоит из естественных
обобщений метода секущих на многомерный случай, мы
предпочитаем называть их методами секущих. Конкретные
варианты методов секущих обычно носят имена своих создателей,
поэтому в тексте неизбежно встречаются соответствующие не
всегда понятные аббревиатуры. Вместе с тем мы пытались
1 0 Предисловие
предложить для них содержательные названия, отвечающие
их месту в общей схеме изложения.
Ядро книги составляет материал по численным методам
решения многомерных задач безусловной оптимизации и
нелинейных уравнений. Он представлен гл. 5—9. Глава 1 —
вводная, она принесет больше пользы студентам,
специализирующимся в чистой математике и информатике, чем читателям,
имеющим некоторый опыт в научных приложениях. Глава 2,
которая посвящена одномерному варианту рассматриваемых
задач, является иллюстрацией нашего подхода и одновременно
его обоснованием. Глава 3 может быть пропущена читателями,
уже изучавшими вычислительную линейную алгебру, а гл. 4 —
теми, кто обладает основательными познаниями в
математическом анализе многих переменных. Глава 10 дает довольно
полное изложение алгоритмов решения нелинейной задачи о
наименьших квадратах, которая относится к важному классу
задач безусловной оптимизации и из-за ее специфики решается
специальными методами. В ней существенно используется
материал предыдущих глав. В гл. 11 указываются некоторые
перспективные направления исследований; здесь отдельные
разделы сложнее, чем предыдущий материал.
Мы использовали эту книгу в учебных курсах для
старшекурсников и аспирантов. Для первых из них гл. 1—9 образуют
фундаментальный курс, а для последних может быть
использована вся книга целиком. При этом если гл. 1, 3 и 4 оставить
для самостоятельного чтения, то курс займет около половины
семестра. Оставшуюся часть семестра легко заполнить
указанными главами или другим материалом, не вошедшим в книгу.
Наибольшую важность среди опущенного нами материала
представляют методы, не связанные с методом Ньютона для
решения задач безусловной минимизации и нелинейных
уравнений. Большинство из них важны только в частных случаях.
Симплексный алгоритм Нелдера — Мида !> [см., например, Ав-
риель (1976)], эффективный для задач с менее чем пятью
переменными, может быть изложен за час. Методы сопряженных
направлений [см., например, Гилл, Мюррей и Райт (1981)]
относятся собственно к курсу вычислительной линейной
алгебры, но благодаря малому объему требуемой памяти ЭВМ они
оказываются полезными и для задач оптимизации с очень
большим числом переменных. Их можно вкратце изложить за
два часа, полное же изложение заняло бы две недели.
Наиболее трудным для нас было решение опустить методы
Брауна — Брента. Их идея изящна и они поразительно
эффективны при хороших начальных приближениях для решения си-
!) Он также известен под названием «алгоритм (демпфируемого)
многогранника» — Прим. перев.
Предисловие ff
стем уравнений, часть из которых линейны. Этим методам в
наиболее распространенной форме нельзя отдать безусловное
предпочтение в задачах общего вида. Они вряд ли где-либо
освещались так же широко, как симплексный алгоритм и
алгоритм сопряженных градиентов. Отсутствие этих методов
можно восполнить одной или двумя лекциями (опуская
доказательства) (см., например, Дэннис (1977)]. Наконец, среди
методов, имеющих важное значение, не нашли отражения
методы типа продолжения или гомотопии, работы по которым
возобновились с новой силой в 70-х гг. Эти изящные идеи
могут пригодиться как крайнее средство в исключительно
трудных задачах, хотя в целом они все же не конкурентоспособны.
На изложение превосходного обзора Алговера и Джорджа
(1980) потребуется по крайней мере две недели.
Книга снабжена большим количеством упражнений, многие
из которых содержат дальнейшее развитие идей, лишь слегка
затронутых в тексте. Большое приложение, написанное Р. Шна-
белем, имеет целью обеспечить как основами для учебных
проектов, так и важным справочным материалом для тех
читателей, кто хочет вникнуть в детали алгоритмов и, возможно,
разработать свои собственные версии. Рекомендуем читателю
на раннем -этапе чтения ознакомиться с предисловием к
приложению.
Некоторые вопросы терминологии и обозначения вызвали
особенные трудности. Ранее уже упоминалось о смешении
понятий «квазиньютоновские методы» и «методы секущих».
Кроме того, в заглавии книги мы использовали термин
«безусловная оптимизация», а в тексте — «безусловная минимизация»,
поскольку в действительности рассматривается только
минимизация, а задача максимизации очевидным образом сводится
к минимизации. Важный термин «глобальный» часто
интерпретируется по-разному, поэтому в разд. 1.1 пояснено, как
именно он понимается в книге. Наконец, основная проблема в
обозначениях состояла в том, чтобы различать между собой
/-ю компоненту л-мерного вектора (скаляр, обычно
обозначаемый как xi) и i-ю итерацию в последовательности таких
векторов х (вектор, также обычно обозначаемый как *,•). После
нескольких неудачных попыток было решено допустить эту
неоднозначность в обозначениях, поскольку подразумеваемый
смысл всегда понятен из контекста. В действительности это
обозначение редко используется в обоих смыслах в одном и
том же разделе.
Нам хотелось без ущерба для изложения сделать книгу
настолько краткой и недорогой, насколько это возможно. Исходя
из этого, безжалостно редактировались некоторые
доказательства и целые темы. Мы старались использовать обозначения,
отвечающие тонкому вкусу и одновременно лучшему понима-
12 Предисловие
нию, и включать доказательства, способствующие хорошему
усвоению предмета, опуская те, которые всего лишь
устанавливают справедливость утверждений. Мы ожидаем больше
критики в отношении того, что было опущено, нежели в
отношении того, что включено. Однако, как известно каждому
преподавателю, наиболее трудной и важной частью составления
учебного курса является решение о том, что следует опустить.
Мы искренне благодарим Идалию Келлар, Арлин Хантер
и Долорес Пендел за перепечатку многочисленных вариантов
рукописи, а также студентов за их поразительную способность
отыскивать неясные места. Дэвид Гэй, Вирджиния Клема, Хо-
мер Уолкер, Пит Стюарт и Лэйн Уотсон использовали
черновой вариант книги в курсах лекций в Массачусетском
технологическом институте, Лоренцевской лаборатории Ливермора,
Университете Хьюстона, Университете Нью-Мексико,
Университете Мериленд и Вирджинском политехническом институте и
внесли полезные предложения. Тронд Стейхауг и Майк Тодд
высказали ряд удачных замечаний по некоторым разделам.
Дж. Дэннис, мл.
Райсовский университет
Р. Шнабель
Университет Колорадо
в Боулдере
Прежде всего одно программное замечание
В первых четырех главах книги содержатся вводные сведения и излагаются
побудительные мотивы к исследованию многомерных нелинейных задач.
В гл. 1 вводятся задачи, которые будут обсуждаться в дальнейшем. Затем в
гл. 2 приводятся некоторые алгоритмы решения нелинейных задач только
одной переменной. Излагая эти алгоритмы так, чтобы отразить основные
идеи всех рассматриваемых далее в книге нелинейных алгоритмов, мы
надеемся тем самым обеспечить читателя доступным и прочным фундаментом
для исследования многомерных нелинейных задач. В гл. 3 и 4 содержится
материал по основам вычислительной линейной алгебры и многомерного
анализа, необходимый для перехода к задачам более чем одной переменной.
1
Введение
В книге приводятся и анализируются методы и алгоритмы
численного решения трех важных нелинейных задач: решение
систем нелинейных уравнений, безусловная минимизация
нелинейного функционала и задача оценки параметров по
нелинейному принципу наименьших квадратов. В разд. 1.1 даются
постановки этих задач и предположения, в рамках которых они
в дальнейшем будут рассматриваться. В разд. 1.2 приводятся
примеры нелинейных задач и обсуждаются характерные
особенности задач, встречающихся на практике. Читатель, уже
знакомый с кругом таких задач, может при желании
пропустить этот раздел. В разд. 1.3 резюмируются особенности
машинной арифметики конечной точности, которые необходимо
знать читателю для понимания машинно-зависимых элементов
обсуждаемых в тексте алгоритмов.
1.1. ПОСТАНОВКИ ЗАДАЧ
В настоящей книге рассматриваются три часто встречающиеся
на практике нелинейные задачи с действительными
переменными. Хотя при довольно естественных предположениях они
с математической точки зрения эквивалентны, мы не будем
применять для всех них одни и те же алгоритмы. Вместо этого
будет продемонстрирована способность наилучших среди
имеющихся в настоящее время алгоритмов учитывать специфику
каждой задачи.
Среди трех задач, с которыми мы будем иметь дело,
решение систем нелинейных уравнений, называемых далее
«нелинейными уравнениями», является самой основной. Вместе с
тем она имеет меньше всего специфических особенностей,
учитываемых в алгоритмах. Задача состоит в следующем:
задано: F:Rn->Rn,
найти ^sR", для которого F (*J = 0 <= R", (1.1.1)
1.1. Постановки задач 15
где Rn обозначает n-мерное евклидово пространство.
Представление (1.1.1) есть один из стандартных способов задания
системы из п уравнений с п неизвестными, при котором правая
часть каждого уравнения полагается равной нулю. Примером
служит
где F (*,,) = 0 при *» = (1,— 2)г.
Несомненно, что х*> являющееся решением (1.1.1), будет
точкой минимума для
t(fi(x))\
где fi(x) обозначает i-ю компоненту функции F. Это частный
случай задачи безусловной минимизации:
задано: /:R*-*R,
найти Jt.eR'1, для которого f(xm)^.f(x) при всех x^Rn.
(1.1.2)
Это вторая из рассматриваемых далее задач. Обычно (1.1.2)
кратко записывается как
min/:R"-*R. (1.1.3)
Примером служит
min / (хи хъ *3) = (*1 - З)2 + (х2 + 5)4 + (х3 - 8)2,
x<=Rn
где решение есть jc# = (3, —5, 8)г.
В некоторых приложениях представляет интерес задача
(1.1.3) с ограничениями
min /:R"->R, (1.1.4)
где Q — замкнутая связная область. Если решение задачи
(1.1.4) лежит внутри Q, то (1.1.4) еще можно считать
задачей безусловной минимизации. Но если л:*—граничная точка
области Q, то минимизация / на Q становится задачей
условной минимизации. Эта задача рассматриваться не будет
потому, что способы ее решения менее изучены, чем в задаче
безусловной минимизации, а, имея дело с последней, нам и
без того есть чем заняться. К тому же техника решения задач
без ограничений служит основой для алгоритмов решения
задач с ограничениями. Многие подходы к решению задачи с
ограничениями фактически сводятся либо к решению некото-
16 Гл. 1. Введение
рой родственной ей задачи безусловной минимизации, чье
решение х по крайней мере очень близко к решению х* задачи
с ограничениями, либо к построению системы нелинейных
уравнений, решение которой совпадает с х+. Наконец, большой
процент задач, которые встречались нам на практике, суть задачи
или без ограничений или же с ограничениями, но очень
простого вида (к примеру: каждая компонента х должна быть
неотрицательной).
Третья из рассматриваемых задач также является частным
случаем безусловной минимизации, но из-за ее важности и
специфичной структуры, она представляет самостоятельный
интерес для исследования. Это нелинейная задача о
наименьших квадратах:
задано: R: Rn -> Rm, m > n,
m
найти x0 e R", для^которого £ (rt (x))2 минимально, (1.1.5)
где через ri(x) обозначена /-я компонента функции R. Задача
(1.1.5) наиболее часто встречается при проведении кривой по
точкам. Она также может возникать всякий раз, когда в
нелинейной системе количество нелинейных связей превосходит
число степеней свободы.
Мы будем иметь дело исключительно с тем весьма общим
случаем, когда нелинейные функции F, f и R
дифференцируемы соответственно один раз, дважды и дважды непрерывно.
При этом нет необходимости предполагать, что имеются
аналитически заданные производные, а всего лишь, что функции
достаточно гладки. Дальнейшие замечания относительно
характерных размеров и других характеристик решаемых на
сегодняшний день делинейных задач можно найти в разд. 1.2.
Весьма типичным при численном решении нелинейной
задачи является такой сценарий. Пользователя просят задать
процедуру для вычисления функции (функций),
фигурирующей в постановке задачи, и начальную точку *0, т. е. грубое
приближение к решению х*. Если это не вызывает особых
трудностей, то пользователя просят задать первые и,
возможно, вторые производные. В книге особый акцент делается на
трудностях, наиболее часто встречающихся при решении
задач. Они укладываются в рамки следующих вопросов: (1) что
делать, если начальное приближение хо не близко к решению х+
(«глобальный метод»), и как это эффективно сочетать с
методом, использующимся вблизи от решения («локальный
метод»); (2) что делать, если в нашем распоряжении нет
аналитически заданных производных; (3) разработка алгоритмов.
эффективных в тех случаях, когда вычисление функции
(функций), определяющей задачу, стоит дорого (часто это именно
1.1. Постановки задач 17
так, причем стоимость порой становится критическим
фактором). Будут рассмотрены основные методы и описаны детали
алгоритмов, являющихся в настоящее время наилучшими для
решения таких задач. Будет также дан анализ того, что, по
нашему убеждению, имеет непосредственное отношение к
пониманию этих методов и к возможности их дальнейшего
обобщения и улучшения. В частности, мы попытаемся выделить,
специально заострив на них внимание, идеи и методы,
которые в результате их развития заняли центральное место в
данной области. На наш взгляд, эта область достигла состояния,
когда упомянутые методы легко выделяемы, и хотя все же
возможны некоторые усовершенствования, в будущем не
следует ожидать новых алгоритмов, которые привели бы к
заметному скачку вперед по сравнению с теми, что считаются
на сегодня наилучшими.
Методы решения нелинейных уравнений и задач
безусловной минимизации тесно связаны. Большая часть книги
посвящена этим двум задачам. Нелинейная задача о наименьших
квадратах есть всего лишь частный случай безусловной
минимизации, однако можно так модифицировать методы
безусловной минимизации, учитывая преимущества специфики
нелинейной задачи о наименьших квадратах, что для нее в
результате получатся более эффективные алгоритмы. Таким
образом, гл. 10 в действительности является развернутым
иллюстративным примером, демонстрирующим то, как
применять и обобщать предшествующий этому материал книги.
Одна задача, к которой мы не обращаемся в книге,
заключается в нахождении «глобального минимума» нелинейной
функции, иными словами, самого наименьшего значения f(x)
в случае, когда имеется много изолированных локальных
минимумов, т. е. решений задачи (1.1.2) в открытых связных
областях пространства Rn. Это очень сложная задача, о которой
нельзя сказать, что она так же широко изучена и успешно
решается, как и рассматриваемые нами задачи. Данной теме
посвящены два сборника статей под ред. Диксона и Сегё
(1975, 1978). На протяжении всей книги используется термин
«глобальный», например в сочетаниях «глобальный метод» или
«глобально сходящийся алгоритм», для обозначений метода,
в котором обеспечивается сходимость к локальному минимуму
нелинейной функции или к некоторому решению системы
нелинейных уравнений почти из любой начальной точки. Было бы
видимо удачнее называть такие методы локальными или
локально сходящимися, однако, согласно традиции, эти термины
уже зарезервированы для использования в другом смысле.
Любой метод, для которого гарантируется сходимость из любой
начальной точки, вероятно, в общем случае весьма
неэффективен [см. работу Алговера и Джорджа (1980)].
18 Гл. 1. Введение
1.2. ХАРАКТЕРНЫЕ ОСОБЕННОСТИ ВСТРЕЧАЮЩИХСЯ
НА ПРАКТИКЕ ЗАДАЧ
В этом разделе мы попытаемся дать некоторое представление
о нелинейных задачах, встречающихся на практике. Сначала
будут приведены три реальных примера нелинейных задач и
некоторые соображения относительно их постановки как
вычислительных задач. Затем будет сделано несколько замечаний
по поводу размера, стоимости и других характеристик обычно
встречающихся нелинейных задач.
Обсуждение модельных задач затруднено тем, что
происхождение и алгебраическое описание задач из этой области
редко оказываются простыми. Хотя все это довольно интересно,
но не для вводной главы книги по численному анализу.
Поэтому наши примеры будут по мере возможности упрощены.
Наиболее простыми среди нелинейных задач являются
задачи с одной переменной. Например, исследователь хочет
определить молекулярную конфигурацию некоторого соединения.
Он выводит выражение f(x), задающее потенциальную
энергию возможной конфигурации как функцию переменной х,
представляющей собой тангенс угла между ее двумя
компонентами. Затем, поскольку природа заставит молекулу принять
конфигурацию с минимальной потенциальной энергией,
желательно найти такое лг, для которого f(x) минимально. Это
задача минимизации с единственной переменной х. Из
физического смысла функции / ясно, что она сильно нелинейна. Верно
и то, что она является задачей безусловной минимизации, так
как х может принимать любое действительное значение.
Поскольку эта задача имеет только одну переменную, она
должна бы легко решаться методами из гл. 2. Однако мы
сталкивались с аналогичными задачами, в которых f была функцией
от 20 до 100 переменных, и хотя эти задачи не были трудными
для решения, но каждое вычисление / стоило от 5 до 100 долл.,
так что они оказались дорогостоящими для решения.
Другой широко известный класс нелинейных задач связан
с выбором в некотором семействе кривых той, которая
наилучшим образом приближает данные эксперимента или
статистической выборки. На рис. 1.2.1 приведен иллюстративный
пример встретившейся нам задачи такого типа. Имелось 20
спектроскопических измерений солнца yif полученных со спутника
для длин волн U. По лежащей в основе этого теории любой
набор из m таких измерений (/i,#i), ..., (tm,ym) может быть
приближен колоколообразной кривой. Однако в полученных
точках содержались экспериментальные ошибки, показанные
на рисунке. Для того чтобы сделать необходимые выводы на
основе данных, желательно найти колоколообразную кривую,
1.2. Характерные особенности задач 19
«наиболее близкую» к т точкам. Поскольку колоколообразная
кривая в общем виде описывается формулой
У{ХЬ *2> Х3, *4, 0 = *1+*2е~('+*з)2/*>
это означает, что Х\У Х2, *з и х\ выбираются так, чтобы
минимизировать некоторую совокупную меру расхождений
(невязок) между точками данных и кривой. Невязки даются
формулой
П(х)Ау(хи *ъ *з. х*> t^ — yt.
В качестве совокупной меры наиболее часто используется
сумма квадратов величин г/, что приводит к определению колоко-
лообразной кривой путем решения нелинейной задачи о
наименьших квадратах:
т т
min / (х) A Z П (х)2= £ h + x2e-(fi+x*Wx* - yt\\ (1.2.1)
xeR'
i~\
i=\
Здесь уместны следующие замечания. Во-первых, причина,
по которой задача (1.2.1) называется нелинейной задачей
о наименьших квадратах, состоит в том, что невязки п(х)
являются нелинейными функциями некоторых из переменных х\,
*2, *э, *4. Фактически п линейны по хх и лег, и некоторые
современные методы используют такую специфику (см. гл. 10). Во-
вторых, существуют функции, иные нежели сумма квадратов,
которые можно выбирать для определения меры отклонения
данных точек от колоколообразной кривой. Два очевидных
выбора суть
т
M*)=£lM*)i
fOQ(x)= max \п(х)\.
J L
J L_
*i h t5
Рис. 1.2.1. Точки данных, которые требуется «наилучшим образом приблизить
колоколообразной кривой.
20 Гл. 1. Введение
Соображения, по которым для минимизации обычно
выбирается /(лс), а не f\(x) или foo(x), иногда связаны со
статистической интерпретацией, а иногда с тем, что получающаяся
задача оптимизации гораздо лучше поддается математическому
анализу, так как сумма квадратов в отличие от двух других
функций непрерывно дифференцируема. На практике
большинство задач о наилучшем приближении данных решается с
использованием принципа наименьших квадратов. Часто /
модифицируется введением «весов» при невязках, однако это не
существенно для наших дальнейших рассуждений.
В качестве последнего примера рассмотрим некоторый
вариант задачи, встретившейся при изучении термоядерного
реактора. Термоядерный реактор можно представить себе
в виде тороидальной камеры с разогретой плазмой внутри
(рис. 1.2.2). Реальная задача в упрощенном (ради
наглядности) виде заключается в нахождении такого сочетания радиуса
тора г, его ширины w и температуры плазмы /, которое
приводило бы к наименьшей стоимости единицы вырабатываемой
энергии. Специалисты установили, что стоимость единицы
энергии моделируется выражением
+ C»(i+'S')<101""'',,• <'-2-2>
где c\t С2, с3, с4—константы. Таким образом, задача состояла
в минимизации / как функции от г, w и /.
Однако имелись и другие важные аспекты задачи. Прежде
всего г, w и t в отличие от переменных из предыдущих
примеров не могли принимать произвольные действительные
значения. Например, г и w не могли быть отрицательными.
Следовательно, это задача условной минимизации. Всего было
пять простых линейных ограничений на три переменные.
/ / г
Температура^)^" Г [ f
Рис. 1.2.2. Термоядерный реактор.
1.2. Характерные особенности задач 21
Важно подчеркнуть, что задача с ограничениями должна
рассматриваться как задача условной оптимизации только
тогда, когда наличие ограничений может повлиять на
получающееся решение, т. е. когда ожидается, что решение задачи
с ограничениями не совпадет с точкой минимума той же самой
функции без ограничений. В задаче о термоядерном реакторе
наличие ограничений обычно имело существенное значение, и
поэтому задача решалась методами, учитывающими
ограничения. Однако многие задачи с простыми ограничениями,
такими, как ограничения снизу и сверху на переменные, можно
решать алгоритмами безусловной минимизации, поскольку
ограничения удовлетворяются в точке безусловного минимума.
Отметим, что, как было написано, ограничения в задаче
о термоядерном реакторе обычно влияли на решение. Это
объясняется тбм, что требовалось решить 625 вариантов задачи,
отвечающих различным значениям констант сь с2> £з и с*.
Значения этих констант зависят от таких факторов, как, например,
стоимость электроэнергии, которая будет постоянной во время
эксплуатации реактора, но которая заранее не известна. Было
необходимо просчитать различные варианты задачи для того,
чтобы увидеть, как изменение этих факторов влияет на
оптимальные характеристики реактора. Часто в практических
приложениях желательно решить много связанных между собой
вариантов задачи. Это повышает требования к эффективности
алгоритма, а также вынуждает проводить предварительные
эксперименты с различными алгоритмами для оценки их
эффективности на данном классе задач.
И наконец, соотношение (1.2.2) было всего лишь простой
моделью термоядерного реактора. При более детальном
изучении выяснилось, что функция, определяющая стоимость
единицы электроэнергии, не задается аналитически как в (1.2.2),
а скорее представляет собой выходной результат некоторой
модели реактора, включающей уравнения в частных
производных. К тому же оказалось на пять параметров больше
(рис. 1.2.3). Такого сорта функции встречаются часто в
нелинейной оптимизации, и это серьезно повлияло на развитие
алгоритмов. Прежде всего подобные функции, по-видимому,
имеют лишь несколько верных десятичных знаков, поэтому не
Определенные
значения
параметров
х\.хг хв
с использованием х
как входных данных
модели
Вычисление
/"(численное решение уравнений)
в частных производных! ^ fix х *
с использованием х 1 ' и j. *2,.. ., л»;
Рис. 1.2.3. Вычисление функции по уточненной модели
термоядерного реактора.
22 Гл. 1. Введение
имеет смысла требовать высокой точности в десятичных
знаках решения. Затем хотя функция / может быть много раз
непрерывно дифференцируемой, ее производные обычно
недоступны. Это одна из причин* по которой аппроксимация
производных становится столь актуальной. И наконец,
вычисление / может оказаться довольно дорогостоящим, что служит
дополнительным стимулом к разработке эффективных
алгоритмов.
Приведенные выше задачи дают некоторое представление
о типичных характеристиках нелинейных задач. Первая — это
ее размер. Хотя существуют, конечно, задачи, имеющие
больше переменных, чем в рассмотренных примерах, но большая
часть имеет, на наш взгляд, относительно немного переменных,
скажем от 2 до 30. Современное состояние дел здесь таково,
что можно надеяться решить большинство малых задач,
имеющих, скажем, от 2 до 15 переменных, но при этом даже
двумерные задачи могут оказаться трудными. К задачам среднего
размера в рассматриваемой области относятся те, что имеют
от 15 до 50 переменных. Современные алгоритмы решают
многие из них. Задачи с 50 и более переменными являются
большими. Если о такой задаче нельзя сказать, что она слабо
нелинейна или имеется хорошее начальное приближение к
решению, то у нас мало шансов решить ее эффективно. Эти оценки
размеров очень изменчивы и зависят от алгоритмов меньше,
чем от наличия быстродействующей памяти и других
возможностей ЭВМ.
Второй вопрос касается наличия производных. Часто
встречаются задачи, в которых нелинейная функция сама
определена как результат численного моделирования на ЭВМ или
задается громоздкой формулой. Таким образом, ситуация
часто такова, что в нашем непосредственном распоряжении нет
аналитически заданных производных, хотя сама функция много
раз непрерывно дифференцируема. Поэтому важно иметь
алгоритмы, эффективно работающие в отсутствие аналитических
производных. Действительно, если библиотека программ для
ЭВМ предоставляет возможность аппроксимировать
производные, то пользователи редко задают их аналитически — кто
упрекнет их в этом?
В-третьих, как указывалось выше, решения многих
нелинейных задач довольно дорогостоящи либо из-за
многократного вычисления дорогостоящей нелинейной функции, либо
из-за того, что сама задача заключается в решении большого
числа взаимосвязанных подзадач. Мы слышали о 50-мерной
задаче, связанной с нефтяной техникой, где на каждое
вычисление функции тратится 100 ч работы ЭВМ IBM-3033.
Эффективность, выражаемая в терминах времени счета алгоритма и ко-
1.2. Характерные особенности задач 23
личества вычислений функции и производных, играет важную
роль в развитии нелинейных алгоритмов.
В-четвертых, во многих приложениях пользователь
рассчитывает получить в ответе лишь несколько верных десятичных
знаков. Это вызвано прежде всего тем, что приближенными
по своей природе являются другие составляющие задачи,
например сама функция, параметры модели, данные. С другой
стороны, пользователи часто требуют больше правильных
десятичных знаков, чем им на самом деле нужно. Хотя желание
иметь более высокую точность разумно, скажем, для того,
чтобы удостовериться, что сходимость достигнута, но дело в том,
что необходимая точность редко бывает близка к машинной
точности.
Пятый вопрос, кстати не проиллюстрированный выше,
связан с плохой масштабированностью многих реальных задач.
Имеется в виду, что переменные значительно отличаются
между собой по порядку величины. Например, одна
переменная может постоянно находиться в пределах от 106 до 107, а
другая — в пределах от 1 до 10. В нашей практике такое
встречалось удивительно часто. Однако большинство работ в
данной области обошло вниманием проблему масштабирования.
В книге мы постараемся обратить внимание на случаи, когда
игнорирование эффекта масштабирования может ухудшить
работу нелинейных алгоритмов, и попытаемся исправить эти
недостатки в рассматриваемых алгоритмах.
И наконец, в этой книге рассматриваются только те
нелинейные задачи, где переменные могут принимать любые
действительные значения, в противоположность задачам, где
некоторые переменные принимают только целые значения.
Сказанное относится и ко всем нашим примерам, однако читатель
может поинтересоваться: реалистично ли вообще это
ограничение. Ответ таков, что существуют, конечно, нелинейные
задачи, где некоторые переменные должны быть только
целочисленными, поскольку они представляют собой такие величины,
как, например, число людей, автомобилей и тому подобное.
Однако поскольку утрачивается всякая непрерывность, то эти
ограничения делают задачу настолько сложной для решения,
что часто самым лучшим бывает решить ее, рассматривая
дискретные переменные как непрерывные и затем округляя до
целых числа, полученные в решении. Теоретически такой
подход не гарантирует получение решения исходной
целочисленной задачи, но на практике он часто дает вполне разумное
решение. Исключение составляют задачи, в которых некоторые
дискретные переменные могут принимать только несколько
значений, например 0, 1 или 2. В этом случае должны
использоваться дискретные методы [см., например, Бил (1977), Гар-
финкель и Немхаусер (1972)].
24 Гл. 1. Введение
1.3. АРИФМЕТИКА КОНЕЧНОЙ ТОЧНОСТИ
И ИЗМЕРЕНИЕ ОШИБОК
Некоторые элементы рассматриваемых вычислительных
алгоритмов, такие, как проверка на сходимость, зависят от того,
насколько точно в ЭВМ представляются действительные числа.
Уместно отметить, что понимание машинной арифметики влияет
на написание вычислительных программ. Поэтому нам
необходимо дать краткое описание арифметики, конечной точности,
являющейся машинной версией арифметики действительных
чисел. Более подробно об этом написано в книге Уилкинсона
(1963).
В так называемой экспоненциальной форме записи1) число
51.75 представляется как +0.5175 X Ю+2. В ЭВМ
действительные числа представляются аналогичным образом с
использованием знака (в нашем примере это «+»), основания системы
счисления (10), порядка (+2) и мантиссы (0.5175). Это
представление становится единственным, если потребовать, чтобы
1/основание ^ мантисса < 1,
т. е. первый «десятичный» разряд справа от десятичной точки
не должен быть нулевым. Длина мантиссы, называемая
точностью представления, особенно важна для численных
расчетов. Это представление действительных чисел в ЭВМ
называется представлением с плавающей точкой. Будем обозначать
через fl(jc) представление с плавающей точкой числа *.
На ЭВМ CDC основание равно 2, а мантисса имеет 48
разрядов. Поскольку 2^^ 10м-4, это означает, что можно точно
хранить до 14 значащих десятичных цифр числа. Порядок
может меняться от —976 до +1070, тем самым наименьшее и
наибольшее числа примерно равны 10-294 и 10322. На ЭВМ IBM
основание равно 16, а мантисса состоит из 6 разрядов в
случае одинарной точности и из 14 в случае двойной точности, что
отвечает приблизительно 7 и 16 десятичным разрядам
соответственно. Порядок может меняться от —64 до +63, так что
наименьшее и наибольшее числа примерно равны 10~77 и 1076.
Хранение действительных чисел только с конечной
точностью имеет серьезные последствия, которые можно легко
изложить в краткой форме. Во-первых, коль скоро не всякое
действительное число может быть точно представлено в машине,
то в лучшем случае можно ожидать, что решение будет
верным с машинной точностью. Во-вторых, в зависимости от
машины и компилятора результат каждой промежуточной
арифметической операции либо округляется, либо усекается до ма-
') В оригинале — scientific notation —Прим. перев.
1.3. Арифметика конечной точности и измерение ошибок 25
шинной точности. Таким образом, погрешность, связанная с
конечной точностью, может накапливаться и еще более
понизить точность результатов. Такие ошибки называются
ошибками округления. Несмотря на то что влияние округления
может быть весьма незначительным, на самом деле существуют
по крайней мере три основные ситуации, в которых оно может
чрезмерно ухудшить вычислительную точность. Первая
возникает при сложении последовательности чисел, в особенности
если числа расположены в порядке убывания их абсолютных
величин. В этом случае из-за конечноразрядного
представления промежуточных результатов происходит потеря крайних
справа разрядов меньших слагаемых (как пример см. упр. 4).
Вторая связана с вычислением разности двух почти
совпадающих чисел. При этом происходит значительная потеря
точности, так как наиболее важные крайние слева разряды разности
имеют нулевые значения (в качестве примера см. упр. 5).
Третья возникает при решении почти вырожденных систем
линейных уравнений. Эта ситуация рассматривается в гл. 3.
Она фактически является следствием первых двух ситуаций, но
вместе с тем она является настолько основополагающей и
важной, что мы предпочитаем рассматривать ее как третью
основную ситуацию. Если постоянно помнить об этих трех ситуациях
при написании и использовании вычислительных программ, то
можно понять и избежать многие проблемы, связанные с
использованием арифметики конечной точности.
Из-за использования арифметики конечной точности, и даже
в большей степени из-за итеративной природы алгоритмов мы
не получаем точного ответа в большинстве нелинейных задач.
По этой причине часто необходимо оценивать близость одного
числа х к другому числу у. Наиболее часто будет
использоваться понятие относительной ошибки величины у при
аппроксимации ненулевой величины х:
\х-у\
1*1 '
Она более предпочтительна при хфО, нежели абсолютная
ошибка:
\х — У\>
так как последняя мера близости зависит от масштабов х и
у у а первая —нет (см. упр. 6).
При измерении ошибок и при обсуждении алгоритмов
будет полезно следующее общепринятое обозначение. Пусть
заданы две последовательности положительных действительных
чисел а, и р„ i= 1,2,3, ...;. тогда будем писать а/= 0(0*)
(читается «а,- есть О большое от Pi»), если существует
некоторая положительная константа с, такая, что а/^с-Р/ для
26 Гл. 1. Введение
всех /, за исключением, быть может, конечного подмножества.
Это обозначение используется для указания того, что
величина каждого а, имеет тот же порядок, что и
соответствующее р„ или, возможно, еще меньше. Дополнительные сведения
можно найти в книге Ахо, Хопкрофта и Ульмана (1974).
Другое последствие арифметики конечной точности состоит
в том, что определенные элементы алгоритмов, такие, как
критерий останова, будут зависеть от машинной точности.
Поэтому важно ввести характеристику машинной точности так,
чтобы рассуждения и вычислительные программы могли быть
довольно независимыми от любой конкретной машины. Обычно
используется понятие машинный эпсилон (machine epsilon)
или кратко macheps. Для конкретной вычислительной машины
оно определяется как наименьшее положительное число т,
такое, что 1 + т> 1 (см. упр. 7). Например, поскольку на ЭВМ
CDC имеется 48 двоичных разрядов, то macheps = 2~47 для
арифметики с усечением и 2~48 для арифметики с округлением.
Величина macheps весьма полезна при рассмотрении
машинных чисел. Например, можно легко сказать, что относительная
ошибка машинного представления П(л:) любого
действительного ненулевого числа х меньше, чем macheps, и, наоборот,
машинное представление любого действительного числа х будет
лежать в пределах (x(l — macheps), x(l + macheps)). АнаЛЪ-
гично, два числа хну совпадают в крайней слева половине
их разрядов, когда
'^'^Vmacheps.
Эта проверка довольно типична для наших алгоритмов.
Другой взгляд на величину macheps служит ключом к
трудному вопросу принятия решения о том, когда в определенном
контексте машинное число могло бы также выступать только
как нулевое. Нулем 0 традиционно считается единственное
решение уравнения х + 0 = х для любого действительного
числа х. В случае представления чисел с конечной точностью роль
нуля в этом тождестве играет интервал 0*, который
содержит 0 и приблизительно равняется (—macheps •*, +macheps-A:).
Нередко в процессе вычислений возникают машинные числа
х и у, имеющие настолько различные порядки величин, что
fl(* + y) = fl(x). Это означает, что в данном контексте у
неотличимо от нуля, и иногда, как, например, в численных
алгоритмах линейной алгебры, полезно контролировать вычисления
и, в самом деле, присваивать у нулевое значение.
И наконец, любому пользователю ЭВМ следует знать о
явлениях переполнения и антипереполнения1), встречающихся,
) Это явление называют также исчезновением порядка. — Прим. перев.
1.3. Арифметика конечной точности и измерение ошибок 27
когда в процессе вычислений возникает ненулевое число,
порядок которого больше или соответственно меньше крайних
значений диапазона, отведенного в ЭВМ под порядки. Например,
антипереполнение возникает при обращении на ЭВМ CDC
числа 10322, а переполнение—при обращении на ЭВМ IBM числа
ю-77.
В случае переполнения почти любая вычислительная
машина прекратит счет и выдаст сообщение об ошибке.
Компилятор часто обеспечивает на случай антипереполнения
возможностью выбора — или прекращать счет, или подставлять
нуль вместо выражения, приведшего к этому. Последняя
альтернатива является разумной, но не всегда (см. упр. 8).
К счастью, если использовать хорошо написанные программы
линейной алгебры, то алгоритмы, рассматриваемые в этой
книге, обычно не приводят к переполнению или
антипереполнению. Так, численная реализация вычисления евклидовой
нормы вектора (см. разд. 3.1)
II v I = У*} + *» + ... +v*n, v е R",
требует особой тщательности.
1.4. УПРАЖНЕНИЯ
1. Дайте стандартную формулировку задачи решения системы
нелинейных уравнений: найти (хи х2)т, такое, что
*? + 2 = 4
2. В лабораторном эксперименте измеряются значения функции f в 20
различных моментах времени t в пределах от 0 до 50. Известно, что /(/)
представляет собой синусоидальную волну, однако неизвестны ее амплитуда
и частота, а также ее смещение в направлении осей f и t Как бы вы
поставили вычислительную задачу для нахождения этих характеристик из ваших
экспериментальных данных?
3. У экономиста имеется сложная вычислительная модель экономики,
которая оценивает темпы инфляции по заданным темпам безработицы,
темпам роста валового национального продукта и по числу строившихся в
прошлом году жилых домов. Требуется определить такую комбинацию этих трех
факторов, которая приведет к наименьшим темпам инфляции. Вам предстоит
поставить и решить эту задачу численно.
(a) К какому типу вычислительной задачи ее можно было бы свести?
Как вы поступите с переменной «число строившихся жилых домов»?
(b) В чем состоят те вопросы, которые*вы хотели бы задать
экономисту, стремясь сделать задачу наиболее удобной для численного решения
(например, относительно непрерывности, производных, ограничений)?
(c) Окажется ли решение этой задачи дорогостоящим? Почему?
4. Предположим, в вашем распоряжении имеется вычислительная
машина, у которой основание системы счисления и точность представления чисел
28 Гл. 1. Введение
соответственно равны 10 и 4. Пусть после каждой арифметической
операции производится усечение, так что, например, сумма 24.57 + 128.3 = 152.87
становится равной 152.8. Каковы будут результаты, если сложить числа
128.3, 24.57, 3.163 и "0.4825 сначала в порядке их возрастания, а затем в
порядке убывания? Как они согласуются с правильным «бесконечно точным>
результатом? Что это вам говорит относительно сложения
последовательности чисел на ЭВМ?
5. Предположим у вас имеется та же вычислительная машина, что в
упр. 4, и вы производите вычисление
(1. _ 0.3300 Vo .3300. Сколько верных
цифр по сравнению с точным ответом вы получите? Что это вам говорит
относительно вычитания на ЭВМ почти совпадающих чисел?
6. Каковы относительная и абсолютная ошибки ответа, полученного
ЭВМ в упр. 5, по сравнению с правильным ответом? Что если заменить
задачу на такую: ((-q— ) — 33]/33? Что это вам говорит о полезности
относительной ошибки в сравнении с абсолютной?
7. Напишите программу вычисления машинного эпсилона имеющейся в
нашем распоряжении ЭВМ или микрокалькулятора. Вы можете
предположить, что macheps будет равен' 2 в некоторой степени, так что ваш
алгоритм мог бы выглядеть следующим образом:
EPS := 1
WHILE 1 + EPS > 1 DO
EPS :=* EPS/2.
Введите счетчик, который позволит узнать в конце программы, какой
степенью двойки является macheps. Выведите на печать его значение, а также
десятичную запись числа macheps. (Замечание. Значение macheps будет
отличаться на коэффициент 2 в зависимости от того, какая используется
арифметика — с округлением или с усечением. Почему?)
Дальнейшая информация о вычислении на ЭВМ характеристик
машинного оборудования имеется в статье Форда (1978).
8. В каждом из следующих выражений произойдет антипереполнение
(на ЭВМ IBM). В каких случаях было бы целесообразно подставить нуль
вместо величины, вызывающей антипереполнение?
(a) a:=^/W+cтf где 6—1, с^Ю"50.
(b) а := ^Ь2 + с2, где Ь = с — 10"50.
(c) v := (ю • х)/(у * г), где w =* 10*"30, х = Ю"60, у = 10"40, г = 10"50.
Почему?
2
Нелинейные задачи с одной переменной
Начнем изучение методов решения нелинейных задач с
обсуждения задач, имеющих только одну переменную, таких, как
нахождение решения одного нелинейного уравнения с одним
неизвестным и нахождение минимума функции одной
переменной. Причина для отдельного изучения задач с одной
переменной состоит в том, что они позволяют увидеть те принципы
построения эффективных локальных и глобальных алгоритмов,
а также алгоритмов с аппроксимацией производных, которые
послужат базисом для наших алгоритмов решения задач с
многими переменными. Для этих целей не требуются знания
линейной алгебры и многомерного анализа. Алгоритмы
решения многомерных задач будут более сложными, чем
рассматриваемые в данной главе, однако понимание изложенной здесь
сути основного подхода окажет несомненную помощь в
многомерном случае.
Вот некоторые ссылки на литературу, в которой подробно
рассматриваются задачи этой главы: Авриель (1976), Брент
(1973), Конт и де Бур (1980), Дальквист, Бьёрк и Андерсон
(1974).
2.1. О ТОМ, ЧЕГО НЕ СЛЕДУЕТ ОЖИДАТЬ
Рассмотрим задачу нахождения действительных корней
каждого из следующих трех нелинейных уравнений с одним
неизвестным:
/i М = х4 - 12JC3 + 47Х2 - 60*,
f2 (х) = х4 - 12JC3 + 47Х2 - 60* + 24,
/3 (х) = х4 — 12Ж3 + 47JC2 — 60х + 24.1
(рис. 2.1.1). Было бы замечательно, если бы мы имели
универсальную программу на ЭВМ, которая говорила нам: «Корнями
30 Гл. 2. Нелинейные задачи с одной переменной
f\(x) являются х = 0, 3, 4 и 5; действительными корнями f2(x)
являются х=\ и хё*0.888; fz(x) действительных корней не
имеет».
Вряд ли когда-либо будет существовать такая программа.
Вообще говоря, вопросы существования и единственности,
типа — имеет ли данная задача решение, и единственно ли оно? —
выходят за рамки возможностей, которые следует ожидать от
алгоритмов решения нелинейных задач. В самом деле, мы
должны с готовностью допускать, что для любого
вычислительного алгоритма найдутся нелинейные функции (если желаете,
то даже бесконечно дифференцируемые), достаточно
замысловатые, чтобы вывести из строя этот алгоритм. Поэтому все,
что может гарантировать пользователю алгоритм, примененный
к нелинейной задаче, заключается в ответах: «Приближенным
решением задачи является » или «Приближенное
решение задачи не было найдено за отведенное время». Тем не менее
во многих случаях постановщик нелинейной задачи знает из
практических соображений, что она имеет решение, и либо
решение единственно, либо требуемое решение лежит в
определенной области. Таким образом, невозможность установить
существование или единственность решения обычно не является
тем, что заботит практиков в первую очередь.
Очевидно также, что для большинства нелинейных задач
представляется возможным найти лишь приближенные
решения. Это следует не только из конечной точности наших
вычислительных машин, но также из классического результата
Галуа о том, что для полиномов степени п ^ 5 невозможно
найти решение в замкнутой форме, использующей только
целые числа, операции +, —, X, -f-, возведение в степень и
извлечение корней целой степени от 2-й до n-й. По этой причине
мы будем развивать методы, нацеленные на отыскание одного
из приближенных решений нелинейной задачи.
Рис. 2.1.1. Уравнение fx (х) — х* — \2х9 + 47х2 — 60*.
2.2. Метод Ньютона 31
2.2. МЕТОД НЬЮТОНА РЕШЕНИЯ ОДНОГО
УРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
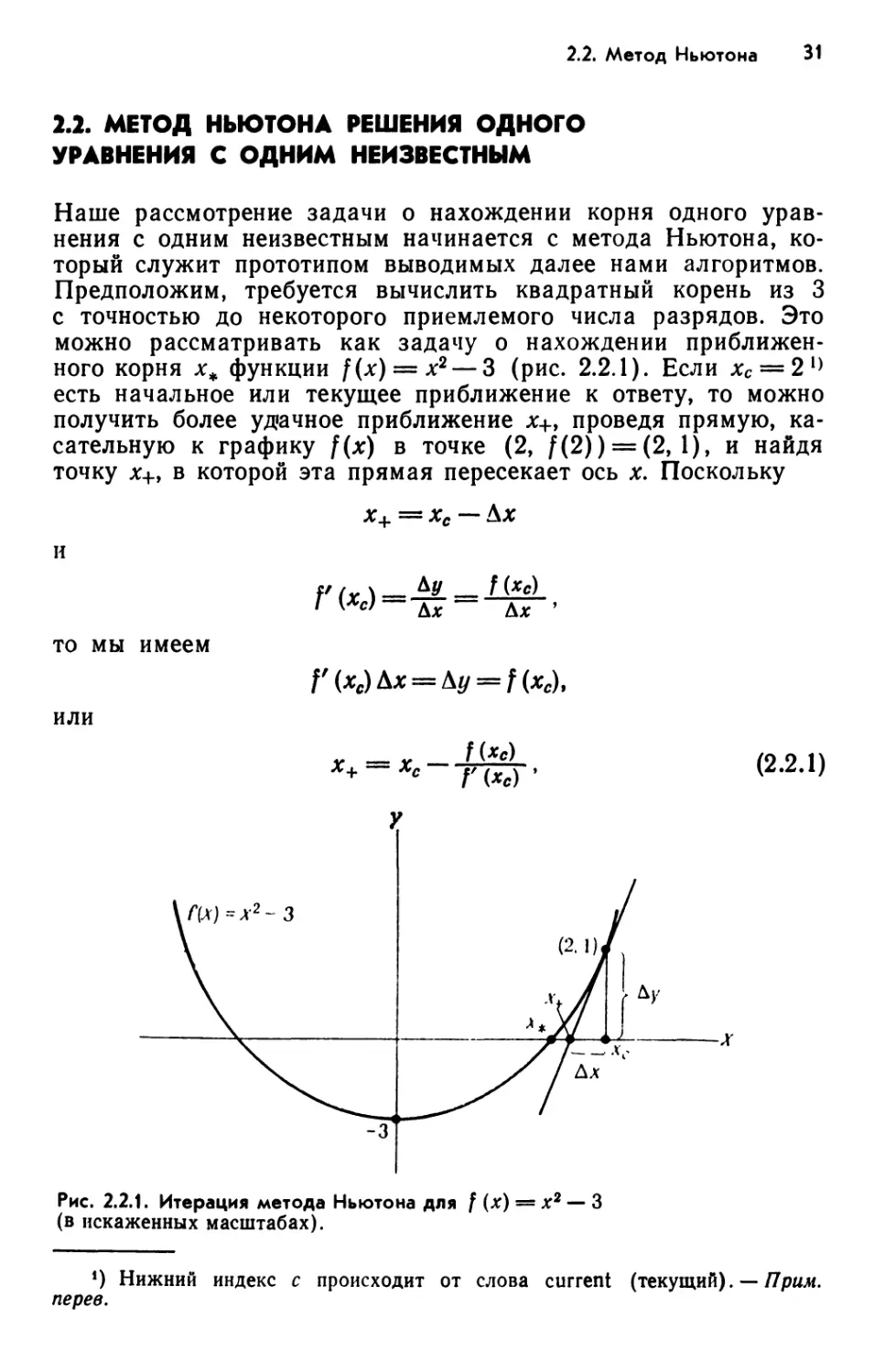
Наше рассмотрение задачи о нахождении корня одного
уравнения с одним неизвестным начинается с метода Ньютона,
который служит прототипом выводимых далее нами алгоритмов.
Предположим, требуется вычислить квадратный корень из 3
с точностью до некоторого приемлемого числа разрядов. Это
можно рассматривать как задачу о нахождении
приближенного корня х* функции f(x) = x2 — 3 (рис. 2.2.1). Если хс = 21)
есть начальное или текущее приближение к ответу, то можно
получить более удачное приближение *+, проведя прямую,
касательную к графику f(x) в точке (2, f(2)) = (2, 1), и найдя
точку х+, в которой эта прямая пересекает ось х. Поскольку
х+ = хс — Ал:
ftr\ — *У — f(*c)
Г К*с) — Дл: — Дл. >
то мы имеем
или
П*с) Л* = Л</= /(**),
Х+ — Хс Г <*«>
(2.2.1)
Рис. 2.2.1. Итерация метода Ньютона для / (х) = х2 — 3
(в искаженных масштабах).
!) Нижний индекс с происходит от слова current (текущий). — Прим.
пере в.
32 Гл. 2. Нелинейные задачи с одной переменной
что дает
1
X
+ = 2-f = ;i.75.
Логично следующим шагом применить тот же прием к но-
ному текущему приближению хс = 1.75. Использование (2.2.1)
дает
х+ = 1.75 - (0.0625/3.5) = 1.732у,
которое уже имеет четыре верных разряда числа д/3. Еще
одна итерация дает х+^ 1.7320508, которое имеет восемь
верных разрядов.
Метод, который мы только что вывели, называется методом
Ньютона — Рафсона, или методом Ньютона. Для лучшего
понимания было бы важно взглянуть на то, что нами сделано,
с более абстрактных позиций. На каждой итерации строилась
локальная модель функции f(x) и решалась задача отыскания
корня этой модели. В данном случае наша модель
Мс (х) = f (хс) + Г (хс) (х - хс) (2.2.2)
представляет собой единственную линейную функцию со
значением f(xc) и наклоном f'{xc) в точке хс (прописная буква М
используется здесь в соответствии с обозначениями в
многомерном случае и во избежание путаницы с задачами
минимизации, где наша модель обозначается через тс(х)). Нетрудно
убедиться в том, что Мс(х) пересекает ось х в точке *+,
определенной в (2.2.1).
Из педагогических соображений надо сказать, что мы по«
лучили метод Ньютона, представляя f{x) в окрестности
текущего приближения Хс в виде ее ряда Тейлора:
f(x) = f(xe) + f'(xe)(x-xe)+ ГМ(х-х.у + _
21
-Z
ГЧхе)(х-хе)< (223)
/-0
и затем аппроксимируя f(x) аффинной1) частью этого ряда,
которая тоже, естественно, задается формулой (2.2.2). Корень
опять же задается формулой (2.2.1). Имеется несколько
причин, по которым мы предпочитаем другой подход. Малопри-
') Будем называть (2.2.2) аффинной моделью, несмотря на то что ее
часто называют линейной моделью. Причина заключается в том, что
аффинная модель соответствует афинному подпространству, проходящему через
(х, f(x))t т.е. соответствует прямой, которая не обязательно проходит через
начало координат, тогда как линейное подпространство обязательно
проходит через начало координат.
2.2. Метод Ньютона 33
влекательно, да и вовсе нет необходимости в том, чтобы
строить предположения относительно производных порядка более
высокого, чем на самом деле используется на итерации. Кроме
того, при рассмотрении многомерных задач производные более
высокого порядка становятся настолько сложными, что их
понимание требует больших усилий, чем любой из приводимых
далее алгоритмов.
Вместо этого метод Ньютона получается просто и
естественно из теоремы Ньютона 1)
X
f(x) = f(xe)+ \f'(z)dz.
хс
Представляется разумным аппроксимировать этот интеграл по
формуле
х
\f'(z)dz~f'(xc)(x-xc)
хс
и еще раз получить аффинную аппроксимацию f{x)9 заданную
в (2.2.2). Такой способ вывода окажется для нас полезным
в многомерных задачах, где различные способы вывода из
геометрических соображений становятся менее успешными.
Метод Ньютона типичен для методов решения нелинейных
задач. Он является итерационным процессом, генерирующим
последовательность точек, которые, как мы надеемся,
становятся все более близкими к решению. Возникает естественный
вопрос: «Будет ли он работать?» Ответом является твердое
«да». Отметим, что если бы f(x) была линейной, то метод
Ньютона нашел бы ее корень за одну итерацию. Теперь
посмотрим, что он будет делать в общей задаче нахождения
квадратного корня:
задано <х>0, найти х, такое, что f(x) = x? — а = 0,
начиная с текущего приближения хсФО. Поскольку
— f(*c) _ *с-а _ ХС i °
*+ — Хс у {Хс) —Хс 2хс — 2 + 2хс ,
имеем
или, используя относительную погрешность, получаем
х, — л/а ( * — л/а \2 / л/а \
^т- - (-V-) • (У • <2-2-4Ь>
*) В отечественной литературе эта теорема известна как формула
Ньютона—Лейбница. При переволе будем придерживаться терминологии
оригинала. — Прим. перев.
34 Гл. 2. Нелинейные задачи с одной переменной
Таким образом, коль скоро начальная погрешность \хс — д/а |
меньше, чем \2хс\, то новая погрешность |л;+ — У<х | будет
меньше старой погрешности |*с — Va I» и в конце концов
каждая новая погрешность будет гораздо меньше предыдущей
погрешности. Это согласуется с нашими наблюдениями при
нахождении квадратного корня из 3 в примере, с которого
начинался данный раздел.
Характер уменьшения погрешности, заданной (2.2.4),
типичен для метода Ньютона. Погрешность на каждой итерации
будет приблизительно равна квадрату предыдущей
погрешности, так что если начальное приближение было достаточно
хорошим, то погрешность будет уменьшаться и в конце концов
уменьшение станет быстрым. Такой характер сходимости
известен как локальная ^-квадратичная сходимость. Прежде чем
получить общую теорему сходимости метода Ньютона,
необходимо обсудить вопрос о скорости сходимости.
2.3. СХОДИМОСТЬ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
Пусть задан итерационный метод, генерирующий
последовательность точек хих2у ... из начального приближения х0. Нам
бы хотелось знать — сходятся ли итерации к решению х„ и
если сходятся, то как быстро. Предположим, что нам известно
то, что подразумевается под записью
lim ak = О
fc-»oo
для последовательности действительных чисел {а*}. Тогда
следующее определение дает необходимые нам в дальнейшем
характеристики свойств сходимости.
Определение 2.3.1. Пусть jc+eK, xk^R, £ = 0,1,2, ... .
Тогда говорят, что последовательность {**} = {дсо, х\,х2, ...}
сходится к х„ если
lim |xk — х0\ = 0.
fc->oo
Если, кроме того, существуют константа се [0, 1) и целое k ^ 0,
такие, что для всех k ^ &
l*A+i —*. К *1 ** — *.!■
то говорят, что {xk} является q-линейно сходящейся к х*. Если
для некоторой последовательности {ck}> сходящейся к 0, имеет
место
1*м-хт\<ск\хк — хл |, (2.3.2)
2.3. Сходимость последовательностей действительных чисел 35
то говорят, что {xk} сходится q-сверхлинейно к х*. Если {xk}
сходится к х* и существуют постоянные р>1, с>0 и й^О,
такие, что для всех k ^ #
\хк+1-х.\^с\хк-хш\р, (2.3.3)
то говорят, что {xk} сходится к4 с q-порядкоМу по меньшей
мере равным р. Если р = 2 или 3, то говорят, что скорость
сходимости является q-квадратичной или q-кубической
соответственно.
Если {л:*} сходится к х* и вместо (2.3.2) выполняется
\xk+J — xj^ck\xk — xj
для некоторого фиксированного целого /, то говорят, что {л:*}
является j-шагово q-сверхлинейно сходящейся к х*. Если {л:*}
сходится к Xk н вместо (2.3.3) для k ^ £ выполняется
I **+/ — *. К *|*Л — xj
при некотором фиксированном целом /, то говорят, что {xk}
имеет j-шаговую сходимость q-порядка, по меньшей мере
равного р.
Примером q-линешой сходимости служит
последовательность
Xq = 2, Х\ = Tj- , Х2 = -£-, *з = "g"» • • • > AT/ = 1 + 2 , ....
Эта последовательность сходится к jt*=l, имея с = у. Нг
ЭВМ CDC потребуется 48 итераций для достижения fl(**) = l.
Примером <7-кваДРатично сходящейся последовательности
служит
y — 1 — 5 — 17 _ 257 _ 1 i о-2*
0 — 2 ' Х{ — 4 ' *2 — ~\6 ' Хз — 256 »•••>** — А i ^ > • • • >
которая сходится к jq* = 1, имея с= 1. На ЭВМ CDC f 1 (дг6)
будет равно 1. На практике ^-линейная сходимость может
быть довольно медленной, в то время как ^-квадратичная или
<7-сверхлинейная сходимость станет в конце концов довольно
быстрой. Однако реальное поведение также зависит от
констант с в (2.3.1—2.3.3), например q-липешая сходимость
с с = 0.001, вероятно, является вполне удовлетворительной, а
с с = 0.9 — нет. (Другие примеры имеются в упр. 2 и 3.) Стоит
подчеркнуть, что эффективность 9_свеРхлинейной сходимости
непосредственно связана с тем, сколько итераций требуется
для того, чтобы ck стало малым.
Когда речь идет о порядках сходимости, следует различать
префикс «9», происходящий от слова quotient (частное), и «г»,
происходящий от root (корень), г-порядок характеризует
скорость сходимости более слабого типа. В этом случае все, что
36 Гл. 2. Нелинейные задачи с одной переменной
можно сказать про погрешности \xk — х*\ последовательности,
имеющей г-порядок, равный р, заключается в том, что они
ограничены сверху другой последовательностью с <7-поРяДком>
равным р. Строгое определение имеется в книге Ортеги и
Рейнболдта (1970). Итеративный метод, сходящийся с
определенной скоростью к истинному решению при условии, что он
стартует в достаточной близости от этого решения, называется
локально сходящимся с упомянутой скоростью. В этой книге
нас будут интересовать главным образом методы, которые
сходятся локально 9-сверхлинейно или ^-квадратично и у которых
такое поведение явно наблюдается на практике.
2.4. СХОДИМОСТЬ МЕТОДА НЬЮТОНА
Здесь будет показано, что для большинства задач метод
Ньютона сходится ^-квадратично к корню одного нелинейного
уравнения с одним неизвестным при условии, что имеется
достаточно хорошее начальное приближение. Однако он может
вообще не сходиться из-за плохого начального приближения, и
тогда необходимо привлекать глобальные методы из разд. 2.5.
Доказательство локальной сходимости метода Ньютона
опирается на оценку погрешностей в последовательности
аффинных моделей Мс(х), рассматриваемых как аппроксимации для
f(x). Поскольку эта аппроксимация была получена с
использованием f'(xc) (х — хс) в качестве аппроксимации для
х
\f'{z)dz,
хс
то нам необходимо сделать некоторые предположения
относительно гладкости р с тем, чтобы оценить погрешность
аппроксимации, равную
х
f{x)-Mc{x)= $ [/'(*)-П*с)]Жг.
хс
Прежде всего дадим определение непрерывности по Липшицу.
Определение 2.4.1. Функция g называется непрерывной по
Липшицу с константой у на множестве X (записывается как
g<=Lipy(X))t если
\g(*) — g(y)\<y\x — y\
для любых х,у^Х.
Для установления сходимости метода Ньютона докажем
сначала простую лемму, показывающую, что если Р(х) непре-
2.4. Сходимость метода Ньютона 37
рывна по Липшицу, то можно получить верхнюю границу
близости аппроксимации f(x)-\-f'(x) (у — х) к f(y).
Лемма 2.4.2. Пусть /: D-+R и //eLipY(D) для открытого
интервала D. Тогда для любых x,y^D
lf(y)-f(*)-n*)(*/-*)l<Y(y2-*)2- (2.4.1)
Доказательство. Как известно из основ анализа, f(y) — f(x) =
у
= \ Y fe) dz, что эквивалентно
х
У
f(y)-f (х) - Г (х) (У~х) = \ W (г) - Y (*)] dz. (2.4.2)
X
После замены переменных
z = x + t(y — x), dz = dt(y — x)
(2.4.2) принимает вид
f(y)-f(x)-f'(x)(y-x)=\[f'(x + t(y-x))-f'(x)](y-x)dt.
о
И, таким образом, используя непрерывность по Липшицу /',
получаем
1Ш-/М-П*)(»-*)К
<\У- x\\y\t(y-x)\dt = y\y-xfl2. П
о
Отметим, что (2.4.1) очень напоминает оценку погрешности,
определяемой остаточным членом в формуле Тейлора, при этом
константа Липшица у играет роль ограничения сверху на
If (5)1» где £eZ). Основное преимущество использования
непрерывности по Липшицу заключается в том, что оно
освобождает нас от необходимости рассматривать следующую по
порядку производную. Это особенно удобно в многомерном
случае.
Теперь мы в состоянии сформулировать и доказать
фундаментальную теорему вычислительной математики. Будет
доказана самая полезная форма этого результата, а более общие
вынесены в упражнения (см. упр. 13—14).
Теорема 2.4.3. Пусть /: D->R, где D — открытый
интервал Д и пусть f eLi/?Y(D). Предположим, что для некоторого
38 Гл. 2. Нелинейные задачи с одной переменной
р > 0 |f(*)I^P ПРИ всех x^D. Если f(x) = 0 имеет решение
**еО, то существует некоторое ц > О, такое, что если |х0 —
— **|<Л> то последовательность {**}, задаваемая формулой
Xk+i = xk— у . . , & = 0, 1, 2, ...,
существует и сходится к х*. Более того, для £ = 0,1, ...
Доказательство. Пусть те(0,1), и пусть т) есть радиус1)
наибольшего открытого интервала с центром в х*,
содержащегося в D. Обозначим rj = min{fj, т(2р/у)}. Покажем по
индукции, что для k = 0, 1, 2, ... выполняется (2.4.3) и
Доказательство по сути просто показывает, что на каждой
итерации погрешность \xk+\ — **| ограничена константой,
умноженной на погрешность, допускаемую аффинной моделью
при аппроксимации / в л% и оцениваемую по лемме 2.4.2 как
О(|агл — х*\2). Для k = 0
X\ x. — Xo *. -jr—--x0 x4 ^,(jCq) —
= 77^-5- [/ (x.) - f (x0) - Г (x0) (x. - *o)].
Выражение в скобках есть f(x+)—M0(xl), т. е. погрешность
в лс* локальной аффинной модели, построенной в хс=х0.
Таким образом, из леммы 2.4.2
1 *1 ~~ х*' ^ 2|f'(*o)l ,Ar°"~ **|2>
и далее по предположениям относительно f'(x)
\x{-xj^-^\x0 — xj2.
Поскольку |л'0 — *«|^Л ^ т -2p/v, мы имеем |*i—л*|^
^т|х0 — хф|<т|. Аналогично проводится доказательство
индуктивного предположения. П
Требование теоремы 2.4.3 о том, чтобы f'(x) имело
ненулевую нижнюю границу в Z), просто означает, что /'(#*) должно
*) Такого рода терминология, присущая скорее многомерному случаю,
чем одномерному, не вызывает серьезных трудностей и используется для
облегчения дальнейшего перехода к случаю пространства многих
переменных. — Прим. перев.
2.4. Сходимость метода Ньютона 39
быть ненулевым для квадратичной сходимости метода
Ньютона. Если на самом деле /'(**)= О, то х* является кратным
корнем, и метод Ньютона сходится всего лишь линейно (см.
упр. 12). Для того чтобы ощутить разницу, мы приводим ниже
пример итераций метода Ньютона, примененного к f{(x) =
= х2—1 и к Ы*) = *2 — 2х+1, начиная в обоих случаях
с лго = 2. Обратите внимание, что метод Ньютона в случае
f2(x) сходится гораздо медленнее из-за f'2(xj = 0.
Пример 2.4.4. Метод Ньютона, примененный к двум
квадратичным функциям (ЭВМ CDC, одинарная точность).
М*) = *2-1 f2(x) = x2-2x + \
2.0
1.25
1.025
1.0003048780488
1.0000000464611
1.0
*о
xt
%2
х3
х4
*5
2.0
1.5
1.25
1.125
1.0625
1.03125
Поучительно также рассмотреть константу у/(2р),
входящую в соотношение для ^-квадратичной скорости сходимости
(2.4.3). Числитель у> представляющий собой константу
Липшица для /' на Z), можно рассматривать как меру
нелинейности f. Однако мера у зависит от масштаба: умножение / или
изменение единиц измерения х на некоторую константу
изменит масштаб /' на эту константу, не делая функцию ни более
и ни менее нелинейной. Мерой нелинейности, не зависящей от
масштаба1), служит относительная скорость изменения /'(*),
которая получается делением у на f'(x). Таким образом,
поскольку р есть нижняя граница для f'(x) при jcgD, то у/р
является верхней границей относительной нелинейности f(x),
и теорема 2.4.3 утверждает, что чем меньше эта мера
относительной нелинейности, тем быстрее будет сходиться метод
Ньютона. Если же / линейна, то у = 0 и х\ = х*.
Теорема 2.4.3 гарантирует сходимость метода Ньютона
только из хорошей начальной точки хо, и, в самом деле, как
легко убедиться, метод Ньютона может вообще не сходиться,
если |л0 — л^| велико. Рассмотрим, например, функцию f(x) =
= arctg* (рис. 2.4.1). Для некоторого jtce [1,39, 1.40]
справедливо следующее. Если х0 = хс, то метод Ньютона будет
генерировать циклически повторяющиеся значения a'i = —л>,
Х2 = хСу хг = —хс, .... Если |лго|<л'с, то метод Ньютона
будет сходиться к л-* = 0, а если |jc0|>xo то метод Ньютона
!) Имеется в гиду лишь независимость от единиц измерения f, а не х.—
Прим. пере в.
40 Гл. 2. Нелинейные задачи с одной переменной
•f(*;«=3rctg х
X
Рис. 2.4.1. Метод Ньютона, примененный к / (х) = arctg х.
будет расходиться, т. е. погрешность \хк — а:«| будет на
каждой итерации увеличиваться. Таким образом, метод Ньютона
полезен быстрой локальной сходимостью, однако нам
необходимо включить его в более надежный метод, который
успешно работал бы и при более удаленных начальных точках.
2.5. ГЛОБАЛЬНО СХОДЯЩИЕСЯ МЕТОДЫ 0 РЕШЕНИЯ
ОДНОГО УРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
Воспользуемся следующим простым принципом включения
метода Ньютона в глобально сходящийся алгоритм: применять
метод Ньютона всякий раз, когда кажется, что он работает
нормально; в противном случае обращаться к более
медленному, но надежному глобальному методу. Такая стратегия
порождает глобально сходящиеся алгоритмы с высокой
локальной скоростью сходимости метода Ньютона. В этом разделе
мы рассмотрим два глобальных метода и затем покажем, как
получить гибридный алгоритм, комбинируя глобальный метод
с методом Ньютона. Будут также обсуждены критерии
останова и другие машинно-зависимые критерии, необходимые для
успешной работы вычислительных алгоритмов.
Простейший глобальный метод—метод деления пополам.
В нем заложено вполне разумное предположение о том, что
имеется начальный интервал (x0t z0), содержащий корень. Он
помещает точку х\ в центре интервала, выбирает в качестве
Рис. 2.5.1. Метод деления пополам.
1) Относительно того, какой смысл вкладывается в понятие «глобальный
метод», см. последний абзац разд. 1.1.
2.5. Глобально сходящиеся методы 41
нового тот из интервалов [*о,Х\] и [jti,Zo]> который содержит
корень, и продолжает делить отрезок пополам до тех пор, пока
не будет найден корень (рис. 2.5.1). Формально это выглядит
так:
заданы дс0, zQ, такие, что / (*0) -f(zo)< 0;
for ft = 0, 1, 2, ... do
r _xk + 4.
xky если f{xk)-f(xk+l)<0;
z*+i = |
zk в противном случае.
Метод деления пополам работает теоретически всегда,
однако гарантированное уменьшение оценки погрешности
составляет только у на каждой итерации. Поэтому с практической
точки зрения метод малопривлекателен. Программы,
использующие деление пополам, выполняют обычно эту операцию до
тех пор, пока не достигнут точки л:*, из которой будет сходиться
некоторый вариант метода Ньютона. Метод деления пополам
не имеет также естественного обобщения на многомерный
случай.
Более наглядное представление о том, как мы будем
поступать в л-мерном пространстве, дает следующий метод.
Представим себе, что метод Ньютона вырабатывает не только шаг
xn = xc — f(xc)/f'(xc)j но также и направление, на которое
этот шаг указывает (предполагается, что У(хс)ф0). Хотя
ньютоновский шаг может в действительности привести к
увеличению абсолютной величины функции, его направление таково,
что вдоль него абсолютное значение функции первоначально
уменьшается (рис. 2.5.2). Геометрически это должно быть
очевидным; простое доказательство дает упр. 16. Таким образом,
Ха/ -Х+.
Х'ы
хс
Рис. 2.5.2. Дробление ньютоновского шага.
42 Гл. 2. Нелинейные задачи с одной переменной
если ньютоновская точка xN не приводит к уменьшению
|/(л:)|, то разумная стратегия заключается в дроблении шага1)
с движением в обратном направлении от xN к xCt пока не
встретится точка jc+, для которой |/(л+) | < \f(xc) |. Возможная
итерация здесь такова:
х+.-хс Г(Хс) ,
while \f(x+)\>\f(xj\ do (2.5.1)
*+ ,— 2 *
Отметим, что эта стратегия не требует начального интервала,
содержащего корень.
Итерация (2.5.1) служит примером гибридного алгоритма,
в котором делается попытка совместить глобальную сходимость
и быструю локальную сходимость, проверяя первым на
каждой итерации ньютоновский шаг, но всегда добиваясь, чтобы
в результате итерации уменьшалась некоторая мера близости
к решению. Разработка таких гибридных алгоритмов позволяет
успешно решать на практике многомерные нелинейные задачи.
Ниже приведена общая формулировка для класса гибридных
алгоритмов для отыскания корня одного нелинейного
уравнения. Этим преследуется цель ввести в рассмотрение и выделить
те основные приемы построения глобально и вместе с тем
быстро локально сходящихся алгоритмов, которые послужат
основой для всех алгоритмов в этой книге.
Алгоритм 2.5.1. Гибридный квазиньютоновский алгоритм
общего вида решения одного нелинейного уравнения с одним
неизвестным:
заданы /: R->R, х0;
for Л = 0, 1, 2, ... do:
1. решить — необходим ли останов; если нет, то:
2. построить локальную модель, описывающую
поведение / вблизи от xk, и найти точку хы, которая является
решением (или близка к тому, чтобы быть решением)
модельной задачи;
3. (а) решить — взять ли xk+\ = xN\ если нет, то:
(Ь) выбрать Xk+u используя глобальную стратегию
(здесь как можно реже прибегайте к решению
модельной задачи).
*) В оригинале — backtrack, что означает движение в обратном
направлении, возвращение. В отечественной литературе принят термин «дробление
шага», его мы и будем придерживаться при переводе, — Прим. перев.
2.5. Глобально сходящиеся методы 43
Шаг 1 обсуждается ниже. В нем мы впервые используем
машинно-зависимые и проблемно-зависимые точности. Шаг 2
обычно включает в себя вычисление ньютоновского шага или
некоторый вариант без вычисления производных (см. разд. 2.6).
Итерация (2.5.1) служит примером шага 3(а — Ь). Мы увидим
в гл. 6, что не нужно выбирать критерий в 3(a) слишком
тщательно, достаточно, чтобы он обеспечивал в большинстве
случаев сходимость гибридного алгоритма к решению.
Принимать решение о том, когда остановиться, приходится
в некоторой степени неформально. Это решение далеко не
всегда безупречно и все же для него требуется четкий критерий.
Поскольку может не существовать машинно-представимого лсф,
такого, что /(х#) = 0, необходимо уметь различать, в каком
случае мы «достаточно близки». Критерий принятия решения
обычно представляется в таком виде: «Получено ли
приближенное решение задачи?» или «Находятся ли результаты
последних двух (или нескольких) итераций практически в одном
и том же месте?» Первый вопрос представляется проверкой
типа: «Имеет ли место |/(*+) | < xi?», где точность xi
выбирается так, чтобы отразить представления пользователя о
достаточной близости к нулю для данной задачи. Например, xi
может быть положено равным (macheps)1/2. Эта проверка,
конечно, очень чувствительна к масштабу f(x), и поэтому важно,
чтобы программа давала пользователю инструкции по
выбору xi или масштаба /, таких, что х+> удовлетворяющее
условию |f(jt+)|<Ti, было бы приемлемым решением задачи.
Уберечься от чрезмерной ограничительности этого условия
помогает второй вопрос, который состоит в проверке соотношения
вида: «Имеет ли место: (|лс+ — хс|/|л:+|) < хг?» Разумной
точностью здесь служит хг = (macheps)1/2, которое соответствует
останову всякий раз, когда совпадает левая половина разрядов
у хс и х+, хотя может быть выбрано любое %2, большее, чем
macheps. Поскольку х+ может быть близким к нулю, то вторая
проверка обычно видоизменяется, скажем, так: «Имеет ли
место: (|*+ — jcc|/max {|*+|, |*с|})<т2. Более удачная
проверка использует в знаменателе вместо \хс\ задаваемую
пользователем величину typx1), которая отражает характерные
значения переменной х (см. упр. 17). Таким образом, критерий
останова на ЭВМ CDC мог бы выглядеть так:
если |/(Jt+)|<l(T5 или 1*/""?1 п <Ю~7>
1 ' v +/ ' ^ max {typ ху | х+ |}
то остановиться.
На практике при решении любой задачи с быстрой локальной
сходимостью значения f(x+) обычно становится малым раньше,
*) Сокращение typ происходит от слова typical (типичный,
характерный).— Прим. перев.
44 Гл. 2. Нелинейные задачи с одной переменной
чем шаг по х, а для задач, на которых скорость лишь линейна,
первым может стать малым шаг по х. Читатель мог уже
убедиться, что выбор критериев останова очень сложен, в особенности
для плохо масштабированных задач. В полном объеме этот
вопрос будет рассмотрен в гл. 7.
2.6. МЕТОДЫ ДЛЯ СЛУЧАЯ, КОГДА ПРОИЗВОДНЫЕ
НЕ ЗАДАНЫ
Во многих практических приложениях функция f(x) не
задается формулой, а скорее представляет собой результат
некоторой вычислительной или экспериментальной процедуры.
Поскольку обычно f'(x) недоступно, то методы, использующие
значения f'(x) для решения f(x) = Q, должны быть
модифицированы так, чтобы обходиться только значением f(x).
Мы использовали f'(x) при моделировании поведения /
вблизи от текущего приближения к решению хс прямой,
касательной к / в хс. Если f'(x) недоступно, то заменим эту модель
секущей, проходящей через значения / в хс и некоторой
близлежащей точке Xc + hc (рис. 2.6.1). Нетрудно убедиться, что
тангенс угла наклона этой прямой равен
.f(xc + hc)-f(xe)
(2.6.1)
и таким образом полученная модель представляет собой
прямую
Mc(x) = f(xc) + ac(x — хс).
То, что нами проделано, эквивалентно, таким образом, замене
производной f'(xc) в исходной модели Мс(х) =/(Хс) +
Рис. 2.6.1. Аппроксимация f(x) с помощью секущей.
2.6. Методы для случая, когда производные не заданы 45
+ Г(хс)(х — хс) аппроксимацией ас. Тогда квазиньютоновский
шаг в нуль модели Мс(х) принимает вид
* - г f(Xc)
*N— *с —•
Тотчас же возникают два вопроса: «Будет ли этот метод
работать?» и «Каким образом следует выбирать Лс?» Из
математического анализа известно, что ас сходится к \'(хс) при
Лс->-0. Если число hc выбирается малым, то ас называется
конечно-разностной аппроксимацией для f(xc). Кажется
разумным, что конечно-разностный метод Ньютона, т. е.
квазиньютоновский метод, основанный на этой аппроксимации,
будет работать почти так же хорошо, как и метод Ньютона.
Позже мы убедимся, что это именно так. Однако этот прием
требует дополнительного вычисления / на каждой итерации, и
если f(x) является дорогостоящей, то дополнительное
вычисление функции нежелательно. В этом случае hc полагается
равным (х- — хс)у где х- есть результат предыдущей итерации,
так что ac = (f{x-) — f(xc))/(x- — хс) и никакие
дополнительные вычисления функции не используются. Получающийся в
результате квазиньютоновский алгоритм называется методом
текущих. Этот метод может показаться излишне надуманным,
тем не менее он работает хорошо. Сходимость метода
секущих немного медленнее сходимости метода с надлежащим
образом подобранной конечно-разностной аппроксимацией,
однако он обычно более эффективен с точки зрения суммарного
количества вычислений функции, необходимых для достижения
заданной точности.
Пример 2.6.1. Конечно-разностный метод Ньютона и метод
секущих, примененные к f(x) = x2—1 (ЭВМ CDC одинарная
точность).
Конечно-разностный Метод секущих
метод Ньютона (Хх выбирается по конечно-
(hk= 10~7«x^j разностному методу Ньютона)
2.0
1.2500000266453
1.0250000179057
1.0003048001120
1.0000000464701
1.0
Ч
Х\
х2
х3
х4
х5
х6
х7
2.0
1.2500000266453
1.0769230844910
U0082644643823
1.0003048781354
1.0000012544523
1.0000000001912
1.0
Пример 2.6.1 содержит образцы сходимости метода
секущих и конечно-разностного метода Ньютона (Ас=10-7) на за-
46 Гл. 2. Нелинейные задачи с одной переменной
даче f(x) = x2—1, л-0 = 2, которая решалась в примере 2.4.4
методом Ньютона. Обратите внимание, насколько похожи
результаты метода Ньютона и конечно-разностного метода
Ньютона; при этом метод секущих сходится несколько медленнее.
Значительное проникновение в суть вопроса дает анализ
влияния величины шага аппроксимации 1гс на скорость
сходимости получающегося конечно-разностного метода Ньютона.
Возьмем
х — * —х f{Xc)
x+ — xN — хс ас .
Тогда
x+-xm = xe-x.-l^ = a7l[f(x.)-f(xe)-aAx.-xe)] =
= a7l[f(x.)-Mc(x,)] =
= a;l{f(x^f(xc)4f(Xc)(x-xc) + [ff(xc)-ac](x^xc)}=
■a7l\\[f'(z)-f'
(xc))dz + [f'(xc)-ac](x.-xc)
Если обозначить ec = | xc — хф\ и e+ = | x+ — xjy то
e+<\a7l\{ie2c + \f'(xc)-°c\ec) (2-6.2)
при тех же предположениях относительно непрерывности по
Липшицу У е LipY(Z)), что и в лемме 2.4.2.
Читатель может заметить, что соотношение (2.6.2)
аналогично приведенному в разд. 2.4 выражению для границы
погрешности, за исключением того, что в правой части (2.6.2)
вместо \У (хс)~х | -стоит \ajx |, и что имеется дополнительное
слагаемое, содержащее разность между f'(xc) и ее
аппроксимацией. Отметим также, что проведенный выше анализ до сих
пор не зависел от значения ас Ф 0. Теперь определим ас
формулой (2.6.1) и введем в рассмотрение предположение о
непрерывности по Липшицу /' (см. разд. 2.4). Получим простое
следствие, которое показывает, насколько близка в зависимости
от hc конечно-разностная аппроксимация (2.6.1) к f'(xc).
Следствие 2.6.2. Пусть /: D->R, где D — открытый
интервал, и у eLipY(D). Пусть, далее хс, .rf + AcED, а ас задано
формулой (2.6.1). Тогда
k-fWK1^1- (2.6.3)
2.6. Методы для случая, когда производные не заданы 47
Доказательство, Из леммы 2.4.2 имеем
\f(Xc + flc)-f(xc)-hcf'(xc)\^^^.
Разделив обе части на |ЛС|, получим желаемый результат. □
Подстановка (2.6.3) в (2.6.2) дает
Если воспользоваться теперь предположением теоремы 2.4.3
о том, что |Г(х)|^р>0 в окрестности точки #*, то на основе
(2.6.3) легко показать, что \а~х |<2р-1 для ,vcgD и для
достаточно малых \hc\. Получаем
e+<%(ec + \he\)ee. (2.6.4)
Теперь довольно легко завершить доказательство
следующей теоремы.
Теорема 2.6.3. Пусть f: D-*~R, где D — открытый интервал,
и f'eLipY(D). Предположим, что |/'(*)|^Р Для некоторого
р > 0 и для каждого xgD. Если f(x) = 0 имеет решение
л% е D, то существуют положительные константы ц и ц',
такие, что если {hk} является последовательностью
действительных чисел, лежащих в пределах 0 < |Ла»| ^: т]', и |лг0 — *#|<л»
то последовательность {xk}f заданная формулами
k k
определена и сходится ^-линейно к х*. Если lim^_>ooA^ = 0, то
сходимость ^-сверхлинейна. Если существует некоторая
константа си такая, что
IК К сх | xk — xm |,
или, что эквивалентно, константа с2, такая, что
\hk\^c2\f(xk)\, (2.6.5)
то сходимость (/-квадратична. Если существует некоторая
константа Сз, такая, что
|Ал|<са|**-**-1|, (2.6.6)
то сходимость является по крайней мере двухшаговой ^-квад-
ратичной, при этом здесь как частный случай содержится
метод секущих, где hk = xk-\ — xk.
48 Гл. 2. Нелинейные задачи с одной переменной
Мы начали это обсуждение с утверждения о том, что
понимание сути вопроса заключено в самом существе анализа
и его простоте. В частности, идея конечно-разностной
аппроксимации выглядела при первом знакомстве с ней как
некоторый специальный прием. Однако можно не только увидеть ее
превосходное с вычислительной точки зрения поведение на
практике, но и получить при помощи анализа, вряд ли более
сложного, чем для метода Ньютона, точную зависимость
сходимости от длины шагов {Л*}. Это всего лишь один из многих
примеров того, когда численный и теоретический анализы
выступают как союзники в деле развития алгоритмов.
Если бы порядок сходимости конечно-разностного метода
Ньютона определялся только выбором {Л*}, то мы попросту
полагали hc = с2 \ f (хс) |, где с2 — некоторая константа, и на
этом заканчивался бы наш анализ, поскольку для хс,
достаточно близких к х«, нетрудно показать, что \f(xc) |^ б\хс— **|
(см. упр. 18). Однако наличие арифметики конечной точности
имеет самые серьезные последствия, на что мы и собираемся
сейчас обратить внимание. На практике, очевидно, hc не
может быть слишком мало по сравнению с хс. Например, если
1\(хс)ФО и |Лс|<|*с| -macheps то il(xc + hc)= 11(хс); таким
образом, числитель р (2.6.1) окажется в результате вычисления
равным нулю, поскольку программа, вычисляющая /, будет в
обоих случаях вызвана с одним и тем же значением аргумента
в представлении с плавающей точкой.
Даже если \hc\ достаточно велико, так что i\(xc + Нс)ф
Ф 11(Хс)у то при вычитании с плавающей точкой, необходимом
для получения числителя в (2.6.1), теряется точность. В конце
концов, если / вычисляется в двух соседних точках, в силу
непрерывной дифференцируемости / получающиеся значения
f(xc + hc) и f(xc) должны тоже быть почти равными. Может
даже получиться, что il{f(xc + hc)) = \\{f(xc)). Если \hc\
мало, то естественно, следует ожидать, что совпадут крайние
слева разряды мантиссы. Например, предположим, что на
ЭВМ с 5-разрядной мантиссой в десятичной системе счисления
имеются f(xc)= 1.0001 и f(xc + hc)= 1.0010, вычисленные для
ЛС=Ю-4 некоторой гипотетической программой. В этом случае
вычисленные значения f(xc + hc) — f{xc) и ас равнялись бы
соответственно 9ХЮ"4 и 9. Таким образом, при получении
разности значений функции было потеряно большинство
значащих цифр.
На практике, более того, если последовательно
просматривать разряды значения функции, то зачастую их достоверность
уменьшается с приближением к правому краю мантиссы. Это
объясняется не только конечной точностью, но также тем
фактом, что функция иногда сама является всего лишь
приближенным результатом, поставляемым вычислительной програм-
2.6. Методы для случая, когда производные не заданы 49
мой. Так, в приведенном выше примере разность f{xc + hc)—
— /(jtc) = 9X 10-4 может отражать только случайные
флуктуации в крайних справа разрядах f и не иметь вообще никакого
смысла. В итоге тангенс угла наклона модели функции / в хс
может даже не иметь того же знака, что и f'(xc).
Очевидный способ более точного вычисления ас состоит
в том, чтобы выбирать \НС\ достаточно большим для того,
чтобы в f{xc-\-hc) и f(xc) совпадали не все из наиболее
достоверных значащих цифр. Вместе с тем \hc\ не может быть
слишком большим, так как конечной целью вычисления
величины ас является ее использование в качестве аппроксимации
для У(хс)у а, как показывает (2.6.3), эта аппроксимация
ухудшается с ростом \hc\. Разумный компромисс заключается в
том, чтобы попытаться сбалансировать ошибку нелинейности,
вызываемую выбором слишком больших значений |ЛС|, с
ошибками арифметики конечной точности и вычисления функции,
проистекающими из возможности выбрать \hc\ слишком
малым. Развитие этого вопроса предлагается в качестве упр. 19.
Далее он будет обсуждаться в разд. 5.4.
Предположим, что f вычисляется настолько точно, насколько
это позволяет машинная точность. Тогда имеется простой
прием, состоящий в том, чтобы внести возмущение примерно
в половину разрядов мантиссы хс:
| hc | = Vmacheps . max {typ x, \xc\},
где typ a: — характерные размеры переменной x (см. разд. 2.5).
Этот часто применяемый прием обычно оказывается
удовлетворительным на практике. Если точность подпрограммы
вычисления f вызывает сомнения, то \hc\ должно быть достаточно
большим настолько, чтобы совпадала только половина
достоверных разрядов f(xc + hc) и f(xc). Если такое \hc\ столь
велико, что" применимость (2.6.1) в качестве аппроксимации
f'(xc) вызывает сомнения, то один из выходов состоит в
использовании центральной разности:
ac=:f(xc + hc)-Hxc-hc) ^ (26J)
Эта формула дает более точную аппроксимацию производной
при заданном hc (см. упр. 20), чем разностная аппроксимация
вперед1) (2.6.1), но вместе с тем она имеет недостаток,
связанный с удвоением затрат на вычисления функции.
*) В литературе вместо «разность вперед» используется также термин
«правая разность». — Прим. перев.
50 Гл. 2. Нелинейные задачи с одной переменной
2.7. МИНИМИЗАЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Завершим изучение одномерных задач обсуждением
минимизации функции одной переменной. Оказывается, эта задача
настолько тесно связана с решением одного нелинейного
уравнения с одним неизвестным, что в сущности уже известно, как
вычислять решения.
Прежде всего необходимо опять признать, что ответить на
вопросы существования и единственности практически
невозможно. Рассмотрим, например, полином четвертой степени,
изображенный на рис. 2.1.1. Его глобальный минимум, где
функция принимает свое абсолютно наименьшее значение,
находится в х ^ 0.943, но он также имеет локальный минимум
в х ^4.60, т. е. точку с минимальным значением функции на
некоторой открытой области. Если разделить функцию на х,
то она станет кубической с локальным минимумом в х ^ 4.58,
но без конечного глобального минимума, поскольку
Hm f(x) = — оо.
JC->-oo
В общем случае практически невозможно убедиться в том,
действительно ли мы находимся в глобальном минимуме
функции. Таким образом, так же как наши алгоритмы решения
нелинейных уравнений могут находить только один корень,
наши алгоритмы оптимизации в лучшем случае могут
определить местонахождение одного локального минимума, причем на
практике этого обычно вполне достаточно. Как и ранее,
вопрос о решении в замкнутой форме не ставится, ибо если можно
было бы находить минимум f(x) в замкнутой форме, то можно
было бы таким же образом решать f(x) = 0y полагая f(x) =
Высказанное выше утверждение о том, что читателю уже
известно, как решать задачу минимизации, основано на том,
что локальный минимум непрерывно дифференцируемой
функции должен приходиться на точку, где /'(*) = 0. Графически
это всего лишь означает, что функция не может начать
уменьшаться из такой точки в любом направлении. Доказательство
этого факта подсказывает нам и алгоритм, так что оно будет
приведено ниже. Полезно ввести обозначения Cl{D) и C2(D)
для множеств соответственно единожды и дважды непрерывно
дифференцируемых функций, действующих из D в R.
Теорема 2.7.1. Пусть f^Cl(D)t где D — открытый интервал,
и z^D. Если f (г)=й=0, то для любого s, такого, что f(z) -s<0,
существует константа / > Q, для которой f{z + Xs) < f(z) при
всех X^(OJ).
2.7. Минимизация функции одной переменной 51
Доказательство. Необходимо лишь, используя
непрерывность /', выбрать такое t, что f'(z + Xs)s<iO и z + Xs^D при
всех ^е(0,/). Остальное следует непосредственно из
математического анализа, так как для всех таких X имеет место
соотношение
л
f{z + ks) — f (z) = J /' (z + as) sda<0. □
о
Теорема 2.7.1 предлагает находить точку минимума х*
функции /, решая //(jc) = 0. С другой стороны, применяя теорему
к g(x) = —f(x), видим, что это условие выделяет также и
возможные точки максимума. Иначе говоря, решение дает
необходимые условия для нахождения точки минимума функции /,
но недостаточные. Теорема 2.7.2 показывает, что
дополнительным достаточным условием является /"(#*) >0.
Теорема 2.7.2. Пусть f^C2(D) для открытого интервала D
и x*eD есть точка, в которой f'(x*)=Q и /"(#*) >0. Тогда
найдется некоторый открытый подынтервал jD'czD, такой, что
^ей'и f{x) > f(x*) для любых других хе D'.
Доказательство. Пусть D' выбирается так, что ^gD' и
/" > 0 на D'. Использование разложения в ряд Тейлора с
остаточным членом не вызовет трудностей позже при изучении
многомерного случая минимизационной задачи. Поэтому
заметим, что для любого x^D' существует х е (**, х) cz D', для
которого
/ (х) - / (*.) = Г (*.) (х - х.) + у Г (х) (х - xf.
Таким образом, утверждение доказано, поскольку f'(x*) = 0 и
х е D' влечет за собой
f(x)-f(x,)=±(x-xff"(x)>0. □
Понимая теперь, что представляет собой решение,
подумаем, как его вычислять. Самый легкий путь, приводящий к
интересующему нас классу алгоритмов, состоит в решении f'(x) = О
с использованием стратегии гибридного метода Ньютона,
которая рассматривалась в разд. 2.5. Для обеспечения
минимизации, а не максимизации, дополним стратегию глобализации
требованием, чтобы /(**) уменьшалось с ростом k.
Итерация гибридного метода начинается из текущей
точки хс с применения к f'(x)=0 метода Ньютона или его мо-
52 Гл. 2. Нелинейные задачи с одной переменной
дификации, рассмотренной в разд. 2.6. Ньютоновский шаг имеет
вид
х+ = хс— у' (хс) * (2-7-1)
Следует взглянуть на суть этого шага с точки зрения
модельных задач. Поскольку (2.7.1) было получено в результате
построения аффинной модели производной f'(x) в окрестности xCt
это эквивалентно построению! квадратичной модели
тс (х) = / (хс) + V (хс) (х -хс) + { Г (хс) (х - хс?
функции f(x) в окрестности хс и выбору в качестве л;+
стационарной точки модели. Для задач максимизации и
минимизации квадратичная модель функции f(x) подходит больше, чем
линейная, поскольку она имеет самое большее одну точку
экстремума. Таким образом, в результате шага (2.7.1) будет
найдена за одну итерацию точка экстремума квадратичной
функции. Кроме того, точно так же как в теореме 2.4.3, можно
доказать, что она сходится локально и <7-кваДРатично к точке
экстремума jc# функции f(x), если У'{х*)Ф0 и f" непрерывно
по Липшицу в окрестности дс*.
Наша глобальная стратегия в минимизации будет
отличаться от приведенной в разд. 2.5 тем, что, принимая решение
о приемлемости ньютоновской точки xN, вместо соотношения
Г(хы) |<|f(*c) |, отражающего степень продвижения к нулю
'(*), будем пользоваться соотношением /(хлг) < f(xc),
указывающим на продвижение к минимуму. Если Цхы)^ f(xc), а
¥(хс) (xn — Хс)< 0, то по теореме 2.7.1 функция f(x) должна
первоначально уменьшаться в направлении от хс к xn, поэтому
следующую приемлемую точку х+ можно найти, дробя шаг в
обратном направлении от xN к хс. Из (2.7.1) видно, что
выражение ¥(xc)(xn — хс) отрицательно тогда и только тогда,
когда Г(хс) (или ее аппроксимация) положительна. Это
означает, что если локальная модель, используемая для получения
ньютоновского шага, имеет минимум, а не максимум, то
гарантируется существование подходящего направления шага
(рис. 2.7.1). С другой стороны, если /"(хс)<0 и f'(xc)(xN —
— хс)>0, то при переходе от хс к xN функция f(x)
первоначально увеличивается, поэтому шаг нужно делать в
противоположном направлении. Одна из стратегий состоит в том, чтобы
сначала проверить, подходит ли шаг длины \хы — хс\, и затем,
если необходимо, дробить его, пока не выполнится неравенство
f(x+)<f(xc). Более совершенные глобальные стратегии для
минимизации обсуждаются в гл. 6.
Критерий останова для оптимизации несколько отличается
от используемого при решении нелинейных уравнений. Здесь
2.8. Упражнения 53
опять возникают вопросы: «Получено ли приближенное
решение задачи?» или «Находятся ли результаты последних
итераций практически в одном и том же месте?» Второй вопрос
проверяется тем же самым условием, налагаемым на
относительную или абсолютную длину шага, что и в разд. 2.5: «Имеет ли
место |jc+ — xc|/max{typ;t, |*+|}<ti?» Первый вопрос можно
просто представить как «Имеет ли место: |/'(*+) I < т2?»>
однако здесь опять просматривается зависимость от масштабов /
и добавляется зависимость от масштабов х. Все же в этом
случае можно кое-что предпринять, а именно потребовать, чтобы
относительная скорость изменения /, равная f'(x)/f(x), была по
абсолютной величине меньше тг, или относительное изменение /,
деленное на относительное изменение х, т. е.
f(*+) +'
было по абсолютной величине меньше т2. Последняя проверка
представляется привлекательной из-за ее попытки учесть
масштабы как /, так и х.
Наконец, возникает вопрос о том, что делать, если
производные f'(x) недоступны. Ответ на него настолько похож на
рассуждения в разд. 2.6, что мы откладываем рассмотрение
этой проблемы до рассмотрения многомерного случая (см.
также упр. 21).
2.8. УПРАЖНЕНИЯ
1. Выполните одну итерацию метода Ньютона из х = 2 для функции
/i(x), заданной в разд. 2.1. К какому корню сходятся итерации? Что
произойдет, если начать из точки х = 1?
ft»*)
f(xc)
\ 1
XN *C
Наличие минимума у локальной
квадратичной модели приводит
сначала к уменьшению f(x) при
переходе от хс к XN
Наличие максимума у локальной
квадратичной модели приводит
сначала к увеличению f(x) при
переходе от хс к х#
Рис. 2.7.1. Соответствие локальной квадратичной модели наклону кривой
в начале перехода от хс к х„.
54 Гл. 2. Нелинейные задачи с одной переменной
2. За сколько приблизительно итераций сойдется к 1 на ЭВМ CDC
(/-линейно сходящаяся последовательность хк = 1 + (0.9)*, k = 0, 1, ...?
(Для ответа используйте бумагу, а не ЭВМ.) Является ли в общем случае
(/-линейная сходимость с постоянной 0.9 удовлетворительной для
вычислительных алгоритмов?
3. Рассмотрим последовательность хк = 1+ 1/£!, k = 0, 1, ... . Сходится
ли эта последовательность (/-линейно к 1? Сходится ли она (/-линейно с
любой постоянной с > 1? Какого типа эта сходимость? Сходится ли {хк} к 1
с (/-порядком / при любом значении / > 1?
4. Докажите, что всегда (/-порядок последовательности не превосходит
ее г-порядка. Приведите контрпример для обратного утверждения.
5. Докажите, что {xk} имеет (/-порядок, по меньшей мере равный р,
тогда и только тогда, когда для нее существует последовательность верхних
оценок погрешности {&*}> где Ьк ^ ек = \хк — х* |, такая, что, {Ьк}
сходится к нулю с (/-порядком, по меньшей мере равным р, и
— Ьк
lim —- < со.
6. (Более трудное упражнение.) Существует интересная связь между
/-шаговым (/-порядком и «1-шаговым» г-порядком. Попробуйте найти эту
связь и провести соответствующие доказательства. Данный результат вместе
с его приложением можно найти в работе Гэя (1979).
7. На ЭВМ IBM серий 360—370 умножение с повышенной точностью
реализовано аппаратно, а деление с повышенной точностью выполняется так:
сначала производится деление с удвоенной точностью, затем используется
итерация метода Ньютона, требующая только умножения и сложения. Для
лучшего понимания этого: (а) выведите итерацию метода Ньютона для
вычисления х* = 1/а, где а — заданное действительное число; (Ь) выполните
три итерации для заданных а = 9 и х0 = 0.1. Какого типа сходимость
наблюдается?
8. Проанализируйте скорость сходимости метода деления пополам.
9. Напишите, отладьте и протестируйте программу для решения одного
нелинейного уравнения с одним неизвестным. Следует придерживаться
гибридной стратегии, изложенной в разд. 2.5. В качестве локального шага
используйте метод Ньютона, конечно-разностный метод Ньютона или метод
секущих. В качестве глобальной стратегии используйте деление пополам,
дробление шага, стратегию интерполирования на отрезке между хы и хк или
какую-либо другую стратегию на ваше усмотрение. Выполните программу
для:
(a) / (х) = sin х — cos 2*, х0 =» 1;
(b) /(*) = *3-7*2+11jc-5, *о = 2, 7;
(c) f (х) = sin х — cos ху jc0 = 1;
(d) f2(x) (задана в разд. 2.1), х0 = 0, 2. (Если используется деление
пополам, то выберите для каждой задачи подходящий интервал и
позаботьтесь, чтобы ни одна из итераций не выходила за его пределы.) Какую
скорость сходимости вы наблюдаете в каждом случае? Она не всегда
должна быть квадратичной. Почему?
10. Воспользуйтесь программой из упр. 9 для нахождения точки с > 0,
на которой метод Ньютона будет зацикливаться при решении уравнения
arctgjc = 0 (см. рис. 2.4.1).
2.8. Упражнения 55
11. Модифицируйте программу из упр. 9 на случай нахождения
минимума функции одной переменной. (Суть модификаций объяснена в разд. 2.7.)
12. Какую скорость сходимости (к х* = 0) имеет метод Ньютона при
решении уравнения х2 = 0? х3 = 0? А при х + *3 = 0? х + хк = 0? Если
нарушаются предположения теоремы 2.4.3, то какие именно в каждом
случае?
13. Докажите, что если /(*♦) = /'(*♦) = 0» /"(**) Ф 0, то метод
Ньютона сходится (/-линейно к *♦, причем lim^^^, вЛ+1/в^= 1/2. [При желании
обобщите этот результат на случай f(x+) = /'(**) = • • • = /"(**) = 0»
/<я+1>(*») =*0.]
14. Докажите, что если /(**) = 0, /'(*♦) Ф 0, /"(**) = 0, f'"(x*) Ф 0,
то метод Ньютона сходится <7-кубически к х*. [При желании обобщите этот
результат на случай /'(**) Ф 0> f (**) = Г2)(*») = • • • = /(я)(*») = 0.
/<"+1>(*«) ¥=0.]
15. Постройте кубически сходящийся метод для решения f(x) = 0,
моделируя / на каждом шаге квадратичной аппроксимацией, получаемой из ее
разложения в ряд Тейлора. В чем основные трудности использования этого
метода? Считаете ли вы, что для этой задачи подходит квадратичная
модель? (См. также метод Мюллера, приведенный в большинстве вводных
курсов по численному анализу.)
16. Заданы feCfD), xc€=D и d=—f(xc)lf'(xe)t причем f(xc)¥=0 и
f (хс) ф 0. Покажите, что существует / > 0, такое, что \f(xc + hd)\<.
<\f(xc)\ для всех А, е= (0, /). [Указание: возьмите t такое, что /'(*с +
+ аЙ) •/'(*<:) > 0 для всех ^ е (0, /), и затем воспользуйтесь техникой
доказательства теоремы 2.7.1.]
17. Рассмотрите процесс решения х2 = 0 методом Ньютона,
начинающимся из Хо = 1. Будут ли любые две последовательные итерации
удовлетворять неравенству \xk+i — **|/тах{|**|, |**+i|} < Ю-7? Что можно
сказать о проверке, содержащей typ х, которая приведена в конце разд. 2.6?
18. Заданы /еС*(/)) и х+ е= Z), причем /(*•) =0. Покажите, что
существуют постоянная а > 0 и интервал D с Д содержащий **, такие, что
I/WI ^ а\х — х*\ для всех х е= и. [Указание: выберите б таким, что
If (*) I < а Для всех х е= D.]
19. Допустим, что /: £>->-R для открытого интервала /), и
предположим, что /' e=LipY(0). Допустим, что программа вычисления f(x) имеет
суммарную погрешность, ограниченную величиной rj |/(*)|, где ^ —
неотрицательная постоянная. Найдите верхнюю границу суммарной погрешности
[f(xc + hc)—f(xc)]lhc при аппроксимации f (хс) как функцию от hc [а
также от у» Л» /(*е) и f(xc + hc)]. Найдите значение hCt минимизирующее эту
верхнюю границу при фиксированных у» "Л и f(xc)- [Предположите здесь,
что f(xc + hc) ^f(Xc).] Как вы думаете, полезны ли конечные разности с
вычислительной точки зрения, когда f'(x) чрезвычайно мало по сравнению
С /(X)?
20. Предположим, что D является открытым интервалом, содержащим
Xc — hc, xc + hc&R, и пусть f": D-+& удовлетворяет условию f" е
eLipY(D). Докажите, что погрешность формулы центральных разностей
(2.6.7) при аппроксимации f'(хс) ограничена величиной y\hc\2/6. [Указание:
56 Гл. 2. Нелинейные задачи с одной переменной
распространите технику доказательства леммы 2.4.2 на получение
неравенства
/(«)-[yw+rW(«,<)+r(x)(«-s)-]<J[i£i^JL
или выведите аналогичную оценку из формулы Тейлора с остаточным
членом.]
21. Предположим, что вы решаете задачу минимизации с одной
переменной, где f(x) и f'(jt) заданы аналитически, но дорогостоящи для
вычисления, а /"(*) не задано аналитически. Предложите локальный метод
решения.
Второе программное замечание
Как явствует из гл. 2, мы предпочитаем получать итерационные алгоритмы
решения нелинейных задач из рассмотрения решений надлежащим образом
подобранных моделей задач. Используемая модель должна принадлежать
классу, для которого существует эффективная вычислительная процедура
решения. Кроме того, она должна выбираться так, чтобы адекватность
моделирования нелинейной задачи обеспечивала сходимость итерационной
последовательности к решению.
В гл. 2 элементарный аппарат математического анализа обеспечил нас
всей необходимой техникой для построения подходящих линейных и
квадратичных моделей и всем необходимым для анализа их погрешностей
аппроксимации на реальном классе нелинейных задач. Для решения модельной
задачи потребовалось всего две арифметические операции. Такая простота
и побудила нас к написанию гл. 2. По-видимому, нет необходимости в
каком-либо другом, более сжатом изложении скалярных итераций.
Существующее изложение позволило без каких-либо затруднений, присущих анализу
функций многих переменных и линейной алгебре, представить идеи, которые
будут распространены далее на многомерный случай.
Модели многомерного случая будут содержать производные функций
многих переменных, а решение модельных задач потребует решения систем
линейных уравнений. В гл. 3 представлен материал по вычислительной
линейной алгебре, касающийся решения модельных задач и извлечения
полезной информации из самих моделей. Глава 4 представляет собой обзор
некоторых теорем анализа функций многих переменных, которые, как нам
представляется, .полезны для построения многомерных моделей и для анализа их
аппроксимационных свойств.
Имеется тонкая и интересная связь между моделями, которые мы строим,
и способами извлечения информации из них. Если модельная задача легко
строится и решается, то нет надобности в том, чтобы она была столь же
хорошей, как в случае, когда решение модельной задачи является
трудоемким. Это подтверждает тот простой факт, что лучше выполнить больше
итераций дешевого метода, чем дорогого. Мы заинтересованы также и в
использовании структуры задачи или по крайней мере той ее части, которая
без труда учитывается в модели. Это делается как в целях улучшения
модели, так и для облегчения получения из нее х+. Интересно также
рассмотреть вопрос о том, что именно из структуры задачи можно благополучно
опустить в модели, облегчая этим ее решение и ожидая тем не менее
значительную сходимость итерации. В подходящий момент будут приведены
примеры обоих подходов.
3
Основы вычислительной линейной
алгебры
В настоящей главе обсуждаются разделы вычислительной
линейной алгебры, необходимые для реализации и анализа
алгоритмов решения многомерных нелинейных задач. В разд. 3.1
вводятся нормы векторов и матриц, предназначенные для
измерения в наших алгоритмах размеров этих объектов, и
приводятся свойства норм, полезные для анализа рассматриваемых
методов. Затем в разд. 3.2 описываются различные матричные
разложения, используемые алгоритмами для решения систем из
п линейных уравнений с п неизвестными. В разд. 3.3 кратко
обсуждается проблема чувствительности к погрешностям,
возникающим при решении таких систем. Наша точка зрения такова:
несмотря на доступность алгоритмов имеющихся в
библиотеках программ, серьезный пользователь нуждается в понимании
принципов, лежащих в основе алгоритмов.
При этом пользователь должен овладеть инструментом
вычислительной линейной алгебры, позволяющим ему выбирать
соответствующие программы, учитывая затраты по их
использованию и величину погрешности.
В справочных целях в разд. 3.5 резюмируются свойства
собственных значений, которые используются в этой книге,
особенно их связь с положительной определенностью. В разд. 3.4 и
3.6 обсуждаются соответственно пересчет матричных
разложений и решение переопределенных систем линейных уравнений.
Поскольку эти темы не понадобятся вплоть до гл. 8 и 11,
ознакомление с ними можно отложить.
Превосходным справочным пособием по этому материалу
служат книги Уилкинсона (1965), Стюарта (1973), Стренга
(1976), Голуба и Ван Лоана (1983).
3.1. Векторные и матричные нормы 59
3.1. ВЕКТОРНЫЕ И МАТРИЧНЫЕ НОРМЫ,
ОРТОГОНАЛЬНОСТЬ
В гл. 2 мы сочли полезным сделать определенные
предположения относительно /, такие, как ограниченность снизу
абсолютной величины производной или выполнение условия Липшица
(2.4.1), что обеспечивало ограниченность величины изменения
производной, деленной на величину соответствующего изменения
аргумента. Впоследствии нам понадобятся аналогичные
условия, но уже в той ситуации, когда абсолютная величина больше
не может служить мерой величин, так как аргументы и
производные больше не являются скалярами. Аналогично, условия,
подобные критерию останова | f(xk) |^ть должны быть
заменены на критерий, подходящий для случая, когда F(xk) есть
вектор.
В гл. 4 мы увидим, что значения функций будут векторами
или скалярами, а производные будут матрицами или векторами.
В данной главе вводятся нормы векторов и матриц как
соответствующие обобщения абсолютной величины действительного
числа.
Существует много всевозможных норм, отвечающих
различным целям, но мы ограничимся лишь некоторыми из них.
Наибольший интерес представляет так называемая евклидова или
/г-норма, которая совпадает с обычным понятием длины
вектора. В настоящем разделе обсуждаются также ортогональные
матрицы. Эти матрицы особым образом связаны с евклидовой
нормой, поэтому они играют важную роль в вычислительной
линейной алгебре.
Напомним, что Rrt обозначает векторное пространство
действительных пХ 1-векторов. Малые греческие буквы будем, как
правило, использовать для действительных чисел, т. е.
элементов множества R, а малые латинские буквы — для векторов.
Матрицы будут обозначаться большими латинскими буквами,
причем множество действительных п X m-матриц будет
обозначаться через RrtXm. Верхний индекс Т будет обозначать
матричное транспонирование. Один и тот же символ 0 будет
использоваться как для векторов, так и для скаляров. Таким образом,
взглянув на приведенное ниже соотношение (3.1.1а), читатель
легко поймет, что ||0||=0.
Определение 3.1.1. Нормой в R" является
действительнозначная функция || • || на R", удовлетворяющая условиям:
IMI ^0 для каждого ugR", причем ||и|| =0,
только если v = 0 е Rn; (3.1.1 а)
||сю|| = |а|-|М1 Для каждого иеКпи aeR; (3.1.1b)
|| v + wIK || о || + 11 w|| для каждого v, w^Rn. (3.1.lc)
60 Гл. 3. Основы вычислительной линейной алгебры
Три наиболее подходящие для наших целей векторные нормы
для fl = (i>i, v2, ..., vn)T^Rn имеют вид
IML = max |0|| (1^- или sup-норма1)); (3.1.2а)
п
|| v ||, = £ | vt | (/гнорма или норма наименьших
'-1 абсолютных разностей); (3.1.2Ь)
1М12 = ( Ys (vi)2) (k'f евклидова или наименьших
^*={ ' квадратов норма). (3.1.2с)
Все они являются отдельными случаями общего класса
векторных /р-норм вида
\\v\\p = [t\Vi\p) \ (3.1.3)
где 1^р<оо. Читатель может доказать, что (3.1.2а)
согласуется с (3.1.3) в пределе при р, стремящемся к оо (упр. 1).
При обсуждении сходимости мы будем говорить о векторной
последовательности {лс*}, сходящейся к вектору хч. Делая такое
высказывание, будем подразумевать определенную норму и
иметь в виду, что
Hm ||**-*J —0.
ft->oo
Будем также говорить о скорости сходимости {xk} к х* и
подразумевать скорость сходимости {И** — д:#||} к 0. Было бы жаль,
если пришлось бы специально оговаривать вид нормы, как это
следовало делать, окажись возможным сходимость в одной
норме, а в другой — нет. Это означало бы, что вывод о том,
сошелся или нет на практике конкретный алгоритм, может
зависеть от того, какая норма используется в его критерии
останова. К счастью, благодаря следующему результату, который
не верен в бесконечномерном пространстве, в Rn нет таких
проблем. Следует подчеркнуть, что ^-линейная сходимость является
свойством, зависящим от нормы.
Теорема 3.1.2. Пусть ||-|| и ||| • ||| —любые две нормы в R".
Тогда существуют положительные константы аир, такие, что
а|М1<||МКР1М1 (3.1.4)
для любого v е R". Более того, если {vk} есть произвольная
последовательность в R", то для и#е Rn
Hm||**-iUI = 0
*) Ее называют также нормой Чебышёва. — Прим. персе.
3.1. Векторные и матричные нормы 61
тогда и только тогда, когда для каждого /, 1 ^ / ^ я,
последовательность (vk)i, состоящая из i-x компонент векторов Vk,
сходится к /-й компоненте (и,),- вектора v*.
Доказательство оставим читателю в качестве упражнения,
поскольку оно не является центральным в нашей теме. Более
простым упражнением будет доказательство справедливости
конкретных соотношений
IMIi>IMI2>IML, 1М1,<У"1М12, ll*k<V*ll*L. (3.1.5)
из которых может быть выведено (3.1.4) для /г, 12- и /«>-норм.
Соотношение || v \\{ ^ л> п || v ||2 можно легко доказать, используя
неравенство Коши — Шварца:
п
vTw = Yj vi^i ^ IIv Ik II ®> ||2 для всех v, a/eR",
Важное следствие из соотношений (3.1.4) и (3.1.5) состоит в
том, что характеристика работы алгоритма вряд ли серьезно
зависит от выбора нормы, и потому такой выбор обычно
основывается на удобстве или на соответствии конкретной задаче.
Ранее уже упоминалось, что нам необходимо уметь измерять
матрицы так же, как и векторы. Это, конечно, можно сделать,
представляя матрицу A=(aij) в виде соответствующего ей
вектора (ап, а2ь ..., апи о>\ъ ...» апп)т и применяя любую
векторную норму к этому «длинному» вектору. Полезная во
многих отношениях фробениусовская норма есть в точности /2-нор-
ма матрицы Л, записанной как длинный вектор:
(п п \1/2
ZSl^i2 . (зл.6)
Принято называть их «матричными нормами», и они вполне
уместны, когда матрица рассматривается как ящик письменного
стола, набитый числовой информацией. Это будет отвечать их
роли в локальных моделях, на которых основываются итерации
наших нелинейных методов.
Надо уметь также измерять матрицы в соответствии с их
ролью операторов. Если v имеет определенную величину ||и||,
то хотелось бы иметь возможность указывать границы для
\\Av\\, величины образа v при отображении с помощью
оператора А. Это окажется полезным при анализе сходимости.
Читатель может вернуться назад, в разд. 2.4, и увидеть, что там
как раз использовалось ограничение р на производную модели.
Нормы операторов должны зависеть от тех конкретных
векторных норм, которые используются для измерения v и Av.
62 Гл. 3. Основы вычислительной линейной алгебры
Естественным определением нормы Л, индуцированной
заданной векторной нормой, является
||Л||= max {^}. (3.1.7)
Это — максимальная величина, на которую А может растянуть
любой вектор в заданной норме ||-||. Вообще говоря, нет
никакой необходимости в использовании одной и той же нормы для
v и Avy однако у нас нет и потребности в соответствующем
обобщении.
Норма (3.1.7) называется операторной нормой,
индуцированной векторной нормой ||-||, и для любой векторной /„-нормы она
обозначается как ||Л||Р. Как нетрудно показать, она
удовлетворяет трем определяющим свойствам матричной нормы, в
точности совпадающим с (3.1.1), если там заменить v, aiGR" на
A, Bg Rnxn. Хотя кажется, что определение (3.1.7) может быть
лишь в малой степени полезным с вычислительной точки зрения,
поскольку оно подразумевает решение оптимизационной задачи,
однако индуцированные матричные /г, /2- и /оо-нормы задаются
следующими формулами:
|| A ||, = max {lla./Ц,}, (3.1.8а)
1</<я
\\А ||2 = (максимальное собственное значение (3.1.8Ь)
матрицы АТАУ12,
ML- шах {|| а,. ||,}, (3.1.8с)
доказательство которых оставляем в качестве упражнения.
Здесь через а.\ обозначен /-й столбец матрицы Л, а через щ.—
ее t-я строка. Таким образом, ||j4||i и ЦЛЦоо нетрудно вычислить,
что же касается ||Л||2, то она оказывается полезной при
анализе.
Иногда линейные преобразования задачи заставляют нас
использовать взвешенную норму Фробениуса:
ИЙ^ЛА^Н^» Wx и W2 — невырожденные лХ ^-матрицы (3.1.9)
(«невырожденные» означает «обратимые»). Несмотря на то что
норма Фробениуса и индуцированная /р-норма удовлетворяют
свойству мультипликативности
||ЛЯ||<||Л||.||В||, (3.1.Ю)
взвешенная норма Фробениуса, за исключением специальных
случаев, не удЬвлетворяет ему.
Некоторые свойства матричных норм и произведений
матрицы на вектор представляют особый интерес для анализа
наших алгоритмов. Эти свойства перечислены ниже. Доказатель-
3.1. Векторные и матричные нормы 63
ства некоторых из них вынесены в упражнения, причем в
необходимых случаях с соответствующими указаниями. Единичная
n-мерная матрица обозначается через /, причем, каково в
каждом случае п, понятно из контекста. След матрицы М,М е Rnxn,
определяется как
tr(A*)=EAf„.
Теорема 3.1.3. Пусть || • || и ||| • ||| суть произвольные нормы
в RnXn. Существуют положительные константы аир, такие,
что
аМ1|<|||Д|||<рМ|| (3.1.11)
для каждого A^RnXn. В частности,
Аг-1/2||Л||/7<||Л||2<||Л||Р, (3.1.12)
а для р = 1 или р = оо
п-ЩА\\р<\\А\Ь<пЩА%. (3.1.13)
Норма Фробениуса матрицы А удовлетворяет соотношению
\\A\\P = [ir(ATA)]112, (3.1.14)
и для любых BGRnx"
\\AB\\F^min{\\A\\2\\B\\F, \\A\\F\\B\\2). (3.1.15)
Кроме того, для любых v, w е Rn имеем
1|Л1Ч|2<||Л|ММ12, (3.1.16)
\\VWT\\F = \\VWT\\2 = \\v\\^\\w\\2. (3.1.17)
Если А не вырождена, то операторная норма, индуцированная
нормой 11-11, удовлетворяет соотношению
min ~7,—!Г"
Следующая теорема утверждает, что операция обращения
матриц непрерывна по норме. Кроме того, она дает
соотношение, связывающее нормы двух обратных к близким между собой
матрицам, которое окажется полезным позже при анализе
алгоритмов.
Теорема 3.1.4. Пусть ||-||—произвольная норма в Rnxn,
такая, что имеет место (3.1.10) и ||/||= 1, пусть также E^RnXn.
64 Гл. 3. Основы вычислительной линейной алгебры
Если ||£||< 1, то существует (/ — Е)~1 и
|(/-£)-'|<—1^-. (3.1.19)
Если А не вырождена и | Л"1 (В — Л)|| < 1, то В не вырождена и
\в~Ч<—г-Ц1^ 1Г- (зл-2°)
" "^ 1-Ц Л"1 (В -Л) II '
Доказательство. Изложим идею, не вдаваясь в детали.
Неравенство (3.1.20) следует из непосредственного использования
(3.1.19) с однократным применением (3.1.10), так что мы
оставляем его как упражнение. Доказательство (3.1.19) во многом
похоже на доказательство равенства
оо
Его схема состоит в доказательстве того, что (/ + £ + Е2 +
... +Ek) = Sk образует последовательность Коши в Rnxn и,
следовательно, сходится. Далее нетрудно показать, что
lim Sk = (I-Erl
и что (3.1.19) следует из соотношения
\\(I-E)-{\\= lim ||S*||<£ IIЯП'- □
В заключение введем понятие ортогональных векторов и
матриц. Некоторые простые свойства ортогональных матриц
в /2-норме показывают, что они будут полезны с
вычислительной точки зрения. Скалярное произведение двух векторов v>
mieR" обозначалось нами как vTw, но иногда будет удобно
пользоваться некоторым специальным обозначением. В
следующих двух определениях происходит наложение двух смысловых
значений vi, и мы еще раз рекомендуем читателю
интерпретировать это по контексту *).
Определение 3.1.5. Пусть v, дое Rn. Скалярное произведение
v и w по определению равно
п
(v, a;> = ora;=S^^ = l^ll2-lltfi;|l2-cose, (3.1.21)
1) См. посвященное этому вопросу замечание в предисловии. — Прим.
перев.
3.2. Решение систем линейных уравнений 65
где 0 есть угол между v и w, если, конечно, v ф О и хюфЪ.
Если (vy w} = 0, то говорят, что v и w ортогональны или
перпендикулярны.
Определение 3.1.6. Говорят, что векторы см, ..., v*€ R"
ортогональны или взаимно ортогональны, если <р/, t//> = 0, / =^= /.
Если, кроме того, <*;,-, У/> = 1, то говорят, что система векторов
{аь • •, ул} ортонормальна, и если £ = /г, то она является орто-
нормальным базисом в Rn.
Пусть Q е RnxP, тогда говорят, что Q является
ортогональной матрицей, если
QTQ = I или QQr = /. (3.1.22)
По определению, эквивалентному (3.1.22), столбцы или
строки ортогональной матрицы образуют ортонормальную систему
векторов. Следующая теорема содержит некоторые свойства
ортогональных матриц, которые делают особенно важным их
значение для практики. Доказательства оставлены в качестве
упражнений.
Теорема 3.1.7. Если матрицы Q, (5 е Рлхл ортогональны, то
матрица QQ тоже ортогональна. Кроме того, для любых i/gR"
и Де Rnxn имеют место равенства
IIQofc'-IHI* (ЗЛ.23)
||Q^||2 = MQ|b = H||2, (3.1.24)
IIQII2=1. (3.1.25)
Равенство (3.1.23) показывает, что ортогональная матрица
соответствует нашим геометрическим представлениям об
операторе отражения и поворота, поскольку он может изменять только
направление вектора v, но не его длину. Равенство (3.1.24)
говорит о том, что ортогональная матрица не изменяет норму
матрицы. Вот те две причины, по которым ортогональные
матрицы с успехом используются в матричных разложениях.
3.2. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
И РАЗЛОЖЕНИЯ МАТРИЦ
Многомерные нелинейные алгоритмы почти всегда требуют на
каждой итерации решения по крайней мере одной системы из п
линейных уравнений с п неизвестными
Ax = b9 As=RnXn, 6, *g=R\ (3.2.1)
66 Гл. 3. Основы вычислительной линейной алгебры
Обычно это связано с нахождением ньютоновской точки путем
решения модельной задачи или некоторой ее модификации.
К счастью, для решения данной задачи доступны превосходные
библиотеки подпрограмм: в Соединенных Штатах, прежде всего
в библиотеках UNPACK и IMSL, а в Великобритании в NAG
и Харвелловской библиотеках. Эти библиотеки содержат
алгоритмы решения задачи (3.2.1) для матриц общего вида, а также
специальные алгоритмы, которые более эффективны для
случаев, когда А имеет структуру особого вида, такую, как
симметричность и положительная определенность (обычные свойства
систем, возникающих в прикладной минимизации). Из-за
доступности этих программ, тщательности труда по их созданию
и тестированию, наша точка зрения такова, что лицу,
решающему нелинейные задачи, нет необходимости, а возможно, оно
и вовсе не должно писать свой собственный «решатель»
линейных уравнений. Скорее, это лицо должно знать, какую из
имеющихся программ использовать для каждого из различных типов
задач (3.2.1), с которыми он или она может столкнуться, а
также знать о затратах и возможных проблемах, связанных
с использованием программ. Важно к тому же иметь базовые
знания по структуре этих программ, с тем чтобы без труда
обращаться с ними и чтобы представлять себе, какие из
технических приемов окажутся полезными в других частях
нелинейных алгоритмов.
В целях экономии места в математических формулах
распространена практика записи A~lb> например хц+\ = Xk — AkXF(xk)
в ньютоновских итерациях для F{x) = 0. Беда в том, что
читатель, не знакомый с численными расчетами, может подумать,
что мы, в самом деле, вычисляем Л^1 и берем ее произведение
на вектор Ъ. Для большинства вычислительных машин всегда
более эффективно вычисление А~ХЬ путем решения линейной
системы Ах = Ь с использованием методов разложения матриц,
хотя это может оказаться неверным для некоторых «векторных
ЭВМ».
Способы представления матриц в виде произведения
сомножителей основываются на разложении А вида
А = А\ • А% • ... • Ат,
где каждое At имеет форму, удобную для решения (3.2.1). В
нашем случае т ^ 5, причем главным образом т = 2 или 3. Имея
разложение А или в процессе ее разложения, мы пытаемся
выяснить вопрос о вырожденности или обратимости Л. Если А
почти вырождена, то задача (3.2.1) не будет хорошо
поставленной с вычислительной точки зрения, и здесь, видимо, более
важно знать это, чем вычислять ненадежное решение.
Подробнее об этом говорится в следующем разделе.
3.2. Решение систем линейных уравнений 67
Если мы хотим приняться за решение Ах = Ь, то нам надо,
«отщепляя» один за другим множители разложения, решить
уравнения в такой последовательности:
АХЬХ = Ь,
A2b2 = blf
АтЬт = 0m_i,
где х = Ьт есть искомое решение. Чтобы убедиться в этом,
отметим, что каждое bi равно AJxAjlx ... АГ1Ь, так что
X — Ат Ащ—1
A7lb = A'lb.
Ниже перечислено шесть наиболее важных вариантов
выбора Ai и кратко упомянуто о характерных особенностях
решения (3.2.1) для каждого из вариантов.
1. Ai представляет собой матрицу перестановок Р. Матрица
перестановок имеет тот же набор строк (и столбцов), что и
единичная матрица, однако расположенных не в таком порядке,
а переставленных. Для любой матрицы М матрица РМ поэтому
является точно такой же перестановкой строк в М, a MP —
такой же перестановкой столбцов в М. Далее, Р~1 = РТ тоже есть
матрица перестайовок. Обычно Р хранится в виде вектора р =
= (рь ..., рп)т, получающегося в результате перестановки в
(1,2,
п)т, причем договоренность здесь такова, что t-я
строка в Р совпадает с р,-й строкой в /. Нетрудно заметить, что
Рх = Ь имеет решение xPi = btt i = 1, ..., п.
2. Ai является ортогональной матрицей, обозначаемой через
Q или U. Поскольку Q~l = Qr, то решение Qx = b сводится
к формированию QT6, а так как Q часто имеет вид произведения
элементарных ортогональных преобразований, то решение, как
правило, можно выполнить эффективным образом, не прибегая
к явному вычислению Q.
3. Ai есть невырожденная диагональная матрица Д du =
= di Ф 0, i=l, ..., n, da = 0, i Ф j. Решением Dx = b является
Xi = bi/diy i = 1, ..., п. Матрица D хранится в виде вектора.
4. At — невырожденная блочно-диагональная матрица De,
у которой на главной диагонали находятся обратимые блоки
размера 1 X 1 или 2 X 2, а вне блоков стоят нули, например,
х х 0
Ои =
X X
X
X
X
X
68 Гл. 3. Основы вычислительной линейной алгебры
Решение йвХ = Ь находится решением соответствующих
линейных систем порядка 1X1 и 2 X 2.
5. At есть невырожденная нижняя треугольная матрица L,
1цф0, i=h ...» я, Л/ = 0, 1 ^ i < / ^ п. Схематично она
выглядит так:
Г* о!
L _ I X X I
~" I X X X Г
I X X X XJ
Если 1ц = 1, i = 1, ..., п, то L называется нижней треугольной
с единичными диагональными элементами. Система Lx = b
решается прямой подстановкой: используя первое уравнение, найти
х\, потом, подставив его во второе уравнение, найти х2, затем,
подставив их в третье уравнение, найти х% и т. д.
6. А\ есть невырожденная верхняя треугольная матрица,
обозначаемая как V или /?. Она является транспонированной к
нижней треугольной матрице. Система Ux = b решается
обратной постановкой с использованием уравнения от л-го до 1-го
для нахождения в том же порядке неизвестных от хп до х\.
Таблица 3.2.1. Арифметическая трудоемкость (главные члены)
решения линейных систем
Матрица
Q
D
D*
L или U
Умножения и деления
п2
п
< 5л/2
п2/2
Сложения и вычитания
п2
—
<Л
п2/2
В табл. 3.2.1 приведена арифметическая трудоемкость1)
решения линейных систем, задаваемых матрицами перечисленных
выше типов. Во всех этих случаях она мала по сравнению с
трудоемкостью разложения матриц. Отметим, что решение Рх = Ь
предполагает лишь п операций присваивания.
Нас будет интересовать разложение матриц трех типов:
общего вида, симметричных и симметричных положительно
определенных. Матрица А е Rnxn симметрична, если А = Ат.
Матрица А положительно определена, если vTAv > 0 для всех
ненулевых v е Rn; в случае симметричности это эквивалентно
условию, что все ее собственные значения положительны.
4) Под арифметической трудоемкостью понимается количество
арифметических операций. — Прим. перев.
3.2. Решение систем линейных уравнений 69
Важное значение имеют PLU- и (^-разложения квадратных
матриц общего вида. PLiZ-разложение имеет вид A=P-L-U
или PTA = LU, где Р — матрица перестановок, L — нижняя
треугольная матрица с единичными диагональными элементами,
U — верхняя треугольная матрица. Это разложение находится
с помощью исключения Гаусса с частичным выбором ведущего
элемента или преобразования Дулитла, где для
преобразования А в U и одновременно для получения разложения
используются стандартные операции над строками (что эквивалентно
умножению слева А на L~XP-X). Далее, QR- или Q/^P-разложе-
ние, где А = QRP, Q — ортогональная, R — верхняя треугольная
матрица, Р — матрица перестановок, получается в результате
преобразования А в R умножением слева на последовательность
из л—1 ортогональных матриц Q,-. Каждая матрица Qt
обнуляет элементы /-го столбца матрицы Q/_i- ... -Q\A, лежащие
ниже главной диагонали, и вместе с тем оставляет неизменными
первые i— 1 столбцов. Матрица Q, называется преобразованием
Хаусхолдера и имеет вид
Qi = I — uiuJt
где (a/)/ = 0, /= 1, ..., /—1, а остальные элементы вектора щ
выбираются так, чтобы Q, была ортогональной и приводила к
появлению требуемых нулей в t'-м столбце. Матрица
перестановок, которая в действительности не всегда используется,
формируется из перестановок столбцов, необходимых для
перемещения на /-и итерации столбца с наибольшим значением суммы
квадратов его элементов, лежащих ниже (i—1)-й строки, на
место /-го столбца.
Преимущество Q/^-разложения состоит в том, что, поскольку
при формировании R оно не приведет к существенному
увеличению в целом элементов преобразуемой матрицы Л. Это делает
его численно очень устойчивым и служит одной из причин, по
которой преобразование Хаусхолдера и другие ортогональные
преобразования играют важную роль в вычислительной
линейной алгебре. С другой стороны, ^(/-разложение является, как
правило, довольно точным, а его трудоемкость составляет
половину трудоемкости Q/^-разложения, так что на практике
используются оба разложения. В алгоритмах секущих будет
использовано <2/?-разложение без перестановок столбцов, поскольку после
внесенных в матрицу изменений малого ранга это разложение
пересчитывается с меньшими затратами, чем PL (/-разложение.
Исходя из соображений реализации, которые изложены Чз
разд. 6.5, мы на самом деле рекомендуем использовать
(^-алгоритм во всех алгоритмах решения систем нелинейных уравде-
70 Гл. 3. Основы вычислительной линейной алгебры
ний с плотно заполненными матрицами. Алгоритм
(^-разложения представлен в приложении алгоритмом АЗ.2.1.
Если матрица А симметрична и положительно определена, то
более эффективным алгоритмом оказывается разложение Хо-
лесского, в котором A=LLT, L — нижняя треугольная матрица.
Матрицу L легко найти, выписав (п2-\-п)/2 уравнений,
выражающих значение каждого элемента нижнего треугольника
матрицы А через элементы матрицы L:
Яц = ('и)2>
#21 ='ll " ^2Ь
#22 = (h\) 4" fe) у
#32 — ^21*31 "Г *22^32>
#л2 — Wnl "Ь Wn2>
азз = (/з.)2 + (/з2)2 + азз)2.
Они решаются в той же последовательности относительно /и,
/гь ..., Inu /22, /32, ..., 1п2, /зз, ..., /пз, ..., причем для
нахождения /// используется уравнение для ац. Этот алгоритм
численно очень устойчив. В нем требуется п извлечений квадратного
корня для получения диагональных элементов ///, /= 1, ..., п\
причем все подкоренные выражения положительны тогда и
только тогда, когда А положительно определена. Иногда
разложение представляется в виде А = LDLT> где матрицы: L —
нижняя треугольная с единичными диагональными элементами, D —
диагональная с положительными диагональными элементами.
Эта форма разложения не требует никакого извлечения
квадратных корней. Алгоритм разложения Холесского является
специальным случаем алгоритма А5.5.2, приведенного в
приложении.
Если А симметрична, но не является знакоопределенной, т. е.
А имеет положительные и отрицательные собственные значения,
то А можно эффективным образом разложить на множители
PLDBLTPTy где Р — матрица перестановок, L — нижняя
треугольная матрица с единичными диагональными элементами, Db —
блочно-диагональная матрица с блоками размеров 1X1 и 2 X 2.
Дополнительные сведения по этому разложению имеются в
работе Банча и Парлетта (1971). Асен (1973) привел вариант,
3.3. Погрешности при решении линейных систем 71
в котором DB заменено на трехдиагональную матрицу Т.
Подробности см. в книге Голуба и Ван Лоана (1983). Детальное
обсуждение PLU-, QR- и 1//-разложений можно посмотреть
в книгах Стюарта (1973) или Донгарры и др. (1979).
Арифметическая трудоемкость всех разложений отличается
от /г3 небольшим множителем. Она приведена в табл. 3.2.2.
Таблица 3.2.2. Арифметическая трудоемкость (главные члены)
разложения матриц
Разложение
A = PLU
A = QR
A = LLT, LDLT
A = PLDBLTPT
A=*PLTLrPT
Умножения и деления
П3/3
2tt3/3
/i3/6
n3/6
n3/6
Сложения и вычитания
rt3/3
2/i3/3
n3/6
Al3/6
Al3/6
В гл. И кратко обсуждаются нелинейные задачи, которые
приводят к разреженным линейным системам, где большинство
матричных элементов нулевые. При их решении следует
пользоваться специальными подпрограммами, предназначенными
для решения разреженных матричных задач. Здесь уместно
упомянуть широко доступные харвелловский и йельский пакеты
программ.
3.3. ПОГРЕШНОСТИ ПРИ РЕШЕНИИ ЛИНЕЙНЫХ
СИСТЕМ
На итерации нелинейного алгоритма будет использовано
решение 5 линейной системы Acs = —F(xc) для определения шага
или направления в точку следующего приближенного решения
jc+. Поэтому важно знать, насколько сильно вычисленный шаг
может быть подвержен влиянию используемой арифметики
конечной точности. Кроме того, поскольку Ас и F(xc) иногда сами
по себе являются аппроксимациями величин, которые в
действительности хотелось бы использовать, то интересно, какова
чувствительность вычисленного шага к изменениям в данных,
определяющих Ас и F(xc). Эти вопросы обсуждаются в
настоящем разделе.
Рассмотрим две линейные системы:
Aix^bl:[4 "|о][£]-[и]-
Г 0.66 3.341 Г *,-| Г 41
Л* = &2:|_1.99 10.01 JUJ-LwJ-
72 Гл. 3. Основы вычислительной линейной алгебры
Обе имеют решение (1, 1)г. Если заменить Ьх на Ь\ —(0.04, 0.06)г,
что соответствует 0.43-процентному относительному изменению
Ь\ в /а-норме, то новое решение первой системы станет равным
(0.993, 0.9968)г, а относительное изменение х в /2-норме
составит 0.51 %. Однако если изменить 62 на ту же самую величину
(—0.04, —0.06)г, что отвечает 0,55-процентному относительному
изменению, то новое решение второй системы будет равно
(6,0)т. Относительное изменение х здесь огромной равно 324 %.
Аналогично, замена первого столбца в А2 на (0.75, 2.00)т также
приводит к тому, что х становится равным (6,0)г. Очевидно,
что вторая система очень чувствительна к изменениям в ее
данных. Естественно спросить, почему? Графическое представление
двух ее уравнений показывает, что они представляют собой две
почти параллельные прямые, так что малое смещение какой-
либо одной из них существенно меняет точку их пересечения.
С другой стороны, первая система соответствует прямым,
пересекающимся примерно под углом в 80°, так что смещение
любой прямой вызывает аналогичное смещение точки их
пересечения (рис. 3.3.1).
Линейные системы, чьи решения очень чувствительны к
изменениям данных в этих системах, называются плохо
обусловленными, и нам нужен способ распознавания таких систем.
Легко показать, что плохую обусловленность может выявить
анализ матрицы системы. Рассмотрим систему Ах = Ь с
невырожденной матрицей А и попробуем найти относительное изменение
решения я», соответствующее заданному относительному
изменению Ь или А. Если изменить Ь на Д6, то новое решение можно
представить как х* + Ах, где
А(х. + Ьх) = Ь + Д6 = Ах, + А6,
Таким образом, в любой векторной норме ||*|| и
соответствующей индуцированной матричной норме
HAjcIkIU-I-hauii-
Д*2 А*2
Уравнения Aix=b] Уравнения кгх=Ь2
Рис, 33.1.
3.3. Погрешности при решении линейных систем 73
Кроме того, из Ах% = Ь имеем
1 ,<М1
так что
ил ^||Л"ЧЛ ■ II Ml •
Аналогично, если изменить А на ДЛ, полагая (А + &А)& = Ь и
* = дс.+ Д£, то
(А + АА)(хт + Ь*) = Ь,
что дает
лд* = — ал • je,
IIAiB<U-!|.||Aiie«ll*IL
JML^niii.lj-il. 1М1
^<11Л||.|Ц-1.1^
II*
В обоих случаях относительное изменение х ограничено
относительным изменением данных, умноженным на ЦЛЦ-УЛ-1!!-
Эта величина известна как число обусловленности матрицы А.
Оно обозначается в случае использования индуцированной
матричной /р-нормы через кр(А). В любой индуцированной
матричной норме число обусловленности представляет собой
отношение максимального и минимального растяжений, вызываемых
матрицей А (см. равенства (3.1.7) и (3.1.18)), и, таким
образом, оно больше или равно 1. В наших примерах m(Ai) =
= (15)(0.14) = 2.1 и xi(i42) = ( 13.35) (300) = 4005, т. е. вторая
система гораздо более чувствительна к изменениям в данных,
чем первая. Так как минимальное растяжение, вызываемое
вырожденной матрицей, равно нулю, то число обусловленности
вырожденной матрицы можно считать бесконечным. Поэтому
число обусловленности невырожденной матрицы служит
степенью близости матрицы к вырожденности. Оно обладает тем
привлекательным свойством, что остается неизменным при
масштабировании матрицы умножением на скаляр, поскольку
х(аЛ) = х(Д) для любого ненулевого aeRn любой матричной
нормы.
Число обусловленности является также мерой
чувствительности решения системы Ах = Ь по отношению к арифметике
конечной точности. Когда линейная система решается на
вычислительной машине, полученное решение, как можно показать,
есть точное решение некоторой возмущенной системы (А +
+ АЛ)дс = &. Этот метод анализа часто называют обратным
анализом ошибок по Уилкинсону, а источником служит книга
Уилкинсона (1965). Можно показать, что для некоторых из
рассматриваемых в разд. 3.2 методов величина ||АЛ||/||Л|| ограни-
74 Гл. 3. Основы вычислительной линейной алгебры
чена сверху константой, умноженной на машинный эпсилон,
причем на практике это почти всегда верно для всех из них.
Поэтому относительная ошибка решения, полученного с конечной
точностью, ограничена сверху константой, умноженной на
(x(/4)-macheps).
Таким образом, число обусловленности матрицы А
оказывается полезной величиной при оценке сверху того, насколько
чувствительным будет решение системы Ах = Ь как к
неточностям данных, так и к влиянию арифметики конечной точности.
Если в этом смысле Л почти вырождена, то можно ожидать
трудностей при решении Ах = Ь. Поэтому в случае плохо
обусловленных линейных систем мы будем настороже при извлечении
информации из наших моделей, поскольку, как бы ни были
просты и точны модели, решение модельной задачи,
чувствительное к малым изменениям, имеет, разумеется, ограниченное
применение в качестве приближения к решению нелинейной
задачи. Если плохая обусловленность встречается вдали от
решения нелинейной задачи, т. е. там, где модель никак нельзя
считать очень точной, то обычно мы просто возмущаем линейную
систему с целью улучшения ее обусловленности и продолжаем
дальше. Если плохо обусловленные системы встречаются вблизи
от решения, где модель, по-видимому, является хорошей1), то
это означает, что решение нелинейной задачи само по себе очень
чувствительно к малым изменениям в данных (рис. 3.3.2). Это
может означать, что исходная задача плохо поставлена.
Нужно, наконец, обсудить то, каким образом мы будем
определять на практике, достаточно ли линейная система (3.2.1)
плохо обусловлена, чтобы следовало избегать ее решения. Со-
fiW-o
хг
Плохо обусловленная система двух
нелинейных уравнений с двумя
неизвестными
Линейная
модель для
\
1Линейная
опель для
f,W«0
Линейная модель этой системы в
близкой к дт* точке (плохо обусловленная
система линейных уравнении)
Рис. 3.3.2. Соответствие между плохой обусловленностью линейной
и нелинейной систем уравнений.
*) Под «хорошей» понимается модель, которая хорошо аппроксимирует
поведение нелинейной задачи. — Прим. перев.
3.3. Погрешности при решении линейных систем 75
гласно анализу, проведенному Уилкинсоном (1965), если к{А)^
^ (macheps)-1, то, вероятно, вычисленное для (3.2.1) решение
будет совершенно ненадежным. На самом деле обычно считают,
что если х(Л)> (macheps)-1/2, то вычисленное для (3.2.1)
решение вряд ли заслуживает доверия. Наши алгоритмы будут
проверять такое условие, и затем возмущением плохо
обусловленных, моделей получать модели с улучшенным1) поведением.
Проблема состоит в том, что вычисление х(Л) включает в
себя нахождение ||Л_1||, а это не только может быть
ненадежным, но и редко когда оправдывает затраты. Поэтому все, что
здесь делается, сводится к оценке к(А) вида
condest = || М || • invest у
где М есть либо Л, либо множитель разложения Л, имеющий
вероятнее всего такую же, как у А обусловленность, a invent
есть оценка для ||ЛМ||. Для наших приложений понадобится
оценить число обусловленности матрицы Л, разложенной в
произведение Q-R. Нетрудным упражнением будет показать, что
в этом случае
X*iH)<*iW)<**iM).
Поэтому мы оцениваем xi(/?), так как /гнорма матрицы легко
вычисляется. Используемый нами алгоритм является
конкретным примером из класса оценок числа обусловленности,
предложенных Клайном, Моулером, Стюартом и Уилкинсоном (1979).
Он представлен в приложении А алгоритмом АЗ.3.1.
Алгоритм сначала вычисляет \\R\\\. Используемый затем
способ оценки ||R~] ||i основывается на неравенстве
справедливом при любом ненулевом г. Алгоритм выбирает z
в результате решения RTz = e, где е есть вектор, состоящий из
единиц с разными знаками, подобранными так, чтобы
последовательно максимизировались значения zb ..., zn. Затем в нем
решается Ry = z и выдается значение condest = l|/?lli(ll*/lli/l|2||i).
Хотя гарантируется, что отношение ||*/||i/||2||i будет оценкой
снизу для И/?"1^» на практике оно довольно близко к
последнему. Одно из объяснений этому основано на том, что процесс
получения у связан с обратным степенным методом,
предназначенным для нахождения наибольшего собственного значения
матрицы (RTR)~l. Другое объяснение таково, что алгоритм, как
!) Улучшенной будет обусловленность модели, но при этом ее
способность аппроксимировать нелинейную задачу может ухудшиться (см.
предыдущее примечание). — Прим. перев.
76 Гл. 3. Основы вычислительной линейной алгебры
оказывается, способен ловко выделять какой-либо из больших
элементов матрицы R-1. Читателям, желающим упрочить свое
интуитивное понимание этого вопроса, настоятельно советуем
проработать пример, приведенный в упр. 19.
3.4. ФОРМУЛЫ ПЕРЕСЧЕТА МАТРИЧНЫХ
РАЗЛОЖЕНИЙ
Позже в книге будут рассмотрены многомерные обобщения
метода секущих, в которых последовательные производные
соответствующих моделей Лс, Л+е Rn*n связаны между собой
особенно просто. В этом разделе мы увидим, как использовать два
наиболее важных соотношения между Ас и Л+ для уменьшения
затрат на получение разложений матриц А+ на основе
разложения матрицы Лс.
В частности, мы хотели бы вникнуть прежде всего в
некоторые детали задачи о нахождении разложения Q+/?+ матрицы
A+ = Ac + uvT, (ЗАЛ)
где uf v е R". Здесь Ас есть некоторая невырожденная матрица
общего вида, для которой уже имеется разложение QCRC- Идея
алгоритма несложна. Для w = Qlu запишем
А+ = QcRc + мт = Qc (Re + wvT),
а затем построим Q/^-разложение
Rc + wvT = QR. (3.4.2)
Тогда /?+ = £ и Q+ = QCQ- Выгода здесь состоит в том, что
Q^-разложение матрицы Rc + wvT стоит намного дешевле, чем
те 5я3/3 операций, которые мы вынуждены были бы потратить
на получение Q+R+, если бы не воспользовались предыдущим
разложением.
Средством, необходимым для получения разложения (3.4.2),
является ортогональное преобразование, называемое вращением
Якоби. Оно по сути представляет собой двумерное вращение,
матрица которого содержится в матрице порядка /г. Вращение
Якоби используется для обнуления одного элемента матрицы,
при этом изменяются только две строки матрицы. Матрица
вращения в двумерном пространстве и матрица вращения Якоби
порядка п определены ниже. Их свойства, имеющие важное
значение, приведены в лемме 3.4.2.
Определение 3.4.1. Матрицей вращения в двумерном
пространстве называется матрица /?(<р)е R2x2 вида
[cosф — sin фI
, <pcsRv
вшф созфГ
3.4. Формулы пересчета матричных разложений
или в эквивалентной записи
Матрица вращения Якоби /(/,/,a,p)eRrtXn такова, что
1</</<л, a, peR, |а| + |Р1*=0,
а
77
[/(/, /, <*, Р)1н = [/(*, h а, Р)],/ = ^==
= а,
-[/(/,-/, а, Р)],/= [/(/, /. a, p)b==^=L= = P,
[/(/, /, а, Р)Ь =1, 1 < k < n, ft Ф /, * ^ /,
а остальные элементы равны нулю.
Она схематично выглядит так:
XU*,P) =
1
1-й столбец
1
j-й столбец
i
« -р
1 О
1
О
1
Ь
1
-*-я строка
-j-Я строка
Лемма 3.4.2. Пусть п !>2, и обозначения /?(<р), /?(a, р),
/(/, /, а, р) имеют прежний смысл. Тогда:
(a) для всех <ре R и ненулевых ueR2 матрица R(<р)
ортогональна, а преобразование /? (ф) • t; поворачивает v на угол ср
против часовой стрелки; кроме того, R(v29 vx)'V = (0, \\v\y)T и
R(vlt -v2)-v = (\\v\\2, of;
(b) для всех целых /, /e[l, n], /</, и a, fsR, где
|a| + IP \¥*0f матрица /(/, /, a, p) ортогональна. Если M + =
= /(/,/, a, р)-М, MeRnXft, то (M+)k=(M)k. для 1<£</z,
i^i и кф \\ кроме того, каждая из строк матрицы М+
с номерами / и / является линейной комбинацией /-й и /-й строк
матрицы М;
78 Гл. 3. Основы вычислительной линейной алгебры
(с) если Мц • Мц ф О, то [/(/, /, MJh Мц) • М]ц = О и
[/ft Л Afn.-AfyiJ.Afl/i-O.
При пересчете (^-разложения матрицы Ас в
(^-разложение матрицы Л+ = QcRc + uvT используются вращения Якоби
для разложения Rc + QTcuvT = Rc + wvT в произведение Q/J
следующим образом. Сначала п—1 раз применяется
вращение Якоби для последовательного обнуления строк матрицы
wvT с номерами п, п— 1, ..., 2. Здесь для обнуления i-й
строки комбинируются строки с номерами / и i— 1. В результате
каждого вращения изменяются некоторые из имеющихся
элементов матрицы Rc и вводится один новый элемент
непосредственно под диагональю в позиции (i,i—1). Таким образом,
п — 1 вращений приводят Rc + wvT к верхнему треугольному
виду с дополнительной диагональю ниже главной. Это есть так
называемая верхняя матрица Хессенберга. Далее опять
применяется п—1 вращений Якоби, но уже для того, чтобы
последовательно обнулить (/, /—1)-е элементы, / = 2, 3, ..., п,
комбинируя строки с номерами i—1 и /. В результате
появляется верхняя треугольная матрица /?, такая, что Rc + wvT =
= QR> где (Q)T есть произведение 2п — 2 вращений.
Читатель может убедиться, что полный процесс пересчета
Q/^-разложения требует только 0(п?) операций. Получение
матрицы Q+ = QcQ, которая хранится до следующего шага,
является наиболее трудоемкой частью разложения. Что касается
другого важного специального соотношения между Ас и Л+, то,
как сейчас будет видно, для него Q+ оказывается ненужным.
При использовании локальных квадратичных моделей для
решения задач безусловной минимизации мы предпочитаем,
чтобы гессианы квадратичных моделей, т. е. матрицы их
вторых производных из RnXrt, были симметричными и
положительно определенными. Мы найдем исключительно целесообразным
выбирать гессиан модели А+ так, чтобы, он обладал
указанными свойствами, если ими обладает гессиан Ас текущей
модели. Более того, получение Л+ из Ас наводит на серьезные
размышления. Дело в том, что если LCLTC есть разложение Хо-
лесского для Д., то А+ =/+/+, где
/+ = Lc + vuT.
Но это прямо говорит нам, как получать разложение Холес-
ского
A+ = L+LT+.
Для получения разложения Q+/?+ матрицы /+ = LTC + uvT из
Q^-разложения QcRc = I • LTC матрицы LTe просто применим
3.5. Собственные значения 79
описанный выше способ. Тогда непосредственно получим
А+ = J+Jl = RT+QT+Q+R+ = RT+R+ = L+LT+.
Процесс пересчета также требует 0(п2) операций. В этом
конкретном случае нам не нужно затрачивать п2 операций на
формирование w = Qlu, поскольку QC = I, а также нет
необходимости строить Q+, так как нам нужно всего лишь /?+ = L+.
Этот алгоритм полностью содержится в алгоритме АЗ.4.1
приложения.
Альтернативой Q^-разложению и обсуждаемым в этом
разделе формулам пересчета является подход, предложенный Гил-
лом, Голубом, Мюрреем и Сондерсом (1974). Он заключается
в использовании разложения A = LDV, где L есть нижняя
треугольная матрица с единичными диагональными
элементами, D — диагональная матрица, а строки матрицы V
образуют ортогональный базис в Rn, но не обязательно ортонорми-
рованный. В этом случае VVT = D представляет собой
диагональную матрицу. Вычисление L+D+V+ = LCDCVC + uvTy где
u,v^Rn, обходится немного дешевле, чем описанный выше
пересчет (^-разложения. В случае симметричных
положительно определенных матриц это соответствует выполнению
£/)//-разложения последовательно для матриц {Ak}. Эти
алгоритмы собраны в работе Гольдфарба (1976).
Последовательное разложение симметричных незнакоопре-
деленных матриц широко исследовалось Соренсеном (1977), и
его до некоторой степени сложный алгоритм представляется
вполне удовлетворительным. Матрицы перестановок
составляют основной источник затруднений. В частности, по этой
причине не известен алгоритм пересчета PLfZ-разложения
матрицы Ас в разложение P+L+U+ матрицы А+ = Ас + uvTy который
был бы удовлетворительным с рассматриваемой точки зрения.
3.5. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И ПОЛОЖИТЕЛЬНАЯ
ОПРЕДЕЛЕННОСТЬ
В этом разделе формулируются свойства собственных значений
и собственных векторов, которые использовались или будут
далее использованы в тексте. Приводятся также определения
положительно определенных, отрицательно определенных, незна-
коопределенных симметричных матриц и их отличительные
признаки в терминах собственных значений. Эти признаки дают
представление о пространственной форме многомерных
квадратичных моделей, введенных в гл. 4 и используемых в
дальнейшем.
80 Гл. 3. Основы вычислительной линейной алгебры
Большинство теорем приводится без доказательств.
Доказательства можно найти в работах, ссылки на которые
имеются в начале этой главы.
Определение 3.5.1. Пусть А е Rnxn. Собственными
значениями и собственными векторами матрицы А называются
соответственно действительные или комплексные скаляры X и
я-мерные векторы v, такие, что Av = Kv и v Ф 0.
Определение 3.5.2. Пусть А е Rnxn симметрична. Будем
говорить, что А положительно определена, если vTAv > 0 для
каждого ненулевого t;eRn. Будем говорить, что А
положительно полуопределена, если vTAv ^ 0 для всех ugR". Будем
говорить, что А отрицательно определена или отрицательно
полуопределена, если —А положительно определена или
положительно полуопределена соответственно. Будем говорить, что
А незнакоопределена, если она не является ни положительно
полуопределенной, ни отрицательно полуопределенной.
Теорема 3.5.3. Пусть А е Rnxn симметрична. Тогда она
имеет п действительных собственных значений Аь ..., Хл и та*
кое множество соответствующих им собственных векторов
v\, ..-, vn, которое образует ортогональный базис в R*.
Теорема 3.5.4. Пусть А е Rnxn симметрична. Тогда
матрица А положительно определена в том и только том случае,
когда все ее собственные значения положительны.
Доказательство. Пусть для А собственными значениями
являются Яь ..., Ял, а соответствующие им ортонормированные
собственные векторы равны vu • • • > vn- Предположим, что
I,- ^ 0 для некоторого /. Тогда v*Avf = 0/(V/) = ^i°Tvt= Л/ ^ °>
что указывает на отсутствие положительной определенности А.
Предположим теперь, что каждое А,, положительно. Поскольку
{vi} образует базис в R", то любой ненулевой уеКл можно
представить как
п
v=Ytaivh
где хотя бы одно щ ненулевое. Тогда
п п п
vTAv = Е S hpptfVf = £ Хр2{ > о
благодаря ортонормированности векторов vt. Таким образом, А
положительно определена. □
3.5. Собственные значения 81
Теорема 3.5.5. Пусть А е Rnxn симметрична. Тогда А
положительно полуопределена в том и только том случае, когда все
ее собственные значения неотрицательны. Матрица А
отрицательно определена или отрицательно полуопределена тогда и
только тогда, когда все ее собственные значения соответственно
отрицательны или неположительны. Матрица А является незна-
коопределенной тогда и только тогда, когда у нее имеются как
положительные, так и отрицательные собственные значения.
Следующие определения и теоремы понадобятся в разд. 5.5.
Теорема 3.5.6. Пусть А е Rnxn симметрична и имеет
собственные значения Ки ..., %п. Тогда
||А||2= max |М.
Если А не вырождена, то
Теорема 3.5.7. Пусть А е Rnxn имеет собственное
значение Xt. Тогда %i + а будет собственным значением для А + а/
при любом действительном а.
Определение 3.5.8. Пусть А е Rnxn симметрична. Будем
говорить, что А является матрицей со строго доминирующей
диагональю, если
\Ф1
для всех /= 1, ..., л.
я« — £ |а//1>0
Теорема 3.5.9 (Гершгорин). Пусть Л е Rnxn симметрична и
имеет собственные значения %\, . • •, hn- Тогда
min А,, ^ min
iin 1а„ —Е а„ I,
iXn\a kk+ /?1 ,а*/'г
max А*< max
Следствие 3.5.10. Если А является матрицей со строго
доминирующей диагональю, то А положительно определена.
82 Гл. 3. Основы вычислительной линейной алгебры
3.6. ЛИНЕЙНАЯ ЗАДАЧА О НАИМЕНЬШИХ КВАДРАТАХ
Заключительной из рассматриваемых тем по линейной алгебре
будет линейная задача о наименьших квадратах:
заданы ЛеГхп, т>л, &€=Rm,
(3.6.1)
min II Ах — Ь ||2,
которая является частным случаем нелинейной задачи о
наименьших квадратах:
заданы rt(x): Rrt->R, /=1, ..., m,
т
min £ гi С*)2
при ri(x) = (at.)x — biy где /=1, ..., m. Основанием для
изучения задачи (3.6.1) служит то, что часто необходимо решать
ее как подзадачу нелинейной задачи о наименьших квадратах
и, кроме того, понимание этой линейной задачи способствует
лучшему пониманию ее нелинейного аналога. В связи с
изучением линейной задачи о наименьших квадратах вводится
понятие сингулярного разложения, представляющего собой
мощное средство вычислительной линейной алгебры, которое
оказывается полезным во многих ситуациях.
К линейным задачам о наименьших квадратах обычно
приводит желание наилучшим образом приблизить набор из т
точек-данных (ti, yi) с помощью функции f(xtt), которая
является линейной относительно ее п свободных параметров
ед^х^+^е*
Рис. 3.6.1. Пример линейной задачи о наименьших квадратах.
3.6. Линейная задача о наименьших квадратах 83
Хи • • •, *п. Предположим, например, что желательно
приблизить три пары (1,2), (2,3), (3,5) с помощью функции f(x,t) =
— xit + x2e* (рис. 3.6.1). Для точного совпадения f(x,ti) = yiy
i = 1, 2, 3, потребовалось бы выполнение равенства Ах = 6, где
4i 1} и;;} -[!]•
(3.6.2)
Так как система уравнений Ах = Ь является переопределенной,
то, не предполагая решать ее в обычном смысле, мы вместо
этого выбираем х, которое минимизирует некоторую меру
величины вектора невязок Ах—6. В (3.6.1) /2-норма выбрана
потому, что получающаяся в результате этого задача обладает
хорошими с математической точки зрения свойствами и, кроме
того, имеет статистическое обоснование.
Отметим, что нахождение решения рассматриваемого
примера задачи (3.6.1) эквивалентно поиску ответа на вопрос:
«Какая из линейных комбинаций векторов (1, 2, 3)т и
(е, е2, е3)т оказывается ближе всего в /2-норме к (2,3,5)7?».
В общем случае можно переформулировать задачу (3.6.1) так:
«Найти линейную комбинацию столбцов а.и •••> <*•« матрицы Л,
ближайшую к Ь в /2-норме». Геометрически это означает
нахождение такой точки в n-мерном подпространстве С (Л),
натянутом на столбцы матрицы Л, которая находится ближе
всего к вектору Ь в евклидовой норме (рис. 3.6.2). Такая
интерпретация приводит к простому решению линейной задачи
о наименьших квадратах.
Известно, что ближайшей к Ъ в С (А) будет точка Лх#е
^С(А)> такая, что Л** — Ь ортогонален ко всему
подпространству С (А). Таким образом, х* должно удовлетворять
равенствам (a.i)T(Ax* — Ь)=0, *=1, ...,/г, что эквивалентно
Ат(Ах* — &) = 0. Ясно, что Ах* единственно, и если столбцы
матрицы Л линейно независимы, то значение х„ которое дает
точку Л**, также единственно и является решением невырож-
Рис. 3.6.2. Решение линейной задачи о наименьших квадратах.
84
Гл. 3. Основы вычислительной линейной алгебры
денной системы уравнении
(АтА)х. = АтЬ. (3.6.3)
Эти сведения резюмируются в теореме 3.6.1, а ее
формальное доказательство оставлено в качестве простого упражнения.
Теорема 3.6.1. Пусть m ^ п > О, А <
решение задачи
min || Ах — Ь\\2
Rmx«, iGRm. Тогда
xesR"
представляет собой множество точек {jc#: Ат(Ах+— Ь) = 0}.
Если столбцы матрицы А линейно независимы, то х*
единственно, А7А не вырождена к х+ = (АТА)-1АТЬ.
Уравнения (3.6.3) известны как нормальные уравнения.
Хотя они и однозначно определяют хщ в случае, когда А
полного столбцового ранга, но не всегда указывают путь, по
которому следует идти при вычислении х*. Это объясняется тем,
что формирование матрицы АТА может привести к
антипереполнению и переполнению, а также к возведению в квадрат
числа обусловленности задачи по сравнению с методами,
которые непосредственно используют А. Если А имеет полный
столбцовый ранг, то можно воспользоваться Q/^-разложением
матрицы Л,
п
m
= m
m
Q
m
n
4 ]
04
0
'}*„
(3.6.4)
R
где ортогональная матрица QsRmxm и верхняя треугольная
матрица R^Rmxn получаются тем же способом, что при
(^-разложении квадратной матрицы. Это разложение
обеспечивает численно устойчивую ортогонализацию столбцов
матрицы А. Следующая теорема показывает, как применять (3.6.4)
для решения (3.6.1).
Теорема 3.6.2. Пусть m ^ л >0, 6 е Rm, и матрица А е
е RmXrt имеет полный столбцовый ранг. Тогда существует
разложение A = QR вида (3.6.4), где тХ т-матрица Q
ортогональна, /?eRWXrt есть верхняя треугольная матрица, и Ru,
образованная первыми п строками матрицы /?, представляет
собой невырожденную верхнюю треугольную матрицу.
Единственным решением задачи (3.6.1) является
xm-Rul(<fb)m,
3.6. Линейная задача о наименьших квадратах 85
где (QTb)u = ((QTb)u ..., (Q?b)n)T. Минимум \\Ах-Ь\й равен
Доказательство. Существование Q/^-разложения матрицы А
вытекает из возможности его получения преобразованиями Ха-
усхолдера, а невырожденность Ru следует из того, что А имеет
полный столбцовый ранг. Используя (3.1.23), получаем
ЪАх-Ъ ||2=]| QRx -b\\2 = || Rx - QTb ||2,
так что (3.6.1) может быть переписано в виде
min||/?*-QrH.
Тогда, если (QTb)i = ((QTb)n+u ..., (QTb)m)T, имеем
ll^-Qr6|l2=l/?^-(Q4l2 + |(Qr6)/t
Ясно, что это выражение принимает наименьшее значение при
x = Rul(QTb)u. П
Если А не имеет полного ранга, то существует целое
множество решений х задачи (3.6.1). Поэтому в задачу можно
внести дополнительное требование найти наименьшее в /2-норме
из этих решений:
заданы A<=RmXnt 6e=Rm,
min {II х Ik: || Ax - b ||2 < \\A* - b ||2 V* e R*}. (3.6.5)
xeR"
Задача (3.6.5) представляет интерес независимо от того,
больше, равно или меньше /л, чем п. Она может быть решена во
всех перечисленных случаях с использованием сингулярного
разложения (SVD1)) матрицы А. Это более трудоемкое
разложение матрицы на множители, нежели обсуждавшиеся до сих
пор разложения, но как средство оно более мощное.
Определение SVD приводится ниже. Характерные свойства множителей
этого разложения приведены в теореме 3.6.4. Теорема 3.6.5
показывает, как использовать SVD для решения задачи (3.6.5).
Определение 3.6.3. Пусть А е RmXrt и k = min{m, п}.
Сингулярным разложением матрицы А называется разложение
вида А = UDVTf где (7eRmXm и Ке Rnxn есть ортогональные
матрицы, a DERmXrt имеет вид d/, = a,^0, /=1, ..., k>
dii = 0, 1Ф\. Величины <Ji, ..., ok называются сингулярными
числами матрицы А
*) SVD-—аббревиатура singular value decomposition. — Прим. перев.
86 Гл. 3. Основы вычислительной линейной алгебры
Заметим, что U используется для обозначения
ортогональной матрицы, несмотря на то что в разд. 3.3 та же буква
использовалась для нижних треугольных матриц. Это прочно
укоренившееся обозначение не должно запутать внимательного
читателя. Кроме того, использование обозначений U и V
традиционно для матриц, столбцы которых представляют собой
собственные векторы, и следующая теорема демонстрирует это.
Теорема 3.6.4. Пусть А е Rmxn. Тогда для А существует
SVD, в котором диагональные элементы а, матрицы D есть
неотрицательные квадратные корни из собственных значений
матрицы ААТ, если т^п, или матрицы АТА, если m^n> а
столбцами матриц U и V являются собственные векторы
матриц ААТ и АТА соответственно. Количество ненулевых
сингулярных чисел равно рангу матрицы А.
Доказательство. Доказательство существования SVD можно
найти в работах, цитированных в начале главы. Так как
AAT = UDDTUT и АТА = VDTDVT, имеем (ААТ) • U = U • (DDT)9
(АТА) V = V (DTD). Таким образом, если м#/ и v.j есть
соответствующие /-е столбцы в U и V, то
(ААТ) u.j = XjU.f, / = 1, ..., m,
(ЛМ)0./ = Л/0./, /=1, ..., п,
где %i представляют собой диагональные элементы матриц DDT
и DTD, причем А,/=(а/)2, /=1, ..., min{m, п}, и Л/ = 0, / =
= min{m, п}+1, ..., max {/л, /г}. Поскольку умножение
матрицы на невырожденную матрицу не изменяет ее ранга, то
rank (Л ) = rank (D), и это равно количеству ненулевых а/. □
Теорема 3.6.5. Пусть А е RmXn имеет SVD вида А = UDVT>
где Uу Д V имеют тот же смысл, что в определении 3.6.3. Пусть
матрица, псевдообратная к Л, определяется как
j4* = KZW, Z)+ =
Й-{
О, <т* = 0, (3.6.6)
I dfj = О, 1Ф у,
D+sR"^. Тогда единственным решением задачи (3.6.5)
является х* = А+Ь.
Доказательство. Из разложения A = UDVT и равенства
(3.1.23) следует, что (3.6.5) эквивалентно
min {II VTx ||2: || DVTx - UTb ||2 < || DVTX - UTb ||2 V* е= R*},
3.6. Линейная задача о наименьших квадратах 87
что для z = VTx эквивалентно
min {||z ||2: || Dz - UTb ||2 < || Di - UTb ||2 V2 е= Rrt}. (3.6.7)
Пусть k равно количеству ненулевых а в D. Тогда
к т
\\Dz-UTb\\22=Z(oizi-(UTb)if+ £ ((£/%)2.
Это выражение принимает минимальное значение при любом г,
таком, что Zi=(UTb)i/Oi, i=l, ...,£. Среди всех таких г
норма ||г||2 минимальна для того из них, у которого zi = О,
/ = &+1, ..., т. Таким образом, решением задачи (3.6.7)
является z'=D+UTb, откуда х*= VD+UTb = A+b. □
Сингулярное разложение находится с помощью
итерационного процесса, тесно связанного с алгоритмом отыскания
собственных значений и собственных векторов симметричной
матрицы, поэтому его труднее получить, чем другие наши
матричные разложения. Этот метод рекомендуется, когда про
матрицу А не известно, имеет ли она полный строковый или
столбцовый ранг. Если т < п и А имеет полный строковый ранг, то
(3.6.5) решается более эффективно с помощью LQ-разложения
(упр. 27). Способ SVD наиболее надежен при вычислении ранга
матрицы, или, что эквивалентно, вычислении количества
линейно независимых векторов в множестве векторов. Можно также
использовать SVD для определения чувствительности х = А~1Ь
по отношению к изменениям в исходных данных Д6, где А есть
квадратная матрица. Кроме того, если А не вырождена, то
х2(А) = 0\/Оп, и тогда SVD представляет собой самый
надежный способ вычисления и2(Л).
Заключительное замечание относительно определения ранга
матрицы на основе ее SVD состоит в том, что D в
действительности дает нам больше информации о линейной независимости
столбцов в Л, чем мы могли бы «втиснуть» в единственное
целое число, отведенное под ранг А. Например, если /г = 3 и
<Ti = l, а2 = 0.1, а3 = 0, то следует согласиться, что А имеет
ранг, равный 2. Если <т3 заменить на macheps, то, вероятно, и
в этом случае следует все же считать, что вся информация
передана фразой «гапк(Л) = 2». Ну а как быть в случае, когда
0i = l, 03 = macheps и 02= (macheps) ^2 или 100-macheps
и т. д.? С увеличением п растет число ситуаций, вызывающих
тревогу из-за более сложного распределения в них сингулярных
чисел. Никто на самом деле не знает, что в таком случае
делать, однако весьма разумным здесь будет подыскать
«разрывы» в расположении сингулярных чисел, и те из них,
которые имеют примерно один и тот же порядок величины, счи-
88 Гл. 3. Основы вычислительной линейной алгебры
тать в зависимости от этого порядка все либо нулевыми, либо
ненулевыми.
Важно, чтобы пользователь программ, имеющихся у него
в записи, понимал суть этих вопросов. Дело в том, что в
пакетах программ ROSEPACK и EISPACK при решении (3.6Л)
с использованием SVD принимается в некоторый момент
решение, по которому А модифицируется так, что ее «малые»
сингулярные числа полагаются равными нулю, и затем
решается модифицированная задача. Несмотря на это, ничего не
происходит в тайне от пользователя, и необходимо всего лишь
прочитать программную документацию для понимания того,
что же в действительности делается. Можно с уверенностью
сказать, что любая подпрограмма, вычисляющая SVD, из
соображений своей эффективности будет присваивать нулевые
значения всем сингулярным числам, которые пренебрежимо
малы с точки зрения проводимых вычислений. Донгарра и др.
(1979) дали очень краткое объяснение типичной проверке на
«пренебрежимую малость».
3.7. УПРАЖНЕНИЯ
1. Докажите, что для любого xeR"
р->оо v °°
Заметим, что здесь на самом деле подразумевается, что для каждой
последовательности действительных чисел {/?*}, стремящейся к оо, имеет место
Нт |х|р -|х|».
2. (Трудное упражнение.) Докажите теорему 3.1.2.
3. Докажите соотношения (3.1.5).
4. Докажите, что для любых р ^ 1 индуцированная матричная /р-нор-
ма (3.7.1) обладает тремя определяющими свойствами нормы Г (3.1.1)
применительно к матрицам] плюс свойство мультипликативности [(3.1.10)].
5. Докажите, что (3.1.8а) правильно вычисляет индуцированную
матричную /i-норму. [Указание: покажите, что для всех v е R",
причем равенство имеет место по крайней мере для одного v.] Проделайте
то же самое для индуцированной матричной /«-нормы.
6. Докажите (3.1.8Ь). (Воспользуйтесь методикой доказательства
теоремы 3.5.4.)
7. Покажите, что tr(АТВ) представляет собой обычное скалярное
произведение А на Б, рассматриваемых как «длинные векторы*. Свяжите это
с нормой Фробениуса, т.е. докажите (3.1.14).
3.7. Упражнения 89
8. Докажите, что IIА || = II Ат || как для /2-нормы, так и для нормы
Фробениуса. Обратите внимание, что (АВ)./ = AB.h и посмотрите, не дадут
ли вам эти факты возможность доказать (3.1.15) и (3.1.16).
9. Докажите (3.1.17).
10. Завершите доказательство теоремы 3.1.4.
11. Докажите, что для любой А е RnXn и любой ортонормированной
последовательности векторов ^ е R", / = 1, ..., я, имеет место
Mft-£M»<i(j
12. Докажите теорему 3.1.7.
13. Решите блочно-диагональную систему Ах = 6, где
ГЗ 1 0
12 0
1 0 0 2
10 0 0
L0 0 0
0
0
0
2
-1
Оп
0 '
0
-1
4.
|. ь =
- 5-1
5
6
3
L i6 J
14. Получите преобразование Хаусхолдера: дано dgR", v Ф 0, найти
weR", такое, что матрица (1 — иит) ортогональна и (/ — иит) v = (а, 0, ...
..., 0)г, а ф 0. [Указание: и должно иметь вид р(у, v2t ..., vn)T, где
15. Примените преобразование Хаусхолдера для разложения А на
множители Q/?, где
1 —1
"
16. Является ли матрица ( 2 з ) положительно определенной? Для
выяснения этого воспользуйтесь разложением Холесского.
17. Найдите разложение Холесского для
Г 4 6 -2-1
I 6 10 1 I
L -2 1 22 J
А если заменить 10 на 7?
18. Докажите, что если А = Q-R, то
1
— Xi(i4)<xi(/?)</ixi(i4).
Докажите также, что Кг(А) = y,z(R).
90 Гл. 3. Основы вычислительной линейной алгебры
19. Найдите число обусловленности в /i-норме для
Оцените число обусловленности этой матрицы с помощью алгоритма АЗ.3.1.
20. Напишите программу для дальнейшего использования в виде
отдельного модуля, которая бы давала оценку числа обусловленности верхней
треугольной матрицы.
21. Та простая форма матрицы R(a, 0), в которой мы представили
вращения Якоби, излишне подвержена воздействию погрешностей
арифметики конечной точности, когда а или 0 малы или велики, либо различны
порядки их величин. Напишите процедуру, которая бы вычисляла /?(а, Р)
с высокой точностью.
22. Найдите матрицу вращения Якоби, которая бы давала нуль в
позиции (3, 1) матрицы
г;; п.
L3 5 9J
23. Докажите теорему 3.6.1. При этом покажите, что если
Ат(Ах+ — Ь)= 0, то || Ах — Ь ||2 ^ II Ах* — Ь ||2 для всех xeR", причем
строгое неравенство имеет место, когда А имеет полный столбцовый ранг и
х Ф х*. Покажите также, что если А имеет полный столбцовый ранг, то
АТА не вырождена.
24. Имеется Q/^-разложение прямоугольной матрицы А полного
столбцового ранга, определенное в теореме 3.6.2. Покажите, что первые п
столбцов в Q образуют ортонормированный базис пространства, натянутого на
столбцы матрицы А.
25. Подберите прямую xi + x2t, приближающую данные (//, yi) =
= (—1,3), (0, 2), (1,0), (2, 4). Выполните поставленную задачу,
используя Qfl-разложение и нормальные уравнения. [Указание: вы делали упр. 15?]
26. Имеются я > m > 0, !ieRm и матрица А €= RmXn полного
строкового ранга. Покажите, как решить задачу
min (О*Ik: Ax=*b),
используя разложение вида А = LQ, где матрица L €= RmX/l —нижняя
треугольная, a Qe риХл _ ортогональная. [Указание: воспользуйтесь
методикой, аналогичной той, что применялась в доказательствах теорем 3.6.2 и
3.6.5.]
27. Покажите, как выполнить LQ-разложение в предыдущем
упражнении, используя преобразования Хаусхолдера.
28. Имеется сингулярное разложение А = UDVT невырожденной
матрицы A g= RnXn. Докажите, что хг(А) = сч/Ол. Пусть u.j и v/ обозначают
соответствующие столбцы матриц V и V. Покажите также, что изменение
А6 = au.f в правой части линейной системы Ах = b приведет к изменению
д* = (a/Oj)v.j в решении.
4
Основы анализа функций
многих переменных
В этой главе содержатся сведения из анализа функций многих
переменных, необходимые в дальнейшем для изучения
вопросов численного решения нелинейных задач. В разд. 4.1
обсуждаются производные, определенные интегралы, ряды Тейлора
и связанные с ними свойства, которые будут впоследствии
использованы при построении и анализе предлагаемых методов.
В разд. 4.2 вводятся формулы для построения
конечно-разностных аппроксимаций производных от функции многих
переменных, а в разд. 4.3 приведены необходимые и достаточные
условия, характеризующие точку минимума при отсутствии
ограничений. Книга Ортеги и Рейнболдта (1970) может служить
подробным справочным пособием как по данной теме, так и по
теоретическому исследованию нелинейных алгебраических
задач общего вида.
4.1. ПРОИЗВОДНЫЕ И МНОГОМЕРНЫЕ МОДЕЛИ
При изучении минимизации функции одной переменной для
построения локальной квадратичной модели минимизируемой
функции использовались производные первого и второго
порядка. Поэтому мы Стремились к тому, чтобы модельная задача
соответствовала реальной задаче по значению, тангенсу угла
наклона и кривизне в точке, которая на текущий момент
является наилучшим приближением к точке минимума. Формула
Тейлора с остаточным членом оказалась полезным
аналитическим аппаратом для оценки погрешности аппроксимации
квадратичной моделью. Она в той же степени будет нам полезна
и здесь.
Мы начинаем этот раздел с описания, без излишних
подробностей, формулы Тейлора второго порядка для скалярной
функции, зависящей от векторной переменной. Затем, для того
чтобы перейти к этапу рассмотрения систем нелинейных уравне-
92 Гл. 4. Основы анализа функций многих переменных
ний, мы изучим задачу построения локальной аффинной
модели для функции F: Rn-vRm. В этом случае подход,
использующий ряды Тейлора, является весьма неудовлетворительным,
потому что здесь не выполняется теорема о среднем. Предвидя
это, в гл. 2 мы использовали теорему Ньютона для построения
аффинных моделей. Вторая часть этого раздела будет
посвящена построению аппарата, позволяющего провести
аналогичный анализ в многомерном случае.
Рассмотрим сначала непрерывную функцию: f: Rn->-R,
п> 1. Если существуют первые частные производные от
функции п переменных / и они непрерывны, то вектор-столбец,
составленный из п частных производных, называется градиентом
Vf(x) функции / в точке х, и он в данном случае представляет
собой то же самое, что и первая производная от функций
одной переменной. В частности, существует соответствующая
теорема о среднем, которая утверждает, что разность между
значениями функции в двух точках равна скалярному
произведению разности между точками на градиент функции в
некоторой промежуточной точке прямой, соединяющей эти две точки.
Аналогично, если п2 вторых частных производных от / также
существуют и непрерывны, то матрица, составленная из них,
называется гессианом1) V2f(x) функции f в точке дг, и он тоже
удовлетворяет условиям теоремы о среднем, представленной
в виде формулы Тейлора с остаточным членом. Точные
определения и леммы приведены ниже. Причины, по которым важные
результаты одномерного анализа остаются справедливыми для
функций многих переменных, состоят в том, что они
используют значения действительной функции в двух точках х и
х + р пространства R", а прямая, соединяющая эти две точки,
может быть параметризована с помощью одной переменной.
Таким образом, результаты следуют непосредственно из
соответствующих теорем одномерного анализа.
Обозначим открытый и замкнутый линейный сегмент,
соединяющий jc, х е R", через (х, х) и [*, х] соответственно, а также
напомним читателю, что DczRn называют выпуклым
множеством, если [х, х] с= D для любых x,x^D.
Определение 4.1.1. Будем говорить, что непрерывная
функция f: Rrt->R непрерывно дифференцируема в jceRn, если
производные (df/dxi)(x)t i=l, ...,п, существуют и
непрерывны. Тогда градиент функции / в точке х определяется как
v/W = [^rW.---.^rW]r- (4-1.1)
*) Гессианом принято называть определитель матрицы Гессе V%f(x).
Однако, учитывая замечание авторов после примера 4.1.8 относительно
терминов «якобиан» и «матрица Якоби», мы все же решили придерживаться
при переводе терминологии, принятой а данной книге. — Прим. перев.
4.1. Производные и многомерные модели 93
Будем говорить, что / непрерывно дифференцируема в открытой
области Dc=Rn, и обозначать это как f^Cl(D)> если она
непрерывно дифференцируема в любой точке из D.
Лемма 4.1.2. Пусть /: Rn-*R непрерывно дифференцируема
на некоторой открытой выпуклой области Dc=Rn. Тогда для
^gD и произвольного ненулевого приращения peRn
производная по направлению р от f в точке х, определяемая как
°Р е->0 8
существует и равна Vf(x)T-p. Для любых ху* + ре£>,
выполнено
1 х+р
f(x + p) = f(x)+\vf(x + tp)Tpdt^f(x)+ J Vf(z)(b9 (4.1.2)
О х
и существует ze(x, х + р), такое, что
f(x + p) = f(x) + Vf(z)Tp. (4.1.3)
Доказательство. Проведем элементарным образом
параметризацию / как функции одной переменной вдоль прямой,
соединяющей х и (х + р),
g:R-+R, g(t) = f(x + tp)
и обратимся к анализу функции одной переменной. Определим
x(t) = x + tp. Затем по цепному правилу дифференцирования
сложной функции для 0 ^ а ^ 1 имеем
п
л
= 2]-e-(*(a))-p, = Vf(* + ep)'p. (4.1.4)
Подстановка a = 0 сводит (4.1.4) к виду
Пользуясь фундаментальной теоремой анализа, теоремой
Ньютона, запишем
8
(\) = g(0)+\g'(t)dt,
94 Гл. 4. Основы анализа функций многих переменных
что по определению g и согласно (4.1.4) эквивалентно
/(* + р)=/(*)+ $ чНх + tpf р Л;
О
тем самым (4.1.2) доказано. Окончательно по теореме о
среднем для функции одной переменной имеем
g(D = g(0) + g'(t), ее (0,1),
что по определению g и согласно (4.1.4) эквивалентно
f(x + p) = f(x) + 4f(x + tp)Tp9 бе (0,1),
и (4.1.3) доказано. □
Пример 4.1.3. Пусть f: R2->R, f(x) = x\ — 2x{ + Sxxxl + Ax\y
jcc = (1, If, р = (-2, Yf. Тогда
[•2^-2 + 341
V'W-[teA+15bi J'
/(**) = 6, f(xc + p) = 23, Vf(xc) = (3,l8f.
В обозначениях леммы 4.1.2
g{t) = f{xc + tp) = f(\-2t, l+t) = 6+l2t + 7t2-2fi.
Читатель может убедиться, что (4.1.3) справедливо для z =
= xc + tp при / = (7 — Vl9 )/б ^ 0.44.
Определение 4.1.4. Будем говорить, что непрерывно
дифференцируемая функция /: R"->R дважды непрерывно
дифференцируема в jceR", если производные (d2f/dxtdxf) (х), 1 ^/,
/ ^ п, существуют и непрерывны. Тогда гессиан функции f в х
по определению есть матрица размера яХя, и ее (*',/)-й
элемент равен
^ W'/=-^e-» 1 <'■ '<п- (4Л-5)
Будем говорить, что функция f дважды непрерывно
дифференцируема в открытой области DczRn, и обозначать это /е
^C2(D), если она дважды непрерывно дифференцируема в
каждой точке D.
Лемма 4.1.5. Пусть /: Rn->*R дважды непрерывно
дифференцируема в открытой выпуклой области D а Кп. Тогда для
любого xgD и для произвольного ненулевого приращения
peR" вторая производная по направлению р от f в точке х,
4.1. Производные и многомерные модели 95
определяемая как
-¥L (х) = lim -^ ^
существует и равна pTV2f(x)p. Для любых хд-fpefl,
существует г е (*, л: + р), такое, что
f(x + p)=f(x) + Vf(xyP + ±pTv2f(z)p. (4.1.6)
Доказательство аналогично доказательству леммы 4.1.2. D
Всякий раз, когда / дважды непрерывно дифференцируема,
гессиан будет симметричен. Именно поэтому мы проявляли
интерес к симметричным матрицам в главе по линейной алгебре.
Пример 4.1.6. Пусть /, хс и р заданы так, как в
примере 4.1.3. Тогда
* «- [ L е.,+w ]• * ы - [ е зо ] •
Читатель может убедиться, что (4.1.6) справедливо для г =
= xc + tp, ^=-3-.
Лемма 4.1.5 наводит нас на мысль, чт*о можно было бы
описывать поведение функции / в окрестности точки хс
квадратичной моделью
mc (хс + P) = f (хс) + V/ (хсУ р + \ PTV2f (хс) р9 (4.1.7)
именно так мы впоследствии и поступим. Действительно, эта
лемма показывает, что погрешность данной модели имеет вид
f {хс + р)-тс (хс + р) = ±РТ (V2/ (г) - V2/ (хе)) р
при некотором 2Е(хс, хс + р). Другую оценку погрешности
дает следствие 4.1.14.
Перейдем теперь к менее простому случаю, в котором
F: R/I->Rm, где пг = п соответствует задачам решения систем
нелинейных уравнений, а т>п — нелинейным задачам о
наименьших квадратах. Было бы удобно иметь специальное
обозначение^ для /-й строки единичной матрицы. Это не должно
вызвать путаницы с основанием натурального логарифма. Так
как значение г-й компоненты функции F можно записать как
fi(x) = ejF(x)yто по правилу дифференцирования произведения
имеем f't (х) = e\F' (х)> что представляет собой /-ю строку F'(x).
96 Гл. 4. Основы анализа функций многих переменных
Таким образом, F'(x) должна быть матрицей размера /иХ«
и ее /-й строкой будет Vfi{x)T. Ниже дается формальное
определение.
Определение 4.1.7. Непрерывная функция F: Ря-^Кт
является непрерывно дифференцируемой в х е РЛ, если каждая
компонента //, *=1, ..., m, непрерывно дифференцируема в х.
Производную от F в точке х иногда называют якобианом
(матрицей Якоби) F в точке х, а транспонированную к ней матрицу
иногда называют градиентом F в точке х. Общепринятые
обозначения таковы:
fW6R"x", F'(x)if = ^(x), F'(x) = J(x)=VF(xY.
Будем говорить, что функция F непрерывно дифференцируема
в открытой области DczRn, и обозначать F^Cl(D), если F
непрерывно дифференцируема в каждой точке из D.
Пример 4.1.8. Пусть F: R2-*R2, fx (х) = е*> — xv f2(x) =
= х21—2х2. Тогда
/е* —1\
'»-(** -»)•
В оставшейся части книги будем обозначать матрицу Якоби
функции F в х через J(х). Кроме того, мы часто будем
говорить о якобиане функции F, а не о матрице Якоби функции F
в точке х. Единственно возможную двусмысленность может
вызвать то, что первый термин иногда используется для
детерминанта матрицы /(*). Однако здесь вряд ли возникнет какая-
либо путаница, поскольку мы редко прибегаем к
использованию детерминантов.
Перейдем теперь к тому, что существенно отличает свойства
скалярных функций от векторнозначных, а именно, для
непрерывно дифференцируемых вектор-функций не существует
теоремы о среднем. Другими словами, может, вообще говоря, не
существовать 2gR", такого, что F(x +p) = F(x) +J(z)p.
Интуитивно понятно, что, несмотря на то что каждая функция /,
удовлетворяет соотношению // (х + р) = fi (х) + V/,- (zi) гр,
точки zi все же могут быть различными. Для иллюстрации
рассмотрим функцию из примера 4.1.8. Не существует ze R", для
которого F(l, l) = F(0,0)+/(z)(l, 1)г, поскольку это означало
бы, что
т. е. eZx = е — 1 и 2zx = 1, а это, очевидно, невозможно.
4.1. Производные и многомерные модели Ф?
Хотя обычная теорема о среднем не выполняется, имеется
возможность заменить ее в нашем дальнейшем анализе
теоремой Ньютона и неравенством треугольника для определенных
интегралов. Эти результаты приведены ниже. Интеграл от
вектор-функции действительной переменной можно понимать как
вектор, состоящий из интегралов Римана от каждой
компоненты функции.
Лемма 4.1.9. Пусть функция F: k"->-Rm непрерывно
дифференцируема в выпуклой открытой области D a Rn. Тогда для
любых х, х + p^D,
1 х+р
F(x + p) — F(x)=\j{x + tp)pdtmm J F'(z)dz. (4.1.8)
О х
Доказательство непосредственно следует из определения
4.1.7 и применения покомпонентно формулы Ньютона (4.1.2). □
Отметим, что соотношение (4.1.8) напоминает теорему
о среднем, если представить его как
F(x + p)-F(x) = Uj(x + tp)dApf
где подразумевается покомпонентное интегрирование матрично-
значной функции. В некоторых случаях эта форма
представления окажется нам полезной. Для использования (4.1.8) в
наших рассуждениях необходимо иметь возможность получать
оценки интеграла в терминах подынтегрального выражения.
Следующая лемма дает как раз то, что нам нужно.
Лемма 4.1.10. Пусть G: D a Rn->RmXrt, где D — открытое
выпуклое множество, причем х, х + p^D. Если G
интегрируема на [х, х -f р], то для любой нормы в Rm
nG(x + tp)pdt \<\\\G(x + tp)p\\dt. (4.1.9)
Во II о
Доказательство оставлено в качестве упражнения. Оно
следует из представления интеграла в виде векторных
интегральных сумм Римана и последующего применения неравенства
треугольника (3.6.1с). Затем можно воспользоваться переходом
к пределу. П
98 Гл. 4. ОсноЕы анализа функций многих переменных
Лемма 4.1.9 наводит на мысль описывать поведение
F(xc + p) аффинной моделью
Mc(xc + p) = F(xe) + J(xc)p. (4.1.10)
Именно так мы впоследствии и поступим. Для получения
оценки разности между F(xc + p) и Мс(хс + р) необходимо
предположить непрерывность J(x) подобно тому, как это делалось
в разд. 2.4. Тогда мы получим оценку, аналогичную данной
в лемме 2.4.2 для функций одной переменной.
Определение 4.1.11. Пусть m, n>0, G: Rn-*Rwxn, хе^л,
и пусть ||-II есть норма в R", а|||-||| —норма в RmXrt. Будем
говорить, что функция G непрерывна по Липшицу в точке jc, если
существуют открытое множество DcR", xel) и константа у,
такие, что для всех v^D
\\\G(v)-G(x)\\\^y\\v-xl (4.1.11)
Константа у называется константой Липшица для G в точке х.
Для любой конкретной D, которая содержит х и для которой
выполняется (4.1.11), говорят, что G непрерывна по Липшицу
в окрестности D точки х. Если (4.1.11) верно для каждого
хеДто _G(=LipY(£>).
Заметим, что величина у в (4.1.11) зависит от нормы, но от
нормы не зависит само существование у.
Лемде 4.1.12. Пусть F: R/,-^Rm непрерывно
дифференцируема в открытом выпуклом множестве D с= R", х е D. Пусть
при заданной векторной норме, индуцированной матричной
норме и константе у якобиан / непрерывен по Липшицу в
окрестности D точки х. Тогда для любых х + Р ^ D
\\F(x + p)-F(x)-J(x)p\\^±\\p\?. (4.1.12)
Доказательство. По лемме 4.1.9
F(x + p)-F(x)-J(x)p = Uj(x + tp)pdA--J(x)p =
= \[J(x + tp)-J(x))pdt.
0
Используя (4.1.9), определение индуцированной матричной
нормы и непрерывность по Липшицу / в окрестности D точ-
4.1. Производные и многомерны» модели 99
ки х, окончательно получаем
1
\\F(x + p)-F(x)-J(x)p\\^\\\J(x + tp)-J(x)nPUt<1
О
1 1
<\v\\tp\\\\p\\dt = y\\P\?\tdt = ±\\p\f. □
о о
Пример 4.1.13. Пусть F: R2-»R2, /, (*) = х\ - х\ — о, f2(x) =
= 2х{х2 — р, а, р е R. [Система уравнений F (х) = 0
эквивалентна уравнению х{ + ix2 = л/а + /р .] Тогда
/(*) = l.2*2 2xJ
Здесь читатель может легкс^ убедиться, используя /гнорму, что
J(x) удовлетворяет (4.1.11) для любых xf tiGR2 при 7 = 2.
Используя непрерывность по Липшицу, можно также
получить полезные оценки погрешности для квадратичной модели
(4.1.7), аппроксимирующей f(xc + p). Это сделано ниже.
Доказательство аналогично доказательству леммы 4.1.12, и поэтому
оно оставлено в качестве упражнения.
Лемма 4.1.14. Пусть f: Rn-*R дважды непрерывно
дифференцируема в открытом выпуклом множестве DaRn и
гессиан V2f{x) непрерывен по Липшицу с константой у в
окрестности D точки х при заданных векторной и индуцированной
матричной нормах. Тогда для любых х + p^D
\f(x + p)^(f(x) + Vf(x)Tp + ^pT^f(x)p)\^l\\pf. (4.1.13)
Мы завершаем этот раздел двумя неравенствами,
связанными с (4.1.12), которые нам понадобятся для оценки
\\F(v) — F(u)\\ в доказательствах сходимости. Доказательство
леммы 4.1.15, обобщающей лемму 4.1.12, оставлено в качестве
упражнения.
Лемма 4.1.15. Пусть F и / удовлетворяют условиям
леммы 4.1.12. Тогда для любых v, u^D
HF(v)-F(u)-J(x)(v-un<y »°-*» + "*-*" ||о-ii||.
(4.1.14)
Лемма 4.1.16. Пусть F и / удовлетворяют условиям
леммы 4.1.12. Предположим, что существует J(x)~l. Тогда суще-
100 Гл. 4. Основы анализа функций многих переменных
ствуют е > 0, 0 < а < р, такие, что
а||о -u||<||F(iO-F(«)||<p||t> -a|| (4.1.15)
для любых v, u^D, удовлетворяющих неравенству тах{||у —
— х\\, Ни —х||}^е.
Доказательство. Используя неравенство треугольника и
(4.1.14), имеем
\\F(v)-F(u)\\<U(x)(v-u)\\ + \\F(v)-F(u)-I(x)(o-u)\\^
<[ll/WII + -|(l|f-*ll + l|u-Jt||)]l|f-«ll<
<ll|/toll + Ye]ll«-"ll.
что доказывает вторую часть (4.1.15) при р=||/(дг)|Ц-уе.
Аналогично,
\\F(v)-F(u)\\>\\J(x)(v-u)\\-\\F(v)-F(u)-J(x)(v-u)\\>
>[(17^чг)-Т(|,0-^| + ||и-^||)]||0-и,|>
Таким образом, если е < 1/(||/(лс)-1|1т), то первая часть
(4.1.15) выполнена при
°-(1лет)-ув>о-р
4.2. КОНЕЧНО-РАЗНОСТНЫЕ ПРОИЗВОДНЫЕ
В МНОГОМЕРНОМ СЛУЧАЕ
В предыдущем разделе мы убедились, что якобиан, градиент
и гессиан будут полезными величинами при построении
моделей нелинейных функций многих переменных. Однако в
приложениях указанные производные зачастую не заданы
аналитически. В настоящем разделе вводятся формулы для
аппроксимации производных конечными разностями и даются оценки
погрешностей этих формул. В разд. 5.4 и 5.6 обсуждаются
вопросы выбора шага конечно-разностных аппроксимаций с
учетом машинной арифметики и вопросы использования конечно-
разностных производных в предлагаемых алгоритмах.
Напомним, что для функции одной переменной / конечно-
разностная аппроксимация производной f'(x) задавалась по
формуле
„_ f(x + h)-f(x)
а~ h
4.2. Конечно-разностные производные 101
где h достаточно мало. Из оценки погрешности аффинной
модели функции f(x + h) мы имели \а — f'(x) | = 0(h) для
достаточно малых Л. В случае когда F: Rn-^Rm, есть смысл
использовать ту же самую идею для аппроксимации (/, /)-й
компоненты J(x) с помощью аппроксимации по разности вперед
fijx + hefi-ftix)
аЧ~ h '
где в\ обозначает у'-й единичный вектор. Это эквивалентно
аппроксимации /-го столбца J(x) по формуле
A.,-'*-*"*-'» . (4.2.Г)
Здесь тоже следует ожидать, что \\Aj — (/(x))./ll= 0(h) для
достаточно малых Л. Этот факт обоснован в лемме 4.2.1.
Лемма 4.2.1. Пусть F: Rrt-*Rm удовлетворяет условиям
леммы 4.1.12 в векторной норме ||-Ц, для которой ||е/||= 1, / =
= 1, ..., п. Пусть, далее, А е Rwxn, где А.\ определены по
(4.2.1), /= 1, ..., п. Тогда
И./-/М./|<1|А|. (4.2.2)
Если пользоваться /гнормой, то
М-/(*)||,<||Л|. (4.2.3)
Доказательство. Подстановка p = hej в (4.1.12) дает
\\F(x + hej)-F(x)-](x)hei\\^\\\hei\? = ±\ht
Разделив обе части неравенства на А, приходим к (4.2.2). Так
как /гнорма матрицы есть не что иное, как максимум /гнорм
ее столбцов, отсюда непосредственно вытекает (4.2.3). П
Следует упомянуть, что хотя, согласно (4.2.3), при
построении всей А используется один и тот же шаг А, из-за
арифметики конечной точности мы будем вынуждены применять шаги
различных размеров для каждого столбца матрицы А
Заметим также, что конечно-разностная аппроксимация якобиана
требует п дополнительных вычислений функции F. Таким
образом, это может оказаться сравнительно трудоемким, если
трудоемко вычисление самой F или п довольно велико.
Если нелинейная задача состоит в минимизации функции
/: R"->R, то может возникнуть необходимость в
аппроксимации градиента Vf(x) и (или) гессиана V2f(x). Аппроксимация
102 Гл. 4. Основы анализа функций многих переменных
градиента всего лишь частный случай рассмотренной выше
аппроксимации ](х) при т—1. В некоторых случаях из-за
конечной точности вычислений приходится подбирать более
точную конечно-разностную аппроксимацию, с использованием
центральных разностей, приведенных в лемме 4.2.2. Отметим,
что такая аппроксимация требует вдвое больше вычислений f
по сравнению с разностью вперед.
Лемма 4.2.2. Пусть f: Рл->-Р удовлетворяет условиям
леммы 4.1.14 в векторной норме с тем свойством, что ||е<|| = 1, i =
= 1, ...,п. Предположим x + hei, x — hei^D, i = l, ...,n.
Пусть fleR", где at имеют вид
q,-'(' + te->-'(->,'). (4.2.4)
Тогда
Если пользоваться /„-нормой, то
ei-V/W,|<-^. (4.2.5)
le-VfWl.^. (4.2.6)
Доказательство. Определим действительные величины аир
следующим образом:
а = f (х + het) - f (х) - Av/ (*), - W (*)„,
P = / (x - tied -f(x) + hVf (*), - AV/ (*)„.
Применение (4.1.13) при p = ±het приводит к
l«K-f и |p|<-£.
и по неравенству треугольника имеем
l—PK-f.
Таким образом, (4.2.5) следует из соотношения а — р =
= 2А(а,— Vf{x)i). Определение /«-нормы и (4.2.5) приводит
к (4.2.6). □
В некоторых случаях градиент V/ задан аналитически, а V2/—
нет. В этих ситуациях V2/ можно аппроксимировать, применяя
формулу (4.2.1) к функции FA.V/, и затем, полагая А =
= у (А + Ат), так как аппроксимация гессиана V2/ должна
быть симметричной. Из леммы 4.2.1 известно^ что ЦА—V2/(*)ll =5S
4.3. Необходимые и достаточные условия 103
= 0(Л) для достаточно малого А. Легко показать, что ||Л —
— V2/(jc)||f^|H — V2/WIIf (см. упр. 12). Таким образом, ||Л —
-V2/(jc)||=0(A).
Если V/ не задан, имеется возможность аппроксимировать
V2/, используя лишь значения f{x)t как это описано в
лемме 4.2.3. Здесь погрешность также имеет порядок 0(h) для
достаточно малых А. Заметим, однако, что такая аппроксимация
требует дополнительно (я2 + Зя)/2 вычислений /.
Лемма 4.2.3. Пусть / удовлетворяет условию леммы 4.2.2
Предположим, что х, х + Ае,-, х + heh х + het + hej е Д 1 ^ /,
/ ^ п. Пусть А е RnXrt, где Ац имеет вид
А __ f(x + h*i + **t)-f(x + **t)-n* + het) + flx) 7)
Тогда
MiZ-^fWi/KyYA. (4.2.8)
Если пользоваться матричной /р, /оо-нормой или нормой Фро-
бениуса, то
IM-V2/(jc)||<|y^. (4.2.9)
Доказательство очень похоже на доказательство леммы 4.2.2.
Для доказательства (4.2.8) вначале подставим
последовательно p = hei + he,-, p = hei и p = hej в (4.1.13). В результате
получим три неравенства. Обозначим величины, стоящие в их
левых частях под знаком модуля, через а, р и г\ соответственно.
Тогда а —р —Tj=(i4// — V2/(jc)//)A2. Используя |а — р — т]|^
^|а| + |р| + М и разделив результат на А2, получим (4.2.8).
Таким образом, (4.2.9) непосредственно следует из (3.1.8а),
(3.1.8с) и определения нормы Фробениуса. □
4.3. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ
В ЗАДАЧАХ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
В этом разделе приведем необходимые и достаточные условия
первого и второго порядков того, что точка х* является
локальным минимумом непрерывно дифференцируемой функции
/: R*-*-R, п ^ 1. Естественно, что эти условия будут ключевыми
в наших алгоритмах решения задачи безусловной
минимизации. Они тесно связаны со следующими условиями,
касающимися задачи с одной переменной, которые уже рассматривались
в гл. 2. Итак, в одномерном случае, для того чтобы хщ была
точкой локального минимума /, необходимо, чтобы /'(*») = 0;
104 Гл. 4. Основы анализа функции многих переменных
достаточно дополнительно выполнения неравенства /"(л'*)>0
и необходимо /"(л*):^ 0. В многомерном случае, для того чтобы
х„ была точкой локального минимума требуется V/(jc#) = 0;
достаточное условие, кроме того, требует положительной
определенности V2/(x»), а необходимое — по крайней мере
положительной полуопределенности V2f(xJ.
Доказательство и интерпретация этих условий по существу,
такие же, как и в случае функций одной переменной.
Равенство нулю градиента просто говорит о том, что не существует
направления из х„ вдоль которого f(x) с необходимостью
начнет увеличиваться или уменьшаться. Таким образом, точка,
имеющая нулевой градиент, является точкой минимума или
максимума / либо седловой точкой, которая представляет
собой точку максимума в одном поперечном сечении
пространства переменных и в то же время точку минимума в другом
(по аналогии с центром седла в двумерном случае).
Положительная определенность V2/(jk*) соответствует геометрическому
представлению о строгой локальной выпуклости и как раз
означает, что / изгибается вверх из точки х* во всех
направлениях.
Лемма 4.3.1. Пусть f: IR^-^IR непрерывно дифференцируема
в открытом выпуклом множестве D cz Rn. Тогда х е D может
быть точкой локального минимума f, только если V/(jt) = 0.
Доказательство. Как и в случае одной переменной, здесь
доказательство от противного предпочтительней, чем прямое
доказательство, потому что сама лемма и доказательство,
вместе взятые, указывают, как распознать возможный минимум
и как улучшить текущее приближение, если оно не является
точкой минимума.
Если V/(jc)=H=0, то выберем произвольное p^Rn, для
которого pTVf(x)<0. Такое р, несомненно, существует, поскольку
достаточно взять р =—v/(jc). В целях сохранения простоты
обозначений, умножим предварительно р на положительную
константу, так чтобы x + p^D. Это можно сделать, поскольку
множество D открыто и выпукло, и поэтому x-\-tp^D для
любых 0 ^ t ^ 1.
Тогда, в силу непрерывности V/ на D, существует
некоторое ?е[0, 1], такое, что V/(.v + tp)Tp < 0 для любых /е[0, t].
Теперь применим теорему Ньютона (лемма 4.1.2), чтобы
получить -
f(x + tp) = f(x)+ \vf(x + tp)Tpdt9
/-о
И таким образом f(x + tp) <f(x). □
4.3. Необходимые и достаточные условия 105
Для целого класса алгоритмов, называемых методами
спуска, характерно то, что они основываются на приведенном
выше доказательстве. Если Ч1(хс)ф0, то они выбирают
направление спуска р, как указано выше, а затем точка х+
определяется спуском в направлении р, так же как указано выше.
Теорема 4.3.2. Пусть /: Rrt-*R дважды непрерывно
дифференцируема в открытом выпуклом множестве DcRn и
предположим, что существует хеД такое, что V/(x) = 0. Если
гессиан V2/(jc) положительно определен, то х является точкой
локального минимума /. Если V2/(x) непрерывен по Липшицу
в х, то х может быть точкой локального минимума /, только
если V2f(x) положительно полуопределен.
Доказательство. Если V2f(x) положительно определен, то
вследствие непрерывности V2/ существует открытое выпуклое
подмножество D, содержащее х, такое, что V2f(z)
положительно определен для всех z из этого йодмножества. Сохраняя
простоту обозначений, переобозначим это множество через D.
Тогда, если psRn таково, что х-\-p^D, то по лемме 4.1.5 для
некоторого 2£[х, х + р] имеем
f(x + p)=f(x) + Vf(xVp + ^pTV2f(z)p =
= f(x) + jPTV2f(z)p>f(x).
Это доказывает, что х есть точка локального минимума /.
Необходимость того, чтобы S72f(x) был положительно
полуопределенным, оставим для упражнения. □
Доказательство данного ниже следствия также является
легким упражнением. Мы приводим его потому, что оно
представляет собой утверждение непосредственно той части
теоремы 4.3.2, которая наиболее соответствует условиям,
обеспечивающим нахождение точки локального минимума методом
Ньютона путем отыскания нуля V/.
Следствие 4.3.3. Пусть f: Rn-^R дважды непрерывно
дифференцируема в открытом выпуклом множестве DczRn. Если
^gD, v/(x*) = 0 и гессиан V2/ непрерывен по Липшицу в **,
причем У2/(#ф) не вырожден, то jc# является точкой локального
минимума / тогда и только тогда, когда Д2/(*#) положительно
определен.
Необходимые и достаточные условия того, чтобы л:* была
точкой лок^л^нргр максимума f, в точности такие же, как для
106 Гл. 4. Основы анализа функций многих переменных
случая, когда jc# является точкой локального минимума для
—/, а именно: V/(x#)*=*0 есть необходимое условие и, вдобавок,
необходимо, чтобы V2/(jc#) был отрицательно
полуопределенным; отрицательная определенность V2/(jc#) является
достаточным условием. Если V2/(x») не является знакоопределенным, то
х* не может быть ни точкой локального минимума, ни точкой
локального максимума.
Достаточные условия минимума частично объясняют
проявленный нами интерес к симметричным и положительно
определенным матрицам в гл. 3. Они приобретают еще более
важное значение из-за того, что предлагаемые алгоритмы
минимизации обычно описывают поведение / при приращении р
к точке хс с помощью квадратичной функции
mc(Xc + p) = f(Xc) + Vf(Xc)TP + YPTHP-
Незначительная модификация доказательства теоремы 4.3.2
показывает, что тс имеет единственный минимум тогда и
только тогда, когда Н положительно определено. Таким образом,
при построении моделей будут часто использоваться
симметричность и положительная определенность матриц Н. Важно
представить себе вид графиков квадратичных функций многих
переменных: они строго выпуклы или выпуклы соответственно
чашеобразны или желобообразны в двумерном случае, когда
Н положительно определена или положительно полуопределена;
они строго вогнуты или вогнуты (в форме перевернутых чаши
или желоба) в тех случаях, когда Н отрицательно определена
или отрицательно полуопределена; они имеют вид седла (в
л-мерном случае), если Н не является знакоопределенной.
4.4. УПРАЖНЕНИЯ
1. Вычислите якобиан следующей системы трех уравнений с тремя
неизвестными:
х\ + *? - х\
Г *i + *2-*3 1
П*) = *t*2*3
L 2*1*2 ~ 3*2*3 + *1*3 J
2. Пусть f: R2->R, f (x)*=x\x\ + x2/x{. Найдите V/(*) и V*f(x).
3. Докажите лемму 4.1.5.
4. Имеется иное определение, согласно которому якобианом функции
F: &п —>• &п в *е Rrt называется линейный оператор 7(х) (если он
существует), для которого
lim
f-*0
r\\F(x + tp) — F (*) — /(*) tp\\l Dn iA.„
i!—i—I—Zl jl-L ' *"' — 0 для »cex petR . (4.4tl)
4.4. Упражнения 107
Докажите, что если каждая компонента F непрерывно дифференцируема в
открытом множестве D, содержащем *, и / соответствует определению 4.1.5,
то J(x) = 7(х). Замечание. Существование такого 7(х) в (4.4.1) является
определением дифференцируемости по Гато F в точке х. Более сильным
условием на F является его дифференцируемость (в х) по Фреше, когда
требуется, чтобы J(x) е RnXn удовлетворяло
IF(x + p)-Flx)-T(x)pl _Q
Р-*о IIP II
[Более подробную информацию см. в книге Ортеги и Рейнболдта (1970).]
5. Пусть
\ х sin —, х Ф 0,
1 0, * = 0.
Докажите, что {(х) непрерывно по Липшицу, но не дифференцируемо в
точке х = 0.
6. Докажите лемму 4.1.14. [Указание: вам понадобится обобщение
теоремы Ньютона на случай двойных интегралов.]
7. Докажите лемму 4.1.15. (Техника доказательства очень похожа на ту,
что использовалась при доказательстве леммы 4.1.12.)
8. Если в определении непрерывности по Липшицу равенство (4.1.11)
заменить на
||G(ti)-G(*)||<Yll<>-*lla
для некоторого а е (0, 1], то говорят, что функция G непрерывна по Гёль-
деру в х. Покажите, что если предположение непрерывности по Липшицу в
лемме 4.1.12 заменить на непрерывность по Гёльдеру, а (4.1.12) заменить на
неравенство
\\F(x + p)-F(x)-J(x)p\\^j^\\p\\l+a,
то утверждение леммы останется в силе.
9. Задано F: R2-*R2,
' Зх? — 2х9
F(X):
/3*f-2*2\
вычислите J(x) в х=(1,1)т. Затем примените формулу (4.2.1) для
вычисления (вручную или на калькуляторе) конечно-разностной аппроксимации
J(x) в jc = (1, 1)г при h = 0.01. Прокомментируйте точность аппроксимации.
10. Обобщите формулу центральной разности по вычислению Vf(x) на
вычисление аппроксимации V2f(x)u по центральным разностям, так чтобы
использовать только значения самой функции и обеспечить при этом
асимптотическую оценку точности О (Л2). (Такая аппроксимация
используется при дискретизации некоторых дифференциальных уравнений в частных
производных.) Можно сделать предположение, что третья производная от
f(x) непрерывна по Липшицу.
108 Гл. 4. Основы анализа функции многих переменных
11. Обобщите методику из упр. 10 на случай нахождения
аппроксимации V2/(*)//, i-Ф /, так чтобы использовались лишь значения самой функции
и асимптотическая точность была при этом О (Л2). Какова по сравнению с
(4.2.7) трудоемкость этой аппроксимации в терминах количества вычислений
функции?
12. Пусть Л, М^&пХп, причем М симметрична, и пусть Д= (А +Ат)/2.
Докажите, что \\М —- A \\F ^ \\М — A \\F.
13. Завершите доказательство теоремы 4 3.2.
14. Докажите следствие 4.3.3.
15. Пусть имеется квадратичная функция п переменных f(x) =
~~хтАх + Ьтх + су где А е= RnXrt симметрична, /igR", cgR.
Докажите, что она имеет единственный минимум тогда и только тогда, когда А
положительно определена. Что здесь является точкой минимума? Как бы
вы ее находили? Напомним, что
V/ (х) = Ах + ЬУ V2f (х) = А.
16. Пользуясь необходимыми и достаточными условиями для задачи
безусловной минимизации, докажите, что любое решение х* е= R" линейной
задачи о наименьших квадратах вида
min \\Ах-Ь\\2, A<=RmXnt b e= Rm,
удовлетворяет соотношению (АтА)х*=АтЬ. [Указание: для случая, когда
А не является матрицей полного ранга, обобщить упр. 15, рассмотрев
положительно полуопределенные матрицы.]
Еще одно программное замечание
Главы с 5 по 9 составляют сердцевину данной книги. В них
рассматриваются вопросы разработки алгоритмов для решения многомерных нелинейных
уравнений и задач безусловной минимизации. В гл. 5 приводится и
обсуждается многомерный вариант метода Ньютона. Этот быстро сходящийся
локальный метод послужит далее базовой моделью для наших алгоритмов.
В гл. 6 представлены основные приемы, используемые в сочетании с методом
Ньютона для обеспечения глобальной сходимости нелинейных алгоритмов.
В гл. 7 обсуждаются практические соображения относительно критериев
останова, масштабирования и тестирования, необходимые для разработки в
законченном виде добротного программного обеспечения ЭВМ. В гл. 8 и 9
рассматриваются многомерные варианты метода секущих, которые
используются вместо метода Ньютона, когда производные недоступны, а
вычисление функции трудоемко.
Структура гибридного алгоритма решения многомерных задач, как
выяснится впоследствии, является по существу той же, что в гибридном
алгоритме для одномерных задач, приведенном в гл. 2. Эта аналогия
прослеживается и на более детальном уровне в определении и анализе локального
шага, за исключением того, что конечно-разностные производные становятся
более дорогими, а аппроксимации по секущим — гораздо менее очевидными.
Однако самое существенное отличие заключается в разнообразии и
возросшей сложности глобальных стратегий в случае многомерных задач.
5
Метод Ньютона решения
нелинейных уравнений
и безусловной минимизации
В этой главе обсуждаются локальные алгоритмы,
предназначенные для решения систем нелинейных уравнений и задач
безусловной минимизации. Тем самым мы приступаем к
рассмотрению многомерных задач. Здесь сначала приводится метод
Ньютона и обсуждаются вопросы его машинной реализации,
а также его достоинства и недостатки.
В разд. 5.2 и 5.3 используются два различных и имеющих
важное значение подхода для доказательства того, что метод
Ньютона локально ^-квадратично сходится для большинства
задач, однако его сходимость не обязательно будет глобальной.
В разд. 5.4 обсуждается конечно-разностный вариант метода
Ньютона решения нелинейных уравнений, включая вопрос
о практическом выборе длины шага в конечных разностях.
Глава заканчивается обсуждением варианта метода Ньютона
решения многомерных задач безусловной минимизации
(разд. 5.5) и обсуждением вопроса об использовании для
этих задач конечно-разностных аппроксимаций производных
(разд. 5.6).
5.1. МЕТОД НЬЮТОНА РЕШЕНИЯ СИСТЕМ
НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Базовой для изучаемых здесь задач является задача решения
системы нелинейных уравнений:
задано F: Rrt->Rn,
найти x$eR", такое, что F(xm) = 0, (5.1.1)
где предполагается, что F непрерывно дифференцируемо.
В этом разделе мы выводим формулу метода Ньютона для
задачи (5.1.1) и обсуждаем налагаемые им условия, вопросы его
реализации и особенности его локальной и глобальной сходи-
5.1. Метод Ньютона решения систем 111
мости. Указанные факторы обусловливают дальнейшую рабрту
в книге, которая разворачивается вокруг метода Ньютона по
его модификации и построения алгоритмов, надежных
глобально и быстрых локально. Мы опять игнорируем вопросы
существования и единственности решения задачи (5.1.1), полагая,
что на практике с этим, как правило, не возникнет никаких
проблем.
Метод Ньютона для задачи (5.1.1) опять получается из
нахождения корня аффинной аппроксимации для F,
соответствующей текущему приближению хс. Эта аппроксимация строится
с использованием тех же приемов, что и в случае задачи с
одной переменной. Итак,
хс+р
F(xc + p) = F(xc) + J J(z)dz. (5.1.2)
хе
Поскольку в целях получения аффинной аппроксимации для F
относительно приращений р к хс мы аппроксимируем интеграл
в (5.1.2) линейным членом J(xc) •/?, то
Mc(xc + p) = F(xc) + J(xc)-p (5.1.3)
(Мс по-прежнему обозначает текущую модель). Затем s*
находится из условия Мс (хс + sN) = 0, что дает нам итерацию
метода Ньютона решения (5.1.1). Таким образом, решается
система
J(xc)s» = -F(xc\
x+=xc + sN. (5.1.4)
Можно эквивалентным образом взглянуть на эту процедуру,
а именно мы находим точку, которая одновременно обращает
в нуль аффинные модели п функций, являющихся
компонентами F. Эти модели имеют вид
(Mc)l(xc + s") = fi(Xc) + Vft(Xc)Ts*9 * = 1, ..., п.
Так как мы не ожидаем, что х+ окажется равным *#, а на
самом деле будет лишь приближением к хщ, более удачным,
чем Хс, то давайте построим на базе ньютоновского шага (5.1.4)
алгоритм, применяя его итеративно из начального
приближения Хо.
Алгоритм 5.1.1. Метод Ньютона для систем нелинейных
уравнений.
Заданы: непрерывно дифференцируемая функция F: R*-vRn
и *0е R"; на очередной, k-ft итерации решить
J(xk)sk = — F(xk\
xk+\ = *Л + Sk-
112 Гл. 5. Метод Ньютона
Например, пусть
*1 + *2 — 3
/7W= 2 . 2 П I'
1х] + х\ — 9 J
Корнями здесь являются (3,0)г и (0,3)г. Пусть лго = (1, 5)г,
тогда первые две итерации метода Ньютона имеют вид
[-—1
П I
хх = х0 + s0 = (-.625, 3.625)г,
[_»-М41 nil
*8 = ^ + 5l « (-.092, 3.092)г.
Метод Ньютона в данном случае, по-видимому, работает
хорошо, ведь х2 находится уже довольно близко к корню
(0,3)т. Здесь проявляется основное преимущество метода
Ньютона: если хо находится достаточно близко к решению х# и
якобиан /(**) не вырожден, то, как показано в разд. 5.2,
последовательность Xk, вырабатываемая алгоритмом 5.1.1,
сходится к х* ^-квадратично. Метод Ньютона будет также
успешно работать на почти линейных задачах, поскольку он находит
нуль (невырожденной) аффинной функции за одну итерацию.
Отметим также, что если какие-либо компоненты-функции в F
аффинны, то каждая итерация, вырабатываемая методом
Ньютона, будет решением этих уравнений, так как используемые
им аффинные модели будут для этих функций всегда точными.
Например, f{ в приведенном выше примере является аффинной,
поэтому
М*1) = Ы*2)(=М*з)...) = о.
С другой стороны, что касается сходимости из плохих
начальных приближений, то, естественно, метод Ньютона будет
вести себя не лучше, чем в случае задач с одной переменной.
Например, если
'«-[£::]•
где х. = (0, 0)т и *0 = (-10, -10)г, то
х, =(-П+е10, -11 + е10)г^(2.2Х104, 2.2 X Ю4)г.
5.1. Метод Ньютона решения систем 113
Про этот шаг не скажешь, что он очень удачен! Поэтому
особенности сходимости метода Ньютона указывают на то, как
его использовать в многомерных алгоритмах. А именно, для
нас всегда будет желательно применять его по крайней мере
на заключительных итерациях любого нелинейного алгоритма,
с тем чтобы использовать его быструю локальную сходимость,
но, для того чтобы он сходился глобально, его нужно будет
модифицировать.
Имеются также две основные проблемы, касающиеся
реализации итерации алгоритма 5.1.1. Во-первых, якобиан
функции F может не быть задан аналитически. Это обычно
встречается в реальных приложениях, когда, например, F сама не
задана аналитически. Таким образом, аппроксимация /(**)
конечными разностями или каким-либо другим, менее дорогим
способом является важной задачей, и она служит предметом
обсуждения в разд. 5.4 и гл. 8. Во-вторых, /(**) может быть
вырожденной или плохо обусловленной, и тогда не
представляется возможным получить достоверное решение sk линейной
системы J(xk)Sk = —F(xk). Как мы видели в разд. 3.3,
описанные нами способы разложения матриц могут успешно
применяться для выявления плохой обусловленности. Таким образом,
возможная модификация алгоритма 5.1.1 заключается в том,
чтобы внести некоторое возмущение в J{xk), достаточное,
чтобы сделать ее хорошо обусловленной, и перейти к дальнейшим
действиям на итерации. Однако такая модификация J(xk) не
имеет убедительного обоснования в терминах исходной
задачи (5.1.1), и поэтому мы ее не рекомендуем. Вместо этого при
плохой обусловленности J(xk) мы предпочитаем переходить
непосредственно к такому глобальному методу решения
нелинейных уравнений (см. разд. 6.5), который соответствует
возмущению линейной модели (5.1.3), вполне осмысленному с точки
зрения исходной нелинейной задачи.
Рассмотренные выше достоинства и недостатки метода
Ньютона служат ключом к развитию наших многомерных
алгоритмов, поскольку они указывают на свойства, которые
желательно сохранить, и на области, где могут потребоваться улучшение
и модификация. Они сведены в табл. 5.1.2.
Таблица 5.1.2. Достоинства и недостатки метода Ньютона
решения систем нелинейных уравнений
Достоинства
1. (/-квадратичная сходимость из хорошего начального
приближения при условии, что /(**) не вырождена.
2 Точное решение за одну итерацию для аффинной F (точное
па каждой итерации для всех аффинных компонент F).
114 Гл. 5. Метод Ньютона
Недостатки
1. Отсутствие глобальной сходимости для многих задач.
2. Необходимость в /(**) на каждой итерации.
3. Необходимость в решении на каждой итерации системы
линейных уравнений, которая может быть вырожденной или
плохо обусловленной.
5.2. ЛОКАЛЬНАЯ СХОДИМОСТЬ МЕТОДА НЬЮТОНА
В этом разделе доказывается локальная ^-квадратичная
сходимость метода Ньютона для систем нелинейных уравнений и
делаются соответствующие выводы. Техника доказательства
аналогична той, что и в случае одной переменной. Она также
служит прототипом большинства доказательств сходимости в
этой книге. Для заданной векторной нормы ||-Ц через N(xtr)
будем обозначать открытую окрестность радиуса г с центром
В X T Р
N(x, r) = {xs=Rn: \\x-x\\<r).
Теорема 5.2.1. Пусть функция F: РЯ-^РП непрерывно
дифференцируема в открытом выпуклом множестве DczR".
Предположим, что существуют ^gR" и г, р > 0, такие, что
N(x*,r)czDy F(x*)=0, существует /(xj-1, причем ||/(дс»)"",1КР
и /е Lipy(N(x*, г)). Тогда существует е > 0, такое, что для
всех x0^N(x*,e) последовательность х\>х2, ..., порождаемая
соотношением
Xk+\ = xk — J(xkrlF(xk), k = 0, 1, ...,
корректно определена, сходится к агф и удовлетворяет
неравенству
ll**+i-M<Pvll**--*X Л —0, 1 (5.2.1)
Доказательство. Выберем е так, чтобы якобиан J(x) был
невырожденным для любых *е #(**, е), и затем покажем, что,
поскольку локальная погрешность аффинной модели,
используемой для проведения всех итераций метода Ньютона, имеет
порядок 0(||дг* — xj|2), сходимость ^-квадратична. Пусть
e = min{r, -щ]. (5.2.2)
Покажем индукцией по ky что на каждом шаге выполняется
(5.2.1), а также, что
11**+! — ХЛ< j \\xk — xj,
5.2. Локальная сходимость метода Ньютона 115
и тогда
хмеЫ(хт9в). (5.2.3)
Сначала покажем, что якобиан /(*о) не вырожден. Из ||jc0—
— х II ^ е, непрерывности / по Липшицу в х* и (5.2.2) следует,
что
|/W"4/W-/Wll<|/W"1ll/(*o)-/(*.)«<
<P-Yll*-*.IKP-Y-e<j-
Таким образом, из соотношения (3.1.20) для возмущенных
матриц вытекает невырожденность J{xo) и
|/(*оГ'1< = 11/1(Х>)"111 ^<2|/(А:Г1|<2.р. (5.2.4)
Следовательно, х\ корректно определено и
Xi — x9 = Xo — xm — J (x0yl F(x0)=x0 — х— J (x0)~l [F(x0) — F(x,)]=
= J (xoV1 [F (xj - F (xQ) - /(x0) (x. - xQ)).
Заметим, что выражение в квадратных скобках как раз
представляет собой разность между F(x+) и значением аффинной
модели Мс{х), вычисленным в хш. Поэтому, используя лемму
4.1.12 и (5.2.4), имеем
IU! — JcJ|<||/(A:oril|F (jcJ _ F(a:0) —/Uo) (^ — л:0)1К
<2p -}\\x0-xJ = fiy\\xQ-xJ.
Это доказывает (5.2.1). Поскольку IU0 — jc»||< e < l/(2pv),
имеем
ll*i —*J<4"ll*b —*Д
что указывает на справедливость (5.2.3) и тем самым
завершает доказательство для случая k = 0. Идентично проводится
доказательство индуктивного предположения. □
Константы v и Р можно объединить в одну константу YRei=
= yP, которая по сути есть константа Липшица для измерения
относительной нелинейности F в х#, так как
\nxrl[J(x)-J(xJ}\<\j(xJ-ltiJ{x)-J(xM<
<PYlU-*JI = YRel||*-*JI
для x^N(x*yr). Следовательно, теорему 5.2.1 можно также
трактовать как утверждение о том, что радиус сходимости
метода Ньютона обратно пропорционален относительной нелиней-
116 Гл. 5. Метод Ньютона
ности F в х#. Относительная нелинейность функции является
основным фактором, определяющим поведение этой функции в
наших алгоритмах, и все наши теоремы сходимости могли бы
быть легко переформулированы и доказаны в терминах этого
понятия. Мы остановились на абсолютной нелинейности только
потому, что это общепринято и, вероятно, поэтому порождает
меньше путаницы.
Читатель мог бы поинтересоваться, достаточно ли близки на
практике к реальной области сходимости метода Ньютона ее
оценки, вытекающие из теоремы 5.2.1. Этот вопрос исследуется
в упражнениях, где показано, что оценка е в теореме 5.2.1
рассчитана на худший случай. Она довольно хорошо отражает то,
насколько далеко распространяется область квадратичной
сходимости в том направлении из л;*, в котором 'F более всего
нелинейна. С другой стороны, в тех направлениях из **, в
которых F менее нелинейна, область сходимости метода Ньютона
может простираться намного дальше. Это один из тех случаев,
когда мы должны платить за использование норм в нашем
анализе.
Ортега и Рейнболдт (1970, с. 411) дали прекрасный
исторический обзор анализа сходимости метода Ньютона, включая и
проведенный Канторовичем анализ, с которым можно
познакомиться в следующем разделе.
5.3. ТЕОРЕМА КАНТОРОВИЧА И ТЕОРЕМА
О СЖИМАЮЩЕМ ОТОБРАЖЕНИИ
В настоящем разделе формулируется второй результат,
касающийся сходимости метода Ньютона. Он отличается от
первого. Этот сильный результат был получен Канторовичем (1948).
Будет также показано, что относящиеся к нему предположения
и методика его доказательства связаны с классическим
результатом, касающимся сходимости итерационных алгоритмов и
известным как теорема о сжимающем отображении. Несмотря на
то что ни один из этих результатов не будет далее
непосредственно использован в книге, они представляют собой две
красивые и сильные теоремы, и их должны знать все те, кто
изучает нелинейные задачи.
Теорема Канторовича отличается от теоремы 5.2.1 главным
образом тем, что она не предполагает существование решения
р(jc^) = 0. Вместо этого она показывает, что, если якобиан J(x0)
не вырожден, / непрерывен по Липшицу в некоторой области,
содержащей лго, и первый шаг метода Ньютона достаточно мал
относительно нелинейности F, то в этой области должен
существовать корень и, более того, быть единственным. За эти
более слабые предположения мы платим тем, что здесь доказы-
5.3. Теорема Канторовича 117
вается лишь r-квадратичная скорость сходимости. Продолжая
знакомство с книгой, читатель увидит, что для большинства
методов получение наилучших оценок скорости сходимости требует
в каждом случае своего отдельного доказательства.
Теорема 5.3.°1 (Канторович). Пусть г > 0, хо е Rn, F: Rn-+ Rn,
и предположим, что функция F непрерывно дифференцируема
в N(xo,r). Пусть для заданных векторной и индуцированной
операторной норм /е LipY((A/(Jto, г)), причем /(лг0) не вырожден,
и существуют константы р, т] ^ 0, такие, что
|/(*аГ'1<Р. lUw^wlkr,.
Введем обозначения YRei = PY> <* = YReiT|- Если а^у и r^rQz=s
s=(l — Vl ~"2a)/(PY)> то последовательность {xk}t задаваемая
соотношением
Xk+i = xk — J(xh)~lF(xk), k = 0, 1,...,
корректно определена и сходится к х*, который является
единственным нулем F в замыкании множества N(xo,ro). Если же
в этом случае a < -у, то лг* будет единственным нулем F в
N(x0, г,), где гх = тт[г, (l + л/1 - 2(x)/(Py)], и
ll*A-JUI<(2a)2*Jf £ = 0,1,.... (5.3.1)
Теорема 5.3.1 имеет довольно длинное доказательство. Его
схема дана в упр. 6—8. В ее основе лежит простая и весьма
здравая идея. Итак, зафиксируем в я-мерном пространстве
итерации лг0, хи • • • и протянем нить, соединяющую их в указанном
порядке. Пометим на нити те места, где находятся xk, а затем
вытянем ее в одну прямую, возможно, при этом немного
растянув ее в длину. То, что в результате получится, представляет
собой линейный сегмент, состоящий из последовательности
верхних оценок для расстояний ||jc*+i—х*||, k = 0, 1, ... .
Доказательство теоремы Канторовича по существу показывает, что для
любой последовательности {xk}, построенной согласно
предположениям теоремы 5.3.1, эти расстояния меньше или равны
соответственно | tk+\ — tk |. Последние получаются, если
применить метод Ньютона, начиная с t0 = 0, к функции
(видно, что она удовлетворяет условиям теоремы 5.3.1).
Поскольку последовательность {tk} сходится монотонно к мень-
118 Гл. 5. Метод Ньютона
шему корню /« = (1 — л/1 — 2а)/(ру) функции /(/), общая длина
части дс-нити, лежащей за хк, не должна превосходить | /* — U | •
Таким образом, {**} является последовательностью Коши и
поэтому она сходится к некоторому **, причем погрешности
\\xk — х#|| ограничены ^-квадратично сходящейся
последовательностью \tk — /*|. Эта методика доказательства называется лш-
жоризацией. Она нигде не использует конечность размерности
пространства Rn. Говорят, что последовательность {/*}
мажорирует последовательность {**}. Дальнейшее развитие
доказательства можно найти в упражнениях или, например, в работе Дэн-
ниса (1971).
Благоприятным обстоятельством в теореме Канторовича
является то, что она не предполагает существования х* и
невырожденности /(**); в действительности существуют функции F
и точки xq, которые удовлетворяют условиям теоремы 5.3.1, хотя
/(*♦) вырожден. Неудачным моментом здесь является то, что
r-порядок сходимости ничего не говорит о продвижениях на
каждой итерации, а даваемые теоремой оценки погрешности на
практике часто слишком неточны. Но это не так важно, так как
Дэннисом (1971) показано, что
■jllsik+i — **IK1*a — *JK 2 ||*ik+l — xk\\.
Кроме того, проверку предположений теоремы 5.3.1 традиционно
представляют себе как выяснение вопроса о том, будет ли
метод Ньютона сходиться из некоторого хо для конкретной
функции F. Однако на практике фактически всегда для тщательной
оценки константы Липшица у требуется больше труда, чем для
того, чтобы просто попробовать метод Ньютона и посмотреть,
сходится он или нет. Так что, за исключением частных случаев,
практическим приложением это не назовешь.
Теорема Канторовича по своему виду очень сходна с
теоремой о сжимающем отображении. Это — другая классическая
теорема. Она рассматривает произвольный итерационный метод
вида Jt*+i = G(Xk) и устанавливает условия, касающиеся О, при
которых последовательность {xk} будет сходиться ^-линейно к
точке jc# из любой точки х0 в области D. Более того,
доказывается, что jc* является единственной точкой в D, такой, что
G(x*) = x+. Таким образом, теорема о сжимающем отображении
представляет собой более общий, но вместе с тем и более
слабый результат, чем теорема Канторовича.
Теорема 5.3.2 (теорема о сжимающем отображении). Пусть
G: D-+D, где D есть замкнутое подмножество Rrt. Если для
некоторой нормы II-II существует ае [0, 1), такое, что
IIG (х) - G (у)]\ < а|| х - у ||, V*, yeD, (5.3.2)
5.4. Методы с конечно-разностными производными 119
то:
(a) существует единственное jt«eZ), такое, что G{x+) = x0\
(b) для любых x0^D последовательность {**},
удовлетворяющая соотношению хк+\ = G{xk)y k = О,1, ..., сходится q-ли-
нейно к jc# с константой а;
(c) для любого Т) ^ ||G(Xo) — X0\\,
Итерационная функция G, удовлетворяющая (5.3.2),
называется сжимающей в области D. Из этого свойства следует, что,
начиная из любой начальной точки хо е £>, длина шага ||jc*+i —
— **Н уменьшается на каждой итерации по крайней мере на
сомножитель ос, так как
II **+i - xh || = || G (xk) - G (xk-{) || < a|| xk - xk-x ||. (5.3.3)
На основе (5.3.3) легко показать, что {лг*} мажорируется
^-линейно сходящейся последовательностью. Отсюда как следствие,
доказательство которого оставляем в качестве упражнения,
вытекает теорема 5.3.2. Таким образом, доказательства теоремы
Канторовича и теоремы о сжимающем отображении тесно
связаны.
Теорему о сжимающем отображении можно применить к
задаче (5.1.1), задав итерационную функцию G(x), так чтобы
G(x) = x в том и только в том случае, когда F(x) = 0.
Примером служит
G (х) = х — AF (х), где i4sRrtXn не вырождена. (5.3.4)
Тогда эту теорему можно использовать для выяснения
существования какой-либо области Z), такой, что точки, генерируемые
итерационной функцией (5.3.4) из х0 е D, будут сходиться к
корню функции F. Однако теорема о сжимающем отображении
может быть использована для установления только линейной
сходимости, поэтому она в целом непригодна для методов,
рассматриваемых в данной книге.
5.4. МЕТОДЫ С КОНЕЧНО-РАЗНОСТНЫМИ ПРОИЗВОДНЫМИ
ДЛЯ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ
УРАВНЕНИЯ
В этой главе обсуждается влияние на метод Ньютона замены
аналитически заданного якобиана J(x) на конечно-разностную
аппроксимацию, построенную в разд. 4.2. Легко показать, что,
если длина конечно-разностного шага выбрана надлежащим
120 Гл. 5. Метод Ньютона
образом, то сохраняется ^"кваДРатичная сходимость метода
Ньютона. Обсуждаются также практические способы выбора
длины шага с учетом влияния машинной арифметики. Для
большинства задач, и это продемонстрировано на одном примере,
метод Ньютона с использованием аналитических производных
и метод Ньютона с надлежащим выбором конечных разностей
фактически неразличимы.
Теорема 5.4.1. Пусть F и *« удовлетворяют условиям теоремы
5.2.1, где ||-II обозначает векторную Л-норму и
соответствующую индуцированную матричную норму. Тогда существуют е,
А > 0, такие, что если {А*} есть последовательность
действительных чисел, причем 0<|Л*|^А и хо^Ы(х^г), то
последовательность х\, Х2, ..., задаваемая формулами
(А \ ^ k ^ k > * k) i 1
*ь ' ' >■■'- (541)
Xk+\ = xk — AklF(xk), k = 0, 1, ...,
корректно определена и сходится ^-линейно к л;*. Если
lim А* = 0,
fc->0
то сходимость ^-сверхлинейна. Если существует некоторая
константа си такая, что
|AaI<*iII*a-*JI. (5.4.2)
или, что эквивалентно, константа сг, такая, что
\hk\^c2\\F(xk)l (5.4.3)
то сходимость ^-квадратична.
Доказательство. Доказательство аналогично тому, что было
дано для теоремы 5.2.1 в комбинации с доказательством
теоремы 2.6.3, где рассматривался конечно-разностный метод
Ньютона в одномерном случае. Выберем е и А, так чтобы
матрица Ak была невырожденной для любых xk^N(x*,z) и
| hk | < Л. Пусть в^ги
е + Л<^г, (5.4.4)
гДе /\ Р, Y определены в теореме 5.2.1. Сначала покажем
индукцией по ky что на каждом шаге
|| **+i - х, || < j \\xk - xm ||, ^isJV (xf, r). (5,4.5)
5.4. Методы с конечно-разностными производными \2\
Для k = Q покажем прежде всего, что А0 не вырождена. Из
неравенства треугольника, леммы 4.2.1, непрерывности / по
Липшицу в хш, \\х0 — *J|<e и (5.4.4) вытекает
|/ (*.)"' Ио - / (х.)] II < II/(хщГ11||| [Л0 - / (jc0)] + [/ (*о) - / (*.)] || <
<P(T"+Ve)<y- (5Л6)
Поступим теперь как при доказательстве теоремы 5.2.1. Из
соотношения (3.1.20) для возмущенных матриц и неравенства (5.4.6)
следует, что А0 не вырождена и
Ыо-'Кгр. (5.4.7)
Поэтому х\ корректно определено и
*i-*. = 4Г1 ([F (*,) - F (х0) - / (х0) (х. - *<>)] +
+ Ш(хо)-А0)(х,-х0)]).
Заметим, что эта формула отличается от соответствующей ей
в анализе метода Ньютона только тем, что J(xo)~l здесь
заменено на AqX и добавлено слагаемое (/(л:о)— А0) (х*— х0).
Используя теперь леммы 4.1.12 и 4.2.1, а также неравенства (5.4.7),
||*о—**ll^ е и (5.4.4), мы убеждаемся, что
\\*i-xJ^\\A0-l\\[\\F(xJ-F(x0)-J(x0)(x.-x0)\\ +
4Ч1Л-'(*о)11К-*о11]<
<2p[|lK~JC0||2 + ^IUo-^ll]<
<lv(* + h)\\x0-xJ<±VLx0-xJ.
Это доказывает неравенство (5.4.5). Идентично проводится
доказательство индуктивного предположения.
Для доказательства ^-сверхлинейной и ^-квадратичной
сходимости, которое мы оставляем в качестве упражнения,
необходимо получить улучшенную оценку величины ||Л* — /(**)||.
Эквивалентность (5.4.2) и (5.4.3) можно просто показать,
используя лемму 4.1.16. □
Как и в случае одной переменной, теорема 5.4.1 не указывает
нам, как в точности следует выбирать длину
конечно-разностного шага на практике. Это вызвано тем, что здесь опять
имеются два взаимно противоречивых источника ошибок,
возникающих при вычислении конечно-разностных производных.
Рассмотрим конечно-разностное соотношение (5.4.1). При этом
опустим ради удобства нижний индекс &, отвечающий номеру
итерации. По лемме 4.2.1 ошибка аппроксимации (/(*))./ с по-
122 Гл. 5. Метод Ньютона
мощью A.j равна 0(yh) в точной арифметике, что наводит на
мысль выбирать h настолько малым, насколько это возможно.
Однако при малых значениях А существенно сказываются
другие ошибки в (5.4.1), связанные с вычислением в арифметике
конечной точности числителя этой формулы. Поскольку там
числитель делится на Л, ошибка б в числителе приводит в (5.4.1)
к ошибке б/Л. Относительно этой ошибки в числителе, которая
проистекает из неточных значений функции и из потери
точности при их вычитании, можно с достаточным основанием
сказать, что она составляет лишь малую часть от F(x). В
действительности если Л слишком мало, то x + hej может быть
настолько близким к х, что F(x + hei)^F(x), и поэтому Ду может
вовсе не иметь достоверных разрядов, или если иметь, то очень
мало. Таким образом, А должно выбираться так, чтобы
сбалансировать в (5.4.1) ошибки 0(yh) и 0(F(x)/h).
Если F(x) имеет t достоверных разрядов, то целесообразно
стремиться к тому, чтобы F(x + hej) отличалось от F(x) правой
половиной этих разрядов. Точнее говоря, если относительная
ошибка при вычислении F(x) равна г\ (т) представляет собой
относительный уровень шума), то мы хотели бы иметь
\\F(x + hef)-F(x)\\^
IF(x)t <ЛЛЬ /=1> ...» "• (5.4.8)
При отсутствии какой-либо дополнительной информации
разумный способ удовлетворить (5.4.8) заключается в использовании
для возмущения каждой компоненты х,- своей собственной
длины шага
A/=V4*/, (5.4.9а)
которая отвечает относительному изменению д/л на величину
xj. Тогда Л./ вычисляется по формуле
f(,+V,)-fW
Л/
Для удобства мы до сих пор предполагали, что используется
одинаковая длина шага h для всей конечно-разностной
аппроксимации, однако нет оснований так поступать на практике.
Более того, единая длина шага может привести к пагубным
последствиям, если компоненты вектора х сильно различаются по
величине (см. упр. 12). Теорему 5.4.1 легко переработать,
оставив ее в силе и в случае, когда для каждой компоненты
используется своя длина шага А/.
В случае когда F(x) задана простой формулой, разумно
полагать т) £ё macheps, и тогда длина шага Л/ есть Vmacheps • */.
5.4. Методы с конечно-разностными производными
123
Пример 5.4.2.
F(x) =
*0 = (2,3)г, х,=
Вычисления на ЭВМ с 48 двоичными
тичных разрядов):
Метод Ньютона,
аналитические производные
" (273)
/0.574655 J 5807608\
V2.1168965612826 )
/0.31178766389307\
\ 1.5241979559460 /
/1.4841388323960\
V 1.1464779176945/
/1.0592959013664\
Vl.0348194625183/
/1.0008031050945\
1,1.0014625483617/
/0.9999987218746 1\
\ 1.0000026672636 /
/0.99999999999548\
\1.0000000000089 /
4
6
2.7182818284590
27
*о
*1
*2
JC.4
Х4
*5
*6
*7
(Ыи
(Л*о)).2
(Ыгх
№р)Ь:
-.)•
= (1, if'
разрядами (sd4.4 деся-
Метод Ньютона
конечные разности
при h,= l0-7\xl\
-—
/0.57465515450268\
V2.H68966735234 )
/0.31178738552306\
Vl.5241981016335 /
/1.4841386151178\
1,1.1464781318492/
/1.0592958450507\
\1.0348195092235/
/1.0008031056081\
V 1.0014625533494/
/0.99999872173640\
V 1.0000026674316 /
/0.99999999999535\
V 1.0000000000091 /
4.0000003309615
6.0000002122252
2.7182824169358
27.000002470838
В примере 5.4.2 сравниваются конечно-разностный метод
Ньютона, использующий (5.4.9) при r\ ^ macheps, и метод Ньютона,
использующий аналитические производные, причем начальная
точка для них одна и та же. Читатель увидит» что результаты,
124 Гл. 5. Метод Ньютона
включая значения производных, фактически неразличимы.
Обычно это имеет место и на практике. По этой причине многие
пакеты программ даже не допускают возможности
использования аналитических производных, вместо которых они применяют
конечные разности. Хотя мы не сторонники таких крайних мер,
все же следует подчеркнуть, что, видимо, основной причиной
ошибок при использовании программного обеспечения по
решению каких-либо нелинейных задач является неверное
программирование производных. Таким образом, если предоставлены
аналитические производные, мы настоятельно рекомендуем,
чтобы они были проверены на соответствие с конечно-разностной
аппроксимацией в начальной точке д:0.
Если F(x) вычисляется очень длинной программой или
итерационной процедурой, то т] может оказаться гораздо больше,
чем macheps. Когда г\ настолько велико, что можно ожидать
неточность в конечно-разностных производных (5.4.9), тогда
следует, вероятно, воспользоваться вместо этого
аппроксимацией J(x) по секущим (см. гл. 8). Это относится и к случаю,
когда недопустимы издержки, связанные с п дополнительными
вычислениями F(x) на каждой,итерации для получения А.
Алгоритм для вычисления конечно-разностных якобианов
представлен в приложении А алгоритмом А5.4.1. Так как
формула (5.4.9а) может дать неприемлемо малое значение А/,
когда Xj подходит близко к нулю, в алгоритме она несколько
видоизменена, так что
Л/ = Ул max {| xt |, typ Xj) sign (*,), (5.4.10)
где typ*/ представляет собой характерный размер */,
задаваемый пользователем (см. упр. 7.1).
В заключение укажем кратко, как длина шага (5.4.10)
может быть отчасти обоснована анализом. Естественно
предположить, что Xj есть некоторое точное машинное число. Для
упрощения анализа предположим, что х\ + Л/ также есть некоторое
точное машинное число, причем Х\ + Л/ ф Х\. Это имеет место,
когда hj вычисляется по какому-либо правилу выбора длины
шага, которое гарантирует, что | Лу1 > macheps |jc/|, и тогда,
прежде чем использовать Лу в (5.4.9Ь),проводятся вычисления1)
temp = Xj + Ay,
Ay = temp — xf.
Этот прием улучшает точность, поэтому мы используем его на
практике. Теперь легко убедиться, что погрешность,
возникающая при вычислении Л.у по формуле (5.4.9Ь) из-за ошибок округ-
) Здесь temp есть сокращение от temporary (временный),— Прим. перев.
5.5. Метод Ньютона безусловной минимизации 125
ления и погрешностей вычисления функции, ограничена
величиной
2 (т) + macheps) F (КЛ11\
|Д/| ' 10.4.1 U
где F есть верхняя граница для Н^ООН при х е [х, х + А/в/].
[Мы не включаем сюда пренебрежимо малые ошибки от
деления в (5.4.9Ь).] Кроме того, по лемме 4.2.1 разница в точной
арифметике между А.,- и /(*)./ ограничена величиной
Щ±, (5.4.12)
где y/ есть константа Липшица, такая, что
|[/(* + te/)-/(*)]e/|<Y/|/l
для всех t е [О, А/]. Значение А/, минимизирующее сумму
величин (5.4.11) и (5.4.12), равно
д. Ц 4 (Л + macheps)^1'2 (5 4 13)
При достаточно разумных предположениях (см. упр. 14) о том,
что
Y/ °l,(max{|x/|, typ*,})2;'
(5.4.13) сводится к (5.4.10) с точностью до некоторого
постоянного множителя со знаком. Заметим в заключение, что
проведенный анализ можно модифицировать с учетом абсолютной
погрешности в вычисленном значении F(x).
5.5. МЕТОД НЬЮТОНА БЕЗУСЛОВНОЙ
МИНИМИЗАЦИИ
Рассмотрим теперь метод Ньютона для задачи
min f: R"->R, (5.5.1)
где предполагается, что J дважды непрерывно
дифференцируема. Точно так же как в гл. 2, мы моделируем / в текущей
точке хс квадратичной функцией
mc(Xc + p) = f(xc) + Vf(xc)Tp+±pT4>f(xc)p
и находим точку х+ = хс + s^. Здесь Vmc(jt+) = 0 является
необходимым условием того, что х+ есть точка минимума для тс.
Это соответствует следующему алгоритму.
126 Гл. 5. Метод Ньютона
Алгоритм 5.5.1 (метод Ньютона для безусловной
минимизации).
Заданы: дважды непрерывно дифференцируемая функция
/: R"->- R и *0е Rn; на каждой итерации к
решить V2f (xk) s% = — V/ (xk)t
xk+\==xk'^" sk-
Алгоритм 5.5.1 просто является применением метода-
Ньютона (алгоритм 5.1.1) ic системе v/(jc) = 0 из п нелинейных
уравнений с п неизвестными, так как в нем на каждой итерации
делается шаг в нуль аффинной модели для V/, определяемой
как
М k (xk + р) = V [mk (xk + р)] = V/ (xk) + V2/ (xk) p.
С этой точки зрения некоторые из достоинств и недостатков
алгоритма для решения задачи минимизации (5.5.1),
несомненно, совпадают с приведенными в табл. 5.1.2. Положительным
здесь является то, что если хо достаточно близко к точке
локального минимума х+ функции / с невырожденной матрицей
V2/(*#) (и поэтому положительно определенной согласно
следствию 4.3.3), то последовательность {**}> генерируемая
алгоритмом 5.5.1, будет сходиться ^-квадратично к х+, что с
очевидностью продемонстрировано примером 5.5.2. Кроме того, если
f — строго выпуклая квадратичная функция, то V/ аффинно и
поэтому х\ будет единственной точкой минимума /.
Пример 5.5.2. Пусть функция
f(xl,x2) = (xl-2y + (xl-2Yxl + (x2+lf
имеет минимум в *#=(2,—1)г. Алгоритм 5.5.1, стартующий из
х0 = (1,1)7', вырабатывает следующую последовательность
точек (с точностью до восьми цифр на ЭВМ CDC при одинарной
точности)'
Л**)
хо = (1.0
Xt =(1.0
х, = (1.3913043
Xj = (1.7459441
х4 = (1.9862783
х5 = (1.9987342
х6 = (1.9999996
1.0 )г
-0.5 )г
- 0.69565217)г
-0.94879809)7
-1.0482081)7
-1.0001700)7'
-1.0000016)''
6.0
1.5
4.09 х 10"'
6.49 х 10"2
2.53 х 10" Л
1.63 х 10"6
2.75 х КГ12
5.5. Метод Ньютона безусловной минимизации 127
Что касается отрицательных сторон алгоритма 5.5.1, то он
разделяет с методом Ньютона для решения F(x) = 0 его
недостатки и имеет к тому же дополнительный минус. Старые
трудности заключаются в том, что метод не сходится глобально,
требует решения систем линейных уравнений и аналитически
заданных производных, причем в данном случае это V/ и V2/.
Указанные вопросы обсуждаются в такой последовательности:
конечно-разностная аппроксимация производных для задач
минимизации в разд. 5.6, глобальные методы в гл. 6, а
аппроксимация гессиана по секущим *) в гл. 9.
Мы должны также принять во внимание тот факт, что даже
как локальный, метод Ньютона не приспособлен специальным
образом для задачи минимизации, поскольку в нем нет ничего,
что удерживало бы его от продвижения в сторону максимума
или седловой точки функции /, где V/ тоже равен нулю. С точки
зрения моделирования трудность в случае алгоритма 5.5.1
состоит в том, что каждый шаг направляется просто-напросто
в сторону стационарной точки локальной квадратичной модели
независимо от того, является ли стационарная точка
минимумом, максимумом или седловой точкой модели. Этот шаг
оправдан при попытке минимизировать /(*), только когда гессиан
V2/(jcc) положительно определен, т. е. когда критическая точка
есть точка минимума. Даже если метод Ньютона рассматривать
прежде всего как локальный метод, который следует применять,
когда хс достаточно близко к точке минимума, где V2/(*c)
положительно определен, то мы все же хотели бы провести
некоторую полезную адаптацию в случае, когда Д2/(*с) не является
положительно определенной.
Имеются, по-видимому, две приемлемые модификации
метода Ньютона для случая, когда V2/(*c) не является
положительно определенной. Первая заключается в попытке
использовать внешний вид модели, в частности «направления
отрицательной кривизну» р, для которых prV2/(jcc)p< 0, с тем чтобы
быстро уменьшить f(x). Было приложено немало усилий к
разработке таких стратегий [см., например, Морэ и Соренсен
(1979)], но они пока еще не оправдали себя! Мы рекомендуем
вторую альтернативу, которая заключается в том, чтобы
изменять модель, когда это необходимо, так чтобы она имела
единственную точку минимума, и затем воспользоваться этой
точкой минимума для определения ньютоновского шага. В
частности, мы увидим в гл. 6, что имеется несколько доводов в пользу
выбора шагов вида — (V2/(*c)+ |Ac/)""!V/(Jcc)f где цс ^ 0, а
^2/(*c)+|ic/ положительно определена Поэтому, когда V2f(xc)
не является положительно определенной, рекомендуется заме-
!> В оригинале secant approximations of the Hessian.—Прим. перев.
12Й Гл. 5. Метод Ньютона
нять гессиан модели на S72f(xc) + \icI, где \лс > 0 в идеале
ненамного превышает то наименьшее jx, которое делает V2/(хс) + \*>1
положительно определенной и достаточно хорошо
обусловленной. Наш алгоритм, выполняющий это, обсуждается в конце
данного раздела. Он представляет собой некоторое
видоизменение модификации разложения Холесского, приведенной в книге
Гилла, Мюррея и Райт (1981, с. 147). Результатом является
следующий вариант метода Ньютона.
Алгоритм 5.5.3. Модифицированный метод Ньютона
безусловной минимизации
Заданы: дважды непрерывно дифференцируемая функция
/: Rn-^R и jc0e Rn; на каждой итерации k:
применить к S72f(xk) алгоритм А5.5.1 для нахождения
разложения Холесского матрицы Hk = V2/(**) + |i*/, где р,* = 0, если
V2f(xk) надежно положительно определена1), n \ik>0
достаточно велико, так что #* надежно положительно определена,
в противном случае:
решить HksNk= -Vf(xk),
xk+\ = xk ~т~ Sk •
Если хо достаточно близко к точке минимума х* функции /
и если V2/(x») положительно определена и достаточно хорошо
обусловлена, то алгоритм 5.5.3 будет эквивалентен алгоритму
5.5.1 и, следовательно, будет ^-квадратично сходящимся.
Пересмотренный вариант доказательства леммы 4.3.1 покажет, что
алгоритм 5.5.3 имеет дополнительное преимущество,
состоящее в том, что модифицированное ньютоновское направление
— H7]yf(xc) является направлением, в котором любая дважды
дифференцируемая функция f(x) начинает уменьшаться из
любой точки хс.
Алгоритм 5.5.3 также имеет две важные интерпретации в
терминах квадратичных моделей функции f(x). Первая
заключается в том, что он полагает х+ равным точке минимума хс + р
для аппроксимации
тс (хс + р) - f (хс) + V/ (*/ р + \ рТНср.
1) То есть не только положительно определена, но также и достаточно
хорошо обусловлена. — Прим. перев.
5.5. Метод Ньютона безусловной минимизации 129
В разд. 6.4 мы убедимся, что х+ есть также точка минимума не-
модифицированной модели
тс (хс + p) = f (хс) + Vf (х/ р + -i р V/ (хс)
при наличии ограничения
\\р\\2<\\(х+-хс)\\2У
что, возможно, является более привлекательным объяснение*м.
Обе интерпретации можно использовать для объяснения
основной проблемы, связанной с модифицированным ньютоновским
алгоритмом: в некоторых ситуациях он может вырабатывать
чрезмерно большие шаги s%. Эта проблема будет рассмотрена
вполне удовлетворительным образом в гл. 6. Длину шага можно
отрегулировать, если поработать с параметрами алгоритма
А5.5.1. Однако любая такая регулировка слишком сильно
зависит от характерных масштабов задачи, чтобы ее включать
в алгоритм общего назначения.
Мы завершаем этот раздел кратким описанием нашего
алгоритма (алгоритм А5.5.1 приложения), в котором определяется
как \ic ^ 0, такое, что Нс = Vf2(xc)+ |*с/ положительно
определена и хорошо обусловлена, так и разложение Нс по Холес-
скому. Хотя этот алгоритм является центральным в нашем
программном обеспечении по минимизации, все же он имеет не
настолько решающее значение, чтобы читатель изучал его в
деталях.
Ясно, что наименьшее среди возможных \ic (в случае, когда
S/2f(xc) не является положительно определенной) несколько
больше, чем абсолютная величина крайнего слева
отрицательного собственного значения матрицы V2/(xc). Несмотря на то
что его можно вычислить без слишком больших хлопот, мы
решили предоставить гораздо более простой алгоритм, который
может приводить к большим jxc. Применим сначала алгоритм
Гилла и Мюррея модифицированного разложения Холесского
к V2/(xc), что даст в результате V2/ {xc) + D = LLTy где D есть
диагональная матрица с неотрицательными диагональными
элементами, которые равны нулю, если V2f(xc) надежно
положительно определена. Если D = 0, то цс = 0, и этим завершаем
работу алгоритма. .Если £>=^=0, то вычисляем верхнюю границу Ь\
для |ic, используя теорему о кругах Гершгорина (теорема 3.5.9).
Поскольку величина
b2= max {du}
1 < i < п
также представляет собой верхнюю границу для цг, то
полагаем (Lie = min{6i, fe2} и завершаем работу алгоритма
вычислением разложения Холесского для Нс = V2f(xc) + \icI.
130 Гл. 5. Метод Ньютона
5.6. МЕТОДЫ С КОНЕЧНО-РАЗНОСТНЫМИ ПРОИЗВОДНЫМИ
ДЛЯ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
В этом разделе рассматривается влияние на метод Ньютона для
безусловной минимизации, которое оказывает замена конечно-
разностными аппроксимациями аналитических производных
Vf(x) и V2/(x), а также практический выбор длины шага при
вычислении этих аппроксимаций. Мы увидим> что здесь имеется
несколько существенных отличий в теории и в практике от
использования конечно-разностных якобианов, рассмотренных
в разд. 5.4.
Обсудим сначала использование конечно-разностных
аппроксимаций гессианов. В разд. 4.2 мы видели два способа
аппроксимации S/2f{xc) конечными разностями: один, когда Vf{x) задан
аналитически, а другой, когда не задан. Обе аппроксимации
удовлетворяют оценке
\\Ac-V2f(xc)\\ = 0(hc)
(he — длина конечно-разностного шага) при стандартных
предположениях, и поэтому, используя ту же технику, что в
доказательстве теоремы 5.4.1, легко показать, что если hc = О(\\ес\\)У
где ес = хс — *♦, то метод Ньютона, использующий
конечно-разностные гессианы, сходится по-прежнему ^-квадратично.
Остается вопрос о выборе длины конечно-разностного шага на
практике.
Если V/(jc) задан аналитически, то Ас вычисляется по
формулам
Л./ = jr , /=1, ..., пу (o.b.ia)
Ac = ±t^. (5.6.1b)
Поскольку (5.6.1а) представляет собой ту же самую формулу,
как в случае конечно-разностных якобианов, то рекомендуется
та же самая длина шага
А, = \An max {| xl |, typ *,} sign (лгу), (5.6.2)
где ц ^ macheps есть оценка для относительной погрешности
вычисления V/(jc). Для этой аппроксимации используется
алгоритм А5.6.1. Напомним, что мы ожидаем получать правильной
примерно первую половину разрядов V2/(jcc) при условии, если
Vf(x) вычисляется точно (см. приведенный ниже пример 5.6.1).
5.6. Методы с конечно-разностными производными 131
Вспомним, что, когда Vf{x) не задан аналитически, Ас
вычисляется по формуле
(Л, _ U (*с + У* + V/) - f (*с + У,)] ~ V (*с + V/) - / (*«)]
{Яс)и Щ •
(5.6.3)
Пример 5.6.1 показывает, что использование длины шага (5.6.2)
в этой формуле может иметь катастрофические последствия.
Пример 5.6.1. Пусть задана f(xux2), как в примере 5.5.2, и
пусть хс =(1,1)г. Тогда
*к*>-[Л -J].
Если V2/(*c) аппроксимируется по формуле (5.6.1) с
использованием Л/=10-7Х/ на ЭВМ CDC с 48 двоичными разрядами
(^ 14.4 десятичных разрядов), то в результате имеем
д Г 13.999999737280 -4.00000018885291
с L - 4.000001888529 4.0000003309615 J '
Однако если V2f(xc) аппроксимируется по формуле (5.6.3) с
использованием той же самой длины шага, то в результате имеем
А
_ 19.895196601283 -5.68434188608081
с~' к 6843418860808 0 J
=г 19
L-5.C
Есл« длину шага в (5.6.3) заменить на h,= Ю-4*,, то в
результате имеем
13.997603787175 —4.00000033096151
Лс~ ■ -4.0000003309611 3.9999974887906 J'
-[
Неверные результаты во втором случае примера 5.6.1 легко
объяснить. Если взять, как это было в примере, ht = д/macheps xi
и Ay = Vmacheps xj9 то знаменатель в (5.6.3) окажется равным
(macheps -XrXj). Поскольку числитель в (5.6.3) будет, вероятно,
вычисляться с ошибками конечной арифметики, по меньшей
мере равными macheps-|/(*с) |, то (Ас)ц будет иметь ошибку в
конечной арифметике, по меньшей мере равную \f(xc) \/\хгХ/\9
что не должно быть малым по сравнению с V2f(xc)ij- Мы часто
сталкивались с тем, что формула (5.6.3) давала полностью
неверные результаты при использовании длины шага (5.6.2),
причем нуль является довольно обычным результатом в нашей
практике. |Если в нашем примере взять A/=10"8jc/, то
получим1) /85.2+ 0 \л
Лс~ V 0 85.2+ )х\
*) Запись «85.2+» означает «85.2 с избытком». —Прим. перев.
132 Гл. 5. Метод Ньютона
Такие же рассуждения и анализ, как и в разд. 5.4,
показывают, что следует выбирать вместо рассмотренного способа
длину конечно-разностного шага в формуле (5.6.3) так, чтобы
этим вносить возмущение в правые две трети достоверных
разрядов f(xc). Это можно обычно сделать, выбирая
Ау = т)1/3 max (| Xj |, typ xf} sign (*,) (5.6.4)
или выбирая во многих случаях просто A/ =(macheps)1/3A:/. Здесь
т] ^ macheps есть по-прежнему относительная ошибка при
вычислении f(x). Эта длина шага довольно хорошо работает на
практике, как продемонстрировано в последнем из
рассмотренных в примере 5.6.1 случаев, где использовалось А/=10-4*/ и
было получено по меньшей мере четыре верных разряда в
каждой компоненте V2f(xc). Алгоритм А5.6.2 в приложении А —это
наш алгоритм для вычисления конечно-разностных гессианов с
использованием значений функции по формуле (5.6.3) с длиной
шага (5.6.4). Заметим, что разумно ожидать получения верных
значений первой трети разрядов V2f(x), причем число верных
разрядов будет даже меньше, если f(x) представляет собой
функцию, вычисляемую с высоким уровнем помех.
Резюмируя, отметим следующее. Когда гессиан
непосредственно не задан аналитически, его аппроксимация либо по
конечно-разностному алгоритму А5.6.1, использующему
аналитически заданные значения Vf{x), либо по алгоритму А5.6.2,
использующему только значения функции, не изменит, как
правило, поведение метода Ньютона. Вместе с тем ясно, что
алгоритм А5.6.1 предпочтительнее, если Vf{x) задан аналитически.
Если f(x) вычисляется с довольно высоким уровнем помех, то
алгоритм А5.6.2 может оказаться неудовлетворительным, и
тогда, вероятно, вместо него следует использовать
аппроксимацию V2f{x) по секущим (см. гл. 9). Аппроксимация гессиана по
секущим должна, несомненно, использоваться, когда слишком
велика стоимость конечно-разностной аппроксимации,
определяемая п вычислениями Vf{x) или (п2-\-Зп)/2 вычислениями
f(x) за итерацию.
Перейдем теперь к конечно-разностной аппроксимации
градиента в алгоритмах минимизации. Читатель может догадаться,
что этот вопрос будет еще более трудным, чем аппроксимация
якобиана и гессиана, так как градиент является величиной,
которую в алгоритмах минимизации мы стараемся сделать
нулевой. Поэтому конечно-разностная аппроксимация градиента
должна производиться с высокой степенью точности.
Напомним; что у нас имелись две формулы для
аппроксимации Vf(xc) по конечным разностям: формула разностей вперед
to))=f(*,+v,)-fw ;=1 я (5в5)
5.6. Методы с конечно-разностными производными 133
которая является как раз частным случаем аппроксимации
якобиана и имеет ошибку О (А/) в /-й компоненте, и формула
центральных разностей
(&с),= [С 2А, ~' /=»• ••- Л, (5.6.6)
которая имеет ошибку О (А/)- Вспомним также, что в случае
конечно-разностных якобианов и гессианов мы видели, что если
длина шага обладает свойством А/ = 0(||ес||), где ес = хс — **,
то при обычных предположениях сохраняется ^-квадратичная
сходимость метода Ньютона. Однако это, вероятно, не имеет
места для аппроксимации градиента по разностям вперед (5.6.5),
так как по мере приближения хс к точке минимума функции
f(x) величина ||V/(jcc)|| ^0(||ес||), и поэтому длина шага порядка
O(lkcll) в (5.6.5) привела бы к ошибке аппроксимации ||gc —
— V/(jcc) II того же порядка, что и аппроксимируемое значение.
Вместо этого можно легко обобщить проведенный в теореме
5.4.1 анализ и показать, что если подправить ньютоновскую
итерацию для минимизации, так что
Х+ = Хс — Ас gc>
где gc и Ас аппроксимируют соответственно Vf(xc) и V2f(xc), то
при аналогичных предположениях
(5.6.7)
(см. упр. 17). Следовательно, для ^-квадратичной сходимости
требуется, чтобы \\gc — V/(xc)ll = 0(||ес||2), а это означает
требование h,-= О (\\ес\\2) при использовании разностей вперед или
Л/ = 0(||ес||) при использовании центральных разностей. Кроме
того, здесь трудно оценить \\ес\\, так как Vf(xc) не задан
аналитически.
На практике этот анализ в действительности не применяется,
в том числе и нами, поскольку мы будем стремиться выбирать
Л/, минимизируя суммарное влияние ошибок, возникающих
из-за нелинейности / и использования машинной арифметики.
Для разностной формулы вперед (5.6.5) это как раз означает
использование той же самой длины шага (5.6.2), как и для
аппроксимации якобиана. Для формулы центральных
разностей (5.6.6) тот же самый анализ, что в разд. 5.4, показывает,
что Л/= 0(т)1/3) оптимально, и мы предлагаем использовать
ту же длину шага (5.6.4), что и при аппроксимации гессиана
с помощью значений функции. В нашей практике
аппроксимация градиента разностями вперед оказывается обычно вполне
достаточной, и поскольку центральные разности в два раза до-
134 Гл. 5. Метод Ньютона
роже, то для аппроксимации градиента рекомендуется
алгоритм А5.6.3, который по сути есть алгоритм А5.4.1 для
аппроксимации якобиана при числе уравнений т = \. Следует,
однако, отдавать себе отчет в том, что точность, с которой
получается решение x«, будет ограничена точностью аппроксимации
градиента. По этой причине, а также для того чтобы охватить
тот редкий случай, когда разности вперед слишком неточны, в
приложении имеется алгоритм А5.6.4, представляющий собой
процедуру аппроксимации градиента по центральным
разностям. В некоторых коммерческих программах автоматически
принимается решение о том, нужно ли переключаться в
аппроксимации градиента с разностей вперед на центральные
разности и когда это делать [см., например, Стюарт (1967) J.
В заключение отметим, что пользователю следует знать
о возможных трудностях, возникающих при использовании в
алгоритмах минимизации конечно-разностных градиентов. Боггс
и Дэннис (1976) для получения приближенных значений точки
минимума проанализировали погрешности, свойственные
использованию таких алгоритмов. Несмотря на то что найденные
ими границы оказываются на практике слишком
пессимистичными, это все же сильно стимулировало пользователя задавать
градиент аналитически всякий раз, когда это возможно.
Пользователь, который получает плохие результаты с
аппроксимацией разностями вперед или которому требуется повышенная
точность, мог бы попробовать взамен центральные разности.
Мы увидим, что вследствие той точности, которая необходима
при аппроксимации градиента, не существует пригодной в
алгоритмах минимизации аппроксимации градиента по секущим.
5.7. УПРАЖНЕНИЯ
1. Система уравнений
2 (л:! + лг2)2 + (д:, — л:2)2 — 8 = 0,
5*1 + (лг2 — З)2 — 9 = 0
имеет решение х* = (1, 1)г. Выполните одну итерацию метода Ньютона из
точки лго = (2, 0)г.
2. Выполните вторую итерацию метода Ньютона для системы
[:: ::ь
начиная из х0 = (—10, —10)г. (Первая итерация была сделана в разд. 5.1.)
Что произойдет, если эта задача будет продолжать решаться методом
Ньютона с использованием машинной арифметики?
Подразумевается, что упр. 3 и 4 дадут представление об области схо*
димости, задаваемой теоремами сходимости для метода Ньютона.
5.7. Упражнения 135
3. Для каждой из функций f(x) = х, f(x) = х2 + xt f(x) =ех—\
ответьте на следующие вопросы:
(a) Чему равно \'(х) в корне *# = О?
(b) Чему равна константа Липшица для f'(x) на отрезке [—а, а]? Чему
равна верхняя граница для | (/'(*) — Г(°))/*1 на этом отрезке?
(c) Какая область сходимости метода Ньютона для f(x)
предсказывается теоремой 2.4.3?
(d) На каком отрезке [Ь, с], b < 0 < с, метод Ньютона для f(x) в
действительности сходится к jc# = О?
4. Используя свои ответы на вопросы из упр. 3, рассмотрите применение
метода Ньютона к
F(x) =
Xi
Х2 ' Х2
в*8- 1
(a) Чему равно J(x) в корне х* = (О, О, 0)г?
(b) Чему равна константа Липшица для J(x) в шаре радиуса а с
центром в **?
(c) Какая область сходимости метода Ньютона для F(x)
предсказывается теоремой 5.2.1?
(d) Какой стала бы область сходимости, если (*о)з — 0? Ну, а если
(аго)2 = (*оЬ = 01)?
5. Покажите, что, если предположение / е LipY (N (х#, г)) в теореме 5.2.1
заменить предположением о непрерывности по Гёльдеру (см. упр. 4.8), то
теорема 5.2.1 останется в силе с той лишь разницей, что вместо (5.2.1)
будет
ll**+.-*.ll<PY||*ft-*.ire. *-0, 1
[Указание: замените (5.2.2) на e = min {г, (а/((1 + а) Ру))1'"}, что означает
PYee<a/(l+a)J
В упражнениях с 6 по 8 излагается доказательство теоремы
Канторовича.
6. Докажите, что условия и заключения теоремы Канторовича
справедливы для квадратичной функции
f«)»-| <*--£ + £. '.=-0.
[Указание: докажите (5.3.1), показав, что выполняется более сильное
неравенство
\ty-t |<2-fc(l-VrTir2a)2fe-3-, *»0, 1,
Для его получения покажите по индукции, что
17'С*)
IГ ('*+,)!
j
') Здесь в первом случае имеется в виду пересечение реальной области
сходимости с координатной плоскостью 1-й и 2-й осей, а во втором —
пересечение с 1-й координатной осью. — Прим. перев.
136 Гл. 5. Метод Ньютона
и, используя это, покажите, что
I'*+i-U<2*~'Py|'*-U2-]
7. Пусть F: R"->Rn и XogR" удовлетворяют условиям теоремы
Канторовича и f(t) и /о определяются как в примере 6. Пусть {хк} и {/*} есть
последовательности, полученные в результате применения метода Ньютона
к F(x) и f(t) из х0 и t0 соответственно. Докажите по индукции, что
II'(**)"' \<\г(<*)"' |. II4+i-ЧII<I<*+. -'*I.
где 6 = 0, 1, .... [Указание: рассматривая индуктивное предположение,
используйте (3.1.20), что поможет доказать первое соотношение. Для
доказательства второго сначала воспользуйтесь равенством
*(**)-'(*/0-'(**-!)-'(**-■) (**-**-.),
с тем чтобы показать что
IIf ЫII <т И **"**-'II2-
Аналогично покажите, что
i/(<*)i-i('*-<*-i)2.
Затем воспользуйтесь этими двумя соотношениями и первым неравенством,
доказанным по индукции, чтобы доказать второе.]
8. Воспользуйтесь упр. 6 и 7 и докажите теорему Канторовича.
9. Прочтите работу Брайяна (1968), и вы получите удовольствие от
красивого приложения теоремы Канторовича.
10. Докажите теорему о сжимающем отображении. Для этого,
предполагая выполненными условия теоремы 5.3.2, покажите:
(а) используя соотношение (5.3.3), что для любых / ^ 0
/
(b) используя (а), что последовательность {**} имеет предел **, так
как {xt} представляет собой последовательность Коши, а также что
<?(*•) =*♦;
(c) используя (Ь) и соотношение (5.3.3), что х# есть единственная
неподвижная точка для G в D и что имеют место ^-линейная сходимость и
оценки погрешностей, приведенные в теореме 5.3.2.
Используя (а), докажите другой вариант теоремы о сжимающем
отображении без предположения о том, что F(D) a D.
11. Пусть f(x) =х2—-1, ogR, а> 1. Докажите, что для некоторого
б > 0 (6 зависит от а) последовательность точек {*/}, построенная,
начиная с .r0 е (1 — б, 1 + 6), по формуле
f(*i)
xi+\—xi —а—*
сходится (/-линейно к .v* = 1. Покажите, что при этом
*i+\~x
lim
f-*oo
если только а Ф 2.
xt —х.
>0,
5.7. Упражнения 137
12. Завершите доказательство теоремы 5.4.1.
13. Пусть F: R2->-R2 таково, что
'«-СП-
Допустим хк = (107, 10_7)г и предположим, что используется ЭВМ с 14
десятичными разрядами. Что получится, если вычислять аппроксимацию для
/(*♦) по формуле (5.4.1) при hk = 1? Ну а при Нк = К)-14? Существует ли
в этом случае какой-либо выбор Л*, который годился бы для аппроксимации
как J(xk)iU так и /(*Л)22?
14. Пусть р е R, р ф О, рф\, ft(x) = хР, f2(x) = е*>*. Полагая
f = f(x) и у = /"(*)> определите по формуле (5.4.13) оптимальную длину
шага для /i(jc), а затем для Ы*)« Как это сопоставляется с длиной шага
(5.4.10)? Какие особые проблемы возникают при конечно-разностной
аппроксимации /2 (х) в случае, когда х равен очень большому положительному
числу?
15. Пусть / (*р дс2) = — (х\ — jc2)2 + -5- (l — JCj)2. Что является точкой
минимума для /(*)? Выполните одну итерацию метода Ньютона для
минимизации f(x) из начальной точки х0 = (2, 2)т. Хороший ли сделан шаг?
Прежде чем ответить, вычислите f(xo) и /(*i).
16. Рассмотрите вопрос применения метода Ньютона к отысканию точки
минимума f(x)=sinx при х0 g= [—я, я]. Искомым решением является
дг* = —я/2. Пусть е есть небольшое положительное число. Покажите, что
если Хо = — е, то метод Ньютона дает xi ^ —1/е. Аналогично выясните, что
произойдет, если взять х0 = +е, но при этом заменить f"(xo) малым
положительным числом?
17. Пусть f j (jc) = — jc2 — jc|» /2 (*) = Jtf — *o- Покажите, что алгоритм
5.5.3 не будет сходиться к точке максимума х+ = (0, 0)г функции fi(x),
если Хо Ф х*. Покажите также, что алгоритм 5.5.3 будет сходиться к седло-
вой точке ** = (0, О)7" функции Ы*)> если только (дго)г Ф 0.
18. На какой-либо ЭВМ по вашему выбору вычислите
конечно-разностную аппроксимацию гессиана функции f(x), заданной в упр. 15, в точке
хо = (2, 2)г, используя формулу (5.6.3) при hj = (macheps) i/2xit а затем
при hj = (macheps) 1/3jc/. Сравните ваши результаты со значением V2f(x0),
полученным аналитически.
19. Пусть f: Rn->R удовлетворяет условию у2/ (*) е Lipy D для
некоторого Dc R". Предположим, что существует х* еД для которого V/(**)=0.
Покажите, что если хс е= D, gc g R", и матрица Лс е= RrtXn не вырождена,
то х+, порождаемое формулой х+ *=хс — А~хgc, удовлетворяет (5.6.7).
20. Покажите, как построить эффективным образом единую
комбинированную процедуру на базе алгоритма для вычисления V/(*) по центральным
разностям (алгоритм А5.6.4) и алгоритма для вычисления V2/(*) по
разностям вперед (алгоритм А5.6.2). Как сопоставляется требуемое в этом случае
количество вычислений функции: (а) с использованием каждой из процедур
в отдельности, и (Ь) с использованием алгоритмов А5.6.3 для
аппроксимации градиента и А5.6.2 для аппроксимации гессиана по разностям вперед?
Какие недостатки проявлялись бы при использовании вашей новой
процедуры на практике?
6
Глобально сходящиеся !)
модификации метода Ньютона
В предыдущей главе было показано, что метод Ньютона
является локально ^-квадратично сходящимся. Это означает, что
если имеется достаточно хорошее текущее приближенное
решение, то оно будет быстро и с относительной легкостью
улучшено. К сожалению, нет ничего необычного в том, что
приходится затрачивать значительные вычислительные усилия на
достижение достаточной близости 2) к решению. Кроме того,
стратегии по достижению такой близости составляют большую
часть вычислительной программы и усилий по
программированию. Эти стратегии могут быть чувствительны к небольшим
отличиям^ в их реализации на ЭВМ.
Эта глава посвящена двум основным идеям относительно
того, как следует поступать в том случае, когда ньютоновский
шаг является неудовлетворительным. В разд. 6.1
устанавливается общая структура класса алгоритмов, которые мы хотим
впоследствии рассмотреть. В разд. 6.2 вводится понятие
«направление спуска», которое уже вскользь упоминалось в
доказательстве леммы 4.3.1. В разд. 6.3 обсуждается первый из
основных подходов по глобализации. Он, по сути, является
современным вариантом известной идеи дробления шага вдоль
ньютоновского направления в тех случаях, когда полный
ньютоновский шаг оказывается неудовлетворительным. В разд. 6.4
рассматривается второй основной подход, базирующийся на
оценке области, в которой можно верить тому, что локальная
модель, лежащая в основе метода Ньютона, адекватно
представляет функцию. Он также опирается на выбор шага,
который приближенно минимизирует модель в этой области. Оба
*) Относительно определения понятия «глобально сходящийся» см.
последний абзац разд. 1.1.
2) Имеется в виду близость текущего приближения, достаточная для
того, чтобы меход Ньютона смог реализовать свою высокую скорость
сходимости. — Прим перев.
6.1. Общая квазиньютоновская схема 139
подхода выводятся сначала для задач безусловной
минимизации. Их применение к решению систем нелинейных уравнений
является темой разд. 6.5.
6.1. ОБЩАЯ КВАЗИНЬЮТОНОВСКАЯ СХЕМА
Основная идея построения успешно работающих нелинейных
алгоритмов заключается в таком комбинировании стратегии
глобальной сходимости со стратегией высокой локальной
сходимости, при котором извлекается польза из них обеих. Общая
схема, реализующая эту идею, представляет собой
незначительное обобщение гибридного алгоритма, рассмотренного в гл. 2
(см. алгоритм 2.5.1). Она описана ниже в алгоритме 6.1.1.
Наиболее важный момент состоит в попытке на каждой
итерации сначала попробовать метод Ньютона или некоторую его
модификацию. Если кажется, что берется приемлемый шаг
(например, если в случае минимизации / уменьшается), то
нужно применить именно его. Если же — нет, то обратиться
к шагу, который предписывается глобальным методом. Такая
стратегия будет всегда заканчиваться использованием вблизи
от решения метода Ньютона, и поэтому будет сохранять
высокую скорость его локальной сходимости. Если глобальный
метод надлежащим образом выбирается и включается в общую
схему, то алгоритм также будет глобально сходящимся.
Алгоритмы, использующие этот подход, будут называться
квазиньютоновскими.
Алгоритм 6.1.1. Квазиньютоновский алгоритм для решения
нелинейных уравнений и безусловной оптимизации [в случае
оптимизации заменить F(xk) на Vf(xk) и Jk на Hk\
Заданы: непрерывно дифференцируемая F: Кя-> Rn и х0^ Rrt.
На k-й итерации:
1. Вычислить F(xk), если этого не было сделано раньше, и
решить — остановиться или продолжить дальше.
2. Вычислить матрицу /*, равную J(xk) или ее
аппроксимации.
3. Применить к Jk некоторый способ разложения на
множители и оценить ее число обусловленности. Если Jk плохо
обусловлена, то внести в нее соответствующее возмущение.
4. Решить Jks% = — F (xk).
5. Принять решение — либо взять ньютоновский шаг xk+l=
= Xk~b~sk> либо выбрать Xk+\ согласно глобальной стратегии.
Этот шаг алгоритма часто дает F(xk) для 1-го шага.
140 Гл. 6. Глобально сходящиеся модификации
К настоящему моменту нами уже были рассмотрены шаги 2,
3 и 4. Шаг 5 служит основной темой данной главы. К концу
этой главы читатель мог бы построить квазиньютоновский
алгоритм в завершенном виде, за исключением критерия
останова, который рассматривается в гл. 7. Формулы пересчета по
секущим из гл. 8 и 9 служат альтернативными вариантами
шага 2.
Напомним читателю, что в приложении А представлена
модульная система алгоритмов для решения нелинейных
уравнений и безусловной минимизации. Она содержит целый ряд
полностью детализированных квазиньютоновских алгоритмов для
решения этих двух задач. Алгоритм 6.1.1 лежит в основе
драйвера (управляющей программы) для этих алгоритмов, который
в приложении представлен алгоритмом D6.1.1 для
минимизации и алгоритмом D6.1.3 для нелинейных уравнений. Основная
разница между приведенным выше алгоритмом 6.1.1 и двумя
драйверами из приложения заключается в том, что данные
драйверы содержат самостоятельную инициализирующую часть,
предшествующую итерационной части.
Назначение, структура и вопросы использования модульной
системы алгоритмов обсуждаются в начале приложения А. Мы
рекомендуем прочитать это обсуждение сейчас, если вы не
сделали этого раньше, и затем обращаться к приложению для
выяснения деталей по мере появления алгоритмов в тексте.
6.2. НАПРАВЛЕНИЯ СПУСКА
Начнем обсуждение глобальных методов с рассмотрения
задачи безусловной минимизации
min /: R"-^R, (6.2.1)
*<eeR"
поскольку для задач минимизации существует естественная
глобальная стратегия, которая состоит в обеспечении того,
чтобы каждый шаг уменьшал значение /. Существуют
соответствующие стратегии и для систем нелинейных уравнений,
обеспечивающие уменьшение каждым шагом значения некоторой
нормы функции F: Rrt->-Rn. Однако использование нормы в
действительности сводит задачу решения системы нелинейных
уравнений F(x) = 0 к задаче минимизации функции вида
/ A ±\\F\\h R"-*R. (6.2.2)
Поэтому на протяжении последующих двух разделов будут
рассматриваться глобальные стратегии для безусловной мини-
6.2. Направления спуска 141
мизации. В разд. 6.5 мы применим эти стратегии к системам
нелинейных уравнений, используя преобразование (6.2.2).
Основная идея глобальных методов для безусловной
минимизации геометрически очевидна: делать шаги, которые ведут
«вниз по склону» для функции /. Точнее говоря, выбирается
направление р из текущей точки хс, вдоль которого / начинает
уменьшаться, и новая точка х+ в этом направлении из точки хс
такова, что f(x+) < /(хс). Такое направление называется
направлением спуска. С математической точки зрения р является
направлением спуска из хс, если производная функции / по
направлению р в точке хс отрицательна, т. е. согласно разд. 4.1,
если
Vf(xc)Tp<0. (6.2.3)
Если выполнено (6.2.3), то гарантируется, что f(xc+Sp)<f(xc)
для достаточно малых положительных б. Направления спуска
лежат в основе некоторых глобальных методов минимизации,
но для всех этих методов они имеют важное значение, и
поэтому они являются темой данного раздела.
До сих пор единственным направлением, которое нами
рассматривалось в задачах минимизации, было ньютоновское
направление sN = — H7lV/(*c)> где Нс есть либо гессиан V2f{xc),
либо его аппроксимация. Поэтому естественно спросить —
является ли ньютоновское направление направлением спуска?
Согласно (6.2.3), это имеет место тогда и только тогда, когда
V/ (хс)т s" = - V/ (хс)т ЯГ1 V/ (хс) < 0.
Данное неравенство справедливо, если матрица Н7Х> или что
эквивалентно, Нс положительно определена. Это вторая
причина, по которой мы в алгоритме 5.4.2 принудительно делали Нс
положительно определенной, если изначально она таковой не
являлась. Это гарантирует не только то, что квадратичная
модель будет иметь единственную точку минимума, но также то,
что получающееся в результате ньютоновское направление
будет направлением спуска для исходной задачи. Это в свою
очередь служит гарантией того, что для достаточно малых шагов
вдоль ньютоновского направления значение функции будет
уменьшаться. Во всех наших методах безусловной
минимизации гессиан Нс модели будет строиться положительно
определенным или принудительно делаться таковым.
Естественно возникает второй вопрос: коль скоро шаги
делаются в направлении спуска, то что представляет собой
направление р, вдоль которого, начиная из х, функция f
уменьшается наиболее быстро? Прежде чем мы сможем ответить на
этот вопрос, необходимо конкретизировать понятие
«направление», так как для заданного вектора вносимых возмущений р
142 Гл. 6. Глобально сходящиеся модификации
производная функции / по направлению р прямо
пропорциональна длине вектора р. Разумный способ действий здесь
состоит в том, чтобы выбрать норму ||-|| и определить
направление произвольного вектора р как р/||р||. Когда мы будем
говорить о направлении р, то будем предполагать, что такая
нормировка уже выполнена. Теперь можно сформулировать наш
вопрос о направлении наиболее быстрого спуска при заданной
норме в виде задачи:
найти min Vf(x)Tp
peRn
при условии ||р ||= 1,
которая в /2-норме имеет решение р = — V/ (х)/\\ V/ (х) l^. Таким
образом, направление антиградиента1) представляет собой в
/г-норме направление наискорейшего спуска из х вниз по склону
и называется направлением наискорейшего спуска.
Классический минимизационный алгоритм, предложенный
Коши, основывается исключительно на направлении
наискорейшего спуска. Ниже дано его формальное описание.
Алгоритм 6.2.1. Метод наискорейшего спуска
Заданы: непрерывно дифференцируемая /: Rrt-*R и x0^Rn.
На k'u итерации:
найти для / в направлении —Vf(xk) из Xk точку,
расположенную ниже всего, т. е. найти А,*, являющееся решением для
minf(xk — kk4f(xk)y,
xk>o
Xk+\ = xk — hkVf(Xk).
Это не является вычислительным методом, так как каждый
шаг включает в себя задачу точной одномерной минимизации,
но его можно реализовать на ЭВМ, выполняя минимизацию
неточно. В обоих случаях при довольно слабых предположениях
можно показать, что они сходятся к точке локального
минимума или седловой точке функции f(x). [См., например, Голд-
стейн (1967).] Однако сходимость здесь только линейная, а
иногда очень медленная линейная. А именно, если
алгоритм 6.2.1 сходится к точке локального минимума jc„ в
которой гессиан V2/(*#) положительно определен, и если
обозначить через evmax и evmin наибольшее и наименьшее собственные
значения для V2/(a:»), тогда можно показать, что последователь-
]) То есть направление, противоположное градиенту. — Прим. перев.
6.2. Направления спуска 143
ность {xk} удовлетворяет
*k+\
— X
fi"» н**-м
■<с,
:А(
evmax evmln Л
min /
evmax + ev-
(6.2.4)
в некоторой специальной взвешенной /2-норме, и показать, что
оценка с достижима для некоторых начальных х0. Если V2/(*«)
прекрасно масштабирован, т. е. evmax = evmin, то с будет мало
и сходимость будет быстрой. Однако если V2/(*#) плохо
масштабирован даже в незначительной степени, например evmax=
= 102evmin, то с будет равно почти 1, а сходимость может
оказаться очень медленной (см. рис. 6.2.1). Случай, когда с = 0.8
и на каждой итерации \\xk+\— **ll= c\\xk — х»||, приведен в
примере 6.2.2. Для вас будет совсем легким упражнением
обобщить это, сделав с сколь угодно близким к 1.
1 9
Пример 6.2.2. Пусть / (х{9 х2) = -^ х\ + у х\ • Это
положительно определенная квадратичная функция с точкой
минимума в хп = (0, 0)г и
V2/ (*) = I 0 9 1 для всех х.
Таким образом, с, определенное в (6.2.4), равно (9—1)/(9 +
+ 1) = 0.8. Читатель также может убедиться, что если f(x)
есть пбложительно определенная квадратичная функция, то
шаг наискорейшего спуска по алгоритму 6.2.1 имеет вид
Xk+\ = Xk
Wnk)8)8'
(6.2.5)
где g = Wf(Xk). Используя (6.2.5), можно легко убедиться, что
при заданных f(x) и jc0 = (9, 1)г последовательность точек,
вырабатываемых алгоритмом 6.2.1, есть
(0.8)*, k=l, 2, .
(6.2.6)
Рис. 6.2.1. Метод наискорейшего спуска в несколько неудачно
масштабированной квадратичной задаче.
144 Гл. 6. Глобально сходящиеся модификации
Поэтому \\Xk+i — xm\\/\\Xk--xJ==\\Xk+i\]l\\Xk\\=zc в любой
/„-норме.
Последовательность {**}, заданная в (6.2.6), представлена
на рис. 6.2.1.
Таким образом, в большинстве случаев методом
наискорейшего спуска как вычислительным алгоритмом пользоваться не
следует, так как квазиньютоновский алгоритм будет гораздо
более эффективным. Однако, когда наша глобальная стратегия
должна делать шаги, существенно меньшие, чем ньютоновский
шаг, она, как это будет видно в разд. 6.4, может делать шаги
вдоль направления наискорейшего спуска или вдоль близкого
к нему направления.
В заключение заметим, что направление наискорейшего
спуска очень чувствительно к изменениям масштаба
переменной х, в то время как ньютоновское направление не зависит
от таких изменений. По этой причине, когда кажется, что в
наших алгоритмах из разд. 6.4 используется направление
наискорейшего спуска, в соответствующих им программных
реализациях из приложения это направление будет на самом деле
предварительно умножено на некоторую масштабирующую
диагональную матрицу. Мы откладываем до разд. 7.1
обсуждение этой важной с практической точки зрения темы, так
называемого масштабирования.
6.3. ЛИНЕЙНЫЙ ПОИСК
Первой стратегией, которая предназначается для продвижения
из приближенного решения, находящегося вне области
сходимости метода Ньютона, является метод линейного поиска. Его
идея выглядит, в самом деле, очень естественной после
обсуждения в разд. 6.2 направлений спуска.
Идея алгоритма с линейным поиском проста: дано
направление спуска рк, мы делаем такой шаг в этом направлении,
который дает «приемлемое» Xk+\- Это означает, что
на k-й итерации:
вычислить направление спуска pk\
положить Xk+\ = xk + hkPk для некоторого Kk > О,
которое делает xk+\ приемлемой следующей
итерацией.
Графически это означает выбор Xk+\ с учетом той половины
одномерного поперечного сечения функции f{x), в котором f(x)
первоначально уменьшается, начиная с хц, как изображено на
рис. 6.3.1. Однако, вместо того чтобы брать, как в
алгоритме 6.2.1, в качестве рк направление наискорейшего спуска
6.3. Линейный поиск 145
—Vf(Xk), мы будем использовать рассмотренное в разд. 5.5
квазиньютоновское направление — HklVf(Xk),rji£ матрица Hk =
= V2f(xk)+ [ikl положительно определена, причем \xk = О, если
V2f(xk) надежно положительно определена. Это позволит нам
сохранить высокую локальную сходимость.
Термин «линейный поиск» относится к процедуре выбора Xk
в (6.3.1). До середины 60-х годов господствовало убеждение,
что Xk следует выбирать исходя из точного решения задачи
одномерной минимизации. Более тщательное численное
тестирование привело к полному пересмотру взглядов1). В этом
разделе будет описан не столь жесткий критерий приемлемости
{Kk}y который приводит к методам, столь же хорошим
теоретически и еще лучше проявляющим себя на практике.
Общая процедура теперь такова: сначала попробовать
сделать полный квазиньютоновский шаг, и если Xk = 1 не
удовлетворяет используемому критерию, то дробить методично длину
шага вдоль квазиньютоновского направления. Вычислительный
опыт показал важность выполнения полного
квазиньютоновского шага всякий раз, когда это возможно. Нарушение этого
правила приводит к потере того преимущества, которое имеет
метод Ньютона вблизи от решения. Поэтому важно, чтобы в
нашей процедуре выбора Xk был предусмотрен выбор Xk = 1
вблизи от решения.
В оставшейся части этого раздела мы обсудим
теоретические и практические вопросы выбора Xk. Поскольку не
существует убедительных причин ограничиваться рассмотрением
линейного поиска лишь вдоль квазиньютоновского
направления, рассматривается поиск х+=хс + Хср вдоль произвольного
направления спуска р из текущего приближенного решения хс.
Правила приемлемости шага, оптимального во всех случаях,
перев.
Цхк+ХРк)
Тангенс
угла наклона=
-Щхк)трк<0-
Рис. 6.3.1. Поперечное сечение для / (х) : R"-> R из х1
в направлении р*.
*) Следует заметить, что существуют методы, например метод
сопряженных градиентов и метод сопряженных направлений Пауэлла, в которых
необходимо производить линейный поиск с высокой точностью. — Прим.
перев.
146 Гл. 6. Глобально сходящиеся модификации
не существует, однако создается впечатление, что требование
f(Xk+i)<f(xk) (6.3.2)
отвечает здравому смыслу. Не будет большим сюрпризом
узнать, что это простое условие не гарантирует сходимость {xk}
к точке минимума функции /. Рассмотрим теперь два простых
одномерных примера, в которых демонстрируются два случая,
когда последовательность итераций может удовлетворять
(6.3.2), но при этом может не сходиться к точке минимума. Эти
примеры приведут нас к полезным критериям приемлемости
шага.
Первый пример. Пусть f{x) = x2, х0 = 2. Если взять {pk} =
= {(-1)*+,}> {**> = {2 + 3(2-<*+'>)>f тогда Ы = {2, —|, |,
—g-, ... J = {(— 1)Л(1 + 2~*)}, каждое рк является
направлением спуска из xk и f(xk) монотонно уменьшается, причем
lim / (xk) = 1
Л-»оо
[см. рис. 6.3.2(a)]. Это, конечно, никакой не минимум для /,
и, более того, {xk} имеет предельные точки ±1, следовательно,
она вообще не сходится.
Теперь рассмотрим ту же самую функцию при том же
начальном приближении и возьмем {р*} = {— 1}, {А*} = {2~*+1}. Тогда
{**} = {2, -g, 4". в"» •••} = (1 + 2~Л}, каждое рк есть опять
направление спуска, f(xk) уменьшается монотонно, и
lim*_Mx>Xfc = 1, что опять не является точкой минимума для /
[см. рис. 6.3.2(b)].
В первом случае проблема состоит в том, что было
достигнуто малое убывание значения / по сравнению с длиной шагов.
ftx) Ш)
Рис. 6.3.2. Монотонно убывающие последовательности итераций, которые
не сходятся к точке минимума.
6.3. Линейный поиск 147
Разрешить эту проблему можно, потребовав, чтобы средняя
скорость убывания от f(xc) до f(x+) составляла заданную долю
от первоначальной скорости убывания в этом направлении1),
т. е. мы задаем ае(0,1) и выбираем %с среди тех А,>0,
которые удовлетворяют неравенству
/ (Хе + М < f (хе) + aXVf (х/ р (6.3.3а)
(см. рис. 6.3.3). Это равноценно выбору Яс из условия
f(x+)<f(xe) + aVf(xtf(x+-xj.
(6.3.3b)
Можно убедиться, что это предотвращает первый из
неудачных выборов точек, но не второй.
Во втором примере проблема состоит в том, что шаги
слишком малы по сравнению с первоначальной скоростью убывания
функции /. Существуют разнообразные условия,
гарантирующие достаточно большие шаги. Мы познакомимся с условием,
которое будет также полезно нам в гл. 9. Потребуем, чтобы
скорость уменьшения функции f вдоль направления р в х+ была
больше, чем некоторая заданная доля скорости уменьшения
вдоль направления р в хс, т. е.
V/(х+)тpAVf (хс + Kpf Р> РV/(х/р, (6.3.4а)
или, что эквивалентно,
V/ (х+)т (х+ - хс) > рV/ (хс)т (х+ - хс) (6.3АЪ)
при некоторой заданной константе ре(а,1) (см. рис. 6.3.4).
Условие р > а гарантирует, что (6.3.3) и (6.3.4) могут быть
^ y-f(*c) + <X>Vf(Xc)Tp
Значения Л, допускаемые условием(6 3 3;(с*=0.1)
Рис. 6.3.3. Значения К, допускаемые условием (6.3.3.) (а = 0.1).
*) Здесь под средней скоростью убывания понимается величина
(f(xc + hp) — f(xc))lh а под первоначальной скоростью убывания —
величина у!(Хс)тр< — Прим. перев.
148 Гл. 6. Глобально сходящиеся модификации
удовлетворены одновременно. На практике выполнение (6.3.4)
обычно не требуется, так как стратегия дробления шага
позволяет избегать чрезвычайно малых шагов. Условие,
альтернативное к (6.3.4), приведено в упр. 7.
В основе условий (6.3.3) и (6.3.4) лежат работы Армийо
(1966) и Голдстейна (1967). В примере 6.3.1 демонстрируется
применение этих условий к простой функции. В разд. 6.3.1
приведены сильные результаты по доказательству сходимости
произвольного алгоритма, удовлетворяющего этим условиям.
В разд. 6.3.2 обсуждаются практические алгоритмы линейного
поиска.
Пример 6,3.1. Пусть / (xv х2) = х\ + х\ + х\> *с = (1, 1)Г>
Р* = (-3,-
Поскольку
1) . Пусть в (6.3.3) а = 0.1, .а в (6.3.4) 0 = 0.5.
V/ (хс)трс = (6, 2) (- 3, - 1)г = - 20,
то рс является направлением спуска из хс для f(x). Рассмотрим
теперь х (X) = хс + Ярс. Если х+ = х (1) = (—2, 0)г, то
V/ (х+)ТРс = (- 36, 0) (- 3, - 1)г = 108 > - 10 = pv/ (х/ Рс.
следовательно, х+ удовлетворяет (6.3.4), но
/(д+) = 20 > 1 = /(хс) + aV/(х/Рс,
и, значит, х+ не удовлетворяет (6.3.3). Читатель может
аналогичным образом убедиться, что х+ = х(0.1) = (0.7, 0.9)г
удовлетворяет (6.3.3), но не (6.3.4) и что д:+ = л:(0.5) = (—0.5,0.5)г
удовлетворяет как (6.3.3), так и (6.3.4). Эти три точки лежат
на рис. 6.3.4 соответственно среди точек справа, точек слева и
в самой «допустимой» области.
Условие (63.4)
(Р=0.5)
А/))
Условие
(6 3.3)
(ot-0.1)
Точки, допускаемые
условиями (6 3 3) и (6 3 4)
Рис. 6.3.4. Два условия линейного поиска.
6.3. Линейный поиск 149
6.3.1. Результаты исследования сходимости
при надлежащем выборе шагов
Использование условий (6.3.3) и (6.3.4) позволяет получить
следующие удивительно сильные результаты:, для любого
заданного направления /?*, такого, что V\(Xk)TPk < 0, существует
кк > О, удовлетворяющее (6.3.3) и (6.3.4); любой метод,
который вырабатывает последовательность {xk}, удовлетворяющую
на каждой итерации неравенствам Vf(xk)T(xk+\ — xk) < О,
(6.3.3) и (6.3.4), является по существу глобально сходящимся;
вблизи от точки минимума функции /, где гессиан V2/
положительно определен, ньютоновские шаги удовлетворяют (6.3.3)
и (6.3.4). Это означает, что мы можем легко создать
алгоритмы, которые сходятся глобально и благодаря тому, что мы
в первую очередь пробуем сделать ньютоновский шаг, обладают
также быстрой локальной сходимостью для большинства
функций.
Теорема 6.3.2, принадлежащая Вольфу (1969, 1971),
показывает, что для любого направления спуска pk существуют
точки Xk + hkpky удовлетворяющие (6.3.3) и (6.3.4).
Теорема 6.3.2. Пусть функция /: R"->R непрерывно
дифференцируема в Rn. Пусть xk е Rn, pk е R* удовлетворяют
условию V/ (xk)T Pk<0, и предположим, что {/ (xk + Xpk) I А > 0}
ограничено снизу. Тогда если 0<а<р<1, то существуют
Хи > А/ > 0, такие, что Xk+\ = Xk + XkPk удовлетворяет (6.3.3) и
(6.3.4) при всех А,£ <= (А/Ди)1*.
Доказательство. Поскольку а < 1, имеем f (xk + Xpk) <
< / fa) + <*^V/ (xk)T Pk для всех достаточно малых X > о. Так
как f(Xk + Xpk) ограничено также снизу, то существует
некоторое наименьшее положительное X, такое, что
/(*) = / (хк + Ш - / (**) + сЛУ/ (xk)T Pk. (6.3.5)
Таким образом, любое x^(xk, х) удовлетворяет (6.3.3). По
теореме о среднем значении существует Ае(ОД), такое, что
f(*)-f (xk) = V/ (xk + kPk)T (* - xk) = V/ (xk + Xpkf XPk, (6.3.6)
и поэтому из (6.3.5) и (6.3.6) имеем
Vf(Xk + Xpk)Tpk = aVf(Xk)TPk > Wf(xk)TPk, (6.3.7)
О Числа А^ и %ц зависят от xk и pk. ■— Прим. перев.
150 Гл. 6. Глобально сходящиеся модификации
так как а<р и Vf(Xk)TPk <0. Согласно непрерывности Vf,
(6.3.7) выполняется еще и для X, составляющих некоторый
интервал (Л/,К), содержащий А. Следовательно, если (fa, К)
ограничить интервалом (ОД), то Xk+\=Xk + hkPk будет
удовлетворять (6.3.3) и (6.3.4) при любых A,*€(%j,&fl). □
Теорема 6.3.3 также принадлежит Вольфу (1969, 1971).
Она показывает, что если вырабатываемая
последовательность {хк} удовлетворяет неравенствам Vf(xk)T(xk+i^-xk)<: 0,
(6.3.3) и (6.3.4) и если угол между Vf(Xk) и (xk+\ — х*) не
стремится к 90° при Л->оо, то либо градиент стремится к 0,
либо / не ограничена снизу. Возможны, конечно, и оба случая
одновременно. Ниже мы поясним, что случай, когда угол
между V/(jc*) и (Xk+\ — Xk) стремится к 90°, может быть
предотвращен самим алгоритмом.
Теорема 6.3.3. Пусть /: Rw->-R непрерывно
дифференцируема в R", и предположим, что существует у ^ 0, такое, что
IIV/ (г) - V/ (х) ||2 < YII г - х ||2 (6.3.8)
для любых л:, 2G Rn. Тогда при произвольно заданном х0^ Rn
либо / не ограничена снизу, либо существует
последовательность {**}, k = 0, 1, ..., удовлетворяющая (6.3.3), (6.3.4),
причем такая, что для каждого к ^ 0 либо
V/(*/**< 0, (6.3.9)
либо
V/(**) = 0 и sk = 0,
где
Sk Axk+[ — Xk. l)
Более того, для любой такой последовательности или
(a) V/ (**) = 0 для некоторого к ^ 0, или
(b) lim f(xk) = — оо, или
£->оо
(c) lim V/^sfe =Q
Доказательство. Каково бы ни было k, если S7f(xk) = 0, то
имеет место (а), и в дальнейшем последовательность не
меняется. Если У!(Хк)фО, то существует pk, например pk —
= — Vf(xk), такое, что Vf(xk)Tpk<0. По теореме 6.3.2 либо /
*) Это утверждение не исключает существование такой
последовательности и в случае неограниченной снизу /. — Прим. перев.
6.3. Линейный поиск 151
не ограничена снизу, либо существует Xk > О, такое, что Xk+\ =
= Xk + hkPk удовлетворяет (6.3.3) и (6.3.4). Без ограничения
общности предположим в целях упрощения обозначений, что
\\Pk\\2=l> Т0ГАа bk = \\Sk\\2-
Мы пока видим, что либо / не ограничена снизу, либо
существует {хк}> и при этом либо {xk} удовлетворяет (а), либо в
противном случае s* Ф О для каждого к. Теперь нам
необходимо показать, что если ни один из элементов в {s*} не равен
нулю, то должно выполняться (Ь) или (с). Было бы полезно
иметь обозначение
Согласно неравенствам (6.3.3) и ХкЬк < 0, справедливым для
каждого k, имеем
/ (*/) - / (*ь) = Е f (хш) - f (Xk) < t aV/ (xk)T sk =
/-1
= a X hifik < 0.
для любого / > 0. Следовательно, либо
оо
!im /(*/) — — оо, либо — £а*6л<оо,
т. е. ряд сходится.
В первом случае справедливо (Ь), что и требовалось
доказать, поэтому рассмотрим второй случай. Мы, в частности,
получаем Нт/5-*оДл6* = 0. Теперь нам хотелось бы сделать вывод,
что Hnu->oo6* = 0, и поэтому необходимо воспользоваться
условием (6.3.4), поскольку оно было принято для предотвращения
чрезмерной малости шагов.
Для каждого k имеем
Vf(xk+\)TSk>Wf(xk)Tsh9
и поэтому, учитывая (6.3.9) и р < 1,
№(**+,) - V/(**)f s*XP ~ l)Vf(xk?sk > 0.
Применение к левой части последнего соотношения неравенств
Коши-Шварца и (6.3.8), а также использование определения
для fi* дают
0<(p-1)*a<yN2=y4.
поэтому
xk>Lz±6k>o
152 Гл. 6. Глобально сходящиеся модификации
И
Таким образом,
0= lim \k6k <-£—!- iim d|<0.
fc->oo Y Л->оо
Это показывает, что
lim 6^ = 0
fc->oo
[т. е. справедливо (с)], и тем самым завершает
доказательство. □
Отметим, что в то время как теорема 6.3.3 без труда
применяется к любому алгоритму с линейным поиском, она
абсолютно не зависит от метода выбора направлений спуска и
длины шагов. Следовательно, эта теорема дает достаточные
условия глобальной сходимости (в слабом смысле) любого
алгоритма оптимизации, включая алгоритмы типа «модель —
доверительная область» из разд. 6.4. Кроме того, в то время как
условие Липшица (6.3.8) предполагается выполненным во всем
Rn, оно используется только в окрестности решения х*.
Наконец, хотя в теореме 6.3.3 {ok}-+0 и не означает, что
обязательно {V/(**)}-> 0, последнее имеет место всякий раз, когда
угол между Vf(Xk) и Sk отграничен от 90°. Можно легко
добиться выполнения этого условия на практике. Например, в
квазиньютоновском алгоритме с линейным поиском, где pk =
= — HklWf (xk) и Hk положительно определено, требуется лишь,
чтобы число обусловленности матриц {#*} было равномерно
ограничено сверху. Таким образом, теорему 6.3.3 можно
рассматривать как утверждение, означающее сходимость к / = —оо
или к V/= 0, однако ее условия слишком слабы, чтобы
обеспечивать сходимость {**}•
Теорема 6.3.4, принадлежащая Деннису и Морэ (1974),
показывает, что наша глобальная стратегия позволит делать
вблизи от точки минимума функции f полные
квазиньютоновские шаги Xk+\ =Xk — HklVf[(Xk), если, конечно, при этом
— HkXVf(Xk)достаточно близко к ньютоновскому шагу.
Теорема 6.3.4. Пусть f: Rrt->R дважды непрерывно
дифференцируема в открытом выпуклом множестве D, и
предположим, что V2/eLipY(D). Рассмотрим последовательность {xk}
вида Xk+\ = xk + %kPk, где Vf(**)rp*<Q Для всех k и Xk
выбирается так, что оно удовлетворяет (6.3.3) при скСу и (6.3.4).
6.3. Линейный поиск 153
Если {л*} сходится к точке ,v»€=D, в которой гессиан \2f(x*)
положительно определен, и если
hm jj—й = 0, (6.3.10)
то существует индекс ко ^ 0, такой, что А,* = 1 является
приемлемым для всех к ^ ko. Более того, Vf(x») = 0, и если Xk = 1
для всех k^koy то {xk} сходится ^-сверхлинейно к х*.
Доказательство. Доказательство является на самом деле
всего лишь обобщением простого упражнения, в котором
требуется показать, что если f(x) есть положительно
определенная квадратичная функция и Pk =—V2f(Xk)~lVf(Xk), то
Vf(xk)Tpk<0 и xk+i = хк + Рк удовлетворяет (6.3.3) при
любых а^у и (6.3.4) при любых Р ^ 0. Некоторые читатели
могут при желании лишь бегло посмотреть его или вовсе
пропустить, так как его детали проясняют не слишком многое.
Положим
. II */(**) + ^ (**)/>* II ил,,
Здесь и далее в доказательстве ||-|| означает ||-||2. Покажем
сначала, что
Пт II р* || = 0.
Л->оо
Если х достаточно близко к лс„ то по уже известным
рассуждениям V2f(x)~l существует и положительно определено, и если
P-I=№f(x.)~ll то y^^lv2/^)"1!*^-1. Отсюда,
поскольку
у/ыгр* pirn**)?* (у(ч)+у2Кч)рк)трк
IIP* II Цр*И II"* II
и PlV2f(xk)Pk >~2 ^ЦР*!2' т0 (6.3.11) и (6.3.10) показывают, что
для достаточно больших k имеет место
- 7/f|^||P* >(|t*-P*)llP*ll>il*HP*ll- (6-3.12)
Поскольку из теоремы 6.3.3 мы имеем
lim —,, „ * =0,
*-»оо \\Pk\\
154 Гл. 6. Глобально сходящиеся модификаций
то (6.3.12) означает, что
lira I рА ||-0.
Покажем теперь, что Xk = 1 удовлетворяет (6.3.3) при всех
&, больших или равных некоторому ко. По теореме о среднем
значении для некоторого xk^ [xk,xk + Pk] получаем
f (** + P*)-f Ы - v/ (хку Pk + j pJV/ (xk) Pk •
или
f(xk + pk)-f(xk)-±Vf(xk)TPk = ±W(xk) + 42f(xk)Pk)Tpk =
=T(v/K) + v2/K)Pft)rPik + TPnv2/(^)-v2/(^)]pfc<
<i-(p* + vIIpJDIIp*II2. (6.3.13)
что имеет место благодаря (6.3.11) и непрерывности V2/ по
Липшицу. Теперь выберем k0 таким, чтобы при k ^ k0
выполнялось (6.3.12) и
Р* + YII Pk II < т »*' min <Р» 1 ~ 2а>- <6А 14>
Если k ^ ko, то Я* = 1 удовлетворяет (6.3.3), так как, согласно
(6.3.13), (6.3.12) и (6.3.14),
f(*k + Pk)-f(Xk)<ivf(xifPb + Y\i-(l-2anpkf<
<±(1 -(1 -2a))Vf (**)rp* = aV/(**)V
Для того чтобы показать, что (6.3.4) выполняется для
Хк = 1 при * ^ £о. воспользуемся еще раз теоремой о среднем
в целях получения для некоторого zk^(xk, хк + рк)
соотношения
V/ (хк + рк)т рк = (V/ (хк) + V2/ (**) рк? рк =
= (V/ (хк) + V2/ (**) Рк)т Рк + Pi (V2/ (г*) - V2f (*.)) Рк-
Следовательно,
I v/ (**+Р/ Рк | < р* и р, н2 + -vii Pk к3 < -f- ii Pk н2 < - m (xk)T Pk
в силу (6.3.11), непрерывности V2/ по Липшицу, (6.3.14) и
(6.3.12). Это дает Vf(xk + pk)Tpk ^ pv/(**)rP/e для £^*0.
Итак, в конечном счете длина шага Xk = 1 удовлетворяет (6.3.3)
и (6.3.4), и с этой точки зрения она приемлема. Простым
следствием из (6.3.10) и \\mk-+<x>pk = 0 является равенство V/(x*) = 0.
Тем самым остается только доказательство <7-свеР*линейной
сходимости в случае, когда Xk = 1 для всех, за исключением конеч-
6.3. Линейный поиск 155
ного числа, членов рассматриваемой последовательности. Мы
откладываем это доказательство до гл. 8, где оно будет
следовать из гораздо более общего результата. □
Выводы из теорем 6.3.3 и 6.3.4, взятые вместе, весьма
примечательны. Они говорят о том, что если / ограничена снизу
и если какой-либо алгоритм делает шаги спуска, у которых
угол, составляемый с градиентом, отграничен от 90° и которые
подчиняются (6.3.3) и (6.3.4), то вырабатываемая им
последовательность {**} удовлетворяет равенству
lim yf(xk) = 0.
Более того, если любой такой алгоритм пробует на каждой
итерации делать прежде всего ньютоновский или
квазиньютоновский шаг, то {xk} будет к тому же сходиться (/-квадратично или
<7-сверхлинейно к точке локального минимума jc# в случае, если
какое-либо Xk окажется достаточно близким к х% и если
выполняются предположения, гарантирующие такую локальную
сходимость ньютоновского или квазиньютоновского метода. Все
эти результаты понадобятся нам для обоснования глобальной
сходимости алгоритмов, рассматриваемых в оставшейся части
книги. (См. также упр. 25.)
6.3.2 Выбор шага дроблением
Поговорим конкретнее о том, как в наших алгоритмах
выбирать Х^ Как мы уже говорили, современная стратегия состоит
в том, чтобы начинать с Xk = 1 и затем, если Xk + Pk
неприемлемо, «дробить» (уменьшать) Xk, пока не встретится
приемлемое Xk + XkPk. Общая схема такого алгоритма приведена ниже.
Напомним, что условие (6.3.4) здесь не используется, поскольку
сама стратегия дробления позволяет избегать чрезмерно
малых шагов. (См. также упр. 25.)
Алгоритм 6.3.5. Общая схема линейного поиска с
дроблением шага
Заданы аб{о,{), 0 < I < и < 1.
** = !;
while f (xk + Xkpk) > f (xk) + aXtff (xkf pk do
Xk = pXk для некоторого p e [/, u];
(*p выбирается в линейном поиске каждый раз заново *)
Xk+i = Xk + XkPk\
156 Гл. 6. Глобально сходящиеся модификации
На практике а берется довольно малым, едва ли большим,
чем требуемое уменьшение значения функции. В нашем
алгоритме используется а=10~4. Теперь остается обсудить
стратегию уменьшения Хк, т. е. выбора р. Определим
/MAffok + bft)
— одномерное сужение функции / относительно прямой,
проходящей через Xk в направлении р*. Если понадобится дробить
шаг, то мы будем моделировать /, используя самую последнюю
информацию о ней, и затем брать в алгоритме 6.3.5 в
качестве Xk то значение Я, которое минимизирует эту модель.
Первоначально у нас имеются две порции информации об
f(X), а именно:
f(0) = f(xk) и f'(0) = 4f(xkfpk. (6.3.15)
После вычисления f(xk + pk) нам известно, что
f(D = f(xk + Pk), (6.3.16)
поэтому если f(xk + pk) не удовлетворяет (6.3.3) [т. е. f(l)>
> f (0) + а/'(0)], то мы моделируем f(X) одномерной
квадратичной функцией
mg(X) = [f(l)-f(0)-f'(0)]X2 + f'(0)X + f(0),
удовлетворяющей (6.3.15) и (6.3.16), и вычисляем точку
-/'(О)
Я = -
(6.3.17)
2[f(U-f(0)-f'(0)]f
для которой тя(к) = 0. Здесь
гй; (Я,) = 2 [f (1) — f (0) — ^ (0)] > 0,
так как f(l)>f (0) + af' (0)>f'(0)+f' (0). Таким образом, X
минимизирует тд(Х). К тому же Л > 0, поскольку /'(0) < °- Поэтому X
Тангенс
угла
нэклона=
?'(0)
Рис. 6.3.5. Дробление шага на первой итерации, используется квадратичная
модель,
6.3. Линейный поиск 157
берется в качестве нового значения А* в алгоритме 6.3.5
(рис. 6.3.5). Заметим, что в силу неравенства/(1) > /(0) + а/'(0),
имеем
к< 2(1-а) •
Действительно, если /(1)^/(0), то A ^-g-- Таким образом,
(6.3.17) задает неявно вполне приемлемую верхнюю границу
и « у для первого значения р в алгоритме 6.3.5. С другой
стороны, если /(1) гораздо больше, чем f(0), то А может
оказаться очень малым. Мы, вероятно, не нуждаемся в слишком
сильном уменьшении Xk на основе Данной информации, так как
это, по-видимому, свидетельствовало бы о том, что f(X) плохо
моделируется в данной области квадратичной функцией,
поэтому в алгоритме 6.3.5 устанавливается нижняя граница
/ = -JQ- • Это означает, что если на какой-либо итерации при
первом дроблении шага было А ^0.1, то следующее пробное
значение А* =-т7г-
ю
Пример 6.3.6. Пусть /: R"->R, хс и р заданы, как в
примере 6.3.1. Поскольку f(xc)=3 и /(лсс + р)=20, то хс + р
не является приемлемым, и требуется дробление шага. Тогда
*я (0) = / (*е) = 3, /й; (0) = V/ (xcf р = - 20, fftq (1) = / (хс + р)=
= 20 и, согласно (6.3.17), А = -^-^0.270. Точка хс + Хро*
^ (0.189, 0.730) теперь уже удовлетворяет условию (6.3.3) при
а = Ю~4, так как f (хс + Xp)j* 0.570 < 2.99946 = f (хс) +
+ aAV/ (хс) р. Поэтому х+ = хс + Ар. В данном случае
минимум f(xc + Xp) находится в Аш^0.40.
Предположим теперь, что f(Xk) = f(xk + Xkpk) не
удовлетворяет (6.3.3). В этом случае опять необходимо дробить шаг.
Хотя можно было бы воспользоваться квадратичной моделью,
тси(?\)
A prey Л 2 prev
I "tcuib)
Х2 prev
Рис. 6.3.6. Дробление шага на основе кубической модели, две возможности
158 Гл. 6. Глобально сходящиеся модификации
как это делалось при первом дроблении, но теперь имеются
четыре порции информации об /(А,). Поэтому на протяжении
всей текущей итерации мы в этом и во всех последующих
дроблениях используем кубическую модель функции /, подбираем
/йси(Я) по /(0)» /'(0) и по последним двум значениям /(Я) и,
устанавливая верхний и нижний пределы того же типа, что
и раньше, полагаем Я* равным значению Я, в котором /йСи(Я)
имеет локальный минимум (рис. 6.3.6). Причина использования
кубической модели состоит в том, что она может более точно
моделировать ситуации, в которых / имеет отрицательную
кривизну, что весьма возможно, когда (6.3.3) не выполнялось для
двух положительных значений Я. Кроме того, такая кубическая
функция имеет единственный локальный минимум, что
наглядно демонстрируется рис. 6.3.6.
Вычисление Я происходит следующим образом. Пусть
Я prev и Я2prev*) —последние два из предыдущих значений А,*.
Тогда кубическая функция, в точности соответствующая
значениям /(0), /'(О), f (Я prev) и f (A,2prev), имеет вид
rhcu (Я) = аЯ3 + И2 + Р (0) Я + f (0),
где
1
ш-
Я prev — Я2 prev
х
X
[Л prev» Х2 prev» 1 Г f (Я prev) — f (0) — f' (0) % prev ]
~ДГ AC- JL n™preT ~} m ~ fm t2 »"J
Я prev2 Я2 prev2
Точкой его локального минимума Я является
35 * (6.3.18)
Можно показать, что если f (Я prev) > f (0), то Я <j Я prev.
Такое уменьшение2) может реально встретиться, но оно
считается незначительным (см. пример 6.5.1). Поэтому
устанавливается верхняя граница и = 0.5, т. е. если Я > -g- Я prev, то мы
полагаем новое ЯЛ = у Я prev. Кроме того, поскольку Я может
составлять произвольно малую долю от Я prev, то опять ис-
!> Здесь prev есть сокращение от previous (предыдущий). —Прим. перев,
"* 2
2) Имеется в виду Ь &^Х prev. — Прим. перев.
6.3. Линейный поиск 15$
пользуется нижняя граница / —-jq (т. е. если A,<-j^-Aprev,
то полагаем новое Я,л =-^-Л prevj . Можно показать, что (6.3.18)
никогда не будет иметь комплексных значений, если а в
алгоритме 6.3.5 меньше -j.
Существует один важный случай, в котором дробление шага
на основе кубической интерполяции можно .использовать на
каждом шаге алгоритма 6.3.5. Иногда имеется возможность
получать Vf(xk + kkPk) за очень малую дополнительную цену
при вычислении f{xk + KkPk)- В этом случае при каждом
дроблении шага можно строить тси(к) на основе f(0), f'(0),
/(Aprev) и /' (Я prev). Ценное упражнение для студентов состоит
в том, чтобы разработать в деталях получающийся в
результате этого алгоритм.
Алгоритм А6.3.1 из приложения содержит нашу процедуру
линейного поиска с дроблением шага. Он имеет две
дополнительные особенности. Так, введена минимальная длина шага,
названная minstep. Эта величина используется для проверки
сходимости в алгоритме А7.2.1, вызывающем рассматриваемый
алгоритм. Если условие (6.3.3) не выполняется, a ||tap*||2
оказывается меньше, чем minstep, то линейный поиск
прекращается, так как сходимость к лс* будет, так или иначе, выявлена
в конце текущей итерации. Этот критерий предотвращает
зацикливание линейного поиска, если pk не является
направлением спуска. (Такое иногда встречается на заключительной
итерации алгоритмов минимизации из-за ошибок конечной
арифметики, особенно когда градиент вычисляется по
конечным разностям.) Поскольку это обстоятельство может также
указывать на сходимость к ложному решению, должно
печататься предостерегающее сообщение. Максимально допустимая
длина шага также устанавливается пользователем, так как на
практике могут встретиться чрезмерно большие шаги, когда
pk = sfl = — H^'Vf (хк) и матрица Нк почти вырождена.
Максимальная длина шага устанавливается специально для того,
чтобы предотвратить выполнение таких шагов, которые могли
бы вывести алгоритм из интересующей нас области, а также,
вероятно, вызвать переполнение при вычислении /(1).
Когда будет использоваться линейный поиск совместно с
алгоритмами секущих из гл. 9, мы увидим, что нам также
необходимо предположить, что на каждой итерации выполняется
условие (6.3.4). Алгоритм A6.3.1mod представляет собой
модификацию алгоритма А6.3.1, которая реализует это условие
в явном виде. Обычно она дает те же самые шаги, что и
алгоритм А6.3.1.
160 Гл. 6. Глобально сходящиеся модификации
6.4. ПОДХОД: МОДЕЛЬ —ДОВЕРИТЕЛЬНАЯ
ОБЛАСТЬ
В последнем разделе рассматривались исключительно
проблемы отыскания приемлемой длины шага в заданном
направлении поиска. Основные предположения заключались в том,
чтобы направлением было квазиньютоновское направление и
полный квазиньютоновский шаг был всегда первым пробным
шагом. Получающийся в результате алгоритм с дроблением
шага объединил в себе эти предположения, с тем чтобы
попытаться достичь глобальной сходимости, не жертвуя при этом
свойствами локальной сходимости квазиньютоновских методов.
Такие цели, очевидно, стоят перед любой глобальной
стратегией. В этом разделе мы преследуем ту же цель, но мы
отходим от предположения, что укороченные шаги должны
обязательно лежать на квазиньютоновском направлении.
Допустим, что квазиньютоновский шаг оказался
неудовлетворительным. Это указывает на то, что наша квадратичная
модель неадекватно моделирует / в области, содержащей
полный квазиньютоновский шаг. В алгоритмах с линейным
поиском сохраняется одно и то же направление шага и выбирается
более короткая длина шага. Эта новая длина определяется с
помощью построения новой одномерной квадратичной или
кубической модели на основе информации, полученной только
при вычислении значений функции и градиента вдоль
квазиньютоновского направления. Хотя эта стратегия имеет успех,
у нее есть и недостаток, состоящий в том, что она никак
больше не использует n-мерную квадратичную модель, включая
гессиан модели. В этом разделе, когда возникнет необходимость
делать более короткие шаги, мы сначала выберем более
короткую длину шага, а уж затем воспользуемся полной п-мерной
квадратичной моделью для выбора направления шага.
Прежде чем приступать к рассмотрению способов выбора
таких направлений, полезно сделать несколько
предварительных замечаний относительно того, как заранее задавать длину
шага. По-видимому, целесообразно после первой итерации
начать придерживаться некоторых соображений относительно
длины шага, который, как мы могли бы с достаточным
основанием надеяться, будет сделан. Например, можно было бы
на основе длины шага, сделанного на &-й итерации, получить
верхнюю границу длины шага, который, вероятно, будет
успешным на итерации k+l. Действительно, в разд. 6.4.3 мы
увидим, как использовать информацию об /, полученную в ходе
итерации, для того чтобы получше оценить длину шага,
который, вероятно, окажется успешным. Имея эту оценку, было бы
желательно начать следующую итерацию с шага
приблизительно такой длины и не тратить вычислении функции, быть
6.4. Подход: модель — доверительная область 161
может очень дорогостоящих, на более длинные шаги, которые
вряд ли окажутся успешными. Это, конечно, означает, что,
исходя из экономии количества вычислений функции, мы могли
бы отказаться от попытки сделать полный квазиньютоновский
шаг на такой итерации, когда он мог оказаться
удовлетворительным. В разд. 6.4.3 будут приведены некоторые
эвристические соображения относительно минимизации вероятности этого
события.
Теперь допустим, что имеются хс и некоторая оценка сверху
6С длины успешного шага, который нам, вероятно, удастся
выполнить из точки хс. Здесь возникает вопрос: как наилучшим
образом выбирать шаг из хс максимальной длины бс?
Существует естественный ответ, если вернуться к идее
использования квадратичной модели. С самого начала мы придерживались
той точки зрения, что квазиньютоновский шаг s% является
приемлемым, так как он представляет собой шаг из хс в точку
глобального минимума локальной квадратичной модели тс
(если гессиан Нс модели положительно определен). Если
добавить идею об ограничении максимальной длины шага
величиной бс > 0, то соответствующий ответ на наш вопрос состоит
в том, чтобы попробовать сделать шаг sc, который является
решением задачи
min тс (хс + s) = / (хс) + V/ (хе)Т s + ^ sTHcs
L (6.4.1)
при условии ||$||2^6С.
Задача (6.4.1) служит основой для подхода «модель —
доверительная область» к решению задач минимизации. Ее решение
приводится ниже в лемме 6.4.1. Это название происходит из
взгляда на 8С, как на величину, порождающую область, в
которой можно доверять тс в том, что она адекватно моделирует /.
В следующей главе мы увидим преимущество
использования масштабированного варианта /2-нормы при ограничении
длины шага, но, поступая так именно сейчас, можно только
запутать дело.
Лемма 6.4.1. Пусть f: Rrt->R дважды непрерывно
дифференцируема, ЯсеРлхя симметрична и положительно
определена, а также пусть ||*|| обозначает /2-норму. Тогда решением
задачи (6.4.1) является
8(v)A-(Ho+VI)-l4f(Xc) (6.4.2)
для единственного ji^O, такого, что ||$(|д,)|| = бс, если только
не имеет место неравенство l|s(0)||^6c, в случае выполнения
которого решением задачи является s(0) = s%. Для любого
р,^0 вектор s(\i) задает направление спуска для / из *с.
162 Гл. 6. Глобально сходящиеся модификации
Доказательство. Формула (6.4.2) вытекает непосредственно
из необходимых и достаточных условий для задач условной
оптимизации, однако нигде в книге нам не требуется привлечения
результатов такой общности. При желании, читая
доказательство, можно обращаться к рис. 6.4.1. На нем изображены дсс,
положительно определенная квадратичная модель тс с
минимумом в точке xN, окруженной линиями уровня для некоторых
возрастающих значений тс, а также изображена граница
шага 6с.
Обозначим решение задачи (6.4.1) через s„ и пусть
xm = xc + sm. Поскольку ньютоновская точка xc + s% служит
точкой глобального минимума для тс, то ясно, что если
|s^|^6c, то s% = sm. Рассмотрим теперь случай, когда xc + s^
выходит за границу шага, как изображено на рис. 6.4.1. Пусть
х — произвольная точка, находящаяся строго внутри
допустимой области, заданной ограничением, т. е. ||ic — jcc||< бс. Тогда
V/7ic (х) Ф О, поэтому имеется возможность уменьшить тс из х,
оставаясь внутри допустимой области и рассматривая точки
вида х — №гпс(х). Отсюда следует, что s не может быть
решением задачи (6.4.1), поэтому s* должно удовлетворять равенству
lls#||=6c если только не имеет место неравенство ||s(0) ||<бс.
Кроме того, поскольку допустимая область задачи (6.4.1)
замкнута и ограничена, то должно существовать решение s,
такое, что ||s ||= 6С.
Рассмотрим теперь s, такое, что ||s||=6c. Для того чтобы s
было решением задачи (6.4.1), необходимо, чтобы при
движении на сколь угодно малое расстояние из хс + s вдоль любого
Рис. 6.4.1. Решение задачи (6.4.1).
6.4. Подход: модель — доверительная область 163
направления, являющегося направлением спуска для тс,
увеличивалось расстояние от лгс. Направлением спуска для тс из
хс + s служит любой вектор р, для которого
О > рТЧтс (хс + s) = pT [Hcs + V/ (хс)]. (6.4.3)
Аналогично, направление р из хс + s увеличивает расстояние
от хс тогда и только тогда, когда
pTs > 0. (6.4.4)
Сказанное сводится к следующему: чтобы s было решением
для (6.4.1), любое р, удовлетворяющее (6.4.3), должно также
удовлетворять (6.4.4). Поскольку известно, что Vmc (хс + s) Ф0,
это может иметь место, только если Vmc(xc-\- s) и —s имеют
одно и то же направление, или, другими словами, если для
некоторого \х > 0
р8 = — Vmc(xc + s) = — (Hcs + Vf(xc)),
что в точности есть уравнение (Нс + \il) s = — V/ (хс). Таким
образом, s, = s(\i) для некоторого \i>0 при ||^|>бс.
Поскольку ji^O и матрица Нс симметрична и положительно
определена, (Нс + \xl) является симметричной и положительно
определенной, поэтому s(n) есть направление спуска для /
из хс. Для завершения доказательства необходимо показать
единственность sm, которая вытекает из более сильного
результата, состоящего в том, что если jii>fi2^0, то ||s(m)||<
< || sM II. Это показывает, что ||s(ji)|| = 6c имеет единственное
решение, которое должно быть решением и для (6.4.1).
Доказательство является простым, поскольку если |i>0 и
Л М А || * (ц) ||2 = | (Нс + ц/Г1 V/ (хс) I
^/„ч_ -Vf(xc)T(liI + Hcr3Vf(xc) __ -s(yi)T(Hc + iiirls(ix)
Ц W II* Mil — ||s(l*)||
и поэтому T)/(|i)<0 всякий раз, когда V/(jtc)¥=0. Таким
образом, т] есть монотонно убывающая функция от ц. П
Трудность использования леммы 6.4.1 в качестве основы
для вычисления шага в алгоритме минимизации состоит в том,
что не существует конечного метода определения \хс > 0,
такого, что \\s([ic)\\2 = Z>c при 6С <|Я71У/(^С)|2. Поэтому в
следующих двух подразделах описываются два вычислительных
метода для приближенного решения задачи (6.4.1). Первый —
метод с локально ограниченным оптимальным (или
«криволинейным») шагом, в котором находится цс, такое, что ||s(|xc)ll2 =
^ 6с, и берется х+ = хс + 5(М- Второй — метод с шагом в виде
ломаной линии, в котором производится кусочно-линейная
аппроксимация кривой s\[x) и в качестве х+ берется точка на
164 Гл. 6. Глобально сходящиеся модификации
этой аппроксимации, удовлетворяющая равенству ||х+ —
— *с11=бс
Нет никакой гарантии, что х+, являющееся приближенным
решением (6.4.1), будет приемлемой следующей точкой,
однако мы надеемся, что она будет таковой, если бс служит
хорошим ограничением шага. Поэтому алгоритм доверительной
области в своем завершенном виде будет выглядеть так:
Алгоритм 6.4.2. Шаг глобальной стратегии на основе
подхода «модель — доверительная область»
Заданы: /: Rn->R, 6С > 0, xc^Rn, симметричная
положительно определенная матрица Нс eRnXn.
repeat
(1) sc = приближенное решение для (6.4.1),
Х+ = хс Т" Sc*
(2) решить — приемлемо ли х+, и вычислить новое
значение 6С9
until х+ — приемлемая следующая точка;
б+=6с.
Описание алгоритма «модель — доверительная область»
завершается в разд. 6.4.3 рассмотрением приведенного выше
шага 2.
В заключение уместно сделать некоторые замечания. Во-
первых, как показал Гэй (1981), даже если Яс имеет отрица-
Рис. 6.4.2. Кривая s (ц)
6.4. Подход: модель — доверительная область 165
тельные собственные значения, решением (6.4.1) является s*,
удовлетворяющее равенству (Яс + ц/)$* = —V/(jcc) для
некоторого ц > 0, такого, что матрица Нс + ц/ по крайней мере
положительно полуопределена. Это приводит к еще одному
обоснованию описанной в разд. 5.5 стратегии внесения
возмущений в гессиан модели, когда S/2f(xc) не является положительно
определенным, таких, что Яс = V2/(xc)+ М'' положительно
определена. Получающийся в результате этого квазиньютоновский
шаг — HclS7f(xc) представляет собой шаг в точку минимума
исходной (неположительно определенной) квадратичной
модели в некоторой сферической области с центром в хс. В
оставшейся части разд. 6.4 предполагается, что Яс положительно
определена.
Во-вторых, важно отметить, что s(\i) непрерывно изменяется
от квазиньютоновского шага — H7lWf (хс)9 соответствующего
у, = 0, до s(m) =—(l/|i,)V/(*c), когда \х становится большим.
Таким образом, когда бс очень мало, решение задачи (6.4.1)
представляет собой шаг длиной бс примерно в направлении
наискорейшего спуска. На рис. 6.4.2 изображена кривая s(m),
0^ \х < оо, для той же самой модели, что и на рис. 6.4.1.
Заметим, что при п > 2 эта кривая, вообще говоря, не лежит в
подпространстве, натянутом на Vf(xc) и #<rV/ (хс) (см. упр. 10).
Флетчер (1980) называет эти алгоритмы методами с
ограниченным шагом. Этот термин отвечает больше всего
рассмотренной в разд. 6.4.3 процедуре пересчета 6С> которая может
быть использована также и в алгоритмах с линейным поиском.
Важной основой для алгоритмов из этого раздела служат
работы, выполненные Левенбергом (1944), Марквартом (1963),
Голдфельдом, Куандом и Троттером (1966). На последующих
страницах приводятся ссылки на более свежие работы.
6.4.1. Локально ограниченный оптимальный
(«криволинейный») шаг
Первый из наших подходов к вычислению шага в
алгоритме 6.4.2 «модель —доверительная область» при l|s(0)||2>6c
состоит в нахождении 5 ЫД — (Нс+ \xl)~l Vf (хс), такого, что
||5(|д)||2 = бс, и далее в выполнении пробного шага в точку лс+=
= *с + 5(м)- В этом разделе рассматривается алгоритм для
нахождения приближенного решения \ic скалярного уравнения
Ф(|*Ш*(|*)Ь-вс = 0. (6.4.5)
Фактически мы вовсе не будем требовать очень точного
решения, но обсуждение этого вопроса откладываем до конца
данного подраздела.
166 Гл. 6. Глобально сходящиеся модификации
Применение идей гл. 2 заставило бы нас использовать
метод Ньютона для решения (6.4.5). Хотя это и оправдало бы
себя, тем не менее можно показать, что Ф'(ц)<0 и Ф"(ц)>0
для всех м ^ О, поэтому метод Ньютона всегда давал бы
оценку снизу для точного решения цш (см. рис. 6.4.3). Поэтому
будет построен другой метод, специально предназначенный для
(6.4.5).
Воспользуемся идеей из гл. 2, заключающейся в
использовании аппарата локальных моделей решаемых задач. В
данном случае одномерный вариант
подсказывает нам общий вид локальной модели
ас
тс0*) — р +>А ~ Ьс
с двумя свободными параметрами аир. Прежде чем обсудить
аир, заметим, что мы незаметно пришли к новым
обозначениям, необходимым нам, когда дело касается итерации по \i,
которая порождается приведенной выше моделью, имеет
место внутри основной итерации по х и предназначается для
отыскания ре, удовлетворяющего равенству (6.4.5). Жирный
шрифт будет использоваться для текущих значений величин
а«.> Р<? и JV которые изменяются на внутренней итерации по ц,
а светлый —для текущих значений величин бс, хс, Vf(xc) и Яс,
которые порождаются на внешней итерации и не меняются на
протяжении решения (6.4.5). Таким образом, \хс получается в
результате внутренней итерации как последнее приближение
1*с к |л#, т. е. к точному решению уравнения (6.4.5). Далее хс
и цс используются для определения х+ = хс + s (|хс).
!№)]!*
Рис. 6.4.3. Метод Ньютона для решения Ф (ц) =
6.4. Подход: модель — доверительная область 167
Модель mc(\i) имеет два свободных параметра ас и Рс,
поэтому, как и при выводе метода Ньютона, целесообразно
выбрать их такими, чтобы они удовлетворяли двум условиям:
Это дает
с= Ф>с) - (6А6)
Р* = Щ^) К • (6-4J)
Заметим, что для вычисления s(jic) требуется разложение
матрицы Яс + Цс/ и, следовательно, на это необходимо
затратить О (л3) арифметических операций. Раз уж мы имеем это
разложение, то вычисление {Hc + Vcl)~{ s(yc) обходится только
в 0(п2) операций, поэтому вычисление Ф'Ол*) сравнительно
дешево.
Теперь, когда имеется модель т«(р), естественно
выбирать ц+ так, чтобы я*Дц+) = 0, т. е.
Читатель может убедиться, что подстановка (6.4.6), (6.4.7) и
(6.4.5) в приведенную выше формулу дает
гф»,) + 6,1ГФ»«П 1ИМ11 Г *(»*«) 1 (648)
что выступает в качестве итерации для решения Ф([ш) = 0. Вид
формулы (6.4.8) показывает, что при р* < рт делается шаг,
больший, чем мог бы сделать метод Ньютона, но при .и* > ц#
шаг оказывается меньшим, чем ньютоновский. По мере
стремления р<? к \im (6.4.8) все более и более напоминает метод
Ньютона и, действительно, локально ^-квадратично сходится
к р..
Остаются невыясненными несколько вопросов, связанных
с превращением (6.4.8) в вычислительный алгоритм.
Дальнейшие рассуждения и наш алгоритм основываются на работах
Хебдена (1973) и Морэ (1977). Можно порекомендовать также
работу Гандера (1978). Читатели, не интересующиеся деталями
численной реализации, могут при желании пропустить
следующие три абзаца.
168 Гл. 6. Глобально сходящиеся модификации
Первое соображение касается начального значения для |ш
при решении (6.4.5). Райнш (1971) показал, что если процесс
(6.4.8) начинается с цо = О, то итерации по jx сходятся
монотонно снизу к |li», но нам хотелось бы начинать еще ближе, так
как каждая итерация в (6.4.8) требует решения линейной
системы. В численной реализации, предложенной Морэ,
используется приближенное решение |i_ последнего варианта
уравнения (6.4.5) для получения начального приближения в текущем
варианте этого уравнения. Способ, применяемый Морэ, прост:
если текущее значение верхней границы шага бс равно
последнему значению верхней границы шага б-, умноженной на р,
то для начала в (6.4.8) используется \ю = ц_/р. Мы
предпочитаем стратегию, отличающуюся от описанной. Напомним, в
какой ситуации мы находимся на итерации: только что был
сделан шаг по лс, равный s(M> из х_ в хс, и хотелось бы
получить *+, причем бс уже получено из б— Перед тем как получить
#с мы все же имеем (#_+|д_/) в факторизованном виде, и
поэтому вычисление
ф All* GO II-а*.
w— |s (МП
обходится только в 0(п2) операций. По аналогии с (6.4.8)
используется
Цо = ц__|££01-*, (6.4.9)
т. е. значение щ полученное на основе ц_, предыдущей модели
и нового радиуса бс доверительной области. Если бс = б_, то
jlao представляет собой в точности то же значение, что мы
получили бы, сделав на основе предыдущей модели еще одну
итерацию по |i. С другой стороны, если на предыдущей
итерации 1) был сделан ньютоновский шаг, то будем выбирать fio
по другому правилу, речь о котором пойдет ниже.
Другая вычислительная деталь, имеющая важное значение
для работы алгоритма по решению (6.4.5), состоит в выработке
и пересчете нижней и верхней границ и+ и /+ для (иц-. Эти
границы используются наряду с (6.4.8) таким же образом, как
границы, которые использовались, чтобы обезопасить процесс
дробления шага в алгоритме 6.3.5, т. е. значение щ-
ограничивается так, чтобы оно принадлежало [/+, и+]. Поскольку
результат ньютоновской итерации, примененной к (6.4.5), всегда
не дотягивает до значения ц., то мы берем 10= — Ф(0)/Ф'(0).
Затем наряду с каждым вычислением (6.4.8) вычисляется
< = цс-Ф(цс)/Ф>,)
') Имеется в виду итерация по х. — Прим. перев.
6.4. Подход: модель — доверительная область 169
и пересчитывается нижняя граница /+ = тах{/с, ц^}, где 1е —
текущее значение нижней границы. Кроме того, поскольку
что следует из положительной определенности Нс и из того,
что ja, >Ь, то || V/ (хс) \уьс берется в качестве начального
значения нижней границы и0 для \i.. Затем на каждой итерации
при Ф (Мс) < 0 пересчитывается верхняя граница по формуле
и+ = т\п{ис, ц^,}, где ис — текущее значение верхней границы.
Если на какой-либо итерации оказывается, что ц+ не
принадлежит [1+у и+], то мы следуем Морэ в выборе ц+ по
формуле
ix+ = max{(l+-u+yi\ 1(Г3и+}> (6-4Л0)
где второй член предохраняет от близких к нулю значений 1+.
На практике к этим границам наиболее часто обращаются при
вычислении Мо- В частности, (6.4.10) используется для задания
Но всякий раз, когда (6.4.9) не может быть использована,
потому что на предыдущей итерации применялся ньютоновский
шаг.
И наконец, мы не решаем (6.4.5) со сколь-нибудь высокой
точностью, довольствуясь вместо этого значениями
||5(ц)||2€=[-тЧ -Is-].
Причина состоит в том, что доверительная область, как это
будет видно в разд. 6.4.3, никогда не увеличивается и не
уменьшается менее чем в 2 раза. Так что если радиус текущей
доверительной области равняется бс, то предыдущий был либо больше
или равен 26с, либо меньше или равен 6с/2. Таким образом, мы
считаем, что фактическое значение 6С является довольно
произвольным в пределах отрезка [Збс/4, Збс/2], который занимает
среднее положение в обоих направлениях, и представляется
разумным допускать любые значения ||s(fi)||2 из этого отрезка.
В некоторых других численных реализациях [см., например,
Морэ (1977)] требуется, чтобы ||s(|i)||2e[0.96c, 1.16с], и не
ясно, какой из этих отрезков лучше. Опыт показывает, что
любое из условий удовлетворяется за число вычислений значения
ц, лежащее в среднем на итерацию по х между 1 и 2.
На этом завершается наше обсуждение алгоритма
приближенного решения уравнения (6.4.5). Ниже приведен простой
пример.
170 Гл. 6. Глобально сходящиеся модификации
Пример 6.4.3. Пусть f (*,, х2) = х\ + х\ + х\, хс = (1, 1)г,
fic = V2f(xc), бс = у, ц_ = 0. Тогда
V/(*c) = (6, 2)г,
Нс==[ 0 П'
*Jr=-Wc-|V/(Jtc)(—f. -1)Г.
КИ 1-088.
Поскольку js^ > 2"6с»то ньютоновский шаг оказывается
слишком большим по длине, и мы стараемся найти некоторое |х > 0,
такое, что
| (Яс + ц/Г' V/ (хс) L е [-^, ^-] = [0.375, 0.75]
(рис. 6.4.4). Поскольку ц- = 0, то вычисления дают
*0 —и ф'(0) = 0.472 = 1"*°»
HW(*c)lk_ 6.325
«о:
дс — 0.5
12.6,
щ = («в-«ё)""а3.97.
Затем вычисляется s(|i0)=— (Яс+ц0/)"'V/(^c)^(—0.334, —0.335)г.
Поскольку
|| s (ц0) Ik « 0.473 е= [0.375, 0.75],
то берем цс = ц0 и х+ = дсс + s (цс) s (0.666, 0.665)7- в качестве
нашего приближенного решения задачи (6.4.1). Заметим, что
^"
^^
^^
•*Г(Хс)
Л
1
-
/
/
/
/
/ >
/ /
/ /
1
\ \
\
\
\
\,
уГ „-»
/ /
/
к: 4-
\
—^ \
'^^ \ \
\ II 2
Xе / / 1
\/ / /
-^У /
/
У
У
^"
_J
1
Рис. 6.4.4. «Криволинейный» шаг из примера 6.4.3.
6.4. Подход: модель—доверительная область 171
в данном случае итерация (6.4.8) не использовалась. Для
наглядности читатель может убедиться, что однократное
применение (6.4.8) дало бы
Ф(ЦП) ||s(fift)|L -0.0271 +0.473
Ц° ф>0) 6с ~ +0528 +0.5 -6А*
и что s 0*0 = (—0.343, -О.Збб)7', || 5 Ы Ik = 0.5006. В данном
случае точное решение уравнения (6.4.5) имеет вид \1тя* 3.496.
Наш алгоритм для вычисления локально ограниченного
оптимального («криволинейного») шага, использующий
описанные в этом разделе приемы, представлен в приложении
алгоритмом А6.4.2. В работе ему предшествует драйверный алгоритм
А6.4.1, осуществляющий полный глобальный шаг с
использованием принципов выбора локально ограниченного оптимального
шага. Полный шаг включает в себя выбор новой точки х+
алгоритмом А6.4.2, проверку приемлемости х+ и пересчет радиуса
доверительной области (алгоритм А6.4.5), а также при
необходимости повторение этого процесса. Все эти алгоритмы
используют диагональную матрицу масштабирования в пространстве
переменных, которое будет рассмотрено в разд. 7.1.
Некоторые недавние исследования [Гэй (1981), Соренсен
(1982)] были сконцентрированы ца приближенном решении
локально ограниченной модельной задачи (6.4.1) с использованием
описанных в этом разделе приемов, распространенных на тот
случай, когда Нс не является положительно определенной. Эти
приемы могут стать важным дополнением к алгоритмам из
данного раздела.
6.4.2. Шаг с двойным изломом
Другой реализацией рассматриваемого подхода «модель —
доверительная область» служит модификация алгоритма
доверительной области, предложенная Пауэллом (1970а). В этой
модификации тоже ищется приближенное решение задачи (6.4.1).
Однако вместо того чтобы находить точку х+= хс + s (\ic) на
кривой 5(|ы), такую, что ||лс+ — Xcll2 = 8c, в ней аппроксимируется
эта кривая кусочно-линейной функцией, соединяющей «точку
Коши» СР.1), т. е. точку минимума квадратичной модели тс
на направлении наискорейшего спуска, с ньютоновским для тс
направлением, как это указано на рис. 6.4.5. Затем в качестве
х+ выбирается точка на этой ломаной линии, такая, что
||х+ — jcc||2 = 6c, если только не имеет место неравенство
\H~lyf (*с)12< *«» причем в последнем случае л+—
ньютоновская точка. Такую стратегию можно еще рассматривать и как
1) с.Р. — сокращение от «Cauchy point» (точка Коши). — Прим. перев.
172 Гл. 6. Глобально сходящиеся модификации
Рис. 6.4.5. Кривая с двойным изломом хс -> СР. -> N -> х^.
простую стратегию поиска в направлении наискорейшего спуска,
если Ьс мало, а по мере роста 6С — в направлении, все более и
более приближающемся к квазиньютоновскому.
Специальный способ выбора кривой с двойным изломом
обеспечивает наличие у нее двух важных свойств. Первое: по
мере продвижения вдоль кусочно-линейной кривой от хс к С. Р.,
затем к if и далее к л;^ расстояние от хс монотонно
увеличивается. Следовательно, для любого d^|#rVf (*с)| существует
единственная точка на кривой, такая, что IU+ — Хс\\2 = 8.
Именно это делает процесс корректно определенным. Второе
свойство состоит в том, что значение квадратичной модели mc(xc+s)
монотонно уменьшается по мере продвижения s вдоль кривой от
хс к СР., затем к if и далее к х^. Это делает процесс вполне
обоснованным.
Точка СР. на рис. 6.4.5 находится путем решения задачи
min тс(хс - Wf (хс)) = f (хс) — ЛЦУ/(хс)||22 + \ ЯМ(хс)т#CV/ (*с),
Xe=R *
которая имеет единственное решение
= №(хс)\\1
* Vf(*c)rtfcV/(jcc) "
Следовательно,
C.P. = xe-kmvf(xe)9
и если
бс < Я,|| V/ (ХС) \\2 - || Vf (Хс) \f2M (хе)т HcVf (Хс),
6.4. Подход: модель — доверительная область 173
то алгоритмом делается шаг длиной 6С в направлении
наискорейшего спуска:
х+=*с- ц7/(хс)Ь vfte>-
Для того чтобы кривая с двойным изломом обладала первым
из сформулированных выше свойств, необходимо показать, что
точка Коши С. Р. находится не дальше от хс, чем ньютоновская
точка xN+. Пусть
sc'Р' = - X.V/ (хс), sN = - H7lVf (хс),
тогда
l|S h-Vf(xcfHcVf(xc)^
\\V(xc)\f2 №(*МНс~1У(*Ж
<
V/ (*/ Я^/ (хс) V/ (*/ Я7^/ (хв)
HV/(*c)ll24
(7f (хе)т НСЩ (хс)) (V/ (*/ H^Vf (*,))
Н^||2А?||^ц2. (6#4Л1)
В качестве упражнения можно показать, что у ^ 1 для любой
положительно определенной матрицы Нс, причем у = 1 тогда
и только тогда, когда sCP- = sN. Мы исключаем из рассмотрения
этот случай до конца данного раздела. Итак,
||5C-P'||2<Y||5^||2<||S^||2.
Точка ft на кривой с двойным изломом выбирается так, чтобы
она имела вид
N = xc — r\Hc~lVf(xc)
для некоторого т], такого, что
и чтобы она обладала свойством
тс(х) уменьшается монотонно вдоль прямой от С. Р. к ft.
(6.4.12)
Поскольку известно, что тс(х) уменьшается монотонно от хс до
СР. и от N до х+, то (6.4.12) будет гарантировать монотонное
уменьшение тс(х) вдоль всей кривой с двойным изломом.
Для того чтобы имело место (6.4.12), т) должно выбираться
так, чтобы производная по направлению вдоль прямой,
соединяющей СР. и ft, была отрицательной в каждой точке этого
линейного сегмента. Параметризуем этот линейный сегмент
следующим образом:
x+(X) = xc + sc-p- + k(r\s»-sc-P-)9 0<Л<1.
1 74 Гл. 6. Глобально сходящиеся модификации
Производная по направлению для тс вдоль этой прямой в лг+(А,)
равна
?me(x+(k))T(risN-sc-p-) =
= [V/(хе) + Нс (5е- р- + X(y\sN - 5е- p))]r{x\sN - sc-p) =
= (V/ (XC) + //,5е- Pf fas" - 5C- P-) + Я (Л5^-5С- Р-)Г Яс (Т15^-5С- Р').
(6.4.13)
Поскольку Нс положительно определена, то правая часть в
(6.4.13) представляет собой монотонно возрастающую
функцию от А,. Следовательно, необходимо потребовать только,
чтобы (6.4.13) было отрицательным для Я=1, что обеспечит ее
отрицательность для 0 <; А, ^ 1. Элементарные преобразования
показывают, что данное условие эквивалентно неравенству
0>(1-Ч)(7/(Хс)г(трлг-вс-р-))-
= 0 - П) (Т - П) (V/ (Xcf H7\f (*)).
которое должно выполняться для всех т)е(у, 1).
Таким образом, в качестве ft можно выбирать любую точку
на ньютоновском направлении хс + r\sN, для которой т| лежит
между 1 и величиной у, определенной в (6.4.11).
Первоначальным выбором Пауэлла было л=1» чему соответствует кривая
с одним изломом. Численное тестирование, однако, показало,
что более ранний переход на ньютоновское направление,
по-видимому, улучшает работоспособность алгоритма. Поэтому
Деннис и Мей (1979) предложили выбор tj = 0.87 + 0.2, который
приводит к кривой с двойным изломом, наподобие той, что
изображена на рис. 6.4.5.
Выбор точек С. Р. и ft полностью определяет кривую с
двойным изломом. Нахождение на кривой точки *+, такой, что
IU+ — *с||2 = бс, представляет собой простую и нетрудоемкую
алгебраическую задачу, что и будет продемонстрировано в
приведенном ниже примере 6.4.4. Отметим, что полные затраты
алгоритма составляют после вычисления s% только О (л2)
арифметических операций.
Пример 6.4.4. Пусть f(x), хс и Нс заданы, как в примере
6.4.3, и пусть 6с = 0.75. Напомним, что
у/(*<) = (6,2)г, Я.-[" I], ^-(-f. -1)Г.
Поскольку J s* Ik = 1.088 > 6С, то алгоритм, использующий
кривую с двойным изломом, сначала вычисляет шаг в точку Коши.
Читатель может убедиться, что она имеет вид
S V512 Д2>/_^-0.15б;
6.4. Подход: модель — доверительная область 175
Так как ||sc-p-||2 = 0.494 < 6С, то далее алгоритм вычисляет шаг
в точку N. Читатель может убедиться, что
Y= (4%2л ^ 0-684,
(512) (f)
t| = 0.8y + 0.2 ~ 0.747,
Й л v (— 0-320 \
Поскольку ||s"\\2££ 0.813 > 6С, то шаг с двойным изломом
должен проходить через прямую, соединяющую С. Р. и N, т. е.
sc = sc-р- + X (sR — $с-р-) для iG(0, 1), такого, что || sc Ik = бс.
Величина А получается в результате нахождения
положительного корня квадратного уравнения
Этим корнем является А, = 0.867. Таким образом,
seeec.P. + 0.8e7(^-sC.P-)«(z2;2S).
- о. _f 0.660 \
Полностью эти вычисления отражены на рис. 6.4.6.
Наш алгоритм выбора точки в соответствии со стратегией
шага вдоль кривой с двойным изломом представлен в
приложении алгоритмом А6.4.4. Вычислительный опыт показывает, что
выбранные, согласно этой стратегии, точки в худшем случае
лишь слегка уступают тем, что выбираются в соответствии с
локально ограниченным оптимальным шагом алгоритма*А6.4.2.
Vf<xc)
Рис. 6.4.6. Шаг с двойным изломом из примера 6.4.4.
176 Гл. 6. Глобально сходящиеся модификации
Однако здесь есть, что сравнивать, а именно сложность и время
счета алгоритма А6.4.4 значительно меньше, чем у алгоритма
Аб.4.2. Это делает привлекательной стратегию поиска вдоль
ломаной, особенно в случае задач, в которых невысока
трудоемкость вычисления функции и производной.
Алгоритм А6.4.3 содержит драйвер для полного глобального
шага, использующего алгоритм поиска вдоль кривой с двойным
изломом с целью нахождения претендента для точки х+. Оба
алгоритма включают в себя диагональное масштабирование
пространства переменных, описанное в разд. 7.1.
6.4.3. Пересчет доверительной области
Для того чтобы глобальный шаг, описанный в алгоритме 6.4.2,
принял завершенный вид, необходимо решить, является ли
точка х+, найденная с использованием техники из разд. 6.4.1
или 6.4.2, удовлетворительным следующим приближением. Если
х+ оказывается неприемлемой, то размеры доверительной
области уменьшаются и производится минимизация той же самой
квадратичной модели на уменьшенной области. Если х+
является удовлетворительной, то нужно решить, увеличивать,
уменьшать, или оставлять неизменной доверительную область на
следующем шаге алгоритма 6.1.1. Основой для такого решения
служат приведенные ниже рассуждения.
Условием приемлемости х+ служит то, что было изложено
в разд. 6.3, а именно:
f К) < / (хс) + о£ (х+ - хе), (6.4.14)
где gc равно Vf(xc) или его аппроксимации, а а — константа из
интервала f О, у J. В нашем алгоритме мы опять полагаем
а=10~4, так что условие (6.4.14) вряд ли более строгое, чем
f(x+)< f(xc). Если х+ не удовлетворяет (6.4.14), то размеры
доверительной области уменьшаются умножением на
коэффициент, лежащий в пределах от -^- до у, и мы снова
возвращаемся к приближенному решению локально ограниченной
задачи минимизации, используя идею локально ограниченного
оптимального шага или шага вдоль кривой с двойным изломом.
Коэффициент уменьшения определяется с помощью той же
самой стратегии дробления шага на базе квадратичной
аппроксимации, которая использовалась в алгоритме А6.3.1 для
уменьшения параметра линейного поиска. Функция f(xc + h(x+ — хс))
моделируется квадратичной mq(k), совпадающей с f(xc) и f(x+),
а также с производной по направлению gj (л:+ — xjj функции f
и хс вдоль направления х+ — хс. Затем мы предполагаем, что
6.4. Подход: модель — доверительная область 177
радиус доверительной области 6+ совпадает с точкой минимума
этой модели, которая находится в
х = -8ГС(Х+-Хс)
• 2[f(x+)-f(Xc)-8Tc.(x+-*c)]
(см. рис. 6.4.7). Таким образом, б+ = А,#||*+ — дсс||2. Если
то вместо этого значения, исходя из тех же соображений, что
и в алгоритме линейного поиска, в качестве 6+ выбирается
ближайший из концов указанного отрезка. Заметим, что если х+
выбирается в соответствии с описанной в разд. 6.4.2 стратегией
поиска вдоль кривой с двойным изломом, то ||х+ — *c||2 = fic, но
если х+ выбирается в соответствии с описанной в разд. 6.4.2
стратегией локально ограниченного оптимального шага, то нам
[3 3 1
Теперь предположим, что уже найдено х+, удовлетворяющее
(6.4.14). Если х+ представляет собой полный ньютоновский шаг
из хс, то этот шаг выполняется, пересчитывается б, строится
новая модель и происходит переход к следующей итерации.
Однако если лг+ — хс не является ньютоновским шагом, то сначала
рассматривается вопрос о том, следует ли пытаться сделать шаг
побольше, используя текущую модель. Довод в пользу того, что
это может быть оправданным, состоит в том, что таким образом
можно избежать необходимости вычислений в *+ градиента
(гессиана), стоимость которых в трудоемких задачах часто является
> у '
Размеры новой доверительной области
(Приблизительные) размеры старой доверительной
I области
Рис. 6.4.7. Уменьшение доверительной области в случае, когда х+
неприемлемо.
178 Гл. 6. Глобально сходящиеся модификации
доминирующей. Причина, по которой возможен более длинный
шаг, заключается в том, что в ходе предыдущей работы
алгоритма доверительная область может стать малой, а в данный
момент может возникнуть необходимость в ее увеличении. Это
имеет место, когда мы выходим из области, где граница длины
шага должна быть малой из-за того, что в ней функция не очень
удачно описывалась квадратичной, и попадаем в область с
более хорошим поведением функции.
Для того чтобы решить — пытаться ли сделать более
длинный шаг из хСу мы сравниваем реальное уменьшение функции
Д/Д/ (*+) — f (хс) предсказанным уменьшением Afpred:4:mc(*+)~~
— f(xc). Берем jc+ в качестве следующего приближения, если
либо соответствие между ними настолько хорошее, т.е. A/Wed —
— Д/|^0.1|Д/|, что величина бс, как мы подозреваем,
недооценивает радиуса области, в которой тс адекватно представляет
/, либо реальное уменьшение / настолько велико, что оно
говорит о наличии отрицательной кривизны, т. е. f(х+) ^.f(хс) +
+ S7f(xc)T(x+ — хс)> и, таким образом, это обещает
продолжение быстрого изменения f(x). В обоих этих случаях
запоминаются значения х+ и f (лс+), однако, вместо того чтобы переходить
непосредственно к *+, сначала удваивается 6С, а затем с
использованием нашей текущей модели вычисляется новое х+. Если
для нового х+ не выполняется (6.4.14), то мы возвращаемся
к последнему хорошему шагу, который уже вычислен, но если
это соотношение выполняется, то производится очередное
удвоение. На практике таким образом можно сэкономить
значительное число вычислений градиента.
Интересная ситуация, в которой граница длины шага
должна сжиматься, а затем увеличиваться, встречается, когда
алгоритм проходит вблизи точки, напоминающей точку минимума.
Ньютоновские шаги становятся все короче, и тогда алгоритм,
выполняя эти ньютоновские шаги, ведет себя так, как если бы
он сходился. Затем алгоритм обнаруживает выход из
сложившегося положения, ньютоновские шаги увеличиваются, и
алгоритм уходит прочь от этого места. Такое поведение является
желательным, так как возмущенная задача могла в самом деле
иметь точку минимума в том месте, на которое было отвлечено
внимание. Для нас желательно, чтобы в этом случае мы могли
быстро увеличивать бс. В одном примере нам встретилось шесть
таких удваиваний границы шага на внутренней итерации после
прохождения точки, привлекшей к себе внимание.
Предположим теперь, что мы уже остановили наш выбор на
х+, как на точке следующей итерации, и поэтому необходимо
произвести пересчет бс в 6+. Для получения б+ допускаются три
варианта: удвоить границу шага, уменьшить ее вдвое или
оставить неизменной. Реальные обстоятельства довольно разнооб-
6.4. Подход: модель — доверительная область 179
разны, однако важно то, что если текущая квадратичная модель
хорошо предсказывает поведение функции, то доверительную
область увеличиваем, но если она предсказывает плохо, то мы
уменьшаем доверительную область. Если квадратичная модель
довольно хорошо предсказала реальное уменьшение функции,
т. е. если Д/ ^ 0.75A/pred, то берется 6+ = 2бс. Если модель
слишком переоценила уменьшение в f(x), т. е. если А/ > 0.1Д/ргесь то
берем 6+ = бс/2. В противном случае 6+ = бс.
Пример 6.4.5. Пусть f(x), хс, Нс и бс задаются, как в
примере 6.4.3. Предположим, что шаг, описанный в этом примере,
уже сделан, т. е.
_. i —(х\ f 0.334 \ _ /0.666 \
x+-xc + sc-{l J-^о.335 J "Ч 0.665 J*
Напомним, что
Мы хотим выяснить, является ли точка х+ удовлетворительной,
и хотим произвести пересчет доверительной области. Сначала
вычислим
/(*+) = 1.083,
/ (хс) + <xV/ (хс)т (jc+ -хе) = 3- 10~4 (2.673) = 2.9997.
Следовательно, х+ приемлемо. Затем мы решаем, нужно ли
попробовать на текущей итерации сделать более длинный шаг.
Для этого вычислим
Af = /(*+)-/(*e)=-1.917
и
Д/pred = "с (*+) ~ / К) = V/ (ХС)Т Sc + ± 8*НЛ -
= -2.673 + 0.892 = —1.781.
Поскольку |Д/—-Д/рге(11/| Д/1 = 0.071 < 0.1, то мы увеличиваем
доверительную область вдвое и возвращаемся к локально
ограниченному оптимальному шагу (см. алгоритм А6.4.1). Читатель
может убедиться, что при новом радиусе доверительной области
6С = 1 алгоритмом А6.4.1 будет сделан ньютоновский шаг.
Оставим в качестве упражнения завершить пересчет доверительной
области на этой глобальной итерации.
Алгоритм пересчета доверительной области представлен в
приложении алгоритмом А6.4.5. Он имеет несколько
дополнительных особенностей.
1. Он использует минимальную и максимальную длину шага,
рассмотренную в разд. 7.2. Радиусу доверительной области не
разрешается выходить за эти пределы. Максимальная длина
180 Гл. 6. Глобально сходящиеся модификации
шага задается пользователем. Минимальная длина шага
служит величиной, используемой для проверки на сходимость в
алгоритме 7.2.1. Если х+ неприемлемо, но размеры текущей
доверительной области оказываются меньшими, чем minstep, то
происходит остановка глобального шага, так как в конце
текущей глобальной итерации была бы обязательно выявлена
сходимость. Эта ситуация может указывать на сходимость к точке,
не являющейся решением, поэтому должно выдаваться
предостерегающее сообщение.
2. Если полученным с помощью алгоритма А6.4.2 или А6.4.4
приближенным решением модельной задачи с ограничением
является ньютоновский шаг, т. е. шаг более короткий, чем
текущий радиус доверительной области, то эти алгоритмы сразу
уменьшают размеры доверительной области до размеров
ньютоновского шага. Затем он все же уточняется алгоритмом А6.4.5.
Это представляет собой дополнительный механизм регулировки
размеров доверительной области.
3. Алгоритм реализован с использованием
рассматриваемого в разд. 7.1 диагонального масштабирования имеющегося
пространства.
В заключение обсудим вопрос о том, как получается
начальная оценка радиуса доверительной области, или, другими
словами, оценка границы шага. Иногда пользователь может сам
задать разумную оценку на основе его знания задачи. Если же
нет, то для этого случая Пауэлл (1970а) предлагает
использовать шаг по методу Коши (см. разд. 6.4.2) в качестве
начального радиуса доверительной области. Возможны и другие
стратегии. Стратегия пересчета в алгоритме А6.4.5 действительно
позволяет алгоритму доверительной области избавиться на
практике от плохого начального значения для б, но обычно за это
надо платить дополнительными итерациями. Поэтому начальная
доверительная область имеет довольно важное значение.
6.5. ГЛОБАЛЬНЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ
НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Вернемся теперь к задаче решения системы нелинейных
уравнений:
задано: F: Rn->Rn,
найти x$GRft, такое, что F(jtj = 0.
В этом разделе будет показано, каким образом можно
объединить метод Ньютона для (6.5.1) с глобальными методами
безусловной минимизации в целях создания глобального метода
для (6.5.1).
6.5. Глобальные методы решения систем 181
Ньютоновский шаг для (6.5.1) имеет вид
x+ = xc-J(xc)~lF(xc)t (6.5.2)
где J{xc) есть матрица Якоби функции F в хс. Из разд. 5.2
известно, что (6.5.2) локально ^-квадратично сходится к х*, но не
обязательно глобально сходится. Теперь предположим, что хс не
находится вблизи от какого-либо решения х* задачи (6.5.1). Как
тогда решать вопрос о том, принять или нет х+ в качестве
следующего приближения? Разумный ответ состоит в том, что в
некоторой норме ||-|| величина ||F(jc+)|| должна быть меньше,
чем ||r(jcc)||, причем подходящим вариантом здесь служит /г-
норма:||/^(л:)||22 = ^(х)^(;с).
Требование, чтобы наш шаг приводил к уменьшению ||F(x)||2,
отвечает тому, что требуется при поиске минимума функции
Н^(*)П2. Таким образом, мы в действительности переключили
внимание на соответствующую задачу минимизации:
minf(x)=±F(x)TF(x)9 (6.5.3)
xeRn Z
где «1/2» добавлено, исходя из удобства дальнейших выкладок.
Заметим, что любое решение (6.5.1) является решением и
(6.5.3), однако (6.5.3) может иметь много локальных
минимумов, которые не'являются решениями для (6.5.1) (рис. 6.5.1).
Поэтому хотя можно было бы пытаться решать (6.5.1), просто
применяя процедуру минимизации к (6.5.3), все же лучше
использовать специфику исходной задачи всякий раз, когда это
возможно, в частности, вычисляя ньютоновский шаг (6.5.2).
Тем не менее наша глобальная стратегия для (6.5.1) будет
базироваться на глобальной стратегии решения связанной с ней
задачи минимизации (6.5.3).
Зададим важный вопрос: «Что является направлением
убывания для задачи (6.5.3)?» Им служит произвольное направле-
\л
/ю-\тгп
Рис. 6.5.1. Нелинейные уравнения и соответствующая задача минимизации,
одномерный случай.
182 Гл. 6. Глобально сходящиеся модификации
ние р, для которого Wf(xc)Tp < 0, где
п п
Следовательно, направление наискорейшего спуска для (6.5.3)
направлено вдоль —J(xc)TF(xc). Кроме того, ньютоновское
направление вдоль sN =—J(xc)~lF(xc) представляет собой
направление спуска, так как
V/(х/sN = -F(хс)тJ(хс)J(хсГ[F(хе) =-F(х/F(хс) < О
всякий раз, когда Р(хс)фО. Этот факт может показаться
удивительным, но геометрически он вполне очевиден. Поскольку
ньютоновский шаг дает корень для
Mc(xc + s) = F(xc) + J(xc)st
он также приводит в точку минимума квадратичной функции
thc(xc + s)AYMc(xc + s)TMc(xc + s) =
= jF(xcVF(xc) + (J(xcfF(xc)fs + ^sT(J(xc)4(xc))s9 (6.5.4)
так как tftc{xc + s)^0 для всех s и ific(xc + sN) = 0. Это
означает, что sN представляет собой направление спуска для /йс, и
поскольку градиенты функций rhc и / совпадают в точке хс, то
оно также является направлением спуска для /.
Полученный выше вывод обосновывает наши дальнейшие
действия по созданию глобальных методов для (6.5.1). Эти
методы будут основаны на применении алгоритмов из разд. 6.3
и 6.4 к квадратичной модели ific(x), заданной в (6.5.4).
Поскольку V2ifi(xc) = J(xc)TJ(xc), то рассматриваемая модель
положительно определена всякий раз, когда J(xc) не вырождено.
Это в данном случае соответствует тому факту, что хс + sN есть
единственный корень для Мс (х), и, следовательно, это есть
единственная точка минимума для thc(x). Таким образом, модель
thc(x) имеет привлекательные свойства, состоящие в том, что
ее направления спуска являются направлениями спуска для
f(x)9 поскольку Viftc{Xc) = Vf(Xc). Поэтому методы,
основывающиеся на этой модели, которые используют направление «вниз
по склону» и минимизацию ffic{x), будут объединять в себе
метод Ньютона для решения нелинейных уравнений с
глобальными методами для решения связанной с ними задачи
минимизации. Заметим, что fhc(x) не тождественно в окрестности точки
хс квадратичной модели
mc(xc + s) = f(xc) + Vf(xc)Ts + ±sTV*f(xc)s
6.5. Глобальные методы решения систем 183
функции f (х) = | F (х)т F (х)9 потому что V2/ (хс) Ф J (хс)т J (хс)
(см. упр. 18 из гл. 5).
Применение глобальных методов из разд. 6.3 и 6.4 к задаче
решения нелинейных уравнений становится теперь вполне
очевидным. Когда матрица J(xc) достаточно хорошо обусловлена,
тогда J(xc)TJ(xc) надежно положительно определена, и
алгоритмы применяются без каких-либо изменений, если определить
целевую функцию как у IIТ7 (*) llj > ньютоновское направление как
—J(x)~vF(x) и положительно определенную квадратичную
модель согласно (6.5.4). Это означает, что в алгоритмах с
линейным поиском этот поиск производится вдоль ньютоновского
направления в целях существенного уменьшения ||F(jc)||2. В
алгоритмах доверительной области приближенно минимизируется
ffic(xc + s) при условии ||s||2 ^ 6с. Если 8С ^ V{Xc)~lF(xc)\\2l
то пробным является ньютоновский шаг, в противном случае
пробным служит локально ограниченный оптимальный шаг
s = - (/ (xcY J (хс) + nJ)~l / (ХсГ F (хе), (6.5.5)
где [хс таково, что ||s||2 = 6c Используя ту или иную глобальную
стратегию, мы ожидаем, что в конце концов начнут выполняться
ньютоновские шаги для F(x) = 0. В примере 6.5.1 показано, как
глобальная стратегия, использующая линейный поиск, работала
бы на примере из разд. 5.4, начиная из другой точки. В этой
точке ньютоновский шаг является неприемлемым.
Пример 6-5.1. Пусть F: R2-> R2
Имеется корень л:+=(1, 1)г. Положим х0 — (2, 0.5)г. Определим
f(x) = ±F(x)TF(x). Тогда
Алгоритм А6.3.1 с линейным поиском вычислит х+ —х0-\- \sjf,
начиная с Я<, = 1 и, если необходимо, уменьшая Я0, пока не
выполнится неравенство f (х+)< f (х0)+ lO~*X0Vf (х0)т So. Для
, дг Г-1.001 _, . Г 1041
184 Гл. 6. Глобально сходящиеся модификации
поэтому очевидно, что ньютоновский шаг неудовлетворителен.
Следовательно, А,0 уменьшается дроблением шага на основе
квадратичной аппроксимации по формуле
^ — У/(^0) s0
1 *[f(*+)-f(*o)-Vf(*o)T4Y
В этом случае /(х+)^5.79Х Ю5, /(*0)«2.89, vf(x0)Ts$ =
= — F(x0)TF(x0)** — 5.77 и тогда (6.5.6) дает Кх ^ 4.99 X Ю"6.
Поскольку А,!<0.1, то алгоритм Л6.3.1 полагает Я1=0.1,
*♦-*+«•'<«[ £?]• '<*♦>«[£?]•
Этот результат все еще не является удовлетворительным, и
поэтому алгоритмом А6.3.2 производится дробление шага на
основе кубической аппроксимации. Читатель может убедиться, что
дробление шага дает hi= 0.0659. Поскольку Я2 > у Я,, то
алгоритм полагает A2 = yA1 = 0.05,
,+ -*0 + o.o^«[J;* ]. />(*+) «[?;£]■
Эта точка все еще не является удовлетворительной, так как
f(x+)^* 3.71 > /(Jto), поэтому алгоритмом производится
следующее дробление шага с кубической аппроксимацией. Это дает
А,з = 0.0116, которое и используется, так как его величина
принадлежит интервалу [Ад/Ю, А,2/2] = [0.005, 0.025]. Теперь
, лл„с v Г 1.9651 р/ ч Г 2.2381
^=x0 + 0.01165o^[0613J, /7(^)^Lo.856j-
Эта точка удовлетворительна, так как
/(*+)« 2.87 < 2.89 ^/(a:0)+10"4(0.01 16) Vf(x0)Ts%9
поэтому мы полагаем х\=х+ и переходим к следующей
итерации.
Интересно проследить дальнейший ход решения задачи. На
следующей итерации
*Г /<*,r'F<*,)ai[-';^],
*?-*. + < «[ИГ]" "WHisZl
что опять является неудовлетворительным. Однако первое же
дробление шага оказывается успешным. Действительно, алго-
6.5. Глобальные методы решения систем 185
ритм А6.3.1 вычисляет Xi = 0.0156, и поскольку это меньше 0.1,
то он полагает Х{ =0.1,
Этот шаг будет приемлемым, так как
/(*+)« 2.63 < 2.87 e/(x1)+10"4(0.1)V/(xi)rsJr.
На следующей итерации
" г г Нг/ \ Г— 0.07561-
s2=-J(x2) F(x2)*[ a0437J,
*з ^2 + 52 — L 1.257 J' *\Х*>*1\ШУ
таким образом, ньютоновский шаг очень хорош. Начиная с этого
момента метод Ньютона сходится (/-квадратично к *„ = (1, 1)г.
Единственное осложнение в этой глобальной стратегии
возникает, когда матрица / почти вырождена в текущей точке хс.
В таком случае мы не можем аккуратно вычислить
ньютоновское направление s^ = —J(xc)~lF(xc)9 и гессиан модели
J(xc)TJ(xc) является почти вырожденным. Для выявления этой
ситуации выполняется Q/^-разложение матрицы J(xc)> и если
матрица R не вырождена, то оценивается ее число
обусловленности по алгоритму АЗ.3.1. Если R вырождена или оценка ее
числа обусловленности больше, чем macheps-1/2, то
производится возмущение квадратичной модели, так что
Лс (*. + s) = g- F {хс)т F (хс) + (/ (хеУ F (хс))т s + -J- sTHcs,
где
Hc = J(xc)TJ(xc) + (n • macheps^l/^/Z^jIt • /.
(Число обусловленности матрицы Нс есть величина порядка
macheps-1/2. Более точное обоснование имеется в упр. 23.) Как
известно из разд. 6.4, ньютоновский шаг в точку минимума этой
модели sN = — HclJ{xc)TF(xc) представляет собой решение
задачи
min thc (хс + s) = || / (хе) s + F (хс) ||*
при условии I S I 2 < й
при некотором б > 0. Он также является направлением спуска
для / (jc) = -j || F (х) \f2. Поэтому мы предпочитаем вместо этого
модифицированного ньютоновского шага использовать некото-
186 Гл. 6. Глобально сходящиеся модификации
рое 5 = —l(xc)-lF(xc), которое бы получалось на основе
возмущенного значения J(xc) Q^-разлож^ния матрицы J(xc).
Дальнейшее обсуждение этого шага можно найти в упр. 24.
В драйвере D6.1.3 можно увидеть наши принципы
использования глобальных алгоритмов безусловной минимизации для
решения систем нелинейных уравнений. В начале каждой итерации
алгоритмом А6.5.1 вычисляется Q^c-разложение для J(xc) и
оценивается число обусловленности матрицы Rc. Если оценка
числа обусловленности меньше, чем macheps-1^ то в нем
вычисляется ньютоновский шаг — J(xc)-lF(xc), в противном случае
вычисляется описанный выше возмущенный ньютоновский шаг.
Затем по выбору пользователя драйвером вызывается алгоритм
линейного поиска, поиска вдоль кривой с двойным изломом или
локально ограниченного оптимального шага. Для всех
глобальных алгоритмов требуется значение Vf(xc) = J(xc)TF(xc),
которое также вычисляется алгоритмом D6.3.1. Кроме того, в
алгоритмах доверительной области требуется разложение Холес-
ского LCLC для Нс = J(xc)TJ(xc) (за исключением случая, когда
в Нс внесено описанное выше возмущение). Поскольку J{xc) =
= QcRcy отсюда сразу же получаем Lc = Rc И наконец, все
наши алгоритмы решения систем нелинейных уравнений
реализованы с использованием диагональной матрицы DF для
масштабирования F(x), рассмотренного в разд. 7.2. Это приводит
к тому, что
/W-ylVWj, Vf(x) = J(x)TD*FF(x)9 H = J(xfDlJ(x).
Имеется один важный случай, в котором эти глобальные
алгоритмы решения систем нелинейных уравнений могут
потерпеть неудачу. Это происходит, когда точка локального
минимума /(*) = уИ^МИг не является корнем F(x) (см. рис. 6.5.1).
Процедура глобальной минимизации, стартующая вблизи от
такой точки, может сойтись к ней1). Не много можно сделать в
такой ситуации сверх того, чтобы сообщить пользователю о
случившемся и предложить ему попытаться начать счет заново
вблизи корня F(x)9 если, конечно, это возможно. Процедура
останова для нелинейных уравнений (алгоритм А7.2.3)
выявляет эту ситуацию и вырабатывает такое сообщение. В
настоящее время проводятся исследования по созданию методов,
которые могли бы сами продолжить счет из таких точек
локального минимума [см. Алговер и Джордж (1980) и Зирилли
(1982)].
1) Одним из признаков этого является вырожденность матрицы J(xc) (см.
упр. 17). — Прим. перев.
6.6. Упражнения 187
6.6. УПРАЖНЕНИЯ
1. Пусть / (jc) = 3jcJ + 2х{х2 + х% л:0 = (1, 1) . Что является
направлением наискорейшего спуска для / в х0? Будет ли (1, — 1)г направлением
спуска?
2. Покажите, что для положительно определенной квадратичной функции
f(Xk + s) = gTs + —sTV2f(Xk)s шаг наискорейшего спуска из Xk задается
равенством (6.2.5).
3. Задано б е (0, 1). Обобщите пример 6.2.2. на случай, когда
последовательность точек, вырабатываемая алгоритмом наискорейшего спуска из
определенной точки х0, удовлетворяет соотношению II Xk+t — х* || =
= cIUa-x*||, * = 0, 1, ... .
4. Пусть / (л:) = х2. Покажите, что бесконечная последовательность точек
Xi = (—\)l(\ 4-2~l), t' = 0, 1, ..., изображенная на рис. 6.3.2, не
удовлетворяет условию (6.3.3), каково бы ни было а > 0.
5. Пусть f(x) = х2. Покажите, что бесконечная последовательность точек
д^=1+2-', ( = 0, 1, ..., допускается условием (6.3.3) при любом а ^Г-^-»
но запрещается условием (6.3.4), каково бы ни было Р > 0.
6. Покажите, что если f(x) является положительно определенной
квадратичной функцией, то ньютоновский шаг из произвольного ^gR"
удовлетворяет условию (6.3.3) при а <-^- и (6.3.4) при любом р > 0.
7. Докажите, что если (6.3.4) заменить на
f(*k+i)>f(*k) + W(xk)T(xk+i-*k)' р^(«. •)>
то теоремы 6.3.2 и 6.3.3 останутся в силе, и докажите, что если, кроме того,
Р > -~-, то также остается справедливой и теорема 6.3.4. Это представляет
собой условие Гольдстейна в его первоначальном виде.
8. Пусть f (х) = JcJ + ^1» *с = (1» 1)Г и направление поиска рс задается
ньютоновским шагом. Что будет представлять собой х+, если использовать:
(a) ньютоновский шаг;
(b) алгоритм линейного поиска А6.3.1;
(c) алгоритм «идеального линейного поиска», полагающий х+ равным
точке минимума f(x) в направлении рс из хс? [Ответьте на (с) приближенно.]
9. Пусть f (*) = — jc^ + jcI» хс = (1, \)т. Каково точное решение (6.4.1)
5
при 6 = 2? А при А = "£"? [Указание: во второй части вопроса попробуйте
взять ц=1.]
10. Докажите, что локально ограниченная оптимальная кривая s(\i),
изображенная на рис. 6.4.2, не обязательно является плоской кривой. Для этого
постройте простой трехмерный пример, в котором хс и какие-либо три точки
кривой не лежат в одной плоскости. [Достаточно рассмотреть f (х) = jCj +
+ 2x1 + 3x1]
11. Пусть матрица // е RnXn симметрична и положительно определена
и 01, ... v 0Л есть ортонормированный базис собственных векторов для Я,
188 Гл. 6. Глобально сходящиеся модификации
которым соответствуют собственные значения Xi, ..., \п. Покажите, что для
ц>0и
п
имеет место соотношение
/=1 '
Как это связано с моделью mc(\i) для \\(Н + \iI)-lg\\ — 6, используемой в
алгоритме локально ограниченного оптимального шага?
12. Пусть Hug заданы, как в упр. 11. Для ц ^ О определим s(\i) =
= (Н + \tl)~lg и т|(|х) = lls(fjL)||2- Используя методику упр. 11 покажите,
что
d ,. g(i*)r(iy + ii/r!g(rt
rfJT^ йШ2 •
[Используя эту методику, вы можете также показать, что (d2ld[i2)r\([i) > О
для всех ц > 0, однако доказательство является громоздким.]
13. Пусть f(x) -1д* + 4 x0 = (\,\f, g = Vf(x0)9 H = V2f(x0). Вы-
числите точку Коши функции / из точки х0 (см. разд. 6.4.2), а также точку
ft = Хо — (0.8у + 0.2) H-lg, которая используется в алгоритме поиска вдоль
кривой с двойным изломом. Затем начертите кривую с двойным изломом и
укажите на ней значения хи соответствующие 6=1 иб=р
14. Пусть матрица Н е= RпХп симметрична и положительно определена,
^eR". Докажите, что (gTg)2 < (gTHg)(gTH~ig). [Указание: положите
и = Hi/2g, v = H~i/2g и примените неравенство Коши — Шварца.]
15. Завершите выкладки в примере 6.4.5.
16. Пусть F(x) = (*i, 2*2)г, Хо — (1, 1)г. Используя технику разд. 6.5,
ответьте, что представляет собой шаг «наискорейшего спуска» из х0 для
системы F = О? Если бы все ваши шаги производились вдоль направлений
наискорейшего спуска, то какую скорость сходимости к корню F вы бы
ожидали?
17. Пусть функция F: Rn->Rn непрерывно дифференцируема и х е= R*
Предположим, что х является точкой локального минимума f (х) &
1 т
a—-F(xy F (х), но F(x) Ф 0. Вырождена ли матрица /(*)? Если J(x)
вырождена, то должно ли х быть точкой локального минимума f(x)?
18. Квадратичной моделью для F = 0, альтернативной к той, что
использовалась в глобальных алгоритмах разд. 6.5, служат первые три члена
разложения в ряд Тейлора функции о-Л ^ С*£ "t- s) |||. Покажите, что эта модель
имеет вид
mc (xc + s)=±F (хс)Т F (хс) + [J (хс)т F (хс)]т s +
+ у sT / {хс)т J (хс) + £ f, (хс) V'fi (Хс) s.
6.6. Упражнения 189
Как ее сравнить с моделью, используемой в разд. 6.5? Совпадает ли
ньютоновский шаг для минимизации тс(х) с ньютоновским шагом для F(x) = О?
Каково ваше мнение относительно достоинств этой модели по сравнению с
той, что использовалась в разд. 6.5? (Аналогичная ситуация, но с другими
выводами встречается при решении нелинейной задачи о наименьших
квадратах (см. гл. 10).)
19. Почему ньютоновский шаг из х0 в примере 6.5.1 является плохим?
[Указание: что произошло бы, если х0 было заменено на (2, е/6)Т ^
~ (2, 0.45) П]
20. Какой шаг был бы сделан из х0 в примере 6.5.1 с использованием
стратегии поиска вдоль кривой с двойным изломом (алгоритм А6.4.4) при
21. Выясните, что представляет собой алгоритм сопряженных градиентов
для минимизации выпуклых квадратичных функций, и покажите, что
ломаная с N = x+ есть результат применения метода сопряженных градиентов
к гпс(х) в подпространстве, натянутом на направление наискорейшего спуска
и ньютоновское направление.
22. Один из часто упоминаемых недостатков алгоритма поиска вдоль
ломаной заключается в ограниченности его шагов тем, что они на каждой
итерации должны лежать в двумерном подпространстве, натянутом на
направление наискорейшего спуска и ньютоновское направление. Предложите
на базе упр. 21 способы смягчения остроты этих критических замечаний [см.
также Штайхауг (1981)].
23. Пусть / е= RrtXrt вырождена. Покажите, что
— \—-T72-<x2(/r/ + («.macheps),'2||/r/||1/)-l<- Г"TTTJ'
п (macheps),/z (macheps)1'^
[Указание: воспользуйтесь (3.1.13) и теоремой 3.5.7.] Обобщите это
неравенство на случай, когда х2(/) ^ macheps-172.
24. Пусть вектор FeR" является ненулевым и матрица / е= RnXn
вырождена. Другим шагом, предложенным для решения нелинейных уравнений,
является решение s задачи
min{||s||2: s есть решение~для min ||f + /s||2}. (6.6.1)
Как было показано в разд. 3.6, решением (6.6.1) является 5 = —/+F, где
/+ есть матрица, псевдообратная к /. Покажите, что при малых а > 0 этот
шаг аналогичен s = — (/r/ + а/)-1/7"/7, доказав для этого, что:
(a) lim (/г/ + а/)"1/г = /+;
а-»+0
(b) для любых а> 0 и i/eR" как (ЛУ + aI)^4Tvy так и J+v
перпендикулярны ко всем векторам w из аннулирующего подпространства
матрицы /.
25. Глобальная сходимость алгоритмов доверительной области с
линейным поиском, описанных в разд. 6.3.2, 6.4.1 и 6.4.2, не вытекает
непосредственно из теории, имеющейся в разд. 6.3.1, так как ни один из этих
алгоритмов не обеспечивает выполнение условия (6.3.4). Тем не менее
теоретически такой же эффект дают имеющиеся в алгоритмах границы каждой
регулировки параметра линейного поиска А, или радиуса доверительной
области 6С. Доказательство того, что все рассмотренные нами алгоритмы имеют
глобальную сходимость, см. в работе Шульца, Шнабеля и Бирда (1982).
7
Критерии останова,
масштабирование и тестирование
В этой главе рассматриваются три вопроса, которые лежат в
стороне от основных математических рассуждений
относительно решения нелинейных уравнений и задач минимизации,
однако эти вопросы существенны для решения на ЭВМ реальных
задач. Первый состоит в том, как приспособиться к решению
задач, плохо обусловленных в том смысле, что зависимые или
независимые переменные сильно различаются по величине.
Второй—как определять, когда останавливать итерационный
алгоритм, работающий в условиях машинной арифметики.
Третий— как отлаживать, тестировать и сравнивать нелинейные
алгоритмы.
7.1. МАСШТАБИРОВАНИЕ
Существенным моментом при решении многих реальных задач
является то, что некоторые зависимые или независимые
переменные могут сильно различаться по величине. Например, нам
могла бы встретиться задача минимизации, в которой первая
независимая переменная х\ лежит в области [102, 103] метров,
а вторая переменная х2 лежит в области [10"7, 1(Н] секунд.
Эти области называются масштабами соответствующих
переменных. В настоящем разделе рассматривается влияние на
наши алгоритмы, оказываемое таким большим разбросом в
масштабах. Одним из мест, где масштабирование будет влиять
на работу наших алгоритмов, является вычисление величин,
таких, как ||х+ — ХсНг, которая использовалась в алгоритмах гл. 6.
В приведенном выше примере любое такое вычисление
фактически не будет учитывать значение второй переменной (время).
Однако существует очевидное средство: перемасштабировать
независимые переменные, т. е. изменить единицы их измерения.
Например, если изменить единицы измерения Х\ на километры
и х2 на микросекунды, то обе переменные будут иметь областью
7.1. Масштабирование 191
изменения [Ю-1, 1] и будет устранена проблема масштабов
при вычислении IU+ — Jtdh. Заметим, что это соответствует
замене независимых переменных на x = Dxx, где Dx есть
диагональная матрица масштабирования вида
Dx = [ Q 1Q6J. (7.1.1)
Здесь возникает важный вопрос. Мы, скажем, преобразовали
переменные нашей задачи так, что х = Dxx, или, в более общей
постановке, преобразовали пространство переменных так, что
£ = Тх, где матрица T^Rnxn не вырождена, затем вычислили
глобальный шаг в пространстве новых переменных, а потом
произвели обратные преобразования. Будет ли результат этого
шага таким же, как и в случае, когда мы вычисляли его в
пространстве старых переменных, используя ту же самую
стратегию глобализации? Ответ довольно неожиданный: в отличие
от ньютоновского шага, который не подвержен влиянию этого
преобразования, направление наискорейшего спуска меняется,
так что на шаг линейного поиска вдоль ньютоновского
направления не влияет изменение единиц измерения, тогда как шаг
алгоритма доверительной области может измениться.
Чтобы убедиться в этом, рассмотрим задачу минимизации
и обозначим х = Тх9 f(£)= f(T-lJc). Тогда, как нетрудно
показать,
Vf (i) = T~TVf (х)l), V2/ (i) = T" V/ (*) T~\
так что ньютоновский шаг и направление наискорейшего спуска
в пространстве новых переменных имеют вид2)
f = - (Г" V/ (х) Г"1)"1 (T~Tvf (*)) = - 7V2/ (хГ1 V/ (х)9
$SD = -T~TVf(x),
или в пространстве старых переменных имеем
sN = T-Y = -V2f(x):lVf(x)t
ssd = t-issd = _ T-*T-Tvf {х) ^ _ {ттт)-1 vf (jc)
Эти выводы действительно находятся в рамках здравого
смысла. Ньютоновский шаг приводит в точку с наименьшим
значением квадратичной модели, которая не меняется с изменением
единиц измерения х. (Аналогично, в случае решения систем
*) Условная запись Т~т используется для обозначения (Т-1)т. — Прим.
перев.
2) Здесь индексы N и SD есть сокращения от Newton и
steepest-descent. — Прим. перев.
/92 Гл. 7. Критерии останова
нелинейных уравнений ньютоновское направление остается
неизменным при преобразовании независимых переменных.)
Однако определение того, какое из направлений считать
направлением «наискорейшего спуска», зависит от того, что понимать
под единичным шагом в каждом направлении. Говорить о
направлении наискорейшего спуска имеет смысл тогда, когда
единичный шаг в направлении переменной хь имеет примерно
такую же относительную длину, что и единичный шаг в
направлении любой другой переменной х\.
По этим причинам наиболее предпочтительным решением
при масштабировании задач, как мы полагаем, будет выбор
пользователем таких единиц измерения в пространстве
переменных, чтобы каждая компонента вектора х имела
приблизительно одну и ту же величину. Однако если это затруднительно,
то равносильный результат можно получить, преобразуя в
алгоритме пространство переменных с помощью соответствующей
диагональной матрицы масштабирования Dx. Это есть та
самая стратегия масштабирования в пространстве независимых
переменных, которая реализована в наших алгоритмах. Все,
что должен сделать пользователь, это установить матрицу Dx
такой, чтобы она соответствовала желаемым изменениям
единиц измерения, и тогда алгоритмы будут действовать так, как
если бы они работали в преобразованном пространстве
переменных. Алгоритмы все же записываются в исходном
пространстве переменных, так что выражение типа \\х+ — хс\\2 принимает
вид \\Dx(x+ — хс)\\2, а шаги наискорейшего спуска и
криволинейный принимают соответственно вид
х+ = Хс — XDx2Vf(xe)>
(см. упр. 3). Однако ньютоновское направление, как мы уже
видели, остается неизменным.
Положительная диагональная матрица масштабирования Dx
задается пользователем как входная информация простым
заданием п значений typjc,, t=l, ..., п, отражающих
«характерные» значения каждого хх. Затем алгоритмом
устанавливается (Dx)ii = (typXi)"lf при этом значения каждой из
преобразованных переменных jci = (Dx)u Xi становятся порядка 1. Если
в нашем примере пользователь задал, скажем typ jci = 103 и
typjt2=10-6, то Dx будет иметь вид (7.1.1). Если считается,
что нет необходимости в масштабировании xt, то typ jc/ должно
быть взято равным 1. Дальнейшие инструкции по выбору
typjCj приведены в руководстве 2 приложения. Естественно, что
наши алгоритмы хранят в памяти не диагональную матрицу £>*,
а вектор Sx (S означает масштаб), где (Sx)i = (Dx)u =
= (typ *,)-■.
7.1. Масштабирование 193
Приведенной выше -стратегии не всегда оказывается
достаточно. Например, имеются исключительные случаи, в которых
необходимо динамическое масштабирование, так как
некоторые xi в них меняются на много порядков величины. Это
соответствует точно такому же использованию матрицы Dx, как
и во всех наших алгоритмах, но она периодически
перевычисляется. Поскольку опыт, накопленный в этой области, мал,
мы не включили динамическое масштабирование в наши
алгоритмы, несмотря на то что достаточно было бы добавить
модуль, производящий периодическое перевычисление Dx с учетом
результатов итерации алгоритма D6.1.1 или D6.1.3.
Пример, иллюстрирующий важность учета масштабов
независимых переменных, приведен ниже.
Пример 7.1.1. Распространенной тестовой задачей для
алгоритмов минимизации является функция Розенброка с линиями
уровня в форме банана
f(x)=l00(x2l-x2f + (l-xlf, (7.1.2)
которая имеет минимум в *# = (1, \)т. Двумя типичными
начальными точками являются х0=(—1.2, 1)гихо=(6.39, — 0.221 )г.
Эта задача хорошо масштабирована, но при а ф 1 масштабы
переменных могут быть ухудшены подстановкой в (7.1.2) aJc{
вместо Х\ и j^/a вместо Хъ> что в результате даст
I (i) = f (a*„ £) - 100 (W - £)' - (Г - a!,?,
*.=(4-°)r-
Это соответствует преобразованию
* Г- ol
St= а \x.
L 0 aJ .
Если приведенные в приложении алгоритмы минимизации
применить к /(£), начиная из jt0 = (— 1.2/a, a)r и x0 = (6.39/a,
a(—0.221 ))г, воспользоваться при этом аналитическими
производными, «криволинейным» шагом глобализации и
параметрами1), значения которых заданы по умолчанию, а также
пренебречь масштабами переменных, положив typjci = typx2 = 1,то
требуемое для сходимости число итераций при различных зна-
*) В оригинале — tolerance, что означает допуск, допустимое отклонение
от чего-либо. Под этим термином подразумеваются задаваемые
пользователем параметры алгоритмов, не всегда имеющие смысл допуска. Сокращение
tol присутствует в именах многих параметров. — Прим. перев.
194 Гл. 7. Критерии останова
чениях а имеет следующий вид (звездочка указывает на
отсутствие сходимости после 150 итераций):
Итерации из Итерации из
а х0 = (-1.2/а, а)т х0 = (6.39/а, а( - 0.221)JT
0.01
0.1
1
10
100
150 + *
94
24
52
150+ *
150+ *
47
29
48
150+ *
Однако если положить typxi = l/a и typx2 = a, то во всех
случаях выдача программы в точности такая же, что и для
a = 1, за исключением того, что значения х преобразуются
с помощью
L 0 aJ
Необходимо также рассмотреть масштабы зависимых
переменных. В задачах минимизации масштаб целевой функции /
имеет значение только в критериях останова, рассматриваемых
в разд. 7.2. Во всех других вычислениях, таких, как проверка
/(*+)</(*) + 10-*Vf(x)T(x+ — х), изменение единиц
измерения f не имеет никаких последствий.
С другой стороны, при решении систем нелинейных
уравнений разброс в величинах компонент функции // может вызвать
такого же типа проблемы, как и разброс в величинах
независимых переменных. Ньютоновский шаг не зависит от
масштабирования (см. упр. 4). Однако стратегия глобализации для
нелинейных уравнений требует уменьшения ИЛЬ, и ясно, что
если единицы измерения двух компонент функции F(x)
существенно различны, то меньшая компонента функции будет в
действительности игнорироваться.
По этой причине наши алгоритмы используют
положительную диагональную матрицу масштабирования DF зависимой
переменной F(x), действие которой такое же, как действие Dx
на х. Диагональная матрица DF выбирается так, чтобы все
компоненты в DFF(x) имели приблизительно одинаковые
характерные величины в точках, не слишком близких к корню.
Затем DF используется для масштабирования F во всех модулях,
связанных с решением нелинейных уравнений. Аффинная
модель принимает вид DFMCy а квадратичная модель функции
в шаге глобализации становится равной tfic = ^\\DPMc\\l. В
таком духе реализован весь наш интерфейс и алгоритмы. В са-
7.2. Критерии останова 195
мом начале от пользователя требуется, чтобы он задал DF. Это
осуществляется вводом значений typ/;, i= 1, ..., п, задающих
характерные величины каждого fi в точках, не слишком
близких к корню. Затем алгоритм полагает (DF)u = typ /Г1- [В
действительности хранится SfgR", где (Sp)i=(DF)u-]
Дальнейшие указания по выбору typfi приведены в руководстве 5
приложения.
7.2. КРИТЕРИИ ОСТАНОВА
В этом разделе обсуждается, каким образом завершать работу
алгоритмов. Критерии останова представляют собой те же
самые условия, которые рассматривались в разд. 2.5 для
одномерных задач и которые вытекают из здравого смысла, а именно:
«Решена ли задача?», «Имеется ли основание для остановки?»
или «Не иссякли ли наши деньги, время и терпение?».
Заслуживают внимания следующие вопросы: как реализовать эти
проверки в конечной арифметике и как уделить надлежащее
внимание масштабам зависимых и независимых переменных?
Обсудим сначала критерии останова для безусловной
минимизации. Наиболее важной является проверка «Решена ли
задача?». В случае неограниченной точности необходимым
условием достижения в х точного минимума f является S7f(x) = 0,
но в итеративных алгоритмах, использующих машинную
арифметику, нужно заменить это условие на V/(x)^0. ХотяУ{(х)=0
может встретиться в максимуме или седловой точке, стратегия
глобализации и стратегия внесения возмущений в гессиан
модели делают фактически невозможной сходимость к точкам
максимума или к седловым точкам. Поэтому в нашем случае
равенство Vf(*) = 0 рассматривается как необходимое и
достаточное условие достижения в х локального минимума
функции f.
Для проверки, выполняется ли приближенное равенство
V/ ^ 0, соотношение
0Vf(*+)IKe (7.2.1)
непригодно, потому что оно в большой мере зависит от
масштабов как /, так и х. Например, если г = Ю-3 и / всегда
заключено в пределах [10~7, 10-5], то вероятно, любое значе*
ние х будет удовлетворять (7.2.1); если же /е[105, 107], то
условие (7.2.1) может оказаться слишком строгим. Кроме того,
если х неудачно масштабировано, например JCie[106, 107] и
Х2^[10г19 1], то (7.2.1), видимо, будет учитывать переменные
неодинаковым образом. Обычно используют неравенство
IV/ (*+)Г V2/ (ж+Г' V/ (х+) | < в, (7.2.2)
196 Гл. 7. Критерии останова
инвариантное относительно любого линейного преобразования
независимых переменных и поэтому не зависящее от
масштабирования х. Однако оно все же зависит от масштабирования f.
Более непосредственная модификация (7.2.1) состоит в
определении относительного градиента функции f в х по формуле
. « , ч Относительная скорость изменения /-
^ ^ 'I Относительная скорость изменения xi
Г(х + Ьй)-Г(х)
= lim tf =Wf£± (7.2.3)
xi
и в проверке неравенства
|| relgrad (х+) t < gradtol. (7.2.4)
Проверка (7.2.4) не зависит от какого-либо изменения единиц
измерения / и х. Она имеет тот недостаток, что идея
относительного изменения xt или / рушится, когда Xi или f(x)
оказываются близкими к нулю. Эта проблема легко решается
заменой xi и f в (7.2.3) соответственно на max{|x/|, typx,} и
max {| / (х) |, typ /}, где typ / является оценкой пользователя
характерного значения /. Получающаяся в результате проверка
неравенства
4f(x)imaxf\(x+) I, typ а:Л I
*' \,7' п—" <gradtol (7.2.5)
max{\f(x ) , typ/} p^6 v '
max
Ki<n
именно та, что используется в наших алгоритмах.
Следует отметить, что проблема определения относительного
изменения в случае, когда z близко к нулю, обычно сводится
к подстановке (|z|+l) или max{|z|, 1} вместо г. Из
приведенных выше рассуждений очевидно, что в обеих этих
подстановках неявно предполагается, что порядок единиц измерения z
близок к 1. Такие подстановки могут также работать
удовлетворительно, когда |г| гораздо больше единицы, но они дадут
неудовлетворительные результаты, если |г| всегда
значительно меньше единицы. Поэтому если имеется значение typ z, то
предпочтение следует отдать подстановке тах{|г|, typz}.
Другой критерий останова в задачах минимизации прост
для объяснения. Проверка достаточности оснований для
остановки алгоритма из-за того, что он либо застопорился, либо
сошелся, имеет вид
|| относительное изменение последовательных значений xll*,^
<steptol. (7.2.6)
7.2. Критерии останова 197
Следуя приведенным выше рассуждениям, измеряем
относительное изменение xi по формуле
Ге1*'-тах{|(дг+)/|,1ур^- <7-2J>
Выбор steptol обсуждается в руководстве 2. В общем случае,
если р есть желаемое число значащих цифр в **, то steptol
следует положить равным 1(Н\
Как принято в большинстве итерационных процедур, мы
указываем количество имеющихся в нашем распоряжении
времени, денег и терпения, задавая соответствующие ограничения
на число итераций. В реальных приложениях эти ограничения
часто определяются стоимостью каждой итерации, которая
может быть высокой, если вычисление функции является
дорогостоящим. В процессе отладки имеет смысл использовать
низкое значение ограничения, с тем чтобы программа, имеющая
ошибку, не работала слишком долго. В алгоритме
минимизации следует также производить проверку на расходимость
итераций Xk, которая может иметь место, когда f не ограничена
снизу или асимптотически приближается сверху к своей точной
нижней грани. Для проверки на расходимость пользователю
следует задать максимальную длину шага, и если пять
последовательно сделанных шагов оказываются столь велики, то
алгоритм останавливается. (См. руководство 2.)
Критерии останова для систем нелинейных уравнений
аналогичны. Сначала проверяем, является ли х+ приближенным
решением задачи, т. е. имеет ли место F(x+)^0. Проверка
||F(x+)||^e также не подходит из-за проблем
масштабирования, но поскольку (DF)u = 1/typ ft выбиралось так, чтобы
(DF)nFi имело величину порядка 1 в точках, не лежащих
вблизи корня, то проверка
||D,FIL<fntol
должна быть подходящей. Рекомендации относительно выбора
fntol приведены в руководстве 5, причем значения порядка КН
типичны.
Затем проверяем, используя (7.2.6) и (7.2.7), сошелся ли
алгоритм или застопорился в х+. Проверка ограничения на
число итераций и проверка на расходимость такие же, как для
минимизации, хотя расходимость алгоритма решения F(x) = 0
менее вероятна.
Наконец, для нашего алгоритма решения нелинейных
уравнений возможно прилипание к найденной точке локального
минимума функции f = у ||DPF\\l, в которой F^=0 (см. рис. 6.5.1).
Хотя алгоритм и будет в этой ситуации остановлен проверкой
198 Гл. 7. Критерии останова
на сходимость (7.2.6), (7.2.7), мы предпочитаем проводить
проверку явно, выясняя, близок ли к нулю градиент функции /
в х+, и используя с этой целью относительную меру градиента,
аналогичную (7.2.5). Если алгоритм достиг локального
минимума функции \\DPF\$, где F=^=0, то все, что здесь можно
сделать, это заново запустить алгоритм в другом месте.
Алгоритмы А7.2.1 и А7.2.3 приложения содержат критерии
останова соответственно для безусловной минимизации и для
решения нелинейных уравнений. Алгоритмы А7.2.2 и А7.2.4
используются перед начальной итерацией для проверки,
является ли начальная точка х0 точкой минимума или корнем.
Руководства 2 и 5 содержат рекомендации по выбору всех
задаваемых пользователем параметров. В нашем программном
обеспечении, реализующем эти алгоритмы [Шнабель, Вайс и Кунц
(1982)], имеются значения по умолчанию для всех параметров,
участвующих в останове и масштабировании.
7.3. ТЕСТИРОВАНИЕ
Если написана вычислительная программа для нелинейных
уравнений или минимизации, то, по-видимому, далее она будет
тестироваться с целью выяснения, правильно ли она работает
и какова она по сравнению с другим программным
обеспечением, решающим эту же задачу. Важно обсудить два аспекта
такого процесса тестирования: (1) каким образом следует
тестировать программное обеспечение и (2) какими критериями
следует пользоваться при оценке его работоспособности? Может
показаться неожиданным, что отсутствует единство мнений по
любому из этих важных вопросов. В данном разделе кратко
излагаются некоторые из основных соображений.
Первым делом при тестировании убеждаются, что
программа работает правильно. Под словом «правильно» здесь
понимается главным образом, что программа работает так, как ей
следует это делать, в противоположность гораздо более
строгому определению понятия «правильность», используемому в
программировании. Это, конечно, непростая задача для любой
программы таких же размеров, что и программы в этой книге.
Мы настоятельно рекомендуем помодульную процедуру
тестирования, т. е. тестирование каждого модуля в том виде, как он
написан, затем фрагментов, составленных из модулей, и в
конце— всей программы целиком. Тестирование всей программы
сразу может чрезвычайно затруднить обнаружение ошибок.
При помодульном тестировании не всегда очевиден подбор
входных данных для тестирования некоторых модулей, таких,
как модуль пересчета доверительной области. Советуем
начинать с данных, получаемых из простейших задач, скажем, раз-
7.3. Тестирование 199
мерностей один или два с единичными или диагональными
якобианами или гессианами, так как в этом случае возможна
проверка вычислений вручную. Затем рекомендуется проверять
модули на более сложных задачах. Преимущество такого по-
модульного тестирования заключается в том, что оно обычно
обогащает наше понимание алгоритмов.
Если все компоненты работают правильно, то следует
протестировать программу на целом ряде нелинейных задач. Это
служит двум целям: убедиться, что вся программа целиком
работает правильно, и затем проследить за ее
работоспособностью на некоторых стандартных задачах. Первые задачи,
которые следует попробовать решить, должны быть самыми
простыми: линейные системы размерностей два или три для
программ по решению систем нелинейных уравнений и
положительно определенные квадратичные функции двух или трех
переменных для программ минимизации. Далее можно было бы
попробовать полиномы или системы уравнений несколько более
высокой степени и малой размерности (от двух да пяти). Если
программа работает на них правильно, то пора прогнать ее на
некоторых стандартных задачах, принятых в данной области
в качестве хороших тестов программного обеспечения
нелинейных уравнений или минимизации. Многие из них довольно
сложны. Часто оказывается полезным запускать эти тестовые
задачи не только из хо, но также из точек, отстоящих от нее
в 10—100 раз далее и находящихся на луче, выходящем из
решения х# пр направлению к стандартной начальной точке хо.
Морэ, Гарбов и Хиллстром (1981) сообщают, что это часто
выявляет в программах важные различия, которые не
обнаруживаются при использовании стандартных начальных точек.
Хотя литература по тестовым задачам пока находится в
процессе развития, приложение В снабжено некоторыми задачами,
общепринятыми на данный момент. Мы даем ядро
стандартных задач для нелинейных уравнений и минимизации,
достаточных для курсовых проектов и для учебно-исследовательской
работы, а также обеспечиваем дополнительно ссылками на
задачи, которые могли бы использоваться в серьезной
исследовательской работе. Следует заметить, что большинство этих
задач хорошо масштабированы. Это свидетельствует о
недостатке внимания, уделявшегося проблеме масштабирования.
Размерности тестовых задач в приложении В соответствуют
размерностям решаемых в настоящее время задач. Набор
задач средней размерности (от 10 до 100) представляется все же
недостаточным, а стоимость их тестирования — весьма
существенная помеха.
Трудный вопрос о том, как оценивать и сравнивать
программное обеспечение по минимизации и нелинейным
уравнениям, является в этой книге побочным. Он осложняется тем,
200 Гл. 7. Критерии останова
что в одних случаях интересуются прежде всего измерением
эффективности и надежности программы при решении задач,
тогда как в других — ее общим качеством как части
программного обеспечения. В последнем случае интересуются также
взаимодействием между программным обеспечением и его
пользователями (документация, простота использования, реакция
на ошибки при вводе, надежность, качество выводимой
информации), а также между программным обеспечением и
окружающей его вычислительной средой (переносимость с одной
ЭВМ на другую). Мы прокомментируем только первую группу
вопросов; что касается всех этих вопросов в совокупности, см.
Фосдик (1979).
Под надежностью понимается способность программы
успешно решать задачи, на которые она рассчитана. Это
определяется прежде всего результатами, полученными на
тестовых задачах, и в конечном счете тем, решает ли она задачи
пользователей. Для пользователя эффективность имеет
непосредственное отношение к вычислительным затратам,
вызванным запуском программы на его задачах. В задачах
минимизации и решения нелинейных уравнений она иногда измеряется
временем счета программы на тестовых задачах. В
вычислительных системах коллективного пользования трудно получить
точные временные данные, однако более очевидное возражение
вызывает довольно распространенное мнение, что тестовые
задачи похожи на задачи пользователя. Другой популярной
мерой эффективности является количество вычислений функции
и производной, необходимых программе для решения тестовых
задач. Оправданием использования этой меры служит то, что
она выявляет стоимость на тех задачах, которые по существу
дорогостоящи, а именно на тех, для которых дорогостоящим
оказывается вычисление функции и производной. Эта мера
особенно подходит для оценки методов секущих (см. гл. 8 и 9),
так как они часто используются для таких задач. Количество
вычислений функции и градиента, используемое при
тестировании и минимизации, иногда объединяется в одну
характеристику
(Эквивалентное количество вычислений функции) =
= (Количество вычислений /) + п(Количество вычислений V/).
Эта характеристика указывает количество вычислений функции,
которые потребовались бы, если бы градиенты вычислялись
с помощью конечных разностей. Поскольку это не всегда имеет
место, предпочтительнее приводить итоги для функции и для
градиента отдельно.
Некоторыми другими возможными характеристиками
эффективности выступают количество требуемых итераций, вы-
7.3. Тестирование 201
числительная трудоемкость одной итерации и требуемая
машинная память. Необходимое число итераций представляет
собой простую характеристику, однако она полезна, если имеется
корреляция со временем решения задачи или с необходимым
для этого количеством вычислений функции и производной.
Вычислительная трудоемкость итерации, если не учитывать
вычисления функции и производной, неизменно определяется
линейной алгеброй, и для методов секущих обычно
пропорциональна nz или п2. После умножения на требуемое число
итераций она дает представление о времени счета для задач, в
которой вычисление функции и производной очень недороги. Объем
машинной памяти обычно не столь принципиален для задач,
размеры которых такие же, как в задачах этой книги, однако
память и вычислительная трудоемкость итерации становятся
решающим по своей важности фактором для больших задач.
Используя указанные выше характеристики, можно
сравнивать две совершенно различные программы по решению задач
минимизации или нелинейных уравнений, но часто интересно
сравнение двух или более версий лишь отдельного сегмента
алгоритма, например линейного поиска. Возможно, в этом
случае стоит протестировать альтернативные сегменты, подставляя
их в программу модульного типа, каковыми являются наши
программы, так чтобы остальная часть программы оставалась
неизменной в течение тестовых проверок. Так организованная
проверка уменьшает доверие к результатам, относящимся к
программам других видов, а сравнение может оказаться
необъективным, если остальная часть программы
благоприятствует одной из альтернатив.
И наконец, читатель должен понимать, что в этом разделе
обсуждались вопросы оценки машинных программ, а не
алгоритмов. Отличие состоим в том, что машинная программа
может содержать много деталей, которые имеют решающее
значение для ее работоспособности, но не являются частью
«базового алгоритма». Примерами служат критерии останова,
подпрограммы линейной алгебры, а также параметры в
алгоритмах линейного поиска или доверительной области. Базовый
алгоритм можно оценить, используя уже обсуждавшиеся
характеристики, такие, как локальная скорость сходимости, свойства
глобальной сходимости, работоспособность на специальных
классах функций. Однако если кто-либо тестирует машинную
программу, как это обсуждалось выше, то он должен сознавать,
что тестируется конкретная программная реализация базового
алгоритма, и что две реализации одного и того же базового
алгоритма могут работать совершенно по-разному.
202 Гл. 7. Критерии останова
7.4. УПРАЖНЕНИЯ
1. Рассмотрим задачу:
найти min (*, - 106)4 + (*i - Ю6)2 + (х2 - 1(Г6)4 + (х2 - 1(Г6)2-
xgR2
С какими проблемами вы могли бы столкнуться, применяя оптимизационный
алгоритм без масштабирования этой задачи? (Рассмотрите направления
наискорейшего спуска, доверительные области, критерии останова.) Какие
значения вы бы дали typ Xi и typ х2 в ваших алгоритмах, чтобы смягчить
остроту этой проблемы? Какое преобразование могло бы оказаться даже более
полезным?
2. Пусть /: Rn->-R, и матрица reR"X« не вырождена. Для любого
jce R" определим х = Txt f(x) = {(Т-*£) = f(x). Воспользовавшись цепным
правилом дифференцирования из анализа многих переменных, покажите, что
Vf (*) _ Т'т Щ (*), V2f (х) = Т~т V2/ (х) Г-1.
3. Пусть feR, ge Rn, Яе RnX/l, где матрица Н симметрична и
положительно определена. Пусть Dg^X" есть положительно определенная
диагональная матрица. Используя лемму 6.4.1, покажите, что решение задачи:
найти min f + gTs + — sTHs
SeRn 2
при условии ||Ds||2<d
дается формулой
s(|i)--(tf + |iZ)*r1*
для некоторого ц ^0. [Указание: сделайте преобразование £ = Ds,
воспользуйтесь леммой 6.4.1 и выполните обратное преобразование.]
4. Пусть F: Rrt->Rrt и, матрицы^ Ти T2e=RnXn не вырождены. Для
любого х g= Rn определим х = Т{х, F (х) = T2F (T^~lx) = T2F (х). Покажите,
что матрица Якоби для F относительно х имеет вид
Что представляет собой ньютоновский шаг в пространстве переменных i?
Если перевести этот шаг обратным преобразованием в исходное
пространство переменных, то как сравнить его с обычным ньютоновским шагом в
исходном пространстве переменных?
5. Что представляют собой некоторые из ситуаций, в которых стратегия
масштабирования, описанная в разд. 7.1, не давала бы удовлетворительных
результатов? Предложите стратегию динамического масштабирования, которая
была бы в этих ситуациях успешной. Теперь опишите ситуацию, в которой
ваша динамическая стратегия не приводила бы к успеху.
6. Предположим, ваша проверка на необходимость останова для задач
минимизации обнаружила, что Vf(xk) « 0. Как можно было бы проверить,
является ли хк седловой точкой (или точкой максимума)? Если xk оказалась
седловой точкой, то как, на ваш взгляд, можно было бы продолжить работу
минимизационного алгоритма?
7. Напишите программу для безусловной минимизации или для решения
систем нелинейных уравнений, используя алгоритмы из приложения А (и
используя точные производные). Выберите для вашей программной реализации
одну из описанных в разд. 6.3 и 6.4 стратегий глобализации. Отладьте и
протестируйте вашу программу в соответствии с рекомендациями разд. 7.3.
...И еще одно программное замечание
В предыдущих главах были разработаны все компоненты системы полных
квазиньютоновских алгоритмов для решения систем нелинейных уравнений и
задач безусловной минимизации. Однако следует обратить внимание на один
тонкий момент: предполагалось, что мы вычисляли требуемую матрицу
производных, т.е. якобиан для нелинейных уравнений или гессиан для
безусловной минимизации, либо аппроксимировали ее с высокой точностью, используя
конечные разности. Это предположение обременительно по той причине, что
для многих задач аналитические производные недоступны, а вычисление
функции обходится довольно дорого. Так, стоимость конечно-разностных
аппроксимаций производных, составляющая п дополнительных вычислений F(x) на
каждой итерации для якобиана и (п2 + Зя) /2 дополнительных вычислений
f(x) для гессиана, высока. Поэтому в следующих двух главах
рассматривается класс квазиньютоновских методов, которые используют более дешевые
способы аппроксимации якобиана или гессиана. Мы называем их
аппроксимациями по секущим1), так как в случае одной переменной они сводятся к
аппроксимации f'(x) по секущей, а использующие их квазиньютоновские
методы мы называем методами секущих. Отметим, что новым будет только
методика аппроксимации производной, остальная же часть квазиньютоновского
алгоритма останется фактически неизменной.
Разработка методов секущих стала областью активных исследований с
середины 60-х годов. В результате появился класс методов, успешно
работающих на практике и чрезвычайно интересных с теоретической точки зрения.
Мы постараемся осветить оба этих аспекта. Как это часто бывает со
многими новыми областями, развитие шло хаотично и было порой весьма
путаным. Поэтому наше изложение будет существенно отличаться от того
пути, на котором были первоначально получены рассматриваемые методы.
Кроме того, будут представлены некоторые новые имена. Мы стремились по
возможности избежать путаницы, с которой новичок традиционно
сталкивается, пытаясь понять методы и взаимосвязь между ними.
Сошлемся на две работы Дэнниса и Морэ (1977) и Дэнниса (1978), п
которых содержится исчерпывающая информация на эту тему. Другую точку
зрения можно найти в книге Флетчера (1980). В основе наших соглашений
относительно даваемых методам названий лежат предложения Дэнниса и
Тапиа (1976).
1) В оригинале — secant approximation. — Прим. перев.
8
Методы секущих для решения систем
нелинейных уравнений
Обсуждение методов секущих начнем с нелинейных уравнений,
поскольку аппроксимации по секущим для якобиана проще,
чем аппроксимации по секущим для гессиана, речь о которых
пойдет в гл. 9. Вспомним, что в гл. 2 мы уже видели, как
можно было бы аппроксимировать /'(*+) по формуле а+=
= (/(*+) — f(xc))/(x+ — хс) без дополнительных затрат на
вычисления функции, и что плата за это сводится к уменьшению
скорости локальной ^-сходимости с 2 до (1 + ^/Ъ)/2. В
многомерном случае идея аналогична: аппроксимируется /(*+) с
использованием только значений функции, которые уже
вычислены. Известны многомерные обобщения метода секущих,
которые, по сути, хотя и требуют дополнительной (по сравнению
с методом Ньютона) памяти под производную, но имеют
/--порядок сходимости, равный наибольшему корню1) уравнения
rn+l — гп — 1 = 0. Однако ни одно из этих обобщений,
по-видимому, не является в общем случае достаточно работоспособным.
Вместо них в данной главе будет описана основная идея класса
таких аппроксимаций, которые не требуют дополнительных
вычислений функции или памяти и которые очень успешны на
практике. Наиболее подробно будет рассмотрена одна из
аппроксимаций. Она имеет ^-сверхликейную скорость локальной
сходимости с г-порядком, равным 21/2л.
В разд. 8.1 мы знакомим читателя с наиболее часто
употребляемой аппроксимацией по секущим, предложенной
С. Бройденом. Методом Бройдена называется алгоритм,
аналогичный методу Ньютона, но использующий эту
аппроксимацию вместо аналитически заданного якобиана. В разд. 8.2
проводится анализ локальной сходимости метода Бройдена, а в
разд. 8.3 обсуждаются вопросы реализации
квазиньютоновского метода в его завершенном виде, использующего упомя-
*) Принадлежит интервалу (1, 2). — Прим. перев.
8.1. Метод Бройдена 205
нутую аппроксимацию якобиана. Глава заканчивается кратким
обсуждением в разд. 8.4 других аппроксимаций якобиана по
секущим.
8.1. МЕТОД БРОЙДЕНА
В этом разделе приводится наиболее удачное обобщение
метода секущих на случай решения систем нелинейных
уравнений. Напомним, что в одномерном случае рассматривалась
модель
М+ (х) = f (*+) + а+ (х - х+),
которая удовлетворяет равенству M+(x+) = f(x+) для любых
а+ е R и приводит к методу Ньютона при а+ = /'(х+). Если
f(*+) было недоступно, то вместо этого требовалось, чтобы
модель удовлетворяла равенству М+{хс) = f(xc), т. е.
/ (хс) = f (х+) + а+ (хс — х+),
что давало аппроксимацию по секущей
f(*+)-f(*«)
а+~ х+-хс '
Следующей итерацией метода секущих было х++, для которого
М+(л;++) = 0, т. е. х++ =х+ — f(x+)/a+.
В многомерном случае аналогичной аффинной моделью
служит
М+(х) = Р(х+) + А+(х-х+). (8.1.1)
Она удовлетворяет равенству М+(х+) = F(x+) для любых Л+е
е Кпхл. В методе Ньютона A+ = J(x+). Если J(x+) недоступно,
то требованием, которое в одномерном случае приводило бы
к методу секущих, является M+(xc) = F(xc), т. е.
F(xe) = F(x+) + A+(xe-x+)
или
A+(x+-xc) = F(x+)-F(xc). [(8.1.2)
Мы будем называть (8.1.2) соотношением секущих. Кроме
того, будем пользоваться обозначением sc = x+ — хс для
текущего шага и yc = F(x+) — F(xc) для результата текущего шага.
Таким образом, соотношение секущих можно записать как
A+sc = yc. (8.1.3)
Основная трудность при обобщении метода секущих на
n-мерный случай связана с тем, что (8.1.3) не полностью
определяет А+ при п>\. Действительно, если sc Ф 0, то
существует п(п—1)-мерное аффинное подпространство матриц,
206 Гл. 8. Методы секущих для решения систем
удовлетворяющих (8.1.3). Построение удачной аппроксимации
по секущим состоит в нахождении подходящего способа выбора
среди этих возможностей. Было бы логично, чтобы этот выбор
расширял набор свойств аппроксимации якобиана Л+ или
облегчал бы его использование в квазиньютоновском алгоритме.
Видимо, наиболее очевидная стратегия состоит в
требовании, чтобы модель (8.1.1) интерполировала F(x) также в
некоторых других предыдущих точках, т. е.
F(x-i) = F(x+) + A+(x-i-x+).
Это приводит к равенствам
A+s-i = у-ь / = 1, ..., m, (8.1.4)
где
s-i Д x-i — х+, У-iAF (x-i) - F (*+)•
Если m = n — 1 и sc, s-i, ..., s_(n-i) линейно независимы, то
n уравнений1) (8.1.3) и (8.1.4) однозначно определяют Л+.
К сожалению, это — та самая стратегия, о которой
упоминалось в предисловии к данной главе и которая имеет г-порядок,
равный наибольшему корню уравнения rn+l — rn—1=0, но на
практике она не приводит к успеху. Одна из трудностей
состоит в том, что направления sc,s-i, ..., s-(n-n стремятся к
линейно зависимым или близки к этому. Это делает
вычисление А+ плохо обусловленной вычислительной задачей. Более
того, такая стратегия требует дополнительно п2 ячеек памяти.
Подход, приводящий к удачной аппроксимации, состоит
совсем в другом. Мы видим, что кроме соотношения секущих
у нас нет никакой новой информации ни о матрице Якоби, ни
о модели, так что желательно сохранить как можно больше из
того, что уже имеется. Поэтому будем выбирать Л+, стремясь
минимизировать изменение в аффинной модели при условии
выполнения равенства A+sc = yc- Разность между новой и
старой аффинными моделями для любого x^Rn равна
М+ (х) - Mc(x) = F(x+) + А+ (х - *+) - F(xc) -Мх- **) =
= /4*+) -F(xc) - Л+ (*+ - хс) + (А+ - Ас)(х - хс) =
= (Л+ — Ас)(х — хс),
где в последнем равенстве использовано соотношение секущих
(8.1.2). Теперь для любого xgR" представим
X — Хе = dSc + t,
где tTs = 0. Тогда выражение, которое необходимо
минимизировать, примет вид
M+(x)-Mc{x) = a(A+-Ae)8e + (A+-Ae)t.
*) Эти п уравнений образуют п2 скалярных уравнений относительно п2
скалярных неизвестных, элементов матрицы А+. — Прим. пере в.
8.1. Метод Бройдена 207
У нас нет никакой возможности влиять на величину первого
члена в правой части, так как из соотношения секущих следует
(Л+ — Ac)sc = yc — AcSc. Однако можно обратить в нуль
второй член для всех хе Rny выбрав А+ так, чтобы (А+ — Ac)t=0
для всех t, ортогональных к sc. Это требует, чтобы Л+— Ас
было матрицей ранга один вида #sj, и е Rrt. Теперь, для того
чтобы удовлетворить соотношению секущих, которое
эквивалентно (Л+ — Ac)sc = ус — AcScy и должно равняться (ус —
— Acsc)/slsc. Это дает формулу
A+=Ac+(yc~?cSc)sTc , (8.1.5)
которая отвечает минимальной поправке в аффинной модели и
удовлетворяет равенству A+sc = ус.
Формула (8.1.5) была предложена в 1965 г. С. Бройденом,
и мы будем называть ее формулой пересчета Бройдена, или,
проще, формулой секущих. Слово пересчет указывает на то,
что мы не аппроксимируем полностью /(*+), а скорее
пересчитываем аппроксимацию Ас матрицы J(xc) в аппроксимацию А+
матрицы J(x+). Это свойство пересчета присуще всем удачным
способам аппроксимации по секущим.
Приведенный вывод формулы соответствует тому способу,
с помощью которого ее вывел Бройден, но его можно сделать
гораздо более строгим. В лемме 8.1.1 будет показано, что
формула пересчета Бройдена отвечает минимальной поправке
матрицы АСу удовлетворяющей равенству A+sc = уСу где эта
поправка Л+— Ас измеряется в норме Фробениуса. После
доказательства мы прокомментируем выбор нормы. Далее будет
полезно еще одно обозначение:
Q(y, s) = {BeR«x«: Bs = y).
Оно означает, что Q(yys) есть множество матриц, которые
действуют как частное от деления у на s.
Лемма 8.1.1. Пусть А е Rnxnt s,y^Rn, s=£Q. Пусть
матричные нормы ||-|| и ||| • ||| таковы, что
11Я-С1КЦЯЦ- ||С|| (8.1.6)
для любых В, CeRnX", и
г
VV
т
V V
= 1 (8.1.7)
206 Гл. 8. Методы секущих для решения систем
для любого ненулевого v е Rrt. Тогда, каковы бы ни были эти
нормы, решением задачи
min ||5- А || (8.1.8)
является
B<=Q(y.s)
sls
(8.1.9)
В частности, (8.1.9) будет решением задачи (8.1.8), когда ||-||
есть матричная /2-норма, причем (8.1.9)—единственное
решение задачи (8.1.8), если ||-|1 есть норма Фробениуса.
Доказательство. Пусть BgQ(j/,s), тогда
1М+-Л|| =
(y-As)sT
т
<\\В-А\\
SS*
т
(В - A) ssT
<ЦЯ-Л||.
Если в качестве ||- || и ||| • ||| взять /2-норму матриц, то (8.1.6)
и (8.1.7) следуют соответственно из (3.1.10) и (3.1.17). Если
II * II и III • III обозначает соответственно норму Фробениуса и
/2-норму матриц, то (8.1.6) и (8.1.7) вытекает из (3.1.15) и
(3.1.17). Для того чтобы читатель убедился в единственности
решения (8.1.9) задачи (8.1.8) в норме Фробениуса, напомним,
что эта норма строго выпукла, так как она является векторной
/г-нормой матрицы, представленной в виде л2-мерного вектора.
Поскольку множество Q{y,s), как аффинное подмножество
множества Rn х п (или R"2), является выпуклым, то решение
задачи (8.1.8) единственно в любой строго выпуклой норме. □
Использование нормы Фробениуса в лемме 8.1.1 разумно,
потому что она способна отражать изменение в любой
компоненте аппроксимации якобиана. Такая операторная норма, как
/2-норма, меньше подходит для этих целей. В самом деле,
интересное упражнение — показать, что (8.1.8) может иметь в
операторной /2-норме целое множество решений, причем
некоторые из них явно менее желательны, нежели пересчет по Брой-
дену (см. упр. 2). Это к тому же указывает на непригодность
использования операторной нормы в (8.1.8).
Теперь, когда мы дополнили нашу аффинную модель (8.1.1)
выбором Л+, очевидный способ использования этого состоит
в выборе корня такой модели в качестве следующей итераций.
Это просто иной способ сказать, что в методе Ньютона J(x+)
заменяется на А+. Получающийся в результате алгоритм имеет
вид
8.1. Метод Бройдена 209
Алгоритм 8.1.2. Метод Бройдена.
Заданы: F: Rn -> Rn, х0 g= R", А0 ERrt^.
for Л = 0, 1, ... do:
Решить Aksk = — F (xk) относительно sk;
xk+\ = xk + sk;
yk = F(Xk+i)-F(xk);
Ak+l = Ak+{y^TAkSk)sl. (8.1.10)
Будем называть данный метод методом секущих. В этом
месте у читателя могут зародиться серьезные сомнения — а
работает ли он? На самом деле локально он работает довольно
хорошо, что будет продемонстрировано ниже при рассмотрении
его поведения на той же задаче, что решалась методом
Ньютона в разд. 5.1. Конечно, для сходимости из некоторых
начальных точек он, как и метод Ньютона, может нуждаться в
использовании способов, описанных в гл. 6.
В алгоритме 8.1.1 имеется одна неопределенность: как
выбирать начальную аппроксимацию А0 матрицы /(*0)? На
практике для обеспечения хорошего начала итерационного процесса
здесь единственный раз используются конечные разности. Это
также делает более привлекательным свойство
минимальности поправки, характерное для формулы пересчета Бройдена.
В примере 8.1.3 для простоты предполагается, что Л0 = /(*о).
Пример 8.1.3. Пусть
Г*|+*2 —31
f(*) = K + *22-9J
Эта функция имеет корни (0, 3)г и (3, 0)г. Возьмем х0 = (1, 5)г
и воспользуемся алгоритмом 8.1.2 с
A.-/(*b)-[a il]
Тогда
fw=[173]. *о=-л"'^(*о)=[:;!;з75]'
*i = *o + s0 = [ з!б25]' F (*,)=Ч 4.53125 J'
Следовательно, (8.1.10) дает
Л, = Ло+1-1.625 -1.375J = L0.375 8.625J'
210 Гл. 8. Методы секущих для решения систем
Читатель может убедиться, что Ais0 = y0. Отметим, что
/(*!) = [_! 25 725J
Таким образом, матрица Ах не очень близка к J(x\). На
следующей итерации
,i-iг./ ч Г 0.5491 , Г-0.0761
8^-Аг F(x{)4-0.549} *2 = xi + sl~[ з.076 J'
F (x2) ~ [ 0466 J, A2 ~ [ _0f799 8#201 J *
Матрица A2 опять не очень близка к
/(*2) = [_0152 6.152 J'
Полностью последовательности итераций, вырабатываемых
методом Бройдена и, для сравнения методом Ньютона, приведены
ниже. Для обоих методов (**) i + (xk) 2 = 3 при k^l, поэтому
ниже приводятся только значения (х*)2.
Метод Бройдена
(1, 5)т
3.625
3.0757575757575
3.0127942681679
3.0003138243387
3.0000013325618
3.0000000001394
3.0
*о
*i
*2
*3
Л4
*5
*6
х7
Метод Ньютона
(1, 5)г
3.625
3.0919117647059
3.0026533419372
3.0000023425973
3.0000000000018
3.0
Пример 8.1.3 является типичным для поведения метода
Бройдена в локальной окрестности корня. Если какие-либо из
компонент функции F(x) линейны, как, скажем, f\(x) в нашем
примере, то соответствующие строки аппроксимации якобиана
будут иметь точное значение при k ^ 0, а отвечающие им
компоненты функции F(xk) будут равны нулю при k ^ 1 (см.
упр. 4). Строки в Л*, соответствующие нелинейным
компонентам функции F(xk)> могут оказаться не очень близкими к
строкам якобиана, однако соотношение секущих все же содержит
достаточно хорошую информацию, обеспечивающую быструю
сходимость к корню. В разд. 8.2 мы покажем, что скорость
сходимости алгоритма ^-сверхлинейна, но не ^-квадратична.
8.2. Анализ локальной сходимости метода Бройдена 211
8.2. АНАЛИЗ ЛОКАЛЬНОЙ СХОДИМОСТИ
МЕТОДА БРОЙДЕНА
В этом разделе исследуются свойства локальной сходимости
метода Бройдена. Будет показано, что если х0 достаточно близко
к корню jt», где матрица /(*») не вырождена, и если А0
достаточно близка к /(хо), то последовательность итераций {xk}
сходится <7-сверхлинейно к х*. Доказательство представляет
собой частный случай более общего способа доказательства,
который применяется также и к методам секущих для задач
минимизации. Здесь излагается лишь частный случай, так как он
проще и легче для понимания, чем общий способ, и, кроме того,
он дает представление о том, как работают многомерные
методы секущих. В гл. 9 результаты, касающиеся сходимости,
будут сформулированы без доказательства. Читателю,
заинтересованному в более глубокой проработке материала,
рекомендуется обратиться к работе Бройдена, Дэнниса и Морэ (1973)
или Дэнниса и Уолкера (1981).
Мы разъясняем наш подход, используя фактически тот же
простой анализ, который использовался при исследовании
метода секущих в разд. 2.6 и метода Ньютона в разд. 5.2. Если
F(x*) = Oy то в результате итерации
Xk+\ = Xk — AklF(xk)
имеем
xk+i — x0 = xk — x. — Akl (F(xk) — F(x0))
или
A k (xk+i — xm) = Ak (xk — xJ — F (xk) + F (xm).
Определение ek^xk — xm, а также прибавление и вычитание
J(x*)ek к правой части приведенного выше равенства, дает
Akek+i = [-F (xk) + F (*.) + / (*J ek] + (Ak-I CO) ek. (8.2.1)
При наших традиционных предположениях
|| - F (xk) + F (xj + J (x.) ek\\ = 0 (|| ek ||2),
поэтому ключом к анализу локальной сходимости метода
Бройдена будет анализ второго слагаемого (Ak — /(.*•))£*. Сначала
мы докажем локальную <7"линейную сходимость {ен} к нулю,
показав, что последовательность {||Л* — /(**)||} остается
ограниченной сверху некоторой подходящей постоянной.
Соотношение
Нт || Л*-/(*.) || = О
212 Гл. 8. Методы секущих для решения систем
может и не выполняться, тем не менее мы докажем локальную
<7-сверхлинейную сходимость, показав, что
lim -
1И1-/(*»>КУ_0>
Отсюда следует, что шаг метода секущих — Л* lF (xk) стремится
к ньютоновскому шагу —J(xk)~lF(xk) по величине и по
направлению. Это есть именно то, что требуется от аппроксимации
якобиана.
Начнем с вопроса о том, насколько хорошей ожидается
задаваемая формулой пересчета Бройдена аппроксимация Л+
матрицы /(*♦). Если F(x) есть аффинная функция с якобианом /,
то / будет всегда удовлетворять соотношению секущих, т. е.
J^Q(yCt sc) (см. упр. 5). Поскольку А+ является ближайшим
элементом в Q(yc,sc) к Ас в норме Фробениуса, то по теореме
Пифагора имеем
\\А+ -/|£ + || А+-Ас |£ = || Ac-Jft,
т. е. IIА+ — J\\f^ НАс — /Hf (рис. 8.2.1). Следовательно, в
аффинном случае формула пересчета Бройдена не может ухудшить
норму Фробениуса погрешности аппроксимации якобиана. К
сожалению, это необязательно имеет место для нелинейных
функций. Например, могло бы случиться, что Ас = /(**), но АС8СФ
фус, и тогда ||А+ — /(х#),|| > \\АС — /(х«)||. В свете такого
примера трудно себе представить, какой полезный результат здесь
можно получить относительно того, насколько хорошо Ak
аппроксимирует /(*»). Все, что можно здесь сделать, это показать
в лемме 8.2.1, что если аппроксимация становится хуже, то она
ухудшается довольно медленно, в той достаточной для нас
степени, чтобы доказать сходимость {**} к jc#.
Лемма 8.2.1. Пусть D^Rn есть открытое выпуклое
множество, содержащее хс пх+, причем хс Ф хт. Пусть F: Р*->1?л,
7(*)eLipY(D), Ac^RnXn9 и А+ определено согласно (8.1.5).
9^с
*-* Q(yc.s)
А+ 'c,Sc)
Рис. 8.2.1. Метод Бройдена в аффинном случае.
8.2. Анализ локальной сходимости метода Бройдена 213
Тогда как в норме Фробениуса, так и в /2-норме матриц, имеет
место
IIЛ+ - / (*+) II < II Ас - / (*,) || + -Й. || х+ _ Хс ц2. (8.2.2)
Кроме того, если x*^D и J(x) удовлетворяет ослабленному
условию Липшица:
Ц/ДО —/(xJIKyII* —*JI Аля всех *sfl,
то
М+ - / (х.) || < || Лс - / (*.) || +1 (|| *+ - х. ||2 + II *« - *, ||2). (8.2.3)
Доказательство. Докажем неравенство (8.2.3), которым в
дальнейшем мы и воспользуемся. Аналогично доказывается
(8.2.2).
Пусть /.Д/(*.)• Вычитая /„ из обеих частей (8.1.5), имеем
"С
scsc
(Jjc - Acsc) 4 , (»«-*.*«)*:
= ^c-/.+ v,c г cc/ c +
Г г Г
5csc 5с5с
= М. - /.) [/ - *$-1 + (''-КМ. (8.2.4)
Теперь для нормы Фробениуса и /г-нормы матриц на основании
(3.1.15), (3.1.10) и (3.1.17) получаем
1/U_y.1<^_/.l|/-^[+ibj^b.
Использование равенства
1'-£1-
[так как / — (scsl/sTcsc) представляет собой матрицу
проектирования в евклидовой норме] и неравенства
IIУс - /A k<i (И*+ - *.»2 + II*• - *.||2) ||5С|Ь,
вытекающего из леммы 4.1.15, завершает доказательство. □
Неравенства (8.2.2) и (8.2.3) служат примером свойства,
названного ограниченным ухудшением. Это означает, что если
аппроксимация якобиана ухудшается, то весьма умеренно. Брой-
ден, Дэннис и Морэ (1973) показали, что любой
квазиньютоновский алгоритм, в котором способ аппроксимации якобиана
214 Гл. 8. Методы секущих для решения систем
удовлетворяет этому свойству, локально q-линейно сходится к
корню х», где /(**) не вырождено. В теореме 8.2.2 приводится
частный случай их доказательства, соответствующий методу
Бройдена. Получив затем более тонкую оценку нормы
выражения
L s'csc J
в (8.2.4), покажем, что метод Бройдена является локально
<7-сверхлинейно сходящимся.
В оставшейся части раздела предполагается, что Хк+\¥=Хк,
k = 0, 1, ... . Поскольку, как показано ниже, наши
предположения гарантируют невырожденность Ak, k = 0t 1, ..., и
поскольку Xk+\ — xk = — AklF(Xk)9 то предположение о том, что
Хк+хФхц, эквивалентно предположению о том, что F(xk)ib0y
k = 0y 1, ... . Следовательно, из рассмотрения исключается
простой случай, когда алгоритм находит корень точно, т. е. за
конечное число шагов.
Теорема 8.2.2. Пусть выполнены все предположения теоремы
5.2.1. Существуют положительные постоянные е и б, такие, что
если ||*о — х^\\2 ^ е и ||Л0 — /(**)||2^6, то последовательность
{xk}> генерируемая алгоритмом 8.1.2, корректно определена и
сходится ^-сверхлинейно к х*. Если предположить лишь, что
{Ak} удовлетворяет (8.2.3), то {xk} сходится к х* по меньшей
мере ^-линейно.
Доказательство. Пусть || • || обозначает векторную и
матричную /2-нормы, ek,&xk — х0У J.AJ(x,)9 Р^Ц/СО"1!- Выберем
в и б так, чтобы
брб<1, (8.2.5)
Зуе < 26. (8.2.6)
Доказательство локальной ^-линейной сходимости будет
состоять в доказательстве по индукции неравенств
М*-/.И<(2-2-*)д, (8.2.7)
Ika+.IK1^- (8.2.8)
для k — 0, 1, ... . Если говорить вкратце, то первое неравенство
доказывается для каждого номера итерации с использованием
свойства ограниченного ухудшения (8.2.3), которое дает
II Ak - /. II < II Ak-i - /. II +1 (II ek |l +1|e*_, ||). (8.2.9)
8.2. Анализ локальной сходимости метода Бройдена 215
Читатель может убедиться, что если
Elk/II
/-о
равномерно ограничено сверху для любого к, то
последовательность {ИЛ* — /J|} будет ограничена сверху. Используя два
предположения индукции и (8.2.6), получаем (8.2.7). Затем нетрудно
доказать (8.2.8), используя (8.2.1), (8.2.7) и (8.2.5).
Для k = 0 неравенство (8.2.7) тривиально выполнено.
Доказательство (8.2.8) идентично доказательству шага индукции,
поэтому мы его здесь опускаем.
Теперь предположим, что (8.2.7) и (8.2.8) справедливы для
всех & = 0, ..., i—1. Для k = i, согласно (8.2.9) и двум
предположениям индукции, имеем
II Л, — /J| ^ (2 — г^'"0) в + -^ || ^_! ||.. (8.2.10)
Из (8.2.8) и неравенства ||£011^8 получаем
||ei-il|<2-('"I)||e0IK2-(|-I)e.
Подстановка этого соотношения в (8.2.10) и использование
(8.2.6) дает
< (2 - 2Ч'"1} + 2"') б = (2 - 2"') б,
что подтверждает справедливость (8.2.7).
Для проверки (8.2.8) мы должны сначала показать, что At
обратимо, так что итерация корректно определена. Из
неравенств H/taJ-HKP, (8.2.7) и (8.2.5) следует, что
|/;l(A-/J|<|/;IIMi-/.l<p(2-2-|)e<2pe<-J-.
Отсюда по теореме 3.1.4 А не вырождено и
д1-1Д< К~'1 < Р _^ /82in
Таким образом, х/+1 корректно определено, и, согласно (8.2.1),
1 еш | < \А711| [|| - F (хй) + F (хт) + /А || + \\Ай- /, IIII е% ||]. (8.2.12)
По лемме 4.1.12 имеем
YII «ill2
II-f^iJ + fw + zaIK^V^.
Подстановка этого неравенства, (8.2.7) и (8.2.11) в (8.2.12) дает
11^1||<|р[|-||^|| + (2~2-0б]||^11- (8.2.13)
216 Гл. 8. Методы секущих для решения систем
Из неравенств (8.2.8), ||е0||<в и (8.2.6) имеем
——^2 Ye^-g-,
что после подстановки в (8.2.13) дает
11*+1В<|-р[у-2"' + 2-2-']в||в|||<Зрв||в1в<-
где последнее неравенство вытекает из (8.2.5). Это доказывает
(8.2.8) и завершает доказательство ^-линейной сходимости. Мы
откладываем на время доказательство ^-сверхлинейной
сходимости и# вернемся к нему позже в этом разделе. D
Мы доказали ^-линейную сходимость метода Бройдена,
показав, что свойство ограниченного ухудшения (8.2.3)
обеспечивает то, что величина \\Ak — /(**)|| остается достаточно малой.
Заметим, что если все известное нам о последовательности
аппроксимаций {Ak} якобиана сводилось к (8.2.3), то мы не
могли рассчитывать на большее, чем доказательство ^-линейной
сходимости, поскольку, например, аппроксимации Ак=А0ф
Ф1(х*); £ = 0, 1, ..., очевидно удовлетворяют (8.2.3), но,
согласно упр. 11 из гл. 5, получающийся в результате метод
сходится не быстрее, чем ^-линейно. Таким образом, та часть
доказательства теоремы 8.2.2, которая относится к ^-линейной
сходимости, представляет теоретический интерес отчасти потому,
что она показывает нам, насколько плохо мы можем
аппроксимировать якобиан и насколько в этом можно преуспеть. Тем не
менее ее реальная польза состоит в том, что она гарантирует
сходимость {xk} к х», такую, что
fl|e*IK°o.
Это неравенство будет использовано при доказательстве ^-сверх-
линейной сходимости.
Как указывалось в начале этого раздела, достаточным для
<7-сверхлинейной сходимости метода секущих является условие
И. »4>-'W»M =0. (8.2.14)
На самом деле мы будем * пользоваться им в несколько
измененной форме. В лемме 8.2.3 показано, что если {**} сходится
^-сверхлинейно к х«, то
Iim пТПГ *»
*->«> ||**||
где Sk = xk+\ — xk и ek = Xk — **. Это наводит на мысль о том,
что можно заменить в (8.2.14) еъ, на Sk и в результате по-преж-
8.2. Анализ локальной сходимости метода Бройдена 217
нему иметь достаточное условие ^-сверхлинейной сходимости
метода секущих. Это доказано в теореме 8.2.4. С помощью
данного условия мы доказываем ^-сверхлинейную сходимость
метода Бройдена.
Лемма 8.2.3. Пусть xk(=Rnt k = 0, 1, ... . Если {**}
сходится <7-сверхлинейно к х% е R", то в любой норме || • ||
HmIf*±LZf*» 1.
Доказательство, Обозначим Sk = xk+\ — xk, ek = xk — x*.
Доказательство наглядно представляется следующим рисунком:
ек + \
Ясно, что если
llm 4^ = 0,
*->оо
II •*«
то limf-4{
= 1.
Формальные выкладки дают
lim
lf*i
Wed
— 1 = lim
1Ы|-|К1
IIе* II
< lim
fc-*oo
<
ll«*+'*ll
«Italgfcii^O.
*->«> ||**||
Здесь последнее равенство есть определение ^-сверхлинейной
сходимости для случая, когда ен Ф 0 при всех k. П
Заметим, что лемма 8.2.3 представляет также интерес и для
критерия останова в наших алгоритмах. Она показывает, что
как только алгоритм достигает по меньшей мере ^-сверхлиней-
ной сходимости, то любой критерий останова, использующий s*,
по сути, эквивалентен тому же самому критерию, но
использующему в*, т. е. ту величину, которая представляет для нас
реальный интерес.
Теорема 8.2.4 показывает, что соотношение (8.2.14) с
заменой ек на sk является необходимым и достаточным условием
<7-сверхлинейной сходимости квазиньютоновского метода.
Теорема 8.2.4 (Дэннис — Морэ, 1974). Пусть D^Rn есть
выпуклое открытое множество, F: Rn-^Rn, /(x)eLipY(D), x#eD,
и матрица J(xm) не вырождена. Пусть {Ак} есть последователь-
218 Гл. 8. Методы секущих для решения систем
ность невырожденных матриц в Rnxn, и предположим для
некоторого xq е Z), что последовательность точек, генерируемая
формулой
Xk+\ = хн — AkXF (xk), (8.2.15)
остается в D и имеет место ** ф хч для любого k9 а также, что
\iTnk^00Xfi = xm. Пусть || • |1 есть какая-либо норма. Тогда {**}
сходится <7-сверхлинейно к х*, и /7(х*) = 0 в том и только в том
случае, когда
Иш^'^'-О, (8.2.16)
*-*°о \\Sk\\
где sk& xk+\— xk.
Доказательство. Обозначим /♦ = /(*♦), ek = Xk — **.
Сначала мы предположим, что имеет место (8.2.16), и покажем, что
F(x*) = 0 и {xk} сходится (7-сверхлинейно к х*. Из (8.2.15) имеем
О = Aksk + F (xk) = (Ak - /,) sk + F (xk) + Jmsk,
поэтому
- F (xk+i) = (Ah - /J sk + [- F (хш) + F (xk) + J.Sk], (8.2Л7)
11F ftw) II ^ II И» - '.) ** II ■ II - F (*»+■) + F (*k) + ^ 11 ^
I Ml ^ II Ml "*" II Ml ^
< '%^'*" + I (II ek II + II еш ||), (8.2.18)
где последнее неравенство вытекает из леммы 4.1.15.
Использование в (8.2.18) соотношений lim^^HM^O и (8.2.16) дает
lim I'f (**+'> 11 =0. (8.2.19)
*-*°о \\Sk\\
Поскольку Нп1Ли>во||5*|| = 0, то это означает, что
F(x,)= UmF(xk) = 0.
Согласно лемме 4.1.16, существуют <х>0 и £0^0, такие, что
IIF (хш) \\ = \\F (хш) - F (xj II > а || еш II (8.2.20)
для всех k^k0. Комбинируя (8.2.19) и (8.2.20), получаем
o_itaJU^>Ita.!g±J.>
*-+оо |И*|| *-*оо \\Sk II
<*"«*+! II _,:„ **_
> Hm т—..", ,. .. = lim
*->~||«fc|l + lle/H-ill »4»'+f»
8.2. Анализ локальной сходимости метода Бройдена 219
где г* A, \\ek+\ И/И ek\\. Отсюда следует, что
lim rk = 0.
Это завершает доказательство ^-сверхлинейной сходимости.
Настоящее доказательство того, что из ^-еверхлинейной
сходимости и равенства F(x+) = 0 следует (8.2.16), почти полностью
повторяет в обратном порядке приведенные выше рассуждения.
Согласно лемме 4.1.16, существуют р >0 и k0^0, такие, что
ll^^+OIKPII^+ill
для всех k ^ k0. Таким образом, ^-сверхлинейная сходимость
приводит к соотношениям
0= „mi^>lim!!^±!>I_ lim ' li£s±il. Ш. (8.2.21)
*->oo \\ek II *->«> H*k\\ *->ooP \\h\\ К II
Поскольку Hm^^ ||s* 11/11 e* || = 1, то из леммы 8.2.3 и
соотношений (8.2.21) вытекает справедливость (8.2.19). Из (8.2.17) и
леммы 4.1.15 окончательно получаем
II (4ь - Л) sk || \\F (*fe+1) || || - F (хш) + F (xk) + /^ ||
II'* II ^ II Ml ^ II Ml ^
11^ (^feH-i)ll t Y ,.. „ , |h
—if*l— 2"
что совместно с (8.2.19) и соотношением Hm^^HMI —0
доказывает (8.2.16). п
Поскольку J(x) непрерывно по Липшицу, нетрудно показать,
что лемма 8.2.4 остается в силе, если (8.2.16) заменить на
Пт ll(*»~ffiK''=(). (8.2.22)
fe-»°o ||5*|l
Это условие имеет интересную интерпретацию. Поскольку
Sjfe = — AkXF(Xk)> то (8.2.22) эквивалентно тому, что
,|тН>.)М-*.)|=0
где s£ = —/(л^)-1/7^) есть ньютоновский шаг из хн. Таким
образом, необходимым и достаточным условием <7-сверхлинейной
сходимости метода секущих является то, что шаги метода
секущих стремятся по величине и по направлению к ньютоновским
шагам из тех же самых точек.
Теперь мы завершим доказательство теоремы 8.2.2. Ему
предшествует лемма, которая имеет методическое значение и
используется в этом доказательстве.
220 Гл. 8. Методы секущих для решения систем
Лемма 8.2.5. Пусть имеются ненулевое ssR" и E^Rnxn9
а также пусть || • || обозначает векторную /2-норму. Тогда
K'-£)H**-(W< <«■*>
«^-■siMW)'- (8-2-МЬ)
Доказательство. Как отмечалось ранее, / — (ssT/sTs) есть
матрица проектирования в евклидовой норме. Таковой является
и матрица ssT/sTs. Поэтому по теореме Пифагора
"*-ИН«('-£)С-
Так как
ssT I №*
то это доказывает справедливость (8.2.23а). Поскольку
(а2 _ р2) i/2 ^ а _ р2/2а для любых а > | р | S£ 0, то из (8.2.23а)
следует (8.2.23Ь). П
Завершение доказательства теоремы 8.2.2 (q-сверхлинейная
сходимость). Обозначим Ek = Ak — /», и пусть ||-|| обозначает
векторную /2-норму. Согласно теореме 8.2.4, достаточным
условием того^ чтобы {xk} сходилось <7-сверхлинейно к **, служит
Hm infill =0. (8.2.24)
Из (8.2.4) имеем
l|Eft+,llf<|^(/-^))+l(yfe"^;)4|p. (8.2.25)
В доказательстве леммы 8.2.1 было установлено, что
("-т'"'н I <>«»+«^.
s\sk \р 2
Использование в (8.2.25) этого неравенства наряду с
неравенством ||е/ж1К1|е*||/2, (8.2.8) и леммой 8.2.5 дает
\Ebsk\f , 3Y
<£-»'<'l£'»'-ratF + T''^
8.2. Анализ локальной сходимости метода Бройдена 221
ИЛИ
\\Eksk\\
IIs* If
• < 21| Ek ||, [|j Ek Ц, -1| Еш \\p + -j || ek ||] . (8.2.26)
Из доказательства теоремы 8.2.2 имеем ||£*||F^26 для всех
£>0 и
Elk*||<2e.
Поэтому из (8.2.26) следует
i^!L < 46 Г|| Ek \\F -1| ЕШ \\р + ^\\ek ||1. (8.2.27)
IIs* II L 4 J
Суммируя левые и правые части (8.2.27) по 6 = 0, 1, ..., /,
получаем
Z1i^<46fii£0iiF-iif/+IiiF+^j;iieftii2]<
<4б[||£0||, + -^]<4б[д + -^]. (8.2.28)
Поскольку (8.2.28) справедливо для любого i ^ 0, то сумма
у WEkskt
к кн2
конечна. Отсюда вытекает (8.2.24), что завершает
доказательство. □
Приведем еще один пример, который иллюстрирует
сходимость метода Бройдена на полностью нелинейной задаче. Этот
пример используется нами как отправная точка, чтобы
выяснить, насколько близким оказывается в решении предельное
значение аппроксимации якобиана Ак к самому якобиану /(х*).
Пример 8.2.6. Пусть
г2 О- v2 .
F(x)-(*l + 4~2 )
имеет корень ** = (1, 1)г. Ниже приведены последовательности
точек, генерируемых методом Бройдена и методом Ньютона из
*о = (1.5, 2)т при A0 = J(x0) для метода Бройдена.
222 Гл. 8. Методы секущих для решения систем
Метод Бройдена
1.5
0.8060692
0.7410741
0.8022786
0.9294701
1.004003
1.003084
1.000543
0.99999818
0.9999999885
0.99999999999474
1.0
2.0
1.457948
1.277067
1.159900
1.070406
1.009609
0.9992213
0.9996855
1.00000000389
0.999999999544
0.99999999999998
1.0
-*о
*1
*2
*3
*4
*5
*6
*7
*8
х9
*10
*11
Метод 1
1.5
0.8060692
0.8901193
0.9915891
0.9997085
0999999828
0.99999999999992
1.0
Ньютона
20
1.457948
1.145571
1.021054
1.000535
1.000000357
10000000000002
10
Последней из аппроксимаций якобиана, порожденных методом
Бройдена, является
МО
тогда как
Г 1.999137 2.021829]
~L 0.9995643 3.011004 J'
В приведенном выше примере максимальная относительная
погрешность для Л10 при аппроксимации /(дс#) составляет 1.1 %.
Это типично для последней из порождаемых методом Бройдена
аппроксимаций якобиана. С другой стороны, нетрудно показать,
что в примере 8.1.3 последовательность {Ak} не сходится к
Их.):
Лемма 8.2.7. В примере 8.1.3
Й> = [!.5 7.5 ]•
тогда как
'W-[J ё]-
Доказательство. В примере 8.1.3 показано, что (Л*)ц =
= (Ak) 12 = 1 для всех k ^ 0:
Л* 40.375 8.625 J *
Fl(xk) = (xk)l + (xk)2-3 = 0
(8.2.29)
для всех k ^ 1. Согласно (8.2.29), имеет место (1, l)rs* = 0 для
всех k^ 1. С учетом формулы (8.1.10) для метода Бройдена
8.3. Реализация квазиньютоновских алгоритмов 223
это означает, что (Аш — Ак)(1, 1)г = 0 для всех Л> 1. Тогда
(А&х + Ш22 = {Ах)2{ + (Л,)22 = 9 (8.2.30)
для всех k^l. Кроме того, в этом случае легко показать, что
соотношение секущих дает
Hm [(Ak)2l - (Л*Ы = - 6. (8.2.31)
Из (8.2.30) и (8.2.31) получаем
lim {Ak)2l =1.5 и lim (Л*)^ = 7.5. П
fc-»oo fc-»oo
Выводы леммы 8.2.7 в точности воспроизводятся на ЭВМ;
так, в примере 8.1.1 получено
^7^ V 1.5 — 10~6 7.5+KTV'
Легко обобщить доказательство леммы 8.2.7 и показать, что
lim Акф](хт)
почти для любой частично линейной системы уравнений,
которая решается с помощью метода Бройдена. Упражнение 11
служит примером полностью нелинейной системы уравнений, для
которой {хм} сходится к корню а:#, однако предельное значение
Ak существенно отличается от /(**).
Резюмируя, заметим, что, когда метод Бройдена сходится
<7-сверхлинейно к корню л:*, нельзя предполагать, что последняя
из аппроксимаций якобиана Ak будет приблизительно равняться
/(#*), хотя часто это именно так.
Если мы могли бы сказать, насколько быстро {||£*s*ll/lls*||}
приближается к 0, то могли бы сказать больше о порядке
сходимости метода Бройдена. Наиболее близким к такому
результату является доказательство, данное Гэем (1979). Он доказал,
что для любой аффинной F метод Бройдена дает х2п+\ = х#, что
эквивалентно ||/?2л$2л11/1|52л|1 =0. Это позволило ему в
предположениях теоремы 8.2.2 доказать 2дг-шаговую ^-квадратичную
сходимость метода Бройдена для общего случая нелинейных
функций. Как следствие из упр. 2.6 это означает, что г-порядок
равен 21/2".
8.3. РЕАЛИЗАЦИЯ КВАЗИНЬЮТОНОВСКИХ
АЛГОРИТМОВ, ИСПОЛЬЗУЮЩИХ ФОРМУЛУ ПЕРЕСЧЕТА
БРОЙДЕНА
В этом разделе обсуждаются два вопроса, касающиеся
использования в одном из наших квазиньютоновских алгоритмов
решения систем нелинейных уравнений вместо якобиана, задан-
224 Гл. 8. Методы секущих для решения систем
ного аналитически или конечно-разностно, его аппроксимации
по секущим. Имеется в виду следующее: (1) детали,
относящиеся к численной аппроксимации, и (2) те изменения, если они
вообще требуются, которые нужно внести в остальную часть
алгоритма.
Первая из проблем использования формул пересчета по
секущим для аппроксимации якобиана заключается в том, как
получать начальную аппроксимацию А0. Мы уже говорили о
том, что нами используется конечно-разностная аппроксимация
якобиана /(*<>), которая вычисляется с помощью алгоритма
А5.4.1. Разработанная Морэ численная реализация HYBRD в
пакете программ MINPACK [Морэ, Гарбов и Хиллстром (1980)]
использует модификацию этого алгоритма, которая более
эффективна, когда J(x) имеет много ненулевых элементов. Его
обсуждение откладывается до гл. 11,
Если формулу пересчета Бройдена реализовывать
непосредственно так, как она записывается, то в данном случае мало
что можно сказать о ее реализации; это просто-напросто
t — y — As,
а = sTs,
Ац — Ац-\——, /=1, ...,л, /=1, ..., п.
Однако, напомним, что первое действие, которое выполнит наш
алгоритм с матрицей Л+, это определение ее Qfl-разложения,
необходимого для вычисления шага •— A+lF{x+). Следовательно,
как читатель уже мог догадаться, поскольку формула пересчета
Бройдена идеально соответствует алгебраической структуре
равенства (3.4.1), то более эффективная стратегия пересчета
состоит в применении алгоритма АЗ.4.1 для пересчета разложения
QcRc матрицы Ас в разложение Q+/?+ матрицы Л+ за 0(п2)
операций. На всех, последующих за первой итерациях это дает
экономию порядка О (л3) на стоимости Q^-разложения Ak.
Читатель может подтвердить, что целиком вся итерация
квазиньютоновского алгоритма, использующего формулу пересчета
Бройдена в форме (^-разложения и линейный поиск или
стратегию глобализации с поиском вдоль кривой, стоит только О (п2)
арифметических операций.
Эти две возможные реализации формулы пересчета Бройдена
будут называться формулами пересчета соответственно в не-
факторизованной и факторизованной формах. Приложение А
содержит обе формы, представленные соответственно
алгоритмами А8.3.1 и А8.3.2. Факторизованная форма делает алгоритм
более эффективным, и ее следует использовать в любой
серьезной программной реализации. Нефакторизованную форму проще
8.3. Реализация квазиньютоновских алгоритмов 225
программировать, и ей можно отдать предпочтение при
предварительной программной реализации.
Обе формы пересчета, представленные в приложении, имеют
еще две особенности. Во-первых, читатель может убедиться (см.
упр. 12), что диагональное масштабирование независимых
переменных, рассмотренное в разд. 7.1, приводит формулу пересчета
Бройдена к виду
А+ = АС+{У<~А?^У . (8.3.1)
SCDXSC
Это та формула пересчета, которая фактически реализована.
Читатель может также убедиться, что формула пересчета не
зависит от диагонального масштабирования зависимых
переменных.
Во-вторых, при некоторых обстоятельствах мы принимаем
решение не менять строку матрицы Ас. Заметим, что если
(ус — AcSc)i = 0, то (8.3.1) вызывает автоматически совпадение
i-x строк в Ас и А+. Наши действия оправданы, так как формула
пересчета Бройдена вносит минимальные1) изменения в /-ю
строку Ас, приводящие к равенству {A+)i.sc = (yc)i, и если
(ус — Acsc)i = Oy то необходимость в каких-либо изменениях
отпадает. Наш алгоритм оставляет также i-ю строку в Ас
неизменной, если | (ус — i4c5c)/| оказывается меньше вычислительной
погрешности в (ус) и измеряемой с помощью л(1М**)| +
+ |//(*+) |), где г\ есть уровень относительной величины шума в
значениях функции (об этом шла речь в разд. 5.4). Это условие
предназначается для того, чтобы в формуле пересчета
препятствовать попаданию в Л+ случайного шума вместо полезной
информации о производной.
Существует еще одна реализация метода Бройдена, которая
тоже требует на итерации 0(п2) арифметических операций. Она
использует приведенную ниже формулу Шермана — Моррисо-
на — Вудбери.
Лемма 8.3.1 (Шерман — Моррисон — Вудбери). Пусть «, уе
е Rn и предположим, что матрица А е RnXn не вырождена.
В этом случае А + uvT не вырождена тогда и только тогда,
когда
Кроме того,
(А + uvT)~l = Л"1 - — A~luvTA-\
*) Это связано с тем, что в норме Фробениуса задача (8.1.8)
распадается на п независимых задач, соответствующих строкам матрицы А. — Прим.
перев.
Гл. 8. Методы секущих для решения систем
Доказательство. Упр. 13. □
Непосредственное применение леммы 8.3.1 показывает, что
если известно ;4J"\ то этим можно воспользоваться, представив
формулу пересчета Бройдена как
tf-A"4(^U№, (8.3.2)
scAc Ус
что требует 0(п2) операций. Тогда направление метода
секущих — A+lF(x+) может быть вычислено умножением матрицы
на вектор, что требует дополнительно 0(п2) операций.
Поэтому, до того как Гиллом и Мюрреем (1972) было введено
понятие последовательности Q/^-разложений, в алгоритмах,
использующих формулу пересчета Бройдена, сначала вычислялось
значение Ао\ а затем применялась формула (8.3.2). Такая реали*
зация обычно прекрасно работает на практике, но у нее есть
тот недостаток, что при ней с трудом выявляется плохая
обусловленность Aj.. Поскольку факторизованная формула пересчета
из Ас в Л+ свободна от этого недостатка и требует по существу
такого же количества арифметических операций, что и (8.3.2),
в готовой программной продукции отдается предпочтение ей, а
не (8.3.2).
В данном разделе дается ответ и на другой вопрос: «Какие
изменения в случае использования формул пересчета по
секущим необходимо произвести в остальной части
квазиньютоновского алгоритма решения нелинейных уравнений?». Исходя из
способа представления общей квазиньютоновской схемы, нам
хотелось бы ответить «никаких», но имеются два исключения.
Первое изменение тривиально: если формула пересчета
используется в факторизованной форме, то на каждой итерации не
производится Q/^-разложение якобиана модели, и на это
настроены отдельные детали реализации в том виде, как это
обсуждается в приложении А.
Второе изменение более существенно: теперь уже не
гарантируется, что квазиньютоновское направление sc= — A7lF(xe)
будет направлением убывания для f (х) = yllFMIi- Вспомним
из разд. 6.5, что Vf(xe) = J(xe)TF(xc), поэтому
sWf (хс) = - F (xcf A7TJ (xcf F (хс).
Если Ac = J(xc), то эта величина неположительна, что
необязательно имеет место в противном случае. Кроме того, не
существует способа, по которому можно проверить, является ли sc
в. алгоритме секущих направлением убывания для f(x), так как
отсутствует возможность вычислить Vf(xc), не используя J(xc).
Это означает, что sc может быть направлением вверх для гра-
8.4. Другие формулы секущих 227
фика f(x), и наш шаг глобализации может потерпеть неудачу
в попытке найти какую-либо подходящую точку. К счастью, на
практике это случается не часто, так как Ас представляет собой
аппроксимацию J(xc). Если же это происходит, то имеется
простой выход: мы восстанавливаем АСу используя
конечно-разностную аппроксимацию для J(xc), и продолжаем счет алгоритмом.
Такая мера предосторожности предусмотрена в драйвере для
нашего алгоритма решения нелинейных уравнений. Это по
существу— то же, что делается в программе Морэ пакета
MINPACK.
8.4. ДРУГИЕ ФОРМУЛЫ СЕКУЩИХ
ДЛЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
До сих пор в этой главе для аппроксимации якобиана
рассматривалась одна формула пересчета по секущим, а именно,
формула Бройдена. Мы видели, что среди всех элементов
множества Q(yc, sc), которое представляет собой аффинное
подпространство матриц, удовлетворяющих соотношению секущих
A+sc = yC9 (8.4.1)
формула пересчета Бройдена дает ближайший к Ас в норме
Фробениуса. В этом разделе упоминаются некоторые другие из
предложенных аппроксимаций, принадлежащих Q(yc, sc).
Альтернатива, может быть, наиболее известная, была
предложена Бройденом в статье, где он предлагал формулу
пересчета Бройдена. Изложенная в предыдущем разделе идея
построения последовательности А£ вместо Ak привела Бройдена
к выбору
i-l л-\
УсУс
A-i = A-i + ('«-ДГ'у,)*? (8 4 2)
Прямое применение леммы 8.1.1 показывает, что (8.4.2) является
решением задачи:
min iB-'-iC'b- (8.4.3)
B<=Q(ye.sc).
В не вырождена
По лемме 8.3.1 равенство (8.4.2) эквивалентно
Л+=Лс+(Ус"УУеЧ. (8.4.4)
что представляет собой формулу пересчета, очевидно отличную
от формулы Бройдена.
228 Гл. 8. Методы секущих для решения систем
Формула пересчета (8.4.2) имеет то привлекательное
свойство, что она непосредственно генерирует значения Л+1 без
каких-либо проблем нулевого знаменателя. Кроме того, она
разделяет с формулой пересчета Бройдена все ее
положительные теоретические свойства. То есть можно модифицировать
доказательство леммы 8.2.1 и показать, что этот метод
аппроксимации J{x)~l обладает с точки зрения аппроксимации J(x*)~l
свойством ограниченного ухудшения. Отсюда можно показать,
что имеет место теорема 8.2.2 с использованием (8.4.2) вместо
формулы пересчета Бройдена. Однако на практике методы,
использующие (8.4.2), оказались значительно менее успешными,
чем те же методы, использующие формулу пересчета Бройдена.
Поэтому (8.4.2) фактически стала известна как «плохая
формула пересчета Бройдена».
Хотя мы не претендуем на полное понимание отсутствия
вычислительного успеха плохой формулы пересчета Бройдена,
интересно то, что хорошая формула пересчета Бройдена
проистекает из минимизации изменения в аффинной модели при условии
выполнения соотношения секущих, тогда как плохая формула
пересчета Бройдена связана с минимизацией изменения в
решении модельной задачи. Возможно, тот факт, что при
формировании модели типа секущих используется информация о
функции, а не о ее решении, служит причиной, по которой первый из
подходов является более желательным. Во всяком случае, мы
встретимся в разд. 9.2 с аналогичной ситуацией, когда формула
пересчета для безусловной минимизации, выведенная из
хорошей формулы Бройдена, превосходит аналогичный метод,
выведенный из плохой формулы Бройдена, хотя оба имеют
аналогичные теоретические свойства.
Существует для нелинейных уравнений множество других
возможных формул пересчета; некоторые из них могут
оказаться в будущем перспективными. Например, формула
пересчета
л —А | (Ук-А*к)°1 (олк\
Ak+l = Ak Н т (8.4.5)
vksk
корректно определена и удовлетворяет (8.4.1) при любых
Vk е Rn, для которых vTksk Ф 0. Хорошая и плохая формулы
пересчета Бройдена отвечают выбору vk = sk и vk = ATkyk
соответственно. Барнес (1965), Гэй и Шнабель (1978) предложили
формулу пересчета вида (8.4.5), где vk является проекцией Sk
в евклидовой норме на ортогональное дополнение к Sk-u • • •
..., s*_m, 0 ^ т < л. Это делает возможным для А+
удовлетворить /л+1 соотношениям секущих Ak+\Si = yt, i = k —
— m, ..., k, означающим, что аффинная модель интерполирует
наряду с F{xk) и F(xh+\) еще и F(xi), i = k — m, ..., k—1.
8.5. Упражнения 229
В программных реализациях, где т < п выбирается так, чтобы
Sk-my ..., sk были сильно линейно независимы1), эта формула
пересчета несколько превосходит в работе формулу Бройдена,
однако опыт здесь все еще ограничен. Поэтому мы все же
рекомендуем формулу пересчета Бройдена в качестве
аппроксимации по секущим для решения систем нелинейных уравнений.
8.5. УПРАЖНЕНИЯ
1. Пусть st, ^gR", /=1, ..., л, и предположим, что векторы Si, ...
..., sn линейно независимы. Как бы вы вычислили матрицу А е= ВпХп,
такую, что Asi = \}и i= 1, ..., п> Почему это является плохим способом
построения модели (8.1.1) в том случае, когда направления s\, ..., sn близки
к тому, чтобы быть линейно зависимыми?
2. Покажите, что если
4-1 !]• «М- >-[Л1
то решением задачи
min ||М-Л||2
является
Л+ = Л + I при любом ае= [—1, 1].
Что представляет собой решение в норме Фробениуса? Если F(x) линейно
по х2, то какому из решений следует отдать предпочтение?
3. (а) Выполните две итерации метода Бройдена для
р{х)-[**+4-*у
начиная из х0 = (2, 7)Т и А0 = J (х0).
(Ь) Продолжите выполнение п. (а) (на ЭВМ) до тех пор, пока не станет
||*fc+i ~~ *fc||^(macheps)^2. Чему равно последнее значение Ak? Сравните
его с / (xj).
4. Предположим, что метод Бройдена применяется к функции F: R*->Rn,
у которой fi, ..., fm линейны, m<n. Покажите, что если А0 вычисляется
аналитически или с помощью конечных разностей, то (Ak)i = / (xk), ,
/ = 1, ..., m, для всех k ^ 0, а при k ^ 1 ft (xk) = 0, i = 1, ..., m.
5. Предположим, что /GRnXn, Ь е Rn, F (х) = Jx + b. Покажите, что
если хс и х+ есть две произвольные несовпадающие точки в Rn, такие, что
sc = х+ — хс и ус = F (х+) — F (хс), то / е= Q {ус, sc).
6. Докажите (8.2.2), используя для этого технику доказательства
леммы 8.2.1.
) В результате m зависит от k. — Прим, перев.
230 Гл. 8. Методы секущих для решения систем
7. Предположим, что s е R", s ^ О, и / есть единичная п X я-матрица.
Покажите, что
-тН--
8. Докажите теорему 8.2.4 с (8.2.22) вместо (8.2.16).
9. Примените при счете на ЭВМ метод Бройдена с целью выяснения его
сходимости на функции из примера 8.2.6, используя начальную точку х0 =
= (2, 3)г (которая использовалась для этой же функции в примере 5.4.2).
Почему мы не воспользовались х0 = (2, 3)г в примере 8.2.6?
10. Обобщите лемму 8.2.7 следующим образом: пусть 1 ^ т < л,
где /,GRmX Л, Ьх е= Rm, и функция F2: Rn -> Rn т нелинейна. Предположим,
что для решения F (х) = 0 используется метод Бройдена, и он генерирует
последовательность аппроксимаций якобиана Ло, Ли Л2, ... . Пусть Л*
разделяется на блоки:
№
Aki<=RmXn, Ak9^Rin-m)Xn.
k2~
Покажите, что если А0 вычисляется аналитически или с помощью конечных
разностей, то Akl~J{ для всех k^0f и (Ak2 — Л12) l\ = 0 для всех £>1.
Какой вывод отсюда можно сделать относительно сходимости
последовательности {Ak2\ к истинному значению г2(х )?
11. Численные примеры плохой сходимости {Л*} к /(**) для полностью
нелинейных функций. Примените при счете на ЭВМ метод Бройдена для
выяснения его сходимости на функции из примера 8.2.6, используя начальную
точку х0 = (0.5, 0.5)Т и выводя на печать значения Л*. Сравните последнее
значение Ак с /(**). Проделайте то же самое, используя начальную точку
*о= (2, гу.
12. Предположим, что мы преобразовали переменные х и F(x) так, что
x = Dx-xt F(x) = DF.F(x\
где Dx и DF — положительно определенные диагональные матрицы.
Произведите пересчет аппроксимаций по формуле Бройдена в новых пространствах
переменных и функции, а затем сделайте обратное преобразование к
исходным переменным. Покажите, что этот процесс эквивалентен использованию
формулы пересчета (8.3.1) в исходных переменных х и F(x). [Указание:
новый якобиан 1(х) связан со старым якобианом J(x) соотношением /(£) =
= DFJ{x)D;1.]
13. Докажите лемму 8.3.1.
14. Воспользуйтесь алгоритмами из приложения, запрограммируйте и
пропустите на ЭВМ алгоритм решения систем нелинейных уравнений,
использующий для аппроксимации якобиана метод Бройдена. Когда ваша
программа заработает нормально, постарайтесь подыскать задачу, в которой методом
секущих вырабатывается направление «вверх по склону графика функции>
[т. е. — P(xk)T AiTJ(xk) F(xk) >0], так что необходимо восстановить Ah
переходом к /(**)•
8.5. Упражнения 231
15. Воспользуйтесь леммой 8.1.1 и покажите, что (8.4.2) есть решение
задачи (8.4.3). Затем, используя лемму 8.3.1, покажите эквивалентность
(8.4.2) и (8.4.4) в случае, когда Ас не вырождена и ylAcsc ф 0.
16. (Трудное упражнение.) Подойдите с более удачным объяснением к
тому факту, что «хороший> метод Бройдена (8.1.5) с вычислительной точки
зрения имеет больший успех, чем сплохой» метод Бройдена (8.4.4).
Упражнения 17 и 18 взяты из работы Гэя и Шнабеля (1978).
17. Пусть Ak^RnX я, sit yi GRn,i = Ji!- 1, k, причем sk_} и $k линейно
независимы, и предположим, что A^k-i^* Uk-v
(a) Получите условие на vk в (8.4.5), такое, что Ak, %sk_. =у
(b) Покажите, что матрица Ak+V заданная в (8.4.5), является при
„ -с Sk-\(SlSk-\)
sk-\sk-\
решением задачи:
найти min \\В — Ak \\р
при условии BeQ (yk, sk)f]Q (yk_v sk_{).
18. Обобщите упр. 17 следующим образом: предположите дополнительно,
что для некоторого т < п существуют s^, у. е Rrt, i = k — m, ..., k, такие,
что sk_m, ..., sk линейно независимы и Aks. = у., * = k — m, ..., k — 1.
(a) Получите условие на vk в (8.4.5), такое, что Лл .Sj = */r / = & —
— m, ..., &— 1.
(b) Найдите такой способ выбора vk, что Ak |t заданная в (8.4.5),
являлось бы решением задачи:
найти min || В — Ak ||_
BeRftXn
при условии BeQ (yv s^), i = k — т, ..., k.
9
Методы секущих для безусловной
минимизации
В этой главе рассматриваются методы секущих для решения
задачи безусловной минимизации. В алгоритмах для этой
задачи в качестве производных использовались градиент V/(x) и
гессиан V2/(x). В алгоритмах минимизации градиент должен
быть известен довольно точно как для вычисления направлений
спуска, так и для критериев останова. Из гл. 8 читатель мог
понять, что аппроксимация по секущим не обеспечивает этой
точности. Поэтому в квазиньютоновских алгоритмах
аппроксимация градиента по секущим не используется. С другой
стороны, гессиан можно аппроксимировать с привлечением идей
метода секущих почти таким же образом, как аппроксимируется
якобиан в гл. 8. Это и является темой настоящей главы. Здесь
будут представлены наиболее успешно работающие формулы
пересчета по секущим для гессиана и сопутствующая им
теория. Формулы пересчета не требуют дополнительных
вычислений функции или градиента и вновь приводят к локально
<7-сверхлинейно сходящимся алгоритмам.
Поскольку гессиан есть не что иное, как якобиан системы
нелинейных уравнений У/(лс) = 0, его можно было бы
аппроксимировать, используя технику гл. 8. Однако при этом не
учитывались бы два важных свойства гессиана: он всегда
симметричен и часто положительно определен. Включение этих двух
свойств в аппроксимацию гессиана по секущим — наиболее
важный новый аспект главы. В разд. 9.1 вводится
симметричная формула пересчета по секущим, а в разд. 9Г2 — формула,
сохраняющая к тому же положительную определенность.
Последняя из формул, называемая положительно определенной
формулой пересчета по секущим (или
BFGS-формулой),—наиболее успешно работающая на практике формула пересчета по
секущим для гессиана. В разд. 9.3 представлен еще один вывод
положительно определенной формулы пересчета по секущим,
который приводит к доказательству ее локальной сходимости.
Вопросы программной реализации обсуждаются в разд. 9.4.
9.1. Симметричная формула секущих Пауэлла 233
Глава заканчивается изложением в разд. 9.5 результатов,
касающихся глобальной сходимости положительно определенной
формулы пересчета по секущим, и кратким обсуждением в
разд. 9.6 других аппроксимаций по секущим.
9.1. СИММЕТРИЧНАЯ ФОРМУЛА СЕКУЩИХ ПДУЭЛЛА
Предположим, что решается задача:
min f: R*->R,
был сделан шаг из хс в *+ и мы хотим аппроксимировать
V2f(x+) матрицей #+, используя технику метода секущих.
Следуя рассуждениям разд. 8.1, выясним сначала, что должно
представлять собой соотношение секущих. Если представить
гессиан как матрицу первых производных для системы
нелинейных уравнений у/(х)=0, то аналогом соотношения
секущих (8.1.3) будет
ff+sc = yCf (9.1.1а)
где
sc = х+ — хс, ус = Vf (х+) — V/ (хс). (9.1.1 Ь)
Будем называть (9.1.1) соотношением секущих для задачи
безусловной минимизации. Заметим, что если #+ удовлетворяет
(9.1.1), то квадратичная модель
т+ (х) = f (х+) + Vf (х+)Т (х - х+) +1 (х - х+)т Н+ (х - х+)
удовлетворяет соотношениям m+(x+) = f(x+), Vm+(x+)=Vf(x+)
и Vm+(xc) = S7f(xc). Это еще один способ объяснения
соотношения (9.1.1).
Мы могли бы теперь воспользоваться формулой секущих из
гл. 8 для аппроксимации V2/(*+) по формуле
(Д+И'Яс+(Ус"?А)^ (9.1.2)
$csc
где ffcGRnXn есть аппроксимация V2f(xc). Основная проблема
в связи с (9.1.2) состоит в том, что даже если матрица Нс
симметрична, то (#+)i не будет таковой, если, конечно, ус — Hcsc
не параллелен sc. Мы уже выявили несколько причин, по
которым аппроксимации гессиана следует быть симметричной.
(См., например, упр. 12 из гл. 4.) Поэтому мы стремимся найти
#+, которая бы наряду с (9.1.1) обладала свойством Н+ = Н+.
Поскольку в гл. 8 проектирование в норме Фробениуса на
Q(ycySc) оказалось удачным способом пересчета Ас, в целях
построения симметричной матрицы (#+)2 на основе (#+)i Ра"
зумной представляется идея проектирования (#+)i в норме
234 Гл. 9. Методы секущих для безусловной минимизации
Фробениуса на подпространство S симметричных матриц.
Нетрудным упражнением будет показать, что это достигается
посредством следующих действий:
т \ 1 (т \ м(и \т\ и ■ (ft-*A)'? + Mft-*A)r
(H+h = — {(n+h + (//+){) = пс-\ ^ .
с с
Теперь (#+)2 симметрична (как и #с), но она в общем случае
не удовлетворяет соотношению секущих. Однако можно
было бы рассмотреть продолжение этого процесса, генерируя
(#+)з, (Н+)А, ... по формулам
(H+)2k+l = (H+)2k
т
8cSc
Здесь каждое (#+)2*+i есть ближайшая в Q(yc,sc) матрица
к (Я+)2л, а каждое (#+)2*+2 есть симметричная матрица,
ближайшая к (//+)2*+i (рис. 9.1.1). Как было показано Пауэллом
(1970b) г эта последовательность матриц сходится к
Н+ = НС
(Ус - Hcsc) sl + sc (Ус - Hcsc)T (yc-Hcsvsc)scsTc
т
sisc
(sTcScf
. (9.1.3)
Будем называть формулу пересчета (9.1.3) симметричной
формулой секущих1). Она известна как симметричная
формула пересчета Пауэлла — Бройдена (PSB). Легким
упражнением можно убедиться, что Я+, заданная согласно (9.1.3),
удовлетворяет соотношению секущих (9.1.1) и Н+ — Нс есть
симметричная матрица ранга два. В действительности Дэннис
и Морэ (1977) доказали следующую теорему.
9(У**с)
Рис. 9.1.1. Процесс симметризации, предложенный Пауэллом.
*) В оригинале. — symmetric secant update. — Прим. пере в.
9.1. Симметричная формула секущих Пауэлла 235
Теорема 9.1.1. Пусть матрица Ясбклхя симметрична, sCf
ус е Rrt, sc Ф 0. Тогда единственное решение задачи:
найти min, ||# — Нс\$
ЯеРлХп
при условии Hsc = yc, (Н — Нс) симметрична,
имеет вид (9.1.3).
Доказательство теоремы 9.1.1 аналогично доказательству
теоремы 8.1.1 и изложено в общих чертах в упр. 4.
Теорема 9.1.1 вытекает также из гораздо более общего результата
Дэнниса и Шнабеля (1979), приведенного в гл. 11. Он
гарантирует, что процесс, изображенный на рис. 9.1.1, будет
сходиться к ближайшей для Нс матрице в пересечении двух
указанных аффинных подпространств.
Свойства локальной сходимости квазиньютоновского
метода, использующего (9.1.3), те же самые, что и у метода
секущих для систем нелинейных уравнений, поэтому мы
ограничимся формулировкой приведенной ниже теоремы.
Доказательство является обобщением техники из разд. 8.2; оно излагается
в общих чертах в упр. 5 и 6. Заметим, что рассматриваемый
алгоритм сходится локально к любому изолированному нулю
градиента Vf(x), так как от V2/(jc*) требуется только
симметричность и невырожденность, а положительная определенность
не обязательна.
Теорема 9.1.2 [Бройден, Дэннис и Морэ (1973)]. Пусть
/: Rn-^R дважды непрерывно дифференцируема в открытом
выпуклом множестве Z)cRn, и пусть V2/eLipY(D).
Предположим, что существует **еД такое, что Vf (х*)=0 и V2/' (**) не
вырождена. Тогда найдутся такие положительные постоянные
б и б, что, если IUo — *»ll2 < е и ||Я0 — V2/(^)||2^6, где
матрица Но симметрична, симметричный метод секущих
xk+{ = xk-HklVf(xk), (9.1.4а)
sk = Xk+\ — Xk, y* = V/(**+i) — Vf(xk)9 (9.1.4b)
"JUl = "к -\ f
sk*k
(yk~Hksk>sk)sksl
(9.1.4c)
236 Гл. 9. Методы секущих для безусловной минимизации
корректно определен, а последовательность {**} остается в D
и сходится <7-сверхлинейно к дс#.
В этот момент может показаться, что мы достигли всего,
чего хотели от аппроксимации гессиана по секущим. Однако
симметричная формула секущих имеет одну важную
особенность, которая на практике отрицательно сказывается на его
работоспособности. Матрица #+, заданная согласно (9.1.3),
может не быть положительно определенной, даже если таковой
является Нс и если в Q(yc, sc)f\S найдутся положительно
определенные матрицы. Рис. 9.1.2 наглядно поясняет причину.
Пусть PD есть множество симметричных и положительно
определенных матриц, a QS = Q{yc, sc)f\ S — аффинное
подпространство симметричных матриц, которые удовлетворяют
соотношению секущих. Тогда мы видим, что ближайшая к Нс матрица
в QS может не быть положительно определенной, даже если
QS(]PD не пусто. Более того, поскольку PD является открытым
выпуклым конусом, то может даже и не существовать
ближайшей к Нс матрицы в Q5 П PD-
Поскольку ранее уже подчеркивалась важность иметь
положительно определенный гессиан модели, хотелось бы, чтобы
в рассмотренной выше ситуации Н+ была положительно
определена. В разд. 9.2 читатель найдет полезный способ,
позволяющий этого добиться. Результатом является формула секущих
для аппроксимации гессиана, которая оказывается наиболее
успешной на практике. Она тоже вносит в Нс симметричную
поправку ранга два.
В заключение упомянем тесно связанную с (9.1.3) формулу,
к которой мы хотим еще вернуться в разд. 9.3. Дж. Гринстад-
Рис. 9.1.2. Объяснение, почему симметричная формула секущих может не
давать положительной определенности.
9.2. Симметричные положительно определенные формулы 237
том (1970) была предложена следующая формула пересчета:
„-1 „-1 , {sc-H^yc)yTc+yc(sc-H-'yc)T
УсУс
{Ус>8с-Н7ХУс)УсУТс ,Q , ~
/ т \2 • la.i.oj
[Ус Ус)
Читатель легко догадается, что (9.1.5) есть результат
применения процесса симметризации, изображенного на рис. 9.1.1,
к плохой формуле пересчета Бройдена (8.4.2) и что Н+
является ближайшей к норме Фробениуса матрицей bQ(sc, yc)f\S к
Нс~\ Теорема 9.1.2 справедлива также и для этой формулы
пересчета, но (9.1.5), конечно, разделяет с симметричной
формулой секущих тот недостаток, что она не обязательно дает
положительную определенность #+, даже если Нс
положительно определена и QS (] PD не пусто. Тем не менее, как это
будет видно в разд. 9.3, (9.1.5) имеет интересную связь с
наиболее успешно работающими формулами секущих для
аппроксимации гессиана.
9.2. СИММЕТРИЧНЫЕ ПОЛОЖИТЕЛЬНО
ОПРЕДЕЛЕННЫЕ ФОРМУЛЫ СЕКУЩИХ
В вопросе решения задачи безусловной минимизации с
помощью квазиньютоновского алгоритма много усилий было
направлено на достижение выигрыша в эффективности,
численной устойчивости и глобальной сходимости, обусловленного
симметричностью и положительной определенностью гессиана
модели. В этом разделе будет показано, как строить
симметричные и положительно определенные аппроксимации гессиана
по секущим. Мы ищем решение задачи:
задано: sC9 j/cgR", sc Ф 0,
найти симметричную и положительно определенную #+eRrtXn,
такую, что H+sc = yc. (9.2.1)
Для обеспечения симметричности и положительной
определенности матрицы Н+ воспользуемся аналогом распространенного
в математическом программировании приема: если некоторая
переменная AgR должна быть неотрицательной, то ее
заменяют на /2, где / е R есть новая независимая переменная, на
которую теперь не накладывается никаких ограничений.
Аналогично, как нетрудно показать, матрица #+ будет симметричной
и положительно определенной тогда и только тогда, когда
Н+ = /+/+ для некоторой невырожденной /+ е Rnxn.
Таким образом, (9.2.1) можно переписать как:
238 Гл. 9. Методы секущих для безусловной минимизации
задано: sc, ус е Rn, sc Ф О,
найти невырожденную /+eRnXn, такую, что J+JT+sc = yc.
(9.2.2)
т
Для любого решения J+ задачи (9.2.2) матрица #+ = /+/+
будет решением для (9.2.1).
Даже для п=\ видно, что не существует решения задачи
(9.2.2), если ус ф О не имеет того же знака, что и sc. Поэтому
мы в первую очередь должны определить условия, при которых
(9.2.2) будет иметь решение. Лемма 9.2.1 дает ответ на этот
вопрос, а также предлагает процедуру нахождения /+.
Лемма 9.2.1. Пусть Scj/cgR", sc¥=0. Невырожденная
матрица /£КлХп, такая, что J+J+sc = yc, существует тогда и
только тогда, когда
s*cyc>0. (9.2.3)
Доказательство. Предположим, что существует
невырожденная /+, такая, что J+JT+sc = yc. Обозначим vc = J+sc. Тогда
О < vTv =sTJJ7Ls =sTy .
Это доказывает ту часть леммы, к которой относится
выражение «только тогда-». Часть, относящаяся к «тогда»,
доказывается с помощью приведенных ниже выкладок, но прежде мы
сделаем некоторое отступление, с тем чтобы обсудить условие
sTcyc>0.
Поскольку ус = V/(x+) — V/(jcc), то условие (9.2.3)
эквивалентно условию
sTc4f(x+)>sTc4f(xc), (9.2.4)
которое просто означает, что производная функции f(x) по
направлению sc больше в х+, чем в хс. Это условие будет
обязательно выполняться, если алгоритмом обеспечивается
выполнение нашего второго условия приемлемости шага из разд. 6.3
sTcVf (*+) > PsJV/ (хс)9 р е= (0, 1), (9.2.5)
которое используется для того, чтобы воспрепятствовать
появлению исключительно малых шагов. Даже если критерий
приемлемости шага не нацелен явно на выполнение (9.2.5), то
производимые нашими алгоритмами шаги будут, как правило,
удовлетворять (9.2.4), если только мы не окажемся в области
со значительной отрицательной кривизной.
Вернемся теперь к первой части доказательства леммы 9.2.1.
Она указывает, что для любой /+, являющейся решением
9.2. Симметричные положительно определенные формулы 239
(9.2.2), найдется vc е R", такое, что
Это подсказывает идею следующей процедуры решения (9.2.2):
1. Выбрать /+£RBXfl, такую, что J+vc = yc. Матрица ./+
будет зависеть от vc и ус-
2. Подобрать vc так, чтобы J^se = ve.
Вспомним, в каком месте нашего алгоритма мы находимся,
когда хотим найти #+. Шаг sc определен с помощью
разложения Холесского LCLTC положительно определенного гессиана
модели Нс. Это, по-видимому, будет полностью соответствовать
духу гл. 8, если выбирать матрицу /+ настолько близкой к Lc,
насколько это возможно. Это означает, что мы удовлетворим
приведенному выше шагу 1, выбирая матрицу
J+ = Le+(y<-L/°)V<, (9.2.6)
которая по лемме 8.1.1 является ближайшей к Lc в Q(yc,vc).
Далее шаг 2 требует, чтобы
°е = Ъ*. - Ф. + vciffc~L//Se •• (9-2-7)
последнее выполняется, только если
v=*cVcsc (9.2.8)
при некотором ac£R. Подстановка (9.2.8) в (9.2.7) после
некоторого упрощения дает уравнение
„*_ Я*с _ УТс8с
с ~ sTL LTs ~ 8ТН s '
sc^c^csc 8cncse
которое имеет действительное решение тогда и только тогда,
когда yTesc > О, так как sTcHcsc > 0. Мы выберем
положительное значение квадратного корня
/ uTs V/2
потому что это делает /+ ближе к Lc при ус = Hcsc. В качестве
упражнения предлагается показать, что /+, заданная согласно
(9.2.6) и (9.2.9), не вырождена и, таким образом, является
решением задачи (9.2.2). Это завершает доказательство леммы
9.2.1, поскольку при любой заданной невырожденной Lc,
согласно (9.2.6) и (9.2.9), справедливо утверждение части «тогда»
леммы 9.2.1. □
Итак, выведена симметричная формула секущих, которая
всякий раз, когда это возможно, сохраняет положительную
определенность путем пересчета сомножителя Lc разложения
240 Гл. 9. Методы секущих для безусловной минимизации
Холесского матрицы Нс в сомножитель /+, такой, что
/+/+ = #+. Однако действительно полезной для /+ была бы
форма нижней треугольной матрицы L+, так как тогда мы
имели бы разложение Холесского для #+. Читатель,
по-видимому, уже догадался, как получить L+ из /+ за 0(п2) операций,
привлекая для этого технику пересчета (^-разложения,
введенную в разд. 3.4 и применявшуюся в разд. 8.3. Если для
получения JT+ = Q+LT+ за 0(п2) операций использовать алгоритм
АЗ.4.1, то H+=J+J^ = L+Q^Q+LTl = L+LT+9 и нет никакой
необходимости накапливать Q+. Аналогично, можно получить
1+£>+/,+-разложение Н+ непосредственно из LsDcLc-разложения
Нс за 0(п2) операций путем пересчета LDV-разложения.
Можно также представить (9.2.6) и (9.2.9) непосредственно
в виде формулы пересчета матрицы Нс в #+. Если построить
#+ = /+/+, используя (9.2.6) и (9.2.9), и вспомнить, что#с =
= Lcl7Cy то в результате получим
Н+ = Нс + ^-Ц^. (9.2.10)
ycsc scHc*c
Этот вид формулы пересчета [или, что эквивалентно, заданный
равенством (9.3.5)] был независимо предложен в 1970 г. Брой-
деном, Флетчером, Голдфарбом и Шанно, и формула пересчета
стала известна как BFGS-формула. Мы будем называть ее
просто как положительно определенна^ формула секущих1).
Процедуру прямого пересчета сомножителя Холесского Lc в L+
можно найти в работе Голдфарба (1976). Читатель может
убедиться, что (9.2.10), как и симметричная формула секущих из
разд. 9.1, удовлетворяет соотношению H+sc = yc, и (#+— Нс)
представляет собой симметричную матрицу ранга не более чем
два.
Является ли вообще пригодной эта положительно
определенная формула секущих? Да, она наилучшая среди известных
в настоящее время формул пересчета аппроксимаций гессиана.
Это иллюстрируется примером 9.2.2, где применяются
квазиньютоновские методы, использующие соответственно
симметричную формулу секущих и положительно определенную
формулу секущих для решения той же задачи, которая решалась
в разд. 5.5 методом Ньютона. По аналогии с гл. 8 полагаем
#o = V2f(x0). Однако в разд. 9.4 мы увидим, что на практике
рекомендуется другая стратегия выбора Н0.
Пример 9.2.2. Пусть функция f(xr х2) = (jCj — 2)4 +
+ (aTj — 2)2х~ + (лс2 + I)2. Она имеет точку минимума х* =
= (2,—1)г. В этом случае последовательность точек, выраба-
1) В оригинале — positive definite secant update. — Прим. перев.
9.2. Симметричные положительно определенные формулы 241
тываемых положительно определенным методом секущих,
xk+i = xk-HkWf(xk), (9.2.11а)
«* = хк+1 — хк, ук = V/ (хк+,) — V/ (хк), (9.2.11Ь)
Н^ = Нк + ^-Цф!± (9.2.11с)
УкЧ skHksk
с начальными значениями х0 = (\,\)т и #o = V2/(jc0) такова
(с точностью до восьми значащих цифр на ЭВМ CDC с 14
десятичными разрядами):
Я**)
*0 =
*1 =
*2 =
Xi-
ХА =
*s =■
хь =
v7 =
■ч =
Л"9 =
*ю =
(1
(1
(1.45
(1.5889290
(1.8254150
(1.9460278
1.9641387
1.9952140
(2.0000653
(1.9999853
(2.0
1 У
-0.5 )г
-0.3875 У
-0.63729087)'
-0.97155747)'
-1.0705597 )г
-1.0450875 )'
-1.0017148 У
-1.0004294 )г
-0.99995203)7
- 1.0 У
6.0
1.5
5.12 х Ю-1
2.29 х 10"'
3.05 х 10"2
8.33 х 10~3
3.44 х 10 "3
2.59 х 10"5
1.89 х 10"7
2.52 х 10~9
0
Последовательность точек, которая вырабатывается
симметричным методом секущих (9.2.4), использующим те же самые х0
и #о> такова:
•ч =
Xl =
х2 =
*3 =
х4 =
*5 =
*6 =
*7 =
*8 =
*9 =
Хю =
*11 =
xi2 =
(1
(1
(1.3272727,
(1.5094933,
(1.7711111,
(1.9585530,
(1.9618742,
(1.9839076,
(1.9938584,
(1.9999506,
(2.0000343,
(2.0000021,
(2.0
1 )Г
-0.5 )г
-0.41818182)г
-0.60145121)г
-0.88948020)г
-1.0632382 )г
-1.0398148 )г
- 0.99851156)г
-0.99730502)7"
-0.99940456)г
- 0.99991078)г
- 0.99999965 )7'
-1.0 У
6.0
1.5
6.22 х 10"1
3.04 х Ю-1
5.64 х 10~2
5.94 х Ю-3
316 х 10~3
260 х 10~4
4.48 х 10"5
3.57 х Ю-7
9.13 х Ю-9
1.72 х 10"n
0
242 Гл. 9. Методы секущих для безусловной минимизации
Для достижения такой же точности методу Ньютона требуется
шесть или семь итераций.
Причины, по которым положительно определенная формула
секущих оказалась столь успешной, все еще до конца не
поняты, хотя в следующем разделе предлагается этому некоторое
объяснение. Там мы также обсудим другой вариант пересчета,
вытекающий из рассуждений, аналогичных тем, которые
используются в настоящем разделе для нахождения H+l =J+TJ+l9
такой, что J+TJ+lyc = sc. Результатом является
,-г ,-г , (sc~L7Twc)wTc
J+ = Lc i f .
WW
/ ut„ y/2 (9.2.12)
c \ylH7xyJ сУс
?c>
где снова Hc = LcLl. Можно показать, что использование
формулы Шермана — Моррисона — Вудбери (лемма 8.3.1) и (9.2.12)
дает
(Ус - нА) УТс + Ус (Ус - Hcscf {ус - Hcsc, sc) усутс
yTcsc {Утс*с)2
(9.2.13)
Н+ = НС
Формулу пересчета (9.2.13) часто называют DFP-формулой
по именам ее авторов: Дэвидона (1959), Флетчера и Пауэлла
(1963). Она была первой среди всех когда-либо
предлагавшихся формул секущих, причем ее первоначальный вывод
полностью отличался от приведенного выше. Как легко показать
из (9.2.12), DFP-формула тоже обладает тем свойством, что
матрица Я+ положительно определена, если положительно
определена Яс> и yTcsc > 0. По этой причине мы иногда будем
называть данную формулу пересчета обратной положительно
определенной формулой секущихх).
В начале 70-х годов было проведено множество
исследований по сравнению квазиньютоновских методов, использующих
две введенные в этом разделе формулы секущих [см.,
например, Диксон (1972) и Бродли (1977)]. Единодушно признается,
по-видимому, то, что положительно определенная формула
секущих (BFQS) работает лучше в совокупности с алгоритмами
из гл. 6 и что DFP-формула иногда вырабатывает
вырожденные с вычислительной точки зрения аппроксимации гессиана.
Тем не менее DFP-формула нашла плодотворное применение
!) В оригинале — inverse positive definite secant update. — Прим. пере в.
9.3. Локальная сходимость 243
во многих хорошо зарекомендовавших себя программах, и в
следующем разделе она также будет играть в анализе
важную роль.
9.3. ЛОКАЛЬНАЯ СХОДИМОСТЬ ПОЛОЖИТЕЛЬНО
ОПРЕДЕЛЕННЫХ МЕТОДОВ СЕКУЩИХ
В этом разделе дается альтернативный вывод положительно
определенной формулы секущих и DFP-формулы. Простой
способ вывода, приведенный в предыдущем разделе, все же не
привел к успеху в анализе сходимости, тогда как способ,
рассмотренный в этом разделе, оказался успешным. Мы. увидим,
что если применить в задаче минимизации некоторое
естественное преобразование пространства переменных, то две
симметричные положительно определенные формулы пересчета из
разд. 9.2 получаются из двух симметричных формул пересчета,
рассмотренных в разд. 9.1, в результате применения последних
к преобразованной задаче. Очень тесно с ним связанное
преобразование приводит к результатам, касающимся сходимости.
В гл. 7 мы увидели, сколь важно иметь дело с хорошо
обусловленной задачей минимизации. Задачу минимизации
квадратичной функции можно было бы считать идеально
масштабированной, если бы ее гессиан был единичной матрицей, так как
это приводило бы к сферическим линиям уровня и к тому, что
методы Ньютона и наискорейшего спуска были идентичны. Это
«идеальное» масштабирование будет ключом к нашим выводам
формул.
В разд. 7.1 было показано, что если преобразовать
пространство переменных по формуле
£ = Тх,
то в новом пространстве переменных квадратичной моделью
в окрестности точки х+ будет
m+ (Jt) = f(x+) + [r"rV/ (х)]Т (i -1+) +
+ y(* - *+? [t-th+t~1] (jt - *+),
где #+ есть гессиан модели в исходном пространстве
переменных. Это означает, что градиент переходит в T-~TVf(x), а
гессиан модели — в Т~ТН+Т-Х. Таким образом,
перемасштабирование, приводящее к единичному гессиану модели, построенной
в окрестности точки i+, удовлетворяет соотношению
Т+тН+Т+1 = 1, т. е. Н+ = ТТ+Т+.
Было бы замечательно построить формулу пересчета Нс по
секущим в пространстве переменных, преобразованном с по-
244 Гл. 9. Методы секущих для безусловной минимизации
мощью этой матрицы Т+> так как для получения новой
квадратичной модели использовалось бы идеальное
перемасштабирование. Однако Т+ и #+ заранее не известны, так что
рассмотрим вместо этого произвольную матрицу масштабирования Г,
такую, что _ _
TTT = HeQ(yetse).
Теперь рассмотрим в этом пространстве переменных
симметричную формулу секущих из разд. 9.1. Она имеет вид
Я+ = Яс+ фс (Щ2 • (9ЗД
где
Sc = л + лс = 1 Д^ц. / #с = 1 SC9
до=r"rv/ (*+) - T"rv/W = f ~тУс,
нс = f"THcf"\ н+ = f"TH+f~l.
Читатель может убедиться, что если воспользоваться
приведенными выше соотношениями, с тем чтобы переписать (9.3.1)
заново в исходном пространстве переменных, то в результате
получится
и __„ , {yc-Hcsc)sTcH + Hsc{yc-Hcsc)T (yc-Hcsc,sc)HscsTcH
(9.3.2)
Поскольку Hsc = HTsc = ус для любой симметричной Я е
^Q(#o sc), соотношение (9.3.2) не зависит от конкретных Я
или Т и принимает вид
„ _ г, , (Ус- Нс*с)у1 + Ус(Ус- Hcsc)T {Ус-Нс5с>Зс)УсУТс /Q Q о\
л + — пс-\ т / т \2 » [?•&•&)
Ус*с [УсЧ
а это и есть DFP-формула! Заметим, что если бы Н+ было
заранее известно, то мы смогли бы воспользоваться
матрицей Т+, такой, что Т+Т+ = Н+, и результат оказался тем же
самым.
Другой способ изложения состоит в следующем. Если Нс
симметрична и yTcsc > 0, то для любого Г£КлХя, такого, что
TTT^Q(yCySc)y (9.3.3) является единственным решением
задачи:
найти min || Т~т (Я+ - Нс) Т~{ \\Р
при условии #+ е Q(ус, sc)ПS. (9.3.4)
9.3. Локальная сходимость 245
Это означает, что DFP-формула представляет собой проекцию
Нс на Q(yc,Sc)(]S в рассматриваемой взвешенной норме Фро-
бениуса.
Если применить то же перемасштабирование, использовать
формулу Гринстадта (9.1.5) для пересчета Н7Х в Я+1 и затем
произвести обратное преобразование пространства, то в
результате получится
я-1 = я-1 , (*с - Нс1Ус) 4 + sc (sc ~ Нс1УсУ _
fee
__ (sc-H7lyC>yc)scsl
(yTcscf
(9.3.5)
Простые, но утомительные выкладки показывают, что (9.3.5)
представляет собой выражение, которое получается после
обращения обеих частей равенства (9.2.10), т. е. Я-представления
положительно определенной формулы секущих (BFGS). Таким
образом, если Нс симметрична и yTcsc > 0, то для любой
матрицы ГеКпхп, такой, что ТТТ е Q(yc, sc), положительно
определенная формула секущих является единственным решением
задачи:
найти min \\Т(Н+1 - Hc~l)fT\\
при условии H+^Q(yCi sc)П5. (9.3.6)
Читатель, вероятно, заметил интригующую двойственность,
которой пронизан в разд. 9.2 и 9.3 вывод положительно
определенной и обратной положительно определенной формул
секущих. Поскольку каждая из этих формул пересчета может быть
выведена с помощью преобразования (масштабирования)
пространства переменных, для каждой итерации своего, то
использующие их методы называют иногда методами переменной
метрики.
В доказательстве локальной сходимости положительно
определенного метода секущих центральное место занимает идея
масштабирования. Доказательство показывает, что
последовательность аппроксимаций гессиана {Hk} обладает свойством
ограниченного ухудшения в виде, приведенном в гл. 8. Для
установления этого факта в доказательстве используется
взвешенная норма Фробениуса, подобная (9.3.6), но с заменой Т
на Г», для которой TlТш = V2/ (*,). Это как раз то
масштабирование, при котором матрица Гессе в точке минимума равна
единичной. Если последовательность аппроксимаций гессиана
сходится к V2/(a:#), то это есть предел матриц
перемасштабирования, которые используются в приведенных выше выводах.
Та же техника применяется для доказательства локальной
246 Гл. 9. Методы секущих для безусловной минимизации
сходимости DFP-метода. В этом случае используется норма из
(9.3.4) с Г, замененным на 7V
Доказательство следующей теоремы основано на технике из
разд. 8.2; его можно найти в работе Бройдена, Дэнниса и Морэ
(1973).
Теорема 9.3.1 (Бройден — Дэннис — Морэ). Пусть
выполняются условия теоремы 9.1.2 и дополнительно предполагается,
что V2/(jc#) положительно определено. Тогда существуют
положительные постоянные е и б, такие, что если ||jc0 — х*\\2 ^ е и
||#о — V2/(jc#)||2 ^ б, где матрица Я0 симметрична, то
положительно определенный метод секущих (BFGS) (9.2.11)
корректно определен, а последовательность {xk} остается в D и
сходится <7-сверхлинейно к х%. То же остается в силе, если (9.2.11с)
заменить обратной положительно определенной формулой
секущих (DFP)
„ _ „ , (Ук - Hksk) у1 + У к (Ук - Hksk)T {Уk - Hks* sk) УОш
Hk+i-Hk+ yrSk {угч)2
Этот результат, касающийся сходимости положительно
определенного метода секущих, не является более строгим, чем
теорема 9.1.2, где сформулирован результат относительно
сходимости симметричного метода секущих. Однако положительно
определенный метод секущих работает на практике
значительно лучше, что воспроизводится ниже в примере 9.3.2S В этом
примере также изучается сходимость последовательности
аппроксимаций гессиана {#*} к значению гессиана в точке
минимума V2/(jc#). В примере видно на промежуточных шагах, что
аппроксимации, генерируемые положительно определенной
формулой секущих, более точны, чем генерируемые симметричной
формулой секущих. Такое поведение, обычное на практике,
частично объясняет превосходство положительно определенного
метода секущих.
Другое преимущество положительно определенного метода
секущих связано с выводом формул, с которых начинался этот
раздел. Не составит труда показать, что положительно
определенная и обратная положительно определенная формулы
секущих инвариантны относительно линейных преобразований
пространства переменных, тогда как симметричная формула
секущих не инвариантна (упр. 13). Благодаря инвариантности,
которая разделяется методом Ньютона, но не методом
наискорейшего спуска, соответствующие машинные программы
почти не зависят от масштабирования задачи минимизации.
Пример 9.3.2. Пусть / (х{9 х2) = х\ + (х{ + х2)2 + (е*> - I)2.
Эта функция имеет точку минимума в х*=(0,0)т. В случаях
9.3. Локальная сходимость 247
х0 = (1, 1)г и jc0 = (— 1, 3)г указанным ниже методам требуется
для достижения точности \\хк — juIIoo^IO-8 следующее число
итераций:
Число итераций из
Метод *ь = (1, 1)г х0 = (-1, 3)т
Метод Ньютона 6 11
Положительно определенный метод
секущих, #0 = v2/(*o) 13 20
Симметричный метод секущих
#o = V2/(*0) И 41
Для jc0 = (—1, 3)г ниже приводятся значения #*,
вырабатываемые двумя методами секущих на некоторых
промежуточных и заключительной итерациях. Значение V2/(x) в точке
минимума равно
ни
Значения Hk на первой из итераций k, для которых
IU*+il!<x:
Положительно
определенный Симметричный
т метод метод
секущих секущих
ю-1
кг3
ю~8
Wl2 =
я16 =
я19 =
"5.485 6.996
6.996 11.78
"2.365 2.264"
2.264 4.160
"2.009 1.993"
1.993 4.004
] н2А =
W34 =
#40 =
"16.86 11.35]
11.35 9.645 J
"3.147 3.783"
3.783 6.797
"2.003 2.02 Г
2.021 4.143
В примере 9.3.2 заключительное значение положительно
определенной аппроксимации по секущим согласуется с
V2f(*») в пределах примерно 0.5%. Такое поведение типично
для формул пересчета аппроксимаций гессиана по секущим:
заключительное значение Нк часто совпадает с V2/(jc#) в
нескольких значащих цифрах. На практике случаи, когда
заключительная аппроксимация гессиана заметно отличается от
V2f(*»), по-видимому, менее распространены, чем случай, когда
заключительная аппроксимация якобиана заметно отличается
от /(*,). Одна из причин состоит в том, что, хотя
последовательность аппроксимаций якобиана по секущим обычно не
сходится к /(*»), когда некоторые компоненты F(x) линейны (что
248 Гл. 9. Методы секущих для безусловной минимизации
мы наблюдали в примере 8.2.7), тем не менее аппроксимации
гессиана из этой главы не имеют такой проблемы в
аналогичном случае, когда у Vf(x) имеются линейные компоненты (см.
упр. 14). Это различие обусловлено симметричностью формул
пересчета аппроксимаций гессиана. Более подробную
информацию по данному вопросу можно найти в работе Шнабеля
(1982).
9.4. РЕАЛИЗАЦИЯ КВАЗИНЬЮТОНОВСКИХ
АЛГОРИТМОВ, ИСПОЛЬЗУЮЩИХ ПОЛОЖИТЕЛЬНО
ОПРЕДЕЛЕННЫЕ ФОРМУЛЫ СЕКУЩИХ
В этом разделе обсуждаются вопросы включения формул
секущих в наши квазиньютоновские алгоритмы безусловной
минимизации. Поскольку наиболее успешной аппроксимацией по
секущим для минимизации оказалась положительно
определенная формула секущих (BFGS), то именно этой аппроксимацией
по секущим снабжены алгоритмы из приложения. Нами
представлены формулы пересчета как в нефакторизованном, так и
в факторизованном видах соответственно в алгоритмах А9.4.1
и А9.4.2. Нефакторизованный алгоритм непосредственно
реализует формулу пересчета ранга два (9.2.10). После обращения
к формуле пересчета вызывается процедура обработки
гессиана модели, которая производит разложение аппроксимации
гессиана модели по Холесскому. Факторизованный алгоритм
реализует формулу пересчета в том виде, в каком она была выведена
в разд. 9.2. В нем производится одноранговый пересчет Lc в /+
[формулы (9.2.6) и (9.2.9)], а затем вызывается алгоритм
АЗ.4.1 для вычисления нижней треугольной матрицы L+=/+Q+.
Коль скоро £+£+ представляет собой разложение новой
аппроксимации гессиана по Холесскому, то в факторизованной
форме формулы пересчета процедура обработки гессиана
модели не используется.
Основное преимущество факторизованной формулы
пересчета заключается в том, что общая трудоемкость пересчета
аппроксимации гессиана и получения его разложения по
Холесскому составляет О (я2), тогда как при использовании не-
факторизованной формулы пересчета — О (я3). Недостатком
является то, что для нее добавляется работа по
программированию и отладке, особенно если уже написана программа
обработки гессиана модели. Кроме того, факторизованную формулу
пересчета трудно совместить с криволинейным шагом, так как
для этого шага требуется Нс в явном виде, а также потому, что
обычно имеется возможность записи на место Lc сомножителя
разложения Нс + ас/ по Холесскому. По этой причине мы
9.4. Реализация квазиньютоновских алгоритмов 249
рекомендуем факторизованную формулу пересчета для
разработки программ, использующих линейный поиск или поиск
вдоль ломаной, но не для криволинейного шага. Что касается
курсовых проектов или предварительной исследовательской
работы, то во всех случаях предпочтение может быть отдано не-
факторизованной форме. При использовании факторизованной
формулы пересчета имеется возможность оценивать число
обусловленности матрицы LCy используя для этого алгоритм АЗ.3.1,
и если полученная оценка превосходит величину (macheps)~l/2,
то можно вернуться к матрице Нс = LcLl и воспользоваться
алгоритмом А5.5.1 для того, чтобы внести поправку к Нс
добавлением к ней единичной матрицы, умноженной на
соответствующий скаляр, и Lc заново положить равной сомножителю Хо-
лесского, но теперь уже для этого измененного гессиана. Ради
простоту мы исключили эту возможность из алгоритмов,
приведенных в приложении.
Единственная дополнительная особенность обоих
алгоритмов, реализующих формулу пересчета, состоит в том, что
пересчет не происходит в следующих двух случаях. В первом он
пропускается, если5*#с^0, так как иначе Н+ не была бы
положительно определенной. В действительности мы пропускаем
формулу пересчета, когда
5^<(macheps)^||5cy|^|^ (9.4.1)
На стадии линейного поиска выполнение этого условия можно
фактически всегда предотвратить, используя алгоритм
линейного поиска A6.3.1mod, который обеспечивает выполнение
условия sTcyc^ — 0.1v/(*c)rsc. Что касается алгоритма
доверительной области, то может встретиться ситуация (9.4.1). Во втором
случае, если ус достаточно близко к Hcsc, то нет никакой
необходимости производить пересчет. Мы пропускаем пересчет, если
величина каждой компоненты ус— Hcsc оказывается меньше,
чем ожидаемый уровень шума в этой компоненте.
Необходимо также обсудить вопрос выбора начальной
аппроксимации гессиана Я0. В отличие от практики решения
систем нелинейных уравнений здесь не принято брать Я0, равной
конечно-разностной аппроксимации гессиана V2/(jc0). Одна
причина заключена в стоимости этой аппроксимации с точки
зрения вычислений функции и градиента. Другая состоит в том,
что методы секущих для минимизации исходят из того, чтобы
начинать с положительно определенной аппроксимации и
затем таковой ее поддерживать, а значит, матрица Н0 должна
быть положительно определенной. Однако нет никакой
гарантии, 4jo V2/(x0) будет положительно определена. Если гессиан
не обладает положительной определенностью, то, используя
250 Гл. 9. Методы секущих для безусловной минимизации
технику разд. 5.5, его можно изменить, внеся некоторое
возмущение, и получить положительно определенную матрицу, но
тогда возникает сомнение—а оправданы ли затраты на
конечно-разностную аппроксимацию.
Вместо этого минимизационные алгоритмы секущих
принято начинать с Н0 = I. Такая Я0, конечно, положительно
определена, и это приводит к тому, что первый шаг делается в
направлении наискорейшего спуска. Вспоминая обсуждение
вопросов масштабирования в разд. 7.1, читатель мог догадаться,
что мы обобщаем этот выбор, полагая #0 = D*, что заставляет
делать первый шаг в масштабированном направлении
наискорейшего спуска.
Одна из проблем, связанных с выбором Н0 = I или £>*,
состоит в том, что при этом не учитывается масштаб f{x). По
этой причине ||//oil может отличаться от ||V2/(jc0)H на много
порядков, что потребует от алгоритма чрезмерно большого
количества итераций. В целях преодоления этих трудностей
предлагались различные стратегии; так, Шанно и Фуа (1978а)
использовали частный случай некоторой более общей идеи Орена
(1974), производя предварительное умножение Я0 на у0 =
«(#o5o/5o^oso) непосредственно перед первым пересчетом. Это
дает то, что Й0 =уоН0 удовлетворяет соотношению sj//0s0 = sj#0,
которое представляет собой некоторый ослабленный вариант
соотношения секущих. Если f(x) есть квадратичная функция,
то гарантируется, что области, в которых лежат собственные
значения Й0 и V2/(*0), перекрываются, и вообще это приводит
к тому, что значения диагональных элементов Я0 в большей
степени начинают походить на диагональные элементы V2/(jco).
После такого предварительного умножения производится
обычный пересчет. Как показывает вычислительный опыт, эта
модификация может улучшить работу минимизационных
алгоритмов секущих.
Из-за наличия некоторых небольших трудностей с
использованием модификации Шанно и Фуа в нашей модульной системе
алгоритмов нами применялась другая модификация. Мы просто
полагали
#0 = max{|/(jc0)|, typ/}•/&
где typ/ есть задаваемое пользователем характерное значение
f(x). Эта формула имеет тот очевидный недостаток, что она
чувствительна к прибавлению константы к f(x). Тем не менее
в экспериментах, выполненных Фрэнком и Шнабелем (1982),
она оказалась наиболее успешной среди различных стратегий,
включая предложенную Шанно и Фуа. Нашими алгоритмами
по вычислению Н0 являются А9.4.3 в нефакторизованном
случае и А9.4.4 в факторизованном случае. Благодаря модульной
9.4. Реализация квазиньютоновских алгоритмов 251
структуре пользователь может также полагать Н0 равной
конечно-разностной аппроксимации гессиана S/2f(x0).
В примере 9.4.1 применяется положительно определенный
метод секущих для решения той же задачи из примера 9.2.2,
используя теперь уже Н0 = 1 и H0 = \f(x0) |/. Результаты
использования #0 = |/(*о)|/ несколько лучше, чем при Я0 =
= V2/(jc0), тогда как при использовании Н0 = 1 они гораздо
хуже. Пример 9.4.2 демонстрирует результаты использования
#о = |/(л:о) |/ вместо Я0 = У2/(х0) на задаче из примера 9.3.2.
При использовании положительно определенной формулы
секущих вместо аналитически или конечно-разностно заданного
гессиана в наших алгоритмах минимизации не нужно делать
каких-либо других изменений сверх тех, что упоминались в этом
разделе.
Пример 9.4.1. Пусть / (хр х2) = (д:, — 2)4 + (*, — 2)2 х\ +
+ (*2 +1)2. Точкой минимума здесь является jc*= (2, — 1)г.
Приведенное ниже количество итераций требуется
положительно определенному методу секущих (9.2.11) для достижения
точности \xk — *J| ^ 10~8 при использовании указанных
значений Я0:
Количество
#0 итераций
V2/(*0) Ю
1/(*Ь>|/ 8
/ 24
Пример 9.4.2. Пусть / {хи х2) = х\+ (х{ + х2)2 + (е*>- I)2.
Точкой минимума здесь является х*=(0,0)г. Указанное
количество итераций требуется положительно определенному
методу секущих (9.2.11) для достижения из *о = (1,1)г и хо =
= (—1,3)г точности \\xk — *«ll^ 10-8 при использовании
следующих значений Я0:
Количество итераций Количество итераций
#0 при х0 = (1, 1)г при х0 = {— 1, 3)г
V7(*0) 13 20
\f(x0)\I И 18
Если Hq = /, то полный шаг метода секущих из х0 в х\ = х0 —
— V/(*0) приводит к увеличению значения /(*).
252 Гл. 9. Методы секущих для безусловной минимизации
9.5. ЕЩЕ ОДИН РЕЗУЛЬТАТ,
КАСАЮЩИЙСЯ
СХОДИМОСТИ ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННЫХ
МЕТОДОВ СЕКУЩИХ
Пауэллом (1976) был получен сильный результат относительно
сходимости положительно определенного метода секущих в
случае, когда он применяется к сильно выпуклой функции и
используется в совокупности с линейным поиском, который
удовлетворяет условиям, приведенным в разд. 6.3.1. Этот результат
приведен ниже. Поскольку здесь имеется линейный поиск, эта
теорема представляет собой результат, касающийся в
некотором смысле глобальной сходимости положительно
определенного метода секущих. Она имеет и другую привлекательную
особенность: в ней не делается никаких предположений
относительно начального значения аппроксимации гессиана Но, за
исключением лишь того, что она должна быть положительно
определенной.
Мы не даем доказательства теоремы 9.5.1, так как оно мало
что добавляет к общему представлению, но интересующимся
студентам рекомендуется все же его в дальнейшем изучить.
Для стимулирования интереса читателя заметим, что остается
неизвестным — справедливо ли утверждение этой теоремы для
DFP-метода.
Теорема 9.5.1 [Пауэлл (1976)]. Пусть выполнены
предположения теоремы 9.3.1, и, кроме того, пусть гессиан V2f(x)
положительно определен для каждого х. Допустим имеются
произвольные xo^Rn и положительно определенная симметричная
матрица Я0. Пусть последовательность {**} определяется
соотношениями
Pk = - Hklvf (**)• xk+i = xk + V*>
где Xk выбирается так, чтобы выполнялись (6.3.3) и (6.3.4),
значение %k = 1 используется всякий раз, когда оно допустимо,
и Hk+i задается согласно (9.2. lib, с). Тогда
последовательности {xk} и {#*} корректно определены, и {#*} сходится ^-сверх-
линейно к х*.
9.6. ДРУГИЕ ФОРМУЛЫ СЕКУЩИХ ДЛЯ
БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
Много формул секущих было предложено для минимизации, не
считая тех, что уже упоминались в этой главе. По-видимому,
ни одна из них не имеет преимущества над положительно
9.6. Другие формулы секущих 253
определенной формулой секущих при использовании их как
средств общего назначения. В данном разделе кратко
упоминаются некоторые из этих «других» формул пересчета в
большей степени из-за того, что они представляют исторический
интерес.
До сих пор наши формулы секущих для минимизации
представляли собой симметричные поправки ранга два к Яс,
которые обеспечивали выполнение соотношения секущих H+sc = ус-
Не составит труда показать, что существует единственная
симметричная поправка ранга один к Н€, которая удовлетворяет
соотношению секущих. Это — симметричная одноранговая
формула пересчета (SRl-формула)
Н,=НС+ ^c-HcSc)(yc-Hcsc)T (g бЛ)
(Ус — HcSc) sc
Неизбежным недостатком этой формулы пересчета является то,
что она не обязательно вырабатывает положительно
определенную #+, если даже Нс положительно определена и s*yc > 0, да
и знаменатель иногда оказывается фактически нулевым, тогда
как в тех же случаях положительно определенная формула
пересчета работает нормально.
Бройден (1970) был первым, кто рассмотрел непрерывный
класс формул пересчета
гг / v „ , (Ус-Нс8с)у1 + Ус(Ус-Нс8с)Т (Ус-Нс8с>5с)УсУ1
я+(ф)=Яс+ г* ш—
- Ф (sIHs) Г-£ ?£££-1 \-¥ f&JT, (9.6.2)
П с сс,1уТс*с sTcHcsc\lyTcsc sTcHcsc\
который включает в себя DFP-формулу при ср = 0,
положительно определенную формулу секущих (BFGS-формулу) при
Ф= 1 и SRl-формулу при 4> = slHcsc/(slHcsc — slyc). Каково бы
ни было феР, матрица #+(ф)—- Нс есть симметричная
матрица ранга два, строки и столбцы которой представляют, собой
линейные комбинации векторов ус и Hcsc. Были проведены
значительные теоретические исследования этого класса формул
пересчета и некоторых его обобщений. Они широко
обсуждаются в работе Флетчера (1980). Однако эти исследования не
привели к появлению формулы пересчета, которая бы
превосходила на практике BFGS-формулу.
Интересно, что все представители класса (9.6.2), такие, что
#+(ф)—Нс имеет одно положительное и одно отрицательное
собственное значение, могут быть эквивалентно выражены как
„ ж/ , {Ус - Hcsc) fc+vc (Ус ~ Hcsc)T (Ус-Нс*с>8с)*Л /Q ~ о\
°cse \°csc)
254 Гл. 9. Методы секущих для безусловной минимизации
где vc есть линейная комбинация векторов ус и H€sc [см. Шна*
бель (1977) или упр. 22]. В частности, положительно
определенная формула секущих (BFGS-формула) соответствует
выбору
"о = Ч7+ТУс + 1^тН*> (9-6-4)
где ac = (#£sc/s£#csc)1/2. Таким образом, положительно
определенную формулу секущих можно получить с помощью
рассмотренных в разд. 9.3 взвешенной нормы или способа вывода,
основанного на масштабировании. С этой целью нужно взять ТТТ
равной соответствующей выпуклой комбинации матриц Нс и //+.
Другой класс формул секущих для минимизации, который
привлек к себе значительное внимание, состоит из так
называемых «проекционных, оптимально обусловленных» формул
Дэвидона (1975) [см. также Шнабель (1977)]. Для методов,
использующих эти формулы пересчета, могут быть тоже
установлены некоторые интересные теоретические свойства, но при
численных проверках [см., например, Шанно и Фуа (1978b)]
они работали не лучше, чем BFGS-метод.
9.7. УПРАЖНЕНИЯ
1. Приведите несколько причин, по которым аппроксимация гессиана по
секущим должна быть симметричной.
2. Покажите, что задача
найти min || В — А \\р при условии, что В симметрична,
B«=R*Xn
имеет решение
Р_ А + Ат
3. Пусть Я+ вычислена по симметричной формуле секущих (9.1.3).
Убедитесь, что H+Sc = ус и что Я+ — Нс представляет собой симметричную
матрицу ранга не более чем два.
4. Докажите теорему 9.1.1. [Указание: воспользуйтесь техникой
доказательства теоремы 8.1.1 и покажите, что если Н+ задано согласно (9.1.3) и
ffeRnx« таково, что Н — Нс симметрично и Hsc = ус> то (Я — Hc)sc =
=*(H+ — Hc)sc и \\(H-He)t\\2> II (Я+ — #с)/||2 для любого /, такого, что
tTsc = 0. Затем для завершения доказательства воспользуйтесь упр. 11 из
гл. 3.]
В упр. 5 и 6 намечается в общих чертах доказательство теоремы 9.1.2.
Она взята из работы Бройдена, Дэнниса и Морэ (1973).
б. Пусть Я+ задано согласно (9.1.3), Яф = У2/(**) и Рс = / — s^/sjsc.
Используя предположения теоремы 9.1.2 и тождество
н^-н—рш rxvn . ftfe-*A)£ , *с(Ус-н**с)Трс /ОТ1.
Я+ — Яф ■- Ре {ifс — Я.) Ре Н f 1 J, , (9.7.1)
sesc sasa
9.7. Упражнения 255
покажите, что Н+ удовлетворяет неравенству
ин+ -н.h<\\нс-н.\\f+i(ii*+ -*л+и*с-х.и <9-7-2)
которое аналогично (8.2.3). Воспользовавшись (9.7.2) и техникой
доказательства линейной сходимости метода секущих (теорема 8.2.2), докажите
локальную ^-линейную сходимость симметричного метода секущих.
6. Воспользуйтесь (9.7.1) для доказательства более сильного, чем (9.7.2),
неравенства
||».-*.|1,<11*«||,-тРЬ7(7Йг)!+
+ \ (11*+ - хЛ + \\хс- xj2), (9.7.3)
где Ес = Нс — //*. Используя (9.7.3) и технику доказательства
сверхлинейной сходимости метода секущих, докажите локальную ^-сверхлинейную
сходимость симметричного метода секущих.
7. Докажите, что матрица #eRrtx« положительно определена и
симметрична тогда и только тогда, когда Н = JF для некоторой
невырожденной /«= R*x«.
8. Покажите, что если матрица /+ задана согласно (9.2.6) и (9.2.9) и
если HC=^LCLTC> то #+ = /+/+ имеет вид (9.2.10) и не зависит от выбора
знака в (9.2.9).
9. Предположим, что Hcsc = ус. Чему равно значение /+, заданное
согласно (9.2.6) и (9.2.9)? К чему приведет изменение знака в правой части
(9.2.9) с плюса на минус? Каким образом это оправдывает выбор знака
в (9.2.9)?
г
'С9
10. Пусть матрица /+ задана согласно (9.2.12), #+ = /+/+ и He=*LcL(
Покажите, что (9.2.12) дает
, _ ! vJ Нд1УсУсН'е
scHc Уснс Ус
Затем покажите, что матрица (9.7.4) представляет собой обратную к (9.2.13).
П. Покажите, что в обозначениях, следующих за (9.3.1), соотношения
(9.3.1) и (9.3.2) эквивалентны.
12. Проработайте доказательство теоремы (9.3.1) с помощью статьи
Вройдена, Дэнниса и Морэ (1973).
13. (а) Покажите, что положительно определенная формула секущих
инвариантна относительно (рассмотренных в разд. 9.3) линейных
преобразований пространства переменных, а симметричная формула секущих — нет.
(Ь) Выведите несимметричную одноранговую формулу, которая
инвариантна относительно линейных преобразований пространства переменных.
14. (а) Пусть функция
f(xv *2)e*l + 2*1*2 + 2*1 + *2-
256 Гл. 9. Методы секущих для безусловной минимизации
Она имеет минимум в дг» = (О, 0)г, и
Для Хо = (1, —1)г и Н0 =* V2/(*o) покажите, что положительно определенный
метод секущих вырабатывает последовательность аппроксимаций гессиана
{Я*}, обладающую свойством
lim #* = V2f(*J,
£->оо
и что симметричный метод секущих вырабатывает идентичную
последовательность итераций {**}, но при этом последовательность аппроксимаций
гессиана {#*} обладает свойством
й.М! ?]•
[Указание: обобщите технику доказательства леммы 8.2.7.]
(b) Обобщите п. (а) на случай произвольной задачи, в которой градиент
Vf(x) линеен в некоторых из его компонент V/(*),-, причем Vf(x<>) имеет
нулевые значения во всех этих компонентах.
(c) Установите экспериментально, как изменятся п. (а) и (Ь), если
V/(jco) имеет ненулевые значения в тех компонентах Vf(x), которые линейны.
15. Дана функция
f (xlt х2) = х\ + х\ + х\.
Она имеет минимум в х+ = (О, 0)г, и
Для Хо = (0, —1)г и Но = I покажите, что положительно определенный
метод секущих и симметричный метод секущих вырабатывают идентичные
последовательности точек {xk} и аппроксимаций гессиана {#*}, а также, что
дия*-[£ Я-
16. Запрограммируйте минимизационный алгоритм из приложения А,
который использует положительно определенную формулу секущих. Сделайте
прогон вашего алгоритма на какой-либо тестовой задаче из приложения В.
Затем замените формулу секущих в вашем алгоритме конечно-разностной
формулой аппроксимации гессиана (оставляя при этом неизменной остальную
часть алгоритма) и сделайте заново прогон вашего алгоритма на той же
самой задаче. Как соотносятся количества итераций, требуемых этими двумя
методами для решения одной и той же задачи? Как соотносятся количества
вычислении функции и градиента? (Не забудьте учесть вычисления функции
и градиента, потребовавшиеся при конечно-разностной аппроксимации
гессиана.) Как соотносятся длительности счета?
17. Запрограммируйте минимизационный алгоритм из приложения А,
который использует положительно определенную формулу секущих и
модифицированный линейный поиск. Сделайте прогон вашего алгоритма на той же
самой тестовой задаче из приложения В.
(а) Как часто происходит обращение к этой модификации линейного
поиска, т.е. как часто точка х+, которую дает традиционный линейный поиск,
не удовлетворяет неравенству
V/ (х+)г (*+ - хс) > (0.9) V/ (хс)т (*+ - хс) ?
9.7. Упражнения 2$?
(b) Насколько близким в ваших тестовых задачах оказывается
последнее значение Нк к V2f(xk)? Попробуйте найти случаи, в которых это
расхождение велико.
18. Пусть /: R"-*R есть положительно определенная квадратичная
функция с гессианом Яе R"X\ хс и х+ — две произвольные несовпадающие
точки в R", s = x+ — Хс, у = Vf(x+)—Vf(Xc). Покажите, что диапазон
собственных значений матрицы Н содержит собственное значение матрицы
(sTy/sTs)I.
19. Что представляет собой шаг метода секущих хх = х0 — HolVf(xQ)
для задачи и начальных точек из примера 9.4.2, если #0 = |/(*0) |/? А если
#0 = /? Прокомментируйте результаты сравнения.
20. Покажите, что //+, заданная согласно (9.6.1), является единственной
матрицей, для которой H+sc = ус, и (Н+ — Нс) представляет собой
симметричную матрицу ранга один.
21. Убедитесь, что SRl-формула (9.6.1) соответствует выбору ф =
= sTcHcsc/(sTeHcsc-sTcyc) в (9.6.2).
22. (а) Покажите, что если vc в у с + oHcsc> где or — решение любого
из уравнений
и чГ , Т =*= (У1*с) (81Нс*с) /07-.
а (ус - Hcscy sc + y'csc = -j-—\—f , , (9.7.5)
то (9.6.3) совпадаете (9.6.2).
(b) Воспользуйтесь (9.7.5) и докажите, что положительно определенная
формула секущих [ф = 1 в (9.6.2)] эквивалентна (9.6.3) при vc, заданном
согласно (9.6.4).
Заключительное программное замечание
На этом завершается изложение основного материала книги, посвященного
методам решения задач безусловной оптимизации и нелинейных уравнений
малой и средней размерности без специальной структуры. В последних двух
главах обсуждаются обобщения этих методов на задачи, существенной
особенностью которых является их специальная структура. Важным примером
служит задача оценивания параметров по нелинейному принципу
наименьших квадратов. Это частный случай безусловной минимизации, который
составляет тему гл. 10. В гл. 11 рассматривается более общий класс задач, где
часть матрицы производных определяется легко, а остальная часть—-нет.
К этой категории относятся задачи с разреженной матрицей производных.
Мы кратко обсуждаем разреженные задачи, а затем даем вывод и анализ
сходимости методов секущих с минимальными поправками, справедливые для
любой задачи из указанного общего класса.
10
Нелинейная задача о наименьших
квадратах
В этой главе обсуждается решение нелинейной задачи о
наименьших квадратах, введенной в гл. 1. Эта задача тесно
связана с задачами, безусловной минимизации и решения
нелинейных уравнений, которые уже обсуждались в книге, и проработка
материала будет состоять главным образом из применения
представленной нами методики. В разд. 10.1 заново вводится
нелинейная задача о наименьших квадратах и обсуждаются
производные, имеющие далее для нас важное значение. В разд. 10.2
и 10.3 объясняются два различных подхода к построению
алгоритмов для нелинейной задачи о наименьших квадратах.
Первый из них наиболее тесно связан с решением систем
нелинейных уравнений и приводит к алгоритмам Гаусса — Ньютона и
Левенберга —Маркварта. Второй, тесно связанный с
безусловной минимизацией, приводит к методу Ньютона для
нелинейных наименьших квадратов, а также к успешно работающим
методам секущих. Конечно, методы этих двух типов тесно
связаны друг с другом, и нами используется эта связь. В разд. 10.4
кратко упоминаются некоторые другие аспекты проблемы
нелинейных наименьших квадратов, включающие критерии
останова и обработку смешанных линейно-нелинейных задач о
наименьших квадратах.
10.1. ПОСТАНОВКА НЕЛИНЕЙНОЙ ЗАДАЧИ
О НАИМЕНЬШИХ КВАДРАТАХ
Нелинейная задача о наименьших квадратах имеет вид
т
найти mins(x) = ±R(x)TR(x) = YYlri№2> (ЮЛЛ)
где т> п, функция невязки
R:Rn-*Rm
260 Гл. 10. Нелинейная задача о наименьших квадратах
нелинейна по х, и черед п(х) обозначена /-я компонента
функции /?(дг). Если R(x) линейна, то (10.1.1) представляет собой
линейную задачу о наименьших квадратах, решение которой
обсуждалось в разд. 3.6. Нелинейная задача о наименьших
квадратах обычно возникает из приложений, связанных с
наилучшим приближением данных, где стараются наилучшим образом
приблизить данные (ti9 yi), i = l, ..., m, с помощью модели
т(х, t)1), которая нелинейна по х. В этом случае ri(x) =
= m(x,ti) — уi и нелинейная задача о наименьших квадратах
заключается в таком выборе х, что приближение является
настолько близким к данным, насколько это возможно с точки
зрения минимизации суммы квадратов невязок ri(x). Обычно т
гораздо больше, чем п (например, п = 5, т= 100). Выбор
суммы квадратов в качестве меры для наилучшего приближения
данных оправдывается статистическими соображениями [см.,
например, Бард (1970)]. В статистической литературе, однако,
та же задача записывается так:
п
найти min S (р) = 1У (/ (р, xt) - yt)\
где р есть переменная, состоящая из р параметров, /((J, х) —
моделирующая функция, и имеется набор данных,
представляющих собой п точек (xt, yi), х\ е Rm, yt-ER, m^l. (Иногда
вместо S и p используются другие символы.) В целях
согласования обозначений с остальной частью книги мы будем
использовать принятую в численном анализе запись (10.1.1).
Нелинейная задача о наименьших квадратах исключительно
тесно связана с ранее изучавшимися в этой книге задачами.
Так, при т — п она включает в себя как частный случай задачу
решения системы нелинейных уравнений, и для любого
значения т она представляет собой лишь частный случай задачи
безусловной минимизации. Причины, по которым мы не
рекомендуем решать ее с помощью программ безусловной
минимизации общего назначения, станут ясными далее в этой главе.
Главным образом это — желание учесть специальную структуру
(10.1.1). Приступая к делу, исследуем производные функции
R(x) и f (x) = -^R(x)T R(x).Пример нелинейной задачи о
наименьших кв.адратах и ее производных дан в конце этого раздела.
Матрица первых производных для R(x) — это просто
матрица Якоби J(x)(=Rmxn, где J(x)if = dn(x)/dxf. Таким образом,
аффинной моделью функции R(x) в окрестности точки хс будет
Mc(x) = R(xc) + J(xc)(x-xc),
*) Не следует путать обозначаемые одним и тем же символом т
количество элементов в наборе данных и модель. — Прим. перев.
10.1. Постановка нелинейной задачи 261
что является обобщением на случай тфп аффинной модели
для системы нелинейных уравнений, которой мы пользовались
на протяжении всей книги. Эта модель будет базовой для
обсуждаемых в разд. 10.2 методов, которые связаны с
интерпретацией нелинейной задачи о наименьших квадратах как
переопределенной системы уравнений.
В разд. 6.5 мы видели, что первой производной от /(*) =
= -^R(x)TR(x) является
т
V/ (х) = Е г, (д) ■ vr, (*) = / (xf R (х).
Аналогично, вторая производная
т
V2/ (х) = £ (Vr, (х) • Vr{ (х)Т + г,(х) • VV, (х)) =
1 = 1
= J(x)TJ(x) + S(x),
где
m
S(x)AZrl(x)-V2rl(x)
обозначает в V2f(x) информацию о производных второго
порядка. Тогда квадратичной моделью для f(x) в окрестности хс будет
тс (х) = f (хс) + V/ (хс)Т (х - хс) + 4 (х - хс)т V2/ (хс) (х - хс) =
= ±R {хс)т R (хс) + R (хс)т J (хс) (х - хс) +
+ j(x-xc)T(J(xc)4(xc) + S(xc))(x--xc), (10.1.2)
что представляет собой специальную форму квадратичной
модели для минимизации целевой функции вида (10.1.1),
полученную из разложения в ряд Тейлора.
Согласно (10.1.2), метод Ньютона применительно к (10.1.1)
имеет вид
x+ = x,-(J(xe)4(xe) + S(xJ)-4(xerR(xe). (10.1.3)
Несомненно, (10.1.3) был бы быстрым локальным методом
для нелинейной задачи о наименьших квадратах, так как он
является локально ^-квадратично сходящимся при стандартных
предположениях. Трудность полномасштабного использования
ньютоновского подхода состоит в том, что S(x) обычно либо
отсутствует, либо получение ее затруднительно, а аппроксимация
262 Гл. 10. Нелинейная задача о наименьших квадратах
с помощью конечных разностей слишком дорога. Хотя
аппроксимация по секущим часто используется на практике, применять
ее ко всему выражению W2f(x) нежелательно, поскольку часть
этого выражения — / (х) TJ (х) — будет в нашем распоряжении.
Это связано с тем, что матрица J(x) должна быть обязательно
вычислена (аналитически или с помощью конечных разностей)
при вычислении Vf(x). Методы разд. 10.3 будут относиться к
методам безусловной минимизации, несмотря на то что мы
будем использовать структуру квадратичной модели (10.1.2) при
решении нелинейной задачи о наименьших квадратах в случае,
если S(x) недоступна в аналитическом виде.
Обсуждая различные методы для нелинейной задачи о
наименьших квадратах, мы хотим различать между собой задачи
с нулевой невязкой, малой невязкой и большой невязкой. Эти
термины относятся к значению R(x) [или f(x)] в точке
минимума хщ для (10.1.1). Задача, для которой /?(**) = 0, называется
задачей с нулевой невязкой; применительно к наилучшему
приближению данных это означает, что модель т(х+, t) точно
приближает yi в каждой точке набора данных. Различие между
задачами с малой и большой невязкой мы поясним в разд. 10.2.
Окажется, что методы из разд. 10.2 работают лучше на задачах
с нулевой и малой невязкой, чем на задачах с большой невязкой,
тогда как методы из разд. 10.3 одинаково эффективны во всех
этих случаях.
Пример 10.1.1. Предположим, что мы хотим наилучшим
образом приблизить данные (/,-, yi), i= 1, ..., 4, с помощью мо-
дели т(дс, t) = etXl -\-etx> исходя из принципа нелинейных
наименьших квадратов. Тогда R: R2-*R4, ri(x) = etiXl=etiX* — yh
i= 1, ..., 4, и нелинейная задача о наименьших квадратах
состоит в минимизации f (х) = -^R(*)TR(*)• Таким образом, /(дс)е
е R4*2,
Г txeUXx txeUXl-\
t2etx> t^-**
tze^ heix-
L /4e'<*« iAetiX7 J
Кроме того, V/ (x) e R2,
V/ (xf = R (x)TJ(x) = (tn (x) ие**\ t rt (x) t^A
и V2fWeR«2. Используя
/(*) =
10.2. Методы типа Гаусса — Ньютона 2бЗ
и 5 (л:) = £Li ri (*) V2r, (л;), имеем
V2fW = J(x)TJ(x) + S(x) =
Г Z &'л (г, (х) + е'А) £ йе** WV ~|
= I *~{ ("1 I
Z &'' (*'+*2) £ /V*(г, (*) + а'Л)
Li=i ,=i J
10.2. МЕТОДЫ ТИПА ГАУССА — НЬЮТОНА
Первый из рассматриваемого нами класса методов решения
нелинейной задачи о наименьших квадратах получается в
результате использования аффинной модели для R(x) в окрестности хс:
Мс (х) = R (хе) + J (хс) (х - хс)9 (10.2.1)
где Мс: Rn->Rm и т>п.
Мы не можем в общем случае рассчитывать найти х+, для
которого Мс(х+)= 0, так как это — переопределенная система
линейных уравнений. Однако логичным здесь будет способ
использования (10.2.1) для решения нелинейной задачи о
наименьших квадратах, состоящий в выборе в качестве следующей
итерации х+ решения линейной задачи о наименьших квадратах:
найти min -J-II Мс (х) Щ А тс (х). (10.2.2)
Предположим, что J{xc) имеет полный столбцовый ранг.
Тогда, как мы убедились в разд. 3.6, решением для (10.2.2)
является
х+ = хе- (J (хе)Т J (хс)Г1 J (хс)Т R (хс). (10.2.3)
Обычно мы, конечно же, не вычисляем *+ согласно (10.2.3), а
вместо этого всегда решаем (10.2.2), используя (^-разложение
для ](хс).
Итерационный метод, состоящий в использовании (10.2.3) на
каждой итерации, называется методом Гаусса — Ньютона. Для
того чтобы понять его поведение вблизи решения х* задачи
(10.1.1), сравним его с методом Ньютона для нелинейных
наименьших квадратов, заданным формулой (10.1.3). Два
выражения отличаются лишь членом S(jc), входящим в методе Ньютона
в матрицу вторых производных J{xc)TJ(xc) + S(xc),uo зато
опущенным в методе Гаусса — Ньютона. Другими словами,
единственное различие между квадратичной моделью тс{х), (10.1.2),
из которой получается метод Ньютона, и квадратичной моделью
/йс(*), (10.2.2), которая дает метод Гаусса — Ньютона, состоит
264 Гл. 10. Нелинейная задача о наименьших квадратах
в том, что слагаемое, соответствующее S(xc) в S/2f(xc),
отсутствует в thc(x). Поскольку метод Ньютона в рамках
стандартных предположений сходится локально и ^-квадратично, то, как
читатель мог догадаться, успех применения метода Гаусса —
Ньютона будет зависеть от того, насколько важным
оказывается опущенное слагаемое S(xc), т. е. от того, насколько
большой вклад оно вносит в V2f(xc) = J(xc)TJ{xc) +S(xc). Это по
существу подтверждается теоремой 10.2.1 и следствием 10.2.2.
В них показано, что если S(jt#) = 0, то метод Гаусса —Ньютона
тоже сходится ^-квадратично. Это происходит в том случае,
когда R(x) линейно, или когда имеет место задача с нулевой
невязкой в решении. Если S(x*) мало по сравнению с
/ (х#)г/ (*»), то метод Гаусса — Ньютона сходится локально
^-линейно. Однако если S(x*) слишком велико, то метод
Гаусса — Ньютона может вообще не быть локально сходящимся.
Далее, сразу после следствия 10.2.2, мы прокомментируем эти
результаты.
Теорема 10.2.1. Пусть R: R"->Rm, и функция f(x) =
= y Я (х)т R (х) дважды непрерывно дифференцируема в
открытом выпуклом множестве DgR". Предположим, что /(дс)е
eLipY(D), причем ||/(*)112^а Для всех x^D, а также, что
существуют xm е D и Я, о ^ 0, такие что / (хУ R (хл) = 0,
Л —наименьшее собственное значение для /(*Jr/(*,), и
II (/ (х) - J (х.))т R (*,) И, < а || х - хл ||2 (10.2,4)
для всех лее/). Если а<Я, то для любого се(1Д/<*)
существует е > 0, такое, что для всех х0 е N(x*, г) последовательность,
порожденная методом Гаусса — Ньютона
xk+i = xh-(J (xk)T J (xk))~l J (xkf R (xk),
корректно определена, сходится к *» и удовлетворяет
неравенствам
иь+1-хЛ<%Ъ**-*Л + 1£Ъхь-хЛ (Ю.2.5)
и
II хш - х. ||2 < ^±± || хк - х, ||2 < || xk - х. ||2. (10.2.6)
Доказательство. Доказательство проводится по индукции.
Мы можем предположить, что А, > а ^ 0, так как утверждения
теоремы относятся только к этому случаю. Пусть с есть
фиксированная константа из интервала (1, Va)> выражения /(хо)>
R(xo) и R(x*) для краткости обозначены соответственно через
/о, Ro и /?*, и через ||-|| обозначена векторная и матричная
10.2. Методы типа Гаусса — Ньютона 265
/г-нормы. Согласно знакомым теперь нам доводам, существует
8i > 0, такое, что /*У0 не вырождена и
к'оЧГ'Ку *ля всех *oetf(*„ е,). (10.2.7)
Пусть
e = min{e1, ^^}. (Ю.2.8)
Тогда на первом шаге хх корректно определено и
х\ ~~ х. = хо "" *, ~"~ (^Uo) ^0^0 ===
= - (W №о + /0Ч (* - *о)] =
= - ТО)"' КЧ - П {R-K-h (* - *»))]. (Ю.2.9)
По лемме 4.1.12
IIR.-Ro-/о(*.- х0)||< 11|х0-х, II2. (10.2.10)
Из (10.2.4), вспоминая, что / (xt)T R (ас,) = 0, имеем
|/J* |<а||*Ь-*.И- (10.2.11)
Объединяя (10.2.9), (10.2.7), (10.2.10), (10.2.11) и неравенство
II /о II ^5°> получим
II ^i — ^!!^11(^^о)"",|| [ 11^^11 -ь Kollll^ — /?0 — ^о (^ — ^о) II ] ^
^j-[o\\x0-xj+^\\x0-xj*\
что доказывает (10.2.5) для случая k = 0. Из (10.2.8) и
приведенного выше соотношения имеем
\\x{-xj^\\x0-xj[^+^\\x0-xj\\^
<\\хо- М[х + "4Я = £^ 11*0 — *.Н< И*Ь-*Л
что доказывает (10.2.6) для случая k = 0. Аналогичным
образом проводится шаг индукции. □
Следствие 10.2.2. Пусть выполнены предположения теоремы
10.2.1. Если /?(**) = 0, то существует е > 0, такое, что для всех
x0eiV(x#, е) последовательность {**}, порожденная методом
Гаусса — Ньютона, корректно определена и сходится ^-кваДРа"
тично к х*.
266 Гл. 10. Нелинейная задача о наименьших квадратах
Доказательство. Если /?(**) = 0, то в (10.2.4) можно
положить а равным нулю. Тогда, согласно (10.2.6),
последовательность {xk} сходится к *#, а согласно (10.2.5), скорость
сходимости будет <7"кваДРатичн°й. П
Из теоремы 10.2.1 видно, что метод Гаусса — Ньютона не
столь хорош, как большинство ранее рассмотренных в книге
локальных методов, потому что на многих задачах с
невырожденной матрицей / (х*) TJ (х+) он обладает невысокой локальной
сходимостью, а на некоторых из них он вообще не является
локально сходящимся. Константа а, входящая в (10.2.4), играет
решающую роль в доказательстве сходимости и заслуживает
дальнейшего исследования.
Удобно рассматривать а как обозначение для ||S(*#)||2, так
как для х, достаточно близких к **, можно показать в качестве
упражнения, что
(/ (х) - J (х.))т R (дО ~ S (х.) (х - *.).
Из этой интерпретации, равно как и из (10.2.4), а является
абсолютной совокупной мерой нелинейности и величины невязки
в решении задачи. Так, если функция R(x) линейна или /?(*») =
= 0, то непосредственно из (10.2.4) следует, что а = 0.
Отношение аД, которое для гарантии сходимости должно быть
меньше 1, может рассматриваться как относительная
совокупная мера нелинейности и величины невязки в решении задачи.
Таким образом, теорема 10.2.1 утверждает, что скорость
сходимости метода Гаусса — Ньютона уменьшается с ростом
относительной нелинейности или относительной величины невязки в
решении задачи, причем если любая из этих двух величин
слишком велика, то метод может вообще не сходиться. Иначе говоря,
это указывает на то, что чем больше S(x*) по сравнению с
/(jc#) TJ(х*), тем, вероятно, хуже будет работать метод Гаусса —
Ньютона.
Хотя метод Гаусса — Ньютона имеет ряд проблем, он служит
основой для некоторых важных и успешно работающих
практических методов решения нелинейных задач о наименьших
квадратах. В табл. 10.2.3 подытожены преимущества метода
Гаусса— Ньютона, которые желательно сохранить, и недостатки,
которые хотелось бы преодолеть. В примерах 10.2.4 и 10.2.5
показано поведение метода Гаусса — Ньютона на простой задаче
с одной переменной.
В примере 10.2.4 исследуется поведение метода Гаусса —
Ньютона при наилучшем приближении моделью etx = y набора
данных вида (/, у): (1,2), (2,4), (3, уг) для различных
значений t/3. Когда уъ = 8, модель точно приближает данные при
х% = In 2 s 0.69315, и в этом случае метод Гаусса — Ньютона
сходится квадратично, По мере уменьшения #3 оптимальное зна-
10.2. Методы типа Гаусса — Ньютона 2*7
Таблица 10.2.3. Преимущества и недостатки метода Гаусса — Ньютона
Преимущества
1. Локальная (/-квадратичная сходимость для задач с нулевой
невязкой в решении.
2. Быстрая локальная <7-линейная сходимость для задач,
которые не являются слишком нелинейными или имеют в решении
достаточно малые невязки.
3. Решает линейную задачу о наименьших квадратах за одну
итерацию.
Недостатки
1. Медленная локальная ^-линейная сходимость на задачах,
которые довольно нелинейны или имеют в решении достаточно
большие невязки.
2. Отсутствие локальной сходимости на задачах, которые сильно
нелинейны или имеют в решении очень большие невязки.
3. Не является корректно определенным, если /(**) не имеет
полного столбцового ранга.
4. Не гарантирована глобальная сходимость.
чение *♦ становится все меньше, невязка R(x*) в решении — все
больше и эффективность метода Гаусса — Ньютона
ухудшается. При (/з = 3 и у$ = —1 метод Гаусса — Ньютона является
все еще линейно сходящимся, хотя в последнем случае
сходимость очень медленная. В случаях у$ = — 4 и у$ = —8 метод
Гаусса — Ньютона вообще не сходится локально.
Для сравнения в примере 10.2.4 показано также поведение
метода Ньютона для нелинейных наименьших квадратов (10.1.3)
на всех этих задачах. Тогда как действие метода Гаусса —
Ньютона сильно зависит от размера невязки, для метода
Ньютона это не существенно, и он работает нормально на всех этих
задачах. Для каждой задачи мы рассматриваем две начальные
точки: Хо= 1 и значение х0, отличающееся от х* не более чем
на 0.1. Поведение алгоритмов при начальной точке, более
близкой к решению, наилучшим образом передает их свойства
локальной сходимости.
Пример 10.2.4. Пусть R: R*->R4, ri(x) = efi —yh /=1, .. .,4,
/ (х) = у/?(х)г/?(*), где tx=l, ух = 2, /2 = 2, у2 = 4, /3 = 3, и
пусть t/з и хо принимают значения, указанные в таблице.
Тогда метод Гаусса — Ньютона (10.2.3) и метод Ньютона (10.1.3)
требуют следующего числа итераций для достижения на каждой
из этих задач точности Wf(xk)|< 10~10 на ЭВМ CDC с 14 +
десятичными разрядами. Для каждой задачи также указаны
точка минимума х0 функции f{x) и величина невязки в
решении /(*.)•
268 Гл. 10. Нелинейная задача о наименьших квадратах
Количество итерации,требуемое для
достижения точности |vt(Xk) I* 10"'°методом
Л
8
3
-1
-4
-8
*©
1
0.6
I
0.5
!
0
1
-аз
I
-0.7
секущих
6
5
8
4
1!
5
13
6
15
8
Ньютона
7
6
9
5
10
4
12
4
12
4
х*
0.69315
0.44005
0.044744
-0.37193
-0.79148
/(*,)
0
1.6390
6.9765
16.435
41 145
В примере 10.2.5 более детально изучаются случаи из
примера 10.2.4, когда метод Гаусса — Ньютона не сходится.
Пример 10.2.5. Пусть f(x) задано, как в примере 10.2.4.
Если у3 = —4, то *,= — 0.3719287. Пусть х0 = х„ + б, тогда
для достаточно малого 161 метод Гаусса — Ньютона дает
х{ ^ х0 — (3.20) б,
так что | х{ — jtjs (2.20)| xQ — хJ. Таким образом, хх находится
дальше от дс„ чем х0. Например, если х0 = —0.3719000, то
atj = —0.3719919. Если */3 = —8, то х0 = —0.7914863, и тогда
для х0 = хш + 6 при достаточно малом |б| метод Гаусса
—Ньютона дает
х{о*х0 — (7.55) б,
так что |*1—*#|£ё (6.55) |*о —*#|. Например, если х0 =
= —0.7915000, то хх =—0.7913968.
Интересной особенностью примера 10.2.5 является то, что
метод Гаусса — Ньютона делает плохие шаги, выбирая их
слишком большими по длине, но верными по направлению. Этот
факт может заинтересовать читателя: действительно ли шаг
по методу Гаусса — Ньютона всегда делается в направлении
спуска? Это, в самом деле, имеет место всякий раз, когда шаг
корректно определен. Доказательство является как раз
обобщением доказательства из разд. 6.5 того, что шаг метода Ньютона
при решении нелинейных уравнений является направлением
спуска для соответствующей задачи минимизации. Если J(xc)
имеет полный столбцовый ранг, так что матрица J(xc)TJ(xc) не
10.2. Методы типа Гаусса — Ньютона 269
вырождена, а шаг метода Гаусса — Ньютона
sQ = -(J (хс)т J (хс)Г1 J (хс)т R (хс)
корректно определен, то J(xc)TJ(xc) положительно определена
и выполняется соотношение
V/ (хс)т sQ = [J (хс)т R (хс))т [- (У (хс)т J (хс))~х J (хс)т R (хс)] =
= - [* (*с)т J (хс)]т (/ (хс)т J (хс)) [J (хс)т R (хс)] < 0,
которое доказывает, что шаг метода Гаусса — Ньютона
находится в направлении спуска. Это указывает на два возможных
пути улучшения алгоритма Гаусса — Ньютона: использование
его с линейным поиском или со стратегией доверительной
области. Эти два подхода приводят к двум алгоритмам, которые
применяются на практике.
Алгоритм, использующий метод Гаусса — Ньютона с
линейным поиском, это просто
х+ = хс - К (J {хс)т J (xc))~l J {хс)т R (хе)9 (10.2.12)
где Кс выбирается методами разд. 6.3. Будем называть (10.2.12)
демпфированным методом Гаусса — Ньютона. К сожалению,
в некоторых работах его называют методом Гаусса — Ньютона.
Поскольку демпфированный метод Гаусса — Ньютона всегда
делает шаги в направлении спуска, которые удовлетворяют
критерию линейного поиска, то метод локально сходится почти на
всех нелинейных задачах о наименьших квадратах, включая
задачи с большой невязкой в решении или сильно нелинейные
задачи. Действительно, по теореме 6.3.3 он обычно сходится
глобально. Однако он все же может сходиться очень медленно на
тех задачах, на которых метод Гаусса — Ньютона сталкивался
с трудностями. Например, если (10.2.12) применяется в четвертой
задаче примера 10.2.4 и используется простой линейный поиск
с делением пополам Гт. е. используется первое подходящее
значение Хс из последовательности!,-^, -j, -g.-.)> то, начиная
из точки с Хо = —0.3, алгоритму требуется все же 44
итерации, 45 вычислений J(x) и 89 вычислений R(x) для
достижения точности |V/(jcc)|^ Ю-10, в то время как методу Ньютона
требуется 4 итерации! Кроме того, демпфированный алгоритм
Гаусса — Ньютона все же не будет корректно определенным,
если Цхс) не имеет полного столбцового ранга.
Другая из предлагаемых нами модификаций алгоритма
Гаусса — Ньютона состоит в выборе х+, согласно подходу
«модель— доверительная область»:
найти min || R (хс) + J (хс) (х+ — хс) ||2
*+SRrt
при условии || х+ — хс ||2 < 6С. (10.2.13)
270 Гл. 10. Нелинейная задача о наименьших квадратах
Как следствие из леммы 6.4.1, легко получить решение для
(10.2.13) в виде
*+ = хс - (/ (хс)т J (хс) + ixcl)'1 J (хс)т R (хс), (10.2.14)
где [1с = 0, если 6С ^ \\(J(xc)TJ(xc))-4{xc)TR(xc)\\2, и \хс > 0 в
противном случае. Формула (10.2.14) была впервые предложена
Левенбергом (1944) и Марквартом (1963) и теперь известна
как метод Левенберга — Маркварта. Много версий метода Ле-
венберга — Маркварта было реализовано в виде программ,
использующих различные стратегии выбора \ic. Так, реализация
формулы (10.2.14) в виде алгоритма доверительной области, где
[ic и 8С выбраны по способам из разд. 6.4.1 и 6.4.3, принадлежит
Морэ (1977). (Морэ использует масштабирование
доверительной области, как это описано в разд. 7.1.) Шаг х+ — хс,
заданный согласно (10.2.14), может быть вычислен более точно путем
решения эквивалентной линейной задачи о наименьших
квадратах (см. упр. 12).
Свойства локальной сходимости метода Левенберга —
Маркварта аналогичны свойствам метода Гаусса — Ньютона и
приведены в теореме 10.2.6.
Теорема 10.2.6. Пусть выполнены условия теоремы 10.2.1 и
последовательность {\лк} неотрицательных действительных
чисел ограничена сверху числом b > 0. Если а < X, то для любого
се(1, (Х + Ь)/(о + Ь)) существует е > 0, такое, что для всех
xq^N(x*> е) последовательность, порождаемая методом
Левенберга — Маркварта
**.+! = **-(/ (*k)T J (xk) + МГ1 / (xk)T R (xk\
корректно определена и удовлетворяет соотношениям
II *»+! - *, И2 < \(х + Ь) И ** "" *« [|2 + 2 (Г+ Ь) Ч ** - Х* »2
и
ll^i-^Jl2<g(a+2^^ + 'Ml^-A:Jl2<|U.~xJb.
Если /?(х#) = 0 и |^ = 0(||/(л:*)г#(**)112), то {xk} сходится
^-квадратично к лг*.
Доказательство. Оно представляет собой простое обобщение
теоремы 10.2.1 и следствия 10.2.2. См. также работу Дэнниса
(1977). □
В теореме 10.2.5 говорится, что алгоритм Левенберга —
Маркварта может все же быть медленно локально сходящимся
на задачах с большой невязкой в решении, а также на сильно
нелинейных задачах, и иногда это действительно так. Тем не
10.3. Методы полностью ньютоновского типа 271
менее многие реализации данного алгоритма, в частности
реализация Морэ, которая включена в пакет программ MINPACK,
как в конечном счете оказалось, очень успешно применяются на
практике, и поэтому указанный алгоритм представляет собой
один из подходов, которые мы рекомендуем для общего решения
нелинейной задачи о наименьших квадратах. Несколько
факторов делают алгоритмы Левенберга — Маркварта на многих
задачах предпочтительней, чем алгоритмы демпфированного
метода Гаусса — Ньютона. Один из этих факторов состоит в том,
что метод Левенберга — Маркварта корректно определен, даже
когда J(xc) не имеет полного столбцового ранга. Другой состоит
в том, что в случаях, когда шаг метода Гаусса — Ньютона
оказывается слишком большим по длине, шаг метода
Левенберга— Маркварта близок к направлению наискорейшего спуска
—J(xc)TR(xc), и это часто лучше, чем шаг демпфированного
метода Гаусса — Ньютона. Для некоторых версий алгоритма
Левенберга— Маркварта доказана глобальная сходимость,
например, Пауэллом (1975), Осборном (1976) и Морэ (1977).
В разд. 10.3 обсуждается другой подход к решению
нелинейной задачи о наименьших квадратах, который является
несколько более надежным, но вместе с тем и более сложным, чем
подход Левенберга — Маркварта.
10.3. МЕТОДЫ ПОЛНОСТЬЮ НЬЮТОНОВСКОГО ТИПА
Другой рассматриваемый класс методов решения нелинейной
задачи о наименьших квадратах основан на использовании
квадратичной модели функции f(x) в окрестности точки хс (10.1.2),
учитывающей полностью все члены соответствующей формулы
Тейлора. Метод Ньютона для нелинейной задачи о наименьших
квадратах состоит в выборе х+, которое было бы стационарной
точкой этой модели, т. е.
x+ = xc-(J(xc)TJ(xc) + S(xc)rlJ(xcYR(xe).
По теореме 5.2.1 он локально <7"кваДРатично сходится к точке
минимума х+ функции f(x), когда гессиан V2f(x) = J(xc)TJ(xc) +
+ S(xc) непрерывен по Липшицу в окрестности точки хс и
V2/(*«) положительно определен. Таким образом, свойства
локальной сходимости метода Ньютона для нелинейной задачи о
наименьших квадратах действительно лучше, чем у методов из
предыдущего раздела, так как метод Ньютона обладает
высокой локальной скоростью сходимости на почти всех задачах,
тогда как демпфированный метод Гаусса — Ньютона и метод
Левенберга — Маркварта могут медленно локально сходиться
при сильно нелинейной функции R(x) или большом значении
272 Гл. 10. Нелинейная задача о наименьших квадратах
Причина, по которой в нелинейной задаче о наименьших
квадратах редко применяется метод Ньютона, состоит в том,
что редко когда имеется возможность за оправданную цену
получить J(Xc)TJ(xc) + S(xc) в аналитическом виде. Если
недоступно аналитическое значение J(xc)> то оно должно
аппроксимироваться конечными разностями так, чтобы yf(xc) =
*B=:J(xc)TR(xc) вычислялось как можно точнее. Это обходится
в п дополнительных вычислений R(x) на каждой итерации.
Однако стоимость аппроксимации V2f(xc) или S(xc) конечными
разностями, составляющая в обоих случаях дополнительные
(п2 + Зл)/2 вычислений на каждой итерации, обычно
непозволительно высока.
Непосредственное применение методов секущих из гл. 9 к
нелинейной задаче о наименьших квадратах также
нежелательно потому, что эти методы аппроксимируют все составляющие
в выражении для V2f{xc). Однако, поскольку в нелинейных
алгоритмах наименьших квадратов, как нами уже отмечалось,
неизбежно должно вычисляться J(xc) либо аналитически, либо по
конечным разностям, составляющая J(xc)TJ(xc) в выражении
для V2f(xc) всегда имеется в нашем распоряжении, и нам
необходимо лишь аппроксимировать S(xc). Так как вдобавок
J(xc)TJ(xc) часто представляет собой преобладающую часть
матрицы V2f(xc)y то методы секущих, которые не учитывают этого
факта и аппроксимируют целиком всю V2f(xc) по секущим, не
показали особой эффективности на практике.
Поскольку
т
S(xc)=Ydri(xc)V2ri(xc),
другой альтернативой служит аппроксимация каждой /гХя-мат-
рицы V2ri(xc) согласно методике гл. 9. Это неприемлемо для
алгоритмов общего назначения потому, что требует хранения
Дополнительно т симметричных /iXя-матриц. Тем не менее эта
Ьдея имеет определенную связь с подходом, который реально
используется.
В удачном подходе к решению нелинейной задачи о наи-
иеныпих квадратах на основе идеи метода секущих
производится аппроксимация V2f(xc) матрицей J(xc)TJ(xc)+ Ас, где Ас
•сть отдельная аппроксимация по секущим для S(xc). Мы будем
■алее рассматривать подход Дэнниса, Гэя и Уэлша (1981), а
всылки на другие методы можно найти в этой же статье.
Нахождение Ас состоит в непосредственном применении методик
пл. 8 и 9. Предположим, что имеется аппроксимация Ас для
${хс), был сделан шаг из хс в х+, и мы хотим построить
аппроксимацию А+ для S(x+). Прежде всего возникает вопрос «Что
представляет собой соотношение секущих, которому должна
удовлетворять Л+?» Вспомним, что для задач минимизации матрица
10.3. Методы полностью ньютоновского типа 273
#+ аппроксимировала V2/(x+), и соотношением секущих было
H+(x+ — xc) = Wf(x+) — Vf(xc).Аналогично если аппроксимацию-
т
s(*+)=£M*+)v2M*+)
временно представить себе в виде матрицы
т
А+=Т,г{(х+)(Н{)+, (10.3.1)
где каждое (#0 + аппроксимирует V2r/(x+), то каждое (#/) +
должно удовлетворять соотношению
(#,)+ (*+ - *с) = Vr, (х+) - Vr, (хс) =
= (/-я строка /(jc+))7' — (/-я строка /(jcc))r. (10.3.2)
Комбинация (10.3.1) и (10.3.2) дает соотношение
m
А+ (х+ - хс) = £ г, (х+) (#,)+ (*+ - хс) =
/-1
m
= 2 Г|(*+)[(*-я строка /(*+))г —(/-я строка /(*с))г] =
= /(л:+)г/?(^)-/(^/?(;с+)А^#, (10.3.3)
служащее для А+ аналогом соотношения секущих. Заметим, что,
хотя это соотношение было выведено из рассмотрения отдельных
аппроксимаций (#*)+> результатом является единственное
соотношение секущих для той единственной дополнительной
матрицы Л+, которая будет храниться в памяти.
В одномерном случае А+ полностью определяется
соотношением (10.3.3). Пример 10.3.1 показывает, как получающийся в
результате метод секущих для нелинейных задач о наименьших
квадратах работает на тех же задачах, что рассматривались в
примерах 10.2.4 и 10.2.5. В целом мы увидим, что метод секущих
лишь несколько медленнее метода Ньютона и что он может
работать лучше, чем метод Гаусса — Ньютона, на задачах со
средней и большой невязкой в решении. В частности, он быстро
локально сходится на тех примерах, в которых метод Гаусса —
Ньютона не сходится вообще.
Пример 10.3.1. Пусть /?(x), f(x), tu yh /2, #2, h и набор
значений для уз и хо такие же, как в примере 10.2.4. Тогда метод
секущих для одномерных нелинейных задач о наименьших
квадратах
**+i = хк- (J(xk)TJ(xk) + AkrlJ(xk)TR(xk),
0 * = 0,
k>0,
Ak=\ in*k)-'(*k-x)]T*{*k\ ^п (Ю-3-4>
I *н-*н-
274 Гл. 10. Нелинейная задача о наименьших квадратах
требует приведенного ниже количества итераций для
достижения точности |V/(xc)|< 10-10 на каждой из следующих задач
на ЭВМ CDC с 14+ десятичными разрядами. Для сравнения из
примера 10.2.4 воспроизведено количество итераций, требуемых
для метода Ньютона, а также решение х* и величина невязки
в решении /(*♦).
Количество итераций, требуемое для
достижения точности | Vf(xk) |410~,0методом
Уз
8
3
-1
-4
-8
*о
1
0.6
1
0.5
1
0
1
-0.3
1
-07
Гаусса-Ньютона
5
4
12
9
34
32
*
*
*
*
Ньютона
7
6
9
5
10
4
12
4
12
4
х*
0.69315
0 44005
0.044744
-0.37193
-0,79148
Дч)
0
1.6390
6.9765
16.435
41.145
* Метод Гаусса-Ньютона не сходится (см.упр 10.2 5),
При п > 1 соотношение (10.3.3) определяет А+ не полностью,
и мы доопределяем Л+, используя методику гл. 9. Поскольку
матрица S(x+) симметрична, то такой должна быть и Л+; тем
не менее в общем случае S{x) может не быть положительно
определенной даже в решении х» (см. упр. 15), поэтому мы не
будем требовать положительной определенности Л+. У нас нет
никакой другой новой информации об Л+, следовательно, как и
в гл. 9, будем брать в качестве А+ наиболее похожую на Ас
матрицу среди множества допустимых аппроксимаций, выбирая
Л+, дающую решение задачи о минимальных поправках;
min \T-T(A+-Ac)T-ll
при условии: А+ — Ас симметрична, A+sc = y*. (10.3.5)
Здесь sc = x+ — xc9 Ус определено в (10.3.3) и Т €=RrtXn не
вырождена. Если выбрать ту же самую матрицу весов 7\ что
обеспечила получение DFP-формулы, т. е. любую 7\ для которой
ТТ\ = ур ус А V/ (*+) - V/ (хс) = J {х+У R(x+)-J (хс)т R (*,),
10.3. Методы полностью ньютоновского типа 275
то, как нетрудно показать, обобщая технику разд. 9.3,
решением для (10.3.5) служит
л _ л , (у? - Л А) у1 + Ус (у? - А а)г
(Ус*-Ас8с'8с)УсУТс /1лоАч
Формула пересчета (10.3.6) была предложена Дэннисом,
Гэем и Уэлшем (1981); она используется для аппроксимации
S(x) в их программе по решению нелинейной задачи о
наименьших квадратах NL2SOL. Как, может быть, читатель уже
догадывается, получающийся в результате метод секущих для
нелинейной задачи о наименьших квадратах, использующий
итерационную формулу (10.3.4) и пересчет Ak, согласно (10.3.6),
локально <7-сверхлинейно сходится при стандартных
предположениях относительно f(x) и Л0. Этот результат получен
Дэннисом и Уолкером (1981) и представляет собой частный случай
теоремы 11.4.2.
Программа NL2SOL, которая реализует только что
описанный метод секущих, имеет дополнительно несколько интересных
особенностей. Для обеспечения глобальной сходимости
алгоритма используется стратегия «модель — доверительная область»,
т. е. на каждой итерации решается задача:
найти min | R (хс)т R (хс) + sTJ (хс)т R (хс) +
+ у *r V (*с)т J (Хс) + Ас] s (10.3.7)
при условии ||s||2^6c
относительно sc, так что
sc = -(J(xc)TJ(xc) + Ac + ixciylJ(xc)TR(xc)t (10.3.8)
для некоторого \лс ^ 0. (В действительности опять же
используется масштабированная доверительная область.) Далее, в
алгоритме иногда вместо расширенной модели (10.3.7) участвует
модель Гаусса — Ньютона (10.2.2), не учитывающая Ас. Из-за
упоминавшейся выше сложности, связанной с аппроксимацией
S(x) конечными разностями, и в связи с тем, что
метод.Гаусса— Ньютона имеет тенденцию хорошо работать в начальной
стадии, NL2SOL использует для А0 нулевую матрицу, так что
в начальной стадии эти две модели эквивалентны. Затем в том
месте каждой итерации, где ограничитель длины шага бс пере-
считывается в 6+ с учетом сравнения действительного
уменьшения значения функции f(xc) — /(*+) с уменьшением,
предсказанным квадратичной моделью, NL2SOL вычисляет уменьшения,
276 Гл. 10. Нелинейная задача о наименьших квадратах
предсказанные обеими квадратичными моделями, независимо от
того, какая из них применялась для выработки шага из хс в х+.
Пересчет Ас в Л+ проводится всегда, но первый пробный шаг
из х+ вычисляется при помощи той модели, в которой
предсказываемое уменьшение функции наилучшим образом согласуется
с действительным уменьшением при переходе от хс к х+.
Характерно, что такое адаптивное моделирование приводит к тому,
что NL2SOL использует шаги по методу Гаусса — Ньютона или
Левенберга —Маркварта до тех пор, пока Ас не накопит
достаточное количество полезной информации о вторых производных,
а затем переключается на шаги, соответствующие расширенной
модели и определяемые согласно (10.3.7), (10.3.8). Для легких
задач с малыми заключительными невязками для сходимости
иногда достаточно лишь шагов метода Гаусса — Ньютона.
И последнее. Перед каждым пересчетом (10.3.6) в NLS2SOL
матрица Ас умножается на «масштабирующий» множитель
т
Ye = min(-|^-,*l}, (10.3.9)
I SCACSC )
который почти такой же, как и множитель Шанно и Фуа,
упоминавшийся в разд. 9.4. Причина, по которой такое
масштабирование необходимо на каждой итерации, состоит в том, что
скалярные компоненты п(х) в
m
S(x)=Ttrl(x)V2rt(x)
иногда изменяются быстрее, чем компоненты вторых
производных W/(jc), а формула пересчета (10.3.6) не может достаточно
быстро реагировать на изменения масштабов. В особенности
это проявляется при довольно малом /?(*#). Масштабирующий
множитель (10.3.9) пробует учесть уменьшение с ||/?(хс)||2 до
Il#(*+)ll2, так что аппроксимация А+ оказывается более точной
в случаях малой и нулевой невязки в решении. Относительно
дальнейших деталей алгоритма NL2SOL, см. Дэннис, Гэй и
Уэлш (1981).
На практике хорошая программа метода Левенберга
—Маркварта (например, программа Морэ в пакете MINPACK) и
хорошая программа метода секущих для нелинейной задачи о
наименьших квадратах (например, NL2SOL) при сравнении
оказываются близкими. На не слишком нелинейных задачах
с малой невязкой в решении обычно нет большой разницы между
этими двумя программами. На задачах с большой невязкой в
решении и на сильно нелинейных задачах программа метода се-,
кущих часто требует меньшего числа итераций и вычислений
функции. Это справедливо в особенности, если необходимо
найти решение х* с высокой точностью, так как в этом случае
10.4. Некоторые другие соображения 277
важное значение приобретает разница между медленной
линейной сходимостью и <7*сверхлинейной сходимостью. С другой
стороны, программа метода Левенберга — Маркварта, такая, как
программа Морэ, требует для ее написания меньшего числа
строк и менее сложна, чем программа метода секущих со всеми
ее особенностями, описанными выше. По этим причинам мы
рекомендуем в общем случае использовать обе программы.
10.4. НЕКОТОРЫЕ ДРУГИЕ СООБРАЖЕНИЯ
ОТНОСИТЕЛЬНО РЕШЕНИЯ НЕЛИНЕЙНЫХ ЗАДАЧ
О НАИМЕНЬШИХ КВАДРАТАХ
В этом разделе мы кратко обсуждаем некоторые другие темы,
связанные с нелинейными наименьшими квадратами, и
читателей, проявивших к этому интерес, адресуем за подробностями
к более полным источникам. Первой темой служит критерий
останова для нелинейных задач о наименьших квадратах,
который отличается несколькими интересными моментами от
критерия, рассмотренного в разд. 7.2 в связи с задачами безусловной
минимизации общего вида. Во-первых, поскольку наименьшим
возможным значением для / (х) = у R (х)т R (х) является нуль,
то проверка вида
/(*+)»0?
служит подходящим критерием сходимости для задач с нулевой
невязкой в решении. Эта проверка реализуется как /(*+) s^toli,
где toll — надлежащим образом выбранная точность. Во-вторых,
градиентная проверка сходимости для нелинейных задач о
наименьших квадратах вида
Vf(*+) = /(*Jrtf(*+)^0? (10.4.1)
имеет благодаря структуре Vf{x) особый смысл, так как его
можно интерпретировать как вопрос о том, является ли R(x+)
почти ортогональным к линейному подпространству, натянутому
на столбцы матрицы /(*+). В качестве упражнения можно
показать, что косинус угла ф+ между R{x+) и этим подпространством
равен
созф+=, *+М^+ГЧ*+ (1042)
|/+('+'+)" '+*+И*+112
где /+ Д/(*+) и /?+Д/?(*+). Если в распоряжении имеется
(/+/+)" У+/?+,как это будет в программе демпфированного
метода Гаусса — Ньютона или метода Левенберга — Маркварта,
278 Гл. 10. Нелинейная задача о наименьших квадратах
тогда вместо (10.4.1) можно использовать проверку cosq>+^
2^ tol2. Другие критерии останова, такие, как (х+ — хс)ё*0,
остаются теми же самыми, что и в задачах безусловной
минимизации. Кроме того, в приложениях, связанных с наилучшим
приближением данных, иногда в качестве критерия останова
используется критерий статистической значимости.
Распространенный критерий такого рода, тесно связанный с (10.4.2),
обсуждается в упр. 18 и в работе Пратта (1977). Обсуждение
критериев останова для нелинейных задач о наименьших
квадратах приведено в работе Дэнниса, Гэя и Уэлша (1981).
Другой важной темой служит вопрос решения смешанных
линейно-нелинейных задач о наименьших квадратах, т. е. тех
задач, в которых функция невязки R(x) линейна по некоторым
переменным и нелинейна по остальным. Типичным примером
является
т
f М = 7 Z г' (*)2' г<М = *1*'Л + **'Л -»«• /= 1..... т.
Здесь переменные хх и х2 входят линейно, в то время как х$ и
ха — нелинейно входящие переменные. Нам, очевидно, нужно
уметь минимизировать f(x) путем решения нелинейной задачи
о наименьших квадратах только относительно двух нелинейно
входящих переменных дс3 и х4, так как для любых заданных
значений хъ и *4 мы можем вычислить соответствующие
оптимальные значения х\ и хг путем решения линейной задачи о
наименьших квадратах. Это действительно так, причем весь достаточно
сложный анализ, требуемый для построения алгоритма, был
выполнен Голубом и Перейрой (1973). Он кратко изложен в
упр. 19 и 20. Имеются некоторые машинные программы, такие,
как алгоритм VARPRO Кауфмана (1975), которые решают
смешанные линейно-нелинейные задачи о наименьших квадратах.
Преимущества их состоят в том, что они решают эти задачи за
меньшее время и при меньшем количестве вычислений функций,
чем стандартные программы для нелинейных наименьших
квадратов, и что для линейно входящих переменных не требуется
никакого начального приближения.
Многие интересные вопросы, относящиеся к решению задач
наилучшего приближения данных по принципу нелинейных
наименьших квадратов, в основном выходят за рамки этой книги.
Один из них касается оценки погрешности получаемых ответов.
В линейных задачах о наименьших квадратах Ах ^ 6,
возникающих в связи с наилучшим приближением данных,
вычисление решения обычно следует за вычислением ковариационной
матрицы о2(АТА)-\ где а есть некоторая статистическая
характеристика. При соответствующих статистических предположе-
10.4. Некоторые другие соображения 279
ниях эта матрица дает дисперсию и ковариацию ответов xt с
учетом ожидаемой неточности в векторе измерений данных 6.
В нелинейных задачах о наименьших квадратах
используются некоторые аналогичные ковариационные матрицы, а
именно b2{jTfJfY , б2 (Ну1) и b2{HJxJTfJfHJx), где xf есть
окончательная оценка для *., Jf = J(xf), Hf = J(xf)T J(xf) + S(xf) (или
аппроксимация этой матрицы) и 6 = 2f(x)/(m — п)—аналог
константы, используемой в линейном случае [см., например,
Бард (1970)]. Несмотря на то что надлежащее обсуждение
ковариационной матрицы выходит за рамки этой книги, важно
предостеречь пользователей программного обеспечения по
нелинейным наименьшим квадратам о том, что ковариационные
оценки для нелинейных наименьших квадратов не столь
надежны, как для линейных наименьших квадратов, и должны
использоваться с осторожностью. На улучшение этой ситуации были
направлены серьезные исследования; см., например, Бейтс и
Уотте (1980).
М наконец, как упоминалось в разд. 1.2, много других мер
величины вектора /?(*), помимо наименьших квадратов, можно
использовать для определения того, что понимается под
выражением «хорошо приближает», причем некоторые из них
становятся все более важными для практики. Действительно, можно
рассматривать нелинейные наименьшие квадраты как частный
случай задачи:
найти min / (*) = р (/? (*)), /?:R"->RW, р: Rm-*R, (10.4.3)
где p(z)=-£ zTz. Другими очевидными возможностями являются
p(2)=||z|li и р(г) = llz||oo, называемые соответственно /г и
минимаксным принципами наилучшего приближения данных. [См.,
например, Мюррей и Овертон (1980, 1981), а также Бартелс и
Конн (1982).] Когда имеются плохие точки данных (так
называемые «выбросы»), то появляется иногда интерес к другим
мерам р(г), которые не так сильно учитывают вклад очень
больших компонент вектора г. Двумя такими примерами
служат функция потерь Хьюбера (1973)
Р(г) =
.(*<) =
= S Pi («|),
Г1
1 *|г,|-
2
Pi
t
:R — R,
|г,|<*.
\zt\>k,
(10.4.4)
280 Гл. 10. Нелинейная задача о наименьших квадратах
линейная по zt для | zt\ > kf и функция потерь Битона-Тьюки
(1974)
т
P(z)=Zp2(z<). p2:R->-R,
P2(zt) = < );ЛУ V KkJJJ (10.4.5)
постоянная при \zi\> k. В каждом из случаев константа k
должна быть выбрана подходящим образом. Они представляют
собой примеры надежных в работе мер, используемых для
наилучшего приближения данных, и здесь уместно сослаться на
Хьюбера (1981). В гл. 11 кратко упоминаются некоторые
вопросы, связанные с минимизацией дважды непрерывно
дифференцируемой функции вида (10.4.3).
10.5. УПРАЖНЕНИЯ
1. Пусть R(x): R^R20, r{ (х) = х{ + */"('<+*з)2/*4 - у(, * = 1, ..., 20,
1 Т
f(x) = —R(x) R{x). (Эта задача обсуждалась в разд. 1.2.) Что
представляют собой /(jc), Vf (jc), S(jc), V2f (jc)?
2. Покажите, что теорема 10.2.1 останется справедливой, если константу
(со + Х)/(2Х) в (10.2.6) заменить на какую-либо другую константу, лежащую
между со/% и 1.
3. Покажите, что в предположениях теоремы 10.2.1 для jc, достаточно
близкого в jc*, имеет место равенство
[/ (х) - / (x.)f R (х,) = S^x.) (х - jc,) + О (|| jc - xjl).
[Указания: запишите
m
/(jc)r/?(*♦) = 5>,(*,)Vr,(*)
i = \
и воспользуйтесь разложением Vrt(x) в ряд Тейлора в окрестности точки av]
4. Вычислите (вручную или с помощью калькулятора) первый шаг
метода Гаусса — Ньютона для задачи из примера 10.2.4, взяв уз = 8 и jc0 = 1.
Вычислите также первый шаг метода Ньютона и два первых шага метода
секущих, записанного в примере 10.3.1.
5. Повторите упр. 4 для случая уз = —8, Хо = —0.7.
6. Пусть *«-*(*«), /с = /(*с), Sc = S(xc), xl = xc-(jTcJcy{JTcRc,
xN+ = хс - (JTCJC + Sc) JTCRC, sQ^x%^ xc, sN = xl - xc. Покажите, что
sO "~5yve(^c О $csN' Используйте это, чтобы показать, что если гессиан
у2 f (x) = J (х)т J (jc) 4- S (x) непрерывен по Липшицу в окрестности точки ми-
10.5. Упражнения 261
нимума х+ функции / {х) = —- R (ху R (х), V f](x>) не вырожден, и хс
достаточно близко к х„ то
I*? - *. %<II(Фс)~Х 1-2II Se ||21| xe - xj2 + О (|| хс - xjg).
В случае // = 1 вы должны уметь показать, что
[(4 - *.) ~ (Sc №)"') (Хс - *.)] - О ( | *с - *. |2). (10.5.1)
7. Вычислите / (xJT J (*J и S (аг+) для двух задач из примера 10.2.5.
Затем, используя (10.5.1), получите два коэффициента отталкивания 2.20 и
6.55, которые приведены в этом примере.
8. Пусть R(x): R2->R4, г, (х) ^е*1**1*2 - */., /=1 4, f (*) =
1 т
= Y /? (*) /? (х). Предположим, что ^ = --2, /2 = — 1» h = 0, /4 = 1> У|- 0.5,
#2 = 1, #з = 2, #4 = 4. [/(*) = 0 в точке *„ = (In 2, In 2).] Вычислите одну
итерацию метода Гаусса-Ньютона и одну итерацию метода Ньютона,
начиная с *0 = (1, 1)Г. Проделайте то же самое, заменив значения ух и уА на 5
и —4 соответственно.
9. Запрограммируйте демпфированный алгоритм Гаусса — Ньютона,
использующий алгоритм линейного поиска А6.3.1, и опробуйте его на задачах
из примера 9.3.2. Как согласуются ваши результаты с результатами,
полученными на этих задачах методом Ньютона и методом секущих?
10. Воспользуйтесь леммой 6.4.1 и покажите, что решением для (10.2.13)
является (10.2.14).
11. Покажите, что для произвольного ц ^ 0 шаг метода Левенберга —
Маркварта х+ — хс, заданный согласно (10.2.14), является направлением
спуска для функции в нелинейной задаче о наименьших квадратах.
12. Задано R е= Rm, / <= RmXn, покажите, что s = — (JTJ + ji/)"1/7'/?
является решением нелинейной задачи о наименьших квадратах
найти min \\As + b\\2y
A e n(m + n)*\ A =
heUm+\ b =
13. Докажите теорему 10.2.6, используя технику доказательства
теоремы 10.2.1 и следствия 10.2.2.
14. Решите задачи из примера 10.3.1 методом секущих для безусловной
минимизации
xk+i = xk-—r-> ak х х —• да«о-М*о).
к k к—\
J
1/2 I '
2
262 Гл. 10. Нелинейная задача о наименьших квадратах
Сравните ваши результаты с приведенными в примере 10.3.1 для метода
секущих для нелинейных наименьших квадратов,
15. Пусть f(x) задано, как в примере 10.2.4, и у$ = 10. Вычислите х*
(с помощью калькулятора или ЭВМ) и покажите, что S(x+) < 0.
16. Пользуясь техникой из разд. 9.3, покажите, что если TTTsc = уСу то
решением для (10.3.5) является (10.3.6).
17. Пусть i?sRm, и / е RmX" обладает полным столбцовым рангом.
Покажите, что проекция R в евклидовой норме на линейное подпространство,
натянутое на столбцы матрицы / есть J(JTJ)-4TR. [Указание: выясните, как
эта задача связана с линейной задачей о наименьших квадратах, в которой
минимизируется \\Jx — /?Иг?] Затем покажите, что косинус угла между R и
этим линейным подпространством имеет вид (10.4.2).
Упражнение 18 описывает в общих чертах статистический критерий
останова для нелинейных наименьших квадратов.
18. (а) Пусть aeR, ssR" и Ме= R"X". Предположим, что М
положительно определена, и a > 0. Покажите, что максимальное значение
функции
равно a (sTM~~ls)
(b) Если M представляет собой ковариационную матрицу нелинейной
задачи о наименьших квадратах, то ф(и)> заданное согласно (10.5 2),
пропорционально проекции s на направление и, деленной на погрешность решения
нелинейной задачи о наименьших квадратах в направлении и, и поэтому
критерий останова
max {ф (v): v е= R"} < tol (10.5.3)
представляет собой вполне осмысленный статистически способ измерения
малости шага s. Покажите, что если s = —(JTJ)-4TR и М = (ЛУ)-1, то
(ГО.5.3) эквивалентно проверке
el/W/^Utoi. <10-5-4>
Покажите, что аналогичное выражение имеет место, если s = —H~4TR и
М = Я"1, где //eR"X" равно гессиану V*f(*) или его аппроксимации.
Сопоставьте (10.5.4) с критерием останова по косинусу угла cos ф+^ tol,
где соБф+ задан согласно (10.4.2).
Упражнения 19 и 20 описывают в общих чертах смешанный линейно-
нелинейный алгоритм наименьших квадратов Голуба и Перейры (1973).
19. Пусть R: R* ->RW, т>п. Кроме того, пусть х«(и, v)T, и е= Rn""p,
0<=RP, 0<р<п, и R(x) = N(v).u-b, где N: Rp->Rm'{r,-p\ Ь е= Rm.
Например, если R: R4 ->► R20, г% (х) = х{е '*3 + х2е i%A — у(, то и = (*г х2)у
v == (дг3, *4), (/-я строка N (v)) =* \е ' 3, е ' 4), Ь( = уг Пусть точкой минимума
для f (х) шт —- R (х)Т R (х) является хт я. (и„ v.). Докажите, что u+=*N (vj+b.
Кроме того, докажите, что задача «найти min Dnf (*)» эквивалентна еле-
дующей:
min i-1| N (v) У (*)* Ь - Ъ \% (10.5.5)
v&Rp
10.5. Упражнения 283
20. С помощью алгоритма Голуба и Перейры (1973) разработайте для
решения задачи (10.5.5) демпфированный алгоритм Гаусса — Ньютона или
алгоритм Левенберга — Маркварта. В частности, опишите, как получаются
в аналитическом виде требуемые производные (это —самая трудная часть)
и как используется <2#-разложение.
21. Модифицируйте так алгоритмы из приложения А для решения
нелинейных уравнений, используя локально ограниченный оптимальный
(«криволинейный») глобальный шаг и аналитически заданный или
конечно-разностный якобиан, чтобы получить алгоритм Левенберга — Маркварта для
нелинейных наименьших квадратов. Вам не нужно будет вносить много изменений
в существующие алгоритмы. Алгоритмы А5.4.1 (конечно-разностный якобиан),
А6.5.1 (формирование якобиана модели), АЗ.2.1 и АЗ.2.2 (Qfl-разложение и
решение) будут отличаться только тем, что / имеет т, а не п строк, и тогда
Q/?-алгоритм будет вычислять решение линейной задачи о наименьших
квадратах [относительно требуемых незначительных изменений см. Стюарт (1973)].
Алгоритмы криволинейного шага остаются без изменений [однако в работе
Морэ (1977) можно найти более эффективную реализацию линейной
алгебры]. Критерии останова .должны измениться, как это обсуждалось в
разд. 10.4 [см. также Морэ (1977), Дэннис, Гэй и Уэлш (1981)]. Вы можете
протестировать свои программы на многих задачах из приложения В, так
как многие из них можно легко переформулировать как нелинейные задачи
о наименьших квадратах.
11
Методы решения задач
со специальной структурой
Эта глава есть нечто вроде приложения к основному материалу
книги в том смысле, что в ней излагаются способы применения
уже изложенной методики к задачам, в которых структура
матрицы Якоби или Гессе имеет важную специфику, часто
встречающуюся на практике.
Учет в квазиньютоновских методах специальной структуры
не является для нас делом новым. В гл. 9, например, в формулы
секущих были включены наследуемые от задач свойства,
сначала симметричности, а затем и положительной определенности.
В гл. 10 были модифицированы методы безусловной
минимизации с учетом специальной структуры нелинейной задачи о
наименьших квадратах.
В этой главе нас будет интересовать тот случай, когда часть
матрицы производных получается легко и точно, а остальная
часть — нет. В наиболее очевидном и, возможно, наиболее
важном случае, когда известно, что матрица производных содержит
много нулей, говорят, что якобиан и гессиан разрежены.
В разд. 11.1 и 11.2 обсуждаются соответственно
конечно-разностный метод Ньютона и методы секущих для решения
разреженных задач.
Обобщением рассмотренного в разд. 11.2 случая выступает
тот, в котором матрица Якоби или Гессе может быть
представлена в виде
J(x) = C(x) + A(x),
где С(х) получается точно с помощью некоторого метода, а для
матрицы А(х) некоторой специальной структуры мы хотим
воспользоваться аппроксимацией по секущим. В разд. 10.3 уже
встречался пример такого типа структуры в методе секущих
для нелинейных наименьших квадратов. В разд. 11.3 приведено
несколько дополнительных примеров структуры этого типа и
представлена весьма общая теория, которая показывает, как
строить аппроксимации по секущим для любой задачи.
11.1. Разреженный метод Ньютона 285
В разд. 11.4 представлена общая теория сходимости любого
метода секущих, который получается с помощью техники из разд.
11.3. Эти результаты включают на самом деле как частный
случай все результаты гл. 8 и 9 по получению методов и
исследованию их сходимости.
11.1. РАЗРЕЖЕННЫЙ КОНЕЧНО-РАЗНОСТНЫЙ
МЕТОД НЬЮТОНА
В этом разделе рассматривается задача решения систем
нелинейных уравнений F(x) = 0, о которой также известно, что
каждое отдельное уравнение зависит от относительно небольшого
числа неизвестных. Другими словами, /-я строка матрицы
производных имеет очень мало ненулевых элементов, и их
расположение не зависит от конкретного значения х. Можно было бы
учесть это, просто игнорируя нули и стараясь решить задачу
методами из гл. 5—9. Однако для многих задач использование
структуры расположения нулей, или, иначе говоря,
разреженности J(x), имеет решающее значение даже для самой
возможности решения задачи. Прежде всего п может быть настолько
велико, что о хранении всей J(x) не может быть и речи, если
не отказаться от хранения нулевых элементов. Кроме того,
экономия количества арифметических операций за счет отказа от
хранения нулей при решении системы линейных уравнений
J(xc)s» = -F(xc) (11.1.1)
относительно ньютоновского шага может оказаться весьма
значительной.
Если ненулевые элементы ](х) легко вычисляются
аналитически, то об этом случае много не скажешь. Следует
пользоваться эффективным способом хранения J(x) наряду с
эффективной программой для решения разреженной линейной
системы (11.1.1). В настоящее время имеются различные пакеты
программ по решению разреженных линейных уравнений, например
пакет в Харвелловской библиотеке или Иельский пакет по
обработке разреженных матриц, доступный через библиотеку IMSL.
Стратегии глобализации из гл. 6 можно без особого труда
приспособить к разреженной задаче, за исключением случая
локально ограниченного оптимального шага, который лишается
своей привлекательности из-за необходимости решения
большого количества линейных систем.
Оставшаяся часть раздела посвящена эффективным
способам аппроксимации с помощью конечных разностей ненулевых
элементов матрицы J(x), если они не заданы аналитически.
В основе этого лежит главным образом работа Куртиса, Пауэл-
ла и Райда (1974).
286 Гл. 11. Задачи со специальной структурой
Приведенные в гл. 4 рассуждения относительно конечных
разностей, включая выбор длины шага Л/, остаются здесь
по-прежнему в силе. Единственное отличие состоит в том, что мы будем
пытаться использовать менее п дополнительных вычислений
F(x) для аппроксимации J(x) путем получения более чем одного
столбца конечно-разностного якобиана на основе одного
дополнительного значения F(x). Для того чтобы увидеть, как это
сделать, рассмотрим следующий пример.
Пусть в\ обозначает /-й единичный орт, и имеются
{2х,+х]\ / 1\
для которых
Непосредственно видно, что элементы (1, 2) и (2, 1) якобиана
нулевые, и поэтому два столбца якобиана обладают тем
основным свойством, что в каждой строке1) содержится не более
одного ненулевого элемента. На гипотетической машине с
macheps = Ю-6, метод из разд. 5.4 выбрал бы й=(1(Н, 1(H),
вычислил
^-^ + *А)-'(Ш1.10)-(,"701).
v2 = F(xc + h2e2) = F(l, 10.01) = (7301)
и затем нашел аппроксимацию первого и второго столбцов
J(xc) по формулам
Pi-F (хе) = ( 4.001 \ v2-F(xc) _(0\
ь V о ;' *2 "vi/
Здесь важно то обстоятельство, что, поскольку нас интересовали
лишь А\\ и Л22, нам потребовались только первый элемент
f\{xc-\-h\ex) в ^! и второй элемент f2(xc + h2e2) в и2. Более того,
поскольку f\ не зависит от х2 и f2 не зависит от хи эти два
значения можно было получить с помощью единственного
вычисления функции
w = F(xc + hlel + h2e2) = F(l.00l, 10.01) = ( 3^0^01)
Тогда An={w{ — f\(xc))/hu A22 = (w2 — f2(xc))/h2, и, таким
образом, мы аппроксимировали J(xc) с помощью только одного
дополнительного к F(xc) вычисления F(x).
*) Имеется в виду строка образованной этими столбцами подматрицы,
которая в данном примере совпадает со всей матрицей. Такие подматрицы
будут играть важную роль в последующем обобщении. — Прим. перев.
11.1. Разреженный метод Ньютона 287
В общем случае действуем так же. Сначала находим
множество номеров (индексов) столбцов Гс={1, ..., п) с тем
свойством, что в каждой строке этого подмножества столбцов
якобиана содержится не более одного ненулевого элемента. Затем
вычисляем
—'(*+,£м)
и для каждой ненулевой строки i столбца /еГ
аппроксимируем J(xc)ij по формуле
Общее число дополнительных вычислений F(x), требуемых для
аппроксимации J(xc), равняется числу таких индексных
множеств Г, необходимых для покрытия всего множества столбцов.
Например, если J(x) есть трехдиагональная матрица:
Пх)ц¥*09 если |/ — Л<1,
Пх)ц = ® в противном случае,
то нетрудно показать, что для любого значения п достаточно
трех множеств индексов {у: / = Amod3}, А = 0, 1, 2. Таким
образом, только три, а не п дополнительных вычислений F(x)
требуется на каждой итерации, чтобы аппроксимировать J(xc).
В общем случае не представляет особого труда группировать
столбцы ленточной матрицы в минимальное число групп таких
индексных множеств и обобщить приведенный выше пример с
трехдиагональной матрицей (упр. 1). К сожалению, не
существует, по-видимому, эффективного способа получения
наименьшего числа таких групп для разреженного якобиана общего
вида. Тем не менее простые эвристические алгоритмы оказались
в конечном счете весьма эффективными. В недавней работе
Коулмана и Морэ (1983) улучшены эвристические приемы Кур-
тиса, Пауэлла и Райда и показано, что общая задача имеет
NP-сложностъ1). Заметим, что если вычисление F(x) может
быть разбито естественным образом на п вычислений его
компонент-функций, то приведенные выше способы оказываются
здесь ненужными, так как мы можем просто аппроксимировать
каждый ненулевой элемент /(**)// по формуле (М*с + Л/в/) —
— fi(xc))/hj. Однако на практике, если J(x) не задано
аналитически, такого рода разбиение F(x) обычно обходится недешево.
Эти способы распространяются и на задачу безусловной
минимизации, где в качестве матрицы производных выступает
гессиан V2f(xc). В квазиньютоновском методе для больших
разреженных задач минимизации нужно эффективно хранить
*) Подробнее об ЛГР-сложности см. Ахо, Хопкрофт и Ульман (1974).—
Прим. перев.
288 Гл. 11. Задачи со специальной структурой
V2f(xc) и использовать программы по решению симметричных
(и положительно определенных, если этим можно
воспользоваться) разреженных линейных систем. Если V2f(xc)
аппроксимировать при помощи конечных разностей, используя лишь
значения функции, то достаточно просто можно аппроксимировать
ненулевые элементы, применяя способы из разд. 5.6. Тем не
менее иногда на практике можно вычислить V/(jc) аналитически
одновременно с f(x) при малых дополнительных затратах.
В этом случае V2f(xc) следует аппроксимировать на основе
дополнительных значений Vf(x), используя в целях обеспечения
эффективности этого процесса процедуру, подобную
приведенной выше. Можно непосредственно использовать способ Кур-
тира, Пауэлла и Райда, а затем для получения разреженной
симметричной аппроксимации гессиана взять среднее из
полученной матрицы и ее транспонированной. Недавнее
исследование Пауэлла и Тоинта (1979), а также Коулмана и Морэ (1982)
сосредоточено на использовании симметричности в целях
получения этой аппроксимации более эффективным образом (см.
упр. 2).
11.2. РАЗРЕЖЕННЫЕ МЕТОДЫ СЕКУЩИХ
В предыдущем разделе мы познакомились с тем, как
использовать разреженность для сокращения количества вычислений
функций, требуемых для аппроксимации ](х) конечными
разностями. Однако если вычисление F(x) обходится дорого, то
такая аппроксимация может оказаться все же слишком
обременительной, и тогда нам, возможно, захочется аппроксимировать
/(jc), привлекая идею метода секущих. При этом для
достижения экономии памяти и числа арифметических операций,
упоминающихся в разд. 11.1, желательно, чтобы аппроксимации
по секущим имели такую же разреженность, как и сам якобиан.
В данном разделе обсуждается разреженная формула секущих,
которая является всего лишь специальным применением
формулы секущих из гл. 8 к разреженному случаю. Кратко
обсуждаются также разреженные симметричные формулы секущих
для задач минимизации.
Напомним, что формула секущих для нелинейных уравнений
(формула пересчета Бройдена)
А+ = Ас+{Ус-А/с)8Тс (11.2.1)
sesc
представляет собой решение задачи о минимальных поправках:
найти min \\В — АС\\Р
при условии Bsc — yc, (11.2.2)
11.2. Разреженные методы секущих 289
где АС9 A+^RnXn аппроксимируют J(xc) и J(x+)
соответственно, sc = x+— хс и yc = F(x+) — F{xc) (для удобства в
оставшейся части этой главы мы будем опускать индекс с величин
A, s и у). В разреженном случае пусть ZeRrtXn есть (0,
^-матрица, задающая структуру расположения нулей в J(x), т. е.
, если / (Jt)jy = 0 для всех х е R",
" — 'в противном случае,
"_1 1
и пусть SP(Z) обозначает множество яХ «-матриц, имеющих
эту структуру расположения нулей, т. е.
SP(Z) = {MeERnXn: Ми = 0, если Z/y = 0, 1</, /</t},
(11.2.3)
Если предположить, что А е SP (Z), то естественным
обобщением (11.2.2) на разреженный случай будет задача:
найти .min \\В — А\\Р
при условии Bs = y, fie=SP(Z). (11.2.4)
Конечно, SP(Z) может не содержать ни одного элемента, для
которого Bs = y> как, скажем, в том случае, когда требуется,
чтобы целая строка в В была нулевой, а соответствующая
компонента в у не равна нулю. Если требуемая разреженность
согласуется с условием Bs = у, то решение (11.2.4) легко
найти, и оно представлено в теореме 11.2.1. Его можно также
получить, используя более общую теорему 11.3.1.
Нам потребуется дополнительно следующее обозначение:
определим оператор матричного проектирования Pz: RnXn->
->Я"ХЛ через
<PzW),( = {u№ '«I* (Ч.2.В)
Это означает, что Pz обнуляет элементы в М> соответствующие
нулевым позициям структуры разреженности Z, и оставляет
без изменения остальные элементы в М. В качестве
упражнения можно показать, что Pz(M) является ближайшей в SP(Z)
матрицей к М в норме Фробениуса. Аналогично, для usR"
определим V| е Rn как
если ZiJ=l.
<*»<-u
Это означает, что vj представляет собой результат наложения
на v структуры разреженности f-й строки матрицы Z.
290 Гл. 11. Задачи со специальной структурой
Теорема 11.2.1. Пусть Z е R"Xn есть (0, 1)-матрица, и пусть
SP(Z) определено согласно (11.2.3), а Р2 —согласно (11.2Г.5).
Пусть i4eSP (Z), s, у е Rn. Определим sh i = 1, ... , /i,
согласно (11.2.6). Если st = 0, только когда *// = 0, то решением
для (11.2.4) будет разреженная формула секущих1)
A+ = A + PZ (D+ (у - As) sT), (11.2.7а)
где D+ определено в (3.6.6) для диагональной матрицы
DgR"x", такой, что
Du = sUh /=!,..., п. (11.2.7Ь)
Доказательство. Пусть Л/., Bit е Rn обозначают 1-е строки
соответственно в Л и В. Тогда, поскольку
\\B-A\&=h\Bi.-Ai.\\l
задача (11.2.4) может быть решена с помощью выбора в
качестве каждого Bit решения задачи:
найти min ||£*. — Л/#||2
при условии (Bi, — At) s = (y — As)h (B{. — A{) e SP (Z)/#,
(11.2.8)
где SP (Z)/# = {v e R*: Vj = 0, если Ztj = 0}. Нетрудно показать,
что решением для (11.2.8) является
В,. = Аи + (sUt)+ (У - -4s), si (U.2.9)
Поскольку i-я строка в Pz(uvT) имеет вид (ut)vi для любых
и,и£Кя, то В,., заданное согласно (11.2.9), в точности
совпадает с *-й строкой матрицы Л+, заданной согласно (11.2.7). □
Пример 11.2.2. Пусть
Г1 0 1-1
Z = \ 110,
Lo l ij
s = (l, -1, 2)r, y = (2, 1, 3)r, A = I. Тогда s, = (l, 0, 2)T, s2 =
= (1, -1, 0)T, s8 = (0, -1, 2)г и (11.2.7) дает
Г 0.2 0 0.41
А+ = А+ 1 -1 0 .
[О -0.2 0.4 J
') В оригинале — sparse secant update. — Прим. nepee.
11.2. Разреженные методы секущих 291
Сравните
дала бы
с формулой пересчета Бройдена (11.2.1), которая
А+ = А +
1
6
1
3
1
6
1
6
1
3
1
6
1
3
2
3
1
3
Формула пересчета (11.2.7) была предложена независимо
Шубертом (1970) и Бройденом (1971), а теорема 11.2.1 была
доказана независимо Райдом (1973) и Марвилом (1979). Эта
формула пересчета кажется эффективной в квазиньютоновских
алгоритмах для разреженных нелинейных уравнений, хотя
имеется мало публикаций по вычислительному опыту их
использования. Если некоторое s/ = 0, то (11.2.4) имеет решение только
тогда, когда соответствующее значение yt = 0. Тем не менее,
если /(jc)eSP(Z), s = x+ — хс и у = F(x+)—F(xc)> то это
имеет место всегда (см. упр. 5). Теорема 11.3.1 обращается
к более общему случаю. В теореме 11.4.1 будет показано, что
квазиньютоновский метод, использующий формулу пересчета
(11.2.7), при стандартных предположениях, локально ^-сверх-
линейно сходится на задачах с /(х)е SP(Z).
К сожалению, применение разреженных формул пересчета
в безусловной минимизации, где аппроксимации должны быть
к тому же симметричными и, возможно, положительно
определенными, не было столь удовлетворительным. Марвил (1978)
и Тоинт (1977, 1978) были первыми, кто обобщил
симметричную формулу секущих на разреженный случай, решая задачу:
найти min \\В — А]\Р
при условии Bs = у, (В — А) е SP (Z), (В — А) симметрична.
Мы приводим эту формулу пересчета в разд. 11.3, а в разд. 11.4
доказывается локальная <7_свеРхлинейная сходимость
использующего ее квазиньютоновского метода. Однако эта формула
пересчета имеет несколько существенных недостатков, о
которых речь пойдет ниже, причем один из них состоит в том, что
порождаемые им аппроксимации не обязательно положительно
определены. Действительно, попытки построить положительно
определенную разреженную симметричную формулу пересчета
пока остаются безуспешными. Шанно (1980) и Тоинт (1981)
получили разреженную формулу пересчета, которая сводится
к BFGS-формуле в неразреженном случае, однако она не
обязательно сохраняет положительную определенность в случаях
наличия разреженности.
292 Гл. 11. Задачи со специальной структурой
Тод* факт, что ни одна из этих разреженных симметричных
формул пересчета не сохраняет положительную определенность,
уже исключает основное достоинство формулы секущих для
задач минимизации. Вдобавок вычисления по любой из
известных симметричных разреженных формул пересчета требуют
дополнительного решения на каждой итерации системы линейных
уравнений с разреженной симметричной матрицей. И наконец,
ограниченный вычислительный опыт работы с методами,
использующими эти формулы пересчета, не дал положительных
результатов. По этим причинам методы секущих, возможно, не
являются перспективным способом решения больших
разреженных задач минимизации.
Вместо этого, как нам кажется, для решения больших
задач минимизации будут использоваться либо
конечно-разностные методы, рассмотренные в разд. 11.1, либо методы
сопряженных градиентов. Методы сопряженных градиентов
несколько отличаются от квазиньютоновских методов по своей
основной структуре, и мы не включили их в книгу. Для задач малой
размерности методы сопряженных градиентов обычно менее
эффективны, чем методы, рассмотренные в этой книге, однако
для задач большой размерности они претендуют на первенство.
Как и методы секущих, они используют при минимизации
только информацию о функции и градиенте, а основным
отличием выступает то, что они не сохраняют никакой
аппроксимации матрицы вторых производных. Относительно дальнейшей
информации см. Бакли (1978), Шанно (1978), Флетчер (1980),
Хестенс (1980) или Гилл, Мюррей и Райт (1981). Что касается
их прямой обработки с помощью аппарата линейной алгебры,
см. Голуб и Ван Лоан (1983). Усеченные методы Ньютона
[см., например, Дембо, Айзенштат и Штайхауг (1982)]
сочетают в себе некоторые черты методов сопряженных градиентов
с особенностями методов доверительных областей из гл. 6.
Другие новые подходы представлены в статьях Гриванка и
Тоинта (1982а, Ь, с).
Завершим обсуждение методов секущих для разреженных
задач упоминанием о преимуществе методов секущих для
неразреженных задач, которое не распространяется на
разреженный случай. Как отмечалось в гл. 8 и 9, мы могли использовать
формулы секущих для сокращения затрат на арифметические
операции с О (я3) до 0(п2) на каждой итерации, используя
либо пересчет непосредственно аппроксимации матрицы,
обратной к гессиану, либо пересчет LU- или Q/^-разложения. В
разреженном случае первая из возможностей не привлекательна,
потому что обратная к разреженной матрице редко бывает
разреженной, тогда как вторая возможность не подходит,
потому что формула пересчета обычно представляет собой
поправку ранга п матрицы Ас. С другой стороны, потеря этого
11.3. Вывод формул с минимальными поправками 293
преимущества, возможно, не столь уж существенна в
разреженном случае, поскольку факторизация и решение
разреженной линейной системы часто требуют лишь О(п) операций.
11.3. ВЫВОД ФОРМУЛ СЕКУЩИХ С МИНИМАЛЬНЫМИ
ПОПРАВКАМИ1)
В оставшейся части этой главы рассматриваются задачи,
определяемые функцией F: Rn->*!Rrt, матрица производных которой
/ (х) = F' (х) имеет вид
J(x) = C(x) + A(x), (11.3.1)
где С(х) находится непосредственно в нашем распоряжении,
тогда как А(х) требуется аппроксимировать, используя
формулы секущих. [Этот случай включает в себя задачи
оптимизации, где F(x) = Vf(x) и J(x) = V2/(jc).] В этом разделе
будет представлено в краткой форме расширенное изложение
результатов Дэнниса и Шнабеля (1979) по выводу в рамках
рассматриваемой общей схемы формул пересчета с
минимальными поправками. Мы опустим длинное доказательство
основной теоремы и приведем лишь простейшие примеры ее
применения, так как читатель, специализирующийся в этих вопросах,
может обратиться к цитируемому оригиналу.
Мы уже видели несколько примеров задач, обладающих
структурой (11.3.1). В разреженных задачах, рассмотренных
в разд. 11.1 и 11.2, где не нужна полная степень общности,
характерная для этого раздела, С(*) = 0, а А(х) содержит
ненулевые элементы J(x) и должно быть аппроксимировано
матрицами, имеющими такую же структуру разреженности.
Близкими к рассмотренному являются два случая: когда некоторые
компоненты функции F(x) линейны или когда F(x) линейна
относительно некоторых своих переменных. Примером в
первом случае служит
1> 2) — \f2(Xl9 х2) = «черный ЯЩИК»(ДС!, *2)/
'<*-{*!&. ди.)-(о оИ*к дЗа)- (»•"»
^ дхх дх2 ' N дхх дх% '
') В оригинале least change secant updates. — Прим tie рев.
294 Гл. 11. Задачи со специальной структурой
Примером во втором случае служит 1)
(Зхх + mess! (х2, *3)\
— ATj + messata, xz) ,
+5xl + mess3(x2, x3)J
J \X\, X2i Хз) —
о dtn\ (x2, x3) dmx (x2, x3)
dx2 dx3
— 1 dm2(*2, *з) дт2(х2, хъ)
дх2 дхъ
с дпн(х2> х3) дт3(х2, х3)
дх2
дхъ
дтх (х2, х3) дтх (х2, х3)
дх2 дхз
дт2(х2, х3) дт2(х2, хэ)
О
0 дх2
п дтг (х2у *з)
U дх2
дхъ
дтз (x2l х3)
дхъ
= С(х) + А(х).
(11.3.3)
В обоих случаях С(х) есть известная постоянная матрица, в то
время как А(х)у возможно, необходимо будет
аппроксимировать с помощью методов секущих.
Другим примером служит нелинейная задача о наименьших
квадратах, рассмотренная в гл. 10, где С(х) = J(x)TJ(x) и
т
A(x)=Zrt(x)1*rt(x).
Напомним, что /(*) вычисляется всегда (аналитически или по
конечным разностям) для того, чтобы вычислить Vf(x) =
= J(x)TR(x). Поэтому С (а:) имеется в нашем распоряжении,
а А(х) обычно аппроксимируется нулевой матрицей или с
привлечением техники метода секущих. Наиболее интересной
представляется функция общего вида, используемая для
наилучшего приближения данных
f(x) = p(R(x)), prR^R1, /?:R"-RnV
о которой речь шла в разд. 10.4. Здесь
V/M = WVP (/?(*)),
(11.3.4)
V*f(x) = J(xYv2p{R(x))J(x) + YJ^£)lV2rt(x) = C(x) + A(x),
i-\
!) Слово mess, используемое здесь для обозначения функции,
переводится как «беспорядок», «путаница». — Прим. перев.
11.3. Вывод формул с минимальными поправками 295
где тХя-матрица / (х) — R' (х). На практике Vp и V2p обычно
получаются тривиально, a J(x) вычисляется аналитически или
по конечным разностям для вычисления V/(x), но о получении
приблизительно тп2/2 различных вторых частных производных
невязки не может быть и речи. Таким образом, мы
непосредственно имеем С(х), и нам необходимо аппроксимировать А(х).
Во всех этих примерах аппроксимация для А (х) по секущим
должна отражать специальную структуру именно этой
аппроксимируемой матрицы. Идея, которая будет использована для
нахождения подходящей аппроксимации для А(х+)9 где х+ —
некоторое приближение, представляет собой естественное
обобщение того, что мы делали до сих пор. Примем относительно
соотношения секущих такое решение, как, скажем Л+ е
s=Q(y*, s)±{MezRnXn:Ms = y*}. Кроме того, выберем
аффинное подпространство «я£, определяемое такими свойствами,
как симметричность или разреженность, которыми должны
обладать все аппроксимации Л*. Затем потребуем, чтобы Л+ была
среди матриц из si> r\ Q (у*9 s) ближайшей кДе^в
соответствующей норме. Это означает, что Л+ будет результатом
применения к А «формулы пересчета с минимальной поправкой»,
обеспечивающей наличие желаемых свойств.
Обсудим для некоторых из наших примеров вопросы выбора
Q(y*> 5), «я£и метрики, необходимой для нахождения
наименьшей поправки. Воспользуемся опять обозначениями s=x+—хс
и y — F(x+) — F(xe) и напомним читателю, что соотношение
секущих в гл. 8, A+s = yy вытекало из того факта, что у =
= J(x+)s, если F(x) линейно, и yo=kJ(x+)s в нелинейном
случае. Здесь желательно, чтобы ## ^ А (*+) s.
Для первого примера (функция (11.3.2)) видим, что s& =
= {ЛеР2Х2:Л,, = (0, 0)} и что норма Фробениуса
представляется приемлемой мерой для определения величины поправки.
Соотношение секущих тоже имеет очень простой вид, так как
А (*+) 5 = ( у/2 {x+fs ) « ( f2 {х+) _ h {Хс)),
поэтому мы берем у* = (0, f2 (*+) — /2 (*с))Т = (0, #г)г.
Во втором примере (функция (11.3.3)) st> = {ЛеРЗХЗ: Ал =
= (0,0,0)7"}, и опять представляется разумным использование
нормы Фробениуса, но соотношение секущих будет несколько
более интересным. Если можно непосредственно вычислять
сложную часть Mess(jt2, #3) в F(x\,X2,Xz)9 то у нас нет особых
трудностей, так как ясно, что логичным будет выбирать
## = Mess((jt+)2, (*+)з) — Mess ((хс)2, (хс)г)- Если мы не можем
разбить функцию F таким образом, то вместо этого нами
используется общая методика, которая работает всегда и которая
296 Гл. 11. Задачи со специальной структурой
в данном случае, равно как и в первом примере, приводит
к тому же самому выбору */#.
Если структура А(х) не подсказывает возможности
недорогого выбора у*, то, коль скоро С(х+) вычисляется всегда,
можно за неимением лучшего перейти к стандартному
соотношению секущих
A+s = y* = y-C(x+)89 (11.3.5)
которое эквивалентно требованию о том, чтобы аппроксимация
всего якобиана /+ = С(х+) +Л+ удовлетворяла стандартному
соотношению секущих
J+s = (C(x+) + A+)s = y.
Читатель может убедиться, что (11.3.5) эквивалентно выбору
у* в рассмотренных выше примерах.
Наш заключительный пример (функция (11.3.4)) является
гораздо более интересным, потому что стандартное ## не
является таким же, как ##, получаемое непосредственно из
рассмотрения A{x+)s. Согласно (11.3.5), стандартное у* имеет вид
У* = J (х+)т VP (R (х+)) - / (xc)TVp(R(xc))-J(x+)TV*P(R(x+))J(x+)s.
(11.3.6)
С другой стороны, прямое обобщение вывода формул (10.3.1)—
(10.3.3) наводит на мысль предложить
m
m
^Zd9T+))&r^-^x<n=
i-l '
= / (*+)г VP (R (x+)) - J (xc)T Vp (R (x+)) = #*, (11.3.7)
что, вообще говоря, отличается от (11.3.6). Отрадно, что
последний выбор */# на практике зарекомендовал себя несколько
лучше.
Для завершения описания условий, налагаемых на
аппроксимацию по секущим для функций (11.3.4), выберем sl> =
= {Ле Rnxn; А = Л7*}, так как А(х) всегда симметрична.
Можно было бы, конечно, взять в качестве метрики для
определения минимальной поправки норму Фробениуса, что привело бы
нашу формулу пересчета при С(х+) = 0 к симметричной
формуле секущих (9.1.3). Однако, коль скоро решается задача
минимизации, здесь пригодятся рассуждения о масштабировании
из разд. 9.3, и они приведут нас к использованию нормы
Фробениуса после проведения масштабирования с помощью 7, где
11.3. Вывод формул с минимальными поправками 29 7
JJTs = y при условии, что yTs > 0. Это сводит нашу формулу
пересчета при С(х+) = 0 к DFP-формуле.
При заданном выборе соотношения секущих i4+eQ(##, s),
подпространства аппроксимаций зФ и взвешенной нормы Фро-
бениуса ||-|| теорема 11.3.1 дает формулу пересчета,
представляющую собой решение задачи:
найти min ||В — Л||
при условии BeQ(j/#, s)r\st,
если, конечно, такая В существует. На самом деле в
теореме 11.3.1 рассмотрен более общий случай, когда Q(y*9 s) ^ s&
может быть пусто. В этом случае в качестве Л+ выбирается
матрица в st, ближайшая к А среди множества матриц из j#,
ближайших к Q(##, s). Для простоты теорема формулируется
в невзвешенной норме Фробениуса, но она остается в силе и
для любой взвешенной нормы Фробениуса. Доказательство
Дэнниса и Шнабеля использует технику итеративного
проектирования, которое является прямым обобщением процедуры
симметризации Пауэлла, рассмотренной в разд. 9.1. Читатель
может вновь обратиться к рис. 9.1.1, подставляя s& вместо S
и у* вместо ус.
Нам понадобится следующий факт: любое аффинное
подпространство st> является сдвигом единственного для него
подпространства 9*. Для любого Л0е«я£ подпространство 9* =
= {А — Л0: А е s&) не зависит от А0.
Теорема 11.3.1 [Дэннис и Шнабель (1979)]. Пусть s#0,
и Р.л и Р& — ортопроекторы на ^ и ^. Пусть, далее, Р есть
п X /г-матрица, у-й столбец которой имеет вид
["(£)]*
и ^Gi, Если v есть произвольное решение задачи
min \\pv-(y*-As)\\2, (11.3.8)
oeRn
или, что эквивалентно, задачи
то
А+ = А + Р*(^ (11.3.9)
298 Гл. 11. Задачи со специальной структурой
является матрицей, ближайшей к А среди матриц из s&,
ближайших kQ(##, s). Если минимум равен нулю, то A+^str\
^Q&#, s).
Комбинируя (11.3.8) и (11.3.9) можно представить нашу
формулу пересчета с минимальными поправками в виде
Л+ = Л + Р^(Я+(у#^Л5)/), (11.3.10)
где через Р+ обозначена матрица, обобщенно обратная к Р
(см. разд. 3.6). Воспользуемся теперь (11.3.10) для вывода
разреженной формулы секущих и симметричной разреженной
формулы секущих, которые рассматривались в разд. 11.2.
Для того чтобы вывести разреженную формулу секущих,
используя теорему 11.3.1, выбираем у# = у, s£ = <?=SP(Z) и
Рл = Р& = Pz, где последний из операторов задан согласно
(11.2.5). Тогда имеет место
следовательно, P = (l/sTs)diag(sTjSj)t и (11.3.10) дает
А+ = А + Pz (diag (sTjSj))+ (у - As) sT,
что экривалентно (11.2.7).
Для вывода симметричной разреженной формулы пересчета
выбираем у* = у, а = 9 = SP (Z) r\ {А е RnXn: А = Л7}. Легко
показать в качестве упражнения, что для любого М е RnXn
Рл (М) = Р& (М) = у Pz Ш + Мт). Читатель затем может
показать, что в этом случае матрица Р из теоремы 11.3.1 задается
формулой
P-^7[diag(^5y) + Pz(ssT)], (11.3.11)
так что (11.3.10) дает
A+ = A + Pz(vsT + svT)9
v = P+(y-As). (11.3.12)
Дальше будет предложено в качестве упражнения показать,
что (11.3.12) сводится при SP(Z) = RnXn и Pz = I к
симметричной формуле секущих (9.1.3). Заметим, однако, что в общем
случае для вычислений по формуле пересчета (11.3.12)
требуется знать вектор v> который в свою очередь требует на
каждой итерации решения новой разреженной линейной системы.
11.4. Анализ методов с минимальными поправками 299
В заключение, используя теорему 11.3.1, дадим формулы
пересчета для трех примеров этого раздела. В качестве простого
упражнения можно показать, что для первого примера (11.3.2)
формула пересчета имеет вид
А+ = А + ( т „° т „ ° V (11.3.13)
+ ^| el(y*-As) ет2 {у*-As) '
\ sTs S{ sTs S2J
а для второго (11.3.12), если Y = [(^)2 +fe)2]4", — вид
(0 ye*(y* — As)s2 ует{ (у* — As) s3\
0 yeT2(y*-As)s2 ye* (у*-As) s А (П.ЗЛ4)
0 yel(y* — As)s2 ye\{y* — As)sJ
Как уже отмечалось в гл. 10, для функции (11.3.4) аналогом
DFP-формулы служит формула пересчета (10.3.6) с j/#,
которое здесь задано согласно (11.3.7) (см. также упр. 16 из гл. 10).
11.4. АНАЛИЗ МЕТОДОВ СЕКУЩИХ
С МИНИМАЛЬНЫМИ ПОПРАВКАМИ
В этом разделе на основе работ Дэнниса и Уолкера (1981)
представлены две теоремы, которые дают необходимые
условия, налагаемые на */# и зФ и гарантирующие локальную
сходимость любого метода секущих, получающегося с
использованием теоремы 11.3.1. Эти теоремы показывают, что любой
представленный в этой книге метод секущих с минимальными
поправками локально и ^-сверхлинейно сходится. Они также
указывают способ построения формул секущих для других
задач со специальной структурой.
Далее предположим, что матрицы J(x) и С(х) удовлетво
ряют условиям Липшица, и что /(**) обратима.
Исходя из наших целей, полезно провести различие между
двумя видами формул секущих с минимальными поправками,
такими как, скажем, метод Бройдена, которые на каждой
итерации при вычислениях по формуле пересчета с минимальными
поправками используют одну и ту же норму Фробениуса, не-
масштабированную или заданную в фиксированной метрике,
и такими, как, скажем, DFP-метод, которые можно представить
себе как результат перемасштабирования задачи на каждой
итерации заново перед вычислениями по формуле пересчета.
Теорема будет сформулирована для каждого из этих двух
типов методов, но из соображений краткости мы не будем
обсуждать методы, подобные BFGS, которые обычно рассматрива-
300 Гл. 11. Задачи со специальной структурой
ются как проекции (в смысле минимальных поправок)
матрицы, обратной к аппроксимации гессиана. Мы также
ограничимся здесь взвешенной и невзвешенной нормами Фробениуса,
хотя статья Дэнниса и Уолкера носит более общий характер.
Упомянутые теоремы можно интерпретировать, грубо говоря,
так, что методы секущих с минимальными поправками
сходятся, если пространство аппроксимаций зФ выбрано
обоснованно и если соотношение секущих, в котором участвует ##,
выбрано должным образом, и что они сходятся сверхлинейно,
если к тому же и ^ выбрано должным образом. Поэтому
выбор соотношения секущих является решающим для
сходимости метода. Этот факт был до некоторой степени завуалирован
той простотой, с которой ## могло выбираться для
традиционных задач или даже для более общих задач из разд. 11.3.
Взаимосвязь между s& и у* выражается в этих случаях всегда
допустимым выбором
#* = pJ( \ J(x + ts)dtj-C(x+)\s, (11.4.1)
который сводится к стандартному выбору
y*=y-C(x+)s,
если А (х) е st> для всех х, как это всегда имело место в
разд. 11.3.
Теорему 11.4.1 предполагается сформулировать с
минимальным, до некоторой степени, предположением относительно *s£.
Оно сводится к предположению о существовании некоторого
A*^st, для которого квазиньютоновская итерация
x+=xc-(C(x*) + A*r*F(xc)
была бы локально ^-линейно сходящейся. Это требование к s4>
является, конечно, довольно незначительным, и если Л(*#)е,я£,
то Л* — А(х*) будет заведомо удовлетворять этому условию.
Требование к ## также достаточно минимально, и его нужно
рассматривать как требование, чтобы расстояние в норме
Фробениуса от А(х*) или от А(х+) до Q(y*, s) уменьшалось как
максимум из ||*+ — х*\\р и \\хс — *Лр для некоторого р > 0.
Другими словами, величина поправки, модели должны становиться
все меньше по мере приближения к решению. Как и в разд. 11.3,
теория включает случай, когда st>r\Q(y#y s) пусто. Этот
случай важен для ряда приложений, относительно которых будут
даны краткие комментарии в конце данного раздела.
Заметим, что 11-11 используется для обозначения
произвольной векторной и подчиненной норм, а ||-||/> по-прежнему
используется для обозначения нормы Фробениуса.
11.4. Анализ методов с минимальными поправками 301
Теорема 11.4.1. Пусть выполнены предложения теоремы
5.2.1. Пусть s&, ^, Q(y, s) и Рл определены как в теореме
11.3.1, P^^Q{0tS) обозначает евклидов проектор на
ортогональное дополнение к 9 r\ Q (0, s) и С: Rn -> RnXn. Предположим,
что Аш = Рл [J (*,) — С (xj] и В, = С (х0) + Аш обладают теми
свойствами, что В0 обратима и существует такое г., для которого
\B:l[J(xJ-{C(xJ + A$\<r.<l. (11.4.2)
Предположим также, что правило выбора y*(s), где 5 = лг+ — л:,
либо является стандартным выбором (11.4.1), либо, в более
общем случае, обладает совместно с si тем свойством, что
существуют а > 0 и р > 0, такие, что для любых х, х+ из
окрестности точки хт имеет место неравенство
\РЬ~ъь9)(0-А.)\<™{х> *+)Р (И.4.3)
по крайней мере для одного G, которое является ближайшей
в si точкой к Q (у* (s), s), где
о(х, *+) = max{|U —*Д ||*+ —*.||}.
При этих предположениях существуют положительные числа
е и б, такие, что если ||#0 — *J|<e и \\А0—- Аф\\< б, то
последовательность, определяемая соотношениями
**+1 = 4 +(С (xk) + Akyl F (**),
Ak+x = (Ak)+e=st9
а также соотношениями, приведенными в теореме 11.3.1,
существует и сходится к хт по крайней мере ^-линейно, причем
цт J_f*±j—fJL = ijm
Л^оо ||**-* || fe->oo
К1 [/ (х,) - (с (xt)+a,)) „**.*;„[ < г..
Отсюда {xk} сходится <7-сверхлинейно к хл тогда и только тогда,
когда
lira [/ (х,) - (С (х,) + А,)] *» ~ ; = 0.
*>оо || ** *J|
В частности, {xk} сходится ^-сверхлинейно к хт, если
J(x.)-C(x.) = A(x,)<=si.
Доказательство теоремы 11.4.1 является сложным, как,
может быть, читатель и предполагает, поскольку из него следует
локальная <7-сверхлинейная сходимость каждого из
обсуждавшихся в этой книге методов секущих с фиксированной
метрикой. Например, для разреженного метода секущих из разд. 11.2
si = SP(Z) и С(х) = 0, поэтому мы тривиально получаем
302 Гл. 11. Задачи со специальной структурой
A(x*) = J(x*)— C(x*) = J(x+)^s&y и (11.4.2) выполняется при
г„ = 0. Кроме того, у* =y — F(x+) — F(хс) представляет собой
стандартный выбор (11.4.1). Таким образом, тривиальное
следствие из теоремы 11.4.1 заключается в том, что разреженный
метод секущих является локально сходящимся, и поскольку
A(x*)^sty то он сходится <7-сверхлинейно к х* при
стандартных предположениях. Тех же рассуждений практически
достаточно для доказательства на основе теоремы 11.4.1 локальной
<7-сверхлинейной сходимости разреженного симметричного
метода секущих. Сходимость неразреженных вариантов метода
секущих и неразреженного метода секущих из гл. 8 и 9
вытекает, конечно, из того, что они просто представляют собой
такие частные случаи, в которых структура разреженности не
имеет нулевых элементов.
Все традиционные методы из гл. 8 и 9 используют
стандартный выбор, и поэтому более общее и несколько
таинственное услойие (11.4.3) оказывается ненужным. С другой стороны,
оно нужно в методах наименьших квадратов с фиксированной
метрикой или с перемасштабированием, использующих у* =
= / (х+)т F (х+) — / (х)т F (х+). Дэннис и Уолкер всесторонне
разработали эту проблему, и мы лишь напомним, что для 9>=
= {Af: М = МТ} достаточно иметь
11*/#-^||<аа(*, x+r\\s\\.
Для 9* общего вида достаточно иметь
## — A;s = Es для некоторой Е^9*9 такой, что
\Р^ЯФ.в)Е\<(ш(х9 *+)'• (П-4.4)
Позже мы действительно увидим пример, для которого
сравнительно легко можно получить более строгий результат: ||£||^
^ао(х,х+)р.
Утверждение теоремы 11.4.2, относящееся к итеративно
перемасштабируемым методам секущих с минимальными
поправками отличается от утверждения теоремы 11.4.1, относящегося
к методам с фиксированной метрикой, тем, что должны
уточняться правила выбора у и у* как функций от s = х+ — х.
Разница простая: матрицы масштабирования принадлежат Q(y,s),
а аппроксимации по секущим принадлежат Q(##, s). Короче
говоря, у стараются выбирать похожим на J(x+)s, а у# — на
A(xm)s.
Для аффинного подпространства Ж и симметричной
положительно определенной матрицы W удобно иметь обозначение
Рл, Wy которое определяет ортогональную проекцию на ^ в
скалярном произведении, порождающем норму ||Af|!v =
= [trace{W-mW-Ш7)]1'2 в К"*". Если W = JJT, а М
симметрична, то полезно иметь в виду, что ||Af||^= \\J~lN[J-T\\F.
11.4. Анализ методов с минимальными поправками 303
Теорема 11.4.2. Пусть выполнены предположения теоремы
5.2.1. Пусть st>, 9 и Q(y, s) определены как в теореме 11.3.1
и ^^Q(o, 5). w обозначает проектор на ортогональное
дополнение к У г>ь Q (0, s) в скалярном произведении, порождающем
норму ||Af|hr, и С: R*-► RnXn. Пусть, далее, матрица J{xm)
симметрична и положительно определена и 9> обладает тем
свойством, что для любых s и у, таких, что sTy > 0, проектор /V, w
не зависит от любой конкретной положительно определенной
симметричной матрицы fsQ(y,s). Кроме того, предположим
относительно st, что
А. = Рл91М[Цхт)-С(х,)] и Вш = Ат + С(х.)
таковы, что В0 обратима, и существует такое гт9 для которого
к-'[/(*.)-(С(*.) + Л.)]1<г.<1.
Предположим также, что существуют а{, а2 ^ 0 и р > 0, такие,
что правило выбора у (s) удовлетворяет условию
II*-/(*.)* II <«i*(*. *+)рН*Н,
а правило выбора у* (s) представляет собой либо стандартный
выбор
y*=PA.w[(\]^Hx + t8)dt)-C(X+j\8
для W = J(xJ или некоторого W^Q(y, s), либо обладает
совместно с s4> тем свойством, что для любых х и х+ из
окрестности точки х9 выполняется неравенство
для любой симметричной положительно определенной матрицы
^gQ(j/,s) и по крайней мере для одной G, которая в W-uop-
ме является ближайшей в s& точкой к Q(y#, 5). В рамках этих
предположений существуют положительные константы е и б,
такие, что если \\х0 — xj<e и ||Л0 — Л*||<6, то существует
последовательность, определяемая соотношениями
**+! = xk — (С (xk) + AkrlJ(xk),
Ak+i = (Ak)+t=st,
в которых ЛЛ+1 получается по формуле секущих с
минимальными поправками, построенной относительно s4> и Q(#*, sk)
в Уд-норме, где ^eQ (yk, sk). Эта последовательность
сходится по крайней мере ^-линейно в х%.
Кроме того,
<Г.< 1.
304 Гл. 11. Задачи со специальной структурой
Следовательно, {xk} сходится <7-сверхлинейно к х, тогда и только
тогда, когда
Иш [/ (*.) - (С (*.) + A.)] „''I*',, = 0.
В частности, {**} сходится ^-сверхлинейно к *,, если (/(*,) —
-C(xm))&st.
Рассуждения относительно условий (11.4.3), следующие за
теоремой 11.4.1, применимы и к условиям (11.4.5). Используя
это, предлагается в качестве упражнения применить
теорему 11.4.2 для доказательства локальной ^-сверхлинейной
сходимости метода секущих Дэнниса, Гэя и Уэлша, приведенного
в разд. 10.3 для решения нелинейной задачи о наименьших
квадратах. Теорема 11.4.2, конечно, доказывает также и
сходимость DFP-метода. В общем случае теоремы 11.4.1 и 11.4.2
говорят о том, что если вы используете правильно построенное
пространство аппроксимаций зФ и при этом знаете, как
правильно выбирать соотношение секущих для этого класса
аппроксимаций, то принцип минимальных поправок является
превосходным способом выбора формул секущих.
В заключение заметим, что открывается ряд интересных
возможностей, если опуотить требование к si>, чтобы A(x)^st
для любых jceRrt. К этому мы приходим, когда решаем
аппроксимировать А(х) последовательностью матриц, имеющих
более простую структуру, чем А(х). Например, в версии
нелинейного алгоритма Якоби, использующего идею метода
секущих, итерация имеет вид
Xk+\ = Xk — AklF(xk)9
где матрица Ak диагональна, даже если J(x) не является
диагональным, т. е. s& = {диагональные матрицы е RnXn}, но
J(x)<£*. Если F(x.) = 0 и l|/-(diag(/(jt,))-V(**)ll<l, то
теорема 11.4.1 говорит о том, что при надлежаще заданном
правиле выбора у* метод будет все же локально сходящимся.
Теорема 11.4.1 наводит нас также на мысль выбирать
величину yf так, чтобы она аппроксимировала
((diag(/(*+)))s), = ^
если st Ф 0, и yf = 0, если s( = 0. В качестве несложного
упражнения предлагается показать, что для такого выбора yt
имеет место (11.4.4), где
Е = <
У?
—, если s{ Ф 0,
si
0, если st = 0,
11.5. Упражнения 305
и поэтому данный метод является при соответствующих
предположениях ^-линейно сходящимся.
В приведенном выше примере следует отметить важный
момент, который заключается в том, что выбор */# отличается от
стандартного выбора (11.3.5), который давал бы у# = у =
= F(x+) — F(x), так как С(х#) = 0. В общем случае
стандартное правило (11.3.5) будет неудовлетворительным при
Л(лг#)^«я0, поскольку это приводит к тому, что у*
аппроксимирует A(x+)Sk, тогда как мы хотим, чтобы оно
аппроксимировало (P*(A(xm)))sk = Amsk. Существуют другие практические
примеры, в которых пространство аппроксимаций $& имеет
более простую структуру, чем {Л(лс)}, и во многих из этих
примеров особенно тяжело подобрать подходящее правило
выбора ## (см., например, упр. 19). Если мы могли бы найти
простую идею относительно подходящего выбора значений */#,
подобную стандартному условию (11.3.5), то теоремы Дэнни-
са—Уолкера подсказали бы нам, что эти методы будут
локально сходящимися, и что скорость сходимости будет
зависеть от того, насколько близко А(х*) находится к з4>. Этот
вопрос служит предметом современных исследований. [См. Дэн-
нис и Уолкер (1983).]
11.5. УПРАЖНЕНИЯ
1. Пусть F: Rn->Rn, и пусть J(x) = F'(x) обладает тем свойством
что /(*)// = 0, если |/ — /| > т, где т < я/2. Используя технику разд. 11.1,
ответьте: сколько требуется вычислений F(x) для получения
конечно-разностной аппроксимации /(*)?
2. [Это упражнение взято из работы Пауэлла и Тоинта (1979).] Пусть
J(x) е R5><5 имеет следующую структуру расположения ненулевых элементов
JW-
X
X X
X X
X X
X X X X
Покажите, что техника разд. 11.1 требует для аппроксимации J(x) полных
пять вычислений F(x) дополнительно к F(xc). Однако если матрица J(x)
симметрична при всех х, то покажите, что J(x) можно аппроксимировать,
используя только два дополнительных вычисления F(x).
3. Пусть SP(Z) определено согласно (11.2.3). Покажите, что решением
задачи:
найти min ||В — А\\р при условии Be SP (Z)
в € Rn*n
является B = PZ(A), где оператор Pz определен согласно (11.2.5).
306 Гл. 11. Задачи со специальной структурой
4. Используя неравенство Коши —Шварца, покажите, что решением для
(11.2.8) является (11.2.9).
5. Пусть F: Rn->Rn непрерывно дифференцируема в открытой
выпуклой области D<zRn, х, x+eZ), s = jc+ — х, у e *(*+) — F (*)» si опреДе*
лено согласно (11.2.6). Докажите, что если ^ = 0, то ^ = 0. [Указание:
воспользуйтесь формулой (4.1.8).]
6. Покажите на примере, что матрица, обратная к разреженной, может
не иметь нулевых элементов. Рассмотрите, например, А е кп*п, такую, что
( 4, /-/,
Ац = \ 1. М-Л-1.
(о, | / — /| > 1.
(Такая матрица возникает при вычислении кубических сплайнов.)
7. Пусть А е RnXrt есть трехдиагональная симметричная положительно
определенная матрица. Постройте алгоритм и организуйте структуру данных
для решения линейной системы Ах = 6, используя 0(п) арифметических
операций и 0(п) памяти. Почему так важно, чтобы А была положительно
определенной?
8. Вычислите Vp (#(*)) и V2p (#(*)) для функций (10.4.4) и (10.4.5),
применяющихся для наилучшего приближения данных. Воспользуйтесь этими
выражениями для вычисления в каждом случае Vf(x) и V2/(jc).
9. Покажите, что значения ##, полученные в разд. 11.3 для функций
(11.3.2) и (11.3.3), эквивалентны стандартному выбору (11.3.5).
10. Пусть / (jc) есть нелинейная функция наименьших квадратов (11.3.4),
1 т
для которой р (R (х)) = —/?(*) R (*). Покажите на примере, что
стандартный выбору* (11.3.6) и выбор (11.3.7), использующийся в разд. 10.3, могут
различаться.
11. Проработайте доказательство теоремы 11.3.1, используя работу Дэн-
ниса и Шнабеля (1979), либо см. работу Пауэлла (1981) и Гриванка (1982).
12. Пусть Л = SPt(Z) г\ {А е= RnXn : А = Ат}. Покажите, что Рл (М) =
= lp2(Af + Afr).
13. Пользуясь теоремой 11.3.1 и упр. 12, завершите вывод разреженной
симметричной формулы секущих с минимальными поправками. Покажите
также, что матрица Р, заданная согласно (11.3.11), положительно определена,
если 81фЪ для всех / [см. Деннис и Шнабель (1979)].
14. Покажите, что разреженная симметричная формула секущих (11.3.12)
сводится к симметричной формуле секущих (9.13) при SP (Z) = RnXn, т. е.
15. Используя теорему 11.3.1, получите формулы пересчета с
минимальными поправками (11.3.13) и (11.3.14) соответственно для функций (11.3.2)
и (113.3).
16. Прочтите статью Дэнниса и Уолкера (1981) и затем попытайтесь
дать доказательство теорем 11.4.1 и 11.4.2. (Эти теоремы представляют собой
незначительное упрощение теорем, приведенных в статье.)
11.5. Упражнения 307
17. Воспользуйтесь теоремой 11.4.2 и докажите локальную <7-сверхлиней-
ную сходимость метода секущих Дэнниса, Гэя и Уэлша для нелинейных
наименьших квадратов
*к+>- **+е (ч)т 1 ы+Ak)~x J (*к)т * (**)•
где Ak пересчитывается согласно (10.3.6), «/* задано в (10.3.3).
18. Покажите, что вариант нелинейного метода Якоби, использующий
идею метода секущих и описанный в разд. 11.4, является ^-линейно
сходящимся. [Указание: покажите, что ||£|| ^ ао(х, х+)р.]
19. В алгоритме Дэнниса и Марвила (1982) разреженная матрица /(**)
аппроксимируется на протяжении конечного числа итераций с помощью
матрицы вида Lot/*, где J(x0) = L0-Uo и 1/*g {матрицы с такой же структурой
разреженности, что и Uo). Затем, когда алгоритм решает, что якобиан стал
слишком плохим, J(Xk+i) = L(Xk+i) -U(Xk+i) перевычисляется с
использованием конечных разностей, и процесс возобновляется сначала. Что утверждает
теорема 11.4.1 относительно того, каким должно быть у# для этого
алгоритма? Как можно было бы реализовать этот выбор? Какой критерий вы
могли бы использовать для принятия решения о том, когда производить
восстановление? Рассмотрите вопрос о привлечении техники выбора ведущего
элемента.
20. В алгоритме Джонсона и Остриа (1983) L^/-разложение
пересчитывается для получения соотношения LUs = у путем пересчета строка за
строкой U и L"1, так чтобы имело место Us — L~ff/ = 0. Напомним, что
матрица L-1 тоже является нижней треугольной. Посмотрите, не сможете ли вы
сами вывести на основе этой подсказки остроумную формулу пересчета
Джонсона и Остриа до того, как вы прочтете их статью.
Приложение А.
Модульная система алгоритмов
безусловной минимизации
и решения нелинейных уравнений1)
ОГЛАВЛЕНИЕ
Предисловие 311
I. Описание . 314
I.1. Назначение модульной системы алгоритмов 314
I.2. Организация модульной системы алгоритмов 316
I.3. Организация отдельных модулей 318
I.4. Ввод и вывод 323
I. 5. Модули для основных алгебраических операций 324
II. Драйверные модули и руководство для безусловной минимизации . . 325
II. 1. Алгоритм D6.1.1 (UMDRIVER). Драйвер модульной системы
алгоритмов безусловной минимизации 325
II. 2. Перечень модулей безусловной минимизации ......... 329
II. 3. Руководство 1. Выбор алгоритмических вариантов для безусловной
минимизации 331
II. 4. Руководство 2. Выбор параметров для безусловной минимизации 333
II. 5. Руководство 3. Соображения относительно памяти для безусловной
минимизации 336
II.6. Алгоритм D6.1.2 (UMEXAMPLE). Драйвер алгоритма безусловной
минимизации, использующего линейный поиск, конечно-разностные
градиенты и факторизованные аппроксимации гессиана по секущим 339
III. Драйверные модули и руководство для нелинейных уравнений . . . 341
III. 1. Алгоритм D6.1.3 (NEDRIVER). Драйвер модульной системы
алгоритмов решения нелинейных уравнений 341
III. 2. Перечень модулей для нелинейных уравнений 346
III. 3. Руководство 4. Выбор алгоритмических вариантов решения
нелинейных уравнений 347
III. 4. Руководство 5. Выбор параметров для нелинейных уравнений . . 349
III. 5. Руководство 6. Соображения относительно памяти для нелинейных
уравнений 351
III. 6. Алгоритм D6.1.4 (NEEXAMPLE). Драйвер алгоритма решения
нелинейных уравнений, использующего поиск вдоль ломаной и
конечно-разностную аппроксимацию якобиана 353
*) Автор — Р. Шнабель.
Модульная система алгоритмов 309
IV. Отдельные модули 354
(U) = использование только для безусловной минимизации
(N) = использование только для нелинейных уравнений
IV. 1. Модули, задаваемые пользователем (требования к ним) .... 354
(U) FN. Подпрограмма вычисления целевой функции f(x) для
безусловной минимизации . . 355
(U) GRAD. Подпрограмма вычисления вектора градиента V/(*)
(необязательная) . 355
(U) HESS. Подпрограмма вычисления матрицы Гессе V2f(x)
(необязательная) 356
(N) FVEC. Подпрограмма вычисления функции F(x), задающей
нелинейные уравнения 357
(N) JAC. Подпрограмма вычисления матрицы Якоби J(x)
(необязательная) 358
IV. 2. Модули, задаваемые разработчиком (частичное описание) . . . 358
(U) UMINCK. Проверка входных параметров для безусловной
минимизации 358
(N) NEINCK. Проверка входных параметров для нелинейных
уравнений 360
IV. 3. Алгоритмические модули (приведены полностью) 362
(N) NEFN. Вычисление суммы квадратов для нелинейных уравнений 362
А 1.3.1 (MACHINEPS). Вычисление машинного эпсилон .... 363
(N) АЗ.2.1 (QRDECOMP). <2#-разложение 363
(N) АЗ.2.2 (QRSOLVE). <Э#-решение . 365
(N) А3.2.2а (RSOLVE). ^-решение для Qfl-решения .... 366
А.3.2.3 (CHOLSOLVE). Драйвер решения по Холесскому . . 366
А3.2.3а (LSOLVE). L-решение 367
A3.2.3b (LTSOLVE). //-решение 368
(N) АЗ.3.1 (CONDEST). Оценивание числа обусловленности верхней
треугольной матрицы 368
АЗ.4.1 (QRUPDATE). Пересчет <Э#-разложения 370
АЗА la (JACROTATE). Вращение Якоби ....... 371
(N) АЗ.4.2 (QFORM). Формирование Q из <2#-разложения .... 372
А5.4.1 (FDJAC). Конечно-разностная аппроксимация якобиана 373
(U) А5.5.1 (MODELHESS). Формирование гессиана модели .... 374
А5.5.2 (CHOLDECOMP). Возмущенное разложение Холесского 377
(U) А5.6.1 (FDHESSG). Конечно-разностная аппроксимация
гессиана с использованием значений аналитически заданного
градиента . . 379
(U) А5.6.2 (FDHESSF). Конечно-разностная .аппроксимация
гессиана с использованием значений функции 380
(U) А5.6.3 (FDGRAD). Аппроксимация градиента по разностям
вперед . 381
(U) А5.6.4 (CDGRAD). Аппроксимация градиента по центральным
разностям 382
А6.3.1 (LINESEARCH). Линейный поиск 384
A6.3.1mod (LINESEARCHMOD). Линейный поиск с условием
на производную по направлению 387
А6.4.1 (HOOKDRIVER). Драйвер локально ограниченного
оптимального («криволинейного») шага 390
А6.4.2 (HOOKSTEP). Локально ограниченный оптимальный
(«криволинейный») шаг 392
А6.4.3 (DOGDRIVER). Драйвер шага вдоль кривой с двойным
изломом 395
А6.4.4 (DOGSTEP). Шаг вдоль кривой с двойным изломом . . 396
310 Приложение А.
А6.4.5. (TRUSTREGUP). Пересчет доверительной области
модели . . 398
(N) А6.5.1 (НЕМОДЕЛ). Построение аффинной модели для
нелинейных уравнений 402
(N) A6.5.1fac (NEMODELFAC). Построение аффинной модели для
нелинейных уравнений с привлечением факторизованных
формул секущих 405
(U) А7.2.1 (UMSTOP). Критерии останова для безусловной
минимизации 408
(U) А7.2.2 (UMSTOP0). Критерии останова для безусловной
минимизации перед начальной итерацией 409
(N) А7.2.3 (NESTOP). Критерии останова для нелинейных
уравнений 411
(N) А7.2.4 (NESTOP0). Критерии останова для нелинейных
уравнений перед начальной итерацией ..... 413
(N) А8.3.1 (BPOYUNFAC). Формула пересчета Бройдена, нефакто-
ризованная форма 414
(N) А8.3.2 (BROYFAC). Формула пересчета Бройдена, факторизо-
ванная форма 415
(U) А9.4.1 (BFGSUNFAC). Положительно определенная формула
секущих (BFGS), нефакторизованная форма ....... 416
(U) А9.4.2 (BFGSFAC). Положительно определенная формула
секущих (BFGS), факторизованная форма 418
(U) А9.4.3 (INITHESSUNFAC). Начальное значение гессиана для
формулы секущих в нефакторизованной форме 420
(U) А9.4.4 (INITHESSFAC). Начальное значение гессиана для
формулы секущих в факторизованной форме 421
Предисловие
Приложение к данной книге преследует различные цели,
которые обсуждаются в разд. 1.1 приложения А. Следующие
замечания касаются того, как использовать приложение при
разработке заданий для самостоятельной работы. Их
рекомендуется прочитать после чтения разд. I. 1 и 1.2 приложения А.
Ежегодно в течение последних пяти лет я использовал
в различных формах псевдопрограммы из приложения А при
разработке заданий для самостоятельной работы группы
старшекурсников, специализирующихся в оптимизации. Студенты,
работая обычно по двое, выбирают определенный метод
безусловной оптимизации или решения нелинейных уравнений и
пишут полностью программу, используя псевдопрограммы из
приложения А. Как правило, каждая группа программировала
только одну глобальную стратегию (например, линейный поиск,
криволинейный шаг или шаг вдоль ломаной), но несколько
вариантов вычисления производных (например,
конечно-разностная аппроксимация и аппроксимация по секущим). Они
писали и отлаживали свои программы в течение семестра, а затем
прогоняли их на различных tecTOBbix задачах, таких, как
задачи из приложения В. Я пришел к выводу, что эти проекты
составляют наиболее полезную часть курса, основанного на
данной книге. Даже если псевдопрограммы и полностью
детализированы, учащиеся должны тщательно в них разобраться,
чтобы успешно реализовать и устранить неизбежно
возникающие ошибки программирования. Наблюдение за работой
алгоритмов в их завершенном виде на тестовых задачах тоже
весьма поучительно. В особенности это справедливо, когда
студенты выводят на печать подробную информацию о процессе
выбора шага, например о пробных значениях параметра
линейного поиска на каждой итерации, и когда они отвечают на
вопросы, возникающие из анализа этой информации (такие,
как скажем «Использовалось ли когда-либо дробление шага
с кубической интерполяцией?» «Как часто брались значения
312 Приложение А.
по умолчанию для шагов дробления?»). Представляется также
поучительным сравнение конечно-разностных методов и
методов секущих на одних и тех же задачах.
Этим проектом можно заниматься в течение семестра. Что
касается начала семестра, то для безусловной минимизации,
например, группы могут написать подпрограммы вычисления
машинного эпсилон и обратного хода решения по Холесскому,
а подпрограммы вычисления конечно-разностных производных
и построения гессиана модели с использованием возмущенного
разложения по Холесскому — после того, как они будут
пройдены в гл. 5. После изучения гл. 6 они могут выбрать
глобальный метод и запрограммировать его вместе с драйверной
подпрограммой. Добавление к ним подпрограмм останова из гл. 7
дает полностью завершенную программу, реализующую
конечно-разностный модифицированный метод Ньютона, которую
учащиеся могут начать тестировать. Ее затем можно заменить
на BFGS-метод после того, как в гл. 8 и 9 будут пройдены
формулы секущих. Аналогичные замечания применимы и к
учебному проекту по решению нелинейных уравнений. Для
учебных проектов полезны следующие два упрощения: можно
пренебречь матрицами масштабирования (т. е. предположить, что
во всех случаях DX = DF = I) и использовать более простой
для понимания, но менее эффективный способ хранения
матриц, принятый в псевдопрограммах (см. руководства 3 и 6).
Исключение масштабирования фактически не влияет на
тестирование задачи, так как почти все стандартные задачи хорошо
масштабированы. Что касается параметров типа допусков, то
проще всего использовать их значения по умолчанию,
приведенные в руководствах 2 и 5.
Поскольку псевдопрограммы использовались в учебных
проектах на протяжении многих лет, в них были внесены
некоторые изменения. Первоначально я строго придерживался
управляющих структур языка Паскаль с операторами BEGIN
и END. Учащиеся, не знакомые с блочно структурированными
языками, с некоторым трудом отслеживали структуру, поэтому
я перешел на гибкую форму «Паскаль/схема нумерации»,
которая лежит в основе теперешних псевдопрограмм. Этот
переход был равнодушно встречен студентами, знакомыми с блоч-
но-структурированными языками, и оказал большую помощь
тем, кому знаком только Фортран. Второе изменение
заключалось в том, чтобы полностью расширить в псевдопрограммах
запись произведений, содержащих матрицы. Первоначально
псевдопрограммы содержали выражения ттта t+-H*s, где Н —
симметричная матрица, у которой хранится только верхняя
треугольная часть, но из-за треугольного способа хранения
матрицы возникало множество ошибок. Мои учащиеся считают
псевдопрограммы в их настоящем виде легкими для использо-
Модульная система алгоритмов 313
вания независимо от того, на чем они пишут программы — на
Фортране или на блочно-структурированном языке. Для
многих из них более трудными оказываются отладка и
тестирование систем программного обеспечения таких размеров. Этим
вопросам посвящены замечания в начале разд. 7.3.
К сожалению, ошибки в псевдопрограммах неизбежны.
Некоторые алгоритмы не использовались моими студентами и
могут содержать алгоритмические ошибки. В остальных
алгоритмах возможны типографские опечатки. Я постарался сократить
число ошибок личным участием в подготовке приложения, и
использовал возможности по редактированию текстов,
предоставляемые операционной системой UNIX на ЭВМ VAX11/780
факультета информатики Университета Колорадо. Я буду
поддерживать в ЭВМ список ошибок и готов выслать их любому,
кто обратится ко мне с такой просьбой, послав готовый к
отправке конверт с обратным адресом. Обращение по поводу
ошибок любого преподавателя, использующего эти
псевдопрограммы для учебных проектов, только приветствуется.
Другая возможность для организации учебных проектов
заключается в том, чтобы получить готовую программу для
решения нелинейных уравнений или безусловной минимизации
и сделать так, чтобы студенты прогоняли ее на тестовых
задачах и, может быть, даже меняли некоторые ее части, если,
конечно, имеется исходный текст программы. В этих целях можно
воспользоваться программой Шнабеля, Вайса и Кунца, почти
полностью соответствующей приведенной в этом приложении
псевдопрограмме для безусловной минимизации. Программу
можно запросить через автора.
Р. Шнабель
I. ОПИСАНИЕ
Назначение модульной
системы алгоритмов
Приложение А содержит модульную систему полностью
детализированных алгоритмов решения задач безусловной
минимизации и систем нелинейных уравнений. Под модульностью мы
понимаем то обстоятельство, что каждая явно выраженная
функциональная компонента этих методов представлена одним
или более отдельными модулями. Например, каждой из таких
компонент, как проверка необходимости останова, вычисление
производной, факторизация матрицы и стратегия выбора шага
(«глобальный метод»), соответствует один или более
отдельных модулей. Слово система отражает тот факт, что для
некоторых стадий процесса минимизации или решения нелинейных
уравнений имеются несколько вариантов модулей, так что
с помощью различных их комбинаций можно получать
разнообразные методы. Кроме того, методы безусловной
минимизации и решения нелинейных уравнений имеют несколько
общих компонент. Существуют, например, три различных способа
глобализации (линейный поиск, поиск вдоль ломаной и
криволинейный шаг), которые можно использовать на принципах
взаимозаменяемости совместно с любыми другими частями
алгоритмов решения обоих типов задач. Имеются также
несколько вариантов для вычисления или аппроксимации
производных (аналитическое вычисление, конечно-разностная
аппроксимация и аппроксимация по секущим). И наконец,
выражение полностью детализированные алгоритмы означает, что
каждый модуль полностью определен, включая память и
любые параметры типа допусков или эвристические решения,
которые обычно опускаются в описаниях более высокого уровня.
Имеется пять основных причин, по которым мы включили
эти алгоритмы в данную книгу:
1) дать полностью детализированное описание каждого рас-
смотренного в книге метода безусловной минимизации или
решения нелинейных уравнений. Алгоритмы в основном тексте
книги излагаются на таком уровне детализации, который мы
считаем достаточным для основательного изучения предмета.
Читатели, желающие познакомиться с деталями, могут найти
их в этом приложении;
Модульная система алгоритмов 315
2) показать, что модульная конструкция квазиньютоновских
алгоритмов (алгоритм 6.1.1), к которым мы обращались на
протяжении всего предыдущего изложения, может быть
доведена до уровня программной реализации. Это подтверждает
ту главную мысль основной части книги, что все
обсуждавшиеся подходы к решению обоих типов задач представляют
собой разновидности одной и той же конструкции;
3) обеспечить методикой преподавания с использованием
учебных проектов. Мы убедились, что программная реализация
одного или более методов из этой системы представляет собой
превосходный способ закрепления материала, представленного
в книге. Учебные проекты обсуждаются, кроме того, в
предисловии к приложению;
4) способствовать использованию структурированного и
управляемого программного обеспечения в тестировании новых
методов оптимизации и решения связанных с этим задач. Если
готовые программы по оптимизации написаны в модульном
стиле, как, например, рассматриваемые нами, то можно
разработать и протестировать много новых методов, изменив
только один или несколько модулей. Это обеспечивает
пользователя простым управляемым средством тестирования.
Упоминающаяся ниже программа Шнабеля, Вайса и Кунца
использовалась именно в таком качестве;
5) помочь тем прикладникам, которым необходимо
разработать свои собственные программы. Подчеркнем, что всякий
раз, когда это возможно, следует пользоваться библиотеками
вычислительного программного обеспечения. Однако из-за
специфики того или иного класса прикладных задач иногда
необходимо разрабатывать специализированные программы на
базе либо копий существующих подпрограмм, либо их
адаптированных вариантов. Эталоном в подобных случаях могут
служить алгоритмы из приложения.
Готовая программа для безусловной минимизации, которая
почти полностью, но не в точности соответствует алгоритмам
в данном приложении, была разработана Шнабелем, Вайсом
и Кунцем (1982). Назначение настоящего приложения вовсе не
состояло в том, чтобы создать эту программу, потому что в
различных библиотеках программного обеспечения содержатся
хорошие программы для безусловной минимизации, включая
библиотеки Harwell, IMSL, MINPACK и NAG. Программа
была разработана для тестирования алгоритмов из
приложения и для того, чтобы обеспечить упоминавшимися выше
средствами для проведения исследований. Ее, как правило, можно
запросить через автора и использовать для учебных проектов
или в качестве дополнительного материала книги.
Алгоритмы представлены в виде псевдопрограмм, а не
программ на реальном языке программирования (например, на
16 Приложение А.
Фортране) в основном ради облегчения их чтения. Алгоритмы
на псевдоязыке программирования отличаются от алгоритмов
на языке программирования для ЭВМ тем, что в первых
сохранены математические обозначения, например греческие
п
буквы (А,), символика суммирования ( £ H[h /])> скалярное
произведение векторов (vTw) и нормы (Ыг). Используемый
нами псевдоязык был разработан так, чтобы его можно было
легко перевести на Фортран или на блочно-структурированные
языки, подобные Паскалю и Алголу, и чтобы он мог быть
реализован в большинстве вычислительных сред. Он связан с
псевдоязыком программирования, использованным Вандерграф-
том (1978).
Оставшаяся часть разд. I, равно как и разд. II и III этого
приложения, будет интересна прежде всего читателям, которые
собираются реализовывать собранные здесь алгоритмы.
В разд. 1.2 объясняется, каким образом объединить части
приложения для создания одного, нескольких или целой системы
алгоритмов решения задач безусловной минимизации и
нелинейных уравнений. Это включает в себя описание структуры
разд. II и III, которые содержат более подробные инструкции
по использованию данного приложения при создании
алгоритмов соответственно безусловной минимизации и решения
нелинейных уравнений. В разд. 1.3 обсуждаются вопросы
перевода отдельных модулей системы на язык программирования
для ЭВМ, включая вопросы влияния вычислительной среды.
В разд. 1.4 и 1.5 кратко обсуждаются два более частных
вопроса программирования этих алгоритмов.
Раздел IV содержит текст полностью детализированных
модулей, соответствующих различным частям наших методов.
Это должно представлять интерес для всех читателей как
дополнение к обсуждению методов в основной части данной
книги. Модули пронумерованы в соответствии с их предыдущим
изложением: первые две цифры из трех, составляющих номер
алгоритма, отвечают номеру раздела, в котором рассматривался
этот метод. Например, алгоритмы с A7.2.I по А7.2.4 являются
алгоритмами останова, рассмотренными в разд. 7.2 основной
части книги. Модулям также даны короткие имена
описательного характера (например, алгоритм А7.2.1 назван UMSTOP),
которые используются внутри псевдопрограмм для повышения
надежности.
1.2. Организация модульной системы
алгоритмов
Организация данной системы алгоритмов безусловной
минимизации и решения нелинейных уравнений отражает общую ква-
Модульная система алгоритмов 317
зиньютоновскую схему, представленную в разд. 6.1 основной
части книги. Методы для обоих типов задач разбиваются на
ряд отдельных функциональных компонент (например,
проверка необходимости останова, вычисление производных,
метод глобализации), и каждая компонента реализуется одним
или более модулями. В некоторых случаях (вычисление
производных или их аппроксимация, метод глобализации) для
одной компоненты дается ряд вариантов, каждый из которых
можно выбрать. Полный метод безусловной минимизации или
решения нелинейных уравнений создается выбором и
программированием алгоритмов для каждой из отдельных компонент,
а затем объединением их со помощью драйверной программы.
Алгоритм 6.1.1 в том виде, как он был представлен в
основной части книги, содержал указания на то, какие требуются
компоненты, а также служил драйвером, однако здесь
требуется более детальное его рассмотрение. В разделе Описание
алгоритмов D6.1.1 и D6.1.3 (см. разд. II. 1 и III. 1) приведены
шаги методов безусловной минимизации и соответственно
решения нелинейных уравнений. Некоторые из этих шагов
являются просто строками программы в драйверном алгоритме,
тогда как другие представляют собой упоминавшиеся выше
компоненты, которые отвечают одному или более отдельным
модулям. В разд. II. 2 и III. 2 приведены отдельные
компоненты и модули, используемые для их реализации, в том числе
и иные варианты, если таковые существуют.
Раздел Алгоритм алгоритмов D6.1.1 и D6.1.3 содержит
псевдопрограммы драйверных алгоритмов, которые следует
использовать для программной реализации всей системы
алгоритмов безусловной минимизации или соответственно решения
нелинейных уравнений со всеми вариантами для метода
глобализации и для вычисления производных. Драйвер для
программы Шнабеля, Вайса и Кунца (1982) аналогичен первому из
них. Для программной реализации одного (или нескольких)
отдельно взятого метода, а не всей системы в целом достаточно
урезанного варианта драйвера. Алгоритмы D6.1.2 и D6.1.4
служат примерами реализации одного метода: безусловной
минимизации и решения нелинейных уравнений. Аналогично можно
создать драйверы для других отдельных методов, выбирая
подходящие части из алгоритма D6.1.1 или D6.1.3.
К каждому головному драйверному алгоритму (D6.1.1 и
D6.1.3) добавляется перечень упоминавшихся выше модулей
и три руководства. Руководство 1 содержит указания по
выбору среди алгоритмических возможностей, предоставляемых
для метода глобализации и для вычисления производных при
безусловной минимизации. Оно задумано как совет
пользователю этой системы и как информация для студентов и
читателей, интересующихся этими проблемами. В руководстве 2
318 Приложение А.
обсуждаются вопросы выбора параметров в критерии останова
и всех других параметров, используемых в алгоритмах
безусловной минимизации. В готовой программной реализации эти
параметры могли бы выбираться пользователем или задаваться
определенными значениями в программе, причем в учебных
проектах обучающиеся выбирали бы их на основе
руководства 2. В руководстве 3 подробно обсуждаются вопросы
хранения матриц, требующихся в программе по безусловной
минимизации. Мы пришли к выводу, что эффективное
распределение памяти представляет собой слишком сложный аспект
алгоритмов, чтобы его можно было полностью отразить в
описании псевдопрограмм, предполагающих главным образом
легкость чтения. В руководстве 3 и в разделах некоторых
модулей памяти мы пытаемся выправить ситуацию.
Руководства 4—6 содержат информацию для решения
нелинейных уравнений, аналогичную приведенной в
руководствах 1—3. В случаях когда информация дублируется, в
руководствах по решению нелинейных уравнений даются ссылки на
соответствующие руководства по безусловной минимизации.
1.3. Организация отдельных модулей
Структура каждого модуля в разд. IV и драйверных модулей
D6.1.1—4 имеет следующий вид:
Назначение
Входные параметры
Входно-выходные параметры
Выходные параметры
Значения кодов возврата
Память
Примечания
Описание
Алгоритм
В разделе Назначение в одном или двух предложениях
кратко излагается назначение модуля. В трех разделах,
рассматривающих параметры, приводятся имена, типы данных и
дополнительная информация нерегулярного характера о всех
параметрах модуля. При вызове модуля другими модулями
в системе порядок следования аргументов в операторе вызова
соответствует порядку следования параметров в этих разделах.
Раздел, посвященный кодам возврата, имеется в таких
алгоритмах, как, скажем, проверки на необходимость останова,
которые возвращают в алгоритм, их вызвавший, некоторую
закодированную целыми числами информацию; во всех других
алгоритмах этот раздел опускается.
Раздел модулей Память вместе с руководствами 3 и 6
определяет требования этих алгоритмов к памяти под матрицы и
Модульная система алгоритмов 319
векторы. В них обсуждаются также иные программные
реализации, дающие более эффективные способы хранения, хотя и
снижающие удобочитаемость программ. В п. 1 раздела Память
каждого отдельного модуля перечисляются все локальные
переменные, которые являются векторами или матрицами. Все
переменные модуля, не перечисленные в этом пункте и не
входящие в список параметров, являются локальными скалярными
переменными (типа real, integer или Boolean). Программы
построены таким образом, что вся связь между подпрограммами
осуществляется через параметры и не требуется никаких
глобальных переменных (типа фортрановских COMMON).
Единственное исключение составляют две переменные, которые
должны передаваться как глобальные переменные между
алгоритмами решения нелинейных уравнений NEFN и D6.1.3 в том
виде, как описано в этих алгоритмах.
Раздел Примечания включается на случай дополнительных
комментариев, относящихся к модулю. Раздел Описание
предназначен для пояснения основной структуры алгоритма,
который за ним следует. Он, возможно, даже слишком упрощает
некоторые детали алгоритма. В очень простых алгоритмах
этот раздел может отсутствовать.
Раздел Алгоритм содержит полностью детализированную
псевдопрограмму модуля. Форма написания псевдопрограмм
рассчитана на то, чтобы быть понятной для всех читателей.
Она аналогична той, что использовалась Вандерграфтом
(1978), и в ее основе лежат кратко описанные ниже
управляющие структуры языка Паскаль, которые были выбраны из-за
того, что их смысл очевиден из написания. (Управляющие
структуры языка Паскаль очень похожи на те, что имеются
в языках Алгол, ПЛ/1 и Фортран-77.) Вместо использования
паскалевских BEGIN и END применяется схема нумерации,
которая указывает порядковый номер и глубину вложения.
С точки зрения нашего опыта, это помогает понимать
псевдопрограммы читателям, не знакомым с блочно-структурирован-
ными языками, и имеет то дополнительное преимущество, что
каждому оператору дается соответствующий только ему номер.
Используется шесть приведенных ниже управляющих
структур. Читателю, знакомому с блочно-структурированными
языками, следует просмотреть их мельком только для того, чтобы
отметить для себя образец схемы нумерации.
i) Оператор IF-THEN
1. IF (логическое условие /)-THEN
1.1. первый оператор внутри IF-THEN
1.5. последний оператор внутри IF-THEN (здесь 5
есть размер блока)
320 Приложение А.
2. следующий оператор
Смысл оператора: если логическое условие i истинно, то
выполнить операторы 1.1—5 и перейти к оператору 2, иначе
перейти непосредственно к оператору 2.
ii) Оператор IF-THEN-ELSE
4. IF (логическое условие и)
4Т. THEN
4Т. 1 первый оператор в THEN-блоке
4Т. 3 последний оператор в THEN-блоке
4Е. ELSE
4Е. 1 первый оператор в ELSE-блоке
4Е. 7 последний оператор в ELSE-блоке
5. следующий оператор
Смысл оператора: если логическое условие И истинно, то
выполнить операторы 4Т.1—3, иначе выполнить операторы
4Е.1—7; затем перейти к оператору 5.
iii) Оператор множественного ветвления
2. последний оператор
За. IF (логическое условие iiia) THEN
операторы с За.1 по За.4
3b. ELSEIF (логическое условие iiib) THEN
оператор ЗЬЛ
Зс. ELSE
операторы с Зс.1 по Зс.12
4. следующий оператор
Смысл оператора: если логическое условие iiia истинно, то
выполнить операторы За.1—4 и перейти к оператору 4; иначе,
если логическое условие iiib истинно, то выполнить
оператор ЗЬЛ и перейти к оператору 4; иначе выполнить
операторы Зс.1—12 и перейти к оператору 4.
Эта управляющая структура с ее характерными ключевыми
словами была включена сюда потому, что она способна
передавать логическую структуру некоторых из наших
алгоритмов лучше, чем оператор IF-THEN-ELSE, у которого
ELSE-ветвь сама представляет собой оператор IF-THEN-
ELSE. Количество вариантов может быть увеличено до
любого желаемого числа, например алгоритм А7.2Л имеет
операторы с 2а по 2f.
iv) Оператор цикла FOR (соответствует оператору цикла DO
в Фортране)
6.2. FOR целая переменная = целое значение М 1 ТО
целое значение № 2 DO
операторы с 6.2.1 по 6.2.9
6.3. следующий оператор
Модульная система алгоритмов 321
Смысл оператора:
a. целая переменная -«- целое значение № 1
b. если целая переменная > целое значение № 2, то
перейти к следующему оператору (6.3), иначе перейти
к шагу с
c. выполнить операторы 6.2.1—9
d. целая переменная*-(целая переменная -+- 1)
e. перейти к шагу b
Заметим, что цикл никогда не выполнится, если целое
значение № 1 > целое значение № 2\ он выполнится один раз,
если эти два значения равны.
Иногда используется оператор FOR ... DOWNTO; его смысл
отличается от приведенного выше только тем, что в шагеЬ
знак > заменяется на знак <, и в шаге d знак +
заменяется на —.
v) Оператор цикла WHILE
7.3.2 WHILE (логическое условие v) DO
операторы с 7.3.2.1 по 7.3.2.8
7.3.3 следующий оператор
Смысл оператора:
a. если логическое условие v истинно, то перейти к шагуЬ,
иначе перейти к следующему оператору (7.3.3)
b. выполнить операторы 7.3.2.1—8
c. перейти к шагу а
vi) Оператор цикла REPEAT
2.3 REPEAT
операторы с 2.3.1 по 2.3.6
2.3U UNTIL (логическое условие vi)
2.4 следующий оператор
Смысл оператора:
a. выполнить операторы 2.3.1—6
b. если логическое условие vi истинно, то перейти к
следующему оператору (2.4), иначе перейти к шагу а
Заметим, что тело оператора цикла REPEAT выполняется
всегда хотя бы один, раз, в то время как тело оператора
цикла WHILE может не выполниться ни разу.
Логическое условие в рассмотренных выше операторах
может быть или простым логическим условием (s2 > х — 2), или
составным логическим условием ((/ = 2)AND((6 < l)OR(b >
> 3))), или же переменной типа Boolean. Составные
логические условия используют операторы AND, OR, а также NOT
и вычисляются в соответствии со стандартным порядком
выполнения действий. Переменным типа Boolean могут быть
присвоены значения TRUE и FALSE; если boo есть переменная
типа Boolean, то boo и NOT boo исчерпывают все возможные
322 Приложение А.
ситуации. Переменные типа Boolean также могут быть частью
составных логических условий.
Поскольку эти алгоритмы не содержат никаких операторов
ввода и вывода (см. разд. 1.4), имеются только два других
типа операторов сверх тех шести, которые приведены выше:
оператор присваивания и оператор вызова подпрограммы.
(Один GO ТО используется в алгоритме D6.1.3, и один
оператор RETURN используется в каждом драйверном алгоритме.)
Оператор присваивания записывается как
переменная -«- выражение
и читается «переменная получает значение выражения».
Оператор «=» зарезервирован для использования в логических
условиях и в операторах цикла FOR. Вызов подпрограммы
выглядит так:
GALL имя модуля (список аргументов).
Имя модуля носит описательный характер (например,
UMSTOP). Номер модуля (А7.2.1) всегда дается как
сопутствующий комментарий. Аргументы соответствуют в порядке
их следования входным параметрам, входно-выходным
параметрам и выходным параметрам вызываемого модуля. Если
тело какого-либо управляющего оператора состоит только из
одного оператора присваивания или вызова подпрограммы, то
ему обычно не дается отдельного номера, например:
3.2 FOR i=l ТО п DO
х [i] <- 1
3.3 следующий оператор
Элементы векторов и матриц обозначаются как в языке
Паскаль: /-й элемент вектора х есть x[i], (/,/)-й элемент
матрицы М есть M[i, /]. Скалярные переменные могут иметь тип
real, integer или Boolean1), причем их тип вытекает из
использования в алгоритме. Иногда имена переменных, когда это
соответствует их использованию в основной части книги,
содержат греческие буквы. В программной версии они могут быть
преобразованы к их эквиваленту на английском языке
(например, а переходит в alpha). Имена переменных носят
описательный характер и некоторые из них оказываются длиннее,
чем это допускают стандарты Фортрана. Все цмена
переменных выделены курсивом.
Точность представления переменных вещественного типа не
указывается. Рассматриваемые методы обычно должны иметь
точность по меньшей мере, в 10—15 десятичных разрядов, от-
*) В этих трех случаях тип переменной указывается соответственно как
е/?, eZ, eBoolean.— Прим. перев.
Модульная система алгоритмов 323
водимых под вещественные числа. Поэтому на ЭВМ CDC, Cray
и им подобных достаточной оказывается одинарная точность,
но на ЭВМ IBM, DEC и аналогичных им вещественные
переменные должны иметь двойную точность. Единственными
машинно-зависимыми константами в программе являются
некоторые функции от машинного эпсилона macheps, который
вычисляется в начале любого метода безусловной минимизации
и решения нелинейных уравнений.
Основная особенность, которая отличает псевдоязык
программирования от существующих языков программирования на
ЭВМ и вместе с тем облегчает его чтение, заключается в
использовании математической и, в частности, векторной
символики. Это, например, знак суммирования, операции max и min,
возведение в степень, присваивание вектора вектору,
умножение векторов, нормы векторов и умножение вектора на
диагональную матрицу (см. разд. 1.5). Для программирования этих
операций потребуется .иногда введение дополнительных
переменных. Операции с недиагональными матрицами
представляются в большинстве случаев покомпонентно. Причина состоит
в том, что обычно возникает слишком много недоразумений
при программировании операции типа t+-H*s, где H^RnXn —
симметричная матрица, причем хранится только ее верхняя
треугольная часть. В сопутствующих комментариях всегда
приводится матричная форма операций.
Комментарии выделяются с помощью обозначений языка
Паскаль: символ (* начинает комментарий, и следующий *),
стоящий не обязательно в той же строке, завершает его.
Операторы RETURN, которые требовались бы в Фортране, но не
в блочно-структурированном языке, указаны в комментариях.
I. 4. Ввод и вывод
Данная система алгоритмов не содержит никаких операторов
ввода (типа read) и вывода (типа write, print). Она связана
с внешним миром исключительно через параметры, которые
перечислены в головной драйверной программе. Это
стандартный и вполне подходящий способ получения входных данных,
и нет никакой необходимости включать в алгоритмы операторы
ввода. Тем не менее большинству из тех, кто займется
реализацией, захочется включить операторы вывода.
Обычно в готовой программе есть несколько уровней
вывода на печать, в том числе и отсутствие вывода на печать
(что иногда желательно, когда программа погружена внутрь
другой программы), а также и малый объем вывода на печать,
скажем: используемый метод, значения функции (и градиента)
в начальной и конечной точках, заключительное сообщение,
324 Приложение А.
потребовавшееся количество итераций и вычислений функции
и производной. Предоставляется еще одна возможность:
печатать также значения функции (и градиента) в конце каждой
итерации. Для отладки и учебных проектов полезно иметь
дополнительную возможность: печатать информацию о процессе
выбора шага, например пробные значения X на каждой
итерации алгоритма линейного поиска, последовательные значения
доверительного радиуса в методе доверительной области,
некоторые подробности итерации по ц в алгоритме
криволинейного шага. Уровнем вывода на печать можно управлять, если
добавить в головном драйвере некоторый входной параметр,
скажем printcode; операторы вывода в программе следует
делать условными, зависящими от значения printcode.
Выходные параметры головных драйверов также
определены не полностью. Они должны включать код завершения
работы1) и заключительное значение независимой переменной х.
Они могут, кроме того, содержать вектор заключительного
значения функции (для нелинейных уравнений) или
заключительные значения функции и градиента (для минимизации). В
случае нелинейных уравнений в заключительной точке вычисляется
якобиан илц его аппроксимация, и, таким образом, он доступен
для вывода. В случае минимизации ни гессиан, ни его
аппроксимация не вычисляются в заключительной точке, поэтому
пользователь, желающий иметь эту информацию, должен несколько
модифицировать соответствующие алгоритмы.
I. 5. Модули для основных алгебраических
операций
Различные алгебраические операции в псевдопрограммах
встречаются достаточно часто, так что программист, реализующий
данные алгоритмы, может захотеть снабдить их специальными
подпрограммами выполнения этих операций. Возможными
примерами служат max и min, скалярное произведение векторов
(vTw), /2-норма вектора и операции с диагональными
матрицами масштабирования Dx и DF. При программировании на
Фортране для реализации некоторых из этих операций может
оказаться полезным использование подпрограмм по основам
линейной алгебры (BLAS), в связи с чем см. работу Лоусон,
Хенсон, Кинкейд и Крог (1979).
Алгоритмы А6.4.1 —5 и А8.3.1 — 2 содержат множество
выражений вида D*v или |D*o^y где k равно +2 или ±1, и
v е Rn. Во всех перечисленных случаях комментарий в псев-
') Имеется в виду информация о причинах завершения работы
подпрограммы, например: достигнута заданная точность решения, сходимость
слишком медленная, имеет место расходимость и т. п. — Прим. перев.
Модульная система алгоритмов 325
допрограмме напоминает читателю, что матрица диагонального
масштабирования Dx как таковая не хранится, а вместо этого
запоминается вектор Sx^Rny где Dx = diag((Sx)\y ... , (Sx)n).
Таким образом, /-й компонентой D\v является (Sx [t])k * v [/].
При программной реализации масштабирования может
оказаться полезным написать одну подпрограмму, которая для
заданных k, Sx и v возвращает значение |D*o|f и другую,
которая возвращает |^^|2.
II. ДРАЙВЕРНЫЕ МОДУЛИ И РУКОВОДСТВО
ДЛЯ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
II. 1. Алгоритм D 6.1.1. (UMDRIVER).
Драйвер модульной системы алгоритмов
безусловной минимизации
Назначение: Попытаться найти точку локального минимума х*
функции f(x): Rn-+R, начиная из х0 и используя один из
имеющегося набора алгоритмов.
Входные параметры: /igZ (п ^ 1), xo^Rn, FN (имя
задаваемой пользователем функции /: /?л->/?, которая по меньшей
мере дважды непрерывно дифференцируема).
Кроме того, необязательные:
i) GRAD, HESS — имена задаваемых пользователем
функций для вычисления Wf(x) и V2f(x) соответственно,
и) global е Z, analgrad е Boolean, analhess е Boolean,
cheapf е Boolean, factsec e Boolean — параметры,
используемые при выборе алгоритмических вариантов. Они
объяснены в руководстве 1. (Параметрам, которые не
введены пользователем, присваиваются значения,
задаваемые алгоритмом UMINCK.)
Hi) typx^Rn, typf^R, fdigits^Z, gradtol^R, steptol^R,
maxstep e /?, itnlimit gZJgJ? - параметры типа
допусков и константы, используемые в алгоритме. Они
объясняются в руководстве 2. (Параметрам и
константам, которые не введены пользователем, присваиваются
значения, задаваемые алгоритмом UMINCK.)
iv) printcode е Z — см. разд. 1.4 приложения.
Входно-выходные параметры: отсутствуют (см. тем не менее п. 2
раздела Память).
Выходные параметры: Xf^Rn (заключительное приближение
к *♦), termcode^Z (указывает на то условие окончания,
которое вызвало остановку алгоритма),
326 Приложение А.
Кроме того, необязательные:
fc^R(=f(xf)), gc^Rn( = Vf(xf)), другие выходные
параметры по желанию того, кто занимается программной
реализацией (см. разд. 1.4).
Значения кодов возврата:
termcode < 0: алгоритм закончил работу из-за ошибки во
входных данных, см. алг. UMINCK.
termcode > 0: алгоритм закончил работу по причине,
приведенной в алг. А7.2.1.
Память:
1) Требования относительно памяти под матрицы и векторы
обсуждаются в руководстве 3. Непременно прочтите п. 5 в
руководстве 3, если вы занимаетесь программной реализацией
этих алгоритмов на Фортране.
2) Имена х0 и Xf используются в этом драйвере только лишь
для большей ясности. В программной реализации х0 и Xf
могут оба занимать одну и ту же память с хс.
Примечания:
1) В разделе «Перечень модулей для безусловной
оптимизации» указано, какие модули соответствуют каждому шагу в
приведенном ниже разделе Описание. Выбор среди имеющихся
в этом перечне вариантов задается описанными в руководстве 1
параметрами, которые определяют алгоритмический вариант.
2) Приведенный ниже Алгоритм используется для реализации
всей системы алгоритмов безусловной минимизации. Для
реализации отдельного алгоритма безусловной минимизации
может быть использован более простой драйвер, как это наглядно
показано на примере алгоритма D6.1.2.
3) На некоторых вычислительных машинах необходимо
снабдить систему фиктивными подпрограммами GRAD и HESS на
тот случай, когда пользователь не предоставляет
подпрограммы вычисления Vf(x) или соответственно V2f(x). Эти
фиктивные подпрограммы требуются единственно для того, чтобы
была возможна трансляция программы.
Описание:
Инициализация:
1) Вычислить машинный эпсилон.
2а) Проверить допустимость входных данных, присвоить
значения по умолчанию тем параметрам, определяющим
алгоритмический вариант, и тем параметрам типа допусков, которые не
были входными для пользователя. (Возвратить в драйвер
значение termcode.)
Модульная система алгоритмов 327
2Ь) Если termcode < 0, то завершить работу алгоритма,
возвратив значения х\ = х0 и termcode. Если termcode = 0, то
положить itncount <-О и продолжить дальше.
3) Вычислить fc = f(xo).
4) Вычислить или аппроксимировать gc = Vf(x0).
5а) Решить, нужно ли остановиться. (Возвратить в драйвер
значение termcode.)
5b) Если termcode > 0, то завершить работу алгоритма,
возвратив значения х\ = хо и termcode. Если termcode = 0, то
продолжить дальше.
6) Вычислить или аппроксимировать Hc = V2f(xo).
7) Положить хс = Хо-
Итерация:
1) itncount«- itncount + 1.
2) Построить гессиан модели Нс (= Яс + ц,/, \х !> О, причем ц = О,
если Нс уже надежно положительно определен) и его
разложение по Холесскому HC = LCLTC, где Lc — нижняя треугольная
матрица.
3) Решить (LCLJ) s„ = - gc.
4) Положить х+ = хс + sc, где sc = s# или равно шагу,
выбираемому в соответствии со стратегией глобализации. В процессе
выполнения этого ijiara алгоритма вычисляется /+ = f(*+)-
5) Вычислить или аппроксимировать g+ = yf(x+).
6а) Решить — нужно ли остановиться. (Возвратить в драйвер
значение termcode.)
6b) Если termcode > О, то завершить работу алгоритма,
возвратив значения Xf = х+ и termcode. Если termcode = О, то
продолжить дальше.
7) Вычислить или аппроксимировать Hc = V2f{x+).
8) Положить хс*-х+, /с-<-/+, gc*-g+ и вернуться к шагу 1
итерационной части.
Алгоритм:
(* Инициализирующая часть: *)
1. CALL MACHINEPS (macheps)
1. CALL UMINCK (список параметров выбирает тот, кто
занимается программной реализацией)
(*см. описание UMINCK*)
3. IF termcode < О THEN
3.1 Xj<—Xq
3.2 RETURN для алгоритма D6.1.1 (*при желании вывести
на печать соответствующее сообщение*)
4. itncout <- О
5. CALL FN (л, x0t fc)
6. IF analgrad
6T. THEN CALL GRAD (n, x0, gc)
328 Приложение А.
6Е. ELSE CALL FDGRAD (п, х0, fc, FN, Sx, r\, gc) (* алг. A5.6.3 *)
7. CALL UMSTOPO (n, x0, fc, gc, Sx, typf, gradtol, termcode,
consecmax) (* алг. A7.2.2 *)
8. IF termcode > 0
8T. THEN xf+-x0
8E. ELSE (* вычислить начальное значение гессиана или его
аппроксимации *)
8E.la IF analhess THEN
CALL HESS (n, x0, Hc)
8E.lb ELSEIF analgrad AND cheapf THEN
CALL FDHESSQ (n, x0, gc, GRAD, Sx, ц, Hc) (* алг.
A5.6.1 *)
8E.lc ELSEIF cheapf THEN
CALL FDHESSF (n, x0, fc, FN, Sx, r\, Hc) (* алг.
A5.6.2 *)
8E.ld ELSEIF factsec THEN
CALL INITHESSFAC (я, fe, typf, Sx, Le) (*алг. A9.4.4*)
(♦замечание: factsec должно быть FALSE, если
global = 2*)
8E.le ELSE (*factsec = FALSE*)
CALL INITHESSUNFAC (n, fc typf, Sx, He) (* алг.
A9.4.3 *)
9. xc+- x0
(* Итерационная часть: *)
10. WHILE termcode = 0 DO
10.1 itncount •*- itncount + 1
10.2 IF NOT factsec THEN
CALL MODELHESS (n, Sx, macheps, Hc, Lc) (* алг.
A5.5.1 *)
10.3 CALL CHOLSOLVE (n, gc, Lc, sN) (* алг. A3.2.3 *)
10.4a IF global = 1 THEN
CALL LINESEARCH(n, xc, fc, FN, gc, sN, Sx,maxstep,
steptol, retcode, x+, f+, maxtaken) (*алг. A6.3.1 *)
10.4b ELSEIF global = 2 THEN
CALL HOOKDRIVER («*, xc, fc, FN, gc, Le, Hc, sN, Sx,
maxstep, steptol, macheps, itncount, bprev, 6, \x, ф, ф',
retcode, x+, f+t maxtaken) (*алг. A6.4:l *)
10.4c ELSEIF global = 3 THEN
CALL DOGDRIVER (n, xc, fc, FN gc, Lc, sN, Sx,
maxstep, steptol, 6, retcode, x+, f+, maxtaken) (* алг.
A6.4.3 *)
10.4d ELSE (* global = 4*)
CALL LINESEARCHMOD (n, xc, fc, FN, ge, analgrad,
GRAD, sN, Sx, maxstep, steptol, retcode, x+, f+, g+,
maxtaken) (*алг. A6.3.1 mod*)
Модульная система алгоритмов 329
10.5 IF global Ф 4 THEN
10.5.1 IF analgrad
10.5. IT THEN CALL GRAD (л, x+, g+)
10.5.1E ELSE CALL FDGRAD (n, x+, f+, .FN, Sx, i\,
g+) (* алг. A5.6.3 *)
(*если используется переключение на центральные
разности, то вместо этого CALL CDGRAD (л, х+,
FN, Sx, r\, g+) — см. алг. А5.6.4 *)
10.6 CALL UMSTOP (л, xc, x+, f+, g+, Sx, (ypf, retcode,
gradtol, steptol,-itncount, itnlimit, maxtaken, consecmax,
termcode) (* алг. A7.2.1 *)
10.7 IF termcode >0
10.7T THEN xf<-x+
10.7E ELSE (* вычислить следующее значение гессиана
или его аппроксимации *)
10.7E.la IF analhess THEN
CALL HESS (л, x+, Hc)
10.7E.lb ELSEIF analgrad AND cheapf THEN
CALL FDHESSG (n, x+, g+, GRAD, Sx,
r\, Hc) (*алг. A5.6.1*)
10.7E.lc ELSEIF cheapf THEN
CALL FDHESSF (n, x+, f+, FN, Sx, r\, Hc)_
(* алг. A5.6.2 *)
10.7E.ld ELSEIF factsec THEN
CALL BFGSFAC (л, xc, x+, gc, g+,
macheps, r\, analgrad, Lc) (* алг. A9.4.2 *)
10.7E.le ELSE (*factsec = FALSE*)
CALL BFGSUNFAC (л, xc, x+, gc, g+,
macheps, t\, analgrad, Hc) (*алг. A9.4.1 *)
10.7E.2 xc^x+
10.7E.3 /сч-/+
10.7E.4 ge+-g+
(*END, цикл WHILE 10*)
(* при желании вывести на печать соответствующее сообщение
об окончании *)
(♦RETURN для алгоритма D6.1.1 *)
(♦END, алгоритм D6.1.1 *)
II..2. Перечень модулей безусловной
минимизации
Шаги в разделе Описание драйвера D6.1.1 соответствуют
следующим модулям. Шаги в этом описании, которые не приведены
ниже, отвечают соответствующим строкам псевдопрограммы
драйверного алгоритма.
330 Приложение А.
Инициализация
Шаг 1 -MACHINEPS
Шаг 2a-UMlNCK
Шаг 3 -FN
Шаг 4 - GRAD или FDGRAD
Шаг 5а - UMSTOP0
Шаг 6 -HESS или (FDHESSG/FDJAC) или FDHESSF
или INITHESSUNFAC или INITHESSFAC
Итерация
Шаг 2 -(MODELHESS/CHOLDECOMP)
Шаг 3 -CHOLSOLVE
Шаг 4 -LINESEARCH или LINESEARCHmod или
(HOOKDRIVER/HOOKSTEP/TRUSTREGUP) или
(DOGDRIVER/DOGSTEP/TRUSTREGUP)
Шаг 5 — GRAD или FDGRAD (или, возможно, CDGRAD,
если используется возможность переключения
на центральные разности)
Шаг 6а - UMSTOP
Шаг 7 -HESS или (FDHESSG/FDJAC) или FDHESSF
или BFGSUNFAC или (BFGSFAC/QRUPDATE)
В том случае, когда какой-либо из приведенных выше шагов
содержит два и более модулей или групп модулей, разделенных
между собой союзом «или», они представляют собой
альтернативные варианты, выбираемые с помощью параметров,
определяющих алгоритмический выбор. Подразумевается, что
конкретный метод использовал бы только один вариант для
каждого такого шага алгоритма.
В том случае, когда два и более модулей перечисляются
выше в скобках и разделяются между собой наклонной чертой
(/), первый из группы модулей, заключенных в скобки,
вызывается драйвером, а остальные модули этой группы вызываются
первым модулем. Например, FDHESSG вызывает FDJAC. Кроме
того, приведенные ниже модули вызывают следующие сервисные
модули и модули вычисления функции и ее градиента:
HOOKSTEP вызывает CHOLDECOMP и LSOLVE
LINESEARCH вызывает FN
LINESEARCHmod вызывает FN и (CRAD или FDGRAD
(или CDGRAD))
TRUSTREGUP вызывает FN
Приведенные ниже модули также вызывают следующие их
подалгоритмы:
CHOLSOLVE вызывает LSOLVE и LTSOLVE
QRUPDATE вызывает JACROTATE
Модульная система алгоритмов 331
II. 3. Руководство 1. Выбор алгоритмических
вариантов для безусловной минимизации
Ниже приведены алгоритмические варианты, имеющиеся в
распоряжении при использовании системы алгоритмов безусловной
минимизации, и указания по выбору этих вариантов.
global — положительное целое, указывающее следующим
образом на то, какую стратегию глобализации использовать на
каждой итерации:
= 1 Линейный поиск (алг. А6.3.1)
= 2 Криволинейный шаг на основе доверительной области
(алг. А6.4.1)
= 3 Шаг вдоль ломаной на основе доверительной
области (алг. А6.4.3)
= 4 Модифицированный линейный поиск (алг. A6.3.1mod)
На некоторых задачах могут существовать большие различия
в точности и эффективности, определяемые сменой способов
глобализации 1, 2 и 3 при сохранении других параметров и
допусков неизменными. Однако ни один из способов не
создает впечатление превосходящего в общем случае остальные
или уступающего им, и каждый из них, вероятно, является
наилучшим на некоторых задачах. Первые три варианта
даны для сравнения и для того, чтобы предоставить
возможность пользователю выбрать наилучший способ для
отдельного класса задач. Способ 4 представляет собой
незначительное расширение способа 1, и ему можно отдать предпочтение
при использовании аппроксимаций гессиана по секущим. По
нашему опыту результаты использования способов 1 и 4
очень похожи.
Предлагаемое значение по умолчанию: global = 1 (так как это,
вероятно, самый простой способ с точки зрения .его
понимания и программирования)
analgrad — переменная типа Boolean, которая имеет значение
TRUE, если пользователем предоставлена подпрограмма
аналитического вычисления градиента V/(jc), и значение
FALSE в противном случае. Если аналитические градиенты
не предоставлены, то на каждой итерации система будет
аппроксимировать градиент по конечным разностям.
Алгоритмы в данной системе обычно способны найти более
точное приближение к точке минимума и иногда могут
выполнить это более эффективно, используя аналитические, а не
конечно-разностные градиенты. Поэтому так важно
предоставить подпрограмму, которая вычисляет аналитический
градиент, если он имеется в распоряжении.
332 Приложение А.
Предлагаемое значение по умолчанию: analgrad = FALSE
analhess — переменная типа Boolean, которая имеет значение
TRUE, если пользователем была предоставлена
подпрограмма аналитического вычисления матрицы Гессе V2/(jc), и
значение FALSE в противном случае. Если аналитические
гессианы не предоставлены, то на каждой итерации система
будет аппроксимировать гессиан по конечным разностям или
по секущим в зависимости от значения cheapf. Алгоритмы
в данной системе могут работать, более эффективно, если
задаются аналитические гессианы. Следует предоставлять
подпрограмму вычисления аналитического гессиана, если он
имеется в распоряжении.
Предлагаемое значение по умолчанию: analhess = FALSE
cheapf — переменная типа Boolean, которая имеет значение
TRUE, если вычисление целевой функции f(x) обходится
недорого, и значение FALSE в противном случае. Если
analhess = TRUE, то значение cheapf игнорируется. Если
analhess = FALSE, то значение cheapf ипользуется для
выбора способа аппроксимации гессиана: конечно-разностные
гессианы используются, если cheapf = TRUE;
аппроксимации гессиана по секущим (BFGS-формуЛы) используются,
если cheapf = FALSE. Методы, использующие
конечно-разностные гессианы, обычно (но не всегда) будут требовать
меньшего числа итераций, чем методы, использующие на той
же задаче аппроксимации по секущим. Методы,
использующие аппроксимации по секущим, обычно будут требовать
меньшего числа вычислений целевой функции, чем методы,
использующие конечно-разностные гессианы (включая
вычисления функции, идущие на конечные разности), особенно
для задач со средними или большими значениями п. Таким
образом, если стоимость вычисления f(x) ощутима или если
аппроксимации по секущим желательны по какой-либо
другой причине, то sheapf следует положить равным FALSE,
а в противном случае cheapf следует положить равным
TRUE.
Предлагаемое значение по умолчанию: cheapf = FALSE.
factsec — переменная типа Boolean, которая используется
только в том случае, когда используются аппроксимации
гессиана по секущим, т. е. когда analhess = FALSE и cheapf =
= FALSE, и которая игнорируется во всех остальных
случаях. Если используется factsec, то ее значение влияет
только на вычислительную трудоемкость алгоритма, причем
результаты и последовательность итераций остаются
неизменными. Если factsec = TRUE, то система использует факто-
ризованную аппроксимацию по секущим, в которой пересчи-
Модульная система алгоритмов 333
тывается L/Лразложение аппроксимации гессиана, и
которая требует 0(п2) арифметических операций на итерацию;
если factsec = FALSE, то она использует нефакторизован-
ную аппроксимацию, требующую О (я3) операций на
итерацию. (Подробности см. в разд. 9.4 основной части книги.)
Если global = 2, то factsec должно быть положено равным
FALSE, потому что алгоритм криволинейного шага в том
виде, как он написан, мог бы сделать запись на место
множителя L разложения аппроксимации гессиана по Холес-
скому. Если global = 1, 3 или 4, то в готовой программе
должно использоваться значение factsec = TRUE, так как
это более эффективно. Во всяком случае, значению factsec =
= FALSE можно отдать предпочтение в учебных проектах,
поскольку эта версия более проста для понимания.
Предлагаемое значение по умолчанию: factsec = FALSE
для учебных проектов или для случая global = 2, в
остальных случаях factsec = TRUE.
II. 4. Руководство 2. Выбор параметров
для безусловной минимизации
Ниже приведены параметры масштабирования, останова и
другие, использующиеся для безусловной минимизации, а также
указания по выбору для них подходящих значений.
typx — массив размерности я, /-я компонента которого есть
положительный скаляр, указывающий характерную величину
x[i]. Например, если предвидится, что* диапазон значений для
итераций по х будет иметь вид
*1е[-1010, 1010], *2е[-104, -102],*3е [-6*1(Г6, 9*1(Г6],
то подходящим выбором здесь было бы
typx = (lOl\ 103, 7'1(Г6).
Параметр typx используется для задания вектора
масштабов Sx и диагональной матрицы масштабирования Dx,
которые в свою очередь используются повсюду в программе;
DJC = diag((S*h, ..., {Sx)n), где Sx[i]=l/typx[i]. Важно
задать значения typx, когда ожидается, что величины
компонент х будут сильно различаться; в этом случае программа
может работать лучше при хорошей информации о
масштабах, чем при Dx = /• Если компоненты х сходны по величине,
то программа будет работать, вероятно, с таким же успехом
при Dx = /, как и при каких-либо других значениях.
334 Приложение А.
Предлагаемое значение по умолчанию: typx[i]= 1, /= 1, ..., п.
tУPf — положительный скаляр, служащий оценкой величины f(x)
вблизи точки минимума л*. Он используется только в
приведенном ниже градиентном условии останова. Если
задаваемое для typf значение слишком велико, то алгоритм может
остановиться преждевременно. В частности, если /(хо)»
>/(**), то значению typf следует быть равным
приблизительно |/(х*) |.
Предлагаемое значение по умолчанию: typf = 1
fdigits — положительное целое, указывающее число достоверных
десятичных разрядов, возвращаемых целевой функцией FN.
Например, если FN представляет собой результат
итеративной процедуры (подпрограмма вычисления квадратуры,
решения уравнений в частных производных), которая, как
предполагается, дает пять верных цифр в ответе, то fdigits
следует положить равным 5. Если ожидается, что FN дает
(с точностью до одной или двух) полное число значащих
цифр, имеющихся на данной вычислительной машине, то
fdigits следует положить равным —1. Число fdigits
используется для установления значения параметра т), который
применяется в программе для указания относительного уровня
шума в f(x); основное применение ц находит при вычислении
длин шага в конечных разностях. Значение г\ полагается
равным macheps, если fdigits = —1, и равным max{macheps,
\Q-fdigits^ в противном случае. Если ожидается, что функция
f(x) будет зашумленной, но приближенное значение fdigits
не известно, то его следует оценить с помощью алгоритма
Хемминга [1973], приведенного в книге Гилл,Мюррей и Райт
[1981].
Предлагаемое значение по умолчанию: fdigits = —1.
gradtol — положительный скаляр, задающий диапазон, в котором
масштабированный градиент считается достаточно близким
к нулю, чтобы остановить алгоритм. Алгоритм
останавливается, если
1</<п1 max {| f |, typf} J ^s
(см.разд. 7.2).Это основной критерий останова для
безусловной минимизации, и величина gradtol должна отражать
представление пользователя о том, что считать решением задачи.
Если градиент аппроксимируется по конечным разностям, то
Ут), вероятно, представляет собой наименьшее значение для
gradtol, при котором приведенное выше условие может
выполняться.
Модульная система алгоритмов 335
Предлагаемое значение по умолчанию: gradtol = machepsl/z
steptol — положительный скаляр, задающий диапазон, в котором
масштабированное расстояние между двумя
последовательными приближениями считается достаточно близким к нулю
для того, чтобы остановить алгоритм. Алгоритм
останавливается, если
(см. разд. 7.2). Значение steptol должно быть по крайней
мере так же мало, как и значение 10-d, где d есть число
верных цифр, которые пользователь хотел бы иметь в
решении х*. Алгоритм может завершить работу преждевременно,
если steptol слишком велико, в особенности когда
используются формулы секущих. Например, steptol = machepsx,z
оказывается часто слишком большим при использовании
методов секущих.
Предлагаемое значение по умолчанию: steptol = macheps2/3
maxstep — положительный скаляр, задающий максимально
допустимое значение масштабированной длины шага \\Dx(x+ —
— хс\\2 на каждой итерации. Величина maxstep используется
для того, чтобы предотвратить появление шагов, которые
могли бы привести оптимизационный алгоритм к
переполнению или к выходу из интересующей пользователя области,
а также для выявления расходимости. Ее следует выбирать
достаточно малой для того, чтобы предотвратить первые два
из этих случаев, но большей, чем любая разумно ожидаемая
длина шага. Алгоритм прекратит работу, если он сделает
шаги длиной maxstep на пяти последовательных итерациях.
Предлагаемое значение по умолчанию: maxstep = 103 *
* max{||Dx*0|l2, IIAJb}
itnlimit .— положительное целое, указывающее максимальное
число итераций, которые могут быть выполнены до того,
как алгоритм прекратит работу. Подходящие здесь значения
сильно зависят от размерности и сложности задачи, а также
от стоимости вычисления нелинейной функции.
Предлагаемое значение по умолчанию: itnlimit = 100
б — положительный скаляр, задающий начальное значение
радиуса доверительной области (см. разд. 6.4). Он используется
только при global = 2 или 3 (методы с криволинейным
шагом или с шагом вдоль ломаной), игнорируется при global=l
или 4 (методы с линейным поиском). Значение б должно
быть таким, какое пользователь считает разумным для
масштабированной длины шага на первой итерации, и должно
удовлетворять условию б ^ maxstep. Если пользователь не
336 Приложение А.
задал никакого значения б или, если б = —1, то вместо него
используется длина масштабированного градиента в
начальной точке. Во всяком случае, радиус доверительной области
впоследствии регулируется автоматически.
Предлагаемое значение по умолчанию: б = —1
II. 5. Руководство 3. Соображения
относительно памяти' для безусловной
минимизации.
Ниже рассматриваются некоторые вопросы памяти, относящиеся
ко всей системе алгоритмов безусловной минимизации. Кроме
того, многие отдельные модули имеют раздел Память,
содержащий комментарии, характерные для этих модулей.
1) Во всей системе алгоритмов безусловной минимизации
используются две яХ /г-матрицы L и Н. Однако в
действительности используются только нижняя треугольная часть в L и
верхняя треугольная часть в #* включая главные диагонали
обеих матриц. Таким образом, вся система алгоритмов могла
бы быть реализована с использованием п2 + 0(п) ячеек
памяти. Мы написали ее, используя отдельно матрицы для L и для
Н, и поэтому затратив сверх необходимого п2 — п ячеек памяти,
так как это упрощает понимание псевдопрограмм. Тем не
менее система написана так, что после некоторых незначительных
модификаций, рассмотренных ниже в п. 2, она в результате
использует только п2 + О(п) ячеек памяти. Для учебных проектов
максимальная размерность задачи п будет, вероятно, мала,
поэтому систему, по всей видимости, следует реализовывать так,
как она сейчас написана, с тем чтобы сделать ее простой для
понимания. При реализации в виде программного продукта
следует, конечно, произвести модификации, приведенные в п. 2.
2) Для того чтобы вся система алгоритмов безусловной
минимизации использовала только одну п X n-матрицу, требуются
незначительные модификации алгоритмов А5.5.1—2, А6.4.1—2,
А6.4.5, А9.4.1 и драйвера D6.1.1 (или используемого
сокращенного варианта драйвера). Они по существу заключаются в
объединении L и Н в одну матрицу, причем главная диагональ
матрицы Н иногда запоминается в отдельном я-векторе hdiag,
а также в соответствующем изменении программы, списков
параметров и последовательностей обращений к подпрограммам.
Модификации таковы:
Алгоритм А5.5.1
i) Заменить выходной параметр L^RnXn на выходной
параметр hdiag^R"
Модульная система алгоритмов 337
и) Между строками 11 и 12 вставить оператор
II1/»- FQR /=1 ТО п DO
hdiag[i\<-H[i9 i]
iii) Заменить строки 12 и 13.8 на
CALL CHOLDECOMP (л, hdiag, maxoffl, macheps, Я,
maxadd)
iv) В строках 13.3.2, 13.3.3 и 13.7 заменить все вхождения
Н [/, i\ на hdiag [i]
v) Заменить оператор 14.1 на
14.1 FOR / = /+1 ТО п DO
H[i, j)+-H[i, f\*sxwsx[i]
14.2. hdiag [i] <- hdiag [i] * Sx [if
vi) В строке 15.1 заменить все вхождения L[i,j] на H[itj]
Алгоритм А5.5.2
i) Заменить входной парамер H^Rnxn на входной
параметр hdiag е Rrt
ii) В строке 2.1 заменить H[i,i] на hdiag [i]
iii) В строке 4.1 заменить #[/,/] на hdiag [j]
iv) В строке 4.3.1 заменить H[i,j] на L[/, i]
Алгоритм А6.4.1
i) Заменить входной параметр H^RnXn на входной
параметр hdiag е Rn
ii) В строках 5.1 и 5.3 заменить параметр Н на hdiag
Алгоритм А6.4.2
i) Заменить входной параметр Я е /?пхя на входной
параметр hdiag е Rn
ii) В строках ЗЕ.8.2 и ЗЕ.8.5 заменить все вхождения Н [i, i]
на hdiag [i]
iii) В строке ЗЕ.8.3 заменить параметр Н на hdiag
Алгоритм А6.4.5
i) Заменить входной параметр H^Rnxn на входной
параметр hdiag е Rn
ii) В строке 9с.2Т.1.1 заменить H[i,i] на hdiag [i]
Алгоритм А9.4.1
i) Добавить входной параметр hdiag е/?л в качестве
последнего входного параметра
ii) Перед строкой 1 вставить оператор
V2. FOR /=1 ТО п DO
H[i9 i]+- hdiag [i]
Драйвер D6.M
i) В строке 1(У.2 заменить параметр Lc на hdiag
ii) В строке 10.4b заменить параметр Нс на hdiag
338 Приложение А.
Hi) В строке 10.7Е.1е вставить параметр hdiag между anal-
grad и Нс
iv) Заменить все остальные вхождения Lc в списках
параметров на Нс. Они встречаются в строках 8E.ld, 10.3,
10.4b, 10.4с и 10.7E.ld.
3) Имеется возможность еще более снизить требование к
памяти до l/2ti2 + 0(n) ячеек в одном частном случае, когда
используются факторизованные аппроксимации гессиана по
секущим. В этом случае Н никогда не участвует; мы имеем дело
лишь с нижней треугольной матрицей L и верхней треугольной
R в алгоритме АЗ.4.1, причем они могут совместно делить одно
поле памяти. В большинстве языков программирования для
того, чтобы фактически занять только (п2 + п)/2 ячеек для
хранения треугольной матрицы, она должна быть реализована как
вектор с (п2 + п)/2 элементами, например с помощью
представления L[iJ] = v[((i2 — i)/2)+j] = R[jyi]yl^j^i^n.
Другие подробности этого преобразования оставляем в качестве
упражнения.
Что касается всех других методов, то для них нужно п2 ячеек
памяти, так как все они используют алгоритм А5.5.1, для
которого надо одновременно знать L и Н. Алгоритмы
криволинейного шага и любые алгоритмы, использующие нефакторизован-
ные формулы секущих, тоже требуют как L, так и Н.
4) Память под векторы, необходимая модулю, определяется
совокупностью векторов в его списке параметров, а также
всеми векторами, участвующими в качестве локальных
переменных. В п. 1 раздела Память каждого модуля перечислены все
векторы, выступающие в качестве локальных переменных. Тому,
кто занимается реализацией, следует определить память под
векторы, требующиеся драйверу.
5) При реализации этих алгоритмов на Фортране все
модули, имеющие среди своих параметров матрицы, могут
потребовать введения дополнительного параметра ndim, задающего
фактическое количество строк матриц. Это нужно всякий раз,
когда размеры матриц в модулях задаются как переменные
вместо того, чтобы задаваться как фиксированные целые.
Например, в готовой программной реализации любая матрица
будет, как правило, передаваться пользователем в качестве
дополнительного параметра головному драйверу. Они будут описаны
в программе пользователя с некоторыми фиксированными
размерностями, скажем, как Я (уО, 50), где размер матрицы (50)
больше или равен размерности задачи п. Тогда все матрицы
в драйвере и модулях системы будут описаны, как H(ndim,n)
или L(ndimy п), где ndim представляет собой дополнительный
параметр, передаваемый пользователем драйверу и системой
Модульная система алгоритмов 339
каждому модулю, имеющему параметр матричного типа. Здесь
ndim содержит количество строк матрицы в программе
пользователя, ndim = 50, в то время как п может быть любым числом
между 1 и 50. Если вместо этого размеры матриц в модулях
задаются как (пу п), то алгоритмы будут работать неправильно.
Причина состоит в том, что по правилам языка Фортран
матрицы располагаются в памяти по столбцам, и компилятору
должно быть известно количество ячеек, отводимых под каждый
столбец (т. е. число строк) для того, чтобы правильно
находить его место в матрице.
В любой версии языка Фортран эти рассуждения применимы
ко всем модулям, в которых размеры матриц заданы как
переменные. Размеры должны иметь вид (ndim, п), где ndim есть
входной параметр модели, содержащий число строк матрицы,
в какой бы подпрограмме или головной программе она ни была
описана с помощью фиксированных целочисленных размеров.
(При реализации нашей системы в учебных целях это должен
быть драйвер.) Для учебных проектов подойдет иной вариант,
при котором матрицы во всех модулях описываются с помощью
одних и тех же фиксированных целочисленных размеров,
скажем, (50, 50). В этом случае дополнительный параметр ndim
не нужен, и не требуется производить никаких модификаций
наших псевдопрограмм, но система будет работать только пои
п ^ 50.
В большинстве языков программирования с полным
контролем типов дополнительный параметр ndim не потребовался бы,
и наши псевдопрограммы можно было бы использовать такими,
как они есть. Например, в языке Паскаль можно было бы
задать тип данных
MATRIX = ARRAY [1..50, 1..50] OF REAL
в вызывающей программе. Размер матрицы (50) опять был бы
большим или равным наибольшей используемой размерности
задач п. Тогда для всех матриц во всех подпрограммах системы
просто был бы задан тип данных MATRIX. Для запуска системы
при п > 50 необходимо было бы изменить только описание типа
данных MATRIX. Недостаток этой схемы заключается в том,
что одно и то же слово MATRIX должно использоваться всеми
подпрограммами системы и вызывающей программой.
II. 6. Алгоритм D6.1.2 (UMEXAMPLE).
Драйвер алгоритма безусловной минимизации,
использующего линейный поиск, конечно-
разностные градиенты и факторизованные
аппроксимации гессиана по секущим
Назначение: Попытаться найти точку локального минимума х*
функции f{x): /?"->/?, начиная из х0 и используя алгоритм
340 Приложение А.
линейного поиска, конечно-разностные градиенты и
аппроксимации гессиана по BFGS-формуле.
Входные параметры: neZ(n>l), х0 е Rn, FN (имя задаваемой
пользователем функции /: Rn->R).
Кроме того, необязательные:^ * typx^ Rn, typf е R, fdigits e Z,
gradtol^R, steptol^R, maxstep^R, itnlimit^Z, print-
code e Z (дальнейшую информацию см. в алгоритме D6.1.1).
Входно-выходные параметры: отсутствуют (см. п. 2 раздела
Память в алгоритме D6.1.1).
Выходные параметры: Xf е Rn (заключительное приближение
к х*), termcode ^Z (указывает, какое из условий
окончания вызвало останов алгоритма).
Кроме того,необязательные:fc^R(=f(xf)), gc^Rn(=Vf(xf))t
другие выходные параметры по желанию того, кто
занимается программной реализацией (см. разд. 1.4).
Значения кодов возврата, память:
такие же, как у алгоритма D6.1.1
Алгоритм:
(* Инициализирующая часть: *)
1. CALL MACHINEPS (macheps)
2. CALL UMINCK (список параметров выбирает тот, кто
занимается программной реализацией)
(*см. описание UMINCK*)
3. IF termcode < 0 THEN
3.1 xf<-x0
3.2 RETURN для алгоритма D6.1.2 (*при желании вывести
на печать соответствующее сообщение*)
4. itncount«- 0
5. CALL FN (п, х0, fc)
6. CALL FDGRAD (п, x0t fc, FN, Sx, т), gc) (* алг. A5.6.3 *)
7. CALL UMSTOP0 (n, x0, fc, gc, SX9 typf, gradtol, termcode,
consecmax) (* алг. A7.2.2 *)
8. IF termcode > 0
8T. THEN xf+-x0
8E. ELSE CALL INITHESSFAC (n, /„ typf, Sx, Le)(* алг. A9.4.4 *)
9. xc<—Xq
(* Итерационная часть: *)
10. WHILE termcode = 0 DO
10.1 itncount <- itncount + 1
10.2 CALL CHOLSOLVE (n, gc, LC9 sN) (*алг. A3.2.3*)
10.3 CALL LINESEARCH (n, xc, fc, FN, gC9 sNt Sx, maxsiep,
steptol, retcode, x+, f+, maxtaken) (*алг. A6.3.1 *)
Модульная система алгоритмов 341
10.4 CALL FDGRAD (л, *+, /+f FN, Sx, t|, g+) (* алг.
А5.6.3*)
10.5 CALL UMSTOP (n, xe, *+, f g+, Sx, typf, retcode,
gradtol, sieptoly itncount, itnlimit, maxlaken, consecmax,
termcode) (* алг. A7.2.1*)
10.6 IF termcode >0
10.6T THEN xf«-*+
10.6E ELSE (* вычислить следующую аппроксимацию
гессиана *)
10.6Е.1 CALL BFGSFAC (я, хсУ х+, gc, g 9 macheps, r\9
analgrad, Lc) (*алг. A9.4.2*)
10.6E.2 xc<-x+
10.6E.3 /,«-/+
10.6E.4 gc<-g+
(*END, цикл WHILE 10*)
(* при желании вывести на печать соответствующее сообщение
об окончании *)
(♦RETURN для алгоритма D6.1.2*)
(*END, алгоритм D6.1.2*)
III. ДРАЙВЕРНЫЕ МОДУЛИ И РУКОВОДСТВО
ДЛЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
III.1. Алгоритм D6.1.3 (NEDRIVER).
Драйвер модульной системы алгоритмов
решения нелинейных уравнений
Назначение: Попытаться найти корень х+ функции F(x): Rn-+Rn,
начиная из хо и используя один из имеющегося набора
алгоритмов.
Входные параметры: n^Z(n^ l),xo^Rn, FVEC (имя
задаваемой пользователем функции F: Rn-+Rny которая по
меньшей мере непрерывно дифференцируема).
Кроме того, необязательные:
i) J АС — имя задаваемой пользователем функции для
вычисления F'(x). (F'(x) обозначается здесь через /(*).)
ii) global е Z, analjac е Boolean, cheap F е Boolean, fac-
tsec e Boolean — параметры, используемые при выборе
алгоритмических вариантов. Они объясняются в
руководстве 4. -(Параметрам, которые не введены пользователем,
присваиваются значения, задаваемые алгоритмом
NEINCK.)
342 Приложение А.
Hi) typ х ^ R", typ F ^Rn,F digits e Z, / uec/o/ e /?, steptol e
e /?, mintol e /?, maxstep e /?, itnlimit eZ, бе /? —
параметры типа допусков и константы, используемые в
алгоритме. Они объясняются в руководстве 5. (Параметрам
и константам, которые не введены пользователем,
присваиваются значения, задаваемые алгоритмом NEINCK)
iv) printcode е Z — см. разд.1.4 этого приложения.
Входно-выходные параметры: отсутствуют (см. тем не менее п. 2
раздела Память).
Выходные параметры: Xf е Rn (заключительное приближение
к х*), termcode ^Z (указывает на то условие окончания,
которое явилось причиной остановки алгоритма).
Кроме того, необязательные:
FV+<=Rn(=F(xf))y Jc<=Rnx»(=J(Xf))f другие выходные
параметры по желанию того, кто занимается программной
реализацией (см. разд. 1.4).
Значения кодов возврата:
termcode < 0: алгоритм закончил работу из-за ошибки во
входных данных, см. алг. NEINCK.
termcode > 0: алгоритм закончил работу по причине,
приведенной в алг. А7.2.1.
Память:
1) Требования относительно памяти под матрицы и векторы
обсуждаются в руководствах 3 и 6. Непременно прочтите п. 5
руководства 3, если вы занимаетесь программной реализацией
этих алгоритмов на Фортране.
2) Имена х0 и Xf используются в этом драйвере только лишь
для большей ясности. В программной реализации хо и х\ могут
оба делить одну и ту же область памяти с хс-
3) Две глобальные переменные (типа COMMON в Фортране)
Sf и FV+ должны передаваться между драйвером и алгоритмом
NEFN. Подробности см. в алгоритме NEFN.
Примечания:
1) В разделе «Перечень модулей для нелинейных уравнений»
указано, какие модули соответствуют каждому шагу в
приведенном ниже разделе Описание. Выбор среди имеющихся в этом
перечне вариантов задается описанными в руководстве 4
параметрами, которые определяют алгоритмический вариант.
2) Приведенный ниже Алгоритм используется для реализации
всей системы алгоритмов решения нелинейных уравнений.
Упрощенный вариант драйвера можно использовать для реализации
отдельного алгоритма решения нелинейных уравнений, как это
наглядно показано на примере алгоритма D6.1.4.
Модульная система алгоритмов 343
3) На некоторых вычислительных машинах необходимо
снабдить систему фиктивной подпрограммой JAC на тот случай,
если пользователь не задаст подпрограмму вычисления F'(x).
Эта фиктивная подпрограмма требуется единственно для того,
чтобы была возможна трансляция программы.
Описание:
Инициализация:
1) Вычислить машинный эпсилон.
2а) Проверить допустимость входных данных, присвоить
значения по умолчанию тем параметрам, определяющим
алгоритмический вариант, и тем параметрам типа допусков, которые для
пользователя не были входными. (Возвратить в драйвер
значение termcode.)
2b) Если termcode < 0, то завершить работу алгоритма,
возвратив значения х\ = л'о и termcode. Если termcode = 0, то
положить itncount-<r-0 и продолжить дальше.
3) Вычислить FV+=F(x0), fc = l/2\\DFFVJ22.
4а) Решить, нужно ли остановиться. (Возвратить в драйвер
значение termcode.)
4b) Если termcode > О, то завершить работу алгоритма,
возвратив значения х\ = х0 и termcode. Если termcode = 0, то
продолжить дальше.
5) Вычислить /с = /(х0) или аппроксимировать его по
конечным разностям.
6) Вычислить gc = JTcD2FFV+.
7) Положить хс = х0у FV± = FV+ и restart = TRUE.
Итерация:
1) itncount •<- itncount + 1.
2) Вычислить ньютоновский шаг sn = — J с Fc или его
некоторый вариант, если матрица /с вырождена или плохо
обусловлена. Построить также связанную с этим минимизационную
модель, если используется алгоритм глобализации, основанный на
построении доверительной области.
3) Положить х+ = хс + Sc где sc = sN или равно шагу,
выбираемому в соответствии со стратегией глобализации. В
процессе выполнения этого шага алгоритма вычисляются F+ = F(x+)
h/+-V.|D^+{.
4) Если /с вычисляется с помощью аппроксимаций по секущим
и алгоритм застопорился, то, используя конечные разности,
положить заново J с равным ]{хс), вычислить также заново gc и
повторить итерацию.
5) Вычислить или аппроксимировать Jc = /(*+).
6) Вычислить gc = JT€&pFV+.
344 Приложение А.
7а) Решить, нужно ли остановиться. (Возвратить в драйвер
значение termcode.)
7b) Если termcode > 0, то завершить работу алгоритма,
возвратив значения Xf = х+ и termcode. Если termcode = 0, то
продолжить дальше.
8) Положить Хс+-х+, /с^-/+» FVC+-FV+ и вернуться к шагу 1
итерационной части.
Алгоритм:
(* Инициализирующая часть: *)
1. CALL MACHINEPS (macheps)
2. CALL NEINCK (список параметров определяет тот, кто
занимается программной реализацией)
(*см. описание NEINCK*)
3. IF termcode < О THEN
3.1 xf^-x0
3.2 RETURN для алгоритма D6.1.3 (*при желании вывести
на печать соответствующее сообщение*)
4. itncount <- О
5. CALL NEFN (л, *0, /,)
(*NEFN вычисляет также значение FV+ = F(x0) и передает
его драйверу через глобальный параметр *)
6. CALL NESTOP0(n, х0, FV+, SF, fvectol, termcode, consecmax)
(* алг. A7.2.4 *)
7. IF termcode > 0
7T. THEN xf+-x0
7E. ELSE (* вычислить начальное значение якобиана*)
7Е.1 IF analjac
7E.1T THEN CALL JAC (n, x0, Je)
7E.1E ELSE CALL FDJAC (n, x0f FV+, FVEC, Sx, i\, Jc)
(*алг. A5.4.1*)
7E.2 FOR /=1 TO n DO
gc[i\^tmi]*FV+[i]*SP[i?
7E.3 FVC+-FV+
8. xc «- x0
9. restart*- TRUE
(* Итерационная часть: *)
10. WHILE termcode = 0 DO
10.1 itncount«- itncount + 1
10.2 IF amtf/ac OR cAeapF OR (NOT factsec)
10.2T THEN CALL NEMODEL (n, fV„ /„ gc, SF, SXJ
macheps, global, M, HC9 sN) (*алг. A6.5.1*)
Модульная система алгоритмов 345
10.2Е ELSE CALL NEMODELFAC (я, FVC, gc, SF, Sx,
macheps, global, restart, M, M2, Jc, Hc, sN) (* алг.
A6.5.1fac*)
10.3a IF global = 1 THEN
CALL LINESEARCH (n, xc, fc, FVEC, gc, sN,
Sx, tnaxstep, steptol, ret code, x+, f+, maxtaken)
(*алг. A6.3.1*)
10.3b ELSEIF global = 2 THEN
CALL HOOKDRIVER (я, xc, fe, FVEC, gc, M, He,
sN, Sx, maxstep, steptol, macheps, itncount, bprev, b,
ц, ф, ф', retcode, x+, f+, maxtaken) (* алг. A6.4.1 *)
10.3c ELSE (* global = 3*)
CALL DOGDRIVER («, xc, fc, FVEC, gc, M, sN, Sx,
maxstep, steptol, 6, retcode, x+, f+, maxtaken)
(* алг. A6.4.3 *)
10.4 IF (retcode = 1) AND (NOT restart) AND (NOT analjac)
AND (NOT cheapF)
10.4T THEN (* обновление в методе секущих: вычислить
заново /с и повторить итерацию *)
10.4Т.1 CALL FDJAC (п, хс, FVC, FVEC, Sx, r\, Jc)
(* алг. A5.4.1 *)
10.4T.2 gc+-JTc*iyF*FVc
(* то же самое, что и в операторе 7Е.2, с точностью
до замены FV+ на FVC*)
10.4Т.З IF (global = 2) OR (global = 3) THEN бч-- 1
10.4T.4 restart«- TRUE
10.4E ELSE (*завершить итерацию*)
10.4E.la IF analjac THEN
CALL JAC (n, x+, Jc)
10.4E.lb ELSEIF cheapF THEN
CALL FDJAC (n, x+, FV+, FVEC, Sx, r\, Jc)
(*алг. A5.4.1*)
10.4E.lc ELSEIF factsec THEN
CALL BROYFAC (я, xc, x+, FVC, FV+, ц, Sx,
SP, Jc, M, M2) (* алг. A8.3.2 *)
10.4E.ld ELSE (*factsec = FALSE*)
CALL BROYUNFAC (я, xc, x+, FVC, FV+,
Л. Sx, Jc) (*алг. A8.3.1*)
10.4E.2 IF factsec
10.4E.2T THEN (* вычислить ge, используя QR-раз-
ложение *)
(* gc^JcDPFV+ =QTDFFV+: *)
10.4E.2T.1 FOR t = l TO я DO
.gcli\^tjc[hJ]*FV+[j]*SP[i]
(*gc^RTgei*)
346 Приложение А.
10.4Е.2Т.2 FOR i = n DOWNTO 1 DO
8с[1\<-£ми,1\'8,Ц\
/=i
10.4E.2E ELSE
gc<-Jl'DyFV+
(* так же, как и в операторе 7Е.2 *)
10.4Е.З CALL NESTOP (я, хе, х+, FV+t /+, ge, SX,SF,
retcode, fvectol, steptol, itncount, itnlimit,
maxtaken, analjac, cheapF, mintol, consecmax,
termcode) (* алг. A7.2.3 *)
10.4E.4a IF {termcode = 2) AND (NOT restart) AND
(NOT analjac) AND (NOT cheapF) THEN
(* обновление *) GO TO 10.4T.1
10.4E.4b ELSEIF termcode > 0 THEN
10.4Е.4Ы.1 xf*-x+
10.4E.4bT.2 IF termcode = 1 THEN
FV+<-FVc
10.4E.4c ELSE restart*-FALSE
10.4E.5 xc*-x+
10.4E.6 /e«-/+
10.4E.7 FVC*-FV+
(* END, операторы IFTHENELSE 10.4 и WHILE 10 *)
(* при желании вывести на печать соответствующее сообщение
об окончании *)
(♦RETURN для алгоритма D6.1.3*)
(*END, алгоритм D6.1.3*)
III. 2. Перечень модулей для нелинейных
уравнений
Шаги в разделе Описание драйвера D6.1.3 соответствуют
следующим модулям. Шаги в этом описании, которые не приведены
ниже, отвечают соответствующим строкам псевдопрограммы
драйверного алгоритма.
Инициализация
Шаг 1 -MACHINEPS
Шаг 2а - NEINCK
Шаг 3 - (NEFN/FVEC)
Шаг 4а - NESTOP0
Шаг 5 — JAC или FDJAC
Модульная система алгоритмов 347
Итерация
Шаг 2 -(NEMODEL/QRDECOMP/CONDEST/QRSOLVE/
CHOLDECOMP/CHOLSOLVE) или (NEMODELfac/
QRDECOMP/QFORM/CONDEST/RSOLVE/
CHOLDECOMP/CHOLSOLVE)
Шаг 3 -LINESEARCH или LINESEARCHmod или
(HOOKDRIVER/HOOKSTEP/TRUSTREGUP) или
(DOGDRIVER/DOGSTEP/TRUSTREGUP)
Шаг 4 — FDJAC (см. приведенное ниже замечание)
Шаг 5 - JAC или FDJAC или BROYUNFAC или
(BROYFAC/QRUPDATE)
Шаг 7а - NFSTOP
В том случае, когда какой-либо из приведенных выше шагов
содержит два и более модулей или групп модулей, разделенных
между собой союзом «или», они представляют собой
альтернативные варианты, выбираемые с помощью параметров,
определяющих алгоритмический выбор. Подразумевается, что
конкретный метод использовал бы только один вариант для каждого
такого шага алгоритма. Заметим, что в перечне, относящемся
выше к итерации, шаг 4 (FDJAC) выполняется только, когда
используются аппроксимации якобиана по секущим.
В том случае, когда два и более модулей перечисляются
выше в скобках и разделяются между собой наклонной чертой
(/), первый из группы модулей, заключенных в скобки,
вызывается драйвером, а остальные модули этой группы вызываются
первым модулем. Например, NEFN вызывает FVEC. Кроме того,
приведенные ниже модули вызывают следующие сервисные
модули и модуль вычисления функции:
HOOKSTEP вызывает CHOLDECOMP и LSOLVE
LINESEARCH вызывает (NEFN/FVEC)
TRUSTREGUP вызывает (NEFN/FVEC)
Приведенные ниже модули также вызывают следующие их под-
алгоритмы:
CHOLSOLVE вызывает LSOLVE и LTSOLVE
QRSOLVE вызывает RSOLVE
QRUPDATE вызывает JACROTATE
III. 3. Руководство 4. Выбор алгоритмических
варрантов решения нелинейных уравнений
Ниже приведены алгоритмические варианты, имеющиеся в
распоряжении при использовании системы алгоритмов решения
нелинейных уравнений, и указания по их выбору.
348 Приложение А.
global — положительное целое, указывающее следующим
образом на то, какую стратегию глобализации использовать на
каждой итерации:
= 1 Линейный поиск (алг. А6.3.1)
= 2 Криволинейный шаг на основе доверительной области
(алг. А6.4.1)
= 3 Шаг вдоль ломаной на основе доверительной области
(алг. А6.4.3)
На некоторых задачах могут существовать довольно большие
различия в точности и эффективности, определяемые сменой
способов глобализации 1,2 и 3 при сохранении других
параметров и допусков неизменными. Однако ни один из способов
не создает впечатление явно превосходящего в общем случае
остальные или уступающего им, и каждый из них, вероятно,
является наилучшим на некоторых задачах. Эти три
возможности даны для сравнения и для того, чтобы предоставить
возможность пользователю выбрать наилучший способ для
конкретного класса задач.
Предлагаемое значение по умолчанию: global =1 (так как
это, вероятно, самый простой способ с точки зрения его
понимания и программирования)
analjac — переменная типа Boolean, которая имеет значение
TRUE, если пользователем была предоставлена
подпрограмма аналитического вычисления матрицы Якоби /(*), и
значение FALSE в противном случае. Если аналитические
якобианы не предоставлены, то на каждой итерации система будет
аппроксимировать якобиан в зависимости от значения cheap Р
по конечным разностям или по секущим. Алгоритмы в
данной системе могут работать более эффективно, если задаются
аналитические якобианы. Следует предоставлять
подпрограмму вычисления аналитического гессиана всякий раз,
когда это возможно.
Предлагаемое значение по умолчанию: analjac = FALSE
cheapF — переменная типа Boolean, которая имеет значение
TRUE, если вычисление функции Р(х) обходится недорого,
и значение FALSE в противном случае. Если analjac =
= TRUE, то значение cheap? игнорируется. Если analjac =
= FALSE, то значение cheap? используется для выбора
способа аппроксимации якобиана: по конечно-разностным
формулам, если cheap? = TRUE; по секущим (формулы
пересчета Бройдена), если cheap? = FALSE. Методы,
использующие конечно-разностные якобианы, обычно будут
требовать меньшего числа итераций, чем методы, использующие
на той же задаче аппроксимации по секущим. Методы с
аппроксимациями по секущим, обычно будут требовать
Модульная система алгоритмов 349
меньшего числа вычислений функции F(x), чем методы с
конечно-разностными якобианами (включая вычисления
функции, идущие на конечные разности), в особенности для
задач со.средними и большими значениями п. Таким образом,
если стоимость вычисления F(x) ощутима, то cheapF
следует положить равным FALSE, а в противном случае
cheap? следует положить равным TRUE.
Предлагаемое значение по умолчанию: cheapF = FALSE
factsec — переменная типа Boolean, которая используется
только в том случае, когда применяются аппроксимации
якобиана по секущим, т. е. когда analjac = FALSE и cheapF =
FALSE, и которая игнорируется во всех остальных случаях.
Если используется factsec, то ее значение влияет только на
вычислительную трудоемкость алгоритма, причем результаты
и последовательность итераций остаются без изменения. Если
factsec = TRUE, то система использует факторизованную
аппроксимацию яо секущим, в которой пересчитывается QR-
разложение аппроксимации якобиана, и которая требует
0(п2) арифметических операций на итерацию; если factsec =
= FALSE, то она использует нефакторизованную
аппроксимацию, требующую 0(п?) операций на итерацию. (Подробности
см. в разд. 8.3 основной части книги.) В коммерческой
программе следует положить factsec = TRUE, так как это
более эффективно. Тем не менее, в учебных проектах можно
отдать предпочтение factsec = FALSE, поскольку эта версия
более проста для понимания.
Предлагаемое значение по умолчанию: factsec = FALSE для
учебных проектов, factsec = TRUE в остальных случаях.
III. 4. Руководство 5. Выбор параметров
для нелинейных уравнений
Ниже приведены параметры масштабирования, останова и
другие параметры, использующиеся при решении нелинейных
уравнений, а также указания по выбору для них подходящих
значений.
typx — см. руководство 2.
tupF—массив размерности п, i-я компонента которого есть
положительный скаляр, указывающий характерную величину
/-и компоненты функции F(x) в точках, которые находятся
не вблизи корня F(x). Параметр typF применяется для
задания вектора масштабов SF и диагональной матрицы
масштабирования Dfj которые используются повсюду в
программе; DF = diag((S/r)b ..., (SF)n), где SF[i) = \/typF\i].
Его следует выбирать так, чтобы все компоненты DFF(x)
350 Приложение А.
имели сходные характерные величины в точках, не слишком
близких к корню, а также следует выбирать в сочетании
с fvectol, как это обсуждается ниже. Важно задать
значения typF, когда ожидается, что величины компонент F(x)
будут сильно различаться; в этом случае программа может
работать лучше при хорошей информации о масштабах, чем
при DF = I. Если компоненты F(x) сходны по величине, то
программа будет работать при DF = I с таким же успехом,
как и при каких-либо других значениях.
Предлагаемое значение по умолчанию: typ F[i] =1, i = 1,..., п.
Fdigits — положительное целое, указывающее число достоверных
десятичных разрядов, возвращаемых функцией FVEC,
задающей , нелинейные уравнения. Если компоненты F(x)
имеют различные числа достоверных разрядов, то Fdigils
следует положить равным наименьшему из этих чисел.
В остальном обсуждение Fdigits аналогично обсуждению
fdigits в руководстве 2.
Предлагаемое значение по умолчанию: Fdigits =—1
fvectol — положительный скаляр, задающий диапазон, в котором
масштабированная функция DFF(x) считается достаточно
близкой к нулю, чтобы остановить алгоритм. Алгоритм
останавливается, если максимальная по модулю компонента
DFF(x+) не превосходит fvectol. Это — основное условие
останова при решении нелинейных уравнений, и величины typF
и fvectol должны выбираться так, чтобы эта проверка
отражала представление пользователя о том, что считать
решением задачи.
Предлагаемое значение по умолчанию: fvectol = machepsl/3
steptol—см. руководство 2.
mintol — положительный скаляр, используемый для проверки
того, не застрял ли алгоритм в точке локального минимума
функции f(x)=x/2\\DFF(x)\\2, где F{x)=£0. Алгоритм
останавливается, если максимальная по модулю компонента
масштабированного градиента функции f (х) в х+ не превосходит
mintol; здесь Vf(x) = J(x) D2FF(x), а масштабированное
значение для Vf(x+) определяется как в случае минимизации
(см. gradtol, руководство 2). Значение mintol следует брать
довольно малым, чтобы быть уверенным, что это условие не
сработало в неподходящей ситуации.
Предлагаемое значение по умолчанию: mintol = macheps2/3.
maxstep — см. руководство 2.
itnlimit — см. руководство 2.
6 — см. руководство 2.
Модульная система алгоритмов 351
III. 5. Руководство 6. Соображения
относительно памяти для нелинейных
уравнений
Соображения относительно памяти для нелинейных уравнений
тесно связаны с теми, которые приведены в руководстве 3 для
безусловной минимизации; прежде чем читать руководство 6,
прочтите, пожалуйста, руководство 3. Ниже даны
дополнительные замечания, применимые к алгоритмам решения нелинейных
уравнений.
1) Во всей системе алгоритмов решения нелинейных
уравнений используется три п X я-матрицы: /, М и Н. Матрица /
предназначается для хранения якобиана, вычисленного
аналитически или по конечным разностям. Если применяются факто-
ризованные формулы секущих, то / также предназначается для
хранения матрицы Z = QTy используемой в алгоритмах АЗ.4.1 и
А8.3.2. В матрице М хранятся (в компактном виде)
(^-разложение /; в нижней треугольной части М также хранится
матрица L, используемая в алгоритмах, связанных с глобализацией.
Матрица Н фигурирует в алгоритмах, связанных с
глобализацией; участвует только верхняя часть Я, включая главную
диагональ. Если используются аналитические якобианы, конечно-
разностные якобианы или нефакторизованные аппроксимации
по секущим (т. е. всё, кроме факторизованных аппроксимаций
по секущим), то Н может легко делить память с Af, если для
этого незначительно модифицировать алгоритмы, как описано
ниже в пункте 2. Это уменьшает требования к памяти под
матрицы до двух п X я-матриц. Кроме того, когда используются
аналитические или конечно-разностные якобианы, матрица /
также может делить память с Af, если сделать несколько
дополнительных модификаций, как указано ниже в п. 3. Это
уменьшает требование к памяти под матрицы до одной я X я-
матрицы, но такое уменьшение невозможно при формулах
секущих. Когда используются факторизованные аппроксимации
якобиана по секущим, Н может делить память с Af, только если
внести некоторые довольно значительные изменения, как
указано ниже в п. 4.
2) Для того чтобы позволить Н делить память с Af в случае
аналитических якобианов, конечно-разностных якобианов или
нефакторизованных аппроксимаций по секущим, должны быть
модифицированы алгоритмы А5.5.2, А6.4.1—2 и А6.4Д как
описано в п. 2 руководства 3. Кроме того, должны быть сделаны
следующие модификации алгоритма А6.5.1 и драйвера А6.1.3:
352 Приложение А.
Алгоритм А6.5.1
i) Заменить выходной параметр Яе^пХл на выходной
параметр hdiag ^Rn.
И) Заменить #[/, /] на М[/, /] в строках 4Т.1.1, 4Т.3.1 и
4Е.5.1.2.
Hi) Заменить Я[1, /'] на М[1, у] в строке 4Т.2.
iv) Заменить #[/, i] на М[/, /] в строке 4Т.3.1.
v) Заменить тело оператора цикла FOR в строке 4Т.4 на
hdiag [i]+-M[/, /]+... (остальное без изменений),
vi) В строке 4Т.5 заменить параметр Н на hdiag.
vii) Заменить #[/, i] на hdiag [i] в строке 4Е.5.1.1.
Драйвер D6.1.3
i) В строках 10.2Т и 10.3b заменить параметр Нс на hdiag.
3) В случае когда используются аналитические или конечно-
разностные якобианы, матрицы / и М могут делить память, если
объединить / и М в один параметр в списке параметров в
заголовке алгоритма Аб.5.1 и при обращении к нему, заменить /[/,/]
на M[i> j] в строке 1.1 алгоритма Аб.5.1 и заменить все
оставшиеся вхождения параметра М в драйвере D6.1.3 на /.
Единственно требуемая дополнительная модификация состоит в
переделке шагов 4Т.1—4 алгоритма Аб.5.1 к виду #-*-/?г/? вместо
Н <-FD2pJ. Поскольку Н и М (которая содержит R в ее
верхней треугольной части) тоже могут делить память, как описано
выше в п. 2, то это несколько нетривиально. Простой способ
достичь этого заключается в использовании нижней треугольной
части матрицы Af, которая в то время не занята, в качестве
временной памяти для Н. Подробности указанного
преобразования, оставлены в качестве упражнения.
4) В случае, когда используются факторизованные
аппроксимации якобиана по секущим, матрица Н может делить память
с Му только если в системе алгоритмов произведены следующие
изменения. Подробности оставлены в качестве упражнения.
i) Не допускается использование факторизованных формул
секущих при global = 2.
ii) Производятся модификации в алгоритме А6.5 Нас и
драйвере D6.1.3, аналогичные тем, что описаны выше в п. 2.
iii) На шагах ЗТ.1—4 алгоритма Аб.б.Иас матрица RTR
формируется в нижней треугольной части М, и
вызываемая на шаге ЗТ.5 подпрограмма CHOLDECOMP
заменяется на такую, которая выполняет разложение на месте
нижней треугольной части матрицы. (CHOLDECOMP,
как она написана, имеет на входе верхнюю треугольную
матрицу, а на выходе — нижнюю треугольную матрицу.)
Модульная система алгоритмов 353
III.6. Алгоритм D6.1.4 (NEEXAMPLE).
Драйвер алгоритма решения нелинейных
уравнений, использующего поиск вдоль
ломаной и конечно-разностную аппроксимацию якобиана
Назначение: Попытаться найти корень х* функции F(x): Rn-+Rn
из начальной точки л'о, используя алгоритм поиска вдоль
ломанной и конечно-разностные якобианы.
Входные параметры: /zeZ(tt^l), x0^Rnt FVEC (имя
задаваемой пользователем функции F: Rn->~Rn, которая по
меньшей мере непрерывно дифференцируема).
Кроме того, необязательные: typx ^ Rn, typF е Rnf Fdigits е
е Z, fvectol ^ R, steptol е R, mintol е R> maxstep е R>
itnlimit gZ, бе/?, printcode e Z (относительно
дополнительной информации см. алгоритм D6.1.3).
Входно-выходные параметры: отсутствуют (см. п. 2 раздела
Память в алгоритме D6.1.3).
Выходные параметры: Xf е Rn (заключительное приближение
к х*), termcode^Z (указывает на то условие окончания,
которое явилось причиной остановки алгоритма).
Кроме того, необязательные:
FV+s=Rn(=F{xf))$ Jcz=RnXn(**J(xf)), другие выходные
параметры по желанию того, кто занимается программной
реализацией (см. разд. 1.4)
Значения кодов возврата, память:
такие же, как у алгоритма D6.1.3.
Алгоритм:
^Инициализирующая часть:*)
1. CALL MACHINEPS (macheps)
2. CALL NEINCK (список параметров определяется тем, кто
занимается программной реализацией)
(*см. описание NEINCK*)
3. IF termcode < О THEN
3.1 Xf *— Xq
3.2 RETURN для алгоритма D6.1.4 (* при желании вывести
на печать соответствующее сообщение*)
4. itncount+-0
5. CALL NEFN(/i, х0, fe)
(*NEFN вычисляет также значение FV+=F(x0) и передает
его драйверу через глобальный параметр *)
6. CALL NESTOP0(/i, xQ, FV+, SP, fvectol, termcode,
consecmax)
(*алг. A7.2.4*)
7. IF termcode > 0
7T.THEN xf+-x0
354 Приложение А.
7Е. ELSE (* вычислить начальное значение конечно-разностноп
якобиана *)
7Е.1 CALL FDJAC(n, х0, FV+, FVEC, Sx, tj, Jc)
(* алг. A5.4.1 *)
7E.2 FOR t=l TO n DO
gcli\<-th[j,i}*FV+[j]*SF[J]2
7E.3 FVe<-FV+
o. Xc <— Xq
9. restart*-TRUE
(* Итерационная часть: *)
10. WHILE termcode = 0 DO
10.1 itncount ■*- itncount + 1
10.2 CALL NEMODEL (я, FVC, Jc, gc, SF, Sx, macheps,
global, M, He, sN)(* алг. A6.5.1 *)
10.3 CALL DOGDRIVER (re, xc, fc, FVEC, gc, M, s„, Sx,
maxstep, steptol, 6, retcode, x+, f+, maxiaken)
(* алг. A6.4.3 *)
10.4 CALL FDJAC(n, x+, FV+, FVEC, Sxr\, Jc)
(*алг. A5.4.1 *)
10.5 gc+-JTc*&P*FV+
(* то же самое, что и в операторе 7Е.2 *)
10.6 CALL NESTOP(n, хс, х+, FV+, /+, gc, Sx, SF,
retcode, fvectol, steptol, itncount, itnlimit, maxtaken,
analjac, cheapF, mintol, consecmax, termcode)
(* алг. A7.2.3 *)
10.7 IF termcode > 0
THEN xf<-x+
ELSE restart+- FALSE
10.8 xc<-x+
10.9 fc<-f+
10.10 FVC^-FV+
(*END, цикл WHILE 10*)
(* при желании вывести на печать соответствующее сообщение
об окончании *)
(* RETURN для алгоритма D6.1.4*)
(* END, алгоритм D6.1.4*)
IV. ОТДЕЛЬНЫЕ МОДУЛИ
IV. 1. Модули, задаваемые пользователем
{требования к ним)
Ниже приводятся спецификации для задаваемых
пользователем функций, которые требуются или же задаются по желанию
Модульная система алгоритмов 355
при использовании системы алгоритмов безусловной
минимизации или решения систем нелинейных уравнений.
Алгоритм FN.
Подпрограмма вычисления целевой функции
f(x) для безусловной минимизации
Назначение: Вычислять значение задаваемой пользователем
функции f(x): Rn ~> R в точке хс.
Входные параметры: «gZ, хс^ Rn.
Входно-выходные параметры: отсутствуют.
Выходные параметры: fc е /?(= f(xc)).
Описание:
Пользователь должен задать эту подпрограмму при
использовании данной системы алгоритмов безусловной минимизации. Она
может иметь любое имя (за исключением имен подпрограмм в
данном пакете); ее имя является входным для драйвера D6.1.1.
Ее входные и выходные параметры должны быть точно такими,
как указаны (в противном случае все обращения к FN в
системе алгоритмов должны быть изменены). Значения входных
параметров п и хс не могут быть изменены этой подпрограммой;
подпрограмма должна присваивать параметру fc значение
целевой функции в хс.
Алгоритм GRAD.
Подпрограмма вычисления вектора градиента
Vf(x) (необязательная)
Назначение: Вычислять значение задаваемого пользователем
градиента Vf(x): Rn-+Rn целевой функции f(x) в точке хс.
W(x)[i\=df(x)/dx[i\).
Входные параметры: п е Z, хс е Rn.
Входно-выходные параметры: отсутствуют.
Выходные параметры: g е Rn(= Vf(xc)).
Описание:
Пользователь по своему усмотрению может задать эту
подпрограмму при использовании данной системы алгоритмов
безусловной минимизации (см. analgrad в руководстве 1). Она
может иметь любое имя (за исключением имен подпрограмм
в данном пакете); ее имя является входным для драйвера D6.1.1.
Ее входные и выходные параметры должны быть точно такими,
как указаны (в противном случае все обращения к GRAD в си-
356 Приложение А.
стеме алгоритмов должны быть изменены). Значения входных
параметров п и хс не могут быть изменены этой подпрограммой;
подпрограмма должна присваивать параметру g значение
градиента целевой функции в хс.
Алгоритм HESS.
Подпрограмма вычисления матрицы Гессе
Т2/(дс) (необязательная)
Назначение: Вычислять задаваемый пользователем гессиан
SJ2f(x): Rn-+Rnxn целевой функции f(x) в точке хс.
(V2/(*) [/,/] = d2f(x)/dx[i]dx[j]\ предполагается, что f(x) по
крайней мере дважды непрерывно дифференцируема, так что
гессиан V2f(x) симметричен.)
Входные параметры: neZ.XcE Rn.
Входно-выходные параметры: отсутствуют.
Выходные параметры: симметричная матрица H^Rnxn(=
Память:
1) Остальной частью системы алгоритмов используется только
верхняя треугольная часть Я, включая главную диагональ.
Поэтому не нужно присваивать никакие значения элементам
нижней треугольной части Я, т. е. элементам #[t, /], где / > /. Если
же нижняя треугольная часть Н заполнена, то она будет
игнорироваться, но никакого вреда остальной части системы
алгоритмов это не принесет.
2) Не требуется никаких изменений этого алгоритма при
использовании экономичного способа хранения матриц.
3) Алгоритму HESS может потребоваться дополнительный
входной параметр ndim, если настоящие алгоритмы реализуются на
Фортране (см. п. 5 руководства 3).
Описание:
Пользователь по своему усмотрению может задать эту
подпрограмму при использовании данной системы алгоритмов
безусловной минимизации (см. analhess в руководстве 1). Она
может иметь любое имя (за исключением имен подпрограмм в
данном пакете); ее имя является входным для драйвера D6.1.1.
Ее входные и выходные параметры должны быть точно такими,
как указаны (в противном случае все обращения к HESS в
системе алгоритмов должны быть изменены). Значения входных
параметров п и хс не могут быть изменены этой
подпрограммой; подпрограмма должна присваивать параметру Н значение
гессиана целевой функции в хс.
Модульная система алгоритмов 357
Алгоритм FVEC.
Подпрограмма вычисления функции F(x),
задающей нелинейные уравнения
Назначение: Вычислять значение задаваемой пользователем
вектор-функции F(x): Rn-+Rn в точке хс.
Входные параметры: п е Z, хс ^ Rn.
Входно-выходные параметры: отсутствуют.
Выходные параметры: Fc ^Rn(=F{xc)).
Описание:
Пользователь должен задать эту подпрограмму при
использовании данной системы алгоритмов решения систем нелинейных
уравнений. Она может иметь любое имя (за исключением имен
подпрограмм в данном пакете); ее имя является входным для
драйвера D6.1.3. Однако если ее имя не есть FVEC, то слово
FVEC в строке 2 алгоритма NEFN должно быть заменено на
имя этой подпрограммы (разъяснение см. в алгоритме NEFN).
Ее входные и выходные параметры должны быть точно такими,
как указаны (в противном случае все обращения к FVEC в
системе должны быть изменены). Значения входных параметров п
и Хс не могут быть изменены этой подпрограммой; подпрограмма
должна присваивать параметру Fc значение в хс
вектор-функции, задающей нелинейные уравнения.
Алгоритм JAC.
Подпрограмма вычисления матрицы Я ко б и /(ж)
(необязательная)
Назначение: Вычислять задаваемый пользователем якобиан
J(x): Rn-+Rnxn вектор-функции F(x) в точке хс. (/[*,/] =
= dfi(x)/dx[j], где fi(x) есть i-я компонента функции F(x).)
Входные параметры: п е Z, хс е /?п.
Входно-выходные параметры: отсутствуют.
Выходные параметры: / е Rnxn(=J{xc)).
Память:
1) Используется вся матрица /.
2) Не требуется никаких изменений данного алгоритма при
применении экономичного способа хранения матриц.
Описание:
Пользователь по своему усмотрению может задать эту
подпрограмму при использовании данной системы алгоритмов решения
систем нелинейных уравнений (см. analjac в руководстве 4).
358 Приложение А.
Она может иметь любое имя (за исключением имен
подпрограмм в данном пакете); ее имя является входным для драйвера
D6.1.3. Ее входные и выходные параметры должны быть точно
такими, как указаны (в противном случае все обращения к
JAC в системе алгоритмов должны быть изменены). Значения
входных параметров п и хс не могут быть изменены этой
подпрограммой; подпрограмма должна присваивать параметру /
значение якобиана вектор-функции, задающей нелинейные
уравнения, В Хс
IV. 2. Модули, задаваемые разработчиком
(частичное описание)
Алгоритм UMINCK.
Проверка входных параметров для безусловной
минимизации
Назначение: Проверить введенные пользователем в драйвере
безусловной минимизации значения параметров,
определяющих алгоритмические варианты, допусков и других
параметров; присвоить значения невведенным пользователем
параметрам алгоритмических вариантов и допускам, а также
константам Sx и т).
Входные параметры: п е Z, macheps е /?, х0 е Rn.
Кроме того, typx е Rn и fdigits е Z, если они введены
пользователем в драйвере безусловной минимизации.
Необязательные входные или выходные параметры: typf е Rf
gradtol е R, steptol e R, maxstep e /?, itnlimit e Z, print-
code eZ (см. ниже примечание 1); 8&R (см. ниже
примечание 2); global^ Z, analgrad e Boolean, analhess e
Boolean, cheap] e Boolean, factsec e Boolean (см. ниже
примечание 3).
Выходные параметры: Sx ^ Rn (см. ниже примечание 4), ц ^ /?,
termcode е Z.
Значения кодов возврата:
termcode = 0: все введено нормально или подкорректировано
данной подпрограммой;
termcode < 0: найдена неустранимая ошибка ввода
следующего типа;
termcode = —1: п < 1;
termcode <—1: другие коды возврата, назначенные тем, кто
занимается программной реализацией алгоритма UMINCK.
Память:
1) Не требуется никакой дополнительной памяти под векторы
или матрицы.
Модульная система алгоритмов 359
2) Если пользователем введен параметр typx> то он может
делить память с Sx, т. е. вместе они могут представлять собой
один входно-выходной параметр данного алгоритма.
Примечания:
1) Значения параметров typf, gradtoU steptoU maxstep, и
itnlimit должны быть либо введены пользователем в драйвере
безусловной минимизации, либо присвоены алгоритмом
UMINCK. Выбор остается за тем, кто занимается реализацией
данной системы алгоритмов. Значения введенных
пользователем необязательных параметров могут проверяться алгоритмом
UMINCK. Значениями, присваиваемыми алгоритмом UMINCK,
могут быть либо значения по умолчанию, приведенные в
руководстве 2, либо другие значения, выбранные тем, кто занимается
программной реализацией. (*0 используется для вычисления
значения по умолчанию для maxstep.) Если printcode
используется в том виде, как обсуждалось в разд. 1.4 настоящего
приложения, то ему тоже должно быть присвоено значение
пользователем или алгоритмом UMINCK.
2) Значение б должно быть задано пользователем или
алгоритмом UMINCK, если global = 2 или 3; оно игнорируется, если
global = 1 или 4. См. ниже шаг 4.
3) При реализации полностью всей системы алгоритмов
безусловной минимизации (драйвер D6.1.1) параметры global, anal-
grad, analhess, cheap] и factsec либо должны иметь
возможность ввода их значений в драйвере D6.1.1, либо им должны
присваиваться значения алгоритмом UMINCK. Здесь применимы
те же рассуждения, что и выше в п. 1. Рекомендации по
выбору значений этих параметров алгоритмических вариантов
приведены в руководстве 1. Если кто-либо занимается программной
реализацией подмножества данной системы алгоритмов
безусловной минимизации, такого, как, скажем, представлено
драйвером D6.1.2, то некоторые или все из этих пяти параметров
могут ему не понадобиться.
4) Если масштабирование во всей системе не реализуется, то
исключаются выходной параметр Sx и приведенный ниже шаг 2.
Описание:
1) Если п < 1, то положить termcode = —1 и завершить
работу алгоритма UMINCK.
2) Если typx был введен пользователем, то положить Sx[i]
равным {l/typx[i])t i = 1, ..., /г, иначе положить Sx[i] = 1, i =
= 1, ..., п.
3) Если fdigits был введен пользователем, то положить г\
равным max {macheps, l(Hd'Ws} или равным maceps, если
fdigits =—1. В противном случае положить ц равным macheps
или оценить его, например, с помощью алгоритма Хемминга
360 Приложение А.
[1973], приведенного в книге Гилл, Мюррей и Райт 11981],
разд. 8.5.2.3. Если tj > 0.01, то, вероятно, должно быть
возвращено отрицательное значение termcode.
4) Если global = 2 или 3, и для б не введено никакого
значения, то положить б = — 1.
5) Присвоить значения параметрам алгоритмических вариантов
и другим параметрам, не введенным пользователем, и проверить
(необязательно) те значения, которые были введены
пользователем, как обсуждалось выше в примечаниях 1 и 3. Замечание:
если global = 2, analhess = FALSE и cheap] = FALSE, то fact-
sec следует установить равным FALSE. (См. руководство 1.)
Алгоритм NEINCK.
Проверка входных параметров для нелинейных
уравнений
Назначение: Проверить введенные пользователем в драйвере
решения нелинейных уравнений значения параметров,
определяющих алгоритмические варианты, допусков и других
параметров; присвоить значения невведенным пользователем
параметрам алгоритмических вариантов и допускам, а также
константам SXy SF и х\.
Входные параметры: /i£Z, machepsе/?, х0еRn.
Кроме того, typx^R", typF^R", и Fdigitss Z, если они
введены пользователем в драйвере решения нелинейных
уравнений.
Необязательные входные или выходные параметры: fvectol^R.
steptol е R, mintol е R, maxstep е /?, itnlimit е Z, printco-
de^Z (см. ниже примечание 1); 6ei? (см. ниже
примечание 2); global е Z, analjac е Boolean, cheap? е Boolean,
factsec е Boolean (см. ниже примечание 3).
Выходные параметры: Sx^Rn, SP^Rn (см. ниже
примечание 4), х\ е R, termcode е Z.
Значения кодов возврата:
termocode = 0: все введено нормально или исправлено
данной подпрограммой;
termcode < 0: найдена неустранимая ошибка ввода
следующего типа:
termcode = — 1: п < 1;
termcode < — 1: другие коды возврата, назначенные тем, кто
занимается программной реализацией алгоритма NEINCK.
Память:
1) Не требуется никакой дополнительной памяти под векторы
или матрицы.
Модульная система алгоритмов 361
2) Если пользователем введены параметры typx или typFy то
они могут делить память соответственно с Sx и S/>, т. е.
каждая пара может представлять собой один входно-выходной
параметр данного алгоритма.
Примечания:
1) Значения параметры fvectol, steptol, mintol, maxstep и
itnlimit должны быть либо введены пользователем в драйвере
решения нелинейных уравнений, либо присвоены алгоритмом
NEINCK. Выбор остается за тем, кто занимается реализацией
данной системы алгоритмов. Значения введенных
пользователем необязательных параметров могут проверяться алгоритмом
NEINCK. Значениями, присваиваемыми алгоритмом NEINCK,
могут быть либо значения по умолчанию, приведенные в
руководствах 2 и 5, либо другие значения, выбранные тем, кто
занимается программной реализацией, (хо используется для
вычисления значения по умолчанию для maxstep.) Если printcode
используется в том виде, как обсуждалось в разд. 1.4 настоящего
приложения, то ему тоже должно быть присвоено значение
пользователем или алгоритмом NEINCK.
2) Значение б должно быть задано пользователем или
алгоритмом NEINCK, если global = 2 или 3; оно игнорируется, если
global = 1. См. ниже шаг 5.
3) При реализации полностью всей системы алгоритмов
решения нелинейных уравнений (драйвер D6.1.3) параметры global,
analjc, cheap? и factsec либо должны иметь возможность
ввода их значений в драйвере D6.1.3, либо им должны
присваиваться значения алгоритмом NEINCK. Здесь применимы те же
рассуждения, что и выше в п. 1. Рекомендации по выбору
значений этих параметров алгоритмических вариантов приведены
в руководстве 4. Если кто-либо занимается программной
реализацией подмножества данной системы алгоритмов решения
нелинейных уравнений, такого, как, скажем, представлено
драйвером D6.1.4, то некоторые или все из этих четырех параметров
могут ему не понадобиться.
4) Если масштабирование во всей системе не реализуется, то
исключаются выходные параметры Sx и Sf, а также
приведенные ниже шаги 2 и 3.
Описание:
1) Если п < 1, то положить termcode = —1 и завершить работу
алгоритма NEINCK.
2) Если typx был введен пользователем, то положить Sx[i]
равным (l/typx[i]), i = l, ..., л, иначе положить S*[f]=l, i =
= 1, ..., п.
3) Если typF был введен пользователем, то положить SF [i]
равным (l/typF[i])9 i = l, ..., л, иначе положить SF[/]=1, / =
= 1, ..., п.
362 Приложение А.
4) Если Fdigits был введен пользователем, то положить х\
равным max{macheps, 10-Fdi^its}y или равным macheps, если
Fdigits =—1. В противном случае положить ц равным macheps
или оценить его, например, с помощью алгоритма Хемминга
[1973], приведенного в книге Гилл, Мюррей и Райт [1981],
разд. 8.5.2.3. Если tj > 0.01, то, вероятно, должно быть
возвращено отрицательное значение termcode.
5) Если global = 2 или 3 и для б не введено никакого значения,
то положить б равным — 1.
6) Присвоить значения параметрам алгоритмических вариантов
и другим параметрам, не введенным пользователем, а также
проверить (необязательно) те значения, которые были введены
пользователем, как обсуждалось выше в примечаниях 1 и 3.
IV. 3. Алгоритмические модули (приведены
полностью)
Алгоритм NEFN.
Вычисление суммы квадратов для нелинейных уравнений
Назначение: Вычислять в х+ значение функции F(x)y задающей
нелинейные уравнения, и вычислять /+«-l/2ll^W(*+)l,2-
Входные параметры: /igZ,x+g Rn.
Входно-выходные параметры: отсутствуют.
Выходные параметры: f+ е R.
Память:
1) В дополнение к перечисленным выше параметрам входная
переменная SF е Rn (DF = diag((Sf)i, ..., (Sf)*)) и выходная
переменная FV+^Rn(= F(x+)) должны передаваться как
глобальные переменные между NEFN и драйвером решения
нелинейных уравнений D6.1.3. (В Фортране это достигается
помещением Sf и FV+ в помеченный COMMON-блок алгоритмов NEFN
и D6.1.3.) Это единственное место во всей системе алгоритмов,
где используются глобальные переменные. Требуется, чтобы
параметры у NEFV и у целевой функции безусловной минимизации
FN были одинаковыми; это дает возможность применять одни и
те же подпрограммы глобализации как к безусловной
минимизации, так и к нелинейным уравнениям.
Примечания:
1) Если имя задаваемой пользователем подпрограммы, которая
вычисляет значение вектор-функции в нелинейных уравнениях,
отличается от FVEC (см. алгоритм FVEC в разд. IV. 1
настоящего приложения), то идентификатор FVEC в строке 2 данного
алгоритма должен быть заменен на имя этой задаваемой поль-
Модульная система алгоритмов 363
зователем подпрограммы. Этого делать не нужно, если имя
задаваемой пользователем подпрограммы для F(x) может
передаваться как глобальная переменная между алгоритмами D6.1.3
и NEFN; в Фортране это невозможно.
Алгоритм:
1. CALL FVEC (n, х+9 FV+){* FV++-F(x+)*)
2. f+^l/2*t((SF[i\*FV+[i])2)
(* RETURN для алгоритма NEFN *)
(*END, алгоритм NEFN*)
Алгоритм Al.3.1 (MACHINEPS).
Вычисление машинного эпсилона
Назначение: Вычислять машинный эпсилон.
Входные параметры: отсутствуют.
Входно-выходные параметры: отсутствуют.
Выходные параметры: macheps <= R.
Память:
1) Никакой памяти под векторы и матрицы не требуется.
Алгоритм:
1. macheps <- 1
2. REPEAT
macheps *- macheps/2
UNTIL (1 + macheps) = 1
3. macheps <- 2 * macheps
(* RETURN для алгоритма Al.3.1 *)
(*END, алгоритм Al.3.1*)
Алгоритм A3.2.1 (QRDECOMP).
Q/7-разложение
Назначение: Вычислять Q/^-разложение квадратной матрицы Af,
используя алгоритм из книги Стюарт (1973). По окончании
работы алгоритма это разложение хранится в Му М\ и М2,
как описано ниже.
Входные парамеры: nGZ.
Входно-выходные параметры: М е Rnxn (на выходе Q и R
закодированы в М, Ml и М2У как описано ниже).
Выходные параметры: ЛП е/?л, M2^Rny sing е Boolean.
364 Приложение А.
Память:
1) Не требуется никакой дополнительной памяти под векторы
и матрицы.
2) На выходе Q и R хранятся, как описано Стюартом: R
содержится в верхней треугольной части М, за исключением ее
главной диагонали, которая содержится в М29 QT=zQn_l. ...
...Q„ где Q/ = /-(^//^), к7М = 0, /=1, ..., /-1,
иу[/] = М[|, /], / = /, ..., л, nf = Ml[j].
3) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководстве 6.
Описание:
Q/^-разложение матрицы М выполняется с помощью
преобразований Хаусхолдера алгоритмом из книги Стюарт (1973).
Разложение возвращает значение sing = TRUE, если
обнаруживается вырожденность М, иначе — значение sing = FALSE.
Разложение выполняется даже в случае обнаружения
вырожденности.
Алгоритм:
1. sing*-FALSE
(* sing принимает значение TRUE, если в процессе
разложения обнаруживается вырожденность М*)
2. FOR k=l ТО /i-l DO
2.1 т]«- max {|ЛГ[/, k]\}
k<i<n
2.2 IFti = 0
2.2T THEN (* матрица вырождена*)
2.2T.1 Ml[k]^0
2.2T.2 M2[k]*-0
2.2T.3 sing ^ TRUE
2.2E ELSE
(* сформировать Qk и умножить M на нее слева *)
2.2Е.1 FOR / —* ТО п DO
M[i,k]+-M[i, k]/i\
2.2Е.2 a4r-sign(M [k, k})* (£ M [/, £]2)
2.2E.3 M[k, k]«^M[k, Л]+"<т
2.2E.4 Ml[k]<-o*M[k9 k]
2.2E.5 M2[k]<- — i\*o
2.2E.6 FOR/ = £+l TO n DO
2.2E.6.1 т +- (J^M [/, k] * M [/, /]) I Ml [k]
2.2E.6.2 FOR i'=k TO n DO
M[t9 j]+-M[i, j]-x*M[i, k]
3. IF M[n, n] = 0 THEN sing*-TRUE
Модульная система алгоритмов 365
4. М2[п]+-М [п, п]
(♦RETURN для алгоритма АЗ.2.1 *)
(* END, алгоритм АЗ.2.1 *)
Алгоритм АЗ.2.2 (QRSOLVE).
(ДО-решение
Назначение: Решать (QR)x = b относительно х, где
ортогональная матрица Q и верхняя треугольная матрица R хранятся
в памяти, как это описано в алгоритме АЗ.2.1.
Входные параметры: «eZ, Me RnXn, Ml e Rn, M2 ^Rn (Q и
R закодированы в M, Ml и M2, как описано в алгоритме
АЗ.2.1).
Входно-выходные параметры: b е Rn (на выходе на месте
вектора Ъ записывается решение л:).
Выходные параметры: отсутствуют.
Память:
1) Никакой дополнительной памяти под векторы и матрицы не
требуется.
2) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководстве 6.
Примечания:
1) Алгоритм А3.2.2а должен быть представлен отдельной
подпрограммой, потому что он отдельно вызывается алгоритмами
АЗ.3.1 и Аб.б.Иас.
Описание:
1) Умножить Ъ на QT. Матрица QT хранится в виде Qn-\- ...
... -Qi, где каждая Q, представляет собой преобразование Хаус-
холдера, закодированное, как описано в алгоритме АЗ.2.1.
Таким образом, этот шаг состоит в умножении слева Ь на Q/, / =
= 1, ..., п—1.
2) Решить Rx = QTb.
Алгоритм:
(*b<-QTb*)
1. FOR /=1 ТО az — 1 DO
(*b+-Qtb*)
1.1 т^(ЕМ[/,/]*6W)/Afl[/]
1.2 FOR/ = / TO n DO
b[i]+-b[i]-r*M[i, Л
(*b+-R~lb*)
366 Приложение А.
2. CALL RSOLVE (п, М, М2, Ь) (* алг. А3.2.2а*)
(* RETURN для алгоритма АЗ.2.2 *)
(* END, алгоритм АЗ.2.2. *)
Алгоритм А3.2.2а (RSOLVE).
/{-решение для Q/f-разложения
Назначение: Решить Rx = b относительно х, где верхняя
треугольная матрица R хранится в памяти, как описано в
алгоритме АЗ.2.1.
Входные параметры: «gZ, М е Rnxn, М2еRn (М2 содержит
диагональ матрицы /?, остальная часть R содержится в
верхней треугольной части матрицы М).
Входно-выходные параметры: Ь е Rn (на выходе на месте Ъ
записывается решение х).
Выходные параметры: отсутствуют.
Память:
1) Никакой дополнительной памяти под векторы и матрицы не
требуется.
2) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководстве 6.
Алгоритм:
1. b[n]+-b[n]/M2[n]
2. FOR i = n — 1 DOWNTO 1 DO
*w-—Чящ
(* RETURN для алгоритма A3.2.2a *)
(* END, алгоритм A3.2.2a *)
Алгоритм A3.2.3 (CHOLSOLVE).
Драйвер решения по Холесскому
Назначение: Решать (LLT)S = —g относительно s.
Входные параметры: п е Z, g е Rn, нижняя треугольная
L е= Rnxn.
Входно-выходные параметры: отсутствуют.
Выходные параметры: s е Rn.
Память:
1) Никакой дополнительной памяти под векторы и матрицы не
требуется.
Модульная система алгоритмов 367
2) В процессе решения g не меняется.
3) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководстве 3.
Примечания:
1) Алгоритм А3.2.3а должен представлять собой отдельную
подпрограмму, потому что он непосредственно вызывается
алгоритмом А6.4.2 (HOOKSTEP).
Алгоритм:
(* Решить Ly = g: *)
1. CALL LSOLVE (л, g, L, s) (*алг. A3.2.3a *)
(* Решить Us = y: *)
2. CALL LTSOLVE (n, s, L9 s) (алг. A3.2.3b *)
(* RETURN для алгоритма АЗ.2.3 *)
(*END, алгоритм АЗ.2.3*)
Алгоритм А3.2.3а (LSOLVE).
L-решение
Назначение: Решать Ly = b относительно у.
Входные параметры: nsZ, b е Rn, нижняя треугольная L е
ge Rnxn.
Входно-выходные параметры: отсутствуют.
Выходные параметры: у е Rn.
Память:
1) Никакой дополнительной памяти под векторы и матрицы не
требуется.
2) Подразумевается, что Ь и у — отдельные параметры. Если
при вызове алгоритма Ь и у соответствуют одному и тому же
вектору, то алгоритм работать будет, но Ь уничтожится в
результате перезаписи.
3) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководстве 3.
Алгоритм:
1. У[1]+-Ь[1]/Ц1, 1]
2. FOR i = 2 ТО п DO
(* RETURN для алгоритма A3.2.3a *)
(* END, алгоритм A3.2.3a *)
368 Приложение А.
Алгоритм A3.2.3b (LTSOLVE). ^/-решение
Назначение: Решать Ux = у относительно х.
Входные параметры: п е Z, у е Rn, нижняя треугольная L е
Входно-выходные параметры: отсутствуют.
Выходные параметры: х е Rn.
Память:
1) Никакой дополнительной памяти под векторы и матрицы не
требуется.
2) Подразумевается, что у и х — отдельные параметры. Если
при вызове алгоритма у и х соответствуют одному и тому же
вектору, то алгоритм работать будет, но у уничтожится в
результате перезаписи.
3) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководстве 3.
Алгоритм:
1. x[n]+-y[n]/L[ny п]
2. FOR i = n-\ DOWNTO 1 DO
УШ- £ (L[j,i]*x[j])
L (/, i)
(* RETURN для алгоритма A3.2.3b*)
(*END), алгоритм A3.2.3b*)
Алгоритм A3.3.1 (CONDEST). Оценивание
числа обусловленности верхней треугольной
матрицы
Назначение: Оценивать в /гнорме число обусловленности
верхней треугольной матрицы R с помощью алгоритма,
содержащегося в работе Клайн, Моулер, Стюарт и Уилкинсон (1979).
Входные параметры: n^Zy Me Rnxn> М2еRn (М2 содержит
главную диагональ матрицы R, остальная часть матрицы R
содержится в верхней треугольной части матрицы М).
Входно-выходные параметры: отсутствуют.
Выходные параметры: est е R (оценка снизу в /i-норме числа
обусловленности матрицы R).
Память:
1) Требуются 3 л-вектора дополнительной памяти для р,рт и х.
2) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководстве 6.
Модульная система алгоритмов 369
Описание:
1) est+-\\R\U.
2) Решить RTx = e относительно х, где е, = ±1, /=1, ..., п,
и знак для а выбирается в соответствии с алгоритмом из ра-
боты Клайн, Моулер, Стюарт и Уилкинсон (1979) с
использованием их соотношения (3.19).
3) Решить Ry = х относительно у. (В приведенной ниже
реализации у записывается на место х.)
A)est<-est*\\yU\x\\x.
Алгоритм:
(* в шагах 1 и 2 положить est<-\\R\\x*)
1. est<-\M2[\]\
2. FOR J = 2 ТО п DO
/-1
2.1 tomp«-|Af2[/]|+ZlAf[/, Л I
/-1
2.2 est*-max {temp, est)
(* в шагах 3 — 5 решить RTx = e, выбирая e в процессе их
выполнения *)
3. x[l]+-l/M2[l]
4. FOR i = 2 ТО п DO
PM*-Af[l,il**[l]
5. FOR } = 2 TO n DO
(* выбрать e, и вычислить x [j] *)
5.1 Xp<-(l-p[j])/M2[j]
5.2 хт«--(-1-р[Л)/А12[Л
5.3 temp<r-\xp\
5.4 tempm «-|*т|
5.5 FOR / = /+1 TO /i DO
5.5.1 pm [i] <- p [i] + M [/, /] **m
5.5.2 tempm «- tempm + (| pm [i] |/| M2 [i] \)
5.5.3 p[i)+-p[i] + M[j,i]*xp
5.5.4 temp «- temp + (| p [/] |/| M 2 [/] |)
5.6 IF temp ^ tempm
5.6T THEN x[/]«-*p (*ey=l*)
5.6E ELSE (*ey = -l*)
5.6E.1 x[j]<r-xm
5.6E.2 FOR / = /+ 1 TO n DO
p И «-pro И
6. xnorm «- Z I x [j] |
/-1
7. est <^ est/xnorm
8. CALL RSOLVE (n, Af, Л12, jc)
(* обращение к алгоритму A3.2.2a для вычисления R~ х *)
370 Приложение А.
9) хпогт <- Ys I X [/] |
10. est+-est* хпогт
(♦RETURN для алгоритма АЗ.3.1*)
(♦END, алгоритм АЗ.3.1*)
Алгоритм АЗ.4.1 (QRUPDATE).
Пересчет Q/J-разложения
Назначение: Для заданного <2/?-разложения матрицы А
вычислять разложение вида Q+/?+ матрицы А+ = Q (R + uvT) за
0(п2) операций.
Входные параметры: n^Z, u^Rn, v е Rn, method£Z (= 1
для нелинейных уравнений, = 2 для безусловной
минимизации).
Входно-выходные параметры: Z е Rnxn (используется только,
когда method = 1, содержит QT на входе и Q+ на выходе),
M^RnXn (верхняя треугольная матрица, содержащая R на
входе и /?+ на выходе).
Выходные параметры: отсутствуют.
Память:
1) Никакой дополнительной памяти под векторы и матрицы не
требуется.
2) При method = 2 Z не используется и данный алгоритм
требует только одну п X м-матрицу, так как вызов алгоритма
АЗ.4.1 алгоритмом А9.4.2 приводит к тому, что Z и М ссылаются
на одну и ту же матрицу.
3) Первая нижняя поддиагональ матрицы М, так же как и
верхняя треугольная часть, включая главную диагональ,
используются на промежуточных этапах данного алгоритма.
4) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководствах 3 и 6.
Описание:
R + uvT умножается слева на 2(п— 1) матриц вращения Якоби.
Первые п— 1 преобразуют uvT к матрице ||w||2eitJr, a R к
верхней матрице Хессенберга Rh. Последние п—1 преобразуют
верхнюю матрицу Хессенберга (Rh+\\и\\2е^Т) к верхней
треугольной матрице /?+. Если method = 1, то QT умножается слева
на те же самые 2 (я—1) матриц вращения Якоби и
преобразуется к виду Qlt Подробности см. в разд. 3.4 основной части
книги.
Модульная система алгоритмов 371
Алгоритм:
(* найти наибольшее k, такое, что и[к]фО*)
0. FOR i = 2 ТО п DO
M[i, /-1]«-0
1. k<-n
2. WHILE (u[k] = 0) AND (ft > 1) DO
(* преобразовать R + tivT к верхней матрице Хессенберга *)
3. FOR i = k—\ DOWNTO 1 DO
3.1 CALL JACROTATE (n, /, u[l\9 —u[i+l], method, Z, M)
(*алг. A3.4.1a*)
3.2 IF u[i] = 0
THEN u[l\<-\u[i+l]\
ELSE и И «- +У(" [i])2 + (u [i + l]f
4. FOR /=1 TO n DO
AJ[1, j]^M[l,j] + u[l]*v[j]
(* преобразовать верхнюю матрицу Хессенберга к верхней
треугольной *)
5. FOR i=l ТО 6-1 DO
CALL JACROTATE {п, /, М [/, i], -М [/ + 1, /], method, Z, М)
(* RETURN для алгоритма АЗ.4.1*)
(*END, алгоритм АЗ.4.1*)
Алгоритм АЗ.4.1 a (JACROTATE).
Вращение Якоби
Назначение: Умножать М, а если method = 1, то и Z, слева на
матрицу вращения Якоби /(/,/+1, а, &), как это описано
в разд. 3.4.
Входные параметры: «g Z, /eZ, а е /?, b е/?, methodgZ(=I
для нелинейных уравнений, = 2 для безусловной
минимизации).
Входно-выходные параметры: Z е Rnxn (используется только
при method =1)Jg /?"X".
Выходные параметры: отсутствуют.
Память:
то же самое, что для алгоритма АЗ.4.1.
Описание:
1) с*-а/л/а2 + Ь2, s^-b/^tf + b2.
2) (новая /-я строка М)*-с*(старая /-я строка Af) — s*(старая
(i+ 1)-я строка А1); (новая (/+ 1)-я строка M)+-s* (старая
1-я строка М) + с*(старая (i'+ 1)-я строка М)
3) Если method = 1, то выполнить шаг 2 с матрицей Z.
372 Приложение А.
Алгоритм:
1. IFa = 0
IT. THEN
1Т.1 c<-0
1T.2 s«-sign (ft)
IE. ELSE
1E.1 den+- + ^a2 + b2
1E.2 с <-a/den
1E.3 s+-b/den
(* умножить слева M на матрицу вращения Якоби *)
2. FOR / = / ТО п DO
2.1 y^M[i, j]
2.2 w<-M[i+l, j]
2.3 M [/, /]«- с * у — s * w
2.4 M[i+ 1, /]«-s**/ + c*ay
3. IF method = 1 THEN
(* умножить слева Z на матрицу вращения Якоби *)
3.1 FOR /=1 ТО п DO
3.1.1 y+-Z[i,j]
3.1.2 w+-Z[i+l, j]
3.1.3 Z[l, j]<^c*y — s*w
3.1.4 Z[f+1, fl«-s*y + c*»
♦RETURN для алгоритма А3.4.1а*)
* END, алгоритм А3.4.1а*)
Алгоритм АЗ.4.2 (QFORM).
Формирование Q из Q/t-разложения
Назначение: Строить ортогональную матрицу QT = Qn-\- ...
... -Qi из матриц преобразования Qb ..., Qn-u
вырабатываемых алгоритмом (^-разложения АЗ.2.1. (Это требуется
только в случае использования формулы пересчета Бройдена
в факторизованной форме.)
Входные параметры: nsZ, М е Rnxnt M\^Rn (Q содержится
в М и All, как описано в алгоритме АЗ.2.1).
Входно-выходные параметры: отсутствуют.
Выходные параметры: Z ^ RnXn (содержит QT).
Память:
1) Никакой дополнительной памяти под векторы и матрицы не
требуется.
2) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководстве 6.
Модульная система алгоритмов 373
Описание:
1) Z+-I.
2) Для ft=l, ..., п—\ умножить слева Z на Qk> где Qk = If
если Afl[ft] = 0, Qfc = / — {ukuTk)jnk в противном случае, мЛИ=
= 0, /= 1, ..., ft— 1, иЛ[*] = Л1[/, ft], / = ft, ..., л, n* = Afl[ft].
Алгоритм:
(♦Z*-/:*)
1. FOR i=l ТО п DO
1.1 FOR /=1 ТО n DO
Z[/, Л«-0
1.2 Z[/, /]ч-1
2. FOR ft = 1 ТО п - 1 DO
2.1 IF All [ft] =^0 THEN
(*Z^Q**Z:*)
2.1.1 FOR /=1 TO n DO
2.1.1.1 T«-(i)Af[/, ft]*Z[/, j]\lMl[k]
2.1.1.2 FOR 'f=ft TO л DO
Z[*,/1«-Z[/f Л-т*А1[/, ft]
(♦RETURN для алгоритма АЗ.4.2*)
(♦END, алгоритм АЗ.4.2*)
Алгоритм А5.4.1 (FDJAC).
Конечно-разностная аппроксимация якобиана
Назначение: Вычислять аппроксимацию по разностям вперед
для J(xc) (матрица Якоби для F(x) в хс), используя
значения F(x).
Входные параметры: /igZ, xc^Rn, Fct=Rn(=F(xc))9 FVEC
(имя для F: Rn -* Rn), Sx <=Rn, r\e= R.
Входно-выходные параметры: отсутствуют.
Выходные параметры: / е RnXn = J(xc).
Память:
1) Требуется один л-вектор дополнительной памяти для Fj.
2) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководстве 6.
Примечания:
1) См. разд. Примечания в алгоритме А5.6.3.
Описание:
/-й столбец J(xc) аппроксимируется с помощью (F (хс + йуеу) —
— F(xc))fhIt где еу есть /-й единичный вектор, и Ау =
374 Приложение А.
= л1/2 * max {| хе [j] |, l/Sx [/]} * sign (хс [/]). Здесь l/Sx [j] есть
задаваемая пользователем характерная величина для |*с[/],
ит]=10~ , DIGITS — число верных десятичных разрядов
в F(x). Соответствующие элементы J(xc) и / будут, что
характерно, совпадать приблизительно в их первых (DIGITS/2)
десятичных разрядах.
Алгоритм:
1. sqrteta<-y\ll2
2. FOR /=1 ТО п DO
(* вычислить /-й столбец / *)
2.1 stepsizej<-sqrteta* max {\xc[j]\, l/Sv[j]} * sign(jcc[/J)
(*для включения другого правила выбора длины шага
изменить строку 2.1*)
2.2 tempj<-xc[j]
2.3 хс [j] <- хс [j] + stepsizej
2.4 stepsizej <- хс [j] — tempj
(* строка 2.4 немного уменьшает ошибки машинной
арифметики; см. разд. 5.4 *)
2.5 CALL FVEC (я, хС9 Fj) (* Fj +- F (хс + stepsizej * е,)*)
2.6 FOR /=1 ТО п DO
/ [i, Л <- (Fi И - Fc И )lstepsizej
2.7 xc[j]<-tempj (* восстановить xc[j]*)
(* END, цикл FOR 2 *)
(♦RETURN для алгоритма A5.4.1 *)
(* END, алгоритм A5.4.1 *)
Алгоритм A5.5.1 (MODELHESS).
Формирование гессиана модели
Назначение: Находить |х ^ 0, такое, что Н + \il е Rnxn
надежно положительно определена, где (ы = 0, если Н уже
является надежно положительно определенной. Затем
положить #-*-// + ц/ и вычислить разложение по Холесскому
LLr для Н.
Входные параметры: п^ Z, Sx^ Rn, macheps е R.
Входно-выходные параметры: симметричная H^Rnxn.
Выходные параметры: нижняя треугольная L е Rnyn.
Память:
1) Никакой дополнительной памяти под векторы и матрицы не
требуется.
2) Используются только верхняя треугольная часть Н и нижняя
треугольная часть L, включая главные диагонали обеих матриц.
Предполагается ради простоты, что каждая из них хранится как
Модульная система алгоритмов 375
полная матрица. Однако можно добиться экономии памяти,
отводимой под матрицы, путем модификации данного алгоритма,
как объясняется в руководстве 3.
Описание:
1) Если Я имеет какое-либо количество отрицательных
диагональных элементов, или если абсолютная величина
наибольшего внедиагонального элемента матрицы Я больше, чем
наибольший диагональный элемент в Я, то Я ч- Я + МаЛ где |jti >• О
выбирается так, чтобы новая диагональ вся была
положительной, причем чтобы отношение ее наименьшего элемента к
наибольшему было ^z (macheps)112 и чтобы отношение ее
наибольшего элемента к наибольшему по модулю внедиагональному
элементу было ^ 1 + 2 * (macheps)1/2.
2) Возмущенное разложение по Холесскому выполняется
применительно к Я (см. алгоритм А5.5.2). Это дает в результате
Я + D = LU, где D представляет собой неотрицательную
диагональную матрицу, которая неявно прибавляется к Я в
процессе разложения и содержит один или более положительных
диагональных элементов, если Я не является надежно
положительно определенной. На выходе maxadd содержит
максимальный элемент D.
3) Если maxadd = 0 (т. е. D = 0), то Я = LU надежно
положительно определена и алгоритм завершает работу, возвращая
Я и L. В противном случае он вычисляет число sdd, которое
должно прибавляться к диагонали матрицы Я для того, чтобы
обеспечить в (Я + sdd*I) надежное строгое диагональное
преобладание. Поскольку как (Я + maxadd */), так и (Я + sdd*I)
являются надежно положительно определенными, алгоритм
вычисляет jut2 = rnin {maxadd, sdd)y Н+-Н + |х2/, вычисляет
разложение Холесского LU для Я и возвращает Я и L.
Алгоритм:
(* приведенные ниже шаги 1, 14 и 15 опускаются, если
масштабирование не применяется*)
(♦масштабирование H+-DxlHD?t где Ac=diag((S*),, .. .,(Sx)n)*)
1. FOR /=1 ТО п DO
1.1 FOR / = / ТО nDO
H[t, /]-я[/, n/(sx[t\msxii\)
(* шаг 1 в описании: *)
2. sqrteps <- (macheps)112
3. maxdiag<- max {Я[/, /]}
4. mindiag<r- mjn {H[iy i]}
5. maxposdiag <- max {0, maxdiag)
6. IF mindiag ^ sqrteps *maxposdiag
376 Приложение А.
6Т. THEN (* fi будет содержать в себе ту величину, которая
прибавится к диагонали Я перед попыткой
разложения по Холесскому*)
6Т. 1 \х +- 2 * (maxposdiag — mindiag) * sqrteps — mindiag
6T.2 maxdiag <- maxdiag + \i
6E. ELSE \i+-0
7. tnaxoff *- max \H [/, /11
8. IF maxoff*(\ + 2*sqrteps) > maxdiag THEN
8.1 \x <- ц + (maxoff — maxdiag) + 2 * sqrteps * tnaxoff
8.2 maxdiag <*- niaxoff * (1 + 2 * sqrteps)
9. IF maxdiag = 0 THEN (*tf = 0*)
9.1 ц<-1
9.2 maxdiag <-1
10. IF ii>0 THEN (*#«-# +ц/*)
10.1 FOR /=1 TO n DO
яр,/]«-#[/, q + ii
11. maxoff I <- Vmax {maxdiag, (tnaxoffIn)}
(* см. алг. A5.5.2 *)
(* шаг 2 в описании: обращение к возмущенному разложению
по Холесскому*)
12. CALL CHOLDECOMP (п, Я, maxoffl, macheps, L, maxadd)
(* алг. A5.5.2 *)
(* шаг 3 в описании: *)
13. IF maxadd > 0 THEN
(* Н не была положительно определенной *)
13.1 maxev <-Н[1, 1]
13.2 minev+-H[l, 1]
13.3 FOR /=1 ТО л DO
13.3.1 offrow «- 11Я [/, /] | + E | Я [/, ДI
13.3.2 maxev «- max {maxev, H[i, i] +offrow}
13.3.3 mmei> <- min {minev, H [/, /] — offrow}
13.4 sdd «- (maxev — minev) * sqrteps — minev
13.5 sdd«-max{sdd, 0}
13.6 ji«- min {maxadd, sdd}
(*H<-H + \xI:*)
13.7 FOR i=l TO n DO
Я[/, l\+-H[i9 q + |i
(* обратиться к разложению Я по Холесскому: *)
13.8 CALL CHOLDECOMP (л, Я, 0, macheps, L9 maxadd)
(* алг. А5.5.2 *)
(* обратное масштабирование Н «- DxHDxy L +- DXL *)
14. FOR /=1 ТО п DO
14.1 FOR / = / ТО я DO
H[i,j]+-H[i9j]*Sx[i)*Sx[i]
Модульная система алгоритмов 377
15. FOR i=\ ТО п DO
15.1 FOR /=1 ТО / DO
L[l, J]+-L[i, j]*Sx[i]
(* RETURN для алгоритма A5.5.1 *)
(*END, алгоритм A5.5.1*)
Алгоритм А.5.5.2 (CHOLDECOMP).
Возмущенное разложение Холесского
Назначение: Находить /-//-разложение для Я + А где D есть
неотрицательная диагональная матрица, которая
прибавляется к Я в случае, когда необходимо позволить
продолжить процесс разложения, используя алгоритм, основанный
на модифицированном разложении Холесского, изложенном
в книге Гилл, Мюррей и Райт (1981).
Входные параметры: /ieZ, симметричная Я е Rnxnt maxoffl^R,
macheps е R.
Входно-выходные параметры: отсутствуют.
Выходные параметры: нижняя треугольная L^RnXn, maxaddl е R
(-««to RID).
Память:
1) Никакой дополнительной памяти под векторы и матрицы не
требуется.
2) Используются только верхняя треугольная часть Я и нижняя
треугольная часть L, включая главные диагонали обеих матриц.
Предполагается ради простоты, что каждая из них хранится
в полной матрице. Однако можно добиться экономии памяти,
отводимой под матрицы, путем модификации данного
алгоритма, как объясняется в руководстве 3.
Описание:
Делается попытка обычного разложения по Холесскому. Однако
если в какой-либо момент алгоритм определяет, что Я не
является положительно определенной, или если оказывается, что
L [/, /] ^ mini, или если при имеющемся значении L [/, /]
некоторые элементы L [t, /], i > /, оказались больше, чем maxoffl, то
некоторое положительное число D[j,*j] неявно прибавляется к
Я [/,/]. Величина D[jtj] определяется так, чтобы L[j9j]
равнялось максимальному среди значения mini и того наименьшего
значения, которое обеспечивает равенство max {|L[/, /]l} =
I<i<n
=maxoffl. Эта стратегия гарантирует, что L [i, i] ^ mini для всех
i и что \L[it j] \^ maxoffl для всех / > /. Это в свою очередь
влечет за собой ограниченность сверху числа обусловленности
матрицы Я + D.
378 Приложение А.
В то же самое время алгоритм построен так, что, если
mini = 0 и Н численно положительно определена, то
производится обычное разложение Холесского без какой-либо потери
в эффективности, приводящее к Я = LU и D = 0. Когда
алгоритм А5.5.2 будет вызываться алгоритмами А6.4.2, А6.5.1 и
Аб.б.Нас, входной параметр maxoffl будет нулевым, и
поэтому будет нулевым mini. Когда алгоритм А5.5.2 будет
вызываться алгоритмом А5.5.1, параметр mini будет положительным,
но D будет все же равным 0, если Н положительно определена
и имеет достаточно хорошую обусловленность. Вообще,
алгоритм старается строить Z), ненамного большую, чем это
необходимо.
Дополнительную информацию, включая объяснение способа
выбора maxoffl, см. Гилл, Мюррей и Райт (1981).
Алгоритм:
1. mini <- {machepsY14 * maxoffl
2. IF maxoffl = 0 THEN
(*это имеет место, когда алгоритм А5.5.2 вызывается при
известном факте положительной определенности Н
алгоритмами А6.4.2 и А6.5.1; данные строки служат
рассчитанной на этот случай мерой предосторожности в машинной
арифметике*)
2.1 maxoffl +- ! max {| Н [/, /] |}
2а. тШ2 -«- (machepsY12 * maxoffl
3. maxadd «- 0
(* maxadd будет содержать максимальную величину,
которая неявно прибавляется ко всем диагональным элементам
матрицы Н при формировании LLT = H + D*)
4. FOR /=1 ТО п DO
(* сформировать /-й столбец L*)
4.1 L[U /Н~#[/, /]-Z(L[/, i\f
4.2 mini jj 4-0
4.3 FOR / = /+1 TO n DO
4.3.1 L [i, j]«- H [j, i] -t(L [/, k] * L [j, *])
4.3.2 mini}}-*-max {| L [i, j] |, tninljj}
4.4 mini]] ^max{ -j^jjf, mini}
4.5 IF L[j, }]>minljf
4.5T THEN (* итерация обычного разложения Холесского *)
L[j, j]+-*/L[j, j)
4.5E ELSE (*увеличить H[j, }]*)
Модульная система алгоритмов 379
4.5Е.1 IF minljj <minl2 THEN
mini]] <- minl2
(* это возможно, только когда введенное
значение maxoffl = 0 *)
4.5Е.2 maxadd+-max {maxadd, minljj2 — L[j, /]}
4.5E.3 L[j9 j]<-minljj
4.6 FOR / = /+1 TO n DO
L[t, j]*-L[i, j]/L[j,j]
(* RETURN для алгоритма A5.5.2 *)
(*END, алгоритм A5.5.2 *)
Алгоритм A5.6.1 (FDHESSG).
Конечно-разностная аппроксимация гессиана
с использованием значений аналитически
заданного градиента
Назначение: Вычислять аппроксимацию по разностям вперед
для V2/(*c), используя аналитические значения Vf{x).
Входные параметры: п е Z, хс е Rn, g е Rn (= V/ (хс))9 GRAD
(имя подпрограммы для V/: Rn->Rn), Sx^Rn, t]^R.
Входно-выходные параметры: отсутствуют.
Выходные параметры: симметричная Н ^ RnXn (^ V2/ (хс)).
Память:
1) Никакой дополнительной памяти под векторы и матрицы не
требуется.
2) Только диагональ и верхняя треугольная часть Я имеют
правильные значения на выходе из алгоритма А5.6.1, потому что
только они составляют те части Я, к которым обращается
остальная часть системы алгоритмов. Тем не менее, на
промежуточном этапе данного алгоритма используется вся -матрица Я.
3) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководстве 3.
Описание:
1) Аппроксимирогать V2f(xc) матрицей Я, используя алгоритм
А5.4.1.
2) Н^(Н + Нт)/2.
Алгоритм:
1. CALL FDJAC (я, хс, g, GRAD, SX9 ть #)
(* алг. А5.4.1 *)
2. FOR /=1 ТО п-\ DO
380 Приложение А.
2.1 FOR / = /+1 ТО п DO
H[l, Л«-<я[/, 1\ + Н\и /]/2
(* RETURN для алгоритма А5.6.1*)
(*END, алгоритм А5.6.1*)
Алгоритм А5.6.2 (FDHESSF).
Конечно-разностная аппроксимация гессиана
с использованием значений функции
Назначение: Вычислять аппроксимацию по разностям вперед
для V2/(ac), используя только значения f(x).
Входные параметры: «gZ, хсе Rn, fc^R(=f (х^)), FN (имя
подпрограммы для /: Rn -►/?), Sx^Rn, rje/?.
Входно-выходные параметры: отсутствуют.
Выходные параметры: симметричная H^RnXn (&V*f(xe)).
Память:
1) Требуются два я-вектора дополнительной памяти для stepsize
и ^neighbor.
2) Только диагональ и верхняя треугольная часть Я
заполняются алгоритмом А5.6.2, поскольку исключительно к этим
частям Н обращается вся система алгоритмов.
3) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководстве 3.
Описание:
Элемент V2f(xc)[i, j] аппроксимируется по формуле #[/, /] =
= (/ (хс + Ал + V/) -/(** + V*) -f(xe + V/) + / (*ЖЬ%),
где е{ есть /-й единичный вектор и ht = т)1/3 * max {| лгс[/] |,
1/SX[/]} * sign(хс[/]). Здесь l/Sx[i] есть задаваемая
пользователем характерная величина для | хс [/] | и т| = 10~D/ /rs, DIGITS —
число верных десятичных разрядов в f(x). Соответствующие
элементы V2/ (хс) и Я будут, что характерно, совпадать
приблизительно в их первых (DIGITS/3) десятичных разрядах.
Алгоритм:
1. cuberteta<-r\ll3
2. FOR /=1 ТО п DO
(♦вычислить stepsize[i] и f(xc + stepsize[i]*ei)*)
2.1 stepsize[i] <- cuberteta * max {| xc [i] |, 1/S* [/]} * sign (xc [i])
(♦для включения другого прагила выбора длины шага
изменить строку 2.1 *)
2.2 tempi<-xc[i]
2.3 хс [i] +- хс [i] + stepsize[i\
Модульная система алгоритмов 381
2.4 siepsize[i] <- хс [i] — tempi
(♦действия в строке 2.4 немного уменьшают ошибки
машинной арифметики; см. разд. 5.4 *)
2.5 CALL FN (л, хс, fneighbor[i\)
(* fneighbor[i] <- f (хс + stepsize[i] * et) *)
2.6 xc [i] <- tempi (* восстановить xc [i] *)
3. FOR i=l TO n DO
(* вычислить /-ю строку H *)
3.1 tempi+-xc[i]
3.2 xc [i] <- jcc [/] + 2 * stepsize[i]
(* или же лгс [/] «- *c [/] —- step size *)
3.3 CALL FN (л, *„ /Й)
(* fit <- f (xc -f- 2 * stepsize[i] * e,) *)
3.4 Я [/, /]«- ((/« - fneighbor[i)) + (fii - fneighbor[i]))J
(stepsize[i] * s/eps/zef/])
3.5 jcc [/] «- tempi + stepsize[i]
3.6 FOR / = /+1 TO n DO
(* вычислить H [/, /J *)
3.6.1 tempj<r-xc[i]
3.6.2 л:с [/] <- xc [j] + stepsize[ji]
3.6.3 CALL FN (я, *c, ///)
(* W «-/(*<? + stepsize[i] *et + stepsize[j] * ej) *)
3.6.4 H [/, /] <- ((/, - /neighbor[i\) + (/// - fneighbor[j]))/
\stepsize[i] * stepsize[j\)
3.6.5 xc[j]<-tempj (*восстановить *Л/] *)
3.7 *c [/] «- temp/ (* восстановить дгс [/] *)
(* END, цикл FOR 3 *)
(♦RETURN для алгоритма A5.6.2*)
(♦END, алгоритм A5.6.2*)
Алгоритм A5.6.3 (FDGRAD).
Аппроксимация градиента по разностям вперед
Назначение: Вычислять аппроксимацию Vf(xc) по разностям
вперед, используя значения /(дс).
Входные параметры: п е Z, хс е /?Л, /с е /? (= Д*с) ), FN
(имя подпрограммы для f: Rn-*~R), Sie/?", tj е/?.
Входно-выходные параметры: отсутствуют.
Выходные параметры: ge /?n(^V/(jcc)).
Память:
1) Никакой дополнительной памяти под векторы и матрицы не
требуется.
Примечания:
1) Данный алгоритм идентичен алгоритму А5.4.1, за
исключением того, что параметры /с£/}и^ейп алгоритма А5.6.3 за-
382 Приложение А.
меняются параметрами Fc^Rn и I ^ Rnxn в алгоритме А5.4.1,
а также, что строка 2.6 алгоритма А5.6.3 заменяется
соответствующим циклом в алгоритме А5.4.1.
Описание:
Элемент V/ (хс) [j] аппроксимируется по формуле g [j] =
= (/ (хс + Л/£у) — / (xc))/hff где et есть /-й единичный вектор и
А/ = т),/2*тах{|*Л/]1, l/Sx[j] }s * sign(xe[j]). Здесь 1/Sx[j] есть
задаваемая пользователем характерная величина для |дсс[/]1>
и т] = lO-^7077^, DIGITS — число верных десятичных разрядов
в f(x). Соответствующие элементы Vf{xc) и g будут, что
характерно, совпадать приблизительно в их первых (DIGITS/2)
десятичных разрядах.
Алгоритм:
1. sqrteta<^r\lt2
2. FOR /=1 ТО п DO
(* вычислить g[j] *)
2.1 stepsizej <- sqrteta * max {| xt [j] |, l/Sx [j]} * sign (xc [/])
(*для включения другого правила выбора длины шага
изменить строку 2.1*)
2.2 tempj <-xc[j]
2.3 хс [j] <- хс [j] + stepsizej
2.4 stepsizej <- xc [j] — tempj
(* действия в строке 2.4 немного уменьшают ошибки
машинной арифметики; см. разд. 5.4 *)
2.5 CALL FN (п, хС9 //) (* // <-f(xc + stepsizej * et)*)
2.6 g[j]+-[fi — fe]/stepsizej
2.7 jcc [/] «- tempj (* восстановить jcc [/] *)
(* END, оператор цикла 2 *)
(♦RETURN для алгоритма A5.6.3 *)
(*END, алгоритм A5.6.3*)
Алгоритм А5.6.4 (CDGRAD).
Аппроксимация градиента по центральным
разностям
Назначение: Вычислять аппроксимацию V((xc) по центральным
разностям, используя значения f(x).
Входные параметры: neZ, хс е /?л, FN (имя подпрограммы
для /: Rn-+R),Sxe= Rn, r\<=R.
Входно-выходные параметры: отсутствуют.
Выходные параметры: g е Rn(^ V/(jcc)).
Память:
1) Никакой дополнительной памяти под векторы и матрицы не
требуется.
Модульная система алгоритмов 383
Примечания:
1) Аппроксимация градиента по центральным разностям может
быть полезной при решении некоторых задач безусловной
оптимизации, как обсуждалось в разд. 5.6. В драйвере D6.1.1 не
предусмотрено использование алгоритма А5.6.4, но он может
быть легко расширен включением в него автоматического
перехода с аппроксимации градиента по разностям вперед на
центральные разности, как указывается ниже. Этот переход
производился бы, когда на какой-либо итерации использование
алгоритмом аппроксимации градиента по разностям вперед не
привело к достаточному убыванию функции, но градиентный
критерий останова еще не выполняется. В этом случае текущая
итерация повторяется с использованием аппроксимации Vf(xc) по
центральным разностям, и затем алгоритм продолжил бы
использование исключительно аппроксимаций градиента по
центральным разностям до тех пор, пока не выполнится какой-либо
критерий останова.
Изменения в драйвере D6.1.1 с целью включения этого
автоматического перехода на центральные разности таковы:
Заменить ELSE-ветвь оператора 6 на:
6Е. ELSE
6Е.1 CALL FDGRAD (n, xQ, fc> FN Sx, ц, gc)
6E.2 fordiff «-TRUE
Вставить между операторами 10.3 и 10.4:
10.372 IF (global = 2) OR (global = 3) THEN trustsave<-6c
Вставить между операторами 10.4d и 10.5:
10.4V2 IF (retcode=\) AND (NOT analgrad) AND (fordiff =
= TRUE) THEN
10.472.1 CALL CDQRAD (n, xc, FN, Sx, r\9 gc)
10.472.2 fordiff^-FALSE
10.472.3 IF (global = 2) OR (global = 3) THEN
6C <- trustsave
10.472.4 IF global = 2 THEN
10.472.4.1 CALL MODELHESS (n, Sx, macheps,
Hc, Lc)
10.472.4.2 ц«-0
10.472.5 GO TO 10.3
Заменить ELSEE-ветвь в строке 10.5.1 на:
10.5.1Е ELSE
10.5.1 ЕЛ IF fordiff = TRUE
THEN CALL FDGRAD (n, x+, /+, FN,
Sx, r\, g+)
ELSE CALL CDGRAD (n, x+9 FN, Sx,
Приложение А.
Описание:
Элемент Vf(xc)[j] аппроксимируется по формуле g[i\=(f(xc+hfii)—
— f(xe^hfiji)l(2*hi)9 где е1 есть у-й единичный вектор, и Лу =
= т|1/3 * max {| хс [j] |, l/Sx [j]} * sign (хс [/]). Здесь l/Sx [j] есть
задаваемая пользователем характерная величина для |*с[/]|, и
r\= W~DI0ITS9 DIGITS —число верных десятичных разрядов
в / (*). Соответствующие элементы V/ (хс) и g будут, что
характерно, совпадать приблизительно в их первых (2 * DIGITS/3)
десятичных разрядах.
Алгоритм:
1. cuberteta <- ц1'3
2. FOR /=1 ТО п DO
(* вычислить g [j] *)
2.1 stepsizej+-cuberteta* max {\xc[j]\9 l/Sx [j]} * sign(xc [j])
(*для включения другого правила выбора длины шага
изменить строку 2.1 *)
2.2 tempj<-xc[j]
2.3 хс [j] <- хс [j] + stepsizej
2.4 stepsizej <- xc [j] — temp]
(♦действия в строке 2.4 немного уменьшают ошибки
машинной арифметики; см. разд. 5.4*)
2.5 CALL FN (п9 хС9 fp) (* fp*-f(xc + stepsizej*ey)*)
2.6 xc [j] <- tetnpj — stepsizej
2.7 CALL FN (n, xC9 fm) (* fm<- f (xc — stepsizej * et)*)
2.8 g [j] «- (fp - fm)/(2 * stepsizej)
2.9 xc [j]+-tetnpj (* восстановить xc [j] *)
(* END, оператор цикла 2 *)
(* RETURN для алгоритма A5.6.4 *)
(*END, алгоритм A5.6.4*)
Алгоритм А6.3.1 (LINESEARCH).
Линейный поиск
Назначение; Для заданных gTp < О и а < у (используется
а=10"4) находить, используя линейный поиск с дроблением
шага, точку х+=хс + Хр9 iG(0, 1], такую, что f(x+)^
<f(xc)-r*bgTp.
Входные параметры: neZ, xc^Rn9 /Ce/J(=f(xc)), FN (имя
программы для /: Rn -► #), g е= Rn (= V/ (xc))9 p e= Rn9 Sx e= Rn9
moxstep^R9 steptol^R.
Входно-выходные параметры: отсутствуют.
Выходные параметры: retcode^Z9 x+^Rn, f+^R(=f(x+))>
moxtaken e Boolean.
Модульная система алгоритмов 385
Значения кодов возврата:
retcode = 0: найдена удовлетворительная *+;
retcode=l: подпрограмме не удалось найти
удовлетворительную х+, достаточно отличающуюся от хс.
Память:
1) Никакой дополнительной памяти под векторы и матрицы не
требуется.
Примечания:
1) Во всех наших обращениях к данному алгоритму (в
драйверах D6.1.1—3) р есть ньютоновский шаг или шаг метода
секущих. Тем не менее данный алгоритм будет работать при
любом р, таком, что gTp < 0.
Описание:
(Пусть х+(Х) обозначает хс + Хр.)
1) Положить X = 1.
2) Установить, удовлетворительна ли точка х+{Х). Если да; то
положить retcode = 0 и завершить работу алгоритма А6.3.1.
Если нет:
3) Установить, не слишком ли мала длина шага. Если да, то
положить retcode = 1 и завершить работу алгоритма А6.3.1.
Если нет:
4) Уменьшить X с помощью множителя, лежащего между 0.1
и 0.5, следующим образом:
(Пусть через f'p(xc) обозначена производная f(x) в хс по
направлению р.)
a. При первом дроблении: выбрать новое значение X таким,
чтобы х+ (А) была точкой минимума квадратичной функции
одной переменной, интерполирующей f(xc), f'p(xc), /(*с + р),
но ограничить снизу новое А, числом 0.1. (Гарантируется,
что новое Х< 1/(2(1—а)) =1/1.9998; см. разд. 6.3.2.)
b. При всех последующих дроблениях: выбрать новое X
таким, чтобы х+ (X) была точкой локального минимума
кубической функции одной переменной, интерполирующей f(xc),
f'P(xc)> /(*+(*))» f(*+(V«))' но 0ГРаничить новое х
^Резком [0.1* (старое Л), 0.5* (старое X)].
5) Вернуться к шагу 2.
Алгоритм:
1. maxtaken*r- FALSE
2. retcode *- 2
3. а«-1(Г4
(*а есть константа, используемая в проверке шага на
приемлемость f (x+)^f (хс) + aXgTp; ее значение можно
изменить, изменив этот оператор *)
386 Приложение А.
4. Newtlen <-\\Dxpi\2
(*Dx = d\ag((Sx)u ..., (Sx)n) хранится как SK^Rn.
Относительно предлагаемой программной реализации выражений,
содержащих Dx> см. разд. 1.5 данного приложения. *)
5. IF Newtlen > maxstep THEN
(* ньютоновский шаг х+ = хс + р больше максимально
допустимого *)
5.1 р <- p*(maxstep/Newtlen)
5.2 Newtlen*-maxstep
6. initslope <-gTp
7. rellength*- max {| p [i] ^(max {| xc [i] |, l/Sx [/]})}
(* rellength есть относительная длина p, вычисляемая как
в подпрограмме останова *)
8. minlambda +- steptol/rellength
(* minlambda есть минимально допустимая длина шага *)
9. Л«-1
10. REPEAT (* ццклом проверить — удовлетворительна ли х+ =
= хс-{-Хр9 и, если требуется, построить новое X*)
10.1 х+<-хс + Хр
10.2 CALL FN (п, х+9 f+) (*/+ +-f (х+)*)
10.3а IF f+^fc + a*X* initslope THEN
(* найдена удовлетворительная х+ *)
10.3a.l retcode+-Q
10.3а.2 IF X = 1 AND (Newtlen > 0.99 * maxstep) THEN
maxtaken <- TRUE
(♦RETURN для алгоритма A.6.3.1 *)
10.3b ELSEIF X< minlambda THEN
(* не удалось найти удовлетворительную х+, достаточно
отличающуюся от хс *)
Ю.ЗЬ.1 retcode <- 1
10.3b.2 х+*-хс
(♦RETURN для алгоритма А6.3.1 *)
10.3с ELSE (* уменьшить X*)
10.3с. 1 IF X=l
10.3с. IT THEN (* первое дробление, квадратичная
интерполяция *)
10.3с. IT. 1 Xtemp < initslope/(2 * (f+ — fc — init slope))
10.3c.IE ELSE (* все последующие дробления,
кубическая интерполяция*)
Га] ! Г 1/Л2 ~1/(Ярг^2)1
Ю.ЗсЛЕ.1 [6J ^" (я -Xprev) * [- Xprev/X2 X/(Xprev2) J
[/+ — fc — X * initslope ~|
f+prev — fc — Xprev * initslope J
10.3c. 1E.2 disc «- b2 — 3 * a * initslope
Модульная система алгоритмов 387
10.3с. 1Е.З IF а = 0
THEN (* кубическая интерполяция
вырождается в квадратичную *)
Метр < initslope/(2*b)
ELSE (* невырожденная кубическая
интерполяция *)
Метр <-(—Ь + (dlsc)^/(3 * а)
10.3ЫЕ.4 IF Метр > 0.5*1 THEN Штр+-0.Ь*Х
10.3с2 kprev+-X
Ю.Зс.З f+prev<-f+
Ю.Зс.4 lFMemp^OA*lTHENh<r-OA*XELSEX<-Memp
(*END, альтернатива 10.3с «уменьшить Л» и оператор
множественного ветвления 10.3)
10U UNTIL retcode<2 (*END, оператор цикла REPEAT 10*)
(* RETURN для алгоритма А6.3.1*)
(*END, алгоритм А6.3.1*)
Алгоритм A.6.3.1.mod (LINESEARCHMOD).
Линейный поиск с условием на производную
по направлению
Назначение: Для заданных gTp < 0, а < у2 (используется
а = Ю-4) и р е (а, 1) (используется р = 0.9) находить точку
х+ = хс + ^Р» Я, > 0, такую, что / (х+) ^f{xc) + aKgTp и
Входные параметры: те же, что и в алгоритме А6.3.1, и, кроме
того, analgrad е Boolean, GRAD (имя подпрограммы для
V/: Rn-+Rn, если analgrad = TRUE, а иначе фиктивное).
Входно-выходные параметры: отсутствуют.
Выходные параметры: те же, что и в алгоритме А6.3.1, и, кроме
того, g+e=R«(=S/f(x+)).
Значения кодов возврата, память, примечания: те же, что и в
алгоритме Аб.3.1.
Описание:
(Пусть через х+(Х) обозначается xc-\-hpf и пусть два
неравенства f(x+)^ f(xc) + aXgTp и Vf(x+)Tp^$gTp называются
соответственно а-условием и р-условием.)
1) Положить К = 1.
2) Если х+(К) удовлетворяет а- и р- условиям, то положить
retcode = 0 и завершить работу алгоритма А6.3. lmod.
3) Если jc+(X) удовлетворяет только а-условию и X ^ 1, то
положить А,-«-2*А, и перейти к шагу 2.
3S8 Приложение А.
4) Если х+(Х) удовлетворяет только.а-условию и Х<1 или
если х+(Х) не удовлетворяет а-условию и!>1, то:
a. Если К < 1, то определить klo = A,, Khi = (последнее из
предыдущих пробных значений К). Если Я> 1, то
определить Ш = А,, Я/о = (последнее из предыдущих пробных
значений X). Замечание: в обоих случаях x+(klo) удовлетворяет
а-условию, a р-условию— нет, x+{Xhi) не удовлетворяет
а-условию, и Klo < Ш.
b. Используя последовательные квадратичные интерполяции,
найти значение A,e(A,fo, Ш), при котором х+{Х)
удовлетворяет а- и р-условиям. Затем положить retcode = 0 и
завершить работу алгоритма A6.3.1mod.
5) В противном случае (х+(А,) не удовлетворяет а-условию и
А,^1) произвести такое же дробление шага, как описано в
шаге 4 раздела Описание алгоритма А6.3.1, и перейти к шагу 2.
Алгоритм:
Такой же, как алгоритм А6.3.1, за исключением того, что шаги
Ю.За.1 и 10.3а.2 заменяются на следующие:
10.3а.1 IF analgrad
THEN CALL GRAD (n, x+, g+)
ELSE CALL FDGRAD (n, x+, f+, FN, Sx, % g+)
(*алг. A5.6.3, аппроксимация градиента по разностям
вперед*)
(* или если вместо этого желательна аппроксимация
градиента по центральным разностям, то CALL CDGRAD
(/г, *+, FN, SX9 т), g+), алг. А5.6.4 *)
10.3а.2 р«-0.9
(*для изменения в данном алгоритме значения р
достаточно изменить эту строку*)
10.3а.3 newslope+-g+p
10.3а.4 IF newslope < р * initslope THEN
10.3а.4.1 IF (X =1) AND (Newllen < maxstep) THEN
10.3a.4.1.1 maxlambda *- maxstep/Newtlen
10.3a.4.1.2 REPEAT
10.3a.4.1.2.1 Xprev<-X
10.3a.4.1.2.2 f+prev*-f+
10.3a.4.1.2.3 A,«-min {2 * A, maxlambda)
10.3a.4.1.2.4 x+*-xc + X*p
10.3a.4.1.2.5 CALL FN (n, *+, f+)(**+«-f (*+)*)
10.3a.4.1.2.6 IF /+</c + а* X* initslope THEN
10.3a.4.1.2.6.1 то же самое, что и выше в
строке 10.3а. 1
10.3а.4.1.2.6.2 newslope+-gT+p
(♦END, оператор IFTHEN 10.3а.4.1.2.6*)
Модульная система алгоритме* 389
10.3a.4.1.2U UNTIL (f+> fc +а* Ь*initslope) OR
(newslope > 0 * iniislope) OR (A, > maxlambda)
<* END, оператор IFTHEN 10.3a.4.1 *)
10.3a.4.2 IF (A, < 1) OR ((A > 1) AND (f+>fc + a*b* initslope))
THEN
10.3a.4.2.1 Uo «-min{A, A,pra>}
10.3a.4.2.2 ЛЛ/f <-1 Я,рга> — A |
10.3a.4.2.3 IF Ж Яргео
10.3a.4.2.3T THEN
10.3a.4.2.3T.l flo<-f+
10.3a.4.2.3T.2 fhi*-f+Prev
10.3а.4.2.3Е ELSE
10.3a.4.2.3E. 1 flo «- f+prev
10.3a.4.2.3E.2 /#*-/+
10.3a.4.2.4 REPEAT
10.3a.4.2.4.1 Шсг^ 9.-™™llpe*№ff)*..m,
2* (fhi — (flo + newslope * Miff))
10.3a.4.2.4.2 IF Utter < 0.2*Xdiff THEN
Mncr+- 0.2 *Xdiff
10.3a.4.2.4.3 к+-Ш+.Шсг
10.3a.4.2.4.4 *+ <- xc + X"p
10.3a.4.2.4.5 CALL FN (л, лс+, /+)(**+«-/(*+)*)
10.3a.4.2.4.6 IF f + > /c + a * A * initslope
10.3a.4.2.4.6T THEN
10.3a.4.2.4.6T.l Xdiff*-kittcr
10.3a.4.2.4.6T.2 fhi+-f+
l0.3a.4.2.4.6E ELSE
10.3a.4.2.4.6E.l то же самое, что и выше в
строке 10.3а. I
10.3а.4.2.4.6Е.2 newslope *- g\p
10.3а.4.2.4.6Е.З IF newslope < fi*initslope THEN
10.3a.4.2.4.6E.3.1 Mo<-A
10.3a.4.2.4.6E.3.2 Xdiff «- Xdiff — Kincr
10.3a.4.2.4.6E.3.3 //o<-/+
(*END, операторы IFTHEN 10.3а.4.2.4.6Е.З и
IFTHENELSE 10.3a.4.2.4.6*)
I0.3a.4.2.4U UNTIL (newslope^ p* initslope) OR
(Kdiff < minlambda)
I0.3a4.2.5 IF newslope < p * initslope THEN
(* не удалось удовлетворить р-условию *)
10.3а.4.2.5.1 f+4-flo
10.3а.4.2.5.2 х+ +-хе + Ш'р
(*END, операторы IFTHEN 10.3а.4.2 и IFTHEN 10.3а.4*)
10.3а.5 retcode+-Q
Ю.За.6 IF (к * Newllen > 0.99 * maxstep) THEN
maxtaken*- TRUE
(* END, добавления в алгоритме A6.3.1mod*)
390 Приложение А.
Алгоритм А6.4.1 (HOOKDRIVER).
Драйвер локально ограниченного оптимального
(«криволинейного») шага
Назначение: Находить точку х+ = хс — (Н + \iDx)~] g, \i ^ 0,
такую, что /(*+)</ (хс) + agT (х+ — хс) (используется а =
= 10~4), и масштабированную длину шага из отрезка [0.756,
1.56), начиная с введенного значения 6, но при необходимости
увеличивая или уменьшая 6. (Ac=diag((S*)i, ..., (5х)п).)
А также вырабатывать начальное значение радиуса
доверительной области для следующей итерации.
Входные параметры: /ieZ, xc^Rn, fc<^R(=f(xc)), FN (имя
подпрограммы /: Rn-+R), g^Rn(=Vf(xc)), нижняя
треугольная L е Rnxn, симметричная Н е Rn><n(= LLT), sN е
ei?n(=-H~lg)9 Sx<EERn, maxstep<=R, steptolt=R, itn-
count eZ, macheps e R.
Входно-выходные параметры: 6e/?, \i e /?, Sprev ей, ф e R>
<p' e R (последние четыре не будут иметь значений при
первом обращении к данному алгоритму; последние два будут
иметь текущие значения на выходе, только если \i Ф 0).
Выходные параметры: retcode е Z, х+ е Rny /+ е R (= /(х+)),
maxtaken е Boolean.
Значения кодов возврата:
retcode = 0: найдена удовлетворительная точка х+;
retcode = 1: подпрограмме не удалось найти
удовлетворительную jc+, достаточно отличающуюся от хс-
Память:
1) Требуются два я-вектора дополнительной памяти для s и
x+prev.
2) Используются только верхняя треугольная часть Н и нижняя
треугольная часть L, включая главные диагонали обеих матриц.
Предполагается ради простоты, что каждая из них хранится
в полной матрице. Однако можно добиться экономии памяти,
отводимой под матрицы, путем модификации данного
алгоритма, как объясняется в руководстве 3.
Описание:
1) Обратиться к алгоритму А6.4.2 с тем, чтобы найти шаг
s = -(H + \LDx)-lg, ц>0, такой, что ||Dxs||2е [0.756, 1.56],
или чтобы положить s = sN9 если ||Z)X%||2^ 1.56.
2) Обратиться к алгоритму А6.4.5 с тем, чтобы решить, при-
Модульная система алгоритмов 391
нимать или нет х+ в качестве следующего приближения, и
чтобы вычислить новое значение б. Если retcode = 2 или 3, то
вернуться к шагу 1; если retcode = 0 или 1, то завершить
работу алгоритма А6.4.1.
Алгоритм:
1. retcode <- 4
(* означает начальное обращение к алгоритму А6.4.2 *)
2. firsthook«-TRUE
3. Newtlen+-\\DxsNft2
(* D* = diag((SJC)1, ..., (Sx)n) хранится как Sx^Rn.
Относительно предлагаемой программной реализации выражений,
содержащих Dx, см. разд. 1.5 настоящего приложения. ♦)
4. IF (itncount=l) OR (6 = — 1) THEN
4.1 jut ^— 0 (* требуется для алгоритма А6.4.2*)
4.2 IF 6 =-1 THEN
(* пользователем не было задано никакого начального
значения радиуса доверительной области (или было
восстановление в методе секущих решения нелинейных
уравнений); положить б равным длине масштабированного
шага по методу Коши *)
4.2.1 a4r-\DxXg%
(* 4.2.2-3 реализуют р <-\LTDx2g\\] *)
4.2.2 р«-0
4.2.3 FOR i=l ТО п DO
4.2.3.1 temp -ȣ{L [/, /] * g [JV(SX [j] * Sx [/]))
/-*
4.2.3.2 $<-$ +temp*temp
4.2.4 6 4-a*a^/p
4.2.5 IF &>maxstep THEN d+-maxstep
5. REPEAT (* вычислить и проверить новый шаг *)
5.1 CALL HOOKSTEP (я, g, L, Я, sN, Sx, Newtlen, macheps,
6, \i, 6prev, ф, ф', firsthooky qfinit, s, Newttaken)
(♦ Найти шаг с помощью алгоритма криволинейного
шага А6.4.2 *)
5.2 6prev*-d
5.3 CALL TRUSTREGUP (л, xCi /с, FN, g, L, s, SXJ Newttaken,
maxstep, steptol, 1, tf, 6, retcode, x+prev, f+prev, x+, /+,
maxtaken)
(* проверить новую точку и сделать пересчет радиуса
доверительной области, алгоритм А6.4.5*)
5U. UNTIL retcode <2
(♦RETURN для алгоритма А6.4.1*)
(♦END, алгоритм А6.4.1#)
392 Приложение А.
Алгоритм А6.4.2 (HOOKSTEP).
Локально ограниченный оптимальный
(«криволинейный») шаг
Назначение: Находить приближенное решение задачи:
mingTs + (l/2sTHs)
s<=Rn
при условии ||Dxs||2<6
путем выбора s = — (# + pDl)~l g, fi>0, такого, что
||Dxs\\2e= [0.756, 1.56], или s = H~lg, если Newtlen^l.56.
(Dx = diag((SJ1, ..., (Sx)n).)
Входные параметры: /isZ, g^Rn, нижняя треугольная
1б/?яхя, симметричная H^Rnxn {=LLT)y sN<=Rn(=—H-1 g),
Sx(=Rnf Newtlen^Rn(=\\DxsN\\2), machepsezR, bprev^R.
Входно-выходные параметры: 6e/?, pe /?, ф£Й, ф'eR,
firsthook^ Boolean, tp'init&R (ф, q/ будут иметь новые
значения на выходе, только если р Ф 0; ф'ш# будет иметь
новое значение на выходе, только если firsthook в процессе
рассматриваемого обращения к алгоритму приняло значение
FALSE.)
Выходные параметры: s е Rn, Newttaken е Boolean.
Память:
1) Требуется один м-вектор дополнительной памяти для tempvec.
2) Используются только верхняя треугольная часть Н и нижняя
треугольная часть L, включая главные диагонали обеих матриц.
Предполагается ради простоты, что каждая из них хранится
в полной матрице. Однако можно добиться экономии памяти,
отводимой под матрицы, путем модификации данного
алгоритма, как объясняется в руководстве 3.
Описание:
1) Если 1.56 ^zNewtlen, то положить s = sN, 6 = min{6, Newt-
len) и завершить работу алгоритма А6.4.2. Если нет:
2) Вычислить начальное значение ц на основе заключительного
значения р на предыдущей итерации, а также нижнюю и
верхнюю границы [ilow и \шр для точного решения р*, как
объясняется в разд. 6.4.1 основной части книги.
3) Если р ф. [plow, \шр], то положить р = max {(\ilow*\iup){i2,
10-*\шр}.
4) Вычислить s = s{[i) = — (H + \iDl)~lg. Вычислить также
Ф = Ф(|х) = ||Z)xs(^*)||2 — к и ф' = Ф'(р).
5) Если ||Dxs\\2^ [0.756, 1.56], то завершить работу алгоритма
А6.4.2. Если нет:
6) Вычислить новые значения р, \ilow и jxwp, как объясняется
в разд. 6.4.1, и вернуться к шагу 3.
Модульная система алгоритмов 393
Алгоритм:
1. ««-1.5
2. lo «-0.75
(* hi и lo есть константы, используемые в проверке
допустимости шага || Dxs Ik е [lo * б, hi * б]; их можно
изменить, изменяя операторы 1 и 2*)
3. IF Newtlen^hi*6
ЗТ. THEN (*5 есть ньютоновский шаг*)
ЗТ.1 Newttaken<-7RUE
ЗТ.2 s+-sN
ЗТ.З \х+-0
ЗТ.4 6«-min{6, Newtlen)
(* RETURN для алгоритма А6.4.2 *)
ЗЕ. ELSE (*найти ц, такое, что \DX{H + !iD^)"1g||2e[/o*6,
А/ * б] *)
ЗЕ.1 Newttaken<- FALSE
(* вычислить начальное значение р, если предыдущий
шаг не был ньютоновским *)
ЗЕ.2 IF \х > О THEN
и <- ц — Г Ф + 6Prg° ] * Г (bprev - б) + Ф I
(* выражение (bprev — б) следует заключать в скобки,
так как возможно равенство 6prev = &*)
(* шаги ЗЕ.З—6 вычисляют нижнюю и верхнюю границы
ДЛЯ fi. *)
ЗЕ.З (р^-Newtlen — б
ЗЕ.4 IF firsthook THEN (* вычислить y'init *)
ЗЕ.4.1 firsthook <- FALSE
(*шаги ЗЕ.4.2—3 дают в результате tempvec*-
ЗЕ.4.2 tempvec <-D2xsN
(* Дс = diag((Sx),, ..., (5*)Л) хранится как S* е Rn.
Относительно предлагаемой программной
реализации выражений, содержащих DX9 см. разд. 1.5
настоящего приложения. *)
ЗЕ.4.3 CALL L SOLVE (/г, tempvec, Lf tempvec)
(* решить L * tempvec = D2xsN с помощью алгоритма
A3.2.3a *)
ЗЕ.4.4 <р'ш# < 1| tempvec \\t/Newtlen
3E.5 \ilow< <p/<p'm#
3E.6 |шр«-|Я*'*к/б
3E.7 4о/г*«-FALSE
394 Приложение А.
ЗЕ.8 REPEAT
(* проверить значение \i и, если необходимо,
выработать следующее \х *)
ЗЕ.8.1 IF (Oi < \xlow) OR (fi > \iup)) THEN
\i <- max {(\ilow * fiwp)1/2, 10_3[iwp}
(*Я*-Я + |а/Й:*)
3E.8.2 FOR /=1 TO n DO
H[i, i]<-H[i, i] + \i*Sx[i]*Sx[i]
(* вычислить /^//-разложение новой Я, используя
алгоритм А5.5.2*)
8Е.8.3 CALL CHOLDECOMP (я, Я, 0, macheps, L,
maxadd)
(* решить (LLT) s = —g, используя алгоритм АЗ.2.3 *)
ЗЕ.8.4 CALL CHOLSOLVE (л, g, L, s)
(* положить Я заново равной ее первоначальному
значению: Я <- Я — \i * D\ *)
ЗЕ.8.5 FOR /=1 ТО /i DO
Я[/, /]^-Я[/, i]-|i«S,PPS,M
ЗЕ.8.6 s/ep/елг <—1| ZJjcS ||2
ЗЕ.8.7 q>+-steplen — 6
(*шаги ЗЕ.8.8—9 дают в результате tempvec*-
+-L~lI?xs*)
ЗЕ.8.8 tempvec *-D2xs
ЗЕ.8.9 CALL L SOLVE (л, tempvec, L, tempvec)
(♦решить L* tempvec = DxsN с помощью алгоритма
АЗ.2.3 *)
ЗЕ.8.10 <р' < 1| tempvec \$/steplen
ЗЕ.8.11 IF ((steplen^lo*6) AND (steplen^hi*6)) OR
(\xup — \ilov < 0)
3E.8.11T THEN (*шаг s является приемлемым*)
ЗЕ.8.1 IT. 1 done <-TRUE
(* RETURN для алгоритма A6.4.2 *)
ЗЕ.8.1 IE ELSE (*шаг 5 неприемлем, вычислить
новое \i9 а также границы \xlow и \шр*)
ЗЕ.8.11 ЕЛ \xlow*- max {plow, ji —(ф/ф')}
ЗЕ.8.11Е.2 IF ф<0 THEN \шр+-Р
3E.8.11E.3^^[i^]*[i]
(*END, оператор IFTHENELSE ЗЕ.8.11*)
3E.8U UNTIL done = TRVE
(*END, оператор IFTHENELSE 3*)
(* RETURN для алгоритма А6.4.2 *)
(* END, алгоритм А6.4.2. *)
Модульная система алгоритмов 395
Алгоритм А6.4.3 (DOGDRIVER).
Драйвер шага вдоль кривой с двойным изломом
Назначение: Находить точку х+ на кривой с двойным изломом,
такую, что /(*+)^ f(xc)+ a>gT(x+ — хс) (используется а =
= 10~4), и масштабированную длину шага б, начиная со
значения б на входе, но при необходимости увеличивая или
уменьшая б. Кроме того, вырабатывать начальное значение
радиуса доверительной области для следующей итерации.
Входные параметры: /isZ, xc^Rn, fc^R(=f(xc)), FN (имя
подпрограммы для /: Rn->R), g е Rn (= V/ {xc))t нижняя
треугольная L е= Rn*n, % s Rn (= - (LLT)~l g)9 SK €= Rn,
maxstep^R, steptol^R.
Входно-выходные параметры: бе/?.
Выходные параметры: retcode^Z, x+^Rn, f+ e R (= / {x +)),
maxtaken e Boolean.
Значения кодов возврата:
retcode = 0: найдена удовлетворительная точка х+;
retcode=l: подпрограмме не удалось найти
удовлетворительную дс+, достаточно отличающуюся от хс.
Память:
1) Требуются четыре /г-вектора дополнительной памяти для s,
ssd, v и x+prev.
2) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководствах 3 и 6.
Описание:
1) Обратиться к алгоритму А6.4.4 с тем, чтобы найти шаг s на
кривой с двойным изломом, такой, что HDxslU = 6, или чтобы
положить 5 = Sn, если ПДгздНг ^ 6- Ф* = diag((Sx) ь • - •
.... (S,)*)).
2) Обратиться к алгоритму А6.4.5 с тем, чтобы решить —
принимать или нет х+ в качестве следующего приближения и чтобы
вычислить новое значение б. Если retcode = 2 или 3, то
вернуться к шагу 1; если retcode = 0 или 1, то завершить работу
алгоритма А6.4.3.
Алгоритм:
1. retcode*-4
(* означает первоначальное обращение к алгоритму А6.4.4 *)
2. firstdog<- TRUE
3. Newtlen<-\\DxsN\\2
(*Dx = diag((SA, ..., (Sx)n) хранится как Sxe=Rn.
Относительно предлагаемой программной реализации
выражений, содержащих DX9 см. разд. 1.5 настоящего
приложения. *)
396 Приложение А.
4. REPEAT (* вычислить и проверить новый шаг *)
4.1 CALL DOGSTEP (п9 g9 L, sN, SX9 Newtlen, max step, 6,
firstdog, Cauchylen, r\, §SD, v9 s, Newttaken)
(* Найти новый шаг вдоль кривой с двойным изломом
с помощью алгоритма А6.4.4*)
4.2 CALL TRUSTREGUP (п, хС9 fC9 FN, g9 Lt s9 Sx>
Newttaken, maxstep9 steptol9 2, L9 6, retcode9 x+prev9
f+prev9 jc+, /+, maxtaken)
(* проверить новую точку и сделать пересчет радиуса
доверительной области, алгоритм А6.4.5*)
(* второе L в приведенном выше списке параметров
является фиктивным параметром *)
4U. UNTIL retcode < 2
(♦RETURN для алгоритма А.6.4.3*)
(*END, алгоритм А6.4.3*)
Алгоритм А6.4.4 (DOGSTEP). Шаг вдоль
кривой с двойным изломом
Назначение: Находить приближенное решение задачи:
min gTs + (1/2) sTLLTs
se=Rn
при условии ||AcS||2^6
путем выбора на описанной выше кривой с двойным
изломом шага 5, такого, что || Dxs ||2 = б, или s = sNf если
Newtlen ^6. (Dx = diag((Sx)l9 ..., (Sx)n).)
Входные параметры: neZ, g^Rn, нижняя треугольная Is
<= RnXn, sN es Rn (= - {lLt)~x g)9 Sx e= Rn9 Newtlen e
e R (= || DxsN ||2), maxstep e R.
Входно-выходные параметры: d e R9 firstdog e Boolean, Cauchy-
ten e /?, т) e R9 sSd e Rn> v^Rn (последние четыре
параметра будут иметь текущие значения на входе и выходе,
только если в тот момент firstdog = FALSE).
Выходные параметры: s е Rn9 Newttaken е Boolean.
Память:
1) Никакой дополнительной памяти под векторы и матрицы не
требуется.
2) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководствах 3 и 6.
Описание:
1) Если Newtlen ^ б, то положить s = s#, б = Newtlen и
завершить работу алгоритма А6.4.4. Если нет:
2) Вычислить кривую с двойным изломом, если она не была
уже вычислена в течение этого обращения к алгоритму А6.4.3.
Модульная система алгоритмов 397
Указанная кривая с двойным изломом представляет собой
кусочно-линейную кривую, соединяющую точки хс, хс + sSd, *с + л^лг
и Хс + Sjf, где ssd есть шаг по методу Коши, в точку минимума
квадратичной модели на масштабированном направлении
наискорейшего спуска, и т| ^ 1. (См. разд. 6.4.2 основной части
книги относительно дальнейших деталей.)
3) Вычислить единственную точку хс + s на кривой с двойным
изломом, такую, что ||Dxs||2 = 6.
Алгоритм:
1. IF Newtlen^b
IT. THEN (*s есть ньютоновский шаг*)
1Т.1 Newttaken+- TRUE
1T.2 s<-sN
1T.3 b+-Newtlen
(* RETURN для алгоритма A6.4.4*)
IE. ELSE
(* ньютоновский шаг слишком длинный, 5 лежит на кривой
с двойным изломом*)
1Е.1 Newttaken+-FALSE
1Е.2 IF firstdog THEN
(* вычислить кривую с двойным изломом *)
1Е.2.1 firstdog*- FALSE
1Е.2.2 a^lDZ'gt
(* Dx = diag ({Sx)x, ..., (Sx)n) хранится как Sx <=
e Rn. Относительно предлагаемой
программной реализации выражений, содержащих Dx>
см. разд. 1.5 настоящего приложения.*)
(* 1Е.2.3-4 реализуют l*-\LTDx2g%*)
1Е.2.3 р«~0
1Е.2.4 FOR i=l ТО п DO
1Е.2.4.1 temp+- £■'(£ [/, /] * g [j]/(Sx [j] * Sx [/]))
/-*
1E.2.4.2 p«-p + temp*temp
1E.2.5 SsD^-W)Klg
(* Ssd есть шаг по методу Коши в
преобразованной метрике; sSd в разделе Описание есть
DX%D*)
1Е.2.6 Cauchylen+-a*aW/£ (* = ||5SD||2*)
1Е.2.7 r,^-0.2 + (0.8*a2/(p*|g^|))
(*т|<1; см. разд. 6.4.2*)
1Е.2.8 v+-r\DxsN — SSD
(* v есть (r\sN — sSd) в преобразованной
метрике*)
398 Приложение А.
IE.2.9 IF 6 = — 1 THEN &<r-ir\m{Cauchylenf maxstep)
(* первая итерация, и пользователем не было
задано никакого начального значения радиуса
доверительной области *)
(*END, оператор IE.2, вычислить кривую с двойным
изломом *)
1Е.За IF r\*Newtlen^6 THEN
(* сделать уменьшенный шаг в ньютоновском
направлении *)
1Е.За.1 s<-(6/Newtlen)*sN
(* RETURN для алгоритма А6.4.4 *)
1Е.ЗЬ ELSEIF Cauchylen^b THEN
(* сделать шаг в направлении наискорейшего спуска *)
1 Е.ЗЬ. 1 5 <- (д/Caucfiylen) * ДГ 1§sd
(* RETURN для алгоритма А6.4.4 *)
1Е.Зс ELSE
(* вычислить выпуклую комбинацию векторов sSd и
Л% (= Dxl§sD + kDxld)> которая имеет
масштабированную длину, равную б *)
1Е.ЗсЛ temp<-vTsSD
1Е.Зс.2 tempv+-vTv
1Е.Зс.З А,«-(—te/np +
+ Vtemp2 — iempv * (Cauchylen2 — 62))/tempv
1E.3C.4 s<-D;x(§sd + M)
(*END, операторы ELSE 1Е.Зс, множественного ветвления
1E.3 и IFTHENELSE 1 *)
<* RETURN для алгоритма A6.4.4 *)
(♦END, алгоритм A6.4.4*)
Алгоритм А6.4.5 (TRUSTREGUP).
Пересчет доверительной области модели
Назначение: Для заданного шага s, выработанного алгоритмом
криволинейного шага или шага вдоль ломаной, решить,
следует ли принимать х+ = хс + s в качестве следующего
приближения. Если нет, то уменьшить или увеличить
доверительную область для текущей итерации.
Входные параметры: neZ, хс е Л", /с е R(=f(xc))> FN (имя
подпрограммы для /: Rn ->/?), g е Rn, нижняя треугольная
L (= Rnxn, s е Rny Sx е Rn, Newttaken е Boolean, maxstep e
e/?, steptol^R, steptupe £Z(= 1 для криволинейного
шага, 2 для шага вдоль ломаной), симметричная H^Rnxn
(используется только при steptype = 1, в этом случае
содержит гессиан модели).
Модульная система алгоритмов 39?
Входно-выходные параметры: бе/?, retcode е Z, x+prev е Rn9
f+prev е R (последние два параметра будут иметь текущие
значения на входе и новые значения на выходе, только если
в тот момент retcode = 3).
Выходные параметры лг+<=/?", /+(=/?(=/(*+)), maxtaken<=
e Boolean.
Значения кодов возврата:
retcode = 0: точка jc+ принята в качестве следующего
приближения, б является радиусом доверительной области
для следующей итерации;
retcode = 1: х+ является неудовлетворительной, однако шаг
глобализации завершен из-за того, что относительная
длина (х+ — хс) лежит в пределах допуска на длину
шага в критерии останова алгоритма, что во многих
случаях свидетельствует о том, что какое-либо
дальнейшее продвижение невозможно; см. случай termcode = 3
в алгоритмах А7.2.1 и А7.2.3;
retcode = 2: значение f(x+) слишком велико, текущая
итерация должна быть продолжена с новым, уменьшенным
значением б;
retcode = 3: значение f{x+) достаточно мало, но шанс
сделать более длинный успешный шаг кажется достаточно
хорошим, чтобы текущая итерация была продолжена
с новым, удвоенным значением б.
Память:
1) Никакой дополнительной памяти под векторы и матрицы не
требуется.
2) Используется только верхняя треугольная часть Я и нижняя
треугольная часть L, включая главные диагонали обеих матриц.
Предполагается ради простоты, что каждая из них хранится
в полной матрице. Однако можно добиться экономии памяти,
отводимой под матрицы, путем модификации данного алгоритма,
как объясняется в руководстве 3.
3) Если steptype = 2, то Н не используется, и данный алгоритм
требует только одной п X /г-матрицы, так как вызов алгоритма
А6.4.5 алгоритмом А6.4.3 приводит к тому, что Н и L ссылаются
на одну и ту же матрицу.
Описание:
1) Вычислить Х+ = Хс + 5, /+ = /(*+)> А/= /(*+) — f(xc).
2) Если retcode = 3 и (f+ ^ f+prev или Д/ > 10-4grs), то
восстановить значения х+ и f+ равными x+prev и f+prev,
положить б = 6/2, retcode = 0 и завершить работу алгоритма А6.4.5.
Если нет:
400 Приложение А.
3) Если Д/> lO~4gTs9 то шаг неприемлем. Если относительная
длина шага слишком мала, то положить retcode = 1 и
завершить работу алгоритма А6.4.5. В противном случае вычислить
А,, при котором хс + Ks есть точка минимума квадратичной
функции одной переменной, интерполирующей f(xc), f(xc + s) и
производную функции / в Хс по направлению s; положить 6 =
= A,|ls||, но проследить, чтобы новое значение б было между 0.1
и 0.5 от старого значения б. Завершить работу алгоритма А6.4.5.
4) А/ ^ l0^gTsy и поэтому шаг является приемлемым.
Вычислить Afpred = (значение f(x+) — f{xc), предсказываемое
квадратичной моделью (=gTs + l/2STLLTs)). Затем выполнить один
из пунктов:
a. Если А/ и bfpred совпадают в пределах относительной
ошибки, равной 0.1, или выявлена отрицательная кривизна,,
и если возможен более длинный шаг, а также если значение
б не было уменьшено в течение этой итерации, то положить
6 = 2*6, retcode = 3, x+prev = х+, f+prev = /+ и завершить
работу алгоритма А6.4.5. Если нет:
b. Положить retcode = 0. Если А/ > Q.l*Afpred, то положить
б = 6/2, иначе если А/ < 0.75*A/pred, то положить б = 2*6»
иначе не менять 6. Завершить работу алгоритма А6.4.5.
Алгоритм:
(* Приведенные ниже шаги 9а.5. и 9с.ЗТ.5 нужно выполнять
только в том случае, когда данный алгоритм используется для
решения систем нелинейных уравнений. *)
1. maxtaken <- FALSE
2. а«-10~4
(*а есть константа, используемая в проверке шага
на приемлемость f(x+)^.f (хс) + agT (х+ — хс); ее
значение можно изменить, изменив этот оператор. *)
3. steplen «-1| Dxs ||2
(* Dx = diag ((Sx)l9 ..., (Sx)n) хранится как Sx e= R\
Относительно предлагаемой программной реализации
выражений, содержащих Dx, см. разд. 1.5 данного
приложения. *)
4. x+4-xc + s
5. CALL FN (я, х+9 f+) (*/+«-/(*+)•)
6. bf^f+-fc
7. imtslope+-gTs
8. IF retcode ФЗ THEN f+prev+-0
(* может понадобиться на случай ошибки при
исполнении следующего оператора *)
9а. IF (retcode = 3) AND ((f+>f+prev) OR (A/ ><x* initslope))
THEN
(* положить заново x+ равным x+prev и завершить
шаг глобализации *)
Модульная система алгоритмов 401
9а. 1 retcode*-0
9а.2 x++-x+prev
9а.3 f + «- f+prev
9а.4 6 «-6/2
9а.5 FV+<-FV+prev
(* fV+ есть глобальная переменная; n-вектор FV+prev
является дополнительной локальной переменной,
используемой только при решении нелинейных
уравнений*)
(* RETURN для алгоритма А6.4.5 *)
9b. ELSEIF Af^a*initslope THEN
(*f(x+) слишком велико*)
9b. 1 rellength<- max { m„ м J mi we rm \
9b.2 IF rellength < steptol
9b.2T THEN
(*дс+ — xc слишком мало, завершить шаг
глобализации*)
9b.2T.l retcode<-l
9b.2T.2 x+<-xc
(* RETURN для алгоритма A6.4.5 *)
9b.2E ELSE
(♦уменьшить б, продолжить шаг глобализации*)
9b.2E.l retcode+-2
ALftrft *, — initslope*steplen
9b.2E.2 Ыетр +- (2 . (д/ JinitJpe))
9b.2E.3a IF Ыетр < 0.1*6
THEN 6 «-0.1*6
9b.2E.3b ELSEIF 6/emp > 0.5 * 6
THEN 6 «-0.5*6
9b.2E.3c ELSE 6<-6te/np
(* RETURN для алгоритма Аб.4.5 *)
9c. ELSE (*/(*+) достаточно мало*)
(* в 9с. 1 — 2 положить Afpred <- gTs + l/2sTHs *)
9с. 1 Afpred «— initslope
9c.2 IF steptype=\
9c.2T THEN (* криволинейный шаг, вычислить sTHs *)
9c.2T.l FOR /=1 TO n DO
9c.2T. 1.1 temp <- 1/2 * H [i, i] * s [i]2
+ t H[l, j\*s\i]*sU\
9c.2T. 1.2 Afpred +- Afpred + temp
9c.2E ELSE (*шаг вдоль ломаной, вычислить sTLLTs*)
9c.2E.l FOR /=1 TO n DO
9c.2E. 1.1 temp «- £ U-1/, 4 * s W)
402 Приложение А.
9с.2Е. 1.2 Afpred «- bfpred + {temp * temp/2)
9с.З IF retcode Ф 2 AND ((| tfpred — А/1 < 0.1 * | А/1) OR
(Д/</ш7slope)) AND (Newttaken = FALSE) AND
(6<0.99*majcste/?)
9c.3T THEN
(* увеличить б вдвое и продолжить шаг
глобализации *)
Эс.ЗТЛ retcode «-3
Эс.ЗТ.2 x+prev<r-x+
9с.ЗТ.2 f+prev<-f+
9с.ЗТ.4 6 «- min {2*6, maxstep)
9с.ЗТ.5 /,l/+pr^^-FK+
(* RETURN для алгоритма A6.4.5*)
9c.3E ELSE
(* взять x+ в качестве нового приближения, выбрать
новое значение 6*)
Эс.ЗЕ.1 retcode*-0
9с.ЗЕ.2 IF steplen > 0.99 * maxstep THEN
maxtaken^- TRUE
9c.3E.3a IF &f>0.l*bfpred THEN 6«-6/2
(* уменьшить б для следующей итерации *)
9c.3E.3b ELSEIF А/< 0.75 * bfpred THEN
б <- min {2 * б, maxstep)
(* увеличить б для следующей итерации *)
(*9c.3E.3c ELSE б не меняется*)
(*END, операторы ELSE 9с.ЗЕ, ELSE 9с и множественного
ветвления 9*)
(* RETURN для алгоритма А6.4.5 *)
(♦END, алгоритм А6.4.5*)
Алгоритм А6.5.1 (NEMODEL).
Построение аффинной модели для нелинейных
уравнений
Назначение: Приводить факторизацию якобиана модели,
вычислять ньютоновский шаг и обеспечивать необходимой
информацией глобальный алгоритм. Если якобиан модели
вырожден или плохо обусловлен, то модифицировать его перед
вычислением ньютоновского шага, как описано в разд. 6.5
основного текста книги.
Входные параметры: /igZ,Fcg Rn(= F(хс))9 J<=Rnxn (=J(xc)
или ее апроксимации), g^ Rn(=JTD2FFc), Sp^Rny SX^R?>
mac heps e R, global e Z.
Входно-выходные параметры: отсутствуют.
Выходные параметры: Me=RnXn, H<=RnXn9 sN€=Rn.
Модульная система алгоритмов 403
Память:
1) Требуются два л-вектора дополнительной памяти для ЛИ
и М2.
2) Используются только верхняя треугольная часть и главна»
диагональ Н. Матрица Н может делить память с М, если внести
некоторые незначительные изменения в этот алгоритм (и в
другие), как объясняется в руководствах 6 и 3.
3) М используется в первой части данного алгоритма для
хранения <2/?-разложения DFJy как описывается в алгоритме АЗ.2.1.
На выходе при global = 2 или 3 ее нижняя треугольная часть и
главная диагональ содержат множитель L разложения Холес-
ского матрицы Я, формирующейся ниже на шагах 3 и 4. Если
global = 2, то эта же самая матрица содержится в верхней
треугольной части и главной диагонали параметра Н на выходе.
(Н может использоваться в пределах данного алгоритма
независимо от значения параметра global.)
Описание:
1) Вычислить (?/?-разложение DFJ. (D/? = diag((Si?)1, ..., {SP)n).}
2) Оценить в ^-норме число обусловленности RDx1. (Dx =
= diag((Sx)i, ...f (Sx)a).)
3) Если RDX l вырождена или плохо обусловлена, то положить
Н = JTD2FJ + л/п * macheps * \jTD2Fj\\ * D2X (см. разд. 6.5),
вычислить разложение Н по Холесскому, положить sN* H~lg$ где
g = J DpFcj и завершить работу алгоритма А.6.5.1.
4) Если RDx1 хорошо обусловлена, то вычислить sN* J"lFc.
Если global = 2 или 3, то записать RT в нижнюю треугольную
часть М. Если global = 2, то положить H = RTR. Завершить
работу алгоритма А6.5.1.
Алгоритм:
(*M^DFJ; DF = diag((SF){, ..., (SP)n)*)
1. FOR i=\ TO n DO
1.1 FOR /=1 TO n DO
M[l9 j]<-SF[i\*J[i, j]
2. CALL QRDECOMP (n, M, Ml, M2, sing)
(♦обратиться к алгоритму АЗ.2.1 для вычисления
(^-разложения М*)
3. IF NOT sing
ЗТ. THEN (* оценить xiCtfDJ1)*)
(*R+-RDx-1*)
3T.1 FOR /=1 TO n DO
3T.1.1 FOR /=1T0/-1 DO
M[i9 j]+-M[i,j]/Sx[j)
3T.1.2 M2[j]+-M2[j]/Sx[j]
3T.2 CALL CONDEST (n, Af, M2, est)
404 Приложение А.
(* обратиться к алгоритму АЗ.3.1 для оценки числа
обусловленности /?*)
ЗЕ. ELSE est*-0
4. IF (sing) OR (est > l/^/macheps)
4T. THEN (* внести возмущение в якобиан, как описано
в разд. 6.5*)
(*#WrD2,/*)
4Т.1 FOR /=1 ТО п DO
4Т.1.1 FOR / = / ТО п DO
H[i, j]+~t J[k,i]*J [k, J]]*SP [kf
(*на шагах 4T.2 —3 вычисляется Hnorm-*-\DxxHDxX\\*)
4T.2 Hnorm+-(l/Sx[l])* t (\H[l, /]|/S,[/])
/-i
4T.3 FOR 1 = 2 TO n DO
4T.3.1 temp+-(l/Sx[t\)*
{i(\H[i,i]\/sx[i\)+ t (\H[t,n\/sxu\)]
4T.3.2 Hnorm■«-max{temp, Hnorm)
(* H <- H + V» * macheps * Hnorm * D\ *)
4T.4 FOR i=\ TO n DO
H [i, i] ■*- H [I, i] + V" * macheps * Hnorm * Sx [i]2
(*на шагах 4T.5 —6 вычислить s^*- H~lg*)
4T.5 CALL CHOLDECOMP (n, H, 0, macheps, M, maxadd)
(♦ Алг. A5.5.2 *)
4T.6 CALL* СHOLSOLVE {n, g, M, %) (*алг. A3.2.3*)
4E. ELSE (* вычислить обычный ньютоновский шаг*)
(♦положить заново R+-RDX*)
4Е.1 FOR /=1 ТО n DO
4Е.1.1 FOR i=l ТО /-1 DO
M[i,j]*-M[i, j]*Sx[j]
4E.L2M2[j]«-M2[j]*Sx[j]
4E.2 sN< DP*FC
(*DF = diag((SP)u ..., (SP)n)*)
4E.3 CALL QRSOLVE (n, M, Ml, M2, sN)
(♦обратиться к алгоритму АЗ.2.2 для вычисления
M~lSff*)
4Е.4 IF (global = 2) OR (global = 3) THEN
(♦(нижняя треугольная часть M)-*-RT*)
4E.4.1 FOR /=1 TO n DO
4E.4.1.1 M[i, i]<-M2\i]
4E.4.1.2 FOR /= 1 TO/-1 DO
M[i, j]+-M[j, i]
Модульная система алгоритмов 405
4Е.5 IF global = 2 THEN
(*H+-LLT*)
4E.5.1 FOR i=\ TO n DO
4E.5.1.1 #[/, iJ«-E (Af[/, k]f
4E.5.1.2 FOR / = /+1 TO n DO
#[U]^£(M[/, £]*M [/.*])
(* RETURN для алгоритма Аб.5.1 *)
(*END, алгоритм A6.5.1 *)
Алгоритм A6.5.1fac (NEMODELFAC).
Построение аффинной модели для нелинейных
уравнений с привлечением факторизованных
формул секущих
Назначение: Этот алгоритм является модификацией алгоритма
А6.5.1, которая используется вместе с факторизованными
формулами секущих. Он отличается от алгоритма А6.5.1
главным образом в способе хранения Q/^-разложения
аппроксимации якобиана.
Входные параметры: «gZ, Fct=Rn{=F(хс))9 g<= Rn, SF e Rn,
Sx e Rnf macheps e R, global e Z, restart e Boolean.
Входно-выходные параметры: Mt=RnX'\ M2<=Rn, J<=RnXn.
Выходные параметры: H^RnXn, sN^Rn.
Память:
1) Требуется один n-вектор дополнительной памяти для Ml.
2) Используются только верхняя треугольная часть и главная
диагональ Я. Матрица Я может делить память с М, если внести
некоторые незначительные изменения в этот алгоритм, как
объясняется в руководствах 6 и 3.
3) В случае восстановления / содержит J(xc) на входе и QT
на выходе, где QR = DFJ(xc). В остальных случаях / содержит
QT на входе, где QR есть факторизованная аппроксимация
Df/(*c) по секущим, и не меняется данным алгоритмом.
Матрица М содержит R в своей верхней треугольной части на
выходе (иногда за исключением своей главной диагонали), а
также на входе (включая главную диагональ), если нет
восстановления. Если global =2 или 3, то главная диагональ и нижняя
треугольная часть М будет содержать на выходе ту же самую
матрицу L, что содержится в М на выходе алгоритма А6.5.1.
Если global == 2, то Я содержит ту же самую матрицу на
выходе, что содержится в Я на выходе алгоритма Аб.5.1.
Описание:
1) В случае восстановления вычислить (^-разложение DFJ,
размещая QT в / и R в М. {DF = diag((SP)lf ..., (SF)n).)
406 Приложение А.
2) Оценить в /(-норме число обусловленности матрицы RDX'.
<0, = diag((S,)„ .... (Sx)n).)
3) Если RDX' вырождена или плохо обусловлена, то положить
Я = RTDFR + У re * macheps ♦ ||RtDfR\i * lfx (см. разд. 6.5),
вычислить разложение Я по Холесскому, положить %•« Я_1£>
где g = RTQTDPFc, и завершить работу алгоритма А6.5.1 fac.
4) Если RDxl хорошо обусловлена, то вычислить sN ■*-
< /?-1Q DFFC. Если global = 2 или 3, то записать RT в
нижней треугольной части М. Если global = 2, то положить Я *- RTR.
Завершить работу алгоритма Аб.б.Иас.
Алгоритм:
1. IF restart
IT. THEN (* вычислить новое Qfl-разложение *)
(*M+-DFJ(xc); Z)F = diag((S„)„ ..., (Sf)„)*)
1T.1 FOR i=l TO n DO
1T.1.1 FOR /=1 TO n DO
M[i,j)^SF[i)*J[i,j]
1T.2 CALL QRDECOMP (re, Af, Ml, M2, sing)
(♦обратиться к алгоритму АЗ.2.1 для вычисления
Q/J-разложения М*)
1Т.З CALL QFORM (re, М, Ml, J)
(♦обратиться к алгоритму АЗ.4.2 для вычисления QT
и размещения ее в /*)
1Т.4 FOR i=\ ТО re DO
M[i,i]<-M2[i]
IE. ELSE (* проверить R на вырожденность*)
1Е.1 smg<- FALSE
1E.1 FOR t=l TO re DO
1E.2.1 IF M[i, /] = 0 THEN s/reg<-TRUE
2. IF NOT sing
2T. THEN (* оценить xi (flDJ1) *)
(*R^RD71*)
2T.1 FOR /=I TO ft DO
2T.1.1 FOR /= 1 TO /— 1 DO
M[l,n*-Mli,]]lSxU]
2T.\.2M2[j)^M2[j]/Sx[j)
2T.2 CALL CONDEST (n, M, M2, est)
(* обратиться к алгоритму АЗ.3.1 для оценки числа
обусловленности R ♦)
(♦положить заново R+-RDX*)
2Т.З FOR / = 1 ТО ft DO
2Т.3.1 FOR /'= 1 ТО /— 1 DO
M[i,j]<-M[i,j]*Sx[j]
2T.3.2 M2 [j] <- M2 [j] ♦ Sx [j]
Модульная система алгоритмов 407
2Е. ELSE est*-0
3. IF (sing) OR (est > U-y/macheps)
3T. THEN (* внести возмущение в якобиан, как описано
в разд. 6.5*)
(*H+-RTR*)
ЗТ.1 FOR t = l ТО п DO
ЗТ.1.1 FOR j = i ТО п DO
H[i,j]^giM[k,i]*M[k,j]
(*на шагах ЗТ.2 —3 вычислить Hnorm<-JDxlHDxlli*)
ЗТ.2 Hnorm^(l/Sx[l])*t(\H[l, Л1/5.Л/])
ЗТ.З FOR / = 2 ТО n DO"
3T.3.1 temp<-(l/Sx[i])*
{ I (|Я[/, <№(/])+ t (\H[i,j№x[j])}
ЗТ.3.2 И norm *- max {temp, Hnorm}
(* H+-H + -\/rt * macheps * Hnorm * D2X *)
3T.4 FOR /= 1 TO n DO
H [i, i] <- H{i, i] + V« * macheps * Hnorm * Sx [i]2
(*на шагах 3T.5 —6 вычислить sN*-H~lg*)
3T.5 CALL CHOLDECOMP (n, H, 0, macheps, M, maxadd)
(* алг. A5.5.2 *)
3T.6 CALL CHOL SOLVE (n, g, M, sN) (*алг. A3.2.3*)
3E. ELSE (* вычислить обычный ньютоновский шаг*)
(*sN< JDFFC; напомним, что / = Qr*)
ЗЕ.1 FOR /=1 TO n DO
%M< t(m, J]*SP[j]*Fc[!])
3E.2 CALL RSOLVE (n, M, M2, sN)
(*обратиться к алгоритму A.3.2.2 для вычисления R~lsN*)
ЗЕ.З IF (global = 2) OR (global = 3) THEN
(♦(нижняя треугольная часть M)-*-RT*)
3E.3.1 FOR t = 2 TO n DO
2E.3.1.1 FOR /=1 TO i-1 DO
M[i,j]+-M[j, i]
3E.4 IF global = 2 THEN
(*H+-LU*)
3E.4.1 FOR t=l TO n DO
3E.4.1.1 FOR j = i TO n DO
Я[/, Л^-Z (Af[/, *]*M[/, *])
(♦RETURN для алгоритма A6.5.1fac*)
(*END, алгоритм A6.5.1fac*)
408 Приложение А.
Алгоритм А7.2.1 (UMSTOP).
Критерии останова для безусловной минимизации
Назначение: Принимать решение, останавливать ли алгоритм
безусловной минимизации D6.1.1 по какой-либо из причин,
перечисленных ниже.
Входные параметры: «gZ, хс е Rn, x+^Rn, f ^R(=f (x+))9
ge=Rn(= v/ (*+)), Sx e= Rn, typf gee R, retcode e= Z, gradtol e R9
steptol e R, itncount e Z, itnlimit e Z, maxtaken e Boolean
Входно-выходные параметры: consecmax e Z.
Выходные параметры: termcode e Z.
Значения кодов возврата:
termcode = 0: не выполнен ни один из критериев останова;
termcode > 0: выполнен некоторый критерий останова, как
указано ниже:
termcode = 1: норма масштабированного градиента меньше,
чем gradtol; х+, вероятно, является приближенно точкой
локального минимума f(x) (если значение gradtol не
слишком велико);
termcode = 2: масштабированное расстояние между
последними двумя шагами меньше, чем steptol; #+ может
оказаться приближенно точкой локального минимума f(x),
но возможно также то, что алгоритм продвигается очень
медленно и что он не находится вблизи от точки
минимума или что значение steptol слишком велико;
termcode = 3: на последнем шаге глобализации не удалось
найти точку со значением целевой функции, меньшим, чем
в хс; либо Хс является приближенно точкой локального
минимума и невозможно достичь более высокой точности,
либо используется неточно запрограммированный
аналитический градиент, либо конечно-разностная
аппроксимация градиента слишком неточна, либо значение steptol
слишком велико;
termcode = 4: превышен лимит на число итераций;
termcode = 5: было сделано последовательно пять шагов
длиной maxstep; либо f(x) не ограничена снизу, либо
/ (лж) имеет конечную асимптоту в некотором направлении,
либо значение maxstep слишком мало.
Память:
1) Не требуется никакой дополнительной памяти под векторы
и матрицы.
Описание:
Параметр termcode полагается равным 1, 2, 3, 4 или 5, если
выполнено соответствующее приведенное выше условие; если ни
Модульная система алгоритмов 409
одно из этих условий не выполнено, то termcode ^-0. Кроме
того, если maxtaken = TRUE, то consecmax увеличивается на
единицу, в противном случае consecmax полагается равным
нулю.
Алгоритм:
1. termcode <- 0
2а. IF retcode=l THEN termcode<-3
( r max { I x. [i] I, 1/S [i]\ )
2b. ELSEIF ,»« {1.И1 iL||/|'w? '}<
^gradtol THEN termcode <-\
(* это максимальная компонента масштабированного
градиента; см. разд. 7.2. ПРЕДОСТЕРЕЖЕНИЕ: если
значение typf слишком велико, то алгоритм может завершить
работу преждевременно *)
2с. ELSEIF max { тяJ^ln'ws \т }<steptol THEN
termcode <- 2
(* это максимальная компонента масштабированного
шага; см. разд. 7.2*)
2d. ELSEIF itncount^itnlimit THEN termcode+-4
2e. ELSEIF maxtaken = TRUE THEN
(* был сделан шаг длиной maxstep; при желании вывести
на печать это сообщение*)
2е. 1 consecmax <- consecmax + 1
2е.2 IF consecmax = 5 THEN termcode+-5
(♦ограничение в пять шагов максимальной длины
совершенно произвольно и может быть изменено заменой этого
оператора *)
21. ELSE consecmax<-0
(* END для оператора множественного ветвления 2 *)
(* при желании в этом месте вывести на печать
соответствующее сообщение об окончании, если termcode > 0 *)
(* RETURN для алгоритма А7.2.1 *)
(*END, алгоритм А7.2.1 *)
Алгоритм А7.2.2 (UMSTOP0).
Критерии останова для безусловной минимизации
перед начальной итерацией
Назначение: Решать, завершать ли работу алгоритма D6.1.1
перед начальной итерацией по причине того, что хо является
приближенно стационарной точкой для f(x).
410 Приложение А.
Входные параметры: AteZ, x0^Rn, f^R(=f(x0)), gG
^flrt(=V/(*0)), Sx<=Rn, typfe=R, gradtol(=R.
Входно-выходные параметры: отсутствуют.
Выходные параметры: termcode е Z, consecmax е Z.
Значения кодов возврата:
termcode = 0: хо не является приближенно критической
точкой для f(x);
termcode == 1: jco является приближенно критической точкой
для f{x).
Память:
1) Не требуется никакой дополнительной памяти под векторы
и матрицы.
Примечания:
1) Если termcode = 1, то возможно, что х0 является
приближенно точкой максимума или седловой точкой f(x). Это можно
определить путем выяснения, является ли V2/(x0) положительно
определенной. В случае отрицательного ответа алгоритм D6.1.1
может быть запущен заново из некоторой точки вблизи хо.
Тогда, вероятнее всего, он будет сходиться опять к х0, лишь если
хо является приближенно точкой локального минимума f(x).
Описание:
Значение termcode полагается равным 1, если абсолютная
величина максимальной по модулю компоненты
масштабированного градиента оказывается меньше, чем \0r**gradtoL (Перед
начальной итерацией используется более строгий допуск на
величину градиента.) В противном случае termcode -<-0.
Алгоритм:
1. consecmax <- 0
(* consecmax будет использоваться алгоритмом А7.2.1 для
проверки на расходимость; он содержит число последних
последовательно сделанных шагов, масштабированная длина
которых была равна maxstep*)
2. IF ™|||И1'=||Ю»1К'Л«
THEN termcode<-1
(* при желании вывести соответствующее сообщение
об окончании *)
ELSE termcode*-0
(* RETURN для алгоритма А7.2.2 *)
(*END, алгоритм А7.2.2*)
Модульная система алгоритмов 411
Алгоритм А7.2.3 (NESTOP).
Критерии останова для нелинейных уравнений
Назначение: Решать, завершать ли работу алгоритма решения
нелинейных уравнений D6.1.3 по какой-либо из причин,
перечисленных ниже.
Входные параметры: n<=Z, хсе= Rn9 х+ е /?*, FgRn(= F(#+)),
Fnorm s R (= (l/2)\\DpF (x+) |), g e Rn (= /^F+), Sx e= Rn,
SF^Rn, retcode^Z, fvectol^R, steptol ^R, itncount^Z,
itnlimit e Z, maxtaken e Boolean, analjac e Boolean, cheapF^
e Boolean, mintol e R.
Входно-выходные параметры: consecmax e Z.
Выходные параметры: termcode e Z.
Значения кодов возврата:
termcode = 0: не выполнен ни один из критериев останова;
termcode > 0: выполнен некоторый критерий останова, как
указано ниже:
termcode =1: норма масштабированного значения функции
меньше, чем fvectol; х+, вероятно, является приближенно
корнем F(x) (если значение fvectol не слишком велико);
termcode = 2: масштабированное расстояние между
последними двумя шагами меньше, чем steptol; х+ может
оказаться приближенно корнем F(x)> но возможно также,
что алгоритм продвигается очень медленно, не находится
вблизи корня, или значение steptol слишком велико;
termcode = 3: на последнем шаге глобализации не удалось
в достаточной степени уменьшить ||F(x)||2; либо хс близко
к корню F(x) и невозможно достичь более высокой
точности, либо используется неточно запрограммированный
аналитический якобиан, либо неточна аппроксимация
якобиана по секущим, либо значение steptol слишком велико;
termcode = 4; превышен лимит на число итераций;
termcode = 5: было сделано последовательно пять шагов
длиной maxstep; либо Ц/7(л:) ||2 асимптотически
приближается сверху к конечному значению в некотором
направлении, либо значение maxstep слишком мало;
termcode = 6: хс> по-видимому, является приближенно
точкой локального минимума ||F(jc)||2, которая не есть корень
F(x) (или значение mintol слишком мало); для
нахождения корня F(x) алгоритм должен быть запущен вновь из
другой области.
Память:
1) Не требуется никакой дополнительной памяти под векторы
и матрицы.
412 Приложение А.
Описание:
Параметр termcode полагается равным 1, 2, 3, 4, 5 или 6, если
выполнено соответствующее приведенное выше условие; если
ни одно из этих условий не выполнено, то termcode ^-0. Кроме
того, если maxtaken = TRUE, то consecmax увеличивается на
единицу, в противном случае consecmax полагается равным
нулю.
Алгоритм:
1. termcode <- О
2а. IF retcode=\ THEN termcode «-3
2b. ELSEIF max {SP[i] *\F[i\\}^fvectol THEN termcode*-I
(* это максимальная компонента масштабированного
значения функции; см. разд. 7.2*)
2с. ELSEIF max ( „Jn^Tu^mx ]<steptol THEN
l<i<n I max {I x+ M |, \/Sx [i]} J ^ r
termcode <- 2
(* это максимальная компонента масштабированного
шага; см. разд. 7.2*)
2d. ELSEIF itncount^itnlimit THEN termcode«-4
2e. ELSEIF maxtaken = TRUE THEN
(* был сделан шаг длиной maxstep; при желании вывести
на печать это сообщение*)
2е. 1 consecmax +- consecmax + 1
2е.2 IF consecmax = 5 THEN termcode <- 5
(* ограничение в пять шагов максимальной длины
совершенно произвольно и может быть изменено заменой этого
оператора *)
2f. ELSE
2f.l consecmax <- О
2f.2 IF analjac OR cheap? THEN
SU.1 ,F max {,гт£^£'Щ}<тШЫ™ВН
1</<л1 max(rnorm, n/2] )
termcode <r- 6
(♦проверка на локальный минимум ||F(*)ll2
опускается при использовании методов секущих,
поскольку в этом случае g может не быть
точным *)
(• END, оператор множественного ветвления 2 *)
(♦при желании вывести здесь соответствующее сообщение об
окончании, если termcode > О*)
(* RETURN для алгоритма А7.2.3 *)
(* END, алгоритм А7.2.3 •)
Модульная система алгоритмов 413
Алгоритм А7.2.4 (NESTOP0).
Критерии останова для нелинейных уравнений
перед начальной итерацией
Назначение: Решать, завершать ли работу алгоритма D6.1.3
перед начальной итерацией по причине того, что х0 является
приближенно корнем F(x).
Входные параметры: «GZ.jcoG^fe Rn(=F(x0))f SF е Rn,
fvectol e R.
Входно-выходные параметры: отсутствуют.
Выходные параметры: termcode е Z, consecmax е Z.
Значения кодов возврата:
termcode = 0: х0 не является приближенно корнем F(x)\
termcode = 1: х0 является приближенно корнем F(x).
Память:
1) Не требуется никакой дополнительной памяти под векторы
и матрицы.
Описание:
Значение termcode полагается равным 1, если абсолютная
величина максимальной по модулю компоненты
масштабированного значения функции меньше, чем 10~2 *fvectol. (Перед
начальной итерацией используется более строгий допуск на
величину функции.) В противном случае termcode •<- 0.
Алгоритм:
1. consecmax «- 0
(♦параметр consecmax будет использоваться алгоритмом
А7.2.3 для проверки на расходимость; он содержит число
последних последовательно сделанных шагов,
масштабированная длина которых была равна maxstep*)
2. IF max {SP[i\ *|F[/]|}< Ю'2* fvectol
THEN termcode*-I
(♦при желании вывести соответствующее сообщение
об окончании ♦)
ELSE termcode*-О
(* RETURN для алгоритма А7.2.4 ♦)
(♦ END, алгоритм А7.2.4 ♦)
414 Приложение А.
Алгоритм А8.3.1 (BROYUNFAC).
Формула пересчета Бройдена, нефакторизованная
форма
Назначение: Производить пересчет А по формуле
Л+~Л+ sTtfxS •
где s = x+— хС9 y = F+ — Fc, пропуская всю или часть
формулы пересчета при выполнении условий, описанных ниже.
Входные параметры: nsZ,xcsRn, х+ еRn, Fc^Rn(=F(хс)),
F+ s=Rn(=F(*+)), т|€#, S,gRn(Dx = diag((Sx)l9 ...,(Sx)n)).
Входно-выходные параметры: A^RnXn.
Выходные параметры: отсутствуют.
Память:
1) Требуется один n-вектор дополнительной памяти для s.
2) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководстве 6.
Описание:
Для каждой /-й строки пересчет i-й строки производится, если
| (у— As) [i] | не оказывается меньше, чем оценка уровня шума
в у[i], которая равна rj*(|F+ [i] \ + \Fc[i]\).
Алгоритм:
1. s<-x+ --хс
2. denom<-\\Dxs\%
(*Dx = diag({Sx)iy •••> (Sx)n) хранится как Sx^Rn.
Относительно предлагаемой программой реализации выражений,
содержащих Dx. см. разд. 1.5 настоящего приложения. *)
3. FOR i=l ТО п DO
(* tempi <- (у — As) [i] *)
3.1 tempi^F+ И - FM - £ A [/, /] * 5 [/]
3.2 IF | tempi \>i\*(\F+[l]\ +1 Fe [i] I) THEN
(* произвести пересчет /-й строки *)
3.2.1 tempi ^-tempijdenom
3.2.2 FOR /=1 TO n DO
A [/, Я +- A [/, /J + tempi * s [/] * Sx [j]2
(♦RETURN для алгоритма А8.3Л *)
(* END, алгоритм A8.3.1 *)
Модульная система алгоритмов 415
Алгоритм А8.3.2 (BROYFAC).
Формула пересчета Бройдена, факторизованная форма
Назначение: Пересчитывать Q/^-факторизацию матрицы Л,
аппроксимирующей DFJ(xc)y в факторизацию вида Q+R+
матрицы
(Dpy-As)(Dxs)T
"*" sTI?xs
аппроксимирующей DFJ (х+), где s = х+ — хс, у = F+ — Fc,
пропуская всю или часть формулы пересчета при
выполнении условий, описанных ниже.
Входные параметры: «gZ, хс еRn, х+ е Rn, Fc ^Rn(=F(хс)),
F+ s=Rn(=F(х+)),r\e=R,Sxe=Rn(Dx = diag((Sx)l9 ....(Sx)n))9
SFt=Rn(DF = diag((SF)ly ..., (SF)n)).
Входно-выходные параметры: Z e RnXn (содержит QT на входе,
Q^ на выходе), M^Rnxn (верхняя треугольная часть и
главная диагональ М содержит R на входе, /?+ на выходе),
М2 е Rn (содержит главную диагональ R на входе, главную
диагональ 7?+ на выходе).
Выходные параметры: отсутствуют.
Память:
1) Требуются три /г-вектора дополнительной памяти для 5. t
и w.
2) Первая нижняя поддиагональ Му а также ее верхняя
треугольная часть, включая главную диагональ, используются на
промежуточных этапах данного алгоритма.
3) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководстве 6.
Описание:
1) Переписать М2 на главную диагональ М.
2) s •<- х+ — Хс-
3) Вычислить / = Rs.
4) Вычислить w = DFy — As = DFy — ZTt. £сли | w [i] | меньше,
чем оценка уровня шума в DFy[i], измеряемого величиной
r\*DF[i]*(\F+[i] \~\-\Fc[i] |), то w[i] полагается равным нулю.
5) Если w = 0, то пересчет не производить. В противном случае:
5а) Положить / = QTw = Zw9 s = DxsjsTDxsy
5b) Обратиться к алгоритму АЗ.4.1 для пересчета Q/J-раз-
ложения матрицы А в разложение вида Q+R+ матрицы
Q(R + tsT)
5с) Переписать новое значение диагонали М в М2.
416 Приложение А.
Алгоритм:
1. FOR /=1 ТО п DO
M[i,i)<-M2[i]
2. s •*- х+ — хе
3. skipupdate*- TRUE
(*t *-Rs:*)
4. FOR /=1 TO n DO
t[i]^^M[i,i]*s[j]
5. FOR 1=1["TO n DO
(* ш [i] +-(DPy-Z4 [/]:*)
5.1 H/J^SH^M'J-SH^J'l-^Zf/, ']*'[/]
5.2 IF w [i] > n * SP [i\ * (| F+ [/] | +1 Fe [iff)
THEN skipupdate*-FALSE
ELSE шИ«-0
6. IF skipupdate = FALSE THEN
(*/«-Z*a>:*)
6.1 FOR /=1 TO n DO
6.2 А?яо/п «HI AtS|g
(♦Dj^diagftS*)! (S*)n)) хранится как Sx s/?n.
Относительно предлагаемой программой реализации
выражений, содержащих Dx, см. разд. 1.5 настоящего
приложения *)
6.3 s*-Dl*s/denom
6.4 CALL QRUPDATE (п, t, s, 1, Z\ M) (*алг. A3.4.1*)
6.5 FOR i=lTO n DO
A*2[t]«-M[i, i]
(* RETURN для алгоритма A8.3.2 *)
(*END, алгоритм A8.3.2*)
Алгоритм A9.4.1 (BFGSUNFAC).
Положительно определенная формула секущих
(BFGS), нефакторизованная форма
Назначение: Пересчитывать Н по BFGS-формуле
„ „ HssTH , уут
s Hs у' S
где s = х+ — хс, y = g+— gc, пропуская пересчет в случае
выполнения условий, сформулированных ниже.
Модульная система алгоритмов 417
Входные параметры: п <= Z, хс <= Rn, х+ е= /?*, gc е #Л, g+ е Rn,
macheps^R, r\^R, analgrad e Boolean (=TRUE, если
используется аналитический градиент, FALSE в противном
случае).
Входно-выходные параметры: симметричная Яе/?ЛХЛ.
Выходные параметры: отсутствуют.
Память:
1) Требуются три л-вектора дополнительной памяти для s>y и /.
2) Используется только верхняя треугольная часть Я, включая
главную диагональ. (Это — единственные компоненты Я, к
которым обращается остальная часть системы алгоритмов.)
3) Если преследуется цель более экономного отношения к
памяти под матрицы, то данный алгоритм следует незначительно
модифицировать, как объясняется в руководстве 3.
Описание:
Указанный выше пересчет не производится, если либо i) yTs <
<.(macheps)l/2\\s\\2\\y\\2> либо ii) для каждого I величина
| (у — Hs) [i] | меньше, чем оценка уровня шума в y[i]. Оценка
уровня шума вычисляется по формуле tol*(\gc[i] \ + \g+[i] |),
где tol = т), если используются аналитические градиенты, tol =
= т)1/2, если используются конечно-разностные градиенты.
Алгоритм:
1 • 5 ^ X + •— Xq
2. y<-g+—gc
3. tempi ■*- yTs
4. IF tempi ^(macheps)112* ||s||2* ||у ||2 THEN
(* ELSE пересчет не производится, и алгоритм завершает
работу *)
4.1 IF analgrad = TRUE
THEN tol4-r\
ELSE *о/«-л1/2
4.2 skipupdate*- TRUE
4.3 FOR i=l TO n DO
(*t[i\^Hs[i\:*)
4.3.1 /и«-£н[j, i]*s[j]+ £ H[i, m*s[i]
/-1 l-i+i
4.3.2 IF | у [i] -1И | > tol * max {| gc Щ |, \ g+ ИI} THEN
skipupdate <- FALSE
4.4 IF skipupdate = FALSE THEN
(* произвести пересчет; ELSE пересчет не производится,
и алгоритм завершает работу*)
4.4.1 temp2*-sTt (*sTHs*)
418 Приложение А.
4.4.2 FOR t=l ТО n DO
4.4.2.1 FOR / = / TO n DO
Hit, /]<-#[*, /1 + -JJ— j—^
(* END, операторы IFTHEN 4.4 и IFTHEN 4 *)
(♦RETURN для алгоритма A9.4.1*)
(* END, алгоритм A9.4.1 *)
Алгоритм A9.4.2 (BFGSFAC).
Положительно определенная формула секущих
(BFGS), факторизованная форма
Назначение: Пересчитывать L/Лфакторизацию матрицы Н
в факторизацию вида L+L+ матрицы
s Hs у s
где
s — x+ — xe, y = g+—gc,
/ = L+(£-g//s)(aZ.V) а=(4±Л1'2,
yls \slHsJ
используя алгоритм АЗ.4.1 для вычисления Q/^-факторизации
матрицы F за 0(п2) операций. Пересчет не производится
в случае выполнения условий, сформулированных ниже.
Входные параметры: п е Z, хс е Rn, х+ е Rn, gc е Rn, g+ е Rnt
macheps g/{, r\ e /?, analgrad e Boolean (= TRUE, если
используется аналитический градиент, FALSE в противном
случае).
Входно-выходные параметры: М ei?nxn (нижняя треугольная
часть и главная диагональ М содержат L на входе, L+ на
выходе) .
Выходные параметры: отсутствуют.
Память:
1) Требуются четыре n-вектора дополнительной памяти для s,
у, t и и. Этот объем может быть уменьшен до двух векторов
простой заменой t на s и и на у во всех их вхождениях в
приведенном ниже алгоритме. (То есть t и и используются только
для того, чтобы сделать алгоритм более простым для
понимания.)
2) На промежуточных этапах данного алгоритма используется
вся матрица Л1, хотя на входе в алгоритм и на выходе из него
Модульная система алгоритмов 419
необходимы только ее нижняя треугольная часть и главная
диагональ.
3) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководстве 3.
Описание:
1) Если yTs <.(macheps)l/2\\s\\2\\y\\2 или если для каждого i
величина | {у — LLTs) [i] | оказывается меньше, чем оценка уровня
шума в y[i], то пересчет не производится. Оценка уровня шума
в y[i\ вычисляется по формуле tol* (\gc[i]\ + |g+M[), где tol =
= т) в случае использования аналитических градиентов и tol =
= т]1/2, если используются конечно-разностные градиенты.
2) Если должен производиться пересчет, то вычисляются
и = LTs/^yTs*sTLLTs nt — y — aLUs, и LT копируется в
верхнюю треугольную часть М. Затем вызывается алгоритм АЗ.4.1,
возвращающий в верхнюю треугольную часть М значение
матрицы /?+, для которой R+R+ = (L + tuT) {LT + uf). Затем R\
копируется в нижнюю треугольную часть М и возвращается как
новое значение L+.
Алгоритм:
1. s<-x+ — хс
2. y<-g+~gc
3. tempi <-yTs
4. IF tempi > (macheps)112 * ||51|2 * ||у ||2 THEN
(*ELSE пересчет не производится, и алгоритм завершает
работу *)
(*t+-LTs:*)
4.1 FOR i=l ТО п DO
/[/]^ZM[/, i]*s[j]
4.2 temp2!<-ltTt (* = sTLLTs*)
4.3 a^-^templ/temp2 (* = *JyTs/srLLTs *)
4.4 IF armlgrad = TRUE
THEN tol*-r\
ELSE /о/ч-п1/2
4.5 skipupdate<-TR\JE
4.6 FOR /=1 TO n DO
(*temp3+-{LLTs)[i]:*)
4.6.1 /бтпрЗ«-£Л1[/, f\*t[j]
4.6.2 IF|у [i] -~temp3\>tol* max {| gc[/] |, |g+ [i] |} THEN
skipupdate <- F AL S E
4.6.3 и И <- у [i] - a * tempS
420 Приложение А.
4.7 IF skipupdate = FALSE THEN
(♦произвести пересчет; ELSE пересчет не производится,
и алгоритм завершает работу*)
4.7.1 tempi <- I/л/tempi * tempi
(* = l/<y/yTs*sTLLTs*)
АЛ.2 FOR /=1 ТО п DO
t\i)*~temp3*t[i]
(* скопировать U в верхнюю треугольную часть М: *)
4.7.3 FOR / = 2 ТО п DO
4.7.3.1 FOR /=1 ТО 1-Х DO
Af [/.(]«-Л! [/,/]
(* обратиться к алгоритму АЗ.4.1 для вычисления Q/J-раз-
ложения матрицы LT + utT: *)
4.7.4 CALL QRUPDATE (я, /, а, 2, М, М)
(* второе Af является фиктивным параметром *)
(* скопировать транспонированную верхнюю треугольную
часть М в М: *)
4.7.5 FOR / = 2 ТО п DO
4.7.5.1 FOR /=1 ТО /- 1 DO
M[i,j]+-M[j,i]
(* END, операторы IFTHEN 4.4 и IFTHEN 4 *)
* RETURN для алгоритма А9.4.2 *)
* END, алгоритм А9.4.2 *)
Алгоритм А9.4.3 (INITHESSUNFAC).
Начальное значение гессиана для формулы
секущих в нефакторизованной форме
Назначение: Полагать Я = max {| / (х0) |, typf) * Z^, где Dx =
= diag((S^)1, ..., (Sx)n).
Входные параметры: /igZ, f^R(=f(x0)), typf^R, Sx^Rn.
Входно-выходные параметры: отсутствуют.
Выходные параметры: симметричная H^Rnxn.
Память:
1) Не требуется никакой дополнительной памяти под векторы
и матрицы.
2) Используется только верхняя треугольная часть Я, включая
главную диагональ. (Это — единственные компоненты Я, к
которым обращается остальная часть системы алгоритмов.)
3) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководстве 3.
Модульная система алгоритмов 421
Алгоритм:
1. temp<- max {|/|, typf)
2. FOR i=\ TO n DO
2.1 H [i, i] +- temp * Sx \i) * Sx [/]
2.2 FOR / = /+1 TO n DO
H[i9 л*-о
(* RETURN для алгоритма A9.4.3 *)
(* END, алгоритм A9.4.3 *)
Алгоритм A9.4.4 (INITHESSFAC).
Начальное значение гессиана для формулы
секущих в факторизованной форме
Назначение: Полагать L = max {| f (*0) |, typf}*Dxf где
Dx = Aiag((Sx)l9 ..., (Sx)n).
Входные параметры: /ieZ, f^R(=f(x0)), typf^R, Sx^Rn.
Входно-выходные параметры: отсутствуют.
Выходные параметры: нижняя треугольная L е RnXn.
Память:
1) Не требуется никакой дополнительной памяти под векторы
и матрицы.
2) Используется только нижняя треугольная часть L, включая
главную диагональ.
3) Этот алгоритм не меняется при использовании экономичного
способа хранения матриц, описанного в руководстве 3.
Алгоритм:
1. temp +-(max{|/|, typf})1'2
2. FOR i=\ TO n DO
2.1 H[i9 i]<-temp*Sx[i\
2.2 FOR /=1 TO /-1 DO
L[l9i\+-0
* RETURN для алгоритма A9.4.4 *)
* END, алгоритм A9.4.4*)
Приложение В.
Тестовые задачи1)
Тестовые задачи обсуждаются в разд. 7.3, так что
интересующемуся этим предметом читателю следует ознакомиться с
разд. 7.3, прежде чем приступать к настоящему приложению.
Морэ, Гарбов и Хиллстром (1981) дают набор приблизительно
из 15 тестовых задач, каждая из которых подходит для
безусловной минимизации, решения систем нелинейных уравнений
и нелинейных задач о наименьших квадратах. Многие из этих
задач можно решать на ЭВМ с различными значениями п. Для
каждой задачи дается начальная точка x0i и большинство
рассчитано на то, чтобы начинать также из 10 *лг0 и 100**0. Таким
образом, число возможных задач, предоставленных Морэ, Гар-
бовом и Хиллстромом, в действительности достаточно велико.
Ниже приводится небольшое их подмножество, которые можно
использовать для тестирования в учебных проектах или для
тестирования нового метода на самой ранней стадии. Всем, кто
заинтересован во всестороннем тестировании, настоятельно
рекомендуется прочитать работу Морэ, Гарбова и Хиллстрома, а
также рекомендуется использовать более широкий набор
содержащихся там тестовых задач. Хайберт (1982) дает
сравнительный анализ программ решения систем нелинейных уравнений,
используя тестовые задачи из работы Морэ, Гарбова и
Хиллстрома, и делает предложения по модификации этих задач,
приводящей к задачам с плохой обусловленностью или к задачам
с зашумленной функцией.
Приведенные ниже задачи 1—4 являются стандартными
тестовыми задачами как для нелинейных уравнений, так и для
безусловной минимизации. В каждом случае задается п
скалярных функций от п неизвестных, fi(x), i = 1, ..., п.
Вектор-функцией в нелинейных уравнениях служит
F(x) = \ ... •
1) Автор — P. Шнабель.
Тестовые задачи 423
тогда как целевой функцией для безусловной минимизации
служит
f(x)=tft(*)2.
Задачи 1—3 могут быть просчитаны на ЭВМ с различными
значениями п. Стандартными размерностями для задач 1 и 2
являются соответственно п = 2 и п = 4, причем с них следует
начинать тестирование. Приемлемым первым вариантом для
задачи 3 является я = 10. Задача 5 представляет собой трудную
тестовую задачу, которая зачастую используется только для
безусловной минимизации.
Следуя Морэ, Гарбову и Хиллстрому, мы приводим для
каждой задачи: а) размерность п\ Ь) нелинейную функцию
(функции); с) начальную точку х0\ d) корень и точку минимума **,
если имеется их точное значение. Минимальное значение f(x)
равно нулю во всех случаях. Решение этих задач можно
начинать из jto, 10*Jt0 или 100*л'0. Ссылку на оригинальный
источник для каждой задачи можно найти в работе Морэ, Гарбова и
Хиллстрома.
1) Расширенная функция Розенброка
a) п — любое положительное целое, кратное 2;
b) для /= 1, ..., я/2:
f«-i W-10(*»-*2i-i).
/2/ (х)= 1 -~x2i-\>
c) *0 = (-1.2, 1, ..., -1.2, 1);
d)*. = (l,l, ..., 1, 1).
2) Расширенная обобщенная функция Пауэлла
a) я — любое положительное целое, кратное 4;
b) для /= 1, ..., л/4:
?41-г (х) = X4iJ=3 + Ю*4*-2>
f«-2(*) = V6 (*«-!—*«).
/4;_1 (х) = (*4*-2 "~ %x4i-\) ,
M*) = VTo(*4,_3--*4*)2;
c) *0 = (3, -U 0, 1, ..., 3, -1, 0, 1);
d) *. = (0, 0, 0, 0, ..., 0, 0, 0, 0);
замечание: F'(x9) и V2/(*J вырождены.
3) Тригонометрическая функция
a) л — любое положительное целое;
b) для 1=1, ..., п:
п
fAx) = n— 2 (cos х\ + * (1 — cos xt) — si*1 xi)>
/-1
c) xo = (l/n, l/n, ..., l/n).
424 Приложение В.
4) Функция типа спиралевидного желоба
a) п = 3;
b) Ы*)=10(*3-10е(*„ *2».
f2(*)=10((*2 + 4)I,2-l)>
где
в fa, лег) = (1/2я) arctg (jCjj/jc,) при дс, > О,
в (хи х2) = (1/2я) arctg (x^i) + 0.5 при хх < 0;
c) *о = (-1, 0, 0);
d)*. = (l, О, 0).
5) Функция Вуда
a) л = 4;
b) / (*) = 100 (*» _*,)» + (1 _ х,)» + 90 (*» - *4)* +
+ (1 - x3f + ЮЛ ((1 - д^)2 + (1 - j^)2) +
+ 19.8(1-*2)(l-*4);
c) *0 = (-3, -1,-3, -I);
d) *. = (!, 1, 1, 1).
ЛИТЕРАТУРА
Асен (Aasen J. О.)
(1971) On the reduction of symmetric matrix to tridiagonal form, BIT 11,
233—242.
Авриель (Avriel M.)
(1976) Nonlinear Programming: Analysis and Methods, Prentice-Hall,
Englewood Cliffs, N. J.
Алговер, Джордж (Allgower E., Georg K.)
(1980) Simplicial and continuation methods for approximating fixed points
and solutions to systems of equations, SIAM Review 22, 28—85.
Армийо (Armijo L.)
(1966) Minimization of functions having Lipschitz-continuous first partial
derivatives, Pacific J. Math. 16, 1—3.
Ахо, Хопкрофт, Ульман (Aho A. U., Hopcroft J. E., Ullman J. D.)
(1974) The Design and Analysis of Computer Algorithms, Addison-Wesley,
Reading, Mass. [Имеется перевод: Ахо А., Хопкрофт Дж., Ульман Дж.
Построение и анализ вычислительных алгоритмов. — М.: Мир, 1979.]
Бакли (Buckley A. G.)
(1978) A combined conjugate gradient quasi-Newton minimization
algorithm, Math. Prog. 15, 200—210.
Банч, Парлетт (Bunch J. R., Parlett B. N.)
(1971) Direct methods for solving symmetric indefinite systems of linear
equations, SIAM J. Numer. Anal. 8, 639—655.
Бард (Bard Y.)
(1970) Nonlinear Parameter Estimation, Academic Press, New York.
Барнес (Barnes J.)
(1965) An algorithm for solving nonlinear equations based on the secant
method, Comput. J. 8, 66—72.
Бартелс, Конн (Bartels R., Conn A.)
(1982) An approach to nonlinear /t data fitting, in Numerical Analysis,
Cocoyoc 1981, ed. by Hennart J. P., Springer-Verlag, Lecture Notes in
Math. 909, 48—58.
Бейтс, Уотте (Bates D. M., Watts D. G.)
(1980) Relative curvature measures of nonlinearity, J. Roy. Statist. Soc.
Ser. В 42, 1—25, 235.
Бил (Beale E. M. L.)
(1977) Integer programming, in The State of the Art in Numerical
Analysis, ed. by Jacobs D., Academic Press, London, 409—448.
Битон, Тыоки (Beaton A. E., Tukey J. W.)
(1974) The fitting of power series, meaning polynomials, illustrated on
hand-spectroscopic data, Technometrics 16, 147—192.
Боггс, Дэннис (Boggs P. Т., Dennis J. E., Jr.)
(1976) A stability analysis for perturbed nonlinear iterative methods, Math.
Сотр. 30, 1—17.
Брайян (Bryan С. A.)
(1968) Approximate solutions to nonlinear integral equations, SIAM J.
Numer. Anal, 5, 151—155.
Брент (Brent R. P.)
(1973) Algorithms for Minimization without Derivatives, Prentice-Hall,
Englewood Cliffs, N. J.
Бродли (Brodlie K. W.)
(1977) Unconstrained minimization, in The State of the Art in Numerical
Analysis, ed. by Jacobs D., Academic Press, London, 229—268.
426 Литература
Бройден (Broyden С. G.)
(1965) A class of methods for solving nonlinear simultaneous equations,
Math. Сотр. 19, 577—593.
(1969) A new double-rank minimization algorithm, AMS Notices 16, 670.
(1970) The convergence of a class of double-rank minimization algorithms,
Parts I and II, J. I. M. A. 6, 76—90, 222—236.
(1971) The convergence of algorithm for solving sparse nonlinear sys
terns, Math. Сотр. 25, 285—294.
Бройден, Дэннис, Морэ (Broyden С. G., Dennis J. E., Jr., More J. J.)
(1973) On the local and superlinear convergence of quasi-Newton methods,
J. I. M. A. 12, 223—246.
Вандерграфт (Vandergraft J. S.)
(1978) Introduction to Numerical Computations, Academic Press, New
York.
Вольф (Wolfe P.)
(1969) Convergence conditions for ascent methods, SIAM Review 11, 226—
235.
(1971) Convergence conditions for ascent methods. II: Some corrections,
SIAM Review 13, 185—188.
Гандер (Gander W.)
(1978) On the linear least squares problem with a quadratic constraint,
Stanford Univ. Computer Science Tech. Rept. STAN-CS-78-697, Stanford,
Calif.
(1981) Least squares with a quadratic constraint, Numer. Math. 36, 291—
307. [Это сокращенная версия работы Гандер (1978).]
Гарфинкель, Немхаусер (Garfinkel R. S., Nemhauser G. L.)
(1972) Integer Programming, John Wiley & Sons, New York.
Гилл, Голуб, Мюррей, Сондерс (Gill P. E., Golub G. H., Murray W.,
Saunders M. A.)
(1974) Methods for modifying matrix factorizations, Math. Сотр. 28,
505 535
Гилл, Мюррей (Gill P. E., Murray W.)
(1972) Quasi-Newton methods for unconstrained optimization, J. I. M. A.
9, 91—108.
Гилл, Мюррей, Райт (Gill P. E., Murray W., Wright M. H.)
(1981) Practical Optimization. Academic Press, London. [Имеется перевод:
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. —- М.: Мир,
1985.]
Голдстейн (Goldstein А. А.)
(1967) Constructive Real Analysis, Harper & Row, New York.
Голдфарб (Goldfarb D.)
(1970) A family of variable metric methods derived by variational means,
Math. Сотр. 24, 23—26.
(1976) Factorized variable metric methods for unconstrained optimization,
Math. Сотр. 30, 796—811.
Голдфельд, Куанд, Троттер (Goldfeldt S. M., Quandt R. E., Trotter H. F.)
(1966) Maximization by quadratic hill-climbing, Econometrica 34, 541—551.
Голуб, Ван Лоан (Golub G. H., Van Loan C.)
(1983) Matrix Computations, the Johns Hopkins University Press.
Голуб, Перейра (Golub G. H., Pereyra V.)
(1973) The differentiation of pseudo-inverse and non-linear least squares
problems whose variables separate, SIAM J. Numer. Anal. 10, 413—432.
Гриванк (Griewank A. O.)
(1982) A short proof of the Dennis-Schnabel theorem. B. I. T. 22, 252—256.
Гриванк, Тоинт (Griewank A. O., Toint Ph. L.)
(1982a) Partitioned variable metric updates for large sparse optimization
problems, Numer. Math. 39, 119—137.
Литература 427
(1982b) Local convergence analysis for partitioned quasi-Newton updates
in the Broyden class, Numer. Math. 39, 429—448.
(1982c) On the unconstrained optimization of partially separable functions,
in Nonlinear Optimization, ed. by Powell M. J. D. Academic Press, London.
Гринстадт (Greenstadt J. L.)
(1970) Variations on variable-metric methods, Math. Сотр. 24,
1 22.
Гэй (Gay D. M.)
(1979) Some convergence properties of Broyden's method, SI AM J. Numer.
Anal., 16, 623—630.
(1981) Computing optimal locally constrained steps, SI AM J. Sci. Stat.
Сотр. 2, 186—197.
Гэй, Шнабель (Gay D. M., Schnabel R. B.)
(1978) Solving systems of nonlinear equations by Broyden's method with
projected updates, in Nonlinear Programming 3, ed. by Mangasarian 0.,
Meyer R., Robinson S., Academic Press, New York, 254—281.
Дальквист, Бьёрк, Андерсон (Dahlquist G., Bjorck A., Anderson N.)
(1974) Numerical Methods, Prentice-Hall, Englewood Cliffs, N. J.
Дембо, Айзенштат, Штайхауг (Dembo R. S., Eisenstat S. C, Steihaug T.)
(1982) Inexact Newton methods, SIAM J. Numer. Anal. 19, 400—408.
Джонсон, Остриа (Johnson G. W., Austria N. H.)
(1983) A quasi-Newton method employing direct secant updates of matrix
factorizations, SIAM J. Numer. Anal. 20, 315—325.
Диксон (Dixon L. С W.)
(1972a) Quasi-Newton family generate identical points, Parts I and II,
Math. Prog. 2, 383—387, 2nd Math. Prog. 3, 345—358.
(1972b) The choice of step length, a crucial factor in the performance of
variable metric algorithms, in Numerical Methods for Non-linear
Optimization, ed. by Lootsma F., Academic Press, New York, 149—170.
Диксон, Cere (Dixon L. С W., Szego G. P.)
(1975, 1978) Towards Global Optimization, Vols. 1, 2, North-Holland,
Amsterdam.
Донгарра, Банч, Моулер, Стюарт (Dongarra J. J., Bunch J. R., Moler С. В.,
Stewart G. W.)
(1979) LINPACK Users Guide, SIAM Publications, Philadelphia.
Дэвидон (Davidon W. C.)
(1959) Variable metric methods for minimization, Argonne National Labs
Report ANL-5990.
(1975) Optimally conditioned optimization algorithms without line
searches, Math. Prog. 9, 1—30.
Дэннис (Dennis J. E., Jr.)
(1971) Toward a unified convergence theory for Newton-like methods, in
Nonlinear Functional Analysis and Applications, ed. by Rail L. В.,
Academic Press, New York, 425—472.
(1977) Nonlinear least squares and equations, in The State of the Art in
Numerical Analysis, ed. by Jacobs D., Academic Press, London, 269—312.
(1978) A brief introduction to quasi-Newton methods, in Numerical
Analysis, ed. by Golub G. H., Oliger J., AMS, Providence, R. I., 19—52.
Дэннис, Гэй, Уэлш (Dennis J. E., Jr., Gay D. M., Welsch R. E.)
(1981a) An adaptive nonlinear least-squares algorithm, TOMS 7, 348—368.
(1981b) Algorithm 573 NL2SOL — An adaptive nonlinear least-squares
algorithm [E4], TOMS 7, 369—383.
Дэннис, Марвил (Dennis J. E., Jr., Marwil E. S.)
(1982) Direct secant updates of matrix factorizations, Math. Сотр. 38,
459—474.
Дэннис, Мей (Dennis J. E., Jr., Mei H. H. W.)
(1979) Two new unconstrained optimization algorithms which use function
and gradient values, J. Optim. Theory Appl. 28. 453—482.
428 Литература
Дэннис, Морэ (Dennis J. Е., Jr., More J. J.)
(1974) A characterization of superlinear convergence and its application
to quasi-Newton methods, Math. Сотр. 28, 549—560.
(1977) Quasi-Newton methods, motivation and theory, SI AM Review 19,
46—89.
Дэннис, Тапиа (Dennis J. E., Jr., Tapia R. A.)
(1976) Supplementary terminology for nonlinear iterative methods,
SIGNUM Newsletter 11:4, 4—6.
Дэннис, Уолкер (Dennis J. E., Jr., Walker H. F.)
(1981) Convergence theorems for least-change secant update methods,
SIAM J. Numer. Anal. 18, 949—987, 19, 443.
(1983) Sparse secant update methods for problems with almost sparse Ja-
cobians, in preparation.
Дэннис, Шнабель (Dennis J. E., Jr., Schnabel R. B.)
(1979) Least change secant updates for quasi-Newton methods, SIAM
Review 21, 443—459.
Зирилли (Zirilli F.)
(1982) The solution of nonlinear systems of equations by second order
systems of o. d. e. and linearly implicit A-stable techniques, SIAM J.
Numer. Anal. 19, 800—815.
Канторович Л. В.
(1948) Функциональный анализ и прикладная математика. УМН 3, No. 6,
89—185.
Кауфман (Kaufman L. С.)
(1975) A variable projection method for solving separable nonlinear least
squares problems, BIT 15, 49—57.
Клайн, Моулер, Стюарт, Уилкинсон (Cline А. К., Moler С. В., Stewart G. W.,
Wilkinson J. Н.)
il979) An estimate for the condition number of a matrix, SIAM. J. Numer.
ла1. 16, 368—375.
Конт, де Бур (Conte S. D., de Boor C.)
(1980) Elementary Numerical Analysis: An Algorithmic Approach, 3d ed.,
McGraw-Hill, New York.
Коулман, Морэ (Coleman Т. R, More J. J.)
(1982) Estimation of sparse Hessian matrices and graph coloring problems,
Argonne National Labs, Math.-C. S. Div. TM-4.
(1983) Estimation of sparse Jacobian matrices and graph coloring
problems, SIAM J. Numer. Anal. 20, 187—209.
Куртис, Пауэлл, Райд (Curtis A., Powell M. J. D., Reid J. K.)
(1974) On the estimation of sparse Jacobian matrices, J. I. M. A. 13,117—120.
Левенберг (Levenberg K.)
(1944) A method for solution of certain problems in least squares, Quart.
Appl. Math. 2, 164—168.
Лоусон, Хенсон, Кинкейд, Крог (Lawsoti С. L., Hanson R. J., Kincaid D. R.,
Krogh F. T.)
(1979) Basic linear algebra subprograms for Fortran usage, ACM TOMS 5,
308—323.
Марвил (Marwil E. S.)
(1978) Exploiting sparsity in Newton-type methods, Cornell Applied Math.
Ph. D. Thesis.
(1979) Convergence results for Schubert's method for solving sparse
nonlinear equations, SIAM J. Numer. Anal. 16, 588—604.
Маркварт (Marquardt D.)
(1963) An algorithm for least-squares estimation of nonlinear parameters.
SIAM J. Appl. Math. 11, 431—441.
Морэ (More J. J.)
(1977) The Levenberg — Marquardt algorithm: implementation and theory,
in Numerical Analysis, ed. by Watson G. A., Lecture Notes in Math. 630,
Springer-Verlag, Berlin, 105—116.
Литература 429
Морэ, Гарбов, Хиллстром (More J. J., Garbow В. S., Hillstrom К. E.)
(1980) User guide for MINPACK-1, Argonne National Labs Report
ANL-80-74.
(1981a) Testing unconstrained optimization software, TOMS 7, 17—41.
(1981b) Fortran subroutines for testing unconstrained optimization
software, TOMS 7 136—140.
Морэ, Соренсен (More J. J., Sorensen D. C.)
(1979) On the use of directions of negative curvature in a modified
Newton method, Math. Prog. 16, 1—20.
Мюррей (Murray W.)
(1972) Numerical Methods for Unconstrained Optimization. Academic
Press, London.
Мюррей, Овертон (Murray W., Overton M. L.)
(1980) A projected Ligrangian algorithm for nonlinear minimax
optimization, SIAM J. Sci. Statist. Comput. 1, 345—370.
(1981) A projected Lagrangian algorithm for nonlinear U optimization,
SIAM J. Sci. Statist. Comput. 2. 207—224.
Нелдер, Мид (Nelder J. A., Mead R.)
(1965) A simplex method for function minimization, Comput. J. 7, 308—
313
Орен (Oren S. S.)
(1974) On the selection of the parameters in self-scaling variable metric
algorithms, Math. Prog. 7, 351—367.
Ортега, Рейнболдт (Ortega J. M., Rheinboldt W. C.)
П970) Iterative Solution of Nonlinear Equations in Several Variables.
Academic Press, New York. [Имеется перевод: Ортега Дж., Рейнболдт В.
Итерационные методы решения нелинейных систем уравнений со
многими неизвестными. — М.: Мир, 1975.]
Осборн (Osborne М. R.)
(1976) Nonlinear least squares —the Levenberg algorithm revisited, J.
Austral. Math. Soc. 19 (Series B), 343—357.
Пауэлл (Powell M. J. D.)
(1970a) A hybrid method for nonlinear equations, in Numerical Methods
for Nonlinear Algebraic Equations, ed. by Rabinowitz P., Gordon and
Breach, London, 87—114.
(1970b) A new algorithm for unconstrained optimization, in Nonlinear
Programming, ed. by Rosen J. В., Mangasarian O. L. and Ritter K.,
Academic Press, New York, 31—65.
(1975) Convergence properties of a class of minimization algorithms,
in Nonlinear Programming 2, ed by Mangasarian O. L., Meyer R. and
Robinson S., Academic Press, New York, 1—27.
(1976) Some global convergence properties of variable metric
algorithm without exact line searches, in Nonlinear Programming, ed. by
Cottle R. and Lemke C, AMS, Providence, R. I:, 53—72.
(1981) A note on quasi-Newton formulae for sparse second derivative
matrices, Math. Prog. 20, 144—151.
Пауэлл, Тоинт (Powell M. J. D., Toint Ph. L.)
(1979) On the estimation of sparse Hessian matrices, SIAM J. Numer.
Anal. 16, 1060—1074.
Пратт (Pratt J. W.)
(1977) When to stop a quasi-Newton search for a maximum likelihood
estimate, Harvard School of Business WP 77—16.
Райд (Reid J. K.)
(1973) Least squares solution of sparse systems of non-linear equations
by a modified Marquardt algorithm, in Proc. NATO Conf.- at
Cambridge, July 1972, North-Holland, Amsterdam, 437—445.
Райнш (Reinsch C.)
(1971) Smoothing by spline functions, II, Numer. Math. 16, 451—454.
430 Литература
Соренсен (Sorensen D. С.)
(1977) Updating the symmetric indefinite factorization with applications
in a modified Newton's method, PH. D. Thesis, U. C. San Diego,
Argonne National Labs Report ANL-77-49.
(1982) Newton's method with a model trust region modification, SIAM
J. Numer, Anal. 19, 409—426.
Стренг (Strang G.)
(1976) Linear Algebra and Its Applications, Academic Press, New York.
[Имеется перевод: Стренг Г. Линейная алгебра и ее приложения.—
М.: Мир, 1980.]
Стюарт (Stewart G. W., Ill)
(1967) A modification of Davidon's method to accept difference
approximations of derivatives, J. ACM 14, 72—83.
(1973) Introduction to Matrix Computations, Academic Press, New York.
Тоинт (Toint Ph. L.)
(1977) On sparse and symmetric matrix updating subject to a linear
equation, Math. Сотр. 31, 954—961.
(1978) Some numerical results using a sparse matrix updating formula
in unconstrained optimization, Math. Сотр. 32, 839—851.
(1981) A sparse quasi-Newton update derived variationally with a non-
diagonally weighted Frobenius norm, Math. Сотр. 37, 425—434.
Уилкинсон (Wilkinson J. H.)
(1963) Rounding Errors in Algebraic Processes, Prentice-Hall, Engle-
wood Cliffs, N. J.
(1965) The Algebraic Eigenvalue Problem, Oxford University Press
London. [Имеется перевод: Уилкинсон Дж. Алгебраическая проблема
собственных значений. — М.: Наука, 1970.]
Флетчер (Fletcher R.)
(1970) A new approach to variable metric algorithms, Comput. J. 13,
317—322.
(1980) Practical Methods of Optimization, Vol. 1, Unconstrained
Optimization, John Wiley & Sons, New York.
Флетчер, Пауэлл (Fletcher R., Powell M. J. D.)
(1963) A rapidly convergent descent method for minimization, Comput.
J. 6, 163—168.
Форд (Ford B.)
(1978) Parameters for the environment for transportable numerical
software, TOMS 4, 100—103.
Фосдик (Fosdick L. ed.)
(1979) Performance Evaluation of Numerical Software, North-Holland,
Amsterdam.
Фрэнк, Шнабель (Frank P., Schnabel R. B.)
(1982) Calculation of the initial Hessian approximation in secant
algorithms, in preparation.
Хайберт (Hiebert K. L.)
(1982) An evaluation of mathematical software that solves systems of
nonlinear equations, TOMS 8, 5—20.
Хебден (Hebden M. D.)
(1973) An algorithm for minimization using exact second derivatives,
Rept. TP515, A. E. R. E., Harwell, England.
Хемминг (Hamming R. W.)
(1973) Numerical Methods for Scientists and Engineers, 2 ed., McGraw-
Hill, New York. [Имеется перевод первого издания: Хемминг Р. В.
Численные методы для научных работников и инженеров. — М.:
Наука, 1979.]
Хестенс (Hestenes М. R.)
(1980) Conjugate-direction Methods in Optimization, Springer Verlag,
New York.
Литература 431
Хьюбер (Huber P. J.)
(1973) Robust regression: asymptotics, conjectures, and Monte Carlo,
Anals of Statistics 1, 799—821.
(1981) Robust Statistics, John Wiley & Sons, New York. [Имеется
перевод: Хьюбер Дж. П. Робастность в статистике. — М: Мир, 1984.]
Шанно (Schanno D. F.)
(1970) Conditioning of quasi-Newton methods for function minimization,
Math. Сотр. 24, 647—657.
(1978) Conjugate-gradient methods with inexact searches, Math, of
Oper. Res. 3, 244—256.
(1980) On the variable metric methods for sparse Hessians, Math. Сотр.
34, 499-514.
Шанно, Фуа (Schanno D. F., Phua К. H.)
(1978a) Matrix conditioning and nonlinear optimization, Math. Prog.
14, 145—160.
(1978b) Numerical comparison of several variable metric algorithms,
J. Optim. Theory Appl. 25, 507—518.
Шнабель (Schnabel R. B.)
(1977) Analysing and improving quasi-Newton methods for
unconstrained optimization, Ph. D. Thesis, Cornell Computer Science TR-77-320.
(1982) Convergence of quasi-Newton updates to correct derivative
values, in preparation.
Шнабель, Вайс, Кунц (Schnabel R. В., Weiss В. E., Koontz J.- E.)
(1982) A modular system of algorithms for unconstrained minimization,
Univ. Colorado Computer Science, TR CU-CS-240-82.
Штайхауг (Steihaug T.)
(1981) Quasi-Newton methods for large scale nonlinear problems,
Ph. D. Thesis, Yale University.
Шуберт (Schubert L. K.)
(1970) Modification of a quasi-Newton method for nonlinear equations
with a sparse Jacobian, Math. Сотр. 24, 27—30.
Шульц, Шнабель, Бирд (Shultz G. A., Schnabel R. В., Byrd R. H.)
(1982) A family of trust region based algorithms for unconstrained
minimization with strong global convergence properties, Univ. Colorado
Computer Science TR CU-CS-216-82.
Добавлено при переводе
Бахвалов Н. С, Жидков Н. П., Кобельков Г. М.
(1987) Численные методы: учебное пособие для вузов. — М.: Наука.
Васильев Ф. П.
(1980) Численные методы решения экстремальных задач. — М.: Наука.
Евтушенко Ю. Г.
(1982) Методы решения экстремальных задач и их применение в
системах оптимизации. — М.: Наука.
Марчук Г. И., Лебедев В. И.
(1971) Численные методы теории переноса нейтронов. — М.: Атомиздат.
Михалевич В. С, Гупал А. М., Норкин В. И.
(1987) Методы невыпуклой оптимизации. — М.: Наука.
Поляк Б. Т.
(1983) Введение в оптимизацию. — М.: Наука.
Пшеничный Б. Н., Данилин Ю. М.
(1975) Численные методы в экстремальных задачах.—М.: Наука.
Самарский А. А., Николаев Е. С.
(1978) Методы решения сеточных уравнений. — М.: Наука.
Сухарев А. Г., Тимохов А. В., Федоров В. В.
(1986) Курс методов оптимизации. — М.: Наука.
432 Литература
Shub М., Smale S.
(1985) Computational complexity: on the geometry of polynomials and a
theory of cost; Part I, Ann. Scf Ecole Norm. Sup. 4 serie t. 18, pp. 107—
142.
(1986) Computational complexity: on the geometry of polynomials and a
theory of cost; Part II, SIAM J. Computing, Vol. 15 (1986), pp. 145—161.
Smale S.
(1985) On the efficiency of algorithms of analysis, Bull. Amer. Math.
Soc. (N. S.) 13 (1985), pp. 87—121.
(1986a) Newton's method estimates from data at one point, Mathematical
Sciences Research Institute, Berkeley, California (April), 16 p.
(1986b) Algorithms for solving equations, Intern. Congress of Math.,
Berkeley, 43 p.
именной указатель
Авриель (Avriel М . ) 10 , 29
Айзенштат (Eisenstat S . С . ) 292
Алговер (Allgower Е . ) 11 , 17 , 186
Андерсон (Anderson N . ) 29
Армийо (Armijo L . ) 148
Асен (Aasen J . О . ) 70
Ахо (Aho A . U . ) 26
Бакли (Buckley A . G . ) 292
Банч (Bunch J . R . ) 70 , 71 , 88
Бард (Bard Y . ) 260 , 279
Барнес (Barnes J . ) 228
Бартелс (Bartels R . ) 279
Бейтс (Bates D . M . ) 279
Бил (Beale E . M . L . ) 23
Бирд (Byrd R . H . ) 7 , 8 , 189
Битон (Beaton A . E . ) 280
Боггс (Boggs P . T . ) 134
Брайян (Bryan C . A . ) 136
Брент (Brent R . P . ) 29
Бродли (Brodlie K . W . ) 242
Бройден (Broyden С G . ) 207 , 211 ,
213 , 235 , 240 , 246 , 254 , 255 , 291
Бур , де (de Boor C . ) 29
Бьёрк (Bjorck A . ) 29
Вайс (Weiss В . E . ) 198 , 315 , 317
Вандерграфт (Vandergraft J . S . ) 316
Ван Лоан (Van Loan C . ) 58 , 71 , 292
Вольф (Wolfe P . ) 149 , 150
Гандер (Gander W . ) 167
Гарбов (Garbow B . S . ) 199 , 422
Гарфинкель (Garfinkel R . S . ) 23
Гилл (Gill P . E . ) 10 , 79 , 128 , 226 ,
292 , 334 , 360 , 362
Голдстейн (Goldstein A . A . ) 148
Голдфарб (Goldfarb D . ) 79 , 240
Голдфельд (Goldfeldt S . M . ) 165
Голуб (Golub G . H . ) 58 , 71 , 79 , 278 ,
282 , 283 , 292
Гриванк (Griewank A . O . ) 292 , 306
Гринстадт (Greenstadt J . L . ) 236
Гэй (Gay D . M . ) 7 , 164 , 171 , 223 ,
228 , 231 , 275 , 278 , 283 , 307
Дальквист (Dahlquist G . ) 29
Дембо (Dembo R . S . ) 292
Джонсон (Johnson G . W . ) 307
Джордж (Georg K . ) 11 , 17 , 186
Диксон (Dixon L . С W . ) 17 , 242
Донгарра (Dongarra J . J . ) 71 , 88
Дэвидон (Davidon W . C . ) 242 , 254
Дэннис (Dennis J . E . , Jr . ) 11 , 118 ,
134 , 152 , 174 , 203 . 211 , 213 , 217 ,
234 , 235 , 246 , 254 , 255 , 275 , 278 ,
283 , 293 , 297 , 299 , 305 , 306 , 307
Зирилли (Zirilli F . ) 186
Канторович Л . В . 116
Кауфман (Kaufman L . С . ) 278
Кинкейд (Kinkeid D . R . ) 324
Клайн (Cline A . K . ) 75 , 368 , 369
Конн (Conn A . ) 279
Конт (Conte S . D . ) 29
Коулман (Coleman T . F . ) 287 , 288
Kpor (Krogh F . T . ) 324
Куанд (Quandt R . E . ) 165
Кунц (Koontz J . E . ) 198 , 315 , 317
Куртис (Curtis A . ) 285 , 287
Левенберг (Levenberg K) 165
Лоусон (Lawson C . L . ) 324
Марвил (Marwil E . S . ) 291
Маркварт (Marquardt D . ) 165
Мей (Mei H . H . W . ) 174
Морэ (More J . J . ) 7 , 127 , 152 , 167 ,
169 , 199 , 203 , 211 , 213 , 217 , 224 ,
234 , 235 , 246 , 254 , 255 , 271 , 283 ,
287 288 422
Моул'ер (Moler С . В . ) 71 , 75 , 88 , 368 ,
369
434 Именной указатель
Немхаусер (Nemhauser G . L . ) 23
Носедал (Nocedal) 8
Овертон (Overton М . L . ) 279
Орен (Oren S . S . ) 250
Ортега (Ortega J . М . ) 36 , 92 , 116
Осборн (Osborne М . R . ) 271
Остриа (Austria N . Н . ) 307
Парлетт (Parlett В . N . ) 70
Пауэлл (Powell М . J . D . ) 7 , 180 , 242 ,
252 , 271 , 285 , 287 , 288 , 305 , 306
Перейра (Регеуга V . ) 278 , 282 , 283
Пратт (Pratt J . W . ) 278
Райд (Reid J . К . ) 285 , 287 , 291
Райнш (Reinsch С . ) 168
Райт (Wright М . Н . ) 10 , 128 , 292 ,
334 , 360 , 362
Рейнболдт (Rheinboldt W . С . ) 36 , 92 ,
116
Сегё (Szego G . Р . ) 17
Сондерс (Saunders М . А . ) 79
Соренсен (Sorensen D . С . ) 7 , 127 , 171
Стренг (Strang G . ) 58 , 71
Стюарт (Stewart G . W . , Ill) 58 , 75 ,
88 , 134 , 283 , 363 , 364 , 368 , 369
Тапиа (Tapia R . А . ) 203
Тоинт (Toint Ph . L . ) 288 , 291 , 292 ,
305
Троттер (Trotter H . F . ) 165
Тыоки (Tukey J . W . ) 280
Уилкинсон (Wilkinson J . H . ) 24 , 58 ,
73 , 75 , 368 , 369
Ульман (Ullman J . D . ) 26
Уолкер (Walker H . F . ) 211 , 275 ,
299 , 305 , 306
Уотс (Watts D . G . ) 279
Уэлш (Welsch R . E . ) 275 , 278 , 283 ,
307
Флетчер (Fletcher R . ) 165 , 203 , 240 ,
242 , 253 , 292
Форд (Ford B . ) 28
Фосдик (Fosdick L . , ed . ) 200
Фуа (Phua К . H . ) 250 , 254
Хайберт (Hiebert K . L . ) 422
Хебден (Hebden M . D . ) 167
Хемминг (Hamming R . W . ) 334 , 359 ,
362
Хенсон (Hanson R . J . ) 324
Хестенс (Hestenes M . R . ) 292
Хиллстром (Hillstrom К . E . ) 199 , 224 ,
422
Хопкрофт (Hopcroft J . E . ) 26
Хьюбер (Huber P . J . ) 279 , 280
Шанно (Schanno D . F . ) 240 , 250 , 254 ,
291 292
Шнабель (Schnabel R . B . ) 7 , 189 ,
198 , 228 , 231 , 235 , 248 , 254 , 293 ,
297 , 306 , 315 , 317
Штайхауг (Steihaug T . ) 189 , 292
Шуберт (Schubert L . K . ) 291
Шульц (Shultz G . A . ) 7 , 189
Ян (Yuan) 8
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Алгоритм гибридный (hybrid
algorithm) 42
— Голуба — Перейры (Golub—Perey-
ra) 282
Алгоритмы квазиньютоновские (qua-
si-Newton) 139
Антипереполнение (underflow) 26
Аппроксимация конечно-разностная
(finit-difference) 45
— с помощью секущей (secant
approximation) 44 , 203
Вращение Якоби (Jacobi rotation) 76
Гессиан (Hessian) 92
Градиент (gradient) 92
Дифференцируемость по Гато
(Gateaux differentiability) 107
Фреше (Frechet) 107
Дробление ньютоновского шага
(backtracking from the Newton step) 41
Задача безусловной минимизации
(unconstrained minimization
problem) 15
— нелинейная о наименьших
квадратах (nonlinear least-squares) 16 , 19
— о минимальных поправках (least-
change) 288
Исчезновение порядка см .
Антипереполнение
Константа Липшица (Lipschitz
constant) 98
Мажоризация (majorization) 118
Масштабы (scales) 190
Матриц разложения (matrix
factorizations) 65
Матрица вращения (rotation matrix)
76
— Гессе см . Гессиан
— незнакоопределенная (indefinite)
80
— отрицательно определенная
(negative definite) 80
полуопределенная (negative se-
midefinite) 80
— положительно определенная
(positive definite) 80
полуопределенная (positive se-
midefinite) 80
— со строго доминирующей
диагональю (strictly diagonally
dominant) 81
— Якоби см . Якобиан
Матрицы сингулярное разложение
(singular value decomposition) 85
— сингулярные числа (singular
values) 85
— собственные векторы
(eigenvectors) 80
значения (eigenvalues) 80
— число обусловленности (condition
number) 73
Машинный эпсилон (machine epsi-
lon , macheps) 26
Метод Гаусса — Ньютона (Gauss —
Newton method) 263
демпфированный (damped)
269
— глобальный (global) 16
— деления пополам (bisection) 40
— локальный (local) 16
— итеративный локально сходящийся
(iterative locally convergent) 36
— Левенберга — Маркварта (Leven-
berg —Marquardt) 270
— Ньютона — Рафсона (Newton —
436 Предметный указатель
Raphson) 32 , 39
сходимость (convergence) 36
— секущих (secant) 45 , 203 , 209
обратно положительно
определенный (inverse positive definite)
242
положительно определенный
(positive definite) 241
— сопряженных градиентов
(conjugate gradient) 292
Методы спуска (descent) 105
Минимум глобальный (global mini-
mizer) 17 , 50
— локальный (local) 17 , 50
Модель аффинная (affine model) 32
Модель—доверительная область
(model — trust region) 161
— локальная (local model) 32
Модульная система алгоритмов
(modular system of algorithms) 314
Направление спуска (descent
direction) 141
наискорейшего
(steepest-descent) 142
Норма (norm) 59
— евклидова см . Норма наименьших
квадратов
— матричная (matrix) 61
— наименьших абсолютных
разностей (least absolut residual) 60
квадратов (least-squares) 60
— Чебышёва 60
Область доверительная (trust region)
161
Оператор матричного проектирования
(matrix projector operator) 289
— множественного ветвления
(multiple branch statement) 320
Ортогональная матрица (orthogonal
matrix) 65
Ортогональные векторы (orthogonal
vectors) 65
Ортонормальная система векторов
(orthonormal set) 65
Ошибка округления (round-off error)
25
абсолютная (absolute) 25
относительная (relative) 25
Перемасштабирование (rescaling) 190
Переполнение (overflow) 26
Поиск линейный (line search) 145
идеальный (perfect) 187
Последовательность сходящаяся
(convergent sequence) 34
с ^-порядком , по меньшей мере
равным р (q-oder at least р) 35
/-шагово <7-сверхлинейно (/-step
<7-superlinearly) 35
— <7-линейно сходящаяся fa-linearly)
34
— <7-сверхлинейно сходящаяся (<7-su-
perlinearly) 35
Представление с плавающей точкой
(floating-point representation) 24
Представления точность (precision)
24
Производная по направлению
(directional derivative) 93
Система нелинейных уравнений
(simultaneous nonlinear equations)
14
Системы плохо обусловленные (ill-
conditioned systems) 72
Скалярное произведение (inner
product) 64
Скорость сходимости ^-квадратичная
(^-quadratic convergence) 35
^-кубическая fa-cubic) 35
След матрицы (trace of matrix) 63
Уравнения нормальные (normal
equations) 84
Ухудшение ограниченное (bounded
deterioration) 213
Формула Дэвидона — Флетчера —
Паиэлла (Davidon — Fletcher —
Powell update) 242
— Ньютона — Лейбница 33
— пересчета Бройдена (Broyden's
update) 207
симметричная одноранговая
(symmetric rank-one (SRI)) 253
— проекционная и оптимально
обусловленная (projected and optimally
conditioned) 254
— секущих см . Формула пересчета
Бройдена
положительно определенная
(positive definite secant update)
240
разреженная (sparse) 290
с минимальными поправками
(least-change) 293
симметричная Пауэлла —
Бройдена (Powell-symmetric-Broyden ,
PSB) 234
— Шермана — Моррисона — Вудбери
(Sherman — Morrison — Woodbury)
225
Функция В уда (Wood's function) 424
— итерационная сжимающая
(contractive iteration) 119
— невязки (residual) 259
— непрерывная по Липшицу (Lipschitz
continuous) 36 , 98
— непрерывно дифференцируемая
(continuously differentiable) 92
в открытой области (open
region) 93
дважды (twice) 94
— Пауэлла обобщенная вырожденная
(extended Powell singular) 423
— Розенброка (Rosenbrock) 193
расширенная (extended) 423
— типа спиралевидного желоба
(helical valley) 424
— тригонометрическая 423
Хаусхолдера преобразование (Hous-
holder transformation) 69
Холесского разложение (Cholesky
decomposition) 70
Шаг криволинейный (hook step) 170
— с двойным изломом (double
dogleg) 171
Шага длина (length) 160
минимальная (minstep) 159
— направление (direction) 160
Якобиан (Jacobian) 96
BFGSFAC 418
BFGSUNFAC 416
BFGS-формула см . Формула секущих
положительно определенная
BROYFAC 415
BROYUNFAC 414
CDGRAD 382
CHOLDECOMP 377
CHOLSOLVE 366
CONDEST 368
DFP-формула см . Формула Дэвидо-
на — Флетчера — Пауэлла
DOGDRIVER 395
DOGSTEP 396
FDGRAD 381
FDHESSF 380
FDHESSG 379
FDJAC 373
FN 355
FOR 320
FVEC 357
GRAD 355
HESS 356
HOOKDRIVER 390
Предметный указатель 437
HOOKSTEP 392
IF-THEN 319
IF-THEN-ELSE 320
INITHESSFAC 421
INITHESSUNFAC 420
JAC 357
JACROTATE 371
LINESEARCH 384
LINESEARCHMOD 387
LSOLVE 367
LTSOLVE 368
/i-норма см . Норма наименьших
абсолютных разностей
/2-норм а см . Норма евклидова
/р-норма (/p-norm) 60
/оо-норма см . sup-норма
MACHINEPS 363
MODELHESS 374
NEDRIVER 341
NEEXAMPLE 353
NEFN 362
NEINCK 360
NEMODEL 402
NEMODELFAC 405
NESTOP 411
NESTOP0 413
NP-полнота (NP-completeness) 287
PLU-разложение (PLU
decomposition) 69
QFORM 372
QRDECOMP 363
QRP-разложение (QRP
decomposition) 69
QRSOLVE 365
QRUPDATE 370
QR-разложение (QR decomposition)
69
REPEAT 321
RSOLVE 366
SRI-формула см . Формула
пересчета симметричная одноранговая
sup-норма 60
TRUSTREGUP 398
UMDRIVER 325
UMEXAMPLE 329
UMINCK 358
UMSTOP 408
UMSTOP0 409
WHILE 321
Оглавление
Предисловие редактора перевода и переводчика 5
Предисловие к русскому изданию 7
Предисловие 9
Глава 1. Введение 14
1.1. Постановки задач 14
1.2. Характерные особенности встречающихся на практике задач 18
1.3. Арифметика конечной точности и измерение ошибок .... 24
1.4. Упражнения 27
Глава 2. Нелинейные задачи с одной переменной . 29
2.1. О том, чего не следует ожидать 29
2.2. Метод Ньютона решения одного уравнения с одним
неизвестным 31
2.3. Сходимость последовательностей действительных чисел . . 34
2.4. Сходимость метода Ньютона 36
2.5. Глобально сходящиеся методы решения одного уравнения с
одним неизвестным 40
2.6. Методы для случая, когда производные не заданы .... 44
2.7. Минимизация функции одной переменной 50
2.8. Упражнения 53
Глава 3. Основы вычислительной линейной алгебры ........ 5§
3.1. Векторные и матричные нормы, ортогональность 59
3.2. Решение систем линейных уравнений и разложения матриц 65
3.3. Погрешности при решении линейных систем 71
3.4. Формулы пересчета матричных разложений 76
3.5. Собственные значения и положительная определенность . . 79
3.6. Линейная задача о наименьших квадратах 82
3.7. Упражнения ' 88
Глава 4. Основы анализа функций многих переменных ....... 91
4.1. Производные и многомерные модели 91
4.2. Конечно-разностные производные в многомерном случае . . 100
Оглавление 439
4.3. Необходимые и достаточные условия в задачах безусловной
минимизации 103
4.4. Упражнения 106
Глава 5. Метод Ньютона решения нелинейных уравнений и безусловной
минимизации 110
5.1. Метод Ньютона решения систем нелинейных уравнений . . 110
5.2. Локальная сходимость метода Ньютона . 114
5.3. Теорема Канторовича и теорема о сжимающем отображении 116
5.4. Методы с конечно-разностными производными для решения
систем нелинейных уравнений 119
5.5. Метод Ньютона безусловной минимизации 125
5.6. Методы с конечно-разностными производными для
безусловной минимизации 130
5.7. Упражнения 134
Глава 6. Глобально сходящиеся модификации метода Ньютона . . . . 138
6.1. Общая квазиньютоновская схема 139
6.2. Направления спуска 140
6.3. Линейный поиск 144
6.3.1. Результаты исследования сходимости при надлежащем
выборе шагов 149
6.3.2. Выбор пиага дроблением 155
6.4. Подход: модель — доверительная область 160
6.4.1. Локально ограниченный оптимальный
(«криволинейный») шаг 165
6.4.2. Шаг с двойным изломом 171
6.4.3. Пересчет доверительной области 176
6.5. Глобальные методы решения систем нелинейных уравнений 180
6.6. Упражнения 187
Глава 7. Критерии останова, масштабирование и тестирование . . . . 190
7.1. Масштабирование 190
7.2. Критерии останова 195
7.3. Тестирование 198
7.4. Упражнения . 202
Глава 8. Методы секущих для решения систем нелинейных уравнений 204
8.1. Метод Бройдена 205
8.2. Анализ локальной сходимости метода Бройдена 211
8.3. Реализация квазиньютоновских алгоритмов, использующих
формулу пересчета Бройдена 223
8.4. Другие формулы секущих для нелинейных уравнений . . . 227
8.5. Упражнения 229
Глава 9. Методы секущих для безусловной минимизации 232
9.1. Симметричная формула секущих Пауэлла 233
9.2. Симметричные положительно определенные формулы секущих 237
9.3. Локальная сходимость положительно определенных методов
секущих 243
9.4. Реализация квазиньютоновских алгоритмов, использующих
положительно определенные формулы секущих 248
440 Оглавление
9.5. Еще один результат, касающийся сходимости положительно
определенных методов секущих 252
9.6. Другие формулы секущих для безусловной минимизации . . 252
9.7. Упражнения 254
Глава 10. Нелинейная задача о наименьших квадратах ....... 259
10.1. Постановка нелинейной задачи о наименьших квадратах . . 259
10.2. Методы типа Гаусса — Ньютона 263
10.3. Методы полностью ньютоновского типа . 271
10.4. Некоторые другие соображения относительно решения
нелинейных задач о наименьших квадратах 277
10.5. Упражнения 280
Глава 11. Методы решения задач со специальной структурой ... 284
11.1. Разреженный конечно-разностный метод Ньютона 285
11.2. Разреженные методы секущих 288
11.3. Вывод формул секущих с минимальными поправками . . . 293
11.4. Анализ методов секущих с минимальными поправками . . 299
11.5. Упражнения 305
Приложение А. Модульная система алгоритмов безусловной минимизации
и решения нелинейных уравнений (Р. Шнабель) . . . 308
Приложение В. Тестовые задачи (Р. Шнабель) 422
Литература 425
Именной указатель 432
Предметный указатель 434
Научное издание
Джон Дэннис, мл., Роберт Шнабель
ЧИСЛЕННЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ
И РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Заведующий редакцией доктор физ.-мат. наук, профессор I Б. В. Шабат I
Зам. заведующего редакцией А. С. Попов *
Ст. науч. редактор И. А. Маховая
Мл. редактор Т. Ю. Дегтярева
Художник В. А. Медников
Худ. редактор В. И. Шаповалов
Технический редактор Е. Н. Прохорова
Корректор С. А. Денисова
ИБ №6285
Сдано в набор 24.06.87. Подписано к печати 22.03.88. Формат 60X90/16. Бумага
типографская № 2. Печать высокая. Гарнитура литературная. Объем 13,75 бум. л. Усл. печ. л. 27,50.
Усл. кр.-отт. 27,50. Уч.-нзд. л. 26,20. Изд. № 1/5470 Тираж 14 000 экз. Зак. 954Цена'2 р. 10 к.
ИЗДАТЕЛЬСТВО «МИР» 129820. ГСП, Москва, И-110. 1-й Рижский пер., 2
Отпечатано с набора Ленинградской типографии № 2 головного предприятия ордена
Трудового Красного Знамени Ленинградского объединения «Техническая книга» им.
Евгении Соколовой Союзполиграфпрома при Государственном комитете СССР по
делам издательств, полиграфии и книжной торговли. 198052, г. Ленинград, Л-52,
Измайловский проспект, 29, в Ленинградской типографии № 4 ордена Трудового Красного
Знамени Ленинградского объединения «Техническая книга» им. Евгении Соколовой
Союзполиграфпрома при Государственном комитете СССР по делам издательств,
полиграфии и книжной торговли, 191126, Ленинград, Социалистическая ул., 14.