в. п. ильин
ЧИСЛЕННЫЕ МЕТОДЫ
РЕШЕНИЯ ЗАДАЧ
ЭЛЕКТРОФИЗИКИ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1985

ББК 22.19
И 46
УДК 519.6
Ильин В. П. Численные методы решения задач электрофизики.— М.:
Наука. Главная редакция физико-математической литературы, 1985—336 с.
Книга посвящена методам расчета электрических и магнитных полей в
различных электрофизических устройствах. В ней содержится описание математических
постановок и алгоритмов для задач электро- и магнитостатики, формирования
плотных пучков заряженных частиц, СВЧ-электроники.
Для различного типа задач применяются методы конечных разностей, конечных
элементов и интегральных уравнений. Даются примеры решения типовых задач.
Рассматриваются вопросы автоматизации расчетов широкого класса приборов
и технологии пакетов прикладных программ.
Для специалистов в области прикладной математики и инженеров.
Рецензент
доктор физико-математических наук Ю. А. Березин
(g) Издательство «Наука»
1702070000—139 Главная редакция
И m е КБ-29-17-85 физико-математической
UOO(U2)-OO литературы, 1985

ОГЛАВЛЕНИЕ
Предисловие
Глава 1. РАЗНОСТНЫЕ МЕТОДЫ РАСЧЕТА ЭЛЕКТРОСТАТИЧЕСКИХ
ПОЛЕЙ И
§ 1.1. Основные понятия и вспомогательные сведения 13
§ 1.2. Способы построения разностных апроксимаций 16
§ 1.3. Свойства разностных операторов и оценки точности разностных
решений 26
§ 1.4. Прямые методы решения разностных уравнений 41
§ 1.5. Итерационные методы решения разностных уравнений 49
§ 1.6. Комбинированные методы решения разностных уравнений .... 73
§ 1.7. Некоторые вопросы расчета характеристик электростатических полей 83
Глава 2. РЕШЕНИЕ ЗАДАЧ МАГНИТОСТАТИКИ МЕТОДАМИ
КОНЕЧНЫХ ЭЛЕМЕНТОВ 93
§ 2.1. Математические постановки задач магнитостатики 94
§ 2.2. Аппроксимация решений в методах конечных элементов 97
§ 2.3. Построение конечно-элементных уравнений 108
§ 2.4. Методы решения систем нелинейных уравнений 113
§ 2.5. Примеры расчетов магнитостатических полей 118
Глава 3. МЕТОДЫ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ ДЛЯ ЗАДАЧ
ТЕОРИИ ПОТЕНЦИАЛА 121
§ 3.1. Интегральные постановки краевых задач 121
§ 3.2. Численное решение интегральных уравнений для потенциала простого
слоя 130
§ 3.3. Примеры решения методических задач 146
§ 3.4. О сравнительной эффективности методов решения интегральных и
дифференциальных уравнений 152
§ 3.5. Краткий обзор других методов решения интегральных уравнений . . 155
Глава 4. МЕТОДЫ РАСЧЕТА СОБСТВЕННЫХ ЧАСТОТ И
ГАРМОНИК ЭЛЕКТРОДИНАМИЧЕСКИХ СИСТЕМ 162
§ 4.1. О постановках задач электродинамики 162
§ 4.2. Разностные аппроксимации проблемы собственных значений для
краевых задач 167
§ 4.3. Итерационные методы решения алгебраической проблемы
собственных значений 178
§ 4.4. Примеры расчета характеристик электродинамических систем . . . 188
Глава 5. МОДЕЛИРОВАНИЕ СИЛЬНОТОЧНЫХ ПУЧКОВ 191
§ 5.1. Описание математической модели 192
§ 5.2. Определение напряженностей электрического и магнитного полей . 201
§ 5.3. Методы интегрирования уравнений движения заряженных частиц . 213
§ 5.4. Вычисление плотности тока и объемных зарядов 226
§ 5.5. Итерационные процессы решения стационарных самосогласованных
задач 233
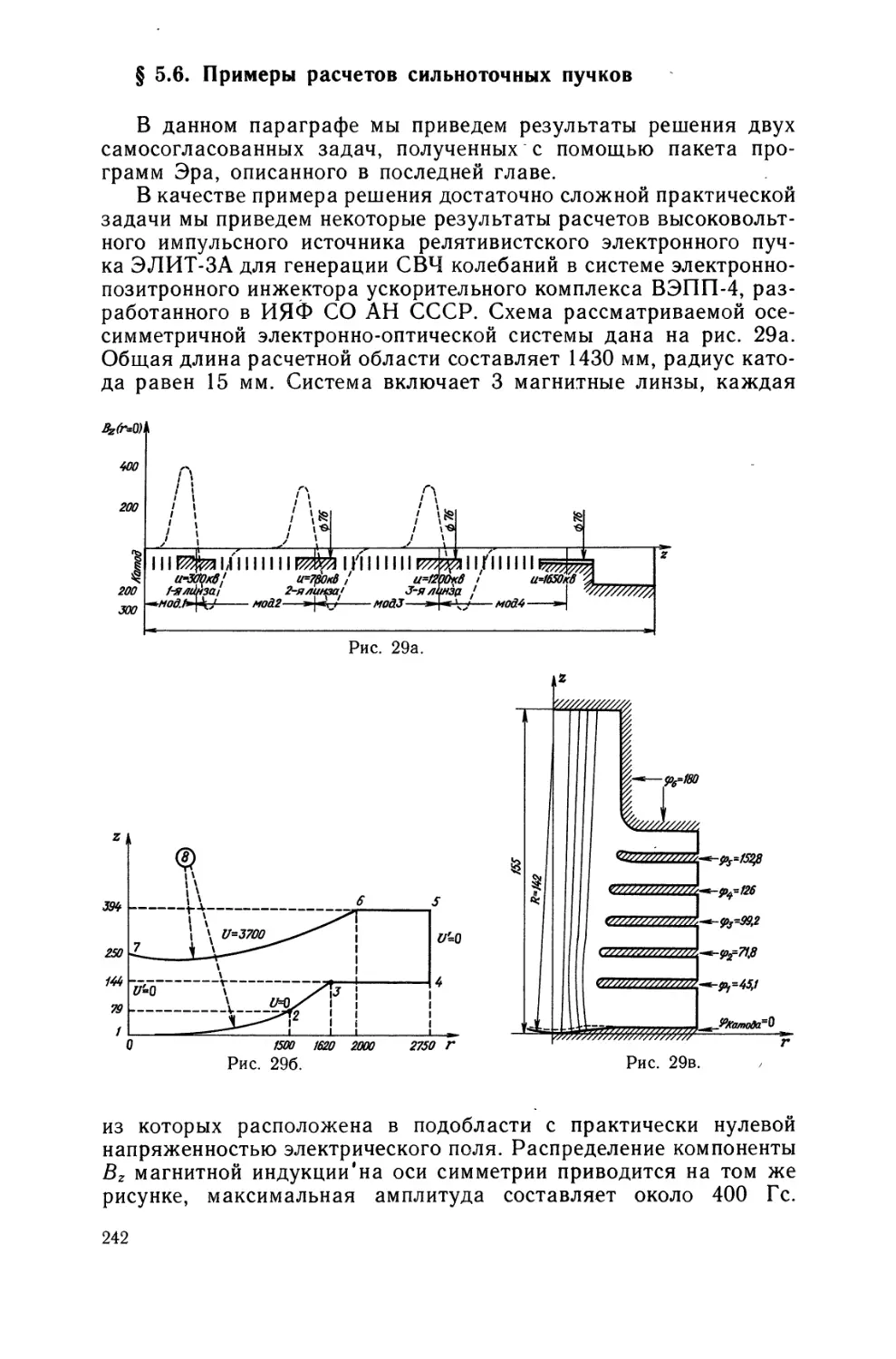
§ 5.6. Примеры расчетов сильноточных пучков 242

Глава 6. ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА ПОЛУПРОВОДНИКОВЫХ
ПРИБОРОВ 247
§ 6.1. Математическая постановка процессов переноса заряда в
полупроводниковых приборах 247
§ 6.2. Разностные методы решения уравнений переноса зарядов в
полупроводниках 254
Глава.7. МЕТОДОЛОГИЯ ПАКЕТОВ ПРОГРАММ ДЛЯ
ПРОЕКТИРОВАНИЯ ЭЛЕКТРОФИЗИЧЕСКИХ УСТРОЙСТВ 268
§ 7.1. Функциональные требования к программному обеспечению САПР . 269
§ 7.2. Технология пакетов прикладных программ 273
§ 7.3. Проблемы автоматизации построения алгоритмов в задачах
электрофизики 288
Приложение. РАСПАРАЛЛЕЛИВАНИЕ АЛГОРИТМОВ В ЗАДАЧАХ
ЭЛЕКТРОФИЗИКИ 312
Список литературы 325

ПРЕДИСЛОВИЕ
К электрофизике традиционно относят задачи, связанные с
определением электромагнитных полей, плотностей токов и
распределения зарядов. Сюда включаются приложения из самых различных
областей науки и техники: высоковольтные конструкции,
электрические машины, трансформаторы, ускорители заряженных частиц,
спектроаналитические приборы, электронно-оптические
преобразователи, приборы СВЧ электроники, устройства формирования
сильноточных пучков, различного типа полупроводниковые
приборы (транзисторы, структуры металл-диэлектрик-полупроводник),
многочисленные плазменные задачи. Это многообразие постановок
мы существенно сузим, исключив из рассмотрения задачи,
сводящиеся к решению уравнений Максвелла, а также те, для которых
существенны столкновительные процессы, описываемые
уравнением Больцмана или его магнитогидродинамическим
приближением.
Однако и при таких ограничениях мы имеем дело с широким
и содержательным классом математических проблем. Одна из них
заключается в эффективном численном решении линейных и
нелинейных эллиптических уравнений в двумерных и трехмерных
областях, как'ограниченных, так и неограниченных, со сложной
конфигурацией границ, в том числе многосвязных, и различными типами
граничных условий. К этому сводятся задачи электростатики и
магнитостатики. Конечной же целью является оптимизация
краевых задач, которая формулируется как минимизация некоторого
функционала от решения при заданных ограничениях на
варьируемые параметры и на какие-либо функциональные
характеристики. Исследования волновых процессов электродинамических
систем приводят к частичной проблеме собственных значений для
краевых задач. Вычислительная работа здесь особенно велика,
если требуется находить большое количество (до нескольких
десятков) собственных частот и гармоник. Принципиальным
моментом является тот факт, что основная цель исследования
численных методов заключается в обеспечении автоматического
построения алгоритмов на ЭВМ для решения широкого класса задач.
Этот подход определяет свои требования к подбору методов,
к самой оценке их трудоемкости и эффективности.
Одной из наиболее сложных является проблема формирования
сильноточных пучков заряженных частиц, которая в общем случае
включает все рассмотренные выше постановки. Моделирование

электронных и ионных потоков, как правило, проводится с
помощью методов больших частиц или трубок тока, которые
позволяют дискретизировать функции распределения частиц по
энергиям и углам. Задачи с сильными нелинейными эффектами могут
иметь неустойчивые режимы, в силу чего сами математические
постановки трудно исследовать в отношении существования и
единственности решения. Зачастую численные алгоритмы
приходится применять без их строгого обоснования; основным критерием
достоверности расчетов является сравнительный анализ
численных экспериментов с натурными или же правдоподобность
получаемых результатов с точки зрения качественных оценок
физических эффектов. Вычислительные трудности возрастают при
наличии следующих факторов: сильные токи, приводящие к
частичному «запиранию» пучков полем объемного заряда и
появлению режима виртуального катода с высокой чувствительностью
решения исходных данных; большие скорости частиц, требующие
учета релятивистских явлений; сильные магнитные поля, когда
ларморовский радиус намного меньше характерных размеров
области и необходимо переходить к дрейфовой теории движения.
Самостоятельную содержательную задачу представляет собой
расчет собственных и внешних магнитных полей. Например,
типичная постановка состоит в нахождении поля по измеренному
с неизбежными экспериментными ошибками полю на оси, в этом
случае приходим к классической некорректной задаче Коши для
уравнения Лапласа.
Интересные и мало исследованные математические постановки
возникают при моделировании процессов переноса зарядов в
полупроводниковых приборах. Основная задача заключается в
расчете характеристик нестационарных процессов, но самостоятельное
значение имеют и стационарные задачи. При различных
физических допущениях возникают задачи со свободной границей,
дифференциальные уравнения с сильными нелинейностями и одна
из трудоемких вычислительных задач — системы уравнений с
малыми параметрами при старших производных. Для таких случаев
типичными особенностями решений является наличие подобластей
с очень большими градиентами, что значительно усложняет
проблему построения хороших аппроксимаций.
Большое внимание в книге уделяется методам расчета полей,
сводящимся к решению краевых задач для уравнений
эллиптического типа. Первая глава посвящена конечно-разностным методам
для уравнения Пуассона в двумерных и трехмерных областях с
различными типами граничных условий. Рассматриваются
способы аппроксимации дифференциальных уравнений, в том числе
повышенной точности, свойства получаемых разностных систем и
методы их решения. Помимо ставших уже классическими
итерационных процессов верхней релаксации, переменных направлений или
неполной факторизации с различными способами ускорения
сходимости, описываются современные комбинированные методы
последовательности сеток и итераций по подобластям с использованием

экономичных прямых алгоритмов типа циклической редукции.
Изложение теоретических результатов по обоснованию или оценкам
' эффективности алгоритмов сопровождается значительным
количеством методических численных экспериментов. В первой главе
значительное место уделяется также общим вопросам методов
дискретизации, аппроксимации уравнений и матричного анализа,
используемым в последующих разделах.
С практической точки зрения рассматриваемые задачи имеют
большое самостоятельное значение, например, при
проектировании высоковольтных конструкций. Основной целью здесь
является нахождение конфигурации электродов и изоляционных
материалов, обеспечивающих наименьшие габариты при
необходимой электрической прочности. Приводятся примеры расчетов
характеристик изолирующих конструкций высоковольтной
подстанции и линии электропередачи.
Вторая глава содержит изложение основ методов конечных
элементов (или же вариационно-разностных схем) на примере
решения двумерных нелинейных задач магнитостатики. Здесь не
ставится цель, конечно, охватить весь круг теоретических и практических
вопросов методов конечных элементов, по которым к
настоящему времени уже имеется большое число прекрасных монографий
советских и зарубежных авторов. Задача заключалась в
наглядном, по возможности, представлении аппроксимационных качеств
и технологических аспектов данного класса алгоритмов,
эффективность которых особенно проявляется при расчетах полей
сложных магнитных линз и других устройств. Описанные же в
отдельном параграфе методы решения систем нелинейных уравнений
могут применяться и для других типов прикладных задач. В качестве
примера достаточно сложной практической задачи приводятся ре-
зультатьграсчетов полей магнитостатическои линзы при различных
токах в катушках, соответствующих случаям слабого, среднего
и сильного насыщения ферромагнитных материалов.
Для расчета полей без нелинейных эффектов во многих случаях
рекордно высокую точность потенциалов и их производных
можно получить сведением дифференциальной задачи к
интегральным уравнениям теории потенциала. Численным методам решения
таких уравнений посвящена третья глава. Эти алгоритмы имеют
пока что меньшее распространение по сравнению с сеточными, но
в последние годы интерес к ним со стороны специалистов по
вычислительной и прикладной математике значительно возрос.
Основное внимание уделено решению двумерных задач с помощью
принципа коллокации и аппроксимации потенциала простого
слоя В-сплайнами.
В четвертой главе рассматривается самостоятельная
физическая задача о расчете свободных колебаний электродинамических
систем. Математически она формулируется как проблема
собственных значений для краевых задач, являющаяся актуальной для
многих других прикладных областей. В методологическом плане
Данная глава является продолжением первой, поскольку в ней ис-

пользуются конечно-разностные методы. Исследуемые здесь
способы построения аппроксимаций с учетом асимптотического
поведения решения в окрестности особых граничных точек
представляют интерес и для расчетов электростатических полей.
Рассматриваются эффективные итерационные методы решения
алгебраической частичной проблемы собственных значений. Для
иллюстрации расчетов характеристик электродинамических систем
приводятся результаты численного моделирования регулярной
структуры волновода и замедляющей системы ускорителя.
Пятая глава посвящена численному решению одной из
наиболее сложных задач о формировании плотных пучков заряженных
частиц. В полной постановке здесь требуются расчеты и
электростатических и магнитостатических полей, и собственных частот и
гармоник резонаторов. Основное внимание в главе уделяется алгог
ритмам интегрирования уравнений движения для разных
постановок (с магнитным полем и без него, релятивистских и н€реляти-
вистских, двумерных и трехмерных), аналитического продолжения
магнитного поля по его компонентам на линии симметрии,
вычисления плотности тока и объемных зарядов, организации
итерационного процесса для решения всей самосогласованной задачи.
Приводятся примеры решения методических задач, а также
результаты расчетов достаточно сложных реальных устройств. Одно
из них — это высоковольтный источник релятивистского
электронного пучка, а второе — электронно-ионная оптическая система
для тлеющего разряда с заранее неизвестной конфигурацией
поверхности плазменного эмиттера.
В шестой главе рассматриваются математические постановки
и численные методы расчета полупроводниковых приборов.
Описываются различные физические модели процессов переноса
основных и неосновных носителей зарядов в полупроводниковых
материалах. Отсюда следуют разной степени адекватности и
разного уровня сложности математические формулировки. Поскольку
наиболее полные и точные постановки являются чрезвычайно
трудоемкими, представляется целесообразным использовать иерархию
моделей таким образом, чтобы решение относительно простой
задачи использовать в качестве начального приближения для более
сложной. Среди исследуемых в главе численных алгоритмов можно
отметить следующие: итерационный процесс для решения задачи
о нахождении свободной границы; построенная на основе
интегрального тождества Марчука разностная схема для
одномерного параболического уравнения с преобладающим
конвективным членом; разностное решение системы уравнений переноса
электронов и дырок в квазистационарном электрическом поле.
Для иллюстрации решения практической задачи приводятся
результаты расчетов установившегося режима для униполярного
транзистора.
Современный уровень развития численных методов и средств
вычислительной техники позволяет осуществлять переход от
решения отдельных задач к разработке пакетов прикладных программ,

обеспечивающих эффективное решение на ЭВМ целых классов
задач, с высоким уровнем автоматизации всего вычислительного
процесса. С инженерной точки зрения это означает подход к
построению системы автоматизированного проектирования различного
типа устройств. Реализация такой системы позволяет в
значительной степени заменить физические эксперименты (что зачастую
связано с созданием дорогостоящих макетов) на оперативное
численное моделирование и, в итоге, сократить сроки и повысить качество
проектирования новых устройств.
Переход от программ исследовательского характера к
разработке производственного программного продукта налагает
жесткие требования на весь технологический процесс
программирования и его конечный результат: гарантирование необходимой
точности, экономичность расчетов, безотказность работы, удобство
в эксплуатации для пользователя без высокой программистской
квалификации, качественное документирование,
приспособленность к расширению программного комплекса и адаптации на
новые технические средства.
Методологическим вопросам всего этого круга проблем
посвящена последняя глава. В ней рассмотрены структура, с^ема
развития и функционирования прикладного программного
обеспечения системы автоматизированного проектирования,
модульный анализ и технология пакетов программ для задач
математической физики, приведены описания ряда пакетов для расчетов
электрофизических устройств.
Вопросы пакетов прикладных программ являются важной
составной частью вычислительной математики. Само современное
понятие эффективности алгоритма неразрывно связано с
особенностями его программной реализации и конфигурации
вычислительных средств: точности машинного слова, объема оперативной
и внешней памяти, характеристик трансляторов, диалоговых и
сервисных средств. В конечном счете хороший алгоритм — это
«дешевый», т.е. позволяющий экономично решать задачи данного класса
на определенном типе ЭВМ.
Рассматриваемые задачи являются одними из трудоемких в
математической физике. Поэтому для проблем
автоматизированного проектирования электрофизических устройств, связанных
с многовариантными расчетами при различных данных,
чрезвычайно актуален вопрос о повышении быстродействия
используемых ЭВМ. В настоящее время однопроцессорные
вычислительные системы близки к предельно возможному быстродействию,
определяемому конечной скоростью распространения
электрического сигнала. Главным резервом повышения скорости
вычислений является распараллеливание алгоритмов на
многопроцессорных вычислительных системах. Эта проблема заставляет или
разрабатывать новые численные методы, или по-новому
рассматривать старые с точки зрения эффективности их реализации.
Этим вопросам посвящено приложение в книге, в котором
исследуются критерии эффективности распараллеливания основ-

ных характерных вычислительных фрагментов: сеточные (конечно-
разностные или конечно-элементные) методы решения краевых
задач, методы решения параболических уравнений в частных
производных, методы решения интегральных уравнений и
уравнений в частных производных. Даются оценки производительности
параллельных вычислительных систем для рассматриваемых нами
задач электрофизики.
В книге сделана попытка, с одной стороны, осветить основные
теоретические проблемы рассматриваемых численных методов,
но без доказательства сложных теорем, а с другой — дать
практические рекомендации по их реализации. Некоторые из
обсуждаемых вопросов содержались в книге автора «Численные методы
решения задач электрооптики», издававшейся в 1974 году.
Излагаемый материал в значительной степени основан на
многолетнем опыте работ лаборатории автоматизации построения
алгоритмов Вычислительного центра Сибирского Отделения
АН СССР. Автор искренне признателен за сотрудничество
А. В. Гаврилину, С. П. Гололобовой, Б. И. Голубцову, Н. И.
Горбенко, Е. А. Ицкович, В. А. Катешову, Г. Я. Куклиной, С. Б.
Кузнецову, Г. С. Поповой, С. А. Сандеру, В. М. Свешникову, А. Л. Урван-
цеву, М. В. Уреву, а также глубоко благодарен Г. И. Нариньяни
и Ф. В. Сартисон, оказавших неоценимую помощь в подготовке
рукописи.
В. П. Ильин

Глава!
РАЗНОСТНЫЕ МЕТОДЫ РАСЧЕТА
ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ
В этой главе мы будем рассматривать методы конечных
разностей решения внутренних краевых задач для электростатических
задач (или магнитостатических задач в линейном приближении).
Постановка формулируется как нахождение функции и (х, у> z),
удовлетворяющей уравнению Пуассона
Да—LJL (^^.)+Л+рЛ ef( } (1Л)
ха dx V °х / ду2 dz2
в ограниченной области G. Здесь (3 = 1 соответствует трехмерным
задачам (при этом а = 0), а |3 = 0 —двумерным; в последнем
случае а = 0 соответствует плоским задачам, а а = 1 — осесим-
метричным. Физический смысл имеет также уравнение с |3 = 0,
а = —1, тогда (1.1) описывает распределение осесимметрично-
го магнитного потока в цилиндрической системе координат. _
Через Г будем обозначать границу области G, а через G =
= G + Г — ее замыкание. Границу области считаем состоящей
из частей Гь Г2, Г3, на каждой из которых заданы граничные
условия 1-го, 2-го или 3-го рода:
и I г, = g\(x, У, А (х, у, z) ge Гь
ди I
дТГ\ г2 = £2 (х, у, z\ (x, у, z) e Г2, (1.2)
+ У{Х У2)
Кроме того, при наличии сред с различными физическими
свойствами на границах их раздела (внутренние границы Г4) ставятся
условия сопряжения — непрерывность решения и скачок его
нормальных производных,— называемые иногда граничными
условиями 4-го рода:
I л- ди \ — ди \ /1 о\
= u\rr, е+_|г<+=е — |гг. (1.3)
Типичный пример условий' 1-го рода в электростатике — это
постоянные заданные значения потенциалов на электродах. К
границе Г2 могут относиться линии или плоскости симметрии, на
которых g2 = 0. Условия 3-го рода могут задаваться, например,
в частях области G с известным характером поведения решения.
11

Решение задачи (1.1) — (1.3) мы считаем единственным и, за
исключением отдельно оговоренных случаев, обладающим
достаточной гладкостью (т. е. ограничены производные до тех порядков,
которые необходимы для обеспечения аппроксимационных свойств
рассматриваемых алгоритмов).
Разностные методы определяются, в первую очередь, способом
дискретизации исходной задачи. Расчетной области G ставится
в соответствие множество дискретных точек (узлов) — сетка Q,
а функциям непрерывного аргумента — определенные на Q
сеточные функции. Дифференциальное уравнение и граничные
условия заменяются алгебраической системой конечно-разностных
уравнений, решение которой дает приближенные значения
решения исходной краевой задачи в узлах сетки.
В теории разностных методов можно выделить следующие
основные проблемы.
а) Каков лучший выбор сетки? Сетка может отличаться
частотой расположения узлов, регулярностью, ориентацией
(прямоугольная, треугольная, шестиугольная и т. д.). Специальным
вопросом является способ выбора сеточного аналога границы
области. Под оптимальной сеткой при некоторых допущениях можно
понимать такую, которая обеспечивает заданную точность
решения при минимальном числе узлов. Ясно, что оптимальная сетка
зависит от решения самой задачи. Например, в области, где решение
меняется слабо, можно брать сетку более редкую. В общем случае
нахождение оптимальной сетки представляет собой нерешенную
теоретическую проблему. Вопросом выбора сеток мы заниматься
не будем и остановимся на использовании самых
распространенных прямоугольных сеток.
б) Какое разностное выражение лучше использовать в
качестве аналога дифференциального уравнения и граничных условий?
Имеется очевидный антагонизм: увеличение числа узлов в
разностном выражении может повысить точность решения, но в то же
время ведет к усложнению метода.
в) Существует ли решение системы разностных уравнений?
г) Сходится ли решение системы разностных уравнений к
решению дифференциальной задачи при сгущении сетки?
д) Какова погрешность разностного решения, т. е. насколько
точное решение системы разностных уравнений отличается от
точного решения дифференциальной задачи?
е) Каков лучший способ решения системы разностных
уравнений?
Конечной целью теории можно считать построение
оптимального метода для данной задачи или для класса задач, т. е. метода,
обеспечивающего получение решения с заданной точностью при
минимальных вычислительных затратах. С этой точки зрения
вопросы выбора сеток, способов построения аппроксимирующих
разностных уравнений и методов их решения оказываются
неразрывно связанными между собой, а также с конфигурацией ЭВМ,
на которой реализуются алгоритмы.
12

Разностные методы за последние двадцать лет стали предметом
самых интенсивных исследований. Основные результаты теории
и обширная библиография приводится в монографиях В. Вазова
и Дж. Форсайта [26], Р. Варги [28], Г. И. Марчука [119], А. А.
Самарского [164, 165, 166], Н. Н. Яненко [204], автора [69, 70] и др.
Основное внимание в настоящей книге обращено на
алгоритмические аспекты методов: вопросы построения разностных
уравнений и способы их решения. Теоретические результаты,
необходимые для обоснования методов и оценок их эффективности,
приводятся, как правило, без громоздких доказательств, с указанием
необходимых ссылок. Исследование разностных уравнений
представляет собой в значительной степени алгебраическую проблему,
и мы будем широко использовать аппарат вычислительных
методов линейной алгебры, см. [38, 151, 188]. Такие сложившиеся
понятия, как разностные решения, погрешности разностных уравнений,
разностные операторы, интерпретируются только как
алгебраические объекты, т. е. как векторы и матрицы.
§ 1.1. Основные понятия и вспомогательные сведения
Рассмотрим сетку, покрывающую область G и образованную
координатными линиями (или плоскостями), параллельными осям:
x=jXi,y = yh z = zkJ = 0f I, ..., /,/==0, 1, ..., m, & = 0, 1, ..., п (для
двумерного случая третья координата отсутствует). Обозначим
Рис. 1.
через (/, /, k) узел с координатами (х/, у/, Zk) и через M/2 = Af-i =
А$ А? h(f hf А$ А?
/ $ hk-i=Zk — zk-\; ft$ = Aj[ = 2*+i —z* —
расстояния от (/, /, k) до соседних узлов (рис. 1). Введем обозначение А =
13

= max {sup h% \ Узел (/, /, k) будем называть внутренним по
i,],k
отношению к области G, если (#,-, г/у, Zk) ^ G, и внешним — в
противном случае. Обозначим через Йо множество всех внутренних
узлов, через Qi — множество внешних узлов, а через ЙГ —
множество граничных точек сетки, т. е. точек пересечения
координатных линий сетки с границей Г области G.
Пусть и = {й (Xi, у\, Zk)} = {uijk} — сеточная функция,
определенная в узлах сетки. Тогда множество ее значений может
рассматриваться как М-мерный вектор, где N — общее число
рассматриваемых узлов. Если номер узла (/, /, k) при каком-либо
упорядочивании равен L, то Щ\к = uL. Например, при естественной
нумерации узлов L = / + jl + klm, / = 0,1,..., /; / = 0, 1,..., m;
* 0 l
, ,,
В вещественном пространстве сеточных функций, определенных
на множестве узлов Q, будем рассматривать скалярные
произведения и нормы:
ijk\ (1.4)
")1/2; (1.5)
,=тах \tiijk I. (1.6)
Векторным нормам (1.5) и (1.6) соответствуют следующие,
подчиненные им, матричные нормы:
/^ /= 1,2, ..., N; (1.7)
=тах S
k /=i
где Я,ул1 — собственное число матрицы АА' ; А ={а*/} — квадратная
матрица, Л/ = {а«}; /г, ^ = 1,2, ..., ЛЛ Собственные числа мы
предполагаем пронумерованными в порядке их убывания (если А —
симметричная матрица, т. е. ani = aik для всех ky l, то )$А, = (А$})2).
Дифференциальные уравнения, определяющие краевую задачу,
запишем в операторной форме:
Lv = g. (1.9)
Дифференциальной задаче (1.9) ставим в соответствие систему
алгебраических конечно-разностных уравнений
Lhu = 1 (1.10)
где и, f — УУ-мерные векторы, компоненты которых определяются
как значения сеточной функции в узлах сетки Q; Lh — квадратная
матрица.
Определение 1.1. Пусть w (ху у, г) — достаточно
гладкая функция, определенная для (х, у, z) e G, a (w)h — сеточная
функция, определенная на сетке Q и принимающая значения,
совпадающие со значениями w (jc, у, г) в узлах сетки. Пусть L —
дифференциальный оператор, определенный на функции w (x, у, z)>
а Lh — конечно-разностный оператор, определенный на (ш)л. Будем
14

говорить, что разностный оператор Lh аппроксимирует в области
G дифференциальный оператор L на функции w(x, у, г) с
погрешностью hy, если при /i-й) для (х, у, z) e G
^ = {Lw)h-Lh (w)h = O(W). (1.11)
Сеточная функция if» называется погрешностью, а у — порядком
аппроксимации.
Обозначив узлы сетки через Qk, систему (1.10) можно записать
в виде
Po(Qk)u (Q0- 2 pi(Qk)u(Qd = KQk\ (1.12)
где D (Qk) — совокупность узлов, используемых в уравнениях для
точки Qk (эти узлы будем называть соседними для Q&), a s(Qk) —
число таких узлов.
Далее, разностное уравнение вида (1.12) для узла Qk будем
называть (s(Qk) + \)-точечным, где s(Q*)+l —число ненулевых
членов в левой части уравнения и, очевидно, число ненулевых
коэффициентов в соответствующей строке матрицы системы
разностных уравнений. Характерным признаком разностных методов
является то, что max s(Qk)<t:N, т. е. плотность матрицы систе-
~ k
мы разностных уравнений (отношение числа ненулевых элементов
к общему числу элементов матрицы) очень мала. Матрицы с малой
плотностью называется редкими.
Матрица системы разностных уравнений будет симметричной
при условии pi(Qk) = Pr(Qk')y если узлы k и Г, W и /совпадают
попарно друг с другом.
Необходимым и достаточным условием существования
единственного решения (1.10) является невырожденность матрицы Lh.
Введем теперь ряд необходимых нам определений.
Определение 1.2. Матрицу А будем называть
положительно определенной, если для любого ифО
(Аи, и)^Ь{и, и\ 6>0. (1.13)
Определение 1.3. Матрица A— {a*/}, fe, /= 1, 2, ..., N
называется матрицей с положительными (неотрицательными)
элементами, если аы>0 (я^/^0) для всех ky l. Соответственно обозначим
Л0
>0или Л>0.
Определение 1.4. Матрица А ={а^} обладает свойством
диагонального преобладания, если
\акк\> 2 \akl\, k = l,2,...,N, -
ИЛИ
S 1ал/|, 1=1,2,..., N,
/5=1
15

причем хотя бы для одного k (или I) выполняется строгое
неравенство. В первом случае мы говорим о диагональном
преобладании по строкам, во втором — по столбцам.
Определение 1.5.-Матрица А называется матрицей
положительного типа, если она обладает свойством диагонального
преобладания и а^>0, а*/<0 для всех k, / при (k=£l).
Аналогично, если для всех узлов Q^Q имеем pi(Qk)>0,
Po(Qk) ^ 2p/(Q), причем хотя бы один раз выполняется
строгое HepaBQelc?BO, то соответствующая система разностных
уравнений типа (1.12) называется системой положительного типа.
Определение 1.6. Матрица А называется монотонной,
если для нее существует обратная матрица и А~1^0.
Определение 1.7. Матрица А называется разложимой,
если перестановкой строк и столбцов она может быть приведена к
виду
II
Л-
DlM
где D\ и D2 — квадратные, М — любая, а 0 — нулевая матрицы.
В противном случае она называется неразложимой.
Приведем без доказательств несколько теорем линейной
алгебры.
Теорема 1.1. (Тауски). Если матрица обладает свойством
диагонального преобладания и неразложима, то она невырождена.
Теорема 1.2. Если А — матрица положительного типа
и неразложима, то она невырождена и А~~1*^0.
Теорема 1.3. Если матрица симметрична, имеет
диагональные положительные элементы и обладает свойством диагонального
преобладания, то она положительно определена.
§ 1.2. Способы построения разностных аппроксимаций
1.2.1. Разностные аппроксимации для уравнения Пуассона.
Построение конечно-разностных аппроксимаций для функций,
обладающих ограниченными производными достаточного порядка,
основывается на применении ряда Тейлора
= и(хи ..., xR)
*
i= 1
При использовании достаточно большого числа узлов
уравнение Пуассона можно аппроксимировать до любой заданной
погрешности с помощью конечно-разностных выражений. Мы
приведем простые, но наиболее часто встречающиеся примеры.
Простейший («одномерный») разностный оператор Лапласа имеет вид
16

(индексы /, k для краткости опускаем)
2щ-х 2и/ 2ц<+|
(Л*И)/ — hf_ i(/rjL t + ^ л*_ |W "I- вд_ i + hf)
В частности, для равномерной сетки (hf=hx) имеем
Аналогично для цилиндрической системы координат получаем
ч 2{Xi-i/2/Xi)Ui-i 2Щ 2
u)i =
hf—hf-i
если Xi=^0. В противном случае имеем Л1 = 2Лх, так как
(х—— )->2—— при л:->0. Здесь и далее обозначается
х д* \ дх ) дх*
Погрешность аппроксимации этих выражений на функциях
иу обладающих ограниченными производными до третьего порядка
включительно, есть O(h). Если-же сетка равномерная и функция
имеет четвертую производную, то погрешность имеет второй
порядок.
Простейшими аппроксимациями для уравнения Пуассона
являются:
для плоской задачи
(A5u)lf=((Ах + Ау)и)и = fa (1.17а)
для осесимметричной задачи
(А1и)ц = ((Ai + Ау)и)ц = fli; (1.176)
для трех переменных
(А7и)цк = ((Л, + Ау + \2)и)цк = fa* (1.17b)
где Ау и Az определяются аналогично Л* из (1.14).
Для двумерных задач формулы (1.17а) и (1.176) выпишем
подробней, используя обозначения в соответствии с рис. 1 и
опуская индексы /, /:
% 2 , 2(xi+]/2/Xi)a
п+ Л3(Л,+Лз)
Здесь а = 0 соответствует плоской задаче, а a=l —осесиммет-
2 В П Ильин 17

ричной, причем в последней при Xi = 0 вместо (1.18). получаем
/ц/Ь,+л,)ц'+ hth*+b) U2+ h3(h*+h3) и*+~й 2 "
Очевидно, все разностные уравнения (1.17) — (1.18)
аппроксимируют уравнение Пуассона с погрешностью первого порядка
на неравномерной сетке, и второго — на равномерной. Точнее
говоря, |г|э|^А1зЛ/3 — для первого случая, I гр | ^Л14Л2/12 —
для второго, где
Mk= max sup —д uh ,
/ stl dxldyk~l
Мы приведем ряд аппроксимаций повышенной точности на
равномерных сетках. Для декартовой системы координат
несложно проверить справедливость следующих соотношений:
для двумерной задачи
(A9u)iik = [(Ах + Ау) Н—х-^~ АхАу]ц =
= \ д2и , д2и .ft д2 / д2и , д2и \ ,
t дх2 ду2 I2 дх2 \ дх2 ду2 )
для трехмерной
= [(Ax+Ay + Az-\—х-рг-?-АхАу-
(|20)
Отсюда следует, что соответствующие разностные уравнения
Пуассона с погрешностью четвертого порядка могут быть
записаны в виде
(Al9u)ijk = fak + T5\-|pr)y* + ~к\^)чк + ~u\jrf)iiv (' *22)
Очевидно, порядок погрешности уравнений останется тем же,
если вместо производных от f брать их конечно-разностные
аппроксимации, т. е. (d2f/dx2) ц заменить на (Л /);/ и т. д. Эта
постановка неизбежна, если значения f известны только в узлах сетки.
18

В покомпонентной записи уравнение (1.21) для/ = 0 и
квадратной сетки имеет вид (девятиточечная схема ящик):
r[i\tji + i+\tj + i + i\tj + \ + i+\,j\ +
on
+ 4(ui-4 + Uitj-x + Ui+4 + Uiti+l) — 20uii\ = 0. (1.23)
Разностный оператор Лд на квадратной сетке обладает тем
замечательным свойством, что для него погрешность
аппроксимации дифференциального оператора Лапласа А = д2/ дх2-{-
+ д2/ ду имеет специальный вид, т. е. если и — достаточно
гладкая функция, то
я|>|7 = (А9и)ц — (Аи)И =
j^ . (1.24)
Отсюда следует, что если и — гармоническая функция, то
уравнение (1.23) имеет погрешность не четвертого, а шестого
порядка.
Аналогично, мы можем на квадратной сетке получить
разностный аналог уравнения Пуассона с погрешностью O(h6):
(1-25)
В правой части этого уравнения можно без понижения
порядка погрешности производные заменить соответствующими
конечно-разностными выражениями, причем необходимо
аппроксимировать предпоследний член с погрешностью О (/г4), а
последний — с погрешностью О (А2).
Для уравнения Пуассона в цилиндрической системе координат
(Д=—— (г—\ -f-^на квадратной сетке г/ = /А, Zj = zoztjh,
/, / = 0, 1, ...) аналогичная аппроксимация с погрешностью
четвертого порядка может быть представлена в виде
Ь + (2+4 W+
*">1. (1-26)
«IJ+l) +
+ uo,j _, + uo.j +1 — 1 Зыо/]=hj+-j^i A/)o;-
В последнем равенстве использовано условие симметрии и_(/=^ы,;.
2* 49'

Мы рассматриваем только один из возможных путей
построения разностных уравнений, основанный на непосредственной
аппроксимации дифференциальных операторов. Он сравнительно
простой, позволяет получать достаточно высокую точность и
вполне достаточен для эффективного решения рассматриваемого нами
класса краевых задач. Другой широко распространенный подход
заключается в построении консервативных, или балансных,
разностных схем на основе интегро-интерполяционного метода,
последовательно изложенного в книгах А. А. Самарского [164, 165].
Существует и другой универсальный подход к построению
разностных аппроксимаций для уравнений Лапласа и Пуассона.
Именно, искомое решение ищется в виде разложения по системе
линейно независимых гармонических функций или просто
алгебраических полиномов. Коэффициенты разностного уравнения
при каком-то фиксированном разложении точек шаблона
находятся из условия, чтобы этому уравнению удовлетворяло как
можно больше членов выбранного разложения. Такой подход
позволяет строить аппроксимации, во-первых, различных
порядков и, во-вторых, для различных типов сеток и сеточных шаблонов.
Останавливаться на них мы не будем ввиду громоздкости
получаемых выражений (см. [50, 69] и цитируемые там работы).
В заключение укажем еще на один метод построения
разностных уравнений, основанный на аппроксимации искомого решения
в виде сплайнов. Коэффициенты алгебраической системы при
этом определяются из условий разрешимости дифференциальных
уравнений (принцип коллокаций) и непрерывности решения и
его производных во вспомогательных точках. Такой подход
позволяет вычислять с высокой, точностью в произвольной точке
области не только само решение, но и его производные, притом
без применения численного дифференцирования, которое
сопровождается накоплением погрешностей. Метод сплайн-коллокаций
интенсивно исследовался для одномерных задач, но
применяется также и для уравнений в частных производных (см.,
например, [51, 65, 85]).
1.2.2. Аппроксимация граничных условий. Приведенные выше
конечно-разностные выражения, аппроксимирующие
дифференциальные уравнения, определены, если используемые точки
принадлежат множеству узлов Qo, внутренних по отношению к
области G. Однако для узлов вблизи границы в разностных
уравнениях могут использоваться точки, лежащие на границе Г
области G или вне области. В этом случае при
аппроксимации дифференциального уравнения предполагаем, что решение
его гладким образом распространяется вне области на расстояние
h. Внешние узлы сетки, входящие в разностные уравнения,
называются иногда" фиктивными. Внутренние узлы, для которых
разностные уравнения содержат точки на границе или вне области,
будем называть околограничными, а остальные внутренние узлы —
регулярными.
20

Для того чтобы система разностных уравнений была
определена т. е. число уравнений равнялось числу входящих в систему
узлов сетки, необходимо использовать конечно-разностные
аппроксимации граничных условий. Методы аппроксимации граничных
условий могут быть различными в зависимости от характера
расположения околограничных узлов относительно границы,
используемых сеточных шаблонов и порядка погрешности
аппроксимации. При этом значительно отличаются задачи, в
которых граничные условия содержат производные, от задач, в
которых это не так.
А. Граничные условия первого рода. Мы
проведем рассмотрение для двух независимых переменных (и\г =
= g(*> У) )• Обобщение методов на трехмерные задачи очевидно.
Интерполяция первого порядка (аппроксимация Коллатца).
В примере на рис. 2 могут быть использованы следующие
соотношения:
U\ =
/01'
= Us'-} -f-Ub-j—^, (1-Z/)
Здесь lpq — расстояние между точками
p и q, причем (как и всюду далее)
предполагается, что при измельчении сетки
расстояния между соседними
точками будут оставаться величинами одного
порядка. При этом экстраполяция производится в узлы,
ближайшие к граничным точкам сетки, т. е. /oi'^ у'01' А^'^у/ог
и т. д. Погрешность аппроксимации, очевидно, равна
Интерполяция полиномами второго и более высокого поряоков.
Логическим развитием является применение экстраполяции
высшего порядка с помощью нескольких внутренних узлов,
лежащих на одной координатной линии. В том же примере может быть
использовано уравнение, имеющее погрешность аппроксимации
О (/г3):
(1.28)
Аналогичные соотношения могут быть выписаны для узлов
5, 2 и т. д. Очевидно, что такие формулы целесообразно
употреблять, если во внутренних узлах сетки используются
разностные уравнения повышенной точности.
21

При использовании формул (1.27), (1.28) предполагается,
что для околограничного узла разностный аналог
дифференциального оператора строится с привлечением соседних узлов сетки,
в том числе и находящихся вне области. Например,
пятиточечное разностное уравнение Лапласа для точки 0 на рис. 2 может
быть представлено в виде
Т7-ч/|+-П-И2+ТТ-аз + 7Т-"4" (тТ~+ТТ-) ио = 0'
4)1 МЗ *02*24 *03ЧЗ '04*24 \ *01 *03 *02*04 / /1 OQ^
Другой подход к аппроксимации граничных условий первого
рода состоит в том, что в околограничных узлах для построения
разностного аналога дифференциального оператора вместо
внешних соседних узлов используются ближайшие точки из Йг,
лежащие на пересечении координатных линий сетки с границей.
Например, пятиточечная аппроксимация Канторовича—Шортли—Уэл-
лера для уравнения Лапласа в точке 0 будет иметь вид (см. рис. 2)
2i* , 2ц2, , 2и3 _|_ 2и4 / 2 _^_ _2 \Uq = Q П 30)
lo2Ub kzku /04/42 V /oiЛоЗ /02'/04/
/О1'/31/ lo2'Ub kzku /04/42/
В этом случае система разностных уравнений содержит
значения и во всех внутренних узлах и в граничных точках сетки,
причем в последних граничное условие можно аппроксимировать
точно (uy = g\>, Ur = g2' и т. д.). Однако при этом погрешность
уравнения в околограничном узле имеет только первый порядок.
Для построения разностных аппроксимаций более высокого
порядка с помощью такого подхода в околограничных узлах
требуется использовать на неравномерных шаблонах разностные
многоточечные уравнения.
Б. Граничные условия, содержащие
производные. В данном пункте речь идет о третьем уравнении из (1.2),
причем для определенности направление нормали п выбираем
внутрь области G. Рассмотрим сначала граничные условия с
нормальными производными, заданными на прямолинейных
границах, параллельных координатным линиям.
Простейший способ аппроксимации состоит в замене
нормальной производной разностью первого порядка и в линейной
интерполяции значений и на границе через два ближайших
узла сетки. В примере на рис. 3,а
/ll'ttO + Zpi'tti ^_ Up-Ui _ (1.31)
/111 /о 1
Значения у, g берутся в точке на границе. Погрешность
аппроксимации такого двухточечного выражения, как легко
проверить, имеет второй порядок, если граница проходит через
середину шага сетки (/ц' = /ог)> и первый порядок — в остальных
случаях.
При произвольном положении точек сетки относительно
границы уменьшить погрешность аппроксимации можно за счет
привлечения дополнительных узлов. Например, для условия Неймана
22

ди/дп = О при /oi = /оз = /i, /ц> = / на рис. 3, а трехточечное
соотношение
имеет погрешность O(h3), если / = (1 —>/3/ 3)Л, и равно O(h2)
для любого другого положения точки Г в отрезке [лс0, *i]. В
частности, при /ц' = /ог аппроксимация (1.32) принимает вид ио = ии
Г 4 „к S Г 4
г
0
2
3
/
6
0
2
J
7
Рис. 3.
б)
а если граница проходит по координатной линии, то мы
получаем другое двухточечное выражение: u$ = U\ (см. рис. 3, б).
Мы выделим особо те задачи, в которых условие Неймана
ставится на плоскостях или линиях, относительно которых
решение обладает симметрией и при этом является достаточно
гладким. Тогда, если линия симметрии проходит через середины
шагов или через узлы сетки (в последнем случае требуется
равенство шагов по обе стороны), равенство нулю центральной
разности на линии симметрии (#о — wi=0 при /и, =/01,)
на рис. 3, а является точной аппроксимацией.
Если граница с условием ди/дп = 0 проходит по
координатной линии и в разностных уравнениях (1.21), (1.22) граничное
условие учитывается с помощью центральной разности вида
ui-i,i — &/+!,/ = 0, то погрешность аппроксимации оказывается
также четвертого порядка (при этом видоизменяется правая
часть в уравнении Пуассона [165]). В примере на рис. 3, б для
квадратной сетки
1 ГЛ/ ' ч " " ~ ' )-2Оио] =
Проведем теперь построение аппроксимаций для общего
случая, ^когда направление нормали к границе не параллельно ни
одной координатной линии.
Во-первых, в околограничном узле разностный аналог
дифференциального уравнения строим с использованием граничных
23

точек сетки из Йг аналогично методу аппроксимации (1.30) для
граничных условий Дирихле. Затем в граничных точках сетки
выписываем разностные уравнения, аппроксимирующие граничное
условие. Для этого из точки на границе проводим вектор п до
ближайшего пересечения с каким-либо отрезком, соединяющим
два внутренних узла. (Заметим, что для применимости метода
должно обязательно найтись такое пересечение.) Далее,
производную на границе по направлению п аппроксимируем
односторонней разностью, причем значение и в точке пересечения п с
линией сетки выражаем (с помощью интерполяционного полинома)
через значения функции во внутренних узлах. Для примера на
рис. 4 получим (значения у, g берутся в точке Г):
/51'
J-U2 + 7—
/23 /23
откуда имеем
(1 —
Для трех независимых переменных алгоритм построения
разностного уравнения остается тем же. Вектор п продолжается
\ \
\
0 J
2
Рис. 4.
до ближайшего пересечения с плоскостью, проходящей через
внутренние узлы. Член ди/ дп аппроксимируется разностью
пеового порядка, а значение во вспомогательной точке с
помощью двумерной интерполяции заменяется через значения во
внутренних узлах сетки. В примере на рис. 5 имеем
их+у{иХ'-иху lUf + g = b (1-35)
U\' = k2ll2 + k3U3 + &5И5. (1.36)
Для подсчета коэффициентов ki, &з, k$ используем формулы
интерполяции двух переменных в плоскости треугольника 2—
3—5:
/,2 _fa—л 1')П5—(hzibW £ __Ei"n5 —TJi'fs й5==Д11 (1.37)
/
24

где fi'= л//?'3 — 111% tii' = 2S2//32, 1б = У/з5 — Л I, T]5 = 2Si//32,
Si и S2 — площади треугольников 2—3—5 и 1—2—3, которые
легко вычисляются по формуле Герона. После подстановки (1.37)
и (1.35) в (1.36) получаем разностное уравнение с погрешностью
первого порядка, аналогичное (1.34) для двумерного случая.
Различные алгоритмы аппроксимации граничных условий с
производными, в том числе с погрешностью высшего порядка,
описаны в статьях многих авторов (см. библиографию в [69,
70]). Мы на них останавливаться не будем, поскольку в
рассматриваемых нами задачах обычно условия Неймана ставятся
только на прямолинейных участках границы.
В. Аппроксимация условий сопряжения на
внутренней границе. Мы проведем построение разностных
уравнений, основанных на непосредственной аппроксимации
условий сопряжения (1.3). Рассмотрим сразу общий случай, когда
нормаль к Г4 не параллельна координатным линиям. В точке
пересечения линии сетки с внутренней границей, ближайшей
к рассматриваемому узлу, производные ди/ дп аппроксимируются
разностью первого порядка с использованием точек пересечения
нормали с отрезками, соединяющими внутренние узлы. В
полученном соотношении значения и в точках, не являющихся
узлами, с помощью интерполяционных соотношений заменйются через
значения и в узлах сетки. В итоге для узлов, в окрестности
которых проходит внутренняя граница,
получаем разностные уравнения,
аппроксимирующие условия сопряжения (1.3) с
погрешностью О(А).
Например, для рис. 6 имеем
е_
(1.38)
(1.39)
1 0
/
* 1
I
2
n
/|4
з Рис. 6.
После подстановки (1.40) и (1.38) в (1.39) в общем случае придем
к пятиточечному разностному уравнению (если нормаль
перпендикулярна к линии сетки, то уравнение может выродиться
в трехточечное):
U\ l 53 7
./йз'-т-^-Из +
-А-иА — и0 = 0.
М4 /
(1.41)
Такой же подход применим и для трех независимых
переменных. При этом используются аппроксимация нормальной
производной и двумерная интерполяция, аналогично тому, как это
делалось для условия Неймана.
25

§ 1.3. Свойства разностных операторов
и оценки точности разностных решений
1.3.1. Примеры разностных операторов и их основные
характеристики. Резюмируем процесс построения разностного аналога
краевой задачи. Во внутренних точках сетки из Qo аппроксимируем
исходное дифференциальное уравнение (за исключением узлов
вблизи внутренней границы, где берется аналог уравнения
сопряжения). При этом для околограничных узлов в полученные
уравнения будут входить члены, относящиеся к внешним узлам Qi или
к граничным точкам сетки пг. Используя граничные условия,
для этих точек строим дополнительные конечно-разностные
соотношения таким образом, чтобы в получаемой алгебраической
системе число уравнений равнялось числу неизвестных (т. е. числу
используемых узлов). Из этой системы мы сразу исключим
неизвестные, соответствующие узлам из Qi и Qr, и будем
рассматривать уравнения только для внутренних узлов сетки.
В качестве простейшего примера рассмотрим одномерное
уравнение Пуассона
52и/3х2 = /(*), *€=(а, Ь\
(1.42)
при трехточечной аппроксимации на равномерной сетке с узлами
Xi = a-\-iht %/ = 0, 1, ..., W+l, h = (b — a)/(N-\-l). Если, например,
на концах отрезка заданы условия Дирихле
и\х=а = иа; u\x==b = ubi (1.43)
то получим систему уравнений
)=/,, /=2, 3
Г—1,(1.44)
или,
где
в векторном
Q(а) _
виде,
== 1/1 —
1
—2
1
С
- иа
1
—2
1
j\a\ i
/А2,...,/
1
2
•
— 1
h-,f
•
2
—
—2
1
«б/А2}
0
1
—2 1
1 —2
(1.45)
(1.46)
26

Рассмотрим смешанную краевую задачу, отличающуюся
граничным условием на правом конце, где предполагаем заданным
условие 2-го или 3-го рода u-{-ydu/dx = g, аппроксимацию
которого можно записать в виде uN+{ cos ф — uNsm ср = 6 (|tgcp|<l;
ф и б выражаются через у, g). При этом система разностных
уравнений для внутренних узлов Qo имеет вид
(Abu)i=Gf\ /=1,2,..., Л/, (1.47)
где № =
coscp
! -2 1
1 —2 1
0
0
1 —2 1
1 tg <p - 2
(1.48)
Опишем свойства трехточечной аппроксимации осесиммет-
ричной задачи
(Х) ^ l0 "! « (149)
Если взять равномерную сетку */ = (/—l/2)ft, h = b/(N-\- 1/2),
/ = 0, 1,..., N-\- 1, то матрица ЛЛ-го порядка системы разностных
уравнений имеет вид (см. (1.18))
—2 2
• 2/3 —2 3/4
О
2/-1
—2
2/-1
О
2N—1
- —2
.(1.50)
Как легко видеть, в рассмотренных задачах матрицы
разностных систем симметричны (кроме (1.50)), трехдиагональны и
обладают свойством диагонального преобладания. Из последнего
свойства с учетом неразложимости матриц следует их
невырожденность, что обеспечивает существование единственных решений
Для систем уравнений (1.45), (1.47), (1.49).
Отметим, что матрицы ( — Та), ( — Ть), ( — То) —
положительного типа, и обратные к ним матрицы имеют неотрицательные
элементы ( — Г"1 > 0, — 7Т1>0, — Т^~1^0). Кроме того, они
27

положительно определены, т. е. для всех и ( — Таи, и) > О,
( — Тьи, и) >0, и их собственные числа положительны.
Свойство симметричности обеспечивает наличие базиса
собственных векторов матрицы, что, как мы увидим, дает аппарат
для обоснования, а иногда и для построения методов решения
систем разностных уравнений. Однако матрица
конечно-разностного оператора, соответствующая неравномерной сетке, вообще
говоря, не симметричная. Например, систему трехточечных
уравнений, определяемую аппроксимацией (1.14) для уравнения
(1.42), с учетом граничных условий можно записать так:
aiUi-i — biUi + CiUi+i = fi9 /=1,2,..., N, a\ = cN = 0, (1.51)
или ,
где F={fii /=1,2, ...,N;
а2 — £
О
Лха = F,
(Г
— bN-\
-bh
. (1.52)
Отметим, что трехдиагональные матрицы вида (1.52)
называются якобиевыми матрицами, если C/a/+i>0. Якобиевы
матрицы симметризуются, т. е. с помощью умножения слева или справа
на диагональную матрицу приводятся к симметричному виду.
Например,
DAX = AX, Ах = Ах (1.53)
где D = {di}—диагональная матрица с элементами
Таким образом, систему уравнений (1.51) легко свести к
системе с симметричной матрицей:
Axu = DF. (1.54)
Охарактеризуем на нескольких примерах свойства матриц для
двумерных краевых задач. Начнем с простейшего случая —
уравнения Пуассона в прямоугольной области, на каждой из сторон
которой задано одно из приведенных выше граничных условий:
2 = f(x1 y\ 0<x<a, 0<y<b. (1.55)
Тогда пятиточечная аппроксимация вида (1.17а) на
прямоугольной неравномерной сетке может быть записана в форме
(Д5и)<7 =
Uiti+\--poiiUij==<I)ij (1.56)
=p3l = p2l='p4m = 0y /
1,2,
/=1,2, ..., /П,
28

где Oij = f(xi> yj) Для регулярных внутренних узлов, а в
околограничных Ф/у изменяется за счет исключения граничных условий,
аналогично одномерной задаче. Значения коэффициентов
определяются с помощью выражений
„ 2 „ 2
(1.57)
рои =
^= р 1
= Р2/
где величины pi/, рз/ равны а,-, с, из (1.51); рй~&/.
В околограничных узлах коэффициенты подправляются с
учетом граничных условий. При естественной нумерации узлов (слева
направо по каждой строке, перебирая их снизу вверх) матрица
системы (1.56) представляется в виде
Д5 = Л,+Л2,
Л2 =
о
Р22Е1 —
О
p4,m-lEt
p2mEt —
(1.58)
где Ei — единичная квадратная матрица /-го порядка, Ai —
блочно-диагональная матрица порядка 1т с блоками Ах порядка
/ на диагонали.
Очевидно, А5 — пятидиагональная матрица порядка 1т.
Матрица ( — Д5) — положительного типа, на равномерной сетке
симметрична и положительно определена. Более того, свойства
симметричности и положительной определенности сохраняются для
равномерной по х и у сетки в областях, составленных из
прямоугольников (со сторонами, проходящими по координатным
линиям) . При этом матрицы Ал и А2 сохраняют тот же блочный вид,
однако порядок каждого блока изменяется и равен числу
внутренних узлов сетки в соответствующей строке.
Если же* в прямоугольной области (или составленной из
прямоугольников) задана неравномерная прямоугольная сетка,
то разностный оператор Лапласа Д5 не симметричен. Однако для
указанных областей матрица системы симметризуется, если
каждое из уравнений (1.56) умножить на (lu + ki)> (/2/ +/4/)/4.
Если же граница области криволинейна, то симметризовать
матрицу пятиточечных разностных уравнений (1.17а) не удается.
Однако для задачи Дирихле с криволинейной границей можно
построить симметризуемую аппроксимацию, если учет граничных
29

условий проводить с помощью «экстраполяции по Коллатцу».
В примере на рис. 2 для околограничного узла 0 можно выписать
уравнение вида (1.29) с привлечением внешних узлов 1 и 2,
которые затем исключаются с помощью соотношений (1.27). В итоге
получаем
Л1+Л3 . Л2 + Л4 . Л1+Л3
++ +
2/г3
, = 0. (1.59)
О/ ' 9/ ' 9/?о 9/ь
01' ^02' ^'*3 z-ii-4
Симметричность разностного оператора А5 не нарушится и
тогда, когда на прямолинейных участках границы области задано
условие Неймана, которое аппроксимируется с помощью разности
первого порядка, как это было рассмотрено выше.
Выражение (1.59), кстати, можно считать аппроксимацией
уравнения Лапласа, погрешность которой, что легко проверить,
есть 0(1), т. е. остается по крайней мере ограниченной при А->0.
Отметим еще одно свойство разностного оператора для
уравнения Лапласа. А именно, в задаче Дирихле для прямоугольника
(и прямоугольной сетки, не обязательно равномерной) полная
матрица системы может быть представлена в виде суммы двух
перестановочных трехдиагональных матриц размерности 1т,
соответствующих «одномерным» операторам:
A5 = Ai+A2; AiA2 = A2Ai; А\~ д2/дх2\ А2~ д2/ду2.
, Свойство перестановочности «одномерных» операторов
сохраняется и тогда, когда на сторонах прямоугольника заданы условия
второго или третьего рода (с постоянными коэффициентами в
граничных условиях).
В общем случае можно утверждать, что разностный оператор
представим в виде суммы перестановочных операторов, если
исходная дифференциальная задача допускает применение метода
разделения переменных.
Отмеченные нами свойства двумерных задач выполняются
и для трех независимых переменных, т. е. свойства
прямоугольной области аналогичны параллелепипедоидальной.
1.3.2. Собственные числа и собственные векторы матриц в
разностных уравнениях. Основным инструментом исследования задач
линейной алгебры является спектральный анализ. Напомним, что
вектор Zi называется собственным для матрицы Л, если Azi — hzu
где ki — число, называемое -собственным числом, соответствующим
Zi. Наиболее поддаются анализу системы линейных уравнений,
которые имеют так называемые нормальные матрицы с базисом
из N линейно независимых собственных векторов (N—порядок
матрицы). Теоретические исследования эффективности методов
решения разностных уравнений практически именно такими
задачами и ограничиваются. К этому классу задач относятся
системы уравнений с симметричными матрицами.
30

Самый благоприятный случай — тот, в котором для матрицы
имеются явные выражения собственных векторов и собственных
чисел. В некоторых простейших разностных задачах это
действительно имеет место, однако чаще всего определение A,/, zi гораздо
сложнее, чем решение самой системы уравнений. При этом для
наших исследований существенны такие свойства: во-первых,
сам факт существования базиса из собственных векторов,
во-вторых, нижняя оценка для минимального модуля собственного
числа, в-третьих, оценка числа обусловленности матрицы,
определяемого как Р= ||Л || • ЦЛ"1!! (для симметричной матрицы можно
положить Р = max |A,/|/ min |А*|).
Мы начнем рассмотрение с одномерных задач предыдущего
пункта. Матрица Та системы уравнений (1.44) для первой краевой
задачи имеет собственные числа
, (1.60)
которым соответствуют собственные векторы
^ /,p=l,2,...,/V, (1.61)
где константа С из условия нормировки 2 u2p{i)=\ равна
i=\
/()
Аналогично, для матрицы Tbi соответствующей системе
уравнений (1.47) в смешанной краевой задаче, известны следующие
собственные числа и векторы (предполагаем tg <р = 1, что
соответствует условию Неймана при х = Ь):
^^ (1.62)
Для матрицы Го, соответствующей осесимметричной задаче,
имеем
А,, = 2(1 -хр\ u{i) = Pp-X(x>), U р= 1, 2,..., N. (1.63)
Здесь Рр^\(х) — полином Лежандра степени р—1, а хр — корни
полинома Лежандра степени N. Явные выражения для них имеют
сложный вид, но нам будет достаточна оценка
^>-4. (1.64)
Общим для всех рассмотренных матриц является то, что все
собственные числа отрицательны.
Если трехдиагональная матрица имеет переменные
коэффициенты a/, bi, Ci, то в общем случае получить выражения для собст-
31

венных чисел и векторов трудно. Для систем уравнений,
аппроксимирующих на неравномерной сетке одномерное уравнение
Пуассона с условием Дирихле хотя бы на одном конце, собственные числа
удовлетворяют неравенству
\к\^ С (max hi/min hi)2, n -^
где С не зависит от А, т. е. если при N-^oo шаги сетки А/ —
величины одного порядка, то оценка для |A,|min не зависит от А.
При аппроксимации же задачи Неймана (условие du/dx — g
на обоих концах отрезка) матрица системы оказывается
вырожденной, так как при этом &,- = а,- + С/ для всех /, и вектор со всеми
единичными компонентами является собственным, а
соответствующее ему собственное число равно нулю.
Для вычисления обусловленности матрицы необходимо найти
верхнюю оценку для модулей собственных чисел. В качестве
оценки для |А,|тах можно взять норму матрицы, например ЦЛЦ^,
которая легко вычисляется. Для матрицы Л* из (1.52) при этом
имеем
Ш<тах(|а,| + |&,| + к,|). (1.66)
Как правило, для разностных уравнений такие оценки вполне
удовлетворительны, а для рассмотренных нами матриц Та, Ть, То
при УУ-> оо они вообще точные.
Рассмотрим спектральные свойства для двумерных разностных
задач на примере оператора A5 = Ai +Л2. Начнем с прямоугольной
области, когда Ai и Л2 перестановочны. Как следует из
предыдущего, матрица Ai порядка lm имеет блочно-диагональный вид,
причем на диагоналях стоят матрицы Ах порядка /,
соответствующие аппроксимации одномерной задачи по х\ количество
таких блоков равно т. Следовательно, собственными числами Ai
являются собственные числа \хр матрицы Ах (р= 1,2,...,/;
каждое из них имеет кратность т).
Перейдем к матрице А2. Очевидно, если компоненты сеточной
функции переобозначить так, чтобы они соответствовали
нумерации узлов по столбцам, а не по строкам, Л2 приводится к блочно-
диагональному виду, в котором на диагонали стоят / матриц Л^,
каждая из которых имеет порядок т и соответствует
одномерной аппроксимации задачи по у. Алгебраически это означает
преобразование подобия с помощью матрицы перестановок Л2 =
= РА2Р~\ которое не меняет собственных чисел.
Следовательно, собственными числами Л2 являются собственные числа v^
матрицы Ау (q= 1,2,..., m; каждое из них имеет кратность /).
Отсюда получаем, что собственные числа А5 можно записать
в виде
A™ = |i, + v,, р=1,2 /, <7=1,2,...,т. (1.67)
32

Несложно проверить, что соответствующие собственные
векторы Аб представляются как
Zpq = (pp^q, р= 1,2,...,/, #=1,2, ...,га, (1.68)
где фр и tyq — собственные векторы матриц Ах и Л^,
соответствующие \хр и v^.
Например, для задачи Дирихле и квадратной сетки имеем
(матричные блоки АХу Ау, из которых составлены А\ и Лг,
представляют собой матрицы вида Та с порядками / и га
соответственно):
л 4
APQ— TV
zpq(i, /) = sin iph sin jqh, i,p= 1,2,..., /, /,<7= 1, 2,..., m.
Если же область не прямоугольная, то матрица Л} имеет
на диагонали разные блоки Л*,, /=1, 2,..., га, каждый из
которых соответствует аппроксимации одномерной задачи на /-Й
строке и имеет порядок, совпадающий с количеством внутренних
узлов // на этой строке. Собственные числа Ai можно выразить
через собственные числа \xpj всех блоков Axj (py-=l, 2, ..., /у,
/=1, 2, ..., га). Аналогично, собственные числа матрицы Л2
можно выразить через собственные числа v^ матриц Ayit каждая
из которых соответствует аппроксимации д2и/ ду на i-м столбце
(^•=1, 2, ..., ти /=1, 2, ..., /).
Явные выражения для собственных чисел матрицы А5 при
некоммутирующих Ль Лг получить очень сложно. Однако, если
Ai и Л2 симметричны, то из минимаксного свойства собственных
чисел можно получить оценку
minimi +min|v^| < |A,Kmax|(jip/| +max|v^| (1.70)
P' / <7' i p, j q, i
для собственных чисел к матрицы Аб через собственные числа
одномерных операторов. Из этой оценки, например, следует,
что для задачи Дирихле в некоторой области G спектр оператора
А5 (если он симметричен) лежит между нижней и верхней
границами спектра матрицы аналогичного пятиточечного
разностного операторадля прямоугольника, описанного вокруг G.
Если матрица А5~не симметрична (например, неравномерная
сетка), но симметризуется с помощью умножения на
диагональную матрицу, то оценка (1.70) остается в силе.
Отметим ряд свойств разностной аппроксимации (1.21)
четвертого порядка на прямоугольной сетке. У матрицы Л9 все
внедиагональные ненулевые элементы отрицательны и имеется
диагональное преобладание, если сетка не очень отличается от
квадратной, а именно, при условии 1/ 5^.hi/ h2y^5. Для
прямоугольной области ее собственные числа выражаются формулой
3 В П Ильин
33

Мы рассмотрели разностные операторы для двумерных плоских
задач, однако аналогичные свойства характерны и для системы
разностных уравнений в цилиндрической системе координат.
Наконец, перейдем к семиточечной разностной аппроксимации
(1.17в) трехмерного уравнения Пуассона.
Перечислим свойства матрицы А7 для трех характерных типов
областей, не зависящие от вида граничных условий
(аналогично двумерной задаче можно написать Д7 = Л1+Л2 + Лз):
а) общий случай (криволинейная граница) — принадлежность
к отрицательному типу и невырожденность (за исключением
задачи Неймана);
б) области, составленные из параллелепипедов — симметри-
зуемость (умножением каждого уравнения на (/if_i + hf) (ftf_i +
-\-hf)(hk-\-{-hk)) и симметричность на равномерной сетке;
в) параллелепипед — перестановочность матриц Ль Л2, Л3;
собственные числа выражаются аналогично двумерной задаче
через сумму собственных чисел одномерных операторов Ах, Ау, Л2.
Если же Ль Лг, Л3 не перестановочны, но симметризуются
при умножении на одну и ту же матрицу, то справедлив
результат, аналогичный предыдущему, т. е. собственные числа
А, матрицы А7 оцениваются через собственные числа ji/ь r\ik,
Vij матриц Axjk, Ayiki A2ij:
Ш >mini у,/,*I +min|r]^| +min|v/7|, (1-71)
/, k i,k i, j
где AXjk — разностный оператор, аппроксимирующий д2и/ дх2 на
k-м слое по z и на /-й строке по у.
1.3.3. Оценки точности решения линейных разностных
уравнений. Пусть краевая задача описывается уравнением
Lv = g, (1.72)
где L — линейный дифференциальный оператор, включающий
граничные условия и определенный в замкнутой области G = G+I\
и пусть система разностных уравнений
Lhu = f (1.73)
аппроксимирует задачу (1.72) на функции со с погрешностью
4>ь> = (— L<* + g)h + Lh((o)h — /.
Определение 1.8. Пусть v — точное решение
дифференциальной краевой задачи (1.72). Будем говорить, что решение
системы разностных уравнений (1.73) сходится в норме || • \\р
со скоростью hy, если при Л->0
\\z\\p=\\vh-u\\p = O(W), (1.74)
где z называется погрешностью разностного решения, а 7 —
порядком скорости сходимости, или порядком погрешности
решения.
34

Вектор ошибки z = Vh — и, очевидно, удовлетворяет
уравнению
Lhz = % ' (1.75)
где ф — погрешность аппроксимации системы разностных
уравнений (1.73) на решении (1.72).
Мы всюду предполагаем, что матрица Lh не вырождена, и,
следовательно, система разностных уравнений имеет
единственное решение, Это условие в наших задачах, как правило, легко
проверяется, поскольку мы не рассматриваем задачи Неймана
(условие 2-го рода задано на всей границе) и наши разностные
уравнения — положительного типа или монотонные.
А. Сходимость в евклидовой норме. Если Lh имеет
ограниченный в какой-либо норме обратный оператор, т. е.
||L/T1 II ^А< сю, то ошибка разностного решения удовлетворяет
неравенству ЦгЦр^ДЦ-фЦр. Из этого непосредственно следует,
что порядок точности будет тот же, что и порядок погрешности
аппроксимации, если А не зависит от h.
Для симметричных разностных операторов естественно брать
евклидову норму 1Mb, а величину Л положить равной
минимальному модулю собственного числа Lh (если Lh
положительно или отрицательно определен).
Таким образом, для рассмотренных нами одномерных задач
(за исключением задачи Неймана) с равномерной сеткой
непосредственно следует сходимость второго порядка, поскольку для
всех собственных чисел Ла, Л*,, Ло справедлива оценка 1М^8,
где б не зависит от h.
Аналогичный результат мы имеем для двумерных и
трехмерных областей прямоугольной или параллелепипедоидальной
формы, если используются соответственно аппроксимации А5 и А7 на
равномерных сетках и если хотя бы на одной из сторон области
задано условие Дирихле, что легко проверить по формулам
для собственных чисел.
При этих условиях разностные операторы А9 и Aig также
имеют ограниченные обратные при любых hx, hy, hz, что легко
проверяется по оценкам собственных чисел, которые выражаются
через собственные числа Л*, Л^, Л2 в силу их перестановочности.
Отсюда, например, следует, что погрешность решения системы
(1.21), (1.22) есть 0(/г4), если граничные условия заданы только
1-го рода и граница области проходит через узлы сетки. В
остальных краевых задачах погрешность лимитируется ошибкой
аппроксимации граничных условий.
Далее, для областей, составленных из прямоугольников или
параллелепипедов со смешанными граничными условиями, на
равномерных сетках сходимость разностных решений в
евклидовой норме для аппроксимации второго порядка (пятиточечные
и семиточечные уравнения) устанавливается аналогично. Для
этого достаточно применить оценки собственных чисел операторов
As и Д7 через собственные числа Л*, Л^, А2 соответственно для
3* 35

прямоугольников и параллелепипедов, описывающих расчетную
область (см. (1.70), (1.71)).
Если же сетка неравномерная, т. е. As и А7 не симметричны,
то можно использовать следующий результат.
Лемма 1.1. Пусть матрица Lh симметризуется умножением
на невырожденную матрицу D, причем
(DLhu, w)>6(w, и), 6>0 (1.76)
для всех и. Тогда решение уравнения (1.75) удовлетворяет оценке
^ (1.77)
. Доказательство следует из цепочки неравенств
82(z, z)2^(DLhz, z)2=(D^ 2)2<(Di|), D4>)(2, z). (1.78)
R
Очевидно, если L/j= 2 ^ и DAk— симметричные положи-
тельно определенные матрицы, т. е.
(DAku, u)^8k(u, u\ 6*>0, k=l, ..., /?, (1.79)
R
то имеет место неравенство 8^ 2 ^.
Таким образом, на неравномер*ных сетках сходимость
разностного решения может быть установлена, если одномерные
операторы Ak симметризуются и если имеются оценки для ||D||2 и
минимальных собственных чисел матриц DAk.
Отсюда непосредственно, с помощью оценки (1.65), следует
сходимость со скоростью O(h) для аппроксимаций (1.17а) —
(1.17в) на неравномерных сетках и областей, составленных из
прямоугольников или параллелепипедов. Необходимо уточнить,
что под скалярным произведением здесь вместо (1.4) понимается
выражение вида (R—размерность области) 2Л$* uukWUjk-
Если же в /?-мерной области погрешность аппроксимации
на подмножестве размерности (/?—1) есть величина порядка
O(hy), а в остальных узлах — О(/гб), то, очевидно, евклидова
норма погрешности равна O(h6-\-hy+0'5). Например, на
прямоугольной сетке с кусочно-постоянными шагами, когда число
линий, на которых меняется шаг, конечно при /i-М), оценка
(1.77) для пятиточечной аппроксимации (1.17а) дает сходимость
()
Б. Равномерные оценки погрешности
разностных решений. Мы будем использовать так называемый
мажорантный метод, основанный на принципе максимума для
конечно-разностных уравнений. В основе его лежат свойства
разностных решений, которые можно резюмировать следующим
образом.
36

Лемма 1.2. Пусть Л — неразложимая квадратная матрица
системы разностных уравнений
Au(Q)=p(Q,QHQ)- 2 P(Q,Q'HQ') = F(Q), QeQ. (1.80)
Пусть также выполняются следующие условия:
а) на множестве Qi^Q разностные уравнения —
неотрицательного типа, т. е.
q(Q)=p(Q,Q)- 2 p(Q, Q')>0, p(Q, Q0>0 (1.81)
всех Q'f=D(Q), QgQ;
б) существует такая неотрицательная в Q функция u(Q),
что a(Q)<Af, Лп(<Э)>Л>0, Q^Qb причем
<; ()
q, A«(Q) Л
в) яа множестве Й2 = й— f2i разностные уравнения
обладают свойством строгого диагонального преобладания:
жо) 2 (1.83)
P(Q, Q)>0, QgS2;
г) правая часть разностного уравнения на множестве Йг
удовлетворяет оценке
\F(Q)\/P(Q>QX*u Q^S2. (1.84)
Тогда решение системы разностных уравнений (1.80)
удовлетворяет неравенству
|«(Q)K ' (4-Al + ei), QeQ. (1.85)
О \ A. '
Хотя для многих задач можно явным образом построить
мажорирующую функцию u(Q), мы ограничимся следующим
допущением. Пусть нам требуется решить уравнение Пуассона в
области G с граничными условиями 1-го рода на участке границы
1\, 2-го или 3-го рода — на Г2 и условиями сопряжения — на
внутренней границе Г3. Тогда мы предполагаем, что существует
ограниченное решение соответствующей краевой задачи (с теми
же значениями а, р, у, е+, е_):
,(1-86)
Поскольку Lh(u) — (Lu)h -► 0 при h -*■ 0, то при достаточно
малых h мы можем в (1.82) принять u(Q) = (u)h, Л = 1/2 и считать,
что существует константа В = М/ А, не зависящая от h.
37

Перейдем непосредственно к оценкам точности наших
разностных уравнений. Рассмотрим отдельно несколько разностных
задач, отличающихся граничными условиями или способом
аппроксимации. Подчеркнем, что везде предполагается
существование достаточно гладкого решения дифференциальной
задачи.
Задача I. Область G — двумерная или трехмерная, с
криволинейными границами. Допускаемые граничные условия: 1-го,
2-го, 3-го рода и условия сопряжения на внутренней границе.
Сетка — неравномерная, прямоугольная или параллелепипедои-
дальная. Разностные уравнения — пятиточечные или
семиточечные типа (1.17а) — (1.17в), с аппроксимацией условий по
формулам вида (1.30), (1.34), (1.35), (1.41).
Теорема 1.4. Погрешность решения разностной задачи
I есть величина 0(h).
Доказательство проводится на основе свойств
рассматриваемых разностных схем и леммы 1.2. Во-первых, погрешность
аппроксимации для всех узлов есть 0(А). Во-вторых, все разностные
уравнения — отрицательного типа (в приведенных формулах они,
наоборот, положительного типа, но перемена знака в уравнениях
роли не играет). За множество Q2 берем совокупность
околограничных узлов, примыкающих к границе Гь с условием 1-го
рода и имеющих величину диагонального преобладания б, как
легко проверить, при любых А больше нуля (мы предполагаем,
что при измельчении сетки величины всех 1Г остаются одного
порядка). Полагая теперь в оценке (1.85) решения системы
(1.80) е = О(А) и 8i = 0(A) при А —►- 0, получаем необходимый
результат.
Задача II. Область G — двумерная или трехмерная, но без
внутренних границ с условиями сопряжения. Граница области
может быть криволинейной, но на таких участках задаются
только условия Дирихле. На прямолинейных участках границы
допускаются условия Неймана. Сетка — равномерная
прямоугольная (параллелепипедоидальная—для трехмерной задачи).
Разностные уравнения — пятиточечные или семиточечные типа
(1.17а) — (1.17в); условия Неймана аппроксимируются
трехточечными выражениями вида (1.32) с погрешностью О(А2),
переходящими в центральные разности, если граница проходит через
узлы или середины интервалов сетки.
Теорема 1.5. Решение разностной задачи II имеет
погрешность порядка О(А2).
Поскольку в узлах вблизи криволинейной границы с
условиями Дирихле, множество которых мы по-прежнему обозначаем
через ^2, погрешность аппроксимации разностных уравнений
удовлетворяет оценке ЦгрЦ^ ^УИ3А/ 3!, а разностные
коэффициенты p(Q, Q) имеют порядок О(А~2), то в (1.85) мы можем считать
si=£iA3, где В{ не зависит от А.
Так как для остальных узлов имеем е = #2А2 (В2 —
некоторая не зависящая от А константа), то решение (1.75) удовлет-
38

воряет оценке
3 + B2h2). (1.87)
Для двумерной задачи, например, можно положить
6 = 0,5(1 + max{h2x/ h% h2y/ /г?})"1,
а значение В2 уточнить, если взять в (1.85) ^за мажорирующую
функцию u = R— (х — хо)2 — (у — у о)2, где R — радиус круга с
центром (*о, уо), описанного вокруг области G.
Задача III. Рассматривается та же дифференциальная
задача и те же се*гки. Единственное отличие состоит в том, что для
околограничных узлов с условиями Дирихле используется вместо
(1.30) пятиточечная симметричная аппроксимация вида (1.29)
с погрешностью 0(1). Очевидно, разница здесь будет в том, что
надо принять e\ = B\h2, после чего для ошибки разностного
решения получаем оценку
/6/, (1.88)
где 6', В\ — некоторые константы, не зависящие от h (в
частности, 6^6').
Задача IV. Геометрия области и допустимые граничные
условия такие же как в задаче II. Равномерную сетку
выбираем так, чтобы прямолинейные границы с условиями Неймана
проходили на расстоянии (1 — УЗ/3) h от узла; тогда
трехточечная аппроксимация нормальной производной вида (1.32) имеет
погрешность |г|)| ^М4Л3/ 4!. Для внутренних регулярных узлов
сетки строим девятиточечную аппроксимацию типа «ящик» (1.21)
(и (1.22) —для трехмерных задач) с погрешностью O(h4) (при
этом мы требуем выполнения условия 1/5<А?/Ау<5, чтобы
разностные уравнения были положительного типа). В
узлах-вблизи криволинейной границы с условием Дирихле, где такая
аппроксимация не может быть построена, используем
пятиточечные уравнения вида (1.17а) (для трехмерной задачи (1.17в)
с погрешностью O(h)).
Теорема 1.6. Погрешность решения задачи IV
удовлетворяет при h -> 0 оценке
\\г\\ ос <-l(Boh4 + Blh3 + B2h% (1.89)
где константы Во, В2 не зависят отк,аЬиВ\ — те же, что и в (1.87).
Здесь слагаемые в правой чаоти характеризуют вклад в ошибку
погрешностей'аппроксимации соответственно в регулярных узлах,
околограничных с условием Дирихле, и в узлах вблизи границы
с условием Неймана. Доказательство проводится аналогично.
Задача V. Расчетная область — двумерная или трехмерная,
с границей, пересекающей координатные линии только в узлах.
Допускаются граничные условия Дирихле или Неймана.
Разностная сетка и аппроксимация те же, что и в задаче IV, за
39

исключением того, что на Г2 используется аппроксимация типа
(1.33) с погрешностью O(h4).
Теорема 1.7. Погрешность решения разностной задачи V
удовлетворяет оценке
(1.90)
Улучшение результатов здесь обязано тому, что мы улучшили
аппроксимацию условия Неймана и что пятиточечные уравнения
для околограничных узлов имеют погрешность 0{h2).
Отметим, что вблизи прямолинейных участков границ,
являющихся линиями или плоскостями симметрии для решения, во всех
рассмотренных задачах целесообразно использовать центральные
разности, которые точно аппроксимируют условие симметрии.
Кроме того, очевидно, что если в какой-то части расчетной
подобласти из априорных оценок можно судить об однородности
решения (т. е. малости его производных), то в этой окрестности
целесообразно строить грубые аппроксимации (например, с
использованием более редкой сетки), так как их вклад в ошибку по
абсолютному значению будет мал.
Рассмотрим теперь на примере двумерной задачи Дирихле
разностные аппроксимации II и III с тем отличием, что вместо
равномерных используем сетки с кусочно-постоянными шагами,
имеющие при А ->- 0 конечное число координатных линий, на
которых меняются величины шагов.
Пусть в расчетной области, заключенной в прямоугольнике
b ^ построена сетка:
/= 1, 2 /ь hXi= (xlx — a)/lu
l,...,/, + /2, hXf = (b-xtl)/l2,
(1.91)
/=1,2,..., mi, hUx={ymx — c)/mu
, а + /ЛХ1, /= 1,
Xi-\Xll+ihXt, * = Z
Погрешность пятиточечной аппроксимации такой задачи
представим в виде <ф = 'ф + 'ф1, где г|) = 0 и |\|?i | ^ipi = C max {IA2 —
— Af|, \hy2 — hyx\} для x = xlx, y = ymi (см. (1.14)), а при хфх1х,
У Ф Упц> ^i — 0; С не зависит от А. Соответственно ошибка
разностного решения имеет вид z = z + z\, где z = О (А2) (см.
теорему 1.5), Аб^1 = i|)i, Z\\r — 0. Для zi, представляющей ошибку
решения, обусловленную погрешностью аппроксимации на линиях
неравномерности сетки, с помощью принципа максимума можно
получить оценку
, (1.92)
*Ь-х\ x>xit9
поскольку подбором значений Ck = O(h2) мы можем определить
40

Z\, удовлетворяющую условиям:
Отсюда следует, что Zi = O(h2). Если сетка имеет линии
неравномерности xlx, xlt, ..., xlp, утх, ут2, ..., ущ, то, очевидно, по принципу
суперпозиции ошибку решения можно представить как z =
+
= 2 Zk + z, где каждое из слагаемых есть величина порядка
O(h2).
Отметим, что мы рассматриваем только те разностные
аппроксимации, которые представляются удобными в программной
реализации для областей сложной конфигурации.
Для задачи Дирихле с криволинейными границами известны
схемы с погрешностью четвертого порядка и выше. Можно
предложить такого типа аппроксимацию: девятиточечные уравнения
(1.21) для регулярных узлов и аппроксимацию на
многоточечном нерегулярном шаблоне — для околограничных. Однако на
неравномерных сетках трудно что-либо сказать о существовании
необходимых свойств этих уравнений или даже о возможности
их построения. Помимо этого, программная реализация
многоточечных разностных уравнений для узлов вблизи
криволинейной границы требует преодоления значительных технических
трудностей.
§ 1.4. Прямые методы решения разностных уравнений
Прямыми методами называются такие, которые дают точное
решение за конечное число арифметических операций (в
предположении, что сами вычисления выполняются без погрешностей).
Мы будем рассматривать специальные алгоритмы решения систем
алгебраических линейных разностных уравнений, основанные
на их специфичной форме и зачастую использующие явные
представления собственных чисел и соответствующих собственных
векторов. Отметим, что непосредственное применение
классических методов исключения Гаусса и других для решения системы
N-ro порядка требует выполнения количества операций Q — O(N3)
и хранения числовой информации объемом P^=O(N2).
В этой главе мы остановимся.только на некоторых
характерных методах; более полный обзор можно найти в [60, 70, 166]
и цитируемых там работах.
1.4.1. Методы факторизации (прогонки). Так называемые
методы прогонки, или факторизации, являются модификациями
метода исключения Гаусса для решения систем уравнений с
матрицами специального вида, а именно, ленточными матрицами.
Напомним, что ленточной матрицей называется такая матрица, у
которой все ненулевые элементы лежат в полосе вблизи главной
Диагонали. При этом предполагается, что ширина ленты, т. е. число
элементов строки, принадлежащих этой полосе, значительно
меньше порядка матрицы.
41

В методе исключения Гаусса исходная матрица
представляется в форме произведения нижней и верхней треугольных матриц.
Таким образом, система уравнений
Au = f (1.93)
приводится к виду LUu = f, (1.94)
где L, U — соответственно нижняя и верхняя треугольные
матрицы. Решение системы (1.94) сводится к легко реализуемому
алгоритму
Lz = f, Uu = z. (1.95)
Для ленточных матриц нижняя и верхняя треугольные матрицы
L, U также являются ленточными, с той же шириной полосы.
Поэтому для семейства матриц различных порядков с шириной
полосы, не зависящей от порядка, возможно строить методы,
требующие количества арифметических операций и объема
запоминаемой информации, значительно меньших по сравнению с общим
случаем.
Рассмотрим систему разностных трехточечных уравнений
Мы не будем связывать систему (1.96) с тем, какую исходную
задачу она аппроксимирует. Предполагаем, что значения
функции ио и uN+x с помощью граничных условий уже исключены
из системы. Тогда решение может быть найдено по единообразным
для всех узлов формулам
., 1. (1.97)
Здесь poZo, uN+l не определены, однако умножакгГся на нулевые
коэффициенты аь cN и не влияют на вычисления в остальных узлах.
Реализация метода для общего вида значений a*, bk, ck требует
проведения 8N арифметических операций и запоминания 2N
вспомогательных величин.
Достаточными условиями устойчивости прогонки по
отношению к накоплению ошибок являются [45]
(1.98)
которые всегда выполняются для приведенных ранее краевых
задач.
Рассмотрим так называемый метод матричной прогонки для
систем пятиточечных разностных уравнений, аппроксимирующих
краевую задачу для уравнения второго порядка в прямоугольнике
ацщ-х^ + Ьцпц -1 + Сцщ+ i,y + dijUitj +1 — ециц = ///, (1.99)
1=1,2,...,/, /=l,2,...,m,
42

где /, т — соответственно число внутренних узлов в строке и
столбце.
Аналогично предыдущему мы предполагаем, что значения
функции, соответствующие граничным узлам с / = 0, /+ 1 или / = 0,
ш+1, с помощью граничных условий исключены из (1.99), т. е.
a{j=ibiX = Cij = dim = O. Введя векторы щ = {щ^ /=1,2,...,/,
состоящие из значений функций на одной строке, систему (1.99) можно
записать в виде
Lkuk-X-Bkuk+Ukuk + i=f9 fe=l,2,...,m, (1.100)
где L*, Bk, Uk — квадратные матрицы порядка /; Lkn Uk —
диагональные матрицы, состоящие соответственно из элементов bjk и
djk\ Bk — трехдиагональная матрица с элементами на строках
a,jk, —e-jk, C\k-
Систему (1.100) можно решать по формулам, являющимся
формальным обобщением метода прогонки (1.97):
Mk= (Bk-LkMk-X)-xUk,
zk= (Bk-LkMk-,)-x(Lkzk-X-fk\ *=l,2,...,m, (1.101)
k = my m— 1,..., 1,
где Mk — матрица порядка /.
Реализация формул (1.101) требует обращения т матриц
порядка / и запоминания их элементов. Таким образом, число
арифметических операций в методе матричной прогонки
пропорционально /Зт. При этом требуется вспомогательная память
объемом порядка 12т ячеек. Эти требования, особенно последние,
делают метод малоэффективным при больших значениях I и т.
Если требуется решать систему при разных правых частях /,
то за счет запоминания матриц Mk число арифметических действий
можно сократить до величины порядка О(12т) (столько
операций требует т умножений матрицы на вектор размерности /).
Положительным качеством метода матричной факторизации
является применимость при переменных разностных коэффициентах,
т. е., например, для неравномерной сетки.
Для устойчивости матричной прогонки, как и для скалярной,
необходимо условие диагонального преобладания. Вопросы
устойчивости методов матричной прогонки и их модификаций для
различных задач исследовались в работах многих авторов (см. [45,
69, 166] и цитируемую там литературу).
1.4.2. Метод циклической редукции. Как видно из предыдущего,
пятиточечная аппроксимация для уравнения Пуассона в
прямоугольной области с граничными условиями первого рода на
равномерной сетке размерности IXт может быть описана системой
векторных уравнений
i uj+i=fh /= 2,3, ... , т — 1, (1.102)
Eum-\+Aum = fmj
43

где Е — единичная матрица порядка /; вектору // определяются
с учетом граничных условий; квадратная матрица А порядка /
может быть представлена в виде A = h2yh.x — 2E, «/ = {«//}, / =
= 1,2,...,/. Мы будем предполагать, что m = 2k+l— 1, k — целое
число. Выпишем три уравнения из системы (1.102) для соседних
значений /:
Euj-2+Auj-\+Euj = fj-\J
(1.103)
Умножая второе уравнение на —А и складывая затем все три,
получаем
-Afi. (1.104)
Аналогичные уравнения можно записать для четных /,
меняющихся от 2 до т — 2, полагая ио = ит + \=О. Такой процесс
понижения порядка системы уравнений называется циклической
редукцией. Заметим, что правая часть уравнения (1.104)* может
быть записана в виде
ifj + fi-l+fi+i-2A-lfh (1.105)
где А(1)=2Е — А2. Если мы положим
(1Л06)
то
/0) = л('М') + ^1). (1.107)
Если в системе уравнений опять исключить половину
неизвестных, т. е. второй раз применить редукцию, то
Аналогично, после r-кратного применения редукции имеем
/5'+') = fW2, + PjrU' -A^ff\ Л^ = 2£-(Л(Г-")2 (1.109)
Выражение для fp можно представить в форме, аналогичной
(1.107):
№ = АЩ) + ф'\ (1.110)
Подставляя (1.110) в (1.109), получаем следующие соотношения:
р('+ ■) = р(') _ (А«)-' {pf(lv + р]%г - <?«), (1.111)
Для вычисления выражения (Лм)~' {р((12' + P{{+v ~ i\r))
необходимо решить систему уравнений
A(rW - pY+iy) = pV-v + Р%- - tf. (1.112)
44

Из определения матрицы А^ следует, что она представима в виде
произведения трехдиагональных матриц
Л<'> = - ПИ + 2cos-££#-£], (1.113)
y-i
легко обращаемых с помощью прогонок. После проведения k
редукций мы имеем A^u2k = A^pP^-q^\ откуда
u2k = p$ + zky А™гк = ($> (1.114)
Здесь Zk легко вычисляется с помощью 2£-кратного применения
метода прогонок (после представления А^ в виде (1.112)). Для
реализации обратного хода решения используем соотношение
Решая систему уравнений
««^ 2,), (1.116)
находим
Uj = p^ + z\r\ (1.117)
Таким образом, метод циклической редукции состоит в
следующем:
а) вычисляется по формулам (1.111) последовательность
векторов p<f\ q\r\ r=l Л, при/7$0) = 0 для/ = 0, ...,2*+I и ^О = /
122*+1 1
б) по формулам (1.114) с помощью прогонок вычисляется w2*;
в) проводится «обратный ход» с нахождением Uj по формулам
(1.116), (1.117) (каждое z^ вычисляется с помощью 2г прогонок,
г = *— 1, ife — 2 1).
Рассмотренный алгоритм был предложен О. Бунеманом. В
применении к уравнению Пуассона он устойчив по отношению к
накоплению ошибок. Имеется ряд модификаций, в том числе для
различных типов граничных условий. Оценки, приведенные в [60],
показывают, что общее количество арифметических операций для
решения разностной задачи в прямоугольнике на сетке / = т равно
(9/2) /2 Iog2 /. Объем вычислений в расчете на один узел можно еще
сократить, если решается несколько однотипных краевых задач,
отличающихся только правыми частями. Имеются модификации
циклической редукции для произвольного числа m [167, 171].
Метод также разрабатывался и для непрямоугольных областей,
но при этом его реализация сильно усложняется.
1.4.3. Методы преобразования Фурье. Решение системы
уравнений (1.102) можно вычислить, используя явное представление
базиса матрицы Л*. А именно, разложим каждый из векторов
45

и;, /; в дискретный ряд Фурье по собственным векторам Л*:
V
(1.118)
p=l,2,...,/. (1.119)
Очевидно, t;p/ для всех р удовлетворяют системе уравнений
— (2 — Xp)v p x + vP2 = h2yfp i,
i=h2yfph / = 2,3,...,m-1,(1.120)
где A,p = -4-(cos w^Ti — 1) собственные числа матрицы /ф\*.
Отсюда, реш'ив / таких систем с помощью прогонок, по формулам
(1.118) вычисляем искомое решение.
Такой метод обладает счетной устойчивостью, поскольку все
уравнения (1.120) имеют диагональное преобладание (в силу
отрицательности кр), а преобразование Фурье (1.118), (1.119)
эквивалентно умножению векторов уу, // на симметричную матрицу
Q = |-w sin ^ k евклидова норма которой равна
единице (fP=Qfj, uf = Qvh vj = {vlh...yVph...,vij}1 fP={fPu...,fPh...,fPi}).
Объем вычислений в данном методе определяется по порядку
для больших /, т выражением 0(1т)-\-0(1т2). Первый член
характеризует трудоемкость решения / систем m-го порядка методом
прогонки, а второй (имеющий преобладающую величину) —
прямое и обратное преобразование Фурье! Алгоритм, как видно, будет
наиболее экономичным при т<^1.
Методы такого типа рассматривались для разного типа
краевых задач, допускающих разделение переменных, и для различных
видов разностных аппроксимаций. Для других Ах требуется также
явное выражение базиса; при этом меняются только формулы
(1.118), (1М20). Оператор Ау может быть более сложным, в том
числе с переменными коэффициентами, поскольку его базис не
используется (это приведет только к изменению системы (1.120),
которая все равно решается прогонками).
К этому классу относятся методы прямых и методы суммарных
представлений. Отличие для последних заключается в том, что
решение систем вида (1.120) проводится не с помощью прогонки,
а путем явного представления через одномерные фундаментальные
решения краевых задач (это позволяет существенно экономить
объем запоминаемой промежуточной информации при отыскании
решения в малом числе точек, но усложняет сам алгоритм). 06-
46

ширная библиография по этим методам имеется в работах
[156, 69].
Методы с разложением по базису разностного оператора
получили наибольшее развитие при использовании быстрого
преобразования Фурье. Идея этого алгоритма основана на том, что при
реализации формул вида (1.118), (1.119), если /+1 не является
простым числом, можно существенно уменьшить объем
вычислений за счет многократно повторяющихся значений sin £^
Мы поясним такой подход на примере вычисления N = 1 сумм
(1.118) при N = 2S с целым s, когда быстрое преобразование Фурье
наиболее экономично и наглядно.
Пусть требуется вычислить
sin иг- р==0' '' -' N~ 1; ^ = 2s-(1-121)
Представляя синусы через экспоненты, запишем
2
где / — мнимая единица. Введя далее обозначения
k = li+2ku /, = 0,1; Л51 —0, 1 ^Vi — 1; N^
p = m\N\+p\, mi = 0, 1; pi == 0, 1,..., N\ —
будем иметь
k,P) = 2(il,p) exp {ikip{ JL}^=z^p)Zl(kuP^
Отсюда выражение для v(p) можно представить в виде двойной
суммы:
v(p) = v{mupx)= S ["я* x{luk{)z\k^}z^\ (1.123)
/,=0 L^,=0 J
Используя теперь обозначения
Pi)= V x{lukx)z\k^\ (1.124)
V
Л0
можем записать
Ф)=/20 vx{luP\)#x*\ (1.125)
Заметим, что последняя сумма включает только 2 слагаемых,
а предпоследняя N\=2S~\ т. е. вдвое меньше, чем исходное
выражение для v(p). При этом Vi(lupi) имеет аналогичную структуру
(Л является просто параметром), и для него можно провести те же
47

преобразования:
, /2 = 0, 1; *2 = 0, 1, ...,ЛГ2—1; N2 = 2
m2 = 0, 1; p2 = 0, I,..., N2— 1,
.126)
1
= vi(lum2,p2) = 2 v2{h,l2,p2)z{h-p0,
/2=0
JVa— 1
luh,p2) = 2 x(h,l2,k2)z2k^\
*2 = 0
Продолжая этот процесс, получим
r, /, = 0,1; fer = 0, I,..., Nr-\; Nr = 2s~r,
O,-l(/,, ...,^-1,^,-0= 2 W,(Z|,...,/,_.,/r,Pr)Z^rl),
Л^г—1
Vr(ll, ..., Ir-U lr, Pr) = 2 *(/|, .... /г-1, /г, Л,)^'».
В частности, при r = s — 1 получаем
Vs-\=(lu..., 4-2, 4-1, Ps-l)W/l,..., /s-2, /s-1, 0)zf-Prl) +
+ x(/b..., /s_2, /s_b l)^-0], (1-128)
где /s_! = 0,1; ps-\ = 0,1; zi^i"p—} = exp{^s_ips_^/2}.
После вычисления us_i находятся последовательно vs~2,
ys_3,'..., Ui, у. Для каждого значения г необходимо вычислять N
величин vr при различных значенияхпараметров /i,..., Zr_i, /r, /7r.
Аналогично находится величина v(p) в формулах (1.123) —
(1.128), надо только заменить 2(ДРг)на z[krPr) и иг на уг. Поскольку
5 = log2A^, то общий объем вычислений оказывается равным
O(N\og2N).
Так как все величины vr, vr, zr, zr — комплексные, то при
реализации рассмотренных формул можно выделять и отдельно
вычислять их действительные и мнимые части. Можно также
непосредственно выписать рекуррентные формулы для
вещественных членов. Это подробно проделано в [166] для разложений по
различным видам тригонометрических функций, соответствующим
собственным векторам Л* для различных краевых задач.
Метод быстрого преобразования Фурье требует примерно
такого же объема вычислений (при детальном подсчете
арифметических действий, но в предположении, что все тригонометрические
функции вычислены заранее), что и метод циклической редукции.
Последний является более устойчивым к накоплению
погрешностей, i
Эффективным приемом является комбинирование редукции и
быстрого преобразования Фурье. А именно, если сделать предва-
48

рительно один или два этапа редукции (больше уже оказывается
нецелесообразным), то в соответствующем измерении порядки
векторов уменьшаются в два или четыре раза, и последующее
преобразование Фурье делается существенно экономичней. Общий
объем вычислений по порядку остается, естественно, O(/mlog2/).
Описание таких алгоритмов подробно изложено в [161, 166].
§ 1.5. Итерационные методы решения разностных уравнений
Теория итерационных методов решения разностных уравнений
за последние десятилетия получила значительное развитие как
специальная область линейной алгебры. По этим вопросам
накоплено огромное количество литературы, и наиболее полное
отражение современного состояния имеется в книгах Г. И. Марчука
[119], А. А. Самарского и Е. С. Николаева [166], Р. Варги [28]
(см. также [69] и цитируемую там литературу).
Целью данного параграфа является обзор основных
эффективных алгоритмов со сравнительным анализом их экономичности.
Мы рассмотрим кратко теоретические оценки скорости сходимости
итерационных методов и условия их применимости, а также
результаты некоторых численных экспериментов для модельных
задач, иллюстрирующих соотношения по количеству итераций,
затрачиваемых разными алгоритмами при различных счетных
параметрах.
1.5.1. Основные свойства итерационных процессов. Общий вид
рассматриваемых нами итерационных процессов для решения
системы уравнений Au — f {и, f — векторы, А — квадратная
матрица N-ro порядка) определяется формулой
l — Aun-1), /i=l,2,..., (1.129)
где ип — вектор я-го приближения'(я-й итерации). Нп —
некоторые невырожденные матрицы, определяющие конкретные
итерационные алгоритмы. Соотношение (1.129) можно переписать в
эквивалентной форме:
l (1.130)
где gn = Hnf, а Вп = Е — НпА называется матрицей перехода, или
итерационного шага.
Для характеристики отклонения я-го приближения от точного
решения вводятся вектор ошибки
у* = и-ип (1.131)
и вектор невязки
rn = f — Au\ (1.132)
связанные очевидным равенством гп = Ауп Вектор ошибки
удовлетворяет соотношению
у«+^у«-НпАуп = (Е-НпА)уп=:Впуп=Тпу\ (1.133)
4 В П Ильин 49

где
Тп= ft (£ - HkA) = П Bk. (1.134)
Для того чтобы итерационный процесс сходился, т. е. уп-*0 при
любой начальной ошибке у°\ необходимо и достаточно выполнения
условия Гл->0. Достаточным i ювием сходимости метода (1.130)
является выполнение для вал п неравенств
||5п||<р<1. (1.135)
В силу неравенства
величина р называется коэффициентом подавления ошибки за
одну итерацию.
При проведении итерационного процесса необходимо знать,
насколько полученное приближение отличается от точного
решения. Мы приведем два неравенства, позволяющих оценивать
достигнутую точность по величине отклонения двух соседних
итераций или по значению вектора невязки.
А. Пусть для итерационного процесса выполняется условие
(1.135) и
\\ип-ип~1\\^г. (1.136)
Тогда справедлива оценка
11^11 <т=78- (1Л37)
Для доказательства достаточно рассмотреть соотношения
откуда непосредственно следует (1.137). -
Б. Пусть матрица А положительно определена, т. е. (Аи, и)^
^8(ик и), 6;>0, для любого ифО, и для невязки выполняется
соотношение
(1.138)
Тогда справедлива оценка
||(/12<е/8. (1.139)
Этот результат выводится из цепочки неравенств
А Ауп)(уп, y")=\\rnh\\ynh.
Из равенства (1.129), которое можно переписать в виде
ип — ип~1 = Нпгп1 и из (1.139) следует также, что при выполнении
неравенства (1.136) справедлива оценка
Н#12< IIЯ^Г11|2е/8. (1.140)
50

Эффективность различных итерационных методов оценивается,
во-первых, по скорости убывания ошибки при проведении
итераций и, во-вторых, по количеству арифметических действий,
необходимых для расчета одной итерации.
Основной характеристикой скорости сходимости
итерационного метода является число итераций п(е), необходимое для
того, чтобы начальная ошибка уменьшилась в г~1 раз:
п(г) = тт{п: \\уп\\/\\у°\\ <е}. (1.141)
С этой величиной связана так называемая средняя скорость
сходимости, определяемая количеством верных знаков (по
основанию е), получаемых в среднем за одну итерацию:
/?я=|1п е|/л(е). • (1.142)
Если при п-^оо существует предел /?д, то он называется
асимптотической скоростью сходимости итераций R.
Если реализация одной итерации в каком-то методе требует
выполнения Qo арифметических операций, то общий объем
вычислений для получения заданной точности 8 (в предположении
°|О(1)) равен величине
Очевидно, для итерационного процесса, удовлетворяющего
условию (1.135),
R>— In p. (1.143)
Если итерационный процесс плохо сходится, т. е. р=1—-6, б <С 1,
то
/?«6. (1.144)
Рассмотрим теперь стационарный итерационный процесс,
определяемый постоянным оператором перехода Вп = В, и
предположим, что матрица В имеет базис из собственных векторов Zi,
22,..., zn, которым соответствуют собственные числа 1 >> I X\ \ >
> |Я2| ^ |А,3| ^ ...^ \Хп\ (максимальное по модулю собственное
число Х\ считаем простым, при этом вектор Z\ будет ортогонален
всем остальным собственным векторам г2, ...,zN). Разлагая вектор
начальной ошибки по базису
° Ni ck = (y°, zk\ (1.145)
для ошибки az-го приближения получим
уп = \lcxz{ + Мс2г2 + ... + bnNcNzN. ■ (1.146)
Отсюда для п-+оо следует выражение
yn = WciZi[l+O№/W)], . (1.147)
т- е- для такого итерационного поцесса асимптотическая скорость
сходимости равна R= — 1п\Х\\у а величина |A,i| является асимп-
4.*
4 51

тотическим коэффициентом подавления ошибки. Если |A,il = l—б
и б<1, то R&8,
Для систем разностных уравнений с малым шагом h обычно
скорость сходимости итераций мала и стремится к нулю при
А->"0. Для ускорения сходимости произвольного стационарного
линейного итерационного процесса, у которого матрица перехода
В имеет простое максимальное по модулю собственное число
А.1, можно применить метод, предложенный Л. А. Люстерником.
Так как уп+{ ж\\С\2\ при достаточно больших значениях я, то
j/n+1«A,i«/n. (1.148)
Далее,
и = ия + уп, u = un+l+kiyn + en. (1.149)
Исключая из (1.149) уп, получаем
Un+[-hun ,
U== 1 5 1
1-Я,, ' 1-Я,,*
Так как по предположению гп мало, то вектор
u = (un+l-Xlun)/(l-h) (1.150)
будет незначительно отличаться от точного решения и. Итак, метод
ускорения заключается в следующем. Сначала делаются итерации
по формуле (1.130) для стационарного процесса. При этом
определяется величина
tffi=\\un--un-l\\/\\un-l--un-2\\9 (1.151)
которая, очевидно, стремится к К\ при я->оо. Когда величина
Мя) меняется от итерации к итерации незначительно, то она
принимается за приближенное значение Х\. После этого рассчитывается
величина un+l и за следующее приближение принимается и по
формуле (1.150). Затем итерации ведутся по обычным формулам, а
через несколько шагов может быть ©пять сделано ускорение.
В частном случае нестационарный итерационный процесс
(1. 129) можно представить формулой
и" = и '+t,,A \i — Aull-x\ м=1,2,..., (1.152)
где К — некоторая невырожденная матрица (будем называть ее
предобуславливающей), а тп — итерационные параметры.
Векторы ошибки при этом, очевидно, удовлетворяют соотношению
уп= (Е - тпК~1А)уп-1 = П (Е - TiK-xA)y\
Выбор оптимальных параметров тл необходимо проводить из
того условия, чтобы для уменьшения нормы ошибки в заданное
число г~1 раз требовалось минимальное число итераций п(г).
Предположим, что матрица К"1 А имеет базис из собственных векторов
Zk, а ее собственные числа вещественны и удовлетворяют условию
0<m<A*<Af, £ = 1,2,...,АЛ
52

Тогда мы можем записать
!,«= 2 ckPn(kk)zk> Ря(к) = П (1 - тД),
где Ck даны в (1.145), а многочлен /г-го порядка РП(А,) целиком
определяется совокупностью значений т/. Выбирая их равными
обратным значениям корней многочлена Чебышева 1-го рода,
наименее уклоняющегося от нуля на отрезке [m, M] и
нормированного условием равенства единице при Х = 0, получим так
называемый итерационный процесс с чебышевским ускорением. При
этом тп можно определять циклически с некоторым периодом s:
\ п=1,2,..., (1.153)
и подавление ошибки за 5 итераций оценивается величиной
|ВД|<2Т7(725+1), Y-(1-VP)/(1+VP), P = m/M.
Отсюда легко находится минимальное число итераций s(e),
необходимое для подавления ошибки в е"1 раз:
5(8) = 1П
!
/1 — 8
Из последнего выражения при e<Cl, р^>\ получаем
следующую оценку для средней скорости сходимости итераций:
Если величина периода s большая (например, s;>40), то
актуальным становится выбор устойчивой упорядоченности тл, при
которой погрешности округлений в процессе итераций не
накапливаются. Эти вопросы рассмотрены подробно в [119, 166], а для
случая s — 2r алгоритм коротко описывается следующим
рекуррентным образом. Пусть {о\, 02, •••, os/2\ — «устойчивая»
последовательность номеров для s = 2r~l. Тогда для s = 2r
соответствующий порядок устанавливается в виде
[О\, 5+1—01, 02, S+ 1—02,...,0s/2, S+l—0s/2}.
1.5.2. Обзор итерационных алгоритмов. Мы остановимся на
тех методах, которые, во-первых, применимы для основных типов
рассматриваемых нами разностных задач, во-вторых, имеют
высокую скорость сходимости и, наконец, достаточно просты при
реализации в универсальных программах, рассчитанных на разные
конфигурации границ и типы граничных условий.
Мы опишем по возможности кратко их основные
алгоритмические особенности и области применимости. Несколько большее
внимание будет уделено представляющимся перспективными
методам неполной факторизации, поскольку они недостаточно
освещены в литературе.
Мы будем описывать методы в векторной форме, а также
иллюстрировать их реализацию на примере системы пятиточечных
53

разностных уравнений вида (1.56), которую запишем в виде
(Аи)ц= —aiii-\ti — Ьиц-1 — cui+{tj — dui,j+ \+еиц = !г, (1.154)
(здесь для краткости опущены индексы /, / при коэффициентах
а, Ь, с, d, е).
А. Метод Зейделя и метод
последовательной верхней релаксации. Пусть матрица А представима
в виде A = D-\-M-\- N, где D — диагональная, М,
N—соответственно нижняя и верхняя треугольные матрицы. Тогда метод
последовательной релаксации определяется следующим образом:
u{(*)un, (1.155)
где число-параметр со называется параметром релаксации.
Для пятиточечных уравнений это сводится к простым
формулам:
u +x)/^ (1Л 56)
в которых предполагается, что счет ведется последовательно для
/=1,2,...,/, /=1,2, ...,т (порядок циклов по / и /
безразличен) .
Если параметр релаксации со равен 1, то мы приходим к методу
Зейделя, для которого сформулируем следующий известный
результат.
Теорема 1.8 Если матрица А положительного (или
отрицательного) типа, то метод Зейделя сходится.
Эта теорема, как нетрудно видеть, устанавливает сходимость
процесса Зейделя для большинства рассматриваемых нами
краевых задач, например, пятиточечных (семиточечных — в
трехмерной задаче) разностных уравнений отриш! ьного типа при
различных граничных условиях, в том числе на внутренних
границах, и при произвольных соотношениях шагов сетки.
Область применимости метода верхней релаксации
характеризует
Теорема 1.9. Если матрица А — симметричная и
положительно определенная, то метод последовательной верхней
релаксации сходится при 0<<(о<;2.
Для большинства рассматриваемых нами систем уравнений,
именно тех, у которых матрица перестановкой строк и столбцов
сводится к блочно-трехдиагональному виду, удается решить
вопрос об оптимизации выбора релаксационного параметра со.
Собственные числа г); оператора перехода метода верхней релаксации
оказываются связанными с собственными числами h оператора
перехода метода Зейделя соотношением
' (ть- + ©-1)7л/ = А (1.157)
Коэффициент подавления ошибки р = тах{|г|Л} достигает миниму-
i
ма при
(0 = 0)0 = 2/(1 -УГ=10 (1.158)
54

i = max 1^-1.(1.159)
i
Практически важным свойством процесса последовательной
верхней релаксации является то, что он позволяет автоматически
в процессе вычислений находить оптимальное значение параметра
релаксации.
Проводя сначала итерации по формулам (1.155) при со = 1,
мы можем приближенно определить А,ь равное значению МП|),
где п\ — минимальное число, для которого
|Mni)/M/Zl"1)-l|<ei. (1.160)
Здесь 8i — достаточно малая величина, a МП|) определяется на
каждой* итерации по формуле
Г) ||Ц ~U И2 -1\2/ Y/,,n-l /#п-2\2\!/2
2\!/2 (л \
) .(1.
/ /
Принимая теперь A,i«A,V4 находим из (1.158) приближенно
оптимальное значение со0, которое и используется в дальнейших
итерациях.
Б. Прогонка по линиям с верхней релаксаци-
е й. Процесс верхней релаксации с прогонками по строкам можно
записать в векторной форме, если совокупность uijf /,•/ в узлах
на /-й строке обозначим через щ, // и проведем разбиение
исходной матрицы на соответствующие блоки:
f+i + Niuf+^fj, / = 2,...,m-l; (1.162)
Мтипт+-\ +Dmunm+l = fm;
и/л+1 = (ой}1+1+(1—©К, /=1,2, ..., m.
Для пятиточечных уравнений (1.154) D} — квадратная трех-
диагональная матрица с элементами — а, е, ~с, порядок которой
равен числу узлов в /-й строке. Матрицы М; и Nf имеют не более
одного элемента на строке, соответственно —Ь и — d. В
покомпонентной записи метод имеет вид
?j — сй?+и 1 = Ь, + Ьи?,}-1 + с1иГ,-[1и (1.163)
} — ы)и?,~1 /=1,..., /, /=1 т.
Вычисление и!) на каждой /-й строке проводится с помощью
прогонки, чем и объясняется название алгоритма (он называется
также блочным методом верхней релаксации).
Сходимость этого метода для симметричных систем
исследуется аналогично поточечной верхней релаксации. При этом
справедливы такие же оценки оптимального параметра
релаксации и скорости сходимости, как (1.158), (1.159), только Х\ есть
спектральный радиус матрицы блочного метода Зейделя (со=1).
Реализация данного алгоритма требует несколько большего
количества арифметических операций при расчете одной итерации,
55

чем в поточечном методе верхней релаксации (в зависимости от
вида коэффициентов разностных уравнений и способов их
вычисления и запоминания). Помимо массива пц при расчетах
требуется хранить дополнительную информацию объемом порядка
количества узлов в двух строках.
В. Неявные методы переменных
направлений. Из большого разнообразия исследований по этому классу
алгоритмов мы приведем только некоторые основные результаты.
Прежде всего рассмотрим схему продольно-поперечных
прогонок Писмана—Ракфорда решения пятиточечных уравнений
для двумерной задачи.
В покомпонентной записи для системы (1.154) этот алгоритм
имеет вид
(1.164)
где ei~\-e2 = e, причем е\ соответствует диагональному члену,
получаемому из аппроксимации д2и/дх2, а е2 — д2и/ду2. Первый
этар (дробный шаг) итерации (1.164) реализуется прогонками
по / для /==1,2, ..., т, а второй — прогонками по / для **= 1, 2, ..., /.
Методы такого типа получили также названия «продольно-
поперечных прогонок», «дробных шагов» и др.
В операторном виде эта итерационная схема имеет форму
-f), (1.165)
которая после исключения промежуточной величины ип+1/2
принимает вид:
un-f), (1.166)
где Tin, x2rt — итерационные параметры; Ai и Л2 определяются из
(1.159).
Если Ль Л2 — симметричные перестановочные матрицы,
имеющие границы спектра соответственно 0 <Cai<;Pi < оо, 0<Сос2<С
<р2<;оо, то алгоритм расчета последовательности параметров,
основанный на минимизации дробно-линейной функции,
характеризующей подавление ошибки, и оценки скорости сходимости
определяются выражениями [164]:
Яп + qn r Я
f\n=-r\ ♦ Т2/г=п , А ^ 1 • П
1-\-(опр \~(опр lnrj yi.
56

» —«О (Р2 —0С2)
_ 1-j /О»
— 1+Е' §~" V (Р, ( )
_2n —1
(1.168)
_ (l+26)(l+ef _2n —
ft)n а~
В частности, если Л[ и Лг имеют одинаковые границы спектра,
т< е. ai=a2 = oc, Pi = р2 = р, причем а^(3, то из (1.167) следует
(М69)
что означает слабую логарифмическую зависимость скорости
сходимости от числа обусловленности матриц.
Если же операторы Ль Л2 не перестановочные, то построить
оптимальную последовательность параметров и получить оценку
скорости итераций вида (1.167) не удается. В общем случае
для стационарного итерационного процесса вида (1.164)
справедлив следующий результат.
Теорема 1.10. Итерационный процесс (1.165) для Ti,n =
= Т2,п==т и операторов Ль Лг, удовлетворяющих для всех
и условиям
(AiU,u) > 64{и, и), . п 170)
(AiUtAiuXtAiiAiUtU), /=1,2, v* ;
сходится при любом т>>0, если хотя бы одна из величин 61,62
больше нуля. При этом для коэффициента подавления ошибки
справедлива оценка
p<(min{Pl, P2})
1/2 Pi =
если итерационный параметр определяется формулой
т=1/У"6Д~ (1.172)
Здесь /= 1 при pi<p2 и / = 2 — в противном случае. Справедлива
также оценка, которая сильнее (1.171) для положительно
определенных Ai, Л2 с близкими границами спектров:
' <U73)
_
т= 1/-\/бА, 6 = min(6i,62), А =
Для двумерной задачи в работах различных авторов (см.,
например, обзор в [69]) предложены модификации методов
переменных направлений, эквивалентные по скорости сходимости
рассмотренному нами алгоритму.
57

Для трехмерных задач известно также несколько
алгоритмов расщепления, из которых мы рассмотрим схему с
дополнительными параметрами:
un+l/p=^un-xn(Alun+i/p + 2 Atun — f),
1=2 (1.174)
un+i/P = un+a- i)/P+pn ._ ,(„«+(*- D/P_ un)-xnAi(un+i/p- и"),
i = 2, 3, .... p.
После исключения промежуточных величин получаем
W-f)- (1Л75)
«=1 1 = 1
Здесь матричные множители в скобках предполагаются
следующими слева направо в порядке возрастания индексов /.
В частности, для двумерной задачи (р = 2) схема (1.175)
сводится к формуле
ы»+> = \Е - ~ (Е - Тп)]и" - сол П (Е + тЛ,)-1/
......
(1.1/О)
(о„=1+р„.
При (оп = 2 эта схема эквивалентна рассмотренному
методу Писмана — Ракфорда (1.165) для Т1П = т2п = т.
Сходимость итерационного процесса (1.175) при р = 3, так
же как и других известных трехшаговых схем, удается ноказать
только при перестановочности операторов Д. А именно, если
при этом Ai—положительно определенные, то итерации (1.175)
СХОДЯТСЯ При ЛЮбыХ Т„ > О И 2 > 0)„ = П(1+ Pni) > 0.
i=l
По поводу реализации неявных методов переменных
направлений можно отметить, что они требуют один или два массива
памяти длиной, равной количеству узлов (в зависимости от
модификации алгоритмов), плюс два-три массива с
размерностью, равной максимальному количеству узлов в строке или
в столбце сетки.
Расчет одной итерации, очевидно, требует примерно в р раз
большего количества арифметических действий, чем метод
прогонок по линиям с верхней релаксацией.
Г. Попеременно-треугольные методы. Мы
напомним, что при решении многомерных задач неявными
методами переменных направлений исходный оператор разбивается
на сумму «одномерных» операторов, а итерационный цикл
представляется в виде последовательности дробных шагов, на
каждом из которых обращается один из «одномерных»
операторов.
В этих эффективных алгоритмах по сравнению с явными
методами Зейделя или верхней релаксации можно, отметить
тот недостаток, что число арифметических операций, необхо-
58

димых для вычисления очередного приближения,
увеличивается из-за необходимости проведения прогонок.
В то же время рассмотренный нами операторный анализ
сходимости итераций при р = 2 требует только условия А = А\+А2
и положительной определенности операторов А\, А2.
В попеременно-треугольных методах, или явных схемах
переменных направлений [64, 166], используются в операторной
записи такие же итерационные процессы, но исходная матрица
разбивается на сумму двух треугольных матриц, которые, как
известно, наиболее легко обращаются. Реализация каждого
дробного шага проводится по явным рекуррентным формулам
и требует столько же арифметических действий, сколько одна
итерация метода поточечной верхней релаксации. Отметим,
что даже для многомерных задач итерационный цикл в этом
случае разбивается только на два дробных шага.
В качестве примера мы приведем явный вариант схемы Пис-
мана — Ракфорда для семиточечных разностных уравнений в
трехмерной задаче
+pouijk = fijk (1.177)
(индексы при ро, Рь ••-, Рь для краткости опускаем).
Операторы Ai и Л2 определяем следующим образом:
Тогда итерационный процесс (1.165) проводится по формулам:
.п+1/2 1 Г/.n \~(г\ ,.л+1/2 | „ ,#я+1/2
Первый дробный шаг реализуется так же, как в методе
Зейделя, с перебором узлов «вправо-вверх» (может быть
выбрана любая последовательность, для которой при вычислении
иц£х/2 значения и^\^к, w£/tYjL u>?.£k-2\ уже определены). При
реализации второго дробного шага счет проводится в обратном
направлении. Очевидно, при вычислениях на ЭВМ требуется
только один массив для хранения пци.
Если матрица Л симметрична и положительно определена,
то при ро=ро =-~- ро и вещественных и имеем
(Л,а, и) = (А\иу и) = (А2и, и)=^{Аи1 t/)>0,
59

что по теореме 1.10 обеспечивает сходимость приближений ип
к точному решению при т;>0.
Поскольку в данном случае операторы Ль Л2 не
перестановочны, то построить оптимальную последовательность
итерационных параметров хп не удается. При т„ = т для оценки
скорости сходимости применима теорема 1.10, как и в неявных
методах. В частности, скорость сходимости попеременно-
треугольного метода для пятиточечной разностной задачи
Дирихле в крадратной области на квадратной сетке вдвое
меньше, чем для стационарного неявного метода Писмана — Ракфорда.
Отметим, что * аналогичные алгоритмы (методы SSOR—
symmetric successive over relaxation) строились зарубежными
авторами из другого принципа — использования
последовательной верхней релаксации с попеременным изменением
направления пересчета неизвестных, см. литературу в [69, 203].
Рассмотрим скорость сходимости явной двупараметрической
схемы переменных направлений для симметричной положительно
определенной матрицы A = Ai + A2, Ai=A2 (см. (1.176)):
ип+1 = [Е—|(£ — Т))ип — сот(£+тА2)~ \Е + тЛi)~7. (1.180)
Легко видеть, что матрица Т симметрична и данный
итерационный процесс будет сходиться при^ т>0, 0<со<4. При
| — j -\/Д/Д
т = то= I—'■ имеем О^ХТ^.ХТ= ¥-Z_ и оптимальное значе-
ние со = соо равно
о 1 4- лШК
<оо = —^- = 4 ^'. (1.181)
1/2 (2- Кг) 1 + 3VVA
а коэффициент подавления ошибки удовлетворяет неравенству
Отсюда для 6/A<Cl скорость сходимости итераций равна
(1.183)
В данном методе при 0<со<2 спектр оператора перехода
лежит на неотрицательной части вещественной оси, и для
ускорения сходимости итераций можно использовать прием чебышев-
ского ускорения в несколько другой форме, чем это описано
в п. 1.5.1 (мы рассмотрим явную схему Писмана — Ракфорда,
т, е. в (1.180) (0 = 2):
urt+1==rt/n+G,
(1.184)
un+l = un+l +an(un+l - ип).
При этом задача отыскания оптимальных значений ап
(л=1, 2, ..., mod (га)) сводится к построению полинома вида
П
Рт = П [к + ая(А,- 1)J, (1.185)
60

наименее уклоняющегося от нуля на интервале [О, ХТ](ХТ—
спектральный радиус Т). Так как
п (*-
то искомые {$„ должны быть корнями многочлена Tm(a
/Tm{a + b), где Tm(aX-\-b) — полином Чебышева степени m на
интервале [—1, 1], а = 2Дг, &= —1:
Н]4{*ЁЧ о-187»
Число итераций п(е), необходимых для подавления начальной
ошибки в е раз, в этом алгоритме равно (при т = п)
'n(e)<ln 8
/inv-VY'-l, Y=r-1- (1-188)
При 6/А<с1 (что соответствует малым h) ХТж1—2-уб/А
и для е<С 1 имеем
что соответствует скорости сходимости
R^2-\J2\jlT^ (1.190)
Отметим также, что применение чебышевского ускорения
требует использования одного дополнительного массива для
хранения в памяти значений u?f~.x
Весьма важно, что метод чебышевского ускорения позволяет
автоматизировать выбор итерационных параметров по
апостериорной информации, без использования значения Хт, которое чаще
всего неизвестно. Для этого сначала выбирается некоторое
значение (поскольку в сеточных уравнениях Хт близко к 1, то можно
смело брать Хо ^ [0.7, 0.9J), и итерации проводятся по формулам
(1.184), (1.187) с заменой Хт на Хо. Поскольку при этом в
последовательных приближениях становится преобладающей
гармоника, соответствующая максимальному собственному числу, то
становится возможным приближенное вычисление ХТу которое
делается следующим образом:
ХтжХР=(1 7гГ)/тА, О-191)
где k — минимальное целое число, при котором
|2Н1М-,|<бь zk=\\uk -tik-xb/\\uk-x -ик~2Ь (1.192)
для некоторого достаточно малого ei.
После этого в итерациях параметры рп вычисляются по формуле.
(1.187) с заменой Хт на X[k\
Д. Вариационные методы переменных
направлений. В последние годы в работах советских и зарубежных
математиков [44, 52, 68; 121, 203] исследовалась оптимизация
61

алгоритмов переменных направлений на основе вариационных
принципов, которая приводит к обобщению известных
градиентных методов. Например, для итерационных процессов вида
ип = ип-{ -(*п-ХН-\Аип-{ -/), (1.193)
где под Нп мы подразумеваем произведение операторов,
соответствующих методам переменных направлений или
попеременно-треугольным, параметры (оп можно выбирать из условия
минимизации какого-либо функционала. Если в (1.193)
минимизировать функцию ошибки Ф(ип) = (Аип, и11) — 2(un,f), то
получим обобщение метода наискорейшего спуска
,vn). ' (1Л94)
Функция ошибки при этом меняется по закону
ф(ип)=ф(ип-1)—{гп-\Н~1гп-1)/{АН-1гп-\ H~lrn~~l). (1.195)
Рассмотрим проведение невязки гп в итерационном процессе
(1.193). Поскольку справедливо соотношение
„я ^п— 1 .ч ylu-Ln-l
Г = Г —(Dn_i/i/7 T ,
то при
<ол = (Л#-1гл, r")/(AH-lrn, AH~lrn) (1.196)
невязка убывает оптимальным образом, причем
(r«+V+')__1 (AH-^\r"f (
4 (r\rn) (rn,rn)(AH-{r\AH~lrnY
Если m, M — минимальное и максимальное собственные числа
матрицы АН~\ то q^(M — m)/(M — m).
Таким образом, формулы (1.193) и (1.196) дают аналог
метода минимальных невязок. Для двух дробных шагов
(А=А\-\-А2) мы полагаем
#:=1(£ + тЛ1)(£ + тЛ2), (1.198)
и реализация рассмотренных двух методов основывается на
решении уравнения
с помощью обращения простых операторов. При этом можно
использовать как неявные, так и явные алгоритмы переменных
направлений, т. е. определять А\, А2 как трехдиагональные или
треугольные матрицы.
Очевидно, эти алгоритмы можно рассматривать как
«классические» релаксационные методы, примененные к решению
уравнения Lu = Gy полученного из исходного умножением
62

"1:
на Я
Отсюда следует, что сходимость таких итерационных
процессов доказывается обычными для этих методов способами,
если Н~1А—положительно определенная матрица.
Эффективность же алгоритмов, очевидно, будет зависеть от
обусловленности Н~1А, которую можно, в свою очередь, оптимизировать
за счет выбора т.
С другой стороны, для градиентных методов существуют
оценки погрешности итераций, непосредственно не зависящие
от обусловленности исходных матриц. Например, в обобщенном
методе минимальных невязок (1.193), (1.196), (1.198) для
вектора невязки справедливо неравенство [52]:
(гл, гп)^4у(Нуо,Нуо)/п\
если Я — симметричная положительная матрица, и ||ЛЯ~1||^7-
Эта оценка характеризует довольно быстрое уменьшение ошибки
на первых итерациях, причем она справедлива даже для
вырожденной матрицы А.
Логическим развитием вариационных методов переменных
направлений являются методы сопряженных направлений.
Таким примером может быть метод сопряженных градиентов,
минимизирующий функцию ошибки Ф(ип) по заданному
начальному приближению и0 (а не по предыдущей итерации ип~\
как в методе наискорейшего спуска):
(1-199)
где Я определяется из (1.198).
В силу самого построения метода сопряженных градиентов
из условия минимальности функции ошибки, скорость его
сходимости по крайней мере не меньше, чем если в методе (1.193)
использовать оптимальную последовательность чебышевских
итерационных параметров соп аналогично тому, как это делалось
выше в п. Г. Кроме того, в итерационном методе (1.193) для
вектора ошибки уп справедлива оценка, аналогичная
предыдущей и не включающая явным образом числа обусловленности
матриц [71]:
Известно также, что метод сопряженных градиентов дает
точное решение за конечное число итераций, равное порядку
системы. Хотя это соображение не дает конструктивной оценки
для разностных уравнений в с^лу большого количества
неизвестных, но свидетельствует о некотором «внутреннем резерве»
алгоритма. По крайней мере численные эксперименты свиде-
63

тельствуют об очень высокой эффективности метода
сопряженных градиентов в сочетании с переменными направлениями.
Исходя из условий минимизации того или другого
функционала, могут быть построены различные алгоритмы сопряженных
направлений. Некоторым сдерживающим фактором для их
широкого распространения является то, что они требуют
большего объема вычислений на одну итерацию и большего объема
памяти, чем метод чебышевского ускорения.
Е. Итерационные методы неполной
факторизации. Рассмотрим систему уравнений блочно-трехдиагональ-
ного вида (см. 1.102), которую мы запишем в форме
=fk, 6 = 2, 3, ..., m-1, (1.200)
— L/Xni — 1 ~\~ B{Xm = /■///.
Здесь Xk, k=l, 2, ..., m,— векторы, каждый из которых имеет
размерность /&. Матрицы Bk предполагаются квадратными,
трехдиагональными и монотонными, т. е. обратные матрицы
Bk~l существуют и имеют неотрицательные элементы. Матрицы
Lfc, Uk считаем неотрицательными, и вся блочно-трехдиагональ-
ная матрица А системы (1.200) предполагается монотонная
(Lk^O, Uk^O, A~x~^0, где матричные неравенства
подразумеваются поэлементно).
Если, например, система (1.200) получена из
аппроксимации краевой задачи в прямоугольной области, то /* = / и L*,
Uk — диагональные матрицы.
Как отмечалось в п. 1.4.1, метод матричных прогонок для
решения такой системы является безытерационным, однако
реализация его требует количества операций О(1гт). Еще
более жестким ограничением является тот факт, что реализация
его требует запоминания вспомогательных чисел О(12т).
Учитывая, что для монотонных матриц с диагональным
преобладанием обратные матрицы имеют положительные
элементы со значениями, убывающими по мере удаления от
главной диагонали, рассмотрим следующий итерационный алгоритм
[75].
, Будем искать решение системы с помощью соотношения
Xk — MkXk+\-\-tjk, после подстановки которого в (1.200) получаем
Gk^Bk-UMk-i), Mk = Gr{Uk. (1.201)
Представим теперь Gk~x в виде суммы Dk + Hk, где Dk —
ленточные матрицы, ненулевые элементы которых равны (или
приближенно равны) соответствующим элементам Gk~l. Переписывая
(1.201) в виде
xk = DkUkXk+\ + HkUkxk+1 + Gr l(fk
64

Представим теперь Gk l в виде суммы Dk + Hk) где Dk — ленточные
матрицы, ненулевые элементы которых равны (или приближенно
равны) соответствующим элементам G&"1- Переписывая (1.201) в
виде
•Xk = DkUkXk+1 + HkUkXk+1 + Gk~ \fk + Lkt/k- i),
можно выписать соотношения
k,
-X + UkXk+\)-DkUkxk+u (1.202)
Gk = Bk-LkDk.xUk-x = Dk + Hk,
"удовлетворяющие, как нетрудно видеть, исходной системе
уравнений. На основе (1.202) определим итерационный процесс
ynx = Gr\n + Uxx$-x)-DxU{xV\
-DkUkxi+\% (1.203)
\, k = 2, 3, ..., га,
k = m—l, ..., 1.
Если в данных соотношениях матрицы Dk взять равными
Gk~l (при этом Hk будут нулевые матрицы), то получим без-
итерационный метод матричных прогонок. Другой предельный
случай, когда Dk = 0, Hk=Gk~l = Bk~l, дает не что иное, как неявный
метод Зейделя с прогонками по линиям, который определяется
из (1.162) при (о=1. Поэтому алгоритм (1.203) при ненулевых Dk
можно еще назвать сверхнеявным методом Зейделя.
Из построения следует, что если последовательность xl
сходится, то предел является решением системы (1.200). Мы
подробней остановимся на реализации метода (1.203) при
Dk = (Gk~l)"3\ где (GrI)(3) означает матрицу, у которой
элементы на трех главных диагоналях те же, что у Gf\ а
остальные — нулевые. В этом случае выполнение итераций требует
предварительного вычисления Dk, что сводится к нахождению
трех главных диагоналей матрицы, обратной к трехдиагональ-
ной матрице Bk — LkDk-\Uk-\. Эту последнюю задачу
рассмотрим на примере трехдиагональной матрицы Т = {—а,-,&/, — С/}.
Вектор-столбец fq) = {t^q] элементов матрицы Г"1, очевидно,
удовлетворяет системе
— ajtj-itq + bjtjq — c}tj + i,q = eq, ai=c/ = 0, /=1, 2, ...,/,
где eq— орт, имеющий единичный д-и компонент, а остальные
компоненты нулевые. С помощью встречных прогонок за 0(1)
арифметических действий могут быть вычислены величины
ri = dl/hu r, = d//(6/-r/_1), di = aj+lch / = 2,...,/,
si = di-x/bu sl = dj-i/{bl — Sj+x)9 / = /—1,/ —2,..., 1,
через которые выражаются элементы трех главных
диагоналей по следующим формулам:
^Н^-^-1-^-ыГ1, <7 = 2, 3, ..., /-1,
tq-\,q = tqqrq-\/aq, q = 2,..., /,
tq+i^—tqqSq+i/Cq, ^—1,2,...,/— 1.
5 В П Ильин 65

Поскольку каждая Gk— трехдиагональная матрица,
умножение векторов на Gr1 в (1.203) также реализуется с помощью
простых прогонок.
Реализация каждой итерации в (1.203) может быть упрощена,
если в качестве Dk брать диагональные матрицы (Gk~l)"{\
ненулевые элементы которых равны диагональным элементам
матриц Gk~x. С другой стороны, усиление «неявности» можно*
достичь при Dk = (Gk~l)(p\ p>3. Например, при р = 5 вычисление
Gk требует нахождения пятидиагональной ленточной части
матриц, обратных пятидиагональным матрицам. Это может
быть несложно осуществлено с помощью встречных пятидиа-
гональных прогонок [15].
До сих пор в этом пункте структуру матриц L&, Bk, Uk и
реализацию алгоритма мы связывали с естественной построчной
упорядоченностью узлов, как и в п. 1.4.1, т. е. Xk из (1.200) равно
Uj = [u,j} из (1.100) при k = j.
Возможен и другой способ представления системы (1.200)
для разностных пятиточечных уравнений (1.99), основанный
на определении векторов Xk как совокупности значений щ на
k-и диагонали сетки с номером k = i-\-j—l. В этом случае
каждая из матриц В^. будет диагональной с элементами e,jy a
Lk и Uk— нижняя и верхняя двухдиагональные матрицы с
элементами a,,, bij и с,/, d,j соответственно. Если мы теперь в (1.203)
определим Dfe = (G^1)(1), то получим итерационный метод
неполной факторизации, предложенный Н.И.Булеевым и развитый
затем многими авторами, см. [69, 24, 124] и цитируемую там
литературу.
Вектор ошибки я-й итерации vn = {xj — xf} в (1.203)
удовлетворяет равенству
где матрицы L, £/, Н имеют следующее блочное представление:
I! я, о
и =
н=
о
о
о
о
-DlUl
-GrlLt
-DkUk
о
Е,
о
нкик
(1.205)
66

Относительно системы (1.200) дополнительно предполагается,
что она обладает диагональным преобладанием, обеспечивающим
выполнение условий устойчивости матричной прогонки М/^0,
||Mfe|| <C 1. Матрицы Mk определяются в (1.101), а за норму
матрицы берем максимальную сумму модулей элементов строки. Далее,
полагая систему отнормированной по условиям ||Lfe||<l, ||(Л||<1,
будем иметь
Gk>0, £>*>0, tf*>0, ||G*L*|I<1, \\DkU\\<l9 Л=1,2,...,т.
(1.206)
Отсюда следует, что матрицы L, U — монотонные, т.е.
итерационный процесс (1.203) реализуем. Его матрица перехода
T=U~lL~lH, очевидно, имеет неотрицательные элементы.
Непосредственным умножением можно проверить справедливость
соотношения
LU-H=G~XA, (1.207)
где G — блочно-диагональная матрица с блоками Gk на
диагонали.
На основе спектральных свойств неотрицательных матриц
несложно доказать следующий результат.
Теорема 1.11. Пусть матрицы Р и N — монотонные,
Q — неотрицательная, R — неотрицательная и невырожденная,
и пусть выполняется соотношение
P-Q = NR. (1.208)
Тогда максимальное по модулю собственное число X матрицы
P~{Q вещественное, простое и удовлетворяет неравенству
0А1
Для частного случая, когда R—единичная матрица, это
утверждение переходит в известный результат о регулярном
расщеплении матриц [28]. По аналогии представление (1.208) будем
называть квазирегулярным расщеплением матрицы N.
Из (1.207) и теоремы 1.11 следует, что максимальное по
модулю собственное число матрицы S = (L')~l(U')~lH
положительное и меньше единицы (штрих означает
транспонирование). Поскольку собственные числа матриц S, Т' и Т совпадают,
получаем, что итерационный процесс (1.204) при выполнении
условий (1.206) сходится.
С целью иллюстрации скорости сходимости данного
итерационного процесса рассмотрим результаты методических
расчетов для разностных уравнений Пуассона,
соответствующих задаче Дирихле в квадрате и квадратной сетке' с числом
внутренних узлов m по каждой координате. В этом случае
Lk и Uk— единичные матрицы порядка m, a Bk— трехдиаго-
нальные матрицы, имеющие «4» на главной диагонали и «—1» —
на соседних с ней диагоналях. Мы применим формальное
обобщение алгоритма, состоящее в определении матриц Dk
по формуле Dk — Q (Gk~[f3\ где Э — некоторый числовой
параметр.
5* 67

Расчеты выполнялись при правых частях fk,
соответствующих точному решению, равному единице. Начальное приближение
выбиралось нулевым. Итераций продолжались, пока
максимальный модуль разности соседних приближений не становился
меньше 10~5.
Для демонстрации влияния параметра 6 в табл. 1 приведены
количества итераций п при разных величинах 9.
Таблица 1
0
т
10
20
30
40
1
16
44
86
141
1,05
13
36
71
116
1,10
10
29
56
91
1,15
12
21
41
67
1,20
17
37
57
75
Итерации
9
17
31
44
Как видно из результатов, оптимальное значение 9 близко
к 1,15 (при этом число итераций сокращается примерно вдвое
по сравнению с 9=1), и его значение слабо зависит от порядка
системы уравнений. Отметим, что при 9>1,25 итерации
расходятся. В последнем столбце таблицы даны результаты по
применению ускорения Люстерника (см. п. 1.5.1). Сначала
ведутся итерации с 9=1 и вычисляются приближения к
максимальному собственному числу Хп= \\хп — хп~1 \\/\\хп~[ — хп~2||. После
выполнения условия \Хп — К-\ I ^s~ 10~3 делается один шаг
ускорения
где хп+{—«обычное» (я+1)-е приближение, а далее итерации
продолжаются при со = 1, 9=1,15. Данный прием сокращает
число итераций примерно в полтора раза. При этом количество
итераций оказывается приблизительно в 3 раза меньше, чем
в методе прогонок с оптимальной верхней релаксацией (1.162).
Отметим, что с учетом возможного вычисления матриц DkUk
до итераций трудоемкость одного приближения не намного
больше, чем в методе блочной релаксаций. По-видимому, если
взять Dk пятидиагональными матрицами, количество итераций
можно существенно уменьшить. Однако увеличение ширины
ленты матриц в пределе (при Я^ = 0, Dk=Gk) приведет к методу
матричных прогонок, не являющемуся оптимальным. Можно
ожидать, что существует «золотая середина» в определении
ширины ленты Dk, при которой эффективность методов данного
класса будет максимальной.
Методы неполной факторизации в рассмотренной форме
даже для симметричной системы имеют несимметричную
матрицу итерационного шага. Это не позволяет эффективно
применять к ним способы повышения скорости сходимости типа
чебышевского ускорения или сопряженных градиентов.
68

Мы теперь остановимся на другой форме алгоритма,
свободной от этого недостатка. Рассмотрим итерационный процесс вида
K(un+{-un) = Tn(f-Aun) (1-209)
с некоторой предобусловливающей матрицей К и параметрами
тп. Выберем К равной
G-lU. (1.210)
Очевидно, при G = B — LG~XU будет К = А и (1.210) представляет
собой не что иное, как блочную факторизацию Гаусса матрицы
А. Тогда итерации в (1.209) сходятся за один шаг, а блочно-
диагональная матрица G = {Gk] определяется из рекуррентных
соотношений G\ = Bu Gk = Bk — LkGiT-\Uk-\, & —2, 3, ..., /.
Если же мы будем использовать только ленточную часть
матриц, обратных к ленточным матрицам
f)U k = % 3, ..., U (1.211)
то формулы (1.209) — (1.211) дают итерационный алгоритм,
реализация которого проводится аналогично (1.203).
Если матрица А симметрична, то Lk=Vk-\ и матрицы G, К
также симметричны. Если к тому же Л — монотонная матрица
и выполняются условия (1.206), то К является положительно
определенной матрицей, а собственные числа К~1А
вещественные и положительные. Кроме того легко показать, что
К—монотонная матрица
и что справедливо соотношение
Отсюда и из теоремы 1.11 следует, что при тп=1 итерационный
процесс (1.209) — (1.211) сходится, поскольку собственные
числа матрицы перехода Т = Е — К~1А = К~1Н будут меньше
единицы по модулю:
1. (1.212)
Спектральный радиус матрицы Т при этом равен
р(Г)=а/(1+а), а =
Теперь для применения чебышевского ускорения' в (1.209)
необходимо определить границы спектра матрицы К~1А.
Непосредственно из (1.212) следует
т=1/(1+а) <ЦК~1А) < (1 +2а) / (1 +сс) =М. (1.213)
Отсюда получаем, что оптимальная циклическая
последовательность (с периодом N) чебышевских итерационных параметров
в (1.209) определяется формулами (1.153), и при а ^> 1 скорость
69

сходимости итераций будет равна
Для модельной разностной задачи (см. (1.69) и ниже (1.214) )
при построчной упорядоченности узлов сетки Lk и Uk будут
единичными матрицами, и величину а= р(А~1Н) можно оценить через
минимальное собственное число матрицы А и норму матрицы
G"1— (G~l)(p). Для р = 3 непосредственные расчеты с помощью
формул (1.203) дают
р^-'ЯХ 0,123/(2А2),
откуда для скорости сходимости метода с чебышевским
ускорением получаем
R
Такая же оценка скорости сходимости будет справедлива и для
метода сопряженных градиентов с использованием предобусловли-
вающей матрицы /Сиз (1.210). Реализацию такого алгоритма
можно провести по формулам (1.199) при Н = К.
Рассмотренные методы имеют нечто общее с появившимися
за последнее время итерационными алгоритмами,
использующими неполное разложение Холесского или Гаусса, когда в матрицах-
множителях «зануляются» относительно малые по величине
элементы (см., например, [2] и цитируемые там работы).
1.5.3. Сравнительный анализ итерационных методов. Одной
из актуальных проблем вычислительной математики, как с
теоретической, так и практической точки зрения, является выбор
оптимальных алгоритмов. Этот вопрос достаточно содержателен при
решении разностных уравнений в силу большого объема требуемых
вычислений и наличия разнообразных итерационных алгоритмов,
имеющих, в свою очередь, свободу в подборе счетных параметров.
Сравнение эффективности итерационных методов можно вести
по теоретическим оценкам скорости сходимости итераций.
Недостатки таких оценок заключаются, как правило, в том,^что они,
во-первых, более или менее точны только для частного круга задач
и, во-вторых, имеют асимптотический характер, т. е. справедливы
при А, 8-^0.
Другой путь заключается в проведении численных
экспериментов. Здесь требуется подбор характерных методических задач
и «чистота» эксперимента, т. е. аккуратность в соблюдении равных
условий при сравнении различных методов.
Понятие оптимального алгоритма имеет смысл в применении
к решению определенного класса задач на конкретной
вычислительной системе. Решить проблему выбора оптимального метода
для частной задачи зачастую не легче, чем просто решить эту
задачу любым имеющимся алгоритмом. Теоретические оценки
и эксперименты на методических примерах не закрывают, конечно,
всей проблемы, но дают первую информацию, которую необходимо
учитывать при анализе эффективности методов.
70

Сравнение итерационных методов решения разностных
уравнений, как правило, проводится на следующей модельной задаче:
(1.214)
/, /=1, 2,..., /, А = я
которая представляет собой пятиточечную аппроксимацию задачи
Дирихле
—\-\ ^=f(x,y), 0<х,
(5л: ду2
= O, в квадрате с
длиной стороны л на квадратной сетке (вид функции f(xyy) не
очень существен, поскольку рассматривается поведение
итерационных процессов).
В табл. 2 приводятся значения асимптотической скорости
сходимости итераций R для рассмотренных ранее методов: Зейделя,
последовательной верхней релаксации, прогонок с верхней
релаксацией, продольно-поперечных прогонок с постоянным значением
итерационного параметра и с последовательностью параметров,
двухпараметрического попеременно-треугольного с постоянными
параметрами, попеременно-треугольного с чебышевским
ускорением и с минимальными невязками, рассмотренного выше метода
неполной факторизации (при р = 3) с чебышевским ускорением,
для которых используются соответственно обозначения ЗЕЙД,
ВР, ПВР, ПШ, ППН, ДПТ, ПТЧУ, ПТМН, НФЗ.
Таблица 2
R
ЗЕЙД
h2
ВР
2Л
ПВР
2л/ТН
ПП1
2Л
ппп
n2/2\\nh\
ДПТ
2h
ПТЧУ
2л/ТГ
ПТМН
2h
НФЗ
4уТ/г
Во всех алгоритмах итерационные параметры предлагаются
оптимальными.
Как видно, при А-►О вне конкуренции оказывается метод
продольно-поперечных прогонок с оптимальной последовательностью
параметров (ППП), а на втором месте стоит
попеременно-треугольный метод с чебышевским ускорением (ПТЧУ).
Если область представляет собой не квадрат, а
прямоугольник, и сетка прямоугольная (равномерная или неравномерная),
то все оценки для R в табл. 2 остаются по порядку теми же (ft в
данном случае есть максимальный шаг сетки). Количественно же
для всех методов значение R будет ухудшаться, если сетка
становится сильно неравномерной, т. е. растет отношение максимального
шага к минимальному.
Для других типов граничных условий, например, если задано
условие Неймана на одной, двух или трех сторонах прямоуголь-
71

ника, скорости сходимости всех методов остаются по порядку
прежними. Общая тенденция поведения R такова: чем на большей
части границы выполняется условие Неймана', тем хуже сходятся
итерации, т. е. R уменьшается.
Для уравнения Пуассона в цилиндрической системе координат
оценки асимптотической скорости сходимости итерационных
методов примерно такие же, как и в декартовых координатах.
Если же рассматриваемая область не является
прямоугольником, то для метода продольно-поперечных прогонок
оптимальная последовательность итерационных параметров неизвестна
и оценка R~(j( .. .] не справедлива. Такая узкая
применимость — главный недостаток этого алгоритма, в то время как для
остальных итерационных процессов оценки из табл. 2 (в том числе
для ПП1) остаются по порядку теми же.
Таблица 3
—^^_^^ Метод
Область ^~"~-~-^-^^^
Квадрат 20x20
Квадрат 30x30
Квадрат 50x50
Уголок 50x50
Кольцо 88x88
ЗЕЙД
319
644
1531
877
1200
ВР
83
147
327
172
478
ПВР
54
90
190
115
272
пш
27
39
60
65
205
дпт
28
42
61
52
—
ПТЧУ
20
31
38
31
50
птмн
15
21
25
23
—
В табл. 3 мы приводим количество итераций, затрачиваемых
рассматриваемыми методами при решении трех характерных
задач. Первая из них—это модельная задача (1.214) с числом
шагов сетки 20X20, 30X30, 50X50 (только граничное условие
п
88 я
бралось ы|г=1). Вторая — «уголок» (см. рис. 7, а) с граничными
условиями #|г=1 и сеткой 50X50: я,- = 0,02г; f// = 0,02/;
/, / = 0, 1, ..., 50. Третья задача — «кольцо» (рис. 7, б) с
граничными условиями ы|г=0, ы|г=1 и квадратной сеткой 88X88: *,• = *,
72

#/=/; *\/ = 0, 1, ..., 88 (радиусы окружностей равны /?i =2,5, R2 =
= 88).
Для всех трех задач решались пятиточечные разностные
уравнения с начальным приближением u?j = O. Итерации
продолжались, пока разность соседних приближений не становилась во всех
узлах меньше 10~5. Расчеты проводились на БЭСМ-6 со
значениями итерационных параметров, для всех методов близкими к
оптимальным.
Как видно из результатов, во всех случаях оотношения
экспериментальной скорости сходимости итераций различных методов
примерно соответствуют теоретическим оценкам. Исключение
составляет попеременно-треугольный метод с минимальными
невязками: число итераций в нем гораздо меньше, чем это следует
из асимптотической оценки скорости сходимости.
Для сравнения практической эффективности алгоритмов имеет
значение количество арифметических действий Q для реализации
одной итерации ичобъем необходимой памяти Р. Соответствующие
данные мы приводим в табл. 4.
Таблица 4
Метод
Q
Р
ВР
12/m
Im
ПВР
15/m
2/4- 1т
пгш
34/т
1т+ 21
ДПТ
25/т
21т
ПТЧУ
33/m
21т
птмн
38/т
3/т
Количество арифметических операций, вообще говоря, можно
примерно в полтора раза сократить, если учесть, что для
регулярных узлов и равномерных сеток коэффициенты имеют простой
вид. Наоборот, необходимость вычисления коэффициентов для
нерегулярных узлов и выполнения логических действий в
программах, рассчитанных на решение краевых задач со сложными
границами, значительно увеличивает фактический объем операций.
Более детальный анализ различных итерационных алгоритмов,
включая теоретические оценки эффективности и обширные
экспериментальные данные, можно найти в работах [18, 69, 166, 26].
g 1.6. Комбинированные методы решения
разностных уравнений
1.6.1. Метод итераций по подобластям. Как видно из
предыдущих пунктов, для прямоугольных областей разностные уравнения
могут решаться почти оптимальным образом с помощью методов
циклической редукции, быстрого преобразования Фурье или
продольно-поперечных прогонок с последовательностью параметров:
число арифметических действий пропорционально /г 21 ln/г |, т. е.
в расчете на один узел слабо зависит от шага сетки. Существенно
более трудоемкими являются задачи с границами сложной
конфигурации, например, криволинейными и многосвязными. При
73

малых h прямые методы в этих случаях слишком громоздкие,
а итерационные требуют проведения большого количества
приближении.
Отсюда, естественно, возникает идея разбить расчетную область
на некоторые подобласти, чтобы одна или несколько из них были
прямоугольные и включали основную часть узлов сетки. Тогда
решение исходной задачи можно свести к последовательному
решению вспомогательных задач в подобластях таким образом,
чтобы итерационные приближения сходились в целом по области
к искомому решению. При этом на границах вводимых
подобластей для каждого приближения необходимо ставить некоторые
специальные граничные условия.
Предпосылками к эффективности такого подхода являются
следующие факторы:
а) скорость сходимости итераций по подобластям должна не
зависеть при /г-^0 от шага сетки;
б) вспомогательные задачи в прямоугольных подобластях
решаются особенно экономично;
в) непрямоугольные подобласти содержат относительно малое
число узлов, и в них разностные уравнения могут быть решены
быстро обычными итерационными методами,
например, верхней релаксации.
Существенным вопросом в данном случае
является построение хорошо сходящихся
итераций по подобластям.
Один из давно известных способов — это
альтернирующий метод Шварца. Для примера
на рис. 8 он формулируется следующим
образом. Расчетная область G представляется в виде
Рис.8. объединения подобластей G = G(1)|JG(2),
G(l)=GiUG3, G(2)=G2UG3, имеющих пересечение Gi= G(1)fl G(2).
Сначала находится п\{х, у)— решение уравнения Пуассона в
G(1) при произвольно взятом начальном граничном значении
на S\ — той части границы G(1), которая принадлежит G(2).
Затем решается задача в G(2), причем для ее решения и2{х,у)
на S2 (определяемом аналогично Si) граничные значения
берутся те, которые получались из предыдущей задачи (мг| s2= ^ij Si)-
Далее процесс продолжается аналогично: вычисляются
приближения мгл-1, u2k, ft = 2, 3, ..., из решения задач в G(l) и G(2), для
которых граничные значения на Si, S2 используются взаимооб-
раЗНО (ll2k-\\ Sl=«2fe-2| s* Ци\ S2==W2/?-l| S) '
Известно, что при некоторых предположениях (в частности,
линии Si, S2 должны подходить к границе G с ненулевым углом)
такой итерационный процесс сходится [61], и для некоторых
частичного вида подобластей несложно дать оценки скорости
сходимости итераций на основе принципа максимума.
Рассмотрим поведение ошибок Z2k — u — U2k, Z2k-i = u — ti2k-\
для примера на рис. 8, предполагая, что го(х,у\=1, (x,j/)6 G(2). На
первом этапе в G(1) имеем Zi(*,{/)<Zi(x,t/), где Z\(x,y) определяется
74

из задачи
z,(jc,j/) = O, (*,*/)£ ГПГь (1.215)
z,(*,{/)=lt (x,y)£ Su
где Г, Tj и Г2 — соответственно границы областей G, G(1) и G(2).
Несложно показать, что значения Z\(x,y) на S2 удовлетворяют
неравенству
z,(x,j/)<<7, = max{l/2, &/4 (*,{/) 6 S2.
Аналогично для второго этапа в G(2) имеем
z2(x,y) < г2{х,у),
где z2(x,j/) определяется из задачи
z2(x,{/) = 0,
z2{x,y) = qi,
Отсюда получаем соотношение
a}, (x,j/)£Si.
Таким образом, после первой итерации, а следовательно и после
каждой последующей, ошибка уменьшается по крайней мере в
q\q2 раз.
Другой перспективный метод заключается в проведении
итераций по подобластям без налегания [196, 174, 123, 168]. Формально
его можно описать для примера на рис. 8 следующим образом
(обозначим при этом G(1)=G!UG3, G(2)=G2).
Пусть имеется какое-то приближение к искомому решению
в G(2) и на границе стыка подобластей
) S,.
Найдем тогда решение и^У+i задачи в G(1) при некоторых краевых
условиях на Si, правая часть в которых зависит от и$ . Затем
находим в G(2) следующее приближение м£$+1) при граничных условиях
на Si, определяемых с учетом m$+u и далее процесс циклически
повторяется:
дп I s^~
(1.216)
5 = 0, 1,2,...
Здесь v i Sr и у | 5[f означают предельные значения функций при
стремлении к Si соответственно из G^l) и G(2). Каждое из
приближений м^У+ь ^22^2 определяется как решение уравнения
Пуассона в G(i), G^2) с исходными граничными условиями на
границе G и (1.216) —на Si. Итерационный процесс может быть
75

модифицирован путем введения релаксационных параметров:
при этом^в левых частях уравнений (1.216) надо заменить и£У+ь
и$}+2 на ЗДУ+i, й^+2- Не останавливаясь на исследованиях такого
вида алгоритмов, отметим главный результат последних работ:
существуют такие значения а,, р,, со*, *=1,2, что итерационный
процесс (1.216), (1.217) сходится к решению исходной задачи,
т. е. u$+i^u(x,y) для (x,j/)6 G(1), u$+2-+u(x,y) для (*,{/)£ G(2) при
ft-*- оо. Один из вариантов граничных условий (1.212) следующий:
для G(1) на S\ ставится условие Дирихле, а для G(2) — условие
Неймана, т. е. |3i =a2 = 0. В общем случае открытой остается проблема
оптимизации значений ab Pi, a2, Рг, coi, 0)2 (они могут быть и
переменными на разных итерациях).
Рассмотренные альтернирующий метод Шварца и итерации
по неналегающим подобластям естественно обобщаются на
случай разбиения исходной области на несколько подобластей и на
трехмерные задачи.
Описание итераций по подобластям мы провели на
дифференциальном уровне, но при решении разностных уравнений
выражения (1.216), (1.217) заменяются, естественно, на
соответствующие конечно-разностные аппроксимации. Этот подход, в сочетании
с эффективными прямыми методами быстрого преобразования
Фурье или циклической редукции при разбиении сложной области
на простые подобласти, представляется одним из перспективных,
так как можно ожидать, что скорость сходимости итераций по
подобластям не зависит от шагов сетки.
1.6.2. Решение разностных уравнений на последовательности
сеток. Одним из самых мощных способов повышения
эффективности методов решения разностных уравнений является
использование вспомогательных сеток. Идея в целом простая: если нам
надо решить краевую задачу на сетке Qh, то можно сначала найти
разностное решение на более редкой сетке QA|, затем проинтерпо-
лировать его в узлы основной сетки Q/, и, приняв полученные
значения за начальное приближение и$\ каким-либо итерационным
алгоритмом найти искомое решение ин с заданной точностью.
Ожидаемый выигрыш в объеме вычислений обязан тому, что, во-
первых, сетка QA| имеет меньшее число узлов, чем Qh
(следовательно, решение соответствующих разностных уравнений требует
меньшего числа итераций и количества арифметических действий
для расчета одного приближения) и, во-вторых, wA0) должно быть
достаточно близко к искомому ин, т. е. «доитерирование» на сетке
Q/z не потребует большого числа итераций. Для решения задачи
на QA| можно, в свою очередь, использовать еще более редкую сетку
Qh2 и т. д., см. [8, 12, 190].
Рассмотрим для простоты последовательность разностных
аппроксимаций Пуассона (1.216) на квадратных сетках Qhk с шагами
76

hk = hk-i/2> ho = h, k= 1, 2, ..., г (на сетке Qhi шаги считаем
величинами одного порядка с характерными размерами области). Если
мы вычисляем разностное решение щ (на сетке Qh «в лоб» с
помощью какого-либо итерационного метода, имеющего скорость
сходимости R=C\h (здесь и ниже Ck — некоторые не зависящие от
h постоянные, например, для оптимальной верхней релаксации
Ci = 2), то асимптотически при h-^О потребуется объем
вычислений Q = C2ft~3 |1п/г | (предполагается, что ошибка начального
приближения есть 0(1), а итерации ведутся до получения решения
исходной системы разностных уравнений с точностью е = С3/г2).
Предположим теперь, что мы сначала решим разностную задачу
на сетке Q\ (с погрешностью 8 = 4Сз^2), затем с помощью
линейной интерполяции определим начальное приближение для сетки
Qh (оно будет иметь погрешность \|) = 8i -\-C^h2 = Csh2, С5 = Сз +
+ С4 по отношению к пи, второй член обусловлен погрешностью
интерполяции) и далее тем же итерационным методом доводим
решение до точности е. В этом случае объем вычислений равен
Q{ = C2(2h)-3 \\nh\ +C5h-2 + C2h-2\n {Съ/Сг): 1-й член
соответствует итерационному решению на сетке Qhl, 2-й — интерполяции
и 3-й — «доитерированию» на Q^. Как видно, при Л->-0 Qi/Q-*-
-^Д- Если, в свою очередь, для вычисления решения uhx на сетке
Qi использовать предварительно сетки Q^, Qhzn т. д., то для Л-►О
несложно получить коэффициент сокращения объема вычислений
Qr/Q-*- \\nh\~l (Qr — трудоемкость решения исходной задачи
на г сетках).
Такой асимптотический подход несложно обобщить на случай
разностных аппроксимаций различного порядка точности, разных
видов интерполяций и итерационных алгоритмов.
Однако более сильные оценки дает спектральный анализ
метода последовательности сеток, предложенного Р. П. Федоренко
[190]. Он основан на следующих качественных рассуждениях.
Классические итерационные методы, например чебышевского
ускорения, быстро подавляют высокочастотные компоненты (т. е.
соответствующие большим собственным числам матрицы системы
уравнений) и сглаживают таким образом приближения, однако
именно потом сходимость к искомому решению, особенно при
малых /г, осуществляется крайне медленно. С другой стороны,
как раз гладкую составляющую решения можно «схватить»
достаточно хорошо из экономичного решения разностных
уравнений на вспомогательной редкой сетке и последующей
интерполяции.
Один из конкретных вариантов такого подхода для решения
уравнения &hUh = fh заключается в последовательном выполнении
нескольких процедур:
а) проводится итерационный процесс
un = un-i + a(Ahunh-{-fh\ /i=l,2, ...,#,, (1.218)
где а и N\ выбираются такими, чтобы высокочастотные компоненты
разложения иЦх в ряд Фурье по собственным векторам матрицы
77

Л^ были достаточно малы, например, для задачи Дирихле в
квадрате собственные числа Д^ равны
p,g=l,2,...,N;
полагая высокочастотными гармониками те, для которых р или q
больше N/2, мы будем иметь для них коэффициент подавления
ошибки qpq=l+aXDq при a = h2/5 меньше числа g ~ О А и
за iVi = 13 итераций можно подавить эти компоненты более чем
в 103 раз;
б) вычисляется невязка полученного приближения
H (1.219)
и определяется вектор rAi, состоящий из компонент, равных
значениям rh в совпадающих узлах сеток Qh и Qhl;
в) на сетке Qhi решается уравнение
А^а, = гЛ1; (1.220)
г) с помощью оператора интерполяции Phuh с сетки Qhl на uh
определяется вектор
zh = Phuhzhi\ (1.221)
если известны значения гц на квадратной сетке только для
четных £,/, то простая интерполяция осуществляется по формулам
{(2, + i,/ + Z;_i,/)/2, i нечетно, / четно,
(2,,/+i + Zrf/_i)/2, -{ четН05 j нечетно, (1.222)
(2/_if/ + 2,-t/ + i + 2(,/_i + 2,+ it/)/4, ^ j нечетны;
д) проводится поправка приближения на сетке Qh'.
u^ + i = uNl + Zh9 (1.223)
Далее проводится Л^2 итераций по формуле (1.208) с
использованием ulfi + l в качестве начального приближения (N2^M\)y
вычисляется снова невязка fh — A^w^l+ +1 и, если она еще велика,
весь цикл повторяется. Как правило, приближение uN{JrNiJr{ уже
совпадает с необходимой точностью с искомым разностным
решением щ.
Решение системы уравнений (1.220) для поправки zhl может
проводиться, в свою очередь, с использованием еще более редкой
сетки йЙ2ит. д. Если при этом полученное решение на редкой сетке
Qhk использовать для построения начального приближения для
Q/jai, то можно показать (путем достаточно сложных выкладок,
которые мы опускаем), что суммарный объем вычислений,
необходимый для получения решения и^ равен О(/г~2), т. е.
пропорционален числу узлов.
Мы теперь рассмотрим модификацию алгоритма, основанную
на использовании вложенных вспомогательных сеток и
решении редуцированной системы разностных уравнений на основной
сетке.
78

Пусть у — решение некоторой краевой задачи, описываемой
операторным уравнением
Ly = fy (1.224)
в которое предполагаются включенными и граничные условия.
Обозначим через
fo (1.225)
систему разностных уравнений, аппроксимирующих на сетке Qo
с характерным шагом h0 исходную дифференциальную задачу
(1.224). Здесь и0, f0 — векторы размерности, равной числу узлов
сетки (мы будем говорить — векторы, определенные на Qo), aL0 —
квадратная невырожденная матрица. Предполагаем, что при
/io->-O погрешность аппроксимаций системы имеет вид
г|)0 = fо - L0(y)0 = ftSDo(<p)o + So. (1.226)
Здесь \ро, So, (г/)о, (ф)о — определенные на Qo векторы; ер —
достаточно гладкая функция непрерывного аргумента; (ф)о означает
вектор, компоненты которого равны значениям ср в узлах сетки Qo;
Do — квадратная матрица с элементами, остающимися
ограниченными при /го->-О. Предполагается, что- норма So достаточно
мала, || So||o = o(fto), причем норма может использоваться разная,
но такая, чтобы ее порядок по hQ был равен порядку компонент
So (например, для двумерных задач можно взять || So ||o = [ujj(So,
S0)]l/2). Кроме того, мы делаем естественное допущение об
ограниченности нормы обратной матрицы, || L5"1 ||о = 0(1).
Вектор ошибки разностного решения Zo = Uo — (у)о
удовлетворяет уравнению LoZo = i|)o, а само разностное решение может быть
представлено в виде
(1.227)
Do((p)o, LoWo — So.
Пусть в расчетной области построена более редкая сетка Q»,
вложенная в Qo и подобная ей, т. е. отношение расстояний от
какого-либо узла в Q\ до его соседей в Qi к соответствующим
расстояниям до соседних узлов в Qo одинаково. Другими словами, на Qo,
Q\ в совпадающих узлах для разностных аппроксимаций мы будем
рассматривать сеточные шаблоны, образующие геометрически
подобные фигуры.
Рассмотрим алгоритм вычисления решения системы
(1.225) с использованием решения разностных уравнений на
сетке Qi
L,a, = f,. ' (1.228)
Пусть нам известен вектор ии для которого справедливо
представление
= Si. (1.229)
79

Здесь S\ — определенный на Qi вектор, для которого || S\ || =
= o(hT). Предполагается также, что элементы диагональных
матриц Di и Do, соответствующие совпадающим узлам сеток Q\ и Qo,
равны между собой, т. е. значения L\V\ и Lovo для совпадающих
узлов одинаковы. Множество точек сетки Qo можно представить
как совокупность двух подмножеств: Q0 = Qi U Qo-
Найдем сначала решение редуцированной системы на густой
сетке, получаемой из (1.225) следующим образом. Решаем только
уравнения, соответствующие узлам из Qo, причем в членах,
соответствующих Qi, значения сеточной функции полагаются равными
соответствующим компонентам и\у и эти члены переносятся в
правую часть. Полученную систему можно представить в векторной
форме
(Louo)Qo = (/o)q8, (wo)o, = и i. (1.230)
Ее решение, как нетрудно показать, можно представить в
виде
H ш (1.231)
где v0 — достаточно гладкая функция.
Рассмотрим теперь вектор невязки (ro)i = f\ — (LoWo)i, для
которого справедливо представление
Отсюда можно сделать естественное предположение, что имеет
место равенство
(ro)i = (г)! + о(А?) (1.232)
с некоторой достаточно гладной функцией г (за исключением,,
возможно, некоторого множества узлов, меньшего по порядку,
чем Qi).
Вектор 2О = ^о — по, очевидно, удовлетворяет системе
Го, Q°o,
Рассмотрим теперь вспомогательную задачу
Lozo = го, (1.234)
где компоненты вектора г0 совпадают с (ro)i в Qi, а в остальных
узлах доопределены специальным гладким образом. Именно,
обозначая через го& компоненту вектора, соответствующую &-му
узлу из Qo, потребуем выполнения соотношения
2_\ ^ok ==
80

где t означает, во сколько раз число узлов в Й0_больше чем
в Qi. Добиться этого можно, например, определив г0 из
уравнения ДдГо = 0 в Q§, где Ah — разностный оператор Лапласа,
соответствующий однородному условию Неймана на границе
расчетной области. Отсюда из выражений 2O=2zo, zo — 2 Zo,
где
= Го,
a rо — вектор с единственной ненулевой k-й компонентой, равной
Гол, получаем равенство
zo=-j-zo + о(А8). (1.235)
Из рассмотренного следует, что решение системы на редкой
сетке
= (ro)i
удовлетворяет соотношениям
гх = (го), + o(Ag) = /[Mi - м,] + о(/га).
Отсюда, наконец, получаем, что для решения системы
Lxux =fx +y(r0), (1.236)
мы имеем
(1.237)
Наконец, решим еще раз редуцированную систему на Q§
с использованием уточненного разностного решения на Йь
(L0Uo)\Qo = f°o, (ffo)|Ql = Mi. (1-238)
С помощью анализа решения системы (1.238), аналогичного
(1.231) — (1.234), несложно установить следующий результат.
Теорема 1.12. Пусть ио, и\ — решения систем разностных
уравнений (1.225), (1.228), аппроксимирующих соответственно на
вложенных подобных сетках Qo, Qi дифференциальную задачу
(1.224), и пусть для них справедливы разложения (1.227), (1.229).
Тогда сеточная функция по, определяемая из уравнений (1.230),
(1.236), (1.238), является приближенным решением задачи
(1.224) на Qo, и для нее 'справедливо разложение
по = (у)о + №о + Ш>о, ||©о||о = о(А8). (1.239)
Следствие 1. Непосредственно из представлений (1.229),
(1.237) с помощью выкладок, аналогичных (1.232) — (1.234),
легко получить, что на сетке Qo можно построить уточненное
разностное решение с погрешностью o(ho). Для этого достаточно после
6 В П Ильин 81

решения системы (1.235) взять на сетке Q\ линейную комбинацию
(так называемая экстраполяция Ричардсона [80]):
ui = [(ao)i—Y"i]/(1—Y). y = (hi/ho)a, , (1.240)
а затем на Й§ решить вместо (1.238) аналогичную
редуцированную систему, которую можно записать в виде
=й>. (1.241)
В итоге мы будем иметь
й (1-242)
(последний несущественный член добавляется за счет
дополнительной погрешности, вносимой при решении (1.241)).
Отметим, что при естественных разностных аппроксимациях
матрица L°o систем (1.230), (1.238), (1.241) имеет конечное число
обусловленности, т. е. || L°o || || (Lo)"1 II =0(1). Это означает на
практике, что при решении таких систем с любой конечной
точностью е каким-либо итерационным методом, например Зейделя,
количество итераций не зависит от шага сетки, тем более, что
с помощью линейной интерполяции по известным значениям на
редкой сетке ошибку начального приближения легко сделать
равной по порядку O(hг). Дополнительную погрешность,
обусловленную «недоитерированием», при анализе (1.232) — (1.234) можно
включить в фЬ2) без нарушения, за счет выбора е, порядка
величины Wo.
Рассмотрим теперь вопрос о решении разностные уравнений
на последовательности вложенных подобных сеток Qo, Й1,..., Й*>.
Как мы видели, решение системы на йо сводится к двукратному
решению систем на Й1. В свою очередь, это можно сделать с
помощью решения систем на Й2 и т. д. В итоге потребуется решать
2k систем на Й^ и на каждой /-й сетке {1 = 0, 1, ..., k) решать 2i + 1 раз
редуцированные системы.
Пусть Q/, Pi означают количество арифметических операций,
необходимых для решения соответственно полной и
редуцированной систем на сетке й,. Тогда, очевидно, имеем
Если последовательность сеток выбрана так, что каждая сетка
й/ строится с помощью деления отрезков между соседними узлами
Й£_1 на целое число частей (3 = 2, 3, ..., то величина Qo, как легко
проверить, будет пропорциональна числу узлов Л/о, если
количество узлов последней сетки конечно. Пусть, например, для
двумерной задачи (3 = 2 и Po = RNo. Тогда, очевидно, будем иметь
Р2
Заметим, что для трехмерных задач и больших значениях (3 от-
82

носительный выигрыш в числе операций возрастет, так как в этом
случае будет Pi = fi-3iRN0.
Во избежание возможного накопления высокочастотных
компонентов погрешностей при использовании нескольких сеток
можно, аналогично [190], на каждой из них уточнять решение
путем проведения нескольких итераций по методу Ричардсона
с использованием т « || Lt \\ ~] и сг?= Si из решения (1.238).
Повышение точности решения по формулам (1.240), (1.241) нужно
проводить только на Qo.
Отметим в заключение, что метод последовательности сеток
можно эффективно применять и при проведении итераций по
подобластям. Большое достоинство алгоритма в том, что помимо
ускорения итерационного процесса, применение комбинаций
разностных решений на разных сетках позволяет повышать порядок
точности результата [80,122].
§ 1.7. Некоторые вопросы расчета характеристик
электростатических полей
Численное решение краевых задач для уравнений Лапласа или
Пуассона для многих электрофизических приложений имеет
самостоятельное практическое значение. Одним из таких актуальных
примеров является расчет электростатических полей
высоковольтных конструкций. Особенностью таких задач является
сложная геометрия расчетных областей, наличие разномасштабных
элементов и сред с сильно различающимися диэлектрическими
свойствами.
Конечной целью являются не сами значения потенциалов в
узлах сетки, а картина эквипотенциальных линий, эпюры
тангенциальных составляющих напряженности поля на поверхностях
изоляторов, линии индукции поля, максимальные напряженности
в критических подобластях и т. д. В силу требований к точности
зачастую расчеты проводятся со значительными затратами
ресурсов ЭВМ как по объему вычислений, так и по оперативной памяти.
Особенно это относится к задачам, когда не просто требуется
определить характеристики заданной конструкции, а найти ее
геометрические или потенциальные параметры, обеспечивающие
необходимые технологические характеристики. В простейшем
случае эта проблема сводится к многовариантным расчетам, а в
целом — к оптимизации решений краевых задач по заданным
функциям цели и ограничениям на варьируемые параметры или
функционалы от решения. Типичным примером для изоляционных
конструкций является задача снижения их габаритов и
материалоемкости при условии гарантированной электрической
прочности.
В"таких условиях «инженерные» расчеты требуют
определенного искусства, опыта и грамотного использования алгоритмов.
6* 83

Основными требованиями к методам можно считать обеспечение
заданной точности, экономичности и надежности. Теоретические
оценки погрешности и объема вычислений носят в основном
асимптотический характер, и расчеты практических конструкций
должны сопровождаться методическими экспериментами или
использовать результаты решения аналогичных задач. В простейшем
случае на их основе требуется выбрать (если не оптимально, то по
крайней мере разумно) разностную сетку, способ аппроксимации
и алгоритмы решения систем уравнений. Задача такого анализа —
оценить примерно число узлов и их расположение для обеспечения
требуемой точности, прикинуть трудоемкость решения задачи
и спланировать проведение численных экспериментов. Зачастую
также возникают нестандартные математические постановки,
в которых решение краевой задачи является только одним из
этапов в достижении конечной цели.
В данном параграфе мы рассмотрим некоторые из
перечисленных вопросов, сопровождая их иллюстрациями расчетов,
выполненных по изложенным выше алгоритмам, реализованным в
пакете программ Эра, описанном в гл. 7 и в КСИ-БЭСМ [10].
1.7.1. Решение методически* задач. А. Задача Дирихле
в кубе. Рассматривается уравнение Пуассона
^+ 4^=
ду2
0 <
<1 -243)
где [ = 0 или f= —3n2s\nnx sinny sirmz, с гранитными условиями,
обеспечивающими точное решение в виде
(1.244)
(здесь р = 0 при f = 0, иначе p = sinjiz). Численное решение
строилось по семиточечным разностным уравнениям на кубической
сетке с шагом /г = 1 /20 и погрешностью итерационного процесса
е = 2~13. В табл. 5 приведены аналитическое решение фа и
относительная погрешность б.
Таблица 5
X
0,05
0,1
0,1
0,85
Y
0,05
0,55
0,1
0,95
z
0,05
0,05
0,05
0,95
f = о
Фа
0,0001290
0,0002547
0,0005031
0,05683
б%
1,01
1,06
1,09
0,14
Фа
0,003958
0,007817
0,01544
0,06794
6%
0,22
0,23
0,23
0,14
Расчеты проводились с помощью попеременно-треугольного
метода. При значениях итерационного параметра 2 ^ т ^ 5
решение требует около 400 итераций.
Б. Задача Дирихле в квадрате. Решалась
аналогичная двумерная задача для уравнения Лапласа в еди-
84

ничном квадрате со значениями ф на границе, соответствующими
решению
(T)(xytj) = s\njix—^- (1.245)
TV ^' slm v ;
на квадратных сетках с числом узлов 20 X 20 и 40 X 40. При
этом использовалась пятиточечная аппроксимация второго
порядка и, кроме того, неоднородная разностная схема с погрешностью
решения О(/г4): пятиточечные уравнения в околограничных узлах
и девятиточечные типа «ящик» — в регулярных. Итерационное
решение проводилось в обоих случаях с помощью попеременно-
треугольного метода с параметром т— 10 и погрешностью г = 2~22.
В табл. 6 даются значения количества итераций п и максимальной
относительной погрешности численного решения б. Результаты
свидетельствуют о значительном превосходстве схемы
повышенного порядка аппроксимации как по точности получаемого
результата, так и по числу итераций.
Сетка
Схема
п
6%
O(h2)
82
0,44
20x20
О (h4)
4 70
0,02
O(h2)
252
0,11
Таблица 6
40X40
О (h4)
211
0,0009
В. Задача Дирихле в кольце. Рассматривается
решение уравнения Лапласа в кольце, см. рис 7, б, с радиусами
окружностей /?i = 2,5; /?2 — 88. Использовались пятиточечные
уравнения на квадратной сетке 88X88, см. п. 1.5.3. В табл. 7
иллюстрируются значения ошибки численных результатов фч;
аналитическое решение имеет вид
"Я?
(1.246)
)=\х\4г-/ \П
Решение этой задачи проводилось также для полукольца
х ^ 44 с граничным условием Зф/дп = 0 при х —44. Когда это
Таблица 7
г
Фа
Фч
3
0,06357
0,06366
0,15
4
0,16388
10,16329
0,36
5
0,2417
0,2411
0,25
10
0,4834
0,4831
0,06
15
0,6248
0,6245
0,05
20
0,7251
0,7249
0,03
условие аппроксимировалось с помощью центральной разности
соотношением cp(ft,j/) —ф( — Л,у) = 0 '(разностная сетка использова-
85

26
лась та же, что и для кольца), полученное численное решение
практически совпадало с предыдущим. А при использовании
односторонней разности, аппроксимирующей условие Неймана с
погрешностью O(h), ошибка численных расчетов на той же сетке
достигала 8,8%.
Г. Расчет ячейки плоского триода. Геометрия
области и граничные условия даны на рис. 9. Эту задачу следует
считать «трудной» для разностных методов, во-первых, _из-за
наличия разномасштабных деталей и,
во-вторых, ввиду большой относительной
длины участка границы с условием
Неймана.
Численное решение этой задачи на
квадратной сетке с числом узлов 54 X 192
и аппроксимацией условия Неймана
центральными разностями дает
максимальное расхождение с аналитическим
решением в 1,9%. Применение более редких
сеток значительно повышает погрешность
расчетов (подробнее см. [70]).
1.7.2. Примеры расчета характеристик
высоковольтных конструкций. При
проектировании новых высоковольтных
систем основной целью является
нахождение геометрии поверхностей и состава
изоляционных материалов,
обеспечивающих наименьшие габариты и вес
конструкций (с этим, как правило, связана их
стоимость) и необходимую электрическую
прочность. Последнее представляет
собой сложную проблему, в которой
необходимо учитывать качественный состав
материалов, чистоту поверхностей и
многое другое. Однако в первую очередь
здесь требуется знать картину
электростатического поля. Напряженность электрического поля может
быть найдена путем численной обработки разностных решений
краевых задач в узлах сетки.
Важной характеристикой является максимальное
значение модуля напряженности поля \Е\ в расчетной области.
Поскольку
' ~ ' "" 1/2
Рис. 9.
вопрос сводится к вычислению производных потенциала по его
значениям в узлах. В § 5.2 подробно рассмотрены формулы
численного дифференцирования с помощью конечных разностей
и сплайновых аппроксимаций, вполне обеспечивающих
необходимую на практике точность.
86

Как правило, в расчетах изоляторов требуется знать
распределение тангенциальной составляющей напряженности Ех на
поверхности диэлектрика. В двумерном случае она легко вычисляется
с помощью разности первого порядка: если Р, Q — две точки
поверхности с достаточно малым расстоянием lPQ между
ними, то
|£т|« \up — uQ\/lpQ.
Для этого требуется предварительно найти значения потенциала
на внутренних границах типа Г4 в точках, не являющихся, как
правило, узлами сетки. Целесообразнее всего в этом случае
использовать те же интерполяционные соотношения, которые
использовались в § 1.2 для аппроксимации условий сопряжения на внутренней
границе. Например, в точке 3' на рис. 6 потенциал может быть
выражен через узловые значения и\у и2, из, и4 по формуле, легко
выводимой из (1.38), (1.40):
Зачастую необходимо знать нормальные производные
потенциала на граничных поверхностях (как правило, металлических,
с заданным потенциалом). Их вычисление наиболее сложно на
криволинейных границах. Проще всего в этом случае использовать
разность первого порядка. Если Р — точка на границе, a Q —
точка внутри области на расстоянии d от Р вдоль нормали Пр, то
приближенно имеем
да/ дп(Р) « (иQ— иp)ld.
Потенциал uQ может быть вычислен с помощью интерполяции
по значениям в соседних узлах сетки. Если уравнение граничной
поверхности имеет вид ф(х,у) = 0, то координаты точки Q могут
быть вычислены по формулам (5.87) из § 5.4. При необходимости
повышения точности можно найти значения потенциала в двух
внутренних точках нормали и аппроксимировать нормальную
производную разностью второго порядка, аналогичным (1.32).
Для наглядного представления картины поля обычно
средствами машинной графики рисуют эквипотенциальные линии в
расчетной области. Здесь требуется вычисление координат эквипо-
тенциалей, что может быть легко сделано с помощью обратной
линейной интерполяции. Если V—значение потенциала данной
изолинии, a tip, uQ—потенциалы в двух соседних узлах сетки
с радиус-векторами zPf rQ, причем аР< V<Mq, to радиус-вектор
г у точки эквипотенциали определяется формулой
rv=rp+{rQ— rP)(V— uP)/(uQ— иР).
Другой удобный способ описания поля заключается в
следующем: рисуют силовые линии, в каждой точке которых касательная
совпадает с вектором напряженности. Уравнение такой ли-
87

нии для двумерного случая можно записать в
параметрическом виде x = x{t), y = y{t). Задав какие-либо начальные данные
x\t==o = xo, y\t = o = yo, координаты силовой линии легко вычислить
с помощью численного
интегрирования
обыкновенных уравнений
dx/dt =
ду/dt = du/ду.
Последняя задача может
решаться каким-либо из
простейших алгоритмов,
например, методом Эйлера:
п, Уп).
В качестве примера
практической задачи мы
приводим
результаты.проведенных В. Н. Гатрич и
В. М. Свешниковым
расчетов опорной
изолирующей конструкции
высоковольтной подстанции. На
рис. 10 изображены
геометрия данной осесиммет-
ричной системы,
эквипотенциальные и силовые
линии. Густой
штриховкой отмечены
поверхности с заданными
потенциалами, а редкой —
изолирующий материал со
значением
диэлектрической постоянной 8=10
(остальная часть области — воздух с 8=1). Высота самой
конструкции около 16 м, а диаметры экранов, сечения которых
представляются заштрихованными кружочками, около 10 см.
Для замыкания краевой задачи потенциал полагался равным
нулю на поверхности цилиндра с радиусом около 16 м и высотой
около 32 м.
Расчеты такой конструкции требуют использования сильно
неравномерной сетки с измельчением шагов около малых деталей.
Для обеспечения практически приемлемой точности численное
решение проводилось на сетке с числом узлов около 10 000. Для
ускорения вычислений использовались три вспомогательные вло-
Рис. 10.

женные сетки, каждая из которых получалась из предыдущей,
более густой сетки увеличением вдвое размеров шагов. Однако
и при этом расчет одного варианта требует около часа времени на
БЭСМ-6 (на каждой из сеток решение разностных уравнений
проводилось с помощью блочного метода оптимальной
последовательной верхней релаксации и точностью итераций около 10~5, см.
подробнее [39]).
1.7.3. Численное решение задачи Робена. Особый вид краевых
задач составляют так называемые задачи Робена, которые
характеризуются наличием в расчетной области изолированных
металлических тел, на которых заданы заряды, но потенциалы
неизвестны. В таком случае, помимо уравнений (1.1) — (1.3), постановка
включает условия (мы считаем, что f(*,j/,z) = O, а количество
граничных участков типа 1\, Г2, Г3, Г4 и вид условий на них не имеет
значения):
\^ , (1.247)
где Si — поверхность тела с неизвестным зарядом q-, и постоянным,
но неизвестным, потенциалом V,. Поскольку рассматриваемая
задача линейная, в силу принципа суперпозиции решение
задачи (1.1) — (1.3), (1.247) можно представить в виде
(1.248)
где фо — решение уравнения (1.1) с заданными граничными
условиями (1.2), (1.3), принимающее нулевые значения на всех S,-;
каждое ф,, е=1,..., N,— тоже решение (1.1), но
удовлетворяющее условиям (1.2), (1.3) с gl = g2 = g3 = 0) и равное единице на
Si и нулю — на всех остальных St-,, U Ф1. Обозначая
dik= \ -—-,мы из (1.247) получаем систему N линейных ал-
гебраических уравнении относительно неизвестных потенциалов
Vi,V2,...,VN:
a,\V\ + al2V2 +....+ alNVN= q, — a,0, i = 1, 2,..., N.
Решив эту систему, мы по формуле (1.248) получаем искомое
решение задачи Робена. Как видно, вычисление всех a,k требует
решения (N-\-l)~u краевой задачи и расчет нормальных
производных от потенциала на всех поверхностях S,.
В качестве примера решения практической задачи Робена мы
рассмотрим расчет изоляционной подвески высоковольтной линии
передачи электроэнергии. Упрощенная осесимметричная модель
конструкции (в действительности она трехмерная) приведена на
рис. Па, а ее узел в окрестности потенциала провода АВ более
подробно изображен на рис. 116.
Подвеска представляет собой двухслойный изолятор с
электрическими постоянными 8i = 5,5, 82 — 3 и радиусами г\ = 11, г2 =
= 23 и металлическими участками АВ (значение потенциала
89,

равно w=l), EF (u = 0) и CD. На последнем из них потенциал
неизвестен, дано только, что он не заряжен (q = 0). Радиусы
проводов, несущих разные фазы тока и изображенных на рис. 11а
точками, равны 10 (все размеры даны в сантиметрах). Краевая
задача замыкается граничным
условием и = 0 на
поверхностях z=0, z = 4000
и г = 2800. Расчеты
проводились на сетке с общим
числом около 6700 узлов
(естественно, сильно
сгущенной около мелких
3/50
-3/00
1000 2000
Рис. Па.
Рис. 116.
деталей) и с использованием четырех вспомогательных,
последовательно разрежающихся сеток. На рис. 11а, 116 приведены
эквипотенциальные линии и распределение модуля
напряженности поля | £ | на критическом участке подвески с координатой
г= Ю. Значение наведенного потенциала на металлическом
участке CD оказалось равным и = 0,115.
1.7.4. Задачи оптимизации электростатических полей.
Проектирование нового устройства по существу всегда представляет собой
задачу оптимизации. Разработчик имеет целью обеспечить какие-
то электрофизические качества, варьируя геометрические,
потенциальные или физические параметры объекта при
технологических, эксплуатационных, финансовых <и других условиях. Эту
проблему можно математически описать как минимизацию некото-
90

рого функционала при линейных или нелинейных ограничениях.
Предполагается, что начальные значения всех параметров
задаются.
Пример задачи оптимизации высоковольтной конструкции:
рассчитать изоляционную систему заданного типа и отыскать
такие конфигурации диэлектриков и электродов, при которых
максимальная напряженность в области или тангенциальная
составляющая напряженности на поверхности изолятора не
превосходили бы заданных критических значений.
Формальнотакая задача может быть описана следующим
образом: найти p\,...,pN такие, что
...,рД (1.249)
при линейных ограничениях на варьируемые параметры
а^Ар^Ь (1.250)
или на некоторые функционалы от решения
ЛЛ<ФЛ(р)<ЯЛ, Л=1,...,М. (1.251)
Здесь a = {ai], b = {bj\, /=Л,..., L, — заданные векторы некоторой
размерности L, р = {ри ..., pN\—вектор параметров, А— в общем
случае прямоугольная матрица с числом строк и столбцов
соответственно N и L, Ak и Bk — заданные числа (таким образом, задано
L линейных и М нелинейных ограничений).
В качестве параметров pL могут быть значения потенциалов
на электродах или количественные характеристики
геометрических вариаций отдельных деталей (сдвиг, поворот, изменение
масштаба и т. д.).
Для решения задачи (1.249) — (1.251) существует большое
количество алгоритмов (и обширная литература; см., например,
[191]). Один из эффективных методов — метод
модифицированных функций Лагранжа, в котором задача разбивается на этапы,
каждый из которых является задачей безусловной оптимизации,
и реализуется по методу сопряженных градиентов.
Особенностью рассматриваемой проблемы является тот факт,
что расчет каждого очередного значения функционала при
текущих значениях параметров является достаточно трудоемкой
операцией, поскольку требует решения краевой задачи u = u(p\....ypN),
а сам функционал зависит последовательно от и: Ф(рь ..., pN) =
= F[u(p\,..., pN)]. Экономичные алгоритмы, требующие
относительно малого числа шагов оптимизации, используют в каждой
очередной точке значения производных функционала по
параметрам.
Для их приближенного вычисления можно использовать
аппроксимацию конечными разностями
91
^ ; PN)— Ф(РЬ ..., Pi— ДР/, .-, PN)

В целях сокращения числа вычисления функционалов можно
использовать следующий подход [137]. В предположении малости
возмущения параметров мы полагаем
р р рд,)
« F[u(pU ..., р„ ..., pN) + /ip;U;(pu ..., р/, ..., р Д (1.252)
где м,- есть функция влияния 1-го параметра, которая представляет
собой враждой точке разностной области производную от
потенциала по pi. Эту величину можно также определять с помощью
аппроксимации конечной разностью, но зачастую ее можно
вычислить, решая вспомогательную краевую задачу.
Так, если р, есть значение потенциала на некотором электроде
Г,, то ut есть решение краевой задачи с единичным значением
потенциала на Г, и однородными условиями на остальной части
границы.
Пусть теперь р, — параметр геометрической вариации
электрода Г, такой, что каждой точке Q невозмущенной поверхности с
радиус-вектором r(Q) соответствует взаимно однозначно точка Q'
возмущенной поверхности Г, с радиус-вектором r'{Q')\
где n(Q) — нормаль к Г, в точке Q, a a(Q) — скалярная функция
координат, зависящая параметрически от р,-. В этом функция
влияния геометрической вариации определяется как решение
уравнения Лапласа с условием
u,(Q) = - a(Q)du(Q)/dnJ Q £ Г,„ (1.253)
(u(Q) — решение невозмущенной задачи) и однородными
краевыми условиями на остальных участках границы.
Для определения всех функций влияния требуется решить N
вспомогательных краевых задач с разными граничными
условиями, но с одинаковой геометрией. Последний фактор позволяет
существенно сэкономить суммарный объем вычислений.
Необходимо отметить, что проводя минимизацию функционала
по некоторому направлению (в пространстве параметров),
выбранном с помощью функций и,, нельзя задавать слишком большие
приращения геометрическим параметрам, поскольку крае-вые
задачи с условиями (1.253) получены в предположении малости
возмущений. Вследствие этого после некоторого числа шагов
оптимизационного процесса требуется пересчитывать геометрические
вариационные функции.

Глава 2
РЕШЕНИЕ ЗАДАЧ МАГНИТОСТАТИКИ МЕТОДАМИ
КОНЕЧНЫХ ЭЛЕМЕНТОВ
В настоящей главе рассматриваются основные
принципы методов конечных элементов и особенности их
реализации при расчетах двумерных магнитостатических полей. Задачи
магнитостатики включают большое разнообразие физических и
математических постановок (см. [178, 56, 181] ). Мы
ограничиваемся достаточно узким типом задач, без учета явлений анизотропии,
гистерезиса и без анализа поведения решений в окрестности
угловых и других особых точек. Однако и рассматриваемая постановка
позволяет рассчитывать с достаточной точностью поля для
широкого класса устройств.
Теория методов конечных элементов для решения
эллиптических уравнений за последние годы нашла исчерпывающее
изложение в монографиях Г. Стрэнга и Дж. Фикса [179], Ж. Обэна
[146], Л. А. Оганесяна и Л. А. Руховца [149], Г. И. Марчука [120]
и других авторов. Мы остановимся только на рассмотрении
аппроксимаций с помощью наиболее простых и распространенных
базисных финитных функций и на формулировках минимального
количества теорем, необходимых для понимания источников
погрешностей и их оценок.
Эффективность реализации методов конечных элементов при
расчете магнитостатических полей в ферромагнетиках
существенно зависит от скорости сходимости итераций для нелинейных
алгебраических уравнений, возникающих в результате
дискретизации исходных задач. По алгоритмам решения нелинейных
уравнений имеется достаточно исследований как общего характера
(достаточно полно представленных в [151] ), так и применительно
к магнитостатическим задачам [198, 41, 105]. В § 2.3 дается
описание наиболее употребляемых итерационных процессов, хорошо
апробированных на практике. Надо сказать, что решение задач
с сильным насыщением остается достаточно трудоемкой
операцией, и по оптимизаций нелинейных итераций можно ожидать
дальнейших разработок.
По расчетам магнитостатических полей на ЭВМ имеется уже
большая практика; см., например, работы [138,-59, 173, 144],
а также труды специально посвященной этим вопросам
международной конференции COMPUMAG [99, 100].
С практической точки зрения особое значение имеет уровень
автоматизации методов конечных элементов (построение сетки,
формирование и решение системы уравнений и т. д.) в пакетах
прикладных программ. На этих вопросах мы остановимся в
последней главе.
93

§ 2.1. Математические постановки задач магнитостатики
Рассматриваемые в данной главе задачи описываются системой
уравнений Максвелла, которые для стационарного случая
сводятся к виду
rot// = ±L/\ (2.1)
0, (2.2)
где В, Н, / — векторы магнитной индукции, напряженности
магнитного поля и объемной плотности тока. Между векторами В
и Н имеется также функциональная зависимость,
характеризующая материальные свойства среды и определяемая, как правило,
из обработки экспериментальных данных. В приближении, когда
можно пренебречь гистерезисом и анизотропией, эта связь имеет
вид
(2.3)
где |io — магнитная проницаемость вакуума, a \i = \x(x,y, z, \В\2) —
относительная магнитная проницаемость.
На бесконечном расстоянии от источников тока магнитное
поле должно обращаться в нуль. В практических задачах
типичным является наличие трех типов сред: воздух (pi=l, / = 0),
проводник из немагнитного материала с током (^=1, j¥=0) и
ферромагнитный материал без тока (^#=1, / = 0). На поверхностях
раздела различных сред ставятся условия непрерывности
нормальной составляющей вектора магнитной индукции и
касательной составляющей напряженности:
п(В+ - В-) = 0, [п X Щ+=[п X #]_ =4я/„/с, (2.4)
где п—нормаль к поверхности, знаки « + » и « —» относятся
к ее различным сторонам, a jn — поверхностная плотность тока.
В силу (2.2) можно ввести в рассмотрение векторный
потенциал А:
B = votA, (2.5)
после чего уравнения сводятся к виду
rot v rot Л = ^L/\ (2.6)
где v=(jjioM')""1 называется магнитным сопротивлением.
Для двумерных плоских задач, когда решение не зависит от
координаты z, а плотность тока и векторный потенциал имеют
только по одной ненулевой компоненте /г = /\ А2 = А, в декартовых
координатах уравнение (2.6) имеет вид
= *!Lj, (2.7)
с h K }
^Л дх) ^ ду\ ду
причем Вх = дА/дх, Ву = дА/ду. •.
94

Другой важный практический класс задач — осесимметричные
поля, когда уравнение
описывает связь между азимутальными компонентами Ад=А,
jQ=j (при этом Л г = Л г = /г = /г = 0, Bz = ЗА/ дг + А/ г, Вг =
В двумерных задачах (2.7), (2.8) соответственно на
плоскостях или на оси симметрии полагается А = 0.
Наиболее простым приближением является |ы=оо для
ферромагнитной среды. В этом случае задача решается только для
немагнитных сред, а на границах с ферромагнетиками ставится
условие Неймана. Следующее приближение заключается в том, что
для каждой ферромагнитной среды полагается [х = const. Тогда
задача остается линейной, и на границах раздела сред ставятся
условия сопряжения (2.4), выраженные через А:
Л| + =Л|_, [nX(v rot A)]\ + =[nX(v rot Л)]|_. (2.9)
В общем случае задача является сугубо нелинейной. Типичная
ситуация связана с определением \х из так называемых £-#-харак-
теристик, типичный вид которых представлен на рис. 12,a, a
О 100
а)
Ю00Н(О/м2) О
Рис. 12.
б)
И
соответствующий вид функции \х(В) — на рис. 12,6. Иногда для
описания этих зависимостей применяются различные
функциональные аппроксимации, например, вида
где а, |3, е, с — параметры, подбираемые из условия' наименьшего
отклонения от экспериментальных кривых.
Двумерные магнитостатические задачи удобно также
описывать в терминах магнитного потока, который для произвольной
поверхности S определяется формулой
(2.11)
95
= \в cos (B,n)dS.

Если в плоскопараллельном поле имеется плоскость
симметрии (пусть это будет x = Ot), то, полагая Л|^=о = О, мы будем
иметь
, У) = \ Bydx' = А{х, у),
о
т. е. г|э(л:, у) удовлетворяет уравнению (2.7).
Для осесимметричных задач, в силу условия А |Г=о = О, можно
г
положить \p(r,z) = 2л [Bz(r', z)r'drf = rA(r, г), причем функция
о
магнитного потока будет удовлетворять уравнению
Дифференциальным уравнениям (2.1), (2.2) соответствуют
интегральные законы сохранения
^-I, (2.13)
\ BndS = 0. (2.14)
S
Здесь L — некоторый замкнутый контур, а /= ( jndS~полный
S(L)
ток, пронизывающий этот контур; в (2.14) через S обозначается
какая-либо замкнутая поверхность. Мы не будем
останавливаться на интегральных постановках задач магнитостатики. Сами же
уравнения (2.13), (2.14) могут служить хорошим средством
контроля численных результатов.
Настоящая глава содержит описание основных
алгоритмических аспектов методов конечных элементов на примере двумерных
уравнений (2.7), (2.8). С одной стороны, эти постановки сами по
себе достаточно актуальны с практической точки зрения, а с
другой — изложение методов решения данных задач позволяет, на
наш взгляд, понять технику реализации конечных элементов
для других дифференциальных уравнений, в том числе и
трехмерных.
Задачи магнитостатики можно формально решать и с помощью
разностных методов, рассмотренных в предыдущей главе. Однако
характерные в данном случае особенности краевых задач —
наличие разномасштабных деталей, подобластей с сильно
различающимися свойствами и разветвленных граничных поверхностей —
требуют подстройки сетки к особенностям геометрии области
и тщательных аппроксимаций в окрестности границы. В принципе
можно для этого строить специальные разностные уравнения
повышенной точности, но сложность их построения и решения
неизмеримо возрастет по сравнению с регулярными прямоуголь-
96

ными сетками, когда простота алгоритмов является огромным
преимуществом. Техника же конечных элементов, несмотря на ее
некоторую трудоемкость, обладает универсальностью,
единообразием и хорошими аппроксимационными качествами именно для
самых разных и сложных задач.
§ 2.2. Аппроксимация решений в методах конечных элементов
2.2.1. Коротко о теоретических основах метода. Методы
конечных элементов основаны на аппроксимации вариационных
постановок задач математической физики. Вариационный принцип
заключается в том, что решение -г- функция независимых
координат — ищется из условия минимума некоторого функционала,
представляемого в виде интеграла. Между вариационными
формулировками и дифференциальными уравнениями существует тесная
связь.
Например, если и(х9 у) е С2 (G) — функция, непрерывная
вместе со своими вторыми производными в ограниченной области
(ху у) е G и принимающая на границе Г области G нулевые
значения, то необходимым условием минимальности интеграла
1(и) = \ F(x, у, и, иХу uy)dx dy (2.15)
является то, что функция и (х, у) удовлетворяет уравнению Эйлера-
Лагранжа
-kF"+-kF"-F'=°- <2Л6>
Если же функция и (ху у) на Г не задается, то необходимое
условие минимальности I (и)у помимо (2.16), включает уравнение
граничных условий
jLC0S {п,х) + IL Sin(/i,x) = 0, (2.17)
где п — нормаль к Г.
Для уравнений (2.7), (2.8) эквивалентная вариационная
постановка сводится к минимизации функционала
= \ [ Т \ v ®d£-M] xadxdy. (2.18)
G О
Здесь единицы измерения полагаются для простоты такими, что
коэффициент \п/с равен единице. Кроме того, мы формально
объединяем случай декартовых и цилиндрических координат, полагая
соответственно а равной нулю или единице ( \В\2 = ( —— +
в п Ильин 97

Если магнитное сопротивление v не зависит от индукции, то
интеграл (2.18) упрощается. Для типичного случая кусочно-
постоянных коэффициентов (v(jc, у) = v,-: для (х, у) £ Giy G;—
некоторая подобласть G = £/G,-, / = 1,2, ..., К) он сводится к виду
Для краевых задач со смешанными неоднородными
граничными условиями
» = &(*> У\ (х,у)*=Ги ^ (2.20)
5I//3/1 + ф, у)и = 6(х, у\ (х, у)*=Г2, Г,UГ2 (2.21)
вариационная постановка несколько меняется. Во-первых, сам
минимизируемый функционал содержит дополнительный член с
интегралом по граничной поверхности Гг с условием Ньютона
(2.21):
Щ = $[\§-J v(E)d£ - jA]x«dxdy + J(|-«2 - *a)rfS. (2.22).
GO F2
Во-вторых, минимум 1(и) ищется среди функций, принимающих
значения g(x,y) на Гь
Решение вариационной задачи мы будем искать в
пространстве Н функций, равных нулю на Fi и имеющих ограниченную
норму
Я (£ ) Ш> (2-23)-
При этом для простоты анализа ограничиваемся однородной
краевой задачей с# = а=6 = 0в (2.20), (2.21). Относительно
функции v(£) мы предполагаем, что она имеет непрерывные первые
производные и удовлетворяет при 0 <£ < оо условиям
0 < v, < v(6) < v2 < оо, v'(£) > 0, . (2.24)
которые выполняются, в частности, если в (2.10) а > 0, р > 0,
с > е > 0.
Справедлив следующий важный результат.
Теорема 2.1. Существует единственная функция и ^ Н
такая, что
I(u) < I(v) для любых v e Я, (2.25)
функционал 1(и) определяется соотношениями (2.18), (2.22).
Доказательство вытекает из того, что при сделанных
предположениях функционал непрерывен в Н, строго выпуклый (т. е.
I(u) + I(v) ^2I(u + v)/2)) и /(»)->■ оо при Mir* оо.
98

Решение задачи (2.25) является также решением уравнения
Lu + } = О,
г . д ( ди , и \ - д ди /о г>£\
LU = —— v(— h»~ +i-V—. - (2.26)
д* \ дх ' х / ду ду
Методы конечных элементов основаны на построении
аппроксимаций решения и е Я вариационной задачи в конечномерных
подпространствах S*, содержащихся в Я. Такие подпространства
строятся с помощью деления области на конечные элементы:
треугольники, четырехугольники и т. д. Наиболее распространенным
является процесс триангуляции (особенно для полигональных
областей), т. е. разбиения области на треугольники. С конечными
элементами связывается совокупность узлов: в простейшем случае
это вершины; иногда используются середины сторон, центры
тяжестей элементов и т. д. На множестве конечных элементов
строятся пространства кусочно-полиномиальных функций таких, что
локально они имеют однотипный вид. Это" могут быть функции
линейные, квадратичные или кубические по каждой переменной
в пределах одного элемента. Их коэффициенты выражаются через
значения самих функций и/или их производных в узлах. Каждая
функция из выбранного пространства может быть представлена
линейной комбинацией линейно независимых функций,
составляющих базис пространства. И что имеет принципиальное значение —
эти функции являются финитными, т. е. отличными от нуля только
в окрестности, ограниченной несколькими соседними элементами.
Простейшие и наиболее распространенные базисные функции —
линейные на каждом треугольном элементе, принимающие
значение 1 в одной из вершин и 0 — в остальных. В общем случае
базисные функции строятся по их заданным значениям в узлах
(вершинах элементов и других вспомогательных точках), а иногда
также по значениям производных или по дополнительно
налагаемым условиям. Количество величин (значения функций или их
различных производных), используемых в одном узле для
построения базисной функции, будем называть его кратностью. Примеры
построения базисных функций и их свойства мы рассмотрим в
следующем пункте.
Через А будем обозначать характерный шаг конечномерной
дискретизации Gh области G. В теоретическом анализе всегда
рассматривается последовательность дискретизаций
соответствующих пространств базисных функций и аппроксимаций исходной
задачи. Все дискретизации предполагаются регулярными в том
смысле, что при А-► О размеры конечных элементов являются
величинами одного порядка, а углы между их сторонами — не
меньше некоторой постоянной
0*> Со, к = 1,2,...,
(2.27)
Cxh < А/< С2А, / = 1,2,...
Здесь и далее через С/ мы обозначаем не зависящие от А константы.
7* 99

Любая функция Vh из пространства Sh, соответствующего
дискретизации (сеточной области) Gh, представляется в виде
линейной комбинации базисных функций:
vh = Cityi + с2г|)2 + ... + cNqN, (2.28)
количество которых определяет размерность пространства и
зависит от количества узлов сеточной области и их кратности. При этом
не учитываются узлы, лежащие на части границы Fi с условием
Дирихле (их совокупность будем обозначать через Г^). Базисные
же функции г|)/ строятся так, что их значения на Г^ равны нулю,
в силу чего любая Vh из Sh будет принадлежать также
пространству Sh.
Существует несколько подходов к приближенному решению
вариационных задач. Если они возникают из самосопряженных
дифференциальных уравнений, что имеет место в нашем случае, то
основным является метод Ритца, заключающийся в нахождении
минимума функционала не в Я, а в конечномерном
подпространстве 5л, точнее, в последовательности таких подпространств.
Функция tih, минимизирующая / на S*:
I(uh) < I(vh) для всех vh e Sh, (2.29)
называется аппроксимацией Ритца вариационной задачи (2.25).
Решение задачи (2.29) определяется из системы уравнений
dl(uh)/dci= 0, 1= 1,2, ...,#.
Отметим, что в пространстве Sh находится и функция йн —
интерполянт точного решения исходной вариационной задачи
(2.25), т. е. такая функция вида (2.28), которая во всех узлах
совпадает с и.
Основными вопросами теории методов конечных элементов
являются:
а) построение приближенного решения iih,
б) оценка нормы погрешности решения Wh = и — tih.
Последний из них решается для наших задач на основе свойств
монотонных отображений.
Определение 2.1. Отображение L строго монотонно, если
существует такая строго возрастающая функция f(t) для 0 <
^ t <С оо, что
/(0) = 0, lim/(0 = оо, (2.30)
t-*-co
и для любых иу v из пространства Н
(Lu - Lv) {u-v)> /(|| и - v\\H)\\u - v\\H. (2.31)
Здесь под Lu(v) понимается скалярное произведение
щ.)- J ,[(£ + «.J.X-& + -т) + Н1
G
100

Определение 2.2. Отображение L непрерывно по
Липшицу для ограниченных аргументов, если для всех u,v e H при
|| и || я <| /?, || 01| я < R существует такая постоянная С(/?), что
\\Lu- Lv\\ < C{R)\\u- v\\H (2.33)
Теорема 2.2. Пусть L — строго монотонное и непрерывное
по Липшицу для ограниченных аргументов отображение. Тогда
существует такая не зависящая от подпространства Sh постоянная
С, что
К\\и- vh\\H) <C inf ||и - vh\\H. (2.34)
Непосредственными преобразованиями можно проверить, что
если v(£) удовлетворяет неравенствам (2.24), то определенный в
(2.26) оператор L соответствует условиям теоремы 2.1. В
частности, если уравнение (2.26) линейное, то f(x) = t, а при v = v (||u\\p)
имеем f(t) = tp+K
Из (2.34) следует важное неравенство
/(II" — ик\\н)< С\\и-йн\\н, (2.35)
где Uh — функция из класса Sh, интерполирующая точное решение
и по его значениям в узлах. Это неравенство позволяет оценивать
ошибку аппроксимации Ритца через погрешность интерполяции в
пространстве S&.
2.2.2. Аппроксимация функций с помощью конечных элементов.
Многоугольная двумерная область наиболее простым образом
разбивается на треугольники. После этого задача аппроксимации
функции может отдельно рассматриваться на каждом отдельном
треугольном элементе.
Пусть Pi, Р2у Ръ — вершины треугольника, в которых заданы
значения и\, и2, иъ функции и(хуу). Простейшая аппроксимация
представляет собой билинейный интерполяционный полином
и(х, у) = он -f а2х + «зУ, (2.36)
коэффициенты которого легко^ могут быть выражены через щ из
решения системы уравнений u{Pt) = uh i — 1,2,3:
ai = -^-[(Xjyk — xkyj)Ui
«2 = -§^[(У! - У*)* + (Ук - yi)ui + {yi - yj)Ukl' (2.37)
аз = -оЦ(** — Xj)Ui + (xi — xk)uj + (xj — xi)uk].
Здесь j, /, k — обозначения каких-либо из вершин,
пронумерованных против часовой стрелки, а S//* — площадь треугольника.
Полином (2.36) может быть также выражен через базисные
101

функции
1=1
(2.38)
где pi есть линейный по лс, у многочлен, равный единице в i-u узле
и нулю в остальных:
( ) C) ( £) = Djk/Cijk,
Tjk = Xjyk — yj
= Xk —
= t// —
1
1
1
X
Xj
xk
У
У1
Ук
, djk =
l
l
l
Xi
Xj
xk
Ui
У\
Ук
(2.39)
Здесь p,i(x, у) определены только в одном треугольнике. Однако
для каждого 1-го узла триангуляции области легко построить
кусочно-билинейную функцию г|)/(х, у), разную единице в /-ом узле
и нулю — в остальных (в каждом из примыкающих треугольников
она определяется по формулам (2.39)). Совокупность таких
пирамидальных функций для всех узлов триангуляции, за исключением
лежащих на части границы Гь образует базис пространства Sh
кусочно-линейных функций, обращающихся на 1\ в нуль. Отметим,
что любая функция из Гн непрерывна, так как значения и(х, у),
построенные для двух смежных треугольников, на их общей
стороне просто совпадают.
Порядок интерполяции легко повысить, если помимо щ в
вершинах треугольников использовать еще значения в серединах сторон
Ра, Рб, Ре, см. рис. 13,а. В этом случае мы имеем
и(х9у) = ро + М + foy +
+
+
где все (3; могут быть определены из уравнений
/= 1,2,..., 6.
а, их,иу
(2.40)
в)
Рис. 13.
Если же ввести функции р[2\х,у\ квадратичные по каждой
переменной, равные единице в рь и нулю — в остальных, то интерпо-
лянт можно представить в виде
й(х, У) =
, у),
(2.41)
где
102
выражаются через р{х,у) из формул (2.39) следующим

образом:
p[*>(x,y) = pl{2pl- 1), /=1,2,3,
(2.42)
р^\х, у) = 4pip2, pi2\x, у) = 4р2рз, Д2) (*, у) = 4р3р1.
Совокупность функций рР (х, у) в треугольниках, имеющих общие
узлы (вершины треугольников или середины сторон), образует
базисную функцию пространства кусочно-квадратичных
непрерывных функций.
Аналогично можно рассмотреть интерполяции и более высоких
порядков. Например, По значениям функции в вершинах
треугольника и точках трисекции сторон и центре тяжести можно построить
бикубическую интерполяцию, имеющую 10 коэффициентов,
которые однозначно определяются по 10 указанным точкам.
В общем случае можно строить полином m-го порядка по двум
переменным, имеющий 4"(т + 0(т + 2) коэффициентов, кото-
1
рые выбираются по условию интерполяции в у(т + \){т + 2)
точках, получаемых при разбиении исходного треугольника на т2
равных треугольников путем деления его сторон на т одинаковых
частей и соединения полученных точек прямыми, параллельными
сторонам.
При построении интерполяционных формул часто
используется предварительное преобразование треугольника к
стандартному, у которого в новых переменных рир2 координаты точек Pi,
Р2, Рз есть соответственно (1,0), (0,1) и (0,0). Эти новые
переменные как раз и выражаются формулами (2.39), поскольку
уравнения р{х,у) = 0 при /= 1,2,3 описывают стороны
треугольника РгЛз, РзР\, Р1Р2, а в вершинах Л имеем Pi(x,y) = 1. Обратное
преобразование плоскости {p\,p<i) в плоскость (х,у) выражается,
как легко видеть, с помощью формул
х = хг + 1\гр\ + £23/02, У = Уз + Ц\зр\ + Ц23Р2. (2.43)
Такого типа интерполяции называются лагранжевыми. Другой
подход заключается в использовании значений не только функции,
но и ее производных. Построенные таким образом
интерполяционные полиномы Называются эрмитовыми.
Класс соответствующих полиномов включает полные
многочлены Qv(x,y) нечетной степени 2v + 1, которыеопределяются
значениями DlQv(Pj) при |/| < V/, / = 1, 2, 3, и DlQv(PA) для |/| < v— 1.
Здесь Р\,р2,Рз — вершины треугольника, Р± — его центр тяжести,
i = (Л, «2), где /i, /2 — целые числа, |/| = i\ + i2, DlQ = d^Q/
/(дх^ду1*).
Простейшую эрмитову интерполяцию представляет
кубический многочлен, десять коэффициентов которого определяются
по значениям функции и ее производных их, иу в вершинах
треугольника, а также по значению и(х,у) в центре тяжести (см.
ЮЗ

рис. 13,6):
Q(x>y)= 2Г^£/(*>У)+ 2 l(ux)i n(xyy) + (uy)iSi(x,y)l
- 7PiPk\ / = 1,2,3,
рд + Ь*р*(р/ - pdl
Ф>У) = PifoaPiiPk - Pi) + 4ikPk(Pj - /?/)].
Интерполяционная функция v(x,y\ построенная с помощью
таких многочленов, будет непрерывна при переходе от одного
треугольника к другому, поскольку вдоль каждой стороны она
представляет собой кубический полином, однозначно определяемый
значениями функции и ее производных в вершинах.
Мы теперь остановимся на прямоугольных элементах, для
которых легко строятся эффективные аппроксимации. Прямоугольные
элементы целесообразно строить для областей, составленных из
прямоугольников. Для областей сложной конфигурации можно
комбинировать прямоугольные элементы внутри области с
треугольными около границы.
Рассмотрим прямоугольный элемент [x/^+i] X [*//,*// +1] с
длинами сторон Ль А2, см. рис. 13, в. Билинейный многочлен,
аппроксимирующий функцию и(х, у) по ее значениям в вершинах, имеет вид
ри(х, у) = ац(х, y)uii + fLi+i,j(x, y)m+ul +
( 0)и/+1./+ь (2.45)
l - y\
- x)(y — yj),
Если в прямоугольной области [*о, хт] х [уо, Ут] построена
прямоугольная сетка х = хи у = уу, / = 0, 1,..., /и, / = 0, 1,..., я, то
кусочно-билинейная аппроксимация во всей области имеет вид
£(*, у)=Ъ 2 Ых, У) uih (2-46)
где каждая базисная функция i|ty строится по формулам (2.45)
из условия, что она равна единице в (/,/)-м узле и нулю в
остальных. При этом г|5//(х, у) отлична от нуля только при *,-_ i <x< xi+1,
с// 1 < у < у/ + ь Нетрудно проверить, что функция р(х, у)
непрерывна во всей области.
Интерполирующую функцию с непрерывными первыми
производными во всей прямоугольной области можно построить с по-
104

3 3
мощью бикубических полиномов вида Q(x, у) = 2 2 ацх1у],
/=0 /-=0
определяемых в каждом прямоугольном элементе по значениям
и, их, иу, иху в четырех вершинах. Для единичного квадрата
O^jc^I, 0^r/^l такой многочлен выражается формулой
ф8» (/) = (1 _ О2 (1 + 2/), Л) = (1 - (ft, (2.47)
^°\о = /2(3 - 20, iri!)(o = t\t - i),
где (D(kyt)u)ij означает dk+lu/dxkdyl в точке с координатами х^ У\-
Бикубическая аппроксимация во всей области может быть
представлена в виде комбинации базисных функций, выраженных
через произведения одномерных функций ^к\х] и ^(у). Теперь
узлу сетки будут соответствовать четыре базисные функции, и
каждая из них имеет носителем четыре прямоугольных элемента.
Построение аппроксимаций на основе интерполирующих
полиномов, построенных непосредственно в четырехугольных
элементах, не являющихся прямоугольниками, связано с той
неприятностью, что при переходе от одного элемента к другому нарушается
непрерывность даже самих функций.
Наиболее распространенным приемом является
преобразование координат с помощью кусочно-полиномиальных функций так,
чтобы в новых переменных четырехугольник переходил в
единичный квадрат. Если для преобразования координат используются
того же вида полиномы, что и для базисных функций, то такое
преобразование называется изопараметрическим. Простейшим
соответствующим примером является отображение квадрата
в четырехугольник с помощью билинейного преобразования.
х(1,г\) = хх + (*2 — х\)1 + (х3 — хх)ц + (ха — хъ — х2 + *i)£t|,
y(l,x\) = У\ + (1/2 — У\)Ъ + {Уг — У\)Ц + {У а — Уз — У2+У\)1г\.
(2.48)
Здесь вершинам единичного квадрата с координатами (0,0), (1,0),
(0,1), (1,1) соответствуют вершины четырехугольника (х\9 у\), (х2, у2\
(*з, */з), (*4, Уа\ а стороны квадрата переходят линейно в
соответствующие стороны четырехугольника. Преобразование (2.48)
обратимо, т. е. каждая точка (jc, у) в четырехугольнике
соответствует одной и только одной точке (£, г\) в квадрате, если
четырехугольник выпуклый, т. е. все его внутренние углы меньше я. Это следует
из того, что в этом случае якобиан преобразования
= 4% - *№ =
г/2 — f/i + Вт) Уз — у\ + #£
где А = х4 — хэ — х2 + х\, В = у4 — уз — У2 + У\, всюду
отличен от нуля.
Другой важный случай преобразования координат связан с
употреблением криволинейных элементов, необходимость которых
105

возникает при наличии областей с непрямолинейными границами.
Мы рассмотрим один простейший, но практически важный
случай — аппроксимацию функции на треугольнике, две стороны
которого прямолинейные, а одна — криволинейная.
Пусть в треугольнике Р\Р2Рз стороны Р2Рз и Р\Рз
прямолинейные и описываются уравнениями 1(х9у) = 0 и т(х,у) = 0, а
криволинейная сторона Р\Р2— уравнением п(х,у) = 0. Функции /, т,
п предполагаем для простоты нормированными условиями
1{хиух) = т(х2уу2) = п(хг,у3) = 1. (2.49)
Преобразуем плоскость (х,у) в плоскость (/, т) по формулам
/ = —!— (т23 + Л2з* — ЬзУ% гп = -Л-(тз1 + Цз\х — 1му),
С 123 С 123
(2.50)
где обозначения взяты из (2.39). В плоскости (/, т) получается
треугольник с вершинами Р\ = (1,0), Р2 = (0,1) и Рз = (0,0), а
уравнение криволинейной стороны принимает вид
n(x(l,m), y(l,m)) = f(l,m) = 0.
Теперь на треугольнике Р[Р2Рз построим лагранжеву
интерполяцию вида
\ (2.51)
где U4 — значение функции в некоторой дополнительной точке Pi,
лежащей на криволинейной стороне Р\Р2, а базисные функции
г|э/ удовлетворяют следующим требованиям:
' a) i^Z, m)=l, t liVtf, m) = I, tm^l9m) = m (2-52)
i=\ i=\ t=l
(//, mi — координаты точек Р[); эти условия означают, что линейные
полиномы в плоскости (/, т) аппроксимируются выражением (2.50)
точно; а поскольку преобразование координат (2.49) линейное, то
в плоскости (х,у) линейные многочлены также интерполируются
точно;
б) базисная функция я|)3(/,т) равна тождественно нулю на
криволинейной стороне Р\Р2\
в) получающаяся из (2.50) кусочно-гладкая функция на сетке
треугольников, каждый из которых имеет не более одной
криволинейной стороны, непрерывна.
Сначала мы построим базисную функцию г|)з,
удовлетворяющую условию б). Для этого рассмотрим семейство поверхностей
z(l, т) = 0, пересекающее плоскость (/, т) по кривой /(/, т) = 0
и описываемое уравнением
(az + р/ + ут + 6)z + /(/,т) = 0 (2.53)
с неопределенными параметрами а, р, у, б. Если мы потребуем,
чтобы фз была линейна на сторонах Р[Р'ъ и Р2Р'з, то есть чтобы
с учетом (2.49) выполнялись соотношения 2=1 — / при т = 0,
106

z = 1 — m при / = 0, то из (2.53) величины р, у, 6 однозначно
выражаются через а, и мы получаем однопараметрическое
семейство поверхностей
+ /(/, т) = 0. (2-54)
Выбирая теперь какое-либо значение а и полагая ^(Z, т) = z,
определяем из соотношений (2.52) остальные базисные функции:
(l-m4)/ + /4rn-/4 /4
♦i('. "О = i-/4-m4 + Т=Р5
— Ц)т — т4 т3
+
1—/—т
В частности, если положить а = 0, а в качестве криволинейной
стороны взять отрезок гиперболы
f(l,m) = aim - I - т +1,
то все базисные функции г|)/(/, /л), как нетрудно проверить,
оказываются многочленами. Это позволяет решать краевые задачи
с криволинейными границами путем аппроксимации их кусочно-
гиперболическими дугами и применяя простые полиноминальные
базисные функции. В общем же случае интерполяция на
криволинейных элементах может привести к более сложным функциям,
например, дробно-рациональным [127].
Отметим, что для трехмерных задач аппроксимации строятся
аналогичным образом, но имеют, естественно, более громоздкий
вид. Типичными конечными элементами являются тетраэдр,
параллелепипед, а также соответствующие фигуры (четырехгранники и
шестигранники) с криволинейными поверхностями. Подобно тому,
как это делается для двумерных элементов, строятся трилинейные,
триквадратичные и более высоких порядков лагранжевы или
эрмитовы интерполяции.
Для оценки ошибок приближенных решений методами
конечных элементов в соответствии с (2.35), необходимо определить
погрешность интерполяции с помощью конечных элементов. Этот
результат устанавливается при наличии следующих свойств
базисных функций:
а) пространство Sh базисных функций % имеет степень &, т. е.
любой полином до &-го порядка может быть представлен в виде
линейной комбинации базисных функций и, следовательно,
принадлежит пространству Sa; это означает, например, что при k = 2
интерполяция с помощью г|эг точна для многочлена вида х2 — ху —
— у ; иногда в таких случаях говорят, что система функций полна
до некоторого k\
б) базисные функции однородны порядка q, т. е. их
производные до g-го порядка равномерно ограничены на последовательно-
107

сти пространств Sh при Л -► 0; это свойство требует, в частности,
невырожденности конечных элементов в смысле выполнения
неравенств (2.27); если же, например, базисные функции строятся
путем сведения криволинейного элемента к стандартному виду, то
якобиан преобразования координат должен быть ограничен и
непрерывен при А -► 0.
Теорема 2.3. Пусть степень пространства Sh равна k, а его
базис однороден порядка q. Тогда для любой функции и,
обладающей k + 1 суммируемой в квадрате производной, справедливо
неравенство при s ^ q:
\и - uh\s < Cshk+ l-*\u\k + u (2.56)
где \v\s = \ \Dav\2dx dy, \a\ = s, a Cs — не зависящие от h
константы.
Неравенство (2.56) означает, что интерполирование базисными
функциями с указанными свойствами обеспечивает погрешность
порядка hk +1 для самих интерполируемых функций и hk + х ~ s—
для их производных порядка s.
Данная теорема в совокупности с оценкой (2.35) позволяет
оценивать погрешность приближенных решений методами
конечных элементов.
Отсюда, в частности, следует, что приближенное решение
задачи (2.25) по методу Ритца при использовании кусочно-линейных
аппроксимаций на треугольниках и представлении функции v(£)
в виде (2.10) имеет погрешность О(А).
При практической реализации методов конечных элементов
могут возникать дополнительные погрешности, связанные с тем,
что приближенное решение ищется не строго из вариационной
постановки (2.29). Зачастую при вычислении интегралов в
функционалах приходится применять приближенные квадратурные
формулы. Кроме того, иногда для упрощения алгоритмов при
наличии криволинейных границ производится их аппроксимация
прямолинейными конечными элементами. Мы не будем проводить
анализ обусловленных этими факторами ошибок. Эти вопросы
достаточно хорошо исследованы, и результат заключается в том,
что точность конечно-элементных решений существенно не
уменьшается, т. е. порядок погрешности при «разумных»
возмущениях вариационной постановки остается без изменений. Например,
если кривую второго порядка аппроксимировать ломаной, то
дополнительная ошибка есть О(А), что вполне допустимо для
кусочно-линейных интерполяций.
§ 2.3. Построение конечно-элементных уравнений
Мы проведем вычисление коэффициентов конечно-элементных
уравнений, получающихся из приближенной минимизации
функционала энергии (2.18) с помощью кусочно-линейных аппроксимаций
на треугольниках. Данный алгоритм используется различными
108

авторами и оказывается достаточно эффективным при расчетах
на ЭВМ магнитостатических полей в средах с нелинейными
характеристиками.
Пусть Gh — сеточная область, представляющая собой
совокупность треугольников Ts(s = 1, 2, ..., k\ на которые разбивается
расчетная область G. Искомое решение представим в виде
Ah(xyy) = ui$\(x,y) + "2ЫХ>У) + - + имЫх>У)> (2-57)
где яр/ — кусочно-линейные базисные функции, отличные от нуля
только на треугольниках, имеющих одной из своих вершин 1-й узел
(значения i|)/(jtr, yt) равны единице при / = /' и нулю — при 1Ф1').
Значение N равно общему количеству узлов триангуляции, за
исключением лежащих на участках границы области с условиями
Дирихле. Предполагается, что триангуляция проведена таким
образом, что граница сеточной области Гл совпадает с границей Г
расчетной области (если последняя есть прямоугольник) или, по
крайней мере, близка к ней. Считаем также, что сеточные узлы из
Га лежат точно или на внешней границе, или на линиях раздела
различных сред (линиях разрыва v(£)).
В (2.57) щ есть искомые значения приближенного решения
в узлах сетки. В пределах отдельного треугольника Тцк с
вершинами Pi, P/, Pk функция Ан(х,у) представляет собой билинейный ин-
терполянт, описываемый формулами (2.38), (2.39). В выбранном
пространстве кусочно-линейных функций минимизируемый
функционал (2.18) заменяется на его аппроксимацию
I(Ah) = 1{ии и2у ..., О, (2.58)
т. е. зависит от конечного числа параметров щ. Система конечно-
элементных уравнений dl/дщ = 0, / = 1,2,..., N, в данном случае
имеет вид
«. _ $ [«1*11(1..*. + В.'*-) - /£]*** = 0. ,2.59,
Gh
где величины Вх, Ву, \В\ в каждом из треугольников выражаются
формулами
".-■£ + «4-*—■£■• !<"'=« +«г-
Мы рассмотрим уравнения подробнее для случая осесиммет-
ричных магнитостатических задач в цилиндрической системе
координат (а = 1).
Для треугольника Тци будем иметь (см. обозначения в (2.39)):
Вх = — (uiljk + tijlki
, у) = т h —2, ui Pi(xy у\
дВх _ In, дВу _ ц,к i дА„ тд + nikx + llky
109

Уравнение для 1-го узла получается после подстановки (2.60)
в (2.59) и проведения интегрирования по треугольникам, имеющим
/-ый узел своей вершиной. Если триангуляция получена путем
предварительного разбиения области с помощью двух семейств
ломаных линий (ломаные одного семейства не должны
пересекаться) на четырехугольники и последующего разбиения их
диагоналями на треугольники, то в каждом уравнении будет
семь ненулевых членов. Такую сетку будем называть
топологически эквивалентной прямоугольной. При использовании
локальной нумерации узлов для такого случая каждое
уравнение можно записать в следующем виде (см. рис. 14):
S prur-pouo = f. . (2.61)
Любой из коэффициентов рг вычисляется из интегралов по
треугольникам, имеющим своими вершинами узлы с номерами
0 и г.
Поскольку функция v имеет сложную нелинейную
зависимость от иГу целесообразно применить простую квадратурную
формулу, а именно считать
величины Ву и дВу/дщ
постоянными в каждом треугольнике,
взяв их значение в центре
тяжести
dm Cijk )
(2.62)
Рис. 14.
В этом случае значение v
постоянно в треугольнике, и
коэффициенты уравнения (2.61) для 1-го узла имеют относительно
простой вид (hr означает расстояние между r-й и 0-й точками,
a vr относятся к треугольникам, пронумерованным в соответствии
с рис. 14, причем треугольники рассматриваются
прямоугольные) :
*/-2Ai/3 A4 , xi-h/3 ,
h2
xi-hx/3
7 —2Ai/3
xth2
i —Л,/3)
+ 7
xth2
3(*, + Аз/3)
]■
h2
/3
lOfa /Q
/i4
hz
A,
- /fci/3).
110

Ръ = Vl
Xz + Лз/З
*/-2Л,/3
(Г+^/з)2
*/ + 2/ЗЛ3
л:2
h4
3
3
Лз
Л, /
л4
9>
JC/ + 2/13
*,-А
УЗ
/з
i/З
- /г
/г4
3 '
л2
л/3)
3/ *J)
\h2
А,
h2
xi + Лз/3 Лз '
Аз/3)^1, (2.63)
6 .
/ = 2 -57 з (т/а + Л/^ +
1
В последнем члене Sr и /г — соответственно площадь и
плотность тока (предполагаемая постоянной) в r-ом
треугольнике, а индексы /, k для каждого из них относятся
соответственно к периферийным вершинам, следуемым в порядке обхода
контура треугольника против часовой стрелки, начиная с
центрального узла «О» (например, для 1-го треугольника / = 3, k = 5,
для 2-го — / = 5, k = 4 и т. д.).
В задачах магнитостатики, как правило, уравнения (2.61)
бывают трех видов. Первый соответствует тому, что все
треугольники относятся к воздушной среде — в данном случае f = 0 и все
vr — одинаковые постоянные, при этом коэффициенты имеют
наиболее простую форму. Второй вид относится к шаблону,
находящемуся в проводнике с током (vr = const, /=т^0), а третий —
к ферромагнитной среде, где vr зависит от значений Ui в
вершинах треугольника. Есть, разумеется, и смешанные узлы, лежащие
на границе раздела различных сред, когда различные
треугольники шаблона имеют раздюго типа функции v и /.
Полученная система уравнений может быть записана в векторном виде
Ku = g, (2.64)
где компоненты векторов и, g соответствуют значениям
неизвестных и правых частей в узлах сетки, а /С, как следует из
построения,— симметричная матрица (с зависящими от и
элементами). Если в функции v(u) зафиксировать какие-либо
значения и, то К является положительно определенной матрицей,
поскольку скалярное произведение (Киу и) есть фактически
функционал
IBI2
Структура матрицы К зависит от упорядоченности узлов сетки
и соответствующих компонентов щ искомого вектора. При есте-
Ш

ственной нумерации узлов сетки, топографически эквивалентной
прямоугольной, К имеет ленточную структуру с шириной полосы
не более 2L + 1, где L — максимальное число узлов в линиях
одного семейства.
Коэффициенты уравнений (2.61), вообще говоря, зависят от
решения, и поэтому К представляет собой нелинейный
оператор, для анализа свойств которого полезно рассмотреть
матрицу Гесса, представляющую собой матрицу вторых производных
от функционала 1(Ап):
дЧ дЧ дЧ
R =
ди\ди2
du\duN
дЧ
дЧ
дЧ
duNdU\ duNdu,2 '" duNduN
Дифференцируя интеграл в (2.59), несложно получить (v'
означает производную по \Вг):
Gh
дВх^2
дВу
9*в*
ав'
где
д2Вх
дВи
= ^i-o.
(2.65)
duf duf duf
Отсюда для уравнений вида (2.61) с коэффициентами (2.63)
матрица R определяется из соотношений
(#w)/=_i=2 prtir — poUo, (2.66)
г= 1
где ро = Ро-\-ро, а величины ро и рг определяются формулами,
которые получаются из выражений для ро и рг заменой
множителей vr на dvr/duo. Если шаблон для /-го узла целиком лежит
в неферромагнитной среде, то ро = ро и все Рг = 0, т. е. в
соответствующей строке матрицы отличен от нуля только
диагональный элемент.
Отметим, что если функционал 1(и) строго выпуклый, то
матрица R является положительно определенной.
Если сетка не является топологически эквивалентной
прямоугольной, то структура матрицы /Сможет существенно усложниться.
Различным узлам могут соответствовать шаблоны с неодинаковым
числом треугольников, и геометрически близко расположенные
узлы могут оказаться имеющими сильно различающиеся номера.
В таких случаях матрица системы конечно-элементных уравнений
будет иметь разное количество ненулевых элементов, и ширина
ленты (максимальная разница номеров компонент неизвестного
вектора, участвующих в одном уравнении) может оказаться
достаточно большой.
Для случая произвольного типа конечных элементов и
базисных функций общая схема построения матрицы системы может
112

быть описана следующим образом. Пусть u(i) = {u({\ и£\..., u\s)} —
совокупность компонентов искомого решения, соответствующего
одному конечному элементу Ts (это могут быть как значения
функции, так и производных). Представляя на элементе Ts
приближенное решение через значения v-t и соответствующие базисные
функции Ап(х, у)= 2 и^к(х, у) и подставляя это выражение
в минимизируемый функционал (2.19), мы можем интеграл по
одному треугольнику написать в форме скалярного
произведения с матрицей /-го порядка, элементы которой зависят от
самих значений иф:
ЦАп)= lT(Ksu^\ u^)-(fs, иМ). (2.67)
Для Ks принято название матрица жесткости. Как следует
из ее построения, при любых «замороженных» коэффициентах,
т. е. когда в функции v берутся произвольные значения Mk, Ks
есть симметричная и положительно определенная матрица.
Матрица же К полной системы уравнений (2.64) складывается из
элементов всех матриц Ks- При построении полной матрицы К
из элементарных необходимо только установить соответствие
между компонентами «локальных» векторов u(s) и вектора и.
§ 2.4. Методы решения систем нелинейных уравнений
Запишем систему конечно-элементных уравнений в виде
f
...+kiN»N = h (2.68)
где kim — зависящие от неизвестных щ величины.
Один из самых очевидных алгоритмов решения системы (2.68)
заключается в проведении итераций с релаксацией по
нелинейности:
/С(л~1)йЛ = /, f/n = cou/l + (l —(й)ип~{. (2.69)
Запись /С^"1) означает, что все элементы матрицы, зависящие
от и, берутся с предыдущего шага. Параметр релаксации со, как
правило, берется в интервале (0,1) и определяется
экспериментально. В зависимости от характера нелинейности задачи его
введение или ускоряет скорость сходимости итераций, или даже
позволяет расходящийся при со = 1 процесс сделать сходящимся.
Если же задача линейная, то при со = 1 процесс дает решение
формально за одну итерацию.
Как видно, в данном случае метод сводится к решению
последовательности линейных задач. При этом актуальным является
вопрос, как решать системы линейных алгебраических уравнений
с матрицами /С(п~!). Напомним, что эти матрицы обычно имеют
порядок N в несколько тысяч и являются ленточными с шириной
8 В П. Ильин 113

ленты L в несколько десятков. Кроме того, К^п~х^ являются
симметричными и положительно определенными. Это обеспечивает
устойчивость метода исключения Гаусса для решения систем даже
без выбора главного элемента. С учетом ленточной структуры
матрицы при больших N, L он требует оперативной памяти ЭВМ
порядка NL ячеек и количества арифметических действий
примерно NL2/3. Если объема оперативной памяти достаточно, то
применение метода Гаусса является эффективным и наиболее
распространенным. Дело в том, что для конечных элементов в
сложных областях (для чего эти методы и наиболее приспособлены)
типичным является большой разброс в шагах сетки, что сильно
ухудшает скорость сходимости итерационных алгоритмов, успешно
применяемых для конечно-разностных уравнений. Кроме того,
часто встречающаяся нерегулярность сетки «портит» структуру
матрицы и делает затруднительным использование ряда экономичных
итерационных процессов, например, неявных методов переменных
направлений.
В методе Гаусса, а равно и в других применяемых прямых
методах (например Холесского), очень актуальным является
выбор такой упорядоченности конечных элементов и узлов сетки,
при которой матрица системы имеет по возможности меньшую
ширину полосы, что позволяет существенно сократить
необходимые для реализации ресурсы ЭВМ как по памяти, так и по объему
вычислений.
Если же в матрице системы линии, огибающие зоны нулевых
элементов, сильно криволинейны, то тщательная реализация
метода Гаусса позволяет еще повысить его экономичность. Пусть
Li = Li — l-\-\ —локальная ширина полуполосы ленточной
матрицу, где L/ — максимальный номер компоненты неизвестного
вектора в 1-ом уравнении, имеющего ненулевой коэффициент.
Тогда реализация метода Гаусса осуществима при использовании
N
только 2 Li ячеек оперативной памяти, что может оказаться го-
/=i
раздо меньше величины NL, где L = max{L/}.
Когда объем оперативной памяти ЭВМ не позволяет
непосредственно применить метод Гаусса, то могут быть использованы
блочные варианты гауссовского исключения с «упрятыванием»
промежуточных данных на внешних запоминающих устройствах.
Однако уже для трехмерных задач с числом узлов в
несколько десятков тысяч реализация даже таких алгоритмов
затруднительна.
В этих случаях при решении системы (2.69) для каждого п
можно применить «внутренние» итерации по методам чебышевско-
го ускорения или последовательной верхней релаксации, или
сопряженных градиентов. При этом фактически производится
приближенное обращение матриц К^п~^ но, если погрешность гп
решения промежуточных систем достаточно мала, то сходимость всего
процесса почти не нарушается. С точки зрения оптимальности
114

алгоритма существенным является вопрос выбора
последовательности е„ такой, чтобы суммарное количество внутренних итераций,
необходимое для обеспечения заданной точности решения
системы (2.69), было минимальным. Теоретически эта проблема трудно
разрешима, и можно только рекомендовать экспериментальный
подбор параметров гп (а также и со, возможно даже различных cort
на разных итерациях) для некоторых классов задач с типичным
характером нелинейности.
Переписав для удобства систему (2.68) в виде g(u) = 0 или
в покомпонентной записи
мы можем указать еще два простых алгоритма, являющихся
непосредственными обобщениями итерационных процессов для
линейных уравнений. Первый из них можно назвать нелинейным
методом Якоби:
giiurK.^ufz^ufuf+i1,..., unN~x) = О,
(2.70)
и? = ай?+(\ —(o)ttf-1, 1= 1,2,..., N.
Здесь на каждой м-й итерации для каждого / необходимо
решать нелинейное (но уже скалярное) уравнение относительно
й?, для чего можно проверить «внутренние» итерации каким-либо
из общепринятых методов: хорд, Ньютона, Стефенсона и т. д.
Параметр релаксации со введен в (2.70) априори для возможного
управления скоростью сходимости.
Второй алгоритм является нелинейной последовательной
релаксацией
g{unu ..., uUu и?, uUx
(2.71)
и?=ай?+(1 -соК /=1,2,..., N,
который при со = 1 является обобщением метода Зейделя. Как
правило, и в (2.70), и в (2.71) значения со подбираются
экспериментально в интервале от 0 до 1 для ослабления влияния
нелинейности. Если в (2.71) для каждого / не проводить точного
вычисления й?, а просто делать фиксированное число т «ньютоновских»
итераций, то получим так называемый m-щаговый метод ПВР-
Ньютона (внешние итерации выполняются с помощью
последовательной верхней релаксации, а внутренние — по методу
Ньютона). Наиболее распространен одношаговый метод ПВР-Ньютона,
который для нашей системы уравнений (с учетом того, что ее
решение минимизирует функционал 1(и)) может быть записан в
следующем явном виде:
d2l/duf(ul....
8* 115

Рассмотренные алгоритмы, каждый своим образом, могут быть
представлены в виде итерационного процесса
ип = В(ип~х) (2.73)
с некоторым нелинейным оператором В в N-мерном пространстве.
Например, если в (2.70) положить со=1 и не делать внутренних
итераций, то в применении к системе (2.68) получим формулы
1), (2.74)
/=1,2 TV.
Относительно итераций (2.73) можно сформулировать
следующий результат.
Теорема 2.4. Если оператор В удовлетворяет условию
\\B(u)-B(v)\\ ^q\\u-v\\, <7< 1, (2.75)
то уравнение и — В(и) имеет решение и
Доказательство начинается с установления неравенств
\\ип+х-ип\\ < \\В(ип)-В{ип~х)\\ < q\\un-un'x\\ <ьЯп\\их — и°\\,
которые следуют из (2.75). Далее для любого целого р > п имеем
\ип+1 — ип
^
Отсюда, согласно критерию Коши, последовательность и11 имеет
предел и*, который является решением, поскольку для любого
п справедливы соотношения
Необходимо заметить, что применение этой теоремы в
конкретных случаях требует «всего навсего» проверить условие (2.75),
что как раз представляет значительные технические трудности.
Одним из самых эффективных методов решения систем
нелинейных уравнений является метод Ньютона — Канторовича
un = un-x—H-\un-{)g(un-x), (2.76)
где матрица Н состоит из производных вектор-функции g: H =
={dgk/duh k, /=1,2,...,ла
Если и* есть решение уравнения g(w) = 0, то через Qa
обозначим множество и, удовлетворяющих условию \\и — и*\\ <Са.
116

Теорема 2.5. Пусть для некоторых положительных чисел
а, аи #2 выполняются условия '
|| Н- \и) || < ах при и 6 Йа, (2.77)
\\g(u)-g(v)-H(v)(u-v)\\ <а2 \\v-u\\2 при u,v 6 Qe,(2.78)
w° б Й&, где ft = min(a,c-1), c = aia2. (2.79)
Тогда итерационный процесс (2.76) сходится и справедлива
оценка
\\и* — ип\\ ^с-1(с\\и1 — и*\\)2. (2.80)
Условия (2.77), (2.78) имеют тот смысл, что для и из некоторой
окрестности решения и* должны быть ограничены все вторые
производные функции gi и матрица, обратная к якобиану Н. Величина
Ь из (2.79) характеризует, насколько начальное приближение
должно быть близко к а*, чтобы метод сходился.
Неравенство (2.80) означает, что за одну итерацию ошибка
убывает квадратичным образом. При этом для того чтобы норма
погрешности я-го приближения была равной || ип — и* || =е, при
е «С 1 требуется количество итераций порядка
п(г) « Iog2log28~1, (2.81)
в то время как для метода простой итерации из теоремы 2.3 имеем
п(г) « Iog28~1.
Таким образом, если начальное приближение выбрано
достаточно близко к точному решению, нелинейные функции в
уравнениях дважды дифференцируемы, а якобиан системы невырожден,
то метод Ньютона сходится и очень быстро.
Одна из сложностей его применения заключается как раз
в выборе начального приближения, а вторая связана с
трудоемкостью реализации самих итераций, которые можно записать
в виде
(2.82)
В данном случае на каждом шаге необходимо решать систему
уравнений с матрицей R^n~{\ Это можно делать или прямыми
методами типа Гаусса, или итерационными. Если применить для этого
m итераций последовательной верхней релаксации (т. е. не решать
точно систему (2.74) на каждом шаге), то получим двуступенча-
тый так называемый m-шаговый метод Ньютона-ПВР. Одна из
трудностей метода (2.73) заключается в необходимости
вычислять для каждого п элементы матриц Я, что может требовать
больший объем вычислений, чем само решение системы (2.74).
В таких случаях применяется модификация метода Ньютона с
пересчетом матрицы R не для каждого я, а через несколько шагов.
Этот прием эффективен тогда, когда приближения ип находятся
в такой окрестности, где их изменение не сильно сказывается на
элементах матрицы R.
117

§ 2.5. Примеры расчетов магнитостатических полей
В этом параграфе мы приведем результаты численных
расчетов, выполненных А. Л. Урванцевым и С. Б. Кузнецовым с
помощью пакета программ Эстамп, описанного в последней главе.
Этот пакет реализует метод конечных элементов с
кусочно-линейной аппроксимацией азимутального компонента осесимметричного
векторного потенциала, описываемого уравнением (2.8). Решение
нелинейных алгебраических уравнений проводится итерационным
методом ПВР-Ньютона (2.72).
Первый пример имеет методический характер. С целью
экспериментальной оценки погрешности метода решается линейная
задача в прямоугольнике 0< г <r3 = 0,117, 0< z < 0,016 с
граничными условиями А = 0 при г = 0, дА/дп = 0 при z = 0 и z = 0,016,
Л=Ло = О,75943 при г = г3. Магнитное сопротивление бралось
равным v = vi = 10~3 при 0 < г < п =0,058, v = v2=l при г>
> 0,058. Плотность тока в (2.8) / = с/о, /о = О,1 для r\<r<L
<:г2 = 0,1 и / = 0 — для г<г\ и г>г2. Точное решение в этом
случае не зависит от z и имеет вид
ег,
где константы a, b, d, e однозначно определяются из условий,
удовлетворяющих исходному уравнению, граничным значениям,
непрерывности величин А и у(дА/дг-\-А/г) при г = Г\ и г2.
Решение задачи проводилось на трех сетках. Одна из них имела
шаги /iz = 0,04, hr = 0,058/13 для r<ru hr = 0,042/4 для ri<r<r2
и /гг = 0,017/3 для г>г2 с общим числом разбиений 4X20. Из
двух других сеток одна имела шаги вдвое большие, а другая,
наоборот, вдвое меньшие, с числом разбиений соответственно
2 X Ю и 8 X 40. Численное решение на сетке 4 X 20 имеет
погрешность в десятые доли процента, причем существенное улучшение
точности дает описанная в гл. 1 экстраполяция Ричардсона (пн —
= 4uh/3 — W2a/3) • Например, в точках г = 0,058 ошибки
равны: для сетки 4 X 20 — 0,2%, для сетки 4 X 20 + 2 X 10 (т. е. с
экстраполяцией Ричардсона) —0,01%, для сетки 8Х40 + 4Х
X 20 —0,0007%.
В качестве примера решения практической задачи мы
рассмотрим расчет поля осесимметричной магнитостатической линзы,
изображенной на рис. 15. Здесь разными штриховками обозначены
области магнитопровода и магнитного наконечника, состоящих из
материалов с различными ферромагнитными свойствами.
Перечеркнутые прямоугольники представляют собой сечения
токонесущих катушек с примерно равными плотностями токов.
Назначением такой магнитостатической линзы является формирование
электронного пучка с заданными оптическими свойствами,
проходящего вдоль оси системы. Основной целью расчетов является
118

нахождение распределения осевой компоненты Bz магнитной
индукции в окрестности зазора линзы (отрезок ВС).
Решение такой задачи является достаточно сложным в силу
ряда специфических особенностей. Отрезок ВС, где требуется
обеспечить наилучшую точность (и не самого решения, а его
производной) составляет около одной сотой части от общей длины
системы АД.
Токи в катушках такие, что возникает сильное насыщение
железа, означающее резкую нелинейную зависимость v(|£|2),
с изменением его значений в
разных подобластях от 1 до 10~5.
Расчеты проводились с
граничным условием Л = 0 на контуре
ADEF, соответствующем
предположению об отсутствии полей
рассеяния вне магнитопровода.
На рис. 15 изображена «редкая»
сетка, используемая в расчетах
(триангуляция области
проводилась путем проведения
диагоналей во всех нарисованных
четырехугольниках). Само решение
вычислялось на густой сетке с числом
узлов около 4000, получаемой
из редкой делением каждого тре- к
угольника на 4 равные части. |
Для повышения экономичности
расчетов решение проводилось в
несколько этапов, с
использованием на каждом из них
вспомогательных подзадач (весь процесс
расчетов автоматизирован):
а) решение задачи на редкой
сетке при кусочно-постоянных
v в железе, выбранных из
априорных предположений;
б) решение нелинейной задачи
на редкой сетке с
использованием решения из п. «а» в
качестве начального приближения;
в) решение нелинейной
задачи на густой сетке с
использованием в качестве начальных приближений значений, полученных
из интерполяции решения в п. «б»;
г) уточнение решения в окрестности зазора линзы. При этом
используется метод «фокусировки»: на границе выбранной
подобласти (прямоугольник KLMN на рис. 15) в качестве граничного
условия берутся значения, полученные с помощью предыдущего
решения, строится еще более мелкая сетка и находится оконча-
Рис 15.
119

тельное решение. Последний этап можно провести экономично
в силу возможности выбора простой подобласти* построения
квадратной сетки и использования специальных алгоритмов решения
алгебраической системы, рассмотренных в гл. 1.
Эффективность расчетов существенно зависит от выбора
релаксационных параметров со в итерациях (2.72), который
может быть осуществлен только экспериментально. Оптимальные
значения зависят и от типа железа, т. е. характера нелинейной
зависимости магнитной проницаемости от величины магнитного
поля, и от величины токов, т. е. от участка кривой v(| В |2),
«работающего» в решаемой задаче. Величины со целесообразно брать
12 Z
разными в «воздухе» и «железе». Для «воздуха» со ^ 1,9 при
достаточно большом числе узлов сетки, в «железе» при слабом
насыщении оптимальные со примерно такие же, а при увеличении тока
уменьшаются и могут быть меньше единицы. Решение обычно
требует проведения нескольких сотен итераций, и сходимость
в целом не является монотонной, т. е. на некоторых шагах ошибка
может расти.
На рис. 16 мы приводим характерный вид зависимости Bz(z) на
оси с началом координат в центре зазора. Три кривые
соответствуют случаям слабого, среднего и сильного насыщений, с
увеличением тока высота пика растет (отношение максимального значения
Bz к значениям на краю подобласти KLMN может составить 103
и более). На рисунке обозначены также экспериментально снятые
значения Bz для рассчитанной магнитной линзы. В районе пика
отклонение составляет 3—5%, а в прилегающих зонах— 1—2%.
С практической точки зрения такое соответствие расчетов и
экспериментов можно считать вполне удовлетворительным.

Глава 3
МЕТОДЫ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
ДЛЯ ЗАДАЧ ТЕОРИИ ПОТЕНЦИАЛА
§ 3.1. Интегральные постановки краевых задач
Пусть Q — ограниченная трехмерная область с достаточно
гладкой поверхностью Г. Для произвольной функции u(x,y,z),
непрерывной вй + Ги имеющей непрерывные производные внутри
Q, справедлива интегральная формула Грина
(3.„
Здесь А — оператор Лапласа, nQ — внешняя нормаль к
границе Г в точке Q, /?(P, Q) — расстояние между точками Р и Q, а со
принимает значения:
[4л, если точка Р лежит внутри Q,
2л, если точка Р лежит на границе Г,
О, если точка Р лежит вне Q.
Для гармонической функции А^ = 0, и из (3.1) для точек Р,
лежащих внутри Q, получаем интегральное представление
- (32)
Аналогичные формулы имеют место и для функций двух
независимых переменных. Пусть S — некоторая область на плоскости
(х,у), ограниченная контуром С, a nQ — направление внешней
нормали к этому контуру в точке Q. Основная интегральная
формула Грина для этого случая имеет вид
(3.3)
( 2я, если Р 6 S,
(о= я, если Р £ С,
I 0, если Pi S + C.
121

Соответственно для гармонической функции во внутренних
точках области S справедливо представление
В данной главе мы основное внимание уделим смешанным
краевым задачам для уравнения Лапласа. Мы отметим несколько
особенностей постановок внутренних и внешних краевых задач
с граничными условиями 1-го рода.
Пусть на границе Г, ограничивающей область G, задана
кусочно-непрерывная функция f(P). Тогда внутренняя задача
Дирихле ставится следующим образом: найти функцию и(Р),
гармоническую внутри области Q, непрерывно примыкающую к граничным
значениям f(P) в точках непрерывности последних и ограниченную
в замкнутой области Q + Г. Требование ограниченности
фактически относится к окрестностям точек разрыва функции f(P). Решение
сформулированной задачи существует и единственно.
Для двумерного случая внутренняя краевая задача ставится
совершенно аналогично. Однако постановки внешних краевых
задач для функций двух и трех переменных существенно
отличаются.
Пусть Q' — дополнение к Q + Г до всего трехмерного
пространства. Первая внешняя краевая задача состоит в следующем:
найти гармоническую функцию и{ху у, г) в неограниченной области
Q', непрерывную вй' + Г, принимающую на поверхности Г
заданные значения g(x, у, г) и равномерно стремящуюся к нулю на
бесконечности. Последнее условие является необходимым для
единственности решения.
Внешняя задача Дирихле на плоскости ставится следующим
образом: требуется найти функцию и(х, у) в неограниченной
области S'— дополнении к S + C, удовлетворяющую в S' уравнению
д2и/ дх2-\-д2и/ ду2 = 0у непрерывную в S' + C, принимающую на
С заданные значения g(x, у) и ограниченную в бесконечности.
Требование обращения решения в нуль на бесконечности здесь
является слишком сильным, так как при нем задача может
оказаться вообще неразрешимой.
Мы будем рассматривать краевые задачи более общего вида,
которые, однако, не сильно усложняют реализацию метода
интегральных уравнений, рассматриваемых в данной главе.
Найти решение уравнения Пуассона
Au = f. (3.5)
в области Q с границей Г, на отдельных участках которой заданы
граничные условия 1-го, 2-го или 3-го рода:
u\Tl = gu (3.6)
122

Кроме того, допускается наличие в области Q «внутренних границ»
Гз, на которых задаются условия непрерывности решения и скачка
его нормальной производной
i i ди | ди I /о о\
«|гз+=*|гз-> 8+^г1гз^-^г|г3^ (3.8)
Границу области мы допускаем кусочно-гладкой и
многосвязной (за исключением отдельных случаев, где делаются
специальные оговорки).
В такой постановке мы будем рассматривать двумерные и
трехмерные задачи, внутренние и внешние. В последнем случае на
бесконечности ставится условие ограниченности и для двумерных
задач и стремления к нулю — для трехмерных. Если участок
границы Tj с условием первого рода присутствует, то решение краевой
задачи единственно. Особый случай представляет задача Неймана,
когда на всей границе задано условие (3.7) при а = 0. Решение
такой задачи определяется с точностью до произвольной
постоянной.
Функция —=—= =-, представляющая по-
R V(*-*')4Qy')2+(2*')2
тенциал поля единичного заряда, помещенного в точке
Q(x\ y\ z'), является решением уравнения Лапласа, зависящим
от параметров х', у\ z'. Если р(х', у', z') есть распределение
объемной плотности зарядов, то обусловленный ими потенциал в точке
Р(х, у, z) определяется интегралом
ёУ^ (3-9)
Для плоских задач аналогично определяется логарифмический
потенциал
и(х,у)=\ в(х',у')\п ,- ' f^dx'dy\ (ЗЛО)
где o(x't у') есть двумерная плотность зарядов.
Отметим, что если объемный потенциал стремится к нулю в
бесконечности, то функция (3.10) имеет логарифмическую
особенность.
Как показывает основная формула Грина (3.2), любая
гармоническая функция может быть выражена с помощью интегралов,
представляющих поверхностные потенциалы.
Потенциал поверхностной плотности зарядов (ji(Q),
распределенных на поверхности Г, описывается интегралом
v(P)=\i^L.dSQ (з.п)
и называется потенциалом простого слоя.
123

Если функция v(Q) описывает поверхностную плотность
диполей, то обусловленный ею потенциал выражается поверхностным
интегралом
S^()S (ЗЛ2)
и называется потенциалом двойного слоя.
Потенциал двойного слоя в некоторой точке Qo на поверхности
Г является разрывной функцией:
(3.13)
Здесь w+(Qo) и w-(Q0) — предельные значения
потенциала двойного слоя при подходе к точке Qo с разных сторон
поверхности.
Потенциал простого слоя непрерывен в точках поверхности Г,
но терпит разрыв его нормальная производная:
(3.14)
где знаками « + , —» обозначены предельные значения
производных, a -^-(Qo) есть так называемое среднее значение
нормальной производной.
Для плоских задач потенциалы простого и двойного слоев
определяются аналогично (3.11), (3.12):
(3.15)
Как и для функций трех переменных, на границе (в данном
случае на кривой С) терпят разрывы потенциал двойного слоя
и нормальная производная потенциала простого слоя. При
этом в формулах (3.13), (3.14) надо только всюду заменить 2я
на я.
Формулы объемного и поверхностных потенциалов позволяют
определить градиенты полей путем непосредственного
дифференцирования подынтегральных выражений в (3.9) — (3.12). Градиент
потенциала объемной плотности зарядов описывается формулой
(3.17)
где rPQ — радиус-вектор точки Q с началом в точке Р. Градиенты
потенциалов простого и двойного слоев представляются соответ-
124

ственно выражениями
^ (3.18)
SQ, (3.19)
где nQ — единичный вектор нормали к поверхности Г в точке Q.
Применение поверхностной плотности потенциалов дает
аппарат для формулировки интегральных уравнений решения краевых
задач.
Будем искать решение трехмерной внутренней первой краевой
задачи (3.5) — (3.6) в виде потенциала двойного слоя
). (3.20)
Полагая при этом / = 0 в (3.5) и считая поверхность Г = Г]
односвязной, в силу условий (3.13) получаем интегральное
уравнение
2nv(P) + \ Kx(P,QWQ)dSQ = gi(P) для Ре Г. (3.21)
г
Если же решается внешняя краевая задача в неограниченной
области Q', являющейся дополнением к Q-f-Г, то вместо
уравнения (3.21) получаем
-2nv(P)+\ Ki(P,Q)v(Q)dSQ = gl(P\ Per. (3.22)
г
Для случая двумерной области вместо уравнений (3.21), (3.22)
будем иметь соответственно для внутренней и внешней краевых
задач интегральные уравнения
nv(P)+ \ K*P,QHQ)dl=gi(P), (3-23)
с
-nv(p)+ \ K2(P,Q)v(Q)dl = gl(P). (з.24)
Здесь ядро каждого из уравнений имеет вид /GCtf, Q) =
dnQ\mR(P,Q))'
Если же для трехмерной смешанной краевой задачи при р = 0
решение внутри Q искать в виде потенциала простого слоя, то
с учетом соотношений (3.14) получаем систему интегральных
уравнений для fui(Q):
\v{Q)Gi(P9Q)dSQ=gl(P\ Per и
125

(3.25)
Здесь ядро записывается в виде G\(P,Q)= \/R{P, Q), а
производные от ядра могут быть вычислены по формулам
9G(PQ) dG dG 0G,
Для внешней краевой задачи'во втором и третьем уравнениях
системы (3.25) перед внеинтегральными членами левых частей
надо поменять знаки.
Для двумерной внутренней краевой задачи аналогичная
система имеет вид
\li(Q)G2(PiQ)dl = gl(P\ Ре Си
с
i = g2(P), P € С2, (з.27)
где G2(P, Q) = ln , а через С\, Съ, Съ обозначены участкитра-
ничных кривых с граничными условиями соответственно (3.6),
(3.7), (3.8).
Мы отдельно рассмотрим также практически важный случай
осесимметричных краевых задач. Переходя к цилиндрическим
координатам г, z, Э и производя в (3.25) интегрирование по углу
0, мы придем к уравнениям вида (3.27), только ядро G2(P,Q) надо
заменить на
П3(РО)=- 4rK^ k= 2^ , (3.28)
V( + ')2 + (')2 1{ + г'Г + (г'Г
где К— полный эллиптический интеграл первого рода, аг,ги г',
г' — координаты точек соответственно Р и Q.
Решение смешанных краевых задач можно также искать,
используя одновременно потенциалы простого и двойного
слоев.
Пусть, например, в краевой задаче (3.5) — (3.7) Г = Г1 + Г2
и р = 0. Тогда, определяя на части границы Г\ плотность простого
слоя |л(Р), а на Г2 — плотность двойного слоя v(Q), и#з граничных
126

условий получаем два интегральных уравнения
Р6Г2. (3.29)
Если плотности \x(Q) и v(Q) из -этих уравнений найдены, то
потенциал определяется из интеграла
Такой подход исследован в работах французских ученых [142, 11].
Рассмотрим еще метод решения внутренней задачи Дирихле,
развитый В. Д. Купрадзе, М. А. Алексидзе [4] и основанный на
интегральном представлении гармонической функции. Введя
обозначение v(Q) = du/ dnQy из (3.1) при Аи = О мы будем иметь для
любой точки Р, лежащей вне Й + Г:
где F(P) = \ u(Q)——(——— )ds — легко вычисляемая функция,
когда u(Q) задана на границе. После нахождения v(Q) из
интегрального уравнения (3.31) решение первой краевой задачи для
уравнения Лапласа определяется из формулы (3.2). Аналогично
можно построить решение и для двумерного случая, надо только
вместо формул (3.1), (3.2) использовать (3.3), (3.4).. Как легко
видеть, ситуация принципиально не меняется для решения
уравнения Пуассона Au = f, при этом в правых частях формул (3.2),
(3.31) достаточно добавить интегралы [ р(р L dVQ.
Отличием интегрального уравнения (3.31) от ранее
рассмотренных является то, что «точки наблюдения» Р не лежат на
поверхности Г, по которой ведется интегрирование. Аналогичный подход
был развит А. X. Рахматулиной и И. И. Кочетовым [ШЗ] на основе
использования фундаментальных решений эллиптических
уравнений. В случае внутренней краевой задачи (3.6), (3.7) для
уравнения Лапласа такой метод описывается следующим образом.
Пусть расчетная ограниченная область Q с границей Г
принадлежит некоторой области Q с границей Г такой, что расстояние
между любой парой точек Pi 6 Г, Р2 6 Г строго больше нуля. Тогда
определяется функция распределения «источников» <x(Q), Q 6 Г,
127

как решение интегрального уравнения
(3.32,
После нахождения o(Q) само решение находится с помощью
интеграла
и(Р)=\
(3.33)
Аналогично можно решать и внешние краевые задачи. Если
решение ищется в неограниченной области Q', являющейся
дополнением к Й, то вспомогательную поверхность Г можно брать
как внутри Q, так и вне. Достоинством такого алгоритма является
то, что поверхность определения «источников» Г можно выбирать
удобной для численной реализации, например, сферу. Однако при
разнесении «точек наблюдения» и «точек интегрирования»
ухудшается устойчивость метода к накоплению ошибок, и решение
интегральных уравнений вида (3.2) требует применения
алгоритмов регуляризации некорректных задач.
В заключение параграфа мы сформулируем актуальную в
электростатике так .называемую задачу Робена. Проблема
заключается в нахождении распределения потенциала, обусловленного
заряженными металлическими телами, на одних из которых заданы
потенциалы, а на других — заряды. В терминах потенциала
простого слоя u(P)=\ MpL dSQ такую задачу можно
сформулировать следующим образом:
\^ РбГо, (3.34)
= <7и Q6T;, /=1,2, ...,m. (3.35)
г,
Здесь Го — часть границы Г с заданными краевыми значениями
потенциала, Г\, Г2,..., Тт — поверхности тел с заданными
величинами зарядов qt. Уравнения (3.35) следуют из применения теоремы
Гаусса к поверхностям, охватывающих тела Q, и стремящихся
к Г/. Потенциал на каждой из поверхностей Г/ должен равняться
постоянной щ, заранее неизвестной:
-^dS^uu РеП i=l,2,...,m. (3.36)
128

Таким образом, задача Робена сводится к системе уравнений
(3.34) — (3.36), решение которой можно записать в виде
.+umu<">, (3.37)
где каждая из функций и^ выражается через «парциальную»
плотность \i^ с помощью интеграла
. / = 0,1,...,т. (3.38)
Для нахождения \i^ надо решить т-\-\ систему уравнений,
первая из которых имеет вид
!И^=Л
\
R(P,Q) ~~« "' * ^ "
а остальные определяются при g(P) = 0:
\
=o, ре То,
Г
где /=1,2,..., m, a 6f/ = l при / = / и б*/ = 0 при /=й/.
После определения всех плотностей [i(/) путем
дифференцирования (3.38) из интегралов вида (3.35) находятся «парциальные»
заряды на поверхностях Г£:
q(» = [ ^—dSQi /=1,2,..., m; / = 0, 1,..., т.
Теперь уже могут быть вычислены неизвестные константы щ
из решения линейных алгебраических уравнений, получаемых из
(3.35):
(3.39)
Окончательно искомое решение определяется по формуле (3.37).
9 В П Ильин 129

§ 3.2. Численное решение интегральных уравнений
для потенциала простого слоя
3.2.1. Двумерные плоские краевые задачи. Мы начнем с
рассмотрения внутренних смешанных краевых задач (3.5) — (3.8)
для уравнения Лапласа в плоскости, когда расстояние между
точками Р(х,у) и Q(x\ у') определяется выражением R(P,Q) =
Границу области считаем кусочно-гладкой и состоящей из
прямолинейных или криволинейных отрезков 5/, /=1,2,..., L,
каждый из которых отличается от других или видом описывающего
его уравнения, или заданным на нем граничным условием. Все
граничные отрезки считаем описанными с помощью параметра
т, имеющего смысл длины и меняющегося на Si в интервале [а/,
Р/]. Для прямолинейного отрезка координаты его точек
определяются через т формулами
х = а1т + Ь1у y = ctt + dh (x,y)eSh а/<т<р,, (3.40)
где коэффициенты а/, bi, с/, di находятся по значениям координат
концов отрезка x(aj)9 y(ai), х(р/), y(fii). Отрезок окружности задается
параметрически соотношениями
(3.41)
где г/ — радиус, a jt0/, Уы — координаты ее центра.
Граница Г может быть многосвязной, а также иметь углы,
в окрестности которых функция плотности имеет особенность. Для
ее устранения на отрезке S/ с граничными условиями 1-го рода,
в окрестности концов которого встречаются такие особенности
(с известным асимптотическим поведением) вводится замена [6]:
№)=, /f(T)T,fif = ifapW' (3-42)
(т — ai) ( — т+P/j
где |л(т) — уже гладкая функция. Значения xi, Х2 характеризуют
порядок особенностей на концах отрезка и определяются
значениями углов соь со2 в концевых точках:
Х/ = (я-о)/)/(2я-о)/), /=1,2. (3.43)
Например, на свободном конце отрезка со = 0 их=1/2. Если
на концах отрезка особенностей нет, то xi = Х2 = 0 и ц(т) = \х(т).
Численное решение интегральных уравнений вида (3.27)
основывается на дискретизации границы С = Si + S2 + ... + S , для
чего каждый из граничных отрезков Si разбиваем точками Pt =
= Р(т/) на Ni частей (проще всего это сделать равномерно по т с
шагом Дт/ = (|3/ — ai)/Ni). Общее количество интервалов разбиения
будет равно N\ + N2+..• +NL.
Совокупность граничных отрезков S/ мы будем называть
граничной ветвью LOT, m = 1,2, ...,Af. Упорядоченность граничных
отрезков Si и их параметрическое представление выберем таким
образом, что на m-й ветви параметр т меняется непрерывно от
130

ат до pm. На каждой ветви функцию |л(т) аппроксимируем с
помощью В-сплайнов:
|im(T)=
k=-p
(3.44)
где Nm — общее количество интервалов разбиения на m-й ветви.
В (3.44) tk есть неизвестные коэффициенты, а В^ (т) —
элементарный В-сплайн п-го порядка, определяемый следующим
образом:
i = k-a
<О/(т) = (т — Т/_а)(т —
Если п+1 — нечетное число, то
(3.45)
, р-а,
в противном случае а = р = (л+1)/2, р = (п— 1)/2. Через т/
обозначаются так называемые узлы сплайна, которые для нечетных п
совпадают с точками т„ а для четных — лежат посередине между
т/_1 и т/. Выражение (/(т))+ равно /(т) при />0и нулю — в
противном случае. На рис. 17 приведены для иллюстрации графики
-2Л
элементарных В-сплайнов 1-го, 2-го и 3-го порядков В[>п)(т),
п= 1,2,3, для случая равномерной сетки с шагом А. Графики
££п) (т) получаются из них простым сдвигом на т*. Соответствующие
формулы для В[)п)(т) имеют следующий вид:
о ,
h + r,
h-x,
О ,
-h,
т;
(3.46)
131

т<-ЗА/2,
-ЗА/2<т<-А/2,
-А/2<т<А/2,
А/2 <т< ЗА/2.,
ЗА/2 < т;
(3.47)
т<-2А,
4А3-6Ат2-Зт3, А<т<о!
4А3 — 6Ат2 + Зт3, 0 < т < А,
6/И (2A —т)3, А<т<2Л,
Д 2А<т.
(3.48)
Поскольку каждый из сплайнов В{)п\т) обладает непрерывными
производными до (п— 1)-го порядка, то такой же гладкостью
обладает и соответствующая аппроксимация \хп(г). Как видно из
(3.44), если граничная ветвь разбита на Nm интервалов, то
функция £п(т) выражается как линейная комбинация Af-f-l +2p
сплайнов. Для однозначного определения сплайновой аппроксимации
на концах отрезка [аот, рт] задаются «граничные условия»
на сплайн, для чего могут использоваться следующие
соотношения:
(3.49)
Здесь а, й, с, d — заданные числа, выбираемые из априорных
соображений о характере поведения аппроксимируемой функции
в окрестности концов отрезка [am, pm]. Если, например,
граничный отрезок подходит перпендикулярно к линии симметрии
потенциала, то на соответствующем конце естественно положить
\i'n=0. Для замкнутых граничных ветвей их концевые точки
совпадают, и тогда на сплайн накладываются условия
периодичности;
McLm) = |I«(Pm), Й(ат)= jU(Pm), |1^(ат)= Й'(Р«). (3.50)
Наиболее просто реализуется, естественно, аппроксимация
сплайнами первого порядка. С точностью до постоянной 1/А_все
tk представляют собой значения интерполируемой функции jli(t^)
в узлах^ Граничных условий на сплайн при п=1 не надо, и в
(3.44) jx(t) фактически есть обычная кусочно-линейная
аппроксимация.
При аппроксимации плотности pi(x) В-сплайнами отдельного
рассмотрения заслуживает случай, когда граничные линии
разветвляются, как это показано, например, на рис. 18. Здесь
изображены характерные эпюры квадратичных сплайнов в окрестности
точки стыка прямых и OL. В плоскости KMN элементарные
сплайны определяются, как в одномерном случае. На луче OL сплайны
132

надо определить так, чтобы они совпали с соответствующими
элементарными сплайнами на ON, если плоскость KOL повернуть
вокруг оси О К до совмещения с плоскостью KON. Если
ломаную NOL описать непрерывным образом с помощью
параметра длины т. то на ней в окрестности точки «О» сплайны
5/(т), / = 1, 2, 3, представляются как обычно. Функция \х в точке
«О» при этом будет аппроксимироваться выражением
t2B2(%)
Здесь параметр т выбирается таким образом, что он представляет
длину как прямой MN, так и ломаной MOL (начиная от
некоторой общей точки на луче ОМ). Аналогично можно определить
J
Л /
M f
к
щ
>>( Ilii^
Рис. 18.
сплайны, когда в одной точке стыкуются три или более граничных
отрезка. Дополнительных граничных условий на сплайны в таких
точках для определения аппроксимации не требуется.
Аппроксимационные качества В-сплайнов являются высокими
не только в отношении приближаемых функций, но и их
производных. Если ип{%) есть интерполяционная аппроксимация функции
и(х) с помощью В-сплайнов /1-го порядка (ип(т/)==и(тг-)), то имеют
место оценки
р = 0, 1,...,п,
где р есть порядок производной, h — максимальный шаг сетки, а
Мр — не зависящие от h постоянные.
Приближенное решение системы интегральных уравнений
строим по принципу коллокаций следующим образом. Подставляя
в интегральные уравнения (3.27) вместо искомой функции |я(т)
ее сплайновые аппроксимации на каждой из граничных ветвей
и требуя точного выполнения граничных условий в точках
дискретизации Pi e Г, получаем систему линейных алгебраических
133

уравнений относительно коэффициентов tki
и
у 2 ЬВР(ъ) + \ 2 tkB<kn\T')Gfa, т') /(х')р(х') dx' = /(x,), (3.51)
Здесь oti, pL — границы отрезка изменения т, на который
отображается вся граница Г при ее параметрическом представлении.
Ради единообразия мы формально объединили все три уравнения
из (3.27). Для точек, лежащих на границе с условием 1-го рода,
внеинтегральный член в левой части (3.51) отсутствует (у = 0),
а для остальных т/ имеем у = л. Правая часть /(х/) равна gi(Pt) или
g^Pi\ если соответствующая «точка наблюдения» лежит
соответственно на участке границы С\ или С2; если Р/еС3, то /(т/) = 0.
7(т') есть якобиан преобразования переменных от х\ у' кт' и
определяется выражением
Функция р(х'), отличная от единицы на граничных отрезках,
в концах которых учитывается особенность плотности,
определяется из (3.42). Суммирование под интегралом проводится по
элементарным В-сплайнам, определенным на всех М граничных ветвях.
Количество уравнений (3.51) равно общему числу точек
дискретизации границы. Правые части уравнения равны
g2(x/), Pi е= С2,
Ядро G2(x/, т') определяется для участков границы с разными
типами граничных условий следующими формулами:
1 _/ о с .— г*
In
Д-1пГ 1
.-8_ д
dnQ
= {cos(nQfx) *—^- +cos (n
причем в последнем выражении надо положить jc = x(x/), f/ = t/(x»),
jc/ = a:(x/), у/==у(т/), а величины cos (nQ, jc), cos (nQ, у) означают коси-
134

нусы углов между осями х, у и нормалью к границе в точке с
координатами х(т'), у{т').
Отметим, что зачастую применяется более грубая
математическая модель без учета особенностей в узловых точках. Если не
требуется вычислять решение в окрестности особых точек или если
вблизи них неизвестно асимптотическое поведение плотности, то
на соответствующих граничных отрезках Si в таких случаях
полагается р(т/)=1.
Как следует из вида ядра интегрального уравнения, при
стремлении точки Q к Р оно имеет логарифмическую особенность,
которую можно устранить с помощью несложного аддитивного
преобразования. Пусть некоторое подынтегральное выражение имеет
вид
ш(т, т') == и(тг, т') + v(t, т') In |т — т'|,
где функции и(т, т'), и(т, т') не имеют особенностей. Тогда интеграл
от w можно вычислить следующим образом:
, т')с1т' = J {ф, т') + [v(t, т') - о(т, т)] In |т — т'|)Л' +
|т —т'|Л/. (3.53)
Последний интеграл берется точно, а в предпоследнем
подынтегральная функция уже «хорошая», и для вычислений теперь
обосновано применение квадратных формул. При вычислении
элементов матрицы указанные преобразования требуется делать
только при интегрировании по интервалам разбиения границы,
примыкающим к точке наблюдения Р,-.
К уравнениям (3.51) для замыкания системы надо добавить
2рМ уравнений, аппроксимирующих граничные условия для
сплайнов, которые получаются как результат подстановки (3.44) в
соответствующие уравнения (3.49) или (3.50). Пусть, например,
краевая задача обладает симметрией относительно какой-то
линии. Если концевая точка, соответствующая значению
параметра т; = ат, принадлежит граничному отрезку, «стыкующемуся»
перпендикулярно с линией симметрии, то для сплайна естественно
поставить граничное условие-~М _ =0. Соответствующее
уравнение алгебраической системы будет иметь вид
Ш±\
где сумма берется фактически по тем элементарным сплайнам,
производные которых не равны нулю в точке т = ат. Для
квадратичного и кубического сплайнов получим уравнение t\-\ — u-|_i = 0.
Таким образом, получаем линейную алгебраическую систему,
в которой число уравнений и неизвестных равно N—{2p-\-\)M-\-
+ 2 Nm. Обозначая через t = {t\, t2, ...,tN) вектор неизвестных
т = \
коэффициентов сплайна, можно записать ее в виде
At = f. (3.54)
135

Здесь / = {/ь /2, ..., Ы есть известный вектор, А — квадратная
матрица порядка N. Если k-oe уравнение этой системы получается
из соотношения (3.51) для точки наблюдения Р(т,-), то /Л = /(т«);
в противном случае fk равно нулю или определяется из правых
частей граничных условий (3.49). Элементы строк матрицы Л,
соответствующие точкам Р(тг) е С, получаются после проведения
интегрирования в (3,51). Иногда это можно выполнить точно,
но зачастую приходится применять численное интегрирование.
В последнем случае можно рекомендовать квадратурные формулы
Гаусса, как имеющие высокую точность при вычислении
подынтегральной функции в достаточно малом числе вспомогательных
точек (на практике 3—5 квадратурных точек на одном интервале
разбиения граничного отрезка является вполне достаточным).
Матрица Л является плотной (малое количество ненулевых
элементов имеется только в строках, соответствующих граничным
уравнениям сплайна) и, вообще говоря, несимметричной.
Решение системы (3.54) с помощью итерационных методов
не представляется нецелесообразным, поскольку спектральные
свойства матрицы Л, необходимые для оптимизации таких
алгоритмов, как правило, неизвестны. При использовании прямых
методов (гауссовского исключения или основанных на ортогона-
лизации) можно рекомендовать итерационное уточнение решения,
заключающееся в следующем. Пусть при решении системы (3.54)
в силу погрешностей округления мы получили не точный
результат, а некоторое приближение /(1). Тогда вычисляем вектор невязки
г(1) = / — Л/(1) и находим поправку к решению
(3.55)
с помощью которой уточняем первоначальное приближение
(з.5б)
Если новая невязка r^ = f — Л/(2) еще велика, то аналогично
можно вычислить новую поправку z^=A~l№ и новое уточнение
£(3) и т. д. Если начальное приближение t^ не совсем уж плохо
и матрица имеет не катастрофически плохую обусловленность,
то процесс итерационного уточнения сходится очень быстро, и на
практике достаточно сделать только одну поправку. Вычисление
невязки дает еще тот дополнительный эффект, что позволяет
осуществлять контроль точности решения. Поскольку
вспомогательная система (3.55) решается с той же матрицей, что и исходная,
это позволяет экономить объем арифметических действий, и
суммарный объем операций при проведении одного итерационного
уточнения увеличивается примерно только на 25%. При
программной реализации этого алгоритма необходимо иметь в виду, что
вычисление невязки обязательно нужно делать с двойной
точностью, поскольку она почти всегда получается как результат
вычитания близких по величине чисел, что приводит к потере
первых значащих цифр.
136

Особый случай представляет собой решение внешней краевой
задачи на плоскости. Дело в том, что если непосредственно из
системы (3.27) найти функцию плотности простого слоя
(напомним, что при этом перед внеинтегральным членом левой части
второго уравнения надо поменять знак), то соответствующий
потенциал, как это видно из (3.15), при- Р-+оо может также
стремиться к бесконечности. В то же время постановка плоской
внешней краевой задачи содержит условие ограниченности
потенциала. Чтобы удовлетворить последнему требованию, можно
поступить следующим образом.
Мы для простоты рассмотрим 1-ю краевую задачу при наличии
внутренних границ с условиями на С3, выраженными третьим
уравнением из (3.27). Определим сначала плотность \х0
непосредственно из системы (3.27) при заданном распределении
потенциала gi(P) на границе (второе уравнение — для Р<=С2 — мы
исключили). Далее найдем функцию \i\ как решение краевой
задачи, в которой потенциал на границе всюду равен единице (в
(3.27) правую часть gx(P) для РееСх надо заменить на 1). Для
этих двух задач найдем соответствующие значения полных
зарядов на границе Qo = J juto(Q) dl, Q\ = \ H-i(Q) dl и определим некото-
c с
рую постоянную б из условия Q0 + 6Qi=0.
Очевидно, что функция
является гармонической функцией, принимает на С\ граничные
значения £i(P) + 6oh обращается в нуль на бесконечности. Легко
также показать, что v\(P)=l, поскольку эта функция есть
единственное решение уравнения Лапласа, равное на всей границе
единице. Отсюда получаем, что потенциал v(P) = v0(P) — б есть
искомое решение внешней краевой задачи, поскольку на границе
он принимает заданные значения g\(P)9 а на бесконечности
стремится к постоянному числу б.
Если функция плотности из решения интегральных уравнений
найдена, то распределение потенциала как для внутренней краевой
задачи, так и для внешней, определяется из интеграла
Кроме того, с помощью дифференцирования подынтегрального
выражения в (3.57) могут быть вычислены производные
различных порядков. Например, первая производная по направлению
/ определяется выражением
(3.58)
137

7 tWt [x-x'(t')]cos(1, x)
— -
Oti
Такая возможность имеет большое значение при
необходимости нахождения производных потенциала, поскольку зачастую
используемое численное дифференцирование с помощью конечных
разностей приводит к потере верных значащих цифр.
Отметим, что для вычисления производных в точках на границе
или вблизи нее при интегрировании по интервалам, близким к
«точке наблюдения» (х, у\ необходимо производить выделение
логарифмической особенности, как и при определении элементов
матрицы А.
Численные методы решения интегральных уравнений для
потенциала простого слоя менее исследованы в теоретическом
плане, чем методы конечных разностей или конечных элементов.
Для многосвязных областей или кусочно-гладких границ оценки
погрешности решения неизвестны.
Мы приведем без доказательств результат, полученный В. В.
Ворониным и В. А. Цецохо [32] для уравнения
К (Л Q)ix(Q)dl=g(P\
где Г — замкнутая гладкая кривая на плоскости, а ядро К(Р, Q)
имеет логарифмическую особенность.
Введя параметризацию кривой, интегральное уравнение
представим в виде
где
a Li — некоторый непрерывный из Ср> а в С7' а оператор, 0<а< 1,
q = тт(р + 2, г). Предполагается, что g(x) принадлежит
пространству СЛ'а периодических функций, r-я производная которых
удовлетворяет условию Гельдера с показателем ос. Норма вводится
следующим образом:
max |g(T)l+suf'
Обозначая через juii(t) приближенное решение интегрального
уравнения, получаемое при кусочно-линейной аппроксимации
\х(т) на сетке с шагом h и использовании метода коллокаций,
138

имеем при г>3 оценку
При кусочно-квадратичной аппроксимации функции \i (т)
получается более точная оценка для приближенного решения \х2 (т):
\\п h\2\\g\\ray
где yrh — hr~l при 2<г<3 и yrh = h3~a при г>4. Через Сь С2
обозначены не зависящие от h постоянные.
3.2.2. Осесимметричные задачи. Решение осесимметричных
задач теории потенциала в цилиндрической системе координат
производится во многом аналогично плоскому случаю с тем
основным отличием, что ядра интегральных уравнений имеют более
сложный вид.
Если r,z — координаты образующих осесимметричных
поверхностей, то после перевода описания граничных отрезков S/ к
параметрическому виду
г = г(т), z = z(t), а/^т^Р/, /=1,2, ..., L,
систему интегральных уравнений (3.27), (3.28) можно привести
к виду
,(t')/(t')G3(t, T')dT' = gi(r), Р(т) е Г,,
О[а G3(t, t') +
-±- G3(P(t), Q(x'))W)dx' = g2(x), P(x) e Г2,
Кт^Оз^т), Q(x'))/(x')rfT' = 0, Р(т)еГ3.(3.59)
Здесь /(т') — шаблон преобразования 7(т/)= ( ^
) т=т/. Ядро и его производные описываются формулами
GT TV
, т') = [г(т). + r'Mf + [z(x) - z'(t')P,
(nQ, Z),
dnQ дг —v-^w I dz
"I \ / С/1*\ Iff иЛ I /л СЛ\
— —^ — t,\k) — Д(«) , (о.,ои)
r'(z'-z)
139

где E(k) — полный эллиптический интеграл второго рода. Во
втором уравнении системы (3.59) знаки «-+-» и « — » относятся
соответственно к внутренней и внешней краевым задачам. Потенциал
плотности простого слоя
) = \ [i(T0G3(
, z,
т'), z'(t')) /C
(3.61)
в данном случае обращается на бесконечности в нуль, и различия
методов решения внутренней и внешней задач, как это было для
плоскости х, у, здесь не имеется.
Численное решение интегральных уравнений (3.59), как и в
предыдущем пункте, проводим с помощью дискретизации границы,
аппроксимации плотности В-сплайнами (3.44) с учетом
особенностей в узловых точках по формуле (3.42) и формировании
алгебраической системы вида (3.51) из условий коллокаций с
добавлением уравнений граничных условий для сплайнов.
Получаемая система линейных алгебраических уравнений (3.54) имеет
матрицу А такой же структуры, только определение ее элементов
требует более сложных вычислений.
Эллиптические функции K{k) и E(k) могут быть
аппроксимированы с высокой точностью известными
полиномиальными представлениями. Одна из таких аппроксимаций,
обеспечивающая максимальную ошибку не более 6ХЮ~~7, имеет
вид
(3.62)
/=0 /=0
Значения коэффициентов а„ bt, ciy dt определяются из табл. 8.
Таблица 8
ai
b,
ci
0
1,386294361
0,5
1,0
0,0
l
0,097932891
0,124750742
0,44479204
0,249697949
2
0,054544409
0,060118519
0,085099193
0,08150224
3
0,032024666
0,010944912
0,040905094
0,01382999
Поскольку вычисление эллиптических интегралов является
трудоемкой и многократно повторяемой операцией при
формировании матрицы системы и расчете потенциалов, то целесообразно
для некоторых интервалов изменения аргумента k использовать
более экономичные формулы. Например, при малых значениях
140

k эффективно использовать ряды [55]:
где k' = -yjl — k2, Ш\ = ((1 — k')/(\ + k'))2. Использование
выписанных пяти членов ряда обеспечивает при k ^ 0,5 величину
погрешности не более 10~10.
Как видно из (3.60), (3.62) ядра интегральных уравнений и в
осесимметричных задачах имеют логарифмическую особенность
при ту'->т. Поэтому при вычислении элементов матрицы Л, когда
интервал интегрирования примыкает к точке наблюдения,
необходимо делать аддитивное выделение особенности по формуле (3.53).
Само численное интегрирование также целесообразно проводить
с помощью квадратурных формул Гаусса.
3.2.3. Трехмерные краевые задачи. Численное решение
интегральных уравнений для трехмерных краевых задач, не отличаясь
по принципиальным моментам от случая двумерных задач,
является гораздо более сложной проблемой в техническом плане. Дело
заключается, естественно, в повышении размерности. Функцию
плотности надо аппроксимировать на двумерных многообразиях,
а численное интегрирование проводить по поверхностям, имеющим
в практических задачах зачастую сложную конфигурацию.
Особенности поверхностной плотности потенциала теперь имеют место
в окрестностях двугранных или трехгранных углов, и ее
асимптотическое поведение имеет более сложный вид. Если характерный
шаг дискретизации границы есть А, то порядок получаемой
системы линейных алгебраических уравнений равен O(h~2). При этом
для обеспечения заданной точности возникает необходимость
решения плотных систем с числом уравнений до тысячи или более,
что требует больших ресурсов ЭВМ.
Система интегральных уравнений в данном случае
описывается формулами (3.25), (3.26), которые мы несколько
конкретизируем:
dGx _ X-X' dGi _y-y> 001 _ z-zf (3-63)
dx ~~ #3 ' Qy #3 ' ~z ~RZ '
Здесь х, у, z и х', у', z' — координаты соответственно точек Р и Q.
Во многих ситуациях оказывается удобным параметрическое
описание граничных поверхностей
x = x(U\ y = y(U\ г = г$Л), (3.64)
141

особенно, если геометрия области позволяет в переменных 5> £
представить границу, состоящей из прямоугольников
a^<g<pP, с42) <£ < |3(m2), /=1,2 Z., m=l,2,...,Af.
Якобиан преобразования (3.64) задается выражением
где в квадратных скобках через дроби обозначены определители
вида
вида
Е. О
В переменных £, £ в окрестности ребер двугранных углов
легко осуществить выделение особенности для граничных условий
1-го рода. Функция плотности представляется в виде произведения
n(g,£) = Й1,£)р(£,£), (3.66)
где первый множитель есть уже гладкая искомая функция,
а второй характеризует асимптотическое поведение плотности
вблизи особенности. В плоскости |, £ части различных граничных
поверхностей будут представляться прямоугольниками или
другими фигурами, и в каждой из них р(£, £) определяется по-своему. В тех
подобластях, на границах которых особенностей нет (или они не
учитываются), полагается р(|, у = 1. Если же, например,
прямоугольник [ii, 62] X [Si, £2] ограничивается ребрами двухгранных
углов | = |i, t == £1 с величинами соответственно соi, C02, то
надо
P(U) = ((Б - БОХ1(Е - ЕО-)-1,
где значения xi, x2, определяются, как и для двумерных задач,
формулами (3.43). В общем, р(£, £) должно содержать столько
множителей, сколько в данной подобласти определения р
содержится разных особенностей.
В плоскости (£, Q построим прямоугольную сетку
I = Ь, £= S/, / - 1,2,..., /, / = 1,2, ..., У, (3.67)
на которой проведем кусочно-полиномиальную аппроксимацию
плотности pi(g, £). Такие аппроксимации — билинейная, биквадра-
тичная, бикубическая — можно строить путем непосредственного
обобщения одномерных В-сплайнов. С другой стороны, фактически
задача аппроксимации здесь стоит та же, что и в хорошо
разработанной теории конечных элементов (см. § 2.2). Используя
технику построения треугольных или четырехугольных конечных
элементов, несложно провести аппроксимацию плотности и в тех
случаях, когда граничные поверхности сложные и в плоскости
142

(I, £) представляются совокупностью фигур различных типов.
Простейший метод заключается в триангуляции отображения
граничных поверхностей в параметрической плоскости и
использовании кусочно-билинейной аппроксимации. На прямоугольной
сетке (3.67) при этом будем иметь
^-^)+ ^Д. (ki+i-Vn), (3-68)
где frj = £,(&, £/), & < | < g/+i, £, < t < S/+i-
Используя середины сторон триангуляции или другие
вспомогательные точки, можно строить конечно-элементные
аппроксимации более высокого порядка точности, как это описано в § 2.2.
Вводя единую триангуляцию точек дискретизации с помощью
индекса «k» и используя финитные базисные функции -ф*(£, £)
конечно-элементной аппроксимации, мы можем записать
Й6,£)~2 скук(ЪЛ), (3.69)
k
где ck — подлежащие определению коэффициенты;
суммирование производится фактически по малому количеству функций г|)ь
отличных от нуля в точке (£,£). В частности, для кусочно-бйли-
нейной аппроксимации, обозначая индексами k\, &2, &з точки (/,/),
(/+1,/), (/,/+1), мы можем для соответствующего треугольника
PkiPk2Pk3 переписать (3.68) в виде
С). (3.70)
Коэффициенты с^ в данном случае совпадают со значениями
ill в соответствующих точках, а базисные функции приводятся к
виду
ь)=1Ы£^)^
Подставляя аппроксимацию ji(^, Q в интегральные уравнения
(3.25), записанные для точек дискретизации границы Р^ k=\,
2, ..., /С, и производя (численно или аналитически) вычисления
необходимых интегралов, получаем систему линейных
алгебраических уравнений для коэффициентов ck. Для задачи Дирихле
систему можно записать в виде
aklci + ... + akkck + ... + akKcK = gi(Pk), k = 1/2,... К, (3.71)
*
где элементы матрицы аы описываются выражением
X Ог(хк, ук, zk, x'(l', £'), У'{1', I'), г\\\ 1')Щ1\ t,')dV dt,'. (3.72)
143

Аналогично с помощью (3.25), (3.63), (3.66), (3.69) могут
быть записаны алгебраические уравнения и для других типов
граничных условий.
3.2.4. Интегральные уравнения для некоторых других
эллиптических задач. Формально близким обобщением уравнения
Лапласа является уравнение Гельмгольца
Аф_й2ф = 0, (3.73)
к которому сводятся, например, задачи об электромагнитных
колебаниях. Решение этого уравнения представляется с помощью
плотности простого слоя в виде
ф(/>)= J KQ) eXPi^'Q)} dS, QzeT. (3-74)
Аналогично рассмотренному выше, для различных краевых задач
могут быть сформулированы интегральные уравнения.
Другим практически важным классом являются задачи,
близкие к осесимметричным. Рассматривая потенциал в
цилиндрической системе координат и представляя его в виде разложения по
азимутальным гармоникам
Ф(г, z, в)=фо(г, z) + q>^(r, z) cos в + ф^(г, z)sin6 +
z) cos2e + q#>(r, z)sin26 + ..., (3.75)
мы получаем, что каждая из них удовлетворяет уравнению
0, /_1. 2. (3.76)
Решение такого уравнения можно искать с помощью
аналога плотности потенциала простого слоя в виде интеграла
фт(Р)= ^^m\Q)G^m\PyQ)dSQy (3.77)
г
где функция G(m)(P,Q) описывается выражением
costnQdd __
я
2г' Г cosm9flf6
(3.78)
O ()
0
Здесь ft определяется формулой из (3.28), как и для осесим-
метричной задачи потенциала, а (г, г) и (г', z'), как обычно,
представляют координаты точек Р и Q.
С помощью этих представлений формируются интегральные
уравнения решения краевых задач для ц)т(г, z), как это делалось
в п. 3.2.2 (в уравнениях (3.59) надо только заменить G на
G(m)). Ядра новых уравнений выражаются через ряды от полных
144

эллиптических интегралов:
ОМ(Р,д)=(_1Г_|_(Л0+ 2 sM
A0 = K(k), At = HK(k)-mi Л, = аИ/_, + р;^-2. / = 2,3,...,
So=l, Sl = sHl[(-l)*jj±zlfo (3.79)
_ 2/-2 1+fe2 o._ 3 — 2/ ._, 2
В частности, для т = 2 эти выражения сводятся к формуле
Для вычисления K(k) и £(й) можно использовать
аппроксимации (3.62), однако при малых значениях аргумента (&<:0,2)
нахождение разности K(k) — E(k) будет сопровождаться
значительной погрешностью. Чтобы этого избежать, следует использовать
представление эллиптических интегралов через степенные ряды,
хорошо сходящиеся при небольших k:
т( т
количество членов можно выбирать автоматически по значению
&, чтобы отброшенные члены не нарушали необходимой
точности.
Для других типов краевых задач можно сформулировать
следующий общий результат [103]. Пусть в области Q с границей
Г ищется решение задачи и(Р), P^Q:
g, (3.82)
где L — эллиптический оператор второго порядка, для которого
известно фундаментальное решение /С(Р,РГ), ди/dl — производная
и по направлению /. Предположим, что условия существования
и единственности решения данной задачи выполнены и что оно
представимо в виде
и{Р)=\ k'(P, P')y{P')dP'. ' (3.83)
г
Тогда для функции <р(Р) из (3.82) получаем интегральное
уравнение
(а + Р -£i)k{P' Р'ЫРУР' = g(P), РеГ. (3.84)
10 В П Ильин 145

Г i
§ 3.3. Примеры решения методических задач
Для иллюстрации точности методов интегральных уравнений
потенциала простого слоя мы приведем несколько результатов
по расчетам задач с известными точными решениями,
выполненных В. А. Катешовым с
помощью описанного в последней
главе пакета программ Эфир.
А. Поле сферического
конденсатора. В
цилиндрической системе координат расчет-
•* ная область ограничивается двумя
z полукругами, см. рис. 19. Точное
решение в указанной на рисунке
системе координат имеет вид
Рис. 19.
Rxz
где
радиусы соответственно
внутреннего и внешнего кругов. Потенциал внутреннего круга
полагается равным единице, а внешнего — нулю, значения
радиусов— /?i = 60, /?2 = 180. В табл. 9 приведены полученные в
расчетах численные значения, а также величины соответствующих
погрешностей в процентах не только для потенциала, но и его
третьих производных (их точные значения описываются
формулой ф"' = — тЛА г?-).
-г)4
Таблица 9
Z
1
2
3
4
5
6
7
8
9
10
11
10- ф
0,2941071
0,6249999
0,9999997
1,428571
1,923076
2,499998
3,181816
3,999997
4,999996
6,249999
7,857229
103-б%
3,7
1,6 • 10~2
3 • 10"2
-7 • 10~2
2,08- 10~'
8 • 10~2
1,3- 10~1
7,5-. 10"2
8,0 • 10~2
1,6- 10~2
-1,1
100 . q>"'
0,3678504
0,4394198
0,5333328
0,6559758
0,8192981
1,041665
1,352364
1,799996
2,469149
3,516313
5,217868
ю4. б%
—4020
76
0,38
1,8
1,1
4,8
4,4
2,2
-3,6
' -197
5700
Эти данные получены из решения интегрального уравнения
(3.59), соответствующего задаче Дирихле для двумерного
уравнения Лапласа в цилиндрической системе координат. Плотность
потенциала аппроксимировалась квадратичными В-сплайнами на
равномерной сетке, полученной разбиением внутреннего круга
на 10 интервалов, а внешнего — на 30. Вычисления
вспомогательных интегралов по контуру проводились с помощью квадратур-
146

ных формул Гаусса, использующих по 4 узла на каждом
интервале разбиения границы.
Как видно из таблицы, расчет потенциала и его производных
осуществляется с достаточно высокой точностью вдали от
границы, однако вблизи нее погрешность существенно повышается.
При проектировании электронно-оптических систем,
формирующих изображения, для определения коэффициентов аберраций
и других оптических характеристик приборов необходимо на оси
симметрии вычислять с высокой точностью потенциал и его
производные до второго порядка, в том числе вблизи границы и даже
на поверхности самих электродов. С целью демонстрации
возможного способа решения такой задачи мы опишем результаты
следующего численного эксперимента. Рассчитывалось поле
сферического конденсатора с теми же параметрами, что указаны
выше. Внутренний полукруг разбивался на 20 интервалов, а
внешний — на 60. Порядок сплайнов использовался второй, а
число гауссовских квадратур 4, как и ранее.
Поскольку вблизи электродов производные вычисляются
непосредственно из интегралов по границе со значительной
погрешностью, применялся следующий прием. На отрезках [О, Н\]
и [L — #2, L] оси симметрии (L = /?2 — R\) вблизи внутреннего и
внешнего электродов потенциал вычислялся с помощью
эрмитовых полиномов 5-го порядка
ф(г) = а0 + ax{z — z0) + a2(z — z0)2 + a3(z — zof +
b(z - z0)5, (3.85)
где Zo = O для левого отрезка и Zo = L — для правого. Для
определения коэффициентов полиномов на каждом из отрезков
использовались, с одной стороны, значения потенциала и
известные соотношения между производными на электродах
ф0 = ф(2о), ф' = -*-<р", <р™ = -*-<р<'"> - -g-ф', (3.86)
где R — радиус кривизны граничной поверхности, а с другой —
вычисленные с помощью интегралов значения потенциала cpk и его
двух первых производных <р£, <р£'. В результате получаем систему
уравнений
ai8k + a28k + ci3bk + a48i + a58l = q)k — <p0,
ах + 2a28k + 3a36f + АаАЫ + ЪаъЬ\ = <р£,
2а2 + 6а36, + 12аЛ + 20а5б1 = q#, (3.87)
а\— /?а2 = 0, а4—-|а3~-|^-=0, 8k==zk — z0.
В целом на отрезке [О, L] потенциал определялся в 121
равномерно расположенной точке (включая граничные), причем на
отрезке [Н\, L — Я2] — непосредственно из интеграла от
поверхностной плотности. Затем по найденным значениям строился
интерполяционный сплайн 5-го порядка с граничными условиями
Ю* 147

вида (3.86), а путем его дифференцирования вычислялись в тех
же узлах первые производные. Результаты расчетов при #i = 15,
#2=10 приведены в табл. 10.
*
Таблица 10
Z
1
3
5
10
16
32
48
64
103-ф
2,793287
8,474550
14,28567
29,41171
48,78047
108,1082
181,8182
275,8622
104 • 6%
3
3
0,3
0,2
0,02
0,01
0
0,003
103 • ф'
2,808892
2,872729
2,938768
3,114189
3,346210
. 4,108852
5,165309
6,688444
Ш4 • 8%
3
3
3
0,7
4
3
4
3
105 • ф"
3,13863
3,24627
3,35892
3,66428
4,08232 ,
5,55146
7,82665
11,5324
ю2. ь"%
0,7
0,7
0,9
1,4
3,7
1,7
0,6
0,5
Приведенные значения вторых производных получены с
помощью центральных разностей от первых («сплайновых»)
производных. Вычисления <p"(z) непосредственно из интерполяционного
сплайна дают очень хорошую точность при точных (p(z,-), а при
наличии ошибки потенциала в 7-м знаке, как это имеет место здесь,
использование сплайна для численного дифференцирования
приводит к погрешности <р" в 10—50 раз больше, чем в табл. 10. В
данном эксперименте были также вычислены из сплайна 3-я и 4-я
производные по г в точке г = 2 = 0. Их расчетные значения
оказались равными 5,14495' 10~~7 и 1,14353-10~8, а соответствующие
погрешности — 0,002% и 0,004%.
Рассмотренные результаты свидетельствуют об очень высокой
достижимой точности данного метода, которой, по-видимому,
трудно достичь в методах конечных разностей или конечных
элементов.
Б. Цилиндрический конденсатор. Для
иллюстрации решения двумерной задачи в декартовой системе координат
мы рассмотрим первую краевую задачу
для области, изображенной на рис. 20.
Радиусы и потенциалы кругов равны
соответственно /?1 = 1, /?2 = 2, ф(/?!)=1,
ф(/?2)=о.
Точное решение в данном примере
описывается формулой
тт Рис. 20.
Численное решение искалось на
окружности радиуса /?=1,5, где точное
решение равно 0,415039. В табл. 11 приведены для различных
координат х значения фЧИСл и погрешности б в процентах (соответ-
148

ствующие значения координаты у определялись из уравнения
окружности). Расчеты проводились при разбиении меньшей
окружности на 20 равных интервалов, а большей — на 40.
Таблица 11
X
—0,3
—0,4
—0,5
—0,6
—0,7
^числ
0,415019
0,415003
0,415020
0,415051
0,415060
Ю3 • 8%
5
9
4,8
—2,8
—5,3
X
—0,8
—0,9
— 1,0
— 1,1
— 1,2
ЧцИСЛ
0,415072
0,415050
0,415044
0,415035
0,415034
ю3 -б%
—7,8
—2,8
—3,8
0,9
1,3
В. Расчет гармоники неосесимметричного
возмущения потенциала в сферическом
конденсаторе. Пусть некоторая осесимметричная поверхность
с заданным потенциалом подвергается малой эллиптической
деформации таким образом, что в поперечном сечении круг радиуса
R превращается в эллипс с длинами полуосей а, 6, где a = R, b =
= R(l—е), е — параметр возмущения. Тогда получаемое
распределение потенциала представимо в виде (3.75). Мы рассмотрим
задачу вычисления первой гармоники <р\1\ которая удовлетворяет
уравнению (3.76) при т=1 и граничному условию ф^) т==—г~| г>
для сферического конденсатора с возмущаемой внешней сферой.
Вычисления проводились при тех же счетных параметрах, что
и в п. А. В табл. 12 даны результаты расчетов первой производной
по г от ф^ при г = 0 и разных значениях г. Через д^\1 обозначены
Таблица 12
Z
0
10
20
30
60
100
110
1С3 . Эф(1)
1,5432
1,5321
1,5181
1,5000
1,4022
9,2648
5,9337
103 . ЭФ<1>
1,5439
1,5324
1,5208
1,5032
1,4051
9,2643
5,9641
\%
0,04
0,02
0,18
0,21
0,21
0,006
Ц,51
ID3. ,ф(1)
1,5432
1,5327
1,5212
1,5036
1,4053
9,2648
5,9644
би%
0,0006
0,04
0,21
0,24
0,22
0,0004
0,52
точные значения ду^/дг, через дф(,1/—численные результаты,
полученные при задании точных граничных условий для (р{1\ и
через Зф^и — расчетные данные, полученные при задании
граничных условий путем нахождения производной по г на границе от
невозмущенного решения фо, также определенного численно.
Величины бт, 6И обозначают соответствующие относительные
погрешности в процентах..
149

Г. Расчет поля двуслойного сферического
конденсатора. Рассматривается задача о, вычислении
поля сферического конденсатора, имеющего радиусы внутреннего
и внешнего электродов с потенциалами Vi = l, K2 = 0
соответственно для R\ = 6, /?3= 18, в котором имеются две среды с
разными диэлектрическими свойствами: е = ei = 1 для /?i <г</?2= 12
И 8 = 82 = 2 ДЛЯ 7?2<^</?3-
Распределение потенциалов в данном случае описывается
формулой
. . [ах/
V } \а2/
(V\-Vt)
ах =
(Л l-+^( J L
\ R\ R2 ^ 82 V /?2 #3
Ri 82 /?з
В табл. 13 приведены точные и расчетные значения
потенциалов и их первых производных по радиусу фт(г), фт(/)> Фр(г)> Фр(г)
для разных значений г (при r = R2 дана полусумма предельных
величин ф^ ф+).
Таблица 13
г
6
7
8
9
10
11
12
13
14
15
16
17
18
фт
1
0,755102
0,571429
0,428571
0,314286
0,220779
0,142857
0,1098*90
0,0816326
0,0571429
0,0357142
0,0168067
0
1,000000
0,754919
0,571443
0,428574
0,314285
0,220791
0,142857
0,109909
0,0816310
0,0571427
0,0357139
0,0168128
ю-11
ф;
0,285714
0,209913
0,160714
0,126984
0,102857
0,0850059
0,0535714
0,0304311
•'0,0262391
0,0228571
0,00200893
0,00177954
0,00158730
0,285714
0,209048
0,160729
0,126990
0,102861
0,0849117
0,0535714
0,0305361
0,0262364
0,0228567
0,00200905
0,00177525
0,00158714
Расчеты проводились при разбиении полуокружностей с
радиусами Ru R2, R3 соответственно на 6, 12 и 18 интервалов.
Аппроксимация плотности осуществлялась с помощью квадратичных
В-сплайнов. Вспомогательные интегралы вычислялись по
квадратурным формулам Гаусса^ с четырьмя узлами. Как видно из
результатов, точность высокая, но она несколько ухудшается для
точек, лежащих вблизи границы, хотя для граничных точек
погрешность очень мала. Это объясняется тем, что в околограничных
точках программная реализация алгоритмов, использованная для
данных расчетов, не предусматривает выделение особенностей
ядра.
150

Д. Некоторые замечания об
алгоритмических особенностях методов интегральных
уравнений. Рассмотренные примеры, а также опыт решения
других методических и сложных практических задач (см.,
например, [6, 32, 71, 197]), свидетельствуют о высокой
эффективности методов интегральных уравнений для решения краевых
задач.
Однако с точки зрения оптимизации этих алгоритмов имеется
много открытых вопросов, которые мы рассмотрим на примере
уравнений потенциала простого слоя. Как видно из предыдущего
параграфа, метод обладает многими «управляющими рычагами»,
что дает дополнительные резервы усовершенствования, но
создает свои проблемы по их квалифицированному освоению.
Первый вопрос — это выбор способа дискретизации границы.
Увеличение числа точек коллокаций должно, естественно,
повышать точность расчетов, но при этом быстро растет объем
вычислений, поскольку формируемая алгебраическая система имеет
плотную матрицу. Далее, маловероятно, что равномерное
расположение граничных точек является наилучшим. Однако какие-либо
рекомендации по их расположению дать затруднительно, кроме
того общего замечания, что точки целесообразно располагать
гуще там, где плотность потенциала должна меняться круче по
априорным соображениям. Надо сказать, что на практике
зачастую эта проблема решается самым прагматичным образом: точки
коллокаций выбираются равномерно (поскольку это проще всего
в программной реализации), а их количество берется по
максимуму такое, сколько позволяет оперативная память ЭВМ. Добавим
к этому, что если точки коллокаций выбираются на поверхности,
не совпадающей с границей (как это делается в описанных в § 3.1
методах Купрадзе, Рахматуллиной и др.), то возникает
дополнительная проблема оптимального расположения этой
вспомогательной поверхности.
Не менее существенный вопрос — способ и порядок
аппроксимации плотности потенциала. При использовании В-сплайнов,
например, следует определить порядок и вид граничных условий
для них. В работах [117, 197] применяются специальные дробно-
рациональные аппроксимации с нелинейными параметрами,
значения которых подбираются экспериментально из решений
характерных задач. Число точек коллокаций и способ аппроксимации,
естественно, — взаимосвязанные факторы. Повышение порядка
аппроксимации в меньшей степени влияет на трудоемкость самого
алгоритма, но может очень сильно усложнить его программную
реализацию.
Точность решения зависит существенно от методов вычисления
вспомогательных интегралов. Можно, конечно, проверить расчеты
«с запасом», используя квадратурные формулы Гаусса высокого
порядка, но при этом значительно возрастает трудоемкость
формирования матрицы алгебраической системы. Сюда же относится
вопрос о способе учета особенностей ядра интегрального уравне-
151

ния, а в осесимметричных задачах — и об аппроксимации
эллиптических интегралов.
Все эти факторы мы рассматривали пока только с точки зрения
повышения точности аппроксимации. Они, однако, неизбежно
влияют на обусловленность матрицы системы, а при ее ухудшении
возникает вопрос о надежном способе решения алгебраической
системы. Исходная задача представляет собой интегральное
уравнение Фредгольма 1-го рода с ядром, имеющим слабую
особенность логарифмического типа; вопросы устойчивости ее
численного решения недостаточно изучены теоретически. Следует
сказать, что в этом отношении имеются обнадеживающие
экспериментальные данные. Для описанных в предыдущем параграфе
алгоритмов, по крайней мере для систем до 300-го порядка,
численное решение является устойчивым и без применения каких-
либо специальных методов регуляризации. В частности, решение
алгебраических систем методами Гаусса или ортогонализации не
приводит к появлению заметных дополнительных ошибок. Однако
на ЭВМ типа ЕС необходимо применять двойную точность (на
БЭСМ-6 в рассматриваемых задачах достаточно и простой
точности).
В целом проблема согласования, оптимизации и
автоматического выбора счетных параметров для обеспечения заданной
точности и экономичности методов интегральных уравнений требует
дальнейших исследований как теоретического, так и
экспериментального характера.
§ 3.4. О сравнительной эффективности методов решения
интегральных и дифференциальных уравнений
Приведенные в предыдущем пункте результаты, а также и
другие имеющиеся в литературе описания численных экспериментов
свидетельствуют, что методы интегральных уравнений позволяют
добиться такой высокой точности решения и его производных,
которой пока что не достигается в методах конечных разностей
или конечных элементов. Для сокращения наименований методов
мы иногда будем употреблять обозначения соответственно МИУ,
МКР и МКЭ.
В силу этого может возникнуть вопрос — а не является ли
метод интегральных уравнений намного эффективнее других
алгоритмов решения краевых задач? И это несмотря на обилие
в мире публикаций и программных реализаций по методам
конечных разностей и конечных элементов. Одним из весомых
аргументов интегральных уравнений является тот факт, что дискретизи-
руется не вся расчетная область, а только ее граница. Это
означает, что искомая функция плотности в двумерных краевых задачах
зависит фактически от одной переменной, а в трехмерных — от
двух.
Чтобы получить сравнительные количественные оценки
экономичности, мы рассмотрим объем вычислений и необходимой опе-
152

ративной памяти для решения с заданной точностью характерной
краевой задачи — уравнения Лапласа в единичном квадрате с
граничными условиями 1-го рода. Сравнение проведем для
интегрального уравнения с кусочно-линейной аппроксимацией
плотности простого слоя и метода конечных элементов с
кусочно-линейными базисными функциями (это эквивалентно также пятиточечной
конечно-разностной аппроксимации оператора Лапласа). Шаг
дискретизации считаем одинаковым и равным А=1/#, где N —
количество разбиений каждой из сторон квадрата.
- Поскольку теоретическое количественное сравнение
погрешности методов провести трудно, мы примем гипотезу, что
получаемая точность решения в данных алгоритмах при равных шагах
примерно одинакова.
В случае малых h количество неизвестных можно считать
равным AN для МИУ и № для МКР или МКЭ. Матрица системы
линейных алгебраических уравнений для МИУ плотная и содержит
16Af2 ненулевых элементов. В МКР порядок матрицы равен N2;
и она является ленточной с шириной полуполосы N и количеством
ненулевых элементов 5N. Реализация МИУ требует 16Af2
машинных слов для хранения элементов матриц и объем вычислений,
равный C\N2 — для формирования матрицы, 16ЛА3/3 — для ее
решения и kC2N — для вычисления значений потенциалов или их
производных в k точках. Здесь С\ и С2 — не зависящие от h
постоянные, причем довольно большие. Например, в случае
цилиндрической системы координат только одно вычисление полного
эллиптического интеграла К при заданном аргументе k требует около
40 арифметических операций (с учетом того, что определение
одного значения логарифма эквивалентно по времени выполнению
примерно 20 умножениям). Реализация МКР с помощью метода
исключения Гаусса требует объем памяти N3 и количество
арифметических действий Лг/3. При использовании метода циклической
редукции или быстрого преобразования Фурье для решения
разностных уравнений эти цифры меняются на Лг и C3Af2log2Af, где
величина Сз в разных реализациях колеблется между 5 и 10. В
итерационных алгоритмах требуется память в N2 слов, а количество
операций меняется в пределах от C3Af3log2Af до CsN2(log2N)2; рекордные
же методы с использованием последовательности сеток сокращают
объем вычислений до C4Af2. Отметим, что при этом в МКР или МКЭ
находится решение во всех N2 узлах сетки.
«Усредняя» эти оценки, можно резюмировать, что при
вычислении в МИУ значений потенциалов примерно для N точек
рассматриваемые алгоритмы близки по экономичности. Если
же решение требуется найти в N2 точках, то метод
интегральных уравнений будет проигрывать, в силу большого
коэффициента С2.
Если решается неоднородное дифференциальное уравнение,
например, уравнение Пуассона вместо уравнения Лапласа, то
ситуация меняется не в пользу МИУ, поскольку при формировании
алгебраической системы расчет правых частей требует для каждой
153

точки дискретизации границы брать интеграл iiO области, что
приводит к дополнительным операциям порядка O(N3). Кроме того, при
вычислении k значений потенциала или производных нужно
дополнительно kC5N2 действий.
Мы рассмотрели простейшие способы аппроксимации для
сравниваемых методов. Повышение. точности аппроксимации в
принципе можно проводить как в конечных элементах, так и в
интегральных уравнениях, в том числе с учетом асимптотического
поведения решения в окрестности особых точек. Однако для МИУ
такие уточнения гораздо легче реализовать технически, поскольку
область определения искомых функций имеет меньшую
размерность.
Значительные преимущества имеет МИУ при решении внешних
краевых задач, так как применение МКР или МКЭ связано с
необходимостью искусственного замыкания расчетной области и
постановки граничных условий из априорных соображений, что не
всегда можно сделать с хорошей точностью.
Решение же трехмерных задач с помощью МИУ
представляется трудоемкой проблемой. Например, если расчетная область —
единичный куб с шагом дискретизации h= \/N> то порядок
алгебраической системы получается 6N2.
Для ее решения требуется память в 36N4 машинных слов,
а объем вычислений равен 72jV6. Это говорит о том, что даже на
современных ЭВМ реально решать трехмерные задачи только
с достаточно большими шагами сетки.
В методах МКР и МКЭ ситуация более благоприятная,
поскольку памяти нужно только N3 слов, а количество операций при
использовании итерационных алгоритмов меняется от C6^3(log2iV)2
до C6Af4log2Af, в зависимости от типа итерационного процесса.
Следует заметить, что МИУ наиболее эффективно применяется
только к относительно узкому классу дифференциальных
уравнений, для которых известны фундаментальные решения. Сюда
входят уравнения, коэффициенты которых или постоянны, или
кусочно-постоянны, или имеют специальный вид. С помощью
различных приемов к интегральным уравнениям можно свести
дифференциальные задачи с переменными коэффициентами общего
вида, но экономичность МИУ будет при этом падать.
В целом же рассмотренное нами подтверждает очевидный факт,
что не существует самого лучшего метода для решения всех
задач. Для каждой задачи, точнее класса задач, имеется свой
предпочтительный алгоритм. И в зависимости от характера задачи
различие в эффективности алгоритмов может быть большим или
меньшим.
Заканчивая сравнительный анализ, необходимо сказать, что
современное понятие алгоритма включает его программную
реализацию. Поэтому окончательное суждение об эффективности
методов надо проводить с учетом разных факторов, в том числе
не являющихся чисто математическими в традиционном смысле,
на которых мы остановимся в последней главе.
154

§ 3.5. Краткий обзор других методов
решения интегральных уравнений
3.5.1. Метод вспомогательных зарядов. В работах В. Т. Овча-
рова, а также и других авторов [141], получил применение
подкупающий своей простотой подход к расчету электростатических
полей на основе представления потенциала в виде совокупности
полей точечных зарядов, располагаемых каким-либо специальным
образом внутри расчетной области или вне ее. Для плоских задач
такое представление имеет вид
Ф,У) = £ qiln I (3.88)
(xf + (yy)2
где Xi, yi — координаты точечных зарядов qt. Зафиксировав
значения Xi, yi и выбрав какие-либо N точек л:/, у\ на граничных
поверхностях с заданными потенциалами ф(х/, yf), для определения
дополучаем систему алгебраических уравнений
2 frln _ * — = qfr;,j/yQ, /,/=l,2,...,JV. (3.89)
V)+(/)
Для осесимметричных задач цилиндрические координаты Г/,
Zi будут соответствовать зарядам, потенциал которых
описывается формулой
_
Система уравнений для qt имеет вид
N
«./=1.2,...,^ (3.91)
Вместо уравнений (3.89), (3.91), фиксирующих значения
искомого потенциала в заданных точках, можно было бы записать
условия минимума среднеквадратичного отклонения ср(х, у) от
значений в точках (jc/, yf). В этом случае количество зарядов и
число «контрольных» точек на границе не обязательно должны быть
равными.
Одна из проблем метода вспомогательных зарядов — это
оптимизация их расположения относительно границы. Если,
например, около прямолинейного электрода с постоянным
потенциалом поле представить как результат действия расположенных
вблизи точечных зарядов, то удовлетворение граничных действий
будет выполняться со значительной ошибкой, поскольку эквипо-
тенциали такого поля около самих зарядов будут существенно
волнистыми линиями. Если же вспомогательные заряды располо-
155

жить дальше от электрода, то ухудшится обусловленность
алгебраической системы, что приведет к погрешности вычисления #/.
Перейдя от «физической» трактовки алгоритма к
математической, легко видеть, что использование вспомогательных зарядов
соответствует кусочно-постоянной аппроксимации плотности в
методе, развитом А. X. Рахматуллиной и И. И. Кочетовым, который
был описан нами в § 3.1.
3.5.2. Аппроксимация потенциала гармоническими
полиномами. В работах А. Г. Власова, Ю. А. Флегонтова и ряда других
авторов [31] получил развитие метод расчета электростатических
полей на основе представления решения уравнения Лапласа в
виде рядов от гармонических функций. Здесь можно выделить два
основных подхода к вычислению потенциалов.
Первый — метод переопределенных рядов А. Г. Власова —
основан на разбиении расчетной области й на ряд подобластей
простой формы так, чтобы в каждой из них решение
представлялось в виде рядов от гармонических функций, точно
удовлетворяющих заданным граничным условиям на той части поверхности
подобласти, которая является границей Q. На поверхностях
сопряжения подобластей выписываются условия непрерывности
потенциала и его нормальной производной, служащие уравнениями для
коэффициентов рядов. Трудности такого подхода заключаются
в реализации задач со сложными конфигурациями границ,
особенно если алгоритм требуется автоматизировать в универсальных
программах, рассчитанных на широкий класс областей.
Второй метод заключается в том, что расчетная ограниченная
область й, имеющая сложную границу Г и, возможно, кусочно-
гладкую и многосвязную, погружается в область Й' простой
конфигурации: прямоугольник — для плоских задач, цилиндр —
для осесимметричных. Приближение ф к искомому решению ф
ищется в виде суперпозиции функций, гармонических в Q'. Если
области йий' имеют общий участок границы S, то приближение
Ф строится так, чтобы удовлетворялось граничное условие ф|5 =
= ф|5. Для Й', представляющей собой цилиндр 0<г</?,
d, можно выбрать следующую аппроксимацию:
+ 2 a|kI>/o(a*r)shp*(c-d)+ S ai2V0(a*r)sha*(d-z) + az + b, (3.92)
где /о, /о — функции Бесселя первого рода соответственно от
вещественного и мнимого аргументов, а* = м*//?, а р* — k-й корень
функции /о. Значения L, М, N определяют точность аппроксимации
и количество неизвестных в получаемой алгебраической системе.
Коэффициенты а$\ ail\ ctp искомого представления ф могут
выбираться из условия минимизации любой из норм функции
невязки граничных условий г = ф|г — <р|г (мы рассматриваем
первую краевую задачу).
156

Авторами показано, что если граница Q состоит из конечного
числа простых поверхностей Жордана с заданными потенциалами,
то можно построить гармоническую функцию ф, равномерно
аппроксимирующую на Г решение ф с произвольной заданной
точностью. То есть обеспечивается выполнение неравенства
1ф — ф1г<е (3.93)
ДЛЯ ЛЮбыХ 8.
Отсюда в силу принципа максимума для гармонических
функций погрешность приближенного решения также не будет
превосходить е и для любой точки расчетной области.
Получаемые в этом методе алгебраические уравнения для
коэффициентов гармонических рядов могут иметь плохую
обусловленность, и тогда применяются методы регуляризации.
Если погрешность получаемого приближенного решения имеет
максимумы в некоторых точках границы, то для повышения
точности в окрестности таких точек можно расположить
вспомогательные заряды, величины которых определяются из условия
минимизации ошибки.
Строго говоря, данный подход можно с одинаковым успехом
считать методом решения как дифференциальных, так и
интегральных уравнений. Мы его относим к последним, поскольку здесь
имеется та общность в технологии, что алгебраические уравнения
формируются из условий удовлетворения граничным условиям
в точках границы.
Мы рассмотрим также относящийся к этому классу метод
Купрадзе — Алексидзе для решения задачи Дирихле [5]. Этот
метод (коротко упомянутый в § 3.2) заключается в следующем.
Пусть требуется найти в ограниченной трехмерной области
G гармоническую функцию, принимающую на границе Г заданные
значения g(P). Обозначим через G\ область с достаточно гладкой
границей Гь целиком включающую в себя область G, и
предположим, что минимальное расстояние между Г и Г\ больше нуля.
Введем функцию v(Q) — -r-^-(Q), Q 6 Г, удовлетворяющую
интегральному уравнению
- Jw=f(p)' Р6Г" f^=$^-4(w)'(3-94)
г г
с помощью которой искомое решение находится по формуле
щР)=— \ ———*-g(Q) (—/—г) dS, P 6 G. (3.95)
г
Приближенное решение уравнения (3.94) ищем в виде отрезка
ряда Фурье
= 2 ъу{Р) (3.96)
157

по специальным образом строящимся ортогональным функциям
Введем функции
)f /=1,2,..., легь (з:97)
где Pi — элементы счетного множества точек, расположенных
всюду плотно на поверхности 1\. Можно показать, что система
функций [ty(P)} линейно независима на поверхности Г, т. е. для любого
N
N из равенства 2
) = 0, Р6Г, следует 2 |а«1=0.
Из
этого вытекает, что можно построить ортонормированную на Г
систему функций
<р/(Р)=2 bik^k{P\ P е Г, (3.98)
удовлетворяющих условиям с ф^ф/ dS = 6ki- Проведение процес-
г
са ортогонализации может быть сведено к формуле
где используются обозначения для определителей
(3.99)
Г
Уравнение (3.94) запишем для точек Pk
= Fk= \g(Q)
-jL
di2 ... d
\ в виде
, (3.100)
\j() (3.101)
Умножая первые / уравнений (3.101) на коэффициенты
(k= I, 2, ..., /) и складывая их, получим
\ v(Q) 2
= ^= 2
r k=x r ^=1
Определяя из этих соотношений с*, искомое приближенное
решение u{N\P) находим из (3.95) после подстановки (3.96) вместо
3.5.3. Применение метода конечных элементов к решению
интегральных уравнений. Мы коротко остановимся на решении
интегральных уравнений с помощью метода Галеркина. Не
останавливаясь на его теоретическом обосновании, которое было
проведено Ж. Неделеком и другими зарубежными математиками
[142], мы только отметим основные алгебраические особенности
на примере трехмерной задачи Дирихле. Для плотности потен-
158

циала простого слоя в этом случае мы имеем интегральное
уравнение первого рода
где ху у означают точки на границе, а \х — у\ — расстояние между
ними.
Как обычно, метод конечных элементов предусматривает
замену расчетной области некоторой ее дискретизацией: в данном
случае поверхность Г аппроксимируется совокупностью элементарных
площадок Г/г. Как было отмечено в § 3.2, при двумерном
параметрическом представлении поверхности Г в плоскости параметров это
может быть простая триангуляция. Далее вводится
конечномерное пространство Vh, имеющее базисом некоторые финитные
функции г|),(х), /=1,2, ..., N, где N — размерность Vh- Вместо
решения уравнения (3.93) ищется ее проекция на Vh в виде
\xh(x)= 2 cft{x\ *е=Гл. , (3.104)
По методу Галеркина искомые c-t определяются из системы
уравнений
-^\ \ 2 cftiy)^(х)/ \x-y\dxdy = \g(xMx)dx. (3.105)
г г /~~1 г
В простейшем случае Yh может представлять собой
совокупность треугольников Tiy a Vh — пространство кусочно-постоянных
функций. Тогда if>/(jt) есть функция, равная единице в Г/ и нулю —
в остальных треугольниках, а уравнение (3.95) записывается в
векторной форме
Ас = g, с = {си с2, ..., cN}9 g = {gu g2, .... gN]. (3.106)
Элементы матрицы пц и правой части g/ описываются формулами
\ \^ $(***• (ЗЛ07)
Данный подход позволяет единообразным способом строить
аппроксимации более высокой точности; в том числе и для других
интегральных уравнений.
3.5.4. О решении интегральных уравнений для потенциала
двойного слоя. Численное решение ряда краевых задач
эффективно осуществляется с помощью потенциала двойного слоя. Мы
рассмотрим коротко его реализацию для внутренней задачи Дирихле
на плоскости в предположении, что граница области односвязная,
гладкая и выпуклая. Уравнение контура С запишем в
параметрическом виде
= х(т), у = у(т)у
159

при этом# считаем, что функции х(т), у(т) имеют непрерывные
производные х(т\ у(т\ не обращающиеся в нуль одновременно.
Потенциал двойного слоя (3.16) в данном случае выражается
формулой
(З.Ю8)
. где (х, у) и (*', у') — координаты точек Р и Q, а ф — угол между
вектором PQ и нормалью в точке Q. Этому же выражению можно
придать вид
где do — усол, под которым элемент дуги контура (1т виден из
внутренней точки Р. В этих обозначениях интегральное уравнение
(3.23) принимает вид
р
\ ^ v(t')</t' = g(r). (3.109)
Если мы поделим последнее уравнение на л, введем ядро
- к(т, х')= - ±£- = - -L-fL arctg ^Р-^,
4 у я d% п d% ъ х(т') — х(т)
и поставим перед интегралом параметр А,, то получим
т>(тО^т'=^(т). (ЗЛЮ)
Можно показать (см., например, книгу Л. В. Канторовича
и В, И. Крылова [86]), что значение X = 1 не является
собственным числом данного интегрального уравнения. Поэтому, на
основании общей теории интегральных уравнений, уравнение (3.110)
имеет единственное решение для любой функции g(r).
Построение приближенного решения этого уравнения
проведено и исследовано Н. М. Крыловым и Н. Н. Боголюбовым.
Оно основано на разбиении всего отрезка [а, (3] на равные
отрезки [т/ — /i/2, т/ + А/2], / = 1, 2,..., N, т, = А/2, h = (р —
— a)/N, и использовании кусочно-постоянной аппроксимации
плотности v(t'). При этом по условиям коллокаций в точках т/ из
(3.110) получаем (при А,= 1) систему алгебраических уравнений
Здесь использованы обозначения
160

Поскольку без ограничения общности мы можем считать все
А/со положительными и в силу равенства
все уравнения системы (3.111) для любого конечного N имеют
строгое диагональное преобладание, если контур имеет всюду
конечный радиус кривизны. Тогда система (3.111) невырождена
и имеет единственное решение при любых gfa).
Погрешность решеция z/ = v(t,-) — v/, как нетрудно показать,
удовлетворяет уравнению
т/) = */, (3.112)
где погрешность аппроксимации -ф/ определяется выражением
1
и, как можно видеть из оценки ошибок квадратурных формул,
удовлетворяет неравенству
max \%\ < Bh\
где постоянная В определяется дифференциальными свойствами
функции v(t) и не зависит от h.
Отсюда следует (см. [86]), что погрешность решения z-t также
есть величина порядка O(h2).
Отметим, что реализация и исследование решения
интегральных уравнений для потенциала двойного слоя существенно
затрудняются при более сложных конфигурациях границ, в
частности, при наличии тонкостенных пластин или незамкнутых
оболочек.

Глава 4
МЕТОДЫ РАСЧЕТА СОБСТВЕННЫХ ЧАСТОТ
И ГАРМОНИК ЭЛЕКТРОДИНАМИЧЕСКИХ СИСТЕМ
§ 4.1. О постановках задач электродинамики
Постановки задач расчета электродинамических систем
чрезвычайно разнообразны, им посвящено много монографий,
например [116, 27, 143]. В этом параграфе мы остановимся только
на некоторых основных моментах — рассмотрим способы
сведения физических постановок к проблеме собственных значений-
для краевых задач.
Задачи электродинамики в общем виде описываются
системой уравнений Максвелла
ot£j/, dv 4np,
с at ^ (4.1)
rot E+ 4"-|f =0' divB==0>
к которым добавляются материальные уравнения
D = eE, B = iiH. (4.2)
Здесь величины £, D, Я, В, с, е, \i обозначают соответственно
напряженность и смещение (индукцию) электрического поля,
напряженность и индукцию магнитного поля, скорость света,
электрическую и магнитную проницаемости.
Систему уравнений (4.1), (4.2) надо дополнить уравнениями,
определяющими распределение плотности тока / и плотности
зарядов р. Однако для целей данной главы их вид не имеет
значения, и мы просто считаем /, р заданными функциями
координат. Величины е, [i будем считать постоянными.
На поверхностях раздела различных сред заданы граничные
условия (мы предполагаем отсутствие поверхностных токов):
£,+ = £Г,. Н? = НГ, (4.3)
где знаки +» — относятся к разным сторонам поверхности, а
индекс / означает тангенциальные составляющие полей. На
металлической поверхности, в предположении идеальной проводимости,
полагаем £"^ = 0.
Рассматривая электромагнитное поле в пустоте (е = |х=1),
удобно ввести скалярный и векторный потенциалы ф, А:
tf = rot Л, £=-grad(p—~~p (4.4)
162

которые удовлетворяют волновым уравнениям
АЛ-4^=-4*//^- ^1?=-4лр' (4-5)
а также соотношению (условию калибровки Лоренца):
В ряде случаев векторы Е и А удобно представить в виде
суммы потенциальных и вихревых компонент (см. [40, 116]):
£ = £<"> + £<*>, А=АМ + АЬ\ (4.7)
удовлетворяющих равенствам
divA<*> = div£(6) = rot£(n) = 0,
£<«=_ 1_^, £<»>=_grad<p, Я=гоМ<Ч (4'8)
Новые Скалярный и векторный потенциалы ф, А^ь\ как следует
из (4.5) — (4.8), удовлетворяют системе уравнений
7-Т = - Ч- +
Особенность данной постановки заключается в том, что
скалярный потенциал ф определяется кулоновским взаимодействием
зарядов и только параметрически зависит от времени.
Векторный потенциал может быть представлен в виде ряда
)= f qk(t)Ak, (4.10)
где Ak — собственные* функции оператора A = grad div — rot rot,
определяемые соотношениями
^ = 0. (4.11)
Последнее условие означает равенство нулю тангенциальной
компоненты вектора Ak на поверхности металлического
проводника. Задача (4.11) определяет дискретный набор собственных
чисел Xk. Собственные функции, соответствующие разным А*,
взаимно ортогональны, и их можно считать нормированными по
условию
В задаче о возбуждении колебаний объемных резонаторов Xk
и Ak представляют собой частоты и гармоники свободных
колебаний. Для определения амплитуд qk(f) первое из уравнений (4.9)
умножим на Ak и произведем интегрирование по объему
резонатора Q. С учетом соотношений (4.10), (4.11) получаем
уравнение
dV, (x)k = Xkc. N (4.12)
11* 163

Здесь также учтено соотношение \ Akgvadtp dV=0, которое
получается, если в векторном тождестве
j (votArotB -\- divAdivB-{- ААВ) dV= \ ([ArotB]-{~Ad\vB)dS
Q Г
положить A=Ak, B = gradcp и учесть свойства функций Л*,<р.
После нахождения векторного потенциала напряженности
электрического и магнитного полей определяются из равенств
Е(ь)= — —2 qLAk, Я = 2 qkrotAk. (4.13)
с к н
Таким образом, основной вычислительной проблемой является
решение частичной проблемы собственных значений (4.11). Для
аппроксимации векторного потенциала конечным отрезком ряда
(4.10) требуется найти несколько наименьших по модулю
собственных чисел Xk и соответствующих собственных функций Ак.
Другая постановка проблемы собственных значений может
быть сформулирована с использованием векторов Герца. Мы ее
рассмотрим для задачи о свободных колебаниях в вакууме при
отсутствии объемных зарядов и токов. При этом используем
широко распространенную комплексную форму уравнений
электромагнитного поля. Представляя зависимость полей от времени в
виде экспоненциального ряда с комплексными показателями,
каждую из гармоник можно записать в виде
4}}, (4.14)
где со есть частота, а ЕШУ Нш — соответствующие векторные
амплитуды колебаний. Из уравнений (4.1) получаем (индекс
со для краткости опускаем):
rotE = ikHy votH=-ikEy к = <ь/с. (4.15)
Введем так называемый электрический вектор Герца,
определяемый соотношениями
£ = grad div П + £2П = пй rot П,
(4.16)
H=-ik rot П.
Очевидно, что векторы £ и Я из (4.16) автоматически
удовлетворяют уравнениям (4.15), если вектор П удовлетворяет
волновому уравнению
ДП + £2П = 0. (4.17)
Аналогично можно определить магнитный вектор Герца
E = ik rot П7, #=grad div n' + £2n' = rot roffl^ (4.18)
Непосредственной проверкой легко убедиться, что если вектор
П' удовлетворяет волновому уравнению
АП/ + ^2П/ = 0, (4.19)
164

то векторы £, Я, определяемые формулами (4.18), будут
удовлетворять системе (4.15).
Одна из типичных задач электродинамики заключается в
расчете распределения электромагнитного поля в волноводе,
представляющие собой полый металлический цилиндр, который
считается бесконечно длинным и имеет поперечное сечение
произвольной формы.
Частные решения уравнений электромагнитного поля внутри
волноводов рассматриваются в виде бегущих волн.
Предполагается, что зависимость амплитуд Еш, Нш от z (ось z выбирается
параллельной образующей цилиндра) описывается множителем'
exp {irz}> где г определяется длиной волны, распространяющейся
вдоль оси.
Класс таких решений (электрические волны) можно получить
с помощью электрического вектора Герца с компонентами
Пх = О, Пу = 0, П2 = Щх, у) exp {irz}, (4.20)
где функция П(х, у) не зависит от г.
Функция Пг должна удовлетворять уравнению ДП &2П
откуда для Щх, у) получаем
(4.21)
Из соотношений (4. 3) следует, что на идеально проводящей
стенке волновода функция П (х, у) удовлетворяет граничному
условию
П|г = 0. (4.22)
Задача (4.21), (4.22) определяет дискретный набор
собственных чисел qn и соответствующих гармоник Пп, д=1,2, ...
Если функция П (х, у) найдена, то составляющие
электромагнитного поля определяются формулами
^, Ey = ir exp{irz} ^, £г =
z}-^-, Hy = ikexp{irz}-^-, #г = 0. (4.23)
оу ох
Другой класс решений (магнитные волны) строится с
помощью магнитного вектора Герца
ГЦ =0, Щ =0, Щ =(х, у) exp{irz}. (4.24)
В силу (4.3), (4.19) получаем, что функция Щх, у)
определяется из задачи на собственные значения
165

Соответствующие компоненты электромагнитного поля
находятся из выражений
Ex = ikexp{irz}dll'/9y, Еу = -ikexp{irz}y E2 = 0, (4.26)
Hx = irexp{irz}dll' /дх, Hy = irexp{irz}dYl' /ду, Hz = q2exp{irz}U\
Другой тип электромагнитных задач состоит в расчете
колебаний поля в объемных резонаторах. Мы рассмотрим
цилиндрический резонатор (с произвольным поперечным сечением),
который можно рассматривать как отрезок волновода, в котором
в плоскостях 2 = 0, z = a поставлены идеально проводящие
металлические стенки. Как и при расчете поля в волноводах,
здесь отдельно рассматриваются электрические и магнитные
волны.
Колебания электрического типа определяются с помощью
электрического вектора Герца с составляющими
П* = 0, П„ = 0, Пг = Щх9у)и(г). (4.27)
Из уравнения (4.17) и условия равенства нулю
тангенциальной составляющей вектора Е на стенках резонатора с помощью
метода разделения переменных получаем, что функция Щх, у)
определяется из задачи на собственные значения (4.21), (4.22),
где Г в данном случае есть боковая поверхность цилиндра.
Функция u(z) определяется из задачи
a = O1 (4.28)
решение которой имеет вид
um(z) = cos \imz9 \im = mn/a. (4.29)
Если через г\ обозначить собственные числа задачи (4.21), (4.22),
то собственные частоты резонатора равны
(Dw« = cVr2 + jiX (4.30)
Магнитная составляющая поля в резонаторе получается с
помощью магнитного вектора Герца
Ш = 0, П£ = 0, Щ = П'(х, у) v(z). (4.31)
Функция П'(х, у), как и для волноводов, определяется
задачей на собственные значения (4.25), а для функции v(z) имеем
задачу
d2v/dz2 + v2v = 0, v(0)=v(a) = 0, (4.32)
определяющую дискретный набор
1 vm = mn/a. (4.33)
Обозначая через q2n собственные числа задачи (4.25), для
волновых чисел резонатора получаем формулу
kmn = л/ql + Vm.
166

Электродинамические задачи могут быть сведены к проблеме
собственных значений и непосредственно для векторов
электрической и магнитной напряженности. При отсутствии свободных
зарядов и токов в вакууме из (4.1), (4.3), (4.15) мы получаем
+ = 0, div£ = O, Et\r = 09
(4.34)
AH+k2H=0, div# = O, (rot#),|r = 0,
где Г обозначает поверхность идеального металлического
проводника, а Е и Н — амплитуды колебаний Еш и Яш.
Мы отметим еще только один тип краевых задач, возникающих
при расчете осесимметричных резонаторов с меридиальным
сечением произвольной формы. В плоскости г, z из (4.34), следует
волновое уравнение
где в случае электрических колебаний функция w определяет
азимутальную компоненту вектора напряженности электрического
поля (w = rEQ) и удовлетворяет граничным условиям
w\r = 0. (4.36)
Для задачи о магнитных колебаниях имеем
w = rHQy dw/dn\r = 0. (4.37)
В обоих случаях функция до, как следует из ее определения,
на оси симметрии обращается в нуль.
§ 4.2. Разностные аппроксимации проблемы
собственных значений для краевых задач
В этом параграфе рассматривается задача на собственные
значения для уравнения
х+^ ы (4 38)
дх \ дх/ ' ду2 х '
где а может принимать значения —1, 0, 1. Требуется найти
значения к и соответствующие функции и(х9 у), удовлетворяющие
в ограниченной области Q уравнению (4.38) и смешанным
однородным граничным условиям на границе Г = Г1иГ2:
и|Г1 = 0, ди/дп\Т2 = 0. (4.39)
Граница области допускается многосвязная и куСочно-гладкая,
причем в угловых точках или точках смены граничных условий
решение может иметь особенность. Случаи а = 0, 1 соответствуют
задачам на собственные значения для оператора Лапласа в
декартовой или цилиндрической системах координат, аа=-1 —
задаче о собственных колебаниях осесимметричного резонатора.
167

Задачу (4.38), (4.39) можно решать различными
алгоритмами, в том числе методами конечных элементов или интегральных
уравнений, см., например, [88, 93]. Мы останавливаемся на
конечно-разностных аппроксимациях только в силу субъективных
интересов. Данный параграф можно считать некоторым
дополнением к §1.2 в плане построения разностных уравнений,
учитывающих асимптотическое поведение решения в окрестности
особых точек. Этот вопрос имеет общий характер как при решении
уравнения Пуассона, так и для задачи на собственные значения.
Построению аппроксимаций с учетом особенностей решения
посвящено большое количество работ по методам конечных
разностей и конечных элементов, см., например, [108, 149, 192] и
цитируемую там литературу. Мы остановимся на одном случае
построения конечно-разностных уравнений, который в
первоначальном виде был предложен И. В. Фрязиновым [192] и далее
развит А. В. Гаврилиным [34]. Положительное качество
рассматриваемых аппроксимаций заключается в их простоте и
достаточной эффективности. Разностные уравнения в окрестности
особых точек остаются пятиточечными, как и вдали от границы,
что позволяет относительно легко автоматизировать их
программную реализацию для сложных краевых задач. Как
показывают численные эксперименты, учет особенностей позволяет
существенно повысить точность как для решения уравнения
Пуассона, так и для вычисления собственных чисел и собственных
функций.
4.2.1. Построение разностных уравнений. Мы рассмотрим
предварительно краевую задачу для уравнения Пуассона
Q, (4.40)
fn\T=q{x,y).
Обозначим через s(P), Р^Г, вектор, касательный к границе Г
в точке Р. При обходе границы вдоль 5 считаем для
определенности, что область Q остается слева. Пусть Qi, i= I, 2,..., N,
означает особые точки границы, которые могут быть вершинами
углов, точками разрыва функций g, q или точками смены типа
граничных условий. Считаем, что в окрестности особой точки
граница Г представляется в виде двух отрезков прямых /i,2 (Qk),
имеющих общую концевую точку Qk и образующих между собой
угол 0o(Q*) = Ji/a*, 0,5<aA-<<2. Около каждой точки Qk построим
в Q сектор a>(Qfc) с углом, образованным отрезками l\,2(Qk) и дугой
окружности с конечным радиусом R. Величину R выбираем
достаточно малой, чтобы секторы (o(QR) не пересекались. Шаги сетки
считаем тоже малыми, чтобы расстояние между разными
секторами было не меньше локального шага сетки. В силу этого мы
далее проведем рассмотрение только для окрестности одной
особой точки Q^ которой соответствует угол 6о. Введем
локальную полярную систему координат с началом в точке ft и с
168

отсчетом угла от положительного направления оси х. Обозначим
через 0i,2 углы, соответствующие отрезкам /i,2, так что Эо =
= 01 — 02, а через Qk— неограниченный сектор, образованный
лучами Li,2, проходящими вдоль /i,2.
Функции g, q из граничных условий в окрестности считаем
линейными по локальной координате r = {[x—*x(Qk)]2-\-
+ [у — y(Qk)f}l/2, т. е. для случая условий 1-го рода на отрезках
/i, /2 будем иметь
gn(r, Qk)=gn(Qk) + bnr, л=1,2, (4.41)
где gn(Qk) означают предельные значения функции g на отрезках
/i,2 при стремлении к точке Qk, а Ъп — константы.
Отметим, что предположения о линейности функций из
граничных условий и о прямолинейности граничных отрезков вблизи
особых точек не являются сильным ограничением. Выбором
достаточно малого R можно добиться, что замена криволинейного
граничного отрезка прямолинейным или линеаризация нелинейной
функции g будет достаточно хорошей аппроксимацией краевой задачи.
Решение задачи (4.40) в секторе co(Q^) представим в виде
(4.42)
где vq — какое-либо частное решение однородного уравнения
(4.40) в Qk с условиями (4.41), a v\ — решение уравнения
(4.40) в (d(Qk) с граничными условиями
tn(r, Q) = vx(r, 02) = O,
(4.43)
Vl(R, 0) = v(R, 0) - 1/о(Л, 0), 0 е [в,,в2].
Для функции v\ в окрестности точки Qk справедливо
разложение (см. [101])
v\= 2 amrwxsinxm(0 —02) + ^2, (4.44)
т=\
где ат — константы, а ^2 — достаточно гладкая функция.
Отсюда для искомого решения в co(Q) имеет место
представление
v = a{rasmyc(Q — 02)+ w(r, 0), (4.45)
где функция ш(г, 0) содержит гладкую часть решения и старшие
гармоники из (4.44), начиная со второй.
В области Q построим прямоугольную сетку с
координатными линиями x=Xi> у = У\у / = 0,1,2,...,/, / = 0,1,2,...,/; с шагами
hf=Xi+\—X/, Щ = t//+i—у}. Все особые точки Q/ считаем
принадлежащими узлам сетки. Разностные уравнения будем строить для
множества узлов Qa, являющихся внутренними по отношению
к области Q. Все внутренние узлы классифицируем следующим
образом:
a) Qa = QJ+Q& гДе ^ — множество регулярных узлов, ай[ —
множество околограничных; регулярным называем такой узел
169

(/,/), у которого все четыре соседних узла (/—1,/), (/,/—1),
(/+1,/), (/,/+1) находятся в Q, если же хоть один «сосед» —
внешний по отношению к Q, то узел (/, /) — околограничный;
б) Qh = Q'h-\-Q'h'y где Q'h является множеством особых узлов,
т. е. принадлежащих одному из секторов co(Q*), a Qa' —
множество обыкновенных узлов, принадлежащих остальной части
области Q.
Смысл такого разбиения заключается в следующем. Для
особых узлов аппроксимацию краевой задачи будем проводить с
учетом разложения (4.45) для искомой функции, а для
обыкновенных узлов — без учета особенностей решения. Кроме того,
как для особых, так и для обыкновенных узлов, если они являются
околограничными, построение разностных уравнений надо
выполнять с учетом граничных условий.
Мы проведем построение аппроксимации для некоторого
особого узла с индексами (/, /), который может быть как регулярным,
так и околограничным. Будем использовать локальную
нумерацию узлов
пятиточечного шаблона в
соответствии с рис. 21, а
индексы /, / в дальнейшем
для краткости
опускаем. Обозначим через Я
ячейку сетки для узла
(/, /), ограниченную ли-
j-i НИЯМИ х = Xi - i / 2,
Рис. 21.
у = У1+1/2 И, ВОЗМОЖНО,
отрезком границы s,
если он пересекает
указанный прямоугольник. На рис. 21 заштрихованы две такие
ячейки — для регулярного и околограничного узлов. Через 1\г U, /з, U
обозначим стороны (а также и их длины) ячейки, параллельные
координатным линиям, а через d — длину отрезка внешней
нормали к ячейке, опущенной из узла (/, /) на граничный отрезок s,
если таковой существует.
Вообще говоря, могут быть и более сложные варианты
пересечения ячейки сетки с границей. Мы их рассматривать не
будем, так как принципы построения разностных уравнений для
всех случаев остаются теми же, что и для рассмотренных ниже
случаев.
Запишем уравнение баланса, для чего проинтегрируем по
ячейке уравнение (4.40), предварительно умножив его на ха:
а -р- dx - \ ха -^- ds = \ xafdx dy. (4.46)
U s н
170

Если ячейка Н не пересекает границу, то последний член в
левой части (4.46) отсутствует.
Аппроксимацию каждого члена в (4.46) будем проводить
так, чтобы она была точна на первой гармонике (4.44), (4.45),
т. е. на функции /(г, 8) = rxsinx(8 — 82). Для этого, например,
выражения \xa~^dy, Kxa-p-ds заменим соответственно на
— v\) /hf-1, cnsxf(vs — v0) /d,
где коэффициенты си сп имеют вид
a^t 1 f a to —1\
dylX
(4-47)
г — \ v*a //с • су*а
а величины xs, vs означают координату и значение функции в точке
пересечения нормали п с граничным отрезком s. Аппроксимацию
интеграла в правой части (4.46) достаточно провести с помощью
формулы прямоугольников (\ xaf dx dyttxtfijHj. В результате для
особого узла получаем разностное уравнение, которое мы
выпишем ради простоты в предположении его регулярности (5 = 0):
fu/4. (4.48)
Легко видеть, что если в (4.48) мы положим Ci = C2== Сз = с4= 1,
то получим обычное балансное пятиточечное уравнение,
рассмотренное в первой главе. Такого вида разностные уравнения, т. е.
без учета особенностей решения, мы будем применять для
обыкновенных узлов.
Отметим, что в секторе (o(Qk) могут быть лучи, соответствующие
некоторым узлам 8, вдоль которых значения t, tXj ty обращаются
в нуль. Если какой-либо отрезок между узлами сетки
пересекается таким лучом, т. е. значения /о, tk в (4.47) имеют разные знаки,
то соответствующие Ck в (4.48) полагаем равным единице. Это
означает, что для таких узлов в разностном уравнении делается
только частичный учет особенностей решения. Если максимальный
шаг сетки h стремится к нулю, то общее количество таких узлов
(будем их называть частично особыми) есть величина порядка
O(h1)
Легко показать, что множители Си в (4.48) имеют вид (шаги
сетки для простоты считаем постоянными, hf=hXy Щ=ку):
,2ч у. //|о/ \ _1_ о h 1 Q
■yjlxxx/ \i6Lx) | bfc, K— А, О,
(4.49)
k = 2, 4.
171

При этом имеют место следующие неравенства:
max[\txxx/tx\, \tyyy/ty\}^l/r2, (450)
\ek\^Bh3/r\ \l—ck\^Bh/r, * = 1,2,3,4, V ' '
где через В обозначается некоторая положительная постоянная,
не зависящая от А и г, а значение г относится к узлу (/, /).
Учет граничных условий как для обыкновенных, так и для
особых узлов, проводим в соответствии с алгоритмами построения
разностных уравнений, рассмотренных в первой главе. Чтобы не
загромождать изложение, мы не будем выписывать аппроксимации
для всех возможных типов узлов, которых набирается достаточно
много: обыкновенные регулярные, обыкновенные околограничные,
особые регулярные, особые околограничные (кроме того, среди
двух последних типов надо выделить частично особые узлы).
В соответствии с обозначениями п. 1.3.3 полную систему
разностных уравнений Пуассона запишем в виде
Lhu=-l
где компоненты вектора правой части имеют вид х*\ц и включают
еще, быть может, члены, обусловленные учетом неоднородных
граничных условий в околограничных узлах. Отметим, что систему
(4.51) мы рассматриваем для удобства как состоящую из
уравнений вида (4.48), поделенных предварительно на объем
ячейки Я,/, при этом также меняем знаки в обеих частях уравнений
(4.48).
При рассмотрении уравнения (4.38) для проблемы на
собственные значения краевой задачи мы используем те же разностные
аппроксимации, что и выше для уравнения Пуассона. При этом
используется тот факт, что собственные функции удовлетворяют
однородным граничным условиям (4.39), и в окрестности особых
точек для них справедливы асимптотические представления
(4.42) —(4.45)/
Таким образом, после аппроксимации уравнений (4.38), (4.39)
получаем алгебраическую задачу на собственные значения
-XhU. (4.51)
4.2.2. Оценки погрешности собственных чисел и функций. Как
и в предыдущем пункте мы сначала рассмотрим разностные
уравнения Пуассона, полученные с учетом особенностей
решения.
Функция ошибки z = u— Vh удовлетворяет уравнению
qy (4.52)
где г|) — вектор погрешности аппроксимации.
В силу линейности уравнения (4.52) погрешность разностного
решения представим в виде суммы z = zQ-\-z\, где член z0
обусловлен ошибкой аппроксимации только для особых узлов, a Z\ — для
остальных. Согласно п. 1.3.3 равномерная норма последнего
слагаемого равна || Z\ ||oo = 0(/i2), поскольку секторы co(Q/) имеют ко-
172

нечный радиус и вне их решение краевой задачи обладает
достаточной гладкостью.
Для анализа г0 необходимо оценить величины ошибок
аппроксимации в особых узлах. Используя разложения в ряд Тейлора,
а также соотношения (4.49), (4.50), можно показать
справедливость неравенств
Bhar~2, 0,E
(4.53а)
Bhra~\ 1<а<2,
для частично особых узлов,
1~{ | ln/г | +га), 0,5<а< 1,
(4.536)
С
\
(B(h2a~
B(r>«
для особых околограничных узлов и
i1+a|ln/i|r-2), 0,5 < a < I,
(4.53в)
для остальных особых узлов.
Мы проведем оценку погрешности z0 в равномерной метрике
с помощью аппарата разностных функций Грина (см. работу Кут-
тлера [108] и цитируемую там литературу), которые определяются
из уравнения
y). (4.54)
Здесь 8pq есть символ Кронекера, а сами величины р, q означают
номера узлов сетки (или номера соответствующих компонент
вектора и), и каждому из них соответствует пара индексов (/, /)
и (*',/').
Для любого узла сетки с номером р компонента вектора
погрешности 2о выражается через функцию Грина формулой
{zo)p = hxhy^Gpqy!(iqy (4.55)
где сумма берется по всем особым узлам.
В силу свойств системы разностных уравнений (4.51)
(монотонность, строгое диагональное преобладание для строк,
соответствующих околограничным узлам, вид множителей Ck) для
разностной функции Грина несложно устанавливаются следующие
свойства:
( flllnAI, a
a>-2,
= -2,
a>0.
173

Здесь величина rq относится к узлу с номером qy первая, сумма
берется по всем регулярным узлам (исключая частично особые),
а вторая — по околограничным и частично особым. Общее число
слагаемых в первой сумме равно O(h~2)y а во второй — O(h~l).
Теперь из равенства (4.55), используя оценки (4.53а) — (4.53в)
для погрешности аппроксимации в особых узлах, а также
неравенства (4.56) для разностной функции Грина, получаем
соотношение
[ 2 + n2h\ 0,5<а<1,
Объединяя эти неравенства, получаем окончательный
результат для полной погрешности разностного решения:
|| z || ос <Ba(/z2 + /i2a I In h I +hl+a In2 A), (4.56)
где величина а определяется «наихудшей» особой точкой, т. е.
k
Перейдем теперь к оценке погрешностей собственных чисел и
функции. Обозначим через А,(/г), v^k\ k—\,2y..., собственные числа
и функции дифференциальной краевой задачи (4.38), (4.39), а
через Х^\ и^ — собственные числа и векторы алгебраической задачи
(4.51). Числа X^k\ Xft считаем пронумерованными в порядке
возрастания их значений, которые неотрицательны, в силу выбранных
знаков при определении дифференциального и разностного
операторов L, Lh. Отметим, что разностный оператор Lh есть матрица,
представимая в виде произведения D~lA, где D — диагональная
матрица, элементы которой есть значения объемов ячеек Нц, а А —
симметричная положительно полуопределенная матрица (А
соответствует непосредственно уравнениям (4.48), до их последующего
деления на (hf-\-{-hf)(hf-\-\-hf)/4). Операторы L, Lh имеют по
одному нулевому собственному числу, если только в исходной
задаче на всей границе заданы условия Неймана.
Уравнение (4.51) эквивалентно обобщенной проблеме на
собственные значения
Au = \hDu. (4.57)
Если Л, D — симметричные матрицы порядка N, и D
невырождена, то всегда существует Af вещественных чисел А,Р и
соответствующих векторов и^к\ удовлетворяющих уравнению (4.57).
Некоторым и^ могут соответствовать одинаковые числа. Векторы
и(к\ соответствующие разным собственным числам, £>-ортогональ-
ны, т. е. (Duik\ t/(/)) = 0 при Х^фХ^.
Оценки погрешности собственных чисел и функций можно
провести с помощью результатов исследований Брэмбла и Куттлера
[108], на которых мы останавливаться не будем. Смысл их
заключается в том, что если разностный оператор обладает теми
свойствами, которые имеют место для рассматриваемого нами опера-
174

тора La, то равномерные оценки погрешности приближенного
решения проблемы собственных значений являются по порядку
теми же, что и для погрешности разностного решения.
Соответствующие неравенства можно записать в следующем виде:
(4.58)
где постоянные Bk не зависят от А, но зависят от номера
собственного числа k. Если к[к) — собственное число кратности mk, т. е.
совпадает с W+1), ...Д^"1""*"0, которым соответствуют u{k+x\ ...
...,a( +m !\ то в (4.58) под u{k) фактически подразумевается
некоторая линейная комбинация собственных векторов,
соответствующих числам Х(п\ ДА^+т*-1)#
В неравенствах (4.58) по сравнению с (4.56) опущен член
A1 + aln2 |Л|. Дело в том, что при выводе оценки погрешности
разностного решения случай а = 1 имеет место только при
неоднородности граничных условий, которой не возникает в задаче на
собственные значения. Если же a<Cl, то при достаточно малых А
имеем AI+a | In2 A | <IA2a| In А |. При а>1 и малых А аналогично
получаем Ai+a| \n2k | <А2.
Заметим, что свойства разностной функции Грина и оценки
погрешности нами были сформулированы ради простоты для
случая равномерной сетки. Однако оценки погрешности уравнения
Пуассона и проблемы собственных значений остаются по порядку
теми же, есл« используется кусочно-равномерная сетка такая,
что при А-^0 в ней остается конечное число координатных линий,
на которых меняются шаги. Качественно это можно объяснить
тем, что количество узлов, лежащих на линиях смены шагов и в
которых аппроксимация хуже, составляет величину О(А~[), т. е.
на порядок меньше общего числа.
4.2.3. Примеры методических экспериментов, В этом пункте
мы приведем результаты по решению уравнения Пуассона и
проблемы собственных значений для краевых задач. Все расчеты, как
с выделением особенностей решения, так и без выделения,
выполнены А. В. Гаврилиным [35].
В табл. 14 приведены ошибки вычисления первого собственного
числа и соответствующей собственной функции для смешанной
краевой задачи в единичном квадрате. На сторонах с
координатами х = 0 и jc= 1 заданы условия Неймана dv/dn = 0, а на сторонах
у = 0 и у=1 —условия Дирихле и = 0. Аналитическое решение
для этой задачи дает А.(1) = 9,8693 и и(1) = /2" sin ш/. Расчеты
проводились на разных сетках с шагами А=1/10, 1/20, 1/40,
1/80. В табл. 14 даны значения 8Х = U(1) — ffl\ и величины
среднеквадратичной (усредненной по всем узлам сетки) абсолютной
погрешности, соответствующей собственной функции Ьи.
Как видно, ошибка вычисления А,(1) убывает примерно
квадратично с уменьшением А, а погрешность Ьи — приблизительно
175

Таблица 14
h
6Л
6а
1/10
0,0809
0,0513
1/20
0,0211
0,0254
1/40
0,0047
0,0126
1/80
0,0005
0,0063
линейно. Последнее можно объяснить тем, что в данных
экспериментах разностные уравнения решались итерационным методом,
и хотя точность А,(1) была достигнута высокая, с точки зрения 8и
имело место «недоитерирование».
В табл. 15 даны погрешности вычислений первых четырех
собственных чисел 6Х(1), 6Ал2), 8Х(3), 6А,(4) для задачи Дирихле в
квадрате.
Таблица 15
h
1/5
1/10
1/20
0,641
0,162
0,040
" вх<2>
5,250
1,495
0,344
5,250
1,495
0,344
9,859
2,564
0,647
Аналитические значения самих собственных чисел равны
соответственно 19,737; 49,348; 49,348; 78,957. Как видно, даже при
небольшом числе узлов сетки точность для всех четырех
собственных чисел (в том числе и для кратных) достаточно высокая.
Теперь мы приведем результаты экспериментов для краевых
задач с особенностями, иллюстрирующими преимущества
рассмотренных выше аппроксимаций с учетом асимптотического поведения
решения перед обычными разностными уравнениями, т. е.
построенных без учета особенностей.
Мы сначала рассмотрим решение задачи Дирихле для
уравнения Пуассона (4.40) при а = 0 в L-образной области, аналогичной
изображенной на рис. 7,а. Конкретнее, выбранная область
представляет собой квадрат с длиной стороны 2, из которого в левом
верхнем углу вырезан единичный квадрат. В качестве искомого
решения выбрана функция
Здесь
tg e = (у - i)/(x - i),
а начало координат выбрано в левом нижнем углу большого
квадрата. Чтобы функция v(xyy) удовлетворяла задаче (4.40), мы
полагаем
) = v(x,y)\r,
176

В табл. 16 для х= 1,2 и разных значений у приведены
следующие данные. В каждой клетке указаны пять чисел, которые в
порядке сверху вниз означают следующее: точное решение задачи в
данной точке, абсолютная ошибка обычного разностного решения
при h = 0,2, то же при А = 0,1, ошибка разностного решения с
учетом особенности при h = 0,2, то же при /г = 0,1.
Таблица 16
х ^^^
1,2
0,6
7,0726
0,0913
0,0389
0,0093
0,0013
0,8
4,2929
0,1427
0,0626
0,0024
0,0003
1,0
1,9489
0,2669
0,1009
0,0479
0,0066
1,2
0,5305
0,0676
0,0296
0,0079
0,0033
Определенные выше особые разностные уравнения строились
при этом только в секторе радиуса 0,5 с центром в угловой точке,
имеющей координаты (1,1). Как показывают результаты, учет
особенности решения позволяет значительно (в 5—10 раз и более)
повысить точность решения. Заметим, что, как показывает
эксперимент, погрешность с уменьшением шага сетки для обычной
аппроксимации убывает примерно линейно, а для аппроксимации
с учетом особенности — квадратично или даже более сильно.
Для такой же L-образной области рассмотрим теперь ошибки
при решении задачи на собственные значения. В случае граничных
условий Дирихле минимальное собственное число
дифференциальной задачи равно к = 9,6397. Расчеты.для такой задачи
проводились на разных сетках как с выделением особенности, так и без
выделения, соответствующие погрешности вычисления к в табл. 14
обозначены через бв и б0.
На обоих типах аппроксимаций был также проведен
эксперимент по применению экстраполяции Ричардсона для уточнения
результатов: на двух сетках с шагами А и 2А находились
приближенные значения кн и А,2л, а далее откорректированное значение
— ~ 4 1
kh определялось по формуле Л.^ = — Хл — — Л,2/г. Строго говоря,
такая операция теоретически обоснована, если справедливо
разложение ^l) = ^1) + aiA2 + O(A2). В данном случае такой факт не
доказан, но сам эксперимент показывает хороший эффект
экстраполяции. Соответствующие ошибки вычисления к обозначены
в табл. 17 через бвз — при аппроксимации с выделением
особенности и боэ — без выделения.
Результаты на самой грубой сетке оказываются не
характерными: погрешность оказывается минимальной для аппроксимации
без выделения особенностей, причем экстраполяция Ричардсона
не дает улучшения точности. Однако при уменьшении шага сетки
расчетные данные приходят в соответствие с асимптотическими
12 В П Ильин
177

Таблица 17
h
1/10
1/20
1/40
0,0487
0,0270
.0,0113
0,0519
0,0198
0,0061
А
0,0530
0,0139
0,0036
0,0033
0,0009
0,0002
оценками ошибок. Отличие численного решения от точного для
разностных уравнений с учетом особенностей гораздо меньше, чем
без учета. Экстраполяция Ричардсона дает значительное
уточнение результатов, и особенно это эффективно для аппроксимаций
с выделением особенности решения.
§ 4.3. Итерационные методы решения
алгебраической проблемы собственных значений
В данном параграфе мы рассмотрим методы решения
обобщенной частной задачи на собственные значения
i= 1, 2,..., N, (4.59)
где Л, D — симметричные матрицы порядка N, А — положительно
полуопределена, afl — положительно определена. В этом случае,
как известно (см. [38]), существует набор из N D-ортогональных
собственных векторов, т. е. (Dziy Zj) = O при 1ф\. Собственные
числа вещественны и неотрицательны, минимальное собственное
число предполагается простым и все они пронумерованы в порядке
возрастания (A,i<A,2< ... <Я#).
Рассмотрим две отдельные задачи: первая — вычисление
минимального собственного числа, вторая — нахождение нескольких
(до 10—20) меньших собственных чисел и соответствующих
собственных векторов.
В рассматриваемых нами приложениях матрица А вырождена,
если только она получается из аппроксимации задачи Неймана.
При этом нулевому собственному числу соответствует только
один собственный вектор со всеми одинаковыми компонентами.
Для других краевых задач матрица А монотонная (Л-1^0), и
минимальное собственное число к\ простое, как это следует из
теории неотрицательных матриц [38] (более того, из нее следует,
что у соответствующего собственного вектора Z\ все компоненты
строго положительны). Отметим, что эквивалентная (4.59)
обыкновенная задача на собственные значения Czi = lkiZi имеет матрицу
C = D~lA, которая имеет вещественный спектр как произведение
двух симметричных матриц. Если исходная краевая задача
рассматривается в области, составленной из прямоугольников, то
матрицу D можно считать единичной и С = А.
Поскольку матрицы систем разностных уравнений имеют
большие порядки (до нескольких тысяч) и являются ленточными и
редкими, то мы остановимся только на итерационных алгоритмах,
178

требующих минимальный объем запоминаемых промежуточных
данных. По этой причине мы не рассматриваем такие известные
методы, как LR- или (^-алгоритмы, методы вращений и др.
4.3.1. Вычисление минимального собственного числа и
соответствующего собственного вектора. Данную задачу мы сформулиру-
ем для удобства как обыкновенную задачу на собственные
значения
CZi = XiZh /=1,2, ...,#, (4.60)
в которой С, Zu ^обладают свойствами: C = D~lA,
... <^, (Dzi9 Zj)=O при 1ф]. Одним из простейших в
теоретическом плане способов вычисления Х\ является степенной метод,
который основан на построении последовательности векторов
хп==С~{хп-{^С-пх\ /1=1,2,... (4.61)
Разложим вектор начального приближения х° в ряд по z,-:
N, ai = (Dx°9 zt),
тогда для п-то вектора последовательности получим
xn = v1axzx+vn2a2z2 + ... +vnNaNzN, v/ = AT1. (4.62)
Отсюда, если начальный вектор не является D-ортогональным
- к первому собственному вектору, т. е. а\Ф0, и если /-я компонента
Z\ ненулевая (а это, как отмечалось выше,-действительно так в силу
неотрицательности матрицы С"1), для любой ненулевой
компоненты хп мы будем иметь
*7 + y*?=v,[l +O(v§/v?)]. (4.63)
Таким образом, если через v(in) обозначить отношение любых
одинаковых линейных комбинаций компонент векторов хп + \ хп,
например, сумму их модулей, то при п-^- оо получаем v^Wvj.
Очевидно также, что в правой части (4.62) при я->оо можно
пренебречь всеми слагаемыми, кроме первого. Это означает, что вектор
хп для достаточно больших п фактически представляет собой
первый собственный вектор. Относительная погрешность компонент
составляет при этом величину O^/vf).
Чтобы избежать чрезмерного роста или уменьшения компонент
хп, можно на каждом шаге вводить нормировку векторов. При
использовании любой из норм для последовательности
J? = C-|jc11-1, xn = xn/\\xn\\J
приведенные выше рассуждения и оценка (4.63) остаются
справедливыми.
В процессе реализации степенного метода итерации (4.61)
ведутся до выполнения неравенства
(4.64)
при достаточно малой величине г.
12* ' 179

Для ускорения сходимости величину v(irt) можно определять
отношением скалярных произведений (Dxf1, xn)=^\\xn\\2D, для
которых, как легко проверить с помощью (4.62), имеет место оценка
v2ln)}. (4.65)
Очевидно, что с помощью выражения (4.65) можно достичь
заданной точности е вычисления vi примерно вдвое быстрее (при
8<Cl), чем из соотношения (4.6S). Отметим, что данный прием
сам по себе никак не влияет на ускорение определения
собственного вектора, так как последовательность хп остается неизменной.
Если имеется какая-либо априорная информация о величинах
A,i, Яг, то дополнительного ускорения можно достичь с помощью
степенного метода со сдвигом, который определяется выражениями
\ G^C-x—il, л = 1,2,..., (4.66)
где т — некоторый итерационный параметр. В то время как раньше
скорость сходимости зависела от v2/vi, теперь определяющей
становится величина
v2-
х =min{ "
v3-t I I vN-
— I}.
13 частности, если v2> v3 и если положить t = v2, to сходимость
степенного метода со сдвигом зависит главным образом от
отношения | (v3 — t)/(vi— т)|.
Применение сдвига будет малоэффективно, если заранее
трудно оценить значение А,2. В этом случае можно использовать
ускорение, которое называется б2-процессом Эйткена. Условием его
применимости является выполнение неравенств | К\ | < I Я21 < I A,31,
а сам алгоритм заключается в следующем.
Пусть на основе последовательности х" определен ряд величин
Упу Уп+и Уп+2, относительно которых известно, что
yn = Civ.nl + C2V& + ... + cN[LnN. (4.67)
Если уп — какая-либо компонента вектора хпу то fi/ = v/, а при
yn=(Dxn, xn) будет \ii = vf, i= 1,2,..., Л^. Обозначим через ип
отношение уп+\/уп и введем величину
рп=(ипип+2 — u2n+i)/(un — 2un+i + un+2). (4.68)
Используя (4.67), несложно проверить справедливость при
i I > I И* I > I M* I отношения
1? Н1). (4.69)
Таким образом, ускорение Эйткена на основе использования
только апостериорной информации позволяет дополнительно
сократить число итераций для вычисления vi, в том числе и по
отношению к (4.65).
Рассмотренный б2-процесс позволяет также уточнить
компоненты первого собственного вектора, если минимальное
собственное число vi уже вычислено с достаточной точностью. Для этого
180

строится аналогичная (4.68) комбинация компонент векторов
хп~~\ хг\ хп + \ умноженных соответственно на vb I, vf1 Исходя
из (4.62), несложно показать справедливость соотношения
^Hv^-'vr1^1- ^/(^Г1- ^x] + vr'^r1) =
= ai2,yv7[l +O(vS/v7)]. (4.70)
Отсюда видно, что числа qn}, /=1,2,..., N, с точностью до
одинакового множителя aivf, дают приближения к значениям Z\\
с относительной погрешностью O(v%/vn\).
Существенным моментом в степенном методе является
необходимость обращения на каждом шаге матрицы С, что эквивалентно
решению системы уравнений
-{ (4.71)
Точное решение таких систем с помощью прямых методов, как
правило, оказывается слишком трудоемким. Поэтому зачастую
используются двойные итерации, состоящие в том, что для каждого
п вектор хп вычисляется с помощью «внутренних» итераций,
выполняемых с помощью какого-либо из алгоритмов, рассмотренных
в гл. 1. На некоторой ai-й «внешней» итерации «внутренние»
итерации ведутся до обеспечения заданной точности гп вычисления
вектора х". Одним из важных вопросов такого метода является
оптимизация последовательности е„, обеспечивающей
минимальное суммарное количество «внутренних» итераций. Мы не будем
останавливаться детально на этой задаче. Очевидно, гп должны
составлять убывающую последовательность, поскольку на первых
внешних шагах не требуется высокая точность определения хп
(исследование этих вопросов можно найти в статьях [170, 110] ).
Для ускорения сходимости степенного метода в (4.66) можно
ввести переменные сдвиги т„, определяемые корнями полиномов
Чебышева 1 -го рода (см. [111] ). Однако мы рассмотрим
применение чебышевского ускорения в алгоритме, аналогичном
используемому при решении систем уравнений и не требующему обращения
матрицы С.
Определим последовательность векторов
х" = х"-1 - тпСха-] = Рп(С)х°, (4.72)
п
РЯ(С)= П (/-т*С), « = 1,2,...,
где тп — итерационные параметры, выбираемые следующим
образом. Определим некоторые положительные числа m, M,
удовлетворяющие неравенствам k\<.m<ks^M. Значения тп выберем
циклическими с некоторым периодом L, равными обратным
величинам корней полинома Чебышева
р м—т
M_m
наименее отклоняющегося от нуля на отрезке [т, М\ и равного
181

единице при v = 0:
тя(т, М, L) = 2[M+m-(M-m)cos я(2^)""1)]"1- (4.73)
Здесь &(я) есть некоторая перестановка первых L чисел
натурального ряда.
При L<30, что обычно достаточно для практических задач,
можно положить £ = modL(n), т. е. k= 1, 2, ..., L, 1,2, ... Для
больших L скорость сходимости итераций (4.72) растет, но в этом
случае для избежания возможной неустойчивости счета требуется
специальное определение последовательности k(ri), на котором
мы не останавливаемся, см. [119, 166].
На каждом шаге итерационного процесса (4.72) будем
вычислять значение величины
а?Р2(У1) + а1^(У2)++а2^(у_1)
()*
Поскольку многочлен Pn(v) строго больше нуля при v = vi (он
имеет корни только на интервале (т, М) и равен единице при v = 0),
то мы имеем
)], (4.75)
где величина р„ определяется равенством
Р„ = Л,(г2)/Р„М (4.76)
при V2<m и
P«=max{|Pn(v)|}/Pn(v,V (4.77)
V 6 [т,М]
если vi<m<Cv2.
В силу свойств многочленов Чебышева и соотношений (4.75) —
(4.77) следует, что
y\n) = {\-gn)/Tn (4.78)
будут стремиться к минимальному собственному числу vi при
n = kLy 6=1,2, ... Скорость сходимости определяется величинами
рп. Полагая для простоты М = 1, из оценок значений чебышевских
полиномов получаем:
Pn<(l-v,/2-y>"~-^r (4.79)
при
при v2<m<l.
Отсюда следует, что скорость выделения минимального
собственного, числа по крайней мере не ниже, чем скорость подавления
ошибки при решении систем линейных уравнений с помощью че-
бышевского ускорения.
182

Обобщением алгоритма (4.72) является итерационный процесс
с переменным сдвигом [36]:
xn = xn-l-TnHnl(A-tin)D)xn-l = Tnxn-\
(4.80)
Х^ = (Ах\ xn)/(Dx\ хп\ п = 1, 2, ...,
где хп — некоторые итерационные параметры, Нп — квадратные
матрицы порядка N, а А,(п) являются приближениями к значению
A,i из задачи (4.59).
Матрица перехода от вектора хп~1 к хп здесь имеет вид
и если какие-то из матриц #„, Л, D не перестановочны, то
собственные векторы матрицы Тп не совпадают с искомыми векторами
zi. Это вносит принципиальное отличие от рассмотренных выше
методов. Например, в (4.72) матрица перехода есть / — т„С, что
позволяет просто проводить анализ сходимости на основе
разложения векторов хп по базису исходной задачи.
Применение же методов типа (4.80) основывается на том
факте, что если последовательность А,(п) сходится к собственному
числу, то векторы хп сходятся к соответствующему собственному
вектору z\ задачи (4.59).
Мы подробнее рассмотрим модификацию алгоритма (4.80),
в котором величины А,(п) пересчитываются не на каждом шаге.
Тогда формально можно записать двуступенчатыи итерационный
процесс (матрицы считаем симметричными, положительно
определенными и не зависящими от п):
лЫ ,л , 1ч „ , (4.81)
Здесь xlo — произвольный начальный вектор, не ортогональный
вектору z\, А,(о) = (Лхо, Хо)/(Вх1, хк), kn — количество «внутренних»
итераций для каждого /г, т4п) — чебышевские итерационные
параметры для интервалов (т„, Мп), границы которых 0<mn<iMn
могут меняться на разных внешних итерациях.
Для произвольного числа А,(о) собственные векторы
спектральной задачи
(A-№D)zt = vPDzi, i=l,2,... ,N, (4.82)
очевидно, совпадают с собственными векторами задачи (4.59),
а собственные числа связаны соотношением vP = Xi — А,(о).
С другой стороны, собственные векторы */[0) матрицы перехода
/#0 = / _ г£я>Я-] (А - ti0)D) (4.83)
итерационного процесса (4.81) при А,(о) определяются
спектральной задачей
i= 1,2,... , N. (4.84)
183

Нетрудно видеть, что v[0) и |40) являются собственными числами
матриц D~l/2{A-X^D)D~l/2 и H~l/2(A ~X^D)H~l/2
соответственно. Отсюда, в силу положительной определенности матриц D, Н
и закона инерции Сильвестра [38] следует, что спектральные
задачи имеют одинаковое число положительных, нулевых и
отрицательных собственных чисел.
Из последнего свойства вытекает, что если значение А,(о)
находится между Xs и A,s+i» I ^s<cN, то для собственных чисел (4.84)
будут выполняться неравенства (с учетом того, что к\ из задачи
(4.59) —простое собственное число):
^<^<...<|40)<0<^,<...<^). (4.85)
Поэтому, если мы выберем то, Мо из условий О^то^м^ь
\х$^Мо, а итерационные параметры т40) возьмем равными обрат-
Ti а пг ( A*o + mo —2v\
ным значениям корней многочлена Чебышева i кЛ—тз— 1
(для этого в формуле (4.73) надо положить п~к, т — тщ, М = т0,
L~ko), to мы получим, что для достаточно больших ко имеют
место неравенства
А/о)2> №ь=(Лх§°, 4°)/(Bxk0\ 4°)>Аи, (4.86)
т. е. значение Я(1) ближе к искомому К\у чем 7S0\ Доказательство
следует из того факта, что в силу (4.85) собственные числа т]10)
матрицы перехода (4.83) удовлетворяют неравенствам
^о)> №> -. > Ч?}> 1 >№х> - > т»(й>. (4.87)
Отсюда, раскладывая векторы Хо из (4.81) в ряд по
собственным векторам yfp задачи (4.84), легко показать, что
последовательность нормированных векторов xq/(Dxo, х§)1/2 сходится к
^/(D/*\ у^у/2. А поскольку величина
(Dxl
с ростом fe стремится к
(Лxk0, x^_ (Q) ((Л-X^D)xi 4)
S)" ~"
то из отрицательности ffl и положительной определенности
матриц Я, 1) получаем (4.86).
Аналогично и для других я можно показать, что если Х^^Хи
to при достаточно большом количестве «внутренних» итераций kn
и соответствующем выборе т„, Мп в итерационном процессе (4.81)
имеем неравенства
Таким образом, получаем, что при я-^оо числа Х^ сходятся
к пределу А,* — Х\ (если Я*>1, то предельное значение \i[n>l
отрицательно, и мы приходим к противоречию). Последовательность
184

векторов t/fi сходится к Z\, так как при п-^оо величина
^я+|> —Л(й)=((Л —Л(я)ад% xfr)/(Dxk0\ 4я)
стремится к нулю и Х{п)-^Х\У хоя-+у\п\
Скорость сходимости алгоритма (4.81), как и в степенном
методе, зависит от соотношения значений к\, А,2. С точки зрения
оптимизации экономичности определяющим является выбор
начального сдвига Я(о), количества внутренних итераций kn,
параметров тп, Мп для вычисления итерационных параметров и самого
вида матриц Я„. Если нет какой-либо априорной информации о
границах спектра матрицы H~l(A — A,(n)D), то значения тп можно
брать нулевыми, а Мп оценить грубо по ее норме.
При выборе Нп в виде единичной матрицы (4.81) мы приходим
к формальному обобщению метода (4.72), заключающемуся в
использовании переменных сдвигов ^"Х Однако как раз в этом
случае простой спектральный анализ показывает, что введение
сдвигов не дает улучшения асимптотических (при больших п) оценок
необходимого числа итераций.
В работах Руэ [162] исследовано применение метода
последовательной релаксации с переменным сдвигом для нахождения
минимального собственного числа и соответствующего
собственного вектора. Формально такой итерационный процесс можно
записать в виде (4.81) с некоторой несимметричной матрицей,
но его реализация более наглядна в следующей записи.
Пусть матрица А из спектральной задачи (4.59)
представляется суммой А = —М-\-В— N, тле В — диагональная, а Ми N—
соответственно нижняя и верхняя треугольные матрицы. Тогда
последовательные приближения определяются формулами
l = Nxkn, k= 1,2,..., *я, (4.88)
Здесь о) — итерационный параметр, a kn — количество
«внутренних» итераций на п-и «внешней» итерации. Как видно,
вычисления векторов Xn+i производятся практически так же, как и при
решении систем линейных алгебраических уравнений методом
последовательной верхней релаксацил. Введение переменного
сдвига изменяет только диагональные члены матрицы перехода,
которая в данном случае определяется из выражений
* = 1,2, ...,*„, (4.89)
В таком итерационном процессе для различных kn и начальных
приближений А,(о) (только матрицы Т$ должны быть
невырождены) при я-> go значения Х^ сходятся к ^, а 4 — к
соответствующему собственному вектору z\.
Мы не будем останавливаться на обосновании метода. Отметим
только, что достаточными условиями сходимости итераций явля-
185

ются те же свойства, что и для методов последовательной
релаксации решения систем уравнений (см. § 1.3): диагональное
преобладание, положительность В и неотрицательность матриц М, N.
У матрицы перехода базис из собственных векторов другой,
нежели в задаче (4.59). Однако если A,(n)->A,i, то минимальное
собственное число матрицы Т$ стремится к нулю, а4 — к ее
соответствующему собственному вектору, который будет при этом
совпадать С Z\.
С точки зрения экономичности алгоритма (4.88) возникает
задача оптимизации параметров со, №\ kn. Теоретически эти
вопросы не исследованы. Практика показывает, что при А,(0) = 0
и выборе со из тех же принципов, как и при решении систем
уравнений, разностные задачи на собственные значения решаются
данным методом с высокой эффективностью (величины kn можно
брать от 1 до 10). Вычисление минимального собственного числа
и соответствующего собственного вектора требует примерно такого
же количества итераций, что и решение системы уравнений с той
же матрицей.
4.3.2. Нахождение нескольких собственных чисел и векторов.
Если мы нашли каким-либо из выше рассмотренных итерационных
процессов Х\ и z\, то его можно продолжить с небольшой
модификацией для определения второго собственного вектора и
собственного числа, если оно простое. Для этого достаточно
использовать свойство D-ортогональности z\ ко всем остальным
собственным векторам задачи (4.59).
Пусть, например, в методе (4.72) при n = tii мы вычислили
с достаточной точностью вектор Z\. Тогда дальнейшие итерации
продолжаем, проводя ортогонализацию векторов хп к Z\\
уп = Рп(С)х\ xn = yn-(Dynfzl)zu n = m + l, лг,+2,... (4.90)
Очевидно, что предельный вектор последовательности хп будет
ортогонален к zu и если собственное число v2 матрицы С простое,
то величины gn из (4.74) для достаточно больших п могут быть
использованы для его вычисления:
v2=\im{(l-gn)/xn}. (4.91)
П-*-оо
При этом предельный вектор хп нам дает 2г.
Типичное использование такого подхода — вычисление
минимального ненулевого собственного числа для вырожденной
матрицы, возникающей из разностной аппроксимации задачи Неймана.
Формально этот процесс можно использовать и для вычисления
нескольких собственных чисел и векторов. Если в задаче (4.59)
уже найдены к\, ...Дг, Zi,..., 2Г, то для нахождения Хг+\ (если оно
простое) можно использовать метод (4.72), в котором векторы
хп D-ортогонализуются к z\,...,zr:
у- = Рп{С)х\ xn = yn-i [Dy\ Zi) и (4.92)
186

Однако применение такого алгоритма к вычислению большого
количества собственных чисел требует высокой точности
определения z\,...,zr, иначе «погрешности ортогонализации» приведут
к большим ошибкам результата. Кроме того, применимость метода
сужает условие некратности вычисляемых собственных чисел.
Эффективным алгоритмом одновременного вычисления
нескольких собственных чисел и векторов для матриц большого
порядка является метод итераций в подпространстве [10],
являющийся одним из вариантов так называемых ступенчатых методов
[183, 188].
Итерационный процесс ведется одновременно с т векторами,
для которых задаются произвольные начальные приближения
xf\ л#>, ...,*2?. Обозначая через Мо прямоугольную матрицу
размера mXN, состоящую из векторов х$\ k= 1,..., m, решение
задачи (4.59) ищем с помощью последовательности
LnDLny (4.93)
= LnZn+\
Как видно из построения, Ап, Вп представляют собой квадратные
симметричные матрицы порядка т, а Ап — диагональная матрица
с элементами Х\п\ ...ДЙ?. Четвертое соотношение (4.93)
представляет собой запись обобщенной проблемы собственных значений
для матриц Л„_|_1, Вп+1, причем столбцы z{n+l\..., z(m + 1) есть
собственные векторы, соответствующие собственным числам Х[п+1\ ...
...,A,fe+1). Для каждого п такая вспомогательная проблема может
быть легко решена «стандартным» алгоритмом (например,
методом Якоби), поскольку для рассматриваемых нами задач m<cN.
Первая строка в (4.93) есть фактически т систем линейных
уравнений N-vo порядка, решение которых может быть выполнено
с помощью итерационных методов, описанных в главе 1.
С помощью спектрального анализа последовательных
приближений можно показать, что значения МЧ-А^ стремятся к
собственным числам A,i,...,A,m исходной задачи (4.59), в том числе и при
наличии среди них кратных значений. Столбцы х^\ &=1, 2,..., т,
матрицы Мп, соответствующие собственным числам Xin\ стремятся
при п-+оо к собственным векторам Zk исходной задачи (4.59).
Скорость сходимости каждой из последовательностей Х\п) для
l^k^m зависит от отношения Xk/km+i. Поэтому с точки зрения
ее увеличения целесообразно брать размерность итерируемого
подпространства с запасом. То есть, если требуется вычислить
г собственных векторов, то значение т берется процентов на 20—
50 больше. Однако надо иметь в виду, что при этом увеличится
трудоемкость каждой итерации.
В целом задача вычисления 5—10 собственных чисел и
векторов остается достаточно «дорогой», и вопрос оптимизации
алгоритмов является чрезвычайно актуальным. Достоинства метода
(4.93) заключаются в возможности его реализации при
относительно малом объеме оперативной памяти и в наличии
опубликованной хорошей программной реализации [10].
187

§ 4.4. Примеры расчета характеристик
электродинамических систем
Мы приведем результаты расчетов ряда практических задач,
выполненных А. В. Гаврилиным с помощью описанного в
последней главе пакета программ Эдип, см. также [37].
4.4.1. Расчет длины волны регулярного волновода. Для
регулярного волновода с П-образной формой поперечного сечения,
см. рис. 22, ставилась задача расчета длины основной волны
электрических колебаний.
Математическая постановка сводится к
решению задачи (4.38) при <х = 0
(декартова система координат)
в области, ограниченной ломаной
ABCDEF. С учетом симметрии
сечения, граничные условия
берутся в виде и —0 на АВ и ди/дп = 0
наBCDEFА.Ллкяа волны /
выражается формулой 1 = 2я/-^Х через
минимальное собственное число X
краевой задачи, для нахождения
которого применялись
рассмотренные выше методы,
и а=1 расчеты проводились с
исвложенных сеток Qh, QA/2,
й
Рис. 22.
Для значений а\=а2 = (
пользованием последовательности
A/2
последняя из которых получалась делением пополам шагов редкой
сетки. Сетки выбирались такими, чтобы граница проходила по
координатным линиям. Аппроксимация условия Неймана
проводилась с погрешностью второго порядка.
Поскольку для данной задачи не известно точное решение,
достоверность расчетов проверялась путем сравнения результатов
на двух типах сеток. Первый вариант рассчитывался на вложенных
квадратных сетках, из которых редкая имела шаг А=1/40. В
результате были получены значения
Kh = 5,5806; Xh/2 = 5,5840;
2 — -L-Xh = 5,5852.
о
Во втором варианте редкая сетка имела следующие шаги:
f 0,05, 0<*<0,25, [ 0,05, 0<у< 0,025,
hx=\ 0,5/30, 0,25<jc<0,75, hy=\ 0,5/30, 0,25<w<0,75,
L 0,05, 0,75 <*<1, I 0,05, 0,75 < у <1.
Соответствующие собственные значения при этом равны:
kh = 5,5828; lh/2 = 5,5849; lh/2 = 5,5857.
Отсюда видно, что для обоих типов сеток проэкстраполиро-
ванные значения кн/2 отличаются друг от друга менее чем на
0,01%, что может служить достаточной гарантией точности
алгоритмов.
188

4.4.2. Расчет коэффициента усиления поля периодической
структуры. В линейных ускорителях заряженных частиц широкое
распространение получили периодические структуры с кольцами.
Схематическое изображение осесимметричного фрагмента одной
из таких структур (вообще говоря, трехмерных) представлено
на рис. 23, а вместе с характерной формой силовых линий
электрического поля.
\\Кп
Рис. 23.
Анализ структуры проводился на основе решения краевой
задачи (4.38) при а = 1 в области, ограниченной контуром
OABCDEFGO с граничными условиями ди/дп — О на ABCD и и =
= 0 — на остальной части границы. Особенностью задачи
является то, что радиусы закругления кольца в точках В и С на два
порядка меньше характерных размеров а или Ь.
Целью расчетов были подбор геометрических параметров для
обеспечения заданной длины волны и нахождение
распределения коэффициента усиления поля ko = Ez/Ec? вдоль поверхности
кольца.
а
Здесь Еср==—\ £г(0, z) dz — среднее значение компоненты
о
напряженности поля на оси,' a Ez = Ez(s)— напряженность как
функция параметра длины контура ABCD. Значения Е2 в узлах
сетки вычислялись с помощью аппроксимации выражения Ez =
=—— по формулам с погрешностью второго порядка, а в
остальных точках использовалась линейная интерполяция. На рис.
23,6 приведён вид зависимости &o(s), имеющий физически
«разумную» форму. Достоверность результата проверялась путем
расчетов с различными счетными параметрами.
4.4.3. Моделирование замедляющей системы ускорителя. На
рис. 24 приведена расчетная ячейка замедляющей системы
ускорителя заряженных частиц. Целью численного моделирования
было нахождение основной частоты электрических колебаний со =
= j/АГи распределения характеристического сопротивления систе-
189

мы, рассчитываемого по формуле
ф) = я( J JL dr' dzj Я^1
Q
dz,
а также определение изолиний азимутальной компоненты
магнитного поля Вф, в данном случае вычисляемого через основную
гармонику и с помощью выражения В^ = и/г.
Рис. 24.
Здесь Q обозначает расчетную область, a Qr — ее часть с
координатами г'^г.
Расчеты проводились на последовательности
кусочно-равномерных сгущающихся вложенных сеток (каждая последующая
сетка имеет шаги вдвое меньше, чем-предыдущая). Самая редкая
из них имела количество узлов около 600, а самая густая — около
10000.
На рис. 24 приведена кривая зависимости характеристического
сопротивления от радиуса, а также характерные изолинии
компоненты магнитного поля Вг Отметим, что полученное в расчетах
значение основной частоты «даже слишком» хорошо совпадает
с экспериментально измеренным числом для данной системы —
отклонение составляет менее 0,01%.

Глава 5
МОДЕЛИРОВАНИЕ СИЛЬНОТОЧНЫХ ПУЧКОВ
Сильноточные пучки заряженных частиц имеют широкое
распространение в различных областях науки и техники.
Математическая постановка здесь заключается в решении так называемых
самосогласованных нелинейных задач, сводящихся к расчетам
электромагнитных полей и движения пучков заряженных частиц
с учетом объемных зарядов и токов. Отдельно следует рассмотреть
стационарные задачи и нестационарные. Описание последних мы
делаем в квазистационарном предположении, что за время
прохождения частицами расчетной области электрическое поле
меняется несущественно и распределение потенциалов описывается
в каждый момент времени уравнением Пуассона.
Рассматриваемые задачи имеют богатое физическое
содержание и в различных приложениях требуют учета многочисленных
эффектов: релятивистских скоростей, вторичной эмиссии,
объемной ионизации, взаимодействия с высокочастотными полями и т. д.,
см. [23, 97, 161, 163].
Численное моделирование плотных пучков заряженных частиц
имеет давнюю историю, восходящую еще к «домашинной» эпохе.
Значительное количество результатов было получено с помощью
приближенных аналитических методов или моделирования на
аналоговых устройствах. Состояние этого этапа работ достаточно
полно отражено в монографии [97].
С освоением ЭВМ образовался поток статей, посвященных
как описанию расчетов различного типа силыюточных приборов,
так и разработке новых алгоритмов. Большая библиография по
этим работам приведена в книгах [70, 138, 161], а также в
обзорной статье [148]. Среди работ за последние годы следует отметить
исследования московских математиков А. Г. Свешникова,
Ю. И. Мокина, Г. Т. Головина и других, в которых
рассматриваются и новые математические постановки, и численные методы,
и результаты численных экспериментов, см. [13, 21, 22, 46, 67,
131 —136], а также цитируемую там литературу.
Можно смело сказать, что расчеты сильноточных
электрофизических устройств представляют собой одну из наиболее
трудоемких задач вычислительной математики, требующую затрат
значительных ресурсов самых современных вычислительных систем.
Достаточно заметить, что в полном объеме эта проблема
включает составными компонентами рассмотренные в
предыдущих главах задачи расчета напряженности электростатического
1Q1

поля, магнитной индукции, собственных частот и гармоник
резонаторов. Кроме того, прикладные требования заставляют
рассчитывать экстремальные режимы сильноточных устройств, что
приводит к решению сильно нелинейных задач, для которых
вопросы существования, единственности или устойчивости решений
являются открытыми. В таких случаях проблемы сходимости или
оценки погрешности алгоритмов практически неразрешимы, и
критерием адекватности расчетов является только сравнительный
анализ численных экспериментов и физических измерений.
§ 5.1, Описание математической модели
Рассмотрим следующую постановку задачи:
а) потенциал электрического поля ср, образованного системой
электродов и объемным зарядом частиц с плотностью р,
удовлетворяет уравнению Пуассона
Аф=—4яр; (5Л)
б) движение частиц массы М и заряда q определяется
уравнением (мы пользуемся гауссовской системой единиц):
где г — радиус-вектор этой частицы, с — скорость света, t —
время, а Я — вектор напряженности магнитного поля;
в) выполняется условие неразрывности токов
div/ = d'wpv = др/dt, (5.3)
где / — плотность тока, a v — средняя скорость, определяемая как
v(r)=hm . (5.4)
Здесь Vi = dr/dt — скорость отдельной частицы, имеющей заряд
qi. Суммы берутся по всем частицам, находящимся в объеме AV.
Соответственно плотность объемного заряда имеет вид
p= lim ^-= lim-у, (5.5)
где Q(AV0 = S<7i• — суммарный заряд в объеме Д1Л
Магнитное поле представляем в виде суммы Н = Нь-\-Нс, где
Нь — напряженность так называемого внешнего поля,
задаваемого или вычисляемого каким-либо образом как функция
независимых переменных. Вектор Нс характеризует собственное магнитное
поле пучка:
КП (г-г')}
\r-r'\
dV. (5.6)
Требуется найти решение, т. е. распределение потенциала,
плотности токов, объемных зарядов и траекторий частиц в замкну-
192

той области G, на границе Г которой заданы условия для ф, / и
начальные данные для координат и скоростей частиц.
Строго говоря, рассматриваемое уравнение неразрывности
плотности тока и сами понятия плотности тока и объемного заряда
имеют смысл только при достаточно высоких плотностях частиц,
что не всегда имеет место в исследуемых задачах. Однако эти
вопросы легко снимаются, если вместо дифференциальных
уравнений (5.1), (5.3) использовать эквивалентные интегральные
законы сохранения: теорему Гаусса
is *v
где As — площадь поверхности объема W, и баланс заряда
i ~ 2 qi= { (Q2 - Q\)dt.
J
AV
Здесь 2 qt означает количество заряда в AV в момент времени
AV
tn, a Q2 и Q\ —заряды, входящие и выходящие, соответственно,
за единицу времени через поверхность As. Используемые ниже
алгоритмы аппроксимируют фактически интегральные
соотношения при малых, но конечных АV.
Для расчета объемных зарядов и плотности тока используем
модель «больших частиц». Предполагается, что элементарные
частицы, влетающие за интервал At в область с некоторой
площадки As со скоростями, находящимися в отрезке [vy v-{-Av],
образуют так называемую большую частицу конечного размера,
которая движется затем как целое, сохраняя свой заряд
неизменным. Начальные координаты и скорости большой частицы
определяем усреднением по всем входящим в нее элементарным
частицам. При необходимости учета распределения частиц по
скоростям проводится разбиение потока на энергетические, а если
нужно, и на угловые группы. Тогда с каждой площадки As
пускаются несколько частиц с начальными значениями скоростей,
усреденными по соответствующей группе.
Для нахождения заряда в некотором объеме АV расчетной
области определяется доля заряда каждой частицы, относящейся
к Д V, и производится простое суммирование. Аналогично, с учетом
скоростей частиц, находятся и элементарные токи в объеме AV.
Для стационарных задач используется более экономичная
модель — метод трубок тока.^ В этом случае предполагается, что
все частицы, входящие в расчетную область через площадку As,
образуют элементарную токовую трубку с неизменным
переносимым ею током
/=$ $ j(r,v)dvds. (5.7)
As Au
13 В П Ильин 193

Форму такой трубки определяем по траектории какой-либо
элементарной частицы, вылетающей с площадки As. При учете
распределения частиц по скоростям также проводятся разбиения
потока на энергетические и угловые группы, и с каждой площадки
запускается несколько трубок, с соответствующими начальными
данными.
Основное различие методов «больших частиц» и «трубок тока»
заключается в объеме необходимой для запоминания информации.
Например, пусть в трехмерной стационарной задаче поток
моделируется 200 трубками тока и каждая соответствующая траектория
содержит в среднем 50 расчетных точек. Тогда требуется
запомнить только начальные значения координат и скоростей частиц,
всего 200 X 6 чисел, в то время как при использовании сравнимой
по точности модели «больших частиц» потребовалось бы 200 X
X 50 X 6 чисел.
Распределение объемного заряда в стационарном случае будем
находить, используя условие неразрывности для отдельных трубок
тока. Если, например, траектория, которой мы ставим в
соответствие бесконечно тонкую трубку с током Л, пересекает некоторый
объем АV за время А/^, то заряд i-и трубки тока, находящийся
в этом объеме, определяется как ЛА/^. Общее количество заряда
в объеме AV ищем с помощью суммирования по всем проходящим
через него траекториям:
2 (5.8)
Отметим, что такой алгоритм универсален в том смысле, что не
предполагает ламинарности потока, допускает пересечения
траекторий и различные типы частиц.
Физический характер рассматриваемых нами задач в большой
степени зависит от типа граничных и начальных условий. В данной
работе мы допускаем следующие возможные случаи.
Расчет проводится в замкнутой двумерной или трехмерной
области, на границах которой задаются или значения потенциала,
или условия Неймана. Если исследуемая система электродов
не замкнута, то требуется провести замыкание расчетной области,
поставив из физических соображений условия на искусственно
вводимых участках границы. Например, если замыкание
проводится достаточно далеко от интересующей нас окрестности, то можно
поставить условие однородности поля дц/дп (здесь и далее п —
внутренняя нормаль к границе). Условия Неймана также ставятся
на линиях или плоскостях симметрии. При наличии сред с
различными диэлектрическими постоянными е+, е_ на границе их
раздела ставятся условия сопряжения (1.3).
Нас будут интересовать, как правило, области со сложной
конфигурацией, в том числе и многосвязные.
Далее, мы будем допускать наличие в области нескольких
пучков частиц различного сорта, т. е. имеющих разные значения
массы и заряда. Мы предполагаем возможным следующие типы
начальных условий для плотности тока.
194

al) Задается плотность тока; если пучок не моноскоростной,
то указывается общая плотность тока, функция распределения
частиц по скоростям и способ разбиения потока на энергетические
или угловые группы. Обозначая tj = cos (и,/г), для этого случая
мы сможем формально записать выражение
/|г€г=/(г,|о(г)|, л(г)). (5.9)
Примерами задач с такого типа условиями может служить
расчет поля в области, в которую влетает односкоростной пучок,
или расчет параметров известной эмиссионной способности катода
с учетом температурного разброса частиц.
61) Ставится условие ограничения плотности тока
пространственным зарядом при нулевых начальных скоростях на эмиттирую-
щей поверхности катода. Это приводит к дополнительному
граничному условию: помимо заданного потенциала фо на катоде
требуется равенство нулю нормальной производной потенциала на
поверхности. Для одномерного случая (плоский диод) такая
задача имеет точное решение: плотность тока пропорциональна
отношению [ф(х) — фо]3/2/х2, а распределение потенциала имеет
вид ф(х)~х4/3 — это так называемый закон «3/2», или Чайльда —
Ленгмюра.
Для цилиндрического или сферического диодов, а также в
случае релятивистских скоростей или наличия внешних магнитных
полей, соответствующие решения имеют незначительные поправки,
см. [113, 163]
Если эмиттирующая поверхность криволинейна, то мы считаем,
что существует на достаточно близком от нее расстоянии d
эквипотенциальная поверхность, «почти параллельная» поверхности
эмиттера, и между ними распределение ф такое же, как для
одномерного случая. При этом учитывается возможность ограничения
плотности тока эмиссионной способностью катода /s, т. е. для
электрона массы т с зарядом е будем иметь
Л лег = mm {/„ -f\J 2 — ), (5.10)
где щ — значение потенциала в точке на расстоянии d по нормали
к поверхности эмиттера.
Рассматриваемая постановка существенно усложняется в
задачах расчета плазменной границы, когда само положение эмитти-
рующей поверхности неизвестно. В этом случае обычно плазма
предполагается квазинейтральной и эквипотенциальной, а
значение потенциала принимается тем же, что и на примыкающем
металлическом электроде. Плотность тока эмиссии из плазмы
считается заданной и определяется ее температурой и плотностью.
Граница эмигрирующей поверхности определяется из условия
равенства кинетического давления плазмы р и давления
электростатического поля:
V дп
13* 195

Если считать переходный слой между плазмой и вакуумом
бесконечно тонким и пренебречь тепловыми скоростями
заряженных частиц, то на границе плазмы можно считать нормальную
производную от потенциала равной нулю. Тогда получаем, что на
малом расстоянии d Ът границы решение приближенно
описывается законом Чайльда — Ленгмюра, как и вблизи обычного катода.
в1) Условие для вторичной эмиссии. В данном случае
плотность тока для вылетающих с поверхности частиц зависит от
энергии и плотности частиц падающего потока. При этом вторичные
частицы могут быть распределены по энергетическим группам:
/вт = /(1/л1, \Vn\, ICbtI, T)X
где vn, jn — скорость и плотность тока падающего потока, а /вт
должна быть задана как функция указанных переменных.
. В простейшем приближении «вторичные» частицы можно
считать вылетающими по нормали к поверхности, причем, как
правило, выделяются упруго отраженные частицы, начальная скорость
которых равна скорости падающих, а также медленные частицы,
обусловленные неупругим отражением. В рассматриваемой нами
формулировке явление поверхностной ионизации понимается как
частный случай вторичной эмиссии, отличающейся только сортом
эмиттируемых частиц.
rl) Мы отметим еще один физический эффект, приводящий
к новому типу задач, — процесс объемной ионизации в
электровакуумных приборах, возникающий из-за остаточного давления.
Предполагаем, что заданы плотность газа, сечение ионизации
и функции распределения частиц после столкновения. По этой
информации в ходе расчета траекторий основного потока
формируются начальные данные для ионизируемых частиц, а их
движение рассчитывается обычным образом.
Решение будем искать в декартовой системе координат х, у, z
для трехмерных областей, а в двумерных используем координаты
х, у для плоских задач и цилиндрические координаты г, z — для
осесимметричных.
Решение самосогласованных стационарных задач проводится
путем последовательных приближений по объемному заряду.
Сначала находится поле при каком-то начальном распределении
р (как правило, нулевом), и в таком поле рассчитываются
траектории, токи и обусловленный ими заряд. Затем определяется поле
с учетом этого заряда, снова рассчитываются траектории и т. д.;
итерации продолжаются, пока соседние приближения не совпадут
с заданной точностью.
Если за период, сравниваемый со временем движения частиц
в расчетной области, существенно изменяются потенциалы на
электродах или какие-либо другие параметры (например,
плотность тока влетающих в область частиц), то мы приходим к
нестационарной задаче. В этом случае будем использовать
квазистационарное приближение, т. е. предполагаем, что скорость изменения
переменных факторов все-таки относительно мала и на каждый
196

момент времени распределение потенциала удовлетворяет
уравнению Пуассона. Решение нестационарной задачи при этом
определяем как последовательность стационарных решений, для каждого
из которых граничные и начальные условия соответствуют моменту
п
времени tn= 2 А/*. Значения Atk выбираются достаточно ма-
k=i
лыми по сравнению с характерным временем изменения
параметров задачи.
Напомним, что в нестационарных задачах поток можно
описывать только с помощью модели больших частиц, а не трубок тока.
Для этого задаются начальные координаты г,- и скорости п
находящихся в расчетной области больших частиц, а также значения
их масс Mi и зарядов qu /=1,2, ...,N. Очевидно, величины г, и N
должны быть такими, чтобы расстояния между соседними
частицами были малы по сравнению с характерными размерами области.
Кроме того, часть границы, являющейся эмиттером или фронтом
входящего пучка, рассматривается как «источник» частиц. С
площадки Ask в каждый момент времени tn выпускается частица
с зарядом AskjkAtn, где jk — средняя плотность тока на As*.
Распределение плотности объемного заряда приближенно
описывается соотношением (5.5), причем AV берется конечным, a Q(AV)
определяется по заряду больших частиц, находящихся в объеме
А V.
Конкретизируем форму дифференциальных уравнений, причем
для удобства введем безразмерные переменные:
х'—— и'—-У- г'—— г'—— V— г ©' — ф
Lq Ьо Lo Lq to фо
dt' vo Но vo /о ро
где Lo, vo, to, фо, /о, ро, Но — некоторые характерные величины
длины, скорости, времени, электрического потенциала, тока,
плотности заряда и напряженности магнитного поля, причем vo =
= Lo/voi (ey m — заряд и масса покоя электрона),
В дальнейшем мы будем все уравнения писать в безразмерном
виде, а штрихи для краткости опускать.
Уравнение Пуассона запишем в форме
для трехмерного Случая и
для двумерного. Здесь а равна нулю для плоских задач и
единице — для осесимметричных, причем ради единообразия перемен-
197

ные г, г заменены на х, у, а 0 = 4пр0Ц/ц)о — безразмерная
константа.
Потенциал ф на разных участках границы удовлетворяет гра-
ничньТм условиям бида (1.2), (1.3), причем функции gi могут
зависеть от t.
Запишем в проекциях на оси координат системы уравнений
движения, выделив для наглядности в дальнейшем те случаи,
которые отличаются алгоритмическими аспектами.
а2) Нерелятивистские задачи без магнитного поля:
х=_р4^, £=-р-^, z=-|A (5.13)
здесь p = zm/(2Af |е|), причем третье уравнение в двумерных
задачах отсутствует (напомним, что в осесимметричном случае
х9 у означают цилиндрические координаты).
62) Плоские нерелятивистские задачи со скрещенными
магнитными полями (НХ = НУ = О):
) ^) (5.14)
здесь Di=HoLoVo/(co(po) — безразмерная постоянная.
в2) Трехмерные релятивистские задачи:
fg] (5.15)
г=pV Т^ [ Ц+d (iH н) ie ]
гдс 82_ e^j
где о - ^ ,w 2 {x dx ty gy
Очевидно, нерелятивистский случай получается отсюда при
6 = 9—0. Решение таких систем может потребоваться даже для
двумерных электрических полей, если НхФ0 или НУФО.
г2) Мы выпишем, наконец, систему уравнений движения в
цилиндрической системе координат для релятивистского случая:
/„, - щНг) - /0 ; (5.16)
дг dz/'
Решение этих уравнений требуется проводить для каждой частицы
198

или траектории при заданных начальных данных
Мы рассмотрим алгоритмы расчета траекторий, объемных
'зарядов, токов и необходимых характеристик электромагнитных
полей. Предполагается, что решение краевых задач для
потенциалов проводится с помощью разностных методов на прямоугольных
(в трехмерном случае — параллелепипедоидальных) сетках
(Гкусочно-постоянными шагами по каждой из независимых
переменных. Соответствующие вопросы мы будем затрагивать в
минимально необходимом объеме, ограничиваясь главным образом
ссылками на первую главу. '
Расчет потенциалов можно бы проводить и по методам
конечных элементов, рассмотренных в гл. 2. Однако при использовании
существенно неравномерных и тем более нерегулярных сеток,
подстраивающихся под геометрию границы, сильно усложняются
алгоритмы вычисления напряженностей электрических и
магнитных полей, являющихся наиболее трудоемкой частью при
интегрировании уравнений движения частиц. В случае же регулярных
прямоугольных сеток конечно-разностные методы более
экономичны, чем конечно-элементные.
Для самосогласованных задач конечно-разностные
аппроксимации имеют преимущество также и по сравнению с методами
интегральных уравнений. Во-первых, при наличии объемных
зарядов в области значительно усложняется формирование
алгебраической системы для определения плотности поверхностного заряда.
Во-вторых, вычисление производных потенциала в каждой точке
(а это необходимо делать многократно при большом числе частиц)
требуется проводить интегрированием по всей границе области,
что тоже является трудоемкой операцией.
Сделаем несколько замечаний о других математических
моделях пучков заряженных частиц. Мы фактически рассмотрели поток
как дискретную совокупность элементарных частиц, а каждую
«большую частицу» определили простым суммированием заряда,
массы и усреднением скоростей элементарных частиц,
находящихся в начальный момент времени в конечном элементе фазового
объема.
Наиболее распространенная модель основана на определении
функции распределения частиц f(t, г, р) в фазовом пространстве
из кинетического уравнения Власова
+v+Fo
« dt dr dp '
где р — импульс, a F — сила, действующая на заряженную
частицу в электромагнитном поле.
Плотности тока и объемного заряда при этом выражаются
интегралами
9(r) = q \ /(г, v)dvf j(r) = q \ vf(r, v)dv,
199

а траекториями движения отдельных частиц являются
характеристики кинетического уравнения, вдоль которых функция
распределения постоянна.
В работах Ю. И. Мокина [131, 133—136] предложена и
исследована еще одна математическая модель, основанная на
определении траекторий заряженных частиц из некоторой системы интег-
ро-Йифференциальных уравнений.
Пусть фо(г) — «лапласовское» электростатическое поле,
определяемое из (5.1) при р = 0 и исходных граничных условиях
рассматриваемой задачи, a G(r, r') — функция Грина,
определяемая уравнением
AG(r, г')=—4я6(г—г')
с соответствующими однородными граничными условиями.
Обозначим через r'(ro, t) радиус-вектор точки траектории
частицы, вылетающей в момент ^ = 0 из точки г0 эмиттирующей
поверхности S, а через t(r0) — момент выхода этой частицы из расчетной
области.
Тогда потенциал — решение уравнения (5.1) —может быть
определен по формуле
/(Го)
G(r,r'(ro,t))dtWS.
s о
Если плотность тока определяется из условия ограничения
пространственным зарядом, то для j(r0) имеем интегральное
уравнение
^\ И Т И = 0. (5.17)
Последние два уравнения в совокупности с уравнениями
движения частиц при начальных данных для всех г0 6 S образуют
замкнутую систему. Если условия задачи требуют учета
собственного магнитного поля пучка, то необходимо добавить аналогичные
уравнения для компонент векторного потенциала. Такая
постановка эквивалентна модели, использующей кинетическое уравнение
Власова. Аналогичная математическая модель была предложена
Ю. И. Мокиным [132J и для задачи о нестационарном движении
пучка заряженных частиц.
Дискретизация системы интегро-дифференциальных уравнений
позволяет получать модели трубок тока и больших частиц. При
некоторых упрощающих предположениях удается также показать
сходимость получаемых приближенных решений к точному [133].
В заключение параграфа отметим, что наиболее сложные из
рассматриваемых задач — это управление пучками заряженных
частиц, или другими словами, оптимизация систем формирования
интенсивных потоков по заданным критериям качества. Некоторые
постановочные вопросы по этой проблеме или примеры решения
отдельных задач рассматривались в работах [21, 116, 114, 147].
200

§ 5.2. Определение напряженностей электрического
и магнитного полей
При расчете траекторий самостоятельной вычислительной
задачей является определение компонент электрического и
магнитного полей. Напряженности находятся, как правило, из численного
дифференцирования сеточных функций,- описывающих
распределение потенциалов или магнитного потока.
5.2.1. Расчет напряженности электрического поля. В данном
пункте мы приводим алгоритмы аппроксимации напряженности
электрического поля по формулам с погрешностью первого или
второго порядка. Рассматриваем также приближение потенциала
бикубическими полиномами (или сплайнами), имеющими
непрерывные производные вплоть до второго порядка и
обеспечивающими погрешность аппроксимации потенциала О(А4), а
напряженности — O(h3).
Для задач с наличием плоского или осесимметричного
внешнего магнитного поля предполагается, что его компоненты заданы
в точках плоскости или оси симметрии. По этим значениям
производится сплайновая интерполяция и далее с помощью ряда Шер-
цера определяется напряженность во внутренних точках области.
Собственное магнитное поле релятивистских пучков находится
из закона Био — Савара — Лапласа или путем численного
дифференцирования функции магнитного потока, определяемого из
решения краевой задачи.
Пусть требуется найти значения д<р/дх, дф/ ду, дф/ дг в точке
(х*, у , z\ расположенной в ячейке разностной сетки
(рис. 25,а).
а?
]
6
3
1
о j
7 а
4 S
1 2
Ч?
Рис. 25.
Производные аппроксимируются с погрешностью О(А)
следующими выражениями:
z—zk
р=-
h2
hx
201

(5.18)
ф^ ф2 — ф1 + ^(ф4 — фз — ф2 + ф1),
ф" = фб — ф5 + ?(ф8 — ф7 — фб + фб),
Фу' = ф7 — ф5 + Р(ф8 — ф7 — фб + фб),
фг^фб —ф1+р(фб —ф5 —ф2 + ф1),
фГ = ф7 — фЗ + Р(ф8 — ф7 ~ ф4 + фз).
Для двух независимых переменных формулы соответствующим
образом упрощаются (г = 0, дц)/дг = 0).
Аппроксимацию производных с погрешностью 0{h2)
проиллюстрируем двумерной задачей. При этом используем
девятиточечный шаблон типа «ящик» с центральным узлом, ближайшим к
точке (а:*, у*) (рис. 25,6). Вдоль ближайших координатных линий
производные аппроксимируются трехточечными выражениями,
а между линиями производится квадратичная интерполяция:
дх
<5ф \
17//-
-J-
2l\—h\
— фо+/
= 0,3,6, / = 0,1,2, /i=a:* — xo, l2 = y*—y0i
\ dx /°
/ dq>
\ дх
/5 |
hxh2
dy
ду
Если ф — решение уравнения Лапласа, то существует
аппроксимация производных по переменным г, z цилиндрической системы
координат, имеющая погрешность O(h2)
в ячейке разностной сетки и
использующая только четыре узла. Это
обусловлено тем, что разложение ф по линейно-
независимым гармоническим
полиномам до третьего порядка
включительно имеет вид
frfz*)
-|а,2»
r
Рис. 26.
azzr2 (5.20)
и содержит только четыре
коэффициента, которые могут быть найдены по
четырем точкам (рис. 26):
202

= фо,
~ ФЗ — ф1
"* h\ ' ° h,h\
Выражения для производных тогда имеют вид:
Если в приведенных примерах некоторые из используемых
узлов разностной сетки внешние по отношению к расчетной
области, то в них значения ф можно предварительно вычислить с
помощью экстраполяции по внутренним узлам (и с учетом граничных
условий). Например, для рис. 2 линейная экстраполяция дает
2 (5.23)
Более точные аппроксимации производных строятся
аналогично с привлечением дополнительных узлов сетки. В этом случае
можно применять эффективные методы интерполяции, описанные
в §2.2 для методов конечных элементов. В частности, самая
простая из них — это кусочно-линейная аппроксимация по
треугольникам (тетраэдрам — в трехмерном случае). В примере на рис.
19 для точек треугольника с вершинами «О», «1», «3» достаточно
положить
дф __Ш-"о ду _ Цз-ао
~д7 hx ' ~di~~ hs ' к }
Аккуратное вычисление напряженности очень важно в
окрестности эмиттирующей поверхности, поскольку ошибка может
повлиять и на форму всей траектории, и на величину вычисляемой
плотности тока. Если эмиттер имеет криволинейную поверхность,
то линейная экстраполяция по формуле (5.23) может дать
значительную погрешность. В этом случае может эффективно
применяться техника интерполирования на криволинейных конечных
элементах. В частности, практически всегда задачу можно свести
к аппроксимации на треугольнике с двумя прямолинейными
сторонами и одной криволинейной. Соответствующие формулы (2.51)
обладают тем хорошим качеством, что обеспечивают точное
согласование заданных значений функции на кривой линии.
Рассмотрим теперь алгоритм сплайновой аппроксимации для
расчета напряженности электрического поля [119]. Остановимся
сначала на функции одной переменной f(x).
Пусть даны N+1 точек хо<.х\<...<%. Функцию у = у(х)
будем называть сплайн-функцией первого порядка (или
кубическим сплайном), если
а) y(Xi) = fiy / = 0, l,...,^, где fi==f(Xi) — заданные числа;
203

б) на каждом отрезке [*/, xi+\]
з
у{х)=у{х) = 2 c№{x-Xl)k; (5.25)
k = 0
в) у(х) имеет непрерывные производные вплоть до второго
порядка;
г) на концах отрезка удовлетворяются условия одного из
следующих типов:
I) y'(Xi) = f't> ; = O,JV;
II) y"(Xi) = f>>9 i = 0,N;
III) на одном*из концов выполняется условие I, а на другом —
условие II.
Из уравнений */(**) = //, yi(xi+l) = yi+l(xi+l)y y((xi+i) = yl + i(xi+i\
yi'(Xi+\) = y!' + \ (Xi+i) получим для коэффициентов формулы (5.25)
следующие уравнения (А/=х/+1— xi):
a$=fh i = O9...,N9 (5.26)
ЗаГЧ-i + aS~l) = a<2, / = 1 ^V — 1, (5.27)
а? = За('-%?-1+2а(>-%1-1 + а«-1\ (5.28)
a«"%3_l + ag-%2_, + a«-%_i + a(/-|> = //, i = l,...,N- Ц5.29)
Исключая из этих соотношений a^ и a^, получим
В уравнениях (5.30) N+1 неизвестных а(^\ На концах
интервала добавим условия одного из следующих типов:
о IN \IN IN
hN-\
III) берется по одному из условий I и II.
Анализ матрицы полученной системы уравнений во всех 3
случаях показывает, что она невырожденная. Следовательно, система
имеет единственное решение.
Когда f(x) четырежды непрерывно дифференцируема, имеем
следующие оценки точности интерполяции:
| у(Р\х) _ fP\x) | = 0{hA~% р = 0,1,2,3, (5.31)
Из системы уравнений (5.30) найдем а%\ / = 0,...,N, методом
прогонки. С помощью этих коэффициентов из (5.27), (5.28)
вычислим а^\ а(*\
204

Перейдем к рассмотрению двумерной задачи. Пусть область
[*о, %]Х[*/о, Ут] разделена линиями, параллельными координатным
осям и имеющими координаты: л;0<••.<*;<...<%,
/
Функцию z = z(x, у) назовем сплайн-функцией второго порядка
(или бикубическим сплайном), если она обладает свойствами:
а) на каждом прямоугольнике [xiy xi+\]X[yj, yj+\]
z(x, у) = 2 S ой» (* - x,)* (у - у/)'; (5.32)
fc=0/=0
6) z(x, у) обладает непрерывными производными вплоть до
второго порядка.
Сформулируем задачу интерполирования. Пусть в узлах
прямоугольной сетки заданы значения функции zij = f(xi, yj). Требуется
построить функцию г(х, у) вида (5.32), совпадающую с f(xi, y\)
в узлах сетки и удовлетворяющую дополнительным условиям на
границах области.
На линиях х = jto, x = xN в точках у} могут задаваться частные
производные df/dx или d2f/dx2 или должна указываться
периодичность функции по х. Аналогичные условия задаются для
переменной у. Всего получается 16 способов задания граничных
условий.
В угловых точках (*<>, Уо), (*о, Ут), (xN, уо) и (xN, ym) должны
задаваться смешанные производные dk+lf/dxkдх\ где k и I —
порядки производных, заданных на границах (при задании
периодичности порядок считается равным нулю). Очевидно, что при
фиксированных у\ 6 [уо, ут] или xt g [х0, xN] функции z(x, у\) и
z(*/, У) — сплайн-функции первого порядка. Основываясь на этом
факте, можно показать существование и единственность z = z(x, у)
с указанными выше свойствами. Оценки точности имеют вид,
аналогичный (5.31).
Построение z(x, у) начнем с построения одномерных сплайнов
по строкам и столбцам сетки. Ввиду единственности они совпадают
со значениями z{xyy) на линиях x = Xi или у = У/. Так, получим
коэффициенты
<tif, aW, аЩ>, aW, afP, <№, 4з;), i=0,1,.... N, } = 0, 1,.... m,
причем
(0,/)_ 1 а2ц I „52 d2z
a°2 -T77l;z*' ^=1Г'^
(5.33)
2 ^ I JI**' ^' dx* или
ц и v выбираются в зависимости от типа условия при x=xNnx=x0.
205

Ясно, что коэффициентов (5.33) достаточно для построения
функций -^-^Vl у=у> в виде Одномерных сплайнов от х. В
результате решения системы типа (5.30) получим значения
а(М\ c&i\ c№\ i=0, 1,..., N, / = 0,1,..., т.
Остальные коэффициенты аиъ и а^ находятся по формулам
вида (5.27), (5.28):
а а*! 3
k= 1,2,3.
В заключение данного пункта можно отметить, что выбор
алгоритма вычисления напряженности электрического поля имеет
важное значение с точки зрения точности и экономичности расчета
траекторий и решения самосогласованной задачи в целом. Однако
проблема выбора оптимального метода остается открытой и
требует систематических численных экспериментов для различных
классов задач. По этому поводу можно дать только рекомендации
общего характера. В расчетах сильноточных приборов, где
требуются в основном интегральные характеристики, такие как общая
сила тока и др., рассмотренные экономичные локальные
аппроксимации 1-го или 2-го порядка дают удовлетворительные результаты.
Однако по мере повышения требований к точности, при
необходимости анализа оптических свойств потока частиц обязателен
переход к более сложным методам аппроксимации, например,
к сплайновым.
5.2.2. Расчет напряженности магнитного поля. Данная задача
распадается на две независимые: вычисление напряженностей
внешнего и собственного магнитных полей.
Внешнее поле, как правило, создается магнитными линзами,
которые можно рассчитывать независимо от электрического поля
и движения пучка. При этом можно применять методы,
описанные в главе 2, и тогда определение компонент напряженности
сводится к численному дифференцированию по значениям
потенциала илк магнитного потока, полученным в узлах сетки
предварительными расчетами.
А. Задача расчета поля по его значениям
на прямой. Зачастую проблема на практике ставится таким
образом, что значения компонент напряженности известны в
некоторых точках из численного эксперимента. В двумерных задачах
это обычно ось или плоскость симметрии. При этом поле во
внутренних точках области определяется с помощью аналитического
продолжения.
Для плоского поля, обладающего симметрией относительно
линии у = 0, с этой целью может быть использован отрезок ряда
206

Щерцера, представляющего разложение гармонической
функции
ф,у)=«х,0)-^°^?+±°&&*-..., (5.34а)
а'для осесимметричного случая — аналогичное соотношение
Выражения (5.34а), (5.346) описывают решение задачи Коши
для уравнения Лапласа соответственно в декартовой и
цилиндрической системах координат, при заданных значениях ф и нулевой
нормальной производной на линии симметрии.
Вычисления по этим формулам требуют предварительного
определения производных на оси. Это должно быть сделано с
возможно большей точностью, поскольку сама задача
аналитического продолжения является условно корректной и незначительные
ошибки в исходных данных могут привести к существенному
искажению результатов. Как видно из приведенных соотношений,
такая неустойчивость будет возрастать при удалении расчетных
точек от прямых с заданными характеристиками полей, т. е. с
увеличением у или г.
Аппроксимацию поля и вычисление производных на линии
симметрии можно эффективно осуществлять с помощью сплайнов.
В качестве иллюстрации достигаемой при этом точности мы
приведем выполненные Г. С. Поповой численные эксперименты
[158] по продолжению заданного на оси симметрии распределения
так называемого колоколообразного поля
Ho/(az2+\\ (5.35)
H2(r,z)=— Ul -a2)"1
имеющего точное решение
Z
A2 + (2arz/a2)2
о
4H0rz С 2\-i/2j (5.36)
1а2(1_а2) 1/2da,
J
Заметим, что функция Hz(rfz) имеет особенности при 2 = 0,
г= \/л[о>у т. е. анализ нисленных расчетов можно проводить только
при г<^\/л[а. Вычисления проводились с помощью аппроксимации
осевого распределения описанным выше кубическим сплайном
на неравномерной сетке, сгущающейся в окрестности точки 2 = 0,
поскольку функция (5.35) имеет там большую крутизну. Значения
207

#г(0, zi) брались на отрезке [0,3], причем на интервале (0,1) было
взято 25 равномерно расположенных точек Zi, а на интервале
(1,3) —20. Вычисленные по ряду (5.346) значения (производные
определялись дифференцированием сплайна и фактически брались
два члена ряда) сравнивались с результатами расчетов по
формулам (5.36), где интегралы брались по формуле Симпсона с
достаточно большим числом узлов, обеспечивающим заведомо высокую
точность.
В табл. 18 приведены погрешности результатов в процентах
для значений Яо=1, а = 0,5, 1,0 (что соответствует разной
крутизне поля) на разных расстояниях г от оси, точнее говоря, для
каждого г приведена максимальная ошибка при z £ [0,3].
Таблица 18
^^"\^^ а
0,125
0,25
0,5
0,5%
0,04
0,16
0,6
1.0%
0,05
0,20
2,6
Ошибки, как видно, можно считать допустимыми, но
необходимо обратить внимание на то, что они заметно растут с увеличением
крутизны поля и удаления от оси.
Были проведены также эксперименты с умышленным внесением
случайной ошибки в исходные данные, когда вместо #г(0, z)
брались значения
где б характеризует масштаб погрешности, а 0 — равномерно
распределенная на отрезке [0,1] случайная величина.
Оказывается, что с использованием неточных данных результаты резко
ухудшаются. Так, при 6 = 0,5% относительная ошибка Hz(ryz)
для а = 0,5, г = 0,25 достигает 30%.
Это свидетельствует о необходимости осторожного
использования аналогичных алгоритмов и о желательности применения
известных алгоритмов регуляризации для задачи продолжения
поля.
Мы опишем коротко такого рода метод, разработанный М. В.
Уревым [158]. Он основан на использовании формулы Пуассона
для потенциала и введении регуляризующего по Тихонову
оператора. Гармоническая функция в точке (г, z) представляется
приближенно в виде
и-
0 -R
q>a(s)ds
_ О^]3/2
= \k(r, zy
sy (5.38)
208

где R — радиус сферы, охватывающей расчетную область, а
фа($) — некоторое «регуляризованное» распределение потенциала
на этой сфере. Для его нахождения составляется интегро-диффе-
ренциальное уравнение
k{0, Z, 5)фа(5)£/5-а[<(5)-фа(5)]=ф(0>
(5.39)
где а — параметр регуляризации. При этом на q>a(s) дополнительно
накладываются естественные условия ф«( — R)=<p'a(R) = 0. Если
ф(0, z) задано в М точках оси, то, аппроксимируя левую часть
(5.39) с помощью квадратурных формул и конечных разностей, мы
можем получить систему линейных алгебраических уравнений
относительно фа($/), i= 1,2,..., М. Решая ее (это можно сделать
методом исключения Гаусса), легко рассчитать фа(г, z) с помощью
применения квадратурных формул к интегралу (5.38). Параметр
а можно выбирать из условия минимальности среднекваДратично-
го отклонения вычисленных значений фа(г, z£-) от заданных ф(0, zj).
Данный алгоритм был апробирован на той же задаче при
значениях вносимой погрешности 6 = 0, 0,5%, 2% (функцию
ф(г, г) в (5.38), (5.39) надо заменить на Hz(r, г)). В табл. 19
приведены результаты (максимальная погрешность), полученные для
а = 0,5 и 1,0 по значениям ф(0, zt) в 41 точке примерно на той же
сетке, что и для табл. 18. Аппроксимация интеграла в (5.39)
проводилась на равномерной сетке по 5 с помощью формул Симп-
сона, а вторая производная заменялась трехточечным конечно-
разностным выражением.
Таблица 19
0,25
0,5
а = 0,5
0%
0,8
2,3
0,5%
1,0
3,2
2%
2,1
4,6
а = 1,0
0%
1,2
3,1
0,5%
1
3,2
2%
2,1
6,1
Эти данные свидетельствуют, что такой алгоритм обладает
хорошей устойчивостью. Однако он более трудоемкий^ чем метод
с использованием сплайнов,, поскольку вычисления фа в точках
окружности Si сводятся к решению системы с пло'тной матрицей,
а определение ее требует проведения интегрирования. Суммарное
количество арифметических действий при этом равно по порядку
О(М3).
Другой подход к решению задачи о продолжении поля при
неточных исходных данных заключается в предварительном
сглаживании значений #z(0, zi) на оси и последующем применении
ряда Шерцера [186].
14 В II Ильин
209

Это может быть сделано с использованием хорошо развитого
аппарата сглаживающих сплайнов. Мы опишем такую технологию
на примере кусочно-кубической интерполяции со сглаживанием.
Задача формулируется следующим образом.
Требуется найти функцию у{х\ минимизирующую на классе
функций, обладающих на отрезке [х0, xN] интегрируемыми с
квадратом вторыми производными, функционал
Р1ШЧ1У, (5.40)
где fi — f(Xi) — значения некоторой функции в точках *,, а рь —
весовые положительные коэффициенты. В такой постановке
скомбинированы условия приближенной интерполяции заданной
кривой f(x) и минимальности «изгибания» функции у(х). Чем больше
значения р,, тем больший вклад в функционал Ф(у) вносят
интерполяционные условия в соответствующих точках xt.
Решением этой задачи является кубический сплайн вида (5.25),
обладающий непрерывными производными второго порядка и
удовлетворяющий граничным условиям y"(xo) = y"(xN) = O. Если
значения */(*/) = *// известны, то такой сплайн однозначно
определяется из формул (5.25) — (5.30).
При этом систему уравнений (5.30) удобно записать в
векторном виде (с заменой Д на у{):
Л^x = Яv, (5.41)
где \л = [аЬ1\ оЦ\ ...,a2k~l\ v = {yo,#i,...,##}— векторы порядка
соответственно N—1 и Af+l, A — квадратная матрица порядка
N — 1, а Н — прямоугольная матрица .из N+1 строки и УУ—1
столбца:
h\ (\
А =
(■=> 42)
Н =
Отсюда мы можем
3
hi-
6
1 А
Ао -
0
о + А,
-А0А,
1
А,
0
написать
6
А,
—
А
А/_1
1
А,
+ А2
А,А2
1
N-2
+ Ы
3
**-
hN-2
6
1
А2
2 + ^
ЛАГ-2
-1 Л
hi
6
3
0
1
ЛГ-1
(5.43)
210

Таким образом, вопрос сводится к нахождению yk, при которых
функционал (5.40) достигает минимума.
Как следует из (5.25), на каждом отрезке [xif Xi+\] функция
у"(х) может быть записана в виде
4V {5M)
Отсюда
'4' (?р ^Y i pfo-ff. (5.45)
Это выражение может быть преобразовано к форме
Ф(У) =Nt
= (Ali,li),+ P((v-f),(v-f), (5.46)
где / = {/о, /i, ..., fN} — вектор, а Р — диагональная матрица
порядка N + 1 с элементами р{.
Поскольку (ш выражается линейно через v, функционал
представляет собой квадратичную положительно определенную форму
от v. Минимум функционала достигается при выполнении условий
3O/0# = O, / = 0,1, ...,ЛЛ (5.47)
Следовательно, уравнения (5.47) в векторной форме имеют вид
H'v + Pv = Pf, (5.48)
в силу соотношений
Умножая (5.48) слева на ЯР"1, получим равенство
HP~xH'v + Hv = Hf, (5.49)
откуда следует уравнение для v:
(A + HP~lH')v = Hf. (5.50)
Матрица этой системы симметрична, пятидиагональна и
положительно определена. Найдя из ее решения вектор v, с помощью
соотношения (5.48) определяем вектор значений сглаживающего
сплайна в узлах:
\i = f-P~lH'v. (5.51)
Отсюда по формулам (5.26) — (5.30) при замене // на у/
определяются все коэффициенты искомого сплайна.
Величины pk здесь фактически являются параметрами
регуляризации. Варьируя их значения, можно выбирать ту или иную
14* 211

гладкость сплайна и точность его совпадения с исходными
данными в узлах сетки.
Аналогично можно строить сглаживающие сплайны более
высоких степеней. Например, аналогично (5.40) определяются
кусочно-полиномиальные аппроксимации порядка 2р—1,
обладающие непрерывными производными до порядка 2р —2 и
минимизирующие функционал
XN N
= \ (0) dx + Z0 P^-f?-
М. В. Уревым проведены эксперименты по продолжению поля
с использованием сглаживающих сплайнов 5-го порядка,
реализованных под руководством В. А. Василенко в составе пакета
программ Лида [29] для аппроксимации функций. Для
рассмотренного выше колоколообразного поля в табл. 20 приведены значения
максимальных погрешностей вычисления для различных
расстояний г от оси симметрии и разных ошибках б в исходных данных.
Таблица 20
"^^\^ б
0,10
0,50
0,75
0%
0,65
2,0
3,9
1%
0,46
1,8
3,5
2%
2,7
5,1
7,7
Расчеты проводились при а=1, /?^=103 и задании начальных
данных на следующей кусочно-равномерной сетке: интервал (0,1)
разбит на 70 равных подынтервалов, интервал (1, 1,5) —на
60 и интервалы (1,5, 2) и (2,3) —на 30 подынтервалов.
Как видно, алгоритм оказывается достаточно устойчивым к
ошибкам исходных данных; он гораздо экономичней метода с
использованием интегрального уравнения, поскольку в данном
случае нужно решать систему уравнений не с плотной матрицей, а с
ленточной.
Б. Определение собственного магнитного
поля пучка. Расчет собственного магнитного поля,
обусловленного распределением плотности тока, можно в принципе
проводить непосредственно по формуле Био — Савара — Лапласа.
Однако непосредственные вычисления интеграла для большого
количества точек, что обычно требуется при моделировании пучков
заряженных частиц, являются достаточно трудоемкими. Если
расчеты проводятся на сетке с числом узлов LXM, то количество
арифметических действий равно по порядку O(L2M2). Возможные
упрощения этой задачи мы укажем для случая осесимметричного
пучка.
Во-первых, зачастую можно учитывать только азимутальную
компоненту магнитного поля И\ определяемую продольной сос-
212

тавляющей вектора плотности тока jz. В этом случае
непосредственное применение теоремы Стокса дает формулу
г
Щ(г, z) =^=4 \ h(r'> z)r'dr'>
о
в которой интеграл можно вычислить методом трапеций или Симп-
сона.
При необходимости учитывать азимутальную компоненту
плотности тока \^ нужно вычислять радиальную и осевую
составляющие напряженности НГу Hz. Это можно сделать с помощью
предварительного определения азимутальной компоненты векторного
потенциала А ^которую можно найти из решения уравнения (2.12)
или выразив ее через функцию магнитного потока Ф = гАв,
удовлетворяющую дифференциальному уравнению
-3-^ ("4)
Решение его можно провести рассмотренными в 1-й главе
разностными методами. Граничные условия достаточно поставить на
поверхности цилиндра, окружающего предполагаемую область
прохождения пучка частиц. Значения Ф или его производных на
границе можно вычислить непосредственно из формулы Био — Са-
вара — Лапласа (что гораздо легче, чем найти поле во внутренних
узлах расчетной области).
§ 5.3. Методы интегрирования уравнений движения
заряженных частиц
Мы рассмотрим некоторые специальные методы решения
систем обыкновенных дифференциальных уравнений, описывающих
движение заряженных частиц в электрических и магнитных полях.
Особенность нашего подхода характеризуется тем, что, во-первых,
нас интересуют алгоритмы расчета траекторий в областях сложных
конфигураций, иначе говоря, методы, относительно легко
реализуемые в программах для решения практических задач. Во-вторых,
градиенты электрического поля рассчитываются по значениям
потенциалов во внутренних узлах разностной сетки с кусочно-
постоянными шагами. В этом случае при численном
интегрировании уравнений движения необходим большой объем операций
для расчета напряженности и проведения анализа положения
точек траекторий относительно области (для окончания счета
траектории, а также «отражения» ее от линий или поверхностей
симметрии). Наконец, сами значения потенциалов вычисляются
приближенно из-за погрешности разностных уравнений и ошибки
итерационного решения.
По этим причинам мы отдаем предпочтение методам,
требующим минимального числа вычислений правой части на одном шаге
интегрирования. Кроме того, мы используем экономичные модифи-
213

кации алгоритмов для отдельных типов задач в зависимости от
наличия магнитного поля, размерности области, учета
релятивистских эффектов и т. д.
Если в задачах, не требующих высокой точности расчета
траекторий, вычисление производных от потенциала производится по
простейшим формулам типа (5.18) — (5.22), то шаг Atn
интегрирования уравнений движения, по-видимому, целесообразно
выбирать так, чтобы частица проходила ячейку разностной сетки за
несколько временных шагов. Тогда условие для определения Atn
имеет вид
^-6А<| г„+1-г„ |< 26/г, (5.55)
где б — задаваемый параметр, а Л — средняя величина шага
разностной сеткив окрестности точки с радиус-вектором rn(h = (hx-\-
-\-hy)/2 или h=(hx-{-hy-\-hz)/3 в зависимости от размерности).
Таким образом, расстояния между соседними точками траектории
примерно равны заданной части б от ближайших шагов сетки.
Условие (5.55) проверяется на каждом шаге. Если
оказывается, что \rn + i — гп|^--бА, то при счете следующей точки шаг
Atn удваивается. Если |rrt+i — rn\^28h, то Atn делится пополам
и данная точка пересчитывается.
5.3.1. Задачи без магнитного поля. В отсутствие магнитного
поля формулы интегрирования уравнения движения d2r/dt2 =
= — Р V Ф (см. (5.13)) с погрешностью О(Дф имеют аналогичный
вид для плоских, осесимметричных и трехмерных задач:
rn+-^-{rn + rn+l). (5.56)
Отметим, что при всей своей простоте этот алгоритм формально
не укладывается ни в один из классических методов решения
обыкновенных дифференциальных уравнений. Назовем его обобщенным
методом Рунге — Кутта. второго порядка.
При расчете траекторий в некоторых типах задач, например,
с тормозящими полями, большое значение может иметь ба-
лансность численного метода интегрирования, т. е. сохранение
энергии:
»2+1-»5 = 2р[ф(гя+1)-Ф(гя)]. (5.57)
Алгоритм в этом случае значительно усложняется. Например,
для двумерного случая формулы (5.56) могут быть
модифицированы к балансному виду, если первое уравнение заменить на
уравнения
хп+\ =хп — А/пР[ф (хп+и Уп+\) —
+\,yn) — q)(Xn,yn)]/[2(Xn+\—Xn)l *
(5.58)
214

При этом на каждом временном шаге требуется проведение
итераций до получения хп+и Уп+\ с нужной точностью. В качестве
начального приближения естественно взять значения xn+\,yn+i
из формулы Эйлера xnl+\=xn-\--^-xru y°n+l=yn+-^- уп.
Нетрудно проверить, что даже при проведении двух итераций
погрешность метода есть O(At%).
Ситуация существенно упрощается, если точки rn, rn+i
находятся в пределах одного треугольника (тетраэдра — в трехмерной
области) разностной сетки, где производные потенциала
считаются постоянными и определяются из формул (5.24). В этом
предположении формулы (5.56) дают точное решение уравнений
движения и являются балансными. Единственная сложность в таком
случае — определение значения Д*„, при котором частица
оказывается на границе треугольника.
Если расчет напряженности проводится по формулам вида
(5.18), т. е. производные представляются кусочно-линейными
функциями типа
0<р/ дх = аи + Ьиу, дц>/ ду = сц + Ьцх (5.59)
для двух переменных ((/, /) — номер ближайшего левого нижнего
узла сетки по отношению к точке (х„, yn) ), то в пределах одной
ячейки балансный алгоритм можно получить в виде (индексы при
а, Ь, с мы опускаем):
^п) (хп+\ — хп)\
(5.60)
Более того, для случая (5.59) уравнения движения (5.13) могут
быть аналитически проинтегрированы в пределах каждой ячейки
разностной сетки. В двумерных задачах расчетные формулы имеют
следующий вид:
4г4 ч
у= — r\c\ert-\-C2e~rt — c3cos rt — c4sin rt)-\-
rt — Cz sin rt + c4 cos rt) +
rt — e~rt-2smrt\ (5.61)
г _ 4'3
(/== — r3(Cl^^_^2^ rf-|_ c3 sin rt—c4 cos r*) +
где г=-л/|р6|; 2с3 = лг0+ —(a + 6(/0); 2c4 =—- + -t. fey0; 4c\ =
г2 г
215

+ ±Ьуо.
Отметим имеющуюся здесь техническую трудность:
интегрирование должно вестись до момента времени t выхода частиц из
данной ячейки разностной сетки, который априори неизвестен.
Поэтому реализацию формул (5.61) приходится вести с помощью
итераций, подбирая значения t до тех пор, пока точка (х, у) не
попадает с заданной точностью на границу ячейки. Начальное
приближение с достаточной точностью может быть вычислено по
формулам (5.56).
5.3.2. Нерелятивистские задачи с магнитным полем. Мы начнем
рассмотрение с простого случая — плоская задача с поперечным
магнитным полем. Соответствующая система уравнений имеет
вид (5.14), причем мы предполагаем характерные размерные
величины выбранными так, что D\ = \. Численное интегрирование
проводим с помощью неявной схемы, имеющей погрешность O(At2):
_ Мп . ^_ Atn .
2 2
Хп-\-1==Хп—рД//2 ——\Хп-\-\12->Уп-\-\1е1) —
уп+1+уп -|
— 2 Л2(Хп+1/2уУп+\/2)1 (5.62)
i -4-х
Уп + \=Уп — г
2
Отсюда выражения для хп+и Уп+i приводятся к явному виду
(значения ду/дх, дц/ду, Н2 относятся по-прежнему к точке (JCn+i/2,
Уп+\/2)):
Хп+1 =
Й
*1я,)].(5.63)
Аналогичная неявная схема второго порядка точности строится
и для трех декартовых переменных х9 у, г с магнитным полем
произвольного вида. Расчетные формулы имеют при этом более
сложный вид (значения ду/дх, ду/ду, дц/dz, НХу Нуу Н2 относятся
216

к промежуточной точке (хп+\/2, Уп+\/2, Zn+i/г)):
A//i • А*л .
(а1+а2аз)(/1 + а2/з) + (1+а2)(/:2 — «з/з)
л+1, /г^.ч
(5.b4)
. ton ,. . . ,
2Л + 1 = Zn + -^- (2Я + Zrt + 1).
Здесь используются вспомогательные величины:
ai = — Р-^-Яг, a2=— P—^Hy, a3 == — Р-^-
f\=xn — рД^я-^.— f/«ai + ina2,
Наконец, мы приведем уравнения движения в цилиндрической
системе координат:
(5.65)
Численное интегрирование в (5.65) можно провести с помощью
следующей схемы типа предиктор-корректор второго порядка
точности. Предварительно находится приближенное значение
угловой скорости $ на (я+1)-м шаге:
& ^ Р(гпЯг - inHr) - 2^я]. (5.66)
Гя+1/2
Здесь, как и ранее, значения Яг, Я2, ду/дг, ду/дг^ относятся
к промежуточной точке (rn+i/2, г„+1/2). Поскольку г() при г->0
не определена, то для достаточно малых г полагаем ipn+i=ipn.
Далее вычисляем
1 = zn — Mn($d<t>/dz + Рг„+ ,/2-фпн- 1/2Яг), (5.67)
217

у Гп+1/2 =у(/'/г +^/2+l), y
+ in+i). После этого корректируется значение угловой скорости:
П[МНН) 2Ъ] (5.68)
и, наконец, находятся величины
Zn+\=Zn-\- htnZn+ 1/2,
|+ф ^я + Ф«+ 0 /2- (5.69)
Расчет угловой скорости в рассмотренных уравнениях может
быть уточнен (и одновременно упрощен), так как в соответствии
с теоремой Буша имеем первый интеграл от уравнения для \f>:
гЧ-(гЧ)<=-^(ф-ф^> (5J0)
где
Ф = 2п\ Hz{r,z)rdr. (5.71)
Если для Н2 используются формулы аналитического
продолжения по его значениям на оси симметрии:
Яг(г, г)«Яг(0, г)—Г1 #£'(0, г), (5.72)
то отсюда получаем (мы для простоты полагаем, что для
координаты 2, соответствующей моменту t0, например на катоде,
магнитное поле отсутствует и Ф,0 = 0):
Ъ= -|[Яг(0, z)—^H'2\Q,z)\ (5.73)
Для этого случая в формулах (5.67) промежуточное значение
угловой скорости вычисляется как
♦«+1/2=-|[Я^0, 2п+1/2)-^1^Я-(0, гя+1/2)1 (5.74)
а вместо (5.68) используется формула, получаемая из (5.74)
заменой гп+\/2 на rn+i- Важным достоинством такого алгоритма
является отсутствие особенности вблизи оси симметрии.
Для построения формул численного интегрирования уравнений
движения при наличии магнитного поля можно использовать
также точное решение для траекторий в постоянных электрическом
и магнитном полях. Если предположить, что величины Ех, Еу, Ег,
Нх, Нуу Hz постоянны на интервале (гп, гп+\\ то скорость частицы
можно определить следующим образом.
Направим ось z' в направлении вектора Я, а оси х'у у' выберем
так, чтобы плоскость х'', г7'содержала вектор Е. Обозначая через
у?/, Vy,, Ex, компоненты скоростей и напряженности в этой вспомо-
218

гательной системе координат, мы получим
vy +' = К' + сЕх>/1Я |) cos сотп - V». sin сот„ - сЕх,тп,
где т„ =/„+! — /„, а со = в |//| /(тос) — так называемая
циклотронная частота. Пересчитывая теперь компоненты скоростей в
основной системе координат pj+1, Vy+ , o?+I, новые координаты частицы
можно определить по формулам
При необходимости несложно перевести координаты и компоненты
скоростей в цилиндрическую систему г, z, -ф.
5.3.3. Уравнения движения релятивистских заряженных частиц.
Если скорости частиц близки к скорости света, то уравнения
движения целесообразно записывать в форме
v=
(5.76)
эквивалентной (5.2). Здесь р означает импульс скорости,
поделенный на то.
Мы рассмотрим алгоритмы для случая цилиндрической
системы координат:
dpr/dt = — $.ду/дг + Щ- p(i//t - п£#г),
i (5.77)
Из этих уравнений следует теорема Буша для релятивистских
частиц
где Ф — поток магнитной индукции.
Для решения этих уравнений построим схему с погрешностью
О(М)2:
,5.79)
я,- °"";+Ч я,).
219

2
__ n+l,k n+l,k л./г+и_Л i Р«+\'Ь \-l/2
—fJr 7 > 7 —I * "1 2 / '
Здесь напряженности электрического и магнитного полей
определяются с помощью численного дифференцирования
потенциала и функции тока:
2я(г* + ! — гя) (r*+i + rn) 2n(zkn+\-zn) (rkn
Данный алгоритм требует для каждого временного шага
проведения итераций. Очевидно, что если шаг Atn достаточно мал,
то итерации будут сходиться быстро. В качестве начального
приближения для всех величин можно взять их значения с
предыдущего момента времени.
Умножив первые три уравнения из (5.79) соответственно на
(Vr + l + Vr)/2y (v1+x-\-vT)/2, (Vy+l-\-Vy)/2 и сложив их, получим
с учетом (5.80) следующее соотношение (индексы k мы опускаем):
ФД (5.81)
которое является разностным аналогом баланса энергии для
релятивистских частиц
Более предпочтительным с точки зрения балансности (в силу
равенства у--£-=—. ( с —У v2 = v2r-\-Vz-\-vl) было бы вы-
at at \ -yjl-— v2/c2 /
полнение соотношений
поскольку они гарантируют сохранение энергии на каждом
временном шаге. Однако обеспечение этого условия несколько
усложняет алгоритм вычисления скоростей. Поскольку левая часть
(5.83) может быть представлена в виде
то определение v?+l (а также и других компонент скоростей)
в этом случае надо проводить не по формулам (5.79), а из
уравнения *
Гр?+1-^(»?+| + ^ = [(»?+1)2-(^2]/^ (5.84)
220

5.3.4. О точности расчета траекторий. Вопрос оптимизации
методов интегрирования уравнений движения имеет существенное
значение для экономичности расчетов самосогласованных задач в
целом, поскольку при прослеживании большого количества частиц
определение их траекторий занимает значительную долю
машинного времени. С этой точки зрения важно выбрать временные шаги
такими, чтобы они обеспечивали необходимую точность, но не были
чрезмерно малыми.
Мы приведем результаты методических численных
экспериментов и анализ погрешности метода (5.56) для двумерных задач без
магнитного поля.
В качестве тестовой задачи мы возьмем движение электрона
в поле сферического конденсатора (симметричном относительно
точки х = 0, у = /?2):
1 J
x u)
^ (yR2)[
при ф1 = 1, ф2 = 0, #i = 2,5, R2= 100, 0<*/</?2 — Ru *>0.
Уравнение траектории в таком поле описывается формулой [84]:
-y)-\f - (C2-B2)(R2-yf
C=
ао = 0,785398, А = (jcg + £/§)/(2 • |р|), Р=—0,5.
Начальные координаты брались равными хо = уо==О. Как
известно из качественного анализа, счет траекторий наименее
устойчив при малых начальных скоростях. Для количественной
оценки этого эффекта расчеты проводились при хо = уо = 7-10"1 и
*о = */о = 7-1О-4.
Сравнительный анализ методов проводился по относительной
погрешности решения б (в %) (для у = 85):
8=\(ха-хч)/ха\ • 100%, -
где ха, хч — аналитическое и численное решения, а также по
абсолютной погрешности выполнение условия баланса
2 +ь Уп+\) — <р(Хп, уп)1
В табл. 21 и 22 приведены значения б соответственно для
начальных скоростей jc0 ==[/0 = 0,7 и хо = уо = 0,0007 при разных
значениях временных шагов т = 50; 25; 12,5; 6,25; 3,125 для четырех
алгоритмов: обобщенного метода Рунге — Кутта второго
порядка (5.56), обозначенного в таблицах буквами ОРК, балансного
метода (5.58) с проведением 2 итераций по дсп+1, уп+\, обозначен-
221

Таблица 21
Метод
РК
ш
ОРК
Б
50
10~5
0,0087
0,06
0,2
25
4 • 10"5
6- 10~5
0,011
0,04
12,5
3 • 10~5
3. 10~5
0,0027
0,01
6,25
3 • 10~5
3 • 10~5
0,00065
0,03
3,125
3 • 10~5
з. ю~5
0,00014
0,0007
Таблица 22
Метод
РК
ш
ОРК
Б
50
0,35
1,5
0,50
22
25
0,047
0,18
0,29
4
12,5
0,0042
0,015
0,10
0,9
6,25
0,00031
0,0010
0,028
0,2
3,125
3,6 • 10~5
5,0 • 10~5
0,0072
0,05
ного буквой Б, стандартного метода Рунге — Кутта 4-го порядка,
обозначенного буквами РК, а также часто применяемого для
интегрирования уравнений движения метода Штермера 4-го порядка
точности [194], обозначенного буквой Ш. Последний алгоритм
применяется только с постоянными шагами At и для нашего случая
в общем виде описывается формулами
_
V фл = V ф(гп), V фп+ 1 = V ф(г«+ l),
Это метод типа предиктор-корректор (или прогноза и
коррекции), в котором сначала вычисляется промежуточное значение
координаты точки гп+х по формуле с погрешностью второго
порядка, а затем — окончательное значение гп+\. На каждом шаге здесь
требуется двукратное вычисление правой части. Поскольку первая
точка Г\ по этим формулам не может быть вычислена, для этого
применяются стандартные формулы Рунге — Кутта четвертого
порядка.
В табл. 23 и 24 приведены аналогичные данные по абсолютной
погрешности баланса энергии 8 для методов ОРК и Б.
Из сравнения результатов можно сделать следующие выводы.
Прежде всего, методы 4-го порядка позволяют, что и следовало
ожидать, получить значительно большую точность, чем методы
2-го порядка. Однако этот эффект проявляется особенно при малых
Таблица 23
Метод
Б
ОРК
50
10~6
2- 10"4
25
4 • 10~8
1(Г4
12,5
3. 10~10
2. Ю-5
6,25
ш- 10
2• 10~6
3,125
5. Ю-12
1 . 10~7
222

Метод
Б
ОРК
5
2
50
. 10~3
• ю-2
6
6
25
• ю-4
. 1(Г3
7
125
. КГ5
1(Г3
6
2
6,25
• 1(Г6
• ю-4
Таблица
3,125
5 • 1(Г7
4•10~5
24
значениях At; для А/= 50 и А/= 25 ошибки всех методов можно
считать сравнимыми (за исключением балансного метода, на
котором мы остановимся особо).
Далее, методы 4-го порядка имеют примерно одинаковую
численную погрешность, поэтому среди них более экономичен метод
Штермера, требующий вычисления правой части уравнения только
в двух точках на каждом шаге (вместо 4-х — в методе Рунге —
Кутта 4-го порядка). При достаточно больших временных шагах
ошибка, с уменьшением Д/, сильно падает (с некоторой натяжкой
ее можно считать в этом случае пропорциональной А/4), однако,
когда погрешность становится очень малой — порядка 10~~5 —
уменьшение At уже не приводит к повышению точности. Можно
предположить, что здесь начинают влиять ошибки округлений.
Для методов 2-го порядка зависимость погрешности б от А/ почти
во всех расчетах близка к квадратичной.
В табл. 21 для всех методов и различных А/ погрешности
оказываются в несколько раз больше соответствующих значений из
табл. 22. Это лишний раз подтверждает ухудшение устойчивости
при уменьшении начальных скоростей частиц.
Из табл. 23 и 24 видно, что погрешность энергетического
баланса е также увеличивается при уменьшении начальных
скоростей. Абсолютные значения 8 с уменьшением А/
уменьшаются, и их значения для всех методов можно считать
удовлетворительными. Отметим, что расхождения между методами 4-го и 2-го
порядков уже не такие разительные, как по значениям б.
Из табл. 21 и 22 видно, что в наименее выгодном свете
представляется балансный метод. Однако необходимо заметить, что его
реализация фактически ^использует аппроксимацию производных
потенциала с помощью конечных разностей первого порядка.
А поскольку с ростом t в данной задаче скорость увеличивается, то
при постоянном At расстояния между соседними точками
траектории сильно растут, что приводит к значительной погрешности
аппроксимации. Для подтверждения этих рассуждений были
проведены эксперименты со значениями А/п, определенными по
формуле
Atn = а/(?п + у*)1'2
из условия приближенного равенства расстояния между точками
траектории заданному значению а. Расчеты показали значительное
повышение точностив этом случае. Например, при выборе а из
условия А*о = 5О (при хо = уо = 7-10"4) значение б равно 0,01 (вместо
6 = 20 для Д4 = 50).
223

Необходимо отметить также тот факт, что во всех методах
использовались точные значения потенциала или его производных.
Для оценки влияния погрешности вычисления правых частей
уравнения движения были проведены следующие эксперименты.
Значения потенциалов находились по точным формулам в узлах
квадратной сетки с некоторым шагом Л, а значения дср/дх, ду/ду
определялись в результате триангуляции сеточной области и
билинейной интерполяции потенциала в каждом треугольнике.
В табл. 25 приведены расчетные значения относительной
погрешности б для метода Штермера при значениях /г, равных 5 и 2,5.
Таблица 25
^^\. А/
5
2,5
' 25
0,0062
0,0067
12,5
0,00019 -
0,0037
6,25
0,011
0,010
3,125
0,0005
0,0008
Результаты показывают, что ошибка существенно возрастает
по сравнению с использованием точных значений производных и
становится того же порядка, что и в методах 2-го порядка. Отсюда
можно предположить, что алгоритмы 4-го порядка наиболее
предпочтительны при возможности вычисления производных
потенциала с высокой точностью. И наоборот, при вычислении напряжен-
ностей из численного дифференцирования разностного решения
для потенциала более экономичен метод второго порядка с
однократным вычислением правой части.
Отметим в заключение, что большая серия численных
экспериментов приведена в работе [58], где рассмотрены различные
методы высокого порядка точности для двумерного случая, когда
потенциалы аппроксимируются многочленами 3-го порядка по их
значениям в 9 узлах разностной сетки.
Мы проведем теперь анализ погрешности обобщенного метода
Рунге — Кутта 2-го порядка (5.56). Рассмотрим частный случай,
когда потенциал представлен гармоническим полиномом 2-го
порядка ф(х, у) = \ax-\-by + cxy+Y(x2~У2) | !. Полагая а = 6 = 0,
что не повлияет на ход дальнейших рассуждений, уравнения
движения приводим к виду
x = dx-\-cyy y = cx — dy.
Решение этой системы можно представить в виде
\ y{t)= m^
где A,i, А,2= ±А,= ±i/c2-f d2, a x\(t), x2(t) — решения задач Коши
224

которые описываются формулами
Xk(tn) = Xk0< к Н ~- К »
г- . Z л[1к 1
Где ak = ± tV^, tn = nTy k = 1,2.
Применяя для каждой из последних систем метод (5.56), мы
получим соотношения
Xk,n+\ =(
Тогда численные решения могут быть записаны в виде
Хкп =
Здесь использованы обозначения
2
Таким образом, получаем следующий результат. Поскольку для
k='2 точное решение системы не превосходит единицы,
компоненты численного решения тоже должны удовлетворять этому
ограничению, и мы получаем условие устойчивости метода:
Непосредственно из выражений для точного и приближенного
решений при т->0 следует оценка погрешности для любого
конечного tn:
6kn= \xk(tn)-xkn\=O(T% k= 1, 2.
я^ более детального анализа ошибки можно рассмотреть
неравенства, получаемые непосредственно из выражений для
Xk(tn) и xkn:
) q
Отсюда, в частности, следует тот естественный результат, что
при увеличении X (это соответствует увеличению производных
потенциала) для сохранения точности необходимо уменьшать
временной шаг.
В целом, конечно, приведенные рассуждения имеют только
наводящий характер, поскольку в расчетах присутствует много
трудно учитываемых факторов: магнитные поля, релятивистские эф-
15 в п Ильин 225

фекты и т. д. В первую очередь сказывается тот момент, что
значения потенциала рассчитываются из разностных уравнений только
в узлах, и при обычно используемых аппроксимациях производные
являются резервными функциями.
На практике в большинстве самосогласованных задач
оказываются удовлетворительными расчеты траекторий при
кусочно-линейной аппроксимации потенциала и выборе шага в схеме (5.56)
по условию (5.55) со значениями 6 ж 0,2-f-0,5.
§ 5.4. Вычисление плотности тока и объемных зарядов
В данном параграфе рассматриваются модели трубок тока и
больших частиц, на основе которых определяются заряды и токи
в ячейках разностной сетки.
5.4.1. Определение начальных данных для трубок тока и
больших частиц. Задача, которую нам сейчас надо решить,
заключается в дискретизации входящего в расчетную область потока
частиц по пространственным координатам, энергии и углам. Мы
начнем с описания стационарных трубок тока. Прежде всего
производится дискретизация по пространственным переменным. Если пучок
частиц входит в расчетную область через какую-либо часть
граничной поверхности, называемую нами начальным фронтом пучка, то
этот фронт разбивается на некоторое количество NT площадок
(в двумерной задаче — интервалов) величины AS/, t = 1,2,..., NT.
Координаты некоторой «серединной» точки каждой площадки — rt
(в двумерной задаче — просто середина интервала) принимаются
за начальные данные для траектории, отождествляемой с
элементарной трубкой тока, включающей в себя частицы, вылетающие
с данной площадки. Толщина
элементарной трубки предпо-
г лагается значительно меньше
Ух
-И
I
, '
шага разностной сетки.
у-ут эды Приведем в качестве
примера разбиение двумерного
фронта на равные части. Пусть
j им будет отрезок кривой Г с
уравнением вида у = у(х) и
значениями xH^ix^Xk (рис. 27).
рис. 27. Тогда численные значения
координат начальных точек
можно найти следующим образом. Отрезок [хя, xk) разбивается на
&
NT равных частей, и вычисляются величины Цх)= \ V 1 +(#*)2 &х,
хи
xr = xH-\-r(xk — хн)/NT, r= 1, 2, ..., NT, LNt—L — общая длина
куска кривой Г; вычисление интеграла проводится по значениям
коэффициентов уравнения кривой с помощью метода трапеций,
причем фактически каждый член квадратурной формулы есть
+max{(y£)2, (л;^)2}Д£, где A£ = Ay, если yi^x'y, и наоборот.

Затем по формулам обратной лицейной интерполяции для
функции L(x) находим координаты xt середин интервалов равной длины
L/NT и yt=y(xt).
Отметим, что для осесимметричных областей значения
соответствующих площадей равны ASt^2nxtL/NT. Наши вычисления,
очевидно, будут оправданы, если величина L/NT достаточно мала по
сравнению с радиусом кривизны кривой Г.
Ток, соответствующий элементарной трубке с номером t,
определяем как
It = jt(rt)&st, (5.85)
где jt — плотность тока, соответствующая серединной точке
интервала. Это выражение можно считать достаточной аппроксимацией
интеграла \ j(r)dsy поскольку плотность тока в большинстве прак-
Ast
тических задач есть слабо меняющаяся функция координат.
Одной из типичных задач является расчет пучков частиц в
режиме ограничения тока эмиссии пространственным зарядом и в
предположении нулевых начальных скоростей. В этом случае мы
предполагаем, что на расстоянии d от эмиттера, достаточно малом
по отношению к радиусу кривизны и характерным размерам
области, распределение потенциала вдоль нормали к поверхности
фронта описывается законом «3/2» для плоского диода. Тогда
с учетом возможного ограничения плотности тока эмиссионной
способностью катода js определяем
Н r
Н rt.>.ww<lw- (5-86)
где с — константа, зависящая от типа частицы и системы единиц
(см. (5.10) для электронов), a q>/(d) — значение потенциала на
расстоянии d по нормали к эмиттеру, восстановленной в точке rt (см.
рис. 27). Величина %(d) вычисляется с помощью линейной
интерполяции по значениям потенциала в узлах ячейки разностной
сетки, которой принадлежит данная точка нормали, координаты
которой для двумерной кривой с уравнением Ф(х, у) = 0 находятся по
формулам
.(587)
Предположим теперь, что заряженные частицы вылетают по
нормали к поверхности фронта с различными начальными
энергиями. В этом случае мы проводим дискретизацию потока по энергии,
используя многоскоростные приближения аналогично тому, как
это денется в расчетах нейтронных потоков ядерных реакторов.
Весь энергетический интервал разбивается на достаточно малые
подынтервалы Aes, s= I, 2, ..., Af9 (jV3 — количество энергетических
групп). Коэффициенты относительного распределения, которые
Для простоты предполагаются независимыми от пространственных
15* 227

координат, определяются как
оо
6, = 5 /(e)de/ $ /(e)rfe, s=l,2 JV,. (5.88)
Aes О
В соответствии с этим распределением вычисляются и
усредненные каким-либо образом абсолютные значения скорости vs для
каждой группы. Из каждой начальной точки фронта выпускается
N3 трубок с величиной тока и начальными скоростями:
Its = Ifis, xts = vscos(nti х\ yts = vscos(nt, у), (5.89)
где nt — нормаль к поверхности фронта в точке с
радиус-вектором ти
И, наконец, дискретизация полного фазового пространства
проводится при необходимости учета углового распределения
влетающих в область частиц. При этом вводятся еще угловые группы,
соответствующие частицам с начальным направлением движения
в интервалах телесного угла Айг и имеющие средние направления
Qn r=l, 2, ..., Ny. Соответствующие коэффициенты
относительного углового распределения равны
xr = J j(Q)dQ/\j(Q)dQy r=l, 2, ..., Ny. (5.90)
Тогда общее количество запускаемых траекторий равно NT N3 Nyy a
начальные данные определяются следующим образом:
Itsr = /*6sxr, xtsr = vscos(Qr,x), ijtsr = vs cos(Qr, y\
(5.91)
ztsr = vscos(Qn z),
где все величины соответствуют точкам (**, yt, zt).
Распределение плотности тока / = /(г, е, Q), за исключением
режима ограничения тока пространственным зарядом, задается
как известная функция координат, энергии и угла. Типичными
примерами являются:
а) катодные системы с полумаксвелловским распределением
тепловых электронов, определяемым температурой эмиттера
(см. следующий параграф);
б) задача о расчете пучка, ранее сформированного какой-либо
электронно-оптической системой, которой и определяется разброс
частиц в фазовом пространстве (простейший пример —
монохроматический пучок с постоянной по сечению плотностью тока).
К другому типу относятся задачи с учетом вторичной эмиссии,
когда плотность эмиттируемых частиц определяется падающим
потоком. В этом случае задаются коэффициенты вторичной
эмиссии, определяющие энергетическое и угловое распределения
вторичного потока. Обычно задается несколько энергетических групп
вторичных частиц, одни из которых имеют энергию вылета,
близкую к энергии падающих частиц (упругое или почти упругое
отражение), а другие — более медленные (неупругое отражение).
228

Для модели больших частиц в нестационарных задачах
необходимо вычислить заряд «большой частицы» и ее начальное
положение. Эти вопросы связаны со способом ее представления.
Простейший подход заключается в следующем.
Считается^ что большая частица в процессе ее движения имеет
постоянный заряд и неизменную форму — прямоугольник в
переменных х, у или г, -г и параллелепипед — в трехмерном случае.
Начальный фронт пучка дискретизируется, как в модели трубок
тока, и в результате определяются прощадки Ask координатами
ri средних точек Mki k= 1, 2, ..., N\. Предполагая, что через
площадку ASk в течение временного интервала [tn, tn-\-Atn]
проходит поток частиц с постоянными плотностью jk и скоростью vly
мы определяем «большую частицу» как прямоугольник
(параллелепипед— для трехмерной геометрии), имеющий равные
основания ASk с координатами средних точек rl и rk-\-Atnvt
Соответствующий заряд полагаем равным Qk = jkASkAtn. Далее
перемещение частицы можно прослеживать по движению ее центра
тяжести, определяемого из интегрирования уравнений движения
при начальной координате г%+1/ =г%+А1пи%/2. В любой
последующий момент времени tm «большая частица» принимается за
прямоугольник с зарядом jknASkAtn, координатой центра г™+1/2,
поперечным размером AS* и высотой длины AtnVk,
ориентированной в направлении скорости у™+1/2.
Если требуется учитывать распределение начальных скоростей
частиц, то, как и для стационарных задач, проводится разбиение
потока на энергетические и угловые группы. В этом случае из
каждой точки Mk начального фронта выпускается несколько
больших частиц с разными зарядами и скоростями, усредненными
по соответствующим группам.
5.4.2. Расчет полного заряда в ячейках сетки. Мы начнем
рассмотрение с модели трубок тока для стационарных задач.
Пусть rn, rrt+i —две точки траектории, полученные в
результате численного интегрирования уравнения движения с временным
шагом Atn. Если в соответствующей элементарной трубке ток равен
/v, то на участке токовой трубки между этими точками находится
заряд
qvn = IvAtn, (5.92)
что непосредственно следует из уравнения неразрывности потока.
Поскольку для решения разностного уравнения Пуассона нас
интересует полный заряд в ячейках разностной сетки, то
параллельно с расчетом траекторий мы определяем время прохождения
ими различных ячеек сетки и, суммируя для каждой ячейки вклад
от всех токовых трубок, находим значения ^м-
Прет этом легко реализуется следующий алгоритм. Отрезок
[гп, гп+{] разбиваем на заданное число Np отрезков [rnp, rn> p+i],
Р=1, 2, ..., Afp, rn0 = rru rrtJVp = rn+i, таких, что в предположении
прямолинейного равномерно ускоренного движения между
расчетными точками траектории частица проходит каждый отрезок за
229

одинаковое время -^ Тогда на одном отрезке находится
заряд
q,np = JAtn/Npi (5.93)
относящийся к ячейке, центральный узел которой является
ближайшим к серединной точке отрезка rn,p+i/2 с координатами,
определяемыми по формуле
rn -\г ——{2р—\)+ —2 [р — (р— 1) J,
Np p (5.94)
р = 1, 2, ..., ЛГр-1.
Таким образом, при расчете траекторий (в том числе для всех
энергетических и угловых групп) одновременно вычисляются
пространственные заряды в ячейках разностной сетки:
Яцы=Ъ ^ (5-95)
Здесь суммирование идет по всем отрезкам всех траекторий,
относящихся к ячейке (/, /, k).
Данный алгоритм обладает свойством сохранения баланса
заряда в области, т. е. с точностью до величины порядка 0(6/ iVp)
выполняется соотношение
v ijk
где U — время прохождения соответствующей траектории
расчетной области, а суммирование ведется: слева — по всем
траекториям, а справа — по всем узлам сетки.
Полная погрешность вычисления объемного заряда г^
зависит, очевидно, от количества траекторий и скоростных групп и от
точности расчета траекторий, которая в свою очередь обусловлена
погрешностью определения электромагнитного поля. Эту ошибку
можно записать формально с помощью выражения
^ ф^ (5.97)
где первые три члена представляют ошибку дискретизации потока
по энергии, угла^ и пространству (для третьего шаг
дискретизации берется по отношению к шагу разностной сетки), следующие
два — ошибка расчета потенциала и численного интегрирования
уравнения движения, и последний — погрешность рассмотренного
выше алгоритма реализации условия неразрывности потока.
Порядки этих членов можно в принципе повысить за счет
применения более точных приближений.
230

Путем некоторого усложнения алгоритма можно уменьшить
ошибку вычисления объемного заряда, обусловленную
представлением пучка конечным числом траекторий. Предположим, что
трубка тока, ограниченная траекториями с номерами v, v+1, несет
ток /v и что плотность тока по сечению трубки постоянна. Пусть г",
rv + 1 и г?+1, г"%\ — расчетные точки v-й и (v + 1)-й траекторий,
время движения частиц между которыми равно Atn (рис. 28).
Четырехугольник с вершинами в этих
точках разобьем на Np частей вдоль
движения частиц и на Nq — в
поперечном направлении. Для этого каждый
из отрезков [г*, r*+I], [г?+ь r£jrj]
разделим точками г"р, a-v+ijP, /?=1, 2,..., Afp,
рассчитываемыми по формуле (5.94),
а на отрезках [rj, Гу+i], И+\ г"Ц]
нанесем равномерно точки r"k, ri£\
k=l,2,...,Nq.
Соединим теперь попарно точки
разбиения сторон прямоугольника,
имеющие одинаковые индексы р и q
соответственно. Очевидно, можно считать, что в каждом из
полученных четырехугольников находится заряд величиной IvAtn/(NpNq),
и можно отнести его к ячейке разностной сетки, в которую
попадает середина этого четырехугольника. Данный алгоритм наиболее
эффективно применяется для ламинарного потока, однако его
можно реализовать и при пересечении траекторий.
Рассмотренные нами методы относились к стационарным
задачам. Если же за время движения частиц меняется существенно
распределение поля в области, то необходимо от трубок тока
переходить к расчету движения «больших» частиц. Пусть на
какой-то момент времени Тп известно распределение поля фЛ
и самих частиц, каждая из которых имеет известную величину
заряда. Из расчета уравнений движения при заданном поле
находим положение частиц на момент времени
Затем определяем соответствующее распределение плотности
объемного заряда pn+i и из решения уравнений Пуассона
Дф=—4ярп+1 с граничными условиями для потенциала на
момент времени Тп+\ находим новое электрическое поле cpn+i.
Величину шага ЛГ„ необходимо выбирать так, чтобы за это время
незначительно изменялись нестационарные параметры задачи
(это могут быть, например, переменное напряжение на электроде
или -зависящая от времени плотность тока пучка на границе
влета его в расчетную область). Значения &Тп и шага численного
интегрирования уравнений движения Atn не обязаны совпадать
(необходимо только условие А^<АГП). Если характерное время
изменения нестационарных процессов мало, а особенности задачи
231

требуют точного расчета траекторий, то целесообразно выбирать
АТп в несколько раз больше, чем Atn.
Аналогию между методами частиц и трубок тока можно
установить для стационарной задачи в примере на рис. 28.
За «большую частицу» можно принять четырехугольник
с вершинами г", г*+1, rj+b r^\ и разносить ее заряд по ячейкам
разностной сетки путем разбиения четырехугольника на NpNq
«микрочастиц», как это делалось выше для стационарного случая.
Считая временные шаги Atn одинаковыми, заряд частиц можно
определить по величине тока, прошедшего через интервал
начального фронта [r$, Tv+i] за тот отрезок времени, когда в расчетную
область входила данная частица.
Если же, как указывалось выше, частица в процессе движения
считается имеющей форму прямоугольника неизменных размеров,
то учет ее заряда проводится по тому же принципу, но реализация
алгоритма несколько упрощается.
Возможны и другие способы представления частиц, но мы на
них останавливаться не будем. Более тонкие модели необходимы
в тех случаях, когда пучок сильно расширяется или сужается,
а также при образовании режима виртуального катода, когда одна
часть пучка резко поворачивает, вплоть до 180°, а другая
проходит имеющийся потенциальный барьер.
Обзор и анализ различных методов «размазывания» зарядов
частиц по ячейкам сетки содержится в [17]. Представляют интерес
также работы Мокина Ю. И. [131, 133], в которых различные
модели частиц и трубок тока следуют как результат применения
разных квадратурных формул к построенной им системе интегро-
дифференциальных уравнений. Однако каких-либо
систематических результатов по сравнению различных способов
представления заряда частиц в ячейках для самосогласованных задач пока
не имеется.
Принципиальное отличие метода частиц заключается в том,
что для' каждой из них на каждый момент времени необходимо
хранить значения координат и скоростей. Если считать, что размер
частицы должен быть меньше или сравним с размером ячейки
разностной сетки, то это налагает большие ограничения на объем
памяти при расчетах на ЭВМ. Если с начального фронта пучка
через каждый временной интервал Atn впускается N частиц,
и каждая из них пролетает расчетную область за L шагов, то
в трехмерных задачах потребуется запоминать примерно 1NL
чисел (координаты, компоненты скоростей и заряд каждой
частицы). Для обеспечения необходимой для практических задач
точности значения L могут достигать нескольких десятков или
сотен, а N — от сотен до нескольких тысяч (при необходимости же
детального анализа энергетического и углового распределения
частиц — до десятков или даже сотен тысяч). В модели трубок
^ока для стационарных задач дополнительной памяти практически
не требуется. •
232

§ 5.5. Итерационные процессы решения
стационарных самосогласованных задач
Мы рассмотрим итерационные методы решения системы
нелинейных разностных уравнений
Д„Ф=-£>р(ф) + /, (5.98)
где Ал — какая-либо разностная аппроксимация оператора
Лапласа, определенная на внутренних узлах сетки с учетом граничных
условий; D — константа, определенная в (5.11) или (5.12);
p = q/ V—вектор значений плотности заряда в узлах сетки
(q — величина заряда в ячейке, V — объем соответствующей
разностной ячейки); f — сеточная функция, отличная от нуля
только в околограничных узлах и появляющаяся за счет
исключения граничных условий.
Во второй главе мы рассмотрели различные итерационные
алгоритмы решения нелинейных уравнений: обобщения методов
Якоби, Зейделя, верхней релаксации, метод Ньютона и его
модификации. Обоснование применимости наиболее эффективных из
этих алгоритмов к решению самосогласованных задач удается
провести только при условиях на правую часть уравнения (5.98),
которые зачастую не выполняются при моделировании
интенсивных пучков заряженных частиц.
Наибольшее распространение в данном случае получили
итерационные процессы с наглядной физической интерпретацией.
Один из них состоит в проведении двойных интераций, в которых
ведутся внешние итерации по объемному заряду, а внутренние
относятся к решению уравнения Пуассона при фиксированной
правой части.
Применяется также метод решения самосогласованных задач,
моделирующий в некотором смысле процесс установления
стационарного пучка после его моментального «включения». В этом
«квазистационарном» процессе задается некоторая
последовательность чисел 0<Г1<:Г2<С... При первых итерациях по
объемному заряду траектории считаются до tn~Tn (кроме тех, которые
выходят еще раньше из области). После проведения некоторого
числа таких итераций, когда соседние приближения станут
достаточно близкими, траектории начинают рассчитывать до момента
Т2 и т. д. На последних шагах этого процесса можно считать
Tk=ooy т. е. все траектории должны оканчиваться пересечением
с границей области. Как показывают расчеты, выбором достаточно
малых &Tk=Tk— Tk-\ можно добиться сходимости итерационного
процесса и для сложных задач с относительно большим объемным
зарядом, но при этом требуется большое число внешних итераций.
Мы будем рассматривать метод релаксации объемного заряда
в виде
-233

где (On — некоторая последовательность релаксационных
параметров; рЛ+1 — функция плотности объемного заряда,
вычисленного для ф = фп+1 по формулам предыдущего параграфа при
расчете всех траекторий до выхода их из области. Такой метод
широко применялся, в том числе и при моделировании задач на
аналоговых устройствах.
Однако строгое доказательство сходимости итерационного
процесса (5.99) (а также существование и единственность самого
решения задачи (5.98)) удается провести только при сильных
ограничениях на величину |др/дф|, выполняющихся для
электронно-оптических систем с незначительным влиянием объемного
заряда.
Мы приведем результаты методических расчетов по решению
самосогласованной задачи с учетом полумаксвелловского
распределения нормальных к катоду компонент начальных скоростей
электронов
и
\[^)', (5.100)
где js — эмиссионная способность эмиттера uo = kT /\e\; k —
постоянная Больцмана; Т — температура катода в Кельвинах.
Объектом численного моделирования избран плоский диод с
расстоянием между катодом и анодом dKa=l04 мкм, потенциалом
анода относительно катода (ра = 1,38« 10~3 в, температурой катода
Г=1100 К и эмиссионной способностью /s = 3 А/см2.
Из аналитического решения такой задачи следует, что минимум
потенциала равен ф=— 0,46 в и достигается на расстоянии от
катода х = 30 мкм [83]. Эта задача может считаться достаточно
«трудной» для итерационного процесса, так как в решение
основной вклад вносят нелинейные эффекты, иначе говоря, в области
образуется большая плотность объемного заряда (до анода
доходит только около 1% общего тока).
Электронный поток разбиваем на 40 энергетических групп с
шагом 0,002 эВ, каждая из которых имеет плотность тока Д/V
Током электронов с начальной энергией более 0,8 эВ пренебрегаем.
Соответствующие значения «удельной» плотности тока —Д- и
Js
средней начальной энергии и* приводятся в табл. 26. Разностная
сетка взята с шагом h\ = l мкм для 0<х<20 и /i2 = 4,2—
в остальной части межэлектродного пространства. Итерационный
процесс заканчивался, когда в двух соседних приближениях
максимальное различие значений потенциала в узлах сетки не
превышало 0,005.
Из априорных физических Соображений ясно, что
итерационный процесс (5.99) при со0»1, ро = О без каких-либо специальных
приемов для данной задачи не сходится, так как в различных
приближениях траектории будут то проходить на анод (внося
в область огромный заряд), то все будут запираться.
234

Таблица 26
k
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1812
1484
1215
994,8
814,4
666,8
545,9
447,0
365,9
299,6
245,3
200,8
164,4
134,6
uk, эв
0,009
0,030
0,049
0,069
0,089
0,109
0,129
0,150
0,169
0,189
0,209
0,229
0,250
0,269
k
15
16
17
18
19
20
21
22
23
24
25
26
27
28
ю*дул//в
110,2
90,2
73,8
60,4
49,5
40,5
33,2
27,1
22,2
18,2
14,9
12,2
9,99
8,18
пк, эв
0,289
0,309
0,329
0,349
0,369
0,389
0,409
0,429
0,449
0,469
0,489
0,509
0,529
0,549
k
29
30
31
32
33
34
35
36
37
38
39
40
6,70
5,48
4,49
3,67
3,01
2,46
2,01
1,65
1,35
1,10
0,90
0,74
uk, эв
0,569
0,589
0,609
0,629
0,649
0,669
0,689
0,709
0,729
0,750
0,769
0,789
Исследуемые нами релаксационные процессы имеют целью тем
или иным способом уменьшить количество объемного заряда в
области на первых приближениях.
Сначала был апробирован метод низкой релаксации, т. е.
использующий значения релаксационных параметров con<Cl.
Прежде всего, эксперименты с постоянным значением соп не дали
удовлетворительных результатов, что можно объяснить тем, что
малые значения релаксационного параметра могут обеспечить
сходимость процесса, но требуют проведения большого числа
итераций. Затем был апробирован метод с поэтапным увеличением
значений con, когда при каком-то фиксированном значении со^
итерации по объемному заряду продолжались до тех пор, пока
соседние приближения ф не становились равными с погрешностью
8<с1, затем использовалось значение параметра со^+1 = со^^,
q> 1 и т. д. В этом случае алгоритм при ооо= Ю~3, q = 2, е= 10~3
требует около 180 итераций, т. е. не является эффективным.
Экономичность расчетов удается значительно увеличить при
более сильном росте значений
(x)n = mm[(dOqn~\ comax], (5.101)
где coo <С 1; q > 1; 0 < comax < 1 (со„ увеличивается на каждом
приближении по объемному заряду). При значениях 2»10~4^
^соо^32« 10~3, 2^q^4, comax= I/ 3 в численных экспериментах
решение задачи достигается за 10—15 итераций. Типичный ход
значений потенциала ип(х) в различных приближениях
иллюстрируется табл. 27.
Мы укажем еще на два подхода к построению релаксационного
процесса, оказавшихся достаточно эффективными на практике.
Один из них связан с тем, что в первых приближениях учитывается
объемный заряд только самых быстрых частиц, а количество
235

Таблица 27
п
1
2
3
4
5
6
7
8
9
10
11
«я
0,001
0,004
0,016
0,256
0,333
0,333
0,333
0,333
0,333
0,333
0,333
х = 3
+ 0,0004
-0,0053
-0,0321
-0,0821
-0,1508
-0,2422
-0,2466
-0,2475
-0,2422
-0,2465
-0,2469
х=\\
+ 0,1014
-0,0176
-0,1000
-0,2338
-0,3683
-0,4818
-0,4488
—0,4468
-0,4174
-0,4335
-0,4339
х = 32,6
+ 0,0041
-0,0385
-0,1963
-0,4053
-0,5440
-0,6158
-0,5320
-0,5225
-0,4806
-0,5055
-0,5052
ЛГ=62
+ 0,0088
-0,0424
-0,1227
-0,3291
-0,4885
-0,4249
-0,3528
-0,3470
-0,3189
-0,3339
-0,3340
рассчитываемых энергетических групп постепенно увеличивается
на каждой итерации по объемному заряду. Другой метод основан
на специальном выборе начального приближения. Расчеты
показывают, что задание начальных значений потенциала даже из
грубых качественных оценок решения самосогласованной задачи
дает значительное улучшение первых приближений по сравнению
с итерационным процессом, в котором траектории вначале
рассчитываются в «лапласовском» поле [70].
Несколько отличным характер итерационного процесса
оказывается для другого класса самосогласованных задач: расчет
катодных систем в режиме ограничения тока электронов
пространственным зарядом при нулевых начальных скоростях.
Приближения по-прежнему строятся по формулам (5.99), однако следует
иметь в виду, что здесь характер зависимости от потенциала
существенно отличается. Это наглядно иллюстрируется
одномерным случаем:
т. е. если в предыдущей задаче от ср зависел только знаменатель,
то здесь — и числитель. Однако, как нетрудно видеть, зависимость
/~ф3/2 «сглаживает» общий нелинейный характер влияния ф" на
распределение pn+1 и итерационный процесс оказывается
«лучше», чем в задачах с энергетическим распределением потока
и потенциальной ямой вблизи катода. Численные эксперименты
свидетельствуют, что такие задачи допускают удовлетворительное
решение для со„«0,3 за 5—15 итераций, что можно считать
достаточно эффективным, см. подробнее [19, 70].
Приведенные выше характеристики справедливы, если
самосогласованные задачи не содержат каких-либо дополнительных
^факторов, усиливающих нелинейные эффекты. Сюда относятся так
называемые задачи с торможением, когда заряженные частицы
в какой-либо части расчетной области (как правило, это
коллекторы электронно-оптических систем) замедляются, что вызывает
236

значительное увеличение плотности заряда в этом месте. Для
таких задач траектории в различных приближениях могут сильно
менять свою форму и сходимость зачастую достигается только
при малых значениях со„ (около 0,1 и ниже) на 20—30 итераций.
Другим примером являются задачи со вторичной эмиссией,
которая может намного увеличить объемный заряд в расчетной
области.
Для решения нелинейной краевой задачи
можно использовать метод Ньютона, в котором строятся итерации
по формулам
зу+7 ^2=^(фп)+(фп+1-фпЫфпХ фп(О)=фо,
(5.102)
и который имеет квадратичную сходимость, если только
выполняется условие достаточной близости приближений ф1 и ф°.
Для самосогласованной задачи расчета плоского диода
с заданной плотностью тока / на катоде и нулевыми начальными
скоростями электронов
) = — а/ л/ф> а = 4я/У т/ ~2е < 0,
этот алгоритм принимает вид
^1-^. (5.103)
Проверка условий сходимости в данном случае
затруднительна, поскольку при положительности фп добавочный член в левой
части (5.103) «портит» дифференциальный оператор.
Представляет интерес итерационный алгоритм, предложенный
в работе [19]. Для плоского диода его можно записать с помощью
выражения (5.102), если только правый член с g'y умножить на
число со = — 2:
=Фь (5.104)
Мы исследуем этот метод уже применительно к решению
разностной задачи (5.98) безотносительно к размерности расчетной
области. Тогда аналог уравнения (5.104) можно представить в
векторной форме:
ДЛф"+1 + /?(фп)фп+1 = -/, "дЛф°=-/. (5.105)
Здесь /?(<р) — диагональная матрица с элементами, равными
значениям Dp(<p)/q> в соответствующих узлах сетки, т. е. для
двумерной задачи (D см. в (5.11)):
(5.106)
237

Если рассматривается движение электронного пучка в области
с положительными значениями потенциалов на электродах, т. е.
/)<0, /;>0, то легко видеть, что значения потенциалов во всех
приближениях будут положительны и итерационный процесс
протекает без вырождения. В самом деле, поскольку ф°:>0, то для
всех п будут выполняться условия
Фя>Фп+1>0, [Ah + R(q>n)]-l<0. (5.107)
Таким образом, если задача (5.98) имеет единственное
положительное решение ф, то последовательные приближения в (5.105)
сходятся, и именно к ф.
Так как все значения /?(фп) отрицательны, то это может
только усилить диагональное преобладание и улучшить
обусловленность матрицы Ah + R(q)n) по сравнению с ДЛ. Для решения
системы алгебраических уравнений (5.105) на каждом
приближении по объемному заряду применимы рассмотренные в первой
главе итерационные алгоритмы, причем скорость сходимости их
должна быть выше, чем при проведении «внутренних» итераций
для уравнения Пуассона в методе (5.99).
Численные расчеты показывают высокую эффективность
метода (5.105), в том числе для задач с ограничением тока на
катоде пространственным зарядом. Например, для плоского
диода о сходимости итераций можно судить по относительным
значениям плотности тока, вычисленным в первых семи
приближениях по закону «3/2»: 14736, 5288, 3151, 2307, 2422, 2412,
2412. В том же диоде с постоянной плотностью тока на катоде
/ = 1165 значения потенциала сходятся за пять приближений с
погрешностью менее 0,1%.
Укажем еще на один вопрос, имеющий значение для решения
дву- и трехмерных самосогласованных задач в режиме
ограничения объемного заряда. Дело в том, что вместо релаксации
объемного заряда на каждой итерации можно проводить релаксацию
плотности тока эмиттера:
где Y — плотность тока, вычисленная с помощью закона «3/2»
по распределению потенциала фп. В одномерном случае, очевидно,
такой алгоритм тождествен с (5.99). Различие в этих двух
методах наиболее существенно, когда от итерации к итерации сильно
искажается форма рассчитываемых траекторий. Систематических
сравнительных экспериментальных данных по таким подходам
не имеется, но, по-видимому, следует отдать предпочтение
релаксации по плотности тока.
Оригинальный и достаточно эффективный алгоритм итераций
по объемному заряду предложен Начамкиным и Хенкоком [140]
для самосогласованных задач с ограничением тока
пространственным зарядом и бесконечной эмиссионной способностью
катода. Идея его заключается в следующем.
238

Обозначим через /? плотность тока в точке ri0 эмиттирую-
щей поверхности, определяемую в соответствии с (5.10) по
распределению очередного приближения для потенциала фп(г):
i=l 2, ..., NT, (5.108)
где предполагается С = 4-"д/-^-> фо = 0, а <рп(п) — потенциал
в точке о, расположенной на расстоянии d по нормали от точки
г/о эмиттера. Функцию фп определяем из решения краевой задачи
для уравнения Пуассона
Дфя=—4яр\ (5.109)
где рп — распределение плотности заряда, вычисленное на основе
плотностей тока /f"1 и траекторий частиц в поле фЛ-1(г).
Решение уравнения (5.109) представим в виде суммы
где ф1 — решение уравнения Лапласа с исходными граничными
условиями для потенциала, а <рп — решение уравнения (5.109)
при соответствующих однородных граничных условиях.
Пусть \л]1~{\ = maxflyf"1!}. В качестве очередного приближе-
/
ния для плотности тока возьмем
]? = а]Г\ /=1, 2, ..., NTf
7 o))/f-1, /1=1, 2,..., 0<(о<1, (5.110)
где значение а выбирается из условия удовлетворения закону
Чайльда—Ленгмюра в окрестности точки г^:
Вводя обозначение а = р3, приводим последнее уравнение к виду
Р3Ф"М - РУ - \rk) + <pt(r*) = 0. (5.111)
Здесь значения ф^(г^) и фп~1(г^) положительны (в противном случае
происходило бы полное запирание тока), а величина $n(rk)
отрицательна в силу ее определения. Поэтому уравнение (5.111) имеет
единственный положительный корень р. Найдя его, мы из (5.110)
определяем плотность тока для последующей итерации. Очевидно,
что в этом методе итерации потенциала ф/г = Ф/, + осфп будут
неотрицательны. Проведенные авторами алгоритма эксперименты
свидетельствуют о хорошей скорости сходимости, причем рекомендуется
брать в (5.110) со = 1 на первой итерации и со = 2/3 — на
последующих.
Отметим, что близкий алгоритм был рассмотрен Г. Т.
Головиным в'работе [47], где коэффициент а линейной комбинации
полей ф^ и фп подбирался из условия равенства нулю напряженности
поля на катоде.
Для одномерного плоского диода удается доказать сходимость
и дать оценку скорости сходимости для следующего алгоритма.
239

Рассматриваемую задачу можно записать в виде
Ф«=/Л/ф. 0<х<Ь, <р(0) = 0, ф) = У, (5.112)
где константа / из условия фя-(0) = 0 равна а= -^—гг- и может
быть представлена как
поскольку само решение при этом равно
Итерационный процесс по объемному заряду представляется
в форме
ф^/^/Уср7-11, (5.114)
где только требует уточнения величина /п. В качестве начального
приближения для плотности тока и потенциала мы полагаем
/о = О, ф°(л:) = Vx/b. Введем вспомогательные величины /«, фЛ:
Непосредственно из решения краевой задачи (5.115) для п=1
следует
Отсюда видно, что если мы положим j\= -j^- ~\/-гЪ> то из
(5.114) получим
Пусть теперь для произвольного п распределение потенциала
имеет вид
Тогда из (5.115) мы имеем-
Отсюда получаем, что при
распределение потенциала на следующей итерации выражается
формулой
% xrt = 2 - Xn-i/2. (5.117)
240

Легко видеть, что последовательность кп при х0 = 1 сходится
к пределу х = 4/3, причем имеет место соотношение
х -и, =.!..(_-l.)", n = l,2,... (5.118)
Функция ошибки я-го приближения для потенциала в таком
итерационном процессе убывает по закону
ф) — уп(х) = gn(x) (х — хп),
gn(x) = -^г(Ь*кпх«»-х - **■)> xJeLl], (5.119)
6 6" L ° J
откуда следует оценка
тах{|ф(х)-фя(х)|}<е/2я, G = sup max {I £*(*)!}. (5.120)
Из выражений (5.118), (5.119) следует очень важное свойство
алгоритма: последовательные итерации <рп(х) дают двусторонние
приближения к точному решению. Для доказательства этого
необходимо показать знакопостоянство gn(x), что действительно имеет
место для достаточно больших я, поскольку b ^ xhxJ>1. Отсюда
следует, что в процессе итераций мы можем контролировать
погрешность решения с помощью неравенства
| фс) — цп(х) К | ф„ + \(х) — ц)п(х) |.
Несложный анализ выражений (5.119) устанавливает
возможность ускорения сходимости итерационного процесса (5.114),
(5.115), (5.116) при помощи линейной комбинации соседних
приближений. А именно, для функций
справедлива оценка
Характер рассмотренного алгоритма не привносит
принципиальных трудностей для применения его к двумерным или
трехмерным самосогласованным задачам.
В работах Ю. И. Мокина [131, 135] рассматривался еще один
метод расчета плотности тока в режиме ограничения
пространственным зарядом, основанный на дискретизации интегрального
уравнения (5.17), в предположении, что траектории частиц
известны. Однако возникающая при этом необходимость решения
вспомогательных краевых задач и применения регуляризующих алго-^
ритмов приводит к сомнению в его практической
конкурентоспособности с вышерассматриваемыми методами, которые дают
хорошие результаты и без использования каких-либо специальных
регуляризации.
16 В П Ильин 241

§ 5.6. Примеры расчетов сильноточных пучков
В данном параграфе мы приведем результаты решения двух
самосогласованных задач, полученных с помощью пакета
программ Эра, описанного в последней главе.
В качестве примера решения достаточно сложной практической
задачи мы приведем некоторые результаты расчетов
высоковольтного импульсного источника релятивистского электронного
пучка ЭЛИТ-ЗА для генерации СВЧ колебаний в системе электронно-
позитронного инжектора ускорительного комплекса ВЭПП-4,
разработанного в ИЯФ СО АН СССР. Схема рассматриваемой осе-
симметричной электронно-оптической системы дана на рис. 29а.
Общая длина расчетной области составляет 1430 мм, радиус
катода равен 15 мм. Система включает 3 магнитные линзы, каждая
Рис. 29а.
\\
7
x\
1 \
1 ^^
—J—V—"^
\
V -
6
^ \
i
i
/\s i
*\г | !
4
1500 1620 2000
2750 Г
Рис. 296.
Рис. 29в.
из которых расположена в подобласти с практически нулевой
напряженностью электрического поля. Распределение компоненты
В2 магнитной индукции'на оси симметрии приводится на том же
рисунке, максимальная амплитуда составляет около 400 Гс.
242

Вдоль всей системы расположено 36 электродов с монотонно
возрастающими значениями потенциалов от 0 до 1,65 МэВ для
обеспечения относительно равномерного распределения поля.
Конструкцию в целом можно представить состоящей из катодного
узла, 4-х ускоряющих модулей и тракта для вывода пучка.
На рис. 296, в изображена схема катодного узла и 1-го модуля,
разделенных эквипотенциальной сеткой, которая считается
прозрачной для электронов. Расчет системы проводился поэтапно:
сначала катодный узел, затем 1 -й модуль, далее 2-й и т. д. На границах
разделения подобластей ставилось условие равенства нулю
осевого компонента электрического поля. Распределение плотности
тока эмиссии и величина полного тока (/^56 А) найдены из
расчета катодного узла в режиме ограничения тока пространственным
зарядом. В каждом последующем модуле начальные данные для
электронов брались из результатов расчетов предыдущего модуля.
Электронный пучок моделировался 120 трубками тока.
В каждой из расчетных областей использовались сетки с числом
узлов около 2500. Разностные уравнения Пуассона решались
блочным методом верхней релаксации с автоматическим выбором
оптимальных итерационных параметров и точностью проведения
итераций е— 10 (при 8= 10 наблюдались существенные
искажения формы траекторий). В каждой подобласти проводилось
около 10 итераций по объемному заряду с параметрами
релаксации со я^ 0,3, что обеспечивало достаточную точность. Например,
при расчете катодного узла значения полного тока эмиссии
принимали следующие значения в итерациях: 169,7; 95,8; 71,1; 62,0;
58,4; 56,9; 56;3; 56,1; 56,0; 56,0. При моделировании пучка
учитывались азимутальная компонента собственного магнитного поля и все
компоненты внешнего поля (последние рассчитывались с помощью
ряда Шерцера и аппроксимации осевого распределения Bz
кубическим сплайном).
Основные требования к данной электронно-оптической системе
заключались в минимизации потерь тока на протяжении всей
области формирования (из условия электрической прочности токо-
осаждение на стенках больше 1% уже недопустимо) и в
минимизации фазового объема пучка на выходе.
Экспериментальные численные исследования, выполненные
В. М. Свешниковым и В. М. Радченко, показали хорошее
согласование с результатами физических измерений. На рис. 30 показан
примерный характер электронных траекторий в 1-м модуле.
Наиболее характерная особенность пучка, обнаруженная в
расчетах,— это отсутствие какой-либо ламинарности потока, начиная
со 2-го модуля.
Рассмотрим пример реальной задачи о формировании
плазменной границы, решение которой было выполнено В. М.
Свешниковым и В. А. Панибрацким [152]. Моделируемая электронно-ионная
оптическая система источника электронов для высоковольтного
тлеющего разряда изображена на рис. 30. Плазма локализована
У анода и имеет равный с ним потенциал ср = О. Изображенная
16* 243

штриховой линией плазменная граница является эмиттером
положительных однозарядных ионов молекулярного азота, которые
летят на холодный катод, находящийся под потенциалами
Ф=—20 кВ. С бомбардируемого участка катода эмиттируется
Рис. 30.
электронный поток, пронизывающий плазму. Электронная
температура и ионная плотность прианодной плазмы принимались
равными Теж3 эВ, tiittlO9 см .
По формуле Бома
ja = 0,43nie(2kTe/mi)l/\
это дает плотность ионного тока с плазменной границы / =
= 5» 10~~5А/ см2. Кроме того, в рассматриваемой модели было
принято, что с участка поверхности, бомбардируемой электронным
пучком, вследствие разогрева плазмы плотность тока в десять раз
больше — / = 5- 10~4А/см2. Плотность объемного заряда
электронного потока считалась пренебрежимо малой, поскольку
скорость ионов в расчетной области намного меньше, чем у электронов.
Конфигурация плазменной границы при получаемой
неравномерной плотности тока эмиссии определялась из условия, что
на малом расстоянии d справедливо одномерное приближение
закона Чайльда—Ленгмюра (напомним, что это соответствует
равенству нулю начальных скоростей ионов и нормальной
производной потенциала на поверхности плазмы).
Расчеты проводились на сетке с числом узлов около 3000.
Ионный поток моделировался 16 трубками тока. Итерации по
объемному заряду проводились с параметром релаксации со = 0,25.
В процессе итераций проводилось варьирование плазменной
границы по следующему алгоритму.
Пусть г?, /=1,2, ..., N, радиус-векторы начальных точек N
ионных траекторий, рассчитанных при распределении потенциала
Фп(г). Соответствующую'форму плазменной границы определяем,
проводя через точки г?так называемый дискретный интерполирую-
244

щий параболический сплайн Г„, обладающий свойствами
монотонной аппроксимации [96]. Найдя при данном положении
эмиттера решение самосогласованной задачи фп(г), координаты новых
точек границ�