ПРИКЛАДНАЯ МАТЕМАТИКА
для ВТУЗов
В.И. КИРЕЕВ
А.В. ПАНТЕЛЕЕВ
ЧИСЛЕННЫЕ
МЕТОДЫ
В ПРИМЕРАХ
И ЗАДАЧАХ
Издание третье, стереотипное
Рекомендовано
Учебно-методическим объединением
высших учебных заведений Российской Федерации
по образованию в области авиаиии, ракетостроения и космоса
в качестве учебного пособия для студентов высших
технических учебных заведений
Москва
«Высшая школа»
2008

УДК 519.6
ББК 22.193
К 43
Рецензенты:
кафедра «Технологии художественной обработки материалов»
Московского государственного горного университета
(зав. кафедрой д-р техн. наук, проф. В.И. Морозов);
д-р физ.-мат наук, проф. М.Я. Иванов
(ЦИАМ им. П.И. Баранова)
Киреев В.И.
К 43 Численные методы в примерах и задачах: Учеб.
пособие/В.И. Киреев, А.В. Пантелеев. — 3-е изд. стер. — М.: Высш.
шк., 2008. — 480 с: ил.
ISBN 978-5-06-004763-9
Пособие охватывает классические разделы численного анализа: методы
алгебры, теории приближения функций одной переменной с их приложениями,
разностные методы решения задач Коши и краевых задач для обыкновенных
дифференциальных уравнений, численные методы решения уравнений
математической физики с двумя и тремя независимыми переменными. Впервые в
учебной литературе наряду с традиционными методами изложены новые
экономичные, устойчивые и простые в реализации методы приближения функций,
численного дифференцирования и интегрирования, решения задачи Коши,
основанные на применении интегрально-дифференциальных сплайнов.
Для студентов математических, инженерно-технических и авиационных
специальностей вузов и университетов, аспирантов и научных работников.
УДК 519.6
ББК 22.193
Учебное издание
Киреев Владимир Иванович, Пантелеев Андрей Владимирович
ЧИСЛЕННЫЕ МЕТОДЫ В ПРИМЕРАХ И ЗАДАЧАХ
Внешнее оформление В.В. Жук. Корректор Г.Н. Петрова
Изд. № РЕНТ-236. Подп. в печать 27.11.07. Формат 60х88'/,6. Бум. офсетная.
Гарнитура «Ньютон». Печать офсетная. Объем 30,00 усл. печ. л., 30,50 усл. кр.-отт.
Тираж 2000 экз. Заказ № 18794 (Kp-sm).
ОАО «Издательство «Высшая школа», 127994, Москва,
Неглинная ул., 29/14, стр. 1.
Тел.: (495) 694-04-56. http://www.vshkola.ru. E-mail: info_vshkola@mail.ru
Отдел реализации: (495) 694-07-69, 694-31-47, факс: (495) 694-34-86.
E-mail: sales_vshkola@mail.ru
Отпечатано с готовых диапозитивов изда1 елылва в ОАО «Смоленский
полиграфический комбинат». 214020, г. Смоленск, ул. Смольянинова, 1.
ISBN 978-5-06-004763-9 © ОАО «Издательство «Высшая школа», 2008
Оригинал-макет данного издания является собственностью издательства
«Высшая школа», и его репродуцирование (воспроизведение) любым способом без согласия
издательства запрещается.

ОГЛАВЛЕНИЕ
Введение 7
Часть I. ЧИСЛЕННЫЕ МЕТОДЫ АЛГЕБРЫ 23
Глава 1. Методы решения систем линейных алгебраических уравнений 23
1.1. Постановка задачи 23
1.2. Прямые методы 25
1.2.1. Метод Гаусса 25
1.2.2. Метод прогонки 31
1.2.3. Метод Z,£/-разложения 36
1.3. Итерационные методы 42
1.3.1. Метод простых итераций 42
1.3.2. Метод Зейделя 50
Глава 2. Методы решения задач о собственных значениях
и собственных векторах матриц 61
2.1. Постановка задачи 61
2.2. Метод непосредственного развертывания 62
2.3. Метод итераций 65
2.4. Метод вращений 68
Глава 3. Методы решения нелинейных уравнений и систем 76
3.1. Методы решения нелинейных уравнений 76
3.1.1. Постановка задачи 76
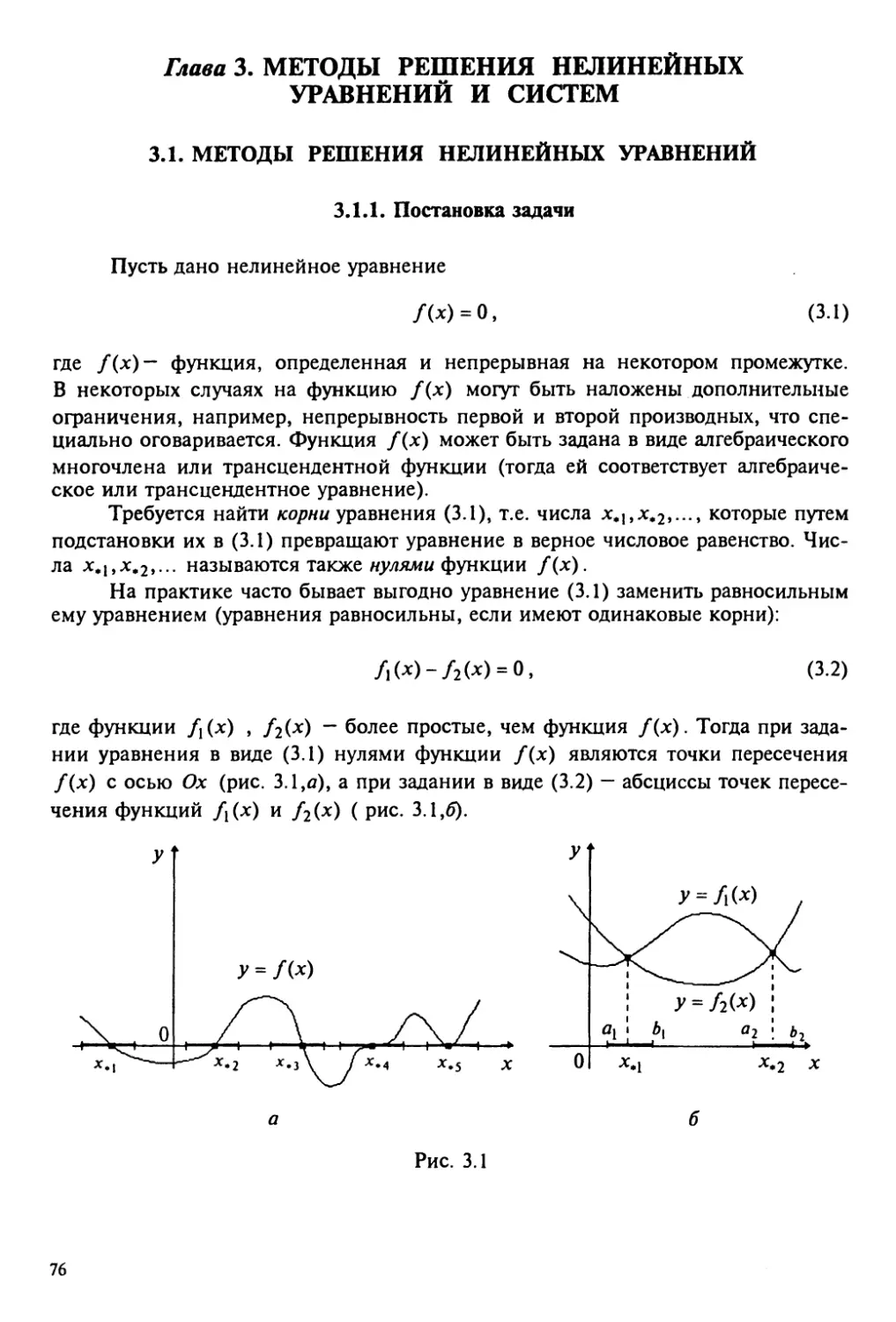
3.1.2. Отделение корней 78
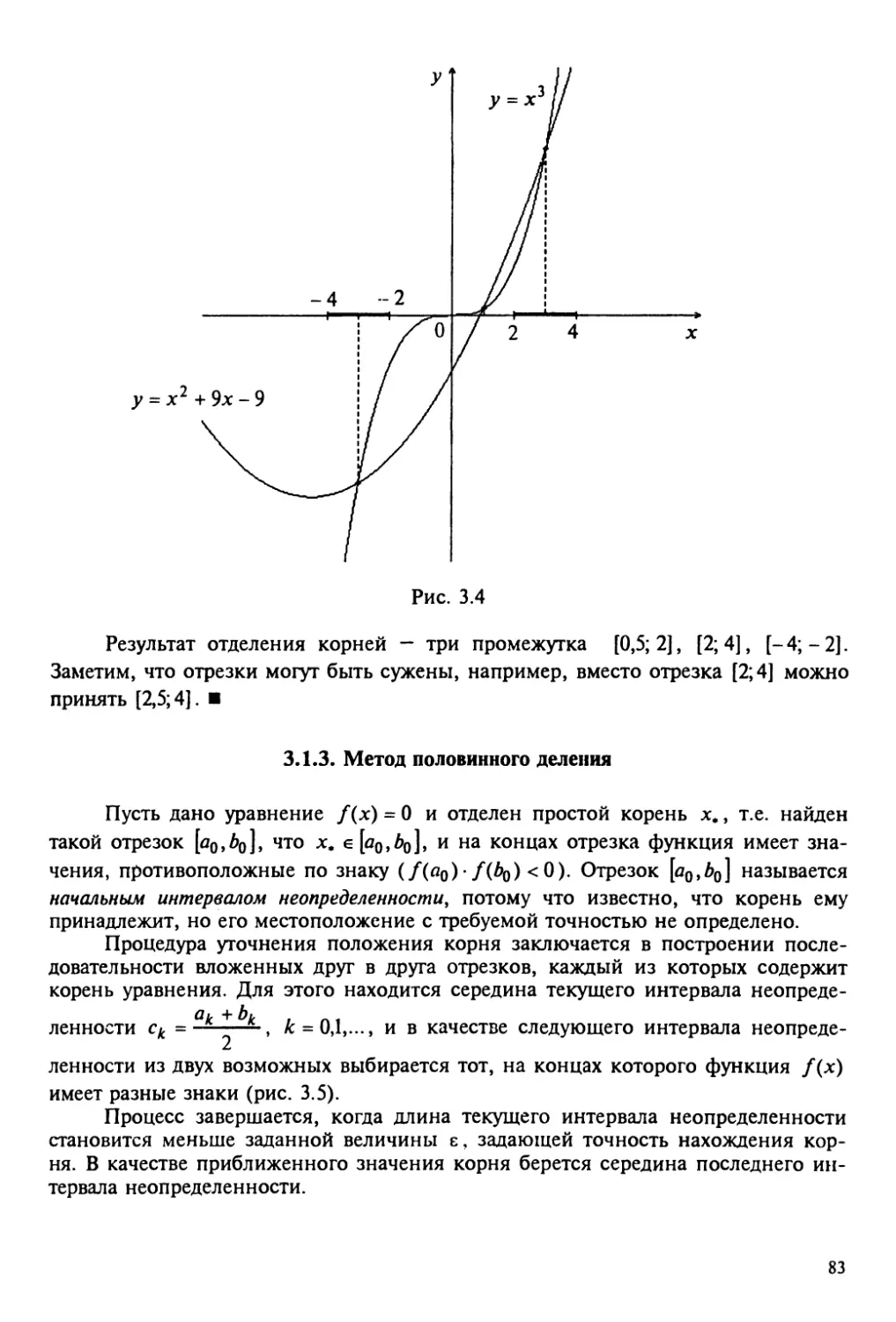
3.1.3. Метод половинного деления 83
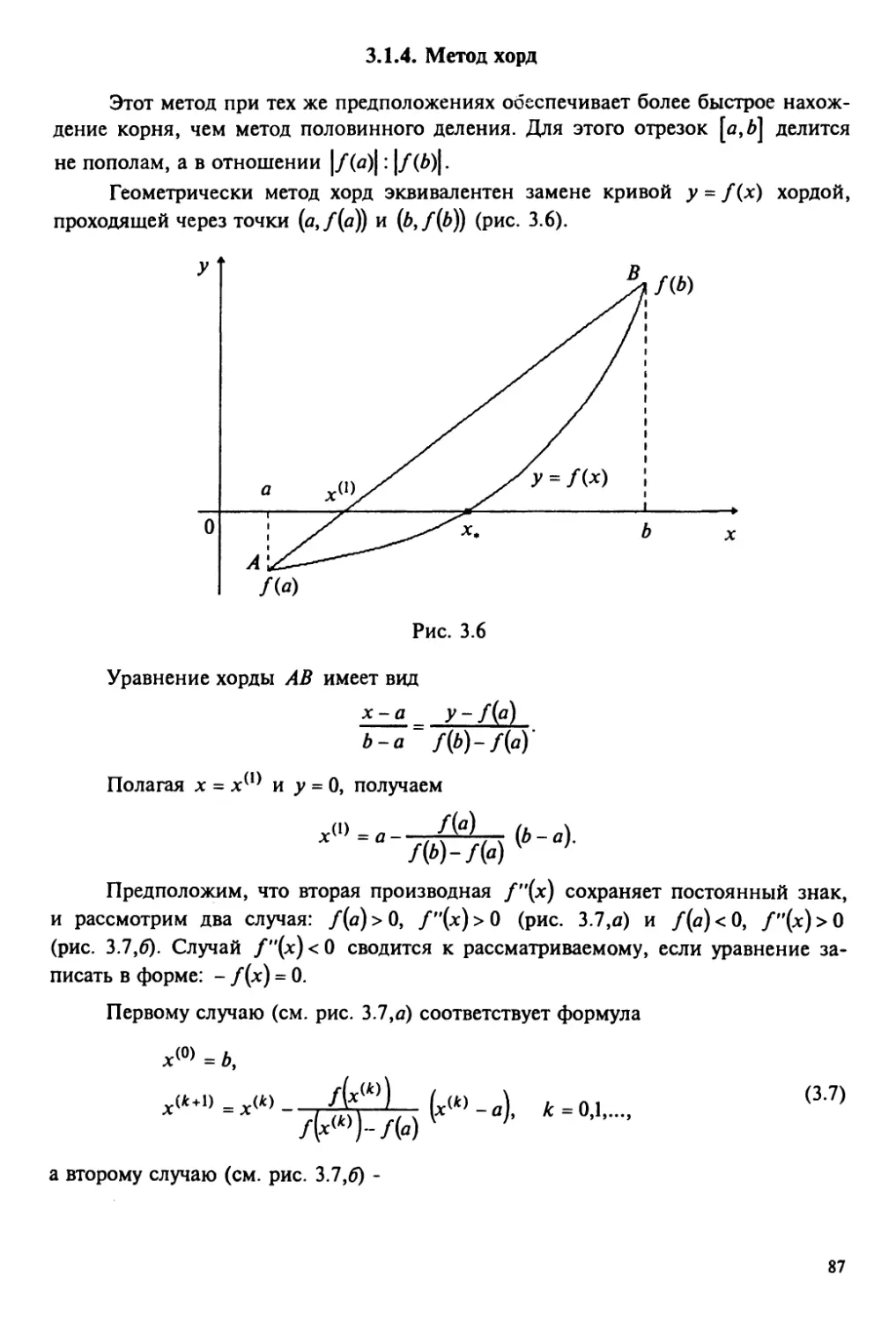
3.1.4. Метод хорд 87
3.1.5. Метод простых итераций 89
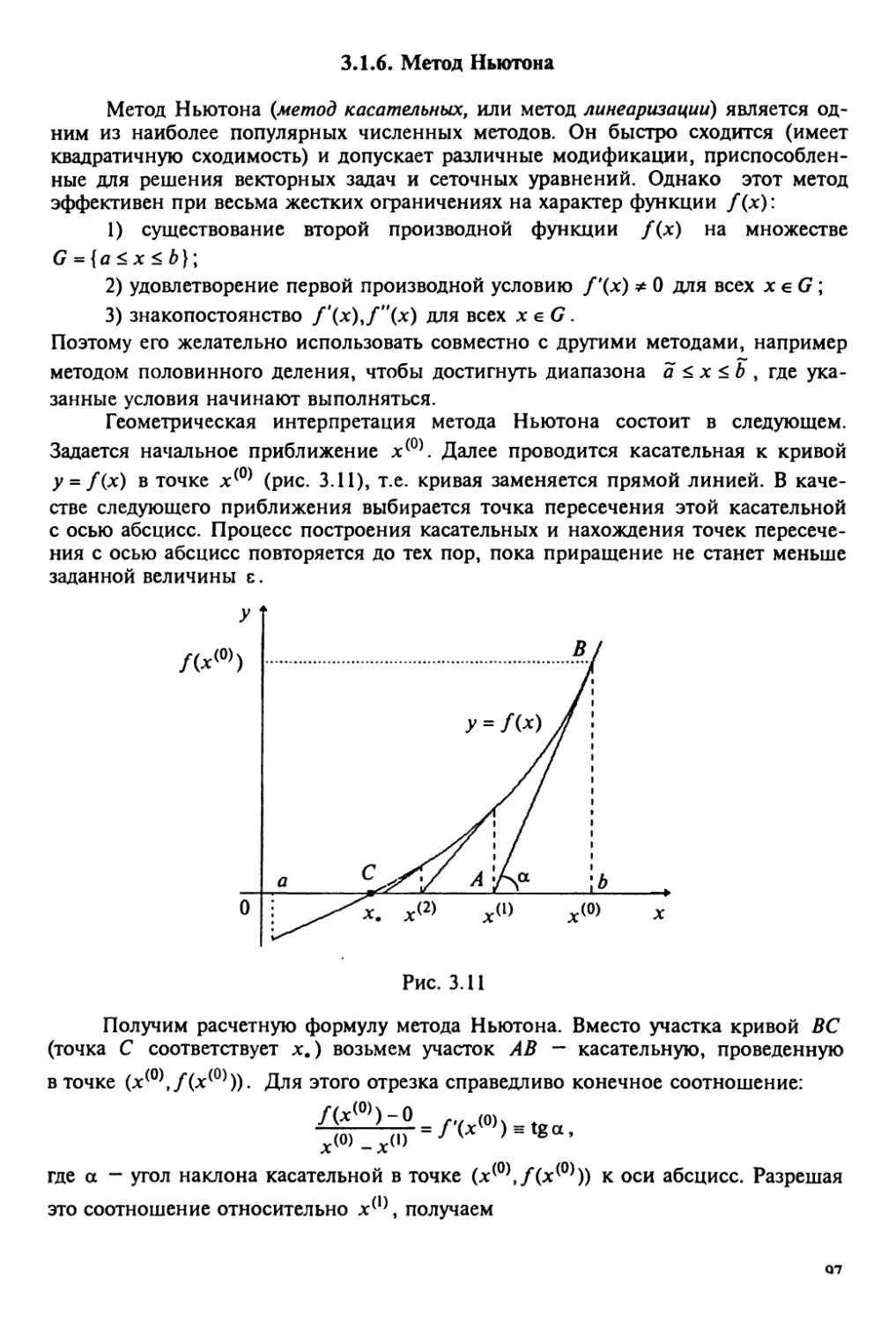
3.1.6. Метод Ньютона 97
3.1.7. Модификации метода Ньютона 104
3.2. Методы решения систем нелинейных уравнений 109
3.2.1. Постановка задачи ... 109
3.2.2. Метод простых итераций 110
3.2.3. Метод Зейделя 113
3.2.4. Метод Ньютона 115
3.2.5. Модификации метода Ньютона 121
3

Часть П. ЧИСЛЕННЫЕ МЕТОДЫ ТЕОРИИ ПРИБЛИЖЕНИЙ 126
Глава 4. Методы приближения сеточных функций 126
4.1. Общая постановка задачи и классификация методов 126
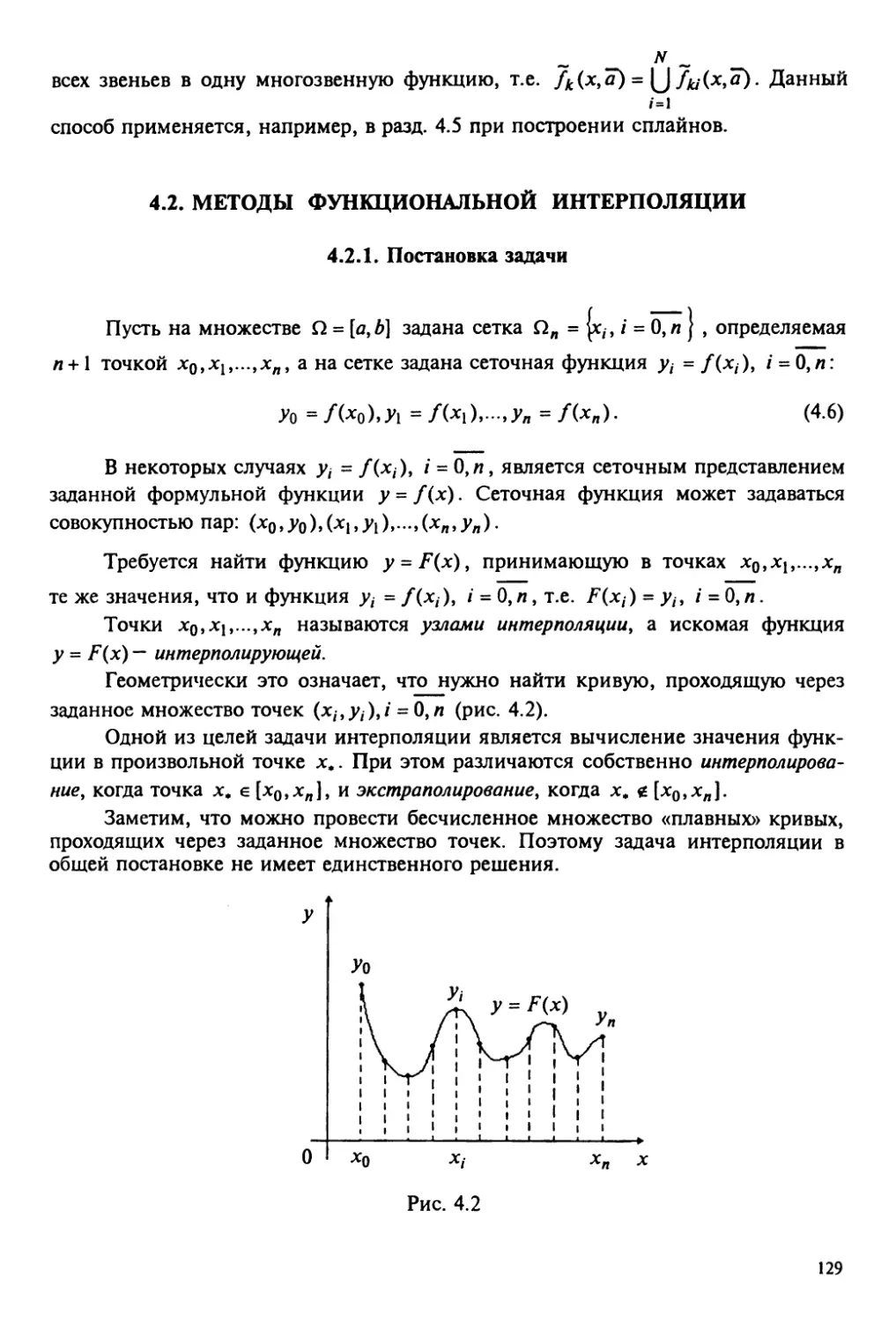
4.2. Методы функциональной интерполяции 129
4.2.1. Постановка задачи 129
4.2.2. Многочлен Лагранжа 132
4.2.3. Многочлены Ньютона 143
4.3. Методы интегрально-дифференциальной интерполяции 154
4.3.1. Постановка задачи 154
4.3.2. Интерполяционный параболический интегрально-
функциональный многочлен 155
4.3.3. Интерполяционный параболический интегрально-
дифференциальный многочлен 159
4.4. Методы интегрального сглаживания 161
4.4.1. Постановка задачи 161
4.4.2. Метод наименьших квадратов 163
4.4.3. Метод наилучшего интегрального приближения 177
4.5. Методы интерполяции и сглаживания на основе сплайнов 183
4.5.1. Постановка задачи и основные положения 183
4.5.2. Интерполяционные дифференциальные
кубические сплайны 188
4.5.3. Интерполяционные дифференциальные
параболические сплайны 196
4.5.4. Восстанавливающие, интерполяционные
и сглаживающие интегрально-дифференциальные
параболические сплайны 202
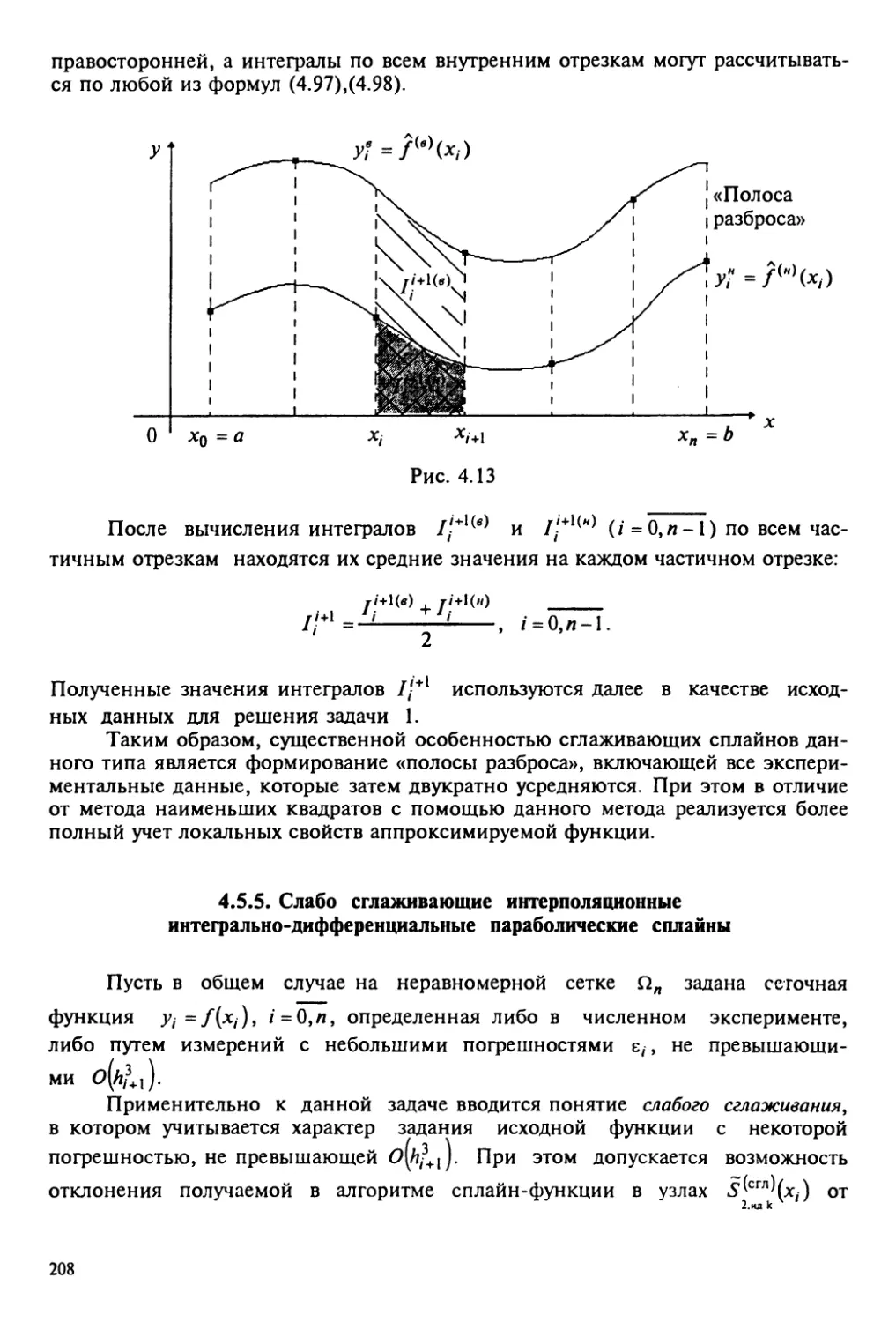
4.5.5. Слабо сглаживающие интерполяционные
интегрально-дифференциальные параболические сплайны... 208
Глава 5. Методы численного дифференцирования и интегрирования 215
5.1. Постановка задачи и принципы конструирования
аппроксимационных формул 215
5.2. Методы численного дифференцирования 218
5.2.1. Формулы, полученные на основе разложения функций
по формуле Тейлора 218
5.2.2. Формулы, полученные на основе разложения первообразных
по формуле Тейлора 232
5.2.3. Формулы, полученные на основе сплайнов 237
4

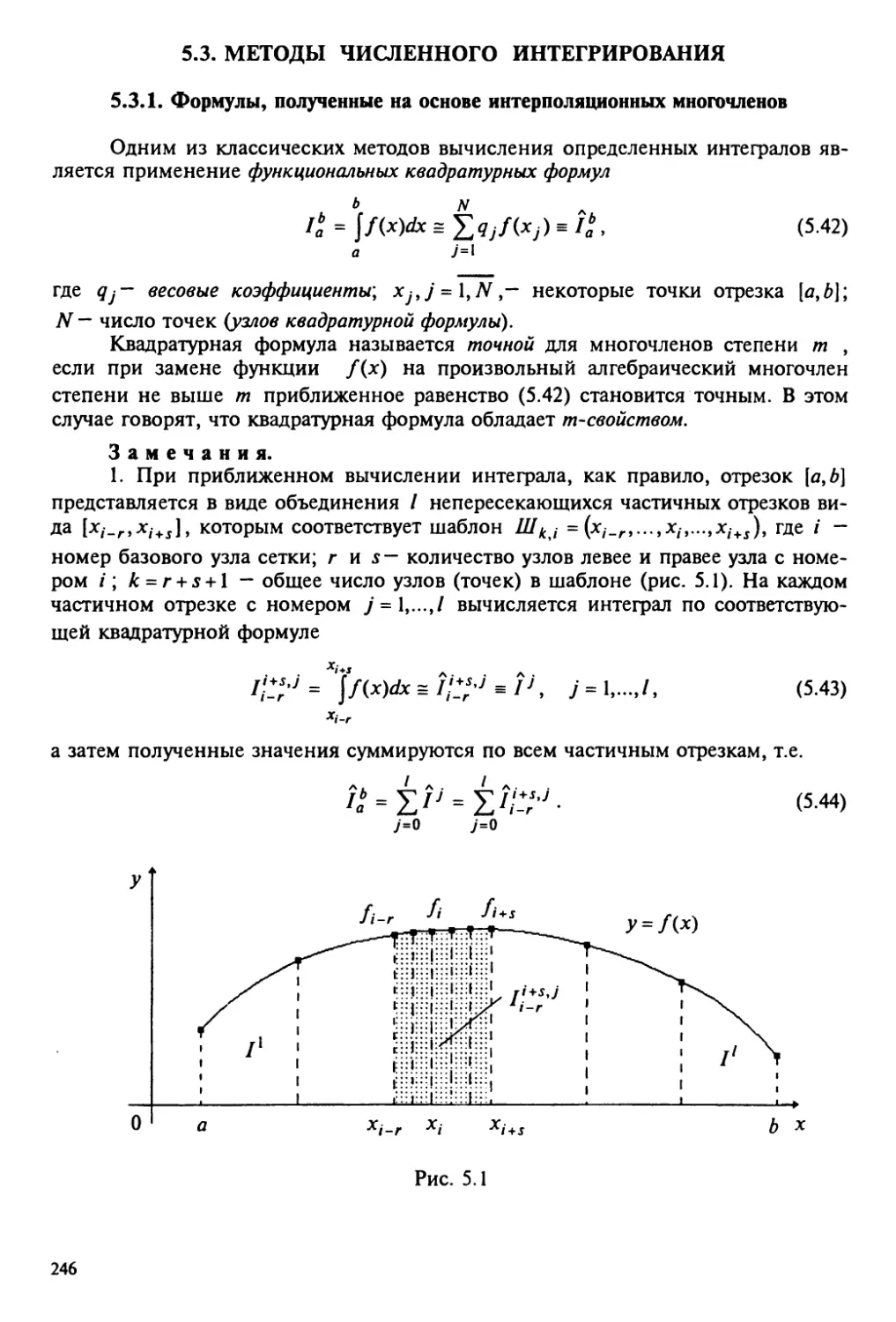
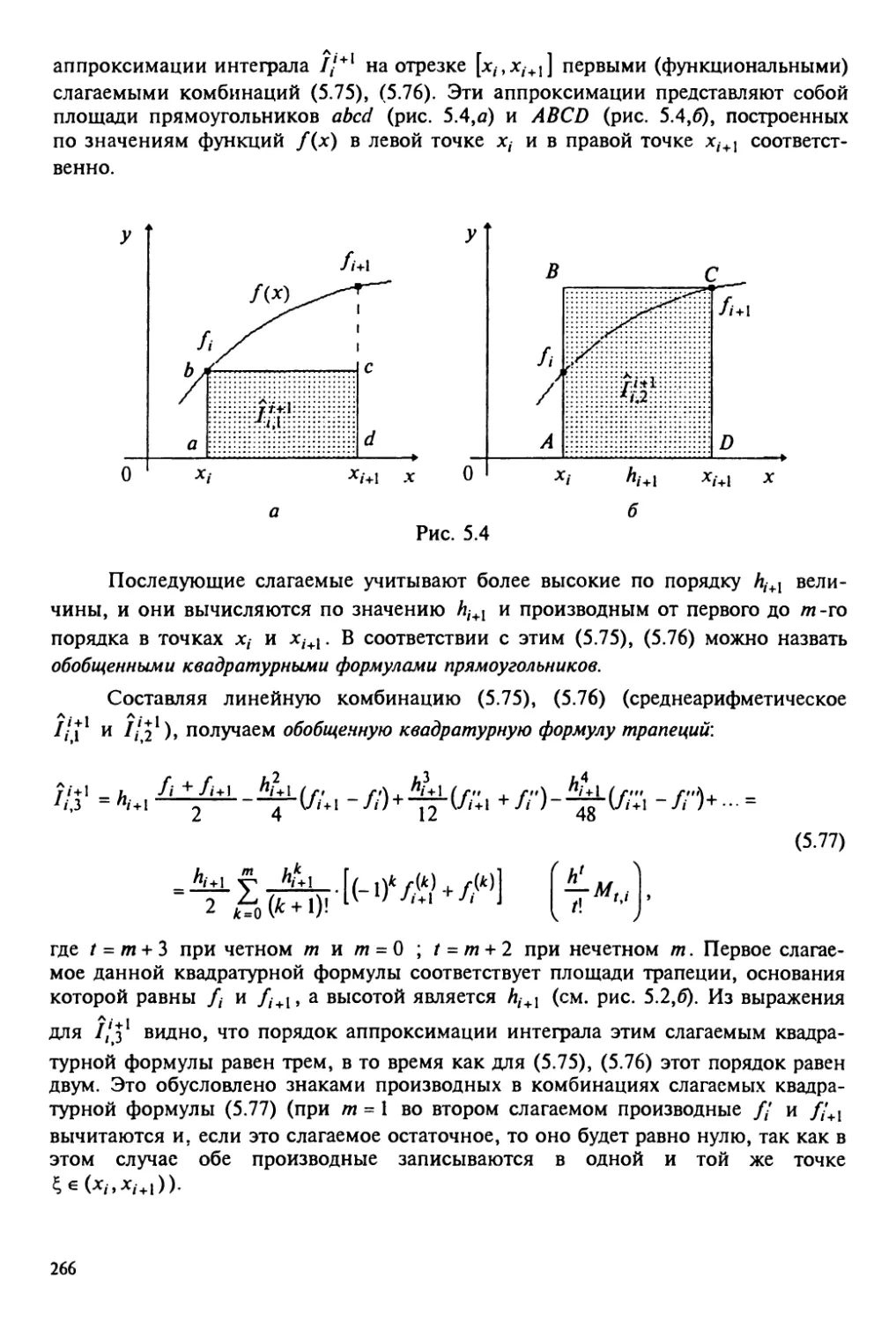
5.3. Методы численного интегрирования 246
5.3.1. Формулы, полученные на основе интерполяционных
многочленов 246
5.3.2. Формулы, полученные на основе сплайнов 257
5.3.3. Формулы, полученные на основе разложения первообразных
по формуле Тейлора 265
5.4. Метод Рунге уточнения результатов численного
дифференцирования и интегрирования 268
Часть III. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 272
Глава 6. Методы решения задачи Коши 272
6.1. Постановка задачи и основные положения 272
6.2. Принципы построения разностных схем 282
6.2.1. Принцип аппроксимаций 282
6.2.2. Интегрально-интерполяционный принцип 289
6.2.3. Принцип согласования с разложением по формуле Тейлора.. 300
6.2.4. Принцип аналогий 308
6.3. Составные схемы 313
6.4. Экстраполяционные методы 320
6.5. Непрерывно-дискретные методы 328
6.5.1. Конструирование последовательных сплайн-методов 328
6.5.2. Схема второго порядка 329
6.5.3. Схема третьего порядка 331
Глава 7. Методы решения краевых задач 337
7.1. Постановка задачи и основные положения 337
7.2. Метод сеток 340
7.3. Методы минимизации невязки 346
7.4. Методы сведения краевой задачи к задаче Коши 354
7.4.1. Метод стрельбы 354
7.4.2. Метод дифференциальной прогонки 359
7.5. Метод конечных элементов 361
5

Часть IV. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ 372
Глава 8. Численные методы решения уравнений математической физики
с двумя независимыми переменными 372
8.1. Постановка задачи и основные положения 372
8.2. Принципы построения разностных схем 383
8.3. Разностные схемы решения уравнений первого порядка 391
8.4. Разностные схемы решения уравнений второго порядка 397
8.4.1. Разностные схемы решения дифференциальных уравнений
параболического типа 397
8.4.2. Разностные схемы решения дифференциальных уравнений
гиперболического типа 405
8.4.3. Разностные схемы решения дифференциальных уравнений
эллиптического типа 411
8.5. Метод прямых 416
8.6. Метод характеристик 420
8.7. Метод Годунова 434
Глава 9. Численные методы решения уравнений математической физики
с тремя независимыми переменными 447
9.1. Постановка задачи и основные положения 447
9.2. Разностный метод 452
9.3. Метод расщепления 459
9.4. Метод переменных направлений 465
9.5. Метод дробных шагов 471
Литература 477

ВВЕДЕНИЕ
В.1. Понятие о численных методах
Проектирование и отработка современных летательных аппаратов, их
отдельных узлов и блоков, а также других технических систем связаны с
теоретическими расчетами и исследованиями, предваряющими выбор определяющих
параметров конструкций. Эти расчеты проводятся с использованием
вычислительных средств (компьютеров и их систем) и вычислительных методов. При
этом обычно выполняются следующие этапы.
1. Физическая постановка задачи. Результатом этого этапа является общая
формулировка задачи в содержательных терминах, т.е. что дано и что требуется
определить. Например, рассчитать траекторию полета ракеты при заданных тяге
двигателей, массе ракеты, ее аэродинамических характеристиках, при
определенных метеоусловиях и др. Как правило, этот этап выполняется специалистом в
конкретной предметной области.
2. Поиск, выбор или модификация некоторой математической модели,
адекватной физической постановке задачи. На этом этапе осуществляются:
— выделение (запись) основных математических уравнений, соотношений,
аппроксимационных формул, описывающих задачу;
— выделение (запись) дополнительных математических уравнений, связей,
граничных или краевых условий;
— предварительное (априорное) обоснование математической модели.
Этот этап является очень важным, так как ошибочная или неудачная
модель, неадекватная физической, сводит «на нет» все дальнейшие усилия по
проектированию изделия. Заметим, что при решении многих задач выбираются, как
правило, общепринятые математические модели.
3. Разработка, выбор или модификация математического (аналитического,
приближенно-аналитического или численного) метода, наиболее целесообразного и
экономичного. Этот этап осуществляется на основе имеющихся у исследователей
знаний (субъективный подход), а также исходя из ресурсов компьютера —
оперативной и внешней памяти, быстродействия, возможностей представления
информации (объективный подход).
4. Составление алгоритма.
5. Разработка программного обеспечения.
6. Решение задачи: апостериорное обоснование модели и метода путем их
методических и параметрических компьютерных исследований в привязке к
реальному объекту. Этот этап включает выдачу рекомендаций и характеристик
объекта в проектно-конструкторские подразделения.
В результате анализа полученного решения задачи может осуществляться
переход к любому из описанных этапов для внесения соответствующих
изменений. Изложенные этапы исследования прикладных задач схематически показаны
на рис. В.1.
Рассмотрим пример простейшей физической и математической моделей.
При заданном количестве микробов или концентрации некоторого вещества у0
7

в начальный момент времени t = t0 получить зависимость, описывающую их
дальнейшее изменение во времени. При t > t0 данная физическая модель
описывается обыкновенным дифференциальным уравнением и начальным условием:
^7-У = 0, (В.1)
at
y(h) = yQ.
(В.2)
Таким образом, уравнение (В.1) и дополнительное (начальное) условие
(В.2) составляют математическую модель (дифференциальную, так как ей
соответствует дифференциальное уравнение). Сопоставление решения задачи
(В.1),(В.2) с результатами эксперимента подтверждает адекватность физической и
математической моделей.
Физическая постановка задачи
>
f
Поиск, выбор или
модификация математической модели
>
!
Разработка, выбор или
модификация математического
метода
^
t
Составление алгоритма
ч
f
Разработка программного
обеспечения
у
f
Решение задачи и анализ |
резул!
>татов 1
Рис. В.1
Другими классическими примерами простых математических моделей
являются: определенный интеграл для нахождения площадей, объемов, длин
кривых, центра тяжести тела и др.; система уравнений движения центра масс лета-
8

тельного аппарата с начальными условиями, заданными на старте; уравнение
теплообмена, например, для изучения процесса охлаждения или нагрева тела при
подводе, отводе тепла.
Классическим средством изучения математических моделей и исследований
на их основе свойств реальных объектов являются аналитические методы,
позволяющие получать точные решения в виде математических формул. Эти методы
дают наиболее полную информацию о решении задачи, и они до настоящего
времени не утратили своего значения. Однако, к сожалению, класс задач, для
которого они могут использоваться, весьма ограничен. Поэтому решение
широкого класса задач при отработке современных технических систем, как правило,
осуществляется численными методами.
Численные методы — это методы приближенного решения задач
прикладной математики, основанные на реализации алгоритмов, соответствующих
математическим моделям. Наука, изучающая численные методы, называется также
численным анализом, или вычислительной математикой.
Численные методы, в отличие от аналитических, дают не общие, а частные
решения, которые определяются не в континуальных (Q),а в дискретных
областях изменения независимых переменных (ПЛ). При этом требуется выполнить
достаточное количество арифметических и логических действий над числовыми
и логическими массивами. В силу приближенного характера вычислений этот
процесс в свою очередь связан с некоторыми основными требованиями или
понятиями, относящимися к конкретным задачам и численным методам (схемам),
— устойчивостью, зависящей от хорошей обусловленности задачи; сходимостью,
высокой точностью, экономичностью, и параметрами методов — шагами
дискретизации /iq или разбиения исходной области Q, в которой решается задача,
количеством итераций (для итерационных методов), соотношениями шагов для
неравномерного разбиения и др.
Некоторые из перечисленных здесь требований являются
противоречивыми, поэтому при выполнении исследований чем-то приходится жертвовать,
например, точностью или экономичностью метода. Часть из указанных понятий
(сходимость, устойчивость, хорошая обусловленность) рассматриваются и
наполняются конкретным содержанием при рассмотрении задач, которые решаются в
основных разделах книги, поэтому дадим только их краткие определения.
Численный метод называется сходящимся, если при стремлении параметров
метода к определенным предельным значениям (например, шагов сетки Hq
к нулю (при Aq->0)) результаты расчета стремятся к точному решению,
т.е.
Лп->0 I
(у и у — приближенное и точное решения соответственно).
Задача является хорошо обусловленной, если при небольших изменениях
входных данных результаты ее решения изменяются незначительно (непрерывная
зависимость решения от исходных данных) и при любых исходных данных из
возможного диапазона их изменения задача однозначно разрешима.
Рассмотрим пример плохо обусловленной задачи.
Пример В.1. Пусть задана система двух линейных алгебраических
уравнений с двумя неизвестными:
300*! + 400х2 = 700,
100*! +133х2 =233. ( "3)
Выяснить, является ли эта задача хорошо обусловленной.
9

□ Система (В.З) имеет точное решение хт = (x^yx#2)T =(1;1)г. Пусть одно
из исходных данных - число Ь - 233 изменилось на доли процента и вместо
него приняли число Ь = 232. Тогда получается решение х0{ = -3; jc#2 =4. Таким
образом, при изменении b на 0,43 % 100% = 100% = 0,43% компонен-
У F \2ЪЪ 233 J
ты решения х.Хухт1 изменились соответственно в 3 и 4 раза. Таким образом,
в соответствии с определением обусловленности задача (В.З) является плохо
обусловленной, так как при небольшом изменении входных данных результаты
ее решения изменились значительно. ■
Численный метод называется устойчивым, если результаты расчета
непрерывно зависят от входных (исходных) данных задачи (т. е. выполняется условие
хорошей обусловленности задачи) и погрешность округления, связанная с
реализацией численного метода, при заданных пределах изменения параметров
численного метода остается ограниченной.
Решения, получаемые численными методами, в силу их приближенности
содержат некоторые погрешности. Рассмотрим их источники и типы.
В.2. Погрешности вычислений
Один из типов погрешностей обусловлен неадекватностью выбранной
математической модели исходной физической. Эта неадекватность в большей или
меньшей степени присуща всем приближенно решаемым задачам. Данная
погрешность является неустранимой, и она определяется апостериорным путем (на
шестом этапе решения задачи (см. рис. В.1)). Остальные три типа погрешностей
являются сугубо вычислительными и обусловлены следующими причинами.
Неточность (неопределенность) задания исходных данных приводит также
к неустранимым погрешностям, связанным с точностью измерений или
вычислений, или округлением данных.
Если мы устраним неопределенность в исходных данных, например, путем
их фиксирования, и найдем решение с помощью какого-либо численного
метода, то получим результат, не в точности соответствующий исходным данным. Это
есть погрешность численного или какого-либо другого приближенного метода
(например, приближенно-аналитического); именно такие погрешности будут
оцениваться при рассмотрении численных методов. Эти оценки могут получаться
до выполнения вычислений (априорные оценки) и после них (апостериорные
оценки).
В компьютере все числа представляются в конечном виде, и поэтому при
использовании вычислительного алгоритма реализуются ошибки арифметических
и других операций над числами, а также ошибки округления.
Дадим некоторые понятия из теории погрешностей вычислительных
действий над приближенными величинами.
Пусть х — точное, но, как правило, неизвестное значение величины, а х
— ее известное приближенное значение.
Абсолютной погрешностью приближения х называется разность
Ах = \х-х\ (в общем случае Ах имеет размерность величины х).
Ю

Относительная погрешность приближения х обозначается 5 и выражается
Ах
отношением 6=-j—г (5— безразмерная величина,х * 0). Часто величина 5 вы-
и
числяется в процентах, и тогда она умножается на сто.
Так как величина х, как правило, неизвестна, а погрешность необходимо
определять, то в рассмотрение вводится предельная абсолютная погрешность Д(х):
Ах = he - х < Д(х).
Раскрывая в этом неравенстве модуль, получаем соотношение, задающее
отрезок, которому принадлежит точное значение: х - Д(х) < х < х + Д(х).
Таким образом, величина х находится в А-окрестности (дельта-
окрестности), определяемой величинами х и Д(х) и составляющей отрезок
[а,Ь] (рис. В.2).
а = х - Д(х) £ Ь = х + А(х)
—I , ^_
А(х) A(Jc)
Рис. В.2
Предельная относительная погрешность приближения х определяется
отношением 6(х) = . . . Отсюда получается часто используемое соотношение
н
А(х) = 5(х).|х|. (В.4)
В дальнейшем рассматриваются только предельные погрешности, и
поэтому в тексте при указании на абсолютную и относительную погрешности для
сокращения слово «предельная» будет опускаться.
Значащими цифрами приближенного числа называют все цифры в его
записи, начиная с первой ненулевой слева.
Первые п значащих цифр приближенного числа называются верными, если
абсолютная погрешность этого числа не превышает половины единицы разряда,
соответствующего л-й значащей цифре, считая слева направо. Излишние
сохраненные цифры, помимо верных, называются сомнительными.
Вычислить приближенное число с точностью е = 10"" означает, что
необходимо сохранить верной значащую цифру, стоящую в /i-м разряде после
запятой.
На практике возникает надобность в округлении приближенного числа, т.е.
замене его числом с меньшим количеством значащих цифр.
Для округления числа до п значащих цифр следует отбросить все его
цифры, стоящие справа от л-й значащей цифры. При этом:
11

а) если первая из отброшенных цифр меньше 5 , то оставшиеся десятичные
знаки сохраняются без изменения;
б) если первая из отброшенных цифр больше 5 либо равна 5 и среди
остальных отброшенных цифр есть ненулевые, то к последней оставшейся цифре
прибавляется единица;
в) если первая из отброшенных цифр равна 5 и остальные отброшенные
цифры нулевые, то последняя оставшаяся цифра не изменяется, если она четная,
и увеличивается на единицу, если она нечетная.
Пример В.2. Найти абсолютные и относительные погрешности числа
я = 3,141592654..., заданного двумя и тремя цифрами после запятой.
□ 1. Пусть х = 3,14. Тогда справедливо
|тг - 3,14| < 0,002 = Д(3,14); 5(3,14) = (0,002 / 3,14) -100% « 0,064%.
2. Если х = 3,141, то
|я - 3,141| < 0,0006 = Д(3,141); 5(3,141) = (0,0006/3,141) • 100% * 0,02%. ■
Абсолютная и относительная погрешности записываются в виде чисел
с одной или двумя значащими цифрами, и они округляются с избытком. В
записи приближенных чисел они указываются так:
х = х±Д; jc=jc(1±5). (В.5)
Например, тг = 3,141 ±0,0006; п = 3,141(1 ±0,02%).
Если Д в записи числа не указано, то подразумевается, что х имеет
точность половины единицы ( 1/2 ед.) младшего разряда. Так, для х = 5,63
абсолютная погрешность Д = 0,005.
Пример В.З. Округлить число х = 3,928525750 до семи, шести, пяти и т.д.
десятичных знаков и до единиц.
□ Пользуясь правилом округления (см.пп."а"-"в"), получаем х = 3,9285258
(согласно п."в", так как первая из отброшенных цифр равна 5 , остальные
отброшенные цифры нулевые, последняя оставшаяся цифра нечетная);
х = 3,928526 (согласно п."б",так как первая из отброшенных цифр больше 5);
х = 3,92853 (согласно п."б", так как первая из отброшенных цифр равна 5 и
среди отброшенных цифр есть ненулевые); х = 3,9285 (см. п."а"); х = 3,929 (см. п."б");
х = 3,93 (см. п."б"); х = 3,9 (см. п."а"); х = 4 (см. п."б"). ■
Пример В.4. Выделить значащие цифры следующих чисел:
2,396037; 0,00167; 3250000; 0,00005.
□ Поскольку значащими являются все цифры в записи числа, начиная
с первой ненулевой слева, то получаем:
2.396037: 000167: 3250000: 0,00005. ■
12

Пример В.5. Выделить верные значащие цифры чисел:
а) х = 0,004507; А = 0,00001 ; б) х = 0,004507; Д = 0,00006;
в) х = 0,0208700; А = 0,0000005; г) х = 12,396; А = 0,03;
д) х = 0,037862; А = 0,007; е) х = 9,999785; А = 0,0004.
D В записи рассматриваемых чисел подчеркнем верные значащие цифры:
а) 0,004507 ± 0,00001, так как А = 0,00001 < 0,5 • 10"4;
б) 0,004507 ± 0,00006, так как 0,5 • 10~4 < А = 0,00006 < 0,5 • Ю-3;
в) 0,0208700 ± 0,0000005, поскольку А = 0,0000005 = 0,5 • 10"6 ;
г) Ш96 ± 0,03, так как А = 0,03 < 0,5 • Ю-1;
д) 0,037862 ± 0,007, поскольку 0,5- Ю-2 < А = 0,007 < 0,5- Ю-1 (все цифры
сомнительные);
е) 9,999785 ± 0,0004, так как А = 0,0004 < 0,5 • 10'3 .■
Погрешности округления в ЭВМ числа х, обусловленные конечностью
разрядной сетки, для различных компьютеров могут быть вычислены по формуле
5(х)= — р-1 , (В.6)
где ат — первая значащая (отличная от нуля) цифра; s — основание системы
счисления, использующееся в компьютере; п — разрядность компьютера (л =32
при стандартной точности и п =64 при двойной — для ЭВМ типа IBM).
Рассмотрим правило вычисления погрешностей арифметических операций
и функций по погрешности аргументов (без учета ошибок округления).
При вычислении абсолютных погрешностей обычно используются
формулы дифференцирования, в которых дифференциалы независимых переменных
заменяются абсолютными погрешностями (dxf = Ах,).
Пусть х{ > 0, х2 > 0 и заданы предельные абсолютные погрешности
А(х{), А(х2), т.е. хх = хх ± А(х,), х2 = х2 ± А(х2). Требуется найти погрешность
СУММЫ X = JCj + х2.
Так как dx = dxx + dx2, то Ах = Ахх + Ах2 < А(х{) + А(х2). Отсюда следует,
что
А(х1+х2) = А(х1) + А(х2). (В.7)
Теперь предположим, что х{ > х2, и найдем погрешность разности
х = Х\| -х2. Тогда dx = dxx-dx2w Ax = Ajc,-Ajc2< А(х,) + А(х2), поэтому
А(хх-х2) = А{хх) + А(х2). (В.8)
Таким образом, абсолютная погрешность суммы и разности двух
приближенных чисел равна сумме абсолютных погрешностей слагаемых.
13

Это правило справедливо для произвольного числа слагаемых. Так, если
хих2,...>х„ имеют одну и ту же погрешность Д(х), то
А(х! + х2 +... + хп) = п • Д(х). Но реально погрешности могут иметь разные знаки
и потому взаимно компенсировать друг друга. По правилу Чеботарева при п >10
можно принять
А(Х] + х2 + ... + хл) = уЗл Д(х).
Для относительной погрешности суммы и разности двух чисел хх ± х2
получаем
с./- + а ч_А(Х| ±х2)_ А(Х!) + А(х2)_ ACxi)^ А(х2)х2
^ 1 ~~ 2/ /А.Л\ /А , А \ /Л1А\А/А.Л\А
(Х!±Х2) (Х,±Х2) (X|±JC2)-JC, (X, ±х2)х2
(х,±х2) (Xi ±х2)
Для произвольного числа слагаемых
5(x)=4s(x1) + ^S(x2)+... + ^-5(x/l), (В.9)
XX X
где х = Xj + х2+...+хЛ; х,- >0, / = 1,...,л.
Пусть max 6(х,) = Л/, min 5(х,) = /я, тогда
Л Xj-Л/ч-...+хп Л/ А х, -т+...+хя т
б(х) <-i -—2 = Л/, 6(х) >-* -—2 = т.
X X
Поэтому
т<Ъ(х)<М. (В. 10)
Аналогично при выполнении умножения и деления получаем погрешности
(при тех же предположениях):
Д(-*1 *2) = A*i х2+Дх2х1 <х1А(х2) + х2А(х1), (В.11)
Stfi • *2> = A(f' "*2> = 5(^1) + «&>, (В. 12)
*1*2
/ А
А
Л\ Л Л. Л Л Л Д/Ач А л/А\
*l А*1 х2 -Ах2 Х| ^ X! •А(х2) + х2А(х1)
i v i А 2 ~ А 2
{Х2) х2 Х2
(В.13)
8||Ч = в<*1> + а<х2). (В.14)
14

Из последних соотношений следует, что относительная погрешность
произведения двух чисел равна сумме относительных погрешностей его сомножителей.
Аналогичное правило выполняется и для частного от деления двух чисел.
Замечание. При вычитании близких чисел на ЭВМ происходит
потеря верных значащих цифр, поскольку разность xj - х2 близка к нулю и,
следовательно, относительная погрешность разности значительно больше относительной
погрешности уменьшаемого и вычитаемого.
Пример В.6. Требуется вычислить разность у = хх -х2 двух близких чисел
хх =0,01234 и х2 =0,01231, для которых Д(х) = 0,000002 (подчеркнуты верные
значащие цифры).
□ Величина у = хх - х2 = 0,00003 имеет только одну значащую цифру, так
как Ь(у) = 0,000004 < 0,5 • 10"5 (А(у) = Л(Х]) + Д(х2)) (абсолютная погрешность
результата удвоилась). Таким образом, произошла потеря трех верных значащих
цифр. Это следует учитывать при составлении алгоритма, по возможности
избегая потери точности с помощью алгебраических преобразований формулы и
изменения в ней последовательности вычислений. ■
Аналогично получаются формулы для погрешностей арифметических
действий при вычислении функций многих переменных. Так, для z = /(х1,х2,...,хЛ)
имеем следующие формулы для погрешностей:
А(£) =
дХ|
•Д(х,) +
дх2
Д(х2) + ...+
д/
дх„
Л(*„),
«(£) =
/ ас,
8(х,) +
к Ж.
f дх2
8(х2) + .
к Ж.
f дх„
6(х„)= (В. 15)
х1
dlnf
дх,
•5(х,) +
*2
д\п/
дх->
■5(х2) + ...+
ain/
дх„
5(хя).
Пример В.7. Стороны треугольника а = 17,3 см, b =23,6 см, с = 14,2 см
замерены с абсолютной погрешностью Д(д) = А(Ь) = А(с) =0,1 см. Определить
абсолютную погрешность периметра р = a + b + с этого треугольника.
D Получаем р = 17,3 + 23,6 + 14,2 = 55,1см; А(р) = 3 0,1 = 0,3см. Таким
образом, р = 55,1 ± 0,3 см (последняя цифра в числе /? = 55,1 сомнительная, так как
Л = 0,3 < 0,5 10°). ■
Пример В.8. Найти относительные погрешности измерения сторон
треугольника в примере В.7 и пределы относительной погрешности для периметра.
□ Вычислим относительные погрешности: 8(a) = —^-. 100% = 0,
1 /,j
№ = ^-100% = 0,42% = m;
23,6
5(c) =-21.100% = 0,70% = Л/.
14,2
15

Пределы изменения относительной погрешности найдем по формуле (В. 10):
0,42% < 6(р) < 0,70% . ■
Пример В.9. Ребра прямоугольного параллелепипеда а = 4,3 см, Ь=1,6 см,
А Л А Л
с = 2,8см замерены с абсолютной погрешностью А(а) = А(Ь) = &(с) =0,1 см.
Определить абсолютную и относительную погрешности его объема V = abc.
□ Воспользуемся обобщением соотношения (В. 12):
* Л л Л л 010101
V = a b • с = 19,264; Ь(У) = 5(19,264) = -^ + ^1 + ^ = 0,121.
4,3 1,6 2,8
По формуле (В.4) имеем Д(К) = V- d(V) = 19,264x0,121 «2,330. Так как в
А . А
А(К) = 2,330 < 0,5 • 10 , то в V = 19,264 верна лишь цифра десятков, а остальные
А
цифры сомнительные. Округляя V, оставим две сомнительные цифры:
V «19,3 см3. ■
Замечания.
1. В арифметике целых чисел на ЭВМ операции сложения, вычитания и
умножения выполняются точно. Деление целых чисел осуществляется с
округлением — заменой частного его целой частью. Если в вычислениях присутствует
большое число операций деления, то в целочисленной арифметике это может
привести к большой погрешности из-за ошибок округления.
2. В арифметике вещественных чисел на ЭВМ все четыре действия, как
правило, выполняются с округлением. Исключение составляют действия над
числами, которые не выходят за разрядность ЭВМ.
3. Оценка погрешностей округлений при решении многих задач на ЭВМ
может быть найдена апостериорным путем с помощью двух повторных расчетов
в арифметике одинарной и двойной точности и составления разности
полученных результатов. Этот прием используется также и для оценки погрешностей
численного метода (модели).
В.З. Некоторые понятия математического анализа,
использующиеся в численных методах
Для получения оценок погрешностей аппроксимационных формул в книге
используются понятия «О большое от А*» (Л — шаг сетки), класс функций
С*[д,£] , разложение функции по формуле Тейлора, теорема о среднем значении.
Рассмотрим эти понятия.
1. Пусть R(h) — некоторая функция переменной h (как правило, R(h) -
остаточное слагаемое некоторой аппроксимационной формулы) с конечной
областью определения DR на полуоси h > 0, причем he DR.
Тогда, если при некотором h < h$ справедливо неравенство \R(h)\ < chk, где
с = const, не зависящая от h, к — целое число, Aq > 0, то пишут R(h) = 0(hk) и
говорят, что R(h) есть «О большое от hk» при И -* 0.
16

В этом случае значение к соответствует порядку аппроксимации аппрок-
симационной формулы (оператора).
Согласно приведенному определению справедливы свойства:
а) если Rl(h) = 0(hk), R2(h) = 0(hk)9 причем DR[=DR2, то
R{(h) ± R2(h) = 0(hk), поскольку справедливо \R{(h) ± R2(h) \ < \R{(h) \ + \R2(h) |, т.е.
0(hk)±0(hk) = 0(hkyt
б)М = адИ) ; Rl(h)hP =0(hk + <>)',
hp
в) если а- произвольная константа, не зависящая от Л, то u.R\(h) = 0(hk)\
г) если Rx(И) = 0(hk*), R2(h) = 0(Л*2), то произведение
R{ (Л) • R2 (h) = 0(hk>+к>), а сумма ^ (Л) + R2 (А) = 0(А*3), где къ = min(A:1, к2).
2. Пусть функция /(х) определена на отрезке [д, ф(?и имеет на нем
непрерывные производные до порядка к включительно. Тогда считается, что f(x)
принадлежит классу Q[<y], и для обозначения этого используется запись
feCk[G]. При к = 0 вместо C0[G] будет использоваться обозначение C[G]
(функция непрерывна на отрезке [a,b]).
Запись / еСк [G] означает, что на некотором интервале G = (А, В),
который включает в себя [a,b], существует к раз непрерывно дифференцируемая
функция, такая, что f(x) = f(x) на G = [a,b]. Тогда значения производных
от/(х) на концах [ayb] будут соответствовать производным функции f(x) в этих
точках (данное обобщение приведено в связи с тем, что в математическом
анализе производные определяются во внутренних точках области определения
функции, от которой вычисляются f^k\x)).
3. Пусть задана функция /(*) е Ск+х\а,Ь]. Тогда в точке х0 е [а,Ь]
справедлива формула Тейлора:
/(*) = /<*b) + /W(*-*o) + ^^
(В.16)
где хе [а,Ь],х * х0; £ — некоторая точка, лежащая строго между точками х и
хо> ^jfc+i(*) = —;—7^~(х-х0)к*1- остаточный член в форме Лагранжа. Индек-
сы, указанные в круглых скобках вверху, здесь и далее означают порядки
производных.
17

Так как по предположению производная /(*+1)(х) непрерывна на отрезке
[а,Ь]9 то она ограничена на этом отрезке, т.е. величина
Mk+l = max /(*+1)(*) < +оо. Поэтому справедлива оценка остаточного члена
К+1(х)|,^.|х-х„Г.
Это неравенство свидетельствует о том, что
|ЛЛ+1(х)| = о(|х-дс0|*+1)=О(АА+1),
где Л = |х-х0|.
Тогда формула (В. 16) может быть записана в виде
к J'-
/W=E7 K*°\x-x0y+O(hk+l). (B.17)
При & = 1 формулу Тейлора можно записать в виде
/(хо+Л) = /(х0) + /'(х0)Л + 0(Л2),
/(*<>-h) = f(x0)-f'(xQ)h + O(h2),
а при к = 2 - в форме
Я*о + Л> = Л*о) + /'(*о) Л + у Г(*о) + ^(Л3),
f(x0-h) = f(x0)-f(x0)h + ^f(x0) + O(h>).
(В.18)
Рассмотрим частный случай формулы (В. 17). Положим дс = х/+1, дс0=дс/,
Л/+1 = х/+1 -X/, где значения xhxi+i задают отрезок [xhxi+l] с: [ауЬ]. Тогда
получаем
/(*/+i) = /(*/) + /'(*/)Л,+1 +^|^ЛД1 +.- + ^^^+1 + 0<tf+Y>- (В.19)
Обозначая /}+1 =/(х/Ч1), /} = /(*,), //^ = /(р)(х;),р = 1,2,..., и учитывая,
что остаточный член в форме Лагранжа имеет вид — ЛД.1 > £ е (*/i*i+i)»
(л + 1).
формулу (В.19) можно записать в форме
18

4. При изложении будет использовано следующее утверждение [6].
Утверждение В.1. Пусть f(x) eC[ayb], ^j e[atb], (/ = 1,я) — произвольные
точки, принадлежащие отрезку [а, Ь]. Тогда существует такая точка £ е [а, Ь],
что
/fti) + .-. + /CU)_/(;)t
п
В.4. Дискретизация и принцип соответствия порядков аппроксимации
дискретных моделей для интегралов, функций и производных
Предметом данной книги является изложение наиболее широко
распространенных математических моделей, увязывающих функции, интегралы,
производные, а также их применение в теории решения обыкновенных
дифференциальных уравнений и уравнений в частных производных. Эта теория тесно
связана с теорией приближения или с заменой непрерывных математических
моделей их дискретными аналогами (дискретизацией задач). Например, для решения
задачи Коши
^ = /(*,>0; У(х0) = Уо, xe[a,b] = Q (В.21)
дифференциальная модель (В.21) (обозначим ее M(Ly,y0 -»>>), где в скобках
слева от стрелки указаны известные данные — дифференциальный оператор Ly
и начальное значение у0, а справа от стрелки - искомая функция) заменяется
дискретной моделью (ДМ) (Lhyty0 ->.?,•), в которой вместо непрерывной
области Q изменения х рассматривается сетка Qn = {х0,х{,...ухп} со значениями
*/+i = xi + fy+i» ' = 0, я -1, hi+{ = xi+l - xi, и с разностным оператором Lhy,
определенным в X/ (узлах сетки).
Данный процесс замены модели M(Ly,y0 -> у) моделью ДМ(Ьну,у0 -> yt),
соответствующей дискретной задаче, называется процессом дискретизации
модели. При этом в книге используются сетки двух типов — равномерные (или
регулярные), если hi+i = const при всех /, и неравномерные (или нерегулярные)
(Л/+1 = var) - в противном случае.
После получения решения дискретной задачи найденные значения yt
могут обрабатываться с помощью других дискретных моделей типа
дифференцирования ДМ1(.р/ -> у-) или интегрирования ДМ2(р,- -> 7/+1). Эти дискретные
модели могут использоваться в составе или независимо от каких-либо более
общих моделей дифференциального типа, на основе которых получаются
решения yt. Подчеркнем, что указанные совокупности операций дифференцирования
и интегрирования выполняются не с помощью классического математического
анализа, приспособленного только к непрерывным функциям, а на основе
аппарата теории приближений сеточных функций, т.е. на дискретных моделях. Класс
этих дискретных моделей (по сравнению с традиционными) расширен за счет
использования теории интегрально-дифференциальных сплайнов (ИД-сплайнов)
в [15-24].
19

Действительно, здесь реализованы модели:
— численного дифференцирования двух типов: ДМ! (j/,//+1-* j/ )
(ft - исходная сеточная функция, р - порядок производных, fW - либо
значение производной, либо ее аппроксимационная формула), flMj (7/+1 -> .// ) ;
— численного интегрирования двух типов: ДМ2 (Л,.// —> //+1)(р = 1,2,3);
ДМ2 (/,->//+1);
— восстановления функций по интегралам и по совокупности интегралов и
производных: ДМ3(//+1 -> /,), ДМ3(//+1,ЛЫ -> /,) и др.
Здесь и далее символом 7/+1 обозначается определенный интеграл
7/+1= //<*)& (у = /<*)),
а символом 7/+1— его приближенное значение, вычисленное, например, по
одной из квадратурных формул (см. главу 5).
Заметим, что часть из указанных моделей может быть использована при
решении какой-либо другой более общей задачи. В этом случае все входящие в
задачу величины определенным образом увязываются между собой в единых
формулах. Кроме того, увязка между функциями, производными и интегралами
существует в вычислительной практике, например, при формулировке задач
обработки данных, аппроксимации результатов экспериментов, анализе силовых и
тепловых характеристик летательных аппаратов и других технических систем.
При решении таких задач необходимо уметь сохранять требуемый порядок
аппроксимации непрерывной модели ее дискретным представлением (о порядке
аппроксимации см. п. В.З введения). Для этого следует увязывать по порядку
аппроксимации все математические объекты, входящие в одну модель, или разные
модели, соединяемые в одну. Данный порядок определяется величинами
Р0)0,Р0)1,Р0>2,... - порядками аппроксимации (точности) исходных данных,
указанных слева от стрелки в приведенных выше обозначениях математических
моделей, и конкретной связью известных и искомых величин, входящих в эту
модель. Для получения Pj - априорно заданной точности результата необходимо,
чтобы Pofl,Poti,Pot2 по величине не были меньше Р{. Без учета этого соответствия
требуемый порядок результата может не достигаться, что приводит к понижению
его точности.
Проблема увязки порядков /Ъ.о^одЛ.г»--- и ^1 Д° настоящего времени
решалась на субъективном (в основном интуитивном) уровне, так как отсутствовал
четкий принцип соответствия между порядками аппроксимации входящих в
различные дискретные модели значений функций, производных, интегралов и
других математических объектов.
Данный принцип следует из представления значения F(xi+l)
первообразной функции F(x) в точке х/+1 на некотором опорном отрезке [*/,х/+1]
относительно ТОЧКИ X/.
20

Действительно, применим формулу Тейлора (В.20) для функции
F(x)eCt+l[e,*]:
F(xul) = F(xi)+F(xi)hul +^рАД, +... + ^РлД, +0(/,*V)-
Так как F(x) первообразная, то справедливы равенства F'(xj) = f(xj),
F"(x, ) = /'(*,), ..., F<*>(x,) = /(*-°(х,). Обозначая FM = F(x/+I),/; = F{x,),
fi = /(*,), fl = /'(*,) = ^"(*,) и т.д., имеем
FM-Fi+hM •/, + ^// + ... + 4|l//*-'> + 0(А*У). (B.22)
Учитывая, что здесь остаточное слагаемое в форме Лагранжа имеет вид
формулу (В.22) можно переписать следующим образом:
Из (В.22) с использованием формулы Ньютона—Лейбница
//+1 = X'\f(x)dx = F(xM)~ F(*i) = ^41 " ^
получается следующее представление интеграла:
О- и*
Л = л/+1 • Л- +-г- Л + -^"ТГ-А + °(Л/Ч1 )•
(В.24)
Формула (В.24), хотя и используется в дальнейшем для построения аппрок-
симационных соотношений для интегралов и производных (см. разд. 5.2.2), здесь
рассматривается только как абстрактная связь между интегралом, функцией и ее
производными различных порядков.
Эта связь фактически фиксирует соответствие порядков аппроксимации
объектов интегрального, функционального и дифференциального типов,
составляющих некоторую, вообще говоря произвольную, модель (аппроксимацию).
Рассмотрим способ использования связи (В.24) для анализа некоторых из
вышеуказанных моделей, например,
ДМ2(./;->//+1). (В.25)
Величины, указываемые в скобках сразу за обозначением модели, будем
называть ее параметрами (в данном случае параметрами аппроксимации).
Включаемый в число параметров моделей интеграл является одноинтервальным, т.е.
он определяется на одном отрезке, однако, его аппроксимация может строиться
не на одном отрезке [х/,х/+1], а на некотором шаблоне или опорном отрезке,
который может включать большее число узлов сетки.
21

л . . л
В модели (В.25) интегралы //+| определяются по значениям функции /)•,
которые измерены или вычислены с некоторой погрешностью. Пусть эта
погрешность составляет величину 0(И?+1)и при вычислении интегралов на каждом
из отрезков [х,,;с/+1] указанную точность необходимо сохранить. Иными слова-
ми, нам требуется найти порядок аппроксимации интеграла // , который
соответствовал бы порядку точности заданной функции, по которой вычисляется
интеграл. С этой целью из (В.24) устанавливается связь между двумя включенными
А . . А А . | А
в модель (В.25) объектами //+1 и /): //+l =hu{ft. Учитывая в правой части
Л
этого равенства остаточное слагаемое для значений /), получаем
1Г1 - */+!<// +0№3+i)) = A,+i// +0(А,4+1).
Таким образом, расчет интегралов //+1 на каждом из отрезков [xhxi+{]
с точностью 0(hf+x) соответствует точности 0(h?+l) для ft (или наоборот).
Если же взять модель ДМ 2 (/,//-> //+1), в которой интегралы определя-
А А
ются по fi и f/, то для соблюдения соответствия порядков аппроксимации
1ГХ ,fi>f{ производные должны быть рассчитаны (аппроксимированы) с
точностью не ниже 0(h?+l).
Для модели ДМ3(//+1 ->/}), являющейся обратной по отношению к
модели (В.25), вышеописанное соответствие также справедливо, т.е. при задании ин-
тегралов // с точностью не ниже 0(Л;-+1) модель обеспечивает вычисление
функции с точностью не ниже 0(h?+l).
Аналогичный анализ может быть выполнен и для других моделей, в
частности для моделей, использующих другие сочетания заданных и определяемых
математических объектов.
В общей форме рассмотренный принцип соответствия порядков
аппроксимации интегралов, функций и производных можно сформулировать в виде
утверждения.
Утверждение В.2. Если некоторая аппроксимационная формула или
дискретная математическая модель содержит в качестве исходных и искомых параметров
сеточную функцию /}, ее одну или несколько производных f№, и одноинтервальные
интегралы 1} , имеющие порядки аппроксимации Pf, Pf{p),Pj соответственноf
то эта модель обеспечивает соответствие указанных порядков в случае, если
Р/ > Pf + 1; Р^р) > Pf + р, где р — порядок производной.
Замечания.
1. В данном утверждении порядок Pf принят как бы в качестве базового,
с которым сопоставляются порядки Pfip) и Р;. В качестве базового порядка
может быть принят также и любой другой.
2. Сформулированный принцип соответствия легко распространяется
также на модели, включающие дифференциальные уравнения.
22

Часть I. ЧИСЛЕННЫЕ МЕТОДЫ АЛГЕБРЫ
Глава 1. МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
1.1. ПОСТАНОВКА ЗАДАЧИ
Прикладные задачи, характерные для проектирования современных
объектов новой техники, часто сводятся к многомерным в общем случае нелинейным
уравнениям, которые решаются методом линеаризации, т.е. сведением
нелинейных уравнений к линейным. В общем случае система п уравнений с п
неизвестными записывается в виде
/1(а1,х2,...дся) = 0,
/2(дс1,х2,...дся) = 0,
fn(x{,X2,..JC„) = 0,
где /|,/2г»/л ~* функции п переменных, нелинейные или линейные (х, в
функции fj входят в первых или частично в нулевых степенях).
Здесь рассматривается частный случай задачи (1.1) — линейная
неоднородная задача для систем линейных алгебраических уравнений (СЛАУ), которая
сокращенно записывается в виде
Л
(ап •• аХп\
Ах = Ь или
*1
(1-2)
где А = (а^) € /?лхл- действительная матрица размера (лх л), i,j — переменные,
соответствующие номерам строк и столбцов (целые числа); Ь - (blt...,bn)T е Rn —
вектор-столбец размера (ях1), х = (xj,...,xw)r е Rn— вектор-столбец
неизвестных, Rn— п-мерное евклидово пространство, верхний индекс "Г" здесь и далее
обозначает операцию транспонирования.
Требуется найти решение хт = (хм,...,х,л)г е R" системы (1.2),
подстановка которого в (1.2) приводит к верному равенству Ах„ = Ь.
Замечания.
1. Из линейной алгебры известно, что решение задачи (1.2) существует и
единственно, если детерминант матрицы А отличен от нуля, т.е. det А = \А \ * О
(А - невырожденная матрица, называемая также неособенной).
2. Поставленная задача часто именуется первой задачей линейной алгебры.
Подчеркнем, что в ней входными (исходными) данными являются матрица А и
вектор b, а выходными — вектор х.
3. Задача (1.2) имеет следующие особенности:
а) задача линейная (все переменные х, , входящие в систему, имеют
степени не выше первой) и неоднородная (Ь ф 0);
23

б) количество уравнений равно количеству неизвестных (система
замкнута);
в) количество уравнений для некоторых практических задач велико:
/i>*.103(* = U103).
г) при больших п использовать формулу х = А~ХЬ не рекомендуется
в силу трудностей нахождения обратной матрицы.
4. Важнейшим признаком любой математической задачи, который надо
в первую очередь принимать во внимание при ее анализе и выборе метода
решения, является ее линейность или нелинейность. Это связано с тем, что
нелинейные задачи с вычислительной точки зрения являются наиболее трудными. Так,
нелинейная задача (1.1) является достаточно сложной при числе уравнений л,
пропорциональном 102, а линейная задача - при л, пропорциональном 106.
Характер задачи и точность получаемого решения в большой степени
зависят от ее обусловленности, являющейся важнейшим математическим понятием,
влияющим на выбор метода ее решения. Поясним это понятие на примере
двумерной задачи (см. также пример В.1):
*11*1+*12*2=*1>
а2\*\ +а22*2 =^2-
Точным решением этой задачи является вектор х, =(хф1,х,2)7,
компоненты которого определяются координатами точки пересечения двух прямых,
соответствующих уравнениям апх{ +д12х2 =^1' а2\х\ +а11х2 =^2 (Рис- 1-lffl).
а2\Х\ + 022*2 = h
det^ = 0
Рис. 1.1
На рис. 1.1,5 применительно к трем наборам входных данных, заданных
с некоторыми погрешностями и соответствующих различным системам
линейных уравнений, иллюстрируется характер обусловленности системы. Если det Л
существенно отличен от нуля, то точка пересечения пунктирных прямых,
смещенных относительно сплошных прямых из-за погрешностей задания А и Ь,
сдвигается несильно. Это свидетельствует о хорошей обусловленности системы.
При det А»0 небольшие погрешности в коэффициентах могут привести
к большим погрешностям в решении (плохо обусловленная задача), поскольку
прямые близки к параллельным. При det А = 0 прямые параллельны или они
совпадают, и тогда решение задачи не существует или оно не единственно.
24

Более строго обусловленность задачи характеризуется числом
обусловленности v(A) = \\A\\' /Г1 , где ||л|| - норма матрицы А, а И"1 ~ норма обратной
матрицы. Чем больше это число, тем хуже обусловленность системы (при
у(Л)« 103 -ПО4 система линейных алгебраических уравнений плохо
обусловлена). В качестве нормы матрицы может быть принято число, являющееся
максимальным из сумм (по модулю) элементов всех строк этой матрицы (подробнее
см. в разд. 1.3.1).
Подчеркнем, что реализация хорошей или плохой обусловленности в
корректной и некорректной задачах напрямую связана с вытекающей отсюда
численной устойчивостью или неустойчивостью. При этом для решения
некорректных задач обычно применяются специальные методы или математические
преобразования этих задач к корректным.
В численном анализе используются два класса численных методов решения
систем линейных алгебраических уравнений:
1. Прямые методы, позволяющие найти решение за определенное число
операций. К прямым методам относятся: метод Гаусса и его модификации (в том
числе метод прогонки), метод LU- разложения и др.
2. Итерационные методы, основанные на использовании повторяющегося
(циклического) процесса и позволяющие получить решение в результате
последовательных приближений. Операции, входящие в повторяющийся процесс,
составляют итерацию. К итерационным методам относятся: метод простых
итераций, метод Зейделя и др.
1.2. ПРЯМЫЕ МЕТОДЫ
1.2.1. Метод Гаусса
Метод Гаусса состоит в исключении слагаемых системы путем ее
равносильного преобразования. При этом в численном анализе с целью хорошей
алгоритмизации задачи преобразованию подвергаются не сами уравнения, а
исходные данные - матрица А и вектор Ь , соединенные в одну (расширенную)
матрицу. В этом случае метод разбивается на две совокупности операций, которые
условно названы прямым ходом и обратным ходом.
Методика решения задачи
1. Прямой ход состоит в исключении элементов, расположенных ниже
элементов, соответствующих главной диагонали матрицы А. Схематически прямой
ход представляется в виде
Л, =
апа[2ап...а1п
а2\а22а2У-а2п
\ап\ап2апЪ-апп
Ь2
Г^12с13...с1л ;</, ^
0 1 c23...c2„ i d2
loo 0 1 \dn)
■А,
(1.3)
где А\ — матрица, которая содержит опорные строки (о.с), получающиеся при
выполнении прямого хода, а затем используется в обратном ходе.
25

Особенности прямого хода:
а) матрица А преобразуется к верхнетреугольному виду с единицами на
главной диагонали;
б) получение матрицы Л{ в прямом ходе включает следующие действия:
— деление на ведущие элементы — на ах х в первой строке, на а22 ~ во вто~
рой, на 5зз "~ в третьей и т.д. (при этом полагается, что они отличны от нуля, и
в этом случае рассматриваемый метод Гаусса называется методом единственного
деления в смысле отсутствия перебора ведущих элементов);
— исключение элементов я/у столбцов, лежащих ниже опорных строк мат-
Л
рицы Ах. Для исключения элементов первого столбца используется первая о.с,
для элементов второго столбца — вторая о.с. и т.д. Все остальные действия
поясним на примере.
Л
2. Обратный ход — от Ах переходим к системе, включающей *],...,*„, и,
начиная с последнего уравнения, последовательно определяем хп,хп_х,...,хх:
*п = dn;
хп-\ =^л-1 ~сп-\,п хп>
хх =d{ -сх2х2-...-с{пхп.
Здесь и далее знак "*" у компонент решения системы опущен.
Пример 1.1. Методом Гаусса единственного деления найти решение
системы линейных алгебраических уравнений (л = 3):
5х{ + 0х2 + х3 = * 1»
2х{ + 6х2 - 2х3 = 8,
-Зх! +2х2 + Юдсз = 6.
□ 1. Прямой ход.
Пояснения действий по преобразованию матрицы А{.
Г0 ° 1 п
Исходная расширенная матрица Ах, в квадрат
заключен ведущий элемент ( в.э.) первой строки.
-3 2 10 6
1 0 0,2 2,2| Поделили первую строку на первый в.э. - получили
первую о.с.
0 6 -2,4 3,6 Умножили первую о.с. на а2\ = 2 и результат вычли из
второй строки.
0 2 10,6 12,6 Умножили первую о.с. на я31 = -3 и результат вычли из
третьей строки.
26

Исключение элементов первого столбца по первой о.с. выполнено. После
этого делением на а22 = 6 готовится вторая ох., и далее исключаются элементы
второго столбца в строках, расположенных ниже второй о.с, и т.д.
Весь прямой ход легко прослеживается по результирующей таблице преоб-
Л
разования матрицы Лх в матрицу Ах.
Начинаем с первой строки.
г—0 0 1 11
2 6-28
-3 2 10 6
Первая о.с. (результат деления 1-й строки на ап =5).
1 0 0,2 2,2
Продолжаем со второй строки.
0 0-2,4 3,6
|—0 2 10,6 12,6
0 1 -0,4 0,6 Вторая о.с. (результат деления на а22 =6).
^ 0 0 111,4 111,4
Продолжаем с третьей строки.
0 0 1
1
Третья о.с. (результат деления на я33 = И>4)-
(10 0,2 2,2^
Таким образом, в результате прямого хода получили А\
0 1 -0,4 0,6
0 0 1 1
2. Обратный ход. По матрице А\ составим систему уравнений:
(1 0 0,2 ^ [х{\ (2,2^
0 1 -0,4
0 0 1
*2
1*3.
0,6
1
Х| + 0 • х2 + 0,2 • х3 = 2,2;
или х2 - 0,4 • х3 = 0>6;
х3=1.
Разрешая эту систему, начиная с последнего уравнения, получаем: х3 = 1;
х2 = 1; хх = 2. ■
Замечания.
1. На основе выполненного прямого хода путем перемножения ведущих
элементов ах\уа22, д3з и Т-Д- вычисляется определитель матрицы А :
\A\ = detA = au.a22.a33-...ann.
Для примера 1.1 : det А = 5 • 6 • 11,4 = 342.
2. Изложенный метод имеет ограничение, связанное с тем, что ведущие
элементы ах{уа22 и т.д. должны быть отличны от нуля и не должны быть малыми
по модулю, поскольку тогда погрешности вычислений будут большими.
27

Поэтому в методе Гаусса-Жордана (с выбором главного элемента) в качестве
ведущих элементов выбираются максимальные по модулю аа путем перебора
этих элементов по столбцу, соответствующему этому в.э., или по всем столбцам.
3. При решении систем линейных алгебраических уравнений методом
Гаусса единственного деления необходимо выполнить количество операций,
пропорциональное л3. Оно может быть существенно снижено, если система
имеет разреженную матрицу А (см. метод прогонки).
Процесс решения иногда удобно представлять в виде последовательности
матриц, получаемых в результате элементарных преобразований.
Пример 1.2. Решить систему линейных алгебраических уравнений
2*! +х2 +4*3 = 16,
Ъхх +2х2 +*з = Ю»
хх + 3х2 + 3х3 = 16
методом Гаусса единственного деления.
□ 1. Прямой ход. Запишем расширенную матрицу и реализуем прямой ход
с помощью описанных преобразований:
(Ш 1
3 2
1 3
16>
10
16J
к = \
->
f
1
1 -
2
0
0
V
1
ш
5
2
\
2
-5
1
8
-14
* = 2
2
-10
-28
78
*=з
*=з
2
-10
1
-28
3
= 4.
При этом в соответствии с вышеизложенным алгоритмом можно
использовать два правила:
каждый элемент строки, в которой находится ведущий элемент, делится
j = 1,...,п +1; к— номер шага (формирование о.с.);
нанего:^ =-Jbl7'
а
кк
- элементы строк, находящихся ниже строки с ведущим элементом, под-
считываются по правилу прямоугольника, схематически показанного на рис. 1.2
(исключение элементов, лежащих ниже в.э. текущей о.с).
Л(*-1)
акк
„(*-1)
*Г}
*<*-■>
i = к + 1,...,л;
j = к,...,п + 1.
Рис. 1.2
28

Поясним алгоритм исключения (второе правило) на рис. 1.2. Пусть
рассчитывается значение а\р на к-м шаге. Следует соединить элемент л^"1* с ведущим
элементом я^-1). Получена одна из диагоналей прямоугольника. Вторую
диагональ образует соединение элементов ^_1) и о^~1К Для нахождения значения
ajV из его текущего значения a)f~X) вычитается произведение элементов я-* _1) и
я**-1) , деленное на ведущий элемент.
2. Обратный ход. По матрице Л{ составим систему уравнений
2
О 1 -10|
0 0 1
( V Л
х2
Л,
' 8 >
-28
1 з J
*1 + 2*2+2хз = 8'
или *2 - Ю*3 = -28,
*3=3.
Решая эту систему, начиная с последнего уравнения, находим: х3 = 3,
*2 = 2, Х| = 1 .■
Пример 1.3. Методом Гаусса с выбором ведущего элемента по столбцам
решить систему:
-Зле, +2,099х2+6хз =3,901;
10х! -7*2+0*3 =7;
5*i - *2 + 5*3 = 6.
D 1. Прямой ход. Реализуем поиск ведущего элемента по правилу: на к-и
шаге переставляются (п - к +1) оставшихся уравнений так, чтобы наибольший
по модулю коэффициент при хк попал на главную диагональ:
(-3 2,099 6 3,90 П
4 =
ю
5
10 -7 0
-3 2,099 6 3,901
5-156
к=1
(\ -0,7 0 0,7 ^
0 -0,001 6 6,001
0 2,5 5 2
)01 Lh
>5jJ
(1
- 0,7 0 0,7
2,5
2,5
[0 -0,001 6 6,001 J
*=2
(I -0,7 0
0 1 2
0 0
6,002
0,7 V ,(1 -0,7 0 0/Л
1 -► 0 1 2 1
6,002) 10 0 11
д.
2. Обратный ход. По матрице Ах составим систему уравнений:
(I -0,7 0^1 (х^ (0,7^
0 1 2
0 0 1
х2
Vx3 J
1
*, -0,7*2 =°>7>
или *2 + 2*з = 1,
*3 = 1.
Решая ее, последовательно получаем: *3 = 1, *2 = -1, *i = 0.1
29

Пример 1.4. Решить систему уравнений
*i - х2 + х3 ~ 4*4 = -2,
2х! + х2 - 5дсз + х4 = 2,
8jq - х2 - *з + 2х4 = И ,
*! + 6х2 - 2*з - 2х4 = -7
методом Гаусса единственного деления.
D 1. Прямой ход.
(Ш -1 1 -4-2^
2 1-51 2
8-1-1 2 11
1 6-2-2 -1)
*=1
*=з
а -1
О 1
о о
о о
1 -4
-1 3
3
1 »
22.
1 -1 1
О Ш -7
0 7-9
1,0 7 -3
-2 ^
2
39
2814
66
22
2814
66 J
-4
9
34
2
-2^
6
27
-5J
*=2
->
Г1
0
0
0
1
-1
1
0
0
1
7
22
40
3
*=4
П -1
о 1
о о
о о
_7
3
1
о
-4 -2
3 2
39 39
22 22
1 1
2. Обратный ход.
'\
0
0
1о
-1
1
0
0
1
7
~3
1
0
-4
3
39
22
1
*2
*3
-2^
2
39
22
И.
или
хх - х2 + х3 ~ 4*4 = ~2,
Х2~-х3+Зх4 =2,
39 =39
*з + 22 *4 ~ 22 '
х4 = 1.
Отсюда х4 = 1, х3
39 39 п
х4 =0,
22 22 4
х2 = 2 +—х3 ~ 3*4 = -1, *! = -2 + х2 - х3 + 4jc4 = 1.
В результате получено решение: хф = (1; -1; 0; \)т .■
30

1.2.2. Метод прогонки
Метод применим в случае, когда матрица А — трехдиагональная. Общая
постановка задачи имеет следующий вид.
Дана система линейных алгебраических уравнений с трехдиагональной
матрицей А. Развернутая запись этой системы имеет вид
ад-1 - М/ + Y/*/+i = 8/» <х, = уя = О, I = 1, л, (1.4)
которому соответствует расширенная матрица
Л. =
Здесь первое и последнее уравнения, содержащие по два слагаемых, могут
рассматриваться как краевые условия. Знак «—» при коэффициенте р,- взят для
более удобного представления расчетных формул метода.
Требуется найти решение х0 = (х,|,...,х«я)гсистемы (1.4) методом
исключения Гаусса.
Если к (1.4) применить алгоритм прямого хода метода Гаусса, то вместо А{
л.
получится А\\
Г-Pi
«2
0
^ о
Yl
-Р2
<*3
0
0
Y2
-Рз
0 •
0 •
Y3 '
• 0
• 0
• 0
• <*„
0
0
0
"РЛ
*А
h
h
s*>
п
At =
(I
О 1 -P2
О 0 1
0 0 0
о
о
1
Qi
Сз
Qn)
Учитывая, что последний столбец в этой матрице соответствует правой части, и
переходя к системе, включающей неизвестные, получаем рекуррентную формулу:
*| =^*/Ч1 +(?/> / = 1,я-1 .
(1-5)
Соотношение (1.5) есть формула для обратного хода, а формулы для
коэффициентов Pj,Qi9 которые называются прогоночными, определяются из (1.4),
(1.5). Запишем (1.5) для индекса / -1:
*,_, = Pj-\Xj +0,_i
и подставим в (1.4). Получим
<*/(Л-1*/ + Qi-\) ~ Р/*/ + У,-*,-+1 = 8/.
31

Приводя эту формулу к виду (1.5) и сравнивая полученное выражение
с (1.5), получаем рекуррентные соотношения для //,£?,:
Y/ п a/Q/-i " 8/
Pi- Llt—, Q,= ' "] п ', / = U-i. (1.6)
Определение прогоночных коэффициентов по формулам (1.6) соответствует
прямому ходу метода прогонки.
Обратный ход метода прогонки начинается с вычисления хп. Для этого
используется последнее уравнение, коэффициенты которого определены в прямом
ходе, и последнее уравнение исходной системы:
хп-\ = ?п-\хп + £л-1>
апхп-\ ~$пхп +0'*Л+1 =5/г
Тогда определяется хп:
^%"Си:8'ай. т.е. xn=Qn. (1.7)
Остальные значения неизвестных находятся рекуррентно по формуле (1.5).
Все соотношения для выполнения вычислений получены. Тогда можно
провести расчеты по методу Гаусса, используя прямой и обратный ход.
Методика решения задачи
Прямой ход.
1. Вычислить Рх = —; Q{ =—- (в (1.6) подставить ах =0).
Pi Pi
2. Вычислить прогоночные коэффициенты Рг&2\ Л>йъ—J Л»-ьСл-1
по формулам (1.6).
Обратный ход.
1. Найти xn = a"Qn-x~h*.
РЛ-алД_,
2. Значения хя_1,хя_2,...,х1 определить по формуле (1.5) :
хп-\ = Рп-\хп +Qn-\> хп-2 = Рп-2хп-\ +Qn-2 >•••, *l=^l*2+ft-
Замечания.
1. Данный метод называется методом скалярной прогонки, так как при
решении задачи на каждом /-м шаге определяется скалярная величина
*/ (' = 1,л).
2. Аналогичный подход используется для решения систем линейных
алгебраических уравнений с пятидиагональными матрицами.
32

3. Алгоритм метода прогонки называется корректным, если для всех
/ = 1, п р; - a/P/_i * 0, и устойчивым, если \Pj\ < 1, / = 1,п -1.
4. Достаточным условием корректности и устойчивости прогонки является
условие преобладания диагональных элементов в матрице А, в которой а, * 0 и
у,* 0 (/ = 2,л-1):
1М*Ы + Ы
(1.8)
и в (1.8) имеет место строгое неравенство хотя бы при одном /.
5. Алгоритм метода прогонки является очень экономичным и требует для
своей реализации количество операций, пропорциональное п.
Пример 1.5. Дана система линейных алгебраических уравнений с трех-
диагональной матрицей Л (п - 4):
5*1 + 3*2 = 8,
3xj + 6х2 + *з = Ю,
х2 + 4*з - 2х4 = 3,
х3 - Зх4 = -2
(а, = 0, у4 = 0). Решить эту систему методом прогонки.
□ Данная система удовлетворяет условию преобладания диагональных
элементов (1.8): в первом уравнении 5 > 3, во втором уравнении 6 > 3 + 1; в третьем
уравнении 4 > 1 + 2, в четвертом уравнении 3 > 1. Далее выполняем прямой и об-
(5 3 0 0 !
ратный ход, учитывая, что матрица Лх =
13 6 1 0 10
0 14-2 3
[о 0 1 -3 -2,
Прямой ход. Вычислим прогоночные коэффициенты
Р.
Д«-
3
'5'
ft-
Pi
8
-5
Г2
1
Р2-«2Л
.,.,-!
2\
5'
02»
<*201
P2"«2fl
5
10
26
6-3
В)2|
Подчеркнем, что ${ =-5; р2 =
втором слагаемом взят знак «минус»:
-6; р3=-4; р4=3, так как в (1.4) во
А=-
J3
Рз-аз/>2
>-Н)
42
79 ;
Сз =
«302 - h
Рз-а3/>2
1.26-
21
-4-1.
Н)
37
79'
33

Обратный ход:
1 Е •>
п а4бз-84 79 , „ о 42 , 37 ,
Р4-«4^3 3-1 [ — 1 9 9
Подстановкой решения дс* = (1; 1; 1; 1)г в исходную систему убеждаемся, что
задача решена верно. Путем анализа всех полученных р, -a,/>_i и />• легко
убедиться также в том, что для данного примера прогонка оказалась корректной и
устойчивой, поскольку р/ - а,/*,! * 0, / = 1,4; |/> | < 1, / = 1,3.
Таблица 1.1
/
1
2
3
4
<*/
0
3
1
1
ft
-5
-6
-4
3
У/
3
1
-2
0
«/
8
10
3
-2
А
-3/5
-5/21
42/79
-
Q
8/5
26/21
37/79
1
Х/
1
1
1
1 |
Прямой ход Обратный
ход
Для наглядности представления информации исходные данные и
результаты расчетов поместим в табл. 1.1, где в первых четырех колонках содержатся
исходные данные, а в последних трех - полученные результаты. ■
Пример 1.6. Дана система линейных алгебраических уравнений с трехдиа-
гональной матрицей А :
*i + 2х2 = 5 ,
2хх - х2 + *з = 3 ,
Х2 - *з + х4 = 3 ,
х3 + х4 - 7 •
Решить систему методом прогонки.
□ Результаты расчетов в прямом и обратном ходе занесены в табл. 1.2.
Таблица 1.2
_
1
2
3
1 4
<*/
0
2
1
1
ft
-1
1
1
-1
Y/
2
1
1
0
5/
5
3
3
7
Pi
-2
1/5
5/4
-
Q
5
7/5
-2
4
*i
1
2
3
4 1
34

В результате получено решение: х„ = (1; 2; 3; 4)т. Заметим, что условие
преобладания диагональных элементов в данном примере не выполнено, но
алгоритм метода прогонки позволил получить точное решение. При этом обратим
внимание на небольшой порядок системы и отсутствие погрешностей
вычислений. ■
Пример 1.7. Решить систему уравнений
2хх + х2 = 4,
2*1 + Зх2 - х3 = 9,
х2 -х3 +3х4 = 12,
х3 -х4 = -4,
или
(2 1 О (П
2 3-1 О
0 1-1 3
[о о 1 -и
методом прогонки.
D Прямой ход. Вычислим прогоночные коэффициенты:
(у Л
*2
*з
{xAj
[ 41
9
12
L--*J
Рг
Pi -2
Y2
Р2-<х2/>,
2 '
Gi=-t- = --t = 2;
-И)
Pi
__1_
= 2;
G2
a2gi-S2_ 22-9
P2-a2P, "
-3-2-1-1
2
2'
Y3
■6; Qi
n % 1 -1-12
«3g2~S3 2
p3-a3/>2
1-1-1
2
= -19.
Рз-^зЛ ,_ь1
2
Обратный ход:
a.j^.H-HJ-M.a.^. ,3 = ^4+Оз=6.3-19 = -1;
p4-a4/>3 1-1-6
х2 =P2x3+Q2 = -(-l) + - = 2; X!
Результаты расчетов приведены в табл. 1.3.
/to+d =--2 + 2 = 1.
Таблица 1.3
1
1
2
3
1 4
а/
0
2
1
1
Р/
-2
-3
1
1
Y/
1
-1
3
0
S/
4
9
12
-4
Pi
-1/2
1/2
6
-
0/
2
5/2
-19
3
*/ 1
1
2
-1
3
Получено решение системы: х„ = (1; 2; -1; З)7
35

1.2.3. Метод LU -разложения
Рассмотрим еще один метод решения задачи (1.2). Метод опирается на
возможность представления матрицы А системы в форме произведения двух
треугольных матриц:
A = LU,
где L-нижняя, a U -верхняя треугольные матрицы, имеющие вид
L =
С учетом (1.9) система Ах = Ь представляется в форме
LUx = b.
(1-9)
(In
hi
Jnl
0 •
/22 •
'„2 •
• (П
• 0
*-nn ,
и =
(\
0
,0
un •
1
0 •
•' Щп
" »2n
1
(1.10)
Решение системы (1.10) сводится к последовательному решению двух
простых систем с треугольными матрицами. В итоге процедура решения состоит из
двух этапов.
Прямой ход. Произведение U х обозначим через у. В результате решения
системы
Ly = b
находится вектор у.
Обратный ход. В результате решения системы
Ux = y
находится решение задачи — вектор х.
В силу треугольности матриц L и U решения обеих систем находятся
рекуррентно (как в обратном ходе метода Гаусса).
Из общего вида элемента произведения А = LU , а также структуры
матриц L и U следуют формулы для определения элементов этих матриц:
///
£ lisusJ, i > 7,
(1-11)
_1_
///
/-1 л
I < J.
Результат представления матрицы А в виде произведения двух треугольных
матриц (операции факторизации) удобно хранить в одной матрице следующей
структуры:
36

h\ hi I ц23 "• и2п
h\ hi 'зз|_*'* "зл
/-i /,
л1 lnl 1пЪ
L
и
Вычисления на к-и шаге метода LU - разложения удобно производить,
пользуясь двумя схемами, изображенными на рис. 1.3.
//I'
h,k-\
М\к
...
ик-\,к
aik
Ы
^'
Г
h,k-\' 1
т*'
#*'*
[_'**_
к*'
'w*-u
akj
к-\
hk = aik -Yilbusk
к-й столбец нижней треугольной
матрицы
ukj
кк
к-\
akj~Y.lksusj
к-я строка верхней треугольной
матрицы
Рис. 1.3
Замечание. Всякую квадратную матрицу Л, имеющую отличные от
нуля угловые миноры А\=ац*09 А2 =
*0, ... , ДЛ=|Л|*0, можно
представить в виде LU -разложения, причем это разложение будет
единственным.
Методика решения задачи
1. Выполнить операцию факторизации исходной матрицы Л, применяя
схемы (рис. 1.3) или формулы (1.11), и получить матрицы L и U.
2. Решить систему Ly = b.
3. Решить систему Vх-у.
37

Пример 1.8. Решить систему линейных алгебраических уравнений
7х\ + х2 +4*з = 16,
3*1 + 2х2 + *з = Ю ,
х1 + 3х2 + 3x3 = 16
методом L U -разложения.
D 1. Выполним операцию факторизации:
(Ш 1 Я (2
3
2 1
1 1J
*=1 )
3,;
J'
,0,5.2^
/' 2 1
з Гз,
ыг 1
ч
2 0,5 ,-2 "|
3 | Q,5 1 — 10
4K'2,5--frJ
*=з
f 2 1 0,5 2
10
3 0,5
U 2,5 26 J
при £ = 1 /п =дп =2; /21 = я21 = 3; 'з! = «3i =i;
1 п< * 4 о
"12 =^«12 = °>5; "13 =-«13 =-j = 2;
при £ = 2 /22 = я22 - /2iw12 = 2 - 3 • 0,5 = 0,5; /32 = аЪ1 -1}\ип = 3 -1 • 0,5 = 2,5 ;
"2з=7"^з-/21«1з) = 7Гг(1-3-2) = -1°;
'22 ^>^
при к = 3 /Зз = язз ~ ^3iwi3 - ^32w23 = 3 -1 • 2 - 2,5 • (-10) = 26.
В результате получены две треугольные матрицы:
(2 0 <П
L = 3 0,5 0
[l 2,5 26j
2. Решим систему Ly = Ь:
(2 0 <М ОЛ П6^
U =
3 0,5 0
1 2,5 26 J
^2
10
v16,
или
(\ 0,5 2 >*
0 1 -10
0 0 1
2У\ =16,
Зл+0,5у2=10,
>>, +2,5 -j>2 + 2б^з =16.
Отсюда у{ = 8, у2 = (10-3• 8)-2 = -28, у3 = 1б 8^70 = 3.
26
3. Решим систему Uх = у:
(I 0,5 2 "| (х^ ( 8 ^
или
хх + 0,5х2 + 2*з = 8,
х2-10х3 =-28,
f щ р __ *з=3.
Отсюда х3=3, х2 =-28 + 10-3 = 2, х, = 8-2-3-0,5-2 = 1. Получен ответ:
0 1
0 0
-10
1
*2
ч*3>/
-28
3
*♦ =(1;2;3)г.
38

Пример 1.9. Решить систему линейных алгебраических уравнений
3xj — х2 ~ 5,
- 2xj + х2 + х3 = 0,
2х{ -х2 + 4х3 = 15
методом LU -разложения.
□ 1. Выполним операцию факторизации:
({Т\ -1 0)
2 П Г
-1 4
*=1
3
^-°)
- 2'Т 1 1
2 ••'' - 1 [~4
1 J
ыг
f^rJ?t4j
* = 3
*=3
(31-Х °1
-2 ОД
I2 -К 5J
при £ = 1 /ц=лц=3; /21=я21=-2; /31-а31=2;
при А: = 2 /22 =fl22-/2iw12 =1-2- = -; /32 = я32-/31н12 =-1 + 2- = --;
"23=7L(fl23--/2i"i3) = l7(1-(-2)0)=3;
/22 Уъ
при к = 3 /33 =^зз-/з1«13-/з2«23 =4-20-3-(-)/)=5.
2. Решим систему Ly = Ь:
3
-2
2
0
К
-К
0
0
hi]
Уг
[Уз)
=
f5l
0
W
или -2^+-^- = 0,
2^1 --Уг+Зуз =15.
Отсюда ^ = -, у2 = 10, уг = 3.
39

3. Решим систему Uх = у:
'l -'о
3
О 1 3
О О 1
\
/
х\
*2
1*3 J
X
=
f5l
3
10|
3
к )
1 5
Х1_Г2 = з'
х2 + Здс3 = Ю,
х3=3.
U у
Отсюда дс3 = 3, х2 = 1, *i = 2. ■
Пример 1.10. Решить систему линейных алгебраических уравнений
2х{ + х2 = 4,
2хх + Зх2 - *з = 9,
х2 ~хз +3х4 = 12,
х3 - х4 = - 4
методом LU -разложения.
П 1. Выполним процедуру факторизации:
[Ш
2
0
10 0^
3-10
1 -1 3
0 1 -1,
к=х >
( 1 1
2 ,- ..0 .-0
•;
V:
? -'
"3
1
0
-1 0
-1 3
1 -I
кт2 >
( 1 "l
2 - 0.0
2"4
..ц^з
ОТ/ f
'••'•'1
г -I з I
I iFiJ
*=3
' 1
2 - 0 .0
2
2 2 -.- 0
О У
^0 0 1
В результате получаем
L =
,-6
*=4
/
2
1
0
1о
2
2
1
0
0
?
1
2
1
N
0
0
-6
5J
'2 0
2 2
0 1
k0 0
0 0^
0 0
-I 0
2
1 5j
(
' U = \
1
0
0
[о
2
1
0
0
0
1
~2
1
0
0
0
-6
1 J
при к = 1 /]
и =2» ^21 =2, /31 =0,
1
/41=0,
1
"12=|-1={, «13=^0 = 0, и14=~0 = 0;
*=з
40

при к = 2
/22=3-2~ = 2,
/з2 = 1-0-т=1> Л
42
0-0^ = 0,
«23 =I(-l-20)=-i, и2А =1(0-2-0) = 0;
при к = 3
/33=-l-lf{) = -f /43=1-0-0-0.(-1) = Ь
«34=-у(3-0.0-10)=-6;
~2
при £ = 4 /44 = -1 - (0 - 0 + 0 - 0 + 1 - (- 6)) = 5.
2. Решим систему Ly = Ь:
(2
2
0
,0
0
2
1
0
0 0
0 0
-± 0
2
1 5
\
/
(V
*2
Уз
^4,
'4>
9
12
.-*J
ИЛИ
2л =4,
2у1+2>>2=9,
1
Jb-J*3 = 12>
Уз+5*4 =-4.
Отсюда ух =2, *2 =-, *3 =-19, у4 =3.
3. Решим систему Uх = у:
(
1
0
о
1
2
1
0
0
1
"2
1
0 0 0
0
0
-6
1,
х\
*2
*3
л,
=
Г 2 1
5_
2
-19
1 з J
ИЛИ
*1+^*2=2>
1
х2--^з=^
х3 -6х4 =-19,
х4 = 3.
Отсюда получаем: х4 = 3, х3 = -1, х2 = 2, Xj =1 или х„ = (1; 2; -1; 3)Т .■
Замечания.
1. При большом числе уравнений (больше 100) прямые методы решения
систем линейных алгебраических уравнений становятся трудно реализуемыми на
ЭВМ прежде всего из-за сложности хранения промежуточных результатов
и операций с матрицами большой размерности.
2. Существуют различные способы представления матрицы А в виде
А = А А
2'--
где каждая матрица А{ имеет форму, удобную для решения системы линейных
уравнений [11]. Как правило, /и<5, причем главным образом m = 2 и /я = 3.
Тогда в результате решения последовательности систем
можно найти искомое решение х„ = bm.
Ambm
41

1.3. ИТЕРАЦИОННЫЕ МЕТОДЫ
1.3.1. Метод простых итераций
Альтернативой прямым методам являются итерационные методы,
основанные на многократном уточнении х*0) — приближенно заданного решения
задачи А х = b. Верхним индексом в скобках здесь и далее по тексту
обозначается номер итерации (совокупности повторяющихся действий).
Суть простейшего итерационного метода - метода простых итераций,
состоит в выполнении следующих процедур.
1. Исходная задача Л х = b преобразуется к равносильному виду:
х = ах + р, (1.12)
где а = {а,у } — квадратная матрица, р = {р,} — вектор, /, у = 1,...,л. Это
преобразование может быть выполнено различными путями, но для обеспечения
сходимости итераций (см. процедуру 2) нужно добиться, чтобы ||а|| < 1 (чтобы норма а
была меньше единицы. Понятие нормы вводится ниже.)
2. Вектор р принимается в качестве начального приближения дс(0) = р и
далее многократно выполняются действия по уточнению решения согласно
рекуррентному соотношению
х(*+1) =ах(*>+р, Л: = 0,1,... (1.13)
или в развернутом виде
х\ -all*l +а12*2 +--- + а1л*л +Р1>
4*+1) = *гАк) + a2i4k)+-+«2п4к)+р2 .
*<*+1> = «„,*<*> + ал2х<*> + ... + «„„*<*> + Ря •
3. Итерации прерываются при выполнении условия
1_||а||Р * II "е' (114)
где е > 0 — заданная точность, которую необходимо достигнуть при решении
задачи, или более простого условия:
|х<*+,>-х<*>|<8. (1.15)
Оба условия носят апостериорный характер (a posteriori — «после»).
42

Замечания.
1. Процесс (1.13) называется параллельным итерированием, так как для
вычисления (& + 1)-го приближения всех неизвестных учитываются вычисленные
ранее их к -е приближения.
2. Начальное приближение х^ может выбираться произвольно или из
некоторых соображений. При этом может использоваться априорная
информация о решении или просто «грубая» прикидка.
При выполнении итераций (любых) возникают следующие вопросы:
а) сходится ли процесс (1.13), т.е. имеет ли место х^ -> хт при к -> оо, где
хф - точное решение?
б) если сходимость есть, то какова ее скорость?
в) какова погрешность найденного решения х(*+1\ т.е. чему равна норма
разности р(А:) -хт ?
Для их разрешения необходимо сравнивать векторы х(Л) и х(*+1). Это
сравнение (а также математическое обоснование и других задач вычислительной
математики) осуществляется на основе норм матриц и векторов. Приведем
основные сведения о них.
Нормой матрицы А = \ау\ (/,у = 1,...,л) называется действительное число
(обозначаемое ||/ф, удовлетворяющее условиям:
1) || Л || > 0 при А*0 и || А || = 0 тогда и только тогда, когда А нулевая
матрица {А = $);
2) ||аА || = | а | • || А || для любого действительного а; (|ос| — модуль а);
3) ||/*i +i42||<||y4i|| + ||>42||> где А\ и А2 — некоторые матрицы (неравенство
треугольника);
4) К4|*Ы-И>1-
Здесь А\ и А2— матрицы, для которых соответствующие операции имеют
смысл.
Условия 1— 4 — это условия нормы, а их непосредственное вычисление
может производиться различными путями. Наиболее употребительными
являются следующие формулы для вычисления значений норм матриц и векторов,
образованных действительными компонентами.
Нормы матрицы А Нормы вектора х
i)|Hli= mfx Zh|; Ikll, =maxK|;
2)fl4=max£h/| ; M2 = I M ;
1 /=i /»i
43

3)NI
-lit*} : Из=Д^
Здесь приведены согласованные нормы матриц и векторов. Согласование
их осуществляется связью:
\Ах\\
M-supl
х*Э
Заметим, что в случае ||х||3 согласованная норма равна у Хтгх(АтА), где
A.max(>4r/0 — максимальное собственное значение матрицы АТА. Однако ее
вычисление связано с весьма трудоемкими операциями. Можно доказать, что
справедливо неравенство
^Xmax(ArA)<U\
Так как величина || А ||. вычисляется относительно просто, то она часто
используется в оценках. Третья норма |||L называется евклидовой, для вектора она
соответствует длине вектора, исходящего из начала координат. В множестве
действительных чисел ||х|| = |х|.
Ответ на вопросы о сходимости дают следующие две теоремы,
приводящиеся без доказательства.
Теорема 1.1 (о достаточном условии сходимости метода простых итераций).
Метод простых итераций, реализующийся в процессе последовательных
приближений (1.13), сходится к единственному решению исходной системы Ах-Ь
при любом начальном приближении х^ со скоростью не медленнее геометрической
прогрессии, если какая-либо норма матрицы а меньше единицы, т.е. ||ос|| <1
(*е {1,2,3}).
Замечания.
1. Условие теоремы 1.1, как достаточное, предъявляет завышенные
требования к матрице а, и потому иногда сходимость будет, если даже || а | > 1.
2. Сходящийся процесс обладает свойством самоисправляемости, т.е.
отдельная ошибка в вычислениях не отразится на окончательном результате, так
как ошибочное приближение можно рассматривать как новое начальное.
3. Условия сходимости выполняются, если в матрице А диагональные
элементы преобладают, т.е.
K^kn| + ... + K,--i| + Ki+i| + «. + K|, / = 1,...,л, (1.16)
и хотя бы для одного / неравенство строгое. Иначе, модули диагональных
коэффициентов в каждом уравнении системы больше суммы модулей
недиагональных коэффициентов (свободные члены не рассматриваются).
4. Чем меньше величина нормы || а ||, тем быстрее сходимость метода.
44

Теорема 1.2 (о необходимом и достаточном условии сходимости метода
простых итераций).
Для сходимости последовательности (1.13) при любых х^ и р необходимо и
достаточно, чтобы собственные значения матрицы а были по модулю меньше
единицы, т.е. |я,/(а)|<1, / = l,...,/i.
Замечание. Хотя теорема 1.2 дает более общие условия сходимости
метода простых итераций, чем теорема 1.1, однако ею воспользоваться сложнее,
так как нужно предварительно вычислить границы собственных значений
матрицы а или сами собственные значения.
Рассмотрим последовательность , сходящуюся к хт. Предположим,
что все ее элементы различны и ни один из них не совпадает с х*. Наиболее
эффективный способ оценивания скорости сходимости состоит в сопоставлении
расстояния между х(*+1> и хт с расстоянием между х^ и хт.
Последовательность называется сходящейся с порядком р, если р —
максимальное число, для которого
1И+,)-**11
0< lim -У !1<оо.
Поскольку величина р определяется предельными свойствами , она
называется асимптотической скоростью сходимости.
Если последовательность (х(Л)) — сходящаяся с порядком р, то число
с = lim
pc(*+l)-;c.
k^\x^-x\P
называется асимптотическим параметром ошибки.
Если р = 1, с < 1 , то сходимость линейная, если р - 2 — квадратичная,
если р-Ъ — кубичная и т.д. Если р > 1 или р = 1, с = 0, то сходимость
сверхлинейная. Линейная сходимость является синонимом сходимости со скоростью
геометрической прогрессии. Сверхлинейная сходимость является более быстрой,
чем определяемая любой геометрической прогрессией.
Теорема 1.3 (о погрешности приближений, вычисляемых методом простых
итераций).
Если в итерационном процессе норма матрицы а, согласованная с нормой
вектора х, меньше единицы (||а|| < 1), то справедлива следующая оценка
погрешности:
И,Ч*т^И,-*<*-,1 "•">
45

Это соотношение может быть переписано через начальное приближение х(0) = р:
\\х
(*).
а
и*+1
х-1-Нй|М- (1Л8)
Неравенство (1.17) позволяет провести апостериорную оценку погрешности
А:-го приближения посредством вычисления нормы разности двух
последовательных приближений х(*\х(*_1) и нормы матрицы а. На основе этой оценки
осуществляется выход из итерационного процесса по результатам расчета (см.
(1-14)):
,^1)_х(*)|| J4HI)
IN
На основе неравенства (1.18) можно записать априорную оценку
погрешности (a priori — «до»)
из которой еще до расчета можно получить число итераций &, требуемых для
достижения заданной точности:
k^b* + w-bf-bH (1Л9)
Преобразование системы Ах = Ь к виду х = ах + р с матрицей а,
удовлетворяющей условиям сходимости, может быть выполнено несколькими
способами. Приведем способы, используемые наиболее часто.
1. Уравнения, входящие в систему Ах = Ь, переставляются так, чтобы
выполнялось условие (1.16) преобладания диагональных элементов (для той же
цели можно использовать другие элементарные преобразования). Затем первое
уравнение разрешается относительно хь второе — относительно х2 и т.д. При
этом получается матрица а с нулевыми диагональными элементами.
Например, система
- 2,8*1 +х2+ 4х3 = 60,
10*! -х2+8х3 =Ю,
- Xj + 2х2 - 0,6х3 = 20
с помощью перестановки уравнений приводится к виду
\0х{ -х2+8х3 =10,
- X! + 2х2 - 0,6х3 = 20,
- 2,8xi + х2 + 4х3 = 60,
где |Ю|>|-1| + |8|, |2| > |-1| +1-0,6|, |4| > |-2,8| + |l|, т.е. диагональные элементы
преобладают.
46

Выражая *, из первого уравнения, *2 - из второго, а *3 - из третьего,
получаем систему
*, =0-*! +0,1*2-0,8*3 + 1,
*2 = 0,5*! + 0 • х2 + 0,3*3 + Ю,
*3 = 0,7*! - 0,25*2 + 0 ■ хъ + 15,
где а =
0 0,1 -0,8^
0,5 0 0,3
[0,7 -0,25 0 J
, Р
10
Заметим, что Ца^ = max {0,9; 0,8; 0,95 } = 0,95 < 1, т.е. условие теоремы 1.1
выполнено.
Проиллюстрируем применение других элементарных преобразований. Так,
система
4*i + *2 + 9*3 = ~ 7»
3*! + 8*2 - 7*3 = - 6,
*i + *2 - 8*3 = 7
путем сложения первого и третьего уравнений и вычитания из второго уравнения
третьего уравнения преобразуется к виду
5*! + 2*2 + *з = 0,
2*j +7*2 +*з = -13,
*! + *2 - 8*3 = 7
с преобладанием диагональных элементов.
2. Уравнения преобразуются так, чтобы выполнялось условие преобладания
диагональных элементов, но при этом коэффициенты а/7 не обязательно
равнялись нулю.
Например, систему
1,02*! -0,15*2 =2>7>
0,8*, +1,05*2 =4
можно записать в форме
*, =-0,02*, +0,15*2+2,7,
*2 =-0,8*i -0,05*2 +4»
для которой ||а||, = max {0,17; 0,85 } = 0,85 < 1.
47

3. Если det А * 0, систему Ах = b следует умножить на матрицу
D - А'1 - е, где {гу } — матрица с малыми по модулю элементами. Тогда
получается система (А~1 - г)Ах = Db или А~] Ах -zAx = Db, которую можно
записать в форме х = сие + р, где а = е Л, р = Db. Если еJ, /, j = 1,...,я, достаточно
малы, условие сходимости выполняется.
Методика решения задачи
1. Преобразовать систему Ах = b к виду х = аде + р одним из описанных
способов.
2. Задать начальное приближение решения х(0) произвольно или положить
х(0) = р, а также малое положительное число е (точность). Положить к - 0.
3.Вычислить следующее приближение х**+1* по формуле х(*+1) = ах^ +р .
4. Если выполнено условие х(*+1) -х(А) < е или (1.14), процесс
завершить и положить х„ = х(*+,). Иначе положить к = к +1 и перейти к п.З.
Пример 1.11. Методом простых итераций с точностью е = 0,01 решить
систему линейных алгебраических уравнений:
2х, + 2х2 + Юх3 = И,
\0х\ + х2 + х3 = 12,
2xj + Kbc2 + *з = 13.
Предварительно определить число итераций.
□ 1. Так как |2| <|2| + |l0|, |l| <|l0| + |l|, |l| <|2| + |l0|, условие (1.16) не
выполняется. Переставим уравнения местами так, чтобы выполнялось условие
преобладания диагональных элементов:
10xj + х2 + *з = 12,
2х{ + 10х2 + х3 = 13»
2хх + 2х2 +10*3 = 14.
Получаем |lC| > |l| + |l|, |l0| > |2| + |l|, |l0| > |2| +12|. Выразим из первого уравнения
Xi, из второго х2, из третьего х3:
Xj = -0,1 х2 -0,1 -х3 + 1,2,
х2 =-0,2-Xi -0,1х3 +1,3, а =
х3 = -0,2х, -0,2х2 +1,4;
г °
-0,2
,-0,2
-0,1
0
-0,2
-0,0
-0,1
oj
; Р =
'1.2>
1,3
М
48

Заметим, что flaflj = max {0,2; 0,3; 0,4 } = 0,4 < 1, следовательно, условие
сходимости (теорема 1.1) выполнено.
По формуле (1.19) вычисляем число итераций, обеспечивающих заданную
точность:
^^-2 + lg0,6-lgl,4=5>95; ^495
lg0,4
Таким образом, для решения задачи необходимо выполнить не менее пяти
итераций.
(12)
. В поставленной задаче е = 0,01.
2. Зададим х(0) = р =
1,3
3. Выполним расчеты по формуле (1.13):
Л*+1)
0 -0,1 -0,П
0,2 0 - 0,1
^-0,2 -0,2 0 J
Ak)
1,3
A: = 0,1,...,
или
x[k+l)=-0,lx[k) -0,lx<*>+l,2;
x<*+1) =-0,2x{k) -0,lx<*> +1,3; A: = 0,1,...,
xf+l) =-0,2x^-0,2x^+1,4;
до выполнения условия окончания и результаты занесем в табл. 1.4.
Таблица 1.4
к
0
1
2
3
4
5
1,2000
0,9300
1,0180
0,9946
1,0015
0,9996
х(к)
х2
1,3000
0,9200
1,0240
0,9934
1,0020
0,9995
х3
1,4000
0,900
1,0300
0,9916
1,0024
0,9993
|L(*)_x(*-i)||
-
0,5
0,13
0,0384
0,0108
0,0027<е
4. Расчет закончен, поскольку условие окончания х(*+1) - х(*ч = 0,0027 < е
выполнено.
Приближенное решение задачи: х* = (0,9996; 0,9995; 0,9993) . Очевидно,
точное решение: хф = (1; 1; \)т.
49

На рис. 1.4 показан характер сходимости х\ ' (к = 0,1,2,3,4,5) к х*3=1.
Видно, что значения х^ получаются то больше, то меньше единицы, но с
увеличением к все меньше отличаются от нее. Это соответствует двусторонней
сходимости метода простых итераций для заданной задачи. В других задачах
может проявляться односторонняя сходимость, когда стремление к xmi
осуществляется с одной стороны от x0i.
Рис. 1.4
Приведем результаты расчетов для другого начального приближения
х(0)=(1,2;0;0)г и е = 0,001 (табл. 1.5).
Таблица 1.5
Г к
0
1
2
3
4
5
6
1 7
х\
1,2000
1,2000
0,9780
1,0108
0,9975
1,0008
09998
U0001
х2
0
1,0600
0,9440
1,0096
0,9963
0,0009
0,9997
ЦЮ01
0
1,1600
0,9480
1,0156
0,9959
1,0012
0,9997
1,0001
|х<»-х<*-">| 1
|
1,1600
0,2220
0,0676
0,0133
0,0053
0,0015
0,0004<е |
Приближенное решение задачи: хт = (1,0001; 1,0001; 1,0001)7 .■
1.3.2. Метод Зейделя
Этот метод является модификацией метода простых итераций и в
некоторых случаях приводит к более быстрой сходимости.
Итерации по методу Зейделя отличаются от простых итераций (1.13) тем,
что при нахождении /' -й компоненты (к +1) -го приближения сразу
используются уже найденные компоненты (& + 1)-го приближения с меньшими номерами
1,2,...,/ -1. При рассмотрении развернутой формы системы итерационный
процесс записывается в виде
50

М+\)
,(*)
апх\К) +апх?> +а13х\К> + ... +а1лхя*' +р,,
<*>.
,<*)
ЛЬ+1)
: ct21pcf
1_
.<*♦!>
|+а22х<* > + a23xf> + ... + а2лхл*> + р2,
(1-20)
г(*+0
(* + 1)
X-j = СХ3lP^i И" «32р2
.(А: 4-1)
+ а33^)+... ч-азяХ^+Рз,
х(*+1)=а ,
лл "-л!
.(* + 1)
+ ая2рс^>
■ «лзМ
Д*+1)
+ -+«лл-1
Сл-1
|+аллхлЛ)+рл.
В каждое последующее уравнение подставляются значения неизвестных,
полученных из предыдущих уравнений, что показано в записи (1.20) стрелками.
Теорема 1.4 (о достаточном условии сходимости метода Зейделя).
Если для системы х = cue + р какая-либо норма матрицы а меньше единицы,
т.е. ||<х|| < 1 (s е {1,2,3}), то процесс последовательных приближений (1.20)
сходится к единственному решению исходной системы Ах-b при любом начальном
приближении х^К
Записывая (1.20) в матричной форме, получаем
*(*+!> =ZJC<*+1)+£/x(*)+p,
где L, U являются разложениями матрицы a:
(1.21)
f 0
a21
«31
^«л1
0
0
«32
«л2
0 .
0
0
«лЗ '
•• 0^
.. 0
•• 0
■■ °>
, u =
'«11
0
0
,0
«12
«22
0
0
«13 •
a23 •
«33 •
0 •
" «In
" «2л
" «Зл
•' «лл
Преобразуя (1.21) к виду х = ах + р, получаем матричную форму
итерационного процесса метода Зейделя:
x(k+l) =(£ - L)'lU х<*> +(£ - L)-lp.
(1.22)
Тогда достаточное, а также необходимое и достаточное условия сходимости
будут соответственно такими (см. теоремы 1.1 и 1.2):
||<х|| = ||(£-1)-'г/|<1, |М«)| = |Ф-£ГЧ|<1-
Замечания.
1. Для обеспечения сходимости метода Зейделя требуется преобразовать
систему Ах = b к виду х = ax + р с преобладанием диагональных элементов в
матрице а (см. метод простых итераций).
51

Например, в системе
2хх + х2 = 2,
*! - 2х2 = -2
диагональные элементы преобладают, так как |2| > 1, |- 2| > 1.
Соотношения метода Зейделя (1.20) принимают вид
„<*+!)
Лк)
-+1,
,(*+1>
-+1.
Выберем в качестве начального приближения х(0) =(0;0)г (рис. 1.5,а). То-
Л0)
гда
х.(1) = —— + 1 = 1. Так как при этом xi0) = 0 , то вычислению х.(1)
соответствует движение по горизонтали до пересечения с прямой, описываемой первым
уравнением. Далее х^ =—— +1 = —. Вычислению х^ соответствует движение
по вертикали до пересечения с прямой, описываемой вторым уравнением.
Продолжая вычисления, получаем xf
(2) -.
4° .3,1
Л2)
т+1:
1 9
= — +1 = — и т.д. В результате имеем процесс, сходящийся к точке х,
о о
"(ИГ-
2х{ + х2
Ху - 2х2 = -2 ^
^-2
*2
= 2
\
2'
1
х(0)
0
\ «- --yf^
\ ^
l\
*1
Рис. 1.5
52

Переставим уравнения в системе:
xj -2х2 =-2,
2xj + jc2 = 2.
В полученной системе диагональные элементы не преобладают. Уравнения
метода Зейделя имеют вид
*<*+1>=2х<*>-2,
х<*+1)=_2х<*+1)+2
При дс*0) = (0 ;0)г получаем xf!)=-2, дс^ = 6 и т.д. В результате имеем
расходящийся процесс (рис. 1.5,6).
2. Условие преобладания диагональных элементов является достаточным
для сходимости, но не является необходимым.
Например, в системе
*! + 2х2 = 3,
Х| - 4х2 = -3
в первом уравнении диагональный элемент не является преобладающим, а
процесс итераций по методу Зейделя сходится (рис 1.6).
Рис. 1.6
3. Процесс (1.20) называется последовательным итерированием, так как на
каждой итерации полученные из предыдущих уравнений значения подставляются
в последующие. Как правило, метод Зейделя обеспечивает лучшую сходимость,
чем метод простых итераций (за счет накопления информации, полученной при
решении предыдущих уравнений). Метод Зейделя может сходиться, если
расходится метод простых итераций, и наоборот.
53

4. При расчетах на ЭВМ удобнее пользоваться формулой (1.22).
5. Преимуществом метода Зейделя, как и метода простых итераций,
является его самоисправляемость.
6. Метод Зейделя имеет преимущества перед методом простых итераций,
так как он всегда сходится для нормальных систем линейных алгебраических
уравнений, т.е. таких систем, в которых матрица А является симметрической и
положительно определенной. Систему линейных алгебраических уравнений с
невырожденной матрицей А всегда можно преобразовать к нормальной, если ее
умножить слева на матрицу АТ. Таким образом, система АтАх = АтЬ является
нормальной, а матрица АтА - симметрической.
Методика решения задачи
1. Преобразовать систему Ах = b к виду х = сие + р одним из описанных
способов.
2. Задать начальное приближение решения х(0) произвольно или положить
х*0) = р, а также малое положительное число е (точность). Положить к = 0.
3. Произвести расчеты по формуле (1.20) или (1.21) и найти х(*+1).
4. Если выполнено условие окончания х(*+1) - х^кЧ < г, процесс
завершить и положить хф s х^к+1К Иначе положить к = к + 1 и перейти к п.З.
Пример 1.12. Методом Зейделя с точностью е = 0,001 решить систему
линейных алгебраических уравнений:
2xj +2х2 +10х3 = 14,
lOxj + х2 + *з =12,
2хх + 10*2 + *з = 13.
D 1. Приведем систему Ах = Ь к виду дс = <хх + р так же, как в примере
1.11:
хх =-0,1х2 -0,1х3 +1,2,
х2 - - 0,2 • х{ - 0,1 • ху + 1,3,
х3 = - 0,2 • хх - 0,2 • х2 +1,4;
/
0 -0,1 -0,Г|
-0,2 0 -0,1
^-0,2 -0,2 0 J
Р =
Так как Ца^ = max {0,2; 0,3; 0,4 } = 0,4 < 1, условие сходимости выполняется.
2. Зададим х(0) = (1,2;0;0)г. В поставленной задаче е = 0,001.
3. Выполним расчеты по формуле (1.20):
х{к+1)=-0,1х(2к) -0,1х<*> + 1,2;
х<*+1) = -0,2х(*+1) - 0,1х<* > +1,3; к = 0,1,...,
х<*+1) = -0,2х<*+1) -0,2х<*+1) + 1,4;
и результаты занесем в табл. 1.6.
54

Таблица 1.6
к
0
1
2
3
[ 4
1,2000
1,2000
0,9992
0,9996
1,0000
v<*)
0
1,0600
1,0054
1,0002
1,0000
х(к)
0
0,9480
0,9991
1,0000
1^0000
И'-*'*-1!
|
1,0600
0,1008
0,0052
0,0004<б ]
Очевидно, найденное решение х, = (1;1;1)г является точным.
4. Расчет завершен, поскольку условие окончания х(*+1) - х^кЧ - 0,0004 < е
выполнено. ■
Пример 1.13. Методом Зейделя с точностью е = 0,005 решить систему
линейных алгебраических уравнений:
4х1 - х2 + х3 =4,
Xj + 6х2 + 2х3 = 9,
- Xj - 2х2 + 5х3 = 2.
□ 1. Так как |4| > |-1| + |l|, |6|>|l| + |2|, |5| >|-l| + |-2|, в данной системе
диагональные элементы преобладают. Выразим из первого уравнения х{, из
второго х2, из третьего х3:
1 1 1
7х2--х3+1,
4 4
1
1
*2=-?х,-Г3+7'
— Xi + —х? +—:
5 l 5 2 5'
л 1
0 -
4
1 л
? °
1 2
5 5
П
4
1
~3
0
)
; Р =
гч
-\
2
2
1л1
2. Зададим х(0) = (0; 0; 0)г. В поставленной задаче £ = 0,005.
3. Выполним расчеты по формулам (1.20):
х\ ~ 4*2 4*з +1>
x<*+1>=-±x<*+I>-Ixf>+|; * = 0д,...,
xf+I>=±x<*+14^x<*+,>+l;
и результаты занесем в табл. 1.7.
55

Таблица 1.7
1 к
0
1
2
3
4
5
х\
0
1,0000
1,0500
0,9896
1,0010
1,0000
т(к)
0
1,3333
0,9473
1,0050
0,9999
1,0000
Y(k)
0
1,1333
0,9889
0,9999
1,0000
1,0000
|х<*>_х<*-1>|
-
1,3333
0,3860
0,0604
0,0114
0,0010<£
Очевидно, найденное решение х, = (1;1;1)г является точным.
4. Расчет завершен, поскольку условие окончания х(*+1) -х^ =0,001 <е
выполнено."
Пример 1.14. Для системы линейных алгебраических уравнений
jcj + 2х2 - 3,
3jtj н- 4jc2 = 7
построить сходящийся итерационный процесс.
(\ 2\
П 1. Матрица А = этой системы не имеет диагонального
преобладания. Достаточное условие сходимости метода простых итераций ||а||<1 не
выполняется. Поэтому сначала проведем нормализацию исходной СЛАУ с
помощью умножения слева на матрицу Ат. Проделав умножение
Б % Ш 90-
получим
Полученная матрица А
Юх{ + 14х2 = 24,
14х, +20х2 =34.
(10 14^
~[l4 20j
является симметрической и положительно
определенной, так как угловые миноры положительны: Ai = 10 > 0,
д2 = И | = 200 -142 = 4 > 0. Поэтому система является нормальной, а для нее
метод Зейделя сходится.
2. Положим х(0) = (2,4;1,02)г.
3. Расчеты произведем по формулам (1.20):
х{к+1) =-1,4x^+2,4,
x<*+1)=-0,7jc|*+i)+1,7.
56

Таким образом, L ■■
О 0^ ГО -1,4^
•0,7 О)' {О О J
Р =
2,4
1,7
Последовательные приближения, получаемые методом Зейделя, приведены
в табл. 1.8.
Таблица 1.8
к
0
1
2
3
4
| 5
Y(*)
2,40000
0,97200
0,97256
0,97311
0,97365
0,97418
*2
1,02000
1,01960
1,019208
1,018823
1,018445
1,018076
р)_х(*-1)|
|
1,42800
0,00056
0,00055
0,00054
0,00053 |
Из табл. 1.8 видно, что норма разности между двумя последовательными
приближениями с увеличением номера итерации уменьшается, что характеризует
сходящийся процесс (этот вывод относится ко всем приведенным примерам).
Видно также, что, начиная со 2-й итерации, х\к) и х^ с увеличением к
увеличиваются и уменьшаются соответственно, и они стремятся к верному (точному)
решению: х^ = 1; х2„ = 1."
Пример 1.15. Решить систему
Х| - х2 + х3 - 4х4 = -2,
2хх + х2 - 5х3 + х4 = 2,
8*! - х2 - х3 + 2х4 =Н,
Xi + 6х2 - 2х3 - 2х4 = -7
методами простых итераций и Зейделя.
□ 1. Переставляя уравнения местами, преобразуем систему к виду с
преобладанием диагональных элементов:
8*1 - *2 " *з + 2х4 =11,
Х| + 6х2 - 2х3 - 2х4 = -7,
2xj + х2 - 5х3 + х4 = 2,
X! - х2 + х3 - 4х4 = -2.
Так как |8| > |- l| + |- l| + |2|, |б| > |l| + |-2| + |-2|,
|-5|>|2| + |1| + |1|, |-4|>|l| + |-l| + |l|,
то условие преобладания диагональных элементов выполняется.
2. Выразим из первого уравнения jq, из второго х2, из третьего х3, а из
четвертого х4:
57

1 1 1 11
Х1=Г2 + 8ХЗ~4Х4+Т'
Х2="бХ1 + зХз + зХ4"б5
*3 = *7Х1 +7*2 + Т*4 -Т»
X4 = 4Xl"4X2 + 4X3 + 2'
3. Зададим начальное приближение х*0' = (0; 0; 1; 2)гие = 0,001.
Расчеты методом простых итераций выполним по следующим формулам
(результаты приведены в табл. 1.9, где А = х(А:) -дс(Л_1) ):
х(*+0 *(*) 1 (*) _1 (*) Л
1 8 2 8 3 4 4 8 '
х(*+0 - _IXW Дх(*) +IXW _Z
Х2 " 6 1 3 3 3 4 6'
х(^\) .1х(к) ,1х(к) +1 (к) _2
*3 -5*1 + 5*2 + 5*4 5>
Таблица 1.9
пг
*1
*2
*3
х4
д
0
0
0
1
2
-
1
1
-0,1667
0
0,75
1,25
2
1,1667
-1,0833
0,1166
0,7916
0,9166
3
1,0562
-1,0583
0,0083
1,0916
0,3
4
0,9708
-0,9760
0,02916
1,0307
0,0854
5
0.9989
-0,9752
-0,0007
0,9940
0,0367
6
1,0045
-1,0021
0,003
0,9933
0,0269
7
1,0018
-1,0019
0,00006
1,0025
0,009
8
0,9992
-0,9995
0,0008
1,0009
0,0024
9
0,99994
-0,9993
-0,00004
0,99986
0.00104
10 |
1,0001
-1,0000
0,00009
0,99979
0,0007
Расчеты методом Зейделя выполним по формулам (результаты приведены
в табл. 1.10):
х(*+0 * (*) +Lx(k) 1 (*) + Д
1 8 2 8 3 4 4 8 '
х(*+1) _ _Iv(*+0 +Iv(*) ЛХМ JL
х2 ~ 6xi +3 3 3 4 6'
x(k + l) -lx(k+l) ,Lx(k+l) I (к) _ 2
х3 ~ 5 х1 5 2 5 4 5'
х(*+0 = Ix(* + D _ J r(*+0 + Ix(* + 0 +I
4 4 1 4 2 4 3 2-
58

Таблица 1.10
к
*\
*2
*3
хА
1 Д
0
0
0
1
2
-
1
1
-0,3333
0,3333
0,9166
1,083
2
1,1458
-0,9409
0,0534
1,0351
0,6075
3
1,0052
-0,9713
0,0148
0,9978
0,1406_
4
1,0059
-0,9967
0,0026
1,0013
0,0254
5
1,0004
-0,9988
0,00067
0,99995
0,0055
6
1,00025
-0,9998
0,000125
1,00005
_0100_Ц_.
7
1,0002
-0,9999
0,00003
0,999999
0,00023 |
Методом простых итераций
хщ z (1,0001; -1,0000; 0,00009; 0,99979)г,
получено приближенное решение
а методом Зейделя решение:
хт = (1,0002; - 0,9999; 0,00003; 0,99999)' . Точное решение: х. = (1; -1;0; I)7
видно, метод Зейделя сошелся за меньшее число итераций.■
Оче-
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Найти численное решение систем, характеризующихся расширенными
матрицами А\, методом Гаусса единственного деления:
1)
5)
9)
13)
17)
21)
Г 5 0 1 1П
13-1 4
1-3 2 10 6 J
Г 3 1-1 П
-2 4 1 5
{ 1 1 3-3J
'4 1-1 7]
2 3 0 7
[\-\ 5 11 J
(3 0-1-4
2-5 1 9
1 2-2 6 8
(3 1 0,5 7,5
13 16
[l 1 4 7
Mil 9 ]
1 5 1 14
I 2 2 5 21J
f
; 2)
; 6)
V
; 10)
;14)
J
; 18)
)
2 0-1-3
-13 12
1-1 4 3
3 1-1 6]
2 4 1 9 ;
1-1 3 4 J
'2 0-1 1
1-4 2 -;
, 1 1 3 (
Mil 9 ]
1 5 1 14
I 2 2 5 21J
[ 3 4 5 26]
2 11 7
I 4 3 7 31J
Л f
; 3)
) \
f
7)
V
5 ;H)
>)
; 15)
; 19)
2 0-1 1N
1-3 12
11 3 4 >
2-1 0-2'
2 5-2-4
1-13 2,
(2-1 0 3
0 5 2 7
ll-l 3 4
f 3 1 1 вл
14 2 9
{ 2 2 5 IAJ
[5 1 2 12]
2 4 1 16
ll 1 4 12 J
; 4)
\ (
; 8)
;12)
)
; 16)
; 20)
-l
l
0
-l
f3
3
12
(2
1
ll
( 3
2
l-l-5>
3 1 5
-2 4 1,
-1 1 n
2-1 3
1 5-5J
1-1-2]
5-18
0 3 1 J
1 0 4]
3 19;
1 4 11J
1 5 2П
117;
3 7 25j
59

2. Дана система с трехдиагональной матрицей А:
2х{ + х2
5 1 м
— + — •#,
2 3
*1 + Зх2 + х3
17 1 л/
- 2х2 + Зх3 + х4 = 1,
х3-2х4 =--+-•#,
где N — параметр, соответствующий номеру по списку группы.
Требуется:
а) убедиться, что матрица А этой системы, если ее представить в виде
Ах = b, трехдиагональная и удовлетворяет условию преобладания диагональных
элементов;
б) решить систему методом прогонки;
в) подстановкой полученного решения в исходную систему убедиться
в правильности результата.
3. Методом простых итераций решить систему линейных алгебраических
уравнений Ах = Ъ, где
(5 1 1]
2 6 -1
2 3 10
£ =
(11 + 0,8.ЛГ|
13 + 0,9-ЛЧ
18-0,5 -N)
предварительно вычислив количество
(N — параметр) с точностью z = 0,001,
итераций по формуле (1.19).
4. Сравнить количество итераций, требующихся для получения решения
системы Ах = b, где
'12 -3 2 -\\ ^^
-16-11
3 2-82
.2 -1 -1 5)
А =
Ъ =
12
-9
U7J
методом простых итераций и методом Зейделя с точностью е = 0,001, прекратив
итерационный процесс апостериорным путем.
5. Методом Зейделя с точностью е = 0,001 найти решение двух систем
линейных алгебраических уравнений, преобразуя их предварительно к виду,
обеспечивающему сходимость:
Ах =
Г 2,7 9,3 1,3 N
3,5 1,7 2,8
[4,1 5,8 -1,7,
, А| =
'2,Г
1,7
м
; л2 =
Г 1,7
2,1
[4,2
-2,8 1,9Ч
3,4 1,8
-1,7 1,3,
• *2 =
Г0,7>
м
[2,8 J
60

Глава 2. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ О СОБСТВЕННЫХ
ЗНАЧЕНИЯХ И СОБСТВЕННЫХ ВЕКТОРАХ МАТРИЦ
2.1. ПОСТАНОВКА ЗАДАЧИ
Пусть А - действительная числовая квадратная матрица размера (пхп).
Ненулевой вектор X = (хь...,л:Л)г размера (лх1), удовлетворяющий условию
АХ = ХХ, (2.1)
называется собственным вектором матрицы А. Число X в равенстве (2.1)
называется собственным значением. Говорят, что собственный вектор X соответствует
(принадлежит) собственному значению X.
Равенство (2.1) равносильно однородной относительно X системе:
(A-XE)X=Of (Х*0). (2.2)
Система (2.2) имеет ненулевое решение для вектора ^(при известном X)
при условии \А - ХЕ\ = 0. Это равенство есть характеристическое уравнение:
\А-ХЕ\ = Рп(Х) = 0, (2.3)
где Рп(Х) — характеристический многочлен п-й степени. Корни Я.1Д2,...,А.Я
характеристического уравнения (2.3) являются собственными
(характеристическими) значениями матрицы А, а соответствующие каждому собственному
значению Xh i = l,...,/i, ненулевые векторы X1, удовлетворяющие системе
АХ* = Х>Х* или (А-Х;Е)Х1 = 0, / = 1,2,...,я, (2.4)
являются собственными векторами.
Требуется найти собственные значения и собственные векторы заданной
матрицы. Поставленная задача часто именуется второй задачей линейной алгебры.
Проблема собственных значений (частот) возникает при анализе поведения
мостов, зданий, летательных аппаратов и других конструкций,
характеризующихся малыми смещениями от положения равновесия, а также при анализе
устойчивости численных схем. Характеристическое уравнение вместе с его собственными
значениями и собственными векторами является основным в теории
механических или электрических колебаний на макроскопическом или микроскопическом
уровнях.
Различают полную и частичную проблему собственных значений, когда
необходимо найти весь спектр (все собственные значения) и собственные векторы
либо часть спектра, например: р(А) = тах|А.;(Л)| и тт|Я./(>4)|. Величина р(А)
' i
называется спектральным радиусом.
Замечания.
1. Если для собственного значения А./ найден собственный вектор X1, то
вектор \\Х1, где ц— произвольное число, также является собственным вектором,
соответствующим этому же собственному значению Ху.
2. Попарно различным собственным значениям соответствуют линейно
независимые собственные векторы; &-кратному корню характеристического
уравнения соответствует не более к линейно независимых собственных векторов.
61

3. Симметрическая матрица имеет полный спектр Xt, / = 1, п,
действительных собственных значений; fc-кратному корню характеристического уравнения
симметрической матрицы соответствует ровно к линейно независимых
собственных векторов.
4. Положительно определенная симметрическая матрица имеет полный
спектр действительных положительных собственных значений.
2.2. МЕТОД НЕПОСРЕДСТВЕННОГО РАЗВЕРТЫВАНИЯ
Полную проблему собственных значений для матриц невысокого порядка
(п < 10) можно решить методом непосредственного развертывания. В этом случае
будем иметь
\ап-Х ап ахг ... аХп
\А - ХЕ\ = °21 ап "^ °23 "' °2п
I ап\ ап2 апЪ •• апп-
Уравнение Рп(к) = 0 является нелинейным (методы его решения изложены
в следующем разделе). Его решение дает л, вообще говоря, комплексных
собственных значений X.1}X2A3vA,i> ПРИ которых Рп(\{) = 0 (/ = 1,л). Для каждого
Xj может быть найдено решение однородной системы (A-\tE)Xl =0, / = 1,л.
Эти решения X1, определенные с точностью до произвольной константы,
образуют систему л, вообще говоря, различных векторов п-мерного пространства.
В некоторых задачах несколько этих векторов (или все) могут совпадать.
Методика решения задачи
1. Для заданной матрицы А составить характеристическое уравнение (2.5):
|Л-А,£| = 0.
Для развертывания детерминанта \А - ХЕ\ можно использовать различные
методы, например метод Крылова, метод Данилевского или другие методы [2,9,14].
2. Решить характеристическое уравнение и найти собственные значения
А.!,А,2»—Ля- Для этого можно применить методы, изложенные в разд.3.1.
3. Для каждого собственного значения составить систему (2.4):
(A-XiE)Xi =0, / = 1,2,..., л,
и найти собственные векторы X1.
= />„(х) = 0. (2.5)
62

Замечание. Каждому собственному значению соответствует один или
несколько векторов. Поскольку определитель l^-X/^l системы равен нулю, то
ранг матрицы системы меньше числа неизвестных: T3.ng(A-XiE) = г < п и в
системе имеется ровно г независимых уравнений, а (я - г) уравнений являются
зависимыми. Для нахождения решения системы следует выбрать г уравнений с г
неизвестными так, чтобы определитель составленной системы был отличен от
нуля. Остальные (п - г) неизвестных следует перенести в правую часть и считать
параметрами. Придавая параметрам различные значения, можно получить
различные решения системы. Для простоты, как правило, попеременно полагают
значение одного параметра равным 1, а остальные равными 0.
Пример 2.1. Найти собственные значения и собственные векторы матрицы
Ле^,где„=(_34 "/J.
□ Воспользуемся методикой.
1. Запишем уравнение (2.5): |Л-А.£|:
3-А. -2
1-4 1 — Х|
получаем характеристическое уравнение Р2(Х) = Х2-4Х-5 = 0.
X2 - 4Х - 5 = 0, отсюда
2. Находим его корни (собственные значения): Х{ = 5Д2 = -1.
3. Составим систему (A-XiE)Xl = 0, / = 1,2, для каждого собственного
значения и найдем собственные векторы:
(Ъ-Хх -2
-4 1-Х*
*1
= 0
или
-2*1-2x1
-4х\-4х12
0,
0.
Отсюда х\ = -х2. Если х\ = ц, то х\
ц. В результате получаем
*'=Ы.**Г = М-1;1)}Г.
Для Х2 = -1 имеем
3 - Х2 - 2
-4 \-Х2
2\
Х\\
хг)
или
4х? - 2х\ =
-4x1+2x1
0.
Отсюда х\ = 2х2. Если х2 = ц, то х\ = 2ц. В результате получаем
*2 = {*?•** Г-Ми2)}г,
где \i— произвольное действительное число.■
63

Пример 2.2. Найти собственные значения и собственные векторы матрицы
(2 -1 П
Л =
-1 2 -1
О 0 1
□ Воспользуемся методикой.
1. Запишем характеристическое уравнение (2.5):
\2-Х -1 1
-1 2-Х -1
О О 1-Х
= 0 или
(l-X)[(2-^-l]=0.
2. Корни характеристического уравнения: Х12 = 1 (кратный корень), Я.3 = 3
— собственные значения матрицы.
3. Найдем собственные векторы.
Для Х]2 =1 запишем системууА - Х} 2Е)- X1,2 =0:
(\ -1 \)
-1 1 -1
[о о о)
системе
0 или х|'2 = *2'2 - *з
( 1 2Л
1,2
х2
V J )
= 0.
имеется одно независимое уравне-
Поскольку хгп%{А -Хх2Е)= 1, в систек
ние jcj1,2 - х^'2 + xj'2 = 0 или х{'2 = х^'2 - х]'2.
Полагая х^2 = 1, х]'2 = 0, получаем xj'2 = 1 и собственный вектор Х{
Полагая х2'2 = 0, х]2 = 1, получаем xj'2 = -1 и другой собственный вектор
(\
\.Ь
о
Для собственного значения Х3
-1 -1 -1
. Заметим, что оба собственных вектора линейно независимы.
3 запишем систему (А - Х^Е)- X2 = 0:
г3
V3 I
*3J
= 0.
0 0 -2)
Поскольку rang(.4 - Х^Е) = 2, то выбираем два уравнения:
- х,3 - х\ + х] = 0 , - 2х33 = С
Отсюда х| = 0, х3 = -х\. Полагая х\ = 1, получаем х3
(-\Л
тор X3 = 1 Л
Ы
3 = -1 и собственный век-
64

2.3. МЕТОД ИТЕРАЦИЙ
Для решения частичной проблемы собственных значений и собственных
векторов в практических расчетах часто используется метод итераций (степенной
метод). На его основе можно определить приближенно собственные значения
матрицы А и спектральный радиус р(А) = max | Xt(A) |.
Пусть матрица А имеет п линейно независимых собственных векторов
Xl,i = lyn, и собственные значения матрицы А таковы, что
р(А) = \х1(А)\>\х2(А)\>...>\хп(А)\-
Методика решения задачи
1. Выбрать произвольное начальное (нулевое) приближение собственного
вектора (второй индекс в скобках здесь и ниже указывает номер
приближения, а первый индекс без скобок соответствует номеру собственного
значения). Положить к = 0.
ХК1)
2. Найти Хт = АХт, Х(Р = -j-т-, где / - любой номер 1 < i < п, и поло-
жить к = 1.
3. Вычислить *1(*+1) = АХт.
х|<*+1)
4. Найти А.(*+1) = ' , где х]^к+1\х]^ - соответствующие координаты
xi
векторов х1(-к+1^ и Х1^кК При этом может быть использована любая координата
с номером /, / = 1, п.
5. Если А = Я.(*+1) -хЩ < е, процесс завершить и положить Х{ s А.(*+1).
Если А > 6, положить к = к +1 и перейти к п.З.
Замечания.
1. Процесс последовательных приближений
ХШ) = АХт, Х1(2) = АХт = А2Хт,...,
Хт =АХКк~1) =А-Ак~1Хт =АкХт,...
сходится, т.е. при к -> оо вектор стремится к собственному вектору X .
Действительно, разложим Аг1(0) по всбм собственным векторам: Аг1(0) = ^с{Х!.
Так как, согласно (2.4), АХ1 = XtXl, то
АХ™ = *1(1) = tcfaX1; АХ™ = Л2*1**» = X1™ = £*/*.?*',...,
/=i i-i
65

АкХ^^Х^^с,\к1Х,'А
eiXl+c2\-f\ X'+...+с,
к
Хп
При большом к дроби — ,...,— малы и поэтому АкХт = схх\Хх,
J(*+D
т.е. Хнк) -> Xх при £ -> оо. Одновременно Хх = lim —'- .
2. Вместо применяемой в п.4 методики формулы для х\ + ' можно взять
среднее арифметическое соответствующих отношений для разных координат.
3. Метод может использоваться и в случае, если наибольшее по модулю
собственное значение матрицы А является кратным, т.е.
A.j = Х2 = ... = Xs, и |Х]| >\Хк\ при /: >s.
4. При неудачном выборе начального приближения Аг1(0) предел отноше-
VK*+D
может не существовать. В этом случае следует задать другое началь-
ния
,К*>
ное приближение.
5. Рассмотренный итерационный процесс для Х{ сходится линейно
с параметром с = — и может быть очень медленным. Для его ускорения исполь-
зуется алгоритм Эйткена.
6. Если А = АТ (матрица А симметрическая), то сходимость процесса при
определении р(А) может быть ускорена.
7. Используя Х{, можно определить следующее значение Х2 по формуле
Я., =
хЦ'+Ъ-Ъх
Ч^/
\(к)
xjM-\lX}<k-l>
(i = lf2,...,/i).
Эта формула дает грубые значения для Х2, так как значение Х\ является
приближенным. Если модули всех собственных значений различны, то на основе
последней формулы можно вычислять и остальные Xj(j = 3,4,...,л).
8. После проведения некоторого числа итераций рекомендуется «гасить»
растущие компоненты получающегося собственного вектора. Это осуществляется
Хт
нормировкой вектора, например, по формуле
Пример 2.3. Для матрицы А =
пенным методом с точностью е = 0,1.
5 1 2"!
1 4 1
2 1 3
хт
найти спектральный радиус сте-
66

□ 1. Выбирается начальное приближение собственного вектора
Х{0) = (1; 1; if. Положим к = 0.
2. Найдем
XW=AXW =
(5 1 2^
1 4 1
[2 1 3j
(Т|
1
W
=
f8l
6
w
x?>
^ 8
ci(0) 1
= 8,
положим к = 1.
3. Вычислим
^2) = ^л-"1> =
f5 1 2)
1 4 1
U ! 3J
f8l
6
k
=
f58l
38
40;
4. Найдем
l(2).
,1(2)
4
Л = 7,25.
5. Так как Ы^ - хЩ = 0,75 > e , то процесс необходимо продолжить.
Результаты вычислений удобно представить в виде табл. 2.1.
Таблица 2.1
*
0
1
2
3
I 4
ГК*)
1
8
58
408
2838
УК*)
1
6
38
250
1682
хЦк)
1
6
40
274
1888
Х<*>
-
8
7,25
7,034
6,9559
1 а<*> №-v
|л1 ~л1
|
-
0,75
0,116
0,078 < 6
Точность по Х^ достигнута на четвертой итерации. Таким образом, в
качестве приближенного значения \х берется 6,9559, а в качестве собственного
вектора принимается Xх = (2838, 1682, 1888) . Так как собственный вектор
определяется с точностью до постоянного множителя, то Xх лучше
пронормировать, т.е. поделить все его компоненты на величину нормы. Для рассматривав-
f 2838^1 ( 1,000 ^
мого примера получим Xх
1
2838
1682
1888
0,5927
l^0,6652j
Согласно замечаниям, в качестве собственного значения Х} можно взять
J(4)
не только отношение
2838
КР) 408
6,9559, но и
г1(4)
1682
cl(3) 250
= 6,7280;
67

rl(4)
1888
,.-. = = 6,8905, а также их среднее арифметическое
xi(3) 274
6,9559 + 6,728 + 6,8905
= 6,8581.
Пример 2.4. Найти максимальное по модулю собственное значение матри-
(2 -1 О
цы А =
и соответствующий собственный вектор.
1-1 2 -1]
0 0 3^
□ 1. Зададим начальное приближение Лг1(0) = (1; -1; if и е = 0,0001.
Выполним расчеты согласно методике (табл. 2.2).
Таблица 2.2
1 к
0
1
2
3
4
5
6
7
8
9
1 ю
YK*)
1
4
13
40
121
364
1093
3280
9841
29524
88573
YHk)
-1
-4
-13
-40
-121
-364
-1093
-3280
-9841
-29524
-88573
х\Ю
х\к)
-
4
3,25
3,0769
3,025
3,00826
3,002747
3,000914
3,000304
3,000101
3,000034
^-х?-»!
-
-
0,75
0,17307
0,0519
0,01673
0,005512
0,00183
0,000609
0,000202
0,000067 1
В результате получено собственное значение Х\ = 3,00003 и собственный
вектор
1
Xх =(88573; -88573; if
или
после нормировки
X1 =
88573
(88573; -88573; \)т = (1; -1; 0,0000113)г (сравните с примером 2.2).1
2.4. МЕТОД ВРАЩЕНИЙ
Метод используется для решения полной проблемы собственных значений
симметрической матрицы и основан на преобразовании подобия исходной
матрицы А е Rnxn с помощью ортогональной матрицы Н.
Две матрицы А и Л(/) называются подобными (А~А{1)или Л(/)~Л), если
А^ = Я-1АН или А = НА^Н'1, где Н — невырожденная матрица.
В методе вращений в качестве Н берется ортогональная матрица, такая,
что ННТ - НтН = Е, т.е. Нт = Я"1. В силу свойства ортогонального преобра-
68

зования евклидова норма исходной матрицы А не меняется. Для
преобразованной матрицы А^ сохраняется ее след и собственные значения X,:
При реализации метода вращений преобразование подобия применяется
к исходной матрице А многократно:
Л<*+1> = (#<*>)~V>#<*> = (tf<*>JV>tf<*>, * = 0,1,.... (2.6)
Формула (2.6) определяет итерационный процесс, где начальное
приближение Л(0) = А. На каждой к -й итерации для некоторого выбираемого при
решении задачи недиагонального элемента ajV, / * j, определяется ортогональная
матрица #(*\ приводящая этот элемент ajk*l) (а также и fljf+1*) к нулю. При
этом на каждой итерации в качестве ajP выбирается наибольший по модулю.
Матрица #(*\ называемая матрицей вращения Якоби, зависит от угла ф^ и
имеет вид
(\
#<*>
0
0
о
1 о о
0 coscp(A:) 0
0 0 1
0 0 0
0 sin у(к) 0
0 0 0
0
- sin ф'
0
0
.<*> 0
0
1 0 0
0 С08ф(*} 0
0 0 1
0 -. 1
i -я строка
j -я строка
0 0 .. 0 0
t t
i -й столбец j -й столбец
В данной ортогональной матрице элементы на главной диагонали
единичные, кроме Л<*} =С05ф(*} и hf} = cos<pik), a h]k) = -shV*\ AJf} =8Шф(А:) (h0 ~
элементы матрицы Н).
Угол поворота ф(Л) определяется по формуле
tg29'
(к) _
2<#>
*(*>=!
^)-^)=^; ^ = 2arCtg^'
(2.7)
где 2ф**ч <—, i < j (atj выбирается в верхней треугольной наддиагональной
части матрицы А) .
В процессе итераций сумма квадратов всех недиагональных элементов
с(А^) при возрастании к уменьшается, так что а(у4**+1*) < а(А^). Элементы
69

ajf\ приведенные к нулю на к-й итерации, на последующей итерации немного
возрастают. При к -* оо получается монотонно убывающая ограниченная снизу
нулем последовательность а(Л(1)) >а(А(2)) > • •• > а(Л(А:)) •■•. Поэтому а(А^)-+0
fh
при к -> оо. Это и означает сходимость метода. При этомЛ^ -> Л =
<П
.0 К)
Замечание. В двумерном пространстве с введенной в нем системой
координат Оху с ортонормированным базисом I i, j > матрица вращения легко
получается из рис. 2.1. , где система координат Ox'y' повернута на угол <р:
-> -* ->
/' = / cos ф + j sin ф,
-► -> -*
/ = - / sin ф + j cos ф.
У
Рис. 2.1
Таким образом, для компонент /',/ будем иметь
' ,У
'>./
[С08ф - Sin ф |
1^тф со8ф/
Отсюда следует, что в двумерном пространстве матрица вращения имеет вид
_^С05ф -БШф^
(зШф С05фу*
Отметим, что при п - 2 для решения задачи требуется одна итерация.
Методика решения задачи
1. Положить к = 0, Л(0) = А и задать е > 0.
2. Выделить в верхней треугольной наддиагональной части матрицы Л^к)
максимальный по модулю элемент ajk\ i < j.
70

Если \ajjk)\ ^ е для всех / * у, процесс завершить. Собственные значения
определяются по формуле Xi[A<-k)j= а\к\ i = 1, л.
Собственные векторы X1 находятся как / -е столбцы матрицы,
получающейся в результате перемножения:
у, = я(0)я(|)я(2)-.я^=(1и2Д3,..Дл).
Если \ajjk)\ > е, процесс продолжается.
3. Найти угол поворота по формуле
<*) * . Нк)
4. Составить матрицу вращения Н^к\
5. Вычислить очередное приближение
л<*+,>=(//<*>е>>//<*>.
Положить к = к + 1 и перейти к п.2.
Замечания.
- MP
1. Используя обозначение Рк = , можно в п.З методики вычис-
лять элементы матрицы вращения по формулам
sin ф(/:) = sign /^ • / —
■ /1(1-1,), cos9») = /1(1+»»).
2. Контроль правильности выполнения действий по каждому повороту
осуществляется путем проверки сохранения следа преобразуемой матрицы .
(2 П
методом вращений найти собственные
Пример 2.5. Для матрицы А
значения и собственные векторы.
□ 1. Положим к = О, А(0)=А=Г Ч.е^НГ10.
2°. Выше главной диагонали имеется только один элемент ац = д12 =1.
3°. Находим угол поворота матрицы по формуле (2.7), используя в
расчетах 11 цифр после запятой в соответствии с заданной точностью:
tg2<p(0)=—^ = -2т = _2; sin Ф(0) = - 0,52573111212; cosФ(0) = 0,85065080835.
аи -ам 2-3
4°. Сформируем матрицу вращения:
( 0,85065080835 0,52573111212")
[-0,52573111212 0,85065080835/
//(0) = fcos ф(0) - sin ф(0)
~Un<p(0) coscp<°>
71

5°. Выполним первую итерацию:
(0,85065080835 -0,52573 И1212 Y2 IV 0,85065080835 0,52573111212^
"1^0,52573111212 0,85065080835 J[l ЗД-0,52573111212 0,85065080835; =
= ( 1,38196601125 - 4,04620781325.10"12
[- 4,04587474634 ■ 1<Г12 3,61803398874
Очевидно, след матрицы с заданной точностью сохраняется, т.е.
2 2
Ша$Р ~ Хо/#0) = ^- Положим Ы и перейдем к п.2.
/-I /»1
21. Максимальный по модулю наддиагональный элемент
|д12| = 4,04620781325 10~12 < е = 10~10. Для решения задачи (подчеркнем, что
п = 2) с принятой точностью потребовалась одна итерация, полученную матрицу
можно считать диагональной. Найдены следующие собственные значения и
собственные векторы:
X, = 1,38196601125; Х2 = 3,61803398874;
, ( 0,85065080835 Л 2 (0,52573111212^1 щ
"[-0,52573111212/ ~[o,85065080835j"
Пример 2.6. Найти собственные значения и собственные векторы матрицы
(5 1 2^
А = \ 14 1.
12 1 V
П 1. Положим к = 0, Аф) =А, е = 0,001.
2°. Выделим максимальный по модулю элемент в наддиагональной части:
а$ = 2. Так как д,3 = 2 > е = 0,001, то процесс продолжается.
3°. Находим угол поворота:
т\ 1 1а\У 1 4 1
Ф<0) = -arctg (Q)J3(0) = -jarctg— = ^arctg2 = 0,553574,
sin <p(0) = 0,52573; cos <p(0) = 0,85065.
4°. Сформируем матрицу вращения: Я(0) =
f 0,85065 0 -0,52573^
0 1 0
[о,52573 0 0,85065 J
72

5°. Выполним первую итерацию:
Л<'> ^<0>)V0>tf<0> =
6,236
1,376
1,376
2,33-10
-6^1
4 0,325
2,33-10~6 0,325 1,764
0)
Положим к = 1 и перейдем к п. 2.
21. Максимальный по модулю наддиагональный элемент а\12} = 1,376. Так
как а[12 > 6, процесс продолжается.
З1. Найдем угол поворота:
<Р0) =^arctg l'°n -larctg 2'1'376 -i-arctg 1,230769 = 0,444239;
2 fl,()-eiV 2 6,236-4 2
41 u22
sin Ф(1) = 0,429770; cos Ф(1) = 0,902937.
41. Сформируем матрицу вращения: Я(1) =
0,902937 -0,429770 й)
0,429770 0,902937 0
0 0 1
51. Выполним вторую итерацию:
( 6,891 2,238-10"4 0,14 "|
a^={h^Ja^h^ =
2,238-10"4 3,345 10,293
0,14 0,293 1,764
Положим к = 2 и перейдем к п.2.
(2)
2 . Максимальный по модулю наддиагональный элемент а% = 0,293 > е
З2. Найдем угол поворота:
п<2>=!
arctg-
2-д(2)
1
■ = —arctg-
2 -0,293 1
*""*<$-<$ 2 ° 3,345 -1,764 2
arctg 0,370651 = 0,177476;
sin Ф(2) = 0,1765460; cos Ф(2) = 0,9842924.
42. Сформируем матрицу вращения #(2*
(\
0
0
0 0,9842924 -0,1765460
^0 0,1765460 0,9842924 J
5 . Выполним третью итерацию:
Г 6,891 0,025
л<3> ^<2>f>>tf <2> =
Положим ЬЗи перейдем к п. 2.
0,138
0,025 3,398 3,375 10~7
(^0,138 3,375-10
-7
1,711
73

25. Максимальный по модулю наддиагональный элемент а\у = 0,138 > г
З3. Найдем угол поворота:
П<3>=:1
arctg-
2я(3)
1 а\ъ
1
■ = — arctg-
2- 0,138 1
2"""0fl{f-flg} 2 6,891 -1,711 2
= -arctg 0,05328 = 0,026615;
sin Ф(3) = 0,026611; cos Ф(3) = 0,999646.
43. Сформируем матрицу вращения: #*3)
53. Выполним четвертую итерацию:
(0,999646 0 -0,026610
0 1 0
[o,0266ll 0 0,999646
a^={h^Ja^h^
6,895
0,025
8,406 • 10
-6 ^
0,025 3,398 - 6,649 10"4
8,406 10'6 - 6,649 10"4 1,707
Положим Ь4 и перейдем к п.2.
24. Так как а$ = 0,025 > е, процесс повторяется.
З4. Найдем угол поворота
ф<4) =—arctg
2-л(4)
1 2 • 0 025
-arctg ,__ :i_ = 0,0071484;
ап-а22 2 6,895-3,398
sin Ф(4) = 0,0071483; coscp(4) = 0,9999744.
44. Сформируем матрицу вращения: Я(4) =
{0,9999744 -0,0071483 $\
0,0071483 0,9999744 0
0 0 1
54. Выполним пятую итерацию:
( 6,895 4,774-10"7 3,653-Ю'6 )
a&={hw)taMhw =
4,774-10"7 3,398 |- 6,649 10"4
3,653 10"6 - 6,649 10"4 1,707
Положим & = 5 и перейдем к п.2.
25. Так как наибольший по модулю наддиагональный элемент
удовлетворяет условию - 6,649 • 10"4 < б = 0,001, процесс завершается.
Собственные значения: Х{ = aff = 6,895; Х2 = а^ = 3,398; Х3 = а$ = 1,707.
74

Для нахождения собственных векторов вычислим
у< = н™.н™.н™.н™.н™
0,753 -0,458 -0,473^
0,432 0,886 -0,171
1^0,497 -0,076 0,864 J
отсюда X1
( 1
(0,753^
0,432
l0,497j
I x
0,5737
^ 0,660 )
(- 0,458^1
0,886
[-0,076j
( -0,517 >*
* =
*2 =
1
*3 =
(- 0,473^
-0,171
( 0,864 J
(- 0,5474^
-0,1979
1
или после нормировки
- 0,0858;
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Для следующих матриц с точностью е = 0,01 определить методами
вращения и непосредственного развертывания собственные значения и собственные
векторы. Методом итераций найти спектральный радиус.
1)
4)
7)
2,1 1 1,П
1 2,6 1,1
1^1,1 1,1 3,1
1,6 0,7 0,8Л
0,7 1,6 0,3
1^0,8 0,3 1,6J
(1,4 0,5 0,6Л
0,5 1,4 0,3
[о,6 0,3 1,4 J
2)
5)
(2,4 1 1,4^
1 2,3 1,4
U4 М 3,4
3)
г2,2 1 2,2'
1 2,7 1,2
<2,2 1,2 3,2,
; 6)
8)
1,7 0,8 0,9"!
0,8 0,7 0,3
^0,9 0,3 1,7 J
9)
(1,3 0,4 0,5^
0,4 1,3 0,3
[0,5 0,3 1,3J
f2,5 1 1,5^
1 1,3 1,5 ;
ll,5 1,5 l,5j
(2,3 1 1,3^
1 2,8 1,3 .
[l,3 13 3,3j
2. Методом итераций найти спектральный радиус для матриц:
^12 3 4^
(а, 2 2Ч
2 5 1
U 1 6J
; 2)
'4 1 0Ч
1 2 1
[о 1 lj
; 3>
4)
1)
(2 3 5
3 1 6
5 6 2
Ч
5)
(1,6 1,2 0,4^
1,2 0,5 1,0
10,4 1,0 0,8 J
2 12 3
3 2 12
1,4 3 2 1
0,2 2,0 0,5^
2,0 1,4 1,7
^0,5 1,7 0,3J
6)
75

Глава 3. МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ
УРАВНЕНИЙ И СИСТЕМ
3.1. МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
3.1.1. Постановка задачи
Пусть дано нелинейное уравнение
/« = 0,
(3.1)
где /(*)- функция, определенная и непрерывная на некотором промежутке.
В некоторых случаях на функцию f(x) могут быть наложены дополнительные
ограничения, например, непрерывность первой и второй производных, что
специально оговаривается. Функция f(x) может быть задана в виде алгебраического
многочлена или трансцендентной функции (тогда ей соответствует
алгебраическое или трансцендентное уравнение).
Требуется найти корни уравнения (3.1), т.е. числа х.|,х,2,..., которые путем
подстановки их в (3.1) превращают уравнение в верное числовое равенство.
Числа хм,х.2,... называются также нулями функции /(*).
На практике часто бывает выгодно уравнение (3.1) заменить равносильным
ему уравнением (уравнения равносильны, если имеют одинаковые корни):
/iW-/2W = o,
(3.2)
где функции fx(x) , f2{x) — более простые, чем функция /(*). Тогда при
задании уравнения в виде (3.1) нулями функции f(x) являются точки пересечения
f(x) с осью Ох (рис. 3.1,д), а при задании в виде (3.2) — абсциссы точек
пересечения функций /i(x) и f2(x) ( рис. 3.1,6).
У = /(х)
У
\
Vs^
0
у AM
щ ; а, в? : ъЛ
Х.1 Х.2 X
Рис. 3.1
76

Замечания.
1. Если f(x) = anxn +an_lxn~l + •• + а0 = Рп(х) - алгебраический
многочлен, то уравнение (3.1) называется также алгебраическим л-и степени:
Pn(x) = anxn+an_lXn-l+.. + a0=0,
(3.3)
где ап,...а0 — действительные числа, коэффициенты уравнения.
2. На практике встречаются задачи нахождения корней уравнения
/(*/) = О, левая часть которого задана сеточной функцией
у, =Ах/),/ = 1,...,7У(рис. 3.2).
У t
ч
\
1 S
ххх2
*♦! X
N»,
*#• : у хт2
XN X
Рис. 3.2
Число х„ есть корень уравнения (3.1) кратности к, если при х = х* вместе
с функцией f(x) обращаются в нуль ее производные до (к -1) -го порядка
включительно, т.е. f(xm) = /'(**) = ••• = /(*_1)0О = 0, а /(А:)(х*)*0. Корень
кратности к = 1 называется простым. На рис 3.1,а простыми корнями являются
jcM,jc*2,x.3> а корни х*4,х*5 ~~ кратные.
В соответствии с классическим результатом Галуа алгебраическое
уравнение (3.1) при п > 5 не имеет решения в замкнутом (формульном) виде. Сеточные
уравнения вообще не имеют формульных решений. Поэтому корни
алгебраических (п > 2), трансцендентных и сеточных уравнений, как правило,
определяются приближенно с заданной точностью.
Решение осуществляется в два этапа:
Первый этап. Находятся отрезки [в/, 6,-], внутри каждого из которых
содержится один простой или кратный корень (x.j б[а,-,6/]) (см. рис. 3.1). Этот этап
называется процедурой отделения корней. По сути на нем осуществляется грубое
нахождение корней х„.
Второй этап. Грубое значение каждого корня xmi уточняется до заданной
точности одним из численных методов, в которых реализуются
последовательные приближения. Порядок (скорость) сходимости метода определяется так же,
как в разд. 1.3.1.
77

3.1.2. Отделение корней
Для отделения действительных корней полезно определять заранее число
корней, а также верхнюю и нижнюю границы их расположения. Для этого
используется ряд теорем.
Теорема 3.1 (о числе корней алгебраического уравнения (3.3)).
Алгебраическое уравнение (3.3) п-й степени имеет ровно п корней,
действительных или комплексных, при условии, что каждый корень считается столько раз,
какова его кратность.
Теорема 3.2 (о свойстве парной сопряженности комплексных корней
уравнения (3.3)).
Если х*/ = <х + р/ — корень алгебраического уравнения (3.3) кратности к, то
число хф/ = а - р/ также является корнем той же кратности.
Следствие. Алгебраическое уравнение нечетной степени имеет по крайней
мере один действительный корень.
Теорема 3.3 (об оценке модулей корней уравнения (3.3)).
Пусть А = max{ K_i|,..,KI}, В = тах{ K|,K_i|> >Ы } ,
где ак, к = 0, п — коэффициенты уравнения апхп + ап_хх + • • • + ахх + а0 = 0.
Тогда модули всех корней х#/ (i = \,...,п) уравнения удовлетворяют неравенству
<\xmi\<l+y-г, i = 1,...,я, (3.4)
hi
т.е. корни уравнения расположены в кольце.
1 А
Следствие. Числа г = — и R = \+ -.—г являются соответственно нижней
ы
и верхней границами положительных корней алгебраического уравнения: г < **• < R.
Аналогично числа -R и -г служат нижней и верхней границами отрицательных
корней уравнения: - R < х^ < -г.
Приведем полезные теоремы, используемые для более точного
установления границ действительных корней алгебраических уравнений.
Теорема 3.4 (теорема Лагранжа о верхней границе положительных корней
уравнения (3.3)).
Пусть й„>0ма/ - первый отрицательный коэффициент в
последовательности ап,ап_1,ап_2,...,а\,ац\ С — наибольшая из абсолютных величин отрицательных
коэффициентов. Тогда за верхнюю границу положительных корней уравнения (3.3)
может быть принято число
д = 1 + л-/|£Г (3.5)
78

Теорема 3.5 (о нижних и верхних границах положительных и
отрицательных корней алгебраического уравнения).
Пусть R — верхняя граница положительных корней уравнения Рп(х) = 0,
Rx — верхняя граница положительных корней уравнения Р (х)
-*'4х)-0'
R2 — верхняя граница положительных корней уравнения Р2(х) = Р„(-х) = 0,
Л3 ~~ верхняя граница положительных корней уравнения Рг(х)-хпРп\ = 0.
Тогда положительные корни **• и отрицательные корни х~ уравнения (3.3)
удовлетворяют неравенствам
-J-<*;,</?, -д2<х-. <--i-. (з.б)
Теорема 3.6 (теорема Декарта о количестве действительных корней
алгебраических уравнений).
Число S{ положительных корней (с учетом их кратностей) алгебраического
уравнения Рп(х) = 0 равно числу перемен знаков в последовательности
коэффициентов ап,ап_|,...,а0 (коэффициенты, равные нулю, не учитываются) многочлена
Рп(х)или меньше этого числа на четное число. Число S2 отрицательных корней (с
учетом их кратностей) алгебраического уравнения Рп (х) - О равно числу перемен
знаков в последовательности anian_i,...,a0 многочлена Рп(-х) или меньше этого
числа на четное число.
Теорема 3.7 ( теорема Гюа о необходимом условии действительности всех
корней алгебраического уравнения).
Если алгебраическое уравнение (3.3) имеет все действительные корни, то
квадрат каждого некрайнего коэффициента больше произведения двух его соседних
коэффициентов.
Следствие. Если при каком-нибудь к выполнено неравенство а\ < ак_{ак+1,
то уравнение (3.3) имеет по крайней мере одну пару комплексных корней.
Для отделения корней применяется следующая теорема.
Теорема 3.8. Если функция f(x), определяющая уравнение f(x) = 0, на
концах отрезка [ahbi\ принимает значения разных знаков, т.е. f(at)- f(bt) < 0, то на
этом отрезке содержится по крайней мере один корень уравнения. Если же f(x)
непрерывна и дифференцируема и ее первая производная сохраняет знак внутри от-
( \
резка [д, ,bf] sign f'(x) - const L то на [oj , bt ] находится только один корень xmi
VM,] )
уравнения.
79

В вычислительной практике обычно используются следующие способы
отделения корней:
1) средствами машинной графики: функция. /(х) представляется на
дисплее и приближенно определяются отрезки, которым принадлежат точки х„- ;
2) средствами математического анализа с помощью исследования функций
и построения графиков (см. рис. 3.1,а);
3) формированием простых функций /i(x) и f2(x) таких, что получается
равносильное уравнение в виде (3.2), и дальнейшим построением графиков этих
функций (см. рис. 3.1,6).
Пример 3.1. Определить число положительных и отрицательных корней,
а также их границы для уравнения
Р5(х) = х5 +2х4 -5х3 + 8х2 -7х-3 = 0.
□ В данной задаче п = 5, а5 = 1, аА = 2, аъ = -5, а2 = 8, ах = -7, а0 = -3.
Согласно теореме 3.1 уравнение имеет пять корней. Поскольку п = 5, то по
следствию из теоремы 3.2 уравнение имеет по крайней мере один действительный
корень.
Оценим модули корней по теореме 3.3. Так как
^ = тах{|2|,|-5|,|8|,|-7|,|-3|} = 8, В = тах{| l|,|2|,|-5|,|8|,| -7| } = 8,
то — < |х„-| < 1 + г—г или — < |х,/| < 9, т.е. все корни лежат внутри дан-
i + рЦ I1! п
I — з |
ного кольца. По следствию из теоремы 3.3 это означает, что положительные
корни удовлетворяют неравенству — < х;( < 9, а отрицательные - неравенству
-9<*.-<-А
Применим теоремы 3.4 и 3.5 для уточнения приведенных результатов.
Найдем верхнюю границу положительных корней. Так как аъ = -5 - первый
отрицательный коэффициент в последовательности 1,2, - 5,8, - 7, - 3 , то / = 3, а
С = тах{ |-5|,|-7|,|-3|}=7 - наибольшая из абсолютных величин
отрицательных коэффициентов. Следовательно, R = 1 + <5-3у — = 1 + Jl = 3,646.
Найдем нижнюю границу положительных корней. Составим уравнение:
= -Зх5 - 7х4 + 8х3 - 5х2 + 2х +1 = 0
или Зх5 + 7х4 - 8х3 + 5х2 - 2х -1 = 0 (старший коэффициент должен быть
положительным). Для этого уравнения / = 3, С = max{| -8|,|-2|,|-l|}=8, поэтому
80

Л, = 1 + (5"3ip = 1 + J- s 2,632. Отсюда 4" = °>38 * **/ ^ * = 3»646 •
■ 3 13 R\
Уточним границы отрицательных корней. Составим уравнение:
Р2(х) = Р5(-х) = -х5 + 2х4 + 5х3 + 8х2 + 7х - 3 = О
или х5 - 2х4 - 5х3 - 8х2 - 7х + 3 = 0. Для этого уравнения i = 4,
С = тах{ | - 21,| - 51,| - 61,| - 71} = 8, поэтому Д2 = 1 + <5"4>/у = 9. Составим
уравнение
,3м. ¥«п[ М_.5рГ n_v5f 1 . 1 , 1 „ 1 П
= -Зх5 + 7х4 + 8х3 + 5х2 + 2х - 1 = О
или Зх5 - 7х4 - 8х3 - 5х2 - 2х + 1 = 0. Для этого уравнения / = 4,
С = тах{|- 7|,|- 8|,|- 5|,|- 2|} = 8, поэтому R3 = 1 + <5-4l/~ = 1 +- = 3,666. Отсюда
находим: - R2 = -9 < хГ, < = -0,272. Заметим, что данный результат совпада-
Яз
ет с полученным ранее.
Исследуем структуру корней уравнения. Так как квадрат каждого
некрайнего коэффициента больше произведения двух его соседних коэффициентов, то
по теореме 3.7 необходимое условие действительности всех корней уравнения
выполняется.
На основе теоремы 3.6 определим число положительных и отрицательных
корней. Выписываем коэффициенты многочлена Рп(х) = Р$(х): 1, 2, -5, 8, -7, -3.
Так как число перемен знака Sx = 3, то число положительных корней равно трем
или меньше на четное число, т.е. равно 1. Далее выписываем коэффициенты
многочлена Р5(-х): -1, 2, 5, 8, 7, -3. Так как число перемен знаков S2 =2, то
число отрицательных корней равно двум или меньше на четное число, т.е. их
вообще нет. ■
Пример 3.2. Отделить корни уравнения х3 - х +1 = 0.
D Согласно теореме 3.1 уравнение имеет три корня, среди которых по
крайней мере один действительный (следствие из теоремы 3.2, поскольку это
уравнение нечетной степени).
Оценим модули корней уравнения по теореме 3.3. Так как
/f = max{|0|,|-l|,|l|}=l, 5 = тах{|1|,|0|.|-1|}=1,то —l— <|х„| < 1 +Л-
"ГО "
или — < |хФ/| < 2. Отсюда — < хф+; < 2 и - 2 < х~ < —.
Определим число положительных и отрицательных корней. Выписываем
коэффициенты многочлена Рз(х): 1, 0, -1, 1. Так как число перемен знака
5*! = 2 (нулевой коэффициент не учитывается), то число положительных корней
равно двум или меньше на четное число, т.е. они отсутствуют. Далее выписываем
81

коэффициенты многочлена jP3(-x) = -x3 + х + 1: -1, 0, 1, 1. Так как число
перемен знака S2 = 1 (нулевой коэффициент не учитывается), то число
отрицательных корней равно единице.
Отделим корни третьим способом. Для этого преобразуем уравнение к
равносильному виду (3.2): х
и у = х -1 (рис. 3.3).
х -1 и найдем точки пересечения графиков у = xJ
у = х-1
Рис. 3.3
Очевидно, корень уравнения х„ е [ - 2; -1 ] .■
Пример 3.3. Отделить корни уравнения х3 - х2 - Эх + 9 = 0.
D Согласно теореме 3.1 уравнение имеет три корня, среди которых по
крайней мере один действительный (по следствию из теоремы 3.2). Оценим
модули корней уравнения по теореме 3.3.
Таккак А = max{| -l|,| -9|,| 9| }= 9, В = тах{| 11,| -11,| - 91 } = 9, то
— < IxJ < 1 + г—; или - < |х.;| < 10. Отсюда - < х+ < 10 и -10 < х' < —.
9 ' ' |1| 2 2 2
1 +
9|
Определим число положительных и отрицательных корней. Выписываем
коэффициенты многочлена Р}(х): 1,-1, -9, 9. Так как число перемен знака
S{ = 2 , то уравнение имеет два положительных корня или ни одного. Далее
выписываем коэффициенты многочлена Р$(-х) - -х3 -х2 +9х + 9: -1, -1, 9, 9. Так
как число перемен знака S2 = 1, то имеется один отрицательный корень.
Отделим корни третьим способом. С этой целью преобразуем уравнение
к равносильному виду: х3 =х2+9х-9. Найдем абсциссы точек пересечения
графиков у = х3 иу = х2+9х-9 (см. рис. 3.4 указаны два из трех полученных
промежутков).
82

-2
у = х + 9х
Рис. 3.4
Результат отделения корней — три промежутка [0,5; 2], [2; 4], [- 4; - 2].
Заметим, что отрезки могут быть сужены, например, вместо отрезка [2; 4] можно
принять [2,5; 4]. ■
3.1.3. Метод половинного деления
Пусть дано уравнение /(*) = 0 и отделен простой корень х,, т.е. найден
такой отрезок [до>^о]> что х* е [flo>fy)L и на концах отрезка функция имеет
значения, противоположные по знаку (f(aQ)- f(b0) <0)- Отрезок [до>^о] называется
начальным интервалом неопределенности, потому что известно, что корень ему
принадлежит, но его местоположение с требуемой точностью не определено.
Процедура уточнения положения корня заключается в построении
последовательности вложенных друг в друга отрезков, каждый из которых содержит
корень уравнения. Для этого находится середина текущего интервала
неопределенности ск =
о к + Ьк
, Л: = 0,1,..., и в качестве следующего интервала
неопределенности из двух возможных выбирается тот, на концах которого функция f(x)
имеет разные знаки (рис. 3.5).
Процесс завершается, когда длина текущего интервала неопределенности
становится меньше заданной величины е, задающей точность нахождения
корня. В качестве приближенного значения корня берется середина последнего
интервала неопределенности.
83

Методика решения задачи
1. Найти начальный интервал неопределенности Lq = [%уЬ^\ одним из
методов отделения корней, задать малое положительное число с. Положить к = 0.
2. Найти середину текущего интервала неопределенности:
Ч
ак +ьк
3. Если f(ak)-f(ck)<09 то положить ok+l=ak, ^*+i=c*» а если
f(ck)- f(bk) < 0, то принять ак+х =ску bk+] = Ьк. В результате находится
текущий интервал неопределенности Lk+i = [ak+\,bk+i).
4. Если bk+i -ак+\ <е, то процесс завершить: хт е Lk+\ = [ok+\,bk+l]. При-
. ак + \ + Ьк + \
ближенное значение корня можно найти по формуле *«. = —— .
Если Ьк+{ - ak+i > е, положить к = к +1 и перейти к п.2.
У
0
<
*0
с1
ц
"^3
V
<
со
>
*0
X
А)
Рис. 3.5
Замечания.
1. Метод имеет линейную, но безусловную сходимость, и его погрешность
I. I №o_flo|
за каждую итерацию уменьшается в два раза: K>i-fli| = 1 ,
\b2 - а2\ = —-— = г—, • ■ •, \bk - ак| = \b0 - а0\ • 2~к . Из последнего
соотношения можно оценить число итераций к для достижения заданной точности е:
|*0-*о|-2-*<е; **log2&^a).
i-з
Отсюда видно, что, например, для достижения точности е « 10 при (Ь0 -а0) = 1
необходимо выполнить примерно десять итераций.
84

2. К достоинствам метода следует отнести то, что он позволяет найти
простой корень уравнения х. e[aQib0] для любых непрерывных функций f(x) при
любых значениях я0А> таких, что f(a0)f(bQ) <0. Недостатки метода - он не
обобщается на системы нелинейных уравнений и не может использоваться для
нахождения корней четной кратности.
Пример 3.4. Найти корень уравнения хг - х +1 = 0 методом половинного
деления с точностью ъх =0,01 и е2 = 0,0005.
□ В примере 3.2 корень уравнения был отделен: х„ €[-2;-l], поэтому
а0 = -2, bQ = -1.
Очевидно, функция непрерывна на отрезке [-2;-l], имеет единственный
простой корень (см. рис. 3.3). На концах отрезка функция имеет значения
/(-2) = -5, /(-1) = 1, противоположные по знаку. Результаты расчетов
приведены в табл. 3.1.
Таблица 3.1
1 *~
0
1
2
3
4
5
6
7
8
9
10
1 11
/(**)
-5
-0,875
-0,875
-0,224
-0,224
-0,08
-0,015
-0,015
-0,015
-0,007
-0,0025
-0,0003
<*к
-2
-1,5
-1,5
-1,375
-1,375
-1,34375
-1,3282
-1,3282
-1,3282
-1,3263
-1,3253
-1,3248
ьк
-1
-1
-1,25
-1,25
-1,3125
-1,3125
-1,3125
-1,3204
-1,3243
-1,3243
-1,3243
-1,3243
№)
1
1
0,2965
0,2965
0,05
0,05
0,05
0,018
0,0018
0,0018
0,0018
0,0018
ск- 2
-1,5
-1,25
-1,375
-1,3125
-1,34375
-1,3282
-1,3204
-1,3243
-1,3263
-1,3253
-1,3248
-
/<<*)
-0,875
0,2965
-0,224
0,05
-0,08
-0,015
0,018
0,0018
-0,007
-0,0025
-0,0003
-
h -ак\
1
0,5
0,25
0,125
0,0625
0,03125
0,0156
0,00781
0,0039
0,002
0,001
0,0005 |
Если гх =0,01, корень х. е [-1,3282; -1,3204], а если е2 =0,0005 -
корень
х. е [-1,3248; -1,3243] или х. = ~ U282-1,3204 = _1ШЪ ^ ^ = QQl.
х. = -1>3248~1>3243 = -1,3245 при е2 = 0,0005. ■
Пример 3.5. Найти корень уравнения лг3 - х2 - 9х + 9 = 0 методом
половинного деления с точностью е = 0,01.
□ В примере 3.3 были отделены корни уравнения. Уточним корень,
лежащий на отрезке [2,5; 4]. Результаты расчетов поместим в табл. 3.2.
85

Таблица 3.2
1 к
0
1
2
3
4
5
6
7
[_8_
/(**)
-4,125
-4,125
-1,3769
-1,3769
-0,3672
-0,3672
-0,0933
-0,0933
-0,02349
**
2,5
2,5
2,875
2,875
2,9687
2,9687
2,9921
2,9921
2,99804
ьк
4
3,25
3,25
3,0625
3,0625
3,0156
3,0156
3,0039
3,0039
№)
21
3,5156
3,5156
0,7815
0,7815
0,1894
0,1894
0,0469
0,0469
ак + ък
к~ 2
3,25
2,875
3,0625
2,96875
3,01562
2,99218
3,0039
2,99804
3,00097
/<<*)
3,5156
-1,3769
0,78149
-0,3672
0,18945
-0,0933
0,0469
-0,02349
0,011647
ък ~ ак
1,5
0,75
0,375
0,1875
0,09375
0,04687
0,02344
0,01172
0,00586 J
В результате найден интервал [2,99804; 3,0039] и приближенное значение
корня х, = 3,00097. ■
Пример 3.6. Отделить корни трансцендентного уравнения
х2 -е~х =0
и найти один из корней с точностью е = 0,01.
1. Можно отделить корни уравнения, преобразовав его к равносильному
виду х2=е~хи определив абсциссу точек пересечения графиков функций
у = /j (х) = х2 и у = /2 (х) = «Гх: х, е [0,5; 1]. При этом /(0,5) • /(1) < 0.
2. Уточним корень. Результаты расчетов приведем в табл. 3.3.
Таблица 3.3
пг
0
1
2
3
4
5
[б_
f(flk)
-0,3565
-0,3565
-0,1446
-0,0301
-0,0301
-0,00069
-0,00069
я*
0,5
0,5
0,625
0,6875
0,6875
0,7031
0,7031
ьк
1
0,75
0,75
0,75
0,7187
0,7187
0,7109
№)
0,6321
0,09013
0,09013
0,09013
0,0292
0,0292
0,0142
ск- 2
0,75
0,625
0,6875
0,7187
0,7031
0,7109
0,7070
/(<*)
0,09013
-0,1446
-0,0301
0,0292
-0,00069
0,0142
0,0067
h ~ак
0,5
0,25
0,125
0,0625
0,0312
0,0156
0,0078 1
Вычисления показывают, что Ьв-ав = 0,7109 - 0,7031 = 0,0078 < б = 0,01 .
„ 0,7109 + 0,7031 п___ т
Поэтому х» = — • = с6 = 0,707. ■
86

3.1.4. Метод хорд
Этот метод при тех же предположениях обеспечивает более быстрое
нахождение корня, чем метод половинного деления. Для этого отрезок [о,£] делится
не пополам, а в отношении \f(a)\: \f{b)\.
Геометрически метод хорд эквивалентен замене кривой у = f(x) хордой,
проходящей через точки (a,/(a)) и {b,f(b)) (рис. 3.6).
/(*)
Рис. 3.6
Уравнение хорды АВ имеет вид
х-а у - f(a)
Ъ-а f(b)-f(a)'
Полагая х = х*1' и у = 0, получаем
r(D
/(«)
(Ь-а).
/(b)-/(а)
Предположим, что вторая производная /"(*) сохраняет постоянный знак,
и рассмотрим два случая: /(а) > О, /"(*)> 0 (рис. 3.7,д) и /(я)<0, /"(*)> О
(рис. 3.7,6). Случай /"(*) < 0 сводится к рассматриваемому, если уравнение
записать в форме: - f(x) = 0.
Первому случаю (см. рис. 3.7,а) соответствует формула
г<0)
Ь,
1<*+» = *<*> ■ Я****) L(k) _а) kz=Ql
(3.7)
а второму случаю (см. рис. 3.7,6)
87

Х<°>=в,
(3-8)
В первом случае остается неподвижным конец а, а во втором случае -
конец Ь.
Рис. 3.7
Замечание. Для выявления неподвижного конца используется условие
/"(*) • /(0 > 0, где / = а или / = Z>. Если неподвижен конец а , применяется
формула (3.7), а если конец b , — формула (3.8).
Пример 3.7. Найти корень уравнения х3 - х +1 = 0 методом хорд с
точностью е = 0,001.
□ Рассмотрим задачу нахождения корня на отрезке [-2;-l] (см. пример
3.2). Так как f(a) = /(-2)= -5, /(b) = /(-1) = 1, а /"(*)= Зх2 -1 > 0 на отрезке
[-2;-l], то /"(*)• f(b) > 0 и, следовательно, имеем второй случай (см.рис. 3.7,6).
Положим х(0) = а = -2, £ = 0. Тогда по формуле (3.8) получаем
/(*)-/(*(0))l ; 1-Й)
Так как А] = х*!) - х(0ч = 0,8334 > е , то положим к = I и продолжим процесс:
*"=*'" "Ti^TiM -*"',=-м666-1^("'"(-M666))= -1даз
Так как А2 = х(2) - хЩ = 0,2287 > е , то положим к = 2 и продолжим процесс:
•(-1-(- 2)) = -1,1666.
88

X(4)=JC0)_.
= -1,2991.
Поскольку A3 = x(3) - x(2) = 0,0962 > с, положим к = 3:
= -1,3347.
Так как А4 = х(4) - х(3) = 0,0356 > е, положим к = 4:
х<5> = -1,3347 - ~°'043 • (-1 - (-1,3347)) = -1,3209.
1 + 0,043 v v 7/
Поскольку А5 = х(5) - х(4) = 0,0138 > е, положим к = 5:
jc<6> =-1,3209- °>0162, •(-!-(-1,3209)) = -1,3261.
1-0,0162 v v "
Так как А6 = х(6) - х(5) = 0,0052 > е, положим к = 6:
х<7) =-1,3261- -°'0059 (-1-(-1,3261)) =-1,3241.
1 + 0,0059 V V "
Поскольку А7 = |х(7) - х(6)| = 0,0020 > е, положим к = 7:
х<8> = -1,3241 - °'00217 • (-1 - (-1,3241)) = -1,3248.
1-0,00217 v v "
Так как А8 = х(8) - х(7) = 0,0007 < е = 0,001, то корень уравнения
х» =-1,3248. Из анализа поведения Ак следует, что сходимость метода хорд
линейная, однако более быстрая, чем сходимость метода половинного деления. ■
3.1.5. Метод простых итераций
Пусть известно, что корень хт уравнения f(x) = 0 лежит на отрезке
G = {a<x<b).
Методика решения задачи
1. Уравнение /(х) = 0 равносильным преобразованием привести к виду
х = ф(х). Это преобразование может быть осуществлено различными путями, но
для сходимости нужно обеспечить выполнение условия | ф'(х) | < % < 1 (х ~
некоторая константа). При этом задача сводится к нахождению абсциссы точки
пересечения прямой у = х и кривой у = ф(х) (рис. 3.8).
89

2. Задать начальное приближение х(0) е [а,Ь] и малое положительное
число б . Положить к = О.
3. Вычислить следующее приближение:
х(*+1) =ф(*(*)).
(3.9)
4. Если х(*+1)-х(А:) <е, итерации завершаются и х0 = х^к+]\ Если
L(*+i) _ х(к)\ > е ^ положить £ = fc +1 и перейти к п.З.
Замечание. 6 качестве условия завершения итераций при известном
значении % может быть использовано неравенство
Проблемы сходимости и единственности численного решения, являющиеся
главными при использовании этого метода, решаются и исследуются с помощью
понятия о сжимающем отображении и теоремы о достаточном условии
сходимости метода.
Отображение (функция) <р(х) называется сжимающим в области G с
коэффициентом % (0 < х < 1), если для любых двух х', х" из G выполнено
неравенство
|9(xV<p(*')|^xj*''-*'|. (3-10)
Теорема 3.9 (о сходимости метода простых итераций и единственности
получаемого численного решения).
Пусть выполнены условия:
1. Нелинейное уравнение х = ф(х) имеет решение хт е G.
2. Отображение <р(х) является сжимающим в области G с некоторым
коэффициентом % (0 ^ X < О •
Тогда:
а) решение х„ является единственным решением в области G ;
90

б) последовательность х(0),х(1),...,х(*+1),... , определяемая по отображению
на основе итерационного процесса, сходится к решению х, со скоростью
геометрической прогрессии, т.е. при выборе х(0) из условия х„ - х(0) < R, где R > 0 -
некоторое малое число, справедливо неравенство х, - х^кЧ < %к \х* - х \» £ = 0,1,...
Теорема 3.9 утверждает, что при выполнении условий 1,2 существует
окрестность G(x.,R), такая, что если взять х(0) в этой окрестности и вычислять
х(,\х(2\... по формуле (3.9), то в результате с любой наперед заданной
точностью можно вычислить х(*+1) « х„, соответствующее искомому (единственному)
корню. Но так как эта окрестность неизвестна, то можно взять произвольное
х(0) eG. Если при этом вычисляется последовательность х(0),х(1),х(2),...,х(*\...,
сходящаяся к некоторому значению х, то в силу теоремы х = х,. Если
сходимость отсутствует, то надо взять другое х(0) е G и повторить расчет.
Теорема ЗЛО (о достаточном условии сходимости метода простых
итераций).
Пусть выполнены условия:
1. Функция ф(х) имеет производные для всех х е G .
2. Существует число % (0 < х < I X = const), такое, что | ср'(х) | < % для всех
xeG.
Тогда отображение ф(х) является сжимающим в G с коэффициентом
сжатия % и последовательность х(0),х(1\...,х( \... , определяемая на основе
итерационного процесса, сходится к решению хт, т.е. х^ -> х, при к -± оо.
Доказательство. В силу условия 1 справедлива теорема Лагранжа о
конечных приращениях:
ср(х") - ф(х') < (х" - х') ф'(5) для Vx\ х" € G,
где 8 — точка, лежащая между х'и х". Но тогда с учетом условия 2 и замены
ф'(5) ее мажорантой % получим
| ф(х") - ф(х') | < х | х" - х |,
т.е. отображение ф(х) — сжимающее, и, таким образом, последовательность
х(0),ха\...,х(*+1),... сходится к некоторому х. Но тогда в силу непрерывности
Ф(х) в G имеет место равенство х = х„.
Геометрическая интерпретация процесса сходимости и расходимости в
зависимости от выполнения или невыполнения достаточного условия сходимости
представлена на рис. 3.9.
Из рис. 3.9 видно, что при 0 < ф'(х) < 1 и при -1 < ф'(х) < 0 (см.рис. 3.9,д,б)
итерационные последовательности х(0),х(1\х(2),... сходятся к хф . Причем в
первом случае реализуется односторонняя (монотонная) сходимость, а во втором —
двусторонняя (немонотонная). При |ф'(*)| > 1 (см.рис. Ъ.Э,в,г) процесс расходится
91

несмотря на то, что точка х( * очень близка к хф . Процессы на рис. 3.9,а,б
соответствуют сжимающему отображению.
I - 1 < ф'(х) < 0 1 у = Х
V
0
1 ф'(*)>1 |/
У = Ф)
/ / х.1 \ !
/ *<°>х«>.
г /
х(2)
/у = х
X
У '
0
\У = Ф)
| ф'М < -1
\ /У = х
k t
\ » У
'а 1
1 1
^
У-—i 1 < \ \—^н
/ ! : : : \х
х<
1)х(0)
'
;
с
Рис. 3.9
Преобразование уравнения f(x) = 0 к равносильному виду х = cp(x) может
быть выполнено неоднозначно. Рассмотрим универсальные практические
приемы равносильного преобразования f(x) = 0, дающие сжимающие отображения.
1. Можно заменить уравнение /(*) = 0 на равносильное х = х + cf(x), где
с = const * О. Тогда, принимая правую часть этого уравнения за ср(х) и раскрывая
|ф'(х)| = |l + cf'(x)\ < 1, получаем условие
-2<с/'(х)<0. (3.11)
92

Таким образом, можно найти константу с на отрезке С7 = [л,/>] так, чтобы
удовлетворялись неравенства (3.11). При этом надо стремиться получить такую
постоянную с, которая бы больше отличалась от нуля, и тогда будет реализовы-
ваться более быстрая сходимость.
Можно показать, что абсолютная погрешность метода оценивается по
формуле (эта оценка выражается через два последовательных приближения)
x(*+1)-xj<
X
1-Х
х(*+1)_х(*)
(3.12)
или по формуле (эта оценка выражается через два приближения х(0) и х(1))
..* + !
X(^D_XJ<I_
1-Х
ijcW-jcW
(3.13)
Из оценки следует условие выхода из итерационного процесса. Если значение %
неизвестно, то выход осуществляется по условию
|Х(^1)_Х(А:)|<8
2. Уравнение f(x) = 0 заменяется равносильным:
= х;-
: ф(х) при х е G ,
тах|/'(*)|
где знак в правой части выбирается из условия ср'(дс) | < 1.
3. Можно выразить х из уравнения f(x) = 0 так, чтобы для полученного
уравнения х = (р(х) выполнялось условие сходимости | ф'(х) | < 1 в окрестности
искомого корня.
Замечание. Выполнение условия А^+1 = х(*+1) -хЩ < е не
гарантирует близости к точному решению (на рис. 3.10 достигается область, где
условие окончания выполняется, но корень хт расположен достаточно далеко от
этой области).
93

Пример 3.8. Методом простых итераций с точностью 6 = 0,001 уточнить
корень трансцендентного уравнения х2 -е~х =0, причем искомый корень
х, е [0,5; 1,0] = G.
X
D 1. Преобразуем исходное уравнение к виду х = ф(х): х = е 2 - ф(х).
Проверкой можно убедиться, что ц'(х) < 1 при х е G .
2. В качестве начального приближения выберем х*°* = — — - 0,75.
3,4. Выполняем последовательные действия по формуле (3.9):
х(*+1) = е 2 Результаты расчетов приведены в табл. 3.4.
Таблица 3.4
к
х(к)
|X(*)_X(*-D|
0
0,7500
-
1
0,6873
0,0627
2
0,7091
0,0218
3
0,7015
0,0076
4
0,7042
0,0027
5
0,7032
0,0010
На пятой итерации выполнилось условие х(5)-х(4) < е = 0,001, поэтому
процесс завершен. В качестве приближенного решения берется х„ = х'5' = 0,703.
Подстановка х(5) в исходное уравнение дает (х(5))2 -е~х =0,00088, т.е.
равенство в уравнении также выполняется с заданной точностью. Видно, что
сходимость двусторонняя (это следует также из неравенства -1 < ср'(х) < 0) и линейная,
так как отношения
r<*+D.
Лк)
ЛЬ)
Лк-\)
при к = 1,2,3,4,5 примерно одинаковые и
равны * 0,35 (знаменатель геометрической прогрессии).»
Пример 3.9. Найти решение уравнения х3 - х +1 = 0 методом простых
итераций с точностью Si =0,01 и б2 =0,001.
□ 1. В примере 3.2 был отделен корень уравнения х« е [-2;-l] .
Преобразуем уравнение к виду х = ф(х). Для этого запишем его сначала в форме
х = х3 + 1. Легко показать, что функция ф(х) = х3 + 1 не удовлетворяет условию
сходимости, поскольку ф'(х) = Зх2, ф'(-2) = 12 > 1, ф'(-1) = 3 > 1. Поэтому
воспользуемся другим преобразованием.
В результате получим х = Ух- 1. Можно проверить, что |ф'(*)| < 1 на
отрезке [- 2; - l], т.е. достаточные условия сходимости выполняются.
2. Зададим начальное приближение х(0)=-1. Решим задачу с различной
ТОЧНОСТЬЮ Б| И Б2 .
94

3,4. Выполним расчеты по формуле (3.9): х<*+1) = Ух^ -1, к = 0,1,2,...
Результаты расчетов приведены в табл. 3.5.
Таблица 3.5
к
XW
|x(*)_x(*-i)|
0
-1,000
-
1
-1,2599
0,2599
2
-1,3123
0,0524
3
-1,3223
0,0100
4
-1,3243
0,0020
5
-1,3246
0,0003
Если et = 0,01, то х„ = -1,3223, а если е2 = 0,001, то хф = -1,3246 .■
Пример 3.10. Найти корни уравнения х3 -х2 -9х + 9 = 0 методом простых
итераций с точностью б = 0,001.
D 1. Преобразуем уравнение к виду х = ср(х): х = vx2 + 9х - 9 .
В примере 3.3 была выполнена операция отделения корней и получены
отрезки [-4; -2], [0,5; 2], [2; 4].
Можно показать, что на отрезках [2; 4], [-4;-2] функция
ф(х) = vx2 + 9х - 9 удовлетворяет условию |ф'(*)| < 1 •
х3 х2
На отрезке [0,5; 2] используем другой вид уравнения: х = +1. Также
х3 х2
легко проверить, что функция ф(х) = + 1 удовлетворяет достаточному
условию сходимости на отрезке [0,5; 2].
2. В качестве начальных приближений выберем:
- точку х(0) = -2 на отрезке [- 4; - 2];
- точку х(0) = 0,5 на отрезке [0,5; 2];
- точку х(0) = 2 на отрезке [2; 4].
В поставленной задаче е = 0,001.
3,4. Выполним расчеты по формуле
xM) = ^/(xW)2+9xW_9,^ = 0,l,2,...,
с начальными значениями х(0) = -2 и х(0) = 2 и по формуле
с начальным значением х(0) = 0,5.
95

Результаты расчетов занесены в табл. 3.6-3.8.
Таблица 3.6
к
0
1
2
3
4
5
6
7
8
9
10
11
12
х<*>
2,0000
2,3513
2,6056
2,7694
2,8682
2,9255
2,9582
2,9767
2,9870
2,9927
2,9959
2,9977
2,9987
\х(к) _х(*-0|
-
0,3513
0,2543
0,1638
0,0988
0,0573
0,0327
0,0185 1
0,0102
0,0057 1
0,0032
0,0018
0,0010 1
Таблица 3.7
к
0
1
2
3
4
5
XW
-2,0000
-2,8438
-2,9816
-2,9979
-2,9997
-2,99997
L(A)_;c(it-l)
|
0,8438
0,1378
0,0163
0,0018
0,00027 1
Таблица 3.8
к
0
1
2
3
4
х(к)
0,50000
0,98611
0,99849
0,99983
0,99998 |
L(*)_x(*-D
-
0,4861
0,01238
0,00134
0,00015
В результате получены приближенные значения корней: xN=-2,99997,
хъ =0,99998, х3. =2,9987.
Обратим внимание на сильное различие в числе итераций,
потребовавшихся для нахождения корней х. = 3 (табл. 3.6) и хф = -3 (табл. 3.7), с помощью
одной и той же формулы. Заметим, что в окрестности корня лгф = 3 значения
модуля производной функции ф(х) = ух2 + Эх - 9 равны: |ф'(2)| = 0,784;
|Ф'(2,3513)| = 0,673; |Ф'(2,6056)| = 0,618; |Ф'(2,9977)| = 0,556. С другой стороны,
в окрестности корня х. = -3 имеем: |ф'(-2)| = 0,206; |ф'(-2,8438)| = 0,124;
|ф'(-2,9977)| = 0,111. Анализ результатов показывает, что чем меньше значения
модуля производной |ф'(*)| , тем быстрее сходимость. ■
96

3.1.6. Метод Ньютона
Метод Ньютона (метод касательных, или метод линеаризации) является
одним из наиболее популярных численных методов. Он быстро сходится (имеет
квадратичную сходимость) и допускает различные модификации,
приспособленные для решения векторных задач и сеточных уравнений. Однако этот метод
эффективен при весьма жестких ограничениях на характер функции /(х):
1) существование второй производной функции /(х) на множестве
G = {a<x<b}\
2) удовлетворение первой производной условию /'(*) * О Для всех х е G;
3) знакопостоянство /'(х) >/'(*) для всех х е G.
Поэтому его желательно использовать совместно с другими методами, например
методом половинного деления, чтобы достигнуть диапазона а < х <Ь , где
указанные условия начинают выполняться.
Геометрическая интерпретация метода Ньютона состоит в следующем.
Задается начальное приближение х(0). Далее проводится касательная к кривой
y = f{x) в точке х(0) (рис. 3.11), т.е. кривая заменяется прямой линией. В
качестве следующего приближения выбирается точка пересечения этой касательной
с осью абсцисс. Процесс построения касательных и нахождения точек
пересечения с осью абсцисс повторяется до тех пор, пока приращение не станет меньше
заданной величины с.
У
/<*(0)>
0
а
с^(/
<^*х. Х<2>
У = /<*)
А'Аа
хт
в
х«
ь
»
X
Рис. 3.11
Получим расчетную формулу метода Ньютона. Вместо участка кривой ВС
(точка С соответствует хФ) возьмем участок ЛВ — касательную, проведенную
в точке (х(0\/(х(0))). Для этого отрезка справедливо конечное соотношение:
где а - угол наклона касательной в точке (х( \/(х(и')) к оси абсцисс. Разрешая
это соотношение относительно х(1), получаем

Х(1)_х(0)_/Л
/'(*<">) •
Повторяя процесс, находим общую формулу:
Подчеркнем, что если отбросить итерационный индекс, то (3.14)
записывается в виде нелинейного уравнения
* = *-7~Ф(х), (3.15)
/(*)
которое, однако, на [a,b] не равносильно исходному, а является таковым только
в одной точке при х = х*. Поэтому данный метод не служит разновидностью
метода простых итераций.
Применим теперь для вывода формулы (3.14) метод линеаризации.
Положим, что итерационный процесс имеет вид
*<*+»> =х<*>+6<*\ к = 0,1,2,..., (3.16)
где 8(Л) - поправка к к -му приближению, которую необходимо найти.
Предполагая, что /(х) имеет непрерывную вторую производную, разложим
/(х(А:) + 5(А:)) по формуле Тейлора относительно точки х^:
/(*<*> + §<*>) = /(*<*>) + 5<*>/'(х«>) + ^—^-Г(0,
где £е (х(*),х(*+1)). Учитывая, что /(х^к) +Ь(к)) = 0 (это соответствует
нахождению точки пересечения с осью абсцисс), и оставляя только линейную
(относительно 5(Л)) часть разложения (отсюда и название — метод линеаризации),
записываем линейное относительно 5(А:) уравнение
/(*<*>)+ 5<*)/'(*(*)) = 0.
Отсюда выражается поправка 5(А:) = - v ' . Подставляя 5(А:) в (3.16),
Г(х{к))
получаем (3.14).
Теорема 3.11 (о достаточных условиях сходимости метода Ньютона).
Пусть выполняются следующие условия:
1. Функция f(x) определена и дважды дифференцируема на [a,b].
2, Отрезку [a,b] принадлежит только один простой корень хф, так что
/<*)•/(*) <0.
98

3. Производные f'(x),f"(x) на [a,b] сохраняют знак, и /'(*) * 0.
4. Начальное приближение jc(0) удовлетворяет неравенству
f(x^)- f'(x^) > 0 (знаки функций f(x) и /"(*) в точке х(0) совпадают).
Тогда с помощью метода Ньютона (3.14) можно вычислить корень уравнения
f(x) = 0 с любой точностью.
Замечания.
1. Метод Ньютона характеризуется вторым порядком сходимости вблизи
корня и первым порядком — вдали от него. Данную оценку проверяем для двух
случаев, когда х^к) находится далеко от корня х. (это возможно на первых
итерациях) и когда х^к) располагается вблизи хт.
Первый случай. Пусть отрезок со = не мал. Тогда на основе теоремы
Лагранжа получим
|/(*(*>)| = |/<х.) - /(*(*})| = \/'&\ • |*. - х(к)\ > тх\хт - х(*>|, (3.17)
где /я, = min |/'(*)|.
О)
Преобразуем с использованием (3.17) итерационную формулу (3.14):
/'(*«>)'
х(к+\) = х(к) fix ) . I {к+{) _ х(к)\
\f(xik))\
\Г(х^)\
тх\х* -*W
где М{ = max |/'(*)| •
Ml
В силу монотонности последовательности х(0),х(1)...
L -х(*+1)| = L - *<*>! -|х<л+,> - *<*>| > L - х<*>| -Щх. _х<*>| =
I II II II I А/. I I
Л/,'
f£)l
X -x(*>
Таким образом, вдали от корня получаем линейную сходимость
|х.-*<*+»>|<с|х,-х<*>|,
где 0<с = 1-—<1.
Л/,
99

Второй случай. Пусть теперь отрезок со = [x**\x.J мал, т.е. итерации
выполняются вблизи корня. Тогда, полагая, что указанные выше предположения
1—4 теоремы ЗЛО выполнены, разложим функцию /(х) в окрестности корня х,
относительно точки х(А:), учитывая члены до второго порядка. Получим
/«
= /(*<*>) + (х. -х<*>)/'(*(А:)) + (х. -х<*>)2£& = 0,
:=х(к) 2
где £ g (х^к) -5,х(А:) + 8) ( 5 > 0 — малая величина). Из данного соотношения
выражаем х.:
х ,.m /(*W> (х.-х<*))2 „
* /'(,<") 2/'(х<*>) ' W"
Но первые два слагаемых в правой части в соответствии с (3.14) равны х(*+1).
Тогда будем иметь
2/(х(*>)
Из последнего соотношения следует оценка погрешности (& +1) - го
приближения через погрешность к -го приближения:
U -*<*+»U*kU _x<*)|2f (3.18)
' I 2m, I i
где принято Л/2 = niax |/"(х)|, #*! = min |/'(х)|. Оценка (3.18) свидетельствует
СО (О
о квадратичной сходимости метода касательных вблизи корня. С
вычислительной точки зрения это означает, что на каждом приближении количество верных
цифр результата удваивается.
2. Для нахождения комплексных корней уравнения f(z) = 0 можно также
использовать (3.14) в форме
z(*+i)-,(*)_ /И) £-012
где г = х + /у — комплексная переменная.
Метод Ньютона может применяться не только для нахождения простых
корней, но для определения кратных корней, т.е. когда на отрезке [д, Ь],
содержащем корень, не выполняется условие f(a)- f(b) <0 (условие 2 теоремы 3.11).
Наряду с теоремой 3.11 удобно также пользоваться следующей теоремой.
100

Теорема 3.12 (достаточные условия сходимости метода Ньютона).
Пусть:
а) дана функция /(х) :/)->/?, где D — открытый интервал, и
/'(*)€ LipyO>);
б) для некоторого р > 0 выполняется условие \f'(x)\ > р при всех х из D.
Если уравнение f(x) = 0 имеет решение х„ е D, то существует некоторое т| > 0,
такое, что если х*0) -xj < л» то последовательность (х*°\х(,\х*2\... },
задаваемая формулой (3.14), существует и сходится к х+. Более того, справедлива оценка
\x<k+l>-x.\*l-\x<k>-x.\2, Л ,0,1,...
Здесь обозначение /'(х) е Lipy(£>) означает, что функция /'(х)
непрерывна по Липшицу с константой у на множестве D, т.е. |/'(*) - f'(y)\ < у - \х - }\ для
любых х,у из D.
Замечания.
1. Требование теоремы 3.12, чтобы производная /'(*) имела ненулевую
нижнюю границу в D, определяет, что значение f'(xm) должно быть ненулевым
для квадратичной сходимости метода Ньютона. Если же /'(**) = 0 , то х,
является кратным корнем, а метод Ньютона сходится лишь линейно.
2. Выполнение условий теоремы 3.12 гарантирует сходимость метода
Ньютона только из «хорошего» начального приближения х(0*.
3. Метод Ньютона является локально сходящимся, так как он сходится с
определенной скоростью к истинному решению при условии, что стартует в
достаточной близости от этого решения.
Методика решения задачи
1. Задать начальное приближение х(0) так, чтобы выполнялось неравенство
/(*(0)) • /"(х(0)) > 0, а также малое положительное число е. Положить к = 0.
2. Вычислить х**+1* по формуле
f\x{k))'
3. Если х(*+|) -хЩ < е , процесс завершить и положить х» = х(*+1).
Если х**+1) - х(*ч > б , положить к = к +1 и перейти к п.2.
Пример 3.11. Методом Ньютона с точностью £ = 0,001 уточнить корень
трансцендентного уравнения х2-е~*=0, причем искомый корень
хфе[0,5;1,0] = <7.
□ Можно проверить, что на множестве G удовлетворяются условия 1, 2, 3
теоремы 3.11, обеспечивающие сходимость метода касательных.
101

1. Зададим начальное приближение из условия 4. Так как для
/(х) = х2 - е~х справедливо /"(*) = 2 - е~х > 0 на множестве (7, /(д) = /(0,5) < 0,
/(b) = /(1) > 0, то /(1) • /"(1) > 0, поэтому х(0) = 1.
2,3. Результаты расчетов по формуле (3.14)
Х(*+П = х(к)
W-
2х<*>.
_-*<*>
■, А: = 0,1,.-,
помещены в табл. 3.9.
Таблица 3.9
1 *
х<*>
L(*) -х^-1)]
/(*<*>)
0
1,000
—
0,63212
1
0,73304
0,27
0,05690
2
0,70381
0,029
0,00065
3 " 1
0,703467
0,00034
8,25-10"7
Из табл. 3.9 можно сделать следующие выводы:
1. Для достижения заданной точности, проверяемой по модулю разности
х(А:) -х(*_1) , потребовалось выполнить три приближения. Если же выход
организовать по условию /(х^) < е , то достаточно двух приближений.
2. Вблизи корня хф количество верных цифр в результатах х(**
удваивается, так что все цифры в х(3) являются верными, тогда как в х(2) верными
являются первые три цифры после запятой.
3. Скорость сходимости метода Ньютона выше скорости сходимости
метода простых итераций (та же точность была достигнута за пять итераций).■
Пример 3.12. Методом Ньютона найти корень уравнения х3 - х +1 = 0.
□ В примере 3.2 корень был отделен: х* € [- 2; -1].
1. Зададим начальное приближение х(0). Так как f'(x) = Зх2 -1,
/"(х) = 6х, то /(-2) = -5, /"(*)< 0 при хе[-2;-1]. Поэтому /(-2)/"(-2) > 0 и
х(0) = -2. Положим е = 0,001.
2,3. Результаты расчетов по формуле (3.14)
х(к+\) = х(к)
(х<*>У
Лк)
+ 1
3(x<*>F-l
, А: =0,1,...,
приведены в табл. 3.10.
Таблица 3.10
к
х(к)
1х<*>-х(*-!>1
0
-2,0000
-
1
-1,545455
0,454545
2
-1,359615
0,185840
3
-1,325801
0,033814
4
-1,324719
0,001082
5
-1,324718 |
0,000001
Найденное приближенное решение х* = -1,3247 2.
102

Пример 3.13. Найти корни уравнения
х3 - х2 - 9х + 9 = О
методом Ньютона с точностью s = 0,001.
□ Процедура отделения корней была выполнена в примере 3.3. В качестве
отрезков [в,-,6J, которым принадлежат корни уравнения, выберем [-4;-2],
[2,5; 4], [0,5; 2].
Так как /(-4) = -3,5; /(-2) = 15, т.е. /(- 4)Д-2) < 0, производные
f"(x) = 6х - 2 < 0, /'(*) = Зх2 - 2х - 9 > 0 сохраняют знак при х е [- 4; - 2], то
условия сходимости выполняются.
Так как /(2,5) =-4,125; /(4) = 21, т.е. Д2,5)/(4)<0, и производные
/'(*)> 0, /"(*)> 0 сохраняют знак при хе[2,5;4], то условия сходимости на
этом отрезке тоже выполняются.
Так как /(0,5) = 4,375; /(2) = -5, т.е. /(0,5)/(2) < 0, и производные
/'(*) < 0, /"(*) > 0 сохраняют знак при х е [0,5; 2], то условия сходимости
выполняются.
1. Зададим начальные приближения: на отрезке [0,5; 2] выберем х(0) =0,5,
так как /(0,5) •/"(0,5) > 0; на отрезке [-4,-2] выберем х(0)=-4, так как
/(4) • /"(4) > 0 ; аналогично на отрезке [2,5; 4] выберем х(0) = 4. В поставленной
задаче е = 0,001.
2,3. Результаты расчетов по формуле (3.14)
с<*+1) = х(к)
(*<*>f-(x<*>f-9x<*>+9
З(х^)2 -2*<*>-9
, * = 0,1,...,
приведены в табл. 3.11—3.13.
Таблица 3.11
к
х{к)
|х(*)_х(*-1)|
0
- 4,00000
-
1
-3,255319
0,744681
2
-3,023383
0,231936
3
-3,000225
0,023158
4
-3,000000
0,000225
Таблица 3.12
к
*<*>
|х<*> -х(к'1)\
0
0,5000
-
1
0,972973
0,472973
2
0,9998246
0,0268516
3
1,0000000
0,0001754
103

Таблица 3.13
1 к
*<*>
!*<*>-х<*-'>|
0
4,0000
-
1
3,322581
0,6774194
2
3,051484
0,2710969
3
3,001674
0,049809
4
3,000002
0,001671
5
3,0000
210"6
В результате получены приближенные значения корней: х#1 = -3,0000;
хт2 = 1,0000; jc,3 = 3,0000 .■
Пример 3.14. Найти корень уравнения х -2х + 1 = 0 методом Ньютона
с точностью £ = 0,01.
□ Очевидно, уравнение имеет один кратный корень хт = 1. Согласно
замечанию к теореме 3.12 применение метода Ньютона для решения поставленной
задачи сопровождается линейной сходимостью (табл. 3.14).
Таблица 3.14
Г к
x(k)
!*<*>-х**-»!
0
2
-
1
1,5
0,5
2
1,25
0,25
3
1,125
0,125
4
1,0625
0,0625
5
1,03125
0,03125
6
1,015625
0,015625
7
1,007813
0,0078125
Полученное приближенное решение хф = 1,007813. ■
3.1.7. Модификации метода Ньютона
Метод касательных, являясь весьма эффективным средством численного
анализа, к сожалению, имеет достаточно жесткие ограничения. Действительно,
он не может применяться для сеточных уравнений (см. рис. 3.2); при нарушении
знакопостоянства производных (рис. 3.12); при существовании неограниченных
вторых производных и др. Так, если даже условие знакопостоянства нарушено
вдали от корня, где выбрано х(0), а вблизи корня выполняется, то все равно
метод касательных неприменим (см. рис. 3.12), если не произвести сужения
начального отрезка.
Рис. 3.12
104

Кроме того, если функция f(x) очень сложная, то будет сложной и ее
производная, и поэтому на каждой итерации приходится рассчитывать две
функции, что снижает эффективность метода касательных.
В силу этого в ряде случаев могут оказаться более предпочтительными
модификации метода касательных. Рассмотрим три из них.
А. Упрощенный метод Ньютона. Методика его применения совпадает с
изложенной в разд. 3.1.6, но вместо формулы (3.14) используется
Л*+1)
*<*>-
7И
А: = 0,1, ..
(3-19)
Отличие от метода Ньютона заключается в том, что производная функции f(x)
подсчитывается только в точке начального приближения, а на последующих
итерациях не уточняется. Процесс последовательных приближений отражен на
рис. 3.13. Первая итерация совпадает с первой итерацией метода Ньютона.
На последующих итерациях соответствующие отрезки параллельны касательной,
проведенной в начальной точке.
Рис. 3.13
Для этой модификации снимаются некоторые ограничения метода
касательных, например условие знакопостоянства производных. Сходимость
упрощенного метода Ньютона линейная.
Пример 3.15. Найти корень уравнения х3 - х +1 = 0 упрощенным методом
Ньютона.
D Корень уравнения отделен в примере 3.2: х„ е [- 2;-1].
1. Выберем начальное приближение х(0) =-2 и зададим ej = 0,01 и
е2 =0,001.
2,3. Выполним расчеты по формуле (3.19):
X(*+D = х(к) _
И)3-:
.(*)
+ 1
Лк)
(*<*>)*-:
Лк)
+ 1
ЗИ)2-! »
Результаты расчетов приведены в табл. 3.15.
к = 0,1,.
105

Таблица 3.15
1 к
0
1
2
3
4
| 5
*<*>
-2,0000 1
-1,5455
-1,4413
-1,3911
-1,3637
-1,3480 |
L(*) _х<*-1)|
-
0,4545
0,1042
0,0502
0,0274
0,0157
1 к
6
7
8
9
10
[ и
*<*>
-1,3388
-1,3333
-1,3299
-1,3279
-1,3267
-1,3259
L(*)_x(*-i)|
0,0092
0,0005
0,00034
0,0020
0,0012
0,0008 |
При е = 0,01 получено решение хФ =-1,3388, а при 8 = 0,001- решение
х0 =■ -1,3259. Очевидно, по сравнению с методом Ньютона сходимость
замедляется (см. пример 3.12).и
Б. Метод Ньютона—Бройдена. Этот метод позволяет увеличить скорость
сходимости последовательных приближений благодаря использованию формулы
х<*+1) = хт.
Ск-
А: = 0,1,...,
(3.20)
где ск— число, которое выбирается на каждой итерации так, чтобы уменьшить
значение Дх(*+1)) по сравнению с /(х^). При ск = 1 метод Ньютона—
Бройдена совпадает с методом Ньютона.
Как правило, при плохой сходимости или ее отсутствии полагают 0 < ск < 1
(рис. 3.14,д), а при хорошей сходимости для ск = 1 полагают ск > 1 (это ускоряет
сходимость (рис. 3.14,6)).
|/(*(1)|>|/(х
Рис. 3.14
На рис. 3.14 прямоугольниками отмечены точки х(1) , полученные при
106

tk\ f(X{k))
c0 = 1, Ь( } ,k = 0,1,..., — поправка, соответствующая методу Ньютона,
f'(x{k))
2l точки jc(I) = x(0) - c05(0) получены по методу Ньютона-Бройдена.
В. Метод секущих. В этом методе производная функции f(x) подсчитыва-
ется с помощью конечно-разностных соотношений:
Л0)
— в точке хх ' используется
где 5 - малая положительная величина;
формула /Уо)),/И)-/И-§),
в точках х^к\ к = 1,2,..., используется формула /'(х(/с))« -^—-^ 1— <■.
х{ ' -х
Вычисленное значение f'(x^) определяет тангенс угла наклона секущей
(рис. 3.15).
У
У = /(х)
Рис. 3.15
Методика применения метода секущих совпадает с описанной в разд. 3.1.6,
но вместо (3.14) используется формула
- I ffiy у.(х<к)-х<к-1)) к-\2
(3.21)
Замечания.
1. Метод секущих является более экономичным по сравнению с методом
Ньютона по количеству функций, подлежащих расчету: на каждой итерации
в методе секущих необходимо рассчитать только значение f(x^), так как
величина f(x^k~l)) уже подсчитана на предыдущей итерации.
2. Метод секущих может применяться и для решения сеточных уравнений.
Для сеточной функции производные в методе секущих определяются так же, но
для определения f(x^) в промежуточных точках осуществляется
аппроксимация (как правило, интерполяция) функции /(*,) (рис 3.16). На этом рисунке
штриховой линией показана аппроксимационная кривая.
3. Для всех описанных модификаций скорость сходимости р по
сравнению с методом касательных снижается: р < 2 . Однако для некоторых из них
107

(метод секущих) значение р > 1 и может достигать р = 1,5.
У '
0
//
-•г / ! i/!
♦ : ; : ^-" х<2> х<'>
4 i
jc(0)
X
Рис. 3.16
Пример 3.16. Методом секущих найти корень уравнения дс3-х + 1=0
с точностью е = 0,001.
□ 1. Зададим начальное приближение х*0) = -2 (см. пример 3.12).
2. Для вычисления /'(*(0)) зададим 6 = 0,1. Тогда
Лх(0))5Л-2)-/(-2.1) = -5-(-6,1б1)=1
0,1 0,1
Отсюда х<" mXi»-j^m-2-^L--l#9*.
Дальнейшие расчеты выполняются по формуле (3.21):
1,29567
Три
Х(2) '- Х(,) - ' 4-/}*<°>)-(*(1) -<0))= -^934-^
704325
X(3)=JC(2)
х(4) = х(3)
0,43066 = -1,41871;
34211;
-T-^^.(x«-x<'))=-l,41871-^^Z8.0,15063 = -«,
f{xW)-f{xM) V ' 0,858893
-г7#^.И-х<2>)=-.,34211-^^.0,0766 = -.,326.3;
/(х(3>)-/(х<2>) V У 0,361404
е<5) ,.(4) Л*(4> f (4) (3)) П2613
. . /j*(S)) .. (х<5> - х(4)) = -1 32474
=-1,32472 = х..
Результаты расчетов приведены в табл. 3.16.
х(6)=х(5)
- 0,00603
0,069348
-0,000139
0,005936
0,01598 = -1,32474;
0,00139 =
Таблица 3.16
1 к
х(к)
\\х(к) _х<*-1>|
0
-2,00000
-
1
-1,56934
0,43066
2
-1,41871
0,15063
3
-1,34211
0,07660
4
-1,32613
0,01598
5
-1,32474
0,00139
6 |
-1,32472
0,00002
Очевидно, метод сходится чуть хуже метода Ньютона (см. пример 3.12),
однако скорость сходимости выше линейной.»
108

3.2. МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
3.2.1. Постановка задачи
Дана система п нелинейных уравнений с п неизвестными:
/1(х1,...,д:л) = 0,
/2(*iv..,*„) = 0,
где fi(xl,...,xn):Rn -> R, i = l,...,/i, — нелинейные функции, определенные и
непрерывные в некоторой области G с Rn, или в векторном виде
F(x) = О, (3.23)
где х = (x,,...,x„)r, F(x) = [/,(х),...,/„(х)]г.
Требуется найти такой вектор х* = (хч,...,х*л)г, который при подстановке
в систему (3.22) превращает каждое уравнение в верное числовое равенство.
Замечания.
1. Проблема решения системы (3.22) возникает при решении многих
прикладных задач, например, поиска безусловного экстремума функций многих
переменных с помощью необходимых условий [31], при применении неявных
методов интегрирования обыкновенных дифференциальных уравнений [33] и т.д.
2. Задача нахождения комплексных корней f(z) = 0 может быть сведена к
проблеме решения двух уравнений с двумя неизвестными. Для этого следует
положить z = х + iy и выделить действительную и мнимую части функции [32]:
f(z) = u(x,y) + iv(x,y) = 0.
Отсюда получаем систему
и(х,у) = 0,
v(x,y) = 0,
которая может быть решена одним из рассматриваемых з данном разделе
методов.
3. Для всех рассматриваемых далее методов требуется находить начальное
приближение х(0). В случае п = 2 это можно сделать графически, определив
координаты точки пересечения кривых, описываемых уравнениями /1(х!,х2) = 0
И /2(*Ь*2) = °-
4. Задача решения системы (3.22) может быть сведена к задаче поиска ми-
п
нимума функции Ч^х) = £.//2(*1>-»*л)- Так как Функция ¥(x) неотрицатель-
ная, ее минимальное значение, равное нулю, достигается в точке х*,
являющейся решением системы (3.22).
109

Для поиска минимума функции Ч'(х) можно применить различные методы
поиска безусловного экстремума функций многих переменных (первого, второго,
нулевого порядков) [31].
Далее рассмотрим основные методы решения задачи (3.22).
3.2.2. Метод простых итераций
Для применения метода требуется привести систему (3.22) к равносильному
виду:
*i =(pi(*i,...,*„),
х2=Ф2(х1,...,хл), (324)
хп =ФЯ(*1>"-,*„),
или в векторной форме
х = Ф(х), (3.25)
где х = (х,,...,хя)г, Ф(х) = [ф,(*),...,фл(х)]г, функции ф,(х) определены и
непрерывны в окрестности изолированного решения х» системы (3.24).
Методика решения задачи
1. Задать начальное приближение х(0^ = (*ю>*20>—»*ло) и малое
положительное число е (точность). Положить к = 0.
2. Вычислить x(*+I) по формуле
х(*+1)^ф(х(*)) (3,26)
или
Xj — Ф1 V^i >*2 > — >хп )>
х(к+1) -а>,(х(к) х<*> х(к))
х2 -4>2\х\ >*2 »—»хл )•> (3 27)
Х(* + 1) -<п (х(*> Х(*> Х(*Ь
3. Если Д(*+1) =тах х^+1) -х\к) <е, процесс завершен и х„ = х(*+1). Если
Д(*+1) > е, то положить к = к + 1 и перейти к п.2.
Замечания.
1. Итерационный процесс, реализуемый согласно (3.27), соответствует
параллельному итерированию, так как для вычисления (£ + 1)-го приближения
всех неизвестных учитываются вычисленные ранее их к -е приближения.
2. Система (3.22) может быть преобразована к виду (3.24) различными
способами, например, с помощью выражения переменных xh i = l,...,/i, таким
образом, чтобы выполнялось условие сходимости.
ПО

Другой способ заключается в замене системы F(x) = 0 системой
х = х + AF(x), где Л - неособенная матрица. В качестве матрицы Л можно ис-
пользовать, например, Л = - ^_1(л:(0)), если det W(x(0)) ф 0 , где
Г*Ш ШхУ]
дхп
Щх) =
дхх
— матрица Якоби.
dfn(x) dfn(x)
к дхх дхп j
В случае, если detH^(jc(0)) = 0, следует выбрать другое начальное приближение.
Заметим, что при таком выборе Л метод простых итераций совпадает с
упрощенным методом Ньютона (см. разд. 3.2.5).
3. В качестве д(*+1) можно использовать различные нормы векторов (см.
разд. 1.3.1).
Теорема 3.13 (о достаточном условии сходимости метода простых
итераций).
Пусть функции ср,(х) и ср/(х),/' = 1,...,л, непрерывны в области G, причем
выполнено неравенство
[ дф/(х)1
max max £
xeG i
;=i
дх:
<q <\,
(3.28)
где q — некоторая постоянная.
Если последовательные приближения х^+1* = Ф(х^), А: = 0,1,..., не выходят
из области G, то процесс последовательных приближений сходится: х„ = lim х**) и
k-too
вектор х„ является в области G единственным решением системы (3.25).
Замечания.
1. Вместо условия (3.28) можно также использовать
max max У
xeG j ^
/=l
дф/(*)
ЭХ;
\q<\.
(3.29)
2. Условия (3.28),(3.29) выполняются, если для любого х е G справедливы
f*Pi(*) <ЫхУ\
неравенства
шыш
дФ
< 1 соответственно, где —:
112 дх
дх,
д<рп(х)
дх„
дх\
дх„
Пример 3.17. Найти корни системы
2*1 -ххх2 -5х, +1 = 0,
х, + 3 • lg X! - х\ = 0,
расположенные в первом квадранте, методом простых итераций с точностью
е = 0,001.
ill

□ Преобразуем систему к виду (3.24) так, чтобы выполнялось условие
сходимости:
ITT
Х{4—Т
= <Pi(*),
х2 = V*i +31gx, = ф2(х).
Найдем частные производные:
д(р\ х2 +5 д<р\ Х\
дхх
1хх(х2 +
5)-1
дх2
\хх(х2 +
5)-1
5ф2
1 +
3- 0,43429
д<Р2
д*1 2^х, +3-Igx1 ' дх2
= 0.
Здесь принято lg е = 0,43429. Далее воспользуемся методикой решения задачи.
1. Для выбора начального приближения найдем координаты точек
пересечения кривых, соответствующих первому и второму уравнениям (рис. 3.17).
2ху -ххх2 -5xj +1 = 0
хх + 3 • lg х\ - х\ = 0
Рис. 3.17
Находим приближенные значения координат решения (по условию задачи
нас интересуют только корни с положительными координатами): л*0) = (3,5; 2,2)г.
Проверим выполнение условий сходимости. Будем рассматривать
окрестность найденной точки х(0): G = {\х{ - 3,5| < 0,1; \х2 - 2,2| < 0,1}. Тогда
112

d<P2
дХ\
( 3-0,43429
3,4
2V3,4 + 31g3,4
: 0,309 < 0,31;
эФ2
дх2
Следовательно, можно получить оценки:
дф,(х)
дх{
дщ(х)
дх2
+
+
5ф2(х)
дх{
дц>2(х)\
дх2 |
< 0,54+ 0,31 = 0,85 <1,
< 0,27 + 0 = 0,27 <1.
Очевидно, условие (3.28) выполняется. Если последовательные приближения не
будут выходить из области <7, то согласно теореме 3.13 итерационный процесс
будет сходящимся. В поставленной задаче е = 0,001.
2,3. Выполним расчеты по формулам (3.27):
,«♦»-/
*}*> •[*<*>
[х\к> + 5] -1
к = 0,1,...,
а результаты поместим в табл. 3.17.
Таблица 3.17
*
XW
х{к)
Д<* + 1>
0
3,5000
2,2000
-
1
3,4785
2,2654
0,0654
2
3,4837
2,2589
0,0065
3
3,4848
2,26049
0,00159
4 '"
3,4957
2,26082
0,0009
Заметим, что величина Д(*+1) при увеличении номера итерации
уменьшается, что характерно для любого сходящегося процесса. Найдено приближенное
решение: х. = (3,4857; 2,2608)г. При этом /,(хф) = -0,0083, f2(x.) = 0,00126. ■
3.2.3. Метод Зейделя
Метод Зейделя предназначен для решения систем, записанных в форме
(3.24). Этот метод является модификацией метода простых итераций, где после
задания начального приближения х(0) вместо параллельного итерирования
производится последовательное итерирование, причем на каждой итерации в каждое
последующее уравнение подставляются значения неизвестных, полученных из
предыдущих уравнений.
in

Методика решения задачи
1. Задать начальное приближение х(0) и малое положительное число е
(точность). Положить к = 0.
2. Вычислить х(*+1) по формулам
r(*) v(*)
= ф1(^,х^,...,х^),
л*+1)
:ф2(
Лк+Щ
I v<*> у(*>\
(3.30)
г(*+1) _
Фя(
,(* + М
X
Л*+1>
Л*+1)
х(*>)
где прямоугольниками отмечены значения, которые берутся из предшествующих
уравнений на текущей итерации.
3. Если Д(*+1* = max х^+1) -xjk^ <е, процесс завершить и положить
хт = х(*+,). Если Д(*+,) > 6, то положить к = к +1 и перейти к п.2.
Пример 3.18. Найти корни системы
/l (*1»xl) = 2jCp - XiX2 - 5jq 4-1=0,
/2(дс,,л:2) = xj + 31gx, -х| =0,
расположенные в первом квадранте, методом Зейделя с точностью е = 0,001.
□ Преобразование системы к виду (3.24) и поиск начального приближения
описаны в примере 3.17.
1. Зададим начальное приближение х(0) =(3,5; 2,2)г. В поставленной задаче
s = 0,001.
2, 3. Выполним расчеты по формулам (3.30):
*,(*+1) = f
.(*) .rY(*)
[xS"'+5]-l
, к = 0,1,...,
x<*+|)=^x{*+1>+3.1gx<*+1>,
а результаты поместим в табл. 3.18.
Таблица 3.18
[" к
Лк)
х\
Лк)
2
I А
0
3,5000
2,2000
-
1
3,4785
2,2588
0,0588
2
3,4821
2,2600
0,0036
3
3,484250
2,260658
_<LQQ215___
4
3,485537
2,261049
JL0Q128
"' 5 1
3,486305
2,26128
0,0007
Найдено приближенное решение х„ = (3,4863; 2,2613)г. При этом
fx(xm) = -0,006425, /2(jO = 0,000007. ■
114

3.2.4. Метод Ньютона
Метод используется для решения систем вида (3.22) или (3.23).
Формула для нахождения решения является естественным обобщением
формулы (3.14):
X(*+D BX(*)-r1(x(*,)7(xw), А: = 0,1,..., (3.31)
где
гдА(х) ШхУ]
дх{ дхп
ЩХ)-
д/п(х) dfn{x)
У дхх dxt
п J
— матрица Якоби.
Так как процесс вычисления обратной матрицы является трудоемким,
преобразуем (3.31) следующим образом:
toik) =-U/-i(x(^))./r(xW)> А: = 0,1,...,
где Ах(Л) = х(*+1) -х^— поправка к текущему приближению х^к\
Умножим последнее выражение слева на матрицу Якоби W(x^):
W(x(k))Ax(k) =-W(x(k))W-l(x(k))F(xik)) = -F(x(k)), к = 0,1,...
В результате получена система линейных алгебраических уравнений
относительно поправки Ах^кК После ее определения вычисляется следующее
приближение х(**1) =х^ +&х^к\
Методика решения задачи
1. Задать начальное приближение х(0) и малое положительное число б
(точность). Положить к =0.
2. Решить систему линейных алгебраических уравнений относительно
поправки Ах^:
W(x{k)) • Ах(к) = -F(x{k)). (3.32)
3. Вычислить следующее приближение:
х(*+1)=х(*Чдх<*>.
4. Если Д**+1) = max Ы*+1) - х\к^< е, процесс закончить и положить
хт = х(*+1). Если д(*+1) > s, то положить к = к + 1 и перейти к п.2.
Теорема 3.14 (о достаточных условиях сходимости метода Ньютона).
Пусть функция F(x) непрерывно дифференцируема в открытом выпуклом
множестве G с R". Предположим, что существуют х+е Rn и г, Р>0, такие,
что N(xmyr) с (7, F(xm) = 0, и существует W~x(x+), причем \\V~x{x*) Ыр и
115

W(x) e L\py(N(x0,r)). Тогда существует e > 0 такое, что для всех х(0) € JV(x,,e)
последовательность х(1\х(2\..., порождаемая соотношением (3.31), сходится к х„
и удовлетворяет неравенству
рс(*+|)-х^Ру|х(*>-х.[2, it = 0,1,... .
Здесь использованы следующие обозначения: N(x,r) - открытая
окрестность радиуса г с центром в точке х: N(x,r) = \x е Rn : \х -х\ < г }; запись
W(x)e Lipy(N(x*,r)) означает, что W(x) непрерывна по Липшицу, где у -
константа Липшица, т.е. || W(y) - W{x) || < у || у - х || Vx, у е N(x0yr).
Замечания.
1. Теорема 3.14 свидетельствует о локальной квадратичной сходимости
метода Ньютона.
2. К недостаткам метода Ньютона следует отнести:
— необходимость задавать достаточно хорошее начальное приближение;
— отсутствие глобальной сходимости для многих задач;
— необходимость вычисления матрицы Якоби на каждой итерации;
— необходимость решения на каждой итерации системы линейных
уравнений, которая может быть плохо обусловленной.
Достоинством метода является квадратичная сходимость из хорошего
начального приближения при условии невырожденности матрицы Якоби.
Пример 3.19. Решить систему
хх + х2 - 3 = 0,
методом Ньютона с точностью £ = 0,001.
□ Очевидно, корнями системы являются хт1 = (3;0)г,хф2 = (0; 3)г. Найдем
приближенно второй корень х,2.
1. Зададим начальное приближение х(0) = (1; 5)Т
6 = 0,001. Положим к = 0.
х?+х%-9-
В поставленной задаче
2°. Составим систему (3.32). Так как W(x) =
\2х
1 Ч
2 10j
ИЧх<0)).Дх(0)
.(0П
/Х*(0))
имеет
Ах,
1
2х2
(0^
, то система
Дх2
(0)
Отсюда
Ах
(0)
АхГ
Ах
(0)
Для вычисления Дх(*\ А: = 0,1,..., здесь и далее
используется метод Гаусса единственного деления (см. разд. 1.2.1).
( \Ъ\ ( 5^
3°. Вычислим х(1) =х(0) + Дх<°> =[Х | +
29
- 0,625
3,625
116

4° Так как Л(1) = тах^
131
8 Г
1 П
1 8
К
то положим к = 1 и перейдем
к п.2.
21. Составим систему W(x(l)) • Лх(1) = -F(xil)):
Г 145 >^
1 П
1~4 4 J
.Дх*»--
О "|
145
К 32
Отсюда Дх(1)
272
145
272>/
0,5333
-0,5333
з'. вычислим х<»=*<■>+дх<»=f-°'t2/Vf 0^]=f;°;
^ 3,625 J l^-0,5333j I, 3,0
-0,625"! ( 0,5333 ^ _ (-0,0919")
J,0919 j
41. Так как Л(2) = 0,5333 > е , то положим к = 2 и перейдем к п.2.
Результаты дальнейших вычислений приведены в табл. 3.19.
Таблица 3.19
к
х(к)
1
Y(k)
Д<* + 1>
0
1
5
-
1
- 0,625
3,625
1,625
2
-0,091911
3,091911
0,5333
3
- 0,002653
3,002653
0,089258
4
- 0,0000023
3,0000023
0,0026507
5
0,0000
3,0000
0,0000023
Найденное приближенное решение х, = (0;3,0000)г. Из анализа решения,
приведенного в табл. 3.19, следует, что количество верных знаков на каждой
итерации удваивается, что соответствует квадратичной сходимости.■
Пример 3.20. Найти решение системы
/i (*) = *, + 3-lgx, -х\ =0,
/2(х) = 2х\ - ххх2 - 5х1 +1 = 0,
расположенное в первом квадранте с точностью е = 10~5.
D 1. Выберем начальное приближение х(0) = (3,5; 2,2)г. В поставленной
задаче е = 10"5. Положим к = 0.
2°. Составим систему (3.32).
Так как
(дЩ дМх))
Щх)-
дхх дх2
д/2М df2(x)
{ дх{ дх2
< 3.0,43429 „
1 + - 2х2
I 4дс, -х2-5
*1
W(x^)
( 3-0 43429
1 + u'^z* -2-2,2
3,5
^4-3,5-2,2-5 -3,5 )
1,372248571 -4,4
6,8 -3,5
117

А.372248571 -4,4V m =_/(х(0)) __
^ 6,8 - 3,5 J
3,5 + 3-lg3,5-2,22
^2-3,52-3,5- 2,2-5-3,5 + 1
Отсюда с помощью метода Гаусса единственного деления находим
-0,29220413^
-0,3 у
Ах
(0) _(-0,011835967^
,062718692 у
I 0,0
3°. Вычислим
X(D _х(0) +дх(0) _f3,5V f-0,011835967^ f3,488l64032^
-х +ах [2,2j Л 0,062718692 J [2,262718691/
Этот же результат может быть непосредственно получен по формуле (3.31):
,0)
(3& 1 Г-3,5 4,4 }
\2Л) 25,11713 [-6,8 1,37248571 J'
"| (- 0,29220413"! _ (3,488164032^
-0,3 J ~(2,262718691/
4°. Так как Д(1) = max {0,011835967; 0,062718692 } = 0,062718692 > е, то
положим к = 1 и перейдем к п. 2.
21. Составим систему (3.32):
f 1,373511678 -4,525437382V (1) ( 0,00394114 "|
[б,689937437 -3,488164032 J** ~[- 0,00102252 J *
Применяя метод Гаусса единственного деления, получаем
Ах
0)
(- 7,21032383-10"4
-0,001089727
З1. Вычислим
[2,261628964/
41. Так как А(2) = max {|-7,21032383 Ю"4]; |-0,001089727| }= 0,001089727 > б,
то положим к = 2 и продолжим решение по алгоритму. Результаты дальнейших
расчетов приведены в табл. 3.20.
Таблица 3.20
Гк
х\
х2
А
0
3,500000
2,200000
-
1
3,488164032
2,262718691
0,062718692
2
3,487443000
2,261628964
0,001089727
3
3,487442788
2,261628631
3,33446159 9 10'7
Из сопоставления полученных результатов с табл. 3.17 следует, что по
методу простых итераций точность б = 0,001 достигается за четыре итерации,
а методом Ньютона точность б = 10~5 достигнута всего за три приближения.»
118

Пример 3.21. Найти решение системы
х\ + х2 + х3 = 1>
2х? + х£ - 4х3 = О,
Зх,2-4х2+*з =0
методом Ньютона с точностью е = 0,005.
D 1. Выберем в качестве начального приближения х(0) = (0,5; 0,5; 0,5)г.
В поставленной задаче г - 0,005. Положим к = 0.
2°, 3°. Воспользуемся формулой (3.31). Матрица Якоби имеет вид
Щх).
(2х, 2х2 2хЛ
4*! 4х2 - 4
[бх] -4 2х3 J
В точке х(0) справедливо
0Ч*<°>) =
11 П
2 1 -4
3-4 1,
/•<х<°>) =
(0,25 + 0,25 + 0,25 -Г)
det^(x(0)) = -40, W^-^x^) = -—
40
0,5 + 0,25-2
^ 0,75-2 + 0,25 )
(Ъ
(-15 -5 -5^
-14 -2 6 =
-11 7 -lj
-0,25'
-1,25
1
8 8
7 1
20 20
И 7
8
20
1
В результате
И0 40 40 J
х<1)=^0>-^-1(х(0))/'(х(0)):
'3 1 1 ^
0,5
JL JL
20 20
11 7
8
_3_
"20
1
'-0,25'
-1,25
I -1 J
=
'0,5>
0,5
,0.5,
+
' 0,375 )
0
l-0,125j
=
'0,875N
0,5
[0,375j
И0 40 40
4°. Так как Л(1) = max {0,375; 0; |- 0,125| } = 0,375 > e, то положим к = 1 и
перейдем к п. 2.
21. В точке jc(,) справедливо
Ж(х(1)) =
(2-0,875 2-0,5 2-0,375) (1,75 1 0,75
40,875 20,5 -4
1,6.0,875 -4 20,375j
3,5 1 -4
1,5,25 -4 0,75j
119

/Х*(1)) =
0,8752+0,52+0,3752-1
2 0,8752+0,52-40,375
3 0,8752-4 0,5 + 0,3752
( 0,15625 "|
0,28125
[ 0,4375 J
Составим и решим систему
(1,75 1 0,75^1
3,5 1 -4
[5,25 -4 0,75J
■Ах
(О
(0,15625 ^
0,28125
( 0,4375 J
С помощью метода Гаусса единственного деления получаем
Ах
(О _
-0,084995
-0,0032467
- 0,0056818J
З1. Вычислим
Х(2)=х(1)+Дх(1)
(0,790005^
0,496753
[o,369318j
41. Так как А(2) = maxlAxf }| = 0,084995 > е = 0,005, то положим к = 2 и
перейдем к п. 2.
22. Составим и решим систему
(1,58001 0,993506 0,738636^
3,16002 1,987012 -4
4,74003 - 4 0/738636J
|Ах<2>=-
(0,007267^1
0,017707
[o,021707j
Применяя метод Гаусса, находим
(-0,004785^
Дх<2> =
0,000136
^ 0,000579 )
З2. Вычислим
х^=х^+Ах(2)
(0,785220^
0,496617
[o,369897j
х. = х
42.Так как Д(3) = max Дх<2) = 0,004785 < 0,005, то процесс завершен и
(3).
120

3.2.5. Модификации метода Ньютона
А. Упрощенный метод Ньютона. В этом методе в отличие от метода
Ньютона (3.31) обратная матрица ищется только один раз в начальной точке х^:
X(*+D = XW _ w-\(;с(0)}. /-(X(*))f к = од,...
(3.33)
Заметим, что при решении одного уравнения f(x) = 0 упрощенным
методом Ньютона производная функции вычисляется также один раз в начальной
точке (см. разд. 3.1.7).
Методика решения задачи аналогична изложенной в разд. 3.2.4, где вместо
(3.32) используется система
и/(х(0)) • Ах(А:) = -Г(х<к)), к = 0,1,...,
матрица которой W(x^) не изменяется от итерации к итерации.
Очевидно, сходимость упрощенного метода Ньютона в общем случае хуже
по сравнению со сходимостью процесса (3.31).
Пример 3.22. Найти положительное решение системы
/1(х) = х12+х22-1 = 0,
/2(Х) = Х!3-Х2=0
упрощенным методом Ньютона с точностью б = 10"4.
□ 1. Выберем начальное приближение. Из рис. 3.18 следует, что для
нахождения положительного решения системы можно принять х(0) = (0,9; 0,5)г.
/1(х) = дс?+х|-1 = 0
/2(х) = х?-х2=0
Рис. 3.18
В поставленной задаче е = 10~4. Положим к = 0.
121

2°,3°.Таккак
то для выполнения вычислений по формуле (3.33) найдем обратную матрицу
U.43 -1/
1 ' 4,23 {- 2,43 1,8 J [0,5
W(*(0)) = [ „7, , |, det W(x(0)) = -1,8 - 2,43 = - 4,23;
(0,2364 0,2364
1,5745 -0.4255J
Поэтому
х(1)=х(0)^и/-1(х(0))./.(х(о)) =
0,9"! _ (0,2364 0,2364 ¥0,060^ _ (0,9) _ ( 0,06832 ) _ (0,83167)
0,5J 1Д5745 -0,4255j[o,229j"[o,5j [- 0,06297J " [о,56298/
4°. Так как А(1) = тах{|- 0,06832|, |0,06297| } = 0,06832 > е, то положим к = 1
и перейдем к п.2.
21.31. По формуле (3.33) получаем
0,83167^ - f0'2364 °'2364 ) (°>008619) _ 1^0,83167^ _ ( 0,004937 ) _ (0,826732)
0,56298J [о,5745 - 0,4255J [о,012267J " [o,56298 J [- 0,000268J ~ 1,0,563246/
41. Так как Д(2) = 0,004937 > е, то положим к = 2 и перейдем к п.2.
22.32. По формуле (3.33) получаем
x<3>=x<2>-^-V0))^(*(2)) =
0,826732^1 _ Г0,2364 0,2364 "] (0,000732^1 _ (0,826732^ _ ( 0,000602 \ _ (0,82613^
0,563246 J [о,5745 - 0,4255j[o,001814j ~ [o,563246j [- 0,000351 J " [о,56359/
42. Поскольку Д(3) = 0,000602 > е , то положим ЬЗи перейдем к п.2.
23.33. По формуле (3.33) имеем
х(4)=х(3)_ И/-1(Х(0)). f{xO)) =
(0,82613) (0,2364 0,2364 Y0,000124^ _ (0,82613) ( 8,524-10"5 ] _ (0,8260447)
[o,56359j [o,5745 -0,4255j[o,000236j "[o,56359j (-2,89692-10"5J "1,0,5636189/
43.Поскольку Л(4) = 8,524-10"5 <e = 0,0001, то процесс завершен и
х.=х<4\
122

Б. Метод секущих. Идея метода секущих (метода Бройдена) заключается
в аппроксимации матрицы Якоби с использованием уже вычисленных значений
функций, образующих систему (сравните с методом секущих для уравнения
/(*) = 0, изложенным в разд. 3.1.7).
Методика решения задачи
1. Задать начальное приближение х^ и малое положительное число е.
2. Положить к - 0 и Aq - W(x^), где W(x) — матрица Якоби.
3. Решить систему линейных алгебраических уравнений
4^ =-/■(*<*>)
относительно sk - поправки к текущему приближению.
4. Вычислить *(*+1) = х^ + sk.
5. Если ||^|| < б, процесс завершить и положить х0 =х(*+,). Если ||5^||>е,
вычислить
„ _ £7v(* + D\ CYv(*h А -А ■ (У к ~Aksk)-Sk
Ук=*\х ')-/Ч* J, Ак + {=Ак + - ,
положить к = к +1 и перейти к п.З.
Замечания.
1. Можно доказать [11], что если х(0) достаточно близко к корню хт, где
матрица Якоби W(x.) не вырождена, и если Aq достаточно близка к JK(x(0)),
то последовательность итераций | х^ ] сходится к хт сверхлинейно.
2. Когда метод секущих сходится к х. сверхлинейно, нельзя предполагать,
что последняя из аппроксимаций якобиана Ак будет приблизительно равняться
W(x0), хотя часто это именно так.
Пример 3.23. Решить систему
/i (х) = х{ + х2 - 3 = О,
/2<*) = Х|2+х|-9 = 0
методом секущих.
D 1. Как следует из примера 3.18, для нахождения корня хт = (0; Ъ)Т
можно выбрать начальное приближение дс(0) = (1; 5)т и е = 0,001.
2. Положим к = 0 и
1 1
[ 2х2 2х2 j
А0=ЩХМ) = [\ М, так как Щх) J
3°. Решим систему Aq sq = -F(x^0)).
Так как F(x™) = Р], то s0 = -ytfW») = ["|'^
123

5°. Поскольку ll^ojlj = 1,625 > е, то вычислим
y0=F(x^)-F(x^)
4,53125
-3
46875)'
sUo = (-1.625 -1,375) | J'™ I = 4,53125,
1,625
Л-^о=(_12~36875)-(.
i i](-ifi*)J -3 W-э
2 10 JU 1,375 J I-12,46875 J 1,-17
1,4,53125 у
fo> - 4>'oY *S = L 53125J(-1625 -1,375);
Aa +
(УО-AqSq)
T
so
)*о)-*о Jl n.f
s0 "b 10J I-1
0 0 W 1 1)
,625 -1,375 J 10,375 8,625 J
Положим Ы и перейдем к п.З.
З1. Решим систему Ах -sx = -F(x^), т.е.
[0,375 8,625/1 = "[4,53125/
Применяя метод Гаусса, получаем
0,549 ) _ Г- 0,076
,549 J " I 3,076
<\ „ (2) т Г- 0,625^1 ( 0,5
41. Вычислим х(2) = х(1) + St = I ' + '
1 [3,625 J [-0,:
51. Поскольку ll^flj = 0,549 > б , то вычислим А2 =
1
, положим
>,799 8,201 J
к = 2 и перейдем к п.З. Результаты вычислений приведены в табл. 3.21.
Таблица 3.21
[ к
1
г(к)
А
0
1
5
-
1
-0,625
3,625
1,625
2
-0,0757575
3,0757575
0,549
3
-0,0127942
3,0127942
0,0629
4
-0,0003138
3,0003138
0,01248
5" ' ~1
0,0000013
3,0000013
„0,00031
Полученное приближенное решение х0 = (0,0000013; 3,0000013).!
124

Пример 3.24. Решить систему
х,2 + х2 - 2 = О,
еХ]~1 ч-д:]-2 = 0
методом секущих с точностью б = 0,01.
□ Очевидно, точное решение системы х.=(\;\)т. Выберем начальное
приближение х(0) = (1,5; 2)т. В поставленной задаче г = 0,01.
Так как W(x) = \х \ , то положим
Результаты расчетов приведены в табл. 3.22.
Таблица 3.22
Г к
1
Лк)
2
А
0
1,5
2
-
1
0,8060692
1,457948
0,69393
2
0,7410741
1,277067
0,18088
3
0,8022786
1,159900
0,11717
4
0,9294701
1,070406
0,12719
5
1,004003
1,003084
0,07453
6
1,003084
0,9992213
0,0038
Найдено приближенное решение: х, = (1,003084; 0,9992213) .■
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Методами половинного деления, хорд, простых итераций, Ньютона,
упрощенным методом Ньютона найти корни уравнений (s = 10"3):
I) х4 -2х-4 = 0(положительный корень); 2) 2-lgx-x = 0
3) tg(l,9x) - 2,8х = 0; 4) sin(2,2x) - х = 0; 5) 1п(8х) = Эх - 3
6) 0,7<Г°'59х - х = 0; 7) 5,6 sin(4,8x) - 4,5* = 0; 8) х4 - 4х -1 = 0
9) tgx = х (наименьший положительный корень);
10) дс4 - Зх2 + 75х -10000 = 0 (отрицательный корень);
II) х4 + 2х3 - х -1 = 0; 12) х3 - 0,2х2 - 0,2х -1,2 = 0 (положительный корень);
13) х5 - х - 0,2 = 0 (положительный корень); 14) х3 - 2х - 5 = 0;
15) х3-2х2-4х-7 = 0 ; 16) х3+2х-7 = 0; 17) х4+Зх-20 = 0.
2. Методами простых итераций, Зейделя, Ньютона, секущих, упрощенным
методом Ньютона решить системы (б = 10"3):
1)
4)
2х,3-х|-1 = 0,
ххх\ -х2 -4 = 0;
tg(X!X2-fO,2) = X2,
х,2 + 2x2 = 1;
sin(x, + 1) - х2 = 1,
2xj + cos х2 = 2;
*!-2*2+1 = 0,
- х2 + 2х2 -1 = 0;
3)
6)
2*, +tg(X!X2)=0,
(jc|-6)2+lnx, =0;
cos(xx + 0,5) - х2 = 2,
sin х2 - 2xj = 1.
125

Часть П. ЧИСЛЕННЫЕ МЕТОДЫ ТЕОРИИ
ПРИБЛИЖЕНИЙ
Глава 4. МЕТОДЫ ПРИБЛИЖЕНИЯ СЕТОЧНЫХ ФУНКЦИЙ
4.1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ И КЛАССИФИКАЦИЯ
МЕТОДОВ
Получаемые при компьютерных вычислениях, в экспериментальных
исследованиях или задаваемые при проектировании элементов конструкций
летательных аппаратов сеточные (табличные) функции
У! «Л*/), */ «Ф,6], / = 0,л,
малоинформативны. Они определены только в узлах х,- (/ = 0, п) сетки Qn, а их
значения в промежуточных точках, а также значения производных в узлах не
известны, интегралы от них нельзя вычислить классическими методами. Каждая
сетка характеризуется шагами hi+{ = х/+1 -х, неравномерного или (Л/+1 = const)
равномерного разбиения.
Однако значения функции должны быть известны при любом значении
аргумента х * х,, а в самих узлах х, требуется знать также первые и вторые
производные, поэтому сеточные функции yf - f(xt) необходимо восполнять. Данная
проблема решается с помощью методов теории приближений (теории
аппроксимации) — одного из важнейших разделов численного анализа.
Для восполнения исходных (аппроксимируемых) функций yt - /(х,), / = 0,л,
искомыми (аппроксимирующими) функциями у = /т(х,Ъ~), как правило,
используются алгебраические многочлены
~ /и
/т (х,д) = Yaajxi =<*0+alx + ... + amxm1 (4.1)
где а = (a0iau...,ат)Т— вектор неизвестных параметров, m — степень
многочлена, подлежащие выбору или определению (обычно т< п).
Замечания.
1. Аппроксимация тригонометрическими многочленами с помощью
рядов Фурье изучается в классических курсах математического анализа.
Алгебраические многочлены являются частным случаем обобщенных многочленов,
рассматриваемых в разд. 4.4. Все понятия, вводимые в данном разделе,
справедливы и для обобщенных многочленов.
2. Иногда в качестве аппроксимируемых функций берутся сложные
формульные функции у = f(x), которые желательно заменить более простыми.
Методы приближения различаются выбором различных по характеру
условий согласования функций fm(x,a) и >>, = Л*/)- В данной книге рассматриваются
два типа условий согласования — точечные (дискретные) и интегральные.
126

Применительно к некоторой точке х,- сетки Q„ = {xh i = 0,л ) дискретные
условия согласования записываются в виде нулевых невязок искомой функции и
ее производных:
Vm('4xha) = /Jp)(xha) - /<»<х/) = 0, (4.2)
где р— порядок производной. При /? = 0 условие (4.2) является функциональным
и оно традиционно называется условием интерполяции:
&fm(xha) = /„<*„?) - f{x,) = 0. (4.3)
Возможны два типа интегральных условий:
1)
J^E[/«(*/,fl>-/<*/)] ->mjn (тйп)\ (4.4)
2) 6/(/*<*') = }/т(х,я)<*х-//+1=0
*/
или (4.5)
*/(*%) = )/т(х*а)<Ь-Н-0>
XU\ xi
где /•+1 = \f(x)dx, /q = \f(x)dx. Условие (4.4) выражает минимум среднеквад-
ратичной погрешности (или отклонения) представления заданной сеточной
функции /(*/),/ = 0,л, с помощью аппроксимирующей функции fm(x,a). Оно
относится, как правило, ко всей области определения функции /(*/), т.е. к отрезку
[ayb]. Сомножитель иногда опускают, так как его наличие или отсутствие
л + 1 _
влияет только на величину погрешности, но не влияет на вектор а,
обеспечивающий ее минимум. Условие (4.5) может относиться как к одному частичному
отрезку [x,,x,+i], так и к отрезку [x0>jcJ , а также ко всему отрезку [a,b].
Условие (4.5) в одномерном случае, когда функция f(x) зависит только от х,
выражает равенство площадей под кривыми f(x) и /т(х,а). В двумерном случае,
когда функция зависит от двух переменных, условие (4.5) обобщается и выражает
равенство объемов (аппроксимация таких функций здесь не рассматривается).
Таким образом, применение условия (4.5) приводит к сохранению интегральных
свойств аппроксимируемой функции, а также предоставляет исследователям
новые ранее неиспользуемые возможности при построении новых нетрадиционных
методов решения задач аппроксимации [15,16,19—21].
Метод приближения, построенный на базе условия (4.3), будем называть
методом интерполяции или функциональным методом (рис. 4.1,а).
Метод, использующий условие (4.2) при р > О, называется
дифференциальным.
Если совместно с условием (4.2) применяется интегральное условие, метод
называется интегрально-дифференциальным.
127

Метод, построенный на базе условия (4.3) и интегрального условия,
называется интегрально-функциональным. Методы приближения, сконструированные
только на базе условия (4.4) или (4.5), выполняют сглаживание исходной
функции (рис. 4.1,6) и поэтому называются методами сглаживания (интегрального
сглаживания).
Если условия (4.5) используются отдельно, метод сглаживания называется
восстанавливающим, а если совместно с условиями (4.3), то — интерполяционно-
сглаживающим.
Названия многочленов, получаемых в результате применения методов,
соответствуют названиям этих методов.
У
0
х
у
Э *1
я
1
*/
У =
■7т(х>а)
*„ х
*0
Рис. 4.1
Можно выделить четыре способа применения методов аппроксимации,
отличающихся областями их «действия».
1. Глобальный способ, в котором для всей области Qs[a,Z>] определяется
одна функция fm(x,a).
2. Локальный способ, когда функция восполняется только в окрестности
некоторой точки х,. Это восполнение обычно осуществляется на основе
формулы Тейлора. Данный способ рассматривается в курсе математического анализа.
3. Кусочный способ, когда ищется одна или несколько функций
Л/(х,а),/ = 0,1,.., каждая из которых является многочленом степени к и имеет
область определения в виде частичного отрезка Qik =[*,-, *,-+*]
(1 < к < п, к = 1,2,..), называемого «окном» аппроксимации, которое составляет
шаблон {xi,xi+l,...,xi+k). Саму функцию /*,(*,я), построенную на одном
шаблоне, будем называть звеном.
4. Кусочно-глобальный способ, в котором область Q представляется сово-
N
купностью N частичных отрезков Qik , таких, что Q = (J Qik. На первом этапе на
каждом из отрезков ищется функция /м(х,а) — i -е звено с применением
кусочного способа аппроксимации. На следующем этапе производится объединение
128

всех звеньев в одну многозвенную функцию, т.е. /*(х,я) = (J/#(x,fl). Данный
способ применяется, например, в разд. 4.5 при построении сплайнов.
4.2. МЕТОДЫ ФУНКЦИОНАЛЬНОЙ ИНТЕРПОЛЯЦИИ
4.2.1. Постановка задачи
Пусть на множестве Q = [а,Ь] задана сетка Qn = |х;, / = 0, л ) , определяемая
л +1 точкой х0,х{,...,хп, а на сетке задана сеточная функция у( = /(х,), / = 0, л:
Уо = /(х0),у{ =/(х\),...,Уп = /(*/,)•
(4.6)
В некоторых случаях ух = /(х,), / = 0, л, является сеточным представлением
заданной формульной функции у = /(х). Сеточная функция может задаваться
совокупностью пар: (x0,y0)f(xl,yl),...i(xn,yn).
Требуется найти функцию y = F(x), принимающую в точках х0,хь...,хп
те же значения, что и функция yt = /(*,), i = 0,л, т.е. F(xt) - yh i = 0,л.
Точки x0,xj,...,xw называются узлами интерполяции, а искомая функция
у = F(x) — интерполирующей.
Геометрически это означает, что нужно найти кривую, проходящую через
заданное множество точек (xhyt)J = 0,п (рис. 4.2).
Одной из целей задачи интерполяции является вычисление значения
функции в произвольной точке х.. При этом различаются собственно
интерполирование, когда точка х„ € [х0,х„], и экстраполирование, когда х„ ч [х0,хл].
Заметим, что можно провести бесчисленное множество «плавных» кривых,
проходящих через заданное множество точек. Поэтому задача интерполяции в
общей постановке не имеет единственного решения.
У
0
Уо
1 1 т^^
1 1 1
1 1 1
1 1 '
1 1 1
*0
A y=Fw v
/ • \ Г~\ Уп
/ 1 \ Л \\ /Л
' j Nn !у!
: i ! ! i i !
, • . • 1 i i
i i i i i i i
x, x„ x
Рис. 4.2
129

Если в качестве интерполирующей функции выбрать алгебраический
многочлен, степень которого связана с числом заданных узлов интерполяции (на
единицу меньше), решение задачи является единственным. Покажем это.
Воспользуемся сначала кусочным способом. Выделим из отрезка [хо,хл]
частичный отрезок [*/,*/+*] и рассмотрим сеточную функцию yt =/(*,), заданную
в (к + 1)-м узле дс/,Х/+1,...,х|-+^(узлы не совпадают):
У\ = /(*/), Ум = f(xul),...9 уик = f(xi+k).
(4.7)
В качестве интерполирующей функции выберем алгебраический многочлен
к -й степени (степень многочлена на единицу меньше количества узлов):
F(x) = fk (х, а) = £ QjXj = а0 + ахх +... + акхк.
у=0
(4.8)
Будем искать неизвестные коэффициенты a0faly...,ak из условия
интерполяции (4.3) , т.е. bfk(xha) = 0:
7к(х»а) = У» 7*(*м.1.5) = .у,ч1>-> fk(xi+k,a) = yi+k. (4.9)
Теорема 4.1 (о единственности решения задачи интерполяции).
_ *
Задача о нахождении интерполяционного многочлена fk(x,a) = Хду*У' удов-
;=о
летворяющего условиям (4.9), «л частичном отрезке \xiyxuk\ по заданной сеточной
функции (4.7) имеет единственное решение.
Доказательство. Запишем условия интерполяции (4.9) с учетом (4.8) и
обозначения yt = /(*,) = /• :
а0 +а^ + а2х? +...+ akx\ = fh
а0 +a{xi+l +a2xi+l +... + акхих = /}+i, {А.Щ
ао + *i*i+* + <*2х?+к +... + akxf+k =fi+k.
Эта система линейных алгебраических уравнений относительно
коэффициентов а0,а{1...,ак имеет единственное решение, так как определитель матрицы
системы
Q(*/>*/ + b — >xj+k) =
ft 2 к \
1 Xt Xj ... xf *
1 *i+l *l+l — */+!
V */♦* Xj+k... Xj+k J
(4.11)
не равен нулю (доказательство последнего факта содержится в курсе линейной
алгебры, где этот определитель называется определителем Вандермонда).
Следовательно, задача интерполяции также имеет единственное решение.
130

Полагая / = 0, к = л, приходим к глобальному способу решения
поставленной задачи. А именно, если задана сеточная функция в (л + 1)-м узле xQ,x{i...fx„
и требуется найти алгебраический многочлен с использованием условий
интерполяции, то единственным решением задачи интерполяции является
интерполяционный многочлен л-й степени:
F(x) = fn(x,a)= Y,ajxi = До+tfi* + - +*/,*"> (4.12)
7=0
коэффициенты которого находятся из системы (4.10) при / = 0, к = п.
Замечания.
1. Матрица (4.11) имеет дискретный (точечный) характер, так как ее
элементы вычисляются по дискретным значениям Jt,,jc/+1,...,;c/+it.
2. При решении поставленной задачи предполагается, что исходная
сеточная функция задана своими точными значениями, хотя класс задач, для которых
используются такие функции, ограничен.
3. Имеются и другие формы записи интерполяционных многочленов. По
теореме 4.1 все эти многочлены степени л, удовлетворяющие функциональным
условиям интерполяции и построенные по одним и тем же точкам, являются
одним многочленом, записанным в разных формах.
4. При большом числе узлов решение системы (4.10) затруднительно.
Искомый интерполяционный многочлен можно построить, не решая этой системы.
Многочлены могут быть построены так, чтобы в самой структуре формулы
многочлена условие интерполяции учитывалось (см. разд. 4.2.2 и 4.2.3).
5. При решении задачи функциональной интерполяции и в ее приложениях
требуется:
а) выбрать наиболее удобную форму и степень интерполяционного
многочлена. При этом можно использовать многочлены Лагранжа (разд. 4.2.2) или
Ньютона (разд. 4.2.3), а также формулу (4.8);
б) оценить погрешность интерполяции;
в) определить значения функции в точках, не совпадающих с узлами;
г) вычислить значения производных или определенных интегралов с
использованием полученных интерполяционных многочленов.
Методика решения задачи интерполяции
1. По заданной сеточной функции составить интерполяционный многочлен
определенной степени. При выборе степени многочлена следует
руководствоваться желаемой точностью интерполяции.
2. Вычислить значения интерполяционного многочлена в заданных точках
xmjyj = !,...,/>, путем их подстановки в формулу многочлена.
131

4.2.2. Многочлен Лагранжа
ПОСТАНОВКА ЗАДАЧИ И ПОСТРОЕНИЕ МНОГОЧЛЕНА
Пусть исходная сеточная функция задана в (п +1) -и точках сетки Q„:
У{ = /(*/),' = 0,/i, где х,- е [а,^] = [х0,дсл] - в общем случае неравноотстоящие
узлы, определяемые шагами й/+1 = х/+1 -х, (А/Ч1 = var).
Воспользуемся сначала кусочным способом. Здесь и далее будем
использовать обозначение /} = /(х,).
Выделим «окно» или частичный отрезок [х/,х/+1], содержащий только две
точки (шаблон (х,,х/+1)). Тогда многочлен Лагранжа, интерполирующий
исходную функцию на данном шаблоне, имеет вид
k W = ,(*~*ы*// + ,{Х~Х'\/м = РиМ ■ f, + flw(x) • /,♦,, (4.13)
^Х, -Xi+\) ^x/+l -X/J
где ^/(х),/^/^.!^) —коэффициенты.
Действительно, легко убедиться в том, что Ц(х) — алгебраический
многочлен первой степени, который удовлетворяет условиям функциональной
интерполяции (4.3) , т.е. Lx(Xj) = /,, ^(xz+i) = fM.
Выделим «окно» в виде двойного частичного отрезка [х/,х/+2] с шаблоном
(x/iJC/"+i»Jci+2)- Тогда многочлен Лагранжа записывается в виде
j , v (х-х<ч1)-(х-х|Ч2) г , (х-х,)(х-х,ч2) ,
\xi ~ xi+l) ' \xi " xi+2) V*/ + l ~ xi) ' W+| ~ *,42 J
(4.14)
(x-X,)(x-X/41)
(x/+2 -*/)(*/+2 -*/ + l)
//+2 = ^2/W * Л + ^2/41 W ' Л+1 + ^2,42(*) ' fi+2>
где ^2/(*)»^2/+1(*)»Л/+2(*)~ коэффициенты.
Легко проверить, что (4.14) — многочлен второй степени и также
удовлетворяет условиям функциональной интерполяции:
£г(*|) = У/i ^2(*/+i) = /i+i> ^2(^*42) = У/+2-
Обобщив запись многочлена на «окно» для к -кратного частичного отрезка
[*/»*/+*] с шаблоном (х/,х/Чj,...,х,+л), можно записать многочлен Лагранжа
в виде
L (дл_ у (x-x/)(x-x/41)...(x-xm.1)(x-xm+1)...(x-x^)
/п=/ (*т " */) * (х/я ~ x/4l)--(xm - хт-\) ' (хт ~ хт+\)-(хт ~ хк)
(4.15)
/Я=/
132

где Phnix) - коэффициенты Лагранжа, которые для внутренних точек шаблона
записываются следующим образом:
РыМ
(x-xi)(x-xul)...(x-xm_l)(x-xm+l)...(x-xk)
(xm -х,)• (хт -хих)...(хт -хт_,) •(хт -xm+1)...(xm -xk)
Легко проверить, что Р^х) удовлетворяют условию
'-(*Но.У-. l<-j<-i + k- (416)
Если положить I = 0, к - п, то приходим к глобальному способу решения
задачи. Тогда интерполяционный многочлен Лагранжа п-й степени имеет вид
L , v _ у (х - Xq)(x - X) )...(х - х,_1) - (х - х/Ч1 )...(х - х„)
1=0
(4.17)
где коэффициенты Лагранжа Pni(x) во внутренних точках отрезка записываются
в форме
(X - Хр) • (X - X) )...(х - X,.!) • (х - х<41 )...(х - хп)
РпМ-
(*/ -Xq)-(xj -xl)...(xi-xi_l)(xi-xul)...(xi -хп)
Очевидно, многочлен Ln(x)y заданный равенством (4.17), является
многочленом степени п и удовлетворяет функциональным условиям интерполяции
(4.3): L„(x/) = y;-,/ = M.
Для записи интерполяционного многочлена Лагранжа удобно пользоваться
табл. 4.1.
Таблица 4.1
х-х0
х\~х0
х2 - х0
хп - х0
Х0 -Xj
X-Xj
х2-х,
хп~х\
х0 -х2
Х\~Х2
х-х2
хп~х2
х0 ~хп
х1 ~хп
х2~хп
х-хп
Пл + 1<*) = (* ~ хо)(х ~xl)(x- xl) • ••• • (х ~ хп)
А>
А
Д2
А,
А
/о 1
А
h
/п
fi 1
Здесь Dj — произведение элементов /-й строки, Пл+1(х) — произведение
элементов главной диагонали, yt = /(*,■) = fjt i = 0,1,...,л.
Тогда многочлен Лагранжа может быть записан в форме
1л(х) = Пл+1(х)£4
/=0 ui
(4.18)
133

Замечания.
1. Если заданная сеточная функция такая, что ff = 1 (/ = 0,л), то из (4.17)
п
следует, что Ln (х) з 1, и поэтому справедливо равенство £ Л» (*) = 1 (сумма всех
коэффициентов Лагранжа в точке х равна нулю), которое можно использовать
для контроля правильности расчетов.
2. Коэффициенты Лагранжа Pni(x) для некоторой функции у,-=/(*,-)
определяются лишь узлами сетки и точкой х , в которой необходимо вычислить
значение многочлена. Если в некоторой точке х„ требуется определить значения
нескольких интерполируемых функций f\(xi)Jf2(xi)y....(i = 1, л), то
коэффициенты Лагранжа для всех исходных функций подсчитываются только один раз.
3. При введении дополнительных узлов интерполяции все коэффициенты
многочлена Лагранжа необходимо пересчитывать заново, что неудобно на
практике. От этого недостатка свободны многочлены Ньютона (см. разд. 4.2.3).
Перейдем к рассмотрению примеров решения задачи интерполяции на
основе вышеизложенной методики.
Пример 4.1. Построить многочлен Лагранжа третьей степени для сеточной
функции, заданной табл. 4.2. Вычислить значение функции в точке хф =2,5. Для
записи многочлена использовать формулу (4.18).
Таблица 4.2
/
Х/
1 /<*/) = //
0
2
7
1
3
5
2
4
8
3 "1
5
7
□ 1. Построим многочлен Лагранжа. Для этого составим табл. 4.3,
соответствующую табл. 4.1.
Таблица 4.3
Г х"2
1
2
3
-1
х-3
1
2
-2
-1
х-4
1
-3
-2
-1
х-5
П4(х) = (х-2)(х-3)(х-4)(х-5)
-6(х-2)
2-(*-3)
-2-(х-4)
6.(х-5)
А
7"
5
8
7
fi
По формуле (4.18) получаем:
г ,. n/Y^/, (x-2)(x-3)(s-4)(x-5)-7 , (x-2)(x-3)(x-4)(s-5)»5
ыо А - 6 • (х - 2) 2 • (х - 3)
(х-2)(х-3)(х-4)(х-5)-8 (х-2)(х-3)(х-4)(х-5)-7
_2-(х-4) + 6(х-5)
134

:-|(x-3)(x-4)(^-5) + -(x-2)(x-4)(x-5)-4(jc-2)(x-3)(x-5) +
6 2
+ |-(х-2)(х-3)(х-4) = --х3+1бх2- — x + 62.
6 2 2
2. Вычислим значение функции в заданной точке: Lj(2,5) = 4,8125. ■
ПОГРЕШНОСТЬ ИНТЕРПОЛЯЦИИ МНОГОЧЛЕНАМИ ЛАГРАНЖА
При определении значения /(х),х*х,, для функции yt =/(х/) (i = 0,/i)
с помощью многочлена Лагранжа возникает погрешность или остаточное
слагаемое Rn (х):
/(x) = L„(x) + /?„(x). (4.19)
Здесь предполагается, что используется глобальный способ интерполяции и
что /(х)бСл+1[й,/>]. Последнее предположение требуется для применения
соответствующих теорем математического анализа, однако, приведенное ниже
соотношение для Rn(x) может использоваться и для сеточных функций.
На основе указанных предположений доказано [2,6,14], что при
интерполяции функции у{ = /(х,), заданной в общем случае на неравномерной сетке
л
Qn, интерполяционным многочленом Лагранжа Ln (х) = J] Pni(х)/} для
произвольного значения х е (х0,х„) возникает погрешность
/=о
RnM=Lr—^гМ*)> (42°)
(л + 1)!
где ю„(х) = (х-х0)(х-Х!)...(х-хл) -многочлен (п + 1) -й степени, а £,е(ауЬ).
Поскольку точно найти Rn(x) нельзя (из-за неопределенности точки £), то при
проведении вычислений обычно находятся только приближенные оценки
погрешностей интерполяции, которые являются априорными.
Оценка погрешности интерполяции в некоторой произвольной фиксированной
точке х„ е [a, b] имеет вид
\fM-Ln(x.)\<-l^\<un(x.)l (4.21)
(Л + 1)!
где Мл+1=тах|/(л+1)(х)|.
М ' ■
Оценка максимальной погрешности интерполяции в любой точке х е [a, b],
т.е. на всем отрезке [a,b]:
\№ - 1„(х) | < т^-max | со„(х)|. (4.22)
{П + 1)! [a,b]
135

Замечание. Для сеточных функций с фиксированными узлами сетки
(узлами интерполяции) также можно проводить оценки погрешности по
формулам (4.21), (4.22), однако для этого необходимо численно определять Мп+\
с помощью аппарата численного дифференцирования. При этом следует
учитывать, что при вычислении производных высокого порядка возникают большие
погрешности (см. гл. 5).
Пример 4.2. С какой точностью можно вычислить значение/(х) = Vx|
|х.=85
если вычисления производить на основе интерполяционного многочлена Ла-
гранжа первой и второй степени, а в качестве сеточной функции принять
(xhyt) = {(16;4),(36;6),(100;10)}, (/ = 0,1,2)?
□ Так как требуется вычислить погрешность только в одной точке х. = 85,
то необходимо использовать формулу (4.21).
Найдем оценку погрешности в точке х„ = 85 для Ц (х). В качестве «окна»
линейной интерполяции (п = 1) выбираем отрезок [хьх2] = [36; 100]. Определим
величину М2 :
/'(*) = -*"2; /"(X) = _IX"2; М = max |/''(jc)|=—L= = -L-
2 J 4 2 [36;ioo]y n 4Jtf 864
Тогда щ(x.) = (85 - 36)(85 -100) = -735; \RX (x)\ < -^-• |a>,(x.)| = -^L. = 0,425.
Найдем оценку погрешности в точке х. для Z^(x). В качестве «окна»
квадратичной интерполяции (п = 2) выбираем отрезок [х0,х2] = [16; 100]. Определим
величину Л/3 •
/"'(*) =-х~ 2; М3 = max 1/'"(х)| = —^= = —-—.
8 3 [i6;ioo],y v п 8^Г 2730,7
Тогда
ю2(х.) = (85 - 1б)(85 - 36)(85 -100) = -50715; |Д2(х)| < _^Мсо2(хф)| = 3,1.
(Л + 1)!
Погрешность для многочлена Li(x) получилась больше погрешности для
многочлена Щх), что обусловлено величиной ю2(х*). ■
О СХОДИМОСТИ ФУНКЦИОНАЛЬНОГО ИНТЕРПОЛЯЦИОННОГО ПРОЦЕССА
ДЛЯ НЕПРЕРЫВНЫХ ФУНКЦИЙ
Как отмечалось выше (см. разд. 4.2.1), выбор сетки и соответствующей
степени интерполяционного многочлена при интерполяции сеточных функций
является одной из важных задач, решить которую можно, рассмотрев проблему
сходимости интерполяционных процессов [6,40] для непрерывных функций
y = f(x)eCn+l[a,b].
136

Будем считать, что интерполяция проводится на последовательности сеток
а,=.|^>, *<'>}, Q2=(42)>*,(M2)). пп = Un),x{»K...,xP } с возрастающим
разбиением к отрезка [a,b]: к^ = 1; к2 = 2;...;&„ = п и т.д.
Если при данных разбиениях при возрастающем к = 1,2,...л,... определяются
значения £*(хф) в некоторой промежуточной точке х«, то реализуется
интерполяционный процесс, характеризующийся последовательностью значений
многочленов: Ll(xm)tL2(xm)i...iL„(x^)i...
Интерполяционный процесс для функции f(x) сходится в точке х0 е [a,b],
если существует lim Ь^(х0) = /(**) (поточенная сходимость).
к-*ао
Для отрезка [a, b] существует понятие равномерной сходимости в некоторой
норме, например max |/(х) - Ln (х)\ -> 0.
хс[а,Ь]
л-юо
Характер сходимости или расходимости интерполяционного процесса
зависит как от гладкости и поведения функции /(х), так и от выбора
последовательности сеток С1п(п = 1,2,...). Так, показано, что если f(x) непрерывна на [a,b],
то найдется такая последовательность Qn(n = 1,2,...), для которой
интерполяционный процесс сходится равномерно на [a,b] (теорема Марцинкевича [40]).
Однако для дискретных функций, рассматриваемых в данном разделе, эта
теорема не применима. Отметим также, что построены расходящиеся
интерполяционные процессы и для формульных функций, например /(х) = | х|, х е [-1; l] и
/(х) = (1 + 25х2)-1, х е [-1; 1]. Кроме того, применение многочленов высоких
степеней приводит к так называемым «провалам» между узлами интерполяции,
часто называемым осцилляциями. Указанные свойства интерполяционных процессов
обусловливают нецелесообразность применения интерполяционных многочленов
высоких степеней. В связи с этим в вычислительной практике для сеточных
функций степень п не берут выше 5 -г- 8 (л < 5 -г 8) и задание частичного отрезка
согласуют с выбранной степенью многочлена.
Рассмотрим часто использующиеся на практике линейную и
параболическую интерполяцию.
ЛИНЕЙНАЯ И ПАРАБОЛИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ
С ПОМОЩЬЮ МНОГОЧЛЕНА ЛАГРАНЖА
В прикладных расчетах часто применяется простейшая кусочная
интерполяция, основанная на многочленах первой степени Ц(х) или второй степени
/^(х). В этом случае функциональная интерполяция называется линейной или
параболической (квадратичной) соответственно. Рассмотрим возможные способы
их реализации и найдем оценки их погрешностей.
Пусть для сеточной функции yt - /(х,), заданной на сетке
С1п = {x0,xi,...,x„} , требуется выполнить интерполяционный процесс для
определения значения /(х*), где хф *хД/ = 0,л), и оценить погрешности. Для
обоснованного выбора степени интерполяционного многочлена необходимо указать,
какую погрешность имеют значения исходной функции /(х,) в узлах. Если эта
137

погрешность составляет величину 0(h}+{) или 0(hf+i)y а в широком классе
вычислительных задач обеспечиваются именно такие погрешности, следует
использовать линейную или параболическую интерполяцию.
Методика решения задачи линейной интерполяции
1. По расположению заданной точки х# на оси Ох выбрать из всех
частичных отрезков [xo>*iM*i>x2]v-Jx/>*^]»->[x/i-i,X/J, заданных своими
крайними значениями и в совокупности образующих сетку Qn, «окно»
интерполяции О = [х,,х/Ч1], такое, что х, < хф < xi+l .
2. Для отрезка [х,,х,ч1] вычислить значения коэффициентов Лагранжа
fl/OO*2—^ — и Л/+1(х*)=—! '~~> входящих в формулу (4.13) для много-
Xj — X/ + j -*/+1 ~ xi
члена Ц(х). Правильность полученных значений Рц(х.)у Рц+\(х+) проверить по
условию Рц(х,) + Рц+\(хт) = 1, которое должно выполняться.
3. Вычислить искомое значение /(х,) согласно (4.13):
/(х.) * Ц(х.) = Ри(хМ+Р1М(х.)/м.
Как показано ниже, порядок этой аппроксимации равен двум, т.е. 0(h?+{).
Уо
1
y = Ldx)^B
Уп
*о
X/ х.
Рис. 4.3
*/+!
Геометрическая интерпретация линейной интерполяции при известной
формульной функции у = /(х) (штриховая линия) изображена на рис. 4.3. Здесь
прямая АВ соответствует графику функции у = Ц(х) на отрезке [х,,х|+1].
Приближенное значение функции равно Ц(х.) ( точка С), и оно отстоит от точного
значения f(x0) на величину CD»0(hl+l) вдоль оси Оу.
138

Методика решения задачи параболической интерполяции
1. Из всей совокупности спаренных частичных отрезков [хо^гЫ^ь^з]»
...,[х/_1,х/+1],[х|,х/+2],",[^л_1,хл], образующих сетку Q„, по заданной величине
хф выбрать два пересекающихся «окна» Ох з [х/_1,х/+1], 02 = [*/,*/+2]
(предполагается, что х, принадлежит внутреннему отрезку [x/,x,-+i]).
2. Для «окон» Ох и 02 вычислить значения коэффициентов Лагранжа:
^(,/-i(^)'^(^)^2(,/ti(^) "Для «окна» О, и Р^(хт)^1х(хт\Р^12(х.) -для
«окна» 02. Путем суммирования проверить правильность полученных значений
/41 /+2
коэффициентов: ( ^P2tk(x*) ~ 1 и Х^2,*(х*) = 1 )•
*=/-1 ' *=/'
3. Используя значения коэффициентов Лагранжа, вычислить значения
4°(^),42)(х*) по формуле (4.14).
Если в расчетах не требуется высокая точность интерполирования, то
можно ограничиться выбором одного «окна», например 02, и тогда /(*♦)« L^2\xm).
Для достижения повышенной точности интерполяцию провести для двух «окон»
и результаты б2\хт),1^\хт) осреднить:
/(х.) * [4°(x.) +42)(*.)]/2 « L2cp(x.).
При этом порядок интерполяции повышается на единицу, т.е. L2c^(xit)
аппроксимирует точное значение с четвертым порядком, поскольку погрешность
составляет величину 0(Я4), где Н = rwLx{hhhi+l,hi+2}.
Замечание. Если хт е [х0,х2] или х, е [x„_i,x„], то выбирается одно
«окно» [х0,х2] или [хл-ьхл] соответственно.
У = /(х)
х*
Рис. 4.4
Геометрическая интерпретация параболической интерполяции изображена на
рис. 4.4. Параболе у = 1^2{х) соответствует кривая ЛХЛ2ВХ, параболе у = li?\x) —
139

кривая А2В1В2. Точка С соответствует значению /§*(хф), точка D - значению
Z^2)(jO, точка Е— значению I^cpOO-
Приведем оценки погрешностей линейной и параболической интерполяции.
Вначале предположим, что сетка Qn равномерная (это имеет значение только
для параболической интерполяции). Формулы (4.13), (4.14) и оценки (4.22),
записанные для «окон» интерполяции, упрощаются, если ввести в рассмотрение
X — Х-
новую переменную — фазу интерполяции и = '-:
п
Ll(u) = (l-u)fi+ufi+l,
г / ч (ы-1)(и-2) г , ~ч<г и(и-\)
£г(«)=- ^ Lfi-u("~2)fi+\+ 2 fi+2-
Здесь учтено, что х - х|Ч1 = х - (дс, + И) = uh - h = h(u -1), х - х/+2 = h(u - 2).
Очевидно, что для Lx(u) величина и изменяется в диапазоне 0<м<1, а для
Li(u) — в диапазоне 0 < и < 2. Для получения мажорант в оценке (4.22)
необходимо найти maxIcojOOl и тах|со2(л:)|. Преобразуя зависимости coj(x) и со2(х)
к новой переменной и , получаем со {(и) = h2u{\ -и), со2(м) = пъи(\ - и)(2- и)
~i i / ч1 h2 ~2 i / ч! 2^3h1
и находим максимумы: Q = max coi (w) = —, Q = max co2(w) = .
Таким образом, реализуются следующие оценки погрешностей линейной и
параболической интерполяции, справедливых для соответствующих «окон»:
\/(и)-Ц(и)\<^М2^ (4.23)
\f(u)-I^(u)\<^^M3Jy (4.24)
где M2j = max |/"(х)|, Л/3/ = max |/'"(х)|. При этом предполагается, что f(x)
[Хпхм] ' к,*,+2]
принадлежит классам функций /(*) € С2[я,£], f(x) е C3[atb] соответственно для
линейной и параболической интерполяции. Таким образом, из оценок (4.23),
(4.24) следует, что линейная интерполяция обеспечивает на частичном отрезке
[*i>*/+i] второй порядок аппроксимации или погрешности по h , а
параболическая (без осреднения) на двойном отрезке [х;,х/+2] — третий порядок. Данные
погрешности, как отмечалось во введении и предыдущих разделах, сокращенно
записываются как 0(h2) и 0(h3). При реализации алгоритма с осреднением
порядок параболической интерполяции становится равным 0(h4).
Замечания.
1. Оценка (4.23) для линейной интерполяции инвариантна по отношению
к виду сетки Qn (равномерной или неравномерной). Параболическая
интерполяция также сохраняет указанную погрешность при выполнении интерполяции
на неравномерной сетке Оя. В [13] для Li(x) при выполнении условия
f(x) е С3[д,б] приведена оценка
140

max |*2(x)|<4"3^3,,. (4.25)
где H = тах(А/+1,Л/+2), hu2 = xu2 -xM, MXi = max |/'"(*)|.
\xhxi+i\
2. Если гладкость функции f(x) не достигает вышеуказанной и класс
гладкости понижен на единицу (/(*) е C2[atb]), то порядок параболической
интерполяции также понижается на единицу:
max \R2(х) \ < 0,1546 • H2M2J. (4.26)
l*i.*/+2l
3. Повышение класса гладкости функции f(x) выше С3[д,б] не приводит
к увеличению порядка параболической интерполяции относительно Н, т.е.
происходит как бы его «замораживание» или «насыщение». Указанные свойства,
вытекающие из оценок (4.25), (4.26), носят общий характер и имеют место в других
оценках аппроксимации многочленов, сплайнов, производных и интегралов.
4. Для произвольной степени интерполяционного многочлена при
h = const,/(*) е Сп+х[а,Ь] погрешность функциональной интерполяции на
отрезке [х0,хл] выражается следующим образом [6]:
|| Дх) - Ln(x) \\м = max | Дх) - Ln(x) \ < hn+l ^f^^n, (4.27)
где Qn = max|co„(w)|, Л/я+1 = тах1/(я+1)(х)|, со„(н) = и(и- 1) -....(и - п). Для
многочленов с п < 5 величины С1п или их оценки являются такими:
Q1 =-; Q2 = -^-; п3 =1; а4 < 3,7; Q5 <17. Из (4.27) следует, что на отрезке
4 9
[х0,;сЛ] величина ||Л„(х)|| есть 0(hn+i) и при уменьшении шага h в два раза
мажоранта уменьшается по крайней мере в 2"+l раз. Отсюда вытекает, что для
непрерывных функций можно по заданной точности интерполяции выбирать шаг
h. При этом можно путем использования кусочной интерполяции в некоторых
пределах изменять степень интерполяционного многочлена. Мажоранту в оценке
(4.27) при кусочной интерполяции можно также снизить путем выбора «окна»
интерполяции [x;,jc/+^] так, чтобы точка хф располагалась как можно ближе
к его середине. Это обусловлено тем, что колебания функции со„(х) вблизи
середины [х,-,Х/+*] меньше, чем у его концов [6] .
5. В широком классе задач математической физики применяются
расчетные схемы в основном второго (и иногда третьего и выше) порядка точности.
При их реализации, как правило, используются встроенные интерполяционные
алгоритмы, основанные на многочленах и сплайн-функциях. Степени
интерполяционных многочленов при этом должны выбираться из условия соответствия
порядков их аппроксимации порядкам точности схем. Если эти порядки
одинаковы, то порядок точности схем сохраняется, хотя константа в оценке
погрешности схемы изменяется. Если же порядок встроенных интерполяционных
алгоритмов хотя бы на единицу выше порядка точности схемы, то вместе с порядком
141

точности схемы сохраняется и указанная константа. Отсюда следует, что
необходимо выбирать такую степень интерполяционного многочлена, которая либо
обеспечивает равенство порядка аппроксимации порядку точности схемы, либо
на единицу превышает последний. Таким образом, использование
параболической интерполяции в качестве встроенных алгоритмов или для восполнения
численных решений, полученных по схемам второго порядка, позволяет сохранить
требуемую точность расчета, а также не дает избыточный порядок и,
следовательно, не усложняет алгоритм. Это замечание носит общий характер и
относится к любым аппроксимационным алгоритмам, выполняющим функцию
восполнения или интерполирования.
Перейдем к рассмотрению примеров решения задач линейной и
параболической интерполяции.
Пример 4.3. Дана сеточная функция, являющаяся сеточным
представлением формульной функции f(x) - х3 (табл. 4.4).
Таблица 4.4
i
*|
1 fi
0
-1
-1
1
0
0
2
1
1
3
3
27
4
4
64
Найти значение /(*♦) при х» = 2 с помощью линейной и параболической
интерполяции.
□ Применение линейной интерполяции. Воспользуемся методикой.
1. Выбираем «окно» интерполяции [*/,x/+J] = [l; 3] (/ = 2, / +1 = 3).
2.Вычислим коэффициенты Лагранжа: Р12 =—: - = 0,5; /fo = —! - = 0,5.
*2"*3
Вычисления выполнены верно, так как Рп + Р\з = 1 •
3. Определим искомое значение /(2) по формуле (4.13):
х3-х2
/(2)«11(2) = Р12/2 + />13/з=14 .
Применение параболической интерполяции с осреднением. Также
воспользуемся соответствующей методикой.
1. Выбираем «окна» интерполяции 0{ = [хх',х3] = [0; 3]; 02 = [х2;хА] = [l; 4].
2. Вычислим коэффициенты Лагранжа Р2\\Р22,Р22 для «окна» 0\ и
Р2?> РП> Р2А Д™ «0КНа» °2 • ПОЛУЧИМ />2({> = --, />£> = 1, />£> = 1,
^22)=Т> ?2?-Ъ ^24)=~Т- Вычисления выполнены правильно, так как
3. Определим значения Щ*(хт), Z£ '(*•) по формуле (4.14):
4° (2) = -|- 0 + Ы Д- 27 = 10; 42)(2) = -• 1 + 1 • 27 --• 64 = 6.
142

Искомое значение получим в результате осреднения:
Z5^(2) + ZJ2*(2)
/(2) « — - = 8. Найдено точное значение /(2) = 8, что объясняется
тем, что оператор осреднения повышает порядок интерполяции. В этом случае
в остаточное слагаемое входит /(4)(£) = О и оно равно нулю. ■
4.2.3. Многочлены Ньютона
РАЗДЕЛЕННЫЕ И КОНЕЧНЫЕ РАЗНОСТИ
В практике функционального интерполирования иногда удобнее
использовать многочлены Ньютона, степень которых можно последовательно повышать
путем добавления очередных слагаемых, имеющих более высокую степень. Такие
несимметричные многочлены, альтернативные симметричным многочленам Ла-
гранжа, основаны на разделенных и конечных разностях, вычисляемых по
интерполируемой сеточной функции.
Разделенные разности вводятся для функции уг = /(х,) = ft, /' = 0, п,
заданной на неравномерной сетке (Л/+1 = var), а конечные разности — для функции
у. = /(х,-) = //,/ = 0, л, определенной на равномерной сетке (Л/+1 = const).
Выбрав внутри неравномерной или равномерной сетки соответствующие
шаблоны интерполяции (xj,Xj+l),(xhxi+{,xi+2),---,(xj,xui,..,xi+k), введем
следующие определения разделенных и конечных разностей:
f — f-
— разделенная разность первого порядка: f(xitxi+\) = —— '-;
*/ + 1 ~xi
— разделенная разность второго порядка: f(xhxux, хи2) = '+Ь ,+2 —" ' ;
xi+2 ~xi
— разделенная разность k-го порядка:
Лу v v ч f(xi+\>xi+2> — >xi+k)~f(xi>xi+\> — >xi+k-\) .
*/»**Ч1 » — >■*/+* J ~ ~ у
xi+k xi
— конечная разность первого порядка: А/) = /}+1 - /];
— конечная разность второго порядка: А /) = А(А/)) = А/)+1 - А/) = fi+2 - 2fi+\ + fi \
/с
— конечная разность к -го порядка: А*/) = A(Ak~lfj) = J](-l)yC/.//+y ,
где С/ =
к\
(k-jy.fi'
143

Последовательность получения разделенных и конечных разностей при
к = 3 для произвольной функции наглядно представляют табл. 4.5 и 4.6.
Таблица 4.5
1 Xj
xi+l -•
*i+3""
fj
-tit....
"Гм
f(Xj>Xj+\)
-А'х;;хт)
-•'/(^r+t^.i)..
f(xj>xj+\,xj+2)
7(*м*Г+-1*-Х|+2.)..._
•—/W+bx/42'X/+3)
/(*/>*/ЧЬ*у+2>*/+з)
:::" /(*/»*/+! >*/+2»*/+з)
ХУ
X/
x/ + l
x/42
x/+3
fj
/m •.•.:■.:::::;
//♦2-•<:::
40
:::::-.a/«i::::;;:
'^■■■-■ап:2
*fj
•>-aI/S
:::::--дау;:;'
Таблица 4.6
A3/;
Для гладких функций числовые значения /(*,,*,+,,...,Xj+k) и А*/} при
возрастании к уменьшаются и стремятся к нулю, т.е. f(xj,Xj+i,...tXj+k) -> 0 и
д*// -> 0 при к -> од.
Связь между разделенными и конечными разностями А:-го порядка при
h = const устанавливается следующим соотношением:
f{xhxM,...,xM) = ±£. (4.28)
Действительно, при к = \ для разделенной разности /(*,-, x,-+i) получаем
f(xifxi+i) = —— L = —7-, т.е. (4.28) при к = 1 справедливо.
h \\hx
Пусть к = 2. Тогда получаем
/Yv v v \ f\xi+\>xUl)- f\xi>xi+\) 1 (Л±2-/±±\ //41 ~У)Л
/ Vх/»*/+i»*#-+2j - = тг J ;— =
xu2~xi 2h\ h h )
2h2 2\h2'
Таким образом, связь (4.28) выполняется и при к = 2. Справедливость
(4.28) при произвольном к можно доказать методом математической индукции.
144

ИНТЕРПОЛЯЦИОННЫЙ МНОГОЧЛЕН НЬЮТОНА
ДЛЯ НЕРАВНОМЕРНОЙ СЕТКИ
Пусть исходная (интерполируемая) сеточная функция yi;=/(хД / = 0,л,
задана на неравномерной сетке Qn = {х0,х{,х2,...,хп} , характеризующейся
шагами А/Ч1 = х/+1 - X/ = var.
Воспользуемся сначала кусочным способом. Из всей совокупности узлов
выбираем шаблон (х/,х/+1,...,х/+л), соответствующий некоторому «окну»
интерполяции [xi9xi+k].
Тогда для функциональной интерполяции может быть использован
многочлен Ньютона, основанный на разделенных разностях:
Nk{*) = ft + f(xi,xUi)-(x-Xi)+ /{х!9х,+ихм) (*-*/)• (х-xi+l) + ...+
(4.29)
+ f(xi,xi+l,...yxi+k){x-xi).(x-xi+l)...-(x-xi+k_{).
Действительно, Nk(x) — многочлен k-й степени, что определяется
сомножителями последнего слагаемого (разделенные разности, входящие в качестве
одного из сомножителей в эти произведения, есть числа). Кроме того, для
многочлена Nk(x) удовлетворяются функциональные условия интерполяции:
Nk[Xj)= fjj = /,...,/ + £. Проверим их справедливость при к = 1 (шаблон
(х,,х/Ч1)) и к = 2 (шаблон (х/,х/+1,х/+2)).
Пусть к = 1. Тогда
Ni{x)=fi + /(х/,х/+1)(х-х/), (4.30)
и поэтому
х/+1 -х,
Таким образом, условия интерполяции для Л^(х) выполнены,
следовательно, многочлен (4.30) может быть использован для линейной интерполяции
кусочным способом.
Пусть к = 2. Тогда
^2 (х) = // + f(xi,xi+x){x - х,) + /(х/,х/+1,х/+2)(х - х,)(х - х/+1), (4.31)
и поэтому
xi+l ~xi
^2(^,42)=// *ItilzlL(xM -Xi) + —l—[f^-fM .Alli|x
■*/ + l xi xi+2 ~ xi \xi+2 ~ xi+\ xi+\ ~ xi)
x (x/+2 - X/)(x/+2 - X/ + 1) = fi+2.
Таким образом, условия интерполяции для многочлена N2{x) также
выполнены и он может использоваться для параболической интерполяции
кусочным способом.
145

Для произвольного к справедливость равенств Nk(xj)= fj, j = /,/ + £,
проверяется методом математической индукции.
Полагая / = 0, к = п, приходим к глобальному способу. Тогда
интерполяционный многочлен Ньютона п-й степени имеет вид
ЛглМ = /0+/(х0,х1)(х-х0) + /(х0,л:1,Х2)(л:-х0)(дс-х1) + ...+
(4.32)
+ /(х0,х1,...,хл)(х-х0)(х-х1).....(х-хл_1).
Замечания.
1. Согласно теореме 4.1 многочлен Ньютона (4.32) является тождественным
~ _ п
многочлену /л(х,д) = Х^у*7 с коэффициентами, получаемыми из системы
у=о
(4.10), либо многочлену Лагранжа, т.е. Ln{x)- Nn(x) = fn(x,a) , если узлы
интерполяции и интерполируемая функция одинаковы.
2. Интерполяционный многочлен Ньютона (4.29) или (4.32) (так же, как и
многочлен Ньютона, выражаемый ниже через конечные разности) записан не
через значения функции, как это имеет место для многочлена Лагранжа, а через
разделенные разности. Поэтому при изменении степени к в процессе
интерполирования у многочлена Ньютона Nk(x) требуется только добавить или
отбросить соответствующее число слагаемых. Это иногда упрощает алгоритм
интерполирования.
3. При интерполяции на основе (4.29) или (4.32) узлы интерполяции
Х/,х/+1,...,х/Ч£ или х0,Х!,...,хл , определяющие шаблоны интерполяции,
целесообразно выбирать так, чтобы точка х„ была расположена возможно ближе к
середине отрезка [х,, х,+* ] ил и [х0, хл ].
4. Остаточное слагаемое многочлена (4.32) совпадает с остаточным
слагаемым многочлена Лагранжа, и оценки (4.21), (4.22), справедливые для точки х# и
всего отрезка [х0,хл], сохраняются.
ИНТЕРПОЛЯЦИОННЫЕ МНОГОЧЛЕНЫ НЬЮТОНА
ДЛЯ РАВНОМЕРНОЙ СЕТКИ
Сначала рассмотрим решение задачи кусочной интерполяции (применение
кусочного способа). Если функция yi;= f(xt) (/ = 0, п) задана на равномерной
сетке Ол, характеризующейся hi+l = const для всех /, то многочлен (4.29),
соответствующий шаблону (x,-,X/+i»—»*/+*)> путем подстановки в него вместо
разделенных разностей их выражений через конечные разности, согласно (4.28),
преобразуется к виду
Ni%)=fi+^q+^q{q-\) + ... + £Aq{q-\)-..A4-k + l), (4-33)
X — X'
где q = — фаза интерполяции, определенная относительно точки х, ;
h
AJfi(j = 1,2,...,А:) — конечные разности.
146

В соответствии с формулой для фазы интерполяции q точка начала ее
отсчета расположена в узле xt и входящие в (4.33) конечные разности относятся к
этой же точке х,. В связи с этим (4.33) удобно применять в начале выделенного
шаблона (л,,*,*!,...,*/**), когда q>0. Если х{ = х0, а х. < х0 , то этот же
многочлен используется и для экстраполяции левее точки х0 (q < 0). Поэтому
многочлен Njf'fa) называется интерполяционным многочленом для интерполяции вперед
(в начале таблицы ) или для экстраполяции назад. В (4.33) этот многочлен
обозначен цифрой I, указанной в скобках вверху. Для определенности назовем его
первым интерполяционным многочленом Ньютона.
Полагая i = 0,k = п , получаем решение задачи глобальной интерполяции
на всем отрезке [х0,хл] :
М%)-/о+^ + ^^-1)+- + ^-^-1)...(»-» + 1). (4-34)
где q = —. Остаточное слагаемое этого многочлена имеет вид
h
nK4J (л + 1)! J ЬУ
где ^е(а,Ь) — некоторое промежуточное значение между узлами xQixlt...,xn и
точкой х.
Если фазу интерполяции определить относительно xi+k некоторой
конечной точки шаблона (x/,x,+i,...,*/+*)> т-е- Я Г*^» то вместо (4.33) получает-
п
ся второй интерполяционный многочлен Ньютона:
*1"Чя) = /,.к + *^$ + ^f*$ti + l) + ... + ^Hq + l)...ti + k-l). (4.35)
Данный многочлен удобно применять в конце выделенного шаблона или
всей таблицы у{ = /(х,) (/' = 0, п).
Если / + /: = л, a jt. > хл, то (4.35) используется для экстраполяции правее
точки xn(q > 0). Поэтому многочлен NJf^(q) называется многочленом для
интерполяции назад (в конце таблицы) или экстраполяции вперед.
Полагая / = 0, / + к = п , получаем решение задачи глобальной интерполяции
— второй интерполяционный многочлен Ньютона п-й степени:
К"Ч1) = /„+^1+Щ^НЭ + 1) + ... + ^($ + 1)...й + п-\), (4.36)
1! 2! п\
а х-хп
где q =
h
Остаточное слагаемое многочлена (4.36) имеет вид
RtS) = hn+l M±1L^115)/(«+0(5),
пН (л + 1)!
где £ е (а, Ь).
147

Схема выбора узлов интерполяции при изменении степеней
интерполяционных многочленов NJf^q), N[U)(q) (Л: = 1,2,3) в одном алгоритме показана
на рис. 4.5. Если точка х# находится в начале отрезка [х0,хя], например на
частичном отрезке [xq,*]], то применяется первый интерполяционный
многочлен Ньютона, а если в конце, например на частичном отрезке [хЛ_1,хл], то -
второй (рис. 4.5,о). Если точка х, находится вдали от концов отрезка [х0,хл], то
может применяться как первый интерполяционный многочлен, так и второй
(рис. 4.5,6).
х0 *•
МУ)(х)
ЩП)(х)
х\
х2
*3
N«\x)
х*
хм
*/+2
*/+3
xi+k-3 xi+k-2 X/+Jk_1 x0
xi+k
Рис. 4.5
Замечания.
1. Из формул интерполяционных многочленов NJ± \q) и N^^(q) видно,
что повышение их степеней в процессе реализации алгоритма не требует
пересчета предыдущих слагаемых, входящих в многочлены с меньшими степенями.
2. Для гладких функций при повышении порядка конечных разностей
справедливо свойство: Д* fi?-> 0 при &-»оо, и поэтому, как только очередное
слагаемое в рассматриваемых многочленах становится меньше требуемой
точности интерполяции, увеличение степени N[n(q), N[n^(q) следует прекратить. Это
замечание справедливо также и для Nk(x).
Пример 4.4. Построить многочлен Ньютона третьей степени для сеточной
функции, заданной табл. 4.7. Вычислить значение функции в точке х„ = 2,5.
Решить задачу интерполяции при включении одного дополнительного значения
сеточной функции: /(1) = 5.
Таблица 4.7
1
xi
1 /(X/)-//
0
2
7
1
3
5
2
4
8
3 " ~~1
5
7
148

□ Построим многочлен Ньютона (4.32), справедливый для произвольного
расположения узлов. Для этого составим табл. 4.8, аналогичную табл. 4.5:
/(*o,*i)=^5y=-2; /(*i,*2)=^tj=3; /(*2>*3)=-jtj=-i;
/(*o,*i,*2)= 4_2 2; ^(дсьх2>^з) = -^3" = -2' /(*о>*ь*2>*з) = 5_22=-2'
Таблица 4.8
Г Х/
2
з "•■■•■■■'
4 ••--::::.
5
fi
7
'■•'■ 5
• &
7
/(XjiXj+O
::::::''"-2
^■—■■э^г:
"••■■■'■■■"•"•"■'■%-i
f(xj>xj+l>xj+2)
5
2
-2
/(xy»x;+i»xy+2'x;+3)
...,,.,.. 2
2
По формуле (4.32) для п = 3 имеем
#з (*) = Л*о) + (* - *о) /(хо> *i) + (х ~ хо) (х - х,) Дх0, х, ,х2) +
+ (х-х0)(х-х1)(х-х2)/(х0,х1,х2,х3) = 7 + (х-2)(-2) + (х-2).(дс-3)-- +
+ (х - 2) • (х - 3) • (х - 4) • (--) = --х3 + 16х2 - — х + 62.
i> 2
Поскольку в данной задаче заданы равностоящие узлы, воспользуемся
также формулой (4.34) для первого интерполяционного многочлена Ньютона:
А/о Л , Д2/о
Д3/о
где q
N\I\q) = f(x0)+^q + ^q(q-\) + -^q(q-\).(q-2)y
- = —— = х-2. Составим табл. 4.9, аналогичную табл. 4.6.
h 1
Таблица 4.9
*'•
2
! з
4
5
Л =/(*,■)
5 -•-•••.'.:..
8 •■<::..
7 "
4/>
..-•-^-2
;^"--::::;-з---:::::;;Г
^■■■••'•"■•■■■■-1
а2/,
:;;;:::::.••• 5
.::::.■.■•■••—--4"""'
А3/,
':::-•••••••' -9
149

Имеем: Д/0 =5-7 = -2; Af{ =8-5 = 3; Д/2 = 7-8 = -1; Л2/о = 3-(-2) = 5;
A2/, = -1-3 = -4; А3/о = -4-5 = -9. Поэтому
^/)(x) = 7 + ^^^^(^-l) + ^9^^-l)4g-2) = -|^+7^-^ + J
3!
х-2
9=-
--(л:3-6х2+12х-8) + 7.(х2-4х + 4)-— (х-2) + 7 = --х3+1бх2- —х + 62.
2 2 2 2
Запишем также второй интерполяционный многочлен Ньютона (4.36):
/(//)
Д/2 . А2/, . .. AJ/o
N?I)(x) = f3+^q+^q-(q + \) + ^±q.(q + l)-(q + 2)\
q=-
(-D
(-9) - ,*
= -^х3+1бх2-^х + 62.
Сравнивая с результатом примера 4.1, можно заключить, что Ь3(х) =
= NV\x) = N(3n)(x). Это еще раз подтверждает единственность решения задачи
интерполяции в классе многочленов, удовлетворяющих условиям теоремы 4.1.
Предположим, что в ходе некоторого эксперимента получен новый
результат /(1) = 5, дополняющий заданную сеточную функцию. Тогда для решения
задачи интерполяции с помощью многочлена Ньютона можно использовать уже
полученный результат. Для этого дополним табл. 4.8. Новый узел и
соответствующее значение функции поместим в конце табл. 4.10.
Таблица 4.10
г*г
2
3-
4-:
1-
У*
--7-
:8...
-Г"
f(Xj>Xj+\)
-••"'-'2
;::::-8--Зг--".'.'.'...
;;.;:.:-^1'---::::
1
'""2"""
/(Ху,ХуЧ1,Ху + 2)
""'Z'::::"±
2
:::-:3
• 1
Т
f(xj > */+1 у */+21 xj+3 )
-;., 2-..
2
.3.
4
/(*0>xbx2>*3>x4)
..... 2
4
150

По формуле (4.34) имеем
N4(x) = N3(x) + (х - х0)(х - х,)(х - х2)(х - х3) f(x0,xl,x2,x3tx4) =
= _£x3 + l6x2_i^x + 62 + (x_2)(x-3)(x-4)(x-5)(-4) =
2 2 4
107
= -ix3+16x2- —х + 62--(х4-14х3+71х2-154х + 120) =
2 2 4
в-2х4+9х3- —x2+62jc-28.
4 4
Легко проверить, что новый узел можно добавить и в начале таблицы, т.е.
будет найден тот же многочлен N4(x). На рис. 4.6 изображены полученные
интерполяционные многочлены.
^ = 1з(х) = N,(x) = N?4x) = ^</7>(х)
| /\У = Х4(х)
Рис. 4.6
Вычислим значение функции в точке х„ = 2,5: N^f)(xm) = N\!I\x.) = 4,8125;
Ar4/)(JC*) = 5»5156-"
Пример 4.5. Для сеточной функции из примера 4.3 найти линейный и
параболический многочлены Ньютона и на их основе подсчитать значение
функции в точке х. = 2,5. Оценить погрешность интерполяции.
□ Так как точка х„ = 2,5 находится вблизи узла х, = х2 и шаблон
(х2,х3,х4) имеет неравномерность по шагу, то для выполнения интерполяции
выбираем многочлен Ньютона (4.29).
151

1. Определим разделенные разности/(x/,x/+i)>/(*/>*/+ь*/+2)(табл. 4.11)
Таблица 4.11
1 /
2
3
4
*/
1
Л
Д
:;••-■•■:::::27^;;;;;;;."'".'
64
/(*/>*/+l)
::::•■•■' 1-3
■■•■■•■■••■■ 37
/(■*i>*i+1»X|+2)
Г-:-- 8
- ,, ч 27-1 ,, ,, ч 64-27 ,_ ,, ч 37-13 _
Здесь /(х2,дс3) = —— = 13, /(х3,х4) = =37, /(х2,х3,х4) = . . =8.
3-1
4-3
4-1
Определим Ni (jc), N2 (х) :
^iМ = Л + /(*2,*3)-(х-х2) = 1 + 13 (jc-1) = 1 Зх-12,
N2{x) = f2+f {х2,х3) (х-x2)+f(x2,x3, х4) (х-х2) (х-хг)=13х-12 +
+ 8(x-l)(x-3)=8x2-19x + 12.
Сравнивая W2(x) с соответствующим многочленом Лагранжа /^(х)
(см. пример 4.3), видим, что они совпадают. Это подтверждает единственность
решения задачи о построении интерполяционного многочлена.
2. Вычислим значения N{(x)\
,N2(x\
7^(2,5) = 13 • 2,5 -12 = 20, Л^2(2,5) = 8 • 2,52 - 19 • 2,5 +12 = 14,5.
Итак, линейная интерполяция приводит к отличию от точного значения
на
20-15,625
15,625
100% = 28%, а квадратичная — на
14,5-15,625
15,625
•100% = 7%.
Таким образом, найдена фактическая погрешность, которая для квадратичной
интерполяции получилась в 4 раза меньше.
3. Найдем априорную оценку погрешности линейной интерполяции на
отрезке [х2,х3] по формуле (4.23). Для этого необходимо сначала оценить
производную M2i. При этом, как и в реальных задачах, будем определять /"(х)
численным дифференцированием. С этой целью используем многочлен N2(x):
N2 (х) = 1бх-19, N2(x) = 16. Приближенно можно принять, что M2i = 16. Тогда
получаем: |.#i(x)| < 16 = 8 или —-—
8 15,625
100% = 51,2%. Заметим, что фактическая
погрешность получилась примерно в два раза меньше априорной.
152

Пример 4.6. Для сеточной функции, заданной в примере 4.4, построить
интерполяционные многочлены первой и второй степени для нахождения значений
в точках *♦! = 2,5; х.2 = 4,5; х,3 = 3,5 > х*4 = 5,5.
□ Для подсчета значения функции в точке хт1 = 2,5 (согласно рис. 4.5,я)
выбираем шаблон (jc0>Xi,jc2) = (2;3;4) для параболической интерполяции
(/ = ОД = 2) и шаблон (х0,х{) = (2;3) для линейной интерполяции (/ = 0, к = 1).
Тогда по формуле (4.34)
х-2
где q = (см. табл. 4.9). В результате подстановки получаем
Nln(x) = -2х +11; W<7)(х) = -х2 -—х + 26.
В заданной точке 7V,(/)(2,5) = 6; Л^7)(2,5) = 5,375.
Для подсчета значения в точке х„2 = 4,5 выбираем шаблон
(3; 4; 5) = (xj, х2, х3) Для параболической интерполяции (/ = 1, А: = 2) и шаблон
(4;5) = (х2,х3) для линейной интерполяции (/ = 2, & = 1). Тогда по формуле (4.35)
N\"\q) = *<">(*) + ^Ч • (я +1) = 7 - £ + ^9 ($ +1) = -2*2 - Зд + 7,
где q = = х - 5. В результате подстановки получаем
h
Nl/r)(x) = -х + 12; Л^/7)(*) = -2х2 +17* - 28.
В заданной точке W,(//)(4,5) = 7,5; jV</7)(4,5) = 8.
Многочлен Л^/7)(х) можно использовать для экстраполяции, т.е. для
подсчета функции в точке х«4 = 5,5: Л^/7)(5,5) = 5.
Чтобы подсчитать значения в точке х,3 = 3,5, сначала выберем шаблон
(3;4;5) = (х1,л:2,хз) для параболической интерполяции (/= 1, к = 2) и шаблон
(3;4) = (xj,x2) для линейной интерполяции (/ = 1,А: = 1). Согласно рис. 4.5,5,
применим формулу (4.33):
^i(/)(^) = /i+~L^ = 5 + ^ = 5 + 3^,
Ny\q) = N\I\q) + ^q(q-\) = 5 + lq + ^-q{q-\) = -2q2+5q + 5,
153

где q = = х - 3. После подстановки получаем
h
^,(/)(х) = Зх-4; ^7)(х) = -2х2+17х-28 и ЛГ<7)(3,5) = 6,5; #<7)(3,5) = 7.
Подсчитать значения в точке х3* = 3,5 (согласно рис. 4.5,5) можно,
использовав шаблон (2;3;4) = (х0,х1,х2) для параболической интерполяции (/ = 0Д = 2)
и шаблон (3; 4) = (х19х2) для линейной интерполяции (/ = \,к = 1). По формуле
(4.35) получаем
N\"4q) = h+&$ = * + \$,
где q --= = х - 4. После подстановки
h
yV,(//)(x) = 3x-4; N(2rn(x) = -x2- — х + 26 и ^(//)(3,5) = 6,5; N[U)(3,5) = 5,875.■
4.3. МЕТОДЫ ИНТЕГРАЛЬНО-ДИФФЕРЕНЦИАЛЬНОЙ
ИНТЕРПОЛЯЦИИ
4.3.1. Постановка задачи
Использование различных сочетаний функциональных, дифференциальных
и интегральных условий согласования (4.2), (4.3),(4.5) позволяет конструировать
различные типы интерполяционных или интерполяционно-сглаживающих
многочленов. В данном разделе рассматриваются задачи построения двух
интегрально-дифференциальных интерполяционных параболических многочленов S^(x)
и S(2fl)(x).
Первый определяется по сеточной функции, заданной не только своими
значениями /}(/ = 0,л-1) , но и значениями интегралов //+1 (/ = 0,л-1). Так
как для нахождения многочлена S^\x) используются совместно
функциональное условие (4.3) и интегральное условие (4.5), то многочлен называется
интегрально-функциональным. Поскольку функциональное условие (4.3) является
частным случаем дифференциального условия (4.2), соответствующий метод
относится к интегрально-дифференциальным.
Второй многочлен определяется по сеточной функции, заданной не только
значениями производных /^р) (/ = 0,л), но и значениями интегралов
/,'+1 (/ = 0,л-1). Так как для нахождения многочлена S^n)(x) совместно
используются дифференциальное условие (4.2) при р = 1 и интегральное условие
(4.5), то многочлен (и соответствующий метод) называется интегрально-
дифференциальным.
154

4.3.2. Интерполяционный параболический интегрально-функциональный
многочлен
Пусть некоторая сеточная функция, определенная в общем случае на
неравномерной сетке Q„ = {x0,xj,...,*„}, задана своими значениями/0,/ь...,/Л и
l\+x = ff(x)dx , которые могут быть предварительно
интегралами 7q, /j[,..., /„_
ч
рассчитаны по одной из квадратурных формул (см. гл.5). Будем считать, что
точность заданных значений /} и вычисленных интегралов 7/+1 для всех узлов
Xj (/ = 0,//) и отрезков [x,-,x,-+i] (/= 0,л-1) не ниже <9(А/+13) и 0(А/Ч14)
соответственно. Это требование следует из утверждения В.2, устанавливающего принцип
соответствия порядков аппроксимации (интерполяции).
Применим кусочный способ интерполяции. Для некоторого отрезка
[x,,x/+i](0 < / < п -1) на двухточечном шаблоне требуется определить многочлен
siJ W = ao,i + aU (* ~xi) + a2j (х ~ xi ?>
где a0j9aiti,a2ti— неизвестные коэффициенты, удовлетворяющие
функциональным (4.3) и интегральным условиям согласования (4.5):
bs£(irl) = X'\s£(x)dx-irl = 0.
Для определения трех коэффициентов параболического интегрально-
функционального многочлена можно получить три линейных уравнения,
являющиеся следствием трех условий согласования:
52,?(*<) = ao,i = fi или flo,/ = Л»
S$(xi+l) = fi+ aXihux + aXih}^ = fM или huxaXi + h?+xa2J = dfh
X'\ [/)• + au{x - Xi)+a2J(x - Xi)2]dx = //+I.
xi
X — X-
Вводя фазу интерполяции и = ——L, последнее условие после интегриро-
А2 А?
вания можно записать в виде huxfj +-Li^aXi + -^a^j = 7/+1.
155

Итак, для оставшихся двух коэффициентов aXi,a2i имеется система
линейных алгебраических уравнений:
ЗАД^у+г/^,. = 6V//+1,
где V//+I =//+1 -hi+{fit А/} =У}+1 -У). Очевидно, определитель этой системы
ЗЛ|Ч1 2Л,Ч1
Л/+1 Л/+1
* 0, что свидетельствует о существовании и единственности
интегрально-функционального многочлена S^)(x) на отрезке [х,,х/Ч1]. В силу
произвольности отрезка [*/,*,•+J данный многочлен S2?(x) существует и является
единственным на каждом частичном отрезке [х/,х/+1], / = 0,л-1. Поэтому
многочлен S$(x) может быть положен в основу кусочной многозвенной
интерполяции, в том числе и сплайн-интерполяции (см. разд. 4.5).
Определяя a{i,a2i из приведенной системы, записываем параболический
интегрально-функциональный многочлен S^)(x) в полиномиальной форме:
4?<*)=// +
\Л2+1 Л/>1
(х-х,)-
-—-V/'
/41
Л/+1
■A/
(х-х,)2. (4.37)
Если в (4.37) подставить вместо (х-х,) произведение ыА/Ч1 и выделить
слагаемые при //+1»У/>Л+1» то получим параболический интегрально-
функциональный многочлен в лагранжевой форме:
S[[}{u) = ^P2J{u)ir{+P2J{u)fi+P2MX(u)fuu
К
(4.38)
Ы
где P2j(u) = 6ы(1 - и); Р2,/ (") = (1 - w)(l - 3w); /^.i+i (и) = w(3tf - 2) - коэффициенты
Лагранжа, удовлетворяющие функциональным и интефальному условиям:
^2,к(хт) = | 0, /я * А: (А: = /,/ + 1); J P2Jc(x)dx = J О, А: = /, (4.39)
[О, А: = /, */ [О, Л = i + l.
Так же как и классические (функциональные) многочлены Лагранжа,
интегрально-функциональный многочлен ^2?М линейно зависит от параметров
//+\//,/,+1- При использовании кусочной интерполяции для определения
значения функции f(x0) в точке хф с помощью многочлена S^)(x) выполняются
действия, аналогичные применяемым при функциональной интерполяции.
156

Методика решения задачи интегрально-функциональной интерполяции
(х.-х)
2. Определить фазу интерполяции и = ^-—— и коэффициенты
Л/Ч1
1. Выбрать «окно» интерполяции [х/,х/+1] так, чтобы х,- < х. < xi+{.
2. Определить
3. По формуле (4.38) вычислить значение f(x0) « S^)(u).
Замечания.
1. Правильность вычисления коэффициентов Лафанжа проверяется по
условию P2j + Pij + ^2,/+i = 1» получающемуся путем подстановки в (4.38) функции
Дх)ш\/
2. При аппроксимации значения /(*») значением многочлена S^J)(x*)
возникает погрешность R\!)(хф): f(x.) = S^1) (х0) + R^f) (дс*). При условии, что
f(x)eC3[aib]) можно получить оценку погрешности на отрезке [x,,x,+i]([18]):
h3
m2ix\f(x)-SW(x)\<-if^MXit (4.40)
[Xi,xM)\ *>' « 72 V3
где MXi = max \f"\x)\.
Если класс гладкости функции f(x) понижен и f(x)eC2[a9b]f то порядок
аппроксимации интегрально-функциональным многочленом S$(x) также по-
нижается на единицу: max \f(x) - ^?(х) ^ l+i- ^2 / •
lXhXM]i *• ■ 25V2
3. Сравним условия применения функционального (классического)
многочлена Лагранжа Z^(x) , определенного на трехточечном шаблоне (x/,x;+i,X/+2)>
и интегрально-функционального многочлена S^)(x):
а) аппроксимируемая функция для применения многочлена Лагранжа
задается только своими значениями /)• (/ = 0, п), т.е. функциональными параметрами,
а для использования S^\x) функция определяется еще и интегралами
//+1(' = 0, п- 1). Если в постановке задачи интегралы неизвестны, то, как
отмечено выше, они вычисляются предварительно по значениям /}(/ = (), л) по тем
или иным квадратурным формулам (см. гл. 5). Интегрально-функциональная
интерполяция предоставляет дополнительные возможности для более полного учета
локальных свойств интерполируемых функций, которые в отдельных точках и
областях могут иметь особенности: разрывы производных, локальные
экстремумы и др. При этом локальные свойства учитываются путем соответствующего
выбора трехточечного шаблона, на котором аппроксимируется интеграл //+|;
б) многочлен Щх) записывается на трехточечном шаблоне (х/,х/+1,х/Ч2)5
а интегрально-функциональный многочлен S^)(x) - на двухточечном (xhxi+i);
в) функциональный многочлен Z^(x) при его записи на одном шаблоне
определяется только функциональными параметрами /,,//+i,.//+2> а интеграль-
157

но-функциональный многочлен S^)(x) - двумя функциональными и
интегральным 7/+I, поэтому при его построении можно учесть интегральные
свойства аппроксимируемой функции;
г) по порядку аппроксимации оба многочлена обеспечивают одинаковый
третий порядок аппроксимации, который при f(x)eC3[a,b) является
максимальным, однако константа в мажоранте для S^)(x) в восемь раз меньше
соответствующей константы в мажоранте для Lq(x):
max \f(x) - 1з(х)| < ^- A/3f/; r max |/(x) - Stf(x)\ < %^&*;,
[*i,*i+iJ 27 [*,-,*ы]' ' i 216
где H = max hk, A/3,- = max |/'"(*)|, M3 <• = max |/"#(*)| •
*=/ + l,/+2 ' I*i.*i+2i ' lxi»**+il
Пример 4.7. Пусть сеточная функция на отрезке [-1; 4] задана
функциональными fj (/ = 0,4) и интегральными параметрами 7/+1,/ = 0,3, приведенными
в табл. 4.12. Данные параметры получены точно путем «обработки» сеточного
представления функции f(x) = jc3 . Интегралы вычислены точно по формуле
Ньютона—Лейбница 7/+1 = 7}+1 -7), где 7) — первообразная. Значения
интегралов в табл. 4.12 помещены посередине между значениями функции.
Требуется найти значение /(*♦) при х* = 2 на основе интегрально-
функционального многочлена S^^x).
Таблица 4.12
/
*'
\ /,
0
-1
-1
1
0
0
2
1
1
3
3
27
4
4
64
l//+1 '■■••••••.:^.><^:::><:::'^><'17^------'1
D 1. По значению х, = 2 выбираем «окно» интерполяции [*2,*3] = [l; 3],
такое, что х2 < х. < х3 •
Т — Y 9 — 1 1
2. Вычислим и = —*—■—- = - (А3 = х3 - х2 = 2) и коэффициенты
Л3 2 2
Лагранжа 7>2>/ = ви-(\-и) = 1; 7>2>2 = (1 -и).(1 -Зи) = -\\ 7>2>3 = и-(Ъи-2) = -I
2 4 4
Так как ]Г7^ * = 1, коэффициенты вычислены правильно.
к
3. Найдем значение /(2) по формуле (4.38) при / = 2:
/(2)»^(2) = ^./2Чл,2-/2 + /'2,з/з=7т-Г1-7-27 = 8-
А3 2 2 4 4
Получилось значение S^(2) = 8, совпадающее с точным значением исходной
формульной функции. ■
158

Пример 4.8. Дана сеточная функция, характеризующаяся
функциональными и интегральными параметрами, заданными в табл. 4.12. Найти
полиномиальный вид интегрально-функционального многочлена на отрезке [х2,хзЬ ВНУТРИ
которого находится точка х. = 2, и вычислить ^7)(2). Результаты сравнить с
решением, полученным с помощью многочлена Лагранжа в примере 4.3.
□ Для решения задачи в соответствии с исходными данными используем
интегрально-функциональный многочлен S^f\x), записанный в форме (4.37).
1. В поставленной задаче «окно» интерполяции, как в примере 4.7, задано
отрезком [х2,х3] = ^ **!» поэтому / = 2.
2. Вычислим значения V/], Д/2, hz и коэффициенты многочлена S$(x):
*з=*з-*2=3-1 = 2; Д/2=/3-/2 =27-1 = 26;
V/23 =/2-Л3/2 =20-2-1 = 18;
До = h = 1; *i = 77v/2 -f-^2 = 1; Д2
Л3 лз
ЧИ+^л/г|=6'
1„,з 2
*з2
Полученные коэффициенты подставим в формулу (4.37):
S{2fJ(x) = \ + (x-\) + 6(x-l)2 = 6jc2-11jc + 6.
3. Определим значение S$(xm): S$(2) = (6х2 -11х + 6) = 8.
Из сопоставления полученных результатов с результатами решения
примера 4.3 следует, что значение »У2/2(2) = 8, полученное интегрально-
функциональным методом, лучше соответствует точному значению, чем
Z^(2) = 6. Это обусловлено тем, что кроме значений функции / = /(*,-) в узлах
задан еще и интеграл, значение которого является точным. В данном случае
значение S$(2) совпало с точным значением, так как х. = 2 находится в середине
отрезка [1;3].и
4.3.3. Интерполяционный параболический
интегрально-дифференциальный многочлен
Пусть некоторая сеточная функция на сетке С1п задана значениями
производных f- - f'(Xj) (/ = 0,л) и интегралами //+| (/ = 0,я), которые либо известны,
либо могут быть предварительно рассчитаны по одной из квадратурных формул.
Так же, как и для многочлена s[r)(x)t рассмотренного в разд. 4.3.2, будем
считать, что fl и //+1 заданы или вычислены с точностью не ниже 0(Л/+12) и
0(Л/+14) соответственно (см. утверждение В.2).
159

Применим кусочный слогов интерполяции. Для некоторого отрезка [x,,x/+i]
(О < i < п -1) на двухточечном шаблоне требуется определить многочлен
S%P(x) = a0i + аи(х -Х;) + a2J(x - х,)2,
где flo,/»flu»fl2,/~" неизвестные коэффициенты, удовлетворяющие
дифференциальным ((4.2) при р - 1) и интегральным (4.5) условиям согласования:
bS'tfHxi) = Sfi'Hx,)- Л = 0, 65^7)(х/Ч1) = S!tfn(xi+l) - /,'+1 = О,
Для нахождения трех коэффициентов многочлена можно получить три
линейных уравнения, являющиеся следствием трех условий согласования, так же,
как это сделано в разд. 4.3.2. В результате имеем выражение для параболического
интегрально-дифференциального многочлена S^P(x) в полиномиальной форме:
$1Ч*)4т-1Г1 -^Л-^^ + /Кх-х§) + -£Я-(х-Х1)29 (4.41)
U+1 2 6 ) 2///Ч1
где А/-=Л+\ -Л-
Если подставить вместо (х-х,) произведение uhi+l (и — фаза
интерполяции) и выделить слагаемые при /,'+1,У}',.//+1» то получим параболический
интегрально-дифференциальный многочлен в лагранжевой форме:
4'Р(") = -Г-7<+' + 7<-3"2 + 6" " ЫмЛ + 7<3"2 - M+i/m• <4-42>
«1+1 о Ь
X — Х-
где и = -, 0 < и < 1.
Замечания.
1. При аппроксимации значения /(хф) значением многочлена 5^7)(х#)
возникает погрешность Ri"\x.): Д.х. ) = £<?>(*. ) + *<">(*.). При условии, что
/(х)€С3[д,б], можно получить оценку погрешности на отрезке [х,,х/+1] ([21]):
max |/(jc) - sflHxi <^-M3i.
[х/.^ыР 2,/ ' 24 3''
2. Алгоритм аппроксимации сеточных функций на основе (4.41), (4,42)
аналогичен изложенному в разд. 4.3.2 для аппроксимации многочленом S^ix).
160

4.4. МЕТОДЫ ИНТЕГРАЛЬНОГО СГЛАЖИВАНИЯ
4.4.1. Постановка задачи
Определение вида функциональных зависимостей, получаемых в
физическом эксперименте, имеет очень важное значение. Обычно экспериментальные
результаты представляются в виде таблиц или сеточных функций yf =/(х/)±б/,
где е, — погрешности измерений. Если их построить на графике, соединяя
экспериментальные точки отрезками прямых, то получится ломаная, не имеющая
ничего общего с той или иной функциональной зависимостью, которая затем
могла бы быть исследована средствами математического анализа. Форма этой
ломаной из-за ошибок измерений при повторном эксперименте не
воспроизводится. Поэтому экспериментатор на основе практического опыта предполагает,
что полученная таблица является реализацией эмпирической гладкой
зависимости fm(x,a) с неизвестным параметром а, являющимся в общем случае
вектором размерности /и + 1(см. рис. 4.1,6). Для его определения используются
различные формы записи зависимости fm(x,a) и различные условия согласования
fm(x,a) с исходной функцией yt =/(jc/)±e/.
На практике удобно представить искомую зависимость в виде обобщенного
многочлена
~ т
fm(x,a) = Y,aj 4>j(x) = a0<p0(x) + alq>l(x) + ... + am4>m(x), (4.43)
где a ={tf0,tfj,...,flm}r— вектор неизвестных коэффициентов, {фу} = {фо,Ф1 >-->Фт} —
заданная система базисных функций. В качестве базисных функций могут
выбираться, например, степенные функции {фу} = {ху}, многочлены Чебышева,
тригонометрические функции {фу} = {cos jx). В первых двух случаях ищется
алгебраический полином, а в третьем — тригонометрический полином. Далее для
решения задачи используются базисные функции только первых двух видов.
В зависимости от используемого условия согласования можно построить
два основных альтернативных метода сглаживания — метод наименьших
квадратов, являющийся традиционным, и метод наилучшего интегрального приближения
или просто метод интегрального приближения, предложенный в работах [15—17,
19—23]. Соответствующий многочлен называется многочленом интегрального при-
ближения.
Метод наименьших квадратов, являющийся методом наилучшего
среднеквадратичного приближения, основан на применении интегрального условия
(4.4), а метод интегрального приближения — на использовании интегрального
условия (4.5).
Оба метода могут быть реализованы глобальным способом, т.е. для всего
отрезка [а,Ь\ может быть получена одна функция /т(х,а~). Как правило,
принимают т < 5 ч-8 (т « п) в связи с отмеченными в разд. 4.2.2 свойствами
многочленов высокой степени. Последнее обстоятельство обусловливает
необходимость использования для сглаживания кусочно-глобального подхода, аналогич-
161

ного сплайн-методу (см. разд. 4.5) , с шаблонами, количество точек в которых
соответствует степени многочлена fm(x,a).
ПОСТАНОВКА ЗАДАЧИ О НАХОЖДЕНИИ СГЛАЖИВАЮЩИХ МНОГОЧЛЕНОВ
МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ
Пусть на множестве Q = [а,Ь] задана сетка Qn = [xh i = 0, л ], определяемая
п + 1 точкой х0,х{,...,хп, а на сетке задана сеточная функция у{ = /(*,), / = 0, л:
Уо = Д*о)> У\ =/(*i),..., Уп = /(*/,)•
Предполагается, что сеточная функция получена, например, в физическом
эксперименте с достаточно большой погрешностью относительно шага, т.е.
у. = f(Xj)±siy причем значения е, превышают 0(Л/Ч1), а узлы сетки могут быть
заданы также с погрешностью. Как и ранее, будем использовать обозначение
В качестве сглаживающей функции будем использовать обобщенный
многочлен (4.43), в котором базисные функции q>/(*) являются степенными
функциями или многочленами Чебышева, причем степень многочлена удовлетворяет
условию 0 < т < п.
Требуется найти такие коэффициенты многочлена а^,аХу...,ат^ чтобы
выполнялось интегральное условие согласования (4.4):
^m(o) = j-^-fj[fm(xha)-fi} ->mjn, (4.44)
т.е. такой вектор а = {а0,аь...,ат}Т, который обеспечивает минимум
среднеквадратичной погрешности 6w (а ).
Метод решения поставленной задачи называется методом наименьших
квадратов или методом наилучшего среднеквадратичного приближения. Согласно
классификации метод является сглаживающим (см. рис. 4.7).
Отметим отличительные особенности решения задачи сглаживания
методом наименьших квадратов по сравнению с решением задачи интерполяции.
1. Метод интерполяции — точечный метод, так как требует выполнения
точечных условий интерполяции. Рассматриваемые здесь интегральные методы
являются альтернативными точечным и не требуют точного удовлетворения
функциональных условий, а требуют выполнения соответствия fm(xta) и yt = y(xt)
в среднем (по интегралу или по интегральной сумме).
2. Исходная функция yt = /(*,) задана не точно, а с погрешностью,
существенно большей, чем в методе интерполяции. Эта функция, как правило,
получена в результате некоторого физического эксперимента.
3. Количество точек х, (/ = 0,л), в которых задана исходная функция, как
правило, значительно больше степени т многочлена (п » т). Поэтому между п
и т нет строгого соответствия, как это имеет место в методе интерполяции.
162

ПОСТАНОВКА ЗАДАЧИ О НАХОЖДЕНИИ СГЛАЖИВАЮЩИХ МНОГОЧЛЕНОВ
МЕТОДОМ ИНТЕГРАЛЬНОГО ПРИБЛИЖЕНИЯ
Пусть на множестве Q = [а,Ь] задана сетка Qm+I = {*,,/ = 0,m +1 j, причем
х0 = а < Х| <х2 < ... < хт+{ = b. Эта сетка, определяемая (т + 2) несовпадающими
узлами, порождает систему (т + 1) частичных отрезков [xhxi+]],i = 0,/я.
На рассматриваемой сетке задана сеточная функция одним из следующих
способов.
Первый способ. На каждом частичном отрезке [xhxi+]]yi = 0,/я, сетки Qm+1
задается величина интеграла //+1.
Второй способ. На частичных отрезках [х0,х1],[х0,х2],..., [х0,хт+|] с
фиксированным левым узлом задаются интегралы /о,/о,...,/™*1.
Третий способ. Сеточная функция задается своими значениями
yt = /(*,-), / = 0,/я + 1. Предполагается, что они известны с погрешностью е,, т.е.
у. = /(*/) ± Б/. Соответствующие интегралы //+1, / = 0, /я, и /q, / = 1,/я +1,
вычисляются по квадратурным формулам (см. гл. 5).
В качестве сглаживающей функции, так же как в методе наименьших
квадратов, будем использовать обобщенный многочлен (4.43) степени /я, в котором
базисные функции (р,(х) являются степенными.
Требуется найти такие коэффициенты многочлена %,ах,...,атУ чтобы
выполнялось интегральное условие согласования (4.5). Для первого способа задания
функции оно имеет вид
)] fm(x,a)dx = //+1, i = 0,1,...,/я, (4.45)
а для второго способа —
х' _
J fm(xya)dx = /J, # = 1,...,/я + 1. (4.46)
*ь
Замечание. Если вместе с интегральными условиями согласования
использовать функциональные, то получаемые в результате многочлены
называются интерполяционно-сглаживающими (см. разд. 4.3).
4.4.2. Метод наименьших квадратов
В соответствии с постановкой задачи найдем коэффициенты а0,аи...,ат
многочлена (4.43), обеспечивающие минимум среднеквадратичной погрешности
(4.44):
bm(°) = i-^tlfrn(xi>°)-fi}2 -> min • (4.47)
| Л + 1 /=о «).fll.•••<*«
163

Очевидно, минимум в (4.47) с учетом (4.43) достигается, если
я
Д=Х [<Po(*/)*0+<Pl(*/)*! +«. + 9m(x/)flm-/j] "> min • (448)
/=0 ^0^1» -ат
Так как на коэффициенты не наложено никаких ограничений, применим
необходимые условия безусловного экстремума:
Я Л
-— = 0, у = 0,1,...,т.
да j
В результате получаем систему
ад Л
— = 2Х [<P0(*/)fl0+<Pl(*/)fll + • » + Vm(xi)am -//]фо(*/) = °>
да0 /.О
ад Л
— = 2Z [фо(*/)*о + <Pi(*/)ai +.» + Фт(*/)Я/я - Л]ф1(^/) = 0 > (4.49)
0*1 /.о
ад л
1 = 2Е [фо(*/)*0+Ф1 (*/)*! +... + Фт(*|)*т-Л]-ф«(*/) = 0.
Для компактной записи полученного результата удобно использовать
скалярное произведение.
Скалярным произведением функций ф*(х) и ф/(х) на множестве точек
{*,.,/= 0,л} называется сумма произведений значений функций, вычисленных
во всех точках, т.е.
л
(ф*>ф/) = £ф*(*/)ф/(*/).
/=0
Число ||фЛ|| = ^(фГ»ф7) называется нормой функции ф*(х) на множестве
точек {*,, / = 0, л ].
Тогда полученную систему (4.49) можно переписать в нормальной форме:
(ф(ъФо)яо +(фо»Ф1)<ч +... + (ф0,Фт)лт =(/,Фо),
(ф1,Фо)до +(Ф1»Ф1)^1 +... + (ф1,Фт)лт =(/,Ф1), (4.50)
(ф/л5Фо)дО + (фщ.Ф1)д1 + - + (фт»Фт)д« = (/,Фт)>
л
где (/,ф^) = ]Г// ф* (*,-). Таким образом, получено (т + \) линейное уравнение
/=о
с (т + 1) неизвестными a0,alt...,am . В силу равенства (ф*,ф/) = (ф/>Ф*) матрица
164

А =
((фО»Фо) (Ф0»Ф1) (фО.Фт) 1
(ФЬФО) (ФЬФ1> (фьФт)
Цфт>Фо) (фт>Ф|) (Фт>ф/я)>/
системы (4.50) является симметрической. Если базисные функции Фо,Фь--,ф/я
линейно независимы, определитель матрицы А не равен нулю (он называется
определителем Грама). Тогда решение системы (4.50) существует и единственно.
Аналогичный вывод можно сделать и о задаче определения многочлена
наилучшего среднеквадратичного приближения.
ПРИМЕНЕНИЕ СТЕПЕННЫХ БАЗИСНЫХ ФУНКЦИИ
В качестве базисных функций используем степенные: ср7(х) = xJ,j = 0,т.
В этом случае обобщенный многочлен (4.43) имеет вид
fm(x,a)= £яуху = а0 + а{х + ... + атхп
(4.51)
Тогда (/,фу) = ЕЛ*/ > (Ф*>Ф/) = Ех/ ' (ФьФ*) = Ех/ и система (4.50)
/=0 /=0 /=0
имеет вид
Г п \ ( п \ ( п
Е ik> + Ех/ н+ Ех'2
Ч/=0 J V/=0 J \i=0
а2 +...+
V#=o у i=0
Е*/ h + Ех/2 р+ Ех'3 к + •••+
V/=0 ) \i=0 J \i=0 J
2>Г' k-Zx/Л, (4-52)
W=0 У ;=0
V/=0 J v/=o J
Обозначим
\a2 + ...+
2m
1*/"к = 5>Г/,-
^/=0 у /=0
50 =/2 + 1, /0 =/o+/l + ■•■ + /«,
5* = *o + x* + •••+ хл > ^ = 1,---,2/я;
'* = *o/o+*i7i +..• + **/„, A: = l,...,m.
Тогда система (4.52) преобразуется к виду
s0fl0 + sici +... + 5mcm = /0,
(4.53)
•VO + sm+\a\ + - + *2«fl« = '/и •
165

Решая систему линейных алгебраических уравнений, находим неизвестные
коэффициенты ao,0i,...,aOT. Подставляя решение в /ш(х,я), получаем искомую
формулу, которая сглаживает экспериментальные данные. Качественный
характер поведения сглаживающей функции fm(xya) относительно исходной функции
показан на рис. 4.7. Подчеркнем, что функция fm(xfa) расположена внутри
полосы «разброса» функции yt = /(*,) и является более плавной по сравнению
с ломаной, проведенной через заданные экспериментальные точки. В этом
состоит сглаживание исходной «пилообразной» функции или функции, заданной
своими значениями с «разбросом».
fm^a)
Рис. 4.7
Методика решения задачи сглаживания
1. Вычислить коэффициенты sk,k = 0,2m; tk,k-0,m, по заданной
сеточной функции и записать систему (4.53).
2. Решить полученную систему одним из методов, изложенных в гл. 1, и
найти коэффициенты aQyali...iam.
3. Записать искомую сглаживающую функцию
fm(x,a) = а0+ ахх +... + атхт.
Замечания.
1. Если для сеточной функции, заданной в (л + 1)-й точке x0ix\,...tx„t
определять многочлен степени т = п методом наименьших квадратов, то тогда
fm(x,a) совпадает с интерполяционным многочленом и метод становится
эквивалентным методу интерполяции. При этом А = 0 и Ът{а) = 0.
2. В каждом конкретном случае может существовать «оптимальная» степень
/я, зависящая от конкретного поведения функции, числа п и вида базисных
функций фу(х). Предположим, что точность задания исходной функции
характеризуется только одним значением 8, т.е. е; = е (е, все одинаковы).
166

Задавшись некоторым числом т и определив я,, j = 0, т, требуется
вычислить среднеквадратичное отклонение Ът(а) и сравнить его с е.
Возможны три случая:
а) если 8т(а)»г , то аппроксимация слишком грубая, степень т мала и
необходимо ее увеличить;
б) если Ът(а) «е , то аппроксимация физически недостоверна, найденная
функция слишком «сплющена», старшие коэффициенты лишние и степень т
надо уменьшить;
в) если 6ш(я)«е , степень многочлена т «оптимальна».
Расчет обычно начинают с /и = 1, когда чаще всего bx(a)»z , и
увеличивают /я, доходя до 6ш(д)«е , если это возможно. Если Ът(а) не становится
близкой 6, то следует искать более подходящий вид базисных функций сру(х)
или использовать, например, двухпараметрические зависимости.
3. Система (4.53) при т » 1 становится плохо обусловленной и
определить полином /т(х,л) практически невозможно. Это связано с тем, что строки
матрицы А при больших т оказываются почти линейно зависимыми и,
следовательно, \А | * 0. Чтобы этого избежать, необходимо вместо степенных базисных
функций использовать полиномы Чебышева, способ реализации которых
изложен ниже, либо строить аппроксимирующие полиномы методом интегрального
приближения.
4. Метод наименьших квадратов реализует наилучшее в среднем
приближение на всей области определения сеточной функции yt = /(*/) и в некоторых
случаях не учитывает локальных свойств аппроксимируемой функции (например,
одиночный резкий «всплеск») [6].
5. Реализация метода наименьших квадратов с использованием степенных
функций связана с решением системы линейных алгебраических уравнений
относительно неопределенных коэффициентов, причем при изменении степени
т все коэффициенты необходимо рассчитывать заново. Этот недостаток
устраняется выбором ортогональных базисных функций фу (х) .
Перейдем к рассмотрению примеров.
Пример 4.9* Решить задачу аппроксимации сеточной функции, заданной
табл. 4.13, при т = 1 и т = 2.
Таблица 4.13
/
*/■
1 /<*/> = //
0
2
7
1
3
5
2
4
8
3
5
7
□ Пусть степень многочлена т = 1, тогда решение ищется в виде
167

1. Для составления системы (4.53):
s0a0 + s{a{ = /0,
sxa0 + s2a{ = tx
найдем ее коэффициенты Sq,sus2. Расчеты поместим в табл. 4.14, где в
последней числовой строке находятся коэффициенты системы.
Таблица 4.14
1 Х{
2
3
4
5
14
si
fi
7
5
8
7
27
'о
1
1
1
1
1
4
*о
*}
4
9
16
25
54
*2
*///
14
15
32
35
96
'i 1
В результате получаем
4а0 +\4ах =27,
14я0+ 54а, =96.
2. Решение системы: а0 = 5,7; я, = 0,3.
3. Искомая сглаживающая функция имеет вид Jx(х,а) = 5,7 + 0,3х, а
среднеквадратичная погрешность 8х(а) = 1,0368.
Пусть т = 2, тогда решение ищется в виде f2(x,a) = д0 + ^х + я2х2 •
1. Составим систему (4.53):
50Д0 + Sxa{ + 52Я2 = /(Ь
^до +52«i +s3a2 =tXi
s2Oq + s^cii + s^a2 = f2 .
Расчеты коэффициентов системы приведены в табл. 4.15.
Таблица 4.15
1 *'
2
3
4
5
14
s\
fi
1
5
8
7
27
>о
1
1
1
1
1
4
so
л1
4
9
16
25
54
*2
х?
8
27
64
125
224
*з
х,4
16
81
256
625
978
54
*ifi
14
15
32
35
96
'i
xfft ]
28
45
128
175
376
'2
168

В результате получаем систему
4я0 + 14flj + 54 а2 = 27,
\4а0+54а{ +224д2 =96,
54с0+224я1+978д2 =376.
7/ -, 169 29 1 2
Мх,а) = х + — х
У2 20 20 4
/,(х,я) = 5,7 + 0,3х
Рис. 4.8
2. Решаем полученную систему методом Гаусса (см. гл.1).
Прямой ход:
(0 14 54 27 ^
14 54 224 96
[54 224 978 376J
Обратный ход:
1 1 21
1 2 2
0 (3 35
21
4
1,5
0 35 249 11,5
(\ 1 21 21\
1 1 2 2 4 '
0 1 7 0,3
[о о 0 1
(\ 1 21 21Л
'22 4 '
0 1 7 0,3
0 0 1 4- у
4 У
1 2 2
0 1 7
0 0 1
V )
м
<*\
1*2 J
=
4
0,3
±
к 4;
ах + 1а2 = 0,3,
169

г* l 3 _ 1 29
Отсюда а2 = —, а, = 7— = ,
2 4 * 10 4 20
= 27_27fl _7fl = 27_27 J__7 29. 169
*° 4 4 *2 2°l " 4 4 4 2 20 20 '
3. Искомая сглаживающая функция /2(х,д) =-—- —x + — x2, а
среднеквадратичная погрешность 52(д) = 1,0062.
На рис. 4.8 изображены заданная сеточная функция, сглаживающие
многочлены при т = 1 и т - 2 , а также интерполяционный многочлен, полученный в
примерах 4.1 и 4.4 (при этом т = 3). ■
Пример 4.10. Пусть сеточное представление формульной функции у = \пх
задано на отрезке [l; 5] с погрешностью 8 = 0,1 (табл. 4.16). По этим данным
найти сглаживающий многочлен f„(xya) методом наименьших квадратов с
использованием последовательного выбора степени т = 1, 2,...
Таблица 4.16
Г /
*/
1 fi
0
1
-0,070
1
2
0,760
2
3
1,000
3
4
1,526
4 1
5
1,449
□ Примем сначала т = 1.
1. Искомая функция fx(x,a) = а0 +а{х определяется из системы (4.53):
i=0 ) u=o ) /=0
( 4 > ( А \ 4
Xх/ г°+ Xх/2 Ь = Х*/Л
/=0
ч/=о ;
5^ + 15^ =4,665,
15а0+55а! =17,799.
2. Решая эту систему, например, методом Гаусса, получаем
а0= -2,2082; я, =0,3804.
3. Сглаживающий многочлен имеет вид f\(x,a) = - 0,2082 + 0,3804 х.
Вычислим среднеквадратичную погрешность Ьх = 0,205 > е = 0,1.
Так как условие 5,- * е не выполнено, возьмем т = 2:
/2(хуа) = а0+а{х + а2х2. Определяя a0iaXla2 из системы (4.53) при т = 2,
получаем
/2(*,я) = -0,9726 + 1,0356* - 0,1092х2.
Поскольку среднеквадратичная погрешность 52 = 0,094 < е = ОД , задача
решена. ■
170

ПРИМЕНЕНИЕ ЭМПИРИЧЕСКИХ ФОРМУЛ
Исходя из приблизительного сходства с экспериментальными данными
выбирается одна из двухпараметрических формул:
/(х,д0,я1) = яо+~;
7(х,а0,а{) = а0а?;
f(x,aQial) = a0 +а{ 1пх;
It \ 1 •
j (х, а0, ах) = ,
а0 + а{х
7(x,fl0,fl1) = ^o^a,x;
7(л:,д0,а1) = —^— ,
7(y п п\ Х
J \Х, %,и\)
а0 + ахх
7/ \ *
J {х, a0iax) = —
aQ + ахе~л
7/ ч аох
f(x,a0iax) = , ....,
ах + х ах + х
где aQiax — неизвестные коэффициенты.
Требуется найти коэффициенты а0,ах, минимизирующие погрешность
сглаживания на основе метода наименьших квадратов:
л== Z[/te'flo»fli)-//J ->min.
Для нахождения коэффициентов а0,ах применяются необходимые условия
экстремума:
-^- = 0, -^ = 0.
да$ дах
В отличие от применения степенных функций, нахождение неизвестных
коэффициентов сводится к решению двух нелинейных алгебраических уравнений
с помощью одного из методов, изложенных в разд. 3.2.
Замечание. В качестве эмпирических формул на практике могут быть
использованы также и трехпараметрические зависимости, например,
f(x,a0ial,a2) = aQxai + а2, f(x,a0,aXia2) = a0eaiX+a2 и др.
ПРИМЕНЕНИЕ ОРТОГОНАЛЬНЫХ БАЗИСНЫХ ФУНКЦИЙ
При нахождении коэффициентов обобщенного многочлена (4.43) с
помощью ортогональных базисных функций нет необходимости решать систему
(4.53).
Функции ф*(х) и <р/(х) называются ортогональными на множестве точек
{дсД/ = 0,1,...,л , если их скалярное произведение на этом множестве равно нулю:
п
(ф*>Ф/) = Еф*(*/)-Ф/(*/) = 0, к */.
Система функций \фу(х) \j = 0,1,...,m, называется ортогональной на
множестве точек {xj },/" = 0,1,...,п, если все функции этой системы попарно
ортогональны на этом множестве.
171

Так, если в обобщенном многочлене
Qm(*) = % Фо(х) + а{ ф,(х) +... + ат фт(х)
система базисных функций ортогональная, то (ф*,Ф/) = 0, к * I, а (4.50)
перепишется в виде
(ф<ъФо)яо =(/>Фо)>
(ФЬФ|)^1 = (/.ф|).
(фт>Фт)^т = (/,Фет)>
т.е. все недиагональные элементы в матрице системы (4.50) становятся равными
нулю. Следовательно, коэффициенты обобщенного многочлена находятся по
формуле
aJ=T-^ = —n • У-0,1,...,«. (4.54)
ь»"* tfa)
i=0
Коэффициенты (4.54) обобщенного многочлена называются
коэффициентами Фурье функции yt - /(*,) относительно ортогональной системы функций.
Теорема 4.2 (о точечном среднеквадратичном приближении функций
ортогональными многочленами [37]).
Для функции yt = /(х(), определенной на множестве точек {х, },/ = 0,1,..., л,
обобщенный многочлен т-й степени Qm(x) с коэффициентами Фурье относительно
ортогональной на этом множестве точек системы функций {(pj (х)} является
многочленом наилучшего среднеквадратичного приближения этой функции, причем
квадрат наименьшего среднеквадратичного отклонения определяется соотношением
P2(f,Qm)-V\2-t°jbj\2- <4-55>
у=0
1 П
где Oj— коэффициенты Фурье, определяемые по формуле (4.54); ||/|| =5]У) ,
/=о
Ikf = t Фу2(*/)> Р(/.0„) = J t [Qm(*i)-fi
i=0 I /»0
p.
Пофешность данного приближения вычисляется по формуле
?</.<?«) =£тпН (4.56)
172

Рассмотрим применение многочленов Чебышева в качестве системы
базисных функций, которая используется для получения многочленов Qm(x).
Многочленами Чебышева go(x),g\(x)i...igm(x) на множестве точек
{*, }, 1=0,1,...,л, называются алгебраические многочлены, которые
ортогональны на этом множестве, с нормой |g*||, отличной от нуля, и определяются
следующими рекуррентными формулами:
Яо(*)31; £i(*) = *-tf; gkM = (x-ak)gk_l(x)-bkgk_2(x)y £ = 2,3,...,/я, (4.57)
п п
2>< • gl-i(Xi) I>/-S*-2(*/)-£*-i(*i)
rae^-L-^x,; ak =&L ; bk =i=2 .
'-0 2>2-i(*,) 2>b(*,)
/=0 /=0
Соотношения для коэффициентов a,ak,bk получены из условия
ортогональности.
Применение ортогональных базисных функций поясним на примере [37].
Пример 4.11. Пусть дана сеточная функция (табл. 4.17).
Таблица 4.17
I
*/
1 fi
0
0
4
1
1
0
2
3
1
3
4
2
Требуется сгладить эту функцию алгебраическими многочленами
наилучшего среднеквадратичного приближения Q0 (х), Qx (х), Q2 (х), <23 (*)» гДе
Goto = flo^W. Gi to = ^oW + fliftW.
£2 to = flo£o to + *i£i to + a2g2(x),
£з to = floftW + fli£i to+ ^£2 to + «з£з(*)»
и найти погрешность каждого из указанных приближений, т.е. р(/,(?о)>
р(/,а),р(/,е2).р(/.Оз).
П 1. Определим ортогональные многочлены Чебышева £oto>£ito>
g2(x), gi(x) на множестве точек {0;1;3;4}.
Сначала найдем go to» £i to- В соответствии с первой формулой из (4.57)
1 п
функция g0(x) = 1, а многочлен gj (х) = х - а, а = У х, . При п = 3 получаем
" + l,to
1 3 1
а = — £х, = —(0 + 1 + 3 + 4) = 2. Таким образом, gQ(x) = 1; gx (х) = х - 2.
4 /=о 4
173

Теперь определим многочлен g2(x) , для которого справедлива формула
gi(x) = (х~а2)8\М~hSo(x)• Функции gQ(x) и g{(x) получены. Требуется
только найти а2 и Ь2 :
а2 =
1>/ *?(*/)
/=о
2>i*o(*/)*l(*i)
*J2 : h = "0 lUof
Вычислим сначала квадраты норм || gQ || и || g{ || :
1*о IP = 2>о<*/) = 4; IUi II2 = i*2U/) = *2(0) + *i2(l) + *i2(3) + ^2(4) =
/=о /=о
= (0 - 2)2 + (1 - 2)2 + (3 - 2)2 + (4 - 2)2 = 10.
Далее найдем а2 и Ь2:
«2 = ^2>«' • *?<*/) = ilO • ft2<°> +! • *?<!) + 3• g?(3) + 4 • g,2(4)] =
1U /=0 IU
= _L(0 + l + 3 + 4) = 2;
^ =7S*/Ы'/)*1(*/) =7[0-Ь(-2) + 1-1-(-1) + 3-Ь1 + 4-1-2] = |.
5 9 5
Итак, многочлен g2(x) = (x-2)gi(x)--g0(x) = (x-2y --.
Определим многочлен £з(х), для которого справедлива формула
^3(x) = (x-fl3)giM-i3^W. Функции #i(x) и ^2W получены. Требуется найти
*з>*з :
3 3
2>/ *2(^/) 5>/ -Sl(*/)-*2(*i)
*3
•; *3=^-
1Ы12 ' 1Ы12
Вычислим сначала квадрат нормы || g2|| :
Ы12 = 2>2(*,) =
/=0
(xo-2)2-f
(х.-2)24
п2
(*2-2)2-|
12
ft2<*2>
(^з-2)2-|
П2
ЗГ* "IT" ""ЗГ" ^1Р
4-|
174

Далее найдем д3> h-
с3 =
91 4 4 4 4J
Iftf
ft I
Итак, £3(x) = (x-2)|
2.
10'
(*-2)2--
--^(х-2) = (д:-2)3-у(х-2).
Аналогичные вычисления выполним для многочлена £з(*):
II*з II2 = £*з<*/) = *э2(*о> + £2(*i) + ft2(*2) + £з2(*з);
/=0
£3(*о)
,34 6 , j t 17 12
, 17 12 2, J о 17 6.
= 1-— = -—; £з(*з) =8-— 2 = -;
х2=з 5 5 '*з=4 5 5
II ||2 _36 144 | 144 t 36 72
II £з || ~ 25 + 25 + 25 + 25 " 5 "
Значения многочленов £о(х)»£1(х)>£2(*)»£з(*) на множестве точек {0;1;3;4}
представлены в табл. 4.18.
Таблица 4.18
1 /
0
1
2
1 3
*,■
0
1
3
4
£о(*/)
1
1
1
1
g\M
-2
-1
1
2
Ы*/)
1,5
-1,5
-1,5
У
£з(*/)
-1,2
2,4 1
-2,4
_.. 1,2 1
2. Определим многочлены наилучшего среднеквадратичного приближения
ft(*).a(*).(fe<*),G3<*):
— многочлен (?о (х):
з
f £//•£<)(*/)
Qo(x) = aQg0(x)\ a0 =U'g°/ si=fi = —(4.1+0-1 + 1-1 + 2-1) = —.
1Ы12 1Ы12 4 4
Таким образом, сглаживающий многочлен Qq(x) = —;
4
175

— многочлен Qx (х):
Ox W = ^oW + *i*i (*); *i = ^Sll = <d^_ :
Ik ill Ikill
_4(-2) + 0(-l) + ll + 2-2 3
10 10'
Таким образом, QAx)= (x-2) = x + —;
1 4 10V 10 20
— многочлен Q2{x)'.
QiM = a0g0(x) + fl,g, (x) + a2g2(x)\ a2
91 2 2 2 2j 6
Ы12
Ibll2
Л / ч 3 47 5
°2(x) = "Tox+^+6
(*-2)24
5 2 109 18
= — x x + —;
6 30 5
— многочлен Сз(х):
*3 =
,, ч £//-*з(*/) .
(/,<Ы_/=0 = J_
Ibll2 " Ы12 "72
4.,.|иЛи(-Ш.,|
2
*3V ' 6 30 5 3
(x-2)2+-^(x-2)
1 3 17 2 13 .
- — x + — x x + 4.
Значения алгебраических многочленов наилучшего среднеквадратичного
приближения в точках х( представлены в табл. 4.19.
Таблица 4.19
/
0
1
2
1 3
Xj
0
1
3
4
G><*/)
1,75
1,75
1,75
1,75
G|(*/)
2,35
2,05
1,45
1,15
ft<*/>
3,6
0,8
0,2
2,4
&<*,•)
4,00
0,00
1,00
2,00
// ]
4
0
1
2
176

3. Найдем погрешности приближений функции у, = f(Xj) многочленами
cbw.aw.e2W.ftw-
Для вычисления погрешности многочлена наилучшего
среднеквадратичного приближения используются формулы (4.55),(4.56).
Определим ||/||: ||/|| = (/, /)^ = j£ /, = ,/(16 + 0 + 1 + 4) = ЛГ.
1/-0
Тогда можно получить численное значение погрешности многочлена
CoW:
p(/.So)=^=Vp2(/.Go) s-j=№ ~а° "g0"2 =
/2Т1 16 V12
Аналогично находятся р(/, (?() * 0,611; р(/, £?2) « 0,276,
-мл)-щ\ы'-Ъ°)Ы-
■■kF
49 л 9 in 25 о ! 721 п
4 + 10 + —-9 + =0.
16 100 36 9 5
Очевидно, при изменении степени т нет необходимости рассчитывать все
коэффициенты заново. Это является одним из преимуществ применения
ортогональных многочленов. ■
4.4.3. Метод наилучшего интегрального приближения
Сначала рассмотрим применение глобального способа. В соответствии с
постановкой задачи, изложенной в разд. 4.4.1, будем искать коэффициенты
сглаживающего многочлена
fm(x^) = SmM = ао +а1х + а2х2 +... + атхт
из условия (4.45), если функция задана первым способом (т.е. интегралами
/o,/i2,...,/^+1) , или из условия (4.46), если функция задана вторым способом
(интегралами /q,/^,...,/™*1) .
Для вычисления коэффициентов многочлена используются интегральные
условия согласования (4.45) или (4.46).
177

Условие (4.45) имеет вид
j (а0 + ахх + а2х2 +... + атхт)dx = /<J,
J (fl0 + a\x + a2x2 +... + amxm) dx = /,2,
j(a0+alx + a2x2+... + amxm)dx = lZ+l
(4.58)
Условие (4.46) приводит к системе
j (д0 + ахх + а2х2 +... + amxm)dx = /<},
*0
*2
f (д0 + щх + а2х2 +... + amxm)dx - /q,
*о
(4.59)
/(А0+А1Х4-О2Х2+... + АтХт)^ = /0т+1.
Интегрируя левые части каждой из систем (4.58),(4.59) и решая
соответствующие системы (т + 1) линейных алгебраических уравнений с (т + 1)
неизвестными, можно найти коэффициенты %,аХуаъ...,ат и искомые сглаживающие
многочлены fm(x,a).
Замечания.
1. Системы (4.58),(4.59) равносильны и получаются одна из другой с
помощью линейных комбинаций (попарного сложения и вычитания уравнений).
2. Системы (4.58),(4.59) имеют единственное решение, так как можно
показать, что определители матриц этих линейных систем не равны нулю, т.е.
jdx jxdx... jxmdx
х2 х2 х2
jdx jxdx ... jxmdx
Xq Xq Xq
X\
\dx
*0
\dx
*i
jxdx...
xq
jxdx...
X[
jxmdx
xo
jxmdx
X\
xm+\ x„+i Xm+\
jdx jxdx ... jxmdx
Хщ *m *m
*0 и
xm+\ *m+l Xm+i
jdx jxdx... jxmdx
XQ Xq Xq
*0.
Таким образом, задача нахождения многочлена наилучшего интегрального
приближения имеет единственное решение [16].
178

3. Как показано в [16], при небольших т(т<1) решать систему (4.58)
необязательно, так как ее решение можно записать сразу, если ввести в
рассмотрение конечно-интегральные разности.
4. При больших т глобальный способ построения многочленов
наилучшего интегрального приближения, как и интерполяционных многочленов,
использовать не рекомендуется.
Применим теперь кусочный способ. Рассмотрим сеточную функцию,
заданную на равномерной сетке (Л = const): yt - /(х,),/ = 0,я. Пусть степень
многочлена равна т , и этот многочлен строится на некотором внутреннем отрезке
ta^jUm+il» А: = 0,1,...,л-/я-1. Этот отрезок, в свою очередь, заключает в себе
(/я + 1) частичных отрезков, на которых заданы интегралы Ik*1 >Ik+\y-*Ik+m+l •
Для большей унификации обозначений индексов будем считать, что для т = 1 на
частичном отрезке [хЛ,Х£+2] опРеДелено дополнительное разбиение этого
отрезка на два подотрезка (р = 2), для т - 2 на частичном отрезке [x*,Xfc+3]
определено разбиение на три подотрезка (р = 3) и т.д.
Конечно-интегральные разности определяются по следующим формулам:
— конечно-интегральные разности первого порядка (т = 1, р = 2):
к+— к+— к+—
*Jk -', \ Jk
к+—
Р
— конечно-интегральные разности второго порядка (/я = 2, /7 = 3):
/с+— к+— к+— к+— к+— к+—
Д2'* '=*' f-A/* '-'* '-2/ f+/ 2';
/> Р Р
— конечно-интегральные разности i -го порядка (т = i, р = i + \):
/С + — fc-i * + — / л+—- -
Здесь для многочленов степени /я = 1, /и = 2, /и = 3 принимается
/? = 2, р = 3, /? = 4 соответственно и т.д.
Тогда, например, для S{(x), S2(x), 53(х) на отрезках [хл,х*+2], [х*,хл+3],
[х*,х*+4] получаем [16]:
hk
( ь 1 ь О
'*2 4А/<2
22 *Д,
+ — д/А 2(*-**), (4.60)
К
179

S2(x)=-
k+7 1 *+7 l 1 *+T
**Р
(x-tk)-*
(4.61)
Г . 1
S3W- —
х(х-Хк) +
*+7 1 *+7 1 -> *+7 1 ■* *+7 42 *+7 -> *+7 11 ■» *+7
(4.62)
3 " 4
hV
12
1 , *+- 3 1 *+7
^А2/, 4 --Д3Л 4
*+-
6/#
Здесь hk = хк+т+1 -хк — шаг, относящийся к внутреннему отрезку
* + ~ к
1хкУхк+т+\]- Для S\(x) используются интегралы 1к 2,/ , , для *У2(х) - инте-
^ 1 * 2
*+- к+-
к+1 к+1 к+1
гралы /73,/~7,/**';для 53(х) - интегралы /*Ч/ +2,/ +,4,/*+з (рис. 4.9).
£+— А+- к+-
к+1 *+э
Узлы разбиения
Узлы формулы (4.60)
Узлы разбиения
Узлы формулы (4.61)
Узлы разбиения
Узлы формулы (4.62)
Хк
хк + \
хк + 2
хк
хк
к + -
2
хк + \
хк + \
Н \
хк + 2 хк+3
—I
Хк
Хк
А + -
3
\ 2
3
хк + \
I f
** + 1 хк + 2 Хк+Ъ хк+4
' —I 1 1
**
к+-
4
2
* 3 ** + 1
4
Рис. 4.9
Коэффициенты многочленов более высоких степеней могут быть получены
рекуррентным способом.
Так, многочлены Sm (х) до степени т = 7 имеют вид
■*«<*)'
f *+1 1
* + -
*+-
*д
*+-
А/, '+тА2/. '--A3/* ^+tA4/, ^-тА5/, *
180

*д
*-о
1 *+~~ 1
+ -Д6/, "--А7/ '
к*-
А/*
12*
*д
-Л2/, "+-ЦД3/, '-4-AV
*Д
*Д
.1|1д5/;+7_4д6/;+7+^Д7/
П
180
10
560
»з
*д
12 *
10
2 * 4 *
*Д
15
*+-
+ -Д4Л р-^-£?1
29
*+-
469
16
+ £Д6/ '--^Д7/,
30 * 480 *
*-0
(х-х,)2+^
6 *
. I*1
--Д4/, '
+ Дд5л '--?-Д6Л '
36
12
1440 *
1 <+i
24 *
Ад5/*'
48 *
144 '
*Д
1008 *'*
"к
(х-хк)4 +
(4.63)
А6
*Д
^//'«U6/
*Д
23 а7/+7
120
40
480
-л'/.
С*-**)5
/
л*7
720 *
1
7 .7**
О
-Д7/* "
1440 *
(*-**)6
I
hi 5040
Д7/, "(х-х*)7,
где р = т + 1.
Для того чтобы воспользоваться формулой (4.63) при т < 7, необходимо
выбрать его конкретное численное значение, найти интегральные разности
порядка т включительно и подставить их в формулу (4.63), в которой учитываются
только слагаемые, имеющие конечно-интегральные разности до порядка т.
Если Sm(x) строится на всем отрезке [а,Ь], то принимается hk =b-a. Правило
усечения формулы (4.63) легко устанавливается путем ее сопоставления с
формулами (4.60)—(4.62), справедливыми при т - 1, т = 2, т = 3.
Подчеркнем, что в отличие от метода наименьших квадратов, метод
наилучшего интегрального приближения при т<1 может быть реализован по
готовым формулам, и поэтому не требуется решать системы алгебраических
уравнений относительно коэффициентов.
Методика решения задачи наилучшего интегрального приближения
1. Выбрать степень т (как правило, т<1) сглаживающего многочлена и
отрезок [*bx*+m+iL на котором он строится. Если многочлен строится на всем
отрезке [я, Ь], то выбрать т = 7.
2. Подсчитать конечно-интегральные разности до /и-го порядка
включительно.
3. Выписать сглаживающий многочлен по формуле (4.63).
181

Пример 4.12. Для задачи, решенной в примере 4.10 методом наименьших
квадратов, построить сглаживающий многочлен наилучшего интегрального
приближения.
□ 1. Сеточная функция, приведенная в табл. 4.16, задана с шагом h = 1 , и
погрешность е, составляет величину 0,1. Выберем степень многочлена т = 3.
Поскольку [х0,хп] = [дс0,х4] > то л = 4. Так как л-/и-1 = 4-3-1 = 0,то £ = 0, а
частичный отрезок [*o>xo+3+i] = [*о>*41 совпадает с отрезком [ауЬ] = [1; 5].
. 1
/+—
2. Рассчитаем интегралы 1{ 4(/= 0,...,4) и конечно-интегральные разности
до третьего порядка (см. рис. 4.9). Для нахождения интегралов используем про-
стейшую квадратурную формулу трапеций: / 4 = —(/} + / \). Результаты расче-
2 /+4
.1.1
/+— , I+—
тов /, 4 и Д*/, 4(£ = 1,2,3) приведены в табл. 4.20.
Таблица 4.20
*/
1
2
3
4
5
у;
- 0,070
0,760
1,000
1,526
1,449
л i
0,3448
0,8800
1,2630
1,4875
Д/,. /4
0,5352
0,3830
0,2245
A*/,'*"
- 0,1522
-0,1585
аз/;+х
- 0,0063
3. Подставляя значения конечно-интегральных разностей, представленных
верхними значениями в колонках табл. 4.19 и ЛЛ =5 — 1=4 в формулу (4.62),
получаем сглаживающий полином
53(х) = 0,2804 + 0,0682 (х-1)-0,07137-(х-1)2 -0,00105-(х-1)3.
Рассчитывая среднеквадратичную погрешность для сглаживающего
многочлена, получаем значение 5 = 0,11, которое приблизительно равно е. Это
свидетельствует об обоснованности применения метода сглаживания многочленом
наилучшего интегрального приближения. Отличие многочлена S$(x) от самой
функции f(x) = \пх на отрезке [1; 5] не превышает 0,064. ■
182

4.5. МЕТОДЫ ИНТЕРПОЛЯЦИИ И СГЛАЖИВАНИЯ НА ОСНОВЕ
СПЛАЙНОВ
4.5.1. Постановка задачи и основные положения
Как отмечалось в разд. 4.1, в вычислительной практике при глобальном
способе аппроксимации высокие степени интерполяционных многочленов
использовать нецелесообразно. Поэтому часто применяется кусочно-глобальный
способ на основе, например, линейной и квадратичной (параболической)
интерполяции. Однако производные таких интерполяционных многочленов,
получающихся на частичных отрезках, в местах их стыка терпят разрывы. На рис.
4.10,д показано поведение совокупности трех таких параболических многочленов
(звеньев). Легко видеть, что производные в точках стыка частичных отрезков
(шаблонов (xi9xi+l,xi+2), (*/+2.*i+3»*i+4). (*|Ч4>*|Ч5»*1+б)) терпят разрывы. Это
является крайне нежелательным, если вся совокупность {JS2ii(x) далее исполь-
зуется, например, для аппроксимации обводов конструктивных элементов
сложных поверхностей. Для изготовления таких поверхностей требуется задание в
узлах не только значений Skj(xj), но и первой производной Ski(xi) или даже
второй производной Ski(xi). Таким образом, вместе с функцией yt = /(*,), /* = 0,л,
требуется достаточно хорошо аппроксимировать и ее производные. Если
восполняемая функция достаточно гладкая, то и ее производные тоже гладкие, и
поэтому они должны быть непрерывными во всех внутренних узлах. В связи с
этим к аппроксимирующим функциям Sm(x) (т— степень многочлена)
предъявляются требования непрерывности Sm{x)y S'm(x) и по возможности S'^x) или
S%(x) во всех точках дсе[я,/>] (рис. 4.10,6). Это и обусловливает необходимость
построения сплайн-функций, обладающих указанными свойствами и имеющих
интерполяционный или сглаживающий характер.
Рис. 4.10
183

Пусть на отрезке [a,b] задана сеточная функция >>,= /(*/) на сетке
Qn. Требуется восполнить ее функцией Sm(*)> где т - степень многочлена,
кусочно-глобальным способом.
Дадим сначала упрощенное определение сплайна, которое затем
уточним.
Сплайн-функцией или сплайном называется совокупность Smi(x)-
алгебраических многочленов степени т (звеньев), определенных на частичных
отрезках [х/,*/+1] ,/ = 0,л-1,и соединенных вместе по всем частичным
отрезкам так, чтобы можно было составить многозвенную функцию
Sm(x)= [JSmj(x), определенную и непрерывную на всем отрезке [a,b] вместе
/=о
со всеми своими производными S%\x) до некоторого их порядка /? = 1,2,....
Разность между т и наибольшим порядком производной,
непрерывной на отрезке [a, b], определяет дефект сплайна q.
Условиями согласования звеньев Smi(x) сплайна с исходной функцией
yf = f(Xf) на соответствующем частичном отрезке [xhxi+{] называются
условия, накладываемые на невязки дифференциального и интегрального типов
bSJfjfc), bSmi(Ilj+l) и использующиеся для вывода формулы одного звена
сплайна на указанном частичном отрезке.
Сплайн, удовлетворяющий условиям (4.3) нулевых функциональных
невязок, называется интерполяционным, а удовлетворяющий только интегральным
условиям (4.5), — сглаживающим или интегрально-сглаживающим.
Сплайн, построение которого основано только на дифференциальных
условиях согласования (4.2) при р - 0,1 или р = 0,2, называется
дифференциальным (Д-сплайном). Если же наряду с дифференциальными условиями
согласования используется интегральное условие вида (4.5), то сплайн
называется интегрально-дифференциальным (ИД-сплайном). Сплайны такого
типа впервые предложены в [16—23].
Количество условий согласования, необходимых для получения
формулы одного звена сплайна, должно соответствовать степени сплайна
(число условий на единицу больше т). После определения формулы Smi(x)
ее правая часть выражается через известные и неизвестные величины
(параметры) : /'^(ху) — для дифференциального сплайна или через совокуп-
ность /^р'(х() и //+| = \f(x)dx —для интегрально-дифференциального. Эти
величины будут называться параметрами сплайна. В зависимости от того,
заданы те или иные параметры сплайна в постановке задачи или нет, они
именуются определенными или неопределенными. Последние вычисляются на
основе условий непрерывности (гладкости) сплайна Sm(x)y которые здесь
называются условиями стыковки. Для некоторого узла х,, общего для звена
/-1 , относящегося к частичному отрезку [х/-!,*,], и звена /', определенного на
частичном отрезке [х/,х/Ч1], это условие имеет вид
184

При решении задачи аппроксимации с помощью сплайн-функций
условия стыковки преобразуются к соотношениям, связывающим
определенные и неопределенные параметры, которые называются параметрическими
соотношениями (уравнениями).
Параметрические соотношения, записанные в виде уравнений, могут
использоваться для нахождения неопределенных параметров применительно к
сплайн-аппроксимации либо для выражения одних параметров через другие.
Последний способ в данной книге применяется для вывода новых типов
формул численного дифференцирования и интегрирования (см. гл. 5).
Кроме того, параметрические соотношения на основе изложенного во введении
принципа согласования порядков численных величин устанавливают
соответствие этих порядков для различных параметров, входящих в то или иное
соотношение.
При решении задачи сплайн-аппроксимации необходимо
предварительно вычислить неопределенные параметры сплайна для всех его звеньев.
Этот этап соответствует решению параметрической задачи. Для пояснения ее
характера введем понятие порядка параметров сплайн-функции, который
обозначим через /. Этот порядок зависит от порядка производных исходной
функции у = /(*): для параметра I}*1 примем / = -1, а для /^'(х,-)
положим / = р(р = 0,1,2,...).
Параметрическая задача называется прямой (обратной), если порядки
всех неопределенных параметров больше (меньше) порядков определенных
параметров. Если в задаче аппроксимации порядки одних неопределенных
параметров больше, а порядки других меньше порядков определенных
параметров, то параметрическая задача называется смешанной. Данная
классификация используется далее при описании конкретных методов
построения параболических интегрально-дифференциальных сплайн-функций.
Две совокупности параметров, относящиеся к параметрическим
уравнениям и сплайнам разных степеней, называются подобными, если они могут
быть получены друг из друга путем соответствующего изменения порядков
параметров / на одинаковую величину.
Параметрические уравнения или их системы, соответствующие двум
сплайнам разных степеней, называются подобными, если они включают
подобные параметры и имеют одинаковые коэффициенты, зависящие от
шагов, определяющих сетку.
Два или несколько сплайнов различных степеней называются подобными,
если формулы звеньев можно получить друг из друга путем
дифференцирования или интегрирования и замены всех параметров одного сплайна
соответствующими подобными параметрами другого сплайна.
Сплайн называется локальным, если все неопределенные параметры,
относящиеся к каждому его звену Smt(x), t = i, при xe[xhxul],
/=0,л-1, находятся локально, т.е. независимо от параметров,
характеризующих все остальные (или почти все остальные) звенья Smt(x)
(f = 0,1,...fi-l,/ + l,...,л-1).
185

Сплайн-аппроксимация (как правило, это интерполяция) локальными
сплайнами сводится, таким образом, к получению конкретных значений
коэффициентов многочленов Smi(x) для каждого звена результирующего
сплайна Sm(x) и неопределенных параметров путем их вычисления по
аппроксимационным формулам. Недостаток локальной интерполяции состоит
в том, что таким способом не удается обеспечить минимальный дефект
сплайна, т.е. максимально возможную его гладкость в смысле
непрерывности производных как можно большего порядка (р = 0,1,2,...).
Альтернативой локальному сплайну является глобальный сплайн, для
которого неопределенные параметры, относящиеся к каждому его звену
^m,/(x)> ' = /"> ПРИ х е [*/i*/+i]> / = 0, л-1, находятся совместно с
параметрами, характеризующими все остальные звенья Sm t [х), / * i .
Неопределенные параметры в глобальных сплайнах для всех звеньев вычисляются, как
правило, путем решения системы линейных алгебраических уравнений трех-
диагонального вида методом прогонки, причем это обеспечивает
непрерывность одной из производных, а именно той, которая не включена в
условия согласования. Если в условие согласования включена производная другого
порядка, то ее непрерывность также гарантируется. Глобальный способ
аппроксимации по сравнению с локальным способом обеспечивает минимально
возможный дефект сплайна. Поэтому глобальные сплайны широко
используются в вычислительной практике.
В заключение данного раздела дадим развернутое определение
глобального интегрально-дифференциального сплайна.
л-1
Функция Sm(x)= \JSmi(x), которая определена на отрезке [a,b] , при-
/=о
надлежит классу гладкости Сг[я,£] и составлена из совокупности звеньев
Smi(x), / = 0,л-1, определенных на каждом частичном отрезке [x/fx/+1]
сетки Оя, называется алгебраическим интегрально-дифференциальным сплайном
степени т и дефекта q (0 < г < /и, q = т-г) с узлами на сетке П„,
если каждое его звено Smj(x) х е [х/,х/+1], / = 0,л-1, представляется в виде
алгебраического многочлена степени т\
V/M= £**./(*-*/)* (4.64)
с коэффициентами aki , выражаемыми из совокупности (т +1)
интегральных и (или) дифференциальных условий согласования:
^-;,(х,,х/+1)= 'j[SmJ{x)-f{x)]dx = 0, (4.65)
Xj
bsM{Xj)= Sj>!,4x)\x^ -/ЫМ|х=х. = 0, j = /,« +1, (4.66)
186

и из условий стыковки (непрерывности) звеньев Smi(x) по производным
Здесь ру (0<р{<г) принимает значения из совокупности нескольких целых
чисел, соответствующих порядкам производных, а р2 - целое число или в
общем случае несколько целых чисел, таких, что 0 < р2 < г, причем ни
одно из этих чисел не равно ни одному значению чисел рх.
Замечания.
1. Данное определение является обобщенным, и оно справедливо как для
интегрально-дифференциального сплайна, так и для классического
дифференциального. В последнем случае условия (4.66) не используются.
2. Условия стыковки (4.67) вместе с дифференциальными условиями
согласования (4.66) обеспечивают непрерывность S)fi\x) , /? = 0,1,...г, во
всех внутренних узлах *,, определяющих точки стыковки звеньев, т.е.
(х,, Sm (х,)), (/ = 1, п -1). Это гарантирует выполнение условия Sm (х) е Cr [a, b].
3. Алгоритм конструирования сплайна сочетает в себе два способа
аппроксимации — кусочный и глобальный и поэтому является кусочно-
глобальным. На кусочном способе основан процесс отыскания звеньев
сплайна Smj(x), т.е. коэффициентов akj многочлена (4.64), а на
глобальном - соединение всех звеньев в единую (многозвенную) функцию Sm(x)
(xe[a,b\) со стыковкой звеньев так, чтобы обеспечивалась непрерывность
S%\x) при р = 0,1,2,..., т.е. непрерывность как самой функции Sm(x), так и
ее производных.
4. Порядки производных рх, выбранных для условий согласования
(4.66), не должны совпадать с порядками производных, используемых
в условиях стыковки (4.67), но вся совокупность порядков производных из
рх и pi должна обеспечивать выполнение условия Sm (х) е Cr [a, b].
5. Интегральное условие согласования (4.65) может быть переписано
в виде jsmj(x)dx = //+1, и тогда //+| вместе со значениями /'^(х,), вхо-
Xj
дящими в дифференциальное условие согласования, причисляется к
параметрам ИД-сплайна. Данные параметры могут быть заданы при
формулировке задачи аппроксимации либо определены при ее решении.
Рассмотрим сначала кубические дифференциальные сплайны,
являющиеся традиционными и широко используемыми при интерполяционном
восполнении сеточных функций [1,2,13,14,25,44].
187

4.5.2. Интерполяционные дифференциальные
кубические сплайны
Рассмотрим задачу восполнения заданной сеточной функции ук - /(*,),
/ = 0,я, Xj е[д,б] на базе интерполяционных глобальных кубических
дифференциальных сплайнов дефекта # = 1, т.е. S3(x)eC2[a,b], которая изучена
в [1,2,13,25] и др. работах. При этом предположим, что восполняемая функция
достаточно гладкая.
Решить эту задачу можно с помощью двух алгоритмов восполнения
исходной сеточной функции, различающихся выбором порядков производных, на
основе которых записываются условия согласования (4.66). Первый способ,
наиболее широко распространенный, соответствует выбору вторых
производных /и,- = //' (/ = 0, п), а второй - выбору первых производных щ = //.
Оба способа основаны на решении параметрически прямой задачи и
весьма близки по характеру вычислительных процедур.
Основные этапы реализации первого способа.
Первый этап. Для алгебраического многочлена (полинома)
^3,/ (*) = «о,/ + *!,,• (* - */) + яг,/ (* - х, )2 + я3./ (* - *i )3 > (4.68)
относящегося к одному /-му звену сплайна, для которого хе [*,,x/+i],
выбираются два дифференциальных условия согласования (4.66) с порядком
/>1 = {0; 2}, каждое из которых относится к концам отрезка [x,,x,+i]:
3S3J(x)\x=Xi =SXi{xi)-f{xi) = Oy
(4.69)
&*зЛ*)|х-х = ъЛ*м)- /fo+i)=о;
(4.70)
s^!/ (*)|х=х+| = ^;,(*,ч,) - r(x/+i)=о.
Выбор значения /7 = 0 обусловлен тем, что отыскивается S$(x) —
интерполяционный многочлен, а выбор производных порядка р = 2 зависит от
выбора способа. Условия (4.69), (4.70) задают параметры сплайна /},
/я, =/"(х;), / = 0,л, первые из которых (функциональные) являются
определенными, а вторые (дифференциальные) — неопределенными.
Подстановка в соотношения (4.69), (4.70) полинома (4.68) приводит
к системе четырех линейных алгебраических уравнений относительно
неизвестных коэффициентов aki (А: = 0,1,2,3). Разрешая их, подставляя получен-
188

ные формулы для aki в (4.68) и распространяя этот результат на все
частичные отрезки, имеем:
*v(*b// +(^V/ -tf-m, -^Дт, j.(x-*,) +
+ ^i-.(x-jc,.)2+ —— Amr(x-Xi)\ / = 1,л -1, (4.71)
2 6Л|Ч1
где Лы = х/+1 - xh Afi = //+1 - /-, Дет, = ет/+1 - ет,-.
Таким образом, найдена общая формула одного звена сплайна, которая
выражается через определенные (/)) и неопределенные (/и,-) параметры (/ = 0,л).
Эти параметры обеспечивают непрерывность сплайна: ^з.мМ] _ =^'з./(;с)| _ >
/ = 1, я — 1, и его вторых производных •S'l'/^Ml = »$з!/М| _ , / = 1, /t — 1, для
всех внутренних узлов.
Второй этап. При вычислении неопределенных параметров ет, (/ = 0, л),
входящих в (4.71), с учетом условия стыковки (4.67) для всех внутренних узлов
устанавливается связь между /) и ет,. Эта связь получается путем записи правой
части (4.71) для звена 53/_](х) при хе[х,ч,х;], ее дифференцирования и
приравнивания производной правой части (4.71) для звена *У3,(х) при хе [x,,x,+i] в
соответствии с условием стыковки (4.67) (р2 = 1). Проведя несложные выкладки
и распространив найденное соотношение на все внутренние узлы, получим
параметрическую систему — трехдиагональную систему линейных алгебраических
уравнений, устанавливающую линейную связь комбинаций определенных /} и
неопределенных параметров ет, во внутренних узлах:
6 3 6 Л/+1 Л/
Данная система относительно ет,(/ = 0,л) является незамкнутой, так как
не хватает двух уравнений. Для ее замыкания используют различные пути
выбора аппроксимаций производных на концах (граничных условий):
1. В простейшем случае вторые производные на концах принимаются
нулевыми, т.е.
Щ =0; т„ = 0.
Такие условия называются условиями натурального сплайна.
189

У-fix)
Из рис. 4.11 видно, что задание условий т0=0 и тп = 0 приводит
к разрыву вторых производных/"(х)1_г и f"(x)\ на концах отрезка [а,Ь],
*X—Xq *Х—Хп
что может вызвать возрастание погрешности интерполирования.
2. Для первых двух и последних двух отрезков можно применить
условие равенства третьей производной. Тогда получается соотношение
Amk_l/hk =Amk/hk+i (& = 1,л-1). Отсюда следуют два трехточечных
уравнения:
пп-г
1 1
-♦^-•!
(4.73)
пп-\
1 1
+ —
К-\ К)
пп-\
= 0.
Соотношения (4.73) позволяют замкнуть систему (4.72) при h = var
(неравномерная сетка). При h = const вторые производные на концах
вычисляются по явным формулам второго порядка аппроксимации [6]:
"o=-j(2/o-5/,+4/2-/3),
п
™п =7т(-^-3+4Л_2-5/л_, +2/J.
/г
(4.74)
190

Отметим, что как (4.73), так и формулы (4.74) для /я0 и тп имеют
порядки аппроксимации, соответствующие порядку сходимости £3(х) к
f(x) (см. п.2 замечаний на стр. 192).
Третий этап. Определяются значения /я, (/ = 0, п) путем решения
систем (4.72), (4.73) (параметрически прямая задача). Для этого используется
метод прогонки, причем необходимо предварительно из первых двух и
последних двух уравнений исключить слагаемые с т2 и т„_2
соответственно. В случае равномерной сетки, как отмечено выше, система (4.72) замыкается
аппроксимацией (4.74).
Четвертый этап. Формируются массивы коэффициентов flo,i»fli,/>fl2,i»fl3,/
для всех звеньев сплайна (/ = 0, п -1) и определяется глобальный ИНТерПО-
л-1
ляционный сплайн S^(x)= \JS3i(x) путем составления многозвенной функции.
/=0
Пятый этап. При необходимости полученная сплайн-функция ^3(х)
используется для вычисления значений функции и производных порядка р :
f(pXx) = slP\x) + o(h^{p) (р = 0,1,2...) в произвольных точках хе[х,,хи1] ,
ь
/ = 0,л-1,или определенных интегралов /* = \S^{x)dx (в приложениях тео-
а
рии приближений).
Основные этапы реализации второго способа.
Первый этап. Для алгебраического многочлена (4.68), обозначаемого
S}j(x)t вместо вторых производных в (4.70) включаются первые производные.
Тогда эти условия определяют параметры сплайна /},/я} = /'(*/),' = 0,я, первые
из которых (функциональные) являются определенными, а вторые
(дифференциальные) - неопределенными (р = \). Проделав выкладки
(аналогично первому этапу первого способа), получим общую формулу /-го
звена искомого сплайна:
•М*) = //+'И/-(*-*|) +
3 3—1 —1
(x-xtf
которая зависит от определенных (/}) и неопределенных (т"• = /■)
параметров сплайна. Данные параметры обеспечивают непрерывность всего сплайна
и его производных J^-iWl =^з,/М| . «Uz-iMl = ^3/(*)| во
всех внутренних узлах (/ = 1, л - l).
Второй этап. С использованием условий стыковки (4.67) по вторым
производным (р2 = 2) во внутренних узлах получается система линейных
191

алгебраических уравнений трехдиагонального типа, выражающая
параметрическую связь между щ и ft■:
±Ц_1+2(±1)Ш1>Шм=3(^ + Ж11=—1. (4.76)
Замыкание системы (4.76) осуществляется аналогично п.2 на втором
этапе реализации первого способа. При h = var получаются два соотношения
(граничные условия), не нарушающие трехдиагональность системы:
- я,2- hHiH^h, 1 )
ff"-'+ш" =!Pr{irAf^ +М^*«4 <477>
пп-\ //л_1 \пп_\ пп )
где Я^_1 = hk_x + hk {к-2, л).
Соотношения (4.77) аппроксимируют производные на концах с
третьим порядком точности, что соответствует четвертому порядку сходимости
S^(x) к f{x) (см. п.2 замечаний ниже). При h = const для определения
значений производных на концах можно использовать соответствующие аппроксима-
ционные формулы (см. гл. 5).
Третий этап. Трехдиагональная система линейных алгебраических
уравнений (4.76), (4.77) при конструировании глобального сплайна решается
методом прогонки (параметрически прямая задача).
Четвертый и пятый этапы аналогичны изложенным для первого способа.
Замечания.
1. Существование и единственность глобальных сплайнов S^(x) и
£з(*) следуют из рассмотренного выше построения общих формул их
звеньев S$j(x), Sij(x) и единственности решения трехдиагональных систем
(4.72), (4.73) или (4.74) и (4.76), (4.77) в силу выполнения условия
диагонального преобладания.
2. Сходимость процесса построения глобальных сплайнов Sy(x)>
^з,/М доказывается для непрерывных (формульных) функций, таких, что
f(x) е С4 [a, b]. Процесс является сходящимся, если при неограниченном
увеличении числа п узлов сетки соответствующая последовательность сплайн-
функций, построенных на этих сетках, сходится к исходной функции
f{x). Доказано, что на равномерной сетке сплайн-функции S3j(x), ^3,/W
сходятся к f(x)eC4[ayb] с четвертым порядком, причем справедливы
оценки
|/<>>(*)-sM(x)\\c[aь] = max |/W(x)-S^(x)\ < МАк*~>, p = 0,1,2. (4.78)
192

Таким образом, при использовании сплайн-функций для вычисления
производных также реализуется сходимость, но ее порядок понижается на
величину р.
3. В соответствии с принципом соответствия порядков аппроксимации
(см. разд. В.4) точность вычисления интегралов на частичном отрезке
[*i>*/+iL те- ^/+1 = j f(x)dx* I-+1 = jS}(x)dx, на основе сплайнов
( \ b
Sy(x), Sy(x) составляет 0[hf+lJ , а интеграла lba = jf(x)dx на отрезке [a,b]
a
составляет o(#4), Я = тахЛ/Ч1 (потеря порядка происходит из-за
суммирования значений //+1 и остаточного слагаемого при переходе от //+|,
Л-1
i = o,/i-i, к /* = £//+').
/=0
4. Выражая из системы (4.72) комбинацию значений функций ft_x,
/1» Л+i через комбинацию /Я/_|, /я,-, т/+1, получаем трехдиагональную
систему линейных алгебраических уравнений относительно ft :
i'<--
С1 И/- ! /•
Г+*—К'+Г~/'+1
(4.79)
•-£mi-i+ з m/4" 6 /yi,4i' |ssl'/l"1 •
Если считать, что вторые производные для некоторой функции
У( =/fa) заданы или каким-либо способом определены, а /0 и /„ на
концах [я,/>] известны, то из (4.79) можно восстановить значения ft во
внутренних узлах х{ (/ = 1, п -1) путем решения параметрически обратной
задачи. В этом случае сплайн 53(х), построенный по fit /я,(/ = 0,л) и
(4.71), является в строгом понимании не интерполяционным, а
восстанавливающим функцию .У/=/(*,)• Единственность решения задачи обеспечивается
преобладанием диагональных коэффициентов в системе (4.79) относительно
значений fr (/ = 0, п).
5. На основе соотношения (4.76) при заданных двух значениях функций
/o,/i или fn-ь/п и всех значениях 5и)(/ = 0,л) можно восстановить
функцию /(*,) во всех точках сетки х, (/ = 2, л). С этой целью система
(4.76) разрешается относительно приращений функций Д/}, которые затем
вычисляются рекуррентно. При задании неравномерной сетки устойчивость
процесса достигается при регулярном сгущении сетки в направлении слева
193

направо 6/+1=—^<1 или при ее регулярном разрежении (б/+1 > 1).
В первом случае восстановление осуществляется слева направо при
заданных /0>/,:
A// =-s/+i А//-1 +Ьк(т^ьт;,ти1),
1
где /,Л=-
1 _ (I I ) - 1 _
л/ \Л hi+\) л/+1
, а во втором — справа
налево при заданных /„,/„_!• Такой алгоритм обеспечивает устойчивость
процесса обратной прогонки.
6. Локальный способ построения интерполяционных кубических
сплайнов для заданной функции >>,=/(*/) основан на многочлене (4.75) и
состоит в определении miy i = 0, п, по аппроксимационным формулам
третьего порядка (см. гл. 5 и [6]), в дальнейшей их подстановке в (4.75) и
в формировании S3(x)= {JS$j(x). Необходимость аппроксимации третьего
/=о
порядка следует из принципа соответствия порядков, изложенного в разд.
В.4, а также из параметрической связи (4.76).
Методика построения интерполяционного кубического сплайна
(первый способ)
1. Используя систему (4.72) , условия т0 = 0, /и„ = О или (4.73) (при
h = const можно использовать условия (4.74)), сформировать замкнутую систему
относительно неопределенных параметров.
2.Вычислить коэффициенты системы (4.72), зависящие от шагов сетки Q„,
и решить ее методом прогонки. В результате найти неопределенные параметры
3. Записать выражения для звеньев сплайна по формуле (4.71):
+ -Г-- {х -Xif + ——Д/и,' (* " */)3» / = 0, л - 1,
2 6л/+1
вычислить коэффициенты звеньев и сформировать многозвенную сплайн-
функцию
*з(*)=йЧ,М>
/=0
являющуюся сплайном дефекта q = 1.
194

Пример 4.13. Для сеточной функции у{ = cosx,, х, =0,—,—,— (/ = 0,3)
найти интерполяционную кубическую сплайн-функцию S^x) первым
способом.
D В поставленной задаче х0 = 0; X! = —-; х2 = —; *з = ~~ > л = 3,
6 3 2
h = я/6 = const; /о = /(х0) = 1; /i = Д х,) = 0,8660254; /2 = Дх2) = 0,50000;
/3=/(х3) = 0.
1. Запишем систему (4.72) для внутренних узлов:
Л1 „ , h\ + h2 т Ьг т fi'fx Л -/о
-щ +-J-IH, + -тг = — —,
Л2 _, . ^2 + h „ , Л3 „, /з ~/2 Л ~/l
"7"/я1 + ; ™2 +Тт1 = 7 7 •
6 3 6 Л3 «2
В силу того, что Л = //j = Л2 = Л3 = л/6 = const, для нахождения значений
щ,т^ выбираются формулы (4.74):
/"о =77(2/0-5/1+4/2-/3),
/г
/"3=-V(-/o+4/,-5/2+2/3).
2. Вычислим коэффициенты системы и значения т0, /л3 :
то = -^-(2/0 - 5/, + 4/2 - /3) = -^-(2 ■ 1 - 5 • 0,8660254 + 4 • 0,5 + 0) = -1,2041589;
71 71
JL„0+|„ltJL„1=V2_2/,./o);
^wi+tm2+um3=!(/3-2/2+/i);
тг = ^-(-/о + 4/, -5/2 + 2/3) = Щ = (-1 + 4.0,8660254 -5 • 0,5 + 0) = -0,1309416.
П 71
Решение этой системы методом прогонки дает: тх =-0,84642;
т2 =-0,4886807.
3. Подставляя параметры т,,/= 0,1,2,3, в формулу (4.71), получаем
следующую трехзвенную сплайн-функцию:
195

S3(x) =
1 + f --0,13397 + — 1,20416 -JL. о,357741 • (x- 0)-
V n 12 36 J
Ш11 (x _o)2+1.0,35774- (x-0)3
2 71
ПрИХ€
0;-
0,86602 + f - — 0,3660 + — • 0,84642 - — • 0,35774 | • f x - -1 -
l я 12 36 J { 6 J
n)2 1
■?J +я
0,84642
-.0,35774-1 x--^
при x e
Л ^ Я
6'T
0,5 + (- - • 0,5 + — • 0,48868 - — • 0,35774] • f x - -] -
{ n 12 36 J I 3j
.^.Ll\\Lo,35mL-f
при x e
я я
У' 2"
или
53W =
1 + 0,02816х-0,60208х1 + 0,11387xJ при хе
\2
*i
0,86602 - 0,50864 |х--| -0,42321 \x-j\ + 0,11387 jc-|| при х е
0,5-0,85821 х-- -0,24434
113871 jc — | прихе
я ш я
яр я
З*'*2
Она является непрерывной и обеспечивает непрерывность первых и вторых
производных. ■
4.5.3. Интерполяционные дифференциальные
параболические сплайны
Выше отмечено, что применение параболических сплайнов более
оправданно при аппроксимационной обработке широкого класса сеточных
функций, например, рассчитанных методами сеток второго и третьего
порядка. Сплайн-методы развиваются и как самостоятельный класс методов
решения задач с обыкновенными дифференциальными уравнениями
(см. гл.6). Следует отметить, что широко распространенные на практике
кубические дифференциальные сплайны теоретически обеспечивают четвертый
порядок сходимости. Однако для их корректного применения необходимо,
чтобы исходные данные (аппроксимируемая функция у/=/(х/)) были
заданы с порядком точности, не меньшим третьего. Это условие при обработке
рассчитанных на основе методов сеток функций J>/=/(*/)» как правило,
196

не выполняется, и поэтому применять кубические сплайны не всегда
целесообразно. Это обусловливает необходимость использования параболических сплайн-
функций. Однако полученные традиционным способом сплайны S2(x)
неустойчивы в смысле отсутствия их сходимости к исходной функции, что связано
с несимметричным характером задания условий согласования и, как
следствие, с аналогичным характером граничных условий. Поэтому для
регуляризации сплайнов S2(x) Шенберг в [49] построил такой алгоритм
аппроксимации с помощью Д-сплайнов, в котором узлы сплайна сдвинуты
относительно узлов сеточной функции. Для нахождения параметров этого сплайна
глобальным способом получается трехдиагональная система линейных
алгебраических уравнений с преобладанием диагональных элементов. Однако такая
модификация существенно усложняет расчетные формулы алгоритма,
и в ней используется дополнительное, обычно в задачах не требующееся
условие непрерывности производных в серединах отрезков между узлами
интерполяции. В ряде случаев это дополнительное требование может
привести к непредсказуемому снижению точности аппроксимации и к
отсутствию сходимости.
Рассмотрим принцип построения параболических дифференциальных
сплайнов со сдвигом узлов сплайна, следуя [44].
Пусть исходная функция .У/=/(*/), / = 0,я, задана в узлах х,е[д,£],
называемых узлами интерполяции и принадлежащими некоторой сетке
А : а = х0 < jc, < ... < хп < b (п>2). Введем также в рассмотрение другую сетку
А: а = х0 < х{ < ... < хп < b = Зся+1 , узлы которой сдвинуты по отношению к
узлам сетки А влево, так что х{_{ < xt< jc,- (i = 1,/i).
л-1
Функция S2(x)= |J S2ti(x) называется интерполяционной параболической
сплайн-функцией, интерполирующей /(*,) на сетке А и принадлежащей
классу гладкости Ci[tf,£], если она составлена из совокупности звеньев
S2i(x) (/ = 0,л + 1), определенных на каждом частичном отрезке [Зс,,Зс/+1]
сетки А и представленных в виде алгебраических многочленов второй
степени:
s2jix) = Zfl*./(* "xtf = a0J + aU (*-*/) + a2j '(x - Xj)2 , (4.80)
*=0
где akj - коэффициенты, которые находятся из дифференциальных условий
согласования
8sM(xk) = sM(x)\ _ -/W(x)| - =° (* = /./ + 1). (4-81)
\x=xk \x=xk
где р\ =0 или рх = 1 . Звенья затем стыкуются по условию непрерывности
(стыковки):
Ф-'.Wl -=sft\x)\ _ (4.82)
с порядками р2у отличными от р{, но такими, что 0<р2<2.
197

В соответствии с этим определением приведем два сплайна S2(x) и
S2{x) и рассмотрим алгоритм построения одного из них , а именно S2(x).
Для некоторого отрезка [3c/,3c/+1] формула S2i(x) имеет вид (4.80)
^2,/(*) = ao,i + ац (*-*/) + a2J (x-Xj)2.
На отрезке [Зс,-,*^J для определения aQh aXi, a2i используются
условия согласования (4.81):
5S2i,(x,) = 0, 65ii/(x/) = 0> 6^,(х,ч1) = 0.
Для простоты предположим, что узлы сплайна расположены в
серединах отрезков [*/,х|Ч1], / = 0,л-1, составленных по узлам интерполяции.
узлы сетки Л
*/-2 Л/-1 *м ^ xi hM хм 4 узлы сетки д
Рис. 4.12
На рис. 4.12 изображена схема расположения узлов сетки А по
отношению к узлам сетки А. Между шагами сеток А и А в этом случае
существует простая связь
h _ h hM _ Н}*
/+i 2 2 2
Из условия 85,2>l(3c/) = 0 следует равенство olt/=/й) рй) =/'(*i))» а из
условия 552,-(3ci+1) = 0 вытекает, что /и) + 2a2i —'■— = /й)+1; д2>/ = —""Г•
2 ' я/+
Из условия интерполяции bS2i (х,) = 0 определяется коэффициент
Итак, звено сплайна ^2,/(х) на произвольном отрезке [х/,х/Ч1]
выражается формулой
S2i(x)ssfi-!!Lml- ^ .+т, ■(*-?,) + ,**' ,(х-Х;)\ (4.83)
2',W Jl 2 ' 4(l + 6/+i) ' v " A,(l+6,4l) V ,У '
где bk=hk+]/hk (А: = 1,2,...,/, / + 1,...).
Подставив (4.83) в (4.82), получим параметрическую систему
относительно т::
198

hi 6,
:Щ
Y-^7rf^jmi-]+T
hi
6/Ч1+1 Л/_1(б/+1)
т. +
(4.84)
^/♦i =A//-i, ' = !,«,
4(5,Ч1+1)
где #2(/-i) = 2//,.! + hj. Система (4.84) обладает свойством преобладания
диагональных элементов, но она незамкнута, так как число неопределенных
параметров равно п + 2. В качестве двух дополнительных уравнений
(граничных условий) могут быть приняты значения производных,
аппроксимированных на концах со вторым порядком аппроксимации (см. гл. 5):
- _ 7г _ Л
Hi
Щ = /о = "ттТ
^i л+М 7,-^+5
!1
Кк
/о
\п2
тп+\ = /л+1 ="=
И
я+1
I Нп +hn+] - \Нп ) - hn+l -
| = /„.,., Jn +-=— /л_1 I
"/! + !
hnhn+\
(4.85)
где Яял+1 = Л„ + Ля+1, fi = Дх,). Здесь шаги Л|,/22,Ля_1,Ля,Ля+| и их комбинации
взяты на сетке А. После определения всех параметров /и) их подставляют
во все звенья S2j(x), / = 0,л, из которых затем формируется
результирующая многозвенная сплайн-функция £2(х), имеющая минимальный дефект
При h = const формулы (4.83), (4.84), (4.85) упрощаются:
^2)/М = Л-^^-^А^+^(^-^) + -^-(^-^)2 (i=0,/i + l);
^+6^.+1=^ (/ = ^
(4.86)
то=^л
= тг("3^ +4/i -Л); ^Л+1 =тг(/л-1 -4/л + з/я+|д).
2/Г
Здесь вместо сетки А используется равномерная сетка Ад = (*0д>*1»—»*Яэ*я+|д)>
h h - -
где х0д =а~^> х*+хд =Ь + ~- дополнительные узлы; /0д = /(ход),/я+1д = /(хл+1д).
Другой параболический сплайн S2i(x) интерполяционного типа
приведен в [44], и он построен для более общего случая, когда узлы х, не
совпадают с серединами отрезков [х/,х|+1]. При этом S2i(x) записывается
для отрезка [х,,х/Ч1] с узлами интерполяции х,,х,Ч1 :
199

^2,/ (*) = fi + Щ(* ~ */) + ci(x - xi? + 4(* " */+i )l з (4.87)
где, как и раньше, *,_! < х,- < х, (/ = 1, п), а
(*-*/*il={ п"Г/+1 ПР-ИХ>^1' (4.88)
v /+1/+ | 0 при х<х/Ч1. '
Здесь коэффициенты при (х-х0)° и (х-х,)1 найдены с учетом
условий согласования 5^, (х;) = 0 и 5^2, (х/) = 0. Коэффициенты с/ и ^/ оп_
ределяются из аналогичных условий согласования, но заданных в точке
х/+1 отрезка [х,,х/+1]:
А
А// "*, + ^/+1 ^
'#41
Л/4ЦЛ/+1 -^/+l) 2 Л/+ЦЛ/Ч1 -^/ + i)
(4.89)
2Л/+1 А|Ч,(а|Ч1 -А/+1) 2(а/+1 -А,Ч1)
Тогда для получения связи определенных и неопределенных
параметров используется условие стыковки (4.82) при р2 = 2, т.е. условие
непрерывности второй производной в точке х,: «Уг'мМ = 4Ч'/М • Учтем,
\х=Х/ ' \x=Xj
что ^2mW| =c/_i+</,-_!, а ^i'/W = с/ в СИЛУ (4-88).
IJf=JC, 1х=х,
Подставляя в выражение с,_! + */,_! = с, соотношения (4.89), получаем
систему линейных алгебраических уравнений относительно параметров
ГА/Ч-А^- 2Af4l -hi+l ) _ А^ -
=7— + 7—* = \\'Щ + 7 ~ = Т^/41 =
(4.90)
А/А/
:2 .|А/у. + . 4£_
А/А/ А|Ч1(А/Ч1 -A/+1jJ
, 1 = 1,/!-1.
В качестве двух недостающих условий могут быть взяты аппроксима-
ционные выражения (4.85). Случаи задания других типов краевых условий
приведены в [44] и здесь не рассматриваются.
Отметим, что алгоритм построения рассмотренного сплайна является
достаточно сложным, так как S2j{x) имеет дополнительное слагаемое
*//(x-X/+i)+ , а коэффициенты сплайна и системы (4.90) зависят от шагов
А и А , характеризующих две сетки А и Л, которые также достаточно
сложны. Кроме того, требование непрерывности второй производной,
присущее сплайну второй степени, может привести не к улучшению качества
аппроксимации, а к ее ухудшению, так как эта производная для ^(х)
является константой.
200

Методика построения параболического сплайна аналогична методике,
изложенной в разд. 4.5.2 для кубических сплайнов.
Замечание. Использование интегрального подхода (ИД-сплайна),
предложенного в [15-21] и изложенного в разд. 4.5.4, 4.5.5, позволяет
строить устойчивые алгоритмы аппроксимации функций параболическими
сплайнами без смещения узлов сплайна относительно узлов интерполяции.
Кроме того, эти сплайны являются консервативными, в том смысле, что
интегралы от S2(x) и У/=/(*/) равны как на [д, b], так и на всех частичных
отрезках [*,,*/+1] (/ = 0,/i-l). С помощью интегрального подхода могут
быть построены замкнутые алгоритмы аппроксимации сплайнами
произвольной четной степени [21].
Пример 4.14. Для сеточного представления функции у = хъ, т.е.
у,=х- (х/=-2; -1; 0; 1; 2), (/ = 0,4), найти интерполяционную
параболическую сплайн-функцию S2{x) со сдвигом узлов на основе формул (4.86).
□ Для построения равномерной сетки Дд введем в рассмотрение
фиктивные узлы Зс0д=-^; и *ьл=у2 со значениями Функции /0д =-15,625
и /5д =15,625. Таким образом, будем определять сплайн S2{x) на отрезке
[- 2,5; 2,5] с сетками Дд = {- 2,5; -1,5; - 0,5; 0,5; 1,5; 2,5}, А = {- 2; - 1; 0; 1; 2}.
1. Запишем систему (4.86):
— _1
2Л
Щ =— (-3/од +4/1 -/2),
/Я/_1 + 6 тк■ + ти1 = —^-К i = 1,4;
h
^5=^(/з-4/4+з/5д).
2. Вычислим значения производных на концах отрезка [- 2,5; 2,5]:
щ =1[-3(-15,625) +4-(-3,375) +0,125] = 16,75;
ть =-(0,125-4-3,375 + 3-15,625) =16,75.
Составим трехдиагональную систему относительно /й):
щ =16,75;
щ + 6ml + т2 = 8 • 7 = 56 (д/0 = 7);
щ + 67п2 + щ =81=8 (л/1 = 1);
т2 + 6т3 + щ =81=8 (д/2 = 1);
щ + 67и4 + Тп5 = 8 • 7 = 56 (д/з = 7);
щ =16,75.
201

Решим систему методом прогонки. В результате получаем значения
производных /й~ (табл. 4.21).
Таблица 4.21
*/•
щ
1 .. 1...
*0д = -2,5
16,75
0
-1,5
6,5061
1
-0,5
0,2134
2
0,5
0,2134
3
1,5
6,5061
4
*5д = 2,5
16,75
5
3. Построим многозвенную (в данном случае пятизвенную) сплайн-
функцию S2{x). Для простоты ограничимся построением многочлена
только для одного звена 520(х):
^2,0 (*) = -! 5,625 - 0,5 • 16,75 - - • (6,5061 -16,75) + 16,75 • (х + 2,5) +
о
+ (6,5061-16,75) .(х + 2)5)2=_22>719 + 16)75 .(х +2,5)-5,1220 (х + 2,5)2.
Остальные звенья строятся аналогично. ■
4.5.4. Восстанавливающие, интерполяционные и сглаживающие
интегрально-дифференциальные параболические сплайны
В разд. 4.3. приведены два интегрально-дифференциальных многочлена
(4.37) (4.41), которые могут использоваться для интерполяции и
сглаживания некоторых функций, заданных своими значениями и интегралами,
либо интегралами и производными.
Здесь рассмотрим основанные на этих многочленах глобальные
способы конструирования различных параболических ИД-сплайнов дефекта q = 1,
позволяющие восстанавливать некоторую функцию либо ее сглаживать.
Рассмотрим применение многочлена (4.37).
ПОСТРОЕНИЕ ВОССТАНАВЛИВАЮЩИХ СПЛАЙНОВ
(задача 1)
Пусть некоторая сеточная функция определена не значениями /J в
узлах л:, в общем случае неравномерной сетки Q„, а значениями
интегралов 7/+| (/ = 0,л-1) .Требуется восстановить эту функцию путем
построения сплайн-функции S2yim\{x) дефекта q = \.
Для решения этой задачи воспользуемся параболическим многочленом
(4.37). Для получения S2tm\{x) при известных параметрах 7/+1 (/=0,л-1)
необходимо сначала определить функциональные параметры ft (/ = 0,л).
Сплайн, составленный из звеньев (4.37), при любых значениях /}
обеспечивает непрерывность S2m\(x). Поэтому для получения параметрической
связи между ft и 7/+l используются условия стыковки S2tWl](x) по
первым производным:
202

■?2./-!.ид1(*)| _ =^UiwlW| _ (r = l,«-l).
(4.91)
Преобразование (4.91) после подстановки многочлена (4.37) приводит
к параметрической системе линейных алгебраических уравнений
относительно /):
Т^+2{|- + ^]л+^/ы»з{^ + ад (/ = l,*-l). (4.92)
Из сопоставления систем (4.92) и (4.76), являющихся следствием
условий стыковки параболических ИД-сплайнов и кубических Д-сплайнов,
видно, что они являются подобными. Действительно, обе системы имеют
одинаковые коэффициенты, а параметры в них, входящие в левую и правую
части, подобны друг другу, так как различаются только порядком р. Если
-1 для
их представить в виде fk*p'(k = i-l,i,i + l) и считать
I}*1 = А/} = Fi+l - Fj (F(x)-первообразная, Ft = F(xt))t то все порядки
параметров, входящих в систему (4.76), будут на единицу больше
соответствующих порядков параметров системы (4.92). Рассмотренные соотношения
соответствуют также подобным звеньям (4.75) и (4.37), относящимся к
кубическим и параболическим сплайнам. Действительно, звено
параболического сплайна может быть получено путем дифференцирования звена
кубического сплайна (4.75) и замены параметров mi9 А/), А/я) на
/„ irl=AFh А/,.
Вернемся к задаче построения параболического сплайна. В качестве
граничных условий, замыкающих систему (4.92), используем интегрально-
функциональные связи:
/о+ ЬА-и?
2Н{ + А,
L/J
hi
"V
Н"-\
пп-\
fn-1+fn
Н*-\
1
(/ = 0),
I h2 ~
]+-
гни+к
ьЗ
/:.
л-1
(4.93)
(/ = *),
являющиеся подобными (4.77) и полученные разрешением системы (4.92)
и соотношений о2,о = fl2,i » а2,п = а2,п-\ у гДе а2,к » А: = 0,1 и к = л, л -1 —
коэффициенты при (дс-х,-)2 (последние равенства для коэффициентов справедливы
в силу постоянства второй производной на двух соседних отрезках). Подчеркнем,
что соотношения (4.93) не нарушают трехдиагональности системы (4.92)
и имеют порядок аппроксимации, равный трем, что соответствует порядку
сходимости выстраиваемых ИД-сплайнов.
203

Разрешение системы (4.92), (4.93) методом прогонки, достаточное
условие устойчивости которого для данной системы выполняется безусловно,
т.е. при любых разбиениях, позволяет вычислить /} (/ = 0, п) (параметрически
прямая задача). Подстановка /},/,'+1 в формулу (4.37) для звеньев
/ = 0, п - 1 определяет интегрально-дифференциальную сплайн-функцию
^2,ид1(х) восстанавливающего типа.
Из подобия параболического ИД-сплайна S2tVlJi\{x) Д-сплайну ^зМ и
возможности его получения путем дифференцирования кубического
Д-сплайна, а также на основе соотношения (4.78), устанавливающего
порядок сходимости Д-сплайна ^(а), можно получить оценку порядка
сходимости параболического ИД-сплайна SljVm\{x) :
|/^*)-^М| <M3h3-r, /> = 0,1,2, (4.94)
свидетельствующую о сходимости $2,ил[(х) с третьим порядком (р = 0), а
производных S^' (х) с порядком (3-р)(р = 1,2).
2,ид1
Методика получения восстанавливающих сплайнов аналогична изложенной
выше для кубического сплайна. Приведем пример построения глобального
интегрально-дифференциального сплайна для функции, заданной интегралами на
частичных отрезках.
Пример 4.15. Пусть исходная функция задана значениями интегралов на
частичных отрезках [x,;x,+1], / = 0,3(табл. 4.22).
Таблица 4.22
/
*'
1 //+'
0
0
1
1
2
2
3
3
4
4
"'■■■"•■•■••^(6)-^
Требуется найти восстанавливающий сплайн ^.ид, (х) дефекта q - 1.
1. Запишем систему (4.92) для внутренних узлов х, (/ = 1,3). При этом
учтем, что шаг сетки постоянный:
1 г 4 г ! /• ilk±lL <• ,ч
т/о+т/i +7-^=3 у2 0 = 0,
h h h h2
т/l +т/2+т/з =3 ' l (/ = 2),
h h h h2
-/2^/3^/4=3-^-0 = 3).
204

Данная система замыкается условиями (4.93), записанными также при
h = const:
2/3+/<4ЬИ4'з4) ('-«>•
2. Подставляя h = 1 и значения интегралов в правые части, получаем
систему линейных алгебраических уравнений, которую в соответствии с методом
прогонки можно записать в виде
а/Л-l -P///+Y/.//+1 =S/ (' = 0,4), а0 =у4 =0.
Коэффициенты системы, прогоночные коэффициенты //,(?, и результат
решения системы методом прогонки приведены в табл. 4.23.
Таблица 4.23
1 /
0
1
2
3
4
<*/
0
1
1
1
2
~"р71
-1
-4
-4
-4
-1
Y/
2
1
1
1
0
8/
2,000
20,000
155,000
611,089
420,574
Pi
-2
-1/2
-2/7
-7/26
-
Qi
2,000
9,000
41,714
153,293
246,974
fi 1
0,94418
0,52791
16,94418
86,69534
247,36348
3. Подставляя значения ft и V//+1 = //+1 - fth в формулу (4.37) на каждом
отрезке [x,,x/+i] / = 0,3, находим искомый параболический восстанавливающий
сплайн.
Для первого и второго отрезков получаем следующие функции:
^2,0(*) = 0,94418 - 8,832536 • х + 8,416264 • х2;
52.| {х) = 0,527908 + 8- (х-\)+8,416264- (х-1)2.
Для остальных двух отрезков выполняются аналогичные действия. Легко
убедиться в том, что полученная сплайн-функция имеет дефект q = 1, т.е. первая
производная во внутренних узлах хх, х2, х3 непрерывна. Таким образом, для хх
имеем
^2,0(*)| =-8,832536+ 2-8,416264-а: |х=1 =8;
^2.1 М| =8 +2-8,416264-(х-1)| х=1 =8.
Аналогичное условие выполняется и для других оставшихся узлов. ■
205

ПОСТРОЕНИЕ ИНТЕРПОЛЯЦИОННЫХ СПЛАЙНОВ
(задача 2)
Пусть на равномерно сгущающейся или разрежающейся сетке Qn заданы
значения сеточной функции /}=/(*,•),/ = 0, л.
Требуется восполнить эту функцию глобальным интерполяционным
интегрально-функциональным сплайном S^m) (х) дефекта q = 1.
Решение этой задачи осуществляется путем объединения многочленов
-звеньев (4.37) после определения интегралов //+I, выраженных из (4.92)
по рекуррентным право- и левосторонним соотношениям (параметрически
обратная задача):
iS+^-blxIU+^Liih,/), i = 1,/i-1 (5,+1<1),
(4.95)
//^-feJ/r^L^A,/), i = „-1,1 (5^<l),
где £/(A,/) = —/м +2- T" + "
hi
3
hu\j
(4.96)
1
fi + У/+1 ~ функция, равная сумме
hi+\
«удельных интегралов» по каждой паре смежных отрезков, 8/+1=Л/+1/Л; —
параметр, характеризующий неравномерность сетки, который называется
параметром нерегулярности. Соотношения (4.95), (4.96) записаны в виде,
учитывающем характер задания сеточной функции на неравномерной сетке,
которая, по предположению, либо равномерно сгущается вправо, либо
равномерно разрежается. Тогда (4.95) соответствует правостороннему обратному
ходу метода прогонки, а (4.96) — левостороннему обратному ходу.
Необходимость такого порядка действий обусловлена достаточным условием
устойчивости прогонки 6/+1 < 1 для (4.95) и 57+i < 1 для (4.96). Заметим, что в
данном случае выполняется только обратный ход метода прогонки.
Соотношения (4.95), (4.96) при f(x)eCm[a,b] (т>3) обеспечивают четвертый порядок
точности вычисления интегралов.
В качестве краевых (граничных) условий для право- и левостороннего
соотношений значения интегралов /<$ и 1Ц_{ вычисляются по однойнтер-
вальным, трехточечным, лево- и правосторонним квадратурным формулам
[17,24] (см. также гл. 5):
//-
вн;
/+1
иГ1) f
и? fi~
я/+1я,3(/Ч1>
fi -т /i+i
Л/Ч1
(/ = 1) , (4.97)
1Г
fy+i
6#;
/41
■ufi-i+-
M/+i
Я2'+|
- f , з/ f
Ji + ,Ji+\
"/41
(i — -l)
(4.98)
206

При h = const (сетка Qn равномерная) данные формулы упрощаются:
'/-1 =]|(5^-1 +8^ -/м); '/+1 =i|(-//-i + 8^ +5/-i)- (4">
В работах [17,24] показано, что квадратурные формулы (4.97), (4.98)
обеспечивают четвертый порядок аппроксимации интегралов на
трехточечном шаблоне (x/_i,x,-,x,-+i), и поэтому порядок аппроксимации //+1
соотношением (4.95) или (4.96) при фиксированном / за счет краевых
условий не понижается. Показано также, что в данном способе построения
интерполяционного сплайна достигается третий порядок сходимости. Однако
способ имеет недостаток, состоящий в том, что при аппроксимации
негладких функций ошибки, возникающие при расчете интегралов по
формулам (4.95) или (4.96), переносятся на последующие значения. Данный
недостаток устранен в задаче построения слабо сглаживающего
параболического сплайна, изложенного в разд. 4.5.5.
ПОСТРОЕНИЕ СГЛАЖИВАЮЩИХ СПЛАЙНОВ
(задача 3)
Пусть в общем случае на неравномерной сетке Пя задана сеточная
функция, определенная, например, в физическом эксперименте с достаточно
большими погрешностями, определяющими разброс значений /(х,), т.е.
/(х/)±Б/ (/ = 0,л), где Б,- намного превышают величину 0[hf+l).
Требуется восполнить эту функцию параболическим сглаживающим
сплайном ^2,ид1 (х) дефекта q = 1.
Поставленная задача решается глобальным способом путем сведения ее к
задаче 1. Рассмотрим его особенности.
Сначала путем визуального изучения исходной функции у{ =/(х/)±б/
исследователь-вычислитель формирует «полосу разброса» данных, ограниченную
двумя функциями — «верхней» у] = /(в)(х,) и «нижней» у" = /*"*(*/) (на Рис-
4.13 квадратиками условно показаны значения, полученные, например, в
результате физического эксперимента). Если на некоторых участках разброс данных не
заметен, функции }>f =/(в)(*у) , У? = /(м)(*/) могут быть совмещены друг
с другом. В случае отсутствия значений /(х,) на концах отрезка [а,Ь] они
определяются приближенно путем линейной или параболической экстраполяции.
Далее на каждом отрезке [х/,х/+1] , / = 0,л-1, по формулам (4.97) или
(4.98) вычисляются интегралы /J+1(e) и /;'+1(н) для функций .V? =/(в)(х,) и
У" =/(м)(*/) соответственно. Недостающие значения функций на линиях,
ограничивающих «полосу разброса», определяются путем дополнительной
интерполяции. Следует также учесть, что интеграл /q на отрезке [x^xj вычисляется
по левосторонней формуле (4.97), интеграл 1"_{ на отрезке [хя_1,хя] — по
207

правосторонней, а интегралы по всем внутренним отрезкам могут
рассчитываться по любой из формул (4.97),(4.98).
«Полоса
разброса»
После вычисления интегралов /!+*(*' и /^М (/ = 0,л-1) по всем
частичным отрезкам находятся их средние значения на каждом частичном отрезке:
/;
/+1
ji+Цв) + j /+!(«)
/ = 0,л-1.
Полученные значения интегралов //+I используются далее в качестве
исходных данных для решения задачи 1.
Таким образом, существенной особенностью сглаживающих сплайнов
данного типа является формирование «полосы разброса», включающей все
экспериментальные данные, которые затем двукратно усредняются. При этом в отличие
от метода наименьших квадратов с помощью данного метода реализуется более
полный учет локальных свойств аппроксимируемой функции.
4.5.5. Слабо сглаживающие интерполяционные
интегрально-дифференциальные параболические сплайны
Пусть в общем случае на неравномерной сетке Q„ задана сеточная
функция у,= /(*/), /=0,л, определенная либо в численном эксперименте,
либо путем измерений с небольшими погрешностями е, , не
превышающими o{hlx).
Применительно к данной задаче вводится понятие слабого сглаживания,
в котором учитывается характер задания исходной функции с некоторой
погрешностью, не превышающей 0[И?+[]. При этом допускается возможность
отклонения получаемой в алгоритме сплайн-функции в узлах 5 (сгл'(*,■) от
208

/fa) на величину не более о(лД|), т.е. реализуется отклонение
max\s^crjl'(x)-f(x) = 0\Нг) по всему отрезку [a,b], включая и узлы интер-
| 2,ид k I
поляции. Здесь индекс «к» (к = 1 или к = 2) соответствует способу построения
сплайна. Подчеркнем, что для традиционных интерполяционных сплайнов
данное отклонение в узлах отсутствует.
Требуется восполнить данную функцию параболическим
интерполяционным слабо сглаживающим сплайном £'сгл'(х) (к = 1,2) , компонующимся на
основе ИД-многочленов (4.37) или (4.41).
Обоснованность такого расширения понятия интерполяции (дополнение
его понятием слабого сглаживания) обусловлена следующими причинами.
1. Интерполяционные сплайн-функции, как и классические
интерполяционные многочлены, часто применяются для восполнения и обработки
сеточных функций, рассчитанных методами сеток второго и третьего порядка, и
потому данные функции (исходные для задачи аппроксимации) неточные, и
их погрешность обычно составляет 0[h?+i). Поэтому применение условий
интерполяции, обеспечивающих нулевые невязки в узлах, вообще говоря, не
является оправданным.
2. Если даже значения исходной функции заданы точно (хотя класс
задач, в которых значения /(*,) являются точными, указать трудно), то
точность сплайн-интерполяции из-за этого не повышается. Для
параболических сплайн-функций порядок сходимости оценивается как третий, а для
кубических - как четвертый.
Построение слабо сглаживающего параболического ИД-сплайна может
быть осуществлено так же, как и построение кубического
дифференциального сплайна (изложенного в разд. 4.5.2) двумя способами,
различающимися порядками производных, заданных в условиях согласования и условиях
стыковки. Это соответствует отмеченному выше (см. разд. 4.5.4) принципу
подобия дифференциальных и интегрально-дифференциальных сплайнов,
описывающихся формулами (4.75) и (4.37). Аналогично легко показать
подобие Д-сплайнов (4.71) и (4.41).
Поэтому, так же как и для Д-сплайнов, здесь рассматриваются два
сглаживающих интегрально-дифференциальных сплайна ^tmi (*) и
Первый способ решения задачи слабого сглаживания (построение сплайна
^2,Сид1 )• Алгоритм восполнения функции yj =/fa) методом слабого
сглаживания аналогичен алгоритму восстановления сеточной функции в задаче 1
(см. разд. 4.5.4) и основан на формуле ИД-многочлена (4.37), принимаемой
в качестве общей формулы звена искомого сплайна и параметрической
системы (4.92), которые имеют вид
209

Щ (*)=// +
6 v/;+1__2_^|.(x_X/) +
"м
-4-v//+i+-|-az-
л/+1
Л/Ч1
(х-х,)2 (/ = 0,/i-l),
(4.100)
1 7 о
fl 1 )7 1 7 1
чл/ Л/+1
г'/+1
••О
Ik
(/ = l,#i-l). (4.101)
Волнистая черта указывает на отличие используемых значений /) от
значений fi исходной функции.
В правой части равенства (4.100) обе группы параметров /j [i = 0,nj
и //+1 (/ = 0,л-1) считаются неопределенными. При этом сначала
вычисляются интегралы //+1 на всех частичных отрезках [х/,х/+1] (/ = 0,л-1] по
одной из явных квадратурных формул (4.97) или (4.98). После этого
проводится пересчет функциональных параметров из системы (4.101), которая
замыкается связями fo,f\JoJ\ и 7Л_1,/л,/лГ2,/л-1 (граничными условиями)
соответственно на левом и правом краях отрезка [я, b]:
/e+T/,-^?i"^?"/eV,J
(' = 0),
(4.102)
*»"-!
/«.
■1+/"'я;.,1
2Я„Л.+А„
'л-2
ул-1
(' = «).
совпадающими с граничными условиями, принятыми в задаче 1 (см. разд. 4.5.4).
Отметим, что оба типа неопределенных параметров находятся путем
решения смешанной параметрической задачи, так как сначала определялись
интегралы //+1 (р = -\), а затем значения функции ft (/> = 0).
Определение /} (/=0,л) из (4.101), (4.102), подстановка /} (/ = 0,л)
и //+I (/ = 0,/z-l) в (4.100) для всех звеньев и их объединение в общую
формулу ^wli (х) завершают решение задачи слабого сглаживания исходной
приближенно заданной сеточной функции, погрешность определения
которой в узлах не превышает 0[И?+{]. Если же погрешность задания исходной
сеточной функции больше 0(л/+1), то погрешность вычисления интегралов
превысит величину 0[h?+i) и третий порядок точности аппроксимации
^2ид1 М не будет Достигнут.
Первый способ решения задачи аппроксимации слабо сглаживающим
сплайном является сходным с решением задачи 2 о восполнении сеточной
210

функции интерполяционным интегрально-функциональным сплайном *S^j] (х).
Различие состоит в том, что для ^"ид! М неопределенными параметрами
являются только //+1 (/ = 0,л-1), а определенными — значения fi (/ = 0,/iJ, и
они не изменяются при решении задачи. Таким образом, задача 2 решается
проще, однако изложенный способ построения сглаживающего сплайна
характеризуется большей устойчивостью, так как он основан на решении
трехдиагональной системы линейных алгебраических уравнений, которая
удовлетворяет условию преобладания диагональных элементов.
В [21] доказана следующая теорема.
Теорема 4.3 (о сходимости глобального параболического ИД-сплайна
Пусть функцию f(x) (xe[ayb])t определенную в общем случае на
неравномерной сетке С1п А, = var, Н = max А, с параметром неравномерности
/ = 1,л
Д = max A, /min А/, аппроксимирует глобальный параболический слабо сглажи-
/=1,л / /=1,л
вающий ИД-сплайн ^2ид1 М- Тогда, если f(x)eC}[atb] и интегралы
//+1 (/ = 0,/j-lj находятся по квадратурным формулам (4.97) или (4.98),
a fj [i = 0,/ij — из трехдиагональной системы (4.101), (4.102), то справедливы
оценки
?Ч?№ W-/WW| ^ Н*-р(тМ + /Г, • Д|+'). Л/3 , (4.103)
где р-порядок производной, Л/3 = max|/'"(jc)|, а константы имеют значения
м
3'° ~llfi' 3J "12' °" 48' *1_24'
Таким образом, при /(х) е С3 [я, b] слабо сглаживающие сплайны
^2ид1 М РавномеРно сходятся к функции f(x) на последовательности
сеток Q^Urt 02={х<2>,х{2\^2>|,....,Пя={х<л>,х}я>,...,х^} с
возрастающим разбиением к отрезка [atb]: кх = 1; к2 = 2;...;А:л = л и т.д. по крайней мере
с кубичной скоростью, а их производные S'2'jjjjy (х) с ростом л равномерно
сходятся к /'(*) по крайней мере с квадратичной скоростью.
Второй способ решения задачи слабого сглаживания (построение сплайна
^2,ид2 (*))• Алгоритм восполнения функции _H,=/(x,) в данной задаче
основан на формуле ИД-многочлена (4.41), принимаемой в качестве общей
формулы звена искомого сплайна, и на трехдиагональной параметрической
системе, вытекающей из условия непрерывности сплайна ^2вд2/М:
211

С (сгл) / \ _
°2,ид2,/ W"
А/4.1 — К
-Am,
ju\ _1H±L^. _^Ш.дй; + m •(*-*,•) +
2Л/.1
^•(x-x,)2 (? = 0,ll-l),
(4.104)
1 1 1 ji + l ji 1 \
^b+\'"i-i+^{bi+hi+l)-mi+-hi+lmi+l =-^ *=*- (/ = l,/i-lj, (4.105)
где /и,= /'(x). Подчеркнем, что формула (4.104) для *?2ид2/М и паРамет-
рическая система являются подобными соответствующим соотношениям
кубического дифференциального сплайна S3(x) (4.71) и (4.72), в которых
порядки всех параметров повышены на единицу.
Аналогично первому способу будем считать, что все параметры,
входящие в (4.104), являются неопределенными. Их значения находятся из
смешанной параметрической задачи, в которой вначале по формулам (4.97)
или (4.98) определяются интегралы //+| (/ = 0,л-1), а затем с
использованием системы (4.105) трехдиагонального типа методом прогонки -
производные 7й)(/ = 0у/|). Для замыкания (4.105) можно использовать два
различных подхода.
В рамках первого подхода производные на концах отрезка [ayb]
определяются по аппроксимационным формулам второго порядка аппроксимации
(см. [17,23] и гл.5):
Щ-\ =
НГ1 +h' f , \ffi*l f hi f (:л\.
hi ЛД+1 hi+l
ni+\
HI
/+i
hr^-i ~TT—Ji + 7 //41 (i = n-\).
{ hi ЛД+i hM J
Во втором подходе при A/+1 = var система (4.105) замыкается двумя
трехточечными соотношениями:
Щ
hi+\
yhi+l hi+2j
л/ + 2
(/-0),
о (/ = «),
вытекающими из условия равенства второй производной на двух первых и
последних частичных отрезках.
В случае, когда h = const (сетка равномерная), производные на
концах могут быть определены также и путем интегральных аппроксимаций,
приведенных в гл. 5:
212

«/--т(-2//+|+з//;,2-//++23) (/-о),
яг, =-i-(//:32-з/й + г//.,) (/ = *)•
h2
Выбор конкретных типов граничных условий обусловливается
особенностью постановки задачи и свойствами аппроксимируемой функции.
Построение слабо сглаживающего сплайна завершается так же, как и в
первом способе. Отличительной особенностью второго способа является то,
что при решении смешанной параметрической задачи (ее прямой части)
вычисляются не сами функции ft, а их производные. Иногда это более
удобно, например, когда в задаче восполнения требуется найти значения
производных в узлах.
Выбор конкретного алгоритма сглаживания зависит от априорной
информации, от аппроксимируемой функции и от требований к выходным
данным.
В заключение отметим, что для сглаживающего сплайна £2 ид2 ^'
как и для сплайна «?2ид1 М' имеет место третий порядок сходимости [20,21].
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Для сеточной функции х0 = -1; у0 = -3; jq = 2 ; у] = 4; х2 = 3; у2 = 5
найти значение у(\) с помощью линейной и параболической интерполяций.
2. Функция /(х) аппроксимируется интерполяционным многочленом Ла-
гранжа второй степени для системы равномерно расположенных на отрезке
узлов. Оценить погрешность интерполяции в точке х*:
а) /(x) = cosx2, х. = -^- |0<х<^|;
б) /(x) = xcosx, хт =yj 0<х<^ ;
в) /(*) = е-*2, хФ = 0,3 (0 < х < 0,4).
3. Сеточное представление функции f(x) = ex приведено в табл. 4.24.
Найти значения многочлена Лагранжа, интерполирующего функцию f(x) в точках
х* = 1,03; х, = 1,07 ; х# = 1,13; х. = 1,18. Полученные значения сравнить с
точными значениями и априорным путем оценить погрешность в указанных точках.
Дать анализ погрешностей.
213

Таблица 4.24
*/
VT
1,00
2,7183
1,05
2,8577
1,10
3,0042
1,15
3,1582
1,20 |
3,3201
4. Пусть сеточные представления функций:
\)у-ех\ 2)>> = shx; 3)y = chx\ 4)y = smx\
5) у = cosx; 6) у = lnx; 7) у - е~х
заданы на отрезке [1,00; 1,20] для равномерного разбиения с шагом h = 0,04.
Построить кубический интерполяционный сплайн способом 1. Задать
граничные условия в следующем виде:
а) /о"-0, /; = 0;
6) аппроксимации (4.73).
Найти значения обоих полученных сплайнов в точках хф = 1,05; хф = 1,09;
х* =1,13; х, =1,15; х*=1,17. Проанализировать результаты для обеих сплайн-
функций.
Получить оценку точности априорным путем по формуле (4.78).
5. Для условия задачи 4 построить кубический интерполяционный сплайн
способом 2. Граничные условия аппроксимировать по соотношениям (4.77).
6. Для условия задачи 4 построить параболический слабо сглаживающий
сплайн по формулам (4.100) - (4.102). Априорным путем оценить погрешность.
Сопоставить полученные результаты с точными значениями функций в
промежуточных точках.
7. Для сеточных функций, заданных табл. 4.25 и 4.26, требуется:
а) решить задачу интерполяции методами Лагранжа и Ньютона;
б) решить задачу сглаживания методом наименьших квадратов при т - 1 и
т = 2;
в) на одном графике построить исходную сеточную функцию, а также
решения задач интерполяции и сглаживания.
Таблица 4.25
*|
1 //
2
5
4
2
6
3
8 " "1
1
Таблица 4.26
*'
1 //
1
4
2
2
3
5
4
8
5 |
2 1
214

Глава 5. МЕТОДЫ ЧИСЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ
И ИНТЕГРИРОВАНИЯ
5.1. ПОСТАНОВКА ЗАДАЧИ И ПРИНЦИПЫ КОНСТРУИРОВАНИЯ
АППРОКСИМАЦИОННЫХ ФОРМУЛ
Если функция /(х) непрерывна на отрезке [а,Ь] и известна ее
первообразная F(x), то определенный интеграл от этой функции может быть вычислен по
формуле Ньютона-Лейбница
ь
\f(x)dx = F(b)-F(a)t
а
где F'(x) = f(x). Однако во многих случаях возникают большие трудности,
связанные с нахождением первообразной, или эта задача не может быть решена
элементарными способами. Например, в элементарных функциях не выражается
\ dx
интеграл .
I \пх
Кроме того, в вычислительной практике часто требуется находить значения
производных и определенных интегралов от сеточных функций, заданных
в общем случае на неравномерной сетке Qn ={x0,Xj,...,xw},x/+| =*,- +huu
/=0,л-1, hul =х/Ч1-х/.
В связи с этим в численном анализе имеется специальный математический
аппарат численного дифференцирования и интегрирования, отличный от
соответствующего аппарата математического анализа.
Традиционно интегралы вычисляются с помощью квадратурных формул
(явно), выражающихся линейными комбинациями значений функции >>, =/(*,)
в узлах сетки Qn , функционально-дифференциальной квадратурной формулы
Эйлера—Маклорена, формул Гаусса—Кристоффеля, Маркова и различных
нестандартных формул [2,4,6,9,14,26,28,29,35]. В данной главе кратко описаны как
классические, так и новые методы численного дифференцирования и
интегрирования, разработанные на основе аппарата интегрально-дифференциальных
сплайнов [15—24]. Приведен ряд обобщенных явных квадратурных формул
функционально-дифференциального типа, а также описан новый способ вычисления
интегралов на основе решения систем линейных алгебраических уравнений.
Последний подход в отличие от способа вычисления интегралов по квадратурным
формулам носит неявный характер и связан с построением неявных алгоритмов.
Особенность аппарата численного дифференцирования и интегрирования,
изложенного в данной главе, состоит в том, что в некоторых аппроксимацион-
ных операторах дифференцирования могут использоваться как значения
сеточной функции в узлах, так и значения определенных интегралов на частичных
отрезках [х,-,х/+|], а в аппроксимационных операторах интегрирования — значения
функции и ее производных в узлах. В соответствии с этим далее выделяются
классические постановки задач численного дифференцирования и
интегрирования, формулируемые обычно на равномерной сетке (А/+1 = const), и обобщенные
постановки, учитывающие связи производных с интегралами в задаче численного
дифференцирования и интегралов с производными в задаче численного интег-
215

рирования, формулируемые на неравномерной сетке. Классические постановки
ниже нумеруются цифрой 1, а обобщенные — цифрой 2. Данные постановки
относятся только к явным аппроксимационным формулам численного
дифференцирования и интегрирования. Соответствующие неявные алгоритмы
рассматриваются отдельно.
ПОСТАНОВКА ЗАДАЧИ 1 ЧИСЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ
Пусть на отрезке [а,Ь] на равномерной сетке Qn(hi+] = h = const) заданы:
а) сеточная функция у, = /(*/),/ = 0, л, своими значениями /} =/(*,) ;
б) точки Xj сетки Qn , в которых требуется найти значения производных;
в) желаемый порядок t точности (аппроксимации) относительно h .
Требуется с заданным порядком точности (аппроксимации) вычислить
значения производных f^p\x)L=x в точках х, сетки, где р— порядок производной.
Иначе требуется получить аппроксимационный оператор f^pH*j),
удовлетворяющий условию \f^p\xj)-Pp\xj) < С Л', где С = const, не зависящая от
величины шага h.
ПОСТАНОВКА ЗАДАЧИ 2 ЧИСЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ
Пусть на отрезке \а,Ь] в общем случае на неравномерной сетке
Пп ={х0,xlv..,x„}, хм = х,+А/+1, i = 0,/i-l, Л/+1 = х/Ч1 -х, (А/+1 =var) заданы:
а) сеточная функция ytf= /(х,),/ = 0,л, своими значениями У/=/(х,) и
(или) значениями интегралов //+| = f/(x)rfx на частичных отрезках [x/,x,-+i];
Xj
б) точки Xj сетки Q„ , в которых требуется найти значения производных;
в) желаемый порядок / точности (аппроксимации) относительно величины
шага.
Требуется с заданным порядком точности (аппроксимации) вычислить
значения производных /(/?)(x)L=x. в точках ху сетки (получить
аппроксимационный оператор), где р— порядок производной.
ПОСТАНОВКА ЗАДАЧИ 1 ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
Пусть на отрезке [а,Ь] на равномерной сетке Q„(/*/+1 - h = const) заданы:
а) сеточная функция у, = /(х,),/ = 0, л, своими значениями /} =/(*/) или
сеточное представление формульной функции у = /(х);
б) желаемый порядок / точности (аппроксимации) относительно величины
шага h .
216

Требуется с заданным порядком точности вычислить значение интеграла
ь
Iab=Iba = \f(x)dx.
а
Иначе требуется получить аппроксимационный оператор интегрирования
/д , удовлетворяющий условию \1Ь - Ib\< С W , где С = const, не зависящая от h.
ПОСТАНОВКА ЗАДАЧИ 2 ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
Пусть на отрезке [ауЬ] в общем случае на неравномерной сетке
Пя ={х0,хь...,хл} (х/+, = х,+Л/+1, / = 0,л-1, /г/+1 = х/+1 -я,- = var ) заданы:
а) сеточная функция у, =/(х,),/= 0, я, своими значениями //=/(х/) и
возможно значениями производных /^р\х{)\
б) желаемый порядок / точности (аппроксимации) относительно шага.
Требуется с заданным порядком точности вычислить значение интеграла
(получить аппроксимационный оператор)
Jb = jb
= j/Mdx
Отметим, что символом «А» здесь и далее обозначаются операторы
дифференцирования и интегрирования.
Построение аппроксимационных формул для производных и интегралов
в данной книге выполняется различными путями на основе:
1) разложения функции /(х) по формуле Тейлора;
2) разложения первообразной функции F(x) по формуле Тейлора;
3) замены заданной функции интерполяционными многочленами и
последующим дифференцированием или интегрированием этих многочленов.
Дополнительные возможности построения аппроксимационных операторов
предоставляют интегрально-дифференциальные сплайны (ИД-сплайны).
Общая интеграпьно-функционально-дифференциальная формула для аппрок-
симационного оператора дифференцирования f*p'\Xj) может быть записана
в форме
{ \ ( \ ( \
2>,./,W
•Г
*2 U )
4+1
Л,+...,(5.1)
гДе в*,,/|(*)>**2.'2^'c*j.'i(*)•— — коэффициенты, индексы при А для упрощения
записи не указаны.
217

Общая функционально-дифференциальная формула для аппроксимационного
оператора интегрирования // может быть записана в виде
/Л1 =*!>*,<«/*, + л2£мл>Д +л31^3(Л)/;; + ..., (5.2)
*| *2 *3
где aki(h),bk2(h),cki(h),... —коэффициенты.
Возможность такого комбинированного представления следует из
разложения первообразной F(x) по формуле Тейлора относительно точки х, и
последующего выражения из него производной некоторого порядка или
определенного интеграла.
В формулы (5.1), (5.2), очевидно, входят суммы нескольких групп
линейных комбинаций. Так, вторая сумма в (5.1) и первая сумма в (5.2) соответствуют
функциональным комбинациям, первая сумма в (5.1) соответствует интегральной
части суммы. Дифференциальным комбинациям соответствуют третья и
последующие части в (5.1) и вторая, третья и т.д. суммы в (5.2) .
Если в (5.1) присутствуют только интегральные комбинации, формула
численного дифференцирования называется интегральной, если только
функциональные комбинации — функциональной (или точечной), а если только
дифференциальные комбинации — дифференциальной. Если же в (5.1) отсутствуют
интегральные комбинации, формула называется функционально-дифференциальной,
если отсутствуют функциональные комбинации — интегрально-дифференциальной,
если отсутствуют дифференциальные комбинации — интегрально-функциональной.
Аналогичная классификация справедлива и для формулы (5.2) численного
интегрирования.
5.2. МЕТОДЫ ЧИСЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ
5.2.1. Формулы, полученные на основе разложения функций по формуле Тейлора
Рассмотрим решение задач 1 и 2 численного дифференцирования на
различных шаблонах.
А. Двухточечный шаблон. Выберем шаблон Я/2>/ =(*/,*/+i) на
неравномерной сетке Qn. Предполагая, что f(x)eC2[a,b], разложим функцию /(х) по
формуле Тейлора (В.20) при к = 1 относительно точки х, с остаточным
слагаемым в форме Лагранжа и найдем выражение для //+J = /(х/+1):
//+!=//+А/+|// + ^-/"(0. (5.3)
где ^ е (xhxi+i), А/+1 = х/Ч1 -х,. Отсюда получаем
218

Очевидно, справедлива оценка
\г%)
<-^- max / (х) =
2 [*/,*/+il ' 2
где Л/2,- = max |/"(*)|.
Отсюда следует функциональная формула (функциональный оператор) для
первой производной:
Гм-f,
(¥"*)■
Ги-1"^- Rr-«v • <")
В скобках справа от аппроксимационных операторов здесь и далее
указываются правые части оценок их погрешностей.
Отметим, что формула (5.4) является несимметричной, односторонней
(левосторонней). Если функцию f(x) разложить по формуле Тейлора
относительно точки х/+1, то получим правостороннюю формулу
fi+lc—J— {^2J
Б. Трехточечный шаблон. На неравномерной сетке Qn выбираем
трехточечный (двухшаговый) шаблон Я/3>/ = (*/-i>*/>*i+i)> характеризующийся шагами
Л/Ч1 = х/+! -х,, А, = х, -*/_, и параметром его нерегулярности 8/Ч1 = -LL4 кото-
рый в общем случае не равен единице.
Аппроксимационные функциональные (точечные) формулы второго
порядка в левой крайней, центральной и правой крайней точках шаблона можно
получить на основе разложения функции f(x) по формуле Тейлора с остаточным
слагаемым в форме Лагранжа. При этом предполагается, что f(x)e С3[я,£]. Это
позволяет получить разностные дифференциальные операторы /'(*/)
(/ = /'-1, /,/ +1) и провести оценки их погрешностей.
Разложим функцию f(x) при х = х, и х = х/Ч1 по формуле Тейлора при
к = 2 относительно точки x,_i с остаточным слагаемым в форме Лагранжа.
В результате находим соотношения, определяющие f,- = /(х,)и ful = /(х/+1):
/, =/м +*///-! +^-//:, +^-/'"fe-). (5.5)
/их =/,-x+Hl+xfU +Z±Y-/!LX + ^^/"'feJ, (5.6)
где #/+I =А, +Л/Ч1, £_ €(xM,x,)f ^ €(х/.1,х/Ч1), /# =/(^)(х/.1), /> = 0,1,2.
Исключая из (5.5), (5.6) слагаемое, содержащее вторую производную, и
выражая из полученного соотношения f[„x, получаем следующую аппроксимацию
первой производной в левой крайней точке (левостороннюю формулу или оператор)
219

//-l,v
Ht
/+!
- (2+ s,4, )/;•_, +
(1 + S/+1)2
S/4I
/• -57+|У/+1
(5.7)
При h = const (б/Ч1 = l) формула (5.7) упрощается и приводится к
известному виду [6]:
Л'-1,с=^(-зу;-,+4у;.-//+1)
^2
%,•
(5.8)
Данную формулу можно записать через конечные разности:
/7-.,с=^(зл/}-1-А/;)-
Здесь нижние индексы v и с, относящиеся к аппроксимационным операторам
(5.7) и (5.8), указывают на тип шаблона — нерегулярный (Л/+, = var) и регулярный
(Л/Ч1 = const)). Остаточное слагаемое для (5.7) получается равным
' г ' 7"'fe) » 4 е (xi-uxi+\) у и поэтому для этой аппроксимации справедли-
Л_1 -//-l,v 7 М3,/>
I I о
где
ва следующая оценка погрешности:
Л/3,= max (/'"(*))-
«%•
Приводимые здесь и ниже остаточные слагаемые для дифференциальных
операторов также получаются путем дифференцирования остаточных слагаемых
R(x) интерполяционных многочленов соответствующей степени. Из (4.20) для
трехточечных формул при п = 2 следует соотношение
RW = —/'"(5) • <Ф0, со(х) = (х - Х/_, )(х - х, )(х - х/Ч1).
Аналогично, разложив функцию f(x) относительно точки xi+l и получив
соотношения для //_!,/} , найдем f/+l - разностный оператор,
аппроксимирующий первую производную /)'+1 в правой крайней точке (правосторонняя
формула):
1 (- , (l+S,4,)2 , k (2+ 6, и) , )
У/'+l.V
н.
/41
5/+1У/-1
°/41 °/41
/Ai,c = Зл (Л-1 - 4Л- + з/,+1) или /;,u = ^(W/ - А/,-1)
(5.9)
/г
Оператор /)'+i v имеет остаточное слагаемое —^—S/+| (l + &/+i )/'"(£)•
6
Разложение функции /(х) относительно центральной точки х,- шаблона,
получение выражений для /}-i>//+i и исключение из них слагаемого со второй
производной приводят к следующим разностным операторам функционального
220

типа, аппроксимирующим первую производную в центральной точке (формула
центрального вида)
Лу
1
я;
/41
Si+iA/1 + А//+
5.
/41
1
) И\
/41
-5/+1Л-1 + ^Si +— Л+
°/41
V
/+1 ;
(5.10)
м-
з,/
//.с = ^ (Л+1 - /i-i) или Дс = ^ (А// + А//-1)
Оператор fis имеет остаточное слагаемое -t"S/+1/'"(4)-
6
Приведенные остаточные слагаемые разностных операторов обусловливают
следующие оценки их погрешностей:
\fU - //-J *^(l + S/4l)^3,/, |У?- /Ц * *jr*MM2J, (5.11)
I lo I i о
\fi\ ~ Л'+i.vl ^ "f 0 + s/4i)s/4i^3,/> ^3,/ = max |/"(x)|.
Замечания.
1. Далее в тексте оценочная константа Мpi для краткости будет
использоваться без дополнительного ее описания. В нижнем индексе этой константы
всюду указывается р — порядок производной.
2. Из оценок (5.11) вытекает, что разностные операторы /м,//,./}+!
аппроксимируют при Л/+1 = var соответствующие производные f\-\JUU\ со вторым
порядком, если шаблон произвольный (безусловная аппроксимация). Если же на
шаблоне с 5/+1 « 1 наложить условие, например 5,+J < /z,, т.е. Л/+1 < h}, то
порядок аппроксимации f\Jl+\ может быть повышен до третьего (условная
аппроксимация). Такая возможность повышения порядка аппроксимации относительно /г,
без увеличения количества точек шаблона обеспечивается введением в
мажоранты, соответствующие аппроксимациям, параметра 8/+1, на который в случае
необходимости можно наложить условие 5/+, < ht. При этом следует иметь в виду,
что данный параметр входит в знаменатель некоторых слагаемых аппроксимаци-
онных формул (5.9), (5.10) и при его уменьшении увеличиваются погрешности
арифметических операций.
3. Аппроксимации (5.8),(5.9) являются условными, так как для них
справедливо условие 5/+| = 1.
Предположим, что /(х)бС4[о,/)1, и разложим функцию /(х) в точках
х/,х/+1 на трехточечном нерегулярном шаблоне Шу =(^m»jc/»jc/+i) до слагаемого
четвертого порядка относительно шага. Складывая эти разложения и выражая из
суммы вторую производную, получаем функционально-дифференциальную формулу
для второй производной:
221

л.= 2(Л.Ч ^ 2/;. + у;.^), 2fe^) ^ , jfe^jy;/- , ^UL^l/(4)fe), (5Л2)
Ьм + hf ЛД, + hf 6(ЛД, + Л/J 4!(АД, + V)
Подставляя в (5.12) аппроксимационную формулу (5.10) для первой
производной, находим разностный аппроксимационный оператор f", выраженный через
параметры 6/Ч1 , hf и аппроксимирующий (безусловно) вторую производную f" на
нерегулярном шаблоне с первым порядком:
J 1,4
1
■f,-l-T-fi +
1
■/м
(5.13)
Выражение (5.13) можно преобразовать к виду
*• __2_(.М._М=1.1 ?-Гй=1. f± + -LV.+=fi±l
Если сетка равномерная (б/+1 = l), то указанный порядок условной
аппроксимации возрастает на единицу, так как третье слагаемое в (5.12) становится
равным нулю. В этом случае из (5.13) получаем широко распространенный
оператор, аппроксимирующий вторую производную на регулярном шаблоне [в] :
file = Tf С//-1 " 2// + fu\) или f"tC = -у (A/ - 4/J-i)
/г /г
12
^4,/
(5.14)
Замечание. Из (5.12) следует, что порядок условной аппроксимации
(5.13) можно повысить на единицу и на нерегулярном шаблоне, если принять
|S/+i ~ l| < hj, т.е. ^ - hf < hi+[ < ht + hf (квазиравномерная сетка).
Как следует из приведенных выше постановок задач, в вычислительной
практике аппроксимационные формулы (операторы) для производных
используются для вычисления значений производных либо для замены ими
соответствующих дифференциальных операторов. В связи с этим приведем методику
вычисления /^(х)
Методика вычисления значений производных
1. Выбрать конкретную аппроксимационную формулу (или несколько
разных формул), в которой порядок аппроксимации должен соответствовать
заданному в задаче порядку точности t.
2. Выбрать наборы точек (шаблоны LUki), которым принадлежат точки Xj
(xj € Шк у), причем для каждого из наборов расположение точки ху должно
быть зафиксировано относительно точек шаблона {к — количество точек,
определяющих шаблон). Эта фиксация определяется структурой формулы. Например,
если формула имеет центральный тип (см. формулу (5.10)), то точка Xj должна
совпадать со средней точкой шаблона, а если формула левосторонняя (см. фор-
222

мулы (5.7) и (5.8)), то точка Xj должна совпадать с левой крайней точкой
шаблона и т.д.
3. В правую часть выбранной формулы (или формул) подставить значения
функций и (или) интегралов, которые соответствуют выбранным точкам шаблона
(шаблонов).
4. Произвести требуемые вычисления с учетом того, что количество
сохраняемых цифр должно приблизительно соответствовать величине остаточного
слагаемого аппроксимационной формулы и порядку точности /.
Пример 5.1. Дана сеточная функция (табл. 5.1), являющаяся сеточным
представлением формульной функции у{х) = —.
Таблица 5.1
/
*'■
1 /
0
1
1,000000
1
1,2
0,83333333
2
1,4
0,7142857
3
1,6
0,6250000
4
1,8
0,5555555
5
2,0
0,500000
Заданы также порядок / = 2 относительно шага h, который необходимо
обеспечить при решении задачи, и точка Xj = 1,4.
Требуется вычислить значение первой производной /'(1,4) и второй
производной /"(1,4) с помощью различных шаблонов и соответствующих формул.
□ Воспользуемся вышеприведенной методикой.
1. Так как шаг задания сеточной функции постоянный h = хих -х, =0,2,
точка Xj = 1,4 находится внутри сетки Qn, то для вычисления производной
в этой точке выбирается вторая формула из (5.10), имеющая второй порядок
аппроксимации относительно шага И . При этом центральная точка шаблона
совпадает с точкой Xj - 1,4.
2. Выберем трехточечный шаблон Шц = (*/_|,*/,X/+i) = (1,2; 1,4; 1,6), в
котором Xj = 1,4 (/ = 2); хм = 1,2 (/-1 = 1); х/+, = 1,6 (/ + 1 = 3). В данном шаблоне
центральная точка х; = 1,4, что соответствует центральному типу
аппроксимационной формулы.
3. Подсчитаем искомое значение производной по формуле (5.10):
f! _ fi+\ ~fi-\ _ 0,6250000-0,8333333
Л'с 2Л 2 0,2
4. Прежде чем выполнить вычисление, необходимо определить количество
знаков, которое сохраняется при этом. Остаточное слагаемое выбранной форму-
И2
лы равно — Л/3 / • Для его вычисления необходимо сначала определить
6
Л/з,/= max |/"'(х)|. Поэтому воспользуемся интерполяционным многочленом
Ньютона с конечными разностями:
y~in urn, ч А /
/г
223

где А3/ - конечная разность третьего порядка. Эта разность может быть
вычислена по значениям функции f( в четырех точках. Возьмем точки х2, х3, х4, х5.
При этом будем считать, что My « /"'(*,) (порядок вычислений конечных
разностей описан в гл. 4 и отображен в табл. 4.2).
Вычисление дает /'"(*/)*-— = -0,741875. Тогда остаточное слагае-
v ,у 0,008
- 0,04 0,74405 лпп.п ЛЛ1
мое по модулю будет равно — -; * 0,0049 < 0,01.
6
На основе полученного приближенного значения остаточного слагаемого
можно заключить, что в вычислениях ожидается одна верная цифра после
запятой. Обычно в расчетах оставляют еще одну или две дополнительные цифры
(в нашем примере это составляет всего 3 цифры). Оставляя три цифры после за-
пятой, получаем результат: / (х)\ - -0,521.
Ijc=1,4
Фактическая абсолютная погрешность составляет
1
-0,521 + -
1,4'
= 1-0,521 + 0,5102 | = 0,0108,
0,0108 1ЛПЛ, -1Л, с
т.е. относительная погрешность равна ~—--100% = 2,1%. Если эта погрешность
не устраивает вычислителя, необходимо повышать порядок точности
относительно h, например, до / = 3. В дальнейшем приводятся соответствующие
примеры с порядком / = 3.
Для вычисления первой производной можно было использовать и другие
формулы. При выборе шаблона Ш^{■. = (х,-_1,х/,х/+1)= (1,4; 1,6; 1,8) по формуле
(5.8) имеем
/U4) = Л\с = ^-(- 3/м + 4/ - //+1 ) = i[- 3/(1,4) + 4/(1,6) - /(1,8)]=
= —— [- 3 • 0,7142857 + 4 • 0,625 - 0,5555] = - 0,496017.
20,2L J
Фактическая абсолютная погрешность составляет |- 0,496017 - 0,510204) = 0,0142,
относительная погрешность равна 2,78%.
Если выбрать шаблон ZZ/3/ = (х/_|,х/,х/+1)= (1; 1,2; 1,4), то по формуле (5.9)
получаем
/'(1,4) = fiu = i(/}., - 4/ + 3/Ч1)= 2^2 t/W " 4/(1,2) + 3/(1,4)]=
= —[1,0 - 4 • 0,83333 + 3 • 0,7142857] = - 0,476187.
0,4L J
Фактическая абсолютная погрешность равна |- 0,476187 -0,510204| = 0,03401,
относительная погрешность составляет 6,66%.
224

Для вычисления второй производной можно взять формулу (5.14) на
шаблоне Шг1 = (x,-i,x/,x/+i) = (1,2; 1,4; 1,6):
//.'с =Л(Л-1 -2//+/m)=t^[^(U)-2-/(1,4) + /(1,6)] =
/г 0,2*
= — [0,8333 - 2 • 0,7142857 + 0,625] = 0,743965.
2
Точное значение / (1,4) = —г = 0,7288629. Фактическая абсолютная
1,4
погрешность равна 0,0151, относительная погрешность 2,07%. ■
В вычислительной практике иногда применяют аппроксимационные
формулы, порядок аппроксимации которых не известен или не приведен в
используемом источнике, и в этом случае, прежде чем использовать эту формулу,
нужно получить оценку ее погрешности.
Данную процедуру можно выполнить с помощью различных подходов,
один из которых основан на разложении функций, входящих в правую часть
оператора, по формуле Тейлора относительно той точки Xj , для которой записан
этот оператор. Другой подход использует анализ остаточного слагаемого,
полученного для интерполяционного многочлена Лагранжа. При этом
рассматривается соотношение (4.19), которое дифференцируется нужное количество раз:
/«(хЫМ + л^М-
Тогда если нужно найти погрешность численного дифференцирования в
точке х = Xj, то осуществляется подстановка х = Xj. В результате находится
оценка погрешности в точке х = Xj:
*М(*)|
> + 1)!
»РЫ.
где п — степень алгебраического многочлена, по которому получен аппроксима-
ционный оператор. Если априори степень п неизвестна, то она может быть
определена путем подстановки в правую часть оператора произвольных узлов х, и
значений f(xt) для многочленов N\(x) = ax + b\ N2(x)- ах2 +bx + c и т. д.
Максимальная степень многочлена Nn(x)f для которого остаточное слагаемое равно
нулю, является искомой.
Если необходимо оценить погрешность аппроксимационного оператора
рр\х) не в точке, а на всем отрезке [а,Ь], то для этого используется неравенство
(4.22), которое дифференцируется р раз:
^fl^wl^^l^wl-
225

Изложим простейшую методику оценки погрешности в точке х = xJt когда
степень многочлена Lk_x{x) и шаблон UIkii на котором этот многочлен получен,
известны.
Методика оценки погрешности аппроксимационного оператора
1. На заданном шаблоне, который в общем случае имеет структуру
UIki = (xi_ri...,xh...txi+s) , k = г + s + 1, записать выражение для оценки
остаточного слагаемого в точке х = Xj■, е IIIki:
«<4J<7fK-H.
k\
Здесь г и s — количество точек, расположенных соответственно левее и
правее точки Xj , которая фиксируется на этом шаблоне.
2. Найти производную со]Д (х) = [(х - *,_,.)(х - х,_г+1)• • • (х - xi+s)}р*.
3. В полученную производную подставить значение Xj . Далее
преобразовать ее, выразив через h (при h = const) или через параметр нерегулярности
S/+1 = hj+Jhj , и записать окончательно оценку погрешности.
Пример 5.2. Для заданного дифференциального оператора (5.8),
записанного для производной в левой крайней точке шаблона Шу - (x/-i,*m*/+i),
требуется найти остаточное слагаемое и оценить погрешность в точке Xj = xt_x.
□ 1. На шаблоне Ш3>/ = (*m,*i,*/+i) записываем выражение (к = 3):
«MU
Л/,
ми
CD2
или
I zv 7|jc=xm| 3!
[(*-*/-l)(*-*/)(*-*/4l)]'
•x=xM
2. Находим производную многочлена co2(x):
®iW = (* ~ xi)(x ~ *i+i)+ (* ~ xi-\)(x ~ */+i) + (x ~ */-i)(* ~ */)■
3. Так как h = const, то
'X-XM
+ (*/-i " */-i )(*/-! - */) = (" A)(- 2Л) = 2Л2.
В результате получаем №(x)| - - ~~^^'
Именно эта оценка и приведена в скобках справа от формулы (5.8).I
226

В. Четырехточечный шаблон. Формулы третьего порядка для первых
производных на регулярном шаблоне III4i = (х,-_2»*м»х«» x/+i) имеют вид [6]:
или
/Uc =Jffrnfi-i + 18Л-1 - V/ +2/м)
7/-2.С =^(HA/5-2-Wm +2A/J);
т^<
/м,с=^(-2/,-2-ЗЛ-,+6/,-//+1)
f/,3
12
4,/'
ИЛИ
itu= ^(246.2+5^-1-40;
//^-^(Л-2-6/м+3/,+2/,+1)
А3 "\
12 4''
(5.15)
или
& = ^(-45-2 + Wm+W/);
ИЛИ
7/Vi,c = ^(- 2//-2 + 9/м -18/. +11//+1)
т^
//+1.с=^(2А//-2-7АГм+ИАЛ-)-
Замечание. Вариант записи производных через конечные разности
здесь и выше приведен для того, чтобы в дальнейшем можно было преобразовать
эти формулы на основе теории подобия для аппроксимации (восстановления)
функций по интегралам (см. замечание в конце данного раздела).
Формулы второго порядка на регулярном шаблоне для вторых производных
имеют вид
//-2^=тт(2Л-2-5/м+4//-//+1)
h2
\\h2
12
Мл
fr-i,c=i2if'-2-2fi-i+fi)
П
>£= £(//-1-2/,+/,+,)
h
/Il\s=M-fi-2+*fi-\-5fi + 2fM)
hr
( h1 \
— M4i
12 4''
7J«v
(5.16)
Uh2
12
MKi l
227

Г. Пятиточечный шаблон. Формулы четвертого порядка для первых
производных на регулярном шаблоне Ш5, = (*/_2>*м>х/>х/+ьх/+2) имеют вид
?1-г,с - j^(- 25/,_2 + 48/,., - 36/ +16/+1 - 3/+2)
fU,c = j^(- З/-2 - Ю/м +18/ - 6/+1 + /+2)
/:с=Т^(/-2-8/-1+8/+1-/+2)
/'+1,с = у^(-/-2 + 6/-! -18/+ Ю/+1 + 3/+2)
/Uc = ^(3/-2 -16/-, + 36/ - 48/+I + 25/+2) (^ М5]
{э )
(И-
(И
[к*
20
>
>
(5.17)
Формулы третьего порядка для вторых производных на указанном шаблоне
имеют вид
/-2,с = TtW(35/-2 -104/-, +114/ - 56/+1 +11/+2),
Yin
_1_
12Л2
f,\c = ТТГТ (*1Л-2 - 20/м + 6/, + 4//+1 - /ч2),
^ = 77ГТ(-Л-2 + l6^-i "30^ + 16Л+1 "/м).
12Л
(5.18)
J_
12Л2
f'^c =Т7П(- fi-2 + 4^-i + 6^ " 2°Л+1 + *^г).
/';2,с = -WO 1//-2 "56/м + 114/, -104/,+| + 35/ч2).
12Л
Пример 5.3. Для сеточной функции из примера 5.1 вычислить значение
первой производной f'(x)\ и второй производной /"(х)| , используя
каждую из приведенных выше формул для четырехточечного и пятиточечного
шаблонов.
□ Для вычисления производных воспользуемся соответствующей
методикой.
228

Используем сначала четырехточечные шаблоны.
Для шаблона UI4i = (х/_2,х/_1,л:/,х/Ч1) = (1,4; 1,6; 1,8; 2) по первой из формул
(5.15) при Х/_2 = Xj имеем
fi-U = ^(" 1 >//-2 + 18/м -9/, + 2/+1) = j!—[-11/(1,4) +18/(1,6)-9/(1,8) + 2/(2)] =
= —[-11 0,7142857+18 - 0,625-9 • 0,5555+2 • 0,5] = - 0,505535.
Фактическая абсолютная ошибка равна 0,00467, относительная
погрешность 0,915%.
Значение второй производной найдем по первой из формул (5.16) при
Xj_2 = Xj:
fi'-U = Л-(2/,-2 "5/м + 4/, - /ы) = -j-j[2/(1,4) -5/(1,6) + 4/(1,8) - /(2)] =
h 0,2
= —[2 • 0,7142857 - 5 • 0,625 + 4 • 0,5555 - 0,5] = 0,639285.
Фактическая абсолютная ошибка равна 0,10468, относительная
погрешность 14,07%.
Заметим, что величина мажоранты в оценке остаточного слагаемого для
использованной формулы в 11 раз больше, чем для двух других формул в (5.16),
аппроксимирующих производные в точках, расположенных внутри шаблона.
Для шаблона UIAi = (х/_2,х/_1,х/,х/Ч1) = (1,2; 1,4; 1,6; 1,8) по второй из формул
(5.15) при х,_] = Xj получаем
file = ^("2/_2 "3/}_i + 6/ - fM) = £^2[-2/(1,2)-3/(1,4) + 6/(1,6)-/(1,8)] =
= —[-2-0,8333-3 0,7142857+6-0,625-0,5555] = -0,51256.
Фактическая абсолютная ошибка равна 0,002357, относительная
погрешность 0,462%.
Значение второй производной найдем по формуле
fi\c = -т(Л-2 - 2/м + /) = -^[/(1,2) - 2/(1,4) + /(1,6)] = 0,743965.
п 0,2
Фактическая абсолютная погрешность равна 0,0151, относительная
погрешность 2,07% (см. пример 5.1).
Для шаблона ША, = (*/_2,*/-i,X/,*/+i) = (1; 1,2; 1,4; 1,6) при х, = Xj имеем
fie = j~h (fi-2 ~ б/м + 3/ + 2fM) = ^ |/(1) - 6/(1,2) + 3/(1,4) + 2/(1,6)] =
= -Ml.O - 6 • 0,8333 + 3 • 0,7142857 + 2 • 0,625] = -0,505785.
*,^
Фактическая абсолютная ошибка равна 0,00442, относительная
погрешность 0,866%.
229

Значение второй производной найдем по формуле
fie = Mfi-i ~ 2// + /41) = iIf 0.2) " 2/d,4) + /d,6)] = 0,743965.
/г 0,2
Фактическая абсолютная погрешность равна 0,0151, относительная
погрешность 2,07% (см. пример 5.1).
Используем формулы (5.17),(5.18) для пятиточечного шаблона.
Для шаблона III5i = (х,--2>*ы»х/»*/+1»*/+2) = (1,2; 1,4; 1,6; 1,8; 2) имеем
/Uc = т^-(- 3/.2 - 10//., + 18/- - б//+1 + /+2) =
12Л
= jj?02 [" 3/(1>2)" Ш/(1,4) + 18/(1'6)" 6/(1'8) + Л2)^=
= -L[_ 3 •0,83333 - 10 • 0,7142857 + 18 • 0,625 - 6 • 0,555 + 0,5] = - 0,5107696.
2,4l J
Фактическая абсолютная погрешность равна 0,000566, относительная
погрешность 0,11%.
Значение второй производной вычислим по формуле
/-1,с = -72 О 1//-2 " 20//., + 6/. + 4//+| - //+2) =
12/г
1 [11/(1,2) - 20/(1,4) + 6/(1,6) + 4/(1,8) - /(2)] =
120,22
= — [11 • 0,83333 - 20 • 0,7142857 + 6 • 0,625 + 4 • 0,5555 - 0,5] = 0,735241.
0,48l J
Фактическая абсолютная погрешность равна 0,00637, относительная
погрешность 0,875%.
Для шаблона IU5i = (*/_2»*i-ii*m*/+i»*/+2) = 0J 1»2; 1,4; 1,6; 1,8) получаем
//.с = ^(Л-2-8/м + V/+1 -/ч2)=Т^[/0)-8/0,2) + 8/(1,6)-/(1,8)] =
= — [1 - 8 • 0,8333 + 8 • 0,625 - 0,5555] = - 0,5092.
2,4L J
Фактическая абсолютная погрешность равна 0,00098, относительная
погрешность 0,192%.
230

Вычислим вторую производную по формуле
12/г
^2
1
120,2
[- /(1) + 16/(1,2) - 30/(1,4) + 16/(1,6) - /(1,8)] =
= —[- 1,0 + 16 • 0,8333 - 30 • 0,7142857 + 16 • 0,625 - 0,5555] = 0,72751.
Фактическая абсолютная погрешность равна 0,00134, относительная
погрешность 0,18%.
Анализ точности аппроксимации показывает, что значения производных в
точках, расположенных вблизи центра шаблона, вычисляются с большей
точностью, чем значения производных в точках, расположенных вблизи концов
шаблона. При повышении порядка аппроксимации точность вычисления
производных возрастает. ■
Замечание. Формулы, записанные выше для аппроксимации
производных через приращения функций, могут быть переписаны для восстановления
функции у = /(х) по значениям интегралов. С этой целью можно использовать
изложенный в гл. 4 метод подобия, состоящий в соответствующем изменении
порядка производной в левой и правой частях аппроксимационного выражения.
А /Ч
Так, из оператора fk (к— номер точки шаблона) можно получить оператор fk
путем замены Afk_{ = fk - fk_x на интеграл Ik_x = Fk - Fk_{. Проделав это, вместо
формулы, следующей за (5.8), вторых из формул (5.9),(5.10) и формул (5.15)
получим операторы, восстанавливающие функцию у = f(x) по значениям
интегралов:
Л-2.С = ^01//-1 - 7//., + 2//+|); /_1>с = ±.(2I& + 5//_1 - //+1);
Дс=^(-//:]+5/^1+2//+1); fi+lc =^(2//:J-7//_, +11//+1).
Первые две формулы имеют второй порядок аппроксимации по h (они
записаны на трехточечном шаблоне), а последние четыре - третий порядок (они
записаны на четырехточечном шаблоне).
Вместо формулы (5.14) имеем следующую:
Лс=^<//+1 -//-!)•
В разд. 5.2.2 эта формула выведена другим способом.
Аналогичным путем можно найти и другие интегральные аппроксимации
первой производной.
231

5.2.2. Формулы, полученные на основе разложения первообразных
по формуле Тейлора
А. Двухточечный шаблон. На неравномерной сетке П„ рассмотрим
двухточечный шаблон IU2jf=(x/,*i4i) с шагом Л/Ч1 = х|+1 -*,. Предположив, что
f(x) eC2[a,b], разложим первообразную F(x) относительно точки х, по
формуле Тейлора при к = 2 и найдем выражение для F(x)\ = Fi+X:
где ^e(xl,xl+1). Выражая из этого разложения сначала первую производную, а
затем интеграл 7/+1 = /}+1 -/), получаем
/£, Л/Ч1 3 2 6
Первые два слагаемых в правых частях последних двух соотношений
представляют собой интегрально-функциональную (интегрально-точечную)
аппроксимацию производной fl и функционально-дифференциальную аппроксимацию
интеграла 7/+1 соответственно:
А
// =
/>'
2//+
А1+1
= Л/+
|//
Л1+1
♦*W?
_2Il (htd
hM I з
—Л/2
Л/2 , (5.19)
(5.20)
Порядки этих аппроксимаций устанавливают остаточные слагаемые в
выражениях для f( и 7/+1, из которых следуют оценки, правые части которых
указаны в скобках рядом с формулами.
Данные оценки свидетельствуют о том, что порядок аппроксимации,
обеспечиваемый (5.19), равен единице, а обеспечиваемый (5.20) равен трем при
условии, что 7/+1 и У) для (5.19) известны с точностью не ниже 0(hf+l) и 0(A,>i), а
fi и f- для (5.20) с точностью не ниже 0(Л^+1) и 0(Л/+1). Этот же результат
следует из рассмотренного в разд. В.4 правила соответствия порядков
аппроксимации математических моделей различного типа.
Замечания.
1. Выразив из разложения для Ful непосредственно функцию /}, получим
еще одно аппроксимационное выражение:
Ji ~ , Ji ~ Ji >
Л/+1 2
232

позволяющее восстанавливать со вторым порядком аппроксимации значение
функции fj в точке х, по значениям 7/+1 и /]•', известным с точностью не ниже
0(h?+\) и ^(^/+1) соответственно.
2. Если в точке х, известны производные более высоких порядков, то
могут быть построены аппроксимации //, 7/+1, /} более высокого порядка,
которые здесь не рассматриваются.
Б. Трехточечный шаблон. Возьмем на неравномерной сетке Qn
трехточечный шаблон UIij - (x|-i,*/»*/+i)» характеризующийся шагами Л/+1 = xi+{ -х±-у
Л/=х/-х/_1 и параметром нерегулярности 5/+1 =-т^-- Предположив, что
hi
f(x)e С3[д,£], найдем разложения для первообразной F(x) при х = х/+1 и
х = х;_| относительно точки х, и выпишем выражения для /r(^/+i),/r(jc/_1) по
формуле Тейлора (В.23) при £ = 3:
fl*i = Ft+w* +^f-/;+^f-/i"+^-/'"в|), 4i е (x„xi+I).
2 6 24
Умножая первое соотношение на Л,, а второе на Л/+1, складывая их с
учетом равенства 7/+l = /}+1 - /) и разрешая относительно // , получаем
//-
А,(1 + 8(+1)
IT—— I ^ Л-12(1 + 8(+1)15'+1/ (^') + / (WJ'
Л/Ч1
Отсюда следует интегрально-дифференциальная аппроксимационная формула
для первой производной f- на нерегулярном шаблоне:
г, i Л Ii-\ 1
Л/0 + 8/+1)^А/+1 ^ J
.M^LZJ)//.. (5.21)
Формула (5.21) при заданных интегралах 7/+1, 7/_| (известных с точностью
не ниже 0(h?+{) и 0(h})) и производной /}" (известной с точностью не ниже
первого порядка) аппроксимирует первую производную f/ на нерегулярном
шаблоне со вторым порядком (безусловная аппроксимация).
При условной аппроксимации, когда 6/+i = 1 (равномерная сетка), из (5.21)
следует интегральная аппроксимационная формула для первой производной/• на
регулярном шаблоне:
fU-jp№-iL) %м\ (5-22>
Эта формула аппроксимирует первую производную // со вторым порядком.
233

Из сопоставления мажорант оценок аппроксимационных операторов f'ic
(см. (5.10)) и f-c (см. (5.22)) вытекает, что они имеют одинаковый (второй)
порядок аппроксимации, однако, мажоранта или остаточное слагаемое оператора
интегрального типа содержит константу — , в два раза меньшую соответст-
J2;
вующей константы в мажоранте оператора точечного (функционального) типа.
Замечание. При условии /(x)eC2[fl,i] на регулярном шаблоне из
разложения первообразных получается аппроксимационная интегрально-
функциональная формула для второй производной:
f^TTli-l-Af* (0(h)), (5.23)
И п
из которой можно выразить интеграл //*/ через значения функции ft и произ-
£_
з
И3
водной //': //+/ = 2hfi +—f".
Пример 5.4. Пусть некоторая функция (взята функция f(x) - х3) на
трехточечном шаблоне хх - 1; х2 = 1,5; х3 = 2 (Л = 0,5 = const) задана двумя
независимыми способами:
1) значениями функции /j =1; /2 = 3,375; /3 = 8;
2) значениями интегралов на двух соседних отрезках: на отрезке
[хх,х2]:1\ =1,015625, а на отрезке [х2,х3]: /2 - 2,734375 (значения функций
/fa) и интегралов вычислены по /(х) = х3 точно).
Требуется найти значение производной /'(*)|x=i,5 с помощью
функциональной и интегральной аппроксимаций.
□ Для определения /'(*)|х=1,5 сначала воспользуемся функциональной
аппроксимационной формулой (5.10):
Применим интегральную формулу (5.22):
fic , /1^.2,734375-1,015625 = ^ {l&%)
h 0,25
В скобках, сразу за численными результатами значений производных
указана относительная погрешность в процентах. Из сопоставления полученных
приближенных значений с точными следует, что интегральная аппроксимация
дает лучший результат. ■
234

Пример 5.5. Пусть сеточная функция (табл. 5.2), являющаяся
представлением /(*)= хА, задана интегралами на отрезках [x,-,X/+i] (/ = 1,2,3), И = 1.
Таблица 5.2
/
*/
/г1
0
0
1
•... <
1
1
2
2
•-""К "'••••...
<
3
3
.211..
5
4
4
.--781
5
Требуется вычислить производную /'(х)|х=2 с использованием
интегральной формулы (5.22), имеющей второй порядок аппроксимации.
D Вычисление производной основывается на методике, изложенной выше.
1. Так как в задаче указан конкретный аппроксимационный оператор, то
выбор формулы осуществлять не нужно.
2. Формула (5.22) записана через значение двух интегралов 1\_х и 7/+I, что
соответствует двухшаговому (трехточечному) шаблону I£I3i = {xi^\fxi,xi+i)9 в
котором Xj =2 (/ = 2), x,_i = 1 (/-1 = 1), х/+1 =3 (/ + 1 = 2). В данном шаблоне
центральная точка х, = 2 совпадает с точкой Xj = 2.
211 31
//+'-//-! 5 "5 180
И2
3. Получим искомое значение /' =
= 36.
1 5
Здесь вычисления выполнены точно, хотя результат является
приближенным.
4. Используя точное значение производной /'(2) = 32, можно получить
32
фактическую погрешность результата
. 100% = 12,5%. ■
Изложенная в разд. 5.2.1 методика определения остаточного слагаемого
основана на соответствующей теореме для интерполяционного многочлена Ла-
гранжа. Полезно рассмотреть и другой способ получения оценки погрешности,
использующей разложение функций по формуле Тейлора.
Методика оценки погрешности дифференциальных операторов
на основе разложения функции по формуле Тейлора
1. Составить разность ffp> - ffp>, где ffp> — обозначение оператора, в
качестве которого может быть принят оператор как функционального типа, так и
интегрального или интегрально-функционального, а /Ур' — точное значение
производной.
2. Все функции, входящие в ffp\ разложить по формуле Тейлора с
остаточным слагаемым в форме Лагранжа относительно точки х;, в которой записан
235

ЛР'. Если оператор f>p' выражается через интегралы, то они записываются
через разности первообразных (F{x)). При этом предполагается, что функции
/(*), F(x) являются непрерывными, и для них существуют непрерывные
производные соответствующего порядка.
3. Подставить разложения функции в разность (см. п. 1) и выполнить ее
преобразование, в процессе которого получается остаточное слагаемое.
4. На основе остаточного слагаемого оценить погрешность аппроксимации.
Пример 5.6. Для заданного дифференциального оператора (5.22)
// = — , записанного на шаблоне Z//3, =(x;-i»*/j*i+i). найти остаточное
/г
слагаемое и оценить погрешность в точке Xj = дс,.
□ 1. Составим разность Л ~ Л = Л—туГ1 ~A'-ij» гДе Л ~~ точное зна-
чение производной, а /) — аппроксимирующий ее оператор.
2. Интегралы заменим разностями первообразных:
Функцию F(x) при х = xh х = х/+, разложим по формуле Тейлора с остаточным
слагаемым в форме Лагранжа относительно точки х, и выпишем выражения для
F{xi+X), Hxi-iY
^,-i) = F, -hfi +^.//.^./r+^/rfe.)f
где ^+ е(х/,х/Ч1), £_ €(дсм>х,-).
3. Подставим данные разложения в разность, составленную в п. 1, и
осуществим преобразования:
( а /,з J.4
н
Fi+hU +у// + у//'+^//"(и-^ -^/ + 1
■V/+y//-|v/'+£/r(U
2
^(rtu+rt-)).
Применяя теорему о среднем (см. утверждение В.1), находим остаточное
слагаемое
Л-Л=^/"Ь), 5/€(х,_„ХЫ).
236

4. С помощью последнего соотношения получим оценку погрешности
аппроксимации // интегральным оператором (5.22):
/y-~r(//+,-//-i)
M±LL2
12
h\
где MXi = max \f'"(x) |.
5.2.3. Формулы, полученные на основе сплайнов
ЯВНЫЕ ФОРМУЛЫ
А. Двухточечный шаблон. Из рассмотрения
интегрально-дифференциальных сплайн-многочленов второй степени в работе [17] получены интегрально-
функциональные аппроксимационные формулы для первых производных на
двухточечном шаблоне Шц =(*/,*/+i):
/м =4-4-1-£(2/,-i+//);
(5.24)
//-f-W-|t2/i)-3-/i'-l-
Формулы (5.24) в силу их одноинтервального характера могут
использоваться при Л/ = var , если значение интеграла 1\_х либо известно, либо заранее
вычислено с точностью не ниже о(А#-4). Для операторов Jl.\Jl справедливы
оценки
\fk-fk\^Mxi, *='-!, /•
Замечание. Из (5.24) можно выразить величину 1\_х , и тогда
получаются следующие функционально-дифференциальные квадратурные формулы:
//-1-^<2/м+/|) + ^-У7-1.
//-1-^(/*-1+2/,)-^-Л'.
Б. Трехточечный шаблон. Из рассмотрения интегрально-дифференциальных
сплайн-многочленов третьей степени на трехточечном шаблоне
^з / = {xi-\>xi>xi+\) получены следующие интегрально-функциональные формулы:
237

— для левой, центральной и правой точек нерегулярного шаблона аппрокси-
мационные формулы для первой производной имеют вид
/7-i,v
я;
/+1
hf ) 1Л/+1 лДч1 ht
1Л+1
//.v =
Я/
/41
ni г/'+1 "/ + 1 r/
V"/41 Л/
Л/+1 ЛД+1 Л/
//'+1.V =
/Г1
-4
[РЯГ+^+П r/+l А+1 г/ I . Р#Г + А+1 /- , 3\/// f r , /fr+j -
—г? у/ +тт"у/-1 г —; л+1+"Т1— Ji+~r~Ji-\
{ Al. " ' /Г'Т[ Ач, "+" ал+1 •"' *'"'
— для левой, центральной и правой точек регулярного шаблона аппрокси-
мационные формулы для первой производной принимают форму
?• —L
■^(/Z*1 + 5//_,)- (/>+1 +12/, +11Л-1)
ъ»«
f = —
j№-iL)-ifM-f,-x)
2Л
|д//+,-(А^+АГм)
^4 N
збо"5-'
//+l.c - 2А
-^Л'+1+//-|)+(11//+1+12Л+/м)
'А3 ^
60^
— для левой, центральной и правой точек нерегулярного шаблона аппрокси-
мационные формулы для второй производной имеют вид
Л-
1.V
НГ
1 П+1 . "2/ ,1
1 ЯГ'(2ЯГ'^) 2H!+l+h,
л:,=
нг
—— 1М 4.J-/'
/'l+l
V
л/+1 л/+1л/
-л*^
//+l,v -"
Я;
i+i
я*4')
/+1 * г/
"/41
+ :: Л+1 + ~~; Л + -г~
fy+l
лА+1
Л/
238

— для левой, центральной и правой точек регулярного шаблона аппроксима-
ционные формулы для второй производной принимают форму
Л-1.С - и2
|.(//+| + з//_,)+ (л+1 + юл + 5Л_, )1 [•
1>Х/
Дс А2
£(//*'+//-i)-(/i+i+«Л +/м)
—А2Л/4
20 4
У/+1.С ="
-J(3//+I+//-i)+(5/w+10//+/M)
,20
Л2Л/,
4,/
Подчеркнем, что правые части данных аппроксимационных соотношений
записаны через интегралы //_i,//+1 на двух смежных отрезках, составляющих
шаблон, и через значения функций в точках этого шаблона. Если известны
интегралы и значения самой функции, то по этим формулам можно вычислить
первые производные с третьим порядком, а вторые производные — со вторым
(остаточные слагаемые некоторых аппроксимационных формул указаны в скоб-
ках, расположенных рядом с этими формулами). При этом формула для f-c,
имеющая симметричный вид относительно центральной точки х, и содержащая
интегральные и функциональные разности, обеспечивает повышенный
(четвертый) порядок аппроксимации. Если интегралы для исследуемой функции
неизвестны, они должны быть предварительно рассчитаны с порядком, по
крайней мере на два превышающим порядок аппроксимации дифференциальных
операторов.
Замечание. В вычислительной практике могут оказаться полезными
еще два аппроксимационных оператора /щп), v> Дс:
/л(П). v =7Г"^''+Л+1)"ТГ"/|'+1 Мг-^з,/ \у
2 vi ^/-н/ з ' I 2
Л/ + 1 Л/+1 ^ z
12 г/Ч1 (Л+1
/^=^г(Л-|+л+|)~//-*1|
_3_
2А2
й"*|.
(5.25)
(5.26)
где //ад. v ~ лево- или правосторонний оператор, а /"с - центральный
оператор, записанный на трехточечном шаблоне при h = const.
В. Четырехточечный шаблон. Выше приведены формулы численного
дифференцирования на трехточечном (или для некоторых формул на двухточечном)
шаблоне, имеющие порядок аппроксимации Л3"'р_1\ где р — порядок
производных, для которых записаны эти формулы. В дополнение к изложенному
материалу приведем формулы, аппроксимирующие производную /^(/? = 1,2)
с порядками къ~\р~{> на четырехточечном шаблоне. Данные формулы получены
239

в работе [17], [23] путем анализа кубических дифференциальных и интегрально-
дифференциальных сплайнов.
1. Формулы для первых производных третьего порядка аппроксимации на
шаблоне LU4i = (x/-2>*/-i>*i>*/+i):
— для лево- и правосторонних внутренних точек x,_i,x, нерегулярного
шаблона справедливы функциональные формулы:
(5.27)
//-.,v = ^{-аДа,У"/+|Г/;-2+/>,+.(а/2(я/+1)2 -аД.^1,-1 )/;■-, н
+ аД,[а/я/_, + Kl_lhi+l]fi -h}hl,HUfM],
f'i.v = — \hihj+lH\*lfi_2 - A,+,(A, Я/+| +Л,-.1А'2/)//+1 +
где в = Я#Я/_,Я/+|п;!|; Kl = At., (Я/.*,1 + 2A,)+ А,(2Я/+| + A,);
*2/-i = A,+i(fl7-i' + 2A,)+ АД2ЯД, + A,J; n{!j = А,_1А,Л/+1; Я/*/ = A,-., + A, + A,+,;
— для левой и правой крайних точек х,_2,х/+1 нерегулярного шаблона
справедливы функционально-дифференциальные формулы рекуррентного типа:
(5.28)
% АД, 2я;.,+ам д/;.,
/'_2'¥ "F~ аз ^'-2 +~ГГ I
я/.,
аГу'-'
/,'-1. (5-29)
2 f-izii+l . и. . ал Л JT'+l
* Л/+1 2ЯГ'+/»,Ч1 А/}_
Л+i.v = "—"Г Г5 А// +
я/
hi
-fi • (5.30)
Яд регулярном четырехточечном шаблоне при Л = const формулы (5.27) -
(5.30) упрощаются и сводятся к формулам (5.15). Можно показать, что (5.27) —
(5.30), так же как и формулы (5.15), имеют третий порядок аппроксимации.
Параболические и кубические интегрально-дифференциальные сплайны
позволяют сконструировать интегральные формулы численного
дифференцирования [15—24].
На четырехточечном нерегулярном шаблоне Ш^и1 = (*/-ь */>*/+ь*/+г)
получаются следующие интегральные и рекуррентные формулы для первых
производных:
240

j, 2 labUhjtf ^ИмНПг +{flli _tf и_7/-. .SEA A, (5.3,)
Af 2 \HJ*lH«M> Ч2 з/^яг'+^-чУ Ч1 hl{-hl2 t 1
Л+1 = "71 7 y/+l ^ Л + 7 '/-If» P-32)
/I, л, Л,- л/ + 1
где А = йД^А, + Л/+1 + 2А/+2)+ /г/Ч1(/»? + аД2)+ M»/+2& + ЗЛ/+1 + А/Ч2).
Формулы (5.31),(5.32) относятся к внутренним точкам шаблона и при
h = const переходят в (5.22), а формулы (5.33) (рекуррентные) — к крайним
точкам шаблона и являются подобными формулам (5.36), справедливыми для
вторых производных.
На регулярном шаблоне из (5.33) при h = const легко получаются явные
трехинтервальные аппроксимации интегрального типа:
fiu = р-(- 2//-, + з//+| - //;,2) (^а2л/з,,-)>
//+2>с = •^•(//., - з//+| + 2//;,2) (^л2л/3,,)-
Последние две формулы могут быть получены также методом подобия
из первой и последней формул (5.16). Их можно записать через интегральные
разности:
//-,.е = -^(2Д//+1-Д//;,2);
/г
//+2,e=-j(2A//++,2-A//+1),
/г
где Д/£+1= /4*+| -/**_,.
2. Формулы для вторых производных второго порядка апппроксимации
на шаблоне Я/4>/ = (^/-2»x/-i»-x:/»x/+i):
— для лево- и правосторонних внутренних точек x,_i,x, нерегулярного
шаблона справедливы следующие функциональные формулы:
241

//;v = -И+1дл1+1л_2+"/-лЖ-А-! - л-/+|ал(+|)л -
а
(5.34)
(5.35)
+ ffrlbi-iKiH*1 + Я/-1дЛ/к - X'i-i&bifux],
где /Г/+1 =п}+1Я/+|; п{+1=ЛД+1; / = /-1,/; Н}[х = Лм + 2Л,;
## = 2Л, + Л/+1; ДЛ|Ч1 = А,+, - ^•; а = Н-1{ Н\_ХН^ П{!,;
— для левой и правой крайних точек нерегулярного шаблона справедливы
дифференциальные формулы рекуррентного типа:
(5.36)
7" - Н** 7" _ fh±L Ь
Формулы (5.27), (5.28) и (5.34), (5.35) могут использоваться для расчета
значений производных во внутренних точках сетки {*,}, / = 1,л-1, а (5.29),
(5.30) и (5.36) — для расчета производных в крайних точках х0,хп сетки Q„.
На регулярном шаблоне при h = const последняя группа формул для
аппроксимации вторых производных во внутренних точках шаблона преобразуется к
традиционным:
#с«^(Л-1-2//+/,+1) [^4,,];
fi"-\,c =-j(fi-2 - fi-\ +fi)>
h
a (5.36) — к рекуррентным формулам:
Л-2,с = Л/i-I.c — Л,с> Л + 1,с = А//,с ~ Л-1,с>
а также к первой и последней формулам из (5.16), имеющим второй порядок
аппроксимации.
242

НЕЯВНЫЕ АЛГОРИТМЫ ЧИСЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ
Путем несложного анализа параболических и кубических
дифференциальных сплайнов получаются нижеследующие неявные алгоритмы вычисления
первых и вторых производных сеточных функций. Значения производных могут
быть получены не по явным формулам, а в результате решения трехдиагональ-
ных систем линейных алгебраических уравнений методом прогонки.
Первые производные по заданной сеточной функции yi■= /(*,•), / = 0, л,
можно вычислить несколькими способами:
а) следствием параметрических соотношений параболических сплайнов
является система линейных алгебраических уравнений относительно первых
производных:
^fU^h^h^fi^fu^tfi,^^ / = 1,11-1, (5.37)
где tfi = fi+l - ft\ hux = x/+1 - Xi.
При заданных значениях производных на концах отрезка [х0,хя] эта
система позволяет со вторым порядком аппроксимации вычислить значения первых
Л.
производных fl во всех внутренних точках.
На регулярном шаблоне при h = const эта система упрощается:
М +2fj +//+1 = - , / = 1,л-1,
h
б) на регулярном шаблоне значения первых производных /■ со вторым
порядком аппроксимации могут быть вычислены также из системы, удовлетворяющей
свойству преобладания диагональных элементов [44] :
8Д/}
//.1 + б//+1 + //л = -Г. ' = М-1 • (5-38)
2 2 2 Л/
Решением этой системы будут производные в узлах, сдвинутых влево на
полшага. Если производные на концах неизвестны, то их необходимо
предварительно вычислить с порядком не ниже второго;
в) первые производные с третьим порядком аппроксимации могут быть
определены из системы, являющейся следствием кубических дифференциальных
сплайнов [1] (см. (4.76)):
hi 1Л+1 hi) ' А/+|
.т^%4 / = 1)Я_1. (5.39)
Данная система, удовлетворяющая свойству преобладания диагональных
элементов, может быть замкнута либо значениями /о,/я, либо двумя
функционально-дифференциальными граничными соотношениями (4.77);
243

г) первые производные со вторым порядком аппроксимации могут вычисляться
также по значениям интегралов с использованием системы, подобной системе
(4.72), в которой порядок производных понижен на единицу (в этом случае
вместо А/) и Д/}_1 следует подставить А/} = 7/+I и Д/}^ = 7/_|):
г/+1 г/
h ч-\
Л//м+2(Л/+^+1)// + ^+1/;+1=6 Ul---j=L I / = 1,и-1. (5.40)
Замыкающие соотношения формируются аналогично предыдущему случаю.
На регулярном шаблоне система (5.40) для f/ записывается через
интегральные приращения:
//-1+4/;+//+1-|(а//+|), i = in~i.
Вторые производные со вторым порядком аппроксимации могут быть
определены из системы, являющейся следствием применения кубических
дифференциальных сплайнов (см. систему (4.72)):
Л1Л-1+2(А,+Л/Ч1)у;"+А(+1Л';1= 6(j^-^H> '-О^П. (5.41)
Данная система, удовлетворяющая условию преобладания диагональных
А Л
элементов, может быть замкнута либо известными значениями /о",/я', либо
двумя граничными соотношениями, следующими из равенства
А£!яА/м.
JM -fi_ Ji " Ji-\
hi+\ ^
которое записывается для трех крайних точек сетки Q„, т. е. для {хо,х{,х2) и
(хп-2>хп-\>хп)-
Подчеркнем, что неявные алгоритмы вычисления производных
предпочтительно использовать в случае, когда для заданной сеточной функции необходимо
определять производные во всех узлах.
Пример 5.7. Проверить соотношение (5.37) при фиксированном / путем
подстановки в него степенной функции.
□ Соотношение (5.37) является следствием применения параболических
сплайнов, поэтому оно должно выполняться для сеточного представления
степенной функции (параболы) f(x) = х2. Возьмем трехточечный нерегулярный
шаблон Шц = (x,-i,*/,*/+i) с шагами Л|+1 = 3; А, = 2; xt_x = 2; х( = 4; х/+1 = 7.
Значения функции f(xk) (к = /*-1,/,/ + 1) и ее производной /'(*)| _ = 2хк
вместе с функциональными приращениями приведены в табл. 5.3.
244

Таблица 5.3
1 ч
*/-1 = 2
*/=4
хм =7
/(**)
4
16
49
АЛ
12
33
/'<**)
4
8
14 |
Тогда соотношению (5.37) при фиксированном / и выбранном шаблоне
будет соответствовать численное равенство
2.4 + 1(2 + 3). 8 + -. 14 = 12 + 33.
2 2 2
В левой и правой частях получаются одинаковые значения, что
свидетельствует о правильности системы (5.37). ■
Методика вычисления производных по неявным алгоритмам
1. С учетом характера задания сеточной функции (заданы значения
функции У{ = f(xj), / = 0,л, или значения интегралов //+1 (/ = 0,л-1)) и порядка
аппроксимации /, который необходимо обеспечить в алгоритме, выбрать
систему алгебраических уравнений относительно значений производных во всех
внутренних узлах сетки. При этом, если эта система является следствием
параболических сплайнов, то для первых производных / = 2, для вторых производных / = 1.
В случае, когда система получена из кубических сплайнов, порядок / возрастает
на единицу. Данные системы являются незамкнутыми (число неизвестных
превышает на два число уравнений).
2. Замкнуть выбранную систему двумя граничными условиями на концах
сетки Qn. Эти условия могут выбираться либо в виде явных аппроксимационных
формул, либо в виде двух дополнительных алгебраических соотношений,
включающих по два слагаемых с /0(/?), f{ip), и /^, /л(/,), р = 1,2. При этом
необходимо соблюсти соответствие порядков аппроксимации последних соотношений
(или формул) и исходного порядка /.
3. Решить полученную замкнутую систему линейных алгебраических
уравнений трехдиагонального вида методом прогонки.
Приведенная методика является составной частью построения кубического
дифференциального сплайна. Она была применена при решении примера 4.13.
245

5.3. МЕТОДЫ ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
5.3.1. Формулы, полученные на основе интерполяционных многочленов
Одним из классических методов вычисления определенных интегралов
является применение функциональных квадратурных формул
ъ
N
1а=\№<1х^Я;Г(Х;)ш1Ьау
а У = 1
(5.42)
где qj— весовые коэффициенты', Xjij = \iN,— некоторые точки отрезка [а,Ь\\
N— число точек (узлов квадратурной формулы).
Квадратурная формула называется точной для многочленов степени т ,
если при замене функции f(x) на произвольный алгебраический многочлен
степени не выше т приближенное равенство (5.42) становится точным. В этом
случае говорят, что квадратурная формула обладает т-свойством.
Замечания.
1. При приближенном вычислении интеграла, как правило, отрезок [я, Ь]
представляется в виде объединения / непересекающихся частичных отрезков
вида [x/_r,*/+J, которым соответствует шаблон IIIki = (x/_r,...,jc/,...,x/+j), где / —
номер базового узла сетки; г и s— количество узлов левее и правее узла с
номером /; k = r + s + l — общее число узлов (точек) в шаблоне (рис. 5.1). На каждом
частичном отрезке с номером у = 1,...,/ вычисляется интеграл по
соответствующей квадратурной формуле
' •* л л
(5.43)
а затем полученные значения суммируются по всем частичным отрезкам, т.е.
ТО
у=0 ,=0
(5.44)
У = /(х)
Ь х
Рис. 5.1
246

2. Далее в силу использования представления (5.44) проблеме вычисления
интеграла (5.43) на частичном отрезке уделяется основное внимание. По
заданной сеточной функции или сеточному представлению формульной функции на
частичном отрезке строится интерполяционный многочлен некоторой степени.
Значение //*/ определяется величиной интеграла от этого многочлена.
Как следует из замечаний, для вычисления интеграла могут использоваться
различные частичные отрезки и соответствующие им шаблоны. Рассмотрим
процедуру получения простейших формул численного интегрирования на
двухточечном и трехточечном шаблонах, наиболее часто описываемых в литературе и
используемых на практике.
А. Двухточечный шаблон. На частичном отрезке [*/>*/+iL которому
соответствует двухточечный шаблон Шц = (x,,jc/41), где г = О, s = 1, заменим
функцию f(x) двумя способами:
а) интерполяционным многочленом нулевой степени:
M*) = /(i5LYi±L).
построенным по значению функции / х = f(x {) в середине частичного отрез-
/'+- /Ч-
2 2
кгх , =*/+*'41 (рис. 5.2,я);
/+2 2
б) интерполяционным многочленом первой степени Ц(х) с узловыми
значениями xhxux :
Xj JCf-+j ДС/+| Xj
X — х-
где q - фаза интерполяции, q =-——-, Л/+1 =xi+1 -дс, (рис. 5.2,6).
Л/Ч1
В результате получим простейшие одноинтервальные квадратурные формулы
прямоугольников и трапеций:
/ft = X%(x)dx = 7 /^iLi^LJA . Л/+1/д, (5.45)
^ ="jA(^)^ = J[o-^>y; +^л^1] ^/+i^ = A/+i^-:^t1-, (5.46)
х, 0 2
где при интефировании учитывалось, что dx = hi+l dq\ q = О при х = jc, и # = 1
при X - X/+i .
Отметим, что понятие одноинтервальной формулы относится не к
шаблону, а к отрезку, на котором вычисляется интеграл. Нижние индексы
соответствуют названию квадратурной формулы.
247

Подчеркнем, что данные формулы справедливы и для нерегулярного
шаблона, хотя последующее их суммирование по всем частичным отрезкам [х/,х/+1]
традиционно выполняется при h = const.
Б. Трехточечный шаблон. Пусть отрезок [а,Ь] разбит на четное количество
одинаковых частичных отрезков, т.е. п = 2к, где к - число пар. Проделав
аналогичные выкладки для многочлена Li(x) второй степени, записываемого при
h = const на шаблоне ШЪ1 = (x/-i,x,-,*/+i) (по одной паре отрезков при
г = 1, s = 1), получим двухинтервальную квадратурную формулу парабол, или
формулу Симпсона:
(5.47)
'/-Ч.пар = i^Mdx=^(у;_1 +4/,. +у;ч1).
Эта же формула может быть получена из (5.23) путем разрешения ее
относительно //*/ и подстановки в нее конечно-разностной аппроксимации второй
производной /)■+! =—г (/}_j - 2/J +//+i), имеющей второй порядок, или из фор-
/г
мулы (4.92) с учетом //*/ = l\_x + I}*1 и h = const.
Дадим геометрические интерпретации квадратурных формул
прямоугольников (рис. 5.2,д), трапеций (рис. 5.2,6) и парабол (рис. 5.2,в).
У t
Рис. 5.2
Интегралы обычно определяются не на частичных отрезках, а на всем
отрезке [a,b], и поэтому путем суммирования левых и правых частей (5.45) - (5.47)
получаются так называемые составные квадратурные формулы.
Для сеточной функции /(*,),/= 0,л, заданной на регулярном шаблоне при
h = const, эти формулы имеют вид
248

Л>,пр = h
/1/2 + /3/2 +... + /
/2 +■■■ + ./ 1
л-1
/^=4^+^+-"+AitA)=f[/o+2(/i+/2+--+/''-i)+/J=
f П-\ \
(5.48)
(5.49)
/ви=|[/Ь+4(Л+/з+... + /2А.1)+2(/2+/4+... + /2А.2) + /я] =
/0+4Е/2/-1+2Е/2/+/2Л
/=1 /=1
(5.50)
Подчеркнем, что в составной квадратурной формуле парабол индекс «к»
указывает на число пар отрезков разбиения, которое предполагается четным
(п = 2к). Если это условие не выполняется, то интеграл вычисляется для четного
количества отрезков и к полученному значению добавляется величина 1„_х,
рассчитанная с порядком 0(h5) по формулам, приведенным далее.
ОЦЕНКА ПОГРЕШНОСТЕЙ КВАДРАТУРНЫХ ФОРМУЛ
Проведем оценку погрешностей одноинтервальных квадратурных формул
1 л ■ 1
прямоугольников и трапеций. С этой целью составим разность /,- - //+i,
которую затем преобразуем путем разложения первообразных и функций по формуле
Тейлора [17,23,24]. Для этого 7/+1 заменим разностью Fi+l -Fifa F(x) и
функции, входящие в правые части квадратурной формулы, разложим по формуле
Тейлора относительно точки х, (F(x) — первообразная, /)=7г(х/)). Так, для
формулы (5.46) при условии, что f(x) е C2[a,b], получим
hi+
АД|
hi
1Г -Ii£=FM-F, -^±L(fi+fi+]) = Fi+hi+l/i +HbLf; + lH±Lf"^)-Fi -
nu\
fi+/i+hl*if! + -f-f%)
hU
Л/+1
^/Ъ)-^/Ъ)=-±&1ГЫ-
где £,- e (x/,x/+1) - одна и та же точка для функций F(x) и f(x). Знак
полученной разности указывает на то, что если вторая производная f"(x) на частичном
отрезке [дс/,х/+1] положительна, то формула (5.46) аппроксимирует //+1 с
избытком. Из полученного соотношения для модуля разности //+| -//;* вытекает
/-/+1 _ //+1
г.тр
оценка |/,'+1 - //?тр| _
/+П^ -ЛД.!, где М2/ = max |/"(*)|, которая означает, что
одноинтервальная формула трапеций аппроксимирует //+1 с третьим порядком
по И.
249

Чтобы перейти к оценке погрешности аппроксимации интеграла /* по
составной формуле трапеций на всем отрезке, соотношения для разности
//+1-//^р= buffet) необходимо просуммировать по всем частичным
отрезкам (при этом полагается h = const):
Применяя к сумме в правой части утверждение В.1, получаем
hi
12
^-/^р=-тт^/т ^М-
Учитывая, что п= , М2 = max |/"(*)| , и переходя к неравенству,
h [a,b]
находим оценку
\lba-lU<^(b-a)h\ (5.51)
Отметим, что для оценки погрешностей квадратурных формул имеются и
другие способы, изложенные, например, в [29,40] .
Оценочная формула (5.51) позволяет сделать следующие выводы:
1. Порядок аппроксимации составной квадратурной формулы трапеций на
единицу меньше порядка аппроксимации одноинтервальной формулы и равен
двум;
2. Величина остаточного слагаемого зависит от длины отрезка
интегрирования [а,Ь] и М2. Константа в правой части равна —— -.
Проделав аналогичные выкладки для одноинтервальной и составной
формул прямоугольников и парабол, получим оценки [40]:
\l>-T!„\*%-{b-a)h>. (5.52)
/в*-#.»р|^(А-в)А4, (553)
где М4 = max /(4)(х) при f(x)eCA[a,b]. Отсюда вытекает, что составная фор-
мула прямоугольников имеет на отрезке [a>b] второй порядок аппроксимации и
М2{Ь-а)
константу —— -, которая в два раза меньше соответствующей константы в
24
оценке погрешности квадратурной формулы трапеций. При /"(*) > 0 на
частичном отрезке [xhxi+{] одноинтервальная формула (5.45) аппроксимирует //+I
с недостатком.
250

Двухинтервальная и составная формулы парабол аппроксимируют //*/ и
/* соответственно с пятым и четвертым порядком по И. Причем повышенный
на единицу порядок аппроксимации формулы (5.47) по сравнению с порядком,
устанавливаемым по правилу соответствия порядков (последний для двухинтер-
вальной формулы парабол равен четырем), получился в силу симметричности
этой формулы при h - const.
Замечание. Между максимальной степенью многочленов, для
которых квадратурная формула является точной, и порядком аппроксимации по
отношению к шагу h имеется связь. Формулы прямоугольников и трапеций
точны для многочленов первой степени и обладают вторым порядком
аппроксимации. Формула Симпсона является точной для многочленов третьей степени и
имеет четвертый порядок аппроксимации.
Вышеприведенные оценки погрешностей аппроксимационных
квадратурных формул позволяют для непрерывных функций априорным путем вычислять
шаг интегрирования, который обеспечивает заданную точность. Для сеточных
функций априорные оценки погрешностей выполняются путем предварительной
аппроксимации функции yf = /(*,) и определения соответствующей величины
Мк (к = 2,3,4) по формулам численного дифференцирования. Далее опишем
методику вычисления интеграла с априорным нахождением шага h.
Методика вычисления определенного интеграла с заданной точностью
и априорным нахождением шага интегрирования
1. Для правой части формулы оценки погрешностей вычислить константу
Мр = max /^(х) • С этой целью необходимо продифференцировать функцию
\оМ ' '
р раз и вычислить ее максимальное значение на отрезке [a,b], где р — порядок
аппроксимации квадратурной формулы.
2. Из условия
^-L{b-a)hP <z ,
А
Мр
где —- - константа, входящая в правую часть оценки погрешностей, определя-
А
I А ■ е
ется величина h: h < р
. Mp(b-a)'
3. По значению h вычислить п — количество разбиений отрезка [a,b] и
сформировать сеточное представление функции у = /(х), т.е. у,- = /(х,-), х0 =а\
х{ -а + h\ х2 = а + 2Л; . . . ; хп = а + п> И (/ = 0,1,...,л).
4. Полученную сеточную функцию подставить в правую часть
соответствующей квадратурной формулы и вычислить искомое значение /J\ При этом
значение интеграла в силу справедливости оценки удовлетворяет заданной
точности е.
251

Замечание. Данная методика может быть использована в основном
для сеточных представлений формульных функций, для которых можно
выбирать величину шага.
Пример 5.8. Вычислить на основе квадратурных формул трапеций интеграл
2
I? = f— с точностью 8 = 0,01. Оценить фактическую погрешность вычислен-
■* X
1 х
ного значения.
□ Воспользуемся методикой.
1. Поскольку /> = 2, вычислим М2 = max /''(*) . Дифференцируя /(х)= —
П;2] ' ' х
2
дважды, получаем /"(*) = —г- Данная функция монотонно убывающая, поэтому
х
она достигает максимума в точке х = 1. Таким образом, М2 = 2.
2. Найдем шаг интегрирования, который обеспечивает заданную точность,
из условия —-(Ь -a)h2 < е. Таким образом, h < J = J — = 0,245.
12 \(b-a)M2 V 1-2
Примем h = 0,2 .
3. По значению h = 0,2 вычислим п = = — = 5 и сформируем сеточ-
h 0,2
ное представление функции, т.е.
/о = — = - = 1, /, =—■— = — = 0,83(3), /2 = Х- = — = 0,7142,
J0 х0 1 Л xQ+h 1,2 J1 x0+2h 1,4
/3= l- = Л- = 0>6250 , /4= = — = 0,5555, /5 = 1- = - = 0,5000.
У3 х0+ЗЛ 1,6 J* x0+4h 1,8 У5 xq+5/i 2
4. Вычислим интеграл по формуле (5.49) при п = 5:
/Ктр=|-1/Ь+2(/1+/2+/з+/4) + /5] =
= 0,1 • [1 + 2 • [0,83(3) + 0,7142 + 0,625 + 0,5(5)] + 0,5] = 0,695.
Точное значение интеграла /j2 = In 2 = 0,693147 . Оценим фактическую
абсолютную погрешность полученного (приближенного) значения:
W = 10,69563 - 0,6931471 = 0,002483.
Из оценки следует, что фактическая погрешность не превышает 0,01 , т.е.
5факг. < 0,01 = е. ■
252

Пример 5.9. Вычислить интеграл /j2 = f— на основе квадратурной фор-
* X
1 Л
мулы парабол с точностью е = 0,01. Результат сопоставить с полученным в
примере 5.8.
□ 1,2. Аналогично примеру 5.8 найдем шаг интегрирования из неравенства
24
:24 ,т.е. h<4 180"е =0,52.
?/ (Ь-а)М4
— Мл < е , Мл = max
180 4,4 (1;2]
Примем // = 0,5.
3. По значению h = 0,5 вычислим п = = = 2 = 2/:. Следовательно,
Л 0,5
к = 1. Сформируем сеточное представление функции:
/о =/(D = l, /i=/0,5) = |, /2=/(2) = |.
Вычислим интефал по формуле (5.50) :
/,2паР. = f[/o + Vi+ /2] = 0,6944.
Фактическая абсолютная пофешность 6фа|ст = |0,69444-0,693147] = 0,001293.
Таким образом, фактическая пофешность не превышает е = 0,01.
Шаг интефирования по формуле парабол получился более чем в 2 раза
крупнее шага Л, соответствующего квадратурной формуле фапеций. Это
является следствием того, что (5.50) имеет четвертый порядок аппроксимации, а (5.49)
— второй. В связи с повышенной точностью квадратурной формулы парабол она
нашла широкое применение в вычислительной практике.■
Замечания.
1. Рассмотренный способ вычисления интефалов, когда с использованием
оценок и точности е предварительно вычисляется шаг интефирования Л,
является способом с априорным определением шага h. В вычислительной практике
большое распространение получил и другой апостериорный способ вычисления h,
основанный на многократном дроблении отрезка [а,Ь]. В этом случае интефал
вычисляется с помощью итерационного алгоритма методом Рунге (см. разд. 5.4).
2. Существуют и другие широко используемые квадратурные формулы.
Одноинтервальная формула прямоугольников (немодифицированная) на
двухточечном шаблоне LLf2j - (*m*/+i), где г - 0, s = 1 (рис. 5.3,а):
itf-h.fi [o(h2)\
Четырехинтервальная формула Воде на пятиточечном шаблоне
lllb>i^(*/-2>*/-ь*м*/Ч1,*/Ч2)> гДе г = 2,5 = 2 (рис. 5.3,в):
h-lc ^Vfi-i+nfi-x+nfi+Vfi+x+Vi+i) {o(h7)).
253

Шестиинтервальная формула Уэддля на семиточечном шаблоне
ШЫ Ч*-з.*-2.*--1.*.*чь*ч2>*чз) > где г = 3, s = 3 (рис. 5.3,г):
ЗА
Л'-3,с = ^"(^-3 + 5^-2 + ^"-1 + 6Л + -Лч! + 5Л+2 + Л+3)
Формулы Ньютона—Котеса (приведем два частных случая):
(о(Л7)).
— трехинтервальная формула на четырехточечном шаблоне
Я/4)/- = (*/_2>*/-b*/>*/4i)> ГДе г = 2ys = \ (формула «трех восьмых», рис. 5.3,6):
i!-{c = у<Л-2 + зУм +3Л +Л+1) (<W5));
— шестиинтервальная формула на семиточечном шаблоне
ши ={xi-i,Xj_2,Xi_i,xhxM,xi+2,xM), где г = 3, 5 = 3 (рис. 5.3,г):
Il-lc =^(41/--з +216У-.2 +27/-.! +272/, + 27/,+| + 216/ч2 + 41/-+3) (о(А9)).
3. Если по условию задачи имеется право выбора узлов и функция обладает
высокой степенью гладкости, то часто применяется квадратурная формула
Гаусса, в которой весовые коэффициенты и узлы подбираются так, чтобы
приближенное равенство было точным для всех многочленов наивысшей степени.
А
У
о~
/о /
f:::::::
*/
А)(*>\
11Ш:11
а
—,/■
i
i
i
i
i
i
i
;;;;:;;
' -»
X 1 х
У
0
Ц(х) ft
f v^
Ji-уГ.. j:..:
fi 2/Ф:^Ш +
У "• ' \ . , ...
f.--::.:;»A---r = :
1 J
*/-2 */-! *i
===== r====ii===.«
= = .::Г::::. H
1P1
*/+l x/+2
0 x,_3 x,_2 x,_, x,- xM x/+2 x/+3 *
Рис. 5.3
254

Пример 5.10. Вычислить интегралы
2 2 2 2
/j = \xdx , /2 = fx2 dx, /3 = Jx3 dx , /4 = J*4 ^
0 0 0 о
по формулам прямоугольников, трапеций, парабол с шагом h = 1. Найти оценки
погрешностей.
□ Точные значения интегралов:
v-l? 2 г3
/, = \xdx = — Г = 2, /2 = fx2rfx = —
1 J 9 0' 2 J 3
о
2 V4 I 9 2 V5
Л TV/ Л J
2 л
0~3'
0 5
Для формул прямоугольников и трапеций порядок аппроксимации р = 2, а
для формулы парабол р = 4. В поставленной задаче я = 0, b = 2. Сначала
получим оценки погрешностей априорным способом.
Найдем М2 = max |/"(х)|:
[0;2]
Л/2 = 0 для функции f(x) = х; М2 =2 для функции f(x) = х2;
М2 = 12 для функции /(х) = х3; Л/2 = 48 для функции /(х) = х4.
Найдем Л/4 = max |/(4)(х) I:
[0;2] * '
Л/4 = 0 для функций /(х) = х; /(х) = х2; /(х) = х3;
Л/4 = 24 для функции /(х) = х4.
Согласно (5.51)—(5.53), справедливы оценки:
K\<-^-aW; \4f\<_^(b-aW; \^\<_^(b-a)h\
Оценки погрешностей формулы прямоугольников:
|епр| = 0 для/(х) = х; |епр| <^-2-12 =0,16(6) для Дх) = х2;
|епр|<^-2.12 = 1 для/(х) = х3; |епр|^-212=8 для/(х) = х4.
Оценки погрешностей формулы трапеций:
|етр| = 0 дляЛх) = х; |етр|^^-2 12=0,3(3) для Дх) = х2;
|Етр|<|~2 12=2 для/(х) = х3; |Етр| £у|-2-12 =8 для/(х) = х4.
255

Оценки погрешностей формулы парабол:
|бпар| = 0 для /(*) = *; Дх) = х2- Дх) = х3;
24
|епар|<-^. 2-12 =0,26(6) для/(х) = х4
180
Таким образом, подтверждается факт, что формулы прямоугольников и
трапеций должны быть точными для многочленов первой степени, а формула
парабол — для многочленов не выше третьей степени.
Теперь рассчитаем значения интегралов по соответствующим квадратурным
формулам.
При h = 1 сеточное представление функций имеет вид
/о=/(0), A=/(U /i=/0), Л=/(|) /2-/(2).
сти:
По формуле прямоугольников (5.48) получаем 7пр = h
/i+/i,
.2 2 J
в частно-
/i=l
1 3
— + —
.2 2
= 2 (0);
/2=1
1 9
- + — i
4 4j
= 2,5 (0,16(6));
I ZZ
i. H
16 ^ 16
= ^ = 5,125 (1,275).
A II // / л
/3=1L8+ 8j=2 = 3'5 (°'5); /4 = 1
Здесь в скобках указана величина фактической ошибки.
По формуле трапеций (5.49) находим /тр = — • [/0 + 2f{ + /2], в частности:
А =-»-[0 + 2 + 2] = 2 (0); /2 Л.[0 + 2 + 4] = 3 (0,3(3));
/3 Л[0 + 2 + 8] = 5 (1); /4 Л[0 + 2 + 1б] = 9 (2,6).
По формуле парабол (5.50), учитывая, что п = 2к = 2 и, следовательно,
к = 1, получаем /пар = - • [/о + 4/J + /2], в частности:
/1=1.[0 + 4 + 2]=2 (0); /2Л.[0 + 4 + 4]Л (0);
/3=i.[0 + 4 + 8] = 4 (0); /4 =-[0 + 4 + 16] = —= 6,6(6) (0,26(6)).
Очевидно, полученные фактические погрешности соответствуют
вычисленным ранее оценкам. ■
256

Пример 5.11. Вычислить интеграл
/ = J smxdx
о
методами прямоугольников, трапеций, парабол, Боде, Уэддля, Ньютона-Котеса
на семиточечном шаблоне, применяя разбиение на 1,2,4,8 частичных отрезка.
Л
□ Точное значение интеграла: / = J sin xdx = 1. Разобьем отрезок 0;— на
/ = 1,2,4,8 частичных отрезка. Применим методы прямоугольников, трапеций,
парабол, используя составные формулы (5.48)—(5.50) . Остальные значения
интеграла подсчитаем по формуле (5.44) при /=1,2,4,8, используя на каждом
частичном отрезке соответствующую квадратурную формулу Боде, Уэддля,
Ньютона—Котеса на семиточечном шаблоне. Результаты расчетов приведем в табл. 5.4.
Таблица 5.4
Метод

Прямоугольников
1 Трапеций
Парабол
Боде
Уэддля
| Ньютона-
Котеса
по 7 точкам
/ = 1
1,110720338230
0,785398006439
1,002279560960
0,999991251569
0,999999293425
0,999999711921
/=2
1,026171820190
0,948059172335
1,000134270907
0,999999562310
0,999999680058
0,999999686177
/=4
1,006454224265
0,987115496263
1,000007981598
0,999999684178
0,999999685980
0,999999686084
/=8 1
1,001607874019
0,996784860265
1,000000202767
0,999999686054
0,999999686082
0,999999686083
Из данного примера видно, что для повышения точности возможны два
альтернативных подхода:
а) увеличивать количество частичных отрезков, и на каждом из них
использовать более простую квадратурную формулу;
б) применять более точные формулы на пяти и семиточечном шаблонах
при малом количестве частичных отрезков. ■
5.3.2. Формулы, полученные на основе сплайнов
ПРИМЕНЕНИЕ ПАРАБОЛИЧЕСКИХ ИНТЕГРАЛЬНО-ДИФФЕРЕНЦИАЛЬНЫХ
СПЛАЙНОВ
Явные формулы
Пусть в общем случае на неравномерной сетке Qn с некоторой точностью
задана сеточная функция yt - /(*,), / = 0,л. Предположим, что точность этого
задания в каждом из узлов не ниже 0\hf+x). В частном случае /(*,■) является
сеточным представлением формульной функции, и тогда сетка может быть
выбрана исходя из характера f(x). Например, в зонах больших изменений f(x) или ее
257

производных, которые могут быть разрывными, шаг сетки желательно
уменьшать. Закон мельчения сетки можно выбирать, например, по формулам
арифметической или геометрической прогрессий. В последнем случае в рассмотрение
вводится параметр нерегулярности сетки 5/+i =—£-L, совпадающий со знаменате-
лем прогрессии. Поэтому данный параметр будем включать здесь в правые части
некоторых квадратурных формул, и с его использованием проводить оценку
погрешности аппроксимации.
Из параболических интегрально-дифференциальных сплайнов путем
анализа их параметрических соотношений на трехточечном шаблоне
^з,/ ~{xi-\*xi>xi+\) получаются следующие лево- и правосторонние безусловные
аппроксимации интегралов //„i,//"1"1 четвертого порядка (одноинтервальные
функциональные аппроксимации):
y/-i,v -7Т77ГГ1"'" Ji+\ + ~J* + Г5*i-\
бнг1
y/,v -
h , У/ + 1 A2/, •" h2
\ "/+l «, Л/Ч1 Л,
/ + 1 "/+1 I ^3/ г . Л/ Д3/ г 1 г
Л+i +—~Г"~ Л -—Ji-i
6Н!
/41
Л/ + 1 Л/Ч1Л/ ni
(5.54)
(5.55)
Предполагая, что /(х)еСъ[а,Ь]у и используя методику оценки
погрешности [40], для данных аппроксимаций нетрудно получить оценки:
|/tf -'/+1|^-^5/+i(5,4i +2).A/3i/, |//.iiV -//-,|^(26/+1 +1)Л/3>/,
где M3J = max .|/'"(*)|.
IXj-I.Xh.iJ
При h = const квадратурные формулы (5.54), (5.55) упрощаются (условная
аппроксимация):
Л4
Их оценки при 6/+1 = 1 становятся одинаковыми (с мажорантой —M3l).
24
Таким образом, из оценок для //* ,//-i,v следует, что при безусловной
аппроксимации обе квадратурные формулы имеют четвертый порядок по И.
Однако для квадратурной формулы (5.55) этот порядок можно повысить, если
применить условную аппроксимацию, в которой положить 5/+i < А,. В этом случае из
формулы 6/+1 =-—-<//, получаем неравенство Л/+1 <Л/2, устанавливающее очень
малый шаг hi+l, такой, что л:/Ч1 отстоит от лс, на величину второго порядка по
Л,-. Этот тип шаблона можно назвать «сильно сжатым», так как он как бы уст-
258

ремляет трехточечный шаблон к двухточечному, и в связи с этим сама величина
интеграла //* является малой.
Суммируя левые и правые части квадратурных формул (5.54), (5.55), после
преобразований получаем компактную, двухинтервальную, трехточечную
обобщенную формулу парабол функционального типа:
7и\ fr(5,4.i+l)L * ч, , (5/+1+Q2 f , f? 1 if
ч-\ = 7 K2-6/+iJ//-i +— Ji + 2~~— Л+i
5/+i
5/+1
(5-56)
Предполагая, что разбиение отрезка [я,£] четное, т.е. п-2к, где X: —
количество пар разбиения, просуммируем (5.56) по к. Получаем обобщенную
составную квадратурную формулу парабол
р М1 + 82)(2-62), , у fa/+1)4-1 г +
6 /=1 6 62/
*г£А
0 + «2/)Л2/-1|2-— K(l + S2/+2)/22/+1(2-62/+2)
(5-57)
+—Г"^-!
б2л,
Известно, что для квадратурных формул важно, чтобы их коэффициенты
были положительны. Это свойство, называемое свойством положительности
коэффициентов, обеспечивает минимум погрешности вычисления интеграла по
данной квадратурной формуле, а также сходимость вычислительного процесса на
последовательно сгущающихся сетках [28]. В квадратурной формуле (5.56)
свойство положительности будет выполнено, если 2-6/+1 > 0, 2 >0. Отсюда
s/+i
вытекают пределы изменения параметра нерегулярности 5/+1: 0,5 < 5/+1 < 2.
Предполагая, что f(x) е С3[я,б], для (5.56) получаем остаточное слагаемое
и оценку погрешности:
\11-1-щ^Щ^^м^)2мх,
(5.58)
Переходя в (5.58) к мажоранте для оценки интеграла на всем отрезке [a,b],
имеем
Ц - М * Щ^(Ат + 1)2Л/з * (' "'J?** (А. + 1)2М3,
72
144
где Нт = max |Л,|, / = 1,л, Ат = max 5?+1 - 1 , Лш = max 6/+1, Л/3 = max !/'"(*)I .
/ i ' ' / [д>] '
259

Приведем анализ соотношения (5.58), устанавливающего порядок
аппроксимации обобщенной квадратурной двухинтервальной формулы парабол.
В общем случае квадратурная формула (5.56) имеет четвертый порядок
аппроксимации (безусловная аппроксимация). Возможны также условные
аппроксимации двух типов:
а) при 8/+1 = 1 реализуется регулярный шаблон и тогда порядок
аппроксимации повышается на единицу, а (5.56) переходит в классическую формулу
парабол (Симпсона);
б) при |б/+1 -1| < hf реализуется нерегулярный шаблон, и тогда порядок
аппроксимации может быть повышен на единицу за счет небольшого отклонения
5/+1 от единицы: А, - h} < hi+l < ht + h}. В этом случае шаблон является
квазирегулярным. Такие разбиения с локальными сгущениями узлов сетки могут
формироваться при численном интегрировании с помощью квадратурной формулы
(5.56) сильно изменяющихся функций или функций, имеющих в некоторых
окрестностях разрывы производных.
Неявные методы
Из анализа параметрических соотношений (4.101) и (4.105) двух типов
параболических интегрально-дифференциальных сплайнов, изложенных в разд.
4.5.5, для внутренних узлов получаются системы линейных алгебраических
уравнений относительно интегралов:
h} hlx h?+2 3[/2;- {^ hi+l [h^ /z,+2J hi+2 J
i = l,/i-2;
Л/ Ai4l Л/Ч2 6
которые при h = const преобразуются к виду
//., + 2//+1 + //;,2 = |[/)_, + 5 • (/, + //+1) + //+2], / = 1^2;
//_, -2//+1 +//;,2 =-у[-^-'+3-<//♦■ -/Я + ЛЛ, ^иП.
Для вычисления интегралов на всех отрезках эти системы необходимо
дополнить двумя граничными условиями. Это можно сделать двумя способами:
1. Системы дополняют значениями интегралов /q и /„_] на конечных
отрезках, которые вычисляются по односторонним формулам (5.54),(5.55)
соответственно.
260

2. Каждая из систем может быть дополнена двумя связями при / = 1 и
2' = п - 1 , которые выражаются из соотношения
— г1 .u-JL/'+i
ht
Л/+1
hi \hi hul) Л/+1
Замечания.
1. Первая из приведенных здесь систем связывает искомые интегралы со
значениями интегрируемой функции, а вторая — со значениями производных.
2. Описанные методы применимы для сеточных функций с п > 3.
3. Полученные системы линейных алгебраических уравнений являются
трехдиагональными и решаются методом прогонки (см. гл.1).
ПРИМЕНЕНИЕ КУБИЧЕСКИХ ИНТЕГРАЛЬНО-ДИФФЕРЕНЦИАЛЬНЫХ СПЛАЙНОВ
Явные формулы
Если кубические многочлены, построенные на [х/,х/+1] с помощью
функциональных, дифференциальных и интегральных параметров /},/}', //+1,
использовать для вывода квадратурных формул, то получаются различные типы одноин-
тервальных функционально-дифференциальных квадратурных формул Эйлера
пятого порядка.
Квадратурная формула Эйлера—Маклорена имеет вид [2]
//+|=А^(л+//+1)-^(//+1-//)
12
720
-Мл
(5.59)
Суммируя (5.59) по всем отрезкам, записываем составную квадратурную
формулу Эйлера четвертого порядка аппроксимации на нерегулярной сетке:
п-\
2
4Л + И/+1// +^-/я -iVZA^Af/Vi •
_1_
12;
(5-60)
Подчеркнем, что производные // для подстановки в (5.60) предварительно
должны быть вычислены по вышеприведенным аппроксимационным формулам
с порядком не ниже третьего. Сокращать производные в последнем слагаемом
составной квадратурной формулы, как это обычно делается в учебниках по
численным методам, не следует, поскольку при этом в сущности предполагается,
что все производные во внутренних узлах известны точно. Это условие для
сеточных функций, от которых рассчитываются интегралы, не должно
использоваться, так как производные этих функций вычисляются с некоторой
погрешностью, порядок которой при суммировании по всем частичным отрезкам
понижается на единицу. Справедливость этого утверждения подтверждается следующим
примером. После суммирования и сокращения в последней сумме квадратурной
формулы (5.60) производных во всех внутренних узлах при h = const формула
(5.60) приобретает вид
.( п-\ \ .2
1° =-
1 п _
/о+2Хл+/л|-^(л;
/о)-
(5.61)
261

Если квадратурную формулу (5.61) использовать для вычисления интеграла
от функции с нулевыми производными на концах или с их одинаковыми
значениями /л = /о, то квадратурная формула четвертого порядка переходит в
квадратурную формулу трапеций, имеющую второй порядок. Таким образом,
реализуется потеря двух порядков, что свидетельствует о необоснованности
проведенного сокращения.
Квадратурную формулу (5.59) целесообразно применить для получения
функциональных квадратурных формул путем подстановки в них конкретных
аппроксимаций fU\>fi- Подставив, например, оператор f(-^^—1^±^ а также
2Л
аппроксимации производных в левой и правой крайних точках четырехточечного
шаблона, получим одноинтервальные функциональные квадратурные формулы —
центральную и лево- и правостороннюю:
/ftU-■£(-//-!+"(Л+Л+1)-Л+2) {-Ш^4'1)' (562)
г '+1 _ _ (Q f . 1 Q f _ * f. _ j_ f A I *" J.5
I'CL = £(V/ + W//+i -5//+2 + /м) Щ^мч)> (563)
//,^-^;(Л-2-5/м+19/,+9/ы) (^А,^4,,| (5.64)
Последние три квадратурные формулы (5.62) - (5.64) могут быть
объединены в единую составную квадратурную формулу.
[ - /о +12/i+ 25/2 + 24§Л + 25/„_2 +12/,., - /„
I /-3 J
ifl - '0, лев. + ~д
"'" 'л-!,прав.
Данная формула для всех внутренних узлов удовлетворяет условию
положительности коэффициентов. Отметим также, что хотя порядок аппроксимации
формулы (5.62) равен порядку аппроксимации квадратурной формулы парабол,
однако их аппроксимационные свойства различаются. Это связано с тем, что
квадратурная формула (5.62) вытекает из полинома третьей степени, а формула
парабол — из полинома второй степени. Поэтому квадратурная формула (5.62)
учитывает, например, наличие точки перегиба, если она имеется в
интегрируемых функциях, в то время как формула парабол этого не позволяет, так как
получается из многочлена второй степени. Это обусловливает преимущество
формулы (5.62) по сравнению с формулой парабол при интегрировании функций,
имеющих указанную, а также другие особенности, присущие полиномам
нечетной степени.
Неявный метод
Неявный метод численного интегрирования получается путем анализа
параметрических соотношений кубических интегрально-дифференциальных
сплайнов. После преобразования соотношения (5.59) путем подстановки в него
производных из разд. 5.2.3 на нерегулярной сетке для внутренних узлов получается
система линейных алгебраических уравнений относительно интегралов
262

fy+1
зл/я/
/41
//-1 +
зя/+1~зя/;2Г злД2я/;,2 /+|
1ВД'*|Ум 2
"/ + 2 . "/ + 1
2 ь2-\
ЛЛ, -А/
2 Tj. tfi + l
6Я/+! 2Л,Я/
/; + (5.65)
+ A+L
\ + hlx-hl:i Jab + frit 7 /ж1Д...,и-2.
2Л/+2я,';,2 6^+,J'+l 12л1+2я/;,2
Яд регулярной сетке эта система преобразуется к более простому виду:
//., +4//+1 +//Л2 =j[//_i +1Ь(Л +//+i)+//+2]. / = 1Д...,#1-2. (5.66)
Для вычисления интегралов на всех отрезках эти системы необходимо
дополнить значениями /q и /J_j , которые могут быть вычислены по квадратурной
формуле (5.59) при Л, = var или по формулам (5.63), (5.64) при h - const.
Полученная в результате система линейных алгебраических уравнений решается
методом прогонки (см. гл.1).
Система (5.65) удовлетворяет условию преобладания диагональных
элементов в следующем диапазоне изменения параметра нерегулярности: б^1 < 5/+1 < б„,
где б, «1,722.
Для системы (5.66) в [24] дана оценка погрешности вычисления интеграла
/д на всем отрезке [а,Ь\, которая имеет вид
\jb_Jb \<hA{a-b)
где Л/4 = max /^4'(х) .
ПРИМЕНЕНИЕ ИНТЕГРАЛЬНО-ДИФФЕРЕНЦИАЛЬНЫХ СПЛАЙНОВ
ЧЕТВЕРТОЙ СТЕПЕНИ
Явные формулы
В данном разделе приводятся функционально-дифференциальные
квадратурные формулы, полученные из интегрально-дифференциальных многочленов
четвертой степени [16]. В соответствии с порядком аппроксимации
многочленами четвертой степени, который равен пяти, порядок аппроксимации интегралов
равен шести.
Одноинтервальные явные квадратурные формулы, представляющие
функционально-дифференциальные аппроксимации на трехточечном шаблоне
шъ,1 = (*м>*м */+i)» имеют вид
263

Л'-l.v = ^0
1
/
(- + —1
/м +
16 18
1Л л/ Л/Ч1 hu\)
ЧЛ, 2A,+1
/•- I 3 9 3
/м- T7 + T^- + -
A? 2A,A,+1 2АД, J
f,"2il/M
(5.67)
Л'v = ^0
tf Л-' +
2 18 16
■ + t— +
l Л/ Л/Л/+1 A/+iJ hi+\\hi hi+\
V 2 I 6 7 I/-
+2^-1+
3 9 3
^2А,2+2АД+,+/£j
tf i 3+_Litf+I
A,+i ^2A, A,+,
(5.68)
где P0 =
30f 1 1
hi
U+W
к = /,/ + 1, соответственно для (5.67), (5.68).
На регулярном шаблоне эти формулы упрощаются:
lUc = ^(13/-i + 16/ + //+i)--j^(/7+i +W!-if!-\)
7200
"%/
, (5.69)
р/+1 Л//- ,^/. ,^/. \ h
/£' =^(Л-1 +16// +13Л+1)-^(7//+1 -18//-//.!)
7200
Л/
5,/
. (5.70)
Суммирование формул (5.69), (5.70) приводит к двухинтервальной
квадратурной формуле (модифицированной формуле Эйлера) :
Il-lc =-^(7//-i +16// +7/Ч1)-^-(//+1 -//_,)
15
15
4725
M5tl I (5.71)
Порядок аппроксимации в этой формуле повышается на единицу из-за
симметричного вида формулы (5.71).
Подставляя в функционально-дифференциальные квадратурные формулы
аппроксимации производных на пятиточечном шаблоне с порядком 0(h4)>
получаем функциональные квадратурные формулы шестого порядка:
Л-1 =75о(_,9/'-2 + 346Л-1 +456у)"74/;+1 + nfi^' (7200 *6"5-') (572)
//*' -^Ol/i-2 -74/,., +456/, +34б//+| -19/,+2),
//-V = ^("//-2 + 34/,., +114/, + 34/,+, -/+2)
756'
Л/,
б,/
(5.73)
(5.74)
264

Подстановка в формулы (5.69), (5.70) лево- и правосторонних
аппроксимаций производных в крайних точках шаблона приводит к лево- и правосторонним
квадратурным формулам шестого порядка:
//-1 =7^(251/;-1 +646Л "264У;+1 +106^2 -19//+3),
//+1 =^о(-19//.з +Ю6Л-2 -264/м + 646/, +251/}+1).
Для расчета интегралов //_i>v » ^/.v1 на нерегулярной сетке по формулам
(5.67), (5.68) предварительно необходимо рассчитать производные в
соответствующих точках с порядком не ниже четвертого. С этой целью необходимо
воспользоваться интерполяционным многочленом четвертой степени.
Неявный метод
В заключение данного раздела приведем неявный метод вычислений
интегралов на всех частичных отрезках путем решения системы линейных
алгебраических уравнений трехдиагонального вида (h = const):
7//_i +19//+1 + 4//;,2 = h ■ (2/,., +15/, + 12/w + fM) (f = 1^2).
Данная система должна быть дополнена значениями интегралов IqJS-\*
которые рассчитываются по вышеприведенным квадратурным формулам.
Можно показать, что неявный алгоритм вычисления интеграла на отрезке
[а,Ь] имеет оценку [24]: I/* -/*| < h {*~^Л/5 .
1 1 I0U
5.3.3. Формулы, полученные на основе разложения первообразных
по формуле Тейлора
Пусть f(x)eCm+{[a,b] - формульная функция. Тогда из разложений
первообразной F(x) по формуле Тейлора относительно точек xt и xi+l и
выражений для Fi+\ = F(xi+l) и Fi - F(Xj) после преобразований получаются одноин-
тервальные обобщенные квадратурные формулы Эйлера, которые имеют
функционально-дифференциальный тип (см. формулу (В.24) и разд. 5.2.2):
2 6 *Го(* + 1)!
(УЛ2Мт+1)
(5.75)
//,2 -W/+1" 2 //+!+—//♦!+...-*+! 1И) ^/W [ (w + 2)j J' ("б)
В скобках справа от квадратурных формул (5.75), (5.76) указаны
мажоранты, характеризующие оценки их погрешностей. На рис. 5.4 показан характер
265

аппроксимации интеграла //+| на отрезке [x,,x/+i] первыми (функциональными)
слагаемыми комбинаций (5.75), (5.76). Эти аппроксимации представляют собой
площади прямоугольников abed (рис. 5.4,д) и ABCD (рис. 5.4,6), построенных
по значениям функций f(x) в левой точке х, и в правой точке х/+1
соответственно.
у
0
л,
ьл
а
X
/
i
fix).
Ji,\
/м
1
1
1
Л
С
d
i+i
JC
Xj Л/Ч1 хм х
б
Последующие слагаемые учитывают более высокие по порядку Л/+1
величины, и они вычисляются по значению Л/+1 и производным от первого до /я-го
порядка в точках х, и х/+1. В соответствии с этим (5.75), (5.76) можно назвать
обобщенными квадратурными формулами прямоугольников.
Составляя линейную комбинацию (5.75), (5.76) (среднеарифметическое
1ц и //J ), получаем обобщенную квадратурную формулу трапеций:
г /+1 _ и fi + fi+\ hi±L( Г г Л . fy+1 //» , /-'Л hi+i.( f" f"^_i_
12
^^•i«-^^>]
48
(5.77)
где t = m + 3 при четном /и и m = 0 ; t = т + 2 при нечетном /л. Первое
слагаемое данной квадратурной формулы соответствует площади трапеции, основания
которой равны ff и /}+1, а высотой является Л/Ч1 (см. рис. 5.2,6). Из выражения
для //з видно, что порядок аппроксимации интеграла этим слагаемым
квадратурной формулы равен трем, в то время как для (5.75), (5.76) этот порядок равен
двум. Это обусловлено знаками производных в комбинациях слагаемых
квадратурной формулы (5.77) (при т = 1 во втором слагаемом производные ff и ff+l
вычитаются и. если это слагаемое остаточное, то оно будет равно нулю, так как в
этом случае обе производные записываются в одной и той же точке
$e(x/,x/+i)).
266

Аналогичным путем на трехточечном шаблоне Ш^ = (*/_i,*/,X/+i) можно
получить двухинтервалъную квадратурную формулу Эйлера:
й^|^Ь *им-'1-л'*»
2Нт+2
{(т + 2)\ т+М
(5.78)
где Н = тах(А,, A/+i).
Замечание. На основе рассмотренных здесь квадратурных формул
дифференциального типа можно строить вложенные алгоритмы численного
интегрирования с заданной точностью, состоящие в том, что на фиксированном
шаге очередное слагаемое суммы вычисляется и добавляется к ранее
вычисленному результату до тех пор, пока абсолютная величина этого слагаемого не
станет меньше заданной величины е > 0.
Пример 5.12. Применяя вложенный алгоритм, вычислить интеграл
л
2
/ = J cos х dx
о
с точностью е = 0,01 на основе обобщенной квадратурной формулы трапеций
(5.77). Результат сравнить с его точным значением.
□ Для функции f(x) с ограниченными производными квадратурная
формула (5.77) содержит слагаемые, которые при Л/Ч1 < 1 уменьшаются по
абсолютной величине при переходе от текущего слагаемого к последующему. Поэтому
достигнутая точность может контролироваться в процессе вычислений по
величине очередного слагаемого (по модулю). Как только это слагаемое по модулю
становится меньше заданной точности е, то вычисления можно закончить.
Проведем вычисления слагаемых: 1,2,3-го и т.д. для заданной в примере функции
/(jc) = cos х . При этом принимается х, = 0; х/+1 = —. В результате имеем
г г (cos 0 + cos —)
h Kk = £ 2_ = £ = 0 78537
/+i 2 2 2 4
%Ч//ц -Л) = —(sini-sinO) = ~7Г = " °>61685;
4 4-4 2 16
^-(/Ki + //") = -^(cos^ + cosO) = -■■£-- 0,32298;
267

Следующее седьмое слагаемое будет по модулю меньше заданной точности
е = 0,01, поэтому его и последующие слагаемые можно не учитывать. Сумма
полученных слагаемых с учетом их знаков и знаков линейной комбинации (5.77)
дает результат :
/| = 0,78537 + 0,61685 - 0,32298 - 0,126834 + 0,039846 + 0,01043 = 1,002682.
Отличие полученного значения от точного не превышает 0,3%. Отметим, что
для данной функции в качестве отрезка \xhxi+l\ выбран целиком весь отрезок
[а,Ь) =
*!
Для достижения заданной точности в примере 5.12 потребовалось
вычислить шесть слагаемых. Если отрезок [а,Ь] разбить на несколько частичных
отрезков, например на два или три, то на каждом шаге потребовалось бы
меньшее количество слагаемых и в результате общее их количество могло бы
уменьшиться. В связи с этим в процессе реализации вычислительного алгоритма
возникает задача выбора оптимальных шагов, которые для достижения той же
точности обеспечивают минимальное общее количество слагаемых и в силу этого
минимальное количество операций.»
5.4. МЕТОД РУНГЕ УТОЧНЕНИЯ РЕЗУЛЬТАТОВ ЧИСЛЕННОГО
ДИФФЕРЕНЦИРОВАНИЯ И ИНТЕГРИРОВАНИЯ
Этот метод является апостериорным, и он основан на получении поправки,
выражаемой через два приближенных результата zhk и zh, получающихся на
двух равномерных сетках с шагами h и kh, где к— коэффициент,
характеризующий уменьшение шага (к <\) или его увеличение (к > 1) при переходе с
одной сетки на другую. Наиболее распространен способ генерации поправки в
итерационном процессе с к - — при необходимости снижения погрешности и к = 2
при возможном ее увеличении.
Общая формула уточненного результата, получающегося на двух сетках с h
и kh, записывается в виде
* = *»* + ,***J**' (5J9)
(±Г-
где р — порядок точности метода, по которому рассчитаны zhk и zh. Второе
слагаемое в правой части (5.79) представляет собой поправку или апостериорную
оценку точности результата, получаемого на сетке с параметром kh. Если
заданная точность не достигается, то при к < 1 процесс продолжается путем
дробления шага и перехода на новую, более мелкую сетку. Если же
указанное.слагаемое намного меньше заданной точности, то в алгоритме необходимо перейти на
укрупненную сетку, полагая, например, к = 2.
Данную методику рассмотрим применительно к расчету производных на
основе сгущающихся сеток \к = — , когда для первоначального вычисления
производных принимается одна из формул (5.10). Схема уточнения приведена
268

в табл. 5.5, где численные значения производных обозначены символом Z
с двумя нижними индексами, первый из которых (т > 1) указывает на ступени
уточнения (т = 1 — первая, т = 2 — вторая и т.д.), а второй — к — на
порядковые номера значений производных, полученных при различных шагах на каждой
ступени уточнения. Начиная с третьей колонки таблицы помещаются значения
Z00, Z0>i, . . ., полученные по некоторой исходной аппроксимационной форму-
В последующих колонках таблицы приводятся значения производных,
рассчитанных по формуле (5.79), которая может быть записана в виде
ле при различных шагах разбиения сетки: Aq , hx =
"тук
= Z,
m-U + l + "
*-!,* + !
-m-U
22m-l
(5.80)
где значение 2m соответствует порядку аппроксимации р.
Таблица 5.5
ГТ~
0
1
2
3
К
К
h\
h
*з
Zq^/c
^0,0
^0,1
^0,2
^0,3
о[нА
Z\,k
^ 2-..0
^ ZLl ^
^ ZU2 ^
оИ
•^г,*
^-» z2ja
^ 2г,х -^
ОЩ
%Ъ,к
^* ^3,0
оШ
Порядок уточнения численных результатов.
Пусть по заданной сеточной функции у, = /(х,) / = 0, п, в некоторой
фиксированной точке Xj = х; производная вначале рассчитывается по формуле (5.10)
второго порядка аппроксимации
Zo,k -
f{xi+hk)-f(x,-hk)
2hk
(42)).
(5.81)
Тогда уточнение до порядка 0[he) производится следующим образом.
1. По формуле (5.81) рассчитываются значения Z00, Z01, Z02
производных в заданной точке с использованием таблицы значений исходной сеточной
функции.
При этом для вычисления Z0 *, к = 0,1,2, берутся значения/(*,) в тех
точках сетки, которые соответствуют шагам h$yh{ и h2. Все величины, входящие
в третью колонку таблицы, имеют порядок аппроксимации 0[И2), что указано
в нижней строке табл. 5.5.
2. Реализуется первая ступень процесса уточнения по формуле (5.80), в
которой следует принять т = 1 (знаменатель второго слагаемого формулы (5.80)
равен 3), а р-2т-2. При этом вычисляются Z10 и Zlt. Порядок
аппроксимации результатов, получаемых в первой ступени уточнения, равен четырем.
269

3. Реализуется вторая ступень процесса уточнения по формуле (5.80), в
которой следует принять т = 2 (знаменатель второго слагаемого формулы (5.80)
равен 15), а р = 2т = 4. При этом вычисляется окончательное значение Z2io,
порядок аппроксимации которого равен шести. Процесс уточнения до заданного
порядка /7 = 6 закончен.
Замечание. 6 случае, когда необходимо обеспечить порядок
аппроксимации, превышающий полученный, например восьмой, производятся
дополнительные расчеты значений Z0k при более мелких шагах и расчеты Z12, Z2>\
по первой и второй ступени уточнения. После этого рассчитывается Z3)0 с
порядком 0\h%) (см. табл.5.5). Данный процесс может быть продолжен и далее.
Пример 5.13. Для сеточного представления функции y = sinx, хе[0;2л/5],
заданной на сетке с шагом А = л/10, на основе применения формулы (5.10)
второго порядка и метода Рунге найти первую производную f'(x)\ * с поряд-
5
ком 0[h4).
П 1. По формуле (5.81) рассчитываются значения Z00 и Z01 производных
в точке х2 = —. При этом Z00 получается при Aq = —, а значение Z0{ при
Л, = —. Записывая формулу (5.81) для указанных шагов, получаем
/и
= Z Л-/о 0,951057-0 0>
2Аь
756827,
Г h в Zw . Az2L в 0,809017-0,309017 = ^^
2Л,
24
10
Исходная сеточная функция и результаты расчетов производной в точке х2
помещены в табл. 5.6.
Таблица 5.6
/
*'"
fi
fih = ^0,0
^2 - = Zo>1
*2
0
0
0^.
1
Л
То
0,309017
ч
2
2л
10
0,587785
0,756827 -
0,795775^
3
Зл
10
0,809017
4
4л
10
^0,951057
Стрелочками от значений производных показаны значения функции,
использованные при расчете.
2. Реализуется первая (в данном случае и последняя) ступень процесса
уточнения по формуле (5.80), в которой т = 1. При этом принимается
f h = zo,i. fih = ^0,0. Тогда
270

Z,„ - /W =Z„,, + £^2£ . o,795775 + °>795775 ~ °'756827 - 0,808758.
Полученный результат соответствует порядку аппроксимации 0[И4).ш
Замечание. Для уточнения результатов численного интегрирования
метод Рунге реализуется аналогично.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
2
1. Вычислить значения интеграла Iq = if(x)dx по формулам трапеций и
о
парабол при h = 1, сравнить полученные результаты с точным значением. В
качестве подынтегральных функций взять:
a)/(jc) = 1 + jc; б)/(х) = 1 + х2; в) /(*) = 1 + х3; г) f(x) = 1 + хА.
1
2. Вычислить значение интеграла l[{ = j(l + х + х2 + х3 + xA)dx методами
-1
прямоугольников, трапеций, парабол при h = 1.
3. Найти значения интегралов в задачах 1 и 2 с точностью е = 0,01,
используя методику априорного выбора шага. Вычислить фактические погрешности.
1
4. Найти приближенное значение интеграла Iq = fsin х dx = 0,45970 мето-
о
дом парабол при h = 0,5. Пояснить, почему получается значение, близкое к
точному.
5. Найти приближенное значение интеграла l\, = f — = 2,30259 методом
' J X
0,1 л
парабол при h = 0,45; h - 0,225 ; h - 0,1125. Пояснить, почему при первом
значении шага получается значительная ошибка. Уточнить результат по методу Рунге
до порядка 0(hs).
ю
6. Найти приближенное значение интеграла /010 = f e~xdx = 0,999955 мето-
о
дами прямоугольников, трапеций, парабол при h = 1. Сделать анализ полученных
результатов.
7. Найти приближенное значение интеграла l\ = f методами прямо-
_* 2 + х
угольников, трапеций, парабол при h = 1. Оценить погрешности методов.
8. Найти значения первой и второй производной функции, заданной табл.
5.7, в точках х = 0; х = 0,1 \х = 0,25. Использовать формулы, соответствующие
двух-, трех-, четырех- и пятиточечным шаблонам.
Таблица 5.7
X
,.У,..
0,00
0,00000
0,05
0,10017
0,10
0,20134
0,15
0,30452
0,20
0,41075
6,25
JL5_2110
271

Часть III. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ
ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
Глава 6. МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ
6.1. ПОСТАНОВКА ЗАДАЧИ И ОСНОВНЫЕ ПОЛОЖЕНИЯ
Обыкновенным дифференциальным уравнением называется уравнение,
связывающее независимую переменную х , неизвестную функцию у(х) этой
независимой переменной и ее производные у'(х), у"(х)у..., у^п\х):
^(х,Ях),У(х),...,Ул)«) = 0, (6.1)
где F(xyyyy\...,y^) — функция указанных аргументов, заданная в некоторой
области их изменения.
Порядком дифференциального уравнения называется порядок старшей
производной, входящей в уравнение.
Если в соотношении (6.1) функция F такова, что его можно представить
в виде
У{а)=Ах,у(х),...,У{я-1Чх)), (6.2)
то уравнение называется обыкновенным дифференциальным уравнением л-го
порядка, разрешенным относительно старшей производной.
Уравнение называется линейным, если функция F линейна относительно
искомой функции и ее производных, т.е. если уравнение может быть записано
в виде
вя(х)Уя> +вя.,(х)/-1> + ... + я0(х)>> = /(*), (6.3)
где an(x)ian_i(x),...fiQ(x)if(x)— известные в общем случае нелинейные функции х.
Решением дифференциального уравнения л-го порядка называется
функция у(х), непрерывная на некотором интервале (ауЬ) вместе со своими
производными до (л-1) порядка включительно, имеющая производную у<<п\х) и
такая, что подстановка у(х) в уравнение обращает его в тождество.
График решения дифференциального уравнения называется интегральной
кривой.
Одной из важнейших задач в теории и приложениях дифференциальных
уравнений является задана Коши {начальная задача), в которой требуется найти
решение дифференциального уравнения, удовлетворяющее заданным начальным
условиям. Для уравнения (6.2) она записывается следующим образом:
У(п)=Дх,У(х)^У(п-1)(х)), (6.4)
У(х0) = Уо,?(хо) = у'0 „.„j^Vo) = jtf"0.
где х0 е (а,Ь), у0,у'0 ,...,д^я_1)- заданные числа.
272

Теорема 6.1 (о существовании и единственности решения задачи Коши
(6.4)).
Пусть выполнены следующие условия:
а) функция f(x,у,...,У""1))определена и непрерывна в некоторой замкнутой
области D , а также имеет в D ограниченные частные производные по переменным
у,? y(-l);
б) точка (х0,у0,у'0 ,.--».Уо ) лежит внутри области D .
Тогда решение задачи Коши (6.4) существует и единственно.
Общим решением дифференциального уравнения л-го порядка в области
G(zD(D— область, в которой выполнены условия теоремы 6.1) называется
функция у = у(х,Сь...,Сп), зависящая от п произвольных постоянных, и такая,
что при подстановке в уравнение она обращает его в тождество при любых
значениях Cl9...,Cn. Геометрически общее решение в области G представляет собой
семейство непересекающихся интегральных кривых, полностью покрывающих
всю область.
Общим интегралом дифференциального уравнения называется соотношение
вида
ф(х,у,Сь...,Сл) = 0,
неявно определяющее общее решение.
При конкретных значениях Cj,...,C„, включая ±оо, из общего решения
выделяется частное решение, а общий интеграл становится частным интегралом.
В каждой точке (х,д>) частного решения или частного интеграла выполняются
условия теоремы 6.1.
Наряду с проблемой решения дифференциальных уравнений л-го порядка
на практике возникает проблема решения систем обыкновенных
дифференциальных уравнений первого порядка, связывающих независимую переменную х,
неизвестные функции У\(х),...,уп(х) и их производные у{(х),...,у'п(х).
В случае, если уравнения разрешимы относительно производных, систему
можно записать в нормальной форме Коши:
-%L = f\(x,yl,...,y„),
dx
^2- = /2(х,У1,.;Уп), (6-5)
ах
^ = Л(х,у1,..,ул),
где fi(x9y\9...,yn), / = 1,л, — известные функции.
Решением системы (6.5) называется совокупность п функций
У\(х),...,уп(х), непрерывных на некотором интервале (а,Ь), такая, что
подстановка этих функций в (6.5) обращает все уравнения в тождества.
Задача Коши для системы (6.5) состоит в нахождении решения системы,
удовлетворяющего начальным условиям:
273

У\(хо) = У\о> Уг(хо) = Jbo»-» Уп(хо) = Упо> (6.6)
где У\о,У2о>->УиО " известные числа.
В векторной форме задача Коши (6.5),(6.6) имеет вид
Y' = F(x,Y), Y(xQ) = Y0, (6.7)
где Y = (уи...,уп)т,F(xJ) = {fx{xJ)y...Jn{xJ)f, YQ = (у10,~,Упо)Т -
Теорема 6.2 (о существовании и единственности решения задачи Коши
(6.5),(6.6)).
Пусть выполнены следующие условия:
а) функции fi(x,yi,...,y„), / = 1,л, определены и непрерывны в некоторой
замкнутой области D , а также имеют в D ограниченные частные производные по
переменным У\,...,уп;
б) точка (х0,.У1о,У20>—>Уяо) лежит внУтРи области D .
Тогда решение задачи Коши (6.5),(6.6) существует и единственно.
Замечания.
1. Во многих практических приложениях независимая переменная
обозначается через / и имеет смысл времени [33], поэтому задача Коши называется
начальной задачей.
2. Понятия общего и частного решений, общего и частного интегралов для
уравнения первого порядка и систем совпадают по форме, если заменить
функцию у(х) на вектор-функцию Y(x), /(х, у) на F(x, Y), а у0 - на Y0.
Численные методы, рассматриваемые в данном разделе, пригодны для
решения задач Коши, записанных в форме (6.5),(6.6). Чтобы решить задачу Коши
(6.4) этими методами, ее необходимо привести к системе п уравнений первого
порядка, т.е. к виду (6.5),(6.6).
Обозначая y,(x) = у(х),у2(х) = у'(х)у...,уп(х) = у(п'1)(х), получаем
'Т'^Уъ У1 (^о) = >^о»
^Г—Д'з, У2(хо) = УЬ> (6-8)
dx
&jL = f(x,yl9...tya), ун(х0) = у<я-1).
Получим точное решение модельного примера, используемого далее для
демонстрации применения различных численных методов.
Пример 6.1. Найти аналитическое решение задачи Коши
7>' + y = l, Я0) = 0,
где Т > 0 - известное число, называемое постоянной времени.
274

D Решение задачи Коши найдем с помощью известной методики [33].
1. Определим общее решение однородного уравнения Ту' + у = 0. По-
1
скольку корень X = соответствующего характеристического уравнения
1
. х
7Х + 1=0 действительный, то у0(х) = Се =Се т — общее решение
однородного уравнения.
2. Частное решение неоднородного уравнения ищется в форме уч(х) = А,
где А = const. После подстановки в решаемое уравнение получаем уч (х) = 1.
3. Общее решение неоднородного уравнения получается как сумма общего
решения однородного уравнения и частного решения неоднородного уравнения:
у(х) = у0(х) + уч(х) = Се~тХ + \.
Ему соответствует семейство интегральных кривых, характеризующееся
параметром С, который может принимать произвольные значения.
4. Частное решение неоднородного уравнения находим из начального усло-
_ j_
вия: у(0) = С + 1 = 0. Отсюда С =-1 и у(х) = \-е Т . ■
Пример 6.2. Записать дифференциальное уравнение второго порядка
2у" + у' + 4у = 6 sin х,
7(0) = 1, У(0) = 2
в виде системы дифференциальных уравнений в нормальной форме Коши.
D Введем обозначения: У\(х) = у(х),у2(х) = у[(х) и запишем уравнение в
форме у" = —/-2y + 3sinjt, разрешенной относительно старшей
производной. Тогда получим
у{ = Уг, У\ (0) = 1,
У\ =-^У2~^У\ +3sinx, у2(0) = 2.ш
Численные и приближенно-аналитические методы решения задачи Коши
в отличие от аналитических методов позволяют найти искомую функцию у(х)
лишь приближенно. Но при этом численные методы являются более
универсальными, так как с их помощью можно приближенно решать многие из задач,
точные решения которых аналитическими методами не могут быть найдены.
Аналитическими методами в основном решаются только линейные задачи и некоторые
типы нелинейных задач, в то время как для численных методов эти ограничения
отсутствуют.
Чтобы упростить изложение и в силу того, что численные методы легко
обобщаются на системы уравнений, в дальнейшем будем рассматривать решение
задачи Коши для уравнения первого порядка
У' = Ах,у), у(х0) = у0 , хе(а9Ь). (6.9)
275

Численное решение задачи ищется в узлах сетки Qn = {х0,хи...,хп}, где
Л/+1 =*/+1-х,, / = 0,л-1, — расстояние между соседними узлами, называемое
шагом интегрирования (параметром сетки). Если Л;+1 -h = const, сетка
называется равномерной (регулярной), а если /z/+1=var — неравномерной (нерегулярной).
В случае равномерной сетки узлы находятся по формуле х, = х0 + ih, / = 0, я, а в
случае неравномерной: Xj = х0 + h{i х2 = *i + h2 = jcj + S2/i|,..., х/Ч1 = х,- + 6/Ч1Л,,...
/г
...,хя = хя_| +5„АЯ_], где 5/+i =—— — параметр нерегулярности.
ni
Решение находится в виде последовательности значений Уо,У\,у2>...,уп,
являющихся приближением значений Уо,у(хх),у(х2),...,у(хп) точного решения
у(х) в узлах сетки П„ (рис. 6.1).
Сеточное представление y(xt), / = 0,л, известной функции у(х) (точного
решения задачи Коши) называется проекцией у(х) на сетку Qn.
У(хм)
У г у№
Численные методы решения обыкновенных дифференциальных уравнений
делятся на две группы:
— дискретные методы, позволяющие найти решение только в узлах сетки.
Эти методы называются еще разностными методами или методами сеток;
— непрерывно-дискретные методы, основанные на использовании
дискретных методов и сплайн-функций для восполнения численных результатов. Они
позволяют найти непрерывные решения дифференциальных уравнений.
Дискретные методы (методы сеток) подразделяются на явные и неявные.
Значение yi+{ на (/ + 1)-м шаге может определяться явно:
Уи\ =<&(xi_k+l,...,xi_l,xi,yi_k+l,...,yi_],yi), (6.10)
где Ф(.) — некоторая функция, зависящая от конкретного метода (кроме
последней рассчитанной точки (х,,.?,) могут использоваться еще (к-\) предыдущих
точек), или неявно:
276

-V/ + 1 =Ф(^/-А + 1» — »^#-1»х;»дс/ + 1»>;/-Л + 1> — »Д'/-1»У|»3'/+1)»
(6Л1)
где искомая величина уи[ входит одновременно и в левую, и в правую часть.
Явные и неявные методы делятся также на одношаговые и многошаговые
(А:-шаговые). В одношаговых методах для расчета очередной точки (х/+1,д>/+1)
требуется информация только о последней рассчитанной точке (*/,р,-).
В к-шаговых методах для нахождения точки (x/+i,j>/+i) требуется информация
о к предыдущих точках (рис. 6.2).
Формулы (6.10),(6.И) в общем случае представляют собой нелинейные
уравнения относительно yi+{ и называются разностными схемами.
*/-*+!
У1-\
т
У\
Рис. 6.2
Ум
Т
*/+!
Численный алгоритм (метод) называется устойчивым, если численные
результаты непрерывно зависят от входных данных и если погрешность остается
ограниченной при заданных пределах изменения параметров численного
алгоритма (шагов сетки, числа итераций и др.).
Сходимость приближенных методов является основной проблемой, от
успешного преодоления которой зависит точность решения всей задачи.
Численный алгоритм называется сходящимся, если при стремлении его параметров к
определенным предельным значениям, например, при И -> 0 (или при s -> «, где s
— число итераций), результаты стремятся к точному решению.
При известном точном решении некоторой модельной задачи сходимость
может быть проверена следующим образом. Фиксируется некоторая точка х> х0
и строится последовательность сеток Qn, таких, что h -+ 0, x = xn=x0+nh. Здесь
для простоты считаем, что все сетки, образующие указанную
последовательность, являются равномерными. Тогда, если \уп - у(хп) -> 0 при Л->0(л-»оо),
то метод является сходящимся в точке jc . Если метод сходится в каждой точке
х € [с, d] с (а, Ь), то он сходящийся на [с, d\.
277

Локальной ошибкой численного метода на (/ + 1) -м шаге называется
величина
ei+iW = &+i -y(xi+l),
где y(Xj+i)— значение точного решения при x = xi+l, а уих - приближенное
решение, получаемое по формуле (6.10) или (6.11) при условии, что вместо
приближенных значений &, &_!,.■.,£,■_*+! используются значения, соответствующие
точному решению, т.е. у(х,?),у(*/-1)>-..,M*i-*+i)-
Глобальной ошибкой называется величина en(h) = у„ -у(хп), где уп—
значение, получаемое по формулам (6.10) или (6.11) при / = п -1.
Глобальная ошибка определяется:
а) ошибками округления и ошибками арифметических действий,
обусловленными числом разрядов компьютера и характером выполняемых операций для
расчета значения искомой функции в очередной точке х/+1;
б) методическими ошибками, определяемыми выбранным алгоритмом;
в) переходными ошибками, обусловленными тем, что при расчете значения
р/+1 вместо точных значений у(х{)%у(хЫ\),...,y(xt_k^) берутся приближенные
значения p/,p/_i,...,p,-_jk+i, полученные на предыдущих шагах.
Локальные ошибки «переносятся» в точку хп и формируют глобальную
ошибку.
Число р называется порядком (точностью) численного метода, если его
глобальная ошибка есть О большое от hp, т.е. en(h) = 0(hp).
На практике в качестве характеристики точности метода часто
используется величина е(А) = max р,- -y(xt) .
/=0,l,...,/i ' '
Рассмотрим введенные понятия более подробно на примере явных одно-
шаговых методов, построенных для задачи (6.9). При этом формулу (6.10)
представим в виде
Р/+1 =Р/ + hy¥(yhxhh),
где ¥( р,-, х,-, А) — некоторая функция, определяемая конструкцией того или
иного метода.
Обозначим y(xyxhyi)— решение задачи Коши
w' = /(x,w), u(xi) = yi.
Тогда локальная ошибка определяется выражением
е,ч1<л) = Р/ + л * У(Р/,*,, А) - M*/+i, *,-,&) •
Геометрическая интерпретация возникновения локальных и глобальной
ошибок изображена на рис. 6.3.
278

Можно показать [53-55], что если локальная ошибка имеет порядок
(/7 + 1), т.е. ги1(И) = 0(Ир+1)у то глобальная погрешность имеет на единицу
меньший порядок, т.е. en(h) = 0(hp).
en(h)
хп-\ Хп X
Рис. 6.3
Перейдем теперь к рассмотрению устойчивости численных методов. Она
проверяется на «тестовом примере»
/ = Ц* y(0) = U (6.12)
где ц — в общем случае комплексная константа. Дифференциальное уравнение
в (6.12) является простейшим линейным уравнением, и для него можно получить
значимые критерии устойчивости в явной форме.
Метод называется устойчивым (ограниченно устойчивым), если существует
такое число Лкр >0, что при использовании метода для решения задачи (6.12),
где Re |i< 0 , с шагом О < h < hKp при / -> оо глобальная ошибка ограничена.
Величина Лкр называется критическим шагом. Если h > hKp , глобальная ошибка
может неограниченно возрастать.
В ограниченно устойчивых методах при задании величины шага h
необходимо учитывать значение критического шага Лкр . Для сложных
дифференциальных уравнений и систем нахождение Акр является самостоятельной задачей, а
свойство ограниченной устойчивости предупреждает вычислителя о возможных
проблемах. Поэтому на практике становится актуальной задача конструирования
таких методов, которые были бы устойчивы при любом значении шага, а его
величина выбиралась бы только исходя из желаемой точности расчетов (при этом
класс решаемых задач может быть ограничен).
Метод называется Л-устойчивым, если при его применении с любым
фиксированным положительным шагом И все численные решения задачи (6.12)
с комплексной константой ц (Re ц < 0) стремятся к нулю при / -> со.
279

Область Л-устойчивости — совокупность значений Лиц,
удовлетворяющих условию Яе(Лц)<0. Она изображена на рис. 6.4,а. Выполнение свойства
^-устойчивости является желательным, поскольку если решение задачи (6.12)
асимптотически устойчиво (в силу условия Re ц < О корень характеристического
уравнения находится в левой полуплоскости), то погрешность численного
решения стремится к нулю при любой величине шага h > 0.
При исследовании устойчивости численного метода необходимо
использовать соответствующую ему разностную схему для решения задачи (6.12) и
привести ее к линейному разностному уравнению с постоянными коэффициентами:
any(i + ri) + an_xy(i + п - 1) +... + a0y(i) = #(/), / = 0,1,...
Известно, что критерием устойчивости решения линейного разностного
уравнения является требование расположения корней А.,- соответствующего
характеристического уравнения апХп +ап_1\п~1 +... + а0 =0 внутри круга единичного
радиуса с центром в начале координат, т.е.
|л,-|<1, / = Ьл. (6.13)
а б в
Рис. 6.4
Замечания.
1. Численные методы, которые можно представить в виде
Z(arA+i-y+*-Pr//+w)-0, (6.14)
где |а0| + |Ро| * 0> fi+\-j■= /(*i4i-y»P/+i_/)> называются линейными /:-шаговыми
методами [54].
к к
Обозначим р(у = £a, ^k'J , oft) = £р, ^'у •
280

Линейный многошаговый метод является устойчивым, если для
фиксированного значения h ц корни уравнения
РЙ) + Л-»х.оЙ) = 0 (6.15)
лежат внутри круга единичного радиуса с центром в начале координат.
2. Для ограниченно устойчивых методов важной задачей является
нахождение величины критического шага Лкр . Если константа ц в уравнении (6.12)
действительная, то можно найти интервал устойчивости.
3. Существуют определения, смягчающие свойство ^-устойчивости [53—55].
Приведем одно из них.
Метод называется А(а)-устойчивым, ae(0,j), если при его применении
все численные решения уравнения (6.12) с фиксированным положительным
шагом И стремятся к нулю при / -» » для всех ц, удовлетворяющих условию
|arg(-n)|<a, |ц|*0,
где arg(-|i)— аргумент комплексного числа (-ц) [32]. Область А(а) -устойчивости
показана на рис. 6.4,6.
Это условие применимо и для линейных систем с постоянными
коэффициентами у' = Ау, где А — матрица коэффициентов, имеющая собственные
значения Xhi = 1,л. Геометрическая интерпретация изображена на рис. 6.4,в.
4. Можно показать, что явные линейные многошаговые методы не могут
быть /1-устойчивыми.
Рассмотрим основные принципы конструирования разностных схем.
1. Производная I —II аппроксимируется на заранее выбранном шаб
\dx)\x=x.
лоне (Х|_*+1,*/-*+2»—»*i+i)i а пРавая часть f(x,y) обыкновенного
дифференциального уравнения заменяется сеточным представлением /(*/,.)>,) в точке
(*/»&)• Условно этот принцип называется аппроксимационным. С его помощью
строятся одношаговые и многошаговые схемы в зависимости от шаблона, по
которому аппроксимируется производная.
2. Дифференциальное уравнение заменяется разностным аналогом на од-
ношаговом (двухточечном) шаблоне (xhxi+l) (возможно использование
дополнительных точек внутри шаблона) путем согласования с разложением функции
у = у(х) при х = х/Ч1 по формуле Тейлора относительно точки jc = дс,. По этому
принципу строятся одношаговые схемы, в частности семейство схем Рунге—
Кутты.
3. Осуществляется интегрирование обеих частей дифференциального
уравнения вдоль решения на выбранном шаблоне. При этом правая часть уравнения
предварительно заменяется интерполяционным многочленом, степень которого
должна соответствовать порядку точности схемы. Данный принцип называется
интегрально-интерполяционным и используется для построения одношаговых и
многошаговых явных и неявных схем, в том числе схем Адамса.
4. Разностные схемы строятся на основе подобия соотношений теории
приближения конструкциям схем. С этой целью используются следствия из ин-
281

тегрально-дифференциальных сплайнов - параметрические соотношения,
формулы аппроксимации производных, квадратурные формулы, записанные в общем
случае на нерегулярном шаблоне. Данный принцип, который можно назвать
принципом аналогий, предложен в [18]. Далее в разд. 6.2.4 он применен для
конструирования двух- и трехшаговых явных и неявных схем.
6.2. ПРИНЦИПЫ ПОСТРОЕНИЯ РАЗНОСТНЫХ СХЕМ
6.2.1. Принцип аппроксимаций
Рассмотрим проблему нахождения численного решения задачи Коши (6.9):
dy
dx
f(x,y), у(х0) = у0.
Для аппроксимации производной
используем формулу (5.4),
записанную на двухточечном шаблоне #/2j/ = (*/,*/+i):
У/+1 -у*
+ 0<А|Ч1)
Pf«„
(6.16)
и формулу (5.10), записанную на трехточечном нерегулярном шаблоне
шг,1 =(x/-i>-x:/»x/+i):
ш
п;
/41
:=xt Hi
/41
hi fy+lj
1
-8/+I-.V/-1 +
(S2/4i-l) 1
4+1
У;+-—Уи\
6/+i
+ 0(И;Ии1)
(h2
-^-§/Ч1^3,/
(6.17)
Tl+l
где H'i = /*, +Al+i, П, = /*Д+1> hux = */+i - */, 8/+1 =-rLL ~ параметр
ni+\ _
При 6/Ч1 = 1 шаблон становится регулярным, а среднее слагаемое с
входящим в него у( — равным нулю. При этом формула (6.17) сводится к
традиционной:
Уи\ -У/-\
2h
+ 0(h2)
(6.18)
282

Аппроксимация формульных функций, входящих в правую часть (6.9),
осуществляется путем перехода к их сеточному представлению.
Методика построения разностных схем
с помощью аппроксимаций производной
1. Вводится в общем случае неравномерная сетка Qn =(x0ixb...^chxi+b...,xn).
Величина шага Л/+! = дс/+! -х,- выражается через узловые точки.
2. Для получения рассматриваемых здесь двух схем (одношаговой и двух-
шаговой) выбирается соответственно двухточечный (одношаговый) и
трехточечный (двухшаговый) шаблоны Ш1х =(х/,х/+1) и HI^j =(*/-i,*/,X/+i)» на которых
в точке х,- производится аппроксимация производной
dx
по формулам
(6.16), (6.17) соответственно в левой и центральной точках х,.
Далее заменяется правая часть уравнения (6.9) ее сеточным
представлением, т.е. f(xyy) -> /(х,,>>,), а вместо у(х) рассматривается сеточная функция
h * y(Xj), которая определяется только в точках сетки.
3. Выполняется подстановка аппроксимаций (6.16), (6.17) и /(*,-, у,-)
в дифференциальное уравнение:
Уи\ ~ У/
Л/+1
• + 0(Л/+1) = /(х,,>>,.);
Я/
i+i
(82/+1-1) 1
S/+1 -У1-\ + У/ +- Ум
4+1
5/+1
+ 0(hihul) = f(Xi,y,)-
После отбрасывания остаточных слагаемых получаются разностные схемы:
— явная схема Эйлера первого порядка (явный метод Эйлера):
Уи\ =yi+hu]f(xhyi)i / = 0,л-1, у0=у0\
(6.19)
— обобщенная на нерегулярный шаблон двухшаговая явная схема Эйлера
второго порядка:
Уи\ =У* -&и\ЬУ1 + НГ%+х/(х19уЛ, i = 1,/i-1,
(6.20)
где byt =у1+{ ->>,.
Обозначим схему (6.20) символами 2Я2Б (суть этого обозначения
поясняется в разд. 6.2.2). Анализ остаточного слагаемого
( п2
~7"8/41^3,/ | обобщенной
схемы Эйлера указывает на то, что при условном выборе шаблона, когда
достигается соотношение bi+l < ht (т.е. hux<hf) , порядок аппроксимации этой
283

схемы повышается на единицу без увеличения количества точек шаблона. Этот
прием повышения точности может быть использован при конструировании
вложенных алгоритмов путем измельчения шага.
При 5/+1 = 1 (регулярный шаблон) схема (6.20) соответствует методу
Эйлера—Коши:
А+i =А-1+2Л •/(*/> А). / = 1,л-1. (6.21)
Для начала расчетов по формулам (6.20),(6.21) требуется иметь две
«разгонные» точки у0, А. Первая определяется известным начальным условием
А) = .Уо» а вторая может быть найдена с помощью другого метода, например, по
формуле (6.19): А = у0 +hlf(x0,y0).
Приведем геометрическую интерпретацию явного метода Эйлера (6.19),
которая показана на рис. 6.5.
У = У(х)
Рис. 6.5
Пусть известна точка (дс,, А) на искомой интегральной кривой у = у(х).
Через эту точку проведем к кривой у = у(х) касательную L , тангенс угла
наклона которой равен /(*,) = /(*,-, А)- Ее уравнение имеет вид
У = А + /(*/)(*-*/) = А +/(*/, А )(*-*/)•
Следующая точка A+i приближенного решения получается при х = х/+1
(в результате нахождения точки пересечения прямых L и jc/41 = const):
A+i =yi+bu{f(xi,yi).
Это соотношение совпадает с формулой (6.19).
Схема (6.19) иногда называется схемой ломаных (рис. 6.6), так как
очередное значение yi+l получается в результате проведения касательной к
интегральной кривой в точке (х,,А)- После выполнения каждого шага метода Эйлера
приближенное решение переходит с одной интегральной кривой на другую, что
обусловлено погрешностью численного решения. Большая погрешность схемы
284

связана с тем, что порядок этой схемы равен единице, и поэтому ломаная,
определяемая по (6.19), довольно значительно отклоняется от точного решения
у = у(х). В связи с этим данная схема используется, как правило, в качестве
вспомогательной при конструировании схем повышенного порядка.
у4
Уо
У Ж А
УАу\
/ | X
/а, !
х0 х{
h
^ ^-~ i
! Лз !
х2 хг
У = У(х)
X
Рис. 6.6
Для анализа устойчивости явного метода Эйлера применим формулу (6.19)
при Л/+1 =А к решению задачи (6.12). В результате разностное уравнение будет
иметь вид
Л. Л . Л
Уи\ =У|+Л-цу,-
ум -(1 + Лц)р, =0.
Корень соответствующего характеристического уравнения Хх = 1 + h ц. Условие
(6.13) принимает форму |l + h ц| < 1. Отсюда следует, что область устойчивости
представляется внутренней частью круга единичного радиуса с центром в точке
(—1; 0) (рис. 6.7). Если ц действительная константа, то можно указать интервал
2
устойчивости - 2 < h ц < 0, т.е. h ц е (-2,0), а при ц < 0 имеем 0 < И < —. По-
этому явный метод Эйлера является ограниченно устойчивым с критическим
. 2
шагом Лкр = —.
1т(Лц)
Яе(Лц)
Рис. 6.7
285

Дадим геометрическую интерпретацию метода Эйлера— Коши (6.21)
применительно к решению задачи (6.9) (рис. 6.8). Пусть известны две точки
(*/-!>Рм )»(*/» .У/) на искомой интегральной кривой у-у(х). Проведем через
точку (xhyt) касательную L , тангенс угла наклона которой равен
y'(xi) = /(*/>h) • После этого через точку (x/_i,j>,_i) проведем прямую Ц ,
параллельную L. Ее уравнение имеет вид
У = Я-\ +f(xi,yi)(x-xi_l).
Следующая точка уи1 приближенного решения получается при х = х/+,:
р/+1 =Я-1 +2hf(xhyi).
Это соотношение совпадает с формулой (6.21).
У
0
/' Уi-\
*М
h
У-i
I
i
i
1
i
i
i
*/
h
*i+
L
Уи\
i
i
i
1
i
i
l
-A
У = У(х)
X
Рис. 6.8
Замечание. Все описанные здесь и далее методы легко переносятся на
системы обыкновенных дифференциальных уравнений (6.7). Под у и f(xyy)
следует подразумевать векторы Y = (уь...,уп)ти F(x,Y) = (f](x,Y),...,fn(x,Y))T.
Например, для системы двух дифференциальных уравнений
y' = f(x,y,z), У(х0) = у0 ,
Z' = g(x,y9z), Z(x0) = z0
явный метод Эйлера (6.19) записывается в форме
.V/41 = h + hux f(xyyhZj), Уо = Уо,
*/+i = Ь + Л/+1 g(x, Pi, Zi), Zo=Z0-
Пример 6.3. Исследовать устойчивость явного метода Эйлера на примере
решения уравнения Ту' + у = 1, у(0) = у0, где Т— действительное положительное
число. Найти приближенное решение задачи Коши
286

0,1/ + у = 1, y(0) = Q
на отрезке [0,1] явным методом Эйлера.
□ Точное решение задачи получено в примере 6.1: у(х) = 1 -е~]0х,
поскольку Т = 0,1. Уравнение Ту' + у = 1 перепишем в виде, аналогичном (6.12):
11 1 . , 2 ._ _
/ = у + —, поэтому ц = , а критический шаг равен пкр = — = 2Т.
Следовательно, при h < 2Т метод устойчив, а при h>2T неустойчив. На рис. 6.9
схематически изображены приближенные решения уравнения Ту' + у = 1, у(0) = 0,
соответствующие устойчивому процессу и хорошей точности численного
решения (рис.6.9,я), устойчивому процессу и плохой точности (рис.6.9,б), а также
неустойчивому процессу и плохой точности (рис. 6.9,в).
Для уравнения 0,1/ + у = 1 постоянная времени Т = 0,1, поэтому Лкр = 0,2.
Решим задачу для значений шага h = 0,05; 0,2; 0,5. При h = 0,05 метод является
устойчивым, при h - 0,2 находится на границе устойчивости, а при h = 0,5
является неустойчивым.
Переписав уравнение в виде / = 10-10>>, получим из (6.19) формулу для
нахождения приближенного решения:
Ум = У'1 + h' 0° ~ 10Я) = ЮЛ + (1 - 10А)&.
Таблица 6.1
*/
0,00
0,05
оло
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
1 0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
1,00
max С/
у, (И = 0,05)
0,000000
0,500000
0,750000
0,875000
0,937500
0,968750
0,984375
0,992187
0,996094
0,998047
0,999023
0,999511
0,999755
0,999877
0,999938
0,999969
0,999984
0,999992
0,999996
0,999998
0,999999
0,117879
Pi (h = 0,2)
0,000
2,000
0,000
2,000
0,000
2,000
1,135335
h (h = 0,5)
0,000
5,000
-15,000
15,99995
X*i)
0,000000
0,393469
0,632121
0,776870
0,864665
0,917915
0,950213
0,969803
0,981684
0,988891
0,993262
0,995913
0,997521
0,998497
0,999088
0,999446
0,999665
0,999797
0,999877
0,999925
0,999955
287

Результаты расчетов, выполненных для различных значений h, приведены
в табл. 6.1. При h = 0,05 приближенное решение достаточно близко к точному,
при h = 0,2 «пила» не сходится и не расходится, а при h = 0,5 «пила»,
аппроксимирующая точное решение, расходится (рис. 6.9, в)М
Рис. 6.9
Замечание. Порядок точности метода, как правило, определяется
порядком аппроксимации схем. Например, для схемы (6.19) первого порядка,
записанной в виде, соответствующем исходному уравнению (6.9), получаем (первое
слагаемое аппроксимирует производную):
y(Xj+\)-y(Xj) ~ * У1+Ь!+1У}+0(Н?+{)-У1
г J(xhyi) = /, = у; -/, +О(Л,ч1) = 0,
Л/+1 Л/Ч1
т.е. у} = fj +0(hi+i). Здесь были использованы формула Тейлора и свойства,
приведенные в разд. В.З.
Для двухшаговой схемы (6.21) аналогично получается второй порядок
аппроксимации. Действительно, воспользуемся частным случаем формулы
Тейлора (см. (В. 18)) при х0 = xi9 xi+i = Xj + //, Xj_Y = Xj - Л,/(х) = y(x):
Уи\ = У* + W +—У"+0(И3), yt_\ = yt - hy] +—y"+ 0(Л3).
Подставляя полученные соотношения в схему (6.21), записанную в виде
Уи\ -У/-1
2Л
- /(л:,, у,) = 0, соответствующем дифференциальному уравнению (6.9),
с учетом свойств, приведенных в разд. В.З, имеем
h2 h2
У\ +hy'i + — y"+0(h2)-yi+hy,i - — y"+0(h3)
Th
-/;=^+0(/i2)-y;=o,
т.е. y\=fi+0(h2).
Также легко проверить, что и схема (6.20) на нерегулярном шаблоне имеет
второй порядок при безусловной аппроксимации. Если же Л/+1 < И2 (условная
аппроксимация), то этот порядок равен трем.
288

6.2.2. Интегрально-интерполяционный принцип
В данном подходе явные или неявные методы соответствующего порядка
получаются путем интегрирования уравнения (6.9) вдоль решения у(х). Так, на
двухточечном шаблоне
]V= '\/(хуу(х))ах. (6.22)
у,- *,
Функция f(x,y(x)) в (6.22) заменяется интерполяционным многочленом
соответствующей степени р (р = О для метода первого порядка,р = 1 для метода
второго порядка, р - 2 для метода третьего порядка и т.д.). Подчеркнем, что
замена /(х,д>) интерполяционным многочленом в (6.22) становится возможной
благодаря тому, что f(x,y) рассматривается не на всей плоскости (х,у), а
только вдоль интегральной кривой у(х). Для вычисления интеграла в правой
части могут быть использованы известные квадратурные формулы
прямоугольников, трапеций, парабол (Симпсона) и др.
Примем х/+1 в качестве узловой точки многочлена Z-o(x), т.е.
Lq(x) = f(xi+\,yi+\). Тогда из (6.22) следует формула неявного метода Эйлера:
Уи\ =h+buxf(xM,yux)m<b(xhxM9yux), / = 0,л-1. (6.23)
Принимая для интерполяционного многочлена Ц(х) в качестве узловых
точек х,- и х/+1 и используя квадратурную формулу трапеций (5.46), получаем
неявную одношаговую схему второго порядка (метод трапеций):
Уи\ =Р/+^1//+/(*|Ч1.Р/+1)]"Ф(^1»^/+!»Р/+1). / = 0,л-1, (6.24)
где fi =/(x/,j)i). Формулы (6.23),(6.24) имеют вид (6.11) при к = 1. Подчеркнем,
что свойство неявности схем (6.23),(6.24) обусловлено наличием искомой
величины уи{ в левой и правой частях в общем случае нелинейных уравнений.
При реализации алгоритма решения задачи Коши неизвестное значение
уи{ вычисляется одним из методов решения нелинейных уравнений (см.гл.З).
Применение метода Ньютона связано с записью уравнения в форме
Уи\ -<D(*/.*,4i,&+i) s Р<Ум) = 0 (6.25)
и с дифференцированием функции /Х.р/+|) , что увеличивает время расчетов из-
за возможной сложности производных или увеличивает погрешность в силу
неточного задания правых частей.
Как правило, используется метод простых итераций:
Р&+1) = <*х„хМ.№1)- к = 0,1,.... (6.26)
289

Таким образом, уравнение (6.24) решается с помощью формулы
(рекуррентного соотношения):
?&+|) =я +^[л +/(*,+!, яЫ * = ол,....
(6.27)
При применении методов Ньютона и простых итераций вначале задается
или находится нулевое приближение решения по формуле у^\ = yt
(так называемый «постоянный» прогноз) или явным методом Эйлера (6.19):
Ум =yi+huxf(xhyi).
Итерации завершаются при выполнении условия окончания
I р<*+1> _ р(*> I < е
где е — малое положительное число.
Для сокращения описания и удобства ссылок получаемые здесь схемы
обозначаются буквенно-цифровыми символами. Первая цифра в нем обозначает
«шаговость» схемы, следующая за ней буква «Я» или буквы «НЯ» — явный или
неявный характер, затем цифра указывает порядок точности схемы и за ней
буква — возможную модификацию. Таким образом, схема (6.24) обозначается
1НЯ2, т.е. она является одношаговой, неявной и имеет второй порядок точности.
Последняя буква указывается только для тех схем, которые имеют модификации.
Приведем геометрическую интерпретацию неявного метода Эйлера (6.23)
(рис.6.10). Пусть известна точка (xhyj) на искомой интегральной кривой
у = у(х). Через эту точку проведем прямую, тангенс угла наклона которой равен
/(*/+i) =/(*/+! >-V/+i)» те- следующая точка уих приближенного решения
берется на той кривой из семейства интегральных кривых, касательная к которой
Л Л
УМ ~ У* _ ft v Г; \
- /1*1 + 1 ^l + l)-
в точке(х/+1,уих)проходит через точку (х,,yt■). Поэтому
Л/+1
Полученное соотношение совпадает с формулой (6.23).
У
h
0
*/
hM
У(хм)
*/ + 1
У = У(х)
X
Рис. 6.10
290

Исследуем устойчивость неявного метода Эйлера и метода трапеций.
Применим формулу (6.23) при Л/+1 =Л к решению задачи (6.12). В результате
получим разностное уравнение
Уи\ =Р/ +Л-ц-р/+| или й+10-Лц)-й =0.
Корень характеристического уравнения Л
-. Условие устойчивости
(6.13) имеет вид
1
\-h\x
< 1 или 11 - h • ц | > 1. Область устойчивости
1 - /г и I
представляется внешней частью круга единичного радиуса с центром в точке
(1;0). Из геометрической интерпретации (рис. 6.11) следует, что неявный метод
Эйлера обладает свойством ^-устойчивости (см. рис.6.4,я), поскольку выделенная
на рис. 6.11 область включает левую полуплоскость.
1т(Лц)
Ке(Лц)
Рис. 6.11
Применим формулу (6.24) метода трапеций при Л/+1 = h к решению задачи
(6.12). Получим разностное уравнение
Ум = Уг + -J (и Л + И Л+1) или ум 11 - -^ I -11 + -2-1 ^ = 0.
Корень характеристического уравнения Xj = -2_. Условие устойчивости
1
Лц
(6.13) принимает вид
1 + ^
2
<1 или |2+Лц| <|2-Лц|. Полученное
неравенство выполняется в области, изображенной на рис. 6.4,я, т.е. метод
трапеций является ^-устойчивым.
Продолжим рассмотрение интегрально-интерполяционного метода.
Использование квадратурной формулы прямоугольников дает модифицированный
метод Эйлера второго порядка:
291

Л/Ч1
2 *
(6.28)
Дадим геометрическую интерпретацию модифицированного метода Эйлера
второго порядка (рис. 6.12).
Рис. 6.12
Пусть известна точка (х,, у() на искомой интегральной кривой у - у{х).
Через эту точку проведем касательную L , тангенс угла наклона которой равен
И-
y'(Xj) = /(*,•, у,-)- При х = Xj +-L±1- получаем точку у {. Далее проведем прямую
2 /♦-
1[ с тангенсом угла наклона Л
( и ^
2 ,+'2j
, а затем прямую Z^,
параллельную ^ и проходящую через точку (xhyt) . Ее уравнение имеет вид
Л -
У = У1 + /
2/
(*-*,).
Следующая точка уи{ приближенного решения находится при х = jci+,:
2 '+Ъ
Это соотношение совпадает с формулой (6.28).
Исследуем устойчивость модифицированного метода Эйлера второго
порядка. Применим формулы (6.28) при hux = h к решению задачи (6.12).
В результате получим разностное уравнение:
292

Уи\ = У! + Лц(У/ + -и И) или у/+1 - у,(1 + яц + —^—) = 0.
Корень соответствующего характеристического уравнения Х{ =1+яц+-—-—
Условие устойчивости (6.13) имеет вид
1 + яц +
2
(М2 '
< 1 . ЕСЛИ |! —
1 1 L (Л^)2 1
действительное число, то, раскрывая модуль, получаем -1 < 1 + я ц + —г— < 1 •
Неравенство 2 + я ц + > 0 выполняется для любых я ц, а неравенство
Лц+ < 0, т.е. я ц • (2 + я ц) < 0 , справедливо при - 2 < я ц < 0. Таким
образом, интервал устойчивости Лц€(-2, 0) модифицированного метода Эйлера
совпадает с интервалом устойчивости явного метода Эйлера (6.19).
Для использования регулярного трехточечного шаблона (Xi^9xi9xi+i)
заменим (6.22) аналогичным выражением:
]*= '\f(x,y(x))dx.
Ум xi-\
Если функцию /(х, у(х)), входящую в правую часть, заменить
многочленом Лагранжа второй степени и применить формулу (5.47), то
получается неявная схема парабол (Симпсона) четвертого порядка (2НЯ4):
У их = А-1 + yl/i-i +V/ +/(х,ч1,&+1)]. (6.29)
Отметим, что схема парабол имеет четвертый, а не третий порядок
точности из-за регулярности шаблона.
В соответствии с классификацией, приведенной в [35], схема (6.29)
относится к классу неявных схем Адамса. Для получения других схем Лдамса
следует переписать (6.22) в форме
Ум *м *м
\dy = \f(x,y(x))dx = \y\x)dx (6.30)
yt X; x;
и заменить y'(x) соответствующим интерполяционным полиномом,
построенным на регулярном шаблоне с h = const.
В силу формулы (4.36) второго интерполяционного многочлена Ньютона
получаем
уХя) ^yt +я ^y^i +-^яЛя + \) + --^д-(я + i)-(g + 2) + ...9
или
293

у (я) = у} + я Art-i + 2 а2у;_2 + ^ 1 11 д^;_3 + ...,
где q = — фаза интерполяции.
h
Подставляя полученное выражение в правую часть (6.30) и учитывая, что
1
dx = hdq , вычисляем \y'(q)-h-dq , поскольку при х - jc, и х = х/+1 справедливо
о
q - 0 и £ = 1 соответственно. В результате имеем
1 S 3
Л+1-& =л.у;+-л.д^;., +—л-а2^;_2+-л-а3>';-з + -
или с учетом (6.9) общую формулу семейства явных схем Адамса:
л л ^ * 5 А9 3 .ч 251 л /^ ->i\
V/+1 = Уг + Л/ +-АЛ/-1 + — А Л/-2 + £ Д Л/-3 +^20 Л'""4 + '"'
где ч/ = hf(xiiyi) = h- /}, а конечные разности вычисляются с помощью табл.
6.2. Подчеркнем, что здесь интерполяционный многочлен записан на шаблоне,
не включающем точку х/+1.
Таблица 6.2
| ч
*/-з
*/-2
*/-1
*'"
А
Ук
И-з
Л
Уг-2
Уг-\
А
Л*
Л/-3
Л/-2
Л/-1 -
л/- "
Ал*
АЛг-3
АЛт^С"""
Апм
Д2Л*
:::..'-а2л^
дЧ-2
А3Л*
;^м
Если взять в правой части (6.31) два слагаемых, то получится явный метод
Эйлера (6.19), если три слагаемых, то явный метод, описываемый формулой
1 h
Ум = А + h'fi +-[hfi-hfi-\] = yi +-РЛ -Л-il.
а если четыре слагаемых, то явный метод вида
= л+£[23/,-1б/м+5/,_21
и т.д.
294

В результате имеем схемы Адамса—Бэшфорта
— второго порядка (2Я2В):
Уи\ = У» + тР// - Л-1 ], / = 1,п -1;
(6.32)
третьего порядка (ЗЯЗА):
У их =3)/+ —123Л-1бЛ-1 + 5Л-2Ь / = 2,я-1;
— четвертого порядка (4Я4):
h+\=h+-fi№fi-&fi-i + ufi-i-*fi-& / = з,/1-1.
(6.33)
(6.34)
Для начала расчетов по формуле (6.32) требуются две «разгонные» точки:
}'0уУ\ , по формуле (6.33) — три «разгонные» точки: Уо,У\,У2, по формуле (6.34) —
четыре «разгонные» точки: Уо,У[,У2,Уз- Их необходимо вычислить с порядком
точности не меньше порядка точности схемы. Далее схема (6.32) обобщается на
нерегулярный шаблон.
Если для построения интерполяционного многочлена использовать
шаблоны, включающие точку xi+^, то получится следующая формула семейства
неявных схем Адамса [2,42]:
Уи\ = Уг + Л/+1 "^АЛ/ - — Л Л/-1 - — А Л/-2 "^Q Л Л/-3 +-. (635)
где т|/+1 = Л■ f(xi+\9yj+i) = Л• /}+1, а конечные разности вычисляются с помощью
табл. 6.3.
Таблица 6.3
**
*/-3
*/-2
*/-!
*'
*/+!
Ра:
У/-3
Л
Н-2
А
Л-1
Г/
Ум
л*
Л/-3
п/-2 <•";.'
Л/-1 -.•::;;;
л/ ■-"
л/+1 ••••"■"'
АЛ к
'".'--••'АЛ/^....
'"Ал^::.::.
"■.;::::Ал/4:::.^
.....Алг ""
А2Л*
^•'•'А2П^......
• :::::А^Й:
■■■■::::А2л7-1
А3Л*
'.>*W
'^Ci
А%*
•••■••А4Л/-з
Если взять в правой части (6.35) два слагаемых, то получится неявный
метод Эйлера (6.23), если три слагаемых, - метод трапеций (6.24):
Уы = У! + h • fi+\ ~ "J \Ь' //+i -bfi\ = Pi + :j L/i + Я*/+ь &+i)] >
295

если четыре слагаемых, — неявный метод, описываемый соотношением
А+1=Л+|(Л+/ч1)~[(Л-//+1-Л-//)-(Л-Л-А-Л-1)] =
*Т.Д.
В результате получаются неявные схемы Адамса—Мултона:
— первого порядка (6.23);
— второго порядка (6.24);
— третьего порядка (2НЯЗ):
Ум =А +—(-Л-1 +8//+5/(x/+|,j>/+,)], / = 1,л-1; (6.36)
— четвертого порядка (ЗНЯ4):
Р/*1=Л+^-[Л-2-5//-1+19Л+9/(х/+1>р/+|)], / = 2,л-1. (6.37)
24
Для расчетов по формуле (6.36) требуются две «разгонные» точки: ро»Л»
по формуле (6.37) — три «разгонные» точки: Уо,у\,У2- Их необходимо вычислить
с порядком точности не меньше порядка точности схемы.
Чтобы найти искомое значение р/+1 с помощью формул (6.36),(6.37), так
же как в неявном методе Эйлера и методе трапеций, требуется решить в общем
случае нелинейное уравнение.
Замечания.
1. Аналогичные методы могут быть получены из интегрального уравнения
Ум *ui
вида \dy = jf(xyy(x))dx, k>2.
Я-k xi-k
2. Области устойчивости методов Адамса—Бэшфорта и Адамса-Мултона
приведены в [54].
Пример 6.4. Найти приближенное решение задачи Коши
/ = *-1, У(0) = 1,
z' = -y-2z, г(0) = -1
на отрезке [0; 1] с шагом h = 0,1 методами Эйлера (неявным и
модифицированным), Адамса—Бэшфорта третьего порядка и трапеций.
□ Путем прямой подстановки в систему легко убедиться в том, что точное
решение задачи имеет вид
y(x) = -2 + 3e~x +хе~х; z(x) = l-2e~x -хе~х.
296

Используя соотношения (6.23),(6.24),(6.28),(6.33), выписываем формулы
для нахождения приближенного решения указанными методами (при этом
применяется векторная форма записи).
Для неявного метода Эйлера из (6.23) имеем
Уи\
Л
+ 0,1
I- Л+1 - 2£,+| J U/ - О'1 • Уи\ ~ °>2 • Ь*\J г0 = г(0) = -1.
Разрешая эту систему относительно у,+\Ли\< окончательно получаем
г,-0,1-j),+0,01
с 0,1 (г,-0,1 .У,+0,001)
Zi+\
1,21
вид
Соотношения (6.28) для модифицированного метода Эйлера принимают
л /ч и,1 ,л 1Ч л и,1 . Л. _Л ч
yUL = Я +-T-U,- -1); z/+i = z,- +—(->'/ - 2*,);
2 2 2 2
Ач1 =P/+o,b[?l4i-ij; £,4i = £/ + 0,1 -^- jJ/+i -2z/+iJ.
Для метода Адамса-Бэшфорта третьего порядка из (6.33) находим
^^ = ^ + *?2"[23 *(£/ -])"1б' (£'-1 " 0 + 5 • (£,.2 ^ 1)],
?i4i = */ +72[23'("^ " 2*^~16' (~^'~1" 2*м) + 5' (~^"2" 2*'~2)''
Для определения «разгонных» точек (*o>Po>2o)>(*i>.Vb2i)>(*2>p2>£2)
воспользуемся модифицированным методом Эйлера. Точка (х0, .?()> ?о)
определяется начальными условиями (0; 1; -1).
Выпишем соотношения для метода трапеций (6.24) и разрешим их
относительно неизвестных:
U/+J U/J 2 lI-u-^J
•^41-2^4,
Я- +0,05£, +0,05£/+i -0,1
■0,05?/-0,05j>/+l+0,9£/-0,tf/+IJ
откуда путем разрешения системы относительно ?/+|,£/+i получаем
а ЛА.А nng-0,1?,+0,8975?,+0,05 П1
У/Ч1 = Л + 0,05г/ + 0,05 И025 0,1;
*/+1 ='
-0,1?/+0,8975?/+0,05
1,1025
297

Таблица 6.4
*l
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
maxe,-
Неявный
метод Эйлера
1,00000
0,80992
0,62960
0,45885
0,29740
0,14500
0,00131
-0,13397
-0,26119
-0,38072
-0,49287
0,03720415
Модиф. метод
Эйлера
1,00000
0,80500
0,61997
0,44479
0,27924
0,12309
-0,02397
-0,16224
-0,29208
-0,41384
-0,52787
0,00067291
Метод Адамса—
Бэшфорта
1,00000
0,80499
0,61991
0,44469
0,27908
0,12285
-0,02428
-0,16265
-0,29257
-0,41441
-0,52853
0,00005942
Метод
трапеций
1,00000
0,80499
0,61991
0,44464
0,279000
0,12273
-0,02444
-0,16284
-0,29279
-0,41465
-0,52879
0,00033550
Точное
решение
1,00000
0,80500
0,61994
0,44470
0,27909
0,12286
-0,02428
-0,16263
-0,29255
-0,41438
-0,52848
-
Таблица 6.5
*/•
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
тах£/
Неявный
метод Эйлера
-1,00000
-0,90083
-0,80316
-0,70753
-0,61440
-0,52408
-0,43684
-0,35287
-0,27229
-0,19518
-0,12158
0,01958133
Модиф. метод
Эйлера
-1,00000
-0,90000
-0,80095
-0,70357
-0,60844
-0,51601
-0,42663
-0,34054
-0,25794
-0,17894
-0,10357
0,00032586
Метод Адамса—
Бэшфорта
-1,00000
-0,90023
-0,80132
-0,70402
-0,60893
-0,51650
-0,42709
-0,34095
-0,25828
-0,17920
-0,10378
0,00012145
Метод
трапеций
-1,00000
-0,90023
-0,80132
-0,70401
-0,60890
-0,51645
-0,42702
-0,34087
-0,25818
-0,17908
-0,10364
0,00003005
Точное
решение
-1,00000
-0,90016
-0,80121
-0,70388
-0,60877
-0,51632
-0,42691
-0,34078
-0,25812 1
-017905
-0,10364
-
298

Результаты проведенных расчетов даны в табл. 6.4 для yity(x) и табл. 6.5
для Zj,z(x) соответственно. Из их анализа вытекает, что наиболее точно
величину yt можно рассчитать методом Адамса—Бэшфорта, а величину £, —
методом трапеций. ■
Пример 6.5. Исследовать устойчивость метода Адамса—Бэшфорта третьего
порядка на примере решения задачи Коши [54]
У = Му-х3) + Зх2, >(-^) =-0,015625
при Л= —, ц = -1 и ц = —100.
Точное решение задачи: у(х) = хъ . При
М)
дифференциальное уравнение имеет вид у'= х3-у + 3х2, а при ц = -100
(hix = -—): / = 100x3-100>> + 3jc2.
Формула (6.33) при h = — принимает форму
Ум-Pi +^<23/, -16/..., + 5/)_2), / = 2,3,...
Положим /о = /(--}■)= 0,1875; у0 = >;0 = -0,15625; /,=/(-1) = 0,046875;
pj = у0 = - 0,001953121; /2 = /(0) = 0 ; ^2=0, т.е. используем в качестве
«разгонных» точек значения, соответствующие точному решению. Результаты
нахождения приближенного решения задачи Коши приведены в табл. 6.6.
Таблица 6.6
/
0
1
2
3
4
5
6
7
8
1 9
А (ь-{)
-0,01562500
-0,001953125
0,0000000
0,00195317
0,01562501
0,05273429
0,12499996
0,24414058
0,42187492
0,66992193
Ошибка
0,00000000
0,00000000
0,00000000
0,00000004
0,00000001
0,00000009
0,00000004
0,00000005
0,00000008
0,00000005
- (и т)
-0,01562500
-0,001953125
0,00000000
0,00195317
0,01562409
0,05275568
0,12449656
0,25408001
0,18516620
6,27264466
Ошибка
0,00000000
0,00000000
0,00000000
0,00000004
0,00000091
0,00002130
0,00050437
0,00993938
0,23670880
5,60272278 1
299

Из анализа решения, приведенного в табл. 6.6, видно, что в случае
А|! = процесс не является устойчивым. Дадим обоснование этому факту.
8
Запишем формулу (6.33) в виде (6.14):
а , ( 23 , 16 , 5 , ^ п
т.е. а0 =l,aj = -1,а2 =а3 =0, Р0 = 0, pf = - —, р2 =—, р3 = ~72'* = 3* ПоэтомУ
рЙ) = ао^3+а^2+а2^аз=^-42,
а(4) = Ро^3+Р,^2+Р24 + Рз=-^(23^- 165 + 5):
Составим уравнение (6.15) при каждом значении Лц.
гг и 1 ,з 73, 16р 5 п
При Лц = — все корни уравнения £ ~7s ~™7^ + ~7 = " лежат внутри
круга единичного радиуса с центром в начале координат, поэтому процесс
устойчив.
п I. 10° сз 2204 с2 1600 с 500 _
При лц = один корень уравнения £ +——-£ 2~^ + Т = ^>
8 96 96 96
- 1 (2204^ _
равныи — • —— , очевидно не лежит внутри указанного круга. Поэтому процесс
неустойчив. Эти выводы подтверждают результаты численного эксперимента.
Ошибка вычисления значении yt при h\i = возрастает (см. правую
8
колонку табл. 6.6).■
6.2.3. Принцип согласования с разложением по формуле Тейлора
Рассмотрим задачу Коши (6.9) в общем случае на неравномерной сетке Qn.
Для получения формулы нахождения последующего значения yUi на шаблоне
(xhxi+i) разложим решение у(х) при х = лс/+1 относительно точки х,- по
формуле Тейлора на промежутке х{ < х < х/Ч1:
Ум = У> + hMy, +\^у'/ +... + -7 АД ,y,(rt + О^1). (6.38)
Входящие в правую часть производные можно определить, дифференцируя
уравнение (6.9) требуемое число раз:
dx'
У' = /(х,у), y" = —f(x,y) = fx +fyy' = fx+ffy ....
300

Если функция f(x,y) имеет /?-е непрерывные производные по обоим
аргументам, то в разложении (6.38) можно учесть слагаемые до Oyij^1). Чем
больше членов разложения используется для вычисления, тем точнее будет
приближение и тем выше порядок схемы. Однако рассчитывать производные
путем дифференцирования правой части уравнения (6.9) невыгодно. Поэтому
Рунге и Кутта независимо друг от друга предложили более удобную и
рациональную форму представления численного решения, при использовании
которой дифференцировать функцию f(x,y) не требуется.
В общем случае методы Рунге—Кутты имеют следующую структуру:
где К и = /(*,,}>,);
*3,i = /(*/ + Mi + b Я + Л/Ч1 Kl*l,/ + fl3,2^2,/) ; (6-39)
**,, =Axi+cshi+lt yi + //,+I (a,AKlti ^ as2K2i+- + ass_xK5_Xi),
где 5- число стадий (этапов), Ksi - значения коэффициентов схемы Рунге-
Кутты, вычисленные на основе правой части уравнения (6.9),
c/-iy = 2,j; alm,l = 2,s;m = 1,5 - 1; &Л,£ = 1,$. Первый индекс в обозначениях
коэффициентов является порядковым номером, а второй соответствует индексу
точки Xj — началу отрезка [лс,,х/+1], на котором производится расчет.
В некоторых методах кроме вычисления приближенного решения yi+l
определяется еще дополнительное значение уих по формуле
Уи\ =Р/+Л/+, •[biKlti+b2K2ti+- + bsKsj]9 (6.40)
порядок которого, как правило, на единицу больше или меньше обеспечиваемого
выражением для j>/+1. Величина j)/+1 -yi+\\ служит для учета погрешности и
управления величиной шага.
Коэффициенты схемы подбираются так, чтобы выражение для j)/+,
согласовывалось с формулой Тейлора (6.38) вплоть до членов степени hf. , где
степень р меняется в зависимости от метода и соответствует порядку схемы.
301

Наибольшее распространение в вычислительной практике нашел метод
Рунге—Кутты четвертого порядка:
Л*1=Л+-£Ч*1,/+2ЛГ2./+2ЛГэ./+*4..-). А>=Л. ' = 0,«-1, (6.41)
где KUI = f, = Дх1гу/),
*2,1=ЛХ1+^У1 +
A/+I
/Г,
1,/ '
*з,, = /fx, +^-,Л +%-*2,1. *4./ = /(*, + W/ + Л,+1 • Кз,,).
Схема (6.41) является четырехчленной, первый коэффициент К\ ,•
относится к точке *,•, второй и третий — к средней точке х, + -^, четвертый -
к точке х/+1. Для этой схемы выбираются следующие параметры, входящие в
(6.39): s = 4, с2 = с3 = -; с4 = 1; <z2ii = ^; "3,1 = fl4.i = 42 = °; сз,2 = j; а4,з = 1 •
Приведем геометрическую интерпретацию метода Рунге—Кутты четвертого
порядка (рис. 6.13). Пусть известна точка (xhyf) на искомой интегральной
кривой у = у(х). Прямая АЕ, проходящая через точку (я,,.?/) и определяющая
величину j?/+j, имеет угловой коэффициент. Этот коэффициент рассчитывается
по угловым коэффициентам касательных в точках A,B,C,D, проведенным
к проходящим через эти точки интегральным кривым (штриховые линии). При
этом коэффициент KXi рассчитывается в точке А, коэффициент K2j ~ в точке
С , коэффициент K$t — в точке В, а коэффициент К4j — в точке D.
Рис. 6.13
302

Замечания.
1. Схемы Рунге-Кутты легко обобщаются на системы дифференциальных
уравнений. Так, применительно к системе двух уравнений
y'(x) = f(x,y,z), y(x0) = yQ,
z'(x) = g(x,y,z), z(x0) = z0
схема Рунге—Кутты четвертого порядка имеет вид
Уи\ = & + -^Ч*1,/ + 2K2,i + 2/T3f/ + *4,i). Уо=Уо>
/ = 0, л - 1 (6.42)
-la* : + 2/7л .. + 7а-> s +ал А. 9* = 7п.
Zu\ = Zi + -^"fel,/ + 2^2,/ + 2?3,i + 04,/)» *0 = Z0
где
*v = /[*/ +"у"' Л + 2Л/+1^2./> */ + 2Л'-+1^2,/1;
4з,/ = *[*/ +~7L' Л + ^Л+Л,/' £,• + 2Л'-+1?2,1 t
^4,/ = /(*/ + л,чь Л + */+1jr3f/, £,■ + л|Ч1^3,/);
Яа,( = И*/ + huu Р/ + Л/+1*з,/> 2/ + Л/+1?з,/)-
2. Соотношения модифицированного метода Эйлера (6.28) можно записать
в форме схемы Рунге—Кутты:
Уи\ = У* + hi+\K2j » i = 0, я -1, у0 = Уо > (6.43)
/Гм = /<*„.?,), *2,, =/<*, +^Lf j)f. + ^*м).
Покажем, что эта схема второго порядка. Разложение (6.38) с учетом
равенства /' = /х + // • /у , где /■ = f(xhyt), частные производные /х,/у и вторая
производная у" вычисляются в точке (х,, у1), принимает вид
Л+1 =Л+^+1Л+|л?+1(/х+у.-/у) + 0(А?+1). (6.44)
Разложение функции f(x,y) относительно точки (x/,j>/) можно записать
следующим образом:
f(x,y) = /<*/,*,■) + (х - х,)/х + (у - я)/, + - (6.45)
где частные производные /х, fy вычисляются в точке (х, ,у().
303

2 '
у = у- +-L±±-f. получаем
Тогда при х = xt; + -
2
2
fr + 1
2
Следовательно, формулу (6.43) можно переписать в виде
йч! = й + W<*,- +А±Ч.?/ +^/(*,,Я)) = А. + W* +|tf+i(A +Л >fy) + o(hlx).
Сравнивая последнее соотношение с (6.44), можно сделать вывод о том,
что схема модифицированного метода Эйлера согласуется с разложением по
формуле Тейлора вплоть до членов степени h}+x и поэтому является методом
Рунге—Кутты второго порядка.
3. Коэффициенты семейства методов Рунге—Кутты (6.39),(6.40) удобно
записывать в виде табл. 6.7. Табл. 6.8 соответствует классическому методу Рунге
—Кутты четвертого порядка (6.41), а в табл. 6.9 приведены коэффициенты
другого метода четвертого порядка (правило —).
0
^2
сз
^
Л
У их
Ум
Таблица 6.7
а7,\
а\\ а3,2
as,\ asy2 - as,s-l
b{ b2 ... bs
b\ b2 ... bs
0
2
2
1
Уи\
Таблица 6.8
2
о I
2
0 0 1
12 2 1
6 6 6 6
0
3
2
3
1
A
Уи\
3
3
1
I
8
Таблица 6.9
1
-1 1
III
8 8 8
Табл. 6.10 соответствует методу Рунге—Кутты (6.43) второго порядка, табл.
6.11 и 6.12 — методам третьего порядка.
Таблица 6.10
0
J_
2
Уи\
Таблица 6.11
0
J_
2
0 1
1
Ум
I 1 I
6 3 6
Таблица 6.12
0
1
3
2
3
•Р/Ч1
1
3
0
1
4
2
3
0
2
4
304

В табл. 6.13 даны коэффициенты метода Фвльберга четвертого порядка, где
формула для J//+i имеет пятый порядок, а в табл. 6.14 — семистадийного метода
Батчера шестого порядка. В табл. 6.15 приведены коэффициенты метода Рунге—
Кутты—Мерсона четвертого порядка, где формула для yi+\ имеет пятый порядок
для систем линейных дифференциальных уравнений с постоянными
коэффициентами и третий порядок для нелинейных систем.
Таблица 6.13
Таблица 6.14
0
4
3
8
12
13
1
2
А
Уи\
Ум
1
4
_3_
32
1932
2197
439
216
_8_
27
25
216
16
135
_9_
32
7200 7296
2197 2197
-8
2
0
0
3680
513
3544
2565
1408
2565
6656
12825
845
4104
1859
4104
2197
4104
28561
56430
40
1
5
_9_
50
0
2
55
0
1
2
2
3
1
3
5
6
1
6
1
1
/ч
-V/+1
1
2
2
9
7
36
35
144
1
360
41
260
13
200
4
9
2
9
55
36
11
36
22
13
0
1
12
35
48
1
8
43
156
И
40
15
8
1
2
118
39
11 4
40 25
1
10
32
195
4
25
80
39
13
200
Таблица 6.15
0
1
3
1
3
1
2
1
Й-1
Й+1
1
3
1
6
1
8
1
2
1
6
1
10
1
6
о
0
0
0
3
8
1
~2
0
3
10
2
2
3
2
5
1
6
1
5
305

Параметры метода Рунге—Кутты—Дормана—Принса пятого порядка
приведены в табл. 6.16. Метод Фельберга седьмого порядка и метод Дормана—Принса
восьмого порядка изложены, например, в [55].
Таблица 6.16
0
5
10
4
5
8
9
1
1
Л
Уи\
Ум
1
5
3
40
44
45
19372
6561
9017
3168
35
384
35
384
5179
57600
9
40
56
15
25360
" 2187
355
33
0
0
0
32
9
64448
6561
46732
5247
500
1113
500
1113
7571
16695
212
729
49
176
125
192
125
192
393
640
5103
18656
2187
6784
2187
6784
92097
339200
84
П
84
187
2100
0
40
4. Для s -стадийных методов Рунге—Кутты справедливо следующее
условие устойчивости, определяемое для задачи (6.12):
Р 2 6 24 5!
<1.
Если ц - действительное число, можно указать интервалы устойчивости:
Лце(-2;0) при 5 = 1,2; Аце(-2,51;0) при 5 = 3; Лце(-2/78;0) при 5 = 4 и т.д.
Пример 6.6. Для задачи Коши
у' = х + у, >>(0) = 1, хе[0;0,2]
выполнить два шага методом Рунге—Кутты второго порядка (6.43) и один
(первый шаг) методом четвертого порядка (6.41). Шаг интегрирования принять
постоянным и равным 0,1. Сравнить оба численных решения с точным
у{х)-2ех -х-1.
306

□ В данной задаче х0 =0,д>0 = 1. Применим схему (6.43).
Первый шаг (/ = 0). В соответствии с постановкой задачи принимается
Л, =0,1. Вычислим ЛГ1|0 ^ f(x0,yQ) = f(x0iy0) = x0 + у0 = 0 + 1 = 1;
*2,о = /<*о + у >^о + у*1,о) = 0,05 + 1,05 = 1,1.
Тогда у{ = у0 + hlK2to = 1 + 0,1 • 1,1 = 1,11.
Второй шаг (/ = 1). Так как шаг постоянный, то h2 = 0,1, а хх = 0,1 и,
следовательно, /Гц = /(xj, pj) = jcj + j>, = 0,1 + 1,11 = 1,12;
^2,i = /<*i+y >Л + y^.i) = o.i + у+ui + o,o5 • i,i2 = i,3i6.
Тогда р2=й +Л2^2,1 =U1 + 0,11,316 = 1,2416. Точное решение: у(х2) = 1,2428055.
Отличие приближенного решения от точного составляет 0,096%.
Выполним теперь первый шаг методом четвертого порядка по формуле
(6.41), записанной при / = 0:
У\ = Уо + mf(K\.o + 2*2,0 + 2*з,о + *4,о)-
При этом вычислим Кх о = х0 + у0 = 0 + 1 = 1;
*2,о=(^о+у) + (Ро+у*1,о) = 0,05 + (1+0,05-1) = 1,1;
*з,о = Uo+y) + (i>o+у*2,о) = 0,05 + (1+ 0,05-1) = 1,105;
*4,о = <*о + hi> + (Уо + Л, • *3,о) = ОД + О + 0,1 • 1,105) = 1,2105;
Р, = 1 +^(1 + 2 • 1,1 + 2 • 1,105 + 1,2105) = 1,1103416.
6
Точное решение: >'(0,1) = 1,1103418.
Сопоставляя точное решения у(х\) в точке х{ с результатами ух,
полученными по схемам второго и четвертого порядка, можно увидеть, что для схемы
четвертого порядка результат ух совпадает с точным решением в семи цифрах, а
для схемы второго порядка — в трех знаках. ■
В заключение данного раздела отметим преимущества и недостатки одно-
шаговых и многошаговых схем:
1. Одношаговые схемы позволяют достаточно легко строить алгоритмы
с переменным шагом и заданной точностью, что необходимо при расчете
функций в областях их больших изменений. Однако они имеют недостаток —
приближенные значения искомой функции, рассчитанные на предыдущих шагах, в
этих схемах не используются.
2. В многошаговых схемах, напротив, учитываются значения искомой
функции, рассчитанные на предыдущих шагах интегрирования, что повышает
порядок точности этих схем без использования дополнительных точек на отрезке
[дс/,х/+1]. Однако эти схемы требуют усложнения расчетных алгоритмов при
реализации переменного шага.
307

Замечание. В явных одношаговых методах обеспечить заданную
точность на каждом очередном шаге из текущей точки (х,,>>,) можно по
следующей методике.
1. Задать начальную величину шага Л(0) = xj®\ -х-, и рассчитать значение
у£\ в точке х^\.
2. Вычислить величину yjlJ{ в точке xjj] с половинным значением шага
/z(1) = (до достижения точки хЦ\ выполняются два шага).
3. Если rp/^j -p/J| < е , то перейти к нахождению приближенного
решения в точке xj^2 = xjl\ + Л(0) . Иначе осуществить еще одно дробление шага, т.е.
вычислить Л(2) = , и найти yjj\ в точке xj1^ = x-t + Л(1).
4. Сравнить решения, полученные с шагом Л(|) и Л(2) в точке х^{. Если
желаемая точность достигнута, расчеты продолжить с шагом Л(,), а если нет, то
процесс дробления шага продолжить до достижения заданной точности.
6.2.4. Принцип аналогий
Данный метод следует из обобщения интегрально-интерполяционного
принципа. Он основан на применении интерполяционных интегрально-
дифференциальных сплайн-функций, преобразования которых —
параметрические соотношения, аппроксимационные формулы для производных и
квадратурные формулы — используются для получения разностных схем решения задачи
Коши [15—24]. Приведем некоторые из этих соотношений, соответствующих
задаче аппроксимации некоторой произвольной функции Ф(х) многочленами
второй степени:
а) параметрическое соотношение, связывающее интерполируемую
функцию Ф(х,) и ее производную w) = Ф'(*/)'
б) формула аппроксимации первой производной в точке jc, на
трехточечном нерегулярном шаблоне (x,-_i,X/,X/+i):
- 1
Ю/Ч1 =
Я,
/41
(нг1¥ я,2"'+1>
5. ,ф. . _i—I—L-ф. +—I ф.
,+| '-' п;>' ' hM ф'+|
^5,4,(1+5,,,)%
(6.47)
где Я*/+|> = * • А, + /> • А,ч1; s,p - целые числа (Я*'+|) = А,(5 + р-8,+1), 8/+1 = 4tL);
308

в) квадратурная формула экстраполяционного типа, имеющая четвертый
порядок:
//♦' =
и?
•i*\
бн;_
н
2(/ + 1)
-Ф
1-2
з(я/_|)2+2^,Я/.,
п;.,
ф
7-1
(6.48)
( 6/»,Я/.1+/1,ч,(3/|,.|+6/»,+2/.)Ч,)ф
п;>'
Эта формула при A/+i = h = const упрощается:
//+| =^(5Ф,-2 -16Ф,., +23Ф,) (|л4Л/3,,];
г) двухинтервальная (трехточечная) обобщенная на нерегулярный шаблон
квадратурная формула парабол четвертого порядка на отрезке [x/_i,x/+l],
выражающая сумму «удельных» значений интегралов через линейную комбинацию
значений Ф/.^Ф^Ф,^:
s,7"-£""
■тф*-*+21т+т-)ф*+т-ф^; (649)
hi \ht hul) hux
д) одноинтервальная (трехточечная) функциональная квадратурная
формула четвертого порядка на отрезке [*/_i,x/+i]
1 6#/+l
//+1I//+1
я*'+|>
1 Lfl + l LfH
1 ^ "/ "3/ ^ 3/
Ф; , + '. , * Ф. + =*(■
п;+Чч1
*♦.
-Ф,
7+1
A fy+1
72
§л+|(§я+1 +2)-M3>/
, (6.50)
которая при hi+l = A = const преобразуется к более простому виду:
//+1=^(-Ф/-1+8Ф,+5Ф/Ч1).
Анализ остаточного слагаемого, получающегося при оценке погрешности
квадратурной формулы (6.50) (см. мажоранту в скобках справа от данной
формулы), указывает на то, что при сгущающейся вправо сетке (условная
аппроксимация интеграла) порядок точности формулы может быть повышен на единицу без
увеличения количества точек шаблона. Действительно, при 6/Ч| < А, легко
получить приближенное условие повышения порядка [18]: А/+1 <А,2. Таким образом,
в данном случае порядок повышается за счет значительного уменьшения шага,
такого, что А/+1 не превышает квадрата шага А,. Этот факт может быть
использован при решении задачи Коши на нерегулярном шаблоне;
309

е) две одноинтервальные (двухточечные) квадратурные формулы
функционально-дифференциального типа:
//+1=^-(ф,+2ф/Ч1)-^-ф;+1 [ън?мч\ (651)
/;+1=/;,+1ф,+%1-(2ф;. + ф;.+1)
24
hfMjj ;
(6.52)
ж) интегрально-функциональнее параметрическое соотношение,
осуществляющее связь интегралов и производных:
^~^&=7(^1^» +2Я<Ы -^+л/ ^-i)-
Л/+1 а,- 6
(6.53)
Дискретные явные или неявные схемы для решения задачи (6.9)
получаются из приведенных соотношений либо посредством аппроксимации производной
(см. разд. 6.2.1), либо путем соответствующей замены одних параметров,
относящихся к параметрическому соотношению или к квадратурной формуле, на
другие параметры. Этот способ построения схем называется способом аналогий.
Так, заменяя в (6.46) ДФ* на Аук, а тк на fk (k = iy /-1) и разрешая
относительно yi+i, получаем двухшаговую явную схему второго порядка (2Я2А):
j?/*i - Л + »?*! AP/.i + лД-1-й—^
'/-И
Л/ )
(6.54)
которая при Л,+1 = h = const преобразуется к виду
Р/+1 =2Я -Р/-1 +А(/}-//-|).
Комбинация схем (6.54) и (6.24) дает обобщенную на нерегулярный шаблон
схему Адамса—Бэшфорта (2Я2В):
У их =У1 +
Л/li
n'+i Л А.. Л"
1п;
Л/
(6.55)
которая при Л/+1 = h = const преобразуется к виду (6.32):
У их = Я + — (ЗЛ ~ /их)-
Аппроксимационная формула (6.47) определяет неявную двухшаговую схему
второго порядка (2НЯ2):
У их
пих
Hf
2(/+D
п/>1 у*-*и\Уих + И*! Лх1+\>У1+\)
i
(6.56)
которая при Л/Ч1 = Л = const принимает вид
310

Замечание. Схема (6.57) является одним из методов Гира, получаемых
на основе формул дифференцирования назад, связывающих значение производной
в точке а*/Ч1 со значениями функции в предыдущих точках */,..., Х/_Л+1(см.
рис.6.2). Схема (6.57) является схемой второго порядка, а неявный метод Эйлера
— схемой первого порядка. Приведем более точные многошаговые схемы,
записанные на регулярных шаблонах:
— схема третьего порядка:
а 18 л 9 а 2л О . г/ лч ,г еп\
Уих = 77 ^"77У1~[ + пу'~2 +7Г Лх'Ч1'>'/+|); ( *
— схема четвертого порядка:
л 48 а 36 л 16 л 3 л 12 , г/ л ч
У их = 2J Л -25^-1 + 25^'2 " 25 Л"3 + 25 Л^(дс'ч|'д'/+|);
— схема пятого порядка:
300 л 300 а 200 а 75 а 12 а 60 . гв а ч
"♦' Я737 " ""137 Л-« +Т37 Л"2 "137Л"3 +Т37Л-4 + Тз7Л'<*'♦''"^
— схема шестого порядка:
360 а 450 а 400 а 225 а 17 а 10 а 60 . г/ а ч
Ум = М7Л ~ М7 ""' + М7Л-2 " 147"» W'"4 " М7Л"5 + M7*/(Ww)-
Известно, что схема (6.58) является А(а) -устойчивой с а = 68°.
Все рассматриваемые ниже схемы получаются из квадратурных формул
(6.48)—(6.52), в которых вместо разности первообразных /)Ч1 - Fi■ = /,-+1
подставляется Aj>,, а вместо Фк (к = / - 2, / -1, /) и Ф'Л подставляются /А и f'k. При этом
порядки точности схем на отрезке [a,b] соответствуют порядкам точности
вычисления интегралов на всем отрезке интегрирования.
Преобразуя таким образом квадратурную формулу (6.48), получаем явную
трехшаговую схему третьего порядка (ЗЯЗ):
Ум = У* +
fy+i
ми
#3?' г з(я/_1)2+2/7/,1Я/.|
J ,-1 '—: //_i +
6/1,Я/.|+/),ч,(язУ,)+2/1,ч,)
(6.59)
n;+1 Л
311

При hu] -h- const она является традиционной, получающейся
интегрально-интерполяционным методом (6.33):
Л+|-Л+^(5//-2-1б//-1+23/,).
Из обобщенной формулы (6.49) следует первая двухшаговая неявная схема
третьего порядка (2НЯЗА)
п2
//-1+2-
, (6.60)
которая при Л/Ч| = h - const преобразуется к виду (6.29).
Одноинтервальная (трехточечная) квадратурная формула (6.50) определяет
вторую двухшаговую неявную схему третьего порядка (2НЯЗБ)
Уи\ = У-t +
бя;+
-Lf , Hi N3i f . П 3/ /vr Л ^
- — Ji-\ + 777- // + -5 ./v*/+i>.V/+i)
(6.61)
Эта схема в соответствии с вышеприведенной оценкой точности интеграла
при 5л+1 < h/ имеет не третий, а четвертый порядок точности. При h = const эта
схема преобразуется к виду (6.36):
И наконец, последние приводимые здесь схемы следуют из квадратурных
формул (6.51), (6.52) (неявные одношаговые схемы) и параметрического
соотношения (6.53) (неявная двухшаговая схема):
Ум « Л + ^-[// + 2/(*/+i,А+,)]-*f-f(xM,ум);
Р/+1 = A +5/4i4?/-i +-у-№Л-1 +2Я/+|У1' + Л/+|/'(х/+1,р/Ч|)],
где /' =/х +/у •/. Эти схемы обозначаются 1НЯЗА, 1НЯЗБ, 2НЯЗД
соответственно.
При Л/+1 = А = const последняя схема преобразуется к виду
Л2
P/+I = " Я-1 + 2й + — [/}'_! + 4/;-' + /'(х/+,, Я+1)] •
Для применения разностных схем, полученных с помощью четырех
различных подходов (см. разд. 6.2.1— 6.2.4), можно использовать общую методику.
312

Методика решения задачи Кош и методами сеток
1. В соответствии с требуемой точностью решения задачи Коши выбрать
численный метод (схему) определенного порядка аппроксимации и типа (явный
или неявный, одношаговый или многошаговый).
2. Задать сетку С1п или выбрать ее параметр (Л, если сетка равномерная;
Л/+,,/ = 0, п - 1 , если сетка неравномерная). Если выбранный метод является
ограниченно устойчивым, то для задания параметра сетки оценить величину
критического шага.
3. Если выбранный метод многошаговый, найти требуемое число
«разгонных» точек.
4. Найти приближенное решение задачи Коши во всех точках сетки Q„.
Если выбран явный метод, каждая следующая точка yj+i рассчитывается по
явной формуле, а если неявный, то с помощью решения в общем случае
нелинейного алгебраического уравнения (6.11) одним из численных методов.
5. Оценить достигнутую точность. В случае невыполнения требований
повторить расчеты, меняя значение шага в соответствии в замечанием в конце разд.
6.2.3 или используя более точный метод.
6.3. СОСТАВНЫЕ СХЕМЫ
Рассматриваемые здесь методы (схемы), называемые составными, известны
под общим названием методов прогноза и коррекции. Из названия следует, что
сначала «предсказывается» значение j)/+1, а затем используется тот или иной
метод для «корректировки» этого значения.
Таким образом, составные схемы включают в себя два шага (этапа) расчета
очередного значения yi+l:
1. Шаг «предиктор» (предсказание), на котором рассчитывается
предсказанное (предварительное) значение yffi.
2. Шаг «корректор» (коррекция), на котором предсказанное значение
уточняется. В результате находится значение yj*}, которое принимается за р/Ч1. Если
промежуток интегрирования не исчерпан, оно далее используется при
реализации очередного шага «предиктор» для нахождения следующего предсказанного
значения у\^\-
Первый шаг реализуется с помощью явных методов, а второй шаг основан
на применении формул неявных методов, в правую часть которых вместо
неизвестного значения yi+{ подставляется результат предсказания. Схемы такого
типа называются также схемами «предиктор-корректор» и в итоге относятся к
явным методам.
Приведем наиболее часто встречающиеся составные схемы.
313

A. Предсказание с помощью явного метода Эйлера (6.19) или метода
Эйлера—Коши (6.21), коррекция по методу трапеций (6.24).
Шаг «предиктор» :
#!V =•?/ + *,>./(*,..?,). (6.62)
или при условии Л/+1 = h = const
#?>=>>_,+2А^(*/^Л (6.63)
где у! и y,_i рассчитаны на предыдущих шагах.
Шаг «корректор» :
Ум -У%\ = Л +^f-lHx„y,) + nxi+hM,y^)\ . (6.64)
Б. Предсказание по методу Адамса-Бэшфорта третьего (6.33) или
четвертого (6.34) порядка, коррекция по методу Адамса-Мултона четвертого порядка
(6.37) (при А/+1 = h - const).
Шаг «предиктор»:
УМ> = У, + ^[23Л - 16/,., + 5/,_2] , (6.65)
или
Ум} = У; + ^-[55/ - 59/., + 37/,_2 - 9/,_31 • (6.66)
Шаг «корректор»:
Ум - Яч/ = Л + ^1/'-2 - V/-i +19/+ 9/(х,+|, #">)] . (6.67)
B. Метод Хемминга четвертого порядка (при A/+j = Л = const).
Шаг «предиктор»:
vt\ = Л-з + у [2// -/-. + 2/-2] • (6.68)
Я/дг «корректор»:
Ум -Ум* =^(9Р, -Р,-2) + у(-/-. +2/ +/(х,Ч1)Р<+п1))1 • (6-69)
Замечания.
1. Разработчикам прикладных программ рекомендуется при решении
конкретных задач выбрать наиболее подходящий составной метод путем
комбинирования схем на шагах «предиктор» и «корректор», соответствующих явным и
неявным схемам. К числу этих схем относятся: П1К2 (1Я1, 1НЯ2), П2К2 (2Я2Б,
1НЯ2), П2КЗ (2Я2Б, 2НЯЗА), ПЗКЗ (ЗЯЗ, 2НЯЗА) и др. (табл. 6.17). Здесь буквы
П и К указывают на шаги «предиктор» и «корректор», рядом с ними приведены
порядки схем, а в скобках - ранее введенные обозначения формул для этих
схем.
314

Таблица 6.17
Предикторы
1Я1 (6.19)
2Я2Б (6.20)
| 2Я2Б (6.20)
ЗЯЗ (6.59)
ЗЯЗА (6.33)
4Я4 (6.34)
Корректоры
1НЯ2 (6.24)
1НЯ2 (6.24)
2НЯЗА (6.60)
2НЯЗА (6.60)
ЗНЯ4 (6.37)
ЗНЯ4 (6.37)
Составная схема
П1К2 (6.62),(6.64)
П2К2 (6.63),(6.64)
П2КЗ
ПЗКЗ
ПЗК4 (6.65),(6.67)
П4К4 (6.66),(6.67)
2. При использовании многошаговых схем (6.63),(6.65)—(6.69) на шаге
«предиктор» и шаге «корректор» необходимо предварительно рассчитать
требуемое число «разгонных» точек (см. разд. 6.2.2). При этом желательно использовать
схемы, порядок которых соответствует порядку основной схемы.
3. Составная схема (6.62),(6.64) является схемой второго порядка и
одновременно относится к семейству схем Рунге—Кутты второго порядка (см. разд.
6.2.3). Она может быть записана в форме
*U = /(*/..?/), *2,/ = /(*/ + Л|Ч1>й + huxKXJ),
Кроме того, данная схема часто называется исправленным методом Эйлера или
схемой Эйлера с пересчетом [35]. Покажем, что эта схема второго порядка, хотя в
ней используется предиктор (6.62) первого порядка. Как и при рассмотрении
модифицированного метода Эйлера (6.43), получим разложение (6.45) функции
Дх, у) при х = х,;+ Л/+1, у = у{,+ hi+xfi:
/(*/ + Л/+1,У/ + huxfi) = fi + hMfx + hMf ■ fy + 0(hul),
где частные производные fx,fy вычисляются в точке (xhyj).
Следовательно,
У их = Р/ +-уЧ// + Я*/ + Л/+,,Я- + hi+lf(xhyi)] = % + -^Ч/, + f + hi+lfx +
+ л/+|у; ./у + о(Л/2+1)] = Р/ +л/+,л +|лД1(Л +frfy) + o(hlx).
Сравнивая последнее соотношение с (6.38), можно сделать вывод о том, что
схема исправленного метода Эйлера согласуется с разложением по формуле Тейлора
вплоть до членов степени hux и поэтому является методом Рунге—Кутты второго
порядка.
Приведем геометрическую интерпретацию схемы «предиктор-корректор»
(6.62),(6.64) (рис. 6.14). Пусть известна точка (xhyt) на искомой интегральной
315

кривой у = у(х). Через эту точку проведем касательную L , тангенс угла
наклона которой равен /(*,) = f(xhyt). Ее уравнение имеет вид
У = У1 +/(*/,А)(*-*/).
5(П)
В качестве результата предсказания берется значение yj+[t получающееся
при х = х, + 1: yffi = у, + hi+lf(xhyt). Далее через точку (x/+i,#"/) к
интегральной кривой проводится прямая Lx с тангенсом угла наклона, равным
л(пк ^ Д*/^/) + /(*/+ьЯч?) г
/(*/+! >>7+i)- Средняя величина LLi— порождает прямую 1^,
проходящую через точку (х/+1,р}п,)). Через точку (x/,j)/) проведем прямую Lj,
параллельную Lq. Ее уравнение: у = у,■ +
Ах19у,) + Дхи19у™)
(X-Xj).
Следующая точка j)/41 = yj*\ приближенного решения (результат
коррекции) получается при х = х,Ч1:
Лч =йк} = Л +^-[/(*/,Р/) + /(х,.^п,))1.
Данное соотношение соответствует (6.64). Если применяется предиктор (6.63)
второго порядка, все приведенные построения сохраняются, только значение
j)y"i находится так же, как на рис. 6.8.
У
У
0
Л
У\л
X,-
**■
^-
^ — -
Л/+1
_>V
— /^ 1
~->^*> f —
1
1
1
1
1
1
1
*/+!
У^
^-"
—*
>v
"Ч
1
У = У(*)
X
Рис. 6.14
316

4. В составных методах может быть использована модификация. Например,
в схеме (6.66),(6.67) после шага «предиктор» вычисляется модифицированное
значение
а(пм) =л(П) + 251_(-(ю_-(П))
где yjK\yjn)~ значения, полученные на шагах «предиктор» и «корректор» в
предыдущей точке.
Затем выполняется шаг «корректор»:
&*,>=;, +£[/,-2 -5/,-, +19/, +9Дхм,$}™>)}.
Следующее значение уи1 вычисляется по формуле
О - 0<к> — fC(K> 0<nh
Уи\ -У/+1 ~ 270 /+I ~"К/+|''
Таким образом, здесь фактически выполняются три приближения.
5. При осуществлении шага «корректор» может быть выполнено несколько
итераций. Например, для корректора (6.64) итерационная формула имеет вид
PJlP'b+tf-imM + fb+h^ffl)], * = 0,I,..; yM-yffl.
Итерации прекращаются либо при выполнении условия \yj+{l) -j?/*| <е для
некоторого положительного £, либо при выполнении ровно т итераций (как
правило, задается т<2). Тогда полагают j)/+1 = <?/f1+l).
Пример 6.7. Найти приближенное решение задачи Коши
/ = х + у, j/(0) = l, хе[0;0,2]
методом «предиктор-корректор» П1К2 (6.62),(6.64) второго порядка. Шаг
интегрирования принять равным 0,1. Сравнить полученное решение с точным
у{х) = 2ех - х - 1.
П Вычислим значения ух и у2 в точках Х\ = 0,1 и х2 = 0,2, полагая _р0 = 1.
Шаг «предиктор» : по формуле (6.62) при Х\ = 0,1 получаем
Pi(n) = i>o + Л - /(*о, Ро) = 1 + 0,1 • (0 + 1) = 1,1 -
Шаг «корректор» : по формуле (6.64) имеем
Первый шаг по выбранной схеме выполнен. Реализуем следующий.
j>, s ylK) = 1 + М[(0 + 1) + (0,1 + 1,1)] = 1,11.
317

Шаг «предиктор»: по формуле (6.62) при х2 = 0,2 получим
#П) = Pi + h.f(xuyx) = 1,11 + 0,1 (ОД + 1,11) = 1,231.
Шаг «корректор»: по формуле (6.64) имеем
у2 = у(2к) = 1,11 + — [(0,1 + 1,11) + (0,2 + 1,231)] = 1,24205.
Точное решение: у(х2) = 1,2428055. Отличие приближенного решения от
точного составляет 0,06%. Так как отрезок интегрирования исчерпан, процесс
закончен, иначе его следовало бы продолжить.■
Пример 6.8. Приближенно решить задачу Коши
/ = -2у-Зх + 2, >>(0) = 0
на отрезке [0; 1] с шагом h = 0,1 различными методами: Эйлера (явным и
неявным), предсказания и коррекции (6.62),(6.64) второго порядка, Рунге-Кутты
четвертого порядка и методом трапеций.
□ Используя исходный вид уравнения (подчеркнем, что оно линейное), из
(6.19) получаем формулу явного метода Эйлера:
Р/+1=Я+0,И-2?,-Зх,+2), р0=0, / = <)£;
из (6.62),(6.64) — формулы метода предсказания и коррекции:
^(")вЛ+0.Ь(-2л-Зх/+2),
Ум = % +-y(~2i)/ "ЗХ/ + 2 " 2?™ "3X/+I + 2);
из формулы (6.41) - формулы метода Рунге-Кутты четвертого порядка:
А+1 = & + ^ки + 2K2.i + 1K\i + ^4,/).
*i,/ = -2р/ " 3*/ + 2. кг; = "2 • (у, + 0,05 • KXJ) - 3 • (х, + 0,05) + 2;
Ку=-2-(у/+0,05-Кг,)-3-(ъ+0,05) + 2\ KAi =-2(х/ н-0,1 • А'з,/)-3-(х,- +0,1) + 2;
из (6.23) — формулу неявного метода Эйлера:
Р/+1 = Р/ + W ' (-2Я-+1 " 3*/+1 + 2),
Я- -0,3х/+, +0,2
откуда yi+] = -i j^j ;
318

из (6.24) - формулу метода трапеций:
Л+1 = >'/ + "Y ■ (~2Я " 3*/ + 2 " 2Яч1 - Зх/+| + 2),
откуда
0,9-Я-f 0,1-х,+2.0,1-|-0,1х/+1
0 2 2
Ум ~ 1,1
Очевидно, в данном примере удалось получить явные формулы для
нахождения j//+j неявным методом Эйлера и методом трапеций лишь в силу
линейности решаемого уравнения. В общем случае применяются методы простых
итераций (6.26) или Ньютона.
Точное решение рассматриваемой задачи Коши: у(х) - 1,75 - 1,5.x -1,75 е~2х.
Результаты расчетов приведены в табл. 6.18, в последней строке которой указаны
фактические погрешности.
Таблица 6.18
х1
1 0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
max 6,
Явный
метод
Эйлера
0,000
0,200
0,330
0,404
0,433
0,427
0,391
0,333
0,256
0,165
0,062
0,068
Неявный
метод
Эйлера
0,000
0,142
0,238
0,287
0,306
0,297
0,264
0,212
0,143
0,061
-0,033
0,059
Метод
Рунге-
Кутты
0,000
0,167
0,277
0,340
0,364
0,356
0,323
0,268
0,197
0,111
0,013
0,0000104
Метод
предсказания и
коррекции
0,000
0,165
0,273
0,335
0,359
0,351
0,318
0,264
0,192
0,107
0,009
0,005
Метод
трапеций
0,000
0,168
0,279
0,342
0,366
0,358
0,325
0,270
0,199
0,112
0,015
0,002
У(х)
0,000
0,167
0,277 1
0,340 1
0,364
0,356 1
0,323 1
0,268
0,197 |
о,ш |
0,013
Анализ результатов показывает, что при решении данной задачи метод
предсказания и коррекции точнее явного и неявного методов Эйлера, но
уступает методу Рунге—Кутты и совсем немного методу трапеций (порядок
погрешности одинаков).»
319

Пример 6.9. Найти приближенное решение задачи Коши
у' = х + у, у(0) = 1 хе [0; 0,4065]
на нерегулярной сетке Q3 = (0,000; 0,150; 0,285; 0,4065) с /;, = 0,15 ;5/+1 =0,9 ; / = 1,2
с помощью методов предсказания и коррекции П1К2, П2К2, П2КЗ, ПЗКЗ.
□ Численные результаты помещены в табл. 6.19.
Таблица 6.19
Тип
схемы
**"
0,150
0,285
0,4065
П1
1Я1
К2
1НЯ2
1,172711
0,08
1,372442
0,15
1,593437
0,20
П2
2Я2Б
К2
1НЯ2
1,174097
0,036
1,375370
0,061
1,597867
0,079
П2
2Я2Б
КЗ
2НЯЗА
1,173700
0,0027
1,374445
0,0057
1,596537
0,0043
ПЗ
ЗЯЗ
КЗ
2НЯЗА
1,1736998
0,0027
1,374467
0,00415
1,596576
0,0019
Точное |
решение
У(Ъ) \
1,1736684
1,374524
1,596576
Для обеспечения расчета на первых шагах всех двухшаговых схем и одной
трехшаговой предварительно рассчитывалось значение у в точке х = 0,01 по
схеме Эйлера П1К2. В последнем столбце табл. 6.19 указано точное значение,
полученное аналитически. Относительные погрешности численных результатов
указаны в строках, расположенных ниже строк, в которых помещены численные
значения yt искомой функции. Анализ результатов свидетельствует об
увеличении точности расчетов при повышении порядков схем как на шаге «предиктор»,
так и на шаге «корректор». Эти результаты оправдывают применение схем
с многошаговым предиктором. Минимальная погрешность обеспечивается
схемой ПЗКЗ, однако схема П2КЗ также приводит к хорошим результатам.■
6.4. ЭКСТРАПОЛЯЦИОННЫЕ МЕТОДЫ
Методы предсказания (см. разд. 6.3) можно рассматривать как методы
экстраполяции, где уи{ экстраполируется по известным предыдущим значениям.
Здесь представлены другие экстраполяционные методы [53-55].
Процедура нахождения очередной рассчитываемой точки (*; + i,p/+i)
состоит из двух этапов.
Первый этап. Получение последовательности решений в точке х = хи]
с использованием некоторой стратегии уменьшения шага.
Второй этап. Уточнение численного решения на основе процедур
полиномиальной или рациональной экстраполяции.
Способы реализации первого этапа. При решении конкретной задачи Коши
следует задать число М, определяемое максимальным допустимым порядком
экстраполяции, осуществляемой на втором этапе.
Рассмотрим процедуру интегрирования дифференциального уравнения (6.9)
на двухточечном шаблоне (xhxi+l) с длиной шага пу называемого базовым.
320

Определим последовательность чисел N0,Nb...yNM , задающую
количество частичных отрезков, располагающихся на промежутке [х/,х/Ч1]:
NM>NM_l>...>Nr>...>Nl>NQ (0<г<Л/), (6.70)
и соответствующую последовательность значений шага hQihli...Jhry...ihM:
/*r=-^-, г = 0,1,..., М. (6.71)
Разными авторами рекомендуются такие последовательности
iVo,^,,...,^:
~ Дойфлхардом: {2,4,6,8,10,12,14,16,18,20,...} или {1,2,4,6,8,10,12,14,16,18,20,...};
«гармоническая» последовательность {1,2,3,4,5,6,7,8,....};
- Ромбергом: {2,4,8,16,32,64,...} или {1,2,4,8,16,32,64,...};
~ Булиршем и Штером: {2,3,4,6,8,12,16,24,32,...} или {1,2,3,4,6,8,12,16,24,32,...}.
Предположим, что точка (х,, р,) известна. При каждом значении г = 0,Л/
генерируем сетку
/, =дс/+5-Лг, * = 0,l,...,jVr, t0=xit tNf=xu{y (6.72)
и, применяя какой-либо разностный метод, интегрируем решаемое уравнение на
отрезке [х/,х/+1] с каждым значением шага Лг, начиная от г = 0 и кончая г = М.
В результате получится (М + 1) значений:
^.о-^ыЛ). г = 0,1,...,Л/, (6.73)
где у(хи\>К)~~ решение задачи Коши в точке х/+1 , найденное при
интегрировании с шагом hr.
Интегрирование рекомендуется проводить следующими методами [53-55]:
а) явным методом Эйлера:
*о = yt, Z5+i =ZS + hrf(tSiZs), s = 0,1,...,Nr -1, (6.74)
Tr,o = Zn, '»
б) методом трапеций:
zq =u, zs+l =^+у[/(/5,0 + А/5+1,г5+1)], 5 = 0,l,...,//r-l,
Tr,o = Zsr \
321

в) методом Эйлера—Коти, модифицированным Грэггом:
*о =&. Z\ = *о+ло/('о>гоЬ
Zs+\ =*,_1+2Аг/(/„г,), 5 = l,...,iVr-l, (6.75)
г) обратным методом Эйлера:
д) по правилу средней тонки (значение zs+\ находится так же, как и в
остальных неявных методах, изложенных в разд. 6.2 и 6.3):
и fit + hr Sj+gj+il
^r.O = Z-N, \
e) методом Бадера и Дойфлхарда [53], который предложен для решения
жестких автономных систем вида Y' -F(Y). Заметим, что неавтономные
системы (6.7) типа У = F(x, Y) всегда можно свести к автономным путем введения
новой переменной, удовлетворяющей уравнению
У'п+\ =1> >Wi(*o) = *o>
и посредством рассмотрения расширенного вектора У =(У,ул+1). С учетом
обозначений
Jl
2г
J = Fy(Y), F(Y) = F(Y)-JY, hr =^-
метод записывается в форме
Ло«£, ^=(E-hrjyllYi^hrF(Yi)]i
i]k+{=(E-hrJyll(E + hrJ)j]k_l+2hrF(r]k)]t * = l,2,...,2r,
ТГ,0 =т(Л2г-1 +Tl2r+l)-
322

В результате применения каждого из методов получается столбец:
'0,0
ho
(6.77)
'Л/-1.0
!м,о-
Способы реализации второго этапа. По полученным на первом этапе
(Л/+1) точкам {hr,y{xM,hr)) могут быть построены либо интерполяционный
полином М -й степени , либо рациональная функция.
Таким образом, для уточнения найденных на первом этапе решений
используются:
а) полиномиальная экстраполяция Эйткена—Невилла:
Tr.o=ylxMthr)9 г = 0,1,...,М;
Т —Т
Tr,s = 27+1,5-1 + т*'5"1 v '''"'> ^ = 1,2,...,Л/; г = 0,1,...,Л/-5; (6.78)
ГА.)
vA+*J
-1
где, как правило, полагают у = 1 или у = 2.
По формуле (6.78) заполняется табл. 6.20.
Таблица 6.20
То.о
! т10
^2,0
Тм-\,о
Тм,о
Тол
7i,i
7л/-2,1
^Л/-!,!
7о.2
^л/-
2,2
^0,Л/-1
^1,Л/-1
То.л/
В качестве уточненного результата р/+1 принимается значение Т0 м ;
323

б) рациональная экстраполяция, предложенная Булиршем и Штером:
7^=0; г = 1,...,Л/; T,tQ =у(х/+,А), г = 0.1 Л/ ;
7/4-1,5-1 ~^Г.5-1
^Г,5 -^Г+1,5-1 +
[ , ^+1,5-1 -Tr,S-\ I
,* = 1,2,...,М; r = 0,l,...fA/-j. (6.79)
V ^+1,5-1 ~ ^r+l.j-2 J
Обычно полагают y = l или у = 2. В результате формируется табл. 6.21.
Таблица 6.21
В качестве уточненного результата уих принимается значение Т0 м.
Замечания.
1. Если на первом этапе применять формулу (6.75), а на втором этапе -
рациональную экстраполяцию, то получаем метод Грэгга—Булирша—Штера.
2. Рекомендуемый максимальный порядок экстраполяции М = 6.
3. Существуют различные модификации экстраполяционных методов,
в том числе с динамическим изменением порядка экстраполяции, контролем
точности, рекуррентной реализацией экстраполяции [53-55].
Алгоритм применения экстраполяционных методов
1. Задать: а) порядок аппроксимации М\ б) базовый шаг //; в)
последовательность N0,Nly...,NM.
2. Выбрать разностный метод для нахождения решений с величинами шага,
равными по,И]у....,Им , и получить значения, составляющие столбец (6.77).
3. Выбрать метод экстраполяции, задать параметр у и получить уточненное
решение Т0 м по формуле (6.78) при полиномиальной экстраполяции или (6.79)
при рациональной экстраполяции. Перейти к следующему промежутку
интегрирования.
324

Пример 6.10. Решить задачу Коши [53]
/ = \+У2, У(0) = \
на отрезке [0; 0,25] с базовым шагом h = 0,25 и порядком экстраполяции, равным
Л/ = 3.
D Точное решение задачи: у(х) = tg(x + —), >>(0,25) = 1,685796417. Будем ис-
4
пользовать последовательность Ромберга. Так как М - 3, выберем из нее четыре
первых числа: 2,4,8,16, т.е. NQ =2, Л^ =4, N2 =8, УУ3 =16. Тогда по формуле
(6.71) получаем: 1ц =—-, Л, = —-, h2 =—-,h3 = -—.
Z 4 О 10
Для нахождения приближенного решения задачи на первом этапе
применим явный метод Эйлера (6.74) , а на втором этапе — рациональную
экстраполяцию (6.79) при у = 1 (табл. 6.22).
Таблица 6.22
1,5703125000 16720018467
0 i,o/zuuiew/ 1б854629545
1,6195625218 1,6814888520 1,6857868712
° 1 6499448310 1,6857435231
0 ' 1,6845757643
1,6670804665
Элементы второго столбца табл. 6.22 получены по формулам (6.74), т.е.
7о.о =У(0,25;Ло) = 1,5703125000,
Г1>0 =у(0,25;Л,) = 1,6195625218,
Г20 = у(0,25; Л2) = 1,6499448310,
Гз,0 = ^(0,25; Л3) = 1,6670804665.
Приведем примеры расчетов по формуле (6.79):
Тол =71о +~—~т
ЧУ
^i.o ~ Tq.o
- = 1,6195625218 +
ч,о -'о.о
-1
7|.о-Г,,.,
1,6195625218-1,5703125000
2Ч1-
1,6195625218-1,5703125000 ^
1,6195625218-0 J
-=1,6720018467;
-1
325

Т\,\ = ^2,0 + "
1 2,0 ~ ' 1,0
__l
h2j
= 1,6499448310 +
'2,0 -'1,0
^2,0 ~ ^2,-1 J
■1
1,6499448310-1,6195625218
241
10,2
1,6499448310-1,6195625218)
1,6814888520 ;
'7i.i +
1,6499448310-0
J'
\h2j
^1,1-7b.il
•=1,6814888520 +
^1,1 ~ 7*1,0
1
1,6814888520-1,6720018467
, . 1,6814888520 - 1,6720018467^
1,6814888520-1,6195625218 J"
1,6854629545 ;
'0,3 = '1,2
r.,+-
4,2 -'0,2
ho] (. _T12 -70,2"I
= 1,6857435231 +
7i.2-7i.i;
■1
1,6857435231-1,6854629545
{ и
,6857435231-1,6854629545^
,6857435231 - 1,6814888520 J"
1,6857868712.
Остальные вычисления аналогичны. Погрешность полученного решения
р(0,25) = 1,6857868712 составляет
| 1,6857868712 -1,685796417 | = 5,2894.10~5.
Если воспользоваться обратным методом Эйлера (6.76) на первом этапе, а
полиномиальной экстраполяцией с параметром у = 1 на втором этапе, то
получим результаты, приведенные в табл. 6.23.
Таблица 6.23
1,8028169014 lf6729289242 ______
1 7Г7Я7?01?я 1,6865256650
\,ШЪШ11* j 683]264798 1,6857760212
1,7104996963 1,6858697276
.,6978418056 1'6851839,5°
326

Здесь результаты экстраполяции находятся по формуле (6.78), например,
'о,з - М,2
7Ь+-
4,2 ~ у0,2
(VI
= 1,6858697276 +
1
1,6858697276 -1,6865256650 ,,Q„7,n010
+ — ■ = 1,6857760212 .
Погрешность полученного решения составляет
| 1,6857760212 -1,685796417 | = 2,039 • Ю-5.
Воспользуемся обратным методом Эйлера (6.76) и рациональной
экстраполяцией при у = 1 (табл. 6.24).
Таблица 6.24
Л 1,8028169014 16774452643
0 i,o//w^o<u ! 6858494038
1,7378729128 1>683975418б
^7104"6963 1,6853698785 1б858°26769
и 1,6978418056
1,6857961912
Фактическая погрешность полученного решения равна
11,6857961912 - 1,685796417 | = 7,2598 • ИГ6.
Применим модифицированный метод Эйлера — Коши и рациональную
экстраполяцию при у = 2(метод Грэгга—Булирша-Штера).
Таблица 6.25
1,6406250000 1>684255б897 ,^75П^
0 1 *7-miRQ^ 1,6857813466
1,6731318956 16856738366 1,6857963393
1,6825207564 1,6857960729
° 1,6849701.71 1'6857881562
Погрешность полученного решения:
| 1,6857963393 - 1,685796417 | = 3,4425 • 1<Г7.
Очевидно, найденное в табл. 6.25 решение точнее остальных.
327

6.5. НЕПРЕРЫВНО-ДИСКРЕТНЫЕ МЕТОДЫ
6.5.1. Конструирование последовательных сплайн-методов
Результаты, получаемые численными методами сеток, имеют
дискретный характер и, как отмечено ранее, требуют восполнения для
определения значений функций в промежуточных точках и, возможно, для
последующей обработки найденного решения. Этого недостатка лишены сплайн-методы
решения задачи Коши. Однако классические сплайн-методы, основанные
на разложении искомой функции в ряд Тейлора, не удобны в практической
реализации, так как для нелинейных задач требуется решать нелинейные
алгебраические уравнения [41]. В данном разделе излагаются непрерывно-
дискретные методы, называемые последовательными сплайн-методами решения
задачи Коши второго и третьего порядков, которые позволяют избежать
решения нелинейных уравнений [18].
Процедура решения задачи Коши при переходе от известного значения у,
в точке х, к очередному рассчитываемому значению yi+l в точке х/+1 состоит из
двух этапов.
Первый этап. Находится дискретное опорное решение задачи Коши с
помощью явных или неявных методов второго и третьего порядков, изложенных
выше.
Второй этап. Полученное на первом этапе опорное решение
подставляется в соответствующую по порядку формулу многочлена (сплайн-функцию).
В качестве этих сплайн-функций могут быть приняты многочлены второй
и третьей степени, использующиеся в теории приближений:
Зц(х) = У1+п1Г{х-х,) + —
П:Л
U
^3,/W = i)/+^?•(*-*/)+
\h щ
ЗДр/ 3m, A/W/ '
(х-х,)2, (/ = 0,1,..., /i-l); (6.80)
(х-х,)2 +
+ ^(-^АЪ+2т1+Ат-\(х-Х;У , (/ = 0,1,...,л-1), (6.81)
Л/+Л Л/Ч1 )
где Щ = у'(х;). Формула для S2j(x) соответствует многочлену, получаемому по
условиям согласования bS2tj(xk) = 0, (к = /,/ + 1); bS^^Xj) = 0 , а формула для
Sij - формуле (4.75).
Таким образом, алгоритм получения непрерывного сплайн-решения
задачи Коши на каждом частичном отрезке [х/,х/+|] (/= 0,1,...,л-l)
разбиения отрезка [a, b] на п промежутков (данное разбиение может
осуществляться как заранее, так и в процессе решения задачи) содержит две
совокупности вычислительных процедур, которые выполняются последовательно и
328

независимо друг от друга. Последовательный характер данных процедур
определяет название данного метода решения задачи Коши.
Рассмотрим совокупности этих процедур отдельно для схем второго и
третьего порядков, так как они имеют некоторые особенности. Здесь, как и
выше, решается задача Коши для уравнения первого порядка
/ = /(х9у)3 у(х0) = у0.
6.5.2. Схема второго порядка
Первый этап. Рассчитывается дискретное решение Уо$\у...>уп по одной
наиболее приемлемой явной или неявной несоставной схеме (см. разд. 6.2)
или по составной схеме, скомпонованной из совокупности явной и неявной
схем (см. разд. 6.3). Решение, полученное на данном этапе, называется
опорным. При выборе конкретной схемы необходимо, чтобы ее порядок
точности равнялся /7-1 = 2, где р = 3 - порядок сходимости сплайн-функции на
отрезке [xi9xl+l] .
Второй этап. Ha каждом очередном отрезке [xitxi+{] дискретное
решение преобразуется в непрерывное путем определения одного из звеньев
сплайн-функции (6.80). Для этого сначала необходимо рассчитать
коэффициенты д0,/' °i,i * °2,/ многочлена
Из сопоставления формул (6.82) и (6.80) видно, что коэффициент aQ i
определяется значением у,, которое известно, а коэффициент ах ., равный
производной /(х, ) = mj, находится путем дифференцирования в точке х = х(
сплайн-функции ^./-iM» рассчитанной на предыдущем шаге
интегрирования. Таким образом, для а0 . и ах . имеем:
Последний коэффициент а2;. вычисляется с использованием
полученного на первом этапе дискретного решения по формуле
следующей из (6.80). Здесь Ар/= U+i-р/ (значения yh i = 1,/i, вычислены
на первом этапе), hi+{ = х/Ч1 - х,.
329

Замечания.
1. При построении функции S20 {х) на первом частичном отрезке
следует положить aQ0 = у0 = у0 ( значение у0 задано в задаче Коши (6.9)), а
а\,о =Лхо>Уо)'
2. Данный алгоритм построения сплайн-функции S2(x) обеспечивает
п-\
непрерывность самого решения у{х) = [jS2i(x) на всем отрезке [a,b], а
также его производной, т.е. ^i./'-iMl _ = ^2,/М| _ (/' = ЬЛ~П- Поэтому
получаемое по данной схеме решение соответствует параболическому сплайну
дефекта q = 1.
Пример 6.11. Для задачи Коши
У' = х + у; у(0)=1
найти численное решение на отрезке [0; 0,4065] последовательным сплайн-
методом второго порядка, задав число частичных отрезков п = 3 ; параметр
нерегулярности сетки 8/Ч1 = 0,9(/ = 1;2), шаг Л| = 0,15.
□ 1. Формирование узлов сетки. С учетом заданных параметров сетки
находим:
х0=0; Х| =дс0+Л, =0,15, h2/h{= 0,9 \ h2 = 0,15 0,9 = 0,135;
х2 =х, + Л2 =0,15 + 0,135 = 0,285; h3/h2 =0,9; А3 = 0,135 0,9 = 0,1215;
х3 =0,285 + 0,125 = 0,4065.
2. Получение опорного решения (первый этап). В качестве опорного
возьмем готовое решение, полученное выше (в разд. 6.3) по схеме П2К2,
имеющей второй порядок точности. Данное решение приведено в табл. 6.19
в третьей от левого края колонке. Нумерацию узлов для данных, помещенных
в эту таблицу, следует начать с / = 1, так как узел х0 = 0 в ней не содержится.
3. Построение формул сплайн-функций на трех частичных отрезках
промежутка [0; 0,4065J (второй этап).
Рассчитаем коэффициенты сплайн-функции на первом частичном
отрезке [0; 0,15]:
°о,о = Уо = Уо = 1; *ii0 = Ахо>Уо)=хо + Уо = 1. Д?о = У\ "Уо = У\ ~1 =
= 1,1740967-1 = 0,1740967,
2-° А, { Л, 1-°) 0,15 (, 0,15 )
330

С учетом этих коэффициентов записываем формулу первого звена сплайн-
*2.о(
функции: 520(x)=l + x + l,0709644x2.
Рассчитаем коэффициенты сплайн-функции на втором частичном
отрезке [0,15; 0,285]:
аол = j>, = 1,174096; ац = S^(х) Ц15 = 1 + 2 • 1,0709644 • х |х=015 = 1,3212893;
1
2'1 И,
^-«»■)- — \1тЗШ" 1Л74096? - *>32128931 - *>2564633-
А2 WJ 0,135 I, 0,135 J
С помощью коэффициентов записываем формулу второго звена сплайн-
функции:
S2l(x) = 1,1740967 + 1,3212893. (х - 0,15)+ 1,2564633 • (х -0,15)2.
Аналогично рассчитываются коэффициенты сплайн-функции и
записывается формула третьего звена:
S22{х) = 1,3753698 + 1,6605343 (х-0,285)+ 1,4050819-{х-0,285)2.
В результате получено непрерывное решение задачи Коши, соответствующее
параболическому сплайну дефекта q = 1 .■
Замечание. В примере 6.11, так же как и в последующих двух,
связанных с применением кубических сплайн-функций S^x), процессы
получения дискретного и непрерывного решений (на первом и втором этапах) для
упрощения полностью разделены. При решении реальных задач Коши
более целесообразно их не разделять, а сразу после определения дискретного
решения на очередном частичном отрезке [х/}х/+1] строить соответствующее
непрерывное решение, т.е. формировать очередное звено сплайн-функции.
6.5.3. Схема третьего порядка
Схема третьего порядка может быть реализована двумя различными
способами, первый из которых основан на использовании формулы (6.71),
а второй на иной конструкции формулы звена сплайна, получаемой в
данном разделе из условий непрерывности первой и второй производной.
Первый способ реализации схемы третьего порядка.
Первый этап. Рассчитывается дискретное (опорное) решение j>/+,
в точке х/Ч1 по одной наиболее приемлемой явной или неявной
несоставной схеме или по некоторой составной схеме, состоящей из явной и
неявной схем. Порядок точности этой схемы должен быть не ниже трех, что
соответствует /?-1, где р = 4 - порядок сходимости сплайн-функции S^x).
331

Второй этап. При выполнении этого этапа дискретное решение yit
j)/+i, соответствующее концам отрезка [x/,x/ + iL преобразуется в
непрерывное путем построения одного звена сплайн-функции (6.81). Для этого, так
же как и для схемы второго порядка, вначале рассчитываются
коэффициенты «о,/»я1,/»^2,/'дз,/ многочлена S$j(x):
^3,1 W = %i + *if/(* ~ Xj)+a2ti(x - ж,-)2 + a2J{x - x,)3, / = 0, л - 1. (6.83)
Из сопоставления формул (6.81) и (6.83) видно, что aQ . определяется
значением >>,, которое рассчитано на предыдущем шаге. Коэффициент л, .
вычисляется по формуле а1 .. = /(*,-,у,), а коэффициенты a2i и я3/ — с
использованием дискретного решения по формулам:
ЗДу, 3m) Am)- . 3 ( 2Ду, - _ ")
Л/+1 Л/Ч1 Л/Ч1 ' Л/+1 I Л/Ч1 J
следующим из (6.81).
Здесь, как и выше, принято обозначение mi=y\xi) . Величина mi+l
вычисляется с использованием правой части исходного
дифференциального уравнения, т.е. т1+{ = /(*/+i>.?/+i)- При построении функции ^з.оМ на
первом отрезке следует положить а00 = у0 = у0 , а ах 0 = /(хо,■?())•
Пример 6.12. Для задачи Коши
У = х + у; Я°) = 1
найти численное решение на отрезке [0; 0,4065] последовательным сплайн-
методом третьего порядка (л = 3,5/Ч1 = 0,9; //j = 0,15) в соответствии с
изложенным первым способом.
□ 1. Формирование узлов сетки осуществляется аналогично примеру
6.11.
2. Получение опорного решения (первый этап). В качестве опорного
возьмем решение, рассчитанное в предыдущем разделе по схеме П2КЗ,
имеющей третий порядок точности. Данное решение приведено в табл. 6.19
в четвертой от левого края колонке. Нумерацию узлов для данных,
помещенных в эту таблицу, следует начать с / = 1, так как узел х0=0 в ней не
содержится.
3. Построение формул сплайн-функции на трех частичных отрезках
разбиения отрезка [0; 0,4065] (второй этап).
Рассчитаем коэффициенты сплайн-функции на первом отрезке [0; 0,15]
(первое звено сплайна):
яо,о = й> = уо = *; ^1,0 = % = /(*о. й>)=! = щ;
332

Щ = /(*1>й)=*1+й =0,15 + 1,1736998 = 1,3236998;
3AJ)0 3m0 Дет0 _ 3(1,1736998-1) 3 • 1 1,3236998-1
"2'0= h? ~ *i - h{
0,152
0,15 0,15
1,0019746;
:'з,о-1Т
( 2др0 0- А-1
— + 2т0 + Дт0 '
I Л1
3 f.2.W23^98 + 2.1 + 0i3236998],o^42332.
0,152
0,15
По значениям рассчитанных коэффициентов записывается формула первого
звена сплайн-функции 530(х)= 1 + х + 1,0019746 • х2 + 0,342332-х3.
Таблица 6.26
Номер звена
0
1
2
ао;
1,0000
1,1737
1,3744
аи
1,0000
1,3237
1,6594
Я2,0
1,0020
1,1419
1,3318
аз,о
0,3423
0,5016
0,4507
Аналогично находятся и два оставшихся звена кубической сплайн-
функции. Коэффициенты всех трех звеньев приведены в табл. 6.26. ■
Второй способ реализации схемы третьего порядка.
При необходимости строгого выполнения условия непрерывности
первой и второй производной в узлах расчетной сетки коэффициенты
искомого кубического сплайна определяются из двух условий интерполяции
(согласования) на концах отрезка [х/,х/+1] и двух условий стыковки
(непрерывности) первой и второй производной в узлах, соединяющих два
соседних отрезка [*,_,,х,] и [x,,X/+i], т.е.
^./-lML. -'fyMLr.. / = 1,я-1,
^м(х)Ц=5з:/(х)Ц, /«1,1,-1.
Производные, указанные в левых частях этих условий стыковки, при
каждом значении / вычисляются с помощью многочлена, полученного на
предыдущем шаге интегрирования, т.е. на отрезке [x/_i,x,].
С учетом отмеченных выше двух условий согласования и двух условий
стыковки нетрудно получить следующую формулу / -го звена сплайна:
где /я,- = у'(х{) = ^з,/-1 (*/) *» Щ - У"(х1)= ^з',/-1 (*/) • Таким образом,
коэффициенты звена сплайна (6.84) находятся по формулам
ззз

— с, , v /Я/ *$3,/-1(*/)
«о,/ = tt, «!,/ = /я/ = ^3,i-i (*/) , д2,/ = у = 2 '
a2J = 7зг(дЛ " «1,/ Л/+1 ~ «2,Л>1), / = 1, л - 1.
На первом отрезке для первого звена сплайна коэффициенты я00, д10,
д2,о вычисляются по формулам
— г, а ч /и0 /'(*о) /'(*о».?о)
«о,о = И> =^о. «1,0 = ™o =/(^о.Уо)> «2,0 = 2 ="2" = 2~"
Пример 6.13. Решить задачу, сформулированную в примерах 6.11 и
6.12, с помощью второго способа реализации схемы третьего порядка.
□ 1. Формирование узлов сетки аналогично примерам 6.11 и 6.12.
2. Получение опорного решения. Осуществляется аналогично
изложенному в примере 6.12.
3. Построение звеньев сплайн-функции на трех частичных отрезках
[0;0,15]; [0,15;0,285]; [0,285; 0,4065].
Рассчитаем коэффициенты сплайн-функции на первом частичном отрезке
[0; 0,15] (первое звено сплайна):
*о,о = уо = уо = 1; «i,o = у'о = /(*о. А>)= i = щ;
2,0 2 2 2 2 2'
л30 = Дг-Гл^о -^Г0 ^ --^-Л!2! = —Ц-(о,1736998-1-0,15- i -0,152) = 0,3554963.
Л| V 2 J 0,15
С помощью этих коэффициентов записываем формулу первого звена сплайн-
функции:
^3,0 М = 1 + х + х2 + 0,3554963 х3.
Рассчитаем коэффициенты второго звена сплайн-функции на втором
частичном отрезке [0,15; 0,285] = [xj,x2] (h2 =0,135). По формуле первого
звена ^зо(х) вычисляются первые и вторые производные «S^oMl
^Vo (х) соответственно:
^.°MLo.i5 =(' + 2х +3-0,3554963 *2)Ц15 = 1,323996 = щ ;
■^'oWL-o.is =(2+ 6-0,3554963 х)|х=015 = 2,3199466 = т,.
334

После этого легко найти все коэффициенты многочлена £3,1 М вто~
рого звена сплайн-функции:
oQl = й = 1,1736998; аи = т, = 1,323996; а2Х = ^ = 2'3199466 = 1,1599733;
0,1353
яз,1 =Тт(Лй -mih2~Yh4 =
(1,374445 - 1,1736998) -1,323996.0,135 - 2>3199466 • 0,1352
= 0,3528836.
С использованием этих коэффициентов записывается формула второго звена
сплайн-функции:
5*3,! (х) = 1,1736998 + 1,323996 • (х - 0,15) + 1,1599733 • (х - 0,15)2 + 0,3528836 • (х - 0,15)3.
Процесс построения последующих звеньев сплайн-функции
выполняется аналогично до конца отрезка [a,b\. В частности, для рассматриваемого
примера получается такая формула последующего третьего звена сплайн-
функции:
Sl2{x) = 1,374445+1,6564827- (х - 0,285) + 1,302912- [х - 0,285)2 + 0,8894584- (х - 0,285)3.
С помощью найденных звеньев формируется многозвенная кубическая
сплайн-функция дефекта q - 1, являющаяся приближенным решением задачи
Коши. ■
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Для решения задачи Коши
/ = -4>/ + sin х, >>(0) = 2,
записать формулы: а) явного и неявного методов Эйлера; б) метода Эйлера—
Коши; в) метода трапеций; г) методов Адамса-Бэшфорта и Адамса-Мултона
третьего и четвертого порядков.
2. Для решения задачи Коши
у = у + 2z - 9х, у(0) = 1,
Z' = 2y + z-4e\ z(0) = 2
записать формулы: а) явного и неявного методов Эйлера; б) метода Эйлера—
Коши; в) метода трапеций; г) методов Адамса-Бэшфорта и Адамса—Мултона
четвертого порядка.
335

3. Используя явный метод Эйлера с шагами h = 1; 0,5; 0,25, найти
приближенное решение уравнения / = 0,04у; у(0) = 1000 , сравнить его с точным
решением у(х) = 1000е0,04х, вычислить значение у(1), проанализировать
сходимость.
4. Найти приближенное решение задачи Коши
/ = -0,01у; Я0) = 100, [я>] = [0;100]
и вычислить >>(100) (точный ответ равен 36,788) с помощью: а) явного метода
Эйлера при h = 25; 10; 5; 1; б) модифицированного метода Эйлера при h = 20; 10;
в) исправленного метода Эйлера при И - 20; 10; г) метода Рунге-Кутты
четвертого порядка при h = 100; 50; д) метода прогноза и коррекции второго порядка
при Л = 20 , если известно значение y(2Q) = 81,8731.
5. Найти приближенное решение задачи Коши
/ = 4-2х, .у(0) = 2, [я,*] = [0;1]
с помощью: а) явного метода Эйлера; б) модифицированного метода Эйлера;
в) исправленного метода Эйлера. Сравнить его с точным решением
у(х) = -х2 + 4х + 2. Исследовать поведение приближенного решения при
изменении величины шага.
6. Найти приближенное решение задачи Коши
/ = -£, ^(0) = 20, [я,£] = [0;12]
У
с помощью: а) модифицированного метода Эйлера при И = 2; б) метода Рунге-
Кутты четвертого порядка при h - 4.
7. Найти приближенное решение задачи Коши
, (6>м-2х + 1) 17
У = , ^(i) = -~, к*1 = [1;4]
х 30
при /; = 1, вычислить у(4) методом прогноза и коррекции второго порадка.
Сравнить найденное решение с полученным при другом начальном условии
,w 30

Глава 7. МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
7.1. ПОСТАНОВКА ЗАДАЧИ И ОСНОВНЫЕ ПОЛОЖЕНИЯ
Рассмотрим двухточечные краевые задачи, часто встречающиеся в
приложениях, например, при решении задач вариационного исчисления, оптимального
управления, механики жидкости и газа и др. Пусть дано обыкновенное
дифференциальное уравнение
F(x,y(x)9/{x),...tyW(x)) = 0, а<х<Ь,
и краевые условия
Vil№.?{fl)r..*y{*'X\a)) = 0, / = 1,2,...,/,,
Vj(y(b\y\b\...,/n-{)(b)) = 0, j = L +1,...,n,
где F(x,yty\...,yMy9 ф/<*/,...,/,,-|)), / = П; М/^У,...,^-»), у = 1 + 1,л -
функции указанных аргументов, заданные в некоторой области их изменения;
L и (л - L) — число условий на левом и правом концах отрезка [а, Ь]
соответственно. Общее количество условий равно порядку дифференциального уравнения.
Требуется найти функцию у = у(х), которая на отрезке [а, Ь] удовлетворяет
уравнению (7.1), а на концах отрезка — краевым условиям (7.2).
Если уравнения (7.1),(7.2) линейны относительно искомой функции и ее
производных, то краевая задача называется линейной.
Для простоты ограничимся частным случаем линейной краевой задачи для
дифференциального уравнения второго порядка (л = 2), которая наиболее часто
ставится в вычислительной практике и записывается в виде
/' + р{х) у' - q(x) у = /(х), а < х < Ъ , (Q = [а, Ь]), (7.3)
а0у(а) + р0у'(а) = А,
a,j(*) + Pi/W = *,
где /?(х), q(x), f(x) е C2[a,b] - заданные функции, а а0,а,,р0,р,,Л, В -
заданные числа, aj + Ру > 0, j = 0,1.
Требуется найти функцию у(х), удовлетворяющую уравнению (7.3) и
краевым условиям (7.4).
Краевые условия при ау * 0, ру * 0, j = 0,1, задают линейную связь между
значениями искомого решения и его производной на концах отрезка [а,Ь].
В простейшем случае, когда р0 = 0, р, = 0, краевые условия задают на
концах отрезка [я, Ь] только значения функции у(а),у(Ь). Такие функциональные
условия называют краевыми условиями первого рода. В этом случае краевая задача
называется первой краевой задачей.
(7.1)
(7.2)
337

В случае, когда а0 = 0, а, = 0, т.е. на концах отрезка заданы только
значения производных, краевые условия являются дифференциальными. Такие краевые
условия называют условиями второго рода или «мягкими». Последнее название
обусловлено тем, что они определяют на концах отрезка [a,b] всего лишь
наклоны интегральных кривых, а не значения функции у(х). В этом случае задача
(7.3),(7.4) называется второй краевой задачей.
В общем случае, когда а0 и (или) а{ ; р0 и (или) Pj не равны нулю,
краевые условия носят функционально-дифференциальный характер и называются
условиями третьего рода. Тогда задача (7.3),(7.4) называется третьей краевой задачей.
Например, условия
у(а) = Л, у(Ь) = В
являются условиями первого рода. Геометрически это означает, что при решении
первой краевой задачи требуется найти интегральную кривую уравнения (7.3),
проходящую через данные точки (а,А),(Ь, В) (рис. 7.1,о).
Условия
/(а) = A, /(b) = В
являются условиями второго рода. Геометрически вторая краевая задача сводится
к отысканию интегральной кривой уравнения, пересекающей прямые
х = а, х = b под заданными углами а, р , где tg а = A, tg р = В (рис. 7.1,6).
Условия
/(а) = А, у(Ь) = В
являются частным случаем краевых условий третьего рода, так как а0 = 0,
р0=1,а1=1,р1=0. Геометрически данная краевая задача сводится к
отысканию интегральной кривой уравнения, проходящей через точку (Ь,В) и
пересекающей прямую х = а под данным углом а, где tg а = А (рис. 7.1,в).
У
в
0
у = Ах)
К а i
i Х%а = А i
i i
a b'x
Рис. 7.1
В общем случае краевая задача может:
а) иметь единственное решение;
б) не иметь решений;
в) иметь несколько или бесконечно много решений.
338

Утверждение 7.1 (о существовании и единственности решения краевой
задачи (7.3),(7.4)) [6].
Для того чтобы существовало единственное решение краевой задачи
(7.3),(7.4), необходимо и достаточно, чтобы однородная краевая задача
у" + р(х)у' - д(х)у = О, а<х<Ь,
аоЗ/(«) + РоУ(д) = °»
имела только тривиальное решение у(х) = 0.
Пример 7.1. Найти аналитическое решение следующих краевых задач:
а) у" + у = 1, 0 < х < —, У(0) = 0, и — - У — = 2 (третья краевая задача);
б) у" + у = -х, 0 < х < 1, >>(0) = 0, у(\) = 0 (первая краевая задача).
D Воспользуемся известной методикой отыскания общих решений
дифференциальных уравнений [33]. Подставив в них заданные краевые условия,
получим аналитические решения данных краевых задач.
1. Найдем общее решение однородного уравнения у" + у = 0, одинакового
для обеих рассматриваемых задач. Так как характеристическое уравнение
X2 +1 = 0 имеет комплексные сопряженные корни А.1>2 = ±/ = ос ± р/ (а = 0, р = 1),
то общее решение будет Уо(х) = е**^ cosрх + С2 sin рх) = Q cosх + С2 sin х.
2. Частные решения неоднородных уравнений находятся методом подбора.
Подставляя уч (х) = С в уравнение у" + у = 1, а ун (х) = Dx в уравнение
у" + у = -х, получаем С = 1,D = -1. Поэтому >\Ддс) = 1 в случае «а», уч(х) = -х
в случае «б».
3. Найдем общее решение неоднородного уравнения как сумму общего
решения однородного уравнения и частного решения неоднородного уравнения:
а) У(х) = Cj cos х + С2 sin х +1; б) у(х) = Q cos х + С2 sin х - х.
4. Определим значения произвольных постоянных из краевых условий
третьего рода (случай «а») и первого рода (случай «б»):
а) найдем у'(х) - - Сх sin х + С2 cos х. Тогда
У(0) = С2=0, ^_у^ = С2+1 + С,=2.
Отсюда Cj = 1 и >>(х) = 1 + cosx - решение краевой задачи «а»;
б) <y(0) = C1=0, y(l) = C,cosl + C2sinl-l = 0. Отсюда С2 =— и
sinl
у(х) = — 1 — решение краевой задачи «б». Таким образом, решение краевой
sin 1
339

задачи представляет собой такое частное решение, которое удовлетворяет
краевым условиям. ■
Рассмотренный метод нахождения аналитического решения краевых задач
применим для ограниченного класса задач. Поэтому в вычислительной практике
используются численные и приближенно-аналитические методы, позволяющие
найти приближенное решение краевых задач, точные аналитические решения
которых не могут быть найдены.
7.2. МЕТОД СЕТОК
Рассмотрим линейную краевую задачу с краевыми условиями первого рода
(первую краевую задачу):
y" + P(x)y'-q(x)y = f(x)y а<х<Ьу
у(а) = Ау у(Ь) = Ву { ' }
где р(х)у q(x)y f(x) е C2[ayb] — заданные функции; Ау В — заданные числа.
Очевидно, любой отрезок [ауЬ]у на котором ищется решение краевой
задачи, можно привести к отрезку [0; 1] с помощью линейного преобразования
х = . Действительно, тогда новая переменная х е [0; 1]. В результате без ог-
Ь-а
раничения общности краевая задача (7.5) может быть решена сначала на отрезке
[0; 1], а затем это решение с помощью преобразования х - а + (Ь - а) • х может
быть записано на отрезке [ayb]. То же относится и к исследованию свойств
полученного решения.
Утверждение 7.2 (о единственности решения краевой задачи (7.5)) [6].
Если функции р(х), q(x), f(x) принадлежат классу С2[0; l], q(x) > 0 на
[0; 1], то краевая задача (7.5) имеет единственное решение у(х) е С4[0; 1].
Для решения задачи (7.5) применим метод сеток, получаемый путем
аппроксимации первой и второй производных (см. также разд. 6.2.1).
Введем равномерную сетку
^я ={хо,хх,...,х„}, Х;=х0+1пу / = 0,я; h = ,
п
где п — число отрезков разбиения.
Функции p(x)yq(x)yf(x) заменяются их проекциями на сетку Q„, т.е.
р(х) -> p(Xj) - Pj, q(x) -> q(xt) = qt-y f(x) -> f(x,) = /,-. Вместо точного решения
y(x) отыскивается некоторое приближение y-t = y(xf) * д/(ху), / = 0,л.
Первая и вторая производные аппроксимируются на трехточечном шаблоне
(х/-1»х/»х/+|) по формулам второго порядка (5.10),(5.14):
340

Краевые условия для этой задачи аппроксимируются точно, т.е. у(а) и
у{Ь) заменяются на у0 и уп. После замены от дифференциальной задачи (7.5)
переходим к разностной схеме:
h2 2h
Уо=А, Уп=В*
представляющей собой систему алгебраических уравнений трехдиагонального
вида:
(7.6)
£о =А Я» = я>
где а,г =—7_ТГ> Y/ =~Т + ТГ> Р/ =Т + ^/» 5/ = •//• Здесь система (7.6) записа-
Л2 2А h2 2Л Л2
на для внутренних узлов сетки Qn. Она является трехдиагональной системой
линейных алгебраических уравнений и решается методом прогонки (см. разд.
1.2.2).
Замечания.
1. Изложенный метод сеток допускает обобщение. Например, его можно
применять для решения нелинейной краевой задачи:
y" = F(xyy)y xe[a,b], у(а) = А, у(Ь) = В, (7.7)
где F(x,y) — нелинейная по у функция (в общем случае, который здесь не
рассматривается, функция F зависит также и от у').
Рассуждая аналогично рассмотренному выше способу, перейдем к
разностной задаче:
Й-1 - 2j>/ + Уи\ = h2F(xity,), i = 1./I-1, (7.8)
Уо = А> Уп=В.
В силу нелинейности правой части полученная алгебраическая система
является нелинейной и для ее решения нельзя использовать метод прогонки в
том виде, в каком он изложен для линейной задачи. Поэтому для ее решения
используем метод простых итераций (см. разд. 3.2.2), с помощью которого при
фиксированном к (к — номер итерации) система алгебраических уравнений
(7.8) превращается в линейную, так как величины, входящие в правую часть
системы, известны из предыдущей итерации. Действительно, для к-й итерации
получается система
#> - 2?<*> + yjt] = h2F(Xi,yjk-\ i = i^rrr,
которая решается на каждой итерации методом прогонки.
341

Можно показать [14] , что итерации сходятся при выполнении условия
q =— (хп -х0)2М{ < 1, Л/i = max — с линейной скоростью.
8 [а,ь] | ду I
2. Краевые условия второго и третьего рода в задаче, аналогичной (7.5),
могут быть аппроксимированы несколькими способами.
Первый способ. Использование аппроксимационных формул (5.4) первого
порядка
h h
В силу первого порядка этих аппроксимаций метод сеток в этом случае также
будет иметь первый порядок аппроксимации.
Второй способ. Применение формулы Тейлора (В. 18) и ее преобразование
с использованием дифференциального уравнения. Таким способом может быть
достигнут второй порядок аппроксимации.
Третий способ. Применение левосторонней (5.8) и правосторонней (5.9)
формул, аппроксимирующих производные со вторым порядком:
% = 2^(-3j)0 +4j), -j>2), у'п =—{уп-2-4Уп-\ + 3j>„). (7.10)
3. Порядок аппроксимации схемы определяется минимальным порядком
аппроксимации дифференциального уравнения и краевых условий.
Алгоритм применения метода сеток
1. Задать сетку Qn на отрезке [а, Ь] или сформировать ее из условий
достижения требуемой точности.
2. Используя аппроксимационные формулы (5.10),(5.14) и один из трех
способов аппроксимации краевых условий (в случае, если они второго или
третьего рода), перейти от исходной дифференциальной задачи к системе
алгебраических уравнений (разностной схеме), неизвестными в которой являются
величины, «близкие» к решению краевой задачи в узлах сетки.
3. Найти решение разностной задачи путем решения трехдиагональной
системы уравнений и таким образом определить приближенное решение краевой
задачи.
Пример 7.2. Найти приближенное решение краевой задачи
у" + у = \, 0<x<-j,
У(0) = 0;
' #у(!
при п = 3, используя первый способ аппроксимации краевых условий. Записать
разностные схемы для второго и третьего способов при произвольном п.
П В поставленной задаче а = 0, b = —, р(х) = 0, q(x) = -1, /(*) = 1,
«о = 0, р0 =1, Л = 0, <Х| = 1, р,=-1, 5 = 2. Для решения задачи воспользуемся
методикой.
342

1. Так как п = 3, то сетка имеет вид Q3 = {х0, х{, х2, х3}, где х, = /Л, / = 0,3,
--0
/»=i—= i Тогда Я0) = у0, уf« 1 = ^,, у у} = у2, у ■j] = >,3- БУДем искать
приближенные значения Уо,У1УУ2,Уз- Проекции функций /?(*),?(*),/(*) на
сетку имеют вид /?, = 0, qt = -1, /, = 1.
2. Составим разностную схему. Согласно (7.6), для внутренних узлов сетки
получаем
Уи\-2у,+У1_х +pfsl$ / = lj2f или д)/_1-(2-Л2)Я+Я+1=Л2, / = 1,2.
Применим первый способ аппроксимации краевых условий. По формуле
(5.4) с учетом условия у'(0) = 0 на левом конце имеем
р6 = Л^ = 0 или р j> о.
я
На правом конце и — = >>з, У — = у\ , и по второй из формул (7.9)
#'S-
Тогда краевое условие у\ — - у'\ — | = 2 аппроксимируется выражением
л л
у3-Уг~У2 =2 или р2-(1-Л)р3 =2Л.
Л
В результате получаем разностную схему первого порядка аппроксимации
(трехдиагональную систему линейных алгебраических уравнений)
Л А л
У\~У0 =0,
Рм-(2-А2)й+ры=А2, / = 1,2.
р2-(1-Л)Р3=2Л.
Сравнивая первое уравнение этой системы с рекуррентным соотношением
Р/= ^ >'/+!+G/ метода прогонки (см. разд. 1.2.2), характеризующим обратный
ход, получаем Р0 = 1, Q0 = 0.
После этого вычисляются все последующие прогоночные коэффициенты
по формулам (см. разд. 1.2.2): Р{ = '—-—, Q,- =—-—— '-, i = 1,2,3. Здесь
а/»Р/»У/ соответствуют коэффициентам левой части полученной алгебраической
системы, а 5, — правой части.
343

Далее выполняется обратный ход: р3 = Сз> Уг = ^Рз + Оъ У\ ~ ?\Уг + Q\ •
Результаты решения краевой задачи приведены в табл. 7.1, в которой
последний столбец соответствует точному решению у(х) = 1 + cosх, найденному
в примере 7.1.
Таблица 7.1
I
0
1
2
1 3
«/
0
1
1
1
Р/
-1,0000
1,72584
1,72584
0,47640
У/
-1
1
1
-
«/
0,00000
0,27415
0,27415
1,04200
Pi
1,00000
1,37771
2,87240
-
Qi
0
-0,37770
-1,87242
1,21853
9i
1,8648
1,8648
1,6277
1,21853
У(х)
2,0000
1,8666
1,5000
1,0000 |
В силу того, что краевые условия аппроксимированы с первым порядком
относительно h, в данном случае получена разностная схема первого порядка,
так как порядок аппроксимации схемы определяется минимальным порядком
аппроксимации дифференциального уравнения и краевых условий.
Воспользуемся вторым способом аппроксимации краевых условий для
построения разностной схемы второго порядка аппроксимации. Разложим у(х)
в точке х = Jtj относительно точки х0 по формуле Тейлора (В. 18):
Л2
У\ =Уо+пУ'(хо) + ^гУ"(хо) + °("г)-
Выразим из этого соотношения у'(х0) и подставим в него вместо /'(*о)
выражение /'(*о) = 1 - .К*о) = 1 - .Уо > определяемое исходным
дифференциальным уравнением:
/(^o)=Z42l-t(1-^o) + W2).
п 2
Как показывает это соотношение, дифференциальное условие на левой
границе аппроксимируется на двухточечном шаблоне (xo>*i) со вторым
порядком аппроксимации двухточечным алгебраическим уравнением:
^^--(1-Ро) = 0 или 21_-L(2_/,2)j>0=A.
h 2V У0; h 2// т 2
Аналогично получается двухточечное алгебраическое уравнение при
/ = п - 1 и / = п . Разложение у(х) в точке jc = хп_{ относительно точки хп по
формуле Тейлора (В. 18) имеет вид
^-1=^-Л/(хл)+у/'(хл) + 0(Л3).
Выражая отсюда у\хп) с учетом связи у"(хп) = 1 -у(хп) = 1 -уп,
следующей из исходного дифференциального уравнения, получаем
344

/^--^-+^-4/-(х.)--^+^4(1-л).
п h 2 п п 2
Подставим это выражение в граничное условие:
У„+^-^-^-Уп) = 2 или 2^. + ±(А2+2А-2)Ря«2 + |.
Таким образом, система линейных алгебраических уравнений в
окончательном виде записывается следующим образом:
1 /, 2 ^\Л 1 Л "
— (Л -2)yQ+-yl =т.
2Л Л 2
Я_,-(2-^)Я+Я+1=^, / = 1, я-1,
>^± + ±(Л2+2Л-2);л=2ч--.
Л 2Л л 2
Эта трехдиагональная система, отличающаяся от полученной первым
способом только первым и последним уравнениями, решается численно методом
прогонки.
Применим третий способ аппроксимации краевых условий для построения
разностной схемы второго порядка. Так, для крайней левой точки используется
левосторонняя формула (5.8):
А. 1 / л А .А Л \
Уо = ^(-ЗУо+*У\ -Уг)-
Тогда получается трехточечное алгебраическое уравнение:
— (-Зр0+4й -у2)=0 или 3p0-4j), + у2 =0.
Алпроксимация производной У — в крайней правой точке по
правосторонней формуле у'п =— (¥ря_2 -4^л_! + 3р„) приводит к трехточечному
алгебраическому уравнению:
Уп - 2^(?я-2 -4рй.| +3ря)= 2 или л_2 -4j)w_, + (3- 2Л)ря =-4Л.
Тогда в этом случае получается следующая система линейных
алгебраических уравнений:
345

3y0 -4yl+y2=0,
f/-|-(2-A2)&+j>/+, =А2, / = 1,я-1;
Л.2-4ув.,+(3-2А)у|,=-4А.
Здесь у2 в первом уравнении и уп_2 в последнем нарушают ее трехдиагональ-
ный характер. В этом случае система приводится к трехдиагональному виду
путем исключения у2 и уп_2 из первых двух и последних двух уравнений
системы и после этого решается методом прогонки. ■
7.3. МЕТОДЫ МИНИМИЗАЦИИ НЕВЯЗКИ
Описываемые здесь методы относятся к приближенно-аналитическим и
могут применяться при решении достаточно широкого класса задач. На основе
одного из приближенно-аналитических методов (метода Галеркина) строится
метод конечных элементов, излагаемый в разд. 7.5.
Рассмотрим линейную краевую задачу (7.3),(7.4). Ее решение будем искать
в виде
УтМ = ФоМ + а\ (pi(*) + ... + flm Фт(х), (7.11)
где ф0(х),ф1(х),...,ф/я(х)— элементы заданной системы функций; Д|,...,дт-
неопределенные коэффициенты. Заданная система функций называется базисной,
и ее элементы должны удовлетворять условиям:
а) ф;(х)еС2[о,/>], У = 0,/я;
б) при любом конечном т функции щ(х),...,фт(х) линейно независимы
на отрезке [я, Ь];
в) Фо(*) удовлетворяет краевым условиям (7.4)
а0 -Фо(я) + Ро Фо(д) = л> (7 п)
<Х| Фо(^) + Р1 -Фо(£) = Я;
г) ф!(х),...,фт(л:) удовлетворяют условиям
а0-фу(л) + РоФу(л) = °. y'sU,
а, фу(^) + р, ф)(^) = 0, у = 1,т.
Функция
г(х\аи...,ат) = у'^(х) + р(х) y'm(x)-q(x) ym(x)-f(x) (7.14)
называется невязкой. Она равна разности левой и правой частей уравнения (7.3),
образующейся при подстановке ут(х) вместо у(х) в дифференциальное уравне-
346

ние, и характеризует степень отклонения функции ут(х) от точного решения
краевой задачи. Если при некоторых значениях коэффициентов аХу...уат невязка
тождественно равна нулю на отрезке [ауЬ]у а именно
г(хуа[у...уат) = Оу а<х<Ьу (7.15)
то функция ут(х) совпадает с точным решением краевой задачи (7.3),(7.4), так
как удовлетворяются и уравнение, и краевые условия.
Однако при решении краевых задач, как правило, не удается получить
невязку тождественно равной нулю. Поэтому ставится задача: вычислить
коэффициенты а{у...уат таким образом, чтобы невязка в каком-либо смысле стала
меньшей. Полученные в результате коэффициенты определяют приближенное
решение (7.11).
Выражение для невязки е(х;Я|,...,дт)с учетом (7.11) удобно записывать
в следующей эквивалентной форме:
т
г(х;ои...уат) = Lym-f(x) = Iq>0(x)+ £я, • L^j00 - f(x), (7.16)
где Lym =у'м (x) + p(x) y'm (x) - q(x) ym (x), L - линейный оператор задачи
(7.3),(7.4) (выполняются равенства L(y + z) = Ly+ Lz, L(Cy) = CLy для любых
yfZ и постоянной С).
Рассмотрим различные методы, минимизирующие невязку.
А. Метод коллокации. На интервале (a,h) задаются т точек хи...,хт
(точек коллокации) и требуется, чтобы в каждой из них невязка (7.14) обращалась
в нуль:
e(x,;flf,,...lflm) = Of
(7.17)
фгш;я,,...,ят) = 0.
С учетом (7.16) эта система принимает вид
alLQi(xl) +... + tfmZxpm(x,) = /(*,) - I<po(xi),
<*\£ф|(*2> + - + атЬ$т(х7) = f(x2)~ ^Фо(^) . (7.18)
a\fy\(xm) + --- + ambpm(xm) = f(xm)-lAp0(xm).
Если полученная система m линейных уравнений совместна, то из нее
определяются коэффициенты а[у...уатУ которые затем подставляются в (7.11).
347

Б. Метод наименьших квадратов (непрерывный вариант). Неизвестные
коэффициенты а{,...,ат должны обеспечивать минимум интеграла от квадрата
невязки:
ь
1= f б2(х,a^...,am)dx -> min .
*' *«
Для решения задачи применяются необходимые условия безусловного
экстремума [31]:
^2)г{г,аи...,ат)д^"-'а^Лс^, j-u,. (7.19)
да; J да.
J a J
Подставляя (7.16) в (7.19), получаем систему т линейных алгебраических
уравнений для нахождения коэффициентов а\,,..,ат:
а{ (Zxp,, £ф!) + ... + ат (Lq>m, Zxp, ) = (/- Lq>0, Цц),
а{(Ьщ, 1ф2) +... + ат(1лрт, 1ф2) = (/ - 1ф0, /хр2), (7.20)
^(/хр,, L<pm) +... + am(L<pm, £jpm) = (/ - /хро, 1ф^),
где (f,g)= jf(x) g(x)dx~- скалярное произведение. В системе (7.20) все скаляр-
а
ные произведения предварительно вычисляются.
В. Метод наименьших квадратов (дискретный вариант). Неизвестные
коэффициенты aXi...,am должны обеспечивать минимум суммы квадратов значений
невязки в заданном наборе точек хи...,хп ; п>т\ т.е. xt е (a,b),i = 1,л:
п
5, = ^Е2(х/,л,,...,дт)-^ min .
/=i fl> fl«
Для решения задачи применяются необходимые условия безусловного
экстремума [31]:
— = 2-2>(*/,fli>...,flw) г = 0, у = 1,т. (7.21)
Отсюда следует система т линейных уравнений для нахождения
коэффициентов tfj,...,0m, которая по форме записи совпадает с (7.20), но скалярное
п
произведение определяется по формуле (/,#) = £/(*/) £(*/) •
/=1
Замечание. При п - т результаты, полученные точечным методом
наименьших квадратов и методом коллокации, совпадают. В этом случае точки
Х|,...,хл являются точками коллокации.
348

Г. Метод моментов (взвешенных невязок). Неизвестные коэффициенты
alt...,am находятся из условия равенства нулю т моментов невязки:
ъ
/= J e(x,a],...,am)-4/j(x)clx = Qi j = l,m, (7.22)
а
где \\/j(x), j -\,т — функции, удовлетворяющие условиям:
а) 1|/у-(х)еС[а,£], j = 1,/я;
б) функции v|/y(jc) являются элементами системы степеней х или системы
тригонометрических функций.
Функции \\ij(x) ,j = 1,/и, называются весовыми, г условие (7.22) является
условием ортогональности невязки к весовым функциям.
Д. Метод Галеркина. Он является частным случаем метода моментов, когда
в качестве весовых функций используются базисные. Коэффициенты alf...,am
находятся из условия ортогональности функций базисной системы
Ф,(х),...,фт(х) к невязке:
ь
J z(x,ab...yam)q>j(x)dx = 0, j = l,m. (7.23)
а
Отсюда следует система т линейных уравнений для нахождения
коэффициентов:
^1 (£<Pi, Ф1) + ... + cim(Lym, q>! ) = (/- Zxpo, Ф]),
с1(/хр1,ф2) + ... + от(1фт,ф2) = (/-1фо,Ф2), (7.24)
о1(^Ф1.Ф/п) + - + «т(^Фт»Фт) = (/-^Ф0»Фт).
Ь
где (/,£) = J/M g(x)dx - скалярное произведение. В системе (7.24) все скаляр-
а
ные произведения предварительно вычисляются.
Известно, что при достаточно большом т условие (7.23) обеспечивает
малость невязки в среднем [10].
Алгоритм применения методов минимизации невязки
1. В выражении (7.11) выбрать систему базисных функций, задать число т
в зависимости от требуемой точности.
2. Найти коэффициенты аи...уат путем решения одной из систем
алгебраических уравнений (7.18),(7.20),(7.24) в зависимости от выбранного метода.
3. Выписать приближенное решение краевой задачи по формуле (7.11).
349

Пример 7.3. Найти приближенное решение краевой задачи
у" + у = -х, 0 < х < 1,
^(0) = 0, у(\) = 0
методом коллокации, интегральным методом наименьших квадратов, методом
Галеркина.
П В поставленной задаче а = О, b - 1, /?(х) = 0, q(x) - -1, /(х) = -jc, а0 = 1,
р0 = 0, А = 0, а, = 1, Pj = 0, В = 0, Ду = у + у • Точное решение найдено в
примере 7.1.
Воспользуемся сначала методом коллокации.
1. Зададим /и = 2 и будем искать решение в виде
У2(*) = ФоМ + *i • <Pi (*) + *2 • Ф2 W»
где ф0(х)гО (эта функция удовлетворяет каждому из краевых условий, т.е.
Фо(°) = 0,ф0(1) = 0). функции ф,(х) = х(1-х), ф2(х) = х2(1-х). Функции
Ф|(х),Ф2(х) линейно независимые, дважды непрерывно дифференцируемые и
удовлетворяют условию (7.13). Действительно,
1ф,(0) + 0ф',(0) = 0, у = 1,2,
1.ф;(1) + 0.ф'7(1) = 0, У = 1,2.
Таким образом, решение краевой задачи ищется в форме
у2(х) = а{ • х(\ -х) + <?2 • х2(1 -х).
2. Так как т = 2 и ф0(х) = 0, то система (7.18) имеет вид
А,/хр1(х1) + д2/хр2(х,) = /(х1),
fl^jto) + a2hp2(x2) = Дх2).
Выберем узлы коллокации: Xi = —, х2 = —. Тогда
4 2
Zxpi (х) = ф5'(х) + Ф1 (х) = -2 + х(1 - х) = -2 + х - х2;
/хр!(х,) = ^Pif-1 = -^г; A>i(*2) = ^Ы = -4 '
^ФгМ = Фг'М + ФгМ = 2-6х + х2 - х3;
/хр2(Х!) = Lq>2f-j = —; Zxp2(x2) = /xp2f~J = --.
350

Таким образом, имеем линейную систему относительно ах и а2:
29 35 1
7 7 1
6 40
решение которой дает ах =—, а2 =—-.
3. Приближенное решение задачи:
j>2«=^D(42 + 40x).
Решим теперь задачу методом наименьших квадратов (см. непрерывный
вариант).
1. Решение краевой задачи ищется в форме (/и = 2):
у2(х) = ах • х(1 - х) + а2 • х2(1 - х).
2. Так как f(x) = -х, <ро(*) = 0, то система (7.20) имеет вид
ах (Ьрх, Ц>{) + а2 (£лр2 , Zxpj) = (-х, hpx),
а1(1ф1,1ф2) + С2(^Ф2»^Ф2) = (-^»^Ф2)э
где
1
(^,,1ф1)= J(-2 + x-x2)2rfx=^; (1ф2,1ф2)= J(2-6x + x2-x3)2rfx=^;
0 3U 0 35
(Lpltbp2)= J(-2 + x-x2)(2-6x + x2-x3)rfx=i£r,
о 60
(-x,Zxp,) = J(-x)(-2 + x-x2)dx=ji; (-х,£ф2)= J(-x)(2-6x + x2-x3)dx=^.
о ^ о 20
Итак, имеем линейную систему относительно Д| и я2 :
101 101 _ П..
30 °х + 60 °2 " 12'
101 131 Jl9
60 °1+ 35 "2 ~20'
решение которой дает ах =0,1875419, а2 =0,1694707.
3. Приближенное решение задачи:
у2(х) = 0,1875419 • х(1 - х) + 0,1694707 • х2(1 - х).
351

Решим задачу методом Гаперкина.
1. Пусть сначала т = 1. Решение ищется в форме ух (х) = а{ • х(1 - х).
2. Тогда система (7.24) преобразуется к виду
ах (hpi, ф,) = (-х, ф,) или ах (ф',' + ф!) = (-х, ф,).
Так как ф| (х) = х(1 - х), £лрх (х) = ф!'(*) + Ф1 (х) - -2 + х(\ - х), получаем
1 1
ах J(-2 + х(1 - х)) • jc(1 - х) dx = - Jx2(l -x)dx.
о о
п 3 15
После вычисления интегралов имеем уравнение ах = , откуда ах = —.
3. Приближенное решение краевой задачи: у{(х) =—х(1 -х).
18
Пусть теперь т = 2.
1. Решение краевой задачи ищется в форме
у2(х) = ах -х(\-х) + а2 х2(1-х).
2. Тогда система (7.24) имеет вид
0|(1ф|,Ф|) + fl2(A>2><Pi) = (/><Pi)>
Я|(£ф1,ф2) + Я2(/лр2,ф2) = (/,ф2).
Так как фДх) = х(1-х), ф2(х) = х2(1-х),
Zxpi(x) = 9i'W + 9i W = -2 + х(1 -х), Ьр2(х) = Ф2М + Ф2М = 2-6х + х2 -х3,
получаем
1 1 1
fl1J[-2 + x(l-x)]x(l-xyx + fl2|[2-6x + x2(l-x)]x(l-x)rfx=-|x2(l-x)dx,
00 о
1 1 1
ах \ [- 2 + х(1 - х)] • х2(1 - x)dx + а2 J [ 2 - 6х + х2(1 - х)] • х2(1 - х)dx = - |х3(1 - х)dx.
00 о
Вычисляя интегралы, находим
3 3 1
10 ' 20 2 12
3 13 1
20 ! 105 2 20
гл 71 7
Отсюда *,= — , fl2= —.
3. Приближенное решение краевой задачи: у2(х) = х(1 - х)
1369 41 J
352

Сопоставим полученные решения с точным (табл. 7.2).
Таблица 7.2
X
1 0,25
0,50
0,75
.Уколлок.
0,045
0,071
0,062
• мет. наим. кв.
0,04311
0,06807
0,05899
.^Галеркина
0,0440
0,0698
0,0600
Точное решение
0,044014
0,069747
0,060050 |
Очевидно, метод Галеркина дал более точный результат. ■
Пример 7.4. Найти приближенное решение краевой задачи [42]
/' + 2ху' - 2у = 2х2, 0 < х < 1,
/(0) = -2, у(1) + /(1) = 0
методом Галеркина.
□ В поставленной задаче а = 0, b = 1, р(х) = 2х, q(x) = 2, /(х) = 2х2,
а0 =0, р0 =1, Л = -2, а, = 1, р, = 1,Я = 0, Ly = у" + 2ху' - 2у.
1. Зададим т = 2 и подберем функции Фо(*),ф|(*),Ф2\*)> используя
систему 1,х,х2,... Функция Фо(х) должна удовлетворять условиям (7.12):
ф'0(0) = -2, фо(1) + ф'о(1) = 0.
Пусть ФоМ = b + сх, где Ь,с- неопределенные коэффициенты. Тогда
Фо(°) = с = -2, ФоО) + ФоО) = b + с + с = 6 + 2с = 0.
Отсюда 6 = 4 и ф0(х) = 4 - 2х.
Функции Ф1(х),ф2(х) должны удовлетворять условиям (7.13):
Ф';(0) = 0, Фу(1) + ф'у(1) = 0, у = 1,2.
Первое условие выполняется для функций вида фу(х) = xy+I + 6,-. Значения
bj находятся из второго условия 1 + bj• + j + 1 = 0, откуда 6у = -у - 2. Тогда
получаем ф1(х) = х2-3, ф2(х) = х3-4.
Таким образом, решение краевой задачи ищется в форме
у2 (х) = 4 - 2х + а{ • (х2 - 3) + а2 • (х3 - 4).
2. Тогда система (7.24) имеет вид
Я| (^Ф|, Ф1) + «2 (^Ф2. Ф1) = (/ - ^Фо > Ф1).
О1(1ф1,ф2) + Д2(^Ф2»Ф2) = (/-^Ф0»Ф2)»
где 1ф0 (х) = фо (х) + 2х ф'0 (х) - 2ф0 (х) = 0 + 2х(-2) - 8 + 4х = - 8;
353

Zxpj(jc) = ф'|'(х) + 2хф|(л')- 2ф|(х) = 2 + 2х2х - 2х + 6 - 2х + 8;
£ф2(х) = ф2(*) + 2хф2(л:)-2ф2(;с) = 6х + 2хЪх2 -2х3 +8 = 4х3 + 6х + 8;
1
(1ф1, Ф,) = J (2х2 + 8)(jc2 - 3) dx = -22,93333;
о
1
(/хр2,Ф,) = J (4х3 +6х + 8)(х2 - 3)dx = -31,16667;
о
i
(1фЬф2) = { (2х2 + 8)(х3 -4)dx = -32,33333;
о
1
(1ф2,Ф2) = J (4jc3 + 6х + 8)(х3 - 4) dx = - 44,22857;
о
1
(/ - 1ф0, Ф1) = J (2х2 + 8)(х2 - 3) dx = -22,93333;
о
1
(/-£ф0,Ф2)= | (2х2 + 8)(х3-4)dx = -32,33333.
о
Окончательно получаем
22,93333- л, + 31,16667 а2 =22,93333,
32,33333 • ах + 44,22857 • а2 = 32,33333.
Отсюда ах = 1, а2 = 0.
3. Приближенное решение краевой задачи у2(х) = х2 - 2х + I .■
7.4. МЕТОДЫ СВЕДЕНИЯ КРАЕВОЙ ЗАДАЧИ К ЗАДАЧЕ КОШИ
7.4.1. Метод стрельбы
Суть этого метода заключается в сведении решения краевой задачи к
многократному решению задачи Коши. Принцип построения метода стрельбы
рассмотрим на примере нелинейной краевой задачи:
У" = /(х,У,/), а<х<Ь, (7.25)
у(а) = А, У(Ь) = В, (7.26)
где f(x,yyy')— нелинейная функция, обусловливающая нелинейность
дифференциального уравнения (7.25).
При введении новой переменой z = у' уравнение (7.25) записывается
в нормальной форме Коши, а краевые условия видоизменяются:
354

У = Z, у(а) = А ,
Z' = f(xty,z), z(a) = r\,
(7.27)
где j] = /(я) = tg а - параметр, равный тангенсу угла наклона интегральной
кривой в точке х = а. Угол а (параметр т\) в процессе многократного решения
краевой задачи должен принять такое значение, чтобы интегральная кривая
«попала в цель», т.е. в точку (6, Я)(рис.7.2,д). В общем случае полученное при
некотором значении ц решение у(х;т)) не будет удовлетворять условию
y(b;r\) = В на правом конце отрезка.
Следовательно, требуется найти такое значение параметра г|, чтобы оно
было корнем нелинейного уравнения
ф(л) = УАп)-я = о.
Для решения этого уравнения, как правило, используются методы
половинного деления (см. разд. 3.1.3) или секущих (см. разд. 3.1.7).
У
в
А
0
i
i
i
а
Ла
i
i
i
i
i
i
i
i
i
b
X
Рис. 7.2
В случае использования метода половинного деления сначала делают
«пробные» выстрелы при выбранных наугад или в соответствии с некоторым
алгоритмом значениях г| до тех пор, пока среди значений Ф(тО не окажется двух
противоположных по знаку. Им соответствует начальный интервал
неопределенности, который далее последовательно сокращается путем деления пополам.
При применении метода секущих используется формула
„<*+!>
,n<*)_<W*')-h
(*> .
n(*-Di
Ф(^к))-Ф(^к~1))
£ = 1,2,...,
где Ti*0),rj(1)— начальные значения параметра, к — номер итерации. Итерации
прекращаются при выполнении условия окончания Ф(л(Аг)) ^ е
или
т^*+1*-т1^ <е с некоторым положительным е, характеризующим точность
решения задачи.
355

Замечание. Точность решения краевой задачи зависит не только от
точности определения параметра rj , но также и от точности решения
соответствующей задачи Коши. Поэтому одновременно с уточнением параметра
л рекомендуется уменьшать шаг при решении задачи Коши, либо выбирать
более точный метод.
Рассмотрим применение метода стрельбы для решения линейной краевой
задачи (7.3),(7.4):
/' + РМ у' - q(x) у = /(х), а<х<Ь
а0у(а) + р0у'(а) = А,
а,у(Ь) + ^у\Ь) = В.
Методика решения линейной краевой задачи
1. Решить две задачи Коши
/' + РМ у' - q(x) у = f(x), а < х < Ь (7.28)
при условии
*оУ(") + Ро/(я) = Л , (7.29)
а именно при Р0*0 задается у(а) = г\, тогда у (а) = — , а при р0=0
Ро
Л
задается у'(а) - л. и тогда у(а) = — с разными произвольными значениями л.,
т.е. т| = ti(0) и г| = г1(1).
2. Найти значения Ф(л(0)),Ф(л(1)) функции Ф(г)) = а, \у(6;л) + Р1 -у'^тЦ-В
и новое значение параметра:
л(2) П) Ф(Л(1)ИЛ(1)-Л(0)]
л л ф(л(1))-ф(л(0)) '
3. Решить краевую задачу (7.28),(7.29) при л. = л(2)- В результате получится
приближенное решение исходной линейной краевой задачи, точность которого
определяется точностью решения задачи Коши при значении г| = г|(2).
Таким образом, в силу линейности поставленной краевой задачи
соответствующая задача Коши решается только три раза.
Пример 7.5. Методом стрельбы найти приближенное решение нелинейной
краевой задачи
УУ"-/2=0, .у(0) = 1, у(\) = 2,718.
Соответствующую задачу Коши решить явным методом Эйлера с шагом Л = 0,01,
а параметр л вычислить методом половинного деления.
356

□ Зададим начальные значения параметра г|: ту' = О, гр' =1,35, которые
обеспечивают разные по знаку значения функции Ф(г|). Они являются
соответственно левым и правым концами начального интервала неопределенности.
Согласно методу половинного деления будем делить текущий интервал пополам и в
качестве нового интервала выбирать тот, на концах которого функция
Ф(ч) = .У(1,т1)-2,718 имеет разные знаки. Процедуру поиска завершим при
выполнении условия h(*+1) -r\ik)\ < е, где положим е = 0,01.
Для применения явного метода Эйлера (6.19) уравнение следует переписать
У'2
в форме /' = -— , а затем с помощью введения новой переменной z = y' — в ви-
У
де (7.27):
У = г, 3>(0) = 1,
z' = —, *(0) = л-
У
Результаты интегрирования явным методом Эйлера с шагом Л = 0,01 с
параметром т], определяемым методом половинного деления, приведены в табл.
7.3. Четыре первых решения у(х,ц) изображены на рис. 7.2Д
Таблица 7.3
Г к
0
1
2
3
4
5
6
7
8
ч(*>
0
1,35
0,675
1,0125
0,84375
0,934375
0,9734375
0,99296875
1,002734375
y(Wk))
1,000000
3,822746
1,959583
2,738495
2,316000
2,534000
2,634597
2,686050
2,712146
ф(л(*})
-1,718000
1,104700
-0,758417
0,020495
-0,402000
-0,184000
-0,083403
-0,031950
-0,005850 1
Таблица 7.4
*/•
у,-
0
1
0,1
1,105
0,2
1,2208
0,3
1,3489
0,4
1,4905
0,5
1,6468
0,6
1,8196
0,7
2,0106
0,8
2,2215
0,9
2,4546
1,0 ~]
2,7121
Последний интервал неопределенности удовлетворяет условию окончания
процесса: 11,0125 - 1,0027343751 = 0,009765625 < е = 0,01. Полученное
приближенное решение приведено в табл. 7.4. ■
Пример 7.6. Найти приближенное решение краевой задачи
у" + у = -х, 0 < х < 1,
у(0) = 0, у(\) = 0
методом стрельбы.
357

D В поставленной задаче а = О, £ = 1, р(х) = 0, q(x) = -1, f(x) = -х, а0 = 1,
Р0 = 0,Л = О, а, =1, Pi = 0,i? = 0. Точное решение найдено в примере 7.1.
Так как задача линейная, то воспользуемся приведенной выше методикой.
1. Решим задачу Коши с начальными условиями, соответствующими
случаю Ро =0:
у" + у = -х, 0 < х < 1,
Я0)= —= 0, У(0) = л
при двух значениях параметра г\: т|(0) =1 и л(1) =-1. Для этого применим явный
метод Эйлера с шагом Л = 0,01. Исходное уравнение с учетом обозначений z~y'
предварительно запишем в форме системы
/ = *, Х0) = 0,
Z' = -y-X, Z(0) = T).
Численные результаты приведены в табл. 7.5.
Таблица 7.5
1 л
1 *'
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
Л<°>=1
;<*,■)
0
9,976 10"2
0,1977231
0,2919084
0,3803712
0,4612217
0,5326446
0,5929167
0,6404248
0,6736817
0,691341
z(x,)
1
0,9910
0,9620968
0,9135469
0,8458201
0,7595744
0,6556531
0,5350776
0,399037
0,2488741
8,6077-10"2
л(,)=-1
УМ
0
9,9999 10"2
-0,2
-0,3
-0,4
-0,5
-0,6
-0,7
-0,8
-0,9
-1
£(*,)
-1
-1
-1
-1
-1
-1
-1
-1
-1
-1
-1
Л(2) =0,18249
УМ
0
1,81074 10'2
3,51523-10"2
4,99637-10"2
6,13916 10"2
6,83188 Ю-2
0,06967-10"2
6,44322 10"2
5,16459 10"2
3,04335 10"2
-8,22125-Ю"7
£<*i>
0,18249
0,17774
0,16008
0,13138
9,13343 10"2
4,03417-10"2
-2Д1013-10"2
-9,23912 Ю-2
-0,17285
-0,261608
-0,35786
2. Запишем функцию
Ф(л) = а, ^;л) + РгУ№л)-^= 1-Я1;л) + 0-0 = >г(1;т|).
Найдем значения Ф(л(0)) = >'(1; 1) = 0,691341 и Ф(г,(,)) = >>(1;-1) = -1, а затем
358

1 ' Ф(л(,))-Ф(л(0)) -1,69134
3. Приближенное решение исходной задачи определяется решением задачи
Коши с ti(2) =0,18249 (две правые колонки в табл. 7.5). Сравнивая его с решением
примера 7.1, можно сделать вывод о близости данного решения к точному.и
7.4.2. Метод дифференциальной прогонки
Отличие метода дифференциальной прогонки [42] от вышеизложенного
метода стрельбы заключается в том, что решаются вспомогательные задачи Коши
не для исходного дифференциального уравнения, а для других уравнений
меньшего порядка. Рассмотрим его применение для решения линейной краевой
задачи (7.3),(7.4).
Методика решения линейной краевой задачи
Первый случай: р0 * 0.
Прямая прогонка. Решить две независимые друг от друга задачи Коши:
Z{ = -Z,2 - p(x)Zx + q(x)t Z, (в) = —S- ;
но
Z'2 = -Z2 .[Z, + p(x)] + /(x), Z2{a) = -p
Po
относительно Zx(x) и Z2(x) на отрезке [a,b].
Обратная прогонка. Решить задачу Коши
y' = Z{(x)y + Z2(x)t a<x<b; y(b) = *"P'*2ff'
a,+p,Z,(A)
Второй случай: a0 * 0.
Прямая прогонка. Решить две независимые друг от друга задачи Коши:
Щ = - и\ ЯМ + Щ р(х) + 1, а<х<Ьу их(а) = -^-;
<*о
и2 = -их(х)[и2 q(x) + f(x)], a<x<by и2(а) = .
<*о
Обратная прогонка. Решить задачу Коши
и\(х)у =у-и2(х), а<х<Ь\ у{Ь)= Jv Pl 2V '.
Р, +a, i/!(A)
Обратная прогонка в обоих случаях дает приближенное решение исходной
краевой задачи.
359

Пример 7.7. Найти приближенное решение краевой задачи
/' + (х + 1)/- 2у = 2, 0<х<\,
У(0)-/(0) = -1, у(1) = 4
методом дифференциальной прогонки. При прямой и обратной прогонке
использовать явный метод Эйлера с шагом h = 0,02.
□ В поставленной краевой задаче а = 0, b - 1, р(х) = х +1, q{x) = 2, f(x) = 2,
а0 = 1, р0 = -1, Л = -1, аj = 1, р, = 0, В' = 4. Так как р0 * 0, воспользуемся
соотношениями для первого случая.
На этапе прямой прогонки решим две задачи Коши на отрезке [0;1]:
Z^-Zf-Z^x + D-f^ ^(0) = --^- = -™1;
Ро ~ *
Z2=-Z2.[Z1+x + l] + 2, Z2(0) = -^ = ^|=1.
Ро _1
На этапе обратной прогонки решим задачу Коши
y-Z.My + ZjW, 0***1; y(i)=B-^K^. = 4.
aj+PjZj^) 1 + 0
Результаты вычислений представлены в табл. 7.6 (в целях экономии места
численные значения приведены в точках, отстоящих друг от друга на 0,1).
Таблица 7.6
Значения
аргумента
1 *''
0,0
1 °Л
0,2
0,3
1 0,4
0,5
0,6
0,7
0,8
0,9
1,0
Прямая прогонка
£|<*/)
1,000000
0,996238
0,984706
0,967711
0,947030
0,924000
0,899611
0,574584
0,849434
0,824526
0,8001108
Z2(x,)
1,000000
0,996238
0,984706
0,967711
0,947030
0,924000
0,899611
0,574584
0,849434
0,824526
0,8001108
Обратная
прогонка
УМ
0,9856163
1,196328
1,427262
1,678383
1,949667
2,241091
2,552642
2,884312
3,236095
3,607991
4,000000
Если при прямой прогонке использовать явный метод Эйлера с шагом h = 0,01, а
при обратной - метод Эйлера—Коши, получается более точное решение [42].■
360

7.5. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
Метод конечных элементов нашел широкое практическое применение при
решении уравнений с частными производными. Здесь описывается его
применение к решению линейной краевой задачи (7.3),(7.4) для обыкновенного
дифференциального уравнения, в которой искомая функция зависит от одной
переменной.
Суть метода конечных элементов заключается в следующем:
а) область определения функции >'(х), удовлетворяющей
дифференциальному уравнению и краевым условиям, разбивается на конечное число
подобластей, называемых конечными элементами;
б) в каждом элементе фиксируется конечное число узловых точеку общих
с узловыми точками соседних элементов, в которых должны быть найдены
узловые значения искомой функции;
в) искомая функция на каждом элементе аппроксимируется линейной
комбинацией базисных функций с коэффициентами, равными узловым
значениям искомой функции;
г) для нахождения коэффициентов применяется метод взвешенных невязок
(метод Галерки на).
Разобьем отрезок [а,Ь] на п конечных элементов (в рассматриваемой
задаче ими являются отрезки) е{,...,еп с (л + 1) нумерованными узлами хьх2,...,хя+1
(рис. 7.3).
е
4-
*/-!
Xj -а х2 xi-\ xi хм хп+1 =Ь
Рис. 7.3
Каждому нумерованному узлу xi9 i = 1, п +1, поставим в соответствие
кусочно-линейную глобальную базисную функцию фДдс), принимающую в данном
узле значение единица, а в остальных - нулевое значение (рис. 7.4):
Ф,(*) =
xi ~ xi-l
*7-l
*/+1
■X
-, XguXUXj+x,
л/+1-л/ / = 1,л + 1. (7.30)
0, X < */_! ИЛИ X > Х/+| ,
Для обеспечения унифицированного определения глобальных базисных
функций необходимо ввести в рассмотрение дополнительные узлы х0 и хп+2-
Тогда глобальные базисные функции q>\(x), уп+\(х) будут определены на
отрезках [х0,х2] и [хя,хя+2] соответственно. Значения функций <Р[(х), уп+\(х) на
отрезках [x0,*i] и [хя+1,хл+2] , примыкающих к отрезку [я,6], в дальнейших
расчетах не используются.
361

у = ф/(*)
Рис. 7.4
Используя глобальные базисные функции, будем искать решение краевой
задачи в виде
л + 1
/=1
(7-31)
где у/ — значения искомой функции в узлах х,, / = 1,л + 1 (коэффициенты).
Требуется найти такие значения >>,, / = 1,л + 1, чтобы выполнялось условие
(7.23) (см. метод Галеркина в разд. 7.3).
Функция, аппроксимирующая искомое решение на каждом конечном
элементе, называется функцией элемента.
Для элемента е, с узлами х,- и х/+1 определим локальные базисные функции
(рис. 7.5):
ф?(х).-*±Ц^_
Ф/V*)-
х-х
•, Х,<Х<Х,Ч1,
(7.32)
xi+\ ~xi
, X/ < X < X/+i,
где нижний индекс у базисной функции соответствует номеру узла, а верхний -
номеру конечного элемента. На каждом элементе е, , / = 1,л , обе локальные
базисные функции линейны, причем в узлах этого элемента одна из них равна
единице, т.е. ф*'(х,) = 1 и ср^(х/+1) = 1. Функция элемента е,- может быть
выражена с помощью локальных базисных функций и узловых значений р,- и уи{ по
формуле
У-, ' Ч>? (*) + ?,ч| • Ф*'+1 (*). Xj <х< х/Ч|; / = 1, п ,
(7.33)
О, X < X/ ИЛИ X > Х/ + 1 .
?"<*) =
362

У
1
0
i
*/•-
y = 4t(x)s
1
$i
i
*/
У'(х)
ф?М <P?ii(*)
^ */ >
i
i
i
i
'^4
i N.
i
I
!
1
1
xi+\
Ч > = Ф/+|М
*/+2
Рис. 7.5
Тогда приближенное решение (7.31) краевой задачи можно представить
в форме
Л*) = ЕР*<*).
(7.34)
В силу свойств локальных базисных функций на элементе е, функция
элемента является линейной и принимает в узле х-, значение у,,ав узле хи{
значение уи1 (рис. 7.5). Если в краевой задаче заданы условия первого рода, т.е.
у(а) = А, у(Ь) = В, то при рассмотрении элемента ех следует положить ух = Л,
так как хх = а, а при рассмотрении элемента е„ положить j)„+1 = В, поскольку
дгл+1 = £. Тогда краевые условия первого рода для решения, записанного в виде
(7.31) или эквивалентном ему (7.34), выполняются автоматически. Для учета
условий второго и третьего рода применяется обобщенный подход (см. пример
7.8). В целом аппроксимация (7.31) является кусочно-линейной. На рис. 7.6
показано применение формулы (7.31) для аппроксимации некоторой произвольной
функции у = у(х).
У
1
0
У2
у\у i \^
i ' i
■ ' i
7$Ы>
х\ = а х2
•^%Л-1
! i
i
i
ФО
*/-!
^ 1
1
1
1
1
.Ф/
*/•
4^/41 у^3
11\Ч ^7*
1 ^?-^ 1
1 1 1
Mi ! !
хм
*\У = У(х)
Т Ря+1
1
\>ч<ри+.(*)
хл+1 =6 X
Рис. 7.6
363

Рассмотрим некоторые теоретические аспекты применения метода
конечных элементов на типовом примере линейной краевой задачи с краевыми
условиями первого рода.
Пример 7.8. Найти приближенное решение краевой задачи
у"-у = 0, 0<х<1,
Я0) = 0, XI) = 1
методом конечных элементов, полагая число конечных элементов, равным трем.
□ В поставленной задаче а = О, 6 = 1, р(х) = 0, q{x) = 1, f(x) = 0, а0 = 1,
Р0 = 0, А = О, а, = 1, pj = 0, В = 1. Точное решение этой задачи (см. пример 7.1):
е г е
УМ"
е2-1
е +-
1-е'
Применим метод Галеркина. Для этого запишем условие (7.23):
1
lly"W-yM}-4>j(x)dx = Q, y = l,#i + l.
(7.35)
Заметим, что базисные функции непрерывны, но в силу кусочной
линейности имеют разрывные производные, а при использовании метода Галеркина
для дифференциального уравнения второго порядка требуется, чтобы
подынтегральные выражения в (7.35) были по крайней мере кусочно-непрерывны.
Поэтому рассмотрим так называемую слабую формулировку метода Галеркина, в
которой требования, предъявляемые к базисным функциям, ослабляются.
Проинтегрируем по частям первое слагаемое в (7.35):
J y"(x).yj(x)dx = <pj(x)
dy(x)
dx
1 _ \dy(x) ^j(x)^
О о Л
dx
Тогда (7.35) запишется в форме
dy(x) d<Pj(x) A/ . , "
dx
dx
dx + y>j(x)
dyM
dx
= 0.
0
(7.36)
Из (7.36) видно, что теперь достаточно, чтобы базисные функции фДх)
принадлежали классу С([0;1]) непрерывных функций.
Задача заключается в следующем: требуется найти такой вектор
У = (У\у->Уп+\)Ту чтобы функция (7.31) удовлетворяла условию (7.36). В этом
заключается слабая формулировка метода Галеркина.
Для решения задачи подставим (7.31) в (7.36):
364

/=1
</jC
<fr
dx = <pj(x)
л + 1
^ ХЛ-ф/W
/И
• (7-37)
0
Полученное равенство запишем в матричной форме:
(7.38)
где К - матрица размера (я + 1) х (я + 1), элемент которой определяется по
формуле
*Л/ = J
dg>j(x) d<Vj(x)
dx dx
+ Фу(*)-Ф/М
dx, у = 1,я + 1; / = 1,я + 1, (7.39)
a / = (/i,.-,/rt+i)r_ вектор, компоненты которого находятся следующим
образом:
/у =фу(*)
л + 1
^ ZU "Ф|(х)
/ = 1
, j = \tn + \.
(7.40)
0
Проанализируем вклад элемента е( с узлами xhxul (см. рис. 7.5).
Единственными отличными от нуля глобальными базисными функциями для
элемента е, будут ф/(х) и Ф,+1(х). Поэтому будем использовать соответствующие
локальные базисные функции <ре/(х),уе/+1(х). С учетом (7.32) и (7.39) определим
элементы матрицы конечного элемента е,:
КЬ = ]
dx
-(ф/w)2
dx,
*ы
*,Ч|
»?t|W <*P?(s)
+ф£,(*)-ф?м
etc,
(7.41)
rfx
* = *«,
<*#(*) ^lW ft/ X ft , X
<** = /:
/ + !,/•
365

В результате можно записать матрицу элемента е( в форме
ГО... О 0.... (П
К1 =
°-*|Ч1,/ ^/Ч1,/Ч1-°
0...0
0 ...
О
(7.42)
Матрица А'системы (7.38) получается суммированием матриц К', / = 1,л.
Этот процесс называется ансамблированием элементов.
Алгоритм применения метода конечных элементов
для решения линейных краевых задач
1. Разбить отрезок [а,Ь] на п конечных элементов еь...,ея и представить
решение в виде (7.31).
2. Для каждого конечного элемента составить матрицу /Г',/ = 1,л, по
формуле (7.42), элементы которой вычисляются согласно (7.41).
3. Сформировать матрицу Къ результате суммирования матриц К1, вектор
/ с учетом (7.40) и составить систему (7.38).
4. Учесть краевые условия и решить систему (7.38). В результате найти
значения У\,...,у„+\ и выписать приближенное решение по формуле (7.31).
Теперь применим описанную методику к решению поставленной задачи.
1. Положим п = 3 при равномерной сетке. Тогда h = xi+l -х, = — = const, а
глобальные базисные функции, определяемые по формулам (7.30), изображены
на рис. 7.7.
Решение задачи ищется в форме
уМ = р, -q>i(x) +j>2 -ФгМ + Рз -Фз(*) + .р4 -ячОО.
(7.43)
где ух, у2, >>з i Уа подлежат определению.
2. Составим матрицу К' для каждого элемента еХуеъе^. С этой целью
вычислим отдельные элементы матрицы по формулам (7.41). Для конечного
элемента ех получим
*2
(dq'Mx)
dx
•k'w)2
1
dx
( V V V
v*2 -*1 J
i2
+
f v y\2
Л2 -л
,*2 ~*1 J
► rfx =
366

-I
9 + 9-I--X
dx-
9x-9
3 = 28.
9 '
0
*2
dx dx
dx-.
-J
о
d ( x2 -x "j Л x-X| "j
*2 ~ * д: - x,
*2 - xl x2~ xl
rfx =
I
з Г
■J-
0 L
-3-3 + 9- \^-x\(x-0)
dx =
53
18'
Kl\ - K\l\ К77 ~ Л,1,
2,2 " л1,1*
Здесь нижние индексы соответствуют связям узлов для элемента,
указанного в верхнем индексе.
Рис. 7.7
367

В результате для конечного элемента et получаем
( 28
АГ1
2 О о"
9 18
£ 28 0 0
18 9
О 0 0 0
О
О 0 0)
Так как сетка равномерная, дифференциальное уравнение с постоянными
коэффициентами и базисные функции «одинаковые», то для конечных
элементов е2,е3 в Решаемои задаче аналогично имеем
К2
0 0 0 0^
0 ii _« о
9 18
о -» » о
18 9
0 0 0 0J
a:j
0
0
0
0
0
0
0
0
0
0
7.8
9
53
18
0 '
0
53
18
28
9 ,
л: =
3. Складывая матрицы элементов еие2,е2 , находим результат ансамблиро-
вания:
^ .« о о'
9 18
_53 56 _53
18 9 18
0 -— — - —
18 9 18
0 0 -» 2
is 9 ;
По формуле (7.40) с учетом (7.43) определим компоненты вектора f
правой части системы (7.38):
/71»! V 1 I
, поскольку ф! (1) = 0, ф! (0) = 0;
/l =<Pi(*)
dy(x)
dx
dy(x)
h =92W'
/з = Фз(*)
</?(*)
dx
= 0'
= 0, так как <р2(1) = 0, Ф2(0) = 0;
U =94W
4?(*)
rfr
0
dy(x)
= 0, так как ф3(1) = 0, ф3(0) = 0;
dx
х = 1
, поскольку ф4(1) = 1, ф4(0) = 0.
368

С учетом полученных результатов запишем систему (7.38):
'2* -* о о
9 18
53 56 _53
"18 9 18
О -— — - —
18 9 18
О 0 -2 28
18 9
\
У
Л
Уз
Л,
/
1
dy(x)
dx
х = 0
dy(x)
dx
1
(7.44)
Из краевых условий у(0) = 0, у(\) = 1 следует, что р, = у(0) = 0, j>4 = ^0) = 1 •
Тогда в системе (7.44) можно исключить первое и четвертое уравнения, положив
в остальных у{ = 0, д>4 = 1 -В итоге получим систему
56
9
53
18
53>
18
56
9 J
р2>
Us J
(°1
53
L18 J
Отсюда у2 = 0,2885; у3 = 0,6088. Точные значения у(х2) = J-1 = 0,2889;
у(хг) = у\— = 0,6102. Приближенное решение задачи имеет вид
>)(х) = 0,2885 • <Р2 (х) + 0,6088 • Фз(х) + ф4 (х). ■
Замечание. В случае краевых условий второго или третьего рода
следует воспользоваться более общей схемой метода Галеркина с учетом невязки
краевых условий, содержащих производные [47]. Например, рассмотрим задачу
У'-Д^О, у(0) = 0, /(1) = 1.
Вместо (7.35) используем следующее условие:
|[Г(х)-р(х)].фу.(дс)Л + [?'(1)-1]-ф;(1) = 0, У = 1,/! + 1, (7.45)
где фу(дс),у = 1,л + 1, ~ весовые функции, задаваемые в общем случае независимо
от функций Фу(х),у = 1,л +1. Как и ранее, краевое условие первого рода на
левом конце может быть выполнено автоматически.
Далее интегрируем по частям:
■J
0 L
dy(x) d<?j(x)
dx
dx
+ Р(*)-Ф;М
dx + фу (x)
dy(x)
dx
1
+
0
/
9yW-
V
dy(x)
dx
x = l
:0
Базисные функции Фу(х),у = 1,л + 1, следует подбирать так, чтобы члены,
содержащие краевые условия с производными, и члены с производными первого
369

порядка, возникающими в той же точке в процессе интегрирования по частям,
уничтожились.
Положим фу(х) = - Ф;(х),У = 1,л + 1. Тогда имеем
dy(x) dyj{x)
dx
dx
+ yM-<Pj(x)
dx = -yj(x)
dy(x)
dx
x = 0
+ Ф./0). у = 1,л + 1.
Полагая /7 = 3 и рассуждая аналогично случаю краевых условий первого
рода с учетом равенств
Ф1(0) = 1,ф2(0) = 0,фз(0) = 0,ф4(0) = 0, Ф,(1) = 0,Ф2(1) = 0,Фз(1) = 0,Ф4(1) = 1,
получаем систему
" ' ' ( <ФЫ\
9 18
53 56 53
О
18
9 18
18 9 18
о о -я М
18 9
\
Л,
=
dx
х = 0
Краевое условие >>(0) = 0 на левом конце учитывается вычеркиванием
первого уравнения и приравниванием ух = 0 в остальных уравнениях.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Решить краевую задачу
у" + у = -х; хе[0;1],
Я0) = 0; /(1) = 0
методом Галеркина. Аппроксимирующую функцию принять в виде
у2(х) = а{х + а2х2 (ф,(х) = х, ф2(х) = х2).
Указание. Данная функция тождественно удовлетворяет условию на левой
границе. На правой границе необходимо использовать взвешенную невязку с
весовыми функциями ф!(х) = -х, ф2М = -х2.
2. Решить краевую задачу
/'-у = 0; хе[0;1],
ЯО) = 0;ЯО=1
методом коллокации и методом Галеркина. Аппроксимирующую функцию при-
т
нять в виде ут(х) = х + ]>] ду sin jnx, удовлетворяющем краевым условиям задачи.
370

3. Решить краевую задачу
y" + y + x = 0; jce[0;l],
методом Галеркина. Аппроксимирующую функцию принять в виде
i)j(x) = aix-М-!]» где ф1(х) = х1 1-^-1,
удовлетворяющем краевым условиям.
4. Решить краевую задачу
y" + y + kx = Q\ xe[0;l],
Я0) = 0, у(\)=\-ку £ = 1-JV, 0,001jV2,
где iVj - номер группы; N2 — номер студента по списку.
Указание. Принимая аппроксимирующую функцию в виде
у3 (х) = х(1 - кх) • (д, + а2х + а3х2),
найти приближенное решение задачи методом Галеркина. Полученное решение
, ч sin* .
сравнить с точным решением у(х) = кх.
sin 1
5. Методом конечных элементов, разбивая [я,£] = [0; 1 - N] на 3, 6 и 12
элементов, решить краевую задачу
У" + У = 0;
*)-.; £
= ctg(l-tf),
где N = N' N° 0,001, N' — номер группы; № — номер студента в группе.
гт с / ч sinx
Приближенные решения сравнить с точным решением у(х) = —-( т.
sin(l-N)
6. Методом конечных элементов решить краевую задачу
У-3/ = 0;хе[0;1],
Яо) = о,Я0=1>
используя четыре конечных элемента. Полученное решение сравнить с точным
. N sh х
решением у(х) = .
sh 1
7. Методом конечных элементов решить краевую задачу
у"-у = 0; хе[0;\],
sh 1
разбивая отрезок Q = [0; 1] на 3 и 4 элемента. Результаты сравнить с точным
решением задачи.
371

Часть IV. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
Глава 8. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ
МАТЕМАТИЧЕСКОЙ ФИЗИКИ С ДВУМЯ НЕЗАВИСИМЫМИ
ПЕРЕМЕННЫМИ
8.1. ПОСТАНОВКА ЗАДАЧИ И ОСНОВНЫЕ ПОЛОЖЕНИЯ
Математические модели современных систем проектирования летательных
аппаратов, а также физические явления в таких областях, как динамика
жидкости, электричество и магнетизм, механика, оптика, теплопередача, описываются
с помощью дифференциальных уравнений в частных производных. В качестве
примеров можно привести уравнения Максвелла, закон теплообмена Ньютона,
уравнения Эйлера, уравнения Навье—Стокса в механике жидкости и газа,
уравнение Шредингера в квантовой механике и др. Производные появляются в
уравнениях потому, что они описывают важнейшие физические величины (такие, как
скорость, ускорение, сила, поток, трение, электрический ток и т.д.). В отличие
от обыкновенных дифференциальных уравнений, в которых неизвестная
функция зависит только от одной независимой переменной, в уравнениях с частными
производными неизвестная функция зависит от нескольких переменных.
В общем случае нелинейное уравнение в частных производных может быть
записано в виде
ди ди д2и д2и дпи
X,,X2,...,Xfc,K,
'ах, '""'ахк 'дх{2'дх\дх2 ''"'дх/'дх/2 ■•дхкРк )
= 0, (8.1)
где хьх2,...уХк — независимые переменные, и(хх,хъ...,хк) — неизвестная
(искомая) функция, р{ + р2 + ...+ рк = п, pt — целые неотрицательные числа.
Во многих практических задачах в качестве независимых переменных
используется время t и пространственные координаты в декартовой, цилиндрической
или сферической системах координат. Задачи с одной пространственной
переменной называются одномерными, с двумя или более — многомерными
(двумерными, трехмерными и т.д.).
Классическим решением уравнения (8.1) называется функция w(xj,x2,...,x^),
имеющая частные производные до требуемого порядка и обращающая это
уравнение в тождество. Общее решение ДУЧП зависит от произвольных функций
с числом аргументов на единицу меньше, чем у функции w(x!,x2,...,x^).
Например, дифференциальное уравнение *' 2 = 1 имеет общее решение
дх2
х2
w(x,,x2) = —+ ф(х2)х! + v|/(x2), где <р(х2), у(х2) — произвольные функции. Для
выделения частного решения необходимо задавать дополнительные условия на
поверхностях размерности к -1 в пространстве независимых переменных
372

х[ух2,...,хк. К этим условиям относятся начальные и граничные (краевые)
условия.
Порядком уравнения называется наивысший порядок частных производных,
входящих в уравнение.
Если функция F линейна относительно искомой функции и(х1,х2,...,хк) и
ее производных, то уравнение (8.1) называется линейным.
Если функция F линейна по высшим производным (л-го порядка), т.е.
коэффициенты при высших производных зависят только от функции и и ее
производных до (п -1) -го порядка, то дифференциальное уравнение называется
квазилинейным.
В данной главе будут рассмотрены численные методы решения
классических линейных одномерных уравнений математической физики, в которых в
качестве независимых переменных, как правило, используется время и одна
пространственная координата.
Пусть D— некоторая односвязная область изменения независимых
переменных х,/. Напомним принципы классификации линейных дифференциальных
уравнений с двумя независимыми переменными на примере линейного
дифференциального уравнения второго порядка, записанного в канонической форме:
дх2 dtdx дГ
+ D(x,t) du{XJ) + Е(х,t) du(xJ) + F(x,t) i#(jc,/) = G(x,t), (x,t)eD,
dx dt
(8.2)
где u(x,t) - искомая функция; A(xit)JB(xit)iC(xit)iD(x1t)iE(x1t)iF(xJ) ~"
коэффициенты, G(xyt) — свободный член (правая часть). Предполагается, что
коэффициенты и правая часть являются заданными дважды непрерывно
дифференцируемыми функциями, причем |Л(х,/)| + |#(-М)| + |С(х,/)| * 0. Если
коэффициенты уравнения не зависят от х и /, то уравнение (8.2) называется уравнением
с постоянными коэффициентами (в противном случае уравнением с переменными
коэффициентами). Уравнение (8.2) называется однородным, если правая часть
G{xy t) тождественно равна нулю для всех х и / (в противном случае
неоднородным). В уравнении (8.2) независимыми переменными являются х и /, но во
многих задачах независимыми переменными являются две пространственные
переменные xHj'.a искомой функцией и(х,у).
Для упрощения записи будем использовать следующие обозначения:
du(x,t) du(x,t) ди(х,у)
Ux = , U, г , Uv s y—±±L
х дх ' dt у ду
_ d2u(x,t) d2u{x,t) d2u(xyt)
ихх = ~~~5 > Utt = „9 ' Uxt = а * * '"*
дх2 дГ dtdx
Тогда уравнение (8.2) записывается в форме
AUn+lBux +Cutt + Dux+Eut + Fu = G. (8.3)
373

Уравнение (8.2) называется уравнением параболического типа в точке
Л/(х0,/0)(в области Z)), если в этой точке (в области D) выполняется условие
В2-АС = 0.
Уравнение (8.2) называется уравнением гиперболического типа в точке
M(x0,t0)(B области /)), если в этой точке (в области D) выполняется условие
В2-АС>0.
Уравнение (8.2) называется уравнением эллиптического типа в точке
Л/(*о>'о)(в области /)), если в этой точке (в области D) выполняется условие
В2 -АС <0.
Заметим, что в различных точках (областях) тип одного и того же
уравнения может быть различным. Если коэффициенты А, В,С постоянные, тип
уравнения (8.2) не изменяется для любых значений независимых переменных в
области D. Он определяется только коэффициентами при вторых производных и
не зависит ни от коэффициентов при первых производных, ни от свободного
члена, ни от самой функции.
Среди задач математической физики, включающих уравнения
гиперболического и параболического типов, выделяются эволюционные (маршевые) задачи.
Для этих задач характерно наличие выделенного независимого переменного -
маршевой координаты, как правило, времени. Если искомая функция зависит от
времени, уравнение называется нестационарным, а если искомая функция не
зависит от времени, то стационарным.
Уравнения параболического типа описывают, например, процессы
теплопроводности и диффузии, гиперболического — колебательные системы и
волновые движения, эллиптического - течение жидкости в стационарных потоках,
стационарное распределение напряженности электрического и магнитного
полей. Тип уравнения определяет формулировку задачи и численные методы его
решения.
Линейное нестационарное уравнение с частными производными первого
порядка имеет вид
А(х, t) их + В(х, t) щ + С(х, /) и = G(xt t), (8.4)
где w(x,/)~ искомая функция; A(xj), /?(*,/), С(х,/) - коэффициенты, G(x,t) -
правая часть. Предполагается, что коэффициенты и правая часть являются
заданными непрерывно дифференцируемыми функциями. Если коэффициенты
не зависят от х и /, то уравнение (8.4) называется уравнением с постоянными
коэффициентами (в противном случае уравнением с переменными
коэффициентами). Уравнение (8.4) называется однородным, если правая часть G(x,t)
тождественно равна нулю для всех х и / ( в противном случае неоднородным).
Пример 8.1. Классифицировать следующие уравнения:
a) ut + их = 0; б) ut -ии^ = sinх; в) и^ + хии = 0; г) ип -с2ихх = 0 ;
д) ut - a2 Uja - О; е) и^ + иуу - 0; ж) х их + / щ + и2 = 0;
з) и^ -0\ и) Ъихх + luXJ + 2utt = 0 ; к) ut и^ - Зх2иuxt + 3 их - и = 0.
□ Для приведения уравнений «е», «з» в соответствие с (8.1),(8.2)
обозначим у = / . Тогда:
374

а) линейное одномерное нестационарное однородное уравнение первого
порядка с постоянными коэффициентами, называемое уравнением переноса)
б) квазилинейное одномерное нестационарное уравнение третьего порядка;
в) линейное одномерное нестационарное однородное уравнение второго
порядка с переменными коэффициентами, где А = 1, /? = 0,С = x,D = Е - F = G = 0.
Поскольку В2 -АС = -х, то при х > О это уравнение эллиптического типа, при
х = 0 — параболического, при х < 0 — гиперболического;
г) линейное одномерное нестационарное однородное уравнение второго
порядка с постоянными коэффициентами, где А = -с2,В = 0, С = 1,
D = E = F = G = 0. Оно называется одномерным волновым уравнением и
описывает распространение плоских звуковых волн в покоящейся среде, продольные
колебания стержня, поперечные колебания струны. Поскольку В2 -АС = с2 > 0, то
это уравнение гиперболического типа при всех jc и /;
д) линейное одномерное нестационарное однородное уравнение второго
порядка с постоянными коэффициентами, где А = -с2, В = 0, С = 0, D = F = G = 0,
Е = 1. Оно называется одномерным уравнением теплопроводности. Поскольку
В2 - АС = 0 , то это уравнение параболического типа при всех х и /;
е) линейное двумерное стационарное однородное уравнение второго
порядка с постоянными коэффициентами, где /4 = 1, В = 0,С = \, D = Е = F = G s 0.
Оно называется двумерным уравнением Лапласа. Поскольку В2 -АС = -1 <0, то
это уравнение эллиптического типа при всех х и у\
ж) нелинейное нестационарное уравнение первого порядка;
з) линейное двумерное стационарное однородное уравнение второго
порядка с постоянными коэффициентами, где А = 0, В = 1, С = D = Е =
= F - G s 0. Поскольку В2 - АС = 1 > 0, то это уравнение гиперболического типа
при всех х и у;
и) линейное одномерное нестационарное однородное уравнение второго
7
порядка с постоянными коэффициентами, где ,4 = 3, В = -, С = 2, D = E =
2 49
= F = G = 0. Поскольку В - АС = 6>0, то это уравнение гиперболического
4
типа при всех х и /;
к) квазилинейное одномерное нестационарное уравнение второго порядка,
так как оно линейно относительно старших производных и^ и и#, а
коэффициенты при этих производных зависят только от м и производных первого
порядка. ■
Математические постановки задач с дифференциальными уравнениями в
частных производных содержат дифференциальные уравнения и дополнительные
условия, позволяющие выделить искомые частные решения среди целого
семейства решений.
В математической физике различают три основных типа задач:
1. Задача Коши (с начальными условиями).
2. Краевые {граничные) задачи с краевыми (граничными) условиями.
3. Смешанные задачи (начально-краевые) с начальными и краевыми
условиями.
375

Количество и характер краевых условий в краевых и смешанных задачах
определяется типом дифференциального уравнения, его порядком и характером
физических процессов, для которых строится математическая модель. Если
количество граничных условий превышает нужное число, то задача становится
переопределенной и, как правило, не имеет решения. Если их меньше, чем
требуется для разрешимости задачи, то ее решение не является единственным. Для
анализа разрешимости задач доказываются теоремы о существовании и
единственности решения (где это возможно). Для любого заданного
дифференциального уравнения целесообразность рассмотрения той или иной задачи
определяется корректностью ее постановки. Задача корректно поставлена, если ее решение
существует, единственно и непрерывно зависит от данных задачи.
Рассмотрим постановки некоторых типовых задач математической физики.
ПОСТАНОВКИ ЗАДАЧ ДЛЯ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
Рассмотрим наиболее типичное уравнение первого порядка — одномерное
уравнение переноса
du(x,t) du(x,t)
dt
дх
■ = 0, 0<x<Lt 0 < / < 7\
(8.5)
являющееся модельным для некоторых процессов в механике сплошной среды.
Оно описывает конвективный одномерный перенос тепла и является
эволюционным. Здесь х = 0 и x-L — левый и правый концы отрезка изменения
пространственной переменной, / = 0 и t -Т — моменты начала и окончания
процесса. Таким образом, задается область D = (0, L) х (0, Т), ограниченная
прямоугольником (рис. 8.1) с длиной L и высотой Т. Соотношения / = 0, 0<x<L
задают нижнюю границу области D, соотношения t = Т, 0 <х < L — верхнюю,
х = 0, 0 <t <Т— левую границу, x-L, 0 < / <Т — правую. Далее на множестве
D = D U dD = [0, L] х [0, Т), где DD — граница области D, рассматриваются
различные начально-краевые задачи для уравнения (8.5).
t
Т V
Рис. 8.1
Начально-краевая задана:
ut +их =0, 0 < х < L, 0 <t <Т,
и(х,0) = i|/(x), 0 < х < L, (начальное условие)
w(0, /) = ф(/), 0 < / < Т у (краевое условие на левой границе)
376

содержит функциональное начальное условие (при / = 0) и функциональное
краевое условие на левой (х = 0) границе области. Здесь и далее ц/(х),ф(/) —
заданные функции, удовлетворяющие условию их согласования в начале
координат [7].
Задача Коши:
ut + их = О, - оо < X < +оо , 0 < / < Г,
w(x,0) = \у(х), - оо < х < +оо , (начальное условие)
содержит только функциональное начальное условие (при / = 0) и
рассматривается в бесконечной области изменения пространственной переменной.
Во всех перечисленных задачах требуется найти функцию u(x,t), которая
удовлетворяет дифференциальному уравнению (8.5) в области D и
соответствующим условиям на ее границе.
ПОСТАНОВКИ ЗАДАЧ ДЛЯ УРАВНЕНИЙ ПАРАБОЛИЧЕСКОГО ТИПА
Рассмотрим наиболее типичное уравнение параболического типа —
уравнение теплопроводности в однородной среде или диффузии
М^ = а2дЩо 0<x<LyQ<t<Ty (8вб)
а/ дх2
где и — температура, а1 = — , к — коэффициент теплопроводности, с - удель-
ная теплоемкость, р - плотность (в задаче диффузии и - концентрация
диффундирующего вещества, а2 = —, d — коэффициент диффузии, с — коэффициент
с
пористости среды, который определяется отношением объема пор к
рассматриваемому объему), х = 0 и х = L — левый и правый концы отрезка изменения
пространственной переменной, / = 0 и t -Т — моменты начала и окончания
процесса. Таким образом, на множестве D = [О, L] х [О, Т] рассматриваются
различные начально-краевые задачи для уравнения (8.6) (рис. 8.1).
Первая начально-краевая задача:
К/=я2"х*> 0 <*</,, 0</<7\
и(хуО) = у(х), 0 < х < L, (начальное условие)
ы(0, /) = ф! (0, 0 < / < Т, (краевое условие на левой границе)
u(L, t) = ф2(/), 0 < / < Т, (краевое условие на правой границе)
содержит функциональное начальное условие (при / = 0) и функциональные
краевые условия на левой (х = 0) и правой (х - L) границах области. Здесь и
далее ц/(х),ф!(0,ф2(0 "~ заданные функции.
377

Вторая начально-краевая задача:
ut = a2 Uja, О < х < L, О < / < Т,
w(x,0) = vj/(x) , О < х < L , (начальное условие)
ди(0,0
ах
du(L,t)
дх
- ф! (/), 0 < / < Г, (краевое условие на левой границе)
= Ф2(0, 0 < / < Т, (краевое условие на правой границе)
содержит функциональное начальное условие (при / = 0) и дифференциальные
краевые условия на левой (х = 0) и правой (х = L) границах области.
Третья начально-краевая задача:
ut=a2uXXi 0 < х < £, 0</<7\
u(xfl) = v|/(x), 0 < х < Z,, (начальное условие)
а0 — + Ро ы(0, t) = ср! (/), 0 < / < Г, (краевое условие на левой границе)
дх
ct| — ' + Pj u(Lyt) = Ф2(0, 0 < / < Г, (краевое условие на правой границе)
дх
содержит функциональное начальное условие (при t = 0) и функционально-
дифференциальные краевые условия на левой (х = 0) и правой (х = L) границах
области. Здесь a0,Po,ct|,Pi — заданные числа (а2 +р? > 0, / = 1,2) либо функции
от / в более общем случае [26].
Задача Коши:
ut=a2uXXi -оо<х<+оо, 0</<Г,
u(xfl) = v|/(x), - оо < х < -и» , (начальное условие)
содержит только функциональное начальное условие (при / = 0) и
рассматривается в бесконечной области изменения пространственной переменной.
Примером физической задачи, приводящей к первой начально-краевой
задаче, может быть процесс теплопередачи по длинному тонкому стержню,
лежащему вдоль оси Ох от х = 0 до х = L (ось стержня совпадает с осью Ох).
Предполагается, что в точке х = 0 температура изменяется со временем по закону
Ф!(/), а в точке х = L по закону Фг(0- В начальный момент времени при / = 0
функцией ц/(х) задано начальное распределение температуры вдоль стержня.
Тогда распределение температуры вдоль него во все последующие моменты
времени определяется решением начально-краевой задачи с уравнением (8.6) , где
w(x,/) — температура стержня в некоторой точке х в момент времени /.
Во всех перечисленных задачах требуется найти функцию и(х,/), которая
удовлетворяет дифференциальному уравнению (8.6) в области D и
соответствующим условиям на ее границе.
378

ПОСТАНОВКИ ЗАДАЧ ДЛЯ УРАВНЕНИЙ ГИПЕРБОЛИЧЕСКОГО ТИПА
Рассмотрим наиболее типичное уравнение гиперболического типа -
одномерное волновое уравнение, которое описывает, в частности, малые поперечные
колебания струны:
Э^__с2Л^ 0<*<L, 0</<Г, (8.7)
где u(xj) — отклонение струны от положения равновесия в некоторой точке х
в момент времени /, коэффициент с2 = —, р — линейная плотность струны,
Р
Т - натяжение, х = 0 и х = L - левый и правый концы отрезка изменения
пространственной переменной, / = О и t -Т — моменты начала и окончания
процесса. Из предположения о малости колебаний следует, что величина натяжения,
возникающего в струне, не зависит от времени. При этом также считается, что
внешние силы, которые могли бы действовать на струну, отсутствуют.
Волновое уравнение описывает также малые продольные колебания
упругого стержня. Тогда с2 = —, к — модуль Юнга, р — плотность. Это же уравнение
Р
описывает распространение звуковых волн в сжимаемой среде и называется
2 УРо СР
уравнением акустики, в котором с =—-, у = —, />о,Ро "" давление и плот-
Ро cv
ность невозмущенной среды, cVicp — коэффициенты теплоемкости при
постоянном объеме и давлении соответственно. Для газовой среды это уравнение
может быть получено из уравнений газовой динамики путем их линеаризации.
Таким образом, на множестве D = [О, L] х [О, Т] рассматриваются различные
начально-краевые задачи для уравнения (8.7) (см. рис. 8.1).
Первая начально-краевая задача:
ии = с Uja , 0<JC<Z/, 0 < / <Т,
ы(х,0) = i|/[ (х), 0 < х < L, (начальное условие)
——— = V2(X)> 0<jc<L, (начальное условие)
dt
w(0, /) = <Pi (01 0 < t < Т, (краевое условие на левой границе)
u(L,t) = (р2(0, 0 < t < Т, (краевое условие на правой границе)
содержит функциональное и дифференциальное начальные условия (при / = 0) и
функциональные краевые условия на левой (х = 0) и правой (х = L) границах
области. Здесь и далее \vi(x)i\v2(x)iyl(t),(p2(t) — заданные функции.

Вторая начально-краевая задача:
ии - с2^, 0 < х < L, 0 < / < Г,
u(xfi) = у, (х), О < х < L , (начальное условие)
—^-2-^ = v|/2(x), 0 < х < L, (начальное условие)
■ = Ф1 (/), 0 < / < Т, (краевое условие на левой границе)
дх
ди(Ц)
дх
= Ф2 W» 0 < / < Г, (краевое условие на правой границе)
содержит функциональное и дифференциальное начальные условия (при / = 0) и
дифференциальные краевые условия на левой (х = 0) и правой (х = L) границах
области.
Третья начально-краевая задача
ии = с2^, 0 < х < L, 0 < / < Г,
u(xfi) = у i (х), 0 < х < Z,, (начальное условие)
du(xfi)
а/
■ = \|/2(х), 0 < х < Z,, (начальное условие)
а0 —^-L-^ + Ро и(0, /) = ф| (/), 0 < / < Т, (краевое условие на левой границе)
дх
cti — ' + pt u(L,t) = ф2(0, 0 < / < Т, (краевое условие на правой границе)
дх
содержит функциональное и дифференциальное начальные условия (при / = 0) и
функционально-дифференциальные краевые условия на левой (х = 0) и правой
(x = L) границах области. Здесь ct0,po,ai,Pi - заданные числа, [ос/1 н-1рхj > 0.
В более общем случае коэффициенты, входящие в краевые условия, являются
функциями времени [26].
Задача Коши:
Utr = С Uja, -оо<Х<+оо, 0</<7\
и(х,0) = у\(х), -оо<х<+оо, (начальное условие)
du(xfi)
dt
■ = 4*2 М» ~ °° < х < +00 » (начальное условие).
380

содержит только функциональное и дифференциальное начальные условия (при
г = 0) и рассматривается в бесконечной области изменения пространственной
переменной.
Во всех перечисленных задачах требуется найти функцию u(xyt), которая
удовлетворяет дифференциальному уравнению (8.7) в области D и
соответствующим условиям на ее границе.
ПОСТАНОВКИ ЗАДАЧ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
Рассмотрим наиболее типичное уравнение эллиптического типа —
уравнение Лапласа
^Ы1 + ^у1 = 0> (x,y)€Q>
дх<
ду'
(8.8)
или более общее уравнение Пуассона
д2и(х,у) д2и(х,у)
дх1
ду'
Ах,У), (х,у)еП,
где Q — некоторая односвязная область на плоскости Оху с простой (без
кратных точек) кусочно-гладкой границей Г (рис. 8.2). В простейшем случае,
рассматриваемом далее, область Q имеет прямоугольную форму.
Уравнение Пуассона описывает стационарное течение идеальной
жидкости, в которой отсутствует вязкость и теплопроводность, стационарное
распределение тепла в теле и др. Это же уравнение описывает стационарное
распределение напряженности электрического или магнитного поля в электродинамике.
Уравнение Лапласа описывает эти явления, когда внутри Q нет источников и
стоков, а уравнение Пуассона — с распределенными по области Q источниками,
задаваемыми правой частью /(х, у).
У •
0
г
V""^::'»ip-:i;;J!.!:;-;H:
\ ^s* п
Рис. 8.2
Поскольку в уравнении (8.8) отсутствуют производные по времени, задача
является стационарной, следовательно, начальные условия в ней не задаются. На
границе Г области Q могут задаваться краевые (граничные) условия трех видов,
что порождает три краевые задачи.
381

Первая краевая задача (задана Дирихле):
uxx+uyy=0, (xj)efi,
и | г = (p(x, у), (х, у) е Г, (краевое условие)
содержит функциональное краевое условие на границе Г области Q, ф(х, у) —
заданная функция.
Вторая краевая задача (задача Неймана):
ихх + иуу = ° > (*» J7) е ^ >
— I г = ф(х, .у), (х, у) е Г, (краевое условие)
содержит дифференциальное краевое условие, в котором задается производная
в направлении внешней нормали п на границе Г области Q (рис. 8.2).
Третья краевая задача:
ихх+иуу=®> (х,у)еС1,
а — |r+Pw|r = ф(*> у) у (х, у) е Г, (краевое условие)
дп
содержит функционально-дифференциальное краевое условие, в котором
задается линейная комбинация производной в направлении внешней нормали и
функции и(х, у) на границе Г области Q. В более общем случае аир зависят от
переменных х и у [26].
В качестве примера задачи Дирихле можно привести задачу о нахождении
стационарного распределения температуры внутри области, если задана
температура на ее границе. Примером задачи Неймана служит задача стационарной
теплопроводности и электростатики, если на границе задан поток (тепла,
электронов).
Во всех перечисленных задачах требуется найти функцию м(х, у), которая
удовлетворяет дифференциальному уравнению (8.8) в области Q и
соответствующему краевому условию на ее границе Г.
Замечания.
1. Тип неравенств (строгое или нестрогое) в краевых и начальных условиях
в каждом конкретном случае определяется особенностями физической задачи.
2. Для существования достаточно гладких решений поставленных задач
требуется выполнение условий согласования начальных и краевых условий в
углах расчетной области [7,8,14].
382

8.2. ПРИНЦИПЫ ПОСТРОЕНИЯ РАЗНОСТНЫХ СХЕМ
Точное решение задач математической физики (в виде явных формул,
рядов и т.п.) можно найти только в редких случаях. Среди приближенных методов,
в результате применения которых получается приближенное (не точное)
решение, представляемое таблицей чисел, наибольшее распространение получили
разностные методы {методы сеток). Сущность разностных методов состоит в том,
что исходная область изменения независимых переменных заменяется
дискретным множеством точек — сеткой, а производные, входящие в уравнение,
аппроксимируются на этой сетке разностными соотношениями. В результате
исходная линейная задача заменяется системой конечного числа линейных
алгебраических уравнений, называемой разностной схемой {задачей). Аналогично
исходная нелинейная задача заменяется нелинейной разностной схемой. За
приближенное решение исходной задачи принимается решение разностной схемы.
Точность приближения зависит от способа аппроксимации и от густоты сетки,
т.е. от того, насколько плотно сетка заполняет исходную область.
Рассмотрим общую запись постановок линейных задач, описанных в разд.
8.1. Пусть дана исходная {дифференциальная) задача в виде
£« = /, (8.9)
где и — искомая функция, определенная на множестве D = D\JY\ D— область
пространства независимых переменных с границей Г; / — заданная функция,
£ — линейный дифференциальный оператор. Предполагается, что все
производные, входящие в дифференциальное уравнение, перенесены в левую часть, а
остальные функции образуют правую часть; дополнительные условия (начальные и
краевые) также включены в оператор £ и правую часть /. Например, начально-
краевая задача для уравнения переноса (8.5) запишется в виде (8.9), если
положить
О, 0<jc<L, 0<t<T
vj/(x), 0 < х < L .
Ф(0, 0 < / < Т
ut + их, 0<x<L, Q<t<T
£и = \ u{x,0), 0<x<L , /:
и(0,0, 0<t<T
Для численного решения задачи вводится сетка /)Л={Л/Л} — конечное
множество точек Mh {узлов сетки), принадлежащих D , плотность размещения
которых характеризуется параметром h — шагом сетки. В общем случае h —
вектор, компонентами которого являются шаги по всем независимым переменным
решаемой задачи, с длиной |Л|. Обычно сетка задается так, что при |Л|->0
множество Dh стремится заполнить множество D = D U Г.
Для определенности далее рассматривается некоторая дифференциальная
задача с двумя независимыми переменными х и /. Для простоты изложения
будем предполагать, что множество D представляет собой прямоугольник длины
L и высоты Т, ограниченный отрезками прямых, параллельных осям Ох и Ot
(рис. 8.3), т.е. задана двумерная прямоугольная сетка
где х-, = /Л, 0 < / < /; tn - пт, 0 < п < N ; N, I - целые положительные числа;
Иух - величины шагов по пространству и времени (для простоты принимаются
383

постоянными); / Л = L, N х = Т. Такая сетка называется равномерной
(регулярной). Здесь можно положить |//| = V/i2+t2 или |//| = V/j2+t. Узлы,
принадлежащие промежуткам {0 < х < L% t = 0}, {х = 0, 0 < / < Г},
{х = L, 0 <t <T}y{t = ТУ 0 < х < L }, называются граничными, а остальные -
внутренними. Слоем \xhtnf, / = 0,...,/-1; п - const называется множество всех
узлов сетки, имеющих одну и ту же временную координату tn.
/ *
Т
Л + 1 '
П '
i
i
0
i
i i
i (
i i
i i
h
1 Т щ ■ 9 ■ 9
1 1
1 1
1 1
1 1
I -
!■■■■■
1 Т
i 1 1 1 1 1
i ■ * ш m m
1
I /
i 111
+ 1 L
—►
Рис. 8.3
Функции, определенные в точках сетки Dh, называются сеточными. Введем
сеточную функцию uh = [и-1 = u(xhtn), Q<i<I,0<n<Nf , которая является
сеточным представлением решения исходной (дифференциальной) задачи или
точным решением дифференциальной задачи в узлах сетки. Как правило, вычислить
uh не удается, поэтому находят другую сеточную функцию uh =uh, приближенно
совпадающую с точным решением в узлах сетки. Она вычисляется как решение
разностной схемы
енч=Гнг (8-Ю)
в некотором смысле соответствующей задаче (8.9). Здесь £h - разностный
оператор, аппроксимирующий линейный дифференциальный оператор £ (он
формируется в результате аппроксимации частных производных, входящих в £,
соответствующими конечно-разностными соотношениями); fh — сеточная
функция, возникающая в результате замены правой части уравнения (8.9)
значениями в узлах сетки. Таким образом, под разностной схемой понимается
совокупность разностных уравнений, аппроксимирующих основное
дифференциальное уравнение во всех внутренних узлах сетки и дополнительные условия
(начальные и краевые) — в граничных узлах. Разностную схему по аналогии с
дифференциальной задачей будем называть разностной задачей.
Обозначим линейное нормированное пространство, образованное
совокупностью функций йИ, определенных на Dh, через Uh, а пространство,
образованное совокупностью функций /Л, через Fh. Пусть в этих пространствах введены
нормы ||-11^,11 .|v
384

Если при \h\ -> 0 выполняется условие
|«*-«*1е,4->0, (8.11)
то решение разностной задачи сходится к решению дифференциальной, а
разностная схема называется сходящейся. Если существуют такие постоянные р > 0 ,
С > 0, не зависящие от \h\, что выполняется неравенство
то схема имеет /?—й порядок сходимости (порядок точности).
Как указано выше, основной идеей разностных методов является
преобразование дифференциальной задачи к разностной задаче для нахождения
сеточного решения, в некотором смысле близкого к точному решению.
Функция bfh в выражении £huh = fh + bfh , получающаяся в результате
подстановки сеточного представления uh в разностную схему (8.10), называется
погрешностью аппроксимации.
Разностная задача (8.10) аппроксимирует дифференциальную задачу (8.9) на
решении и(х, t), если
\bfk\h-*b при|Л|->0.
Если существуют такие постоянные к > 0 , Л/>0, не зависящие от |/г|,
что выполняется неравенство
\bf4FhSM\h\k, (8.12)
то разностная схема имеет к -й порядок аппроксимации.
Одновременное выполнение условия Цб/дЦ^ =0(хр+ hq) означает, что
схема имеет р-й порядок аппроксимации по времени и ^-й по пространству.
В случае трех независимых переменных аналогичное условие имеет вид
|%|^-0(х'+А,«+А/)-
Разностная схема называется устойчивой^ если существует постоянная
К > 0, не зависящая от |Л|, что при любых /Л е Fh справедливы условия:
1) разностная схема (8.10) имеет единственное решение;
2>l**Usjr|yiU-
Замечания.
1. Свойство устойчивости какой-либо задачи означает, что при небольшом
изменении исходных данных решение изменяется мало. Таким образом, для
исследования устойчивости необходимо рассматривать уравнение, которому
удовлетворяет погрешность, возникающая в результате возмущения исходных
данных. Однако в случае линейного оператора структура уравнения для
погрешности та же, что и исходного уравнения (8.9). Действительно, рассмотрим
уравнение £И ц =fh> отличающееся от (8.10) правой частью. Вычитая его из (8.10), по-
385

лучаем уравнение €h zh = bfh, описывающее изменение погрешности zh -uh -ih
в силу наличия возмущения bfh =//,-//, правой части. Тогда если выполнено
условие 2) определения устойчивости, то одновременно fle/,11^ < А'Цб//, Ц^ и,
следовательно, || ел Ц^ -> 0 при || 6/л Ц^ -> 0. Это означает, что задача
устойчива.
2. Свойство устойчивости связано с понятием норм, вводимых в
пространствах UhiFh. Возможны случаи, когда условие 2) будет выполняться для одних
норм и не выполняться для других. Если это условие не выполняется ни при
каком разумном выборе норм, то схема неустойчива.
Разностные схемы, устойчивые при любом соотношении шагов h и т,
называются абсолютно устойчивыми.
Разностные схемы, неустойчивые при любом соотношении шагов Лит,
называются абсолютно неустойчивыми.
Разностные схемы, устойчивые лишь при некотором ограничении на
отношение шагов по пространству и по времени, называются условно устойчивыми.
Сходимость и устойчивость связаны теоремой, играющей основную роль
при анализе разностных схем.
Теорема [40]. Пусть дифференциальная задача (8.9) поставлена корректно,
разностная схема (8.10) устойчива, аппроксимирует дифференциальную задачу (8.9)
и имеет к -й порядок аппроксимации. Тогда решение разностной задачи сходится к
решению дифференциальной задачи, причем порядок точности совпадает с порядком
аппроксимации.
Установить устойчивость разностной схемы с использованием определения
на практике затруднительно. Поэтому предложен ряд методов, позволяющих
получить необходимые (иногда необходимые и достаточные) условия устойчивости
разностных схем: спектральный признак устойчивости, метод гармоник Фурье,
принцип максимума, метод операторных неравенств [14,35,40]. В данной книге
эти методы не рассматриваются.
Схема называется явной, если оператор £ аппроксимируется с
использованием известных значений функции u(xhtn) на л-м слое, а аппроксимирующее
уравнение содержит только одно неизвестное значение функции на следующем
(л +1) -м слое, которое нетрудно выразить явно. Схема называется неявной, если
оператор аппроксимируется с использованием нескольких неизвестных значений
искомой функции на (л +1) -м слое. Узлы сетки Dh, значения в которых
используются при аппроксимации оператора €, образуют шаблон. При изображении
шаблона светлыми кружочками обозначаются узлы, соответствующие всем слоям
с известными значениями функции, а зачерненными - узлы с неизвестными
значениями функции, подлежащими определению. Шаблон, содержащий р
узлов, называется р-точечным.
Получим некоторые разностные формулы для аппроксимации частных
производных первого и второго порядков, входящих в уравнения видов (8.3),(8.4)
и в соответствующие дифференциальные задачи, рассмотренные далее.
386

Пусть имеется функция и(х,/), имеющая непрерывные производные по
всем переменным до (к + \)-го порядка включительно. Выберем узел (xhtn)
сетки £)Л. Сначала рассмотрим разности в направлении д:.
Применим формулу Тейлора (В.16)-(В.18) разложения функции u(x,tn)
одной переменной х в окрестности выбранного узла (xhtn).
При к = 1 имеем
Л2
u(xi+hytn) = u(xhtn) + ux(xittn)h + uxx(B3litn) — t 5i €<*/,*/+«, (8.13)
h2
^/-Л,Гл) = ^(д:/,Гя)-^(д:/,/',)/; + ^(42,/л)у, $2е(*/-М/). (8.14)
Из (8.13) следует
Очевидно, справедлива оценка
"«(4ь'л)|
<- max 1и«(х,/я) =-Л/2,
1 xelx/.x^+Z»]1 I 2
где М2 = max м^ (*,/"). Отсюда получаем формулу (аппроксимационный
xe[xitXj+h)l I
оператор)
а^,/")-^^^-^'^, (£*,) (8.15)
которая аппроксимирует частную производную их с первым порядком
аппроксимации на двухточечном шаблоне. Она называется правой разностью.
Аналогично из (8.14) получается формула
их{х^)-и{Х,'П-и^-Н',П\ (8.16)
п
также аппроксимирующая частную производную их с первым порядком
аппроксимации на двухточечном шаблоне. Она называется левой разностью.
Получим еще одну формулу для аппроксимации частной производной их.
При к = 2 из формулы Тейлора (В. 16)—(В. 18) получаем
h1 h3
u(xi+hjn) = u(xiitn) + ux(xhtn)h + uxx(xiJn) — + uxxx£ljn)?-, (8.17)
2 6
^ e(xi9Xj +/z),
h2 h3
u(xi-h>tn) = u(xi3tn)-ux(xhtn)h + uxx(xiJn) — -uxxx^2>tn) — i (8.18)
l о
£2e(x,—/i,x,).
387

Вычитая (8.18) из (8.17), имеем
u(xi+h,tn)-u(xi-h,tn) = 2ux(xhtn)h + luJoa^l,tn) + uxxx^2,tn)}^.
Но, согласно утверждению В. 1, существует точка 4 е (х, - h, х, + /;), что
~ — иххх VS»' ) •
Поэтому
/ ,«ч u{xi+hytn)-u{xi-h>tn) „ h2 . , L i.v
ux\xi»1 /~ г*.
(И
(8.19)
где Л/3 = max 1/АЗСС(х,/л) . Эту формулу называют центральной разностью,
xe[Xj-h,Xi + h]* '
которая аппроксимирует частную производную их со вторым порядком
аппроксимации на трехточечном шаблоне.
Обозначая u(xhtn) = и?, w(x, + hytn) = u"+l, w(x, - /;,г") = w/!_,, перепишем
(8.15),(8.1б),(8.19)вформе
Ux(xht")=U"*;U> 9 (8.20)
Л
ах(х/,/»)=и""""-', (8.21)
Теперь получим формулы для аппроксимации производных второго
порядка. При к = 3 формула Тейлора (В. 16)—(В. 18) имеет вид
h2 h3
u(Xj + h,tn) = u(xhtn) + ux(xhtn) h + u^iXiJ") — + Uxxx{xhtn) — +
z о
+ *w(^'")—> ^(^^Л). (8.23)
Л2 Л3
u(xi-h,tn) = u(xhtn)-ux(xhtn)h + uxx(xntn) — -Uxxx(xi3tn) — +
Z О
+ «х=с«(42.'п)^. ^e^-A.x,). (8.24)
388

Сложим (8.23) и (8.24):
x..tn) + u„Jx:.tn)h2 +\и (Ei.tn) + u (E^tn)\
24
u(xi+hJn) + u(xi-hjn) = 2u(xiJn) + u^(xiJn)h2+lu^(^Jn)^uxxxx^2itn)]
и (E tn} + и (E tn)
Поскольку, согласно утверждению B.l, -sss-— ^^ — = uxxxx(E31tn), где
^ e (Xj - Л, Xj + h), то перепишем полученное равенство в виде
Ц(х/+/?>/я)-2^(х/)/я) + Ц(х/-/2,^) Л^
"дос V-*/ у1 ) — 9 "досхх vS>' / , ~
/Г 1^
или окончательно
ихх\х1>* ) = Г5 ТТМ4
Л
Г 1.2 ^
12 — Г (825)
где М4 = max Uxm(^i^) • Формула (8.25), называемая центральной разно-
хе[хк-h, *, + /»]' '
cm б/о второго порядка, аппроксимирует и^ со вторым порядком аппроксимации
и может быть записана аналогично (8.20)-(8.22):
п Iv *п\ UU\ -2ui +ui-\ /ола
Л
Так же получаются разности в узле (xhtn) в направлении /:
а,ь,п-и1х,-'в*х)-«х"''\ адх|./")-^^. (8.27)
X X
и,(Х,П=и^'П)-и{Х»'П-*\ fi,(„.,->-£u£L, (8.28,
х х
a^,,")^-'"^;^''""^ *,<,|Г).«£^, (8.29)
2х 2х
а ,v ,Лч фс/,/"+х)-2ф:/,;',) + ц(х/,/"-х)
X
М*/.'я)=- ^——
X
(8.30)
Формулы (8.27),(8.28) аппроксимируют производную и, с первым порядком
аппроксимации, а (8.29),(8.30) аппроксимируют соответствующие производные со
вторым порядком аппроксимации. Все вышеприведенные формулы записаны на
л-м временном слое. При необходимости (например, при конструировании
неявных схем) вместо л-го используется (п + 1) -й и (п- 1)-й временные слои.
389

Теперь получим выражения для аппроксимации смешанной производной.
Применим (8.27) к оператору, заданному (8.15):
du(xhtn)
дх
u(x,+h,tH + i)-u(xhtn +т) u(xi+h,tn)-u(xiita)
u(Xj + h,tn +T)-u(xht" +т)~м(х/ +h,tn) + u(xi9tn)
hi
или
я + l ,." + l ,." , ,."
uxt(xhtn) = Ui^ ~Щ ~и^+и< , (8.31)
hi
Получим еще одну формулу. Для этого применим (8.29) к функции,
заданной (8.19):
и(х; + h, t" + т) - u{Xj - /?, tn + т) u(Xj + hy tn - i) - u(xt - h,tn - i)
du(xhtn)) 2Л 2h
dx J 2t
u(Xj +h,tn + т)- w(x7- - Л, /" + т) - w(x, + Л, /" -t) + i/(x/ -/?,/л - т)
4Лт
или
,.л+1 л+1 ..л-1 л-1
£„(*/,'*)-"' "' '*' "' • (8-32)
4Ат
Можно показать, что (8.31) аппроксимирует производную uxt с первым
порядком, а (8.32) - со вторым порядком аппроксимации [27].
Замечания.
1. Поскольку при численных расчетах вместо точного решения u(xhtn) в
узлах (xhtn) известно не точное, а приближенное решение u{xhtn), то в
формулах (8.20)—(8.22),(8.26)—(8.32) следует ставить знак л над и.
2. Здесь рассмотрены аппроксимационные формулы на равномерной
сетке. С использованием (5.7),(5.10) можно построить аналогичные формулы при
неравномерной сетке.
В заключение раздела сформулируем основные этапы решения задач с
линейными дифференциальными уравнениями в частных производных разностными
методами:
1. Выбрать сетку Dh , соответствующую расчетной области D .
2. Заменить дифференциальные операторы в уравнении и дополнительных
условиях разностными, а функции — их сеточными представлениями, т.е.
построить разностную схему. Установить ее порядок аппроксимации.
3. Исследовать сходимость разностной схемы, проверив устойчивость
схемы.
4. Задать величины шагов сетки по всем независимым переменным,
обеспечивающие сходимость. Решить разностную задачу одним из известных
методов. В результате находятся значения u(xhtn) приближенного решения в узлах
сетки.
390

8.3. РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ
ПЕРВОГО ПОРЯДКА
Рассмотрим проблему конструирования разностных схем для решения
уравнения (8.4):
Л(х, /) их + В{х, 0 щ + С(х, /) и = G(x, t),
где u(x,t)~ искомая функция; /l(x,/),i?(x,/),C(jc,0 - коэффициенты, G(x,t) -
правая часть, /?(*,/) *0. Это уравнение относится к эволюционным. Основная
идея состоит в том, что после замены дифференциального уравнения его
конечно-разностной аппроксимацией получаются формулы, явно или неявно
выражающие значения решения для одного момента времени через значения
решения в предыдущий момент времени. Таким образом, если известно решение в
начальный момент времени, можно шаг за шагом найти решение для всех
последующих моментов. Чтобы проиллюстрировать общий подход, рассмотрим
типичную задачу для уравнения переноса.
Пример 8.2. Построить разностные схемы для задачи
ut + их = О, -оо<х<оо, 0 < / < Г ,
w(x,0) = \j/(x), - оо < X < оо ,
где v|/(x) - заданная функция.
□ Решается задача Коши, в которой A(x,t) = 1, B(x,t) = 1, С(х,/) = 0,
G(xyt) = 0. Для анализа различных разностных схем, используемых для
нахождения приближенного решения, найдем сначала аналитическое решение
поставленной задачи. Оно может быть найдено различными методами, в частности
методом характеристик, который опирается на следующий факт: начальное
условие в некоторой точке х при / = О переносится в плоскости Oxt вдоль линии,
называемой характеристикой. Рассмотрим один из вариантов этого метода
[7,14,46].
1. Решаем систему двух обыкновенных дифференциальных уравнений
(уравнений характеристик):
^ = Л(*,0, х(0) = ц,
ds
(8.33)
^ = Я(х,/), /(0) = 0,
as
где 5,\л - параметры, 0 < .у < оо, - оо < ц < оо.
Поскольку A(x,t) = 1, B(xj) = 1, то система имеет вид
^ = 1, *(0) = и,
ds
^ = 1, '(0) = 0.
ds
391

Отсюда x(s) = s + C\, t(s) = s + C2 и x(0) = Cj = ц, f (0) = C2 = 0. Следовательно,
характеристики описываются уравнениями
x(s) - s + ц, Г = j .
Заметим, что в общем случае результатом п.1 будут формулы связи
переменных х,/ и 5,ц:
Х = х(5,ц), / = /(5,ц),
где параметр s изменяется вдоль характеристик, а параметр ц изменяется вдоль
прямой линии / = 0.
Исключая s, получаем х = / + ц, -оо<ц<оо, т.е. каждому значению ц
соответствует прямая линия (рис. 8.4).
/ = х-\х
-2 -1
/ А
А
0
H = -z
1
ц = -
2
1 Я к
3
1 = и
/Ц = 2
/^
4
X
Рис. 8.4
2. Используя координаты 5,ц и то, что с учетом (8.33) справедливо
du dx dt ., . n/ .
— = ux — + ut — = A(x, t) ux + B(x, t) ut, сведем исходное уравнение в частных
ds ds ds
производных к обыкновенному дифференциальному уравнению
du
— + C(x(s, у), /(5, ц)) и = G(x(s, ц), /(*, ц)),
ds
n(0)«Vfti).
Для рассматриваемого примера уравнение (8.34) имеет вид
n(0) = v(*i).
(8.34)
S--
Отсюда w(s, ц) = С, w(0, ц) = С = ц/(ц), следовательно, u(s, ц) = ц/(ц).
3. Найдем решение ы(х,/) исходной задачи, выражая s и ц через х и /
(см. п.1). Так как s = /, ц = х - /, то ы(х,/) = ц/(х-/). На каждой характеристике
значение решения постоянно, определяется значением параметра ц и равно
1|/(ц). Например, значение решения в точке В то же, что и в точке А, и равно
у(0)(рис. 8.4).
392

о л, / ч / ч fVoM*°> *<0,
Заметим, что если функция ш(х) имеет вид vj/(x) = t
[О, х > О,
решение задачи в точках, расположенных на характеристике, проходящей через
точки А и В, и правее этой характеристики, равно нулю, а в точках,
расположенных левее этой характеристики, не равно нулю.
Перейдем к конструированию различных явных и неявных разностных
схем. В качестве сетки Dh возьмем совокупность точек (х,,/л), где х,=/Л,
tn = лх, / = 0,±1,±2,...; л = 0,1,2,...,TV; Т = Nx. При построении разностных схем
производную их можно аппроксимировать по формулам (8.20)—(8.22), а
производную щ — по формулам (8.27)—(8.29). Сформируем некоторые из них.
Для получения первой схемы применим (8.20), (8.27):
Ш HL. + Ш+1 '- = о, / = 0,±1,±2,...; п = 0,1,2,..., TV -1;
х h
«Nvf*/), / = 0,±1,±2,...
Полученную схему здесь и далее можно представить в форме £h uh = /Л, где
ij, Щ_^им щ ^ / = 0>±1±2j . „ = 0,1,2,...,ЛГ-1;
х Л
#>, / = 0,±1,±2,...;
Г0, / = 0,±1,±2,...; л = 0,1,2,...,ЛГ-1;
/й J v(x,), / = 0,±1,±2,....
и,"*1 = firf 1 +1j - fi,"+I I, У = 0,±1,±2,...; л = 0,1,2,...,ЛГ -1.
Решение на (л +1) -м слое запишется в виде
(8.35)
Узлы, участвующие в расчетах, образуют трехточечный шаблон
Шз(х/»/Я) = {(*/>/Л)Л*/+1>0>(*/,'л+1)}> изображенный на рис. 8.5, а.
Проанализируем эту схему, используя выводы, полученные при применении метода
характеристик.
с , , ч , ч IVo(*)*0» *<0,
Если функция у(х) имеет вид у(х) = \
[0, х > 0,
то «Р = 0,
i = 0,1,2,... Тогда по формуле (8.35) при любом соотношении между х и h
получаем и?=0, / = 0,1,2,...; /7 = 1,2,..., т.е. в первом квадранте решение уравнения
тождественно равно нулю. Это противоречит точному решению (см. рис. 8.4),
следовательно, сходимость решения разностной задачи к решению
дифференциальной задачи отсутствует. Таким образом, схема (8.35) имеет первый порядок
аппроксимации по х и по h и является абсолютно неустойчивой [35,42].
Следовательно, она не может быть использована на практике и приведена здесь из
методических соображений.
393

/, п + I
/, п + I
Сн^—О
а
i.n + l
i +1, л
О—^—6
/-1,я i,n
б
/, я +1
(У-^^-О
i -1, n
в
■О
/ +1, /I
/, Л + 1 / + 1, /2 + 1
О
a
/-l,/2 I, Л
г
/ - 1, л + 1 /, л + 1
-О
/ + 1, /I
6
/,Л
е
/, л + 1 / + 1, л + 1
Для получения второй схемы применим (8.21) и (8.27), т.е. в отличие от
предыдущего случая производная их аппроксимируется левой разностью:
Ля+1 А/? Лл Лл
^—Zii. + ui ~и*-\ = о, / = 0,±1,±2,...; л = 0,1,2,..., ;V - 1; и? = v|/(x,-), / = 0,±1,±2,...
394

Решение на (п + 1)~м слое запишется в виде
йГ1 = й/л[ 1 - j) + "/-1 ^ '' = 0,±1,±2,...; п = 0,1,2,..., N -1.
(8.36)
Узлы, участвующие в расчетах, образуют трехточечный шаблон
Ш3(х/,/") = {(х/_1,/л),(х/,/л),(х/+|,/,|+1)}, изображенный на рис. 8.5,5. Схема
имеет первый порядок аппроксимации по х и по h и является условно
устойчивой (является устойчивой при — < I) [35,42].
И
Правая часть формулы (8.36) является формулой линейной интерполяции.
Она определяет значение функции, отстоящей от точки (х,,/я) на расстояние,
равное т. Это значение переносится по характеристике в точку (х/,/п+1).
Поведение характеристик в данной задаче изображено на рис. 8.6. Проанализируем
более подробно свойства этой схемы для трех случаев соотношения шагов Лит
сетки Dh.
При - = 1 разностная схема в данной задаче дает точное решение, так как
h
и"*1 = й"_{, т.е. решение на следующем временном слое, передающееся вдоль
характеристик (помечены на рисунке пунктирной линией), остается постоянным
(рис. 8.6, а).
/, п +1
/, я +1
/, п +1
i=i
О-
<i
о о-*1
/-1.Й
1,11
i-Ln
-о
1>1
-хю—о
я б в
Рис. 8.6
При - < 1 и — > 1 по характеристике переносится значение, соответст-
h h
вующее точке, отмеченной крестиком (рис. 8.6, б и в). При - < 1 разностная
h
схема дает решение, соответствующее истинному с точностью, которой обладает
линейная интерполяция. При — > 1 можно получить решение, существенно от-
п
личающееся от точного. Например, пусть начальное условие задано в виде
, Ч [VOW*0» ^<0. _ *0 Л • ЛП А. п
VWH^ л Тогда и. =0, /=0,1,2,.., и, следовательно, и = 0 при
[0, х > 0,
395

/ = 1. Точное решение в этом узле определяется значением ч/0(Л-ц) (см. п.З
метода характеристик), поэтому погрешность может быть практически любой.
Для получения третьей схемы применим (8.22) и (8.27):
щ щ_хщ+\ "/-1_ = 0> / = о,±1,±2,...; л = 0,1,2,...,//-!; (8.37)
х 2Л
и? = Ч>(*/), / = 0,±1,±2,...
Узлы, участвующие в расчетах, образуют четырехточечный шаблон
Ш4(х/,ГЛ) = {(х/_1,/"),(х/,/л),(д:/Ч1,/я),(х/,/Л+1)}, изображенный на рис. 8.5,в.
Схема является абсолютно неустойчивой [35] и имеет первый порядок
аппроксимации по т и второй — по h.
Для получения четвертой схемы {схемы Лакса) применим (8.22) и модифи-
кацию (8.27), где вместо и" берется среднее -^ —:
J 2 + "/+i-"/-i =0> / = о,±1,±2,...; /I = 0,1,2,...,iV - 1; (8.38)
х 2Л
«?=*/), / = 0,±1,±2,...
Узлы, участвующие в расчетах, образуют трехточечный шаблон
Шз(х/>гЛ) = {(*/-1»'я)»(*/+1>0>(*/»/Л+1)} > изображенный на рис. 8.5,г. Схема
является условно устойчивой (является устойчивой при — <1) [35]. Заметим, что
h
простейшая модификация схемы (8.37), а именно использование среднего
значения, привела к тому, что разностная схема из абсолютно неустойчивой
превратилась в условно устойчивую.
Формулы (8.35)—(8.38) явно выражают решение на (л + 1)-м временном
слое через решение на п -м слое. Поэтому соответствующие им схемы
называются явными двухслойными.
Для получения пятой схемы применим формулу (8.20), записанную на
(п + 1) -м временном слое, и (8.27):
+ '+1 '— = 0, / = 0,±1,±2,...; п = 0,1,2,...,// -1; (8.39)
х h
uf =v(*/). / = 0,±1,±2,...
Эта схема относится к неявным, использует трехточечный шаблон
Шз(x/,/л) = {(x/,rл),(x/,/',+1),(x/Ч,,/л+,)} (рис. 8.5,д) и является абсолютно
устойчивой [35]. Схема (8.39) имеет первый порядок аппроксимации по х и по h.
396

Для получения шестой схемы применим (8.21), записанную на (л + 1)-м
временном слое, и (8.27):
щ Щ_^Щ ^bL = 0> / = 0,±1,±2,...; л = 0,1,2,..., jV -1; (8.40)
т //
W =v(Xi), / = 0,±1,±2,...
Эта схема также относится к неявным, использует трехточечный шаблон
Ш3(х/,/") = {(х/.,)//,+|),(х/)/й+1))(х/,/я)} (рис. 8.5,е) и является абсолютно
устойчивой [35]. Схема имеет первый порядок аппроксимации по т и по л.
Для получения седьмой схемы будем использовать средние значения
выражений, определяемых формулой (8.20), записанной на (л + 1)-м и л-м
временных слоях, и формулой (8.27), записанной при х = х, и х = хих:
1 2 + Й Й = 0, / = 0,±1,±2,...;
л = 0,1,2,...,ЛГ-1;
«/°=VU/). / = 0,±1,±2,...
Эта схема относится к неявным, использует четырехточечный шаблон
Шз(х/,/я) = {(х|-,/я)>(дс/,/я+,),(дс/Ч1>/я),(^/+,>/я+|)} (рис. 8.5,ж) и является
абсолютно устойчивой. Схема имеет второй порядок аппроксимации по т и по л
[14]. Второй порядок аппроксимации обеспечивается путем применения
оператора осреднения аппроксимационных операторов на (л + 1)-м и л-м временных
слоях.
Пятая, шестая и седьмая схемы относятся к неявным двухслойнымМ
8.4. РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ
ВТОРОГО ПОРЯДКА
8.4.1. Разностные методы решения уравнений параболического типа
Сначала рассмотрим проблему конструирования явных разностных схем.
Основная идея состоит в том, что после замены дифференциального уравнения
параболического типа его конечно-разностной аппроксимацией получаются
формулы, явно выражающие значения решения для одного расчетного
временного слоя через значения решения на предыдущем временном слое. Таким
образом, если известно решение в начальный момент времени, можно шаг за шагом
(послойно) найти решение для всех последующих моментов. Чтобы
проиллюстрировать общий подход, рассмотрим типичную задачу теплопроводности.
397

Пример 8.3. Построить явную разностную схему для решения задачи
теплопроводности в стержне, начальная температура которого равна нулю. Пусть
температура левого конца (х = 0) фиксирована, а на правом конце (х = L)
происходит теплообмен с окружающей средой, так что тепловой поток
пропорционален разности температур конца стержня и среды (определяется функцией
*(0).
□ Решается третья начально-краевая задача:
ut =ихх> 0 < х < L, 0 < / < Г,
и(х,0) = 0, 0 < х < L, (начальное условие)
и(0, /) = 1, 0 < / < Т, (краевое условие на левой границе)
ux(Ly t) = -[ u(L, t) - g(t) ], 0 < / < T, (краевое условие на правой границе).
Сравнивая с общей постановкой задачи (см. разд. 8.2), получаем а1 = 1,
у(х) s 0, а0 = 0, Ро = 1, ф](/) = 1, aj = 1, Pj = 1, cp2(0 = g(t); L,T — заданные числа.
Для аппроксимации производных в решаемом уравнении будем
использовать (8.27),(8.26):
йр^-й? йД1-2^+1//,.|
т " h2
Отсюда
^^^^1-2^,^, / = 1,...,/-1.
(8.41)
Эта формула при фиксированном значении / выражает решение на (п +1) -
м временном слое через решение на л-м слое. Ей соответствует
четырехточечный шаблон, изображенный на рис. 8.5, в.
При записи в разностной форме начальное условие u(xfl) = 0, 0 < х < L,
запишется в следующем виде:
«°=0, / = 0,1,...,/, (8.42)
краевые условия на левом конце (х - 0):
йЦ=\, A7 = l,...,yV, (8.43)
краевые условия на правом конце (x = L) определяются левой разностью по
формуле (8.21):
^-^ = -[«7-*(>")]•
h
Отсюда
1 + Л
398

Заметим, что соотношения (8.42),(8.43) точно аппроксимируют начальное и
соответствующее краевое условие. Соотношения (8.41)—(8.44) образуют явную
двухслойную разностную схему, имеющую первый порядок аппроксимации по т и
второй — по И.
"о
Щ
л1
N f
«о°
«,» и°2
UI-\
ffj
Рис. 8.7
Замечания.
1. Данная схема условно устойчива (устойчива при выполнении условия
— <— , т.е. при т<—). Тем самым накладываются серьезные ограничения на
выбор шага по времени. Например, если шаг сетки по переменной х выбрать
равным h = 0,1, то шаг сетки по времени не должен быть больше, чем
т = 0,5 • (0,1)2 = 0,005 (это означает, что отрезок [0;1] будет пройден за 200 шагов).
Наилучшим с точки зрения минимизации ошибок является соотношение
' = Т127'.
2. Разностная схема для уравнения ut =a2(x,0wxx строится аналогично и
является устойчивой при — < —, где А = max д2(х,/)[42].
h2 1А (x,t)eD
МЕТОДИКА ВЫЧИСЛЕНИЙ ПО ЯВНОЙ СХЕМЕ
1. Задать значения шагов сетки Л,т так, что /h = L, TVт = Г, где I,N—
целые положительные числа, причем значение шага по времени выбрать из усло-
вия устойчивости т<—. Вычислить w,° =0, / = 0,1,...,/; wq =1, л = 1,...,#.
Положить л = 0.
399

2. Найти решение на (п + 1) -м слое (рис. 8.7):
«7+| = -т «А. + (i - 2 -т] «7 + -V «7+i, / = 1..... / -1,
Дя «7-1 -Ag(wr)
"/ = ГТл •
3. Если п = N, вычисления завершить. Иначе положить п = п + 1 и перейти
к п. 2. ■
Пример 8.4. Пользуясь явной схемой, используемой в примере 8.3, найти
приближенное решение первой начально-краевой задачи вида [10]:
"/ -"xxi
0<х<1, 0 < г < 0,01,
u(xfl) = 4х (1 - х), 0 < х < 1, (начальное условие)
//(0, /) = 0, 0 < / < 0,01, (краевое условие на левой границе)
и(1, /) = 0, 0 < / < 0,01, (краевое условие на правой границе).
□ Сравнивая с общей постановкой задачи (см. разд. 8.2), получаем
д2=1, ij/(x) = 4x(l-x), <p,(/)s0f ф2(/)н0, L = l, Г = 0,01.
1. Зададим шаг по пространству: h = 0,1, следовательно, / = — = — = 10.
Выберем шаг по времени из условия обеспечения устойчивости и минимизации
И2 0,01 1 .. Т 0,01 с _
ошибок х = — = -2— = -—, поэтому N = — = -у— = 6. Таким образом, получа-
6 6 600 т ут
ем х/ =0,1/, /=0,1,...,10; ,« =-JL-,,, = 0,1,...,6.
Вычислим значения решения на нулевом слое:
и? =4х/(1-х/) = 40,1./ (1-0,1/), /=0,1,...,10 (/ = 10).
Краевые условия на левой и правой границах записываются в виде:
£0"=0, // = 1,...,7V = 6; i/7=0, л = 1,...,6 (TV = 6).
2,3. Поскольку — = -^^ = -, решение на следующих слоях при п = 0,1,...,5
h 0,01 6
находится по формуле, следующей из (8.41):
*п+\ 1 ля 2 ля 1
= g",-i+j"" + g«"+i, ' = 1,-,9,
и занесено в табл. 8.1.
400

Таблица 8.1
L х
0
1
2
3
4
5
6
0
0
0
0
0
0
0
0
1
0,360
0,347
0,336
0,326
0,317
0,309
0,302.
2
0,640
0,627
0,613
0,600
0,588
0,576
0,564.
3
0,840
0,827
0,813
0,800
0,787
0,774
.0,761
4
0,960
0,947
0,933
0,920
0,907
0,894
0,881
5
1,000
0,987
0,973
0,960
0,947
0,934
0,921
6
0,960
0,947
0,933
0,920
0,907
0,894
0,881
7
0,840
0,827
0,813
0,800
0,787
0,774
0,761
8
0,640
0,627
0,613
0,600
0,588
0,576
0,564
9
0,360
0,347
0,336
0,326
0,317
0,309
0,302
10
0
0
0
0
0
0
о 1
Подчеркнем, что полученное решение на каждом из временных слоев
является симметричным. ■
Теперь рассмотрим проблему конструирования неявных разностных схем.
Для их получения все производные, входящие в дифференциальное уравнение,
заменяются конечно-разностными аппроксимациями. Однако значения решения
на (л +1) -м слое уже не выражаются в явном виде через значения на
предыдущих слоях. В неявных схемах для нахождения решения на следующем временном
слое необходимо решать систему линейных алгебраических уравнений.
Для иллюстрации общего подхода решим следующую задачу
теплопроводности.
Пример 8.5. Построить неявную разностную схему решения задачи
теплопроводности в стержне, начальная температура которого равна 1, а температура
левого и правого концов равна нулю.
□ Данным физическим условиям соответствует первая начально-краевая
задача:
ut =ихх> 0 < х < L, 0 < / < Г,
u(xfi) = 1, 0 < х < L, (начальное условие)
ы(0, /) = 0, 0 < / < Т, (краевое условие на левой границе)
u(L,/) = 0, 0 < / < Г, (краевое условие на правой границе).
Сравнивая с общей постановкой задачи (см. разд. 8.2), получаем а2 = 1,
\\f(x) = 1, ф, (0 = Ф2(О s 0; £> Т — заданные числа.
Для аппроксимации производных в решаемом уравнении будем
использовать формулу (8.27) и формулу (8.26), записанную на (п +1) -м временном слое:
h2
Отсюда
-■^^V+(l + 2^-j«rl-^-^V="7. /-1...../-1. (8.45)
401

Эта формула выражает решение на (я + 1) -м временном слое через решение
на л-м слое. Ей соответствует четырехточечный шаблон, изображенный на рис.
8.8, а.
/- \3п + 1
/', п +1
/ + 1, п + 1
■1,л + 1 /, л + 1 / + 1,я + 1
О
/ -1, п
I + 1, Л
Рис. 8.8
При записи в разностной форме начальное условие u(xfi) = 1, 0 < х < L,
запишется в следующем виде:
краевые условия:
и? =1, / = 0,1,...,/,
й5=0, /i = l,.-.,iV,
Й7л=0, лН iV.
(8.46)
(8.47)
Соотношения (8.45)—(8.47) образуют неявную двухслойную разностную
схему, имеющую первый порядок аппроксимации по т и второй - по h. Она
является абсолютно устойчивой и сходящейся [35].
МЕТОДИКА ВЫЧИСЛЕНИЙ ПО НЕЯВНОЙ СХЕМЕ
1. Задать значения шагов сетки Л,т из условия обеспечения требуемой
точности решения так, что / h = L, N т = Т, где I,N — целые положительные
числа. Вычислить и? =1, / = 0,1,...,/; ufi =0, л = 1,...,УУ; и" =0, л = 1,...,/У.
Положить /? = 0.
2. Сформируем систему линейных алгебраических уравнений для
некоторого временного слоя, записывая уравнение (8.45) при / = 1,...,/ -1 (рис. 8.9):
-р-и0 +^1 + 2—J«, -—н2 -и,,
402

Согласно п.1, uq = 1, /i = l,...,N; и" = 0, n=\,...,N. Поэтому для нахождения
решения на следующем временном слое требуется решить трехдиагональную
систему (/ -1) линейных алгебраических уравнений с (1-1) неизвестными
Ал + 1 Ал+1 .
1 + 2—|wf - —"i'
:«i
А2 ^ I А2
uI-2 + 1 + 2ТТГ/-1 ~ w/-l '
Методы решения таких систем рассматривались в гл.1.
3. Если п = N, вычисления завершить. Иначе положить п = п +1 и перейти
к п. 2.
Методику вычислений по неявной схеме можно проследить на рис. 8.9, где
выделен используемый четырехточечный шаблон. Заметим, что в неявной схеме
объем вычислений на каждом шаге больше, чем в явных, но хорошую точность
можно получить при гораздо большем шаге по времени.
"б
А2 ж
и0 f
л1
"О
|у£ А0 ,л0
1 Ul
"Л
1 «I
* х
и1-\ и)
Рис. 8.9
Получим еще одну неявную схему. Для аппроксимации производной ut
применим (8.27), а для аппроксимации и^ взвешенное среднее выражения
(8.26), записанного для узлов (xhtn)y(xht"+l) на л-м и (л + 1)-м временных
слоях (см. рис. 8.8,6):
ц/+1 ~ lui +ui-\
А2
403

fin+l *)fin+l , fin+l fin ^fin fin i
т.е. wJOC=X-LtJ ^ LJ- + (1-X)-J±J з —, где Хе[0;1]. При X = -
h2 /r 2
получается обычное среднее, при X = - одна из разностных производных берется
4
с весом —, а другая — с весом —. В результате получаем разностную схему:
4 4
£/1 + 1 fin fin+\ 0/)я + | j. ил+1 #0" 1и"л.пП
т h2 h2
uf=\, / = 0,i,..,/;
и0я=0, n = \,...,N; й,л=0, « = 1,...,7V.
Перенесем в первых (/ -1) уравнениях все неизвестные в левую часть.
Тогда получаем
- X ± fitf +[l + 2K±yrl-l-p «Д+|' = (8-48)
= (1 -x)-I.fi* , +[i _2(l-X)-yW +(1 -Х)-уЙД,. / = 1,...,/ -1;
h V А / я
w,° = l, / = 0,1,...,/;
ug = о, л = 1,..., iV; й; = о, п = 1,..., w.
Эта схема абсолютно устойчива и сходится [46]. Для нахождения решения
на следующем слое, как и ранее, требуется решать трехдиагональную систему
(/ -1) линейных алгебраических уравнений. При X = - схема называется схемой
Кранка—Николсон. При X = 0 из (8.48) следует явная схема (8.41), а при X = 1 -
неявная схема (8.45). Шеститочечный шаблон, соответствующий схеме (8.48),
изображен на рис. 8.8, б. При X = - схема имеет второй порядок аппроксимации
по т и по h, а при X * — — первый порядок аппроксимации по т и второй — по
h [14].
Методику вычислений, совпадающую с уже описанной для схемы (8.45),
продемонстрируем на примере.
1. Зададим Л = 0,2; т = 0,08; L = 1; Г = 0,8. Тогда /0,2 = 1, #0,08 = 0,8,
т.е. / = 5, N = 10. Тогда начальные и краевые условия примут вид:
и?=1 / = 0,1,...,5;
w0"=0, л = 1,...,10; й?=0, л = 1,...,10.
404

Положим /2 = 0, А. = -. Вычислим — = -~—
2 А2 0,04
2.
2. Запишем систему (8.48) , принимая / = 1,2,3,4 (/-1 = 4) с учетом п.1:
и1 ~и2
Л0 А0 Л0
- й/ + Ъи\ - й] = «|° - й£ + «з »
Л| _Л| Л| /4Q aq ло .
- HJ + 3"4 ~ w5 = w3 ~ w4 + "5 i
1, / = o,i,...,5; «i=o, «j=0.
Тогда получаем
или в матричной форме
f Ъ
-1
0
1о
о А1 Л1
Ъи\-и\ =
1,
Ai oAi А1 1
- и[ + 3^2 - wj = 1,
Al оА1 А1 1
- «2 + 3^3 - «4[ = 1,
А1 оА1 1
- Ыз + 3^4 = 1
-10 <П
3-10
-1 3 -1
0 -1 3 J
fAl>
«1
А1
"2
А1
"3
А1
=
т
1
1
Л
В результате имеем и\ = 0,6; и\ = 0,8; й\ - 0,8; й4* = 0,6.
3. Далее, полагая п = 1, можно сделать следующий шаг по времени, решая
новую систему алгебраических уравнений. Аналогичный процесс продолжается
до достижения значения N = 10. ■
8.4.2. Разностные методы решения дифференциальных уравнений
гиперболического типа
Методы сеток для решения гиперболических уравнений имеют много
общего с соответствующими методами для параболических уравнений. Однако они
имеют и свои особенности, связанные с типом уравнения.
Сначала рассмотрим проблему конструирования явных разностных схем.
Основная идея состоит в том, что после замены дифференциального уравнения
гиперболического типа его конечно-разностной аппроксимацией получаются
формулы, явно выражающие значения решения для одного расчетного
временного слоя через значения решения на предыдущем временном слое. Таким
образом, если известно решение в начальный момент времени, можно шаг за шагом
(послойно) найти решение для всех последующих моментов. Чтобы
проиллюстрировать общий подход, рассмотрим типичную краевую задачу для волнового
уравнения.
405

Пример 8.6. Построить явную и неявную разностные схемы для решения
задачи, в которой имеется струна длиной L, натянутая между двумя точками оси
Ох , точкой х - 0 и точкой х = L. Концы струны закреплены, начальное
смещение струны описывается функцией f(x), а начальная скорость — функцией g(x).
□ Решается первая начально-краевая задача (см. разд. 8.1):
utt - ихх » 0 < х < L, 0 < / <Т,
и(ху0) = f(x), 0 < х < L, (начальное условие)
ut(xfl) = g(x), 0 < х < L, (начальное условие)
w(0,0 = 0, 0 < / < Г, (краевое условие на левой границе)
w(L, /) = 0, 0 < / < Т, (краевое условие на правой границе).
Сравнивая с общей постановкой задачи (см. разд. 8.1), получаем с2 = 1,
ц{(х) = f(x), v2(x) = g(x),cpi(0 =Фг(0 s 0; L,Г—заданные числа.
Для аппроксимации производных в решаемом уравнении будем
использовать (8.30) и (8.26):
*л+1
~ lui +ui ui+\ - 1и\ +Ц/-1
Отсюда
*л+1
1\
1--
/г
/ = 1,...,/-1.
(8.49)
Эта формула выражает решение на (п + 1) -м временном слое через решение
на п -м и (л -1) -м слоях. В отличие от схем для уравнения теплопроводности,
в которых использовались только два временных слоя (я-йи (л + 1)-й) , здесь
требуется использовать три слоя: (л-1)-й, л-йи (/г + 1)-й. Ей соответствует
пятиточечный шаблон, изображенный на рис. 8.10, а , называемый «крест».
/', п +1
■1,/f + l
/, п +1
/ + 1, л + 1
о-
/ -1, п
-о
-О
'. л I + 1, я
6 /,и-1
о
;-1,л
а
■о-
-о-
-о
'." / + 1.Л
-о
1-1,/1-1 /,/f-l / + 1,71-1
5
Рис. 8.10
406

При записи в разностной форме начальное условие u(xfi) = f(x),
О < х < L, запишется в следующем виде:
и? =/т, / = !,...,/-!, (8.50)
начальное условие ut(xfi) = g(x), 0 < х < L, с применением (8.27) при п = 0
в виде
Л} AQ
и - иу
■■ g(ih), / = 1,..., / - 1, или, используя предыдущее соотношение,
и] = /(/Л) + т*(/Л), / = !,...,/-!,
(8.51)
краевые условия представляются в форме:
£0Л=0, й/Л=0, rt = 0,...,yv.
(8.52)
Соотношения (8.49)—(8.52) образуют явную трехслойную разностную схему.
Эта схема имеет первый порядок аппроксимации по / и второй -по х, так как
соотношение (8.51) аппроксимирует дифференциальное начальное условие с
первым порядком.
Замечания.
1. Данная схема условно устойчива (устойчива при выполнении условия
7*1) [27].
п
2. Разностная схема для уравнения ип = с2 (х, /) и^ строится аналогично и
т2 1 9
является устойчивой при — < —, где С = max cz(x,/)[42].
h2 С {x,t)zD
3. Простейшая замена (8.51) имеет первый порядок аппроксимации.
Поскольку разностная схема (8.49) аппроксимирует дифференциальное уравнение
со вторым порядком, желательно, чтобы разностное начальное условие также
имело второй порядок аппроксимации. Для этого запишем аналог формулы
Тейлора (8.17) в направлении / при к = 2:
u(x,t°+T) = u(xtt0) + ut(x,t0)T + utt(x,t0) I- +„,„(*, 5) L_,
I о
$е(Л/°+т), 0<x<L.
Если функция /(х) имеет ограниченную вторую производную, то в силу
исходного
дифференциального
уравнения
получаем
ы„(х,г) = uxx(xit ) = f"(x). Из предыдущего соотношения получаем
или
,,(x,/o)^^<0+T)-"(x',0)+/"wii
т 2
И|(х,,0) sh(s,/0+t)-B(s,/°) + /,,(jc) ti>
т 2
"///(*. У-
^т2
ТЛ/3
407

где Л/3 = max \utJt(xj)\. В результате соответствующее начальное условие в
/€[/°,/0+т]
Л1 А0
разностной форме имеет вид — — - /"(/Л) - = g(ih), / = 1,..., / - 1.
т 2
Так как щ = /(/Л), / = 1,..., / - 1, то
u}=fW + xg№ + f"№j, / = !,..,/-!.
(8.53)
Если в разностной схеме используется (8.51), схема имеет первый порядок
аппроксимации по т и второй — по Л, а если (8.53), то имеет второй порядок
аппроксимации по т и по Л.
МЕТОДИКА ВЫЧИСЛЕНИЙ ПО ЯВНОЙ СХЕМЕ
1. Задать значения шагов сетки А, т так, что / h = L, N т = Т, где IyN -
целые положительные числа, причем значение шага по времени выбрать из
условия устойчивости х < h. Вычислить
u?=f№, i = !,...,/-!; и} = /(/Л) + т*(/А), i = !,...,/-!,
ЭД =0, uj = 0, /* = 0,...,7V.
Приведенные выражения дают решение задачи для первых двух слоев сетки (рис.
8.8). Положить /7 = 1.
2. Найти решение на (л + 1) -м слое (рис. 8.11):
т2 ( т2>>
ЛЛ + 1 _ Л_ил хО 1 _
"' -а'*-|+2Га',
/г
/ = 1,...,/-1.
^=о |—т—т—т—т—т—г
Йо2=0
Я»0[
0°=0 ±—Щ
Й1°-/(Л)
"/-1
^=0
й)«о
1— *
/ Й/°-0
Рис. 8.11
3. Если п = N, вычисления завершить. Иначе положить л = л +1 и перейти
к п. 2.
408

Теперь рассмотрим проблему конструирования неявных разностных схем.
Для их получения все производные, входящие в дифференциальное уравнение,
заменяются конечно-разностными аппроксимациями с использованием (п +1) -
го слоя для аппроксимации и^. Однако значения решения на (п + 1) -м слое уже
не выражаются в явном виде через значения на предыдущих слоях. В связи с
этим в неявных схемах для нахождения решения на следующем временном слое
необходимо решать систему линейных алгебраических уравнений.
Для иллюстрации общего подхода получим неявную схему для волнового
уравнения. При аппроксимации производных в уравнении будем использовать
(8.30) и формулу (8.26), записанную на (п - 1)-м, w-ми (п + 1) -м слоях:
Uj - lit; +Uj Л Ц/+1 -Щ +Ц/-1 , ,т ПЛ чЫ/+1 -Щ +Uj_x
Т h , h (8.54)
Лл-1 9£л-1 ,f)n-\
h
где X - параметр, 0 < X < -. Значения приближенного решения на нулевом и
первом слоях вычисляются по формулам (8.50)—(8.52), как и в явной схеме. На
остальных слоях схема представляет собой линейную систему алгебраических
уравнений с трехдиагональной матрицей, в которой диагональные элементы
преобладают. Решение этой системы существует, единственно и вычисляется
методом прогонки (см. разд. 1).
Формула (8.54) выражает три неизвестных значения решения на (л + 1)-м
временном слое через решения на я-м и (л-1)-м слоях. В отличие от схем для
уравнения теплопроводности, в которых использовались только два временных
слоя (л-й и (л + 1)-й) , здесь требуется использовать три слоя: (л-1)-й, я-йи
(п +1) -й. Поэтому такая схема называется неявной трехслойной. Ей соответствует
девятиточечный шаблон, изображенный на рис. 8.10, б. При X = 0 схема (8.50)-
(8.52),(8.54) переходит в явную схему «крест».
При - < X < - схема абсолютно устойчива, а при 0 < X < — схема условно
4 2 4
-- 1 1
устойчива (устойчива при выполнении условия — < (1 - ЛХ) 2) При — < X < -
схема имеет второй порядок аппроксимации по т и по h [14].■
Пример 8.7. Пользуясь явной схемой, найти приближенное решение
первой начально-краевой задачи [10]:
utt =Wjoc, 0<х<тг, 0</<^,
u(xfi) = х(л-х), 0<x<7i, (начальное условие)
ыДх,0) = 0, 0<х<л, (начальное условие)
П
5*
18
и(0, /) = 0, 0 < t < —, (краевое условие на левой границе)
18
и{п, /) = 0, 0 < / < —, (краевое условие на правой границе).
409

D Сравнивая с общей постановкой задачи (см. разд. 8.1), получаем
с2=1, у{(х) = х(п-х), ч/2(*) = 0> Ф1(0=Ф2(0 = 0; L = n, Т = -^.
1. Зададим шаг по пространству, равным h- —, шаг по времени выберем
18
из условия устойчивости: \<h. Положим т = Л = —. Тогда дс, =—, tn =—,
i = 0,1,...,/ = - = 18 ; п = 0,1,...,// = - = 5.
И т
По формулам (8.50), (8.52), (8.53), учитывая, что f(x) = х (п - х),
f'\x) = -2, g(x) s 0, получаем значения приближенного решения на нулевом и
первом слоях:
"N/(^) = ^(^-^) = ^(n-^j, / = 1,..Д7,
us =0, й;=о, л = о,...,5,
2 т2
«/«лад + т^ЭД + Паду^хДя-^ + о-гу
2SL L.5L . JL1 / = i,...,i7.
18 I 18J 118J
2,3. Поскольку — = 1, решение на последующих слоях вычисляется по
h2
формуле, следующей из (8.49):
В табл. 8.2 приведены результаты расчетов при / = 0,1,...,9, так как решение
u(x,t) симметрично относительно х = - (/ = 9) при фиксированном / .■
Таблица 8.2
Р^<
0
1
2
3
4
5
0
0
0
0
0
0
0
1
0,518
0,487
0,426
0,366
0,305
0,244_
2
0,975
0,944
0,853
0,731
0,609
0,487
3
1,371
1,340
1,249
1,097
0,914
0,731
4
1,706
1,675
1,584
1,432
1,218
0,975___
5
1,980
1,950
1,858
1,706
1,493
1,218
6
2,193
2,163
2,071
1,919
1,706
1,432
7
2,346
2,315
2,224
2,071
1,858
1,584
8
2,437
2,406
2,315
2,163
1,950
_1_,6_75
9
2,467
2,437
2,346
2,193
1,980
1,706
410

Замечание. В практике применения численных методов существует
полезный прием, позволяющий на основе результатов расчетов судить о том, с
какой точностью они получены. С этой целью используется правило Рунге,
изложенное выше применительно к уточнению результатов численного
дифференцирования и интегрирования (см. разд. 5.4). Аналогичный подход можно
использовать для оценки точности решения задач математической физики [26]. Опишем
идею его реализации:
а) находится численное решение с шагом И по пространственной
переменной х и шагом т по времени /;
б) расчет повторяется с шагами — и - с тем, чтобы образовывались слои,
некоторые из которых совпадали бы со слоями, полученными ранее;
в) сравниваются оба численных решения в одинаковых узлах сетки (им
соответствуют одни и те же значения пространственной координаты и времени).
Если отклонение удовлетворяет заданным требованиям, то процесс завершается
и в качестве приближенного решения задачи принимается полученное в п.б.
Иначе шаги снова делятся пополам и процесс продолжается.
8.4.3. Разностные методы решения уравнений эллиптического типа
Рассмотрим проблему решения краевых задач для уравнений
эллиптического типа. Эти задачи являются стационарными, так как в них отсутствует
временная переменная. В них требуется найти решение уравнения с частными
производными в данной области пространства, если на границе области решение
или его производная заданы. Разностные схемы получаются путем замены
производных их конечно-разностными аппроксимациями. В результате
приближенное решение эллиптических задач сводится к решению системы линейных
алгебраических уравнений для значений искомой функции во внутренних узлах сетки.
Чтобы проиллюстрировать общий подход, рассмотрим задачу Дирихле для
уравнения Лапласа.
Пример 8.8. Построить разностную схему для решения задачи Дирихле:
ихх +иуу = 0, 0 < х < L, 0 < у < М,
"(О, ^) = ф(0,^, 0<у<Му
u(L,y) = (p(Lyy)f 0<у<М,
и(х,Л/) = ф(л:,М), 0<x<L,
и(х,0) = ф(х,0), 0<jc<L,
где y(x,y) — заданная функция, L,M' — заданные числа.
□ В данном случае задача решается в области Q прямоугольной формы,
краевые условия заданы на сторонах прямоугольника. В плоскости Оху
построим сетку Dh={(xi9yj)}, где х,;= ihx , yj=jhy, i = 0,1,...,/; j = 0,1,...,/; hx,hy-
величины шагов по x и у\ I hx = L, J hy = М , / и / — целые положительные
числа.
411

Заменим дифференциальные операторы в уравнении Лапласа по формулам,
следующим из (8.25) при замене переменной tn на переменную уу:
u(xt +hXiyj)~ 2и(х, ,yj) + ц(х, - hx, yj)
hi
Uxx(*i>yj) = - 2
u(Xj,yj+hy)-2и(х{,yj) + u(Xj,yj -hy)
uyy\xi>yj) 2
*;
Применяя краткую запись u(xhyj) = ы, у, получаем
л _/ч л л _ л л
"/+1 У " 2и, / + и/-1 7 И/ # + 1 " 2W/ / + Ui /-1
jr+L/ *А ,-Ы + -Ы11 'Л ^zL = o, / = 1,...,/-1; у = 1,...,/-1,
^
h
2 #,2
У /) . "У
л2
",-,=0, (8.55)
/ = 1,...,/-1; у = 1,...,/-1.
Полагая ф/у- = <p(ihXijhy), краевые условия можно записать в виде:
"о,; =Фо,у> у = 1,...,У-1;
"Л/=Ф/,у» У = 1,...,/-1; (8.56)
"/,у =Ф/,у. / = 0,1,...,/;
"/.о = Ф/,о> / = 0,1,...,/.
Для нахождения искомого решения требуется решить систему
(/ -1) х (/ -1) линейных алгебраических уравнений. Схема (8.55),(8.56) имеет
второй порядок аппроксимации по т и по И, является абсолютно устойчивой и
сходится [14]. Ей соответствует пятиточечный шаблон, изображенный на рис.
8.12.
При hx -hy, т.е. одинаковых шагах в горизонтальном и вертикальном
направлениях, получаем
uMJ +«/-1,у+£и+1 +"/,y_i -4й,у =0, / = 1,...,/-1; у = 1,...,/-1. (8.57)
Разрешив относительно uf •, имеем
Sij = 4(Si+\j+«t-iJ+«ij+\+«ij-\)* / = 1"">/-1' y = U^-l. (8-58)
Это означает, что решение и;. аппроксимируется средним значением по
четырем соседним узлам. Как правило, для решения системы (8.58) применяются
различные итерационные методы, например, метод простой итерации или метод
Зейделя (см. разд. 1).
412

/,y + i
о о—х—о
i-lj I '»-/ / + 1,7
О /,7-1
Рис. 8.12
Рассмотрим частный случай поставленной задачи при L = 1, Л/ = 1,
sin тис, у = 0, 0 < х < 1,
на остальных границах прямоугольной области Q.
У
чек (/ = 1,2; у = 1,2):
"2,1 + "о,1 + "i,2+"i,o-4"i,i =0, (/ = 1,7 = 1)
"2,2 + "0,2 + "l,3 + "l,l ~4"l,2 =0> (/ = 1,7 = 2)
/ = / = 3
Так как Их - hy = -, то запишем систему (8.57) для четырех внутренних то-
"3,1 + "U + "2,2 + "2,0 ~4"2,1 = 0> (/ = 2,7 = 1)
"3,2 + "1,2 + "2,3 + "2,1 -4"2,2 =0' (/ = 2,7 = 2)
Краевые условия (8.56) запишутся в форме
1/о,у=0, 7 = U; «з,7=°. > = 1'2
W/з = 0, / = 0,1,2,3; и,о = sin(nihx) = sin —, / = 0,1,2,3.
С учетом краевого условия система может быть записана в следующей
матричной форме
4 1 1 (П
1-401
10-41
^0 1 1 -4)
(Л Л
и,
*1,2
'2.1
Л2Л)
п
•sin —
3
0
. 2л
sin —
3
I 0 )
В результате имеем й{ { = 0,325; и, 2 = 0,108; и2 { = 0,325; и2 2 = 0,108.
413

МЕТОДИКА ВЫЧИСЛЕНИЙ
1. Задать сетку Dh = {(х,, у})}, где х, = ihx, у} = jhy,
/ = 0,1,...,/; у = 0,1,...,/; hx,hy— величины шагов по х и у; I hx = L, J hy - М,
I и / — целые положительные числа; е > 0 — желаемую точность.
Вычислить
"о,у=Фо,>> / = 1,...,/-1; и/.у=Флу. У = 1,...,/-1;
£/,/=ф|,/» / = 0,1,...,/; ",,о=ф,,о, / = 0,1,...,/.
Положить £ = 0; задать начальное приближение искомого решения во
внутренних узлах: uj^j, / = 1,...,/ - 1; / = 1,...,/ - 1.
2. Вычислить ы/*+1) одним из двух методов (рис. 8.13):
а) методом простых итераций:
£<*+!>-!(/;<*> + £<*> + £(*> .£<*> ) ;_i /-I- /-I /.1.
'.У ~ 4^ / + 1^' '-1>J '.7+1 iJ-\ Г ~ '"'J l* J ~ 1* — >J 1'
б) методом Зейделя:
Шаг 1. Положить / = 1.
Шаг 2. Вычислить
'.У " 4^ /+1-/ '-]>J Лу'+1 Лу-1 А '-1»-,/ а.
Шаг 3. Если у = / -1, процесс завершить. Иначе положить j = j + \ и
перейти к шагу 2.
3. Если выполняется условие окончания max w/*+I) ~"/V - е> процесс
завершить. Иначе положить к = к + \ и перейти к п.2.
"о,/ = Фо.у
"0,У-1 = Ф0./-1
h
«o,i = Фол
wo,o = Фо.о
К
Рис. 8.13
+ uI,J-\ =Ф/,У-1
"/-1
UJ,J =Ф/,У
"/,1 = ф/,1
и/,0 = Ф/,0
414

Замечания.
1. Метод Зейделя обеспечивает движение по узлам слева направо, начиная
с первого слоя сетки по переменной х. Использование значений с (к + \)-и
итерации, как правило, улучшает сходимость.
2. Вместо метода Зейделя можно использовать более эффективные
релаксационные методы:
;(*+!)
'»*#*
1 -со
\ui+\J+ui-\J +ui,j+\+uiJ-\ )>
где со — параметр релаксации. Член сом/*-* характеризует «память» алгоритма о
значении решения на предыдущей итерации. При со > 1 итерационный метод
называется методом верхней релаксации, при 0 < со < 1 — методом нижней
релаксации, при со = 0 совпадает с методом Зейделя. Существует оптимальное значение
со* параметра релаксации, зависящее от шагов сетки и способа получения ы/*+1),
при котором достигается максимальная скорость сходимости метода.
3. При решении задачи Неймана или третьей краевой задачи производные,
входящие в краевые условия, следует также заменить их конечно-разностными
аппроксимациями.
4. Если область Q, в которой решается задача, имеет неправильную форму,
можно покрыть ее сеткой (рис. 8.14) и найти решение в ближайших к границе
точках, а затем рассчитать значения искомой функции на границе, например,
с помощью линейной интерполяции [10] .
Рис. 8.14
5. В данной главе рассмотрены принципы конструирования разностных
схем для простейших линейных начальных, краевых и начально-краевых задач.
Для нелинейных задач, которые решаются при расчетно-теоретической
проработке современных технических систем, применяют те же разностные схемы, что
и для линейных задач.
415

8.5. МЕТОД ПРЯМЫХ
Основная идея метода состоит в сведении проблемы решения уравнений
в частных производных к решению системы обыкновенных дифференциальных
уравнений. Он используется в основном для решения уравнений эллиптического
и параболического типов. В методе прямых, в отличие от метода сеток, не все
дифференциальные операторы, входящие в исходную дифференциальную задачу,
заменяются разностными. Обычно для аппроксимации выбирается оператор,
соответствующий пространственной переменной в задаче теплопроводности или
соответствующий неравноправному направлению в задачах с эллиптическими
уравнениями. Тем самым дифференциальная задача заменяется
дифференциально-разностной с меньшим числом непрерывных переменных (понижается
размерность дифференциальной задачи). В связи с этим данный метод можно
рассматривать как предельный случай метода сеток, когда шаги сетки по
определенным независимым переменным стремятся к нулю.
Основную идею конструирования метода прямых рассмотрим на примере
нахождениия решения и(х,у) уравнения:
А(х,у)
д2и(х,у)
дх2
+ 2В(х,у)
д2и(х,у)
дудх
+ С(х,у)
д2и(х, у)
эу2
+ D(x,y)
Мх, у)
дх
+ Е(х,у)^^- + Г(х9у)и(х,у) = С(хуу), (x,y)€n = (0,Z,)x(0,A/),
ду
(8.59)
с краевыми условиями
u(xfl) = ф(х), и(х, М) = у(х),
(8.60)
и(0,у) = Ф(у), иЦ,у) = Пу)
на границах области прямоугольной формы (рис. 8.15), где (p(x),\\t(y),0(x)f4,(y)-
заданные функции. Пусть выполнено условие В2 - АС < 0 эллиптичности
уравнения для всех (х, у) € Q. Отсюда следует, что А(х, у) ф 0, С(х, у) * 0.
М
Q
уj = const
yj+l = const
yj = const
yy_i = const
- Уо = const
Рис. 8.15
416

Для решения задачи выберем на отрезке [О, М] точки Уу =//r, 0</</,
Jh-M, и проведем через них прямые, параллельные оси ШГ. На каждой
прямой дифференциальное уравнение в частных производных (8.59) приближенно
заменим обыкновенным дифференциальным уравнением для функций и(х,д/у).
Для этого аппроксимируем частные производные по у (см. разд. 8.2):
ди(х,у)\ u(x,yj+\)-u(x>yj-i)
ду \У = Уj ~ 2Л
д2й(х,у)
ду2
u(x,yj^)-2u(x,yj) + u(xiyj.x)
\У = У] " А2
(8.61)
а2£(х,у)
дудх
Введем обозначения
u(x,yj) = uj(x),
У = У1
"х(х,у]+1)-их(х>У]-\)
2h
ди(х,У]) А a2w(x,yy)
—— = "у (*), у2- = "у (*) >
дх J дх2 J
A(xiyj) = Aj(x)y B(X>yj) = Bj(x)t C(x,yj) = Cj(x) и т.д.
На прямых, описываемых уравнениями yj = const, j = 1,...,/ -1, получаем
Aj(x)U';(x) + Bj(x)
Uj+\(x)-"j-\W
+ Cj(x)
Цы(*)~2"7 +"y-l(*)
+ Dj(x)uj(x) +
(8.62)
+ £,(*)
uj+i(x)-uj„i(x)
2h
+ Fj(x)Uj(x) = Gj(x)t y = l,...,/-l; 0<*<Z,.
Здесь u{(x),...tuj_i(x) — приближенное решение задачи на прямых
у = ух= const,...,у = yj_i = const, Aj(x),...,Gj(x) — коэффициенты уравнения
(8.59) на этих прямых.
В силу краевых условий находим
й0(х) = и(х,0) = ф(х), uj(x) = и(х, М) = i|/(x),
(8.63)
«у(0) = Ф(^) = Ф(уЛ), ^а) = ЧУ(^.) = ^(у//), у = 1,...,/-1.
Таким образом, от линейного дифференциального уравнения в частных
производных (8.59) и краевыми условиями (8.60) переходим к дифференциально-
разностной краевой задаче (8.62),(8.63) для системы из (л-1) обыкновенных
дифференциальных уравнений (8.62) относительно (п -1) неизвестных функций
^ (*),..., иу_,(х). В результате ее решения можно найти законы изменения
искомой функции и(х,у) вдоль прямых yj = const, У = 0,1,...,/, т.е.
u(x9yj),j = QX...fJ. Значения функции в промежуточных точках по у может
быть найдено с помощью интерполяции. Система (8.62),(8.63) называется
системой уравнений метода прямых.
417

Замечания.
1. В зависимости от выбора аппроксимационных формул для производных
по у можно получить различные системы метода прямых, отличающиеся
порядком аппроксимации.
2. Метод прямых удобнее применять в том случае, когда коэффициенты
в уравнении (8.59) не зависят от х. Тогда система (8.62) будет системой с
постоянными коэффициентами.
3. Если расчетная область отлична от прямоугольника, при реализации
метода возникают трудности, связанные с тем, что функции и,(х) определены на
различных множествах [10].
4. При решении нестационарных уравнений дискретизация проводится по
пространственным переменным, а время / остается непрерывной переменной.
5. На практике система дифференциальных уравнений (8.62) из-за
большого числа / должна решаться численно, поэтому потребуется вводить шаг не
только по у.
6. Если изменение искомой функции внутри множества Q в направлении
у не велико, то можно ограничиться одной или двумя прямыми.
Пример 8.9. Составить уравнения метода прямых для решения одномерной
задачи теплопроводности [4]
ut = а2цхх > 0 < х < 1, 0</<1,
w(x,0) = у(х), 0 < х < 1,
н(0,/) = 1/(1,0 = 0, 0</<1,
где у(х) — заданная функция.
□ Для решения задачи выберем на отрезке [0,1] точки х,- = /Л, / = 0,1,...,/;
/Л = 1 и проведем через них прямые, параллельные оси Ot (рис. 8.16). На
каждой прямой приближенно заменим уравнение теплопроводности обыкновенным
дифференциальным уравнением для функции u(xht). Для этого заменим
частную производную Uja по формуле
дх2
u(Xi_{,t)-2u(xift) + u(xi+ut)
И2
и введем обозначения ы(х,, 0 = щ (0, '-2— = и] (0 •
dt
Тогда на прямых х, = const, / = 1,...,/ -1, получаем систему
#(/) = а2 Ц(*/-1>0-2"(*/>0+ "(*/+!>0 1 < / < / _ 1,
А2
ц,(/) = и(0,/)-0,
«,(/) = «(1,0 = 0,
»
0</<1
0</<1
(8.64)
с начальными условиями
«,(0)-v(^)-v('A). / = 1,..,/-1.
418

/
Г = 1
х0 = const
h
1 = 1
*1
х, = const
Рис. 8.16
X/ - const
Полученную систему дифференциальных уравнений можно записать в век-
(-2 1 ... О 0^
торно-матричной форме: —
dt
и\
К"1-\
1 -2 1 .. 0
11-21
0 С -. 1 -2)
щ
\ui-\
Задача имеет аналитическое решение [4]
«(/) = н-
г "2
0
0
о
о
0 е Л2
■Я и(0),
где и(0) =
Г ¥(Л) 1
Ч*(2Л)
, X/ = - 2 cos — + 2 , / = 1,..., / -1, — собственные значе-
ния матрицы системы, элементы матрицы Я (собственные векторы матрицы Л)
nik
равны Я,* = sin , / = 1,...,/-1, Л = 1,...,/-1.
Заметим, что при численном решении системы обыкновенных
дифференциальных уравнений при увеличении числа / (улучшении точности)
коэффициент жесткости S системы увеличивается [4,33]. При больших значениях п спра-
тах|Х/|
ведливо S = —'■—:—г
min |Я./|
ЛГ
419

8.6. МЕТОД ХАРАКТЕРИСТИК
Данный метод применяется при численном решении уравнений
математической физики, описывающих различные процессы в газовой динамике, теории
упругости, прочности и других прикладных областях. При его использовании в
процессе решения задачи имеется возможность выделять в расчетных областях
особые поверхности или линии, отделяющие области с одними свойствами от
областей с другими свойствами.
Рассмотрим основные идеи метода на примере задачи Коши для
квазилинейной системы дифференциальных уравнений т -го порядка с двумя
независимыми переменными x,t:
dux(xyt) dum(xyt) dux{xyt) dum{x,t) w ч
a\ 1 ™ + - + a\m — + °\ 1 Z + — + 0\т Z ~ /1 \x> *> uh
dt dt дх dx
(x,t)eD
*m\
to\(x*') , ,a dum(xyt) du{(xyt) dum{xyt) , ,
— +... +tfmm - +Dmi - + ... + 0mm - - Jm[XytyU)y
dt dt дх dx
dt "" dx """ dx
w1(x,0) = 9,(x), xe Ry
где a0 =a0(xytyu)y b0,= bjj(xytyu)y / = \,...,m;j = l,...,/w; D = Rx(OyT)y T>0 -
заданный момент времени.
Перепишем систему в векторно-матричном виде
A{x,t,u)^^ + B{x.t,u)^^ = f(x.t,u), (х,/)е D,
dt дх
м(х,0) = ф(дс), х е Ry
(8.65)
где А(ху ty и) = (ау (ху ty и)), В(ху ty и) = щ (х, /, и)) — матрицы размеров (тхт)у
f{xyt,u)-
{fm(x>t>u)j
мая вектор-функция, ср(х) =
- вектор-функция правых частей, ы(х,/) =
{"mix*'))
иско-
l<Pm(*)J
— заданная вектор-функция.
420

Пусть известно, что система (8.65) имеет гладкое решение в области D и
на некоторой кривой у оно задано и равно и(х,/) (рис. 8.17). Рассмотрим зада-
чу о нахождении решения в окрестности кривой у.
/1
Выберем на кривой у произвольную точку (x0,tQ)y а вектор бесконечно
малого смещения вдоль этой кривой из точки (х0,/0) обозначим (dx,dt).
Присоединим к уравнениям (8.65) выражение для полного дифференциала
(для упрощения записи опустим аргументы):
Ади Ddu г
А— + В— = /,
dt dx
, ди , ди ,
аи = —ах + — at.
дх dt
ди
Умножим первое уравнение на dt, а из второго выразим —dt:
A*±dt + B^dt = fdt,
dt дх
— dt = du dx.
dt dx
Подставляя второе уравнение в первое, имеем
Adu-A — dx + B — dt = fdt
дх дх
{Bdt - Adx)— = fdt - Adu.
дх
(8.66)
421

Если определитель матрицы (Bdt-Adx) отличен от нуля в каждой точке
ди ди
кривой у, то частная производная — и, следовательно, частная производная —
дх dt
определяются однозначно. В этом случае можно найти решение в окрестности
кривой у : и(х,t) = и(х,t)\ + du, что соответствует разложению искомого реше-
\У
ния по формуле Тейлора до членов первого порядка.
Если определитель матрицы (Bdt - Adx) в каждой точке кривой у равен
нуди ди
лю, то в силу предположения о существовании решения производные —,— и,
дх dt
следовательно, функция u(x,t), находятся неоднозначно. В этом случае кривая у
называется характеристикой.
Приравнивая определитель матрицы (Bdt - Adx) к нулю и предполагая, что
dt * О вдоль кривой у, получаем соотношение
В-А^
dt
О или \В-А\\=0, (8.67)
dx
где Х(х,t,и) = —-. Линии, задаваемые дифференциалами смещения dxydt, вдоль
at
которых справедливо (8.67), являются характеристиками. Анализ разрешимости
уравнения (8.67) позволяет ввести классификацию систем вида (8.65).
Если уравнение (8.67) имеет т различных действительных корней, то
система (8.65) называется гиперболической', если их число меньше т, то система
называется параболической', если уравнение не имеет действительных корней, то
— эллиптической.
В дальнейшем будем рассматривать только гиперболические системы, т.е.
имеющие т различных характеристик:
f^l =М*>'>4 / = 1,...,/и, (8.68)
где функции Xj(x,t,u) задают характеристические направления в каждой точке
кривой у.
Вдоль характеристик решение системы должно удовлетворять
характеристическим соотношениям (соотношениям совместности), которые получаются в
результате приравнивания к нулю определителя т -го порядка расширенной
матрицы, т.е.
(Bdt - Adx, fdt - Adu). (8.69)
При этом следует избегать случаев получения тривиальных тождеств.
Характеристические соотношения связывают дифференциалы искомых функций с
дифференциалами независимых переменных вдоль характеристик.
Этот способ получения характеристических соотношений основан на
применении теоремы Кронекера—Капелл и: решение системы (8.66) существует тогда
и только тогда, когда ранг матрицы Bdt - Adx этой системы равен рангу расши-
422

ренной матрицы. Предполагается, что решение существует и определитель
матрицы системы (m-го порядка) вдоль характеристик равен нулю. Поэтому должен
быть равен нулю определитель расширенной матрицы, составленный из
произвольных т столбцов.
В результате описан принцип получения характеристических уравнений
(уравнений характеристик и характеристических соотношений). Их вывод
составляет первый этап метода характеристик. Основные идеи первого, а также
второго этапа, связанного с конструированием численной схемы, рассмотрим на
примере линейной задачи Коши для одномерного волнового уравнения,
описывающего распространение плоских звуковых волн в покоящейся среде.
Пример 8.10. Получить соотношения метода характеристик для решения
линейной задачи Коши
ЩА = ЁЩ1)у (Х,,)€/?Х(0;Г),
dt2 дх2
ф(х,0) = х2 + х, х е R,
ср, (х,0) = cos х, х е R.
□ Данная задача, в частности, описывает процесс распространения
звуковых волн в спокойной среде (отсутствуют источники и стоки), следовательно,
решаемое уравнение можно рассматривать как уравнение акустики.
Для применения метода характеристик сначала сведем задачу к виду (8.65),
т.е. к системе двух уравнений первого порядка. Для этого введем новые искомые
функции
Здесь v(x,/),/?(*•,/)— отклонения скорости и давления от их значений в
невозмущенной среде, вызванные распространением звуковых волн, ф(х,/) — потенциал
функции v(x,t). Тогда уравнение можно представить в форме
(drfxtt))_ аГ*р(х,/У| или dv(xj) dp(x,t)_0
{ dt ) дх{ дх J dt дх
Предполагая, что задача имеет гладкое решение (т.е. рассматриваемая
функция имеет столько непрерывных производных, сколько нужно для
законности приводимых преобразований), воспользуемся свойством, справедливым для
дважды непрерывно дифференцируемых функций:
а2<р(*,0 = з2фМ или dpfat) = avfcQ
дх dt dtdx dt дх
423

В результате от исходной задачи для волнового уравнения переходим к
задаче для системы двух дифференциальных уравнений с начальными условиями
относительно новых искомых функций:
М^_М^ = 0, v(*,0) =
dt дх » v . /
COSX,
dt дх
Запишем систему в виде (8.65)
где
Ади Ddu (cosx^
А— + В— = 0, w(x,0) = l I,
dt дх ' [2х +1J
<-(i3-(-.V) ■-(;)->•
(8.70)
Для решения задачи (8.70) применим метод характеристик, содержащий
два этапа.
Первый этап. Нахождение характеристик и вывод характеристических
соотношений. Для этого решим уравнение (8.67), записанное для (8.70):
\В-АХ\
-X -1
-1 -X
= 0.
Получаем X -1 = 0, Х\ 2 = ±1 > т.е. два направления характеристик:
(£Ь-* а
1-г,..,.
(8.71)
Интегрируя, найдем общие решения полученных дифференциальных
уравнений. Для первого уравнения * = / + const, а для второго x = -t + const. Им
соответствуют два семейства характеристик (в данной задаче прямых линий).
Их принято обозначать буквой «С+» с верхним индексом «+» для семейства
характеристик, имеющих меньший угол с положительным направлением оси 0х
по сравнению с соответствующим углом для характеристик семейства «С-».
В данной задаче характеристики семейства «С+» имеют положительный наклон,
а характеристики семейства «С"» - отрицательный наклон (рис. 8.18). Условно
их также называют характеристиками первого и второго семейств
соответственно.
Для получения характеристических соотношений запишем расширенную
матрицу (в решаемой задаче / = ):
(Bdt-Adxjdt-Adu)--
•dx -dt - dv\
-dt -dx -dp)
424

Рис. 8.18
Приравнивая определитель матрицы, составленной из последних двух
столбцов, нулю, получаем
- dt -dv
-dx -dp
= dpdt-dvdx = Q.
Поделив на dt (предполагается, что dt * 0), имеем
dp-dv— = 0.
и dt
Так как на прямых семейства С+ выполняется равенство — 1 = Хх = 1, то
соответствующие характеристическое соотношение имеет вид
(8.72)
Аналогично на прямых семейства С справедливо
—1
dtl
■Xj =-1 и
dp + dv = 0.
(8.73)
Обыкновенные дифференциальные уравнения (8.71)—(8.73) образуют
систему уравнений метода характеристик. Полученные характеристические
соотношения (8.72), (8.73) в данной задаче могут быть проинтегрированы.
В результате получаются конечные соотношения
р - v = const (вдоль семейства С+),
р + v = const (вдоль семейства С~),
называемые инвариантами Римана. Далее они будут использованы при
построении численной схемы.
425

Результатом первого этапа является получение уравнений характеристик и
характеристических соотношений (следствий из них):
— |=1 (или х = / + const) ;
р - v = const,
(8.74)
=-1 (или х = -/ + const) ; /? + v = const.
К системе (8.74) следует добавить начальные условия
v(jc,0) = cos х, p{*fi) = 2х + 1.
Второй этап. Конструирование численной схемы и вычисление значений
искомых функций.
1. Для простоты изложения выделим на оси Ох отрезок [0;l] и на нем
зададим три точки 0; 0,5; 1 (рис.8.19, а). Они соответствуют нулевому временному
слою. Значения функций /?(х, t\ v(x,/) в этих точках будем обозначать p?,v?y
i = 0,1,2, а сами точки (х,,/") парами индексов (/,/i), где /' - номер точки по
переменной х , а п — номер временного слоя.
Для п = 0 с учетом начальных условий v(x,0) = cos х , /?(х,0) = 2х + 1
получаем
v# = v(0; 0) = 1; v? = v(0,5; О) = 0,8776; v£ = v(l; 0) = 0,5403;
/>о°=/>(0;0)=1; /?l°=/7(0,5;0) = 2;
P°2=p(l,0)=3.
(0,0)
(2,0) (ifii) 1
Рис. 8.19
2. Выведем разностные уравнения, определяющие положение точек на
следующем временном слое и значения искомых функций в них. Система (8.74)
заменяется системой разностных уравнений. Численное решение задачи строится
на характеристической сетке, которая формируется одновременно с процессом
нахождения решения. При этом обычно рассматривается трехточечный угловой
шаблон с узлами «1»,«2»,«3», составленный отрезками характеристик
426

(из семейств С+ и С"), пересекающихся в рассчитываемой точке «3» (рис.
8.19,6). Назовем этот шаблон базовым. Предполагается, что положение узлов
«1» , «2» и значения решения в узлах известны из начальных условий или
рассчитаны на предыдущем шаге. Положение узла «3» и значение решения в нем
подлежат определению.
Аппроксимируя производную по формулам
Vdt)\ 'з-'i
'dx
,dt
получаем
_. *3 - *2
'3">2
(вдоль характеристики из семейства С* с Х{ = 1),
(вдоль характеристики из семейства С" с Х2 = -1),
хз ~х\ ='з ~ч>
*3-*2=>2-'з-
(8.75)
Условие /? - v = const вдоль характеристик из семейств С+ записывается
для лежащих на ней узлов «1» и «3»:
Рг - v3 = Р\ ~ vi, (8.76)
а условие р + v = const вдоль характеристики из семейства С" записывается для
лежащих на ней узлов «2» и «3»:
Рз + v3 = />2 + v2- (8-77)
Система (8.75)—(8.77) является замкнутой относительно искомых значений
х3,/з,/?з>уз ПРИ известных x1>4,x2,/2,/?i,V|,P2»v2- Формулы (8.75)—(8.77) являются
базовыми для расчета всех точек, принадлежащих области D. После совмещения
узлов «1» и «2» базового шаблона с выбранными очередными узлами сетки в
(8.75)—(8.77) подставляются конкретные величины в соответствии с принятыми
обозначениями.
3. Производится расчет первого временного слоя.
В решаемой задаче на нулевом временном слое угловой шаблон может
занимать два положения (рис. 8.20, а,б).
427

Для точки с номерами (0,1) первого рассчитываемого слоя узлы «1» и «2»
углового шаблона совмещаются с узлами (0,0) и (1,0) (рис. 8,20,я). Поэтому
система (8.75)—(8.77) имеет вид
*o,i -*о,о= 'o,i - 'о,о> *0,1 - х1,0 = 'i.o - '0,1 у
J „1 «о „0 «1 х „1 «о , „о
Ро - vo = Ро - vo» Ро + v0 = Pi + vl •
Подставляя t0 0 =0, /j 0 = 0, х0>о = 0; хх 0 = 0,5 и известные значения
Po>Pi0>vo>vi° на нулевом слое (см. п.1), получаем
xo,i-° = ro,i-°> *o,i-°.5 = °-'o,i;
^ - vi = 1 - 1 = 0; р4 + vi = 2 + 0,8776 = 2,8776.
Решение этой системы:
х0>1 = 0,25; /ол = 0,25; р\ = 1,4388; vj = 1,4388.
Для второй точки первого слоя (рис. 8.20,6) с номерами (l;l) узлы «1» и «2»
углового шаблона совмещаются с узлами (1,0) и (2,0). Тогда система (8.75)—(8.77)
имеет вид:
*1,1 ~ xi,o = 'и ~ 'i,o ; *1,1 ~ *2,0 = '2,0 ~ 'i,i i
Р\ ~ vj = Р\ - v,0.; р\ + v\ = /?2 + ^2-
Подставляя /1>0 = 0, /2,о = 0> х1,о = ^,5; х2$ = 1 и известные значения
Pi°>vi0>P2>v2 на нулевом слое (см. п.1), получаем
*i.|-0,5 = /IiI-0; х1Д-1 = 0-/1Л;
р\ -v} =2-0,8776 = 1,1224; р\ + vj =3 + 0,5403 = 3,5403.
Отсюда jc,tl =0,75; /м =0,25; д1 =2,33135; vj =1,20895.
4. Для расчета точки (0,2) следующего временного слоя узлы «1» и «2»
углового шаблона совмещаются с узлами (0,1) и (l,l) (рис.8.20,в). Тогда система
(8.75)—(8.77) принимает вид:
*0,2 _ *0,1 = *0,2 ~ 'О.Ь *0,2 _ *1,1 = h,\ ~ *0,Ъ
Ро - vo = Ро - vi; Ро + vo = Л1 + vi •
428

Подставляя значения с предыдущего слоя, имеем
х0,2 - 0,25 = /0§2 - 0,25; х0>2 - 0,75 = 0,25 - r0f2;
Р% - v02 = 14388 -1,4388; р$ + v02 = 2,33135 + 1,20895.
Отсюда л0,2 = 0,5; tQ2 = 0,5; pi = v02 = 1,77015.
Очевидно (см. рис. 8.19,а), количество узлов на каждом последующем слое
уменьшается на единицу. Расчет продолжается до замыкания области, так как на
последнем слое останется один узел. В данном примере этим узлом является
точка (0,2).■
Замечание. Рассмотренная в примере 8.10 задача является всего лишь
модельной, выбранной для пояснения основных принципов конструирования
метода характеристик и его численной реализации. В вычислительной практике,
как правило, ставятся нелинейные задачи. Проиллюстрируем некоторые
особенности их решения на следующем примере.
Пример 8.11. Получить соотношения метода характеристик для решения
нелинейной задачи Коши
дщ{х,1) du2(x,t) dUl(x,t) du2{x,t) ,
а\\ —г;— + а\2——— + д\\ —;— + ^12—-— = /1 »
dt dt дх дх
{x,t)eD
du{(xj) dum{x,t) diijfat) du2(x,t)
al\ Г + «22 ~ + ^21 ~ + ^22 " = Jl >
dt dt дх dx
и,(х,0) = ф|(х), и2М) = ф2й, xeR,
где a0 = a&(x,t,u), bQ = b&(x9t9u)t /, = fi(x,t,u), i = 1,2; j = 1,2; <p,(x),<p2(x) -
заданные функции; D - Rx (0,Г), T > 0 — заданный момент времени.
D Поставленная задача является частным случаем задачи (8.65) при m = 2.
Применим метод характеристик, включающий два этапа.
Первый этап. Нахождение характеристик и характеристических
соотношений. Уравнение (8.67) имеет вид
\В-А\\--
Ь\\-Щ\ ьп-^ап
Ь2Х-Ха2Х Ь22-Ха12
= 0
или
.2
аХ1 + ЬХ + с = 0,
где а = апа22 - аХ2а2Х, Ь = а2ХЬХ2 + апЬ21 -апЬ22 -а22Ьп> с = bub22 - bX2b2X.
429

Решая полученное уравнение, находим выражения для двух
характеристических направлений в каждой точке расчетной области:
— = Хх(х,/,их,и2) = "^ ч" 1Ш. (определяет семейство С+);
\dt )х *~
-ь + 4ь2 ■
-ь-
2а
-J*
-4ос
-Аас
(8.78)
rdx\ „ !7 ~
I— = X2(x,t,их,и2) = —-— -^- (определяет семейство С ).
i, dt )2 2а
Сформируем расширенную матрицу
(Bdt-Adx,fdt-Adu) =
bxxdt-axxdx bx2dt-ax2dx fxdt-axxdux -aX2du2\
b2Xdt-a2xdx b22dt-a22dx f2dt - a2Xdux - a22du2)
Характеристические соотношения получаются в результате приравнивания
нулю определителя второго порядка (т - 2), составленного из второго и третьего
столбцов расширенной матрицы:
bx2dt - aX2dx fxdt - ах xdux - aX2du2
b22dt - a22dx f2dt - a2Xdux - a22du2
= 0.
Раскрыв определитель и поделив на dt ф 0, получим
\е - а — \dux + g du2 + hdt + qdx = 0 ,
где e = axxb22 -a2Xbx2i g = ax2b22 -a22bx2, h = bX2f2 -b22fx, q ^a22fx-aX2f2.
Последние два слагаемых перепишем в эквивалентной форме
hdt + qdx = (h + qj-)d*-
Поскольку для семейства характеристик С+ выполняется равенство
(dx\ л w ^_ (dx\ Л
— = Хх, а для семейства С - равенство — = Х2, то характеристические
\dt )х \dt )2
соотношения имеют вид
(е - аХх)dux + gdu2 +(h + qXx)dt = 0 (для семейства С+);
(8.79)
(е - aX2)dux + gdu2 +(h + qX2)dt = 0 (для семейства С").
430

В результате получена характеристическая система (8.78), (8.79) из четырех
обыкновенных дифференциальных уравнений. Они позволяют найти значения
/, х, w,, и2 вдоль характеристик.
Второй этап. Конструирование численной схемы.
Как и в предыдущем примере, будем использовать трехточечный угловой
шаблон (рис. 8.19, б). Предполагается, что в точках «1» и «2» известны значения
t,x,ul,u2 из начальных данных или из расчета предыдущего слоя, т.е.
/1,x1,wn,w2i для точки «1» и t2,x2iuX2ju22 Для точки «2». Здесь при обозначении
значений функций их,и2 , а далее и при обозначении других функций в точках
шаблона первый нижний индекс соответствует номеру самой функции, а второй
индекс - номеру точки в шаблоне. Требуется найти значения ^*хУ>и13»и23*
определяющие положение точки «3» и значения искомых функций в ней.
Предполагается, что точки «1» и «2» близки друг к другу, поэтому заменим
дифференциалы конечными приращениями, а производную — — конечно-
dt
разностным отношением:
dt = At = /3 - tx, dx = Ах = *з " xl » dux = Ащ = Wj3 - Щ |, du2 = Аи2 - и2Ъ - и2Х,
fdx\ __х3-х{
(для семейства С+);
dt = At = /3 - f2, dx = Ax = x3 - x2 , dux = Д^ = ы13 - w12, */w2 = Aw2 = ы23 - u22,
— = — (для семейства С").
В итоге уравнения характеристик являются уравнениями прямых,
соединяющих точки «1» и «2» с точкой «3», а характеристическая система (8.78), (8.79)
преобразуется к виду
хъ-хх =(*.,), (/3-'i),
*з-*2 =(^2)2(^3 -'2). (8.80)
{е-аХх\ («i3-«n) + te)i -(«23 -«2i) + (^ + ^Xi), (/3 -/i) = 0,
(е - в Х2)2 (i/I3 - их2) + (g)2 • (и2г -u22) + (h + q Х2)2 (t3 - /2) = 0.
Здесь нижние индексы 1 и 2 указывают, что значения всех функций,
входящих в соответствующие выражения, подсчитываются в точке «1» или «2».
Решая систему (8.80), можно найти значения 'з'^з^и^з» определяющие
положение точки «3» и значения искомых функций в ней. Сначала обычно
решаются первые два уравнения и определяются значения /з,*3, а затем ~"
последние два уравнения, откуда находятся их^уи2^.
431

Опишем теперь общую схему численного решения поставленной задачи
Коши.
1. При / = 0 на оси абсцисс задаются точки с некоторым шагом. В этих
точках (на рис. 8.21 выделен фрагмент, содержащий точки 1-6) значения
функций их,и2 определяются начальными данными, т.е. функциями (Pi(x),(p2(x).
2. В соответствии с изложенной методикой последовательно
рассчитываются координаты точек 7-11 и приближенные значения решения в них. При этом
точки «1» и «2» углового шаблона последовательно совмещаются с точками 1 и 2,
затем с точками 2 и 3, 3 и 4, 4 и 5, 5 и 6. Узлами выстраиваемой
характеристической сетки служат точки пересечения характеристик (они образуют следующий
временной слой).
3. Расчет слоев продолжается до достижения последней точки (точки 21)
треугольной области.
/ '
0
19/
16 /
12 А 13Х
7 / 8Y 9 J
1 2 3
21
Л17
4
*20
Л18
14 Д5
Yio Д"
5 6
X
Рис. 8.21
Отметим, что дифференциальным уравнениям (8.78) соответствуют
криволинейные характеристики, а точка «3» должна быть точкой пересечения
этих криволинейных характеристик. При переходе от дифференциальных
уравнений (8.78),(8.79) к разностным дифференциалы были заменены конечными
разностями, а производные конечно-разностными отношениями. Вследствие
этого криволинейные характеристики были аппроксимированы отрезками
прямых. Решение системы (8.80) объявляется первым приближением, т.е.
.0)
з
h
r(i)
*з
:*з> ип ="13>
-,0)
w23 = w23, и может возникнуть необходимость
в уточнении координат точки «3» и значений искомых функций в этой точке.
Ограничимся изложением одного из возможных способов уточнения [3,26].
432

После нахождения первого приближения следует найти средние
арифметические значения:
Xi- , Х2= , *,= - ,
_(е-а\2)2+(е-аХ2)3 _ (g){ + (g)3 , _ (g)2 + (#)з
2 2 l 2 » Ч. 2
(/* + <7>ч)| +(/г + ^Я.|)3 .. (h + q\2)2+(h + qk2)3
мх = , м2 = ,
где нижний индекс 3 указывает, что соответствующее выражение подсчитывается
в найденной точке «3». Эти соотношения получаются, если при интегрировании
дифференциальных уравнений применять правило трапеций [26].
Затем решается система
х<2)-х2 =X2(/f -/2),
*1 («{? »l/il) + Il -(4? -«2l) + ^l (f} "/.) = 0,
*2 С",? - "12) + к ' ("$ " «22) + ^2 ('f ~ /2) = 0
относительно нового (второго) приближения /з2),х^2), иЦ\ и$. Описанный
процесс продолжают до тех пор, пока решения, полученные при двух
последовательных приближениях, не будут совпадать с заданной точностью. Как правило,
если расстояние между точками «1» и «2» невелико, достаточно сделать два
уточнения.
Замечания.
1. Приведенные примеры иллюстрируют важное свойство метода
характеристик, отличающее его от ранее рассмотренных разностных методов. Оно
заключается в том, что расчеты осуществляются вдоль характеристик — линий, по
которым распространяется информация об исходных данных, что придает методу
четкий физический смысл.
2. Описанный метод расчета, когда точки следующего слоя заранее
неизвестны, а вычисления ведутся вдоль характеристик семейств С+ и С",
выделяемых в процессе расчета, называется классическим методом характеристик.
Существуют модификации этого метода, когда точки следующего слоя задаются
заранее, а для нахождения значений искомых функций в них характеристики
выпускаются в направлении к известному слою. Такие методы называются сеточно-
характеристическими [22].
433

8.7. МЕТОД ГОДУНОВА
В механике сплошных сред при решении задач, описывающихся
квазилинейными дифференциальными уравнениями в частных производных, в
расчетных областях могут возникать поверхности сильного разрыва, к которым относятся
ударные волны, центрированные волны разрежения, поверхности контактного
разрыва. На этих поверхностях терпят разрыв как искомые функции,
характеризующие исследуемые процессы, так и их производные. При решении таких
задач используются два класса численных схем, в одном из которых с
использованием законов сохранения явно выделяются поверхности разрыва, а в другом эти
поверхности явно не выделяются, а рассчитываются «насквозь» вместе с
областями непрерывности. К последнему классу методов относится метод С.К.
Годунова [50]. Идею его конструирования рассмотрим на примере решения
смешанной краевой задачи для уравнений акустики.
Пример 8.12. Получить соотношения метода Годунова для решения задачи
du(xj) ( 1 dp(x,t) _0
dt ро дх
dp(x,t) , . ,2ди(х,0 п
-^г-+Ро*°-^г-=0
с начальными условиями
u(xfl) = Ij/^x) , p(xfi) = V2(x), 0 < х < 1,
и краевыми условиями
/>(0,/) = Ф,(0, />(U) = Ф2('), 0</<7\
Система двух дифференциальных уравнений описывает распространение плоских
звуковых волн (малых возмущений) в покоящейся среде. Здесь и(х, t), р(х, /) -
малые отклонения скорости и давления от их значений в невозмущенной среде,
вызванные распространением звуковых волн; р0 - плотность невозмущенной
среды; а0 — скорость звука.
D Рассмотрим основные этапы конструирования метода Годунова.
1. Введем разбиение отрезка [0;1] с шагом h = —, где п — число промежут-
п
ков. В результате получим узлы х,, / = 0,1,...,я, определяемые соотношением
х/+1 = х/ + h, i = 0,1,..., п -1; х0 = 0 , хп = 1.
2. Заменим функции v|/i(x),v|/2(x) на начальном слое / = 0 кусочно-
постоянными (пример описанной замены для некоторой произвольной функции
\\i\(x) изображен на рис. 8.22) путем их интегрального осреднения по формулам
"i=T \v\(x)dx, P. i =T fv2(*)<** . / = 1,2,...,л. (8.81)
i-z h rJ i-- h /
2 */_i 2 *j_i
434

Здесь и далее все заданные или ранее рассчитанные функции снабжаются
нижними полуцелыми индексами. Из рис. 8.22 видно, что полученная кусочно-
постоянная функция имеет в узлах разрывы первого рода.
/С
JS \
\ \ h
j , 1 ,
и. 1
\ч\(х)
^^^ 1
1
1
►
х0=0
*/-!
Xj */+!
Рис. 8.22
*„=1
3. Выберем шаг х по времени / и образуем следующий расчетный слой
(/j = т) с теми же узлами х, (рис. 8.23). Таким образом, образуется совокупность
прямоугольных ячеек. Предполагается, что искомые функции на горизонтальных
и вертикальных границах образованных ячеек также являются постоянными.
На рассчитываемом слое при / = т приближенное решение задачи также
представляется в виде кусочно-постоянной функции, имеющей разрывы в узлах
сетки, совпадающих с узлами на предыдущем слое. Это означает, что во времени
на слоях / = const сохраняется структура решения, изображенная на рис. 8.22.
Значения искомых функций на рассчитываемом слое (верхних границах ячеек)
i
/-—
обозначаются верхними полуцелыми индексами: и 2,/? 2, / = 1,2,...,п. На
вертикальных границах ячеек значения функций обозначаются прописными
буквами с нижними целыми индексами: UhPh i = 0,...,л.
h
Щ 1
Ut-i
i 1
и 2
p 2
u,
Pi
vM
i ' I
I I
l ■ ►
<i-\ Ui-\ X, UUL XU{
M
M
Рис. 8.23
435

При / = 0 , / = п значения Р0 и Рп определяются краевыми условиями по
формулам, аналогичным (8.81):
/Ъ— J<Pi(0</>, />„=-)ф2(')</'.
1 о т о
(8.82)
Значения U{i...,Un_XyPXi...tPn_{ находятся в результате решения вспомогательной
задачи о распаде произвольного разрыва, описанного в п.4, а значения UQ,Un
определяются в п.5.
4. Выберем две соседние ячейки с узлами Х/.^х,- и х/}х/Ч1 (эти ячейки
выделены на рис. 8.23 жирными линиями). С целью нахождения значений UitPf
на внутренней границе ячеек при х = х, рассмотрим решение вспомогательной
задачи, называемой задачей о распаде произвольного разрыва [7,50].
Дана система уравнений
ди(х, /) 1 dp(x,t)
dt ро дх
(8.83)
0,
dp(xyt) ш _ _2Mx,t)
с начальными условиями вида
u(xfl) = I
U ,, X/., <х<Х,,
'"2
и ,, х,<х<х/+1,
/+2
/>(х,0) =
/? ,, X/., <Х<Х„
"2
р ,, X/ <x<x/ + i.
' + 2
Требуется найти решение w(x,/),/>(x,/) при / > 0 и х = х,-, т.е. u(xht) = [/,-,
/>(*/,/) = fl.
Заметим, что в данной задаче начальные данные имеют разрыв первого
рода в точке X/. При / > 0 они трансформируются, т.е. происходит распад
разрыва, что обусловливает название рассматриваемой задачи.
Для ее решения применим метод характеристик (см. разд. 8.6). Перепишем
систему (8.83) в матричной форме
Адфьй + вМх10=0>
где А
-С?)--
f 1 ^
0 —
Ро
UW ° )
а/
, и =
ах
(8.67):
Для нахождения характеристических направлений используем условие
436

\В-АХ\ =
-X —
Ро
Ро^о -*•
= 0.
Отсюда X = ± а0 и
Ш-*
:^о»
(§) —
Интегрируя последние уравнения, имеем
х - a0t - const (для семейства С+),
х + a0t = const (для семейства С).
Если при / = 0 выполняется условие х = х,, то из последних соотношений
выделяются две прямые, исходящие из точки х,- на начальном слое:
х - a0t - х{ (прямая семейства С+),
х + a0t = X/ (прямая семейства С").
Для получения характеристических соотношений запишем расширенную
матрицу (8.69) (учитывая, что / = 0):
< 1 ^
Bdt - Adx,
■ MY
-dx —dt -du
Ро
Lpo^o^ "dx -dp)
Приравнивая определитель матрицы, составленной из двух последних
столбцов, нулю, получаем
dpdt-dxdu = 0.
Ро
Полагая dt * 0, разделим уравнение на dt:
Ро dt
dx
Подставляя вместо — сначала Х+ = а0, а затем X = -а0, получаем
*/м + dp = 0 (соотношение вдоль семейства С+),
Ро ао
du-
Poflo
-dp = 0 (соотношение вдоль семейства С").
437

Так как коэффициенты обоих уравнений постоянны, то их можно
переписать в эквивалентной форме
1
Ро До
1и-
1
= 0 (соотношение вдоль семейства С+),
: 0 (соотношение вдоль семейства С).
Ро °о )
Интегрируя и обозначая постоянные интегрирования /+,/~, имеем
и + р = /+ (соотношение вдоль семейства С+),
Ро^о
и р = /~ (соотношение вдоль семейства С").
Ро^о
(8.84)
Полученные соотношения называются инвариантами Римана. Они
показывают, что величина ил- р = 1+ остается постоянной вдоль семейства С+, а
Ро°о
величина и р = /" остается постоянной вдоль семейства С".
Ро^о
Теперь, используя направления характеристик и сохраняющиеся вдоль них
инварианты, построим численную схему решения задачи о распаде разрыва.
х + a0t = xj+l х - aQt = */_,
х - a0t = x,
Рис. 8.24
438

Рассмотрим две характеристики х-я0/= Х/_| и х-a0t = Xj из семейства
С+, исходящие из узлов .*,■_[,*/, а также две характеристики x + a0t = xi и
x + aQt = jc/41 из семейства С", исходящие из узлов xhxi+{ (рис. 8.24). В
результате пересечения указанных характеристик образуются области I, II, III , первые
две из которых представлены треугольниками, а третья - четырехугольником.
Вертикальная граница (х, = const) , разделяющая ячейки, на которой ищется
решение задачи, располагается в области III. Покажем, что на этой границе
искомое решение постоянно. Для этого выберем на ней произвольную точку
(назовем ее точка 3) , а решение в ней обозначим UhPt. В эту точку приходит
характеристика семейства С+, исходящая из точки 1 промежутка (x/_i,X/). Точке
1 соответствуют заданные значения и [ур { . Вдоль этой характеристики оста-
'"2 '"2
ется постоянной величина и + р = /*, т.е.
Ро^о
Uj+ Р, =и , + р ,
"2 P0fl0 '"2
P0fl0 '"о P0fl0 '-г
Кроме того, в точку 3 приходит характеристика семейства С", исходящая из
точки 2 промежутка (х/,я:/+1). Точке 2 соответствуют заданные значения
и |, р j . Вдоль этой характеристики остается постоянной величина
/+2 /+2
1
и р = I , т.е.
Ро^о
Ut — />=*. , !-Л ,.
РО^О , + 2 p0fl0 / + 2
Разрешая систему из двух последних уравнений относительно UhPt ,
получаем
". 1 +и. 1 Р. 1 "Л 1
2 2р0 д0
/ = 1,...,л-1. (8.85)
/>. I + Л 1 и. i -". \
ч = z Ро ао z
Поскольку точка 3 была выбрана произвольно на вертикальной границе
ячейки, то полученные выражения определяют решение в любой точке этой
границы (очевидно, решение постоянно вдоль границы), за исключением самой
точки х, и точки пересечения характеристик, исходящих из точек x/_i,xl+|.
Таким образом, формулы (8.85) определяют «большие» величины UhPt на всех
внутренних вертикальных границах ячеек.
439

Результаты решения данной вспомогательной задачи определяют шаг т по
времени. Действительно, влияние каждого из разрывов, относящихся к соседним
узлам х,_1,Х/ на слое / = 0, ограничивается характеристиками, исходящими из
этих узлов. Физически это означает, что разрывы, возникшие при / = 0,
распространяются со скоростью звука а0. Характеристики, исходящие из соседних уз-
, h
лов навстречу друг другу, пересекутся в точке с координатами / = ,
2а0
х = —^ l.Ot этой встречи разрывов возникнут новые волны, которые через
следующий отрезок времени длительностью достигнут вертикальных границ
2а0
(*/_! = const, X/ = const) соседних ячеек. Именно до этого момента, т.е. в
течение времени — = + , значения UhPt будут сохраняться неизменными и
а0 2а0 2а0
определяться по формулам (8.85). Таким образом, величина шага по времени
должна выбираться из условия т < —.
5. При / = 0 для нахождения величины U0 при известном Р0 используется
инвариант Римана и р = /" вдоль семейства С" (рис. 8.25). Поскольку на
РоЛо
промежутке (0,*|) заданы значения их,р\ , то U0 Р0 =их рх. От-
2 2 Р°а° 2 Ро°° 2
сюда получаем
1
1
U0 = Р0 +wt
P0fl0 2 Ро°0 2
-Р\
(8.86)
х0=0
Рис. 8.25
При / = п для нахождения величины Uп при известном Рп используется
инвариант Римана и + р = 1+ вдоль семейства С+(рис. 8.25). Поскольку на
Ро^о
440

последнем промежутке (хп_\,1) заданы значения и х,р j, то
П~2 П~1
ип+-
Ро^о
■А=и
! + р !. Отсюда получаем
л~2 РО °0 Л~2
£/„=■
1 D 1
PK+U , + /> ! .
Poflo
я"2 РО а0 п~2
(8.87)
На рис. 8.25 показаны две крайние ячейки с тремя характеристиками, одна
из которых (верхняя) ограничивает область влияния начальных данных,
заданных на промежутках (х0,х,) и (xn^tx„) соответственно.
6. Перейдем к задаче расчета искомых величин на следующем временном
слое. Для этого рассмотрим одну ячейку (рис. 8.26), для которой известны
значения приближенного решения и х,р { на нижней границе и #,_!,//_!,£/,,//,
/* = l,...,/i, на левой и правой вертикальных границах (см. п.4). Требуется опреде-
.1 .1
лить значения р 2,и 2 на верхней границе ячейки.
Рис. 8.26
Для решения поставленной задачи перепишем уравнения (8.83) в так
называемом дивергентном виде
du(x,t) , [ Ро
О
dt
Ро_
дх
= 0,
dp(xj) t а(р0 а$и(х, /)) _0
а/ дх
(8.88)
Запишем двойной интеграл от левой и правой частей уравнений по поверхности
ячейки. Для его нахождения применим формулу Грина перехода от двойного
интеграла к криволинейному интегралу второго рода:
Я(^*^)*М(ф.*-«мг).
441

где -5* — поверхность ячейки, а у — ее граница, обходимая против часовой
стрелки. Таким образом, вместо системы (8.88) получается система интегральных
уравнений
cf иdx - — dt = 0 , <fpdx-p0ciQudt = Q.
Ро
Проводя интегрирование, имеем
и xh-^-x-u 2Л + ^-х = 0,
Ро Ро
2
Р \h-poa5UjT-p 2Л + р0Я() ty-i * = 0.
'"2
Из этих уравнений получаем
. j_
'"2 ЛР0
/ = 1,...,л. (8.89)
/> 2 =Л i -7-Poflo(^/-^/-i).
Таким образом, получены формулы для расчета первого временного слоя
112 2 „Л „_1
(f = x). После нахождения значений и2,р2,и2,р2,...,и 2,р 2 из условия
х < — выбирается очередной шаг и формируется новый временной слой
До
(/2 = *i +х). Найденные значения используются в качестве опорных (они
переобозначаются путем присвоения им соответствующих нижних индексов) для
нахождения приближенного решения на следующем слое по формулам (8.85)-
(8.87), (8.89). Заметим, что для вычисления P^tPn вместо (8.82) используются
формулы интегрального осреднения, аналогичные (8.81). Для расчета, например,
второго временного слоя они имеют вид
Ро=~ }ф1(')Л. Л=- J Ф2 (')<*• (8.90)
h h
Изложенная схема метода Годунова имеет первый порядок апроксимации
по т и h [7,50].
Замечание. Из процедуры интегрирования следует, что искомые зна-
/-- /--
чения и 2,р 2 соответствуют среднеинтегральным величинам
/-I 1 * *-± 1 *
и 2=- fu(x,x)dx,p 2=- \p(x,t)dx.
xi-i xi-\
442

Приведем пример расчета по описанной схеме для частного случая
рассматриваемой задачи:
du(xj) i 1 dp(x,t) _0
dt
Ро дх
0<х<1, 0</<1,
dp(x,t) гди(х,0
—т— + Ро ао —-— = °
dt дх
u(xfi) = \\t\(x) = sinx, р(ХуО) = \\i2(x) = p0xsmx, 0^х<1,
p(Q9t) = ф,(/) = ОД/ + ро flo sin'> P&t) = Фг(0 = 0.1' + Ро 4 sin>> 0 < / < 1,
где р0 = 0,123; а0 = 0,25.
/ -
1
0,5
т
о 1
С
А
[ Л
0
,5
D
В
1
*
Рис. 8.27
А. Выберем число промежутков п = 2. Тогда находится шаг h = — = 0,5 и
вводятся узлы х0 =0; х{ = 0,5; х2 = 1. Зададим шаг т = 0,5 по времени из условия
т < — = __l_ = 2. Сформируем две ячейки «А» и «В» первого временного слоя
а0 0,25
tx = х = 0,5 (рис. 8.27).
Б. Заменим функции \\t\(x) = sinx, ц/2(х) = Ро xsinx кусочно-постоянными
по формулам (8.81). Для вычисления интегралов используются квадратурные
формулы трапеций (см. разд. 5.3.1):
'. 1 =
1 "'•-' +Uj h- Ui~{ + щ
1 Pi-\ + Pi , Pi-i + Pi . }1
P. l =T ~ Л = z . ' = 12,
i-- h 2 2
443

где и, = sin xh Pj = po jc,- sin xf. Поэтому
0 + 0,479 n07Q 0,479 + 0,841
uL = = 0,239 , W3 = = 0,660;
2 2
0 + 0,0294 nm/17 0,0294 + 0,1035 пп„л
/?! = = 0,0147 , /73 = = 0,0664.
2 2
В. Найдем значения Pq,Pi по формулам (8.82). Для вычисления
интегралов, как и ранее, применяется формула трапеций:
0 + 0,0537 ^ 0 + 0,0463 ^
О 2 2 2
Рассчитаем значение U0 на левой границе ячейки «А» по формуле (8.86):
UQ = Po+u\ Р\ =0,635 и значение U2 на правой границе ячейки
Ро ао 2 Ро а° 2
«В» по формуле (8.87): U2 = Р), + и?> + Ръ = 1,476.
Ро^о ^ poflo 2
Г. Вычислим значения Ux, Р\ на правой границе ячейки «А» (левой границе
ячейки «В» ). По формулам (8.85) получаем
ul+ul Pi" Pi PL+Pl ul~ul
tf1=-I_2.-.I Is. 0,392, Л=ЛГ^-Ро«оЛГ1 = 0,0341.
2 2p0fl0 2 2
112 2
Д. Вычислим значения u2yp2\ w2,/?2 на верхних границах ячеек:
1 I
„2=Wl -_^(/>-/>0) = 0,1805, />2=/>, -fPo«02(^-^o) = 0,0226,
2 ЛР0 2 h
2 2
«2=«3-7T-(^-fl)s 0,749, ^2=/>з-~р0я02(^2-^) = 0,0521.
2 ЛР0 2 Л
Таким образом, первый слой полностью рассчитан.
Е. Для расчета второго слоя (/2 = t\ +т) с шагом х = 0,5 полученные значе-
I i 2 2
ния и2,р2; и2,р2 переобозначим, для чего верхние индексы заменяются
нижними: и{ =0,1805; рх =0,0226; иъ =0,749; />з =0,0521 . Сформируем две ячей-
2 2 2 2
ки «С» и «D» второго временного слоя (см. рис. 8.27).
444

Ж. Найдем значения Р$,Рг по формулам (8.82). Для вычисления
интегралов, как и ранее, применяется формула трапеций:
0,0537 + 0,1065 0,0463 + 0,00935
0 " 2 2 2
Рассчитаем значение U0 на левой границе ячейки «С» по формуле (8.86):
UQ = Р0 +u{ р{ =2,0504 и значение U2 на правой границе ячейки
РоЛо 2 p°fl° 2
«D» по формуле (8.87): U2 = Р2 + "з + Ръ = 0*8651.
Родо 5 РоЛо 2
3. Вычислим значения UltP{ на правой границе ячейки «С» (левой границе
ячейки «D»). По формулам (8.85) получаем
UL+U1 P1~PL PL+P1 ul~ul
tf1=-L-I-^I Is-0,0150, Р^Лг^-Ро^о-1^-1^0'02861-
112 2
И.Вычислим значения u2yp2\ u2,p2 на верхних границах ячеек «С» и «D»:
"2="i -7r-(fl-fl))s 0,599, р2=рх -fp0ao2(^i-^o) = 0,0385,
2 АР0 2 h
3 3
"1= "3-7^(^2-^) = 0,7556, ^2=P3-fpoflo(^2-^i) = 0,04533.
2 ЛР0 2 Н
Таким образом, второй слой полностью рассчитан и найдено
приближенное решение поставленной задачи. ■
Замечание. Здесь рассмотрен пример методики конструирования
метода С.К. Годунова и ее реализации для относительно простой линейной задачи.
В нелинейном случае метод существенно усложняется. Для более глубокого
изучения проблемы авторы рекомендуют [22,36,50], где данный метод применяется
для различных классов нелинейных задач и задач с тремя и четырьмя
независимыми переменными.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Составить явную и неявную схемы для решения задач 1—4.
lw/=wxx» 0<х<1, 0</<0,08;
u(Q,t) = t, «(1,0 = 0,5 + /, 0 < / < 0,08;
х2
и(х,0) = ±-, 0<х<1.
445

2. ut = u^ + x2 - 2/, 0 < x < 1, 0 < t < 0,02;
w(0,/) = 0, n(l,/) = /, 0</<0,02;
w(x,0) = 0, 0 < x < l.
3.utt=uxx> 0 < x < 1, 0</<l;
w(0,0 = 0, w(l,/) = 0, 0</<l;
u(xfl) = 0, w, (x,0) = я sin ях, 0 < x < 1.
4. ",/ =wxc + ex/, 0<x<l, 0</<0,5;
w(0,0 = arctg /, i/(l, 0 = 1, 0 < t < 1;
i/(x,0) = x, щ (x,0) = Vx, 0 < x < 1.
Составить явную схему решения задач.
5. и^ + иуу = 0, 0 < х < 0,8, 0 < у < 0,8;
и(х,0) = х2, и(х;0,8) = х2 - 0,64, 0 < х £ 0,8;
и(0,у) = -у2, и(0&у) = 0у64~У2, 0<у<0,8.
6. и^ + иуу = 4, 0 < х < 0,8, 0 < ;/ < 0,8;
w(x,0) = х2, ы(х;0,8) = х2 +0,64, 0 < х < 0,8;
и(0, у) = у2, и(0,8; у) = 0,64 + у2, 0 < >> < 0,8.
7. Методом сеток найти решение задачи
ип=ихх> 0<х<1, 0 < / < 0,5;
*/(0,О = 0, 1/(1,0 = 0, 0 < Г < 1;
w(x,0) = 0,2 х(1 - х) sin ях, щ (х,0) = 0, 0 < х < 1.
8. Методом характеристик решить задачу Коши
ии - ихх> 0 < х < я, 0 < / < 0,5;
ы(х,0) = х(я - х), и,(х,0) = 0, 0 < х < 1.

Глава 9. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИИ
МАТЕМАТИЧЕСКОЙ ФИЗИКИ С ТРЕМЯ НЕЗАВИСИМЫМИ
ПЕРЕМЕННЫМИ
9.1. ПОСТАНОВКА ЗАДАЧИ И ОСНОВНЫЕ ПОЛОЖЕНИЯ
Рассмотрим задачи с тремя независимыми переменными *,>>,/, где х,у —
пространственные переменные, а /- время, / = 0 и t-T- моменты начала и
окончания процесса. В качестве примера расчетного множества, в котором
ищется решение задачи, используем цилиндр (рис. 9.1). В начальный момент
времени / = 0 множество задано односвязной областью Q с кусочно-гладкой
границей Г.
/ t
♦ х
Рис. 9.1
Приведем обобщения задач, поставленных в разд. 8.1, на случай трех
независимых переменных.
ПОСТАНОВКА ЗАДАЧИ ДЛЯ ДВУМЕРНОГО УРАВНЕНИЯ ПЕРЕНОСА
Рассмотрим двумерное уравнение переноса
^х1^ + ча»с^ + ^а!«сьми/(я>л0> (XtJ,>o.Qx(ot70f (9Л)
dt
дх
ду
447

где q,c2 — скорости переноса по осям ОхуОу, f(xyyyt) — заданная функция.
Оно является модельным для математического описания многих физических
процессов (нейтронных потоков в реакторе; теплопроводности в газах,
обусловленной диффузией атомов и электронов, и др.).
Начально-краевая задача:
и, +их +иу = /, (xyyyt)eQx(QyT)y
и(х,у,0) = \\i(xyу), (х, у) е П U Г, (начальное условие)
"(х, у, t) = ф(х, yyt)y (х, у) е Г, 0 < / < Т, (краевое условие)
содержит функциональное начальное условие (при / = 0) и функциональное
краевое условие. Здесь и далее y(x9y)9<p(x,y9t) — заданные функции.
Требуется найти функцию и(ху у9 t), удовлетворяющую дифференциальному
уравнению (9.1), начальному и краевому условиям.
ПОСТАНОВКИ ЗАДАЧ ДЛЯ ДВУМЕРНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
Рассмотрим двумерное уравнение теплопроводности
ди(х,
dt
^ = аг(вМ^+дМь^\ (х,у,1)еПх(о,Т), (9.2)
И (, дхг дуг )
где и — температура, а2 — коэффициент температуропроводности, а2 =—, к -
рс
коэффициент теплопроводности, с — удельная теплоемкость, р — плотность.
Оно описывает, например, распределение температуры на плоской пластине при
отсутствии тепловых источников.
Первая начально-краевая задача:
ut ^^(Uxx+Uyy), (*,>>,/) еПх (О, Г),
и(х, у90) = v|/(x, у), (х, у) е Q U Г, (начальное условие)
и(х, У, 0 = ф(*, У9 0, (х, у) е Г, 0 < / < Т, (краевое условие)
содержит функциональное начальное условие (при / = 0) и функциональное
краевое условие на границе Г. Здесь и далее y(x,y),<p(x,y,t) - заданные
функции.
Вторая начально-краевая задача:
Щ =a2(Uxx+uyy)> (x9y9t)eQx(0yT)y
w(x, yfi) = у(х, у) у (ху у) е Q U Г, (начальное условие)
du(xyyyt)
дп
'■ ф(*, У у 0, (х, У) е Г, 0 < / < Т, (краевое условие)
448

содержит функциональное начальное условие (при / = 0) и дифференциальное
краевое условие на границе Г, задающее производную в направлении внешней
нормали.
Третья начально-краевая задача:
Щ =Я2(";сс + «jy). (xj,/)6Qx(0J),
и(х, yfl) = у(х, у), (х, у) е Q U Г, (начальное условие)
а — + р и = ср(х, >>, /), (х, >>) g Г, 0 < / < Г, (краевое условие)
дп
содержит функциональное начальное условие (при / = 0) и функционально-
дифференциальное краевое условие, задающее линейную комбинацию
производной в направлении внешней нормали и функции на границе Г. Здесь а,р —
заданные числа (а2 +р2 > 0) либо функции от / в более общем случае [26].
Во всех перечисленных задачах требуется найти функцию и(х,>>,/), которая
удовлетворяет дифференциальному уравнению (9.2) в области D = Qx (0,Г) и
соответствующим условиям на ее границе.
Примером физической задачи, приводящей к первой начально-краевой
задаче, может быть процесс изменения распределения температуры в плоской
пластине, на границе которой поддерживается заданная температура, определенная
функцией <р(х, у, t). В начальный момент времени при t = 0 функцией \|/(х, у)
задано начальное распределение температуры на поверхности пластины.
Искомая функция u(x,yj) характеризует температуру пластины в точке с
координатами (х, у) в некоторый момент времени /.
ПОСТАНОВКИ ЗАДАЧ ДЛЯ ДВУМЕРНОГО ВОЛНОВОГО УРАВНЕНИЯ
Рассмотрим двумерное волновое уравнение:
2..,„ .. a Г*2..,„ ,. a *2.,/v „ ,Л
d'u(x,y,t) 2
а/2
д*и(х,у, t) + д'и(х,у, /)
ах2 ду2
, <*,*/) 6 Пх (0,7*), (9.3)
где u(x,y,t) - величина смещения точки (х,у) в момент времени /, с2 = —, f-
Р
проекция вектора натяжения на плоскость Оху, р — поверхностная плотность
мембраны. Волновое уравнение описывает малые поперечные колебания
мембраны.
449

Первая начально-краевая задача:
ип =c2(wxx +иуу), (х,.у,/)еОх(0,Г),
и(х,yfi) = ц!{(х,у), (xjJeQUr, (начальное условие)
— = vj/2(x,,y), (x,>>)€QUr, (начальное условие)
"(*, У, 0 = ф(*> Уу*) , (х, >>) е Г, 0 < / < 7\ (краевое условие)
содержит функциональное и дифференциальное начальные условия (при / = 0) и
функциональное краевое условие. Здесь и далее у\(х,у)у\\12(х,у),у(х,у^) —
заданные функции.
Вторая начально-краевая задача:
ип = с2("хх +"уу)> (*.У,0 е О х (0, Г),
и(х, у,0) = \|/! (х, у), (х, у) е Q U Г, (начальное условие)
— = v|/ 2 (*, у), (х,;/) е Q U Г, (начальное условие)
dt
'•^ = ф(х, у, /), (х, у) е Г, 0 < t < Т, (краевое условие)
содержит функциональное и дифференциальное начальные условия (при / = 0) и
дифференциальное краевое условие на границе Г, задающее производную в
направлении внешней нормали.
utt = с2Кх + иуу) » (*.У>0 е П х (0, Г),
Третья начально-краевая задача
Ыуу)
ы(х, у,0) = у j (х, у), (х, у) € О U Г, (начальное условие)
ди(х,у,0)
dt
du(x,y,t)
■ = \\t 2 (х, у), (х, >>) е Q U Г, (начальное условие)
дп
+ р и = ф(х, >>, 0, (х, у) е Г, 0 < / < Т, (краевое условие)
содержит функциональное и дифференциальное начальные условия (при / = 0)
и функционально-дифференциальное краевое условие, задающее линейную
450

комбинацию производной в направлении внешней нормали и функции на
границе Г. Здесь а,р - заданные числа (а2+р2 >0) либо функции от / в более
общем случае [26].
Во всех перечисленных задачах требуется найти функцию м(х, у, t), которая
удовлетворяет дифференциальному уравнению (9.3) в области /) = Пх(0,Г) и
соответствующим условиям на ее границе.
ПОСТАНОВКИ ЗАДАЧ ДЛЯ ТРЕХМЕРНОГО УРАВНЕНИЯ ЛАПЛАСА
Рассмотрим трехмерное уравнение Лапласа
d2u(x1y1z) , d2u(x,y,z) , д2и(х, y,z)
дх2 ду2 dz2
или более общее уравнение Пуассона
= 0, (xyy,z)eQ, (9.4)
d2u(x,y,z) d2u(x,y,z) d2u(x,y,z) ft ч , ч _
f + , + T = f(x,y,z)9 (x,y,z)eQy
дх2 dy2 dz2
где Q. — некоторая односвязная область пространства Oxyz с кусочно-гладкой
границей Г, /(х, yt z) — заданная функция.
Поскольку в уравнении (9.4) отсутствуют производные по времени, задача
является стационарной, следовательно, начальные условия в ней не задаются. На
границе Г области Q могут задаваться краевые (граничные) условия трех видов.
Первая краевая задача (задача Дирихле):
uxx+uyy+uzz=0y (х,у,z) е Q,
и | г = Ф(*> У у z), (х, у, z) е Г, (краевое условие)
содержит функциональное краевое условие на границе области, y(xyyyz)~
заданная функция.
Вторая краевая задача (задача Неймана):
ихх +иуу +uzz =0> (x,y,z)eQ,
ди |
— г = ф(*> У у z) у (ху У у z) G Г > (краевое условие)
дп
содержит дифференциальное краевое условие, в котором задается производная
в направлении внешней нормали на границе Г области Q.
451

Третья краевая задача:
ихх +иуу +uzz =0> (x,y9z)eQ,
а — |г -н р wIг = ф(х,у,z), (х,у,z) е Г, (краевое условие)
дп
содержит функционально-дифференциальное краевое условие, в котором
задается линейная комбинация производной в направлении внешней нормали и
функции и(х, у) на границе Г области Q.
Во всех перечисленных задачах требуется найти функцию и(х, у), которая
удовлетворяет дифференциальному уравнению (9.5) внутри области Q и
соответствующим условиям на ее границе.
В качестве примера задачи Дирихле можно привести задачу о нахождении
стационарного распределения температуры внутри объемной области, если
задана температура на ее границе.
9.2. РАЗНОСТНЫЙ МЕТОД
Принципы построения разностных схем изложены в разд. 8.2. Для
простоты изложения будем предполагать, что в двумерных начально-краевых задачах
для уравнения переноса, уравнения теплопроводности и волнового уравнения
множество D представляет собой параллелепипед длины L , ширины Л/ и
высоты Т, ограниченный отрезками прямых, параллельных осям Ох, Оу и Ot в
пространстве трех независимых переменных х, у и / (рис. 9.2). Поэтому
зададим сетку Dh =\xhyj,tn\, где x,=ihxy 0</</; >>у = jhy, 0<j<J; tn=n%,
0<n<N't iV,/,/ — целые положительные числа; hXihy,T - величины шагов по
пространственным координатам и времени (для простоты принимаются
постоянными); //*X=L, Jhy = М, Nt = T. Такая сетка называется равномерной
(регулярной).
t
Т
О
452
Рис. 9.2

Введем сеточную функцию
uh=[u?j;=u(xhyJytn), 0</</, 0<7<У, 0</i</v},
которая является сеточным представлением решения исходной (дифференциальной)
задачи или точным решением дифференциальной задачи в узлах сетки. Как
правило, вычислить uh не удается, поэтому находят другую сеточную функцию
uh =uh, приближенно совпадающую с точным решением в узлах сетки. Она
ищется как решение разностной схемы. Под разностной схемой, как и ранее,
понимается совокупность разностных уравнений, аппроксимирующих основное
дифференциальное уравнение во всех внутренних узлах сетки и дополнительные
условия (начальные и краевые) — в граничных узлах.
Для аппроксимации частных производных можно использовать
естественные обобщения формул (8.20)-(8.22), (8.26)—(8.32):
и»+] -и" и" -и"~]
Ut(*i>yj>t")=— -, ut(*i>yj>t )=— —
и?+,х-иГ{ ••"+I
(9.5)
"',7 "'J
u,(Xi,yj,tn)= 'J , '" , u„(xityj,tn)
u?- -2u? • + u?~-
n\_ uij *uij *ui,j
2x ' "v/"J' ' T2
ux(xhyjytn) = 'У, U , ux(xhyj*tnV-
K
(9.6)
T-K hr2
Sy(xhyjJn)= '''*' ''', Uy(xhyjitn)^
hy r j /^
(9.7)
Заметим, что приведенные в (9.5)-(9.7) операторы, в знаменателе которых
находятся T,hxthy, имеют первый порядок аппроксимации по
соответствующим шагам, а операторы с т2,Их,Иу,2х,2пх,2пу в знаменателе -
второй порядок.
453

Пример 9.1. Построить разностную схему для задачи:
и,+их + и, =/(*,*/), (x,y,t)e(Q,L)x(Q,M)x(0,T),
и(*у У>®) = Ч>(*> JO > (*> У) е [О, L] х [О, М], (начальное условие)
и(0, у, /) = ф(у, /), >> е [О, М], 0 < / < Т, (краевое условие)
u(xfi, t) = Ф(х, /), х е [О, Z,], 0 < / < Т, (краевое условие)
где/(х, у, /), vj/(x, .у), ф(у, /), Ф(х, /) — заданные функции.
D Решается первая начально-краевая задача для двумерного уравнения перс-
носа (9.1), где с, = с2 =1. Построим аналог абсолютно устойчивой схемы (8.40).
Для этого используем сетку Dh и четырехточехный шаблон (рис. 9.3).
Для аппроксимации производной и, используем первую формулу в (9.5) и
вторые формулы в (9.6) и (9.7), записанные на (л +1) -м временном слое:
.Ы LL + JU 1-Ь± + -Ы Ы-± = /* \<i<t/-\f \<j<J-\y (9.8)
т hx hy
\<n<N -1,
где fij = f{xhyj,tn) — сеточное представление правой части.
i-l,y,/i + l h /, У, л +1
/, у - 1, я + 1
о
Рис. 9.3
Начальные и краевые условия представляются в виде
"U = V/,y. 0</</, 0 < у < /,
"о.у =Ф". О^у^У, 1<л7<//, (9.9)
ЭД> = Ф?> 0 < / < / , \<n<N ,
где Ф? =ф(^-,/я), Ф," = Ф(х,,/л), у,-, =ф(х/,уу).
454

Совокупность соотношений (9.8),(9.9) составляет неявную двухслойную
разностную схему. Можно показать, что она абсолютно устойчивая и имеет первый
порядок аппроксимации. Следовательно, она сходится с первым порядком
точности [14]. Последовательность вычислений по разностной схеме может быть
различной. Достаточно, чтобы она соответствовала какому-либо порядку
заполнения первого координатного угла в пространстве (x,yj) ячейками, при
котором новая ячейка прикладывается тремя гранями к ранее уложенным ячейкам
или координатным плоскостям. ■
Пример 9.2. Построить разностные схемы для решения первой начально-
краевой задачи для двумерного уравнения теплопроводности:
(x,^/)€(0,L)x(0,A/)x(0,:T),
w(x,yfl) = vj/(x,у), (x,y) e [0,L]x[0,M], (начальное условие)
w(x, у у t) = ф(х, yy t), (xj)er, 0</<Г, (краевое условие)
где Q = (О, L) х (0, М), Г - граница области Q; i|/(x,>0,<p(.M) ~~ заданные
функции; L, Л/, Т — заданные числа.
□ Для решения задачи зададим сетку Dh. Сначала построим явную схему.
Для аппроксимации уравнения используем шеститочечный шаблон (рис. 9.4,а).
/,./,/2 + 1
i.y + l,/!
/'-1,у,/| + 1
/, у +1, п +1
/,У,л + 1Х / + 1,У,л + 1
/ + 1,У,л
1,7-1,11 + 1
Рис. 9.4
Для аппроксимации производных используем первую формулу в (9.5) и
четвертые формулы в (9.6),(9.7):
U'J " UiJ _^ Ui+\J ~ lUi,J + Ui-lj UiJ+\ ~ lUiJ + UiJ-\
(9.10)
1 < /</-!, 1 < 7 < / -1,
\<n<N -\.
455

Начальные и краевые условия представляются в виде
u?j=Vij, 0</</, 0<у</,
"о,,=Фо,у, "7,у=Ф/,у> 0^'^> 1<л<#, (9.11)
й"о=Ф?.о. й"у=фГ.у. 1</</, 1<л<ЛГ,
где <р£у- = ф(х/,^у-,/я), \|//у = \\f(xhyj). Начальные условия задают значения
искомой функции на нижнем основании параллелепипеда, а краевые условия - на
боковых гранях.
Соотношения (9.10),(9.11) образуют явную двухслойную разностную схему.
Можно показать, что она условно устойчива (устойчива при выполнении условия
<-) [14]. При hx=hv=h имеем условие — <-. В этом случае
2 ' Л2 4
hx hy j
(9.10) принимает вид
Ui+\J +Ui-\J +UiJ-\ +UiJ+\ ~^Ui,j
h2
1 < / < / -1, 1 < у < / - 1, \<n<N-\.
Из этого соотношения следует, что при фиксированных /,у',л искомое
значение u"jl определяется явным образом через известные значения на л-м
слое:
UiJ ~ UiJ + 77 Г' + 1,У + W'-l.y + UU-l + W'.y+1 " 4W'J J •
/г
Построим неявную схему, применяя шеститочечный шаблон,
изображенный на рис. 9.4,5. Для аппроксимации производных используем первую формулу
в (9.5) и четвертые в (9.6),(9.7), записанные на (л + 1)-м временном слое.
£л+1 /)л *п+\ о/)я+1 . ,0я+| f0w+1 о£я+1 _1_ /)я+1
Ц',У ~UiJ _Ui+lJ-2ui,j +Ui-\J uiJ+\-2ui,j + ui,j-l {Q m
x - A,' */ ' (912)
1</</-1, 1 < у < У -1, 1 < л < W - 1.
Соотношения (9.12),(9.11) образуют неявную двухслойную схему. Можно
показать, что она является абсолютно устойчивой [35]. Соотношение (9.12),
записанное для всех внутренних узлов (л + 1)-го слоя, порождает систему
линейных алгебраических уравнений для определения значений искомой функции в
456

узлах. Каждое уравнение этой системы содержит только пять неизвестных.
Следовательно, матрица системы является пятидиагональной и сильно разреженной.
Для решения системы применяются, как правило, итерационные методы и метод
прогонки.
Получим еще одну неявную схему, используя десятиточечный шаблон,
изображенный на рис. 9.5. Он является обобщением шеститочечного шаблона (см.
рис. 8.8,6) на двумерный случай.
I, j + 1, п + 1
i -1, у, п + 1 /, У, п + \/^ i + 1, у, п + 1
_ . _ /,у' + 1,л
1 ~£s
1-1,У,я ^/S i,j,n i + \J,n
i,j-\,n
Рис. 9.5
Аппроксимация уравнения имеет вид
uiJ - ui,j
= х
Ui+\J
•ж
-л+1
Ui-\J
£л+1
■2u
л+1
+ Ut
л+1
+ (1-W
iO" Э/)л л. Л" /0Л
И/+1.7 ~^ц/,у +Ui-\J uiJ+\
2йГ,
"ij-x
(9.13)
1 < / < / -1, 1 < у < / - 1, 1 < л < /V -1,
где 0 < X < 1 — параметр схемы. При X = 0 схема становится явной и значение
решения на (л +1) -м слое непосредственно вычисляется по известным
значениям с предыдущего слоя, а при Х = \ совпадает с неявной схемой (9.12),(9.11).
Начальные и краевые условия записываются в виде (9.11). Соотношения
(9.13),(9.11) образуют неявную двухслойную разностную схему. Можно доказать,
что схема имеет второй порядок аппроксимации по hx,hy, а по т — первый
порядок при X * — и второй при Х = ~. Схема является условно устойчивой
(устойчивой при А. > ^г + —т
2 4т /,2 И2
у J
-1
) [14].l
457

Пример 9.3. Построить разностные схемы для первой начально-краевой
задачи для двумерного волнового уравнения:
utt = с2(Uxx +иуу), (х, ytt)eClx (О, Т),
и(х,У,®) = V1 (*»У)> (х,у)еС1[)Г, (начальное условие)
ди(х,у,0)
dt
= У2(Х>У)> (*>.v)eQUr, (начальное условие)
и(х, уу t) = ф(х, у, /), (х, j/) € Г, 0 < / < Т, (краевое условие)
где Q = (0, L)x(0,AZ), Г - граница области Q; \|/1(х,.у)>Ч'2(*».У),ф(*..УэО -
заданные функции.
□ Сначала построим явную схему. Для этого воспользуемся шаблоном,
изображенным на рис. 9.6,д, обобщающим шаблон «крест» , применяемый для
решения одномерного волнового уравнения (см. разд. 8.3.2). Для аппроксимации
частных производных будем использовать четвертые формулы в (9.5)—(9.7):
п-\
■ 2u?j + "и
Ui + \J - luiJ +ui-\,j uiJ+\ ~Zui,j +uiJ-\
1 < / < / -1, 1 < у < / - 1,
(9.14)
1<л<ЛГ-1.
Функциональные начальное и краевое условия представляются так же, как
и в примере 9.1. Дифференциальное начальное условие следует
аппроксимировать со вторым порядком, чтобы не ухудшать свойств схемы (см. пример 8.6).
В результате имеем явную трехслойную схему, имеющую второй порядок
аппроксимации и условно устойчивую (устойчивую при выполнении условия
1
(
\ х
1 1
Ну J
) [14].
i,j,n + \
/,у' + 1,л
/-1,у,л
i + lj,n
/-1,у> + 1
/, у +1, п + 1
ij,n+l/ i + \J,n + \
/,у-1,л + 1
/-1.У.Я О
/ + 1,у,л-1
458

Построим неявную схему, используя пятнадцатиточечный шаблон,
изображенный на рис. 9.6,6.
л-1
i,j i.j i j
■ = X
-n+l
>+i
.^/i+i
Ui+\J - luiJ +Ui-\J uiJ+\ "Iui,j +uiJ-\
>-rt+1 + /}.Л+1
+ 0-X)
/)л п*л , /)л *л о/)я о./)"
Ц/+1,у ~^/,у +Ui-\J ui,j+\ ~ZuiJ +UiJ-\
(9.15)
+ X
ui+\J~ZuiJ +Ui-\J uiJ+\ ~Zui,j +ui,j-\
1 < / < / - 1, 1 < у < У - 1 ,
]<n<N-\.
Схема (9.15),(9.11) имеет второй порядок аппроксимации и является
трехслойной. При X = О она переходит в явную. При -<>.<- схема абсолютно ус-
4 2
тойчива, но относится к неэкономичным [14].и
9.3. МЕТОД РАСЩЕПЛЕНИЯ
При решении многомерных задач теплопроводности, в которых число
независимых переменных больше двух, объем вычислений методом сеток
существенно возрастает. Для его снижения Н.Н.Яненко предложил весьма
эффективный метод расщепления, который наряду с устойчивостью обладает свойством
минимальности объема вычислений [51]. Такие методы принято называть
экономичными.
Рассмотрим методику конструирования одной схемы расщепления на
примере модельной задачи Коши для двумерного уравнения теплопроводности.
Пример 9.4. Построить схему метода расщепления для решения задачи
Коши:
и1=ихх+иуу> (x3y,t)e R*Rx(0,T),
w(x, yfi) = \|/(x, у), (x, y) e R2, (начальное условие),
где y(x,y) — заданная функция.
□ Следуя [51], введем в рассмотрение дифференциальный оператор
Ли = ихх+ иуу. Тогда решаемое уравнение записывается в операторной форме:
ut=c/Iu. Предположим, что решение u(x,y,tn) поставленной задачи известно
в момент времени / = /". Выразим решение u(xfy>tn+l) при / = /л+1 для
фиксированных х и у через решение u(x,yttn), пользуясь формулой Тейлора:
459

u(x,y,ta*1) = u(x,y,tn + т) - u(x,y,tn) + j<8u(\y',nKo(i1) =
1! ot
= u(x,yJn) + ±c*u(x,yJn) + 0(x2) = (g + TcA)u(x,yJn) + 0(T2)y
ди(х,уу1п)
где производная —L-L:L!—- во втором слагаемом заменена правой частью исход-
dt
ного дифференциального уравнения, записанного в операторной форме, а £ -
тождественный оператор (£к(х, >>,/") - u(x,yjn)).
Зададим сетку Dh ={xi,yjitn), где х, =///, у,- = уЛ, f" =лт, /,у = 0,±1,±2,...,
л = 0,1,...,//; Г = М.
Оператор правой части исходного уравнения представим в виде суммы двух
операторов:
Л - <А4 + Л2, Л^и^, сЛ2 = иуу •
Наряду с исходной задачей рассмотрим две вспомогательные задачи Коши:
— задача 1, в которой решается уравнение
5/ ах2
с начальным условием
v(x,y,tn) = и(х,.Мя), (х,>>) € R\ при л = 1,2,..., tf -1,
v(x,y,/°) = i|/(x,y), (х,у)€Л2, при Л = 0,
— задача 2, в которой решается уравнение
JHfeM^^y) <х,Л/)€ЛхЛх</\/"*«),
dt ду2
с начальным условием
уфг,д/,/л) = у(х,.Мл+1), (х,у)€Л2, /2 = 0,1,...,jV-1.
Поставленные задачи могут быть решены последовательно: сначала задача
1, а затем задача 2. Решая задачу I, можно найти функцию v(x,y,tn+{) на
(п +1) -м слое, которая определяет начальное условие задачи 2. Решая задачу 2,
можно найти функцию w(x,.y,//,+1) на том же слое. Задача 1 при фиксированном
у и задача 2 при фиксированном х фактически являются одномерными.
Установим связь между функциями v(x,y,//7+l), w(x,yttn+l) и решением u(x,y,tn+])
исходной задачи на (п + 1) -м слое.
Пользуясь формулой Тейлора, для функции v(x,y,tn+l) получим
соотношение v(x,y,tn+l) = (e + T<44)v(x,y,tn) + 0(T2) = (e + TcA4)u(x9y,tH) + 0(T2) , где
функция v(x, y>tn) заменена на u(x,y,tn) в силу начального условия в задаче 1.
460

Для функции w(x,y,tn+l) можно получить аналогичное выражение
w(xiyitn+l) = ^ + T^2)w(x,yJtn)^0(T2) = ^ + T^2)v(xiy,tn+l) + 0(z2);
yv(xyyJn+l) = ^ + x^2)[^^T^,)u(xiy,tn) + 0(x2)}^0(z2) =
= е2и(х,у^п) + т(сД<+сЛ2)и(х,у,1п) + х2сЛ2сЛ<и(х,у,1п) +0(х2) =
= (£ + тсЛ)и(хуу,Г) + 0(х2) = и(х,у,1п+{) + 0(т2), (9.16)
так как g2u(x,yjn) = $и(х,у^п), \2<Л2<А4 u(x,y,tn) = 0(т2). Таким образом,
в результате последовательного решения задач 1 и 2 при t - tn+l получаем
функцию н'(л,,<у,/л+1), которая отличается от решения исходной задачи u(x,y,tn+l)
лишь на величину 0(т2). Поэтому можно положить
i^c,^"*1)^*,^1).
Следовательно, здесь процесс решения исходной двумерной задачи
заменен процессом решения двух задач в силу расщепления дифференциального
оператора <А на сумму двух операторов *А4+<А2.
Замечания.
1. В описываемом методе расщепление произведено на уровне задач. В
методе переменных направлений (см. разд. 9.4) расщепление на уровне задач не
делается, но слагаемые оператора Л аппроксимируются на различных временных
слоях.
2. Имеется модификация данного метода, в которой расщепление
осуществляется по физическим процессам, когда отдельные слагаемые оператора с/1
соответствуют различным физическим явлениям (например, неравновесным
химическим или колебательным процессам, процессам подогрева, двухфазным
процессам и т.д.).
Сформируем две схемы расщепления, заменяя задачи 1 и 2 разностными
аппроксимациями. При построении явной схемы применим шаблоны,
изображенные на рис. 9.7. Для аппроксимации частных производных по времени
применим первую формулу в (9.5), а для аппроксимации пространственных
производных — последние формулы в (9.6) и (9.7), имеющие второй порядок
аппроксимации.
Тогда для задачи 1 получаем (шаблон на рис. 9.7,а)
v/,7l-v/,i v/*+ii-2v;/+v"
JU и=^Ы ы. «_У., /,у = 0,±1,±2,..., л = 0,1,...,#-1; (9.17)
т /Г
v?J =4>/,у> /,7=0,±1,±2,...,
4j = Ki > '"> J = 0,±1Э±2 п = U, N - 1,
где y/fy =\v(xhyj).
461

Для задачи 2 аналогично получаем (шаблон на рис. 9.7,6)
А/1 + 1 Ая Ал <^АЯ Ая
1 , /,у = 0,±1,±2,..., л = 0,1,...,#-1; (9.18)
»/\; =^+1> /,7 = 0,11,12,..., /i«0,l,...,tf-l.
Заметим, что (9.17) с учетом условия v"7 = w/j можно переписать в форме
АЯ+1 Ал
Ал ^Ал Ал
Ц/ЧЦ -^•,> +Ui-\J
а (9.18)-в виде ^s№'+tVi Zwu+w'J-i
hr
С учетом (9.16) и того, что начальные условия при п = 0
аппроксимируются точно, эта явная двухслойная разностная схема аппроксимирует исходную
задачу с порядком 0(т2 + А2). Схема является условно устойчивой (устойчивой при
т<^)[26].
/,Л/| + 1
/,у,/| + 1
а
/,7 + 1, л
/-1,7,я / ij,n / + 1,7, л i-\J,n /ij,n
ij + l,/i
/ + l,y,ii
i,y-l, я
/,7-1,/f
Рис. 9.7
МЕТОДИКА ВЫЧИСЛЕНИЙ ПО ЯВНОЙ СХЕМЕ
1. Задать значения шагов сетки Л, т так, что N т = Г, где W — целое
положительное число, причем значение шага по времени выбрать из условия устой-
А2
чивости т < —. Вычислить v°y = ufj = v|/;- у, /,7 = 0,±1,±2,..., где
V/.y = v(*/»Уу)• Положить л = 0.
462

2. Найти решение на (п + 1) -м слое.
Первый этап. Решить задачу 1 при каждом j = 0,±1,±2,...:
_ui+i,j ~ZuiJ +Ui-\J
yiJ ~"ij
-, /=0+l,±2,..
Второй этап. Решить задачу 2 при каждом / = 0,±1,±2,...:
к п. 2.
^'-^U,^'-2W^+^-', У = 0>±.,±2,...
h
Положить u?f =w"}!, ij = 0,±1,±2,...
3. Если п = N, вычисления завершить. Иначе положить п = п + 1 и перейти
При построении неявной схемы применим шаблоны, изображенные на рис.
9.8. Для аппроксимации частных производных по времени применим первую
формулу в (9.5), а для аппроксимации пространственных производных —
последние формулы в (9.6) и (9.7), записанные на (п + 1) -м временном слое.
/, j + 1, п + 1
/, j + 1, п + 1
i-Ly.if + l h ij,n+y' i + W./i + l i-l,y,#i + l iJ,n+)^i + ljtn + \
i, у -1, л +1
1,7-1,1 + 1
Рис. 9.8
Тогда для задачи 1 получаем (шаблон на рис. 9.8,с)
*л+1 *п Лл+1
чу v/>y=v^ 2v + v,.,^ u = 0±1>±2> ? л = о,1,...,*-1; (9.19)
t Л2
*U=ViJ> ',7 = 0,±1,±2,...,
*/J = "U' '•./ = 0,±1,±2,..., л = 1,...,/V - 1,
где \j//fy =ч/(х/,.уу).
463

Для задачи 2 аналогично получаем (шаблон на рис. 9.8,6)
_ы ^ = _лу11 ц ^ /,у = 0,±1,±2,..., /i = 0,U,tf-l; (9.20)
т Л2
w/\; = v# > ЛУ = o,±if±2 л = о,1,...,л^-1.
Приведенные соотношения образуют абсолютно устойчивую двухслойную
неявную разностную схему метода расщепления, имеющую порядок
аппроксимации 0(т2 + Л2)[26].
МЕТОДИКА ВЫЧИСЛЕНИЙ ПО НЕЯВНОЙ СХЕМЕ
1. Задать значения шагов сетки Л, т так, что Nx = T, где N— целое
положительное число, причем значения шагов выбрать из условия достижения
заданной точности. Вычислить v-j = ufj = \\f,j, /,у = 0,±1,±2,..., где \|/у у = \\>(xhyj).
Положить п = 0.
2. Найти решение на (л + 1) -м слое.
Первый этап. Решить задачу 1 при каждом j = 0,±1,±2,...
_L(^+i--(—+ Лу-ят
1 и •
+ — Vy.j ,- = , / - U,±l,±2,...,
Ji^ J т
применяя метод прогонки для системы линейных алгебраических уравнений
с трехдиагональной матрицей (система получена из (9.19) при v"y = ufj).
Второй этап. Решить задачу 2 при каждом / = 0,±1,±2,...:
-L^t» _[ JL + I|£!»+i J.-zit1, =-1-уП+1 / = o+i+2
Л2 U2 TJ Л2 т ' u'-b-z'--,
применяя метод прогонки для системы линейных алгебраических уравнений
с трехдиагональной матрицей (система получена из (9.20) при iv"y- = v/j1).
Положить u?f =w?jl, /,У = 0,±1,±2,...
3. Если п - N, вычисления завершить. Иначе положить п = п + 1 и перейти
к п. 2. ■
464

Замечания.
1. Для решаемых на первом и втором этапах методики систем линейных
алгебраических уравнений выполняется условие преобладания диагональных
элементов, следовательно, метод прогонки устойчив.
2. Для пояснения общей схемы вычислений здесь рассматривалась задача
Коши, поэтому индексы / и j были не ограничены. Однако эти схемы могут
быть легко приспособлены для решения смешанных краевых задач с
ограниченным множеством D [26].
9.4. МЕТОД ПЕРЕМЕННЫХ НАПРАВЛЕНИЙ
Рассмотрим идею метода переменных направлений, относящегося к классу
экономичных схем, применительно к решению первой начально-краевой задачи
для двумерного уравнения теплопроводности.
Пример 9.5. Построить разностную схему метода переменных направлений
для решения первой начально-краевой задачи для уравнения теплопроводности:
щ = Uxx + Uyy + Дх, у, /), (х, у, t) е (О, L) х (О, М) х (О, Т),
и(х, yfi) = у(х, у), (х, у) е [О, L] х [О, М], (начальное условие)
и(*> у, t) = (р(л\ у, t), (х, у) е Г, 0 < / < Т, (краевое условие)
где Q = (О,L)х(О,М), Г— граница области Q (прямоугольника); f(x,y,t) —
плотность источников тепла; y\f(x,y),q>(ytt) — заданные функции; L,M,T—
заданные числа.
□ Как и в методе расщепления, исходное уравнение аппроксимируется
совокупностью двух разностных схем, каждая из которых соответствует только
одному пространственному направлению. Однако оператор Л здесь не
расщепляется на сумму Л4 + сЛ2 двух операторов на уровне задач, а каждый элемент
суммы аппроксимируется с помощью явных и неявных конструкций. Для этого
наряду со слоем / = /л+1, расчет которого осуществляется на данном этапе, вводит-
1
ся один дополнительный (промежуточный) слой / = / 2. Тогда для перехода от
I
слоя t = t" к слою / = /л+1 с использованием слоя / = / 2 исходное
дифференциальное уравнение аппроксимируется двумя разностными уравнениями, одно
1 1
л+- л-»-- .
из которых связывает слои / = г и / = t 2, а второе — слои t = t 2 и / = гя+|.
При реализации метода используем девятиточечный шаблон,
изображенный на рис. 9.9. Переход с л-го временного слоя на (п + 1) -й разбивается на два
этапа.
465

/,У,я + 1
/,у-1,л + 1
/,У+ 1,я +1
о-=ц-о
/ + 1,7,л + -
'»У + 1, я
/,У-1,л
Рис. 9.9
Первый этап. Переход на дополнительный промежуточный я + - -й
слои
с шагом —. Частная производная по времени аппроксимируется по первой
формуле в (9.5), производная по х аппроксимируется на
и-
м слое,
производная по у — на п -м слое. Входящая в правую часть исходного уравнения
функция f(x,y,t) заменяется своим сеточным представлением. Соответствующая
разностная схема имеет вид:
1
и • 1 —и!
1 1
гл. и 2 -2и 2+и 2 /0я ?£я 4./)" «4.1
ij _ "/+!.; z"/,y +Ui-\J ui,j+\ ~ luiJ + uiJ-\ ^ fn+2
+ //,y2, 1</</-1,(9.21)
\<j<J-l
n+i- ( \ \
где fj;= f\ Xi,yj,tn + — т , или в традиционной записи:
2Л
7 им.Г
1 + -
1 1
>чЛ + Г т лл+т
ы 2 + —— и 2 _ pp. 1 < / < / _ 1
2Л* 1 < У < / - 1,
где /7яу- = --fiJ 2 Tr/J+i ~"2ы,лу +"Лу-1/""Лу- Заметим, что вместо значе-
2А,
ния У) , 2 в (9.21) можно использовать У}^ [14].
Для каждого j = 1,...,/ - 1 требуется решить трехдиагональную систему
линейных алгебраических уравнений, так как каждое уравнение содержит три неиз-
466

1 1 I
ЛЛ+- A"+- лЯ+т
вестных значения ^Д, ul. ,и/Ч,2., а остальные значения берутся с л-го слоя
1
или вычисляются, например f. ~ 2. Иными словами, при таком переходе схема
является неявной по направлению х и явной по направлению у. Искомые
значения на промежуточном слое вычисляются методом прогонки по направлению
х, т.е. продольному направлению.
Второй этап. Переход на (л + 1)-й временной слой с промежуточного
\п + - -го с шагом -. Частная производная по времени аппроксимируется по
первой формуле в (9.5), производная по х аппроксимируется на л + - -м слое,
производная по у — на (л + 1)-м слое. Соответствующая разностная схема имеет
вид:
i i +! +!
йП{ -О"]2 С2 ~2и"]2 +Л #+[, -2U?? +#711 я+1
2 +' ,2
2 "
1 < / < / - 1, 1 < у < / - 1,
или в традиционной записи:
2А,' "'^
Я + -
НУ )
й?*1 + Т й-\ =ф'.".2 1</< /-1
2А/ 1 < у < / - 1,
1 f 1 1 1
/-1,7 '.7 т / + 1,7
-V-i«-3fr
1
Ля+г
- й, ,2 . Заметим, что вместо зна-
1
чения f"j в (9.22) можно использовать /; 2 [14].
Для каждого значения / = 1,...,/-1 требуется решить трехдиагональную
систему линейных алгебраических уравнений, так как каждое уравнение
содержит три неизвестных значения й"]\\, w/j1, й?у]\\, а остальные значения берутся с
\п + - -го слоя. Иными словами, при таком переходе схема является явной по
направлению х и неявной по направлению у. Искомые значения на целом слое
вычисляются методом прогонки по направлению у, т.е. в поперечном
направлении. Диагональные элементы в системах (9.21),(9.22) преобладают,
следовательно, процесс прогонки устойчив, а решение разностной задачи существует и
единственно. К достоинствам метода, достигнутым благодаря введению
промежуточного слоя, следует отнести расщепление исходной задачи на две более
простые, решаемые с помощью алгоритма скалярной прогонки.
467

Начальные и краевые условия представляются в виде
ufj = \\ijj, 0 < / < /, 0 < у < /, (нулевой слой)
"oj = Фо.у > "л; = Ф/,у> О < у < У , 1 < я < /V, (на плоскостях, (9.23)
перпендикулярных оси Ох)
И/?о = Ф?,о у "и ~ Ф?,/ > 1 < / < / , 1 < л < N , (на плоскостях,
перпендикулярных оси Оу)
где <р£у- = ф(дсу,у,,/"), vj//y = v(jcf-,yj).
I
Для промежуточного слоя требуются значения ui 2 на сторонах расчетной
области, определяемых уравнениями х = 0 и х = L. Вычитая (9.22) из (9.21),
получаем
/)Я+2 _ L(nn + l л. пп \ Т (£п + [ Ъ0Л + 1 j. #0Л + 1 \ _i_-_I_/,iO" 9|0Л х/)Л \
2 4Л/ 4A/
Отсюда при / = 0 (х = 0) имеем
ио j o'w<U + UQJ'—ГТ^о.7+1 ~Zuo,j +uoj+\) + ~j(uoj+\-2uoj+uoj+\)-
1 4A/ 4Л/
Такой способ обеспечивает второй порядок аппроксимации. Аналогично
получается соотношение при / = / (х = L).
Схема (9.21)—(9.23) метода переменных направлений имеет второй порядок
аппроксимации и является абсолютно устойчивой [14].
МЕТОДИКА РАСЧЕТОВ
1. Задать сетку Dh = \xi,yj,tn\i где х, = ihx% 0 < / < / ; у} = j hy, 0 < j < J;
/л=ят, 0<n<N; /V,/,/ — целые положительные числа; hx,hy,x - величины
шагов по пространственным координатам и времени (для простоты принимаются
постоянными); I hx = L, J hy - М , Nт = Г.
2. Вычислить
££,. = у,-j, 0 < / < /, 0 < у < / ,
"о,у=Фо,у, "7,у=ф7,у> °^^> 1^л</У,
468

*%=Ф?.о. «*/=<?i.J> 1</</, \<n<N,
где ф£у = ф(х,, уу, /л), V/ty. = \|/(х,,>>,).
Положить п = О.
3. Найти решение на (л + 1) -м слое.
Первый этап. Перейти на дополнительный промежуточный | л + — -й слой
с шагом —: для каждого j = 1,...,/-1 решить трехдиагональную систему
линейных алгебраических уравнений
т ,п,- _
2hx
1
2И/-1.У
( \
I л,2
2/г
1 1
АЯ+, 1
4Л
4Л,
1
£ +2 _ /£я+1 . £я \ т /Ля+1 ъЛя+' . мя+1 \ . т /Ля о.0я . £л \
* 4Лу 4/^
1 i 1
ЛЯ+- АЛ+Т АЯ+7
Искомые значения и^2.-, "/>у >"/+i .• на промежуточном слое вычисляются
методом прогонки по направлению х.
Второй этап. Перейти на (я + 1)-й временной слой с промежуточного
л + - -го с шагом - : для каждого значения / = 1,...,/-1 решить
трехдиагональную систему линейных алгебраических уравнений
Ж
т ля+1
-juij-\
Ч ИУ J
Лл+1 т Ля+1
" 2А„2
I я* —
(/."t1. =ф.2 1 < # < J-1
ui,j+\ ^ij » 1-У-'' *»
1
я+- т я+- х
где Ф,,,2 в д . 2
2А*
1 1 П
л"+2 о-"+2 лЯ+2
Ui-\J2uiJ+UHrlJ
"/,У
Искомые значения й"]1\, й/JJ1, м"у|] на целом слое вычисляются методом
прогонки по направлению у.
469

4. Если п = N, вычисления завершить. Иначе положить п = п + 1 и перейти
к п. 3. ■
Замечания.
1. При решении двумерных задач со смешанными производными по
пространственным переменным и трехмерных задач изложенная схема становится
условно устойчивой.
2. Описанные в разд. 9.2 и 9.3 алгоритмы решения двумерного уравнения
теплопроводности могут применяться для решения двумерных уравнений
эллиптического типа.
Рассмотрим задачу Дирихле для уравнения Лапласа с двумя независимыми
переменными (см. разд. 8.1):
ихх+иуу=®> (х,у)еП,
и | г = ф(дс, у), (х, у) е Г, (краевое условие)
где ф(х,у)— заданная функция.
Наряду с этой стационарной задачей рассмотрим нестационарную задачу
для двумерного уравнения теплопроводности с теми же краевыми условиями и
произвольно заданными начальными условиями:
ut = ы^ + иуу, (х, у, Г) е Q х (0, + оо),
w(x, ^,0) = ц/(х, у), (х, у) е Q U Г , (начальное условие)
и(х, yt t) | г = ф(х, у), (х, у) е Г, 0 < / < +оо (краевое условие).
Таким образом, вводится дополнительная независимая переменная / и
исходная задача усложняется, так как увеличивается ее размерность. Однако при
этом становится возможным выбор наиболее экономичной разностной схемы
решения уравнения теплопроводности. Можно доказать, что решение
нестационарной задачи при / -> +оо сходится к решению стационарной задачи, а при
достаточно большом / = Т может быть принято за приближенное решение задачи
Дирихле [14,35]. Такой метод называется методом установления. Для
прекращения вычислений можно использовать, например, условие max\и"У - и".Л< z,
где 6 > 0, /— положительное целое число (порядка нескольких десятков).
Для решения нестационарной задачи можно использовать схемы
(9.21),(9.22) и метод переменных направлений. В последнем случае существует
I
1 1и2 и2 ( 1 1 V2
наилучший шаг по времени: т = — ^п$ + п* — + —- , при котором
нестационарное решение выйдет на стационарное за наименьшее число шагов [14].
470

9.5. МЕТОД ДРОБНЫХ ШАГОВ
Рассмотрим методику конструирования схемы метода дробных шагов на
примере модельной задачи Коши для двумерного уравнения теплопроводности.
Пример 9.6. Построить схему метода дробных шагов для решения задачи
Коши:
ut = и^ + иуу, (x,y,t)e RxRx(0,T),
и(х,yfl) - у(х,у), (х,у) е R2, (начальное условие)
где у(х,у) - заданная функция.
□ Зададим сетку Dh = {xifyJttn), где xt = /Л, yj = jh, tn = лт,
/,y = 0,±l,±2,..., az = 0,1,...,jV; T = Nt.
Оператор правой части исходного уравнения, как в методе расщепления,
представим в виде суммы двух операторов:
Далее они аппроксимируются отдельно друг от друга. В отличие от метода
расщепления вводится вспомогательный (промежуточный) слой, соответствующий
1
значению / = / 2. Как в методе переменных направлений, сначала
осуществляется переход на промежуточный \п + — -й слой с дробным шагом -, а затем с
тем же шагом на целый (п +1) -й слой.
Наряду с исходной задачей рассмотрим две вспомогательные задачи Коши:
— задача 1, в которой решается уравнение
dv(x,y,t) dzv(x,y,t)
I
. (x,y,t)eR*Rx(t\t 2),
dt дх2
с начальным условием
v(xyy,tn) = u(x9ytt") (х,у) е R\ при п = 1,2,..., jV -1,
v(x,y,/°) = у(х,у) (xty)e R2, при л = 0,
- задача 2, в которой решается уравнение
MfiM^My), (х,^,о^хЛх(Л2,/я+1),
dt ду2
с начальным условием
I I
w(x,y,tn*i) = v(x,y,t"*i) (xyy)eR2, п = 0,1,.., W -1.
471

Поставленные задачи могут быть решены последовательно: сначала задача
1
1, а затем задача 2. Решая задачу 1, можно найти функцию v(x, у, t 2) , которая
определяет начальное условие задачи 2. Решая задачу 2, можно найти функцию
w(xty,tn+l). Задача 1 при фиксированном у и задача 2 при фиксированном х
фактически являются одномерными. Как и в методе расщепления, функция
w(xty,tn+l) является приближенным решением исходной задачи на (л + 1)-м
слое, т.е. можно положить и(х, у, /Л+1) = w(x, у, tn+l).
При реализации метода используем семиточечный шаблон, изображенный
на рис. 9.10. Переход с л-го временного слоя на (л + 1)-й разбивается на два
этапа.
/,У-1,л +
1 а
/-1,у,л + -
/,У,/1 + 1
/,у + 1,я + 1
/ + 1,У,я + -
Первый этап. Переход на дополнительный промежуточный
Н)-й
слой
с шагом -. В задаче 1 частная производная по времени аппроксимируется по
первой формуле в (9.5), производная по х аппроксимируется по последней
формуле в
(9.6) на (п
+ — I -м слое. Соответствующая разностная схема имеет вид:
1 ill
V .2 _$/«. у. 2 _2v. .2 +v. 2
, /,y = 0,±l,±2,..., л = 0,1,...,/У-1;
^y=n;, /,y = 0,±l,±2,...,
Kj =4j> /,7=0,±1,±2,..., ai = 1,...,/V-1,
(9.24)
472

где \\fjj = y(xhyj), или в традиционной записи:
2Л
2 Vi-U
1 + -
',У
Т л
+ rv
2Л,
2 r/+W
/,У = 0,±1,±2,...
Для каждого j требуется решить трехдиагональную систему линейных
алгебраических уравнений, так как каждое уравнение содержит три неизвестных
1 1 1
■2 й"+Т fl-I
значения ^.Д, vy , ,v/+12., а остальные значения берутся с л-го слоя. Иными
словами, при таком переходе схема является неявной. Искомые значения на
промежуточном слое вычисляются методом прогонки по направлению х.
Второй этап. Переход на (п +1) -й временной слой с промежуточного
Ю-
го с шагом -. Частная производная по времени аппроксимируется по
первой формуле в (9.5), производная по у аппроксимируется по последней
формуле в (9.7) на (п + 1)-м слое. Соответствующая разностная схема имеет вид:
т
2
".7
иг;ii -2w; ;•■ +W-;;:,
w,
i,j
i.j
/,y = 0,±l,±2,..., л = 0,1,...,/У-1;
/,y = 0,±l,±2,..., n = 0,l,...,iV -1,
(9.25)
или в традиционной записи:
1 -wrl
Ж
lwu-\
1 + -
"у )
Ля+1 ^ лл+1 А
гк
/,у=0,±1,±2,...,
л = 0,1,...,7У-1.
Для каждого значения / требуется решить трехдиагональную систему
линейных алгебраических уравнений, так как каждое уравнение содержит три
неизвестных значения w"}ii, w"}1, ^/ly+i» а остальные значения берутся с \п + - -го
слоя. Иными словами, при таком переходе схема является неявной. Искомые
значения на целом слое вычисляются методом прогонки по направлению у.
Далее полагают u[*jl =vv/|}1, /,У = 0,±1,±2,...
Можно показать, что схема (9.24)—(9.25) метода дробных шагов имеет
первый порядок аппроксимации по т и второй по Л и является абсолютно
устойчивой.
473

Диагональные элементы в системах (9.24),(9.25) преобладают,
следовательно, процесс прогонки устойчив. К достоинствам метода, достигнутым благодаря
введению промежуточного слоя, следует отнести расщепление исходной задачи
на две более простые, решаемые с помощью алгоритма скалярной прогонки.
К недостаткам метода относится сравнительно низкая точность из-за того, что
на каждом дробном шаге аппроксимируется только один пространственный
оператор.
МЕТОДИКА РАСЧЕТОВ
1. Задать сетку Dh = {xhyjytn)t где х,- =/Л, yj = jh, tn = от, ij = 0,±1,±2,...,
п = 0,1,...,^; T = Nz. Величины шагов в силу абсолютной устойчивости метода
выбрать из условия удовлетворения точности расчетов.
2. Вычислить
«и = *и =v/,y U = 0,±l,±2,...,
где \yltJ =\\t(xhyj).
Положить п = 0.
3. Найти решение на (п + 1) -м слое.
Первый этап. Перейти на дополнительный промежуточный \п + - -й слой
с шагом —: для каждого j решить трехдиагональную систему линейных
алгебраических уравнений с учетом п.2:
i ( \
v. .z. -
2А > ''-'•'•
.п+- т ля+-
V- 2+—^—v 2=-мл. //=0+1+2
2rlY
1 1 1
Искомые значения v,.,2 vjj *vj+\j на промежуточном слое вычисляются
методом прогонки по направлению х.
Второй этап. Перейти на (п +1) -й временной слой с промежуточного
( П т
\п + — -го с шагом — : для каждого значения / решить трехдиагональную
систему линейных алгебраических уравнений
2h> 'J-[
wn+x + -^— w?+-K =-v"+2 i / = 0+1+2
2hv
"у
474

Искомые значения w/J}Ii, w/JJ1, iv"yj_! на целом слое вычисляются методом
прогонки по направлению у.
Положить uff =w?j\ /,у = 0,±1,±2,...
4. Если п = N, вычисления завершить. Иначе положить п = л +1 и перейти
к п. 3. ■
Замечания.
1. В приведенной методике для простоты можно сразу положить
1 1
лп+- лп+- . .
V. .2 =п. .2 £"+1 = „" + l
Лу Лу ' '•■/ '-У '
2. При применении метода дробных шагов к решению уравнения с тремя
пространственными переменными
ut=uxx+ иуу + uzz
1 2
л+- л+-
используются два промежуточных слоя: / = / 3 и f = / 3. Тогда на дробных
шагах реализуется следующая аппроксимация дифференциальных операторов:
1 ill
v/.m-v'.m v,4i.M-2v/ji+v»-U.* о» г.
; = 71 • vU.k = иШ •
— пх
3
2 12 2 2
Л"+Т аЯ+Т аЛ + 7 „ал+Т ая+Т 1 1
wij-wij wiJ\.k-2wu +wij-\,k ^~ъ *»+-,
—— —— =———■ — ——■— vy. . J = v. ..
т .2 ' ".У \j,* '
з *'
2
,я+1 _ЛЯ+3 Л/i+l i*/i+l . Лл+l _2 2
ля+-
uij,k ujj,k uiJ,k + \ ~luiJ,k +uiJ,k-\
т л 2 ' "ЛЛ* " WW'
3
3. Метод дробных шагов по сравнению с методами расщепления имеет
недостаток, состоящий в том, что в нем имеет место только частичная
аппроксимация пространственных операторов на каждом дробном временном слое.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Построить разностную схему для решения начально-краевых задач 1-3.
1. щ +их +иу =/ + 1, (x,y,t)e(09L)x(09M)x(09T),
и(х, у ft) = х + у, (х,у)е [О, L]x[0,M],
w(0,j>,/)=.y + /2, уе[0,М], 0</<7\
u(xfl,t)=xt, xe[0,L], 0</<7\
где L, Л/, Т— заданные числа.
475

2. ut =uxx+3uyyi (х,>;,/)е(0,1)х(0,Л/)х(0,Г),
u(x9 у ft) = 2x + y, (x,y)e [0, L] x [0, M],
w(x,^,/)=2, (х9у)еГ, 0<r<7\
где Q = (0, L) x (0, Af), Г - граница области Q; L,M,T- заданные числа.
3. «ff =4(i#xx+mw,), (х,д/,/)бПх(0,Г),
к(х,д>,0) = х2+Д (x,y)eQ\jrt
с/
и(х,^,/) = /, (х,у)еГ, 0<Г<Г
где Q = (0,Z,)х(0,Л/), Г — граница области Q; L,M,T- заданные числа.
4. Построить схему метода расщепления для решения задачи Коши:
ui - 2^хх + 3Uyy, (x,yj) е Rx Rx(0,Г),
i/(x,y,0) = x + 2y, (х,у)€/?2,
где Г — заданное положительное число.
5. Построить разностную схему метода переменных направлений для
решения первой начально-краевой задачи:
Щ = «« + "уу + 3/, (*,*/) е (0, Z,)х (0, М) х (0,Г),
и(х, у,0) = 2х + 5у, (х, у) е [0,1] х [0, Л/],
u(x,ytt)=sint, (xj)er, 0 < / < 7\
где Q = (0, L) х (0, М), Г — граница области ft; LyM,T- заданные числа.
6. Построить схему метода дробных шагов для решения задачи Коши:
и, =2^+*/^, (х,д/,/)б/?х/?х(0,Г),
«(х,у,0) = х2+^2, (*,>>) е Я2,
где Т — заданное положительное число.

ЛИТЕРАТУРА
1. Алберг Дж., Нильсон Э., Уолш Дж. Теория сплайнов и ее приложения. -
М.: Мир, 1972.
2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. - М.:
Наука, 1983.
3. Березин И.С, Жидков Н.П. Методы вычислений.—Т. 1,2.—М.: Наука, 1960.
4. Боглаев Ю.П. Вычислительная математика и программирование. — М.:
Высшая школа, 1990.
5. Вержбицкий В.М. Основы численных методов.—М.: Высшая школа,2002.
6. Волков Е.А. Численные методы. -М.: Наука, 1987.
7. Годунов С. К. Уравнения математической физики. - М.: Наука, 1971.
8. Годунов С.К., Рябенький B.C. Введение в теорию разностных схем. - М.:
Физматгиз, 1962.
9. Демидович Б.П., Марон И.А. Основы вычислительной математики. — М.:
Наука, 1966.
10. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа.
- М.: Физматгиз, 1963.
И. Деннис Дж., Шнабель Р. Численные методы безусловной оптимизации и
решения нелинейных уравнений. — М.: Мир, 1988.
12. Дьяконов В.П. Справочник по алгоритмам и программам на языке
Бейсик для персональных ЭВМ.— М.: Наука, 1987.
13. Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн-
функций. — М.: Наука, 1980.
14. Калиткин Н.Н. Численные методы. -М.: Наука, 1978.
15. Киреев В.И. Интегродифференциальный метод приближения функций
алгебраическими многочленами // Вычислительные технологии. - Новосибирск,
МВТ СО РАН, 1993. Т.2, №6.
477

16. Киреев В. И. Интегральный метод приближения функций
алгебраическими многочленами и биквадратными сплайнами // Вестник МАИ, 1994. Т.1,
№1.
17. Киреев В.И. Интегродифференциальные сплайны и их приложение
к численному дифференцированию и интегрированию. — Деп. в ВИНИТИ
№ 1675-В93, 1993.
18. Киреев В.И. Многошаговые дискретные схемы и явные,
последовательные сплайн-методы решения обыкновенных дифференциальных
уравнений на нерегулярном шаблоне// Вычислительные технологии. — Новосибирск,
ИВТ СО РАН, 1996. Т.1, №2.
19. Киреев В.И. Численные методы решения задач алгебры и теории
приближений. —М.: Изд-во МАИ, 1991.
20. Киреев В.И., Бирюкова Т.К. Интегродифференциальные сплайны и их
применение в интерполяции, численном дифференцировании и интегрировании
// Вычислительные технологии. — Новосибирск, ИВТ СО РАН, 1995. Т.4, №10.
21. Киреев В.И., Бирюкова Т.К. Полиномиальные
интегродифференциальные одномерные и двумерные сплайны в задачах интерполирования и
сглаживания одномерных и двумерных функций // Вестник МАИ, 1997. Т.4, №2.
22. Киреев В.И., Войновский А.С. Численное моделирование
газодинамических течений.—М.: Изд-во МАИ,1991.
23. Киреев В.И., Формалев В.Ф. Методы алгебры и теории приближений. -
М.: Изд-во МАИ, 1985.
24. Киреев В.И., Цирков Т.В. Вычисление интегралов по явным
квадратурным формулам и неявным алгоритмам, построенным на основе интегродиффе-
ренциальных сплайн-функций на нерегулярной сетке. - Деп. в ВИНИТИ
№ 3206-В97, 1997.
25. Корнейчук Н.П. Сплайны в теории приближения. — М.: Наука, 1984.
26. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы:
В 2 т. - М.: Наука, 1976 - 1977.
27. Мак-Кракен Д., Дорн У. Численные методы и программирование на
ФОРТРАНе. - М.: Мир, 1977.
478

28. Мысовских И.П. Интерполяционные кубатурные формулы. - М.: Наука,
1981.
29. Никольский СМ. Квадратурные формулы. — М.: Наука, 1979.
30. Пантелеев Л. В., Бортаковский А.С Теория управления в примерах и
задачах. — М.: Высшая школа, 2003.
31. Пантелеев A.B.t Летова Т.А. Методы оптимизации в примерах и задачах.
— М.: Высшая школа, 2002.
32. Пантелеев А.В., Якимова А.С. Теория функций комплексного
переменного и операционное исчисление в примерах и задачах. — М.: Высшая школа,
2001.
33. Пантелеев А.В., Якимова А.С, Босов А.В. Обыкновенные
дифференциальные уравнения в примерах и задачах. — М.: Высшая школа, 2001.
34. Плис A.M., Сливина Н.А. Лабораторный практикум по высшей
математике. - М.: Высшая школа, 1994.
35. Пирумов У.Г. Численные методы. — М.: Изд-во МАИ, 1998.
36. Пирумов У.Г., Росляков Г.С Численные методы газовой динамики. — М.:
Высшая школа, 1987.
37. Ракитин В.И., Первушин В.Е. Практическое руководство по методам
вычислений с приложением программ для персональных компьютеров. — М.:
Высшая школа, 1998.
38. Рябенький B.C. Введение в вычислительную математику. - М.: Наука,
1994.
39. Самарский А.А. Теория разностных схем. — М.: Наука, 1983.
40. Самарский А.А., Гулин А.В. Численные методы. -М.: Наука, 1989.
41. Саульев В.К. Современные вычислительные методы. - М.: Изд-во
МАИ, 1977.
42. Сборник задач по методам вычислений / Под ред. П.И. Монастырного.
- М.: Физматлит, 1994.
43. Сигорский В.П. Математический аппарат инженера.—Киев: Техшка,
1977.
479

44. Стечкин СБ., Субботин Ю.Н. Сплайны в вычислительной математике.
- М.: Наука, 1976.
45. Фаддеев Д.К., Фаддеева В.П. Вычислительные методы линейной
алгебры. — М.: Физматгиз, 1963.
46. Фарлоу С. Уравнения с частными производными для научных
работников и инженеров. — М: Мир, 1985.
47. Формалев В.Ф. Метод конечных элементов в задачах теплообмена. — М.:
Изд-во МАИ, 1991.
48. Хайрер Э., Нерсетт С, Ваннер Г. Решение обыкновенных
дифференциальных уравнений. Нежесткие задачи. - М.: Мир, 1990.
49. Холл Дж., Уатт Дж. Современные численные методы решения
обыкновенных дифференциальных уравнений. - М.: Мир, 1979.
50. Численное решение многомерных задач газовой динамики/Под ред.
С.К.Годунова.—М.: Наука, 1976.
51. Яненко Н.Н. Метод дробных шагов решения многомерных задач
математической физики.- Новосибирск: Наука, 1967.
52. Butcher J.Ch. The numerical analysis of ordinary differential equations:
Runge-Kutta and general linear methods.-Wiley, Chichester.-1987.
53. Fatunla S. O. Numerical methods for initial value problems in ordinary
differential equations.— Academic Press, 1988.
54. Gear C.W. Numerical initial value problems in ordinary differential
equations- Prentice-Hall, 1971.
55. Hairer R, Norsett S.P., Wanner G Solving ordinary differential equations.
Nonstiff problems.— Springer-Verlag, 1991.
56. Henrici P. Elements of numerical analysis.— McGraw-Hill Book Co.,New
York, 1964.
57. Lambert J.D. Computational methods in ODEs.- John Wiley,New
York, 1973.
58. Lapidus L., Seinfeld J. Numerical solution of ordinary differential equations.-
Academic Press, New York, 1971.
59. Schoenberg I.J. Cardinal interpolation and spline functions. -
J.Approximation Theory, V.2, №2, 1969.—P. 167-206.

ПРИКЛАДНАЯ МАТЕМАТИКА
для ВТУЗов
В.И.КИРЕЕВ
А.В.ПАНТЕЛЕЕВ
ЧИСЛЕННЫЕ
МЕТОДЫ
В ПРИМЕРАХ
И ЗАДАЧАХ