Ю. М. Колягин,
Ю. В. Сидоров, М. В. Ткачева,
Н. Е. Федорова, М. И. Шабунин
Д л геб ра
и начала
математического
анализа
JlpOCpUXbHblU
уровень

M(cosa; sin a)
x
У i
0 1
x
У
x

Ю. М. Колягин,
Ю. В. Сидоров, М. В. Ткачева,
Н. Е. Федорова, М. И. Шабунин
Длгебра
и начала
математического
анализа
УЧЕБНИК
для учащихся
общеобразовательных
учреждений
JlpOCpUXbHbLU
уровень
Рекомендовано
Министерством образования и науки
Российской Федерации
8-е издание, стереотипное
Москва 2009

УДК 373.167.1:512+517.1
ББК 22.141я721+22.161я721
К62
Колягин Ю. М.
К62 Алгебра и начала математического анализа. 10 класс : учеб.
для учащихся общеобразоват. учреждений (профильный
уровень) / Ю. М. Колягин, Ю. В. Сидоров, М. В. Ткачева,
Н. Е. Федорова, М. И. Шабунин. — 8-е изд., стер. — М.: Мне-
мозина, 2009. — 366 с. : ил.
ISBN 978-5-346-01315-0
В учебнике представлен в целостном виде раздел по тригонометрии.
Много внимания уделяется алгебраическим, показательным,
логарифмическим и тригонометрическим примерам и задачам различного уровня
сложности для самостоятельного решения.
Разделы «Производная» и «Интеграл» изложены в учебнике для
11-го класса.
УДК 373.167.1:512+517.1
БВК 22.141я721+22.161я721
© «Мнемозина», 2001
© «Мнемозина», 2009
© Оформление. «Мнемозина», 2009
ISBN 978-5-346-01315-0 Все права защищены

ПРЕДИСЛОВИЕ
Данный учебник является первой частью курса «Алгебра и
начала математического анализа» для 10—11-го классов средних
общеобразовательных учреждений различного типа, в которых на
изучение математики отводится 4—5 часов в неделю.
В новом учебнике изложены элементы теории действительного
числа, представленного в виде бесконечной десятичной дроби. В
целостном виде также представлен раздел тригонометрии, начиная с
определения синуса, косинуса, тангенса и котангенса угла и
кончая решением тригонометрических неравенств и изучением
обратных тригонометрических функций. Широко представлены разные
типы тригонометрических уравнений и методы их решения
(уравнения, сводящиеся к алгебраическим; линейные уравнения
относительно sin х и cos x; уравнения, содержащие корни и модули; метод
разложения на множители, метод замены неизвестного, метод
оценки левой и правой частей уравнения). Включена глава, в которой
изложены основные методы решения систем уравнений
(рациональных, иррациональных, показательных,
логарифмических и др.), приведены примеры решения текстовых задач с помощью
систем уравнений. Кроме того, отдельная глава посвящена изучению
степенной функции, где рассматриваются вопросы, связанные с
понятиями обратной функции, равносильности и следствия. В каждой
главе учебника имеется краткая историческая справка.
Наконец, важная особенность учебника — расширенная
система задач и упражнений с учетом уровневой дифференциации
обучения и потребностей учащихся в получении знаний, необходимых
для поступления в вузы.
Для удобства учителей и учащихся в тексте книги выделены:
1) названия параграфов, материал которых обычно изучается
учащимися, проявляющими повышенный интерес к математике;
2) номера задач в тексте и в конце параграфов, для решения
которых требуется применение различных приемов и методов, не
входящих в перечень обязательных для всех учащихся.
Упражнения «до черты», расположенные после каждого
параграфа, соответствуют обязательному уровню усвоения материала;
1* 3

упражнения «за чертой» — продвинутому уровню усвоения. Задачи
повышенной трудности обозначены одной или двумя звездочками.
В учебнике для 11-го класса наряду с традиционными
разделами курса «Алгебра и начала математического анализа»
(производная и ее применение, интеграл) представлены главы, связанные с
изучением комплексных чисел, элементов комбинаторики и теории
вероятностей.
Авторы
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ:
л Начало решения задачи
▲ Окончание решения задачи
О Начало обоснования утверждения или вывода формулы
• Окончание обоснования или вывода

ГЛАВА
Ll
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА.
СТЕПЕНЬ С ДЕЙСТВИТЕЛЬНЫМ
ПОКАЗАТЕЛЕМ
§ 1. Рациональные числа
Напомним и систематизируем те сведения о действительных
числах, с которыми вы уже знакомы. Изучение математики вы начали
с натуральных чисел, т.е. с чисел 1, 2, 3, 4, 5, ....
При сложении и умножении натуральных чисел всегда
получаются натуральные числа. Однако их разность и частное могут не быть
натуральными числами.
Добавлением к натуральным числам отрицательных чисел и
нуля множество натуральных чисел расширяется до множества
целых чисел, т.е. О, ±1, ±2 , ±3, ....
Для любых целых чисел их разность является целым числом.
Однако частное двух целых чисел может не быть целым числом.
■^ т
Введение рациональных чисел, т.е. чисел вида — , где т — це-
п
лое и п — натуральное, позволило находить частное двух
рациональных чисел при условии, что делитель не равен нулю. Заметим,
что каждое целое число т является рациональным, так как его
т
можно представить в виде — .
Итак, при выполнении четырех арифметических действий
(кроме деления на нуль) над рациональными числами всегда
получаются рациональные числа.
т
Если рациональное число можно представить в виде дроби тт*- ,
где т — целое и k — натуральное, то его можно записать в виде
327
конечной десятичной дроби. Например, число —гг можно записать
23
так: 3,27; число -— можно записать так: -2,3.
Существуют рациональные числа, которые нельзя записать в
1 2 3
виде конечной десятичной дроби, например —, -—, — •
1 3 9 7
Если попытаться записать число - в виде десятичной дроби,
используя известный алгоритм деления уголком, то получится
бесконечная десятичная дробь 0,333... .
Бесконечную десятичную дробь 0,333... называют
периодической, повторяющуюся цифру 3 — ее периодом и кратко записывают
так: 0,(3); читается: «Нуль целых и три в периоде».

Вообще периодическая дробь — это бесконечная десятичная
дробь, у которой, начиная с некоторого десятичного знака,
повторяется одна и та же цифра или несколько цифр — период дроби.
Например, десятичная дробь 23,14565656... = 23,14(56) —
периодическая с периодом 56; читается: «23 целых, 14 сотых и 56 в
периоде».
27
3 а д а ч а 1. Записать число — в виде бесконечной десятичной
дроби.
А Воспользуемся алгоритмом деления уголком:
27
22
11
2,4545...
50
"44
60
55
50
44
6...
Остатки повторяются, поэтому в частном повторяется одна и та
же группа цифр: 45. Следовательно, — = 2,4545... = 2,(45). а
Отметим, что при делении целого числа т на натуральное
число п всегда получается бесконечная периодическая десятичная
дробь, так как каждый из остатков меньше п и поэтому при
дальнейшем делении в частном будет повторяться одна и та же группа
цифр. Так, период может быть равен нулю, т.е. может получиться
целое число или конечная десятичная дробь.
Например:
36 1
-— = -6 = -6,000...; - = 0,2 = 0,2000...;
о 5
^ = -3,75 = -3,75000...; 0 = 0,000... .
4
Вообще каждое рациональное число можно представить в виде
бесконечной периодической десятичной дроби.
Справедливо и обратное утверждение: каждая бесконечная
периодическая десятичная дробь является рациональным числом,
т
так как может быть представлена в виде дроби —, где т — целое, а
п
п — натуральное числа.

3 а д а ч а 2. Представить бесконечную периодическую
десятичную дробь 0,2(18) в виде обыкновенной.
ДПусть* = 0,2(18) = 0,2181818... .
Так как в записи этого числа до периода содержится только
один десятичный знак, то, умножая на 10, получаем:
10* = 2,181818... . (1)
Период этой дроби состоит из двух цифр. Поэтому, умножая обе
части последнего равенства на 102 = 100, находим:
1000* = 218,181818... . (2)
Вычитая из равенства (2) равенство (1), получаем: 990л: = 216.
216 12
Отсюда: *= — =-.
Ответ: 0,2(18)= —. А
55
3 а д а ч а 3. Показать, что 2,999... = 3.
А Пусть х = 2,(9). Тогда 10* - х = 29,(9) - 2,(9) = 27, откуда:
х = З.А
Аналогично можно показать, что любую конечную десятичную
дробь можно записать в виде бесконечной дроби двумя способами:
с периодом 0 и с периодом 9.
Например:
1,75 = 1,75000... = 1,74999..., - 0,2 = -0,2000... = -0,199999....
Условимся в дальнейшем не использовать бесконечные
десятичные дроби с периодом 9. Вместо таких дробей будем записывать
конечные десятичные дроби или бесконечные десятичные дроби с
периодом 0.
Например: 5,2999... = 5,30000... = 5,3.
Упражнения
1. Записать в виде конечной (если это возможно) или бесконечной
периодической десятичной дроби:
1)|; 2)£; 8)|; 4)-±; 5)-з1; б) £.
2. Выполнить действия и записать результат в виде конечной или
бесконечной десятичной дроби:
"Ti + V 2>iH; 3>i + 1'25; 4>i + 0'33;
5)^ 1.05; 6)J-3,7.

3. Записать в виде обыкновенной дроби бесконечную
периодическую десятичную дробь:
1)0,(6); 3)0,1(2); 5)-3,(27);
2)1,(45); 4)-0,(7); 6)-2,3(32).
4. Вычислить:
1) (5,4 1,2 - 3,7 : 0,8) (3,14 + 0,86): 0,25;
2) (20,88 : 18 + 45 : 0,36): (19,59 + 11,95);
3) (3,14 : (8,7 - 2,42) + 5,2): (7,86 - 0,26 (1,38 + 28,12));
\2) 71
5)9 + 8 + .
' 36 32 10 18
5. Вычислить:
6 8) 4 1,20 18 J 41
16 72 12 J (5 23 115 J (18 24
3) Гз±+0,241 2,15 + f5,1625-2—) -;
^ 25 ) { 16 J 5
4) 0,364 : — + — : 0,125 + 2- 0,8;
25 16 2
(з,25--)б,25 (5,5-3^) :5
\ ±1 + A i/_
4 3
(2-0,75):- (2-0,8) 1-
5 4
§ 2. Бесконечно убывающая
геометрическая прогрессия
Напомним: геометрической прогрессией называется такая
числовая последовательность bx; b2; bs;...; bn;..., что для всех
натуральных п выполняется равенство
Ьп+1 = Ьп<1>
где Ъп Ф 0, q Ф 0. Например, таковы последовательности:
5 25 125 \5/
2; -4; 8; -16; ...; -(-2)"; ... (Ьг = 2,q = -2).

По формуле
— h лП-1
вычисляется n-й член геометрической прогрессии, а по формуле
сумма ее первых п членов, если q Ф 1.
Среди геометрических прогрессий особый интерес представляют
бесконечно убывающие прогрессии.
Вначале рассмотрим квадраты, изображенные на рисунке 1.
Сторона первого квадрата равна 1, сторона второго -» сторона третьего
Li
-~2 и т.д. Таким образом, стороны квадрата образуют геометричес-
1
кую прогрессию со знаменателем -:
lf 2'2*'F'""'^'"" (1)
Площади этих квадратов образуют геометрическую прогрессию со
знаменателем -у:
,111 1
^'^V'- '^Т"- (2)
Из рисунка 1 видно, что стороны квадратов и их площади с
возрастанием номера п становятся все меньше, приближаясь к нулю.
Поэтому прогрессии (1) и (2) называются бесконечно убывающими.
Отметим, что у этих прогрессий знаменатели меньше единицы.
Рассмотрим теперь геометрическую прогрессию
1 -I J. -JL (-1)""
' з'з2' З3"*" З"-1
(3)
Знаменатель этой прогрессии
_ 1 _ 1
Q-~9 а ее члены Ьл = 1, ^2-~~»
о о
. _1 . _ 1
^~9' ^--^гит.д.
С возрастанием номера п члены
этой прогрессии приближаются к нулю.
Прогрессию (3) также называют
бесконечно убывающей. Отметим, что
модуль ее знаменателя меньше единицы:
IL
О 1
I I
4 2
Рис. 1

Геометрическая прогрессия называется бесконечно убывающей,
если модуль ее знаменателя меньше единицы.
Задача 1. Доказать, что геометрическая прогрессия,
заданная формулой п-го члена Ъп = —, является бесконечно убывающей.
5
о о о Ъ Л
А По условию fy. = —у Ь2= — = —, откуда Q = т~ = 7*
о 5 25 t\ Ь
Так как | q \ < 1, то данная геометрическая прогрессия
является бесконечно убывающей. ▲
На рисунке 2 изображен квадрат со стороной 1. Отметим
штриховкой его половину, затем половину оставшейся части и т.д.
Площади заштрихованных прямоугольников образуют бесконечно
убывающую геометрическую прогрессию
I I I J_ _L
2*4*8*16*32*""
Если заштриховать все
получающиеся таким образом прямоугольники, то
штриховкой покроется весь квадрат.
Естественно считать, что сумма площадей
всех заштрихованных прямоугольников
равна 1, т.е.
11111
— + — + — + —+ —+ ... =1.
2 4 8 16 32
рис. 2 В левой части этого равенства стоит
сумма бесконечного числа слагаемых.
Рассмотрим сумму первых п слагаемых:
Sn+++...+.
2 4 8 2п
По формуле суммы п членов геометрической прогрессии имеем
2"
2
Если п неограниченно возрастает, то ~ как угодно близко при-
ближается к нулю (стремится к нулю). В этом случае пишут:
— -> 0 при гс->оо или lim —= 0
1 п~*°°2
(читается: « — стремится к нулю при п, стремящемся к бесконечнос-
1 1
ти» или: «предел — при п, стремящемся к бесконечности, равен
нулю»).
10

1 / 1 \
Так как — —> О при я—>«>, то II -I—>1 при п—>«>, т.е.
^ \ £ I
Sn—>1 при я—>оо или limS,j=l. Поэтому бесконечную сумму
11111 Л~*°°
~+ ~+ ~+ •" + ••• считают равной 1.
2 4 8 16 32
Говорят, что сумма бесконечно убывающей геометрической
прогрессии есть предел последовательности Sx; S2; S3; ...; Sn; ....
Например, для прогрессии
I--I.I. _JL. f_±
х 3 9 27 ^ 3
где&1 = 1, q = -^y имеем
.12^ .117
3 3 3 9 9
1
о I 3 У /" 1 ЛЛ
Поэтому HmS^ =—, так как lim — =0.
л->°° 4 л->оо^ 3J
Выведем формулу суммы бесконечно убывающей
геометрической прогрессии.
Воспользуемся формулой Sn = ———. Запишем ее так:
Так как \-q \ < 1, то qn -^ 0, если п неограниченно возрастает.
Поэтому Qn также стремится к нулю при п —»°о . Первое слагае-
1-q
мое в формуле (4) не зависит от п. Следовательно, Sn стремится к
ЧИСЛУ При П -¥ оо .
1-q
Таким образом, сумма S бесконечно убывающей
геометрической прогрессии равна
1-g
(5)
В частности, при Ьг = 1 получаем S = . Это равенство обычно
записывают так:
1-q
Подчеркнем, что это равенство и равенство (5) справедливы
только при| q\ < 1.
11

Задача 2. Найти сумму бесконечно убывающей геометричес-
111 1
кой прогрессии —> ~т»тт:> ~тт> ••• •
с* о 1о э4
. 1 , 1 _ Ь2 _ 1
Д Так как 0\-—у02-—, то "~~Г~ ~^у и по формуле
^~ ПОЛУЧИМ
Задача 3. Найти сумму бесконечно убывающей
геометрической прогрессии, если Ьг = -1, Я = — •
А Применяя формулу Ъп = blqn~1y при п = 3 получаем
/1 \з-1 1
-1 = ^ • - у -1 = &[•■—, откуда Ьл =-49.
\7/ 49 1
По формуле (5) находим сумму S
1-1 в
7
Задача 4. Пользуясь формулой (5), записать бесконечную
периодическую десятичную дробь а = 0,(15) = 0,151515... в виде
обыкновенной дроби.
А Составим последовательность приближенных значений
данной бесконечной дроби:
a1 = 0,15 = —,
1 100
+
a2 =0,1515 =
+
100 1002
a3 = 0,151515 = — + — +
100 1002
100 ЮО2 100J
Запись приближений показывает, что данную периодическую
дробь можно представить в виде суммы бесконечно убывающей
геометрической прогрессии:
. 15 15 15
а~юо юо2 ЮО3
По формуле (5) получим 15
а =
г J_ 99 33
100
12

Упражнения
6. Является ли геометрической прогрессией последовательность,
заданная формулой п-го члена:
l)bn = -22n; 2)bn = 33n?
7. В геометрической прогрессии найти сумму ее первых пяти
членов, если:
8. Доказать, что геометрическая прогрессия является бесконечно
убывающей:
1)1 Л, ),...; 3)-81,-27,-9, ... ;
*>-АЬ~"; 4)-16,-8,-4,....
9. Выяснить, является ли геометрическая прогрессия бесконечно
убывающей, если:
1 = 40, Ь2 = -20; 3)&7 = -30,Ь6 = 15;
10. Вычислить:
l)lim—; 2)lim(0,2)n; 3)lim(l+—1; 4)lim ((-)" -21
11. Найти сумму бесконечно убывающей геометрической прогрессии,
если:
12. Найти сумму бесконечно убывающей геометрической прогрессии:
l)l,i,i,...; 2)6,1±..; 3)-25, -5, -1, ...; 4) -7, -1, --,....
3 9 6 7
13. Записать бесконечную периодическую десятичную дробь в виде
обыкновенной дроби:
1)0,(5); 2)0,(9); 3)0,(12); 4)0,2(3).
14. Является ли последовательность бесконечно убывающей
геометрической прогрессией, если она задана формулой п-го члена:
1)ЬЛ = 3.(-2)Я; 3)ЬЯ = 2.(~) ;
2)&„ = -3-4»; 4) Ьп = 5 (-1)"" ?
13

15. Найти сумму бесконечно убывающей геометрической прогрессии:
1) 12, 4, |, ... ;
2) 100, -10, 1, ... .
16. Найти сумму бесконечно убывающей геометрической прогрессии,
если:
17. Сумма бесконечно убывающей геометрической прогрессии равна
150. Найти:
1)&1,если 9 = "^>
18*. Вычислить:
2) д, если Ь1 = 7Ь.
2) lim
Зп
3)
4) lim
(541)2
(2"-3)(22n+3 2"+ 9)
19*. На куб со стороной а поставили куб со стороной —, на него куб
а а
со стороной —, затем куб со стороной — и т.д. (рис. 3). Найти
высоту получившейся фигуры.
20*. В угол, равный 60°, последовательно вписаны окружности,
касающиеся друг друга (рис. 4). Радиус первой окружности Rv
Найти радиусы #2, Rs, ..., Rn, ... остальных окружностей и
показать, что они образуют бесконечно убывающую
геометрическую прогрессию. Доказать, что сумма Rx + 2(R2 + R3 + ... + Rn + ...)
равна расстоянию от центра первой окружности до вершины
угла.
Рис.3
Рис.4
14

§ 3. Действительные числа
В § 1 было показано, что любое рациональное число можно
записать в виде бесконечной периодической десятичной дроби и
каждая бесконечная десятичная периодическая дробь — рациональное
число. Если же бесконечная десятичная дробь не периодическая,
то она не является рациональным числом. Например, дробь
0,101001000100001..., в которой после первой цифры 1 стоит один
нуль, после второй цифры 1 — два нуля и вообще после п-й цифры
1 стоит п нулей, не является периодической. Поэтому такая дробь
не представляет никакого рационального числа. В этом случае
говорят, что данная дробь является иррациональным числом.
Иррациональным числом называется бесконечная
десятичная непериодическая дробь.
Иррациональные числа, так же как и рациональные, могут
быть положительными и отрицательными.
Например, число 0,123456..., в котором после запятой
записаны подряд все натуральные числа, является положительным
иррациональным числом. Число -5,246810..., в котором после запятой
записаны подряд все четные числа, является отрицательным
иррациональным числом.
Числа л/2,^/7, -^3 , к также являются иррациональными, так
как они могут быть записаны в виде бесконечных десятичных
непериодических дробей.
Рациональные и иррациональные числа образуют множество
действительных чисел.
Таким образом, действительными числами называют
бесконечные десятичные дроби, т.е. дроби вида
+ао'а1а2аз ••• ' ~ао'а1а2аз
где а0 — целое неотрицательное число, а буквы av a2, ...
обозначают какие-либо из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Например, в записи действительного числа к = 3,1415... число
ао= 3, а первые три десятичных знака таковы: ах - 1, а2= 4, а3 = 1.
В записи действительного числа -^/234 = -15,297058... число
а0 = 15, а десятичные знаки таковы: а1 = 2, а2= 9, а3 = 7, а4 = 0 и т.д.
В записи действительного числа 37,19 = 37,19000... число а0 = 37,
а десятичные знаки таковы: ах = 1, а2 = 9, ап= 0 при п > 3.
Действительное число может быть положительным,
отрицательным или равным нулю.
Бесконечная десятичная дробь равна нулю, если все цифры в ее
записи — нули.
15

Положительное действительное число — это десятичная дробь,
не равная нулю, со знаком «+», а отрицательное — со знаком «—».
Знак «+» перед дробью обычно опускается.
Вам известно, как выполняются действия над конечными
десятичными дробями. Арифметические операции над
действительными числами, т.е. бесконечными десятичными дробями, обычно
заменяются операциями над их приближениями.
Например, вычислим приближенные значения суммы у[2 + </3 .
С помощью микрокалькулятора находим
^2 = 1,4142135..., J3 = 1,7320508... .
Поэтому с точностью до единицы:
,/2 + ^/3-1,4 + 1,7 = 3,1 = 3;
с точностью до одной десятой:
^2 + ^3 = 1,41 + 1,73 = 3,14 « 3,1;
с точностью до одной сотой:
72 + ^3 - 1,414 + 1,732 = 3,146 - 3,15
и т.д.
Итак, при сложении числа ^2 и 73 заменялись их
приближениями — рациональными числами, сложение которых выполнялось
по известным правилам.
Аналогично, вычисляя произведение ^2-yjZ , например, с
точностью до 0,1, получаем
72 • ^3« 1,4 1,7 = 2,38-2,4.
Вообще пусть xv x2, ..., хпУ ... — последовательные
приближения действительного числа х с точностью до 1, до 0,1, до 0,01 и т.д.
Тогда
lim xn = х,
так как погрешность приближения \х — дгл| —> 0 при л, стремящемся
к бесконечности.
Например, зная, что у7 = 2,6457513..., при вычислении
значений числовых выражений, содержащих у]7, можно
воспользоваться любым его рациональным приближением: хх =3; х2 = 2,6;
х3=2,65; ... .
Отметим, что все основные свойства действий над
рациональными числами сохраняются и для действительных чисел (перемести-
тельный, сочетательный и распределительный законы, правила
сравнения, правила раскрытия скобок и т.п.).
16

Модуль действительного числа х обозначается | х | и
определяется так же, как и модуль рационального числа:
Например, если х = -0,1010010001..., то\х\ = -х = 0,101001... .
Геометрически действительные числа изображаются точками
числовой прямой (рис. 5, а).
-3
-2 -42 -1 -0,5 0 0,5 1 41 2
Рис. 5, а
Покажем, например, как можно
геометрически указать на числовой оси i
точку с координатой д/2 . Построим 1
квадрат со стороной 1 (рис. 5, б) и с по- 0 1 42 х
мощью циркуля отложим диагональ рис ^ ^
О А на числовой оси.
Заметим, что если бы не было иррациональных чисел и
соответствующих им точек числовой оси, то прямая оказалась бы с «дырками», в
частности, не было бы на числовой оси точки с координатой д/2 .
Множество действительных чисел «заполняет» всю числовую
прямую, каждому действительному числу соответствует
единственная точка числовой прямой, и, наоборот, каждой точке числовой
прямой соответствует единственное действительное число.
Точку, изображающую число а, также обозначают буквой а.
Отметим, что если а < Ь, то точка а лежит левее точки Ь.
Множество всех действительных чисел обозначается R. Запись
х е R (читается: «х принадлежит R») означает, что х является
действительным числом.
Упражнения
21. (Устно.) Выяснить, какие из данных десятичных дробей
являются иррациональными числами:
1) 16,9;
2) 7,25(4);
3) 1,21221222... (после п-й единицы стоит п двоек);
4) 99,24681012... (после запятой записаны подряд все четные
числа).
Хнгщные полщ сообщества
17

22. Установить, какая из пар чисел 4,4 и 4,5 или 4,5 и 4,6 образует
десятичные приближения числа -^21 с недостатком и с избытком.
23. Какое из равенств | х | = х или | х | = -х является верным, если:
24. Выяснить, каким числом (рациональным или
иррациональным) является числовое значение выражения:
1) ф - 3)(3+ 2^2); 4) (5^3 + ^27): ^;
2) (727 + 2)(2 - а/3); 5) (^3 -1)2 + (^3 +1)2;
3) (,/50 + <ку[2)V2; 6) (^5 -1)2 - (2^5 +1)2.
25. Вычислить:
1) /7л/28; 2)720-75; 3)^2-^4; 4)^81-^9;
5)750:78; 6) fi2:Jzt; 7)^16:з/54; 8)^500:^108.
26. Сравнить числовые значения выражений:
1) 7^9+78 и 7п+7i7; 2)7П-72д и
27. Упростить:
2)
3) а/75-276+75 + 276+4;
4) J(78 + 2^-78-2^)'2 + 7;
(л/2-л/з)(5+л/6)+л/27 (V3+2)(7-Vl2)-8
V 2V2-2 ' з712+6л/3-9
§ 4. Арифметический корень
натуральной степени
Задача 1. Решить уравнение
х4=81.
А Запишем уравнение в виде
*4-81=0
18

или
(*2
Так как х2 + 9 Ф О, то х2 -9 = 0, откуда хг = 3, х2 = -3. д
Итак, уравнение х4 = 81 имеет два действительных корня хг = 3,
х2= -3. Их называют корнями четвертой степени из числа 81, а
положительный корень (число 3) называют арифметическим корнем
четвертой степени из числа 81 и обозначают ^81. Таким образом,
^81 =3.
Можно доказать, что уравнение хп = а, где п — натуральное
число, а — неотрицательное число, имеет единственный
неотрицательный корень. Этот корень называют арифметическим корнем п-й
степени из числа а.
Определение. Арифметическим корнем натуральной
степени п> 2 из неотрицательного числа а называется
неотрицательное число, п-я степень которого равна а.
Арифметический корень п-й степени из числа а обозначается
так: ца . Число а называется подкоренным выражением. Если
п = 2, то вместо $[а пишут у[а .
Арифметический корень второй степени называют также
квадратным корнем, а корень третьей степени — кубическим.
В тех случаях, когда ясно, что речь идет об арифметическом
корне п-й степени, кратко говорят: «корень п-й степени».
Чтобы, используя определение, доказать, что при а > 0 tfa
равен Ь, нужно показать, что:
l)b>0; 2)bn=a.
Например, ^64 = 4, так как 4 > 0 и 43 = 64.
Из определения арифметического корня следует, что если а > 0,
то
=а, V/a* =a.
Например, (^7)5 = 7, ^1? = 13.
Действие, посредством которого отыскивается корень п-й
степени, называется извлечением корня п-й степени. Это действие
является обратным к действию возведения в п-ю степень.
Задача 2. Решить уравнение
х3 = 8.
А Запишем уравнение в виде
19

или
Так как (х + I)2 +3 * 0, то х - 2 = 0, откуда х = 2. А
Итак, уравнение х3= 8 имеет один действительный корень л: = 2.
Так как 2 > 0, то это число — арифметический корень из 8, т.е.
^8 =2.
Задача 3. Решить уравнение
Xs =-8.
А Запишем уравнение в виде
*3+8=0
или
Так как (х - 1)2+ 3 Ф О, то х + 2 = 0, откуда х = -2. А
Итак, уравнение jc3 = -8 имеет один действительный корень х = -2.
Так как -2 < 0, то число -2 является корнем из числа -8, но оно не
является арифметическим корнем. Число -2 называют корнем
кубическим из числа -8 и обозначают так:
-^8 =-2.
Вообще для любого нечетного натурального числа 2& + 1
уравнение x2k+1 = а при а < 0 имеет только один корень, причем
отрицательный. Этот корень обозначается, как и арифметический
корень, символом 2k+^fa . Его называют корнем нечетной степени из
отрицательного числа.
Например, ^-27 = -3, ^32 = -2.
Корень нечетной степени из отрицательного числа а связан с
арифметическим корнем из числа -а = | а \ следующим равенством:
Например, ^-243 = -^243 = -3.
Задача 4. Вычислить:
-0,027 - ^0,0016 - ^729 - 1FA2&.
Д ^-0,027-^0,0016-
= -0,3-0,2-3
20

Арифметический корень п-й степени обладает следующими
свойствами.
Если а)0,&>0 и л, т — натуральные числа, причем п > 2,
т > 2, то
В свойстве 1 число b может также быть равным 0, в свойстве 3
число т может быть любым целым, если а > 0.
Докажем, например, что
О Воспользуемся определением арифметического корня:
1) tfatfb > 0, так как а > 0 и Ъ > 0;
2) (^ЩП = аЬ, так как (^Щ* = (^f (Щ* = о». •
Аналогично доказываются и остальные свойства.
Приведем примеры применения свойств арифметического корня:
1)
2)
= 3;
256 /4 /256~4 Ш 4
V625 V5 V625 5
4)
181 3
Задача 5. Упростить выражение
, где а > 0, Ь > 0.
А Используя свойства арифметического корня, получаем
ab
21

Отметим еще одно свойство арифметического корня четной
степени.
При любом значении а справедливо равенство
О Воспользуемся определением арифметического корня:
1) | а | > О по определению модуля;
2) | a \2k = a2k, так как | а |2 = а2. •
Задача 6. Упростить выражение
если 3 < х < 5.
Д
Так как 3 < х < 5, то
\х-5\ =-(х-6) =
Поэтому
Упражнения
28. (Устно.) 1) Найти арифметический квадратный корень из числа:
1; 0; 16; 0,81; 169; ^
5| + | jc — 3 |
х-3\ =х-3.
-3=2. A
2) Найти арифметический кубический корень из числа: 1; 0; 125;
—; 0,027; 0,064.
3) Найти арифметический корень четвертой степени из числа:
16 256
0; 1; 16; —5 5 0,0016.
Вычислить (29-31).
2) 1^?; 3) 4/1 — I ; 4)
29. 1) ^363
30. 1)
31. 1)
5)^
4) ^/-1024;
6) %
22

32. Решить уравнение:
2)
хъ - •
х — ,
32
3)5*5=-160;
Вычислить (33—37).
33.1) 3/-125+^#64;
8
2) ^/32-0,5^-216;
3) —^81 + ^625;
3
4) ^-1000 --^/256;
4
5) #0,0001 - 2VO25 + бСХ;
V 32
6) 5 —+ 3У-0,001-4/0,0016.
V243
34.1) ^343 0,125;
3) ^256 0,0081;
2) ^512 216;
4) ^/32 100000.
35.1) ^53-73; 2)^/ll434; 3) ^(0,2)5-85; 4) Jf-1 -217.
36. 1) Щ $ЙЮ; 2) $02 ^004; 3) 4/324 -Щ; 4)^2
3) МЦ; 4) «к30-
} 13 i I
37. 1) ^310-215; 2) л/23 • 56;
381. Извлечь корень:
20
39. Упростить выражение:
2) tf
40.1)
Вычислить (40-41).
4) зр^ • з -^.
\ Ь2 V2ab
1125 V81 '^ 8 Ч 32
^16 ^
41.1) 4/324 : ^4; 2) ?/l28 : ^2000; 3) -^-J 4)
5) (725-745): 75; 6) $625 - ^5): ^5.
1
Здесь и далее буквами обозначены положительные числа, если нет
дополнительных условий.
23

42. Упростить выражение:
2)
3)
2b
Вычислить (43—44).
43. 1)
2)
44. 1)V^729; 2)
45. Упростить выражение:
3)
4)
4)
4)(4a'-W) ; 5) V« ; 6)
46. При каких значениях х имеет смысл выражение:
-3;
3)
4)
2jc-4
Вычислить (47—48).
47. 1) V9 + V17 • V9-VI7;
48.1) шш~2
2)
3) (V5 + V21 + V5 -
V3 + V2 V3-V2
^250 '
4)
4)
5)
л/З-л/2 л/З+л/2*
3)
Упростить выражение (49-50).
6) ^17-733 •
3)
24

50.1)
2)
52. Упростить:
1) tf(x - 2)3 при: а) х > 2; б) х < 2;
2) V(3-*)6 при: а) х < 3; б) х > 3;
3) л/Сг + б)4 + yJ(x-3)29 если -1 < л: < 2;
4) ^/(2jt +1)6 - ^(4 + х)4, если -3 < х < -1.
53*. Сравнить значения выражений:
1) >/з + ^30 и ^63; 2)
54*. Доказать, что:
1) yJ4 + 2V3 - yJ4 - 2V3 = 2; 2)
55*. Упростить выражение:
}
3)
a-fc
a+fc
§ 5. Степень с рациональным показателем
Задача 1. Вычислить v 5 .
А Так как 512 = (53)4, то ^5^ = ^(53)4 =53 = 125. А
Таким образом, можно записать v512 = 125 = 53 или v512 = 5 4 ,
12
так как 3 = —.
4
25
12

15
Точно так же можно записать, что \7~15 = 7 5.
Вообще если п — натуральное число, п > 2; т — целое число и
т Л
частное — является целым числом, то при а > О справедливо
равенство
а" =аг
, , (1)
т
По условию — — целое число, т.е. при делении тнапв резуль-
п
т
тате имеем целое число k. Тогда из равенства = k следует, что
п
т =kn. Применяя свойства степени и арифметического корня,
получаем
т ^
Если же частное не является целым числом, то степень ап,
где а > 0, определяют так, чтобы осталась верной формула (1), т.е.
и в этом случае считают, что
ап =:
Таким образом, формула (2) справедлива для любого целого
числа т и любого натурального числа п > 2 и а > 0.
Например,
.
З2 9
Напомним, что рациональное число г — это число вида — , т.е.
_ т п
г » где т — целое, п — натуральное числа. Тогда по формуле
п — nl—
(2) получаем аг= ап = Чат. Таким образом, степень определена для
любого рационального показателя и любого положительного
основания. Если г = — > 0, то выражение \1ат имеет смысл не только
п
при а > 0, но и при а = 0, причем v0m = 0. Поэтому считают, что
при г > 0 выполняется равенство 0г= 0.
Пользуясь формулой (2), степень с рациональным показателем
можно представить в виде корня и наоборот.
26

т _ mk
Так как ~ ~~~» где п — натуральное число, тик — целые
П ПК
числа, к Ф О, то при любом а > О
т mk
з 6 ъ_ ап =апк.
Например, 74 = 78 = 712.
Можно показать, что все свойства степени с натуральным
показателем верны для степени с любым рациональным
показателем и положительным основанием. А именно для любых
рациональных чисел р иди любых а > О и b > О верны равенства:
Эти свойства получаются из свойств корней.
Докажем, например, свойство apaq =apH1.
О Пусть р = —, q = —, где пи1 — натуральные, тик — целые
числа. Требуется доказать, что
anal = ar
(3)
т k
Приведя дроби — и ~ к общему знаменателю, записываем ле-
п I
вую часть равенства (3) в виде:
т k
ml kn
anal = anlanl.
Используя определение степени с рациональным показателем,
свойства корня и степени с целым показателем, получаем
т k ml kn
^ml+kn
ml+kn
-а
m k
= an ~l.
Аналогично доказываются остальные свойства степени с
рациональным показателем.
Приведем примеры применения свойств степени:
1 з !+.?
1) 74 74=74 4=7;
2 1 2 1 1
2) 93 :96=936 = 92=>/9 = 3;
9 I £ 3 1 4 -
3) ^) 4
27

2 2 3 2 2
4) 243=(23 3)3 = 2 3 33 =
273 (З3)3 3
Задача 2. Вычислить 255 1255.
А 255 1255 = (25 125)5 = (55)5 = 5.
1 1
a3b+ab3
Задача 3. Упростить выражение ————.
Ча + ЩЪ
1 i f I i)
Л ^J
Задача 4. Упростить выражение
II -I 1
дЗ_дЗ д 3_дЗ
I Z _1 ^
дЗ_дЗ д 3_ дЗ
а3-а3 а3+а 3 а3(1-а) а
Задача 5. Вкладчик помещает в банк 1000 р. Банк ежегодно
выплачивает ему 3% от суммы вклада. Какую сумму денег
получит вкладчик через 3 года и 5 месяцев?
А Искомая сумма вычисляется по формуле сложных процентов
*■— , (4)
100 J
где а — первоначальная сумма денег; р — число процентов,
начисляемых банком в год; t — число лет, в течение которых деньги
находились в банке.
В данной задаче а = 1000, р = 3, t = 3—- . По формуле (4) находим
S = 1000 1,03*12.
Вычисления можно провести на микрокалькуляторе. Например,
на МК-54 это можно сделать по следующей программе:
5 [iT]l2 0 3 S 1,03 [F] 0 1000 0 1106,2684.
Ответ. 1106р. 27 к.
28

Упражнения
56. (Устно.) Представить в виде степени с рациональным
показателем:
57. (Устно.) Представить в виде корня из степени с целым
показателем:
1) х4; 2) „*. 3) а~«; 4) Ь~3; 5) (2*)2; 6) (ЗЬ)Ч
Вычислить (58-62).
J_ J_ £ 3
58. 1) 642; 2) 27»; 3) 8»; 4) 81^; 5) 16-°'75; 6) 9~15.
1 11 1 £ ^ 2
59.1)2525; 2)5757; 3) 93 :96;
15 -- —
4)43:46; 5) (7"3)"3; 6) (812Г4.
2 9 9 9 Я. Я. Ч Ч
60.1) Ф ■ 27^; 2) 73 493; 3) 144^ : 9^; 4) 1502 : б2.
-0,75 f ч-i 2 2 6 4
Пз; 3)87:87-35-35;
16
2 _2 3
2) (0,04Г1>5-(0,125)" 3; 4) (5
( 1 V0'75 ( 1QV
62.1) А + 8100000'25 - 7— в;
16 { 32)
-I 2 _Х1
2) (0,001)3-2"2(64)3-8 3;
2
i1
4)(-0,5)-4-625°-25-f2il 2;
5) (0,0625)0>25 + (-2Г2 + ^/25-53.
63. Найти значение выражения:
1) Ча% при а = 0,09; 3) при & = 1,3;
^ г-
2) V& : ^/& при Ъ = 27; А)ЩаЦа- Щаь при а = 2,7.
64. Представить в виде степени с рациональным показателем:
1 11 1
1) а3 ■ Та; 2) &2. ьз . §/£. 3) ^ :«,«;
5 : ^; 5) ^ -х^'М; 6) (j/"3'8 : у2-3)
4) «5 : ^; 5) ^ -х^'М; 6) (j/"3'8 : у2-3) •
29

65. Вынести общий множитель за скобки:
1 3
1
1) х2 + *;
3) у
4-у'4;
11 11
2) (ab)*+(ac)*; 4) 12ху2 -Зх2у.
66. Пользуясь тождеством a2-b2 = (a -b)(a + b)> разложить на
множители:
j. j. 2 2 1
I)a2-b2; 2) у3-1; 3)a3-63;
11 11
4)х-у; 5) 4а2-б2; 6) 0,01т6 -п6.
67. Разложить на множители, используя тождества
а3 + Ь3 = (а + &)(а2 - а& + &2) или а3 - &3 = (а - Ь)(а2 + а& + &2):
зз 2 1 1
1)а-х; 2)jc2-z/2; 3)а2-62; 4) 27а + с2.
Упростить выражение (68—69).
68.1) (а4
1/ .1
Ла 3
аЛа
69.1) 1/ з
al
1/ з j
4la4+a 4
2)-у
70. Вычислить:
( 5 _1 5 _1\
1) 23-3 3-33-2 3 -^6
71. Упростить выражение:
1
2) 6
72. Сократить дробь:
1)-Рр
л:2 + 1/2
2)-^-4;
2>H,F
1
3)
5 __1
4)
/ j. з l з
2) 54:24-24:54
3)
4)
3)
4)
4.
т+2у[тп+п
i
с-2с2+1
л/с-1
30

Упростить выражение (73-76).
74 U х~у х~у •
Х2_у2 ^2+^2
1
cb2
с-Ь
74.1) \1-2А- + - :«■-*;
1 1
19 13
2) а3+&3 :
75. 1)
2)
76*. 1)
2)
а&2 2a2-4ab
о\ q4-q4 Ь 2-
6> — 5
4)
a-b
_ _ yyfx
x-y yfx-yfy <Jx+y[y'
a-b
a+b
T Г
a + b
a-b
£ 1^ 1^ 2 2 11 2
77*. Упростить:
3)
4)
3)
4)
2 2
1
Ь2 + Ь~
ai-i
2
a+b
I I'
TT IT*
1)
JC3-I/3 ^
Z) 3 3 ^
а2-&2
£ J_ J_ 2^ j_ J_
-у3 xz-y3
a2-b2
3)
4)
n-1
2 1
jc+1
2
_
1-л^
1
JC3 + 1
1 2
1
П2-1
9
4x^+4+-^-
X
со|
78*. Вкладчик вложил в банк 5000 р. под 2% годовых. Сколько
денег он получит через 3 года?
79*. Банк выплачивает ежегодно 3% от суммы вклада. Сколько
денег получит вкладчик через 2 года 7 месяцев, если
первоначальная сумма вклада составляла 2000 р.?
31

§ 6. Степень с действительным показателем
Покажем, как можно определить степень с иррациональным по-
казателем на примере о .
Пусть rv г2, г3, ..., гя, ... —последовательность десятичных
приближений числа V2 (например, с недостатком):
гх= 1,4; г2= 1,41; г3= 1,414, ... .
Эта последовательность стремится к числу л/2 , т.е.
lim rn = V2.
П—>оо
Числа rv г2, г3, ... являются рациональными, и для них
определены степени 3Г1, 3Г2, 3Гз, ..., т.е. определена последовательность
ql,4 ol,41 ql,414
Можно показать, что эта последовательность стремится к
некоторому действительному числу, которое обозначают 3> , т.е.
Пусть а > 0 и х — произвольное иррациональное число.
Рассмотрим последовательность xv xv xv ..., хп, ... десятичных
приближений числа л:. Эта последовательность имеет предел
lim jc^ = jc.
Можно показать, что последовательность а4, а*2, а*3,..., аХп,...
также имеет предел. Этот предел обозначают ах и называют
степенью числа а с показателем х:
ах = lima*".
Таким образом, степень ах определена для любого а > 0 и
любого действительного показателя х.
При любом х е R и любом a > 0 степень а* является
положительным действительным числом:
ах > 0 при л: g Д, а > 0.
Если основание степени а = 0, то степень 0* определяют только
при х > 0 и считают, что 0* = 0 при х > 0. Например, 0 = 0; О01 = 0.
При х < 0 выражение 0х не имеет смысла. Например, выражения
О"1, 0 , 0° не имеют смысла.
При таком определении степени с действительным показателем
сохраняются все известные свойства степени с рациональным
показателем. Сформулируем эти свойства.
32

Пусть а > О, Ь > О, х, х1 и х2 — любые действительные числа.
Тогда справедливы равенства:
' (1)
(2)
(3)
(4)
(5)
Доказательство этих равенств основывается на свойствах
степени с рациональным показателем и на теории пределов
последовательностей, которая изучается в курсе высшей математики.
Задача 1. Упростить выражение vs-з 4-Т5 *
А Применяя свойства степени с действительным показателем,
получаем
/aV3-iW3+i a(V3-i)(V3+i)
xl
а
(аЪ)х
ш
= аХ1+Х29
= аХ1Х\
= axbx,
' _ах
r,V5-3f4-V5
• = — = а. ▲
Приведем еще одно свойство степени, доказываемое в курсе
высшей математики с помощью теории пределов: для любого а > 1 и
любого х > 0 число ах больше 1, т.е.
' (6)
1приа> 1, х>0.
С помощью свойств (1) — (6) доказываются следующие свойства
степени.
Теорема. Пусть а > 1 и хг < х2. Тогда а*1 < а*2.
О По условию х2 - хг > 0. Поэтому по свойству (6)
аХ2-*>1.
Умножим обе части этого неравенства на положительное число а*1:
Отсюда по свойству (1) получим аХ2 >aXl. •
Следствие 1. Пусть 0 < а < 1 и хг< х2. Тогда а*1 > а*2.
О Так как 0<а<1,то~>^- Поэтому из теоремы следует, что
а
;t
2-Ю. М. Колягин, 10 кл.
33

1\х 1 11
С
(1\ 1 11
По свойству (5) степени — =—. Следовательно, ~Г ~7~9 от-
\а) ах а1 а2
куда а*1 >а*2. •
Следствие 2. Пусть а > О, а Ф 1, а*1 = а*2. Тогда хх - х2.
О Предположим, что равенство хх = х2 не выполняется, т.е.
хг < х2 или хх > х2 . Пусть, например, хх < х2. Тогда при а > 1 по
теореме должно быть а*1 <аХ2> а при 0 < а < 1 по следствию 1
должно быть а*1 >а*2, что противоречит условию а*1 =а*2. •
Задача 2. Сравнить числа б2^ и б3^.
А Сравним показатели 2>/3 и 3V2 . Так как 2>/3=>/l2,
3V2 = Vl8 и 12 < 18, то 2>/3 < 3>/2. Поэтому по теореме б2^ < б3^. А
/ \л/8 ^
Задача 3. Сравнить числа — и —
А Так как 0 < Ж 4, то 0 < -г < 1.
4
Сравним показатели: V8 < V9, т.е. V8 < 3.
/ \л/8 / \3
К] К
Применяя следствие 1, получаем — > —
И / \4
Задача 4. Решить уравнение 4* = 2^ .
А По свойствам степени 4* = (22)х = 22х. Поэтому уравнение
можно записать так: 2 =2^ . Применяя следствие 2, получаем
2х = 4>/3, откуда х = 2>/3 . А
Следствие 3. Пусть 0 < jcx < х2. Тогда еслир > 0, то х{ < х2,
аеслир<0, то х^>х2.
О По условию > 1- 1) Если р > 0, то по формуле (6) имеем
— > 1- По свойству степени -j > 1> откуда х2 >х^, т.е. х^ <х2.
2) Если р < 0, то -р > 0 и по формуле (6) имеем h^2- > 1,
откуда ~7>lj ^rf>:L» xl>xl- •
Таким образом, при возведении неравенства с
положительными левой и правой частями в положительную степень знак
неравенства не меняется, а при возведении в отрицательную степень знак
неравенства меняется на противоположный.
34

Задача 5. Сравнить числа V2 и у/3 .
А По свойствам степени получаем
(V2)6 = (22 )6 = 23 = 8; (%/3)6 = (3*)6 = З2 = 9. Так как 0 < 8 < 9, то
1 1
86<96, т. е. V2 < $3 . А
Упражнения
Вычислить (80-83).
ол л \ о>5 о~v5 . о\ o2V2 . rw2 q\ /Kv3 \V3 . y|\ //л c\V2 \V8
ol. 1) z • о ; 4) (э ) ;
3) 61+2VS :
82 1)2i-272.4
2)
4»fV2
83.1)
2)
4)
o2fV5 ol+V5
84. Выяснить, какое из чисел больше:
7 8
1) ОД8 или ОД9;
2 3
2) 5~3 или 54 ;
5) 4"73 или
,7з
if (if
- или - ;
3 1 О
) \о )
85. Сравнить число с единицей:
1) 2"2; 2) (0,013т1;
5)2"^; 6)U) ;
86. Упростить выражение:
6) 2V* или 21J;
4)
,75-2
о/8-З
3)
4)
: b2.
2*
35

87. Сравнить числа:
Упростить выражение (88—89).
88.1) A"!; 3)
2*^
2) 25*^ = 5V5; 4)
92. Сравнить числа:
1) ^10 и fe 3) л/17 и
2)^и|7; 4) ^13 и
93. Решить уравнение:
3)
V3 ^
^ J л/3
2) ^-(|f ^
Упражнения к главе I
94. Вычислить:
5,48+8,02 20,88:18+45:0,36
1) —■ ; 2) — ;
(7,97+8,77): 3,72 19,59+11,95
3) fo,645 : 0,3- 1—1 -f4: 6,25-1: 5 + -1,9б1;
I 180 Л 1 )
4) (А-0,3751: 0,125 + f--—) : (0,358-0,108).
U J U 12 J
2) ^-4^; 4)
(xyf
89.1) (а1+^ )х-^; 3)
2) ( b/s\5 M 4)
90. Решить уравнение:
Ш (а) : 3)9Х=*2^2' 4> 16* = 2е".
91. Решить уравнение:
36

95. Представить в виде обыкновенной дроби:
1) 1,3(1); 2) 2,3(2); 3) 0,(248); 4) 0,(34).
Вычислить (96-99).
96. 1) 152; (0,5)2; Р J ; (-1Д)2; (-1-1 ; (0,2)4;
2)48°; 10"2; (-1 ; (0,3)"3; (-1.2Г2; (^
3) №; Ш; Ш;
I 2 I 2 Л ( \
4) 83; 273; 100004; 325; 32"5; —
!-73; ИШ-ifi; Wl5^ : Wi;
V 8 \5
2) 56° : 8"2; 164 • 252; — : 92; 83\-\ : 16"1;
273 i :814; VlOO 492 Зб"1;
3) (16 81 625) 4; (27 0,008 125)3;
. Г0,25-64VI.
1 Л 7 4
54-5 4 73-7~3
~¥~; 72 ;
,-l
4)
4 Uy
4) (0,01)"2 :100 г;
]3
(0,3)03 (0,3)-'
(0,3)13
2) f— 125-
127
0,01
2
-1
3)
6)
27
99.1)
4)
100. Расположить числа в порядке возрастания:
Q 1
1 ; 2)98°, (-] у 325.
101. Сравнить числа:
2) — и (0,41) <;
3) (4,09)^ и (4—
{ 25
Jf-fM
.12J 13
37

102. Упростить выражение, представив его в виде степени с
основанием а:
il 7-
1)
2)
3)
5)
6)
аа
103. Упростить выражение:
2)
V3-1
104. Сравнить числа:
105. Решить уравнение:
1
1)62*=6*; 2)3* = 27;
4)22*+1 = 32; 5)42+х=1;
106. Сократить дробь:
,4х-3
= 5.
4 4
У-161/2.
1)
107. Упростить:
з 1
2)
1)
ab2-b2
а-Ь
Проверь себя!
1. Вычислить:
2 7
_ 153 З3
5 3
»isf-i=
2. Упростить выражение: ?
с V с2
38

3. Сократить дробь
а-9а2
7а* + 21
' 2 Т п 1 Т
4. Сравнить числа 5|| — и|- .
U9j V^ 4 )
5. Упростить выражение (^а + Щ>)2 - (\[а - \[b)2.
108. Показать, что геометрическая прогрессия является бесконечно
убывающей, если:
1) Ь2 = -81, S2 = 162; 3) Ьг + Ъ2 = 130, Ьх - Ь8 = 12°;
2) Ь2 = 33, S2 = 67; 4) Ь2 + Ь4 =68, &2-&4=60.
109. Записать бесконечную периодическую десятичную дрюбь в виде
обыкновенной:
1) 1,10(209); 2) 0,108(32).
110. Проверить равенство:
= 1; 2)
> _7 — 9
111. Освободиться от иррациональности в знаменателе дроби:
г—
2
1)
л/2-л/з'
2)
5)
5+-Л0'
з
7*)
112. Вычислить:
6) з
8*)
11
113. 1)
2)
114. 1)
2)
2)
Упростить выражение (113—114).
■Jx-Jy Jx
4 4
2 2 2
3)
a3+b3
a-b
1 1 1
4 4
4)
39

Упростить выражение (115—116).
2)
(oft)
"1
117*. Доказать, что:
П-бл/2
3-V2
; 2)^20+1472 + ^20-1472 = 4.
ИСТОРИЧЕСКАЯ СПРАВКА
1. История действительных чисел
Еще в V в. до н. э. в школе Пифагора было доказано, что
множества рациональных чисел не хватает для точного измерения
длин любых отрезков. Одной из первых задач, выводящих на
понятие несоизмеримости отрезков, была задача нахождения
стороны квадрата, площадь которого равна 2. Тем самым было
доказано существование несоизмеримых отрезков. Идею доказательства
методом от противного факта несоизмеримости диагоналей
квадрата и его сторон можно найти в «Началах» Евклида (IV в. до н. э.).
Все последующие после Евклида годы, вплоть до XII в.,
математики Индии и Востока использовали иррациональные величины для
нужд математической науки и астрономии, но не признавали их за
числа. В начале XII в. персидский и таджикский поэт, математик и
философ Омар Хайям (ок. 1048 — после 1112) теоретически
расширил понятие числа до положительного действительного числа.
В XV в. самаркандский ученый аль-Каши стал применять
десятичные дроби для увеличения точности извлечения корней. В 1594 г.
40

нидерландский математик и инженер Симон Стевин (1548-1620) в
книге «Приближения к алгебре» показал, что десятичные дроби
можно использовать для бесконечно близкого приближения к
точному значению иррационального числа. Позже французский
математик, философ, физик и физиолог Репе Декарт (1596-1650)
показал, что иррациональные числа, как и рациональные,
изображаются точками на числовой оси и образуют вместе с рациональными
числами множество действительных чисел.
2. История числовых последовательностей
В древности уже употребляли понятие последовательности —
были известны бесконечные последовательности натуральных,
четных и нечетных чисел, последовательности простых чисел и
обратных натуральным. Различали последовательности возрастающие и
убывающие, для некоторых последовательностей умели находить
выражение-формулу их общего члена. Для последовательности
простых чисел формула общего члена неизвестна, но еще в III в. до н.э.
александрийский ученый Эратосфен указал способ (названный
позднее «решетом Эратосфена») получения простых чисел.
Упоминания о прогрессиях, частных видах
последовательностей, восходят ко II тысячелетию до н.э. Примеры арифметических
и геометрических прогрессий найдены в клинописных табличках
вавилонян и в египетских папирусах. Знакомую нам формулу
суммы геометрической прогрессии можно найти в «Началах»
Евклида. Идея нахождения предела убывающей последовательности
появилась в V-IV вв. до н.э. В книге Архимеда «Квадратура
параболы» (III в. до н.э.) присутствует сумма бесконечно убывающей
геометрической прогрессии
а а а а 4
а + - + — + — +... =—г = -а.
4 42 43 i_I 3
4
Интересно, что лишь в 1484 г. французский математик Н. Шю-
ке в своей книге «Наука о числах» дает правило для нахождения
суммы любой бесконечно убывающей геометрической прогрессии.
3. История понятия предела
До наших дней дошли 9 апорий (затруднительных положений-
парадоксов) элейского философа Зенона (V в. до н.э.). В апории
«Дихотомия» (от греч. — «деление пополам») Зенон утверждал, что
движение вообще невозможно, так как для того, чтобы пройти
1
расстояние от одной точки до другой, надо сначала пройти ~ этого
41

Ill
расстояния, затем ~> 7> 77 > ••• этого расстояния. Но последова-
4 8 16
тельность таких отрезков бесконечна, значит, конечная точка пути
не будет достигнута. Парадокс, представляемый как логическая
безысходность, заключается в том, что рассматриваемая сумма
2 4 8 16
бесконечного числа слагаемых конечна.
Несмотря на то что парадоксы Зенона оставались
неразрешимыми, они не уничтожили идею бесконечности в математике. Первое
теоретическое исследование, в котором в неявном виде
использовались предельные переходы (при вычислении площадей и объемов
криволинейных фигур), было проведено древнегреческим
математиком и астрономом Евдоксом Книдским в IV в. до н.э. В XVII в.
метод Евдокса назовут методом исчерпывания. В нем фактически речь
идет о пределе возрастающей последовательности площадей
правильных вписанных многоугольников: пространство между кругом
и вписываемыми в него многоугольниками как бы
«исчерпывается при их «возрастании».
В начале XVIII в. многие математики, еще не имея строгой
теории действительного числа, работали со степенными функциями
и выводили многие свойства этих функций. Понятие же степени аа
с любым действительным показателем а окончательно
сформировалось только в XIX в., когда в математику прочно вошло понятие
предела.

глава II J [ ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
§ 7. Показательная функция,
ее свойства и график
С понятием функции вы познакомились в курсе алгебры 7—9
классов.
Если каждому значению х из некоторого множества
действительных чисел поставлено в соответствие по определенному правилу
число у, то говорят, что на этом множестве определена функция.
При этом х называют независимой переменной или аргументом,
а. у — зависимой переменной или функцией.
Множество значений х, для которых определены значения у(х),
называют областью определения функции.
Для обозначения функции обычно используют буквы f,g,Fn т.д.
Например, говорят: дана функция у = f(x), или функция g(x) = 2jc — 1,
или функция F(x) = х2.
Функции могут быть заданы формулами, графиками,
таблицами. В 7—9 классах вы познакомились с некоторыми функциями,
изучили их свойства и строили графики. Нижеприведенная
таблица напомнит вам о них.
В § 6 степень была определена для любого положительного
основания и любого действительного показателя. Пусть основание
степени а > 0. Тогда каждому х е R соответствует одно определенное
число у = ах. Тем самым задана функция у = ах. Если а = 1, то
функция у = ах принимает одно и то же значение у = 1 при всех х.
I Функцию у = ах,
где а > 0, а Ф 1, называют показательной функцией.
Такое название функции объясняется тем, что ее аргументом
является показатель степени.
Показательная функция обладает следующими свойствами.
Свойство 1. Область определения показательной функции
у = ах — множество R всех действительных чисел.
Это свойство следует из того, что степень с положительным
основанием определена для любого действительного значения показателя.
Свойство 2. Множество значений показательной функции
у = ах — множество положительных чисел.
Второе свойство следует из того, что если а > 0 и а * 1, то
уравнение ах = b имеет корень при любом b > 0, т.е. функция принимает
любое положительное значение. Это доказывается в курсе высшей
математики.
43

Функция
y = kx+b
у = xs
У = v X
k
У=х
Область
определения
функции
R
R
R
х>0
Множество
значений
функции
R
у>о
R
у>о
График
функции
к>
к<
\
0
у[
о,
/
0
У
\
!ч
У
1
0
У
7
у
0
/.
1 *
0 х
\
У
/
1 л:
0 л-
X
к>0
К-
А
X'
Интервалы
знакопосто-
янства
функции
у > 0 при х > - -
К
Ь
у < 0 при х < - т
/г
г/ = 0прил:= "-
I/ > 0 при jc < -~
К
у < 0 при jc > --
/г
1/ = 0прил:= ~-
г/ > 0 при
jc> 0, х< 0
г/ = 0 при jc = 0
у > 0 при jc > 0
I/ < 0 при jc < 0
г/ = 0 при х = 0
г/ > 0 при jc> 0
i/ = 0 при jc = 0
z/ > 0 при х> 0
I/ < 0 при jc < 0
I/ > 0 при jc < 0
г/ < 0 при х> 0
Промежутки
возрастания
(убывания)
функции
Возрастает
на всей
числовой
прямой
Убывает
на всей
числовой
прямой
Возрастает
на
промежутке х > 0,
убывает на
промежут-
Возрастает
на всей
числовой
прямой
Возрастает
на
промежутке
х>0
Убывает
на
промежутках
х>0
Возрастает
на
промежутках
44

Функция
Ив
§§?
4 ft К
jo д >»
О о €<
Множество
значений
функции
График
функции
Интервалы
знакопосто-
янства
функции
Промежутки
возрастания
(убывания)
функции
у = ах2 +
+ Ъх + с,
*0;
R
У>Уо
где
xlf *2 -
корни
уравнения
c2 + Ъх +
+ с = 0 при
У>Уо
У>0
У<0
а>0,
D = Ъ2 - 4ас> О
х0
у > 0 при
JC < JCj, JC> JC2,
i/ < 0 при
^! < X < Х2,
у = 0 при
Возрастает
на
промежутке х>х0,
убывает на
промежутке
:о
у > 0 при
xl<x < х2,
у < 0 при
х < xv х> 1
у = 0 при
'2»
Возрастает
на
промежутке jc<jc0,
убывает на
промежутке
х>х0
у>0
при х е R
Возрастает
на
промежутке х>х0,
убывает на
промежутке
О х0
а < О, D < О
у <о
при jc g R
Возрастает
на
промежутке jc<jc0,
убывает на
промежутке
х>хп
у > 0 при
i/ = 0 при
JC =
Возрастает
на
промежутке х>хх,
убывает на
промежутке
х, х
а < О, D = О
у < 0 при
0
у = 0 при
Возрастает
на проме-
жуткел: <x
убывает на
промежутке
х> хл
45

При b < О уравнение ах = Ь не имеет корней, так как ах > 0 при
любом х.
Свойство 3. Показательная функция у = ах является
возрастающей, если а > 1, и убывающей, если 0 < а < 1.
Третье свойство следует из теоремы и следствия 1, доказанных в § 6.
Задача 1. Построить график функции у = 2х.
А Составим таблицу:
X
у = 2*
-3
1
8
-2
1
4
-1
1
2
0
1
1
2
2
4
3
8
Построим эти точки и проведем через них кривую, учитывая, что
функция у = 2х возрастает (рис. 6). А
Вообще график показательной функции у = ах, где а > 1, имеет
вид, представленный на рисунке 7.
Этот график расположен выше оси Ох, так как ах > 0 при jcei
С возрастанием аргумента значения функции увеличиваются, так
как у =ах — возрастающая функция, если а > 1.
Задача 2. Построить график функции у = - .
А Составим таблицу:
X
-3
8
-2
4
-1
2
0
1
1
1
2
2
1
4
3
1
8
Построим эти точки и проведем через них кривую (рис. 8). А
Рис.6
Рис.7
Рис. 8
46

Вообще график показательной функции у =ах, где 0 < а < 1,
имеет вид, представленный на рисунке 9.
Этот график расположен выше оси Ох> так как ах > 0 при х е R.
С увеличением аргумента значения функции уменьшаются, так как
у = ах — убывающая функция, если 0 < а < 1.
Из свойств 2 и 3 следует, что уравнение ах = Ь, где а > 0, а Ф 1,
b > 0, имеет единственный корень, т.е. по заданному значению b
степени ах показатель степени х однозначно определяется.
Геометрически это означает, что прямая у-b пересекает график функции в
одной точке, абсцисса которой является корнем уравнения ах = b
(рис. 10).
(1\х 2
Задача 3. Решить графически уравнение - = х .
I 3 J 3
А Построим графики функций у =
пу=х-- (рис. 11). Из
о
рисунка 7 видно, что графики этих функций пересекаются в одной
точке. Следовательно, данное уравнение имеет один корень —
абсциссу этой точки. Из рисунка видно, что х = 1. Проверка
показывает, что х = 1 является корнем уравнения. А
Показательная функция часто используется при описании
различных физических процессов. Так, радиоактивный распад
описывается формулой:
t
(1)
где m{t) и т0 — массы радиоактивного вещества соответственно в
момент времени t и в начальный момент времени t = О, То — период
полураспада (промежуток времени, за который первоначальное
количество вещества уменьшается вдвое).
Рис.9
Рис. 10
Рис. 11
47

С помощью показательной функции выражается давление
воздуха в зависимости от высоты и подъема, ток самоиндукции в
катушке после включения постоянного напряжения и т.д.
Задача 4*. Альпинист, находясь на высоте hx - 1100 м над
уровнем моря определил, что давление воздухарх =741 мм рт. ст., а
температура 15°С. Каково давление воздуха на высоте h2 = 2300 м
при той же температуре?
А Известно, что давление р2 находится по следующей
барометрической формуле:
Р2 = Рх- (0,8886)Л2"Л1.
Подставляя в эту формулу данные из условий задачи, имеем
р2-741(0,8886)2300-1100.
Выполнив вычисления с помощью микрокалькулятора, получим
р2 ~ 639 мм рт. ст. А
Задача 5*. Период полураспада плутония равен 140 сут.
Сколько плутония останется через 10 лет, если его начальная масса 8 г?
А Воспользуемся формулой (1). В данной задаче т0 = 8 г,
t = 10 365 (считаем, что в году 365 дней), Т = 140. Тогда
3650
Выполнив вычисления с помощью микрокалькулятора, получим
Упражнения
118. Построить график функции:
1)0 = 3*; {1)
119. Используя график функции (рис. 12), указать:
1) значения аргумента, при которых значение функции равно 0;
г)
Рис. 12
48

2) значения аргумента, при которых функция принимает
положительные (отрицательные) значения;
3) промежутки возрастания (убывания) функции.
120. Найти область определения функции:
9)У =
6) g(x) = yJ2x2 + 5x-3; 13) у =
7) y(x) = 4оГл + VIT2; 14) у = 0,2^.
121. Построить график функции у = 3* и, используя этот график,
найти приближенно:
1)л/8; 2)з1; 3) ^ 4) З15.
122. Изобразить схематически график функции:
1)» = (0,4)*; 2)у= (V2 )*; 3) z/ = f-| j ; 4) у = (л/3 )*.
123. Для данной функции выяснить, является ли она возрастающей
или убывающей:
=[l|]X; 2) у = (0,57)*; 3) у= U=) ; 4)у=[з|]*.
124. (Устно.) Используя свойство возрастания или убывания
показательной функции, сравнить числа:
1) 1,73 и 1; 2) 0,32 и 1; 3) 3,215 и 3,216;
/iv/2 /W.4
4) 0,2"3 и 0,2"2; 5)J и ^ ; 6) ЗЛ и зЗД4«
125. Сравнить число с 1:
)^ 3)(5rt 4)я5; 5) (f) ; 6) ^
126. На одном рисунке построить графики функций:
и у = 2'; 2)у=(±Ч и у=(
49

127. Найти координаты точки пересечения графиков функций:
128. (Устно.) Решить уравнение:
1)5* = ^; 2) 7х = 49; 3
5
129. Решить графически уравнение:
(1\х
1) - =* + 1; 3)2* = 3*-2;
\ «5 I
130. Используя графики функций, решить неравенство:
1)3*<1; 2)2*>1; 3)4*>4;
131. Решить графически неравенство:
1)2*>-* + 3; 2)^-
132. Выяснить, возрастающей или убывающей является функция:
133. Найти множество значений функции:
134. Построить график функции:
= 3--2; 2) у = ^ j + 3; 3) у = 2*+1; 4) у = З-2.
(if
135. Доказать, что графики функций у = 2х и у = — симметрич-
V2
ны относительно оси ординат.
136. Построить график функции:
l)i/ = 2l*l; 2)y= i ; 3) у = |3*-2|;
137*. При радиоактивном распаде количество вещества уменьшается
вдвое за сутки. Сколько вещества останется от 250 г через
1,5 сут.; 3,5 сут.? Вычисления провести на микрокалькуляторе.
50

138*. Налесном участке можно заготовить 4105 м3 древесины.
Ежегодный прирост деревьев составляет 4%. Сколько можно
заготовить древесины на этом участке через 5 лет? Вычисления
провести на микрокалькуляторе.
§ 8. Показательные уравнения и неравенства
Рассмотрим несколько примеров показательных уравнений и
неравенств, в которых неизвестное содержится в показателе степени.
Решение таких показательных уравнений часто сводится к
решению уравнения
ах=а\
где а > 0; а Ф 1. Так как из равенства степеней с одинаковыми
основаниями следует равенство показателей, то уравнение имеет
единственный корень х = Ь.
Например, уравнение 3х = 81, т.е. уравнение 3х = З4, имеет
единственный корень х = 4.
Задача 1. Решить уравнение 4-2*=1.
А Запишем уравнение в виде 2*+2 = 2°, откуда х + 2 = 0.
Ответ. х = -2. А
Задача 2. Решить уравнение 23х 3х = 576.
А Так как 23х = (23)* = 8х, 576 = 242, то уравнение можно
записать в виде 8х 3х = 242 или в виде 24* = 242. Отсюда х = 2.
Ответ, х-2. А
Задача 3. Решить уравнение Зх+1 - 2 • 3*~2 = 25.
А Вынося в левой части за скобки общий множитель 3*~2,
получим З*"2 (З3 - 2) = 25;
З*"2 25 = 25, откуда З*"2 = 1, х - 2 = 0, х = 2.
Ответ, х-2. А
Задача 4. Решить уравнение 3* = Iх.
3*
А Так как Iх Ф 0, то уравнение можно представить в виде — = 1,
(SY
откуда 1-1 =1,л: = 0.
Ответ. х = 0. А
Задача 5. Решить уравнение 3 • 2Х+1 + 2 • Ъх~2 = Ъх + 2Х~2.
А Запишем уравнение в виде 3 • 2Х+1 - 2Х~2 = Ъх - 2 • 5х"2, откуда
(2\х~2
2*"2(3 23 - 1) = 5*"2(52 - 2), 2*"2 23 = 5*"2 - 23, ^J = 1, х - 2 = 0.
Ответ, х-2. А
51

Задача 6. Решить уравнение 9х - 4 • 3х - 45 = 0.
А Заменой 3х = t данное уравнение сводится к квадратному
уравнению
*2-4*-45 = 0.
Решая это уравнение, находим его корни tx = 9, t2 = -5, откуда
3х = 9, 3х = -5. Уравнение 3х = 9 имеет корень х = 2, а уравнение
3* = -5 не имеет корней, так как показательная функция не может
принимать отрицательные значения.
Ответ. х = 2. А
3 а д а ч а 7*. Найти все значения а, при которых уравнение
9х-аЗх + 3-а = 0 (1)
имеет хотя бы один действительный корень.
А Пусть 3х = ty тогда уравнение (1) примет вид
t2-at + 3-a = 0. (2)
Задача равносильна следующей: найти все значения а, при
которых уравнение (2) имеет хотя бы один положительный корень.
Дискриминант квадратного уравнения (2) D = а2 - 4(3 - а) = а2 +
+ 4а - 12 = (а + 6)(а - 2) неотрицателен при а < -6 и при а > 2.
Если а < -6, то -а > 0, 3 - а > 0 и по теореме, обратной теореме
Виета, оба корня уравнения (2) отрицательны.
Пусть а > 2. Тогда при 2 < а < 3 оба корня уравнения (2)
положительны (-а < 0, 3 - а > 0); при а = 3 один из корней равен нулю, а
другой равен 3); если а>3, тоЗ-а<0и поэтому корни уравнения
(2) имеют разные знаки (один из них положителен, а другой —
отрицателен).
Ответ. а>2. А
Рассмотрим теперь примеры решения показательных неравенств.
Такие неравенства часто сводятся к простейшим неравенствам
ах > abj ах < аь.
При решении таких неравенств используется свойство
возрастания функции ах при а > 1 и убывания при 0 < а < 1.
Задача 8. Решить неравенство 3х < 81.
А Запишем неравенство в виде 3х < З4.
Так как 3 > 1, то функция у = 3х является возрастающей.
Следовательно, при х < 4 выполняется неравенство 3х < З4, а при х > 4
выполняется неравенство 3х > З4 . Таким образом, при х < 4 нера-
52

венство является верным, а при х > 4 — неверным, т.е. неравенство
3* < 81 выполняется только тогда, когда х < 4.
Ответ, х < 4. А
[1 Лх
- > V8.
2У
А Запишем неравенство в виде
if . «I __fi
f iТ з
Так как - — убывающая функция, то х < --.
[2) з
Ответ, jc <~"5"' ^
Задача 10. Решить неравенство 16* + 4* - 2 > 0.
А Обозначим 4* = t> тогда неравенство запишется в виде
t2+t-2>0.
Это неравенство выполняется при t < -2 и при £ > 1. Так как
£ = 4*, то получим два неравенства: 4* < -2 и 4х > 1. Первое не имеет
решений, так как 4х > 0 при всех хбй. Второе неравенство можно
записать в виде 4х > 4°, откуда л: > 0.
Ответ. л:> 0. А
Упражнения
Решить уравнение (139-145).
139. 1)4х1 = 1; 2)0,33*"2=1; 3)22*=24V3; 4(J)* (^)
140.1)27-4 2)400*=^; 8) g)*=25; 4(|
141. 1)3-9*= 81; 2) 2 4*= 64; 3) 3*+2 • 3*~2 = 1;
4) 0,5* +7 С51-2* = 2; 5) 0,6* +3 = 0,62* "5; 6) б3* х = б1"2*.
142. 1) Ш ^ 8х = 32; 3) 36 б^2 =36* б3;
2) 2^=4 2; 4)8*+2 = 2 64*.
143. 1) З2*1 + З2* = 108; 4) З*1 - 3*+ 3*+1 = 63;
2) 2 3*+2 - 23*"2 = 30; 5) 7 2*+1 + 2х - 2*+1 = 52;
3) 2*+1 + 2*1 + 2* = 28; 6) 25 3* - 10 3*+1 + 3*+2 = 36.
144. 1)5*= 8*; 2) (^f = (|f 5 3)3* = 52*; 4) 4* = 31
53

145. Решить уравнение:
1)9^4343 = 0;
2) 16*-17 4*+16 = 0;
146. Решить неравенство:
2)",
3)25*-6 5*+5 = 0;
4) 64* - 8х - 56 = 0.
3)
Решить уравнение (147—155).
1)3*2+*-12=1;
2) 2х2~7х+ю =1;
147. 1) 3*2+*-12=l; 3) 2X"2 =4;
,3_„2,
148. 1) 0,3' -* +*"1
(
2>(2
=1}
149. 1) 10х = ^100;
2) 10* =^10000;
3) 2252дс2"24=15;
4) 0,5* =4x+l.
(3)
4)
4)10* =
-0,06
6)
3)(jJ
4) 0,7v
о\ 97* 93* — Qfi.
Ol £1 I * ^ — OQt
4) 32Л 25^=225.
150. 1)2*
2)
151. 1) 2х2 5*2=100;
152. 1) Iх - lx~l = 6; 3)53* + 3 53*"2
2) З2^1 + 32^"2 - 32^"4 = 315; 4) 2X+1 + 3 2xl -5246 = 0.
1 *хЯ. 1 \ 7^-2 _ q2-jc. q\ q 4 _ кл^+2.
ХЭО. 1.) i —о 9 о) О —D у
лг-3
2) 2х"3 = З3^ 4) 4 2 =32(х"3).
154. 1) Зх+3 + 3* = 7*+1 + 5 7х;
2) 3*+4 + 3 5Х+3 = 5*+4 + Зх+3;
3) 2*~х + 73"* = 74~х + 23"* 11;
4) 2Х+1 + 2*"1 - 3х"1 = 3х"2 - 2х"3 + 2 3*~3.
54

155. 1)8 4*-6 2*+1 = 0; 4) 32x+1 - 10 3х + 3 = 0;
1 -6=0, 5)23* + 8 2*-6-22*=0;
3) 132*+1 - 13* -12 = 0; 6) 53*+1 + 34-52l-7-5I=0.
Решить неравенство (156—158).
156. 1) 5х"1 ^ 75; 2) З2 > 9; 3) З^"4 > 1;
157. 1) Зх+2 + 3х"1 < 28; 3) 22х~1 + 22х"2 + 22*"3 > 448;
2) 2х-1 + 2*+3 > 17; 4) 53*+1 - 53jc"3 < 624.
158. 1)9*-3*-6>0; 3)5м + 45'-1>0;
2)4*-2*<12; 4)3 9*+11 3х < 4.
159. Решить графически уравнение:
Jx+l; 3) 2х=-х-\;
=x-i; 4) 8*= 11-х.
160. Решить графически неравенство:
x+l; 3)2<9-ix;
161. Решить графически уравнение:
162. При каких значениях х сумма чисел 2х"1, 2Х~4 и 2*~2 равна
сумме бесконечно убывающей геометрической прогрессии 6,5;
3,25; 1,625; ... ?
Решить уравнение (163-165).
163. 1) З2*443 = 2*+3; 3) 2* 3*= 36х2;
164. 1) 3 16*+ 36*= 2 81х; 2) 25х + 13 10* = 7 22х+1.
165. 1) 811*2-11 =27; 2) б'2*"6! =25Х-5*-4.
55

Решить неравенство (166—167).
) -£— < 4;
4 -о
166. 1) 0,4' - 2,5*+1 > 1,5; 3) -£— < 4;
4 -о
2) 25 0,04 2х > 0,2*(3-х>; 4) ^j - 3L ^
167. л/27 3~6*2 >9*х.
168*. Найти все целые значения а, при которых функция
принимает значения, меньшие 3.
169*. Найти значения а, при которых имеет корни уравнение:
2)а 4*-4*-4 2
Упражнения к главе II
170. Сравнить числа:
/ 1 ЛЯ /^ 1 N3'14
2) 2V3 и 21'7;
171. Сравнить с единицей число:
| , 3,(1) ; 4,
172. (Устмо.) Является ли функция возрастающей или убывающей:
1) у = 0,78х; 2) у = 1,69х; 3)»=(|) ; 4) у = 4"*?
173. В каком промежутке находятся значения функции при ж € [-1; 2]:
1)0 = 5*; 2) у = 5"*?
Решить уравнение (174—178).
174. 1) 5*2-9-1 = 0; 2) г*2"1^ 3) 1,55*"7
4) 0,75"*-» = (lip; 5) 5'2-5-6=1; 6) g
175. 1) 10'2-3=0,01; 3) 24д:2 =42*"15;
2)5'2"5=^; 4) 16я2 =64»-*.
176. 1) 2х + 2*"3 = 18; 5) 2 3*+1 - 6 3х"1 -3х = 9;
2) 3* + 4 3*+1 = 13; 6) 5*+1 + 3 5х"1 - 6 • 5х + 10 = 0;
3) Iх + 2 7*+1 = 15; 7) Зх+3 - Зх+1 + 3х = 75;
4) 5 2*"2 + 3 2Х+1 = 29; 8) Зх+1 + 5 • 3х - 3 • 3х"1 = 21.
56

177. 1) Ъ2х -5х- 600 = 0; 3) 3* + 9*1 - 810 = 0;
2)9*-3*-6 = 0; 4)4*+2*+1-80 = 0.
178. 1)2 16Х-3 4Х = 2; 3)3 81*-8 9* = 3;
2)2 -4х + 2 2*-4 = 0; 4)4 16*-17 4* +4 = 0.
179. Решить неравенство:
2>9; 3) 0,7*2+2*<0,73;
180. Решить графически уравнение:
2) (±Х =
ПРОВЕРЬ СЕБЯ!
1. Построить схематически графики функций:
/хч0,2 /хч1,2
2. Сравнить числа: 1^1 и I -^ J ;5 0>2и5 1>2.
3. Решить уравнение:
2*+з _ 2^+1 =i2; 4 -22х - 5 2Х+ 1 = 0.
4. Решить неравенство:
7*"2>49; (0,5)*2"2>!.
181. Доказать, что последовательность значений функции у = 2х при
натуральных значениях jc составляет геометрическую прогрессию.
182. За первый год работы предприятие имело а рублей прибыли. В
дальнейшем каждый год прибыль увеличивалась на р%.
Какой станет прибыль предприятия за п-й год работы?
183. Найти область определения функции:
1)у= 2^; 3) z/=0,2^+V^T;
2) у=3^; 4) У=(|
184. Найти множество значений функции:
= 1-3*; Z)y = 2x~l; 4)у = 0,Ъ1~х+ 2.
57

185. Построить график функции:
(1Y
1; 3)i/=l-J -2;
Решить уравнение (186-188).
186. 1) 0,6* (|П "12 = (^)3; 2)
^ 9 J \125/
2
187. 1)233xl + 27х"3 = 9х1 + 2 З2*1;
2) г^^-
3) 22 9х-1-- 3x+3+i 3*+2=4;
3 3
4) 5 4*"1 - 16' + 0,25 22х+2 + 7 = 0.
188. 1) 2Х+4 + 2Х+2 = 5Ж+1 + 3'5';
2) 52* - 7' - 52' • 17 + Iх ■ 17 = 0;
4) 3-4*+i-9ae+2=6-4I+1-i-9x+1.
3 2
189. Решить неравенство:
2) 2х2 -б*2 <Ю-^Ю3-*)2; 4)
190. Построить график функции:
Решить уравнение (191—194).
191. 1) У = 5 0,04х; 3) 2 4* - 3 10* - 5 25* = 0;
л/5
X X
2) 4 3х - 9 2х = 5 З2 22 ; 4) 4 9х + 12х - 3 16* = 0.
192*. 1) 4х + 25х =29; 2) 3х + 4х = 91.
193. 1) 2l*+5l = 8; 3)31Х-11 = 31Х"21;
2)5l2^l = 125; 4)4l3+^ = 4l^-2L
194*.
58

Решить неравенство (195—196).
195. 1) 31*-21 < 9; 3)2l*-2l>4l*+1l;
2)4l*+1bl6; 4)5lx+4l<254
1Qft 1 ^ М- ^ о|Зд:-12 + 2jc o\ **
9j ' " ' ' 3-32*
Историческая справка
В письмах немецкого философа, физика-изобретателя и
математика Г. Лейбница (1646—1716) к голландскому ученому X.
Гюйгенсу (1629—1695), датированных 1679 г., можно найти
использование (без пояснений) переменной величины в показателе степени.
Начиная с XVIII в. европейские математики, еще не имея
строгой теории действительных чисел, изучали отдельные свойства
показательной функции. В XIX в., после того как в математике
упрочилось понятие предела и было введено понятие степени с
действительным показателем, удалось строго обосновать и свойства
показательной функции.
Теория показательной функции имеет огромное прикладное
значение. Известно, что многие природные и общественные явления
происходят по законам показательной функции. Например, при
радиоактивном распаде вещества его масса уменьшается за равные
промежутки времени в одно и то же число раз. Если через То обозначить
период полураспада вещества, то через Т лет оставшаяся масса
вещества М выражается формулой М = Мо - , где Мо — первона-
чальная масса. Размножение живых организмов в природе также
находится в показательной зависимости от времени.

глава III J [ СТЕПЕННАЯ ФУНКЦИЯ
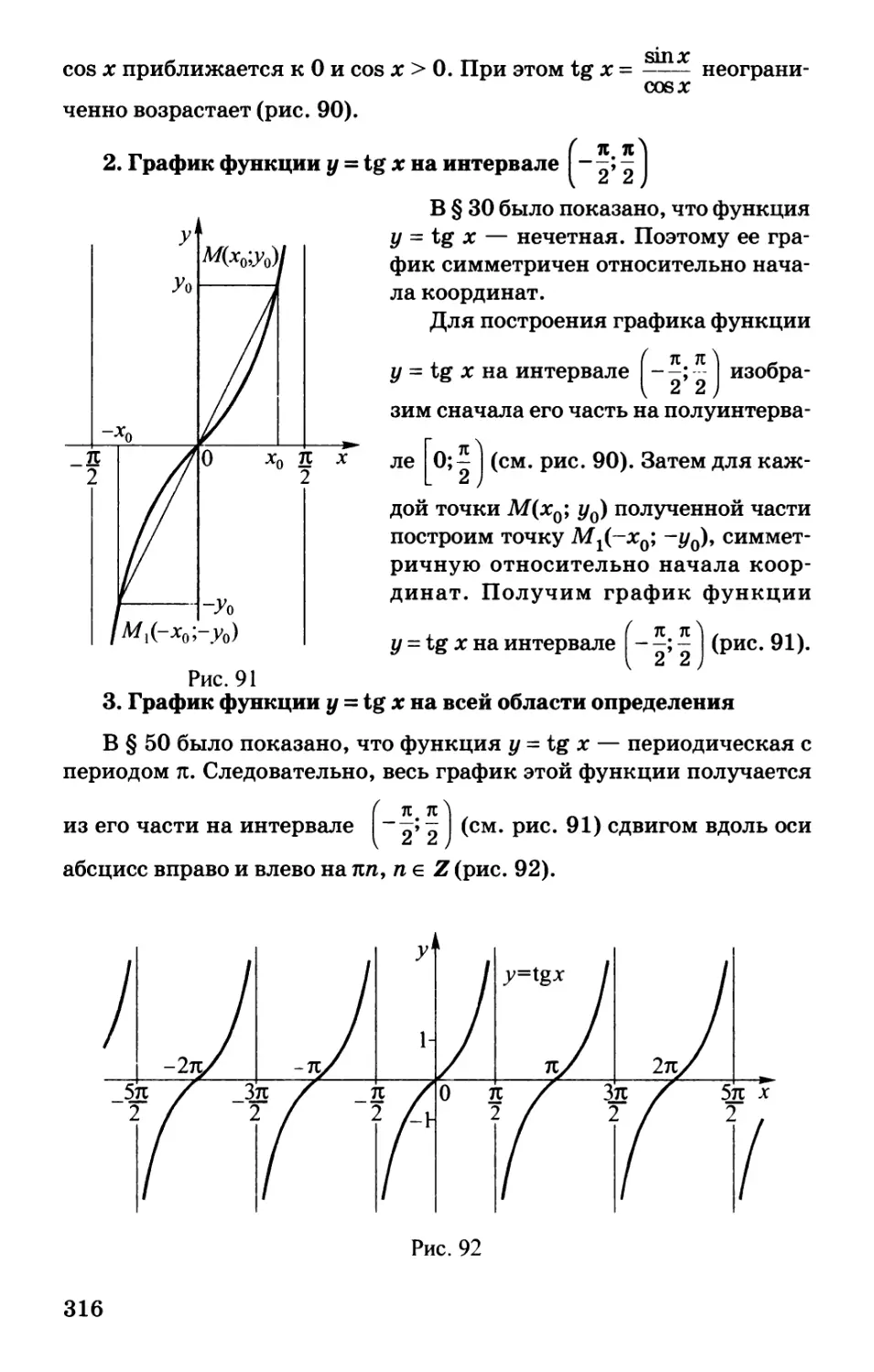
§ 9. Степенная функция, ее свойства и график
Вы знакомы с функциями у = х, у = х2у у = х3, у = — и т.д. Все эти
функции являются частными случаями степенной функции, т.е.
функции
У = хР, (1)
гдер — заданное действительное число.
Свойства и график степенной функции (1) существенно зависят
от свойств степени с действительным показателем и, в частности,
от того, при каких значениях х ир имеет смысл степень хр.
Перейдем к подробному рассмотрению различных случаев в
зависимости от показателя степени р.
1. Показатель р = 2п — четное натуральное число.
В этом случае степенная функция у = х2п, где
п — натуральное число, обладает следующими
свойствами:
— область определения — все
действительные числа, т.е. множество R;
— множество значений — неотрицательные
числа, т.е. у>0;
— функция у = х2п — четная, так как
О
(-х)2п = х2п;
Рис. 13, а — является убывающей на промежутке х < О
и возрастающей — на промежутке х > 0.
График функции у = х2п имеет такой же вид, как, например,
график функции у = х2 (рис. 13, а).
2. Показатель р = 2п — 1 — нечетное натуральное число.
В этом случае степенная функция у = х2п~г, где п —
натуральное число, обладает следующими свойствами:
у=х — область определения — множество R;
— множество значений — множество R;
— функция у = х2п~1 — нечетная, так как
У
v — является возрастающей на всей
действительной оси.
График функции у = х2п~1 имеет такой же
вид, как, например, график функции у - х3
Рис. 13, й (рис. 13, б).
60

3. Показатель р = — 2п , где п — натуральное число.
В этом случае степенная функция у - х~2п = —^ обладает
следующими свойствами:
— область определения —
множество Ry кроме х = 0;
— множество значений —
положительные числа у > 0;
1
— функция у = ~2^ — четная, так
как
— является возрастающей на
промежутке х < О и убывающей на промежутке х > 0.
График функции у = —^ имеет такой же вид, как, например,
график функции у = —- (рис. 14, а).
х
4. Показатель р = - (2п - 1), где п — натуральное число.
В этом случае степенная функция
у = x-2(n-i) _ 2я1 обладает
следующими свойствами:
— область определения —
множество R, кроме х = 0;
— множество значений —
множество R, кроме у = 0;
1
— нечетная,
У
— функция у =
1
х2п-1
1
так как . \2n-i 2n-i »
— является убывающей на
промежутках х < 0 и * > 0.
1
Рис. 14, б
График функции у =
х2п-1
имеет
такой же вид, как, например, график функции у=— (рис. 14, б).
5. Показатель р — положительное действительное нецелое число.
В этом случае функция у = ^обладает следующими свойствами:
— область определения — неотрицательные числа х^0;
— множество значений — неотрицательные числа у^0;
— является возрастающей на промежутке х > 0.
61

График функции у = хр, гдер — положительное нецелое число,
1
имеет такой же вид, как, например, график функции у = х3 (при
4
О < р < 1) или, как, например, график функции у = х3 (при р >1)
(рис. 15, а—б).
yix
V=JC3
О
о
Рис. 15, а Рис. 15,6
6. Показатель р — отрицательное действительное нецелое число.
В этом случае функция у = хр обладает
следующими свойствами:
— область определения — положительные
числа х > 0;
— множество значений — положительные
числа у > 0;
— является убывающей на промежутке х > 0.
График функции у = хР, где р — отрицательное
нецелое число, имеет такой же вид, как, напри-
1
Рис. 15,
мер, график функции у = х = -у (рис. 15, в).
Задача 1. Решить неравенства:
1) х3 >х;
2) х3 > х.
А 1) Неравенство х3 > х имеет смысл при х > 0. При х = 0
неравенство не выполняется. При х> 0, возводя неравенство в куб,
получаем
х > х3, т.е. х(1 - х2) > 0.
Так как х > 0, то 1 - х2 > 0, откуда х2 < 1, | х \ < 1.
Следовательно, 0 < х < 1. 4
2) Аналогично, возводя неравенство х3 > х при х>0в куб,
получаем
х4>х3, т.е. х\х-1)>0.
62

Так как х > О, то х - 1 > 0, т.е. х > 1.
Ответ. 1)0<х< 1; 2)х>1. А
Решение этой задачи показывает, что график функции у = х*
лежит выше графика функции у = х при 0 < х < 1 и ниже — при х > 1
(рис. 16, а); график функции у = х3 лежит выше графика функции
у = х при х> 1 и ниже — при 0 < х < 1 (рис. 16, б).
Рис. 16
Задача 2. Сравнить числа (3,2)3"л и (3,5)3~л.
А Так как 3< я < 4, то 3 - я <0. Функция у = х3~к убывает на
промежутке х> 0. Поэтому
(3,2)3-7C>(3,5)3"7t. A
Задача 3*. Найти точки пересечения графиков функций
4
у=у[х и у= х3.
А Для нахождения точек пересечения этих графиков решим
уравнение
&с = А
Левая часть этого уравнения имеет смысл при всех х> а
правая — только при х > 0.
При х > 0 функция у=у[х совпадает с функцией у=х*>
поэтому уравнение можно представить в следующем виде:
Возводя это уравнение (при х > 0) в куб, получаем
х = х4,
откуда х(х3 - 1) = 0, х1 = 0, х2 = 1.
Ответ. (0;0),(1;1). А
63

Задача 4*. Построить график функции
А Заметим, что эта функция четная, так как | -х \ = х. Поэтому
достаточно построить ее график для х > О, а затем симметрично
отразить его относительно оси ординат.
1 1
При х > 0 имеем у =1 + \xf = 1 +х* . Строим график функции
у = х^ (при х > 0), сдвигаем его вверх на единицу и отражаем
полученный график относительно оси ординат (рис. 17). А
у1
з-
^\ 2
\
-6-5-4-3 -2 -1 0
^
/''* У Х ('°0)
1 2 3 4 5 6 jc
Рис. 17
Упражнения
197. Изобразить схематически график функции и указать ее область
определения и множество значений:
2)у=х5;
3)у=х~2;
• х-2; 6)у=хК
198. (Устно.) Является ли функция у = хр возрастающей
(убывающей), если:
е
2-я; 6)р = е?
/С
199. Изобразить схематически график функции:
2)у=х2; 3) у =
64

200. Пользуясь свойствами степенной функции, сравнить с едини-
ЦеЙ: / г-чО,2
1)4,12'7; 2)0,20'3; 3)0,791; 4) (л/З) .
201. Пользуясь рисунком 15, б, найти промежутки, на которых
графики функций: 1) у = х ; 2)у = хк — лежат выше (ниже)
графика функции у-х.
202. Пользуясь рисунком 15, а, найти промежуток, на котором
графики функций: 1) у - хп ; 2) у = хsin 45° — лежат выше (ниже)
графика функции у-х.
203. Сравнить значения выражений:
. ,\"2
1) 3,17'2и4,37'2;
\2,3 /1Оч2,3
_. /10f° /12f* „ /14\4 /15\4
2) hpr и тт ; 6) — и — ;
7 \11/ \11/ 7 \15/ \16/
2 2
3)0,30'3 иО,2°»3; 7) (4>/з)5 и (ЗлД)5 ;
4) 2,5"зд и2,6"зд; 8) (2^6) и
204. В одной системе координат построить графики функций:
1.
1) у = хг и у = х3 ; 3) z/ = х2 и z/ = х~2;
1
2)у = х4и у= х4; 4) у = х5 и у = х~5\
205. Пользуясь рисунком 15, в, найти промежуток, на котором
графики функций:
лежат выше (ниже) графика функции у = х.
206. Изобразить схематически график функции:
1
1)х = х*+1; 2)у=х~'-1; 3)у = (х-2)е
7)у=3х«;
3-Ю. М. Колягин, 10 кл. 65

207*. Построить график функции:
1
1)у=\х\»;
= \х\5;
4)у=\х\ъ -2;
= \х-1\3;
= \2х
\~3
208*. Используя графики функций, выяснить, сколько корней
имеет уравнение:
§ 10. Взаимно обратные функции
Если задана функция у = f(x)> то для каждого значения х из
области определения функции можно найти соответствующее
значение у. Нередко приходится решать обратную задачу — по
данному значению функции у находить соответствующее значение
аргумента х.
Примером может служить формула v = v0 - gt, которая
выражает зависимость скорости v движения тела, брошенного вверх с
начальной скоростью i>0, от времени движения t. Из этой формулы
можно найти обратную зависимость — времени t от скорости v:
t
g
В рассмотренном примере каждому значению функции
соответствует одно определенное значение аргумента. Для таких функций
можно выразить обратную зависимость значений аргумента от
значений функции. Поэтому такие функции называют обратимыми.
Если функция у = f(x) принимает
каждое свое значение у только при одном
значении xf то эту функцию называют
обратимой.
Например, функция у = 2х - 2
обратима, так как каждое значение у
принимается при единственном значении
аргумента х. Это значение можно найти, решая
_^ уравнение у = 2х-2 относительно х.
х Функция у = х2 не является обратимой,
так как, например, значение у = 1 она
принимает при х = 1 и при х = -1 (рис. 18).
-1 О
1
Рис. 18
66

Пусть у = f(x) — обратимая функция. Тогда каждому у из
множества значений функции соответствует одно определенное число
х из области ее определения, такое, что f(x) = у. Это соответствие
определяет функцию х от у, которую обозначим х = g(y). В этой
записи, в соответствии с принятыми обозначениями, поменяем
местами х и у. Получим
Функцию у = g(x) называют обратной к функции у = f(x).
Задача 1. Найти функцию, обратную к функции
у = Зх + 5. (1)
А Решая это уравнение относительно х, получаем
В этой формуле поменяем местами х и у
У=\{х-Ь). (2)
Функция (2) является обратной к функции (1).
Если обратимая функция у = f(x) задана формулой, то для
нахождения обратной функции надо решить уравнение f(x) = у
относительно х и затем поменять местами х и у.
Заметим, что рассмотренная в задаче функция у = Зх + 5 являет-
1
ся обратной к найденной для нее обратной функции у = ~ (х - 5).
о
Поэтому эти функции называют взаимно обратными.
Из определения обратной функции следует, что область
определения обратной функции совпадает с множеством значений
исходной, а множество значений обратной функции совпадает с
областью определения исходной функции.
Задача 2. Найти функцию, обратную к функции у =
х-2'
А Решая это уравнение относительно ху получаем х = 2+ - . За-
у
менив х на у и у на х, находим у = 2+ — .
В этой задаче область определения функции у = ^ есть мно-
х—&
жество действительных чисел, не равных 2, а множество ее
значений — все действительные числа, не равные 0. График этой
функции представлен на рисунке 19.
3* 67

Для обратной функции у = 2 + — область определения —
множество действительных чисел, не равных 0, а множество
значений — все действительные числа, не равные 2. График обратной
функции изображен на рисунке 20.
Рис. 19
Рис. 20
| Теорема 1. Монотонная функция является обратимой.
О Пусть, например, функция у = f(x) возрастает и пусть у0 — ее
значение в некоторой точке х0, т.е. yo=f(xo). Тогда если
хпринадлежит области определения функции, то при х > х0 выполняется
неравенство f(x) > f(x0) = yQJ а при х < х0 — неравенство f(x) < f(x0) = у0.
Следовательно, значение у0 рассматриваемая функция принимает
только в одной точке и поэтому является обратимой. •
Например, функция у = х3 возрастает, и поэтому она обратима,
о/
обратной к ней является функция у=у/х (рис. 21, а).
Если функция у = f(x) возрастает, то с увеличением х значения у
возрастают и, наоборот, с увеличением у возрастает х. Это
означает, что обратная функция также возрастает. Аналогично если
функция у = f(x) убывает, то обратная к ней функция также убывает.
Например, функция f(x) = 1 - 2х убывает, и обратная к ней
1-х
функция g(x) = также убывает. Функция, не являющаяся мо-
нотонной, может не иметь обратной.
Например, функция у = х2, рассматриваемая на всей числовой
оси, не имеет обратной. Однако если функцию у = х2 рассматривать
только при х > 0, то на этом промежутке она возрастает и,
следовательно, имеет обратную у = у[х (рис. 21, б).
Функция у = х2, рассматриваемая при х < 0 , убывает и также
имеет обратную у = - \[х (рис. 22).
68

У1
1
/'
0
2
у=х 1
У
1
/
/
/
.У- х
Рис. 21, a
Рис. 21,6
-1
7
о •
/
Cgix)
;о х
Рис. 22
Рис. 23
•с
I Теорема 2. Если функция имеет обратную, то график
обратной функции симметричен графику данной функции
относительно прямой у =х.
О Если точка (х0; у0) принадлежит
графику функции у = f(x), то точка (у0; х0)
принадлежит графику обратной функции
у = g(x) (рис. 23), а точки (х0; у0) и (у0; х0)
симметричны относительно прямой у = х
(рис.24). •
Рисунки 21, б; 22 иллюстрируют эту
теорему.
Отметим, что степенная функция у = хр
с областью определения х> 0 и р Ф 0
обратима, так как по свойству 3 § 9 она
монотонна. Обратной к ней является функция у = хр .
Рис. 24
69

Упражнения
209. (Устно.) Выяснить, является ли обратимой функция:
8)*=-;
= х4,х<0.
l)y = 3x-l;
4)у= Л\
210. Найти функцию, обратную данной:
г = 2лг- 1;
Злг-1
211. Найти область определения и множество значений функции,
обратной данной функции:
6)!/ =
х-4'
212. Функция у = f(x) задана своим графиком. Построить график
функции, обратной данной (рис. 25).
1 х
1 х
б)
Рис. 25
213. Являются ли взаимно обратными функции:
3)у =
= -хг и у = -у[х;
214. Найти функцию, обратную данной:
1)у=-х*;
3)у=х~2;
70

215. На одном рисунке построить график данной функции и
функции, обратной данной:
1= Зх lj о) у= х 2а\
6)у = (х-1)3;
3
= х2-1
= (х- 1)2прил:> 1;
7)у=
8)у=
— 1;
+ 1.
§11. Равносильные уравнения и неравенства
1. Равносильные уравнения
Задача 1. Найти точки пересечения графиков функций
У = Зу/х иу = х + 2.
А Если (х; у) — точка пересечения данных графиков, то у = 3 у[х =
= х + 2. Следовательно, для нахождения абсцисс точек пересечения
надо решить уравнение
"" :*+2. (1)
Возводя обе части уравнения (1) в
квадрат, получаем 9х = х2 + 4х + 4,
откуда х2 - Ъх + 4 = 0. Корни этого
квадратного уравнения хх = 1, х2 = 4.
Проверка показывает, что оба эти корня
являются также и корнями уравнения
(1).
Теперь находим ординаты точек
пересечения данных графиков
У1 = Зу[х1 = 3, у2 = З-y/jc^ = 6. Итак,
данные графики пересекаются в двух
точках (1; 3) и (4; 6) (рис. 26).
Ответ. (1;3);(4;6). А
При преобразовании исходного уравнения
получили
У'
6-
з-
4
0
&
/
1
У
\
z
X
Рис. 26
х2 - Ъх + 4 = 0.
Все три уравнения имеют одни и те же корни хг = 1, х2 = 4. Такие
уравнения называют равносильными.
71

I Уравнения, имеющие одно и то же множество корней,
называются равносильными.
Например, уравнения 4х - 3 = 2х + 3 и 2х = 6 равносильны, так
как каждое из них имеет только один корень х = 3. Уравнения
(х - 2)(х + 5) =0 и х2 + Зх - 10 = 0 также равносильны, так как
они имеют одни и те же корни хг = 2, х2 = -5.
Из определения равносильности уравнений следует, что два
уравнения равносильны, если каждый корень первого уравнения
является корнем второго и, наоборот, каждый корень второго
уравнения является корнем первого. Уравнения, не имеющие
корней, также считают равносильными.
Из курса 7 класса вы знаете, что можно сделать следующие
преобразования уравнений:
любой член уравнения можно переносить из одной части в
другую, изменив его знак на противоположный;
обе части уравнения можно умножить или разделить на одно
и то же число, неравное нулю.
При этих преобразованиях исходное уравнение заменяется на
равносильное ему уравнение.
Заметим, что если некоторое выражение в левой или правой
части уравнения заменить тождественно равным ему выражением, то
получится уравнение, равносильное исходному. Однако не при
любом преобразовании уравнение заменяется на равносильное.
Например, при возведении в квадрат обеих частей уравнения
4х =х-2
получается уравнение
х = (х-2)2,
не равносильное исходному: первое уравнение имеет только один
корень х = 4, а второе — два корня хг = 4, х2 = 1.
В этом случае второе уравнение называют следствием первого
уравнения.
Если при переходе от одного уравнения к другому не
происходит потери корней, то второе уравнение называют следствием
первого. Другими словами, если все корни первого уравнения
являются корнями второго, то второе уравнение называется
следствием первого уравнения.
Из этого определения и определения равносильности уравнения
следует, что:
1) если два уравнения равносильны, то каждое из них
является следствием другого;
2) если каждое из двух уравнений является следствием
другого, то эти уравнения равносильны.
72

При решении уравнений главное не потерять корни, а наличие
посторонних корней можно установить проверкой. Поэтому
важно следить за тем, чтобы каждое уравнение, полученное при
преобразовании данного уравнения, было его следствием.
Задача 2. Решить уравнение
2*
х-2 х-1 (х
А Умножим обе части уравнения на общий знаменатель всех
трех дробей, т.е. на (х - 1)(х - 2). Получим
2х(х - 1) - (х + 1)(х - 2) = 4, (3)
откуда
х2-х-2 = 0, хг = 2, х2 = -1.
Проверка. 1) При х-2 знаменатели двух дробей уравнения
равны нулю. Поэтому х = 2 не является корнем данного уравнения.
2) При х - -1 левая часть уравнения равна
2(-1) -1+1^2
-1-2 -1-1 3'
правая часть равна
(-1-1Н-1-2) 3*
Ответ. х = -1. А
Заметим, что для проверки корня х = -1 достаточно увидеть, что
знаменатели дробей уравнения при х = -1 не равны нулю (если,
конечно, при решении уравнения не допущены ошибки в
преобразованиях и вычислениях).
При решении этой задачи из равенства (2) получено
уравнение (3), которое является следствием уравнения (2). Корень хг = 2
уравнения (3) не является корнем уравнения (2). Его называют
посторонним корнем для уравнения (2).
(Посторонние корни могут получиться при умножении обеих
частей уравнения на выражение, содержащее неизвестное.
Задача 3. Решить уравнение
х2- 4 = 7х- 14.
А Преобразуем данное уравнение так:
(х + 2)(х-2) = 7(х-2), (4)
(х - 2)(х + 2 - 7) = О,
(х-6)(х-2) = 0,
откуда хх- 5, #2 = 2. А
73

Если обе части уравнения (4) разделить на х - 2, то получится
уравнение х + 2 = 7, которое имеет только один корень х = 5, т.е.
произойдет потеря корня х = 2 и решение задачи будет неверным.
I Потеря корней может произойти при делении обеих частей
уравнения на выражение, содержащее неизвестное.
Итак, при решении уравнения можно делать только такие
преобразования, при которых не происходит потери корней. Если при
этом получаются уравнения-следствия данного, то необходима
проверка найденных корней.
2. Равносильные неравенства
Аналогично определяется равносильность неравенств с
неизвестным.
Неравенства, имеющие одно и то же множество решений,
называют равносильными.
х — 3
Например, неравенства —^— <0 и * - 3 < О равносильны,
неравенства х2 - 4х < х - 6 и х2 - Ьх+ 6 < О также равносильны.
При решении неравенств обычно данное неравенство
преобразуется в равносильное ему.
Задача 4. Решить неравенство
Бх-3 Л
А Так как х2 + 1 > 0 при всех действительных значениях х, то,
умножая данное неравенство на х2 + 1, получаем неравенство
5х-3>х2+1,
равносильное данному.
Решая это неравенство, получаем
х2-5х+ 4<0,
откуда 1 < х < 4. А
Задача 5*. Решить уравнение
2
4 5
А 1) Зх - 4 > 0, но Зх - 4 Ф1, т.е. х> -, но хФ -, тогда 2х2+ 2
О О
5
2) Зх - 4 = 1, т.е. д:2 = -z , так как 1У = 1 при любом i/.
74

3)3*-4 = 0, т.е. х =-. Выполним проверку: 0 9 =0, О3 =0,
о
4
х3 = - — корень уравнения.
4
4) Зх - 4 < 0, но Зх - 4 Ф -1, т.е. х < -, но х * 1, тогда 2х2 + 2 = 5х,
о
5 5
1 о14т> Г 5^2 Г 5^2
лс = - или л: = 2; -<— . Выполним проверку: — ф\ — , так
5
как I — Г не существует.
5) Зх - 4 = -1, т.е. х = 1. Выполним проверку: (-1)21+2 = (-1)4 > 0,
(-1)5 <0, х = 1 — не корень.
5 4
Ответ. лгх = 2, х2=-,х3= ^. *
Упражнения
216. Решить уравнение:
JC —
2)Х +х2-4~4+х2-4' 4)(
217. Выяснить, равносильны ли уравнения:
1)2*-7 = 4*+5 и 2х +12 = 0;
2) |(2х-1)=1 и ^^ = 15
) = 0 и х2 ;
4)(х- 2)2 = 3(х- 2) и х-2 = 3;
5)х2+1 = 0 и 2^ = 0;
6) | jc - 2 | = -3 и 3* = (-1)3.
218. Выяснить, равносильны ли неравенства:
1)2х-1>2 и 2(х-1)>1;
2)<0 и Jt2 + x<2;
1)<3jc + 3 и jc-2<3;
4)х(х + 3)>2х и х2(х + 3)>2х2.
219. Установить, какое из двух данных уравнений является
следствием другого уравнения:
75
-3 = 0 и х2-5х + 6 = 0; 2) *-3* + 2 = 0 и x2-
JC-1

220. Решить уравнение:
х 2х 4х
х + 1 х-1 xz-l
2) —-- = -J_;
х-2 х х-2
221. Решить неравенство:
>1.
Выяснить, равносильны ли уравнения (222—224).
222. 1) | 2х - 11 = 3 и 2х - 1 = 3;
Зх-2_4-,Зх5 10
3 2
2;с2и2х + 3
3 2 6 3
223. 1) - =0их2 + 1 = 0; 3)х2 = 2х и х =
х
2)^=-2ил: + 3 = х; 4)32д:2"5д: = - и
9
224. 1) 2х-1 = 4- 1,5* и 3,5х-5 = 0;
2х + 5 и *2-Зх-5 = 0;
) и Зх+1 = 3;
4) Vx + 2 =3 и х + 2 = 9.
225. Установить, какое из двух данных уравнений является
следствием другого уравнения:
1)|х| = 5 и 4х2 =5;
2)— = — и *2 = 4;
jc + 2 jc + 2
3)(х- 5)(х + З)2 =2(jc + 3)2hjc-5 = 2;
4)^^ = —- и (х - 2)(х + 2) = (х - 3)(х + 3).
jc + З х + 2
ЛЛЛ х. 1 2 Ъх Зх2
226. Решить уравнение — = -.
3 + 1 3jc-1 9л:2-1 1-9jc2
227. Найти корни уравнения:
3 4х-1х2+5
'
1) 2)
х-1 х + \ х2-1 ' х-2 х2-4 х + 2 4-х2
76

228. Решить неравенство:
1) х3 - Зх2 + 2х - 6 > 2хг - х2 + 4х - 2;
2) х3 - Зх2 - 4х + 12 > -Зх3 + х2 + 12* - 4.
229*. Решить уравнение:
у2_х_2 9
2) (j^-jc-I)^"1 = 1; 4)
§ 12. Иррациональные уравнения
В уравнениях VJt+T = х - 1, V5jc-4 = 2 + Vx неизвестное jc
находится под знаком корня. Такие уравнения называются
иррациональными.
Приведем еще примеры иррациональных уравнений:
Иррациональные уравнения часто получаются при решении
разных задач. Их решение основано на следующем свойстве.
1При возведении обеих частей уравнения в натуральную
степень получается уравнение-следствие данного.
О Пусть х — корень уравнения
т.е. f(x) = g(x) — верное числовое равенство. Тогда по свойствам
верных числовых равенств fn(x) = gn(x) — также верное числовое
равенство, т.е. х — корень уравнения
Обратное утверждение неверно.
Например, уравнение у/б-х = х имеет один корень х = 2, а
уравнение 6 - х = х2 имеет два корня хг = 2, х2 = -3.
При возведении обеих частей иррационального уравнения в
натуральную степень могут появиться посторонние корни, поэтому
необходима проверка.
Например, при возведении обеих частей уравнения
yjx2+x-l=y[x
в квадрат получим уравнение
х2 + х-1=х, т.е. х2= 1.
Это уравнение имеет два корня хх = 1, х2 = -1. Второй корень
является посторонним для исходного уравнения, так как подкоренные
выражения при х= -1 отрицательны.
77

Задача 1. Решить уравнение
у1х + 6-у/х + 1
А Возводя обе части уравнения в квадрат, получаем
х + 6 -2yJ(x+6)(x+l)
откуда yj(x+6)(x+l) =6.
Возведем обе части последнего уравнения в квадрат
х2 + 7х + 6 = 36, или х2 + 7х - 30 = 0.
Корни этого уравнения хх = 3, х2= -10.
Проверка показывает, что х2= -10 — посторонний корень.
Ответ. jc= 3. А
Задача 2. Решить уравнение
^с2 + 12 = *. (1)
А Возведем обе части уравнения в четвертую степень
х2 +12 = л:4,
откуда х4 - х2 - 12 = 0.
Решим это биквадратное уравнение
1±7
2 2 '
т.е. JC2 =4 или jc2=-3.
Уравнение л:2 = 4 имеет два корня: х = ±2. Уравнение л:2 = -3
не имеет действительных корней.
Так как при возведении обеих частей уравнения (1) в четвертую
степень могли появиться посторонние корни, то нужно сделать
проверку. При х = 2 обе части уравнения (1) равны 2, т.е. х = 2 —
корень уравнения (1).
При х = -2 левая часть уравнения (1) равна 2, а правая равна
-2, т.е. х = -2 не является корнем уравнения (1).
Ответ. х = 2. А
Задача 3. Решить уравнение
у1х3-19=х-1. (2)
А Возводя обе части уравнения в куб, получаем
откуда
78

Корни этого уравнения: хг = 3, х2 = -2. Проверка показывает, что
оба эти значения неизвестного являются корнями уравнения (2).
Ответ. х1 = Зух2 = -2. А
Иногда при решении иррационального уравнения полезно
использовать графики функций.
Задача 4. Выяснить с помощью
графиков, сколько корней имеет
уравнение у[х = 1 - х2. Найти приближенные
значения этих корней.
А Построим на одном рисунке
графики функций у = у/х и у = 1 - х2 (рис. 27).
Графики пересекаются в одной точке при
х -0,5.
Ответ, х~ 0,5. А
Рис. 27
Задача 5*. Решить относительно х уравнение
(3)
А Возводя обе части уравнения в квадрат, получаем
(х + 2)(х - 3) = а2,
откуда
х2-х-6-а2 = 0,
(4)
Для проверки отметим, что 25 + 4а2 > 25 и л/25 + 4а2 > 5 при
любых действительных значениях а. Из формул (4) получим хх > 3,
*2<-2.
При х - хх оба подкоренных выражения в уравнении (3)
неотрицательны, а при х - х2 подкоренное выражение второго корня
отрицательно: х2 - 3 < -5 < 0. Следовательно, х2 — посторонний корень.
Для окончательной проверки корня х1 достаточно заметить, что
при х = х1 левая часть уравнения (3) неотрицательна,
следовательно, правая часть также должна быть неотрицательной, т.е. должно
выполняться неравенство а > 0.
Ответ. Если а > 0, то х = —(1 + v 25 + 4а2 ); если а < 0, то
корней нет. А
79

Упражнения
230. (Устно.) Решить уравнение:
1)л/^=2; 2)7^=7; 3)^=2;
Решить уравнение (231—240).
231. 1) V*7l = 3; 3)
2)7^2 = 5; 4)
Zoz. ij v^^ + o = i; oj \ji~4x = *
4)
233. 1)
4)
234. 1)
235.
2)
3)
236. 1)
2)
237. 1)
2)
3)
238. 1)
2)
3)
4)
239. 1)
2)
4)3/3*2-3 = ^.
2) x =
5)
2)
5)
- 36,75 = x- 3,5;
4)
5)
6)
3)
6)
3)
в) 7б+д
4^ = 8;
-20 =
3)
4)
4)
5)
6)
3)
4)
80

ОАС1 Л\ iV-v^ 9 -v О» O\ л/'У^ tiv^xifiv f\ -v 9
u4U. ±) У]X —Z — X — Ct\ ct) \X —OX ~r 1OX — О—X — Z.
241. Выяснить с помощью графиков, сколько корней имеет
уравнение, и найти приближенные значения этих корней:
&) SX — \Х L) , 4JX 1 — л/Л — 1 .
242*. Решить уравнение:
3) V*2 + Зх +12 - \/х2 + Зх = 2;
2) 3-x = yl9-4s6x2-6x4; 4) л/*2 + 5х + 10-л/*2 +5х + 3 =1.
243*. Решить относительно Jt следующее уравнение:
1) y/x + l-Jx-2=a; 2) y[x-Jx + 2=a-l.
§13. Иррациональные неравенства
Задача 1. Стрельба из спортивного пистолета по круглой
мишени диаметром 1 м ведется из точки прямой, перпендикулярной
плоскости мишени и проходящей через ее центр. На каком
расстоянии от мишени должна быть точка выстрела, чтобы разность
расстояний от нее до края мишени и до
центра была не больше 2 см?
А Пусть А — точка выстрела, О —
центр мишени, В — точка на окружности
мишени (рис. 28, а). По условию ВО = 50
см. Обозначим АО = ху тогда
АВ= Vx2+2500. По условиюАВ -АО < 2,
т.е. Рис-
л/*2+2500-х<2,
или
V*2+2500 <х + 2. (1)
Так как по смыслу задачи х > 0, то левая и правая части
неравенства (1) положительны. Следовательно, обе части неравенства (1)
можно возвести в квадрат, при этом знак неравенства не изменится
и получится равносильное неравенство
откуда 4х > 2496, х > 624 см.
Ответ. Не меньше 6,24 м. А
81

В этой задаче пришлось решать неравенство (1), содержащее
неизвестное под знаком корня. Такие неравенства называют
иррациональными.
Рассмотрим примеры решений иррациональных неравенств.
Задача 2. Решить неравенство
V5^<4. (2)
А Найдем область определения неравенства (2), т.е. множество
таких значений ху при которых имеют смысл обе части
неравенства. Правая часть неравенства определена при всех значениях х,
а левая — при 5 - х > 0, т.е. при х < 5. Следовательно, область
определения неравенства (2) — луч х < 5.
При х < 5 обе части неравенства (2) неотрицательны, и поэтому
при возведении в квадрат обеих их частей получается
равносильное (на множестве х < 5) неравенство 5 - х < 16.
Таким образом, неравенство (2) равносильно системе
неравенств
Решая эту систему, получаем -11 < х < 5.
Ответ. -11 <х<5. А
Рассуждения, приведенные при решении задачи 2, можно
провести устно и сразу записать, что неравенство (2) равносильно
системе неравенств
[5-Ж16.
Задача 3. Решить неравенство
Vx2-3x<2. (3)
А Неравенство (3) равносильно системе
\х2-Зх>09
Решая первое неравенство системы (4), получаем х < 0 , х > 3.
Решая второе неравенство системы (4), получаем -1 < х < 4. Оба
неравенства системы (4) выполняются при -1 < х < 0, а также при
3<х<4(рис. 28, б).
Ответ. -1<х<0, 3<jc<4. A
-2-1012345 х
Рис. 28, б
82

Задача 4. Решить неравенство
л]ю+х-х2>2. (5)
Д Это неравенство равносильно системе
\l0+x-x2>0,
t (6)
Так как каждое решение второго неравенства системы (6)
является решением первого неравенства системы (6), то эта система
равносильна одному второму неравенству
10 + x-x2>4. (7)
Следовательно, неравенство (5) равносильно неравенству (7).
Решая неравенство (7), получаем -2 < х < 3.
Ответ. -2<х<3. А
Задача 5. Решить неравенство:
1) yJSx-4 < -5; 2) V2*2+5*-3 < 0.
4
А 1) При всех допустимых значениях ху т.е. при х > - значения
3
л/Злг-4 неотрицательны. Поэтому неравенство у/Зх - 4 < -5
решений не имеет.
2) Неравенство v 2х2 + Ъх - 3 < 0 выполняется только тогда, когда
yj2x2 + 5jc - 3 = 0 , т.е. если 2х2 + Ъх -3 = 0, откуда хг = -3, х2= -. А
Задача 6. Решить неравенство
л/Зх + Кх + 1. (8)
А Область определения этого неравенства — луч х > — . При
3
этих значениях х правая часть неравенства (8) положительна.
Следовательно, неравенство (8) равносильно системе
Решая эту систему, получаем — < х < 0, х > 1.
о
Ответ. — <д:<0, jc> 1. А
3
83

Задача 7. Решить неравенство
у/х+3>х+1. (9)
А Область определения этого неравенства — луч х > -3. При всех
х > -3 левая часть неравенства неотрицательна, правая же часть
этого неравенства отрицательна при х < —1. Поэтому все значения
х из промежутка -3 < х < -1 являются решениями неравенства (9).
Рассмотрим случай, когда х > -1. Тогда обе части неравенства
(9) неотрицательны, и поэтому обе части этого неравенства можно
возводить в квадрат: х + 3 > (х + I)2. Решениями этого неравенства
являются значения х из промежутка -2 < х < 1. Отсюда,
учитывая, что х > -1, получаем -К х < 1.
Итак, решениями неравенства (9) являются все значения х из
промежутка -3 < х < 1, а также из промежутка -1 < х < 1, т.е. из
промежутка -3 < х < 1.
Ответ. -3< х< 1. А
Неравенство (9) проще решать с помощью графиков. На
рисунке 29, а построены графики функций у = Jx + З и у = х + 1. Из
этого рисунка видно, что решениями неравенства (9) являются
значения х из промежутка -3 < х < 1.
Задача 8. С помощью графиков решить неравенство
у[х<2-х.
А На одном рисунке построим графики функций у = у[х и
у = 2 - х (рис. 29, б) и выясним, при каких значениях х точки
графика функции у = у[х лежат ниже точек графика функции у = 2 - х.
Из рисунка видно, что эти графики пересекаются в одной
точке, абсцисса которой является корнем уравнения \[х -2-х. Этот
корень х- 1.
-3
Рис. 29
84

График функции у = у[х лежит ниже графика функции у = 2 - х
приО<л: < 1.
Ответ. 0<х< 1. А
Задача 9. Решить неравенство
у12х2-Ьх-3>х-1. (Ю)
А Найдем область определения этого неравенства, т.е. решим
неравенство 2л:2 - Ъх - 3 > 0. Так как корнями уравнения 2л:2 - Ъх - 3 = 0
являются числа хг= — , х2 = 3, то неравенство 2х2 - Ъх - 3 > 0 вы-
полняется при х < — и при х > 3 (рис. 30).
Таким образом, для решения неравенства надо выбирать только
такие значения х, которые принадлежат его области определения.
1) Если х - 1 < 0, т.е. х < 1, то из этого промежутка области
определения неравенства (10) удовлетворяют только числа х < —
(рис. 31). 2
_1 _1
2 2
Рис.30 Рис.31
2) Если х -1 >0, т.е. х> 1, то, возводя обе части неравенства
(10) в квадрат, получаем
2х2-Ьх-Ъ >х2-2х+1,
откуда
х2 - Зх - 4 > 0.
Так как корнями уравнения х2 - Зх - 4 = 0 являются числа хг = -1,
х2 = 4, то неравенство х2 - Зх - 4 > 0 выполняется при хх < -1, х2 > 4.
Из этих двух промежутков области определения неравенства и
условию х > 1 удовлетворяют только числа х > 4 (рис. 32).
Ответ. х< — , jc>4. A
2
3 4
Рис. 32
85

Задача 10*. Решить относительно х неравенство
yj2ax-x2>a-x, (11)
если а > 0.
А Найдем область определения этого неравенства, т.е. решим
неравенство 2ах - х2 > 0. Так как корнями уравнения 2ах - х2 = 0
являются числа хг = 0, х2 = 2а и а > 0, то областью определения
неравенства (11) является промежуток 0 < х < 2а.
1) Если а - х < 0, т.е. л: > а, то из этого промежутка области
определения неравенства (11) удовлетворяют только числа а < х < 2а.
2) Если а - х > 0, т.е. л: < а, то, возводя обе части неравенства
(11) в квадрат, получаем
2ах - х2 > (а - х)2,
откуда
2ах- х2>а2-
Так как корнями уравнения 2л:2 - 4ах + а2 = 0 являются числа
jq = -(2- V2), х2 = -(2+V2) и а > 0, то неравенство 2х2 - 4ах + а2 < 0
2 2
выполняется при — (2-v2)<jc<— (2+v2). Из этих значений надо
2 2
выбрать те, которые принадлежат области определения, т.е.
промежутку 0 < х < 2а и удовлетворяют условию х < а, т.е. из
промежутка 0 < х < а (рис. 33).
Так как 0< <1, >1, то из рисунка 33 видно, что
2 2
в этом случае решениями неравенства (11) являются числа
-(2
Объединяя оба случая, получаем
Г £,„„„„7>к Л 2а _
Рис. 33
86

Упражнения
244. Решить систему неравенств:
3) J2
2) Г3-
J
J
\х>2;
4) j9-x2<0
U + 5<0.
Решить неравенство (245—250).
245. 1) V*>2; 2) Vjc<3; 3)
4)
246. 1) Vjc-2>3;
4)7i^>3;
5)V3jc>1; 6)
Q\ I ~. О ^ 1 • Q\ /Q
la) \iX — ^4 1, O) ~\J О —
5) V2jc-3>4; 6)
7)V3x-5<5; 8)V4x+5<-.
2
247. 1) Vx2-l>l; 2)л/1-д:2<1; 3) V25-*2>4;
4) V25-x2<4; 5)Vx2-8x>3; 6)
7) Vl-
8)
248.
249.
250*
1)
2)
3)
4)
1)
2)
3)
4)
• 1)
sj2x2+3x-2>0;
yj2+x-x2 >-l;
л/блг-х2 <л/5;
yjx2-x>j2;
7^2>V4^;
7зТ2^>ч/^Т1;
V2^5<75^T4;
7з!Г2>*-2;
\Ix + 1-tJx<Jx-1;
5)
6)
7)
8)
5)
6)
7)
8)
2)
8) \lx2-x-2>-l-x2.
87

Решить неравенство, используя графики функций (251—252).
251. 1) у[х > х\ 2)у[х<х; 3)у[х>х-2; 4)у[х<х-2.
252. 1) Jx<2x; 2) Vx>0,5x; 3) yfx>2x-l; 4)y[x>x2.
253*. Решить неравенство:
1) у/х-1 < а; 2) ^2ах-х2 >а-х, еслиа<0.
Упражнения к главе III
254. Изобразить схематически график функции, указать ее область
определения и множество значений:
.1
г = х7; 2)j/=7*; 3)z/= x~2;
в)У = х-\
255. На одном рисунке построить графики функций у = х2 и у-2х.
3
Сравнить значения этих функций при х - 0; 0,5; 1; -; 2; 3; 4; 5.
256. Расположить числа в порядке возрастания:
2
1)0,3*; 0,30'5; 0,3*; 0,33'1415;
2) V2 ; 1,9Л;
1
' ' [5) '
2
4) 0,5 ^; 1,3 3; я 3; V2 з.
257. Решить уравнение с помощью графиков:
258. Найти область определения функции:
2)y=(2-x2f; 4) j/ =
88

259. Найти функцию, обратную данной, ее область определения и
множество значений:
; 2)у =
х-3
3) I/ = (jc + 2)3;
= х3-1.
260. Изобразить график функции, обратной к функции у = Дх),
график которой изображен на рисунке 34, а и б.
У
б)
Рис. 34
261. Выяснить, являются ли равносильными уравнения:
2) \1х2+Зх=у/2 и х2 + 3л: = 2;
4) ^x + 18=3/2-x и л: +18 = 2-х.
262. Решить уравнение:
2)
3) у/3-4х = 2х;
4) ylbx-1 + Зх2 =Зх;
263. Решить неравенство:
5) V2x-l =
6) V2-2jc=
7) у1х2-17=2;
4/^.2
8) л/^+17=3.
2) Vl^
3)
4)
89

ПРОВЕРЬ СЕБЯ!
1. Найти область определения функции:
3(х-1Г3; 2)y=$lx2-Zx-4.
2. Построить график функции:
\)у =
2)у = ;
S)y=-.
Для каждой функции указать область определения и
значения х, при которых у > 0.
3. Решить уравнение:
2) у]з-х-х2=х.
4. Решить неравенство:
1) л/2* + 1<1;
264. На одном рисунке изобразить схематически графики
функций:
1)!/=
265. Являются ли заданные функции взаимно обратными:
10-3* 4* + 10
и у =
х-4
3*-6
* + 3
6-х
J^i И!/=з-з*;
2-х 2(jc-1)o
4)z/=- и z/=- ?
2 + jc l + jc
266. Найти функцию, обратную данной, ее область определения и
множество значений:
3)z/= л/3-jc -1;
Решить уравнение (267—268).
267. 1) Jx-4 = >Jx-3-yl2x-l; 3) Vx-3 = V
2) 2Vx + 3-V2x + 7 = Vjc; 4) j9-2x =
90

268*. 1) V* + 4-3#t + 4 + 2 = 0; 3) %l^x-5Щ^х = -6;
2) 7^3 = 3^x^3 + 4; 4) x2 + 3*W*2 + 3* =2.
Решить неравенство (269—270).
269. 1) Vx + l<Jt-l; 3)
2) >/l^x>x + l; 4)
270*. 1) *13*+4°<O; 2)
271*. При различных значениях а решить неравенство:
Историческая справка
Учение о степенных функциях развивалось параллельно с
расширением понятия степени (начиная со степеней с натуральными
показателями и заканчивая понятием степени с любым
действительным показателем). Так, равенством а0 = 1 (где а Ф 0)
пользовался в начале XV в. самаркандский ученый ал-Каши. В XV же веке
французский математик Н. Шюке ввел понятие отрицательного
показателя степени. Идея введения дробных показателей
встречается еще в XIV в. в работах французского ученого Н. Орема, где в
словесной формулировке он описал правила действий со степенями.
Современную символику степеней с нулевым, отрицательным и
дробным показателями начал использовать английский математик
Д. Валлис (1616—1703), а общепринятой эта символика стала
после употребления ее И. Ньютоном (1643—1727) в своих работах.
В начале XVII в., в результате открытия метода координат и
аналитической геометрии, появились графический метод
исследования функций и графический способ решения уравнений.
Ньютон называл все кривые, задаваемые функцией
у = ах + Ьх2 + сх3 + ... +рхп>
параболическими кривыми, хотя традиционно все же этим
термином называют графики функций
у = схт,
где с — положительное действительное число, т — положительное
рациональное число. Если т < 0, то графики функций у = схт
называют гиперболическими кривыми.
91

ГЛАВА |v J [ ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
§ 14. Логарифмы
3 а д а ч а 1. Найти положительный корень уравнения jc4 = 81.
А По определению арифметического корня имеем
х= ^81 =3. А
Задача 2. Решить уравнение 3*=81.
А Запишем данное уравнение так: 3х = З4, откуда х = 4. А
В задаче 1 неизвестным является только основание степени, а
в задаче 2 — показатель степени.
Способ решения задачи 2 состоял в том, что левую и правую
части уравнения удалось представить в виде степени с одним и тем же
основанием 3. Но уже, например, уравнение 3х = 80 таким
способом решить не удается. Однако вы знаете, что это уравнение имеет
корень. Чтобы уметь решать такие уравнения, вводится понятие
логарифма числа.
В § 5 было сказано, что уравнение ах = Ь, где а > 0, а * 1, & > 0,
имеет единственный корень. Этот корень называют логарифмом
числа b по основанию а и обозначают logfl b. Например, корнем
уравнения 3х = 81 является число 4, т.е. log3 81 = 4.
I Логарифмом положительного числа b no основанию а, где
а > 0, а Ф 1, называется показатель степени, в которую надо
возвести число а, чтобы получить Ь.
Например, log2 8 = 3, так как 23 = 8; log3 - =-2, так как 3"2= -;
log7 7 = 1, так как 71 = 7, log4 1=0, так как 4° = 1.
Определение логарифма можно кратко записать так:
a}oe«b=b.
Это равенство справедливо при b > 0, а > 0, а * 1. Его обычно
называют основным логарифмическим тождеством.
Например,
С помощью основного логарифмического тождества можно
показать, например, что х = log3 80 является корнем уравнения 3х = 80. В
самом деле, 3log380=80.
92

3 а д а ч а 3. Вычислить log64 128.
А Обозначим log64 128 = х. По определению логарифма 64* = 128.
Так как 64 = 26, 128 = 27, то 26х = 27, откуда 6х = 7, х = - .
о
Ответ. log64 128= -. А
3 а д а ч а 4. Вычислить З"2 log3 5 .
А Используя свойства степени и основное логарифмическое
тождество, находим
д-2 log3 5 _ /3loS3 5 \"2 _ g-2 _ J^ д
3 а д а ч а 5. Решить уравнение log3 (1 - х) = 2.
А По определению логарифма З2 = 1 - ху откуда х = - 8. А
х-1
3 а д а ч а 6. При каких значениях х существует log5 TjTT^ ?
А Так как основание логарифма 5>0 и5^1,то данный лога-
х-1
рифм существует только тогда, когда tjt~^ > 0.
Решая это неравенство, находим 1 < х < 2. А
Упражнения
Найти loga х, исходя из равенства х = ау (272-273).
272. 1) х = 27, а = 3, у = 3; 3) х = 9> а=-, у = -2;
о
2) д: = 625, а = 5, i/ = 4; 4) х = 2, а= |, у = -|.
273. 1)х = 4, а=16, i/=|; 3)х = 7, а = 7, у=1;
2)х = 9, а = 27, у=-; 4) х = 1, а = 16, у = 0.
Проверить справедливость равенства (274—276).
274. 1) log15 225 = 2; 3) log3 ^ = -5;
2) log4 256 = 4; 4) log7 ^ = -3.
275. 1) log! 64 = -3; 3) logl ±- = 3;
4 3 г1
2) log! 81 =-4; 4)logli-=6.
3 2 "'
93

276. 1)
2)
lognl = C
Iog77=l
1; 3) log
; 4)log279 =
1664=2;
2
3'
277. Найти логарифмы чисел по основанию
Вычислить
278. 1) log2 16;
4)
279. 1)
4)
280. 1)
4)
log2 1;
log3 27;
log3 1;
logi ^;
2
4.5 9 =
(278-285).
2)log264;
5)log2|;
2)log381;
5)log3^;
2) log! 4;
2
5)iog0,5 i;
3)
6)
3:
log2 2;
logi.
3) log3 3;
6)
3)
6)
lOgg з •
log05 0,125;
logi л/2 .
2
281. 1) log5 625; 2) log6 216; 3) log4 ^ ; 4) log5 y^ .
282. 1) logx 125; 2) logi 27; 3) logl -J-; 4) logi 36.
5 3 4 64 6
283. 1) 31огз18; 2)5logs16; 3) 10logl°2; 4) (^
284. 1)351окз2;- 2)(|)^; 3) 0,321ок°з6;
285. 1) 8log2 5; 2) 9log312 ; 3) 16log4 7; 4) 0,125loeo-51.
286. Решить уравнение:
l)log6x = 3; 2)log5x = 4; 3)log2(5- x) = 3;
4)log3(x + 2) = 3; 5)logifx-^l = -2; 6)logi (0,5 + x) = -l
287. Выяснить, при каких значениях д: существует логарифм:
1) logi (4 - х); 2) log0 (7 - х); 3) log6 -J— ;
2 * \— £*Х
94
4) log8 2^4; 5) logi i-x2); 6) log0 7 (-2x3).
4X1 4

Вычислить (288-294).
288. 1) log2 $2 ; 2) log3 ^; 3) log0 5 -|= ; 4) log7 Ц
289. I)log3264; 2)log27243; 3)log8127; 4)log1288.
290. 1) log,. -L=; 3) log , 25^/5 ;
3^3 7
2) lo8jE "Л=; 4) log-L
291. l)log10 (0,01); 3)log
2) logio 7^ ; 4) log10 (100 Ш )•
luuu
292. 1) (ОДГ1ов1о0>3; 2) 1O"1(«io4; 3) 5"Iog53; 4)
oi s /1\11овз4 /ir51og23
293 1)92iog35. 2) (I)" 3)(i)
4)27 3 ; 5)103-|ogl°5; 6) l±
294. 1) log2 log3 81; 4) - log9 log2 8;
2) log3 log2 8; 5) log4 log16 256 + log4 J2 ;
3) 21og27 log10 (1000); 6) 31og2 log4 16 + logi 2.
2
295. Решить уравнение:
1) log, 27 = 3; 2)logz| =-1; 3)logxS = \;
4) log, S = -4; 5) log, (7з)3 = |; 6) log, 8 = -0,6.
Выяснить, при каких значениях х существует логарифм
(296-298).
296. 1) log6 (49 - х2); 3) log3 (2 - х - х2);
2)log7(jc2 + x-6); 4)log3(x2-3* + 2).
297. 1) log9 (х 2 + 4 х + 4); 4) logi (6 ж - 10 - х2);
2) log0 5 (i x2 + х +1); 5) logi (*2 + 4);
3) log5 (6x -x2- 9); 6) log;t (2x2 -x + 10).
95

у. О y fyY 4- Л- 4 ОС
298. 1) Iog0,5 2^1; 2) logH -^- ; 3) log36 ^ ; 4) log6
Решить уравнение (299-303).
299. 1) log^ (2x - 1) = 4; 2) log^ (3x - 4) = 6.
300. 1)2* = 5; 2) (1,2)* = 4; 3)34*=10; 4)23*=3.
301. 1)42*+3 = 5; 3)(1,3)3*"2=3;
\5f4x
302. 1)72*+7*-12 = 0; 5) 25*+2 5*-15 = 0;
2) 9* - 3* - 12 = 0;
3) 16* - 4*+1 -14 = 0; 7) 9*+1 - 3*+1 9 = -8;
303*. 1) (3* + 2 *) (3*+ 3 2*) = 8 6*;
2) (3 5* + 2,5 3*) (2 • 3*- 2 5*) = 8 15*.
304*. Выяснить, при каких значениях х имеют смысл выражения:
l)logx(2x-l);
305**. Найти все значения а, при которых уравнение
9*+9а(1-а) 3*"2-а3 = 0
имеет корни, и решить это уравнение.
§ 15. Свойства логарифмов
При выполнении преобразований выражений, содержащих
логарифмы, при вычислениях и при решении уравнений часто
используются разные свойства логарифмов. Рассмотрим основные из
них.
Пусть а>0, а * 1, Ь> 0, о 0, г — любое действительное
число. Тогда справедливы формулы:
Ь
\oga - =\ogab-\ogac,
logabr=rlogab.
(1)
(2)
(3)
96

О По основному логарифмическому тождеству
аХо^ь=Ьу (4)
aloe°c=c. (5)
1. Перемножая равенства (4) и (5), получаем
откуда по определению логарифма loga b + loga с = loga (be).
Формула (1) доказана.
2. Разделив равенства (4) и (5), получим
откуда по определению логарифма следует формула (2).
3. Возводя основное логарифмическое тождество aloga ь = b в
степень с показателем г, получаем
откуда по определению логарифма следует формула (3). •
Приведем примеры применения формул (1) — (3):
1) log6 18 + log6 2 = log6 36 = 2;
2) log12 48 - log12 4 = log1212 = 1;
g. Iog34 = Iog34 =7
Iog347 ^bg34
1
Задача 1. Вычислить log5 ^/jj - - log5 12 + log5 50.
А Применяя формулы (1) — (3), находим
1 Уз 50
log*; л/3 ~ о 1о£* 12 +1°£* 50 = log. т=~ = log. 25 = 2. А
3 а д а ч а 2. Доказать, что если а > 0, a * 1, b > 0, р Ф 0, то
к«вРЬ=р1ов«Ь-
А Пусть log р b = х, тогда по определению логарифма fr = ap*, а
loga ft = loga apx , по свойству (3) loga apx =px loga a = px,
следовательно, loga b =p • logap ft или logaP * = - loga ft- A
4-Ю. М. Колягин, 10 кл. 97

306.
307.
308.
309.
311.
Упражнения
Вычислить (306-310).
1) log8 16 + log8 4;
2)log68 + log627;
1) log2 15 - log2 — ;
2) log5 75 - log5 3;
1) log13 ^/169 ;
2) logn #121;
I)log812-log815 + log820;
2) log915 + log918 - Iog910;
3) | log7 36 - log7 14 - 31og7 $.
4) 2 logi 6 logi 400 + 3 log
3 2 3 i
5)4log! 3-f logi 27-2logx
2 2 2
6) | log10 0,001 + log10 ЩШ
n ioS38 . Зч log
logo 16
оч log5 27 . 4)
3)log122 + log1272;
4)log36 + log3-.
3) log! 54 - log! 2;
3 3
3) log! ^243 ;
3
1
4) log2 fi/
7 D2 6/190
21;
s
6;
3 ,
- - iog10 Vioooo.
;536-log512.
!lg578
Iog59 ' "*' Iog715-log730*
Найти x по данному его логарифму (а > 0, b > 0):
1) log3 x = 41og3 a + 7 log3 ft;
2) log5 x = 21og5 a - 31og5 b;
3) log! x = -logx a--
2 3 2 5
1 4
4) log2 x = -log2 a + -
3 4 3 7
2
6.
3
312. Выразить log2 x через log2 a, log2 b, log2 с, где a > 0, ft > 0, c> 0:
98

Вычислить (313-315).
to»«a4-jl0g'72
log318 - - log3 72 ' l0&2 20 + 3 log2 2'
3
log7 14 - i log7 56 3 log7 2 - i log7 64
2) ^ ; 4) \
log6 30 - - log6 150 41og5 2 + - log5 27
314. 1
2) I 81^"^Og94-h25log1258 |.49log72;
1
4) 72
315. I)log362-ilogl3;
* e
2) 21og25 30 + log0 2 6;
3) log^ 7 + log9 25 + log81 16 - log3 1470;
4) log0 01 0,64 + log100 0,16 + log^ V20 .
316. Выразить данный логарифм через логарифм с основанием 2:
1) log4 7; 2) logi 5; 3) log^ 15; 4) log8 0,1.
2
317. Доказать, что при а > 0, а * 1, х > 0, р * 0 справедлива
формула
logaPxp =logax.
318. Вычислить:
log±7
}
J Iog49 * J -31ogA2'
3
319. Выразить через аиЬ:
1) log^ 50, если log3 15 = a, log3 10 = b\
2) log4 1250, если log2 5 = a.
4*

320. Доказать, что при а > 0, а * 1, х1 * 0, х2 * 0 справедливы
формулы:
1) loga | ххх21 = logo | хх | + loga | х21;
2)logfl
Хл
loga
321. Решить уравнение:
4 = 2;
3) log^ 5 + log^ 64 = 3;
4) 2 log, 7 - ilog^ 16 + ^log^ 64 = 2;
5) logi 5 + logj_ 12 + - log, 3 = 1;
X X2
6) \ log, 7 - log_i_ 3 - log^ 28 = 1.
§ 16. Десятичные и натуральные логарифмы.
Формула перехода
Для логарифмов чисел составлены специальные таблицы
(таблицы логарифмов). Логарифмы также вычисляют с помощью
микрокалькулятора. И в том и в другом случае находятся только
десятичные или натуральные логарифмы.
Десятичным логарифмом числа называют логарифм этого
числа по основанию 10 и пишут lg b вместо log10 b.
Натуральным логарифмом числа называют логарифм этого
числа по основанию е> где е — иррациональное число,
приближенно равное 2,7. При этом пишут In b вместо loge b.
Иррациональное число е играет важную роль в математике и ее
приложениях. Число е можно представить как сумму
Вычисление числа е на микрокалькуляторе проводится по
программе
1 Ш 0 2,7182818.
100

Отметим, что в записи числа е « 2,718281828 после первого
десятичного знака 7 два раза подряд записан год рождения Л.Н.
Толстого.
Вычисления на микрокалькуляторе lg Ъ и In Ъ проводятся
соответственно по программам (если на МК есть специальные клавиши
F, lg и In):
Например, вычисляя lg 13, получаем
13 Ш [jg] 1,1139433;
вычисляя In 13, получаем
13 [F] [In] 2,5649493.
Оказывается, что достаточно знать значения только десятичных
или только натуральных логарифмов чисел, чтобы находить
логарифмы чисел по любому основанию. Для этого используется
формула перехода от логарифма по одному основанию к логарифму по
другому основанию
logca'
(1)
где&>0,а>0 а *1, с>0, с*1.
Докажем справедливость формулы (1).
О* Запишем основное логарифмическое тождество aogab = b.
Возьмем от обеих его частей логарифмы по основанию с
Используя свойство логарифма степени, получаем
logafelogca =logcfe, откуда 1о£а& = ^^- #
Из формулы (1) при с = 10ис = е получаются формулы
перехода к десятичным и натуральным логарифмам
I, . lgfe . . lnfe /оч
1о^Ь= l°gft= (2)
Из той же формулы (1) следует формула
log b= . (3)
101

Задача!..С помощью микрокалькулятора МК-54 вычислить
log3 80.
А 1) С помощью десятичных логарифмов
80 Ш\п$\ 3 ШШ S 3,9886927.
2) С помощью натуральных логарифмов
80 [F] [In] 3 [F] [In] 0 3,9886928.
Ответ. Iog380 = 3,99. A
Формула перехода от одного основания логарифма к другому
используется иногда при решении уравнений.
о
3 а д а ч а 2. Решить уравнение log2 jc + log4 x = - .
А По формуле перехода
1О*4* Iog24" 2 '
1 3
Поэтому уравнение примет вид log2 х + - log2 jc = -, откуда
3 а д а ч а 3. Решить уравнение log3 x + 2 log^ 3 = 3.
А По формуле (3) имеем log 3 = . Уравнение примет вид
х 1о£зх
2
log3 х + = 3 или (log3 х)2 - 31og3 х + 2 = 0. Решая это квадрат-
ное уравнение относительно log3 х, получаем: 1) log3 х = 1, хх = 3;
2)log3* = 2,*2 = 9.
Ответ. jcx = 3, jc2 = 9. A
3 а д а ч а 4. Двухпроцентный вклад в Сбербанк, равный а руб.,
через п лет становится равным а(1,02)'\ а трехпроцентный вклад
становится равным а(1,03)п. Через сколько лет каждый из вкладов
удвоится?
А 1) Для первого вклада 2а = а (1,02)л, откуда (1,02)л = 2,
п = logj 02 2. Вычисления проведем на МК-54:
2 [ЩЫ| 1,02 [F|[E| 0 35,002788.
2) Для второго вклада п = logj 03 2, и программа вычислений такова:
2 Щ[Ы| 1,03 [HGn| 0 23,449772.
Ответ. По первому вкладу приблизительно через 35 лет, а по
второму — через 23,5 года. ▲
102

Упражнения
Вычислить с помощью микрокалькулятора (322—323).
322. 1) lg 23; 2) lg 7; 3) lg 0,37; 4) lg |.
323. 1) In 81; 2) In 2; 3) In 0,17; 4) In - .
324. Выразить данный логарифм через десятичный и вычислить на
микрокалькуляторе с точностью до 0,01:
I)log725; 2)log58; 3)log90,75; 4)log0751,13.
325. Выразить данный логарифм через натуральный и вычислить
на микрокалькуляторе с точностью до 0,01:
1) log7 5; 2) log8 15; 3) log0 7 9; 4) loglд 0,23.
326. Выразить данный логарифм через логарифм с основанием 7:
I)log53; 2)lg6; 3)log27;
4)log5|; 5)lg7; 6) log3 7.
327. Дано: lg 2 - 0,301; lg 5 - 0,699; lg 3 - 0,477. Вычислить
приближенно:
I)log52; 2)log23; 3) log2 ^5;
4) log5 0,25; 5) log2 25 + log5 0,5; 6) log3 Vl25 + log5 27.
328. Вычислить:
Ig625
1)5^; 2)logi(log34 Iog23).
4
Решить уравнение (329—330).
329. 1) log5 x = 21og5 3 + 41og25 2; 4) log9 x2 + log^ x = 3;
5 x = 21og5 3 + 41og25
2) log3 x = 91og27 8 - 31og3 4; 5) log2 x + log8 x = 8;
3) log2 x- 21ogi x = 9; 6) log4 x - log16 x = -.
2 4
330. 1) log3 x + log9 x + log27 x = — ; 3) log3 x log2 x = 4 log3 2;
2) log3 jc+log^ x+logi ^ = 6; 4) log5 л: log3 x = 9 log5 3.
331. Дано: log3 17 = т. Найти: log3 51; log27 17; log27 51; 21og9 153.
332. Дано: log7 2 = т. Найти: log49 28.
333. Дано: lg 3 = m, lg 5 = п. Найти: log15 30.
334. Дано: log6 2 = т. Найти: log24 72.
335. Дано: log36 8 = т. Найти: log36 9.
336. Дано: log4 125 = т. Найти: log10 64.
103

337. Вычислить:
Iog3216 Iog324. Iog2192 Iog224
log8 3 log72 3 ' log12 2 log96 2 '
338. Выразить число с через а и Ь, если:
1) с = log900 600; а = log2 3, Ъ = log5 2;
2) с = log350 140; а = log5 2, Ь = log7 5.
Решить уравнение (339—340).
339. 1) log| х-9 log8 х = 4; 3) log| * + 5 log9 jc - 1,5 = 0;
2) log| *-151og27* + 6 = 0; 4)161ogf6 x + 3 log4 *- 1 = 0.
340. 1) log2 jc + 61ogx 2 = 5; 3) log^ x - 51ogx 3 = 9;
2) log5 x - Slogx 5 = 2; 4) 21ogx 3 - log^ x = 5.
341*. Вычислить (не используя микрокалькулятор):
Iog62 Iog43. 21og23.
J Iog56 Iog46' J Iog49 '
' Iog34
342. Найти:
1) logb (a3 fe), если loga b = 3; 2) loga (fe3 a), если logb a = 9.
343**. Число жителей города-новостройки увеличивается
ежегодно на 8%. Через сколько лет их число удвоится?
344**. При одном качании поршневого насоса из сосуда удаляется
1,2% имеющегося в нем воздуха. Через сколько качаний
насоса в сосуде останется т^п часть первоначальной массы
воздуха?
345**. Вычислить на микрокалькуляторе приближенное значение
числа е по формуле
2 23 234 2 34 ... л
при: 1) д= 7; 2)л = 8; 3)л = 9; 4)л=10.
346*. Известно, что при больших положительных значениях п чис-
(л JT
ло е можно приближенно находить по формуле е ~ 1+~~ .
I п)
Вычислить по этой формуле на микрокалькуляторе
приближенное значение числа е при: 1) п = 100 000; 2) п = 1 000 000.
104

§ 17. Логарифмическая функция,
ее свойства и график
Вы знаете, что выражение loga x определено при a > О, аФ1,х>0.
Пусть задано основание логарифма а > О, а Ф 1. Тогда каждому
х > О соответствует число у = loga x. Тем самым задана функция
I Функцию у = loga х, где а>0,а?1, называют логарифмической.
Логарифмическая функция обладает следующими свойствами:
Свойство 1. Область определения логарифмической
функции — множество всех положительных чисел, так как логарифм
определен только для положительных чисел.
Свойство 2. Множество значений логарифмической
функции — множество R всех действительных чисел.
О Пусть задано у е R. Тогда функция loga x принимает
значение у при х = ауу так как loga ay = у. Таким образом, любое
действительное число у принадлежит множеству значений
логарифмической функции. •
Задача 1. Построить график функции у = log3 x.
А Составим таблицу ее значений:
X
У = log3 х
1
9
-2
1
3
-1
1
0
3
1
9
2
27
3
Построим найденные точки и
проведем через них кривую, учитывая, что
функция у = log3 х определена при х > О
(рис. 35). А
У1
3-
1-
0_
-2-
v=log3x
y^T^i i i i i i
/13 9 х
Рис. 35
Задача 2. Построить график функции у = log! x.
"о
А Составим таблицу ее значений:
У =
X
logi х
3
1
9
2
1
col
1
1
0
3
-1
9
-2
27
-3
Построим найденные точки и
проведем через них кривую, учитывая, что
функция у = logi х определена при х> О
(рис. 36). А 3
У
з-
i-
0_
-2-
9
: х
"~ ;
V=l0g |Л'
я
Рис. 36
105

I Свойство 3. Логарифмическая функция у = loga x является
возрастающей, если а>1>и убывающей, если О < а < 1.
О Докажем, что при а > 1 функция у = loga x является
возрастающей. Рассмотрим любые два числа из области определения
данной функции, т.е. хх > О, х2 > 0.
Пусть хх < х2. Требуется доказать, что \oga хх < \oga x2.
По основному логарифмическому тождеству
Х-^ — а , х2 — а
По условию хх < xv поэтому aloga Xl < aloga *2 .
Из этого неравенства и из свойств степени с действительным
показателем и основанием а > 1 следует требуемое неравенство
loga хх < loga х2. Аналогично доказывается, что при 0 < а < 1
функция у = loga х является убывающей. •
Свойство 4. Если а > 1, то функция у = loga x принимает
положительные значения при х > 1, отрицательные — при
О < х < 1. Если 0 < а < 1, то функция у = loga x принимает
положительные значения при 0 < х < 1, отрицательные — при х> 1.
Это следует из того, что функция у = loga x принимает значение,
равное нулю, при х = 1 и является возрастающей на промежутке
х> 0, если а > 1, и убывающей, если 0 < a < 1 .
Из рассмотренных свойств логарифмической функции у = loga x
следует, что ее график расположен правее оси Оу и имеет вид,
указанный на рисунке 37, если а > 1, и на рисунке 38, если 0 < а < 1.
Отметим еще раз, что график любой логарифмической функции
у = \oga х проходит через точку (1; 0).
Рис. 37
106

I Свойство 5. Логарифмическая функция у = loga x и
показательная функция у = аху где а > О, а Ф 1, взаимно обратны
(рис. 39 а, б).
О Из формулы у = ах выразим х через у. По определению
логарифма у = loga у. Меняя местами х и у, получаем у = loga x. •
У
v—a ,
-1-
-1-
а>\
а)
\
\
v=a \
0<a< V
\
ь
0
A-
\
/v
Рис. 39
Так как функции у = loga хиу = ах взаимно обратны, то свойства
любой из них можно установить, зная свойства другой. Например,
множеством значений функции у = ах является множество у > О,
поэтому областью определения функции у = loga x является
множество х> 0; функция у = ах возрастает, если а > 1, поэтому функция
у = loga х также возрастает, если а > 1.
3 а д а ч а 3. Сравнить числа:
I)log53 и Iog56; 2) logi 3 и logi 5; 3)log35 и Iog53.
2 2
А 1) Так как 5 > 1, то функция у = log5 x возрастает и поэтому
log5 3< log5 6.
2) Так как 0< - < 1, то функция у = logi x убывает и поэтому
>log5 2
2 2
3) Заметим, что log3 5 > 1, так как log3 3 = 1 и функция у =
= log3 х возрастает. Аналогично log5 3 < 1, так как log5 5 = 1 и
функция у = log5 х возрастает. Поэтому log3 5 > log3 3. А
3 а д а ч а 4. Сравнить числа а и Ь, если:
I)a = 71og52, Ь = 3; 2)a=ilog465, fe = log5ll.
Al)a = log527 = log5128, fe = 3 = log5125, a > b.
107

2)a=-log465; 2a = log465; fe = log5ll; 2fe = 21og5ll = log5121;
Iog465 > Iog464 = 3; Iog5121 < Iog5125 = 3. Таким образом,
2a = Iog465 > 3, 2b = Iog5121 < 3, следовательно, а > b. A
Задача 5*. Построить график функции:
A 1) График функции у = \ogs(x + 2) получается сдвигом
графика функции у = log3 х влево вдоль оси Ох на 2 единицы, так как
эти функции принимают одинаковые значения, если аргумент
первой из них на 2 единицы меньше соответствующего аргумента
второй, т.е. log3(JC0 + 2) = log3 xv если х0 + 2 = хх или х0 = хх - 2
(рис. 40, а).
2) График функции у = 2 + logi x получается сдвигом графика
ъ
функции у = logi х вверх вдоль оси Оу на 2 единицы, так как при
3
одном и том же значении х значение первой функции на 2 больше
значения второй функции (рис. 40, б). А
У.
2-
1-
2-
1-
/\
1 »■
2 3 х
б)
Рис. 40
Упражнения
347. Построить график функции:
1) У = log2 х; 2) у = logi #.
2
Какие из данных функций являются возрастающими?
убывающими? При каких значениях х каждая функция
принимает положительные значения? отрицательные значения?
значения, равные нулю?
108

348. По графику функции у = log2 x найти приближенно:
Iog23; Iog20,3; log2 5; Iog20,7.
349. Изобразить схематически график функции:
2) y = lognx; 4)y= logi x.
о
350. Сравнить числа:
1) log3 - и log3 -; 3) log! в и log! я;
DO 2 2
2) logi 9 и logi 17; 4) log2 ^ и log2 ^ .
3 3 Z Z
351. Выяснить, является ли положительным или отрицательным
число:
1) log3 4,5; 2) log3 0,45; 3) log5 25,3; 4) log0 5 9,6.
352. Сравнить с единицей число х> если:
1) log3 х = -0,3; 3) lg x = 0,2;
2) logi * = 1,7; 4)log2jc = l,3.
з
353. Выяснить, является ли возрастающей или убывающей
функция:
1) у = log0 075 х; 2)у= log^ x; S)y = lg х; 4) у = In x.
2
354. Решить графически неравенство:
1) log3 х > 3; 2) log2 x < 1; 3) logi * < 2;
2
4) log! jc> 1; 5)log5 jc > -1; 6) logi x<-2.
2 2
355. Найти область определения функции:
1) У = log3 (x - 2); 3) у = log5 (x2 - Sx);
2)у = log0 5 (2 + *); 4) у = log^ (9 - х2).
356. Доказать, что:
1) функция у = log2 (х2 - 1) возрастает на промежутке х> 1;
2) функция у = logi (#2 ~ 1) убывает на промежутке х > 1.
2
357. Сравнить числа а и Ь, если:
1) а = log5 6 + log6 5, b = 2; 3) а = 21og2 7, fe = 1 + 21og2 5;
2) а = log9 36, & = log36 288; 4) a = log3 5, b = log2 3.
109

358. Сравнить значения выражений:
1) | + Ig3 Hlgl9-lg2; 3)3(lg7-lg5)H2filg9-|lg8J;
2)lg5^gV7Hlg5^; 4)lg(lg4)Hlgl.
359. Сравнить числа а и Ь, если:
2) а =
360. Построить график функции:
l)y = logz(x-l); 4) j/=
з
2)i/=logi(* + l); 5) y= l + log3(*-l);
з
3) y = l + log3x; 6) i/=logi (* + l)-l.
з
361. Найти область определения функции:
= log8 (x2 - 3* - 4); 5) у = log0 з (| 4* - *21);
= log7(2x2-7\x\
= 1°g(),7
x2-4
x + 3
x-4 *
4) у = logi -~2 ; 8) у = log3 (2X l - 4).
362*. Решить графически уравнение:
1) log2 x = - x + 1; 5) lg x = 4x ;
2) logx
2
3) logi
2
4)log3
x =
x =
x = \
2x-
Axh
'-\
5;
xh
7)log2(jc-2)=|;
2
363*. Построить график функции:
1) у = | log3 * |; 4) у = 11 - log2 x |;
8
3) у = log2 | 3 - x |; 6) у = 3log3 (3-*> + 5log5 (1-*>.
364*. Показать, что графики функций i/ = log2 x и y= logi л:
симметричны относительно оси абсцисс. 2
110

365*. Найти область определения функции:
l)i/ = log21 3 - jc | - log2 | jc3 - 81;
2)y = log0S ViTl + log04(l-8*3).
§ 18. Логарифмические уравнения
При решении логарифмических уравнений часто используется
следующая теорема.
IT е о р е м а. Если loga хх = loga х2, где а > О, а Ф 1, хг > О, х2 > О,
то хг = х2.
О Предположим, что хх Ф х2. Если а > 1, то из неравенства
хх < х2 следует, что loga хх < loga х2; если 0 < а < 1, то из
неравенства хх < х2 следует, что loga xx > loga x2. В обоих случаях имеем
противоречие с условием loga xx = loga x2. Следовательно, хх = х2. •
3 а д а ч а 1. Решить уравнение log5 (Зх - 2) = log5 7.
А Используя доказанную теорему, получаем Зх - 2 = 7, откуда
3 а д а ч а 2. Решить уравнение
А Следствием уравнения (1) является уравнение
Умножая это уравнение на jc + 1, получаем
jc + 9 = *(* + 1), (3)
которое является следствием уравнений (1) и (2). Решая уравнение
(3), находим х + 9 = х2 + х, х2 = 9, откуда хх = 3, х2 = -3. Проверка
показывает, что корнем исходного уравнения (1) является только
*1 = з.
Ответ. х = 3. А
При решении логарифмических уравнений также часто
переходят от уравнения loga f(x) = Ьк уравнению f(x) = ab, где а > 0, а Ф 1.
Теорема. Пусть а > 0, а Ф 1. Пусть дана функция у = f(x)
и действительное число Ъ. Тогда уравнение
logj(x) = b (4)
и уравнение
f(x) = ab (5)
равносильны.
111

О Докажем, что каждый корень уравнения (4) является корнем
уравнения (5) и, наоборот, каждый корень уравнения (5) — корень
уравнения (4).
1) Пусть х0 — некоторый корень уравнения (4), т.е. f(x0) > 0 и
равенство loga f(x0) = b верное. Тогда по определению логарифма
верно равенство f(x0) = аь, т.е. х0 — корень уравнения (5).
2) Пусть х0 — некоторый корень уравнения (5), т.е. верно
равенство f(x0) = аъ. Так как а > О, а Ф 1, то f(x0) > 0 и по
определению логарифма верно равенство loga f(x0) = Ъ, т.е. х0 — корень
уравнения (4). •
3 а д а ч а 3. Решить уравнение log3 (х2 + х + 3) = 2.
А Исходное уравнение равносильно уравнению х2 + х + 3 = З2,
откуда х2 + х - 6 = 0.
Решая это квадратное уравнение, находим корни хх = 2, х2 = -3.
Ответ: хх = 2, х2 = -3. А
Рассмотрим часто используемые преобразования
логарифмического уравнения, которые заменяют данное уравнение его
следствием.
1. Если в уравнении сумму логарифмов двух выражений
заменить логарифмом их произведения, то полученное уравнение
будет следствием данного.
Поясним на примере уравнения
logaf(x) + logag(x) = b. (6)
О Если х0 — корень уравнения (6), то по определению
логарифмов f(x0) > 0, g(x0) > 0. Поэтому f(x0) g(x0) > 0 и выполняется
равенство loga f(x0) + logfl g(x0) = loga [ f(x0) ■ g(x0)]. Следовательно,
x0 — корень уравнения
loga[/W g(x)] = b9 (7)
т.е. уравнение (7) — следствие уравнения (6). •
Отметим, что уравнение (7) может иметь корень, который не
является корнем уравнения (6). Это объясняется тем, что
неравенство f(x) • g(x) > 0 может выполняться не только при f(x) > 0,
g(x) > 0, но и при f(x) < 0, g(x) < 0.
3 а д а ч а 4. Решить уравнение
Iog2(l-x) = 3-log2(3-x).
А Перенесем логарифм из правой части в левую:
log2(l-Af) + log2(3-x) = 3,
откуда
Iog2(l-x)(3-x) = 3,
112

Решая это уравнение, получаем хх = 5, х2 = -1.
Число хх = 5 не является корнем исходного уравнения, так как
при х = 5 левая и правая части уравнения теряют смысл. Проверка
показывает, что число х = -1 является корнем исходного уравнения.
Ответ. х = -1. А
2. Если в уравнении разность логарифмов двух выражений
заменить логарифмом их частного, то полученное уравнение будет
следствием данного.
3 а д а ч а 5. Решить уравнение
log4 (xs -x)- log4 x = log4 3. (8)
А Заменяя разность логарифмов логарифмом частного,
получаем уравнение
о
^=log43, (9)
которое является следствием уравнения (8).
Уравнение (9) равносильно уравнению
Решая это уравнение, находим его корни хх = 2, х2 = -2.
Проверкой убеждаемся, что хх = 2 — корень уравнения (8), ах2 = -2 не
является корнем уравнения (8).
Ответ. х = 2. ±
При решении задачи 5 посторонний корень х2 = -2 появился
при переходе от уравнения (8) к уравнению (9), т.е. оба уравнения
неравносильны.
Отметим, что при решении логарифмических уравнений
замена логарифма произведения (частного) суммой (разностью)
логарифмов может привести к потере корней.
Например, уравнение log2 (х + 1) (х + 3) = 3 имеет два корня хх = 1
и х2 = -5, а уравнение log2 (х + 1) + log2 (х + 3) = 3 имеет только
один корень хх = 1. При переходе от первого уравнения ко второму
теряется корень х2 = -5.
Рассмотрим еще примеры логарифмических уравнений.
3 а д а ч а 6. Решить уравнение
*2 = 4. (10)
А По определению логарифма это уравнение равносильно
уравнению х2 = 74, откуда х = ±72 = ±49.
Ответ. хх 2 = ±49. ▲
113

Отметим, что уравнение (10) нельзя заменять уравнением
21og7 х = 4, так как при этом теряется корень х = -49. Однако
уравнение (10) равносильно уравнению 21og7 | x | = 4, откуда \х\= 49,
х = ±49.
3 а д а ч а 7. Решить уравнение
log4 (2* - 1) log4 x = 21og4 (2x - 1). (И)
А Преобразуем данное уравнение
log4 (2х - 1) log4 х - 21og4 (2x - 1) = 0,
Iog4(2*-l)(log4*-2) = 0.
Приравнивая каждый из множителей левой части уравнения
нулю, получаем:
1) log4 (2х - 1) = 0, откуда 2х - 1 = 1, хг = 1;
2) log4 х - 2 = 0, откуда log4 * = 2, *2 = 16.
Проверка показывает, что оба значения х являются корнями
исходного уравнения.
Ответ. хг = 1, х2 = 16. ▲
Отметим, что если обе части уравнения (11) разделить на
выражение log4 (2х - 1), то будет потерян корень х = 1.
3 а д а ч а 8*. Найти все значения а, при которых уравнение
log2 х + loga x + log4 x =1 имеет корни.
А Перейдем к основанию 2
Следствиями этого уравнения будут уравнения
log2 a log2 х + log2 x + - log2 x log2 a = log2 a,
-log2 a +1 • log2 jc = log2 a, log2 jc2 = log2 a, x2 = a,
^ )
откуда x = aslog2a+2 . Так как параметр а стоит в основании логариф-
2
ма, тоа> 0, а*1, т.е. 31og2a + 2^0 иа± 2 3.
2
Ответ. При а>0, а^1, аФ 2 * . А
114

Упражнения
Решить уравнение (366—375).
366. 1) log3 (5* - 1) = 2; 4) log7 (x + 3) = 2;
2) log5 (Зх + 1) = 2; 5) lg(3* - 1) = 0;
3) log4 (2х - 3) = 1; 6) lg (2 - 5х) = 1.
367. 1) log3 (5* + 3) = log3 (7x + 5);
2) logi (3x-l)=logi (6*+ 8).
368. 1) log2 ^ = log2 *; 3) ^|
2) logl -^- = logl x; 4) lg^i = lg*.
2 2 * ~~
369. I)log4(x2-x) = l; 4) log2 (x2 + 2x - 4) = 2;
2) log7 (x2 + 3x) = 2; 5) logi (д;2 + Зд; - 6) = -2;
2
3) log3 (x2 - 4* - 2) = 1; 6) log! (x2 -5x + 33) = -3.
з
370. l)log2(*-5) + log2(x +2) = 3; 3)lg(x+ у/з ) + lg(x- S
2)log3(x-2) + log3(* +6) = 2; 4)\g(x- l) + lg(x + l) = 0.
371. I)lg(;c-l)
3) log7 (2*2 - 7x + 6) - log7 (jc - 2) = log7 *;
4) lOgg (X3 -X)- lOgg X - lOgg 3.
372. I)\lg(x + x5) = lg5x + lg;
373. l)log5*2 = 0;
2)log4*2 = 3;
374. 1) log7 (x - 1) log7 д; = log7 x;
2) logi x logi (3* - 2) = logi (3x - 2);
3 3 3
3) log2 (3* + 1) log3 x = 21og2 (Зд; + 1);
4) log^ (x - 2) log5 x = 21og3 (x - 2).
375. I)lgx4 + lg4x = 2 + lgx3; 2) lgд; + lg x2 = lg 9x.
115

Решить уравнение (376-388).
376. 1) log4 (x + 2)(х + 3) + log4 ~ = 2; 3) log3 x2 - log3 ~ = 3;
2) log2 |^4 + 1{*2 (* " !Х* + 4) = 2; 4) log2 ~ + log2 *2 = 5.
377. 1) 231ех -5lg* =1600; 3) —|— + ^г~
4+lgx 2-lgx
2) 2log3 х* 5log3 * = 400; 4) —{— + ^-f—
5-lg* 1+lgx
378. 1) logf (* " 1)" 3bg2 (jc - 1) = 4;
379. 1) log3 (x - 1) + 21og9 (17 + x) = 7 + logi 9;
з
2) log3 * + log^ x - logi л; = 6;
з
3) log^2 x + 4 log^ ac + logg * = 16;
4) log 0 5(x + 2) - log2 (x - 3) = |log! (-4x - 8).
2 V2
380. l)*lga:=10; 4) х31
3) ОД я16*'3 =1000; 6)д;" 2 =8.
381. I)log2*-21og;c2 = -l; 3)log3A;
2) log2 x + log^ 2 = 2,5; 4) log3 x - 61ogx 3 = 1.
382*. 1) log^ 9 + log^ 4 = 2; 2) log^ 16 - log^ 7 = 2.
383*. 1) lg (6 5* - 25 20*) - lg 25 = x;
2)\g(2x + x + *) = x - x\gb.
384. Dl+loge^ilog^-l)2; 2)
385. 1) \ogx_2 (x - 4) - log^, (7 - x) = 0;
2) 1<*Л7х_з Д:2 + log^ (*2 + 7д: - 3) - 2 = 0;
3) log^j (2x - 3) = Iog2;c.3 (2x - 1);
4) log;e+1 (д: - 0,5) = logx_05(x + 1).
386*. 1) lg2 (x + 1) = lg (x + 1) lg(* - 1) + 21g2 (x - 1);
2) 21og5 (4 - x) Iog2x(4 -x) = 31og5 (4-х)- log5
116

387*. 1) log4 [log3 (log2 x)] = \ ; 2) log2 [log9 (logf (x - 3))] = 0.
388*. 1) ^log.,.25 + 3 = -—; 2) yJ2logl x + 31og2 x-5 = log2 (2x).
389*. Найти все значения параметра а, при которых уравнение
51og5 х + \oga x - 41og25 x = а имеет корни, и решить это уравнение.
§ 19. Логарифмические неравенства
При решении логарифмических неравенств часто используется
следующая теорема.
IT е о р е м а. Пусть а > 0, а Ф 1, хг > 0, х2 > 0. Если
loga хх < loga х2у то хх < х2 при а > 1 и хх > х2 при 0 < а < 1.
О Пусть, например, а > 1. Предположим, что неравенство
jCj < jc2 не выполняется, т.е. хг > х2. Тогда по свойству возрастания
функции у = loga х при а > 1 должно выполняться неравенство
loga xx > loga x2, что противоречит условию. •
Задача 1. Решить неравенство log2 х < 3.
А Заменяя 3 на log2 8, запишем неравенство в виде
log2 х < log2 8.
Так как функция у = log2 x определена при х> 0 и возрастает, то
неравенство log2 x < log2 8
выполняется тогда и только тогда, когда х > 0 и
х<8, т.е. приО<*<8.
Ответ. 0<jc<8. A
Графически решение неравенства
log2 х < 3 сводится к нахождению тех
значений х, при которых точки
графика функции у = log2 х лежат ниже
прямой у = 3 (рис.41, а). Рис- 41> *
Задача 2. Решить неравенство logi x>-2.
з
А Так как -2 = logi 9, то данное неравенство примет вид
з
logi x> logi 9.
з з
Функция у = logi х определена при х > 0 и убывает, так как
1 з
0 < - < 1. Следовательно, неравенство logi x> logi 9 выполняется
d зз
тогда и только тогда, когда 0 < х < 9.
Ответ. 0<*<9. А
117

3 а д а ч а 3. Решить неравенство
lg(*+l)<2. (1)
А Правая часть данного неравенства имеет смысл при всех
значениях ху а левая часть — при х + 1 > 0, т.е. при х> -1.
Промежуток х > -1 называют областью определения неравенства (1). Так
как логарифмическая функция с основанием 10 возрастающая, то
неравенство (1) при условии х + 1 > 0 выполняется, если х + 1 < 100
(так как 2 = lg 100). Таким образом, неравенство (1) равносильно
системе неравенств
Г*>-1,
[jc + KIOO, (2)
т.е. неравенство (1) и система (2) имеют одно и то же множество
решений. Решая систему (2), находим -1 < х < 99. А
Приведем примеры решения более сложных логарифмических
неравенств. Обычный способ решения таких неравенств
заключается в переходе от них к более простому неравенству или системе
неравенств, имеющей то же самое множество решений.
Например, неравенство lg (х + 1) < 2 имеет то же множество
решений, что и система неравенств
Г
3 а д а ч а 4. Решить неравенство
log2(*-3)<l-log2(*-2). (3)
А Логарифмическая функция определена при положительных
значениях аргумента, поэтому левая часть неравенства имеет
смысл при х - 3 > 0, а правая часть — при х - 2 > 0.
Следовательно, обе части неравенства одновременно имеют
смысл при х > 3. Поэтому в дальнейшем будем считать, что х > 3.
Неравенство (3) при х> 3 можно записать так:
log2 (х - 3) + log2 (х - 2) < 1
или
log2(*-3)(*-2)<log22. (4)
Логарифмическая функция с основанием 2 возрастающая.
Поэтому при х> 3 неравенство (4) выполняется одновременно с
неравенством
(х-3)(х-2)<2.
Таким образом, исходное неравенство (3) равносильно системе
неравенств |(я-8Х*-2)<2,
1*>3. (5)
118

Преобразуем первое неравенство системы (х - 3)(х - 2) < 2,
х2 - Ъх + 6 < 2, х2 - Ъх + 4 < 0.
Решая квадратное неравенство, получаем 1 < х < 4.
Учитывая, что х> 3, получаем 3 < х < 4.
Ответ. 3<*<4. А
Обычно при решении логарифмического неравенства сначала
находят область определения данного неравенства.
3 а д а ч а 5. Решить неравенство
logi (х + 15) > logi (x - 1) - 2. (6)
3 3
А Найдем область определения данного неравенства. Логарифм
в левой части неравенства имеет смысл при х > -15, логарифм в
правой части — при х > 1. Следовательно, оба логарифма
определены при х > 1, т.е. область определения неравенства (6) — луч х> 1.
При х> 1 неравенство (6) можно записать в виде
logi (* + 15)- logi (x-l)> logi 9,
з з з
т.е.
, # + 15
log
> logi 9.
3 Х Х 3
Так как основание логарифма — < 1, то при х > 1 имеем
о
<9
JC-1
Таким образом, неравенство (6) равносильно системе
(7)
Умножим обе части первого неравенства системы на х - 1, при
этом знак неравенства не изменится, так как х - 1 > 0. Получим
Следовательно, неравенство (6) равносильно системе
>1, т.е. системе
Ответ. x>Z. ^
119

3 а д а ч а 6. Решить неравенство
(8)
Область определения неравенства находится из условия
*2 + 2*-8>0.
Неравенство (8) можно записать в следующем виде:
logi (*2 + 2*-8)> log! 16.
2 2
Так как логарифмическая функция с основанием - является
Li
убывающей, то для всех х из области определения неравенства
получаем
*2 + 2*-8<16.
Таким образом, исходное неравенство (8) равносильно системе
неравенств
О
Jjc2+2x-8>0,
1
-4
-6
Рис.
'///A
Рис.
2
41,6
0
41,e
//////At
X
/\ ^
4 x
или
_6 -4 0 2 4 х
Рис. 41, г
Решая первое квадратное
неравенство, получаем х < -4, х > 2 (рис.
41, б). Решая второе квадратное
неравенство, получаем -6 < х < -4 (рис.
41, в). Следовательно, оба
неравенства выполняются
одновременно при -6 < х < -4 и при 2 < jc < 4
(рис. 41, г).
О т в е т. -6 < х < -4, 2 < х < 4. А
3 а д а ч а 7*. Решить неравенство
3 - х < log5 (20 + 5*).
А Данное неравенство равносильно каждому из следующих
неравенств:
log5 53х < log5 (20 +5*), 53* < 20 + 5*, Ъ2х + 20 5* - 125 > 0,
(5х - 5)(5* + 25) > 0, 5х > 5, откуда х>1.
Ответ. х> 1. А
3 а д а ч а 8*. Решить неравенство при разных значениях а:
loga* + logfl(*+l)>2. (9)
120

А Областью определения неравенства являются все
действительные значения х > 0, параметр а может принимать значения: а > О,
а Ф 1, так как стоит в основании логарифма.
При всех # > О, а > 0, а * 1 данное неравенство можно
представить в виде
loga(*(* + l))>logaa2. (10)
Рассмотрим два возможных случая решения неравенства: при
а> 1и0<а< 1.
1) Если а>1, tojc>Oh х(х + 1) > а2, так как логарифмическая
функция с основанием больше единицы возрастающая. То есть
неравенство (10) равносильно системе неравенств
1 (11)
\х(х-1)>а2.
Уравнение х2 + х - а2 = 0 имеет корни хх =
х2 = ^г , где хх < 0, х2 > 0. Следовательно, множество ре-
/,,ч -1 + V1 + 4O2
шении системы (11) — промежуток х > х2, или х > — .
2) Если 0<а<1,тол:>0и х(х + 1) < а2, так как
логарифмическая функция с основанием меньше единицы убывающая. То есть
неравенство (10) равносильно системе неравенств
\( 1)2
Множество решений неравенства х2 + х - а2 < 0 — интервал
(хг; х2)9 а решением системы будет лишь интервал (0; х2).
Ответ. Нет решений при а < 0, а = 1; х> - при а > 1;
-l + Jl + 4a2
О <л: < ^ приО<а<1. А
Упражнения
Решить неравенство (390—391).
390. 1)log5 jc> log5 3; 3)lgjc<lg4;
2) log! x < logi |; 4) In x> In 0,5.
5 5 8
391. 1) log3 x < 2; 3) logi * > 16;
2
121

392. Найти область определения функции:
l)y = lg(Sx-2); 3)y=logi (х2~2);
2
2) у = log2 (7 - 5jc); 4) у = log7 (4 - х2).
Решить неравенство (393—395).
393. 1) log3 (х + 2) < 3; 4) log! (* - 1) > -2;
з
2) log8 (4 - 2х) > 2; 5) log! (4 - 3*) > -1;
5
3) log3 (x + 1) < -2; 6) logz (2 - 5x) < -2.
g3
з
394. I)lg*>lg8 + 1; 3)log2(x-4)<l;
2) lg x > 2 - \g 4; 4) logi (3x - 5) > logi (x + 1).
5 5
395. 1) log15 (x - 3) + log15 (x - 5) < 1;
2) logi (x - 2) + logi (12 - *) > -2;
3 3
3)lg(3*-4)<lg(2;c + l);
4) logi (2* + 3)> logi (x+1).
2
396. Найти область определения функции:
5)y=Jlgx+\g(x+2);
6)у=
Решить неравенство (397—411).
397. 1) log5 Щ=£ > 0; 2) log, ^^ < °-
2 % *
398. 1) log8 (х2 - 4х + 3) < 1; 3) log3 (х2 + 2х) > 1;
2) log6 (д:2 - Зх + 2) >1; 4) loga (х2 - 2,5х) < -1.
з
399. 1) lg (х2 - 8х +13) > 0; 3) log2 (*2 + 2*) < 3;
2) logi (х2 - Ъх +7) < 0; 4) logi (*2 - 5* - 6) > -3.
5 2
400. 1) log0 2 * - log5 (x - 2) < log0 2 3;
2) lg * - log0л (x - 1) > log0 j 0,5.
122

401. 1) logi bg2 x2 > 0;
2) log3 logi (*2 - 1) < 1.
402. 1) \ogl>2 x - 51og0 2 x < -6;
2) log^ x + 31og0л *> 4.
403.
404.
5-lgx 1+lgx
^ + -^— <1.
lg* 1-lgx
2)log2(6
4 - x.
405. 1) log3 (26 + 3-*) < x + 3; 2) log2 (3 - 4*) < log2 11 - 2x - 4.
406*. 1) log^2 з (4х + 7) > 0;
2)logx.i (л/б-2х) <0;
407*.
408*.
409*.
3)
4)
(3x + 6) < 1;
- 2) > -1.
S1"37 -1 + 2J < 4|4*- 1|.
7
-1 9*-2*
410*. 1) log|3;c+2| x2 > 2;
2) log|2;c+1| д:2 > 2.
x +
411*. 1) 7log3 (9* +18) < log3 (x + 2); 2)
412*. Решить неравенство при различных значениях а:
l)loga(*~
Упражнения к главе IV
Вычислить (413-417).
413. I)log15225; 2)log4256;
2 >
VI-
3)iog3^;
414. 1) logi 64;
415. l)lognl;
416.
2) logi 81;
з
2)log77;
417. 1) 41ogi 3-flogi 27-logi 6;
2 6 2 2
3) logi
5 27'
3) log16 64;
3) 5"log53;
4)1ое7з1з
4) logi ^r.
-2 64
4)log279.
/1
4)
2) |lg 0,001+lg ^/1000--lgJlOOOO.
3 5
123

418. Сравнить числа а и Ь, если а = 21og3 4, Ъ = 3 log х — .
27 17
419. Вычислить с помощью микрокалькулятора:
1) log8 7; 2) Iog312; 3) loglf8 0,17; 4) log0 381.
420. Построить графики функций:
l)y = log4x; 2)у = logi x.
4
Какая из данных функций является возрастающей?
убывающей? При каких значениях х каждая функция принимает
положительные значения? отрицательные значения? значения,
равные нулю?
421. Выяснить, является ли возрастающей или убывающей
функция:
l)y = log02x; 2)y=\og^x; 3) i/= logi *; 4)y=log^x.
e T
422. Решить графически уравнение:
1) log3 x = 5 - x; 2) logi x = Sx.
з
423. Найти область определения функции:
1) У = bg7 (5 - 2х); 2)у = log2 (х2 - 2х).
Решить уравнение (424—426).
424. 1) log3 (3* - 1) = 2; 3) 2 logi x = logi (2*2 - х);
2 2
2) logi (7 - Sx) = -2; 4) lg (x2 - 2) = lg x.
2
425. 1) lg (x2 - 2х) = lg 30 - 1; 3) lg2 x - 31g x = 4;
2) log3 (2x2 + x) = log3 6 - log3 2; 4) log| x - 51og2 x + 6 = 0.
426. 1) log2 (x - 2) + log2 (x - 3) = 1;
2)log3(5-*)
4)
Решить неравенство (427—429).
427. 1) log2 (x - 5) < 2; 3) logi (2x + 1) > -2;
2
2) log3 (7 - jc) > 1; 4) logi (3 - 5*) < -3.
2
428. 1) log3 (5 - 4*) < log3 (x - 1); 2) log0 3 (2x+ 5) > log0 3 (x + 1).
429. l)lg(*2 + 2* + 2)<l; 2) log3 (jc2+7jc - 5) > 1.
124

ПРОВЕРЬ СЕБЯ!
1. Вычислить:
log5 125; lg 0,01; 2log2 3; 321og3 7; log2 68 - log2 17.
2. Построить схематически график функции:
У = 1о£о,2 х> У = 1о^2 х-
3. Сравнить числа:
log0 2 3 и log0 2 2,5; log2 0,7 и log2l,2.
4. Решить уравнение:
Iog5(3* + 1) = 2;
log3(* + 2) + log3* = l;
In (x2 - 6* + 9) = In 3 + In (x + 3).
5. Решить неравенство:
log3 (*-!)< 2; log! (2-*)>-!.
Вычислить (430-431).
; 2
4) 3,6log3'6l0+1; 5) 21og5 S + 31og2 8; 6) log2 log2 log2 216
431 1) 1Og53° log5l5°; 2) Iog342 Iog3378
Iog305 Iog65 ' Iog1263 Iog143 '
432. Сравнить числа:
21og25+logi9
l)log!- nlogi-; 2)2 ~9 ил/8.
2 6 3 Z
433. Упростить выражение .
434. Выразить log30 64 через числа a = lg3n fe = lg5.
435. Выразить log30 8 через числа a = lg5n fe = lg3.
436. Выразить log175 56 через числа а = log14 7 и b = log14 5.
437. Найти значения х, при которых справедливо неравенство:
1) log^ 8 < log^ 10; 2) log^ -- < log^ - .
438. Решить графически уравнение:
1) Iog3*= ?; 2)2^= logi x.
x
2
125

Решить уравнение (439—445).
439. 1)34* = 10; 2) 23х = 3; 3) 1,33*"2 = 3;
5)16*-4*+1-14 = 0; 6)25Л
440. 1) log3 x + log9 x + log27 x = —;
2)
i л:=6;
з
4) (J) = 1,5;
2 5х-15 = 0.
3) log3 jc • log2 x = 41og3 2;
4) log5 x - log3 x = 91og5 3.
2)log3log2log4(*2-48) = 0.
442. 1) log3 (2 - x2) - log3 (-д;) = 0;
2)log5(*2-12)-log5(-;c) = 0;
3)log2 y/x-3 + log2 у/Зх-7 = 2;
4) lg(x + 6) - lg y/2x-3 = Ig4.
443. 1) log^ л + 41og4 x + log8 x = 13;
2)log05(x + 2)-log2(;c-3)=
444. 1) log! 5 + log x 12 + - log^ 3 = 1;
7 2
2) - log^ 7 - logA 3 - log^ 28 = 1;
3)61og4;c2-51og;c2 = 0;
4)log5-
(-4*-8).
445. l)log2
3)lg
x+8
—
2)
10
2 i X
= log! x;
X—
Решить неравенство (446—448).
446. 1) logjg (x - 4) + log^ (x + 1) < 2;
2) log^ (jc - 5) + log^ (jc + 12) < 2;
3) log3 (8jc2 + jc) > 2 + log3 x2 + log3 jc;
4) log2 x + log2 (x - 3) > log2 4;
5)
(x- 10)- logi (* + 2)>-l;
5 5
6) log± (л:+10)+ log! (jc + 4)>-2.
V7 77
126

447*. 1) 41og4 x - SS\ogx 4 < 1; 2) logx 3 < 4 1 + logi x .
{ J
448*. 1) log! flog2 -itf" 1 > 0; 2
2\ 1 + 1,0* j 3
449*. Доказать, что если последовательность положительных
чисел является геометрической прогрессией, то их логарифмы по
одному основанию образуют арифметическую прогрессию.
450*. Найти три последовательных члена геометрической
прогрессии, если их сумма равна 62, а сумма их десятичных
логарифмов равна 3.
451*. Построить график функции:
Решить уравнение (452—454).
452**. 1)a;1s9 + 91s* = 6; 2)
453**. 1) 3 + 2logx+1 3 = 21og3 (x + 1);
454**. 1) log2 (2х - 5) - log2 (2* - 2) = 2 - *;
2) log2 (2'+ 1) ■ log2(2x+l + 2) = 2;
4) log3;c+7 (5* + 3) = 2 - log5;c+3 (3* + 7).
Решить неравенство (455—456).
455**. 1) logi (2X+2 - 4*) > -2; 2) logj_ (6*+1 - 36*) > -2.
456**.
457**. Решить уравнение:
jc+4.
2) log2 * • log2 (x - 3) + 1 = log2 (*2 - Sx).
458**. Найти все значения а, при которых уравнение 1&кил') = 2
имеет только один корень.
459**. Решить неравенство н ъ— < 1.
logax-l loga;<r + l
127

Историческая справка
Еще древнегреческий ученый Архимед в III в. до н.э. в своем
сочинении «Псаммит» («Исчисление песчинок») рассматривал
последовательность степеней одного и того же числа (основания):
а0, а1, а2, а3, ... ,ал,...
и высказал утверждение, которое в современной символике
выглядит как
ап- ат —ап+т.
Идея сведения действия умножения чисел, представленных в
виде степеней одного и того же числа, к сложению их показателей
появлялась в математических исследованиях ученых отвлеченно и
вплоть до XVI—XVII вв. и не находила реального применения.
В эти века практика поставила перед математиками задачи
упрощения громоздких вычислений, связанных с расчетами сложных
процентов в финансовом, страховом и кредитном делах.
Вычислительные средства тогда были ограничены — использовались в основном
операции с целыми числами и обыкновенными дробями, а
десятичные дроби только входили в практику.
Чтобы воспользоваться обозначенной идеей, нужны были
таблицы, в которых сопоставлялись бы последовательности степеней
чисел с последовательностями их показателей. Первые таблицы
сложных процентов составил в начале XVII в. нидерландский
ученый и инженер С. Стевин. Эти таблицы были аналогичны по
структуре таблицам логарифмов, которые практически одновременно
закончили составлять швейцарец И. Бюргли (1552—1632) и
англичанин Дж. Непер (1550—1617). Однако автором изобретения
логарифмов и составителем первых таблиц логарифмов история считает
Непера, так как он раньше Бюргли опубликовал (в 1614 г.) свою
работу в этой области под названием «Описание удивительной таблицы
логарифмов». Следует отметить, что термин «логарифм» первым в
употребление ввел также Непер (слово «логарифм» возникло из
сочетания греческих слов ho'yoc — отношение и apiGjio'o — число).
Для десятичной системы счисления, которой мы пользуемся,
самым удобным основанием для таблиц логарифмов является число
10. Действительно, любое положительное число N можно
представить в стандартном виде N = а 10л (п — целое число, 1 < а < 10).
Так как порядок числа легко определяется, то для нахождения
логарифма числа (lg N = п + lg а) достаточно иметь лишь таблицу
мантисс (таблицу чисел lg a, где 1 < а < 10).
128

Усовершенствованные таблицы десятичных логарифмов,
которыми пользовались в России десятки лет (пока их не вытеснили
калькуляторы) были составлены отечественным педагогом-математиком
ВМ.Брадисом.
На основе той же идеи замены произведения степеней —
суммой, частного — разностью показателей основана была
конструкция логарифмической линейки, которой пользовались инженеры и
математики всего мира более 300 лет. Изобретателем
логарифмической линейки (в 1624 г.) считается английский ученый Э. Гунтер.
Десятичные логарифмы и сегодня часто используются в силу
исторических традиций и удобств практики. Однако для
математической науки и ее приложений более значимыми являются
натуральные логарифмы. Важность логарифмической функции у = In x
объясняется тем, что в математике чаще всего используются
показательные функции с основанием е, поэтому важны и обратные им
функции.
Если считать, что идея логарифмической функции возникла у
Непера при решении кинематических задач (эти задачи он решал
ради составления таблиц логарифмов), то законченный вид теории
логарифмической функции придал выдающийся математик XVIII в.
Л. Эйлер (1707—1783). Отметим, что значительную часть своей
жизни Эйлер, сын небогатого пастора из Базеля, провел в России,
приняв в 1727 г. приглашение работать в только что
организованной в Петербурге Академии наук. Ему принадлежат общие
определения показательной и логарифмической функций как взаимно
обратных, введение символа е для обозначения основания
натуральных логарифмов.
После Эйлера развитие теории логарифмических функций
происходило в основном в рамках математического анализа.
Логарифмические функции, помимо кинематической, впоследствии
приобрели геометрическую и аналитическую интерпретации.
Для любознательных продемонстрируем, как с помощью
четырехзначных таблиц Брадиса школьники предыдущих поколений
находили, например, значение произведения N = ^513,2 • 0,505:
1
\gN= lg$513,2 0,505) = lg(513,2)5 + lg(5,05 101 ) =
= | lg (5,132 102) + lg (5,05 101) =
= | (lg 5,132 + lg 102) + lg 5,05 + lg 101 =
= \ lg 5,132 + \ 2 + lg 5,05 - 1 = -0,6 + I lg 5,132 + lg 5,05.
0 0 О
5-Ю. М. Колягин, 10 кл. 129

После выполнения этих преобразований в разделе таблиц
«Мантиссы логарифмов» надо было найти значения lg 5,132 и lg 5,05.
Приводим «нужную» часть этих таблиц, в которой подчеркнута
мантисса-логарифм числа 5,132 («поправка» на четвертую
значащую цифру 2 находится в правой части таблицы и прибавляется к
последнему разряду подчеркнутого четырехзначного числа
основной части таблицы). Мантисса-логарифм числа 5,05 в таблице
выделена жирным шрифтом:
а
50
51
52
0
6990
7076
1
6998
7084
2
7007
7093
3
7016
7101
4
7024
7110
5
7033
7118
6
7042
7126
7
7050
7135
8
7059
7143
9
7067
7152
123
123
123
456
345
345
789
678
678
Итак, lg 5,132 - 0,7101 + 0,0002 = 0,7103,
lg 5,05 - 0,7033.
Окончательно: lg N « -0,6 + - 0,7103 + 0,7033 - 0,2454.
о
После нахождения lg N с помощью раздела «Антилогарифмы»
(в этих же таблицах) по числу 0,2454 находится число N « 1,759.

главаV J [ СИСТЕМЫ УРАВНЕНИЙ
В этой главе вы познакомитесь с разными полезными приемами
решения систем уравнений, часть из которых вам известна.
§ 20. Способ подстановки
Задача 1. Решить систему уравнений
\Зх-у-6 = 0,
А Из первого уравнения выразим у через х
у = 3х-6 (2)
и подставим это выражение во второе уравнение
х2 + 4х(3х - 6) - 2 (3* - б)2 = -29. (3)
Упростив это уравнение, получим
Ъх2 - 48* + 43 = 0, (4)
откуда хх = 1, х2 = 8,6. Подставляя эти значения в формулу у = Зх - 6,
находим ух = -3, у2 = 19,8.
Ответ. (1;-3), (8,6; 19,8). А
Способ подстановки вам знаком, он является одним из самых
простых и надежных способов решения систем уравнений.
Приведем его обоснование на примере решения задачи 1.
О Предположим, что существует решение (х; у) системы (1), т.е.
х и у — такие числа, что оба равенства (1) верны. Тогда из них по
свойствам верных числовых равенств получается, что равенства
(2)— (4) также верны. Из равенств (2) и (4) найдены хх = 1, ух = -3,
*2 = 8,6, у2=19,8.
Итак, предположив, что система (1) имеет решения, мы
установили, что этими решениями могут быть только две найденные
пары чисел. Но, может быть, наше предположение неверно?
Поэтому докажем, что найденные две пары чисел в самом деле
являются решениями системы (1).
Это можно сделать обычной проверкой: подставить найденные
значения х и у в уравнения системы (1) и убедиться, что
получаются верные числовые равенства. Однако можно доказать, что
такая проверка необязательна, так как полученные данным способом
пары чисел всегда являются решениями системы (если, конечно,
не допущены ошибки при вычислении).
5* 131

Приведем это доказательство.
Пусть х — корень уравнения (4), т.е. х — такое число, что
равенство (4) является верным. Из него по свойствам верных
числовых равенств получаем верное равенство (3). Считая у равным Sx - 6,
т.е. верным равенство (2), из равенств (2) и (3) имеем верные
равенства, образующие систему (1). •
Заметим, что приведенное рассуждение состояло из двух
частей. Сначала, предположив, что данная система имеет решения,
было установлено, какими они могут быть. Во второй части было
показано, что решения системы существуют и найденные две пары
чисел в самом деле являются решениями исходной системы.
Таким образом, способ подстановки обосновывается
свойствами верных числовых равенств. Поэтому этот способ можно смело
применять, не приводя каждый раз подробные доказательства.
Задача 2. Решить систему уравнений
А Подставляя х = у 2 + 1 во второе уравнение, получаем у3 + у =
2 + УЪ, откуда у(у -1) = 09у1 = О, у2 = 1.
По формуле х = у2+1 находим хх = 1, х2 = 2.
Ответ. (1;0), (2; 1). А
Задача 3. Решить систему уравнений
\j/i-2xy-3x2 = 0.
А Выразим из второго уравнения у через х, решая это уравнение
как квадратное относительно у:
у = х± \lx2 + Sx2 =x±2x,
т.е. или у = Sx, или у = -х.
1) Подставляя у = Sx в первое уравнение системы (5), имеем
16*2=16,*12 = ±l,i/12 = ±3.
2) Подставляя у = -хв первое уравнение системы (5), получаем
О т в е т.4(1; 3)', (-1; -3), (2; -2), (-2; 2). А
Задача 4. Решить систему уравнений
{Sx - 4у = 2,
9х2 - 16/ = 20.
132

А Пусть (х; у) — решение этой системы. Заметим, что второе
уравнение можно записать так:
а так как из первого уравнения Зх + 4z/ = 2, то
(3* - 4z/) 2 = 20,
т.е.
Зх-4у=10.
Получилась система
3* + 4у = 2,
3*-4i/ = 10, (7)
которая имеет то же самое решение (х; у).
Наоборот, если (х; у) — решение системы (7), то, умножая
второе уравнение этой системы на первое, получаем систему (6), т.е.
(х; у) — решение системы (6).
Итак, обе системы (6) и (7) имеют одни и те же решения. Такие
системы называют равносильными. Решая систему (7), находим
х = 2уу = -1.
Ответ. (2;-1). А
Проведенными при решении задачи 4 рассуждениями
обоснована возможность подстановки значения выражения,
содержащего неизвестные, из одного уравнения в другое.
Задача 5. Решить систему уравнений
А По формуле суммы кубов второе уравнение запишем так:
(х + 2у)(х2 - 2ху + 4у2) = 35.
Отсюда и из первого уравнения системы получаем
откуда х = 5 - 2z/.
Подставляя это значение х в первое уравнение исходной
системы, получаем
(5-2z/)2-2z/(5-2z/) + 4z/2=7.
После упрощения этого уравнения находим
6z/2-15z/ + 9 = 0,
У\ = 1> У2 = 1>^' а из формулы: х = 5 - 2у находим хх = 3, х2 = 2.
Ответ. (3; 1), (2; 1,5). ▲
133

Задача 6. Решить систему уравнений
А Первое уравнение системы имеет смысл, если х > О, у > 0. При
таких значениях х и у имеем
х-у=
поэтому система такова:
откуда
Решая эту систему, находим >/# = 7, у[у =5. Следовательно,
Ответ. (49; 25). А
Задача 7. Решить систему уравнений
Jlog2^-log2 z/ = l,
[4у2+х-12 = 0.
А Первое уравнение системы имеет смысл, если х> О, у > 0. При
таких значениях х и у выразим х через у из первого уравнения си-
X X
стемы log2 — = log2 2, — = 2; х = 2у. Подставляя х = 2у во второе
г/ У
уравнение системы, получаем 4у2 + 2у - 12 = 0, откуда i/j = -,
о
у2 = -2. Так как у > 0, то у2 = -2 — посторонний корень. При ух = -
из формулы х = 2у находим хх = 3.
Ответ. (з;-1. А
V 2)
Задача 8. Решить систему уравнений
134

Д Так как 4 = 22, 27 = З3, то по свойствам степени систему можно
записать так:
т.е.
\
[ у
Решая эту систему, находим х = 1, у = 3.
Ответ. (1;3). А
Упражнения
Решить систему уравнений (460—470).
460.
461.
462.
463.
1)
1)
2)
3)
4)
1)
2)
3)
1)
\х-у = 2,
[Зх + 2у = 16;
[ху = 7;
[х + у = 1,
\ху = -6;
f* + 3i/ = 10,
1*0 = 3;
\х-2у = -7,
\ху = -6;
\х2+у2 = 41,
\у-х = 1;
\2х2-у2= 46,
\х2+у2=25;
\х + у = Ъ,
\х3+у3=35;
2) (х + у = 3,
[5х-2у = 1.
5) \х2-у2 = 20
\х + у = 20;
6)\х2-у2=9,
\х-у=1;
7) \х2+у2= 10
\ху = -3;
8) \х2+у2=13
\ху = 6.
4) \х-у = 3,
{х2+у2=5;
5)Ux-y)2 = 4,
2) Г*-у = 1,
1*3-у3=19
135

464. 1) [\gx-\gy = l,
\\gx + \gy = b;
2) Jlog2* + ilog2i
[xy = 2;
465.1) J>£ + ^ = 8,
466.
2) \2x-y = 5,
2x2y-xy2=15;
467.1)
468. 1)
469.
470.
3 3
x2-y2=7,
I l
x + x2y2 +y = 7;
jg* gi/
\lgx-lgy =
3) (lgx-lgy =
4) 3
\x2y-2y + 9-0.
2)\Jx~-Jy~ = l,
U-J/-5.
3)
4) ixy(x + y) = 6,
\x3+y3=9.
2)\y2 + 2xy-15x2=0,
\x2 + 2xy+2y2 = 25.
2)
2) J3*-9^=27,
t
§ 21. Способ сложения
Задача 1. Решить систему уравнений
(1)
А Прибавим к первому уравнению второе, умноженное на 2, а
второе уравнение оставим без изменений:
136

х2+2ху + у2 =25,
Докажем, что системы (1) и (2) равносильны.
Пусть (х; у) — решение системы (1), т.е. оба равенства (1)
верны. Тогда по свойствам верных числовых равенств верны оба
равенства (2), т.е. (х; у) — решение системы (2).
Пусть, наоборот, (х; у) — решение системы (2), т.е. верны оба
равенства (2). Прибавим к первому из них второе, умноженное на (-2).
Получим верные равенства (1), т.е. (х; у) — решение системы (1).
Решим систему (2). Первое уравнение системы (2) запишем так:
(х + у)2 = 25, откуда х + у = ±5, т.е. или у = 5 - х, или у = -5 - х.
1) Подставляя у = 5 - х во второе уравнение системы (2),
получаем х(Ъ - х) = 6, откуда х2 - 5х + 6 = 0, хх = 3, х2 = 2. По формуле
у = Ь-х находим у1 = 2, у2 = 3.
2) Подставляя у = -5 - х во второе уравнение системы (2),
получаем х(-Ъ - х) = 6, откуда х2 + 5х + 6 = 0, х3 = -3, у3=-2и х4 = -2,
О т в е т. (3; 2), (2; 3), (-3; -2), (-2; -3). А
Приведенные при решении задачи 1 рассуждения обосновывают
следующее свойство систем двух уравнений с двумя неизвестными.
Если к одному из уравнений данной системы прибавить дру-
гое, умноженное на число, не равное нулю, и составить систему
из полученного уравнения и любого из уравнений данной системы,
то получится система, равносильная данной.
Аналогично доказывается и следующее свойство таких систем.
Если каждое из уравнений данной системы умножить на не
равное нулю число (оба уравнения на одно и то же число или на
разные числа), то получится система, равносильная данной.
Заметим, что вместо слов «умножить обе части уравнения на
число» кратко говорится: «умножить уравнение на число». Так же
вместо слов «сложить левые и правые части уравнения» кратко
говорится: «сложить уравнения».
Задача 2. Решить систему уравнений
А Умножив первое уравнение на 3, а второе на (-2), получим
137

Складывая уравнения системы (4), получаем
х2-у2 = 0,
откуда у = х или у = -х.
1) Подставляя у = х в первое уравнение системы (3) (можно в
любое из уравнений систем (3) и (4)), имеем:
хг-2х2 + Зх2 = 2,
откуда х2 = 1, х1 = у1 = 1, х2=у2 = -1.
2) Подставляя у = -х в первое уравнение системы (3), получаем
х2+2х2 + Зх2 = 2,
2=1,х3=±,у3 = -± и X4=-±,y4=^L.
Задача 3. Решить систему уравнений
1х-ху-у = -7у
А Для того чтобы исключить из этих уравнений произведение ху,
прибавим ко второму уравнению первое, умноженное на 2. Получим
Зх - Зу = -9, откуда
х-у = -3,у = х + 3.
Подставляя это выражение у через х в первое уравнение
системы, имеем
х - х(х + 3) - (х + 3) = -7,
откуда х2 + Зх - 4 = 0, хх - 1, х2 = -4. По формуле у = х + 3
находим i/j =4, z/2 = -l.
Ответ. (1; 4), (-4;-1). А
Задача 4. Решить систему уравнений
2JC2 + 2*у- у2 - 2х+6у=8.
А Вычтем из первого уравнения второе, получим
х2 + у2 + 2х - 4у = -5.
Это уравнение можно преобразовать так:
х2+ 2х + 1 + у2 - 4у + 4 = 0, (х + 1)2 + (у - 2)2= О,
откуда х = -1, z/ = 2. Проверка показывает, что (-1; 2) — решение
системы.
Ответ. (-1; 2). ▲
138

Задача 5. Решить систему уравнений
А Применяя свойство степени, запишем данную систему так:
[З-З*-2*^ = 1.
Прибавляя к первому уравнению второе, умноженное на 2,
получаем 7 3* = 7, откуда х = 0. Подставляя х = 0 в первое
уравнение исходной системы, получаем 1 + 2 у+1 = 5, откуда у = 1.
Ответ. (0; 1). А
Задача 6. Решить систему уравнений
А Умножим первое уравнение на (-2), а второе на 3 и сложим
полученные уравнения:
5V2x-l = Зх
Решаем последнее уравнение: 25(2* - 1) = 9х2, 9х2 - 50х + 25 = 0,
Подставляя хх = 5 в первое уравнение исходной системы,
находим
5
Подставляя х2 = - в первое уравнение исходной системы, на-
*7
ходим: 2/^-1-3^/3-1/ =0,
2
У
4
81'
81
Проверка показывает, что обе найденные пары являются
решениями исходной системы.
Ответ.(5;-1), f-;2— \ A
9 81
139

Задача 7. Решить систему уравнений
flog2:x; + log4 y = 5,
Оба уравнения системы имеют смысл, если х> 0, у > 0. При этих
значениях ху у, используя формулу перехода к логарифмам по осно-
log х
ванию 4, получаем log2 х = , 2 = 21og4 *, log2 z/ = °g*y = = 21og4y.
Поэтому система уравнений такова:
г v = 5,
= 1 (5)
Вычитая из первого уравнения этой системы второе,
умноженное на 2, находим -31og4 у = 3, log4 z/ = -1, у = 4"1 = ~ .
Вычитая из второго уравнения системы (5) первое, умноженное
на 2, находим -31og4 х = -9, log4 х = 3, # = 43 = 64.
Проверку можно не делать, так как найденные значения х, у
положительны.
Ответ. f64;-l. A
Упражнения
Решить систему уравнений (471—479).
471. 1) |3* + 5i/ = 10, 2) Ux-6y =
|3* + 5i/ 10,
[2x-7y = U;
472. 1) \x2 + у2 =10, 2) fjc2 + у2 =13,
W = -3; W = 6.
473. 1) (x + xy + y = -l, 3) J2
\
2) |jc-jcz/-i/ = -7, 4)
\x + xy-y = l;
474. 1) j*2 + 3jq/ = 54, 2)
140

-2t/2 = 0,
3)
475. 1) |7х2-19лл/-3«/2 =
2)
476*.
477*.1)
478*.
479*.
+ г/2 - ДС1/= 3.
2) |5^2
[4х2-ху-4х+2у=27.
2) jlog9 дс2 + log3 (дс-1/) = 1,
log9x-log3i/ =
4) |31og5x-log5j/
§ 22. Решение систем уравнений
различными способами
Задача 1. Решить систему уравнений
\ху = -10.
(1)
А Эту систему можно решить, например, способом подстановки.
Однако вы знаете, что если х и у таковы, что равенства (1) верны,
то по теореме, обратной теореме Виета, х и у являются корнями
уравнения z2 - З2 - 10 = 0. Решая это уравнение, находим его
корни: zx = 5, 22 = -2. По теореме Виета найденные числа 5 и -2 —
удовлетворяют системе (1). При этом х может равняться 5, тогда у - -2,
или х = -2у у = 5.
Ответ: (5;-2), (-2; 5). А
141

Задача 2. Решить систему уравнений
х </3
J__J__8
х2 у2~9'
1 1
Д Для краткости записи введем новые неизвестные: и = — , v = ~.
х у
Получим
4
Решая эту систему, например, способом подстановки, находим
и- 1, v- — . Атак как х- — , у- - , то jc= I, y = 3.
о и v
Ответ. (1;3). А
Приведем еще примеры, когда для краткости записи полезно
ввести новые неизвестные.
Задача 3. Решить систему уравнений
\х- 1
(2)
х2+у2 +ху = 3.
А Введем новые неизвестные: х- у = и, ху =v. Заметим, что при
этом
х2 + у2 = (х - у)2 + 2ху = и2 + 2v.
Поэтому систему (2) можно записать так:
J
\u2+3v = S.
Решая эту систему, например, способом подстановки, находим
их = 0, vx = 1, и2 = 3, v2 = -2.
Возвращаясь к старым неизвестным, получаем две системы:
-у = 0, 2) h-y = Sy
\ху = 1; \ху = -2.
Из первой системы находим хх = 1, ух = 1; х2 = -1, у2 = -1, а из
второй системы находим jc3= 2, уг = -1; jc4 = 1, у4 = -2.
О т в е т. (1; 1), (-1; -1), (2; -1), (1; -2). А
142

Задача 4. Решить систему уравнений:
[4х+ 9"-7 2*-5 3^ + 18=0,
А Введем новые неизвестные: 2х = и, Зу = v. Так как 4* = (2х)2
и2, 9У = (Зу)2 = v2, то в новых неизвестных система (3) такова:
u-v = l.
Решим эту систему способом подстановки. Из второго уравнения
имеем v = u- 1. Подставляя это значение v в первое уравнение
системы (4), получаем
и2 + (и - I)2 - 1и - Ъ(и - 1) + 18 = О,
откуда
и2 + и2 - 2и + 1 - 1и - I
^ = 4,1^2 = 3.
По формуле v = u- 1 находим vx - 3, v2 = 2.
Возвращаясь к старым неизвестным, получаем две системы:
Из первой системы находим хг = 2, х2 = 1, а из второй системы:
l l
О т в е т. (2; 1), (log2 3; log3 2). А
Рассмотрим примеры, когда при решении системы полезно
перемножить или поделить ее уравнения, т.е. перемножить или
поделить ее левые и правые части.
Задача 5. Найти действительные решения системы уравнений:
у
А Перемножая уравнения (5), получаем
(5)
откуда
х2у2 + 18ху- 144 = х2у2,
(6)
143

Подставляя (6) в систему уравнений (5), получаем систему:
—
У?
— = 32,
(7)
Умножая первое уравнение системы (7) на уравнение (6),
получаем х4= 8 • 32 = 44. Так как требуется найти только
действительные решения, то хх 2 = ±4. Из уравнения (6) находим У12 = ±2.
Решение системы (5) нельзя считать законченным, так как был
использован новый для вас прием — умножение уравнений
системы. Следует убедиться в том, что, по крайней мере, уравнения (6)
и (7) являются следствиями системы (5). Покажем это.
Пусть (х; у) — решение системы (5), т.е. оба равенства (5)
верные. Заметим, что тогда х Ф О и у Ф О (на нуль делить нельзя!). Из
равенств (5) получены верные равенства (6), (7) и хх = 4, ух = 2 и
х2 = -4, у2 = -2. Обратный переход от этих пар чисел (х; у) к
равенствам (7), (6) и, наконец, к (5) в общем виде трудно доказать. В
таких случаях проще сделать проверку. Подставляя каждую из
найденных пар чисел в оба уравнения (5), получаем верные числовые
равенства.
Ответ. (4; 2), (-4;-2). А
Задача 6. Решить систему уравнений
У2 = 3, (8)
zx = 2.
А Перемножая все три уравнения, находим х2 у2 г2 = 36, откуда
= ±6.
1) Пусть
6. (9)
Подставляя поочередно в равенство (9) каждое из уравнений (8),
находим хх = 2, ух - 3, z1 = l.
2) Если xyz = -6, то аналогично находим х2 = -2, у2 = -3, z2 = -1.
Проверкой убеждаемся, что обе тройки чисел являются
решениями системы (8).
Ответ. (2;3; 1), (-2;-3;-1). А
Задача 7. Решить систему уравнений
{2х 9^ = 5832.
144

Л Разложим правые части уравнений системы на множители:
1728 = 64 27 = 26 З3, 5832 = 729 8 = 272 23 = З6 23. Исходная
система такова:
| ~ ' (10)
Умножив и разделив уравнения этой системы, получим систему
6*+2i/=69,
(И)
Заметим, что если (х; у) — решение системы (10), т.е. оба
равенства (10) верные, то левые и правые их части не равны нулю.
Поэтому верны равенства (11), т.е. (х; у) — решение системы (11).
В этом случае систему (11) называют следствием системы (10).
Отметим также, что уравнения системы (10) получаются
умножением и делением уравнений (11), т.е. система (10) является
следствием системы (11). Поэтому эти системы равносильны.
Теперь отметим, что в системе (11) равенство 6х+2у = б9 по
свойствам степени является верным только тогда, когда х + 2у = 9, так
как 6 > 0, 6*1. Аналогично второе равенство (11) верно только
при х - 2у = -3. Следовательно, система (11) равносильна системе
J
\х-2у = -3.
Решая эту систему, находим х = 3, у = 3.
Ответ. (3;3). А
Задача 8. Найти действительные решения системы уравнений
А Заметим, что если (х; у) — решение этой системы, то х Ф 0,
так как при х = 0 из первого уравнения системы получается, что
у = 0, но при х = 0, у = 0 второе уравнение системы не является
верным равенством.
Разделив обе части первого уравнения системы (12) на х2,
получаем
^-3 * =0,
х *
145

т.е.
Решая это квадратное уравнение относительно — , получаем
У 2 у 2
- = - или - = -1, т.е. у = - х или у = -х.
X О X О
2
1) Подставляя у--х во второе уравнение системы (12), полу-
о
чаем
откуда
-1*2— 1
jc2=9,
2
По формуле у = - x находим ух = 2уу2 = -2.
2) Подставляя у = -х во второе уравнение системы (12),
получаем
т.е.
Это уравнение не имеет действительных корней.
Ответ. (3; 2), (-3;-2). А
Задача 9. Найти действительные решения системы уравнений
А Заметим, что если (х; у) — решение этой системы, то левые и
правые части системы не равны нулю. Поэтому уравнения (13)
можно разделить.
Разделим второе уравнение на первое:
146

Теперь отметим, что если (х; у) — решение системы (13), то х Ф О,
так как если х = О, то из первого уравнения (13) получается у2 = — ,
а из второго — у2 = 6. Поэтому числитель и знаменатель дроби,
стоящей в левой части уравнения (14), можно разделить на х2:
2 — 2— — — I
откуда
3\У.\ -8^
у
Решая это квадратное уравнение относительно — , получаем
у и 2 2
— = 2 или — = -, т.е. у = 2х или у = - х.
X X 3 о
1) Подставляя у = 2х в первое уравнение (13) (можно во второе —
получится то же самое), имеем
х2 - 3*(2*) + 2(2*)2 = 3,
откуда
*2(1-6 + 8) = 3,
х2- 1, хх- 1, х2 = -1.
По формуле у = 2х находим ух = 2, у2 = -2.
2
2) Подставляя у = - х в первое уравнение системы (13), получаем
о
v2 '
х —«
откуда
Это уравнение не имеет действительных корней.
Ответ. (1; 2), (-1;-2). А
Системы уравнений настолько разнообразны, что практически
невозможно дать какие-либо общие рекомендации по способам их
решения. В каждом конкретном случае нужно использовать свой
147

опыт решения систем, желательно находя наиболее простой способ
их решения. Поэтому при решении полезно накапливать такой
опыт.
Приведем еще несколько примеров решения разнообразных
систем уравнения (без подробных объяснений).
Задача 10. Решить систему уравнений
|3*-2 6* 2^+612^=0,
[2-У+ 4.6" 2*-12*=0.
А Используя свойства степени, запишем данную систему
уравнений так:
|
[2.941+2-2^) = 12*.
Умножая уравнения этой системы, получаем
откуда
1-4.4
4х4* = 1,
Подставляя у = -хв первое уравнение исходной системы,
получаем
3*-2 6* 2*-6 12*=0,
откуда
3*-2 3* 2*-6 12*=0,
3х =6 12 "х,
3х-12х =6,
36^=6=362,
1 „ 1
х = - . Поэтому у = -х = - - .
Ответ. —;— . А
(2 2)
Задача 11. Решить систему уравнений
[lO(y-x)-x4=9,
148

А Запишем второе уравнение системы в виде у/у-2х = >/2-у[у, и
возведем обе части данного уравнения в квадрат:
откуда yjty = # +1.
Возведя обе части этого уравнения в квадрат, получаем
2
Подставим значение у в первое уравнение исходной системы
После преобразований этого уравнения имеем
откуда хх = 1, х2 = -1, х3 = 2ух4 = -2.
(х+1)2 9 1
По формуле у = 2 находим уг = 29у2 = 09у3=-9 у4 = - .
Проверкой устанавливаем, что (xv yx)y (х2> у2) — решения
системы, а (х3, у3)9 (х4у у4) — посторонние решения.
Ответ. (1;2), (-1; 0). ▲
Задача 12. Решить систему уравнений
А Запишем первое уравнение системы в виде yj7x-^y = 5-y/2x+y
и возведем обе части этого уравнения в квадрат:
7* + у = 25 -10^/2^+
откуда
10^2х+у =25-5*,
Подставляя значение у]2х+у во второе уравнение системы (15),
получаем
5-* i
откуда
х = 2у-3.
149

Подставляя значение х во второе уравнение системы (15),
получаем
Возведя обе части этого уравнения в квадрат, получаем
5у-6=16
откуда
у2 = 11, у2 = 2.
По формуле х = 2у-3 находим хх = 19, х2 = 1.
Проверкой устанавливаем, что (19; 11) — постороннее решение,
а (1; 2) — решение системы (15).
Ответ. (1; 2). А
Задача 13. Решить систему уравнений
А Первое уравнение системы имеет смысл только при х > О,
хф\у у > О, уф\. При таких значениях х, у по формуле перехода
log х = . Поэтому первое уравнение системы таково:
У log* У
откуда
2(logxy)2-blogxy + 2 = 0.
Решая это квадратное уравнение относительно log^. у, находим
1
log у = 2 или log у — — •
1) Если log^. у = 2, то у = х2 и второе уравнение исходной
системы таково: Xs = 27, откуда д^ = 3, а по формуле у = х2 получаем ух = 9.
1 у—
2) Если log^. i/ = — , то у = у/х и второе уравнение исходной сис-
3
темы таково: х* = 27, откуда х2 = 9, а по формуле у = л[х получаем
у2 = 3. А
Ответ. (3; 9), (9; 3).
150

Задача 14*. При каких значениях а система уравнений
J
\х+у=1
не имеет решений?
А Вычитая из первого уравнения второе, умноженное на 2,
получаем
(9a2-4)i/ = 3a-2.
Это уравнение не имеет решений, если 9а2 -4 = 0,а За-2*0.
Из равенства 9а2 -4 = 0 находим а = ± - .
3
2
Из неравенства За - 2 Ф 0 находим аФ - .
о
2
Следовательно, система не имеет решений при a = - - . к
о
Упражнения
Решить систему уравнений (480-495).
480. 1) Г* + у = 4, 3)
2)
481. 1)
1 - 1 -5-
? 2' '
4) ГЗдгг/ = -1,
2)
482.
483.
1)
1)
2)
\х-у + ху = 2,
12 2 г\
[х +у -ху = о;
\2х-у = \,
|5х+»=2б-
\х-у=2,
2)
3)
4)
\ХУ
и
\х-
[22>
\2х
+ х + у =
+ У2+Х1,
■3«/ = 2,
^=0,5;
+у=з,
{г1-2» =16.
151

484. 1) J5* + 2y = 7, 2) Гзх + 4У = 7,
{б*-2» =10; 1з*-4? = 12.
485. 1) |log2 (дс2 + у2) = 7, 2) jlog3 * + log3 у = 2+log3 7,
[log2x+21og4i/=6;
486.
1+1 = 1;
2)
5)
1зх2-у+2х=-1;
6)
3) |x2 - y2 = 0,
4)
V 16;
487*. 1) \x2+y2=x+y,
2) \x4
488.
489. 1) f 5* - б" = 100,
7) (xy(x + y) = 84,
\
8)
3)
4)
y(x2-l)_4
+ 10=0,
3) |Xf-U*+M = 1,
2) \2X-9-3^=7,
|2*-3*'=—;
4) j/-4*+3=l,
1
152

490. 1) j642*+642j/ =
[64*f
3) llog2
4)
-,
\xy = 2;
Шх1 + ^3у
[6x + y-2xy = 7;
491*.
492*.
493*. 1) J5(log!/ s + log, y) = 26,
2)
2) Jj/4
2)
Z)\\ogxy-2\ogyx=l,
4)
494*.
495*. [logf (*+z/)+log!(*-i/)-logf (2*)=
1 l
2 {x-y)-\og2
3 3
496. Найти все действительные значения а, при которых система
Ах2-у2=\,
уравнении < имеет действительные рюшения при лю-
[у = ах + Ь
бом действительном значении Ь.
497. Найти все значения а, при которых не имеет решений система
уравнений
l(3a+14)x+(a+8)i/=5a2 + 5.
153

§ 23. Решение задач с помощью систем уравнений
Решение многих задач сводится к решению системы двух
уравнений с двумя неизвестными. Рассмотрим примеры.
Задача 1. Пассажирский и товарный поезда одновременно
отправились от двух станций навстречу друг другу. Расстояние
между станциями, равное 120 км, пассажирский поезд прошел на 1 ч
быстрее товарного. С какой скоростью двигались поезда, если они
встретились через 1 ч 12 мин после начала движения?
(Предполагается, что каждый поезд двигался с постоянной скоростью.)
А Обозначим скорости движения пассажирского и товарного
поездов соответственно * и у (в км/ч). Тогда расстояние 120 км они
120 120 120 120 1
прошли соответственно за и ч. По условию = 1.
* У У х
За время движения до встречи, равное 1 ч 12 мин = - ч, пасса-
о
жирский и товарный поезда прошли соответственно - * и - у км,
о о
а вместе — расстояние 120 км, т.е.
5 5
Таким образом, получилась система уравнений
120 120.
-у~ * •
Решим эту систему. Первое уравнение умножим на ху (по смыс-
5
лу задачи ху Ф 0), а второе — на - :
jl20x-120y = xy>
[* + z/ = 100.
Из второго уравнения выразим у через х
у=100-х
и подставим в первое уравнение. Получим
120* - 120(100 - х) = *(100 - х).
Упростим это уравнение:
120* - 12 000 + 120* = 100* - *2,
*2 + 140* - 12 000 = 0.
154

Решим полученное квадратное уравнение:
* =-70 ±74900+12000 =-70±130,
^ = 60, *2=-200.
По смыслу задачи скорость положительна; следовательно,
х- 60. Подставляя это значение в формулу у = 100 - х, находим
# = 100-60 = 40.
О т в е т. 60 км/ч, 40 км/ч. ▲
Задача 2. Гипотенуза прямоугольного треугольника равна
10 см, а его площадь 24 см2. Найти его катеты.
А Пусть катеты равны х и у сантиметров. Используя теорему
Пифагора и формулу площади прямоугольного треугольника,
запишем условие в виде
Решим эту систему. Из второго уравнения выразим у через х:
48
и подставим в первое уравнение. Получим
4
х
Упростим это уравнение:
х4 + 2304 = 100*2,
*4-100*2+ 2304 = 0.
Решая полученное биквадратное уравнение, находим:
х2 = 50 ± V2500-2304 = 50 ± 14,
Так как по смыслу задачи х > 0, то выбираем только
положительные корни: хх = 8, х2 = 6. Подставляя эти значения в
выражение для у, т.е. в формулу (1), находим ух = 6, у2 = 8. В обоих
случаях один катет равен 8 см, другой — 6 см.
Ответ. 8см, 6см. А
Задача 3. Бассейн наполняется с помощью двух труб за 7,5 ч,
причем первая труба, работая одна, наполняет на 8 ч быстрее, чем
вторая. За сколько часов первая труба может наполнить бассейн?
А Пусть первая труба заполняет бассейн за х, а вторая за у
часов. Примем вместимость бассейна за единицу. Тогда за 1 ч первая
труба заполняет — часть бассейна, а вторая , а вместе обе тру-
* 1 1 у
бы за 1 ч заполняют ~ + ~ часть бассейна.
155

По условию первая труба заполняет бассейн на 8 ч быстрее,
отсюда
1 2
а обе трубы заполняют за 1 ч —г = — бассейна. Следовательно,
1+1=1
х у 15'
Таким образом, получаем систему уравнений
[х у 15*
Решим эту систему:
2x2-Ux- 120 = 0,
*i,2 = | (7 ± V49 + 240 ), xx = 12, jc2 = -5.
По смыслу задачи х> 0.
Ответ. 12ч. А
Задача 4. Теплоход прошел расстояние между двумя
пристанями за 7 ч, а обратно за 9 ч. Найти расстояние между
пристанями и собственную скорость теплохода, если скорость течения
реки 2 км/ч.
А Пусть х километров — искомое расстояние, у километров в
час — собственная скорость теплохода. По условию:
* =7,
У + 2
х
= 9.
У-2
Решим эту систему уравнений. Разделим первое уравнение на второе:
j/-2=7
9'
откуда 9у - 18 = 1у + 14, 2у = 32, у = 16.
156

Подставляя у = 16 в первое уравнение системы, находим
х - = 7, *=126.
16+2
Ответ. 126 км, 16 км/ч. А
Задача 5*. Бак объемом 425 м3 из двух кранов был
наполнен водой, причем первый кран был открыт дольше второго на 5 ч.
Если бы первый кран был открыт столько же времени, сколько
второй, а второй кран был бы открыт столько же времени, сколько
первый, то из первого крана вытекло бы в 2 раза меньше воды, чем из
второго. Если одновременно открыть оба крана, то бак
наполнится за 17 ч. Сколько времени был открыт второй кран?
А Пусть х часов — искомое время, на которое был открыт
второй кран, v кубических метров в час — скорость поступления воды
из первого крана, w кубических метров в час — скорость
поступления воды из второго крана.
Составим систему уравнений:
= w(x+5), (1)
(v+w) 17 = 425.
Решая эту систему, нужно найти только х.
Второе и третье уравнения системы (1) можно представить так:
Из этой системы выразим v и w через х, т.е. решим систему (2)
относительно v и w.
Сначала прибавим к первому уравнению системы (2) второе,
умноженное на (х + 5):
2vx - w(x + 5) = О,
+ v(x + 5) + w(x + 5) = 25(* + 5)
5) = 25(* + 5)
250с+5)
откудау=-з^Г-
Затем прибавим к первому уравнению системы (2) второе,
умноженное на (-2*):
2vx - w(x + 5) = О,
+ -2vx - w2x = -50*
-а>(3* + 5) = -50*
50*
отсюда w = .
*ix+о
157

Подставляя найденные значения v и w в первое уравнение
системы (1), имеем
Злг + 5
После преобразований этого уравнения получим
З*2-41*-60 = О,
откудахх = 15, х2= -- .
Так как по смыслу задачи # > 0, то д: =15.
О т в е т. 15 ч. ▲
Упражнения
498. При делении двузначного числа на сумму его цифр в частном
получается 6, а в остатке 4. При делении этого же числа на
произведение его цифр в частном получается 2, а в остатке 16.
Найти это число.
499. Если двузначное число разделить на сумму его цифр, то в
частном получится 4, а в остатке 12. Если же это число разделить
на произведение его цифр, то в частном получится 1, а в
остатке 20. Найти это число.
500. Из пункта А в пункт В отправился автомобиль, а навстречу ему
из пункта В одновременно отправился автобус. Автомобиль
прибыл в Б, а автобус — в А спустя соответственно 40 мин и
1,5 ч после их встречи. Найти скорости автомобиля и
автобуса, если расстояние между пунктами А и В равно 100 км
(скорости автомобиля и автобуса постоянны).
501. Две машинистки, работая вместе, могут перепечатать
рукопись за 6 ч. Одна машинистка, работая отдельно, может
перепечатать ее на 5 ч быстрее, чем другая. За сколько часов
может перепечатать рукопись каждая из них, работая в
отдельности?
502. Двое рабочих в течение 45 мин выполняли одну работу, затем
первый из них ушел, а второй закончил работу за 2,25 ч.
Сколько времени понадобилось бы каждому рабочему в
отдельности на выполнение всей работы, если первый мог бы ее
выполнить на час раньше?
503. Катер прошел расстояние между поселками за 4 ч и вернулся
обратно за 6 ч. Каково расстояние между пристанями, если
скорость катера в стоячей воде составляет 20 км/ч?
158

504. Расстояние от А до Б по течению реки теплоход проходит в
1,5 раза быстрее, чем катер, причем за каждый час катер
отстает от теплохода на 8 км. Против течения реки путь от В до
А теплоход проходит в 2 раза быстрее катера. Найти их
скорости в стоячей воде.
505. От пристани А одновременно направились вниз по течению
реки катер и плот. Катер, пройдя 96 км, повернул обратно,
встретил плот на обратном пути в 24 км от А и вернулся в А,
затратив на весь путь (туда и обратно) 14 ч. Найти скорость
катера в стоячей воде и скорость течения реки.
506. Комплект журналов может полностью заполнить 13
стандартных полок. В продаже были полки, на каждую из которых
помещалось на 2 журнала меньше, чем на стандартную.
Поэтому пришлось купить 17 полок, и при этом осталось свободное
место для двух журналов. Сколько журналов было в
комплекте?
507. Бригада рабочих строит мост за 14 дней. Если бы в бригаде
было на 4 человека больше и каждый работал бы на один час
в день дольше, то та же работа была бы выполнена за 10 дней.
При увеличении же бригады еще на 6 человек и рабочего дня
еще на один час вся работа была бы выполнена за 7 дней.
Сколько человек было в бригаде и сколько часов в день они
работали?
508*. Бассейн наполняется водой из двух кранов. Сначала был от-
1
крыт только первый кран на — того времени, которое потре-
о
бовалось бы для наполнения бассейна лишь вторым краном.
Затем был открыт только второй кран на - того времени, ко-
торое потребовалось бы для наполнения бассейна лишь пер-
13
вым краном. В результате оказалось наполненным — бассей-
1о
на. За какое время каждый кран в отдельности наполнит его,
если оба крана наполняют бассейн за 3 ч 36 мин?
509*. Один вкладчик положил в банк некоторую сумму денег,
другой — вдвое большую сумму. Сумма первого вкладчика через
т лет составила р руб., а второго через п лет (где п Ф т) —
q руб. Определить, какова первоначальная сумма денег
первого вкладчика и сколько процентов в год выплачивает банк.
159

Упражнения к главе V
510. Выяснить, какая из данных пар чисел (1; 3), (1; >/3 ), (-1; - >/з )
является решением системы уравнений
Uv-з.
511. Выяснить, какая из двух систем уравнений
\х-у = 2, „\*-У = 2,
[х2-у2=Зх-Зу [х + у = 3
является следствием другой.
512. Выяснить, являются ли равносильными следующие системы
уравнений:
\х2-4у2=15
Решить систему уравнений (513—516).
513. 1) \х-у = 2, 4) ix-y = l,
\
15*-у = 24; \х2-у2=-Ъ;
3)U + y = l, 6) \x-y = 3,
514. 1) |2дг-£/ = 5, 3)
18л + 2у = 11;
2) |3*-2у = 5, 4)
к.к 1Ч fl 1 3 оч Г1 1 5
515. 1) - + - = -, 2) - + - = —,
<х у 8 * у 12
[
160

516. 1) Гз*-5» = 75, 4)
|зг/-5* = 45; \\gx + lgy = 2;
2)i2?& = 12, 5) |log2 x + log2 у = log212,
[г8'-3^ = 18; [log2(*+i/) = 3;
3) jу - x = 9, 6) Jlog3 *+log3 i/ = log3 63,
\lgx-lgy = l; \\og2(x-y) = l.
517. 1) Среднее арифметическое двух чисел 25, а их среднее
геометрическое равно 15. Найти эти числа.
2) Найти двузначное число, которое в 3 раза больше суммы его
27
цифр ив — больше произведения его цифр.
1.
2.
ПРОВЕРЬ СЕБЯ!
Решить систему уравнений:
\х2-у2
2) flog2 х
Разность двух
сумма этих чисел в 5
= 12;
+ 1о&2 У = log2 6,
14'
чисел в 24 раза меньше
раз больше их разности
их произведения, а
. Найти эти числа.
518. Выяснить графически, сколько решений имеет система
уравнений:
+y2=4, 3)
xy = l; \y-log1(x-l) = 0.
2
6-Ю. М. Колягин, 10 кл. 161

Решить систему уравнений (519—531).
519.
\х2-ху + у2=52;
520. 1) \х2 + ху+2«/2 = 74,
[2х2 + 2ху+у2 = 73;
2) {Ъх2 -бху+бу2 = 29,
[7Х2-8^+7^ = 43;
521.
2)
522.
523. 1) 1хг-уг=9,
\ху = -2;
524. 1)
525*.
526. 1) |3 5*-2-3" = 21,
[5*-3^=675;
527. 1) 12*3^= 1152,
\
528.
lgx-lgy = l;
2) \х +2ху + у =1-ху,
\х + у = -2.
3) \5х2-х+у2 = 4,
{8х2-ху+2у2 = 8;
4) \х2-3ху+2у2 = 3,
[2х2-2ху-у2 = -6.
з) \±--±-=1
\ху х + у 2
[х2у + ху2=2;
4)
2) J2i/2-4*i/+3x2 = 17,
1^-^ = 16.
2){х4+у4=17,
\ху = 2.
2) р!+$/ = 5,
2)
2)
2) J3*-9^ = 27,
2) jlog3 x + log3 у = 2 + log3 2,
162

529. 1) jig (x2 + у2) = 1+21g 2, 2) |log9 x2 + log3 (x- y) = 1,
j [log2 y=log4 (дя/-2).
530*. 1)
log2 — 2 - log2 у = 21og4 (у +1),
У
x 14
x2 =21og3
|
[log3 (x- 2y)+log3 (3x+2y)=3.
532. Два пешехода вышли одновременно навстречу друг другу,
первый — из пункта А, второй — из пункта В. До места их
встречи первый прошел на 1 км больше, чем второй. Первый
пешеход прибыл в пункт В через 45 мин после их встречи, а
второй — в пункт А через 1 ч 20 мин. Найти расстояние от А до В.
533*. Два спортсмена бегают по замкнутой дорожке стадиона.
Скорость каждого постоянна, и на пробег всей дорожки один
тратит на 5 с меньше другого. Если они стартуют одновременно
и в одном направлении, то окажутся рядом через 30 с. Через
какое время они встретятся, если побегут одновременно с
общей линии старта в противоположных направлениях?
534*. Бассейн наполняется тремя насосами за 3 ч, причем первый
насос вдвое производительнее второго. Если бассейн сначала
наполнить на 0,5 объема первым и третьим насосами, а затем
0,5 объема вторым и третьим, то он наполнится за 5 ч. За
какое время наполнится бассейн, если будет работать только
третий насос?
535*. Имеются два сплава, состоящие из железа, никеля и хрома.
Процентное содержание хрома в первом в 5 раз больше, чем
никеля во втором сплаве. Кусок первого сплава массой 200 г
сплавили с куском второго сплава массой 400 г и получили
сплав, содержащий q% никеля. Сколько граммов железа
содержит новый сплав, если первый сплав содержит 30%
никеля, а второй — 40% железа?
6* 163

Историческая справка
Еще со времен вавилонян и древних индусов считается, что
одной из основных целей алгебры является решение уравнений и их
систем.
В Древнем Вавилоне более 4000 лет назад умели решать
уравнения первой, второй и некоторые уравнения третьей степени.
Однако общей теории решения уравнений в те времена еще не было.
Приведем задачу, найденную в папирусе Кахуна (XVIII—
XVI вв. до н.э.). Задача сформулирована в современных
обозначениях и сводится по существу к решению системы уравнений: «Най-
Q
ти числа х и у у для которых х2 + у2 = 100 и х : у =1 : -».В
папирусе задача решена методом «ложного положения». «Положим х = 1,
3 f5f
тогда у=-их2 + у2=\—\. Но в условии х2 + у2 = 102, значит, в
4 [4)
качестве х нужно брать не 1, а 10 : - =8. Тогда у = 6».
4
В древности уравнениям придавалась геометрическая форма.
Сегодня напоминание о «геометрической алгебре» встречается,
например, в терминах «квадрат числа», «куб числа» и др. (22 мы читаем
как «два в квадрате», 23 — как «два в кубе», уравнение вида ах2 +
+ Ъх + с = 0 называем «квадратным» и т.д.).
Известно, что впервые правила преобразований уравнений,
обосновав их, правда, геометрически, разработал выдающийся
узбекский ученый первой половины IX в. аль-Хорезми. В XII в. труды аль-
Хорезми были переведены на латинский язык и долгое время в
Европе являлись основным руководством по алгебре. Арабское
название операции «восполнение» («перенесение отрицательных членов
уравнения в другую часть») звучало как «ал-джебр», что и дало
название разделу математики, занимающемуся решением
уравнений, — «алгебра».
Начало освобождения алгебры от геометрической формы в III в.
связывают с именем древнегреческого ученого Диофанта. Однако
лишь после того, как французский математик Ф. Виет (1540—
1603) ввел буквенные обозначения для неизвестных и известных
величин, и после появления трудов Р. Декарта (1596—1650) и
других европейских ученых XVI—XVII вв. процесс освобождения
алгебры от геометрической терминологии был завершен. Этот процесс
способствовал расцвету алгебры и развитию различных ее
направлений: теориям уравнений, многочленов, функций и пр.
164

ГЛАВА
Vll
ТРИГОНОМЕТРИЧЕСКИЕ
ФОРМУЛЫ
§ 24. Радианная мера угла
Пусть вертикальная прямая касается в
точке Р окружности с центром О радиуса 1
(рис. 42). Будем считать эту прямую
числовой осью с началом в точке Р, а
положительным направлением на прямой —
направление вверх. За единицу длины на
числовой оси возьмем радиус окружности.
Отметим на прямой несколько точек: ±1, ±—,
±3, ±71.
Напомним, что число п — отношение
длины окружности к диаметру этой
окружности. Число п является иррациональным,
причем к = 3,14. Вообразив эту прямую в
виде нерастяжимой нити, закрепленной на
окружности в точке Р, будет наматывать
ее на окружность. При этом точки
числовой прямой с координатами, например, 1,
— , -1, -2 соответственно перейдут в точки
Li
окружности Mj, M2, М3, М4, такие, что
длина дуги РМХ равна 1, длина дуги РМ2
равна — и т.д. Таким образом, каждой
Li
Рис. 42
точке прямой ставится в соответствие
некоторая точка окружности.
Так как точке прямой с координатой 1 ставится в соответствие
точка Mv то естественно считать угол РОМХ единичным и мерой
этого угла измерять другие углы. Например, угол РОМ2 следует
считать равным — , угол POMS — равным -1, угол РОМ4 — равным
Li
-2. Такой способ измерения углов широко применяется в
математике и физике. В этом случае говорят, что углы измеряются в ра-
дианной мере, а угол РОМХ называют углом в 1 радиан (1 рад).
Отметим, что длина дуги окружности РМХ равна радиусу.
Рассмотрим окружность радиуса R и отметим на ней дугу РМ,
длина которой R, и угол РОМ (рис. 43).
165

Центральный угол, опирающийся на дугу, длина которой
равна радиусу окружности, называется углом в 1 радиан.
Найдем градусную меру угла в 1 рад. Так как
дуга длиной kR (полуокружность) стягивает
центральный угол в 180°, то дуга длиной R стяги- / R/
вает угол, в п раз меньший, т.е.
Гр
180
Так как к « 3,14, то 1 рад « 57,3°.
Если угол содержит а радиан, то его
градусная мера равна
Рис. 43
а рад
■№'■
(1)
Задача 1. Найти градусную меру угла, равного:
2) - рад;
3) — рад.
1)лрад;
А По формуле (1) находим:
п Зя /180 Згс\°
1) п рад = 180°; 2) - рад = 90°; 3) — рад = -j I = 135°. А
Найдем радианную меру угла 1°. Так как угол 180° равен к рад, то
1° =
180
рад.
Если угол содержит а градусов, то его радианная мера равна:
ос°=
180
а рад.
(2)
Задача 2. Найти радианную меру угла, равного: 1) 45°; 2) 15°.
А По формуле (2) находим:
1) 45° = ^ • 45 рад = ^ рад;
2)15°= ^
Приведем таблицу наиболее часто встречающихся углов в
градусной и в радианной мерах:
Градусы
Радианы
0°
0
30°
я
45°
я
1
60°
я
90°
я
180°
к
Обычно при обозначении меры угла в радианах наименование
«рад» опускают.
166

Радианная мера угла удобна для вычисления длины дуги
окружности. Так как угол в 1 рад стягивает дугу, длина которой равна
радиусу R, то угол в а рад стягивает дугу длиной
l = aR. (3)
Задача 3. Конец минутной стрелки кремлевских курантов
движется по окружности радиуса R « 3,06 м. Какой путь проходит
конец этой стрелки за 15 мин?
А За 15 мин стрелка поворачивается на угол, равный — рад. По
я ^
формуле (3) при а = — находим
Li
/=^йа-^- 3,06м *4,8м.
l\ l\
Ответ. 4,8м. ▲
Особенно простой вид формула (3) имеет в случае, когда радиус
окружности R = 1. Тогда длина дуги равна центральному углу,
стягиваемому этой дугой (в радианах), т.е. I = а. Этим объясняется
удобство применения радианной меры в математике, физике, механике
и т.д.
Задача 4. Доказать, что площадь кругового сектора радиуса
R, образованного углом в а рад, равна
R2
S = —а, где 0 < а < п.
l\
R2
А Площадь кругового сектора в п рад (полукруга) равна п— . По-
Li
R2
этому площадь сектора в 1 рад в п раз меньше, т.е. я— : п. Следо-
Li
R2
вательно, площадь сектора в а рад равна —а. ▲
Li
Упражнения
536. Найти радианную меру угла, выраженного в градусах:
1)40°; 2)120°; 3)105°; 4)150°;
5) 75°; 6) 32°; 7) 100°; 8) 140°.
537. Найти градусную меру угла, выраженного в радианах:
5)2; 6)3; 7)1,5; 8)0,36.
538. (Устно.) Определить градусную и радианную меры углов:
а) равностороннего треугольника; б) равнобедренного
прямоугольного треугольника; в) квадрата; г) правильного
шестиугольника.
167

539. Вычислить радиус окружности, если дуга длиной 0,36 м
стягивает центральный угол в 0,9 рад.
540. Найти радианную меру угла, стягиваемого дугой окружности
длиной 3 см, если ее радиус 1,5 см.
Зя
541. Дуга кругового сектора стягивает угол в — рад. Найти
площадь сектора, если радиус круга 1 см.
542. Радиус круга 2,5 см, а площадь кругового сектора 6,25 см2.
Найти угол, который стягивается дугой этого кругового
сектора.
543. Заполнить таблицу:
Градусы
Радианы
0,5°
36°
159°
108°
5
3
10*
2,5
1,8
544. Заполнить таблицу:
Угол,град.
Угол, рад
Радиус, см
Длина дуги, см
Площадь сектора, см2
30°
2
я
5^
2
10
5
5
50
2
25
10
50
§ 25. Поворот точки вокруг начала координат
В предыдущем параграфе использовался наглядный способ
установления соответствия между точками числовой прямой и точками
окружности. Теперь покажем, как можно установить соответствие
между действительными числами и точками окружности с помощью
поворота точки окружности.
Рассмотрим на координатной плоскости окружность радиуса 1
с центром в начале координат. Ее называют единичной
окружностью. Введем понятие поворота точки единичной окружности
вокруг начала координат на угол а рад, где а — любое действительное
число.
168

1. Пусть а>0. Предположим, что точка, двигаясь по
единичной окружности от точки Р против часовой стрелки, прошла путь
длиной а (рис. 44). Конечную точку пути обозначим М. В этом
случае будем говорить, что точка М получена из точки Р поворотом
вокруг начала координат на угол а рад.
2. Пусть ос<О.В этом случае поворот на угол а рад означает,
что движение совершалось по часовой стрелке и точка прошла путь
длиной |ос| (рис. 45). Поворот на 0 рад означает, что точка остается
на месте.
yi
а<0
Рис. 44
Рис. 45
Примеры
1) При повороте точки Р(1; 0) на угол — рад (рис. 46) получает-
ся точка М с координатами (0; 1).
2) При повороте точки Р(1; 0) на угол -— рад (см. рис. 46) по-
Li
Зя
лучается точка N(0; -1).
3) При повороте точки Р(1; 0) на угол -^ рад (рис. 47)
получается точка К(0; -1).
4) При повороте точки Р(1; 0) на угол -п рад (см. рис. 47)
получается точка L(-l; 0).
У{
K(O-l)
Рис. 47
169

В курсе геометрии рассматривались углы от 0° до 180°.
Используя поворот точки единичной окружности вокруг начала
координат, можно рассматривать углы, большие 180°, а также
отрицательные углы. Угол поворота можно задать как в градусах, так и в
радианах. Например, поворот точки Р(1; 0)
Зл
на угол — означает то же самое, что и
У±
6
п
4
3
2
271
-71
30°
45°
60°
90°
180°
270"
360°
-90°
-180°
поворот на 270°; поворот на - — — это по-
Li
ворот на-90°.
Приведем таблицу поворотов на
некоторые углы, по модулю меньшие 2 л,
выраженные в радианной и градусной
мерах (рис. 48).
Отметим, что при повороте точки
Р(1; 0) на 2л, т. е. на 360°, точка
возвращается в первоначальное положение.
При повороте этой точки на -2л, т. е. на
-360° , она также возвращается в
первоначальное положение.
Теперь рассмотрим примеры
поворотов точки на угол, больший 2л, и на
угол, меньший -2л. Так, при повороте
9л о о л
на угол —=2 2л + -
точка совершает
два полных оборота против часовой
стрелки и проходит еще путь — (рис. 49).
9л о о л
При повороте на угол --—=-ZZn- —
точка совершает два полных оборота по
часовой стрелке и еще проходит путь —
в том же направлении (рис. 50).
Заметим, что при повороте точки
9л
Р(1; 0) на угол — получается та же са-
l\
мая точка, что и при повороте на угол —
9л
(см. рис. 49). При повороте на угол - —
Li
получается та же самая точка, что и при
повороте на угол - — (см. рис. 50).
Рис. 48
170

Рис. 49
Рис. 50
Вообще если а = а0 + 2nky где k — целое число, то при повороте
на угол а получается та же самая точка, что и при повороте на угол о^.
Итак, каждому действительному числу а соответствует
единственная точка единичной окружности, получаемая
поворотом точки (1; 0) на угол а рад.
Однако одной и той же точке М единичной окружности
соответствует бесконечное множество действительных чисел
а + 2nky где k — целое число, задающих поворот точки Р(1; 0) в
точку М (рис. 51).
М
Рис.51
Задача 1. Найти координаты точки, полученной поворотом
точки Р(1; 0) на углы: 1) 7л; 2) -— .
Li
А 1) Так как 7 л = л + 2к • 3, то при повороте на 7к получается та
же самая точка, что и при повороте на п, т. е. получается точка с
координатами (-1; 0).
2) Так как - — = - — - 2л, то при повороте на - — получается
та же самая точка, что и при повороте на -
ка с координатами (0; -1). А
, т. е. получается точ-
171

3 а д а ч а 2. Записать все углы, на которые нужно повернуть
точку (1; 0), чтобы получить точку —; — .
V 2 2)
А Из прямоугольного треугольника
ЛОМ (рис. 52) следует, что угол АОМ
я
— , т. е. один из возможных углов пово-
я
рота равен — . Следовательно, все углы,
на которые надо повернуть точку (1; 0),
чтобы получить точку 2*2' выРа"
жаются так: — + 2nk, где k — любое це-
о
лое число, т. е. k = 0; ±1; ±2; .... А
У
Рис. 52
Упражнения
545. Найти координаты точки единичной окружности, полученной
поворотом точки (1; 0) на угол:
1)4я;
л
5)
4'
6)
3) 3,5я;
7) 225°;
4) -6,5я;
8) -45°.
На единичной окружности построить точку, полученную
поворотом точки (1; 0) на угол (546—548).
546.
547.
1)
5)
1)
2)
Я
4я<
я
~3
2)-
; 6)-
,2п;
±2к;
к
з ;
!*
3)
4)-
3) —;
3
7)315°;
—- ±8я.
о_
548. 1) — + 2nky k — целое число;
Li
з
2) - ^^ + 2яА:, А: — целое число;
Li
3) - я + 2яА:, А: — целое число;
4) - — + 2nk9 k — целое число.
4
4)-¥л;
8) -225°.
172

549. Найти координаты точки, полученной поворотом точки Р(1; 0)
на угол:
1)3л; 2)-|л; 3)-уя;
4) 5л; 5) 540°; 6) 810°.
550. Найти координаты точки, полученной поворотом точки (1; 0)
на угол (k — целое число):
l)~+2nk; 3)у+
Li
551. Найти координаты точки, полученной поворотом точки (1; 0)
на угол (k — целое число):
1) | ±к; 3)^
2) -А ±к; 4) -
4
552. Найти все углы, на которые нужно повернуть точку (1; 0),
чтобы получить точку с координатами:
1) (-1; 0); 2) (1; 0); 3) (0; 1); 4) (0; -1).
553. Определить четверть (квадрант), в которой расположена
точка, полученная поворотом точки Р(1; 0) на заданный угол:
1)1; 2)2,75; 3)3,16; 4)4,95.
554. Найти число ху где 0 < х < 2я, и натуральное число k, такие,
чтобы выполнялось равенство: а = х + 2nk, если:
1)а = 6,7л; 2)а = 9,8л; 3)а=4-л;
Li
4)7| 5)^ 6)*
555. На единичной окружности построить точку, полученную
поворотом точки Р(1; 0) на заданный угол:
l)J±2n; 2)-^±2п; 3) |л ±6я;
4)-^±8л; 5) 4,5л; 6) 5,5л;
4
7)-6тс; 8)-7л.
173

556. Найти координаты точки, полученной поворотом точки Р(1; 0)
на угол (й — целое число):
2)f +2nk;
3) у+
4)-f
557*. Записать все углы, на которые надо повернуть точку Р(1; 0),
чтобы получить точку с координатами:
2) "
л/2. _л/|
2 ' 2
§ 26. Определение синуса, косинуса
и тангенса угла
В курсе геометрии были введены синус, косинус и тангенс угла,
выраженного в градусах. Этот угол рассматривался в промежутке
от 0° до 180°. Синус и косинус произвольного угла определяются
следующим образом (рис. 53):
Определение 1. Синусом угла а
называется ордината точки, полученной
поворотом точки (1; 0) вокруг начала
координат на угол а (обозначается sin a).
Определение 2. Косинусом угла а
называется абсцисса точки, полученной
поворотом точки (1; 0) вокруг начала
координат на угол а (обозначается cos a).
В этих определениях угол а может
выражаться как в градусах, так и в
радианах.
Например, при повороте точки (1; 0) на угол — , т. е. угол 90°,
получается точка (0; 1). Ордината точки (0; 1) равна 1, поэтому
sin |- =sin90° = l;
абсцисса этой точки равна 0, поэтому
cos - = cos 90° = 0.
Рис. 53
174

Отметим, что приведенные определения синуса и косинуса в
случае, когда угол заключен в промежутке от 0° до 180°, совпадают с
определениями синуса и косинуса, известными из курса геометрии.
Например:
sin — = sin 30° = — ;
D Z
cos к = cos 180° = -1.
Задача 1. Найти sin (-л) и cos (-к).
А Точка (1; 0) при повороте на угол -л перейдет в точку (-1; 0)
(рис. 54). Следовательно, sin (-л) = 0 и cos (-л) = -1. ▲
Задача 2. Найти sin 270° и cos 270°.
А Точка (1; 0) при повороте на угол 270° перейдет в точку (0; -1)
(рис. 55). Следовательно, cos 270° = 0 и sin 270° = -1. А
Рис. 54
Задача 3. Решить уравнение sin x = 0.
А Решить уравнение sin х = 0 — это значит найти все углы,
синус которых равен нулю.
Ординату, равную нулю, имеют две точки на единичной
окружности: (1; 0) и (-1; 0) (см. рис. 54 ). Эти точки получаются из точки
(1; 0) поворотом на углы 0, л, 2л, Зл и т. д., а также на углы - л,
-2л, -Злит. п.
Следовательно, sin х = 0 при х = nk, где k - любое целое число. ▲
Множество целых чисел обозначается буквой Z. Для
обозначения того, что число k принадлежит Z, используют запись k e Z
(читается: «k принадлежит Z»). Поэтому ответ к задаче 3 можно
записать так:
х = nk,ke Z.
175

Задача 4. Решить уравнение cos x = 0.
А Абсциссу, равную нулю, имеют две
точки единичной окружности: (0; 1) и
(0; -1) (рис. 56). Эти точки получаются из
точки (1; 0) поворотом на углы — , — + тс,
— + 2лит. д., а также на углы — -тс, — -2я
и т.п., т.е. на углы — + kn, где k е Z.
Li
Ответ. х= — +nk, ke Z. A
Задача 5. Решить уравнение:
1) sin x=l; 2) cos x = 1.
А 1) Ординату, равную единице, имеет точка (0; 1) единичной
окружности. Эта точка получается из точки (1; 0) поворотом на
углы — +2nk, k е Z.
Li
Ответ. х- — + 2тсk, ke. Z.
Ci
2) Абсциссу, равную единице, имеет точка, полученная из
точки (1; 0) поворотом на углы 27С Ar, k e Z.
Ответ, х = 2&7Г, ke Z. а
I Определение 3. Тангенсом угла а называется отношение
синуса угла а к его косинусу (обозначается tg a).
Таким образом,
tgoc =
sinoc
cosa
Например:
. я
sin —
«■••-
tg4 =
= 2 =
4 2
Иногда используется котангенс угла а (обозначается ctg а),
который определяется формулой
ctg a =
cosa
sina
Например:
ctg 270° =
cos270° = 0
sin270° " -1
= 0,
«»■=!■
= 1.
Отметим, что sin a и cos a определены для любого угла, а их
sina
значения заключены от -1 до 1; tg a = определен лишь для
176

тех углов, для которых cos а Ф 0, т. е. для любых углов, кроме
а = — + nky k g Z; ctg а = определен лишь для тех углов, для
2 sinoc
которых sin а Ф 0, т. е. для любых углов, кроме а = nk, ke Z.
Приведем таблицу часто встречающихся значений синуса,
косинуса, тангенса и котангенса:
а
sin а
cos а
tgoc
ctg а
0
(0°)
0
1
0
Не

ществует
я
~6
(30°)
1
2
V3
2
1
V3
V3
я
(45°)
V2
2
V2
2
1
1
к
(60°)
V3
2
1
2
V3
1
Я
(90°)
1
0
Не

ществует
0
К
(180°)
0
-1
0
Не

ществует
Зя
2
(270°)
-1
0
Не

ществует
0
2л
(360°)
0
1
0
Не

ществует
Задача 6. Вычислить:
4sin - + V3 cos - - tg - .
А Используя таблицу, получаем
4sin
cos J -tg |=4 i
о 4 2
л/з
Значения синуса, косинуса, тангенса и котангенса для углов, не
вошедших в эту таблицу, можно найти по четырехзначным
математическим таблицам В.М. Брадиса, а также с помощью
микрокалькулятора.
Задача 7. Вычислить на микрокалькуляторе с точностью до
0,01:
1) sin 25°; 2)cos^; 3)tg5.
о
А На любом микрокалькуляторе вычисления проводятся с
помощью одних и тех же клавиш: |sinl, |cos|, |tg|, перед которыми
нужно нажимать клавишу [f| . Перед вычислением надо
установить переключатель Р—Г (радиан — градус) в нужном положении:
1)25 [fJ [sin] 0,42261825.
Ответ. 0,42.
177

2)@0 5 0 @ [cos] 0,80901703.
Ответ: 0,81.
3) 5 ЦЩ [tg] -3,380514.
Ответ: -3,38. А
Упражнения
558. Изобразить на единичной окружности точку,
соответствующую числу а, если:
l)sinoc= 1; 5) sin а = -0,6;
2) sin а = 0; 6) sin а = 0,5;
3) cos а = -1; 7) cos а = - ;
3
4) cos а = 0; 8) cos а = -0,25.
559. Вычислить:
1) sin - + sin — ; 4) sin 0 - cos 2к;
Li Li
/ \
2) sin — + cos — ; 5) sin к + sin 1,5k;
\ 2) *
3) sin к - cos к; 6) sin 0 + cos 2к.
560. Найти значения синуса и косинуса числа р, если:
rt 5
1) р = Зк; 4) р = -п;
2) р = 4л; 5) р = Kky k g Z;
3) p = 3,5л; 6) p = (2k + 1)tc, keZ.
Вычислить (561 - 562).
561. 1) sin Зк - cos — ;
Li
2) cos 0-
3) sin Kk + cos 2ttAj, где k e Z;
(2fc+l)rc . (4Лг+1)я
4) cos — sin —-— , где ke Z.
Li Li
562. I)tgrc + cos7c; 2) tg 0° - tg 180°;
3) tg к + sin л; 4) cos к - tg 2к.
563. Найти значение выражения:
1) 3 sin ^ + 2cos ^ - tg ^ ;
2) 5 sin - + 3 tg — - 5 cos — - 10 ctg — ;
4 4 4 4
178

4) sin - • cos - - tg - .
о О 4
564. Решить уравнение:
1) 2 sin x = 0; 3) cos x - 1 = 0;
2) - cos x = 0; 4) 1 - sin x = 0.
565. Может ли sin а или cos a быть равным:
1) 0,49; 2) -0,875; 3) - л/2 ; 4) 2 -Vl
566. Найти значение выражения при данном значении а:
1) 2 sin а + V2 cos а при а = — ;
4
2) 0,5 cos а - >/3 sin а при а = 60°;
3) sin За - cos 2а при а = — ;
.. а . а я
4)cos - + sin - при а= - .
567. Найти значение выражения:
1Ч . п я . я я
1) sin — cos — - sin — cos — ;
4 4 3 6
о Я . о Я .Я Я
«> (*!-<*!)(•««!
4) 2 cos2 - - sin2 - + tg - ctg - .
568. Доказать, что
я я^( . я . п} 2я
cos - - cos -J ^sxn - + sm -J - cos—.
569. Решить уравнение:
1) sin x = -1; 4) cos 0,5* = 0;
2) cos x = -1; 5) sin — + 6я = 1;
\2 )
3) sin 3jc = 0; 6) cos (5x + 4rc) = 1.
179

570. Используя микрокалькулятор, проверить равенство:
1) sin 60° - 0,866; 3) cos £ - 0,996;
о
2) cos 45° - 0,707; 4) sin ^ - 0,225.
571. Используя микрокалькулятор, вычислить с точностью до 0,01:
1) sin 1,5;
2) sin 0,866;
3) sin 3,53;
4) sin 8,071;
5) cos 0,5;
6) cos 0,138;
7)cos 4,81;
8) cos 10,035;
9) sin 38°;
10) sin 13°;
11) sin 51° 15';
12) sin 60° 20';
13) cos 12°;
14) cos 42°;
15) cos 45° 12';
16) cos 30° 10'.
572. Используя микрокалькулятор, вычислить с точностью до 0,01
Dsinf;
2) cos - ;
10
3) cos у л ;
4)tg-rc;
5)tg^;
6) ctg J ;
27
11tc-
9) sin 368°;
10) cos 1025°;
Il)tg773°;
12)tg423°.
§ 27. Знаки синуса, косинуса
и тангенса угла
1. Знаки синуса и косинуса
Пусть точка (1; 0) движется по единичной окружности против
часовой стрелки. Для точек, находящихся в первой четверти
(квадранте), ординаты и абсциссы положительны. Поэтому sin a > 0 и
cos а > 0, если 0 < а < — (рис. 57, 58).
Li
Для точек, расположенных во второй четверти, ординаты
положительны, а абсциссы отрицательны. Следовательно, sin a > 0,
cos а < 0, если — < а < к (см. рис. 57, 58). Аналогично в третьей
Li
четверти sin а < 0, cos а < 0, а в четвертой sin а < 0, cos а > 0
(см. рис. 57, 58). При дальнейшем движении точки по
окружности знаки синуса и косинуса определяются тем, в какой четверти
окажется точка.
180

У
sin ос
cos a
X
Рис. 57 Рис. 58
Если точка (1; 0) движется по часовой стрелке, то знаки синуса
и косинуса также определяются тем, в какой четверти окажется
точка; это показано на рисунках 57, 58.
3 а д а ч а 1. Определить знаки синуса и косинуса углов:
1)^; 2)745°; 3)-^.
А 1) Углу — соответствует точка единичной окружности,
расположенная во второй четверти. Поэтому sin —- > 0, cos — < 0.
4 4
2) Так как 745° = 2 360° + 25°, то повороту точки (1; 0) на угол
745° соответствует точка, расположенная в первой четверти.
Поэтому sin 745° > 0, cos 745° > 0.
3) Так как -к < < -— , то при повороте точки (1; 0) на угол
—— получается точка третьей четверти. Поэтому sin —- < 0,
2. Знаки тангенса
cos -— < 0. А
По определению tg a =
sinoc
cosa
. Поэтому
tg a > 0, если sin а и cos а имеют одинаковые
знаки, и tg a < 0, если sin a и cos a имеют
противоположные знаки. Знаки тангенса
изображены на рисунке 59.
3 а д а ч а 2. Выяснить знак тангенса
угла: 1)260°; 2)3.
А 1) Так как 180° < 260° < 270°, то
tg 260° > 0.
2) Так как - < 3 < к> то tg 3 < 0. А
tga
Рис. 59
181

Упражнения
573. В какой четверти находится точка, полученная поворотом
точки Р(1; 0) на угол а, если:
1)а=§; в)а=-£;
2)а=^; 7)а = 3,5;
3)a = -J; 8)а = 4,8;
4)а=-^; 9) а = -1,31;
5)а=у; 10)а = -2,7?
574. Пусть 0 < а < — . В какой четверти находится точка, получен-
ная поворотом точки Р(1; 0) на угол:
1)|-а; 2) а-л; 3>Т"а;
4) | + а; 5) а - |; 6) тс - а?
575. Определить знак числа sin a, если:
5л п. 5л „ч 13 л^ 33л
1)а = т; 2)а = —; 3)а = —л; 4)а = -—;
f\ A 7
5)а = --7с; 6)а = --7с; 7) а = --я; 8)а = -0,1я;
о о 4
9)а = 4; 10)а=5,1; 11)а = -7,3; 12)а = -6,1;
13) а = 210°; 14) а = -230°; 15) а = 850°; 16) а = -470°.
576. Определить знак числа cos a, если:
2 7 Зя 2
1) a = -п; 2) a = -тс; 3) a = -—; 4) a = --тс;
5) a = 2; 6) a = 4,6; 7) a = -4; 8) a = -5,3;
9) a = 290°; 10) a = -150°.
577. Определить знак числа tg a, если:
5 12 3 5
1) a = -тс; 2) a = —тс; 3) a = --тс; 4) a = --тс;
6 5 5 4
5)a=l; 6)a = 3,7; 7)a = -3,4; 8)a = -l,3;
9) a =190°; 10) a = 283°.
182

578. Определить знаки чисел sin a, cos а, tg а, если:
1) л < а < -л; 2) -л < а < —;
3) -£■ < а < 2л; 4) 2л < а < 2,5л.
579. Определить знаки чисел sin a, cos а, tg а, если:
1)а=1; 2)а = 3; 3)а = -3,4; 4)а = -
580. Пусть 0 < а < - . Определить знак числа:
1) sin - - а ; 2) cos - + а ; 3) cos (а - л);
6)sin(n-a).
581. Каковы знаки sin a, cos a, tg a, ctg a, если:
3 2 4
582. Для каких значений аргумента а, заключенных в
промежутке от 0 до 2 л, знаки синуса и косинуса совпадают (различны)?
583. Определить знак числа:
. 2л
l)sin^sin^; 3) £;
о 4
ЛЧ 2л л .ч , 5л . л
2) cos — cos-; 4) tg—- + sin-.
3 6 4 4
584. Сравнить значения выражений:
1) sin 0,7 и sin 4; 2) cos 1,3 и cos 2,3.
585. Решить уравнение:
1) sin (5л + х) = 1; 3) cos (- л + х | = -1;
V2 )
2)cos(х + Зл) = 0; 4) sin -л + х \= -1.
I2 )
586*. В какой четверти находится точка, соответствующая числу
а, если:
1) sin а + cos а = -1,4; 2) sin а - cos а = 1,4?
183

Mfcosoqsina)
Рис.60
§ 28. Зависимость между синусом,
косинусом и тангенсом
одного и того же угла
Выясним зависимость между
синусом и косинусом.
Пусть точка М(х; у) единичной
окружности получена поворотом точки (1; 0)
на угол а (рис. 60). Тогда по определению
синуса и косинуса
х = cos a, у = sin a.
Точка М принадлежит единичной
окружности, поэтому ее координаты (х; у)
удовлетворяют уравнению х2 + у2 = 1.
Следовательно,
sin2 a + cos2 a = 1.
(1)
Равенство (1) выполняется при любых значениях а и
называется основным тригонометрическим тождеством.
Из равенства (1) можно sin a выразить через cos a и cos a
через sin a:
sin a = ± у 1 - cos2 a,
cosa= ± >/l-sin2 a.
(2)
(3)
В этих формулах знак перед корнем определяется знаком
выражения, стоящего в левой части формулы.
Задача 1. Вычислить sin а, если cos а=--ил<а<— .
О Z
Зя
А Воспользуемся формулой (2). Так как к < а < — , то sin a < О,
поэтому в формуле (2) перед корнем надо поставить знак «минус»:
sim
V х
Задача 2. Вычислить cos а, если sin а = - и -- < а < 0.
о Z
А Так как -- < а < 0, то cos а > 0, поэтому в формуле (3) перед
z
корнем нужно поставить знак «плюс»:
cosa =
2V2
3
184

Выясним теперь зависимость между тангенсом и котангенсом.
По определению тангенса и котангенса
tga= **а
(4)
cosa sum
Перемножая эти равенства, получаем
tga ctga=l.
Из равенства (4) можно выразить tg a через ctg a и наоборот:
tga =
ctga'
ctga=-—.
tga
(5)
(6)
Равенства (4)—(6) справедливы при аФ-k, k e Z.
Задача 3. Вычислить ctg a, если tg a = 13.
А По формуле (6) находим:
1 1 А
Задача 4. Вычислить tg а, если sin а = 0,8 и — < а < к.
По формуле (3) находим cos а. Так как — < а < л, то cos а < 0.
Поэтому
cos
a = -^/l-sin2a = -^/1-0,64 = -0,6.
sina _ 0,8 _4
tga= ^^"^06" 3'
Следовательно,
Используя основное тригонометрическое тождество и
определение тангенса, найдем зависимость между тангенсом и косинусом.
Разделим обе части равенства sin2 a + cos2 a = 1 на cos2 a,
предполагая, что cos a Ф 0.
Получим равенство
cos2a+sin2a _ 1
cos2 a cos2 a'
откуда
tg2a=
cos2 a
(7)
Эта формула верна, если cos a * 0, т. е. при a * — + nk, ke Z.
Li
Из формулы (7) можно выразить тангенс через косинус и
косинус через тангенс.
185

Задача 5. Вычислить tg а, если cos а = — и - < а < л.
о Л
А Из формулы (7) находим
* 2 1 1 1 . 16
tg2a= —л 1 = ?-1 = —.
cos2a ( зТ ^
Ь> 4
Тангенс во второй четверти отрицателен, поэтому tg а = —. А
О
Задача 6. Вычислить cos а, если tga = 3n7C<a< —.
2
А Из формулы (7) находим
cos2 a =
l+tg2a 10'
Так как к < а < —, то cos a < 0 и поэтому cos a = -^/0,1. ^
Упражнения
587. Может ли синус (косинус) принимать следующие значения:
пПо. ?, 5 11 13 г-
U)Ud) 3' 3' 13' 11 ' V '
588. Могут ли одновременно выполняться равенства:
V2 V3 . V3 V23
=^^ ncosa=-T-; 4) sin a =-— ncosa=—— ;
3 3 5 5
оч • 4 3 Кч • 2 3^
2)sina=-- ncosa=--; 5)sina=- ncosa=—;
0 0 7 7
1 2
3) sin a = - - и cos a = ~z ; 6) sin a = 0,2 и cos a = 0,8?
О О
589. Вычислить:
1) sin a, tg a, ctg a, если cos a= — и — < a< л ;
5 2*
2) cos a, tg a, ctg a, если sin a= — и rc<a< — .
5 2
590. Вычислить значение каждой из тригонометрических функций,
если:
l)cosa= —и — <ос<2л; 3)tga=— и л<ос<— ;
13 2 8 2
2)sina = 0,8n -<a<rc; 4)ctga = -3 и — <а<2п;
186

5) cos a = 0,8 и 0<а<- ; 7)tgoc = -2,4 и ^
6)sincc=-—и ^<а<2л; 8)ctga= ^т и л<а<—.
13 £ с\\ 2
591. Какие значения могут принимать:
п /о О
1) cos a, если sin a = ; 3) sin a, если cos a = - ;
5 3
2) sin a, если cos a = —j=; 4) cos a, если sin a = --rr ?
592. Могут ли одновременно выполняться равенства:
1 1 1ч *\
1) sin a = - и tg a = -j— ; 2) ctg a = — и cos a = - ?
593. Пусть a — один из углов прямоугольного треугольника. Най-
2VI6
ти cos a и tg a, если sin a = .
594. Угол при вершине равнобедренного треугольника имеет
тангенс, равный 2>/2 . Найти косинус этого угла.
595. Найти cos a, если cos4 a - sin4 a = - .
о
596*. Известно, что tg a = 2. Найти значение выражения:
-v ctga + tga. «v 2sina + 3cosa.
ctga-tga' 3sina-5cosa'
2^ sina-cosa. ,, sin2a + 2cos2a
sina + cosa' sin2 a-cos2 a
597*. Известно, что sin a + cos a = - . Найти:
1) sin a • cos a; 2) sin3 a + cos3 a.
598*. Решить уравнение:
1) 2sin x + sin2 x + cos2 x = 1;
2) sin2 x - 2 = sin x - cos2 x;
3) 2 cos2 x - 1 = cos x - 2 sin2 x;
4) 3 - cos x = 3 cos2 x + 3 sin2 x.
187

§ 29. Тригонометрические тождества
Задача 1. Доказать, что при а Ф nk, k e Z справедливо
равенство
а тт j. cosa
А По определению ctg a = — , поэтому
sina
9 , cos2a sin2a + cos2a 1
1 + ctg^ a = 1 + т~2~" = r~2 = —2~ •
sin a sin a sin a
Эти преобразования верны, так как sin a Ф О при аФкк> k e Z. А
Равенство (1) справедливо для всех допустимых значений а, т.е.
таких, при которых его левая и правая части имеют смысл. Такие
равенства называют тождествами, а задачи на доказательство
таких равенств называют задачами на доказательство тождеств.
Обычно при доказательстве тригонометрических тождеств или
при упрощении выражений допустимые значения углов не
устанавливают, если это не требуется в условии.
Задача 2. Доказать тождество
cos2 a = (1 - sin a) (1 + sin a).
A (1 - sin a) (1 + sin a) = 1 - sin2 a = cos2 a. A
Задача З. Доказать тождество
cosa _l + sina
1-sina cosa
А Чтобы доказать это тождество, покажем, что разность между
его левой и правой частями равна нулю:
s2 a (1 sin2 a) cos2 a cos2
cos
a I + sin a _ cos2 a - (1 - sin2 a) _ cos2 a - cos2 a _ ~
(li) (li)
1 - sin a cos a cos а (1 - sin a) cos а (1 - sin а)
При решении задач 1—3 использовались следующие способы
доказательства тождеств: преобразование правой части к левой;
преобразование левой части к правой; установление того, что
разность между правой и левой частями равна нулю. Иногда удобно
доказательство тождества провести преобразованием его левой и
правой частей к одному и тому же выражению.
Задача 4. Доказать тождество
-^С- = cos4oc - sin4 a.
l + tg2a
sin2 a
l-tg2a cos2 a cos2 a-sin2 a 2 • 2
A V- = 2~- = —2 o—=cos a~sin a»
1 + tg a sin a cos a + sin a
9
cos a
188

cos4 a - sin4 a = (cos2 a - sin2 a) (cos2 a + sin2 a) = cos2 a - sin2 a.
Тождество доказано, так как его левая и правая части равны
cos2 a-sin2 a. A
1
Задача 5. Упростить выражение , + ctff .
А 1 1 sinacosa
tga + ctga sina t cosa su
cosa sina
Упражнения
599. Доказать тождество:
cos2 a
1) (1 - cos а) (1 + cos а) = sin2 а; 4) ~л <г~ = ctg2 а;
J. — COS ОС
2) (1 - sin а) (1 + sin а) = cos2 а; 5) ^ t 2 + sin2 а = 1;
sin2 a
6)
600. Упростить выражение:
2
1) cos a • tg a - 2sin a; 3) a ;
1 + cos a
04 . , .v cos2 a
2) cos a - sin a ctg a; 4)
1 - sin a
601. Упростить выражение и найти его числовое значение при
заданном значении а:
1Ч sin2oc-l я
1) g— приа= -;
1-гога 4
2) cos2 а + ctg2 а + sin2 а при а = -;
6
оч 1 Я
3) —2 1 ПРИ а = ^»
cos а 3
4) cos2 а + tg2 а ctg2 а + sin2 а при а = —.
о
602. Доказать тождество:
1) (1 - sin"2 a) (1 + tg^ а) = 1;
2) sin2 а (1 + ctg2 а) - cos2 а = sin2 а.
189

603. Упростить выражение:
l)(l + tg2a)cos2<x-l; 3)l + tg2a +
i 9
2) 1 - sin2 a (1 +ctg2 a); 4)
sin2 a
604. Доказать тождество:
1) (1 - cos 2a) (1 + cos 2a) = sin2 2a;
sin a -1 1
2)
cos2 a 1 + sin a'
3) cos4 a - sin4 a = cos2 a - sin2 a;
4) (sin2 a - cos2 a)2 + 2 cos2 a sin2 a = sin4a + cos4 a;
r4 sina 1+cosa 2
5) +
6)
7)
1+cosa
sina
1-cosa
1
sina
1+cosa.
sina
1
sina
= 1;
l+tg2a l+ctg2a
8) tg2 a - sin2 a = tg2 a sin2 a.
605*. Найти значение выражения sin a cos a, если sin a - cos a = 0,6.
606. Найти значение выражения cos3 a - sin3 a, если cos a - sin a = 0,2.
607. Известно, что tg a + ctg a = 3. Найти tg2 a + ctg2 a.
608. Решить уравнение:
1) 2 sin x + sin2 x + cos2 x = 1;
) ;
3) 3 cos2 JC-2sinjc = 3-3 sin2 x;
4) cos2 x - sin2 jc = 2sinjc-l-2 sin2 x.
§ 30. Синус, косинус, тангенс
углов а и -a
Рис. 61
Пусть точки Мх иМ2 единичной
окружности получены поворотом точки
Р(1; 0) на углы а и -а соответственно
(рис. 61). Тогда ось Ох делит угол
МХОМ2 пополам, и поэтому точки Мг
и М2 симметричны относительно оси
Ох. Абсциссы этих точек совпадают, а
ординаты отличаются только
знаками. Точка Mj имеет координаты
(cos a; sin a), точка M2 имеет координа-
ты (cos (-a); sin (-a)). Следовательно,
190

sin (-a) = -sin a, cos (-a) = cos a.
(1)
Используя определение тангенса, имеем
, . ч sin(-a) -sina
tg(-a)= —)—- = =-tga.
&v ' cos(-a) cosa &
Таким образом,
tg (-a) = -tg a.
(2)
ос* -
2
Формулы (1) справедливы при любых а, а формула (2) — при
, ke Z.
Можно показать, что если а Ф nk, k e Z, то ctg (-а) = -ctg а.
Формулы (1) — (2) позволяют сводить вычисление значений
синуса, косинуса и тангенса отрицательных углов к вычислению их
значений для положительных углов.
Например: sin [ - - | = -sin - = - - ;
, к\ я V2
cos | - - I = cos - = — ;
Упражнения
609. Вычислить:
l)coe(-|)8ln(-f)+tg(-f);
4) cos (-П) + ctg (-1 j - sin (- |л j + ctg f-1
\ 6i
2С-Н)
f
6)2sin(-j]-3ctg^ 4
h7,5tg(-n)+|
1 , „
cos | - -к
191

610. Упростить выражение:
1) tg (-a) cos а + sin а;
2) cos а - ctg а (-sin а);
_. cos (-а) + sin (-а) #
cos2 а - sin2 а
4) tg (-а) ctg (-а) + cos2 (-а) + sin2 а.
611. Доказать тождество
cos2 а - sin2 а л . ,
——г + tg (-а) cos (-а) = cos а.
cos а + sin (-а)
612. Вычислить:
о f «1 • ( Л
2cos — +sin —
L з j [ e
2) л/3 sin (-1) + 3tg (-^) - 2ctg (-1) + 4cos (-1
613. Упростить:
sin3 (-а) + cos3 (-а) # 1 - (sin а + cos (-a))2
1 - sin (-a) cos (-a)' - sin (-a)
614. Доказать тождество:
1) cos a sin (6rc - a) • (1 + ctg2 (-a)) = ctg (-a);
2) l-sin(-«).sin(a-2K)
} cos(4rc-a) l-cos2(-a) *
615. Решить уравнение:
1) sin (-x) = 1; 4) sin (-2x) = 0;
2) cos (-2x) = 0; 5) cos2 (-x) + sin (-x) = 2- sin2*;
3) cos (-2x) = 1; 6) 1 - sin2 (-x) + cos (4я - jc) = cos (jc - 2n).
§ 31. Формулы сложения
Формулами сложения называют формулы, выражающие cos (a ± P)
и sin (a ± P) через косинусы и синусы углов аир.
Теорема. Для любых а и Р справедливо равенство:
cos (a + Р) = cos a cos P - sin a sin p.
(1)
О Пусть точки Ma, Mo и Ма+р получены поворотом точки
Мо (1; 0) на углы а, ~Р и а + Р радиан соответственно (рис. 62).
192

По определению синуса и косинуса эти
точки имеют следующие координаты:
Ма (cos a; sin а);
M_p(cos(-p); Sin(-P));
Ма+р (cos (а + р); sin (а + р)).
Так как ZMQOMa+^ = ZM_p OMa, то
равнобедренные треугольники М0ОМа+„
и Ма ОМа равны и, значит, равны их
основания М0Ма+п и М_« Ма.
Следовательно,
Рис.62
Применяя формулу для расстояния между двумя точками,
известную из курса геометрии, получаем
(1 - cos (a + p))2 + (sin (а + р))2 =
= (cos (-Р) - cos а)2 + (sin (~P) - sin а)2.
Преобразуем это равенство, используя формулы (1) из § 30:
1 - 2 cos (ос + Р) + cos2 (а + Р) + sin2 (а + Р) =
= cos2 Р - 2cos P cos а + cos2 а + sin2 Р + 2sin p sin а + sin2 а.
Применив основное тригонометрическое тождество, имеем
2-2 cos (а + Р) = 2 - 2 cos а cos Р + 2sin а sin p,
откуда cos (а + Р) = cos а cos P - sin а sin p. •
Задача 1. Вычислить cos 75°.
А По формуле (1) находим
cos 75° = cos (45° + 30°) = cos 45° cos 30° - sin 45° sin 30° =
V 2 v 3 v 2 1 _ V6 — V 2
= T T~~2~ 2" 4 "
Заменив в формуле (1) P на -р, получим
cos (a - P) = cos a cos (-p) - sin a sin (~P),
откуда
cos (a - P) = cos a cos P + sin a sin p.
(2)
Задача 2. Вычислить cos 15°.
А По формуле (2) находим:
cos 15° = cos (45° - 30°) = cos 45° cos 30° + sin 45° sin 30° =
= V2 V3 V2 1 = V6 + V2
" 2 2 + 2 2 4 '
7-Ю. М. Колягин, 10 кл.
193

Задача 3. Доказать формулы:
л \ . .к
cos —a =sinoc, sin —а = cosoc. (3)
\ 2 J [ 2
А При а = — по формуле (2) получим
cos —Р =cos — cosP + sin — sinP = sinP, т.е.
у2 J 2 2
cosf|-pj=sinp. (4)
Заменив в этой формуле (3 на а, имеем
(к
cos —а |=sinoc.
Полагая в формуле (4) Р = — - а, получаем
• (* Л
sin —a = cosoc. ▲
Используя формулы (1)—(4), выведем формулы сложения для
синуса:
sin(a+p)=cos[|-(a+p)j=cosj[|-aj-p j=
= cos —a cosB+sin —a sinB =
U J U J
= sin a cos P + cos a sin p.
Таким образом,
sin (a + P) = sin a cos P + cos a sin p. (5)
Заменяя в формуле (5) P на ~Р, имеем
sin (a - P) = sin a cos (~P) + cos a sin (~P),
откуда
sin (a - P) = sin a cos P - cos a sin p. (6)
Задача 4. Вычислить sin 210°.
A sin 210° = sin (180° + 30°) = sin 180° cos 30° + cos 180° sin 30° =
Задача 5. Вычислить:
.8л л . л 8л
sin — cos — sin — cos —.
7 7 7 7
A . 8л л . л 8л (&п п\
A sin — cos — sin— cos — = sin =smrc =
7 7 7 7 17 7
194

Задача 6*. Доказать равенство
Л \&( (VI- S^n(ot + P) _sinacosp + cosasinp
cos(a + P) cosacosp-sinasinp"
Разделив числитель и знаменатель последней дроби на
произведение cos a cos P, получим формулу (7). А
Формула (7) может быть полезна при вычислениях. Например,
по этой формуле находим
)
l-tgl80°tg45°
Упражнения
616. С помощью формул сложения вычислить:
1) cos 135°; 2) cos 120°; 3) cos 150°; 4) cos 240°
617. He пользуясь таблицами, вычислить:
1) cos 57°30' cos 27°30' + sin 57°30' sin 27°30';
2) cos 19°30' cos 25°30' - sin 19°30' sin 25°30';
оч 7л 11л . 7л . 11л
3) cos — cos sin — sin ;
У У У У
.ч 8л л . 8л . л
4) cos — cos- +sin— sm-.
7 7 7 7
618. Вычислить:
1) cosf^ + a , если sina = -7= и 0<a< ■£;
I3 ) V3 2
2) cos a— , если cos a=-— и —
619. Упростить выражение:
1) cos 3a cos a - sin a sin 3a;
2) cos 5p cos 2p + sin 5p sin 2p;
3) c
A. (In \ (2n ~] . Г7л А . (2к \
4) cos —+a cos — + a +sm —+a sin — + a L
I5 Jl5 ) I5 Jv5 )
620. He пользуясь таблицами, вычислить:
1) sin 73° cos 17° + cos 73° sin 17°;
2) sin 73° cos 13° - cos 73° sin 13°;
O4 . 5л л . л 5л
3) sln-cos-+sin-cos-;
А, . 7 л л .л 7л
4) sin_cos_-sin-cos-.
7* 195

621. Вычислить:
14 • ( *\ 3 ЗК
1) sin а + — , если cos а=--ил<а<—;
у о ) о Z
2) sin ^-а , если sin а= -- и — < ос < тс.
\4 ) 6 *
622. Упростить выражение:
1) sin (а + р) + sin (-а) cos (~P);
2) cos (-а) sin (-р) - sin (а - Р);
3)cosf|-ajsinf|-pj-sin(a-p);
4) sin (a + р) + sin (- - а 1 sin (- р).
у2 )
3 3
623. Вычислить cos (а + Р) и cos (а - Р), если sin а= --, -п <а<2к
о Z
и sin р = — , 0<Р<-.
624. Вычислить sin (а - Р), если cos а = -0,8, - < а < к и
Li
T
625. Вычислить tg (a + P), если sin a = -, - < a < к и cos P = — ,
О Z 17
626. Упростить выражение:
1) cos (a -- P) - cos (a + P); 3) cos 3a + sin a sin 2a;
2) cos —+ a cos --a +-sin2 a; 4) cos 2a - cos a cos 3a.
V4 ) V4 ) 2
627. Доказать тождество:
si
si
sin(a-p) tga-tgp'
2) ^
cos(a + p) ctgactgp-1'
3) cos - + a 1=—(cos a-sin a);
cos(aH^ =
cosasmp
5) cos a cos P = - [cos (a + P) + cos (a - P)];
6) sin a sin P = - [cos (a - P) - cos (a + P)].
196

628. Вычислить:
г) Jg29° + tg31° . 3) l + tglO°tg55° .
l-tg29°tg31°' tg55°-tglO° '
2) ^le'^ll71 ; 4) l-tgl3°tgl7°
l+tg-*tg-*' tgl7°+tgl3°
16 16
629. Вычислить:
Q
1) tg (a + p), если tg a = -- и tg p = 2,4;
4
4
2) ctg (a - p), если ctg a= - и ctg p = -1.
630. Упростить выражение
. (к ) (n
sm - + a -cos - + a
6 3
. (n ) (к
sin — + a +cos - +
U J U
631. Упростить выражение:
1) sin a cos 2a + sin 2a cos a;
2) sin 5p cos 3p - sin 3p cos 5p.
632. Решить уравнение:
1) cos 6x cos bx + sin 6x sin bx = -1;
2) sin Sx cos bx - sin bx cos Sx = -1;
3) V2cos(-- + jcI -cosjc=1;
И
§ 32. Синус, косинус и тангенс
двойного угла
Выведем формулы синуса и косинуса двойного угла, используя
формулы сложения.
1) sin 2a = sin (a + a) = sin a cos a + sin a cos a = 2 sin a cos a.
Итак,
sin 2a =2 sin a cos a. (1)
2) cos 2a = cos (a + a) = cos a cos a - sin a sin a = cos2 a - sin2 a.
Итак,
I cos 2a = cos2 a - sin2 a. (2)
197

Задача 1. Вычислить sin 2а, если sin а = -0,6 и к < а < —.
А По формуле (1) находим
sin 2a =2sinacosa = 2 • (-0,6) • cos a =-l,2 cos a.
Так как л < a < —, то cos a < 0, и поэтому
cosa= - >/l - sin2 a = -Vl - 0,36 = -0,8.
Следовательно, sin 2a = -1,2 • (-0,8) = 0,96. A
Задача 2. Вычислить cos 2a, если cos a = 0,3.
А Используя формулу (2) и основное тригонометрическое
тождество, имеем
cos 2a = cos2 a - sin2 a = cos2 a - (1 - cos2 a) = 2 cos2 a - 1 =
= 2 (0,3)2-l = -0,82. A
o o лт sin a cos a
Задача 3. Упростить выражение «—.
l-2sin a
sin a cos a 2 sin a cos a sin 2a
A
1-2 sin"5 a 2(shr a + cos"5 a - 2 sin"5 a) 2(cos^ a - sin"5 a)
2cos2a 2
Задача 4. Вычислить tg 2a, если tg a = - .
А Полагая в формуле tg (a + P) = ———^Цг (см. § 31) p = a, no-
1-tgatgp
-tgatgp
лучаем
tg2a =
2tga
l-tg2a*
(3)
Если tg 2a = - , то по формуле (3) находим
2~ 4
tg2a=—-*r = -. A
1-(2,
Задача 5*. Вычислить sin За, если sin а = - .
4
A sin За = sin(a + 2а) = sin a cos 2а + cos a sin 2a =
= sin a (cos2 a - sin2 a) + cos a 2sin a cos a =
198

= sin a cos2 a - sin3 a + 2sin a cos2 a = 3sin a cos2 a - sin3 a =
= 3sin a (1- sin2 a) - sin3 a = 3sin a - 4sin3 a = sin a (3 - 4 sin2 a).
При sm a = - получаем sin 3a = - о --=-—. A
4 4^ 4J 16
Упражнения
Используя формулы двойного угла, преобразовать (633 — 634).
633. 1) sin 48°; 2) cos 164°; 3)tg92°;
4) sin 45°;
634. 1) si
5) sin
3 ;
6) COS у .
4) cosf— + a'
I 2
5) sin a; 6) cos a.
He используя таблицы, вычислить (635 — 637).
635. 1) 2 sin 15° cos 15°; 3) 2tg15 ;
l-tg215°
2) cos2 15° - sin215°; 4) (cos 75° - sin 75°)2.
636. 1) 2sin- cos-; 3)
8 8
2) cos --siiT-;
637. 1) 2sin 75° cos 75°; 3)
2) cos2 75° - sin2 75°; 4)
638. Вычислить sin 2a, если:
,ч . З я
l)sma= - и - <a<л;
4 Зя
2) cos a = - - и Ж a < —;
э £
639. Вычислить cos 2a, если:
2tg
8 .
>
V2 ( я
— ^cos- + s
6tg75°
l-tg275° '
tg222°30'-l
. я
Ш8
tg22°30'
3) sin a + cos a = -;
4) sin a - cos a = - - .
о
l)cosa= -;
Э
2) sin a = - -
5
199

640. Вычислить tg 2а, если tg а = 0,5.
Упростить выражение (641—642).
641. 1) 2 cos 40° cos 50°; 3) sin 2a + (sin а - cos а)2;
2) 2 sin 25° • sin 65°; 4) cos 4а + sin2 2а.
642. 1) sin2a 2 ; 2) 1+CQ62a.
(sin a + cos a) -1 1 - cos 2a
643. Доказать тождество:
1) sin 2a = (sin a + cos a)2 - 1; 3) cos4 a - sin4 a = cos 2a;
2) (sin a - cos a)2 = 1 - sin 2a; 4) 2 cos2 a - cos 2a = 1.
644. Вычислить sin 2a, если:
1) sin a + cos a = - ; 2) sin a - cos a = -- .
645. Доказать тождество:
cos 2a
1) — —9— = ctg a - 1;
sin a cos a + sin a
rt4 sin2a-2cosa rt ,
2) — r-y— = -2ctg a;
sin a - sin a
3) tg a (1 + cos 2a) = sin 2a;
.4 l-cos2a + sin2a
l+cos2a + sin2a
5)(1"2^W2ga"1)=Ctg22a;
6)l-2sin2fj-|l =sina;
q q sin 4a
7) cosd a sin a - sind a cos a = —-— ;
sina + sin2a _
646. Доказать тождество
sin2 a cos2 a
2>/2sir
sin I a —
cos a (1 + ctg a) sin a (1 + tg a) sin 2a
647. Решить уравнение:
1) sin 2jc - 2 cos x = 0; 4) sin2 x = -cos 2x;
X X 1
2) cos 2x + sin2 x = 1; 5) sin — cos — + - = 0;
x x
3) 4cos x = sin 2x; 6) cos2 — = sin2 — .
200

§ 33. Синус, косинус и тангенс
половинного угла
По некоторым значениям sin а и cos а можно найти значения
. а а , а
sin — , cos — и tg — , если известно, в какой четверти лежит угол а.
Ct Ct Ct
Из формулы cos 2x = cos2 x - sin2 х при х = — имеем
2 а • 2 а /14
cos а = cos2 — - sin2 — . (1)
Запишем основное тригонометрическое тождество в виде
1 = cos2 — + sin2 — . (2)
Ct Ct
Складывая почленно равенства (2) и (1) и вычитая почленно из
равенства (2) равенство (1), получаем
l + coscc = 2cos2 —, (3)
1 - cos a = 2 sin2 —. (4)
Формулы (3) и (4) можно представить так:
(5)
(6)
Формулы (5) и (6) называют формулами синуса и косинуса
половинного угла. Иногда их называют также формулами понижения
степени.
Если известен cos a, то из формул (5) и (6) можно найти sin —
и cos — с точностью до знака. Знак может быть определен, если из-
вестно, в какой четверти лежит угол — .
Задача 1. Вычислить cos — , если cos a = -0,02 и 0 < a < к.
Ct
А По формуле (5) находим
9 a 1 + cosa 1-0,02 Л АГ.
COS 2=^~ = —2~ = 0'49'
Так как 0 < a < я, то 0 < — < -,и поэтому cos — > 0. Следова-
Ct Ct Ct
тельно, cos — = 70,49 = 0,7. А
Ct
201
cos2
sin2
a
2
a
2
1 + cos a
2 '
1 - cos a
2

Разделив почленно равенства (6) и (5), получим формулу
тангенса половинного угла:
2 а _ 1-cosa
г£ 2 " 1 ■ -™~ " * '
Задача 2. Вычислить tg — , если cos a = 0,8 и к < а < 2к.
А По формуле (7) имеем
2 а 1-cosa = 1-0,8 _ 0,2 = 1
tg 2 " l+cosa"l+0,8"l,8"9'
По условию к < а < 2я, поэтому -< — <7cntg— <0. Следо-
вательно, tg - = -у- = -- . А
Задача 3. Упростить выражение
1-cosa ,2 al+cosa
1+cosa C^ I 2
А Используя формулы (7) и (5), получаем
1-cosa 2
2 a_l + cosa=2sin2.ct 2 a_
l + cosa 2 2 2cos2a 2
,2a, 2a 2CC-I 20C -20CA
= tg - ctg --cos - = l-cos - = sin -. A
Задача 4. Решить уравнение 1 + cos 2x = 2 cos x.
А Так как 1 + cos 2x - 2 cos2 я, то данное уравнение примет вид
2cos2 x - 2 cos Xj откуда cos x (cos x - 1) = 0.
1)cos;t=0, x= - +nk, ke Z;
Ct
2) cos *: =1, x = 27m, ne Z.
Итак, исходное уравнение имеет две серии корней: х = - + к k,
ke Zи х = 2пп> ne Z.
В ответе можно записывать обе серии с одной буквой (k или п).
Ответ. х= - +nk, x = 2nky keZ. A
a
Задача 5. Выразить sin a, cos a и tg a через tg — .
2sin —cos— 2sin —cos —
Al)sina=sin 2-И =2sin-cos-=2^ 22
2sincos
2i 2 2 ! sin2«+cos2«
(8)
202

„ „ cos2 — - sin2 — cos2 — sin2 —
2)cosa=cos|2-^|=cos2--sin2^= ^ ^ = ? 2- =
I 2
1-tg2
_2_. Итак,
cosa =
(9)
a
3)tgo=tg|2-||= ^r. Итак,
(10)
Эту формулу можно также получить почленным делением
формул (8) и (9). А
Итак, по формулам (8)—(10) можно находить синус, ко-
a
синус и тангенс угла а, зная тангенс угла —.
Упражнения
648. Выразить через двойной угол:
1) sin2 15°; 2) cos2 ^; 3) cos2 (- - а \ 4) sin2 (- + a \
649. Найти значение выражения:
1) 2 cos2 J - 1; 3) ^ + 2 sin2 15°;
2) 1 - 2 sin2
-,
4) -^ +2 cos2 15°.
650. Пусть cos a = 0,6 и 0 < a < —. Вычислить:
1) sin |; 2) cos |; 3) tg |; 4) ctg |.
Q —.
651. Пусть sin a = - и - <a< ^.Вычислить:
1) sin -; 2) cos -;
4) ctg -.
203

652. Вычислить:
1) sin 15°; 2) cos 15°; 3) tg 22°30'.
653. Вычислить:
1) sin а, если tg — = 3; 3) tg 2a, если tg a = - ;
2) cos a, если ctg — = -; 4) ctg 4a, если ctg 2a = - .
Упростить (654 — 655).
654. 1) 1+C06a; 3) (1+cos 2a) tg a;
1-cosa
2) l+sin2a + cos2a. _cqs 2 a
sina + cosa
655. 1) 1-°06a; 3) Ч
sina si
; 3) Ч ;
sina sin4a
sina e 4ч l-cos2a + sin2a
1+cosa' l+cos2a + sin2a '
656. Найти:
.ч , a . « З к
1) tg it , если sin 2а=-иО<а<~.
2 5 4
a 5 Зя
2) sin 2a и sin —, если tg a = — и л<а< —.
Li \.Li Li
Доказать тождество (657—659).
657. 1) 2 cos2 7 ~ -^ = 1 + sin a; 3) 2 cos2 7 + ^ = 1 - sin a;
2) 2 sin2 4 - -^ = 1 - sin a; 4)2 sin
2 4 + 2 = 1 + sin a*
658. 1) !=£«§*±«£ = tg*a; 2) 1±^+оов& =
3+4cos2a + cos4a ь l+sin2acos2a
659. l)k«a«.ctea=l;
sin2a
2) ^L2^ =tga; 4) It™»» =tg fj
; 1-Hcos2a s ; cos2a e И
660*. Доказать, что если 0 < a < -, то v1 + sin a.~ V1 ~ sin a = 2sin
661*. Упростить выражение .
tg4a-tg2a
204

662. Решить уравнение:
х
2 ;
х
2;
1) 1 -cosл: = 2 sin
2) 1 + cos x = 2 cos
3) 1 - cos 6x = 2 sin Sx;
4) 1 + cos 8л: = 2 cos 4x;
5)l-cos|=2cos(|--*-|;
^ч л x n . (x Sk
6)l+cos-=2sin(j-T
X 1
7) 2 sin2 - + - sin 2x = 1;
8) 2 cos2 x - - sin 4* = 1.
§ 34. Формулы приведения
Таблицы значений синуса, косинуса, тангенса и котангенса
составляются для углов от 0° до 90° (или от 0 до —). Это объясняется
тем, что их значения для остальных углов сводятся к значениям для
острых углов.
Задача 1. Вычислить sin 870° и cos 870°.
А Заметим, что 870° = 2 • 360°+ 150°. Следовательно, при
повороте точки Р(1; 0) вокруг начала координат на 870° точка
совершит два полных оборота и еще повернется на угол 150°, т. е.
получится та же самая точка М, что и при повороте на 150° (рис. 63).
Поэтому sin 870° = sin 150°, cos 870° = cos 150°.
Рис. 63
Рис. 64
Построим точку Мj, симметричную точке М относительно оси
Оу (рис. 64). Ординаты точек М и Мх одинаковы, а абсциссы
отличаются только знаком. Поэтому sin 150° = sin 30° = -, cos 150° =
= -cos30°=-f.
Ответ: sin 870°= \, cos870°=-^. A
205

При решении задачи 1 использовались равенства
sin (2 • 360°+ 150°) = sin 150°, cos (2 360°+ 150°) = cos 150°, (1)
sin (180° -30°) = sin 30°, cos (180° - 30°) =-cos 30°. (2)
Равенства (1) верны, так как при повороте точки Р(1; 0) на угол
ос+ 2nk9 k g Z, получается та же самая точка, что и при повороте
на угол а.
Следовательно, верны формулы
sin (ой- 2nk) = sin a, cos (а + 2nk) = cos а, ke Z.
(3)
(4)
Равенства (2) являются частными случаями формул
sin (я - а) = sin а, cos (я - а) = -cos а.
Докажем формулу sin (я - а) = sin а.
О Применяя формулу сложения для синуса, имеем
sin (я - а) = sin я cos а - cos я sin а =
= 0 cos а - (-1) sin а = sin а. •
Аналогично доказывается и вторая из формул (4). Формулы (4)
называются формулами приведения.
Вообще формулами приведения для синуса называют следующие
шесть формул:
sin | — a | = cos a, sm
=cosa;
sin (я - a) = sin a, sin (я + a) = - sin a;
sin a = - cos a, sin —
V 2 ) \ 2
I = - cos a, sm I — + a I = - cos a.
(5)
Следующие шесть формул называют формулами приведения для
косинуса:
cos I - - a = sm a, cos - + a | = - sin a;
2 ) V2
cos (я - a) = - cos a, cos (я + a) = - cos a;
(Sn Л (Зк
cos a = - sm a, cos —
= sin a.
(в)
Формулы (5) и (6) справедливы при любых значениях а.
Задача 2. Вычислить sin 930°.
А Используя из формул (3) первую, получаем
sin 930° = sin (3 360° - 150°) = sin (-150°).
206

По формуле sin (-a) = - sin а имеем
sin (-150°) = -sin 150°.
По формуле (4) находим:
- sin 150° = - sin (180° - 30°) = - sin 30° = - \ .
Ответ, sin 930°= -|. А
Задача 3. Вычислить cos —г-.
4
15л (А кЛ ( пЛ к V2 .
A cos = cos 4л — = cos - — = cos - = — . А
Покажем теперь, как можно свести вычисление тангенса
любого угла к вычислениям тангенса острого угла.
Отметим, что из формул (3) и определения тангенса следует
равенство tg (a + 2nk) = tga9ke Z.
Используя это равенство и формулы (4), получаем
tg (а + л) = tg (а + л - 2л) = tg (а - л) =
, , ч sinfrc-a) sina ,
= -tg(n-a)= ) { = =tga.
cos(7i-a) -cosa
Следовательно, справедлива формула
' (7)
Аналогично доказывается формула
ctg (a + nk) = ctg a, k e Z. (8)
Следующие четыре формулы называют формулами приведения
для тангенса и котангенса:
ctga, tg(|-a|=
ctga,
\к \ (к \ (
ctg ^- + a =-tga, ctgf|-aj=tga.
Формулы (9) справедливы при всех допустимых значениях а.
3 а д а ч а 4. Вычислить: 1) tg -=- ; 2) tg —- .
207

Формулы приведения для синуса и косинуса доказываются с
помощью формул сложения аналогично тому, как доказана первая
формула (4).
Формулы (9) можно получить из формул (5) и (6), зная, что
tgoc =
cosot
Формулы приведения необязательно запоминать. Для того
чтобы записать любую из них, можно руководствоваться
следующими правилами:
1) В правой части формулы ставится тот знак, который имеет
левая часть при условии 0 < а < - .
2) Если в левой части формулы угол равен - ± а или — ± а, то
синус заменяется на косинус, тангенс — на котангенс и
наоборот. Если угол равен к ± а, то замены не происходит.
Например, покажем, как с помощью этих правил можно
получить формулу приведения для cos I — + a . По первому правилу в пра-
вой части формулы надо поставить знак «-», так как если
О < a < - , то - < - + a < я, а косинус во второй четверти отрица-
телен. По второму правилу косинус нужно заменить на синус,
следовательно, cos I — + a = - sin a.
V2 )
Итак, формулы (3), (7) и формулы приведения позволяют
свести вычисление синуса, косинуса, тангенса и котангенса любого угла
к вычислению их значений для острого угла.
Упражнения
663. Найти острый угол а, при котором выполняется равенство:
1) cos 75° = cos (90° - a); 5) sin - к = sin (к + a);
2) sin 150° = sin (90° + a); 6) tg | = tg (| - a 1;
3) sin 150°= sin (180°-a); 7) cos Ц- = cosffre+a];
4) cos 310° = cos (270° + a); 8) ctg у к = ctg (2л - a).
208

664. Привести к углу а, где 0 < а < -:
1) cos 110°;
5)tg291°;
41
9) cos — n;
2) sin 148°;
6) ctg 305°;
10) sin — к;
3)sin
7) ctg
ID tg
5
5
sK;
8
sn;
4
4) cos - n;
5
8) sin - к;
28
12) ctg — n.
Используя формулы приведения, вычислить (665—666).
665. 1) cos 150° ; 2) sin 135°; 3) ctg 135°; 4) cos 120°;
5) cos 225°; 6) sin 210°; 7) ctg 240°; 8) sin 315°.
666. 1) tg f; 2) sin Ц ; 3) cos f ; 4) ctg f ;
5)sm[- —j; 6)cos[-yj; 7)te[- —J; 8)ctg[~J.
Упростить (667-668).
ctg —a -tg(K + a) + sin —-a
667. 1) i2 I L^
cos (7i + a)
sin (я - a) + cos —+ a + ctg (я - а)
2> 7Г l
. f Зтс ^ fie
sm — + a tg —+a
668. 1) l 2 J 12
ctg (2л - a) sin (я + а)
sin2 (я + a) + sin2 I -+a
cos —+a
I2
669. Привести к углу а, где 0 < a < —, и вычислить:
4
1) cos 750°; 2) sin 1140°; 3) tg 405°; 4) cos 840°;
еч . 47л 25л 27л оч 21л
5) sm — ; 6) tg —; 7) ctg — ; 8) cos — .
209

670. Найти числовое значение выражения:
1) cos 630° - sin 1470° -ctg 1125°;
2) tg 1800° - sin 495° + cos 945°;
3) 3 cos 3660° + sin (-1560°) + cos (-450°);
4) cos 4455° - cos (-945°) + tg 1035° - ctg (-1500°).
671. Вычислить:
1Ч 23л . 15л , ( 11л
1) cos — sin - ctg -
4 4 V 2
оч . 25л ( ПпЛ , Юл
2)Sin — -cos[-— j-tg—;
3) sin (—7jc) - 2cos — tg —- ;
о 4
лх / л ч о • ( 497О , ( 2\ъ\
4) cos (-9л) + 2 sin -— - ctg -— L
Доказать тождество (672 — 673).
(п Л (к \
672. l)sin 4 + а -cos 4~а1=0;
3) ctg a-ctg I Y + otJ=-l;
sin —-cc ctg —+а
i2 ) \\
4) i2 )■ \\ =-sina.
tg(n+a) f^]
673. l)sin|y +
^ + o|=-sin^-a|;
. ( л
с—— | =-cos - + a
V3
4) cos а = cos a + —
674. Доказать, что синус суммы двух внутренних углов
треугольника равен синусу его третьего угла.
210

675. Решить уравнение:
l)cos \--х | = 1; 3) cos (x - п) = 0;
V2 )
5) sin (2x + Зя) sin (Sx + —) - sin Sx cos 2x = -1;
I 2 J
6) sin f 5x - — ) cos (2л: + 4л) - sin (5x + к) sin 2x = 0.
2
676**. Доказать, что вычисление значений синуса, косинуса и
тангенса любого угла можно свести к вычислению их значений
для угла, заключенного в промежутке от 0 до - .
§ 35. Сумма и разность синусов,
сумма и разность косинусов
При различных преобразованиях тригонометрических
выражений бывает полезно представлять сумму или разность синусов и
косинусов в виде произведения.
Так, для суммы синусов справедлива формула
. о о . ос + Р сс-р
sin a + sin р = 2 sin —s- cos —г1-
(1)
О Обозначим —г— = х, —^- = у. Тогда х + у = а, х - у = $, и по-
этому
sin a + sin р = sin (х + у) + sin (x - у) =
= sin х cos у + cos x sin у + sin x cos у - cos x sin у =
= 2 sin x cos у = 2 sin ——- cos —^- . •
Ct Ct
Заменив в формуле (1) p на (-р), имеем
• о о • а~Р
sin а - sin В = 2sm —- cos
~ О
(2)
Аналогично выводится формула для суммы косинусов:
cos a + cos р = cos (х + у) + cos (x - у) =
- cos х cos у - sin x sin у + cos x cos у -/-sin x sin у =
= 2 cos x cos у =2 cos ^J- cos
211

Итак,
cos а + cos p = 2cos
cos —-— .
2 2
Точно так же выводится формула
cos а - cos р = -2 sin — J- sin ^—- .
2 2
Задача 1. Вычислить sin 75° + sin 15°.
Д sin 75° + sin 15° = 2 sin t cos -^-r
(3)
(4)
= 2 sin 45° cos 30° =
о or» 11я 5я
Задача 2. Вычислить cos —— cos — .
11я 5я _ . 8я . Зя _ . 2я . к
A cos гг^— cos — = ~2 sin — sin — = -2 sin — sin — =
_ >/5 .
Задача З. Доказать равенство
q_
sin(ot + p)
cosa cosp
sinp _ sinacosp + sinpeosa _ sin(a + p)
cosa cosp cosacosp cosa cosp"
Задача 4. Решить уравнение cos Sx - cos x = 0.
Используя формулу (4), получаем -2 sin 2x sin л: = 0.
l)sin2;t = 0,
= nk,x= —9keZ;
2) sin x = 0, л: = яп, пе Z.
Каждый корень из второй серии содержится среди корней
первой серии, так как пп - — при k = 2n. Поэтому в первой серии со-
держатся все корни исходного уравнения.
Ответ. х= — у ke Z. А
Задача 5. Преобразовать в произведение 2 sin a + >/з .
А 2 sin a + >/з = 2 sin a + — = 2 sin a + sin - =
A . (a , k\ (a n
= 4sin - + 6-cos ---
212

Задача 6*. Доказать, что наименьшее значение выражения
sin a + cos а равно -v2 , а наибольшее равно V2 .
А Преобразуем данное выражение в произведение:
sin a + cos а = sin а + sin - - а = 2 sin - cos а — =
= V2 cos [а—£ I.
I 4J
Так как наименьшее значение косинуса равно -1, а
наибольшее— 1, то наименьшее значение этого выражения равно
л/2 • (-1) = - V2 , а наибольшее равно V2 • 1 = V2. А
Упражнения
677. Вычислить без таблиц:
1) cos 105° + cos 75°; 5) tg 267° + tg 93°;
2) sin 105° - sin 75°; 6) tg Щ + tg ^ ;
Пл 5л _ч . 7л . л
3) cos — + cos — ; 7) sin — - sin —;
4) cos ^ - cos ^ ; 8) sin 105° + sin 165°.
678. Упростить выражение:
2)cos I -4-P I -cos I ^ + P |; 4)cos2 | «-- | - cos2
679. Доказать тождество:
cosct + cos3a cos2a-cos4a
680. Упростить выражение:
1Ч 2(cosa + cos3a) Оч 1 +sin a-cos 2a-sin 3a
2sin 2a + sin 4a 2 sin2 a + sin a -1
681. Доказать тождество:
1) cos4 a-sin4 a + sin 2a = V2 cos I 2a-- I;
V 4J
2)cosa + cos I — + a +cos a | =0;
3 I 3
213

3)cos2a + cos2 fj + al + cos2 (jj-
.v sin2a + sin4a-sin3a
cos 2a + cos 4a-cos 3a
682. Преобразовать в произведение:
1)1 + 2 sin a; 5) 1 + sin a;
2) 1 - 2 sin a; 6) 1 - sin a;
3) 1 + 2 cos a; 7) 1 + cos a + sin a;
4) >/з - 2 cos a; 8) 1 - cos a - sin a.
683. Доказать тождество:
1) cos a + cos 2a + cos 6a + cos 7a = 4cos — cos — cos 4a;
2) cos 2a + cos 5a - cos 3a - cos 7a = - 4sin — sin a cos — .
684. Упростить выражение:
1 + sin a - sin 3a - cos 2a
1)
2sin a + sina-1
685. Решить уравнение:
1) sin Sx + sin x - 0;
2) cos 4jc + cos x = 0;
3) sin Sx = sin л:;
4) tg x + tg 3* = 0;
Зя
tg(a + p)-tga
1 + tga
2)
6) cos (2x - к) - sin (4x + — ] = 0;
I 2
7) sin Sx + sin x = 2 cos x;
8) cos bx - cos x - 2 sin Sx;
9)cos
5)sin bx + cos х-— =0; 10)sin 2*-^ -sin
x--]=0;
4
^ 1=0.
686*. Разложить на множители:
1)1- cos a + sin a; 3) 1 + sin a - cos a - tg a;
2) 1 - 2 cos a + cos 2a; 4) 1 + sin a + cos a + tg a.
687*. Вычислить без таблиц:
1) tg 9° - tg 27° - tg 63° + tg 81°; 2) cos 36° + cos 108°.
214

§ 36. Произведение синусов и косинусов
В ходе преобразований тригонометрических выражений бывает
также полезно представлять произведение синусов и косинусов в
виде суммы или разности.
Так, для произведения синуса и косинуса справедлива формула:
sin a cos p = - [sin (a + p) + sin (a - p)].
О По формулам сложения имеем
sin (а + р) = sin а cos p + cos а sin p;
sin (а - р) = sin а cos p - cos а sin p.
Складывая почленно эти равенства, получаем
sin (а + р) + sin (а - р) = 2sin а cos p,
откуда следует формула (1). •
Аналогично доказываются формулы:
sin a sin р = - [cos (а - р) - cos (а + р)],
cos а cos p = - [cos (а + р) + cos (а - р)].
(1)
(2)
(3)
Задача 1. Доказать тождество:
4 sin a sin — + а sin — - а = sin 3 а.
А Применяя формулу (2), имеем
2 sin I - + а I sin I - - а I = cos 2а - cos -у = cos 2а + - .
Тогда левая часть примет вид 2sin a cos 2а + sin а. Используя
формулу (1), находим 2sin a cos 2а = sin За - sin а, откуда следует,
что левая часть тождества равна sin За. А
Задача 2. Вычислить 4 cos
А По формуле (3) получаем
5л л
—
л. A
cos
А
4coS
= 2| cos- + cos- =
215

Задача 3. Решить уравнение
2 sin 2x cos х = sin Sx.
А По формуле (1) находим
sin Sx + sin x = sin Sx,
откуда sin x = 0, x = nk, ke Z. A
Упражнения
Представить произведение в виде суммы (688—690).
688. 1) sin 4° sin 6°; 3) cos 7° cos 90°;
2) sin 11° sin 13°; 4) cos 15° cos 3°.
689. 1) sin (a + P) sin (a - p); 3) sin (a + P) cos (a - p);
2) cos (a - p) cos (a + p); 4) cos (a + p) sin (a - p).
690. 1) 4 sin 10° cos 50° cos 40°; 2) 4 cos 15° sin 15° sin 100°.
691. Вычислить: sin (60° + a) sin (60° - a), если cos 2 a = -.
о
692. Доказать тождество:
1) 2 sin x sin 2x + cos Sx = cos x;
a к ^ (a , к } . .я
6 '
693. Вычислить cos I 7 + a cos т" a L если sin a = - .
^4 ) 6
694. Вычислить sin I '~k + a I cos I т + a , если cos a = - .
{6 ) [b ) 4
695. Решить уравнение:
1) 2sin Sx sin 2x = cos x; 3) sin 2 x cos x = sin x cos 2x;
2) 2 sin Sx cos x = 2 sin x cos x; 4) sin x cos Sx - sin Sx cos x.
696. Преобразовать произведение в сумму:
1) sin a cos 3a cos 4a; 2) cos 3a cos 5a cos 7a.
Упражнения к главе VI
697. Найти:
л/3 к
1) cos a, если sin a = — и - < a < к;
у[Е ЗЯ
2) tg a, если cos a = —— и к < a < — ;
о Z
216

3) sin а, если tg a = 2>/2 и 0 < a < -;
4) cos a, если ctg a = V2 и ж a < —
698. Упростить выражение:
'л
2
1) 2 sin (-a) cos | *-a| - 2cos(-a)sinf--al;
I2 )
2) 2 sin (n - a) cos (- - a ) + 3 sin2 (| - a 1 - 2;
tg2(-a))' X
l + ctg2(-a)J'
sin(7i + a)cos —-a tg a--
V 2 i v 2
cos - + a cos —
2 )
V2 ) V2
Вычислить (699-700).
699. 1) sin ^E; 2)tg^; 3)ctg^; 4) cos
D 4 4
700. 1) cos ^ - sin ^ ; 3) cos 3660° + sin (-1560°);
4 4
25л Юл
2) sin — - tg — ; 4) cos (-945°) + tg 1035°.
Упростить выражение (701—702).
гтг\ч 1ч fl + cos2a . ^1, o. , fl + sina .
701. 1) sina -^а; 2) ctga cosa .
I sina 12 I cosa
fn Л . (n } { n
-cos - + a sin --a
sin - + a -cos - + a sin --a +cos --a
702. 1) У У ; 2) 4
. (n ) (к ) . (n ) In
sin —+ a +cos - + a sin —-a -cos —-a
и ) {* ) U J и
703. Доказать тождество:
cosacosp
cosacosp
217

Вычислить (704-705).
704. 1) 2sin 6a cos2 I - + За - sin 6а при а = -^ ;
И ) 24
2) cos За + 2 cos (п - За) sin2 - - 1,5а при а = — .
[4 ) 36
V3(cos75°-cosl5°) о,
7051)
l-2sin215° l + 8sin2-cos2-
8 8
706. Доказать тождество:
2sin2a-sin4a 2cos2a-sin4a fn
г) 2sin2a + sin4a =tg a; 2) 2cos2a + sin4a =tg (4"a
707. Показать, что:
1) sin 35° + sin 25° = cos 5°; 2) cos 12° - cos 48° = sin 18°
ПРОВЕРЬ СЕБЯ!
4 к
1. Вычислить sin а, tg а, cos 2а, если cos а = -^ и - < а < я.
2. Найти значение выражения:
1) cos 135°; 2) sin ^ ; 3) tg Ц-; 4) cos2 \ - sin2 Ц-.
о о о о
3. Доказать тождество:
1) 3 cos 2а - sin2 а + cos2 а = 2 cos 2а;
оч sin5a-sin3a
2) — = sin a.
2cos4a
4. Упростить выражение:
1) sin (a - р) - sin - - a sin (-p);
2)cos2 (jc-a)-cos2 [^~a
3) 2 sin a sin p + cos (a + p).
708. Упростить выражение
fcosp sinp ^ l-cos4a
l^sina cosaj (р
218

Доказать тождество (709—710).
sin (2a - Зл) + 2cos I — + 2а
709. 1) ^ г L? J- =-V3ctg2a;
2cos I - - 2а |+ >/3 cos (2a - Зя)
I6 )
2\ 4sin4(a-l,5K) =
sin4 (а-2,5л) + cos4 (а + 2,5л)-1
gv -2соб4(а-л)
cos4 (а - 1,5л)+sin4 (а + 1,5л) -1
2cos|--2a ]-V3sin(2,5n-2a)
cos (4,5л - 2а) + 2cos (- + 2а ' ^
[ 6
sm2a"sma
711. Вычислить:
=
-v , ex 1 5л Зл
1) ctg — , если cosa=- и—- < а < — ;
Z о 4 ^
2) tg — , если cos a = - - и - < a < к.
ct & 2
^,-л ^ sin2 a cos2 a
712. Вычислить значение выражения : , если
cos a sin a
sin a - cos a = - .
_^o ^ 4sin2a + 5cos2a , 1
713. Вычислить значение выражения _ . .— —, если ctg a = -.
2sin2a-3cos2a 3
Доказать тождество (714—715).
714. 1) sin2 (a + p) = sin2 a + sin2 p + 2 sin a sin p cos (a + p);
2) sin a + 2 sin 3a + sin 5a = 4 sin 3a cos2 a ;
3) \=*?£ = ctg2|^ + a\ 4) **а+У9а =2ctg2a.
l + sin2a [4 j l+tgatg2a
-1K 14 cos2 a + sin4 a-cos4 a o 2 ex
715. 1) = 2cos —;
1-cosa 2
9ч sina + sin3a + sin5a
219

716*. Найти значение выражения:
1ч sin а , о
х) т-8 о—Г"> если tg а = 2;
sin ot + 3cos а
оч sin2 2а , о
2) —j г~з , если tg а = 3.
cos a + sina cos a
Доказать тождество (717 — 718).
2)sin2 a + cos --a cos - + a 1 = -;
I3 J I3 ) 4
718*. 1) sin6 a + cos6 a = ~ (5 + 3 cos 4a);
о
2) sin8 a + cos8 a = -rz (cos2 4a + 14 cos 4a + 17);
3) sin 3a sin3 a + cos 3a cos3 a = cos3 2a ;
Историческая справка
Как и многие разделы математики, тригонометрия возникла в
древние времена из потребностей людей при ведении расчетов,
связанных с земельными работами (для определения расстояния до
недоступных предметов, составления географических карт и пр.).
Еще древнегреческие ученые создали «тригонометрию хорд», в
которой выражались зависимости между центральными углами
круга и хордами, на которые они опираются. Этой тригонометрией
пользовался во II в. до н. э. в своих расчетах древнегреческий
астроном Гиппарх. Во II в. н. э. греческий ученый Птоломвй в своей
работе «Алмагест» («Великая книга») вывел соотношения в
круге, которые по сути своей аналогичны современным формулам
синуса половинного и двойного углов, синуса суммы и разности двух
углов.
Долгие годы тригонометрия служила и развивалась благодаря
астрономии. В VIII в. усилиями математиков Ближнего и Среднего
Востока тригонометрия выделилась из астрономии и стала
самостоятельной математической дисциплиной. К этому времени хорды в
220

тригонометрии были заменены синусами (отношениями половины
хорды к радиусу круга), были введены понятия косинуса и
тангенса, а также составлены таблицы значений тригонометрических
функций.
Слово «синус» произошло от латинского sinus («перегиб»),
которое, в свою очередь, происходит от арабского слова «джива»
(«тетива лука»). Слово «косинус» — сокращение словосочетания
complementi sinus («синус дополнения»), объясняющего тот факт,
к
что cos а равен синусу угла, дополняющего угол а до - , т.е.
-~~ °Ч. Латинское слово tangens переводится как
«касательная» («касательная к окружности»).
Идея введения тригонометрических понятий с помощью круга
единичного радиуса получила распространение в X-XI вв.
Первый научный труд, в котором тригонометрия утвердилась
как самостоятельная ветвь математики, был создан в 1462-1464 гг.
немецким астрономом и математиком И. Мюллером, известным в
истории под псевдонимом Региомонтан (1436-1476). После Регио-
монтана значительный вклад в тригонометрию внес польский
астроном и математик Н. Коперник (1473-1543), посвятивший этой
науке два раздела своего знаменитого труда «Об обращениях
небесных тел» (1543). Позже, в сочинениях И. Кеплера (1571-1630),
Й. Бюрги (1552-1632), Ф. Виета и других известных математиков,
встречаются сложные преобразования тригонометрических
выражений и выводятся многие формулы. Интересны, например,
рекуррентные формулы, полученные Ф. Виетом:
cos та = 2 cos a cos (m - 1)а - cos (m - 2)а;
cos та = -2 sin а sin (m - 1)а + cos (m - 2)а;
sin ma = 2 cos a sin (m - l)a - sin (m - 2)a;
sin ma = 2 sin a cos (m - l)a + sin (m - 2)a.
Тригонометрическая символика с годами совершенствовалась и
лишь в трудах Л. Эйлера в XVIII в. приобрела современный вид,
удобный для решения вычислительных задач.
Следует отметить, что помимо «плоскостной» тригонометрии,
изучаемой в школе, существует сферическая тригонометрия,
являющаяся частью сферической геометрии. Сферическая
тригонометрия рассматривает соотношения между сторонами и углами
треугольников на сфере, образованных дугами больших кругов сферы.
Исторически сферическая тригонометрия возникла из потребностей
астрономии фактически раньше тригонометрии на плоскости.
221

ТРИГОНОМЕТРИЧЕСКИЕ
глава VII ] [ УРАВНЕНИЯ
Об определении тригонометрических функций
Вы знаете, что каждому действительному числу х соответствует
единственная точка единичной окружности, получаемая поворотом
точки (1; 0) на угол х радиан. Для этого угла определены sin x и cos x.
Тем самым каждому действительному числу х поставлены в
соответствие числа sin х и cos x, т. е. на множестве R всех действительных
чисел определены функции
у - sin хиу = cos х.
Каждая из этих функций принимает значения от -1 до 1, т. е.
-1 <sin;t< 1, -1 < cos;t<l.
m , sinx
Так как tg x = , то тангенс числа х определен для тех х, для
COSJC
которых cos х •*■ 0, т. е. для всех действительных значений х, кроме
х = - +nk, k e Z. Функция у = tg x принимает все действительные
значения.
^ , cosjc
Функция ctg х = —— определена для всех действительных зна-
sinx
чений х9 кроме х = nk, k e Z, и принимает все действительные
значения.
Функции у = sin х, у = cos х, у = tg х, у = ctg х называют
тригонометрическими, а уравнения sin х = a, cos х = а, tg х = а, ctg х = а
называют простейшими тригонометрическими уравнениями.
Решить тригонометрическое уравнение, например уравнение
cos х = а, — это значит найти все его корни, т. е. найти числа х,
которые обращают уравнение в верное числовое равенство, или
установить, что таких чисел нет.
222

§ 37. Уравнение cos x- a
Рассмотрим уравнение
cos х = a. (1)
Так как множество значений косинуса — отрезок [-1; 1], то
уравнение (1) имеет корни только при -К a < 1.
Корни уравнения (1) при а = О, а = 1,а = -1 были найдены в § 26:
cos х = 0
COS X = 1
cos;t = -l
х- — +ЛЛ, neZ
х = 2лп, га е Z
х = п + 2пп, пе Z
(2)
(3)
(4)
2кп
Задача 1. Решить уравнение cos Зх - 1.
А По формуле (3) имеем Зх = 2пп, п е Z, откуда л: = -тг1
пе Z. А
Задача 2. Решить уравнение cos х = -
А Напомним, что cos x — абсцисса
точки единичной окружности,
полученной поворотом точки Р(1; 0) вокруг
начала координат на угол х радиан. Абсцис-
1
су, равную - , имеют две точки
окружности Мг и М2 (рис. 65). Так как
- = cos - , то точка Мг получается из
точки Р(1; 0) поворотом на угол хг = —,
а также на углы х = - + 2nk9 где k = ±1, ±2,
Рис. 65
Точка М2 получается
из точки Р(1; 0) поворотом на угол х2 = — —, а также на углы
-— + 2nk9 где k = ±1, ±2, ... . Итак, все корни уравнения cos x - -
можно найти по формулам х= — + 2nk9 х = - — + 2я£, ke Z. Вместо
о о
двух этих формул обычно пользуются одной:
П ~ -,keZ. A
223

Задача 3. Решить уравнение cos x = — -
л/,
Рис. 66
А Абсциссу, равную - - , имеют две
точки окружности Mj и М2,
симметричные относительно оси абсцисс (рис. 66).
m 1 2к 2л
Так как -- = cos —, то хл - —,
Z о х 3
х2 = - — . Следовательно, все корни
уравнения cos х = - - можно найти по фор-
2л
муле х = ±— +2nk, ke Z. A
Таким образом, каждое из уравнений cos х = - и cos х - - -
имеет бесконечное множество корней.
На отрезке 0 < х < п каждое из этих уравнений имеет только один
к 1 2л
корень: хл = - — корень уравнения cos х= - и х.= — — корень
1 о 2 о
1 тт к г
уравнения cos х = — —. Число ~ называют арккосинусом числа — и
2 о 2
1 л 2л ( \\
записывают: arccos - = - , а число — — арккосинусом числа —-
z о б у 2)
( \\ 2л
и записывают: arccos — = — .
Вообще уравнение cos х = а, где -1 < а < 1, имеет на отрезке
О < х < п только один корень. Если а > 0, то корень заключен в
промежутке
°#
если а < 0, то в промежутке
(И
. Этот корень
называют арккосинусом числа а и обозначают arccos а (рис. 67).
Арккосинусом числа а, модуль которого не больше единицы,
называется такое число х из промежутка 0 < х < я, косинус
которого равен а:
' ' (5)
arccos а = х, если 0 < х < п и cos x = а.
Например:
1ч V3 я л л V3
1) arccos — = -, так как 0 < - < к и cos g = — ;
2)arccos
= —-, так как
4
—- < к и cos —
4 4
224

arccos я,
б)
Рис. 67
Формулу (5) можно также представить в виде:
cos (arccos a) = а, если | а | < 1.
(6)
Например, cos (arccos 0,3) = 0,3.
Задача 4. Найти приближенное значение arccos (-0,75).
А Значение arccos (-0,75) можно
приближенно найти на рисунке 68,
измеряя угол РОМ транспортиром.
Приближенные значения
арккосинуса можно также находить с
помощью специальных таблиц или
микрокалькулятора. Например, значение
arccos (-0,75) можно вычислить на
микрокалькуляторе МК—54 по программе
0,75 [7-7
24188583.
Рис. 68
Итак, arccos (-0,75) « 2,42.
В данном случае переключатель микрокалькулятора Р-ГРД-Г был
установлен в положение Р (радиан).
Если вычисления проводить в градусной мере, то переключатель
микрокалькулятора Р-ГРД-Г следует установить в положение Г
(градус). Программа вычислений остается прежней:
138,59038.
0,75 /-/
cos
-1
Итак, arccos (-0,75) « 139°. А
Задача 5. Решить уравнение
cos х = cos a,
где а — заданное действительное число.
А Запишем уравнение (7) в виде
cos л:-cos a = 0.
(7)
8-Ю. М. Колягин, 10 кл
225

1 Y -X- (Y X. (Y
По формуле разности косинусов получаем — sin sin = О,
откуда:
l)sin ^-^ =0, ^^ =nk>
x = -a + 2nk, keZ; (8)
оч . X~a л Х~а
2) sin -y- = 0, -y- = 7c/e,
x = a + 2nk9 ke Z. (9)
Объединяя формулы (8), (9), имеем: л: = ±а + 2nk, ke Z. A
Отметим, что если в уравнении (7) а = arccos а, где | а \ < 1, то
его можно записать так: cos x = а.
Результаты решения задач 1—3 позволяют сделать следующий
вывод:
I Все корни уравнения cos х = а, где \а\ < 1, находятся по формуле
= ± arccos a + 2rcfe, feeZ. (10)
Отметим, что формулы (2) - (4) являются частными случаями
формулы (10).
>/з
Задача 6. Решить уравнение cos х = — .
Li
Jo
А По формуле (10) находим х = ± arccos — + 2nk.
Так как arccos -=- = - ,то х = ±- + 2nk, k e Z. А
2 о о
V2
Задача 7. Решить уравнение cos х- —— .
( л/2 ^
А По формуле (10) получаем х = ± arccos —— + 2nk. Так как
( >fe} Зтг Зя о и и „ А
arccos —it =-—,tox=±-—+ 27c/e, k e Z. A
^ ^ ) 4 4
Задача 8. Решить уравнение cos х = —— .
Ci
А Так как V5 > 2, то - V5 < -2, поэтому - — < -1. Следователь-
но, уравнение не имеет корней. А
226

Докажем, что для любого а е [-1; 1] выполняется равенство
(И)
arccos (-а) = я - arccos а.
О Обозначим arccos a = х. По определению арккосинуса числа
имеем:
1)0<*:<я; 2) cos x = а.
Тогда:
1) по свойствам неравенств -я < -х < 0, откуда 0 < я - х < я;
2) по формуле приведения cos (я - х) = -cos x = -а.
Следовательно, по определению арккосинуса числа имеем:
arccos (-а) = я - х = я-arccos а. •
„ ( S)
Например, arccos —— = п - arccos
л/3
я 5л
= к - - = — .
Формула (11) позволяет сводить значения арккосинуса
отрицательных чисел к значениям арккосинуса положительных чисел.
Поэтому в таблицах обычно даются значения арккосинуса только
для неотрицательных чисел.
Приведем таблицу часто встречающихся значений арккосинуса:
а
arccos a
0
к
2
1
2
к
3
V2
2
к
4
V3
2
к
6
1
0
Задача 9. Решить уравнение cos x = --.
о
А По формуле (2) находим х = ± arccos | —- | + 2кп, п е Z или
э
х = ± я - arccos - + 2яи, л е Z. А
5J
Задача 10. Решить уравнение 1 + 2cos (2х - 1) = 0.
А Данное уравнение можно представить в виде
Отсюда 2х - 1 = + arccos ~ + 2пп = ± я-arccos - + 2кп =
z) \ 2 )
= ±
, 2х = 1 ± Щ-
: = - ± ^
2 о
, n g Z. А
8*
227

Отметим, что корни тригонометрических уравнений обычно
записываются действительными числами, выраженными с помощью
числа я. Это связано с тем, что значения тригонометрических
функций повторяются через промежутки, кратные я.
Так, корнями уравнения cos х = cos 5 являются числа х = ±5 + 2яА,
ke Z.
Приведем еще несколько задач на применение рассмотренных
формул.
Задача 11. Решить уравнение cos Зх cos х = 1 - sin Зх sin x.
A cos Зх cos х + sin Зх sin x = 1, cos 2x = 1,
2х = 2пп> х = кпу пе Z. А
Задача 12. Решить уравнение (4cos х - 1) (2 cos 2х + 1) = 0.
А 1) 4cos х - 1 = 0, cos л: = - , х = ± arccos - + 2кп, пе Z.
4 4
2)2cos2;t + l = 0, cos 2* = -- , 2х = ± у +27m, x = ±-+nn,neZ.
1 я
Ответ. jc = ±arccos - + 2кп9 х = ± - + 7m, neZ. A
4 о
Задача 13. Вычислить sin | arccos | - - 11.
о
А Так как 0 < arccos | - - 1 < я, то sin arccos --- 11 > 0. Следо-
3 У 3,
вательно, sin arccos -- = + /1-cos2 arccos [-- 11 =
I I *)) V I V 6
Задача 14. Вычислить arccos | cos — |.
4
А Сначала вычислим cos — . По формуле приведения cos —
4 4
= cos \K + т =-cos - =-— . Следовательно,
( Ьп\ { &) V2 к Зя
arccos cos — = arccos ~~~о~ \ =к- arccos —--= я --=-—
{ 4 ) { г ) 2 4 4
228

(о \
cos— .
3 )
лгр 2я 1 ( 2к\ ( 1) 2к
А Так как cos — = - - , то arccos cos — = arccos | "о = "«Г •
3 2 ^ 3 J V z) **
Вообще
arccos (cos x) = х при 0<л:<я. (12)
О По определению арккосинуса числа равенство
arccos a - х (13)
означает, что:
1)0<л:<я; 2) cos x = а.
Подставляя в равенство (13) а = cos x, получаем формулу (12). •
Например, по формуле (12) находим
arccos cos— = — , arccos (cos 2) = 2.
I 5 J 5
Эту же задачу можно также решить с помощью формулы (12).
Задача 16. Вычислить arccos cos —
I 4
А Так как — > я, то нельзя сразу применить формулу (12).
4
Заметим, что cos — = cos ^"""7" = cos — . Теперь формулу
(12) можно применить, так как 0 < —- < я. Получим arccos cos — =
4 I 4 J
( Зя "\ Зя
= arccos cos — = — . a
I 4 J 4
Задача 17. Вычислить arccos (cos 4).
А Так как 4 > я, то нельзя сразу применять формулу (12).
Сначала надо заменить cos 4 косинусом числа, принадлежащего
отрезку [0; я]. Отметим, что я < 4 < 2я, откуда -2 я < -4 < -я,
0<2я-4<я.
Так как cos (2я - 4) = cos (-4) = cos 4, то по формуле (12) находим
arccos (cos 4) = arccos (cos (2я - 4)) = 2я - 4.
Упражнения
Вычислить (719-720). г-
719. 1) arccos 0; 2) arccos 1; 3) arccos —- ;
1 ( л/з) ( л/2
4) arccos -; 5) arccos —■- ; 6) arccos ——
2 12 2
229

720. 1) 2 arccos 0 + 3 arccos 1; 2) 3 arccos (-1) - 2 arccos 0;
Тз
3) 12 arccos — - arccos | -- |;
{ Я)
4) 4 arccos ^~ + 6 arccos
Вычислить (721-723).
Я
721. 1) cos arccos — ; 4) sin arccos — ;
2) cos arccos - ;
3)sin arccos - I;
722. 1) cos 6arccos
2) cos [ 3arccos -
3) sin 4arccos -
I 2
723. 1) arccos I cos —
5)tg arccos- ;
V *)
6) tg arccos -^ .
cos — ;
2 )
724. Сравнить числа:
1) arccos — и arccos - ;
2 £
V2
2) arccos — и arccos 0;
725. Сравнить числа:
1) arccos - и arccos \~~Л\
Решить уравнение (726-728).
.Го
726. ]
4) sin (5 arccos 0);
5) tg [ 2arccos ^
6) tg | 3arccos —
3) arccos I cos -n
3
13
4) arccos | cos —n
3) arccos —— и arccos — ;
12] [2)
4) arccos (-1) и arccos I .
2) arccos "т и arccos (-1)
2) cos x - - ;
4) cos *: = -
7з
2 '
1
230

727. 1) cos x = - ;
о
3
2) cos x = - ;
728. I)cos4*=l;
2) cos 2x = -1;
3) V2cos - =-1;
4
3) cos* = -0,3;
4) cos* = -0,2.
4) 2 cos ^ = >/з ;
+ ^1=0;
6)cos \2x~ | = 0.
Вычислить (729-732).
729. 1) arccos cos-я ; 2) arccos cos-я I; 3) arccos | sin-
6 ) [ 3 ) 13
4) arccos | sin-я |; 5) arccos | 2cos^ |; 6) arccos [ -tg- ].
730. 1) cos (arccos 0,2);
2) cos | arccos I--
3
3)cos [ я+arccos -
I 4
731. 1) sin [arccos |-|
2) sin arccos- ;
2
3)sin [ arccos- I;
1
732. l)sin | arccos - + arccos
3 о
4) cos (я - arccos 0,3);
5) sin —+arccos-7= ;
[2 V3 J
6)sin --arccos-— |.
I Z о
4) sin | arccos- |;
3
( 2
6)tg arccos-^ ,.
arccos—arccos- .
5 5 )
733. Упростить выражение, если -1 < a < 1:
1) cos (я + arccos a); 3) cos (2 arccos a);
2) sin [ -H-arccosa |;
4) sin | — H-arccosa
z
734. Решить уравнение:
1) cos x cos Sx = sin Sx sin x;
2) cos 2x cos x + sin 2* sin x = 0.
231

735. Выяснить, имеет ли смысл выражение:
1) arccos (>/б - 3); 4) arccos (1 - V5);
2) arccos (V7 - 2); 5) tg 2arccos \-
3arccos^
Решить уравнение (736 — 737).
736. 1) cos2 2x = 1 + sin2 2х\ 3) 2 cos2 x = 1 + 2 sin2 x;
2) 4 cos2 * = 3; 4) 2 V2 cos2 x = 1 + V2 .
737. 1) (1 + cos *) (3 - 2 cos *) = 0;
2) (1 - cos x) (4 + 3 cos 2*) = 0;
3) (1 + 2 cos x) (1 - 3 cos *) = 0;
4) (1 - 2 cos x) (2 + 3 cos x) = 0.
738*. Решить уравнение:
1) arccos (2x - 3) = - ;
о
2) arccos
3 '
739. Найти все корни уравнения cos 2х = - - на отрезке --; —
г i г г
у[2
740. Найти все корни уравнения cos 4л: = — , удовлетворяющие не-
Li
равенству | х \ < -.
741*. Доказать, что если -1 < а < 1, то 2 arccos
= arccos a.
§ 38. Уравнение sin х = а
Рассмотрим уравнение
sin л: = а. (1)
Так как множество значений синуса — отрезок [-1; 1], то
уравнение (1) имеет корни только при -1 < а < 1.
Корни уравнения (1) при а = 0, а = 1, а = -1 были ранее найдены:
sin х = 0
sin x = 1
sin;t = -l
л: =
л: =
х =
к
= 2
я
= ~2
7т, пе
+ 27СП,
+ 2пп>
Z
пе
пе
Z
Z
(2)
(3)
(4)
232

Задача 1. Решить уравнение sin 2х = 1.
А По формуле (3) имеем 2х = — + 2пп, пе Z, откуда
х = — + 7т, пе Z. А
4
Задача 2. Решить уравнение sin х = - .
А Напомним, что sin x — ордината точки единичной
окружности, полученной поворотом точки Р(1; 0) вокруг начала координат
на угол х. Ординату, равную - , имеют две точки окружности М. и
М2 (рис. 69).
Так как - = sin -, то точка
по-
лучается из точки Р(1; 0) поворотом на
к к
угол хл = —, а также на углы х = - + Znk,
1 о о
где k = ±1, ±2, ... . Точка М2 получается
из точки Р(1; 0) поворотом на угол
5я
о
5я
—
о
Рис. 69
т. е. на углы х = к- — +2nk, где k = ±l9 ±2,... .
Итак, все корни уравнения sin x = - можно найти по формулам:
х= - + 2nk, х = к - - + 2nk9 ke Z.
о о
Эти формулы объединяются в одну:
6
В самом деле, если п — четное число, т. е. п = 2k9 то из формулы
9 пе Z.
(5)
(5) имеем х = — + 2nky а если п — нечетное число, т. е. п = 2k +1, то из
о
этой же формулы получаем х = п - — + 2nk.
Ответ. х = (-1)п - +пп9 пе Z. А
233

Задача 3. Решить уравнение sin х = - — .
м
Рис. 70
А Ординату, равную - - , имеют две
точки единичной окружности Мг и М2
(рис. 70), где хх = - -, х2 = - — . Следо-
1
вательно, все корни уравнения sin х--
можно найти по формулам: х - - — + 2яА,
5я
х = - — + 2nk, ke Z.
о
Эти формулы объединяются в одну:
(6)
В самом деле, если п = 2/е, то по формуле (6) имеем х = - — + 2nk,
5л
а если п = 2k - 1, то из этой же формулы находим л: = - — + 2nk.
Ответ. х = (-1)п (-^
пп, пе Z. *
Итак, каждое из уравнений sin х = - и sin x = -- имеет бесконеч-
ное множество корней. На отрезке - — < х < - каждое из этих урав-
нений имеет только один корень: хл = — — корень уравнения
1 о
1 я 1 тт к
sin х- - и jc2 = - — — корень уравнения sin х = - - . Число - - называ-
1 . 1 я к
ют арксинусом числа — и записывают так: arcsin - = -; число --
1 . ( 1) л
называют арксинусом числа - - и записывают: arcsin \~ \=- — и
2 V *) ь
Вообще уравнение sin х = а, где -1 < а < 1, на отрезке - - < х < -
Ct Ct
имеет только один корень. Если а > 0, то корень заключен в
промежутке 0; — ; если а < 0, то в промежутке - -; 0 . Этот ко-
L 2J [ 2 )
рень называют арксинусом числа а и обозначают arcsin а (рис. 71).
234

Рис. 71
Арксинусом числа а, модуль которого не больше единицы, на-
к
зывается такое число х из промежутка - —
равен а:
п
— , синус которого
к . . к
arcsin а = х, если - — < х < - и sin x = а.
(7)
Например:
1Ч . у[2 п к к к . к >/2
1) arcsin — = - , так как --< - < -nsin- = — ;
оч - (
2) arcsin -
=--, так как
-f<-i<i-eIn(-f)=-T-
Задача 4. Найти приближенное значение arcsin -
А Значение arcsin- можно приближенно найти из рисунка 72,
измеряя угол РОМ транспортиром.
Значения арксинуса можно находить
по специальным таблицам или с
помощью микрокалькулятора. Например,
2
значение arcsin - можно вычислить на
о
микрокалькуляторе МК—54 по
программе:
ВТ
з Ы
sin
-1
7,2972769 • ИГ1.
Рис. 72
235

2
Итак, arcsin - ~ 0,73. При этом переключатель микрокальку-
о
лятора Р-ГРД-Г был установлен в положение Р (радиан). А
Формулу (7) можно записать и так:
' (8)
sin (arcsin a) = а, если | а | < 1.
Задача 5. Решить уравнение
sin х = sin a, (9)
где а — заданное действительное число.
А Запишем уравнение (9) в виде:
sin х - sin a = 0.
По формуле разности синусов имеем
1 . х-а х + а ~
-sin— cos —= 0,
откуда:
14 • Х~а л Х~а
l)sm ~y~ =0, —£-
2nk, ke Z; (10)
x + a л Jt + a к
2)cos ~y~ =0, --- = g + nb9
x = -a + n(2k + l), ke Z. (11)
Объединяя формулы (10), (11), получаем
:c = (-l)"a + 7m, neZ. A
Отметим, что если в уравнении (9) a = arcsin а, где | а \ < 1, то
его можно представить так: sin x = а.
Результаты решения задач 2, 3 и 5 позволяют сделать
следующий вывод.
Все корни уравнения sin х = а, где | а \ < 1, находятся по формуле
= (-1)п arcsin a + 7m, neZ. (12)
Отметим, что формулы (2) — (4) являются частными случаями
формулы (12).
7з
Задача 6. Решить уравнение sin х = —г .
А По формуле (12) имеем х - (~1)л arcsin -— + пп. Так как
arcsin — - -,тол: = (-1)л « +яп, пе Z. А
2
236

V2
Задача 7. Решить уравнение sin x = - —.
( у/2
А По формуле (12) находим х = (-1)" arcsin - — | 4- кп. Так как
arcsin I -
4
= (-1)п+1 -л +пп,пе Z. А
4
Vio
Задача 8. Решить уравнение sin x = —т—.
о
А Так как л/10 > 3, то —— > 1, и поэтому данное уравнение не
о
имеет корней. А
Докажем, что для любого а е [-1; 1] выполняется равенство
arcsin (-а) = - arcsin а. I
(13)
О Обозначим arcsin a = а. По определению арксинуса числа это
означает, что:
2) sin a = а.
Тогда:
1) по свойствам неравенств - - < -ос < - ;
2) используя формулу sin (-a) = -sin а, получаем sin (-a) = -а.
Следовательно, по определению арксинуса числа:
arcsin (-а) = -а = -arcsin а. •
и . I Тз! .
Например, arcsin —— = -arcsin
1
7з
к
3*
Формула (13) позволяет сводить значения арксинуса
отрицательных чисел к значениям арксинуса положительных чисел.
Поэтому в таблицах обычно даются значения арксинуса только для
неотрицательных чисел.
Приведем таблицу часто встречающихся значений арксинуса:
а
arcsin a
0
0
1
2
к
6
V2
2
к
4
7з
2
п
3
1
тс
2
237

2
Задача 9. Решить уравнение sin х = - .
о
2
А По формуле (12) находим х = (~1)п arcsin - + кп, пе Z. А
Задача 10. Решить уравнение 1-2 sin (Sx + 4) = 0.
А Данное уравнение можно записать в виде sin (Sx + 4) = - .
Отсюда Sx + 4 = (-1)" arcsin - +nn = (-l)n - + 7m,
Зл: = -4 + (-1)" ^ + nn,
Задача 11. Решить уравнение sin 5л: cos 2x - cos 5л: sin 2x.
A sin 5л: cos 2x - cos 5л: sin 2л: = 0, sin Sx = 0, Sx = ли,
л: = — , и g Z. А
о
Задача 12. Решить уравнение (3 sin х - 1) (2 sin 2л: + 1) = 0
А 1) 3 sin л: - 1 = 0, sin х = - , х - (-l)n arcsin - + пп, пе Z;
2) 2 sin 2л: + 1 = 0, sin 2л: = - - , 2л: = (-1)Л arcsin -^ + пп =
-arcsin ij +nn = {-l)n+1 J +nn,
x = (l) + f,neZ.
Ответ, x = (~l)n arcsin - + nn, x = (~l)n+1 — + — , n e Z. A
о 1Z Z
Задача 13. Вычислить cos arcsin — .
I V 5))
А Так как - - < arcsin (- - I < - , то cos arcsin - - | ] > 0.
2 15 12 I 15
Следовательно, cos arcsin — = + 11 - sin2 arcsin - - I =
5 5
238

in [sin|].
Задача 14. Вычислить arcsin
AT . я V3 . ( . кЛ . л/3 я
А Так как sin - = — , то arcsin sin — = arcsin — = —.
о 2» 13) & о
Вообще
arcsin (sin x) = х при - — < х < —.
Ct Ct
О По определению арксинуса числа равенство
arcsin а = х
означает, что:
к к
1)-2<X<2
; 2) sin x = а.
(14)
(15)
Подставляя в равенство (15) а = sin x, получаем формулу (14). •
Например, по формуле (14) находим arcsin sin — = —,
arcsin (sin (-1,5)) =-1,5.
( . Ъ \
Задача 15. Вычислить arcsin sm ^ я .
А Сначала вычислим sin — . По формуле приведения имеем
о
. 5л . ( к\ . я 1
smT =sm^--j=sin- = -.
Следовательно,
. ( . Ъп\ .1 я А
arcsin sm — = arcsin - = —. А
Задачу 15 можно также решить с помощью формулы (14).
А Так как — > -, то нельзя сразу применить формулу (14).
6 2
Заметим, что sin — = sin \к— = sin - . Теперь формулу (14)
6 I 6J о
можно применить, так как - - < - < - . Получаем
с\ О с\
arcsm sm — = arcsin sm - = - . A
6 6)6
239

Задача 16. Вычислить arcsin (sin 5).
Q
А Так как - л < 5 < 2л, то - - < 5 - 2л < 0, т. е. 5 - 2л е
Следовательно,
arcsin (sin 5) = arcsin (sin (5 - 2л)) = 5 - 2л. А
Упражнения
—£> ^ .
Вычислить (742-749).
742. 1) arcsin 0; 2) arcsin 1;
3) arcsin
2 '
л\ • ! кч • (
4) arcsin - ; 5) arcsin -
2 \
7з
6) arcsin | - — |.
743. 1) arcsin I - arcsin (-1);
2) arcsin —f= + arcsin [--/= ; 4) arcsin
v2 I v2 )
( y/s) ( V2I
744. l)sin arcsin— ; 4) cos arcsin— ;
1 л/3
3) arcsin - + arcsin — ;
& 2
+ arcsin | -~z |.
2) sin arcsin- |;
I 2
5)tg|arcsin^|;
3) cos arcsin - ; 6) tg
v 2)
745. 1) sin (4 arcsin 1); 4) cos (6 arcsin 1);
2) sin I 3 arcsin — I; 5) tg | 2arcsin- |;
3) cos I 5 arcsin — ; 6) tg 4 arcsin —
746. 1) cos (arcsin 0,6); 2) cos arcsin-= .
I v3 J
747. 1) arcsin | sin - |; 3) arcsin | sin ■£ |;
2) arcsin I sin - |;
748. 1) arcsin cos- |;
V 3
4) arcsin | sin — |.
2) arcsin I cos- |.
240

2)arccos | sin
749. l)arccos sin- ;
750. Сравнить числа:
1 f И ( 31
1) arcsin - и arcsin -— ; 2) arcsin "- и arcsin (-1).
Решить уравнение (751—755).
751.
752.
753.
754.
755.
1) sin x = — ;
2) sin x = — ;
3
1) sin x = - ;
2
2) sin л: = - ;
I)sin3*:=l;
2) sin 2л: = -1;
3) V2 sin | =-1;
2
3 '
2)sinx = _^;
l)sin(2x-l)=|;
3) sin x =
4)sinx =
3) sin x =
4) sin x =
4) 2 sin |
5)sin(*-
6)sin |2*
3) sin л: =
4) sin л: =
2) sin (3*
1
"V2;
1
2*
1
4;
V5
3 "
= 7з
1 + V5
3 5
l-Vio
2
+ 2) =
Вычислить (756-759).
756. l)arcsin|sin^
p
2) arcsin | sin —- |;
3
3)arcsin I cos-^ I;
6
4) arcsin | cos— |;
5) arccsin | 2sin —
6) arcsin
Г к
7) arcsin (sin 4);
8) arcsin (sin 7).
241

757. l)sin I arcsin- |;
3
4) sin к + arcsin - ;
I 3)
2) sin I arcsin -- ||;
3) sin к - arcsin -
6)ooe [f-anrin^];
758. 1) cos arcsin - I;
6) cos (- + arcsin - ].
12 5 J
4) cos arcsin:
2) cos arcsin --
I 5
3)cos |arcsin|--
3
759. l)sin arccos- |;
v 3
760. Вычислить:
5)tg|arcsin-^|;
6) tg I arcsin-^ |.
2) sin arccos -
2V2
l)sin I arcsin - + arccos
3 3
2) cos arcsin - + arccos -
^ 5 5
761. Вычислить:
( 2V2 11
3)cos arcsin + arcsin- ;
( A. \
4) sin arccos - + arccos - |.
15 5
2) cos 2arcsin - .
762. Выяснить, имеет ли смысл выражение:
1) sin 2arcsin - I;
I 3J
1) arcsin (y[E - 2);
2) arcsin (>/б -3);
3) arcsin (3 - Vl7 );
Решить уравнение (763—765).
4) arcsin (2 - VlO );
5) tg |6arcsin- I;
/9
6)tg |2arcsin —
763. 1) 1 - 4 sin x cos *: = 0; 3) 1 + 6 sin — cos — = 0;
4 4
2) 7з + 4 sin x cos x = 0;
764. 1)1+ cos bx sin 4x = cos 4x sin bx\
2) 1 - sin x cos 2x = cos x sin 2x.
4) 1 - 8 sin ^ cos f = 0.
О о
242

765. 1) (2 sin x - 1) (3 sin x + 1) = 0;
2) (4 sin x - 3) (2 sin * + 1) = 0;
3) (2 sin 2x - 1) (sin 4* + 1) = 0;
4) (4 sin Sx - 1) (2 sin x + 3) = 0.
766. Найти все корни уравнения sin 2x = - , принадлежащие
отрезку [0;2л].
767. Найти все корни уравнения sin — = — , удовлетворяющие не-
равенству \ogK (х - 4л) < 1.
768. Найти наименьший положительный корень уравнения
769*. Решить уравнение:
1) arcsin f--з! = ^; 2) arcsin (3 - 2х) = - -л .
[2 ) 6 4
770*. Доказать равенство:
1Ч . 4 ( 11 "I Зя
Darcsin^ -arccos ^-7Ш]=-Т;
2) arccos - + arccos - - = arccos - — .
771*. Доказать, что если 0 < а < 1, то 2 arcsin a - arccos (1-2 а2).
§ 39. Уравнение tg х = а
Напомним, что значения синуса и косинуса можно находить
геометрически, измеряя ординаты и абсциссы соответствующих точек
единичной окружности. Покажем, как можно геометрически
находить значения тангенса.
Рассмотрим сначала случай, когда 0 < х < — . Пусть точка Мх
получена поворотом точки Р(1; 0) вокруг начала координат на угол
х радиан (рис. 73). Соединим отрезком точку Мг с точкой О и
проведем МгА _1_ ОР. Тогда ордината точки Мх равна АМХ = sin x9 а
абсцисса АО = cos х.
Поэтому
243
tgX cosx АО

a=tgx
V/
A
M
7x\x
/
N
0 A i
^
M
Д1;
/
0)
X
_
" tg Х'
Теперь через точку Р(1; 0) проведем
прямую I перпендикулярно РО и
продолжим прямую ОМг до пересечения с
прямой I в точке М (см. рис.73). Из
подобия треугольников МгЛ0 и МРО
получаем
АМг _ РМ
~Ю ~ ~РО
Так как РО = 1, то
РМ = tg х.
Итак, в этом случае значение tg x
Рис. 73 можно найти геометрически, измерив
длину отрезка РМ, т. е. ординату
точки М (см. рис. 73).
Рассуждения и построение можно провести в обратном порядке
и найти геометрически угол х по значению tg x> т. е. найти корень
уравнения
tg х = а,
где а — любое заданное положительное число. А именно: на прямой
I построим точку М с ординатой а, соединим точку М с точкой О и
измерим угол х = ZPOM транспортиром (см. рис. 73).
Таким образом, между числами х, где 0 < х < — , и точками пря-
мой Z, лежащими выше оси абсцисс, установлено взаимно
однозначное соответствие.
Так как tg 0 = 0, то, естественно, числу х - 0 поставим в
соответствие точку Р(1; 0) прямой /.
Напомним, что тангенс угла — не существует. Это видно и гео-
метрически: если точка Мх лежит на
оси ординат, то прямые ОМХ и /
параллельны и поэтому точки пересечения М
не существует.
Теперь рассмотрим случай, когда
-- < х < 0. Сделаем аналогичные
построения (рис. 74). Тогда sin х = -AMV
cos x = АО.
Поэтому
Рис.74
(\
a=tgx
0
Л
A
f *
\
W
/
_ sin* АМХ
244

Из подобия треугольников МгАО и МРО имеем
АМг РМ
~AO=~¥6='igX'
а так как РО - 1, то
PM = -tgx.
Отметим, что и в этом случае tg х = -РМ — это ордината точки М.
к к
Итак, между числами х из интервала — — < х < — и всеми точ-
ками прямой I установлено взаимно однозначное соответствие.
Прямую I называют линией тангенсов.
Кроме того, показано, что уравнение
где а — любое действительное число, имеет единственный корень х
на интервале - - < х < —. Этот корень называют арктангенсом
числа аи обозначают arctg а (рис. 75).
а) б)
Рис. 75
Арктангенсом числа ае R называется такое число х е . 2
тангенс которого равен а:
к к
к к
arctg а = х, если - - < х < - ntgx = a.
(1)
Например:
^Ч1/—Я К К К Л К г-
1) arctg V3 = з , так как - - < -; < - и tg - = V3 ;
2) arctg (-1) = -^, так как -
245

У
2
1
V °
У
м
arctg 2
Р(1;0)
X
Задача 1. Найти приближенное
значение arctg 2.
А Значение arctg 2 можно
приближенно найти из рисунка 76, измеряя
угол РОМ транспортиром.
Приближенные значения
арктангенса можно также найти по
таблицам или с помощью
микрокалькулятора.
Например, значение arctg 2 можно
вычислить на МК—54 по программе
Рис. 76
1, 1071486.
Итак, arctg 2 « 1,11. А
Из формулы (1) следует, что
tg (arctg a) = a,ae R.
(2)
Например:
tg (arctg 12) = 12, tg (arctg (- V7 )) = - V7 , tg (arctg 0) = 0.
Задача 2. Решить уравнение
tg x = tg a,
где a — заданное число, a Ф — + nk9 ke Z.
А Преобразуем это уравнение:
tg x - tg a = 0,
(3)
sin л:
since
= 0,
cosjc cosa
sin jccos a - cos Jtsin a
cos ;t cosa
sin (л:-a)
cos ;t cosa
= 0,
= 0.
(4)
Заметим, что cos a Ф 0, так как a Ф - + nk, k e Z. Кроме того, и
cos x Ф 0, так как при cos x = 0 левая часть уравнения не определена.
Следовательно, sin(х- а)-0, откуда;с-а=ля, х = а + кп ,пе Z.
Ответ. х = а + пп ,пе Z. ±
Отметим, что если в уравнении (3) a = arctg a,aeR, то
уравнение (3) можно представить так:
tgx = a.
246

Результат решения задачи 2 приводит к выводу:
все корни уравнения
tgx = a, ае R
находятся по формуле
х = srctg а-\-кп , пе Z. (5)
Задача 3. Решить уравнение tg х = 1.
А По формуле (5) находим х = arctg 1 + кп = — + кп, пе Z. А
4
л/3
Задача 4. Решить уравнение tg л: = - — .
о
А По формуле (5) имеем х = arctg \+кп = -- + кп, пе Z. А
{ 2 ) Ь
Задача 5. Решить уравнение tg x = 5.
А По формуле (5) находим л: = arctg 5 + кп, пе Z. А
Задача 6. Решить уравнение (tg х + 1) 2cos— - v3 = 0.
I 3 )
А 1) tg х + 1 = 0, tg х = -1, х = - - + кп, п е Z.
4
Эти значения х являются корнями исходного уравнения, так
как при этом выражение в первой скобке левой части уравнения
равно нулю, а во второй — не теряет смысла.
2) 2 cos д - 7з = 0, cos - = — , - = ±- + 2кп, х = ±- + бкп,
пе Z.
При этих значениях х выражение во второй скобке левой
части исходного уравнения равно нулю, а в первой — не имеет
смысла. Поэтому эти значения не являются корнями исходного
уравнения.
Ответ, jc = - - + кп, пе Z. А
4
Докажем, что для любого действительного числа а
выполняется равенство
arctg (-a) = -arctg а. (6)
О Обозначим arctg a = а. По определению арктангенса числа
имеем:
<< ^; 2)tga = a.
247

Тогда:
1) по свойствам неравенств - - < -а < - ;
2) используя формулу tg (-а) = -tg а, получаем tg (-a) = -а.
Следовательно, по определению арктангенса числа
arctg (-а) =-а =-arctg а. •
л/3 я
. ( Я] +
Например, arctg - — = -arctg
I О I
Формула (6) позволяет сводить значения арктангенса
отрицательных чисел к значениям арктангенса положительных чисел.
Поэтому в таблицах обычно даются значения арктангенса только для
неотрицательных чисел.
Приведем таблицу часто встречающихся значений арктангенса:
а
arctg a
0
0
V3
3
к
6
1
к
4
к
3
Задача 7. Вычислить arctg tg — .
V 6)
А Так как tg - = — , то arctg tg ^ I = arctg — = -. А
о о ^ о j о о
Вообще
arctg (tg x) = х
(7)
О По определению арктангенса числа равенство
arctg a = х (8)
означает, что:
1)~1<х<1; 2)tgx = a.
Подставляя в равенство (8) а = tg x, получаем формулу (7). •
Например, по формуле (7) находим arctg | tg[ -— ] | = - -,
arctg (tg 1,5) = 1,5.
248

Задача 8. Вычислить arctg I tg — .
I 4 )
А Сначала вычислим tg — . По формуле приведения
j -tg-=-l.
Следовательно, arctg I tg — I = arctg (-1) = - -. A
Задачу 8 можно также решить с помощью формулы (7).
А Так как —- > - , то нельзя сразу применить формулу (7).
4 &
Заметим, что tg — = tg \ п- — \ = tg -— . Теперь можно при-
4 { *) v 4;
менить формулу (7), так как - — < - — < - . Получаем
Ct 4 £t
arctg (tgf}=arctg(tg[-^]]=-f. A
Задача 9. Вычислить arctg (tg 3).
А Так как - < 3 < я, то - - <3-7С< - . Следовательно,
arctg (tg 3) = arctg (tg (3 - к)) = 3 - п. А
Упражнения
Вычислить (772-773).
772. 1) arctg 1 - arctg (-1); 3) arctg 0 + arctg (->/3);
2) arctg -j= + arctg >/з ; 4) arctg ~ "Tg + arctS °-
773. 1) 6 arctg 7з - 4 arcsin
in - -щ I;
2) 2 arctg 1 + 3 arcsin
in -- ;
v 2)
( l ^ (-&
3) 3 arctg \--j= +2 arccos
{ V3J
4) 5 arctg (-V3) - 3 arccos
I * )
249

774. Сравнить числа:
г ( >/з
1) arctg V3 и arctg 1; 4) arctg (-1) и arcsin - —
I г
2) arctg -75 и arctg V3 ; 5) arctg 1 и arccos -- ;
Vo \ *)
(f^\ ( l\ i— 1
- — и arcsin -- ; 6) arctg V3 и arccos - .
3 J { 2) z
775. Вычислить:
_ ( i Л
1) ctg (arctg J3 ); 4) sin arctg —r= ;
I V3j
2) ctg (arctg 1); 5) cos (arctg 1);
3) sin (arctg (- л/3)); 6) cos (arctg (S)).
Решить уравнение (116—111).
776. l)tgx=-^; 4)tg* = -l;
2)tg*= >/3; b)tgx = 4;
S)tgx=S; 6)tgx = -5.
111. l)tg2* = 0; 3)l + tgf =0;
2)tg3x = 0; 4) V3 +tg f = 0.
Вычислить (778-781).
3
6
778. 1) tg (arctg 5); 5) tg (n - arctg f |;
v
2) tg (arctg 3,5); 6) tg ( к + arctg -
I 4
3)tg (arctg (-12));
4) tg (arctg (-9)); 8) ctg f | - arctg 2 j.
779. 1) arctg (tg ^ ); 5) arctg {2sin ^ 1;
I 4 J I 6 )
( Ьп\ ( к Л
2) arctg tg — ; 6) arctg 2sin - ;
I 6 ; v 3;
3) arctg (ctg у j; 7) arctg (cos Ц j;
4) arctg I ctg ~ I; 8) arctg f cos (- ™
250

780. 1) tg (arctg 2,1); 3) tg (я - arctg 7);
2) tg (arctg (-0,3)); 4) ctg [j +arctg 61.
781. 1) 3 arctg (tg 5 j; 3) arctg f tg
2) 4 arctg (tg 0,5); 4) arctg (tg 13).
Решить уравнение (782—783).
782. l)(tg*-l)(tg;t+ V3) = 0; 4)(tg* - 4,5)(1 + 2 sin x) = 0;
2)(V3 tgx + l)(tgx- V3) = 0; 5)(tg* + 4)ftg--ll=0;
I 2 )
3) (tg x - 2) (2 cos * - 1) = 0; 6) (tg| + 1 j(tg * - 1) = 0.
783*. 1) arctg (5* - 1) = ^; 2) arctg (3 - 5*) = - jj.
784. С помощью микрокалькулятора решить уравнение:
785. Найти наименьший положительный и наибольший
отрицательный корни уравнения 3 tg x - V3 =0.
786*. Доказать равенства:
1) arctg 2 + arctg 3 = —; 2) arctg - + arctg - = —.
4 2 о 4
ah
787*. Доказать, что если ab Ф 1, то tg (arctg a + arctg b) = .
1—ab
788*. Доказать, что при любом действительном значении а
справедливо равенство cos (arctg a) =
§ 40. Уравнение ctg х = а
Рассмотрим уравнение
ctg х = а.
Используя формулу приведения, запишем это уравнение так:
tg\»-x\=a. (1)
251

В § 39 показано, что уравнение (1) при любом заданном действи-
к к}
тельном значении а имеет единственный корень в интервале ■ 27 2 1'
т. е. тогда, когда
к к к
откуда
-я < -х < О,
0< х<к.
Итак, уравнение ctg x = a, ae R имеет единственный корень на
интервале 0 < х < п. Этот корень называют арккотангенсом числа
а и обозначают arcctg a.
Арккотангенсом числа а е R называется такое число х е (0; я),
котангенс которого равен а:
arcctg а = х> если 0 < х < п и ctg x = а.
(2)
Например:
1Ч , V3 к к к V3
1) arcctg — = —, так как 0 < — < к и ctg — = -5- ;
2) arcctg (-1) = -7-, так как 0 < —- < п и ctg — = -1.
4 4 4
Из формулы (2) следует, что
ctg (arcctg a) = a,ae R. (3)
Например: ctg (arcctg 15) = 15; ctg (arcctg (-7)) = -7;
ctg (arcctg 0) = 0.
При определении арккотангенса числа а формулой (2) было
установлено, что х = arcctg а является единственным корнем уравнения
ctg х = а
на промежутке 0 < х < п.
Так же, как и в § 39, доказывается, что все корни уравнения
ctgx = a, ae R
находятся по формуле
х = arcctg а + кп, пе Z. (4)
Задача 1. Решить уравнения:
l)ctgx= V3;2)ctgx = -1; 3)ctg* = 0.
252

А По формуле (4) находим:
1) х = arcctg у/з + ял = — + пп, пе Z;
о
2)х = arcctg(-1) + ял = — + 7m, neZ;
4
3)л: = arcctg0 + кп = — + лл, пе Z. А
Докажем, что для любого ае R выполняется равенство
arcctg (-а) = к - arcctg а.
(5)
О Обозначим arcctg a = х. По определению арккотангенса числа
имеем:
л; 2) ctg x = а.
Тогда:
1) по свойствам неравенств -л < -х < О, откуда 0 < л - х < л;
2) по формуле приведения ctg (л - х) = -ctg x = -а.
Следовательно, по определению арккотангенса числа:
arcctg (-а) = л - л: = л - arcctg а. •
Рассуждая аналогично, можно также показать, что
arctga + arcctga= -,ae R.
(6)
Формула (5) позволяет сводить значения арккотангенса
отрицательных чисел к значениям арккотангенса положительных
чисел.
Приведем таблицу некоторых значений арккотангенса:
а
arcctg a
0
я
"2
7з
3
к
1
я
1
S
к
6
Аналогично тому, как это сделано в § 39 для арккосинуса,
можно доказать, что
arcctg (ctg x) = х, если 0 < х < п.
(7)
При решении уравнений, содержащих котангенс, можно исполь-
зовать формулу ctg а =
КП
1 КП гш
при а * — , пе Z.
tga 2
253

Задача 2. Решить уравнение ctg х-- —^ .
А Если х — корень уравнения cosx = —=, то cos jc/Ои sin x * 0.
sin* V3
Поэтому можно воспользоваться формулой ctg х = т— и записать
igx
данное уравнение в виде tg л: = - V3 . Отсюда
х = arctg (- V3 ) + ял =-arctg >/з + пп = - - + ял, пе Z. А
о
Вообще уравнение
ctg л: = а (8)
при а * 0 равносильно уравнению tg х = -, и поэтому корнями
уравнения при а Ф 0 являются числа х = arctg - + пп, п е Z.
Задача 3. Решить уравнение (tg л: + 4) (ctg jc - >/з ) = 0.
А 1) tg л: + 4 = 0, tg л: = -4, л: = arctg (-4) + пп = -arctg 4 + пп, пе Z.
При этих значениях х выражение в первой скобке левой части
исходного уравнения обращается в нуль, а во второй не теряет
смысла, так как из равенства tg х = -4 следует, что ctg х = - — .
Следовательно, найденные значения х являются корнями
исходного уравнения.
г- г- 1 1
2) ctg х - V3 = 0, ctg х = V3 , tg x = -j£ , х = arctg ^yg + пп =
= - + nn9 пе Z.
6
Эти значения х также являются корнями исходного уравнения,
так как при этом выражение во второй скобке левой части
уравнения равно нулю, а в первой не теряет смысла.
О т в е т. х = -arctg 4 + пп, х = - + пп9 п е Z. А
Л „ 2я
Задача 4. Вычислить arcctg tg
V 5
А По формуле приведения
2л . fn 2n^ , я
t t~.
254

По формуле (7) находим
. (> 2кЛ , ( . к Л
arcctg tg — = arcctg ctg —- .
V 5 ) V 1U)
Эту задачу можно иначе решить.
А По формуле (6) имеем
arcctg [tgT j= ^ -arctg [tgTj= 2 " T = 10 ' A
Итак, в этом и предыдущих параграфах показано, как
решаются простейшие тригонометрические уравнения sin x = a, cos x = а,
tg х = а, ctg л: = а.
Все другие тригонометрические уравнения с помощью
тригонометрических и алгебраических преобразований сводятся к
простейшим. В следующих параграфах будут рассмотрены некоторые типы
тригонометрических уравнений и способы их решений.
Упражнения
Вычислить (789—793).
789.1) arcctg 1; 3) arcctg у/з ;
л/3
2) arcctg (-1); 4) arcctg — .
(Го
790.1) 3 arcctg >/з - 4 arccos ^
2) 2 arcsin I -- I + arcctg 1;
3) - arctg >/3 + 2 arcctg -j= + arcctg (-1);
• V2 ( n , 7з
4) arcsin — + arccos -- + arcctg — .
В)
791.1) arcctg (- л/3 ); 2) arcctg f -^ J.
792.1) ctg (arcctg 1); 2) ctg (arcctg >/з ).
793.1) arcctg (ctg J1; 2) arcctg f ctg J1.
794. Сравнить числа:
1) arcctg V3 и arcctg 1; 3) arcctg 1 и arctg ^ ;
1 yfs
2) arcctg (- >/з ) и arcctg (-1); 4) arccos - и arcctg -r-
& о
255

Решить уравнение (795—801).
795. l)ctgx = -l; 2)ctgx = l; S)ctgx=S;
= -^; 6) ctg* = 7.
796.1) 1 + ctg | = 0; 2) ctg Sx = 0.
о
797.1)2 -ctg 2x-^ =0; 2)l-ctg
798.1) ctg I 2x -1 j = 7з ; 2) ctg Ых
799. l)6ctg| 1-^1-7 = 0; 2)5ctg(l + - 1+6 = 0.
V 4J V 3)
800.1) (tg x - 5) (ctg x + 7з ) = 0; 2) (ctg x + 3) (tg x + 1) = 0.
801. l)(ctgx- >/3)f2sin^- + ll=0;
3)
4) fl-V2cos-l(l+ V
802*. Вычислить:
1) arcctg tg -тс ; 2) arcctg tg -к .
803*. Доказать, что если -1 < а < 1, то
а
ctg (arccos a) = / .
л/1-а
§ 41. Уравнения, сводящиеся к квадратным
Рассмотрим тригонометрические уравнения, которые сводятся
к квадратным относительно синуса, косинуса или тангенса.
Задача 1. Решить уравнение sin2 x + sin х - 2 = 0.
А Это уравнение является квадратным относительно sin x.
256

Поэтому
откуда sin x = 1 или sin x = -2.
Уравнение sin х = 1 имеет корни х = — + 27m, ne Z; уравнение
sin х = -2 не имеет корней.
Ответ, х = — + 27cn, neZ. A
Задача 2. Решить уравнение 2 cos2 х - 5 sin х + 1 = 0.
А Заменяя cos2 х на 1 - sin2 x, получаем
2(1 - sin2 х) - 5 sin х + 1 = 0 или
2 sin2 х + 5 sin х - 3 = 0,
-5±J25 + 24 -5±7
откуда sin л: = -3, sin x = - .
Уравнение sin x = -3 не имеет корней, а уравнение sin х = - име-
ет следующие корни:
х = (-1)" arcsin - + кп = (-1)" ^ + пп, ne Z.
2 о
Ответ, х = (-1)" - + ял, neZ. A
о
Задача 3. Решить уравнение cos2 х - 2 cos л: - 3 = 0.
А Это уравнение является квадратным относительно cos x, его
корни: cos х = -1, cos x = 3. Уравнение cos л: = -1 имеет следующие
корни: л: = п + 2тш, я е Z, а уравнение cos x = 3 не имеет корней.
Ответ: л: = я + 27m, neZ. A
Задача 4. Решить уравнение 2 sin2 л: - cos х - 1 = 0.
А Используя формулу sin2 л: = 1 - cos2 x, имеем
2(1 - cos2 х) - cos л: - 1 = 0 или
2 cos2 л: + cos х - 1 = 0,
откуда cos л: = -1, cos х = - .
Ответ. х = к + 2кп, х = ±- +2пп,пе Z. А
о
9-Ю. М. Колягин, 10 кл. 257

Задача 5. Решить уравнение 3 tg2 x + 5tgx-2 = 0.
А Это уравнение является квадратным относительно tg x, его
корни: tg х = -2 и tg х = -, откуда получаем две серии корней:
о
х = -arctg 2 + пп9 х = arctg - + 7m, ne Z.
о
Ответ, х--arctg 2 + кп, х = arctg - + кп, ne Z. А
о
Задача 6. Решить уравнение tgx-2 ctg x + 1 = 0.
А Так как ctg л: = -— , то уравнение можно представить в виде
Умножая обе части уравнения на tg х, имеем
tg2 х + tg x - 2 = 0,
откуда
tg л: = 1, tgх = -2, * = - + 7m, л: = -arctg 2 + 7m, neZ.
Отметим, что левая часть исходного уравнения имеет смысл,
если tg х Ф 0 и ctg х * 0. Так как для найденных корней tg x Ф 0
и ctg Jt Ф 0, то исходное уравнение равносильно уравнению
tg2 х + tg x - 2 = 0.
Ответ. *=т+ яя> * = -arctg 2 + лл, ne Z. А
Задача 7. Решить уравнение 3 cos2 6x + 8 sin Sx cos За: - 4 = 0.
А Используя формулы
sin2 бх + cos2 6jc = 1, sin 6x = 2 sin Sx cos Sx,
преобразуем уравнение
3(1 - sin2 6x) + 4 sin 6x - 4 = 0,
3 sin2 6л: - 4 sin 6л: + 1 = 0.
Обозначив sin 6л: = i/, получим уравнение Sy2 - 4i/ + 1 = 0,
откуда yx = l9y2=-.
1) sin 6 x = 1, 6л: = - + 2nn9 x= — + — ,ne Z.
£ 1Z О
2) sin 6 л: = - , 6л: = (-1)" arcsin - + nn9 x = J arcsin - + — ,
3 3 6 3 6
ne Z.
_ к кп (~l)n . 1 кп
Ответ. X=U+Y'X= 6 arcsm з + ~Ъ~ ' П G A
258

Упражнения
Решить уравнение (804—816).
804.1) sin2 х = |; 3) 2 sin2 x + sin x - 6 = 0;
2) 2 sin2 x + sin x - 1 = 0; 4) 3 sin2 л: + 2 sin л: - 8 = 0.
805. 1) cos2 x = - ; 3) 2 cos2 x + cos x - 6 = 0;
2) 2 cos2 * - cos x - 1 = 0; 4) 3 cos2 x - 5 cos x - 12 = 0.
806. 1) 2 cos2 x - sin x + 1 = 0; 3) 4 sin2 x - cos x - 1 = 0;
2) 3cos2 * - sin x - 1 = 0; 4) 2 sin2 x + 3 cos x = 0.
807. 1) tg2 * = 2; 3) tg2 * - tg x + 1 = 0;
2) tg2 * - 3 tg * - 4 = 0; 4) 3 tg2 x - 4 tg x + 5 = 0.
808. l)tg* = ctg;t; 3)tg*- >/з ctg* + 1 = >/з ;
2) tg * + 3 ctg * = 2 >/3 ; 4) ^з tg x = 2 + >/з ctg *.
809. 1) cos 2x + 8 sin x = 3;
2) 8 cos x = 7 + cos 2x;
3) 5 cos 2x + 7 cos f x + - ] + 1 = 0;
2)
4)2cos2
810.1) 2 sin2* + sin2 2* = 2; 2) cos 4* + 2 sin2 * = 0.
811.1) ctg4 2x+ -г-k- =25; 2> —^ = tI +<«*•
sin 2jc cos jc 16
812.1) 2 cos 2x + 4 cos * = sin2 x; 2)2sin2;t+ —г~~ =3-
cos jc
813. 1) 16 sin4 x - cos2 x = sin2 *; 2) 16 cos4 * - sin2 x = cos2 *.
814.1) sin4 x + 3 sin2 * = 4; 2) 2 cos4 x + 3 cos2 * - 2 =0.
815. 1)cos 2x + 20cos2 | +3sin [ * + ^ j = 3;
2) 2 cos 4л: + 3 cos2 x + cos 2x = - .
816. 1) sin4 л: + cos4 x = - sin 2x; 2) sin4 л: - cos4 x = cos я.
817*. Найти все значения а, при которых уравнение
4 sin2 x + 2(a - 3) cos x + 3a - 4 = 0
имеет корни, и решить это уравнение.
818*. Найти все значения а, при которых уравнение
4 cos 2л: + (2 - 4a) sin л: = а + 3
имеет единственный корень на интервале ~~~^>(
V z
9* 259

§ 42. Уравнения, однородные
относительно sin x и cos x
Рассмотрим уравнение
a sin х + b cos x = О, а Ф О, Ь Ф О, (1)
которое называют однородным относительно sin x и cos x (1-й степени).
Разделив обе части уравнения (1) на cos x, получим
a tg х + Ь = О, (2)
откуда
tg Jt = — , х = -arctg - + ял, пе Z.
a a
В процессе решения обе части уравнения были разделены на
cos х. Поэтому проверим, не являются ли корнями исходного
уравнения те значения х, при которых cos x обращается в нуль. Если
cos х = О, то из уравнения следует, что и sin х = О, так как а Ф 0. Но
равенства sin x - 0 и cos x = 0 одновременно выполняться не могут,
так как sin2 x + cos2 x = 1.
Таким образом, при переходе от уравнения (1) к уравнению (2)
корни не теряются и посторонние корни не появляются, т. е.
уравнения (1) и (2) равносильны.
Задача 1. Решить уравнение sin x + cos x = 0.
А Данное уравнение равносильно уравнению tg х + 1 = 0, откуда
я
tg х = -1, х= -— + кп.
О т в е т. х = — + nn> ne Z. А
4
Уравнение
a sin2 л: + & sin л: cos х + с cos2 л: = 0 (3)
также называют однородным относительно sin л: и cos x (2-й степени).
Если а Ф 0, то, разделив обе части уравнения (3) на cos2 x,
имеем равносильное уравнение
a tg2 х + & tg * + с = 0,
которое является квадратным относительно tg л:.
Задача 2. Решить уравнение 2 sin2 х + 3 sin x cos л: + cos2 x = 0.
А Данное уравнение равносильно уравнению
2 tg2 х + 3 tg * + 1 = 0.
Решая это квадратное уравнение относительно tg x, находим
t
Ответ, х - -— + 7т, х = -arctg - + 7m, n E Z. А
4 ct
260

К уравнению (3) сводится уравнение
a sin2 х + b sin x cos x + с cos2 x + d = O.
Для этого достаточно воспользоваться основным
тригонометрическим тождеством, заменив d на d(sin2 х + cos2 x).
Задача 3. Решить уравнение
sin2 х + 2 sin x cos x - 3 cos2 л: + 2 = 0.
А Заменив 2 на 2(sin2 x + cos2 х), запишем уравнение в
следующем виде:
sin2 х + 2 sin Jt cos л: - 3 cos2 л: + 2(sin2 x + cos2 x) = 0,
откуда 3 sin2 x + 2 sin x cos x - cos2 x = 0.
Разделив обе части этого уравнения на cos2 x> имеем уравнение
3 tg2 х + 2 tg x - 1 = 0,
равносильное исходному.
Отсюда находим tgx= -9tgx = -l.
о
1 К
Ответ, х = arctg - + пп, х = -— + пп, пе Z. А
Задача 4. Решить уравнение
3 sin2х + sin 2x + 2 cos2 л: = 4.
А Это уравнение равносильно каждому из следующих уравнений:
3 sin2 х + 2 sin Jt cos л: + 2 cos2 л: = 4(sin2 x + cos2 x);
sin2 a: - 2 sin x cos л: + 2 cos2 x = 0;
tg2 * - 2 tg * + 2 = 0;
(tg*-l)2 + l=0.
Это равенство не выполняется ни при каких значениях tg x, так
как (tg х - I)2 > 0. К этому же выводу можно прийти, заметив, что
дискриминант квадратного уравнения tg2 x-2tgx + 2 = 0
отрицателен.
Ответ. Уравнение не имеет корней. А
Упражнения
Решить уравнение (819—822).
819.1) >/з cos х + sin x = 0; 3) sin x = 2 cos x;
2) cos Jt = sin x; 4) 2 sin x + cos л: = 0.
820. 1) 4 sin2 *: - 5 sin x cos л: - 6 cos2 x = 0;
2) 3 sin2 jc - 7 sin x cos л: + 2 cos2 л: = 0;
3) 3 sin2 x + sin a: cos x - 2 cos2 x = 0;
4) 2 sin2 a: + 3 sin x cos x - 2 cos2 л: = 0.
261

821.1) 4 sin2 x - 8 sin x cos x + 10 cos2 x = 3;
2) 3 sin2 x - 4 sin л: cos л: + 5 cos2 л: = 2;
3) 2 sin л: cos л: + 5 cos2 x = 4;
4) 3 sin2 л: - 2 sin л: cos x = 1;
5) 1 - 4 sin л: cos л: + 4 cos2 x = 0;
6) 1 + sin2 л: = 2 sin л: cos л\
822. 1)1 + 7 cos2 x = 3 sin 2x;
2) 3 + sin 2x = 4 sin2 *;
3) cos 2л: + cos2 x + sin л: cos x = 0;
4) 3 cos 2л: + sin2 л: + 5 sin x cos л: = 0;
5) sin 2x + 2 cos 2* = 1;
6) cos 2x + 3 sin 2x = 3.
823*. Найти все значения а, при которых уравнение
sin2 x - sin x cos л: - 2 cos2 л: = a
не имеет корней.
824*. Найти все значения а, при которых уравнение
(а2 + 2) sin2 x + 4a sin л: cos л: = а2 + 3
имеет корни, и решить это уравнение.
§ 43. Уравнение, линейное
относительно sin x и cos x
Уравнение
a sin х + Ь cos x = с, (1)
где а ^ 0, & ^ 0, называют линейным относительно sin x и cos л:.
Покажем на примере, что уравнение (1) можно свести к
квадратному относительно tg — . При с - 0 уравнение является однород-
ным и сводится к уравнению tg х = — (см. § 42).
а
Задача 1. Решить уравнение
4 sin х + 3 cos л: = 5.
А Пользуясь известными формулами и заметив, что л: = 2 • - , за-
XX XX
пишем: sin х - 2 sin — cos — , cos x = cos2 — - sin2 — , 5 =
- 5 sin — + cos — . Тогда данное уравнение можно представить так:
v ^ & I
262

откуда
8sin ^ cos -| + 3 cos2 —-sin2 — = 51 sin2 — + cos2 — ],
2 21 2 211 2 2 j
8 sin2 — - 8 sin — cos - + 2 cos2 — = 0.
ct ct c\ ct
X
Полученное уравнение является однородным относительно sin —
Ct
X
и cos — и приводится к уравнению
Ct
4tg2|-4tg|+l = 0.
Отсюда находим tg — = -, — = arctg - + кп.
Ответ. х = 2arctg — + 2пп, пе Z. А
с\
Задача 2. Решить уравнение
sin х -cos x - 1. (2)
А Используя формулы двойного угла, так же как и при решении
задачи 1, получаем
_ . X X п X . (\ X , п л п X
2 sin — cos — - cos'2 — + sin"* — = sin^ - + cos'2 — ,
Ct Ct Ct Ct Ct U
откуда
XX X
sin — cos — - cos2 — = 0.
В последнем однородном уравнении коэффициент при sin2 —
равен нулю. Поэтому уравнение не сводится к квадратному отно-
сительно tg — , так как при делении на cosz — потеряются корни.
тт» х ( - х х\ t\
Дальнейшее решение можно провести так: cos - sin — cos - | = 0,
^12 2
х . х х
откуда cos — = 0 или sin — - cos — = 0.
Ct Ct Ct
1) cos - = 0, — = - + 7m, x = к + 27m, ne Z;
_JC X X . X К К
2) sin - = cos - , tg — = 1, — = - + тт, x = - + 27m, n s Z.
Ответ. x = n + 27m, x = — + 2кп, ne Z. A
Ct
263

Уравнение (2) можно было иначе решить.
А Заметив, что 1 = tg —, запишем уравнение (2) так:
sin х - tg — cos x = 1,
4
к . к к
откуда sin х cos — - cos x sin — = cos —;
4 4 4
*,„.!). Л.
71 71
X = — + (~~1) "7 + 7Ш, Л Е Z. A
4 4
Задача З. Решить уравнение
>/3 sinx + cosx = 2. (3)
А Разделим обе части уравнения на 2:
V3 . 1 1
— sin х + - cos х = 1.
Q л/3 71 1 . Я
Заметив, что — = cos —, - = sin -, представим уравнение так:
к . к
sin х cos — + cos х sin - = 1,
о о
откуда
sin
х + - = - ;
х = - + 27m, neZ. A
о
Покажем, что любое линейное уравнение
a sin х + Ъ cos x = с, (4)
где а Ф О, Ь Ф 0, с * 0, можно решить таким же способом, как и
уравнение (3).
О Разделим обе части уравнения (4) на л/а2 + Ь2 :
a b с
I 2 о sin х + -т-j—- cos x = -т=—- . (5)
1г+Ь2 l2b2 12Ь2
jcos x = т
la2+b2 \1а2+Ь2
264

ч2 , ч2
Так как | —^—- I ч / | =1, то точка с координатами
Ja2+b2
I лежит на единичной окружности. Следовательно,
существует такое число ф (такой угол ф), что
а . b
Ja2+b2 y]a2+b'
Поэтому уравнение (5) можно записать так:
СО8<Р=-НГ7!Г' 8ШФ= ,.,,
с
sin х cos ф + cos х sin ф = I
V2
откуда
Последнее уравнение является простейшим
тригонометрическим, решение которого известно. •
Задача 4. Решить уравнение
6 sin х - 8 cos x = 3.
А Поделим обе части уравнения на v62 + 82 =10. Получим
3.4 3
-sin*--cos*=-.
3 4
Тогда cos ф = - , sin ф = - —, поэтому уравнение можно предста-
э э
вить так:
3
sin х cos ф + cos x sin ф = — ;
3
sin (x + ф) = — ,
откуда
. _3_
ф-1 ) 10 »
3
х = -ф + (-1)" arcsin — + ппу пе Z.
Q А
Так как cos ф = - > 0, sin ф = - - < 0, то угол ф лежит в четвер-
5 5
той четверти и поэтому ф = arcsin \Т = -arcsin - .
A Q
О т в е т. х - arcsin - + (-1)" arcsin — + пп, пе Z. А
о 1U
265

Упражнения
Решить уравнение (825—828).
825. 1) sin х + cos x = 1; 3) sin x + >/з cos x = 1;
2) sin л: + cos х = V2; 4) >/з sin л: + cos x = 1.
826. 1) >/3 sin л: - cos л: = 2; 2) V2 cos л: - V2 sin л: = 2.
827. 1) sin Зх - cos 3* = 0,5 >/б; 2) >/з cos Ъх - sin 5* = - 4s.
828. 1) 4 sin ^ + 3 cos f = 2; 3) 8 sin 3* - 15 cos Sx = 1;
2) 12 cos - - 5 sin — = 1; 4) 24 cos - + 7 sin - = 5.
829. Найти наибольший отрицательный корень уравнения
>/б cos х + V2 sin Jt = 2.
830. Найти наименьший положительный корень уравнения
>/3 sin Sx - cos Sx - >/з .
831*. Решить уравнение:
1) sin3 x - cos3 Jt + sin x cos2 л: - cos x sin2 jc = 1;
2) sin3 x + cos3 a: + sin x cos2 x + cos x sin2 jc = 1.
832*. Найти все значения а, при которых имеют корни уравнения:
1) sin х + a cos х = 2; 2) cos л: + a sin л: = 2.
§ 44. Решение уравнений методом
замены неизвестного
Задача 1. Решить уравнение sin 2х - sin х - cos х - 1 = 0.
А Выразим sin 2x через sin x + cos x, используя тождество:
sin 2х - (sin х + cos x)2 - 1.
Обозначим sin х + cos х = t. Тогда (sin х + cos х)2 = t29 sin2 x +
+ 2 sin x cos Jt + cos2 x = t29 sin 2л: = t2 - 1. Уравнение примет вид
t2 - t - 2 = 0, откуда tx = -1, *2 = 2.
Задача свелась к решению следующих уравнений:
sin х + cos x = -1, sin x + cos л: = 2.
Решим первое уравнение:
V2 . V2 V2
266

л/2
х + - = (-l)k arcsin ——
x = -^+(-l)k+1 ^+nk; keZ.
Отсюда при четном k получаем х = — — + 2nk9 а при нечетном k
x = n + 2я£. Второе уравнение не имеет корней, так как sin x < 1,
cos х < 1 и равенства sin х = 1, cos л: = 1 не могут одновременно
выполняться.
Ответ. х = к + 2кп, х = -- + 2кп, neZ. А
Задача 2. Решить уравнение
sin 2x + 3(sin х - cos x) = 1.
А Обозначим sin х - cos x = t. Тогда (sin x - cos x)2 = £2, sin2 x -
- 2 sin х cos Jt + cos2 x = t2, sin 2л: =1 - t2. Данное уравнение можно
записать так:
Решая его, находим t (-t + 3) = 0, tг = 0, t2 = 3.
Задача свелась к решению следующих уравнений:
sin х - cos x - 0, sin x - cos x = 3.
Решая первое уравнение, получаем
tgx = ly х= - + 7т, neZ.
Второе уравнение не имеет корней, так как | sin х \ < 1, | cos х \ < 1
и, следовательно sin х - cos х < 2 < 3.
_ к „
Ответ. х= - +яп, пе Z. А
4
Задачи 1 и 2 решены с помощью замены неизвестного.
Вообще уравнение
a(sin х + cos x) + Ь sin 2л: + с = 0, a * О
заменой t = sin x + cos л: сводится к квадратному уравнению
at + b(t2-l) + c = 0;
уравнение
a(sin х - cos л:) + b sin 2л: + с = 0, a * О
заменой t = sin x - cos л: сводится к квадратному уравнению
at + b(l-t2) + c = 0.
При решении некоторых тригонометрических уравнений
бывают полезны замены и других выражений, содержащих неизвестное.
267

Задача 3. Решить уравнение
: + ctgf =2.
А Воспользуемся формулами
2tg£
■ 2 + * 1
sin х = ^- ; ctg - = —
*f 2 f
X X
Обе эти формулы верны, если sin — Ф О и cos — Ф 0. Заметим,
что значения х, при которых sin — = 0 или cos — = 0, не являются
корнями данного уравнения. Поэтому можно сделать замену
х
tg — = t и свести данное уравнение к виду
i+t2 + 7"2'
Так как t Ф 0, то имеем
2*3-3*2 +2^-1 = 0;
(2t3- 2t2)- (t2- t) + (t - 1) = 0;
(t-l)(2t2-t + l) = 09
откуда
*-l = 0, 2t2-t + l = 0.
Из первого уравнения получаем t = 1, а второе не имеет
действительных корней.
Если t = 1, то tg - = 1, — = - + 7m, x = - + 27m, и е Z.
Ответ, jc = - + 2кп, пе Z. а
2 1
2 л: + —9~~ = sin jc :— + - -.
2 sin л: 4
Задача 4. Решить уравнение
JL 7_
! jc sinx 4
А Пусть sin л: :— = t; тогда t2 = sin2 л: + —р 2 и уравнение
sinx sin х
7 f \^? 1
преобразуется к виду t2 + 2 = £ + - или ^ — =0, откуда t=-9 т.е.
4 [ 2) 2
sin л: ;— = - , 2 sin2 х - sin л: - 2 = 0,
268

1±Л7
sin х = —-— .
4
1+V17 „ 1+Vl7 ^ 1
Уравнение sin х - —-— не имеет корней, так как —-— > 1.
4 4
1 1Л7 1 . 1-V17
Учитывая, что -1< —-— < 1, из уравнения sin х = —--— имеем
4 4
+гет1, пе Z.
1л rr _ -I
Ответ. x = (-l)n+1 arcsin —-— +ли, пе Z. А
4
Задача 5. Решить уравнение
„ к х Зл л (к х}
А Положим - - - =t; тогда х-^—- =к-2 ---- \=n-2tn урав-
О а О I О £t J
нение примет вид
sin (я - 2t) = 2 sin t или sin 2* = 2 sin £,
или
Если sin t = 0, то t = nn> а если cos t = 1, то t = 2nn. Так как корни
второго уравнения содержатся во множестве корней первого
уравнения, то t = nn, пе Z9 или \-~ = 7т, откуда x = 2\- + nn\yneZ.
5 2 ^5
Ответ. x = 2\- + nn\,neZ. A
V5 )
Упражнения
Решить уравнение (833—844).
833. 1) 2 sin 2х - 3(sin х + cos х) + 2 = 0;
2) sin 2х + 3 = 3sin х + 3cos x;
3) sin 2х + 4(sin х + cos л:) + 4 = 0;
4) sin 2л: + 5(cos л: - sin х + 1) = 0;
5)1 + 2 sin л: = sin 2х + 2 cos л:;
6) 1 + 3 cos л: = sin 2х + 3 sin л:.
834. sin3 л: + cos3 х = 1 + sin 2x.
835. tg2 л: + ctg2 л: = tg л: + ctg x.
269

836.tg42x+ —*— =25.
cos 2x
837. 2 cos2 x + —V- =5.
sin x
838. cos2 x + = cos x 2~ = 2.
cos x cos x
839. sin 2x + ^p =2 sin | x-- |.
840. sin f 2x - — I = 2 cos
I 9 J
841. sin4x + cos6x = l.
842. «"2* + -^= 1.
2
843. sin x + —— = sin2 x + —
sinx sin2 x '
844. cos4 x + sin8 x = 1.
845*. Найти все значения а, при которых уравнение
sin 2х - 2а л/2 (sin х + cos х) + 1 - 6а2 = О
имеет корни, и решить это уравнение.
§ 45. Решение уравнений методом
разложения на множители
Одним из наиболее применяемых методов решения
тригонометрических уравнений является метод разложения на множители.
Задача 1. Решить уравнение
sin 2х - sin х = 0.
А Используя формулу для синуса двойного аргумента, запишем
уравнение в виде 2 sin x cos x - sin x = 0.
Вынося общий множитель sin x за скобки, получаем
sin x(2 cos х - 1) = 0.
l)sinx = 0, x = nn9 ne Z;
2) 2 cos х- 1 = 0, cosx= -, х = ±- +2кп, ne Z.
2i о
Ответ, х = ял, х = ±- + 2лл, ne Z. А
о
270

Задача 2. Решить уравнение
2 sin х cos 2л: - 1 + 2 cos 2л: - sin x = 0.
А Вынося общий множитель первого и третьего слагаемых,
запишем уравнение в виде
2 cos 2x (sin х + 1) - (sin л: + 1) = 0
или
(2 cos 2л: - 1) (sin х + 1) = 0.
1 я я
1)сов2л:= -, 2х = ±- +2пп, х = ±- + 7m, wgZ;
2 о о
2) sin л: = -1, х = - - + 27т, neZ.
~ я я
Ответ. л: = ± - + 7т, л: = - - + 27т, пе Z. А
о ^
Задача 3. Решить уравнение cos Зл: + sin 5л: = 0.
А Применяя формулу приведения sin a = cos — а |, запишем
V2
уравнение в виде
cos Зл: + cos — 5л: = 0.
V2 )
Используя формулу для суммы косинусов, имеем
' \ (
2 cos \--x cos 4л:-- I =0.
l)cos —x\ = 0, х- - = - +7m, x= -n +7m;
[4 ) 4 2 4
Л 3 3 ял
Ответ. jc = —п + 7т, л: = —к + — 9пе Z. А
4 16 4
Задача 4. Решить уравнение sin 7х + sin Зл: = 3 cos 2x.
А Применяя формулу для суммы синусов, запишем уравнение
в виде
2 sin Ъх cos 2л: = 3 cos 2x
или
/ 3^\
cos 2л: sin5л:-- =0.
V 2)
Уравнение cos 2л: = 0 имеет корни х = - + -г- , а уравнение
4 2
. с 3
sin 5л: = - не имеет корней.
л к кп
Ответ. х= - + — ,пе Z. А
4 £
271

Задача 5. Решить уравнение cos Зх cos х = cos 2x.
А Так как cos 2х = cos (Зх - х) = cos Sx cos x + sin Зх sin х, то
уравнение примет вид:
sin х sin Зх - 0.
l)sinx = 0, x = nn;
2) sin Зх = 0, л: = — .
3
Заметим, что числа вида кп содержатся среди чисел вида
кп _ кп _
л: = — , п е Z, так как если п = 3«, то — = nk. Следовательно, пер-
о О
вая серия корней содержится во второй.
~ кп „
Ответ, х——9neZ. A
3
Задача 6. Решить уравнение
cos3 х + sin3 x = cos 2x.
А Левая и правая части уравнения имеют общий множитель
cos х + sin Xj так как
cos3 x + sin3 Jt = (cos x + sin x) (1 - sin x cos x);
cos 2x = (cos *: + sin x) (cos x - sin x).
Поэтому данное уравнение таково:
(cos x + sin x) (1 - sin x cos x + sin x - cos x) = 0.
1)cosx + sinx = 0, tgx = -1, # = -7+ яя> «gZ;
2) 1 - sin a: cos a: + sin x - cos x - 0.
Заменой sin x - cos x = t получаем уравнение t2 + 2t + 1 = 0,
откуда f = -1, т. e.
shut -cosx = -l
или
sin x + 1 - cos x = 0;
2 sin - cos — + 2 sin2 — = 2 sin - cos - + sin - 1 = 0.
Z ^^2 2)
X XXX
Если sin — = 0, то x = 27m, а если cos — + sin — = 0, то tg — = -1,
К
откуда х = - — + 2кп.
Ответ, jc = --т + 7m, x = 2nn, x = - — + 2яп, пе Z. A
4 ^
272

Задача 7. Решить уравнение cos x sin 7x = cos Зх sin 5л:.
А Выражая произведения тригонометрических функций через
суммы, запишем уравнение в виде
- (sin 8л: + sin 6л:) = - (sin 8л: + sin 2л:),
откуда
sin 6л: - sin 2x = 0.
Используя формулу разности синусов, получаем
2 sin 2л: cos 4л: = 0:
1) sin 2л: = 0, х = — ;
2) cos 4х = 0, х = - + — .
Л ЯЯ Я ЯЛ ,,
Ответ. * = "^г ; х=з + "4"'Пе
Упражнения
Решить уравнение (846—856).
846. 1) >/з sin х cos x = sin2 х; 5) sin Зх = 3 sin л: cos2 л:;
2) 2sin x cos л: = cos x; 6) sin 4л: = sin 2л:;
3) sin 4л: + sin2 2x= 0 ; 7) cos 2л: + cos2 x = 0;
4) sin 2л: + 2 cos2 x = 0; 8) sin 2л: = cos2 x.
847. 1) cos x - cos 3x; 3) sin 2л: = cos 3x;
2) sin bx = sin x; 4) sin x + cos Зл: = О.
848.1) cos x sin 9x = cos Зл: sin 7x; 3) sin x sin Зл: = - ;
Li
2) sin x cos 5л: = sin 9x cos Зл:; 4) cos x cos Зл: = - - .
A
849.1) cos Зл: - cos 5л: = sin 4л:; 3) cos x + cos Зл: = 4 cos 2л:;
2) sin 7x - sin x = cos 4л:; 4) sin2 x - cos2 x = cos 4л:.
( x xf
850.1)1- sin 5л: = cos - - sin - ; 4) sin 2л: + cos 5л: = 0;
[2 2 )
2) 2 sin2 x = 1 + \ sin 4л:; 5) 2 cos2 2л: + 3 cos2 x = 2;
о
3) 2 cos2 2л: - 1 = sin 4л:; 6) (sin x + cos л:)2 = 1 + cos x.
851.1) cos x cos 2л: = sin x sin 2л:; 4) cos 5л: cos x = cos 4л:;
2) sin 2л: cos x = cos 2л: sin x; 5) cos Зл: cos x - cos 2л:;
3) sin Зл: = sin 2л: cos x; 6) 2 cos 2л: = sin x cos 2л:.
273

852.1) cos x + cos 2x + cos 4x = 0;
2) cos x + sin x + cos 3x + sin Sx - 0.
853.1) sin 2x = 1 + cos 2х + V2 cos я;
2) sin 2* + cos 2* = V2 sin 3*.
sin — -x
854.1) ctg x = 1 + 2 cos 2x\ 2) —И <( = cos 2x.
sin — + jc
I4
855.1) cos2 x = sin x(l + cos 2x);
2) sin3 л: + cos3 x - sin л: - cos x = 0.
856*. 1) sin 3* = 2 sin 2*;
2) sin x(l + cos ;t) = 1 + cos x + cos2 x.
§ 46. Различные приемы решения
тригонометрических уравнений
Задача 1. Решить уравнение
3 cos4 л:+ 4 sin4 л: = 3.
А Решить это уравнение можно с помощью формул понижения
степени:
9 1 +cos 2а 9 1-cos 2а
cos*5 а = , sinz а = ,
которые получаются из формул половинного угла. Используя эти
формулы, имеем
о (1+ cos2х)2 A(l-cos2х)2 о
3 4 +4 4 =3'
7 cos2 2* - 2 cos 2x - 5 = 0.
Решая это квадратное уравнение относительно cos 2x, находим:
1)cos 2х = 1, 2х-2пп> х = пп> пе Z;
5 ( 5\ If 5
2)cos2;t = --, 2;t = ±arccos -- +27m, л:= ±- я-arccos-
7 V 7 / 2V '
Ответ. x = 7m; л: = ±- 7C-arccos- \+nn, ne Z. A
Задача 2. Решить уравнение sin4 x + cos4 \ x - - = - .
I 4J 4
А Применяя формулы понижения степени, получаем
2 1 + COS2 \Х--
1-cos2jc^
2 )
274
4*

Отметим, что cos 2 х— = cos 2x— = cos \--2x = sin 2x.
{ 4J { 2) U j
Поэтому, освобождаясь от дробей, имеем
1 - 2 cos 2х + cos2 2х + 1 + 2 sin 2х + sin2 2х = 1;
1 + sin 2x - cos 2x = 0;
2 sin л: cos л: + 2 sin2 л: = 0;
sin х (sin Jt + cos x) - 0,
я ~
откуда находим х = nn; x = - - + nn, ne Z.
4
Ответ. х = пп; x = -- +кп, ne Z. A
4
Задача З. Решить уравнение
sin10 x + cos10 x = 1.
А Решить это уравнение с помощью формул понижения
степени непросто. Проще использовать следующие рассуждения.
Известно, что | sin х | < 1 и | cos х \ < 1. Пусть выполняются
строгие неравенства | sin х \ < 1 и | cos х \ < 1. Тогда sin2 х < 1, cos2 x < 1
и тем более sin8 х < 1, cos8 х < 1, и поэтому sin8 л: < sin2 x,
cos8 л: < cos2 х. А так как sin2 х + cos2 л: = 1 для любого значения х,
то sin8 х + cos8 Jt < 1.
Итак, если имеют место строгие неравенства | sin х \ < 1 и
| cos х | < 1, то данное уравнение не имеет корней.
Осталось лишь рассмотреть случаи, когда или | sin х \ = 1, или
| cos х | = 1, т. е. или х = — + пп, или л: = п + 7m, ne Z. Эти значения
и есть корни данного уравнения.
Ответ. х= - + пп9 п g Z. А
Задача 4. Решить уравнение
2 sin4 л: + 3 cos4 4х = 5.
А Так как | sin х \ < 1 и | cos 4х \ < 1, то sin4 х < 1 и cos4 4л: < 1.
Если выполняются строгие неравенства, то 2 sin4 х + 3 cos4 4л: < 5
и уравнение не имеет корней. Следовательно, sin4 х = 1 и cos4 4jc = 1.
Корнями уравнения sin4 л: = 1 являются числа х = — +пп. При
этих значениях х верно и второе равенство: cos4 4x - 1.
Ответ. *=- + кпу ne Z. А
275

Задача 5. Решить уравнение
2 sin х + 7 cos 8л: = 9.
А Воспользуемся односторонней оценкой значений синуса и
косинуса: sin х < 1 и cos 8л: < 1. Поэтому 2 sin х < 2, 7 cos 8л: < 7,
откуда 2 sin л: + 7 cos 8л: < 9.
Следовательно, уравнение обращается в верное равенство
только тогда, когда sin x = 1 и cos 8x = 1. Решая уравнение sin x = 1,
получаем л: = — + 2яп. При этих значениях х находим cos 8л: =
= cos 8 I — + 2пп = cos (471+ 16кп) = 1, т. е. корни уравнения sin x = 1
V2 )
являются и корнями уравнения cos 8л: = 1. Если вместо проверки
решить также и уравнение cos 8л: = 1, то, получив его корни х = -т-,
пришлось бы дополнительно устанавливать, какие из них
являются корнями уравнения sin х = 1, т. е. не являются посторонними для
данного уравнения.
Ответ, х- - + 2пп, пе Z. А
Задача 6. Решить уравнение
sin х sin Ъх sin 9л: = 1.
А Уравнение может иметь корни только в случае, когда | sin х \ = 1.
Если sin л:=1,тол:=^+ 2кп9 пе Z, откуда следует, что sin Ъх = 1,
sin 9л: = 1.
Если sin х = -1, то х = - — + 27m, n e Z, и тогда sin 5л: = -1, sin 9л: =
= -1 и поэтому sin х sin 5л: sin 9л: = -1.
Ответ. х=^ + 2кп, пе Z. А
Задача 7. Решить уравнение
А Исходное уравнение равносильно каждому из уравнений
1 - cos 4л: 1 - cos 8л: _ cos2x
2 2 ~ cos Зх '
cos 4л: + cos 8л: cos 2* cos 2x
' cos 6*cos 2x= ^~^
276

а при выполнении условия cos Зх Ф О равносильно уравнению
cos 2a:(cos Sx • cos 6x - 1) = 0.
Уравнение cos 2x = 0 имеет корни *:= — + -, ne Z, а уравнение
4 2
cos За: cos 6x = 1 может имеь крни только в случае, когда | cos Sx \ = 1.
Если | cos Зх | = 1, тогда cos 6х = 2 cos2 3jc - 1 = 1, и поэтому
cos За: cos 6л: = 1 только тогда, когда cos Зх = 1, откуда х = —г- .
о
~ к кп 2кп __ А
Ответ, л: = — + — , х= , пе Z. k
4 2 3
Упражнения
Решить уравнение (857—864).
857.1) 8 sin х cos x cos 2x = 1; 3) cos3 x sin x - sin3 л: cos x = -;
4
2)1+ cos2 Jt = sin4 x; 4) sin3 a: cos x + cos3 л: sin x = -.
4
858.1) sin2 * + sin2 2x = 1; 3) sin 4* = 6 cos2 2x - 4;
2) sin2 x + cos2 2* = 1; 4) 2 cos2 3x + sin bx = 1.
859.1) 2 cos2 2x + 3 sin Ax + 4 sin2 2* = 0;
2) 1 - sin x cos a: + 2 cos2 л: = 0;
3)2sin2*+icos32;t = l;
4
4) sin2 2x + cos2 3x = 1 + 4 sin a:.
860. 1) 2 cos2 x = 1 + 4 sin 4x; 2) 2 sin2 x = 1 - 3 sin Ax.
861.1) sin8 x + cos8 x = 1; 2) 3 sin6 jc + 4 cos6 * = 7.
862.1) 2(sin4 x + cos4 *) = 6 sin 2x - 5 sin2 2x;
2) 8(sin5 *: cos x + cos5 л: sin x) + 3 sin 2л: = О.
863.1) sin3 x cos Зл: + cos3 x sin Зл: = - -;
о
2) sin6 л: + cos6 x = 1 + 2 sin2 a: cos2 л:.
864.1) sin a: sin bx = 1; 3) cos x sin 5л: = -1;
2) sin a: cos 4л: = -1; 4) sin x cos 3x = -1.
277

865*. Найти все значения а, при которых уравнение sin4 х + cos4 х = а
имеет корни, и решить это уравнение.
866*. Решить уравнение:
l)cos;tcos 3;tcos Ъх = -1; 2) sin л: sin 3;tsin 7x= 1.
§ 47. Уравнения, содержащие
корни и модули
Задача 1. Решить уравнение
7l-2sin2jt = 2 sin x - cos x. (1)
А Возводя обе части уравнения в квадрат, получаем
1 - 2 sin 2x = (2 sin x - cos x)2, (2)
откуда
1-4 sin х cos x = 4 sin2 x - 4 sin л: cos л: + cos2 л:;
1 - cos2 x - 4 sin2 Jt = 0;
sin2 x - 4 sin2 a: = 0;
sin a: = 0, x = nk, ke Z.
Напомним, что при возведении обеих частей уравнения в квадрат
могут появиться посторонние корни, поэтому необходима проверка.
При х = nk, ke Z левая часть уравнения (1) равна y]l-2sin2nk = 1,
а правая равна 2 sin nk - cos nk - ~(-l)k - (-l)fe+1. Значение, равное
единице, правая часть принимает только при k = 2n +1, где пе Z.
Поэтому корнями уравнения (1) являются числа х = п(2п + l),neZ.
Отметим, что в данном случае для проверки достаточно было
установить, при каких найденных значениях х правая часть
уравнения (1) неотрицательна (конечно, если не допущены ошибки в
преобразованиях или в вычислениях).
При х = nk, k g Z правая часть положительна, если k = 2n +1,
п g Z, и отрицательна, если k = 2п, пе Z.
Кроме того, отметим, что знак подкоренного выражения
уравнения (1) при найденных значениях х не нужно устанавливать, так
как правая часть уравнения (2) неотрицательна и поэтому
корнями этого уравнения являются только такие значения х, при
которых 1-2 sin 2х > 0, т. е. подкоренное выражение уравнения (1)
неотрицательно.
Ответ, х - л(2и + 1), п е Z. А
Задача 2. Решить уравнение
77-cosjc-6cos2jc = 4 sin x.
А Возводя обе части уравнения в квадрат, имеем
7 - cos х - 6 cos 2x = 16 sin2 x.
278

Используя формулу косинуса двойного угла, это уравнение
приводим к квадратному:
4 cos2 х - cos x - 3 = О,
3
откуда cos х = 1, cos x = - — .
1) cos x = 1, х = 2кп, ne Z;
2)cosx = — , Jt = ±arccos —- + 2кп9 ne Z.
Проверим, при каких из найденных значений х правая часть
исходного уравнения неотрицательна, т. е. sin x > 0:
1) при х - 2пп получаем sin x = 0;
2) угол arccos — лежит во второй четверти, в которой синус
положителен.
Угол -arccos — лежит в третьей четверти, в которой синус
отрицателен.
Ответ, х = 2пп, х = arccos —- + 27tn, ne Z. А
I 4
Задача 3. Решить уравнение
2-3sin2*: = 2|cos;t|.
По определению модуля числа следует рассмотреть два случая:
1) | cos х | = cos х, если cos x > 0;
2) | cos х | = -cos x, если cos x < 0.
Рассмотрим первый случай. При cos x > 0 имеем
2-3 sin2 х = 2 cos x;
3 cos2 x - 2 cos x - 1 = 0;
cos jc = 1, cos jc = - - .
о
Второе значение не годится, так как cos x > 0. Из уравнения
cos х = 1 находим л: = 2я£, ke Z.
Во втором случае, т.е. если cos л: < 0, имеем
2-3 sin2 х = -2 cos ;t;
3 cos2 Jt + 2 cos a: - 1 = 0;
cos x = -1, cos x = - .
3
Второе значение положительно, т. е. не удовлетворяет условию
cos х < 0. Из уравнения cos х - -1 находим л: = я + 2nk, k e Z.
Объединяя формулы л: = 2я£ и л: = я + 2я£, получаем л: = лд,де Z.
Ответ. х = пп, ne Z. А
279

Задача 4. Решить уравнение
4-2 cos2 х = 5 | sin x |.
А 1) sin х > 0;
4-2 cos2 Jt = 5 sin x;
2 sin2 jc - 5 sin x + 2 = 0;
sinx = 2, sinx= -.
Li
Уравнение sin x = 2 не имеет корней;
sin Jt = - > С
Li
2) sin x < 0;
sin л: = - > 0, x = (-1)" - + 7m, ^
^ о
4-2 cos2 x = -5 sin я;
2 sin2 л: + 5 sin x + 2 = 0;
sin x = -2, sin x - - — .
Li
Уравнение sin x - -2 не имеет корней;
sin x = - - < 0, x = (-1)"+1 - + 7m, ne Z.
Z О
Ответ, x = (-1)п-г + 7m, л: = (~1)"+1^ + 7m или х = ±- + 7Ш,
О DO
Упражнения
Решить уравнение (867-874).
867.1) ylcos2x = sin x; 2) ^/l-sinjc = 2 cos *.
868.1) V2 cos л: = - /3sinjc; 2) yjcos2x = 1 + 2 sin *.
869. 1) | sin x | = sin x + 2 cos *; 3) | 2 tg * - 81 = 3 tg * + 1;
2) | 3 sin x - 5 | = 2; 4) 2 | cos * | - cos x - 3 = 0.
870.1) yjsm2x =
2) V4+3cosJt-cos2jc = >/б sin x.
/3 2
871.1) J- + COS x = sin л: -cos x;
2) >/sin3jc-sinjc = -jr sin л:.
872.1) 75cosjc-cos2jc = -2 sin л:;
2) ^cosjc+cosSjc = - V2 cos л:;
280

3)
4) Vctg2x-ctgx =
COS*
873*. l)4|cosx| + 3 = 4sin2x; 2)|tg2x|
COS c\X
874**. 1) ^/5+cos2jc = sin x + 3 cos *;
(Уз + l)sin 3jc + sin bx j-
2)
Isinjcl
§ 48. Системы тригонометрических
уравнений
Задача 1. Решить систему уравнений
lsimccosj/=--,
[ctgxtgy=l.
А Из первого уравнения следует, что sin х^Ои cos у Ф 0.
Поэтому, умножая почленно второе уравнение на первое, имеем систему,
равносильную данной:
1
sin a: cos i/ = —,
cos л: sin i/=—.
Складывая и вычитая почленно уравнения этой системы,
получаем
Jsin х cos у + cos Jt sin i/ = 1,
[sin x cos i/- cos a: sin i/ = 0
или
откуда
{ 2, ne Z,
Решая последнюю систему, находим х = л:я+ —, у = кп ——,
ne Z,ke Z.
Ответ. jc = m+—,i/ = jw —— ,/ig Z, ke Z. A
281

Отметим, что в записи решения целые числа пик могут быть
как одинаковыми, так и разными. Употребление только одного
обозначения целого числа (только п или только к) привело бы к потере
корней.
Задача 2. Решить систему уравнений
{sin у = 5 sin х,
/ = 2-3cos;t.
А Возведем обе части уравнения в квадрат и сложим
полученные уравнения. Отсюда имеем
25 sin2 х + (2 -3 cos xf = 1,
откуда
8 cos2 x + 6 cos x - 14 = 0;
cos x = 1 или cos x = - — .
4
Уравнение cos x - - - не имеет корней.
Из уравнения cos x - 1 находим х = 2пп, п е Z. Подставляя эти
значения х в исходную систему, получаем
fsini/ = O,
[cosi/ = -l,
откуда у = п+ 2nkj ke Z.
Ответ. (27m; n + 2nk)9 n9keZ. A
Задача З. Решить систему уравнений
sinx=-sin2j/,
[cosjc=sinj/.
А Возведем оба уравнения в квадрат и сложим полученные
уравнения:
откуда
sin2 х = - sin2 2i/,
cos2 x = sin2 у
1 = sin2 у + - sin2 2i/
cos2 i/ = - • 4 sin2 у cos2 i/;
cos2 i/ l--sin2 у 1=0;
v y ;
282

cos2 у \ — sin2 у I = 0.
И )
g
Так как | sin у | < 1, то - - sin2 у Ф 0.
Следовательно, cos2 y = 0,y= — + nk> ke Z.
Рассмотрим два случая: k — четное и k — нечетное числа.
1) Если k = 2п, то, подставляя у = — + 2пп в исходную систему, име-
ем
Jsin;t = O,
[cos х = 1,
откуда х = 2к1, le Z.
2) Если k = 2п + 1, то, подставляя у = — + п + 2яя в исходную
систему, получаем
[sin л: = 0,
|cos;t = -l,
откуда х - я + 2я/, Z e Z.
Ответ. |2л/;^ + 27т I, \ъ+2тй\ — + 2пп ], /, пе Z. А
3 а д а ч а 4. Решить систему уравнений
fsin i/ = 3sin x,
А Для исключения неизвестного у из данной системы
преобразуем второе уравнение, возведем оба уравнения в квадрат и почленно
их сложим:
| = l-2cos;t,
|sin2j/=9sin2jc,
[cos2 у = 1 - 4cos x + 4cos2 x\
1 = 9 sin2 x + 1 - 4 cos x + 4 cos2 я,
откуда
9-9 cos2 a: - 4 cos a: + 4 cos2 л: = 0;
283

5cos2 x + 4 cos x - 9 = 0;
9
cos x - 1, cos л: = - - .
о
1) cos x = 1, x = 27m, ne Z;
9
2)cosx = -- <-l, корней нет.
э
Подставляя cos x = 1 во второе уравнение исходной системы,
находим
cos у = -1, у = п + 2nk, ke Z.
Так как в ходе решения системы уравнения возводились в
квадрат, необходима проверка.
Найденные решения удовлетворяют второму уравнению
системы, так как оно было использовано для нахождения значений у при
найденных значениях х.
Проверяем первое уравнение: его левая часть равна
sin (к + 2nk) = 0,
правая часть
3 sin (2nk) = 0.
Посторонних корней нет.
Ответ. х = 2пп, у = к + 2nk, ne Z, ke Z. А
Упражнения
Решить систему уравнений (875—887).
875.1) Jsin (х + у) = 0, 2) fcos (х + у) = 0,
|sin(;t-i/) = 0; |cos(*-i/) = l.
876.1)
sina:sini/ = -, 2)
4
я
sin2 лг + cos2 у = -,
К
877. [sinjt+cosj/=l,
\ • 2 2 1
sin jc+cos j/=-.
878. [sin x - sin i/ = 1,
[sin2 x + cos2 y =
879.
sin:ccosi/ = -
2
1.
2'
284

880.
[5cos x cos у - 3sin x sin у = 3.
881. cosu:cosrc£/
882. j4sin;t-2sini/ = 3,
|2cos;t-cos # = 0.
883.
[4cos ял: cos яг/ = 3.
884. sin x = + sin y9
sin*
cos x + cos y.
cos*
885. rcosjc-sinjc=l+cosy-sin[/,
[3sin2jc-2sin2j/=|.
886*. [ctg4 2x + 32sin2 у = 55,
1
887*.
. -4cosi/ = 5.
sin 2л:
я
sin 3jc+—
= S111J/-COSJ/,
sin 2j/+2sin2jc=- + 2sin3 2x.
§ 49. Появление посторонних корней и потеря
корней тригонометрического уравнения
При решении тригонометрических уравнений (как и при
решении иррациональных или логарифмических уравнений) некоторые
преобразования не приводят данное уравнение к равносильному ему.
Например, при возведении обеих частей уравнения в квадрат
получается уравнение — следствие данного, т. е. могут появиться
посторонние корни. При умножении обеих частей уравнения на
выражения, содержащие неизвестное, также могут появиться посторонние
285

корни, а при делении обеих частей уравнения на выражение,
содержащее неизвестное, может произойти потеря корней.
Если в процессе решения уравнения получается уравнение —
следствие данного, надо проверить, не появились ли посторонние
корни. Потерю корней обнаружить труднее. Поэтому
преобразования уравнения, которые могут привести к потере его корней,
нужно проводить осторожно.
Рассмотрим случаи приобретения посторонних корней или
потери корней при решении тригонометрических уравнений.
Задача 1. Решить уравнение
2 tg х sin — + 4 sin — - tg x - 2 = 0.
О О
А Способом группировки разложим левую часть уравнения на
множители
( х \
(tgx + 2) 2sin—1 =0.
I 3 J
1)tgx + 2 = 0, tgx = -2, x = -arctg 2 + кп, ne Z;
2) 2 sin - - 1 = 0, sin - = -, - = (-l)n - + 7m, x = (-l)n - +
+ 37m, ne Z.
Так как левая часть данного уравнения содержит tg x, который
не имеет смысла при х = — + nk> k e Z, то необходимо проверить, не
появились ли в связи с этим посторонние корни. Выполним
проверку:
1) если х = -arctg 2 + 7m, n e Z, то tg x существует и левая часть
данного уравнения не теряет смысла;
2) если х = (-1)п -х + 37т, то tg x не существует и левая часть ис-
ходного уравнения не имеет смысла.
О т в е т. х = -arctg 2 + 7m, n e Z. А
Задача 2. Решить уравнение
' +1 = 0.
sin х
А Пусть sin х Ф 0, т. е. х Ф nk, he Z. Умножая обе части
уравнения на sin х, получаем
2 sin Зх + sin Ъх + sin x = 0.
Используя формулу суммы синусов, имеем
2 sin Зх + 2 sin Зх cos 2x = 0;
sin3*(l
286

nk
1) sin Sx = 0, Sx = nk, x = —, k e Z;
о
2) 1 + cos 2x = 0, cos 2x = -l,2x = n + 2nk, x = ^ + nk, k e Z.
Так как при решении уравнения обе его части умножались на
sin х, возможно появление посторонних корней. Выполним проверку:
1) если х = —, k е Z, то sin х = 0 при k = Зп, т. е. при х = кп, но
о
sin х ■*■ 0 при £ * Зи, т. е. при £ = Ъп + 1 и при k = Зп + 2;
2) если л: = — + я£, /г е Z, то sin л: * 0.
^ л 2л к _
Ответ. л:= — + 7т, л: = — + 7т, л: = — + 7m, ne Z. а
о о 2
Задача 3. Решить уравнение
2 - cos х
= 2.
COSJC
А Пусть cos х Ф 0. Тогда
2 - cos л: = 2 cos x;
2
cos л: = -;
2
л: = ±arccos — + 27m, ne Z.
о
2 2
Выполним проверку. Если х = ±arccos — + 27m, то cos x = — Ф 0.
о о
2
О т в е т. х = ±arccos — + 27m, ne Z. A
о
Задача 4. Решить уравнение
, sin x - cos x
tgx= : .
sinjc
А Так как tg x = , то, умножая обе части уравнения на про-
COSJC
изведение sin x cos x Ф 0, получаем
откуда
sin2 х = sin x cos x - cos2
sin2 Jt + cos2 x = sin a: cos x;
sin a: cos x = l;
2 sin л: cos л: = 2;
sin 2x = 2.
287

Последнее уравнение является следствием исходного. Оно не имеет
корней, следовательно, и исходное уравнение не имеет корней.
Ответ. Корней нет. А
= cos х.
Задача 5. Решить уравнение
/1+COSJC
V 2~
А Возводя обе части уравнения в квадрат, имеем
1 + cos*=cosa*>
откуда
2 cos2 х - cos х - 1 = 0, cos х = 1, cos х = - — .
1) cos x = 1, х = 27m, ne Z;
1 271
2)cos*: = --, x = ± — + 27m, /igZ.
Z о
Так как при решении обе части уравнения возводились в
квадрат, то выполним проверку: выясним, при каких из найденных
значений х правая часть исходного уравнения неотрицательна.
2л 1
Если х = 27т, то cos х = 1 > 0; если х = ±— + 27т, то cos х = -- < 0.
о 2t
Ответ. х = 2яп, ne Z. А
Рассмотрим теперь примеры уравнений, при решении которых
может быть потеря корней.
Задача 6. Решить уравнение
tg х = sin 2x.
А Запишем это уравнение так:
sin л:
= 2 sin х cos x.
Пусть cos х Ф 0, тогда
sin х = 2 sin x cos2 x;
sin x (1 - 2 cos2 ;t) = 0.
1)sinx = 0, a: = 7m, ne Z;
2) 1 - 2 cos2 *:, 2 cos2 x = 1, 1 + cos 2x = 1, cos 2x = 0, 2x = - + 7m,
Проверка показывает, что в обоих случаях cos x Ф 0.
_ к кп
Ответ. л: = 7т, х= - + — ,neZ. A
288

Замечание. Если обе части исходного уравнения
= 2 sin х cos x
cosx
разделить на sin x, т. е. перейти к уравнению
= 2 cos х,
cos л:
то будут потеряны корни уравнения sin х = О, т. е. х = кп, пе Z.
Задача 7. Решить уравнение
tg х - sin x = 1 - cos x.
А Представим это уравнение так:
tg х - 1 = sin x - cos x;
sinx
1 = sin x - cos x.
cos л:
Если cos x Ф О, то
sin x - cos x = cos a: (sin x - cos x);
sin x - cos a: - cos x (sin a: - cos x) = 0;
(sin x - cos л:) (1 - cos x) = 0.
1) sin x - cos x = 0, tg a: = 1, x = — + яп, ^eZ;
2) 1 - cos x - 0, cos x=l, x = 2nn, ne Z.
Проверка показывает, что в обоих случаях cos x Ф 0.
Ответ, л: = т+ пп, х = 2кп, пе Z. А
4
Отметим, что если промежуточное уравнение
sin х - cos x - cos Jt (sin x - cos я) = 0
разделить на разность sin x - cos л:, то будут потеряны корни
к
х- — +7m, ne Z.
4
Задача 8. Решить уравнение
4 cos х + sin 2л: = 4 + 2 sin л:.
А Преобразуем это уравнение следующим образом:
4 cos х + 2 sin Jt cos л: = 4 + 2 sin л:;
cos Jt (2 + sin ;t) = 2 + sin a:.
Заметим, что 2 + sin x Ф 0, т. e. sin x * -2, при любом значении
x. Поэтому не произойдет потери корней, если обе части уравнения
разделить на (2 + sin x). Получим
cosx=l,x = 2nn> ne Z.
Ответ. х = 2ппу пе Z. А
10-Ю. М. Колягин, 10 кл. 289

Задача 9. Решить уравнение
sin х-2 cos л: = 2.
А Воспользуемся формулами
cos x =
Однако эти формулы следует осторожно применять, так как они
не при всех значениях х верны. Эти формулы верны, если tg —
существует, т. е. cos — Ф 0, х Ф к + 2кп9 пе Z. Поэтому требуется про-
верить, не являются ли значения х =п + 2пп, ne Z корнями
исходного уравнения. Проверка показывает, что эти значения х и есть
корни исходного уравнения. Запомним это.
При других значениях х можно использовать эти формулы для
решения уравнения. Применяя формулы и заменяя tg — = t, имеем
2t 2(1"t2)2
i+t2
Так как 1 + *2*0, то
< = 2,T.e.tg| =2;
— = arctg 2 + пп, х = 2 arctg 2 + 2пп, пе Z.
Ct
Ответ. х = к + 2кп9 х-2arctg2 + 2кп9 пе Z. А
Задача 10. Решить уравнение
2ctg*-tg | *+
А Воспользуемся формулами
Эти формулы верны при хф — >хф — +nk,ke Z.
290

„ nk к , , „
Проверим, не являются ли х = —, х = -- + nky k e Z корнями
с» 4
nk
исходного уравнения. Проверка показывает, что х = — являются
корнями исходного уравнения только при k = 1 + 2п9 т. е. при
х = — + кп, так как при k = 2п ctg х не существует; х - — + nk не
являются корнями исходного уравнения, так как при этих значе-
ниях не существует tg
Запомним это и продолжим решение.
Применяя формулы и заменяя tg x = t, получаем
2
В ходе предварительной проверки получилось, что если t = tg x Ф О
и £ = tg;t* 1, то
2-2t-t-t2 = t-t2;
t = - , т. е. tg х = - , х = arctg - + пп, п е Z.
я 1
Ответ. *=о+ ли, л: = arctg - + 7m, neZ. A
Итак, рассмотренные примеры показывают, что при решении
тригонометрических уравнений могут появиться посторонние
корни, если:
1) уравнение содержит тангенс или котангенс;
2) обе части уравнения умножаются (или делятся) на
выражение, содержащее неизвестное;
3) обе части уравнения возводятся в квадрат.
Потеря корней при решении тригонометрических уравнений
может произойти, если:
1) обе части уравнения делятся (или умножаются) на
выражение, содержащее неизвестное;
2) используются тригонометрические формулы, которые
справедливы не при всех значениях неизвестного;
3) при решении системы тригонометрических уравнений для
обозначения целого числа в найденных значениях хиу
употребляется только одна буква.
10* 291

Упражнения
Решить уравнение (888—895).
ллл 2cos3x+cos5x
888. +1 = 0.
cos л:
jcos2* = sin2*
cos* sin*
890. tg 2x = 3 tg x.
1+eos.r
892. tg |x-^) -2ctgx=l.
COS oX uwu л-
|cosjc| cos3x ~
894. V7-cosjc-6cos2jc = 4 sin x.
qok J5 + 3cos4x
Упражнения к главе VII
896. Вычислить:
1) 2 arcsin — + 3 arcsin (""„); 4) arccos (-1) - arcsin (-1);
2) arcsin 7/^-4 arcsin 1; 5) 2 arctg 1 + 3 arctg ("~"7«);
3) arccos I" «I ~ arcsin — ; 6) 4 arctg (-1) + 3 arctg V3 .
Решить уравнение (897—906).
897.1) cos (4 - 2x) = - \; 3) Л cos \гх + j) + 1 = 0;
-^; 4)2cos (|-8x) - V3 =0.
898.1)2 sin (Зл:--) +1 = 0; 3) 3 + 4 sin (2x + l) = 0;
2)1 -sin (^ + ^)=0;
292

899.1) (1 + л/2 cos x) (1 - 4 sin x cos x) = 0;
2) (1 - л/2 cos x) (1 + 2 sin 2x cos 2x) = 0.
-i; 3)V£-t*
±; 4)l-tg(* + -j =
901. 1) 2 sin2 л: + sin л: = 0; 3) cos2 x - 2 cos x = 0;
2) 3 sin2 x - 5 sin x - 2 = 0; 4) 6 cos2 x + 7 cos x - 3 = 0.
902. 1) 6 sin2 x - cos x + 6 = 0; 2) 8 cos2 x - 12 sin x + 7 = 0.
903.1) tg2 x + 3 tg x = 0; 3) tg x - 12 ctg x + 1 = 0;
2)2tg2x-tg;t-3 = 0; 4) tgx + ctg;t = 2.
904. 1) 2 sin 2x = 3 cos 2x; 2) 4 sin 3x + 5 cos Sx = 0.
905.1) 5 sin x + cos x = 5; 2) 4 sin л: + 3 cos л: = 6.
906. 1) sin Sx = sin bx\ 2) cos л: = cos Sx;
907. 1) cos2 Sx - cos Зл: cos bx = 0; 2) sin x sin 5x - sin2 bx = 0.
ПРОВЕРЬ СЕБЯ!
1. Найти значение выражения:
1) arccos I + arcsin 0;
2) arccos ("о/ ~ arcsin ~^~ >
3) tg (arctg V3 );
4) sin arccos —
I 2
2. Решить уравнение:
1) sin Sx cos x - sin x cos Зл: = 1;
2) 2 cos2 x + 5 cos x = 3;
3) tg x - 3 ctg x = 0;
4) sin Sx - sin x = 0;
5) 2 sin x + sin 2x = 0.
Вычислить (908-909).
908.1) cos arccos — ; 2) cos (arccos - J; 3) sin (arccos -);
4)sin arccos-— ; 5)tg (arccos^); 6)tg arccos
I z ) v 2/ ^
—-
293

909.1) sin larcsin-j; 4) sin Irc + arcsin-J;
2)sin (arcsin — I; 5)cos I — arcsin-7=);
\ \ 4 )J V 2 v 5 /
3)sin (rc-arcsin-l; 6) cos f- + arcsin-J.
Решить уравнение (910—927).
910. 1) sin 2x + 2 cos 2x = 1; 2) cos 2x + 3 sin 2x = 3.
911. l)3tg4*:-10tg2;t + 3 = 0; S)ctgx
SllUt
2) 3 tg x + 1 = 2~ ; 4) sin4 x = 1 + cos4 x.
912. 1) sin2 x + sin2 2x = 1; 2) 13 sin2 x + cos 4* - 2 = cos 2*.
913. 1) 8 sin4 л: + 13 cos 2x = 7; 2) tg * + ctg x = 3 + 2 sin 2*.
914. 1) tg x (3 ctg * - 16 sin x cos3 x) = 0;
2) 2 tg x + —!— = -r^z- .
sin* sin2x
915. 1) 3 sin2 x + sin x cos л: - 2 cos2 x = 0;
2) 2 sin2 л: + 3 sin x cos л: - 2 cos2 л: = 0.
916.1) 1 + 2 sin x = sin 2* + 2 cos *;
2) 1 + 3 cos x = sin 2л: + 3 sin л\
917. 1) sin (* + ^) + cos (* +1) = 1 + cos 2x\
2) sin I*-?) +cos (я-т) = sin 2л:.
918. 1) cos3 Jt sin x - sin3 л: cos x = - ;
2) sin3 л: cos л: + cos3 л: sin x - - .
919.1) sin2 x + sin2 2x = 1; 3) sin 4* = 6 cos2 2* - 4;
2) sin2 л: + cos2 2x = 1; 4) 2 cos2 Зх + sin 5л: = 1.
920. 1) sin2 x - cos x cos Sx = — ;
2) sin Зл: = 3 sin л:;
3) 3 cos 2x - 7 sin x = 4;
4) 1 + cos x + cos 2x = 0;
5) cos 4x - sin 2л: = 1;
6) 5 sin 2л: + 4 cos3 x-8 cos x = 0.
294

921.1) sin x + cos x - л/2 sin 7x;
2) sin x + sin 2x + sin Sx = 0;
3) sin x - sin Sx = sin 2x - sin 4л:;
4) cos x - cos Зл: = cos 2x - cos 4л:.
922. sin Зл: + sin 4x + sin 5л: = cos x + cos 2x + cos Зл:.
923. sin2 2x + sin2 Зл: = sin2 4x + sin2 6x.
924. sin л: sin 7x = sin Зл: sin 5л:.
6\/3
926.
927. | cos x | - cos Зл: = sin 2л:.
Решить систему уравнений (928—929).
928. 1) I cos x sin у = -, 2) [sin x + sin i/ = 1,
929.1)
[sin2xsin2j/ = 0; [cosx-cosz/ =
5
^ -, 2) fsinjc+cosjc=2+sinj/-cosj/,
sin г/ о <
[2sin2jc-sin2j/=l.
cosi/ 3'
Решить уравнение (930—938).
930*. 4 sin Зл: sin 4л: = cos x (tg x + tg Зл:).
931*. cos л: - 2 cos Зл: + cos bx = tg x cos Зл:.
933**. 1) sin x sin bx = 1; 3) cos x sin bx = -1;
2)sinxcos4x = -l; 4) sin xcos 3x = -l.
934* ^Зх + cos3x = _2_
cos2bc sin2x вшЗл:
935*- q^^^o^ = ct^ 2x-
nO£J. вшЗл: sinx
936*. —: r-5- = 2 cos 2л:.
sinx вшЗл:
937*. V5tgx+10 = - sin л: +
2 ~ собл:'
295

sin 4x
938*-4smx-sin3x=cos^
939*. Решить систему уравнений:
1)
2) Ul + sin xsiny= cos jc,
tg — - 2sin л: = 6sin (i/ + x);
940*. Найти все значения а, при которых уравнение
sin10 x + cos10 Jt = а имеет корни.
Историческая справка
Очевидно, что еще древнегреческие математики, используя
элементы тригонометрии для решения прямоугольных треугольников,
фактически составляли и решали простейшие тригонометрические
_ я I I „
уравнения типа: sin х = а, где 0 < л: < - и | а | < 1.
Исторически учение о решении тригонометрических уравнений
формировалось параллельно с развитием теории
тригонометрических функций, а также черпало из алгебры общие методы их
решения. Как мы видим, часть тригонометрических уравнений
непосредственно решается сведением их к простейшему виду, иногда —
с предварительным разложением левой части уравнения на
множители, когда правая часть равна нулю. В некоторых случаях удается
произвести замену неизвестных таким образом, что
тригонометрическое уравнение преобразуется в «удобное» для решения
алгебраическое уравнение. Иногда удается решить
тригонометрическое уравнение, анализируя его левую и правую части. Например,
для решения уравнения sin4 х + cos4 х = л/2 следует понять, что
sin4 х < sin2 х, cos4 x < cos2 x, т. e. sin4 x + cos4 x < sin2 x + cos2 x = 1,
а так как 1 < v2 , то уравнение не имеет решений. Многие
тригонометрические уравнения в традиционном понимании вообще
неразрешимы, и для них можно лишь указать метод приближенного
решения. Такое часто, например, происходит, когда в уравнении
неизвестная величина встречается и под знаком тригонометрической
функции, и вне ее (примером такого уравнения может быть
К сожалению, нельзя указать общего метода решения
тригонометрических уравнений, почти каждое из них (кроме простейших)
требует особого подхода.
296

ТРИГОНОМЕТРИЧЕСКИЕ
главаVIIIJ [ ФУНКЦИИ
В этой главе будут рассмотрены основные свойства и графики
тригонометрических функций у = sin х, у - cos x,y = tgx,y = ctg х.
Напомним, что при изучении различных функций (линейной,
квадратичной, степенной и т. д.) выяснились такие их свойства,
как область определения, множество значений, возрастание или
убывание, наибольшие и наименьшие значения, промежутки зна-
копостоянства, четность или нечетность, нули (корни) функции
(точки пересечения графика функции с осью абсцисс).
Для тригонометрических функций, кроме этих свойств,
характерно свойство периодичности.
§ 50. Периодичность тригонометрических
функций
Вы знаете, что для любого значения х верны равенства
sin (х + 2п) = sin xt cos (x + 2я) = cos x.
Из этих равенств следует, что значения синуса и косинуса
повторяются при изменении аргумента на 2я. Такие функции
называют периодическими с периодом 2к.
Функция f(x) называется периодической, если существует
такое число Г^О, что для любого х из области определения этой
функции выполняется равенство
f(x-T) = f(x) = f(x+T).
Число Т называют периодом функции f(x).
Из этого определения следует, что вместе с каждым х значения
х + Т и х - Т также входят в область определения периодической
функции f(x). Поэтому все точки х + kT9 ke Z также принадлежат
области определения, и в этих точках значения функции равны,
т.е. f(x + kT) = f(x).
На рисунке 77 изображены графики некоторых периодических
функций.
Периодическими функциями описываются многие физические
процессы (колебание маятника, вращение планет, переменный ток
и пр.).
Покажем, что число 2к является наименьшим положительным
периодом функции у = cos x.
297

У
7
ЛЛЛЛ'ЛЛЛЛ
Рис.77
О Пусть Т > О — период косинуса, т. е. для любого х
выполняется равенство cos (х + Т) = cos х. Положив х - О, получаем cos T = 1.
Отсюда Т = 2nk, ke Z. Так как Т > О, то Т может принимать
значения 2л, 4л, 6л,... и поэтому период не может быть меньше 2л. •
Можно доказать, что наименьший положительный период
функции у = sin х также равен 2л.
3 а д а ч а 1. Доказать, что fix) = sin Sx — периодическая функ-
2л
ция с периодом — .
о
А Если функция fix) определена на всей числовой оси, то для
того, чтобы убедиться в том, что она является периодической с
периодом Ту достаточно показать, что для любого х верно равенство
fix ± Т) = fix). Данная функция определена для всех х е R и
:±у) =sin3(*± ^j=sin(Sx-2n) = smSx = fix). A
Покажем, что функция tg x является периодической с
периодом л. Если х принадлежит области определения этой функции,
т. е. х Ф — +пп> пе Z, то по формулам приведения имеем
tg (х - л) = -tg (л - х) = -(-tg х) = tg х, tg (х + п) = tg х.
Таким образом, tg (х - л) = tg х - tg (х + л). Следовательно, л —
период функции tg x.
298

Покажем, что я — наименьший положительный период
функции tg х.
О Пусть Т — период тангенса, тогда tg(x + T) = tg x, откуда при
х = О получаем
tgT = O, T = nk, ke Z.
Так как наименьшее целое положительное число k равно 1, то
я — наименьший положительный период функции tg x. •
х
Задача 2. Доказать, что tg — — периодическая функция с
о
периодом Зя.
х
то tg — — периодическая функция с периодом Зя. А
о
Задача 3. Найти наименьший положительный период функ-
Зх
ции у = cos — .
А Пусть Т > 0 — период этой функции, т. е. для любого значе-
З(х + Т) Зх _ Л
ния х выполняется равенство cos —-— = cos — . Положив х = О,
ЗТ л ЗТ Л 14л/г
имеем cos -— = 1, откуда — = Znk, Т = —г— , k e Z. Среди этих
( 7 о
чисел наименьшее положительное число получается при k = l. Про-
14л
3
3/ , 14я\1 (Зх , о \ Зх
верим, что число —г- является периодом данной функции:
о
14я
Ответ, —г- . А
о
Аналогично тому, как это было сделано при решении задач 1—3,
можно доказать более общее утверждение: если функция у - f(x)
периодическая с периодом Т9 то функция у = cf(ax + &), где а * О,
Т
является периодической с периодом Т1 = — .
Например, функция у = 3 ctg (5л: - 4) является периодической
с периодом Т = —, так как функция у - ctg л: периодическая с пе-
о
риодом я.
299

Упражнения
941. На рисунке 78 на отрезке [0; 2] построен график периодической
функции с периодом Т = 2. Построить график этой функции на
отрезке [-2; 6]:
\ /
-3 -2
2 3 4 5 6 7
Рис. 78
942. На рисунке 79 на отрезке - - Т; -Т\ построены графики пери-
одических функций с периодом Т. Построить графики этих фун-
—Т; -Т .
2 2 J
У
1
-2 \-1
О
-1
б)
-2 -II
-2 -1
-1
Рис. 79
300

943. Доказать, что данная функция является периодической с
периодом 2я:
1) у = cos х- 1; 2) y = sinx + I; 3)i/ = 3sinx;
у 5) i/= sin (*-^j; 6) i/= cos (*+y)-
944. Доказать, что данная функция является периодической с
периодом Т, если:
I)y = sm2x, T = n; 3)y = tg2x, T= у,
2)y = cos ^,Т = 4п; 4) y = sin -у , Т = -п.
Найти наименьший положительный период функции (945—
946).
2 х
3) t
945. l)i/ = cos*; 3)y = tg;
Q
2) i/ = sin - x; 4) i/ = | sin jc |.
946**. 1) i/ = sin x + cos jc; 2) у = sin jc + tg x.
§ 51. Функция у = sin x, ее свойства и график
Функция у - sin х определена на всей числовой прямой и
является периодической с периодом 2я. Поэтому подсчет значений этой
функции для любого аргумента можно свести к вычислению ее
значений для аргумента, принадлежащего какому-нибудь отрезку
длиной 2я, например отрезку -я < х < я.
В § 34 было отмечено, что с помощью формул приведения
подсчет значений этой функции для любого аргумента можно свести
к вычислению ее значений для аргумента от 0 до -.
Следовательно, весь график функции у = sin x можно построить
с помощью части графика, построенного на отрезке 0 < х < -. По-
кажем, как последовательно строится график этой функции:
сначала на отрезке 0; — I затем на отрезках [0; я], [-я; я] и, наконец,
на всей числовой прямой.
301

1. График функции у = sin х на отрезке 0; —
Докажем, что функция у = sin х возрастает на отрезке 0; — .
О Пусть хх и х2 — любые два числа, принадлежащие отрезку
0; - и удовлетворяющие неравенству хх < х2, т. е. 0 < хх < х2 < -.
Требуется доказать, что sin хх < sin x2.
... Хо ~ Хл Хо "♦" JC-i __
Рассмотрим разность sin x2 - sin хх = 2 sin cos . Так
Л Я Л *2~*1 ТС _ Хо + Х\ К „
как 0 < хх < х2 < -, то 0 < z < - и 0 < z < -. Поэтому
sin 2 г > 0 и cos -^-z— > 0. Следовательно, sin x2 - sin хг > 0,
т. е. sin хх < sin x2.
Для построения графика функции у - sin х на отрезке 0; —
составим таблицу ее значений:
X
у = sin х
0
0
п
6
0,5
л
4
п
3
| = 0,в7
2
1
тывая
Построим найденные точки и проведем через них кривую, учи-
, что на отрезке 0; - функция у = sin x возрастает (рис. 80).
Для более точного построения графика нужно составить более
подробную таблицу, находя значения синуса еще для некоторых
значений аргумента, например, по таблицам В.М. Брадиса.
Приближенно значения функции у = sin x можно
геометрически находить и затем строить график этой функции. Поясним этот
способ построения графика функции у = sin х на отрезке 0; -- .
Построим окружность радиуса 1 с центром в точке А оси
абсцисс, лежащую левее оси ординат (рис. 81). Разделим первую
четверть этой окружности, например, на 8 равных частей и через
точки деления проведем прямые, параллельные оси абсцисс. Отрезок
0; — оси абсцисс также разделим на 8 равных частей и из точек
302

деления восстановим перпендикуляры к ней до пересечения с
соответствующими прямыми, проведенными параллельно оси
абсцисс так, как показано на рисунке 81. Построенные точки
пересечения прямых по определению синуса числа являются точками
графика функции у = sin x. Проведем через эти точки кривую,
учитывая, что функция у = sin х возрастает на отрезке 0; — , получим
график этой функции на данном отрезке (см. рис. 81).
0,5
КПП
6 4 3
К X
Рис.80
Рис.81
2. График функции y = sinx на отрезке [0; тс]
Докажем, что график функции у = sin x симметричен
относительно прямой х = -, т. е. прямой, параллельной оси ординат и про-
ходящей через точку — оси абсцисс.
О Надо доказать, что для любых двух точек а и Ь, лежащих на
оси абсцисс и симметричных относительно прямой х = -, выполня-
ется равенство sin a = sin Ъ.
Пусть расстояние от точек а и Ъ до
прямой х = - равно а. Тогда а = - - а,
b = — + а (рис. 82) и по формулам приве-
У1
1
0
/
а=2~а
\ .
Рис. 82
дения sin f--cx) =sin 1- +
Для построения графика функции у = sin x на отрезке [0; я]
сначала построим его часть на отрезке Ф^ (см. рис. 80). Затем
303

эту часть графика отобразим симметрично относительно прямой х = —.
Получим график функции на отрезке [0; я] (см. рис. 82).
3. График функции у = sin х на отрезке [—тс; тс]
В § 30 было показано, что функция у = sin x — нечетная,
поэтому ее график симметричен относительно начала координат.
Для построения графика функции у = sin x на отрезке [-я; я]
построим сначала его часть на отрезке [0; я] (см. рис. 82). Затем для
каждой точки М(х0; у0) полученной части построим точку М(-х0; -у0),
симметричную относительно начала координат, и получим график
функции у = sin х на отрезке [-я; я] (рис. 83).
Рис. 83
4. График функции у = sin x на всей числовой прямой
В § 50 было показано, что функция у = sin x является
периодической с периодом 2я, т. е. для любого х выполняется равенство
sin (х + 2я) = sin х. Отсюда следует, что sin (х + 4я) = sin x,
sin (х - 2я) = sin х и вообще sin (х + 2кп) = sin х для п = 0, ±1, ±2, ...
и любого х. Следовательно, график функции у = sin x периодически
повторяется с периодом 2я, т. е. на отрезках [я; Зя], [Зя; 5я],
[-Зя; -я] и т.д. график такой же, как и на отрезке [-я; я] (рис. 84).
У1
1
г Ч^
"I
У =
0 2
• sin х
г 2п/
У i
Рис. 84
304

Кривая, являющаяся графиком функции у = sin х, называется
синусоидой.
Итак, весь график функции у = sin x построен геометрически,
исходя из его части на отрезке 0; — . Следовательно, свойства
функции у = sin х можно получить из построенного графика, опираясь на
свойства этой функции на отрезке 0;— . Например, из рисунка 82
L J Г* ^
видно, что функция у = sin х положительна на полуинтервале г^»я \,
Гд 1 1 }
равна нулю при х = пи убывает на отрезке nSn . Из рисунка 83 вид-
к к \
но, что функция у = sin х возрастает на отрезке ~"?'"? • Из рисунка
84 видно, что функция у = sin x возрастает на отрезках
-- + 2пп;- + 2пп \ п е Z, убывает на отрезках - + 2ял; —+ 2ял 9
пе Z. Перечислим основные свойства функции у = sin x.
5. Основные свойства функции у = sin x
1. Область определения — множество R всех действительных
чисел.
2. Множество значений — отрезок [-1; 1].
3. Функция у = sin х — периодическая с периодом 2я, т. е.
sin (л: + 2я) = sin x.
4. Функция у = sin х — нечетная, т. е. sin (-х) = -sin x.
5. Функция у = sin x:
возрастает на отрезках —- + 2кп;—+2кп \,пе Z;
убывает на отрезках —+2ял;—+2ял \9пе Z.
|_2 2 J
6. Функция у = sin х принимает:
наибольшее значение, равное 1, при х = — + 2пп ,neZ;
наименьшее значение, равное -1, при х = -— + 2пп ,пе Z;
значение, равное нулю, при х = пп, пе Z.
Задача 1. Разбить отрезок —; 2я на два так, чтобы на
одном из них функция у = sin х убывала, а на другом — возрастала.
А Из рисунка 84 видно, что при увеличении аргумента от — до
— значения функции у = sin х уменьшаются от 1 до -1. При уве-
11-Ю. М. Колягин, 10 кл. 305

личении аргумента х от — до 2я значения функции у = sin x увели-
чиваются от -1 до 0.
Ответ. На отрезке —; — функция у = sin x убывает, а на
отрезке —;2я — возрастает. А
Задача 2. Сравнить числа sin 2 и sin 3.
А Так как я «3,14, ^ «1,57, то ^ <2<3<я.
Из рисунка 84 видно, что на отрезке — ;я функция у - sin x
убывает. Следовательно, sin 2 > sin 3. А
3 а д а ч а 3. Найти все числа х на отрезке —; — , для которых
выполняется неравенство: sin х < — .
А На отрезке г^-^- функция у - sin x убывает (см. рис. 84) и
V2 Зя
принимает значение — при х = —. Следовательно, неравенство
^ V2 Зя . ^ Зя
sin х < — выполняется при — < х < — . А
Задача 4*. Построить графики функций:
= sin
2) i/ = 2 + sin x;
3)у = 2 sin x;
4) у = sin 2л\
А 1) График функции у = sin I х + -1 получается сдвигом графика
функции у = sin х вдоль оси абсцисс влево на — ед. (см. рис. 85, а).
2) График функции у = 2 + sin x получается сдвигом графика
функции у = sin х вдоль оси ординат вверх на 2 ед. (см. рис. 85, б).
3) График функции у = 2 sin jc получается растяжением
графика функции у = sin х вдоль оси ординат от оси абсцисс в 2 раза
(см. рис. 85, в).
4) График функции у = sin 2x получается сжатием графика
функции у = sin х вдоль оси абсцисс к оси ординат в 2 раза
(см. рис. 85, г). А
306

\
ч
ч
ч
У1
3-
2i
/
у
0
у =2+sin л:
\
ч
ч
ч
/
/ х
У
ч\
\-
V
У1
2-
1.
л
К"
0
-1
-2
y=2s\n х
<\^ y=sin;c
V-7
1_
^ /\"2
f/
0
-1
в
?\
у-.
уТу
5in 2jc
\f
2щ
X
г
Рис. 85
11*
307

Упражнения
Пользуясь графиком функции у = sin x, выполнить упражнения
(947-954).
947. (Устно.) Выяснить, при каких значениях х, принадлежащих
отрезку [0; Зя], функция у = sin x принимает значения:
1) равные 0; 1; -1; 2) положительные; 3) отрицательные.
948. (Устно.) Выяснить, возрастает или убывает функция у = sin x
на промежутках:
2>(§4
5)[2; 4]; 6) (6; 7).
949. Разбить данный отрезок на два так, чтобы на одном из них
функция у = sin х возрастала, а на другом убывала:
1) [0; 71]; 2) [|;2я] ; 3) [-я; 0]; 4) [-2я; -я].
950. Используя свойство возрастания или убывания функции
у ~ sin x9 сравнить числа:
1Ч . 7 л . 13л .
1) sin — и sin -ZT7T ; 5) sin 3 и sin 4;
ЛЧ . 13л .11л „ч . „ . „
2) sin -з- и sin -=- ; о) sin 7 и sin о;
3) sin (-^) и sin {—); 7) sin (-3) и sin (-2);
4) sin I—^J и sin I——I; 8) sin (-1) и sin (-1,5).
951. Найти все решения неравенства, принадлежащие отрезку [0; Зя]:
1) sin х > - ; 3) sin x > - - ;
2) sin x < — ; 4) sin x < - — .
952. Выражая косинус через синус по формулам приведения,
сравнить числа:
л л л 5л
1) sin - и cos -; 3) sin - и cos — ;
У У D 14
. 9л 9л .л Зл
2) sin — и cos —; 4) sin - и cos —.
308

953. Найти все решения неравенства, принадлежащие промежутку
1 v fo
I)sin2x>--; 3)sin -^ > — ;
954. Построить график функции и выяснить ее свойства:
l)i/= I-sin л:; 5)i/ = sin (*-^J;
2) i/ = 2 + sin x; 6) у = sin (*+1);
3) у = sin 3jc; 7) у = sin (x - 2);
4) у = 2 sin x; 8) i/ = sin (x + 4).
955*. Найти множество значений функции у = sin x, если х
принадлежит промежутку:
2)|_Т'Т_|; 3
956**. Построить график функции:
1)y = sin \x\; 3)y = sin
2) i/ = | sin x |; 4) i/ =
sm-
957**. Сила переменного электрического тока — функция,
зависящая от времени, выражается формулой
где А — амплитуда колебания, со — частота, ф — начальная
фаза. Построить графики этой функции, если:
jj
*; 2)A=l,<D=2,<p=jj.
§ 52. Функция у = cos x, ее свойства и график
Функция у = cos х определена на всей числовой прямой, четная
и периодическая с периодом 2я. Ее график можно построить таким
же способом, каким в § 51 был построен график функции у = sin x.
Однако проще воспользоваться следующей формулой приведения:
309
cosjc = sm U + I.

Эта формула позволяет построить график функции у = cos x и
получить ее свойства из графика функции у = sin x и свойств этой
функции.
1. График функции у = cos x
Покажем, что график функции у = cos x получается из графика
функции у = sin х сдвигом вдоль оси абсцисс влево на — (рис. 86).
У
1
-1
(
0
/
\ ^
!Ч
sin.v
V У
y = sin х
*ч
Зл
\ X
Рис. 86
О Рассмотрим любую точку х0 оси абсцисс. Точка х0 + - лежит
тс
правее точки х0 на —. Надо доказать, что значение функции у = cos x
в точке х0 равно значению функции у = sin х в точке jc0 + -
(см. рис. 86). По формуле приведения имеем cos х0 = sin lx0 + -1. •
График функции у = cos x изображен на рисунке 87. Перечислим
основные свойства этой функции.
' Ч
-2я _3jTV-я!
У
1
/2
-1
ч
0 |\
S i4
^\S 7 7 N^ : ^
Рис. 87
2. Основные свойства функции у = cos x
1. Область определения — множество R всех действительных
чисел.
2. Множество значений — отрезок [-1; 1].
3. Функция у = cos х — периодическая с периодом 2я, т. е.
cos(jc + 2n) = cosx.
310

4. Функция у = cos x — четная, т. е. cos (-х) = cos x.
5. Функция у = cos x:
возрастает на отрезках [-я + 2пп; 2пп], пе Z;
убывает на отрезках [2кп, я + 2пп], пе Z.
6. Функция у = cos х принимает:
наибольшее значение, равное 1, при х - 2пп, пе Z;
наименьшее значение, равное -1, при х = я + 2пп, пе Z;
_ я „
значение, равное0, прих = — + пп, пе Z.
Задача 1. Выражая синус через косинус по формуле приве-
я . Зя
дения, сравнить числа cos - и sin — .
7 о
А „ , . Зя /я Зя\ я __
А По формуле приведения sin — = cos I — - —- = cos —. Числа
о \ Z о / о
- и - принадлежат отрезку [0; я] и - < —. Из рисунка 87 видно,
О I О (
что функция у = cos х убывает на отрезке [0; я]. Следовательно,
я я Зя я
cos - > cos -, т. е. sin — > cos -. А
О I О I
Задача 2. Найти все решения неравенства cos х > - - ,
принадлежащие отрезку -я < х < 2я.
А Из рисунка 88 видно, что график функции у = cos x лежит выше
^ 1 / 2я 2я\ /4я
графика функции у = - — на промежутках I —^>~^\ и
2я 2я 4я
Ответ. -~г <х< —, —<х<2п. А
о об
y=cosx
Рис.
Задача 3. Найти область определения функции
1
У = .
sinx+cosx
А Найдем значения х, при которых выражение
не
SJJ1X + СОоХ
имеет смысла, т. е. значения х, при которых знаменатель равен
311

нулю. Решая уравнение sin x + cos x = О, находим tg x = -1,
Х---Л- пп, п е Z. Следовательно, областью определения данной
функции являются все значения ХФ-- + ял, пе Z. А
Задача 4. Найти множество значений функции
у = 3 + sin х cos x.
А Нужно выяснить, какие значения может принимать у при
разных значениях х, т. е. установить, для каких значений а
уравнение 3 + sin х cos x = а имеет корни. Применяя формулу синуса
двойного угла, запишем уравнение так: 3 + «sin 2x = а, откуда
sin 2x = 2а - 6. Это уравнение имеет корни, если | 2а - 6 | < 1, т. е.
если -1 < 2а - 6 < 1, откуда 5 < 2а < 7, т.е. 2,5 < а < 3,5.
Следовательно, множеством значений данной функции является
промежуток 2,5 <у <3,5. А
Задача 5*. Построить график функции
у = -3 cos (х- 1).
А График функции у = -3 cos (x - 1) можно получить из графика
функции у = cos х следующими преобразованиями:
1) сдвигом вдоль оси абсцисс вправо на 1 ед.;
2) растяжением графика функции у = cos (x - 1) вдоль оси
ординат от оси абсцисс в 3 раза;
3) симметричным отображением графика функции у = 3 cos (x - 1)
относительно оси абсцисс (рис. 89). А
У
з.
/\*"
/ \'
/ \
/ \
\
-3
1+
0 1
-1
1
—2 1
j/ = 3cos(;c-l)
i
f
I
/
и
I
1
9.1 .
\
/ п 1+я х
1
Рис. 89
312

Упражнения
Пользуясь графиком функции у = cos x9 выполнить упражнения
(958-962).
958. (Устно.) Выяснить, при каких значениях х, принадлежащих
отрезку [0; Зя], функция у = cos x принимает значения:
1) равные 0; 1; -1; 2) положительные; 3) отрицательные.
959. (Устно.) Выяснить, возрастает или убывает функция у - cos x
на отрезке:
1) [Зя; 4я]; 2) [-2я; -я]; 3) \^Щ 5
4)[-|;0J; 5)[1;3]; 6) [-2;-1].
960. Разбить данный отрезок на два так, чтобы на одном из них
функция у = cos х возрастала, а на другом — убывала:
961. Используя свойство возрастания или убывания функции
у = cos х, сравнить числа:
1) cos - и cos —; 4) cos -— и cos -— ;
i У \ l ) \ { )
2) cos — и cos —— ; 5) cos 1 и cos 3;
( 6п\ ( пЛ
3) cos —— и cos —- ; 6) cos 4 и cos 5.
962. Найти все решения неравенства, принадлежащие отрезку [0; Зя]:
1) cos х > -; 3) cos x < - — ;
2) cos x > - —; 4) cos x < — .
963. Найти область определения функции:
I)y = sm2x; 2) у = cos--; 3)y = cos—;
Z x
2 r-
4) у = sin — ; 5) у = sin Vjc; 6) у = cos
964. Найти множество значений функции:
1) у = 1 + sin х; 4) у = 1 - 4 cos 2x;
2)у=1- cos х; 5) у = sin 2x cos 2x + 2;
3) у = 2 sin х + 3; 6) у = — sin x cos jc — 1.
313

965. Выражая синус через косинус по формулам приведения,
сравнить числа:
л . к . Зл Зл
1) cos — и sm —; 4) sin — и cos — ;
о о о о
ЛЧ . л л л . 5л
2) sm - и cos -; 5) cos — и sin — ;
7 7 о 14
5л . 5л л Зл
3) cos — и sm — ; о) cos - и sin — .
о о о 1U
966. Найти все решения неравенства, принадлежащие промежутку
_п Зл
2<Х< 2 :
1 V2
1) cos 2х < - ; 2) cos 3* > — .
967*. Построить график функции и выяснить ее свойства:
1) у = 1 + cos х; 4) I/ = 3 cos x;
2)у = cos х - 2; 5) i/ = cos 3jc - 1;
6) у = 2 cos
968*. Найти множество значений функции у = cos x, если х
принадлежит промежутку:
i)[f;«]; 2Ат>Ч)-
L«> J \ 4 4 /
Найти область определения функции (969-970).
969*. 1)у= Vsin*+1;
2)у= vcosx-l; 5)у = lgsin x;
970*Л)у=
3)у= y/2cosx-l; 6) у = In cos jc.
1
о . 2
2sin jc-
2)г/=—г r~2~ ; 4)у=—з •
COS JC-Sin JC * COS Jt + COSJt
971*. Найти множество значений функции:
1) у = 2 sin2 x - cos 2x; 4) у = 10 - 9 sin 3*;
2) у = 1 - 8 cos2 x sin2 x; 5) у = 1 - 2 | cos x |;
оч l+8cos2x „.
3)у= ; о) у = sin х + sin
972**. Построить график функции:
1) у = | cos х |; 2) i/ = 3 - 2 cos (* -1).
314

§ 53. Функции у = tg х и у = ctg x,
их свойства и графики
Функция у = tg х определена на всей числовой прямой, кроме
точек х = — + кп, пе Z, нечетная и периодическая с периодом я.
Построим последовательно график этой функции: сначала на полуинтер-
( п кЛ „ -
, затем на интервале "т:5 т: и, наконец, на всей области
v & 2)
вале
определения
1. График функции у = tg х на полуинтервале 0; - I.
Докажем, что функция y=tgx возрастает на полуинтервале
0; - I.
я
О Пусть 0 < хх < х2 < -. Тогда 0 < sin хх < sin xv cos jcx > cos x2 > 0.
sin xt sin jc2 sin x2
Следовательно,tgx,= < < =tgx9,T.e.tgx* <tgx0. •
x cos jcx cos xx cos jc2 2 ^1^2
Составим таблицу значений функции у = tg x для нескольких
значений х из полуинтервала 0;- ]:
X
y = tgx
0
0
я
6
|.0,58
Я
4
1
я
3
V3-l,7
Построим найденные точки и проведем
через них кривую, учитывая, что на
полуинтервале 0; - ] функция у = tg х возрас-
тает (рис. 90).
Для более точного построения графика
надо составить более подробную таблицу,
находя значение функции у = tg x еще для
нескольких значений аргумента, например,
по таблицам В.М. Брадиса или на
микрокалькуляторе.
Отметим, что если х приближается к
- и х < -, то sin х приближается к 1, а
к к к к х
6 4 3 2
Рис. 90
315

cos x приближается к 0 и cos х > 0. При этом tg x =
SU1JC
COSJC

неограниченно возрастает (рис. 90).
2. График функции z/ = tg х на интервале - -; - I
У1
Уо
В § 30 было показано, что функция
у = tg х — нечетная. Поэтому ее
график симметричен относительно
начала координат.
Для построения графика функции
у = tg х на интервале —; изобра-
V 2 2)
зим сначала его часть на полуинтерва-
х ле 0;^ ] (см. рис. 90). Затем для каж-
L 2)
дой точки М(х0; у0) полученной части
построим точку Мг(-х0; -y0),
симметричную относительно начала
координат. Получим график функции
у = tg х на интервале [--;-] (рис. 91).
V 2 2 у
Рис.91
3. График функции у = tg x на всей области определения
В § 50 было показано, что функция у = tg x — периодическая с
периодом л. Следовательно, весь график этой функции получается
из его части на интервале ~^» ^ (см. рис. 91) сдвигом вдоль оси
абсцисс вправо и влево на пп, пе Z (рис. 92).
-Уо
1-
y=\gx
Рис. 92
316

Итак, весь график функции у = tg x строится геометрически,
исходя из его части на полуинтервале 0;- . Следовательно, свойства
L 2)
функции у = tg х можно получить из ее графика. Например, из
рисунка 91 следует, что функция у = tg x возрастает на интервале
, а из рисунка 92 видно, что эта функция возрастает на
интервалах \-- + пп;- + пп , пе Z.
\ 2 2 )
Перечислим основные свойства функции у = tg x.
4. Основные свойства функции y = tgx
1. Область определения — множество всех действительных чи-
К г,
сел, кроме чисел — +кп, пе Z.
2. Множество значений — множество R всех действительных
чисел.
3. Функция у = tg х — периодическая с периодом к.
4. Функция у = tg х — нечетная, т. е. tg(-jc) = -tg x.
5. Функция y = tgx возрастает на интервалах - - + пп; - + пп ,
V 2 2 )
пе Z.
6. Функция у = tg х принимает значение, равное 0, при х = пп,
пе Z.
5. Функция у = ctg х
По формуле приведения ctg х = -tg \х + —
V 2
Следовательно, график функции у = ctg x и ее свойства можно
получить из графика функции y = tgx и свойств этой функции.
График функции у - -tg \х + -- получается из графика функции
у = tg х сдвигом вдоль оси абсцисс влево на - и затем симметрией
относительно оси абсцисс. График функции у = ctg x изображен на
рисунке 93.
317

Рис. 93
Задача 1. Найти все решения неравенства tg x < 2,
принадлежащие отрезку -я < х < —.
А Из рисунка 94, а видно, что график функции y = tgx лежит не
выше прямой у = 2 на промежутках [-я; х3], —;хг и —; х2 ,
V 2 J V2 J
где хг = arctg 2, х2 = я + arctg 2, jc3 = - я + arctg 2.
Ответ. -7C<x<-7C+arctg2, -— <Jt<arctg2, — <л:<я+arctg2. А
Задача 2. Решить неравенство tg x> 1.
А Построим графики функций i/ = tgjcni/=l (рис. 94, б).
Рисунок показывает, что график функции у = tg x лежит выше прямой
1 ( [
у =1 кз. промежутке —; — , а также на промежутках, полученных
V4 2 )
сдвигом его на я, 2я, Зя, -я, -2я и т. д.
Л к п
Ответ. -+пп<х<-+ кп, пе Z. А
Задача 3*. Построить график функции у = tg \2x +
А График функции y = tg \2x + - =tg2ut + - , которая
является периодической с периодом —, можно получить из графика функ-
ции y = tgx следующими преобразованиями:
1) сдвигом вдоль оси абсцисс влево на - ед.;
2) сжатием графика функции у = tg \х + - вдоль оси абсцисс к
оси ординат в 2 раза (рис. 94, в). А
318

f
J
yl
2
r
j
0 x
y=tgx
J
y=2
Зл x
2
Отметим, что построение графика функции у = tg \2х + - мож-
V 2 У
но иначе осуществить, записав данную функцию так: у - - ctg 2jc.
В этом случае можно сначала выполнить сжатие графика функции
319

у = ctg x (рис. 93) вдоль оси абсцисс к оси ординат в 2 раза, а затем
график функции у = -ctg 2х получить из графика функции у - ctg 2x
с помощью симметрии относительно оси Ох.
Тригонометрические функции широко применяются в
математике, физике и технике. Например, многие процессы, такие, как
колебание струны, колебание маятника, напряжение в цепи
переменного тока и т. д., описываются функцией, которая задается
формулой у = A sin (cojc + ф). Такие процессы называют
гармоническими колебаниями, а описывающие их функции — гармониками (от
греч. harmonikos — соразмерный). График функции у = A sin (сол: + ф)
получается из синусоиды у = sin x сжатием или растяжением ее
вдоль координатных осей и сдвигом вдоль оси Ох. Обычно
гармоническое колебание является функцией времени: у = A sin (art + ф),
где А — амплитуда колебания, со — частота, ф — начальная фаза,
период колебания.
Упражнения
Пользуясь графиками функций у = tg x и у = ctg x, выполнить
упражнения (973—976).
973. (Устно.) Выяснить, при каких значениях х из промежутка
-я < х < 2я функция у = tg х принимает:
1) значение, равное 0; 2) положительные, 3) отрицательные
значения.
974. (Устно.) Выяснить, является ли функция у = tg x
возрастающей на промежутке:
} (Л} 4>'2;3>-
975. (Устно.) Выяснить, при каких значениях х из промежутка
-2я< х < п функция у = ctg х принимает:
1) значение, равное 0; 2) положительные, 3) отрицательные
значения.
976. (Устно.) Выяснить, является ли функция у = ctg x убывающей
на промежутке:
977. Сравнить числа:
l)tgl5°Htg25°; 3)tg
2) tg (-80°) и tg (-50°); 4) tg \ и tg у ;
320

5)tg2Htg3; 7)tg(-l)Htg(-l,5);
6)tglHtgl,5; 8) tg (-2) и tg (-3).
978. Сравнить числа:
1) ctg 35° и ctg 67°; 4) ctg f-| 1 и ctg |;
2)ctg95°Hctgll7°; 5) ctg 1,2 и ctg 1,5;
3)ctgf-y)Hctg y; 6) ctg 2 и ctg 3.
979. Выяснить, выполняется ли неравенство tg x > О во всех
точках промежутка:
«(of); »(*?); «[-£-?]; «[-?#
5) [-1; 1]; 6) [2; 4]; 7) (-3; -2); 8) (0,5; 1).
980. Найти все решения неравенства, принадлежащие промежутку
(-я; 2л):
l)tgx>l; 3)tgx<-l;
981. Найти все числа х интервала (0; я), для которых выполняется
неравенство:
1) ctg х > - V3 ; 4) ctg х < V3 ;
2) ctg х > -1; 5) -1 < ctg x < 0;
3)ctg*<l; 6)0<ctgx<l.
982. Найти все решения неравенства, принадлежащие промежутку
[0; Зя]:
l)tg*>3; 2)tgx<4; 3)tgx<-4;
4)tgJC>-3; 5)ctgjc>2; 6)ctgx<-3.
983. Найти все решения неравенства, принадлежащие промежутку
-н
I)tg2x<l;
2)tg3x<-V3;
321

984*. Построить график функции и выяснить ее свойства:
X
tg2;
= tg x - 2;
1
= ctg|x-- |;
6)y = ctgx+ 1.
985*. Найти множество значений функции у = tg х, если х
принадлежит промежутку:
4 ' 2
Построить график функции (986—988).
986*. l)y = tg\x\; 2) у = | tgx|; 3) i/ = ctgx;
1
г = tg х ctg jc; 6) i/ = sin x ctg jc.
ctgx'
987*. 1) у =
988*.
sinx при —<jc<—,
tg* при 4
3x--
cosjc при —<x<-,
2 2
При -
§ 54. Тригонометрические неравенства
Рассмотрим примеры тригонометрических неравенств. При их
решении используются свойства тригонометрических функций и их
графики.
V3
Задача 1. Решить неравенство cos x <
2 *
А Так как косинус — периодическая функция с периодом 2л, то
достаточно найти решения неравенства на отрезке длиной 2я. В
качестве такого отрезка возьмем отрезок [0; 2я]. Рассмотрим на от-
7з
резке [0; 2л] график функции у = cos x и проведем прямую У=~^
(рис. 95).
322

Надо найти все те значения х из
отрезка [0; 2я], для которых
соответствующие точки графика
функции у = cos х лежат ниже прямой
у= — и на этой прямой. Прямая -1-
V3
V=COSJC
j = -^ пересекает при х е [0; 2я] Рис. 95
график функции у = cos x в точках А и В, абсциссы которых есть
л/3
корни уравнения cos х = — на отрезке [0; 2я]. Одно из решений
у[3 К _ 11Я „
этого уравнения: хг = arccos — = -, другое: х2 = 2я - хг = — . Если
, то cos х < — .
Следовательно, на отрезке [0; 2я] все решения неравенства
. л/3 к Пк
cos х < -jr- определяются условием - < jc < -т- .
^ 0 0
Ответ. \
о
-£■ +2nk,ke Z. А
о
Задача 2. Решить неравенство cos х > - .
А Рассмотрим график функции у = cos jc на отрезке [-я; я] и
проведем прямую у = - (рис. 96).
Прямая у = - пересекает на этом отрезке график функции у = cos x
в точках Аи В, абсциссы которых хх= —, х2 = -.
3 3
Из рисунка 96 видно, что все решения неравенства образуют интер-
п п
вал
» т-е.
отрезке [-я; я]
все решения данного неравенства оп-
к ^ к
ределяются условием — < х < -.
3 3
71 7С
Ответ. -- + 2nk < х < - +
о о
keZ. A
Рис. 96
323

Неравенство cos x > - можно также решить с помощью
единичной окружности.
А На единичной окружности строим угол, косинус которого
равен -. Для этого на оси Ох отметим точку с абсциссой, равной - , и
через эту точку проведем прямую, параллельную оси Оу (рис. 97).
Эта прямая пересекает единичную
окружность в двух точках Мг и М2. Точке Мг
соответствует угол в -— рад. (или в
5л
— рад.), точке М2 соответствует угол в
— рад. Из рисунка видно, что все точки дуги
о
МХРМ2 единичной окружности, кроме ее
концов, имеют абсциссу, большую - .
Поэтому на отрезке [-я; к] все решения
данного неравенства заключены в промежутке
Рис. 97
-- < х < -. На множестве действительных чисел все решения не-
о о
равенства можно записать так: -— + 2nk < х < — + 2я&, k e Z. А
о о
Задача 3. Используя единичную окружность, решить
неравенство cos х < - .
А Из рисунка 98 видно, что все точки дуги M2NMX единичной
окружности имеют абсциссу, меньшую или равную - . Поэтому на
отрезке [0; 2я] все решения данного
неравенства образуют отрезок — < х < — .
о о
На множестве действительных чисел все
решения неравенства можно представить
так: - + 2nk < х < —
о о
Ответ. £
о
, k e Z.
-~+2nft,fteZ. A
о
324

X
Задача 4. Решить неравенство sin х < ~тт .
А Построим графики функций у = sin х и у = —гт (рис. 99). Сна-
1
чала найдем все решения неравенства sin х < —^ , принадлежащие
1
отрезку
—;—
длиной 2я. На этом отрезке уравнение sin х =
Зя 9я ЛЛ
имеет два корня: х = —- и х = —. На рисунке 99 видно, что решени-
4 4
ями неравенства sin х < —г= на отрезке
[я 5я
2;Т
являются все числа
(Sn 9я^
интервала —; — .
I 4 4 )
Так как функция sin x периодическая с периодом 2я, все
решения неравенства sin х < -?- — это числа х из интервалов
V2
^+2яп;^ + 2я711 п е Z(cm. рис. 99).
_
4 2
Рис. 99
^ Зя л 9я л „
Ответ. — + 2кп < х < —- + 2яя, п е Z. А
4 4
Заметим, что решение задачи 4 можно начать с рассмотрения
другого отрезка длиной 2я, например отрезка ——; — .
Из рисунка 99 видно, что на этом отрезке решениями неравен-
ства sin х < -j= являются числа интервала ;- . Следователь-
v2 ^ 4 4 )
5я _ я _ _
но, ответ можно записать в виде —— + 2пп < х < — + 2ял, пе Z.
4 4
325

Задача 5. Решить неравенство cos х > - -т= .
А Построим графики функций у = cos х и у - -—j= (рис. 100). На
отрезке [-я; я] уравнение cos х = --?= имеет два корня: х = —— и
Зл 1
х = — . Из рисунка 100 видно, что решениями неравенства cos х > - -т=
Г 1 Г ЗЯ ЗЯ1
на отрезке [-я; я] являются все числа х отрезка ——; — .
Рис. 100
Так как функция cos x периодическая с периодом 2я, то все ре-
. 1
шения неравенства cos х > ~~щ — это числа х из отрезков
I ~ + 2пп\ -j + 2пп\, д е Z (см. рис. 100).
Ответ. —— + 2ял < л: < —- + 2яя , пе Z. А
4 4
Задача 6. Решить неравенство tg x> 1.
А Построим графики функций у = tg х и у = 1 (рис. 101). На ин-
( л л ^ „ , .
тервале --; — длиной я уравнение tg x = 1 имеет один корень
V 2 2 У
л
х - —. Из рисунка 101 видно, что решениями неравенства tg x > 1
Г л л ^ (л л )
на интервале —; - являются все числа х интервала -; - .
326

Рис. 101
Так как функция tg x периодическая с периодом я, то все
решения неравенства tg х > 1 — это число х из интервалов
)
е Z(cm. рис. 101).
Ответ. - +пп<х< - + пп, пе Z. А
Задача 7*. Решить неравенство sin2 х < - .
А Это неравенство можно представить в виде | sin х \ < —г= .
Построим график функции у = | sin x |. Для этого сначала
построим график функции у = sin x и затем часть графика, лежащую
ниже оси Ох, отразим симметрично относительно этой оси
(рис. 102). На этом же рисунке построим прямую у= -щ .
1-
\Xl ГЧ/1
_7n _5n
4 4
y=\fsmx\
IX/1 1\/
Ш
4
Рис. 102
Функция у = | sin х | периодическая с периодом я. На отрезке
[л л] , . , 1 п
--; - длиной я уравнение | sin х \ = —гт имеет два корня: х = —- и
4
327

х = -. Из рисунка 102 видно, что решениями неравенства | sin х \ < —?=
Г к я
-—;—
|_ 2 2
Г к я1 ( п-п) о
на отрезке -—;— являются все числа интервала ~Т»Т • Следова-
| 2 2J v 4 4
тельно, все решения неравенства | sin х \ < -у— — это числа х из
интервалов | -— + пп;—+пп , п е Z(cm. рис. 102).
Ответ. -— +пп<х< — + пп, пе Z. А
4 4
Задача 8*. Решить неравенство 4 sin2 х - 8 sin х + 3 < 0.
А Обозначая sin x = t, имеем квадратное неравенство 4t2 - St +
+ 3 < 0. Разложив квадратный трехчлен 4t2 - St + 3 на множители,
запишем неравенство в виде 4 £-— *-— < 0. Заменяя ^ на sin x,
\ 2 А 2)
( 1 \( 3 ^ 3
получаем неравенство sin х— sin х— < 0. Так как sin х - - < 0
при всех х, то исходное неравенство равносильно неравенству
sin х - - > 0 или sin х > - .
Решениями последнего неравенства являются числа х из
отрезков -+ 2пп\—+ 2лл \,пе Z.
L6 6 J
Ответ. — + 2яя < х!
о
Решить неравенство
989. l)sin*<0;
2) sin x > 0;
3)sinx>-|;
4) sin x < 2;
/—
990.1)sinx<-^;
1
2) sin x > -j^ ;
^^+2n^,^eZ.
о
Упражнения
(989-998).
5)sinx> 1;
6) sin x < -2;
7)sinx<-l;
8)sinjc>l.
3) sin x
4) sin x
A
328

991.1)cosx<0;
2) cos x > 0;
3) cos x< v3;
4)cosx>-2;
992. 1)cosjc<--t=
2) cos x> \-;
3) cos x < - ;
993. l)tgJt<0;
V3;
V3;
994. 1)1-2 sin 2л: > О;
2) 2 cos 2x + 1 < 0;
995. 1)2 sin
t >i;
5) cos x < -2;
6)cosjc> 1;
7)cosjc>1;
8)cosjc<-1.
4)cosx>--;
5) cos x>--;
о
6) cos x > - .
о
6)tgx>-l;
7)tgx<3;
S)tgx>-2.
3)3tg|<V3;
3)4cos2jc<3;
-? > -V; 4)4sin2jc>l.
996.
997*. 1) tg x + ctg x > 0; 3) sin x - cos x > 0;
2) cos 2x + cos x < 0; 4) sin 2x + sin x < 0.
998*. 1) 2 cos2 x - sin x > 2; 2) cos 2x - 5 sin x < 3.
999*. Найти область определения функции:
2)y=
1000. Решить неравенство:
1) yj5-2sinx >6sin:c- 1; 2) 1 + 6 cos x < 2 ^/2+ 4cos x.
329

§ 55. Обратные тригонометрические функции
1. Функция у = arcsin x
По определению арксинуса числа для каждого х е [-1; 1]
определено одно число у = arcsin x. Тем самым на отрезке [-1; 1] задана
функция у = arcsin х, -1 < х < 1.
Покажем, что функция у = arcsin x является обратной к функ-
к . .к
ции у = sin х, рассматриваемой на отрезке - — < х < -.
О Рассмотрим уравнение у = sin x, где у — заданное число из
отрезка -1<у<1,&х — неизвестное. На отрезке - - < х < — это урав-
нение по определению арксинуса числа имеет единственный
корень:
х = arcsin у.
В полученной формуле меняем местами х и у:
у = arcsin х. •
Таким образом, свойства функции у = arcsin x можно получить
из свойств функции у = sin х. График функции у = arcsin x
симметричен графику функции у = sin х9 - — <х< — относительно прямой
у = х (рис. 103, 104).
Перечислим основные свойства функции у = arcsin x:
-1
0 1 х
у = arcsina:
Рис. 103
2
Рис. 104
330

1. Область определения — отрезок [-1; 1].
2. Множество значений — отрезок --; — .
3. Функция у = arcsin x возрастает.
4. Функция у = arcsin x является нечетной:
arcsin (-х) = -arcsin x.
2. Функция у = arccos x
По определению арккосинуса числа для каждого х е [-1; 1]
определено одно число у = arccos x. Тем самым на отрезке [-1; 1]
определена функция у = arccos х, -1 < х < 1. Эта функция является
обратной к функции у = cos х, рассматриваемой на отрезке 0 < х < я.
График функции у = arccos х симметричен графику функции у = cos x,
О < х < я относительно прямой у = х (рис. 105, 106).
Перечислим основные свойства функции у = arccos x:
-1 /
/ -\
-i
Рис. 105
Рис. 106
1. Область определения — отрезок [-1; 1].
2. Множество значений — отрезок [0; я].
3. Функция у - arccos x убывает.
3. Функция у = arctg x
По определению арктангенса числа для каждого действительного
х определено одно число у = arctg x. Тем самым на всей числовой
прямой задана функция у = arctg дг, х е R. Эта функция является
обратной к функции y = tgx9 рассматриваемой на интервале - - < х < - .
График функции у = arctg x получается из графика функции
331

y = tgx, - - < x < — (см. рис. 92) симметрией относительно прямой
у = х (рис. 107).
У
п
К
2
о "
Рис. 107
Перечислим основные свойства функции у = arctg x:
1. Область определения — множество R всех действительных
чисел.
2. Множество значений — интервал
v 2 2
3. Функция у = arctg x возрастает.
4. Функция у = arctg х является нечетной: arctg (-х) = -arctg x.
Функции у - arcsin x, arccos x, у = arctg x называются
обратными тригонометрическими функциями.
Задача 1. Сравнить числа:
1) arcsin - и arcsin --;
о 4
/о /о
2) arccos —г и arccos — ;
4 о
( 2\ ( 1
3) arctg -- и arctg --
)
А 1) Так как - > - и функция у = arcsin x возрастает, то arcsin -
о 4 о
> arcsin - .
4
2) Так как
V3 . V2
< -^ и функция у = arccos x убывает, то
V3 V2
arccos — > arccos — .
2 1
3) Так как -- < -- и функция у - arctg x возрастает, то
О с*
arctg [-- Uarctgf--
332

Задача 2. Решить уравнение arccos (2х + 1) = — .
4
А Так как — € [0; я], то по определению арккосинуса числа дан-
ное уравнение равносильно уравнению 2х + 1 = cos — , откуда
i-_^ _ 2+V2 А
х-1
Задача 3. Найти область определения функции у = arcsin —г— .
о
А Так как функция у = arcsin х определена при -1 < х < 1, то функ-
. х-1
ция у = arcsin —г— определена для тех значении х, для которых
о
выполняются неравенства -1 < —г— < 1. Отсюда -3 < х - 1 < 3,
-2<х<4. А
Упражнения
Сравнить числа (1001-1003).
2 3 ( 1 ^ ( Л
1001. 1) arcsin - и arcsin -; 3) arcsin —j= и arcsin -
о 4 ^V3J V
2) arcsin -7= и arcsin ~ттт ; 4) arcsin --и arcsin -- .
V3 л/10 { S) [4)
1 2 ( S\ ( (s^\
1002.1) arccos - и arccos - ; 3) arccos —- и arccos -J-- ;
2) arccos —j= и arccos -j= ; 4) arccos --и arccos -— .
V3 V5 \ ь ) V 6)
1003. 1) arctg - и arctg - ; 3) arctg (-Зл/i) и arctg (-4>/з);
2) arctg 2л/3 и arctg Зл/2 ; 4) arctg —j= и arctg —\= .
V ^2 ) V ^5 J
Решить уравнение (1004-1006).
1004. 1) arcsin (2 - 3*) = ~ ; 3) arcsin X-~- = - 7 ;
о 4 4
2) arcsin (3 - 2jc) = --; 4) arcsin —-— = - - .
4 Z о
333

1005.1) arccos {2x + 3) = |; 3) arccos ^y- = у ;
я 2jc-1
2) arccos (3jc + 1) = -; 4) arccos —— = л.
Z о
1006. 1) arctg -^ = ^ ; 3) arctg (2x + 1) = - jj;
1 ■+■ 2jc те те
2)arctg —— = -; 4) arctg (2 - 3x) = - - .
1007. Найти область определения функции:
1) i/ = arcsin ^— ; 5) у = arcsin —— ;
2) i/ = arcsin —r— ; 6) i/ = arccos (2yfx - 3j;
3) у = arccos (2jc - 3); 7) i/ = arccos (x2 - x + 1);
2x2-5
4) i/ = arccos (2 - Sx); 8) i/ = arcsin —^— .
о
1008. Доказать, что график функции у = arccos x симметричен от-
носительно точки | О; — .
2 i
Упражнения к главе VIII
1009. Найти область определения функции:
1) у = sin х + cos x; 4) у = yjcosx;
2*
2) у = sin х + tg x; 5) i/ =
2sinx-r
COSJC
2sin2 jc-sinjc *
1010. Найти множество значений функции:
l)i/=l-2sin2x; 4) i/= 2 cos2*+ 5;
2) у = 2 cos2 jc — 1; 5) у = cos 3jc sin x - sin 3jc cos x + 4;
3) i/ = 3 - 2 sin2 x; 6) i/ = cos 2jc cos jc + sin 2x sin jc - 3.
1011. Выяснить, является ли данная функция четной или нечетной:
1) У - х2 + cos х; 3) у = (1 - jc2) cos jc;
2) г/ = xs - sin x; 4) у - (1 + sin x) sin jc.
1012. Найти наименьший положительный период функции:
I)i/ = cos7x; 2) у = sin - .
334

1013. Найти корни уравнения, принадлежащие промежутку [0; Зя]:
1) 2 cos х + >/з = 0; 3) 3 tg х = >/§ ;
2) >/з - sin л: = sin х; 4) cos х + 1 = 0.
1014. Найти все решения неравенства, принадлежащие
промежутку [-2л; -я]:
1) 1 + 2 cos х > 0; 3) 2 + tg x> 0;
2) 1 - 2 sin * < 0; 4) 1 - 2 tg x < 0.
1015. Выяснить графически, сколько корней имеет уравнение:
1) cos х = х2; 2) sin x = 1 - х.
ПРОВЕРЬ СЕБЯ!
1. Найти область определения функции у = tg 4д\ Является
ли эта функция четной?
2. Построить график функции у - sin x (или i/ = cos x) на
отрезке [-я; 2я]. При каких значениях х из этого отрезка i/(x) = 1,
у(х) = -1, у(х) = 0, y(x) > 0, у(х) < 0? Разбить данный отрезок на
отрезки возрастания и убывания функции.
3. Построить график функции у = tg x на отрезке
Г Зя я]
L" 2 ;2j-
При каких значениях л: из этого отрезка tg х - 0, tg х < 0, tg x> 0?
4. Решить неравенство tg х^-1.
1016. Найти область определения функции:
2)y=yjtgx;
1017. Найти наибольшее и наименьшее значения функции:
1) у = cos4 jc - sin4 x; 3) i/ = 1 - 2 | sin Зх |;
+-7 sin \ х-- I; 4)y = sin2x- 2 cos2*.
4J I 4J
7 sin \ х
4J I 4
1018. Выяснить, является ли данная функция четной или нечетной:
1) у = sin х + tg х; 3)у = cos х +1 sin л: |;
2)у = sin jc tg x; 4) i/ = sin jc | cos x |.
1019. Найти наименьший положительный период функции:
= 2sin(2jt+l); ^
1020. Выяснить графически, сколько корней имеет уравнение:
1) cos х = | х |; 2) sin x = \ х + 11.
335

1021. Найти нули функции:
1) у = sin2 х + sin x; 3) у = cos 4jc - cos 2x + sin x;
2)у = cos2 x - cos jc; 4) у = cos jc - cos 2x - sin 3jc.
1022. Решить неравенство:
1) ctg x cos x > 0; 2) tg jc sin jc < 0.
1023*. Найти все значения х, при которых функция у = 1,5 - 2 sin2 -
принимает положительные значения.
1024*. Найти все значения х, при которых функция у = tg 2x - 1
принимает отрицательные значения.
1025*. Построить график функции:
2; 6) i/ = 2 ctg (x~
3) i/ = sin л: +1 sin x |; 7*) i/ = 2 arcsin (x + 1);
4) у = cos jc - ycos2 л:; 8*) i/ = 3 arccos (x - 2).
1026*. Найти множество значений функции:
1) у - 12 sin x - 5 cos x; 3) i/ = arcsin (x2 - 2);
2) i/ = cos2 x - sin x; 4) у = 2 arccos (x2 - 1).
1027*. Решить неравенство:
1) sin x > cos x; 3) cos x - V3 sin x < V2 ;
2) tg jc> sinx; 4) V3 sinx + cos jc < 1.
1028*. Найти область определения функции:
1) У = 73sin2o:-cos2jc ; 3) у = arcsin (*2 - 1);
2)у= Jem2 x-3cos2 х ; 4) у = arccos (*2 -4).
Историческая справка
Тригонометрические функции (получившие название от греч.
trigonon — треугольник и meteo — измеряю) играют огромную роль
в математике и ее приложениях.
Исследованием тригонометрических функций практически
занимались еще древнегреческие математики, изучая взаимное
изменение величин в геометрии и астрономии. Соотношения между
сторонами в прямоугольных треугольниках, которые по сути своей
являются тригонометрическими функциями, рассматривались уже
336

в III в. до н. э. в работах Евклида, Архимеда, Аполлония и других
ученых.
Учение о тригонометрических величинах получило развитие в
VIII — XV вв. в странах Среднего и Ближнего Востока. Так, в IX в.
в Багдаде ал-Хорезми составил первые таблицы синусов. Ал-Бузд-
жани в X в. сформулировал теорему синусов и с ее помощью
построил таблицу синусов с интервалом 15', в которой значения
синусов приведены с точностью до 8-го десятичного знака. Ахмад-ал-Бе-
руни в XI в. вместо деления радиуса на части при определении
значений синуса и косинуса, сделанного до него Птоломеем, начал
использовать окружность единичного радиуса. В первой половине
XV в. ал-Каши создал тригонометрические таблицы с шагом Г,
которые были непревзойденными по точности последующие 250 лет.
Самым крупным европейским представителем той эпохи, внесшим
вклад в развитие исследования тригонометрических функций,
считается Региомонтан.
В начале XVII в. в развитии тригонометрии наметилось новое
направление — аналитическое. Если до этого учения о
тригонометрических функциях строились на геометрической основе, то в
XVII—XIX вв. тригонометрия постепенно вошла в состав
математического анализа и стала широко использоваться в механике и
технике, особенно при рассмотрении колебательных процессов и
иных периодических явлений.
О свойствах периодичности тригонометрических функций знал
еще Ф. Виет. Швейцарский математик Я. Бернулли (1642—1727)
в своих работах начал применять символы тригонометрических
функций. Однако близкую к принятой теперь символику ввел Л. Эйлер
в 1748 г. в своей работе «Введение в анализ бесконечных». Он в этой
работе рассмотрел вопрос о знаках всех тригонометрических
функций любого аргумента.
Тригонометрические функции Эйлер рассматривал как особые
числа, называя их общим термином «трансцендентные
количества», получающиеся из круга. Для вычисления приближенных
значений sin x и cos x он получил их разложения в ряды:
1 ** X4 X6
1+ (1)
х3 хъ х7
8Ш*=Х-3! + 5Г7!+"- (2)
На рисунке 108 показано, что графики функций, образованных
различным числом членов ряда (1), постепенно приближаются к
графику функции у = cos x.
12-Ю. М. Колягин, 10 кл. 337

-1-
у=\
Рис. 108
Дальнейшее, после Эйлера, развитие теории тригонометрических
функций было продолжено в XIX в. в работах русского математика
Н.И. Лобачевского (1792—1856), а также в трудах других ученых,
например в работах профессоров МГУ ДЛ. Меньшова и HJC. Бари.

ОТВЕТЫ
Глава I
1. 2) 0,(27); 4) -0,25; 6) 0,(0990). 2. 1) 0,(29); 2) 0,(855); 4) 0,44(1);
6) 2,8(7). 3. 2) g ; 4) -\ ; 6) -2gj . 4. 2) 4; 4) 0. 5. 2) io| ; 4) 5,8. 6. 2)
Является. 7. 2) 341. 8. 2) g = « ,
< 1. 9. 2) Является;
27 2 11
4) является. 10. 2) 0; 4) -2. 11. 2) ^; 4) ^ . 12. 2) 7^ ; 4) -8^ . 13. 2) 1;
4) gQ . 14. 2) Не является; 4) является. 15. 2) 90,(90). 16. 2) 4 л/3 +8.
17. 2) |. 18. 2) 9; 4) з . 19. 2а. 22. 4,5 и 4,6. 23. 2) | х \ = -х; 4) | х \ = -х.
24. 2) Рациональное число; 4) рациональное число; 6) иррациональное
число. 25. 2) 10; 4) 9; 6) ^ ; 8) ^ . 26. 2) VTI - ^24 > VlO - ТЗД . 27. 2) 3;
4) 2 + 73; 6) 1. 29. 2) 2; 4) 15. 30. 2) 81; 4) ^J . 31. 2) -1; 4) -4; 6) -8.
32. 2) jc = - \; 4) хг = 2, *2 = -2. 33. 2) 5; 4) -11; 6) ^ . 34. 2) 48; 4) 20.
35. 2) 33; 4) 7. 36. 2) 0,2; 4) 2. 37. 2) 50; 4) 16. 38. 2) а2Ь3; 4) а2Ь3. 39. 2) ЗаЬ;
4) ^ . 40. 2) з ; 4) g . 41. 2) 0,4; 4) 2; 6) 4. 42. 2) 3*; 4) — . 43. 2) 3 ; 4) ^ .
44. 2) 2; 4) 5. 45. 2) у2; 4) a8b9; 6) За. 46. 2) При * > -3; 4) при | < * < 2.
47. 2) 2; 4) 4 >Уб . 48. 2) 6; 4) |; 6) 4. 49. 2) аЬ2с; 4) 2лч/. 50. 2) 3*; 4) 0;
6) а - 1. 51. 2) 7; 4) 1. 52. 2) а) (3 - *)3; б) (х - З)3; 4) - Зх - 5.
53. 2) ^7 + >/15<78 + ^28. 55. 2) 2^Ь; 4) 1. 58. 2) 3; 4) 27; 6) ^ . 59. 2) 5;
4) \; 6) \ . 60. 2) 49; 4) 125. 61. 2) 121; 4) 150. 62. 2) 5^ ; 4) ю|? .
ill 11 11
63. 2) 3; 4) 2,7. 64. 2) Ь; 4) а; 6) 1. 65. 2) а3( Ь3 +с3 ); 4) Зх2у2 ( 4jc2 -у2 ).
1 1 Ilii JJL L L
11 11 JL1 2 11 1
67. 2)(x2-i/2)(jc +x2y2+y); 4) (За3+сё) (9а3-3а3с6+с3 ). 68. 2) а2Ь.
li l 11
69. 2) 1; 4) а3Ь3. 70. 2) 3. 71. 2) Ь2 ; 4) а + Ь. 72. 2) а4 +Ь4 ; 4) Vc - 1.
12* 339

73. 2) Зс. 74. 2) -^щ; 4) 2 V& . 75. 2) 2i/; 4) 2%b . 76. 2)2^6;4)
А 1 *3
77. 2) 2(а2 -Ь2); 4) —^ . 78. 5306 р. 4 к. 79. 2158 р. 70 к. 80. 2) 1; 4)
624
2 3 , л х V3 /1 n V2 ,_ / i \л /1 \3»14
81. 2) 3; 4) *; 6) -^ • 82. 2) 9; 4) 8. 83. 2) 18; 4) 0,75.
о ozo
84. 2) 5"з>5"4; 4) [{} <[{} ; 6) 2®>&7; 8) к < о -
85. 2) (ОДИЗ)"1 > 1; 4) 271'5 > 1; 6) {^1 < 1; 8) {^1 > 1. 86. 2) а2^ ; 4) Ь.
8V5-15
o/.Z) \fO < v i • об. Zl W; 4) 4Д ~ —t/ . о*7. ct) ТП ', *±) п . Уи. б/л- о ,
9 ^
o/rt 1
/1\ -v — 9тг О1 9\ -v — . /4\ -v — 1 О*> 9^ ^/^ ^ Зг7 • А\ 4/i Q ^ 5/oQ QQ 9^ -v — — •
о о
29 34 3 1 25 16
4) x = 1. 94. 2) 4; 4) 2. 95. 2) 2— . 4) ^ . 96. 2) 1; 0,01; ^ ; 37^=; ^ ; — ;
4) 2; 9; 10; 4; ^ ; ^ . 97. 2) 64; 10; 5; 2; 1; 2; 4) ^ ; ^; 11^ . 98. 2) 15;
81 3 3 1 -1 г
4) 105; 6) Vf^ . 99. 2) « ; 4) ъ ; 6) 4. 100. 2) 98°; 325 ; = . 101. 2) A 4 <
zoo ££ i 7 J 12
А ГиГ^ Г19Г^
А ГиГ Г19Г - -
<(0,41)4; 4) ^ > lii) • Ю2. 2)^!; 4) a7; 6) a2. 103. 2) a2.
104. 2) 5/1 i4_i± I > 5i| li-ljf . Ю5. 2) ^ = 3; 4) x = 2; 6) * = |.
2 2
106.2) а5+Ь5. 107.2)
а-Ъ'
Проверь себя!
5.
109. 2) ^ . Ш. 2) ^ ; 4) Щ ; 6) 1M^±^. 8)
112. 2) 7. 113. 2) 2$G^; 4) ^Л . 114. 2) (^а-^fe) ; 4) a2 + b2. 115. 2) 1.
116. 2) a'1; 4)1.
340

Глава II
120. 2) х е R; 4) jc > 6; 6) jc < -3, jc > |; 8) 0 < jc < 2; 10) jc < 0, 0 < jc < |;
l
12) jc > 0; 14) jc Ф 0. 123. 2) Убывающая; 4) убывающая. 125. 2) (V2)2 > 1;
2
4) я5 > 1; 6) \-7=\ < 1. 127. 2) -1; -i ; 4) (-2; 9). 132. 2) Возрастающая;
[yJo ) у 6)
4) убывающая. 133. 2) у > 0; 4) у < 2; 6) у > 1. 137. 88,39 г; 22,1 г.
138. 486 661,161 м3. 139. 2) х = |; 4) х = -|. 140. 2) * = -0,5; 4) х = 4.
2
141. 2)* = 2,5; 4)* = 9; 6)* = 0,4. 142. 2) jc= I; 4)jc= I g . 143. 2)*= 1; 4) jc = 3;
6) jc = 2. 144. 2) х = 0; 4) х = 0. 145. 2) jcx = 0, jc2 = 2; 4) * = 1. 146. 2) * < 2;
4) х < -0,5; 6) х >3. 147. 2) jcx = 2, *2 = 5; 4) * = - ^ . 148. 2) *х = 1, х2 = -3;
4) jcx = -0,5, jc2 - 3. 149. 2)х = 0,8; 4) * = -1; 6) хг = 0,5, х2 = -3. 150. 2) *х = 0,3,
jc2 = -0,2; 4) х = 4. 151. 2) * = -1; 4) х = 1. 152. 2) i/ = 3; 4) * = 2. 153. 2) * = 3;
4) х = 3. 154. 2) jc = -3; 4) х = 4. 155. 2) х = -1; 4) *х = 1, х2 = -1; 6) х = -1.
156. 2) jc> 4; 4) * < 1, х> 2; 6) 1 < х < 2. 157. 2) * > 1; 4) х < 1. 158. 2) * < 2;
4) х < -1. 162. jc = 4. 163. 2) jc = 2; 4) х = 3,25. 164. 2) * = 0. 165. 2)х=~.
э
166. 2) -2 < * < 1; 4) -| < jc < 2. 167. -<j < х < * . 168. -1, -2, -3, ±4, ±5,
±6, ... (т. е. для а < 0 и а > 3, где а е Z). 169. 1) -2 < а < 2; 2) -2 < а < 2.
/ 1 чя м чЗД4 , 1 у/3 х 1 у/8-3
170. 2) 2^3 > 2"; 4) (|) <^) . 171. 2) (|) < 1; 4) (I) > 1.
173. 2) 0,04 < у < 5. 174. 2) хг = -1, *2 = 1; 4) х = -2; 6) хх = 3, х2 = -1.
8) х = 1. 177. 2) х = 1; 4) х = 3. 178. 2) х = 0; 4) хх = -1, х2= 1.
179. 2)x<-l;4)-2<x<2.
Проверь себя!
2. ^ j > (± J , 5-°-2 > 5"Ь2. з. * = 2; ^ = -5, jc2 = 1; х = 1; хх = 0,
jc2=-2.4. jc>4;-2<jc<2.
182. ail + COW1.183.2) jc * -2; 4) x < 1.184 2) у < 1; 4) i/ > 2.186.2) jc = 24.
187. 2) jc = 9; 4) jc = 1. 188. 2) jc = 0; 4) jc = -0,5. 189. 2) -3 < jc < 1; 4) -1 < jc < 1.
191.2)jc = 4;4)jc=1. 192.2) д: = 3. 193.2) jCj = -1,jc2 = 5; 4) jc = -|. 194. jc = -2,
jc > 0.195. 2) jc < -3, jc> 1; 4) jc < -|, jc> 4. 196. 2) jc < 0, jc> |.
341

Глава III
О 2
200. 2) 0,203 < 1; 4) (7з) ' > 1. 201. 2) Выше — при х > 1, ниже — при
fiof-3
0 < х < 1. 202. 2) Выше — при 0 < х < 1, ниже — при х> 1. 203. 2) ^у <
<f^V ; 4) 2.5-3-1 > 2.6-3-1; 6) №f < (ЩТ4 ; 8)
205. 2) Выше — при 0 < х < 1, ниже — при х > 1. 208. 1) Два; 2) один.
210. 2) I/ = -g- ; 4) у = —д—; 6) у = у/х+3 . 211. 2) Все действительные
числа; 4) все действительные числа; 6) множество значений: все
действительные числа, кроме у = 4; область определения — все действительные числа,
кроме х = 0. 213. 2) Нет; 4) нет. 214. 2) у = -у[х* ; 4) у = -хг. 216. 2) Нет
корней; 4) нет корней. 217. 2) Равносильны; 4) не равносильны; 6)
равносильны. 218. 2) Равносильны; 4) не равносильны. 219. 2) Второе. 220. 2) Нет
корней; 4) х = 4. 221. 2) 3,5 < х < 5. 222. 2) Равносильны. 223. 2)
Равносильны; 4) равносильны. 224. 2) Равносильны; 4) равносильны. 225. 2)
Второе; 4) оба. 226. х = 3. 227. 2) * = 6. 228. 2) -2 < * < 1, х> 2. 229. 1) xt = -1,
jc2 = 2, jc3 = 4; 2) хг = -1, *2 = 1, х3 = 2; 3) хх = -4, *2 = -3, х3 = -2, *4 = 1;
4)jc1 = -2,jc2 = -1,jc3 = 3.231.2)jc = 27;4)jc = 5.232.2)jc =-7; 4)*1 = 3, *2 = -д .
233. 2) jc = 5; 4) х = 5; 6) *х = -3, х2 = 4. 234. 2) х = 4; 4) * = 5; 6) х = -1.
235. 2) jc = 7; 4) jc = 5; 6) хх = -3, *2 = 1. 236. 2) Нет решений; 4) нет
решений. 237. 2) х = -3; 4) х = 18; 6) * = 20. 238. 2)х = -4; 4) х = 5. 239. 2) * = 10;
4) х12 = ±Vl7 , *3>4 = ± V2. 240. 2) *х = -1, х2 = -3. 241. 2) Два; 4) один,
jc = 1. 242. 1) хх = 0, х2 з = ± 2; 2) jcx = 0, *2 = 2; 3) *х = -4, *2 = 1; 4) хх = -6,
jc2 = 1. 243. 1) х = -Il+V4a2 + 9J при а > 0, нет корней при а < 0;
2) jc = -l + Va2-2a + 2 при a > 1, нет корней при а < 1. 244. 2) 1 < * < 1,5;
4) х < -5. 245. 2) 0 < * < 9; 4) х < 13,5; 6) 0 < х < 2. 246. 2) 2 < х < 3; 4) * < -5;
5 5 19
6)jc>-q;8)-^ <Jc<-jg.247.2)-Kjc<0,0<JC<l; 4)-5<jc<-3, 3<jc<5;
6) jc < - g , jc> 9; 8) нет решений. 248. 2) -1 < jc < 2; 4) * < -1, x> 2; 6) 0 < x <
< 4; 8) x < -1, jc > 2. 249. 2) * > -1; 4) 3 < x < 6; 6) -3 < x < 1; 8) 2 < * < 3.
250. 1) jc> -7=; 2) -2,8 < x < 6. 253. 1) 1 < * < a2 + 1 при а > О, нет решений
f 1 f к --
при a < 0; 2) |(2+V2)<jc< 0. 256.2) U= , (V2) , (1,9)*, nK; 4) я"3,
342

(>/2)"3, (1,3) з, (0,5)"з. 257. 1) л: = 1; 2) х = -1. 258. 2)-V2 <х< ^;
2
4) jc < 1, х > 2. 259. 2) у = — + 3 — обратная функция; область
определения: все действительные числа, кроме х = 0; множество значений: все
действительные числа, кроме у = 3; 4) у = у/х+1 — обратная функция;
область определения и множество значений — все действительные числа.
261. 2) Да; 4) да. 262. 2) х = 21; 4) хг = \, х2 = |; 6) х = -1; 8) х12 = ±8.
263. 2) -8 < х < 1; 4) -3 < х < 1. 265. 2) Да; 4) нет. 266. 2) у = х2 - 4ху
область определения — х < 2, множество значений — у < -4; 4) у = 6х -
- х2 - 8, область определения — х > 3, множество значений — у < 1.
267. 2) jc = 1; 4) * = 0. 268. 2)х = 259; 4) х12 = ~S±^1S . 269. 2) л: < 0; 4) х > -\.
1 8
270. 1) 6 < х < 8; 2) * < -4, т> <х < ^ . 271. 1) Если а < 2, то решений нет;
если а>2, to6<jc< ^~2 > 2) —т^ < х < | а | при а * 0, нет корней
при а = 0.
Глава IV
272. 2) 4; 4) - ~ . 273. 2) ^ ; 4) 0. 274. 2) Верно; 4) верно. 275. 2) Верно;
4) верно. 276. 2) Верно; 4) верно. 278. 2) 6; 4) 0; 6) -3. 279. 2) 4; 4) 0; 6) -1.
280. 2) -2; 4) 1; 6) -|. 281. 2) 3; 4) -3. 282. 2) -3; 4) -2. 283. 2) 16; 4) 6.
284. 2) 64; 4) 3. 285. 2) 144; 4) 1. 286. 2) х = 625; 4) х = 25; 6) х = 5,5.
287. 2) х < 7; 4) х > |; 6) * < 0. 288. 2) -1,5; 4) -1 ^ . 289. 2) g ; 4) ^ .
290. 2) -4,5; 4) -2,8. 291. 2) -3; 4) 2,2. 292. 2) ^ ; 4) 4. 293. 2) ^ ; 4) 512;
6) l|. 294. 2) 1; 4) ^ ; 6) 2. 295. 2) х = 7; 4) *= щ; 6) *= ^ . 296. 2) * < -3,
х > 2; 4) х < 1, # > 2. 297. 2) jc € Д, х * -2; 4) не существует ни при каких х;
6) х е R. 298. 2) 0 < х < 2; 4) -- < * < 4. 299. 2) * = 4. 300. 2) * = logx 2 4;
4)jc= " log2 3. 301. 2) jc = - - - Iog72;4)jc = -- + -logxl,5 . 302. 2) x =
о z z 4 4 з
= log3 4; 4) xx = - , x2 = log8 60; 6) xx = -1, *2 = logx 2; 8) ^ = log8 3, x2 = log8 5.
3 з
343

303.1) хг = 0, x2 = \ogl5 3; 2) х = log0 6 2. 304.1) - < х < 1, х> 1; 2) К х < 2,
jc> 2; 3) -1 < х < 0, 0 < х < 2, * > 2; 4) * < -3, -3 < х < -2, -2 < * < -1,
-1 < х < 1. 305. Если а = -1, то х = 0; если а > 0, то jc = log3 а2; если а < 0,
2
а * -1, то хг = log3 а2, *2 = log3 (-в). 306. 2) 3; 4) 2. 307. 2) 2; 4) -3. 308. 2) - ;
4)^
о
312. 2) 4 log2 а + - log2 Ь - 3 log2 с; 4) - log2 с log2 а - - log2 Ь.
3 4 5 5
1 1
313. 2) 1 - ; 4) 0. 314. 1) 3; 2) 19; 3) 475; 4) 22,5. 315. 1) - ; 2) 1; 3) -1; 4) 1.
о z
316. 2) -log2 5; 4) - log2 0,1. 318. 2) - - ; 4) - - . 319.1) 2(а + Ь - 1); 2) 2а + -.
321. 1) х = 4V3 ; 2) х = - ; 3) х = 10; 4) х = 14; 5) х = 0,1; 6) х = 4,5.
322. 2) 0,845; 4) -0,176. 323. 2) 0,693; 4) -0,154. 324. 2) 1,29; 4) -0,42.
325. 2) 1,3; 4) -15,42. 327. 2) 1,58; 4) -0,861; 6) 4,25. 328. 1) 25; 2) --.
329. 2) jc = 8; 4) х = 3; 6) х = 2. 330. 2)х = 27; 4) *х = 27, х2 = — . 331. 1 + ш,
1 тп+1 1 1+т 2+т 2
- т, ^^ , т + 2. 332. - + т. 333. . 334. —г- . 335. 1 - - т. 336.
3 3 2 л+т 1+2т з
. 337. 1) -2; 2) -3. 338. 1) ^^^ ; 2) **±*±1. 339. 2) ,, = 9,
2Ь+2аЬ+2 ab+2b+l x
х2= 27; 4) хг = ^ . *2= & • З40- *) *i = 4> Х2= 8' 2) *i = 5> *2 = 125» 3) xi = 819'
х2= ^;4)хх= -,х2= Щ. 341. 2) 1; 4) 0,5. 342. 1) 2; 2) - . 343. 9 лет.
344. 3052 качания. 345. 2)2,7182788; 4) 2,7182819. 346. 1) 2,7182682;
2) 2,7182805.350. 2) logi 9 > logi 17; 4) log2 — > log2 ^ • 35L 2) log3 0,45 < 0;
о
4) log0 5 9,6 < 0. 352. 2) jc < 1; 4) x > 1. 353. 2) Убывающая; 4) возрастающая.
354. 2)0<jc<2;4)0<jc<-;6)jc>4. 355. 2) x> -2; 4) -3 < x < 3. 357. 2) a > b;
4) a < Ь. 358. 1) | + Ig3 < Igl9 - Ig2; 2) lgb+^ < ig ^^ ; 3) 3 (Ig7 -
-Ig5)> г[IIg9--\gs]; 4)lg(lg4)> lg - . 359.1)a <b; 2)a< b. 361.1)x< -1,
^ 2 3 j d
jc> 4; 2) -1 < jc < 6; 3) -3 < x < -2, x> 2; 4) *> 4; 5) * * 0, x * 4; 6) * < -3,
344

-« <х< «, *> 3; 7)х> 1; 8)х > 3. 365. 1) х Ф 2, х Ф 3; 2) -1 < х < « •
366. 2) jc = 8; 4) х = 46; 6) * = -1,6. 367. 2) Корней нет. 368. 2) xt = 5, х2 = 2;
4) корней нет. 369. 2) *х 2 = —^ ; 4) хх = 2, х2 = -4; 6) хх = 3, *2 = 2.
370. 2) jc = 3; 4) х = V2 . 371. 2) Корней нет; 4) х = 2. 372. 2) * = 5. 373. 2) xlf2 =
= ±8; 4) х = 16. 374. 2) * = 1; 4) хх = 3, *2 = 5. 375. 2) * = 3. 376. 2) * = 3;
4) хх = 4, х2 = -8. 377. 2) * = 9; 4) хх = 100, *2 = 1000. 378. 2) хх = 1 — , х2 = 0.
379. 2) jc = 9; 4) корней нет. 380. 2) хх = -, х2 = 3; 4) хх = 3, х2 = 9; 6) хх = 4,
у
/s 12
х2=64.381.2)х1 = 4,х2= V2; 3)х1 = 3, х2= 9; 4) хх = 27,х2= ~.382.2)jc= ^.
383. 2)х = -4. 384. 1) хх = -11, х2= -1, х3 = 5;2)х= -5. 385. 1) jc = 5,5;
2) * = |; 3) х = 1 + -jg ; 4) * = 1. 386. 1) хг = V2 , jc2 = 3; 2) *х = |, jc2 = 2.
1 1
387.1) jc = 512; 2) х1 = 3-=- , х2 = 128. 388.1) х = 53; 2) х = 4. 389. Если а > 0,
1^э
^ 5 3 ,tojc= б3"10^5 . 390. 2)х> g ; 4)jc>0,5. 391. 2)0 <*<0,16;
7
4) jc > 0,16. 392.2) jc < -; 4) -2 < x < 2. 393. 2) * < -30; 4) 1 < x < 10; 6) x < - 0,05.
э
5
394. 2) jc> 25; 4) - < x < 3. 395. 2) 2 < * < 3, 11 < x < 12; 4) решений нет.
о
396.2)-| <х<1; 4)х<--,х> ~;6)х> у/2. 397. 2) х> 7. 398. 2)jc<-1,
jc>4; 4) jc< -0,5, jc> 3. 399. 2)* < 2,*> 3; 4)-2<х <-1, 6<х< 7. 400. 2)х>
3 3
>2.401.2)-V2 <JC<-^/I'^7I<JC< >/2.402.2)0<л;<0,1;*>
403. 2) 0 < х < 1, jc> 10. 404. 2) х > 1. 405. 2) jc < -1, log4 ^ < * < log4 3.
406. 2) jc < ^^ ,|<jc<^;4)i<jc<l,jc>3. 407. jc < log2 (V2-1),
x > g . 408. 2 - log4 5 < jc < 1. 409. -log3 2 < x < 0, tj log3 2 < x < 1.
410. 1)-|<jc<-|;2)-3 < x < 0. 411. 1) x > 7; 2) 1 < x < ^2, x > 8.
l+Jl+4a 1+J1+4a2 , , r-
412.1) 1 < jc < —^2 при 0 < a < 1, x> ——^ ПРИ л > 1; 2) | x | > va ,
0 < | x | < ~r , если a > 1; 0 < | x | < Va,|x|> -т=, если 0 < a < 1. 413. 2) 4;
va Va
2 1
4) -3. 414. 2) -4; 4) 6. 415. 2) 1; 4) - . 416. 2) - ; 4) 4. 417. 2) -2,2. 418. a<b.
345

419. 2) 2,39; 4) -3,65. 421. 2) Возрастающая; 4) убывающая. 423. 2) х < О,
х> 2. 424. 2) jc = - ; 4) х = 2. 425. 2) *х = 1, х2 = - - ; 4) хх = 4, х2 = 8.
8 2
426. 2) jc = -4; 4) х = 2. 427. 2) * < 4; 4) * < -1. 428. 2) Решений нет.
429. 2) jc < -8, х> 1. 430. 2) -4,5; 4) 36; 6) 2. 431. 1) 1; 2) 2. 432.1) logi - >
1 £ /^ 6(1-Ь) 3(1-а)
> logi - ; 2) 2 9 > V8 . 433. loga Ь. 434. -^—z . 435.
; 2) 2 > V8 . 433. \ogn b. 434. . 435. 7^
2 л+1 1+0
3
3-2a
436.
1 if 1
. 437. 2) 0 < x < 1. 439. 2) x = - log2 3; 4) x = - logi 1,5-5 ;
4 [ )
[ 3 )
6)x = log5 3. 440. 2)x = 27; 4) jtj = 27, *2 = —. 441. 2) xlf2 = ±8. 442. 2)x = -4;
^7
4) xx = 14, jc2 = 6. 443. 2) Корней нет. 444. 2) x = 4,5; 4) jcx = —, x2 = 5.
25
445. 2) Jtj = 2, jc2 = 5; 4) корней нет. 446. 2) 5 < * < 6; 4) x> 4; 6) -4 < x < -3.
-— 1
447. 1)0<jc<4 4,1<*<64;2)0<jc<1,jc=V3. 448. 1) -- < x < 0;
2)V6<jc<3, -3<jc<-V6. 450. 2, 10, 50 или 50, 10, 2. 452. 2) xx = 10,
x2 = 0,1. 453. 2) jcx = 23, x2 = -1,8. 454. 2) x = 0; 4) * = 2. 455. 2) * < 0,
log6 5 < x < 1. 456. jc < log13—^—, x> 1. 457. 1) д: = |; 2) jc = 5. 458. a < 0,
1 i-£ i + ^ i + ^
a = 4. 459. 0 < jc < ~7= ,a 2 < jc < a, jc> a 2, если a> l;0 < x < a 2,
va
1-^ 1
a < x < a 2 , x> -/= у если 0 < a < 1.
Глава V
460. 1) (4; 2); 2) (1; 2). 461. 1) (1; 7), (7; 1); 2) (3; -2), (-2; 3); 3) (1; 3),
f 9;|1; 4)(-3; 2), f-4;|l; 5)(15; 5); 6)(5; 4); 7)(1; -3), (-1; 3), (3; -1), (-3; 1);
8) (2; 3), (3; 2), (-2; -3), (-3; -2). 462. 1) (4; 5), (-5; -4); 2) (5; 2), (-5; -2);
3) (3; 4), (4; 3); 4) (1; -2), (2; -1); 5) (2; 4), (4; 2); 6) (2; 3), (-2; 3), (V3; 4),
(-V3 ; 4). 463.1) (2; 3), (3; 2); 2) (3; 2), (-2; -3). 464.1) (106; 0,1); 2) f 8;^!;
3) (1000; 10); 4) (1; 9). 465. 1) (25; 9); 2) (9; 4). 466. 1) (3; 5), (5; 3); 2) (3; 1),
[ "i;"6]; 3) (3; ~1)f {~2;f }4) (1; 2)> (2; 1}*467'1} (2; 2)> (~2; ~2)> (1; ~3)>
f 5 25 W 5 25 ^
(-1; 3); 2) (l; 3), (-1; -3), ^-^ . ("^ ^J } 468. 1) (4; 1);
346

2) (2; 8), (8; 2). 469. 1) (100; 10), (0,1; 0,01); 2) (2; 1). 470.1) (1; 3); 2) (1; 1).
if'"fl) 2) (I; I
2) (3; 2), (2; 3), (-3; -2), (-2; -3). 473. 1) (2; -1), (-1; 2); 2) (1; 4), (-4; -1);
3)(0; 2); 4) (5; 1), (1; 5), (-5; -1), (-1; -5). 474.1) (3; 5), (-3; -5), (36;~\
f-36;^l; 2) (5; 8), (-5; -8), (2; -1), (-2; 1); 3) (2; -1), (-2; 1), ^ \2 '
3-J2 S) ( 372 V2
; J [;
( 2. 1 W 2 . 1 ^
476.1), 2) Нет решений. 477.1) (0; -2); 2) (4; 1). 478.1) (0; 1,75); 2) (1; 0,75).
479.1) (2; 3); 2) (3; 2); 3) (9; 1); 4) (125 V5; V5). 480.1) (1; 3), (3; 1); 2) (2; 3), (3; 2);
3) (3; 0,5), (0,5; 3); 4) (l;-|l. f-|;1V 481> 1} (|;|); 2) fi;1l'
),(-l-V5;l-V5),
-3-V5
4) (2; -1). 484.1) (1; 1), (log5 2; log2 5); 2) (1; 1), (log3 4; log4 3). 485.1) (8; 8);
2) (7; 9), (9; 7). 486.1) (2; 2); 2) (2 7б; 7б), (-2 7б; - 7б); 3) (2; -2), (-2; 2);
4) (1; 4); 5) (-1; 2), Г|; ^1; 6) (2; 4), (4;2); 7) (3; 4), (4; 3), (6 + V29;
6 - V29), (6 - V29; 6 + V29); 8) (3; 1), (-1; -3), [ * + ^-; -^ + ^1,
3 V11 |.487.1)(0;0),(l;l);2)(0;0),(l,-2),(-2;l),(3;6),(6;3);
^2 2 2 2
3) (2; 3), (-2; 3); 4) (3; 1), I ^;-l I. 488. 1) (1; 1), (Iog32; 0); 2) (Iog34; 1).
489. 1) (3; 2); 2) (3; -2); 3) (2; 7), (3; 8), (1; 6), (-1; 4); 4) (1; 5), (3; 1).
490. i) [-;-]. [-;-); 2> (J; 2У<3> [8;-]; 4>(2; 4>'
491.1) (1; -1), (2,5; 2); 2) (0; 1), (2; -1). 492.1) (-1; 1); 2) (2; 2). 493.1) (2; 32),
347

(32; 2); 2) (3; 27), (27; 3); 3) (л/2;4Л 4) (3; 73), (73; 3). 494. (^j,
(2+ V7;2+ V7).495. [ 1;- 1 [ 1;-- |. 496. -К а < 1. 497. а = -6. 498. 64.
499. 68. 500. 40 км/ч, 60 км/ч. 501. 10 ч, 15 ч. 502. 3 ч, 4 ч. 503. 96 км.
504. 20 км/ч, 12 км/ч. 505. 14 км/ч, 2 км/ч. 506. 117. 507. 20 чел.,
6чвдень.508.9ч,6ч. 509.
^rm,ioo
%.510.(1; V3),
(-1; - л/3). 511. Каждая из двух. 512. 1) Да; 2) да. 513. 1) (0; -2); 2) (5; 1);
3) (2; -1), (-1; 2); 4) (3; 2), (-2; -3); 5) (2; -3); 6) (2; -1). 514.1) (3; 1); 2) (1; -1);
3) (2; 2), (-2; -2); 4) (2; 4), (4; 2), (-2; -4), (-4; -2). 515. 1) (4; 8), (8; 4);
2) (4; 6), (6; 4). 516.1) (1; 2); 2) (2; 1); 3) решений нет; 4) (25; 4), (4; 25); 5) (2; 6),
(6; 2); 6) (9; 7). 517. 1) (5; 45); 2) 27. 518. 1) Два; 2) одно; 3) одно; 4) одно.
519.1) (6; -2), (-2; 6); 2) (1; -3), (-3; 1). 520.1) (3; 5), (-3; -5), (8; -5), (-8; 5);
2) (2; 3), (3; 2), (-2; -3), (-3; -2); 3) (0; 2), (0; -2), (1; 0); 4) (1; 2), (-1; -2).
521. 1) (5; -1), (-1; 5); 2) (3; 2), (2; 3), (5; 1), (1; 5); 3) (1; 1), (1; -2), (-2; 1);
4) (4; 2), (-4; -2). 522.1) (4; 5), (-4; -5), (3 >/3 ; 73), (-3 л/3; - 73); 2) (3; 5),
(-3; -5), |-5; — ], (--;- — ]. 523. 1) (2; -1), (1; -2); 2) (2; 1), (1; 2),
(-2; -1), (-1; -2). 524.1) (4; 9), (9; 4); 2) (8; 27), (27; 8). 525.1) (3; 1); 2) (2; 2).
526. 1) (2; 3); 2) (-9; 3). 527. 1) (7; -2); 2) (1; 1), (9; -3). 528. 1) (100; 10),
(ОД; 0,01); 2) (6; 3), (3; 6). 529.1) (6; 2); 2) (3; 2). 530.1) (4; 1); 2) (3; 18), (1; -6).
531. 1) (4,5; 0,5); 2) (3; -3). 532. 7 км. 533. 6 с. 534. 12 ч. 535. 15(30 - q),
10<д< 19 g .
Проверь себя!
1.1) (4; 2); 2) (3; 2), (2; 3); 3) (2; 7), (7; 2). 2. 12 и 8.
Главы VI - VII
536.2) |;4)£;в)|;8)£.537.2)20°;4) 135°;6)
539. 0,4 м. 540. 2 рад. 541. -^ см2. 542. 2 рад. 545. 2) (0; 1); 4) (0; -1);
(1 S] fV2 J2)
6) I г: т 1; 8> I т; ~т I-549-2) (°?!):4) (-1; °); 6> (°5 !)• 55°-2) (°; v>
4) (0; -1). 551. 2) - V» ""V ; 4) (1; 0), (-1; 0). 552. 2) 2яЛ, где k — любое
{ * г )
целое число; 4) — ■« + 2nk, где Л - любое целое число. 553. 2) Вторая;
348

4 5
4) четвертая. 554. 2) х = 1,8л, k = 4; 4) х = « я, k = 3; 6) х = « я, k = 2.
556. 2) (0; 1); 4) (0; -1). 557. 2) — + 2я/г, /г = 0, ±1, ±2, ...; 4) -^ + 2я/г,
/г = 0, ±1, ±2, ... . 559. 2) -1; 4) -1; 6) 1. 560. 2) sin Р = 0, cos P = 1; 4) sin Р = 1,
cos р = 0; 6) sin Р = 0, cos Р = -1. 561. 2) 2; 4) -1. 562. 2) 0; 4) -1. 563. 2) -7;
4) -^ . 564. 2) х = ^ + я/г, k = О, ±1, ±2, ...; 4) х = ^ + 2я/г, fc = 0, ±1, ±2, ... .
566. 2) -|; 4) ^^. 567. 2) ~ ; 4) ^ • 569. 2) * = я + 2я£, /г = 0, ±1, ±2, ...;
2
4) х = я + 4я/г, k = 0, ±1, ±2, ...; 6) * = * nk, k = 0, ±1, ±2, ... . 573. 2) Во вто-
э
рой; 4) в третьей; 6) во второй; 8) в четвертой; 10) в третьей. 574. 2) В
третьей; 4) во второй; 6) во второй. 575. 2) Плюс; 4) минус; 6) плюс; 8) минус;
10) минус; 12) плюс; 14) плюс; 16) минус. 576. 2) Минус; 4) плюс; 6)
минус; 8) плюс; 10) минус. 577. 2) Плюс; 4) минус; 6) плюс; 8) минус;
10) минус. 578. 2) Минус, плюс, минус; 4) плюс, плюс, плюс. 579. 2) Плюс,
минус, минус; 4) минус, плюс, минус. 580. 2) Минус; 4) минус; 6) плюс.
581. 2) Плюс, минус, минус, минус. 583. 2) Минус; 4) плюс.
584. 2) cos 1,3 > cos 2,3. 585. 2) х = | + я/г, k = 0, ±1, ±2, ...; 4) х = я + 2я/г,
k = 0, ±1, ±2,.... 586. 2) Во второй. 588.2) Да; 4) нет; 6) нет. 589.2) cos а = - ±=- ,
и
2 V21 3 4 3 1
tga=^j-,ctga= — .590.2)cosa=-g,tga= -g ,ctga= —^ ;4)tga= -g,
3 1 12 5 12 24
cosa= ^yjg ,sina= -^jg- ;6)cosa= jg , tga= -j^ctgo^ -у; 8)tga= у ,
24 2 /2 9
591 2) ± 4) ± J 592 2) Н 593
7 24 2 /2
cos a = - 25 , sin a = —^ . 591. 2) ±^g ; 4) ± Jg . 592. 2) Нет. 593. cos a =
tga= -^ . 594. |. 595. ±|. 596. 2) |; 4) 2. 597. 2) ^ . 598. 2)*= -| + 2тс/г,
k = 0, ±1, ±2, ...; 4) jc = | + я/г, k = 0, ±1, ±2, ... . 600. 2) 0; 4) 1 + sin a.
601. 2) ^2- , 4; 4) 2. 603. 2) 0; 4) tg2 a. 605. ^ . 606. ^ . 607. 7.
608. 2) jc = ~ + я/г, /г = 0, ±1, ±2, ...; 4) x = \ + 2я/г, /г = 0, ±1, ±2, ... .
609. 2) |; 4) -3; 6) 2. 610. 2) 2 cos a; 4) 2. 612. 2) -~. 613. 2) -2 cos a.
615. 2) jc = ^ + ^ , /г = 0, ±1, ±2, ...; 4) * = ^ , /г = 0, ±1, ±2, ...; 6) x = | + я/г,
/г = 0, ±1, ±2, ... . 617. 2) -2- ; 4) -1. 618. 2) ^^. 619. 2) cos 3p; 4) -1.
349

620. 2) ^ ; 4) 1. 621. 2) - ^14 . 622. 2) -sin a cos Р; 4) sin а cos p.
QA Q/» f*Q Г7Г7 Л
623. g5 » g5 • 624. - gg . 625. ^ . 626. 2) g cos2 a; 4) sin a sin 3a. 628. 2) 1;
4) л/3 . 629. 2) ^ . 630. л/3 tg a . 631. 2) sin 2p. 632. 2) x = ^ + я/г, k = 0, ±1,
±2, ...; 4) x = 4я/г, /г = 0, ±1, ±2, ... . 633. 2) cos2 82° - sin2 82°; 4) 2 sin 22°30' x
x cos 22°30'; 6) cos2 -jjr - sin2 -j^ . 634. 2) 2 sin f+ 2 cos I+2 ;
4) cos* (?+f) -sin* (f + f); 6)003* f -sin^.635.2) f; 4) \.
636. 2) ^ ; 4) -1. 637. 2) -^ ; 4) -2. 638. 2) ~; 4) |. 639. 2) ^ .
640. з . 641. 2) sin 50°; 4) cos2 2a. 642. 2) ctg2 a. 644. 2) ^ . 647. 2)x = я/г,
k = 0, ±1, ±2, ...; 4) x = | + я/г, /г = 0, ±1, ±2, ...; 6) * = ^ + я/г, /г = 0, ±1, ±2, ... .
1 + cosi l-cosf£+2a
1 + cosi l-cosf£+2al /5 .
648. 2) 2.; 4) li? 1. 649. 2) ^ ; 4) 1. 650. 2) 7^8 ; 4) 0,5.
2 2 2
651.2) ^; 4) ^. 652.2) J^
a 120 5
4) sin 2a. 655. 2) tg ^ ; 4) tg a. 656. 2) ^ , ^щ . 661. cos 4a. 662. 2)x = 4я/г,
nk n nk
x = n + 2я/г, ke Z;4)x= -£ yx= £ + -j-, /г e Z; 6) jc = 8я/г, jc =2я + 4я/г, /г е Z;
8)jc= ^ + ^,fte Z. 663. 2) 60°; 4) 40°; 6) ^; 8) ^ . 664. 2) cos 58° = sin 32°;
4) -cos |; 6) -tg 35° = -ctg 55°; 8) sin |; 10) sin |; 12) -tg ^ . 665. 2) ^ ;
|^^)-|;4)-^;6)|;8)1. 667. 2)-l. 668. 2) ^
669. 2) ^ ; 4) -\ ; 6) 1; 8) -^ . 670. 2) -V2; 4) ^ - 1. 671. 2) -^ ;
4) -1. 675. 2) jc = я + 2я/г, /г g Z; 4) x = я + 2я/г, fc€Z;6)jt=^ + ^-,UEZ.
Jfi ч/б
677. 2) 0; 4) -^- ; 6) 0; 8) ^- . 678. 2) V2sin p; 4) sin 2a . 680. 2) 2 sin a.
( к а} ( п аЛ ( а п Л ( a n \
682. 2) 4 sin [12-2J cos [l2+2j; 4) 4 sin [ 2 + 12j sin ( 2"l2j;
6)2sin2 f-j-a I; 8)2>/2 sin I ^ 1 sin ^-7 I. 684. 2) tg p. 685.2)*= \ +
v4/ vzyvZ4y ^
2я/г я 2я/г я я/г я/г
+ -д- , jc = "к + -g- , /г € Z; 4) jc = я/г, jc=^+ -^ , k e Z; 6) jc = -q~ , «eZ;
350

8) х = -у , x = - ^ + л/г, k € Z; 10) x = 4 + -у , /г € Z. 686. 2) -4 cos a sin2 -g ;
cosa
689. 2) co
693. ^g . 694. - |g . 695. 2) x = ^ , /г € Z; 4) * = у , fteZ. 696. 2) ^ (cos a +
+ cos 5a + cos 9a + cos 15a). 697. 2) -=- ; 4) - J« . 698. 2) cos2 a; 4) ctg2 a.
э V о
699.2) 1; 4)-^ . 700.2)-^ ; 4)-^y?. 704. 2) \ . 705. 2) ^ . 708. -4sin2a.
711. 2) 2. 712. ^. 713. -1. 716. 2) |. 719. 2) 0; 4) |; 6) ^ . 720. 2) 2л; 4) 8л.
721.2) g ; 4) g ; 6) 1.722.2)-1; 4)1; 6)-1.723.2) |;4) ^л . 724 2) arccos ^ <
< arccos 0; 4) arccos (-1) > arccos ~2 у 725. 2) arccos ~ 4 < arccos (-1).
я Зя З
726. 2)jc = ±g +2л/г, k e Z; 4) x = ±-£ +2nk, k g Z. 727. 2)jc= ±arccos ^ +
+ 2л/г, /г € Z; 4) x = ±arccos (-0,2) + 2л/г, k e Z. 728. 2) x = ■£ + л/г, Л € Z;
4)x = ±| +6л£, ftG Z;6)jc=^ + ^,^€Z. 729. 2) ^; 4) ^; 6) J.
2 Js 3 2>/2 1 24
730. 2) --; 4) -0,3; 6) ^- . 731. 2) ^ ; 4) ^-; 6) -.732. 2) —. 733. 2) a;
4) -a. 734. 2) x = | + лЛ, Л € Z. 735. 2) Да; 4) нет; 6) да. 736. 2) х = ±| + nk,
ke Z; 4) х = ±^ +nk, k e Z. 737. 2) х = 2nk, k e Z; 4) х = ±?г + 2nk,
о о
= ±arccos |-|]+2лЛ, ke Z. 738. 2) jc = -2,5. 739. ±£, -^, ^, -^, ^.
740. ±^ . 742. 2) |, 4) J, 6) -|. 743. 2) 0; 4) -|. 744. 2) \; 4) ^ ;
6) V3. 745. 2) 0; 4) -1; 6) 0. 746. 2) ^| . 747. 2) |; 4) |. 748. 2) ^ .
(о
--g
(
--g > arcsin (-1). 751. 2) х = (-1)л ^ + лд,
пе Z; 4) х= (-1)л+1 ^ +пп9 tig Z. 752. 2) * = (-1)л arcsin ^ + пп, п € Z;
о •
351

75 я 2л
4) х = (-1)л arcsin -g- +кп9пе Z. 753. 2) * = - ^ + яд, л € Z; 4) * = (-1)" -д- +
+ 2ял, л е Z; 6) jc = - ^ + -«г , л е Z. 754. 2) jc = (-1)л+1 arcsin jg + ял, л € Z;
4) нет корней. 755. 2)х = -^ + (-1)л+1 ^ + ™ , л g Z. 756. 2) ^ ; 4) - ^ ;
7 7 тг
760. 2) 25 ; 4) 1. 761. 2) g . 762. 2) Да; 4) нет; 6) нет. 763. 2) х = (-l)n+1 g +
ял 3 1 Зял я 2ял
+ -у , л € Z; 4) jc = (-1)" g arcsin ^ + -у ,neZ. 764. 2) х = g + -у , л € Z.
765. 2) jc = (-l)n+1 g + ял, х = (-1)п arcsin -i +nnfneZ;4)x = (-l)n arcsin -z +
772. 2) | ; 4) - ^ . 773. 2) 0; 4) - -^ . 774. 2) arctg ^g < arctg 73 ;
( S) r- 1 11
4) arctg (-1) > arcsin —^ ; 6) arctg V3 = arccos ^ . 775. 2) 1; 4) ^ ; 6) ^ -
776. 2) jc = о + tc^» Л€ Z; 4) x = - ~z + ял, n e Z; 6) x = -arctg 5 + ял, n e Z.
777. 2) jc = ™ , л e Z; 4) * = -2я + бял, л € Z. 778. 2) 3,5; 4) -9; 6) ^ ; 8) 2.
779. 2) -^ ; 4) -\ ; 6) |; 8) 0. 780. 2) -0,3; 4) -6. 781. 2) 2; 4) 13 - 4я.
782. 2) x = g + ял, jc = - ^ + ял, л e Z; 4) x = arctg 4,5 + ял, x = (-l)n+1 g + ял,
ne Z;6)x= ^ + ял, х = -^п + бял, neZ. 783. 2) +5 . 784. 2) x « -1,44 +
я 5я Зя я я 5я 2я
+ ял, л € Z. 785. g , - -g-. 789. 2) -j ; 4) д . 790. 2) - ^ ; 4) -j". 791. 2) -д-.
792. 2) 73. 793. 2) ^ . 794. 2) arcctg (-73) > arcctg (-1); 4) arccos ^ =
= arcctg -5- . 795. 2) х = ~i + nnf п е Z; 4) ^ = ~ g + ял, л е Z; 6) х = arctg ^ +
+ ял, л g Z. 796. 2)*=g + -g-^EZ. 797. 2) jc = gg + ял, л g Z.
798. 2) jc = ^ + -^ , л g Z. 799. 2) jc = -3 - 3 arctg g + Зял, л g Z.
800. 2) x = -arctg g +ял, x = -^ +nn,ne Z. 801. 2) * = - у +6ял, jc= ^ +
+ ял, ne Z; 4) * =+я + 8ял, * = -g +кп>пе Z. 802. 2) ^ . 804. 2)x=-^ +2ял,
352

я 2л
х = (-1)л g + ял, л е Z; 4) корней нет. 805. 2) х = 2ял, х = ± -у + 2ял, neZ;
2 27i
4) корней нет. 806. 2) х= (~1)п arcsin g + ял, ne Z; 4) х = ±-^ + 2ял, п е Z.
807. 2) х = - -1 + кпу х = arctg 4 + ял, ne Z; 4) корней нет. 808. 2) jc = ^ + ял,
ле Z;4)x= g +яд,л:=-^ +7m,rt€Z.8O9.2);c=27m,rtEZ;4)jt=±2 + 2ял,ЛGZ.
± z 811 2) t t
810. 2) jc = 2 + "о"» * = ± e + Kn> n e z- 811. 2) jc = arctg ^ + nnf x = arctg
n€Z. 812.2)jc= ^ + ^, n€Z.813.2)jc = ±^ +яд, д € Z.814. 2)jc= ^ +
+ -у , д € Z. 815. 2) jc = ±g + яд, n e Z. 816. 2) x = n + 2яд, x =± g + 2яд,
a 3 я
nGZ.817.-2<a<2,Jt=iarccos g +27W,neZ. 81&a<l,a= ^>a>3.819.2)jc= ^ +
л g Z;4)x = -arctg « + ял, л g Z. 820. 2) x = arctg 2 + ял, x = arctg « + ли,
1 я 3
ne Z;4)jc=arctg « + лл,x = -arctg2+nnfne Z.821.2) jc= -т + ял,x = -arctg -A +
Z 4 4
+ ял, л g Z; 4) x = arctg -^— + ял, л g Z; 6) корней нет. 822. 2) jc = - -z +
+ ял, x = arctg 3 + ял, л g Z; 4) x = arctg 3 + ял, х = -arctg т> + ли, n e Z;
6) jc = -г + ял, x = arctg о + ял, л g Z. 823. a < «— , a > —«— .
4 ^2 Л Л
824. a < -1, a > 1; jc = arctg (2a ±л/3а2-3) + ял, л e Z. 825. 2) * = ^ + 2ял,
л g Z; 4) jc = 2ял, x = -у + 2ял, л e Z. 826. 2) jc = -^ + 2ял, л е Z.
2я 2ял я 2ял 12 t
827. 2) jc = y^ + -g- , jc = g + -g- , л g Z. 828. 2) jc = 3 arcsin jg + (-l)n+1 x
1 24 1
x 3 arcsin уд + Зял, л g Z;4)x = -2 arcsin gH + (~l)n 2 arcsin gH + 2ял, ne Z.
.= ? . 831. 2) jc = 2ял, jc = | + 2ял, л е Z. 832. 2) | а | > >/3.
833. 2)x = 2ял, jc = « + 2ял, л g Z; 4) x = я + 2ял, jc = « + 2ял, л e Z; 6) jc = ~i +
+ ял, л g Z. 834. x = -~i + ял, jc = 2ял, jc = « + 2ял, л g Z. 835. x = -г + ял,
л g Z. 836. jc = ±^ + ^ , л g Z. 837. x= ^ + ™ f n e Z. 838. * = ял,
x = ztarccos —^— + 2ял, л g Z. 839. x = ~ + ял, л g Z. 840. jc = т^ + ял, л g Z.
353

яд 2я я
841. х= -w,ne Z. 842.х = 2яд, х = ±-^ + 2яд, пе Z. 843.*= ~ + 2яд, Д€ Z.
844. jc = -у , д g Z. 845. | а | < 1; если |а| < « » то * = ~ 7 + (~^)n+1 arcsin а + кпу
я 1 я t
jc = - -т + (-1)л arcsin За + яд; если « <а<1, то х = - 7 + (-1) arcsin а +
4 v ' 3 ' ' 4 v '
+ яд, д € Z. 846. 2) х = о + яд, х = (-1)п g + яд, д € Z; 4) х = « + яд, х = - ^ +
яд я я 1
+ яд, д е Z; 6) х = -у , х = ± g + лд» ^ € Z; 8) jc = о + ли, jc = arctg «
я яд я Зя яд
847. 2) х = кп, х = g + -r^€Z;4)jt=7 + лл» х = -jt + -^ , п е. Z.
яд я яд я я яд
848. 2)jc= -g-, Д€ Z;4)jc= ^ + у »* = ±з +7СЛ»ле Z. 849. 2)jc= g + -j-,
jc = (-1)л ^+^,дGZ; 4)JC=^ + ^,Д€Z. 850. 2) jc = ^ +
яд я 2яд Зя 2яд я я
+ -у ,Д€ Z;4)x= g + -у, jc = ^ + -у, д € Z; 6) jc = g + яд, jc = (-If ^ +
яд я яд
+ яд, д € Z. 851. 2) jc = яд, д € Z; 4) х = -^-, д € Z; 6) jc = -т + -5-, д е Z.
852. 2) jc = т> + яд, jc = — т; + ~^~, д € Z. 853. 2) х = ~: + 2яд, дс = т^л + к >
Z о Z 4 ZU Э
д € Z. 854. 2) х = \ +пп9х=^г ,пе Z. 855. 2) * = - -т + яд, jc = -5-, Д е Z.
856. 2) jc = | + 2яд, д € Z. 857. 2)х=^ +кп,пе Z;4)x = (-1)" ^ + у ,
яд я я 2яд
д е Z. 858. 2)jc=-g-,neZ;4)jc=2 + 2ял, х = —gg + -jj- , л е Z. 859. 2) Кор-
яд я яд 1 1 яд
ней нет; 4) х = —г , п е Z. 860. 2)jc=-7 + ~o~»jc= (~1/ о arcsin ^ + -^-, д е Z.
4 4 Z Z О Z
861. 2) Корней нет. 862. 2)jc=^,jc=| + ^^gZ. 863. 2) jc = у , д € Z.
я 11
864. 2) jc = - g + 2ял, д е Z; 4) корней нет. 865. « <а<1, jc = ±^ arccos(4а - 3)+
яд я я 3
+ -jt , Д е Z. 866. 2) х = о + 2яд, д € Z. 867. 2) х = « + 2яд, jc = -arcsin -г + 2яд,
д € Z. 868. 2) x = nnf пе Z. 869. 2) jc = g + 2яд, пе Z; 4) jc = я + 2яд, д € Z.
870. 2) jc = я + 2яд, х = arccos -z + 2яд, n e Z. 871. 2) x = яд,
2 я 2я
x = (-l)n arcsin о + яд, n e Z. 872. 2) x = « + лл> jc = ±-5- + 2яд, д € Z;
о z о
354

4)jt=-arctg g + 2лл, ne Z. 873. 2)x = ~2~>* = ±g + ~2~»де Z. 8742)*= ^ +2лл,
Зя я 5я 7я
х = -j- + 2ял, х = --п + 2ял, х = -То + 2ял, jc = -То + 2ял, л g Z.
875.2) (£ + ^(Л + 2л), £+"(£-2/1)1,Л е Z, л g Z. 876. 2) (ял, —я/il, ле Z.
v4 ^ 4 ^ / V4;
877. ((-1)л^ + ял, ± J + 2ic*l, л е Z, Л е Z. 878. ((-«"J + jcM-I)**1 J
. 879. (^ + я( *+^\-т + я(т5-*Т1 л е Zyke Z.880. Г±-
И I 2) 4 I2 JJ I 6
Zyke Z.SS1. f л,л +jl, f л-j,nl, ле Z.882. f(-l)n
^ 1, л € Z, /г g Z. 883. Г 1
I 6
^ + ял1, л € Z, /г g Z. 883. Гл + Л-1,л-Л-11,
4 J I 6 6J
i,n-A + il,neZ,AeZ.884. f^ + ^, ^ + f2ft+^
6 6J 1^4 2 4 (^ 2
885. f^ + (-l)n+1arxsm-L + 7m, 5 + (-l)*arcsin-i- + 7c*l> n e Zt k e Z.
886. fe|arctgV5, 2K/?±arccos^j, д e Zf k e Z. 887. f(-l)*JL + ^f
fneZ,ke Z.888.x = n + 2nn,x= « +ял, jc= -^- +ял, л g Z.
DO
889. Корней нет. 890. x = nnt x = ± g + ял, л e Z. 891. * = (-1)" g + ял,
t % ®^
ne Z. 892. x= -n + nnf x = -arctg « + nnf ne Z. 893. x = ± —г + 2ял, ne Z.
894. x = 2ял, jc = arccos --г + 2ял, ne Z. 895. jc = « + 2ял, jc = -г + 2ял,
Зя 7я Зя я 2ял
jc= -j- + 2ял, л g Z. 896. 2) --j-; 4)-g-; 6) 0. 897. 2) jc = -2 ± ^ + -g- , л е Z;
4) jc = g ± jg + -g- , л g Z. 898. 2) jc = g + 4ял, л e Z; 4) x = ^ + (-1)л х
1 2 ял лл л я я ял
х « arcsin ^ + -^ , л g Z. 899. 2) jc = ± ^ + 2ял, х = -т. + -% > п е Z.
900. 2) jc = gg + -g-, л g Z; 4) jc = 2з + ял, л g Z. 901. 2) х = (-l)n+1 arcsin g +
1 /qq q
+ ял, л g Z; 4) х = ±arccos « + 2ял, ne Z. 902. 2) х = (-1)п arcsin —-л— + ял,
о 4
л g Z. 903. 2) х= - -г + ял, jc = arctg 1,5 + ял, л е Z; 4) jc = 7 + лл> neZ.
1 5 ял ял
904. 2) х = - о arctg 7 + ~о"» л g Z. 905. 2) Корней нет. 906. 2) х = -^ ,
О 4 О Z
355

д g Z. 907. 2) x = Щ-, x = ^ , x = I + ^ , д g Z. 908. 2) tj ; 4) 73 ; 6) 1.
909. 2) - 7 ; 4) - « ; 6) - к . 910. 2) x = ~A + яд, x = arctg 75 + яд, д g Z.
911. 2) x = nny x = arctg 3 + яд, д g Z; 4) x = ^ + яд, д g Z. 912. 2) ±2 x
x arccos —^-— + яд, д g Z. 913. 2) jc = (-1)" ^ +y,raeZ. 914. 2) jc =
2я 1
= ±-«- + 2яд, д g Z. 915. 2) x = arctg 73 + лл> ^ = -arctg 2 + яд, д g Z.
916.2)*= ^ +яд, nG Z.917.2)x = nnyx = ± ^ +2яд, nG Z.91S.2)x = (-l)nx
к nn я я я
x j2 + у , n g Z. 919. 2) jc = яд, jc = ± « + яд, д g Z; 4) x = 73 + 2яд, ^ = ~22 +
2яд я 2я
2яд п 2п
+ ТГ ' n G Z' ^^' 2) x = nn> n G z> 4) x= о + яд, jc = ±-«- + 2яд, д € Z;
я я яд 2я
6) jc = 2 + яд, х = (-1)л g + яд, д € Z. 921. 2) х = w , х = ± -«- + 2яд, д g Z;
я 2яд 2я я яд я
4) jc = 2яд, jc = g + -g-, д € Z. 922. jc = ±-«- + 2яд, х = j + -^ , х = (-If т« +
+ -у , д g Z. 923. jc = g + лд, х = -у , д € Z. 924. х = -^ , д € Z. 925. * =
= (-1)л « + у , л 6 Z. 926. jc = о + л^» Jt = arcsin 7 + (2д + 1)я, п g Z.
927. jc = | + яд, х = 2яд, х = ^ + яд, д € Z. 928. 2) Г(-1)Л+л Д-^ +
, ,vV. „A, k e Z, n e Z. 929. 2) (-1)лarcsin^-^ +яд,
о j [34
(-1)л+1 arcsin—- + ^ + я/г |, k g Z, д g Z. 930. jc = яд, x = -^ + -^ , n g Z.
931. х = ±^+яд, x = (-l)n+1j^ +■ ™ ,x = nny nG Z.932.2)jc = ±^ +яд, де Z;
4) x = ± g + яд, д g Z; 6) корней нет. 933. 2) jc = - « + 2яд, п g Z; 4) корней
нет. 934. x = ± 77 + яд, n g Z. 935. jc = т + -5- , дс = (-1)" g + яд, д е Z.
356

936. х = -z + ~2 у n g Z. 937. x = arctg 2 + 2nn> x = -arctg 2 + nn, n e Z.
938. x= I + ™, д g Z. 939. 2)
ne Zfke Z. 940. jg < a < 1.
Проверь себя! (гл. VI)
3 3 7 -v/2 Гч
1. sin a = g , tg a = -^ , cos 2a = ^ . 2. 1) - -у ; 2) у ; 3) >/3;
jo
4) у-. 4.1) sin a cos P; 2) cos 2a ; 3) cos (a - P).
Проверь себя! (гл. VII)
|/^ \ e Z\2)x = ±\ +2nn,
п € Z; 3) х - ±g + ял, п € Z; 4) # = пп, х = ^ + -^ , п е Z; 5) х = пп,
neZ.
Глава VIII
945. 1) 5л; 2) у; 3) 2я; 4) я. 946. 1) 2л; 2) 2л. 949. 1) [o;|j , [J;7iJ ;
Зл о 1 Г л! Г л Л1 Г о Зл1 Г Зл 1
7л 13л 13л 11л ( 7л ^ f 8л^
950. 1) sin Tq > sin -=q- ; 2) sin -=r- > sin —=r ; 3) sin ~~g" < sin ~"g" U
4) sin —s- > sin —q- ; 5) sin 3 > sin 4; 6) sin 7 > sin 6; 7) sin (-3) > sin (-2);
V • ) V ь )
8) sin (-1) > sin (-1,5). 951. 1) ^ < x < -^ , ~ < x < ~ ; 2) 0 < x < ^ ,
Зл 9л 11л 7л 11л 4л 5л
-£ < д: < -|-, -|- < jc < Зя; 3) 0 < х < -^ , -^- < * < Зл; 4) -у < х < у .
952.1) sin g < cos g ; 2) sin -тг > cos у; 3) sin ^ > cos T7 ; 4) sin g < cos Tq .
357

Зя 17л 13л 5л л 7л 11л
953. 1)-^ < х<-^2>~12 < х<-г2>-12< х<п> ~12 < х< п;
Зл 11л 10л 5л 4л л 2л 7л 8л
2)~1><х<~~сГ>~~9~ < х<~~9>~~9 К х<9'~9 К х<~9'~9 < х<к;
4) -1 < у < 1. 960. 1) Г5;я] , \п>4\; 2) I -|;о] , Го;|1; 3) [0; к], \ъЩ\ i
4) [-я; 0], 0; -Ц I 961.1) cos % > cos -£■; 2) cos n? < cos -=r; 3) cos —=- <
L *\ ( У / / \ * )
( пЛ ( 8л ^ f 9л "i
< cos - g ; 4) cos ~y < cos -y ; 5) cosl > cos 3; 6) cos 4 < cos 5.
л 5л 7л 2л 4л 8л Зл 5л
962.1)0 < х< ъ, ^ < х<~^;2)0< х< -^, ^ < х< ^;3) -г < х< -г f
11л л 11л 13л
-j- < jc < Зя; 4) ^ < jc < -0- , -g- < jc < Зя. 963. 1) х е R; 2) х е R; 3) х Ф 0;
4) jc * 0; 5) jc > 0; 6) х < -1, х > 1. 964. 1) 0 < у < 2; 2) 0 < i/ < 2; 3) 1 < i/ < 5;
4) -3 < у < 5; 5) g < У < ^ \ 6) -1,25 < i/ < -0,75. 965. 1) cos | > sin |;
л л 5л 5л Зл Зл л 5л
2) sin у < cos у ; 3) cos -g- < sin -g-; 4) sin -g- > cos ~r ; 5) cos g < sin тт ;
л Зл л л л 5л 7л Зл
6) cos g > sin до . 966. 1)-2<JC<~6'6<JC<~6~'~6~< x< ~2;
л л 7л Зл 5л 17л 1 72
2)"12 <дс< 12' 12 < ДС< Т» Т < дс< 12"968Л)"1<^/< 2;2)"Т <
< I/ < — . 969.1) х е R; 2) х = 2яд, п е Z; 3) - \ + 2пп < jc < ^ + 2яд, д € Z;
4) --£- + 2яд < х < g + 2яд, п е Z; 5) 2яд < jc < л + 2пп> neZ;6)-n + 2яд <
< х < о + 2лл, д € Z. 970. 1) jc Ф яд, jc ^ (-1)п g + яд, д € Z; 2) jc ^ 7 + "о"»
(1 + 2д)я л
n e Z\2) хф nn, x Ф —— , д € Z; 4) x Ф « + яд, n e Z. 971.1) -1
4 z
19 /— /—
2) -1 < у < 1; 3) ^ < i/ < ^ ; 4) 1 < у < 19; 5) -1 < у < 1; 6) - V3 < у < V3.
358

977. 1) tg 15° < tg 25°; 2) tg (-80°) < tg (-50°); 3) tg f ~y j > tg у;
4) tg ^ > tg -y ; 5) tg 2 < tg 3; 6) tg 1 < tg 1,5; 7) tg (-1) > tg (-1,5);
8) tg (-2) > tg (-3). 978. 1) ctg 35° > ctg 67°; 2) ctg 95° > ctg 117°;
3) ctg [--jr J > ctg y ; 4) ctg ^-| J < ctg ^ ; 5) ctg 1,2 > ctg 1,5; 6) ctg 2 >
> ctg 3. 979. 1) Да; 2) да; З) нет; 4) нет; 5) нет; 6) нет; 7) да; 8) да.
Зя я я я 5я Зя л 5я я я
980.1)-^- <Jt<-2,4<JC<2'T<JC<T;)~K<JC<~lf'~2 <x< 6;
я 7я Зя я я я Зя Зя 7я
<23)
я я я 2я Зя 5я л 5я
4)-^<jc<-2,-3<jc<2'T<jc<~2~'T<jc< 1) 0 < jc < у ;
Зя я я я Зя я я
2)0<JC<-^;3)^<Jt<K;4)g <jc<k;5)2<^<^-;6)4<^<2*
я Зя 5я
982.1) arctg 3 < х < ^ , л + arctg 3 < х < -у , 2л + arctg 3 < * < ^ ; 2) 0 < * <
< arctg 4, « < х < к + arctg 4, -у < jc < 2л + arctg 4, -g- < x < Зл; 3) -^ < х <
Зя 5я я
< л - arctg 4, -у < х < 2л - arctg 4, -у < jc < Зл - arctg 4; 4) 0 < х < ^,
к - arctg 3 < х < -<г , 2л - arctg 3 < х < ~к , Зл - arctg 3 < х < Зл; 5) 0 < х <
< arcctg 2, л < х < к + arcctg 2, 2л < х < 2л + arcctg 2; 6) arcctg (-3) < х < л ,
л + arcctg (-3) < х < 2л, 2л + arcctg (-3) < х < Зл. 983. 1)-^ <*<--^,
я я 5я Зя я 4я я я
< 8'4<де< "8"'Т<ле<71;2)~2<ле<~"9"'~6<дс<~9
2я я 5я 5я 8я л 2я я Зя
<<<<3)0<<4)<<0
< jc < л. 985. 1) -1 < х < 73 ; 2) у > -1; 3) i/ < 0; 4) у < -1. 989. 1) л + 2лд <
< х < 2л + 2лд, пе Z;2) 2кп < х < л + 2лд, д g Z; 3) х е R; 4) jc e R; 5)
решений нет; 6) решений нет; 7) х = -тг + 2лд, п g Z; S) х = -^ + 2лл, п е Z.
4я 5я я Зя
990. 1) -д- + 2лд < jc < -у + 2лд, д € Z; 2) ^ + 2лд < jc < -|- + 2лд, п е Z;
359

3) - g + 2ял < x < -g- + 2nn, n e Z; 4) - -g- + 2ял < jc < g + 2ял, n e Z.
991. 1) g + 2ял < л; < -у + 2ял, пе Z;2)--^ + 2ял < л: < ^ + 2тш» л g Z;
3) jc € Д; 4) jc € Л; 5) решений нет; 6) решений нет; 7) х = 2ял, ле Z; 8) jc = я +
+ 2ял, л € Z. 992. 1) -£■ + 2ял < * < -^ + 2ял, л € Z; 2) - ^ + 2ял < jc < g +
+ 2ял, л € Z; 3) д + 2ял < jc < -у + 2ял, л € Z; 4) - -у + 2ял < jc < -у +
+ 2ял, л € Z; 5) (2я + 1)я - arccos « < х < (2л - 1)я + arccos « , л € Z;
6) -arccos « + 2ял < х < arccos « + 2ял, л е Z. 993. 1) т> + ял < jc < я + ял,
л € Z; 2) ял < jc < g + ял, л € Z; 3) - о + ял < jc < « + ял, л € Z; 4) ^ + ял <
^71 п ^ К Зя л Зя Зя
< х < 2 + ял, n g Z; 5) п +ял<дс<-^+ ял, л € Z; о) -j- +ял<дс< у + ял,
л € Z; 7) - л + ял < jc < arctg 3 + ял, л е Z; 8) -arctg 2 + ял<#< « + ял,
5я 13я я 2я
л € Z. 994. 1) т« + пп < х < -у£ + ял, nGZ;2)«+it/i<jf<-n-+ ял,
л € Z; 3) -я + 2ял < jc < « + 2ял, n g Z; 4) т <JC^18 +"Т»де^-
995. 1) - j2 + 2пп <х< Jji + 2пп> пе Z;2) j2 + 2ял < х < ^ + 2ял, л € Z;
я 5я я 5я я
3) g + ял < х < -g- + ял, л € Z; 4) g + ял < х < -g- + ял, л € Z. 996. 1) - ^ +
я я Зя
+ ял < х < -г + ял, л е Z; 2) пп < х < -г + ял, -j- +ял<дс<я + ял, п е Z.
997. 1) ял < jc < g + ял, л е Z; 2) д + 2ял < jc < у + 2ял, л € Z; 3) ^ +
5я 2я 2я
+ 2ял < х < -j- + 2ял, л е Z; 4) -у + 2ял < jc < я + 2ял, - у + 2ял < х <
< 2ял, пе Z. 998. 1) я + 2ял < х < у + 2ял, - g + 2ял < jc < 2ял, л € Z;
2) - g + 2ял < х < -^ + 2ял, л € Z. 999.1) т +ял < х< « +ял, « +ял <
360

^ Зя п лч ^ Я 571
< jc < -г- + яд, д е Z; 2) яд < jc < g + яд, -^-+ял<#<я + яд, п е Z.
5я 13я я 2я
1000. 1) -g- + 2яд < jc < -g- + 2яд, д € Z; 2) ^ + яд < х < -^ +кп,пе Z.
2 3 1 2 f П
1001. 1) arcsin о < arcsin ^ ; 2) arcsin 775 < arcsin -jctt ; 3) arcsin ""Ж >
(_[2) (2} ( ЗЛ 1 2
> arcsin у 5 ; 4) arcsin I ~ 3 I > arcsin I - ^ . 1002.1) arccos « < arccos ~ ;
1 1 ( Ъ\ {_ (S) ( 4\
2) arccos "7g < arccos 7^ ; 3) arccos I -g I > arccos уg ; 4) arccos I "5 >
> arccos -« L 1003. 1) arctg « > arctg -r ; 2) arctg 2л/3 < arctg 3 V2;
3)arctg(-3V4)> arctg(-4 V3); 4) arctg f--jLl< arctg f--^ j. 1004.1) x= \ ;
2)jc= ^^;3)jc = 2-2>/2; 4) jc = -3 - >/3 . 1005. 1) x = -\ ; 2) x = -^ ;
= -1. 1006.
1007. 1) - g < x < 1; 2) 1 < x < 5; 3) 1 < x < 2; 4) g < x < 1; 5) 0 < x < 9;
6) 1 < x < 4; 7) 0 < jc < 1; 8) -2 < x < -1, 1 < jc < 2. 1009. 1) x g R;
2)хф о + яд, д € Z; 3) 2яд < jc < я + 2яд, д е Z; 4) - т> + 2яд < jc < «
п е Z; 5) х Ф (-l)ng + яд, п е Z; о) х * кп, х * (-l)ng + яд,
д е Z. 1010.1) -1 < у <1;2)-1< у < 1; 3) 1 < у <3;4)5< у <7;5)3<i/< 5;
6) -4 < у < -2. 1011. 1) Четная; 2) нечетная; 3) четная; 4) не является
четной и не является нечетной. 1012. 1) -=-; 2) 14я. 1013. 1) -g-, -g-, -g- ;
я 2я 7я 8я я 7я 13я 4я
2) « , -«■, -«■, -«■; 3) о , -*■, -£- ; 4) я, Зя. 1014. 1) -2я < х < - -«■;
О о О О О О О о
2) - -^- < х < - -х-; 3) -2я < х <--«-, -тс - arctg 2 < jc < -я; 4) arctg « - 2я <
<х<--йг. 1015.1) Два; 2)один. 1016.1)х* ? + ^-, Д€ Z;2)Tcn<x< ? +тсд,
д € Z; 3) jc € Д; 4) « + яд < jc < « + яд, - « +яд<х<-^ + яд, п е Z.
361

1017. 1) 1 и -1; 2) g и - g ; 3) 1 и -1; 4) 1 и -2. 1018. 1) Нечетная;
2) четная; 3) четная; 4) нечетная. 1019.1) я; 2) 4л. 1020.1) Два; 2) корней нет.
1021. 1) х = пп, х = у + 2лл, п е Z; 2) х = 2яд, х = « + кп, п е Z; 3) х = кп,
я пп п 2яд я Зя
х = (~1)лТо + "о" , л е Z; 4) jc = —«- , х = -г + яд, у + 2яд, п е Z.
1022. 1) 2яд < jc < я + 27Ш, д е Z; 2) « + 2яд < jc < -g- + 2кпу п е Z.
2я 2я я яд я яд
1023. - "з" + 2яд < х < -у + 2яд, д € Z. 1024. - ^ + -у <*<g + "2 »«^Z.
1026. 1) -13 < i/ < 13; 2) -1 < i/ < -g ; 3) -| < у < \ ; 4) 0 < у < 2я.
1027. 1) 4 + 2яд < jc< -£ + 2яд, ne Z;2)nn < x < g + яд, д € Z; 3)-^ +
+ 2яд < jc < тл + 2яд, д g Z; 4) -тг + 2яд < jc < (1 + д)2я, д e Z. 1028. 1) g +
5я n:
-g- + яд, л e Z; 2) ft
V2;4)-V5 < jc< -V§, y/S<x< V5.
5я n:
яд < x < -g- + яд, л e Z; 2) ft +яд
Проверь себя!
1. х * Ъ + ~/г у п g Z; нет, не является. 2. Для синуса: у(х) = 1 при
я я Зя
о » У(х) = ~* ПРИ Х - ~ 9 ' ~9~ » ^(Х) = ^ ПРИ Х = ~Я» ^» Я» 2Я, 1/(JC) > 0 При
0 < х < я, z/(jc) < 0 при -я< jc < 0, я < jc < 2я, отрезки возрастания - « ^ х < «»
Зя я я Зя
у < jc < 2я, отрезки убывания -я < # < - т>» q ^^^ ~о"» Для косинуса:
i/(jc) = 1 при х = 0; 2я, i/(jc) = -1 при jc = ±я, i/(jc) = 0 при х = - « ; о » "о"»
я я Зя я я Зя
у(х) > 0 при ~2<*<2,у<*<2я, i/(jc) < 0 при -п<х< - g , g < x < у,
отрезки возрастания -я< jc< 0, я < jc< 2я, отрезок убывания 0 < х < я.
3. tg jc = 0 при jc = -я, 0; tg jc < 0 при -у < jc < -я, - „ < ^ < 0, tg jc> 0 при
я я я я

ПРИЛОЖЕНИЕ
Формулы сокращенного умножения
(а ± bf = a2± 2ab + Ь2
а2 - Ь2 = (а- Ь)(а + Ь)
(а ± bf = as± 3a2b + 3ab2 ± Ьг
as±bs = (a± b)(a2 T ab + b2)
Свойства степени
ат • ап = ат + п
(ат)л = атп
(ab)m = ambm
[а\т _ дГ_
\bi " Ь"1
Свойства квадратного корня
4ab = VaVfe, а > 0, b > О
Арифметическая прогрессия
Sn = j- ■ n,Sn= g ' п
п ~ 2
Геометрическая прогрессия
л~ q-l ' п~ 1 - q
363

Таблица квадратов чисел до 30
Десятки
0
1
2
0
0
100
400
1
1
121
441
2
4
144
484
3
9
169
529
4
16
196
576
5
25
225
625
6
36
256
676
7
49
289
729
8
64
324
784
9
81
361
841
Таблица некоторых степеней однозначных чисел
Основание
2
3
5
6
7
Показатель
2
4
9
25
36
49
3
8
27
125
216
343
4
16
81
625
1296
5
32
243
3125
6
64
729
7
128
8
256
9
512
10
1024

Оглавление
Предисловие 3
Глава I. Действительные числа.
Степень с действительным показателем
§ 1. Рациональные числа 5
§ 2. Бесконечно убывающая геометрическая прогрессия 8
§ 3. Действительные числа 15
§ 4. Арифметический корень натуральной степени 18
§ 5. Степень с рациональным показателем 25
§ 6. Степень с действительным показателем 32
Упражнения к главе I 36
Историческая справка 40
Глава П. Показательная функция
§ 7. Показательная функция, ее свойства и график 43
§ 8. Показательные уравнения и неравенства 51
Упражнения к главе II 56
Историческая справка 59
Глава III. Степенная функция
§ 9. Степенная функция, ее свойства и график 60
§ 10. Взаимно обратные функции 66
§ 11. Равносильные уравнения и неравенства 71
§ 12. Иррациональные уравнения 77
§ 13. Иррациональные неравенства 81
Упражнения к главе III 88
Историческая справка 91
Глава IV. Логарифмическая функция
§ 14. Логарифмы 92
§ 15. Свойства логарифмов 96
§ 16. Десятичные и натуральные логарифмы. Формула перехода 100
§ 17. Логарифмическая функция, ее свойства и график 105
§ 18. Логарифмические уравнения 111
§ 19. Логарифмические неравенства 117
365

Упражнения к главе IV 123
Историческая справка 128
Глава V. Системы уравнений
§ 20. Способ подстановки 131
§ 21. Способ сложения 136
§ 22. Решение систем уравнений различными способами 141
§ 23. Решение задач с помощью систем уравнений 154
Упражнения к главе V 160
Историческая справка 164
Глава VI. Тригонометрические формулы
§ 24. Радианная мера угла 165
§ 25. Поворот точки вокруг начала координат 168
§ 26. Определение синуса, косинуса и тангенса угла 174
§ 27. Знаки синуса, косинуса и тангенса угла 180
§ 28. Зависимость между синусом, косинусом и тангенсом
одного и того же угла 184
§ 29. Тригонометрические тождества 188
§ 30. Синус, косинус, тангенс углов а и -а 190
§ 31. Формулы сложения 192
§ 32. Синус, косинус и тангенс двойного угла 197
§ 33. Синус, косинус и тангенс половинного угла 201
§ 34. Формулы приведения 205
§ 35. Сумма и разность синусов, сумма и разность косинусов ... 211
§ 36. Произведение синусов и косинусов 215
Упражнения к главе VI 216
Историческая справка 220
Глава VII. Тригонометрические уравнения
§ 37. Уравнение cos х = а 223
§ 38. Уравнение sin х = а 232
§ 39. Уравнение tg х = а 243
§ 40. Уравнение ctg x = a 251
§ 41. Уравнения, сводящиеся к квадратным 256
§ 42. Уравнения, однородные относительно sin x и cos x 260
§ 43. Уравнение, линейное относительно sin x и cos x 262
§ 44. Решение уравнений методом замены неизвестного 266
§ 45. Решение уравнений методом разложения на множители ... 270
§ 46. Различные приемы решения тригонометрических уравнений 274
§ 47. Уравнения, содержащие корни и модули 278
§ 48. Системы тригонометрических уравнений 281
§ 49. Появление посторонних корней и потеря корней
тригонометрического уравнения 285
Упражнения к главе VII 292
Историческая справка 296
366

Глава VIII. Тригонометрические функции
§ 50. Периодичность тригонометрических функций 297
§ 51. Функция у = sin х9 ее свойства и график 301
§ 52. Функция у = cos x, ее свойства и график 309
§ 53. Функции у - tg х и у = ctg x, их свойства и графики 315
§ 54. Тригонометрические неравенства 322
§ 55. Обратные тригонометрические функции 330
Упражнения к главе VIII 334
Историческая справка 336
Ответы 339
Приложение 363

Учебное издание
Колягин Юрий Михайлович, Сидоров Юрий Викторович,
Ткачева Мария Владимировна и др.
АЛГЕБРА
И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
10 класс
УЧЕБНИК
для учащихся общеобразовательных учреждений
(профильный уровень)
Генеральный директор издательства М. И. Безвиконная
Главный редактор К. И, Куровский. Редактор Е. В. Смольникова
Оформление и художественное редактирование: И. В. Цыцарева
Технический редактор И. Л. Ткаченко
Корректоры И. Н. Баханова, Л. В. Дьячкова
Компьютерная верстка: Т. В. Батракова
Санитарно-эпидемиологическое заключение
№ 77.99.60.953.Д.003577.04.09 от 06.04.2009.
Подписано в печать 30.06.09. Формат 60x90 Vie- Бумага офсетная № 1.
Гарнитура «Школьная». Печать офсетная. Усл. печ. л. 23,0.
Тираж 25 000 экз. Заказ № 23168 <к-сы).
Издательство «Мнемозина». 105043, Москва, ул. 6-я Парковая, 29 6.
Тел.: 8(499)367 5418, 367 5627, 367 6781; факс: 8(499)165 9218.
E-mail: ioc@mnemozina.ru www.mnemozina.ru
Магазин «Мнемозина»
(розничная и мелкооптовая продажа книг, «КНИГА — ПОЧТОЙ»).
105043, Москва, ул. 6-я Парковая, 29 6.
Тел./факс: 8 (495) 783 8284; тел.: 8 (495) 783 8285.
E-mail: magazin@mnemozina.ru
Торговый дом «Мнемозина» (оптовая продажа книг).
Тел./факс: 8(495)665 6031 (многоканальный). E-mail: td@mnemozina.ru
Отпечатано в ОАО «Смоленский полиграфический комбинат».
214020, г. Смоленск, ул. Смольянинова, 1.

sin2a + cos2a =
in a = ± V1--
sin
cos* a
cos a = ± Vl-sin2a
tg a + ctg a = 1
*ga = ;^, ctga =
ctg a
tga
cos2 a'
sin2 a
cos (a ± P) = cos a cos p + sin a sin
sin (a ± P) = sin a cos p ± cos a sin
1+tgatgp
sin 2a = 2 sin a cos a
cos 2 a = cos2 a - sin2 a
l-tg2a
1 - cos a
t 2a _ 1 - cos a
g 2 " 1 + cosa
cos x = a
x - ± arccos a + 2nn, neZ
sin x - a
x = (-l)warcsina + nn, neZ
tgx -a
x = arctga + nn, tigZ
loga(bc) = logab + logaC
loga%r=\ogab-logac
alogab=b, \ogabr=rlogab
- 1°ёсЬ

Длгебра
и начала
математического
анализа
Jlpocp ильный
уровень
ISBN978-5-346-01315-0
785346
013150