Author: Киселев В.В.
Tags: общая механика механика твердых и жидких тел физика квантовая механика
ISBN: 978-5-94057-497-2
Year: 2009
Text
В. В. Киселёв
Квантовая механика
Курс лекций
Москва
Издательство МЦНМО
2009
УДК 531:530.145
ББК 22.314
К44
Киселёв В. В.
К44 Квантовая механика. Курс лекций. (Учебное пособие) —
М.: МЦНМО, 2009.-560 с.
ISBN 978-5-94057-497-2
В первой части книги в рамках аксиоматического подхода изложены
основные принципы квантовой механики и их следствия в объеме первой
части годового курса. Материал включает в себя детальное рассмотрение
логических и математических принципов квантовой механики в форма¬
лизме Дирака, вывод основных свойств одномерного движения, гармони¬
ческий осциллятор и голоморфное представление для него, непрерывные
и дискретные симметрии пространства в квантовой механике, квантова¬
ние момента количества движения, введение спина, рассмотрение атома
водорода, квазиклассическое описание частицы и метод интеграла по тра¬
екториям.
Во второй части изложена теория возмущений, процедура сложения
моментов, релятивистская квантовая механика свободных скалярных, спи-
норных и векторных частиц на основе группы Пуанкаре и метода вторич¬
ного квантования, нерелятивистский переход для спинора Дирака и ре¬
лятивистские поправки в атоме водорода, качественная теория сложных
атомов, некоторые вопросы феноменологии атомов во внешних полях, тео¬
рия квантового излучения в дипольном приближении, рассеяние в подходе
«^-матрицы и метод фазовых сдвигов.
Пособие рассчитано на изучающих теоретическую физику студентов
младших, старших курсов и аспирантов физических специальностей уни¬
верситетов, а также преподавателей и научных работников.
ББК 22.314
Киселёв Валерий Валерьевич
КВАНТОВАЯ МЕХАНИКА
Редактор К. В, Парфенов
Корректор Т. Л. Коробкова
Технический редактор Д. Е. Щербаков
Подписано в печать 3/VIII 2009 года. Формат 70 х 100 Vi6.
Бумага офсетная № 1. Печать офсетная. Объём 35 печ. л.
Гарнитура ITC Charter. Тираж 1000 экз. Заказ № 17696
Издательство Московского центра непрерывного математического образования.
119002, Москва, Большой Власьевский пер., 11. Тел. (499) 24174 83.
Отпечатано по CtP-технологии в ОАО «Печатный двор» им. А. М. Горького.
197110, Санкт-Петербург, Чкаловский проспект, 15.
ISBN 978-5-94057-497-2
© Киселёв В. В., 2009.
© МЦНМО, 2009.
Оглавление
Предисловие
9
Часть I
Тема 1. Принципы квантовой механики
Лекция 1
15
15
1.1. Формализм Дирака: бра и кет (20). 1.2. Проектор и полнота (23).
1.3. Операторы: эрмитово сопряжение, унитарность (26). 1.4. Наблюдаемые
и эрмитовость (27). 1.5. Собственные векторы, дисперсия и непрерывный
спектр (28). 1.6. Коммутатор (31). 1.7. Соотношение неопределенностей (32).
1.8. Гипотеза де Бройля: координата и импульс (34).
Лекция 2 38
2.1. Канонический формализм квантования (38). 2.2. Оператор эволю¬
ции (40). 2.3. Теорема Эренфеста (41). 2.4. Полный набор наблюдаемых (42).
2.5. Аксиоматика (44). 2.6. Консервативные системы и спектральная задача,
вакуум (46).
Лекция 3 51
3.1. Уравнение непрерывности: поток вероятности (51). 3.2. Волновой па¬
кет (55). 3.3. Интегралы движения, условия вырождения (57). 3.4. Соотно¬
шение неопределенностей энергия-время (59). 3.5. Г-инвариантность (60).
3.6. Представление Гейзенберга (62).
Лекция 4 65
4.1. Вариационный принцип (65). 4.2. Калибровочная инвариантность (66).
4.3. Импульсное представление (69). 4.4. Р-четность (70). 4.5. Оператор
трансляций, квазиимпульс, номер зоны (72).
Тема 2. Одномерное движение 77
Лекция 5 77
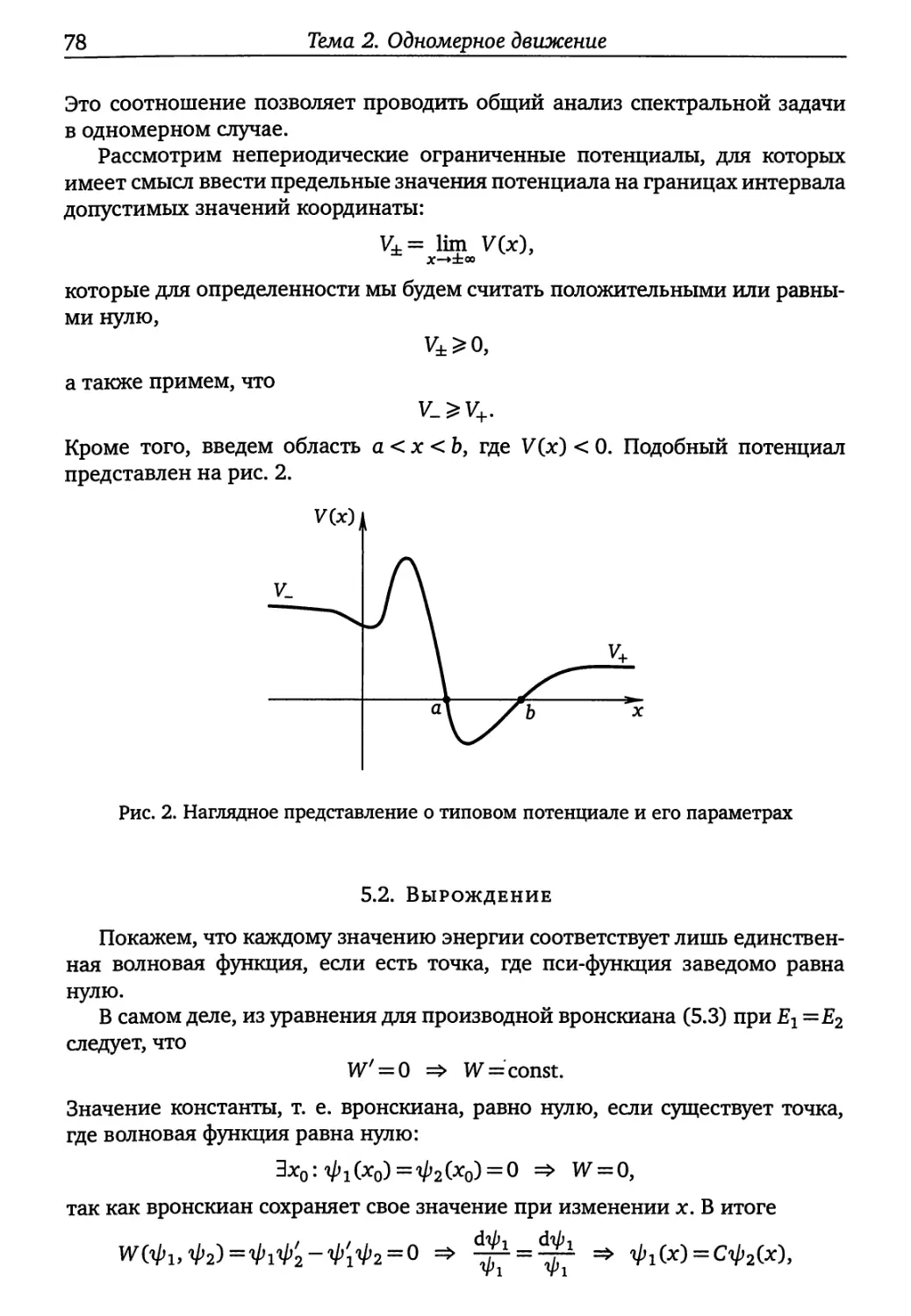
5.1. Одномерное движение: исходные положения (77). 5.2. Вырождение (78).
5.3. Связанные состояния, осцилляторная теорема (80). 5.4. Коэффициенты
отражения и прохождения (82). 5.5. Резонанс (84). 5.6; Скачок производ¬
ной (90).
4
Оглавление
Тема 3. Гармонический осциллятор 91
Лекция 6 91
6.1. Каноническое квантование (91). 6.2. Стационарные уровни, операторы
рождения и уничтожения (93). 6.3. Собственные функции, полиномы Эрми-
та (96). 6.4. Когерентные состояния (98).
Тема 4. Непрерывные симметрии пространства 105
Лекция 7 105
7.1. Трансляции (105). 7.2. Вращения (109).
Лекция 8 115
8.1. Момент импульса, квантование (115). 8.2. Орбитальный момент, соб¬
ственные функции (118).
Лекция 9 125
9.1. Спин матрицы Паули (125). 9.2. Спинорная метрика (127). 9.3. Прин¬
цип запрета Паули, перестановки тождественных частиц (130). 9.4. Ферми-
онный осциллятор, гр£ссмановы переменные (133).
Лекция 10 136
10.1. Оператор конечных поворотов, углы Эйлера (136). 10.2. Задача двух тел,
разделение переменных (140). 10.3. Относительное движение в центральном
потенциале (141).
Тема 5. Атом водорода 149
Лекция 11 149
11.1. Набор квантовых чисел и атомные единицы (149). 11.2. Связанные состо¬
яния (151). 11.3. Вырождение (154). 11.4. Средние, рекуррентное соотношение
Крамерса (157). 11.5. Волновая функция в нуле (160).
Тема 6. Квазиклассика 163
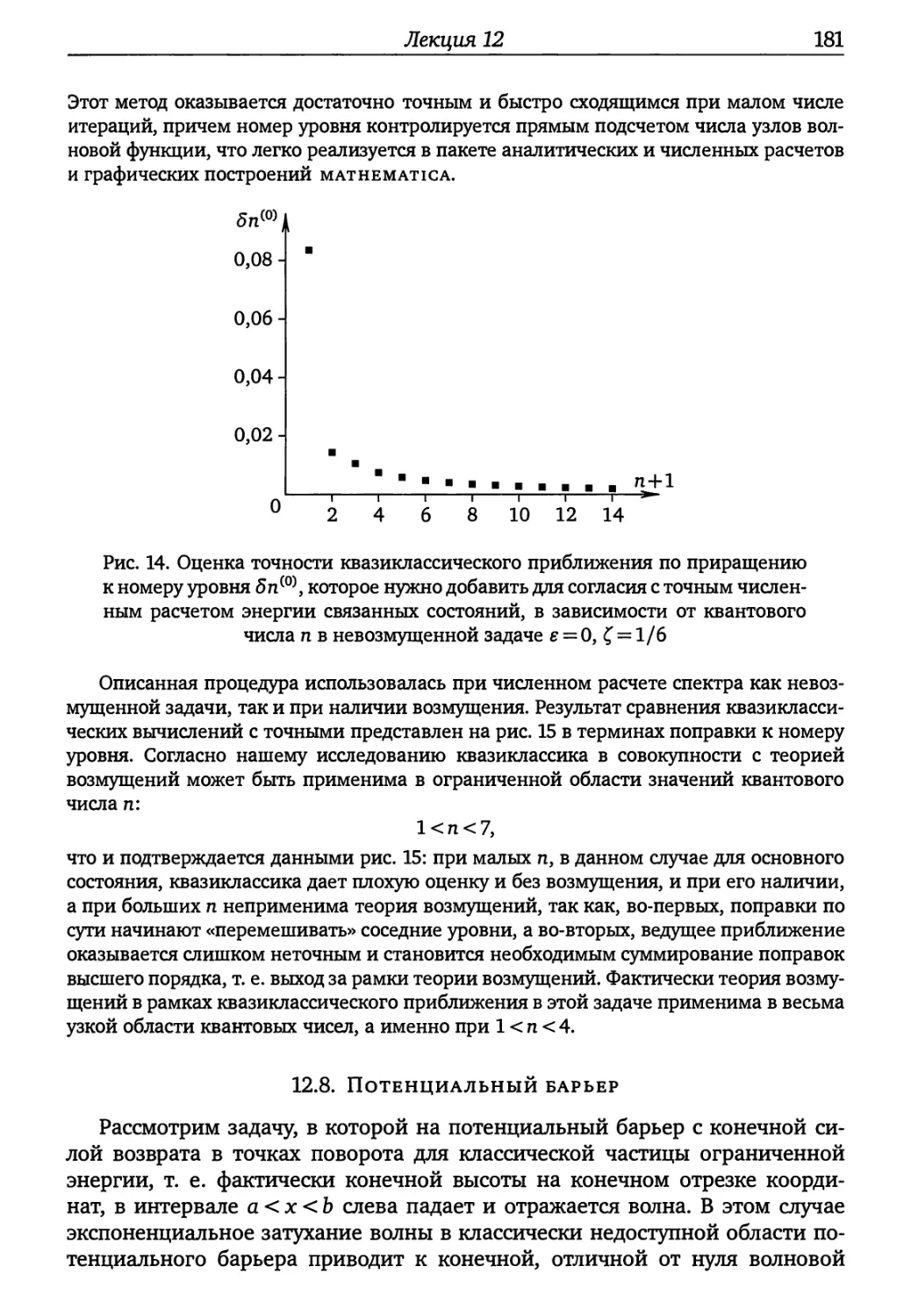
Лекция 12 163
12.1. Классический предел: h—>0 (163). 12.2. Метод JWKB (165). 12.3. Условия
отражения, сшивка решений в точках поворота (170). 12.4. Правило кванто¬
вания Бора—Зоммерфельда (172). 12.5. Плотность состояний (173). 12.6. Нор¬
мировка (173). 12.7. Возмущение (174). 12.8. Потенциальный барьер (181).
Тема 7. Интеграл по траекториям 191
Лекция 13 (дополнительная) 191
13.1. Фейнмановский интеграл (191). 13.2. Источник и производящий функци¬
онал (19 7).
Лекция 14 (дополнительная) 206
14.1. Т-произведение (206). 14.2. Граничные условия: осциллятор в голоморф¬
ном представлении (208). 14.3. Функционал У -матрицы (216).
Оглавление
5
Часть II
Тема 8. Теория возмущений 223
Лекция 15 223
15.1. Стационарная теория (223). 15.2. Нестационарная теория (229).
Тема 9. Сложение моментов 245
Лекция 16 245
16.1. Сложение двух моментов: базис состояний (246). 16.2. Тензорные опера¬
торы: правила отбора (251).
Тема 10. Релятивистская квантовая механика 255
Лекция 17 255
17.1. Вращения (255). 17.2. Бусты (259). 17.3. Собственная ортохронная группа
Лоренца (261). 17.4. Дискретные преобразования (262). 17.5. Классификация
состояний: представления (265).
Лекция 18 270
18.1. Группа Пуанкаре (270). 18.2. Ковариантный вид коммутаторов и дис¬
кретные симметрии (274). 18.3. Скалярное поле (277).
Лекция 19 288
19.1. Вейлевские спиноры (288). 19.2. Дираковские спиноры (294). 19.3. Май-
орановские спиноры (304).
Лекция 20 306
20.1. Безмассовое векторное поле (306). 20.2. Связь спина со статисти¬
кой (311). 20.3. Калибровочное взаимодействие (313). 20.4. «Релятивистский»
атом водорода: спектр (318).
Тема 11. Нерелятивистское приближение: эффективная теория 325
Лекция 21 325
21.1. Построение эффективного действия (325). 21.2. Интерпретация попра¬
вок (329). 21.3. Атом водорода: поправки (331). 21.4. Аномальный магнитный
момент (335).
Тема 12. Атом гелия 341
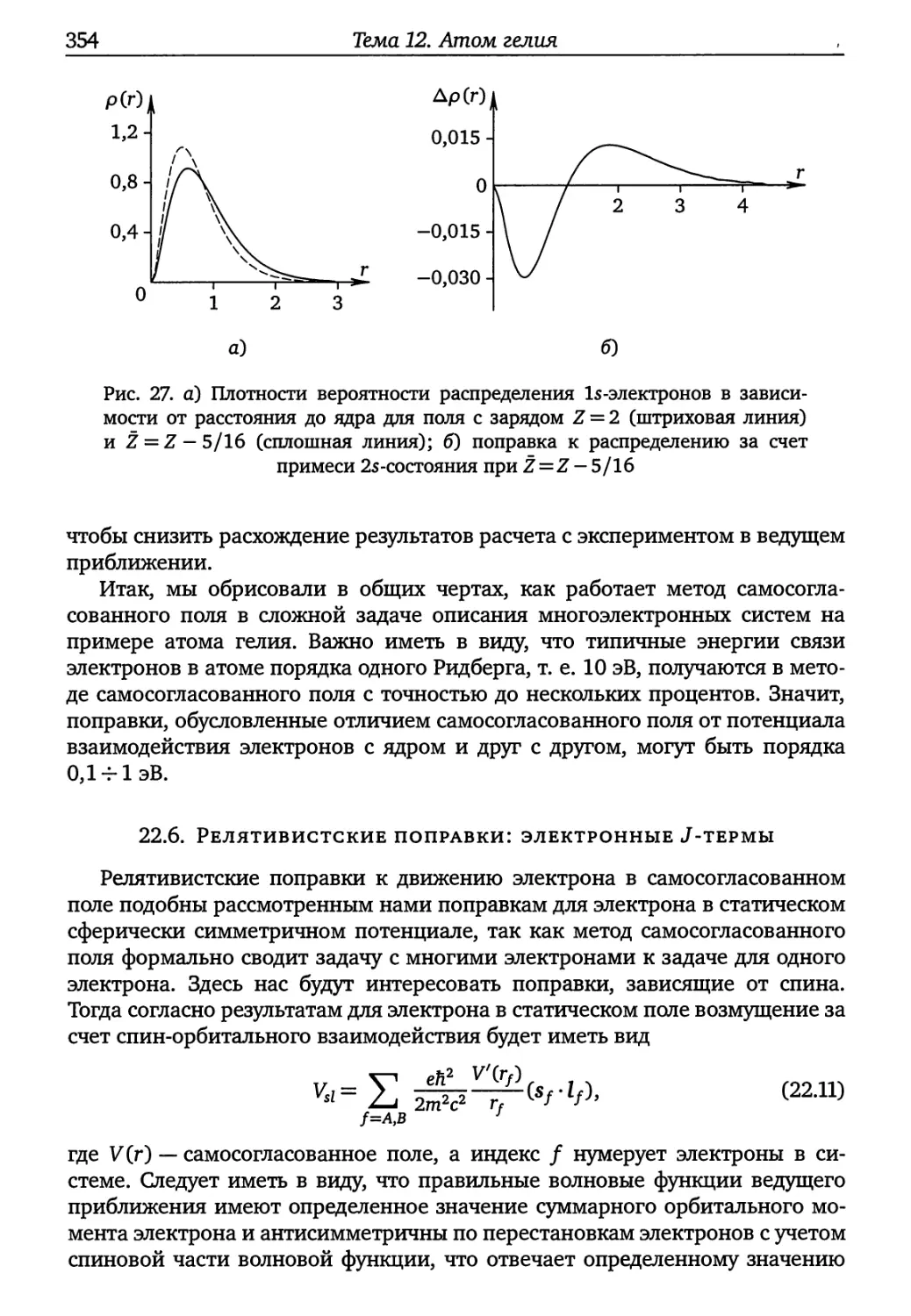
Лекция 22 341
22.1. Нерелятивистская задача (341). 22.2. Обменное взаимодействие (344).
22.3. Уравнения Хартри—Фока (346). 22.4. Самосогласованное поле: конфи¬
гурация электронов, термы (348). 22.5. Основное состояние (350). 22.6. Реля¬
тивистские поправки: электронные J-термы (354).
6
Оглавление
Тема 13. Сложный атом 357
Лекция 23 357
23.1. Определитель Слетера (357). 23.2. Поправки к центральному потенциа¬
лу: термы (359). 23.3. Релятивистские поправки (361).
Тема 14. Феноменология: атом во внешнем поле 369
Лекция 24 369
24.1. Атом в магнитном поле: энергия взаимодействия электронов (369).
24.2. Аномальный эффект Зеемана (371). 24.3. Диамагнетизм (372). 24.4. Па¬
рамагнетизм ван Флека (373). 24.5. Эффект Пашена—Бака (374).
Тема 15. Спонтанное излучение 377
Лекция 25 377
25.1. Дипольное приближение (377). 25.2. Дипольные переходы в атомах:
правила отбора (382). 25.3. Индуцированное излучение и поглощение коге¬
рентного поля (385).
Тема 16. Рассеяние 389
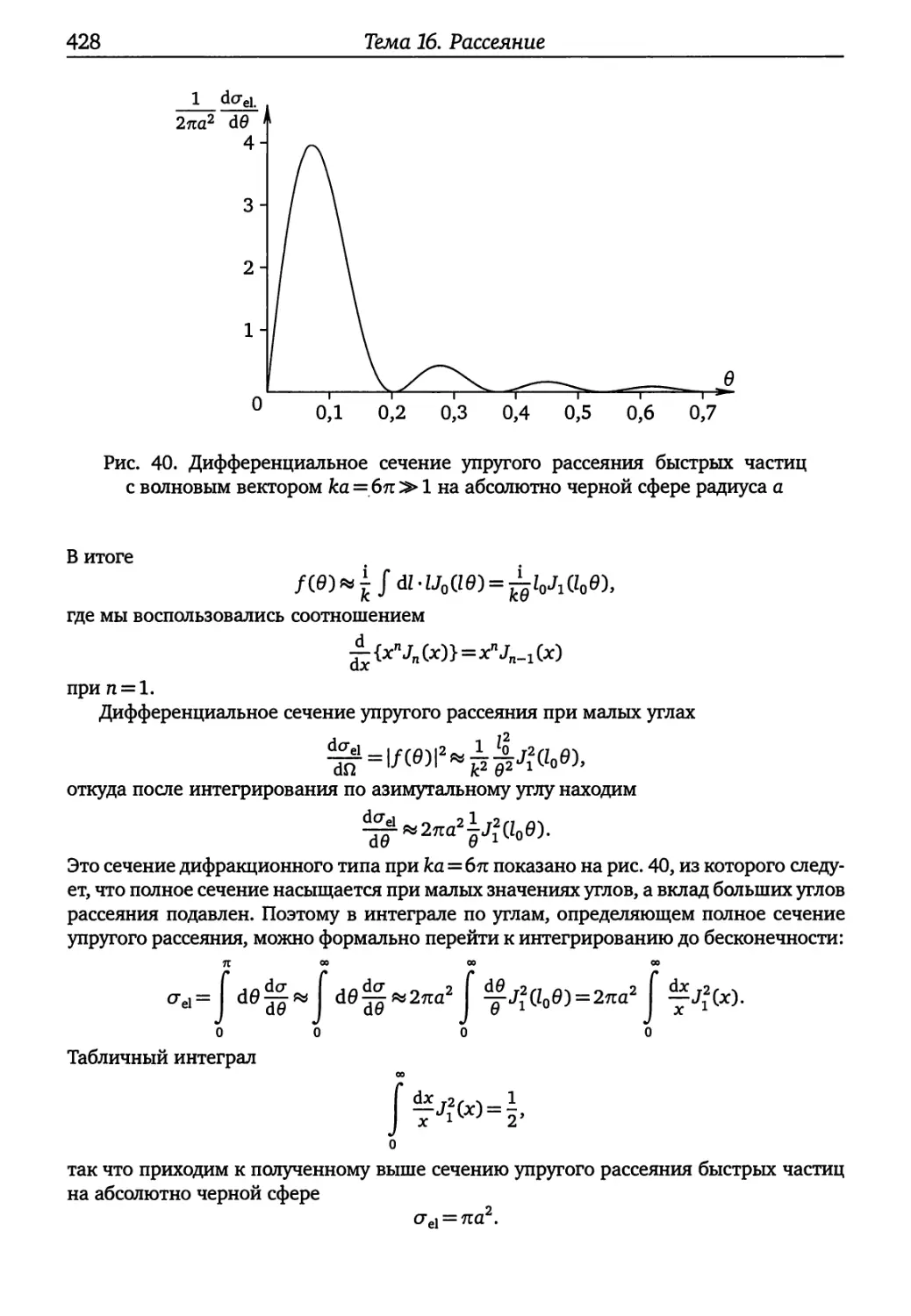
Лекция 26 389
26.1. Асимптотические состояния и 5?-матрица (389). 26.2. Функция Гри¬
на (392). 26.3. Функция Грина свободной частицы (394). 26.4. Интегральное
уравнение (396). 26.5. Асимптотическое поведение на больших расстояниях
и формула для сечения (397). 26.6. ^-матрица, унитарность и оптическая
теорема (399). 26.7. Борновское приближение (403).
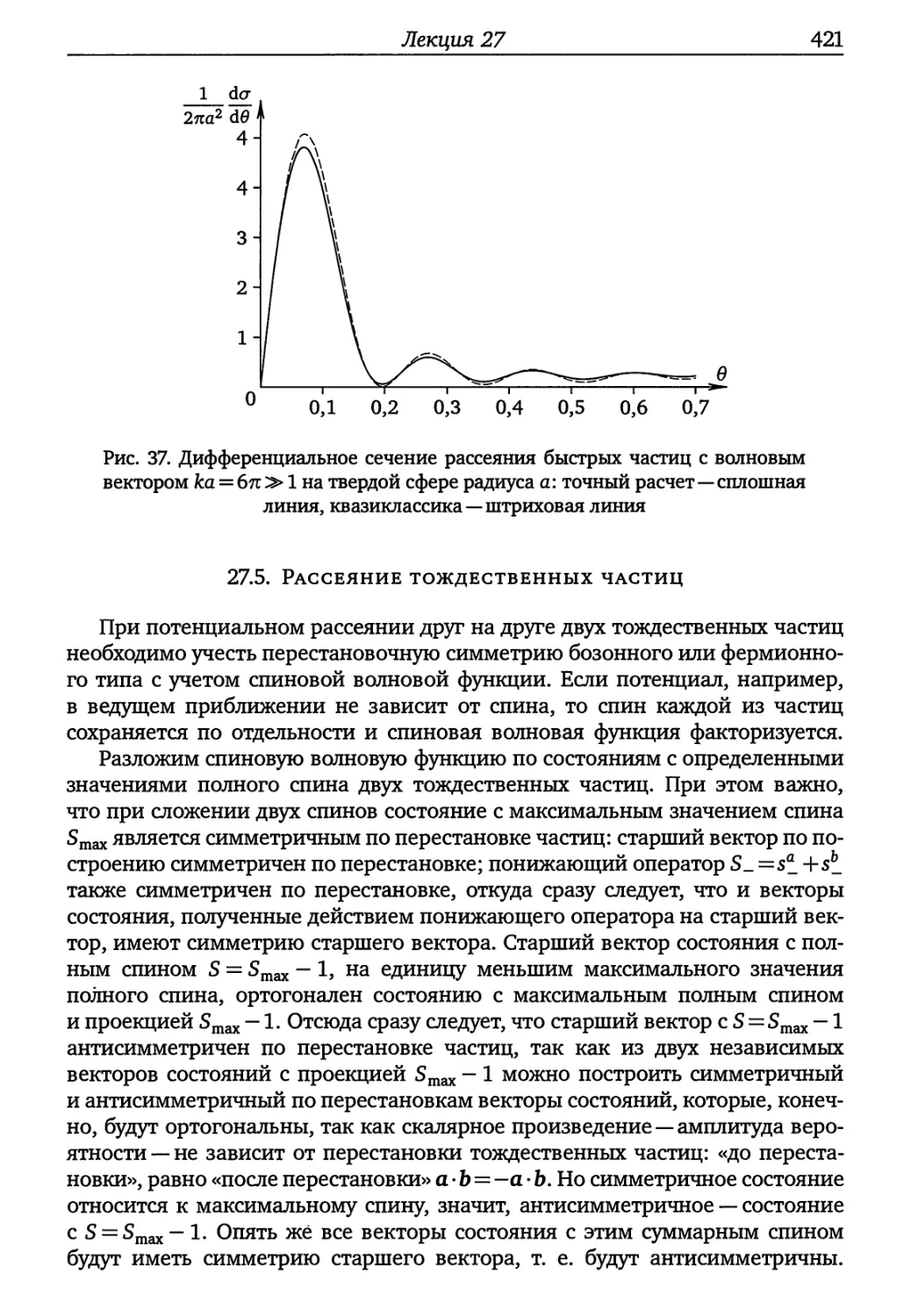
Лекция 27 405
27.1. Сферические волны свободной частицы (405). 27.2. Разложение волны
де Бройля по парциальным волнам (408). 27.3. Фазовые сдвиги и парци¬
альные сечения (411). 27.4. Свойства фазовых сдвигов (412). 27.5. Рассеяние
тождественных частиц (421). 27.6. О кулоновском потенциале, резонансах
и неупругих столкновениях (423).
Приложения
Послесловие 431
Основные формулы курса 433
Вопросы по курсу «Квантовая механика» 451
Дополнение I. Соотношение неопределенностей и корреляции 481
Дополнение II. Матрица плотности, квантовая запутанность
(entanglement), статистические ансамбли и энтропия 483
Дополнение III. Парадокс Эйнштейна-—Подольского—Розена 491
Оглавление 7
Дополнение IV. Неравенства и теорема Белла 498
Дополнение V. Эйконал в рассеянии 504
Дополнение VI. Кулоновское рассеяние 510
Дополнение VII. Уровни Ландау 538
Литература 541
Предметный указатель 543
Предисловие
Материал этой книги представляет собой расширенный вариант лекций,
предлагаемых автором студентам Московского физико-технического инсти¬
тута (Государственного университета) в качестве годового курса квантовой
механики на кафедре теоретической физики.
Целью первой части этих лекций является достаточно строгое теорети¬
ческое обоснование основных положений квантовой механики, начиная с
принципов и их последовательного применения в одномерных задачах, для
важнейших систем: осциллятора и атома водорода, при введении спина и
описании частицы в квазиклассическом приближении, т. е. относительно
стандартного набора ключевых знаний, характерного для курса квантовой
механики в рамках теоретической физики.
При этом необходимо иметь в виду, что студенты получают достаточно
детальное представление о квантовомеханических явлениях на качествен¬
ном уровне в курсе общей физики, так что из этой части курса полностью
исключен описательный феноменологический материал, который обычно
предваряет введение «новых квантовых величин и понятий». Поэтому этот
курс лекций построен не по традиционной схеме индуктивной логики от
частного к общему, характерному при первом знакомстве учащегося с ма¬
териалом. Следование по такому стандартному пути приводит к проблеме
«естественного обоснования понятий, не вписывающихся в схему старой
физики», и к представлению исторического развития квантовой механики
в виде революционного переосмысления концептуальных понятий, которое,
в действительности, как всякая революция, противоречит логике нормально¬
го, т. е. эволюционного, развития, а следовательно, как раз и не может быть
«естественным» с точки зрения парадигмы, оказавшейся в итоге не полной
в своем описании явлений природы.
Изложение курса ведется дедуктивно, посредством аксиоматического вве¬
дения основных принципов, которые не могут быть выведены из прежнего
состояния науки, а возникают, по мысли Гильберта, как новые идеальные
объекты, причем действия с ними и их отношения с прежними твердо уста¬
новленными законами должны быть строго определены в согласии с опытом.
Подобный метод открывает возможность более элегантного и последо¬
вательного изложения материала с указанием тонких взаимосвязей меж¬
ду понятиями, но, с другой стороны, однозначно является более сложным
для восприятия студентом: утешительным призом в этом случае становится
лишь привлекательность самого стиля лекций, который, как известно, —
дело вкуса, а также необходимость иметь разные точки зрения на предмет,
если студент желает его основательно изучить. Нужно ещё учесть закон
инвариантности: стандартная сумма знаний по курсу квантовой механики
10
Предисловие
содержится в любом из учебников, хотя каждый из них излагает материал
по-своему, со специфическими деталями.
Весенний семестр довольно скоротечен, в соответствии с этим в основе
первой части курса —12 лекций, которые читаются до майских праздников.
Мы добавили еще 2 дополнительных лекции об интеграле по траекториям
для любознательных (после майских праздников), т. е. для тех, у кого совре¬
менное звучание квантовой механики в научных исследованиях вызывает
живой интерес.
Во вторую часть курса, наряду со стандартным представлением теории
возмущений, сложения моментов, качественного описания сложных атомов,
взаимодействия атомов с магнитным полем, квантового излучения в ди-
польном приближении и теории упругого рассеяния, включен существенно
расширенный материал по релятивистской квантовой механике свободных
частиц с последующим нерелятивистским переходом, а также У -матричный
подход в теории рассеяния.
Автор сознательно пошел на такое «усложнение», потому что широко
распространенное эвристическое построение уравнения Дирака путем «ли¬
неаризации» уравнения Клейна—Гордона—Фока для скалярной частицы, на
мой взгляд, уже превратилось в рудимент, представляющий интерес скорее
в плане предметного изучения истории физики, а главное, оно порождает
искаженное представление об истинном состоянии квантовой теории, раз¬
витие которой концептуально давно ушло вперед по сравнению с простыми,
но фантастически точными шагами Дирака на заре квантовой эры. На смену
отживших свое время конструкций типа «моря Дирака» и Zitterbewegung
(«циттербевегунг» — дрожание) электрона встали четкие и логически стро¬
гие представления, основанные на группе Пуанкаре и квантованном локаль¬
ном поле. Уравнение Дирака не угадывается, а последовательно выводится
из этих квантово-релятивистских предпосылок. Та же программа реализуется
и для безмассового векторного поля, для которого, как следует из релятивиз¬
ма, с необходимостью имеют место калибровочные преобразования (автор
подсмотрел этот ход у Стивена Вайнберга в его трехтомнике «Квантовая
теория поля»). Предмет квантованных свободных полей так обширен, что,
несмотря на явно увеличенный объем четырех лекций по релятивизму, в них
не вошли многие важные вопросы, такие, как, например, малая группа Виг¬
нера.
Нерелятивистскому переходу придано современное звучание в свете по¬
строения эффективного действия: от релятивистских лагранжианов к ря¬
ду в терминах нерелятивистских полей, в котором выделен ведущий вклад
и малые возмущения. Здесь опущено из рассмотрения преобразование Фол-
ди—Ваутхойзена со всей его арифметической механикой разделения боль¬
ших и малых компонент, а упор сделан на физическом содержании нереля¬
тивистского перехода.
При изложении рассеяния автор посчитал нужным расширить раздел,
посвященный функциям Грина, настолько, чтобы стали возможными введе¬
ние ключевых понятий асимптотических состояний и У -матрицы, а также
Предисловие
11
последовательный вывод оптической теоремы из унитарности, наряду со
стандартным анализом связи полных сечений с мнимой частью амплитуды
рассеяния вперед при рассмотрении суммы парциальных сечений.
Следует особо подчеркнуть, что лекции составляют необходимую теоре¬
тическую платформу для семинаров по квантовой механике в упражнени¬
ях и задачах, а также для решения двух заданий, без которых немыслима
полнота курса и в отрыве от которых лекции превращаются в бесплодное
схоластическое теоретизирование. Планы семинаров, упражнения и задачи
для заданий по квантовой механике содержатся в методических изданиях
МФТИ.
Что касается сложности содержания курса для слушателей, то здесь прин¬
ципиально отметить следующее: в отличие от распространенного мнения
о том, что материал лекций не должен сколько-нибудь превышать тот объем
знаний, который будет затем запрошен к ответу у студентов на зачетах и эк¬
заменах, дабы лектор не «читал лекции для самого себя», автор этого курса
придерживается другой точки зрения. Во-первых, лекции университетского
цикла образования призваны представлять предмет как науку, т. е. отражать
его логическую и концептуальную целостность наряду с методами получения
основных фактов и результатов. Во-вторых, исключение лектором из мате¬
риала курса ряда ключевых логических элементов и методов по причине их
сложности или «заведомой ненадобности» для использования большинством
студентов в их будущей жизни, что вполне приемлемо, например, в выс¬
шей инженерной школе, ограничивает свободу выбора студентом степени
своего кругозора и наносит удар по самому научному подходу к образова¬
нию в университете. Кроме того, если с некоторыми понятиями студенту
действительно в дальнейшем и не придется столкнуться в практической
жизни, то это скорее можно считать аргументом в пользу необходимости
знакомства с ними на университетской скамье, что обеспечивало бы полноту
его образования, того, что остается в памяти среди забытого через многие
годы, чем поводом ограничиться вещами сугубо прагматическими.
В свете такого взгляда на проблему автор полагает, что, имея курс лекций,
построенный по научному принципу, а значит, в целом довольно строгий
и сложный, студент способен самостоятельно варьировать глубину изучения
того или иного вопроса курса, вникая более подробно в одни из них и зна¬
комясь с другими лишь вскользь, но оставаясь при этом в логическом поле
целостного научного взгляда на материал курса.
Автором выделены три уровня сложности, которые определяются сводкой
вопросов, сгруппированных по следующему принципу: от студента требуется
1) знание основных фактов и умение оперировать ими, 2) понимание ло¬
гики и взаимосвязи понятий, обоснование важных результатов, 3) владение
методами построения логической структуры предмета и умение доказывать
результаты. Они отвечают программам бакалавра, магистра и аспиранта.
На практике заинтересованный студент, к которому и адресована эта книга,
вначале читает весь текст бегло в течение семестра и только затем при под¬
готовке к контрольным мероприятиям углубляется в те или иные вопросы.
12
Предисловие
Таким образом, автор посчитал нужным поместить вопросы не частями по¬
сле каждой из лекции, а собрать их в виде единого списка в конце книги. Ряд
вопросов, как и некоторые части текста, могут все же показаться излишне
сложными, но не стоит забывать, что эта книга трактует теоретическую
физику, саму по себе непростую, и это, как говорят,—«книга второго чтения»,
которую стоит брать в руки после первого знакомства с квантовой теорией
в рамках курса общей физики.
Автор благодарен профессору Ю. М. Белоусову за постоянную поддержку
и разъяснения. Я признателен профессорам С. П. Аллилуеву, Г. С. Ирошникову
и доцентам С. Н. Вергелесу, С. А. Гордюнину и В. П. Кузнецову за помощь
при обсуждении решений задач и за интересные беседы, а также академику
С. С. Герштейну за поддержку и Н. Н. Пастушковой за теплую атмосферу на
кафедре.
Особую благодарность автор выражает научному редактору книги доцен¬
ту кафедры квантовой теории и физики высоких энергий физического фа¬
культета Московского государственного университета им. М. В. Ломоносова,
кандидату физико-математических наук К. В. Парфенову, который внима¬
тельно прочел рукопись и в краткие сроки на высочайшем уровне квалифи¬
кации подробно сформулировал свои замечания, позволившие существенно
улучшить изложение как по стилю, так и по содержанию, а также устранить
в тексте не замеченные автором неточности в формулировках и фактах.
Я сердечно признателен К. В. Парфенову за плодотворное сотрудничество при
работе над книгой.
Прошу читателей направлять свои замечания и отзывы о книге по элек¬
тронному адресу Valery.Kiselev@ihep.ru с пометкой «Курс квантовой
механики».
Часть I
...Наука... не в состоянии озарить светом душу, которая
лишена его, или заставить видеть слепого; ее назначение
не в том, чтобы даровать человеку зрение, но в том, чтобы
научить его правильно пользоваться зрением, когда он дви¬
жется...
Мишель де Монтенъ
Тема
1
Принципы квантовой механики
Лекция 1
Логические принципы, интерференция, суперпозиция, корпускулярно-волно¬
вой дуализм, состояние, амплитуда вероятности, средние значения, принцип
соответствия, уравнение эволюции, гильбертово пространство, обозначения
Дирака, формализм, эрмитово сопряжение, унитарность, наблюдаемые, ком¬
мутационные соотношения, соотношение неопределенностей, волны де Брой¬
ля, геометрическая оптика, принцип Ферма, оператор импульса, гамиль¬
тониан.
Концептуальная проблема корпускулярно-волнового дуализма, заключа¬
ющегося в том, что одна и та же физическая сущность обладает как свой¬
ствами дискретности, характерными для частиц, так и свойствами интерфе¬
ренции, присущей волнам1, получила окончательное решение после форму¬
лировки копенгагенского стандарта квантовой механики. Фундамент кван¬
товой механики как последовательной теории был заложен в работах Бора,
де Бройля, Гейзенберга, Борна, Шрёдингера и Дирака, наряду со множеством
оригинальных работ, посвященных конкретным явлениям квантовой приро¬
ды и выполненных другими учеными, среди которых следует особо отметить
Планка, который впервые ввел в физику постоянную h в пионерской работе
о квантовом характере излучения абсолютно черного тела2.
Согласно современному пониманию частица с набором характеризующих
ее наблюдаемых величин представляет собой фундаментальную физическую
сущность, непосредственно доступную для измерительных приборов, посред¬
ством которых детектируются значения присущих частице наблюдаемых ве¬
личин. Состояние частицы полностью определяется амплитудой вероятно¬
сти Ф(д) того, что частица имеет точные значения своих наблюдаемых {q}.
Эхо состояние удовлетворяет динамическому уравнению, детерминирующе¬
му эволюцию корректно заданного начального состояния со временем3. От¬
сюда сразу следует, что в динамическое уравнение входит только первая
производная состояния по времени: только в этом случае начальное состо¬
яние определяет всю его последующую эволюцию.
качественная физическая картина явлений корпускулярно-волнового дуализма детально
излагается в курсах общей физики.
2Планк нашел формулу, описывающую спектр излучения абсолютно черного тела, буквально
в течение одной недели после публикации достаточно точных экспериментальных данных своих
берлинских коллег-экспериментаторов.
3Мы рассматриваем здесь нерелятивистскую квантовую механику, так что время играет
выделенную роль по сравнению с координатами пространства.
16
Тема 1 Принципы квантовой механики
Амплитуда вероятности1 Ф(д) определяет волновую сущность состояния
частицы, так как она с необходимостью по построению квантовой меха¬
ники обладает свойством интерференции: амплитуды вероятности физиче¬
ских состояний, являющихся решениями уравнения эволюции, можно склады¬
вать с произвольными комплексными коэффициентами, удовлетворяющими
условию корректности, так что такие их линейные комбинации вновь яв¬
ляются физическими состояниями для данного уравнения эволюции, т. е.
имеет место принцип суперпозиции состояний. Вероятность того, что частица
имеет заданные значения физических наблюдаемых, определяется квадра¬
том модуля амплитуды вероятности2: w = | Ф(д) |2, так что для суперпозиции
состояний имеет место интерференция волн амплитуд состояний, например,
при интерференции двух состояний вероятность w = \c1'&1 (q) + с2Ф2С<?) I2-
Принцип суперпозиции математически означает, что, во-первых, уравне¬
ние эволюции, которое называют также уравнением Шрёдингера, линейно по
Ф-функции, во-вторых, физические состояния образуют комплексное вектор¬
ное пространство, спецификой которого в отличие от векторных пространств
линейной алгебры с конечным числом базисных векторов является понятие
о корректности элементов этого пространства и действий с ними.
Корректность начального состояния Ф(д, t0) включает в себя два основ¬
ных требования: 1) в этом состоянии амплитуда вероятности должна иметь
ненулевые значения только в допустимой области вещественных значений
набора физических наблюдаемых3; 2) вероятность того, что наблюдаемые
принимают значения в области допустимых значений, равна единице:
2 |^Cq,t0)|2 = l.
Для всякого линейного пространства, каковым согласно принципу супер¬
позиции является пространство квантовых состояний физической системы,
встает вопрос о количестве линейно независимых векторов, которые могут
образовывать базис в этом пространстве. С физической точки зрения изме¬
рение вероятностных характеристик частицы или их совокупности может
быть только счетным по своему количеству, так же как и число самих изме¬
рительных приборов, определяющих наблюдаемые величины с малыми, но
конечными погрешностями. Значит, наблюдательная информация о системе
будет полной только в том случае, если число линейно независимых кван-
1Эквивалентное название амплитуды вероятности—пси-функция; оно широко применяется,
но, однако, несколько затеняет физическое содержание этого понятия.
2Это утверждение является точным, если все наблюдаемые принимают значения в дис¬
кретном множестве, в противном случае речь идет о плотности вероятности для непрерывно
меняющихся переменных.
3В понятие допустимой области может входить и ограничение, связанное с абсолютны¬
ми законами сохранения, типа закона сохранения электрического заряда, в том смысле, что
говорить о состоянии, которое с некоторой вероятностью имеет заряд Q1 или Q2, просто
бессодержательно. Поэтому в таких случаях формулируют принцип суперотбора, который по
определению сужает рассмотрение на подпространство квантовых состояний с одинаковыми
сохраняющимися зарядами.
Лекция 1
17
тоных состояний максимально будет счетным. В противном случае знание
о квантовой системе никогда не может считаться вполне достоверным. По¬
этому специфическим является требование предельной разложимости (iсепа¬
рабельности) начального состояния по счетному базису1 решений уравнения
Шрёдингера
fc=i
где сходимость подразумевается в квадратичном смысле (в смысле вероятно¬
сти):
К примеру, индекс к может нумеровать уровни энергии консервативной
системы, заключенной в пространственной области конечного размера: свя¬
занные состояния или стоячие волны с учетом возможного вырождения этих
состояний и допустимого перехода к пределу бесконечного объема. Другими
словами, сепарабельность означает, что всякое физическое состояние харак¬
теризуется счетным числом амплитуд вероятности иметь точные значения
наблюдаемых величин, даже если формально они лежат в непрерывной,
континуальной в смысле мощности множества, области. Отметим, что, как
мы неоднократно увидим в ходе дальнейшего изложения, именно наличие
сепарабельности обеспечивает тождественность свойств возникающих поня¬
тий, операций с ними и конструкций, определенных дискретным и непре¬
рывным образом (например, сумм и интегралов) в пространстве амплитуд
вероятности. Поэтому его можно считать формализованным отражением
представления о корпускулярно-волновом дуализме поведения квантовых
объектов.
Корректность уравнения эволюции означает, что оно сохраняет нормиру¬
емость состояния на единицу, их суперпозицию, сепарабельность и оставляет
значения наблюдаемых в области их допустимых значений. Дополнитель¬
ным является требование полноты: пространство состояний содержит в себе
все свои предельные точки в смысле квадратичной сходимости. Важно по¬
вторить, что эволюция состояния детерминирована: если задано состояние
физической системы в начальный момент времени, то уравнение эволюции
однозначно определяет состояние во все последующие моменты времени.
Математически это означает, что уравнение включает в себя только первую
производную состояния по времени, и вдобавок, согласно принципу супер¬
позиции, эта производная линейно входит в уравнение эволюции.
Принципиальным в квантовой механике является введение понятия ве¬
роятности и амплитуды вероятности. Только многократное измерение иден¬
тичных состояний дает возможность получить полную информацию об этом
п
lim V nKq, to) - V скФк(q, t0) = 0.
R—>00 f | ( d
{q} k=1
1Читателю, знакомому с функциональным анализом, конечно, известна традиционная,
строгая формулировка этого понятия: бесконечномерное евклидово пространство называют
сепарабельным, если в нем существует всюду плотное счетное множество.
18
Тема 1 Принципы квантовой механики
состоянии экспериментально1. Здесь существенно отметить факт, следую¬
щий из различия понятий вероятности и амплитуды вероятности: поскольку
измеряется модуль амплитуды вероятности, значение ее глобальной фазы не
имеет физического смысла,
|е^Ф(д)| = |Ф(9)|,
содержательным же является лишь понятие относительной фазы состояний,
которая наблюдается при интерференции:
Ic^iCq) + с2Ф2(д) | = | |c1^1(q)| + eia|c2^2(q)) 11,
где а —относительная фаза. Поэтому говорят, что в пространстве состояний
наблюдаемыми являются не сами векторы, а лучи, так как есть соотношение
эквивалентности векторов за счет глобального фазового сдвига2
Ф(д)*е*Ф(д).
В силу вероятностного смысла состояния среди характеристик физической
системы появляются такие понятия, как среднее значение наблюдаемой ве¬
личины (q), ее дисперсия Aq, корреляции величин и т. п. Например, среднее
значение определяется согласно обычным формулам теории вероятности
(q>=5j9l*(9) I2,
{«>
где состояние системы можно представить в виде разложения по заданному
полному набору решений уравнений Шрёдингера, т. е. по базису состояний:
ФСд) = S cfc^fcCq)- Как видим, пространство квантовых состояний строится
в полной аналогии с комплексным3 векторным пространством с введением
понятия нормы, с той лишь разницей, что размерность этого пространства
является не строго заданным конечным натуральным числом, как в конечно¬
мерном евклидовом пространстве, а определяется характеристиками самой
физической системы.
Итак, квантовая механика имеет дело с физическим объектом — части¬
цей—и состоянием объекта—волной амплитуды вероятности. В этом заклю¬
чается единство существования волны и корпускулы и противоположность
их сущности в составе полной системы объект-состояние.
В дальнейшем под физической системой мы будем понимать либо ча¬
стицу, либо набор частиц. В некоторых случаях говорят также о макро¬
скопическом квантовом состоянии, как это имеет место при рассмотрении
сверхтекучести или сверхпроводимости, а также при образовании других
конденсатов. Мы будем полагать, что такая физическая система характери¬
зуется набором независимых «координат» {q} и канонически сопряженных
им импульсов {р}.
Исключение составляет случай собственных состояний, в которых соответствующие физи¬
ческие величины имеют точные значения.
2 Другое естественное ограничение, задающее луч состояния, — нормировка вероятности на
единицу.
3Норма вектора задается произведением амплитуды вероятности на комплексно сопряжен¬
ную амплитуду с суммированием по области допустимых значений наблюдаемых величин.
Лекция 1
19
Здесь просматривается аналогия с классической механикой. Эта аналогия
не случайна. Она является выражением еще одного принципа построения
кпантовой механики—принципа соответствия: квантовая физическая систе¬
ма строится путем процедуры квантования классической системы с иден¬
тичными наборами наблюдаемых величин, причем для квантовой системы
существует предел, в котором классическое описание становится с высокой
степенью точным. Этот предел классического описания, очевидно, имеет
место тогда, когда дисперсия наблюдаемой несущественна при описании
динамики среднего значения наблюдаемой. Его обычно называют также пре¬
делом больших квантовых чисел, так как в случае наличия дискретного мно¬
жества значений наблюдаемой п среднее значение обычно становится много
больше дисперсии при п—»оо. Сама процедура квантования включает в себя
построение корректного уравнения эволюции и способа вычисления всех
иероятностных характеристик наблюдаемых величин.
В качестве иллюстрации принципа соответствия рассмотрим пример
квантовой системы — электромагнитное поле, состоящее из квантов — фо¬
тонов. Состояние поля характеризуется амплитудой вероятности, так что
полное описание предполагает многократные измерения с регистрацией
каждого фотона и его характеристик. Однако если квантов много (п -* оо)
и прибор регистрирует в области детектирования также много квантов,
флуктуации числа которых малы (т. е. дисперсия несущественна), то поле
с высокой точностью описывается классически, а именно, профиль амплиту¬
ды вероятности соответствует профилю поля.
Здесь важно остановиться на часто встречающейся концептуальной
ошибке, ведущей к непониманию важнейшего принципа квантовой механи¬
ки, —к неверному отождествлению волн амплитуды вероятности с волнами
материи. Такое отождествление кажется естественным с позиций, основан¬
ных на восприятии волн в классическом понимании: приборы фиксируют
распределение электромагнитного поля в пространстве, т. е. распределение
волн электромагнитной материи. Но такое представление справедливо
только в классическом пределе. Также неверно представлять себе электрон
в атоме водорода в виде размытого облака, так как в действительности
электрон как физический объект является точкой, частицей, и лишь в клас¬
сическом приближении, т. е. при многократном взаимодействии прибора
с атомом, электрон может выступать в виде облака (как в химических
процессах, где имеется много идентичных атомов).
Итак, суммируя, можно отметить следующие основные характеристики
понятия состояния в квантовой механике:
a. Принцип суперпозиции: состояние является элементом векторного
комплексного пространства 0состояния интерферируют, уравнение эволю¬
ции является линейным по квантовому состоянию).
b. Базис: в пространстве состояний физической системы существует пол¬
ный базис, размерность которого мы считаем счетной Ссепарабельность).
20
Тема 1 Принципы квантовой механики
c. Эквивалентность: состояние определено с точностью до комплексной
фазы, общей для всех состояний (луч в пространстве состояний).
d. Нормируемость: состояние имеет норму — вероятность обнаружить
физическую систему в области допустимых значений наблюдаемых величин;
эта норма является евклидовой: счетная сумма квадратов.
e. Физический смысл: каждое состояние однозначно характеризуется
амплитудой вероятности Ф(д), которая задает вероятность w(q) того, что ча¬
стица имеет точные значения наблюдаемых физических величин {q}: w(q) =
= l*(q)|2.
f. Динамика: состояние удовлетворяет уравнению эволюции во времени,
уравнению Шрёдингера, причем это уравнение детерминировано: начальное
состояние физической системы в исходный момент времени полностью опре¬
деляет состояние во все последующие моменты времени (уравнение линейно
относительно производной состояния по времени).
Указанные нами требования к квантовому описанию физической систе¬
мы относятся к случаю, когда мы оперируем полным знанием об этой систе¬
ме и о внешнем влиянии на нее. В классике это отвечало ситуации, когда
о системе известны все начальные данные о всех степенях свободы и все си¬
лы, действующие как в самой системе, так и извне. Тогда траектории системы
строго детерминированы. Если часть информации становилась недоступной
наблюдению, например, при колоссальном числе степеней свободы в систе¬
ме, то приходилось говорить о статистическом, вероятностном, описании
из-за неполноты наблюдательных данных. В этой связи законы классиче¬
ской механики самодостаточны и первичны, хотя для статистических систем
имеют место и свои специфические законы. В квантовой механике вероят¬
ностный характер физических наблюдений не устраним по своей сути и в
случае полного знания о всех степенях свободы и всех силах в системе. В этом
смысле мы приступили к описанию, как говорят, «чистых состояний», инфор¬
мация о которых полна. Особенности систем, часть информации о которых
не наблюдается, относящихся к «смешанным состояниям», мы опускаем,
поскольку они обычно излагаются в курсах квантовой статистики.
1.1. Формализм Дирака: бра и кет
Состояние физической системы можно описывать эквивалентными набо¬
рами наблюдаемых величин, что в классике просто соответствует обратимым
заменам координат и, следовательно, импульсов при описании одной и той
же траектории частиц в фазовом пространстве. Поэтому вектор состояния
обычно характеризуют не конкретной амплитудой вероятности для задан¬
ного набора координат-наблюдаемых {q} —> ^(q), а абстрактным элемен¬
том пространства состояний в квантовой механике, которое по набору его
свойств (бесконечномерное линейное пространство с комплекснозначным
Лекция 1
21
скалярным произведением) в математике называют гильбертовым простран¬
ством Н.
Согласно обозначениям Дирака пишут
|Ф) — кет-вектор, |Ф) е Н, (1.1)
в полной аналогии с конечномерным векторным пространством V, где
а — контрвектор, а е V.
Поскольку такая аналогия гильбертова пространства Н с комплексным
векторным евклидовым пространством V весьма наглядна и полезна, мы
будем ее в дальнейшем детально прослеживать при введении основных поня¬
тий формализма Дирака. Выбор заданного набора наблюдаемых сопровож¬
дается решением уравнения Шрёдингера в этих переменных, среди которых
можно определить базис — набор состояний с различными значениями на¬
блюдаемой, которую для определенности мы обозначим п:
\п)- базис, (1.2)
в пространстве V:
еп — базис.
Такую наблюдаемую называют квантовым числом п, если она принимает
дискретные значения, или спектральным параметром v, если область зна¬
чений непрерывна. Квантовых чисел может быть несколько.
По определению гильбертова пространства каждый элемент разлагается
по базису:
И: 1*)=2Ф»1П> ~ V:a = 2anen- С1-3)
П П
Коэффициенты разложения Фп и ап имеют смысл проекций вектора на ба¬
зисные орты. В квантовой механике они имеют физический смысл: Фп —
амплитуда вероятности того, что в состоянии |Ф) наблюдаемая имеет зна¬
чение п. Для определения проекции необходимо ввести понятие скалярного
произведения, которое в комплексном евклидовом пространстве V с орто-
нормированным базисом задается в виде
(a,b)=2<bn
П
и определяет положительно определенную норму вектора
(а, а) = ^ а*ап ^ 0, (а,а) = 0 => а = 0.
П
В гильбертовом пространстве скалярное произведение векторов состояний
|Ф) и |Ф) записывается как
<Ф|Ф>=2ФпФп,
п
(1.4)
22
Тема 1 Принципы квантовой механики
а норма—
(ф|ф) = 2]ф;1фп^0, (Ф|Ф> = 0 => |Ф>=0. (1.5)
и
Ортонормальность означает, что базис выбран согласно
V: (вп, ej = 5пт «-» Н: (п\тп) = 5пт. (1.6)
Введение скалярного произведения сопровождается определением сопря¬
женного (дуального) векторного пространства:
V: а <—> а* — ковектор; (а, Ь) = а* ■ Ъ, а* € V,
К: |Ф)<—»(Ф| -бра-вектор; (Ф|Ф)=^Ф*ФП, (Ф^#,
причем1
Если представить себе кет-векторы в виде столбцов с компонентами Фп
а бра-векторы в виде строк с компонентами Ф*,
«-(?)
<Ф| = (ф;, ...),
то операция сопряжения векторов является комбинацией транспонирова¬
ния (т) и комплексного сопряжения (*), которая называется эрмитовым
сопряжением векторов и обозначается символомt:
<ф| = |ф>*. |ф) = (фГ, (0+=((.)т)*.
Это построение находится в полной аналогии с векторным пространством,
где векторы представлены в виде столбцов, а ковекторы в виде строк. Если
базис выбрать вещественным, то векторы в пространстве V
ГЛ
V:e1 =
? , ..., а=( j V aeCN,
w
N—размерность V, а ковекторы в дуальном пространстве V
?:аМа;,...,а;).
Поскольку коэффициенты разложения вектора по базису суть его проекции
на эти базисные векторы, то их следует отождествить со скалярными произ¬
ведениями
V: ап = (е„, а), П: Фп = (п|Ф>. (1.8)
1Поскольку скалярное произведение обычно обозначается скобками, так что в V: («, >), а в
Н\ (<|>), — Дирак ввел для объектов, составляющих скалярное произведение в гильбертовом
пространстве в квантовой механике, обозначения согласно английскому слову bracket (скобка):
(bra|cket), откуда и проистекают названия бра- и кет-векторов.
Лекция 1
23
Физический смысл этих соотношений в квантовой механике очень прост: для
того чтобы вычислить амплитуду вероятности того, что в состоянии |Ф) на¬
блюдаемая имеет определенное значение п, необходимо взять проекцию, или
скалярное произведение, состояния |Ф) на состояние с заданным значением
наблюдаемой |гг).
Из общего определения скалярного произведения следует, что
<п|Ф) = <Ф|п>* = (Ф|п)П
где в последнем равенстве мы использовали то, что скалярное произведение
или, что то же в квантовой механике, амплитуда вероятности есть число (или
функция от значений наблюдаемой), так что транспонирование переводит
число в себя, и в этом случае операции комплексного и эрмитова сопряжения
совпадают: (<|>)* = (<i|>)t.
1.2. Проектор и полнота
Итак, мы установили, что важную роль при рассмотрении состояний
и амплитуд вероятности играет проецирование: операция выделения компо¬
нент вектора состояния в заданном направлении с определенным значени¬
ем наблюдаемой величины. В результате проецирования в терминах строк
и столбцов получаем (нет суммирования по п)
V: ап=епап = еп(е^-а) => Н: |Фп) = |п)т/>п = |п)(п|Ф).
Это действие, которое переводит один вектор состояния |Ф) в другой вектор
состояния |ФЛ) в том же гильбертовом пространстве, т. е. оператор, называ¬
ется оператором проецирования Рп:
|ф)^|ф„Ь
что записывают в виде
РП|Ф) = |Ф„) Ф* Р„|Ф) = |п)<п|Ф).
В обозначениях Дирака пишут
Р„ = |п)(п|.
Очевидно, что повторное проецирование вектора состояния на то же направ¬
ление даст ту же проекцию, что и при однократном проецировании:
р„|фп) = |фп> <=> р„2|ф)=р„|ф> V |Ф> ФФ р2=рп.
Поэтому оператор называют проектором, если его квадрат равен ему само¬
му1:
Р — проектор: Р2=Р.
Обязательным является условие эрмитовости оператора проецирования, которое мы опре¬
делим ниже, хотя введенное эрмитово сопряжение бра- и кет-векторов состояния позволяет
установить для проектора Р* = (|n)(n|)t = \п)(п\=Рп.
24
Тема 1 Принципы квантовой механики
Согласно постулату о полноте базиса в гильбертовом пространстве, произ¬
вольный вектор из пространства представйм в виде разложения по базису,
так что
у|ф) |Ф)=2|п)^„=2]1г1)иф>=2]рп|ф)=1|ф)’ (1-9)
п п п
где 1 — единичный оператор, и полнота базиса эквивалентна записи
1=2рп=2|п><„|. (1.10)
п п
Конечно, под п мы понимаем такой набор независимых измеряемых ве¬
личин, который однозначно характеризует состояние заданной физической
системы.
Если же система характеризуется непрерывным спектральным парамет¬
ром v, принимающим значения на отрезке v е [vmin, vmax], то поступим со¬
гласно следующей схеме.
— Выберем конечные значения riN) < и затем по счетной последо¬
вательности устремим их при N —»оо соответственно к vmin и vmax, которые,
вообще говоря, могут принимать и бесконечные значения.
— Разобьем отрезок [viN), v+N)] на N равных отрезков точками vk=+
+ fce, где
e = Av = j±1(.viN)-v™), k = l, ...,N — 1.
— Построим базис состояний |vfc), отвечающий тому, что спектральный
параметр принимает при измерении значение на отрезке [vk, vfc+1], где vfc,
vk+1 нормированны условием
(VnWm) ^
— Определим проектор соотношением
откуда, действительно, следуют свойства проектора:
Pk = Ivk)Av (vfc|vfc)Av(vfc| =Рк, р£=рк.
4 V ^
1
Тогда разложение квантового состояния |Ф) по базису |vfc) дает
1ф) = 2 lvfc>77T7T = 2 Фк = К|Ф>.
i {Vk'Vk> Ы
В пределе N —»оо и е —»0 находим
^ ^ ^тах
|Ф)=Нт 2^ |vfc)AvV»fc= J |v)dv0(v),
£—>0 к=1 vmin
Лекция 1
25
где (г|Ф> называют волновой функцией. Аналогично для проектора
N—1 v+0
P(v) = lim V |vfc)Av(vfc|= / |v)dv(v|, vfc-»v,
N—»oo ( *
e-»0 *:=! v_0 ' 4 ^
X V
и для нормы состояния
N-1
(Ф|Ф) = lim / (Ф|ук)Ау(уц.|Ф) = f dv |Ф(у)|2 = 1,
iV—>00 J
£—»0 k=l vmin
так что p(v) = |Ф(г)|2 —это плотность вероятности (см. также формулы для
иычисления средних значений наблюдаемых, из которых последнее утвер¬
ждение следует еще более явно).
Например, для одномерного движения в качестве наблюдаемой можно
выбрать координату частицы х, так что
|Ф) = / сЪсФОО!*), (Ф|Ф) = / сЬсФЧхЖх), (х|х/) = 5(х-х/)
и Ф(х) —-амплитуда плотности вероятности р(х) = |\К*)|2 обнаружить ча¬
стицу в точке х, если она находится в состоянии |Ф).
Для состояния с определенным значением спектрального параметра |/х>
запишем
|д) = / dv |v)(v|ju),
откуда немедленно получаем соотношение ортонормированности базиса с
непрерывным спектральным параметром в терминах дельта-функции Дира¬
ка:
(v|jLl) = 5(V-jLl). (1.11)
Значит, при предельном переходе от бесконечно счетного (сепарабельного)
базиса к непрерывному спектру мы получаем состояния, ненормируемые
в стандартном смысле, и приходим к понятию обобщенных функций. Фор¬
мальное и физическое содержание этих понятий подробней обсуждается
ниже после введения операторов физических величин. Здесь же отметим, что
невозможность нормировать вектор состояния на единицу с учетом физиче¬
ского смысла амплитуды указывает на невозможность практической реали¬
зации соответствующего идеализированного состояния квантовой системы.
Например, невозможно перевести точечную квантовую частицу в состояние
со строго определенным значением координаты. Тем не менее, во многих
случаях использование базиса с непрерывным спектральным параметром
формально оказывается и удобным, и полезным в полной аналогии с подоб¬
ным же случаем в теории волн: вряд ли стоит сомневаться в невозможности
практического создания идеальной монохроматической волны, но это не
мешает использовать разложение реальных волновых пакетов в интеграл
Фурье.
26
Тема 1 Принципы квантовой механики
С учетом дискретного и непрерывного спектров условие полноты базиса
состояний запишется в виде
Vmax
1 = 2] WN+ / |v)dv(/i|. (1.12)
1.3. Операторы: эрмитово сопряжение, унитарность
Среди операторов А, преобразующих одни векторы состояния в другие,
|Ф>Д|ФА): |Фа)=А|Ф),
выделяют те, что сохраняют свойство суперпозиции:
^(cl№l) +c2^2)) =cl^№l) +c2^l^2) ^|Ф1>2),
их называют линейными1. Например, проекторы, рассмотренные выше, по
построению являются линейными.
Оператор эволюции £/(t) переводит состояние |Ф) в момент времени t = t0
(для краткости последующих обозначений мы полагаем без ограничения
общности рассмотрения t0 = 0) в состояние |Ф(0) в момент времени t, так
что
\Ш)=Ш\я>). (1.13)
Так как U(0 по определению сохраняет суперпозицию состояний, он—ли¬
нейный оператор. Поскольку U (t) сохраняет нормировку состояния на еди-
НИЦУ’ (Ф(0|Ф(0) = 1. (1.14)
Для произвольного оператора А его действие на вектор состояния в гильбер¬
товом пространстве записывают в виде
А|Ф) = |ФА) = \Агр),
при этом естественным образом вводят эрмитово сопряженный оператор А*
согласно формуле
(Ф|АТФ) = (Ф1ЛФ)1 У|Ф), |Ф). (1.15)
Это определение в точности согласуется с определением для матриц в ко¬
нечномерном векторном пространстве. Действительно, для двух базисных
векторов \п) и \т), если учесть, что эрмитово сопряжение числа совпадает
с его комплексным сопряжением, определение эрмитово сопряженного опе¬
ратора переписывается в виде
(m|Atn) = (п|Л т)* <=> А*т = (АПтУ,
так что в правой части последнего равенства стоит элемент транспониро¬
ванной и комплексно сопряженной матрицы Апт, что и отвечает эрмитову
сопряжению этой матрицы.
1Антилинейными называют операторы со свойством + c2|^2)) = ci^l^i) + с2^1^г)
У|Ф12), т. е. они заменяют коэффициенты разложения на комплексно сопряженные.
Лекция 1
27
Взяв эрмитово сопряжение (1.15), получим другую запись этого же опре¬
деления эрмитова сопряженного оператора
(А+Ф|Ф) = (Ф|ЛФ), У|Ф), |Ф).
Тогда действие оператора эволюции можно переписать, используя эрмитово
сопряженный оператор
(Ф(0|ф(0) = (иш\иш) = (U'www,
но с учетом сохранения нормировки
(Ф(0|Ф(0) = {Ф|Ф) = 1 У|Ф),
получаем операторное равенство
(171'(0и(0Ф|Ф) = (Ф|Ф) Ф=> йЮ = 1.
Поскольку последнее равенство означает, что эрмитово сопряженный опера¬
тор является и обратным, а также верно и обратное, то для произвольного
оператора, удовлетворяющего равенству
А*А=АА*=1, (1.16)
говорят, что оператор А называется унитарным. Итак, унитарные операторы
сохраняют нормировку волновой функции. Согласно этому определению,
оператор эволюции является унитарным.
1.4. Наблюдаемые и эрмитовость
Среднее значение наблюдаемой величины q в теории вероятности, как мы
знаем, записывается как
(<1> = 2 ql^Cq) I2=2 q^*(q)^(q).
iq} {<J>
В дираковских обозначениях эта запись преобразуется к виду
(q)=J]q(mW)-
iq>
Введем для наблюдаемой {q} оператор Q:
&\q)=q\q), (1-17)
т. е. его действие на вектор состояния, в котором наблюдаемая имеет значе¬
ние q, дает значение этой наблюдаемой в этом состоянии |q). Тогда выраже¬
ние для среднего значения наблюдаемой в произвольном состоянии запишем
в виде
<д)=2(ф|(2д)^|ф>’ (118)
ю
28
Тема 1 Принципы квантовой механики
или, с учетом полноты базиса (единичный оператор можно «вставлять» и «со¬
кращать»)
Х>}<<?1 = 1,
{q}
найдем наиболее общий вид для среднего наблюдаемой в терминах операто¬
ра О:
<?) = (Ф |Q*). (1.19)
У наблюдаемой среднее должно принимать только вещественные значения,
так что
(q) = (q>* ^ <Ф|<гФ) = («да>+.
Пользуясь определением эрмитово сопряженного оператора (1.15), запишем
равенство =
справедливое для любого вектора состояния: У|Ф) е W. В итоге
(Ф|аФ)=(Ф|аЧ),
и мы получаем операторное равенство1
Q = Qf. (1.20)
Такие операторы называются эрмитово самосопряженными или просто эр¬
митовыми. Итак, физическим наблюдаемым отвечают эрмитово самосопря¬
женные операторы.
Для эрмитовых операторов F = F* использование определения эрмитова
сопряжения дает цепочку
(ф|р-ф) =f (F+Ф|Ф) = ^Ф|Ф).
Поэтому действие оператора «налево» и «направо» эквивалентно, так что для
эрмитовых операторов пишут
<Ф|#|Ф>
и называют это число матричным элементом оператора F.
1.5. Собственные векторы, дисперсия и непрерывный спектр
Для наблюдаемой {q} соответствующий ей эрмитов оператор Q в бази¬
се |q> может быть представлен диагональной матрицей, так как
(<Z'lQlq>=qSqV
2Из равенства диагональных матричных элементов оператора и его эрмитово сопряженного
оператора следует и равенство недиагональных матричных элементов этих операторов. Дей¬
ствительно, выбирая в качестве состояния |Ф) сначала |Ф) = |Ф) + |Т), а потом |Ф) = |Ф) + i|T)
и записывая условие равенства диагональных матричных элементов операторов Q и Q*, легко
приходим к равенству (Ф|<2|Т) = (Ф|<2*|Т) У|Ф>, |Т).
Лекция 1
29
где 5(Jtq имеет смысл символа Кронекера в случае дискретного спектра {q}
и дельта-функции Дирака для непрерывного спектрального параметра. В
произвольном базисе |/), который получается суперпозицией исходного ба-
:шса,
i/>=2№> (/I/)=Е=5//>
iq} {q} Щ iq}
матричные элементы оператора составляют, вообще говоря, недиагональ-
иую матрицу
</lQl/> =2 2 /4*(qlQ|q) =2 ffy * QV)5ff.
iq} iq} iq}
Основное равенство (1.17), определяющее оператор для наблюдаемой, как
мы знаем из линейной алгебры, называется уравнением на собственное
значение.
Если вектор |Ф) — собственный для эрмитова оператора F, то дисперсия
среднего для F равна нулю. В самом деле, дисперсия1 — флуктуация физиче¬
ской величины возле ее среднего значения:
(AF)2=f (4'|(F-F)2|'I')j F = ('I'|F|'I').
Но для собственного вектора, нормированного на единицу,
£|Ф)=/|Ф) <=> р = (ф|#|ф)=/, (F-F)|Ф) = 0,
так что дисперсия равна нулю. Другими словами, если состояние является
собственным для заданной наблюдаемой, т. е. в этом состоянии наблюдаемая
имеет определенное значение, то дисперсия для среднего этой наблюдаемой
равна нулю. Верно и обратное: если дисперсия наблюдаемой равна нулю,
то состояние — собственный вектор для этой наблюдаемой. Действительно,
в силу эрмитовости оператора для вектора
|#) = (F-F)|'I') => ($| = |#>t = (^|(Ft-F) = (^|(F-F),
норма
(Ф|Ф) = (Ф|(#-Я2|Ф) = (ДР)2 = 0 => (F —F)|'I') = 0,
так как вектор имеет нулевую норму, если он сам равен нулю, откуда
#|Ф)=£|Ф),
а значит, вектор — собственный. Итак, при нулевой дисперсии наблюдаемая
не флуктуирует возле среднего, т. е. имеет определенное, точное значение,
равное ее среднему в этом состоянии, которое является собственным для
наблюдаемой. Наблюдаемая измерима точно, если состояние—собственное.
При наличии непрерывного спектра со спектральным параметром v мы,
прежде всего, воспользуемся описанной выше процедурой предельного пере¬
хода от сепарабельного базиса состояний |vfc) к состояниям, которые всюду
1 Дисперсией часто называют величину cr(F) = (AF)2.
30
Тема 1 Принципы квантовой механики
плотно покрывают область допустимых значений спектрального параметра.
Затем отметим, что наблюдаемая N, для которой построенный базис являет¬
ся собственным,
tf|vfc)=vfc| vk),
в произвольной степени т также удовлетворяет уравнению на собственные
значения:
tfm|vfc)=vfcm|vfc),
а значит, и функция оператора /(N), представимая в виде ряда Тейлора по
степеням оператора, дает
/(tf)|vfc}=/(vfc)|vfc).
Значит, для среднего значения оператора при наличии только непрерывного
спектра находим
vmax
(Ф|/($)|Ф)= lim V(^|/(N)|vfc)Av(vfc^)= j dv |4»(v)|2/(v), (1.21)
/V—>00 i i u
£—♦0 Vmin
откуда заключаем, что Ф(у) = (у|Ф) есть амплитуда плотности вероятно¬
сти p(v) = |^(v)|2 измерения спектрального параметра в бесконечно малой
окрестности значения v.
Пространство физических состояний непрерывного спектра, которое мы постро¬
или с помощью сепарабельного базиса покрытия области изменения спектрального
параметра v счетным числом малых окрестностей1 точек vk в пределе бесконечно
малых отрезков (е -> 0) и бесконечного числа точек разбиения N —> оо, обычно обо¬
значают символом Г2. Гильбертово пространство реальных физических состояний,
очевидно, содержит в себе всякое пространство состояний с таким счетным разбие¬
нием отрезков непрерывного спектрального параметра, т. е. Н 2 П.
По сути, гильбертово пространство физических состояний и при наличии непре¬
рывного спектра является сепарабельным, что отвечает физической процедуре изме¬
рений, в которой приборы всегда обладают конечным разрешением для непрерывных
переменных. Это свойство является важным, поскольку верно следующее математиче¬
ское утверждение: гильбертово пространство является сепарабельным тогда и только
тогда, когда оно обладает ортонормированным счетным базисом. Эта теорема позво¬
ляет строго обосновать введенное выше требование сепарабельности пространства
физических состояний в качестве одного из постулатов, устанавливающих связь меж¬
ду понятийным и формальным аппаратом квантовой теории.
Именно, физические наблюдаемые принимают определенные значения на счет¬
ном числе нормированных квантовых состояний, по которым можно построить су¬
перпозиции произвольных допустимых квантовых состояний, т. е. имеется счетный
нормируемый базис. При этом по физическому смыслу такие состояния ортогональ¬
ны. В самом деле, скалярное произведение двух таких состояний определяет амплиту¬
ду (плотности) вероятности обнаружить в состоянии с заданным точным значением
наблюдаемой величины ее же с другим, отличным от заданного значением, так что
*Как говорил Кронекер: «Бог создал натуральные числа, все остальное выдумал человек», —
нанося чувствительный удар по авторитету Вейерштрасса с его анализом бесконечно малых.
Лекция 1
31
,тга амплитуда, очевидно, должна обращаться в нуль. Это свойство означает, между
прочим, что пространства кет-векторов Н и бра-векторов Н по своей структуре
ннляются эквивалентными, т. е. Н = Н, поскольку они совершенно эквивалентно
определяют друг друга с помощью скалярного произведения которое мож¬
но рассматривать и как линейную комплекснозначную функцию бра-типа ТС2 над
произвольными кет-элементами Нъ и как линейную комплекснозначную функцию
кот-типа Hi над произвольными бра-элементами Н2-
Ситуация кардинально меняется при рассмотрении скалярного произведения как
билинейной операции над пространством Г2: {|П2>, (fi2l^ib определяющей
и элементы пространства бра-векторов (П2| ей, поскольку такая операция уже при¬
нимает значения в пространстве комплекснозначных обобщенных функций, т. е.
функциональных операторов. Так как обычные комплекснозначные функции явля¬
ются подмножеством обобщенных функций, находим, что Й2Й, т. е. пространство
бра-векторов П шире пространства реальных физических состояний. Такая детально
описанная нами явно конструкция из трех пространств состояний ПС.'Н = 'Н^й
и математике называется оснащенным гильбертовым пространством (rigged Hilbert
space), которое представляет собой идеализацию реального пространства состояний
квантовой механики в пределе бесконечно точного измерения непрерывных спек¬
тральных параметров1.
1.6. Коммутатор
Поскольку разным операторам наблюдаемых Q, F, ... соответствуют мат¬
рицы, умножение операторов, вообще говоря, может быть неперестановоч-
HO: А А А А
Q-F^F-Q,...
В этом случае вводят определение коммутатора операторов
[Q,P]=Q-P-P-&. (1.22)
Очевидно, что коммутатор
— антисимметричен
[&£] = -[£,&,
— линеен по сумме операторов
[&+р,р]=[й,р]+[Р,р-\
— и удовлетворяет тождествам Якоби2
[& [Р, F]] + [Р, [F, Q]] + [F, [Q, Р]] =0.
Для эрмитовых операторов
_ A A J. ^ Л А А А ^ 4. AJ. Л J. A 1 А1 А Л А А _ Л А.
[Q, FV = (Q'F-F-Q^=F^-Q1f-Qt-Fi=F-Q-Q-F = -[Q, F].
1Благодаря основополагающим работам Пуанкаре знатокам математических тонкостей
должно быть совершенно ясно, что само понятие непрерывности неразрывно связано с нали¬
чием окрестности точки в топологическом смысле.
2Векторное пространство (определены сложение элементов и умножение элементов на
число), снабженное билинейной операцией с перечисленными свойствами, носит название
алгебры Ли.
32
Тема 1 Принципы квантовой механики
Здесь мы использовали выражение для эрмитова сопряжения произведения
операторов:
* * A A J. А1 Л 1
(Q-F)t = Ft-Qt,
которое легко доказать, последовательно пользуясь определением эрмитова
сопряжения:
(Ф|(Q-F)%) = (Q - РФ|Ф) = (F<£|Qt^) = ($|Ff • Q4) У|Ф), |Ф).
Итак, эрмитово сопряжение коммутатора эрмитовых операторов дает
[Q, F]f = -[Q, F],
поэтому, используя очевидное тождество для мнимой единицы if = i* = — i,
вводят обозначение
[Q,F] = ihC,
где h — постоянная Планка «с чертой»: й = й/(2тг), a C = Ct — некий эрмитов
оператор, так что
(тсУ = -тс,
что и требовалось по построению. Значит, коммутатор эрмитовых опера¬
торов выражается через другой эрмитов оператор с точностью до мнимой
единицы.
Для линейных операторов, с которыми мы имеем дело в квантовой меха¬
нике, комплексные числа выносятся из-под знака действия оператора:
Fc = cF, се С.
Это эквивалентно, в наших обозначениях, тому, что комплексные числа ком¬
мутируют со всеми линейными операторами:
[с, F] = 0.
Отсюда немедленно следует, что коммутатор линеен по сумме операторов
с произвольными комплексными коэффициентами
[ClQ + с2Р, F] = сг [Q, F] + с2 [Р, F].
Кроме того, сдвиг оператора на комплексное число не меняет его коммута¬
тор:
[Q + с, F] = [Q, F].
1.7. Соотношение неопределенностей
Рассмотрим эрмитовы операторы А=At, В=В* со сдвигом на их средние
значения в заданном состоянии |Ф)
а = А-А, Ь = В-В: Л= <Ф|А|Ф>, В = (Ф|В|Ф).
Лекция 1
33
Коммутатор операторов
[А, В] = i ПС
после сдвига не изменяется, так что
[a, b] = ihC.
Средние «маленьких» операторов по построению равны нулю:
(Ф|а|Ф) = (Ф| (А - А) |Ф) = О, (Ф|Ь|Ф) = (Ф| (В - В) |Ф) = О,
в то время как их дисперсии совпадают с дисперсиями «больших» операто¬
ров, к примеру:
(Да)2 = (Ф|а2|Ф) = (Ф|СА-Л)2|Ф) = (ДА)2,
и аналогично для Ь.
Составим вектор1
|Ф) = (а-1^)|Ф),
£еЕ—вещественное число, и найдем его неотрицательную норму
(Ф|Ф>^0,
<Ф|(а - i£b)+(a - ^Ь)|Ф) = (Ф|{а2 - i £(аЬ - Ъа) + ?2Ь2}|Ф) ^ О
ввиду эрмитовости операторов, что с учетом коммутатора
[а, Ь]=ШС
дает полином по
£2 (Д В)2+П(С) I + (ДА)2 ^ 0.
Другими словами, это квадратное уравнение по ^ либо не имеет веществен¬
ных корней, либо два вещественных корня совпадают. Такая ситуация имеет
место тогда и только тогда, когда дискриминант неположителен
V^O <=> Й2(С)2-4(ДА)2(ДВ)2^0.
Отсюда получаем соотношение неопределенностей для дисперсий (флуктуа¬
ций) наблюдаемых (эрмитовых) величин АиВ
ДАДВ^||(С)|, или ДАДВ^||([А,В])|, (1.23)
которое называют еще соотношением неопределенностей Гейзенберга. Та¬
ким образом, если наблюдаемым величинам АиВ отвечают эрмитовы опера¬
торы, коммутатор которых не равен нулю, так что в заданном состоянии |Ф)
и среднее от коммутатора не равно нулю, (Ф|С|Ф) ^0, то эти величины не
могут быть совместно измерены точно: если дисперсия одной наблюдаемой
стремится к нулю, то значение флуктуаций другой становится бесконечно
большой, либо каждая из этих величин имеет конечную неопределенность.
Проведенное построение носит название метода Вейля.
34
Тема 1 Принципы квантовой механики
В итоге не все величины могут совместно входить в полный набор на¬
блюдаемых, характеризующих состояние частицы, так как по построению
в квантовой механике состояние частицы задается амплитудой вероятности
того, что частица имеет точные значения наблюдаемых в допустимой обла¬
сти.
Очевидно, что соотношение неопределенностей минимизируется, если
детерминант равен нулю и существует единственный вещественный корень
для параметра £; = у е R. При этом значении параметра составленный нами
вектор состояния |Ф) имеет нулевую норму, а значит, и сам он равен нулю,
|Ф) = 0, т. е.
(a-iyb)|Ф) = 0 <=> (Л-Л)|Ф) = 1‘г(В-В)|Ф), уем. (1.24)
Примечательно, что это уравнение линейно по операторам наблюдаемых
величин. Равенство нулю детерминанта определяет значение у, так как урав¬
нение принимает вид
И2 (С)2?2+4(АА)2 (С) I + 4(ДЛ)4 = О
с единственным корнем
r=“2Wi =» lrl = fs- а25)
Поскольку для заданного состояния (С) — некоторое число, то физический
смысл параметра у сводится к тому, что он пропорционален дисперсии на¬
блюдаемой А.
Вообще говоря, вероятностные характеристики в приведенных выше
уравнениях с минимизацией неопределенностей могут зависеть от времени,
так как само состояние эволюционирует. Особо выделяют случай, когда
средние и дисперсия сохраняют свои значения. Тогда говорят, что имеет
место когерентное состояние, так как минимизированные флуктуации на¬
блюдаемых не изменяются со временем.
1.8. Гипотеза де Бройля: координата и импульс
Рассмотрим простейшую классическую систему—частицу с обобщенной
координатой q и канонически сопряженным ей импульсом р. В рамках га¬
мильтонова формализма динамика классической частицы полностью задает¬
ся гамильтонианом H(q, р; t). Квантовая система полностью характеризует¬
ся амплитудой вероятности найти частицу в заданной точке Ф^) и зависи¬
мостью этой амплитуды от времени. Другими словами, построим квантовую
систему, взяв в качестве базиса набор состояний \q) и задавая корректные
правила вычисления оператора эволюции и вероятностных характеристик
импульса (среднее, дисперсия, другие флуктуации). Поскольку базис состоя¬
ний фиксирован, имеет смысл все рассуждения проводить в терминах ампли¬
туды вероятности ^|Ф) = Ф(д), так что для операторов введем представления
в этом базисе
<д|д|Ф> = 4,Ф(д), <д|р|Ф> =#q*(q),
Лекция 1
35
где операторы в координатном представлении действуют на пси-функцию,
стоящую справа от них, причем ввиду (q\q = q{q\ получим
qq=<z,
т, с. в координатном представлении оператор координаты — просто число,
рпиное значению этой координаты. Вид оператора импульса в координатном
представлении определим согласно принципу соответствия.
В классическом пределе квантовой системы, когда многократное повторе¬
ние опытов с частицей аналогично наблюдению за ансамблем таких частиц с
пренебрежимо малыми флуктуациями средних значений наблюдаемых, вви¬
ду корпускулярно-волнового дуализма необходимо получить согласованное
совместное описание системы и как потока частиц, и как интерферирующих
иолн материи.
Поэтому, с одной стороны, классическая система описывается в рамках
гамильтонова формализма, так что
dq_dH dp _ дН
dt “ Эр’ dt—lj’ (L26)
или в терминах действия
S(q,t)= f {pdq-Hdt},
QoJo
так что имеют место уравнения Гамильтона—Якоби
Щ=Р, f = (1.27)
С другой стороны, волны материи, как в теории распространения света,
могут описываться лучами, т. е. опять же траекториями корпускул с малыми
флуктуациями, в рамках геометрической оптики с помощью принципа Гюй¬
генса, который утверждает, что фаза волны
Ф(д, 0^е1ф
задается формулой
Ф= J {fcdq-codt},
<2o»fo
где о> — фазовая частота волны, а к = 2п/Х—волновое число (или волновой
вектор), и Я —длина волны, которая зависит от частоты v = со/(2п) и ско¬
рости распространения волны v: X=v/v. Эта фаза определяется принципом
стационарности, сформулированным Ферма,
5Ф = 0,
в полной аналогии с принципом наименьшего действия для классических
частиц
5S = 0.
36
Тема 1 Принципы квантовой механики
Указанная аналогия действия классической частицы и фазы волны в гео¬
метрической оптике приобретает особенно простую форму в случае движе¬
ния свободных частиц и лучей, так как при таком движении сохраняются
энергия+импульс и частота+волновой вектор соответственно, так что S и Ф
легко получить в явном виде:
S = pq-Et, Ф = kq — cot.
Подобие этих функций приводит к введению универсального, единого для
всех физических систем постоянного фактора Й, имеющего размерность дей¬
ствия, так как фаза безразмерна. Тогда запишем
ф = \s, (1.28)
так что в случае свободного движения немедленно получим соотношения де
Бройля:
Е = hco, р = hk, (1.29)
которые обобщают связь энергии с частотой, установленную Планком в ра¬
боте о спектре излучения абсолютно черного тела и Эйнштейном в теории
фотоэффекта.
Поскольку в классическом приближении волны материи тождественны
волнам амплитуды вероятности, находим пси-функцию в приближении гео¬
метрической оптики (т. е. классического описания)
ф(дд)?^с=е»5(<,’°. (1.30)
Тогда из уравнений Гамильтона—Якоби (1.27) следует, что в координатном
представлении для оператора импульса имеем цепочку равенств
pqФ(д, О = ^-^(q, О = t). (1.31)
Поэтому положим, что
/>,—!»£ аз»
в операторном смысле.
Кроме того, уравнения Гамильтона—Якоби определяют и эволюцию вол¬
новой функции, потому что, во-первых, дифференцирование дает
Цф(<?> 0 = -ihfte^ “ t), (1.33)
а во-вторых, из уравнений следует
ih^Vtq, О =H(q, Pq, t)*(q, О, (1.34)
где Я — оператор гамильтониана, так как в нем в качестве аргумента сто¬
ит оператор импульса. Дифференциальное уравнение эволюции (1.34) на¬
зывается уравнением Шрёдингера. Обобщение операторных соотношений
с классического приближения на общий квантовый случай требует проверки
Лекция 1
37
основных требований корректности, предъявляемых к операторам импульса
и гамильтониана.
Покажем, например, что оператор импульса эрмитов на функциях, доста¬
точно быстро убывающих на бесконечности. Согласно общему определению
эрмитова оператора следует показать, что
(Ф|рФ>=(рФ|ф>-
И координатном представлении запишем
J dq Ф* (q){—ifi}^/(q) = (интеграл по частям) =
= -J dq$,*(q){-iftWq) = J dq
ч то и требовалось доказать. При этом в ходе выкладок мы полагали, что
интегралы сходятся, а функции на концах интегрирования равны нулю, что
гарантирует корректность применения интегрирования по частям.
Найдем коммутатор координаты и импульса. Действуя на пси-функцию,
запишем
Ид, Pqmq)=qi-m±*(.q) -{-ift^q'Kq) =
= q{-ift}^*(q)+q{ift}^*(q) + {ift}*(q),
так что
[qq> РдЖ q) = ifi«f(q),
и в операторном виде
= (1.35)
Тогда из общих соотношений неопределенностей (1.23) для случая координа¬
ты и импульса с оператором С = 1 получим
AqAp^f. (1.36)
Заметим, что собственные функции оператора импульса в координатном
представлении найти очень легко: очевидно, это экспоненты
Фр^)~е-»и,
которые подчинены условию нормировки на дельта-функцию Дирака
/ dq ^*,(q)^p(q)~5(p-p0.
Однако следует обратить внимание на то, что эти функции не принадлежат
пространству квадратично интегрируемых волновых функций и поэтому не
описывают физически реализуемые состояния квантовых частиц. Это видно
и из соотношения неопределенностей: в таких состояниях частица имела бы
бесконечную неопределенность координаты. Таким образом, для корректно¬
го решения спектральной задачи для импульса надо использовать описанную
выше конструкцию «оснащенного гильбертова пространства».
38
Тема 1 Принципы квантовой механики
Что касается гамильтониана, то в простых случаях, таких как свободное
движение или движение в потенциальном поле,
его квантовое обобщение вполне однозначно. Проблемы возникают в двух
обстоятельствах. Во-первых, у классической физической системы вклад в га¬
мильтониан могут давать члены с произведениями координат и импульсов.
Например,
что неэквивалентно, так как операторы не коммутируют, и это обычно назы¬
вают проблемой упорядочивания некоммутирующих операторов при кван¬
товании классической системы. Каждый способ упорядочивания может ока¬
заться корректным, так что при квантовании классической системы могут
быть сформулированы различные квантовые обобщения.
Во-вторых, классическая система может включать в себя связи. Квантова¬
ние систем со связями также можно провести в общем случае, но простей¬
шим является тот, в котором связи разрешаются в явном виде до квантова¬
ния. Такое разрешение связей в явном виде не всегда возможно и удобно,
поэтому в квантовой механике разработана общая процедура квантования
систем со связями.
Скобки Пуассона, флуктуации, каноническое квантование, производная опе¬
ратора по времени, динамическое уравнение для оператора эволюции и его
решение, теорема Эренфеста, совместная измеримость наблюдаемых, полный
набор, принципы квантовой механики в картине Шрёдингера, спектральная
задача, стационарное уравнение Шрёдингера и уровни энергии.
В классической механике физические величины как функции обобщен¬
ных координаты q и импульса р удовлетворяют динамическим уравнениям
Гамильтона. Действительно, если /=/(q, р, t), то
H(q,p) = ^ + V(q)
qp => qp или pq
Лекция 2
2.1. Канонический формализм квантования
(2.1)
где, как обычно, точка над символом означает производную по времени на
траектории. Пользуясь уравнениями Гамильтона для производных по време¬
ни координаты и импульса (1.26), находим
Лекция 2
39
Для выражения в фигурных скобках вводят термин — скобка Пуассона: для
дмух величин / и g
Xf = — (2 3)
dqdp dpdq3 1J
глк что
% = |+(/, H>p. (2.4)
Наш величины / и g не зависят от времени явно, то скобка Пуассона возника¬
ет также и при рассмотрении следующих вариаций переменных. Допустим,
что дифференциал / обращается в нуль:
d/ = |d4 + |di’=°-
Тогда для дифференциала g находим
dg=Mdq+^dp=dq{^£Z_^i£/l 1 ,
6 dq 4 dp F 4 \ dq dp dp dq) df/dp ’
•r. e.
dg = dq{g,/>P^.
Заменяя символы дифференциалов на флуктуации, получаем
5g5f^{g,f}р 5q 5р. (2.5)
Вводя стандартное обозначение для элемента фазового объема системы
ДГ = 5q 5р,
находим
5g5f*{g,f} РДГ, (2.6)
т. е. произведение флуктуаций наблюдаемых величин в классике пропорци¬
онально их скобке Пуассона и флуктуации фазового объема системы, име¬
ющего размерность действия. Этот факт следует сравнить с результатом
анализа соотношения неопределенностей в квантовой механике. Для кван¬
товых операторов тех же наблюдаемых произведение дисперсий задается
коммутатором:
AgAfc*\[gJ] |. (2.7)
Аналогия становится явной, если применить приведенный анализ непосред¬
ственно к координате и импульсу, для которых
{q,p}Р = 1 [q,p] = ift,
так что, полагая ДГ^Й, находим, что классические и квантовые флуктуации
согласуются, если считать, что квантовый коммутатор можно построить из
соответствующей скобки Пуассона для классических наблюдаемых:
[/, Я = {/,*}?• У*. (2.8)
40
Тема 1 Принципы квантовой механики
Это соответствие скобки Пуассона и коммутатора было предложено в каче¬
стве процедуры канонического квантования1 Дираком. Отсюда, например,
автоматически получаем уравнение, задающее производную оператора по
времени согласно (2.4), умноженному на фактор Ш,
= + (2.9)
которое называют уравнением Гейзенберга.
2.2. Оператор эволюции
Зависимость состояния от времени согласно уравнению Шрёдингера
т±\т))=А\ш), (2.Ю)
как мы установили выше, можно переписать в терминах оператора эволю¬
ции U (t):
|Ф(0) = 0(0|Ф) У|Ф)<Е7*.
Действительно, подставляя определение оператора эволюции в уравнение
Шрёдингера при произвольных допустимых корректных начальных услови¬
ях, находим
ih^-U=HU => -ihjrtP^A, (2.11)
ot ot
где мы использовали эрмитову самосопряженность гамильтониана, причем
0(0) = 1,
так как в начальный момент времени исходное состояние преобразуется
само в себя. Для бесконечно малого смещения dt получим
U(dt) = 1 - dt + 0(dt2) = е~*й dt + 6>(dt2).
При этом мы ввели общее определение функции от оператора в виде разло¬
жения Тейлора по степеням операторного аргумента.
Решение дифференциального уравнения для оператора эволюции легко
найти в случае, если гамильтониан не зависит от времени, так что
иЮ=е-*ЙС, (2.12)
при этом оператор эволюции и гамильтониан коммутируют и в исследуемом
уравнении с ними можно обращаться как с числами.
Если же гамильтониан зависит от времени, то осложнения возникают
из-за того, что в разные моменты времени гамильтониан не коммутирует сам
с собой:
*В уравнении (2.8) в левой части стоят операторы, а в правой классические величины,
которым необходимо придать операторное значение. Здесь мы опять сталкиваемся с проблемой
упорядочивания, если только ситуация не является простой и скобка Пуассона наблюдаемых не
равна числу, как в случае с координатой и импульсом.
Лекция 2
41
В подобной ситуации можно поступить следующим образом. Разобьем
интервал интегрирования [0, t] на N малых отрезков. Тогда, пренебрегая
изменением гамильтониана за время от tk до tfc+1, посредством малых сме¬
щений получим, что
°<0=й1. С1 - dt) - яй('1>dt)=П *>•
к=1
где символ f означает упорядочивание по времени: каждый фактор зависит от
момента времени, большего, чем времена справа, и меньшего, чем времена
слева. Такой предел (если он существует вне зависимости от разбиения)
обозначают символом «Т-экспоненты»:
U(t) = t{е- / i6(f) dt}. (2.13)
Конечно, если гамильтониан не зависит от времени, то мы возвращаемся
к обычному выражению экспоненты в (2.12).
Найдем производную по времени среднего значения физической наблю-
даемой / (q, р, t):
1й£(Ф(0|/|*(0) = ih±(*\u4t)fu(t№ =
•г. е.
ift£(*(t)lM(t)> = <*(0|{iftf£ + [/, Я]}|Ф(0>,
так что, определяя производную оператора по времени как
ihftf = ih& + [f,H] (2.14)
и согласии с каноническим квантованием, находим, что среднее от произ¬
водной по времени наблюдаемой равно производной по времени от среднего
значения наблюдаемой:
/d/\ _d(/)
\dtl dt *
2.3. Теорема Эренфеста
Проведенное рассмотрение производной среднего значения оператора
в сочетании с каноническим квантованием физической системы позволяет
установить простое, но важное соотношение. Действительно, для координа¬
ты и импульса, которые не зависят явно от времени, в квантовом случае
имеем
= {[q, Я]) = ift(iq, Я}р) = ift ( ^ )
И
in^ = ^А]> = Щ{р, Я}р) = - iй ( f|) >
42
Тема 1 Принципы квантовой механики
где в конце цепочек равенств стоят средние от операторов, которые получа¬
ются из соответствующих классических выражений подстановкой операто¬
ров координаты и импульса, скажем, в координатном представлении. В итоге
динамика средних значений координаты и импульса определяется средними
значениями скорости и сил:
что и составляет содержание теоремы Эренфеста. Значит, каноническое кван¬
тование гарантирует, что в случае, когда дисперсии несущественны, динами¬
ка квантовой системы в среднем в точности совпадает с динамикой исходной
классической системы, и требования принципа соответствия квантовой
и классической систем автоматически удовлетворяются при каноническом
квантовании.
Поскольку по построению квантовой механики амплитуда вероятности
задает вероятность того, что наблюдаемые имеют некоторые точные зна¬
чения, пары некоммутирующих наблюдаемых ввиду соотношения неопре¬
деленностей не могут совместно входить в состав аргументов амплитуды
вероятности: если значение одной из таких наблюдаемых точное, т. е. ее
дисперсия равна нулю, то другая наблюдаемая флуктуирует, а значит, ее
значение не является точным. Другими словами, невозможно определить
Покажем, что, если две наблюдаемых / и g точно измеримы совместно,
то их коммутатор равен нулю. В самом деле, мы уже вывели выше, что если
наблюдаемая измерима точно, то состояние является для нее собственным
вектором, а значит, в рассматриваемом нами случае
которые с учетом возможности наличия и других квантовых чисел состав¬
ляют полный базис состояний в гильбертовом пространстве. Поэтому ра¬
венство нулю коммутатора на базисных векторах означает его операторное
равенство нулю:
lf,g] = 0.
Если теперь коммутатор наблюдаемых равен нулю, то базис состояний
можно выбрать так, что наблюдаемые измеримы точно. Действительно, пусть
(2.15)
2.4. Полный НАБОР НАБЛЮДАЕМЫХ
откуда
= (&-*/)№> = 0.
Значит, состояние характеризуется парой собственных значений
|ф> = !/,*>,
Лекция 2
43
состояние является собственным для наблюдаемой /:
Рассмотрим состояние
Носпользуемся коммутативностью / и g в цепочке равенств
№*))=&№)=&№=№№)),
т. е. состояние £|Ф) — собственное для наблюдаемой /. Здесь возникают две
иозможности.
Во-первых, собственное состояние может быть невырождено, т. е. данно¬
му собственному значению отвечает единственный вектор |Ф) = |/). Тогда
g|/) = const|/),
где значение постоянной, очевидно, задает собственное значение наблюда¬
емой g в этом состоянии, так что обе наблюдаемых измеримы точно в этом
состоянии с квантовыми числами / и g: |Ф) = |/, g).
Во-вторых, состояние может быть вырожденным: заданному собственно¬
му значению отвечает набор собственных векторов, который мы пометим
индексом а, так что |Ф) = |/, а). Тогда действие оператора g дает вектор из
того же подпространства:
g\f, а) = сар\Г,Р),
где подразумевается суммирование по повторяющемуся индексу р. Однако
из эрмитовости оператора g = g* следует эрмитовость матрицы с: caj9 =c^a,
гак что эту матрицу можно диагонализовать, т. е. перейти от базиса векто¬
ров |/, а) к базису собственных значений матрицы |/, Я{), в котором
^1/, Я£)=Я£|/, Я£>.
Последнее равенство означает, что А* — собственные значения g, и мы по¬
строили базис, в котором пара коммутирующих наблюдаемых измерима сов¬
местно.
Таким образом, полный набор наблюдаемых квантовой системы состав¬
ляет максимально возможное множество функционально независимых по¬
парно коммутирующих физических величин, характеризующих заданную си¬
стему.
В частности, полный набор после квантования могут составлять обобщен¬
ные координаты классической системы1, в то время как канонически сопря¬
женные им импульсы составляют полный набор дополнительных перемен¬
ных. Из проведенного доказательства следует, что мы не можем расширить
такой набор наблюдаемых координат добавлением одного из канонически
Подчеркнем, что мы ограничиваем себя случаем систем без связей, которые приводят
к функциональной зависимости между наблюдаемыми величинами, например между обобщен¬
ными координатами.
44
Тема 1 Принципы квантовой механики
сопряженных импульсов, так как он не коммутирует со своей координатой.
Но мы можем попарно заменять переменные координат и импульсов в до¬
полнительных наборах переменных.
Отметим также простое свойство базисных векторов состояний: собствен¬
ные вектора наблюдаемой с различными собственными значениями ортого¬
нальны. В самом деле, действуя эрмитовым оператором в скалярном произ¬
ведении направо и налево, находим для
/1Л)=Л1/>, /1Л>=Л1/> => (Л1/1Л) =Л</21Л) =/2<Л1Л>,
и если /j Ф/2, то
(/21Л)=о.
2.5. Аксиоматика
Суммируем, наконец, в сжатом виде основные положения квантовой ме¬
ханики в форме Шрёдингера.
Пусть дана классическая система, которая допускает гамильтоново описа¬
ние в терминах обобщенных координат {q} и сопряженных им импульсов {р}
с гамильтонианом Я (q, р, 0 без связей.
Постулат 1. Принцип суперпозиции. Квантовое состояние системы в мо¬
мент времени t—вектор гильбертова пространства: |Ф(t)) еН.
Постулат 2. Наблюдаемые. Физическим величинам, построенным из
обобщенных координат и импульсов, соответствуют наблюдаемые—эрмито¬
вы линейные операторы, действующие в гильбертовом пространстве состоя¬
ний, причем коммутационные соотношения для наблюдаемых определяются
согласно формализму канонического квантования по скобкам Пуассона в ис¬
ходной классической системе.
Постулат 3. Полнота описания. Среди наблюдаемых существует пол¬
ный набор {/}—максимальный набор функционально независимых взаимно
коммутирующих наблюдаемых, так что собственные вектора для полного
набора наблюдаемых образуют базис в гильбертовом пространстве:
|f)en: |ФЮ>=2|/)(/|Ф(0>. (2.16)
{/}
Выбор полного набора неоднозначен, что определяет свободу различных
представлений квантовомеханической системы.
Постулат 4. Динамика. Эволюция вектора состояния по времени задает¬
ся уравнением Шрёдингера
т^|Ф(0)=Н(4,р,С)|Ф(0>, (2.17)
при этом решается спектральная задача—определяется область допустимых
собственных значений полного набора наблюдаемых, среди которых выде¬
ляют: 1) квантовые числа п — дискретные значения наблюдаемых, 2) спек¬
тральные параметры v— непрерывные значения наблюдаемых; {/} = {п, v}:
Лекция 2
45
4'„(v, t) = (п, у|Ф(£)). Квантование, т. е. дискретная область значений на-
Олюдаемой, отвечающей непрерывной переменной в классической систе¬
ме, возникает как следствие корректного решения уравнения Шрёдингера:
решения должны принадлежать гильбертову пространству состояний, что
п мависимости от свойств системы может иметь место только при дискретных
шачениях классических физических величин.
Постулат 5. Физический смысл — вероятностная интерпретация. Ам-
11литуда вероятности Фп (v, t) = (n, v | Ф (£)) определяет плотность вероятности
но спектральным параметрам v и долю вероятности по квантовым числам п:
dwn = |ФП(v, О|2 dv, (2.18)
е нормировкой вероятности на единицу:
2/dv|«n(v,t)|2 = l, (2.19)
П
где гг и v могут быть многомерными.
Принцип соответствия. Динамика средних значений наблюдаемых кван¬
товой системы в пределе малых флуктуаций (предел больших квантовых
чисел) тождественна динамике соответствующих физических величин клас¬
сической системы.
Принцип соответствия также можно отнести к системе постулатов, ес¬
ли не оговаривать заранее способ квантования. Однако, как мы видели,
при каноническом квантовании имеет место теорема Эренфеста, так что
принцип соответствия, по сути, доказывается как следствие введенной нами
аксиоматики.
Итак, если волновые свойства физического объекта-состояния полностью
определяются вероятностной трактовкой гильбертова пространства состоя¬
ний, то природа дискретности в квантовой механике двойственна: во-пер-
ных, первичные объекты, частицы, уже сами по себе кванты, так как ча¬
стица либо присутствует в системе, либо ее в ней нет1; во-вторых, по своей
структуре динамическое уравнение в квантовой механике может приводить
1 Представление о частице как объекте квантовомеханического описания вполне естествен¬
но в нерелятивистской теории по самому построению физической системы, но оно остается
справедливым и при квантовании релятивистской теории классических полей, где введение
частиц уже выглядит менее тривиально и, по сути, может означать добавление дополнительного
постулата о возможности «корпускулярной интерпретации» результатов измерений, производи¬
мых над квантовыми системами с помощью макроскопических измерительных приборов. Речь
фактически идет о принципе дополнительности Бора, который до сих пор по-разному трактуется
различными авторами и иногда сводится просто к рассуждениям о ключевой роли соотношения
неопределенностей Гейзенберга. С нашей точки зрения этот принцип в развернутом виде звучит
следующим образом: реальные физические приборы измеряют матричные элементы наблюда¬
емых величин для квантовой системы частиц в вероятностном смысле при многократном по-
нторении опытов с идентичными состояниями системы. Эти измерения позволяют определить
зависимость матричных элементов от времени, которая находится в согласии с принципом де¬
терминизма и уравнениями эволюции. Вероятностные характеристики измеряемых матричных
элементов связаны между собой в соответствии с соотношениями неопределенностей. Поэтому
46
Тема 1 Принципы квантовой механики
к дискретности точных значений наблюдаемой, которая рассматривалась
как непрерывная переменная в классике. Это второе свойство, обусловлива¬
ющее динамическое квантование, и есть центральная проблема квантовой
механики.
2.6. Консервативные системы и спектральная задача, вакуум
Квантовая система называется консервативной, если ее гамильтониан не
зависит явно от времени: H=H(q, р). Тогда энергия системы—сохраняюща¬
яся величина, так как
т^ = [А,н]=о.
Уравнение Шрёдингера с определенным значением энергии
Йг|Ф(0)=В|Ф(0) (2.20)
принимает вид
ift^|*(t)>=fi|*(t)>. (2.21)
Последнее уравнение легко интегрируется:
|Ф(0) = е“*а|Ф), (2.22)
где |Ф) — вектор состояния, не зависящий от времени. Если рассмотреть
плотность вероятности для непрерывной наблюдаемой q
р(.ч)=\№т2=\(т\2=\*т2,
то, как видим, она не зависит от времени, т. е. профиль распределения для
стационарного состояния не изменяется со временем.
Уравнение (2.20) на собственные значения гамильтониана, не зависящего
от времени, называется стационарным уравнением Шрёдингера. В коорди¬
натном представлении
<q|A|*(t)> =Hq(q\nO) =Hg^(q, О
с учетом сокращения зависящего от времени фактора в обеих частях уравне¬
ния (2.20) получим
Hq^(q)=E^(q).
Решение стационарного уравнения Шрёдингера определяет спектр состоя¬
ний, которые тем самым дают решение спектральной задачи — фиксируют
область допустимых точных стационарных значений полного набора наблю¬
даемых.
В стационарных состояниях энергия принимает точные значения, т. е.
имеет нулевую дисперсию, так как эти состояния — собственные. Но это не
полное знание о системе, формируемое при измерениях, предполагает дополнительность са¬
мого процесса измерения для величин, совместно не измеримых. Принцип дополнительности
представляет собой согласованное объединение понятий детерминизма и корпускулярно-веро¬
ятностной трактовки концепции измерения в квантовой механике.
Лекция 2
47
чтчит, что у системы в общем случае не может быть энергий вне стационар¬
ных уровней. Действительно, можно построить суперпозицию, скажем, двух
собственных состояний с разными энергиями (а значит, двух ортогональных
состояний):
Viq, t) =c1e-»Blt4'1(q) + c2e~hE^^2(.q), \сг\2 + |c2|2 = 1.
Средняя энергия такого состояния
(А) = |с1|2Б1 + |с2|2£2^£1>2,
но в этом состоянии профиль распределения вероятности меняется со време¬
нем, так как
|Ф(д, t)|2 = |)с1Ф1(д)|е-н^-^+1д“-№+1д^ + |с2Ф2(д)||2,
где Да12(д) — разность комплексных фаз первого и второго состояний в су¬
перпозиции, а Д/312 — разность комплексных фаз постоянных коэффициен¬
тов съ с2. Поэтому интерференционная картина двух амплитуд зависит не
только от координат q, но и от времени.
Важнейшим понятием консервативной системы является вакуум — состо¬
яние с минимальной конечной энергией. Существование такого состояния
является, по сути, еще одним постулатом квантовой механики: если энергия
стационарного состояния неограничена снизу, то такая система считается
несовместной с квантовой теорией, и, следовательно, само существование
подобной системы запрещено.
Энергия вакуума Evac является минимально допустимой средней энергией
квантовой системы одинаково в стационарном или нестационарном состоя-
пии: {Е)^Ечас.
Задача 1.1. Найти стационарные уровни энергии частицы в потенциальном од¬
номерном ящике:
Г О, 0<х<а,
У(*) = <
( оо, х^а, х^О,
м также их волновые функции, средние значения координаты, импульса, их дисперсии
и сравнить с классическими выражениям для этих средних и флуктуаций.
Решение. Потенциал в этой задаче показан на рис. 1, где мы полагаем, что
потенциальные барьеры слева и справа от ямы стремятся к бесконечности, образуя
тем самым потенциальный ящик, вне которого волновая функция обращается в нуль:
гф(х^О)='ф(х^ а) = 0.
Волновая функция, определяющая локальную плотность вероятности, должна быть
непрерывна. Поэтому
0)=-ф(а) = 0,
а стационарное уравнение Шрёдингера в интервале 0 < х < а
-^гр"=Бгр, Е> О,
имеет решения в виде
h2k2
'ф 00 = Сг sin(foc) + С2 cos (foe), —— =Е.
48
Тема 1 Принципы квантовой механики
Однако условие зануления волновой функции на концах интервала приводит к усло¬
виям
ka = nn, n€ N, С2 = 0. (2.23)
Это определяет дискретные значения квантованной энергии, которая принимает
2т а2
задающие среднее значение квадрата импульса частицы на n-м уровне
{р2) = {2тЕп) = ^п2п2.
Волновые функции принимают вид
грМ = С1 0 <х<а.
Нормированное на единицу решение получается, если положить
Заметим, что условие (2.23) означает, что в потенциальном ящике укладывается
целое число полуволн, поскольку волновой вектор к связан с длиной волны Я соот¬
ношением к = 2п/Х, так что а/Л = п/2. Средние значения координаты и ее квадрата
после простейшего интегрирования
<*> = Jd* 1Р2Ш = §, (х2) = f dx 1/>2(х)х2 = £-
которые можно сравнить со средними в классической теории, где частица совершает
периодические движения со скоростью v:
е=!ТГ' т=Т■ *Ю={И' г Т\ °<tS2'
так что
Mclass = h J dt X(0 = (-^2) class = I J dt *2(0 =
Лекция 2
49
Кик видим, и в квантовой механике, и в классической частица в среднем находится
н центре потенциального ящика, а флуктуации возле среднего определяются диспер¬
сией
(Ах2) = {(х - (х))2) = (х2 - 2х(х) + (х)2) = (х2) - (х)2,
•гп к что в квантовом случае
(Дх)2= —
и дисперсия стремится к классическому выражению при больших квантовых числах
п -► а> в согласии с принципом соответствия. Поскольку среднее значение импульса
ривно нулю:
а а а
(р) = J dx\j)(x){—ih\p/(x)}=—{-ift}/ dxrsin(bc) cos (/ос) = -ih- J dx sin(2foc) = 0,
о a о a о
дисперсия импульса равна среднему от его квадрата
(Ар)2 = (р2) = (2 тЕп) = ~2 п2п2,
а произведение неопределенностей для координаты и импульса—
(Дх)2(Др)2 = £ (я2 п2 -6)2^,
что согласуется с общим рассмотрением для координаты и импульса. Величину
Ах Ар = АГ
называют элементом объема фазового пространства. При п —> оо на одно состояние
Ап = 1 приходится фазовый объем
Л„1 dAr л h
АГ к = ——Ап->——71.
1Дп=1 d п 2V3
Задача 1.2. Докажите операторное тождество
00
едВе-А=В + У’ [А, [А, ...[А, В]...]].
n=lN v '
п
Решение. Вычислим производные операторной функции
F(A) =емВе_ЛА
по параметру Я в нуле:
п п
dnF(A)
А=
dA"
= У AkeXABe~XAAn~k (-l)n~k . =V АкВАп~к(-1)П-к.
я=о j—L я=о
fc=0 fc=0
Значит, искомый оператор можно записать в виде разложения в ряд Тейлора опера¬
торной функции при значении Я = 1
п
eABe~A=F( 1) = 2 ^ YjAkBAn~k(-l)n~k.
п=0 * к=О
При п = О
о
^АкВАп_Ч-1)п_,:=В.
к—О
Докажем методом индукции равенство
п
= [А, [А, ...[А, В]...]].
' '
к=О
50
Тема 1 Принципы квантовой механики
Действительно, при n = 1 имеет место тождество
1
AkBAn~ki-1)"-* = -ВА+АВ= [А, В].
к=0
При п = т^1 верно
т
J]AkBAm-k(-l)m-k = [A, [А, ...[А, В]...]],
fc=0 4 ^ '
Ш
так что при п = т +1, выделяя первый и последний члены суммы, получим
Ш+1 /■ Ш \ /• Ш \
5] AfcBAm+1-4-l)m+1"'c = - (2 AkBAmk(~tynk )A+A{Y^ АкВАт~к(.-1)т-к ) =
fc=0 W=o j У k=0 '
= [a, 2 AkBAm~k(—l)m-,: j = [А, [А, ...[А, B]...]] = [A, [A, ...[A, B]...]] .
fc=0 m (m+1)
Таким образом, утверждение доказано.
Задача 1.3. Докажите операторное тождество для функции F(B)
eAF(B)e-A=F(eABe"A).
Решение. Согласно общему определению функция от оператора записывается
в виде ряда Тейлора
F(B)=2 iF(n)(0)Bn,
так что рассмотрим выражение
елвп е-А = еАВе-А еАВе-А = (еЛВе-А)П
V V, ' 4 У ’
п
где мы учли, что
еАе“л = 1.
Значит, действительно,
00
eAF(B)e_A = ^] ^jF(n) (0)(еАВе_Л)" =F(eABe“A).
п=О
Задача 1.4. Докажите, что для операторов Л и В, перестановочных со своим
коммутатором [А, В], имеют место равенства
еАеВ = е[А,В]еВеА
и
£еАеВуп _ е|п(п-1)[ДВ] епВепА
Решение. Согласно предыдущей задаче
еАеве“АеА = ехр(еАВе_А)еА.
Как мы доказали выше,
00
еАВе~л=В + V [А, [А, ...[А, В]...]],
Ь1, • '
П
но этот ряд по условию задачи обрывается на первом слагаемом:
еАВе~А = В + [А, В].
Лекция 3
51
Значит,
еАеВ =еВ+[А,В]еА = е[А,В]еВеА9
поскольку [В, [А, В]] = [А, [Л, В]] =0, и первая часть утверждения доказана. Далее,
__ ^AgBjn-lgAgB __ ^eAeBjn-l0[A,B]eBeA =е[А,В] ^AgBjn-lgBgA
Уже доказано, что
eAQkB =ек[А,В] екВеА
где /с —число. Значит,
п
^еАеВ^п = е^к1А,В]епВепА=е1п{п-тА,В}епВепА^
где мы использовали известное выражение для суммы арифметической прогрессии.
Задача 1.5. Докажите, что для операторов Л и В, перестановочных со своим
коммутатором [А, В], имеет место тождество Бейкера—Хаусдорфа
gA+В = е 2 [А,В] qBqA '
Решение. Вычислим ехр(АН-В) как предел
еА+в = lim (l + -(A+B)V = lim(eA/neB/n)",
П-*oo \ Jl J П—*oo
где порядок сомножителей под знаком степени, конечно, можно было выбрать и об¬
ратным, что не умаляет общности дальнейшего рассмотрения. В предыдущей задаче
мы показали, что
^eA/neB/n^n = е jnCn-l) [А,В] евеА^
так что
еА+в = Um е’n(n“1) £[дв] евеА = ег № евел.
Лекция 3
Плотность потока вероятности, уравнение непрерывности, свободная нереля¬
тивистская частица, волновой пакет, фазовая и групповая скорости, неопре¬
деленность координаты и импульса, интегралы движения и инвариантность
классического действия, условия вырождения состояний, неопределенность
энергия-время, обращение стрелы времени, Г-четность, представление Гей¬
зенберга, матричная динамика.
3.1. Уравнение непрерывности: поток вероятности
Рассмотрим нерелятивистскую частицу в потенциальном поле с гамиль¬
тонианом в координатном представлении
H = J^ + V(r), р2 = (—iftV)2 = —h2A.
Базис на непрерывных координатах |г) задает волновую функцию, амплитуду
вероятности (г|Ф(0) = Ф(г, t), которая, следовательно, является непрерыв-
52
Тема 1 Принципы квантовой механики
ной1. Определим зависимость плотности вероятности от времени
^р(г,0 = ^{Ф*(г,0Ф(г,0}
с помощью уравнения Шрёдингера, так что, для краткости опуская аргумен¬
ты,
= 1{(яф*)ф - ф*(яф)}=
= S {+v*")'*-**(-+'}=
= -^{(ДФ*)Ф - Ф*(ДФ)> = Д V • {Ф^Ф) - ^Ф*)Ф>.
Zm Zm
Введем вектор потока вероятности2
; = -^|{Ф*^Ф) - (УФ*)Ф} (3.1)
и получим в этих обозначениях уравнение непрерывности для плотности
вероятности
^ + v-j=0 фф ^ + divj=0. (3.2)
Интегрирование уравнения непрерывности по объему V в области допусти¬
мых значений координат дает, с одной стороны,
— Г d3rp = —1 = 0,
dt J н dt ’
так как вероятность нормирована на единицу, а с другой стороны,
J d3r diу j=§ j-ds,
V dV
где dV — поверхность-граница объема V. Поэтому из уравнения непрерыв¬
ности и сохранения вероятности следует, что поток вероятности через по¬
верхность объема, где находится квантованная частица, должен обращаться
в нуль.
Рассмотрим, к примеру, свободную нерелятивистскую частицу в коорди¬
натном представлении. Гамильтониан —
Поскольку
т^=[р,й0]=о,
Наблюдаемая плотность вероятности |Ф(г, t)|2 в непрерывной области переменной г по
своему физическому смыслу может быть только непрерывной функцией от г.
2В терминах оператора скорости v = p/m вектор потока j есть просто оператор скорости
«в обкладках волновой функции и ее комплексного сопряжения», т. е. оператор, подействовав¬
ший налево и направо: на волновую функцию Ф и Ф*, - так, чтобы результат был заведомо
вещественным, а именно, j = ^{Ф*в>Ф) + (£Ф)*Ф}, и значит, поток вероятности отвечает плот¬
ности скорости.
Лекция 3
53
у свободной частицы сохраняются и энергия, и вектор импульса, причем они
могут быть измерены совместно. Поэтому выберем в качестве базиса полного
набора наблюдаемых импульс частицы, так что
р|р>=р|р>, Н0\р) = ^\р).
Для удобства отнормируем состояния согласно1
(р/|р) = (2яЮ35(р/-р) Ф* J 1р>сЙ)з(р1 = 1-
Тогда справедливо равенство
V)=j
как это и должно быть согласно требованию о полноте базиса. Найдем вол¬
новую функцию свободной нерелятивистской частицы
Фр(г) = <г|р),
где в координатном представлении нормировка состояний задана соотноше¬
ниями
(r'lr) = 6(1^ —г) <=> J |r) d3r (г| = 1.
Используем координатное представление для оператора импульса:
(г|р|р) = (г|р|р) <=> рФр(г)=рФр(г)
ФФ — iftV'I'p(r) =р'1'р(г) => Фр(г) =7Vrenpr.
Нормировочную константу N выберем вещественной и положительной (гло¬
бальная фаза ненаблюдаема), исходя из нормировки состояний:
(р'\р) = (2яК)3 5(р'-р) <=>
<^=> / (p'\r) d3r <r|p) = J Ф*,(г) d3r Фр(г) =
=М2 f d3r ел(р-р ) г=Я2(2пК)3 5(р'-р),
так что Я = 1, и
Фр(г) = е^г.
Таким образом, состояние свободной нерелятивистской частицы описывает¬
ся волной де Бройля
Фр(г, t) = enip'T~Et\
Для этого состояния из (3.1) легко получить вектор потока вероятности
j=P
J тп}
который совпадает с вектором скорости классической частицы.
1Трехмерный спектральный параметр — вектор v = и для состояний |v> стандартная
2 пп.
нормировка (v|у') = 5(у -v') = (2пК)3 5(р-р')-
54
Тема 1 Принципы квантовой механики
Задача 1.6. Выведите выражение для матричного элемента (г|р|г'), исходя из
канонического квантования, т. е. из коммутатора координаты и импульса.
Решение. Согласно каноническому квантованию коммутатор координаты и им¬
пульса покомпонентно равен
Va, Рр\ = Ш5ар>
где 5ар — символ Кронекера в 3-мерном евклидовом пространстве (индексы а, /3
пробегают значения от 1 до 3). Вычислим матричный элемент этого коммутатора,
(г| • |г'). С одной стороны,
(НЕra> PplW) = (r\faPfi-P^aW} = (r-r,')a(r\pp\r'},
поскольку базис построен из собственных состояний эрмитова оператора координа¬
ты, т. е. его действие дает числа
Ur')=r'a\r'), (r\ra = ra(r\.
С другой стороны, в силу нормировки базиса с непрерывным спектральным парамет¬
ром
{г\ШарУ) = Ша0 бСг-г7).
В итоге находим равенство в смысле обобщенных функций
(г-г')а(г\рр\r') = ih5af} 5(г —г').
В фурье-представлении
d3fc ,ifc-(r-r')
(2л:)3
Введем представление в виде интеграла Фурье для матричного элемента
8(г-г')= |
-rt-J
теграла $
<r|p|r') = J (0eik^V(fc),
ю необходимо установить.
(r-r%{r\Pf,\r') = -i J (Цз//>№)
где /(fc) — функция, которую необходимо установить. Тогда запишем
jLpiHr-r7)
дка
и после интегрирования по частям с нулевым вкладом граничных членов (в этом
можно убедиться позже, установив явный вид функции /) находим
(г __ г'\ /Г|А IfA —i Г pifc-Cr-r') д//з№)
(Г г)а(г|р^|г)-1 J (2я)3е дка ,
так что полученное выше соотношение для обобщенных функций дает
id-^- = ihSaP =» m=hk,
где мы положили константу интегрирования равной нулю. Значит,
(r|p|r') = ft J ^3eifc(r-r/)fc=—invr J -^eik^ = -ihvr5(r-r'),
где мы указали у символа набла аргумент дифференцирования. Совершенно анало¬
гично в импульсном представлении
(р|г|р'> = iftVp 5(р-р0.
Лекция 3
55
3.2. Волновой ПАКЕТ
Теперь мы можем представить волновую функцию стационарного состоя¬
ния в виде
Ф(г, 0 = <г|Ф(0> = J* <г|р)^з<р|Ф(0),
где
(г|р) = Фр(г) = е»рг,
о
(р|Ф(0> = е-»*(р|Ф) = е"»йФ(р).
Последнее выражение справедливо не только для стационарной волновой
функции, но и для частицы с заданным законом дисперсии, т. е. зависи¬
мостью энергии от импульса Е = Е(р) (энергия точно задается значением
импульса, что имеет место, например, для свободной частицы). В итоге
получаем представление для волновой функции в виде волнового пакета
ф(гд)=/ (^ф(р)е"Ср'г“£0
с амплитудой Ф(р) —пси-функцией в импульсном представлении. Запишем
амплитуду в виде
Ф(р) = |Ф(р)|е1а(р),
так что комплексная фаза </?/Й в подынтегральном выражении1 для волнового
пакета задается выражением
<р = р • г — Et + fia(p). (3.3)
Фронт волны задается поверхностью постоянной фазы ip = const, откуда на¬
ходим, что точки этой поверхности движутся по траектории
17
r(t) = ^2pt + r0 => </>=p-r0 + fta(p)= const.
Скорость движения фронта волны называется фазовой скоростью:
Для того чтобы определить характеристики движения пакета как целого,
рассмотрим вклады в интеграл от двух областей. Во-первых, если фаза (/?
меняется в некоторой области импульсов достаточно быстро по сравнению
со скоростью изменения модуля амплитуды, то подынтегральное выражение
быстро осциллирует и вклад этой области в интеграл подавлен. Во-вторых,
фаза может иметь стационарную точку
13десь, в отличие от изложения квантовой гипотезы де Бройля, мы переходим от безразмер¬
ной фазы к величине ip с размерностью действия.
56
Тема 1 Принципы квантовой механики
В этом случае вклад области вблизи стационарной точки доминирует, т. е.
он определяет область, где в координатном пространстве волновая функция
существенно отлична от нуля. Из явного выражения для фазы условие стаци¬
онарности фазы запишется в виде
r-jpt + ft|2 = 0,
др др ’
что можно переписать как
r(t)=Vgrt+r0,
где мы ввели групповую скорость
1/ -25
Ph~ др’
которая показывает, с какой скоростью перемещается волновой пакет как
целое.
Для свободной частицы
e=pL
2т9
так что
1, __Е __Р_ _ _ Р
Ph р2Р 2m5 V*h др т9
т. е. фазовая и групповая скорости существенно отличаются, и волновой
пакет в ходе эволюции довольно быстро расплывается.
Волновой пакет представляет собой пример преобразования Фурье. Легко
оценить область вблизи стационарной точки, которая определяет основной
вклад в интеграл. Очевидно, что только при изменении комплексной фазы
порядка единицы (или 2 п) экспонента еще не начинает сильно осциллиро¬
вать и дает существенный вклад. В терминах (р:
А y?~ft.
Вариация фазы под знаком интеграла определяется зависимостью от импуль¬
са, так что
Ду«ЦдР,
но в первом порядке из-за стационарного условия эта флуктуация равна нулю
в центре волнового пакета. Отличие от нуля возникает, если сдвинуть точку
координат с траектории центра волнового пакета, т. е. положить
AV * др^АРаАГр = АРаАГ“ ~ П’
где производная второго порядка для </> подставлена в явном виде. Поэтому
из общих свойств преобразования Фурье заключаем, что характерные раз¬
меры пакета в координатном и в импульсном пространствах покомпонентно
связаны соотношением
АхАрх ^ ft,
согласно принципу неопределенности.
Лекция 3
57
3.3. Интегралы движения, условия вырождения
Согласно уравнению Гейзенберга для полной производной оператора по
иремени (2.9)
mdF = mfF + [^]’
среднее значение, дисперсия наблюдаемой и все ее статистические момен¬
ты распределения (средние высших степеней оператора) сохраняются, если
полная производная оператора по времени df/dt тождественно обращается
и пуль, а значит,
ih% + U, Н]=0. (3.4)
11ри этом распределение вероятностей реализации значений наблюдаемой
и ее спектре остается постоянным во времени, а сама наблюдаемая называ¬
ется интегралом движения1.
В частности, для оператора, не зависящего явно от времени, следует
положить
U,H]= 0.
Постоянные операторы, коммутирующие с гамильтонианом, сохраняются.
Этот факт находится в полном согласии с каноническим формализмом
п классической механике. В самом деле, динамической переменной /(q, р)
соответствует, после замены координат, канонически сопряженная величи¬
на (р, которую можно отнести в ряд обобщенных координат2, так что
dt- dip-"’
/Для интеграла движения скобка Пуассона обращается в нуль, что после ка¬
нонического квантования отвечает сохранению квантовой наблюдаемой. С
другой стороны, как мы видим, обращение в нуль скобки Пуассона связано
с тем, что гамильтониан классической системы не зависит от обобщенной ко¬
ординаты ip, т.е. имеет место инвариантность гамильтониана относительно
сдвигов
(// = ip + и. (3.5)
Пара {/, ip} называется переменными действие-угол.
Согласно теореме Нётер параметрическая замена координат ip' = ip'(ip, и)
приводит к вариации действия в виде
—= Г
dи J dt Удф ди )’
гВ качестве примера интеграла движения, явно зависящего от времени, приведем галилеев
момент замкнутой системы частиц K=2(mara - fPa)-
а
2Можно так условиться для определенности.
58
Тема 1 Принципы квантовой механики
где L — функция Лагранжа, связанная с гамильтонианом Я преобразованием
Лежандра, но в исследуемом нами случае (3.5)
V.
ди 3
а по построению канонически сопряженный к </? импульс-—это /:
дЬ_ _ г
дф
и он сохраняется, так что
I=J
а значит, действие инвариантно относительно трансляций переменной (/?.
Таким образом, мы установили, что инвариантность действия классиче¬
ской системы отвечает интегралу движения и в квантовой механике1. Однако
проведенное нами выше исследование относилось к наблюдаемой, соответ¬
ствующей непрерывным преобразованиям классических обобщенных коор¬
динат, в то время как преобразованиям, связанным с дискретными симмет¬
риями, отвечают исключительно квантовые интегралы движения, с приме¬
рами которых мы встретимся ниже.
Теперь рассмотрим консервативную систему с интегралами движения /
и g:
[/,Я]= о, [g, Н]=0.
Как мы знаем, если / и g коммутируют, то в полный набор наблюдаемых
консервативной системы можно включить совместно измеримые значения
энергии, / и g. Если же
[/,g] = iftC^0,
то / и g не измеримы точно совместно: имеют место флуктуации. Составим
набор наблюдаемых из собственных векторов энергии и / и рассмотрим
состояние |Ф):
Я|Ф)=Е|Ф>, />)=/0|Ф).
Тогда вектор
№)
является собственным для энергии, так как Hg = gH и
Hg\*)=gH\*)=Eg\V).
Итак, мы имеем два собственных вектора энергии |Ф) и £|Ф) с одним и тем же
значением энергии. Но мы строили базис по совместным собственным век¬
торам энергии и оператора /. Поэтому рассматриваемый вектор состояния
разлагается в этом базисе как
m=Y>c№’fk>> 1ф>=|я,/о>- (з.б)
к
1Если инвариантность классической системы после квантования не приводит к соответству¬
ющему интегралу движения, то говорят, что имеет место квантовая аномалия.
Лекция 3
59
Нектор состояния g\E, /0) не может быть представлен как суперпозиция соб¬
ственных векторов оператора / с одним и тем же значением /0, так как в этом
случае, как мы показывали, коммутатор fug должен обращаться в нуль.
!)то означает, что в сумме (3.6) имеются вклады от кф О, т. е. состояние
с энергией Е вырождено: состояние с заданной энергией имеет несколько
собственных значений оператора /.
3.4. Соотношение неопределенностей энергия-время
Если система неконсервативна, то среднее значение энергии зависит от
иремени, так как ЬН/Ъгф0. Рассмотрим оператор Л(д, р), среднее которого
также зависит от времени. Тогда согласно уравнению Гейзенберга
[A,H] = ih^. (3.7)
Как мы показали в общем случае, из (3.7) следует, что флуктуации энергии
и наблюдаемой А связаны соотношением
AAAEZ|
(£>
(3.8)
Особый интерес представляет ситуация, когда временная зависимость
энергии и оператора А приводит к их малым флуктуациям АЕ, АЛ вблизи
средних значений Ё, Л, а характерное время изменения средних—At. Тогда
можно положить
АЛ
At ’
и в этом случае из (3.8) следует соотношение неопределенностей энергия-
премя для неконсервативных систем:
AEAt> |. (3.9)
В качестве примера рассмотрим переход квантовой системы с одного
квазистационарного уровня на другой. Квазистационарность означает, что
в пренебрежении взаимодействиями, обусловливающими редкие переходы
между уровнями, квантовая система с хорошей точностью описывается как
стационарная, т. е. как система с неким спектром уровней энергии. При пе¬
реходах изменяется и энергия, и другие характеристики квазистационарных
уровней. Если At—характерное время изменения наблюдаемых параметров
квазистационарных уровней, то его называют временем жизни квазистаци¬
онарного уровня т. Флуктуация же энергии отвечает неопределенности в ча¬
стоте перехода между уровнями v = (Ег — Е2) /Й. Поэтому точность измерения
частоты перехода ограничена шириной Г, а соотношение неопределенно¬
стей энергия-время устанавливает связь флуктуации энергии излучения при
переходе между квазистационарными уровнями с временем жизни возбуж¬
денного состояния: тГ~Й.
60
Тема 1 Принципы квантовой механики
3.5. Г-ИНВАРИАНТНОСТЬ
Классическая система без диссипации энергии (т. е. без трения) облада¬
ет инвариантностью относительно обращения времени t —> —t. Рассмотрим
соответствующую консервативную квантованную систему в координатном
представлении1
t) =H(q, Д,Жд, О-
Отсутствие диссипации отвечает вещественности гамильтониана2:
Я*=Я.
Инвариантность квантовой системы относительно обращения стрелы вре¬
мени означает, что действие оператора обращения времени Т на волновую
функцию
f'Kq, 0 = ФГ(9, -t)
дает волновую функцию, удовлетворяющую уравнению Шрёдингера
Фг(д, -t) =H(q, Д,)ФТCq, -t).
Уравнение для ФтСд, следует сравнить с уравнением Шрёдингера, в ко¬
тором мы заменим t—» — t и возьмем комплексное сопряжение обеих частей
с учетом вещественности гамильтониана:
ift£**(q, — О =H(q, Pg)^*(q, -t).
В итоге заключаем, что преобразование волновой функции при инверсии
времени имеет вид
f*(q, t) = **(q, -О, ФтСд, t/) = »*(q, -t), = (3.10)
Поскольку гамильтониан для исходной волновой функции и обращенной по
времени один и тот же (по построению), это можно записать как3
ТН = НТ ФФ [Г, Я] =0,
т. е. Т — интеграл движения. Таким образом, инвариантность классической
системы относительно дискретной операции обращения стрелы времени
1 Изложение в этой лекции касается только однокомпонентных, скалярных, волновых функ¬
ций без внутренних квантовых чисел вроде спина и т. п. В противном случае необходимо
определять, как операция обращения стрелы времени действует и на эти квантовые числа.
2В противном случае передача энергии во внешнюю по отношению к рассматриваемой
системе среду означало бы возбуждение в ней квантовых состояний, так что равная единице
вероятность найти систему и окружающую среду складывалась бы из вероятности обнаружить
саму систему и вероятности найти возбуждения внешней среды, которая становится отличной
от нуля, так что в полной вероятности обнаружить исходную систему возникали бы вклады, даю¬
щие убывание этой вероятности со временем, т. е. появились бы мнимые добавки к собственным
значениям гамильтониана — энергии, которые определяют зависимость плотности вероятности
от времени: |Ф(д; t)l2 = l^(q)2| expj-^(E —£*)t|.
3В этом можно убедиться и просто пользуясь уравнением Шрёдингера.
Лекция 3
61
приводит к возникновению нового квантового числа, которое называют
Т-четностъ.
Для стационарного состояния фактор временной зависимости под дей¬
ствием Т
fe-iEt = e-iEt
сохраняет свой вид, а координатная часть волновой функции просто ком¬
плексно сопрягается
t9(q) = 9*(q).
Значит, квадрат оператора обращения времени в квантовой механике равен
единице:
Г2 = 1,
а его собственные значения
Хт = ±1.
Отсюда следует, что вещественные волновые функции стационарных состоя¬
ний являются, как говорят, Г-четными:
f*(q)=*(q), ®*(q) = *(q),
а чисто мнимые Г-нечетными:
Гф(д) = -ф(д), ф*(д) = -ф(д).
Так как после преобразования Г волновая функция удовлетворяет уравне¬
нию Шрёдингера, обращенные по времени состояния также обладают свой¬
ством суперпозиции, а значит, оператор обращения времени сохраняет прин¬
цип суперпозиции, но при этом
f [c^a(q, t) + с2Ф2^, ОП =с*Ф*(q, -t) +с*Ф*(q, -t),
то есть оператор t является антилинейным.
В обозначениях Дирака преобразование имеет вид
(q|f*(t))=**(q,-t).
Тогда
<ТФ(0|ГФ(0) =2,(r*(t)|q)(q|T»(t)> = J dq №*(q, -t)]***(q, -t) =
= / dq #(q, -t)«*(q, ~0 = <Ф(-0|Ф(-0).
В частности,
<гф(0|гф(0) = <Ф(—0|Ф(—1)> = 1.
В итоге оператор обращения времени, конечно, сохраняет нормировку состо¬
яния, так что он является антилинейным унитарным оператором.
62
Тема 1 Принципы квантовой механики
3.6. Представление Гейзенберга
С помощью оператора эволюции £7(t) матричный элемент произвольного
Поэтому динамику квантовой системы можно рассматривать в терминах
операторов в представлении Гейзенберга:
причем все вероятностные характеристики таких операторов вычисляются
по не зависящим от времени состояниям, в отличие от рассматриваемых
нами ранее состояний в представлении Шрёдингера:
Итак, в представлении Гейзенберга векторы состояний не эволюциони¬
руют, вместо этого динамикой обладают операторы. Запишем динамические
уравнения для операторов в представлении Гейзенберга. Для этого продиф¬
ференцируем оператор по времени и воспользуемся известным уравнением
движения для оператора эволюции:
т. е. получаем коммутатор операторов в представлении Гейзенберга. В итоге
а значит, получается обычное уравнение Гейзенберга для производной опе¬
ратора по времени только в представлении Гейзенберга.
Если оператор эрмитов в представлении Шрёдингера, то он эрмитов и в
представлении Гейзенберга:
В представлении Гейзенберга наблюдаемые зависят от времени, они удовле¬
творяют уравнению Гейзенберга. Если наблюдаемая не зависит от времени
явно, то можно взять матричный элемент уравнения Гейзенберга по состоя¬
ниям (п\ • \т), откуда получаем
Вставляя единичный оператор в виде l = 2fc 1Ж^1 в произведение операто¬
ров, матричный элемент коммутатора представим в форме
FHV = u4t)FU(.t),
(3.11)
|ф)н=£Ч0|ф(0)=|ф>.
(3.12)
= ihufi£u+&(-йР+Рн)и.
at dt
(3.13)
р*=р <=> F£ = (t>W = t>+Ft/=FH.
(п|#н(2 |ВД)ЯН-ЯН(2] \k)(k\)PH\rn)=FnkHkm-HnkFkm,
k k
Лекция 3
63
где справа подразумевается суммирование по повторяющемуся индексу к.
11озтому уравнения эволюции для оператора примут вид
i h^=FnkHkm-HnkFkm> (3.14)
и и таком виде они являются основными динамическими уравнениями мат¬
ричной механики, сформулированной Гейзенбергом, Борном и Йорданом.
Ксли система консервативная, то базис строится по собственным векторам
оператора Гамильтона, т. е.
Н-кт Ет&кт>
матрица диагональна и уравнения Гейзенберга для наблюдаемых принима¬
ют вид
^Цг=Рпт(.Ет-Еп), (3.15)
что необходимо также дополнить выражением для гамильтониана, т. ё. энер¬
гии. Например, для осциллятора с массой m и частотой со в матричном виде
гг, л р2 , mco2q2 _ 1 , mсо2
H(q, р) 2m 2 > п 2т^п^^п 2 0-пкЧкпв
!)то позволяет приравнять правые части в уравнениях (3.15), т. е. коммута¬
торы в матричном представлении, их явному выражению. Например, для
координаты получим
(n\[q,H]\m) = ih(n\^\m) = ih{n\£\m) = ih^,
так что
ih^ = qnm(Em-En) = ih^-,
и аналогично для импульса
(п\[р, Й]\т) = -ift(n|^|m) = -ih(n\ma>2Q\m) = -ihrnco2qnm,
откуда
^ Рпт№m — Er) —iftmct) qnm-
Уравнения матричной механики для осциллятора были решены Гейзенбер¬
гом еще до того, как Шрёдингер сформулировал свою волновую квантовую
механику, поскольку этот вопрос, собственно говоря, составлял содержание
первой статьи Гейзенберга, положившей основу матричной механики. Важно
подчеркнуть, что в представлении Гейзенберга квантование не может воз¬
никнуть в качестве ограничений на волновую функцию, которые следуют из
ее физического смысла, как это происходит в представлении Шрёдингера.
Поэтому в качестве «условия квантования» в матричной механике выступает
связь между матрицами координат и импульсов, а именно их коммутатор,
который фактически был введен в упомянутой статье Гейзенберга.
64
Тема 1 Принципы квантовой механики
В самом деле, из уравнений для производных координаты и импульса элемен¬
тарно заключаем, что, например, подстановка выражения для матричного элемента
импульса через матричный элемент координаты дает
qnm{(.Em-E„)2-h2a>2} = О,
откуда qnn = 0 и qnm # 0, если \Ет — Еп \ = hco. Будем считать спектр связанных ста¬
ционарных состояний осциллятора дискретным и невырожденным1. Тогда каждому
значению энергии Еп соответствует пара состояний с энергиями
* En + hco = En+1,
Еп ч
Еп Ь.о) — Еп_ 1,
где мы воспользовались свободой в выборе системы нумерации состояний. Именно
для таких состояний не равны нулю матричные элементы qn>n±1. Далее, диагональный
матричный элемент соотношения неопределенностей координата-импульс в матрич¬
ных обозначениях принимает вид
(гг|[д,р]|п) = Ш => qnkpkn-pnkqkn = ih.
Опять выражая импульс через координату, находим
ft2 ft
ЧпкЧкп (Рк *„) 2m ^ Q.n,n+l4n+l,n 4n,n-l4n-l,n 2тсо *
Определим комплексные фазы состояний2 так, чтобы ненулевые матричные элементы
координат оставались вещественными: qnm=q*m- Тогда в силу эрмитовости коорди¬
наты qnm = q*mn находим qnm = qmn. Значит, положительно определенные величины
8п =<?пп-1 =(?n,n-i<Jn-i,n образуют арифметическую прогрессию, так как для них мы
установили рекуррентное соотношение
_ ft
gn+1 Sn 2mш'
Для основного состояния с наименьшей энергией положим п = 0, и, следовательно,
g0 = 0, поскольку состояния с энергией Е_г =E0-hco не существует. В результате,
ft v I ft v . I mhco
*" = 2^П => 4nji-i ~ у 2тсоП =* Pn.n-l = lV—
Эти значения устанавливают матричные элементы в момент времени t=0, а их зави¬
симость от времени легко получается интегрированием записанных выше уравнений
Гейзенберга, так что
Наконец, элементарное суммирование в выражении для энергии по к=п± 1 приводит
к выражению
En = ha>(n+l).
1Это доказывается в лекции о свойствах одномерного уравнения Шрёдингера.
2В момент времени t = 0.
Лекция 4
65
Лекция 4
Уравнение Шрёдингера из вариации «квантового действия», вариационная
задача, глобальная и локальная калибровочная инвариантность, закон со¬
хранения заряда, минимальное взаимодействие нерелятивистской скалярной
частицы с электромагнитным полем, стационарное уравнение Шрёдингера
в импульсном представлении, пространственная четность, трансляции, ква¬
зиимпульс, функции Блоха, номер зоны.
4.1. Вариационный принцип
Волновую функцию можно рассматривать и как «поле» с действием1
S = J d3r dt Ф*(г, -я}ф(г, t). (4.1)
Действительно, считая ФиФ1 независимыми переменными варьирования2,
найдем уравнения Лагранжа—Эйлера согласно принципу экстремального
действия:
р~ = 0 <=> Щ=0 => ih^-H^ = 0;
бфТ ЭФ* dt ’
!f = 0 ф=> = 0 =* -&A-ihjrVf = 0.
<5Ф ЭФ dt ЭФ dt
Как и следовало ожидать, вариация дает уравнения Шрёдингера для волно¬
вой функции и комплексно сопряженной к ней. Заметим, что для динамиче¬
ской переменной q —> Ф стандартное определение канонически сопряженно¬
го ей импульса дает
р=|4 -»v=^=
* dq ЭФ
Это подтверждает обоснованность независимой вариации поФи Ф1*, как это
имеет место в гамильтоновом формализме.
Для стационарного состояния действие принимает вид
Sstat = / d3r«t(r){£ —А}Ф(Г),
где мы «убрали» тривиальный фактор интегрирования по времени. В этой
форме вариационную задачу часто используют для приближенных оценок
энергии стационарного состояния и его волновой функции, находя минимум
действия в классе пробных функций с конечным числом параметров.
1При этом не следует забывать, что волновая функция —это не волна материи, а амплитуда
вероятности!
2При варьировании, строго говоря, необходимо учитывать то, что в гамильтониан входят
частные производные по координатам, но мы воспользуемся эрмитовостью гамильтониана, т. е.
тем, что его действие «направо» эквивалентно действию «налево», так что при варьировании,
иапример, по Ф будем считать, что гамильтониан со всеми своими производными действует
на Ф*, и т. п.
66
Тема 1 Принципы квантовой механики
Задача 1.7. Найти энергию стационарного состояния осциллятора в классе проб¬
ных функций
Ф(д)~е 2о2.
Решение. Действие гамильтониана осциллятора на пробную функцию дает
Производные равны
ЯФ(д)=■
Ф'(д) = -4е-^, ®"(q) = «L£ie-&.
O’ сгч
Прежде чем находить минимум действия по параметру пробной функции <т, необхо¬
димо отнормировать волновую функцию:
N=J dq|^(q)|2= J dqe”^ = jj dqdq'e-4^ J ?
— 00 — 00 — 00
так что, вводя на плоскости {q, q'} полярные координаты
q = r cosip, q' = r sin ip,
находим стандартное выражение для гауссова интеграла
f2n <Х> ^2 ^1/2
N = | J d(/? J г dr е-^ | = у/па2.
оо
Тогда действие примет вид
00
г _ 1 f J -4 Гг. й2 Ч2Г_ 2 fi2 11 _г, ft2 а2 г_ 2 ft2 1
t_ а/гё J 4'6 а Г 2шсг2 2 [т<° mcr4 J J — 2тсг2 4 1”“° тег4!’
— 00
где мы использовали интегрирование по частям. Найдем экстремум по а2. Диффе¬
ренцируя и приравнивая производную нулю, получаем:
S' - fi2 ma>2-0 => <т2 = —
stat 4тсг4 4 тсо *
В итоге значение гамильтониана в экстремуме
Вторая производная
s" =—<о
stat 2mcr
строго меньше нуля, т. е. мы имеем максимум действия, что отвечает минимальному
значению гамильтониана в классе заданных пробных функций. Заметим, что, как
и должно быть для осциллятора, средняя кинетическая энергия в стационарном со¬
стоянии равна потенциальной:
h2 mo)2cr2 1
— ■ = -псо.
4 тег2 4 4
4.2. Калибровочная инвариантность
Как мы уже упоминали выше, вектор состояния в гильбертовом про¬
странстве определен с точностью до глобальной комплексной фазы, так как
Лекция 4
67
подобная фаза входит в общий фактор всех состояний и не влияет на ин¬
терференцию, а вероятность задается модулем амплитуды. Вариационная
формулировка динамики волновой функции позволяет воспользоваться тео¬
ремой Нётер для параметрических преобразований динамических перемен¬
ных, которые в нашем случае имеют вид
Фи(г, t) = е-1иФ(г, t), *1 (г, О = е‘иФ+(г, t), (4.2)
где фаза не зависит от координат
Такие преобразования называют глобальными калибровочными преобразо-
ипниями. Очевидно, что они образуют группу по умножению.
Кроме того, согласно определению волновой функции Ф(г, t) = (г|Ф(0)
ее преобразование эквивалентно введению преобразования базиса в коор¬
динатном представлении
\ru) =e"iu|r), Фи(г, 0 = (г“|Ф(0). (4.3)
На уравнениях движения по теореме Нётер производная действия, ин-
нариантного относительно таких параметрических преобразований, равна
пулю1:
ds_ [ А+лзгЯ Г ас эф„ . эс
du J *НЭЭМФ ди ддцФ* Эи J
Если инвариантность установлена для произвольной области интегрирова¬
ния, то имеет место локальный закон сохранения—равенство нулю 4-дивер¬
генции тока:
а — л /ти— I д£
-и’ J -ээ„ф Эи ээдф+ эи •
Если же интегрирование идет по всему 3-мерному объему пространства
и интервале времени от до t2, то
J dtd3rd0J° + J dtd3rV-(/ = J d3^! +/dt <f> d2s-l/ = 0,
где мы воспользовались теоремой Гаусса—Остроградского для объемного
интеграла от дивергенции тока. Если поток через сферу на бесконечности
равен нулю, то сохраняется заряд
Q = / d3r J0.
В исследуемом случае при и —> 0
Дф ЭФ* *
Эи ’Эи ’
гКак принято, мы вводим нулевую компоненту х0 =ct.
68
Тема 1 Принципы квантовой механики
для нерелятивистскои частицы в потенциальном поле лагранжиан—
с=туЧ - (уф1) • (v^) - уф%,
zm
а компоненты тока—
J0 = chv4, / = -^[Ф+УФ-(УФ+)Ф],
т. е. этот 4-ток составлен из плотности вероятности и компонент потока
вероятности, введенных выше:
j^=h(cp,j),
что в точности совпадает со стандартным током для заряженной частицы.
Таким образом, глобальная калибровочная инвариантность приводит к за¬
кону сохранения вероятности и уравнению непрерывности, который также
можно интерпретировать и как закон сохранения электромагнитного тока,
если частица заряжена.
Рассмотрим теперь обобщение на случай локальной калибровочной инва¬
риантности, т. е. с параметром, который зависит и от времени, и от коорди¬
нат. При этом частные производные, отвечающие ковариантному 4-вектору
импульса частицы
р„Ф=тэмФ=1й(и,УФ), рм=св/с,-р),
при локальном преобразовании принимают вид
p^u = e~iu(ih д^ + h ajLtu)'I'.
Обычно вводят размерный параметр калибровочного преобразования /:
е г
где е —электрический заряд рассматриваемой частицы. Тогда
РцФц = e-iu (j>n + 2 дц/) Ф •
После локального калибровочного преобразования с параметром / лагран¬
жиан для волновой функции заряженной частицы примет вид
Cf = сФ^ (ро + §Эо/)фи + ^ (рФи - fV/Фu)f • (рФи - f V/Ф»).
Этот лагранжиан можно сделать инвариантным, если ввести векторное ка¬
либровочное поле Ам = (А0, —А), так что
а . л е а
Pfl ^ Рц~ cAli*
с законом градиентного преобразования
Л£=ЛМ + ЭМ/. (4.4)
Это эквивалентно введению ковариантной или, как говорят, «длинной» про¬
изводной
= + (4.5)
Лекция 4
69
гмк что с учетом калибровочного преобразования для поля (4.4) действие
копариантной производной сохраняет групповые свойства, т. е. экспонен¬
циальный фактор выносится за знак дифференцирования и при локальном
преобразовании:
^Фи = е"!,%Ф. (4.6)
Тогда лагранжиан
С = сФ* (ро - § А>) *+ 2^ (р*- §Аф)+ • (рФ -1 Аф) (4.7)
инляется калибровочно инвариантным относительно локальных преобразо-
нпмий. Калибровочное векторное поле определяет 4-вектор потенциала для
лисктромагнитного поля.
Лагранжиан (4.7) согласно принципу наименьшего действия приводит
к уравнению Шрёдингера для однокомпонентной волновой функции заря¬
женной частицы в электромагнитном поле:
1Й^Ф(г, 0 = 2^(р-~сА)2*(г> О + еА0Ф(г, t). (4.8)
Калибровочный принцип лежит в основе теории всех известных взаимо¬
действий не гравитационного типа: электромагнитных, слабых и сильных.
Описание каждого из этих взаимодействий связано с введением сохраня¬
ющихся зарядов и взаимодействующих с ними векторных калибровочных
нолей. Отличие же разных теорий состоит в различном выборе унитарной
группы калибровочных преобразований полей материи. Как мы видели вы¬
ше, электромагнитному взаимодействию отвечает преобразование волновых
функций унитарными множителями — комплексными числами е-ш, то есть
группа U(l).
4.3. Импульсное представление
В уравнении Шрёдингера (2.10)
У1^|Ф(0)=А|Ф(0),
возьмем проекцию на состояние с определенным значением импульса |р),
т£<р|ф(0>=<р|Д|Ф(0),
и для простоты ограничимся рассмотрением стационарных состояний
(р|Ф(0) =е~*Бс(р|Ф),
где амплитуда вероятности в импульсном представлении
(р|Ф) = Ф(р).
Тогда, пользуясь полнотой базиса в импульсном представлении, получаем
ЕФ(р) = |(р|Н|к)^|з<*с|Ф) ЕФ(р) = |<р|Н|к>^|зФ(к).
70
Тема 1 Принципы квантовой механики
Для нерелятивистской частицы выделим в матричном элементе гамильто¬
ниана вклад кинетической и потенциальной энергии. Для первого из них,
очевидно, имеем
=ё*=2^(2nh)3 5(р ~ ю’
где первое равенство получается ввиду того, что мы выбрали собственные
векторы состояний для оператора импульса, а второе есть принятое нами
условие нормировки состояний в импульсном представлении.
Вклад потенциальной энергии в матричный элемент можно представить
в виде
<p|V(f)|fc> = /(p|V(f)|r) d3r (r\k),
где мы воспользовались полнотой базиса в координатном представлении:
/ |r) d3r (г| = 1.
Векторы состояний в координатном представлении — собственные для опе¬
ратора координаты,
f|r) = r|r) => V(r)|r) = V(r)|r).
Как мы выяснили при рассмотрении волнового пакета,
(r|k) = e»fc'r, (p|r) =е“»рг,
так что
(p|V(r)|fc> = J d3r V(r)e«(fc_p) r = V(p — fc) (4.9)
есть не что иное, как преобразование Фурье для потенциала.
Собирая вклады кинетической и потенциальной энергий, получим урав¬
нение Шрёдингера в импульсном представлении
я*(Р) = |^(р) + J Пр-к)Ф(к)•. (4.10)
4.4. Р-четность
Если классическая система имеет потенциал, инвариантный при зеркаль¬
ном отражении всех трех декартовых координат, т. е.
V(r) = V(-r),
то в квантовом случае эта симметрия приводит к возникновению нового
квантового числа, Р-четности.
Действительно, введем оператор1 Р: Р|Ф) = |РФ),
(г|РФ) = Ф(-г). (4.11)
1Как и при рассмотрении Т-инвариантности, изложение строится для скалярных волновых
функций.
Лекция 4
71
11оскольку
*(-!•) = <(-г)|Ф) => (г|РФ) = ((-Г)|Ф),
длн двух произвольных состояний
<Ф|РФ> = /(Ф|г) d3r (г|РФ) = /(Ф|г) d3r (с—г)|Ф> =
= / <Ф|(—r)> d3r (г|Ф) = (РФ|Ф>,
г. с. оператор P-четности эрмитов, и
Р|г) = |(-г)>.
Н частности,
(г\Рр) = Фр(-г) = e~hpr = (г|( р)),
откуда
Р|р) = 1С-р)).
Тиким образом, оператор зеркальной инверсии пространства меняет знак
координат и импульсов.
Очевидно, что квадрат оператора Р-четности равен единице
Р2 = 1,
поэтому собственные значения P-четности могут быть только
Яр = ±1.
Соответственно собственные функции оператора P-четности в координат¬
ном представлении будут либо четными, либо нечетными.
Действие оператора на координату и импульс имеет вид
Pf4r) = rP|r) = r|(-r)M .
> => Рг= —гР
№|r)=*|(-r)) = -r|(-r))J
и аналогично
Рр = -рР.
Поэтому
м-н&+т}~{ы+п~п}р=йр-
так как по условию задачи потенциал инвариантен относительно зеркальных
отражений всех координат. Отсюда следуют два заключения. Во-первых, как
и следовало ожидать, оператор P-четности коммутирует с гамильтонианом,
и значит, он—интеграл движения. Во-вторых, волновая функция, полученная
при действии оператора Р-четности, удовлетворяет уравнению Шрёдингера
с тем же гамильтонианом.
Напомним, что условием вырождения уровней энергии является наличие
двух наблюдаемых — интегралов движения, которые не коммутируют друг
с другом. Как мы видели, импульс и P-четность не коммутируют, хотя оба
они могут быть интегралами движения, например, для свободной частицы с
V(r) = 0. Поэтому состояния свободной частицы с заданной энергией вырож¬
дены: инверсия пространства меняет знак импульса.
72
Тема 1 Принципы квантовой механики
4.5. Оператор трансляций, квазиимпульс, номер зоны
По определению, оператор пространственных трансляций Га сдвигает
аргумент волновой функции на вектор а:
(г|ГаФ) = Ф(г+а). (4.12)
Разлагая в ряд Тейлора
оо
Ф(г+а)= J] (а• V)Ф(г) = e(aV)Ф(г),
к=О
находим, что в координатном представлении оператор конечных трансля¬
ций1
<г|ГвФ) = ?вФ(г)
принимает вид
fa = e(aV).
Используем выражение для оператора импульса в координатном представле¬
нии
p = -ihv,
откуда
ta = e*ap,
а значит, оператор конечных трансляций определяется оператором импуль¬
са. При этом инфинитезимальные преобразования имеют вид
ra^l + ^a-p + (9(a2), a-*0.
Поскольку оператор коммутирует с любой степенью самого себя (на любом
собственном векторе оператора это верно с очевидностью), коммутатор им¬
пульса с оператором конечных сдвигов равен нулю:
[Та)р]= 0.
Найдем оператор, эрмитово сопряженный к fa. По определению для про¬
извольных состояний
(Ф|гаФ) = (г2Ф|Ф>.
Распишем левую часть этого равенства, пользуясь единичным оператором
в координатном представлении:
(Ф|ГаФ) = /(Ф|г> d3r (г|ГаФ) = J d3r Ф*(г)Ф(г+а)
и совершим замену переменных г —> г — а, так что
(Ф|ГаФ) = / d3r ф*(г—а)Ф(г) = (Га*Ф|Ф).
Следовательно,
<г|Г» = Ф(г-а)
ХВ отличие от инфинитезимальных, т. е. бесконечно малых, трансляций.
Лекция 4
73
и армитово сопряженный оператор трансляций сдвигает аргумент волновой
функции в обратную сторону. Отсюда легко заключаем, что
Ttf =1
т. с. оператор трансляций унитарен.
Рассмотрим собственные векторы унитарного оператора А
А|А)=А|А).
Для унитарного оператора
(АЯ|АЯ> = (Я|Л+ЛЯ) = (Я|Я>.
11одставляя в это равенство собственный вектор оператора А, находим
А*А(А|А) = (А|А) =» А*А = 1.
Следовательно, собственные значения унитарного оператора суть комплекс¬
ные числа единичного модуля:
A = elv, y?eR (mod27r).
По сути, мы привели доказательство следующего утверждения: унитар¬
ный оператор А представим в виде
А = е'1ф, ф = ф^,
где ф — эрмитов оператор. В самом деле, в базисе своих собственных век¬
торов унитарный оператор—диагональная матрица1, образованная числами
A = elv>, поэтому можно определить оператор ф как оператор, который в том
же базисе имеет вещественные собственные значения, равные у. В итоге
введенный оператор по построению эрмитов и имеет необходимую для сде¬
ланного нами предложения связь с исходным унитарным оператором2.
В случае унитарного оператора конечных трансляций
Га=е^
оператор фазы ф записывают в виде
где оператор к называют оператором квазиимпульса. Его отличие от опера¬
тора импульса обусловлено тем, что фаза определена по модулю 2п, и, сле¬
довательно, квазиимпульс имеет собственные значения, определенные по
модулю 2nh/a по каждой из компонент.
Собственные волновые функции оператора трансляций
Та |Ф> = е*“*|Ф)
1Если собственное значение вырождено, то необходимо выбрать ортонормированный базис
в подпространстве, отвечающему этому собственному значению.
2Мы привели типовую схему доказательств связей между операторами: в базисе собствен¬
ных векторов оператора необходимые операторные соотношения сводятся к соотношениям
между комплексными числами.
74
Тема 1 Принципы квантовой механики
в координатном представлении
(г|Га|Ф) = е»а*<г|Ф)
удовлетворяют уравнению
Ф(г + а) = е»а’*Ф(г).
Такие функции представимы в виде
Ф(г) =ейг*Ф(г), Ф(г+а) = Ф(г).
Подобные функции называют функциями Блоха. Они находят свое примене¬
ние в задаче с периодическим потенциалом:
V(r + a) = V(r). (4.13)
Прежде чем рассматривать такую квантовую задачу, изучим действие опе¬
ратора конечных трансляций на базисные вектора состояний и операторы
координаты и импульса.
Волновая функция состояния |г') в координатном представлении
(r\r') = 5(r-r/)
согласно общему определению оператора трансляций (4.12) преобразуется
как
(r\Tar') = 5(r-r/ + a),
откуда заключаем, что
fa|r') = |r'-a).
или, эквивалентно,
Г» = |г+а>.
Эти соотношения показывают, что базисные векторы в гильбертовом про¬
странстве под действием преобразования смещаются в обратную сторону по
сравнению с векторами состояния системы, или, что то же, по сравнению
с волновыми функциями. Поэтому можно эквивалентно говорить либо о том,
что преобразование переводит одну физическую систему в другую (активная
картина преобразований), либо о том, что система остается неизменной,
а базис преобразуется обратным смещением (пассивная картина преобразо¬
ваний).
Поскольку волновые функции полностью аналогичны координатам век¬
тора в комплексном векторном пространстве, обе эти картины хорошо зна¬
комы из линейной алгебры, где преобразования координат вектора мож¬
но считать результатом, скажем, либо поворота самого вектора в неизмен¬
ном базисе, либо смены базиса в пространстве под действием обратного
поворота. Это соответствие активной и пассивной картин преобразований
в векторном пространстве является точной аналогией для преобразований
в гильбертовом пространстве.
Лекция 4
75
Теперь запишем
Таг\г)=гТа\г)=г\г-а)А
rta\r) = r\r-a) = (r-a)\r-a)j
Аналогично,
tavm=v(r+d)ta,
тик что для периодического потенциала (4.13) коммутатор равен нулю:
[Та, V(г)] = 0.
It итоге для гамильтониана с периодическим потенциалом
[fa, Н] = [fa, + vm] = 0. (4.14)
Тпким образом, гамильтониан для волновой функции, полученной действи¬
ем оператора сдвига на период потенциала, тождественно равен исходному
гамильтониану, т. е. если волновая функция удовлетворяет уравнению Шрё¬
дингера с периодическим потенциалом, то и волновая функция, полученная
h:i этого решения уравнения Шрёдингера оператором сдвига, также является
рсчиением этого уравнения.
В классике инвариантность энергии при сдвигах на период потенциала
очевидна.
Поскольку при квантовании оператор сдвига на период потенциала ком¬
мутирует с гамильтонианом и эрмитов оператор квазиимпульса коммути¬
рует с гамильтонианом, т. е. квазиимпульс — интеграл движения, то базис
можно строить по совместным собственным векторам энергии и оператора
трансляций. Как мы видели, собственными функциями оператора трансля¬
ций являются функции Блоха. Инвариантность классического гамильтониа¬
на относительно сдвигов приводит к сохранению нового квантового числа —
квазиимпульса.
Если потенциал периодичен, то сдвиг можно проводить и в обратную
(reverse) сторону:
а-^-а. (4.15)
!)та операция, очевидно, сохраняет гамильтониан, т. е. энергию:
[R, Я]=0. (4.16)
11оэтому мы имеем новый квантовый интеграл движения, не имеющий ана¬
лога в классической физике, скажем, R-четность, так как R2 = 1. Однако эта
операция изменяет собственные значения оператора конечных смещений:
Я = е»ак е“ »a'fe = Я*,
Значит, коммутатор R-четности с операторами трансляций и, следовательно,
квазиимпульса не равен нулю:
[R, fa] ф 0, [R, к] ф 0, если к ф 0.
76
Тема 1 Принципы квантовой механики
Итак, у нас есть два интеграла движения, которые не коммутируют между
собой: имеет место условие вырождения уровней энергии. Именно, каждому
значению энергии частицы в периодическом потенциале соответствуют два
значения квазиимпульса {к, —к}, если его значение не равно нулю1. Другими
словами, энергия—функция квадрата квазиимпульса, Е=Е(к2).
То, что фаза оператора трансляций определена по модулю 2тг, также
приводит к нетривиальным последствиям в квантовой механике. Действи¬
тельно, определим параметр сдвига как
а-^а + 2тгйп||, ne N, (4.17)
где квазиимпульс к, естественно, не равен нулю. Кроме того, если добавка
кратна стандартному шагу потенциала, то повторяется ситуация со сдви¬
гом на несколько периодов (что не несет новой информации о волновой
функции). Мы положили п натуральным, так как введенная выше операция
R-четности позволяет избавиться от рассмотрения отрицательных целых зна¬
чений. Очевидно, операция Dn введена так, чтобы оставить инвариантными
собственные значения оператора сдвига:
Л = е»а*^е»а*+2™ = Л, к-^к.
Значит,
[Ta,Dn] = [k, Dn]=0. (4.18)
По построению, собственные состояния операторов Та иГ)п нумеруются спек¬
тральным параметром квазиимпульса к и новым квантовым числом п, кото¬
рое называют номером зоны.
В общем случае энергия изменяется под действием зонных сдвигов (4.17),
так как потенциал имеет фиксированное значение периода, не равное вели¬
чине в (4.17), Л Л
[D„,H]#0. (4.19)
Итак,
[ta,Dn]=0, [Га,Я]=0, [А, А,]/ 0.
Рассмотрим собственные состояния оператора конечных трансляций. Они
характеризуются вектором квазиимпульса. Вдобавок мы имеем пару дру¬
гих операторов — зонные сдвиги и гамильтониан, — которые коммутируют
с трансляциями, но не коммутируют друг с другом. Следовательно, налицо
условие вырождения собственных значений квазиимпульса. Именно, каждо¬
му значению квазиимпульса отвечает бесконечное счетное множество значе¬
ний энергии: состояния можно пронумеровать непрерывным спектральным
параметром к (квазиимпульсом) и квантовым числом п (номером зоны);
базис— |к, п). С учетом R-четности, энергия частицы в периодическом потен¬
циале имеет вид 0
я=ВД2),
где п—номер зоны.
1Описанное действие оператора R на энергию и квазиимпульс можно записать в виде Е(к) =
Тема Одномерное движение
2
Лекция 5
Вид потенциала, вронскиан, двукратное вырождение состояний энергии
и непрерывном спектре, невырожденность в случае ограниченного движения,
сиязанные состояния частицы в потенциале, дискретный спектр, осциллятор-
ная теорема, задача рассеяния, соотношения взаимности для коэффициен¬
тов прохождения, сохранение потока вероятности, явление резонанса, время
жизни возбужденного состояния, амплитуда Брейта—Вигнера, скачок произ¬
водной.
5.1. Одномерное движение: исходные положения
Одномерное движение в квантовой механике является полигоном, упраж¬
нения на котором подготавливают сдобренную конкретными примерами
и расчетами почву, призванную составить культурный слой для роста каче-
ггменно новой квантовой интуиции в описании физических явлений. Эта
интуиция не может быть заимствована из опыта изучения классических
систем. Кроме того, одномерное движение может служить и моделью фи¬
зической системы со связями, приближенно ограничивающими движение
чпетицы одномерной линией.
Итак, квантовая система в одномерном случае описывается единственной
непрерывной наблюдаемой — координатой частицы х (или сопряженным
к ней импульсом). В этом случае амплитуда вероятности в координатном
представлении —волновая функция ^(х), а стационарное уравнение Шрё¬
дингера для нерелятивистской частицы в потенциале имеет вид
- (X) + У(х)'ф(х)=Е'ф (х),
где штрих означает дифференцирование по координате. Это уравнение обыч¬
но переписывают как
1/>" + |^[Е-У(л:)]я/> = 0. (5.1)
Если *ф19 /ф2—решения уравнения Шрёдингера с энергией Еъ Е2 соответ¬
ственно, то величина
W0ф1г V’a) = V>2 - ^2 = det Q (5.2)
называется вронскианом или определителем Вронского. Производная врон¬
скиана по координате, очевидно, выражается формулой
W = М" - ip"ip2 = Щ (El - £2)^2- (5.3)
78
Тема 2. Одномерное движение
Это соотношение позволяет проводить общий анализ спектральной задачи
в одномерном случае.
Рассмотрим непериодические ограниченные потенциалы, для которых
имеет смысл ввести предельные значения потенциала на границах интервала
допустимых значений координаты:
V±= lim VQt),
*—►±00
которые для определенности мы будем считать положительными или равны¬
ми нулю,
V±£0,
а также примем, что
Кроме того, введем область а<х<Ъ, где У(х)<0. Подобный потенциал
представлен на рис. 2.
Рис. 2. Наглядное представление о типовом потенциале и его параметрах
5.2. Вырождение
Покажем, что каждому значению энергии соответствует лишь единствен¬
ная волновая функция, если есть точка, где пси-функция заведомо равна
нулю.
В самом деле, из уравнения для производной вронскиана (5.3) при Ег =Е2
следует, что
W' = 0 =Ф W = const.
Значение константы, т. е. вронскиана, равно нулю, если существует точка,
где волновая функция равна нулю:
3х0:гр1(х0)='ф2(х0) = 0 => W = 0,
так как вронскиан сохраняет свое значение при изменении х. В итоге
W(T/>i,4/>2)=V’lV,2-',/’i1/’2 = 0 => = ^ =
Лекция 5
79
где* С — постоянная, т. е. функции гр1 и 'ф2> отвечающие одному и тому же
пшчению энергии, пропорциональны друг другу, если у них есть общий
|«>рснь. Отсюда, в частности, следует, что такую волновую функцию можно
пыЛрать вещественной. Действительно, пусть гр (х) — комплексное решение
урпинения Шрёдингера, имеющее по условию рассмотрения нуль. Значит,
общественная и мнимая части этой волновой функции обращаются в нуль
и одной точке, при этом мы можем положить грг = Re|/0(x)], ^2=ImWW]j
ко торые в силу принципа суперпозиции также являются решениями уравне¬
нии Шрёдингера с той же энергией;
Tpi=lmx)+i>*m, я/>2=^'Фм-'ф*т,
п является решением уравнения Шрёдингера в силу обратимости по
нремени (см. Т-инвариантность в лекции 3). Но мы показали, что в этом
случае пропорциональны друг другу, так что комплексная фаза реше¬
ния не зависит от х, и, следовательно, от нее можно избавиться за счет
глобального калибровочного преобразования.
Рассмотрим теперь, при каких обстоятельствах волновая функция обра¬
щается в нуль. Пусть Е < V_, т. е. энергия меньше асимптотического значения
потенциала на бесконечности (движение финитно хотя бы в одну сторону).
Тогда при х—> — оо уравнение Шрёдингера принимает вид
t/>" + |£[E-V_Ji/> = 0, (5.4)
где
j£-[E-V_] = -x2_<0, х_>0,
так что решение имеет асимптотику
%1)М = С^~х-х + С2ех~х, х-* -оо.
Однако экспоненциальный рост первого слагаемого приведет к тому, что
иолновая функция не может быть нормирована на единицу, т. е. наличие
ненулевого Сг выводит такое решение из гильбертова пространства кванто-
иой механики: у решения нет физического смысла. Поэтому
Сг = О
и
'ф(х)с*С2ех~х —>0, х—> — оо. (5.5)
Значит, если движение финитно хотя бы в одну сторону, т. е. энергия меньше
асимптотического значения потенциала на бесконечности, то уровень энер¬
гии невырожден.
Если энергия больше асимптотических значений потенциала на бесконеч¬
ности Е > У_ (движение инфинитно в обе стороны), то, например,
'ф" + к2_'ф = 0) Х-+-О0, (5.6)
где
^[Е-у_]=к2_ >0, к_> О,
80
Тема 2. Одномерное движение
так что решение имеет асимптотику
гр(х)^С~е~1к-х+ С2 elk~x, х—►—оо. (5.7)
Аналогичные выражения получаются и при х—>+оо с подстановкой
|г[Е-У+]=*ч>0, К>0,
И
я/>(х) c*C+e~lk+x + С* elk+x, X—>+оо. (5.8)
Следовательно, на бесконечности имеет место суперпозиция волн де
Бройля для свободной частицы с двумя значениями проекции импульса на
ось х. Если рассматривать уравнение Шрёдингера в этой области энергий как
задачу Коши с начальными данными С^, С2 при х—> — оо, т. е. в виде (5.7),
то при любом значении /с_ уравнение приведет к решению в виде (5.8) при
х —> “Ь00, так что параметры С^, С2 являются функциями начальных данных
Ci, С2:
^2 = С^2(С-2).
Поскольку никаких ограничений на коэффициенты С+, С2 при х—>+оо нет,
приходим к выводу: если движение инфинитно в обе стороны, т. е. энергия
больше асимптотических значений потенциала на бесконечности, то уро¬
вень лежит в непрерывном спектре с двукратным вырождением по знаку
импульса частицы на бесконечности.
Если значение энергии лежит в промежуточной области
V+<E<V_,
то, комбинируя (5.5) и (5.8), заключаем, что в этом случае уровень энергии
невырожден, так как волновая функция обращается в нуль при х —»—оо, а при
х —> +0° имеется свободная волна, которую можно сделать вещественной.
В этом случае спектр непрерывный: его можно «пронумеровать» импуль¬
сом к+.
5.3. Связанные состояния, осцилляторная теорема
Если энергия находится в интервале
^min < V+,
то в качестве начальных данных в задаче Коши можно рассматривать гранич¬
ное условие1 (5.5) с С2 = 1. В полной аналогии с получением этого условия,
при х —> +оо уравнение Шрёдингера принимает вид
1Константу С2 без потери общности рассмотрения можно положить равной единице, так как
ее всегда можно будет перемасштабировать в случае, если решение имеет конечную норму, так,
чтобы полная вероятность была равна единице.
Лекция 5
81
^[E-V+] = -x2+<0, х+>0,
е решением в виде
яр (х) ^ е~х+х + С2 ех+х, х —>+оо,
П|)ичем коэффициенты являются функциями начальных данных:
С+ = С+(Е), С+ = С+(Е).
Для нормируемости волновой функции необходимо положить
что и определяет квантовый невырожденный спектр связанных состояний,
т. е. состояний, плотность потока вероятности для которых равна нулю,
II плотность вероятности стремится к нулю при х-*±оо? что выполняется
и рассматриваемой области энергий.
Допустим, что уравнение (5.9) имеет два решения при значениях энергии
/?! <Е2. Пусть Xi, х2 — последовательные узлы решения гр^х): <0(х1)= О,
Ф (х2)=0. Такие узлы всегда есть, так как по меньшей мере волновая функция
связанного состояния должна обращаться в нуль в конечных точках х-*±оо.
Кроме того, как мы показали, наличие этих нулей позволяет считать вол¬
новые функции связанных состояний вещественными. Тогда согласно (5.3)
инкремент вронскиана имеет вид
Поскольку узлы волновой функции грг (х) последовательные и для опреде¬
ленности хг < х2, эта непрерывная волновая функция не меняет знак на
интервале между корнями, т. е., например, она является положительной при
Xi < х < х2, причем, очевидно, в этом случае
Пользуясь методом «доказательства от противного», допустим, что волновая
функция гр2(х) на интервале хг < х < х2 также является знакоопределенной,
скажем, положительной. Тогда левая часть уравнения (5.11)
С+(£) = 0,
(5.9)
WO0i>’/’г) 2 = ^р1^р2У 2 = тг(£1-£г) / dxxp1xl>2, (5.Ю)
или с учетом я/>г (х1>2) = 0
■ф[ V’i (*2) ^ 0.
-V>iV>2 2^о,
(5.12)
в то время как правая часть
(5.13)
82
Тема 2. Одномерное движение
так как под интегралом стоит положительное произведение непрерывных
функций, а разность энергии по построению отрицательна. Противоречие
(5.12) и (5.13) говорит о том, что непрерывная функция г/)2М должна менять
знак между двумя последовательными узлами волновой функции с меньшим
значением энергии.
Поскольку проведенное исследование справедливо для любой пары по¬
следовательных узлов волновой функции грг (х), а тг узлов этой функции,
включая две конечные точки, разбивают интервал — оо < * < +оо на п — 1
последовательных интервалов, волновая функция имеет как минимум
п +1 узел.
Итак, мы пришли к утверждению о том, что связанное состояние с боль¬
шей энергией имеет большее количество узлов волновой функции. Более то¬
го, можно нумеровать невырожденные связанные состояния количеством
внутренних узлов: по мере последовательного возрастания количества узлов
последовательно увеличивается и энергия связанного состояния. Это утвер¬
ждение и составляет осцилляторную теорему.
С учетом непрерывности волновой функции количество узлов, а следова¬
тельно, и количество связанных состояний может быть только счетным,
а значит, спектр связанных состояний—только дискретным.
Замечание о Р-четности. Если потенциал инвариантен относительно
операции зеркального отражения
V(x) = V(-x),
то, как мы выяснили, уровни энергии можно классифицировать дополни¬
тельно новым квантовым числом, Р-четностью. В сочетании с осцилляцион-
ной теоремой, очевидно, получаем следующее утверждение: волновые функ¬
ции уровней энергии с четным числом узлов имеют положительную чет¬
ность, а с нечетным числом узлом—отрицательную четность.
5.4. Коэффициенты отражения и прохождения
Если энергия состояния лежит в непрерывном дважды вырожденном спек¬
тре, то ставят задачу рассеяния волны на потенциале.
Запишем решение в виде
fe-ik+X+R ik+X X_>+W
uO)H .. (5.14)
\ Sue •*, x—oo.
В этих асимптотиках рассмотрим потоки вероятностей
№0с)1 = -§{['Ф*Мг1>\х) - 0ф\х)Гх1>Ш,
которые связаны с каждым из вкладов. Поскольку мы рассматриваем супер¬
позицию свободных волн, изученных нами выше, легко убедиться, что
j [e-ifc+JC] = = "k+
Лекция 5
83
это поток волны, падающей из положительной бесконечности на потенци-
ил (поток направлен в отрицательную сторону);
j [Rueifc+x:] = j'back = \RU I2 щ k+
- это поток волны, отраженной от потенциала (поток направлен в положи¬
тельную сторону); и, наконец,
j [Sue-ifc--] = jout = - |SU |2
-это поток волны, прошедшей через потенциал. Очевидно, из закона сохра¬
нения вероятности следует, что входящий и выходящий потоки равны:
Jin Н" Jback Jout ^ k+(l “ l-^ul ) ^_|SU| •
Коэффициент прохождения определяется как
J out
т =
1и
Jin
(5.15)
и в нашем случае он равен
Коэффициент отражения
и в этой задаче он
ти=^К\2.
Jback
Jin
= 1 — т
*ц = 1 RJ2-
Аналогично можно рассмотреть волну, падающую на потенциал из отри¬
цательной бесконечности:
Г Sveik+X, х —* +00,
ik х -Ikx (5-16)
[ e-+Rve , х —* —оо.
В этой ситуации можно также ставить задачу о рассеянии—отражении и про¬
хождении волн. Например, коэффициент прохождения
r„=^|s„|2.
И тут возникает вопрос: совпадают ли в общем случае, для потенциала
общего вида, коэффициенты прохождения и отражения в прямую и обратную
стороны?
Для ответа на этот вопрос напомним, что вронскиан для двух решений
с одной и той же энергией остается постоянным, не зависящим от х. Для
рассматриваемых решений мы можем вычислить вронскиан для пары волно¬
вых функций при х —> — оо и х —»+00, а затем приравнять эти величины. Так,
например,
W(u, v)x__00 =
=Sue-ifc-x (ifc_eifc-* - ifc_R„e-ifc-*)-Su(-ik_)e~ik-x(.eik-x+R„e-ifc-;c),
84
Тема 2. Одномерное движение
так что
W(u, !/)*_>_«> = 2ik_Su.
Совершенно так же
W(и, i/)^+00 = 2ik+Sv.
Сохранение вронскиана означает, что
k_Su = k+Sv => Tv = ^|S,|2 = ^|Su|2 = ru,
т. е. действительно имеет место соотношение взаимности: коэффициенты
прохождения волной потенциала в прямом и обратном направлении совпа¬
дают.
Отметим, что волновые функции, полученные операцией обращения стре¬
лы времени:
Т * Т *
и—>Ц*, V—>1/*,
также являются решениями уравнения Шрёдингера с той же энергией. Ко¬
нечно, ввиду того, что уровни энергии дважды вырождены, эти новые реше¬
ния можно выразить через пару {u, v}. Однако сохранение вронскианов
W(u,u*) и W(y,v*)
позволяет установить также и закон сохранения потока вероятности.
5.5. Резонанс
Рассмотрим непрерывный спектр невырожденных уровней энергии в по¬
тенциале
VL ->+оо, х<0,
V 00 = Vb < 0, 0 ^ х ^ а, (5.17)
V+ = 0, х> а,
показанном на рис. 3. По условию задачи
V+<E<V_.
Интервал значений координаты естественным образом разбивается на
три области.
I) х < 0. Согласно общему рассмотрению в (5.5) решение уравнения Шрё¬
дингера затухает на бесконечности экспоненциально, причем коэффициент
затухания стремится к бесконечности1:
X2_ = ^(V_-E)^+co,
1В случае конечного интервала по х решение представляется в виде суммы растущей
и затухающей экспонент, и этот же коэффициент определяет степень экспоненциального роста.
Поэтому в пределе бесконечно высокого потенциального барьера растущий вклад необходимо
занулить, так как иначе волновая функция становится бесконечно большой.
Лекция 5
85
так что при наличии в некотором интервале конечной ширины бесконечно вы¬
сокого потенциала волновая функция обращается внутри этого интервала
в тождественный нуль:
гр100=0, х<0.
II) 0 ^ х ^ а. Решение осциллирует, но поскольку в силу непрерывности
волновой функции
яК0)=0,
решение уравнения можно выбрать с точностью до множителя веществен¬
ным, так что с учетом наличия узла в нуле
Vn(*)=Asin(fcoX). %kkl=E~Vo> (5.18)
где связь волнового вектора к0 с энергией следует из уравнения Шрёдингера.
III) х > а. Запишем решение в виде
xpmM = e-ikx+Reikx, |iк2=Е, (5.19)
где первый вклад отвечает падающей из бесконечности на потенциальную
яму волне, а второй — отраженной от стенки волне. Поскольку поток про¬
шедшей волны равен в этой задаче нулю, коэффициент отражения равен
единице и
|R| = 1 => R = eilfi,
т. е. отраженная волна приобретает дополнительную фазу рассеяния </?.
Для получения связи неизвестных параметров в волновой функции необ¬
ходимо потребовать непрерывности волновой функции и ее производной
в точке сшивки решений
я/»п(а)=^ш(а), ■0(1(а)='0'п(а).
(5.20)
86
Тема 2. Одномерное движение
Отсюда
Asm(k0a) = e-ika + ei(-ka+,f\
к0А cos(к0а) = -ifce-lfca + ifcel№a+¥,)
A=—2ik
fc0 cos(k0x) — i/c sin(k0x)9
ei$ _ _e-2ifca fcp cos(fcpjc) + ifc sin(fc0x)
fc0 cos(k0x) — ifc sin(fc0x)'
(5.21)
Модуль амплитуды Л, которая определяет вероятность нахождения частицы
в потенциальной яме, задается величиной
4 к2 _ 4 к2
|Л|2 = :
(5.22)
к2 + (к2 - к2) cos2(fc0a) к2 - ^V0 cos2(kQa)'
Как видим, квадрат модуля осциллирует в границах 0 ^\А\2 ^ 4. Характерный
график этой функции в зависимости от волнового вектора показан на рис. 4.
Рис. 4. Нормировка плотности вероятности обнаружить частицу в потенци¬
альной яме в зависимости от волнового вектора падающей волны (в едини¬
цах a = 10, — 2mV0/h2 =200)
Пики распределения расположены при
к0а = ^ + пп, п€ N.
Эти пики сглаживаются, если их амплитуда мала, т. е. при
2m Vq
(5.23)
При обратном же соотношении пики хорошо разделены и ярко выражены.
Это имеет место при
fc2<fc2 vCv0,
где v и Vq — скорости движения волны при х > а и в потенциальной яме.
Другими словами, при наличии пиков потенциальная яма выглядит глубокой
для рассеивающейся частицы. С ростом энергии, естественно, потенциаль¬
ная яма будет восприниматься как мелкая.
Лекция 5
87
Совершенно аналогично фаза
4> = -n-2ka + 2arctgtg(fc0a)]
иблизи пика испытывает существенное изменение. В качестве более объ¬
ективной характеристики обычно рассматривают разность фаз падающей
и отраженной волны, например, на границе потенциальной ямы, т. е. при
х = а:
Aip = 2 arctgtg(fc0a)J - п. (5.24)
Эго же значение комплексной фазы получается при умножении найденного
нами решения на фактор exp(i2fca), т. е. при переопределении глобальной,
ненаблюдаемой фазы волновой функции в целом.
Говорят, что пики амплитуды и быстрая смена фазы отвечают возбужде¬
нию резонансов в глубокой потенциальной яме. График разности фаз пред¬
ставлен на рис. 5, откуда видно, что вблизи пика комплексная фаза быстро
меняется на 2п. Соотношение (5.23) показывает, что резонанс имеет место
при условии, что в яме укладывается нечетное число четверть-волн, что
в случае ямы с бесконечными стенками, т. е. потенциального ящика, соответ¬
ствовало бы положению ровно посредине между стационарными уровнями
энергии1.
Рис. 5. Разность фаз (по модулю 2л) в зависимости от волнового вектора
Групповая скорость волны определялась из условия стационарности фазы
d(p(x,t)
др
так что для отраженной волны с учетом переопределения фазы, как это было
сделано при выводе Aip,
4>(.x,t)=px-Et + h(p, р—Кк,
*В потенциальном ящике sin(fc0a) =0, в то время как в рассматриваемой задаче | sin(fc0a)| =
= 1. Дополнительная фаза «набегает» за счет того, что одна из стенок не является бесконечно
высокой.
88
Тема 2. Одномерное движение
и
ЭЕ д£
др дк’
что можно переписать в виде
x=Vp(t-At),
где запаздывание по времени определим по разности фаз А(р
дА<р/дк _ дАу
дЕ/др дЕ •
В явном виде в рассматриваемой задаче производная
дАу _ 2 f ак2 ,kl ~fc2
дк Л-18
в пике имеет значение
ЭД (/?
2 Г ак k.Q — K |
к2 tg2 (fc0a) + к% 1 cos2 (kQa) к0 ^^оа) |
2а,
dfc Ipeak
а между пиками при sin(fc0a) = О
^а2аЦ<2а-
Эти соотношения можно проинтерпретировать следующим образом. В клас¬
сике частица проходит от одного конца ямы до другого за время
^=1=т/!- (5-ад
В пике, когда частицу с высокой вероятностью можно обнаружить в глубокой
потенциальной яме, в квантовом случае получаем
Atquant = m§ = m^^>Atdass. (5.26)
Это означает, что в случае резонанса частица многократно отражается от
стенок ямы. Величину т = Atquant/4 называют временем жизни резонанса
в глубокой потенциальной яме1. Вне резонанса время пребывания частицы
в яме даже меньше, чем в классике.
Рассмотрим поведение амплитуды резонанса вблизи пика с fc* фО. При
этом
| sin(fc0a) | —»1, соs(fc0a) —> О,
так что, вводя малый параметр разложения A fc,
fc = fc* + Afc, Afc—>0,
находим
fco=^/-^+^-y~^ + fc* + 2fc*Afc^fco + FAfc’
1Время многократного прохождения половины длины ямы.
Лекция 5
89
vj\vt /Cq = k0№*)* Поскольку в пике
cos (fc^a) = 0, k^a = ^ + nn,
и окрестности пика получим
fc0 cos(fc0a) —»(—l)n+1fc* sin^aAfc^ —► (—l)n+1k*aAfc.
Тогда согласно выражению для амплитуды (5.21) вблизи пика резонанса
e-ifc*a ^
А~ cos(fc0Jc)-ifc sin(fc0x) ~ (-l)n+1Jc*aAfc- (-l)"ifc*’
где мы учли, что sin(fcga) = (—1)". Выразим А к через разность энергий
П2 ,Ь2 ъгл-? ". , ».
откуда
Стандартная запись подобной амплитуды резонанса в виде
А (5.28)
(£-£*)+ ^ Г
называется приближением Брейта—Вигнера. Величину Г называют шириной
резонанса. Квадрат модуля амплитуды —
^ ~(ДЕ)2 + ±Г2’
так что при АЕ = ±Г/2 плотность вероятности обнаружения резонанса пада¬
ет вдвое. Поэтому Г еще называют шириной на полувысоте. В рассматривае¬
мой нами задаче
г. ofr2k*
Г = 2—-.
та
Амплитуда Брейта—Вигнера как функция энергии представляет собой
полюс в комплексной плоскости энергии при
£poie=E*-|r. (5.29)
Поэтому считают, что временная зависимость волновой функции резонанса
~e~nEp°let = e~bE*te~ibrt
имеет затухающий фактор, так что плотность вероятности падает со време¬
нем как
\гр\2 ~е~*п.
Величину
т = £ (5.30)
90
Тема 2. Одномерное движение
называют временем жизни резонанса. Тогда
M2~e-t/T.
В нашем случае
та
2КК’
что находится в полном согласии с приведенной выше интерпретацией вре¬
мени запаздывания сигнала в терминах комплексной фазы за счет возбужде¬
ния резонанса.
5.6. Скачок производной
В ряде задач узкий потенциал вблизи некоторой точки х0 с конечной
площадью иногда аппроксимируют 5-образным потенциалом:
V(x)*-Vo5(x-x0) => JdxV(x) = -V0.
В этом случае уравнение Шрёдингера
iР" + ^[E + V05(.x- хь)]1р = 0
показывает, что вторая производная волновой функции содержит вклад
5-функции, а следовательно, у первой производной пси-функции есть скачок.
Его легко определить, если проинтегрировать уравнение в пределах х0 — е <
< х < х0 + е, где е —> +0:
J dx {%p" + jp-[E + V0 5(х-х0)]гр}ъ
Xq-E
^ ^'\х-е + ' 26 + = °’
откуда при e —> +0
\ hp'(x0 + 0) - \p'(.x0 - 0)] + V0ip (x0) = o.
Выражение в квадратных скобках и есть скачок производной. При этом,
конечно, сама волновая функция остается непрерывной.
Тема Гармонический осциллятор
3
Лекция 6
Канонический формализм, теорема вириала, характерные значения коор¬
динаты, импульса и энергии, операторы рождения, уничтожения и числа
квантов, спектр, полиномы Эрмита, когерентные состояния, распределение
Пуассона по числу квантов, голоморфное представление.
6.1. Каноническое квантование
Одномерный осциллятор в классической гамильтоновой механике описы¬
вается следующим гамильтонианом
ТУГ л Р2 , ™.“>2Ч2 г*
HCq,p) = 2^ + -1—, (6.1)
где {q, р} — пара координата-импульс, со — фазовая частота колебаний, так
как уравнения движения сводятся к виду
Г q=™ = L
вРанШ ^ 4 + с°2я=0. (6.2)
p = -— = -mco2q
Соответствующая скобка Пуассона
{q,p} Р = 1
переходит согласно формализму канонического квантования в квантовый
коммутатор наблюдаемых
[q, р] = ift.
6.1.1. Соотношение Фейнмана—Хеллманна и теорема вириала. Сред¬
ние значения кинетической и потенциальной энергии в квантовой механике
связаны между собой так же, как и в случае классической системы, согласно
теореме вириала. Для ее доказательства покажем сначала справедливость со¬
отношения Фейнмана—Хеллманна, которое устанавливает зависимость соб¬
ственного значения наблюдаемой от параметра:
Ц = f\n)=fn\n), (6.3)
л
где /—наблюдаемая величина, fn—ее собственное значение на собственных
векторах |п), а Я—параметр. Тогда
й-=А{п^п)={пФп)+Шп1)^п)+(п|^(й|п)) •
92
Тема 3. Гармонический осциллятор
Пользуясь уравнением на собственные значения, запишем далее
Ж = + /" (Й<п0|п) +^"<п| (ж|п>) = <п|5Х|п) +^<n'n>’
где последнее слагаемое равно нулю, так как состояние нормировано на
единицу при произвольных значениях параметра
(п|п) = 1,
так что соотношение Фейнмана-—Хеллманна доказано.
Рассмотрим теперь нерелятивистскую частицу с гамильтонианом
Я = г + У = -Цд + Пг),
в котором мы проведем замену переменных
г = Аг'.
В штрихованных координатах
Й=-шЬА'+П^-
Найдем собственные векторы гамильтониана |п). Очевидно, что собствен¬
ные значения энергии Еп не зависят от того, в каких координатах мы решаем
стационарное уравнение Шрёдингера, так что
^=0
дХ и<
Воспользуемся соотношением Фейнмана—Хеллманна при Я = 1:
/ril ЭЙ|_\
ЭХ ^ дХ I }
А=1
где, очевидно,
ЭЙ
дХ
= 2——А'+дУаг,) ЭАг'
я=1 2 т Я3 ЭХ г' дХ
=_2 ?+г*ш
Я=1 Эг
В итоге взяв среднее по стационарному собственному состоянию, находим
-2<f) + (rf£)=0, (6.4)
связь1
которая и устанавливает теорему вириала2 в квантовой механике: среднее
значение кинетической энергии в стационарном состоянии связано с рабо¬
той потенциальных сил.
1К тому же результату придем, если рассмотрим производную по времени оператора D=г • р
с помощью уравнения Гейзенберга и его среднее по стационарному состоянию. При этом
нужно учесть, что среднее коммутатора произвольного оператора с гамильтонианом в стацио¬
нарном состоянии обращается в нуль, и в частности, (n|[D, Я]|п> = 0.
2Термин «вириал» происходит от латинского слова vires — «силы».
Лекция 6
93
Особую изящность теорема приобретает, если потенциал — однородная
функция координат, когда производная потенциала, определяющая силу, лег¬
ко вычисляется. Например,
V = V0(i*y => (f) = a(V).
В частности, для осциллятора а = 1, и
(T) = (V), (6.5)
т. е. в среднем кинетическая энергия равна потенциальной.
6.1.2. Характерные значения координаты, импульса и энергии; заме¬
на переменных. Воспользуемся теоремой вириала для того, чтобы оценить
характерные размерные параметры в задаче с квантовым осциллятором.
Равенство кинетической и потенциальной энергий дает
2
Р 2 2
— ^mcL>zqz,
т 4 3
в то время как согласно соотношению неопределенностей при колебаниях
вблизи нулевых значений координаты и импульса
откуда характерные значения координаты и импульса в осцилляторе—
Ро = \/ mcoh, =
а его энергия
Е0 = § = Псо.
т
?= а=-Г> HQ = ТГ- (6.6)
Введем безразмерные величины
Р. о-1 и
п ’ п ’ nQ~ F •
Ро Яо йо
Тогда
Hq = \{V2 + &2}, Я = HcoHq, (6.7)
а коммутационные соотношения принимают вид
_а_
ldQ*
6.2. Стационарные уровни,
ОПЕРАТОРЫ РОЖДЕНИЯ И УНИЧТОЖЕНИЯ
Стационарное уравнение Шрёдингера в координатном представлении для
квантового осциллятора принимает вид
AeV>(O)=«K0, *=£;>
94
Тема 3. Гармонический осциллятор
и оно представляет собой дифференциальное уравнение второго порядка.
Наиболее эффектный способ решения спектральной задачи для осциллятора
основан на введении операторов1
' й = -±=&+ iV),
t 1 * . (6-8)
A' = ±«2-iP)
со следующими коммутационными соотношениями
[&, af] = \{(й + iff)(й- iP) - (ё - i£) (3+i£)> = - §i • 2[Q,V] = 1,
а значит,
[а,а+] = 1. (6.9)
Преобразования, обратные к (6.8),
£ = -т=(аЧа),
\2 (6.10)
Р = -^-а),
дают возможность найти оператор гамильтониана (6.7) в терминах a, at:
Я2 = i {_ (а+ - а)2 + (af+ а)2} = \ {afa+aaf}=а+а+ \ [a, af] =afa + |. (6.11)
Введем эрмитово самосопряженный оператор
N = aTa, (6.12)
тогда
(6.13)
Следовательно, решение задачи на собственные значения оператора N
N\n)=n\n)
дает и решение стационарного уравнения Шрёдингера с собственным значе¬
нием энергии
Е = Ксо(п + \).
Волновые функции таких стационарных состояний—
Фп(2) = (е|п>.
Найдем произведение
Na = а*аа = (aaf — 1 )a = a(N — 1).
aB классической механике траектория гармонического осциллятора в фазовой плоскости
переменных {Q, *Р} представляет собой окружность, по которой точка движется равномерно.
Поэтому для подобного движения выглядит естественным введение соответствующей комплекс¬
ной переменной a = (Q + iV)/V2, в точности отвечающей точке на окружности в фазовой
плоскости.
Лекция 6
95
Аналогично
No* = ataat = a1" (a^a +1) = a1* (N +1).
Отсюда следует, что вектор состояния а\п) является собственным для опера¬
тора N:
Na|n) = a(N — 1) |п) = (п — l)a|n)
с собственным значением (гг — 1), причем соответствующее связанное стаци¬
онарное состояние частицы при одномерном движении невырождено, т. е.
имеет единственный нормированный базисный вектор, так что состояние
а\п) = Ьп\п-1),
а его норма—
(атг\ап) = (д|п»*й|п) = (п\а*а\п) = (n|N|n) = п
поэтому
а\п) = л/7г|п. — 1). (6.14)
В частности, при п = О
а|0) =0. (6.15)
Совершенно аналогично находим
а*\п) = у/пЛЛ \п +1). (6.16)
Соотношения (6.14), (6.16) позволяют ввести следующие определения опера¬
торов a, af:
— оператор а понижает значение энергии осциллятора на величину Йсо,
это—понижающий оператор;
— оператор дР повышает значение энергии осциллятора на величину hco,
это—повышающий оператор.
Квантование уровней. Квантование уровней, т. е. определение допусти¬
мых значений наблюдаемой N, возникает вследствие положительности энер¬
гии осциллятора. Действительно, согласно определению эрмитово сопряжен¬
ного оператора и в силу положительной определенности нормы вектора
устанавливаем, что спектральный параметр не может принимать отрица¬
тельных значений,
(n|N|n)=n Ф=» {n\tfan) = {an\an)=n^0.
Теперь воспользуемся понижающим оператором для того, чтобы построить
из |п) цепочку собственных состояний
|п), а\п), а2\п), ..., ат\п), ...
со значениями энергии
+ hco(n-l +hco^n — 2 + ^j, kco(n-m + ^j, ...
96
Тема 3. Гармонический осциллятор
Для того, чтобы энергия принимала только положительные значения, необ¬
ходимо, чтобы цепочка оборвалась, т. е. существовало такое натуральное
значение т, что
ат+1|п) = 0, п-т^О.
Это возможно только в случае, если
am+1|n)~a|0) = 0,
а значит,
am+1|n) =а(атШ=й\/п(п-1 )...(п-т + 1) |п-т)
И
п = т, mGN.
Таким образом, собственные значения оператора N должны быть только
натуральными, а энергия стационарных уровней —
E = ha>(n + ^, neN. (6.17)
Энергия связанных состояний осциллятора принимает дискретные значения.
При этом квантовое число п называют числом заполнения. Квант энергии,
т. е. инкремент изменения энергии при изменении числа заполнения на
единицу Ап = 1, равен АЕ = ha>, поэтому говорят, что п-й уровень содержит
п квантов, а операторы а+, а называют еще операторами рождения и уничто¬
жения квантов.
6.3. Собственные функции, полиномы Эрмита
Волновые функции стационарных состояний осциллятора можно постро¬
ить, воспользовавшись свойствами операторов рождения и уничтожения,
именно:
|п> = ^|0>, (6.18)
причем
а|0) =0, (6.19)
и в представлении {Q} последнее уравнение для вакуумного состояния, т. е.
состояния с минимальной энергией, принимает вид
(s|ao)=o => ^(е+э|)1/’о(е)=о.
Преимущество излагаемой процедуры ясно видно из этого уравнения: оно
является уравнением первого порядка в отличие от исходного стационарного
уравнения Шрёдингера для осциллятора! Решение имеет вид гауссова рас¬
пределения
т<о 2
Ф0(д) =Ае" 2 =Ае~~*q , (6.20)
Лекция 6
97
где постоянная А определяется единичной нормировкой
о Г - т{0 -2
A2 J dq е * 9 = 1,
откуда
Вакуумное состояние, нормированное в пространстве {Q},—
(6.21)
В этом же пространстве волновые функции n-го уровня получаются согласно
так что в этих обозначениях волновые функции осциллятора выражаются
через полиномы Эрмита в виде
Так как потенциал осциллятора инвариантен при зеркальном отражении
оси q, невырожденные уровни связанных состояний имеют определенное
значение P-четности: число заполнения п равно числу внутренних узлов1
волновой функции стационарного состояния, и пространственная четность
совпадает с четностью числа узлов.
Эволюция по времени. Зависимость волновых функций стационарных
состояний от времени является стандартной: фактор ехр[—iEnt/h]. Интерес
представляет эволюция операторов рождения и уничтожения. Согласно урав¬
нению Гейзенберга (2.9)
(6.18):
(6.22)
Заметим, что
(е - Jo)x(Q) = (-l)e^ (Q)},
так что
(fi - Й) VS) = C-Dne^^|r{e-^^(Q)},
откуда
Полиномами Эрмита называют функции
(6.23)
(6.24)
Ш^ = ШЭ? + [/Л’Й3’
1Не считаем зануление волновых функций на концах интервала — оо <q< +оо.
98
Тема 3. Гармонический осциллятор
с учетом того, что
находим
Коммутатор вида
IАВ, С]
часто встречается в задачах, так что рассмотрим его в общем виде:
л Л Л Her АЛЛ Л л Л Л Л л ЛЛ ЛЛ АЛА АЛЛ АЛА
[АВ, С] = ABC - CAB=А(ВС - СВ) - (СА-АС)В=А[В, С] - [С, А]В.
В итоге
[AB,C]=A[B,C]-[£i]il. (6.25)
Поэтому
ГА Л+ЛТ ГЛ+Л А1 А+ГЛ А1 , Г Л + АЛЛ А
[а, а'а] = —[а'а, а] = —а1 [а, а] + [а1, а]а = а.
Значит,
.da
1dF = wa>
и решение этого уравнения имеет вид
a(t) =e_ia>ta. (6.26)
Совершенно аналогично находим
dt(t) = eia»tat (6.27)
6.4. Когерентные состояния
Как мы показали в лекции 1, соотношение неопределенностей для двух
наблюдаемых Л и В минимизируется, если (см. (1.24)—(1.25))
(А — А) |Ф) = ir (В — В) |Ф>, у е R, (1.24)
где
r = - 2iTTTC => 1г1 = т4- (1.25)
<[А, В]) 1,1 ДВ-
Для операторов Q и V в представлении {Q} со средними значениями (Q) = Q0
и (V)=V0 в состоянии |a): (Q|a) = <i/>a(Q), минимизирующем соотношение
неопределенностей, уравнение (1.24) перепишется в виде
(S-So)V>a(Q) = ir(-i^-'Po)V’a02) <=> (6-28)
<=> (Q-r^)V>e(Q) = (eo-ir^o)V»e(G)- (6-29)
Это обыкновенное дифференциальное уравнение легко решается в общем
виде, так как
&Фа
^ = dQ±(Q-Q0 + im>),
Лекция 6
99
откуда
(Q~Qp)^ I q
V'a(S) = '0Oe * +1PoS,
и с учетом
г = -2-^rOr— = —2(AQ)2
r m,v])\
находим
(Q-Qp)2 , n
'ФаШ)='Фое "^"+lP°Q. (6.30)
Значит, в общем случае соотношение неопределенностей координата-им-
пульс минимизируется на волновых функциях гауссова типа с учетом нали¬
чия ненулевого среднего импульса, что приводит к стандартному фактору
в виде комплексной фазы, зависящей от координаты.
Итак, для произвольной системы мы можем изготовить состояние гауссо¬
ва типа, которое минимизирует соотношение неопределенностей координа-
та-импульс в начальный момент времени. Но это не значит, что составленный
таким образом волновой пакет сохранит это свойство минимизации в ходе
эволюции: волновой пакет может расплыться в зависимости от гамильтони¬
ана физической системы и параметров начального состояния. Особый инте¬
рес представляют системы, для которых можно в явном виде построить ди¬
намически устойчивые волновые функции, минимизирующие соотношение
неопределенностей координата-импульс, т. е. с минимальными неопределен¬
ностями во все моменты времени. Такие волновые функции представляют
собой не расплывающиеся со временем волновые пакеты, в максимальной
степени соответствующие движению исходной классической системы.
В случае осциллятора заметим, что вакуумное состояние (6.21) является
гауссовым волновым пакетом с
(AQ)2 = | => Y = ~ 1.
Этот волновой пакет—стационарное состояние, т. е. распределение не изме¬
няется со временем, и свойство минимизации является динамически устой¬
чивым. С этим параметром у = — 1 уравнение (6.29) перепишется в виде
(e+^)^a(e)=(So+iWa(Q)- (6,31)
Учитывая явное выражение для оператора а в представлении {Q}, находим
а'фаШ) = а'фаШ), a = -j=(Q0 + iVo). (6.32)
В обозначениях Дирака основное уравнение
а\а) = а\а) (6.33)
представляет собой уравнение на собственные значения оператора уничто¬
жения, причем комплексное собственное значение имеет вполне определен¬
ный физический смысл: с точностью до фактора д/2 вещественная часть соб¬
ственного значения есть среднее значение координаты осциллятора, а мни¬
мая часть —среднее значение импульса.
100
Тема 3. Гармонический осциллятор
Кроме того, вычисляя квадрат вектора состояния (6.33), находим, с одной
стороны,
(а|а))+й|а) = (a|afa|a) = (a|N|a),
а с другой—
(а|а»+а|а) = |а|2(а|а) = \а\2,
где мы учли нормировку состояния на единицу. Значит,
(N) = |а|2, (6.34)
т. е. среднее число квантов в таком состоянии определяется квадратом моду¬
ля собственного значения оператора уничтожения.
6.4.1. Разложение по базису. Коммутатор оператора уничтожения с га¬
мильтонианом
[Я, а] = h<o[a*a, a] = —hoo[a, at]a = —hcocL
не обращается в нуль (за исключением среднего значения для вакуумного
состояния). Поэтому энергия в состоянии |а) флуктуирует вблизи своего
среднего значения, определенного согласно (6.34): (£) = fta>((N) +1/2). Раз¬
ложим это состояние по базису стационарных состояний
п
и с учетом уравнения на собственные значения
Сп(а) = (п|а) = ^(п\аа) = 1(&п\а),
где мы воспользовались также определением эрмитово сопряженного опера¬
тора. По построению
а}\п) = у/~пЛЛ |п + 1),
так что получаем рекуррентное соотношение
aC„(a) = д/п + 1Сп+1(а),
которое можно разрешить в явном виде:
Cn(a) = -^=C0(a).
Разложение принимает вид
\а) = C0(a) 7=Н =Со(«) £ ^Ю) = С0(а)е^|0),
п * * п
где мы использовали соотношение
Лекция 6
101
Коэффициент С0(а) можно определить из условия единичной нормировки
состояния
<а|а> = |C0(a)|2(0|e“*ae“at|0> = |С0(а)|2 £ ^ = 1,
П
где мы учли ортогональность стационарных состояний. Отсюда
|C0(a)|2e|a|2 = l => C0(a)=e_12",
и в это определение включено соглашение о фазе состояния. Окончательно,
|a) = e-tre“at|0)=e-^ S^T|n)- (6-35)
6.4.2. Распределение по числу квантов. Доля вероятности того, что в
состоянии |а) имеется п квантов, естественно, задается квадратом модуля
коэффициента в разложении состояния по базису (6.35):
pn = |(n|a)|2 = ^e-l“l2.
Вспоминая, что
получим
гг!
(N) = |a|2,
Pn = ^e~W, (6.36)
т. е. распределение Пуассона для числа квантов со средним значением (N).
6.4.3. Эволюция. Разложение по стационарным состояниям однозначно
задает зависимость вектора состояния |a(t)) от времени
|a(t)) =е"^ -^=е-»я"Чп), (6.37)
где теперь необходимо учесть явный вид спектра Еп = hco(n + 1/2), так что
Теперь введем зависящий от времени параметр
a(t) = e~lwta. (6.38)
Тогда зависимость состояния от времени сводится к
|a(t)) = e_i&>te"!^L ^=Нп). (6.39)
Учитывая зависимость оператора уничтожения от времени и сравнивая
(6.39) с (6.35), замечаем, что
a|a(t)) = a(t)|a(t)), a(t)|a(t)) = a|a(t)>, (6.40)
102
Тема 3. Гармонический осциллятор
т. е. в ходе эволюции состояние остается собственным состоянием зависяще¬
го от времени оператора уничтожения. Это означает, что с учетом динамики
сохраняется минимизация неопределенностей для координаты и импульса,
и состояние является когерентным.
Так как изменения сводятся к зависимости комплексной фазы собствен¬
ного значения от времени
то среднее значение частиц в когерентном состоянии остается неизменным
Сохраняется, следовательно, и распределение Пуассона по числу квантов.
Наконец, распишем собственное значение через средние значения коор¬
динаты и импульса
но это есть не что иное, как решение уравнений движения для классиче¬
ского осциллятора: в когерентном состоянии осциллятора средние значения
координаты и импульса совершают классическое движение1. Поэтому коге¬
рентное состояние осциллятора с минимальными флуктуациями координаты
и импульса максимально соответствует классическому движению частицы.
6.4.4. Полнота. Согласно (6.35) найдем скалярное произведение двух ко¬
герентных состояний
Значит, когерентные состояния неортогональны. Кроме того, базис гиль¬
бертова пространства осциллятора составляют собственные состояния энер¬
гетического спектра, т. е. счетное число векторов, в то время как число
когерентных состояний является континуумом в квадрате. Тем не менее,
покажем, что сумма проекторов на когерентные состояния дает соотношение
полноты2
янии средние значения координаты и импульса удовлетворяют классическим гамильтоновым
уравнениям движения, так как эти уравнения линейны, но в стационарных состояниях сред¬
ние значения тождественно равны нулю, так что теорема Эренфеста сводится к тривиальным
тождествам нулей. В других же, не когерентных, состояниях дисперсии координаты и импульса
неминимальны.
2Под элементом площади в комплексном пространстве понимается площадь параллело¬
грамма, натянутого на векторы da •-> ех dx 4- iey dу и da* = da -»ех dx - iey dy в двумерном
пространстве с ортами по осям х и у, так что da da=2i dx dy.
|a(t)| = |a|,
(JV(t)) = |a(t)|2 = |a|2 = (N).
(6.41)
(6.42)
П
(6.43)
13аметим, что согласно теореме Эренфеста для гармонического осциллятора в любом состо-
Лекция 6
103
где а = а* — комплексно сопряженное число. Для любых собственных состоя¬
ний энергии |n), |т) с учетом (6.35) матричный элемент (6.43)
. _ I /_i~\dada,_l_\ _ | dada_-ial2 атап
тп~] J -Щ-е
после замены переменных
а = re1{p, da da = 2i dip r dr
сводится к
00 2п
1 — 2 I dip
Cmn= I rdre r y== -^-[cos(m —n)y + i sin(m —n)t/j].
0 0
Так как {m, n} € N, интеграл по углам идет по полному периоду, и
2п
dip
I
[cos(m-n)y + isin(m — n)</>]=26„
Тогда
ос
I _ 2 »*2m
dr2 е~гГ-г = 5
. = 5mn J
mj —''mn>
0
что и требовалось показать.
6.4.5. Голоморфное представление. Выведенное выше соотношение
полноты можно использовать для построения голоморфного представления.
Введем волновые функции комплексной переменной
фп(.а) = {а\п) • е“ = =, (6.44)
где экспоненциальный фактор сокращает зависимость от комплексной пере¬
менной а:
— свойство голоморфности. Тогда скалярное произведение базисных функ¬
ций в голоморфном представлении можно построить, вставляя единичный
оператор, записанный через когерентные состояния, в соотношение орто-
нормированности базиса (т\п) = 5пт,
a)V>n(d)e-““ = Sn
В голоморфном базисе действие операторов рождения и уничтожения дает
&*'фп(.а) = (al^n) • е^ = (a|a»t|n) • е^ = а(а\п) • е^ = dipn(a), (6.45)
й'фп (а) = (а|ап) • е^ = л/п{а\п -1) • ef = п а =-^-у=, (6.46)
^/(п —1)! daVn\
104
Тема 3. Гармонический осциллятор
а значит,
В этом случае действительно
[а, а+] = , а] =1,
и
afi/)n(a) = да/>„(а) = \/п + 1-Д^= = ■\/n + l ipn+1(a),
>/(п+1)!
dn-l
а-фпСа) = п-^=г = Vnip^id),
как это и должно быть для собственных векторов энергии. Легко также
показать, что с введенным скалярным произведением
(■фт^Чп) = (tymWn) = у/п + 1 5mn+1,
т. е. операторы рождения и уничтожения действительно являются эрми¬
тово сопряженными друг другу. Произвольные операторы в голоморфном
представлении строятся в виде матриц с базисом функций {'фп(а)} (см.,
например, [17,19]).
Тема
4
Непрерывные симметрии
пространства
Лекция 7
Трансляции с непрерывным параметром сдвига, генераторы инфинитези-
мальных преобразований, общий вид преобразования операторов, связь
с классическими преобразованиями физических величин, вращения декарто¬
вых координат, спиновая матрица для вектора, генераторы вращений, момент
импульса, коммутационные соотношения генераторов вращений с векторны¬
ми и скалярными наблюдаемыми, преобразование волновых функций ска¬
лярных и векторных частиц, полный момент количества движения, спин
векторной частицы.
В классической механике евклидово пространство обладает непрерывны¬
ми симметриями—трансляциями и вращениями—наряду с дискретной сим¬
метрией зеркальных отражений, которые сохраняют инвариантными длины
векторов. Рассмотрим, как эти непрерывные преобразования действуют на
состояния и операторы в квантовой механике.
В лекции 4 мы изучили трансляции с фиксированным шагом а. В классике
соответствующее преобразование координат Та записывается в виде
Мы показали, что в квантовой механике оператор трансляций, сохраняющий
нормировку состояния и, следовательно, являющийся унитарным,
в которых действие оператора конечных трансляций на волновую функцию
можно представить в виде
7.1. Трансляции
г
—> га = г - а.
а на состояния как
(г|?в|Ф)=Ф(г+а).
Введем обозначения
(7.1)
(гв|Фа> = (»•№) *=> Фа(»’а) = Ф(г).
(7.2)
106
Тема 4. Непрерывные симметрии пространства
Это означает, что волновая функция после действия оператора трансляций
в преобразованных координатах получается просто заменой переменных в
исходной волновой функции. С другой стороны, соотношение (7.2) есть вы¬
ражение унитарности оператора трансляций:
<Га|Фа) = = <Г|Ф>.
Равенство (4.12) можно теперь записать и в виде
ФаОО = ?аФ(г) = ф(г+а),
откуда в координатном представлении мы нашли явный вид оператора транс¬
ляций через оператор импульса
Матричный элемент оператора F
(r'|F|r) =&(/, г)
есть не что иное, как операторная функция1 двух переменных. Это клас-
сическая величина, зависящая от координат. Поэтому вполне естественно
положить, что преобразование трансляции приводит к матричному элемен¬
ту, который получается просто заменой переменных функции, т. е.
&aK,ra)=&{r,,r), (7.3)
точно так же, как это было при определении преобразования волновой функ¬
ции. В обозначениях Дирака последнее равенство запишется в виде
K\Pa\ra) = (l'\P\r), (7.4)
т. е. матричный элемент преобразованного оператора Fa в преобразованных
координатах совпадает с матричным элементом исходного оператора F в ис¬
ходных координатах (можно говорить и о базисе состояний). Это утвержде¬
ние вполне согласуется с физической интерпретацией матричного элемента
и волновой функции: результаты измерения наблюдаемых характеристик
оператора (т. е. его матричные элементы) не зависят от того, в каких коор¬
динатах проводятся измерения.
В принятых нами обозначениях (7.1) равенство (7.4) запишется в виде
(r'\Wa\r) = (r'lFlr), VIг), И, (7.5)
откуда
Fa = faFtl (7.6)
Кроме этого, покажем, что равенство (7.4) допускает решение в виде
Ра = Т;ЧР), (7.7)
:В матричный элемент, вообще говоря, могут входить производные по координатам и т. п.
Лекция 7
107
где Га(/) —преобразование величины f в классической механике при трансля¬
ции, а Т~х — обратное преобразование. В самом деле, для оператора коорди¬
наты в этом случае имеем
(<|га|га) = (Та(г/)|Та-1(г)|Та(г)) = г(Та(г,)|Та(г)},
так как мы имеем дело с собственными значениями оператора координаты
на собственных векторах1. В силу унитарности оператора трансляций
(Та(г/)|Га(г)) = (г'|г),
и мы приходим к необходимому равенству
(г;|ГаМ=Иг|г>.
Справедливость (7.7) для некоторого эрмитова оператора наблюдаемой сле¬
дует из того, что матричный элемент можно строить по собственным векто¬
рам этой наблюдаемой, так что доказательство дословно повторяет рассмот¬
ренную нами логическую цепочку для оператора координаты2.
В итоге
Fa = faFPa=T;\F). (7.8)
Например, для оператора координаты, в силу того, что в классике
Га(г) = г—а => Га_1(г) = г+а, (7.9)
находим
ra = tarf^ — r+a. (7.10)
В справедливости этого утверждения мы убедились путем явных выкладок
в лекции 4.
Другой пример—оператор импульса. В классике импульс при трансляци¬
ях не изменяется
Та(р)=р => Т~1(р)=р,
откуда
Pa = WZ=P-
Вообще, для произвольных обратимых преобразований классической на¬
блюдаемой величины /
/g = G(/), (7.11)
следуя (7.8), в квантовом случае имеем
FG = GFGf = G_1(F), (7.12)
где F—квантовая наблюдаемая для /, G—унитарный оператор преобразова¬
ний, соответствующий классическому преобразованию G.
Согласно определению функции от оператора в виде ряда Тейлора /(F) =Xm
на собственных векторах этого оператора F\Fn)=Fn\Fn) получим элементарно f(F)\Fn) =
=/(Fn)|Fn). Значит, действуя в той же схеме, найдем для обратимой функции /_1(^)|/(^п)) =
=/_1(/(fn))l/(f„)) =fnl/Cfn)>. что и требовалось.
2В действительности компоненты, скажем, векторного оператора не обязательно комму-
тируют друг с другом, как это было в случае координат, так что возможна ситуация, когда
компоненты одного оператора не имеют общих собственных векторов. Тогда можно считать по¬
лученную связь определением закона преобразования операторов, обобщенного на квантовый
случай.
108
Тема 4. Непрерывные симметрии пространства
7.1.1. Инфинитезимальные преобразования, генераторы. Поскольку
мы рассматриваем преобразования, зависящие от непрерывного параметра,
в данном случае а, изучим предел бесконечно малого параметра трансляций,
а-» 0:
t.-1 + jfP-a- (7-13)
Тогда преобразование называется инфинитезимальным, а эрмитов оператор,
определяющий разложение унитарного оператора в виде (7.13),
г = \р (7.14)
— генератором преобразований (здесь —трансляций): f(a)-»l + ir-a, где
а-»0.
Отметим, что преобразования трансляций образуют группу Ли, так как
1) произведение трансляций определяется как последовательное применение сло¬
жной функции на координатах: Та о Тъ(г) = Га(Гь(г)), и по построению это произведе¬
ние ассоциативно:
Та о (Тъ о Гс) = (Та о Тъ) оТс = ТаоТьоТс = Га(Ть(Гс(г)));
2) существует единичный элемент: Га=0 = 1;
3) у всякой трансляции существует обратная трансляция:
ТаоТ_а = 1.
Генераторы же бесконечно малых преобразований образуют алгебру Ли. В самом
деле, так как произведения двух операторов группы в прямом и обратном порядке
могут отличаться только на элемент в той же группе:
(ТаоТь) = Гсо(ГьоТа),
то отсюда для инфинитезимальных операторов при {а, Ь, с} 0
—ГаГь = — ГьГа + iTc,
где Га = Г • а и т. п., так что
1Та> ГЬ] = -1ГС,
т. е. коммутатор генераторов лежит в векторном пространстве, натянутом на базис
генераторов. Кроме того, из ассоциативности следует справедливость тождеств Якоби
для коммутаторов
[[Га, Гь], Гс] + [[Гь, Гс], Га] + [[Гс, Га], Гь] =0
(циклическая перестановка индексов). Итак, у нас определено векторное простран¬
ство, образованное линейной оболочкой генераторов, так что в нем задан комму¬
татор, для которого справедливы тождества Якоби — это пространство называется
алгеброй Ли генераторов группы Ли.
В пределе бесконечно малого параметра преобразований соотношение
для преобразования оператора координаты (7.10) сводится к
![pa>r*V = a0,
откуда
[Pa> =
Лекция 7
109
т. е. приходим к стандартному выражению для коммутатора импульса с ко¬
ординатой.
В самом общем случае проведенное выше рассмотрение позволяет утвер¬
ждать справедливость следующего положения:
если у классической системы {£I, Р} — пара канонически сопряженных пе¬
ременных координата-импульс, то после канонического квантования генера¬
тором трансляций координаты является величина Г = Ф/Н.
В частности, если (р — угол вращения частицы относительно некоторой
оси, а [л — проекция момента импульса на ось вращения, то, поскольку угол
и момент образуют каноническую пару переменных, оператор вращения во¬
круг заданной оси имеет генератор F = fi/h. Впрочем, рассмотрим вращения
в евклидовом пространстве более подробно.
7.2. Вращения
Прежде всего напомним, как можно параметризовать бесконечно малые
повороты в евклидовом пространстве, так как согласно процедуре, описан¬
ной в предыдущем разделе (см. (7.11), (7.12)), это позволит нам определить
вид преобразования операторов в квантовой механике.
При вращениях длина вектора г не изме¬
няется, так что малое приращение вектора 5г
ортогонально самому вектору
г-бг=0.
Если е — единичный вектор вдоль оси враще¬
ния, а 5</? —-малый угол поворота вокруг этой
оси, то, выделяя проекцию радиус-вектора на
ось вращения гм = е(е • г) и поперечную к оси „ , ..
г 11 г j рис ^ Малое вращение
компоненту г± = г - гц, находим, что векторы
{е, г1з5г} образуют правую тройку и, очевидно, направление оси вращения
задается векторным произведением г± на 5г, а длина вектора приращения
равна \5г\ = г±5(р, так что1
е 5ц> = \(г1 х 5г).
г±
Определим вектор малых углов поворотов как вектор, направленный по оси
вращения, с модулем, равным углу поворота:
5<р = е5<р, (7.15)
тогда малое смещение вектора при вращении можно переписать в виде
векторного произведения
5r = —rx5ip, (7.16)
:Во избежание путаницы мы обозначаем векторное произведение не квадратными скоб¬
ками, которые в курсе квантовой механики отвечают коммутатору двух величин, а крестом:
векторное произведение а х Ь, а также часто выделяем эту величину круглыми скобками в фор¬
мулах с несколькими множителями.
110
Тема 4. Непрерывные симметрии пространства
где мы воспользовались ортогональностью радиус-вектора и его инкремента.
В тензорных обозначения это векторное произведение перепишется в виде
5га = -еарггр 5 ipr, (7.17)
где еарг—полностью антисимметричный тензор Леви-Чивита.
Как и для трансляций, определим матрицу инфинитезимальных преобра¬
зований координаты при вращениях на угол у —> 0 как1
га = ®арг13 = га + «а/3ГГ/3 Vr, * 5щ0 + Y4>r = 5а/3 + i(s • <p)af},
где векторная (3 х 3)-матрица s в координатном представлении покомпо¬
нентно определяется тензором Леви-Чивита:
(sr)a0 = (7.18)
Эта матрица эрмитова:
(spa0 = (sp,3e = (sr)aj3>
здесь мы использовали антисимметрию тензора Леви-Чивита. Покажем, что
для этой матрицы имеют место соотношения коммутации
[Sa>S/3] = i£a/3rV (7.19)
В самом деле, слева в этой формуле стоит матричное выражение с индексами
{М,А}
(— i) 8vA ^/xv^avA)
= &арйцх — + 5ajl5pX = 5ajX5px ~
Справа же имеем
i(-i)ea/3rerM = 8ац?>1ЗА “ ^аЯ^ц/3>
и тождество доказано.
В матричных обозначениях
+ <р—>0, (7.20)
откуда для конечных вращений находим
ЗД) = еиГ (7.21)
Поскольку длина вектора при поворотах сохраняется, получаем:
(rV)2 = r2 =Ф Г*Г* = = ГрГр => £%ap&ap' = 5pp',
или в матричных обозначениях
= (7.22)
1Обратите внимание на изменение знака в первой формуле по сравнению с формулой
(7.17) по аналогии с трансляциями, так как вращение (трансляция) на отрицательный угол
(вектор) в классике соответствует вращению (трансляции) на положительный угол (вектор) для
оператора наблюдаемой угла (координаты). Это следует из общей формулы для преобразования
квантового оператора (7.12), где стоит обратное преобразование.
Лекция 7
111
Значит, матрица вращений ортогональна: обратная матрица равна транспо¬
нированной. Кроме того, детерминант матрицы
det St = \,
что определяет отсутствие зеркальных отражений, для которых det SI — —1.
В итоге мы находим трехпараметрическую группу ортогональных преобра¬
зований с детерминантом, равным единице: группа вращений трехмерного
евклидова пространства—SO (3).
В классической механике установлено, что канонически сопряженный
к углу вращения обобщенный импульс—орбитальный момент импульса:
L = rxp.
Действительно, кинетическая энергия вращения с угловой частотой ф
T_mv2 _ тг2ф2
2 2 ’
так что обобщенный канонически сопряженный импульс
дТ о «
L = —r = mr<p=rx mv=rxp.
dip
7.2.1. Преобразование операторов. Согласно общей схеме при канони¬
ческом квантовании оператор вращений в квантовой механике имеет гене¬
ратор
А 1 А
г=^
так что
k=enLv. (7.23)
Для операторов преобразование имеет вид
Fv = RFRr = (F). (7.24)
Рассмотрим два важнейших случая.
1 Скалярная наблюдаемая С. В классической механике скалярные вели¬
чины не преобразуются при вращениях. Поэтому
<%(С) = С => 52-1(С)=С.
Значит, и в квантовой механике скалярная наблюдаемая не преобразуется
при действии оператора вращений
ev=C. (7.25)
Подставляя в (7.24) инфинитезимальный оператор вращений
R=l + if.-y>, <р^ 0, (7.26)
находим коммутатор оператора орбитального момента с произвольной ска¬
лярной наблюдаемой
[1,С]=0. (7.27)
112
Тема 4. Непрерывные симметрии пространства
2. Векторная наблюдаемая А. В классической механике векторные вели¬
чины преобразуются так же, как и координаты:
А^ЯарАр => т-\А)а = ^1рАр, (7.28)
так что квантовый векторный оператор преобразуется при вращениях как
А1=йАа& = !%1§Ар. (7.29)
Для бесконечно малых поворотов в правой стороне (7.29) получаем
®1(}АрЪАа-еа1}гАр<рг, <р->0,
в то время как
ЛЛЛф А 1_Л Л _
RAaRf ъ Аа + ^ [Lr<pr, Ла].
Сравнивая два предыдущих выражения, находим
Аа] lfiSQpyApj
так что после переобозначения индексов суммирования получаем общее вы¬
ражение для коммутатора момента импульса с векторной наблюдаемой:
[La, Ар] — iheapyAy. (7.30)
Обычно определяют безразмерный векторный оператор
l=\t, (7.31)
так что, в частности, из (7.30) следуют коммутационные соотношения для
оператора момента импульса
= (7.32)
Последнее равенство можно также установить посредством выкладок в яв¬
ном виде, пользуясь выражением для оператора
La = еа ругрРу
Важным приложением общих результатов являются коммутационные со¬
отношения генераторов поворотов с квадратом момента импульса
[1аЛ2] = 0, (7.33)
как и должно быть для скалярного оператора Z2.
7.2.2. Преобразование состояний. Как мы знаем, в классическом при¬
ближении волновая функция состояния, амплитуда вероятности, переходит
в волну материи, фаза которой пропорциональна классическому действию
для корпускул, которые движутся по лучам согласно законам геометрической
оптики. Однако пример поля — электромагнитные волны — показывает, что
амплитуда волны обладает еще и такой характеристикой, как поляризация.
Действительно, электрическое и магнитное поля являются векторами. Следо¬
вательно, амплитуда вероятности при квантовании будет характеризоваться
Лекция 7
113
не только своими модулем и фазой, зависящими от координат и импульсов,
но и поляризацией. Поэтому частицы, составляющие, например, электромаг¬
нитное поле в квантовой механике, кроме координаты и импульса имеют
еще и наблюдаемую величину Я, которая в классике соответствует поляри¬
зации волн. Для частиц с поляризацией базисом состояний может служить
набор векторов с определенными значениями координаты частицы и ее по¬
ляризации
|г,А).
Тогда состоянию |Ф) соответствует волновая функция
(г, А|Ф) = Фя(г).
Особенностью преобразования квантовых состояний при вращениях являет¬
ся определение закона преобразования поляризаций частиц.
Скалярные частицы. Скалярными называются частицы, у которых нет
поляризации, так что имеет место стандартное определение преобразований
состояния при вращениях:
(г*|Ф*) = (г|Ф), Ф*(г*) = Ф(г),
где
k\*) = m, K|r> = |r*) = |^r>,
где 9t — матрица поворотов в классике. Отсюда можно также записать
^(г) = Ф(^тг).
С другой стороны,
Ф*(г) = (г|А|Ф) =е«£^Ф(г)
есть не что иное, как координатное представление оператора вращений, где
i = -ih(rx V).
В итоге
'К (г) = е»^Ф(г) = Ф(^тг). (7.34)
В справедливости этого тождества можно убедиться прямыми вычисления¬
ми. Например, при у —> О инфинитезимально находим
{1 + ц>- (гхУ)Жг) = Ф(г-гх</?),
и, переставляя порядок вычисления смешанного произведения слева, полу¬
чаем верное тождество
Ф(г)-(гх v?) • УФ(г) = Ф(г-г х </>).
Векторные частицы. Векторными называются частицы, поляризация и
состояние которых характеризуются вектором s. Поэтому волновая функция
векторной частицы—вектор:
(г,5Я|Ф) = Фя(г) или (г, з|Ф) —S' Ф(г). (7.35)
114
Тема 4. Непрерывные симметрии пространства
Вектор поляризации при вращениях преобразуется так же, как координата,
так что
R\r, s) = И, sv) = |mr, 01s). (7.36)
В силу унитарности оператора вращений
Ш = 1
по-прежнему имеет место тождество
{rv, sv’|'I'v’) = (г, «|Ф). (7.37)
Отсюда
(ад-Ф^(^г)=5-Ф(г),
или после подходящей замены переменных г -»Й2тг и использования равен¬
ства
{0ts • Ф) = &xpsp<S>x = = s • (52ТФ)
получаем
5гтФ^(Г)=ф(^тг) ^ фУ(Г)=^ф(^тг)> (738)
или в тензорной записи
ф£(г)=^лрфр0%тг). (7.39)
Далее используем матричную запись для М
& = eiiv
и операторное равенство (7.34)
Ф(^тг) = еп^Ф(г), (7.34)
так что (7.38) эквивалентно
Ф? (Г) = е»(Ш)'^Ф(г), (7.40)
где матричный оператор размерности действия
S=hs (7.41)
называется спином векторной частицы, а сумма
M=t + S (7.42)
— полным моментом импульса частицы. В принятых обозначениях преоб¬
разованная при вращениях волновая функция выражается через исходную
волновую функцию действием оператора вращений с генератором полного
момента количества движения
Ф? (Г) = е»й^Ф(г), (7.43)
так что физический смысл оператора спина, возникающего из-за введения
поляризации волновой функции, есть собственный момент количества дви¬
жения частицы.
Лекция 8
115
Так как в координатном представлении дифференциальный оператор ор¬
битального момента коммутирует с постоянной матрицей спина
[1а,^]=0, (7.44)
а коммутационные соотношения для спиновой матрицы идентичны соотно¬
шениям для орбитального момента, для полного момента импульса1 получа¬
ем
[Ма, Мр] = i heaj3rMr, (7.45)
которые совпадают с коммутационными соотношениями как орбитального
момента, так и спина.
Лекция 8
Квантование момента импульса, повышающий и понижающий операторы,
старший и младший вектор представления, вырождение квадрата момен¬
та по значениям проекции на ось, полуцелые значения момента импульса,
допустимые значения орбитального момента, базис в полярных координа¬
тах, компоненты оператора орбитального момента в полярных координатах,
сферические гармоники, полиномы Лежандра, присоединенные полиномы
Лежандра, P-четность сферических гармоник, число узлов.
8.1. Момент импульса, квантование
Полученные нами в предыдущей лекции коммутационные соотношения
для компонент момента количества движения составляют основу для про¬
цедуры построения полного набора наблюдаемых, например, для свободной
частицы2 в 3-мерном евклидовом пространстве:
L/a* jp'i ^apyjy>
А Ал
U«J2] =о,
lLp2]=o,
(8.1)
Ua; Pp]-i£aprPr-
Кроме того, если энергия является скаляром3, то
[ja,H]= 0. (8.2)
гЧасто используют обозначения hj=J=M.
2При наличии взаимодействия, т. е. при включении потенциала в гамильтониан, необходим
мо анализировать и перестановочные соотношения генераторов симметрий с потенциалом.
3Для частицы в потенциальном поле это всегда имеет место, если силы, действующие на
частицу, центральные.
116
Тема 4. Непрерывные симметрии пространства
Тогда полный набор наблюдаемых может включать в себя для свободной
частицы следующие операторы1:
Действительно, все эти операторы коммутируют, так что они могут быть
измерены точно совместно, т. е. они имеют общие собственные векторы
состояния. Важно подчеркнуть, что компоненты момента импульса, вообще
говоря, не могут быть измерены точно совместно, так как их коммутатор не
равен нулю. Исключение составляет случай
т. е. если орбитальный и спиновый момент импульса тождественно равны
нулю в данном состоянии.
Рассмотрим задачу на собственные значения квадрата импульса и одной
из его компонент, для определенности компоненты по оси z:
так как выполнено условие вырождения: оператор j2 коммутирует со всеми
компонентами j, но эти компоненты не коммутируют друг с другом.
Введем операторы
массу частицы в качестве величины, задающей связь между энергией свободной частицы и ее
импульсом.
(8.3)
j2|A,ju) = A|A,ju),
А|А,м)=м|А, м).
(8.4)
Сразу отметим, что собственные состояния j2 являются вырожденными по ju,
(8.5)
Тогда легко видеть, что
и аналогично
А Л Ал Aq А
j~j+=j;+jy-jz.
В итоге
Ал I Л Л Л Л Ал
j =^U+j- +)-)+)+j2-
Коммутатор этих операторов с компонентой jz легко вычисляется
Uz, j±] = lL )х ± i/y] = i/у ± i(-ijx) = ±j±.
Это позволяет установить, что векторы /±|Я, /i) также являются собственны¬
ми векторами заданной пары наблюдаемых:
jJ±|A, ju) =L(i ± 1)1 А, ц) = (jU± l)j±|A, ju).
хМы включили в полный набор энергию частицы, но вместо нее можно было поставить
Лекция 8
117
Итак, операторы j± являются соответственно повышающим и понижаю¬
щим на единицу значение проекции момента импульса операторами. Значит,
J± I я, М) =Л4 (А, /х) | А, д ± 1),
где нормировочные множители Л4 легко определить, взяв модуль каждого
из состояний:
(А, /х|/_/+ (А, (л) = (А, д|(j2 -)2 - jz)|A, ju) = А - ц2 - /х ^ О
и аналогично
(A, /х| /+ /_ | А, д) = (А, ц\ (/2 - j2 + jz) I A, ju) = А - ц2+ц 2 О,
откуда
/±|А, ju) = \/А —juCju±l)|A, д±1). (8.6)
Так же, как и в случае гармонического осциллятора, использование повыша¬
ющего и понижающего операторов позволяет провести квантование спектра
собственных значений пары {j2, jz} с помощью условия неотрицательности
нормы вектора состояния. В самом деле, повышающий оператор переводит
ц -* ju +1 и изменяет норму вектора
N2 —> Л/*2 [А — ju(ju +1)] ^ 0.
Для того чтобы норма вектора состояния после многократного действия по¬
вышающего оператора оставалась положительно определенной, необходимо,
чтобы цепочка многократного повышения прервалась, т. е. чтобы существо¬
вал старший вектор состояния:
J+ |А,мя) = 0, А = /ха(/хл-Ы). (8.7)
Составим цепочку состояний, многократно действуя на старший вектор по¬
нижающим оператором:
|А,/*я). /-|А,Ма>, -
с собственными значениями проекции
Мя> ...
Для того чтобы норма векторов в этой цепочке состояний оставалась положи¬
тельно определенной, необходимо, чтобы она оборвалась, т. е. существовал
бы младший вектор:
j_|A,v*)=0, A = va(va-1), (8.8)
но при этом мы получаем собственное значение для младшего вектора пу¬
тем целого конечного числа шагов из собственного значения для старшего
вектора:
vx=nx-n, neN.
Собственное значение А оператора j2 при действии повышающего и пони¬
жающего операторов не изменяется (соответствующий коммутатор равен
нулю), так что согласно (8.7), (8.8) имеет место тождество
Мя(Мя +1) = (Мя - п) (/хя - п -1)
118
Тема 4. Непрерывные симметрии пространства
с единственным решением
Таким образом, проекция момента импульса на заданную ось принимает
полуцелые значения, и состояния можно полностью охарактеризовать зна¬
чением проекции для старшего вектора /хя=j, так что
J2\j, m)=j(j + l)\j, т),
Jz\j> тп)=т\j, т),
* , ' (8.9)
]-\j> -j) = o,
причем количество состояний с заданным j равно числу шагов от старшего
вектора к младшему п = 2j плюс одно начальное состояние построения це¬
почки (старший вектор), т. е. вырождение j2 по числу проекций есть
k = 2j +1, (8.10)
где {j, т}—полуцелые числа,
j = |(fc-1), fceN,
и fc—кратность вырождения j2. В частности, при k = 1 имеем j = 0.
Кроме того, мы нашли, что матричные элементы повышающего и пони¬
жающего операторов задаются формулами
(j, n\L\j, т) = Vi0' + l)-m(m±l)5nm±1. (8.11)
8.2. Орбитальный момент, собственные функции
Допустимые значения орбитального момента. Совершим поворот неко¬
торой физической системы, у которой нет поляризации, т. е. спин системы
тождественно равен нулю, вокруг некоторой оси на угол 2тс. При этом пре¬
образуются только координаты системы, так что система после поворота
тождественно эквивалентна исходной системе до поворота. Другими слова¬
ми, поворот физической системы с нулевым спином вокруг некоторой оси на
угол 2п приводит к тождественному преобразованию для волновой функции
этой системы. Даже отличие волновых функций до и после такого поворота
на глобальную фазу запрещено, потому что при наличии такой фазы можно
было бы ее обнаружить по интерференции с неким другим состоянием при
составлении одинаковых суперпозиций стороннего состояния с двумя состо¬
яниями системы до и после поворота.
Итак, если е — единичный вектор вдоль оси поворота, то вектор углов
4> = 2пе, и согласно закону преобразования волновой функции состояния без
спина при вращениях, поворот на угол 2п дает
Ф(г) = е2^'еФ(г),
Лекция 8
119
где мы положили преобразованную функцию тождественно равной исход¬
ной. Квантование системы можно провести, положив в качестве проекции
орбитального момента компоненту вдоль оси вращения,
Л А
k = l-e,
так что для базисных состояний
\l,lz)=e2nil‘\l,lz),
откуда
lz = me N,
т. е. орбитальный момент может принимать только целые значения.
Если у системы есть ненулевой спин, то совершим преобразование коор¬
динат путем поворота вокруг некой оси на угол 2тг, при этом сохраняя по¬
ляризации частиц. Такое преобразование также сводится к тождественному,
так как мы получаем систему в тех же координатах и с теми же поляризация¬
ми. Поэтому приведенные выше формулы остаются в силе, так как спиновые
степени свободы не преобразовывались по построению. В итоге приходим
к тому же выводу о целочисленном значении собственных значений проек¬
ции орбитального момента.
Собственные функции. Для построения собственных функций орбиталь¬
ного момента в координатном представлении используют полярную систему
координат, так что вектор в декартовых координатах
в = а*ех + ауеу + ажеж,
где базисные векторы имеют вид
ех = (1, 0,0), еу = (0,1, 0), ez = (0,0,1),
выражают через базис в полярных координатах
а = агег + + а^е^,
где уже
ег = (cos ip sin 0, sin ip sin 0, cos 0),
ee = (cos ip cos 0, sin (p cos в, -sin 0),
= (-sin (/?, cos (p, 0).
При этом элемент длины
dr2 = dr2 + г2 d02 + r2 sin2 0 dtp2 = dl2 + dt2e + dt2
сохраняет форму евклидовой метрики в терминах дифференциалов dtk, где
индекс к принимает значения г, 0, </?. Тогда вектор набла имеет вид
с суммированием по немому индексу к, а радиус-вектор—
г=егг.
120
Тема 4. Непрерывные симметрии пространства
Выразим компоненты орбитального момента в полярных координатах.
Например,
tz = ez • I=- iez • (г x V), (8.12)
где векторное произведение запишем в полярных координатах
г хЧ = е^гкгщ = евевг9г-£- + е9е9гвгщ, (8.13)
где полностью антисимметричный тензор Леви-Чивита определен стандарт¬
но, так что для правой тройки базисных векторов
erOip = l-
Отсюда для s-й компоненты находим
I =—i —
£* 1д(р*
(8.14)
что и следовало ожидать из канонического квантования, так как проекция
орбитального момента на ось z как раз отвечает поворотам со сдвигом угла
(р. Этот оператор эрмитов на функциях, периодических по </? с периодом 2тг.
Для оставшихся компонент прямые вычисления после несложных выкла¬
док, которые мы здесь опускаем, дают
lx = +i sin 4>jQ + i cos ctg 0^,
откуда
Zy = -icos<^ + i sin <p ctg 0^,
г±=е±,’’(±зИ
(8.15)
(8.16)
Как видим, компоненты орбитального момента зависят только от углов.
Лекция 8
121
(8.18)
Для справок приведем также вид оператора квадрата орбитального мо¬
мента в угловых переменных:
Р = —Afsin0:^l \-ZTT2- (8.17)
Sin в дв V. дв J sin в дф
Собственные функции
12щ1т(е,<р)=щ+1щт(в,<р),
Ъ‘Щ,т(в>Ч’) = ™Щ,т(в> V),
нормированные на единицу,
1 2 п
/ d cos в j d(p 9Cn(0,v)^(0.V) = l,
-1 О
называются сферическими гармониками. В угловых переменных уравнение
на собственные значения для проекции момента на ось z
ЪЧт(0> V) = -i^^,mC6, у) = ТПЩ'т(в, (?)
легко интегрируется при разделении переменных, так что
^(0,V) = eimvyljm(0).
Функции ^>т(0) проще всего найти, используя повышающий оператор, кото¬
рый зануляет старший вектор:
?+e£z(0,¥O=о,
откуда
дв•
с решением
^Yu«9)-Zctg6>fy(e) = 0,
&ц(9, ip) = С; sin1 0el!v, (8.19)
где нормировочную константу Q определим, взяв интеграл
2 п
Ii = J dcos0 J dip sin2*(0).
о
Проведем интегрирование по частям:
1 о
Ii=2n J sin21 в d cos в = -2n 21 J cos в sin2Z_1 в cos 9 de=2l[Ii_1 - 1г],
-1 n
где после изменения порядка пределов интегрирования мы ввели
Ii=2tc J sin2H_1 в d0.
о
Для этого интеграла аналогично находим
к п
Ii = —2n j sin2* 0dcos0=2Z J cos2 в sin2*-1 d6 =2Z[Iz_1 — Jz].
122
Тема 4. Непрерывные симметрии пространства
Получаем рекуррентное соотношение
21 ~ 2212
1, = 21 + 17,-1 = (21) (21 +1)/)_1’ ZeN’
причем
/0 = 4я,
и, следовательно,
?_ 22|ао2
' (2i+i)i
Отсюда
В итоге нормированная на единицу сферическая функция для старшего
вектора—
ip) = (-1)'sin! 0е^, (8.20)
где фактор (—I)1 определяет общепринятое соглашение о фазе. Сферические
гармоники с меньшими значениями проекции момента получаются действи¬
ем понижающего оператора:
Li I, I)=Jki+d-ki-d I и i -1>,
L| l, l-1) = y/l(l + l)-(l-l)(l-2) 11,1-2) = \/ 2(21 — 1) 11,1 - 2),
так что
t*\l, i) = V21(21 —1)2 \l, I — 2),
L\U 1-2) = Ji(i+i)-(i-2)(i-3) 11, i- 3) = л/з(2г-2) IZ, г - з),
или
ti\l, l) = 21(21-1) (21 -2)2-3 |Z, 1-3).
По индукции
В частности,
®{jO(0, V?) = —^=Zi^(6>, ¥>).
VC2Z)!
В явном виде
“8 9)Ч»С6)==to"M,(ted)^r^bsta" e) W»>-
Отсюда находим
sin' ^•'(9)=c^sin2' *•
Лекция 8
123
Собирая множители, получаем
Согласно стандартному определению полиномами Лежандра называют функ¬
ции
ЖО = ^^г(1-£2)г, (8.21)
И
m=jmPl,0S в).
Так как сферические гармоники, являющиеся собственными векторами, ор¬
тогональны и нормированы на единицу, для полиномов Лежандра автомати¬
чески находим
Кроме того, отметим следующее свойство этих полиномов:
ргш=1, ргс-1)=(-1)г,
что следует из того, что ненулевой вклад при |£| = 1 дает лишь слагаемое
с нулевой степенью фактора (1 — £2), и поэтому нужно многократно диф¬
ференцировать лишь степень этого фактора, что и приводит к сокращению
численного множителя в (8.21).
Состояния Щут(6, <£>) с т > 0 обычно выводят с помощью действия повы¬
шающего оператора на функцию Щ}0(в, </?). Для этого найдем
1+%т(в, Ч>)= eiv + i ctg 0^)eim^,m(0) =
= ei(m+1* :m ctg 0)^,m(0) =
= -е«т+1^ {(sin 0)m+1 —!Ц- -r^rs Ь/т(б) =
(. dcos0sinm0J L’m
= y/l(l +1) - m(m + 1)Щ т(6, </>)•
Значит, с одной стороны,
= eim4-irj^fsinm 9j£^Pi(cos в),
а с другой—
о(д)=у/щ+1) Va - D«+2).. Va - m - mi+тщ^в, <*>)=
124
Тема 4. Непрерывные симметрии пространства
В итоге
Щ>т(в, ip)=eim4-l)m]/2l4+n1 g-gK-Ccos в), (8.22)
где присоединенные полиномы Лежандра—
%(€) = (1 - ?2)т/2^гРг(?). (8.23)
Совершенно аналогично строятся сферические гармоники Щ-т(.д, </>) с
отрицательной проекцией орбитального момента на ось z, где т > 0:
»u(e.v)=e"imv/^iiSp,-m(cos0)j (Km^> (8-24)
так что имеет место элементарное соотношение комплексного сопряжения
^,-m(0^)=(-Dm^m(6^).
Р-четностъ. При зеркальном отражении всех осей евклидова простран¬
ства г-^-> —г углы преобразуются как
р р
V?—»^ + я, 0—*п-в,
или
eimy> JU eim(V>+") = (—l)meim('’, cos 0 - cos 0.
Присоединенные полиномы Лежандра суть производные функции четности
(—1)г, так что их четность определяется просто числом производных, и
Pi m(cos 0) (-l)i_mPi m(cos 0).
Собирая факторы, находим
^>m(0, v) -L (-1 )1Щ1т(в, у). (8.25)
Другими словами, Р-четность сферических гармоник равна
АР = (-1)'.
Отметим, что уравнение на собственное значение квадрата орбитально¬
го момента при условии справедливости уравнения на собственное значе¬
ние проекции орбитального момента (см. (8.17)—(8.18)), очевидно, сводится
к одномерному уравнению второго порядка для присоединенных полиномов
Лежандра. Это уравнение можно проанализировать стандартными метода¬
ми, рассмотренными нами при изложении квантовой механики в одном
измерении. В частности, можно установить, что присоединенный полином
Лежандра Р*>т(£) имеет I - т узлов на интервале — 1 < £ < 1, т. е. четность
числа узлов этой волновой функции совпадает с ее Р-четностью.
Лекция 9
125
Лекция 9
Спин спинор и матрицы Паули, преобразование спинора при вращениях,
поворот на угол 2п, эквивалентные представления группы вращения спино¬
ров SU(2), зарядово сопряженный спинор, спинорная метрика, индексы с точ¬
ками и без точек, тождественные частицы и принцип запрета Паули, опера¬
тор перестановок тождественных частиц, антисиметричные и симметричные
волновые функции, фермионы и бозоны, «духи», фермионный осциллятор,
антикоммутационные соотношения операторов рождения и уничтожения,
голоморфное представление и переменные Грассмана.
9.1. Спин матрицы Паули
Рассмотрим собственный момент импульса частицы, спин, s = В этом
случае соответствующая спиновая матрица представляется в виде
s = l&, (9.1)
где а — матрицы Паули1. Найдем явный вид матриц Паули, используя общие
выражения для матричных элементов момента импульса (8.9), (8.11). Базис
спиновых состояний для краткости обозначений записывают как
f,+f) = l+>, = (9-2)
причем это —собственные векторы проекции спина
s*l+) = |l+)> Sz|-) = -i|-). (9.3)
Следовательно, эта матрица в рассматриваемом базисе имеет диагональный
вид
2 U -1) •
Согласно (8.11) ненулевые матричные элементы повышающего и понижаю¬
щего операторов
<+|S+|-> = V/i(i + l)-(-1)1 (-5 +1) = 1, (9.4)
(-|5_|+> = «+|1+|-)^ = 1, (9.5)
откуда
*♦=$£)> *-=(!!!)• <9«
Тогда
l, = |(St + 8.) = | (» J) (9.7)
хМы часто в дальнейшем будем опускать «шляпку» над сигма-матрицами как символ, ука¬
пывающий, что мы имеем дело с оператором, потому что у матриц Паули нет классического
числового аналога.
126
Тема 4. Непрерывные симметрии пространства
»,=£»♦-*->=!(? -»)• <9-8>
Поэтому сигма-матрицы Паули—это
&* = (л о) ’ &y = G "о) ’ *• = (J -!) • С9-9)
Поскольку частица со спином которую называют спинором, обладает дву¬
мя поляризациями1
0а =(£))> « = {1,2},
волновая функция нерелятивистского спинора2
(г, ба|Ф) =я/>а(г) (9.10)
— это так называемый двухкомпонентный спинор Паули.
При вращениях спинор преобразуется согласно
V»S(»#) = {eu-»}gV»/j(r), (9.11)
где мы указали матричные индексы в явном виде. Так как по построению
(г,0|Ф) = 0“г/>а(г)
— инвариант при вращениях, спинор поляризации 0“ преобразуется как
00 = 0«{е“ч'}£ 0£ = 0“{е-*П£. (9.12)
В матричных обозначениях
xl>'f=Rs-i>, ev = e-Rl, fi.s = ei*'4>, (9.13)
причем ipa — столбец, а 0a — строка.
Для вычисления матричной экспоненты установим два факта:
1) коммутационные соотношения
№а> = 2iеарг°г (9*14)
следуют из коммутационных соотношений для момента импульса;
2) антикоммутационные соотношения
{&а> У = &а&1} +°f}°a = 25а0 (9.15)
устанавливаются прямыми вычислениями произведений матриц Паули.
Поскольку
<7а<7/3 = \ \&а> + |{0-а, &/}},
1 Далее будем использовать для спинорных индексов греческие буквы в начале алфавита:
а, /3,— а для векторных индексов греческие буквы в середине алфавита: д, v,...
2В отличие от векторов, для которых в евклидовом пространстве метрика в декартовых
координатах—единичная матрица, так что можно не делать различий между верхними и ниж¬
ними индексами, для спиноров, как будет ясно ниже, верхние и нижние индексы несут разную
информацию: метрика для спиноров отличается от единичной матрицы.
Лекция 9
127
(9.16)
(9.17)
где справа стоит векторное произведение векторов (не путать с коммутато¬
ром!). В частности,
п=О
четные степени разложения пропорциональны единичной матрице, а нечет¬
ные — оператору
где е — единичный вектор вдоль оси поворота. Тогда суммирование четных
и нечетных степеней дает
т. е. волновая функция спинора меняет знак после поворота на угол 2п. Это
свойство, очевидно, является общим для всех частиц с полуцелым спином,
которые называются фермионами.
а матрица ау чисто мнимая, и
Для того чтобы отличать фиксированный набор матриц (9.9) от матриц, кото¬
рые получаются при проецировании на произвольно заданные оси декарто¬
вых координат {сгх, сгу, crz}, часто для матриц Паули используют обозначения
С учетом антикоммутационных соотношений элементарно находим
су-а')2 = ч>2.
Тогда в экспоненте оператора вращений
00
(</> • O') = I </> I (е • <т) = (V? • е) (е • <х),
ei* v’=cosQ(v>-e)j + i(e-d) sin(^(v?-е)).
(9.18)
При повороте вокруг оси на угол 2п = (<р • е) получаем rv =г и
(9.19)
Значит,
(9.20)
9.2. Спинорная МЕТРИКА
Заметим, что матрицы ах, az вещественные, так что
а2о,*а2 = а2аТа2 = —а.
(9.21)
128
Тема 4. Непрерывные симметрии пространства
Отсюда немедленно следует, что
cr2{eiS'v }тсг2 = e_iiv> фф a2RTsa2=Rl (9.22)
и совершенно аналогично
a2R*s<r2=Rs. (9.23)
Говорят, что соотношения (9.22) и (9.23) устанавливают соответственно эк¬
вивалентность транспонированного представления группы вращения спино¬
ров эрмитово сопряженному представлению этой группы и эквивалентность
комплексно сопряженного представления исходному спинорному представ¬
лению.
Действительно, рассмотрим, например, спинор-столбец, построенный по
комплексно сопряженному спинору:
'фс = 1<Г2‘Ф*-
При вращениях он переходит в
'Фс = i^2 (^s^)* = cr2R*sa2{i(T2%p*') =Rs'ij)c,
где мы воспользовались тем, что = 1, и соотношением (9.23). Значит, этот
спинор при вращениях преобразуется так же, как и сам спинор гр. Поэтому
произведение двух любых спиноров
*l>lX =i>T(-i<r2)X =^а(- 1<Г2)аРХр
является скаляром, т. е. инвариантом группы вращения спиноров. Итак,
последняя формула определяет скалярное произведение двух спиноров. По¬
этому согласно общему представлению о метрическом тензоре (как о квад¬
ратичной линейной функции) введем метрическую матрицу для спиноров
6 = ia2=(_; J), (9.24)
что является не чем иным, как полностью антисимметричным тензором
второго ранга:
{£}“/» = е“0 = -е0“, е12 = 1.
В терминах метрики скалярное произведение двух произвольных спиноров
гр их
-ф-Х = ^ЖХр- (9-25)
Метрика определяет спиноры с верхними индексами
ярр = ера\ра,
так что скалярное произведение
раХа-
Обратная метрика еа$ определяется согласно
Лекция 9
129
но так как
(io-2)C-io-2) = 1»
то, очевидно,
еар = -еар = ера, е12 = -1.
Определенный выше спинор-столбец грс называют зарядово сопряженным
спинором, и его обычно обозначают спинором с чертой, который имеет
верхний индекс с точкой:
^ = Ца2гР*Г = (еа^рГ. (9.26)
Как мы показали, этот спинор при вращениях преобразуется так же, как
и обычный спинор1. Поэтому скаляром будет величина
х'■'Фс = Ход*>
где мы ввели обозначение для спинора-строки с нижним индексом с точкой
как эрмитово сопряженного к обычному спинору:
Ха = (Ха)Г- (9.27)
Элементарно получаем
Xt = iX*}T = {-102(1О2**)}Т = {-102*}Т-
Поэтому
Х"Ф = еар Х*#&> еар = -Иог2}ф е12 = -1,
т. е. метрика еаР в спинорных индексах с точкой совпадает с метрикой
в индексах без точек.
Метрика остается инвариантной при вращениях спиноров. Действитель¬
но, общий закон преобразования метрики дает
es —RTssRs = etr'Rl^Rs = = 6,
где мы воспользовались тождеством (9.22). Группа инвариантности спинор-
ной метрики с det Rs = 1 называется специальной унитарной группой на
двухкомпонентных спинорах: SU(2). Это трехпараметрическая группа. Мы
уже исследовали алгебру генераторов группы при построении вращений
спиноров. Эта алгебра совпала с алгеброй группы вращений трехмерного
евклидова пространства SO(3). Тем не менее, сами группы не совпадают, так
как в SU(2) допустимы и полуцелые собственные значения генератора sz,
а в SO (3) — только целые значения jz. Это особенно ярко проявляется при
проведенном выше рассмотрении вращения на угол 2п: для спиноров это
вращение дает фактор —1, а для бозонов, частиц с целым значением спина, —
фактор +1.
ХВ релятивистской теории с бустами (преобразованиями Лоренца) зарядово сопряженный
спинор преобразуется при действиях бустов иначе, чем обычный спинор.
130
Тема 4. Непрерывные симметрии пространства
9.3. Принцип запрета Паули, перестановки
ТОЖДЕСТВЕННЫХ ЧАСТИЦ
Рассмотрим два тождественных1 фермиона. Их волновая функция —
(гъ пг; r2, ef2y п2|ф) =я/'5’П2)(г1, г2),
где мы указали возможные многомерные квантовые числа (п1, п2), не свя¬
занные со спинорными характеристиками. После поворота на угол 2п коор¬
динаты первой частицы гг и ее поляризации эта функция меняет знак2
СГ1» Г2) ^Т"П2) (Г1’ Г2) = ~^аР (Г1»
Подобное отличие в фазе волновой функции фермионов после вращения на
угол 2п может быть обнаружено при интерференции с исходным состояни¬
ем3. Теперь рассмотрим ситуацию, когда квантовые числа двух фермионов
тождественно совпадают:
г1 = г2 = г, 0^ = 0^ = в1, п1 = п2 = п,
т. е., другими словами, поместим тождественные частицы с одним и тем же
набором значений наблюдаемых величин в одну точку пространства. В пол¬
ной аналогии с выводом допустимых значений квантованного орбитально¬
го момента потребуем выполнение следующего принципа: если состояния
каждой из двух тождественных частиц неотличимы, то вращение одной из
них на угол 2п ненаблюдаемо, т. е. должно приводить к тождественному
преобразованию состояния. По сути, речь идет о вращении одной частицы
относительно другой. Если две частицы находятся в тождественных кванто¬
вых состояниях (и, в частности, в одной точке), то такое вращение не имеет
физического смысла, т. е. ненаблюдаемо. Следовательно, исходная волновая
функция
•фи'п) (г, г)
буквально термин «тождественность» означает, конечно, что совпадают как полные наборы
наблюдаемых для двух частиц, так и квантовые числа, которые принимают эти наблюдаемые
в рассматриваемом квантовом состоянии. Мы же трактуем здесь это понятие несколько шире,
а именно подразумевая под ним «неразличимость» частиц, т. е. совпадение их полных наборов
наблюдаемых и спектров этих наблюдаемых, сохраняя, таким образом, в принципе и потен¬
циальную возможность для точного совпадения квантовых чисел этих частиц в квантовом
состоянии. В такой ситуации у наблюдателя отсутствует всякая возможность определить, кван¬
товые числа какой из двух неразличимых частиц он измерил. Далее мы ставим вопрос о том, как
полная тождественность спектров двух частиц сказывается на их квантовом состоянии.
2Такой формальный поворот соответствует реальной ситуации, когда две физические систе¬
мы пространственно разделены, так что одну из них можно повернуть на угол 2п независимо
от другой. Для независимых подсистем доли вероятности обнаружить тот или иной эффект
в каждой из них умножаются, что соответствует факторизации волновой функции невзаимо¬
действующих частиц в произведение волновых функций для каждой из частиц по отдельности:
^ь"2)(п, Г2) =№(п)^(г2).
3Наблюдаемые эффекты тесно связаны с действием так называемых обменных сил, возника¬
ющих вследствие составления суперпозиции состояний тождественных частиц (см. ниже).
Лекция 9
131
должна тождественно совпадать с волновой функцией после вращения коор¬
динат одной из частиц на угол 2п:
(г, г) = —(г, г) = О,
что достигается только в случае равенства нулю волновой функции тожде¬
ственных фермионов с тождественными квантовыми числами.
Принцип запрета Паули. Два тождественных фермиона, т. е. две тож¬
дественных частицы с полуцелыми спинами, не могут находится в тожде¬
ственных квантовых состояниях.
Этот принцип автоматически удовлетворяется, если волновую функцию
тождественных фермионов антисимметризовать:
^’П2\гъ г2) = ±{-ф§’П2\гъ Г2)-^\г2, Г,)},
так как она обращается в нуль, если квантовые состояния фермионов тожде¬
ственны1;
Антисимметризованная волновая функция двух фермионов являет собой
пример общего принципа, возникающего в квантовой механике с тожде¬
ственными частицами. В самом деле, физическая система из тождественных
частиц не изменится, если поменять местами пару этих частиц. В квантовой
механике это утверждение означает, что состояние системы тождественных
частиц не изменится при перестановке двух частиц из системы:
|Ф: {Qi, Q* ..•}> = А|Ф: {Q2, Q1} ...}>, |А| = 1, (9.28)
где {Ql5 Q2,...} — полный набор наблюдаемых для частиц {1, 2,...}. В этом
уравнении мы требуем, чтобы при перестановке квантовых чисел первой
и второй частиц вектор состояния остался прежним с точностью до фазово¬
го множителя (нормировка остается без изменения). Если ввести оператор
перестановок
: Q* ...}) = |Ф: {Q2> Qi, - Л), (9.29)
то (9.28) есть не что иное, как уравнение на собственные значения для 5К
Двукратное применение перестановки возвращает систему к исходному со¬
стоянию:
5*5* = 1, (9.30)
откуда немедленно следует, что спектр собственных значений оператора
перестановок тождественных частиц
Я2 = 1 <=> А = ±1. (9.31)
Поскольку перестановки не изменяют никаких наблюдаемых характеристик
системы тождественных частиц, оператор перестановок коммутирует со все¬
ми наблюдаемыми2:
[У, Я] = [У, р] = [У, }] = ... = 0.
1Фактор 1/\/2 обеспечивает единичную нормировку состояния.
2Это и есть, собственно говоря, строгое определение понятия тождественности частиц.
132
Тема 4. Непрерывные симметрии пространства
Значит, собственное значение оператора перестановок тождественных ча¬
стиц является квантовым числом в любом полном наборе наблюдаемых,
и все квантовые состояния можно строго разделить на состояния с симмет¬
ричными по перестановкам тождественных частиц волновыми функциями
и с антисимметричными волновыми функциями.
Антисимметричные волновые функции, очевидно, обращаются в нуль,
если квантовые числа двух тождественных частиц совпадают. Как мы видели,
это имеет место для фермионов—частиц с полуцелым спином. В этом случае
А = е2™, (9.32)
где 5—значение спина каждой из тождественных частиц. Эта формула, полу¬
ченная для полуцелых значений спина частиц, остается справедлива и для
целых значений спина, т. е. для бозонов, которые, таким образом, имеют
симметризованные по перестановкам волновые функции. Именно, в природе
не наблюдаются псевдобозоны целого спина с антисимметричными по пере¬
становкам волновыми функциями. Тем не менее, поля таких частиц исполь¬
зуются для вспомогательных целей в квантовой теории поля для наиболее
наглядной формулировки некоторых принципов симметрии. Поля псевдо¬
бозонов называют «гостами» (от английского ghost, что значит «дух») или
просто «духами». При этом, однако, полагают, что число духов в начальном
и конечном состоянии равно нулю, т. е. в полный набор наблюдаемых вклю¬
чают число духов, тождественно равное нулю.
Подчеркнем, что рассмотренная связь спина со статистикой1 возникла
благодаря пространственной вращательной симметрии2 для спиноров, т. е.
благодаря группе SU(2). Однако это не значит, что присутствие какой-либо
другой симметрии со спинорами в группе SU(2) также неминуемо приведет
к антисимметризации волновых функций. Например, в стандартную модель
взаимодействий элементарных частиц включено скалярное, а следовательно,
бозонное, поле со спином 0, которое является спинором по калибровочной
группе SU(2). Как мы показали, наличие калибровочной группы симмет¬
рии отвечает сохранению заряда, который в данном случае — заряд части¬
цы в слабом взаимодействии. Эта калибровочная группа никак не связана
с пространственными вращениями, и поэтому она не означает введения
каких-либо дополнительных ограничений на волновую функцию, связанных
с симметрией по перестановкам. Такие группы, не связанные с вращения-
1 Связь спина со статистикой — это сформулированное выше однозначное соответствие
между собственными значениями оператора перестановок тождественных частиц в состоянии
и целым или полуцелым спином этих частиц. Антисимметрия по перестановкам приводит
к статистике Ферми—Дирака, а симметрия — к статистике Бозе—Эйнштейна.
2Проведенное рассмотрение, как мы видели, представляет собой лишь аргумент в пользу
такой связи спина со статистикой, поскольку никак не ограничивает симметрию по переста¬
новкам бозонов, и оно не является полным в математическом смысле необходимого условия. На
теоремном уровне эта связь устанавливается при вторичном квантовании полей релятивистских
частиц: для положительной определенности энергии частицы необходимо установить бозе-
и ферми-статистику для частиц с целым и полуцелым спином соответственно (см. вторую часть
лекций).
Лекция 9
133
ми и трансляциями пространства, называются группами внутренней сим¬
метрии, генераторы которых, следовательно, коммутируют с генераторами
трансляций и вращений.
9.4. Фермионный осциллятор, грассмановы переменные
При рассмотрении стационарных состояний гармонического осциллятора
мы выяснили, что уровень энергии характеризуется числом тождественных
кпантов Йсо. Число этих квантов принимало произвольное натуральное зна¬
чение или нуль в случае вакуума. Поэтому, как мы теперь понимаем, гармо¬
нический осциллятор соответствует системе квантов-бозонов, число которых
н состоянии определяет квантовые уровни энергии.
Обобщение осциллятора на случай фермионных квантов нетрудно по¬
строить в уже изложенном формализме с операторами рождения и уни¬
чтожения. Действительно, предположим, что мы рассматриваем фермион
с заданной проекцией спина на ось z и фиксированным набором неспиновых
квантовых чисел. Теперь уже число квантов
п = а+а (9.33)
должно иметь спектр собственных значений
п = {0,1}, (9.34)
•гак как согласно принципу запрета Паули в состоянии с фиксированным
набором квантовых чисел может находится максимум один квант. Значит,
у фермионного осциллятора базис образуют только два кет-вектора
|0), |1). (9.35)
Для этого необходимо, чтобы действие повышающего оператора на век¬
тор состояния |1) не приводило к возникновению нового состояния:
df|l) = 0. (9.36)
Но это есть не что иное, как уравнение на старший вектор. В то же время
верно и определение вакуума
а|0) =0, (9.37)
что, очевидно, можно трактовать как уравнение на младший вектор. В итоге
мы имеем квантовую систему с двумя уровнями со старшим и младшим
векторами состояний. Такая квантовая систем уже была нами построена —
это, по сути, спинор. В ней операторы представляются в базисе (9.35) как
матрицы 2x2. Легко провести следующее отождествление
n = l+sz, (9.38)
так как в заданном базисе оператор числа квантов диагонален по построе¬
нию, как и матрица sz с собственными значениями откуда
*-аа-
134
Тема 4. Непрерывные симметрии пространства
так что
и состояния представлены столбцами1
Аналогично повышающий и понижающий операторы становятся оператора¬
ми рождения и уничтожения:
af=s+, a=s_. (9.39)
Для них имеет место антикоммутационное соотношение
{a, a+} = {(s* - isy), (s* + isy)> = {s*, sx} + {sy, §y} = 1.
Значит, для фермионного осциллятора
= (9.40)
Когерентные состояния определяются по-прежнему:
а|6>) = 0|6>>, (9.41)
где необходимо осторожно обращаться с числами нового типа в, свойства
которых мы выясним при построении голоморфного представления.
Разложим когерентные состояния по базису. Для этого рассмотрим
<0|а|в> = (^|0>т = (1|е),
откуда с учетом условия когерентности (9.41) находим
С1 = (1|0) = б(О|0) = 0Со.
Так как разложение включает в себя только два члена,
|0) = Со(|О) + 0|1)). (9.42)
Нормировка на единицу дает
(0|0)= |Со|2(1 + 00), 0 = 0*.
Разложение по базису позволяет построить голоморфное представление
в полной аналогии со случаем бозонного осциллятора. Действительно, опре¬
делим базисные голоморфные функции согласно
(п|0) = Со^*(0), п = {0,1}. (9.43)
Значит,
^о(0) = 1, ^(0) = 0. (9.44)
Отсюда получаем голоморфные представления операторов. Для оператора
рождения имеем
&гр0(в)='ф1(.в) => af = 0.
1 Очевидно соответствие с состояниями спинора |-Н) —> |1>, |-> -> |0).
Лекция 9
135
Однако, поскольку
а^0х(0)= О,
получаем необычное свойство числа в:
в2 = 0 <=> {0,0} = О. (9.45)
Взяв комплексное сопряжение, находим также
{0,0} = О. (9.46)
Для оператора уничтожения
ai/>i(0)=i/>o(0) => а = Л,
откуда автоматически
ai/>o(0) = O,
как и должно быть.
Для операторов рождения и уничтожения в голоморфном представлении
справедливы антикоммутационные соотношения
{a,at> = l,
так как на базисных функциях действительно легко вычислить с учетом
антикоммутационных соотношений для переменной 0
{a, &Уф0 (б) = 1=ip0 (0)
и
{a,at>v»1(0) = 0=i/>1(0).
С учетом того, что все функции от 0 и 0 разлагаются в ряд только до линей¬
ных по каждой из переменных членов, можно записать, что
1 + вв=еёв,
откуда
\С0\2 = е~ёв,
т. е. имеет место прежнее выражение для вклада вакуума в когерентное
состояние.
Условие полноты когерентных состояний запишем в виде
Jd0d0 |0)(0| = 1, (9.47)
где необходимо определить правила интегрирования так, чтобы выполня¬
лись соотношения ортонормированности базисных векторов. Именно,
Jd0d0 (n|0)(0|m) = 5nm, п, m = {0,1}. (9.48)
Интеграл можно переписать с помощью голоморфных волновых функций как
/ d0 d0 е-ё91р*п(в)трт(в) (9.49)
136
Тема 4. Непрерывные симметрии пространства
и в матричном виде получить равенство
I
Ав 6в е~ёд
(1 0 = (1<Л
Ув eej vo \)
(9.50)
Справедливость этого равенства имеет место, если принять следующие пра¬
вила интегрирования:
и их дифференциалов.
Совокупность соотношений антикоммутативности (9.45), (9.46), (9.53)
и правила интегрирования (9.51), (9.52) полностью определяют алгебру пе¬
ременных Грассмана, или грассмановы переменные.
Углы Эйлера, спиновая и координатная части оператора конечных вращений,
вращение спинора и матриц Паули, спинорная матрица конечных поворо¬
тов, собственные векторы матрицы а • п, выделение движения центра масс
в задаче двух тел, факторизация волновой функции, относительное движение,
центрально-симметричный потенциал, квантовые числа, радиальная волно¬
вая функция и ее уравнение Шрёдингера, оператор радиального импульса,
редуцированное одномерное стационарное уравнение Шрёдингера и специ¬
фическое граничное условие при г 0, асимптотическое поведение радиаль¬
ной волновой функции вблизи нуля.
10.1. Оператор конечных поворотов, углы Эйлера
Вращения евклидова пространства принято характеризовать последова¬
тельностью трех поворотов так, как это показано на рис. 8: сначала совер¬
шается вращение вокруг оси z на угол а; при этом оси х и у перемещаются
в своей плоскости в положения, которые обозначены новыми осями х' и у1
соответственно; затем совершается поворот на угол /3 вокруг новой оси у;,
причем ось z перемещается в положение z\ а ось х' уходит под плоскость
{х, у}; наконец, третье вращение —на угол у вокруг оси z\ Такая совокуп¬
ность вращений называется параметризацией Эйлера1.
Оператор вращений в параметризации Эйлера, очевидно, запишется в ви¬
де ассоциативного умножения
(9.51)
(9.52)
а также антикоммутативность переменных
{в, в} = 0
(9.53)
Лекция 10
Д(а, р, г) =RAr)'Ry'Q3) -Я2(а),
(10.1)
1В технической терминологии угол а — рысканье, /3 — тангаж, у — вращение.
Лекция 10
137
Рис. 8. Углы Эйлера
где мы указали в качестве аргументов углы поворотов, а соответствующие
оси вращений как нижние индексы.
Точный вид первого операторного фактора нам уже известен, это-—
A,(a) = eu*“, $, = \<т3. (10.2)
Для определения второго фактора необходимо знать выражение для генера¬
тора syi. Запишем его в виде
= ‘ву/),
где еу — единичный вектор вдоль оси у', а а' — матрицы Паули в базисе
{*', у', z}. Таким образом, это—оператор, который получается при вращении
вокруг оси z на угол а исходного оператора
*, = §(*•«,).
Согласно закону преобразования операторов
(&' ■ еу) = Rz (a) • (<т • еу) • А* (а), (10.3)
откуда сразу получаем
Ry,(p)=k2(a)-kyW)-Rl(a). (10.4)
Совершенно аналогично учтем, что ось z' получается при вращении на угол /3
вокруг оси у', так что
Значит,
Д^(г)=Ау05)-А«(г)-А/05).
(10.5)
А(о, 13, у) =Rz>(r)-RyW) -4(a) =А/С/8) • А,(г) • AJ,(/8) • (/8) • Д,(а).
138
Тема 4. Непрерывные симметрии пространства
Унитарность оператора вращений дает
г,
так что
R(a, /3, у) =Ry(/3)-R2(r) -Kz(a) =Rz(a)-Ry(P) • Д*(а) -Я2(г) • K2(a).
Легко сообразить, что при вращении вокруг одной оси углы складываются
и, следовательно,
^(a)-R2(r) •£*(«) =£*(Г)>
так как вращение на угол а компенсируется обратным вращением. Оконча¬
тельно находим
R(a,/3,r)=K^a)-Ry(0)-Kz(r).
(10.6)
Очевидно, что вывод этого выражения нигде не опирался на свойства опера¬
торов спина так что полученная формула справедлива для частиц произ¬
вольного спина. В этом выражении все факторы строго определены.
Например, спинорный оператор конечных вращений получается последо¬
вательным перемножением матриц
a a /cos- + isin-
Rz(a) = cos - + ia3 sin - = I
P
f 0 /• gia/2 о \
cos | - i sin | J V 0 e~ia/2) ’
Ry(a) = cos - + ia*2 sin тг =
P . 0'
cos sin “■
2 2
В явном виде умножение матриц дает
Г
Rs(a,P,Y) =
cos — •
2
sin|-ei(a"^2
Л
(10.7)
(10.8)
- sin £ • el(r a^2 cos ^ • e *fr+a)/2 .
\ Л Z /
Поэтому преобразование спинора запишется в виде
^(r) = {Rs(a,/3,r)}^b(^Tr),
где мы записали спинорный оператор вращений в матричной форме и ис¬
пользовали латинские спинорные индексы, чтобы не возникло путаницы
с греческими обозначениями углов Эйлера. Здесь матрица вращений в ко¬
ординатном пространстве
^т = ^т(а, 13, r)=<(a)^y(/3)^J,(r)
определяется теми же углами Эйлера. При этом пространственная часть
оператора вращения дает
£r(a, р, r)V>b(r) =iРьШг),
Лекция 10
139
где
Яг(а, /3, г) =%(а)-Rry(/3)-Rrz(y)
определяются операторами орбитального момента. В итоге преобразование
спинора представляется в факторизованной форме как произведение завися¬
щих от углов Эйлера спинорного и орбитального операторов
г/>*(г) =RS-Rrxp(f), R=R(_a, /3, у) =RS-Rr.
Действие пространственных и спинорных операторов можно продемон¬
стрировать следующим образом: рассмотрим оператор
ап,
где а—матрицы Паули, а вектор п—единичный вектор вдоль радиус-вектора
г. Вектор п есть результат действия оператора пространственных вращений
на единичный вектор ez, определяющий ось z:
n = Rrez{Rr)\
где вращение производится, как мы видели, на утлы Эйлера в обратном
порядке1: сначала вокруг оси z на угол у, потом на угол /3 и затем лишь вокруг
оси самого вектора п на угол а,—так что координаты вектора п в исходной
системе—
п = {cos у cos /3, sin у cos /3, sin /3},
при этом, конечно, значение угла а никак не сказывается на координатах
вектора п, так как он задает вращение вектора п вокруг его собственной оси.
Найдем собственные векторы
(.a-n)X(k) = hX(k),
где нет суммирования по к, который задает номер собственного значения
спинора ха с индексом а = {1, 2}. Подействуем на предыдущее уравнение
спинорным оператором вращений Rs и учтем его унитарность:
Rs(a • пЩRsxik) = Яk&sX(ky
Но согласно общему формализму
Rs(.a • n)Rl=RsRr(a ■ e2)^(Rr)f = • e,.
Значит, спиноры удовлетворяют уравнению на собственные
значения
Собственные значения известны: Я12 = ±1, так как у спинора могут быть
только две проекции спина на заданную ось. Поэтому в базисе собственных
векторов
<rz'-eg’ = a3
хПо этой причине часто пишут оператор вращений с заменой а<—*у, чтобы произведение
операторов повторяло порядок записи углов.
140
Тема 4. Непрерывные симметрии пространства
и
т. е.
v»i=(j), м;).
Тогда собственные векторы для матрицы о1 • п даются спинорами
*1,2 =^1,2,
так что
*1 =
^cos — *е ^а+т)/2^
2
vsin J.e-i(a-r)/2
*2:
(-sinLe*«-ryA
cos — • ei(r+a)/2
2
В справедливости этих выражений для собственных спиноров матрицы ст • п
можно убедиться прямыми вычислениями1. Подчеркнем, что вращение век¬
тора п вокруг собственной оси на угол а приводит к введению общей фазы
у этих собственных векторов.
10.2. Задача двух тел, разделение переменных
В задаче двух тел с массами т1 и т2 оператор кинетической энергии
в координатном представлении
Pi
Н0 = т£- +
Р\
2 т1 2 т2
обычно переписывают в новых координатах
т 1
г = Гг-г2) R=
ri + :
т7
-г2,
(Ю.9)
(10.10)
mi + m2 m1-hm2
где г—относительная координата двух частиц, а R—координата центра масс
частиц. Приведенная масса двух частиц определяется согласно
_щггь_
т! + т2'
Тогда замену переменных можно представить в матричном виде
откуда
СЭ-(4
№НЧ£)-
Кинетический вклад
•№)
1Проще всего поменять местами углы а <—> у.
Лекция 10
141
после замены переменных сводится к преобразованию
(Vr,VR)-G-
Г 1)'°тй).
2 m2J
Г12
гак что элементарное умножение матриц дает
-J—V2 + 'V2 = —V2 Н V2
2т! 1 2т2 2 2т г 2(т1 + т2) R*
Поэтому, если полный гамильтониан есть сумма кинетической энергии
и двух потенциалов
H = H0 + y(r) + W(K),
то его можно представить как
а=-1а+ум+{-5(^^л*+и'(Ч
где первые два члена дают вклад в энергию относительного движения частиц
с приведенной массой:
й = £+У(г)> P = ~ihVr,
а выражение в фигурных скобках — вклад движения центра масс системы
двух частиц
#k = |^ + W(K), P=-ihVR>
где М = т1 + т2 — масса системы. Если W = 0, то движение центра масс
является свободным и суммарный импульс частиц сохраняется.
Так как энергия движения в центральном потенциале является суммой
независимых вкладов для энергии относительного движения и энергии дви¬
жения центра масс, стационарное уравнение Шрёдингера
Hi/»(r, R) = £i/>(r, R)
имеет решения в виде произведения волновых функций
Ф(г,Я) = ^(г)ФСК),
так что
Нг1/> (г) = Егр (г), Йк Ф(К) = ЛЖЮ (10.11)
И £=Е + М. (10.12)
10.3. Относительное движение в центральном потенциале
Исследуем относительное движение в консервативной системе с цент¬
ральным потенциалом, т. е. потенциалом, который зависит только от рассто¬
яния между частицами. Стационарное уравнение Шрёдингера для нереляти¬
вистской частицы с нулевым спином—
{^ + У(г)}гР(г)=ЕгР(г), г = |г|. (10.13)
142
Тема 4. Непрерывные симметрии пространства
Очевидно, что в этом случае гамильтониан является скаляром, так что
[1а,Н]=0,
т. е. полный набор наблюдаемых могут составить энергия, орбитальный
момент и его проекция на ось z:
{.H,P,lz} h/>) = |E,l,m),
причем операторы г и lZ) как мы показали, зависят только от углов, так
что волновая функция факторизуется в произведение радиальной волновой
функции и сферической гармоники
{r\E, I, m)=*f(r)^jm(e,v>),
и уравнения на собственные значения
12Щ,ш= Щ + 1р') = тЩ т(.6, </?)
удовлетворяются. Поскольку коммутатор
[Я, Р]=0
и момент импульса—псевдовектор:
[Pjj= О,
Р-четность может быть измерена точно совместно с моментом импульса
и энергией, т. е. пространственную четность также можно рассматривать как
квантовое число. Однако мы уже получили простую формулу для собствен¬
ных значений Р-четности
яР=С-1)1,
так что она однозначно задается орбитальным моментом.
Найдем
I =L-L = eaprrppreapyrplpY' = (5рр>5п> - 5ру-5гр>)гррггр,рг,
и воспользуемся перестановочными соотношениями для координаты и им¬
пульса
PrV = _ift6rj8' + VPr’
так что
L2 = - ift(r• р - Зг • р) + г2р2 - бр^бур.гргрф^, =
= 2ihr ■ р + г2?2 - ihr ■ р - (г • р)2 = г2?2 + ihr • р - (г • р)2.
Теперь вычислим в полярных координатах
г • р = — ihr • V =—ihrer • V = —iftr Jp.
Отсюда
Лекция 10
143
В итоге
n2l2 = r2p2 + 2h2rl+h2r2^,
г дГ дг2
ИЛИ
• &
^2=«2{?-7 Tr-Ы- (10J4)
Пользуясь собственным значением квадрата орбитального момента на сфе¬
рических гармониках I2 1(1 +1), получаем уравнение для радиальной вол¬
новой функции
“ TJF - М + V(r)Rf (г) =ERf(r). (10.15)
Обычно вводят определение оператора радиального импульса
рг = - ift(p + £), (Ю.16)
квадрат которого
й2 = -п2 (- + - — + — - + —1 = -п2 ( - — + —)
Pr п v г2 г 9г 9г г дг2 J Кгдг^дг2)
в точности совпадает с выражением, которое входит в уравнение для ради¬
альной функции. Поэтому
+y(r)+К1[r)=ERi'Сг)- (10-17)
Таким образом, потенциал ползает добавку за счет орбитального момента
количества движения (центробежный потенциал)
ДПг)=^щ+ц
Подчеркнем, что оператор радиального импульса является эрмитовым,
например, в классе функций, достаточно быстро стремящихся к нулю на
бесконечности. В самом деле, скалярное произведение для радиальных вол¬
новых функций из-за интегрирования по 3-мерному евклидову пространству
в полярных координатах d3r = r2 dr dQ задается формулой
00
i <ФГ|ФГ> = J Ф*(г)Ф(г)г2 dr,
о
поэтому
00
(Фг|ргФг) = | $*(r)(-ift){p + J:}'Hr)r2dr,
о
и после интегрирования по частям
00
144
Тема 4. Непрерывные симметрии пространства
так что
оо
(^rl^r) = J + |:}ф(г)) Ф(г)г2<1г=(ргФг|Фг}.
О
Значит, этот оператор—эрмитов.
Наконец, заметим, что
prpu(r) = -iftV(r) =» pfju(.r) = -h2ju"(r),
где штрих означает, дифференцирование по г. Это свойство позволяет нам
произвести эффективную подстановку
Д?(г) = £и(г), (10.18)
где мы опустили индексы энергии и орбитального момента. Тогда стационар¬
ное уравнение Шрёдингера для функции и (г) принимает вид
-|V+{nr) + !!^±!i}u=Eu. (10.19)
Но это есть не что иное, как стационарное уравнение Шрёдингера для одно¬
мерного движения, свойства которого нам хорошо известны. Единственное
отличие обусловлено подстановкой функций (10.18) и связано с граничным
условием при г = 0:
ц(г) —>0, u(r) = 0(r), г->0, (10.20)
так как радиальная волновая функция должна оставаться конечной при г—»0.
Более точно, в случае, когда орбитальный вклад доминирует1:
|v(r)l<^Ei^’ г^0’ 1*0>
асимптотически уравнение сводится к
_fa»+«22+!)u=o,
2т 2 тг2
и оно имеет два решения
щ = г1+1, и2 — г 1,
второе из которых недопустимо или некорректно, потому что сингулярно
в нуле. Поэтому асимптотическое поведение радиальной волновой функ¬
ции— .
«г(г)~г!, г —>0. (10.21)
Подстановка для радиальной функции означает также, что скалярное про¬
изведение для функций и имеет стандартный одномерный вид:
00
(ф) = J v*(r)u(r) dr. (10.22)
1Поиск стационарных состояний в потенциалах, ведущих себя более сингулярно, чем
0(1 /г2), не имеет физического смысла (см. падение частицы на центр, рассмотренное у Ландау
и Лифшица в § 35 [1]).
Лекция 10
145
Задача 4.1. Решите спектральную задачу для 3-мерного изотропного гармониче¬
ского осциллятора в полярных координатах.
Решение. Гамильтониан 3-мерного изотропного гармонического осциллятора
имеет вид 9 9 0
pz , тсоV
2т 2 '
Это — центральный потенциал. Набор квантовых чисел включает в себя энергию
Еу орбитальный момент Z, его проекцию т и P-четность Яр = (—1)*. Уравнение для
радиальной волновой функции R(r) = u(r)/r согласно общему формализму сводится
к виду
„ , Г(тсо}2 2 , Ш +1)1 2тЕ
~и + UirJ r +— \U=1FU-
При г-*оо асимптотически получаем уравнение
„ . С тсо Л2 2 л
\ТГ) г и = 0’
для которого решение, отвечающее связанным состояниям, т. е. обращающееся в нуль
на бесконечности, ведет себя как
та> _2
Ц ~е 2Й ? Г—>00.
Учитывая асимптотическое поведение при г—>0, u~rz+1, проведем подстановку
u=i/(r)r'+1e"!^r2,
где v(r) — новая неизвестная функция, удовлетворяющая условиям
i/(0) = a0^0, i/(r)e_!^r2->0, г—»оо.
Элементарное дифференцирование приводит радиальное уравнение Шрёдингера к
виду
v» + 2V'{l-±^-^fr}+V{e-^f(.2l + 3)}=0,
где е = 2mE/h2 — параметр энергии. Будем искать функцию v(r) в виде ряда
00
Кг)=]>]акг\ а0Ф 0.
к=О
Тогда подстановка ряда в уравнение дает
00
'У \ rk |afc+2 (к + 2)(к + 21 + 3) + ак —— (2Z + 3 + 2fc)J } =
к=0
Этот ряд тождественно обращается в нуль, если каждый его член равен нулю, т. е.
имеет место рекуррентное соотношение
e-uf-(2l + 3 + 2k')
ак+2 = ~аЬ (к + 2)(к + 21 + 3) *
При к —> оо асимптотически имеем
O-k 2тсо
а*+2~Т—>
что отвечает связи между коэффициентами разложения при асимптотическом пове¬
дении фуНКЦИИ 2т&) 2
е л ,
которое является недопустимым для функции i/(r), отвечающей связанным состоя¬
ниям. Единственная возможность, исключающая подобное асимптотическое поведе¬
ние, — конечность ряда для z/(r), что имеет место, если в рекуррентном соотношении
146
Тема 4. Непрерывные симметрии пространства
Е
Рис. 9. Спектр низших состояний для 3-мерного изотропного гармонического
осциллятора
есть нулевой элемент, т. е.
ЭпгеМ: а„г+2=0.
Значит,
е = “jpT = “jr~(2Z + 3 + 2nr) => E=ftw(z + nr + |).
Поскольку в рекуррентном соотношении инкремент равен 2: ак ак+2, а а0 Ф 0,
необходимо, чтобы радиальное квантовое число пг было четным, в то время как
все коэффициенты ряда с нечетными номерами тождественно обращались в нуль:
иначе, так как невозможно оборвать рекуррентную цепочку сразу и для четных и для
нечетных степеней, соответствующие члены ряда дали бы функцию, асимптотически
ведущую себя как г exp{2r2mo>/ft}, что совершенно недопустимо для заданного клас¬
са функций i/(r).
Итак, главное квантовое число1
n = Z + nr + l, nr = 2р, р€{ 0,N},
определяет спектр2
E = ha)(ji + ^, пе N,
причем четность главного квантового числа противоположна четности орбитального
момента. Это означает, между прочим, что энергетический спектр невырожден по
P-четности, но вырожден по орбитальному моменту с шагом 2. Степень вырождения
легко вычислить с учетом 21 +1 состояний проекции момента при заданном Z. Так,
13десь радиальное квантовое число пг—степень полинома от г, определяющего радиальную
волновую функцию, а следовательно, и число ее узлов. Однако поскольку это квантовое число
четное, полином фактически зависит от квадрата расстояния, так что половина его узлов
расположена зеркально относительно нуля при отрицательных значениях г, т. е. вне физической
области. Поэтому фактическое число узлов радиальной волновой функции равно пТ/2=р.
2Подчеркнем, что в отличие от одномерной задачи с идентичной формулой для уровней
энергии квантовое число п для изотропного трехмерного осциллятора начинает свой отсчет не
с нуля, а с единицы!
Лекция 10
147
при нечетном главном квантовом числе и I = 2q степень вырождения
(л—1)/2
k= ^ (4q + l) = -n(n + l),
ч=о
что остается верным, как легко убедиться непосредственным расчетом, и при чет¬
ном п. Спектр низколежащих состояний 3-мерного изотропного гармонического ос¬
циллятора в классификации1 nl приведен на рис. 9.
гВ спектроскопии принято обозначать значения орбитального момента частицы в централь¬
ном поле 1 = {0,1,2,3,...} латинскими буквами {s, р, d, соответственно.
Тема Атом водорода
5
Лекция 11
Квантование связанных состояний, атомные единицы, асимптотическое по¬
ведение, главное и радиальное квантовые числа, полиномы Лагерра, спектр
связанных состояний, вырождение уровней энергии по орбитальному момен¬
ту и Р-четности, интеграл движения для замкнутых орбит в кулоновском
потенциале, рекуррентное соотношение Крамерса для средних значений сте¬
пени радиуса (rs), классический предел, среднее (г-2), волновая функция
s-состояния в нуле.
11.1. Набор квантовых чисел и атомные единицы
Кулоновский потенциал притяжения электрона и протона в атоме во¬
дорода в ведущем приближении, т. е. без учета релятивистских поправок
и спинов этих фермионов, является центрально-симметричным,
V(r) = -j, (11.1)
так что стационарное уравнение Шрёдингера имеет решения, которые раз¬
лагаются по базису собственных функций следующих операторов:
1) Н — энергия стационарного уравнения Шрёдингера для радиального
движения
-£“" + {"7 + ^Ba}u=£u- <“-2)
так что радиальная волновая функция
«f(r) = pu(r), (11.3)
где
u(r)~r/+1, г-+ 0; (11.4)
массовый параметр—приведенная масса электрона и протона:
тетр
т= — •
те + тр’
Да
2) г — орбитальный момент, так что зависящая от углов часть волновой
функции дается сферическими гармониками
12Щ,т(в> vO=W+l)9U(0, ¥>); (11.5)
3) lz — проекция орбитального момента с собственными функциями —
сферическими гармониками:
Ы,т(в, Ч>)=тЩ>т{в, V?); (11.6)
150
Тема 5. Атом водорода
4) Р-четность с собственными значениями
АР = (-1)'. (11.7)
Для полного определения волновой функции стационарного состояния
*I>m(r)=Rf(r)^,m(0,¥>)
необходимо решить радиальное уравнение (11.2) с эффективным потенциа¬
лом, учитывающим вклад орбитального движения, как показано на рис. 10.
Рис. 10. Потенциал для радиального движения при нулевом орбитальном
моменте в сравнении с кулоновским потенциалом (штриховая кривая)
Но прежде чем это сделать, определим характерные значения размерных
физических величин в задаче об атоме водорода: скорости движения элек¬
трона v0, его импульса р0 = mi/0, размера волнового пакета а = г0 и энергии
mi/2
*o = Y-
Атомные единицы.
• Скорость t/0.
Если воспользоваться теоремой вириала, которая для кулоновского по¬
тенциала дает
1 / , rnvl е2
т—\т ■*
и соотношением неопределенности координата-импульс (по порядку величи-
НЫГоРо = Ю
то сразу найдем
mvn
е2
V0=~b'
(U.8)
• Постоянная тонкой структуры
Лекция 11
151
которая построена как отношение скорости и0 к скорости света: aem =v0/c.
Полезно убедиться, что ает есть величина безразмерная. В самом деле, по¬
скольку потенциальная энергия V ~е2/г, квадрат заряда имеет размерность
[е2] = [Я]-[г]
т. е. размерность произведения энергии на длину, так же как и
№] = №]• И, [с] = [г]/М => [йс] = [В]-[г].
Численно ает ^ 1/137,04. Отсюда следует, что электрон в атоме водорода
движется нерелятивистски:
7 = «ет<1.
• Импульс
Ро = ™0 = тсает = . (11.10)
• Боровский радиус
„=»=-»-= 4. ош
Ро тсает те2
Если считать массу протона бесконечно большой1 (или ядро бесконечно тя¬
желым), то численно а «0,5291772 • 10-8 см « 0,53 А, т. е. примерно пол-анг¬
стрема.
• Энергия связи—«один ридберг»
F -ть— mvQ-Po - тс2гЛ - те4 _ 1 П112')
E0-Ry- — - — -—aem-^-^^. (11.12)
Численно Ry«й 13,61 эВ (электрон-вольт). В атомных единицах стандарт¬
ную энергию обычно полагают равной Ё0 = 2Е0.
11.2. Связанные состояния
Стационарное уравнение радиального движения с использованием во¬
ровского радиуса можно записать в виде
и" + ^и- ^4r^u = —ей, (11.13)
где е = 2mE/h2. Введем безразмерный параметр v, так что для энергии связи
Е< 0
и
e=JLJ.=_JL
а2 Е0 a2v2'
Поправки за счет отличия приведенной массы от массы электрона составляют величину
порядка отношения масс электрона и протона те/тр «1/1836.
152
Тема 5. Атом водорода
Совершим замену переменной
(11.14)
Тогда
u(x) = u(r(x)) => и' = й'~ = 2-й' ы" = _£_*//
dr va ’ v2a2 ’
где штрих означает производную по аргументу функции. Тогда уравнение для
ц(х) примет вид
й//+{1_га+1)_1}й=о (и15)
Допустимая асимптотика функции ц(х) при х ^ 0 нам уже известна
й~х1+\
На бесконечности уравнение
й"~\й = 0г х^+00>
для связанного состояния должно иметь затухающую асимптотику, так что
допустимое поведение
й(х)~е-*/2, *^+оо.
Поэтому будем искать решение в виде
й(х) =v0c)x!+1e“*/2, (11.16)
где для функции v(x) есть ограничение, так как не допускается ее экспонен¬
циальный рост на бесконечности. Элементарная подстановка дает
xv" + (21 + 2- x)v' - (I +1 - v)v=0. (11.17)
Будем искать решение в виде степенного ряда
к
откуда после прямых вычислений производных получаем
2 ак{к(к -1)**"1 + 2« +1 - кхк - а +1 - v)xk} = О,
к
так что, приравнивая нулю коэффициенты ряда при степени хк, находим
рекуррентные соотношения для коэффициентов ак:
afc+i{Cfc + Dfc + 2(fc + l)a + i)}_afc{fc + z + 1_v} = 0j
или
= С1Ш>
Значит,
ак+1=а°(^тШш^у
Лекция 11
153
Если ряд бесконечный, то
Qfc+i 1
ak fc’
т. е. ряд асимптотически ведет себя как экспонента
i/(x) ~ е*.
При такой асимптотике волновая функция расходится на бесконечности,
так что подобные решения не принадлежат гильбертову пространству (не
имеют физического смысла). Однако существуют такие значения энергии
связи (параметра v), при которых ряд обрывается, т. е. содержит конечное
число членов. Это возможно, только если
3 пг € N: аПг+1 = 0, (11.20)
т. е. если v(x)—полином степени пг. Натуральное число пг называется ради¬
альным квантовым числом. Условие (11.20) согласно (11.18) означает, что
v = nr +1 + 1 е N, (11.21)
т. е. параметр v=п—натуральное число, которое называют главным кванто¬
вым числом:
n = nr + l + l€N. (11.22)
Квантование (11.21)—(11.22) дает уровни энергии связанных состояний
ИЛИ
Еп = -^а 1 = -
2п2 ет 2n2h2'
Полиномы, которые возникают при квантовании энергии связанного со¬
стояния в кулоновском поле
v(x) = CnrLll+1_1(x), (11.24)
называют присоединенными полиномами Лагерра1. Их определение мы, по
сути, дали в рекуррентной форме. Единственная неопределенность связана
с нормировкой, т. е. коэффициентом а0. Его значение задается формальным
определением не нормированных на единицу полиномов Лагерра, которое
мы приведем здесь без доказательства:
М:-e'&fe-W. LJ М =
В итоге для 1^1Х
_ [(n+Q!]2
0 (n —Z —1)!(2Z + 1)!*
гМы следуем обозначениям, пришлым у А.Мессиа [2], которые отличаются от определения
индексов полиномов Лагерра у Ландау и Лифшица [1].
154
Тема 5. Атом водорода
Нормировочный коэффициент СпЬ обеспечивающий единичную нормировку
волновой функции, приводится в справочных разделах учебников по кванто¬
вой механике (например, у А. Мессиа в дополнении Б в первом томе [2]).
Важно отметить, что полином Лагерра имеет ровно пг узлов при 0 < г <
<+оо, в то время как вещественная или мнимая части сферических гармоник
имеют Z узлов (т у функции по </? и Z — т у присоединенных полиномов
Лежандра). В итоге можно сказать, что главное квантовое число показывает,
что волновая функция связанного состояния имеет п -1 узлов.
11.3. Вырождение
Из общих установленных нами ранее свойств мы можем утверждать,
что при фиксированном значении орбитального момента I уровень энергии
вырожден по проекции орбитального момента, т. е. кратность вырождения
равна 2Z +1, а радиальная волновая функция при фиксированном Z невырож¬
дена, так как радиальное движение описывается одномерным стационарным
уравнением Шрёдингера и является ограниченным г > 0, т. е. все функции
и (г) имеют общий узел и(0) = 0.
Однако энергия вырождена по Z, так как уровень задается главным кван¬
товым числом
п = nr + Z +1
и оно может оставаться неизменным при
1 = 0,1,..., n-1, nr = (n-1), (п-2), ...,0,
т. е. если квантовые числа Z и пг коррелируют должным образом. Значит,
кратность вырождения определяется суммой по допустимым уровням Z, каж¬
дый из которых вырожден 2Z +1 раз1:
п—1
fc=J](2Z + l) = n2.
1=0
Поэтому для того, чтобы отличать уровни энергии по I, их обозначают двумя
квантовыми числами: главным квантовым числом и орбитальным момен¬
том — nl, причем для низших значений орбитального момента электрона
используют строчные буквы латинского алфавита согласно договоренности:
Z = {0,1,2,3,...} l = {s, р, d,f,...}.
О состоянии с Z = 0 говорят как о 5-волне и т. п. Спектр низших состояний
в атоме водорода схематически показан на рис. 11.
Природа кулоновского вырождения имеет глубокую причину: существу¬
ют только два типа центрально-симметричных потенциалов, у которых все
*Сумма арифметической прогрессии Sn = а0 + (а0 + с) +... + (а0 4- пс) = ~ (п +1) (2а0+сп).
Лекция 11
155
1=0
1 = 1
1=2 I
•3s
■2s
■3p
• 2 p
•3d
Is
Рис. 11. Спектр низших состояний для кулоновской системы
ограниченные орбиты замкнуты. Это — кулоновский потенциал и потен¬
циал гармонического осциллятора1 (см. курс классической механики Ар¬
нольда [21]). Именно для этих потенциалов энергия связанного состояния
вырождена по орбитальному моменту. В классической механике замкнутость
произвольной ограниченной траектории в кулоновском потенциале притя¬
жения отвечает сохранению величины вектора2
В самом деле,
Й(1хр)=1хр = (гхр) х р = (г р)р-р2г.
Уравнения движения—
r=v= p = -W(r) = -~r.
т г г3
Тогда
si= jj - \ (r • r)r+ {(r■ p)p + (r■ p)p + (r■ p)p - 2(p • p)r-p2r} =
r r me
= p - p-(r-i/)r+ ^|mv2v- Zy-v— ^f-(r-y)r+2^|-Cr-i;)r-m2v2v| = 0.
Значит, s/ — интеграл движения. Физический смысл этого вектора прост.
В точке минимального удаления от фокуса эллипса радиус-вектор ортогона¬
лен импульсу, так что если е = rmin/rmin — единичный вектор в направлении
1Орбиты — эллипсы, для кулоновского притяжения центр расположен в фокусе, для осцил¬
лятора—в центре эллипса, т. е. на пересечении большой и малой осей.
2Вектор Рунге—Ленца, известный в аналогичной кеплеровой задаче небесной механики еще
Лапласу.
156
Тема 5. Атом водорода
от фокуса до точки минимального удаления, то
" ^г) l=rmta=e(1+4) Lmin’
где T/V — отношение кинетической энергии к потенциальной. При мини¬
мальном удалении кинетическая энергия принимает значения Т ^ — ^V, так
что при равенстве орбита круговая. Поэтому выражение в круглых скобках
не положительное. Поскольку этот вектор сохраняется, точка минимального
удаления не перемещается со временем и орбита замкнута.
В квантовом случае необходимо сначала записать вектор s# в таком виде,
чтобы при подстановке операторов, например, в координатном представле¬
нии получающийся оператор был эрмитов. Поэтому перепишем его как
^ = f + ^{ixp-pxi}, (11-25)
так что покомпонентно оператор наблюдаемой в координатном представле¬
нии
Ч = Т + ivn IvPa+PaU (11.26)
и это, очевидно, эрмитово самосопряженный оператор. Скобка Пуассона
{Я, jzf}p = О,
где стоит гамильтониан для атома водорода. Согласно каноническому кван¬
тованию соответствующий коммутатор также должен обращаться в нуль
[Я, J2?\ =0.
В этом можно убедиться прямыми вычислениями. Поскольку в классической
механике j#—вектор, по общему правилу
[la, = ieaprJ2/r, (11.27)
и мы имеем ситуацию, когда пара интегралов движения I и не ком¬
мутируют, и, следовательно, уровни энергии вырождены по орбитальному
моменту I.
Кроме того, в отличие от орбитального момента, являющегося псевдо¬
вектором, j# — вектор, и он меняет свой знак при операции зеркального
отражения всех осей пространства. Значит, коммутатор с оператором Р-чет¬
ности также не равен нулю
\Р,Я\Ф о,
и уровни энергии вырождены и по Р-четности.
Лекция 11
157
Алгебра операторов л$ и ее следствия детально исследованы1 у Ландау
и Лифшица (см. § 36 в [1]). Приведем для справок только их коммутатор
11.4. Средние, рекуррентное соотношение Крамерса
Теорема вириала о связи средней кинетической энергии в состоянии со
средней потенциальной энергией (6.4)
Обобщение этой формулы на другие степени радиуса г было получено Кра-
мерсом в виде рекуррентных соотношений.
Вывод рекуррентных соотношений Крамерса. Исходным пунктом вычис¬
ления средних значений является уравнение радиального движения для фун¬
кций и (г) (11.13), в котором подставлено проквантованное значение энергии
связанного состояния
1В рамках матричной квантовой механики В. Паули использовал этот интеграл движения
и коммутационные соотношения для него, чтобы рассчитать спектр атома водорода в нереля¬
тивистском приближении, и сделал это буквально за пару недель до появления первой статьи
Э. Шрёдингера по волновой механике с решением той же задачи после введения стационарного
уравнения Шрёдингера (точнее, статьи поступили в редакции журналов с разницей в 10 дней).
в случае кулоновского потенциала дает
(п, I, т\Т\п, I, m) = -|(n, I, m\V(r)\n, I, m),
так что энергия связанного состояния
En = (T) + {V) = l{V),
т. е.
и с использованием атомных единиц
(11.28)
(11.29)
Домножим это уравнение на rsu(r) и проинтегрируем по г. Отсюда
00
J dr • rsuu" + \ (г5-1) -1 (I +1) (г5"2) - ~(г°) = О,
о
(11.30)
158
Тема 5. Атом водорода
где введены обычные обозначения для средних значений
00
J dr-rsu2(r) = (rs).
о
Поскольку и(г) экспоненциально убывает при г—► +<», записанные выше
интегралы сходятся на верхнем пределе. Поэтому важно проследить за по¬
ведением подынтегральных функций при г —>0. С учетом того, что
u(r)~rz+1, г—>0,
наиболее сингулярное поведение имеет вклад
00
(rs-2) = J dr-rs-2u2(r),
о
в котором подынтегральная функция ведет себя как
rs~2u2(r)~rs+2', г—»0.
Для сходимости интеграла на нижнем пределе необходимо наложить условие
s + 2l>— 1, т. е.
s > —21 — 1. (11.31)
Интегрируя по частям, найдем простое вспомогательное соотношение
Отсюда
(rs)=J dr • r$u2 = J u2dr$+1 =—J dr-rs+1uu'.
0 s 0 s 0
/ dr-rs+1uu' = -^(rs). (11.32)
0
Теперь найдем, интегрируя по частям,
оо оо оо оо
IS = J dr-rsuu" = f du'-rsu = — J dr-rs(u')2 — s f dr-rs~1uu'.
ooo о
Для второго члена воспользуемся связью (11.32), а первый перепишем так,
чтобы проинтегрировать его по частям:
00 00
= I drs+1-(u')2 + ^s(rs-2) = j^1 f dr ■ rs+1u'u" + |s(s -1) (rs~2).
0 0
Подставим под интеграл выражение для и" из уравнения радиального дви¬
жения (11.29):
00
=ттт /dr • UU'H г*+ю+Dr5"1+^rs+1}+|s(s - D(r-2)
о
и снова воспользуемся выражением (11.32) для интеграла от ии', так что
2* = ТХТ^"1) - 7Z7«l +1 )(rs-2) - -^<r*> + is(s - 1)<г-2).
Лекция И
159
Подставляя это выражение в формулу (11.30) и приводя подобные члены,
находим
+г-чХш+2)+<^2> [-'«+ « 0 + Si) +!s(s - «] =°-
Домножив на — (s + 1)а2/2, получаем рекуррентные соотношения Крамерса
(rs) - a(2s +1) (rs_1) + |a2{( 21 +1)2 - s2}(rs_2> = 0, (11.33)
причем
5>—2Z —1. (11.31)
Иллюстрации.
1. Положим s = 0:
Л-а(Г-1)=0 => (r-1> = ^,
n anr
и мы получили уже выведенное нами посредством теоремы вириала выраже-
ние для среднего значения обратного радиуса.
2. При s = 1
^(г)-За + Щ + 1)(г-1> = 0,
откуда с использованием предыдущего примера
(r) = §[3n2-Z(Z + l)]. (11.34)
3. При s = 2
^ (г2) - 5 a(r) + |a2(4Z2 + 4Z - 3) = 0,
так что приведение подобных членов в конце концов дает
(r2) = ^[5n2 + l-3Z(Z + l)]. (11.35)
При больших квантовых числах Z —> оо, пг < Z, п ~ I легко находим, что
(г) ~ ап29 (г2) ~ a2n4,
и, следовательно, дисперсия
(Дг)2 = (г2)-(г)2<(г)2,
т. е. имеет место классический предел: флуктуации средних значений стано¬
вятся несущественными, и среднее значение радиуса совпадает с классиче¬
ским выражением
<r)*an2 = —
т. е.
е2
Еъ--
2(г)'
4. Для вычисления среднего (г-2) соотношения Крамерса неприменимы,
так как не удовлетворяется ограничение на степень радиуса. Поэтому иссле¬
дуем соотношение Фейнмана—Хеллманна в случае
дЕп_/эЙ\
160
Тема 5. Атом водорода
В левой части стоит выражение
h2 д 1 h2 1
2та2 dl (nr + Z +1)2 та2 гг3 *
В правой—среднее от
Поэтому
1_\ 2_ 1
г2! a2 n3(2Z + l)’
(11.36)
С учетом этой формулы можно затем применять соотношения Крамерса
и для отрицательных s при условии, конечно, Z > —(s +1)/2.
При выводе соотношений Крамерса мы полагали, что интегрирование
по частям не содержит конечных вкладов при подходящих ограничениях на
степень усредняемого значения радиуса. Если на бесконечности волновые
функции убывают быстрее любой степени радиуса и такое положение имеет
место почти автоматически, то вклад при г = 0 может оказаться не равным
нулю. Это обстоятельство позволяет получить связь между волновыми функ¬
циями в нуле и средними значениями степеней радиуса.
Например, уравнение для s-волнового стационарного состояния в потен¬
циале У (г) имеет вид
где мы учли, что при г —► оо волновая функция связанного состояния стремит¬
ся к нулю, а при г —>0 функция u(r) =rR(r) дает u'(0) =R(0), т. е. выражается
через радиальную волновую функцию s-состояния в нуле. Та же операция над
правой частью (11.37) аналогично приводит к
где вклад конечных членов равен нулю на обоих концах интегрирования: при
г —> оо в силу зануления волновой функции связанного состояния, при г —>0—
если потенциал ведет себя менее сингулярно, чем 1 /г2.
В итоге, так как для s-волновых состояний Я(0) = д/4тс|Ф(0) |, получаем1
11.5. Волновая функция в нуле
и//(г) = -^{Е-У(г)}и(г),
(11.37)
так что умножение на 2и! и интегрирование по г дает слева
2 Г и'и" dr = Г d(u02 = (u02 °° = -Я2(0),
п J о
-Щ ]{Е - V(r)} dи2 = ~^{Е - V(r)}u21“ - Щ / uV(r) dr=-^(V/(r)),
l*(0)|2 = r£b<V'>.
(11.38)
Считается, что этот результат впервые был получен Ю. Швингером и излагался в его
лекциях, которые впоследствии не были опубликованы.
Лекция 11
161
Задача 5.1. Рассмотрите связь волновой функции в нуле со средними в наиболее
общем виде.
Решение. Запишем стационарное радиальное уравнение Шрёдингера в виде1
и" (г) = —С(г) • u(r), £(r) = |£{E-V(r)}-^t!2. (11.39)
Домножим его на фактор 2rsu' и проинтегрируем по радиусу. Тогда получим равен¬
ство
оо оо
/ г1 d(u')2 = - J г*£(г) dи2. (11.40)
О о
Интегрируя слева по частям с учетом конечных вкладов, найдем для интеграла
-sj г5-1 (и')2 dr.
(11.41)
I=rs(u')2
Для последнего интеграла интегрирование по частям дает
00 00 00 00
-s J rs-1(u')2dr = —s J rs-1u'du = -srs-1u/u + s(s-l) J г*~Чиdr +
о о 0 о
00 00
+s Г rs-1u"udr = -sr5-1u'u +s(s-l) f rs~2u'u dr — s(rs_1£(r)),
о 0 о
где в последнем слагаемом мы воспользовались уравнением Шрёдингера, подставив
значение второй производной функции и (г). Воспользуемся вспомогательным выра¬
жением для среднего с учетом конечных членов интегрирования по частям
00 00 00
(г5) = Г rsu2 dr= —-rs+1u2 - Дг Г rs+1u'u dr,
J 5 + 1 л с-4-1 J
S +1
что сводится к
J rs+1 u'udr = -~(rs) + ^rs+1 и2
(11.42)
(11.43)
2 2
U
В итоге (11.41) дает
j=|rs(u/)2-srs-1u'u+|s(s-l)rs-2u2}|”-s(rs-1£(r))-|s(s-l)(s-2)(rs-3). (11.44)
С другой стороны, интегрирование по частям правой части уравнения (11.40) элемен¬
тарно приводит к
+s(rs-1£) + (rs£/). (П.45)
Z=-rsu2£ +s Г u2rs-1£dr+ Г u2rs£/dr = -rsu2£
0 о о ^
Учитывая, что на бесконечности волновая функция связанного состояния затухает
быстрее любой степени радиуса, и приравнивая (11.44) и (11.45), находим для конеч¬
ных вкладов
|r5(u')2-5rS 1U/U+^5(s-l)rS 2U2-rV'uJ =
= —2s(r5_1£) - {г5С') - ~s(5 — l)(s — 2) (rs-3). (11.46)
1Дальнейшее изложение следует обзору Q u i g g С., R о s п е г J. L. Quantum mechanics
with applications to quarkonium // Phys. Rept. 1979. Vol. 56. P. 167.
162
Тема 5. Атом водорода
Далее, при г -> О согласно общему результату при фиксированном значении орбиталь¬
ного момента запишем
и — atrl+1, и' -> ах (Z+1 У, и" -> azZ(Z + Цг1’1,
где а{ — неизвестные константы, которые полностью определяют поведение волновой
функции вблизи нуля. Левая часть (11.46) не имеет сингулярности только при s ^ -21,
а при 5 > —21 она обращается в нуль. В итоге приводя подобные члены при s = —21,
получаем общее соотношение
(21 +1 )2a?5s+2(i0 = —2s(г5-1 С) - (r*d) -\sb- l)(s-2)(rs"3). (11.47)
Пример s = О, Z = 0. В этом случае
C' = -2*V\r),
а
а0=К(0) = л/4гёФ(0),
откуда, считая волновую функцию вещественной, получаем
|ф(0)|2=^(у,)- (11-38)
Для атома водорода V' = е2/г2, и, подставляя при i = 0 среднее значение
(1/г2) =2/(a2n3), с учетом e2m/ft2 = l/a находим для s-волновых состояний
1*пЛ°)12 = г4-з- (11-48)
па°п°
Пример s = 1. В этом случае левая часть тождества (11.47) обращается
в нуль при любом целом значении орбитального момента, а равенство
2(C) + (г£') = 0
сводится к теореме вириала.
Тема Квазиклассика
6
Лекция 12
Малые дисперсии и предел h —> 0, амплитуда и фаза волновой функции
в классическом пределе, волновой фронт в геометрической оптике, уравнение
непрерывности, разложение волновой функции по h методом итераций, метод
ВКБ, классически доступная и недоступная области, нулевая и первая итера¬
ции, квазиклассическое приближение и необходимые условия его примени¬
мости, отражение волны от потенциального барьера, фаза отражения, сшив¬
ка возле точек поворота, вывод правила квантования Бора—Зоммерфельда,
плотность энергетического спектра связанных состояний, нормировка вол¬
новой функции, малое возмущение и сдвиг уровня связанного состояния,
туннельный эффект, коэффициент прохождения.
12.1. Классический предел: ft—► О
Согласно принципу соответствия у квантовой системы должен существо¬
вать классический предел, в котором дисперсии физических величин малы
при рассмотрении динамики их средних значений. Как мы отмечали, такой
предел обычно имеет место при больших квантовых числах п —> оо, когда
дисперсией можно пренебречь. Принцип соответствия использовался при
построении основных операторов физических величин в приближении гео¬
метрической оптики, которая как раз дает предельный случай волновой
механики, когда пренебрежение эффектами интерференции позволяет гово¬
рить о траектории корпускул, составляющих свет.
Другой аспект принципа соответствия открывается, если взглянуть на
соотношение неопределенностей физических наблюдаемых А и В:
ДА-ДВ^||(С)|.
Можно считать, что флуктуации наблюдаемых малы, если
0. (12.1)
Кроме того, дискретность спектра физической величины, как мы видели,
связана с конечностью значения постоянной Планка, так что этой дискрет¬
ностью можно пренебречь, если верно (12.1). Конечно, это условие является
лишь необходимым, но не достаточным (знак неравенства в соотношении
неопределенностей). Тем не менее, исследование предела (12.1) позволяет
установить и достаточные признаки применимости классического описания
и приближений к нему.
164
Тема 6. Квазиклассика
Запишем волновую функцию как
Ф(г, О =А(Г, t)e»s(r’°, {A(r, t), S(r, t)}eR, (12.2)
т. e. в виде вещественной амплитуды А и фазы S. Подставляя это выражение
в уравнение Шрёдингера
dt 2т
вычислим прежде всего
ДФ = v2# = V • {е»5(г’° VA +1 Ae»s(r>t) vs} =
= е»5(г’°{2^У5 • VA+ДА - ^A(VS)2 + ^AAs},
а затем
eMS + bSH**'
так что, сократив экспоненциальный фактор и после этого взяв мнимую
и вещественную части от полученного уравнения, легко находим1
R ^ {2 V S • VA+A AS}, (12.3)
_Alf = “£AA + ^(VS)2 + VA (12-4)
Эти уравнения можно переписать в форме
M + ivS-™+AAS„o, (12.5)
g + _L(VS)i + V = |i^. (12.6)
В первое из этой пары уравнений постоянная Планка не входит. Для его
анализа вычислим плотность потока вероятности
j=-v* - (v*m=^ vs
2лп т
и его дивергенцию
div j = Vj= -AVS • VA + —AS.
m m
Поэтому, домножая (12.5) на 2А, получаем
2Af^ + div j = 0
и с учетом того, что плотность вероятности
р = |ф|2=А2,
1К таким же уравнениям мы придем, если перейдем от комплекснозначной функции Ф
не к двум вещественным функциям А и S, а к комплекснозначным функциям А и S, которые
являются четными по h.
Лекция 12
165
находим, что это уравнение сводится к уравнению непрерывности
^+divj = 0.
Уравнение (12.6) содержит квадрат постоянной Планка. В пределе h —> О
оно сводится к
ff + ^(VS)2 + V = °, (12.7)
т. е. к уравнению Гамильтона—Якоби в классической механике. Как и следо¬
вало ожидать, мы пришли к классическому пределу уравнения Шрёдингера.
При этом комплексная фаза волны S/h удовлетворяет принципу Ферма.
Для стационарного состояния
— 0 — = —Е
dt ’ dt
и
А А
(VS)2-2m(E-V')=h2— (12.8)
вместе с уравнением нулевой дивергенции потока вероятности. Классиче¬
ский импульс можно представить как обратную длину волны:
р2 = 2т(£-У) = (|)2.
Поэтому
(vs)2=|0+*2ir).
Следовательно, классическое приближение применимо, если
А2^<1. (12.9)
Тогда имеет место уравнение для волнового фронта в геометрической опти¬
ке:
(V*)2 = -p, Ф = Js. (12.10)
12.2. Метод JWKB1
Уравнения (12.5), (12.6) являются эквивалентными уравнению Шрёдинге¬
ра/Их решение можно представить в виде рядов по Й. В этом и состоит метод
JWKB, который мы проиллюстрируем на примере одномерного движения
стационарного состояния.
Уравнение непрерывности (12.5) для стационарных состояний сводится
к виду
2S'A'+AS" = 0,
1По фамилиям Jeffries, Wentzel, Kramers, Brillouin—Джеффрис, Вентцель, Крамере, Бриллю-
эн. Широко распространено сокращение ВКБ по фамилиям трех авторов, которые совместно
детально разработали этот метод в квантовой механике в отличие от Джеффриса, применявшего
его в 1923 г. до создания строгой теории. Отметим, что еще в 1912 г. лорд Рэлей использовал
некоторые математические приемы ВКБ при решении задач о распространении волн.
166
Тема 6. Квазиклассика
где, как обычно, штрих означает дифференцирование по координате частицы
х. Это уравнение элементарно интегрируется:
А(х) = ~7£=. (12.11)
Значит, амплитуда волновой функции однозначно (с точностью до нормиров¬
ки С) задается ее фазой.
В уравнение
АД
(VS)2 - 2m (Е - V) = Тг2 =р (12.8)
теперь необходимо подставить вторую производную амплитуды согласно
(12.11) (поскольку нормировка А выпадает, положим С = 1):
v= s" Л„= з as")2 s'"
2v/CS0?> ijvw
Значит, основное уравнение имеет вид
(S')2 - 2 т(Е - V) = ^^{3(S")2 - 2S'S"'}. (12.12)
Отсюда следует, что фаза раскладывается в ряд по степеням ft2:
S = S0 + h2S1 + h4S2 + ...
Поскольку волновую функцию можно теперь записать как
Ф(х) = expjjrS(x) + ln A(x)J = С exp j^S(x) -1 InS'j, (12.13)
ясно, что разложение фазы приводит и к разложению амплитуды по степеням
ft2, а вещественного аргумента экспоненты—по нечетным степеням ft.
Выражение с правой стороны (12.12) можно считать малым возмущением
и решать уравнение методом итераций.
Нулевая итерация:
{Sg(x)}2=p2(x), p2 = 2m[E — V(x)],
причем необходимо выполнение условия вещественности фазы, так что
р2(х)=г о Ф=> EZVCx).
Это значит, что пока нулевая итерация справедлива только в области, доступ¬
ной для классической частицы. При этом
р (х) = ± ^2т[Е - V(x)],
и возможно существование двух линейно независимых решений (в зави¬
симости от значения энергии в согласии с общими свойствами решений
одномерного уравнения Шрёдингера).
Решение уравнения имеет стандартный вид координатной части действия
классической частицы:
S0(x) = J р dx. (12.14)
Лекция 12
167
С учетом вклада энергии в комплексную фазу стационарного состояния
S0(x, t) = J pdx — Edt
получаем волновую функцию в классическом пределе
Ф(х, t) = Cexp|^S0(x, t)}=Cexpj^ / pdx-Edt}.
В итоге фаза волновой функции осциллирует в области, доступной для клас¬
сической частицы, например, между точками поворота, как показано на
рис. 12.
Рис. 12. Пример потенциала и классически доступной для частицы обла¬
сти а^х^Ь. Осциллирующее поведение волновой функции в этой области
показано волнистой кривой, а в запрещенной для классического движения
области пси-функция убывает экспоненциально
Продолжение в классически недоступную область. Заметим, что выве¬
денная нами пара уравнений не изменится, если получать их, выделяя не
мнимую и вещественную части в уравнении Шрёдингера, а вклады в виде
четной и нечетной функций по ft. В самом деле, считая, что А и S — четные
функции по ft, опять приходим к (12.3) и (12.4). Значит, нулевая итерация
в классически запрещенной области координаты дает решение в виде
Ф(х) = ! л/2т[Пх)-Я] dx + Сге-А J у/2m[V(x)-E] dx>
причем значения коэффициентов Съ С2 зависят от налагаемых на волно¬
вую функцию граничных условий. Например, на рис. 12 волновая функция
должна экспоненциально убывать на бесконечности, так что поведение при
х —> +«> требует Сг = 0.
168
Тема 6. Квазиклассика
Квазиклассическое приближение. Учтем линейный по h вклад в аргумент
экспоненты для волновой функции, т. е. подставим выражение для функции
А через S0. Тогда
(12.15)
где импульс р(х) = у/2т[Е- У(х)] уже вычисляется как комплекснозначная
двулистная функция, т. е. имеется пара решений уравнений Шрёдингера в
квазиклассическом приближении. При этом необходимо помнить, что гра¬
ничные условия, а именно наличие классического финитного движения при
заданной энергии, могут приводить к фиксированной суперпозиции этих
решений, так как при финитном движении в одномерном случае состояние
энергии невырождено.
Первая итерация и условие применимости квазиклассического приближе¬
ния. Уравнение для первой итерации, которая дает квадратичный по h вклад
в S, очевидно, имеет вид
(S;+?i2S')2 ър2 (х) + ^{3(S")2 - 2SqSq'}
Поскольку с заданной точностью до ft2
(S£> + ft2S' )2 (S')2 + 2 h2S'0S'2
и S'0=p(x), из (12.16) следует, что
S'2 = -^{3(p')2-2pp"}.
(12.16)
(12.17)
Нулевая итерация является достаточно хорошим приближением, если этот
вклад мал в сравнении с ведущим членом:
П2
/\2
(р о
а также
Величина
:|р21
р2 р
р р
<1,
<1.
(12.18)
(12.19)
р'1=р'Х = 5р
есть изменение импульса на расстоянии в длину волны в первом порядке.
Поэтому разложение по h оправдано, если
5р
Р
<1,
(12.20)
т. е. если относительное изменение импульса на длине волны пренебрежимо
мало в первом порядке. Второе условие (12.19), очевидно, дает
52Р
<1, 52р~р"Х2,
(12.21)
Лекция 12
169
т. е. относительное изменение импульса на длине волны должно быть прене¬
брежимо мало и во втором порядке.
условия применимости квазиклассического приближения можно записать
в виде
что, по сути, означает, что относительное изменение длины волны на рассто¬
янии в длину волны в первом и втором порядке должно быть пренебрежимо
мало. Первое из условий (12.22) можно также переформулировать так: если
£—интервал, на котором потенциал изменяется настолько существенно, что
изменение длины волны сравнимо с длиной волны, то
а значит, существенное изменение потенциала в условиях применимости
квазиклассики происходит на расстояниях £, в которые укладывается боль¬
шое число длин волн. Другими словами, потенциал должен изменяться до¬
статочно медленно.
Кроме того, используя явный вид функции р (х), запишем
Р
есть работа, совершаемая силой на расстоянии 5х = h/p = А, т. е. на длине
волны. С учетом выражения для кинетической энергии
условие применимости квазиклассики в первом порядке принимает вид
т. е. работа, совершаемая силой на длине волны, должна быть пренебре¬
жимо мала в сравнении с кинетической энергией частицы. Поэтому ясно,
что вблизи точек поворота, где кинетическая энергия и импульс стремятся
к нулю, а сила остается отличной от нуля, квазиклассическое приближение
неприменимо.
С учетом
|Я'|<1, \Х"Х\ < 1,
(12.22)
откуда сразу находим
(12.23)
_/ _ 2m V' т т?
р—ir~pF’
где F = —У' — сила, действующая на частицу. Тогда
-F*5x-F~5A
(12.24)
170
Тема 6. Квазиклассика
12.3. УСЛОВИЯ ОТРАЖЕНИЯ, СШИВКА РЕШЕНИЙ В ТОЧКАХ ПОВОРОТА
Вблизи точек поворота вместо квазиклассического приближения необхо¬
димо точно решить уравнение Шрёдингера. Тогда
где в точке поворота У (а) =Е, и мы приходим к уравнению Шрёдингера для
частицы, на которую действует постоянная сила F(a). Точное решение выра¬
жается через спецфункцию Эйри, которую необходимо затем сшить с квази-
классическим приближением возле точки поворота. Результат такого строго¬
го рассмотрения в точности согласуется с более наглядным методом сшивки
квазиклассических решений вблизи точки поворота, который мы и приведем
ниже. По сути, речь идет об отражении частицы от потенциального барьера
в квазиклассическом приближении.
Пусть слева от точки поворота х = а расположена недоступная для клас¬
сической частицы область вплоть до х—> — оо, как это показано на рис. 12.
Волновая функция при х < а в запрещенной для классической частицы об¬
ласти имеет вид затухающей экспоненты
так что аргументы корней положительны.
Совершим переход в классически доступную область х > а по двум конту¬
рам в комплексной плоскости х, как показано на рис. 13.
Е - V(х) м Е - V(a) - V'(а) (х - а) = F(a) (х - а),
где
V'CaXO,
а
х
а
Рис. 13. Контуры обхода точки поворота
Для этого сделаем замену переменных
х — а = — ре1^, р = const > 0,
(12.26)
где для левого контура
а для правого
05? </? 5? —п.
Лекция 12
171
При таком обходе точки поворота соответственно получаем пару вкладов при
х>а
p-irc/4
*lW = 2^exp{5bfe)djt}’
=§7=§f *ч>Н/ »w dx}-
где уже
p(x) = \J 2m [E - VOOL x>a, Е>У(х),
— вещественная функция импульса. Каждое из этих решений можно про¬
должить по тем же контурам в обратную сторону в область х < а, поменяв
контуры обхода местами. При этом, однако, возникает вклад, экспоненциаль¬
но растущий при х —> — оо:
С е!я/2
VIpWI а
Легко заметить, что этот недопустимый растущий вклад сокращается для
суперпозиции
X
ФМ». = Фа(х) + Ф2(х) = -jL=. cos{i J р(х) dx - 5}. (12.27)
V рОО а
Таким образом, поскольку волны Ф2 и можно соответственно рассмат¬
ривать как падающую на потенциальный барьер волну и отраженную от
него волну, при отражении от классически недоступной области потенциала
возникает относительная фаза волн1
Совершенно аналогично при отражении от потенциального барьера спра¬
ва при х = Ъ затухающая волновая функция в классически недоступной обла¬
сти
ъ
*(*)*>(, = § ехр{ я f WI d*} (12.28)
переходит в
*Мх<ь = cos{| / p(x)dx-^Y (12.29)
Снова убеждаемся, что фаза падающей на потенциальный барьер волны на
— больше фазы отраженной волны.
Подчеркнем, что в случае отражения от бесконечно высокого в точке по¬
ворота потенциального барьера конечной ширины2 волновая функция долж¬
1При этом мы молча полагали, что в точке поворота на классическую частицу действует
конечная, ограниченная по величине сила.
2Точнее, на границе барьера сила возврата обращается в бесконечность.
172
Тема 6. Квазиклассика
на обращаться в нуль в точке поворота, так что, например, если V(x < а) =
= +оо, то
Пх)х>а=^Щcos^ Ipix) dx±^’
и относительная фаза падающей и отраженной волн равна ±п, т. е. вдвое
больше, чем в случае потенциального барьера конечной высоты в точках
поворота, отличных от бесконечности.
12.4. Правило квантования Бора—Зоммерфельда
Рассмотрим потенциальную яму, изображенную на рис. 12. Согласно по¬
лученным нами условиям сшивки решения внутри ямы с затухающими на
бесконечности решениями получаем
х
*(x)x>a = -^=cos{| J p(x)dx-f } (12.30)
a
И
м D
Ф(х),<ь = -j£== cos{± f p(x) dx - f }, (12.31)
где С и С — нормировочные константы для решений, затухающих соответ¬
ственно при х—>+оо. Эти выражения должны быть тождественно равны
друг другу, так как они описывают волновую функцию внутри классически
доступной для частицы области. Значит,
тЬ c°s(5 ! рМ = “8(я ! *»*-*}. (12.32,
Это равенство имеет место, если, во-первых, амплитуды косинусов равны по
модулю:
|С| = |С|, (12.33)
а во-вторых, зависящие от координат фазы косинусов совпадают с точностью
до знака и сдвига на пп:
i Jp(x)dx-^ = ±{j^ Jp(x)dx-^} + 7m, неZ. (12.34)
a x
Знак «плюс» дает
1 х 1 *
^ J р(х) dx+£ j p(x) dx = nn,
a b
так что слева стоит функция от х, а справа —постоянная: это уравнение не
имеет решений (р(х) = 0 не имеет физического смысла). Взяв знак «минус»,
находим
Лекция 12
173
Здесь интеграл берется по полупериоду движения классической частицы
в потенциальной яме. Переходя к интегрированию по полному периоду,
находим правило квантования Бора—Зоммерфельда:
р(х) dx = 2nh(n + ^, п€N. (12.36)
Интеграл по циклу есть не что иное, как адиабатический инвариант — фа¬
зовый объем внутри траектории. Поэтому квазиклассическое квантование
связанных состояний частицы показывает, что квантовое число п задает
число ячеек фазового пространства АГ = 2nh, приходящихся на данное ста¬
ционарное состояние (с точностью до вклада основного состояния). Ясно,
что фазовый объем равен целому числу ячеек только при некоторых дискрет¬
ных значениях энергии частицы.
12.5. Плотность состояний
Продифференцируем формулу квантования Бора—Зоммерфельда по энер¬
гии
f И<Ьг=2"в1§- <12-37>
Здесь, очевидно, — плотность спектра состояний по энергии, а = v —
скорость движения частицы. Так как dx=v dt, интеграл по периоду сводит¬
ся к
f $k=$dt=T’
т. е. он равен периоду движения классической частицы. Отсюда
= (12.38)
и плотность состояний определяется круговой частотой движения со = 2п/Т.
Эта частота не зависит от энергии у гармонического осциллятора, так что
квазиклассика воспроизводит точный результат для разности энергий между
двумя соседними уровнями:
ДЕ = §|дп|Дп=1 = Йсо.
В произвольном потенциале частота движения и расщепление между уров¬
нями связанных состояний зависят от энергии.
12.6. Нормировка
При нормировке волновой функции связанного состояния в квазиклас-
сическом приближении необходимо учесть два факта: 1) плотность вероят¬
ности обнаружить частицу вне классически доступной области пренебрежи¬
мо мала (экспоненциально подавлена); 2) само приближение справедливо
174
Тема 6. Квазиклассика
лишь при п »1, т. е. когда число волн между точками поворота велико
(в противном случае длина волны заведомо сильно изменялась бы за период
колебаний от бесконечности в точке поворота до конечного значения внутри
допустимого интервала координат). Значит,
ь
J |Ф(х)|2сЬ:*/ |Ф(х)|2 dx = |C|2 J |cos{-}|2^y. (12.39)
а
Здесь под косинусом стоит фаза, которая совершает большое количество ко¬
лебаний гг, а амплитуда этих колебаний, обратно пропорциональная импуль¬
су, по условию применимости квазиклассики медленно меняется. Значит,
квадрат косинуса можно заменить его средним за период колебания:
cos2{-}->|.
Тогда с учетом dx=v dt и р = mv нормировка
jLWPdx-gjd.-gl-. (12.40,
—оо а
где опять Г — полный период движения частицы в связанном состоянии.
Волновая функция нормирована на единичную вероятность, так что
\C\2 = f. (12.41)
12.7. Возмущение
Рассмотрим задачу квазиклассического квантования связанных состоя¬
ний системы с гамильтонианом
н = ^ + V0 М + 5 V(x) (12.42)
с малым возмущением 5У<У0 в смысле малого отличия интегралов от
функций V0 и V0 + 5V на разумных конечных интервалах координаты1. Будем
считать, что решение задачи с гамильтонианом
а2
Ho = fe + Vo00 (12.43)
известно, так что
§ р$(х) dx = 2пП (n +1), (12.44)
где, естественно,
Ро ОО = y/2m[En-V0Ml (12.45)
1Наивное сравнение значений функций в точках не соответствует представлению о малости
возмущения, так как потенциал У0 может просто обращаться в нуль там, где 5V ф 0. То же
можно сказать и в отношении сравнения приращений, так как V0 может иметь экстремум, не
совпадающий с экстремумом 5V.
Лекция 12
175
и интеграл берется между точками поворота (а, b). В задаче с возмущением
правило квантования Бора—Зоммерфельда дает
§ рЕ+5Е(х) dx = 2nh(n + ^, (12.46)
где импульс—
рЕ+5Е(х) = ^2 т[Еп + 5Еп - У0(х) - 5У(х)]. (12.47)
Здесь
Еп + 5Еп=Ёп
— значение уровня энергии в потенциале с возмущением, и мы полагаем,
что 5Е —малая поправка. Пределы интегрирования, конечно, несколько ме¬
няются: (а + 5а, Ъ + 5Ь), — но вклад вблизи точек поворота в квазиклассике
пренебрежимо мал, так что в (12.44) и (12.46) мы будем полагать пределы
интегрирования одинаковыми (в рамках ведущего приближения это оправ¬
дано).
Вычтем (12.44) из (12.46) при фиксированном п. Тогда имеем
§{рЕ+5Е(х)-рЕ(х)} dx = 0. (12.48)
Выражение для импульса можно разложить по малому возмущению энергии
и потенциала:
рЕ+5ЕМ = \/2т[£„ + 8Еп - V0(x) - 5V(x)] =
= ]j2т[Еп - V0(x)]{l + } Po + fo[5£" " 5Vl
Значит,
Переходя к интегралу по времени, находим
т
5£п = ^/ df 5V[*(t)L (12.50)
о
или
5£" = 7|ш51,М- №51)
Первая из этих формул показывает, что среднее значение возмущения за
период определяет сдвиг энергии связанного состояния, а вторая дает прак¬
тический рецепт расчета этого сдвига.
Критерий применимости. Проведенное рассмотрение расчета поправ¬
ки к энергии стационарного состояния за счет возмущения в квазиклассиче-
ском приближении следует считать справедливым только в том случае, если,
прежде всего, изменение волновой функции 5%р в задаче с возмущением
176
Тема 6. Квазиклассика
в некотором смысле мало по сравнению с самой волновой функцией гр0
в исходной задаче: \5гр\ = |*0 - 1 < |я/>0|. Так, потребуем, чтобы в ходе вре¬
менной эволюции, выраженной в волновой функции фактором exp{-i£t/ft},
за время периода колебаний частицы в потенциальной яме Т была мала
поправка к волновой функции за счет разности энергий:
Последнее возможно, только если фаза под знаком экспоненты мала по срав¬
нению с 2тг, т. е.1
где стандартным образом фазовая частота со = 2тс/Т. Как мы показали, ве¬
личина поправки к энергии определяется средним значением возмущения
на классической траектории с энергией уровня в системе без возмущения:
5Е = (У), в то время как hco задает инкремент в дискретном спектре энергий
системы АЕ. Поэтому критерий применимости теории возмущений в квази-
классическом случае (12.52) можно записать в виде
Таким образом, теория возмущений применима при условии малости возму¬
щения по сравнению с разностью энергий между соседними стационарными
уровнями.
При выводе критерия применимости методом рассмотрения временного
фактора волновой функции мы по сути полагали, что в некоторой точке
пространства в области, доступной для классической частицы и удаленной от
точек поворота, где квазиклассика заведомо неприменима, пространствен¬
ные волновые функции в задаче с возмущением и без возмущения практи¬
чески совпадают, что и позволило рассмотреть лишь разность временных
факторов. Но для этого необходимо, чтобы и пространственная зависимость
этих волновых функция мало отличалась друг от друга. Поэтому запишем
более подробно вид координатной зависимости волновой функции в квази¬
классике, используя разложение импульса по малым поправкам при наличии
возмущения:
Как мы уже установили, переход к временной зависимости на траектории
дает
|е лЕТ — е й£оТ|<1 Ф=> |е *5Е'Т —1|<1.
<2я <=> \5E\Cho),
(12.52)
(12.53)
exp
{i J p(x) dxj^expj^ J p0(x) dx} expj^ J ^y(5£-V(x))J.
10тметим, что «набегание» фазы, кратное 2п, за время периода означало бы, что волновая
функция в задаче с возмущением существенно отличается от исходной.
Лекция 12
177
где, конечно, время на верхнем пределе интегрирования параметрически
зависит от координаты, t=t(x). Значит, координатная зависимость волновой
функции в задаче с возмущением может быть представлена в виде
причем первое слагаемое под знаком экспоненты по сути повторяет поправ¬
ку во временном факторе за счет малого сдвига энергии стационарного
состояния, и мы знаем, что возникающей за счет него фазой за период
колебаний можно пренебречь. Поэтому критерий применимости теории воз¬
мущений, учитывающий малое отличие пространственной зависимости вол¬
новой функции в задаче с возмущением от зависимости исходной волновой
функции, можно представить в виде
что опять же справедливо, только если на всем периоде колебаний набегаю¬
щая фаза мала по сравнению с 2я, т. е.
В итоге и рассмотрение пространственной зависимости волновых функций
приводит к тому же критерию теории возмущений в квазиклассике: харак¬
терные значения возмущения на интервале классического движения частицы
должны быть существенно меньше разности энергий между соседними уров¬
нями. При этом не следует, конечно, забывать и о критерии применимости
самого квазиклассического приближения, а именно об условии большого
числа колебаний за период движения между точками поворота: п »1.
Еще более наглядно критерий применимости теории возмущений в ква¬
зиклассике можно представить, если определить при больших квантовых
числах малую вариацию номера уровня 5п:
ще dE^/dn —обратная плотность состояний в спектре энергии, посредством
которой расстояние между двумя соседними уровнями можно вычислить как
Тогда условие применимости теории возмущений АЕ^>\5Еп\ представится
в виде
•0 (х) = 1/>0 (х) ехр{ ^5Е • (t -10) - ^ (V (t)> • (t -10)},
(У(У'Г <2n <=> |(У)|«|ДЕ| = Йй>.
(12.54)
(12.55)
AE = -т-^-Ап приДп = 1.
(12.56)
|5n|<l,
(12.57)
т. e. возмущение эффективно сводится к малому сдвигу номера квантового
состояния в задаче без возмущения, так что не происходит перекрытия с со¬
седними уровнями.
178
Тема 6. Квазиклассика
Задача 6.1. Вычислить поправку к энергии осциллятора за счет возмущения
5V = em2co3x4/h, где е —> 0, и определить условие применимости метода теории воз^
мущений для конечных значений е.
Решение. Согласно общему правилу квантования Бора—Зоммерфельда (12.36),
спектр невозмущенной задачи — гармонического осциллятора — задается условием
f p0№dx = 2nh(n+^, =
так что с помощью параметрической замены
Х=]]2Е™
находим
Х-М
V mar
0 sin (Z?
mar
9р.(0) 2я
f РоОО d* = -2- / cos2 </> dy> = -jE™.
o
В итоге спектр осциллятора в квазиклассике
Е® =fia>(n+i)
совпадает с точным выражением1.
Поправку к энергии
5Е =
J РО
определяют интегралы
X ^ = J_ Jd 2я
J р0 тсо JQ тсо
и
X л 4(е£0))2 2|? . 4 з 2яЙ f , 1^2
| T.SVM=’-M lsm *Л*=?-^Г + г) ■
В итоге
5En = leh<o(n+l)2.
Критерий применимости теории возмущений в квазиклассике, 5Е < hco, дает2
е • п2 < 1 при условии п »1.
Отсюда, между прочим, следует, что требование точности вычислений по теории
возмущений в квазиклассике на уровне, скажем, порядка нескольких процентов при
конечном значении параметра малости е~0,1 может оказаться совершенно недости¬
жимым, поскольку для этого квантовое число п должно принимать слишком малые
значения, что недопустимо в квазиклассическом приближении.
Комбинированный критерий применимости квазиклассического приближения и
теории возмущений приводит к двустороннему ограничению на квантовое число
1«П«4г,
V®
1Надо иметь в виду, что «точное совпадение» выглядит менее «солидно», если помнить
о критерии применимости квазиклассики тг» 1.
2Заметим, что наивное требование условия малости абсолютной величины поправки в виде
5Еп < Еп привело бы к неверной оценке области применимости теории возмущений: е • п < 1,
что ошибочно увеличило бы верхнюю границу для допустимых значений квантового числа п.
Лекция 12
179
что, впрочем, совершенно ясно, поскольку четвертая степень координаты в конце
концов начинает доминировать над квадратом при больших значениях х, где, сле¬
довательно, возмущение велико.
Задача 6.2. Провести квазиклассическое квантование спектра частицы, движу¬
щейся в потенциале
Решение. Введем безразмерную координату и = х/а, в терминах которой стаци¬
онарное уравнение Шрёдингера для ip (и) запишется в виде
или после использования безразмерных параметров глубины потенциальной ямы f
и энергии v=E/U0
В задаче без возмущения (е —> 0) правило квантования Бора—Зоммерфельда
Свойства гамма-функции zY{z) = T(z +1), Г(г)Г(1 — z) = n/ sin(Trz) позволяют запи¬
сать
Эта формула достаточно точно описывает систему уровней в задаче без возмущения
уже при п > 1, что видно из рис. 14, где в случае £ = 1/6, е = 0 представлена величина
5п(0), которая определена как приращение к номеру уровня, необходимое для полу¬
чения спектра, рассчитанного численно, и задана согласно формуле
считая е малым параметром. Провести сравнение с точным спектром при
ip" + и0(м4 + еи^хр = Егр,
дает
§ p0(u)du = § \/2(Cv — С^4) du=4-\/2f / duy/v-u4,
о
что введением переменной i/=u4/v сводится к бета-функции
§ p0(u)du=y2Cv tpv / dv-v = .
так что в итоге
Введем число
и запишем спектр невозмущенной задачи
180
Тема 6. Квазиклассика
так что
Для расчета поправки используем ту же замену переменных в интегралах:
X du V-J }Л ,_1 v-?r(l)r(l)
Ф —TT = -^J dv'v 4(l-v) 2=“F=— /Зч
J PoOO V2?J0 72? Г(|)
X du e fj J i v? Г(|)Г(|)
Ф T7TTU ~F= J dvtM(l-v) 2==-——^—^-,
J PoM y/2Z 0 \/2? r(f)
откуда по общей формуле
c зГ(2)Г(|) з |Г2(|) 8 3 9Г4(|)
— с у 2 -— = PV 2 — = PV 2 —
r(f)r(i) flr2(l) 15eV 4** •
В итоге
5v" = ^eg4|(n + i)2.
Вычислим эффективный сдвиг номера уровня
5vci) 2 %. (п\\ ( 1Л з
5n=5^v^ = Ieg4?J v 2J <<L
Значит, теория возмущений применима при
Подчеркнем, что прямое сравнение поправки к энергии уровня со значением энергии
в невозмущенной задаче привело бы к ошибочной оценке верхней границы области
применимости теории возмущений по квантовому числу п, так как необходимо срав¬
нивать поправку с расстоянием между соседними уровнями.
При заданных значениях параметров задачи £=1/6, е=0,1 для сравнения прибли¬
женных оценок в квазиклассической теории возмущений с точным расположением
уровней следует провести численный расчет спектральной задачи. Стандартный при¬
ем состоит в том, чтобы построить схему итераций, реализуемую в виде алгоритма.
Мы использовали следующий метод: при заданном начальном значении энергии
вычислялись точки поворота а < Ь, после чего в качестве начальных значений задачи
Коши бралось квазиклассическое выражение достаточно глубоко в области затухания
волновой функции, скажем, правее Ъ; тем самым определялась необходимая для ре¬
шения уравнения второго порядка первая производная волновой функции в исходной
точке х0 > Ъ с произвольной нормировкой *ф(х0). Затем вычислялось значение волно¬
вой функции в зеркальной точке гр (—x0) и определялось значение асимметричности
d = \‘if> (х0) \-\ip (—х0) |.
В изучаемой задаче потенциал—четная функция координаты, так что при верном
выборе энергии в спектре уровней асимметричность d должна обращаться в нуль;
при этом затухание волновой функции при отрицательных х также гарантировано
выбором квазиклассического условия затухания при положительных х. Выбирая пару
значений энергии Еъ Е2, легко провести линейную итерацию в точку, где асиммет¬
ричность должна обратиться в нуль:
dfcEfc+i - dk+iEk
Ei
k+2 dk-dk+1
Лекция 12
181
Этот метод оказывается достаточно точным и быстро сходящимся при малом числе
итераций, причем номер уровня контролируется прямым подсчетом числа узлов вол¬
новой функции, что легко реализуется в пакете аналитических и численных расчетов
и графических построений mathematica.
Рис. 14. Оценка точности квазиклассического приближения по приращению
к номеру уровня 5п®\ которое нужно добавить для согласия с точным числен¬
ным расчетом энергии связанных состояний, в зависимости от квантового
числа п в невозмущенной задаче е = О, £ = 1/6
Описанная процедура использовалась при численном расчете спектра как невоз¬
мущенной задачи, так и при наличии возмущения. Результат сравнения квазикласси-
ческих вычислений с точными представлен на рис. 15 в терминах поправки к номеру
уровня. Согласно нашему исследованию квазиклассика в совокупности с теорией
возмущений может быть применима в ограниченной области значений квантового
числа п:
1 < п < 7,
что и подтверждается данными рис. 15: при малых п, в данном случае для основного
состояния, квазиклассика дает плохую оценку и без возмущения, и при его наличии,
а при больших п неприменима теория возмущений, так как, во-первых, поправки по
сути начинают «перемешивать» соседние уровни, а во-вторых, ведущее приближение
оказывается слишком неточным и становится необходимым суммирование поправок
высшего порядка, т. е. выход за рамки теории возмущений. Фактически теория возму¬
щений в рамках квазиклассического приближения в этой задаче применима в весьма
узкой области квантовых чисел, а именно при 1 < п < 4.
12.8. Потенциальный барьер
Рассмотрим задачу, в которой на потенциальный барьер с конечной си¬
лой возврата в точках поворота для классической частицы ограниченной
энергии, т. е. фактически конечной высоты на конечном отрезке коорди¬
нат, в интервале а<х<Ъ слева падает и отражается волна. В этом случае
экспоненциальное затухание волны в классически недоступной области по¬
тенциального барьера приводит к конечной, отличной от нуля волновой
182
Тема 6. Квазиклассика
функции и в области х>Ъ, где появляется уходящая на бесконечность волна,
прошедшая через барьер (см. рис. 16).
Волновая функция
^>b=7fe)exp^/pWd^
имеет асимптотику прошедшей через барьер волны с потоком, направлен¬
ным в положительном направлении х. Пользуясь методом сшивки реше¬
ний в квазиклассическом приближении, описанным в предыдущем разделе,
мы получим в области а<х<Ъ суперпозицию экспоненциально падающего
и растущего с ростом х вкладов. Оба вклада нормированы так, что они
равны одной и той же константе С при х = Ь. Значит, в области а<х<Ъ
возле х = а в рамках погрешности самого квазиклассического приближения
следует пренебречь тем вкладом, который экспоненциально подавлен, так
как его учет означал бы превышение точности метода расчета. Поэтому
х
VWa<x<b= ~f==e~ln/4 еХр{~| J d*} =
VIpWI Ь
=ехр{-н S 'рdx+я / d*} ^
а
=> УМа<х<Ь= еХР\Й -С dX}>
где
ъ
С = Се-1Я^4 ехр|^ J |р(х)| dxj. (12.58)
а
Эта волновая функция повторяет ситуацию с отражением волны от потенци¬
ального барьера при х = а справа, так что
ФСх)х<а=27Шcos^ Iр(х) dx~^'
Коэффициент прохождения потенциального барьера Т определяется от¬
ношением потоков вероятности в прошедшей и падающей волнах:
7- =7- jclzjcl
J out Jx>b р m m >
и здесь при вычислении потока в волне дифференцируется только экспонен¬
та, а предэкспоненциальный множитель в квазиклассике изменяется очень
медленно, т. е. выносится из-под знака дифференцирования, а после пред¬
ставления косинуса в области х < а в виде суммы двух экспонент с падающей
и отраженной волнами, получаем
Лекция 12
183
Рис. 15. Приращение к номеру уровня 5п за счет поправки в теории возму¬
щений (квадраты) и дополнительный вклад, который нужно добавить для
согласия с точным численным расчетом энергии связанных состояний (тре¬
угольники), в зависимости от квантового числа п
Рис. 16. Туннельный эффект — проникновение волны через потенциальный
барьер
184
Тема 6. Квазиклассика
так что
(12.59)
Отметим, что в квазиклассике коэффициент отражения тождественно равен
единице (разложение косинуса на две экспоненты с одинаковыми амплитуда¬
ми). Это не противоречит наличию ненулевого коэффициента прохождения,
так как он экспоненциально подавлен, так что в разности 1 — Т сохране¬
ние второго члена являлось бы превышением точности. Экспоненциальное
подавление обусловлено условием достаточной ширины барьера, так как
ширина должна превосходить несколько длин волн для применимости ква¬
зиклассики вдали от точек поворота:
где t = b — а — характерная длина, на которой потенциал существенно изме¬
нился, что находится в согласии с общим условием применимости квазиклас¬
сики: длина волны существенно меняется на расстояниях, много больших
длины волны, А/£ <С 1.
Строго говоря, при выводе коэффициента прохождения потенциального
барьера, т. е. при рассмотрении эффекта туннелирования, для примени¬
мости квазиклассического приближения необходимо, чтобы потенциал до¬
статочно плавно вел себя вблизи точек поворота, так что, например, для
потенциала на рис. 17 в области 0 < х < а нужно уже использовать точ¬
ное решение уравнения Шрёдингера. Это, однако, сказывается только на
предэкспоненциальном множителе в коэффициенте прохождения (12.59), ко-
ъ
а
V(x)
WWW
х
а
Ъ
Рис. 17. Квазистационарное состояние в потенциальной яме и проникновение
волны через потенциальный барьер
Лекция 12
185
торый становится отличным от единицы1. Поэтому по-прежнему
Т~expj-| J |pOO|dx}.
а
Туннельный эффект был использован Гамовым для объяснения законо¬
мерностей а-распада квазистационарных состояний ядер в соответствии с
расчетом коэффициента прохождения в потенциале типа рис. 17, где притя¬
жение (яма) обусловлено короткодействующими ядерными силами, а оттал¬
кивание—кулоновским взаимодействием положительного ядра и а-частицы.
В этой связи заметим, что квазистационарными состояниями называют
долгоживущие резонансы, возникающие в процессах рассеяния, о которых
мы упоминали в лекции 5. К теории рассеяния и распадам квазистационар¬
ных состояний мы обратимся несколько позднее во второй части курса. Здесь
же укажем на то, что резонансы могут образовываться как при упругом рас¬
сеянии, когда начальное и конечное состояния описываются одним и тем же
набором частиц, так и при неупругом, когда набор частиц изменяется. Долгое
время жизни резонанса позволяет рассматривать его безотносительно к про¬
цессу его происхождения, а задачи описания квазистационарных состояний
составляют отдельный класс, который мы не рассматриваем в этом курсе.
Флуктуации и виртуальные частицы. Физический смысл туннельного
эффекта становится более ясным, если ввести понятие виртуальных частиц.
В области потенциальной энергии, недоступной для классических частиц,
имеют место существенные флуктуации, обусловленные тем, что операторы
кинетической и потенциальной энергии по отдельности не коммутируют
с гамильтонианом:
[Tip), Я] = [|^, V(r)] = 2^(р[р, VCr)] + [р, V(r)]p) =
= - J^AV(r) - f {W(r)> p
и [V(г), Я] = — [Т(р), Я] Ф 0, так что значения кинетической и потенциаль¬
ной энергии имеют неопределенности в случае стационарного состояния
с точно заданной энергией. Этими флуктуациями можно пренебречь в об¬
ласти, доступной для классической частицы, потому что —W = F — сила,
действующая на частицу, и второе слагаемое в коммутаторе имеет порядок
£{VV(r)> • р • J £ ~ SA • ГИп,
771 771 р ТП
где, как и выше, 5А — работа силы на длине волны. Эта работа совершается
за характерное время
5- Я ft 771 h
Q [ Л; — r>sj — • rsj
v P P W
1Впрочем, подчеркнем, что если движение частицы квазиклассично по обе стороны от
барьера, то отличие предэкспоненциального множителя от единицы оказывается также экспо¬
ненциально подавлено.
186
Тема 6. Квазиклассика
Первое слагаемое в коммутаторе того же порядка, что и второе: используя
определение силы F=dp/dt=—VV, находим
zm zm т
Поскольку коммутатор с гамильтонианом определяет производную операто¬
ра по времени, для флуктуаций за время 5t находим
=> ТШ-5ТШ~5А-ТШ)
а значит, согласно условию применимости квазиклассического приближения
7t m Xj
kin ikin
и флуктуациями как кинетической, так и потенциальной энергии в классиче¬
ски доступной области необходимо пренебречь. Поэтому можно проводить
рассуждения в терминах импульса, зависящего от потенциальной энергии,
как мы это делали при построении квазиклассического приближения.
Ситуация коренным образом меняется в области, недоступной для клас¬
сической частицы, когда понятия кинетической и потенциальной энергии
плохо определены по отдельности. Итак, имеется вероятность такой флук¬
туации потенциальной энергии, при которой частица может проникнуть
в классически недоступную область с некоторым положительным значением
кинетической энергии. Эта вероятность в квазиклассике определяется коэф¬
фициентом прохождения
—2-
w ~е я,
где S — действие, зависящее от координаты частицы в глубине потенци¬
ального барьера. Частицы, проникающие под барьер за счет флуктуаций
потенциальной и кинетической энергии, называют виртуальными. Таким
образом, при наличии внешнего поля его потенциал испытывает флукту¬
ации, приводящие к распространению виртуальных частиц. Если внешнее
поле меняется, скажем, адиабатически в зависимости от времени или рас¬
стояния, то виртуальные частицы могут попасть в классически доступную
область, т. е. наблюдаться, как это имеет место при прохождении через по¬
тенциальный барьер: если потенциал медленно уменьшается ниже значения
полной энергии в некоторой области пространства, то в ней наблюдается
туннельный эффект — виртуальные частицы за счет флуктуаций проходят
барьер и регистрируются в классически доступной области как реальные.
Задача 6.3. В рамках квазиклассического приближения для туннельного эффекта
оценить вероятность образования электрон-позитронных пар в постоянном электри¬
ческом поле за счет флуктуаций вакуума во внешнем поле.
Решение. Квантовые флуктуации вакуума, которые приводят к рождению пар
частица-античастица, возможны, если энергия флуктуации порядка массы частицы
АЕ ~ тс2,
Лекция 12
187
а значит, время такой флуктуации согласно соотношению неопределенностей
Atc^ ~2 •
тсг
Если на электрон-позитронную пару в вакуумной флуктуации действует внешнее
электрическое поле 8, то возникающие силы разводят электрон и позитрон в разные
стороны, так что эти виртуальные частицы могут перейти в состояние реальных,
наблюдаемых частиц, т. е. может произойти туннельный переход — пробой вакуума.
Вероятность туннельного перехода задается квазиклассической формулой
—2-
w~e ft,
где S—действие виртуальной частицы
S^p- Ах.
Импульс в последней формуле по порядку величины задается энергией покоя
рс^тс.
Его вариация входит в уравнение движения: производная импульса по времени равна
силе электрического поля;
л л
-=е£ => Др*—2.
Но флуктуация импульса связана с флуктуацией координаты соотношением неопре¬
деленностей
Ар • Ах ^ h,
откуда действие
с т2с3
~ е£ *
а вероятность рождения электрон-позитронной пары в постоянном электрическом
поле
. .t m2c3
W ~ е eft£ .
В квантовой теории поля вычисляется и постоянная const = п, и предэкспоненци-
альный множитель. Здесь же отметим лишь то, что введение комптоновской длины
волны электрона
Ае = —-
тс
позволяет записать аргумент экспоненты в виде фактора
тс2
е£Ле’
т. е. он задается отношением массы покоя электрона к работе сил постоянного элек¬
трического поля на комптоновской длине волны электрона Ае. Рождение пар из
вакуума становится статистически значимым, если значение этого фактора сравнимо
с единицей, а значит, когда поле настолько велико, что его напряженность «разрыва¬
ет» вакуум на комптоновской длине электрона. Численно это поле чудовищно велико:
S ~ 1014 В/м.
При осмыслении полученного результата следует обратить внимание на то, что
рождение пар частиц в течение бесконечного времени существования поля неми¬
нуемо приведет к необходимости учета обратного влияния рождающихся частиц на
источники поля (согласно закону сохранения энергии), поэтому в действительности
процесс рождения частиц носит существенно нестационарный характер, и при стро¬
гом подходе надо рассматривать поля с конечным временем существования.
188
Тема 6. Квазиклассика
Задача 6.4. В рамках квазиклассического приближения для туннельного эффекта
определить энергетическую зависимость вероятности рождения пар фотонов в грави¬
тационном поле черной дыры вблизи поверхности Шварцшильда за счет флуктуаций
вакуума, если гравитационное ускорение возле сферы Шварцшильда равно хс2 (для
х вводят термин «поверхностная гравитация»).
Решение. Предположим, что в вакууме в течение времени At имеет место флук¬
туация: образуется пара фотонов с энергией Е > 0 и — Е < 0. На фотон с энергией Е
и гравитационной массой т=Е/с2 действует сила гравитационного поля
F = хс2 • т = хЕ,
где, как видим, вместо массы покоя в релятивистском случае стоит энергия частицы.
Эта сила направлена к центру черной дыры. На фотон с энергией — Е действует такая
же по модулю сила, направленная в другую сторону, от центра, так как энергия
отрицательна. Таким образом, гравитационные силы растаскивают фотоны из ваку¬
умной флуктуации в разные стороны, так что может иметь место «пробой вакуума»,
что, естественно, невозможно в отсутствие внешних сил. Поэтому говорят, что под
действием гравитационного поля имеет место туннельный переход флуктуации в со¬
стояние с реальными фотонами.
Сила определяет изменение импульса, так что в конечных приращениях
Ар
c^F — xE,
At
а изменение импульса для фотона связано с энергией флуктуации
А Е
Ар — -.
с
Отсюда время флуктуации, в течение которого фотон приобретает энергию Е,
At i
За это время фотон проходит расстояние
At~ —.
хс
Ах ^ с At ^ -.
х
Поэтому характерное значение действия S для такой флуктуации
С А Е 1
Sczp-Axc* ,
с х
а вероятность туннельного перехода в квазиклассике
w~e я
дает
w ~ e-constife = е~РЕ,
где точное значение постоянной const=2п было рассчитано Хокингом (Hawking), так
что
В итоге энергетическая зависимость вероятности наблюдения флуктуации повто¬
ряет распределение Гиббса для излучения абсолютно черного тела с температурой
кТ = 1/13,
т— — —
к ' 2п'
где к — постоянная Больцмана и мы выделили фактор из фундаментальных постоян¬
ных, который обычно полагают равным единице за счет выбора единиц измерения
температуры, длины, времени и энергии.
Лекция 12
189
Значит, гравитационные силы способны приводить к детектированию удаленным
наблюдателем фотонов со спектром излучения абсолютно черного тела. При этом,
конечно, необходимо, чтобы фотон с отрицательной энергией никогда не попадал
в область действия измерительных приборов вне черной дыры. Это действительно
возможно при наличии сферы Шварцшильда: тогда при квантовой флуктуации вбли¬
зи этой сферы фотон с положительной энергией достигает удаленного наблюдателя,
а фотон с отрицательной энергией падает в черную дыру. В результате энергия черной
дыры уменьшается ровно на столько, сколько ее унес с собой фотон к стороннему
наблюдателю в измеряемом им спектре излучения. Качественно описанный процесс
есть квантовый эффект испарения черных дыр, который носит имя Хокинга.
Отметим, что, подобно предыдущему примеру с рождением пар частица-анти-
частица в электрическом поле, в наших оценочных рассуждениях мы не учитывали
нестационарность задачи о возникновении и существовании черной дыры, что в дей¬
ствительности весьма существенно в последовательной теории эффекта Хокинга.
Наконец, определим значение поверхностной гравитации из качественных сооб¬
ражений. Фотон не может покинуть черную дыру, так как работа сил гравитации на
расстоянии порядка размера черной дыры rg равна его энергии
хЕ-г„с^Е => х^—,
О Г
rg
так что температура черной дыры обратно пропорциональна размеру черной дыры1.
Для примера, гравитационный радиус Солнца (М0 ^ 2 • Ю30 кг)
2GM©
f©= ^
а температура черной дыры с массой Солнца была бы лишь
Г0^ 5-10"8 К,
но масса Солнца недостаточно велика, чтобы гравитационные силы необратимо сжа¬
ли бы его в черную дыру после исчерпания запасов термоядерного топлива (коллапс
Солнца по современным представлениям невозможен).
1Точная формула для черной дыры Шварцшильда l/x = 2rg.
Тема Интеграл по траекториям
7
Лекция 13 (дополнительная)
Вывод представления оператора эволюции в виде интеграла по траекториям
в фазовом пространстве, граничные условия, квантовый принцип Гюйгенса—
суперпозиция вкладов всех траекторий, классический предел, интегрирова¬
ние по траектории импульсов для квадратичных гамильтонианов, поворот
Вика, континуальный интеграл при наличии источника, уравнения Швин-
гера—Дайсона, производящий функционал, роль решения свободных класси¬
ческих уравнений движения при заданных граничных условиях, двухточеч¬
ная функция Грина, производящий функционал функций Грина, диаграммы
Фейнмана, ангармоничный осциллятор, квантовое эффективное действие,
квантовые поправки в функциональном уравнении Швингера—Дайсона, вер¬
шинные функции, графическое представление квантового уравнения для
двухточечной вершины в виде диаграмм Фейнмана, петли, связь вершин со
связными функциями Грина, введение возмущения для осциллятора.
Рассмотрим эволюцию состояния, заданного в начальный момент време¬
ни t = t! в координатном представлении
I*(t = t')> = / |q'} dq' Ф(д', t'), Ф(Ч', t') = (q'l'Kt')), (13.1)
где q'—обобщенная координата (для простоты—в одномерном случае). Тогда
согласно общему формализму состояние в момент времени t получается
в результате действия оператора эволюции U(t, t')
Здесь оператор эволюции записан в общем виде как символ «Т-экспоненты»,
т. е. понимается в виде предела произведения бесконечно малых сдвигов по
времени, строго упорядоченных в порядке возрастания моментов времени,
а нормировка записана с учетом ненулевого значения исходного момента
времени. В соответствии с таким разбиением интервала t — t' на N отрезков,
так что dt = (t - t')/N, при N -» » бесконечно малый сдвиг по времени
t' —»tx = t' + dt дает
13.1. Фейнмановский интеграл
|фсо)=era, t')i^(t')>,
(13.2)
где (см. (2.13))
192
Тема 7. Интеграл по траекториям
и, подставляя единичные операторы в координатном и импульсном представ¬
лениях, находим
l*fti)) = J d<2i l<2i)(<2ilPi)|^x
х (p-у| expjtj) dt}|q'^ dq' tfCq', t') + 0(dt2).
Для квадратичных по импульсу гамильтонианов вида
H(q,p,t) = |^+V(q,t),
очевидно1,
(р|Н(<2, р, О|q) = H(.q, р, t)(p|q), (13.3)
где ft(q, р, £) —гамильтониан классической системы. Поэтому, опуская члены
второго порядка малости по инкременту времени, с учетом (p|q) = eipq/fi
1В общем случае при переходе от классического гамильтониана к квантовому возникает
проблема упорядочивания некоммутирующих между собой наблюдаемых — координаты и им¬
пульса — так, чтобы оператор гамильтониана был эрмитовым. При этом выбор той или иной
процедуры упорядочивания, конечно, приводит к различным квантовым обобщениям клас¬
сической теории. Мы фактически полагаем, что после принятия некоторого выражения для
гамильтониана затем производятся перестановки импульса и координаты так, чтобы в итоге все
операторы имульса оказывались бы левее всех операторов координаты.
Что касается самой процедуры упорядочивания, то укажем, к примеру, обычно принимаемую
стандартную схему — анзатц Вейля. Пусть дана классическая величина как функция импульса
и координаты, F(p, q). Вычислим ее фурье-образ
Ни, v) = / dp dq el(up+l/q)FCq, р)
и построим оператор, упорядоченный по Вейлю, как обратный образ с операторами в экспонен¬
тах
Этот оператор заведомо эрмитов, если исходная величина F вещественна.
Вычислим, например, оператор, соответствующий упорядочиванию Вейля для величины
F = pq. Преобразование Фурье для линейной функции
J dp peiup = J dp eiup =2ят^5(и),
дает фурье-образ
Пи, V) = -(2n)28'(u)5'(v).
Тогда обратное преобразование приводит к
F(p,q) = - Г )25'(u)6'(v) =——
J (2 я)2 dud v lu=i/=0
так что
^=^(.рч+чр')-
Ясно также, что для функций коммутирующих наблюдаемых, например, для функции, завися¬
щей только от импульса или только от координаты, упорядочивание Вейля сводится к стандарт¬
ной подстановке в функцию соответствующего оператора (импульса или координаты).
Лекция 13 0дополнительная)
193
получаем1
l*(ti)> = J dq' Ф(Ч', t'). (13.4)
Повторял эту процедуру N раз, приходим к выражению
г N
|Ф(0) =^lim |qN) Р| ^^e№kbk-4k-0-n(qk,pk,tk)dt] dg/ ф(д/) ^ (13 5)
~~>°° J fc=l
где qo = q'- Введем скорость
q(tfc) = ^if^. (13.6)
1Вычислим матричный элемент
Hio = Ы#(р, q, t)ko) = J(qilp>^(pl^(p, q, t)|q0)
в схеме с упорядочиванием по Вейлю. Для этого следует записать гамильтониан в виде
Н(р, q, t) = J ^e-w+^jecu, V, О,
где Ж(u, v, О — фурье-образ функции Гамильтона в классической механике H(q, р, t). Следова¬
тельно, необходимо найти матричный элемент
(ple-^+^lqo),
который легко вычисляется согласно общей формуле Бейкера—Хаусдорфа для произведения
экспонент операторов АиВ, коммутирующих с их коммутатором [Л, В],
еАеВ=е\[А,В]еА+В
так что
e-i{up+v4) _ е- \ i2uv[p,4] e-iupe-iv4
и в силу [р, q] = -ih получаем
<Ple_i(“^+1'^|qo>=e-^ifiui,e-iupe_i‘'l,o<p|qo>-
Значит,
н10= Г iL^е^(Ч1-Чо-ВДе-^ое-|^^(и, V,о.
J 27ш (2тг)
Однако интегрирование по импульсу дает дельта-функцию для переменной и:
j ^е*рС,1",0"Ли)=5(91-чо-ад.
так *гго под интегралом в Я10 можно сделать соответствующую подстановку, что приводит к
>'(qo + =«'(чо + \(Я1 -<Зо)) = ^(<h +5о)
И
Н10= Г ^eSPt«i-4o)^e-i(uP+,'«o)^f(u)v,0,
J 2яН (2я)2
где мы ввели срединную точку q0 = (qa +q0)/2. В итоге обратное преобразование Фурье берется
для классических величин, и
<<h|tf(p, Я, 0Ы = J ^e>^-«o)W(q0, Р, t).
Таким образом, упорядочивание Вейля приводит к тому, что классический гамильтониан бе¬
рется в срединной точке координаты. В остальном проведенный в основном тексте вывод
матричного элемента гамильтониана остается в силе.
194
Тема 7. Интеграл по траекториям.
Тогда множество точек {qk} образует ломаную траекторию, которая показана
на рис. 18. Точно так же вводится и траектория в импульсном пространстве
Рис. 18. Ломаная траектория в координатном пространстве
Тогда произведение экспоненциальных факторов под интегралом в (13.5)
сводится к
expj^ J[p(t)q(t)-H(q(t),p(t),t)] dt} = ехрt)}, (13.7)
t'
где S(t', t) — классическое действие на траектории в фазовом пространстве
{q(t), p(t)} с граничными условиями в координатном пространстве q(t')=q'
и q(t) =qN. Получающееся выражение для состояния
|Ф(£")> = Um f \qN) dq' Ф(д', t') ]~[(13.8)
J k=l
обозначают как интеграл по траекториям
I'Kt")) = J dqN \qN) dq' ^(q', t') J ©q Q>p ел5[<!'р:с'’с"], (13.9)
где (первый и последний раз) указана функциональная зависимость класси¬
ческого действия S от траектории в фазовом пространстве, а мера интегри¬
рования получается при предельном переходе к континууму
<шо>
k=1
и поэтому фейнмановский интеграл по траекториям называют также конти¬
нуальным интегралом.
Матричный элемент (q"|Ф(с7/)), как видим, сводится к вычислению выра¬
жения
(q"|Ф(г")> = f{q"\U(.t", OlqO dq' V{q', t% (13.11)
Лекция 13 (дополнительная)
195
где
(q"|U(t", t')\q') = f Щ 9p e»^'0 (13.12)
есть интеграл по траекториям, причем интегрирование по qN «снялось»
вследствие
(ч"к w) = 5(q//-qN)>
так что траектории движения в координатном пространстве имеют гранич¬
ные условия
q(t/)=q/, q(t")=q". (13.13)
Подчеркнем, что матричный элемент — это число или числовая функция,
т. е. классический объект, и континуальный интеграл построен из чисто
классических величин: траекторий и действия на них.
Физический смысл такого представления матричного элемента в виде
интеграла по траекториям прост: амплитуда перехода из точки q(t') = q'
в точку q(t") = q" есть суперпозиция амплитуд для всех траекторий из ис¬
ходной точки в конечную, так что каждая траектория в фазовом простран¬
стве дает вклад ехр{iS/ft}, где S —действие на траектории. Как видим,
в фейнмановской формулировке прослеживается явная связь с принципом
Гюйгенса в теории волн, а именно, интеграл по траекториям устанавливает
квантовый аналог принципа Гюйгенса.
Оператор эволюции можно представить как
U(t”, t')= / dq" |q")(q"|C>(t", t')\q') dq' (q'|,
откуда1
U(t", t') = J dq" dq' |q")(q7| J ®q <2p (13.14)
1 Классический предел. При h-> О под интегралом стоит функция с быстро
осциллирующей фазой S/ft, за исключением случая, когда у действия имеется
стационарная точка:
5S = 0, 5q(t') = 5q{t")= 0, (13.15)
1 Обычно вводят запаздывающую функцию Грина уравнения Шрёдингера
ihG(q"y tq', t') t')Iq'),
где ^(0 — ступенчатая тэта-функция Хевисайда. Эта функция Грина удовлетворяет уравнению
{ifi J_ р", t")}g(q", t"; q\ -1') S(q"-q'),
так как дифференцирование тэта-функции дает дельта-функцию от разности времен, а опера¬
тор эволюции, во-первых, удовлетворяет уравнению Шрёдингера, а во-вторых, при равенстве
времен обращается в операторную единицу, матричный элемент которой в координатном пред¬
ставлении равен дельта-функции от разности координат. В терминах функции Грина эволюция
состояния вперед во времени дается соотношением
ф(д" t") =/ g(q", t"; q', г'Жд', t') dq', t" > t'.
В простейших случаях, например для свободной частицы, можно решить это уравнение
в явном виде. Однако в этом разделе мы исследуем метод континуального интеграла, оставляя
изложение аппарата запаздывающей функции Грина до рассмотрения теории рассеяния.
196
Тема 7. Интеграл по траекториям
т. е. вариация действия на траектории с фиксированными концами обраща¬
ется в нуль. Но это есть не что иное, как принцип наименьшего действия
в классической механике. Значит,
Z0 = f Siq Sfp ^Aefi5o(t ,t/ ) + квантовые поправки,
где S0— действие на «прямой» классической траектории.
2. Интегрирование по импульсу. Интеграл по импульсам можно взять, так
как
+ 00 +00
где нормировочная константа ЛГ не зависит от траектории. Тогда
г0=Л / Щ е* s(£''t"), (13.16)
где уже действие зависит только от траектории в координатном простран¬
стве:
t"
S(t', t") = J dt - V[q(t), t]}, (13.17)
t'
a
N
сЛ— lim Г\лг.
N->00 1 1
fc=1
3. Поворот Вика. Для интегрирования, в частности, для оценки констан¬
ты Я часто используют поворот Вика контура интегрирования по времени.
Формально полагают, что
dt=idt£, (13.18)
где tE—«евклидово время» (см. рис. 19). Для правомерности такого поворота
необходимо, чтобы на пути смещения контура не было особых точек. Обычно
полагают, что это условие выполнено. Тогда
+ 00
кг- Г dP* 1 (Рк-Щк)2 / т
J 2nh Pi h 2т Е) у 2nhdtE’
— 00
Отсюда видно, что, во-первых, нормировочный фактор действительно не
зависит от параметров траектории и его можно вынести из-под знака кон¬
тинуального интеграла. Во-вторых, корректное определение континуального
предела подразумевает «регуляризацию» этого расходящегося вклада.
Лекция 13 Сдополнительная)
197
Рис. 19. Поворот Вика
13.2. Источник и производящий функционал
Рассмотрим теперь частицу, на которую действует внешняя сила ДО,
зависящая от времени, так что
n=^+V(q)-j(t)q. (13.19)
В этом случае говорят о гамильтониане с источником j. В присутствии источ¬
ника интеграл по траекториям функционально зависит от j
t"
Z(j) =<yrj&q exp ji J dt - V(q(t)) + j(t)q(t)] J, (13.20)
t'
ИЛИ
Z(j) = Jf J ®q exp{£s(t', t", j)}. (13.21)
Функциональная замена переменных
qW^№=qV + 5q(t), Sq(t') = 5q(t") = 0,
представляет собой сдвиг, который не изменяет ни меры интегрирования
Щ = Щ, (13.22)
ни значения функционального интеграла
Z(j) J Щ exp{|s(t', t", j)}. (13.23)
Вычитая из функционала (13.23) самого себя в записи (13.21), находим при
5q(t)-> 0
(13.24)
198
Тема 7. Интеграл по траекториям
Сюда нужно подставить вариацию Эйлера
5S ■ = —mq (t) — V' (q (t)) + j (t),
5q(t)
где V'—производная потенциала по координате, так что
/ Щ {mq(t) -t-y'CqW) -j(t)}e«s(t'’t"J') = 0. (13.25)
Значит, мы установили квантовый аналог уравнения Лагранжа—Эйлера: ура¬
внения движения остаются справедливыми в смысле интеграла по траекто¬
риям.
Наличие источника позволяет преобразовать квантовые уравнения Эйле¬
ра-Лагранжа. Действительно,
= ^ $ ®<J,<Z(t)e»s(t,’t'/,j)) (13.26)
поэтому (13.25) представимо в виде
тё{-ш1м}=-'''(-иш)2о>+^,>2ог аз.27)
Принято делать подстановку
Z(;) = ^Ke»G0), (13.28)
тогда
}=-''|вду(-1(щ)"ВД+т' (1329)
Уравнения в функциональных производных (13.27) и (13.29) суть уравнения
Швингера—Дайсона.
Для иллюстрации приведем пример гармонического осциллятора:
тсо2
V(q) = ~2^Ц2 => V/(q) = mo)2q,
откуда уравнение на G(j) для осциллятора принимает вид
d2 f5GQ'))_ 25gQ) i nooni
dt2l 5jit) )~ 0 5j(t) (13.30)
Это—функциональное уравнение с источником.
Функционал G(j) можно разложить в функциональный ряд
GO) = 0о + J Sa)(t)j(t) dt + i J a(2)(ti, t2)j(ti)j(t2) dtj dt2 + ... (13.31)
Очевидно,
So = ■-ift In
Zo
JT
а основное уравнение (13.30) содержит в себе уравнения на все остальные
функции Gn(t\,..., tn), потому что его можно дифференцировать и полагать
j = 0. Так, при j = 0 в (13.30) находим
d2,7(1)/■*■»_ 2
Лекция 13 Сдополнительная)
199
— уравнение для свободного классического осциллятора. Его решение — это
e^(t) = q0(t)9 т. е. классическая траектория с заданными граничными усло¬
виями. Вариационная производная основного уравнения дает
_d2 Г 62G(j) 1 , _ 2 S2GO)
mdt21{5j(t1)5j(.t2)\ + m<°°5j(t1)5j{t2) 5(tl t2)’
так что, полагая j = 0, находим
тdtf1^(2) ^ + тсоо$(2) t2) = 5(tj -12),
т. е. уравнение для двухточечной функции Грина. Домножая это уравнение
на j(t2) и интегрируя по t2i очевидно, находим уравнение движения для
осциллятора с внешней силой (источником)
m{dtj + а)о} $ dt2=j(ti),
и решение этого уравнения записано в виде вынужденных колебаний
q(j; t)=f g(2)(t, t2)j(t2) d t2,
причем общее решение получается суммированием свободных колебаний
q0(O и вынужденных q(j; t). Поскольку исходное уравнение для двухточеч¬
ной функции содержит оператор, симметричный по аргументам и t2, и за¬
висит от источника с аргументом tx —12, его общее решение можно предста¬
вить в виде
а(2) (h, t2)=а(2) (tx -12)+с • gm (tjgm (t2),
т. e. с точностью до вклада свободной волны с произвольной нормировкой С.
Последний вклад просто дает добавку к траектории
Aq(t) = С • q0(t) J q0(t2); (t2) dt = С • q0(t),
и эта добавка заменяет уже имеющийся вклад q0(t) от с?(1) (t)
qoCO-^qoWd + C),
что несовместимо с заданными граничными условиями, если только С не
равно нулю. Значит, для осциллятора имеем точное равенство
s(24ti,t2)=a(2)(ti-t2). (13.32)
Точно так же при О 3 уравнение Швингера—Дайсона означает, что
т^2^(п)^1> •••> fn) +mct)2a(n)(ti,t„) = 0,
и, следовательно, многоточечные функции Грина для осциллятора удовле¬
творяют свободному уравнению и могут быть построены в виде компози-
ций gm(.tk), что опять приводит к нулевым коэффициентам нормировки
из-за граничных условий (свободное движение уже включено в линейный
вклад £(1)), так что
о, з.
200
Тема 7. Интеграл по траекториям
Для осциллятора
G(j) = <?o + / S(1)(0j(t) dt +J 0C2)(ti-t2)j(ti)j(t2) dtx dt2.
Это есть исключительное свойство гармонического осциллятора—системы,
гамильтониан которой квадратичен как по импульсу, так и по координате.
Подынтегральные выражения принято изображать в виде диаграмм Фей¬
нмана согласно правилам:
1) источнику j(tk) сопоставляется луч, показанный штриховой линией
с началом в точке tk;
2) одноточечной функции Грина 0(1)(**) сопоставляется отрезок, показан¬
ный сплошной линией с началом в точке tk и концом в точке, помеченной
знаком <8>, который обозначает зависимость от граничных условий;
3) многоточечная функция Грина 5(n)(ti,..., tn) изображается отрезками
сплошной линии с началами в точках tl3..., tn и общим концом в точке,
показанной кружком.
Например, в разложении функционала G(j) для свободного осциллятора
есть только два вклада:
Qmj —* <8>;
0*2 _ . + . .
В общем случае G(j) называют производящим функционалом для связных
функций Грина так как по построению в нем не содержатся вклады, ко¬
торые можно представить в виде произведения интегральных множителей,
которым соответствуют диаграммы Фейнмана, не соединенные никакими
линиями. Если же рассмотреть разложение функционала Z(;‘)
Z(j)=X>0-ift I X>(1)(t)j(0 dt+ Цг" J ^(ti’ t2)j(ti)Kt2) dt1dt2 + ..„
то в нем, несомненно, есть факторизуемые вклады, так как Z(j)=exp £ —jp~ ] •
Действительно, для двухточечной функции V имеем
чему соответствует диаграмма
—ift • • 1 -•—® 0—•-—
Очевидно, что вторая диаграмма не является связной (у нее есть разрыв).
Точно так же четырехточечная функция V может быть представлена, в
частности, вкладами произведений £(2)С/(2) с различными комбинациями
аргументов, что дает члены типа
т. е. опять же несвязные диаграммы.
Лекция 13 0дополнительная)
201
Ситуация с разложением производящего функционала и, следовательно,
со множеством допустимых диаграмм существенно изменяется, если ввести
ангармоничность осциллятора. Для определенности, пусть
mcoi 0 Ха
V(q) = ^q2 + ±q4,
где Я —постоянная, задающая степень ангармоничности. Тогда в уравнении
Швингера—Дайсона вклад потенциала задается величиной
=‘»3ИадгМШ-р(!?)>ад}=
.«.3 Я f i 83G 3 5G52G i f 5G\3) _ X Г 5G\3 \.r8G82G \r283G
Ш 3! U 8j3 h2 Sj 5j2 h3 V 5j J J “ 6 U j) 2 Ш 8j 5j2 + 6n 5f '
Отсюда
m/d2 x^2l5G Xf8G\3 X.h5G52G , Afi253G_ . m
id? °J 5j 6 vSjJ ~2 ~8f~8j2 6 ~5p~ (13<33)
В этом случае уже не приходится говорить, что многоточечные функции Гри¬
на равны нулю, так как получающиеся уравнения существенно нелинейны
и содержат вклады, зависящие от источника. Однако по-прежнему можно
утверждать, что многоточечные функции не содержат вкладов, построенных
в виде произведения одноточечных функций.
Вид уравнения Швингера—Дайсона для производящего функционала G(j)
на примере осциллятора показывает, что естественно определить квантовый
аналог классической траектории как
= (13.34)
так что
5GW
= <?о(0,
)- 0
j—0 5j(t)
т. е. без источников в случае осциллятора получаем свободное движение,
как это и должно быть, а при наличии, скажем, ангармоничности из (13.33)
следует, что величина qd(t) удовлетворяет уравнению
m{^ + Wo}qd(t) + -1iftqdCOnfp ■+=j> (13.35)
а значит, в пределе h —* 0 получаем решение классического уравнения для q (t)
при наличии источников. Вклады с Й приводят к квантовым поправкам.
Преобразование Лежандра от j к qci приводит к функционалу
r(qd) = “ J <Zci(Oj СО dt + G(;), (13.36)
202
Тема 7. Интеграл по траекториям
который называют квантовым эффективным действием. Оно раскладывает¬
ся в функциональный ряд по траекториям qd (t)=qd (t) — q0 (t) наподобие ряда
для G(;), причем по построению
В разложении
r(qci) = r(0) + J r(14t)qd(t)dt + ^ J ГС25(tx, t2)qcl(ta) qd(t2) dtxdt2 + ...
коэффициентные функции называются многоточечными вершинами:
г(п) = б^Г
12...п 5qd(t1)5qcl(t2)...5qcl(tn) qa=qo’
где мы ввели сокращенное обозначение для аргументов многоточечных фун¬
кций. Поскольку при j = 0 имеем qd(t) = q0(t) или qd = 0, замечаем, что
разложение функционала Г происходит также при нулевом значении источ¬
ника j. Поэтому
5Г
Г(1) (t) =
1 J 5qcl(t)
= —J (t) lj=o = 0.
j=о
qcl=0
С учетом этих обозначений дифференцирование уравнения (13.35) при
t = по qd(t2) и условие j = 0 дают
т{^2 + шо}^12 + f 9o(fi)5i2 - +
+ f ifiq0(ti" |й^шзгз2 = “1ц, (13-37)
где мы использовали равенство
5 _ 5j3 5 р(2)_5_
5q2 5q2 5j3 32 6j3
и определения функций Грина. При этом, конечно,
512 = 5(fi — t2)> 4oCti) = ^i1^
и мы использовали сокращенное обозначение для «свертки» индекса 3, на¬
пример,
0шгз2 = I е(3) (h, h, t3)r(2) (t3 -12) dt3.
Вариация второго порядка при нулевых источниках, очевидно, связана
с обратной двухточечной функцией Грина:
гса_ 52г gj(ti) _ Гбдdfe)]-1,
12 5qd(t1)5qd(t2) 5qd(t2) L 8j(ti) J
L5j'(ti)5j'(t2)
в смысле интегрального выражения
12 ^23 °13*
Лекция 13 0дополнительная)
203
Уравнение (13.38) справедливо не только при нулевом источнике, так что
дифференцируя
<52Г 52G
5qt5q2 5j25j3 513
еще раз по qd(t5), находим
■р(З) /^(2) р(2) л
1 12'5У2'3 1 12 ^234 45 ""и’
или с учетом обратного двухточечного оператора
г-(З) - _лО) Г(2)г(2)г(2) _г(3) г^(2)1-1гг?(2)-|-1Гг(2)-,-1
1 12'5 “ у2341 12 1 32 45 “ ^234Li/12 J Ly32'J Lb/45 J J
и т. п. Поэтому говорят, что вершинные функции—усеченные функции Гри¬
на, т. е. функции внешние, исходящие из кружка, линии которых отсечены
обратными двухточечными функциями Грина. Действительно, если прене¬
бречь квантовыми поправками (ft —> 0) и взять третью производную уравне¬
ния (13.37) по qcl, то получим вершину четвертой степени в эффективном
действии Г
^1234 ** ^^12 613614,
а соответствующая функция Грина
После этого уравнение для двухточечной вершиной функции (13.37) при¬
нимает вид
+
+ f ihg™g™ [g™]-1 - Wgr1. (и.39)
Это уравнение можно изобразить графически, если условиться обозначать
вершинные функции так же, как и функции Грина, но с перечеркнутыми
линиями. Итак,
где мы ввели обозначение
d2
(“т{^2+й)о}_|+ )512 * * А-О-+-
Этот вклад можно также выразить в виде
■ / » / • =
204
Тема 7. Интеграл по траекториям
Здесь же введена двухточечная вершинная функция для свободного осцилля¬
тора или, как говорят, собственная энергия осциллятора
d2
_m{dt2 + a)o}5i2 —* *—
Напомним, что этот вклад — квадратичный член в квантовом эффективном
действии, т. е. просто
Г(2)
= -f Jdtqd(t){^^ + «gqd(C)} = J d
Подчеркнем, что каждая замкнутая петля приводит к фактору h.
Графическое представление уравнения Швингера—Дайсона (13.39) для
двухточечной вершинной функции становится еще более наглядным, если
использовать тривиальное тождество
У41 -Оц'.
Умножая уравнение на это тождество и интегрируя по t^, видим, что вклад
с дельта-функцией не изменяется, а квантовые поправки теперь можно пред¬
ставить с использованием дополнительной усеченной двухточечной функции
Грина («ампутированная нога»), так что
—• = •—+-0-t—• +
Эта запись «читается» так: двухточечная вершинная функция равна сумме
вкладов собственной энергии с учетом квантовых эффектов самодействия
и квантовых поправок за счет петель, причем однопетлевой вклад опреде¬
ляется трехточечной функцией Грина (кружок с тремя линиями) и «голой
вершиной» д4-взаимодействия Я (точка с четырьмя линиями), а двухпетле¬
вой—«голой» четверной вершиной (точка с 4 линиями) и полной 4-точечной
функцией Грина (кружок с 4 линиями).
Совершенно аналогично собственная энергия с квантовыми поправками
представляется как
Я
= —/ Т /
Значит, наряду с собственной энергией свободного осциллятора есть вклад
от «голой» вершины Я с учетом граничных условий и однопетлевой вклад
(так называемый «головастик»).
Наконец, укажем исходное положение способа построения теории возму¬
щений в терминах континуального интеграла и, следовательно, диаграмм
Лекция 13 (дополнительная)
205
Фейнмана. Пусть гамильтониан представлен в виде
о2 тш2
2т + ~2
где У — малое возмущение. Тогда производящий функционал
t"
Z0‘)=^J 9>q expjl J dt [^^^_^q2(t)_V(q(t))+j-(t)q(t)] J
t7
можно переписать в виде
г
Z0')=^exp[-i | dt v(-Wj^)} x
t'
t"
x J @q exp{^ J dt ~~~Y2q2(0+J,(t)q(t) j,
t7
где мы воспользовались тем, что значение координаты на траектории под
знаком интегрирования получается при вариации континуального интегра¬
ла. Значит, производящий функционал при наличии возмущения выражается
через действие дифференциального оператора на производящий функционал
для свободного осциллятора:
t"
Z(j) = expj-i J dt V}zosc(j), (13.40)
t7
где, как мы выяснили,
^oScO') = e»GU)
И
GO')=G0+Jacl)(t)j(t)dt+^ J aC23(ti-t2)j(ta)j(t2) dtj dt2.
Дальнейшая процедура построения правил Фейнмана для многоточечных
функций Грина задается вариационным дифференцированием в последо¬
вательном порядке малости по возмущению. Мы не будем рассматривать
здесь теорию возмущений в рамках интеграла по траекториям, поскольку это
обычно относят к курсу квантовой теории поля.
Итак, фейнмановский интеграл по траекториям позволяет, во-первых,
эффективно строить теорию возмущений при введении малой добавки к по¬
тенциалу. Во-вторых, по своему определению он дает метод численного ин¬
тегрирования квантовых задач, не поддающихся анализу в рамках теории
возмущений. В-третьих, континуальный интеграл в квантовой теории поля
позволяет наиболее наглядно и просто получать соотношения между функ¬
циями Грина при наличии симметрий исходного классического действия
206
Тема 7. Интеграл по траекториям
и выявлять квантовые аномалии, т. е. случаи принципиально непреодолимо¬
го нарушения симметрии классического действия при квантовании, и т. п.
Лекция 14 (дополнительная)
Хронологическое упорядочение операторов и интеграл по траекториям, го¬
ломорфное представление для интеграла по траекториям, нормальное упо¬
рядочение, асимптотические состояния, стабильность вакуума, 5?-матрица,
переходы вакуум-вакуум при наличии источников, фейнмановские гранич¬
ные условия, причинный пропагатор Фейнмана, физический смысл двухто¬
чечной функции Грина, античастицы как кванты отрицательной энергии,
движущиеся обратно по времени, Sf -матрица как функционал от свободного
классического решения, физический смысл коэффициентных функций, их
связь с многоточечными функциями Грина, графическое представление ре¬
дукционных формул, пример введения взаимодействия осцилляторов.
14.1. Т-ПРОИЗВЕДЕНИЕ
Представление оператора эволюции в виде континуального интеграла
= J dq"\q")(q"\U(t",t')\q')dq' (q'\ =
= J dq" dq' |q//)(q/| / ©q enS(t ,t"\ (13.14)
очевидно, дано в представлении Гейзенберга, т. е., во-первых, в базисе не
зависящих от времени состояний, а во-вторых, в терминах оператора, за¬
висящего от времени. Для оператора эволюции переход к представлению
Гейзенберга
AH = u4t", t')AU(t", t')
дает
0H(t", t') = U4t”, Otfct", to = U(t", о
в силу унитарности оператора эволюции. Значит, оператор эволюции при
смене представления со шрёдингеровского на гейзенберговское остается
прежним.
Рассмотрим связь интеграла по траекториям от физических наблюдаемых
с операторным представлением этих величин. Если задан континуальный
интеграл от двух величин F и G в моменты времени > t2
T-Ffi = f@q@P e»s<-t ,c"->F[q(t1), p(tj), ti]G[q(t2), p(t2), t2], (14.1)
то по построению интеграла по траекториям его можно представить как
1f,g = (q"\W, h)M(ti, t2)Gt)(t2, t')|q'), (14.2)
Лекция 14 Сдополнительная)
207
так как действие операторов на состояния в соответствующие моменты вре¬
мени как раз и дает значения координат и импульсов в эти моменты времени.
В этом выражении порядок операторов строго задан условием t1>t2 \ Введем
6H(.t2) = U4t2,t')GU(t2,t')
и воспользуемся, во-первых, унитарностью оператора эволюции и, во-вто-
рых, его основным свойством сдвига квантового состояния по времени, на¬
пример,
&(t1,t2)&(t2,t') = fr(t1,f').
Тогда
С>(t", tJFUity, t2)GU(t2, = t^FiU^, t2)[/(t2, t')} x
x {U4t2, t')GU(t2, t')} = Uit", tJFUit!, t'-)6H{t2) =
= {U(t", t')}Fjf(ti)Gfj(t2) = U(t", t')FH(tj)Gj-f(t2).
В итоге при tj > t2
J Siq Sip e»s(t/,t/)F[q, p, t]
G[q, p, t]
ti
Если ввести обозначение для начального состояния в момент времени t!
Iq/) = |in/),
а для конечного в момент времени tn
Ю = lout'7),
то обратная эволюция дает
|q/'> = |in,/).
Поэтому получаем матричный элемент операторов в представлении Гейзен¬
берга по базису в начальный момент времени при строгом упорядочении
операторов по времени
' J 9qSpe^sV^F[q,p,f] G[q,p,t] =(m"\FH(t1)GH(t2)\m'). (14.3)
h t2
Как мы уже знаем, такой оператор хронологического упорядочивания обозна¬
чается символом f, так что при произвольных значениях моментов времени
континуальный интеграл XF G равен матричному элементу «Т-произведения»
операторов
1 J I (in ^(^„(t^lin), t2>ti.
Обобщение на случай нескольких операторов очевидно.
208
Тема 7. Интеграл по траекториям
14.2. Граничные условия: осциллятор
В ГОЛОМОРФНОМ ПРЕДСТАВЛЕНИИ
Для построения интеграла по траекториям в голоморфном представле¬
нии, как теперь понятно из проведенного выше общего анализа, необходимо
рассмотреть оператор эволюции на fc-м шаге разбиения интервала времени
от t' до t":
U (tfc + dt, tfc) = J |afc+1) d<X|l2^a|c+1 (ak+i \U(.tk + dt,tk-)\ak) d(X2n“k (afcl-
Матричный элемент гамильтониана сводится к функции
(ak+1\H(a\ a, tfc)|afc) =П(ак+ъ ак, tk)(ak+1\ak), (14.5)
если гамильтониан, как говорят, нормально упорядочен: все операторы рож¬
дения стоят слева от операторов уничтожения. В этом случае действие
операторов уничтожения на кет-вектор когерентного состояния дает соб¬
ственные значения
а\ак) = ак\ак),
и аналогично для бра-векторов
(afc+i |6f = («fc+i I «it+i •
Например, для свободного осциллятора
Йо = Ла)од?й + 1н<0о,
и
(ак+1\Н0\ак) = \ha>0ak+1ak + \ha>0} {ак+1\ак).
Матричный элемент {ак+1\ак) был определен при построении когерентных
состояний осциллятора (см. (6.42)):
(«fc+il«fc) =ехр{--~— - + ак+1ак},
который можно представить в виде
<«fc+il«fc> = exp{|(afc+1 - ак)ак - \ак+1(ак+1 - afc)}.
Поскольку множества точек {ак, ак} по построению соответствуют траекто¬
риям {a(t), a(t)}, естественно ввести скорости изменения параметров траек¬
торий
(afc+i - afc) = a(tk) dt, (ak+1 - ak) = a(tk) dt.
Значит,
(“fc+il«fc) = exp{||a(tfc)a(tfc) -a(tfc)a(tfc)] dt}. (14.6)
Лекция 14 (дополнительная)
209
Таким образом, бесконечно малый шаг эволюции представим в виде
fr(tfc + dt,tfc) = J \ак+1)Щ^Щ^{ак\х
х expj^ dt [-y[d(tfc)a(tfc) -a(tfc)a(tfc)]-H(.a(tk), a(tk), tfc)] j, (14.7)
а на конечном интервале времени
N—1
j f n
J J fc=2
2Tii
fc=2
x expji J dt [-§ [S(t)a(t) - a(t)act)] -W(a(t), a(t), t)] J, (14.8)
t'
где, как нетрудно показать, интегрирование по времени дает действие на
траектории в классической механике. В самом деле, вклад
/ p(t)q(t) dt
можно после интегрирования по частям представить как
\ /[pCOq(t) — q(t)p(t)] dt.
Тогда стандартная замена переменных
q(t) = + «СО], Р(0 = \/Нтсо0-±= [a(t) - a(t)]
после приведения подобных членов дает
\ J[p(t)q(t) — q(t)p(t)] dt = - J dtf [a(t)a(t) -a(t)d(t)]. (14.9)
В пределе получаем интеграл по траекториям в представлении когерентных
состояний
U(t",t') = f / 9а Si а -е^'Л
где действие на траектории
t"
S(.t", t')= J dt [-§ [fi(t)a(t) - a(t)a(t)] -H№), a(t), t)]. (14.10)
t'
Так же, как в координатно-импульсном представлении континуального ин¬
теграла интегрирование в фазовом пространстве по траектории импульса
было независимым от интегрирования по траектории координаты (импульс
не определяется скоростью!), в голоморфном представлении траектории a(t)
210
Тема 7. Интеграл по траекториям
и а([) не связаны комплексным сопряжением, а являются независимыми
однопараметрическими кривыми в двух комплексных плоскостях: z для а и w
для а.
Ядро оператора. Для определения голоморфного представления запишем
для оператора А:
A = j |ctout)^^2B(aoutlA|ain)^^(ain|, (14.11)
причем матричный элемент можно определить с помощью полного набора
собственных состояний энергии для осциллятора
(a0Ut|A|ain) =2KutW(n|A|m)(m|ain) =
п,т
п,т
где мы стандартно ввели матричные элементы оператора Апт = (п\А\т) и
воспользовались голоморфным представлением для волновых функций соб¬
ственных состояний энергии осциллятора. Поэтому голоморфное ядро опе¬
ратора определяют в полной аналогии с волновыми функциями
(«out. «in) = <«outlA|ain) • = 2 ^j=Anm (14.13)
n.m
и оно действительно, как мы только что показали, является функцией только
от aout и ain и не зависит от переменных, комплексно сопряженных к ним!
В частности, голоморфное ядро оператора эволюции имеет вид
°U(aout, ain) = J 9а 9а- eis(t" ° (1414)
где граничные условия задаются равенствами
«out = «(£")> «ш = «(0- (14.15)
Для рассмотрения граничных условий при наличии источников мы бу¬
дем полагать, что t' —*• —оо и t" —> +оо, а сами источники отличны от нуля
только при конечных временах (или достаточно быстро стремятся к нулю
на временной бесконечности). Тогда состояния осциллятора в бесконечном
прошлом и бесконечном будущем представимы в базисе собственных век¬
торов энергии свободного осциллятора, т. е. в базисе с заданным числом
квантов в начальном и конечном состоянии эволюции. Этот базис опре¬
деляет асимптотическое пространство состояний, а матричные элементы
оператора эволюции
ynm = (n\U(.t",t')\m)
, t'—»—00, t"—»+00, (14.16)
j=0
Лекция 14 0дополнительная)
211
называют элементами «У-матрицы»1. У-матрица не является уже, вооб¬
ще говоря, диагональной, так как при наличии взаимодействия количество
квантов разного сорта (если осцилляторов несколько) может изменяться
(поглощаться и излучаться). Особый случай—вакуум. Мы будем считать, что
вакуум стабилен. Это означает, что в ходе эволюции вакуум переходит в себя
с вероятностью, равной единице, а значит, модуль амплитуды перехода равен
единице:
Другими словами, эволюция вакуума сводится к введению фазового множи¬
теля, который вообще зависит от источников как функционал, и этот фактор
обычно полагают равным единице в отсутствие источников2. Поэтому для
вакуума
т. е. состояния «in» и «out» совпадают с точностью до фазы—производящего
функционала связных функций Грина. Значит,
Поэтому Т-произведения операторов, которые выражаются через интеграл
по траекториям, при > t2
Элементы У -матрицы можно выразить через производные голоморфного
ядра оператора эволюции при нулевых источниках, поскольку
1Гипотеза существования асимптотических состояний является ключевой при формулиров¬
ке квантовой теории взаимодействующих полей, и фактически она может быть обоснована
только после нахождения точного решения динамических уравнений теории, что на практике
редко представляется возможным для реальных физических ситуаций, предоставленных нам
природой [имеются искусственные примеры точных решений, например, электродинамика
частицы с половинным спином в одном пространственном измерении (модель Швингера)].
Математически строго этот вопрос рассматривается в рамках аксиоматического подхода (см.,
например, Боголюбов Н. Н., Логунов А. А., Оксак А. И., Тодоров И. Т. Общие
принципы квантовой теории поля. М.: Наука, 1987). ^
2Это означает, что мы производим сдвиг энергии вакуума: Е0 = -h<o0 ->Еуас = 0> — так что
она принимается равной нулю.
I (о\йь", to к» |=i, е - оо, t" -+оо.
(14.17)
|out) = t/|in) = enGCj-* |in), |in) = |0),
(out\UFH(t1)GH(t2')\^) = (ш|#н(^)^н(е2)|т).
(14.18)
(14.19)
так что
i an+m
rz737 Япп n
Vn\m\ 3“Cuta!n
“^(«out, «in)
aOut=ain=0
'out in
1
. (14.20)
</Шт! дапоша™
“out=“in=0
212
Тема 7. Интеграл по траекториям
При расчете переходов из вакуума в вакуум дополнительные множители
исчезают, a ain, aout—>0:
<0|£|0) = ^(0,0), (14.21)
и при наличии источников так же.
Поскольку в голоморфном представлении состояния с заданным числом
квантов являются собственными векторами оператора рождения с собствен¬
ными значениями а:
&-фп(а) = спрп(с0,
зависимость от времени параметров а повторяет зависимость от времени
оператора рождения
af(t) = е1С°0^ => a(t) = elc0ota, a(t) = e“lc0ota,
так что с учетом граничных условий находим
— при t —> t", т. е. в асимптотическом будущем1,
q(0 =х0№) + a(t)] ^*0[е~^а (14.22)
с зачетом aout —»0 означает, что
д(0^х0е-^о^, (14.23)
т. е. в асимптотическом будущем распространяются только положительно
частотные моды;
— при t —»tт. е. в асимптотическом прошлом,
q(t) =x0[a(t) + a(t)] ^ХоСе^^^а^ + е^а] (14.24)
с учетом ain —► 0 означает, что
д(0^*0е^а, (14.25)
т. е. в асимптотическом прошлом распространяются только отрицательно
частотные моды.
Эти граничные условия позволяют однозначно определить двухточечную
функцию Грина для осциллятора.
Вынужденные колебания задаются сверткой двухточечной функции Гри¬
на с источником
q(t) = J S(2)(t-ti)j(ti) dtx,
причем обратная к ней вершинная функция
r(2)(ti -12) = + со2} 5(tx -t2)
в импульсном представлении имеет вид
Г^(со) = / r(2)(0eia,tdt=m(a>2-a>2). (14.26)
1Для краткости обозначим х0 = у/h/(2moj0).
Лекция 14 Сдополнительная)
213
Поэтому запишем вынужденные колебания в импульсном представлении
9(0 = | Ш dtj J = J j(
Здесь
0®(й>) = -
т(а>2-со%)
(14.27)
имеет полюса при со = ±о>0, обход которых должен быть согласован с гранич¬
ными условиями в асимптотическом прошлом и будущем. Решение в виде
контура интегрирования в плоскости комплексной со показано на рис. 20.
Рис. 20. Контуры интегрирования в плоскости комплексной переменной со
при t—►+ оо (слева) и t—»—оо (справа)
В самом деле, при £—>+оо контур можно замкнуть в нижней полуплоско¬
сти, так как отрицательная мнимая добавка к частоте в экспоненте приводит
к нулевому вкладу по полуокружности, и полюс при со = со0 - iO в экспонен¬
те дает положительно частотную моду. Аналогично, при t —> —оо вклад по
полуокружности в верхней полуплоскости обращается в нуль, и полюс при
со = —coq + iO дает отрицательно частотную моду.
В итоге получаем так называемую причинную двухточечную фейнманов-
скую функцию Грина, которую также называют пропагатором:
е(2)(о>)=-
т со2 — col + iO'
(14.28)
Описанные граничные условия, очевидно, можно получить, заметив, что
они выводятся посредством замены со0 —> а>0(1 — ie), где е —> +0, т. е. добавкой
бесконечно малого затухания. Мы видели, что это затухание связано с ши¬
риной резонанса. Поэтому ясно, что физически малое значение е приводит
к вымиранию возбуждений вакуума, т. е. следует из условия стабильности
вакуума. Этот же аргумент приводит к математическому обоснованию по¬
ворота Вика в плоскости частот (соответствующие интегралы по контуру
214
Тема 7. Интеграл по траекториям
при вращении от вещественной оси к мнимой на угол, п/2 не встречают
полюсов).
После преобразования Фурье
+ 00
g®(t) = J" j£.e-ia*g™(£0),
которое можно найти, взяв при t > 0 интеграл Коши по контуру, изображен¬
ному слева на рис. 20,
= e-W t>0j
2со0т ’ 5
и при t < 0 по контуру справа на рис. 20,
получаем
а(2) (О = 2^e_i"olt|- (14.29)
Подчеркнем, что эти выражения получены в пределе бесконечно удален¬
ных прошлого и будущего. Если интервал эволюции конечен, соответствую¬
щие формулы можно найти, например, в курсе квантовой электродинамики
С. Н.Вергелеса [22].
Итак, общее выражение для производящего функционала связных функ¬
ций Грина при наложении причинных фейнмановских граничных условий
приобретает вид
go*)=J g(1Kt)j(t) dt+± f gwcb-byctjjctj dt, dt2,
где мы положили б0 = 0, а £(2) (tx -12) задается формулой (14.29). Единствен¬
ный оставшийся вопрос — решение свободного уравнения £(1)(0- В случае
перехода вакуум вакуум, который является основным состоянием для ос-
циллятора, очевидно, средние значения координаты и импульса тождествен¬
но зануляются, так что
(Ч) = (Р)=0 => a(t)=0, q0CO=S(1)(O=0
и
GO) = / aC2)(t! - dt! dt2, (14.30)
откуда функционал
zosc0) = exp{^G(j)} = exp{^y / £(2)(ti - t2)j(ta)j(t2) dtj dt2|, (14.31)
и именно по этому функционалу строится теория возмущений для осцилля¬
тора.
Лекция 14 (дополнительная)
215
Согласно связи континуального интеграла с Т-произведением операто¬
ров,
(in|f{4(t1)4(t2)}|in)=-ft2 52z(j)
Поскольку
= -ma(2)(t i-t2). (14.32)
j=0
(in|T{q (t1)qCt2)}-|in) = (in|f {(ar (ti) + a (tx)) (a+ (t2) + a (t2))} |in)
и вакуум переходит в вакуум, в этом Т-произведении члены, квадратичные
по at и а, дают нулевой вклад, и, следовательно,
(in|f{at(t1)a(t2) +a(t1)at(t2)}|in) = -2im<o05(2)(ti -12) =e"ic°o|tl“t21. (14.33)
Эта формула показывает физический смысл двухточечной функции Грина
в квантовой механике: двухточечная функция Грина —12) (с точно¬
стью до фактора —2imco0) задает амплитуду вероятности последователь¬
ного рождения кванта с энергией hco0 в момент времени t2 и его поглощения
в момент времени tx > t2 (второе слагаемое), и аналогично при < t2 (первое
слагаемое). Именно поэтому двухточечную функцию называют пропагато-
ром, т. е. функцией распространения квантов. Этим обосновывается также
графическое изображение пропагатора как линии из точки t2 в точку t1}
которая тем самым дает «линию жизни» кванта.
Наличие двух слагаемых в формуле (14.33) обусловлено вещественностью
волновой функции одномерного осциллятора, т. е. неразличимостью яp(q)
и гp*(q). Как мы знаем, комплексное сопряжение связано с операцией об¬
ращения времени. При обращении времени движение осциллятора остается
инвариантным, т. е. полученная формула связи Т-произведения с пропагато-
ром не изменяется. Однако при этом
a(t)-^af(-t),
Поэтому можно также сказать, что формула (14.33), а именно первое слага¬
емое в ней, задает и амплитуду вероятности последовательного рождения
кванта с отрицательной энергией —hco0 в момент времени t' = —t2 (опера¬
тор а уменьшает энергию) и его поглощения в момент времени t[ = —t1 < t2 =
=>—t2 (оператор a1*). Такие кванты с отрицательной энергией, движущиеся
обратно по времени, Фейнман предложил считать античастицами. Для
вещественной волновой функции кванты частиц и античастиц неразличимы.
Поэтому они на равных правах входят в выражение для пропагатора (как
это имеет место, например, для фотона, волновая функция которого веще¬
ственна). Если кванты частиц и античастиц различимы, как, например, при
наличии ненулевого заряда, то обобщенные координаты таких квантов, т. е.
динамические переменные, не могут быть просто вещественными числами.
Динамические переменные заряженных частиц — классические поля — ком¬
плексные или многокомпонентные. Вопрос квантования классических полей
(вторичное квантование) относится к курсу квантовой теории поля.
216
Тема 7. Интеграл по траекториям
Фейнмановская трактовка квантов отрицательной энергии в качестве
античастиц, конечно, тесно связана с введенными граничными условиями:
положительно частотные решения (частицы) распространяются вперед по
времени, отрицательно частотные — назад по времени. Другими словами,
источники излучают частицы в будущее или поглощают античастицы из
прошлого.
14.3. Функционал ^-матрицы
Для граничных условий в голоморфном представлении введем решение
классического уравнения движения для свободного осциллятора
q0(t) = *o(aine-io>ot + “oute‘“ot)> *о = {1Л.2Л)
и рассмотрим голоморфное ядро Sf -матрицы как функционал от этого реше¬
ния, т. е. запишем его в виде
г
•5"(aout. ain) = ^[q0(t)] = expj-£ J dt jzosc(j)
(14.35)
j=о
где
2OSC0')=exp{ J emW№ dt+hJ gi2)(t' - dt! dt2} (14.36)
И
a(1)(t)=q0(t).
Разложение этого функционала в ряд
00 # п
=2 О П 9o(tfc) dtfc (14.37)
П=1 * fc=l
имеет наглядный физический смысл: коэффициентные функции 5*(л) задают
амплитуды перехода одного асимптотического состояния в другое с общей
суммой квантов в исходном и конечном состояниях, равной п. В самом деле,
дифференцирование по параметру начального состояния ain и конечного aout
можно представить как вариационную производную
да™дап
-г
n=“om=0 J
5т+пУ[д0]
“in=“om=0 J ^3o(^l)-"^4o(^m+n) lq0=0
dqofo) j* ft ^qp(ti)
out
<**>
fc=l 111 1=1
Лекция 14 (дополнительная)
217
так что в правой части (14.38) стоит фурье-образ коэффициентной функции
..., tm+n) fl dtk f] e1^ dt, =
fc=i (=i
= 5?(m+n)(a>0,..., oj0, -co0,..., -co0).
I
m n
С левой же стороны (14.38) согласно (14.20) стоит производная от голоморф¬
ного ядра оператора эволюции при нулевых источниках, т. е.
dm+n5?[q0]
да™дап .
rn out
= Vn\m\ynm.
ain“«out—0
При этом матричный элемент
ynm = (n\U(t",t')\TTl), t"->+oo, t'-+-оо,
и есть амплитуда перехода в ходе эволюции из начального состояния с m
квантами в конечное состояние с п квантами1.
Редукционные формулы. Найдем теперь связь между амплитудами перехо¬
дов и функциями Грина Для этого заметим, что
J ea)(t)j(t)dt+i J aC2)(ta -t2)j(t1)j(t2) dta dt2=
= j (ti - t2)/(t1)/(t2) dtx dt2, (14.40)
где
J(t)=j(t) + J[^(t-t)]"^00© dt, (14.41)
причем возникающий дополнительно вклад
J ta^a-t)]-1 aa)(t)ea)(t) dtdt=o,
так как (t) =q0(t) —решение уравнения свободного движения осциллято¬
ра2.
Поэтому вариация функционала ^-матрицы согласно (14.35) сводится
к вариации производящего функционала функций Грина Z(j)
Sq0(t)
Но так как
5j(t)
~«Г
j=o J
5Z(j) 5j(t) d-
5j(t) 5q0(t)
;=o
(14.42)
5q0(t)
интегрирование «снимается», и
= [a(2)(t -1)]"1 = rn{ ^ + co2}s(t -t),
Sy[q0]
5q0(t)
= m{
j=о I
d2 , *1 52(J)
dP+""JsJW
3
j=0
(14.43)
1B действительности многие подобные амплитуды могут оказаться равными нулю в силу
законов сохранения энергии и т. п.
2В других вкладах необходимо аккуратно обращаться с произведением двухточечной функ¬
ции Грина на обратную к ней.
218
Тема 7. Интеграл по траекториям
а значит,
tn) = (П т{^ + ^о})^(п)(^ - О- (14.44)
Это и есть редукционные формулы: матричные элементы У -матрицы полу¬
чаются из функций Грина для производящего функционала оператора эволю¬
ции V усечением каждой линии фактором обратной связной двухточечной
функции Грина для свободного осциллятора Если графически представить
функции V аналогично функциям Грина G, заменив кружок на квадрат, на¬
пример, для двухточечной функции
р(2)= Щ
а усечение внешних линий свободным пропагатором осциллятора двойным
перечеркиванием, то, к примеру,
.
При этом, конечно, нужно помнить о том, что многоточечные функции V
построены из связных функций Q и поэтому включают в себя несвязные
диаграммы.
Нормальный символ. Наряду с голоморфным ядром оператора А часто рас¬
сматривают и его нормальный символ, определенный разложением операто¬
ра в ряд по нормально упорядоченным произведениям операторов рождения
и уничтожения:
лы (^)п ат
п,т
где коэффициенты разложения А„т, конечно, не совпадают с матричными
элементами оператора. Матричный элемент по когерентным состояниям—
п,т
Величину
(«out. “in) 2 ^пт Ут! (14.47)
П,ТТ1
называют голоморфным ядром нормального символа оператора1. Тогда из
(«ошЮ = exp{-a°u^a°ul - + aout«m}
и определения ядра оператора следует связь
d(“out. «in) = ea°AAN(aout, ain), (14.48)
1Голоморфность является явной по построению.
Лекция 14 Сдополнительная)
219
которая устанавливает соотношение между голоморфным ядром оператора
и ядром его нормального символа. В литературе, использующей голоморф¬
ные представления, часто цитируется эта формула (развитие формализма
континуального интеграла в квантовой механике и теории поля см. в учеб¬
ном пособии [19]).
Фермионный осциллятор. Построенное нами ранее голоморфное пред¬
ставление для фермионного осциллятора позволяет повторить для него про¬
цедуру введения интеграла по траекториям с той лишь разницей, что инте¬
грирование ведется по грассмановым переменным.
Взаимодействие осцилляторов. Рассмотрим пример. Допустим, что физи¬
ческая система включает в себя два различных осциллятора: обобщенные
координаты — q1 и q2) частоты свободных колебаний — сог и со2• Если мы
знаем, что сог = 2со2 и при этом условии квант первого осциллятора мо¬
жет переходить в пару квантов второго осциллятора (сохранение энергии)
с амплитудой Я, то как выглядит потенциал взаимодействия этих осциллято¬
ров? Очевидно, что описанный процесс распада кванта первого осциллятора
(штрихпунктирная линия) на пару квантов второго (сплошные линии) соот¬
ветствует диаграмме
которая показывает уничтожение кванта типа 1 и рождение двух квантов
типа 2. Эту амплитуду можно записать как
Но это есть не что иное, как амплитуда перехода, которая возникает при
введении взаимодействия
где мы добавили эрмитово сопряженный вклад для вещественности потен¬
циала и не приводим зависимость операторов от времени. Постоянная взаи¬
модействия Я, очевидно, должна иметь размерность частоты. Значит,
{2"\й\1') = а,
или в рамках теории возмущений
= (0|a2(t")a2(t")e-s f dtJ^(t')|0) м
t"
«<0|a2(t")d2(t"){l-£ JT dt (-DSAa^O^WaiWja^tOlO).
V = +h.c.,
220
Тема 7. Интеграл по траекториям
где мы учли связь операторов рождения и уничтожения с динамиче¬
ской переменной, а также ввели параметр энергии V0 = —ЯЙ и длину i =
= (h3/8m1mlco1o)l')1/6t
Таким образом, эмпирические наблюдения, т. е. измерения эффективного
квантового действия, позволяют в рамках теории возмущений вводить члены
с взаимодействием квантовых систем.
Часть II
Кто хочет знания, пусть ищет его там, где
оно находится...
Мишель де Монтенъ
Тема Теория возмущений
8
Лекция 15
Стационарная задача и разложение по базису стационарных состояний исход¬
ного гамильтониана, ряд по малой константе связи возмущения, рекуррент¬
ные формулы для поправок к энергии и к состояниям, критерий применимо¬
сти теории возмущений, вырожденный случай и правильные волновые функ¬
ции ведущего приближения, секулярное уравнение, точное решение задачи
с двумя уровнями: отсутствие перекрытия уровней, задача теории возмуще¬
ний в нестационарном случае, представление взаимодействия, ведущее при¬
ближение, постоянное возмущение и соотношение неопределенностей вре¬
мя-энергия, периодическое возмущение, резонансный вклад при бесконечно
длительном воздействии возмущения, сохранение энергии, индуцированное
излучение и поглощение, «золотое правило Ферми» для плотности вероят¬
ности перехода в непрерывный спектр, мгновенное включение возмущения
и «замороженное состояние», критерий мгновенности, адиабатическое изме¬
нение со временем параметров гамильтониана, адиабатическое приближение
для исходного состояния, критерий адиабатичности, фаза Берри для цикличе¬
ского изменения параметров гамильтониана, ковариантная производная как
генератор трансляций правильного адиабатического состояния, калибровоч¬
ная инвариантность в пространстве параметров, теорема о телесном угле,
задача о спине во вращающемся магнитном поле.
Точно решаемые квантовомеханические задачи скорее исключение, чем
правило. Поэтому на практике часто приходится использовать приближен¬
ные методы нахождения состояний и их квантовых чисел. Стандартный под¬
ход в этом смысле —теория возмущений для стационарного и нестационар¬
ного уравнений Шрёдингера.
15.1. Стационарная теория
4
15.1.1. Невырожденный случай. Пусть известны точные решения ста¬
ционарного уравнения с гамильтонианом Я0:
Н0\пт)=Е™\пт), (15.1)
где |п®) —невырожденные состояния дискретного спектра с энергией
Рассмотрим спектральную задачу с гамильтонианом
H=H0 + AV, А->0, (15.2)
где возмущение V не зависит от времени, так же как и исходный гамиль¬
тониан Н0. В силу предельного перехода Я—»0 будем полагать, что базис
224
Тема 8. Теория возмущений
гильбертова пространства |п(0)) полон и в гильбертовом пространстве в за¬
даче с возмущением. Это предположение является центральным в теории
возмущений! Если оно a posteriori оказывается неверным, то теория возму¬
щений теряет всякий смысл.
Далее нас будет интересовать только дискретный спектр в задаче с возму¬
щением, так как в силу центрального предположения метода области непре¬
рывного спектра в задаче с возмущением и без него совпадают, в то время
как дискретные уровни энергии могут смещаться при введении возмущения.
Будем искать собственные значения
Н\п)=Еп\п) (15.3)
в виде ряда по Я —»0:
00
Ял=£п0)+ЕЯРеР> (15-4)
Р = 1
где ер — поправка p-то порядка. Собственные векторы состояний также мож¬
но записать в виде ряда
00
H = |n(0)>+][V|n(p)>. (15.5)
р=1
Однако собственные состояния гамильтониана допускают несингулярное
преобразование
\п) -> /(Я)|п).
Поэтому для того, чтобы разложение состояния в ряд по Я было однознач¬
ным, необходимо зафиксировать амплитуду вероятности одного из базисных
векторов исходного гильбертова пространства, например, |п(0)), что пред¬
ставляется вполне естественным. Пусть
(п(0)|п> = 1. (15.6)
Подставляя сюда разложение состояния |п) в виде ряда по степеням Я и рас¬
сматривая его последовательно в каждом порядке, находим, что
(п(0)|п(р)> =0, (15.7)
т. е. каждая поправка к состоянию не содержит вклада |п(0)) и, следователь¬
но, ортогональна исходному невозмущенному состоянию. Конечно, выбор
условия однозначности в форме (15.6) приводит к собственному вектору,
норма которого, вообще говоря, отлична от единицы, но эта проблема легко
решается последовательно в любом заданном наперед порядке по Я.
Подставляя представление состояний и энергии в виде рядов, находим
(Н0 + AV){|n«»> +2 Ар|п(р))|= (е«> +2 А%) {|п<Ю> +£ Ар| п
1 р=1 } V Р=1 J К р=1
так что последовательно в каждом порядке по Я получаем рекуррентную
Лекция 15
225
систему уравнений:
Я°: H0|n(0))=£f |п(0)),
Я1: H0|n(1))+y|n(0))=£f |п(1))+гг|п(0)>, (15g)
Яр: Н0|п(р)> +V\n(p-») =£®)|п(р)) + ... + ер|п(0)).
Пользуясь ортогональностью поправок и состояния |п(0)) и исходным уравне¬
нием (n(0') |Н0 = (nt0) IE®-1, возьмем проекцию уравнений (15.8) на это состоя¬
ние: (п(0)|-), так что
ei = (n(0№0)> = Vnn,
,2 = (n<»|V|„n>),
£p = (n<0>|V|H»-1>),
т. е. опять-таки рекуррентную схему вычисления поправок к энергии, если
известны поправки к состоянию.
Поправки к состоянию в силу их ортогональности к уровню в базисе
исходной задачи раскладываются в виде
I„(Р)) = £ IfcW)) (fcCW |nw), (15.10)
кфп
где амплитуды разложения легко найти, проецируя уравнения (15.8) на со¬
стояния базиса (fc(0)|-):
(fc(0)|V|n(0)) = (Е®-е£0))(/с(0)|п(1)),
(fc(0)|V|nCp)) = СЕ®» -Ej™)<fc(0)|n(p)> + e1(fcC0)|n(P-1)> + ... + £p_1(fc(0)|n(1)),
или с учетом e0 = 0
<fc(0)|n(p)) = I m{Vkn - ei(fc(0)|n(p_1)) -... - ep-:L<fc(0)|na)»5 (15.11)
п к
гдер^1, кфп.
Для примера,
(1512)
кфп Ч
откуда
, V У«Мп
Z-JL Е(0)_ЕС0)’
fc#n п *
и в силу ynfc = (7i(0)|y|fc(0)) = (fc(0)|v|n(0))* = yfc*n,
^ IVJ2
226
Тема 8. Теория возмущений
Отсюда, в частности, следует, что для основного состояния с наименьшей
энергией Е£0) - Е£0) < 0 поправка второго порядка всегда отрицательна, если
не равна нулю.
Подчеркнем, что ведущая поправка к энергии уровня задается средним
значением возмущения. По смыслу теории возмущений поправки высших
порядков становятся существенны, если поправки низшего порядка обраща¬
ются в нуль или необходимо получить значение с высокой точностью.
15.1.2. Условия применимости. Необходимым условием применимости
теории возмущений является сходимость рядов для энергий и собственных
состояний системы с Я = Н0 + ЯУ. Мы установили, что поправки к состояни¬
ям строятся по степеням малого отношения матричного элемента возмуще¬
ния к инкременту уровней в исходной системе
Wkn\
<1.
Значит, возмущение можно считать малым, если его характерная величина,
т. е. модуль его матричных элементов между векторами стационарных со¬
стояний невозмущенной задачи, отвечающими различным уровням энергии,
существенно меньше типичного расстояния между этими уровнями. С фи¬
зической точки зрения это означает, что возмущение не приводит к «пере¬
крытию уровней» исходной системы. В этом случае вклад высших поправок
к состояниям подавлен степенями этого малого параметра, так что из вы¬
ражения для поправок к энергии (15.9) следует, что и они также подавлены
в зависимости от порядка р теории возмущений.
15.1.3. Вырожденный случай. Если уровень исходной системы Е£0) яв¬
ляется вырожденным и кратность его вырождения равна fc, то предел Я —> О
в системе с возмущением также можно определить однозначно, фиксировав
вклад базисных собственных векторов в fc-мерном подпространстве с энер¬
гией Е£0)
Н0|п(0), а) =Е(0)|п(0)> а), ае{ 1, fc}, (15.14)
в состояние
|п) =2 Са|п«» а) + 2 AVP)>, (15.15)
а=1 р=1
т. е. задав «вектор»
Са = {п(-°\ а\п). (15.16)
Отсюда опять следует, что поправки по построению ортогональны подпро¬
странству состояний с энергией Е®\
Используя разложение в ряд энергии и состояния, в полной аналогии
с невырожденным случаем в первом порядке по Я находим
к к
Н0|л(1)> + V 2 са|п(0), а) =Е®> |пш) + в1 2 Са|п(0), а). (15.17)
а=1 а=1
Лекция 15
227
Проецируя это уравнение на (п(0), Ь|«) с учетом уравнения на собственные
значения гамильтониана Н0 и ортогональности поправок ведущему вкладу
за счет |п(0), Ь), получаем уравнение
к
YSvba - е15ъа}Са = 0, vba = b|V|n(0> а), (15.18)
а=1
которое говорит о том, что вектор Са является собственным для эрмитовой
матрицы Vab, и его собственное значение ег дает величину ведущей поправки
к энергии этого состояния. Секулярное уравнение для матрицы ||У||ьа = Vba
в подпространстве собственных состояний энергии Е
det(V-e) = 0 (15.19)
имеет к собственных значений, которые, вообще говоря, тоже могут быть
вырождены. Выбирая значения Са в виде собственных векторов матрицы У,
находим «правильные» функции ведущего приближения
Ift®, g), V|n(0), g) = в® |Ц0» g), (15.20)
где g нумерует собственные значения матрицы У. Поскольку правильные
функции составляют ортогональный базис, задача нахождения высших по¬
правок теперь сводится к решению тех же рекуррентных соотношений, что
и в невырожденном случае, для каждого из собственных векторов матри¬
цы У:
Й0\п^) +У|п(р-1)> =£<0)|пСр)> + е1(гУР-1)> + ... + ejfV0), gb (15.21)
Дальнейшее построение повторяет рассмотрение невырожденного случая.
При этом поправки к состояниям могут включать в себя и вырожденные
состояния уровней энергии исходного гамильтониана, отличных от рассмат¬
риваемого уровня е£0).
15.1.4. Задача с двумя уровнями. Если спектр квантовой системы за¬
ведомо включает в себя только два уровня, то задачу для гамильтониана
Я0 + ЯУ можно решить точно. В самом деле, в этом случае решение представ¬
ляется в виде разложения
IV>)=c1|l)+c2|2)
по базисным состояниям исходной системы
А0\1)=Б™\1), H0|2)=Ef|2>.
Тогда проекция стационарного уравнения
#|т/>) =Е|я/>)
на базисные векторы дает
НцС 1 + AVi2c2=Ес1г
Н22с2 "I" ^21с1 = Ес2,
(15.22)
(15.23)
(15.24)
(15.25)
228
Тема 8. Теория возмущений
или в матричном виде
т. е. уравнение на собственные значения матрицы 2 х 2. В стандартной про¬
цедуре
det{H — Е} = [±(ЯП +Н22)-Е] 2 -\(Ни-Н22)2 - Я2|У12|2 = 0.
Решения этого уравнения
Е± = \Шп + Н22) ± \/\Wn-H22)2 + X2\V12\2 (15.27)
суть искомые значения энергии стационарных состояний, а соответствую¬
щие состояния в исходном базисе удобно выразить в виде унитарного пово¬
рота
№+> =elv/2 sin ||1> +е-^2 cos §|2),
|гр_)=е1*12 cos f |1> -е"^/2 sin ||2),
(15.28)
где мы ввели фазу матричного элемента V12 = |Vi2|elv>, и
toa = Ajvy
2 i(Hn-Я22)- +
откуда
tga = -^. 05.29)
■“11 — rt22
Здесь, конечно, равны значения энергии уровней с учетом поправки ве¬
дущего приближения
Ни = Ej0) + ЯУи, Н22=Е™ + ЯУ22
(при Е® т^Е®). При достаточно большой константе связи возмущения Я
поведение, описываемое (15.27), будет качественно отличаться от этих зна¬
чений. Например, при некоторых фиксированных Е£0) фЕ®\ Vn > ^22 < О
и V12 Ф 0 зависимость от Я для диагональных элементов гамильтониана и его
собственных значений проиллюстрирована на рис. 21.
Как видим, возмущение может быть настолько сильным, что в ведущем
приближении диагональные матричные элементы имеют точку пересечения.
Однако точное решение показывает, что истинные значения собственных
значений гамильтониана не пересекаются. Поскольку допустимая область
изменения угла ае [0, тс], собственные состояния гамильтониана являются
смешанными за исключением исходной задачи с Я = 0 и при а —► тг, если
\v12\<\vn — V22\ и Я—>00, когда состояния |1) и |2) меняются местами: первое
имеет большую энергию, чем второе.
Задача с двумя уровнями находит применение не только в случае, напри¬
мер, двух спиновых состояний для частицы со спином 1 /2, но и в таких ситуа¬
циях, когда энергетическая щель между парой низших уровней энергии и их
Лекция 15
229
Е±> Яц, Н22
£1(0)
Я
Рис. 21. Зависимость собственных значений гамильтониана Е± (жирные ли¬
нии) и диагональных элементов Яи, Я22 (тонкие линии) от константы связи
возмущения Я
возбуждениями достаточно велика, чтобы можно было пренебречь вкладами
от высших поправок от возбужденных состояний, в то время как эффекты
смешивания за счет введения V велики и не могут быть рассмотрены как
малые поправки в системе двух низших состояний.
Постановка задачи в нестационарной теории несколько отличается от
стационарной, так как в последнем случае нам достаточно было определить
поправки к энергиям и состояниям для того, чтобы до конца решить задачу
нахождения состояний в произвольный момент времени в виде суперпози¬
ций стационарных.
При введении возмущения, зависящего от времени,
Пусть до «включения» возмущения система находилась в одном из стацио¬
нарных состояний гамильтониана Я0:
так что |i) — начальное (initial) состояние эволюции, которое определялось
согласно
15.2. Нестационарная теория
Я = Я0 + ЯУ(0,
полагают, что в начальный момент времени t!
V(t') = 0.
H0\x)=E™\i),
(15.30)
где оператор эволюции
230
Тема 8. Теория возмущений
При включении возмущения, зависящего от времени, оператор эволюции
в общем виде принимает вид «Т-экспоненты»:
U(t, t') =f ехр{-| J H(t) dt} (15.31)
t'
и удовлетворяет уравнению
iП^г=Йи, U(t', = (15.32)
dt
Состояние в момент времени t —
|i(t)) = l/(t,t,)|i).
Рассмотрим эволюцию в базисе состояний «представления взаимодействия»
|i(t))/ = U0+(t, t')|i(t)> = Uj(t, (15.33)
откуда
C/Ct, to = LT0ct, Ct, to. (15.34)
Если возмущение мало, то состояние |i(t)>7 мало отличается от начального
И>.
Подставляя определение оператора эволюции (15.34) в уравнение (15.32),
легко находим
+и0т^ =н0и0и,+и0тд-£,
так что вклад с Я0 с обеих сторон уравнения сокращается и
dU
ih-^ = XVIUl, (15.35)
где потенциал в представлении взаимодействия
Vi = UqVUq. (15.36)
Разложение в ряд по Я решения уравнения для оператора эволюции в пред¬
ставлении взаимодействия
Ujit, t') =Т ехр{-|я / ВД dt}
t'
дает построение последовательных приближений по степеням константы
связи Я —> 0.
Ведущее приближение. В первом порядке по Я
t
u,(t, tO = l-£Aj V;(t) dt. (15.37)
t'
Пусть |f) — состояние из спектра исходного гамильтониана. Значит, амплиту¬
да вероятности найти начальное состояние в момент времени t в конечном
(final) состоянии |f) в ведущем порядке по константе связи равна
tO|i> -Ai /<f|V^C0|i> dt, |f>^|i>. (15.38)
t'
Лекция 15
231
Для матричного элемента, очевидно, имеем
(flVKOli) = <f|Uo(t, t')V(t)U0(t, t')|i> = (flVWlOe1"»'^
где
Если конечное состояние находится в дискретном спектре, то, возводя
в квадрат модуль амплитуды
получаем вероятность перехода из начального состояния в конечное
где состояния нормированы стандартным способом: (v'|v) = 5(v' — v).
15.2.1. Постоянное возмущение. Если
то квадрат модуля амплитуды
характерное поведение которого на конечных временах показано на рис. 22.
Значит, постоянное возмущение с ненулевыми недиагональными мат¬
ричными элементами по состояниям исходного гамильтониана за конечное
время At приводит к переходам с частотой
в то время как переходы с другими частотами подавлены.
Если трактовать измерение спектра системы как введение малого воз¬
мущения, то, как видим, только бесконечно длительное наблюдение за
стационарным состоянием позволяет избежать возбуждения других состоя¬
ний, и при конечном времени измерения всегда возникает неопределенность
энергии за счет переходов на другие уровни, причем имеет место соотноше¬
ние неопределенности время-энергия1.
1По сути, амплитуда вероятности в данном случае воспроизводит спектральную плотность
функции-ступеньки, которая при конечной временной длительности имеет вклады частот, от¬
личных от нуля.
(15.39)
(15.40)
и в случае непрерывного спектра—плотность вероятности
(15.41)
(15.42)
(15.43)
232
Тема 8. Теория возмущений
Рис. 22. Поведение квадрата амплитуды перехода на конечных временах
в зависимости от частоты перехода
При t7—»—оо, £—>+ оо возмущение действует бесконечно долго, так что
амплитуда перехода
и она формально обращается в нуль при соух фО на фоне вклада начального
состояния, в то время как
2 я <5 (со)
t—>+00
СО—>0
= / eicot dt
t'—* — оо
= (t —t')—
и мы получаем поправку к эволюции за счет смещения уровня
е{=е10)+%
так как
U0(t, t'W'dt, t') ~ ехр{ - £(Е.(0) + (t -1')}.
При конечных временах и co^(t — амплитуда перехода—
Afi = -^Vfi{l
Заметим, что в представлении взаимодействия матричные элементы опера¬
торов отличаются от матричных элементов по состояниям в представлении
Гейзенберга, которое фактически используется в стационарной теории воз¬
мущений:
<f|[7,[(t, t')FU0(t, t')|i> = ei"<>(t"t')(f|F|i),
что, естественно, никак не сказывается на вероятности, определяемой моду¬
лем амплитуды.
Поэтому вычисленная нами выше амплитуда может быть связана с ампли¬
тудой смешивания стационарных состояний Afi согласно
Лекция 15
233
где уже
Ati = - е-1"»*»"0}, (15.44)
и это—величина, которая сильно осциллирует при малом изменении интер¬
вала времени, и значит, имеет смысл взять ее среднее значение по периоду,
так что экспонента «выпадает», и в среднем амплитуда не зависит от време-
ни:
^ = “ = £«»-£«»’ (15.45)
что, конечно, воспроизводит результат стационарной теории возмущений
для амплитуды примеси к начальному состоянию. Поэтому критерий приме¬
нимости теории возмущений в этом случае остается без изменений.
Итак, мы убедились, что подстановка постоянного возмущения согласует¬
ся с теорией возмущений в стационарном случае.
15.2.2. Периодическое возмущение. Амплитуда перехода за счет пери¬
одического возмущения, равного нулю при t = t/9
XV(t) =
принимает вид интерференции двух вкладов
Ап = —i{ t-r ■ v (1 - еЦй>('+й,К(-(,)) - —г(1 - ei("n-“>(t-t,:))},
'l {Н(соп + соу ' h(con-co)K 'У
анализ каждого из которых вполне аналогичен рассмотрению постоянного
возмущения, но физические выводы существенно отличаются. Так, во-пер-
вых, при |(cofi ± o>)(t -10| 1 сильно осциллирующие со временем экспо¬
ненты «вымирают», и амплитуда обращается в нуль в силу эрмитовости
возмущения.
Во-вторых, при а>^ ± со 0 имеет место резонанс, который мы рассмот¬
рим при длительном действии возмущения: t' —»—оо, t -* +оо. Тогда интегри¬
рование в (15.39) дает
Afi = ±%{2п5(а>п + со)~ 2n5(a>fl - со)}. (15.46)
Считая частоту возмущения положительной по определению, заключаем,
что один из вкладов отличен от нуля либо когда имеет место возбуждение
уровня o>fi = со — вынужденное поглощение энергии квантовой системой за
счет возмущения, либо когда происходит переход с вышележащего уровня
на нижележащий cofi = — со — вынужденное излучение энергии квантовой
системой. При этом мы установили, что амплитуды индуцированного1 погло¬
щения и излучения по модулю равны друг другу.
В случае излучения, например,
IAfiI2 = I%\22п5(й)р + о>)2п5(cofi + со) ^ ^ |Vfi|22я5(cofi + <x>)(t-1'),
1То есть вынужденного.
234
Тема 8. Теория возмущений
где мы опять воспользовались выражением для дельта-функции от частоты
при нулевом значении аргумента через полный временной интервал дей¬
ствия возмущения. Поэтому имеет смысл говорить о вероятности (плотности
вероятности) перехода системы за единичное время:
wn = = ^2п5 (£f0) “ Ei0)+hco)’ (15-47)
причем мы внесли Й под знак дельта-функции. Если конечное состояние
находится в непрерывном спектре, то получаем «золотое правило Ферми» для
дифференциальной вероятности перехода за единичное время:
dwfi = ||Vfi|22 я5(Е}0) -Е® +йй>) dv(Ef(0)), (15.48)
где dvCEf(0)) — дифференциальная плотность состояний с заданной энергией
конечного состояния.
Подчеркнем, что согласно формулам (15.47), (15.48) бесконечно длитель¬
ное воздействие периодического возмущения приводит к точному закону
сохранения энергии для уровней исходной системы в смысле квантового
характера поглощения и излучения энергии.
Если интегральная вероятность перехода из одного состояния в другое за
единицу времени wfi, то вводят величину т с размерностью времени
1
т‘
Тогда, если рассмотреть N идентичных систем в момент времени t, то за
время dt вероятность распада
dn(t) __ dt
«И-,- О5'50)
что легко интегрируется, и
N(t)=N0e"x. (15.51)
Согласно этому уравнению т называют временем жизни системы, если имеет
место индуцированное излучение, или временем возбуждения, если проис¬
ходит вынужденное поглощение. При этом совершенно ясно, что по проше¬
ствии времени т вероятность индуцированного излучения или поглощения
становится близка к единице. Поэтому логично считать критерием приме¬
нимости теории возмущений для периодического возмущения не малость
вероятности перехода, а несколько иной показатель. Именно, единственным
условием, которое должно с необходимостью выполняться в ходе вывода
выражения для вероятности перехода в единицу времени, будет достаточная
длительность воздействия возмущения, много большая, чем период колеба¬
ний возмущения1. Этого всегда можно достичь, если только время жизни
уровня много больше периода колебаний возмущения:
т»—. (15.52)
СО
ХС точки зрения динамики возникновение дельта-функций при предельном переходе к бес¬
конечным временам означает пренебрежение вкладом нерезонансных переходов на фоне резо¬
нансных при больших временах: интервал времени, на котором мы изучаем эволюцию системы,
Лекция 15
235
Поскольку частота колебаний связана с разностью энергий уровней соотно¬
шением ho> = |£f(0) - £;(0) | = АЕ, условие применимости расчета вероятности
перехода за счет периодического возмущения можно представить в виде
Г<ДЕ, (15.53)
где
Г = | (15.54)
называют шириной перехода. В задаче с постоянным возмущением мы виде¬
ли, что дельта-функция, отвечающая закону сохранения энергии, возникает
в пределе бесконечно длительного воздействия возмущения. В случае же
конечного времени воздействия имеется конечная ширина распределения по
энергии, которая связана с временем воздействия соотношением неопреде¬
ленности время-энергия. Этот вывод, очевидно, остается справедлив и для
периодического возмущения: просто центр распределения на рис. 22 сме¬
щается с нуля к величине AE/h. Поскольку характерное время перехода
равно т, соответствующая неопределенность в значении энергии перехода
есть Й/т = Г. Поэтому, например, ширина перехода определяет в процессе
вынужденного излучения точность определения энергии распадающегося
уровня, т. е. ширину уровня.
Другое условие применимости теории возмущений —сходимость ряда по
константе связи Я. Степень сходимости можно установить, только вычислив
следующую по Я поправку к ширине перехода Г(2) и убедившись, что Г(2) < Г.
15.2.3. Мгновенное включение возмущения. При рассмотрении посто¬
янного возмущения мы полагали, что в момент включения возмущения от
нулевого значения до V состояние системы точно совпадало с одним из кван¬
товых уровней невозмущенной, исходной системы с гамильтонианом Я0.
Однако это предположение нуждается в более детальном исследовании, так
как необходимо установить точность такого приближения, учитывая факти¬
ческую конечность интервала времени изменения потенциала, и обсудить
возможную связь с соотношением неопределенности время-энергия.
Для простоты обозначений будем считать, что в начальный момент вре¬
мени t' = 0 возмущение быстро возрастает от нуля до величины V за малое
время 5t:
ЯУ(0 = У(5), t = 5t-s, 5£ [0,1]. (15.55)
должен быть существенно больше периода колебаний, чтобы произошло выделение резонансной
динамики на фоне нерезонансной, т. е. \t-1'\»1/со^. С другой стороны, вероятность перехода
остается малой, если интервал времени наблюдения за системой мал по сравнению со временем
перехода: |t —1'\ < т. В итоге совместное выполнение этих требований означает введение крите¬
рия применимости нестационарной теории возмущений в виде т»1/а^. В этом, собственно,
и состоит отличие стационарной теории возмущений от нестационарной: для применимости
первой достаточно потребовать малости возмущения, а во второй необходим еще и анализ роли
резонансов. При описании переходов в состояния непрерывного спектра при выводе «золотого
правила Ферми» мы объединяем теорию возмущений с выделением резонансных переходов, что
и приводит к появлению ограничений на его применимость типа (15.52).
236
Тема 8. Теория возмущений
Гамильтониан как функция параметра s равен
H(s)=H0 + V(s).
Оператор эволюции в первом приближении по малому 5t —
. 1
U(5t) = 1 - i J H(s)5t ds = l — ±5tH, (15.56)
0
где мы ввели «среднее значение» гамильтониана
1
Я = / H(s) ds. (15.57)
О
Теперь сразу видно, что
lim I7(5t) = l, (15.58)
6t-> о
т. е. при мгновенном изменении потенциала начальное состояние действи¬
тельно не изменяется.
Вычислим вероятность найти систему в момент времени 5t в состоянии,
отличном от начального:
w = Yi Kfl^C5t)|i)|2 = 2]<i|t7tC5t)|f>{f|LrC5t)|i). (15.59)
В силу полноты базиса
2><fl=i-|i>(i|=A
есть проектор на пространство, ортогональное исходному состоянию, так что
w== (i|I/t(5t)j\U’(5t)|i).
В ведущем приближении использование ортогональности дает
(i| UfCSt)Pl = jj5t{HHPu PiUCStM = -±5tPlH\i),
и значит,
W = ^(6t)2(i|HPiH|i) = ^(5t)2{(i|HH|i) - (i|H|i)2}.
Но выражение в фигурных скобках есть не что иное, как квадрат флуктуации
5Н среднего значения гамильтониана,
w = ^(5t-5H)2, (15.60)
ПГ
поэтому вероятность возбуждения состояний, отличных от начального, пре¬
небрежимо мала, w < 1, если
(15.61)
Ясно, что флуктуация среднего значения гамильтониана 5Н ~ 5Е определя¬
ется величиной малого возмущения 5Е ~ У.
Лекция 15
237
Согласно соотношению неопределенности время-энергия при флуктуа¬
ции энергии на величину 5Е состояние, а значит, его волновая функция
существенно, т. е. физически значимо, изменится за время
Таким образом, включение возмущения можно считать мгновенным, если
состояние не успевает измениться за время 5t,
т. е. интервал времени для инициации возмущения много меньше характер¬
ного времени изменения волновой функции за счет изменения энергии1.
15.2.4. Адиабатическое возмущение. Рассмотрим задачу определения
состояния системы в результате медленного изменения со временем пара¬
метров гамильтониана.
Пусть гамильтониан зависит от р параметров {а= а, где [л = {1, р},
и нам известны нормированные собственные состояния этого гамильтони¬
ана
Я(а) №„(а)> = Еи(а)|я/>п(а)), (15.63)
причем состояния являются невырожденными ни при каких а, т. е. любые
две функции из набора Еп(а) не пересекаются.
Будем считать, что параметры медленно меняются со временем, если
Построим по собственным состояниям гамильтониана «адиабатические» со¬
стояния, удовлетворяющие уравнению
одним типом взаимодействий, существенного, скажем, на больших расстояниях, а возмущение
задается другим взаимодействием, ограниченным на малых расстояниях. Тогда распростране¬
ние этих взаимодействий со скоростью порядка скорости света, приводит к иерархии времен
взаимодействия, отвечающей мгновенному включению возмущения. Классическим примером
такого рода является задача о состоянии электрона в атоме с ядром трития после его /3-рас-
пада в ядро гелия: атомные размеры существенно превосходят радиус распространения слабых
взаимодействий. Кроме того, /3-электрон является релятивистским и покидает атом, не успевая
провзаимодействоватъ с ним.
5t<C At~ Д=-,
(15.62)
a = a(s), t = T-s, s€[0;l], Г —> оо.
(15.64)
а именно,
a)) =H(a)\xpA(,t, а)),
S
№n(t>a)) = expj-ir J En(s) ds}|i/>n(a)),
(15.66)
(15.65)
где
En(s)=En(a(s)).
Введем обозначение для интегральной фазы размерности частоты
s
(15.67)
о
1Подобная ситуация является типичной в случае, когда квантовое состояние определяется
238
Тема 8. Теория возмущений
так что
IVtffc a)) = e-i7V"(*)|V>n(a)).
Однако построенные таким способом «адиабатические» состояния не удо¬
влетворяют уравнению Шрёдингера (!), так как полная производная состо¬
яния по времени включает в себя и вклад за счет изменения параметров
гамильтониана
a)) = ft, a)) + a)> =
=En(s)|^(t, a)) + ift£d^|V£(t, a)),
где a=da/ds. Как видим, возникающая поправка может быть мала при Г—> оо
как О0-/Т), если параметры имеют конечные производные по s и состояния
также умеренно зависят от а. Производную по параметрам доминирующего
при заданном п состояния можно разложить по базису |я/^(а)). Поэтому
будем искать решение уравнения в виде
№„(0) =c„(s)|^(t, a))+Jcfc(5)e-ir(^(s)-^<i»|^(t) a)), (15.68)
кфп
где по построению
cn(s)=ei’r« + o(i), |eir(s)| = l, с„(0) = 1
И
kfc(s)| = e>(j), кфп, cfc(0)=0,
причем, в отличие от стационарного случая, мы не можем нормировать
ведущий вклад |cn(s)| точно на единицу при любом значении s, потому что
уравнение Шрёдингера не допускает перемасштабирование состояний фак¬
торами, зависящими от времени.
Адиабатическое приближение. Оставляя лидирующий член в разложе¬
нии (15.68) и подставляя его в уравнение Шрёдингера, найдем
a)) + ia^|i/>*(t, a)) =0,
так что проецирование на основное состояние (^„(а)!*) дает
dy = i daM(i/>„(a)|d“|i/>„(a)), 3“ = ^.
Значит, в адиабатическом приближении
|'фп(0) = ехр{—i7Vn(s) + i / daMM(a)}|i/>„(a)),
о
где «поле»
Ai(a) = i(i/’n(a)|d“|i/’n(a)).
(15.69)
(15.70)
(15.71)
(15.72)
Лекция 15
239
Проецирование уравнения (15.69) на состояние, отличное от основного,
дает «невязку», которая может быть компенсирована поправкой первого по¬
рядка. Действительно, оставляя с обеих сторон уравнения Шрёдингера после
проецирования (i/>fc(a)|-) только вклады порядка 1/Т, находим
£ сп№Ша)тп(.<0) = ck(s){Ek(s)-En(s)}. (15.73)
Недиагональный матричный элемент {'фк(а)\д*\'фп(а)) можно вычислить,
дифференцируя по параметру уравнение на собственные значения гамиль¬
тониана (15.63)
{д^ЙСаШпШ +Н(а)д1Ша)) = {д1Еп}\грп(а)} +ЕпЭ£№„(а)>
и проецируя на
fc (а) | { Э ° Я (a)} | п (a)) = {Еп (s)-Ek(s)}(ipk(a)\d°№n(a)). (15.74)
В итоге
Ск(з) = ~ТщЮ=Е,^у2^Ша)\{дайН(аШп(а)) = о(^. (15.75)
Подчеркнем, что cfc(0) = 0, если только начальная скорость изменения па¬
раметров обращается в нуль: ам(0) = 0. В противном случае на малом ин¬
тервале 5s система эволюционирует долгое время 5Т = 5s • Г —> оо, так что
в состоянии появляется примесь состояний с другими квантовыми числами
и уже ск(0) Ф 0, но тогда достаточно считать, что ск (0) ~ 0(1 /Г), т. е. опять же
бесконечно малая величина в адиабатическом пределе.
Критерий адиабатичности изменения параметров гамильтониана немед¬
ленно следует из выражения для амплитуд примеси состояний, отличного от
исходного (15.75), если считать, что
|cfc(s)|<l.
Поскольку As ~ 1, а адд“Н ~ (Аа/As) (АЕ/Аа) ~ АЕ, обозначая разность энер¬
гий Ек — Еп = hco, заключаем, что
Гсо2^»1, (15.76)
или, вводя характерное время изменения состояния At = h/AE при изме¬
нении энергии на ДЕ и период излучения для переходов между уровнями
Тш ~ 1/со—период собственных колебаний в системе, находим
r»At^~7^, (15.77)
т. е. время изменения параметров Т должно быть много больше характерного
времени изменения состояния At при изменении энергии с учетом факто¬
ра квадрата отношения периода собственных колебаний к времени измене¬
ния состояния, или время изменения параметров должно быть существенно
больше периода собственных колебаний с учетом фактора отношения пери¬
ода к характерному времени изменения состояния при флуктуации энергии.
240
Тема 8. Теория возмущений
Критерий выглядит намного проще, если изменение энергии порядка
расстояния между уровнями (которые сдвигаются так, чтобы по-прежнему
не пересекаться), т. е. если АЕ ~ hco или, что то же, ~ At:
Г» 7^ <=> сот <С со, (15.78)
а значит, время адиабатического изменения гамильтониана должно быть
много больше периода собственных колебаний в системе, или частоты соб¬
ственных колебаний много больше характерной частоты изменения пара¬
метров.
Таким образом, мы обосновали законность адиабатического приближе¬
ния
i/da^Ca)
|г/>„(0)*е о |i/>£(t,a)), ^M(a) = i(a/>n(a)|d“|V>n(a)), (15.79)
согласно которому состояние аппроксимируется единственным собственным
адиабатическим вкладом с точностью до фазы, определяемой зависимостью
базиса состояний от медленно меняющихся параметров.
Фаза Берри. Правильное адиабатическое состояние |я/>„ (а)) отличается
от исходного статического состояния \^n(a)) экспоненциальным фактором
i J daM Ац(а)
l^„(a)) = e 0 №„(<*)) (15.80)
с фазой
s
r(5)=J daM Лм(а). (15.81)
о
Рассмотрим эту фазу более подробно в случае, когда адиабатическое измене¬
ние параметров гамильтониана является циклическим, т. е. по прошествии
времени Т параметры принимают свои начальные значения
a(l)=a(0).
Тогда
г(1) = ДсГ = f da" дм(а) (15.82)
есть цикл фазы, выражаемый циркуляцией вектора поля по контуру в про¬
странстве параметров а, и этот цикл называют топологической или геомет¬
рической фазой Берри. Естественно, фаза Берри определена по модулю 2тг,
т. е. с точностью до ненаблюдаемого сдвига на 2тт, п е Z.
Переопределим фазу исходного состояния как функции в пространстве
параметров, сохраняя тем самым нормировку,
IV>n(a))u = e-iu(a)|i/>n(a». (15.83)
Тогда изменится и поле:
Д“(а) = iu(V'n(a)|a“|i/)n(a))u = ^fl(a) - в“и(а), (15.84)
что есть не что иное, как калибровочное преобразование с функцией u(а).
Лекция 15
241
Поэтому цикл фазы станет равным
АсГи = АсГ-Аси. (15.85)
Таким образом, фаза Берри определена с точностью до геометрической фазы
исходного состояния, которая, в силу произвольности, не несет на себе дина¬
мического смысла. Поэтому имеет смысл выбирать фазу исходного состояния
в виде однозначной функции в пространстве параметров, а также считать
и калибровочную функцию и (а) однозначной.
Итак, если исходное состояние имеет тривиальную геометрическую фазу
при циклическом изменении параметров гамильтониана, то это состояние
при адиабатическом циклическом изменении параметров гамильтониана во
времени приобретает нетривиальную геометрическую фазу, которая носит
имя Берри.
Если условие тривиальности топологической фазы исходного состояния
выполнено (интегрирование по частям имеет место с нулевыми граничны¬
ми вкладами), то можно воспользоваться теоремой Стокса для контурного
интеграла вектора, выразив его через интеграл от ротора по поверхности,
границей которого является контур. При произвольном числе измерений
параметрического пространства эта процедура наиболее корректно запи¬
сывается в терминах дифференциальных форм. В трехмерном же случае
получаем
f da j^(a) = / ds rot j^(a), (15.86)
dS s
что указывает на калибровочную инвариантность интеграла (ротор градиен¬
та равен нулю), если калибровочная функция и (а) является однозначной.
Из-за наличия динамической фазы бесконечно малые трансляции пра¬
вильного адиабатического состояния в пространстве параметров за¬
даются оператором
Г( da) = 1 + d a** V*, V‘ = Э* + UM, (15.87)
где называется ковариантной производной. Инфинитезимальные транс¬
ляции правильного адиабатического состояния из одной точки в другую по
двум путям отличаются друг от друга только фазой—циклом по замкнутому
пути:
T(da)T(db) = T(db)T(da)eiAcr,
откуда
iAcy = daM dbv [VM, Vv] = i da^ dbv(flMA, - dyAJ. (15.88)
Можно ввести тензор напряженности поля через коммутатор ковариантных
производных:
= ддЛ - dvAц = - i[VM, Vv], (15.89)
так что, переходя от бесконечно малых замкнутых петель к конечным, на¬
242
Тема 8. Теория возмущений
ходим, что интеграл поля по замкнутому контуру сводится к интегралу от
калибровочно инвариантной напряженности поля по площади, «натянутой»
на контур.
В трехмерном случае, если параметры изменяются на сфере, то площадь
петли определяется телесным углом, поэтому говорят, что геометрическая
фаза Берри пропорциональна телесному углу, заметаемому петлей на сфере
(теорема о телесном угле).
Задача 8.1. Найти фазу Берри для спинового состояния электрона, ориентирован¬
ного по магнитному полю, которое адиабатически вращается по окружности вокруг
оси z (см. рис. 23).
Рис. 23. Вращение магнитного поля вокруг оси z
Решение. Исходное состояние спина 1/2, ориентированного вдоль единичного
вектора магнитного поля п = 3tf/H = (sin в cos у, sin в sin </>, cos в), имеет вид
IТ>=cos ||+)+eiv sin||-),
где |±) — состояния с положительной и отрицательной проекциями спина на ось z
и мы выбрали фазовый фактор так, чтобы он давал однозначную функцию угла </>,
так как при адиабатическом вращении магнитного поля вокруг оси z именно этот
угол и является параметром изменения гамильтониана. Тогда поле
A> = i<TKIt> = —“п2 ! = |(cos0 —1)
не зависит от </?, и фаза Берри равна
2 я
Асу = / dip А.у = тс (cos 0 — 1).
о
Заметим, что окружность, описываемая вектором магнитного поля на сфере, «заме¬
тает» телесный угол
1 2 п
П= J dcos0 J d</? = 2rc(l-cos 0),
cos в О
так что фаза Берри
Асу = -зП}
где s=1/2—проекция спина на ось магнитного поля. Можно убедиться, что последняя
Лекция 15
243
Q
формула справедлива и для в = —1/2: состояние против оси поля Ц) = — sin —1+) +
+ eiv cos |-|-), откуда ^ = -(cos 0Н-1)/2 и Acy = -7r(cos 0 + l)+27r = --7r(cos д -1),
где мы добавили ненаблюдаемую фазу 2п.
Фаза Берри наблюдается экспериментально, как, например, в опытах по
вращению спина нейтрона в адиабатически вращающемся магнитном поле,
так и в ставших классическими экспериментах по вращению поляризации
света при движении по изогнутому световолокну.
Тема
9
Сложение моментов
Лекция 16
Тензорное произведение векторных величин в классической физике и нагляд¬
ное представление о разложении произведения в сумму по неприводимым
тензорам, постановка задачи о сложении моментов в квантовой механике,
базис состояний и квантовые числа суммарного момента, допустимые значе¬
ния проекции и модуля суммы моментов, коэффициенты Клебша—Гордана,
число состояний, задача о сложении j = 1 и j = 1/2, закон преобразования
неприводимых тензорных операторов с заданным моментом и его проекцией
в стандартном представлении, коммутационные соотношения с моментом,
самый общий вид неприводимого тензорного оператора и теорема Вигне¬
ра—Эккарта, сферические гармоники как неприводимые тензорные функции
в стандартном представлении, правила отбора для матричных элементов тен¬
зорных операторов и запрет перехода 0—> О7.
В классической физике тензорное произведение двух векторных величин
аа и в 3-мерном евклидовом пространстве можно представить в виде
суммы по тензорам:
aabP = Р (а • Ь) + \eafir (а хЪУ + ±{а“ЬР + аЧ* - §5^(а • Ь)}, (16.1)
которые преобразуются при вращении координат системы независимо друг
от друга, т. е. только через свои собственные компоненты, так что эти ком¬
поненты уже не раскладываются на независимые, а значит, как говорят
в математике, тензорное произведение векторов раскладывается в прямую
сумму неприводимых тензоров. В самом деле, во-первых, скалярное произве¬
дение является инвариантом, а тензор Кронекера, или евклидова метрика—
также инвариант вращений, т. е. не зависит от системы координат. По¬
этому первый вклад удовлетворяет указанному свойству неприводимости.
Во-вторых, псевдовектор векторного произведения также преобразуется при
вращениях только через свои компоненты: он неприводим. В-третьих, след
тензора—инвариант, поэтому бесследовый симметричный тензор сохраняет
нулевое значение следа так же, как и симметричность: он независим. Однако
разбиение на независимые тензоры — это достаточное, но не необходимое
условие неприводимости, так как оно еще не означает, что каждый из них
уже невозможно далее так же разложить на независимые, т. е. инвариантные,
подпространства. В группе вращений путеводной нитью построения непри¬
водимых тензоров является наличие единственного инварианта — квадрата
векторного генератора вращений j2, а также базиса состояний с определен¬
ной проекцией ;3, элементы которого переходят друг в друга под действи¬
ем операторов j±, так что в этом пространстве нет инвариантных подпро¬
246
Тема 9. Сложение моментов
странств: только тензорные величины, имеющие определенное значение j2,
являются неприводимыми1! В разложении (16.1) мы записали сумму скаляра
(спин 0), вектора (спин 1) и тензора (спин 2).
В квантовой механике преобразование эрмитовых операторов, сопостав¬
ленных векторным или тензорным наблюдаемым, с одной стороны, в точ¬
ности соответствует классическим преобразованиям, а с другой, задается
действием операторов вращения
RAaRt = 32%A(>,
где 91 — матрица вращения операторов координат. В инфинитезимальном
виде
R^l + i(s •</>),
где оператор s берется в представлении, отвечающем оператору Аа. Это
справедливо и при рассмотрении действия оператора вращений на состоя¬
ния с определенным значением спина и орбитального момента. Уже в этом
случае возникает задача определения суммарного значения j = 1 + s.
Для произведения операторов АаВР оператор бесконечно малых поворо¬
тов—
R = l + i(sA + sB)-y?.
Но разложение произведения тензорных величин в сумму неприводимых
тензоров означает, что эти неприводимые тензоры преобразуются как ве¬
личины с соответствующим значением квадрата спина Поэтому встает
задача нахождения суммы
SA + SB =SAB'
Для построения базиса в пространстве состояний достаточно знать дей¬
ствие операторов суммируемых моментов на состояния с заданным значе¬
нием полного момента, так как это позволит для тензорного произведения
операторов вычислять матричные элементы по этим базисным состояниям.
16.1. Сложение двух моментов: базис состояний
Пусть заданы моменты jA и jB, которые действуют в пространстве базис¬
ных состояний | jA, тА) и |;в, тв). Сумма моментов, как мы видели, является
генератором вращений в пространстве тензорного произведения состояний
IjA, тА) ® \jB, тв) = |;А, mA)\jB, тв),
Доказательство этого важного факта является довольно элементарным: тензорные вели¬
чины с определенным значением j2 принадлежат (2j +1)-мерному векторному пространству,
построенному, как мы помним, из старшего вектора действием понижающего оператора; если
е — единичный вектор вдоль оси вращения на угол (р, то в векторном пространстве можно
перейти к базису из собственных векторов генератора вращений j • е, так что действие матрицы
вращений 9L =exp{i(j'e)ip} на векторы такого базиса сводится к умножению на фазовый
множитель exp{im</?}, где т — значение проекции момента на ось вращения, и, таким образом,
дальнейшее приведение становится невозможным.
Лекция 16
247
где мы опускаем знак тензорного произведения для краткости записи. В этом
пространстве можно выбрать базис так, чтобы оператор1
J=jA+f
имел на базисных векторах определенные значения своего квадрата и проек¬
ции на ось z:
J2\J, М) =J(J + 1)|J, М), J3\J, М) =M\J, М).
Другими словами, ставится задача найти для двух физических систем А
и В с моментами импульса jA и jB волновую функцию полной физической
системы с определенным значением суммарного момента J, построенную
в виде суперпозиции произведений волновых функций систем Л и В.
Заметим, что
^зИА> mA)\jB, тв) = О'з+;|)|jA, mA)\jB, тв) = (.mA + mB)\jA, mA)\jB, тв),
т. е.
h\jA>mA)\jB,™-B)=M\jA,mA)\jB,mB), М = тА + тв. (16.2)
Значит, состояния произведения являются состояниями с заданной проекци¬
ей суммарного момента.
Найдем, сколько состояний исходной системы отвечают заданной вели¬
чине М и какова область ее допустимых значений. Для этого рассмотрим
диаграмму на рис. 24. Легко заметить, что М принимает значения в области
-jA-jB^M^jA+jB (16.3)
с шагом ДМ = 1.
Пусть для определенности jA ^ jB. Тогда согласно диаграмме кратность
вырождения М по тА и тв в исходном базисе зависит от значения М. Так,
кратность fc(M) остается постоянной при
-jA+jB^M^jA-jB, fc(M) = 2jB + l, (16.4)
т. е. кратность определяется числом базисных векторов для меньшего из двух
моментов.
В других случаях
\M\=jA+jB, fc(M) = 1,
\M\=jA+jB-l, fc(M) = 2,
\M\=jA-jB + l, fc(M)=2jB,
ИЛИ
k(M)=jA+jB + l-\M\, jA-jB + l^\M\^jA+jB. (16.6)
Тривиальное, но важное замечание состоит в том, что оператор суммарного момента имеет
те же коммутационные соотношения, что его составляющие, которые, по построению, взаимно
коммутируют.
248
Тема 9. Сложение моментов
mBi
1 M=jA+jB
\ \
\ \
Jb
\ \
\ \
\ \ mA
-Ja
Ja. \
—Jb
\
M=jA+j„- i
Рис. 24. Диаграмма допустимых значений проекций суммарного момента М
на плоскости (тА, тв) с характерными линиями постоянной суммы проекций
М = тА + тв
Для старшего вектора
J+\jA, iA)\jB, f) = и^+)вЖ, iA)\jB, jB)=о.
Отсюда заключаем, что это собственный вектор состояния | J, J) с моментом
1J — j^-j-те
I/, )А)\)В, }В) = \jA+jB, jA+jB). (16.7)
Поскольку
^±=J±+J±,
действие этих операторов на исходные состояния \jA, mA)\jB, тв) дает состо¬
яния из того же пространства. Поэтому в силу1
| J, J) = )/j(J + l)-J(J-l) | J, J -1) = л/27 I J, J -1)
состояние
J_ | jA + jB, jA+jB) = \/2(jfA+JB) |j A+jB, jA+jB -1)
СВОДИТСЯ к
0*+j*)I./a, jA> |jB, jB) = ViA0'A+i)-iA0'A-D ljA, iA - i>l;B, jb> +
+ +«-№-1) Ija. jaWb. f -1) =
= ^ l;'A,jA- i)l;B, jB) + JWB IjA, jA)\jB, jB-1).
Значит,
i jA+jB, ja+f -1>=ьл ja - Di jB, jB)+
+/ijA’jB-i}- (i6-s)
1Применяем общую формулу j±\j, m) = у/j(j+ 1)— \j, mil).
Лекция 16
249
Но в пространстве с М = jA + jB — 1 есть еще одно независимое состояние,
которое можно выбрать ортогональным к | jA+jB, jA+jB — 1), например,
И+ (16.9)
Действие на это состояние оператора J+ переводит его либо в состояние
с М=jA + jB, либо дает нуль1. Прямым вычислением2 легко убедиться в том,
что J+|o) =0. Поэтому заключаем, что состояние (16.9) есть старший вектор
|о) = | J, J) с моментом J=jA + jB — 1.
Эта процедура может быть продолжена рекуррентно вплоть до значений
М = jA — ;в. Итак, при М = jA — jB мы имеем 2jB + 1 состояний, которые
отвечают базису состояний с суммарным моментом J = {jA+jA — jB}-
Последующее действие понижающим оператором, во-первых, оставляет со¬
стояния в исходном пространстве и, во-вторых, не приводит к увеличению
независимых состояний. В итоге указанные нами значения суммарного мо¬
мента полностью исчерпывают его допустимые значения. Таким образом,
сложение моментов jA и jB приводит к суммарному моменту, который при¬
нимает значения
J=jA+f, jA+jB-1, .... \jA-jB\- (16.10)
Этот вывод допускает простую наглядную интерпретацию: максимальная
длина суммы векторов достигается, когда они параллельны, а минималь¬
ная—когда они антипараллельны.
Преобразование базиса от \jA, mA)\jB, тв) к |J, М) сохраняет нормировку
состояний и является линейным. Это—унитарное преобразование
|J, М) = 2 IjA, тА)IjB, mB)CJ.fmA..B<mB, (16.11)
та,тв
где амплитуды
тА> Л ПВ^> М>
носят название коэффициентов Клебша—Гордана, и они приводятся в табли¬
цах для практически применяемых значений моментов. Чтобы избавиться от
произвольных фазовых множителей, полагают, что число
CJJ >0
1Первая возможность исключена, так как обратное действие понижающим оператором дало
бы независимое ортогональное состояние, что невозможно. Действительно, если |а) — состояние
с определенным значением момента и J+\a) /0, тогда J_J+|a) ~ \а). Пусть |Ъ) ортогонально
|а), поэтому (a|J_J+|b) =0. Значит, состояния J+\b) и J+\a) ортогональны. В нашем случае
вектор состояния, получающийся действием повышающего оператора на (16.9), ортогонален
единственному состоянию с максимальным значением проекции суммарного момента, значит,
повышение (16.9) дает тождественный нуль.
2Тем не менее, доказательство, приведенное в предыдущей сноске, необходимо для последу¬
ющей рекурренции.
250
Тема 9. Сложение моментов
т. е. значение заданного коэффициента разложения является положительным
числом. Тогда по построению (понижающие операторы) все коэффициенты
Клебша—Гордана—вещественные числа.
В силу ортогональности
{J', M'\J, М) = 5jji5mmi
находим
2 С^МшА;)в,твС?,тА;)Ыв = 5^'5ММ'- (16-13)
тА,тв
В силу полноты базиса в подпространстве
J=jA+jB M=J
J=\jA-jB\ M=-J
и ортогональности исходного базиса состояний, получим
J=jA+jB M=J
SV CJ¥ .» CJf i .r , = 5m m/ 5m m/. (16.14)
/ J )A,mA;jB,mB jA,m'A;jB,m'B mAmA твтв v J
J=\jA_jB\ M=~J
Число состояний. В исходном базисе было (2jА 4*1) (2jB 4- 1) ортонор-
мированных состояний. В разложении этих состояний по базису с опреде¬
ленными значениями суммарного момента и его проекций мы получаем
соответственно
2(;A+jB) + l, 2(jA+jB~) — 1, ..., 2(jA — jB) +1
состояний. Суммируя члены арифметической прогрессии1, находим
\ {2(jA+JB) +1 + 2(ja - jB) + 1>(2;в +1) = (2jA +1) (2jB +1),
т. e. то же число базисных состояний, как этого и следовало ожидать.
Задача 9.1. Провести сложение моментов jA = 1 и jB = 1/2.
Решение. Состояние |1,1)|+) дает старший вектор с моментом 3/2
|,|)=11.1)1+).
Понижающий оператор дает, с одной стороны,
j |3 3\уз 3 1\
|2*2/ 2’2/’
а с другой —
0* +J-)U,1)1+) = 0>1+> + II, DH-
Значит,
|,1> = /||1,0)|+)+У||1,1)Н.
1«Первый плюс последний на число членов пополам».
Лекция 16
251
Ортогональный ему вектор —
Ц)—ДММ + ДЧ.1)\-).
Действие понижающим оператором дает, во-первых,
оператором дает, во-первых,
и
at + jf)|l, 0)1+) = л/2|1, -1)1+) + |1,0)|-),
0*+j!)|l> 1>|-> = V2|1,0)|-),
откуда
Во-вторых, аналогично,
5--5) — -/fl1. ->>!+> + i/ll»- »>l->-
!'-D—
Наконец, очевидно, младший вектор —
Итак, мы построили базис ортонормированных состояний с суммарным спином 3/2
и 1/2.
переводит скалярное состояние в состояние с заданным моментом j и его
проекцией т. По построению это неприводимый тензорный оператор. При
вращениях он преобразуется как кет- и бра-векторы, т.е. согласно
где 3L — матрица вращения состояний с моментом j, и мы подразумева¬
ем суммирование по повторяющемуся индексу т'. Отсюда видно, что f не
может зависеть от т, так как иначе вид преобразований при вращениях
не соответствовал бы состоянию с заданным значением момента, что есть
частный случай теоремы Вигнера—Эккарта, примененной для данного опе¬
ратора.
Коммутаторы тензорного оператора с моментом легко вычисляются по
известному результату действия компонент момента на кет- и бра-состояния:
Соотношения (16.16) и (16.17) — закон преобразования и следующие из
него коммутационные соотношения—представляют собой самое общее опре¬
деление для неприводимых тензорных величин. Обобщая (16.15), можно за¬
писать неприводимый тензор порядка j с компонентой т, который действует
16.2. Тензорные операторы: правила отбора
Тензорный оператор
(16.15)
(16.16)
(16.17)
252
Тема 9. Сложение моментов
на состояния произвольного момента импульса, в виде
(16.18)
J,M
Закон его преобразования при вращениях
Но матрица вращений состояний является унитарной
и мы получаем в точности
т mm m
(16.16)
При этом существенно, что величина % не зависит от проекций моментов.
Доказательство коммутационных соотношений (16.17) также не вызывает
никаких затруднений1. Итак, выражение (16.18) определяет самый общий
вид неприводимого тензорного оператора2 порядка j с проекцией т (это
представление обычно называют стандартным).
Теорема Вигнера—Эккарта. Матричный элемент неприводимого тен¬
зорного оператора Т® порядка j с проекцией m по состояниям с заданны¬
ми значениями момента выражается через коэффициенты Клебша—Гордана
в виде
где (J\\Т^||Jf) —приведенный матричный элемент оператора, который за¬
висит только от J и J', но не зависит от проекций моментов. Здесь фактор
1/a/2J + 1 введен согласно общепринятому соглашению для удобства при
вычислениях.
Мы по существу доказали эту теорему явным построением неприводимых
тензорных операторов общего вида3, затем определив их трансформацион¬
ные свойства. Обычно поступают наоборот, постулируют закон преобразо¬
вания величин при вращениях и отсюда получают общий вид оператора, т. е.
его матричный элемент, отвечающий теореме.
Пример. Сферические гармоники можно представить как матричный элемент
неприводимого тензорного оператора вида (16.15):
1Для повышающего и понижающего операторов нужно провести подходящую замену пере¬
менной суммирования М—>М 1.
2Мы здесь опустили в бра- и кет-векторах обозначения для других возможных квантовых
чисел, остающихся неизменными при вращениях (для скаляров).
V2J+1
(16.19)
Лекция 16
253
Значит, эти гармоники — стандартное представление для неприводимых тензоров
порядка I. Для I = 1 легко найти
Приведенные формулы для стандартного вида сферических гармоник полезно срав¬
нить с результатом суммирования двух моментов ; = 1, которые дают тензор j = 2:
что в точности совпадает с выражениями через функции # при очевидном соответ¬
ствии состояний момента и компонент Ф.
Правила отбора. Коэффициенты Клебша—Гордана принимают ненуле¬
вые значения, только если моменты и их проекции при сложении пробега¬
ют допустимую область своего изменения. Поэтому и матричные элементы
неприводимых тензорных операторов, пропорциональные, как мы убеди¬
лись согласно теореме Вигнера—Эккарта, коэффициентам Клебша—Гордана,
отличны от нуля, если, во-первых,
Значит, для оператора ранга j с произвольной допустимой проекцией имеет
место, как говорят, правило отбора по проекции момента
В противном случае матричные элементы этого оператора заведомо равны
нулю.
причем
что отвечает принятому соглашению о фазах: = (— 1)тЩ _т.
Для 1 = 2
так что стандартное представление получается согласно
Здесь мы учли, что
п2 = папр5ар = —п+п_ — п_п+ + п3п3,
откуда следует, что 5ар имеет диагональный вид с
5+_ = <5_+ = — 533 = — 1.
|2,2) = |1, +1)|1, +1), |2, -2) = |1, -1)|1, -1),
|2,1) = j={\l, +1>|1,0) +11,0)|1, +1)},
|2,0) = ±{\1, +1)|1, -1) +11, -1)|1, +1) + 2|1,0)|1,0)},
М'=М + т, me{-j,-j +1,..., j-1, j}.
(16.20)
254
Тема 9. Сложение моментов
Во-вторых, так как
правило отбора по модулю момента принимает вид
\AJ\zZj, j^J+J'. (16.21)
Как следствие, получаем правило запрета: если j Ф 0, то матричные
элементы с 3 = J' = 0 тождественно равны нулю, или, как говорят, переход
О -»O' запрещен.
Тема Релятивистская квантовая
1 /ч механика: поле и вторичное
^ квантование
Лекция 17
Генераторы вращений, их коммутатор, спин векторной частицы, полный
момент количества движения, генераторы бустов и полная алгебра группы
Лоренца, собственные ортохронные преобразования, дискретные операции
инверсии пространства и времени, классификация преобразований полной
группы Лоренца, базис полей и группа SL(2, С), релятивистские спиноры,
индексы с точкой и без точки.
Квантовая механика релятивистских частиц строится в 4-мерном про-
странстве-времени Минковского, которое обладает симметриями—преобра¬
зованиями координат, оставляющими инвариантными метрику, т. е. интер¬
вал
ds2 = c2 dt2-dr2.
Соответствующая группа преобразований включает в себя зависящие от не¬
прерывных параметров трансляции, вращения и бусты (переходы от одних
инерциальных систем к другим), а также дискретные преобразования зер¬
кального отражения пространства, обращения стрелы времени и зарядового
(комплексного) сопряжения.
17.1. Вращения
Бесконечно малые вращения координат 3-мерного евклидова простран¬
ства вокруг оси, направленной вдоль единичного вектора е, на угол ip —»О
в декартовой системе координат задаются векторным произведением
5r=[tp,r],
где псевдовектор поворота—
ip = ipe.
Преобразованные координаты можно записать покомпонентно
га = (г+бг)а = (5аг + еарг(рр)гг,
256
Тема 10. Релятивистская квантовая механика
или в матричном, операторном, виде1
r^Cl-is* у?)г,
(17.1)
причем компоненты матрицы 5, очевидно, задаются явно как
—1£рау.
Эти матрицы эрмитовы.
Коммутационные соотношения для этих матриц
tsa> = ieaPrSY
(17.2)
(17.3)
легко установить прямым вычислением коммутатора матриц: слева в (17.3)
имеем
т. е. имеет место тождество. Кроме того, квадрат вектора s в матричной
форме равен
Произвольный вектор, не зависящий от координат, преобразуется при
малых вращениях по тому же закону, что и сами координаты:
Согласно коммутационным соотношениям для вектора 5 (17.3) и (17.4) в век¬
торном пространстве можно выбрать базис из собственных векторов матриц
sz и s2. Собственные векторы матрицы
1Напомним, что, как было показано в лекции 7, преобразования квантовых величин —
операторов координат — и классических величин являются взаимно обратными, поэтому если
преобразования базиса Л|г) = |л?г), где — матрица преобразований координат в классике, то
для операторов координат г' = АгА~г = В принятых в этой лекции обозначениях заданы
бесконечно малые преобразования классических координат, т. е. матрицы для базиса («пас¬
сивная» картина преобразований). Переход к «активной» картине преобразований получается
простой заменой параметров на обратные, в частности, для поворотов (р -»— ip, или, что то же,
заменой знаков перед генераторами преобразований.
^a/xp^apv ^apyi^apv 25^v,
а значит, он пропорционален единичной матрице, и
s-s = 2.
Очевидно, что скалярная величина не изменяется при вращениях:
[S2, Sa]=0.
(17.4)
A' = (l — is- ip) А.
(17.5)
Лекция 17
257
легко найти: собственным значениям Я = ±1 и Я = 0 (матрица эрмитова)
соответствуют ортонормированные векторы
е-=л(-1)' Ч;)’ (1ад
так что
А = А_е+ + А+е_ + А0е0,
где связь с компонентами в исходном базисе декартовых координат, очевид¬
но,
А± ^—{Ах i i Ay}, Aq Az.
Вектор, зависящий от координат, называется векторным полем. Для него
инфинитезимальные преобразования записываются в том же виде
A/(r/) = (l-is-^)A(r). (17.7)
Поскольку для малых смещений координат
А'(г') =A'(r) + jg-5xa=А'(г) + 5хадаА(г),
где мы опустили «штрих» во втором слагаемом в силу того, что это приводит
к поправкам второго порядка малости по углу поворота. Затем необходимо
подставить вращения 5ха = ё0аРгфрХг, где мы перешли к релятивистским
тензорным, индексным, обозначениям, так что Ч>р = —уР,ху = —xr, a emnkl —
полностью антисимметричный тензор Леви-Чивита с нормировкой ё0123 = 1.
Тогда с учетом антисимметрии символа emnkl
А'(г') =А'(г) + ^е0аРг<рр{хгда - хадг)А(г),
или
AV) = A! if) + И • ipA(r), (17.8)
так что с учетом 1-ц> = —1ауа
1а = У0арЧхрдг - хгдр} = i (X х РУ = ±La, (17.9)
где мы приняли во внимание релятивистские обозначения для верхних и
нижних индексов: хр = —х@ и — idy =—iVr=pr/fi, откуда L=xxp—оператор
орбитального момента (мы использовали (• х •) для обозначения векторного
произведения, чтобы не путать его с коммутатором [•, •]).
Тогда согласно (17.7) и (17.8) преобразование функции поля в заданной
точке есть
А'(г) = (1 - i(Z + s) • ¥>)А(г), (17.10)
и, следовательно, можно ввести оператор
j = l + s, (17.11)
258
Тема 10. Релятивистская квантовая механика
х'а=ха + соаРхв, соаР = -соРа.
ИЛИ
J=hj.
Этот оператор называют полным моментом импульса поля, который состав¬
лен из суммы оператора орбитального момента L и спина векторного поля
S = hs. Полный момент имеет те же коммутационные соотношения, что и со¬
ставляющие его коммутирующие между собой слагаемые:
If, /] = H0aprf, [j2, Л = 0, (17.12)
т. е. генераторы вращений на векторных полях образуют алгебру группы
SU(2).
В релятивистских обозначениях вводят тензорный оператор
Lap = ih{xadp -хрда} = {харр - хрра}, ра = ih да, (17.13)
так что
l-ip = -lr(pr = -±^6°^ = ±LafS<o'*,
где тензор углов вращений
coat5 = -e0a/3rwY = e0apripr. (17.14)
В этих обозначениях при бесконечно малых вращениях координаты преобра¬
зуются согласно
. Ja а I . .ав _
ХР>
Откуда следует, что с необходимой точностью первого порядка по со
х/ах'а = ХаХа + 2сОаРхаХр = хаха,
т. е. сохраняется релятивистская мера—интервал, как это и должно быть.
Тогда и спиновую часть момента можно преобразовать, если записать
5А& = — i(s)^r • ч>Аг = i(s)^r • <рАг
и
(s)^ • <р = -i i0aP4-Va) = - 8^}^.
Введение спинового матричного тензора векторного поля
s^ = ih{slsr-sp6r} (17.15)
позволяет записать оператор инфинитезимальных преобразований в вектор¬
ном пространстве в виде
Rita) = 1 - ^{LMV + S„v}w^v, (17.16)
так что обьгчно вводят тензор момента
M/iV = ^jLlV + S/XV> (17.17)
или JMV =МДУ. В этих обозначениях
5аНх) = -^v(M^vfrAr(x).
Лекция 17
259
17.2. Бусты
Конечные преобразования Лоренца от одной инерциальной декартовой
системы координат к другой—бусты—имеют вид
r*'=x0chtf-(fe)shtf,
у г' = г+е{ (г • е) (ch ■& — 1) — х0 sh ft},
где e — единичный вектор в направлении скорости движения штрихованной
системы отсчета относительно начальной,
v — ev,
а модуль скорости связан с углом гиперповорота ft
-=thft.
с
Для бесконечно малых бустов, очевидно, разложение по ft дает
( х! = х0-(г-#),
(1719)
^ Г — Г XqU,
где мы ввели вектор гиперповорота ft = eft.
Это преобразование в индексных обозначениях имеет вид
х,к=хк + {5*5" - 5%5ka}ftaxn = xk-i (Ж)кп • ftxn, (17.20)
где введены антисимметричные генераторы бустов в векторном простран¬
стве
G*ra)fcn = i{5^-5^}, (17.21)
или в контравариантном виде
Wa)kn = H5k8Z-g0ngka}, (17.22)
где gmn = diag{l, —1, —1, —1} — метрика пространства Минковского в декар¬
товых координатах, a gnk = diag{l, —1, —1, —1}—обратная метрика: gmngnk —
= 5к
TTL
Если ввести антисимметричный тензор инфинитезимальных бустов
со0а = -соа0=$а, (17.23)
то,
х/к = хк + сокпхп,
или
х'к=хк _ ^{(Xa)knCO0a + WarkCOa0}xn = хк - ±&т{)кпСОт1Хп,
где тензор генераторов бустов есть
07.24)
В итоге произвольное 4-векторное поле преобразуется при бустах согласно
закону
А'к(.х') = {1 - ЦЖ-ткпАп(х) = {l - ±comlSml}knAn(x). (17.25)
260
Тема 10. Релятивистская квантовая механика
=A'k(x) + -Xldm}Ak Ос).
Разлагая находим
A'V) =А/\х) + 5хпдпА\х) =А/к(х) - ±(Sml)nqcomlxqdnAk(x) =
=А,к(х) + ^сот1т{5пт5^ - 8l5?}xndqAk(x) =
— Л/кГ^Л J
2 h
В итоге
А,к (х) = {l - ^coml (Lml + Sml) }ЫАп (jc), (17.26)
и полный тензор момента для бустов равен сумме коммутирующих друг
с другом пространственного и спинового вкладов
Mmi = Lmi + Smi. (17.27)
Коммутатор генераторов буста Ж легко вычислить в матричном представле¬
нии для векторного пространства:
[Жа, ЛГ*]* = (Xa)fcm(J^)mn - (^)fcm(Jfa)mn =
= (—i)2({5p5™ - 5^5ka}{gm0gnp-gn0gmp}-{5k5^ - <5™5*}{gm0gna-gn0gma}) =
= 5Unp ~ 5pgna = ie0aPY(.-ie°rkn') = -iea/}r(sr)kn.
В итоге
[Жа, = —ieapysr. (17.28)
Совершенно аналогично можно показать, что для полных генераторов,
включающих в себя пространственную и спиновую части:
hKa=L0a + S0a=L0a + КЖа
и
hf = |e0a^(I^r + Spr) = \eaprLpY + hsa=Ma + hsa,
имеют место следующие коммутационные соотношения:
[ja,/]=+ie^r/,
[ja)K/5]=+iea/3rKr, (17.29)
[Ка, К^] =—ieapYjr.
Эти коммутаторы можно легко вычислить, пользуясь операторным представ¬
лением для пространственных членов генераторов, т. е. полагая спиновые
части равными нулю:
j-»— iQtx V), К—»i(ctV + “dt^.
Полученные коммутационные соотношения показывают, что генераторы бу¬
стов по своему закону преобразования при вращениях являются трехмерны¬
ми векторами. Кроме того, коммутатор двух бустов по разным осям сводится,
вообще говоря, к повороту.
Лекция 17
261
17.3. Собственная ортохронная группа Лоренца
По построению генераторы вращений и бустов для 4-векторов можно
объединить в антисимметричный тензор
Jkn=Lkn + Skn, Lkn = ih(xkdn-xndk), Sfcn = ih{8™ 5ln — 5™5[}, (17.30)
где уже индексы пробегают все возможные значения в пространстве Минков-
ского, так что векторное поле инфинитезимально преобразуется согласно
Am(x) = [5ml - ±^соы}Мх). (17.31)
Антисимметричный тензор параметров преобразований связан с углами по¬
ворота (рг и направлением малого буста #а
o>afs = eafSy, а>0а=#“.
Шестипараметрическое преобразование координат—
х'т=хт + сот1х1, О)ml = -COlm.
Конечные элементы группы преобразований сохраняют интервал, так что
при
dx/m = A™ dxn
находим, что инвариантность
ds2=gmn d*/m dx/n = gmnA™Anq dxp dxq =gpq dxp dxq
в матричных обозначениях
g = AT-g-A
имеет место при
(det A)2 = 1, (17.32)
а также
goo = l=gmnKK = ОО2 - СДо)2- (17.33)
Отсюда
|A°|^1. (17.34)
Преобразования, включающие в себя исследованные нами бесконечно
малые вращения и бусты вблизи тождественного преобразования, очевидно,
имеют
det Л = 1, Л°5*1. (17.35)
Такие преобразования не содержат инверсии пространства и не меняют
стрелу времени, и поэтому они образуют соответственно собственную орто-
хронную группу Лоренца—SO+ (3,1).
Элементы группы могут быть записаны в виде решений уравнений, зада¬
ющих бесконечно малые преобразования. Например, для конечных бустов
имеем
Л($) = ехр{—\Ж •
262
Тема 10. Релятивистская квантовая механика
как решение уравнения с постоянной величиной Ж-е:
dA №
В координатах {х0, е • г, гх> матрица X • е имеет блочный вид
Л) 1 О (Л
ЛЖ-е — —
10 0 0
0 0 0 0
Vo о о о у
Поэтому поперечные координаты, естественно, не преобразуются, а для вре¬
менной и продольной компонент получаем
exp{-iJ*r-#} = ch#-Oi sh#=(_shtf _ch?) » С17-36)
как и должно быть для преобразования буста с параметром /3 = v/с = thtf.
Совершенно аналогично можно представить и конечные повороты вокруг
произвольно направленной оси.
17.4. Дискретные преобразования
Несобственные ортохронные преобразования SOl(3,1) с
detA = —1, Л°^1, (17.37)
получаются из собственных ортохронных домножением на фактор отраже¬
ния координат пространства г —> —г,
0
0 -1
0
V0
0 0^
0 0
0-10
о о -1J
(17.38)
Эти преобразования сохраняют метрику Минковского, но сами по себе, изо¬
лированно, не являются группой, так как последовательное действие пары
несобственных преобразований является собственным.
Действие собственных антиортохронных преобразований SO+(3,1) с
det Л = 1, Л°^-1, (17.39)
связано с обращением стрелы времени t-> — t. Элементы этих преобразова¬
ний строятся введением фактора
(-1 0 0 0Л
0 10 0
0 0 10
V ооо1)
sr=
(17.40)
в произведение элементов SO+(3,1).
Преобразование вещественных тензорных полей под действием операций
дискретных симметрий ^и5“ строится в соответствии с обычными правила¬
ми преобразования тензоров: по каждому из векторных индексов проводится
Лекция 17
263
умножение на соответствующие матрицы и при этом выделяются величины
с положительной и отрицательной пространственной четностью, а также
с положительной и отрицательной четностью по отношению к обращению
стрелы времени согласно стандартному правилу: величины с отрицательной
четностью меняют знак при соответствующей инверсии.
Однако генераторы инфинитезимальных преобразований группы Лорен¬
ца включают в себя мнимые единицы, т. е. комплексные факторы, а зна¬
чит, соответствуют комплекснозначным тензорным величинам. В этой связи
в квантовой механике возникает дополнительный вопрос о том, является ли
оператор дискретной симметрии линейным — сохраняющим суперпозицию
с заданными комплексными коэффициентами — или антилинейным, т. е.
переводящим суперпозицию в суперпозицию с комплексно сопряженными
коэффициентами.
Проиллюстрируем этот вопрос на двух примерах. Так, с одной стороны,
генератор пространственных вращений —орбитальный момент—
L = -iUxx V)
является в классической физике псевдовектором:
Поэтому действие квантового оператора Р на координаты
Р х Р-1 = -х, Р V Р-1 = -V,
и на генератор вращений
PLP_1=L
согласовано, если
Р i Р"1 = i,
значит, оператор линейный.
С другой стороны, при обращении стрелы времени движение частицы
заменяется на противоположное, так что «в классике»
С учетом естественного определения действия обращения времени на коор¬
динаты
ТхТ~г=х, TVT_1 = V,
находим, что
Т L Т~1 = —L,
если только
Т i Т-1 = —i,
а значит, оператор обращения времени антилинейный. К такому же выводу
об антилинейности инверсии времени можно прийти, если рассмотреть пре¬
образование энергии и импульса частицы, которая движется по траектории
264
Тема 10. Релятивистская квантовая механика
в обратную сторону, а именно
& &
Ро *Ро> Р *~Р-
Из антилинейности следует, например, что вектор, отвечающий генера¬
тору бустов для скалярных полей (спиновая матрица тождественно равна
нулю)
JC=i(ctV + fat),
вопреки наивным ожиданиям, сохраняется:
ГКТ~1=К,
так как
т t Т"1 = -t, Т dt ТГ1 = -dt.
Полное отражение пространства-времени строится как произведение Р • Т.
Произведение этой дискретной симметрии на элементы SO+(3, 1) дает эле¬
менты несобственных антиортохронных преобразований SOi(3,1) с
det Л = —1, Л^-1. (17.41)
Под действием оператора РТ генераторы преобразований группы Лорен¬
ца меняют знак:
РТ L (РТ)-1 = —L, РТ К (РТ)'"1 = —К.
В результате действия операции полного отражения мы получаем движение
в зеркальном мире с обращенной стрелой времени, т. е. обратно по времени.
Введем операцию комплексного сопряжения К, которая, очевидно, не ме¬
няет координаты и метрику пространства Минковского, но также формально
обращает знаки генераторов:
К L К"1 = —L, К К К-1 = -К.
Поэтому действие комбинированного оператора КРТ на генераторы пре¬
образований группы Лоренца сводится к тождественному: отсюда следует,
что величины, инвариантные относительно собственной ортохронной груп¬
пы Лоренца, например, вещественное действие для скалярных полей, после
преобразования операции ЮРТ остаются инвариантными относительно этой
же группы. Это утверждение есть качественное указание на СРТ-теорему
в релятивистской квантовой механике, где оператору комплексного сопря¬
жения соответствует оператор зарядового сопряжения С, действующий на
состояния частиц (в отличие от его представления в виде комплексного
сопряжения, действующего на поля и генераторы группы Лоренца).
Полная группа вращений и бустов пространства Минковского включает
в себя и дискретные симметрии, т. е. все компоненты: собственные и несоб¬
ственные вращения, ортохронные и антиортохронные бусты.
Лекция 17
265
17.5. Классификация состояний: представления
Действие преобразований группы Лоренца на классические поля класси¬
фицируется введением базисов собственных функций для генераторов груп¬
пы. Для этого необходимо выделить допустимые совместно измеримые, т. е.
взаимно коммутирующие, величины. Введем комбинации генераторов
j?± = l(j±iK). (17.42)
Тогда коммутационные соотношения для этих величин получаются подста¬
новкой известных коммутаторов для генераторов вращений и бустов (см.
(17.29)), так что (здесь индексы в 3-мерном евклидовом пространстве распо¬
ложены снизу для упрощения записи)
[/£./?]=°> (17.43)
а также
[(/+)2,/£]= 0, [(/-)2,/^]=0. (17.44)
Эти соотношения показывают, что алгебра генераторов группы Лоренца
SO(3,1) эквивалентна (изоморфна) паре алгебр произведения групп враще¬
ний SU(2) <8> SU(2): so(3,1) =su(2) Фзи(2). Поэтому поля можно разлагать по
базису собственных значений операторов
(/+)2*(х) = Я+(Я+ + 1)*(х), Я+ - полуцелое,
/з*(*)=т+*00, т+€{Я+, Я+-1,..., 1-Я+, -Я+>,
(17.45)
и
(17.46)
)20(х) = Я_(Я_ + 1)0(х), Я_ - полуцелое,
0(х) = т_0(х), т_е{А_, А_-1,..., 1 -Я_, -Я_}.
Значит, базис полей можно характеризовать парой чисел (А+, А_), имея
в виду возможность вырождения по проекциям т±: поля % и 0 могут иметь
2А+ +1 и 2А_ +1 компонент соответственно.
Обратные преобразования
J=/++/~, i К=/+-/- (17.47)
показывают, во-первых, что генератор вращений принимает вещественные
значения, а генератор бустов—чисто мнимые: такие представления группы
Лоренца называются неунитарными. Во-вторых, компонентные поля
допускают затем еще и разложение по базису с определенными значения¬
ми j.
Спиноры: от SO(3,1) к SL(2, С). Наличие полуцелых значений А± указы¬
вает на важнейший факт: подобно тому, как группа вращений 3-мерного ев¬
клидова пространства SO(3) при введении спиноров обобщалась до группы
вращений спиноров SU(2), так и группа Лоренца пространства Минковского
266
Тема 10. Релятивистская квантовая механика
обобщается до группы преобразований релятивистских спиноров SL(2, С).
В самом деле, рассмотрим поля—релятивистские спиноры-столбцы, которые
характеризуются парами (А+, А_)
хА~ (i°)
и
(°,|),
где индексы а, а принимают значения 1, 2. Для спинора %
= /"=0,
где <г—матрицы Паули, так что
!-\о, к=-|<т.
Совершенно аналогично для спинора 9
Jf~ = l а, /+ = 0
и
Матрица преобразований для 9 записывается в стандартном виде
Л_ = exp{-i(j• ip +К•'^)> = ехр|-|сг • <р + -а •#)}. (17.48)
В силу тождества, которое легко доказать, переходя к базису собственных
значений матрицы А,
deteA = etrA,
где tr А означает взятие следа матрицы А (сумма собственных значений),
матрицы 2x2 самого общего вида = (Л_)£ имеют единичный детерми¬
нант:
det М = 1
(для обозначение таких специальных матриц используется символ S). Ра¬
венство tr А = 0 следует из того, что матрицы Паули образуют базис для
комплекснозначных матриц (символ С) со следом, равным нулю. Поскольку
матрицы задают линейные преобразования спиноров (символ L), группа
преобразований спиноров носит название SL(2, С).
Матрица преобразований для спиноров %
Л+ = ехр{—i(j- ip +K-tf)} = expj“0- •</> - •#)} (17.49)
может быть получена, как и в случае нерелятивистских спиноров, с помощью
сопряжения
А+ = а2-А*_-а2. (17.50)
Лекция 17
267
Поэтому спиноры1
вй = {(нг2в)в>* = K(i<720)o = 0ср
преобразуются как спиноры 0^, а спиноры
Ха = {(-i°2 хГУ = K(-i <т2хУ = Ш
ср
преобразуются как спиноры (о>
Кроме того, из явного вида матриц следует, что
Л1 = Л;1. (17.51)
Определим матрицы
Тогда
(стт)ай = ( 1,+а), (17.52)
(ат)йа = (1,-а). (17.53)
(сгт(7п + <тпстт)“ = 2gmn5p, (17.54)
(<7тстп + стпстт)“ = 2gmn5% (17.55)
'Р * Р
а также введем антисимметричные символы
^ (сгт(7п - апат)р = (сгтп)^, (17.56)
t(.aman-an<7m)j = (amn)°:. (17.57)
Отсюда легко заметить, что для пространственных компонент
= ац,у = -е ар
2 3
а для временных
<т°м = —cr0fl = ^о-й.
Поэтому матрицы преобразований представимы в виде
Л_ = ехр{ - ± сгтпо>тп}, Л+ = ехр|" атпсотп }.
Спинорная метрика
J)
поднимает индекс спинора 6р и переводит его в спинор-строку:
ва=еа?вр=а о-2е)т=е* = -eTi<r2=-ер8Ра.
Поэтому преобразование по верхним индексам без точки производится мат¬
рицей
-io*2Alio,2 = AI1 <=> eAr_e = AZ1,
1Мы ввели здесь индекс ср, смысл которого будет выяснен и обоснован ниже.
268
Тема 10. Релятивистская квантовая механика
откуда следует, что, во-первых,
9a^a = 6^ = im
является инвариантом относительно группы SL(2, С) и, следовательно, груп¬
пы Лоренца, а во-вторых, спинорная метрика также сохраняется при дей¬
ствии группы релятивистских преобразований спиноров:
е«х(> =e»v(AZ1)“(A71)Z = KAZ1)TiAZ1}ap = eaf}.
(J, У
Аналогичные конструкции метрики и инвариантной свертки имеют место и
для спиноров с точечными индексами: инвариантная спинорная метрика еаР
С нормировкой е12 = 1, спиноры-строки Ха = СарХ1* = {(-10*2ШТ = {(z)cp>t
преобразуются матрицей А"1 =л1, и ХаФ° = ХсР V = inv*
4-вектор. Произвольная эрмитово самосопряженная величина V в пред¬
ставлении т. е. несущая пару индексов {аа}, может быть разложена
по базису матриц сгп:
№аа = °ПааУп> С17.58)
причем
так как, очевидно,
tr{CTmcrn} = 2 gmn. (17.60)
Согласно установленным нами законам преобразования верхних и нижних
спинорных индексов, преобразования группы SL(2, С) переводят V в эрми¬
тову величину
У/ = Л_УЛ1, (17.61)
которая опять может быть разложена по исходному базису:
Заметим, что
det = det{A_ УЛ1} = |det A_ |2 det V = det V. (17.62)
При этом
P_fV0+V3 Vi-iVj'V
+ V0-V3J>
так что
/W \У — \,o
det V = Vq— V2,
а равенство детерминантов (17.62) означает, что преобразование сохраняет
лоренц-инвариантную длину 4-вектора, т. е. представляет собой элемент
группы Лоренца на 4-векторах. Это представление является двузначным, так
как матрицы А_ и —А_ приводят к идентичным преобразованиям 4-вектора.
Лекция 17
269
В случае инфинитезимальных преобразований cokl —> О,
A_ = l — ^(7kiCoklj Al = 1-1- ^aklcokl
находим, что
у/m _ ут + ]_ tr{o-fcio-mCTn - aklanam}coklVn,
где, например, разложение на симметричную и антисимметричную по пере¬
становке индексов части
атсгп = gmn — 2iamn
приводит к
tr{aklaman} = -2i tr{aklamn},
и затем, как легко заметить, используя явный вид генераторов, получаем
tr{<7W<7mn} = \{5™5Ч - 545?} - У™.
Совершенно аналогично
tr{akl(Tmn} = 1{5£8? - 5пк5{“} +
В итоге приведение подобных членов дает
V/m = Vm + a>mnVn,
т. е. инфинитезимальное преобразование 4-вектора. Отсюда, в частности,
следует, что величины
в(7тх = ваа^хй и ватх = 0ь(ат)йаха
ведут себя как 4-векторы.
Таким образом, мы построили схему представления полей в базисе, ха¬
рактеризуемом парой {Я+, Я_} в группе SL(2, С), и продемонстрировали
процедуру применения этой схемы на примере полей спиноров и 4-векторов.
Подчеркнем, что действие группы на релятивистских полях не сводится, во¬
обще говоря, к унитарным преобразованиям, как это имело место, например,
в нерелятивистской квантовой механике с трансляциями и вращениями.
Поэтому сами эти поля, скорее всего, не могут рассматриваться в качестве
волновых функций или векторов состояний релятивистских частиц в гиль¬
бертовом пространстве. Например, в случае спиноров, поскольку (бд)1* = вй
и (хаУ = Ха> величины
в^в = 5йавйва = ва°в
и
хЧ = 5а<хХаХ“ = Х°0Х
преобразуются как нулевые компоненты 4-векторов и не являются скаляра¬
ми. Впрочем, их можно рассматривать как пространственные плотности, так
как интегралы
J d3x 0<7°0 и J d3x ха°Х
270
Тема 10. Релятивистская квантовая механика
являются релятивистскими инвариантами. Поэтому для окончательного ре¬
шения вопроса о возможности считать эти инварианты вероятностями необ¬
ходимо построить уравнения движения для полей, исходя из вариационного
принципа, с каноническим определением положительно определенного га¬
мильтониана и рассмотреть его совместимость с положительной определен¬
ностью вероятностей.
Лекция 18
Трансляции и неоднородная группа Лоренца, коммутаторы генераторов, век¬
тор Паули—Любанского, классификация Вигнера для массивных и безмассо-
вых полей, спиральность, киральные поля, действие дискретных преобразо¬
ваний на генераторы, СРТ-теорема, свободные классические вещественное
и комплексное скалярные поля, положительно- и отрицательно-частотные
решения, совокупность осцилляторов, динамические переменные поля и их
квантование, операторы рождения и уничтожения скалярных частиц, их
зависимость от времени и координаты, классическое поле как среднее зна¬
чение оператора поля по когерентным состояниям, вторичное квантование
и пространство Фока, оператор заряда, античастицы, зарядовое сопряжение
и инверсии пространства и времени в фоковском пространстве и их действие
на квантованное скалярное поле.
18.1. Группа Пуанкаре
Трансляции декартовых координат пространства Минковского
х'к=хк + ак = ехр {дпап}хк = ехр{ - ±рпап }xfc, (18.1)
где генератор сдвигов —оператор 4-импульса
Рп~ <ЭП,
не преобразуют тензорные индексы полей, так что, например, для векторно¬
го поля
А/к(х/)=Ак(х).
С учетом
А'к (х') =A'k(x + cQ = expj—^рпап j А'к (х)
находим
А'к (х) = expj ±рпап j Ак (х). (18.2)
Полная группа Пуанкаре есть объединение группы трансляций и группы
Лоренца. В таком случае говорят также о неоднородной (Inhomogeneous)
группе Лоренца: ISO(3,1).
Для того чтобы определить допустимый базис разложения полей, теперь
необходимо установить и коммутационные соотношения для генераторов
Лекция 18
271
трансляций и генераторов группы Лоренца. Поскольку генераторы трансля¬
ций—линейные дифференциальные операторы, они, естественно, коммути¬
руют между собой, а также со спиновыми генераторами, которые представ¬
ляют собой числовые матрицы:
Остальные коммутаторы легко найти, используя их явный вид, так что
Значит, 4-вектор импульса преобразуется при вращениях и бустах, как это
и должно быть, причем
т. е. квадрат 4-импульса—релятивистский инвариант.
Другой инвариант был введен Паули и Любанским. Псевдовектор Пау¬
ли—Любанского определяется как
компоненты этого псевдовектора естественным образом преобразуются при
действии группы Лоренца.
Теория группы Пуанкаре в квантовой механике была построена Вигне¬
ром. Согласно Вигнеру, вакуумному состоянию (без частиц) приписывается
нулевая энергия, а физическим состояниям релятивистской частицы отвеча¬
ют положительные значения энергии на фоне вакуума:
(гипотетические частицы с р2 < 0 называют тахионами). Тогда значение W2
задается детерминантом
w2 = -\{PnPnSkiSkl+pnplSklSnk+pnpkSklSln -
-PnPlSklSkn-PnPkSkiSnl-PnPnSklSlk},
[РьРп] = 0, [рь Smn]=0.
(18.3)
[f,P^ = ^aprPr> [ДРо]=0,
[Ka,pP] = i5aflp0, [Ka,poi = ipa.
(18.4)
[Др2] = [К“,р2]=0,
(18.5)
Wm = -±i™>*pnSkI,
(18.6)
(18.7)
Po^°>
а также 4-импульсы с неотрицательной инвариантной массой:
р2^ О
что можно представить в виде
272
Тема 10. Релятивистская квантовая механика
и после использования антисимметрии тензора спина получаем
w2 = -\{p2S2 - 2pnpkSklSnly.
Затем рассматривают случаи массивных и безмассовых частиц.
18.1.1. Массивные частицы. При р2=т2с2> 0 квадрат 4-вектора W2, яв¬
ляющийся релятивистским инвариантом, удобно вычислить в системе покоя
частицы. Тогда р = (тс, 0), и
W2 = ~lm2c2{SklSkl -2S0aS0a} = -|m2c2Sa/3Sa/3 =
= —m2c2h2s2 = —m2c2h2s(s +1).
Значит, при заданной массе собственное значение W2 определяется квадра¬
том спина. В итоге все состояния свободной частицы заданного типа отвеча¬
ют одинаковым значениям релятивистских инвариантов: массы и квадрата
спина, — отличаются же они. значениями импульса и проекции спина на
выделенное направление. Таким образом, состояние свободной массивной
частицы можно характеризовать полным набором попарно коммутирующих
наблюдаемых—масса, импульс, спин и его проекция на выделенное направ¬
ление: {т, р, 5, sz}.
18.1.2. Безмассовые частицы. При р2 = 0 распишем в компонентах
W2=PnPkSkiSnl=pnpkSkoSn0+pnpkSkaSna =
= -papPS0aS^+p2S0aSQa-prpPsraSpa+p0p4SpaS0a-S0asPa) =
= Й2{(р • Ж)2-р2УС2 - (р х s)2 + pop • {(s х X) - (X х s')}}.
Раскрывая квадрат векторного произведения, находим
w2 = -Ро (s2 + Ж2) + (р • s)2 + (р • X)2 + pop • {(s х Ж) — (Ж х 5)}.
Выражая генераторы спина и бустов через эрмитовы векторы и
получаем
Ж2 = -4р2Й2{/+-/"-^(р-/+)(р-/-)-^р-(/+х/-)}.
Выберем ось проецирования спина вдоль пространственной компоненты им¬
пульса: р = (0,0, ро), откуда р / = р0/з, тогда
w2=-4p02ft2{/aVr+А+А“ - iCA+A“ - Л+/Г)}>
ИЛИ
W2 = -4р2Й2{/+ + i/2+H/r - i/2“> = -4p^2AV-~.
В искомом базисе поля удовлетворяют уравнению на собственные значения
оператора W2. Но у повышающего оператора в группе SU(2) существуют
только два собственных вектора: во-первых, это «вакуум» с нулевым момен¬
том
/*10) = 0, (18.8)
Лекция 18
273
а во-вторых, это старший вектор с нулевым собственным значением
/++|А+,А+)=0. (18.9)
Точно так же для понижающего оператора есть два собственных вектора:
вакуум (18.8) и младший вектор с нулевым собственным значением
/_~|А_, -А_)=0. (18.10)
При этом, конечно, на этих полях (т. е. при действии операторов на поля)
проекция спина на ось импульса или, как говорят, спиральность имеет зна¬
чения .
р '<? — jr± — ±х,
Ро S3
причем на физических полях W2 = 0.
Таким образом, среди безмассовых полей со спином базис составляют
так называемые киральные поля полуцелого спина и поляризованные поля
целого спина:
правые поля с положительной киральностью и спиральностью s = А+:
/-=0 => Ж = —is, /+=s, (18.11)
левые поля с отрицательной киральностью и спиральностью s = -А_:
J+ = 0 => JXT = is, /~ = s, (18.12)
а также их произведения и вакуум.
Рассмотрим компоненты псевдовектора Паули—Любанского для кираль-
ных и поляризованных полей. С учетом
Spr = heprpsP
нулевая компонента
W0 = ~l^rpaSpY=hPs=±p0hX±.
При вычислении пространственной компоненты необходимо использовать
то, что
is0r = JTr = Tisr,
откуда
wa = _ 1 ё«<>Ргро8рг - ^2eaP°rP/3S0r =h{p0sa т i(p х «)“}•
Поэтому при р ТТ z
^(3)=Ро/з± = ±Я±Ро,
I w(2) = Ро/з* =F iPoJi = ±ip0/± = о,
^W(1)= ± ipo/^=р0/± = 0,
274
Тема 10. Релятивистская квантовая механика
где равенства понимаются в слабом смысле, т. е. они имеют место при
действии операторов на поля. Эти результаты представимы в простой кова-
риантной форме в виде пропорциональности 4-векторов
±Wk=spk, s = ±A±. (18.13)
Это согласуется с установленными нами условиями для ненулевых 4-векто¬
ров:
р2 = о, W2 = О, p-w = 0,
откуда следует их пропорциональность (18.13).
18.2. Ковариантный вид КОММУТАТОРОВ
И ДИСКРЕТНЫЕ СИММЕТРИИ
Собирая приведенные выше покомпонентные коммутационные соотно¬
шения для генераторов группы Пуанкаре, выпишем в целях полноты изло¬
жения эти коммутаторы в ковариантном виде
№тп> ^^Smk^nl ~ Sml^nk Snl^mk ““ Snk^ml}> (18.14)
что можно также установить непосредственно, используя явный вид генера¬
торов Lmn. Аналогично,
Umnf PkJ ”ift{SmkPn “ (18.15)
Относительно зеркальных инверсий пространства операторы спина и мо¬
мента являются тензорами
(18.16)
где & =diag(l, -1, -1, —1)—симметричная диагональная матрица преобра¬
зований координат при инверсии (см. явный вид матрицы & в лекции 10,
раздел 17.4, формула (17.38)). Напомним, что оператор спина sr = ie“^rSa(3 —
псевдовектор. Импульс является вектором:
РртР"1=^рь (18.17)
и соответственно вектор Паули—Любанского—псевдовектор:
Р№тРч = -^. (18.18)
Из последних двух уравнений (18.18) и (18.17) заключаем, что спиралъностъ
безмассовой частицы меняет знак при пространственных инверсиях:
р
S >—5.
Аналогично, для действия оператора обращения стрелы времени с учетом
его антилинейности находим, что импульс является вектором с отрицатель¬
ной Т -четностью
Трт Т-а = -^рь (18.19)
Лекция 18
275
а генераторы 4-вращений — тензором 2-го ранга с отрицательной Г-четно-
стью
TJmn (18.20)
где S' — соответствующая матрица преобразований декартовых координат
пространства Минковского. Вектор Паули—Любанского также имеет отрица¬
тельную Г-четность:
Т Wm Т-1 = —&£wk. (18.21)
Поэтому спиралъностъ безмассовых частиц сохраняется при обращении стре¬
лы времени: т
S >5.
С учетом матричного произведения
т L т
действие антиунитарного преобразования полной инверсии пространства
Минковского РТ дает
РТр" (РТ)_1=рп, PTJmn (Ff)-1 = -Jmn, PTVT (PT)_1 = -Wn (18.22)
и обращение спиральности
РТ
5 >—$.
Действие для полей строится как функционал, зависящий от самих по¬
лей и генераторов группы Пуанкаре в соответствующих представлениях так,
чтобы оно было инвариантно относительно преобразований собственной
ортохронной группы Лоренца и пространственно-временных трансляций,
т. е. так, чтобы действие было скаляром. Это, в частности, означает, что
спинорные поля (фермионы) входят в виде билинейных комбинаций, кова-
риантным образом преобразующихся при действии собственной ортохрон¬
ной подгруппы Пуанкаре. Второе важнейшее свойство —действие является
вещественным скаляром. Наконец, в-третьих, действие зависит от зарядов
частиц g = Ye, которые являются лоренцевыми скалярами, но при этом зна¬
чение безразмерных зарядовых констант Y может зависеть от поляризации
поля1. Поэтому после полного пространственно-временного отражения мы
приходим к действию
РТ
' S[*(х), Рп, Jmn, Wn, Y, е] —>S„=S№„(-x), pn,-Jmn,-wn, Y„, e],
а условие его вещественности
S* = S,
с учетом действия комплексного сопряжения на генераторы
КрпК-1 = -рп, К JmnK-1 = -Jmn, КП'^Г,
1Например, левые и правые киральные поля могут обладать разными зарядами, как это име¬
ет место в стандартной модели электрослабого взаимодействия, где в слабых взаимодействиях
с передачей заряда (заряженные токи, как при бета-распаде нейтрона) участвуют лишь левые
спиноры, в то время как заряд правых спиноров принят равным нулю.
276
Тема 10. Релятивистская квантовая механика
означает, что
S№(X), рп, Jmn, Wn] -Рп, Jmn,-Wn].
Воспользуемся тем, что действие является функционалом, так что замена
переменных с единичным якобианом
xk^-xk
оставляет инвариантным и само действие, и лагранжиан и согласно этой
подстановке дает
РП^-РП, Jmn - Jmn,
так что
S№(x), р\ Jmn, wn] pn, Jmn, W"].
Но комплексное сопряжение меняет знак комплексной фазы поля, а значит,
и знак заряда, если понимать его как параметр некоторого калибровочного
преобразования. В самом деле, при комплексном сопряжении калибровочное
преобразование трансформируется согласно
^u(x) = e“iu^'I'00 -> Ф*00 = е"|лФ*00,
так что соответствующий ток меняет знак
-/п[Ф 00] = ^ _> ijn£!— _Ijn[ф*
c) L^uWJ 5dnVuM du cjkl*«wJ 5dnV*uM du cJ LV«WJl
Поэтому говорят, что действие, полученное операцией полного простран-
ственно-временного отражения РТ, описывает зарядово сопряженные по¬
ля, для которых мы имеем те же значения генераторов группы Пуанкаре.
Следовательно, движение в зеркальном мире с обратной стрелой времени
описывает движение античастиц — частиц противоположного знака заряда.
В итоге комбинация комплексного сопряжения с полной инверсией про¬
странства-времени после описанной замены координат дает для веществен¬
ного действия
РТ
S№00, р\ Jmn, Wn, Y, е] —,S№^(JC), рп, Jmn, wn, У„, -е].
Как мы увидим ниже, возможно введение независимой линейной опера¬
ции, действующей на поля так, что сохраняются значения генераторов
СрпС~1=рп, CJmnC~1=Jmn, CWnC~1 = Wn (18.23)
и спиральности на преобразованных полях
с
5 >5,
но меняющей знаки зарядов
Лекция 18
277
и восстанавливающей безразмерные зарядовые константы
^СГГ = Y•
Поэтому для действия получим
(Гртг
S№(X), р\ Jmn) Wn, У, е] —^Scpr = S№jpr(*), рп, Jmn, W", 7, е]. (18.24)
Значит, операция СРТ приводит к действию на полях ФСРТ которые удовле¬
творяют тем же уравнениям движения, что и исходные поля Ф, поскольку
действие является СРТ-инвариантным, так как все генераторы преобразо¬
ваний и заряды остаются равными исходным значениям, что составляет
содержание СРТ-теоремы Паули—Людерса—Вигнера.
18.3. Скалярное поле
У скалярного поля </?(*), которое реализует базис для полей (0, 0) в пред¬
ставлении группы SO(3,1), спиновые генераторы тождественно равны нулю,
так что тождественно равен нулю и 4-вектор Паули—Любанского. Поэтому
единственное уравнение для такого поля—уравнение на собственное значе¬
ния квадрата 4-импульса:
(р2 — т2с2) <р (х) = 0, (18.25)
где, как обычно, х = (ct, дс), а генераторы трансляций задают 4-вектор
pn = ih^ = ih дп.
Уравнение для скалярного поля, которое носит имя Клейна—Гордона—Фока,
может быть получено вариацией по полю (/?(*) действия, инвариантного от¬
носительно преобразований группы трансляций и собственной ортохронной
группы Лоренца:
S = ^2 / d4* фМ (р2 - пг2с2) у Сл:). (18.26)
Решение волнового уравнения для свободного вещественного скалярного
поля можно представить в виде разложения по плоским волнам с положи¬
тельными и отрицательными частотами и волновым вектором k=p/h:
<p(t, х) = J 2^2nreikX{aic0> fc)e-i<ut + /3(«. k^iwty> (18.27)
где
cl> = ■§• л/ m2c2 + h2k2.
n
Комплексное сопряжение дает
4>\t, x) = J 2^kse~ikX{a4<0’ + fc)e_ie,t},
278
Тема 10. Релятивистская квантовая механика
и условие вещественности поля
</>*(t, *) = </? (t,x)
означает, что
Р (со, к) = а*(со, -fc), (18.28)
и в результате
Ч>(t,х) = J* 2^2п)з{а(й°’ к^Ы~кХ) + «*(«. Юе1(ш‘~кх)}• (18.29)
Обычно определяют положительно и отрицательно частотные поля
</>(±)(t,x) = J 2ш(2т03 а(±0>> ±k)e:fll<ot~k'x), (18.30)
где
а.(—со, —к) = а*(со, к).
При этом «плюс»- и «минус»-поля переходят друг в друга при комплексном
сопряжении:
[</_) (*)]* = </> (+)(х).
Переходя к 4-векторным обозначениям, получим явно ковариантную за¬
пись для вещественного скалярного поля
V>W = VC+)W + V(-)W=J -0^а(тп5(к2-т2с2/Н2)е~[кх, (18.31)
причем
а(-к) = а*(к)
5(^-mV/rt = 5jL{6(k0-f)+5(k0 + f)}.
Действие для вещественного скалярного поля может быть представлено
в лагранжевом виде
S = f dtL = j dt J d3x|{^2-(VV)2-^Y>2}, (18.32)
так что функция Лагранжа—
а энергия задается гамильтонианом, который получается обычным методом
преобразования Лежандра в классической механике:
H = J = i J + + 08.33)
Лекция 18
279
Интегрирование по координатам х сводится к интегралу по волновому век¬
тору по следующей схеме:
/ d3jt/2W=J d>*J jgj/оо.»* J
где фурье-образ функции —
/(fc) = J d3jc/(x)e~ifc*.
Переставляя порядок интегрирования, с учетом
/ d3x ет+к') х = (2я)3<5(к+к0
находим
Jd3x/2(x) = j ^L/(fc)/(-k).
Используя эту процедуру, вычислим энергию волнового пакета свободного
скалярного поля:
Е=\/ ?5l^{(-^+fc2+!§!)e"2icl)ta^fc)«^-fe)+
+ [~^ + к2 + ^^е2Ша*(а>, к)а*(о>, ~Ю +
+ + к2 + [<*(<о, Юа*(<о, к) + а*(а>, к)а(<о, fc)]|.
Осциллирующие со временем вклады зануляются вследствие уравнения дви¬
жения
-*Т + к2 + ф^ = 0.
сг п2
Поэтому окончательно получаем
Ч
<1834)
Отсюда видно, что по своему физическому смыслу величина
п0(к) = ^\а(со,к)\2 (18.35)
I
представляет собой плотность состояний с энергией е(к) =Ксов пространстве
волнового вектора. Определим комплексные параметры а0(к) с нереляти¬
вистской нормировкой
а0(к) = —=L=a(co, к) => n0(fc) = |a0(k)|2. (18.36)
V 2e(fc)
В полной аналогии с классическим осциллятором введем пару вещественных
канонических переменных: динамическую координату q(fc) и сопряженный
ей импульс р (к):
q(fc) = -^{a*(fc) + a0(fc)>, p(fc) = ^{a*(fc)-a0(k)}, (18.37)
280
Тема 10. Релятивистская квантовая механика
так что
|ct0Cfc)|2 = |{q2(fc) +p2(k)},
и гамильтониан для осциллятора1 с волновым вектором fc—
f>(fc) = e(fc)f{q2(fc)+p2(fc)}. (18.38)
Тогда энергия вещественного скалярного поля представима в виде суммы
гамильтонианов элементарных осцилляторов
н=\ (жз9)
Квантование канонической пары {q(fc),p(fc)} эквивалентно введению опе¬
раторов рождения и уничтожения квантов {aj(fc), a0(fc)} с коммутационным
соотношением
[a0(fc), aj(fc')] = (2л)35(к-к'). (18.40)
Это следует из принятой нами нормировки одночастичных состояний в не¬
прерывном спектре, так что матричный элемент единицы—
(k\k') = (2л)3 5 (к — к'),
так как
|fc/) = a+(fc/)|0), (fc| = (0|ao(fc),
где |0) — состояние вакуума, для которого, как обычно, o0(fc)|0) =0, и, следо¬
вательно,
{к\к') = (0\a0(k)al(k')\0) = (0|[a0(к), aj(k')]|0> = (2л)3 5 (к-к').
Вводя когерентные состояния2 | a0(fc)),
a0(fc)|a0(fc)) = cc0(fc) |a0(fc)) • (a0(fc)|a0(fc)),
находим, что классические величины пары канонических переменных зада¬
ются средними значениями в когерентном состоянии:
ч№) - -к ытм) (°.№)Ka*№)+ao«)K№)>.
т = Тг WhU) «>•
1Для того чтобы убедиться в гамильтоновости системы, необходимо «восстановить» зави¬
симость от времени: а(со, к) •-> а(со, fc)e”1£0t, — и, соответственно, использовать эти величины
в определении зависящих от времени координат q и импульсов р, а также показать, что имеют
место уравнения Гамильтона q = df)/dp, р = — dfj/dq.
2В отличие от случая гармонического одномерного осциллятора мы ввели фактор нормы
когерентного состояния релятивистского поля, причем эта норма формально не равна единице,
а определяется так же, как и для одночастичного состояния. Это связано с тем, что оператор
уничтожения кванта с другим значением волнового вектора при действии на когерентное
состояние просто зануляет его, а отличное от нуля значение получается только при совпадении
значений волнового вектора в аргументах оператора уничтожения и когерентного состояния.
Лекция 18
281
Зависимость операторов рождения от времени дается уравнением Гейзен¬
берга:
ift^ = [a(fc),$(fc)], a(k)|t=0 = a0(fc), a(k) = е-,л>Ч(к),
где решение легко полнить, действуя обеими частями уравнения Гейзенбер¬
га на одночастичное состояние |fc), для которого 0(fc)|fc) = hco\k), а энергия
вакуума полагается равной нулю О(к)|0) =0. Последнее условие выполняется
автоматически, если принять нормальное упорядочивание операторов для га¬
мильтониана: нормальный символ оператора :F: получается перестановкой
всех операторов рождения налево от операторов уничтожения, причем каж¬
дая операция перестановки операторов из исходного выражения сопровож¬
дается умножением на фактор перестановки бозонного или фермионного
оператора. Например,
•МкУ- = \ :{aj(fc)a0(fc) + a0(fc)aj(fc)}: = aj(fc)a0(fc).
Эта операция позволяет также избавиться от формально бесконечной суммы
вакуумных энергий элементарных осцилляторов1.
При выводе уравнения Гейзенберга используется оператор сдвигов по
времени—оператор эволюции для бесконечно малых преобразований:
0=l-j§dt,
так что, опуская функциональную зависимость от волнового вектора, полу¬
чаем
da = L/ta0L/-a0 = —^[a0, f)] dt.
Совершенно аналогично оператор сдвига по координате—оператор трансля¬
ции для бесконечно малых преобразований
t = 1 + ifc-djc
приводит к зависимости от сдвига координат
da=fta0f’ —a0 = i[ao, fc] • dx.
1Отметим, что вычисление энергии вакуума с помощью неупорядоченного гамильтониана
привело бы к формально бесконечной сумме вакуумных энергий элементарных осцилляторов.
Поэтому соглашение о нормальном упорядочивании есть в сущности простейший вариант так
называемой перенормировки, то есть переопределения «физических» операторов наблюдаемых
с целью устранения формальных расходимостей. В локальной квантовой теории полей при нали¬
чии взаимодействия проблемы, связанные с появлением расходимостей, решаются существенно
более сложными методами. Именно, в квантовой теории поля было разработано несколько схем
перенормировочных процедур, которые обладают групповыми свойствами (ренормгруппа).
При этом требование устранения расходимостей за счет введения перенормировки лишь конеч¬
ного числа физических величин (напрмер, массы, заряда и нормировки волновой функции, как
в квантовой электродинамике) стало центральным при анализе теоретической самосогласован-
ности квантовой теории взаимодействия элементарных частиц (условие перенормируемости).
Затем для устранения расходимостей стали использовать симметрию бозонных и фермионных
мод в теории (суперсимметрия) и переход к рассмотрению нелокальных теорий (теория струн).
Можно утверждать, что именно обсуждение этой проблемы определило направление развития
релятивистской квантовой теории во второй половине XX века.
282
Тема 10. Релятивистская квантовая механика
Отсюда
—iVa=[o, fc], о|х=0 = О0. (18.41)
Решение этого уравнения легко получить, действуя обеими частями равен¬
ства на одночастичное состояние |fc) с учетом того, что
fc|k) = k|k), fc|0) = 0 => [a, k]|fc) =ka|fc).
Поэтому
—iVa=fca => a=elfcxo0.
Значит, оператор динамической координаты
q0(fc) = -^{aj(fc) + a0(fc)}
приобретает зависимость от времени и координаты в виде
№ = j={eikxal(k)+e~ikxa0m. (18.42)
Тогда после перехода к релятивистской нормировке операторов рождения
и уничтожения
ао = -=й => [a(.k), a4k')]=2hco(2n)35(k-k')
л/2 hco
усреднение оператора
ф{к) = ^q(fc) = ^{eikxa4k)+e~ikxam
по когерентным состояниям
(Ф(Ю) = (a(fc)|a(fc)) (а(Ю\ф(к)\а(к)) = ^{eikxa*(k) + e~ikxa(k)}
в точности дает классическое поле
Квантованное поле в релятивистской нормировке имеет вид оператора
<£(*) = J 2^£)3{eibCat(fc) + e"ifc*a(fc)}- (18-43)
Подчеркнем, что классическое поле не имеет смысла амплитуды вероят¬
ности, т. е. волновой функции. Оно является средним значением оператора
квантованного поля по когерентным состояниям. Согласно принципу со¬
ответствия, при большом количестве квантов |a(fc)|2»l флуктуациями их
количества можно пренебречь, и мы имеем наблюдаемое классическое поле.
По построению гамильтониан квантованного поля получается из гамиль¬
тониана классического поля подстановкой квантованного поля и взятием
нормального символа:
Ж = \ j d3x:{^(<K*))2 + (V<£(jt))2 + ^<£2(x)}:. (18.44)
Лекция 18
283
18.3.1. Фоковское пространство. Состояния, порождаемые действием
операторов рождения квантов поля на вакуум, составляют базис фоковского
гильбертова пространства в релятивистской квантовой механике свободных
вторично квантованных полей.
Релятивистски инвариантная нормировка одначастичных состояний
acfc)|o)=|fc>,
очевидно, имеет вид
{k\k')=2h(o(2n)35(k-k'). (18.45)
Поскольку дельта-функция при нулевом значении волнового вектора выра¬
жается через объем пространства V,
(2O36(fc)|fc=0 = / d3x e~ifc'*|fc_0 = V,
величина
1 Wfc)
2e(k) V
имеет смысл нормировки одночастичного состояния в виде 1 частицы на
объем всего пространства.
Задача 10.1. Найти поток частиц с релятивистской нормировкой состояний
(18.45).
Решение. Релятивистская нормировка задает число частиц, которое равно
(k\k) = 2e(fc)(2^)35(fc)|fc=0 = 2e(fc)V.
Для свободных частиц вектор потока направлен по волновому вектору j = j • п, где
n = k/k. Тогда за время Т —> оо через площадь S = S n с нормалью, параллельной
потоку, пройдет число частиц
jY=j-ST=jST.
Но если V—скорость движения частицы, то
Т = ~, V = SL,
V
и, следовательно,
VJ
а значит,
j = 2e(k) -V.
Подчеркнем, что плотность релятивистски нормированных состояний с
определенной энергией задается инвариантной величиной
dffc ^ 1= Г |fc)dffc (fcj
2hco(2n)3 J 2ha>(2n)3
так что состояния из фоковского пространства представляются в виде супер¬
позиций многочастичных состояний, например,
*">■
J 1=1
где в волновой функции Ф(fcl5..., fcn) еще необходимо учесть симметрию по
перестановкам тождественных частиц.
284
Тема 10. Релятивистская квантовая механика
18.3.2. Комплексное поле. Комплексное скалярное поле с массой т яв¬
ляется суперпозицией двух вещественных полей (рг, ц>2 с той же массой,
Ф(х) = (*) +1^2 W}, (18.46)
так что сумму действий для вещественных компонент можно представить
в виде
S = ^ J й4х Ф^х) (р2 - т2с2)Ф(х). (18.47)
Выделение в комплексном поле пары динамических вещественных полей
(18.46) допускает введение произвольной глобальной комплексной фазы и:
Фи (х) = e_iue/(fic)#(x), (18.48)
что, как говорят, определяет калибровочные преобразования поля, остав¬
ляющие инвариантным действие. Мы ввели в определение фазы фактор
^ в том же виде, что и при определении калибровочных преобразований
нерелятивистской волновой функции.
Согласно теореме Нётер калибровочной инвариантности действия отве¬
чает сохраняющийся 4-вектор тока
5S 5S ЭФ„(Х) м
cJ ди дд^Ф^Сх) 5дцФи(х) ди ’
(18.49)
Находим
^ = 1^{Ф+ЭмФ-(адФ)+Ф>. (18.50)
Соответствующий сохраняющийся заряд—
Q = f d3xj0(x). (18.51)
Введем для комплексного квантованного поля операторы, составленные
из операторов рождения и уничтожения вещественных полей,
a(fc) = -^{a1(fc) + ia2(fc)}, al(k) = j={al(.k) + ial(k)}. (18.52)
Тогда для этих операторов справедливы следующие коммутационные соотно¬
шения:
[a(fc), а4k')l = [ac(fc), aj(fc')] =2Псо(2пУб(к - к'), (18.53)
im, ас(к')] = [a(fc), а](к')] = 0. (18.54)
Квантованное поле запишется через эти операторы в виде
Ф(Х) = / й|^{е1ЬСас(к)+е"^ада>-
(18.55)
Энергия поля задается гамильтонианом
^ = / 2Йс£г)з ho>ti4k)m + al(k)ac(k)}. (18.56)
Лекция 18
285
В то же время квантованный заряд—это нормальный символ
Q = Jd3x:j0(x):, (18.57)
который равен
Q = eJ 2^я)3 {аЧкЖЮ ~ ЬКЮаШ, (18.58)
где осциллирующие со временем вклады сократились.
Полученные выражения для полной энергии и заряда квантованного поля
говорят о том, что в пространстве волнового вектора
n+(k) = ^аЧкЖЮ, п_(к) = ^aj(fc)ac(fc),
— это плотности квантов с зарядом еи—е соответственно, так что в реляти¬
вистской нормировке a1" (fc) — оператор рождения кванта с зарядом е, а a* (fc) —
оператор рождения античастицы с зарядом —е.
18.3.3. Зарядовое сопряжение. Построим линейный оператор зарядово¬
го сопряжения, который оставляет инвариантным вакуум
С|0) = |0)
и переводит состояние частицы в состояние античастицы, сохраняя норми¬
ровку:
C|fc)=7)|fcc), |т)| = 1,
где
|fc)=at(fc)|o>, |fcc)=aJ(fc)|o).
Отсюда легко получить
с at№) с_1с|о)=r}aJ(fc)|o>,
и наконец, действие зарядового сопряжения на оператор рождения частицы
с af(fc) с-1=r)aj(fe). (18.59)
Поскольку двукратное применение зарядового сопряжения возвращает со¬
стояние в исходное с точностью до фазы,
С2 = £, |£| = 1 => СГ2 = Г- (18.60)
Тогда из (18.59) следует, что
т)са^дас_1=а+да са^юс-^^аЧю.
Совершенно аналогично из инвариантности вакуума получаем
с a(k) c_1c|fc)=с ада c_1rj|fcc) = |о).
Поэтому
с a(fc) с-1=т?*ас(к), (18.61)
286
Тема 10. Релятивистская квантовая механика
и, как следствие,
cac(fc)c_1=rja(k). (18.62)
В итоге очевидно, что зарядовое сопряжение меняет знак заряда Q: С Q С-1 =
= —Q, оставляя инвариантным гамильтониан. Кроме того, легко заметить,
что действие зарядового сопряжения на квантованное поле практически
сводится к его эрмитовому сопряжению:
С Ф (х) С-1 = т?*Ф (х)+. (18.63)
При этом, конечно, квантованное действие остается инвариантным.
18.3.4. Инверсия времени. При построении оператора обращения вре¬
мени т
t—=
необходимо учесть зависимость состояний фоковского пространства от вре¬
мени. Итак, положим, что инверсия времени сохраняет вакуум
Т|0> = |0>
и изменяет направление движения на противоположное, так что для одноча¬
стичного состояния
T\k,t) = Z\-k9t'), T|fcc,t) = Cc|-kc,t'>, Ifl = If cl = 1. (18.64)
Поскольку в явном виде, например,
|k, t) = e~i(0t\k) =e-i£Otat(fc)|0>, (18.65)
действие оператора Т приводит к
Т е~ш Т-1Т аЧЮ Т_1|0) = Ce_i<at'at(-fc)|0).
Отсюда выводим, во-первых, что
т af(fc) тг-1=саЧ-к), (18.66)
и, во-вторых, вследствие t' = —t,
Te-i£l>t T-1=elb>t, (18.67)
т. e. оператор обращения времени является антилинейным: он переводит
число в комплексно сопряженное;
ТяТГ1 =** = *.
Сохраняющий нормировку состояния антилинейный оператор называется
антиунитарным. Действие такого оператора обладает следующими свойства¬
ми:
ПсМ +с2|я/>2» = с;|Т^!> + с*|Тя/>2), (18.68)
и
(ТФ|ТФ) = (Ф|Ф) = (Ф|Ф>*. (18.69)
Лекция 18
287
Эрмитово сопряженный оператор для антилинейного определяется соотно¬
шением
(Ф|ТФ) = (Ф|Т+Ф). (18.70)
Далее тем же способом, что и при построении соотношений для опера¬
тора зарядового сопряжения, находим с учетом антилинейности оператора
инверсии времени
т асад т"1=с*ас—fc),
та^дат-^са^-к), (i8.7i)
тадк) г1=£&(-«.
Тогда в силу
Т а+(к)а(к) т-1 = af(—fc)a(—к),
т aj(k)ac(k) т"1=aj(-k)ac(-k)
(18.72)
гамильтониан Ж и заряд поля Q останутся эрмитовыми операторами, и они
остаются инвариантными при обращении стрелы времени, как этого и сле¬
довало ожидать.
Действие оператора инверсии времени на квантовое поле с учетом t •-» t'
Т Ф(с, х) ТГ1 = J* 2^§)з+ei(tot'"kx)rа(-к)} =
{ei(-o,t'-fc.x)^at(fc)+e-i(-a,t'-fc.,)ra(fc)}
=1
2й)(2я)3
можно свести к
Т l>(t, х) Т"1 = Фт(с', х) = С*Ф(-t', х),
только если
Г = Сс- (18.73)
С другой стороны, можно считать, что
т Фа, х) т-1=Фта', х)=с*Ф*а', *),
где действие комплексного сопряжения на операторы рождения и уничто¬
жения формально считается эквивалентным действию операции инверсии
стрелы времени (18.72). Последняя запись допускает прямую аналогию с вол¬
новой функцией в нерелятивистской квантовой механике.
С учетом (18.73) квантовое действие свободного комплексного скалярно¬
го поля останется инвариантным относительно инверсии времени.
18.3.5. Инверсия пространства. Зеркальное отражение пространства
р
X—> —х
в квантовой механике свободной релятивистской скалярной частицы соот¬
ветствует линейному оператору, сохраняющему вакуум
Р|0) = |0) (18.74)
288
Тема 10. Релятивистская квантовая механика
и преобразующему, например, одночастичное состояние, сохраняя его нор¬
му:
Р|к) = £|-к>, |5| = 1, (18.75)
и аналогично для античастицы.
Тогда та же схема рассуждений, что и в двух предыдущих разделах, при¬
водит к следующим соотношениям:
Га*(ЮГ1 = ?af(-fc), Pa(fc) Р"1 = £*a(—fc),
paj(fc)p_1=§caj(-fc), pac(fc)p-J=£*ac(-fc).
Поле преобразуется согласно
РФ(С, лОР"1 = £*Ф (t, —дс), (18.76)
если = £с, что дает также инвариантность действия.
Лекция 19
Уравнения движения для киральных безмассовых спиноров Вейля, действие
кирального поля, гамильтониан и заряд, базисные спиноры и квантова¬
ние вейлевского спинора, античастицы с противоположной спиральностью
и CP-инвариантность, инверсия времени, безмассовый биспинор Дирака
и операция пространственной инверсии, гамма-матрицы и их алгебра, ки-
ральные проекторы, дираковски сопряженный спинор, зарядовое сопряжение
биспинора, дираковский спинор с массой, уравнение Дирака, квантование,
проекторы на состояния с заданным значением спина, сумма по поляриза¬
циям, представление Дирака для гамма-матриц, дискретные симметрии для
поля Дирака, зарядово самосопряженные спиноры Майораны, майорановская
масса.
19.1. Вейлевские спиноры
Правое киральное безмассовое поле ха(х), преобразующееся по представ¬
лению 0^ группы SL(2, С), согласно общему формализму удовлетворяет
уравнению
spkx =
где спиральность s = а оператор Wk задается покомпонентно, так что для
временной компоненты
\w* = \p.<r,
а уравнения для пространственных компонент, как мы показали, являются
следствием заданного представления для безмассового поля. В явном виде
уравнение для р0 принимает вид
РоХ=Р'ОХ,
(19.1)
Лекция 19
289
или с учетом определения 4-вектора сигма-матриц
рксткх = 0 ** РксгкаАх* = 0. (19.2)
Уравнение (19.1) может быть представлено как «релятивистское уравнение
Шрёдингера» для правого кирального фермиона
Hr=сР'а> (19-3^
причем «гамильтониан» HR—эрмитов оператор.
С учетом того, что (^a)t = %а, уравнение (19.2) может быть получено
вариацией действия
SR = J d4x {xpkcrkx } (19.4)
по ха> причем, как мы видели, это действие является релятивистским инва¬
риантом.
Выписывая обобщенный импульс
^- = Шхас,
5x00
находим гамильтониан классического поля
HR = J d3x{ihxcr0x-cXPkvkX}=c J d3x {xp axh
Глобальные калибровочные преобразования
Хи = е~ш*‘Х (19.5)
определяют сохраняющийся ток
l.fc_ 5SK дХи_е к-
с 5дкхи Эи сх z
и заряд
Q = / d3x j°(x)=ef d3x {xa°x}=e J d3x {*+*}.
Найдем решения уравнения для спинора (19.1) в импульсном представле¬
нии, т. е. в виде плоской волны
jW=e‘ipa^%)(p);
я
где
р-х=р0х0-р-х.
Как нам известно, матрица
р-(Т = СТр
имеет пару собственных векторов-столбцов, так что в их базисе
р-<7 = |р|Оз = |р| (J
290
Тема 10. Релятивистская квантовая механика
и, принимая условие нормировки xfX = 2|р|,
X Ср) = уШ (J) , Р ■ <?Х Ср) = \р\х Ср),
ЛГсрСр) = \/2|р| (5) , -Р • <т*ср С-р) = \p\Xcp С-р),
где сопряжение1
^сР(-р) = -ад*(р)
дает левый спинор-столбец. Формально спинор ^ср(—р) отвечает правому
спинору при проекции спина на импульс —р и соответствует отрицатель-
но-частотным решениям р0 = —\р\. Меняя знак 4-импульса, приходим к ле¬
вому спинору ^ф(р) с положительной энергией.
В итоге разложение классического правого спинорного поля по модам
принимает вид
*Cx) = J 2po(2^)3{е~«рхх(.р)$(.р) +е*рхXcp(P)v(p)}, С19.6)
где уже энергия р0 принимает только положительные значения
Ро = \Р\> р-х = р0х0-р-х,
а #(р) и г; (р) — комплекснозначные параметры.
С учетом ортогональности базисных спиноров находим для гамильтониа¬
на
HR = J еСр)щ^{#СрЖр)~г>СрЖр)}, 09.7)
где е(р) = с|р| = ср0 > 0 — положительно определенная энергия спинорной
моды. Аналогично, заряд классического поля
Q = e j 2Р^2ПЮ^РЖР) + У(РЖР)}- (19’8)
Классические выражения для гамильтониана и заряда допускают логиче¬
ски непротиворечивую интерпретацию, если параметры #(р) и г>(р) являют¬
ся грассмановыми переменными, так как только в этом случае гамильтониан
является положительно определенной величиной: можно ввести соответству¬
ющие плотности гамильтониана в импульсном пространстве для спинорных
мод
*кСр) = ^(рЖр)*°, С19.9)
tfT(p) = ^O(p)v(p)£0, (19.10)
Независимо от базиса решение хСр С~Р) с отрицательным собственным значением матрицы
р • а, или с «отрицательной энергией», можно записать в виде Хср(~Р) = ~i°2Х(р)> поскольку
— —СТ.
Лекция 19
291
поскольку для грассмановых переменных
г)(рМр) = -г;(рЖр),
так что величины
п0(р) = ^г-'&СрЖр),
Р° (19.11)
п<о (Р) = 2^v(p)v(p),
определяют соответственно плотности состояний правых спиноров и СР-со-
пряженных к ним спиноров, обладающих левой спиральностью и противо¬
положным значением заряда, так как
Q=eJ (^з^о(р)-ПоР(Р)>- (19.12)
Квантованное правое спинорное поле — правый вейлевский спинор —
запишем в виде
X GO - J Ypo(2nh)3 {е~*Р ХХ+ е*Р'ХХср(р)4,срср)>. (19.13)
где а[ ср — оператор рождения квантов античастиц (заряд —е) с отрицатель¬
ной киральностью, a aR — оператор уничтожения квантов с положительной
спиральностью (заряд +е), причем имеют место антикоммутационные соот¬
ношения, характерные для фермионов:
{«L,cp(P)> °1,ср(рО} = 2р0(2тгТг)35(р -рО,
{aR(p), a£(p')} = 2p0(2nh)35(p -р'),
в то время как другие антикоммутаторы обращаются в нуль, например,
К,сР(Р), aLiCp(p/)} = {aR(p), aL>cp(p/)> = {aR(p), a*cp(p')} =
= К,сР(Р)>4(р/)} = 0. (19.15)
Усреднение операторов по когерентным состояниям фермионного осцилля¬
тора
«L,cp(p)Kp)> = i>(p)Kp))> aR(p)|tf(p))=tf(p)|tf(p))
дает классические фурье-компоненты поля:
(U(^^><«Cp)l<q,Cp)|vCp))=«Cp),
тртр))тр)ЫрШр)}=#Ср)-
Квантование приводит к положительно определенным гамильтонианам
Ш = ^4(РК(Р) и bCLP(p) = j^alcp(P)aUcp(P). (19.16)
Выражение для квантованного заряда достаточно очевидно.
292
Тема 10. Релятивистская квантовая механика
Повторяя ту же процедуру для левых вейлевских спиноров-столбцов ва,
которые удовлетворяют уравнению
pkak6 = 0 <=> рк(ак)йада = 0, (19.17)
находим действие
SL = f 64х{вркакв} (19.18)
и квантованное поле
^М = J 2ро(2яЮз{е~"Р*0(р)аь(р) + е"Р'%СР)4л»СР)}, (19.19)
где а^ср — оператор рождения квантов античастиц (заряд —е) с положитель¬
ной киральностью, aaL- оператор уничтожения квантов с отрицательной
спиральностью (заряд +е), причем имеют место стандартные антикоммута-
ционные соотношения для фермионных (грассмановых) операторов.
Действие дискретных симметрий на состояния фоковского пространства
для вейлевских спиноров обладает существенными отличиями от их дей¬
ствия на состояния скалярных частиц. В самом деле, унитарная операция
зарядового сопряжения сохраняет киральность частицы, но существует лишь
одно состояние с заданной спиральностью и положительной энергией. Про¬
странственная инверсия меняет спиральность частицы, так что она пере¬
водит правые спинорные поля в левые и обратно, но при этом остается
неизменным знак заряда, что, как мы видели, не согласуется с последова¬
тельным квантованием кирального поля. Это означает, что действие одного
киралъного поля с определенной спиральностью принципиально не может
быть инвариантно относительно С- или P-сопряжения по отдельности.
Рассмотрим операцию комбинированной CP-четности, изменяющей спи¬
ральность, на примере правого кирального поля. Установленные нами свой¬
ства импульса, энергии и спиральности означают, что
СР 4(р) (СРГ1 = T)cpalcp (-Р), (19.20)
где |rjcp| = 1, и, как следствие процедуры, повторяющей рассмотрение для
скалярных полей,
CP aR(p) (СР)"1 = 1?*рaLcp(-р). (19.21)
Такое сопряжение оставляет инвариантным гамильтониан и меняет знак
заряда поля (операторы плотности частиц и античастиц меняются местами).
Сопряженное свободное поле должно удовлетворять исходному уравнению
движения (19.2). Поэтому сопряжение операторов рождения и уничтожения
(19.20), (19.21) с необходимостью сопровождается и сопряжением спино-
ров-столбцов с помощью линейного матричного оператора, так что
Лекция 19
293
Значит, CP-преобразование поля дает
*„»,*>=сг footer»-1=J
х {VcPe~*p xX(-p)aL,cp(-р) + VcPe”P'XZ(-p)a-i(-p)}. (19.22)
В итоге можно записать
Хср&*) = -X), (19.23)
где операция х* означает комплексное сопряжение для комплексных чисел
и эрмитово сопряжение для операторов рождения и уничтожения. Из явного
вида сопряженного поля (19.22) следует, что оно, конечно, удовлетворяет
исходному уравнению движения, но соответствует квантам с противополож¬
ным значением заряда. Подчеркнем также, что действие киралъных спиноров
инвариантно относительно операции СР (19.23): действительно, поскольку
для спиноров-столбцов
Хср = (Хср? = 'ПсрХТ1<72>
находим
XcpPk°kXcp = -f^2Pk^k^2X* = f&fPnfr^X* =
= {ХТ&кпРп(°к)ТХ*}Т = X&knPn<rkX,
так что замена переменных интегрирования в действии согласно операции
пространственной инверсии
x/k = &>kxn
оставляет действие кирального спинора инвариантным.
Антилинейная операция обращения стрелы времени сохраняет спираль-
ность, энергию и обращает импульс, так что, следуя процедуре, разработан¬
ной для скалярных полей, находим
T4(p)T-1 = Ca^(-p), Так(р)Т"1 = Гак(-р),
Т а* ср(р) Т-1 = £ср<ср(—Р), Т aLср(р) Т-1 = CPaL,cp(-p),
гдё |£| = |£ср1 = 1- Тогда гамильтониан сохраняется вещественным, а заряд
остается инвариантным, как этого и следовало ожидать.
Квантованное поле преобразуется по закону
Т X(t, X) Т-1 = -Ciaj4-t, X), (19.25)
причем необходимо положить fcp = f*. Легко показать, что действие сво¬
бодного кирального поля инвариантно относительно операции обращения
стрелы времени.
Обобщая экспериментальные данные, Ландау, а также, независимо от
него, Ли и Янг предложили рассматривать нейтрино, участвующие в слабых
взаимодействиях, в качестве левых вейлевских спиноров.
294
Тема 10. Релятивистская квантовая механика
Подчеркнем, что вейлевские спиноры с необходимостью обладают заря¬
дом, но необязательно электрическим, обусловленным калибровочной ин¬
вариантностью преобразования фазы комплексного числа, т. е. симметрией
по отношению к группе U(l) независимо от киральности поля. В частности,
нейтрино являются электрически нейтральными, но они несут как гипер¬
заряд, (группа U(l) с различными значениями заряда у левого и правого
вейлевских спиноров), так и заряд электрослабой группы SU(2), в которой
нейтрино представляет собой компоненту дублета (спинора) по слабому
изоспину и является партнером левого электрона.
19.2.1. Безмассовое поле. Поскольку пространственная инверсия меня¬
ет знак спиральности безмассового поля, сохраняя его заряд, а зарядовое со¬
пряжение сохраняет спиральность, изменяя знак заряда, свободное спинор-
ное поле, действие которого симметрично относительно операций простран¬
ственной и зарядовой четности по отдельности, с необходимостью должно
включать в себя как левые, так и правые спиноры одного знака заряда,
и, следовательно, такое поле преобразуется относительно группы SL(2, С)
как прямая сумма (расширенный столбец)
т. е. дираковский бистгинор имеет индексы и правого, и левого спиноров.
Такой безмассовый биспинор, очевидно, удовлетворяет системе уравнений
Уравнения движения в терминах дираковского спинора можно также запи¬
сать в виде
где матрица р понимается в блочном смысле. Она переводит биспинор в би¬
спинор, так как
Pk аа 0а — правый спинор,
pfccr^d^a—левый спинор.
Обычно вводят блочные матрицы Дирака в киральном представлении
19.2. Дираковские СПИНОРЫ
(19.26)
(19.27)
которая получается из действия
SD = j d4x(xPkVkX + 6Pk°k0)-
(19.28)
(19.29)
(19.30)
Лекция 19
295
Тогда1
P=PkYk=PoYo-P'Y- (19-31)
Безмассовый биспинор имеет два собственных состояния киральности
r5</>D=±^D> (19.32)
где в киральном представлении
Г5 = (о -?) •
Если обозначить матрицы Паули, образующие блоки2, символом т, чтобы не
путать их с а-матрицами в группе SL(2, С), то, очевидно,
Го = *1> Г5 = *3>
и для полноты базиса
ГоГ5 = -**2>
так что
Г = ТоТ5сг-
Тогда 4-вектор гамма-матриц Дирака с учетом различия верхних и нижних
спинорных индексов с точками и без точек запишется в виде
(Уо> Г) = Тк = т+ ® &к + ® °к> (19.33)
где т± = (тх ± iT2)/2. Произведения
т+т- = (оо)’ Т-Т+= (о l)
образуют эрмитовы матрицы—проекторы на киральные состояния
Р^ = |(1±Г5). (19-34)
причем
PR=PK> P?=Pl> Pr+Pl = 1-
Тогда, используя антикоммутационные соотношения для сигма-матриц, мгно¬
венно находим
{rm,Yn} = 2gmn, (19.35)
а с помощью коммутатора вводим дираковские матрицы <тшп,
\ lrm, Гп] = PrV™+Рь°тп = (^7 атп) = \&тп, (19.36)
которые, очевидно, образуют представление спиновых генераторов группы
Лоренца на дираковских спинорах.
1Вместо перечеркнутого символа в отечественных изданиях используют символ со шляпкой.
2Умножение блочных матриц с точки зрения математической грамотности принято записы¬
вать в виде прямого произведения обычных, не блочных, матриц: <=>Tfc 0crf.
296
Тема 10. Релятивистская квантовая механика
Отметим, что согласно алгебре матриц Паули
Го = Г5 = _Гр = 1. {rs»r"} = 0, р = {173}, п = {073},
где нет суммирования по р.
Произвольный элемент группы Лоренца на дираковских спинорах по их
построению имеет вид
А=ГЛ+ М
О Л_ у ’
а обратный элемент
л-=(л;л0:-)
может быть представлен в виде
Л" = (Ло л») =г»л’г-
Поэтому дираковски сопряженный спинор
$о = 1>1го (19.37)
преобразуется обратной матрицей. Используя это свойство и расписывая
билинейные комбинации дираковских спиноров через вейлевские, получаем
трансформационные свойства для следующих величин (опуская маркер D
для дираковских спиноров):
'Ф'Ф = вх+хв —скаляр,
я/>утя/> = х°тХ + Оатв — вектор, (19.38)
|'0(ТтП/0 = в(7тп% + %omnQ — антисимметричный тензор.
Действие оператора пространственной инверсии изменяет спиральность, так
что
и
р р р
Я«—►-*, Рь<—>Pr, Y5 4 * Y5*
При этом фазы преобразования спиноров можно определить таким образом,
что операция инверсии запишется в виде1
яpv(t, х) = Yolp(t, -ж), (19.39)
причем, как и должно быть,
ГоГ5 = -Г5Го-
1В самом деле, матрица преобразования в общем виде запишется в виде Q ®iu eQ ^, но
фазы и можно занулить, переопределяя глобальные комплексные фазы киральных спиноров
Вейля.
Лекция 19
297
Тогда легко заметить, что следующие билинейные комбинации преобразуют¬
ся как псевдовеличины:
'фГБ'Ф^дх-хд — псевдоскаляр,
4pYsYmip = Х<УтХ — 6&т9 —псевдовектор.
Поскольку шестнадцать матриц
(1, г5, rm, r5rm, &тп)
образуют базис в пространстве матриц 4x4, мы получили исчерпывающий
набор всевозможных билинейных дираковских выражений и их характери¬
стики относительно преобразований группы Лоренца, включая дискретную
операцию инверсии пространства.
Операция зарядового сопряжения сохраняет спиральность, т. е. переводит
правый спинор в правый и аналогично действует на левый спинор, а также
меняет знак комплексной фазы поля, которая связана со знаком заряда, так
что, опуская фазу преобразования,
х*~^ёй=(«“* е.?=(а<г2е)тг=ia2e*,
@а ~~~* Ха ~ (в*Д*)f = СС—icr2^)T)f = -i(T2x*.
Значит,
CV- = (_i°a2 7) М>* = - iТ2Г- (19-41)
Действие спинора, инвариантное относительно каждого из дискретных
преобразований группы Лоренца по отдельности, принимает вид
SD = J d4x 'фр'ф. (19.42)
Таким образом, безмассовое поле Дирака по сути представляет собой си¬
стему из двух вейлевских спиноров, переходящих друг в друга при инверсии
пространства и сопряжении заряда.
19.2.2. Массивное поле. Дираковское поле с массой можно построить
посредством действия буста на состояния базисных полей с нулевым импуль¬
сом
кп = (тс, 0)
и с'заданными проекциями спина на ось z
s3u±(0) = ±|u±(0).
Важно, что пространственная инверсия, обращающая импульс и сохраняю¬
щая энергию и спин,
р р р
Р< * ~рз Ро 4 * Ро> s 4 > s>
в случае нулевого импульса может быть дополнительно включена в полный
набор наблюдаемых, так как она коммутирует с энергией и спином, посколь¬
ку инверсия сводится к матричному умножению
Pu±(O) = r0u±(O).
298
Тема 10. Релятивистская квантовая механика
Значит, пространственная четность—квантовое число для массивного поля
с нулевым импульсом. Собственные значения матрицы у0 = т1®1 известны:
Я = ±1. Поэтому вводят два типа дираковских спиноров с заданными проек¬
циями спина и пространственной четности:
Гои(0)=+и±(0),
roKO) = -v±(0).
Преобразования Лоренца для дираковского спинора задаются трансфор¬
мационными свойствами столбца 0^ 0 (0, ^), так что для буста вдоль
единичного вектора п имеем для правых спиноров
A+(tf) = expjio--ntf j = ch | + <7-nsh |,
а для левых спиноров
Л_С&) = ехр• п& j = ch ^ — а • п sh
причем
сЬ#= —, shtf = —,
тс тс
где рп = (р0, р) — 4-импульс дираковского спинора в результате действия
буста, так что р = птс sh #. Элементарные преобразования, согласно соотно¬
шениям
— тс
так что
(19.44)
(19.45)
2 тс
приводят к
Л+ (#) = 1 =(р0 + тс + а-р),
i/2mc(p0 + mc)
А- (!&) = (р0 + тс-<т-р),
у 2тс(р0 + тс)
Л»)=(Л0 А_) = у5=Щ<Ро + тс+Г5» Р).
Тогда для покоящихся спиноров действие буста сводится к
Л(#)и(0) = -у * =Ср+тс)ц(0),
^/2тс(р0 + шс)
так как
Р=РоГо “ Г • Р=РоГо + Гзо- * РГо-
Аналогично,
AWKO) = .. 1 (-у+тсМО).
^/2тс(р0 + тс)
Ввиду того, что
(р- тс)(р+ тс) = PnPirnYl ~ (.тс)2=pnpi^{yn, Г1У~ Ос)2=р2 - (тс)2 = 0,
Лекция 19
299
базисные спиноры с заданным 4-импульсом
u(p) = Л(#)и(0), v(p) = Л(#МО),
удовлетворяют уравнениям
(р — тс)и(р) = 0, (p+mc)v(p) = 0.
Их суперпозиция—поле Дирака—
d3p
'•/’(*)
■/
г{е »p*u±(p)№±(p) +e»poci/±(p)b±(p)}
(19.46)
(19.47)
2p0(2nh)3
удовлетворяет уравнению Дирака
(РпГп ~ тс)я/>(*) = 0, (19.48)
где рп = ihdn — оператор 4-импульса в координатном представлении, а го, b —
комплексные параметры в алгебре Грассмана.
Уравнение Дирака получается вследствие принципа наименьшего дей¬
ствия, имеющего вид
SD = / d4x 'ф (х) (р - me) ip (л:). (19.49)
Обычно принимают релятивистски инвариантную нормировку спиноров
массивного поля
й± (0) и± (О) = й± (р) и± (р) = 2 тс,
2/±(0)i/±(0) =z/±(p)v±(p) = —2тс,
так как в явном виде в киральном представлении
(19.50)
u.(0) = \/тс
ЛЛ
0
1
voy
u_(0) = \/mc
Г 0\
1
0
V17
и
( л
(
v+(0) = Vmc
0
-1
, v — (0) = л/тс
1
0
Для спиноров с ненулевым импульсом после учета соотношения
у0Л(#) = Го (ch | + у5(о- • n) sh |) = Л(-#)г0
получаем в силу Л-1 = Yo^Yo и Л”1= Л(—#)
ГоМр) = м±(~Р), Го^±(р) = -v±(“P),
как это и должно быть для операции пространственной инверсии, которая
меняет знак импульса и сохраняет спин
rl
Заметим, что знак «минус», который появляется перед спинором v± (р) при действии
матрицы пространственной инверсии у0, означает, что дираковская античастица имеет про¬
тивоположный знак, как говорят, «внутренней» четности по сравнению с частицей (см. ниже
раздел о действии оператора пространственной честности).
300
Тема 10. Релятивистская квантовая механика
После простейших выкладок легко найти гамильтониан поля
Hd = $ d3x i/i (хХр • Г + mc) 'Ф (*) =
= J ^^f^cpoi^±(Pi«>±(P)-b±(p)b±(p)}. (19.51)
Ток определяется стандартным образом вариацией действия по комплексной
фазе поля ^j)u = ехр{—ieu/hc}ip:
7>"=ш^г=с'}г''ф- а952)
а заряд задается выражением
Q = J d3x j°(x)=e J {*±(р)»±(р) + b±(p)b±(p)}. (19.53)
После этого процедура квантования согласованным образом приводит,
конечно, к оператору поля
^(*) = J 2ро(2пЮ3^е~*Р'Уц±(Р)°±(Р) +е"Р'Ху±(Р)а1±(Р)>> 0-9.54)
где ас,±(р) — оператор рождения античастиц с импульсом р, зарядом —е
и проекцией спина на ось z, равной ±^, а а±(р) — оператор уничтожения
частиц с импульсом р, зарядом +е и проекцией спина на ось z, равной ±i.
Когерентные состояния, определенные по этим операторам уничтожения,
соответствуют классическим полям, которые получаются усреднением по та¬
ким когерентным состояниям. Безусловно, произвольное классическое поле
можно представить как суперпозицию усредненных когерентных состояний,
что приводит к непуассоновскому распределению по числу квантов и их
флуктуациям.
19.2.3. Собственные состояния спина. В приложениях приходится опе¬
рировать спинорами, вектор поляризации которых направлен не вдоль за¬
данной оси (мы использовали ось z)} а вдоль произвольного 4-вектора, что
позволяет проводить расчеты в явно ковариантном виде. Построим проекто¬
ры на состояния с заданным значением вектора поляризации, т. е. состояния
с проекцией спина на заданный вектор, свойства которого мы определим
в ходе его построения в явном виде.
Пусть в системе покоя массивного спинорного поля Дирака спин направ¬
лен вдоль единичного вектора е, т. е. имеет место уравнение на собственное
значение оператора спина
£-au(0) = Аия(0), А = ±1, в2 = 1, (19.55)
причем в этой системе произведение 4-векторов поляризации е11 = (0, е)
и импульса рп = (тс, 0) равно нулю
епРп = 0.
Лекция 19
301
С учетом определения гамма-матриц Дирака Y=YoYs°' и того>что спинор в систе¬
ме покоя является собственным для матрицы Yo> находим равенство
е • сти(0) = € • ГГзГоиС0) = * * ГГз^СО) = -$у5и(0) = г5*и(0).
Произведем операцию буста, так что
Ау5еи(0) = Ау5еА~1и(р),
где, как мы выяснили (19.45),
Л= . * ==(р0 + тс + у5<т-р)
л/2тс(р0 + тс)
И _ 1
Л 1=r0Atr0= , , ■ •(Ро + тс — у5а -р),
у/2тс(р0 + тс)
откуда
ЛГзвА-1 = 2'mc(^+"j {(Ро + тс)2Го (е • <Т) + Го (р • O') (е • O') (р • о-) +
+ (ро + mc)rsYo((P • о-) (с • а) + (е • <т)(р • а))}.
Это выражение существенно упрощается, если провести преобразования согласно
алгебре сигма-матриц
(p-<r)(e-aXp-<r) = {(p-e) + i(pxe)-o'}(p-cr) =
= (Р'£Хр-о-)-((рхе)хр)-(г=2(р-£)(р-(г)-р2(£-сг)
и
(р-(т)(е •о,) + (в-о,)(р-ог) = 2(р-в).
Используя связь энергии с импульсом р2 =р2 + (тс)2, находим
Лг5гЛ-1 = ГоО- • (в + { ^ -1 }п(п • е)) + YsYo (п ■ е)
где п = р/|р| — единичный вектор в направлении буста. Теперь заметим, что преоб¬
разование Лоренца, переводящее 4-импульс покоящейся частицы в 4-импульс движу¬
щейся,
Ро = me ch ft, р = птс sh #,
для вектора поляризации еп = (0, е) имеет вид
ё0 = (п-е) shtf, ё = е + {chtf-l}n(?w),
причем
shtf=—, chtf=—.
тс тс
Кроме того,
Г5ё = Г5Го£о + Го(<г-*),
так что в итоге получаем
Лу5*Л~1=у5*,
т. е. буст просто преобразует 4-вектор поляризации в систему движущейся частицы.
Поэтому уравнение на собственные значения проекции спина на вектор
поляризации в произвольной системе отсчета принимает ковариантный вид
Г5гил(р)=Яия(р), А = ±1, е2 = —1, е-р = 0, (19.56)
где мы опустили знак тильды, указывающий на то, что вектор поляризации
спинора записывается в системе отсчета движущейся частицы.
302
Тема 10. Релятивистская квантовая механика
Совершенно аналогично для спиноров античастиц получим
ГбЯ'лСр^-ЯуяСр), А = ±1, е2 = —1, е-р = 0. (19.57)
Значит, проекторы на состояния с заданной проекцией спина частицы на
вектор поляризации имеют вид
P± = i(l±rs*), (19.58)
а для античастиц —
Р± = |(1ТГ5*). (19.59)
19.2.4. Сумма по поляризациям. Для покоящихся спиноров сумму по
поляризациям—матрицу
П(0)=2“л(0)йя(0)
Я
можно вычислить в явном виде как прямое произведение строк и столбцов
ЛЛ
П(0) = тс(1, 0,1, 0)<8>
+ тс(0,1, 0,1) ®
ГоЛ
(1 0 1 0\
1
0 10 1
0
= тс
10 10
9
V0 1 0 1J
или в ковариантном виде
П(0) = тс(т'0-Ы) = (У + тс), р' = (тс, 0).
Поскольку преобразование Лоренца для матрицы Л сводятся к преобразова¬
нию 4-вектора Ал в движущуюся систему отсчета (проделайте это упражне¬
ние самостоятельно):
ЛА'А-1 ->Л,
сумма по поляризациям для движущихся частиц —
П(р) = (р+тс) (19.60)
и аналогично для античастиц
Пс (р) = 2 i/я (р)^я (Р) = СР - тс). (19.61)
я
19.2.5. Представление Дирака. В оригинальной работе Дирака, посвя¬
щенной выводу уравнения для релятивистского электрона, он использовал
не киральное представление для гамма-матриц, введенное выше, а нашел
другой вид гамма-матриц, удовлетворяющих определяющему их соотно¬
шению антикоммутации (19.35). Представление Дирака для гамма-матриц,
естественно, эквивалентно киральному, так как оно может быть получено
унитарным преобразованием с
W = j=(r0 + r5), = *и2 = \, (19.62)
так что
rnD=wrnw'-
Лекция 19
303
Тогда легко найти, что
°и °и
У о * Г 5> Г 5—>Го, Г
т. е. матрицы у0 и у5 меняются местами, а у меняет знак, и в представлении
Дирака (опускаем маркер D, указывающий на представление)
ro=(;_°o. rs-(;j), (19-6з)
19.2.6. Дискретные симметрии. В отличие от случая скалярного поля
комплексные фазы преобразования операторов рождения и уничтожения
при наличии ненулевого спина могут, вообще говоря, зависеть от проекции
спина. Для того чтобы определить вид этой зависимости, воспользуемся со¬
отношением для базисных состояний оператора спина у массивной частицы,
а именно,
5+ |s, ms) = i/s(s +1) -ms(ms +1) |s, ms + 1), 5± = sx±isy. (19.64)
Тогда, действуя на это равенство линейным оператором пространственной
инверсии, сохраняющим спин, находим, что если
ms)y l£mj
TO
?ms ^ms+Ъ
т. e. фаза для действия оператора пространственной инверсии не зависит от
проекции спина. Значит, пространственная инверсия действует на спинор-
ные операторы рождения и уничтожения как
Ро+(р)р-1 = ?а^(-р), РаЦ(р)Р"1 = ^саЦ(-р), (19.65)
а поле преобразуется как
Р 'ф (t, х) Р"1 = Г Го^ ft, (19.66)
если £с = -£*, откуда £*§с = —1, а значит, как говорят, дираковская анти¬
частица имеет противоположный знак внутренней, отвечающей спиновым
степеням свободы, пространственной четности по сравнению с четностью
частицы.
Поскольку зарядовое сопряжение сохраняет спин, заключаем, что фаза
этого линейного преобразования также не зависит от значения проекции
спина. Поэтому
Co^(p) C_1 = rjaJ±(p), СаЦ(р)С_1 = 17*<4(р), (19.67)
и
С 4>it, х) С"1 = х), (19.68)
где комплексное сопряжение действует как эрмитово сопряжение на опера¬
торы рождения и уничтожения.
304
Тема 10. Релятивистская квантовая механика
Аналогично, для фазы антилинейной операции инверсии стрелы време¬
ни, которая меняет знак спина, из (19.64) в силу
TsT_1 = -s, Т i Т_1 =—i, T|s,ms) = CmJs,-ms), ICmsl = l
получаем условие
Cm* Cms+1>
(19.69)
которое удовлетворяется, если положить
ст=а-1У~щ,
(19.70)
где £—значение фазы инверсии времени при ms=s. Значит,
т 4(р) ТГ-1 = С±4(-р), Т аЦСр) Т"1 = ?с,±<т(-р),
(19.71)
а поле преобразуется согласно
Т '</’(£, х) Т-1 = £”Чсг2я/>*(—t, х),
(19.72)
причем £* = С с- В самом деле, при нулевом импульсе легко найти,
что
ia2u*±m = ±uT(0) => ш2и*щ(0) = (-1 У~т‘и_щ(0),
io-2v±(0) = ±i/T(0) => icr2v*ms (0) = (-l)s_msy_mj (0),
и в силу свойства преобразования Лоренца А(р)
сг2А*(р)=А(-р)сг2
находим
io2<(p) = (-Ds"m^-ms(-p), ioii^Cp) =
Поэтому действие антилинейного оператора инверсии времени дает
1Ш хП-1 = С J {e»pxio-2umi(p)(-l)s-m‘a_mj(-p) +
+ e~npxia2vms (р) (-l)s_mi4_mj (—р)},
так что после использования
[(-l)s_m‘]2 = l
и замены переменной интегрирования р^-р получаем равенство (19.72),
где операция комплексного сопряжения относится лишь к числовым фак¬
торам, а операторы рождения и уничтожения преобразуются согласно дей¬
ствию инверсии времени.
19.3. Майорановские спиноры
Идею абсолютно нейтрального спинора сформулировал итальянский фи¬
зик Майорана. Поскольку нейтральное поле должно переходить само в себя
при зарядовом сопряжении и оно, следовательно, с необходимостью является
Лекция 19
305
собственным для оператора зарядового сопряжения, в майорановское поле
должны входить как правые, так и левые спиноры, а значит, относительно
действия группы SL(2, С) оно должно преобразовываться так же, как и дира-
ковский биспинор
(|, °) ® (°, !)=(£)= 'Ни- (19.73)
Операция зарядового сопряжения в киральном представлении, как мы выяс¬
нили, имеет вид
Ct/>M = -ir2V'M=(_122V) •
Тогда уравнение на собственные значения для оператора зарядового сопря¬
жения
^'Фм = ^'Фм
имеет решения
e = ±x = Ti<т2х*-
Значит, майорановские спиноры с положительной и отрицательной зарядо¬
вой четностью имеют вид
V»m=(4). (19.74)
т. е. они построены из вейлевского спинора и сопряженного к нему вейлев¬
ского спинора.
Вектор электрического тока
ih=‘Фмгп'1>м=х°пх +х°пх
тождественно обращается в нуль
Зы = °>
если принять во внимание перестановочные соотношения для грассмановых
величин:
ХСТпХ = Ка^Хре^Хр = (ё'^ХрХр = -Х°пХ>
где (<тп)^ = cr*deaPeaP = (—ia2crnicr2)T-
Действие для массивного майорановского спинора можно легко получить
из действия дираковского спинора, расписанного в киральном представле¬
нии
SD=f d4:>cipD(p-mc)'ipD=f <14х{хрксткх + вркб-к6-тс(.х9 + 6ЮУ> (19.75)
если учесть условие зарядовой самосопряженности, так что
Su = S d4* ‘4>M(p-mc)xpM = j d4x iXPk^X + XPk^XTmcixX + XX')},
(19.76)
где последний вклад носит имя майорановского массового члена. Как видим,
майорановская масса вводится для абсолютно нейтральных спиноров, так
306
Тема 10. Релятивистская квантовая механика
как ее вклад нарушает инвариантность относительно преобразований ком¬
плексной фазы поля: действительно, вещественная величина
XX + XX = fi°2X* + XTicr2x = 2 Re^io^*]
изменяется при введении дополнительной фазы у спинора %.
В научной литературе рассматриваются модели с правым нейтрино, ко¬
торое не участвует в сильных, слабых и электромагнитных взаимодействиях,
т. е. не несет никакого из известных зарядов. Поэтому такое правое, как
говорят, «стерильное» нейтрино можно считать майорановской частицей.
Лекция 20
Векторное поле и уравнения Максвелла, циркулярная поляризация, продоль¬
ное поле, преобразования Лоренца и калибровочная инвариантность, дей¬
ствие для поперечных мод, квантованное поле, массивное векторное поле,
уравнение Прок£, калибровочное преобразование базиса гильбертова про¬
странства в нерелятивистской и релятивистской квантовой механике, опе¬
рация трансляций и ковариантная производная, калибровочное поле, тензор
напряженности как коммутатор ковариантных производных, минимальное
взаимодействие заряженных релятивистских частиц с калибровочным полем,
спектр атома водорода из релятивистского уравнения для скалярной частицы,
сведение к нерелятивистскому уравнению, расщепление уровней по орби¬
тальному моменту, спектр уровней из уравнения Дирака, квантовые числа
состояний, важность Р-четности, расщепление уровней по полному моменту.
20.1. Безмассовое векторное поле
Спиновый оператор векторного поля матрица
не имеет временных компонент, т. е. не приводит к смешиванию 3-мерного
поля с Л0. Поэтому общие операторные уравнения
±Wn=spn,
где
j:W0=p-s, jr W=pQs - sign (5) i (p x s),
в случае безмассового векторного поля, во-первых, не содержат компонен¬
ты А0, которая тем самым не имеет отношения к динамике свободного
векторного поля, а во-вторых, в силу $ = Я = ±1 принимают простой вид
PoA^ = UpsXAv, XpaA* = ро(saXAv -XieaprpP(s^Av.
Подставляя операторы 4-импульса (р0, р) = ift(d0, -V) и выражение для опе¬
ратора спина, находим из первого уравнения
id0j2/ = Xrot j4.
(20.1)
Лекция 20
307
Второе уравнение
= eailvd0Av + iA{5»dvAv - Э„Ла)
содержит симметричную и антисимметричную части тензора, которые соот¬
ветственно дают
dvAv = div s/ = 0, -iArot л/ = д0л/.
Последнее соотношение повторяет полученное выше (20.1), так что, сумми¬
руя все связи для безмассового векторного поля, получаем систему
_1М = 1Я rot sf, div л/= 0, Ао = 0, (20.2)
где первое уравнение динамическое, так как оно содержит производную по
времени, а два последних—условия, исключающие компоненты 4-векторно-
го поля, не имеющие отношения к безмассовому векторному полю.
Из (20.2), конечно, следует уравнение массовой поверхности
4г ^-гт- = - rot rot s4 => Пл? = 0.
С2 dt2
Основные уравнения (20.2) имеют нековариантный вид: два последних из
них, очевидно, не могут выполняться в произвольной системе отсчета. Одна¬
ко можно, во-первых, записать их ковариантно, если перейти в импульсное
представление, так что
divj?^ = 0 >-* к-л/(к) = 0,
т. е. поле является поперечным. Уравнение массовой поверхности примет вид
(fc2-fc2)^(fc) = fcV(fe) = 0.
Поэтому с учетом
До = 0
находим ковариантную форму поперечности
кпАп = 0 <=» дпАп = 0, (20.3)
и это уравнение уже справедливо в произвольной системе отсчета.
Во-вторых, динамическое уравнение также можно записать ковариантно,
если ввести антисимметричный тензор напряженности поля
hn = дк^п “ &П'(20.4)
откуда
Fq^ = — д^Ао •—> —dojtf1*,
если учесть условие Ао=0. Стандартным образом определяют электрическое
поле
£а=*0а
и магнитное поле
— ~2£аРг^ар} Fap = •
308
Тема 10. Релятивистская квантовая механика
Подставляя определение тензора напряженности поля, находим
Ж = rot jz? => diVc^f = 0.
Тогда динамическое уравнение примет вид
& = (20.5)
Отсюда
div<£ = 0.
Кроме того, динамическое уравнение (20.2) устанавливает операторное ра¬
венство для линейных уравнений поля
л,/ • л 1 д
rot = 1Л-Т7.
с dt
Тогда уравнение (20.5) дает
С dt’ С dt
В итоге мы получили уравнения Максвелла для свободного электромагнит¬
ного векторного поля, которые могут быть записаны ковариантно
dkFkn = 0, dkFmn + dmFnk + dnFkm = 0 (20.6)
при условии
dkAk = 0, Л0 = 0.
Эти уравнения, как известно, как раз и описывают две поперечных поляри¬
зации безмассового векторного поля.
Заметим, что уравнение (20.2) является равенством между вектором и
псевдовектором и содержит псевдоскалярную величину поляризации Я. По¬
этому определим псевдотензор, дуальный тензору напряженностей:
ртп=1 е™ьрркр} (20.7)
у которого компоненты имеют вид
F0а ^ > Fa[3 €<х(3у^ ’
т. е. имеет место подстановка—преобразование дуальности:
1—* 1—* —(?.
Тогда основное уравнение безмассового поля с заданной спиральностью при¬
мет ковариантный вид
Fkn = iXFkn. (20.8)
Решение уравнения в виде плоской волны с положительной энергией
можно представить в виде
так что подстановка дает
~£± = iAk х s_l, со = с\к\.
Лекция 20
309
Если fcttz, то ортонормированные базисные векторы, отвечающие положи¬
тельной и отрицательной киральности,—
При этом, конечно, для 4-векторов поляризации еп = (0, е, 0)
е*пеп = -е*-е = -1.
Вещественное поле, являющееся решением уравнений движения, согласно
принципу суперпозиции имеет вид
"J
Ж*)=| щЬ?{е"1к'*«я№)ая№)+е1кХ(к)«А№)}. (20.9)
20.1.1. Преобразования Лоренца и калибровочная инвариантность.
В произвольной системе отсчета у векторного поля появляется ненулевая
временная компонента, так как преобразование Лоренца имеет вид
Л/п(х/) = А^Дгп(х).
В импульсном представлении это преобразование будет иметь тот же вид,
но нам необходимо также принять во внимание дополнительное условие
кпАп=к0А0 - к • л/=0, которое в силу своей ковариантности справедливо и в
штрихованной системе. Значит,
xJLjL
0 К ’
и вследствие к'0 = |fc'| поле можно представить в виде
, w к'-Л' + ./1
п п (К)2 п ’
где уже
A'j- = 0, к'-л/'± = 0.
В итоге динамическое поле выражается следующим образом:
A'n1(x/) = A,n(x/-)-d'nf(.x/),
где / — подходящая функция, удовлетворяющая условию □/ = 0. От этого
условия можно избавиться, если помнить, что продольные компоненты поля
не являются физическими. Но именно эти компоненты не входят в тен¬
зор напряженности, поэтому формулировка уравнений движения вектор¬
ного безмассового поля в терминах тензора напряженности автоматически
исключает нефизические продольные компоненты. Отсюда заключаем, что
динамическое безмассовое векторное поле является калибровочным и оно
удовлетворяет уравнениям
dkFkn = 0, dkFkn = 0, (20.10)
причем состояния с положительной и отрицательной киральностью А = ±1
удовлетворяют условию
Fkn = iXFkn. (20.8)
310
Тема 10. Релятивистская квантовая механика
20.1.2. Действие и квантование. Найденные нами поперечные моды с
заданной спиральностью удовлетворяют уравнению массовой поверхности.
Поскольку спиральность входит в полный набор наблюдаемых, ее коммута¬
тор с гамильтонианом равен нулю, и, следовательно, она является интегра¬
лом движения. Поэтому построение действия для каждой поляризации по
сути повторяет процедуру, проведенную для скалярных полей, с той лишь
разницей, что квадрат вектора поляризации равен — 1. Тогда уравнение мас¬
совой поверхности
р2Лп±(х) = 0, Д" (х) = (gnk -
где оператор
nnnfc
р/сп _ пк _ У У -ркп пт _ ркт
г & р2 3 г гп ~г >
называют проектором на поперечные моды. Действие, приводящее к задан¬
ным уравнениям для векторного калибровочного поля, в полной аналогии со
случаем скалярного поля имеет вид
W = "^2 /^Л1(Х)Р2Л1>П(Х),
где мы ввели знак минус, отвечающий указанной нормировке 4-вектора
поляризации. Подстановка поперечного проектора, выражение оператора
4-импульса через частные производные и однократное интегрирование по
частям дают
Sgauge = ~Ycf d4* дкЛЧдкА*п ~ дпЛ*к-),
так что с учетом антисимметрии полученного тензора находим хорошо из¬
вестное выражение для действия вещественного калибровочного поля1
W = -£ Jd4*Fbfb (20.11)
Квантованное поле в полной аналогии со случаем скалярного поля имеет
вид
4l(*)=J 2kf(2n)3 {е~!^я(fc)flA№) + (fc)°i(fc)>, (20.12)
где 4-векторы поляризации являются поперечными
епрп = 0, е0 = 0.
Электрическое поле
= -до*00 = J 2kf(2n)3 ^0{e-ikxex(k)ax(lc) - eikx£*х(к)а{(к)}
*B принятой нормировке полей — системе Хевисайда — электрический заряд нормирован
условием е2/(4тгйс) ^ 1/137, а потенциальная энергия двух зарядов имеет вид V = e1e2/4nr.
Лекция 20
311
дает гамильтониан свободных волн
:Н: = / <13х:£(х)^(х): = | ^^зко^)ч(к),
если учесть ортонормированность векторов поляризации
*x-*v = Sw.
Релятивистская нормировка операторов рождения и уничтожения имеет ста¬
ндартный вид
[ая(*0, а^; (к')] = 2ho>(2n)35xx,5(k - к').
На этом мы завершаем рассмотрение безмассового вещественного калибро¬
вочного векторного поля, которое мы провели в формализме канонического
квантования, вследствие чего изложение велось в нековариантном виде, так
как мы выделили в явном виде динамические переменные — поперечные
компонентные поля. Вопросы ковариантного квантования калибровочных
полей обычно относят к курсу квантовой теории поля.
В заключение приведем без вывода действие для массивного векторного
поля Vn:
S = J d4* {-^Ffcn(V)Ffcn(V) + \ (f)Vvn} =
= d4* {V2?2V" — Vn(mc)2V„},
где условие поперечности поля dnVn=0 является следствием уравнений дви¬
жения, полученных из вариационного принципа—уравнений Прока:
anFnfc = -(^)V,
поскольку dkdnFkn = 0 как свертка симметричного тензора с антисимметрич¬
ным.
20.2. Связь спина со статистикой
Необходимость квантования операторов рождения и уничтожения в фор¬
ме коммутаторов для частиц с целым спином и антикоммутатора для частиц
с полуцелым спином определяет однозначную связь спина со статистикой:
тождественные частицы с целым спином имеют симметризованные по пере¬
становкам квантовые состояния и подчиняются статистике Бозе—Эйнштей¬
на, а тождественные частицы с полуцелым спином имеют антисимметризо-
ванные по перестановкам квантовые состояния и подчиняются статистике
Ферми—Дирака.
В самом деле, если а и а1* —операторы уничтожения и рождения частицы
с полуцелым спином и фиксированным набором квантовых чисел (заряд,
312
Тема 10. Релятивистская квантовая механика
проекция спина, импульс и т. п.), то для гипотетического состояния с двумя
тождественными квантами
|2>=Й|1)=Л"|0)
легко находим, что в силу свойства вакуума и оператора а: а|0) = 0, а также
и вследствие антикомутации аа' + а*а = 1,
д/2а|2> =aaf|l) = (1 -afa)|l) =at(l -aaf)|0) = <ЛЛх|0) = 0, (20.13)
и поэтому его норма равна нулю:
(2|2) = -^(1|а|2) = 0, (20.14)
т. е. и само это состояние — нуль. Значит, для антикоммутирующих опера¬
торов рождения и уничтожения устанавливается принцип запрета Паули,
и они подчиняются статистике Ферми—Дирака: состояния двух тождествен¬
ных фермионов с идентичными квантовыми числами запрещены, квантовое
состояние является антисимметричным по перестановкам тождественных
частиц.
Аналогично, для случая частиц с целым спином и коммутатора операто¬
ров рождения и уничтожения находим, что норма состояний с произвольным
числом п тождественных квантов не равна нулю, и построенные действием
операторов рождения состояния являются симметричными по перестанов¬
кам.
Собственное значение оператора перестановок тождественных частиц не
зависит от изменения квантовых чисел этих частиц, отличных от спина, так
как оператор перестановок коммутирует со всеми квантовыми числами по
самому определению тождественных частиц. А значит, установленные нами
свойства симметрии и антисимметрии по перестановкам для частиц с иден¬
тичными неспиновыми квантовыми числами являются такими же и для
произвольных квантовых чисел, отличных от спина.
Таким образом устанавливается теорема о связи спина со статистикой:
фермионы обладают полуцелым спином, а бозоны—целым.
Кроме того, мы по сути получили и недостающие соотношения коммута¬
ции и антикоммутации для операторов рождения:
[at (fc), at,(fc7)] = 0 для бозонов,
t + / (20.15)
{а^ (fc), ajy (fc)} = 0 для фермионов,
и после применения эрмитова сопряжения точно такие же соотношения для
операторов уничтожения
[ao (fc), av(fc7)] =0 для бозонов,
, (20.16)
{ая(fc), аЯ/ (fc )} = 0 для фермионов.
В самом деле, для состояния, в котором мы выделим пару тождественных
частиц,
|i2a,i22,->=aIc4|0,0,->, (20.17)
Лекция 20
313
где SI обозначает набор квантовых чисел, например, импульс, спиральность,
заряд и т. п., {fc, Я, е,...}, а фоковское состояние других квантов произвольно,
симметрия или антисимметрия по перестановкам тождественных частиц
очевидно, означает, что соответственно
a\al = ±а\а\, (20.18)
откуда сразу следуют соотношения коммутации для операторов рождения
бозонов и фермионов с произвольными квантовыми числами.
Мы установили связь спина со статистикой для свободных релятивист¬
ских частиц, но в силу коммутативности оператора перестановок тожде¬
ственных частиц со всеми наблюдаемыми включение взаимодействий не
может изменить собственных значений этого оператора, так что фермионы
и бозоны подчиняются соответствующей статистике и при наличии взаи¬
модействий между частицами или полями.
20.3. Калибровочное взаимодействие
Глобальная инвариантность действия релятивистских полей относитель¬
но преобразований комплексной фазы определяет, согласно теореме Нётер,
сохраняющиеся токи и, как следствие, интегралы движения — заряды, ко¬
торые мы использовали при построении квантованных полей для описания
частиц и античастиц. В нерелятивистской квантовой механике волновая
функция Ф(лг) = (х|Ф) приобретает комплексную фазу, если произвести заме¬
ну базисных кет-состояний
\х) ~ Ю=еыУ^|х), (20.19)
где У — оператор, который имеет фиксированное значение для заданного
типа частицы, так что
Фи(х) = (хи|Ф> =е-1иУ^Ф(лг). (20.20)
Если и—глобальный параметр, т. е. он не зависит от координат и времени, то
приобретаемая всеми базисными состояниями комплексная фаза не может
быть наблюдаемой, так как она всегда сокращается при определении ампли¬
туд вероятностей или матричных элементов операторов.
Если параметр преобразования и локальный, т. е. зависит от координат
и времени и = и(х), то состояния частицы в разных точках приобретают,
вообще говоря, относительную фазу, которая уже в принципе может быть
наблюдаема. Выяснение вопроса о наблюдаемости фазы — предмет этого
параграфа.
Важно, чтобы переход от одного базиса состояний к другому осуществ¬
лялся унитарным преобразованием, сохраняющим нормировку состояний.
Отсюда следует, что оператор Y должен быть эрмитовым. Мы остановимся
на простейшем случае — группе U(l), для которой Y = Q — диагональный
314
Тема 10. Релятивистская квантовая механика
оператор, равный значению заряда частиц в единицах е, как мы это видели
при квантовании свободных полей.
В релятивистской теории обобщением преобразования комплексной фа¬
зы базиса \х) является унитарное преобразование комплексной фазы одноча¬
стичного состояния в фоковском пространстве1:
IР> ~ lpu> = eiuy£|p), (20.21)
что можно свести к переопределению оператора рождения частицы af(p):
^u(p) = a4p)emYnc => au(p) = a(p)e~m7£. (20.22)
Для античастиц Ус = —У, так что релятивистское квантованное поле, постро¬
енное, как мы видели, из спиновых мод и операторов рождения античастиц
и уничтожения частиц, подвергается тому же преобразованию (20.20), что
и классическое.
Оператор заряда Y обладает простыми свойствами относительно группы
Пуанкаре: Y является скаляром, т. е. он коммутирует со всеми генераторами
группы Пуанкаре, так как он не изменяет квантовых чисел состояний, связан¬
ных с пространственно-временными характеристиками поля. При этом, как
мы уже отмечали, его трансформационные свойства относительно дискрет¬
ных операций инверсии пространства и времени задают тип взаимодействия
различных киральных компонент полей. В простейшем случае группы [/(1)
мы в дальнейшем опускаем Y для упрощения записи.
Говорят, что преобразования (20.20) образуют группу преобразований
внутренней (не связанной с пространством-временем) симметрии, если дей¬
ствие поля остается относительно таких преобразований инвариантным. Рас¬
смотрим калибровочные преобразования более подробно.
Оператор пространственно-временных сдвигов состояний в инфинитези-
мальной форме
T = t-^pkdxk, Pk =
действует на оператор уничтожения согласно
6a(p) = rto(p)r-a(p)=Vfca(p)dxfc => iftVfca(р) = [&, a(p)].
Тогда, как мы уже показали, в силу
lPk> a(p)] = a(p)pfc,
где pk = (р0, р) - 4-импульс одночастичного состояния, находим
iftVfca(p) = a(p)pb
т. е.
^k = dk>
1Мы считаем здесь, что вакуум инвариантен относительно преобразований комплексной
фазы: заряд вакуума равен нулю. Вакуумные состояния, не инвариантные относительно калиб¬
ровочных преобразований, рассматриваются в квантовой теории поля, и они отвечают теориям
со спонтанным нарушением калибровочной симметрии.
Лекция 20
315
и при трансляциях оператор приобретает фазу
а(р) -► e~#pd*a(p).
После калибровочного преобразования оператора уничтожения (20.22)
получим
i^V“au(p) = [pfc, au(p)].
Отсюда, вычисляя простейший коммутатор
[Pk,e-iu*‘] = ^-iu*<dku,
находим
i?iV“au(p) = au(p) (pfc + ^kuj,
так что трансляции дают
au(p) - e-№+ea«u/c)dxkau(p),
что и следовало ожидать, поскольку изменение дополнительной фазы, обу¬
словленной калибровочным преобразованием, и должно быть
ie г- ie ~ л к
-■г-ои = —т-дки ах .
пс пс *
При этом, однако, приходится переопределять ковариантную производную
^к = дк ^к = дк~^дки>
куда входит теперь продольное поле дки, которое является нефизическим,
потому что смена базиса состояний не может приводить к новым наблюда¬
емым физическим явлениям. Это означает, во-первых, что действие остается
инвариантным при калибровочных преобразованиях
5“S = 0 =* -Мо=1сдк>к(-Х) = 0> (20>23)
т. е. имеет место закон сохранения тока. Во-вторых, продольное поле, как
мы видели, является нефизическим, если только оно является компонентой
4-вектора, представляющего собой безмассовое калибровочное векторное
поле. Значит, ковариантная производная—
Vk = dk + i j-Ak, (20.24)
так что при калибровочных преобразованиях
А% = Ак + дки, (20.25)
и, следовательно, ковариантная производная сохраняет свой вид
Vfc“ = 3fc + i
Тогда при трансляциях оператор уничтожения, а значит, и цоле приобретают
фазу
а(р) е~*(-Рк~1'Лк) ^aip).
316
Тема 10. Релятивистская квантовая механика
Значит, для определения фазы поля при трансляциях необходимо просто
задать калибровочное поле или, как говорят математики, связность А^х).
Для пары бесконечно малых сдвигов
Tij2 = l + dx£2Vfc
последовательное действие двух трансляций из точки хк в точку хк + dxk +
+ dxk2 в прямом и обратном порядке дает поле, которое может отличаться
только фазой
r27i = lir2ft>(x), со = е~'5иь.
Эта разность фаз 5 и наблюдаема, потому что перенос одного и того же
физического состояния системы по двум путям из одной точки в другую
приведет, вообще говоря, к наличию интерференции состояний. В пределе
инфинитезимальных трансляций
ТгТ2 - Т2Тг = [7i, г2] = [Vfc, Vn] dxk d4
И при
со = 1 — \5Utt~
пс
находим
i5u^ = [VbVn]dx1fccbc2n.
Коммутатор выражается через напряженность калибровочного поля:
[Vb VJ = [дк + i±Ak, дп + i^А,] = i]tc(hAn~дпА0 = i^Fkn,
так что
5u=Fkndxkdx%.
Таким образом, разность фаз, а значит, и интерференция возникают, только
если напряженность калибровочного поля не равна нулю, т. е. в системе есть
динамическое безмассовое векторное поле. Если же калибровочное поле —
«чистая калибровка», то никаких наблюдаемых эффектов не возникает.
Подчеркнем также особый случай: контур трансляций охватывает об¬
ласть, где напряженность поля не равна нулю, в то время как на самом кон¬
туре напряженность поля — тождественный нуль. Тогда говорят, что имеет
место ситуация «пространства с дыркой». Ее можно осуществить физически,
скажем, помещая в систему бесконечно длинный соленоид с магнитным
полем вне пределов движения частиц, например, за экраном, но так, чтобы
траектории могли охватывать этот соленоид (см. рис. 25). При этом калибро¬
вочное поле —«чистая калибровка» вне соленоида, нр внутри соленоида оно
отвечает наблюдаемому магнитному полю, так что непрерывная функция
поля не является калибровкой во всем пространстве. Тогда изменение фазы
является наблюдаемым: это —эффект Ааронова—Бома.
Итак, локальное калибровочное преобразование базиса состояний в фо-
ковском пространстве приводит к необходимости введения в теорию дина¬
мического безмассового векторного поля путем «удлинения производных»,
Лекция 20
317
с двумя экран
щелями
Рис. 25. Схема эксперимента по дифракции электронов на экране с двумя
щелями. При включении магнитного поля W, заключенного в соленоиде
внутри области распространения электронов, изменяется разность хода для
верхних и нижних траекторий, т. е. имеет место эффект Ааронова—Бома
т. е. введения обобщенного импульса1
Рк •“> А = Рк “ “Ль Рк = ift дк, (20.26)
который дает взаимодействие заряженных полей с калибровочным полем.
Такой вид взаимодействия называют минимальным, так как, наряду с та¬
кими взаимодействиями, калибровочная инвариантность не запрещает вво¬
дить дополнительные калибровочно инвариантные слагаемые в действие.
Второй важнейший вывод—калибровочное поле Ак является динамическим
безмассовым векторным полем, и, следовательно, у него есть собственный
кинетический член, который определяется коммутатором ковариантных про¬
изводных
[Vfc,VJ = i^Ffcn, (20.27)
т. е. напряженностью поля, уже известным нам образом
Sgauge = ■J d4xFknFkn. (20.28)
Действие для поля Дирака, взаимодействующего с калибровочным полем:
S = J d4x {р~\А — mcjя/»| + Sgauge. (20.29)
Член с взаимодействием представйм в виде
Sint = -f J d4x ■фЛгр = -i J d4x Akjk,
где, конечно,
jk = expYkip
1Ковариантная производная определяет кинетический импульс Рк = muki где ик — ковари-
антный вектор 4-скорости, а собственно обобщенный импульс — оператор рк = ihdk.
318
Тема 10. Релятивистская квантовая механика
есть 4-вектор тока фермиона. Значит, взаимодействие построено по типу
ток-источник.
Для скалярного комплексного поля Клейна—Гордона—Фока
s=|d4* Ыр (к- !•*] ФУ [г* -1д‘]ф - Kf )2ф,ф}+w
Отметим, что взаимодействие для скалярного поля содержит вклад, квадра¬
тичный по калибровочному полю.
20.4. «Релятивистский» атом водорода: спектр
20.4.1. «Скалярный» электрон. Исторически Шрёдингер при формули¬
ровке волновой квантовой механики решил задачу о релятивистском атоме
водорода для случая скалярного поля.
Фиксируем калибровку электростатического поля условием
^ = 0,
так что
— —-
есть кулоновский потенциал притяжения для заряда е. Тогда уравнение Клей¬
на—Гордона—Фока для стационарных связанных уровней примет вид
{(po + ff) — р2 - (тс)2|ф(дг) = 0, (20.30)
где Ро = Е/с выражается через искомую энергию Е,
Ч>(х) = е~*Е(Ф(г),
а р—оператор импульса. Тогда основное уравнение сводится к виду
Это — уравнение со сферической симметрией, так что его решения можно
искать в виде
♦(r) = ^9U(0,y),
где Щ т — сферические гармоники. Радиальное уравнение для функции и (г)
принимает вид
ГРг2 Ее2, h2 Г1П . е4 >1 , , Е2-(тс2)2 , л
{ 2т тс2 г + 2mr2 V( +15 ft2c2 J }U(r) 2тс2 “(г)’
или после введения постоянной тонкой структуры и «энергии связи» е:
е2 _ _Е2-(тс2)2
he ает’ 6 2 тс2
находим
Лекция 20
319
Таким образом, мы свели задачу к решению того же уравнения, что и в тео¬
рии нерелятивистского атома водорода, с точностью до нормировки заряда
кулоновского притяжения
2 Е 2
ez —> —~ez
mcL
и переопределения орбитального квантового числа
Щ +1) ~ А(А + 1)=га + 1)-а2т,
так что
А = l-5h (20.33)
и уравнение для бг
5f - бг (2*+ 1) + 4п = 0
имеет решение, отвечающее положительным значениям Я, что необходимо
для регулярности функции и (г) в нуле1:
51 -1 + \ - V0 + i) _aem- (20.34)
Нормируемые решения уравнения отвечают уровням
е = -—а2 -* е - g2 „2 _ °£п Д2
2n2 em v_ 2v2 m2c4 ет — 2v2 тс2’
где
n = l + Z + nr •-» v = l + A + nr, nr€{0,N}.
Подставляя определение е через энергию, легко находим «точную формулу»
для энергии связанного состояния
или энергию связи
&V=E — тс2 = — тс2
Е= ,тс , (20.35)
П?
_£Ш.
v2
Во втором приближении по малому параметру а\т разложение в ряд Тейлора
дает
А
1Если заряд ядра равен Z, то выражение для сдвига 5\ принимает вид
Si -z2aL■
При Zaem >1/2 величина 50 приобретает мнимую добавку. Тогда говорят о катастрофе, свя¬
занной со слишком большим вкладом притягивающего потенциала 1 /г2. Физической причиной
для возникновения такой формальной катастрофы служит некорректность применения одноча¬
стичного уравнения в сильных электрических полях, которые приводят к большим флуктуациям
поля, в том числе и числа частиц.
320
Тема 10. Релятивистская квантовая механика
где еще необходимо провести разложение
v2 (n-5i)2 п2\ nj
где
а2
57^г ет
2Z + 1’
В итоге
С2036)
Как видим, релятивистская поправка снимает вырождение по орбитально¬
му моменту I между уровнями с заданным значением главного квантового
числа п. Однако эксперимент однозначно опровергает такое значение рас¬
щепления, например, для уровней 2s и 2р. Поэтому Шрёдингеру пришлось
ограничиться ведущим нерелятивистским приближением в задаче для атома
водорода. Причина расхождения кроется, конечно, в наличии спина у элек¬
трона.
20.4.2. «Релятивистский» электрон. Стационарное уравнение Дирака
для электрона в кулоновском поле протона имеет вид
(Р—тс)'ф(г) = 0,
где „ 2
р0=-+~,
и с сгу
и
1/>(x)=e"ȣtiKr).
Умножение уравнения на (РЛ-тс) дает
{(ро + -р2-(пгс)2-г-рГо^}^С»*) = 0,
где дополнительный по сравнению с уравнением для скалярного поля вклад
после дифференцирования сводится к
• ft2aem ^ ч
где п = г/г. Этот член сохраняет пространственную четность, так как при
отражении пространства у5 —> —75, — п, а псевдовектор спина s = со¬
храняется. В итоге в полной аналогии со случаем скалярного поля приходим
к уравнению на собственные значения энергии
Й- М - ^irs^ ")]}v-(r)=^(r). (20.37)
Поскольку
[1а, (а • n)] = ieaprOpnr, [sa, (а • n)] = ieaprnp(TY,
Лекция 20
321
в задаче сохраняется полный момент
j = Z + s
и его квадрат. Кроме того, инвариантность относительно пространствен¬
ной инверсии означает, что Р-четность — квантовое число. При сложении
орбитального момента со спином 1/2 при заданном j допустимы только 2
значения
i±=j±|,
которые отличаются знаком P-четности. Поэтому будем характеризовать со¬
стояние полным набором {Е, j, m, Z}, где j — полный момент, т — его проек¬
ция на заданную ось, I — орбитальный момент, дающий Р = (—1)г.
В киральном представлении гамма-матриц Дирака матрица у5 диаго-
нальна
поэтому уравнение (20.37) для биспинора
разделяется на пару независимых уравнении для двухкомпонентных спино¬
ров Ф±(г):
<2аз8>
Двухкомпонентные спиноры можно представить в виде суперпозиции состо¬
яний с заданным орбитальным моментом I:
Ф±(г) = a±^;m(r) + b±Y>/;m(r),
так что пространственная инверсия биспинора дает
р a_^'m(r)-b_^,m(r)N
т/>(г) —> у<Ж-г) = (~1)1+
Va+W+m (г) — Ь+ (г) у
Значит, биспинор имеет четность (—1)г+, если
а_=а+, Ь_ = -Ъ+, Р = (-1)1+,
и (—1)L, если
a_ = -a+, b_ = b+, Р = (- 1)L.
Сами спиноры ipf’"1 построены согласно правилам сложения двух моментов.
Поэтому
i24>i’m=i± a±+D^m.
Так как оператор (а • п) обладает отрицательной Р-четностью и его квад¬
рат равен единице, можно выбрать фазы спиноров так, чтобы
(а-п)(р£п = (р£т.
322
Тема 10. Релятивистская квантовая механика
Значит, этот оператор смешивает состояния в уравнении (20.38), причем
матрица, соответствующая вкладу орбитального движения
ft2 [l2-a2pmTiaem(a-ti)]
2 mr2
в базисе имеет вид
h2 м+(/+ + 1) — а2
2 тг2
Tiae
Tiae
Z_(L + 1)-с&
ft2
2 mr2
A.
Найдем собственные значения z для
Л =
О2+ 2/ + f — а2
Tiae
em 1 —em
У2-- —a2 ,
4 em у
Tlaem
где мы подставили l± = j± 1/2. Уравнение
detCA —z)= [(j + l) -aem_Z+J + |] • [0 + |) +aem = 0
легко решается, так что
(j + l)2-aL-Z = ±]l 0' + i)2-«em’
и
2=i/0'+I)2-<(i/0'+1)2-o,-±1)-
Значит, собственные значения можно представить в виде
z = A(A + l), А=;±| - 5j = Z± —5j-,
(20.39)
где уже
5J-j + l~ \lO + l) “aem-
(20.40)
Собственные значения для верхних и нижних спиноров, очевидно, совпа¬
дают, причем коэффициенты смешивания а± и Ь± удовлетворяют условиям
построения биспиноров с заданной четностью.
В базисе собственных векторов матрицы получаем уравнение, опять име¬
ющее вид уравнения для нерелятивистского атома водорода
"2 - *2 П2
^ + 2^A(A + 1)}U(r) = <?U(r)’
12m me2
и, повторяя выкладки, аналогичные случаю скалярного поля, находим спектр
связанных состояний
Е =
тс*
№
(20.41)
Лекция 20
323
где уже
v = 1 + nr +1± - 5j = п± - 5j.
Поэтому для заданного главного квантового числа гг мы имеем двукрат¬
ное вырождение по орбитальному моменту I (разные значения радиального
квантового числа пГ) при фиксированном значении полного момента j, если,
конечно, п > 1 и п > j +1/2, потому что в случае равенств возможны только
значения Z = 0 и Z = j —1/2 соответственно, при пг = 0.
Разложение энергии связи в ряд по константе тонкого расщепления ает
дает
Теперь значение расщепления уровней с заданным п в зависимости от j дает
прекрасное согласие с экспериментами по измерению спектров в атоме во¬
дорода. Состояния электрона принято характеризовать тройкой квантовых
чисел: главное квантовое число гг, орбитальный момент Z, полный момент
количества движения j,—которые объединяют в виде символьной записи rtlj,
носящей название ;-терма.
Поправки высшего порядка имеют, однако, уже другую природу: они
определяются не только высшими членами разложения релятивистского вы¬
ражения, но и обусловлены взаимодействием спина электрона со спином
ядра—сверхтонкое расщепление—и флуктуациями электромагнитного поля
при наличии зарядов—лэмбовский сдвиг 5-волновых уровней.
Проведенное нами рассмотрение спектра атома водорода из релятивист¬
ского уравнения Дирака укрывает от глаза осознание динамической природы
поправок в терминах, допускающих ясную физическую трактовку. Поэтому
проведем систематическое построение гамильтоновой динамики электрона
путем последовательного учета релятивистских эффектов в виде возмущения
к ведущему нерелятивистскому вкладу.
(20.42)
Тема Нерелятивистское приближение:
11 эффективная теория
Лекция 21
Операторное уравнение для двухкомпонентного спинора во внешнем поле
в одночастичном приближении, разложение операторов в ряд по малому от¬
ношению v/c, ведущий вклад в нерелятивистское приближение, эффективное
действие для спиноров Паули, магнитный момент электрона и фактор Ланде
g = 2, поправки к эффективному действию в случае движения в статическом
потенциале, роль нормировки заряда на единицу, природа кинетической
поправки, спин-орбитального взаимодействия и дарвиновского члена, учет
томасовского вращения спина при неинерциальном движении, локализация
электрона и область применимости нерелятивистского приближения, комп-
тоновская длина, релятивистские поправки как возмущение в атоме водорода,
квантовые числа электрона и формула для поправки к энергии, снятие вы¬
рождения по полному моменту и остаточное вырождение по орбитальному
моменту, введение аномального магнитного момента, швингеровское зна¬
чение, полученное в теории возмущений из квантовых петлевых поправок,
задача о магнитном моменте протона и нейтрона в кварковой модели.
21.1. Построение эффективного действия
Рассмотрим массивную частицу Дирака во внешнем поле в случае, когда
энергия частицы мало отличается от энергии покоя, т. е. сделаем подстанов¬
ку
^t,r)=e-imA(j((;;;|), (21.D
где (р и % — двухкомпонентные спиноры в представлении Дирака для гам-
ма-матриц, так что уравнение Дирака СР — тс)я/> = 0 с обобщенным импуль¬
сом Vk = ihdk — принимает вид
^ (<7S>) -po+U-mcJ W ’
где ро = тс + £/с и оператор ё = ih dt) так что получаем систему
(ё - еФ)ср — с(а • х = О,
(21.3)
с(а - (2тс2 + ё-еФ)х =0,
которую можно разрешить относительно х •
326 Тема 11 Нерелятивистское приближение: эффективная теория
причем здесь необходимо внимательно следить за тем, чтобы соблюдать
порядок следования операторов. Обозначим для упрощения записи
1
Тогда
1,l=£i=1 + >V. (21.5)
2т<?
Z=a+W><z£iv.
Используя этот результат, запишем
cipCP — тс)тр = ipf{(e — еФ)<р — с(а • 9)хУ =
= (/?t{ё — еФ - 2“(<г • 9)(1 + W)(сг • 9)
Значит, действие для спинора Дирака во внешнем поле примет вид
SD = J д4х'фСР-тс)гр =
= J dt J d3r —еФ —+ (21.6)
Плотность заряда ej° = етру°гр = е^яр = e(sp*ip + х*Х^ запишется как
е;° = е</>*{1 + ^^(а-^)(1 + >У)2(<г •£»)}</>. (21.7)
Выражения для действия и плотности заряда (21.6) и (21.7) являются точ¬
ными, но они содержат обратные операторы, которые формально можно
разложить в ряд. Например,
1 +W=—W = l-4rl£f+ ••• (21.8)
Следует ожидать, что ряд сходится, если вклады
е — еФ
<1.
2 тс2
Очевидно, это имеет место, если поле слабое и энергия частицы в нем мала
по сравнению с массой покоя. Таким образом, проведенные преобразования
поля Дирака могут служить основой для нерелятивистского приближения.
Ведущее приближение. Полагая W —> 0, с точностью до вкладов порядка
0(1/с2) находим для плотности тока
ej°*seip*(p, (21.9)
а значит, нормируя двухкомпонентный спинор ip условием
/ d3r ¥>V = 1,
получаем поле с единичным зарядом, что эффективно соответствует одноча¬
стичному приближению1.
1Нормировка заряда на единицу, очевидно, останется той же и при рождении электрон-по-
зитронных пар за счет энергии внешнего поля. Поэтому условие нормировки заряда на единицу
Лекция 21
327
Отметим, что в нерелятивистском разложении нижняя компонента %
дираковского биспинора подавлена по сравнению с верхней компонентой ц>
отношением \р\/тс, т. е. как 0(у/с), где v — скорость движения частицы.
Поэтому верхнюю компоненту часто называют «большой», а нижнюю—«ма¬
лой».
В том же порядке по обратной скорости света действие SNR для нереляти¬
вистского спинора (/? принимает вид
SNr = J dt J d3r —еФ —(21.10)
Согласно алгебре сигма-матриц Паули
(сг •&')2 = &2 + ia(& х0>).
Векторное произведение
(£? X ^)а — €ару ( ” ^ ~ с^О ^ — ^ ~ с*^0 = ~ ^Г^Р^’
так что
В итоге
(0» x0*) = iy = (21.11)
Srai=J dt J dsrV*{«-et-|J + ^Ca-^)}V. (21.12)
Вариация действия по приводит к уравнению Паули для нерелятивистско¬
го спинора
т^ч>=ншч> (21.13)
с гамильтонианом
С2Ш)
где оператор спина s=^cr и «g-фактор» Ланде
g=2.
Этот результат явился ярчайшим успехом теории Дирака: он позволил объяс¬
нить наблюдаемое экспериментально значение фактора Ланде, исходя из ре¬
лятивистского уравнения с минимальным взаимодействием калибровочного
типа. Кроме того, поскольку Дирак вывел свое уравнение эвристическим пу¬
тем, именно нерелятивистское приближение позволило ему установить, что
полученное им релятивистское уравнение описывает частицу со спином 1/2.
еще не означает нормировку числа электронов. Однако, как будет ясно ниже, процессы флук¬
туации числа квантов поля становятся заметными лишь при неопределенности координаты
порядка комптоновской длины волны электрона, что согласно соотношению неопределенностей
отвечает флуктуациям импульса порядка 5р~тс, т. е. в релятивистском случае, когда нереля¬
тивистское приближение становится неприменимым.
328 Тема 11 Нерелятивистское приближение: эффективная теория
Релятивистские поправки для статического потенциала. В случае
J2? = 0 с учетом поправок порядка 1/с2 плотность тока имеет вид
е?ъеу'{1 + -^}ч>. (21.15)
Введем
+ (2116)
Тогда с точностью до высших поправок
9°weVMiVNR> (21-17)
а значит, нормировка
I d3r V’nrY’nr^I (21.18)
обеспечивает интерпретацию (рш в качестве волновой функции одночастич¬
ного состояния с точностью до 1/с2.
С учетом ведущего приближения и первой поправки к
2 тс2
действие
Очевидно, что
(<г • р) е (cr • р) = ёр2,
в то время как
(а • р)Ф(сг • р) = Фр2 — 1Й{УФ • р + i<x • (УФ х р)},
где V действует на потенциал Ф. Значит,
S*JdtJd3rV{e(l +
_ (Фр2 "Р+ i<T'(V* Х Р)}) }'У'
Теперь в этом выражении необходимо перейти к нормированному нереляти¬
вистскому спинору
Тогда вклад энергии с заданной точностью
вклад кинетического члена
Лекция 21
329
и наконец, вклад потенциала
{ф-5^(,,!ф+фр2)}''’»-
Простым дифференцированием находим
р2Ф = ф р2 - 2ihV$ ■ р - П2 АФ.
Для поправки порядка 1/с2
<^-^Ф • р + i<7 • (УФ х p)}ip ъ </>nR{V Ф • Р + io- • (УФ х р)}(/?ш-
Суммируя подобные члены, находим эффективное действие для нереляти¬
вистского спинора
Sl" J dt / d3r <{<■- - ё + Ш? - ■ &* х - 5&
Если потенциал является центрально-симметричным, то
VФ(r) = ^^r,
и с учетом определения орбитального момента I = (г х р)
S-J dt J +
В итоге гамильтониан нерелятивистской частицы в статическом централь¬
но-симметричном потенциале с учетом релятивистских поправок вплоть до
порядка 1/с2 принимает вид
Н = ^- + еФ- + е\ 2 Ф (-г-) (s-I) + -^ДФ. (21.19)
2т 8т3с2 2т2с2 г 8т2с2
Общий формализм построения эффективного гамильтониана произвольно
заданного конечного порядка по обратной скорости использует преобразова¬
ние Фолди—Ваутхойзена (Foldy—Wouthuysen), которое мы здесь не рассмат¬
риваем.
21.2. Интерпретация поправок
Каждый из трех членов релятивистских поправок к движению частицы со
спином 1/2 в гамильтониане (21.19) допускает вполне ясную интерпретацию.
Прежде всего, разложение релятивистского выражения для кинетической
энергии по скорости
Б=д/(тс2)2 + с2р2 = тс2(1 + ^-|^ + ...)^тс2 + ^-^
в точности воспроизводит релятивистскую поправку к кинетической энер¬
гии.
330 Тема 11 Нерелятивистское приближение: эффективная теория
Вклад спин-орбитального взаимодействия требует более тщательного
рассмотрения. Во-первых, электрическое поле статического потенциала 8 =
= — УФ = — гФ'(г)/г при переходе в систему, сопутствующую электрону, кото¬
рый движется со скоростью v} согласно преобразованию Лоренца в нерелл-
тивистском пределе дает магнитное поле
#=-1 (vxS)=-mCrXp)=_mL.
с mcr г тег
Потенциал взаимодействия магнитного диполя электрона /х с внешним по¬
лем t/mag = -(/х* Ж) принимает вид
ТТ - ф/(г) geh T^ — J&L&Sllrc тл
mcr 2mc^S ^ 2m2c2 r ^ ^
что, однако, вдвое больше результата, выведенного из уравнения Дирака
в нерелятивистском пределе, так как g = 2. Причина расхождения—не инер-
циальное, а вращательное движение электрона в статическом потенциале,
вследствие чего спин испытывает прецессию Томаса.
В нерелятивистском пределе частота прецессии равна
Ускорение можно выразить из второго закона Ньютона
*=i.*=_i£Cr)r>
m m г
так что
е Ф'(г) ( л _ е ФЧг)т
со — оо х mv) — л о о Ь.
2m2c2 г v 2т2с2 г
Вращение спина описывается уравнением
ds
d^=6,xs-
В квантовой механике это уравнение получается из уравнения Гейзенберга
ds а
-^Thomas
если добавка к гамильтониану равна
^Thomas = ^(s • Ci>),
ЧТО СВОДИТСЯ К
zj efi Ф (г) ^ -v
17Thomas ~ 2т2С2 Г ’
и суммарный вклад спин-орбитального взаимодействия
^ = (g~1)2mV^r(r)(5'I) (2L20)
совпадает с результатом нерелятивистского приближения уравнения Дирака
при g = 2.
Лекция 21
331
Наконец, дарвиновский вклад
Нп • = — АФ
Darwin 8 тп2с2
возникает вследствие ограниченности области применения нерелятивист¬
ского одночастичного приближения. В самом деле, если частицу локализо¬
вать на расстояниях порядка комптоновской длины %c = h/(mc), то согласно
соотношению неопределенности флуктуации импульса достигают реляти¬
вистских значений р ~ тс, что несовместимо с принятыми предположениями
о сходимости разложения действия по обратным степеням скорости све¬
та. Другими словами, нерелятивистский электрон во внешнем поле можно
считать точкой только с точностью до флуктуаций на масштабах порядка
комптоновской длины волны. Поэтому и локальный потенциал нереляти¬
вистского приближения — это усредненная величина. Поправка к усреднен¬
ной величине потенциала за счет флуктуаций равна
(ф(г)) = Ф(г) + (5г) • V<Kf) + 1(5га8г^)дадр Ф(г) +
где г = (г). Очевидно, что
(бг) =0, (бгабг^) = |сбг)2ба^,
и при 5r~h/(mc) поправка сводится к
ебФ~ т^-^ДФ,
6 тгсг
что с точностью до коэффициента дает дарвиновский вклад, точное значение
которого выведено из уравнения Дирака.
Таким образом, все релятивистские поправки для частицы спина 1/2
имеют вполне ясное динамическое происхождение.
21.3. Атом водорода: поправки
В атоме водорода потенциал притяжения
Поэтому
Ф = --.
Ф '(г) = АФ(г) =4тге5(г),
г*
так что возмущение в виде релятивистских поправок имеет вид
V = --xK^ + ^rTl\(-s'L^ + ^rT-2n5^- (ZL2$
8m3c2 2т2с2 г3 4 2т2с2
Как видим, для кулоновского случая дарвиновский член сводится к дель-
та-функции, поэтому его еще называют контактным. Отметим здесь, что
точность в измерении спектров атома водорода столь высока, что она позво¬
ляет выделить вклад за счет неточечности ядра, в частности, протона: в этом
332 Тема И Нерелятивистское приближение: эффективная теория
случае необходимо вместо дельта-функции поставить распределение заряда
в ядре конечного радиуса.
Связанные состояния исходной системы —нерелятивистского уравнения
Шрёдингера для атома водорода — характеризовались набором квантовых
чисел: главного квантового числа п, орбитального момента I и его проек¬
ции т. При этом четность состояния определялась через I как (—1)*.
Теперь из вида возмущения (21.21) видно, что квадрат орбитального мо¬
мента по-прежнему является квантовым числом, так как он коммутирует с У.
Четность определяется тем же соотношением и так же сохраняется, потому
что возмущение как функция координаты центрально-симметрично, а ска¬
лярное произведение спина на момент—скаляр. Однако ни оператор спина s,
ни оператор орбитального момента l = L/h по отдельности не коммутируют
с этим скаляром:
[sa, (s • 0] = ieaprLpSr> [la, (s • Z)] = iheaPrlYsp.
Зато отсюда следует, что сохраняется полный момент
j = s + l,
так же как и его квадрат. Значит, связанные состояния имеют следующие
квантовые числа: главное квантовое число п, орбитальный момент I и чет¬
ность (—1)г, полный момент j и его проекция т;-.
Квадрат полного момента равен
j2 — I2 + 2(1- s) + s2. (21.22)
Значит, значение скаляра
(1-е) = \{;(; +1) -Щ +1) -1} (21.23)
полностью определяется квантовыми числами состояния, так что возмуще¬
ние является диагональным в этом базисе (секулярное уравнение тривиаль¬
но).
Для вычисления спектра с учетом релятивистских поправок остается вы¬
числить матричные элементы возмущения по базису.
Кинетический вклад при усреднении по состоянию с квантовым числом
п с помощью нерелятивистского уравнения Шрёдингера для энергии
feln, I, j, т}) -у\ п, I, j, mj) = I, j, mj),
можно представить как
—/—£^-\ = —( С-Ш!-а2 +£Г)2\ = _™!а 4
\8m3c2 / 2тс2 \ v 2п2 г J 1 8п4 ет+2п2 \ г / 2тсЛг2 Г
Воспроизводя результаты для атома водорода с учетом ае2 = h2/m, получаем
\ а2 1 тп/'З
х2
ет}
/е2\_е2 1 _ тс2 о
\ г / ап2 п2 е
е4 / 1 \ _ е4 2 1_ _
2тс2 \ г2 / 2тс2 a2 n3(2l + l) п3(21 + 1)“ет'
:at
Лекция 21
333
Приведение подобных членов дает поправку к энергии
= C2L24)
Именно эта поправка возникала из решения задачи о связанных состояни¬
ях в кулоновском поле согласно релятивистскому уравнению Клейна—Гор¬
дона—Фока, потому что оставшиеся вклады спин-орбитального взаимодей¬
ствия и дарвиновский член обусловлены спином электрона.
Спин-орбитальное взаимодействие отлично от нуля только при 1ф 0. Из
рекуррентных соотношений Крамерса для средних по волновой функции
атома водорода находим
Ш-иЫФ.
откуда
/1\ = JL 2
\ г3 / a3n3(2f+i)za+i)’
а значит,
я Р — / g2ft2 -L fc. I) \ = mg2 /у4 J 0‘ ~Ш ~ Z (Z +1) — 3/4 q е л qi 95^
sZ \ 2т2с2 г3 V 2п2 ет n(2Z + l)Z(Z + l) ( (21.25)
где последний фактор обращается в нуль при Z = 0 и равен единице при Z Ф 0.
Наконец, контактный вклад
пропорционален квадрату волновой функции в нуле, а значит, отличен от
нуля только при 1 = 0. Нормированные волновые функции имеют
1*П00(0)|2 = ^, (21.26)
так что контактный член равен
5Darwin£ = ^«em^i0. (21.27)
Суммируем полученные результаты сначала для L = j — 1/2^0. Тогда
в склу 2L +1 = 2j и L (Z_ +1) = j2 -1/4 легко находим
Я F + x F_ тс2 4 1 fn 3n J —1/2 п ) _ тс2 4 1 Г п 31
ошг.-го51п- 2пгаетп\у 4 _!/42jJ 2л2 етп21 j +1/2 4Г
Аналогично при Z+ = j +1/2 в силу 2l+ + 1 = 2 (j + 1) и j (j +1) = Z2 — 1/4
получим
334 Тема 11 Нерелятивистское приближение: эффективная теория
т. е. мы получаем одно и то же выражение при l± = j ± 1/2 #0. Не составляет
труда убедиться в том, что и при I = 0 остается справедлива формула для
ведущей релятивистской поправки к спектру в атоме водорода
г*=-=Й4{7тЬ-!}' C2L28)
что, конечно, воспроизводит результат, полученный при разложении выра¬
жения для энергии связи в атоме водорода из релятивистского уравнения
Дирака со статическим кулоновским потенциалом по (определяющей ско¬
рость движения электрона в атоме) постоянной тонкой структуры ает 0.
Рис. 26. Уровни связанных состояний электрона в атоме водорода в нереля¬
тивистском приближении (штриховые линии) и с учетом расщепления из-за
релятивистских поправок (сплошные линии)
Тонкое расщепление уровней с заданным значением главного квантового
числа л в зависимости от j схематически показано на рис. 26. Напомним,
что при j <п — 1/2 (при l = n — 1 и; = п-1/2 состояние невырождено
по I) сохраняется двукратное вырождение состояний nlj по орбитальному
моменту Z =; ± 1/2, так как энергия зависит только от главного квантового
числа и полного момента электрона j.
Итак, мы установили динамическую природу релятивистских поправок
к спектру связанных состояний в атоме водорода. Учет спина электрона поз¬
волил достигнуть согласия с экспериментальным исследованием спектров
переходов между уровнями с точностью, соответствующей сделанным тео¬
ретическим расчетам ^(а^т). Как уже упоминалось выше, поправки высших
порядков включают в себя сверхтонкое расщепление за счет взаимодействия
спина электрона со спином ядра и лэмбовский сдвиг 5-волновых уровней за
счет флуктуаций электромагнитного поля. Еще один источник поправок по¬
рядка 0(а1т)—аномальный магнитный момент электрона: отличие фактора
Ланде от 2.
Лекция 21
335
21.4. Аномальный магнитный момент
Как мы видели, значение фактора Ланде g = 2 есть прямое следствие
калибровочной инвариантности взаимодействия с безмассовым векторным
полем и рецепта минимальной связи заряда с полем: длинная ковариантная
производная или обобщенный импульс. Однако при наличии спина суще¬
ствует также возможность введения калибровочных взаимодействий посред¬
ством связи инвариантного тензора напряженности Fkn с тензором спина
&кп, так как каждый из них антисимметричен. Дополнительный вклад в дей¬
ствие для спинора Дирака запишем в виде
В нерелятивистском приближении р —> 0 биспинор Дирака сводится к нере¬
лятивистскому спинору гр ъ (</?, 0). Поэтому в аномальном взаимодействии
(21.29) ненулевой вклад дает только диагональный член с аа&
так что стандартная связь компонент тензора напряженности с магнитным
полем Fapeapr = —2Нг приводит к
Таким образом, вообще говоря, магнитный момент за счет аномального
вклада мог бы принимать произвольные значения. Однако в квантовой тео¬
рии поля, учитывающей петлевые поправки в теории возмущений, прямое
включение члена с аномальным магнитным моментом недопустимо, так как
он приводит к так называемым неперенормируемым поправкам: петлевые
поправки могут принимать конечные значения только при введении беско¬
нечно счетного числа новых членов взаимодействий с соответствующими
новыми константами. Чтобы избежать подобного логического тупика, сво¬
дящего предсказательную силу теории к нулю, необходимо положить исход¬
ный или, как говорят, затравочный аномальный магнитный момент равным
нулю. Тогда учет петлевых поправок становится однозначным (теория пере¬
нормируема), и эти поправки в теории возмущений приводят к малому по
(21.29)
Матрицы &кп в представлении Дирака имеют вид
(21.30)
т. е. к аномальному магнитному моменту частицы со спином 1/2:
д=(1 + а)^-(8-ЖУ
(21.31)
336 Тема 11 Нерелятивистское приближение: эффективная теория
константе взаимодеиствия ает аномальному магнитному моменту частицы
со спином 1/2, так что согласно Швингеру
а = ^, (21.32)
что согласуется с экспериментом.
Поскольку отклонения аномального магнитного момента от расчетного
свидетельствовало бы о наличии неизвестного типа взаимодействий, изме¬
рения аномального магнитного момента с высочайшей точностью находятся
на переднем фронте современных экспериментальных исследований: точ¬
ность для мюона достигла двенадцати порядков значащих цифр. В настоящее
время данные согласуются с расчетами на основе калибровочных теорий
электромагнитных, слабых и сильных взаимодействий.
Задача 11.1. Вычислить магнитные моменты барионов в составной модели «кон-
ституэнтных» (составных) и-, <2- и s-кварков: протона р = (uud), нейтрона п = (ddu)
и заряженных сигма-гиперонов Е+ = (uus), XT = (dds). Считать, что барионы явля¬
ются антисимметричными состояниями кварков трех цветов: квантовое число а =
= {1,2, 3} = {синий, красный, желтый}, так что, например, цветовое состояние про¬
тона1 |color) = -^=eapruaupdr. Заряды кварков положить равными Qu = 2/3, Qd = 0* =
v6
= —1/3 в единицах заряда протона е, в то время как массам кварков сопоставить
реалистические значения mu = md= 330 МэВ, ms = 480 МэВ. Массу нуклона считать
efi
равной mN = 940 МэВ. Выразить результат в единицах ядерного магнетона /% = .
2ГТ%С
Сравнить с экспериментальными данными: /хр =2,79/%, /хп = -1,91/%, /хЕ+ = 2,46/%,
/хЕ- = —1,16/%. Какой вывод можно сделать о значениях g-факторов конституэнтных
кварков в барионах?
Решение. Барионы, рассматриваемые в задаче, являются основными состояни¬
ями для каждой из заданных кварковых систем, т. е. кварки находятся в s-волновых
конфигурациях с нулевым орбитальным моментом. Более того, модель конституэнт¬
ных кварков предполагает, что движением кварков в барионах можно пренебречь:
кварки покоятся в системе покоя бариона, так что энергия связи мала, и масса
бариона приближенно дается суммой масс конституэнтных кварков, MB&'£tqmq.
Поэтому в задаче о магнитных моментах пространственная часть волновой функ¬
ции кварков несущественна (она симметрична по перестановкам тождественных
кварков), и вектор состояния бариона по сути сводится к произведению состояний,
факторизованных по цвету и спину:
|baryon) = | color) | spin).
Цветовое состояние определено условием задачи. Оно является нормированным на
единицу. Важно, что это состояние является антисимметричным по перестановке
кварков, так как в каждом из рассматриваемых барионов есть по паре тождественных
кварков, которые являются фермионами.
1Волновые функции зависят также и от координат, что не указано в цветовой функции; это
приводит к ненулевой цветовой волновой функции.
Лекция 21
337
Состояние тождественных фермионов, согласно принципу Паули, должно быть
антисимметрично по перестановке частиц. Отсюда с учетом антисимметрии цвето¬
вой части состояния следует, что спиновая часть волновой функции должна быть
симметричной относительно перестановки тождественных кварков. Поэтому спино¬
вое состояние, скажем, пары u-кварков имеет спин S = 1, т. е. является векторным,
а состояние с нулевым спином, скалярное состояние, запрещено. Полный спин ис¬
следуемых барионов равен 1/2. Его можно представить как сумму спина двух тожде¬
ственных кварков и третьего кварка, т. е. как результат сложения спина 1 и спина 1/2.
Например, для состояния протона \j, т)
\1/2, +1/2)р = У§|1, +l)|->d - У||1,0)|+)d,
где |±)d — спиновое состояние d-кварка, а спиновые состояния пары u-кварков зада¬
ются стандартным образом:
|l>+l) = l+)u1l+)u2>
|1> 0) = -j= (l+)ua I”)u2 + l”)ui l+)u2) •
Найдем магнитный момент бариона как среднее значение суммы проекций магнит¬
ных моментов кварков на ось z в заданном нами состоянии:
= 2^(S =Mn(E
q 4 q 4 я 4
где g « 2 для дираковской частицы. Для протона, очевидно, действие операторов
спина кварков с соответствующими факторами дает
2 ?Qu^|l,+l) = gu^Qu|l,+l),
flijl 1%
Ч=Щ,и2
S ^TduguSlИ,0)=0,
т
q=ubu2
В итоге магнитный момент протона равен
Совершенно аналогично для нейтрона1 тг = (ddu)
Г 2 1 Г71дг 1 Г 2 ТП-N 1 'j
1Эти же результаты принято записывать в виде соотношений между магнитными момента-
* 4 14 1
ми кварков и барионов (лр = ~[Ли — [лп = — ~[ли и т. п., где магнитныи момент кварка q
eQqh i
338 Тема 11 Нерелятивистское приближение: эффективная теория
для гиперона Е+ = (uus)
Г 2 mN 1 mN 1 Г 4 . 1 ]
- Млг {£« з —Qu - & g —Qs} - Mw {&, 9 — + & 18 — },
для гиперона XT = (dds)
В ведущем приближении положим g-факторы для всех кварков равными 2. Тогда
в сравнении с экспериментом получим
— ведущее приближение:
Мр = 2,85/%, /хп = -1,90/%, /хЕ+ =2,75/%, /хЕ- = 1,05/Хд^;
— эксперимент:
Мр = 2,79/%, /хп = -1,91/%, /хЕ+ = 2,46/%, jUs- = -1,16/%.
%
Это сравнение указывает на то, что g-факторы близки к теоретико-полевому значе¬
нию, которое не учитывает квантовые эффекты. Оценим величину этих эффектов.
Для этого составим следующие правила сумм, которые позволяют получить значения
g-факторов из экспериментальных данных путем разрешения выражений для магнит¬
ных моментов как уравнений для g-факторов. В самом деле, например,
1 ,Л , -V 5 гт%
—(4Mp+Mn) = xgu-f.
Маг «3 mu
Отсюда получаем, что с экспериментом согласуется значение
gu ** 1>97.
Аналогично, для d-кварка находим
^-(МР+4Мп) = -|&?1 => gd w 2,04.
Hn о md
Однако эти поправки лишь слегка уменьшают разногласие в значениях магнитных
моментов для гиперонов. Конечно, согласие применяемой модели с экспериментом
можно улучшить, учитывая, например, энергию связи кварков: эффективные массы
кварков будут несколько больше для более тяжелых по сравнению с нуклонами гипе¬
ронов, —и вводя другие поправки1.
1Вместо «конституэнтных», т. е. эффективных, практически свободных кварков, квантовые
числа которых аддитивно в виде суммы по кваркам определяют квантовые числа бариона,
такие, например, как электрический заряд, масса, изотопический спин, странность и т. п., в ло¬
кальной квантовой теории первичными являются кварковые поля с идентичными спиновыми
и зарядовыми квантовыми числами. Эти кварки называют «токовыми». Токовые кварки взаимо¬
действуют сильным образом, обмениваясь глюонами — безмассовыми векторными частицами,
аналогичными фотонам в квантовой электродинамике, но обладающие цветовым зарядом (по¬
добные калибровочные теории описываются неабелевыми группами преобразования полей).
Теория цветовых взаимодействий — квантовая хромодинамика — характеризуется таким явле¬
нием, как конфайнмент, т. е. невылетание кварков из бесцветных адронов в свободном виде.
Конфайнмент обеспечивается ростом силы взаимодействия с увеличением расстояния между
цветовыми объектами, так что на масштабе порядка 1 ферми происходит интенсивное обра¬
зование кварк-антикварковых пар и глюонов, а также могут образовываться кварк-глюонные
конденсаты, и токовые кварки, двигаясь в среде конденсатов, приобретают эффективную массу,
так что в этом грубом приближении допустимо их описание как конституэнтных. Систематиче¬
ское же изучение характеристик адронов предполагает последовательный учет взаимодействий
кварков и глюонов в среде конденсатов, что осложняется трудностью описания собственно
конфайнмента в неабелевой теории, для которой характерно явление асимптотической свобо¬
Лекция 21 339
Тем не менее, можно считать, что упрощенная картина представления сложных
барионных систем в виде трех покоящихся конституэнтных кварков дает правильные
качественные результаты с точностью лучше 10% для магнитных моментов с g-факто¬
рами кварков, близкими к 2.
ды—уменьшение заряда на малых расстояниях, где становится применима теория возмущений.
В этой связи весьма актуальными становятся компьютерные симуляции—вычисления на решет¬
ке континуальных интегралов Фейнмана для различных физических величин.
Тема Атом гелия
12
Лекция 22
Потенциал в атоме гелия и сохранение суммарного орбитального момен¬
та, статистика Ферми для электронов с учетом спина: орто- и парагелий,
потенциал ведущего приближения, обменное взаимодействие и отталкива¬
ние электронов, теорема об отрицательной разности энергии связи триплета
и синглета, приближение факторизации и уравнения Хартри, обобщение
с учетом обменного члена — метод Хартри—Фока, самосогласованное поле —
сферически симметричный потенциал ядра и его экранировка электрона¬
ми, сведение задачи к одноэлектронной: конфигурация электронов, диаго-
нальность поправки по полному орбитальному моменту и обменный вклад:
термы, расчет основного состояния атома гелия в модели с эффективным
экранированным зарядом ядра, интегралы, точность метода и относительная
величина поправок, задача о поправке второго порядка по возмущению,
роль экранировки ядра, величина релятивистских поправок и электронные
J-термы.
Для того чтобы продемонстрировать трудности, возникающие при опи¬
сании многоэлектронных атомов и молекул, которые составляют предмет
науки квантовой химии, рассмотрим простейшую систему — атом гелия,
считая неподвижным его ядро с зарядом 2, взаимодействующее с двумя
электронами.
22.1. Нерелятивистская задача
Опуская релятивистские поправки к движению электронов, запишем га¬
мильтониан электронов в атоме гелия как сумму кинетических энергий элек¬
тронов с потенциальными энергиями притяжения к ядру и отталкивания
между электронами:
™2 "2 7о2 а2
Ра _|_ Рв_ _ Ze_ _ Ze _j е
2т 2т rA rB \гА-гв
координаты и операторы импульсов помечены индексами А и Б, относящи
мися к двум электронам.
Коммутаторы орбитальных моментов электронов с гамильтонианом лег
ко вычисляются:
#Nr] = -leaPrrA |r.-rR|] = _1|Гд-Г„|з(-Га X Гв)0’
|гл-гви |гл-Гв|3
UB, -^Nld ~~^eafirrB [at jrT—rj ] =— * |гл — Гв|3 ^X Г’
342
Тема 12. Атом гелия
откуда сразу следует, что сохраняется суммарный орбитальный момент
[Z“ + Z“,HNR]=0. (22.2)
Поэтому в принятом приближении связанные состояния электронов в атоме
гелия характеризуются значением энергии, полного орбитального момента Z
и его проекцией т.
К ним можно добавить еще значения проекций спина каждого из элек¬
тронов. Однако такая схема, вполне приемлемая для частиц разного сорта,
очевидно нуждается в корректировке, так как электроны являются тожде¬
ственными частицами. Поэтому состояния электронов, подчиняющихся ста¬
тистике Ферми, должны быть антисимметричными по перестановке частиц.
Спиновые состояния двух электронов с суммарным спином S = О и S = 1
согласно правилам сложения двух моментов имеют вид:
S = l: |1, +1) = |+Ы+)5,
|1> 0) = ^={|+)а1~)в + 1“)а1+)в}>
И, -1) = ИлНв,
S = 0:|0,0> = -^{|+)A|-)B-|-)A|+)B>,
а значит, они являются симметричными по перестановкам при S = 1 и ан¬
тисимметричными при S = 0. Это обстоятельство упрощает поиск волновых
функций стационарных состояний, потому что сам гамильтониан (22.1) яв¬
ляется симметричным по перестановкам электронов1. С учетом того, что
операторы спина коммутируют с орбитальным моментом, всегда имеется
возможность соответствующей суперпозицией выбрать волновые функции
так, чтобы они обладали заданными значениями полного спина и полного
орбитального момента и симметрией пространственных частей по переста¬
новкам электронов: если волновая функция 'фО'д, гв) удовлетворяет стаци¬
онарному уравнению Шрёдингера с гамильтонианом (22.1), то и волновая
функция гр (гв, гА) также удовлетворяет этому уравнению, что позволяет опе¬
рировать функциями, симметричными по перестановкам:
■Фо^а, ГВ) = ~j=ty(rA, rB)+i>(.rB, ГА)}
для состояний с полным спином S = 0 и
V>1гв) = -1={ф(гА, гв) -гр(гв, гА)}
для состояний с полным спином S = 1. Тогда полные волновые функции
'«/’оСга, гв)|0, 0>, V'iOa» гв)|1> Щ)
обладают антисимметрией по отношению к перестановкам электронов.
гВ силу тождественности электронов гамильтонианы, не симметричные по перестановкам,
запрещены: иначе имелась бы возможность отличить один электрон от другого.
Лекция 22
343
Состояния с 5 = 0 называются уровнями парагелия, а с S = 1 — орто¬
гелия. Ортогелий в нерелятивистском приближении трижды вырожден по
значениям проекции полного спина, поэтому его еще называют триплетным.
Отметим, что в случае
<Ф(.гА,гв) = гр(гв,гА)
необходимо, во-первых, подправить нормировку состояния парагелия (под¬
становка 1/л/2 —»1/2), а во-вторых, установить запрет на состояния ортоге¬
лия, так как его волновая функция тождественно обращается в нуль.
Задачу нахождения волновых функций стационарных состояний решают
методом введения такого сферически симметричного потенциала ведущего
приближения, который эффективно включал бы в себя как взаимодействие
электрона с ядром, так и экранировку ядра другими электронами. Подобный
потенциал называют самосогласованным полем в том смысле, что оно учиты¬
вает коллективную экранировку потенциала ядра для заданного электрона
облаком распределенного заряда других электронов в соответствии с при¬
ближенной, усредненной волновой функцией электронов в атоме. В таком
подходе с последующим применением теории возмущений для остаточного
взаимодействия полагают, что в ведущем приближении имеет место факто¬
ризация волновых функций электронов:
'ФО'а, гв) *я/и(гА)я/>в(гв). (22-3)
Здесь функции %pA, грв являются собственными состояниями специально
выбранных гамильтонианов ведущего приближения, записанных в атомных
единицах1, с самосогласованным полем V(r):
На = -|да + У(га), яв = -|ав + у(гв),
так что
На'Фа=Еа'Фа> Нв'фв=Ев'фв,
причем гамильтониан в атоме гелия в атомных единицах
1 л 1д Z Z
2 2 3 гА гв |гл-гвГ
естественно, после тождественного преобразования представйм в виде
#не = На + Нв + У(?а> гв)>
где остаточное взаимодействие электронов описывается потенциалом
V(rA, ГВ) = + r-±— - V(rA) - V(rB),
rA rB \rA~rB\
который при удачном выборе самосогласованного поля является малой по¬
правкой, т. е. может быть учтен в теории возмущений. Поправка к самосо¬
гласованному полю обладает свойством инвариантности относительно пере¬
становок координат электронов гА <—»гв
V( га,гв) = У(гв,га).
Расстояния измеряются в единицах боровского радиуса a=h2/(me2), а энергия в удвоенных
ридбергах Е0 =h2/(ma2), так что уровни атома водорода в атомных единицах Еп = — 1/(2п2).
344
Тема 12. Атом гелия
Вопросы о методах построения потенциалов ведущего приближения1 мы
опишем ниже: важно, чтобы поправка за счет возмущения была мала, —но
прежде остановимся на общих свойствах такого подхода к задаче в целом.
22.2. Обменное взаимодействие
Пусть волновые функции электронов в ведущем приближении различны
'ФаЮФ'ФвЬг),
т. е. электроны находятся в различных стационарных состояниях гамильто¬
ниана НА:
f «13Г'0*СГ)Я/)В(Г)=О.
Для краткости записи введем обозначения для произведения волновых функ¬
ций:
’Фав=‘Фа(Га),Фв(Гв), ’Фва = ‘Фв(Га)'Фа(Гв'),
причем эти состояния ортогональны:
(M>ab\^ba) = J d3rAi/>*(rA)i/>B(rA) J d3rB^(rB)i/»A(rB) = 0.
Тогда состояниям с суммарным спином S = 0 и S = 1 отвечают нормирован¬
ные пространственные волновые функции
'Фол = ~^=^AB =*= 'ФваУ-
По построению
На'Фол = '^{^а'Фав^^в'ФваУу Нв'Фол = "^{Ев'Фав^Еа'ФваУ)
так что
(Нд + од = №а ВДод •
Значит, в теории возмущений поправка к энергии дается матричными эле¬
ментами
№o\V\*l>o) ~ ('Фав^'Фав) + (^ab\V\*Pba)>
(^ilvl^i) = {'фabWI^ab) ~ ('Фав^^ва))
где мы учли симметричность возмущения по перестановкам координат элек¬
тронов, откуда
('Фав^^ав) — ('Фва^^ва)» ('Фав^'Фва) = {'Фва^'Фав)-
В итоге энергия связи пара- и ортогелия дается выражением
Еод =Еа + Ев + ('ФавЩ'Фав) ± {'Фав^'Фва)- (22.4)
1В простейшем, но не в лучшем случае можно, конечно, просто положить V(г) = — Z/г.
Лекция 22
345
Член
Урегт = ('Фав^'Фва) = / d3rA d3rB гр*А(гА)гр*в(гв)У(гА, гв)(гА)^А(гв) (22.5)
возникает вследствие антисимметризации полной волновой функции тожде¬
ственных фермионов-электронов посредством перестановок (permutations)
и называется вкладом обменного взаимодействия.
Введем «плотность»
Рав(г)='Фа(г)'Ф*в(г)
с нулевым зарядом
/ d3rpAB(r) = 0.
Тогда в интеграле
J d3rB V(rA, rB)pAB(rB)
выпадают вклады в V, зависящие только от гА. Аналогично в интеграле
J d3rA V(rA,rB)p*B(rA)
выпадают вклады в V, зависящие только от гв. Значит, в обменном члене
остается только вклад за счет взаимодействия электронов друг с другом
wf A. (22.6)
Теперь заметим, что
есть статический потенциал зарядов с плотностью рАв(гв)• Для него имеет
место уравнение Пуассона
-А(р=Лпрлв,
и поэтому
Vperm = J d3rA v(rA)p*B(rA) = J d3rA ip(rA)Aip*(rA),
так что, проводя интегрирование по частям с нулевым поверхностным чле¬
ном (потенциал обращается в нуль на бесконечности, потому что электроны
находятся в связанном состоянии), получаем
vpenn = ^ J d3rA {Vv>(rA)}Vy>*(rA) = ±J d3rA IV</?(rA)I2 > 0. (22.7)
Строгое неравенство, естественно, следует из того факта, что потенциал
создает не равное нулю электрическое поле.
В силу установленной положительности обменного вклада заключаем,
что состояние ортогелия имеет меньшую энергию, чем состояние парагелия.
346
Тема 12. Атом гелия
22.3. Уравнения Хартри—Фока
Уравнение Шрёдингера для статических состояний получается вариацией
«действия» за время Т
по /0*(гА, гв). Если принять в ведущем приближении факторизацию волно¬
вых функций электронов ^p(rAf rB) ^я/;А(гА)я/>в(гв), то вариация
где в гамильтониан для электрона входит потенциал его взаимодействия
с распределенным зарядом другого электрона
Записанная система уравнений носит имя Хартри. Ее физический смысл
достаточно прозрачен: энергия электрона определяется суммой его кине¬
тической энергии и потенциала притяжения к ядру, которое экранируется
«облаком» другого электрона. Для наглядности такой трактовки мы ввели два
параметра ЕаиЕв, которые в действительности не являются независимыми,
как это следует из вариации исходного действия, так что
— это гамильтониан для электрона, взаимодействующего с ядром. В выраже¬
ние входит среднее значение по волновой функции электрона, как это отме¬
чено соответствующим индексом А или В, например, (Н(0))А = (я/>А|НС0)|я/>А).
S = T J d3rA d3rB xj}*(rA, rB){E -HHe}ip(rA, rB)
d3rA d3rB 'ф*А(?А)'фв(гв){ЕА+Ев — ЙНе}'фА(гА)/фв(гв) —
= J d3rArA(.rA)(EA-{-lAA-f-})ipA(rA) +
+ j d3rB 1>*в(.гв-)(ев — | — 2 Дв — ^г})1/’в(гв)—
- J d3rA d3rB я/>А(гА)^;(гв)|^^-|я/>А(гА)т/>вСгв)
+ const
по гр*А и грв дает систему связанных уравнений
(22.8)
здесь в атомных единицах плотность зарядов
Рл(гА) = №а0л)12, Рв(»в) = I V’bOb)!2-
Еа=Е — (Н(0))в, Ев=Е — (я(0))а,
где
Н(0) = —^Д ——
2 г
Лекция 22
347
Тем не менее, величины Еа, Ев имеют определенный физический смысл:
они дают энергии ионизации электрона с соответствующими квантовыми
числами.
Однако решать подобную систему приходится численными методами.
Подчеркнем, что в уравнениях Хартри никак не отражено свойство тожде¬
ственности электронов. Конечно, учет статистики Ферми для электронов
может быть затем достигнут путем соответствующей симметризации про¬
странственных волновых функций в зависимости от значения суммарного
спина электронов. Еще одна трудность—уравнения для электронов, находя¬
щихся в разных состояниях, отличаются за счет потенциала экранировки,
уА (г) Ф ¥?в(г)> и поэтому собственные функции для двух разных уравнений
с различными квантовыми числами, вообще говоря, не ортогональны.
Обобщением уравнений Хартри являются уравнения Хартри—Фока, в ко¬
торых напрямую учитываются правильные свойства пространственных вол¬
новых функций по отношению к перестановке тождественных электронов.
Для вывода этих уравнений, очевидно, необходимо в действии провести
подстановку волновой функции в факторизованном виде1
'Ф(ГА> Гв) «V’oGa, гв) = {'Фав-'ФваУ/^
ИЛИ
V» с г А, гв) « о/»! (гА, г в) = {ФаВ + 'ФваУ/^
в зависимости от полного спина электронов. Тогда в действии появится вклад
обменного взаимодействия
Sperm I j3 ,3 Рав(га)Рав^Гв) f ч , \ I * г \
— =T dVAdVB—|г^_гд|—, pAB(r)=rpA(r)ipB(r),
а также, возможно, недиагональные члены из-за неортогональности функ¬
ций ярА и *фв
Т f d3rA d3rB Гав{Е-Н^ -Н^УФва,
куда входит интегральный «заряд»
Qab = J d3r РавОО-
Вариация действия по яр*А и с учетом обменного вклада приводит
к системе уравнений в приближении Хартри—Фока
( Еа'Фа = {-\Дл " + </>в(гА)}^А±Мгл) + ЬЕаУФв(Гл),
V Бв-фв = {-|ЛВ - ^ + (pAirB)}i>B ± V(rB) + АЕв}ч/)а(гв),
где комплекснозначный «потенциал» обменного взаимодействия имеет
прежний вид
гКак при рассмотрении обменного вклада во взаимодействие, введем произведения
‘Фав=‘Фа(.Га')‘Фв(гв') и 1/’ва=,0в(га)1/>а(гв)-
348
Тема 12. Атом гелия
а «сдвиги энергий» возникают из-за недиагональных вкладов
АЕа = WbIH (0)№л>-EQab, АЕв = (грА\Н^\хрв)-EQ*BA.
Взяв матричные элементы уравнений (22.9) по грА и ярв соответственно, лег¬
ко убедиться, что энергии ионизации принимают вещественные значения,
несмотря на то, что в эти уравнения входят комплексные параметры.
Полагают, что решение уравнений Хартри—Фока дает ортогональные вол¬
новые функции для электронов с разными квантовыми числами. Тогда вкла¬
ды с = 0 выпадают, и связь энергий ионизации с энергией связи атома
сохраняет прежний вид.
Важно подчеркнуть, что потенциалы экранировки ядра и обменного вза¬
имодействия не произвольны, а определяются распределениями электронов,
которые сами получаются из уравнений, т. е. эти потенциалы задаются само¬
согласованным образом и зависят от состояния электронов.
Как видим, полученная система уравнений для пространственных волно¬
вых функций двух электронов в приближении Хартри—Фока может учиты¬
вать отличие этих волновых функция для пара- и ортогелия, но она неимо¬
верно сложна с точки зрения проблемы ее решения в аналитической форме1,
так что для качественного и количественного анализа многоэлектронного
атома часто используют комбинацию методов априорного непертурбативно-
го введения самосогласованного поля и теории возмущений. Один из вари¬
антов такого подхода мы приводим ниже.
22.4. Самосогласованное поле:
КОНФИГУРАЦИЯ ЭЛЕКТРОНОВ, ТЕРМЫ
Будем считать, что каждый из электронов движется в сферически сим¬
метричном поле У (г), которое учитывает как потенциал притяжения ядра,
так и отталкивание от коллективного, распределенного заряда других элек¬
тронов в атоме. Поскольку это распределение заранее неизвестно и, вообще
говоря, зависит от состояния электронов, приходится моделировать этот
потенциал некоторой функцией, что дает модель самосогласованного поля.
Конечно, как мы видели, модель можно считать удачной, если поправки по
теории возмущений за счет отличия потенциала в гамильтониане от само¬
согласованного поля оказываются малыми: по сути мы рассмотрели схему
самосогласованного поля с начала постановки задачи для нерелятивистских
волновых функций в атоме гелия. Указанием на вид самосогласованного поля
могут служить итерации в решении уравнений Хартри—Фока, которые дают
некие приближения для распределения зарядов электронов в атоме. У само¬
согласованного поля есть разумные асимптотики в нуле и на бесконечности:
вблизи нуля определяющим является потенциал ядра, а на бесконечности
1 Современная вычислительная техника позволяет решать подобные системы уравнений
либо непосредственно численно с высокой точностью, либо вариационным методом с многопа¬
раметрическими классами пробных функций и численными методами нахождения экстремума
в пространстве параметров.
Лекция 22
349
электрон движется в поле притяжения единичного заряда, так как другие
электроны экранируют ядро.
Однако методически оказывается более важным другой факт: в едином
для каждого из электронов центрально-симметричном поле, приближенно
учитывающем коллективную плотность заряда, легко провести классифика¬
цию уровней и квантовых чисел электрона, так как она фактически повто¬
ряет классификацию одноэлектронной системы в атоме водорода с той лишь
разницей, что решение радиального уравнения с потенциалом самосогласо¬
ванного поля необходимо проводить численно.
Итак, каждому электрону ставится в соответствие главное квантовое чис¬
ло гг, орбитальный момент I и его проекция т. Но согласно принципу запрета
Паули для каждого значения проекции орбитального момента допустимы
лишь два состояния электрона с противоположной ориентацией спина. По¬
этому для каждого значения Z, т. е. для электронной оболочки, возможное
число заполнения уровня не превышает 2(2Z +1). Электроны, заполняющие
одну и ту же оболочку, называются эквивалентными. Набор квантовых чи¬
сел nl с указанием степени заполнения оболочки составляет конфигурацию
электронов в ведущем приближении самосогласованного поля.
Например, в атоме гелия основное состояние отвечает конфигурации Is2,
а первые возбужденные состояния—ls2p и ls2s.
Так как возмущение, учитывающее отличие центрально-симметричного
потенциала и вклада отталкивания электронов от самосогласованного поля,
в атоме является диагональным в базисе с заданным значением суммарного
орбитального момента электронов, то правильные функции ведущего при¬
ближения — состояния с определенным значением орбитального момента
и коммутирующего с ним полного спина электронов:
I « м • \ I « г с \ / 1соп%; L> щ; ortho),
Iconfig) Ispin)«Iconfig; L, mt; S, ms> ~ | |сш1%. ^
где еще необходимо учесть принцип запрета Паули — антисимметризовать
состояние по перестановкам электронов.
Итак, состояния с различными значениями полного орбитального момен¬
та диагонализуют гамильтониан атома гелия, имея, вообще говоря, различ¬
ные значения поправок к энергии. Значит, состояния необходимо характери¬
зовать квантовым числом L. Мы видели также, что обменный вклад приводит
к меньшему значению энергии для ортогелия, чем для парагелия. Отсюда
следует, что для полной характеристики уровня в атоме необходимо указать
наряду с конфигурацией пару квантовых чисел: полный орбитальный мо¬
мент L и суммарный спин S. Эта пара, как говорят, определяет терм, который
принято записывать в виде 2S+1L, где, как обычно, для момента L вместо
чисел используются буквенные обозначения, но в отличие от конфигурации,
где пишут строчные буквы, здесь употребляют заглавные. Например, упомя¬
нутым выше конфигурациям соответствуют следующие термы:
is2 —»xs, ьгр-*1?,3?.
350
Тема 12. Атом гелия
22.5. Основное состояние
Для иллюстрации метода самосогласованного поля на примере атома ге¬
лия введем простейший центрально-симметричный потенциал кулоновского
вида
V(r) = -f,
где Z—некий эффективный заряд, который позволяет промоделировать поле
ядра и его экранировку на масштабах порядка боровского радиуса, так что
мы не будем беспокоится о правильном асимптотическом поведении вблизи
нуля и на бесконечности, где этот потенциал явно модифицируется, но для
наших целей это не очень важно, так как вероятность обнаружить электрон
вдали от средних размеров атома мала. Поэтому можно ожидать, что ошибка
в расчетах будет подавлена. Кроме того, по-видимому, значение Z близко
к заряду ядра: |Z — Z|/Z<1.
Поскольку основное состояние обладает минимальной энергией из всех
связанных состояний, можно считать параметр самосогласованного поля Z
свободным и использовать это обстоятельство для минимизации энергии
связи основного состояния.
В заданном поле энергия основного состояния равна удвоенной энер¬
гии связи основного состояния в одноэлектронном, водородоподобном атоме
с зарядом ядра^:
E0 = ~Z2.
В электронной конфигурации Is2 каждый из электронов имеет простран-
ственную волновую функцию (в атомных единицах)
Для пары электронов
’ф(гА,гв) = гр(гА)'ф(гв)
—это правильная волновая функция с полным орбитальным моментом, рав¬
ным нулю. Поскольку она симметрична по перестановкам электронов, пол¬
ный спин может быть равен только нулю и его спиновая функция анти¬
симметрична. Основное состояние гелия — синглет, парагелий, а состояние
ортогелия запрещено в конфигурации Is2.
Вычислим матричный элемент возмущения
y=tlZ + LiZ 1
г* «в |rA-rB|
по состоянию электронной конфигурации основного состояния, для того
чтобы получить поправку к энергии в первом приближении. Для централь-
но-симметричного вклада согласно общим выражениям для средних в атоме
водорода легко находим
(Ц1- + Ц^)=2 Z(Z-Z).
\ ГА ГВ /
Лекция 22
351
Для потенциала отталкивания электронов запишем
1 , . - / 1 \ -1! Г c-2Z(r,+r„)d3^d3rB
^repulsive \ |гЛ — Гв| / 7Г2 J 1Гд-Гв| *
Замена переменных
ГА = Гв = Дг V
2Z 2Z
дает
г -_L_ Г -fa+y)d3xd3y
repulsive 25я2 J |*-у|*
Вычислим интеграл по косинусу угла х между векторами, введенному соглас¬
но \х - у| = у/х2-2 хух + у2:
+1
dx
I
-1
\] х2 — 1хух+у2 +1 1
——{х+У—Х—у}.
XV _1 XV ^ 1 у 1
-1
Из-за модуля интегрирование по х и у разбивается на две области: х > у
и х < у. Однако в силу симметрии интеграла по перестановке переменных
можно ограничиться лишь одной из областей, удвоив результат. Именно,
в области у < х интеграл по косинусу угла равен
±<Х+у-Х+у} = 1
Тогда
Repulsive = ■2п J 2d* *е_дс / dy y2e~y=Z j dxxe~x J dy y2e~y,
о о о 0
где мы учли элементарное интегрирование по углам. Оставшиеся интегралы
легко берутся по частям:
X
J dy у2е~у = —х2е~х — 2хеГх — 2е~х + 2,
о
00
‘ f dx {—х3е~2х - 2х2е~2х - 2хе-2* + 2хе~х} = -|g-^-| + 2 = |.
О
Т — —7
1 repulsive g"*
В итоге энергия отталкивания
С учетом поправки
(V)=2Z(Z-Z) + |Z
энергия основного состояния атома гелия
Е = Е0 + (V) = -Z2 + 2Z(Z -Z) + § Z.
352
Тема 12. Атом гелия
Найдем экстремум этого выражения: он отвечает минимальному значению
энергии основного состояния,
^| = -2Z + 4Z-2Z + | = 0 => Z=Z-j£.
В экстремуме (V) = 0, так что энергия связи
E = -(z-^y. (22.10)
Численно для гелия
Е ^ —2,85,
что следует сравнить с экспериментальным значением
^exp w —2,90.
Различие этих чисел составляет менее 2%, что, с одной стороны, выглядит
неплохо, но с другой, если учесть высокую точность экспериментальных
данных, совершенно недостаточно для того, чтобы считать такой расчет
успешным.
Конечно, можно продолжить расчеты, оценив вклад второй поправки,
которая, как помним, для основного состояния всегда отрицательна.
Задача 12.1. Вычислить вклад конфигурации ls2s в поправку второго порядка для
энергии связи основного состояния атома гелия.
Решение. Найдем матричный элемент кулоновского вклада в возмущение
где волновая функция 25-уровня
Тогда
(ls|^|2s> = ^Pz(Z-Z).
Вклад энергии отталкивания электронов вычисляется так же, как и в случае матрич¬
ного элемента для конфигурации Is2, с тем отличием, что теперь уже интеграл не
является симметричным по перестановке электронов. Тогда элементарное интегри¬
рование дает
<ls2|i^|ls2s)=^-
Возмущение не зависит от спинов электронов, поэтому его матричный элемент от¬
личен от нуля только для состояний с одинаковым суммарным спином электронов —
правило А5 = 0. Значит, в конфигурации ls2s необходимо взять состояние с полным
спином 5 = 0, как и в основном состоянии. Таким образом, антисимметричное по
перестановкам электронов спиновое состояние задает симметричную пространствен¬
ную волновую функцию
'Фо2* = ■^={'Фъ,(Га)‘Ф2!(Гв') + 'Фъ(га)'Фъ(гв)}.
Лекция 22
353
Легко заметить, что это приводит к дополнительному фактору л/2 для уже вычислен¬
ных матричных элементов по конфигурациям:
Отметим, что так же, как и в основном состоянии, вклад притяжения компенсируется
отталкиванием электронов. Поскольку разность энергий уровней
иторая поправка к энергии основного состояния атома гелия за счет конфигурации
\ s2s имеет величину
Как видим, с одной стороны, эта поправка достаточно мала, чтобы считать схо¬
димость ряда теории возмущений достаточной быстрой, а с другой стороны, она,
очевидно, улучшает согласие оценки энергии основного состояния атома гелия с экс¬
периментальным значением, если принять во внимание и вклады других электрон¬
ных конфигураций: в проведенном расчете вклады притяжения и отталкивания по
отдельности составляют -0,02 и -0,04, но они деструктивно интерферируют, хотя
абсолютные величины этих вкладов указывают на то, что принципиально можно
существенно приблизить теоретические расчеты к экспериментальному значению.
Впрочем, выбранный нами класс самосогласованного поля существенно ограничен
однопараметрической функцией, так что разумное расширение этого класса приво¬
дит к более точному результату уже при учете поправки первого порядка по воз¬
мущению. Наконец, отметим, что согласие теоретических оценок с заданной экс¬
периментом точностью достигается, например, вариационным методом в некоем
классе восьмипараметрических пробных функций, что, конечно, эквивалентно рас¬
четам в первом порядке теории возмущений с самосогласованным полем, зависящим
от восьми же параметров.
Отметим, что сделанная нами оценка энергии связи в атоме гелия в пер¬
вом порядке совпадает, как нетрудно видеть, с расчетом вариационным ме¬
тодом, если искать волновую функцию в классе пробных функций основного
состояния атома водорода со свободным параметром — эффективным заря¬
дом ядра Z.
На рис. 27 показаны плотности вероятности распределения 15-электронов
в зависимости от расстояния до ядра для поля с зарядом Z = 2 и Z = Z — 5/16.
Из этого рисунка (а) видно, что волновая функция существенно моди¬
фицируется за счет экранировки ядра: электрон в среднем дальше от ядра.
Поэтому приближение без учета поля электронов не может быть достаточно
точным: в ведущем приближении энергия основного состояния за счет при¬
тяжения к ядру Е0 »-> —Z2 = —4, что слишком сильно (на 30 %) отличается от
экспериментального значения.
Таким образом, метод самосогласованного поля позволяет существенно
улучшить численные оценки для энергии связи в многоэлектронных атомах.
На рис. 27 (б) показано, насколько модифицируется распределение элек¬
трона из-за возмущения за счет примеси 25-уровня. Отсюда видно, что само¬
согласованное поле нужно очень тонко подстроить с процентной точностью,
'2
354
Тема 12. Атом гелия
p(r)J
1,2-
Лр(г)
0,015 -
0,8-
0
г
0,4-
-0,015 -
0
-0,030 -
12 3
Рис. 27. а) Плотности вероятности распределения ls-электронов в зависи¬
мости от расстояния до ядра для поля с зарядом Z — 2 (штриховая линия)
и Z = Z-5/16 (сплошная линия); б) поправка к распределению за счет
примеси 25-состояния при Z=Z - 5/16
чтобы снизить расхождение результатов расчета с экспериментом в ведущем
приближении.
Итак, мы обрисовали в общих чертах, как работает метод самосогла¬
сованного поля в сложной задаче описания многоэлектронных систем на
примере атома гелия. Важно иметь в виду, что типичные энергии связи
электронов в атоме порядка одного Ридберга, т. е. 10 эВ, получаются в мето¬
де самосогласованного поля с точностью до нескольких процентов. Значит,
поправки, обусловленные отличием самосогласованного поля от потенциала
взаимодействия электронов с ядром и друг с другом, могут быть порядка
0,1Ч-1эВ.
22.6. Релятивистские поправки: электронные J-термы
Релятивистские поправки к движению электрона в самосогласованном
поле подобны рассмотренным нами поправкам для электрона в статическом
сферически симметричном потенциале, так как метод самосогласованного
поля формально сводит задачу с многими электронами к задаче для одного
электрона. Здесь нас будут интересовать поправки, зависящие от спина.
Тогда согласно результатам для электрона в статическом поле возмущение за
счет спин-орбитального взаимодействия будет иметь вид
где У (г) — самосогласованное поле, а индекс / нумерует электроны в си¬
стеме. Следует иметь в виду, что правильные волновые функции ведущего
приближения имеют определенное значение суммарного орбитального мо¬
мента электрона и антисимметричны по перестановкам электронов с учетом
спиновой части волновой функции, что отвечает определенному значению
(22.11)
Лекция 22
355
полного спина. Это термы—2S+1I. Спин-орбитальное возмущение, очевидно,
коммутирует с квадратами суммарного орбитального момента I2 и полного
спина S2 , так что I и S—квантовые числа даже с учетом возмущения.
Однако спин-орбитальное взаимодействие сохраняет только вектор пол¬
ного момента электрона jf=lf+Sf. В итоге единственная величина, которая
сохраняется для электронной системы—это полный момент всех электронов
J='^i(lf+sf) = L + S, meL = '^ilf, S=^s/.
/ f f
Значит, термы потенциального описания 2S+1L будут, вообще говоря, рас¬
щепляться в зависимости от значения полного момента J. Величина рас¬
щепления за счет релятивистских поправок, как мы уже знаем, имеет от¬
носительную величину порядка a2m ~ 10”4, т. е. 10“3 эВ, что намного мень¬
ше расщепления за счет отличия потенциала от центрально-симметричного
самосогласованного поля. Таким образом, после учета спин-орбитального
взаимодействия электронные термы обозначают символом
2S+1 т
LJ-
Обсуждение технического вопроса расчета спин-орбитального расщепления
мы отложим до следующей темы, посвященной многоэлектронным атомам.
Тема Сложный атом
13
Лекция 23
Факторизация волновой функции для электронов в самосогласованном цен-
трально-симметричном поле, статистика Ферми и определитель Слетера,
разложение состояния конфигурации по базису с допустимыми значениями
полного спина электронов и их суммарного орбитального момента, кванто¬
вые числа заполненной оболочки, иерархия термов — первое правило Хунда
и аргументы в его пользу, задача о термах атома углерода, оценка спин-орби-
тальных релятивистских поправок, усреднение по конфигурации и LS-связь,
J-термы и правило интервалов Ланде, понятие «дырки», знак константы
спин-орбитального взаимодействия и второе правило Хунда.
Как мы убедительно показали на примере атома гелия, наиболее ясное
и последовательное построение теории сложного атома—многоэлектронной
системы с неподвижным ядром — основано на методе самосогласованного
поля. Поэтому в ведущем приближении состояние электронов характеризу¬
ется конфигурацией, т. е. пространственной волновой функцией, которая
представляется в факторизованном виде как произведение одноэлектронных
состояний с набором квантовых чисел: главного п, орбитального I и маг¬
нитного т, к = {тг, Z, т}. После этого необходимо учесть принцип Паули для
фермионов, т. е. статистику Ферми.
23.1. Определитель Слетера
В атоме с N электронами конфигурация считается заданной, если указаны
квантовые числа каждого из электронов {къ к2,..., kN}, а значит, и отвечаю¬
щий этому набор пространственных волновых функций {‘0k1(ri)>'Фк^и'^У-
В ведущем приближении спин электрона коммутирует с гамильтонианом, по¬
этому состояние электрона факторизуется на произведение пространствен¬
ной и спиновой волновых функций: |fc, m5). Для удобства обозначений вводят
«координату»
x = {r, ms},
так что состояние описывается волновой функцией, составленной из произ¬
ведений типа
^kSrЪ msN) ='ipki(x1')...xpkti(xN),
358
Тема 13. Сложный атом
которую необходимо антисимметризовать по перестановкам электронов. Ре¬
зультатом антисимметризации является определитель Слетера
(V'fcj (*i) - 'ФкцЧхг)']
(23.1)
который антисимметричен по перестановке xt <—> Xj вследствие свойства
определителя по перестановке любой пары строк. Здесь нормировка фикси¬
рована для случая ортонормированных состояний.
Затем, следуя той же схеме, что и при рассмотрении атома гелия, спино¬
вые состояния в определителе Слетера разложим по состояниям с допусти¬
мыми значениями полного, суммарного, спина электронов. Это, очевидно,
всегда можно сделать, следуя той же методе, что и при сложении моментов:
любое состояние из спинового базиса тензорного произведения состояний
можно разложить по базису состояний с допустимыми значениями суммы
спинов, только если в случае двух электронов коэффициентами разложения
были уже известные нам символы Клебша—Гордана, то для большего коли¬
чества слагаемых спинов решается аналогичная задача, сложность которой
возрастает с ростом числа электронов.
Те же аргументы справедливы и для преобразования базиса для орбиталь¬
ных моментов электронов.
В итоге определитель Слетера разлагается по базису состояний с допу¬
стимыми значениями суммарного орбитального момента электронов L и их
полного спина S:
«V.jfc/Xi, •••> = 2 •••» rw)li> м‘> s>Ms), (23.2)
где М—проекция суммарного орбитального момента, Ms—проекция полно¬
го спина, а суммирование ведется по L и S с учетом перестановок квантовых
чисел в конфигурации и проекций орбитального момента и спина электро¬
нов.
Безусловно, решение такой задачи разложения конфигурации по бази¬
су с допустимыми значениями суммарных спина и орбитального момента
строится в каждом конкретном случае, но имеется одно исключительное
обстоятельство, когда решение известно и определено однозначно. Именно,
рассмотрим оболочку nl. Проекции момента имеют 21 + 1 значений. Каж¬
дой проекции момента отвечают два допустимых значения проекции спина
электрона, так что максимальная степень заполнения оболочки согласно
принципу Паули 2(2Z +1). Пусть конфигурация имеет вид nl2(-2l+1\ т. е. все
возможные состояния заняты. Это — заполненная оболочка. Ей отвечают
значения
М = 0, Ms = О,
потому что заняты все состояния проекции I и все состояния проекции спина
электрона.
Лекция 23
359
Действие на такое состояние повышающих операторов полного спина
и суммарного орбитального момента сохраняют конфигурацию, ее кванто-
пые числа nl9 а также и S, но либо дают состояние сМ5 = 1иМ = 1 соответ¬
ственно, либо нулевые векторы. Первая возможность исключена принципом
запрета Паули, так как мы уже установили, что значения суммарных про¬
екций спина и орбитального момента для заполненной оболочки строго
фиксированы. Значит, операции повышения, а равно и понижения, дают
тождественные нули, что отвечает единственному состоянию cL = 0hS = 0.
Поэтому конфигурация заполненной оболочки имеет фиксированные нуле¬
вые значения суммарных спина и орбитального момента.
Таким образом, вклад заполненных оболочек в разложение конфигурации
в сумму по термам строго определен и всегда отфакторизован, так как за¬
полненные оболочки дают нуль при расчете полного спина и орбитального
момента конфигурации.
23.2. Поправки к центральному потенциалу: термы
Как мы уже знаем, в силу обменного взаимодействия состояния с различ¬
ными значениями полного спина электронов обладают разными значениями
энергии связи. Мы убедились на примере атома гелия, что минимальное
значение энергии имеет состояние с максимальным допустимым значением
спина (все спины направлены в одну сторону). Физическое обоснование это¬
го факта вполне прозрачно: состояние с максимальным спином симметрично
по перестановкам электронов1, а это означает, что вероятность обнаружить
электроны в одной точке равна нулю—пространственная волновая функция
антисимметрична, и, следовательно, вероятность найти электроны близко
друг к другу подавлена, откуда мы заключаем, что положительный вклад
в энергию за счет отталкивания электронов подавлен. Если значение сум¬
марного спина меньше максимального, то спин хотя бы одного из электро¬
нов обращен в противоположном направлении к спинам других, и поэтому
этот электрон, вообще говоря, может находиться вблизи других электронов
с ненулевой вероятностью, что увеличивает вклад энергии отталкивания
электронов.
* Кроме того, парные потенциалы взаимодействия электронов друг с дру¬
гом коммутируют с суммарным орбитальным моментом, так что правильные
волновые функции, для которых возмущение в виде парных взаимодействий
диагонально, — состояния с заданным значением полного орбитального мо¬
мента L. В итоге после учета поправок к центральному самомогласованному
1Такое состояние заведомо не запрещено для оболочек, заполненных не более чем наполо¬
вину, так как принцип запрета Паули не накладывает в этом случае никаких жестких условий на
корреляции спинов. Если же оболочка заполнена более чем наполовину, то необходимо перейти
к представлению, основанному на понятии «дырки» (см. ниже), так что опять получаем ситу¬
ацию с оболочкой, заполненной дырками менее чем наполовину, и рассуждение о симметрии
состояния с максимальным значением суммарного спина остается справедливым.
360
Тема 13. Сложный атом
полю приходим к уровням энергии конфигурации, которые расщепляются по
термам 2S+1L.
Для порядка следования термов установлено эмпирическое правило Хун-
да.
Первое правило Хунда. Энергия конфигурации минимальна при мак¬
симально допустимом значении полного спина S; при фиксированном зна¬
чении полного спина минимальную энергию имеет терм с максимально
допустимым значением суммарного орбитального момента электронов L.
Требование максимального значения орбитального момента по своей
природе аналогично рассуждениям о подавлении энергии отталкивания
электронов: при большем орбитальном моменте электроны реже находятся
вблизи друг друга. Действительно, при заданном значении орбитального
момента парное отталкивание электронов удерживает их на неком рас¬
стоянии, в то время как при уменьшении орбитального момента хотя бы
один электрон должен начать вращаться в обратную сторону по сравнению
с вращением других электронов, так что встреча с движущимися навстречу
электронами становится неизбежной и более частой, а значит, вклад в энер¬
гию парного отталкивания возрастает.
Это правило в сочетании с установленным нами свойством заполненной
оболочки позволяет установить основное состояние-терм для атома химиче¬
ского элемента в периодической системе элементов Менделеева.
Задача 13.1. Определить термы и основное состояние атома углерода: конфигу¬
рация ls22s22p2.
Решение. В этой конфигурации две заполненных s-оболочки, которые не участву¬
ют в определении термов. Пара 2р-электронов может быть распределена по 2(21 +1)
состояниям с различными проекциями спина и орбитального момента I = 1
способами.
Максимальное значение спина электронов S = 1 является симметричным по пе¬
рестановкам электронов. Сложение орбитальных моментов электронов 1 + 1 дает
L = 0, 1, 2, причем максимальное значение 1 = 2 также является симметричным
по перестановкам, значит, оно запрещено для 5 = 1, так как в противном случае
состояние было бы симметричным, что противоречит статистике Ферми. Состояние
с L = 0 также является симметричным по перестановке двух электронов, поэтому оно
также запрещено для S = 1. В итоге получаем единственный триплетный терм
3Р.
Число таких состояний (2S +1) (2L +1) = 3 • 3 = 9.
При 5 = 0 спиновое состояние является антисимметричным по перестановкам,
поэтому допустимы только симметричные орбитальные состояния двух электронов,
т. е. 1 = 0, 2. Соответствующие термы
1S,
имеют вырождение по проекциям спина и момента
1 + 5 = 6.
Лекция 23
361
Суммарное число вырождения конфигурации 15 совпадает с суммарным числом
состояний термов, которые расщепляются вследствие учета поправок к самосогласо¬
ванному полю.
Основное состояние согласно правилу Хунда —3Р.
Приведенное рассуждение является специфическим для двух электронов, посколь¬
ку для них за исключением случая заполненной s-оболочки всегда реализуются все
состояния, получающиеся сложением орбитальных моментов этих электронов, что,
как мы увидим на примере следующей задачи, не имеет места для большего числа
эквивалентных электронов, так что приходится использовать наиболее общий метод
определения термов.
23.3. Релятивистские поправки
Масштаб релятивистских поправок в атоме определяется, вообще говоря,
величиной Zaem. Этот параметр может быть довольно большим для тяжелых
ядер по сравнению с рассмотренным нами случаем атомов водорода и гелия,
где электроны заведомо двигались нерелятивистски. Но при этом необхо¬
димо принять во внимание эффект экранировки ядра: электроны внешних
незаполненных оболочек, определяющие термы, взаимодействуют не только
с ядром, но и с электронами заполненных оболочек, находящихся ближе
к ядру, так что фактически заряд центрально-симметричного самосогласо¬
ванного поля для внешних электронов невелик, и, кроме того, как мы увидим
в дальнейшем, вклад релятивистских поправок для электронов на запол¬
ненных оболочках с нулевыми значениями полного спина и орбитального
момента не может зависеть от спин-орбитальных характеристик терма, т.е
приводит к смещению терма как целого.
В самосогласованном поле У(г) зависящие от спина электронов реляти¬
вистские поправки обусловлены потенциалом
<23-3>
где / нумерует электроны в системе. Мы показали, что это возмущение со¬
храняет для каждого электрона в отдельности его полный момент jf = lf+Sf.
Поэтому для терма в целом сохраняется только полный момент всех электро¬
нов
J='^i(lf+sf)=L + S, где! = ^]1/, S = ^sf.
f f f
Значит, термы потенциального описания 2S+1L будут, вообще говоря, расщеп¬
ляться в зависимости от значения полного момента J.
Спин-орбитальные операторы в возмущении (23.3) не выражаются че¬
рез полный спин и орбитальный момент электронов. Но для расчета по¬
правки к энергии за счет этого возмущения необходимо взять его среднее
по правильным функциям ведущего приближения. Мы будем полагать, что
362
Тема 13. Сложный атом
расщепление термов за счет релятивистских поправок мало1 по сравнению
с расщеплением конфигурации по термам в самосогласованном поле 2S+1L.
Тогда среднее можно вычислить в два этапа.
На первой стадии усредним по пространственной волновой функции кон¬
фигурации с фиксированными значениями квантовых чисел терма. В итоге
должен получиться оператор, зависящий только от суммарного орбитального
момента I и полного спина S, причем этот оператор должен быть скаляром,
линейным по спину, так что
(L, М; S, Ms\Vsl\L, М; S, Ms) = AIS(L • S). (23.4)
Значение константы спин-орбитального взаимодействия ALS в (23.4) опре¬
деляется расчетом средних для конкретных конфигураций, но его масштаб
и знак можно оценить также из следующих соображений.
Во-первых, вклад в спин-орбитальное взаимодействие электронов на за¬
полненных оболочках равен нулю, потому что их спин и орбитальный мо¬
мент равны нулю. Значит, необходимо рассматривать только внешние элек¬
троны на незаполненных оболочках. Во-вторых, если внешняя оболочка за¬
полнена не более чем наполовину, принцип запрета Паули не приводит к су¬
щественным корреляциям спина электронов, поэтому в среднем можно счи¬
тать, что для электрона на внешней оболочке с rif электронами его спин
s f & —S,
/ nf
т. е. каждый электрон несет равную часть полного спина на внешней оболоч¬
ке. При этом, конечно, среднее расстояние электронов на внешней оболочке
от ядра можно считать примерно одинаковым: ту —> (г). Значит,
Поскольку электроны притягиваются к центру самосогласованного поля,
справедливо неравенство
e(V')>0,
причем для внешних электронов заряд экранированного ядра равен — enf9
т. е. потенциал V^—enf/r. Значит, константа спин-орбитального взаимодей¬
ствия оказывается положительной порядка
^ls~~з ~mc2aem>0> nf^2l-Ы. (23.6)
Конечно, точное значение вычисляется в зависимости от самосогласованно¬
го поля и конфигурации атома.
1Напомним, что мы опускаем за скобки случай, когда эффективный заряд притяжения
настолько велик, что релятивистские поправки оказываются сравнимы с поправкой к самосо¬
гласованному полю.
Лекция 23
363
После этого второй этап усреднения довольно прост, так как возникший
оператор диагонален в базисе с допустимым значением полного момента
.шектронов J=L + S:
J2 = (I + S)2 => J(J + 1)=L(L + 1) + 2(L‘S) + S(S + 1). (23.7)
11оэтому
(vis> = |AiS{J(J +1) -1(1 +1) - S(S +1)}. (23.8)
Отсюда следует
Правило интервалов Ланде. Расщепление термов вследствие спин-ор-
битального взаимодействия происходит с регулярными интервалами по J:
разность энергий соседних термов 2S+1Lj и 2S+1LJ_1 растет пропорциональ¬
но J, так что расщепление A(Уь) =E(2S+1Lj) — £(2S_hlit/_1),
MVis)=ALSJ. (23.9)
Теперь рассмотрим ситуацию, когда оболочка заполнена более чем напо¬
ловину: Tif > 21 +1. В этом случае существенным становится правило запрета
Паули, которое особенно ярко проявляется, если оболочка заполнена пол¬
ностью: спины электронов строго коррелированы так, что дают в сумме
нуль. Заполненная оболочка не участвует в формировании сдвига уровней за
счет спин-орбитального взаимодействия. Если с заполненной оболочки снять
один электрон, то получится незаполненная оболочка, причем операция сня¬
тия электрона очевидно эквивалентна представлению, когда к электрону на
заполненной оболочке добавляется «дырка» (hole) — частица, движущаяся
совместно с электроном по той же траектории, заряд которой полностью
компенсирует заряд электрона: это эффективная частица противоположного
заряда eh = —г. Спин дырки компенсирует спин электрона. Значит, если снять
с заполненной оболочки nh электронов, число которых меньше половины
максимальной степени заполнения оболочки, nh = 2(2Z +1) — Uf < 21 -I-1, то
это эквивалентно добавлению к заполненной оболочке nh дырок, спин кото¬
рых компенсирует спин снятых электронов (знак тильды):
П/i Щ
25/+2sh=°-
/=1 /1=1
Тогда, с одной стороны, спин электронов на оболочке, заполненной более чем
наполовину,
s=2s/’
/
а с другой — его можно получить, добавляя сначала электроны, чтобы пол¬
ностью заполнить оболочку, а потом дырки, чтобы вернуться к исходной
конфигурации:
nh ч
s=Ss/+Ss/+Z^
/ /=1 h=1
364
Тема 13. Сложный атом
Но на заполненной оболочке спин равен тождественному нулю
ч
Zs/+2s/=0’
/ /=1
так что
ч
3 = У^Sh = sh-
h=1
Значит, полный спин электронов на заполненной более чем наполовину обо¬
лочке равен полному спину дырок на этой оболочке. И аналогично для орби¬
тального момента
I-£l„ L = Z
/ /=1 h=1
так как дырки повторяют траектории экранируемых ими электронов на за¬
полненной оболочке (знак тильды). Тогда, поскольку на заполненной оболоч¬
ке L = О,
1 + 1 = 0
и
L = L + L —Lh = —Lh.
Поэтому задача о спин-орбитальном расщеплении в этом случае сводится
к задаче о движении дырок на этой оболочке, причем дырочная оболочка
оказывается заполненной менее чем наполовину, а спин дырок равен спину
электронов, в то время как их орбитальный момент противоположен орби¬
тальному моменту электронной оболочки. В итоге решение задачи об оценке
константы спин-орбитального взаимодействия повторяет проведенное выше
рассмотрение для оболочки, заполненной менее чем наполовину, и после
замены спина и орбитального момента дырок на равный спин и противопо¬
ложный по знаку орбитальный момент электронов находим
(L, М; S, Ms\Vsl\L, М; S, Ms) = AhLS{Lh ■ Sh) = -AhLS(L • S), (23.10)
где a£s > 0 — положительная константа спин-орбитального взаимодействия
ДЛЯ дырок при rif > 21 +1.
Таким образом, устанавливается следующее
Второе правило Хунда. Если оболочка заполнена не более чем наполо¬
вину, то после учета релятивистских поправок наименьшее значение энер¬
гии имеет терм с минимальным допустимым значением полного момента
J = \L — S\, а если оболочка заполнена более чем наполовину, то наименьшее
значение энергии имеет терм с максимальным допустимым значением пол¬
ного момента J = L + S.
В самом деле, из формулы для поправки за счет спин-орбитального взаи¬
модействия (23.8) следует, что при Als > 0 наименьшая энергия—у состояния
с минимальным значением полного момента, а при ALS < 0 наименьшая
Лекция 23
365
энергия —у состояния с максимальным значением полного момента, что
и имеет место при соответствующих условиях заполнения оболочки.
Например, в атоме углерода основное состояние отвечает терму 3Р0, а тер¬
мы 3РЪ 3Р2 находятся последовательно выше согласно правилу интервалов
Ланде. Схема расщепления электронной конфигурации углерода при после¬
довательном учете поправок показана на рис. 28.
lsa 1)
г
/
/
/
/ гР(5)
/ /
/ /
Р2(15) >/
•^oCL)
/ / ■L/2
/ /
^2(5)
гР(9) - 3Р2(5)
3Pi(3)
Зр0а)
Рис. 28. Последовательное расщепление электронной конфигурации внешней
электронной оболочки углерода в теории возмущений: в самосогласован¬
ном поле — р2, с учетом парных взаимодействий электронов и обменных
вкладов—термы 2S+1L согласно первому правилу Хунда, тонкое расщепление
за счет релятивистских спин-орбитальных взаимодействий — термы 2S+1Lj
согласно второму правилу Хунда и правилу интервалов Ланде. В скобках
указана степень вырождения терма
Порядок получения термов с учетом релятивистских поправок, рассмот¬
ренный нами, носит название метода LS-связи, или рассель-саундеровского
подхода. Он применим в тех случаях, когда расщепление термов из-за об¬
менного взаимодействия и поправок к самосогласованному полю намного
больше расщепления за счет взаимодействия спин-орбита. Мы уже упомина¬
ли, что в редких случаях имеет место обратная картина: спин-орбитальные
взаимодействия больше поправок к самосогласованному полю, — тогда го¬
ворят о jj-связи, так как доминирующие операторы в возмущении имеют
вид (IfSf), и они диагональны в базисе полных моментов для электронов
jf = l/+sf. Поэтому правильные функции ведущего приближения — состоя¬
ния с заданными моментами электронов, и поэтапное усреднение по этим
состояниям сводится к сложению моментов электронов j + j, а не к сложению
их орбитального и спинового моментов L + S. Мы не будем здесь останавли¬
ваться на более подробном описании свойств jj-связи.
В заключение мы изложили в этой лекции лишь качественные основы тео¬
рии многоэлектронных атомов, ибо сам этот предмет, лежащий в основе пе¬
риодической системы химических элементов Менделеева, наряду с теорией
366
Тема 13. Сложный атом
молекул безусловно заслуживает более подробного освещения в отдельном
курсе квантовой химии.
Кроме того, подчеркнем, что использованная нами схема исследования
(комбинация приближения самосогласованного поля и теории возмущений)
очень эффективна для большинства атомных и молекулярных задач, но не яв¬
ляется универсальной. В поведении многочастичных квантовых систем ино¬
гда существенную роль играют коллективные эффекты (эффекты кластериза¬
ции нуклонов в атомных ядрах, куперовское спаривание в ферми-жидкостях
с притяжением и другие), которые невозможно учесть как малое возмущение
задачи с самосогласованным полем, ибо они зачастую качественно изменя¬
ют спектр и динамику системы. В этом случае обычно используют методы,
построенные на базе схемы вторичного квантования, которые с математиче¬
ской точки зрения близки к методам квантовой теории взаимодействующих
полей.
Задача 13.2. Определить термы атома азота: конфигурация ls22s22p3.
Решение. Три 2р-электрона на незаполненной оболочке могут быть распределе¬
ны по 2(2Z +1) состояниям с различными проекциями спина и орбитального момента
1 = 1
Cl = — = 20
6 3!3!
способами.
Максимальное значение спина электронов S = - является симметричным по пере¬
становкам электронов, и оно возможно, только если электроны с проекцией полного
спина | занимают состояния с различными значениями проекции орбитального
момента: схема расположения р-электронов с различными проекциями орбитального
момента т =
+1
-1
т
т
т
, а значит, при проекции
в этом случае —
суммарного орбитального момента только М = О, т. е. исключительно1 при L = 0.
Поэтому при максимальном значении спина электронов единственный терм
4S ~ 4s3/2.
Число таких состояний (2S +1) (2L -f 1) = 4 • 1 = 4.
При S = ^ допустимые значения суммы проекций орбитального момента М = ±2,
±1, ±0. Термы с максимальными значениями |М| = 2 отвечают L = 2:
2D 2&5/2> 2^3/2>
1Для этого необходимо убедиться, что указанное состояние с М = 0 является одновременно
и старшим, и младшим вектором. Это ясно, во-первых, из того, что другие значения проекции
суммарного орбитального момента просто запрещены. Во-вторых, чисто формально мы можем
3 СП
подействовать на состояние с М = 0 повышающим оператором L+=Yi ч• Повышающий
/=1 .
оператор отдельного электрона сдвигает «стрелку» этого электрона в состоянии | Т I Т I Т~|
на одну клетку влево. Для первого электрона такой клетки нет, и получается нуль; сдвиг второго
электрона приводит к двум одинаковым стрелкам в первой клетке, что запрещено принципом
Паули (значит, получаем нуль); сдвиг третьего электрона приводит к аналогичной ситуации
с двумя одинаковыми стрелками во второй клетке. В итоге оператор повышения дает нуль,
и вектор состояния действительно старший. Доказательство того, что состояние — младший
вектор, проводится почти дословно так же, как для старшего вектора.
Лекция 23
367
и они имеют вырождение по проекциям спина и момента
2-5 = 10, или ^(2J + 1) = 6+4=10.
Состояния с Ms = +- и М = +1 — это
U
т
и
т
п
. Одна из
суперпозиций отвечает терму с S = - и L = 2, описанному выше, но просто с другим
значением проекции М, а другая, следовательно, терму с S=| и L = l. Значит,
в конфигурации есть еще и терм
2Р ~ 2Р3/2,2РЦ2,
который имеет вырождение по проекциям спина и орбитального момента 2*3=6 или
по проекциям полного момента 4 + 2 = 6.
Состояния сМ5 =+|иМ = 0 включают в себя три спин-орбитальных конфигура¬
т
1
т
}
1
I
?
и
т
т
1
ции TIT, ITT и Т Т 4 . Из этих трех состояний можно
составить только три суперпозиции, отвечающих уже найденным нами термам 2D,
2Р и 4S. Поэтому независимых состояний, отвечающих каким-то новым термам,
больше нет. В этом можно убедиться, суммируя количество состояний в термах:
2D+2P+4S = 10 + 6+4=20, которое исчерпывает степень вырождения конфигурации
по проекциям орбитального момента и спина.
Основное состояние азота согласно правилам Хунда—4S3/2.
Схема расщепления электронной конфигурации азота при последовательном уче¬
те поправок показана на рис. 29.
р3(20) !/
/
/
/
/
/ /
//
/
/
2Р( 6)
2D(10)
■2Рз/2(4)
■2Рцг(2)
•4Г>5/2(6)
‘ 2^з/г(4)
4S(1)
■4S3/2(4)
Рис. 29. Последовательное расщепление электронной конфигурации внешней
электронной оболочки азота в теории возмущений: в самосогласованном по¬
ле—р3, с учетом парных взаимодействий электронов и обменных вкладов —
термы 2S+1L согласно первому правилу Хунда, тонкое расщепление за счет
релятивистских спин-орбитальных взаимодействий — термы 2S+1Lj согласно
второму правилу Хунда и правилу интервалов Ланде. В скобках указана сте¬
пень вырождения терма
Тема Феноменология:
-а л атом во внешнем поле
Лекция 24
Взаимодействие атома с постоянным магнитным полем, магнитный момент
электронов, наведенный диамагнитный вклад, масштаб сильного и слабого
магнитных полей, расщепление терма с J Ф 0 в слабом поле — аномальный
эффект Зеемана, применение теоремы Вигнера—Эюсарта для матричного
элемента полного спина, фактор Ланде для терма, снятие вырождения, диа¬
магнетизм атомов с заполненными оболочками, явление парамагнетизма ван
Флека для терма с J = 0, расщепление терма в сильном магнитном поле —
эффект Пашена—Бака, остаточное вырождение.
24.1. Атом в магнитном поле:
ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ электронов
Гамильтониан взаимодействия электронов атома с постоянным внешним
магнитным полем включает в себя вклад вектор-потенциала за счет кова-
риантной производной и ведущую поправку взаимодействия собственного
магнитного момента с полем Ж
H = S{2^(P/-?^(r/))2-(ilxf^ + eA(r/)} + V) (24.1)
где V — потенциал, включающий в себя как нерелятивистские вклады ку-
лоновского взаимодействия электронов с ядром и попарно друг с другом,
так и релятивистские поправки, зависящие от спина. Магнитный момент
электрона, обусловленный спином, согласно уравнению Дирака eg = 2 есть
Калибровка обычно фиксируется так, чтобы
^(г) = |(.МГхг), (24.2)
откуда заключаем, что
div М(г) = \еаргдаЩхг = \еаРгЩ5аг = 0.
Поэтому при возведении в квадрат обобщенного импульса
(р- f^(r))2=р2 -~с{(р-Л) + Ы-р)}.+
вклад
(р • sf) + (л/ • р) = ■ р) — ih div sj
370
Тема 14. Феноменология: атом во внешнем поле
сводится к
2(л/-р) = eaprHaXppr = • (г х р) = ПЖ ■ I,
т. е. возникает член взаимодействия с магнитным моментом вращения:
Значит, гамильтониан атома в постоянном внешнем магнитном поле прини¬
мает вид
где —гамильтониан атома в отсутствие внешних источников, а магнетон
Бора fi0 = |е|Й/2тс.Суммирование орбитального момента и спина очевидно
приводит к возмущению в виде взаимодействия магнитного поля с магнит¬
ным моментом электронов атома:
обусловливает диамагнитные свойства электронов, потому что коэффици¬
ент при квадрате поля имеет положительный знак: наведенный магнитный
момент пропорционален внешнему полю = ЪЖ, и он дает вклад в по¬
тенциальную энергию L7ext = • Ж), так что если Ъ < 0, то наведенный
магнитный момент направлен против внешнего поля и соответствующая
энергия диамагнитной системы Vd = —ЪЖ2 > 0, т. е. она квадратична по полю
и положительна.
Оценим по порядку величины вклад во взаимодействие магнитного мо¬
мента электронов и диамагнитный член. Для этого прежде введем напряжен¬
ность поля, характерную для атома:
и, если L Ф 0 или S Ф 0, энергия взаимодействия магнитного момента с посто¬
янным магнитным полем при Н < aem^at ~ Ю5 Гс оказывается существенно
меньше энергии спин-орбитального взаимодействия за счет релятивистских
поправок.
Для диамагнитного вклада
^mag — Й)«^ ■ № + 2S),
а квадратичный по полю член
(24.5)
(24.6)
Тогда
-т— — тс
Лекция 24
371
Отсюда немедленно следует, что если магнитный момент электронов не
равен тождественно нулю, то диамагнитным вкладом заведомо можно пре¬
небречь, поскольку он сравнивается с членом магнитного момента только
при гигантских полях порядка
Н~^~109Гс,
®еш
при которых и поправки за счет магнитного момента становятся сравнимы¬
ми с энергией связи в атоме, т. е. поля становятся настолько велики, что
приводят к ионизации атома, которую мы не рассматриваем.
Далее исследуем различные условия взаимодействия атома с внешним
магнитным полем, используя теорию возмущений.
24.2. Аномальный эффект Зеемана
Если магнитный момент терма не равен нулю, то взаимодействие атома
со слабым внешним магнитным полем ТС < aem^at ~ Ю5 Гс является ма¬
лым возмущением по сравнению с релятивистскими спин-орбитальными
поправками. Это означает, что в качестве волновых функций ведущего при¬
ближения следует рассматривать термы 2S+1Lj.
В возмущении (24.5) магнитное поле задает выделенное направление,
которое примем за направление оси z. Коммутатор
[Ja, ('X’-{J + S})] = ieaf}rHf}{J + S}r
обращается в нуль для Jz. Далее, используя алгебру коммутаторов для произ¬
ведения, легко найти, что
[J2, Or-{J+S»]=0.
Таким образом, квантовыми числами терма по-прежнему будет пара {J, М/},
но вырождение по MJf которое имело место в отсутствие магнитного поля
вследствие того, что сохранялись и компоненты J±: [J±, Я*] =0, некомму¬
тирующие с Jz: [J±,JZ] #0, теперь оказывается «снятым»: энергия зависит
ОТ Mj.
Для вычисления матричного элемента возмущения заметим, что опе¬
раторы полного момента и спина являются неприводимыми тензорными
операторами первого порядка, т. е. момента 1, так как при вращениях они
преобразуются соответствующим образом — как векторы. Отсюда следует,
во-первых, элементарно
{J,Mj\Jz\J,M'j)=Mj5MjM>, (24.7)
а во-вторых,
[J2,SJ = 0,
и значит, Sz—это нулевая компонента векторного оператора в стандартном
представлении, и согласно теореме Эккарта—Вигнера
(J, Mj\Sm\J, Mj) = Mj\J, М'у, 1, m), m = {z, ±>, (24.8)
372
Тема 14. Феноменология: атом во внешнем поле
где коэффициент Клебша—Гордана отличен от нуля при J Ф 0 (правило за¬
прета переходов 0—>07 за счет тензоров, не являющихся скалярами). В этом
параграфе мы будем иметь в виду это условие. Совершенно аналогично для
полного момента
(J, Mj\Jm\J, M'j) = Mj\J, Mji 1, m), m = {z, ±}, (24.9)
откуда заключаем, что для одного и того же терма оператор полного спина
S пропорционален оператору полного момента J:
S = AJ, (24.10)
где параметр А определяется значениями приведенных матричных элемен¬
тов для заданного терма
>(J\\s\\J)
тт
и не зависит от величины проекции Мj. Определим А, рассчитав матричные
элементы
((S-J))=A(J2) => ((I-S)+S2)=AJ(J + 1),
откуда
а J(J + 1)—£(L + 1)+S(S + 1) (0АЛЛЛ
2JG/ + 1) •
В итоге матричный элемент возмущения есть
<W=Mo (24.12)
где фактор Ланде
_ , J(J+1)-L(L + 1)+S(S + 1)
gLSJ = 1 + 27(7+1) • (24-13)
В терминах ларморовской частоты £1=е'Н/(2тс) получаем расщепление уров¬
ней в терме:
(24.14)
Итак, атомный терм в слабом магнитном поле расщепляется на 2J +1 уров¬
ней, т. е. вырождение терма снимается полностью.
24.3. Диамагнетизм
Если оболочки атома заполнены полностью, как, например, у инертных
газов, то L = 0, S = 0 и магнитный момент электронов тождественно обра¬
щается в нуль. Поэтому взаимодействие такого атома с магнитным полем
целиком определяется диамагнитным вкладом: атомы с заполненными элек¬
тронными оболочками диамагнитны.
Поскольку состояние является сферически симметричным, усреднение по
углу между полем и радиус-вектором электрона проводится элементарно:
(sin2 в) = ^ J d cos в • sin2 в = |,
-1
Лекция 24
373
так что зависимость энергии от поля в первом порядке теории возмущении
f
Отсюда магнитная восприимчивость
X = -^e1(H) = -£iS('/><°. (24.16)
и атомы диамагнитны.
24.4. Парамагнетизм ван Флека
Если J=0, но L=S ^ 0, то согласно проведенному рассмотрению поправка
первого порядка по магнитному полю тождественно обращается в нуль:
«работает» правило запрета переходов 0 —> (У за счет векторного оператора.
Поправка второго порядка
=Е
1ЧыР
£(0) _ рС°)
кфп
включает в себя сумму по состояниям, отличным от исходного. Здесь матрич¬
ный элемент, как мы уже выяснили, имеет порядок
\Vkn\~VoH~mc2alm£-,
' Lat
а вот расщепление уровней существенно отличается: в терме 2S+1L расщеп¬
ление за счет релятивистских поправок в а2т раз, т. е. на четыре порядка
меньше, чем между уровнями в нерелятивистской системе с самосогласован¬
ным полем, и приблизительно на два—три порядка меньше, чем расщепление
конфигурации электронов за счет обменных сил и парных взаимодействий.
Поэтому с довольно высокой точностью сумму можно аппроксимировать
вкладом J-состояний, принадлежащих одному и тому же терму 2S+1I. Тогда
согласно правилу интервалов Ланде AE(J') = —ALSJ'(J' +1)/2
2 2-1 -AuJ'U' + l) _ ■ t J
J'eterm
Подобная поправка имеет место для основного терма с минимальным из
возможных1 значением J = 0, т. е. если оболочка заполнена не более чем
наполовину, а значит, при Als > 0, и поправка к энергии отрицательна2
и квадратична по магнитному полю, что отвечает парамагнетизму атома:
д2е2 „ „
X = —> 0. В самом деле, в отсутствие внешнего магнитного поля ненуле-
дгС
вые спиновые и орбитальные магнитные моменты электронов атома в сред¬
нем полностью компенсируют друг друга, поскольку полный момент атома
1Кроме основного состояния атома согласно условиям задачи имеются и другие термы,
например, с J' = L + S = 2S Ф 0.
2Поправка второго порядка к основному состоянию, напомним, всегда отрицательна.
374
Тема 14. Феноменология: атом во внешнем поле
равен нулю, в то время как включение внешнего поля приводит к тому, что
эти моменты ориентируются вдоль поля в разной степени выстроенности,
давая вклад в ненулевой наведенный магнитный момент. Такой механизм
магнитной поляризации носит имя парамагнетизма ван Флека. Поскольку
константа спин-орбитального расщепления ALS ~ тс2а*т, a /Xo^at~mc2aem>
этот парамагнитный вклад имеет порядок
е2 ~ тс2 a2 тс2 а4 -5-,
z ет п-/ 2 а ет qj 2 >
' at ' at
т. е. он в 1 /а2т ~ 104 раз больше диамагнитной энергии.
Таким образом, атомы с термом J=О, hocL=S^0h оболочкой, заполнен¬
ной не более чем наполовину, в слабом магнитном поле проявляют свойства
парамагнетика.
24.5. Эффект Пашена—Бака
В1912 году немецкие физики Пашен и Бак, наблюдая спектральные линии
кислорода в магнитном поле, установили, что в слабых полях расщепление
пропорционально величине поля в согласии с теорией эффекта Зеемана,
но с его увеличением до 10 тесла эта зависимость становится существенно
нелинейной, линии спектра перемещаются друг относительно друга, часть
из них исчезает, и лишь в сильных полях более 10 тесла зависимость рас¬
щепления уровней от поля вновь становится линейной. Подобное поведение
расщепления линий спектров атома в магнитном поле получило название
эффекта Пашена—Бака.
Ясно, что в слабых полях, когда энергия взаимодействия электронов ато¬
ма с магнитным полем существенно меньше величины спин-орбитального
расщепления термов, имеет место аномальный эффект Зеемана. При увели¬
чении поля до 10 тесла происходит выравнивание по величине магнитного
и спин-орбитального взаимодействий: при этом задача расчета энергии элек¬
тронов приобретает существенно нелинейный по полю характер. И нако¬
нец, в сильных полях1 энергия магнитного взаимодействия преобладает над
спин-орбитальным вкладом, так что имеет место нормальный эффект Зее¬
мана, который мы рассмотрим в конце данного раздела. Важно подчеркнуть,
что иерархия двух типов взаимодействия электронов: спин-орбитального и с
магнитным полем, — определяет вид как возмущения в атомной системе
электронов, так и выбор правильных волновых функций в вырожденном
случае теории возмущений.
Итак, нормальный эффект Зеемана наблюдается в сильных магнитных
полях, если спин-орбитальное взаимодействие в атоме подавлено. Понятие
сильного магнитного поля задается масштабом Н ~ aemHat ~ 105 Гс=10 тесла.
1При этом мы полагаем, конечно, что энергия взаимодействия электронов с внешним
магнитным полем все же существенно меньше величины поправок к энергии электронов в са¬
мосогласованном поле за счет обменных сил или, точнее, остаточного взаимодействия.
Лекция 24
375
Такие поля являются рекордными для соленоидов из сверхпроводящих ма¬
териалов, поэтому на практике в большинстве атомов в сильных полях не
удается получить ситуацию, когда взаимодействие магнитного момента элек¬
тронов с магнитным полем доминирует над спин-орбитальным потенциа¬
лом, что осложняет расчеты и делает их громоздкими. Однако в некото¬
рых конфигурациях спин-орбитальное взаимодействие оказывается подав¬
ленным, и тогда им можно пренебречь. В этом случае описание эффекта
Пашена—Бака становится элементарным.
В самом деле, отсутствие пренебрежимо малого спин-орбитального взаи¬
модействия означает, что волновые функции ведущего приближения—термы
2S+1I, а среднее от возмущения для этих состояний легко вычисляется:
(L, М'; S, M/s\ix0H{Lz + 2SZ)|L, М; S, Ms) = К1т + 2М8)6ША.6щщ.
Расщепление терма снимается лишь частично: остается комбинаторика пе¬
рестановок значений проекций орбитального момента и полного спина при
заданном значении М + 2Ms. При этом, как и при аномальном эффекте
Зеемана, спектр расщеплений является эквидистантным с инкрементом, ко¬
торый отличается от случая аномального эффекта Зеемана отсутствием фак¬
тора Ланде. Невырожденными являются, очевидно, низшее и высшее состо¬
яния.
Тема Спонтанное излучение
15
Лекция 25
Квантовые переходы между уровнями атома в ведущем приближении, элек¬
трический диполь и квантованное электромагнитное поле, вид возмущения,
задача о распаде 2р-уровня атома водорода в основное состояние, матрич¬
ный элемент перехода в нестационарной теории возмущений, усреднение по
поляризациям начального состояния атома, время жизни, интенсивность из¬
лучения, дипольная формула и принцип соответствия, характерные частоты,
ширины и времена жизни, сумма по поляризациям фотона, угловое распреде¬
ление спонтанного излучения в дипольном приближении, правила отбора по
полному моменту, спину, орбитальному моменту и четности в общем случае,
серии Лаймана и Бальмера в атоме водорода, индуцированное излучение
и поглощение атомом в когерентном электромагнитном поле, интенсивность
вынужденного излучения и ее пропорциональность числу квантов поля.
Рассмотрим взаимодействие атома с квантованным электромагнитным
полем, т. е. учтем квантовое излучение зарядов, которые движутся нереля¬
тивистским образом, что заведомо имеет место для электронов в атоме из
верхней части периодическом таблицы химических элементов Д. И. Менделе¬
ева. В отличие от классического описания в квантовой механике состояния
электронов в атоме лежат в области дискретных значений энергии. Поэтому
излучение электромагнитного поля соответствует переходам между уровня¬
ми квантовой системы заряженных частиц.
25.1. Дипольное ПРИБЛИЖЕНИЕ
Прежде всего запишем гамильтониан взаимодействия нерелятивистских
электронов и ядра с внешним полем, как это делается в классической элек¬
тродинамике. Поскольку система является нейтральной, вклад в потенциаль¬
ную энергию полного заряда системы равен нулю, и в первом приближении
V£1 = -d-*(t), (25.1)
где d = e^]rf —дипольный момент атома в системе отсчета с центром в точ-
/
ке, где покоится неподвижное ядро: сумма берется по электронам атома,
а электрическое поле в центре системы г = 0 в момент времени t. Последу¬
ющие члены высших порядков включают в себя энергию квадруполя (Е2)
и других 2£-польных электрических моментов (Е£), а также магнитный мо¬
мент (Ml) и высшие магнитные мультиполи.
Условие применимости дипольного приближения заведомо выполнены,
если длина волны излучения много больше атомного размера, Я » а. Кроме
378
Тема 15. Спонтанное излучение
того, поскольку электроны движутся нерелятивистски, смещение зарядов за
период излучения всегда много меньше длины волны, так что дипольное
приближение вполне законно, а высшие мультиполи подавлены, если только
вклад электрического диполя в матричный элемент перехода не равен нулю
(см. правила отбора ниже).
Для квантованного электромагнитного поля необходимо записать элек¬
трическое поле во вторично квантованном виде
ОД = -d0j*Oc) = J* 2^)3 ihiz-ikxex(Vax(k) - eikxel(k)a{(k)},
так что
т = i J ^3 {е-^*л(к)ал(к) - еше1(.Юа1(К)},
где операторы рождения и уничтожения нормированы условием
[ая(Ю, а[,(к')] = 2П<о(2п)35хх,5(к-к'),
и возмущение за счет дипольного взаимодействия принимает вид
VEi(t) = -iJ ^-{е~1“с(1-ех(к)ах(к) -ei<utd• «* (fc)4(k)}. (25.2)
25.1.1. El-переход 2р —> Is в атоме водорода. Вычислим матричный эле¬
мент перехода атома водорода из состояния 2р в состояние 15 за счет ди¬
польного излучения кванта электромагнитного поля в рамках формализма
нестационарной теории возмущений. Поскольку спин электрона коммути¬
рует с оператором возмущения, для простоты опустим его из рассмотрения
в этом параграфе.
Начальное состояние квантовой системы—атом водорода в состоянии 2р
с проекцией орбитального момента т и вакуум в фоковском пространстве
для фотонов
|i) = |vac)|2p,m) -> (r|i) = |vac)-02p>m(r) = |vac)R2p(r)^im(0, у).
Угловую часть волновой функции, как мы выяснили в лекции 2, можно
записать в векторном виде
Ъ,а&> =
где п — единичный радиус-вектор.
Конечное состояние квантовой системы включает в себя 15-уровень атома
водорода и один квант электромагнитного поля с волновым вектором
и поляризацией Af:
|f) = |kf,Af)|ls) - (r|f) = |kf, Af)-^==Rls(r).
Матричный элемент перехода в первом порядке нестационарной теории
возмущений
00
Afi = -| J dt eia)ilt<f|y^i(t)|i),
Лекция 25
379
где
°>П = \{Еи-Е2рУ < О,
после подстановки дипольного взаимодействия, начального и конечного со¬
стояний принимает факторизованный вид:
оо
Afi = i J dt ei("«l+"f)t j ^0pef(k)(kf,xyx(k)\vac)x
— 00
x J d3r -±=Rls(r)R2p(.r)&lia(e, 4>)dP. (25.3)
Здесь последний интеграл есть матричный элемент оператора электрическо¬
го дипольного момента электрона d = er = егп:
/— 00
(ls|d^|2p, а) = еЦ J d2ft папР J dr • r2Rls(r)R2p(r)r. (25.4)
4тг
о
Усреднение на сфере выполняется элементарно:
Г d2£2 nan^ = UaP,
4п J 3 9
а интеграл по радиусу вычисляется довольно просто, если подставить извест¬
ные выражения для радиальных волновых функций в атоме водорода
Rls(r) = -p=e_r/a, J?2D(r) = —F=re"r/2a,
откуда
rfi = J dr • r2Rls(r)R2p(r)r = -^= J dx-x4e-3x/2=a(iy^ = a]/l-^.
В итоге матричный элемент диполя равен
<ls|d* |2р, а) = j=5aperfi. (25.5)
Матричный элемент в фоковском пространстве1 —
(fcf, Af|o^(fc)|vac) =2h<Of(2n)38XfX5(kf-fc).
Поэтому интеграл по волновому вектору «снимается» дельта-функцией
/ 2§^£** (fc)^f’ Aflal® lvac) =hcoief, (25-6)
1Мы действуем здесь оператором рождения «направо», т. е. на вакуум. Действие же этим
оператором налево приводит к его эрмитову сопряжению и к выражению
ах(кЩ, Af> = |vac)2ficof(2Tr)35Xf-Ю = |vac)(k, A|kf, Af),
что еще раз подчеркивает, что действие операторов рождения и уничтожения квантов поля
в отличие от случая одномерного гармонического осциллятора сопряжено с аккуратным учетом
нормировки состояний.
380
Тема 15. Спонтанное излучение
Значит, матричный элемент—
+ *«(*,). (25.7)
Значение матричного элемента, как видим, зависит от проекции вектора
поляризации фотона на направление вектора поляризации 2р состояния:
в амплитуде перехода стоит компонента вектора поляризации фотона, соот¬
ветствующая поляризации исходного состояния. Поэтому угловые распреде¬
ления и модуль амплитуды определяются скалярным произведением поля¬
ризаций начального и конечного состояний. Для упрощения оценок в даль¬
нейшем проведем расчет вероятности распада, усредненной по поляризации
исходного состояния атома водорода в состоянии 2р, т. е. проведем сум¬
мирование по проекции орбитального момента и разделим на число таких
состояний 21 +1 = 3.
При возведении амплитуды перехода в квадрат возникает знакомое нам
выражение
2п5 (со)
~Г,
со-»0
где Г —> оо — время наблюдения за системой. Поскольку фотонное состояние
находится в непрерывном спектре, квадрирование амплитуды дает плот¬
ность вероятности перехода в единицу времени
1 \А \2 dЗк e2r2. dЗк
dwn = 2l + l Т 2^f(27t)3=27l5(a>fi + Ct>f)_9La>f2fia)f(27t)3’ (25‘8)
где мы учли, что вектор поляризации нормирован на единицу: ё* • е = 1, если
провести суммирование по всем проекциям орбитального момента в состоя¬
нии 2р. Интегральная вероятность в единицу времени, или обратное время
жизни уровня, вычисляется как
i = J dwfi,
так что с учетом |fcf | = a>f/c,
d3fcf = -^d2ft • coj dcof
легко находим
где
- = ^ja>fd2^-, (25.9)
Т з С3 f ixh(Df}
j _ e ’n
fi V4ZV3
есть усредненный по поляризации начального состояния атома матричный
элемент модуля электрического дипольного момента электрона, если учесть,
что мы проводили расчеты в системе Хевисайда, в которой е=е0 л/4тг, где е0 —
заряд электрона в системе СГСЭ.
Лекция 25
381
Интенсивность излучения фотона с заданной поляризацией определяется
как произведение энергии кванта на вероятность излучения в единицу вре¬
мени:
Ло1(^) = ^Г = !зЧ4’ (2S.10)
где, очевидно, отвечает второй производной по времени дипольного
момента в частотном представлении, так что воспроизводится классическая
формула для интенсивности излучения электрического диполя, но на месте
модуля диполя стоит его матричный элемент перехода.
Полученная выше интенсивность выведена для фотона с заданной поля¬
ризацией, так что полная интенсивность распада получается суммированием
по количеству поляризаций фотона, т. е. умножением выражения (25.10) на
фактор 2:
^f) = ^d2. (25.11)
Кажущееся «удвоение» классического результата обусловлено переходом от
диполя как функции времени к спектральному представлению: если /(£) —
вещественная моногармоническая функция времени,
т=/ае~ш+/.аеш,
то усреднение квадрата функции
/2(0 =2/w/_^+/2e-2i"t+/2a>e2ia>t
по достаточно длительному по сравнению с периодом интервалу времени
приводит к константному вкладу
</2(t)) = 2|/J2,
что как раз и имеет место при рассмотрении квантового перехода в диполь-
ном приближении, где
d (£) 21 — a>2dfi|2.
Оценим полную ширину 2р-уровня
(25.12)
С учетом значения ft = 6,58 • 1СГ16 эВ • с, по порядку величины частоты пере¬
хода
cofi ~ |rnc2a2m ~ 1016 с-1, fta>fi ~ 25 эВ,
дипольный момент
e0fi
dfi~e0a'
тсает'
так что полная ширина перехода
Г ~ тс2а5ет < Vsl ~ тс2 а* (25.13)
382
Тема 15. Спонтанное излучение
т. е. ширина на два порядка (aem ft* 1/137) меньше спин-орбитального рас¬
щепления уровней в атоме.
В рассматриваемом случае
г=(1)‘тс!“™-
так что численно
Г w 4,1 • 10-7 эВ, т «1,6 • 1(Г9 с, (25.14)
в прекрасном согласии с экспериментом.
Таким образом, мы показали, что спонтанное излучение приводит к ме¬
тастабильности возбужденных уровней в атоме водорода, и сделали оценку
характерного времени жизни на примере 2р-уровня. Конечно, переходы со
спонтанным излучением фотонов происходят не только вследствие диполь¬
ного взаимодействия, но и с учетом других электрических и магнитных
мультиполей.
25.2. Дипольные переходы в атомах: правила отбора
Поскольку, как мы видели, ширины переходов между атомными уровнями
со спонтанным излучением фотонов на пару порядков меньше спин-орби-
тального расщепления, матричные элементы таких переходов следует вычис¬
лять по состояниям термов 2S+1Lj. Поэтому начальное и конечное состояния
атома—
|iat) = |L, S; J, Mj), |fat> = 11', S'; f, Mj),
а начальное и конечные состояния в фоковском пространстве для фотонов
остаются такими же, как и в рассмотренном нами примере для самопроиз¬
вольного перехода 2р —> Is в атоме водорода.
Отсюда совершенно аналогично с предыдущим разделом находим
= 2n5(.a>fi + (fcf) <fat|d“|iat) • (25.15)
Введем матричный элемент дипольного момента
d“ = (fatl<Hiat>.
Тогда дифференциальная вероятность перехода в единицу времени
dwfi = ^г- ь ^ --з =2п5(ооп + а>')о>? ^ ^ d“d!f.
Г 2Йа>,(2я)3 fl ' >2Й<о,(2я)3 h h f1 f‘
Проведем суммирование по поляризациям фотона в конечном состоянии
п1 (25Л6)
h
где единичный вектор щ = /fcf направлен по волновому вектору фотона.
Тогда
Е C/xStf=i,r -ij, - W,r n,) w„ •„,)* =
= (dfi X nf) (dfi x nf)* = |df, |2 sin2 в. (25.17)
Лекция 25
383
Значит, интегрирование по телесному углу и частоте
d3fcf = • о»2 daif, d2ft = dcos в dip, J d cos 0-sin2 0 = |
элементарно приводит к вероятности распада в единицу времени
I = JL w4 |£fiL 1 . (25.18)
т Зс3 f 4тг
Переходя к единицам СГСЭ согласно соотношению
Щ-ld |2
приходим к стандартной формуле для обратного времени распада за счет
электрического дипольного взаимодействия
»SJS0
и его интенсивности
^(cof) = ^<^|dfi|2. (25.20)
Правила отбора для дипольного момента определяются тремя фактами.
Во-первых, согласно теореме Эккарта—Вигнера матричный элемент вектор¬
ного оператора дипольного момента не равен нулю только в случае, если
\AMj\^ 1, |AJ|^1, l^J + J'. (25.21)
Отсюда специально отмечаем правило запрета для переходов 0 —»(У: матрич¬
ные элементы с J = J' = 0 тождественно равны нулю.
Во-вторых, оператор полного спина электронов коммутирует с диполь-
ным моментом
[Sa,dp]= 0, [S2,dj=0,
так что, взяв от этих коммутаторов матричный элемент по начальному и ко¬
нечному состояниям атома, например,
(L', S'; J', Mj\[S2, dj|I, S; J, Mj) =
= {S'(S' +1) - S(S +1)} x U, S'; J', M'j\da\L, S; J, Mj) = 0,
заключаем, что если
AS т^О, AMS Ф 0,
то матричный элемент дипольного момента обращается в нуль. Значит, пра¬
вило отбора по полному спину имеет вид
AS = 0. (25.22)
Из этого факта диагональности матричного элемента по полному спину и
независимости от значения спина сразу следует, что правила отбора по сум¬
марному орбитальному моменту повторяют правила отбора по полному мо¬
менту
|ДМ|«=1, |AI|^1, IsZL+L' (25.23)
и, как следствие, правило запрета переходов с L=L' = 0.
384
Тема 15. Спонтанное излучение
Наконец, в-третьих, гамильтониан атома, свободных фотонов и их вза¬
имодействия сохраняет пространственную четность1. Следовательно, мат¬
ричный элемент перехода отличен от нуля, если только он является про¬
странственно четной величиной. Другими словами, четности начального
и конечного состояний полной квантовой системы, включающей атом и по¬
ле, должны совпадать.
Вектор поляризации фотона является пространственно нечетной вели¬
чиной: он меняет свой знак при полном зеркальном отражении простран¬
ства. Значит, как говорят, внутренняя пространственная четность фотона
отрицательна. Отрицательной является и четность однофотонного состояния
в конечном состоянии: она является произведением внутренней простран¬
ственной четности фотона на пространственную четность его координатной
волновой функции, которая определяется орбитальным моментом движения
фотона относительно центра масс системы, т. е., в нашем случае, относи¬
тельно атома, импульсом отдачи которого мы пренебрегаем, так что в при¬
ближении электрического дипольного излучения поле в возмущении берется
в точке покоя атома (см. (25.2)), а значит, оно не зависит от координат
и обладает сферической симметрией, что, в итоге, и дает положительное
значение для четности пространственной части волновой функции фотона.
Поскольку четность состояния определяется произведением четностей атома
и фотона, отсюда следует, что начальное и конечное состояния атома отлича¬
ются пространственной четностью, т. е. правило отбора по четности гласит,
что
Pf = -P{. (25.24)
Значение четности состояния атома определяется конфигурацией:
к
где 1к — орбитальные моменты электронов в самосогласованном поле.
Обычно это правило отбора по четности конфигурации выводят из того
факта, что дипольный момент является вектором, а значит, его перестано¬
вочное соотношение с оператором пространственной инверсии I имеет вид
Id = -dl. (25.25)
Возьмем матричный элемент этого операторного равенства по конечному
и начальному состояниям атома (fat| • |iat) и учтем, что эти состояния, отвеча¬
ющие заданным электронным конфигурациям, являются собственными для
эрмитова оператора инверсии:
^Kat) =^iftat)> (fatl^= (fatl-fy
так что
^f(fat|d|iat> = -^i(fatld|iat). (25.26)
1Учет слабых взаимодействий приводит к переходам с нарушением пространственной чет¬
ности.
Лекция 25
385
Значит, матричный элемент дипольного момента не равен нулю, если только
Pf = -Pi5 (25.27)
т. е. пространственные четности начального и конечного состояний имеют
противоположные знаки.
Итак, мы установили основные характеристики спонтанного излучения
атомов в дипольном приближении Е1, которое приводит к метастабильно¬
сти возбужденных уровней атома. Эта метастабильность наблюдается в ви¬
де спектральных линий излучения атомов. Например, в простейшем слу¬
чае атома водорода переходы возбужденных состояний на основной уро¬
вень соответствуют серии Лаймана в ультрафиолетовом диапазоне частот
с Я ^1500 ангстрем (1А=10-8 см), а на уровень с главным квантовым
числом п = 2 — серии Бальмера, которая находится в видимой части спектра
А ~ 4500 4-7500 А.
25.3. Индуцированное излучение и поглощение
КОГЕРЕНТНОГО ПОЛЯ
Если квантованное электромагнитное поле находится в когерентном со¬
стоянии, отличном от вакуума, то имеет место индуцированное поглощение
и излучение квантов поля атомом при переходах между термами, которое
легко вычислить, используя результаты двух предыдущих параграфов.
В самом деле, вместо матричного элемента оператора рождения кванта
электромагнитного поля при расчете излучения единичного фотона
<fcf, Afl4(fc)|vac) =2hcof(2n)35XfX5(ki -fc) = (fc,, A,|fc, A)
следует рассмотреть величину
<^Af(fcf)|aXCfc)l«Al(fct)) =^f(fcf) • <fcf, Aflfcj, А;) • (fc,, A,|fc, A) • {p\a), (25.28)
в которой состояние вакуума в фоковском пространстве заменяется на на¬
чальное когерентное состояние фотонов |ая. (]к{)) с импульсом к{ и поляриза¬
цией
аЯ(*0К (*0> = «я,№i)K (fci)> • (К МК Я,), (25.29)
а конечное однофотонное состояние на когерентное состояние фотонов
|/3Af(fcp) с импульсом и поляризацией Яр В случае же поглощения нужно
вычислить аналогичный матричный элемент оператора уничтожения фотона
(fttf (fcf)|aA(fc)|aAi (*c,)> = афО • (fcf, Я, ft, Я.) • (fcf, Я,|к, Я) • ф\а). (25.30)
При этом мы кратко записали стандартный фактор неортогональных коге¬
рентных состояний с одинаковым значением волнового вектора и поляриза¬
386
Тема 15. Спонтанное излучение
ции в виде
(Р\а)=е-^~^.
В результате в выражении для вероятности и интенсивности индуцированно¬
го излучения появляется дополнительный фактор
|0я, (fcf)|2 • |(/3|а)|2 = (25.31)
где х — относительная фаза комплексных параметров а и /3. Максимум этого
множителя, очевидно, имеет место, во-первых, при % = 0, а во-вторых, если1
^ (N{). Таким образом, дополнительный фактор задается средним чис¬
лом фотонов в когерентном состоянии, которое определяет интенсивность
электромагнитного поля: плотность потока энергии S~{N). Это утверждение
справедливо и для вынужденного поглощения, вероятность которого, соглас¬
но общим свойствам и из явного вида формул, совпадает с вероятностью
вынужденного излучения2. Подчеркнем, что вероятность и интенсивность
вынужденного излучения пропорциональна интенсивности электромагнит¬
ного поля, которое индуцирует это излучение, что контрастирует со спон¬
танным излучением, которое не зависит от интенсивности внешнего поля.
В итоге вероятность излучения оказывается больше вероятности поглощения
за счет вклада спонтанного излучения.
Важно отметить, что постановка задачи о вынужденном излучении су¬
щественно отличается от постановки в случае спонтанного перехода: в по¬
следнем случае измеряется вероятность излучения кванта метастабильной
системой в единицу времени, в то время как индуцированные переходы пред¬
полагают измерение потока частиц, падающих на изучаемую систему, так
что вероятность излучения обычно нормируют на падающий поток. Это есть
прямое следствие полученного нами вывода о пропорциональности инте¬
гральной вероятности вынужденного излучения числу падающих на систему
квантов.
Описанное явление индуцированного излучения когерентным электро¬
магнитным полем лежит в основе действия лазеров —усилителей когерент¬
ного электромагнитного излучения за счет переходов из возбужденных мета-
стабильных состояний, количество которых увеличивают за счет механизма
«накачки»: сначала импульсом энергии переводят атомы в возбужденное
состояние, которое быстро распадается в долгоживущее метастабильное со¬
стояние, редкий спонтанный распад которого дает затравочное когерентное
состояние поля, индуцирующее переход других таких состояний.
Наконец, произвольное поле можно представить в виде суперпозиции ко¬
герентных состояний, так что задачу вынужденного излучения и поглощения
можно считать решенной и в общем случае.
Укажем, однако, одно элементарное приложение, когда начальное и ко¬
нечное состояния задаются точным числом квантов поля: при излучении п
1Точнее, необходимо установить положение экстремума х* для функции f(x) = х2 х
х ехр[—(х—х0)2]. При xQ »1, т. е. если среднее число квантов велико, легко найти х* ъх0 + 1/х0.
2Необходимо поменять местами начальное и конечное состояния: |а) <—* \/3).
Лекция 25
387
квантов до перехода ип + 1 после перехода. Тогда схематически
(п + llc^ln) = д/п + 1,
так что вероятность пропорциональна числу квантов в конечном состоянии
п + 1 для перехода |тг) —► \п + 1), а в случае поглощения |п) —> |п — 1) она
пропорциональна числу квантов в начальном состоянии п.
Несложно также указать амплитуду для перехода когерентного состояния
в состояние с фиксированным числом квантов и обратно.
Тема Рассеяние
16
Лекция 26
Асимптотические состояния в задаче рассеяния, 5/-матрица и определение
дифференциального сечения рассеяния, предельное значение оператора эво¬
люции на больших временах и функция Грина стационарного уравнения
Шрёдингера, контур интегрирования, запаздывающая функция Грина, раз¬
ложение функции Грина по базису стационарных состояний, функция Грина
свободной частицы, интегральные уравнения для функции Грина стационар¬
ного уравнения Шрёдингера, для запаздывающей функции Грина и волновой
функции в задаче рассеяния, волновая функция как решение стационарной
задачи с источником, асимптотическое поведение на больших расстояниях,
падающий и рассеянный потоки вероятности, амплитуда рассеяния /(0)
и формула для дифференциального сечения, ^-матрица рассеяния, тождество
унитарности для матрицы рассеяния и оптическая теорема, интегральное
уравнение для 5"-матрицы, амплитуда рассеяния в борновском приближении
и условие его применимости для медленных и быстрых частиц.
26.1. Асимптотические состояния и У-матрица
Пусть в задаче о рассеянии мишень, помещенная в центр координат, со¬
здает сферически симметричный потенциал V(г), который обращается в нуль
на бесконечности1, и в начальный момент времени t; —>—оо вдали от мишени
частица находится в состоянии |i(tO), отвечающем свободной волне де Брой¬
ля с волновым вектором к{, направленным к мишени, т. е.
1р<ЯЩ, г) = (r|i) = eifci'r • (26.1)
Поскольку такое состояние не является решением стационарного уравнения
Шрёдингера с гамильтонианом
H=H(0) + V(r), = £
оно может служить лишь асимптотическим приближением для точного реше¬
ния в ограниченной области, а именно, вдали от мишени, где потенциалом
можно пренебречь, если радиус его действия ограничен. Поэтому говорят,
что такие начальные состояния образуют пространство асимптотических
in-состояний. Обычно полагают, что in-состояния можно представить в виде
волнового пакета достаточно большого размера далеко от мишени в малом,
13адача о разделении движения центра масс и относительного движения двух тел решается
стандартным образом, поэтому мы сразу полагаем, что мишень покоится, а частица, рассеива¬
ющаяся на ней, имеет массу, равную приведенной массе в нерелятивистской задаче двух тел.
390
Тема 16. Рассеяние
но макроскопическом телесном угле в направлении —щ, где щ = к{/к{ —
единичный волновой вектор исходного состояния, так что отличием этих
состояний от волн де Бройля можно пренебречь.
Для консервативной системы эволюция состояния во времени определя¬
ется действием унитарного оператора эволюции
Uit”, t') =е~пЙ(с"~п,
так что в момент времени t" —»оо получается состояние
|i(t//)> = LT(t//, tOIKO).
Результат эволюции начального состояния исследуют вдали от мишени, где
опять можно пренебречь потенциалом, регистрируя частицы, отвечающие
де-бройлевским состояниям |f(t/7)) с волновым вектором fcf, направленным
от мишени, т. е.
г/»;о) Ct", г) = (r|f(t")) = eik' r •
Такие конечные состояния также не могут быть точными решениями стаци¬
онарного уравнения Шрёдингера, и их рассматривают как асимптотические
оШ-состояния, имеющие область применения, ограниченную малым телес¬
ным углом в направлении nf = kf/kf вдали от мишени (см. рис. 30)1.
1По сути мы ставим задачу рассеяния в рамках нерелятивистской квантовой механики
для консервативных систем в ее стационарной формулировке, условия применимости которой
можно резюмировать следующим образом:
а) взаимодействие частицы с мишенью «достаточно быстро» убывает на бесконечности; это
требование с математической точки зрения позволяет определить асимптотические in- и out-o6-
ласти и на каждом уровне точности описания задать «радиус взаимодействия» как расстояние,
при превышении которого взаимодействием уже можно пренебречь;
б) апертура пучков должна быть много больше радиуса взаимодействия, что позволяет пре¬
небрегать «краевыми» искажениями волн;
в) разброс импульсов частиц в пучке должен быть мал, на уровне неопределенности импульса
при локализации частицы в области взаимодействия;
г) пучки должны быть разреженными для того, чтобы взаимодействиями частиц собственно
в пучке можно было пренебречь.
Ясно, что реальная задача рассеяния волновых пакетов является в действительности суще¬
ственно нестационарной, поскольку такие пакеты характеризуются как групповой, так' и фа¬
зовой скоростью движения, которые в общем случае не совпадают, и происходит зависящее
от времени расплывание волнового пакета частиц в пучке. Однако перечисленные требования
позволяют использовать принцип суперпозиции и свести задачу к рассеянию стационарных
волн де Бройля на статическом потенциале так, как будто мишень постоянно подвергается
бомбардировке частиц пучка и формируется стационарная волна рассеяния.
На самом деле, как установлено, конечность полного сечения (что соответствует конечному
радиусу взаимодействия) обеспечивается лишь для потенциалов, убывающих на бесконечности
быстрее, чем 1 /г2. Поэтому кулоновское рассеяние, например, на самом деле принципиально
нестационарно. Кроме того, кулоновское дальнодействие, как мы увидим, приводит к неустра¬
нимому искажению волны де Бройля вдали от мишени, так что волновой пакет приходится
раскладывать по специфическому набору искаженных волн.
Вообще, задача рассеяния в квантовой механике при становлении теории сыграла ключевую
роль в обосновании Максом Борном вероятностного физического смысла волновой функции
в его споре с Эрвином Шрёдингером, который до конца своих дней придерживался трактовки
волновой функции как материальной волны. С точки зрения Шрёдингера, которую, кстати,
Лекция 26
391
детектор
Рис. 30. Схема рассеяния пучка на мишени. Идеальный детектор максималь¬
но «покрывает» всю 4тг-геометрию по телесному углу
Амплитуду вероятности
lim (fCt'OlL/a7', tOliCt')) (26.2)
t—> —00
t"-»+00
называют элементом У -матрицы.
Так как энергия консервативной системы сохраняется, элементы 5^-мат¬
рицы по состояниям с разной энергией обращаются в нуль и отличны от нуля
только при Е^ = Е{, а значит,
yn~5(Ef-E0.
Поэтому квадрат матричного элемента определяет плотность вероятности
перехода из начального состояния в конечное, лежащее в непрерывном спек¬
тре, в единицу времени, так что
I Ф I2 H3fr
<4t=l j:' (2<tj3> T = t"-tf- со, T = 2nh5{E)
Дифференциальное сечение рассеяния определяют согласно
Е—*0
dwf:
dcr = —Д, (26.3)
Л
разделяли такие гранды, как Эйнштейн и Планк, то, что называют частицей, в действительно¬
сти есть достаточно локализованный пакет материальной волны, описываемый пси-функцией,
причем все изменения этого пакета происходят без каких-либо квантовых скачков, а плавно
и непрерывно. Явление расплывания волнового пакета при соответствующем законе дисперсии,
а значит, и катастрофическое превращение «частицы» в «сгусток» нисколько не убеждало сто¬
ронников материальной волны в изъяне их концепции, поскольку расплывание всегда можно
устранить подобающим выбором закона дисперсии. Однако если в задаче рассеяния частиц
начальное состояние трактовать как материальный волновой пакет, то уже рассеянная по всему
пространству волна никак не может ассоциироваться с локализованным пакетом, представ¬
ляющим частицу, которая, между тем, наблюдается экспериментально, к тому же в строгом
соответствии с распределением волновой функции, рассчитанной в квантовой механике.
Интересно отметить, что упомянутые нами знаменитые противники вероятностного решения
проблемы корпускулярно-волнового дуализма в рамках квантовой механики сами при этом
внесли определяющий вклад в рождение теории квантов.
392
Тема 16. Рассеяние
где j{—модуль вектора потока вероятности в начальном состоянии в момент
времени £'—>—00. Размерности величин в формуле для дифференциального
сечения
№**>] = Ш=н%}>
так что сечение имеет размерность площади.
Таким образом, решение задачи рассеяния и вычисления сечений сводит¬
ся к задаче расчета элементов У -матрицы
26.2. Функция Грина
Для консервативных систем оператор эволюции при £—>+оо можно про¬
сто выразить в виде преобразования Фурье для оператора
+ 00
■А'=ф
d Е e~i*
= i , (26.4)
1 2тг E — H + iO
где знак бесконечно малой мнимой добавки в знаменателе позволяет, во-пер-
вых, замкнуть контур интегрирования в нижней полуплоскости, как это по¬
казано на рис. 31, поскольку
e-et->0, t->+oo, £-*+0,
и интеграл по полуокружности обращается в нуль, а во-вторых, формально
вычислить интеграл в теории вычетов с помощью формулы Коши по замкну¬
тому контуру с ориентацией по часовой стрелке:
d Е—=
Е-Н+Ю
При £-* — оо контур замыкается в верхней полуплоскости, и интегрирование
по контуру, не содержащему полюсов, дает нуль.
Оператор
Ge = г (26.5)
ь Е-Н+Ю
Рис. 31. Контур интегрирования в плоскости комплексной энергии Е
Лекция 26
393
называют резольвентой. Очевидно, что резольвента удовлетворяет оператор¬
ному уравнению
(E-H)Ge = 1, (26.6)
и матричный элемент этого уравнения в координатном пространстве (г| • |г')
легко вычислить, если ввести обозначение для функции Грина
£?я(г, г7) = (r\GE\r') (26.7)
и учесть тождество
(r|l|r7) = S(r-r7),
так что
(Е -НгШг, г') = б(г- г7). (26.8)
Таким образом, мы пришли к уравнению для функции Грина стационарного
уравнения Шрёдингера.
Матричный элемент оператора эволюции дает запаздывающую функцию
Грина
+ 00
a(t", г; е, r') = -j:{r\U(t", t')\r') = J Це4^"-^я(Г, г'), (26.9)
— 00
*// */
которая обращается в нуль при t" — t'< 0. Вводя ступенчатую функцию Хеви¬
сайда, запишем
(t" - t7)(r|[/(t", г; t', г7). (26.10)
Разрыв функции Хевисайда при нулевом значении аргумента существенно
влияет на то, какому уравнению удовлетворяет запаздывающая функция
Грина. Дифференцирование по времени дает
+ 00
ifi£a(t, г; t', г') = J* ^е-^-[,\Й+Е-Н)дЕ(г, г') =
— 00
+ 00
=HQ(t, г; t', rO + J* е~»Е(с~с )5(г — г') =HS(t, г; t', г') + 5(t- ^)5(г-г0.
К этому же результату придем, если будем дифференцировать рассматривае¬
мый оператор #(t77 — tOl/ft", О с учетом уравнения для оператора эволюции
и начальных данных к нему U (t7, t7) = 1, а также принимая во внимание свой¬
ство тэта-функции Хевисайда d^(x)/dx = 5(x) и затем возьмем матричный
элемент полученного операторного равенства. В итоге используя компакт¬
ные обозначения х= (t,r) = (t, jc) , принятые в пространстве Минковского,
находим
ih-ЦгвОс; х') -нд(х; х') = S(4)(х -х'). (26.11)
01
394
Тема 16. Рассеяние
Запаздывающая функция Грина уравнения Шрёдингера позволяет нахо¬
дить волновую функцию состояния в произвольный момент времени t > t
так как она дает координатное представление для оператора эволюции:
%p(x) = ih J d3x'g(x; x'Wx'). (26.12)
Значит, элементы У-матрицы выражаются через матричные элементы
функции Грина по асимптотическим состояниям:
Уп = Л lim J dV d3x" г/>*(0) (*")£(*"; x'^^ix'). (26.13)
Г—*—00
t"—> + 00
Если известны точные решения стационарного уравнения Шрёдингера,
(г) =Еп'фп(г),
образующие базис в гильбертовом пространстве, то, естественно, в силу
полноты базиса1
2>|п> <пИ = 2= ■6(1*-;г'),
п п
легко найти и формулу для функции Грина <ЭЕ. В самом деле,
GE(.r,r'') = Yt(r\GE\n)(n\r'),
П
и так как
GE\n) = г 1 п) = -=—J1 .Jn),
ь Е-Н+ iO £-£n + i0'
получаем
п г /-, V ГЪС.ЛЛ\
0в(г,г) = 2, E_E +i0- (26.14)
П
Отсюда методом вычетов находим для запаздывающей функции Грина
вСх"; х') = ~^(t"-1') Yt (26.15)
Tl
где #0) — ступенчатая тэта-функция Хевисайда.
Однако, как известно, точные решения удается найти редко. Поэтому
приходится использовать приближенные методы расчетов. Для этих целей
исследуем функцию Грина свободной частицы, решение уравнения Шрёдин¬
гера для которой хорошо известно.
26.3. Функция Грина свободной частицы
Базис стационарных состояний свободной нерелятивистской частицы с
гамильтонианом Н(0)
(r\k) =eikr
1Для простоты записи проводим суммирование по квантовым числам, среди которых могут
быть и непрерывные спектральные параметры.
Лекция 26
395
позволяет вычислить функцию Грина G®\r, г') по общей формуле, так что
d3fc
где
E(k) =
(2я)3 Е —E(fc) + iO’
h2k2
2m
Интегрирование по углам выполняется элементарно
2 п +1
J d<^ / d cos 0elfcp cos e = jj~{elkp ~ e
где p = |r — r'l. Далее,
,,r/)_ 4я2р J
fcdfc
lm
I
dfc
Jpy/k*
k2-k2-i09
L£-E(k) + Ю 4я2П2р
о с
где kg=2mE/h2, а интеграл берется по верхнему и нижнему «берегам» разре¬
за в плоскости комплексной переменной к2, как это показано на рис. 32. При
этом у/к2 принимает положительные значения на верхнем берегу разреза
и отрицательные на нижнем. Контур интегрирования может быть замкнут
по окружности на бесконечности, поскольку комплексная фаза квадратного
корня на этой окружности имеет положительную чисто мнимую часть, так
что экспонента обращается в нуль.
Рис. 32. Особенности подынтегрального выражения для функции Грина сво¬
бодной нерелятивистской частицы в плоскости комплексной переменной
к2 = к2 и контур интегрирования
Тогда по формуле Коши для вычетов находим для функции Грина выраже¬
ние
r(°v_ „Л _ т eifcE|r~r'1
$е (г>г) 2nh2 Ir-r'l ' (26.16)
Отметим, что функция Грина свободной нерелятивистской частицы обладает
трансляционной инвариантностью: она зависит только от разности векторов
г —г' = р.
396
Тема 16. Рассеяние
26.4. Интегральное уравнение
Реперное уравнение для резольвенты свободной частицы
1 = G® (Е - Н(0)) = G® (Е - Я + У) (26.17)
позволяет установить тождество для функции Грина стационарного уравне¬
ния Шрёдингера с гамильтонианом Я:
Ge = 1-Ge = G® ев ■- Я+ V)Ge = G® (1 + VGjj),
т. е.
GE = G<0)+G<0)VGE, (26.18)
а значит, в координатном представлении это уравнение является интеграль¬
ным:
вЕ(Г, г')=дс°\г-г') + f ejPCr-rOVWSjiCri, rO d3r2. (26.19)
Очевидно, что это уравнение для функции Грина можно решать методом
итераций, т. е. находить решение с любой точностью по степени потенциала.
Такой подход эффективен, если ряд последовательных приближений быстро
сходится, и этот метод лежит в основе теории возмущений.
Аналогичную процедуру можно провести и для запаздывающей функции
Грина, если ввести состояния \х), нормированные согласно
<jc|jcO = 5е45 (л: — л:').
Тогда
G = G(0) + G(0) VG, (26.20)
и в интегральном виде1
в(.х, х') = д(0)(х-х') + / д(0) (х - х1)У(ха)5(х1; х') d4xx. (26.21)
Запаздывающая функция Грина переводит начальное состояние в состоя¬
ние в момент времени t > t', так что
ip{0) (х) = ift / дсо)(х - x')i/\(0) (хО d3x',
а также
■фЮ (х) = iAf д(Хг (х') d3x/5 (26.22)
где, как следует из определения функции Грина, гр.+)(х) — решение уравне-
ния Шрёдингера при t > tf.
*В отличие от выражения в виде «Т-экспоненты» для оператора эволюции, в случае по¬
тенциала, зависящего от времени, метод функций Грина приводит к обычным интегральным
выражениям. Однако сложности с упорядочиванием по времени проявляют себя и здесь при рас¬
четах петлевых квантовых поправок: возникающие интегралы могут содержать расходимости,
методам устранения которых посвящена теория перенормировок, выходящая за рамки данного
курса.
Лекция 26
397
Используя пару последних уравнений и интегральное уравнение для за¬
паздывающей функции Грина, легко находим интегральное уравнение для
запаздывающей волновой функции
■ф{+)(х) =1р\0)(х:) + / g^ix-xjvixjxpl^ixj dV (26.23)
В стационарном случае, во-первых, потенциал не зависит от времени:
V(x) = У(л:), а во-вторых, начальное асимптотическое состояние с энергией
Е{ дает стационарное решение уравнения Шрёдингера с той же энергией:
V,(+)(x)=e-«B'tyi+)(*). (26.24)
Поэтому интегральное уравнение сводится к виду
е-№-ф[+\х) = е-*£'Ч/>[0)(*) + J х
х J gj® Cx-x1)V(x1)^+4x1)d3x1,
или после сокращения временных факторов
■ф{+) (X) = V>[0) С*) + J gf (х - Xl)V(Xl)ip{+) (*j) d3xb (26.25)
Это — интегральное уравнение1 для стационарной волновой функции в за¬
даче рассеяния. Физический смысл этого уравнения становится ясным, если
записать стационарное уравнение Шрёдингера для хр[+\х):
СЕ - Н(0))г/>[+) (х) = V(x)xp{+) (ж), (26.26)
которое, естественно, следует из интегрального уравнения. Поэтому правую
часть можно рассматривать в качестве источника в уравнении Шрёдингера
(Е-Н(0)Ж*)=Дх),
общее решение которого представляется в виде суммы решения для однород¬
ного уравнения без источников, т. е. гр[°\х)} и частного решения
/ е£0)(х-*!);(*!) d3Xj.
Тогда подстановка в это соотношение источника j (дс) = V (дс)я(дс) приводит
к интегральному уравнению для стационарной волновой функции.
26.5. Асимптотическое поведение на больших расстояниях
и формула для сечения
Интегральное уравнение
1р{+) (г) = V\(0)(Г) + J Qf>(г - r')V(r')^l+)(rO dV (26.25)
Сравнение Липпмана—Швингера.
398
Тема 16. Рассеяние
позволяет установить асимптотическое поведение волновой функции в зада¬
че рассеяния при г-* оо. Оставляя вклад падающей волны1 (г), исследуем
интегральный член. При г —»оо и ограниченном г' < а функция Грина свобод¬
ной частицы ведет себя как
г(0)Гггл_ ТП eill*|r-r'1 m е^г~п^ п_г 9Г1
GB (г, г)- 2п%2 [г _ “ 2nh2 г ’ п г' (26,27)
Поэтому для потенциалов ограниченного радиуса действия или достаточно
быстро убывающих с ростом расстояния асимптотическое поведение волно¬
вой функции можно представить в виде
я/,[+Чг)^[°Чг) + ^/(0), г > оо, (26.28)
где
/(0) = -^/dVe-^VfrO^+V). (26.29)
Здесь в силу сохранения энергии2 кЕ = к{, и кЕ = пкЕ. Поскольку скалярная
величина / зависит от двух векторов3 к{икЕ, она может определяться только
скалярными величинами: квадратами векторов и их скалярным произве¬
дением кх кЕ = fc? cos 0, а значит, / является функцией угла между этими
векторами, как мы и записали выше.
Если фиксировать нормировку падающей волны, как мы ее определили
при постановке задачи рассеяния, то асимптотический вид волновой функ¬
ции—
,/,[+>(r)~eik‘r + ^/(e), г^~.
Величину /(б) часто называют амплитудой рассеяния. Ее можно записать
согласно (26.29) в виде
/(0) = ~^2 I dV (rOVfrO$+) (rO, (26.29)
где свободная волна
гр®~> (г') =e~ik£'r'.
Поток начальной волны t/>[0)(r), как известно,
ji = ~K
J\ m X
1Точнее было бы говорить не о падающей волне, а о волне, прошедшей без рассеяния: если
потенциал выключить, то эта волна отвечает точному решению уравнения Шрёдингера, при
наличии же потенциала интегральный член соответствует рассеянию, причем в силу сохранения
вероятности (нормировки состояния) в члене с рассеянием с необходимостью присутствует
волна, рассеянная вперед (с тем же импульсом, что и в начальном состоянии), которая ин¬
терферирует с исходной волной, уменьшая ее вклад в нормировку ровно настолько, с какой
вероятностью происходит рассеяние. О точном математическом выражении этого факта —
оптической теореме — речь пойдет ниже.
2Потенциал на бесконечности обращается в нуль, так что полная энергия определяется
кинетической энергией.
3Если потенциал не является центрально-симметричным, как, например, в случае потенци¬
ала в постоянном электрическом поле У (г) = -е(г • <£), интеграл зависит от трех векторов.
Лекция 26
399
Для расчета потока вероятности
вычислим в асимптотической области г —> оо градиент вклада рассеяния.
В полярных коордианатах
v=ere?+ee7h+ev Г sine at •
Поэтому при г —> оо угловые компоненты малы как 0(1 /г2), и вклад дает
только компонента вдоль радиус-вектора ег = п:
«ikir
V^-/(0) и ^^/(0)п= ifcE^-/(0).
Следовательно, поток вероятности рассеяния
Jout = ^fcB^l/C0)l2 (26.30)
зависит от угла рассеяния б и является симметричным по полярному углу
ф (в случае сферически симметричного потенциала). В асимптотической
области в малом телесном угле этот поток можно аппроксимировать плоской
волной с волновым вектором fcf = и нормировкой, которая определяет
вероятность рассеяния. В самом деле, за счет потока вероятности через пло¬
щадь на сфере радиуса г в телесном угле d£2
ds = n • г2 dfi
вероятность рассеяния в единицу времени составляет
dw=j0M-ds = %lki\fm2 dn. (26.31)
Следовательно, дифференциальное сечение рассеяния1
dcr = —7— = |/(0) |2 dfi. (26.32)
J i
В итоге мы вывели формулу для дифференциального сечения в терминах
амплитуды рассеяния /(0).
26.6. «^-МАТРИЦА, УНИТАРНОСТЬ И ОПТИЧЕСКАЯ ТЕОРЕМА
Матричный элемент У -матрицы
Уп= lim М®Ю№{+)(0>
Г—>+оо I
1Для волн де Бройля мы фиксировали нормировку (k\kf) = (2я)350е —fc'), которая отвечает
норме состояния (27036(fc)|fc_*0=V, где V —объем пространства. При нормировке состояния на
единицу |fc) •-> \к)/ Vv плотность потока имеет привычную размерность: j>-+j/V=hk/mV — ско¬
рость, деленная на объем, т. е. вероятность на единицу площади в единицу времени. Очевидно,
что тот же фактор необходимо ввести и для рассеянной волны (она получается в ходе эволюции
падающей волны), так что выражение для сечения не изменится.
400
Тема 16. Рассеяние
можно вычислить, подставив выражение для |т/>[+) (t)) согласно интегрально¬
му уравнению. Тогда
= (<} IV\(0)) + J (0) MS(0) (X - хх) V(Xj)V»i(+) (Ха) d4*! d3x. (26.33)
Здесь, во-первых,
=e-i®‘-B»)t(fcf|fc1> = (2я)35(к, — fcj).
Во-вторых, при t > tj
ift J ^ООЛх-х,) d3x=J (fcf|fc)^3(fc|xi>eH(E'-£)t+HEtl=^;(0)Ua).
Это есть функциональное выражение тождества для унитарного оператора
эволюции
l7(t,t/)[/(t/,t) = l => l/(t,t') = t/t(t/,t),
которое означает, что этот оператор описывает также и эволюцию назад
по времени. Поэтому интегральный член в матричном элементе Sfy (26.33)
записывается в виде
/ a/)*(0)(x1)V'(x1)a/)[+)Ui)d4xa.
Однако в стационарном случае потенциал не зависит от времени, а волновая
функция (х) является решением стационарного уравнения Шрёдингера
с энергией начального асимптотического состояния Еи так что интегрирова¬
ние по легко выполняется
J dt: e^E'~E,)t = 2nH5(Ef — Et).
В итоге матричный элемент имеет вид
5^ = (2тг)35(kf — fc;) — i2n5(Ef — E{) J xp*(0)(r)V(.r)^[+\r) d3r. (26.34)
В этом выражении первый член отвечает вкладу за счет падающей на ми¬
шень волны в задаче рассеяния
(2п)35(к^ — fcj) = (fc, |к(),
а второй можно записать через амплитуду рассеяния /(0) согласно ее опре¬
делению (26.29):
j xpf0)(r)V(r)xp[+\r) d3r = J d3r e_ifci'rV(r)'0[+)(r) = (0).
Важно подчеркнуть, что интегральное представление для волновой функции
и матричного элемента позволило нам доказать сделанное при постановке
задачи рассеяния утверждение, что амплитуда перехода пропорциональна
дельта-функции от разности энергий начального и конечного асимптотиче¬
ского состояний, так что ее квадрат определяет вероятность перехода в еди¬
ницу времени.
Лекция 26
401
Поскольку У -матрица есть предельное значение оператора эволюции при
бесконечном времени эволюции, она, как частный случай оператора эволю¬
ции, унитарного в любой момент времени, также является унитарной
5'5't = l. (26.35)
Обычно вводят понятие ^-матрицы рассеяния, чтобы исключить тривиаль¬
ный вклад падающих на мишень волн из У -матрицы
У = 1-&. (26.36)
Унитарность «^-матрицы приводит к соотношению
откуда следует операторное тождество — соотношение унитарности для &-
матрицы
STST^ = -2П Im ST. (26.37)
В стационарном случае
= (fcflfci) - = (fcflfci)" ^2пП5(Щ-Е,Щт{+)),
ИЛИ
= (kf \P\kJ = -2 Яйб(£, -£,)^/(0). (26.38)
Если взять диагональный матричный элемент соотношения унитарности
для ^-матрицы
(fci|^t|fci) = -2RIm(fci|^|fci),
то в правой части будет стоять величина
-2ft = 2nh5(E)\E^o^f Im /(0),
где /(0) — амплитуда упругого рассеяния вперед, и, как обычно, формально
2nh5(E)\E_>0 = Г-»оо — время наблюдения за частицей при рассеянии. Для
левой части тождества унитарности «^-матрицы запишем1
Г d3k С d3k
(fci|^t|fci) = J (fci|^|fcf>^3<fcfl^t|fci)=J
Заметим, что вероятность рассеяния в единицу времени—
иа2 d3fcf i^fii2 d3fcf
fi T (2n)3 h2T (2л)3’
1Вообще говоря, необходимо «вставить единицу» как сумму проекторов на базисные состо-
яния в асимптотическом пространстве. Если имеются только упругие столкновения, то это —
сумма по волнам де Бройля для рассеянной частицы, как мы это записываем ниже. Но формула
остается справедливой и для столкновений с образованием других частиц: пространство асимп¬
тотических состояний необходимо расширить, включая все возможные конечные состояния,
так что наличие неупругих столкновений не вносит изменений в вывод связи полного сечения
с амплитудой упругого рассеяния вперед.
402
Тема 16. Рассеяние
а полное сечение рассеяния1 —
a = I-f dWfi=Tft2j4 J (2я)3'^^2,
В итоге время наблюдения Г в равенстве сокращается, и унитарность приво¬
дит к тождеству
Й2Л(Т = Im / (0),
так что с учетом ]{ = Нк{/т окончательно находим
ст = ^1т/(0). (26.39)
Это тождество составляет содержание оптической теоремы, или соотноше¬
ния Бора—Пайерлса—Плачена, связывающего полное сечение рассеяния с
мнимой частью амплитуды упругого рассеяния вперед.
Наконец, введем стационарную ^-матрицу
ST = 2nh5(Ef - Е0&е. (26.40)
Тогда интегральное уравнение для состояния
l^r)> = IV>r)) + Gi0V|a/,[+))
позволяет установить для матричного элемента ЗГЕ
(fcf|^|fci) = (fcf|V|^[+))
следующее равенство
= (kflvlkj + (fcj|VGg°^V|i/)[+)> =
= (fcflVlfcJ + J <fcf|VGf |fc)^ <fc|V|^[+)) =
= (fcflVlfct) + J <fc,|VGf Ifc)^ mifcj.
Это интегральное уравнение можно записать в операторной форме
STE = V+VGf &Е, (26.41)
что позволяет строить итерационный ряд, сходящийся в теории возмущений
по малому потенциалу2.
1 Дифференциальное сечение da = dw^/j{ после подстановки матричного элемента ^ со¬
гласно (26.38) и d3kf = km d£2 dE^/h2, конечно, сводится к стандартному виду dcr = |/(0)|2 dn.
2 Обычно потенциал записывают в виде V —> XV, где Я — константа связи взаимодействия,
которую считают малой: Я —► 0.
Лекция 26
403
26.7. Борновское приближение
В ведущем приближении итераций в уравнении для ЗГЕ-матрицы или, что
то же, в интегральном уравнении для волновой функции рассеяния
&E*V, (fcjl^lfct) «(*£,№), (26.42)
так что
(fcf|V|fci> = / d3r V(r)e~i(k>~kl)'r = V(kf — k{),
где V есть не что иное, как фурье-образ потенциала, зависящий от передан¬
ного импульса q=h(kf — kj. В итоге амплитуда рассеяния
/(0)*-^V(fcf-fci). (26.43)
Это приближение называется борновским.
Критерий применимости борновского приближения включает в себя два
аспекта. Поскольку итерации в исследуемых интегральных уравнениях пред¬
ставляют собой разложение решения в ряд по теории возмущений, где в ка¬
честве такого возмущения выступает потенциал, степень сходимости ряда
можно оценить, во-первых, по малости самой борновской поправки к волно¬
вой функции свободной частицы, а во-вторых, по относительной величине
поправок высших порядков по возмущению к волновой функции или к сече¬
нию рассеяния.
На практике обычно ограничиваются первым условием:
№[+) (х) - V»,® (*) I < №,(0) (*) I, (26.44)
а значит, согласно интегральному уравнению
|i/»[+)(x)-я/>[0)(х)| = |/ Qe)^x-x1)V(.x1)%PI+\x1') d3*!|яа
«|/ Sf (x - xJVixJipf Qcj) d3xa | < 1. (26.45)
Указанное ограничение должно иметь место при любых х.
В качестве грубой оценки интеграла сверху можно взять интеграл от
модулей сомножителей:
|/ a£0)(x-x1)y(xa)i/>®)(x1)d3>r1|^ / |^0)(х- хг) 11 У(хг) ||a/i[0)(дсх) | d3*!.
Тогда для потенциала, отличного от нуля в ограниченной области г <а,
с характерным масштабом энергии |V(r)| ~У0, из
^(x-xOlw^i \^°\Xl)\ = l
находим
^a2< 1. (26.46)
Если ввести обозначение А0 для характерной длины волны частицы с энер¬
гией V0:
v»=£l- <26-47)
404
Тема 16. Рассеяние
то условие применимости борновского приближения принимает вид
з£<1. (26.48)
Это означает, например, что в случае притягивающего потенциала частица
с длиной волны Л0 не помещается в яме размером а, т. е. в яме нет связанных
состояний. В этом же приближении амплитуда рассеяния
с т ,, 4тг _з а2
f o—*s2 VO о а ^ о 2 *
и полное сечение
2rt?v°Tu
ст~4я|/|2«*47га2^4.
Величину
^geom 4яа
обычно называют геометрическим сечением. Поэтому условие применимо¬
сти борновского приближения еще записывают в виде
<7<°-geom> (26.49)
т. е. рассчитанное в борновском приближении полное сечение должно быть
существенно меньше геометрического сечения1.
Полученные ограничения на применимость приближения Борна можно
ослабить, если рассмотреть различные кинематические условия рассеяния.
Медленные частицы (kr~fca< 1). В этом случае экспоненциальные
множители в функции Грина и в падающей волне можно заменить едини¬
цами
eikr &е'каъ1.
Но это, по сути, повторяет общие рассуждения, приведенные выше, где был
взят модуль этих экспоненциальных факторов, также равный единице, так
что ограничение на величину потенциала остается прежним.
Быстрые частицы (kr~fca> 1). Функция Грина при |г -г'| «а
а волна де Бройля
^С°) _ giкг' cos в' ^ gifca cos в'
быстро осциллирует как функция от г' ~ а и зануляет интеграл везде, кроме
узкой области по углам:
gifcacosO'^ |COS0/|<^<1.
*На самом деле ограничение на применение борновского приближения в форме (26.48)
является более строгим, так как малым параметром в нем является не площадь сг в относитель¬
ных единицах, а линейный размер л/а~а2/Лц. Однако если считать, что достаточное условие
применимости борновского приближения дается малостью вероятности рассеяния, а не его
амплитуды, то форму (26.49) следует признать более реалистической.
Лекция 27
405
Ограничивая область интегрирования по телесному углу этим конусом, легко
находим критерий применимости борновского приближения для быстрых
частиц
^а2^<1 ФФ j^Cka, (26.50)
что, конечно, значительно слабее условия для медленных частиц.
Лекция 27
Движение частицы в сферических координатах в области с нулевым по¬
тенциалом, рекуррентные соотношения для радиальных волновых функций
с различными I, асимптотическое поведение при г —> оо, сферические волны
свободной частицы, сохранение потока вероятности на бесконечности при
упругом рассеянии и фазовые сдвиги, разложение волны де Бройля по пар¬
циальным волнам, парциальные амплитуды рассеяния и их связь с фазовыми
сдвигами, парциальные сечения и оптическая теорема, интегральное пред¬
ставление для парциальных амплитуд, борновское приближение для сдвига
фаз, зависимость фаз рассеяния от энергии, постоянное сечение для медлен¬
ных частиц, длина рассеяния, вклад парциальных волн для быстрых частиц,
свойства симметрии по перестановкам для тождественных частиц с четным
и нечетным спином при потенциальном рассеянии и выражение для сечения,
роль обменных сил, качественные замечания о дальнодействующих силах ку-
лоновского типа: искажение асимптотических состояний; о резонансе в Z-ка-
нале: диаграмма Аргана, брейт-вигнеровское сечение, особенности функции
Грина при наличии резонанса; о неупругих столкновениях: полное сечение
неупругих каналов и оптическая теорема для полного сечения рассеяния.
В центральном поле сохраняется вектор орбитального момента. Поэтому,
наряду с волнами де Бройля с заданным волновым вектором, асимптотиче¬
ские состояния в задаче рассеяния можно разлагать по базису сферических
волн: состояниям с определенными значениями орбитального момента I
и его проекции m на заданную ось. Такой подход называют парциально-вол-
новым анализом.
27.1. Сферические волны свободной частицы
В области, где потенциалом можно пренебречь или он равен нулю, урав-
^21^2
нение для стационарного состояния с энергией Е(к) = и заданным зна¬
чением орбитального момента I и его проекции т
гр(г) =Rfc;(r)^im(0, ip)
имеет вид
+ f*и(г) + (к2 - ^±±2)йи(г) = 0, (27.1)
406
Тема 16. Рассеяние
т. е. является уравнением для свободной частицы, которое мы и исследуем
более детально в этом параграфе.
Согласно общему свойству радиального уравнения при г —> 0
Rki(r)~rl,
так что проведем замену функции
Rki(.r) = rlXki(.r). (27.2)
Тогда элементарное дифференцирование
KiW = г1Хы+1г1-'хкь R,;i(r) = rlx''l+2lrl-1x/kl + ia -1 )rl~2Xki
после приведения подобных членов приводит к уравнению
^ + ^a + l)4, + fc2^ = 0. (27.3)
Введем
Хк1(.г)=”к№> z = r2.
Тогда
Хы = 2rvki> *w = 44i + 2l/w>
где штрих у функции от z означает дифференцирование по z: i/ = dz//dz.
Уравнение для vkl(r2) примет вид
4zv"t + 2(2 Z + 3)v'kl + k2vkl = 0. (27.4)
Дифференцирование этого уравнения по z дает
4si/"' + 2(2(Z +1) + 3)v" + = 0.
Это уравнение тождественно удовлетворяется, если vfkl является решением
уравнения для Ущ+Г), т. е.
^fcd+D(z) = Bv'M(z) => Xk(.i+1)(г) = §:Хн^-
Положим В = 2 и запишем выведенные нами рекуррентные соотношения
для радиальных волновых функций с различными значениями орбитального
момента в виде
ЫП=С1^(}±)1Яко(г). (27.5)
Здесь Rk0 (г) — решение радиального уравнения для 1 = 0, фактор к~1 введен
для удобства, а сх—нормировочные постоянные. Для Rk0(r) =u(r)/г стандарт¬
но имеем
и!1 + к2и = 0, (27.6)
откуда ясно, что функция и (г) представима в виде суперпозиции двух неза¬
висимых решений
и = с0{—e~ifcr+S0eifcr}, (27.7)
Лекция 27
407
или
Kfco(r) = |{-e-ifcr + S0eifcr},
(27.8)
где S0 — константа относительной нормировки расходящейся части волны.
Полагая с0 = 1, находим общее точное выражение для волновой функции
в области, где центральный потенциал обращается в нуль, и в частности,
в асимптотической области г—► оо,
При г —»оо ведущий вклад получается дифференцированием экспонент, так
что
Rki(r)^cij{(-l)l+1e-ikr+Sleikr} = cl^-{-e~i(kr-2l) +Slei(kr~21)}. (27.10)
Если потенциал тождественно равен нулю, то уравнение справедливо во
всем пространстве, и приведенное общее выражение необходимо ограни¬
чить на случай свободной частицы: волновая функция должна вести себя
как г1 при г—>0. Экспоненты в радиальной функции общего вида (27.9)
можно разложить в сумму синуса и косинуса от кг, из разложения которых
в ряд Тейлора сразу следует, что вклад косинуса необходимо занулить, так как
он приводит к члену 1 /г, дифференцирование которого дает сингулярность
при г = 0. Напротив, для вклада синуса получим
так что радиальная волновая функция имеет правильное поведение в нуле.
Итак, для отсутствия сингулярности в нуле необходимо, чтобы для свободной
частицы1
Для центрального потенциала, достаточно быстро обращающегося в нуль
на бесконечности, радиальная волновая функция общего вида (27.9) в задаче
рассеяния описывает в асимптотической области суперпозицию падающей
Различные выборы постоянных S[ определяют радиальные функции, которые отвечают
(27.9)
1 d У (kr)2l+1
г dr) r(2Z + l)! r_0
_r ylk2l+1 (20!!
^ A.J /Ч. Г07_Ь-П1 J
(21 + 1)!
(27.11)
и тогда2
(27.12)
что в асимптотической области г —> оо дает
(27.13)
сферическим функциям Бесселя j[ (кг) (Rk0 ~ функциям Неймана щ (кг) (Rk0 ~
gXl/CT
функциям Ганкеля к^(кг) (Rk0 ~
2Мы сделали подстановку с/ —»с[°^(—1)*.
408
Тема 16. Рассеяние
на мишень и рассеянной волн со сферическим фронтом (27.10). В силу уни¬
тарности падающий и рассеянный потоки равны друг другу для упругого
рассеяния, т. е.
|S(| = 1, S; = е2'5', S,€R, (27.14)
где 5г — фазовые сдвиги, зависящие от потенциала, энергии и орбитального
момента. По построению
5te[ 0,тг]. (27.15)
Значит, при г —»оо волновая функция в разложении по парциальным волнам
имеет вид
RH(r)~c®i{-e-i(fcr-?0 +S/ei(fcr-iO} = ci(0)yei5' sin(fcr- fi + S;). (27.16)
Подчеркнем, что в этой формуле коэффициенты с[0) те же, что и в разложении
по парциальным волнам волновой функции свободной частицы, так как
в задаче рассеяния падающая волна в стационарном out-состоянии должна
тождественно совпадать с падающей волной свободного in-состояния.
Итак, мы установили, что в случае исключительно упругих столкновений
процесс рассеяния описывается парциальными фазовыми сдвигами, и опре¬
делили асимптотический вид волновой функции в задаче рассеяния. Теперь
для расчета сечения необходимо отнормировать парциальные потоки так,
чтобы они отвечали потокам падающей волны де Бройля, потому что в экс¬
перименте осуществляется только такая возможность, когда состояниями
асимптотического in-пространства являются именно свободные монохрома¬
тические волны, а для out-состояний возможен парциально-волновой анализ:
наблюдается разложение по орбиталям.
27.2. Разложение волны де Бройля по парциальным волнам
Разложим состояние |fc) с заданным волновым вектором к по базису сво¬
бодных сферических волн |fc; I, т) с энергией Е = h2k2/2m и орбитальным
моментом I с проекцией т в координатном пространстве:
(r\k) =]T](r|fc; I, т) (к; I, т\к). (27.17)
1,т
Обычно вводят единичные векторы
П=Г~, П*> = £.
г9 к
Тогда, очевидно, волна де Бройля
(r\k)=eikrnnm. (27.18)
Состояние {r\k; I, т) есть не что иное, как решение стационарного уравнения
Шрёдингера для свободной частицы в координатном представлении
{r\k; I, т) =Ки(гЖт(п),
Лекция 27
409
где ЩгГП(п)—сферическая гармоника, которая зависит от угловых координат
единичного радиус-вектора n, a (k; Z, т\к) —эрмитово сопряженное решение
стационарного уравнения Шрёдингера в импульсном представлении (пред¬
ставлении волнового вектора):
(к; Z,m|fc)=R*;(fc)^m(n№)).
Переопределим радиальную волновую функцию, поглощая фактор Rju(fc),
так что в согласии с общим рассмотрением свободных сферических волн
разложение примет вид
eifcrn.„<‘> =4я ^ К(0)(гщтСпщ*т(п(к))} (27.19)
1,т
где
ян М = с/С0)(-1)'i (f Ю' f{-e_ifcr + eifcr}, (27.12)
с неизвестными коэффициентами с[0), задачу определения которых мы сей¬
час решаем.
В волне скалярное произведение векторов п • n(fc) симметрично по пере¬
становке единичных векторов, в разложении же стоит произведение сфери¬
ческих гармоник ^>m(n)^*m(n(fc)), которое можно преобразовать, пользуясь
свойством комплексного сопряжения сферических функций
%n(n) = (-l)m^*_m(n),
откуда
®u(n)®cm(n№))=&;-т(п)Щ'_мк)ъ
и значит, суммирование по т в правой части разложения (27.19) дает резуль¬
тат, симметричный по перестановке единичных векторов, как это и должно
быть.
Вычислим коэффициенты разложения с[0) в случае, когда волновой вектор
направлен вдоль оси z, откуда п• = cos в, т. е. =0, и в разложе¬
нии участвуют только вклады с т = 0
^:т("°°) - 9Со(°’ о)=id)=
и
®im(n) - ^г,о(0, V) = У^Р((СОЗ 0).
Тогда разложение принимает вид
gifcrcose =^(2г + 1)рг(С08 6)R®(r). (27.20)
I
Из ортогональности полиномов Лежандра
г 2
J dcos в ' Р[/(COS 0)P;(COS Q) = 2/-I-1
410
Тема 16. Рассеяние
и принятого разложения следует, что
1
/ d cos 0 • Р, (cos 6)e'kr cos 6 = 2R^ (r). (27.21)
-1
Рассмотрим обе части этого равенства при г-» оо. Тогда слева интегрирова¬
ние по частям дает
1
J d cos в ■ Pi (cos 0)eifcrcose = t^P;(cos 0)eikra*e
+1
-1
1
- jjg: / d cos 0 -P/Ccos 0)eifcrcos0.
Очевидно, что интегрирование по частям следует повторить еще I — 1 раз, так
как полином Лежандра Рг является полиномом степени I. Однако в пределе
г —> оо каждый дополнительный шаг интегрирования по частям приводит
к вкладам (9(1/г2). Таким образом,
/ dcos0-P,(cos0)eifcrcos0 = T|;P;(cos0)eifcrcose (27.22)
По построению Рг( 1) = 1 и Pz(—1) = (—l)z, так что окончательно асимптотиче¬
ски получаем
/ d cos 0 • Рг(cos 0)eifcrcos е а eikr - (-1 Ye~ikr}. (27.23)
С другой стороны, асимптотическое поведение радиальной волновой функ¬
ции сферической волны было нами установлено в предыдущем параграфе:
Rj™(r) ~с\°\-1)1±{е1кг - (—1)ге-*г>.
Значит, из (27.21) находим
ci°) = i!2lfc- (2Z24)
Таким образом, разложение окончательно принимает вид1
eib-co.e=2(2l + 1)fl(Cos0)(-i)I5igTr(i|:)li{-e-,fcr + eU[r}
I
с асимптотикой при r—> оо
eifcrcos в ^(21 + l)P;(cos 0) 2^{eifcr - (—l),e-ifcr} =
I
= J](2Z + 1)P, (cos 0) i' • Sm^fcr~^ • (27-25)
1Обычно вводят безразмерную переменную р = кг, от которой только и зависит разложение
плоской волны по сферическим.
Лекция 27
411
27.3. Фазовые сдвиги и парциальные сечения
Стационарная волновая функция в задаче рассеяния имеет асимптотиче¬
ский вид
ifer
,/,[+>(,.)-e^' + ^/tf), fc = |fe.|
Выберем в качестве оси z направление волнового вектора начального состо¬
яния и разложим амплитуду рассеяния по базису полиномов Лежандра
m^mcosv. (27.26)
I
Асимптотическое разложение волновой функции по сферическим волнам
согласно общему рассмотрению имеет вид
*/>[+}(г) -^(2* + 1)Жсоз в) 2^{S,eifcr - C-l)le~ikr}. (27.27)
I
С другой стороны, разложение плоской волны свободной частицы и ампли¬
туды рассеяния по полиномам Лежандра дает
eifc‘r+^/(0) +1)p!(cos ш{ (r+w+i)eikr - C_1)!e_ifcr}-
Значит,
S' = 1 + I?T « (27.28)
Выражая S; через фазовые сдвиги
S, = e2i5',
легко находим
/i = ^ei5'sin5,. (27.29)
Дифференциальное сечение рассеяния по общей формуле
= fipi (cos Щ*р1' (cos 0) (27.30)
Ц'
имеет характерную зависимость от углов, которая и подвергается парциаль¬
но-волновому анализу при исследовании экспериментальных данных. В силу
ортогональности полиномов Лежандра полное сечение рассеяния—
=4я Z Ш+Т = F Е(2г+sin2 5'- (27-31)
г. /
Обычно вводят понятие парциального сечения
<т, = (2Z +1) sin2 5г, (27.32)
которое принимает максимальное значение при 5г = я/2. Отметим, что для
рассеяния вперед Pt (cos б = 1) = 1 и
т_ г 2Z 4-1
IHL Ji — —г— Sin О/,
412
Тема 16. Рассеяние
так что
т. е. оптическая теорема справедлива для каждого парциального сечения
упругого рассеяния в отдельности.
27.4. Свойства фазовых сдвигов
Согласно интегральному уравнению для амплитуды рассеяния
/(0) = - / dV e~i,t£rV(rOV\(+) (г7) (26.29)
несложно получить выражение и для фазы рассеяния, если воспользовать¬
ся разложением по парциальным волнам для волны де Бройля и точного
решения стационарного уравнения <0[+) (г) с подходящими граничными усло¬
виями. В самом деле,
е-ifcV = (gifc-ry = Я*®
1,т
где ^*m(n') = Ц*т(в', ip% Щ>т(п<-Ю) = Щ>т(в, <р), и
гр[+)(г') =^(2^ + DP/'(cos e')RkV(r'),
V
так что интегрирование по телесному углу в выражении для амплитуды
рассеяния (26.29) элементарно дает
J сКУ • i'(cos 00 = (I, т\1', 0) = 5ц,5т0.
Поэтому амплитуда выражается в виде ряда
/(0) = -§гЕ( 2Z + 1)P((COS0) J dr-r2R*[0)(r)V(r)Rfc,(r). (27.34)
Следуя определению, парциальные амплитуды запишем в виде:
/, = -|P(2Z + l) J dr-r2R*f}(r)V(r)R«(r). (27.35)
Функция R^^r) — решение одномерного радиального уравнения Шрёдинге¬
ра, комплексная фаза которого фиксирована асимптотическим условием
, sin (kr-^l)
R(0) frl ~ i* ^
nkl —1 £г
так же, как и фаза точного решения стационарного уравнения Шрёдингера
с потенциалом
:£. , sin (kr-^l + 5t)
Лекция 27
413
Поэтому можно перейти к вещественным волновым функциям Ф (г) в ради¬
альных уравнениях с заданными асимптотиками на бесконечности, так что
Л® (г) = i! • Ф® (г), Ли(г) = ei5' i' • Фи (г).
Тогда
fl = -^{2l + l)eiS> J ёгт2Ф™(г)У(г)Фы(г). (27.36)
Сравнивая последнее выражение с формулой для парциальной амплитуды
в терминах сдвига фазы (27.29), получаем интегральное представление для
фазы
sin5, = -^ / с1гт2Ф®(г)Пг)Фы(г). (27.37)
В борновском приближении, очевидно,
sinS^-^Jdr-{гФ® (r)}2V(r). (27.38)
Интегральное представление позволяет установить некоторые свойства сдви¬
гов фаз, причем, поскольку основные свойства радиальных волновых функ¬
ций для свободных волн и точного решения уравнения Шрёдингера с потен¬
циалом качественно по своему поведению вблизи нуля и периоду осцилля¬
ций практически совпадают, выводы о парциальных амплитудах, сделанные
на основе борновского приближения и точного интегрального представле¬
ния, мало отличаются друг от друга, за исключением важного случая резо¬
нансов.
Пусть потенциал имеет характерную величину |У| ~ У0, и он существенно
отличен от нуля только в области г < а. Как мы выяснили, вблизи нуля
поведение радиальной волновой функции1 определяется выражением:
(21 +1)! (2г + 1)2i+ie-2i-i ^2тг(2г + 1) ^ 21 J ^ 1 J
где мы воспользовались формулой Стирлинга для оценки факториалов2 и
опустили несущественные числовые множители. При этом удобно считать
для общности рассмотрения, что эти выражения остаются справедливыми
и при Z —> 0, если формально положить I1 —► const, в оправданности чего
можно убедиться, непосредственно подставив Rk0 ~ const. Значит, интеграл,
определяющий фазу, можно оценить как
/ dr-{^®(r)}2V(r)~^(f )2i+\
1Из этого выражения видно, что радиальная функция становится сравнимой с единицей при
kr^l. Ho R^i (г) ограничена по модулю величиной порядка единицы, и поэтому она получает
поправки, которые останавливают ее рост, так что функция становится убывающей и осцилли¬
рующей при kr^l. Это означает, что асимптотическое выражение для радиальной пси-функции
в парциальной волне при г —► °о становится справедливым при kr »I, что может быть важно,
если задача рассеяния решается приближенно для быстрых частиц ка »1: тогда можно считать,
что Rid ~ sin(fcr — + 5i)/(fcr) при г ^ а, если I < ка.
2Именно, п\ъппе~пл/2ппу л» 1.
414
Тема 16. Рассеяние
откуда
. с 2mV0 2^CLkЛ2l+1 . с 2тУ0 31
sm5z J и sm50~-^ax (27.39)
Из этих оценок заключаем, что рассеяние частиц с I» ка подавлено. Этот
факт согласуется с классическим рассмотрением, поскольку орбитальный
момент падающей на мишень частицы можно оценить как произведение
волнового вектора (импульса) на прицельное расстояние Ь, так что
l~kb^>ka => b»a,
т. е. прицельное расстояние много больше радиуса действия потенциала,
и рассеяния не происходит.
С другой стороны, малый вклад в сечение парциальных волн с I>fca
можно понять, исходя из относительного вклада центробежного потенциала
в энергию частицы при больших I 1:
ау;(г)= пч2
Е 2mEr2 'SJ\krJ
Значит, вклад орбитального момента в энергию радиального движения со¬
здает при r = a потенциальный барьер относительной высоты
I2
(ка)2
При I <С ка происходит надбарьерное рассеяние, и частица достигает потен¬
циала, отличного от нуля при г <а. При I» ка проницаемость высокого
и широкого барьера сильно подавлена, вероятность проникновения на рас¬
стояния г <а крайне мала, так что частица практически рассеивается так
же, как и в случае свободного движения: вклад области, где существенно
наличие потенциала, пренебрежимо мал, т. е. фазы рассеяния близки к нулю
(см. рис. 33).
Медленные частицы (ка С1). В этом случае доминирует рассеяние с I ^
^ ка < 1, т. е. с I = 0: 5-рассеяние. Амплитуда рассеяния не зависит от углов,
и при 50 ~ ка —> 0 единственная фаза, отличная от нуля, является веществен¬
ной:
/о = I sin60ei5°= —а0, (27.40)
где а0 — длина рассеяния1. Итак, для медленных частиц дифференциальное се¬
чение рассеяния является изотропным, а полное равно постоянной величине
сг=4тг |/о |2 |fc_0 = 4лйд, (27.41)
которая не зависит от энергии.
Задача 16.1. Найти сечение рассеяния медленных частиц на твердой сфере ради¬
уса а0.
1Длина рассеяния может быть и отрицательной, что очевидно, например, из выражения для
фазы рассеяния в борновском приближении: если потенциал притягивающий, то фаза заведомо
положительна.
Лекция 27
lT(r)+AVi(r)
415
Рис. 33. Потенциал радиального движения для I = 0 (нижняя кривая), I = 0,7/са
(средняя кривая) и I = 2ка (верхняя кривая)
Решение. Потенциал твердой сферы
>+оо, г^а0,
»{.*■
г>а0,
в области г < а0 непроницаем для частиц, т. е. на границе он создает бесконечно
большую силу отталкивания, так что С70 обращается в бесконечность при г < а0.
Значит, волновая функция тождественно равна нулю при г ^ а0. Для медленных
частиц существенным является вклад с I = 0, радиальная волновая функция которого
при г > а0, где потенциал равен нулю, известна:
, sin(fcr + 50) 7 2 2тЕ
кг ’ К ~ h2
По непрерывности волновой функции
Rko(r)
откуда
= 0 =» sin(fca0 + 50) = 0,
r=a0
50 = -ka0, f0*>Y = ~a°-
Эта аналогия с рассеянием на твердой сфере и послужила аргументом для того
определения длины рассеяния, которое мы дали выше. Сечение, очевидно, а = 4па2.
Исключение возникает в случае, если по каким-либо причинам длина
рассеяния обращается в нуль, например, при деструктивной интерференции
в интеграле для сдвига фазы, когда рассеяние происходит на потенциале,
в котором притяжение компенсируется отталкиванием. Тогда полное сече¬
ние определяется подавленными высшими парциальными волнами, и диф¬
ференциальное сечение перестает быть изотропным, а полное зависит от
энергии (например, сг1 ~Е2). Такое аномальное поведение сечения для мед¬
ленных частиц называется эффектом Рамзауэра.
416
Тема 16. Рассеяние
Задача 16.2. Найти сечение рассеяния медленных частиц на глубокой сфериче¬
ской яме радиуса а0.
Решение. Потенциал ямы
Г/(г)
J ~ио>
1°.
г^а0>
г>а0.
Решение уравнения Шрёдингера для радиальной волновой функции при I = 0 запи¬
шется в общем виде как
„ sin(fcur) , 2 _ 2т(Е + и0)
А~к~г> п2 ' r^a°
sin (fcr+5o) 2_2mE
kr ’ h2 ’ 0
где А, В — константы, которые можно определить исходя из условия непрерывности
волновой функции. Фазу вычислим из условия непрерывности логарифмической про¬
изводной радиальной функции
KfcoOO
г—ад—0 -Rfco(r)
г=ао+0
причем для медленных частиц ка0 < 1 дифференцирование при г = а0 + 0 дает
*и>00 cos« - sin(-)}.
а при г = a0 — 0 в глубокой яме fcua0 :>1
*£«,« ~ ки = ф{киГ C0SW ~ SinW>-
Тогда непрерывность логарифмической производной дает
к Г к 1
tg№a0 + 50) = — tg(fcua0) =» 50 = -ка0 + arctg tg(fcua0)J.
Если tg(kua0) —> ±°°, то вкладом fca0 —> 0 следует пренебречь и 5q —» ±тг/2, так что име¬
ет место резонанс: сечение рассеяния принимает максимально допустимое значение
для парциальной волны I = 0, и оно существенно больше геометрического значения:
(7 о = 4 я/k2 = 4тш2/ (7са0)2 » 4тга2.
В противном случае, когда tg(kua0) принимает конечные значения, в пределе
малых импульсов к —> 0 в яме fcu —> 2mU0/h, и фаза
5° Wfc{ Ь tg(fc°ao) " a°} = ^^Као) - fcua0>-
При условии
tg(k0ua0) = k°ua0 (27.42)
фаза 50, а значит, и длина рассеяния обращаются в нуль, т. е. имеет место эффект
Рамзауэра: сечение рассеяния определяется высшими парциальными волнами, так
что оно аномально мало зависит от энергии и от углов. При этом (27.42) совпадает
с условием появления в яме связанного состояния.
Быстрые частицы (fca» 1). Как мы уже выяснили, для быстрых частиц
вклад в полное сечение дают парциальные волны с
I ^ ka »1.
Лекция 27
417
При этом, поскольку максимальное значение парциального сечения, равное
сг™ах=4п(21 +1) /fc2, достигается при sin 5Z = 1, полное сечение не превышает
величину
ka
a < W S(2Z + 15 = Щ (fea + 1)2 * 4л°2 = а8еот’
1=0
т. е. оно ограничено геометрическим сечением, и этот предел достигается
в случае наличия резонанса в каждой парциальной волне.
Задача 16.3. Найти полное сечение рассеяния быстрых частиц на твердой сфере
радиуса а. При ка = 6п провести численный расчет для фаз рассеяния и парциальных
сечений, сравнить его с квазиклассическим приближением, численно найти диффе¬
ренциальное сечение при малых углах рассеяния.
Решение. Вклад частиц с !>fca в сечение рассеяния пренебрежимо мал. Для
частиц с I ^ ка, определяющих сечение, радиальные волновые функции при г > а в
нулевом приближении мало отличаются от своих асимптотических выражений, спра¬
ведливых при кг »I,
По непрерывности волновой функции
ЯиМ
откуда
Для вклада парциальной волны
sin2 5t -
Поэтому в полном сечении
5,«-fca + |z.
sin2 5; = |(1 —cos25() = |{l —(—1)! cos 2ка}.
fca»l
O’ = У] (2.1 + 1) sin2 5,
1=0
можно выделить два вклада: первый дает
fca> 1
fj £](2Z + l) = 27ra2,
fc2 ,=о
а второй
Jea» 1
-ffcos(2Jfca) J] (21 +«(“I)1
k2
l=o
можно легко оценить согласно разбиению на четные и нечетные Z:
J](2Z+ !)(-!)'= J] (4n + l)- J] (4n + 3) wn(2n +1) — n(2n + 3)
г=о n=о
и
= —fca,
n=^fca»l
fca» 1
-ffcos(2fca) ]T(2Z + lX-l)'«2rai2^g^,
1=0
cos (2 fca)
ka
<1,
418
Тема 16. Рассеяние
Рис. 34. Фазовые сдвиги в задаче рассеяния быстрых частиц с волновым
вектором ка = 6л »1 на твердой сфере: ломаная—квазиклассический расчет,
квадраты — точные значения
а значит, этот вклад подавлен по сравнению с первым, и им можно пренебречь.
В итоге сечение определяется геометрической величиной (точнее, половиной геомет¬
рического сечения)
сгъ2па2.
Расчеты можно сделать несколько точнее, если при записи радиальной волновой
функции от нулевого приближения перейти к квазиклассическому. Тогда при стан¬
дартной подстановке
*.00=^
функция ц(г) при г >а удовлетворяет радиальному уравнению Шрёдингера с потен¬
циальной энергией центробежных сил
и"_(У_Ш+1Г)и=0
и обращается в нуль на границе твердой сферы г = а, так что в квазиклассическом
приближении при 1(1 + 1)^ка
г
и (г) ъА1 sin <^(r) =А{ sin J dr ^к2 -
а
причем нас интересует поведение </?(г) при г—> оо. Заменой переменных
VW+1) .
г = ch z
к
интеграл под знаком синуса сводится к виду
<р(г) = у/Щ+Ъ f thzdchz=y/l(l + l) f{l + (thz — 1)}dchz,
где интегрирование no ch z идет в пределах [ка/y/l(l-Ы), кг/у/1(1 +1)], так что
ц>(г) = кг — ка+ у/1(1 +1) / dz thz(shs —chz).
Лекция 27
419
Рис. 35. Парциальные сечения в задаче рассеяния быстрых частиц с волновым
вектором ка = вп »1 на твердой сфере: ломаная—квазиклассический расчет,
квадраты—точные значения
Полагая у = ехр{—z}, находим при г —>»
У(г)
ф(г) = кг-ка+у/щ +1) J dy "-^"2 = fcr - fca + +1) (у + 2 arctg ^ ) j
y(a)
Via+u
так что
lim у (г) = +0,
(/?(г) = fcr - fca - я VZO + I) + >/l(l +1) (у(a) + 2 arctg ).
Значит, асимптотически при г —> оо находим
sin (кг — %l + 5i)
ДЫ(г)^А, V fcr2
причем
5, = ■-fca +1 a -20(1 + 1)) + 0(1 + 1) (у (a) + 2 arctg .
У(а)>
Если Z <fca, то возвращаемся к результату нулевого приближения б* = — fca+ ^Z,
в противном случае возникают поправки. При Z ^ ка »1 получаем у (a) ^ 1 и 5Z ^ 0, т. е.
фазовый сдвиг обращается в нуль, что и следовало ожидать из общих соображений.
Зависимость фазовых сдвигов от орбитального момента показана на рис. 34, где про¬
водится сравнение квазиклассического расчета с численными оценками, полученны¬
ми из уравнения Rkl (a)=0 для точных радиальных волновых функций при ка=вп »1.
Парциальные сечения в квазиклассическом приближении также достаточно точно
420
Тема 16. Рассеяние
Рис. 36. Интегральное парциальное сечение в задаче рассеяния быстрых
частиц с волновым вектором ка=6п »1 на твердой сфере: сплошная линия—
квазиклассический расчет, квадраты—точные значения, штриховая линия —
«сглаженное» нулевое приближение
воспроизводят довольно сложную зависимость от орбитального момента, получен¬
ную при точном численном расчете (рис. 35).
Чтобы сравнение квазиклассического приближения с точным расчетом стало еще
более наглядным, удобно ввести в рассмотрение интегральное сечение с орбиталь¬
ным моментом, меньшим или равным Z, посредством выражения:
i
O-mt(0=X]O'i-
1=0
Это сечение графически представлено на рис. 36, где показано также «сглаженное»
интегральное сечение нулевого приближения с парциальными сечениями, усреднен¬
ными согласно формуле:
(о-,) = \ (о-,-! + 2а, + а,+1) =
= §{\(21 + 1)-(-1)' cos(2ка)[-(21 -l) + 2(2Z + l)-(2Z + 3)]} = ||(2Z + l)i.
В итоге мы приходим к выводу, что при ка »1 «сглаженное» нулевое приближе¬
ние дает хорошую (но хуже, чем квазиклассика) аппроксимацию для интегрального
сечения.
Дифференциальное сечение, полученное в результате численных оценок, показа¬
но на рис. 37, из которого видно, что оно имеет характер дифракции на сферическом
препятствии.
Заметим, что изучение зависимости амплитуды рассеяния от энергии
составляет предмет специальных исследований, которые мы оставляем вне
рамок этих лекций.
Лекция 27
421
Рис. 37. Дифференциальное сечение рассеяния быстрых частиц с волновым
вектором ка = вп »1 на твердой сфере радиуса а: точный расчет—сплошная
линия, квазиклассика — штриховая линия
27.5. Рассеяние тождественных частиц
При потенциальном рассеянии друг на друге двух тождественных частиц
необходимо учесть перестановочную симметрию бозонного или фермионно-
го типа с учетом спиновой волновой функции. Если потенциал, например,
в ведущем приближении не зависит от спина, то спин каждой из частиц
сохраняется по отдельности и спиновая волновая функция факторизуется.
Разложим спиновую волновую функцию по состояниям с определенными
значениями полного спина двух тождественных частиц. При этом важно,
что при сложении двух спинов состояние с максимальным значением спина
Smax является симметричным по перестановке частиц: старший вектор по по¬
строению симметричен по перестановке; понижающий оператор S_ =s“ +sb_
также симметричен по перестановке, откуда сразу следует, что и векторы
состояния, полученные действием понижающего оператора на старший век¬
тор, имеют симметрию старшего вектора. Старший вектор состояния с пол¬
ным спином S = Smax — 1, на единицу меньшим максимального значения
полного спина, ортогонален состоянию с максимальным полным спином
и проекцией Smax — 1. Отсюда сразу следует, что старший вектор с S=Smax — 1
антисимметричен по перестановке частиц, так как из двух независимых
векторов состояний с проекцией Smax - 1 можно построить симметричный
и антисимметричный по перестановкам векторы состояний, которые, конеч¬
но, будут ортогональны, так как скалярное произведение — амплитуда веро¬
ятности — не зависит от перестановки тождественных частиц: «до переста¬
новки», равно «после перестановки» а • b = -а • Ь. Но симметричное состояние
относится к максимальному спину, значит, антисимметричное — состояние
с S = Smax — 1. Опять же все векторы состояния с этим суммарным спином
будут иметь симметрию старшего вектора, т. е. будут антисимметричны.
422
Тема 16. Рассеяние
Повторение этой процедуры1 приводит нас к важному выводу: спино¬
вые состояния с максимальным спином — симметричны по перестановкам,
а последующее уменьшение спина на единицу приводит к последователь¬
ному чередованию симметрийных свойств, т. е. спиновые состояния фер¬
мионов с нечетным спином симметричны по перестановкам, а состояния
с четным спином — антисимметричны. Поэтому пространственные части
волновых функций фермионов с нечетным спином должны быть антисим¬
метричны по перестановкам, а состояния с четным спином—симметричны.
Точно так же для бозонов: спиновые состояния с четным спином симметрич¬
ны по перестановкам, а состояния с нечетным спином —антисимметричны,
и пространственные части волновых функций с четным спином должны быть
симметричны по перестановкам, а состояния с нечетным спином—антисим¬
метричны. В итоге пространственные волновые функции для пары фермио¬
нов и для пары бозонов обладают одинаковыми свойствами по перестановке
частиц: пространственные волновые функции с четным спином должны быть
симметричны по перестановкам, а с нечетным спином—антисимметричны.
Согласно этому для четных и нечетных значений полного спина S асимп¬
тотическое поведение волновых функций в задаче рассеяния в системе цен¬
тра масс определяется выражением
i Jkr
1/>(+) (г) * eikr + (—l)se-ikr + ^{/(б) + (-1)S/(7T - 0)}, (27.43)
так как перестановка частиц в системе центра масс соответствует замене
г •-> —г, а значит, в »-> п — в. Дифференциальное сечение рассеяния дается
выражением
dCT = |/(0) + (-l)s/(7t-0)|2dn, (27.44)
потому что падающий поток остается прежним. Важно подчеркнуть, что для
тождественных частиц в сечении возникает интерференция за счет обменно¬
го взаимодействия.
Мы записали дифференциальное сечение в случае с заданным значением
суммарного спина двух тождественных частиц в начальном состоянии для
потенциала, не зависящего от спина. Если же начальное спиновое состоя¬
ние не фиксировано, то каждая проекция спина на некоторую ось является
равновероятной. Например, для фермионов со спином 1/2 имеется 4 конфи¬
гурации проекций: 2 • 2, если рассматривать произведение спиновых проек¬
ций для каждого фермиона. С другой стороны, суммарный спин принимает
значения S=1 и 5 = 0 с числом проекций 2S +1, т. е. 3 и 1 соответствен¬
но. Поскольку каждая проекция равновероятна, дифференциальное сечение
с вероятностью 3/4 и 1/4 отвечает рассеянию этих фермонов в состоянии со
спином 1 и 0. Поэтому оно запишется в виде
da= (fl/(0) - Д^-в)|2 + ^1/(0) +/(Я- 0)|2) da (27.45)
Предлагаем читателям самим провести построение для спиновых состояний с меньшим
значением спина.
Лекция 27
423
27.6. О КУЛОНОВСКОМ ПОТЕНЦИАЛЕ, резонансах
и НЕУПРУГИХ СТОЛКНОВЕНИЯХ
В заключение этой темы сделаем несколько замечаний о важных вопро¬
сах, которые мы опустили.
Кулоновские силы. В проведенном нами изложении теории рассеяния
мы полагали, что потенциальные силы являются короткодействующими. То¬
гда установленные асимптотики для волновой функции в задаче рассеяния
являются точными, а интегралы, определяющие амплитуду рассеяния, схо¬
дятся на верхнем пределе. Например, для фазы рассеяния подынтегральное
выражение ведет себя при г —> оо как
г 2 (г) Ф w (г) V (г) ~ г2 ^ sin (kr -11 j sin (kr - I + 5t j V (г) ~ V (r).
Поэтому, так как |sin(x)| ^ 1, интегралы заведомо сходятся на верхнем пре¬
деле и фазы оказываются конечными, если потенциал У (г) убывает быстрее,
чем 1/г, т. е. если силы действительно короткодействующие. Отсюда стано¬
вится ясно, что физически актуальный случай дальнодействующих сил куло-
новского типа требует специального рассмотрения. Этого следовало ожидать
и из того факта, что дальнодействующие силы искажают свободные волны
и на больших расстояниях, так что аппроксимация асимптотических состоя¬
ний волнами де Бройля в этом случае может оказаться некорректной.
В самом деле, уже при классическом рассмотрении можно установить, что
частицы одной энергии, падающие из бесконечности на центр кулоновских
сил с импульсами, параллельными заданному направлению, с одинаковым
удалением по оси импульса и различными прицельными параметрами на
больших, но конечных расстояниях уже образуют фронт, отличный от плос¬
кого. Это искажение фронта в кулоновском случае может быть установлено
точно, потому что квантовомеханическая задача рассеяния решается до кон¬
ца в терминах спецфункций. В частности, оказывается, что асимптотическое
поведение для рассеянной волны принимает вид
Rki 00 ~ “ sinjfcr + c(fc) ln(2fcr) -1Z + 51 j,
и аналогично для прошедшей волны с той разницей, что под логарифмом
появляется зависящий от угла фактор. Дополнительная логарифмическая
фаза искажает фронт падающей волны и модифицирует асимптотическое по¬
ведение рассеянной волны, но этими искажениями можно последовательно
пренебречь при вычислении потоков вероятности, так как они оказываются
подавленными как 1/г. При этом оказывается, что точное выражение для
дифференциального сечения стационарного кулоновского рассеяния воспро¬
изводится в борновском приближении: формула Резерфорда.
Резонансы. Парциальное сечение достигает своего максимума, равного
at = 4n(2l +1 )/fc2, при энергии, соответствующей значению = п/2. В этом
случае говорят о наличии резонанса в Z-канале. Запишем парциальную ам¬
424
Тема 16. Рассеяние
плитуду:
к г _ sin _ sin 5t _ i
21 +1 ~~ e~i5i ~ cos 5t - i sin ~ ctg 5t — i ’
Котангенс парциального сдвига 5г обращается в нуль, если энергия близка
к резонансной ЕъЕ*, т. е.
(27.46)
где мы ввели величину размерности энергии Г и положили, что в ведущем
приближении зануление происходит линейно по энергии. Значит,
5'*arCtg2(Br=£) (27'47)
при вариации энергии вблизи резонанса в малой области размером в не¬
сколько Г пробегает значения от нуля до п. Для парциальной фазы можно
записать:
^_/i = qpl = i-ie^. (27.48)
Это показывает, что в комплексной плоскости парциальная амплитуда с ро¬
стом энергии пробегает против часовой стрелки по окружности, центр ко¬
торой смещен из нуля на чисто мнимую ось, как это показано на рис. 38.
Подобный график называют диаграммой Аргана (Argand plot). Окружность
на таком графике практически замкнутая, если вдали от резонанса сдвиг
фазы относительно мал.
Рис. 38. Диаграмма Аргана — зависимость комплексной парциальной ампли¬
туды от энергии вблизи резонанса
Парциальное сечение рассеяния
2Z + 1
стг = оПГт1//12
Лекция 27
425
вблизи резонанса
,~я+1 i
» «.-Ж-.5 (27-49)
как функция энергии приобретает зависимость брейт-вигнеровского типа
^ _tt(2Z + 1) г2 Г97 w
1 k2(E) (Е*-Е)2 + Г2/4’ U/.bUj
т. е. имеет вид пика с шириной Г на полувысоте. Однако пикообразная форма
зависимости сечения от энергии сама по себе может возникать по различ¬
ным динамическим причинам, поэтому для идентификации резонансов при
парциально-волновом анализе экспериментальных данных по рассеянию по¬
точечно строят диаграмму Аргана, что в случае характерной зависимости
и служит достоверным доказательством наличия резонанса в том или ином
канале.
Выше мы молчаливо полагали, что ширина Г положительна. Это отвечает
тому, что амплитуда рассеяния (27.49) имеет полюс в комплексной плоскости
энергии при Е=Е* — ir/2, т. е. полюс смещен в нижнюю полуплоскость. Этот
вопрос тесно связан с исследованием аналитических свойств как амплитуд
рассеяния, так и функции Грина стационарного уравнения Шрёдингера, что
выходит за рамки нашего изложения. Вкратце же отметим, что, в частности,
на примере функции Грина свободной частицы мы видели, что по энергии
она имеет разрез в комплексной плоскости вдоль вещественной оси от нуля
до бесконечности, т. е. при значениях энергии в непрерывном спектре. При
наличии связанных состояний функция Грина, как следует из разложения
по базису стационарных состояний, приобретает полюса на вещественной
оси в точках дискретного спектра. Резонансы имеют место в непрерывном
спектре, так что отмеченный полюс расположен «за» разрезом, т. е. на нефи-
зическом листе двулистной функции Грина, зависящей от k = \j2mE/h2.
Рис. 39. Особенности функции Грина: полюса на вещественной оси, отве¬
чающие связанным состояниям, разрез в непрерывном спектре и полюс
резонанса под разрезом на нефизическом листе
При этом мы показали, что для запаздывающей функции Грина мнимая
добавка к энергии в полюсе должна быть отрицательной, что соответствует
426
Тема 16. Рассеяние
распаду метастабильного состояния — резонанса. Тогда величина т = Н/Г
определяет время жизни резонанса.
Неупругие столкновения. При изложении фазовой теории рассеяния
мы полагали, что поток вероятности сохраняется: число падающих на ми¬
шень частиц равно числу рассеянных, так что имеет место тождество
|S, I = 1,
и рассеяние происходит упругим образом. Однако, если в процессе столкно¬
вения образуются частицы, отличные от исходных, то говорят, что откры¬
ваются неупругие каналы рассеяния: пространство асимптотических состоя¬
ний двух частиц становится неполным, часть падающего потока инициирует
неупругие процессы, и
|S,| < 1. (27.51)
Тогда сечение упругих (elastic) столкновений с /, = (21 + 1)(S, - l)/(2ifc)
CTel = § S(2Z + 1}lS‘ - Х|2’ (27-52)
так как амплитуда рассеянной волны пропорциональна разности амплитуд
расходящихся волн в (г) и ■ф{0\г), т. е. S, -S,(0) = S, -1, а недостающий
поток вероятности в рассеянной волне, пропорциональный фактору 1 - |S,|2,
естественно отнести к сечению неупругих (inelastic) столкновений, так что
его полное сечение
(7ind = §Yi& + l)a-\Sl\2). (27.53)
Полное (total) сечение
<Г«* = о* + ^inel = § Yp.1 + 1){|S, -1|2 +1 - |S,I2}. (27.54)
Преобразуем:
|S, —1|2 +1 — |S,I2 = (S, - 1)(S* -1) +1 - IS,I2 = 2 - (S, + Sp = 2(1 - Re S,).
В итоге
о-tot = ff 2](2Z +1) (1 - Re S0- (27-55)
I
Заметим, что
Im/, = ^Imy(ReS,-l-HImS,) = ^±l(l-ReS,).
Тогда по-прежнему справедлива оптическая теорема
(27-56)
i
что отражает факт сохранения вероятности с учетом вклада неупругих столк¬
новений.
Наконец, отметим, что резонанс при наличии неупругих каналов рассея¬
ния на диаграмме Аргана проявляется в виде витка неправильной спирали.
Лекция 27
427
Задача 16.4. Найти полное и дифференциальное сечения рассеяния быстрых
частиц на абсолютно черном шаре радиуса а.
Решение. Будем называть абсолютно черным тело, которое поглощает при рас¬
сеянии все падающие на него волны, т. е. оно не отражает волны, достигшие его
поверхности. Как мы видели, центробежные силы создают потенциальный барьер,
который непроницаем для волн с I» ка. Поэтому для этих волн отражение происходит
так же, как и в свободном случае: St = 1. При I ^ ка волны достигают поверхности
черного шара, и отражения не происходит: St = 0, а значит, имеет место неупругое
рассеяние (|SZ | < 1). В этом случае сечение упругого рассеяния
= £ Z(2Z + DIS, -1|2 = р +1) = па2,
К ыо к 1=0
а неупругого —
ка ка
o-ine.= § +ш - Is' l2) = £ 1>г+ 1У= па2=
К 1^0 к ЫО
Итак, упругое и неупругое сечения равны друг другу. Найдем мнимую часть упругого
рассеяния вперед:
В итоге для каждого парциального сечения устанавливаем равенство
°i=a*+aLi=Tlmfi=i?(-2l+1)’
т. е. соотношение оптической теоремы для заданного типа рассеяния.
При I»1 от суммирования по парциальным амплитудам упругого рассеяния в
данной задаче
можно перейти к интегрированию по Z:
ка . /0
f(0) = '^if,Pl(cos / dZ-ZP,(cos в), l0tvka.
1=0 о
Полиномы Лежандра удовлетворяют уравнению на собственные значения квадрата
орбитального момента
l2Pt (cos 0) = I(1+1 )Pt (cos 0),
где оператор I2 при малых значениях углов принимает вид
i2 1 аг. д2 1 д
sineaelsm дв2 в дв'
Поэтому, вводя х = 1в, находим
{*2l^+*£+4p'(cosf)=0’
что есть уравнение для функции Бесселя J0(x):
428
Тема 16. Рассеяние
Рис. 40. Дифференциальное сечение упругого рассеяния быстрых частиц
с волновым вектором /са = 6тг» 1 на абсолютно черной сфере радиуса а
В итоге
/(*)*£ J и-и0ав)=-^10^(.10е),
где мы воспользовались соотношением
1(*)
при п = 1.
Дифференциальное сечение упругого рассеяния при малых углах
= l/(^)|2 W ^2
откуда после интегрирования по азимутальному углу находим
^^2яа2-|^2а0е).
Это сечение дифракционного типа при ка=6п показано на рис. 40, из которого следу¬
ет, что полное сечение насыщается при малых значениях углов, а вклад больших углов
рассеяния подавлен. Поэтому в интеграле по углам, определяющем полное сечение
упругого рассеяния, можно формально перейти к интегрированию до бесконечности:
71 оо оо оо
сте1 = J сШ^|*2яа2 J ^-J*(J.06)=2na2 j
ООО о
Табличный интеграл
00
I
о
так что приходим к полученному выше сечению упругого рассеяния быстрых частиц
на абсолютно черной сфере
сте1 = яа2.
Приложения
Послесловие
Признаваться в незнании, на мой взгляд, — одно из
лучших и вернейших доказательств наличия разума.
Мишель де Монтенъ
В этом курсе лекций автор старался начертать теоретические основы
квантовой механики в замкнутой форме на умеренно высоком уровне стро¬
гости логических конструкций, стремясь сохранить ясность изложения, что
неминуемо привело к потере многих, может быть, и важных деталей.
Это становится достаточно очевидным, если упомянуть хотя бы даже
те «стандартные вопросы», которые «выпали» из базовой части курса: так,
феноменология, т. е. приложение теории к актуальным и важным задачам,
представлена лишь фрагментарно; опущены подробная теория измерений
и обсуждение методически важных и исторически наглядных квантовых па¬
радоксов; не изложен формализм сложения трех и более моментов, нет тео¬
рии неупругих столкновений и анализа аналитических свойств амплитуды
рассеяния; выведены за рамки курса и систематическое изложение форма¬
лизма вторичного квантования, и метод квазичастиц... И этот список мо¬
жет быть продолжен. Однако автор полагает, что исчерпывающее изложение
предмета в одном учебнике является методически ущербным, потому что
материал действительно усваивается и становится рабочим инструментом,
если у студента возникает о нем собственное мнение, а это практически
становится возможно при знакомстве с разными точками зрения на пред¬
мет. Поэтому тотальный охват вопросов одним автором создает иллюзию
законченности изучения, в то время как пробелы в тематике курса невольно
побуждают студента обратиться к другим учебникам и пособиям и при этом
не только «вычитать» вопрос из программы, но и пролистать их, а значит,
увидеть многое в ином свете и под другим ракурсом, что часто служит
катализатором качественного скачка в понимании.
С другой стороны, не нашли отражения в основных, отвечающих деле¬
нию на семестры, двух частях курса (лекции 1—14, лекция 15—27) и «новые
достижения», такие как неравенства Белла, позволяющие научно строго ис¬
ключить возможность вероятностного описания природы за счет введения
«скрытых параметров» взамен понятия амплитуды состояний и их гильберто¬
ва пространства1; бурно развивающаяся теория квантовых вычислений и т. п.
Однако нужно иметь в виду специфику университета, студентам которого
предлагаются эти лекции, а именно, то, что курс квантовой механики по
*Этот вопрос освещен в дополнении IV к базовой части курса.
432
Послесловие
кафедре теоретической физики составляет лишь один из элементов базис¬
ного образования, в котором есть также и общая физика с качественным
рассмотрением множества феноменологических задач, и лабораторные заня¬
тия, и семинары по решению задач, где упоминаются типовые приложения
квантовой механики. Еще важнее, что старшекурсники физтеха продолжа¬
ют затем свое специализированное, углубленное образование на базовых
кафедрах в исследовательских организациях, где формируются конкретные
научные интересы студентов и соответственно этому расширяется их круго¬
зор и знания.
Именно в свете этих аргументов и фактов автор и не ставил себе целью
создание энциклопедического труда по квантовой механике, что просто было
бы ему явно не по силам. В свое оправдание могу привести лишь слова
все того же Мишеля де Монтеня: «Рука, что дает нам истину, —■ смертная,
и смертная же рука принимает ее».
Основные формулы курса
Часть I
Волновая функция
Волна де Бройля:
фр(г,0 = <г|р, t)=e“«(£t_p'r).
Условие нормировки:
{р\р') = / d3r Ф* (г, ОФр'(г, ^ = (27rfi)3 5(р -рО.
Волновой пакет:
Ф(р) = (P. t|*(t)) = / d3r е»(££-рг)Ф(г, t) = f d3r Ф* (г, ОФ(г, t).
Условие единичной нормировки:
(Ф|Ф) = J d3r Ф*(г, ОФ(г, t) = J ^^зФ*(р)Ф(р) = 1.
Средние значения координаты и импульса:
(г) = (Ф|г|Ф) = f d3r Ф*(г, ОФ(г, t)r, r=r,
<р) = (Ф|р|Ф> = | ^^зФ*(р)Ф(р)р, p = -ifiV.
Уравнение непрерывности, поток вероятности:
р = |Ф(г, t)|2, ; = -^{Ф*^Ф)-(УФ*)Ф}, ^+divj = 0.
Операторы физических величин и состояния
Эрмитово сопряжение состояний:
<ф|=|ф)+, |ф) = <фГ, (•)t=(0T)*-
Эрмитово сопряжение операторов:
#1ф)=|рф), <ф|рф) = (^ф|ф)=(ф|р+ф)*.
434
Основные формулы курса
Физические величины = наблюдаемые:
#t = р, (F) = (Ф|РФ) = (Ф|РФ)* = (Ф|#|Ф).
Дискретный спектр:
£|n)=/Jn), neN, (п\тп) = 5пт.
Непрерывный спектр:
F|v)=/(v)|v), v€E, (v|ju) = 5(v —ju).
Условие полноты базиса:
Y, H(n| + J |v) dv (v| = l.
П
Проекторы на состояния с заданным значением наблюдаемой F из ее спек¬
тра:
r v+0
Р„ = Н(п|, Р2-Р„, Ру= f |v)dv(v|, P2=PV.
v-0
Разложение по базису («вставка единицы»):
|ф>=Z 1п)(п1ф>+J И dv (*|ф).
п
Физический смысл коэффициентов разложения—амплитуд: вероятность
^П = |ф„|2 = |<п|ф>|2,
плотность вероятности
рОЮ = |Ф(у)|2 = |(у|Ф)|2,
среднее
(F) = (*\F\*) = 'ZfnWn + S dvp(v)/(v).
Tl
Коммутатор:
[Р,6]^Рд-6Р.
Дисперсия наблюдаемой:
(AF)2 = {(# - (F))2) = (F2) - (F)2.
Соотношение неопределенностей для наблюдаемых:
(AF)2(AG)2^([F,6]>2.
Эволюция СОСТОЯНИЙ и ВЕЛИЧИН
Уравнение Шрёдингера:
т£|Ф(0>=#|Ф(0>.
Основные формулы курса
435
Гамильтониан нерелятивистской частицы в потенциальном поле V:
А-|1 + У(г).
Стационарное уравнение Шрёдингера:
Н|Фе)=Е|Фе>, |Ф£(0)=е-я*|Фя>.
Уравнение Гейзенберга:
Эволюция средних:
d(F) /d F'
d(F) / dF \
dt \ dt /■
Интеграл движения (если наблюдаемая не зависит от времени явно, dF/dt=
=0):
[F, Н] = О f = 0.
Оператор эволюции:
|ф(0)=Ш|ф>, ишЧо=иЧоШ=1,
Консервативные системы:
0(.t) = e
Общий случай:
[>(0=Техр{-| Jdt#(t)}.
Представление Гейзенберга:
|фн) = u+(t)|Ф(с)), fh = йЧоРйю.
Гармонический осциллятор
Гамильтониан:
тте ч р2 , mwV
H(4,p) = 5j + -2-.
Осцилляторные единицы:
Ро
= V&, Чо=\[^, Е0 = ^ = П<о.
436
Основные формулы курса
а = А=(.й+1'Р),
^ ГА
Операторы рождения и уничтожения:
[a, aT] = 1;
а|п) = л/п |n — 1), аг|п) = Vn+T |п + 1), а|0) = 0.
Спектр:
E=hco(n + ^j, п е {О, N}.
Базис:
|п)=лГ|0>’
т)=п‘1т - 7гЫ°- и)'е'* "
Полиномы Эрмита:
Нп00 = (.-irez2^{e-z\ Kn(Q) = -p^=e"^Hn(Q).
Когерентные состояния:
а|а) = а|а>, a = -^(Q0 + iP0)> (Д02 = (ДР)2 = |.
Среднее число квантов:
(a|tf|a) = |a|2.
Распределение по числу квантов:
Рп = |(пИ|2 = ^е-М
Момент импульса
Коммутационные соотношения для J=hj:
Ua> Jp] ^eapyjy
Базис:
j2\j> m) = jO + 1)1Л m>» J = |, fc€{0, N},
J*|J. ™) = mlj> m>> m e -j + •••> j - Я-
Повышающий и понижающий операторы:
j±=jx±ijy>
j+\j, m) = a/ j (j +1) — m(m +1) |j, m +1),
./-Lb m) = ^(j + ij-mCm-i) |j, m-1).
Основные формулы курса
437
Старший и младший векторы представления:
j+\j,j)=°>
Орбитальный момент:
t = hl = rx р,
= i2 = -±a4j(s
z dtp’ sm в дв \ дв J sin2 в dip2
Сферические гармоники:
%т(в, <р) = (в, <р\I, т), Щ т(,в, </>) = eim<%n(0),
4>) = mWl>m(G, ip), 12Щ,т(в, ip) = l(.l + 1Щ^в, ip).
A 1 A
2
Матрицы Паули cr:
М?Э- *,-GD- *.-6-3
Базис:
12* +2 ) = (2’ 2 ) = l—
Коммутационные соотношения:
^/j] = 2iSapr**r•
Антикоммутационные соотношения:
*pY= 6a*p+*p*a = 28al>-
Разложение произведения:
&a&P — ieapr^r ■*" ^“0-
Спинорная метрика:
«=io-2=(_; j).
Фермионный осциллятор:
a+=i+, a=s_, {Mf}=i.
Атом ВОДОРОДА
Атомные единицы:
— постоянная тонкой структуры
е2 . 1 .
em he 137,04’
438
Основные формулы курса
— скорость
е2
v0 = aemc = j;
— импульс
те2
p0 = mv0 = mcaem = -^;
— боровский радиус
а — — = —= -^5 « 0,5 • 10~8 см;
Ро тсает те2
— энергия связи—«один ридберг», Е0 = Ry,
Е - Ро _
0 — 2т ~
Гамильтониан и спектр:
Eo=f = nfa2 !ng=fiЦ = |1*13,61эВ.
0 2m 2 em 2fi2 2m a2 2a ’
R_P p_
2m г-’ “Не¬
квантовые числа: n = nr + i +1 — главное квантовое число, nr — радиальное
квантовое число, i—орбитальное квантовое число, т—магнитное квантовое
число; базис: (r|n, I, т) = -фп1т(г),
'ФпыЮ =RniO")%m(.e, <р), Rnl(р) ~plwnl(p)e-Zp/n,
где и/п(—обобщенные полиномы Лагерра.
Основное состояние (при Z = 1):
’/’юоС»*) = 7=е_г/а.
утгег
Степень вырождения (без учета спина электрона): п2.
КВАЗИКЛАССИКА
Классически доступная область:
w, (Х) 2* £+ . ен / Р[w d* + ik. е-я/ j»1w
* VP а/Р
Критерии применимости:
|А'|<1, |-^|«1.
Ip Р I
Правило квантования Бора—Зоммерфельда:
р(х) (1х = 2тгЙ^п + “^, ne{0, N}.
Плотность состояний:
дп _ 1
ЭЕ hco(E) '
Вероятность проникновения через потенциальный барьер:
Т~ехр{-| / |р(х)| dxj~exp|—2^}«С1.
а
Основные формулы курса
439
Часть II
Теория возмущений
Поправки к энергии в стационарной теории возмущений для невырожденно¬
го случая:
ei = (n(0)|V|n(0)) = Vnn,
кфп *п Ч
Критерий применимости:
1М<1.
дс
Секулярное уравнение в теории возмущений для поправки к энергии в пер¬
вом порядке:
det(V-e1) = 0, ^Ьа = (п(0), Ь|У|п(0), а), ае{1,
«Правильные» функции ведущего приближения:
fc к
In) =2 са|п(0), а), _ ех5Ъа}Са = 0,
а=1 а=1
Представление взаимодействия:
|i(t)>7=ujct, tO|i(t))d= 17/Ct, t') |i),
U(t, t') = UoCt, t% U0(t, t') =
Оператор эволюции:
ihd-^-=xvIuI, v^ulvuo,
( . t t
0=f exp{--U J V,(t)dt}«l-jjA J ВД dt.
t' t'
Амплитуда перехода:
t'
top = i(Ef(0) -fif), (f|V(t)|i)=Vfi(t).
«Золотое правило Ферми»:
<4 = JlVftl2 • 2я5(£{0) - В® +Йо>) dv(Ef(0)),
где dv(Ef(0)) — дифференциальная плотность состояний с заданной энергией
конечного состояния.
Критерий применимости:
440
Основные формулы курса
Адиабатическое приближение (при ЕпфЕт, если пфт)\
s
—i7Yn(s)+i Г да^ЛЛа)
\ipn(t)) = e ° №«(«)).
где
t = T-s, se[0;l], Г-ю°, a=a(s), {all} = a, jue{l , ...,p},
H(aMn(a))=EniaMn(.a))> <^„(s) = J J En(s) ds
0
и
Лм(а) = i('0nCa)|3“|'i/»n(ct)).
Критерий применимости адиабатического приближения:
г»-,
СО
со—частота собственных колебаний в системе.
Фаза Берри:
Дсу = $ daMM(a).
Сложение моментов
Сумма J=jA+jB, допустимые значения:
J=jA+jB, jA+jB~ 1, |jA-jB|, -jA-jB^M^jA+jB,
с шагом ДМ = 1.
Состояния:
|J,M}= J] |jA, тв)С^тд..в>тв.
та,тв
Коэффициенты Клебша—Гордана:
Cj\rnA;jB,mB = (jA> тА> ^’ ШВ \J> М)’ Cj\jA-,jB,J-jA > °'
Число состояний: (2jA +1) (2jB +1).
Неприводимый тензорный оператор в стандартном представлении, закон
преобразования:
т тт т 3
где — матрица вращения состояний с моментом j; коммутационные соот¬
ношения:
mil*
Основные формулы курса
441
Теорема Вигнера—Эккарта:
(J, M\T<P\J', М'> = M\f, М'; j, т),
где {J\\T^\\Jf) —приведенный матричный элемент оператора, который зави¬
сит только от J и J7.
Правила отбора:
|ДМ| ^ j, \AJ\^j, j^J + f.
Релятивистская квантовая механика: группа Лоренца
Спиновая матрица для векторной частицы:
(s0)ar = "~iej3ar
Оператор орбитального момента и тензор спина для векторной частицы:
Lap ХрдоУ ^.^аРр ^СрРаУ> Ра ~~
Sg = ift{5j5J-5^r>.
Преобразование векторного поля при бесконечно малых преобразованиях
группы Лоренца x/k=xk + <oknxn с параметрами сокп = —сопк:
А'\х) = {l - ±coml(Lml + Sml)}knAn(x).
Полный набор коммутационных соотношений для генераторов вращений ja
и бустов К&:
Ua,f]=+ieaPrf, [f,K^^+ieaPrKJ, [Ka,K^] = -ieaPrf.
Собственная ортохронная группа Лоренца:
dx'm=A™ dxn, det A=1, Л°>1.
Генераторы:
Коммутаторы:
№а> = *еаРгс^г 5 №а> ~ *еарус^Г’ №а’ р^ = ®’
VJ+?,Sp=o, L(J-)2,Jp=о.
Базис:
(/+)2* М = Я+ (А+ + 1)х М, А+ — полуцелое,
з
и
= m+€{A+, А+-1,..., 1-А+, —А+},
С^-) 0(х) = Я_(Я_ + 1)0(х), Я_ —полуцелое,
^J0(x) = m_0(x), т_е{Я_, Я_ — 1,..., 1 — Я_, — Я_}.
Матрицы:
(o-m)aa = (1> +о0> (o-m)da = (l,-О-).
442
Основные формулы курса
Релятивистская квантовая механика: группа Пуанкаре
Коммутационные соотношения 4-импульса (р0, ра) с генераторами враще¬
ний j* и бустов КУ:
if, РР1 = 1£а/3ГРГ> If, Ро] = О»
[KaV] = i5a%, [Ka)Po] = ipa.
Псевдовектор Паули—Любанского:
wm=-\imMPnskl.
Инварианты группы:
У“, Р2] = [Ка, р2] = 0, [ja, W2] = [Ка, W2] = [Pk> W2] = 0.
Массивные частицы: инварианты
р2 = т2>0, W2 = -m2h2s(s + l);
квантовые числа {т, р, s, sz}.
Безмассовые частицы: инварианты р2 = 0, W2 = 0;
квантовые числа—спиральность s и импульс р:
±Wk=spk, 5 = ±Я±.
Релятивистская квантовая механика
Уравнение Клейна—Гордона—Фока:
(р2-т2с2)</>(л:) = 0.
Коммутационные соотношения для операторов рождения и уничтожения
частиц вещественного скалярного поля:
[&(fc), a+(fc')] =2hco(2n)3 5(fc —fc').
Квантованное поле:
фМ = J 2~ejS)3{eife3Cat(fc) + e~ikXW»-
4-вектор тока для комплексного скалярного поля:
)ц = “ (3M¥>)V>-
«Уравнения Шрёдингера» для правого и левого вейлевских спиноров % и в:
рох=р-°х, ро0=-р-о-е.
Уравнение Дирака:
(рпГп - = 0; р=ркук=РоГо-Р-Y•
Основные формулы курса
443
Матрицы Дирака {ут, у"} = 2gmn:
Г'-в-V. T.-QS). г-Ц-Я-
Дираковски сопряженный спинор:
i>=^Yo-
Билинейные величины:
‘ф'ф —скаляр,
%pym\p —вектор,
^'ф&тп'ф — антисимметричный тензор,
'ФТб'Ф —псевдоскаляр,
'4>YsYm'lP — псевдовектор.
Сумма по поляризациям массивного поля Дирака
П(р) ия(р)йя(р) =f>+mc.
А
Квантованное поле Дирака:
= J 2р0(2яЮ3*6~*Р*Ц±(р)а±(р) + е*р*У±(р)а£±(р)}.
Перестановочные соотношения для частицы со спином
{ая(р), а*, (р')} = 2р05ЯЯ/ (2яй)3 5(р - р')-
Безмассовое векторное поле со спиральностью Я:
~с^Г = 1Яг(*^’ div.*^ = 0, Л0 = 0,
8 = 1Я^4Р, Fkn = iXFkn.
Квантованное безмассовое векторное поле:
Лм = | zSk?{e~ik'X£*Cfc^W + e^MCWa^fc)},
где 4-векторы поляризации являются поперечными:
епкп = О, е0 = 0.
Калибровочное преобразование:
|pu)=eiur£|p), aj(p) = at(p)eiurk => оц(р) = a(p)e_iuy£.
Ковариантная производная:
= + •4fc=^fc + djicu.
444
Основные формулы курса
«Релятивистский» атом водорода: спектр
Вырождение по орбитальному моменту:
Энергия связи:
J±=j±§.
— тс2, v = 1+ nr +1± — 5j = п± — 5j,
I 2~
53 + ]10 + |) _ает-
Ведущая поправка:
*nj ™-^а1т{1 + -jjjr (_2j+i ~ I) }•
Нерелятивистское приближение: эффективная теория
Уравнение Паули для нерелятивистского спинора:
Й™ = |^+«Ф-!&(*■*)■
Фактор Ланде:
8=2.
Релятивистская поправка к кинетической энергии электрона:
5Еш = ~8^
Спин-орбитальная поправка во внешнем статическом центральном потенци¬
але <р(г):
v‘'=(s-1)dbiT2(s-I)-
Дарвиновский вклад:
Нп • = е^2 АФ
Dar™ 8 m2c2
Атом гелия
Гамильтониан для электронов в атоме гелия в нерелятивистском приближе¬
нии:
й 2__Z£,_£_ 7_0
ш 2т 2т rA rB \гА-гв\’
Основные формулы курса
445
Уравнения Хатри (в атомных единицах):
ЕаФа~ { — — ~ + Ч>в(га)}‘Фа>
Ев'Фв = { “ - ув + 4>A(.rB)}^B,
где экранирующие ядро потенциалы
Ра(га) = I’/’aOa)!2, Рв(гв) = |-i/»BCrB)|2.
Сложный АТОМ
Определитель Слетера:
1 (Фк^XI) ... rpkN(xХ)Л
(*i>..., xN) = -= det * = <r’ m*>-
Конфигурация: эквивалентные электроны, оболочки в самосогласованном
поле п1к.
Термы с учетом поправок к самосогласованному полю: 2S+1L,
состояния \п1к,L, М; S; Ms).
Термы с учетом релятивистских поправок: 2S+1Lj.
Правило интервалов Ланде:
A(Vls) =E(2S+1Ij) — £(2S+1Ij_1) =AlsJ.
Атом ВО ВНЕШНЕМ ПОЛЕ
Гамильтониан:
H=S{^ {.Pf ~ -c^frf ~ +eMrf)} + V,
в магнитном поле: взаимодействие магнитного момента электронов (магне¬
тон Бора ц0 = еН/2тс)
^mag = М0^ ’ № + 2S),
диамагнитный член
Аномальный эффект Зеемана:
(Mj) = hClgLS]Mj, а = еН/ (2 тс).
446
Основные формулы курса
Фактор Ланде:
J(J + 1)-L(L + 1)+S(S+1)
Slsj 2J(J + 1)
Эффект Пашена—Бака:
(I, М'; S, M>0«az + 2SZ)|I, М; S, Ms> = ftn(M+2Ms)5MM,5MsM,.
Спонтанное излучение
Вероятность спонтанного излучения в единицу времени—дипольное прибли¬
жение:
матричный элемент дипольного момента:
^ = (fat|da|iat).
Интенсивность излучения:
Правила отбора: по полному моменту (и его проекции)
|ДМ,|г$1, |AJ|^1, l^J+J',
по спину
AS = 0, AMs = 0,
по орбитальному моменту
|ДМ|^1, |Д1|^1, lsSL+L',
по четности
Pf = -Pt.
Индуцированное излучение и поглощение: вероятность и интенсивность
= Л ,Г,л.Л = /ЛЛ \Й..\2
^ind
=w^o>;\dfi\idfii2
Рассеяние
Оператор функции Грина—резольвента:
Ge = г .
E-H+iO
Уравнение для функции Грина стационарного уравнения Шрёдингера:
(.Е-НгШгУ) = 5(.г-г').
Основные формулы курса
447
Запаздывающая функция Грина
+ 00
0(t", г; е, г') = 4<r|L/(t", tOliW-1') = J r']’
— 00
ih-%QOc; х')-Йд(х; x/) = 5(4)(x-x/), x = (t, r).
Эволюция волновой функции:
ifi(x) = ift J dV £(*; x'Wix').
Разложение по базису стационарных состояний:
QE(r,r)-2_, £_£n+i0 •
П
Функция Грина свободной частицы
e(0)Cr r/) = __jn_e^
** ir’rj 2ягЙ2 Ir-r'l '
Интегральное уравнение Липпмана—Швингера:
V>[+)(X) = ^[0)(*) + J sf>(X - хх) V(Xj)V»{+)(Xj) d3xv
Асимптотическое поведение при г—> оо:
(г) * V»{® (Г) + ^/(0), Г - 00,
где
/(60 = _2^ J* dVe-^VCrO^CrO.
Дифференциальное сечение рассеяния:
da = |/(0) |2 dfi.
Соотношение унитарности для ^-матрицы:
STSf* = —2ft Im 2Г.
Оптическая теорема:
сг = ^1ш/(0).
Борновское приближение:
условие применимости: медленные частицы (кг ~ ка < 1)
быстрые частицы (кг ~ ка »1)
mVoa2 1
448
Основные формулы курса
Парциальные волны
Свободная частица:
асимптотически при г —> оо:
R®>(r)*c»>^Sm(*r-fl),
в волне де Бройля:
СО) = iiJ_
1 1 2ik'
В задаче рассеяния:
Упругое рассеяние:
|S, 1 = 1, s, = e2i5', 5,6 [0, я].
Асимптотически при г—> оо:
%(r)^c,(0)yei5' sin(fcr- |Z + 5,).
Парциальные амплитуды:
/(0) = 2 /i^Ccos 0), /, = ^±iei5' sin 5,.
I
Парциальные сечения:
Оптическая теорема при упругом рассеянии:
ai=Tlmfl-
Фазовые сдвиги (зависимость от кинематики):
. _ 2mV0 2fak\2l+1 . г 2mV0 3.
sin 5, у—J и sm50'—а к.
Медленные частицы (ka<C 1): длина рассеяния
/о = ^ sin50е‘5°й| = —а0,
полное сечение
о-=4я|/0|2|^0 = 4яа2.
Рассеяние тождественных частиц с суммарным спином S (потенциал не за¬
висит от спина):
dcr = 1/(0) + (-1)S/(7T - 0)|2 da
Основные формулы курса
449
Фазовый сдвиг и амплитуда вблизи резонанса:
г
г
5г га arctg
2 СЕ.-Е)’ 2г + 1л ijf
* 2
Сечение Брейта—Вигнера:
_ 7t(2Z +1) Г2
°l к2{Е) (Е*-Е)2 + Г2/4’
Неупругие столкновения |S?| < 1:
упругое сечение
CTel = f X|C2Z + 1)|SI-1|2,
неупругое сечение
^inel=f S(2Z + 1)(1"IS'|2)-
I
Вопросы по курсу
«Квантовая механика»
Вопросы для контроля усвоения материала студентом разбиты на 3 груп¬
пы по степени сложности:
уровень А: аспирантский, или advanced (повышенной сложности), отве¬
чает глубокому пониманию предмета, необходимому для дальнейшего обу¬
чения соискателя на звание кандидата физико-математических наук;
уровень М: отвечает твердому усвоению и пониманию предмета при
обучении магистра физико-математических наук, который готовится к науч¬
ной работе;
уровень Б: отвечает усвоению предмета при обучении бакалавра физи-
ко-математических наук.
Вопросы уровня Б поставлены так, чтобы ответ на них не требовал ника¬
ких выкладок, а мог быть сформулирован буквально в одну строку практиче¬
ски без времени для раздумий и подготовки, т. е. усвоение предмета бакалав¬
ром предполагает режим «блиц»: вопрос—ответ. Вопросы уровня М допуска¬
ют минимальное время на подготовку в зависимости от сложности: часть из
них также не требует выкладок. Уровень А предполагает ответ в несколько
логических шагов и требует небольшого времени для подготовки.
Для удобства вопросы сгруппированы по лекциям согласно нумерации
последних.
Часть I
Принципы квантовой механики
Лекция 1
Б1. Какая величина задает квантовое состояние частицы?
Б2. Как связана амплитуда вероятности с плотностью вероятности?
БЗ. Сформулируйте принцип суперпозиции для двух амплитуд вероятно¬
сти квантовых состояний физической системы.
Б4. Сформулируйте принцип соответствия для динамики квантовой си¬
стемы.
Б5. Из какого принципа следует линейность уравнения Шрёдингера по
волновой функции?
Б6. Из какого принципа следует разложимость амплитуды вероятности
квантового состояния по базису?
Б7. Из какого принципа следует линейность уравнения Шрёдингера от¬
носительно производной волновой функции по времени?
452
Вопросы по курсу «Квантовая механика»
Б8. Из какого требования следует нормируемость амплитуды вероятно¬
сти?
Б9. Дайте определение линейного унитарного оператора.
Б10. Каков результат действия оператора эволюции U (t) на состояние |Ф),
заданное в момент времени t = О?
Б11. Чему равен оператор если U(t) — оператор эволюции?
Б12. Какие операторы соответствуют наблюдаемым физическим величи¬
нам?
Б13. Какому числовому множеству принадлежат средние значения эрми¬
това оператора в общем случае?
Б14. Дайте определение коммутатора двух операторов в гильбертовом
пространстве. Перечислите три основных свойства коммутатора. Чему равен
коммутатор линейного оператора с числом?
Б15. Запишите соотношение неопределенностей для двух наблюдаемых.
Б16. Запишите уравнение Шрёдингера для волновой функции.
Б17. Запишите гамильтониан нерелятивистской частицы в операторном
виде.
Б18. Чему равен коммутатор координаты и канонически сопряженного
к ней импульса [q, р]?
Б19. Чему равен коммутатор компонент декартовых координат и импуль-
са [га,Рр]?
Б20. Запишите соотношение неопределенностей координата-импульс.
Ml. Каков физический смысл амплитуды квантового состояния?
М2. Какой физический смысл имеют коэффициенты Фп в разложении
кет-вектора |Ф) состояния по базису |п) с заданным квантовым числом гг?
М3. Запишите коэффициенты в разложении кет-вектора |Ф) по бази¬
су \п) в терминах дираковских бра и кет.
М4. Какой операцией связаны состояния бра и кет? Запишите эту связь.
М5. Чему равно число (Ф|Ф)*?
Мб. Запишите условие полноты базиса в гильбертовом пространстве ква¬
нтовых состояний с квантовым числом п и спектральным параметром v.
М7. Запишите условие нормировки состояний в дискретном и непрерыв¬
ном спектре.
М8. Дайте определение эрмитово сопряженного оператора в дираков¬
ских обозначениях.
М9. Запишите среднее значение эрмитова оператора F и его дисперсию
в дираковских обозначениях.
М10. Запишите уравнение на собственные значения эрмитова операто¬
ра F в обозначениях Дирака.
Вопросы по курсу «Квантовая механика»
453
Mil. Чему равна дисперсия наблюдаемой F в состоянии, которое является
для нее собственным? Докажите.
М12. Что можно сказать о квантовом состоянии, если в нем наблюдае¬
мая F имеет нулевую дисперсию? Докажите.
М13. Докажите, что (F • G)1" = G1" • F* в дираковских обозначениях.
М14. Чему равно [F, G]1" для двух эрмитовых операторов?
М15. Запишите уравнение для состояния, минимизирующего соотноше¬
ние неопределенностей для двух наблюдаемых величин.
М16. Как связано действие классической частицы S(q, t) с комплексной
фазой </?(q, О волны для этой частицы в пределе «геометрической оптики»,
т. е. в пределе распространения лучей по принципу Ферма? Запишите эту
связь для свободной частицы. В чем состоит гипотеза де Бройля?
М17. Покажите, что оператор импульса в координатном представлении
эрмитов. Как следует ограничить класс волновых функций?
М18. Вычислите коммутатор координаты и канонически сопряженного
к ней импульса в координатном представлении.
А1. Какое соотношение эквивалентности задает понятие луча в простран¬
стве квантовых состяний физической системы?
А2. Сформулируйте понятие сепарабельности и полноты пространства
квантовых состояний.
АЗ. Дайте определение проектора как оператора. Запишите проектор на
состояние |п) в дираковских обозначениях.
А4. Выведите необходимое и достаточное условие точного измерения
наблюдаемой F в дираковских обозначениях.
А5. Докажите соотношение неопределенностей для двух эрмитовых опе¬
раторов методом Вейля в обозначениях Дирака.
А6. Получите уравнение на состояние, которое минимизирует соотноше¬
ние неопределенностей для двух наблюдаемых.
А7. Введите универсальную постоянную Планка h согласно принципу со¬
ответствия классического движения частицы пределу «геометрической оп¬
тики» для волны, допускающей описание распространения лучей согласно
принципу Ферма.
А8. Выведите выражение для оператора импульса, действующего на вол¬
новую функцию, которая записана в пределе «геометрической оптики» со¬
гласно гипотезе де Бройля и уравнениям Гамильтона—Якоби. В этом же
формализме получите уравнение Шрёдингера. Как задается гамильтониан
квантовой системы?
Лекция 2
Б1. Запишите уравнение Гейзенберга для производной оператора по вре¬
мени.
454
Вопросы по курсу «Квантовая механика»
Б2. Запишите уравнение для оператора эволюции и начальные данные
к нему.
БЗ. Запишите оператор эволюции в случае консервативных систем.
Б4. Как определяется функция от оператора /(F)? Чему равно /(F) \Fn) на
собственном векторе оператора F, т. е. если F\Fn) =Fn\Fn)?
Б5. Чему равно среднее от производной эрмитова оператора по времени?
Б6. Запишите теорему Эренфеста.
Б7. Если две наблюдаемые / и g измеримы точно совместно, то что
можно сказать о значении их коммутатора [/, £]?
Б8. Дайте определение полного набора наблюдаемых.
Б9. Чем задается представление квантовой системы?
Б10. Запишите стационарное уравнение Шрёдингера в формализме Ди¬
рака.
Б11. Чему равна дисперсия энергии АЕ в стационарном состоянии?
Б12. Как зависит от времени плотность вероятности р (г, t) квантовой
системы в стационарном состоянии?
Б13. Запишите связь волновой функции стационарного состояния в мо¬
мент времени t с волновой функцией в начальный момент времени t0.
Ml. Запишите соответствие между коммутатором и скобкой Пуассона
двух наблюдаемых согласно методу канонического квантования.
М2. Запишите оператор эволюции для системы с гамильтонианом, зави¬
сящим от времени, в виде предела и его символического обозначения.
М3. Выведите соотношение для среднего производной эрмитова операто¬
ра по времени.
М4. Докажите теорему Эренфеста в методе канонического квантования.
М5. Докажите, что если коммутатор [/, g] = 0, то в гильбертовом про¬
странстве существует базис, в котором наблюдаемые fug измеримы сов¬
местно точно.
Мб. Докажите ортогональность двух квантовых состояний, которые явля¬
ются собственными для наблюдаемой / с разными собственными значения¬
ми /1>2, в обозначениях Дирака.
М7. Сформулируйте постулаты квантовой механики при каноническом
квантовании классической системы в картине Шрёдингера.
А1. Покажите, что связь коммутатора двух физических величин с их скоб¬
кой Пуассона может быть выведена из требования согласования флуктуаций
этих величин в квантовой и классической механике.
А2. Выведите необходимое и достаточное условие совместной точной
измеримости двух наблюдаемых.
Вопросы по курсу «Квантовая механика»
455
Лекция 3
Б1. Запишите уравнение непрерывности для нерелятивистской частицы.
Запишите выражение для плотности вероятности р и потока j в терминах
волновой функции частицы.
Б2. Запишите поток вероятности для свободной волны де Бройля.
БЗ. Запишите волновую функцию свободной частицы в состоянии с за¬
данным значением импульса, нормированном на (р|р/) = (2пК)3 5(р — р7).
Б4. Запишите выражение для волнового пакета частицы с заданным за¬
коном дисперсии Е = Е (р).
Б5. Запишите выражение для фазовой скорости в волновом пакете i/ph.
Б6. Запишите выражение для групповой скорости в волновом пакете vgr.
Б7. Как связаны ширина волнового пакета в координатном и импульсном
пространствах?
А dF
Б8. Какому уравнению удовлетворяет интеграл движения F, если — = О?
dt
Б9. Эрмитовы операторы / и g коммутируют с гамильтонианом Я:
[/, Н] = [£, Я] =0,
но [/, g] ф0. Что можно сказать о базисе стационарных состояний |Е, /)?
Б10. Запишите однокомпонентную волновую функцию, отвечающую со¬
стоянию, обращенному по времени.
Б11. Как связаны операторы в представлении Гейзенберга с операторами
в представлении Шрёдингера?
Б12. Как связаны состояния в представлении Гейзенберга с состояниями
в представлении Шрёдингера?
Ml. Выведите уравнение непрерывности для плотности вероятности не¬
релятивистской частицы, движущейся в потенциале, из уравнения Шрёдин¬
гера.
М2. Чему равны матричные элементы (г|р|г7) и (р|г|р7)?
М3. Покажите, что уравнение Шрёдингера для нерелятивистской части¬
цы в потенциале, не зависящем от времени, инвариантно относительно об¬
ращения стрелы времени.
М4. Запишите производную оператора по времени в представлении Гей¬
зенберга в базисе стационарных состояний.
А1. Выведите выражение для матричного элемента (г|р|г'), исходя из
канонического квантования, т. е. из коммутатора координаты и импульса.
А2. Докажите условие вырождения базиса стационарных состояний с
энергией Е по значениям оператора /, коммутирующего с гамильтонианом.
456
Вопросы по курсу «Квантовая механика»
АЗ. Выведите соотношение неопределенности энергия-время из уравне¬
ния Гейзенберга для незамкнутых систем.
А4. Дайте определение антилинейного унитарного оператора. Рассмот¬
рите операцию обращения стрелы времени для уравнения Шрёдингера с од¬
нокомпонентной волновой функцией.
А5. Запишите уравнения движения для гармонического осциллятора в
представлении Гейзенберга. Какое уравнение служит условием квантова¬
ния? Вычислите матричные элементы координаты и импульса и получите
спектр энергии квантового осциллятора.
Лекция 4
Б1. Запишите «квантовое действие» для «поля» Ф(г, t), из которого сле¬
дует уравнение Шрёдингера для нерелятивистской частицы. Какая величина
является обобщенной координатой?
Б2. Запишите глобальное калибровочное преобразование для волновой
функции.
БЗ. Запишите уравнение Шрёдингера для нерелятивистской бесспиновой
частицы в электромагнитном поле.
Б4. Запишите стационарное уравнение Шрёдингера в импульсном пред¬
ставлении.
Б5. Запишите оператор координаты в импульсном представлении.
Б6. Запишите действие оператора зеркальной инверсии пространства на
однокомпонентную волновую функцию в координатном представлении.
Б7. Запишите оператор трансляций координат на вектор а. Чему равны
собственные значения этого оператора трансляций?
Б8. Какие квантовые числа определяют энергию стационарного состоя¬
ния в периодическом потенциале?
Ml. Сформулируйте вариационную задачу для основного стационарного
уровня квантовой системы.
М2. Запишите калибровочное преобразование для координатного базиса
и определение «длинной производной».
М3. Выведите импульсное представление стационарного уравнения Шрё¬
дингера из его операторного вида в обозначениях Дирака.
М4. Докажите эрмитовость оператора пространственной четности и
определите его собственные значения.
М5. Запишите определение функции Блоха с параметром квазиимпуль¬
са fc и периодом а. Каков результат действия оператора трансляций с векто¬
ром сдвига а на функцию Блоха?
Вопросы по курсу «Квантовая механика»
457
А1. Выведите закон сохранения тока вероятности и электромагнитного
тока, исходя из калибровочного принципа и теоремы Нётер для «квантового
действия».
А2. Каким свойством обладают собственные значения унитарного опера¬
тора? Докажите его.
АЗ. Докажите, что энергия стационарного состояния в периодическом
потенциале зависит от квадрата квазиимпульса и каждому значению ква¬
зиимпульса соответствует счетное число значений энергии, т. е. существуют
зоны.
Одномерное движение
Лекция 5
Б1. Запишите уравнение Шрёдингера для стационарных состояний нере¬
лятивистской частицы, совершающей одномерное движение в потенциале
VM.
Б2. Дайте определение вронскиана.
БЗ. Чему равна степень вырождения стационарных квантовых состояний
одномерного движения, инфинитного в обе стороны? Каков спектр таких
состояний?
Б4. Чему равна степень вырождения стационарных квантовых состояний
одномерного движения, финитного хотя бы в одну сторону? Каков спектр
состояний, инфинитных в одну сторону?
Б5. Каков спектр связанных состояний (одномерное финитное движение
в обе стороны)?
Б6. Запишите выражение для асимптотического поведения волновой
функции в непрерывном спектре при одномерном движении в инфинитную
сторону.
Б7. Запишите выражение для асимптотического поведения волновой
функции при одномерном движении в финитную сторону.
Б8. Асимптотическое поведение волновой функции на бесконечности при
одномерном движении в задаче рассеяния.
Б9. Дайте определение коэффициентов отражения и прохождения в за¬
даче рассеяния при одномерном движении. Как эти коэффициенты связаны
согласно сохранению потока вероятности?
Ml. Запишите производную вронскиана по координате W/(xplf\p2) на
функциях-решениях уравнения Шрёдингера с энергией Еъ Е2 соответственно.
М2. Докажите, что два решения уравнения Шрёдингера я/^Ос), гр2(х)
с энергией Е пропорциональны друг другу, если у них есть общий узел х0.
М3. Докажите, что спектр стационарных состояний при инфинитном од¬
номерном движении хотя бы в одну сторону непрерывен.
458
Вопросы по курсу «Квантовая механика»
М4. Сформулируйте осцилляторную теорему.
М5. Сформулируйте следствие осцилляторной теоремы в случае потенци¬
ала, инвариантного относительно зеркальной инверсии координаты.
Мб. Что такое соотношение взаимности для коэффициентов прохожде¬
ния в одномерном случае?
М7. Запишите амплитуду Брейта—Вигнера для резонанса. Как ширина
резонанса связана с временем его жизни?
А1. Докажите осцилляторную теорему.
А2. Докажите соотношение взаимности для коэффициентов прохожде¬
ния в одномерном случае.
Гармонический осциллятор
Лекция 6
Б1. Запишите гамильтониан гармонического осциллятора как функцию
импульса и координаты и как оператор в координатном представлении.
Б2. Запишите соотношение Фейнмана—Хеллмана для производной соб¬
ственного значения наблюдаемой по параметру.
БЗ. Запишите теорему вириала в квантовой механике нерелятивистской
частицы в общем случае и для однородного потенциала степени 2а.
Б4. Чему равны характерные значения координаты, импульса и энергии
осциллятора с массой т и частотой со (осцилляторные единицы)?
Б5. Запишите гамильтониан гармонического осциллятора в терминах
безразмерных координаты Q и импульса V.
Б6. Запишите определения операторов повышения af и понижения а
числа квантов гармонического осциллятора в терминах безразмерных коор¬
динаты Q и импульса V.
Б7. Запишите коммутационное соотношение для операторов [а, а1"].
Б8. Запишите оператор числа квантов осциллятора в терминах повыша¬
ющего и понижающего операторов.
Б9. Запишите гамильтониан гармонического осциллятора в терминах
операторов рождения и уничтожения.
Б10. Запишите результат действия повышающего и понижающего опера¬
торов на стационарное состояние с п квантами. Чему равно а|0)?
Б11. Запишите спектр энергии гармонического осциллятора.
Б12. Запишите выражение для состояния осциллятора с п квантами в ви¬
де действия оператора, зависящего от операторов рождения и уничтожения,
на основное состояние.
Вопросы по курсу «Квантовая механика»
459
Б13. Запишите волновую функцию основного состояния гармонического
осциллятора в координатном и импульсном представлениях в терминах без¬
размерных координаты и импульса.
Б14. Сколько узлов и какова четность у полинома Эрмита Нn(z)?
Б15. Запишите общий вид волновой функции, минимизирующей соотно¬
шение неопределенностей координата-импульс. От скольких параметров она
зависит и каков их физический смысл?
Ml. Докажите соотношение Фейнмана—Хеллмана для производной соб¬
ственного значения наблюдаемой по параметру.
М2. Докажите теорему вириала.
М3. Выведите результат действия повышающего и понижающего опера¬
торов на стационарное состояние с п квантами.
М4. Выведите выражение для волновой функции состояния гармониче¬
ского осциллятора с п квантами в терминах полиномов Эрмита.
! М5. Выведите выражение для произведения дисперсии координаты и им¬
пульса в стационарном состоянии гармонического осциллятора с п кванта¬
ми.
Мб. Выведите выражения для операторов рождения и уничтожения кван¬
тов гармонического осциллятора в представлении Гейзенберга.
М7. Какому уравнению удовлетворяет волновая функция, минимизирую¬
щая соотношение неопределенностей координата-импульс?
М8. Запишите основное уравнение, определяющее когерентное состоя¬
ние гармонического осциллятора с комплексным параметром а. Какой фи¬
зический смысл имеют Re а, Im а, |а|2?
М9. Каково распределение вероятностей рп обнаружить п квантов в ко¬
герентном состоянии осциллятора?
М10. Получите выражения для зависимости средних координаты и им¬
пульса осциллятора в когерентном состоянии от времени, исходя из зависи¬
мости от времени комплексного параметра a(t) и его физического смысла.
А1. Выведите разложение когерентного состояния по базису стационар¬
ных состояний гармонического осциллятора.
А2. Докажите, что когерентное состояние гармонического осциллятора
остается таким в ходе его эволюции по времени.
АЗ. Докажите соотношение полноты когерентных состояний гармониче¬
ского осциллятора.
А4. Выведите волновые функции стационарных состояний гармониче¬
ского осциллятора в голоморфном представлении, а также вид операторов
рождения и уничтожения в этом представлении. Получите выражение для
скалярного произведения волновых функций в голоморфном представлении.
460
Вопросы по курсу «Квантовая механика»
Непрерывные симметрии
Лекция 7
Б1. Запишите преобразование трансляции в классике, действие операто¬
ра трансляции fa на базис в координатном представлении и на волновую
функцию в этом представлении.
Б2. Запишите оператор трансляций Та в виде функции от оператора им¬
пульса.
БЗ. Запишите бесконечно малое преобразование вектора координат при
вращении на угол 5 у.
Б4. Чему равен коммутатор орбитального момента L со скалярной вели¬
чиной С?
Б5. Чему равен коммутатор орбитального момента La с векторной вели¬
чиной А^?
Б6. Запишите коммутационные соотношения [1а, 1^] для оператора орби¬
тального момента, где l = L/h.
Б7. Запишите коммутационные соотношения [Za, I2] для оператора орби¬
тального момента и его квадрата, где Z = L/fi.
Б8. Запишите оператор орбитального момента в координатном представ¬
лении.
Б9. Запишите преобразование координат в классике при вращениях в
матричном виде, если —матрица вращений, действие оператора вращений
на базис в координатном представлении и на волновую функцию скалярной
частицы (без поляризации) в этом представлении.
Б10. Запишите связь оператора вращений вокруг оси на угол ip с опера¬
тором орбитального момента.
Ml. Запишите связь матричного элемента (r'|F|r) оператора F в коорди¬
натном базисе с матричным элементом оператора, получаемого после транс¬
ляций, в базисе преобразованных координат.
М2. Запишите преобразование оператора F при действии трансляций ta.
М3. Как связан оператор Fa, полученный из F при трансляциях Га, с об¬
ратным преобразованием классической величины F?
М4. Какой оператор является генератором трансляций?
М5. Запишите вектор-матрицу, которая является генератором вращений
для координат.
Мб. Запишите матрицу конечных поворотов на угол </> для вектора коор¬
динат и ее основные свойства.
М7. Какая величина является канонически сопряженной вектору угла
поворотов вокруг заданной оси? Какая наблюдаемая является генератором
вращений?
Вопросы по курсу «Квантовая механика»
461
М8. Запишите преобразование координат в классике при вращениях в
матричном виде, если 9L — матрица вращений, действие оператора вращений
на базис в координатном представлении и на волновую функцию векторной
частицы в этом представлении.
М9. Запишите оператор вращений на угол (р для векторной частицы. Что
является оператором спина в этом случае?
М10. Чему равен коммутатор орбитального момента со спином [La, S^]?
А1. Выведите связь генератора трансляций обобщенной координаты с ка¬
нонически сопряженным к этой координате импульсом в квантовой механи¬
ке.
А2. Покажите, что генераторы непрерывных преобразований образуют
алгебру Ли.
АЗ. Выведите коммутационные соотношения орбитального момента со
скалярными и векторными наблюдаемыми.
А4. Выведите оператор спина для векторной частицы при получении за¬
кона преобразования волновой функции векторной частицы при вращениях
на угол (р.
Лекция 8
Б1. Дайте определение повышающего и понижающего операторов мо¬
мента импульса /±.
Б2. Запишите выражение для квадрата момента импульса j2 через опера¬
торы }z и /±.
БЗ. Запишите коммутационные соотношения для компонент момента
импульса [/*,/±].
Б4. Какие значения может принимать проекция момента импульса на
ось z?
Б5. Какова область допустимых значений орбитального момента?
А
Б6. Запишите оператор проекции орбитального момента lz в полярных
координатах.
Б7. Как действуют операторы орбитального момента I2 и lz на сфериче¬
ские функции-гармоники Щ}т(в, ip)l
Б8. Какая функция является собственной для оператора орбитального
момента lz с собственным значением т?
Ml. Запишите результат действия операторов момента импульса на ба¬
зисные состояния j2\j, m).
М2. Запишите результат действия операторов момента импульса на ба¬
зисные состояния jz\j, m).
462
Вопросы по курсу «Квантовая механика»
М3. Запишите результат действия операторов момента импульса на ба¬
зисные состояния j+\j, j).
М4. Запишите результат действия операторов момента импульса на ба¬
зисные состояния j_|j, —j).
М5. Запишите результат действия операторов момента импульса на ба¬
зисные состояния j+\j9 т).
Мб. Запишите результат действия операторов момента импульса на ба¬
зисные состояния j_\j, m).
М7. Чему равен матричный элемент (j, n\j±\j, т)?
М8. Запишите выражение для V в полярных координатах.
М9. Запишите операторы проекций орбитального момента Z± в полярных
координатах.
М10. Запишите функциональную зависимость от углов 0 и ip сфериче¬
ской гармоники </?).
Mil. Чему равна четность полинома Лежандра Рг(£)?
М12. Запишите связь сферической гармоники ip) с полиномом Ле¬
жандра P/Ccos 0).
М13. Чему равна четность присоединенного полинома Лежандра Pi>m(£)?
М14. Чему равна четность сферической гармоники ^>т(0, </0?
М15. Каким соотношением связаны сферические гармоники Щт(0,<р)
и ip)?
А1. Проведите квантование момента импульса, исходя из коммутацион¬
ных соотношений.
А2. Выведите выражения для операторов орбитального момента lz, l±, I2
в полярных координатах.
АЗ. Получите выражение для сферической гармоники ip) через по¬
линомы Лежандра. Обоснуйте соотношение ортонормируемости полиномов
Лежандра.
А4. Постройте связь сферической гармоники Щ}ТП(в9 ip) с присоединен¬
ными полиномами Лежандра при m > 0.
Лекция 9
Б1. Дайте определение о--матриц Паули в явном виде.
Б2. Запишите коммутационные соотношения [&а, о^] для <т-матриц Пау¬
ли.
БЗ. Каков физический смысл двухкомпонентного спинора Паули?
Б4. Чему равно (а • е)2, где о-—матрицы Паули, а е—единичный вектор?
Б5. Как преобразуется спинор Паули я/*а(г) при повороте вокруг некото¬
рой оси на угол 2тг?
Вопросы по курсу «Квантовая механика»
463
Б6. Чему равна волновая функция двух тождественных частиц с полуце-
лым спином, находящихся в тождественных квантовых состояниях?
Б7. Сформулируйте принцип запрета Паули.
Ml. Каковы симметрийные свойства волновых функций для двух тожде¬
ственных фермионов и бозонов?
М2. Запишите антикоммутационные соотношения {&а,&р} для сг-мат¬
риц Паули.
М3. Раскройте произведение матриц Паули &а&р.
М4. Раскройте произведение (а• <т)(Ь• а), где а-—матрицы Паули, а а
и Ъ — векторы.
М5. Раскройте выражение для оператора вращения спинора Паули elS v>
на угол </? = (ре, где е — единичный вектор вдоль оси поворота.
Мб. Запишите спинорную метрику ёа& в явном виде как матрицу.
М7. Запишите скалярное произведение яр • % двух спиноров Паули яр а и Хр
покомпонентно.
М8. Как связан сопряженный спинор г/iа со спинором Паули яра?
М9. Чему равны собственные значения оператора перестановки двух тож¬
дественных частиц для фермионов и бозонов?
М10. Чему равны коммутаторы оператора перестановки двух тождествен¬
ных частиц с наблюдаемыми физической системы?
Mil. Запишите перестановочное соотношение для операторов рождения
и уничтожения фермионного осциллятора а и а1. Чему равны квадраты этих
операторов?
М12. Запишите уравнение, определяющее когерентное состояние ферми¬
онного осциллятора. Чему равен квадрат грассмановой переменной?
А1. Выведите выражения для о*-матриц Паули, исходя из общих выраже¬
ний для матричных элементов оператора момента импульса в случае спина
-!•
А2. Выведите соотношения, устанавливающие эквивалентность транспо¬
нированного представления группы вращения спиноров эрмитово сопряжен¬
ному представлению этой группы и эквивалентность комплексно сопряжен¬
ного представления исходному спинорному представлению.
АЗ. Логически обоснованно введите спинорную метрику, сопряженные
спиноры Паули и спинорную метрику для них. Покажите, что спинорная
метрика инвариантна относительно действия операции вращения.
А4. Покажите тождественные свойства и отличия групп вращения SU(2)
и SO(3).
464
Вопросы по курсу «Квантовая механика»
А5. Постройте соответствие между операторами числа квантов, рожде¬
ния и уничтожения квантов фермионного осциллятора и операторами спина
ч-
А6. Постройте разложение когерентного состояния фермионного осцил¬
лятора по базису с определенным числом квантов.
А7. Постройте голоморфное представление для фермионного осциллято¬
ра. Получите полноту когерентных состояний, подходящим образом опреде¬
лив интегрирование грассмановых переменных.
Лекция 10
Б1. Запишите матрицу поворота спинора на угол а вокруг оси z.
Б2. Запишите оператор кинетической энергии двух частиц с массами тг
и т2 через относительные координаты и координаты центра масс (дайте
определение этих координат).
БЗ. Перечислите квантовые числа частицы, совершающей движение в
центральном потенциале.
Б4. Запишите стационарное уравнение Шрёдингера для радиальной вол¬
новой функции R(r) частицы, движущейся в центральном потенциале с за¬
данным орбитальным моментом I.
Б5. Запишите вклад в потенциальную энергию радиального движения
частицы в центральном потенциале за счет центробежных сил при заданном
орбитальном моменте Z.
Б6. Запишите асимптотическое поведение радиальной волновой функ¬
ции R(r) при г —»О для частицы, движущейся в центральном потенциале
с орбитальным моментом Z.
Ml. Запишите матрицу конечных поворотов спинора в виде произведе¬
ния матриц вращения на углы Эйлера.
М2. Запишите выражение для квадрата импульса р2 через оператор орби¬
тального момента и операторы дифференцирования по радиусу (разделение
переменных в полярных координатах).
М3. Дайте определение оператора радиального импульса в полярных ко¬
ординатах.
М4. Запишите стационарное уравнение Шрёдингера для зависящей от
модуля радиуса функции u (г) = rR(r), определенной посредством радиальной
волновой функции R(r) для частицы, движущейся в центральном потенциале
с заданным орбитальным моментом I. Какому условию должна удовлетво¬
рять и (г) при г —> О?
А1. Выведите выражение для матрицы конечных поворотов спинора че¬
рез углы Эйлера.
Вопросы по курсу «Квантовая механика»
465
А2. Выведите выражение для оператора кинетической энергии двух ча¬
стиц с массами тг и т2 через относительные координаты и координаты
центра масс.
АЗ. Выведите выражение для квадрата импульса р2 через оператор орби¬
тального момента и операторы дифференцирования по радиусу (разделение
переменных в полярных координатах).
А4. Докажите эрмитовость оператора радиального импульса в полярных
координатах.
Атом ВОДОРОДА
Лекция 11
Б1. Перечислите квантовые числа электрона в атоме водорода.
Б2. Запишите атомные единицы скорости, импульса, энергии (один Рид-
берг), боровский радиус и постоянную тонкой структуры через заряд элек¬
трона, его массу и постоянные Й, с.
БЗ. Запишите спектр уровней атома водорода.
Б4. Как связано главное квантовое число с радиальным квантовым чис¬
лом и орбитальным моментом в атоме водорода?
Б5. Какую характеристику радиальной волновой функции электрона в
атоме водорода указывает радиальное квантовое число пг?
Б6. Чему равна степень вырождения уровня энергии в атоме водорода
с главным квантовым числом п (без учета спина электрона)?
Б7. Чему равно среднее значение обратного радиуса (1 /г) в состоянии
атома водорода с главным квантовым числом п?
Ml. Сколько узлов имеет полином Лагерра для квантового состояния
атома водорода с главным квантовым числом п и орбитальным моментом I?
М2. Запишите выражение для вектора Рунге—Ленца.
М3. Запишите асимптотическое поведение радиальной волновой функ¬
ции электрона в атоме водорода с главным квантовым числом п и орбиталь¬
ным моментом I при г —> + оо.
А1. Выведите выражение для спектра связанных уровней электрона в ато¬
ме водорода.
А2. Покажите с помощью вектора Рунге—Ленца, что уровни энергии в
атоме водорода вырождены по орбитальному моменту и по четности.
АЗ. Выведите рекуррентные соотношения Крамерса для средних значе¬
ний радиуса в атоме водорода.
А4. Выведите выражение для связи радиальной волновой функции в нуле
со средними от степеней радиуса, получите формулу для |ФП5(0)|2 в случае
атома водорода.
466
Вопросы по курсу «Квантовая механика»
Квазиклассика1
Лекция 12
Б1. Запишите выражение для импульса частицы в квазиклассическом
приближении.
Б2. Запишите выражение для стационарной волновой функции в класси¬
чески доступной области в квазиклассическом приближении.
БЗ. Запишите условие применимости квазиклассического приближения.
Б4. Запишите правило квантования Бора—Зоммерфельда для частицы
в потенциальной яме.
Б5. Чему равен фазовый объем АГ на одно квантовое состояние в квази¬
классике?
Б6. Запишите коэффициент прохождения потенциального барьера в ква¬
зиклассике.
Ml. Как связана амплитуда АО) волновой функции стационарного состо¬
яния грОс) = A(x)e*SM с ее фазой S(x), если А(х) и S(x) —четные функции ft?
М2. Запишите квазиклассическое выражение для волновой функции
справа от потенциального барьера с конечной силой возврата в классически
доступной области.
М3. Запишите квазиклассическое выражение для волновой функции сле¬
ва от потенциального барьера с конечной силой возврата в классически
доступной области.
М4. Запишите квазиклассическое выражение для волновой функции в об¬
ласти потенциального барьера с конечной силой возврата в классически
недоступной области, простирающейся до бесконечности.
М5. Запишите выражение для волновой функции справа от потенциаль¬
ного барьера с бесконечной силой возврата в классически доступной области
в квазиклассике.
Мб. Запишите выражение для энергетической плотности состояний в
квазиклассическом приближении.
М7. Запишите поправку к уровню энергии за счет введения малого воз¬
мущения к потенциалу 5V(x) в квазиклассическом приближении.
М8. Запишите условие применимости формулы для вероятности туннель¬
ного перехода в квазиклассике в терминах длины волны.
А1. Получите систему уравнений для амплитуды и фазы волновой функ¬
ции в классически доступной области. Покажите, что одно из них эквива¬
лентно уравнению непрерывности, а второе при ft —> 0 сводится к уравнениям
Гамильтона—Якоби.
ХВ вопросах, если специально не указано, имеется в виду одномерное движение частицы.
Вопросы по курсу «Квантовая механика»
467
А2. Проведите разложение JWKB для волновой функции стационарного
состояния при одномерном движении вплоть до членов первого порядка
ПО Й2.
АЗ. Выведите правила квантования Бора—Зоммерфельда.
А4. Выведите выражение для энергетической плотности состояний в ква-
зиклассическом приближении.
А5. Выведите условие нормировки волновой функции в квазиклассике.
А6. Рассмотрите влияние возмущения потенциала на уровень связанного
состояния в квазиклассике.
А7. Рассмотрите флуктуации кинетической и потенциальной энергии в
области, доступной для классической частицы, и вне ее в рамках квазиклас¬
сического приближения.
Часть 2
Теория возмущений
Лекция 15
Б1. Запишите формулу для поправки первого порядка к энергии в стаци¬
онарной теории возмущений для невырожденного случая.
Б2. Запишите формулу для поправки второго порядка к энергии в стаци¬
онарной теории возмущений для невырожденного случая.
БЗ. Запишите критерий применимости стационарной теории возмуще¬
ний в первом порядке в невырожденном случае.
Б4. Запишите секулярное уравнение в теории возмущений для поправки
к энергии в первом порядке.
Б5. Что определяют собственные векторы матрицы возмущений первого
порядка в вырожденном случае?
Б6. Запишите решение для оператора эволюции в представлении взаимо¬
действия в первом порядке теории возмущений.
Б7. Запишите амплитуду перехода между начальным и конечным кванто¬
выми состояниями в первом порядке нестационарной теории возмущений.
Б8. Запишите «золотое правило Ферми» для дифференциальной вероят¬
ности перехода в единицу времени между начальным и конечным квантовы¬
ми состояниями в непрерывном спектре в первом порядке нестационарной
теории возмущений.
Б9. Запишите критерий применимости нестационарной теории возму¬
щений в первом порядке.
Б10. Запишите критерий применимости приближения мгновенного вклю¬
чения взаимодействия.
468
Вопросы по курсу «Квантовая механика»
Ml. Запишите формулу для поправки первого порядка к исходному кван¬
товому состоянию в стационарной теории возмущений для невырожденного
случая.
М2. Каким условием однозначно фиксируется ряд разложения квантово¬
го состояния по малому параметру (константе связи) возмущения в невырож¬
денном случае стационарной теории возмущений?
М3. Запишите уравнения для оператора эволюции в представлении взаи¬
модействия. Как определяется потенциал в представлении взаимодействия?
М4. Как связан оператор эволюции в представлении взаимодействия с
операторами эволюции системы без возмущения и с возмущением?
М5. Запишите общее решение уравнения для оператора эволюции в пред¬
ставлении взаимодействия.
Мб. Запишите вероятность перехода между квантовыми состояниями за
конечное время в случае постоянного, не зависящего от времени возмуще¬
ния.
М7. Запишите квантовое состояние в адиабатическом приближении для
гамильтониана, зависящего от параметра, медленно меняющегося со време¬
нем, в случае, если известны собственные состояния этого гамильтониана
в каждый момент времени и эти состояния никогда не вырождены.
М8. Запишите критерий применимости адиабатического приближения
в терминах частот, характеризующих квантовые переходы в системе и зави¬
симость параметров гамильтониана от времени.
А1. Выведите рекуррентные соотношения для поправок к энергии и кван¬
товому состоянию в стационарной теории возмущений в невырожденном
случае.
А2. Рассмотрите теорию возмущений для вырожденных уровней энергии
в первом порядке, выведите выражение для правильных функций ведущего
приближения и секулярное уравнение.
АЗ. Рассмотрите точное решение задачи стационарной теории с возмуще¬
нием для системы с двумя уровнями в случае, когда уровни находятся близко
друг к другу.
А4. Дайте определение представления взаимодействия для операторов
и квантовых состояний.
А5. Выведите вероятность перехода между квантовыми состояниями за
конечное время в случае постоянного, не зависящего от времени возмуще¬
ния.
А6. Покажите, что для периодического возмущения амплитуды индуци¬
рованного излучения и поглощения равны друг другу.
А7. Выведите критерий применимости приближения мгновенного вклю¬
чения возмущения.
Вопросы по курсу «Квантовая механика»
469
А8. Выведите адиабатическое приближение для квантовой системы с га¬
мильтонианом, зависящим от параметра, медленно меняющегося со време¬
нем, в случае, если известны собственные состояния этого гамильтониана
в каждый момент времени и эти состояния никогда не вырождены.
А9. Введите понятие фазы Берри для квантового состояния в адиабатиче¬
ском приближении.
Сложение моментов
Лекция 16
Б1. Запишите допустимые значения суммы J двух моментов j\ и j2 и ее
проекции М.
Б2. Сколько состояний имеет сумма J двух моментов j\ и j2?
БЗ. Запишите правила отбора для матричных элементов неприводимого
тензорного оператора Т® в переходе J -> У по проекции момента и его
модулю. Какие переходы запрещены при j Ф О?
Ml. Дайте определение коэффициентов Клебша—Гордана в терминах ска¬
лярного произведения базисных состояний двух моментов jl9 j2 и их сум¬
мы J.
М2. Сформулируйте теорему Вигнера—Эккарта.
А1. Выведите соотношения для коэффициентов Клебша—Гордана, исходя
из ортогональности и полноты базиса состояний.
А2. Введите неприводимый тензорный оператор момента j с проекцией
m в стандартном представлении в терминах базисных состояний; выведите
коммутационные соотношения этого оператора с оператором момента и его
трансформационные свойства при вращениях.
Релятивистская квантовая механика
Лекция 17
Б1. Запишите покомпонентно спиновую матрицу (sa)igr для векторной
частицы.
Ml. Дайте определение тензорного оператора орбитального момента Lap
и тензора спина для векторной частицы.
М2. Запишите преобразование векторного поля Ак(х) при бесконечно
малых преобразованиях группы Лоренца х/к = хк + сокпхп с антисимметрич¬
ными параметрами сокп = — <опк.
М3. Запишите полный набор коммутационных соотношений для генера¬
торов вращений ja и бустов К?.
470
Вопросы по курсу «Квантовая механика»
М4. Запишите условия на матрицу преобразований дифференциалов ко¬
ординат Л™, задающие собственную ортохронную группу Лоренца.
М5. Запишите выражения для инвариантов группы Лоренца в терминах
генераторов вращений j и бустов К.
Мб. Какими квантовыми числами характеризуется частица относительно
преобразований группы Лоренца?
М7. Какие квантовые числа имеют спиноры с индексами с точками %а
и без точек ва?
М8. Запишите генераторы вращений j и бустов К для спиноров и 0а.
М9. Запишите определение 4-векторов сгт и <тт в терминах матриц Паули.
М10. Чему равны выражения (ат<тп + ап<тт)2 и (<ттстп-{-<тГ1<тт)??
р р
А1. Введите понятие собственной ортохронной группы Лоренца.
А2. Определите дискретные преобразования инверсии пространства и
стрелы времени пространства Минковского и соответствующие компоненты
группы Лоренца, а также действие инверсий на генераторы преобразований
группы и мнимую единицу.
АЗ. Обоснуйте введение группы SL(2, С) для релятивистских спиноров.
А4. Как связан 4-вектор Vm с его представлением в группе SL(2, С)? Обос¬
нуйте.
А5. Введите генераторы преобразования релятивистских спиноров сгтп
и <гтп и запишите их покомпонентный вид в терминах матриц Паули.
Лекция 18
Б1. Запишите коммутационные соотношения 4-импульса (р0, р“) с гене¬
раторами вращений и бустов Ю.
Б2. Какими инвариантами относительно преобразований группы Пуан¬
каре характеризуется релятивистская частица?
БЗ. Перечислите квантовые числа свободной массивной релятивистской
частицы.
Б4. Перечислите квантовые числа свободной безмассовой релятивист¬
ской частицы.
Б5. Запишите уравнение Клейна—Гордона—Фока. Какими квантовыми
числами обладает частица, поле которой удовлетворяет этому уравнению?
Ml. Дайте определение псевдовектора Паули—Любанского Wm.
М2. Запишите действие для вещественного скалярного поля.
М3. Запишите коммутационные соотношения для операторов рождения
и уничтожения частиц вещественного скалярного поля.
М4. Запишите 4-вектор тока для комплексного скалярного поля.
Вопросы по курсу «Квантовая механика»
471
А1. Проведите классификацию квантовых чисел массивных и безмассо-
вых частиц относительно преобразований группы Пуанкаре.
А2. Какими уравнениями характеризуются киральные и спиральные по¬
ля?
АЗ. Выведите ковариантный вид коммутационных соотношений для ге¬
нераторов группы Пуанкаре, исходя из их покомпонентного определения
с разделением на пространственную и временную части.
А4. Как действуют дискретные операции инверсии пространства и вре¬
мени на генераторы группы Пуанкаре, спиральность и вектор Паули—Любан-
ского?
А5. Обоснуйте СРТ-теорему для эрмитова действия.
А6. Исходя из действия для вещественного скалярного поля, получите
выражение для его гамильтониана.
А7. Определите положительно и отрицательно частотные компоненты
вещественного скалярного поля.
А8. Запишите энергию вещественного скалярного поля в терминах его
фурье-компонент а(7с).
А9. Введите динамические координаты и импульс для вещественного ска¬
лярного поля и проведите их квантование в терминах операторов рождения
и уничтожения.
А10. Определите операцию нормального упорядочивания оператора.
All. Какие состояния образуют фоковское пространство для квантового
вещественного скалярного поля? Запишите общий вид элемента этого про¬
странства.
А12. Запишите квантованное комплексное скалярное поле в терминах
операторов рождения и уничтожения.
А13. Получите выражение для оператора заряда для комплексного ска¬
лярного поля.
А14. Запишите действие операторов зарядового сопряжения, инверсии
времени и пространства на одночастичные состояния и вакуум в фоковском
пространстве для комплексного скалярного поля и на само это поле.
Лекция 19
Б1. Запишите уравнение Дирака для спинора я/>(х).
Б2. Распишите покомпонентно символ р в терминах матриц Дирака.
БЗ. Запишите матрицы Дирака в дираковском представлении в терминах
матриц Паули.
Ml. Запишите «уравнение Шрёдингера» для правого вейлевского спино¬
ра
472
Вопросы по курсу «Квантовая механика»
М2. Запишите «уравнение Шрёдингера» для левого вейлевского спино¬
ра в.
М3. Дайте определение дираковски сопряженного спинора.
М4. Чему равны у\, у2, у2?
М5. Какими тензорными свойствами относительно преобразований гру¬
ппы Лоренца обладают величины 'ф'ф, ipym,xp, грсгтп'ф, •фуз'ф, “фуьУт,ф1
Мб. Запишите действие для массивного спинора Дирака.
М7. Запишите сумму по поляризациям для частиц массивного поля Дира¬
ка П(р) = 2 ия(р)йл(р).
я
М8. Чему равен заряд майорановской частицы?
А1. Запишите действие, гамильтониан и заряд для классического правого
вейлевского поля.
А2. Запишите выражение для квантованного правого вейлевского поля
в терминах операторов рождения и уничтожения.
АЗ. Запишите (анти)коммутационные соотношения для операторов рож¬
дения и уничтожения частиц вейлевского поля. Покажите, что последова¬
тельное квантование вейлевского спинора имеет место только для фермион¬
ного типа коммутационных соотношений.
А4. Рассмотрите действие операции комбинированной CP-четности и ин¬
версии стрелы времени на вейлевский спинор.
А5. Введите безмассовый дираковский спинор в киральном представле¬
нии.
А6. Запишите матрицы Дирака в киральном представлении.
А7. Запишите проекторы на киральные состояния для спинора Дирака
в терминах матрицы у5 и ее явный вид в киральном представлении.
А8. Дайте определение генераторов группы Лоренца &тп для дираковско¬
го спинора через матрицы Дирака.
А9. Введите операции инверсии пространства и заряда для безмассового
дираковского спинора.
А10. Выведите уравнение Дирака, исходя из трансформационных свойств
и квантовых чисел массивного поля со спином
All. Запишите квантованное поле Дирака в терминах операторов рожде¬
ния и уничтожения, указав их физический смысл.
А12. Получите проекторы на состояния с положительной и отрицатель¬
ной проекцией спина дираковской частицы на заданный вектор поляриза¬
ции е.
А13. Выведите выражения для суммы по поляризациям для дираковской
частицы и античастицы.
Вопросы по курсу «Квантовая механика»
473
А14. Рассмотрите действие дискретных симметрий инверсии простран¬
ства, времени и заряда на квантованное дираковское поле.
А15. Запишите действие для майорановского спинора. Обоснуйте это вы¬
ражение.
Лекция 20
Б1. Запишите калибровочное преобразование для одночастичного состо¬
яния с заданным импульсом в фоковском пространстве и для операторов
рождения и уничтожения.
Б2. Запишите выражение для ковариантной производной при наличии
калибровочного векторного поля.
Ml. Запишите уравнения для безмассового векторного поля со спираль¬
ностью Я, которые следуют из релятивистского формализма группы Пуанка¬
ре.
М2. Как связаны тензор напряженности Fkn и дуальный к нему Fkn для
безмассового векторного поля со спиральностью Я?
М3. Запишите действие для безмассового векторного поля.
М4. Запишите связь коммутатора ковариантных производных с тензором
напряженности калибровочного поля.
М5. Запишите действие для поля Дирака во внешнем калибровочном
поле в минимальной схеме взаимодействия.
А1. Покажите, что преобразования Лоренца безмассового векторного по¬
ля приводят к требованию калибровочной инвариантности уравнений дина¬
мического поля.
А2. Запишите выражение для квантованного безмассового векторного
поля в терминах операторов рождения и уничтожения. Какие условия нала¬
гаются на вектор поляризации?
АЗ. Запишите коммутационные соотношения для операторов рождения
и уничтожения безмассового векторного поля.
А4. Запишите уравнения Прока и действие для поля массивной вектор¬
ной частицы.
А5. Выведите связь разности фаз двух трансляций в прямом и обратном
порядке с тензором напряженности калибровочного поля и ее приложение
к эффекту Ааронова—Бома.
А6. Запишите действие для заряженного скалярного поля во внешнем
калибровочном поле в минимальной схеме взаимодействия.
А7. Запишите выражение для энергии связи скалярной релятивистской
частицы в кулоновском потенциале и его разложение по малому парамет¬
ру а2т вплоть до второго порядка малости. Какое вырождение снимает вто¬
рой член приближения? Приведите схему вывода этого результата.
474
Вопросы по курсу «Квантовая механика»
А8. Запишите выражение для энергии связи релятивистского электро¬
на в кулоновском потенциале и его разложение по малому параметру а*т
вплоть до второго порядка малости. Какое вырождение снимает второй член
приближения?
Нерелятивистское приближение
Лекция 21
Б1. Запишите уравнение Паули для нерелятивистского спинора.
Ml. Запишите релятивистскую поправку к кинетической энергии элек¬
трона.
М2. Запишите релятивистскую спин-орбитальную поправку к энергии
электрона во внешнем статическом центральном потенциале </>(г).
М3. Запишите релятивистскую поправку — дарвиновский вклад к энер¬
гии электрона во внешнем статическом центральном потенциале
М4. Какова степень вырождения по орбитальному моменту I состояния
электрона в атоме водорода с заданным значением полного момента j, если
главное квантовое число п > 1? Каковы значения I?
А1. Постройте эффективное действие для нерелятивистского спинора
вплоть до членов второго порядка малости по скорости.
А2. Обоснуйте динамическую природу введения релятивистских попра¬
вок к энергии электрона во внешнем статическом центральном потенциа¬
ле </?(г).
АЗ. Рассчитайте релятивистские поправки в атоме водорода в формализ¬
ме нерелятивистских спиноров.
А4. Запишите действие, приводящее к аномальному магнитному момен¬
ту электрона. Рассмотрите нерелятивистский предел этого действия.
Атом ГЕЛИЯ
Лекция 22
Б1. Запишите гамильтониан для электронов в атоме гелия в нереляти¬
вистском приближении. Сохраняет ли этот гамильтониан орбитальные мо¬
менты электронов по отдельности и суммарный орбитальный момент элек¬
тронов?
Б2. Какое квантовое число электронов задает состояния пара- и ортоге¬
лия и чему оно равно в этих случаях?
БЗ. Какой симметрией по перестановкам электронов обладают простран¬
ственные волновые функции электронов в атоме пара- и ортогелия?
Вопросы по курсу «Квантовая механика»
475
Б4. Какое из состояний гелия имеет меньшую энергию связи—пара- или
ортогелий? За счет какого взаимодействия?
Б5. Дайте определение понятия самосогласованного поля. Что учитывает
этот потенциал наряду с притяжением к ядру атома?
Б6. Какие квантовые числа и для какого гамильтониана определяют кон¬
фигурацию электронов в атоме?
Б7. Вследствие какого взаимодействия состояния электронов с различ¬
ным суммарным спином в атоме имеют различные энергии?
Б8. Какие поправки вызывают расщепление термов электронов в атоме
по суммарным орбитальному моменту и спину?
Б9. Какие поправки вызывают расщепление термов электронов в атоме
по суммарному моменту J?
Ml. Запишите уравнения Хартри для электронов в атоме гелия. Какой
физический смысл имеют энергии связи электронов в этих уравнениях?
М2. Запишите уравнения Хартри—Фока для электронов в атоме гелия.
М3. Вычислите энергию основного состояния атома гелия методом само¬
согласованного поля кулоновского типа с эффективным зарядом Z в первом
порядке теории возмущений.
А1. Покажите, что интеграл обменного взаимодействия в атоме гелия
положителен.
Сложный АТОМ
Лекция 23
Б1. Запишите волновую функцию состояния электронов в атоме в веду¬
щем приближении с учетом спина, если пространственные степени свободы
характеризуются наборами квантовых чисел {къ к2)..., fcn}, а спиновые чис-
ла—{msl, ms2, msn}.
Б2. Запишите определитель Слетера и укажите условия его применения.
Как определяется координата х?
БЗ. Какие квантовые числа имеет заполненная оболочка эквивалентных
электронов?
Б4. Сформулируйте первое правило Хунда.
Б5. Сформулируйте правило интервалов Ланде.
Б6. Сформулируйте второе правило Хунда.
Б7. Укажите характерные значения в электрон-вольтах для энергии связи
электрона на внешней оболочке в атоме в самосогласованном поле, величину
расщепления термов по суммарным орбитальному моменту и спину и рас¬
щепления за счет релятивистских поправок.
476
Вопросы по курсу «Квантовая механика»
Ml. Обоснуйте первое правило Хунда.
М2. Обоснуйте правило интервалов Ланде.
А1. Обоснуйте второе правило Хунда.
Феноменология: атом во внешнем поле
Лекция 24
Б1. Запишите гамильтониан для электронов атома во внешнем электро¬
магнитном поле.
Б2. Запишите гамильтониан для электронов атома во внешнем постоян¬
ном магнитном поле.
БЗ. Запишите магнитный момент электрона в атоме во внешнем посто¬
янном магнитном поле.
Б4. Чему равна атомная единица магнитного поля в гауссах?
Б5. При каких значениях магнитного поля (в гауссах) имеет место ано¬
мальный эффект Зеемана?
Б6. Какие термы испытывают расщепление при аномальном эффекте
Зеемана? По какому квантовому числу происходит расщепление?
Ml. Запишите квадратичный по полю диамагнитный вклад энергии элек¬
тронов атома во внешнем постоянном магнитном поле.
М2. Запишите фактор Ланде в случае аномального эффекта Зеемана и
энергию взаимодействия электронов атома с магнитным полем.
М3. Запишите магнитную восприимчивость для атомов cL = 0hS = 0.
М4. При каких условиях возникает парамагнетизм ван Флека?
М5. При каких условиях возникает эффект Пашена—Бака? Запишите фор¬
мулу для расщепления энергии.
А1. Оцените дипольный магнитный и диамагнитный вклады в энергию
взаимодействия электронов атома с внешним постоянным магнитным полем
в сравнении с энергией связи электронов.
А2. Выведите формулу для аномального эффекта Зеемана, используя тео¬
рему Вигнера—Эюсарта.
Спонтанное излучение
Лекция 25
Б1. Запишите обратное время спонтанного излучения фотона атомом
в дипольном приближении в терминах частоты перехода и матричного эле¬
мента электрического дипольного момента.
Вопросы по курсу «Квантовая механика»
477
Б2. Чему равно характерное время жизни 2р-уровня атома водорода из-за
электрического дипольного излучения?
БЗ. Какими квантовыми числами характеризуются серии Лаймана и
Бальмера в спектрах излучения возбужденных состояний атома водорода?
Б4. Как модифицируется формула для обратного времени спонтанного
дипольного излучения в случае индуцированного излучения и поглощения?
Ml. Запишите потенциал электрического дипольного взаимодействия си¬
стемы электронов со вторично квантованным электромагнитным полем.
М2. Запишите интенсивность спонтанного излучения фотона атомом в
дипольном приближении в терминах частоты перехода и матричного элемен¬
та электрического дипольного момента.
М3. Запишите правила отбора по проекции полного момента электронов
атома при электрическом дипольном излучении.
М4. Запишите правила отбора по проекции суммарного спина электро¬
нов атома при электрическом дипольном излучении.
М5. Запишите правила отбора по полному моменту электронов атома
при электрическом дипольном излучении.
Мб. Какие переходы запрещены при электрическом дипольном излуче¬
нии атома?
М7. Запишите правила отбора по пространственной четности электронов
атома при электрическом дипольном излучении.
А1. Выведите формулу для времени жизни 2р-уровня атома водорода и
интенсивность спонтанного излучения фотона атомом в дипольном прибли¬
жении и рассмотрите общий случай.
А2. Выведите правила отбора и запрета для электрического дипольного
излучения атома.
АЗ. Рассмотрите индуцированное излучение и поглощение когерентного
электромагнитного поля атомом в дипольном приближении.
Рассеяние
Лекция 26
Б1. Запишите оператор функции Грина в стационарной задаче рассея¬
ния—резольвенту Ge.
Б2. Запишите уравнение для функции Грина стационарного уравнения
Шрёдингера GE(r, г').
БЗ. Запишите функцию Грина GE(r, г') в виде разложения по известным
волновым функциям стационарных состояний грп с энергиями Еп.
Б4. В чем заключается борновское приближение в задаче рассеяния?
478
Вопросы по курсу «Квантовая механика»
Б5. Запишите амплитуду рассеяния /(0) на центральном потенциале V
в борновском приближении.
Б6. Запишите условия применимости борновского приближения для мед¬
ленных и быстрых частиц.
Ml. Какие волновые функции отвечают асимптотическим in- и out-состо-
яниям?
М2. Дайте определение элемента У -матрицы рассеяния в терминах опе¬
ратора эволюции и асимптотических состояний.
М3. Запишите плотность вероятности рассеяния частицы в единицу вре¬
мени dvt/fi, если известен элемент У-матрицы.
М4. Дайте определение сечения рассеяния, если известна вероятность
рассеяния частицы в единицу времени dwfi.
М5. Дайте определение запаздывающей функции Грина б it, г; t\ г0 через
матричный элемент оператора эволюции.
Мб. Запишите уравнение для запаздывающей функции Грина уравнения
Шрёдингера б it, г; t;, г7).
М7. Запишите в задаче рассеяния связь волновой функции 'фСх) в про-
странственно-временной точке x = {t, г} с волновой функцией исполь¬
зуя запаздывающую функцию Грина.
М8. Запишите элемент У -матрицы в терминах запаздывающей функции
Грина и волновых функций начального и конечного состояний.
М9. Запишите выражение для функции Грина свободной нерелятивист¬
ской частицы 0£О)(г, г7).
М10. Укажите контур интегрирования и особенности в плоскости ком¬
плексной переменной энергии E = h2k2/2m при вычислении функции Грина
свободной нерелятивистской частицы.
Mil. Запишите интегральное уравнение Липпмана—Швингера для вол¬
новой функции в задаче рассеяния.
М12. Запишите выражение для асимптотического поведения волновой
функции на больших расстояниях в задаче рассеяния.
М13. Запишите формулу для дифференциального сечения рассеяния в
терминах амплитуды /(0).
М14. Запишите формулу оптической теоремы. Какие величины она свя¬
зывает?
А1. Получите формулу для запаздывающей функции Грина Q (х хг) в ви¬
де разложения по волновым функциям стационарных состояний.
А2. Выведите интегральное уравнение для функции Грина бЕ стационар¬
ного уравнения Шрёдингера с потенциалом V и для запаздывающей функции
Грина б М.
Вопросы по курсу «Квантовая механика»
479
АЗ. Выведите выражение для амплитуды рассеяния /(0) в интегральном
представлении для центрального потенциала.
А4. Выведите выражение для дифференциального сечения в терминах
амплитуды рассеяния /(0).
А5. Запишите связь У-матрицы с ^-матрицей рассеяния и соотношение
унитарности для ^-матрицы.
А6. Выведите оптическую теорему в терминах ^-матрицы.
А7. Введите стационарную ^-матрицу и интегральное уравнение для
нее.
Лекция 27
Б1. Запишите радиальную волновую функцию Д^(г) для свободной ча¬
стицы при I = 0.
Б2. Чему равны факторы рассеяния для свободной частицы в централь¬
ном потенциале?
БЗ. Чему равны модули факторов рассеяния в центральном потенциа¬
ле \St \ при упругом рассеянии?
Б4. Запишите определение парциальной амплитуды рассеяния /г в виде
коэффициентов разложения по парциальным волнам амплитуды /(0).
Б5. Запишите связь парциального сечения сгг с фазовым сдвигом 5г.
Б6. Частицы с какими орбитальными моментами I не рассеиваются на
потенциале с радиусом действия а, если их энергия задается волновым век¬
тором к? Почему?
Б7. Какое условие определяет медленные частицы в задаче рассеяния?
Б8. Какие орбитальные моменты доминируют при рассеянии медленных
частиц?
Б9. Какой величиной характеризуется рассеяние медленных частиц? Как
она связана с фазой рассеяния и сечением?
Б10. Какое условие определяет быстрые частицы в задаче рассеяния?
Б11. С какими орбитальными моментами рассеиваются быстрые частицы
на потенциале с радиусом действия а?
Ml. Запишите радиальную волновую функцию Я&(г) для свободной ча¬
стицы.
М2. Запишите асимптотическое поведение радиальной волновой функ¬
ции Rki(r) при г —> оо при рассеянии в центральном потенциале в терминах
фаз рассеяния.
М3. Запишите разложение плоской волны по парциальным волнам (по¬
линомам Лежандра).
М4. Запишите связь парциальной амплитуды рассеяния /г с фазовым
сдвигом 5г.
480
Вопросы по курсу «Квантовая механика»
М5. Запишите оптическую теорему для парциальных сечений упругого
рассеяния.
Мб. Запишите интегральную формулу для сдвига фазы 5г в борновском
приближении.
М7. Как ведет себя фазовый сдвиг как функция волнового вектора к и ор¬
битального момента I при рассеянии в центральном потенциале радиуса а?
М8. Запишите волновую функцию рассеяния тождественных частиц в
центральном потенциале, не зависящем от спина, с четным и нечетным
значением их суммарного спина, а также формулу для дифференциального
сечения.
М9. Запишите формулу Брейта—Вигнера для парциального сечения резо¬
нанса.
М10. Какие значения принимают факторы рассеяния парциальных волн SL
при наличии неупругих каналов рассеяния?
Mil. Запишите парциальные сечения упругого и неупругого рассеяния
в терминах факторов
А1. Получите формулу для радиальной волновой функции Rju(r) для сво¬
бодной частицы в центральном потенциале.
А2. Выведите асимптотическое поведение радиальной волновой функ¬
ции Rki(r) при г-* оо при рассеянии в центральном потенциале в терминах
фаз рассеяния.
АЗ. Выведите разложение плоской волны по парциальным волнам (поли¬
номам Лежандра).
А4. Выведите связь парциальной амплитуды рассеяния с фазовым сдви¬
гом
А5. Докажите оптическую теорему для парциальных сечений упругого
рассеяния.
А6. Выведите интегральную формулу для сдвига фазы 5* и ее вид в бор¬
новском приближении.
А7. Определите понятие диаграммы Аргана для упругого рассеяния и по¬
ясните его физический смысл.
А8. Как расположены особые точки функции Грина в комплексной плос¬
кости энергии при наличии резонансов?
А9. Докажите оптическую теорему при наличии неупругого рассеяния
в терминах парциальных сечений и факторов рассеяния Sj.
Дополнения
После завершения текста лекций в той форме, что изложены в частях I и II,
автору поступили предложения и настоятельные рекомендации включить
в текст книги в качестве дополнений целый ряд вопросов, которые находятся
несколько в стороне от учебного плана, положенного в основу лекции, но
послужили бы в качестве инструмента улучшения цельности и более полного
освещения сути квантовой теории. Не все эти рекомендации могли быть
удовлетворены, поскольку я старался не включать в эту книгу те темы, ко¬
торые традиционно излагаются достаточно полно в других курсах, например,
в статистической физике (скажем, метод квазичастиц) или квантовой теории
поля (лэмбовский сдвиг уровней или принцип причинности в квантовой ре¬
лятивистской теории), а также темы, сами по себе образующие семестровые
курсы, как квантовые вычисления. Поэтому список дополнений выглядит
довольно субъективно и обусловлен лишь степенью готовности автора сжато
и в короткие сроки изложить тот или иной вопрос. Среди вопросов есть
как принципиально-концептуальные, так и иллюстративно-феноменологи-
ческие, а также математически-технические, как, например, кулоновское
рассеяние, которое очень важно и имеет довольно большую область физи¬
ческих приложений.
Дополнение I. Соотношение неопределенностей
и корреляции
Соотношение неопределенностей, полученное нами методом Вейля, ука¬
зывает наименьший предел произведения дисперсий двух наблюдаемых фи¬
зических величин А=А* и В = Bt, которые не коммутируют друг с другом:
(ДЛ)2( AB)2z\([A,Bi)2.
Однако этот предел может быть принципиально недостижим в квантовых
системах, если, как мы покажем ниже, между наблюдаемыми имеется кор¬
реляция.
Как и прежде, введем операторы
а=А — А, Ъ = В-В: А=(Ф|А|Ф), Б = (Ф|В|Ф),
причем
[A)B'] = ihC => [a,b] = ihC,
482
Дополнения
а средние и дисперсии
(Ф|а|Ф> = 0, (Да)2 = (ДЛ)2,
(Ф|6|Ф)=0, (ДЬ)2 = (ДВ)2.
Составим вектор состояния
|Ф) = (аа + /ЗЬ)|Ф),
с комплексными коэффициентами, {а, /3} еС, и найдем его неотрицательную
норму
<Ф|Ф>£0,
так что ввиду эрмитовости операторов
а*а(а2) + /3*13 (b2) + а*/3(аЪ) + /3*а(Ьа) ^ 0. (Д1.1)
Неравенство (Д1.1) можно представить в виде квадратичной формы на дву¬
мерном комплексном пространстве
(Д1.2)
где эрмитова матрица G определяется средними
а_((ДЛ)2 (ah) (т
I <ьа> wtfj' OT'3)
Запишем произведение операторов как сумму их коммутатора и антикомму¬
татора
Тогда
где величину
aS = |{a,S} + i[a, Ь].
обычно нормируют на произведение неопределенностей, так что
\{{А,Ё})-{А){й)
Г ЛАЛВ ^ ^
называют коэффициентом корреляции величин Л и Б. После этого матрица
рассматриваемой квадратичной формы сводится к сумме матрицы корреля¬
ций неопределенностей и квантовой поправки
А А Л
® ^согг ^quant*
где матрица корреляции
_ f (ДА)2 гАААВ\
^гДЛДВ (ДВ)2 )
Дополнение П. Матрица плотности, квантовая запутанность..
483
а квантовая поправка вследствие некоммутативности наблюдаемых
{ о ЫсЛ
Gquant= i 2 • (Д1.6)
^-iS(C) о J
Рассматриваемая квадратичная форма положительно определена, если
собственные значения эрмитовой матрицы G неотрицательны: в базисе соб¬
ственных векторов это утверждение становится элементарным. Собственные
значения Я определяются корнями секулярного уравнения
det{G^} = 0,
откуда
Я2 - Я{(ДА)2 + (ДВ)2} + (АА)2(АВ)2(1 -r2)-j (С)2 = О,
так что согласно теореме Виета для положительной определенности корней
необходимо
Яа + Я2 = (ДА)2 + (ДВ)2^0 (Д1.7)
И
ЯгЯ2 = (ДА)2(ДВ)2(1 - г2) -j(c)2 2 0. (Д1.8)
Условие для суммы корней (Д1.7) удовлетворяется автоматически, в то время
как ограничение на произведение корней (Д1.8) дает искомое соотношение
неопределенностей при наличии корреляций
(АА)2(ДВ)2 £ 4(1^г2)([Д В]}2. СД1.9)
Это соотношение было установлено независимо Робертсоном и Шрёдинге-
ром в 1930 году (см. ссылки в [24], где приведены также и примеры фи¬
зических квантовых состояний с не равной нулю корреляцией наблюдае¬
мых, так что модификация соотношений неопределенности становится суще¬
ственной).
Дополнение II. Матрица плотности, квантовая
запутанность (entanglement), статистические ансамбли
и энтропия
Чистые состояния. В рамках матричной реализации квантовой механи¬
ки Ландау, Блох и фон Нейман независимо друг от друга предложили вместо
векторов состояния ввести эквивалентное описание с помощью матрицы
плотности, которая в формализме Дирака определяется как проектор на
квантовое состояние системы |Ф):
р = |*)(Ф|, р* = р, р2 = р.
СДИ.1)
484
Дополнения
Согласно свойству сепарабельности, квантовое состояние разложимо по счет¬
ному базису,
I *>=!>»,
п
где для упрощения записи мы приняли, что спектр задачи описывается кван¬
товыми числами п, имея в виду, что среди них могут быть и спектральные
параметры (непрерывные переменные). Тогда
P = 2ln)<mlcnC СДП.2)
п,т
а значит, при фиксированном базисе описание квантового состояния сводит¬
ся к введению матрицы с элементами
Рпт = спс*т> СДП-3)
причем выполняются условия (ДП.1), наложенные требованием того, что
данная матрица—проектор. Кроме того, по построению рпп = |сп|2 ^ 0.
Нормировка состояния на единицу может быть представлена в виде
(Ф|Ф) = ]>](Ф|п)(п|'1') = ^(п|Ф)(Ф|п> =2 Рпп = tr Р>
п п п
откуда заключаем
trp = l. (ДИ.4)
Итак, матрица плотности, как говорят, чистого состояния, т. е. состоя¬
ния, представленного в полном гильбертовом пространстве сепарабельным
образом, является проектором с единичным следом.
Средние значения наблюдаемых в заданном состоянии вычисляются со¬
гласно общему предписанию как
(Ф|А|Ф)=2№1т)(т|Л|п>(п|Ф)=2]рптАтп=»{рА>. (ДП.5)
п,т п,т
Наконец, динамика матрицы плотности чистых состояний в согласии
с уравнением Шрёдингера для состояния, образующего проектор р, задается
уравнением1
m^p(o = [H,p(t)L (ди.б)
так что в случае стационарных состояний
Pnm(t) = pnm( 0)е-й(£"-Е-» (ДП.7)
Подчеркнем, что и в стационарном случае недиагональные по энергетическим
уровням элементы матрицы плотности чистого состояния зависят от вре¬
мени. Блок матрицы плотности, составленный по состояниям с заданной
энергией при наличии вырождения, остается не зависящим от времени.
Сравнение Лиувилля.
Дополнение П. Матрица плотности, квантовая запутанность..
485
Запутанность и статистические ансамбли. Рассмотрим чистое состоя¬
ние системы, образованной двумя подсистемами АиВ, квантовые состояния
которых принадлежат гильбертовым пространствам НА и Нв, т. е.
l*)=EcJa)A|b}B. (ДП.8)
а,Ь
Матрица плотности такого состояния—
р = |Ф)(Ф|= cabc*,b,|a>A{|b)B B(b/|>A(a/|. (ДП.9)
a,b;a',b'
Для измерения средних наблюдаемых, действующих в пространстве состо¬
яний подсистемы А, достаточно знать эрмитову матрицу плотности этой
подсистемы
Ра = Р = J] cabc*a,b|а)А А(а'\, (ДП.10)
а,Ь;а'
так как
<QA)=tr{pQA} = J] cabc*a,b,(a'\QA\a){b/\b) =
а,Ь;а',Ь'
= 2 cabc*v(a'|QA|a)5w = trA{pAQA}.
afoa'yb'
Если матрица плотности подсистемы рА является проектором, то говорят,
что состояние подсистемы является сепарабельным, т. е. чистым:
Л 9 А
Ра~Ра-
Если же
р\ФрА, СДИ.11)
то говорят, что имеет место entanglement, т. е. запутанность (переплете¬
ние), состояния подсистемы с другой подсистемой, замыкающей физическую
систему до полной в квантовомеханическом понимании состояний. Такие
квантовые состояния подсистемы называют также смешанными.
Поскольку матрица плотности подсистемы А является эрмитовой
{РлУаа' ^ ] СаЬСа'Ъ {РлУа'а3
а,Ь;а'
ее можно заменой базиса привести к диагональному виду в некотором базисе
собственных векторов состояния \п):
ipA}nm=Wn5nm, (ДП.12)
причем, очевидно, из общего вида элементов матрицы рА следует, что
wn^ 0.
По-прежнему имеет место нормировка вероятности
trAPA = trAtrBP=trP = 1 => 2И'П = 1- СДП-13)
486
Дополнения
Если отлично от нуля только единственное собственное значение wn = 5ПоП, то
матрица плотности—проектор, и состояние сепарабельное. Если же отлична
от нуля хотя бы пара или более собственных значений, то имеет место за¬
путанность, и состояние подсистемы А характеризуют как статистический
ансамбль. С точки зрения нормировки вероятности величина wn по-прежне-
му есть вероятность обнаружения подсистемы в квантовом состоянии |п),
но при этом сама подсистема уже не может характеризоваться квантовым
состоянием в смысле амплитуды вероятности, сепарабельно разложимой по
базису, а описывается матрицей плотности. Отличие таких квантовых систем
становится существенным при вычислении средних значений наблюдаемых,
которое особенно ясно видно в случае выбора базиса собственных векторов
матрицы плотности, так как тогда
(Qa) = trA{pAQA}=2 wn<n|QAW, СДИ.14)
П
где в сумме нет недиагональных матричных элементов оператора QA, кото¬
рые, вообще говоря, не равны нулю в базисе | п) и дают вклад при вычислении
среднего по чистому, сепарабельному состоянию подсистемы Л!
Пример. Состояние двух частиц спина | с суммарным спином S = О
10, 0) = j={\+)A\-)B - |->л1+)В} (ДП.15)
дает матрицу плотности для частицы А
рА = trB{|0, 0)(0, 0|} = {в(+|0, 0)(0, 0|+)в} + {вН0, 0)(0, 0|-)в} =
= ^{|+)аа("Н} + (ДП.16)
Значит, частица А характеризуется смешанным квантовым состоянием, в ко¬
тором каждая из проекций спина на ось % равновероятна.
Если подсистема, матрица плотности которой рассматривается, замкнута,
то, даже если подсистема образует статистический ансамбль, т. е. несепара¬
бельна, очевидно, имеет место то же самое уравнение движения для матрицы
плотности, что и в сепарабельном случае (ДП.6).
Термодинамический ансамбль и энтропия. Набор квантовых систем
{А, В, С,...}, помещенный в термостат, т. е. внешнюю систему, которая ха¬
рактеризуется макроскопическими величинами, находится в тепловом рав¬
новесии по отношению к каждой из подсистем и к термостату, если ее
статистический ансамбль является термодинамическим, т. е. он удовлетво¬
ряет требованиям
— стационарности,
— независимости статистических ансамблей каждого элемента набора,
— универсальности параметров каждого статистического ансамбля, отве¬
чающих наблюдаемым величинам по отношению к термостату.
Дополнение II. Матрица плотности, квантовая запутанность... 487
Из стационарности сразу следует, что матрица плотности каждой из
подсистем не зависит от времени
±рх = О, Х = {А,В,С,...}. (ДИ.17)
Независимость статистических ансамблей означает, во-первых, что эволю¬
ция матрицы плотности подсистемы описывается уравнением для замкнутых
систем
т±рх = [нх,рх],
что при условии стационарности дает
[Нх,рх] = 0. (ДИ.18)
Отсюда сразу же заключаем, что в базисе собственных стационарных состоя¬
ний гамильтониана подсистемы оператор матрицы плотности также являет¬
ся диагональным:
Рх = 2 wn^’0\n, ?>(?', п|, %|п, £)=£>,£), (ДП-19)
П
где <^ —набор квантовых чисел в случае вырождения состояний энергии.
Во-вторых, независимость подсистем означает, что для подсистемы, со¬
ставленной из элементарного набора {А, В, С,...}, ее матрица плотности есть
произведение матриц плотности компонент:
Рав...х=РаРв---Рх> (ДИ.20)
так что статистические веса w* перемножаются, а результирующая матрица
плотности опять же диагональна по собственным состояниям ее гамильтони¬
ана.
Наконец, в-третьих, из независимости подсистем следует, что гамильто¬
ниан составной подсистемы равен сумме гамильтонианов ее компонент
НАВ...х = НА+ Нв +... ■+ Нх, (ДП.21)
т. е. энергия такой подсистемы равна сумме энергий ее компонент. Такие же
соотношения справедливы и, при наличии их у системы, для ненулевых адди¬
тивных интегралов движения, которые сводятся к скорости поступательного
движения системы как целого, угловой скорости ее вращения вокруг некой
оси, заряду, скорости равновесных химических реакций и т. п.
Далее мы рассматриваем только случай, когда все аддитивные интегралы
движения системы как целого, за исключением энергии, тождественно рав¬
ны нулю, а химические реакции отсутствуют. Это означает, в частности, что
термостат регулирует только количество тепла, т. е. энергии, в системе, и его
системы способны измерять количество тепла в любой «точке» системы, так
что эта характеристика остается стационарной и одинаковой независимо от
точки измерения. Тогда требование универсальности статистических ансам¬
блей приводит к единому выражению для статистических весов
(ДП.22)
488
Дополнения
где факторы Zx определяют нормировку следа матрицы плотности подси¬
стемы X на единицу и, следовательно, зависят от структуры уровней этой
подсистемы и их вырождения. Факторы и/(Е) уже не зависят от специфиче¬
ских квантовых чисел, определяющих возможное вырождение стационарных
состояний подсистем, и определяются универсальной функцией энергии со¬
стояния. Это справедливо в силу того, что, во-первых, зависимость от дру¬
гих аддитивных, а значит, универсальных интегралов движения исключена
наложением условия равенства нулю соответствующих величин (скорость
поступательного движения, скорость углового вращения системы как целого
и т. п.). Во-вторых, введение в функцию статистического веса w парамет¬
ров в виде специфических квантовых чисел вырождения состояний энергии
каждой из подсистем нарушала бы требование универсальности. Тогда сама
система становилась бы зависимой от характеристик, не измеримых термо¬
статом, т. е. она не была бы термодинамической.
Далее, стандартным образом, рассмотрим систему, составленную из эле¬
ментов А и В. Ее матрица плотности, как мы выяснили,
Рав = РаРв
диагональна в базисе стационарных состояний гамильтониана
Нав=На + Нв, |п, m)AB = \n)A\m)B,
причем статистические веса определяются выражением
Чтобы исключить переопределение функции w(E) умножением на произ¬
вольный числовой фактор, что допускается уравнением (ДП.23), положим
так что решение уравнения (ДИ.23) полностью определяется параметром /3:
откуда с учетом нормировки в нуле находим термодинамическое распределе¬
ние
(ДП.23)
Тогда из (ДИ.23) следует
м/(0) =w2(0) = 1.
Обозначим значение производной функции w(E) в нуле как
w'(0) = -j8,
(ДП.24)
м/(Е) = е"0£.
(ДИ.25)
Нормировочный фактор Z называют статистической суммой
г = ае~рЙ, (ДП.26)
Дополнение II. Матрица плотности, квантовая запутанность..
489
где суммирование ведется по стационарным состояниям подсистемы с га¬
мильтонианом Я. Окончательно матрица плотности термодинамического
ансамбля принимает вид
р = (ДП.27)
После этого все физические характеристики квантовой системы в тепловом
равновесии по сути определены: известны правила их расчета. Так, напри¬
мер, для средней энергии находим
(Б) =tr{pH} = Япе-^ =
Т1
Определение статистической суммы (статсуммы)
П
позволяет записать
г = е~тЛ,
где величина Jf, очевидно, имеет смысл числа состояний со средней энер¬
гией (Е). По сути, Jf указывает меру термодинамического хаоса в системе:
чем больше число состояний со средней энергией, тем больше возможностей
у системы находится в различных состояниях. Величину
<S = fc In сЖ (ДИ.28)
называют энтропией, где к — постоянная Больцмана. Термодинамический
потенциал Т в выражении для статсуммы
In Z = -f$T (ДП.29)
называют свободной энергией Гельмгольца. Тогда
{E)=F+±S, (ДП.30)
так что
£ = СДП.31)
где Т — температура, а значит, стандартно,
(E)=F+TS.
Наконец, температура1 должна быть положительной, так как в противном
случае состояния с большей энергией были бы более вероятны, что создает
ситуацию, нестабильную по отношению к спонтанным переходам между
уровнями системы, в то время как положительная температура гарантирует,
что высшие состояния по энергии возбуждаются вследствие установления
равновесия, т. е. в ходе вынужденного поглощения энергии состояниями на
нижних уровнях.
1И, следовательно, параметр р.
490
Дополнения
Статистический вес состояния с энергией Е
(Е) = СДП.32)
как функция энтропии растет с ростом <S: увеличение энтропии есть наи¬
более вероятный процесс эволюции термодинамической системы. В этом
смысле выделяют обратимые процессы с постоянной энтропией и необрати¬
мые, в вероятностном понимании, процессы с ростом энтропии, так как ее
макроскопическое, в единицах постоянной Больцмана х, уменьшение крайне
маловероятно. Такая статистическая необратимость, возникающая в теории,
которая изначально описывалась уравнениями с инвариантностью по отно¬
шению к обращению стрелы времени, связана, на мой взгляд, с необратимо¬
стью спонтанного излучения в том смысле, что начальное и конечное состоя¬
ния спонтанных переходов по построению неэквивалентны. Действительно,
само понятие спонтанности излучения предполагает наличие вакуума для
квантов излучения в начальном состоянии, а значит, начальное и конеч¬
ное состояния неперестановочны, т. е. необратимы по времени. При этом
в стационарной системе в тепловом равновесии по определению началь¬
ное и конечное состояния тождественны, так что требование стабильности
термостата и термодинамической системы, т. е. отсутствие искусственной
накачки возбужденных уровней, подверженным спонтанным переходам1, по
сути означает введение граничных условий необратимости по времени. Это
можно также понимать и следующим образом: тождественность начальных
и конечных состояний термодинамически равновесной системы предпола¬
гает равенство нулю вероятности спонтанных переходов. Но обратимая по
времени теория должна включать в себя и процессы спонтанного излучения,
так что такие граничные условия несовместимы с инвариантностью по отно¬
шению к операции обращения стрелы времени.
Итак, мы установили, что матрица плотности термодинамической систе¬
мы в базисе стационарных состояний имеет диагональный вид:
рт = \*Г*\ 2au, = L (ДП.ЗЗ)
п
Отсюда
РЕп = — In Z — In рпп. (ДП.34)
Поэтому выражение для энтропии сводится к виду
<S = fc(lnZ + /3 (Б)) = к (in Z + =
П
fc ^ln Z — 2> Z -\-1и РппУРпп) —^ ^ 1 Рпп I** Рпт
п п
Искусственно созданная инверсная заселенность уровней в лазерах иногда трактуется как
наличие отрицательной температуры в системе, что, как известно, и приводит к спонтанному
излучению, т. е. нестабильности.
Дополнение III. Парадокс Эйнштейна—Подольского—Розена 491
т. е.
<S = -fctr{plnp}. (ДН.35)
Таким образом, в (ДИ.35) мы пришли к выражению для энтропии уже для
произвольного статистического ансамбля, характеризуемого матрицей плот¬
ности1, а не только для термодинамической системы. Значит, в единицах
постоянной Больцмана энтропия есть среднее значение логарифма статисти¬
ческого веса состояний системы. Напомним, что для термодинамического
ансамбля энтропия —логарифм среднего числа состояний системы со сред¬
ней энергией.
Информация как мера хаоса в статистическом ансамбле. В теории
информации обобщение энтропии дается формулой для количества инфор¬
мации в статистической системе с матрицей плотности р
J = - tr{p log2 р }, (ДП.36)
которое называют также энтропией Шеннона. Выбор основания логарифма
связан с простым соображением: в системах с двоичным кодом удобно пред¬
ставить статистический вес диагональной матрицы плотности в виде
_ 1
Рпп 2тп 9
где тп — число двоичных разрядов в состоянии | п), так что
1= ~ 2 2^ log2 =2 тпРпп = (тп)>
п п
а значит, энтропия Шеннона есть просто среднее число двоичных разрядов
в статистической системе, а среднее число вариантов передачи информации
по среднему каналу—2х.
Дополнение III. Парадокс Эйнштейна—Подольского—Розена
В 1935 году Эйнштейн, Подольский и Розен опубликовали статью, в ко¬
торой был сформулирован парадокс (ЭПР-парадокс), поставивший под во¬
прос концептуальные основы квантовой механики как физической теории,
удовлетворяющей целому ряду естественных и интуитивно ясных эмпири¬
ко-аксиоматических требований, в частности наличию причинно-следствен¬
ных связей с учетом конечной скорости распространения влияния одно¬
го явления на другое (локальный принцип причинности). Из этой работы,
по мнению авторов, следовало, что квантовая механика либо несовмести¬
ма с принципом причинности, либо неспособна дать описание механизма
возникновения локальных причинно-следственных связей в предложенном
1Если состояние чистое (сепарабельное), то в базисе собственных состояний матрицы плот¬
ности отличен от нуля только единственный матричный элемент, равный единице, так что
энтропия равна нулю.
492
Дополнения
классе явлений, а значит, неполна, т. е. не может быть окончательной, ис¬
тинной физической теорией. На эти две трактовки ЭПР-парадокса принято
ссылаться как на альтернативы «квантовой нелокальное™» и «локального
реализма», причем в последнем случае имеется в виду, что все физические
характеристики системы строго определены и детерминированы по време¬
ни, но часть из них скрыта от измерений в квантовой механике (теории со
скрытыми параметрами).
Мысленный эксперимент. Рассмотрим одномерную квантовую систе¬
му. Пусть источник излучает две частицы1 в противоположные стороны так,
что их центр масс покоится, т. е. суммарный импульс Р тождественно равен
нулю: Р=рА+рв = 0. Значит, волновая функция центра масс
Ч,С.Ш.5.~5(Р)=б(рЛ+рВ),
а в координатном пространстве ^c.m.s. (ха + хв) ~ const. Относительное дви¬
жение частиц характеризуется тем, что в момент измерения они находятся
на строго заданном расстоянии I друг от друга, т. е. волновая функция их
относительного движения
Фге1(*А (ХА +
В итоге
(хА, хв |Ф) = фге1. (хА - хв) Фс.т.5. (хА+хв) = «Ж 5 (хА - хв +1). (ДШ.1)
Отсюда
(Ра> Рв1ф) = / dxA (PaI*a) (Рв1*в) (*а> ^в№> =
= «Ж J dxA dxB е~» (раха+рвХв) g— хв+^) =
=Jf / dxA е-п^л+РвХл+РвП _ jY2nh 5(рА+рв) е*(р''“РвК, (ДШ.2)
что подтверждает реализуемость описанной ситуации в квантовой механи¬
ке2.
Пусть физические величины первой частицы измеряются приборами на¬
блюдателя А, а второй — В (см. рис. 41)3. Описанные волновые функции
в координатном и импульсном пространствах говорят о следующем:
1) если наблюдатель А измеряет координату первой частицы хА, то резуль¬
тат измерения наблюдателем В координаты второй частицы строго предопре¬
делен4: хв = ха+£;
2) если наблюдатель А измеряет импульс первой частицы рА, то результат
измерения наблюдателем В импульса второй частицы строго предопределен:
Рв = ~Ра-
1Для простоты массы частиц одинаковы.
2Гамильтониан подобной квантовой системы, а следовательно, и ее динамика не обсужда¬
ются!
3В западной литературе общепринято давать наблюдателям имена «Алиса» (Л) и «Боб» (В).
4 Суть ситуации, конечно, нисколько не изменится, если поменять местами порядок наблю¬
дателей, т. е. В.
Дополнение III. Парадокс Эйнштейна—Подольского—Розена
493
Подобные результаты полностью согласуются с интуитивными ожидани¬
ями из локального принципа причинности: частицы образуются с проти¬
воположными импульсами, сумма которых сохраняется, так что измерения
и должны давать противоположные значения импульсов; то же можно ска¬
зать и об относительной координате, значение которой строго фиксировано.
При этом не возникает никаких неопределенностей в значениях измеряемых
физических величин у второй частицы.
Рис. 41. Схема мысленного эксперимента Эйнштейна—-Подольского—Розена
Однако ситуация кардинально меняется, если
10 наблюдатель А измеряет координату первой частицы хА, а наблюда¬
тель В измеряет импульс второй частицы рв;
2') наблюдатель А измеряет импульс первой частицы рА, а наблюдатель В
измеряет координату второй частицы хв.
Интуитивно согласно принципу локального реализма следовало бы ожи¬
дать, что измерение в случае V дает точные значения координаты второй
частицы хв=хА+1 и импульса первой частицы рА = —рв, так как эти величи¬
ны строго коррелируют друг с другом. Если наблюдатели АиВ встречаются
после проведения измерений, это могло бы дать способ точного измере¬
ния координаты и импульса частицы, что, однако, отрицается принципами
квантовой механики: именно, при одном и том же значении измеренной
первым наблюдателем координаты хА многократное повторение измерений
импульса второй частицы наблюдателем В привело бы к неопределенности
значения рв, связанной в соответствии с соотношением неопределенностей
с погрешностью измерения координаты хв (в частности, точное значение хА
приводило бы к бесконечной неопределенности в значении рв, см. ниже).
Аналогичные результаты с неопределенностями координата-импульс возни¬
кали бы согласно квантовой механике и в случае 2'.
Допустим, что наблюдатели АиВ заранее не договаривались о том, какие
характеристики частицы они будут измерять, и объединили результаты своих
измерений только после их проведения при встрече. Но тогда различие в ре¬
зультатах измерений в сериях экспериментов 1,2 и 1', 2' становится парадок¬
сальным: измерения проводились практически одновременно приборами,
разделенными расстоянием порядка I; выбор наблюдателями АиВ приборов
для измерения координаты или импульса в одной и той же физической
системе проводился независимо друг от друга; каким образом информация
494
Дополнения
о том, какие приборы выбрал для измерения характеристик первой частицы
наблюдатель А, сказалась на результатах измерения характеристик второй
частицы наблюдателем В, пространственно отделенным от наблюдателя А?
Как информация о процедуре измерения одним наблюдателем может влиять
на результаты измерения другим наблюдателем?
По мнению Эйнштейна, Подольского и Розена ответ на эти вопросы мо¬
жет быть только в виде двух альтернатив:
— либо квантовая механика существенно нелокальна, т. е. противоречит
принципу локальной причинности1,
— либо она неполна, т. е. неспособна дать основанного на принципе
локальной причинности описания физического механизма возникновения
или отсутствия неопределенностей в измерениях в зависимости от выбора
приборов пространственно разделенными наблюдателями, а значит, долж¬
на существовать теория локального реализма, в которой все физические
величины строго детерминированы в согласии с принципом причинности
в каждой точке траектории, а статистические неопределенности возникают,
как и в любой классической статистической теории, вследствие неполного
знания параметров траектории и, в частности, всего многообразия началь¬
ных данных, т. е. истинная теория, лежащая в основе явлений, описываемых
«неполной» квантовой механикой, должна быть теорией со «скрытыми» па¬
раметрами.
Подчеркнем, что в принципе авторы ЭПР-парадокса не оппонируют экс¬
периментальному факту наличия неопределенностей типа координата-им-
пульс. Они ставят проблему логического обоснования этих неопределенно¬
стей согласно принципу причинности.
Формулировка Дэвида Бома. Оригинальная формулировка ЭПР-пара-
докса оставляет открытыми вопросы о реализации условий мысленного экс¬
перимента, в частности, гамильтониана, описывающего воображаемую ситу¬
ацию распространения двух частиц с заданными свойствами. Однако основ¬
ные характеристики мысленного эксперимента ЭПР:
— наличие двух аддитивных интегралов движения для пары наблюдае¬
мых (у ЭПР сумма импульсов и разность расстояний частиц),
— некоммутативность этих наблюдаемых друг с другом, влекущая за со¬
бой соотношение неопределенностей (у ЭПР неопределенность координа-
та-импульс),
позволили Дэвиду Бому указать полный аналог мысленного эксперимента
ЭПР, обладающий тем достоинством, что его можно реализовать практиче¬
ски.
Пусть частица спина нуль распадается на две частицы спина ^ с отно¬
сительным орбитальным моментом, равным нулю, так что приборы, рас¬
положенные на некотором расстоянии от источника распада вдоль оси у,
1 Эйнштейн называл такую ситуацию «spooky action at the distance», что часто переводят
как «кошмарное дальнодействие», хотя слово «spook» вернее трактовать как «привидение», т. е.
кошмар вполне определенного рода.
Дополнение III. Парадокс Эйнштейна—Подольского—Розена 495
Рис. 42. Эксперимент ЭПР с измерением спиновых корреляций — формули¬
ровка Д. Бома
регистрируют эти частицы, определяя проекции их спина на заданную ось
(см. рис. 42), например, с помощью метода Штерна—Герлаха (отклонение
заряженной частицы в неоднородном поле за счет взаимодействия с магнит¬
ным моментом). Тогда спиновая волновая функция в терминах проекций на
ось z имеет вид
|0, 0) = ^={|+}д|-)в - |-)а1+)в>- СДП1.3)
Это означает, что
1) если наблюдатель А измеряет значение проекции спина первой ча¬
стицы на ось z, равное ms, то результат измерения проекции спина второй
частицы на ось z наблюдателем В строго предопределен и равен —ms (закон
сохранения проекции спина).
Затем, если перейти от базиса {|+), |—)} к базису состояний с определен¬
ной проекцией спина частицы на ось п, которая получается вращением орта1
ez вокруг оси у на угол /3:
|t) = + cos ||+)+sin||-),
|i) = -sin||+)-l-cos||-),
то это же состояние запишется как
|о> о) — у={|Т)аЦ)в ~~ Ц)а1Т)в}-
(ДШ.4)
(ДШ.5)
Значит,
2) если наблюдатель А измеряет значение проекции спина первой ча¬
стицы на ось п, равное т5, то результат измерения проекции спина второй
частицы на ось п наблюдателем В строго предопределен и равен —ms (закон
сохранения проекции спина).
Однако полагая, что /3 Ф nk, fceZ, заключаем, что
1') если наблюдатель А измеряет значение проекции спина первой ча¬
стицы на ось п, равное т5, то результат измерения проекции спина второй
гЭта задача решена в лекции 10.
496
Дополнения
частицы на ось z наблюдателем В даст неопределенное значение, поскольку
состояния (Д1И.4) представляют собой не собственные состояния с заданны¬
ми проекциями спина на ось z3 а суперпозиции таких состояний, в которых
значение проекции не определено, а флуктуирует в соответствии с соотноше¬
нием неопределенностей;
2') и аналогично, если наблюдатель А измеряет проекцию спина первой
частицы на ось z, а наблюдатель В проекцию спина второй частицы на ось п,
то результаты таких измерений будут находится в согласии с соотношением
неопределенностей.
Здесь опять возникает вопрос о реализации принципа локальной причин¬
ности в таких ситуациях: каким образом измерения наблюдаемых величин
испытывают столь различные корреляции в зависимости от выбора про¬
странственно разделенных приборов регистрации их характеристик? Если
эти корреляции причинно обусловлены, то либо эта причинная связь яв¬
ляется нелокальной и противоречит конечной скорости распространения
влияния одних событий на другие, либо квантовая механика не содержит
в себе информации об установлении таких причинно-следственных связей
путем распространения взаимодействий с конечной скоростью, т. е. непол¬
на, а истинная теория является локально-причинной теорией со скрытыми
параметрами.
Парадокс ЭПР вызвал дискуссию об основаниях квантовой механики,
что плодотворно сказалось на более детальной разработке и формализации
некоторых ее аспектов, особенно связанных с процессом и самим поняти¬
ем измерения. В частности, было дано обобщенное определение понятию
единичного измерения как оператора, действующего на квантовое состояние,
т. е. амплитуду вероятности.
Понятие амплитуды вероятности, как следует из постулатов квантовой
механики, предполагает серию многократных измерений, или эксперимен¬
тов с идентичными квантовыми системами, которые и позволяют определить
ее, а значит, квантовое состояние, эмпирически. Нет сомнения, что этот
постулат находится в непререкаемом согласии со всем многообразием опыт¬
ных данных. Осмысление акта единичного измерения привело к следующему
представлению его как оператора:
прибор имеет на входе некое собственное состояние |q) наблюдаемой
величины Q: Q\q) = q\q)y на выходе же он выдает сигнал, значение
которого трактуется как само значение q (естественно, с некоторой
погрешностью).
Общая процедура формирования такого сигнала зависит от конкретного
прибора. Например, фотоумножитель, имея на входе фотон с частотой в пре¬
делах своей чувствительности, выдает на выходе электрический импульс, ам¬
плитуда которого соответствует по шкале калибровки этого аппарата вполне
определенному значению энергии фотона с точностью до погрешности са¬
мой калибровки и измерения этой амплитуды. Поскольку полный набор
наблюдаемых величин квантовой системы может быть шире, чем единствен¬
Дополнение III. Парадокс Эйнштейна—Подольского—Розена 497
ная физическая величина q, измеряемая данным прибором, то, естественно,
возникает вопрос о том, каким является состояние системы в результате
действия на него прибора, определившего значение q. Поскольку состояние
нормировано на единицу, описанная нами процедура единичного измерения
эквивалентна записи оператора, действующего на состояние системы |Ф>,
в виде
где Pq =?* =Р2—проектор на состояние с заданным значением наблюдаемой,
которое определилось прибором, р — матрица плотности состояния, так что
знаменатель дроби обеспечивает правильную нормировку при действии на
состояние:
Приведенное определение оператора единичного измерения применимо не
только к чистым (сепарабельным) состояниям, но и к запутанным (состояни¬
ям с запутанностью). Тогда
Поскольку проектор «вырезает» лишь одну из компонент в суперпозиции
состояний, образующих исходное |Ф), принято говорить, что оператор изме¬
рения приводит к «редукции» или «коллапсу» волновой функции.
Например, в изложенной нами выше формулировке парадокса ЭПР, дан¬
ной Дэвидом Бомом, измерение наблюдателем А проекции спина первой
частицы на ось z, равной +|, дает состояние
где состояние |0, 0) и матрица плотности рА заданы в (ДП.15) и (ДИ.16), так
что в результате единичного измерения получается состояние
и редукция волновой функции обозначена явно. Таким же образом изме¬
рение наблюдателем А положительной проекции спина первой частицы на
(ДШ.6)
(ДШ.7)
откуда
(ДШ.9)
Так как проектор Pq действует только в пространстве, независимом от дру¬
гих наблюдаемых N полного набора системы {Q, N}, след можно вычислить
в два этапа:
tr{pPq} = trQ trN{pPq} = trQ{pQPq}. (ДИШ)
(ДШ.Ю)
-А+|0> 0) — |+)дд(+|0> 0)
1
•\/1та{Ра1+)м(+|}
Л+|0,0) = |+)А|-)в,
498
Дополнения
ось п приводит к состоянию
Ат|0,0) = ||Шв = IT>a{- sin f |+>в + cos f |->в},
откуда следует, что отрицательная проекция спина второй частицы на ось п
будет измерена с вероятностью, равной единице, в то время как положи¬
тельная и отрицательная проекции спина второй частицы на ось z будут
измерены наблюдателем В с вероятностью sin2 ^ и cos2 соответственно.
Таким образом, изложенная процедура единичных измерений позволяет
строго описывать утверждения в рамках квантовой механики, в том числе
и в случае парадокса ЭПР, суммировать основные выводы которого можно
следующим образом в виде двух взаимоисключающих альтернатив:
Парадигма квантовой механики. Квантовое состояние изначально со¬
держит в себе информацию о всех возможных способах вероятностного из¬
мерения своих характеристик, так что нелокальная реализация какого-либо
из них не означает мгновенного распространения причинно-следственного
влияния пространственно разделенных частей измерительного прибора друг
на друга, а связана с осуществлением вероятного исхода избранного набора
измерений наблюдаемых величин с учетом соотношений неопределенности
(квантовая нелокальность).
Парадигма локального реализма (теорий со скрытыми параметра¬
ми). Все физические величины частиц строго определены локально, в каж¬
дой точке детерминированной по временной эволюции траектории, но часть
из них скрыта от наблюдения (современными приборами), так что при мно¬
гократном повторении «идентичных» по отношению к измеряемым вели¬
чинам опытов вариации начальных данных для скрытых параметров могут
приводить к статистическим «неопределенностям» наблюдаемых величин,
хотя их истинные значения всегда строго определены и детерминированы
в согласии с локальным принципом причинности.
Эти две парадигмы1 оставались действительно альтернативами вплоть до
1964 года, когда Джон Белл сумел формализовать их следствия в виде нера¬
венств для статистических корреляций измеряемых физических величин,
которые открыли путь для эмпирического утверждения истинности кванто¬
вой механики и отвержения парадигмы теорий со скрытыми параметрами,
удовлетворяющим локальному принципу причинности (теорема Белла).
Дополнение IV. Неравенства и теорема Белла
Рассмотрим физическую величину некоторой частицы — а, спектр зна¬
чений которой лежит на отрезке [—1; 1], а среднее значение равно нулю2.
1Эйнштейн настаивал на справедливости принципов локального реализма, считая кванто¬
вую механику промежуточным, заведомо внутренне противоречивым этапом на пути к истин¬
ной теории. Он выражал свою позицию известным изречением: «Бог не играет в кости».
2Этого всегда можно добиться, выбрав подходящее взаимно однозначное отображение некой
наблюдаемой на заданный отрезок.
Дополнение IV. Неравенства и теорема Белла
499
Обозначим значение этой величины, измеренное наблюдателем А как А (а) е
е [-1; 1]. Введем для той же частицы аналогичную величину а', которая
с точки зрения квантовой механики не коммутирует с а, и обозначим резуль¬
тат ее измерения наблюдателем А, как А (а'). Для другой частицы и наблюда¬
теля В построим такую же пару величин ЬиЬ'и обозначим результаты их
измерения через В(Ь) и В(Ь').
Пусть эти частицы излучаются некоторым источником в стороны наблю¬
дателей А и В, которые разделены пространственно, но прежде чем прово¬
дить измерения, договорились вести таблицы одновременных измерений,
каждый раз произвольно определяя измеряемую каждым из них величину.
Тогда после многократных опытов при встрече эти наблюдатели могут соста¬
вить следующие средние величины
(А(а)В(Ь)), (A(a)B(Z/)}, (А(а')В(Ь)), (A(a')B(b')), (Д1У.1)
которые называют корреляторами и часто обозначают символом1 с[Л(а)В(Ь)].
Поскольку частицы излучаются единым источником, между коррелятора¬
ми может существовать причинно-следственная связь. Так, в теориях локаль¬
ного реализма, т. е. в детерминированных теориях со скрытыми параметра¬
ми Я на траектории, измеряемые величины принимают точные значения на
каждой из траекторий, а корреляторы, как и другие средние, вычисляются
согласно формуле
с[Л(а)В(Ь)] = / dАр(А)Л(а, А)В(Ь, А) - (АШ(В(Ь)), (Д1У.2)
Л
где р (Я) — плотность вероятности найти скрытый параметр со значением Я
в области его допустимых значений Л. Далее полагаем, что средние значения
наблюдаемых величин равны нулю.
Составим цепочку неравенств
*(Я) = А(а, Я){В(Ь, Я) + В(Ь', Я)} +А(а', Я){В(Ь, Я) -В(Ь', Я)} *5
^ |А(а, Я){В(Ь, Я) + В(Ь', Я)}| + |А(а', Я){В(Ь, Я)-В(Ь', Я)}| ^
^ |В(Ь, Я) + В(Ь', Я)| +1В(Ь, Я)-В(Ъ', Я)|, (Д1У.З)
где мы воспользовались ограничением на спектр наблюдаемых |А(*)| ^ 1,
|В(-)| ^ 1. Далее, для двух вещественных чисел {х, у} €М
К = (|х+у| + |х-у|)2 = (х+у)2 + (х-у)2 + 2|(х+уНх-у)| =
= 2(х2+у2) + 2|х2 —у2|, (Д1У.4)
откуда при у2 ^ х2 ^ 1
К = 4х2 ^ 4, (ДГ/.5)
и при jc2 ^ у2 ^ 1
К=4у2 ^ 4, (Д1У.6)
1Напомним, что в точном определении коррелятора стоит выражение с [Л (a) 5(b)] =
= (А(а)В(Ь)) - (А(а))(В(Ь)), но в нашем случае средние положены равными нулю по условию
задачи.
500
Дополнения
так что из (ДГ/.З)—(Д1У.6) следует, что
F(A)s; 2. СД1У.7)
Домножая (Д1У.7) на положительно определенные плотность вероятности
р(А) и меру интегрирования dA, находим
J dAр(A)F(A) ^2 J dAp(A). (ДГУ.8)
л л
Согласно нормировке вероятности на единицу
J dAp(A) = l,
Л
а интеграл в левой части неравенства (Д1У.8) сводится к комбинации корре¬
ляций
J dA p(A)F(A) = / dAp(AM(a, A)B(b, A) + J dAp(A)A(a, A)B(b', A) +
A A A
+ J dA p(A)A(a', A)B(b, A) - J dA p(A)A(a', A)B(b', A) =
Л Л
= c[A(a)B(b)] +c[A(a)B(b')] +c[A(a')B(b)] -сЕАСа'ЖЬ')].
Тогда
c[A(d)B(b)-\+c[A(.d)B(b')] + с[А(а')В(Ь)] - c[A(.a')B(b')] sS 2. СД1У.9)
Подстановка a *-♦ —a, a' •-» —a' приводит к неравенству с левой частью проти¬
воположного знака:
—с[А(а)В(Ь)] - с[А(а)В(Ь')] - с[А(а')Вт + сШа'ШЬ')] ^ 2, (ДШО)
так как средние значения линейны по каждой из физических величин, изме¬
ряемых разными наблюдателями. Поскольку
fxsS|a|,
\ . <=> \х\£\а\,
из (Д1У.9) и (Д1У.10) приходим к неравенству Белла в форме1 Клаузера—
Хорна—Шимони—Холта [Clauser, Horne, Shimony, Holt] (CHSH)
\c[A(ci)Bm +с[А(.а)В(Ъ'Я +c[A(.a')B(b)] -c[A(a')B(b')]\^2. (fllV.ll)
Итак, парадигма локального реализма теорий со скрытыми переменными
приводит в математическом выражении к ограничению на корреляции из¬
меряемых величин в виде неравенства (Д1\Ш).
2В литературе выведен целый класс неравенств, которые по имени их первооткрывателя
носят имя Белла. Сам Белл получил в 1964 году оригинальное неравенство, связывающее кор¬
реляции для величин, которые принимают значения ±1 и строго антикоррелируют в случае,
если характеристики двух частиц а и Ъ одинаковы, т. е. при а = Ь имеется строгое равенство
А (а) + В(Ь) = 0, откуда с[А(а)В(а)] = — 1. Собственно неравенство Белла (1964) может быть
получено из неравенства Белла (ДГ\Ш), если в последнем положить сначала о! — Ъ! = — с и учесть
линейность коррелятора по каждому из его аргументов, например, с[А(—а)В{Ь)] = —с[А(а)В(Ь)]у
откуда с[А(а)В(Ь)] - с [А (а) В (с)] ^ 1 + с[А(с)В(Ь)]. Если теперь еще сделать подстановку Ъ —► -Ь,
с•—* —с, то приходим к искомому неравенству |с[А(а)В(Ь)] -с[А(а)£(с)]| ^1 + с[А(с)В(Ь)].
Дополнение IV. Неравенства и теорема Белла
501
Теорема Белла. Теории локального реализма со скрытыми параметрами
неспособны воспроизвести все предсказания для физических величин, следую¬
щие из квантовой механики.
Для доказательства этой теоремы достаточно построить пример кванто¬
вой системы, в которой нарушается одно из неравенств Белла, например,
в форме (Д1\Ш), установленных для теорий со скрытыми параметрами. Для
этого рассмотрим опыт, соответствующий мысленному эксперименту ЭПР
в формулировке Дэвида Бома, а именно, измерение спиновой волновой функ¬
ции двух спиноров, излучаемых единым источником в состоянии с суммар¬
ным спином, равным нулю. Пусть наблюдатель А измеряет проекцию спина
первой частицы в двух ортогональных направлениях п и п\ полученных
вращением вокруг оси у на угол /3 и /3' = /3 + ^:
а = сгА-п, а' = сгА • п\ (Д1У.12)
а наблюдатель В измеряет компоненты спина второй частицы на оси z их:
Ъ = а*, Ъ' = авх. (Д1У.13)
Собственные векторы операторов определены в базисе собственных векто¬
ров для сгг: |+) и |-), так что состояния с положительной и отрицательной
проекциями для первой частицы имеют вид
_ I |t) = + cos§|+)+sm§|->,
' I U) = -sinf|+) + cosf|-),
I in=+cos§|+> + sinf|->,
I |J/) = — sin у|+) +cos у |—).
Тогда измерения в состоянии
|0, 0) = ^{|Т)АЦ)В - ИШВ} = j={\Y)A\l')B - 1Пл1Пв>
дадут следующие средние значения:
— наблюдаемая а будет иметь значения ±1 с вероятностью
— при А(а) = +1 положительное значение наблюдаемой Ъ будет измерено
•2 Р 2 Р
с вероятностью sinz а отрицательное—с вероятностью cosz что отвеча¬
ет разложению состояния ||) по базису {|+), |—)};
— при А (а) =—1 положительное значение наблюдаемой Ъ будет измерено
2 Р • 2 Р
с вероятностью cosz , а отрицательное с sm что отвечает разложению
состояния |Т) по базису {|+), |—)},
так что коррелятор
(А(а)В(Ь)) = |{+1 • (sin2 ^ - cos2 §) -1 • (cos2 ^ - sin2 = - cos/3.
(Д1У.15)
502
Дополнения
Совершенно аналогично
(А(,а')В(Ъ)) = - cos
(ДШ6)
Далее, базис для наблюдаемой ах получается при вращении на угол —
вокруг оси у, так что он имеет вид
я
У:
Ь'|1> = +|1>, Ъ' |2> =—12>,
(Д1У.17)
откуда
|+) = -L{|2) + |l», |-) = -L{j2)-|i)},
и мы находим представление для
Р
а:
= М (cos II) и+-sin j) '4
11) = тЫ(с“ §_si" j)|2> “ (cos й11*}'
WIV.18)
и аналогично для а'. Тогда несложно вычислить средние
(А(а)В(Ъ/)> = +|{+1-(cos ^ + sin -1-(cos^-sin^) j -
- \ {+1’ (cos 2 -s^ f) -1'(cos 2+sin 2) } = sin^> WIV.19)
{Aia'^BQ}')) =sin /3'.
В итоге корреляции сводятся к
\{А(а)В(Ь)) + (А(а)В(ЬО) + (А(а ')В(Ь)) - (A(a/)B(b'))\ =
= | — cos /З + sin Р — cos f3' — sin/3'| = 2\/2 cos sin(^ у— ^ .
Подстановка (3' = (3 + ^- дает
|(А(а)В(Ь)) + (А(а)В(ЬО) + {А(аОВ(Ь)) - <А(а/)В(Ь/)) | = 2a/2|cos(^ +|.
{7Т ЗтГ 1
——, —j приходим к явному нарушению неравенства Белла
(CHSH), полученному в теории локального реализма:
|с[А(а)В(Ь)]+с[А(а)В(Ь/)]+с[А(а/)В(Ь)]-с[А(а/)В(Ь/)]|=2л/2>2. (Д1У.20)
Таким образом, теорема Белла доказана.
Можно показать, что в рассмотренном примере измерений спиновых кор¬
реляций был получен верхний предел для модуля суммы корреляторов в кван¬
товой механике. Для этого перейдем к векторным обозначениям наблюдае¬
мых:
а = (о’А-а), а2 = 1,
b = (crB-b), Ъ2 = 1,
Дополнение IV. Неравенства и теорема Белла
503
где планарные1 векторы а и Ъ характеризуют ориентацию, вдоль которой
измеряется проекция спина первой и второй частицы. В компонентах, напри¬
мер,
г А \ ( а* йх-ЫуЛ
(«, + ia, -а» )■
так что, вводя столбцы
элементарно находим
аЪ\0,0) = (аА ■ а)(ав ■ Ъ) ^{|+)АИв - Иа1+)в} =
J_{ ( а,-1аЛ m J Ъ2 bx-iby\ г0л
V2{ + ~az J VOj \J}X + iby -bz J UJ
_( az ах-1аЛ ЛЛ f К bx-iM m \
^ax + iay -az J UJ + iby -bz J VCM J
в то время как
(0, 0| = -^{(1, 0) ® (0,1) - (0,1) ® (1,0)}
и, следовательно,
(0, 0|ab|0, 0) = \{-azbz - (ax - iay)(bx + iby) - (ax + iay)(bx - iby) - azbz}
а значит, коррелятор спинов в квантовой механике выражается в виде ска¬
лярного произведения векторов, задающих ориентацию проекции измеряе¬
мого спина,
(А(а)В(Ь)) = —а-Ь. (Д1У.21)
Тогда
| с[А(а)В(Ъ)]+с[А(а)В(Ъ')] +с[А(а')В(Ь)]-с[А(а/)В(Ь/)]\ =
= | - а • Ъ - а • У - о! • Ы- о! • У | = \а • (Ь + Ь7) + а' • (Ь - Ь') |.
Модуль суммы скалярных произведений принимает максимальное значение,
если эти скалярные произведения имеют один знак, а векторы, составля¬
ющие скалярные произведения, параллельны или антипараллельны, т. е.
имеет место цепочка неравенств
la-Cb + bO+a'-Cb-bOl^la-Cb + bOl + la'-Cb-bOl^lb + b'l + lb-b'l.
1Лежащие в плоскости, т. е. двумерные векторы.
504
Дополнения
Для единичных векторов, образующих угол % у
cosf
of
\Ъ + Ъ'\ = V2(l + cos^) = 2
|b-b/| = V2(l-cos^) = 2
Без потери общности рассмотрения1 можно считать, что косинус и синус
половинного угла имеют положительный знак, так что
г£2л/2.
\Ь + Ь'\ + \Ь-Ъ'\^2
cos |-+sin|-
= 2V2U(f + f)
Значит, в квантовой механике имеется неравенство для спиновых корреля¬
ций
\сШаЖЪ)]+с[А(аЖЬ/)]+с[А(а'ЖЪ')] -с[А(.а'ЖЪ')]\^2^2, (Д1У.22)
а максимальное значение достигается при х = у т. е. когда векторы
bib' =ф b + b'lb-b' => ala',
причем
Ы-Ь'ТТа, Ь-Ь'Па',
ИЛИ
Ь + Ь7 ti а, Ь-Ь'Ца',
что воспроизводит ситуацию, рассмотренную нами выше. Как и следовало
ожидать, в квантовой механике реализуются системы, для которых наруша¬
ются неравенства Белла для теорий локального реализма.
Теорема Белла открывает путь эмпирического подтверждения несостоя¬
тельности претензий теорий локального реализма со скрытыми параметра¬
ми на превосходство в истинном описании природы по сравнению с кванто¬
вой механикой как источника неопределенностей в измерении физических
величин. Эксперимент надежно опровергает парадигму локального реализ¬
ма2 и утверждает истинность квантовой механики.
Дополнение V. Эйконал в рассеянии
При высоких энергиях
E^V0, V0~|VCr)|, (ДУ.1)
рассеяние на короткодействующем потенциале происходит, главным обра¬
зом, на малые углы, поскольку характерная сила, действующая на частицу
в потенциале с радиусом действия а,
Z7 У0
р r^J
а
Неравенства остаются в силе при перемене мест а <—»а', Ъ«—»Ъ'.
2Опыты с максимальным уровнем достоверности проводились на парах фотонов во вполне
аналогичном квантовом состоянии: вместо спина фигурировала линейная поляризация фото¬
нов.
Дополнение V. Эйконал в рассеянии
505
в течение времени, за которое частица со скоростью v испытывает на себе
действие потенциала,
At ~ —
v
приводит к характерному изменению импульса
и отклонению на угол
= => Д0<1. (ДУ.2)
р mv mv2 Е
Подчеркнем, что условие большой кинетической энергии (ДУ.1) еще не озна¬
чает выполнение условия применимости борновского приближения для быс¬
трых частиц ka :>1, так как условие высокой энергии можно представить
в виде
2
"" т'^У° ^ ka:>Voh2ka’
в то время как критерий применимости борновского приближения для быст¬
рых частиц требует более жесткого ограничения
h2ka
т. е. при высоких энергиях допустимо и
У0~£г*а, CflV.3)
что несовместимо с рассмотрением в борновском приближении.
Амплитуда упругого рассеяния выражается в общем виде через волновую
функцию стационарной задачи (26.29), так что для потенциала общего вида
/ = -^5 J dV e-ife£'rV(r/)'0[+)(V), (ДУ.4)
где волновой вектор рассеянной частицы кЕ = кп, п = г/г. В борновском
приближении мы полагали
(г') eik>r',
т. е. считали, что отличием между истинной волновой функцией и падающей
волной можно пренебречь в первом порядке по малости потенциала. При
условии (ДУ.З) такое предположение становится некорректным. Для пре¬
одоления этой проблемы заметим, что волна де Бройля представляет собой
частный случай классического приближения, или приближения геометриче¬
ской оптики, для свободной частицы, которое в случае свободного движения
оказывается точным:
iKr)~ei/fc(r)dr~eifc>'r, (ДУ.5)
где интеграл берется по классической траектории r=r(t), а функция
Ф = f k(r) dr СДу.6)
506
Дополнения
традиционно называется эйконалом. Напомним, что при формулировке при¬
нципов квантовой механики мы исходили из того, что приближение геомет¬
рической (волновой) оптики отождествляется с гамильтоновой (корпуску¬
лярной) механикой посредством связи эйконала Ф с действием на траекто¬
рии1 S
Эйкональное приближение в теории рассеяния при высоких энергиях заклю¬
чается в том, чтобы в формулу для амплитуды рассеяния в качестве волновой
функции подставить ее выражение через эйконал2
if) (г) >-» е1 k(r) dr (ДУ.7)
с учетом малого искривления траектории частицы по сравнению со свобод¬
ным движением dгъкх drjkb так что
Т dгъу- dгъ dri3
к кх 1
в то время как волновой вектор можно разложить до членов первого порядка
малости отношения потенциальной энергии к полной:
*4V2m{E-nr)>4v^-^nr)=fc,-^(r),
откуда
Ф = / k(r) dr=jr J* ^/2m{E — V(r)}^ dr&
WJ fci dri_ i" v(r)dri = ki-r~j^ J V(r)dr„ CflV.8)
где потенциал зависит от радиус-вектора
r = b + rt|, bkt = 0, (ДУ.9)
а вектор Ъ, лежащий в плоскости, ортогональной волновому вектору свобод¬
ной частицы на бесконечности, называют прицельным параметром.
Представление для эйконала в форме (ДУ.8) применимо, если, во-первых,
энергия велика (ДУ.1), а во-вторых, вклад в эйконал от поперечного движе¬
ния мал, т. е. вклад поперечного движения в фазу экспоненты от эйконала
несущественен:
ДФх-С2 п.
Этот вклад легко оценить как произведение отклонения по импульсу и по
координате:
1 1 Vn2
ДФХ ~ ^Др Дг± ~ s Др • г, Д0 ~ ^г„
1Мы опускаем здесь зависящий от времени вклад для стационарных состояний в эйконал:
-Et/h = -cot.
2Выбор нормировочной константы перед экспонентой очевиден: он соответствует норми¬
ровке потока вероятности на бесконечности.
Дополнение V. Эйконал в рассеянии
507
так что при Е ~ h2k2/m, v ~ hk/m,
г,«Ц. (ДУЛО)
Если для оценки максимальной величины потенциала взять границу приме¬
нимости высокоэнергетического приближения (ДУ.З), то принятое прибли¬
жение справедливо в области
r{<ka• а, (ДУ. 11)
а значит, в силу ka »1, им можно пользоваться достаточно далеко за преде¬
лами действия потенциала г{» а. Это становится существенным при вычис¬
лении амплитуды рассеяния в эйкональном приближении
/*-5^2 I dV е-^уУ(гО expjikrr'-^- f VCr') dr,}, (ДУ.12)
где интегрирование вдоль траектории по г{
dV = d2b dт-
можно проводить в интервале (—оо, +оо), так как короткодействующий по¬
тенциал V «обрезает» интегрирование в пределах г{ < а, т. е. в области при¬
менимости сделанных приближений (траектория мало отличается от прямо¬
линейной). Тогда
+ 00
1
dr- V(г') expj-g- J V(r') drt} =
= ■ПГ | d'Ц-ЦIv^ I VOO dr,} -1.
Стандартно вводят обозначение
25(b) = rr-ЦЬ- f VCr') dr,, (ДУ.13)
i _oo
которое отвечает разности эйконалов падающей и прошедшей волн, т. е.
в точности соответствует удвоенному фазовому сдвигу в задаче рассеяния.
В рамках этой же аналогии факторы рассеяния
У (b) = e2i5(b\ (ДУ.14)
Далее, переданный волновой вектор
q = kE-kt
при малых углах рассеяния лежит в плоскости, ортогональной к траектории
свободной частицы, а значит,
q-r'^q-b.
508
Дополнения
В итоге амплитуда рассеяния в эйкональном приближении принимает вид
/(«)» - ^ / d2b • e-iq b = (e2i5(b) -1). СДУ.15)
При вычислении полного сечения упругого рассеяния
<* = ! I/I2
в эйкональном приближении необходимо принять во внимание, что домини¬
рует рассеяние на малые углы, а значит,
сШ = sin в d0 dip ъ в d0 dip,
так что с учетом
q2 = 2к2(1 - cos 0) = 4к2 sin2 | м к2в2
находим в полярных координатах в плоскости прицельного параметра
dSl^^qdqdip = ^d2q,
что, впрочем, справедливо не только для малых углов рассеяния, поскольку
можно записать точно
d2q = £jq dq dip = 2 sin ^ cos ^ d0 dip = sin 0 d0 dip = dfi, G4V.16)
и
о- „ J *3- d2b d2b' е_‘ч'(Ь_Ь ) • (e2i5® -1) • {e~2iS^ -1).
В силу
j
(здесь не путать фазовый сдвиг 5 с дельта-функцией Дирака 6D!) получаем
сг = / d2b • 4 sin2 5 (Ь). (ДУ.17)
Амплитуда упругого рассеяния вперед (q = 0) имеет в эйкональном прибли¬
жении согласно (ДУ.15) мнимую часть
Im / (0) = ^ / d2b • sin2 5 (b), (ДУ.18)
что позволяет записать соотношение оптической теоремы в случае отсут¬
ствия неупругих каналов
cr = ^Im/(0), CAV.19)
которое несложно обобщить и при наличии неупругого рассеяния:
— в рамках представления прицельного параметра амплитуда упругого
рассеяния с переданным волновым вектором q = kE — k{ имеет вид
fW = ~^ I d2b-e~iqb{y(b)-l}, |5ЧЬ)|«а; C4V.20)
Дополнение V. Эйконал в рассеянии
509
— сечение упругого рассеяния вычисляется согласно формуле
aei = -£2 I dVl/(q)l2 = J d2b-ll-y(b)l2;
i
№21)
— сечение неупругого рассеяния—
СПУ.22)
— имеет место оптическая теорема для полного сечения рассеяния
cr = crel + ainel = ^Imf(0) = 2 f d2b-{l-Re[y(b)]}. (ДУ.23)
Итак, стартовав с рассеяния при высоких энергиях и эйконального при¬
ближения для волновой функции в амплитуде рассеяния, мы пришли к пол¬
ноценному представлению для этой амплитуды в терминах прицельного па¬
раметра, так что выполняется оптическая теорема, т. е. сохраняется веро¬
ятность, а значит, это представление никак не ограничивает общность рас¬
смотрения. Представление прицельного параметра бывает особенно удобно,
если заранее неизвестен потенциал взаимодействия и приходится модели¬
ровать поведение «эйконала», т. е. функции 5ЧЬ) = exp{2i 5(b)}, из каких-то
феноменологических соображений, которые могут быть естественными или,
другими словами, обладать рядом свойств, следующих из характера физиче¬
ской задачи. Конечно, запись фазового сдвига через эйконал в виде (Д\Л13)
с заданным потенциалом возвращает нас к эйкональному приближению для
рассеяния на малые углы при высоких энергиях.
В случае центрально-симметричного потенциала представление прицель¬
ного параметра для амплитуды упругого рассеяния на малые углы при высо¬
ких энергиях можно получить непосредственно из общей формулы
поскольку при малых углах полиномы Лежандра аппроксимируются функци¬
ей Бесселя нулевого порядка (см. лекцию 27 и задачу о рассеянии быстрых
частиц на черной сфере)
а от суммирования по орбитальному моменту можно перейти к интегриро¬
ванию
/(в)=Е ^{S‘ - 1}р>(cos в)>
Р[ (cos в) ^J0(ie), в<1,
1р 10
1=0 0
так что, вводя обозначения
= bk, Sz = S(b),
запишем
00
00
2п
r-ikb9 cos у
2п
о
о
о
510
Дополнения
При малых углах переданный волновой вектор по модулю равен
\q\ = \kE-ki\ = 2k sin ^ъкб,
а показатель экспоненты представим в виде скалярного произведения в плос¬
кости прицельного параметра, которая совпадает с плоскостью переданного
волнового вектора, ортогональной к волновому вектору рассеиваемой части¬
цы,
кЪв cos ip «\q\b cosip=q-b,
где ip —угол между передачей q и введенным таким образом вектором при¬
цельного параметра Ь.
В итоге приходим к сферически симметричному варианту выражения для
амплитуды упругого рассеяния в эйкональном приближении (ДУ.20):
[q) = / d2fe'е_1,'Ь^(Ь) -1>. WV.24)
Повторим, что эйкональное приближение дает не только весьма эффектив¬
ный метод расчета амплитуды упругого рассеяния при высоких энергиях
с заданным потенциалом, но и является инструментом исследования свойств
этой амплитуды, в том числе путем моделирования эйконала в случаях, когда
собственно потенциал неизвестен.
Дополнение VI. Кулоновское рассеяние
Кулоновское взаимодействие относится к важнейшему классу дальнодей-
ствующих: переносчиком такого взаимодействия является безмассовая ча¬
стица, в случае электромагнетизма — это фотон, а статический потенциал
убывает с ростом расстояния как К Это приводит, прежде всего, к искаже¬
нию асимптотических in- и out-состояний, так что их аппроксимация вол¬
нами де Бройля становится физически неприемлемой: она приводит к рас¬
ходящимся интегралам, например для фаз рассеяния, и не может считаться
сколько-нибудь точным приближением для волновой функции даже на очень
больших расстояниях. С другой стороны, специальный вид статического по¬
тенциала позволяет обойти эту трудность, так как задача решается матема¬
тически точно.
Асимптотические состояния. Поскольку потенциал стремится к нулю
на бесконечности, на достаточно больших расстояниях имеет место условие
B»|V(r)|, «VI.1)
которым можно воспользоваться для того, чтобы найти асимптотическое
поведение волновой функции в кулоновском поле путем расчета эйконала.
При условии (ДУ1.1) волновая функция, с заданным волновым вектором к[}
имеет вид
яКг)^е‘ф, Ф = кгг-^ / nb + ktf/fcOdr,, (ДУ1.2)
Дополнение VI. Кулоновское рассеяние
511
где траектория частицы мало отличается от прямолинейной вдоль волнового
вектора, Ъ — прицельный параметр, и в случае кулоновского потенциала
отталкивания
У(Ь + к;Г.А;) = -^=, (ДУ1.3)
у/Ь2 + г?
так что интеграл
в результате замены переменных
r{ = Ъ sh и
легко вычисляется:
ri
C(rs) = e2J ^J£=e2u = e2arcsh^[ = -e2ln{^ + l-|}[.
R
Тогда, возвращаясь к полярным координатам
г= д/ rt2 + b2, r^rcosO,
находим
Ф = fc.. г+у 1п{кхг(1 - cos 0)} + const, fflVI.4)
где константа не зависит от расстояний и углов, а также введен стандартный
параметр в задаче кулоновского рассеяния
те2 е2 тс с rirxrt
Г “ h% ~ he hk, ~ “em Vi ’ C4VI.5)
который есть отношение постоянной тонкой структуры к скорости движения
частицы в начальном состоянии, выраженной в единицах скорости света.
Этот параметр мал в случае применимости борновского приближения, но
при малых скоростях он указывает на то, что необходимо проводить сумми¬
рование всех членов, как говорят, «по степеням a/v».
Полученное выражение для эйконала (ДУ1.4) справедливо при
lr-rj-юо, (ДУ1.6)
так что асимптотические in-состояния в кулоновской задаче имеют вид
(г) a* eifci‘r+ir ln(fcir-fci*r\ (ДУ1.7)
где мы выбрали нормировочную постоянную так, чтобы выражение для по¬
тока вероятности для этих состояний совпадало с потоком вероятности вол¬
ны де Бройля с точностью до членов порядка
Л = ^ + о(^). WVI.8)
512
Дополнения
Как видим, логарифмический вклад в эйконал для асимптотических состо¬
яний приводит к несущественной для нас поправке к потоку вероятности,
однако, как мы увидим ниже, ее необходимо учитывать при расчете ампли¬
туды рассеяния.
Асимптотические in- и аналогично построенные out-состояния в кулонов-
ском рассеянии мы будем обозначать дираковскими символами
а точные решения кулоновской задачи с заданными граничными условиями
как
Для того чтобы указать асимптотическое поведение \яр^ ) с учетом рассеяния,
необходимо также вычислить эйкональную поправку для рассеянной волны.
При движении вдоль радиуса прицельный параметр равен нулю и
ка, что и рассеянная волна, явный вид которой для нас несущественен.
Амплитуда рассеяния. В кулоновском потенциале величина /(0) может
быть вычислена точно. Для этого мы используем связь стационарной ^-мат¬
рицы с амплитудой
где 0 —угол рассеяния между волновыми векторами в начальном и конечном
асимптотических состояниях. Однако расчет матричного элемента произво¬
дится не по асимптотическим состояниям, а в импульсном представлении
матрицы рассеяния, поскольку эта процедура может быть проще формали¬
зована математически. Значит, мы получим матричный элемент (к^Е\к{)}
который связан с искомой величиной соотношением
«VI.9)
(flVLlO)
Г
V (г) dr = е — = е In г + const, (ДУШ)
так что с учетом рассеянной волны
(ДУ1.13)
Дополнение VI. Кулоновское рассеяние
513
причем для конечных и начальных состояний имеет место асимптотическое
нормировочное условие, отвечающее сохранению импульса на больших рас¬
стояниях, где можно пренебречь потенциалом:
(k\kc) = (203 5(k — кс) [3fc(fc)]1/2, (ДУШ)
что просто отражает тот факт, что кулоновские асимптотические состояния,
нормированные на стандартный поток вероятности на бесконечности, как
в волне де Бройля, на самом деле имеют отличную от стандартной норму:
(fcc|fc/c) = (2л)3 5(кс — к/с) 2е (кс).
Отсюда
(fcfl^lkf) = (fcf|^|fci) • [^(.k^ikj]112. (ДУ1.15)
Следовательно, задача приобретает два аспекта: вычисление величин {kf\^E\k{)
и йfc(k). Для решения первой задачи необходимо «проинтегрировать» урав¬
нение для оператора ^-матрицы
&E = V + VGf*TE (Д\Л.16)
в импульсном представлении. Для получения нормировочной «константы»
рассмотрим выражение для функции Грина стационарного уравнения Шрё¬
дингера при наличии только непрерывного спектра1
с»=/ + W"-17»
и матричный элемент
<r|G,|fc')=J «V1-18)
в асимптотической области \гк" — г к!'| —> оо, где точную волновую функцию
можно заменить на ее асимптотическое выражение: |г/>£) —»\кс), так что
согласно подстановкам
<r|fc") = eirfc", (^|k'> (кс\к') = (2тг)3 5(к — к!) • [&с(к')]1/2
находим в асимптотике
{r\GB\k') ^ eifc'r+ir ^к'г~к^ ^&) + iO • (ДУ1.19)
Значит, нормировочная константа определяется асимптотическим поведени¬
ем функции Грина стационарного уравнения Шрёдингера
/
.ir-fc" d3fc" р ,,// i/ч _ ifc'-r+ir lnffc'r-fe'-r) [2?С(к )]
■ (2n)3W’K)-e Е-Е(.к') + Ю*
гВ потенциале притяжения появляется вклад дискретного спектра связанных состояний, од¬
нако он не сказывается на проводимых ниже выводах для состояний с положительной энергией.
514
Дополнения
В последнем асимптотическом равенстве или в (ДУ1.19) фигурирует опять
же функция Грина в импульсном представлении. Заметим в связи с этим,
что задачи расчета ^-матрицы рассеяния и функции Грина стационарного
уравнения Шрёдингера по сути эквивалентны друг другу, поскольку эти опе¬
раторы связаны соотношением
Ge = G<0) + GfSTEGf, (ДУ1.20)
откуда, между прочим, согласно уравнению для матрицы рассеяния (ДУ1.16)
следует, что
GfSTEGf = GfVGf* + GfV{GfSTEGf + G<0) - G®} = GfVGE,
и мы приходим к верному уравнению для стационарной функции Грина
Ge = Gf + Gf VGe. (ДУ1.21)
В импульсном представлении уравнение для матрицы рассеяния имеет
вид
(fcf l^lfci) = <fcf ivlfcj + J (kf\V\k) -03 ^ -.Q (k\srE\fej. cqvi.22)
Аналогично можно записать и интегральное уравнение для стационарной
функции Грина в импульсном представлении.
Интегральные уравнения можно решать методом итераций. При этом
удобно изображать элементы соответствующих произведений в виде диа¬
грамм Фейнмана согласно следующим правилам:
— потенциал изображается волнистой линией переносчика взаимодей¬
ствия — фотона, соединяющей вершины частиц с входящим и выходящим
импульсами и источник потенциала, изображенный жирной линией:
к к'
(k'|V|k) (ДУ1.23)
— свободная функция Грина отвечает линии с идущим по ней импульсом
и соединяет вершины:
= + ю WI.24)
Тогда итерационный ряд для матрицы рассеяния
&Е = у + VG® V + VG® VGfv + ...
представйм в виде так называемых «лестничных» диаграмм:
к, к. к. к. h к.
Дополнение VI. Кулоновское рассеяние
515
Отметим, что петля на подобной диаграмме Фейнмана соответствует ин¬
тегрированию по 3-мерному промежуточному импульсу.
Диаграммы Фейнман для итерационного ряда, отвечающего стационар¬
ной функции Грина GE, повторяют приведенную выше картину для матрицы
рассеяния с той лишь разницей, что внешние линии с входящим и выходя¬
щим импульсами соответствуют факторам в виде свободных функций Грина
и имеется дополнительное слагаемое—распространение без взаимодействия
[рисунок в (ДУ1.24)], которое в импульсном представлении включает в себя
дополнительный фактор сохранения импульса (2тг)3 5(к{ -kf):
(fcf |G<0) |fc,) = Gf (fct) (2nf 5 (fcf - kj.
Для кулоновского отталкивания
Тогда интегральное уравнение для матрицы рассеяния (ДУ1.22) запишется
в виде
ц,\*Г\и 4яе2 . Г 4пе2 dЗк {к\^Е\к,)
^1 £l i> (fcc-fci)2 (к.—к)2(2п)3Е — Е(к) + iO' CflVI.26)
Поворот Вика. Разность энергий Е — Е(к), стоящую в знаменателе инте-
гранда (ДУ1.26), обычно переписывают в виде
вводя параметр1 е. Следовательно, выражение функции Грина свободной
частицы принимает вид
1 _ 2 m 1
Е — E(fc) + iO h2 г2 — fc2 + iO
Напомним, что при интегрировании по импульсам и вычислении этой функ¬
ции Грина в координатном пространстве мы установили, что как функция
энергии она имеет разрез вдоль вещественной оси, т. е. на линии непре¬
рывного спектра, как это указано на рис. 43, причем физическое значение
берется на «верхнем берегу разреза». При переходе к переменной е фи¬
зический лист комплексной плоскости энергии сворачивается в верхнюю
полуплоскость, а нефизический отображается в нижнюю. Следовательно,
нужно считать, что е е + iO.
Введем теперь переменную ё так, чтобы
h2s2_ -
2m
Соответствующие плоскости комплексных переменных —Еиё с обозначени¬
ем на них сингулярностей свободной функции Грина и расположения физи¬
ческого и нефизического листов приведены на том же рис. 43. Из рисунка
ХВ обозначениях волновой теории е = со/с, где с — скорость распространения волны.
516
Дополнения
физ.
лист
1®
■lie
нефиз.
лист
нефиз.
лист
(i)
ж
ЧТУ
физ.
лист
т.
Рис. 43. Сингулярности свободной функции Грина как функции комплексной
переменной энергии (физическое значение берется на верхнем берегу разре¬
за) и их отображение в плоскости переменных е = ~ V2 тЕ ие = ^ \!—2тЕ
очевидно, что физическое значение при положительной энергии, указанное
стрелкой, соответствует чисто мнимому отрицательному значению ё + 0.
Переход отеке называется поворотом Вика.
При таком повороте
*=-> т.27)
а выражение для резольвенты свободной частицы
1 2тп 1
Е-Е(к) + Ю h2 ё2+к2 CflVI.28)
формально не имеет полюсов и соответствует 4-мерному евклидову про¬
странству (4Б-пространству) для волновых векторов
к£ = (ё,к), к2£ = ё2 + к2. (ДУ1.29)
Поэтому последующие расчеты проводятся именно в 4-мерном евклидовом
пространстве, что отвечает отрицательной энергии Е, а результаты для Е > 0
получаются аналитическим продолжением согласно (ДУ1.27) в окончатель¬
Дополнение VI. Кулоновское рассеяние 517
ных выражениях. Такой прием широко распространен в теоретической фи¬
зике.
Заметим, что, если в системе есть связанные состояния, т. е. стационар¬
ные уровни с Е < О, то они будут отвечать полюсам при положительных ве¬
щественных значениях ё, т. е. на физическом листе, а возможные полюса при
отрицательных значениях ё являются нефизическими, т. е. не соответствуют
связанным состояниям, хотя они определяют поведение функции Грина и на
физическом листе и оказываются существенными при рассмотрении задачи
рассеяния.
Другим объектом, специфическим для статического дальнодействия, в
уравнении для матрицы рассеяния является функция
(k-k')2’
которую можно представить в виде
1
к2 + к'2 -2(к- к') k2a + t2-2txY
где, считая для определенности, что \к\ > |к'|, мы положили
,=М<1 х=<кИ
№1 ’ IM-lfc'l
Функция (1 + t2 — 2tjc)_1 является производящей для полиномов Чебышева
второго рода Wn(x)
оо
^=Z (до-30)
1 + - -- п=0
то есть1
щ (V) —jLitl 1
*nW п\ dtn 1 + t2 — 2tx
(ДУ1.31)
t=о
Именно разложение по полиномам Чебышева, которые образуют «базис»,
и позволяет точно решить задачу кулоновского рассеяния.
Однако при интегрировании по импульсам их отношения принимают
значения как большие, так и меньшие единицы, что осложняет применение
указанного разложения по базису полиномов Чебышева второго рода. Го¬
раздо удобнее перейти к векторам, нормированным на единицу. Это можно
сделать, опять-таки проводя рассмотрение в 4-мерном евклидовом простран¬
стве. Но именно в этом пространстве, как мы покажем ниже, и полиномы
Чебышева приобретают особую роль, а их свойства формулируются наиболее
эффективно.
1Несколько первых полиномов: ^0ix) = 1, %(х) = 2х, °U200 = 4х2 — 1.
518
Дополнения
40-обозначения. В 4-мерном евклидовом пространстве введение поляр¬
ных координат для 4-вектора г£ = (г, г) производится стандартным образом
r = |re|cos*,
г = |ге| sin я,
x=r sin в cos ip,
y = r sin в sin ip,
z=r cos в,
СДУ1.32)
где \г£| = \[Щ—длина вектора, а {х, в, ip}—полярные углы. Тогда
dr dr =
так что
Э(г, г)
д(.\г£\,х)
d\r£\dX=det d\r£\dx = \r£\d\r£\dx,
d4rf = dr d3r = r2 dr dr d cos в dip = |r£|3 d|r£| dQ3(rf),
где дифференциал по 3-мерному телесному углу
dft3 = sin2 х sin в dx dв dip.
(Д\Л.ЗЗ)
Для того чтобы записать 3-мерное интегрирование в 4Б-обозначениях,
введем единичный вектор v£ = (v, v):
v = •
ё2-к2
ч
v=wk
Ч
vf = l.
C4VI.34)
В терминах полярных углов cos х = ё/\к£\, sin х = 1^1/1^г1 для 4Б-вектора к£
(ДУ1.35)
v = cos2 х ~ sin2 х = cos 2Х>
|v| = 2sin* cos* = sin 2x,
так что с учетом единичнои длины вектора
d3v = dn3(v£) = sin2 2х sin в d2x dв dip = 23 cos2 x dTl3(k£).
Поскольку все расчеты проводятся при фиксированном значении энергии
de = 0 => cosх d|fcf|-sin^|fcf| d*=0,
так что
dfc = sin x d\k£| + cos x\k£I dx = IM dX + cosx\k£\dx = dx
И
cos*
d3fc = fc2 dfc d cos в dip = dJ23 (k£).
cos x
cos x
В итоге с учетом cos х = ё/\к£\ находим
d3fc=(^-) dfi3(v£).
im.36)
Дополнение VI. Кулоновское рассеяние
519
Наконец, вычислим величину
• ~2 _ 7,2 ~2 _ ъ'2
Tv v^2_? п(ё -к2 ё2-к2 Лё П ,/Л _
Ws Vg) 2 21 ,2 /2 1(2 is'i )
\ IV л IV /» IV л iv At X
= + fc72 - 2Cfc • fc')} = ^ (fc - fc')2.
В 4Э-обозначениях интегральное уравнение для «^-матрицы рассеяния
принимает вид
4яе2 4ё2 Г&еЛ*4П*<Уе) ШЕ\к,)
(2я)3 fc|
/1г|д-|7г\_ 4яе2 4ё2 2т Г 4яе2 4е2 (к1у
f Е (yfe-vie)2 k2sk2e h2 J (.Vfe-Vg)2 k2£k2\2ej
Введем обозначение
(fcf|^|fci)=47re2r|^Tfi) C4VI.37)
'Cf£,Ci£
где величина Tfi = T(vf£: • vi£) кинематически зависит только от скалярного
произведения единичных векторов. Тогда основное уравнение примет вид
nv’£v-)=^?-f/ ww-38)
Заметим, что
n п 2п
J сШ3 = j sin2 % dх J sin в dd J d</? = 2я2,
ООО
так что интегрирование в (ДУ1.38) ведется с усреднением по телесному углу.
Согласно определению полиномов Чебышева второго рода
оо
t=1=XX(v£,V£)’
п=О
(v£-v')2 1 + t2 — 2t(v£ • v')
в то время как искомую величину можно представить в виде разложения по
этому же базису в виде
00
Т(Уе'v's) =S 8nWn(.v£ • v'), (ДУ1.39)
п=О
где gn—неизвестные коэффициенты. Тогда
*/ £ 71=0 n'=0 J
так что решение проблемы кулоновского рассеяния сводится к вычислению
стандартного интеграла
J
dfio fvp)
^nCVfg • Vg)^(Vg •
для нахождения которого необходимо знание основных свойств полиномов
Чебышева второго рода.
520
Дополнения
4Б-вращения. В 4-мерном евклидовом пространстве генераторы 6-параметриче-
ской группы вращений записываются в том же виде, что и в пространстве Минковско-
го, с той лишь разницей, что верхние и нижние индексы декартовых ко- и контравек-
торов эквивалентны:
Lab I'aPb ^ъРа» ^ab ^ab 0,3.
Введем вектор—генератор 3-мерных вращений (греческие индексы «бегают» в 3-мер-
ном пространстве)
Za=|<WiLiV’ l = —irx V,
и 3-вектор «пространственно-временных» вращений
u = -i(rV-rd),
откуда элементарно вычисляются коммутационные соотношения
> ly] i^/zvo^aJ Uv] ^ixva^ay ^v-1
так что, вводя линейные комбинации генераторов
j(±) = i(Z±u),
(ДУ1.40)
C4VI.41)
(ДУ1.42)
(ДУ1.43)
находим
СДУ1.44)
т. е. стандартную алгебру для пары независимых моментов. Следовательно, в общем
случае мы имеем два инварианта — /~)2}, которые выражаются через исходные
генераторы
/±>2 = I{I2 ± (I • u + и • I) + и2}.
Однако, используя явный вид генераторов 4Б-вращений, элементарно получим
Zu = -f(r х V)- V + (rx V)-r§ = 0
и аналогично
а значит,
и • Z = —f V • (г х V) + г • (г х V)5 = 0,
/+)2=/-)2 = |{12 + и2}.
Обозначим квантовое число инварианта1 как
j=jw = пе{0, N},
(Д\Л.45)
(ДУ1.46)
(ДУ1.47)
так что значение инварианта
IV2 = I2 + u2 = 4j O’+1) = П(п + 2),
а базис состояний можно характеризовать квантовыми числами «моментов»: абсо¬
лютным значением векторов и их проекцией на заданную ось
I „,(+) Г-)\ П г±) ГС
\пу 771 J), ~2^т 2 ’
Однако, поскольку
[I, и^]=0, C4VI.48)
взаимно коммутируют операторы инварианта w2, орбитального момента I2 и его
проекции на заданную ось, например lz. Так что удобнее пользоваться обычными
квантовыми числами
IП, I, т), C4VI.49)
1 Инвариант может принимать как целые, так и полуцелые значения.
Дополнение VI. Кулоновское рассеяние
521
где т — собственное значение проекции орбитального момента, причем, так как
орбитальный момент выражается в виде суммы моментов
его допустимые значения определяются границами сверху jt+) +j(_) = 2j = п и снизу
| j(+) _ j (-) | = \j _ j | = о, т. e.
О^Ып. (Д\Л.50)
Легко посчитать число базисных векторов
П
х = ]^(2Z +1) = (n +1)2,
1=0
что, естественно, совпадает с числом векторов исходного базиса состояний в стан¬
дартном представлении х = (2j(+) +1) (2+1) = (n +1)2.
Генераторы вращений зависят только от угловых переменных, так что если |Г23) —
координатное состояние с заданным единичным вектором на 3-мерной сфере, т. е.
в телесном угле, то
&Ыт(.Х> 0> <£) = Фз1л. I, т)
суть сферические гармоники в 40-пространстве. Они удовлетворяют уравнениям на
собственные значения
w2%lm=n(n + 2)%lm, f%lm=l(l + l)2%lm, lz%lm=m%lm, (ДУ1.51)
так что, записывая операторы в терминах угловых переменных1 и пользуясь стан¬
дартным методом введения старшего и младшего векторов, можно построить сфе¬
рические гармоники в виде явных функций от углов. В последних двух уравнениях
операторы не зависят от угла и их решения, следовательно, выражаются через
знакомые нам сферические гармоники, зависящие от двумерного телесного угла:
а функции связаны с полиномами Гегенбауэра %п(х)> построением которых
мы здесь не занимаемся2:
Of) ~ sin* X %п (c°s X) •
Условие полноты базиса сферических гармоник для функций, зависящих от поляр¬
ных углов в 40-пространстве, запишется в виде
00 п I
ЕЕ 2(Пз1пЛ,т)(п,г,т|п;> = 5(П3-П,3). (Д\Л.52)
п=0 1=0 т=-1
Как и в трехмерном евклидовом пространстве, распишем операторы I2 и и2,
исходя из их определений: как и прежде,
i2=- г*дю+г*£+2г£.
где Д(3) — оператор Лапласа в 3-мерном пространстве, а
и2 = -(гV - гд)(г V - гд) = -г 2Ат - г2!2 + 3fd + r^-+2rr^-.
J дг дгдг
Учтем теперь, что
г2 = г2 + г2, Д(3) = Д(4)-Э2,
1То, что эти операторы не зависят от длины 4D-BeKTopa, следует из их инвариантности
относительно масштабного преобразования г£^Хг£.
2Заинтересованный читатель может обратиться к математическим справочникам.
522
Дополнения
так что для инварианта находим
I2 + и2 = -г\ Д(4) + г2 ^2 + г2 ^2 + Эг § + Зг^ + 2гг .
Из соотношений
(|r^afe)2=(fl+r|:)2=F2^+r2£+2rf!^
следует, что
I2 + и2 = -г2 Д(4) + |ге |2 ^ + 3\re |^. CflVI.53)
В итоге 40-оператор Лапласа связан с инвариантом группы вращений соотношением
Д(4) = 1^ +(ДУ1.54)
() д\ге\2 |г£|Э|г£| г| ^
Задача 16.1. Выразить оператор w2 в терминах дифференцирования по углам,
определив оператор Лапласа на сфере в двумерном, 3-мерном и 4-мерном простран¬
ствах.
Решение. Двумерный случай. Для определения угловой части лапласиана запи¬
шем оператор V(2) в полярных координатах
__ а , а
(2)_Сгаг +е^гэу’
так как элемент длины имеет вид
dr2 = dr2 + r2 dip2.
В криволинейных координатах, частным случаем которых и являются выбранные
нами полярные, базис векторов в отличие от декартовых ортов не остается посто¬
янным при смене точки его приложения; ортонормированный базис криволинейных
координат вращается при сдвигах, т. е. при дифференцировании1. В евклидовом про¬
странстве геометрическая связь полярного базиса с декартовой системой позволяет
наглядно получить изменение базисных ортов при дифференцировании. При сдвиге
вдоль радиус-вектора базис полярных ортов не изменяется:
тА«=0-
Сдвиг по углу эквивалентен вращению вокруг воображаемой оси — нормали к по¬
верхности, так что для единичного радиуса
&г=е„,
в то время как для касательного к окружности орта — это движение вектора скоро¬
сти при вращении, и его изменение есть центростремительное ускорение единичной
скорости на единичной окружности2:
_д
Значит, лапласиан
= (?*-+*
Гдф ) дг2 ' Г2 dip2 ' v гдф V. г дг V rdip ,
вг*
А гг 2 ( д , д Л2 д2 . 1 д2 , д ( д , д \
(2) ~ (2) “ (л дг + еч> гдш ) ~ дг2 г2 дч>2 ^ гдч> 1вг дг + С* гдш ) ’
ХВ дифференциальной геометрии подобные вращения базиса описываются введением кова-
риантной производной, а значит, и соответствующих символов Кристоффеля.
2Формула для модуля ускорения a=v2/г.
Дополнение VI. Кулоновское рассеяние
523
и в согласии с полученными выражениями для дифференцирования ортов и их орто-
нормированностью получаем
д -v2 -ii + iJi+Ii.
(2) (2) аг2 г2 dip2 г вг'
Отметим, что для расчета лапласиана достаточно знать такие изменения ортов ба¬
зиса, которые направлены по орту варьируемого параметра полярных координат:
другие скалярные произведения базисных векторов в лапласиане обращаются в нуль.
Трехмерный случай. Элемент длины
dr2 = dr2 + r2{d02 + sin2 в d</?2}
задает
тт э , э , 1 а
^сз)=ег5;+ев^?+е,)^г?—.
При смещении вдоль радиуса базис не изменяется и, как и прежде,
5 Л
дгег,<р,е
Сдвиг по углу в эквивалентен вращению вокруг орта ev, так что в полном соответ¬
ствии с 2-мерным случаем
Ивег~ев’ дёев~~вг’ aeef~0'
Сдвиг по углу ip эквивалентен вращению вокруг оси z: у орта ет вращается ком¬
понента, спроектированная на плоскость {х, у}, длина которой sin в, направление
ортогонально ev, а смещение параллельно е^,, т. е.
^er = sin0V
Аналогично, длина проекции ев в той же плоскости равна cos 0, эта проекция ортого¬
нальна смещению вдоль ev, и
^e9=coseV
Смещение ev по ip ортогонально е^, и для нас оно не существенно. Собирая необхо¬
димые нам результаты (смещение по углу параллельно его орту),
^ег=ев, j^er=sin 0ev, ^efl=cos0ev,
найдем
v2 =fe±+eeJ-+e
v(3) V*'dr sin 6 d<p)
_ a2 l a2 l д2 ев a a <у a a а a _
dr2 г2 дв2 r2 sin2 в dtp2 r dOCr dr rsint? dipCr dr rsin0 dipSerdd
_ a2 1 a2 l a2 . 2 э . l a
dr2 r2 de2 r2 sin2 0 dtp2 r dr r2 g dO ■
Выделяя радиальную и угловую части лапласиана, можно записать
^>=£+^£+М^+да-2)^*»-*>з^}' «и-5»
где D — размерность пространства, {X{d-d> •••» ХгУ — полярные углы, определяющие
последовательное проецирование радиусов евклидовых пространств
Гф-k) = rw-k+i) sin Xw-k), к6{1,..., D -1},
524
Дополнения
а А(г>—1) C^cd-2)> • • •> £ц)) —угловая часть лапласиана в D — 1 измерении. Например, при
D = 3 мы обозначили Х\ — Ч>> Хг = а Д(2) Gf(i)) = I/7*2 s*1*2 0 * д2/дц>2. Справедливость
формулы (ДУ1.55) следует непосредственно из способа введения полярной системы
координат—последовательного проецирования из большей размерности в меньшую:
при этом радиальный орт имеет D — 1 проекцию в низшие измерения, которые
вращаются при изменении углов так, что длина радиуса вращения компенсируется
коэффициентом при частном дифференциале угла, а направление изменения при
сдвиге угла как раз определяется соответствующим угловым ортом; орт (D — 1)-го
угла имеет D — 2 проекций в низшие размерности с длиной первой проекции, равной
cos Хф-1), в то время как при дифференциале (D —2)-го угла стоит при
дальнейшем проецировании эти факторы сохраняются, а направление изменения
при сдвиге угла опять же задается ортом соответствующего угла; лапласиан в низших
размерностях не изменяется. Для убедительности приведем необходимые формулы
для 4-х измерений.
Четырехмерный случай. Дифференцирование базисных ортов, которое необхо¬
димо учесть при записи лапласиана, сводится к набору, который следует из прямого
обобщения 3-мерного случая:
Jjer=ex> jger = siaXee, ^er=sin* sin 0е„,
Jeex =cos xee> ^e,=cos*sineev„
^e0=sin^cos 0ev,
откуда легко находим
Д Э2 3 Э 1 Г Э2 cosX д 1 ( д2 cos в д 1 д^_Л\
(4) дг2 г дг г2 Id*2 sin* дх Sin2*vd02 sin 9 дв sin2 0 dip2 J J ’
Отсюда сразу следует выражение для инварианта w2, которое записывают также
в несколько иной форме, в терминах дифференцирования по косинусам:
v д2 . о д . 1
h o’ Н- 3 cos * Ь ~ о
д COS х д cos X sin2 *
w2 = -(1 - COS2 x)T~Z2 + 3 cos *77^7 + ^ГГт}2’ C4VI.56)
где
I2 = — (1 — cos2 в)—2+2cos 6-
d cos в2 d cos в sin2 в dip2 ’
Построим базис решений уравнения для гармонических функций
А(4)Ф = 0 (ДУ1.57)
в терминах сферических гармоник, т. е. с учетом уравнений на собственные значения
инварианта вращений, орбитального момента и его проекции (ДУ1.51). Тогда общее
решение уравнений на собственные значения имеет вид
ф=Ж|гг|)уяЬ1(*,е,у),
где уже St удовлетворяет уравнению однородной функции от длины 4D-BeKTopa
+ ill afel" }^(|Ге!|} = °’
которое легко решается стандартной подстановкой
®(\г£\) = \г£\с,
откуда
с(с-1) + Зс + п(п + 2) = 0 => с12 = —1 =Ь(п +1).
Дополнение VI. Кулоновское рассеяние
525
Значит, базис гармонических функций составляют решения вида
*i = \re\n*hm(X, О, у), ^2 = \ге\~п~2^лпСх, 0, у). C4VI.58)
Функция Грина. В 4-мерном евклидовом пространстве оператор Лапласа Д4 име¬
ет функцию Грина
А(4)5(г£) = 5(4)(г£) (ЛУ1.59)
вида
6ы=-£?]§’
Действительно, интегрируя (ДУ1.59) по 40-шару V4 и пользуясь теоремой Гаусса—Ост¬
роградского, находим
-^2 Jd4r£A(4)^ = -^2
V4 dV4
где
d53 = |rf|3 dn3 -er
иег = г£/\г£\ — единичный радиус-вектор в 40-пространстве, а
V7 1 - 2
(4) 2 г3 '6г
£ £
так ЧТО
• VC4) \ = —2 J (Ш3 = —4п2,
Гг
dV4
и мы приходим к верному тождеству1
I
d4r£ Д(4) -j -1.
г£
V4
С другой стороны, вводя единичные 40-векторы v
r£ = |rfi|vfi, r' = |r£|v'
и пользуясь определением полиномов Чебышева второго рода, запишем
Сг i^a “ lrf 1)Т7 ~Vl r+^(lril “ М) —-f Г2 1. , Г =
=#(|reI - |i£|) J] jjsL■%(vf • v£) + ■&(\r'£| -\reI)ф 2 (Уе ■ v'e),
где, как обычно, ft обозначает тэта-функцию Хевисайда. Согласно (ДУ1.59) и (ДУ1.60)
запишем равенство
-^л»0^7р=5<4>'1-'-р. 0W-®
а значит, при \г£\> |г'| находим
А(4) ^ | |п+2 ^П (Уе * vf) = О,
п=0 1 51
1По сути мы указали способ построения функции Грина оператора Лапласа в D ^ 3 измере¬
ниях, так что Q{d) (г) = -^*, где x~l = (D-2) J dHD_!.
526
Дополнения
А(4) ^ у |П+2 (У£ ’ V£) О,
а при |г£|<|г'|-
Ы"
=3 w
откуда фазу следует, во-первых, что согласно построенному выше базису для гармо¬
нических функций и полиномы Чебышева можно разложить в этом базисе:
п I
W„Cve .vp=£ 2 cnlm(x\ o', 0, <PX
1=0 m=—l
так что
W2%(v£ • v') = n(n + 2)%(ve ■ v'), cqvi.62)
и поскольку полиномы зависят только от угловых переменных,
JLX(*'-V=0.
а значит,
Aw%(vs • v^ = -±n(n + 2)%(ve -v'). СДУ1.63)
re
Выбирая v' = (1,0,0,0) и обозначая £ = v£ • v' = cos *, запишем уравнение (ДУ1.62)
в виде
(1 - £2)<(£) - З^'СО + п(п + 2)^п(0 = 0. fflVL64)
Во-вторых, так как уравнение для функции Грина (ДУ1.61) симметрично отно¬
сительно перестановки штрихованных и нештрихованных переменных (оператор
Лапласа может действовать и в пространстве 4D-BeKTopa г'£), аналогичное условие
гармоничности имеет место и для штрихованных переменных, а значит, полиномы
Чебышева раскладываются по базису сферических гармоник, который удобно вы¬
брать комплексно сопряженным:
Cnlm(x',0',<p') = £| X Сп!тЧ1'Ж’ &> <А
z'=0 m/=—I'
а значит,
Wn(.ve-v'£)= ^ (n3(v£)|n, г, т)с‘'^(п, V, m'|n3(v')>, WVI.65)
,т!
где {Z, ш} и {Г, т'} «пробегают» допустимые значения.
Действие лапласиана с учетом условия гармоничности дает
Д(4) (г£-г')2 = {(ij^ja + “|r*|}} § ‘V>£) +
+ {(э|г£|2 + |Г£| Э|Г£|)^Г^ |Г£,)} 2 |r'|n+2^n(VfVp +
“ _М
Дополнение VI. Кулоновское рассеяние
527
Однократное дифференцирование тэта-функций дает
- |г^|) = 5(|г£| -\г£\),
- |r£|) = -5(|rf | - \г'£\),
а значит, однократное и повторное дифференцирование только тэта-функций приво¬
дит к нулевой сумме двух вкладов, в то время как, дифференцируя дробно-степенные
функции, элементарно находим для левой стороны уравнения для функции Грина
(ДУ1.61)
00
LHS = 1^3 5<|ге|-1Г^ (-2) I> + D^Cve • v').
Для правой стороны этого уравнения получаем
RHS = S(4)(ге -:r'£)= ^ 5(|re | -1r'e|) 5(3)(v - v'),
НО
d3v = dn3 (ve), 5(3) (v-v') = 5{fi3 (v£) - n3 (v' )>,
где, очевидно,
5{ft3(v£) -n3(v')}= —- . д Six “ *') S(0 - 0') S(fp - <A
sm x sin “
т. e.
RHS = 5^rs\- lr£l) 5{n3(vfi) -n3(v')}.
В итоге равенство левых и правых частей при произвольном 40-векторе v' означает
00
^2 2(п + 1)^(уе,у£) = 5{Пз(у«)_ПзСу£)}> (ДУ1.6б)
п=0
что есть не что иное, как условие полноты базиса полиномов Чебышева в 3-мерном
угловом пространстве телесных углов для функций, зависящих от скалярных произве¬
дений единичных 4D-eeKmopoe.
В силу полноты базиса сферических гармоник в пространстве функций, зависящих
от углов,
00
2 1> т^п’1> т1пзОг)) = 5{n3(vf) -n3(v')},
n=0 l,m
из разложения полиномов Чебышева по гармоникам (ДУ1.65) и (ДУ1.66) сразу нахо¬
дим
1'т* 2п2 с с
Сп1т “ п _|_ I ^тт'>
а значит,
J](n3(v£)|n, а)(п, a|n3(v')} = ^%ive • v'), (ДУ1.67)
a
где a = {Z, m} в области их допустимых значений: Z€{0,..., п}, m€{-Z,..., Z}.
«Нормировка» состояния легко определяется согласно
2>, a|n, a) =2] J df23 (п, а|П3)(П3|п, а) =
а а
=2 / dn3 <пз1п> а>(п, а|«з) = f dn3 %(ve-v£),
528
Дополнения
но
Wn(vs-v£) = %(l).
Значение
Id" 1 I _ (-1)" d" 1
%(V = :
— П+ 1,
t=0
n! dt" (1 -1)2 |t=o n! d(l - t)n (1 -1)2
так что
^]<п,а|п, а) = (п + 1)2,
а
и поскольку базис был выбран ортонормированным (п, а\п, а) = 1, его вырождение,
как и должно быть, равно (n +1)2. Следовательно,
^](п)а|п/)а> = (п + 1)25пп/. СДУ1.68)
а
Теперь легко установить тождество
J (v£ • vp (v" • v') = Йт (v£ • V'). (ДУ1.69)
В самом деле, левую часть равенства можно записать в виде
LHS' = E f (а3\п,а)^(п,а\0!1)^Щп',Ъ)^1(п',Ъ\0!3),
а,Ъ J
где
|£2з) dfig (П31 = 1, f(n, а|П") dO" (П" |n', b) = (n, a\n\ b) = 5nn,5ab,
так что
LHS'=J](n3|n, a)(n, а\Щ-^5пп, = |ssl^n(v£ • v').
a
Решение уравнения для матрицы рассеяния. Уравнение на матрицу
рассеяния
при решении методом итераций — суммировании лестничных диаграмм —
приводит в j-й итерации к вкладу вида
2 2я2 (Va> - у®)2
1 dHaCv^) 1
... х
ОГ15 - vf)2 2п2 (vf - vi£)2
•/ j n0,...,Tlj
п л П.. •' n—n
n0,...,Tij J n=0
Дополнение VI. Кулоновское рассеяние
529
В итоге получаем
СО 00 ^ . 00
Г(Vfg • Vie) (Vff • Vi£) = 2 ^n(vf£ • vi£) —.
n=0 ;=0 n=0 n+1
(ДУ1.70)
С другой стороны, это решение может быть получено и непосредственно
после учета выведенного свойства ортогональности полиномов Чебышева
(ДУ1.69) и подстановки в уравнение разложения матрицы рассеяния
00
Т(Уе ■ vp = • vp, WVI.39),
п=0
так что для неизвестных коэффициентов gn легко находим
8п = 1~?-^> №1Л)
а сама матрица разлагается в ряд1
00
nv£ • vp = 2 ^Wn,-iiv£.vp. СДУ1.72)
п'=1 1
Эта матрица имеет полюса в точках f = —п!:
ё=-Р§, №73)
расположенные на отрицательной полуоси ё в случае потенциала отталки¬
вания, т. е. на нефизическом листе комплексной переменной Е = —К2ё2/2т.
Если же перейти к потенциалу притяжения e2—>q1q2e2, qxq2 = —1, то эти по¬
люса лежат на положительной полуоси, т. е. на физическом листе, и отвечают
связанным состояниям с энергией
En = -%$*L> WVI.74)
как это и должно быть в кулоновском потенциале. Отсюда видно, что нату¬
ральное п' = п +1GN имеет смысл главного квантового числа для связанных
состояний в случае притяжения2.
Для проведения суммирования в (ДУ1.72) заметим, что
SrfTf=/d5'5"+f.
1Начало суммирования сдвинуто: n' = п +1.
2Если подставить разложение полиномов Чебышева по сферическим гармоникам ^п/т, то
несложно вывести и нормированные волновые функции связанных состояний ^pnim (р) в тер¬
минах ^nim. Однако мы здесь этого не делаем, потому что не строим гармоники в явном
виде, к чему следовало бы еще добавить аккуратное описание перехода от матрицы рассеяния
к функции Грина, связь которой с нормированными волновыми функциями известна, а кроме
того, задача нахождения волновых функций уровней энергии в кулоновском потенциале была
рассмотрена ранее в координатном пространстве.
530
Дополнения
откуда
1
Г 00
T(y£-v'e)= Jf(n+l)^(v£-vp.
j n=0
0
По построению,
— = g ^%(YS • v').
Значит,
2 Zn(n + 1)%(Vf • V£) = -j|£ ^ ?n<^n(Vf • vf) = 3£1 + ?2_2£(v .V')-
n=0 п=0 ъ ъ £ £
Дифференцирование элементарно дает
d g . i-g2
d? 1 + ? - 2 £(v£ • v') {1 + £2 - 2£(ve • v')}2 ’
так что, учитывая единичную нормировку 4Б-векторов,
2Ое • v'£) = 2 - (ve - v')2,
запишем
1 + £2 - 2£(v£ • v') = (1 - O2 + ?(v£ - v')2,
и в итоге приходим к интегральному представлению:
1
W2
{(1-€)2 + £(v£-v')2}2
о
в котором несложно выразить квадрат разности 4Б-векторов через исходные
волновые векторы,
Пу£ • v') = | d? • (ДУ1.75)
(V£-Vp2 = ^2(fc-fc/)2,
е
что решает задачу нахождения матрицы рассеяния в общем случае посред¬
ством связи
<fcf folk.) =W-^rT(vff • vi£). (ДУ1.37)
Однако нам необходимо исследовать реальную ситуацию рассеяния, когда
длины волновых 4Б-векторов начального и конечного состояний стремятся
к нулю, поскольку
к\ = ё2 + к2 -> + fc2 = ~^{Е -Е(к)}, Е(к) =
так что асимптотически на больших расстояниях, где вклад потенциальной
энергии стремится к нулю, получаем
kf£,ki£^0 => (у£ — v'g)2 ► оо, WVI.76)
Дополнение VI. Кулоновское рассеяние
531
и, как говорят, матричный элемент берется на массовой поверхности. Прове¬
дем в интегральном выражении для матрицы рассеяния замену переменных
£ = ?( v£-v')2,
откуда в искомом пределе (ДУ1.76)
где интеграл выражается в терминах бета-функции после стандартной под-
х t
становки £ = :
00 1 ММ
jV(l + СГ2 df = J(1 - trW dt = r(1 + wll(1~f) = Г(1 + f )Г(1 -f).
О о
Значит, «вблизи массовой поверхности» амплитуду рассеяния можно запи¬
сать в виде формулы:
(ЩШК) = ГГ(1 + г)Г(1-г). WVI.77)
Перенормировка асимптотического состояния. Для расчета амплиту¬
ды рассеяния необходимо, как мы выяснили, вычислить стационарную функ¬
цию Грина, которая позволяет найти перенормировочную постоянную i2fc(fc)
для асимптотических начального и конечного состояний. Поскольку
Ge = Gf + Gf*rEGf, (ДУ1.20)
взятие матричного элемента в импульсном представлении приводит к выра¬
жению
(.2n)35(kf-k;) (feJW
Е' *' hV. ft2*? r rfitf .„V
£-l^ + 10 (£-l^ + l0)(E-l^ + l0J
Теперь следует перейти к 40-обозначениям. Для этого выразим дельта-функ-
цию, воспользовавшись равенством
d3fc 5(к-к') = dП3Ск£) 5{П3(к£) -П3(к'£)},
откуда
5(к-к') = 5{П3(к£)-П3(к'£)}
Следовательно, уравнение для функции Грина примет вид
(fcf|GE|fci) = -^i(^)2(203 5{Пз№*)-Пз№е)} +
532
Дополнения
так что, вводя обозначение
<к,|СЕ|к;) = -Лп£-ё (]^)2G(vfe • vif), (flVI.78)
найдем, что
G(yfe • vi£) = 2тг2 5{fi3(fcf) - П3(к'£)} - fT(yfe • vif), (ДУ1.79)
где уже и дельта-функция, и матрица рассеяния выражаются через полиномы
Чебышева второго рода (см. (ДУ1.66) и (ДУ1.70)):
2п2 5{П3(к£) -Пз(ф}- YS* +
а
Значит, функция Грина представима в виде ряда
00 2
G(vfe • vif) = J] ^±lL^n(Vff • vif), СДУ1.80)
n=0
где опять можно провести суммирование тем же методом, что и выше, так
что
1
W2
4(1-£>2 + £(v5-v')2}2
о
а «вблизи массовой поверхности» прежняя замена переменной интегрирова¬
ния £ = E>{ys — v')2 приводит к представлению:
1
4)=Jd?-r^
c(v£ • v') = а? • г :~*w. mvlsd
00
G(vf£-vi£) = {(^_^)2}1+f
0
и после интегрирования по частям находим формулу
00
G(vf£-vl£) = — {(Vff_^)2}1+r J = “f
r(i+f)rq-f)
{(vf£-vi£)2}1+f
0
В итоге «вблизи массовой поверхности» матричный элемент принимает вид:
lit IГ \h\ = m2 4яе2 Г 4g2(fcf — fcj)2 л -Г 4g2
(fcf|GB|fci) fc2ffc2£ J fc2£fc2£r(1 + r)ni r)-
Однако для исследования асимптотического поведения матричного эле¬
мента (r\GE\k;) на больших расстояниях удобнее воспользоваться выражени¬
ем (ДУ1.81) и произвести замену переменных
Иё2 _ ..,Л2_.Лк-к')2
Дополнение VI. Кулоновское рассеяние
533
Тогда при kf —> 0 можно записать выражение:
оо
G(vf-v') = (||-) (fc2)2 J dr?-r?r^T){k2+r]il_m2>
О
откуда находим матричный элемент:
00
WHM - -4*й (f Г J d„ ■ i4s|_i_)!)2.
0
Для расчета матричного элемента
(r\GE\k')= I 7^3 (fc|GB|k/)eifcr
необходимо взять интеграл
d3fc ifc.r
(2 я)3 {k*+r)(k-k')2}2’
где k2 *-> ё2 + fc2 — iO, поскольку при положительных энергиях и при условии
2тЕ + iO _ ь/2 ;
&
—»• —fc/z + кг — iO. Значит, интеграл представим в виде:
массовой поверхности следует считать ё2 >-> ^— = —к'2 — iO, так что
Ч
d3fc j кг
) С
(2я)3 {(т) + 1)к2 -2г)(к-к') + (rj - l)fc'2 - iO}2 ‘
Поскольку справедливо равенство
(г? + l)fc2 - 2rj (fc • fc') + (tj - l)fc/2 = (n +1) (fc - :2 - ^jfc'2
проведем замену переменных интегрирования
и обозначим
q = fc rrfc/
4 17 + 1
я2 1 fc/2
qo (TJ + l)2* ’
после чего искомыи интеграл сводится к выражению
а— 1 ifc'nj/Cn+l) Г d3q iq.r 1
(7j + l)2 J (2я)3 {q2 — q§ — iO}2
_ 1 -ifc'-m/fa+l) 1 d j d3q iq.r 1
(77 +1)2 2q0 dq0 J (2л)3 q2 - q2 - iO ‘
534
Дополнения
Заметим теперь, что в лекции 26 мы рассмотрели функцию Грина свободной
частицы
а м-( d3q г‘ог 1
УеКГ) (2я)3 £-£(q) + iO 2яЙ2 г ’
где
E=nv в(в)=йг
2т 9 14J 2m ’
так что легко устанавливаем
I
d3q io-r 1 _ 1 eiq°r
(2я)3 q2-ql~iO 4я г ’
eia/(T?+l)^
и далее элементарно находим
0 _ i rik'-r iCk'r-k'-ri/Cn+l)
* 8тг(г7 Н- 1)/с' е
В асимптотике a = (к'г — к' • г) —> +°° матричный элемент равен
00
о
Введем переменную
a W -
t=— => —— —>1,
rj 17 + I
так что интеграл преобразуется согласно выражению:
00
J dT?'T?f^^+Ieia/(T,+1)^_iaf J
о
Здесь оставшийся интеграл сводится к гамма-функции поворотом контура
интегрирования t = i£, откуда получаем
оо оо
J dt-rV^i1"? J df-fV^ie-^rd-f).
О о
Поскольку справедлива формула
О? = еГ 1п( fc'r-fc'-r)^
окончательно находим матричный элемент:
<r|G*|k'> = - (|J) 1_reik'-r+? in№'r-fc'-De-if*/2r(1 _ f) (ДШ.82)
Как и следовало ожидать, в асимптотике мы получили искаженную дально¬
действием волну, которую мы нашли выше методом эйконала:
ifc'-r+irlnCfc'r-fc'-r)
Дополнение V7. Кулоновское рассеяние
535
если, в согласии с поворотом Вика, положить при положительных энергиях
f = ir, e = -ie. (ДУ1.83)
Значит, в силу k'= e = ie можно записать
(r|GE|k'> = -2^2 (^S)-f ). (ДУ1.84)
Для нахождения нормировочной константы выделим свободный пропагатор
откуда согласно
(r\G |//\-- 1/2 pifcV+f InCfcV-kV)
(r|GE|fc;-£_E(fc/) + .oe
приходим к выражению
[2fc(k/)]-1/2= (^)_Ге-^я/2Г(1-у). (ДУ1.85)
Остается только использовать найденные выражения для перенормиро-
вочной константы (ДУ1.85) и матрицы рассеяния в импульсном представле¬
нии (ДУ1.77) в формуле для кулоновской матрицы рассеяния (ДУ1.15), чтобы
получить
(fcf№lfcf> = (fc^efc.)2 ((fcf^,)2) r(i-f)* wvi.86)
куда следует подставить при положительных энергиях
ё2 •-» —к^
и f из СДУ1.83).
В итоге матрица кулоновского рассеяния имеет вид:
= WVL87)
а амплитуда (ДУ1.13) равна
*сГт_ 2те2 ( 4kf угГ(1-НГ) f Rft.
7 ( ^ fi2(fc, - fc;)2 I (fc, - kj)2 J r(l-ir)' WVI.88)
Она отличается от борновской амплитуды
гВГдч _ 2 те2
7 1 ; fi2(fc,-fci)2
только фазовым множителем
exp iy In ^’2^ +2i5q j = exp£-iy lnsin2 |+2i5^],
•»2
4Jc?
где
(fcf - fct)2 = 2k? (1 - cos 0) = 4kf sin2
536
Дополнения
5S = argr(l + ir) (Д\Л.89)
есть кулоновская фаза рассеяния при 1 = 0 (см. ниже).
Дифференциальное сечение дается формулой Резерфорда:
dcr е4 1
4Е2 sin4 * ’
2
WVI.90)
Кулоновские фазы рассеяния. Вычислим парциальные амплитуды рас¬
сеяния согласно общей процедуре:
1
2
-i
Для этого проведем замену переменной интегрирования
в
2
cos 0 = l-2sin2 f = 1-2£.
Полиномы Лежандра запишем в виде
f,(cose) = (2,;>'dc^e,(l-cos2a)1,
где
1 — cos2 0 = (1 — cos 0)(l + cos б) = 2 sin2 ^2^1 — sin2 ^ = 22£(1 — £).
Значит, полиномы Лежандра можно выразить в терминах
Р,(СО8 0) = ^?'(1-Ог.
Амплитуда в тех же терминах равна
fC Т с—1—iy Ч~ iyO
* 2k> r(l-ir)‘
Значит, парциальная амплитуда определяется выражением:
1
f _ 2Z + 1 Г(1 +iy) 1 Г j г. с—
Г 2fcj Г(1 — iy) Z! J d£'^ ^ ’
о
где легко провести Z-кратное интегрирование по частям, что приводит к
1
1 Г d£ • Г1-‘г^£'(1 - О1 = Й±1гЪ(!±!±М } dt-c^a-D1.
J о
о
Используя бета-функцию
Дополнение VI. Кулоновское рассеяние
537
а также свойства гамма-функции
r(Z + l) = ZI, zr(z) = r(l + z),
легко собираем множители, так что кулоновские парциальные амплитуды
равны
fC_2l + l Г(1 + ту)
“ 2ifc, га+z-iy)* wvi.yij
что следует сравнить со стандартным выражением
/1=^{e2i5,-i>-
«Недостающий» вклад в амплитуду кулоновского рассеяния
5/(0) = "Ш S Р'(cos вК21 +13
1 I
отличен от нуля только при в = 0, т. е. при рассеянии вперед, которое мы не
рассматривали в силу его сингулярности в случае дальнодействия.
В самом деле, действуя по той же схеме, что и для 4В-векторов, т. е.
рассматривая функцию Грина оператора Лапласа в 3-мерном евклидовом
пространстве, несложно показать, что для единичных векторов пип7
i I
^±1р,(п-п')= 2 ^m(„)^(n/)=2] (n\l,m)(l,m\ri).
т=-1 т=—1
Значит, в силу полноты базиса сферических гармоник в классе функций,
зависящих от углов, имеет место тождество:
I
У^(21 +1 )Pi(n-ri)=4n^ ^ (n|Z, т)(Z, m\ri) = 4п 5(2)(n-ri).
I I т=—1
Поэтому при ненулевых углах рассеяния справедлива формула для парци¬
альных амплитуд (ДУ1.91), согласно которой кулоновские фазы рассеяния
определяются как
5f = argr(l + Z-Hr). C4VI.92)
В случае потенциала притяжения проведенное рассмотрение остается
в силе, если провести подстановку—сменить знак параметра у: у^—у.
Итак, проводя расчеты в импульсном представлении, мы точно решили
нерелятивистскую задачу кулоновского рассеяния, которая может служить
примером настоящей лаборатории теоретической физики, демонстрирую¬
щей красоту и силу ее методов. При этом, добавив для логической замкнуто¬
сти изложения несколько педагогических отступлений, мы следовали канве
оригинальной работы Юлиана Швингера 1964 года, который изящно изложил
этот свой результат1 на трех страницах научного журнала [26].
1В координатном представлении амплитуда рассеяния была точно вычислена существенно
раньше Моттом и Гордоном в 1928 году. Это решение в терминах вырожденной гипергеометри-
538
Дополнения
Дополнение VII. Уровни Ландау
Определим квантовый спектр заряженной частицы с нулевым спином
в постоянном магнитном поле. Гамильтониан в этом случае имеет вид
Я= 2~Р2, P=-ift3-^(r). CZWILl)
Вычислим оператор скорости согласно уравнению Гейзенберга
v=b=-^[r,A],
используя равенство [А, В2] = [А, В]В + В[А, В], так что
[Га> ~^~^Р ^Р^
и с учетом стандартного коммутатора
1га>Рр1 = 1Л5ар
находим
V=^P. (Д\Ш.2)
Таким образом, мы установили выражение для кинетической скорости v для
заряженной частицы в магнитном поле и, следовательно, для кинетического
импульса mv, отличного от обобщенного р = — ihd.
Наличие вектор-потенциала приводит к тому, что компоненты скорости
уже не могут быть в общем случае измерены точно совместно, поскольку
коммутатор равен
[Ра, Pfi] = if([da, + [Аа, др]) = i*idaAp - даАа) = if Safir(xot *ПГ.
Но по определению магнитного поля rot = Jtff, так что окончательно
[Pa)P0] = ifea/Srttr, [va,Vp] = i-^-ceaprnr (ДУ11.3)
Если магнитное поле постоянное, то его направление можно отожде¬
ствить с осью z. Тогда не равный нулю коммутатор равен
U>x,vy] = i-^-Hz. (Д\Ш.4)
J тс
Отсюда следует, что [Д, Я] = 0 и z-компонента импульса — интеграл движе¬
ния Pz — pz — const.
Определим характерные значения х- и у-компонент импульса, полагая
Р° = Р° и пользуясь их связью согласно соотношению неопределенности,
х у
которое следует из коммутатора (ДУП.З):
APx-APyzfn,
ческой функции представлено в большинстве стандартных учебников по квантовой механике.
Однако, на наш взгляд, оно не демонстрирует каких-либо физических идей и выглядит чересчур
формально как некое математическое свойство спецфункции, полученное методами, которые
вводятся в дисциплинах, далеко отстоящих от теоретической физики, так что предложенное
здесь рассмотрение в импульсном представлении обладает тем достоинством, что оно прово¬
дится на основе ясных и логически уместных физических идей.
Дополнение VII. Уровни Ландау
539
откуда Р®Ру — ehH/c. Тогда, вводя частоту вращения в магнитном поле1
Пн = ±, WVII.5)
найдем, что
(Р°)2 = тНПп.
Введем безразмерные операторы
-.Рх, йу= J—PY, (ДУП.б)
х у/тМ1п ХУ У y/mh£ln
для которых коммутационные соотношения приобретают «канонический»
вид
[йХ9йу] = и (ДУ11.7)
Записав гамильтониан в терминах переменных й±:
й=£+Щ*-(й2х+й2у), шт
замечаем полную аналогию со случаем гармонического осциллятора. Имен¬
но, введем операторы рождения и уничтожения квантов
й=-±=(йх+1йу), (д\л1.9)
и найдем их коммутатор
[а, а+] = 1 WVII.IO)
и гамильтониан
2
Й = ^+ППп(а'а + 1У OWII.ll)
В итоге спектр энергии заряженной частицы в постоянном магнитном поле
определяется уровнями Ландау
Еп = ^+ППп{п + 1), 0WII.12)
где pz—непрерывный спектральный параметр.
Итак, мы нашли спектр уровней энергии заряженной частицы с нулевым
спином вне зависимости от выбора калибровочного условия для вектор-по-
тенциала. Однако от этого условия, естественно, зависит выбор полного
набора наблюдаемых, а значит, и вид волновой функции. В самом деле,
положим для определенности
— (0, Нх, 0) =Ф Hz = дхАу — дуАх — Н.
13десь для определенности записи мы полагаем, что заряд положителен и, следовательно,
частота — тоже положительно определенная величина, однако это, естественно, нисколько не
ограничивает общности рассмотрения: переобозначения в случае отрицательного заряда оче¬
видны.
540
Дополнения
Тогда
К-Рх = - iRa*, Py^Py-fHx, h=Pz
откуда сразу следует, что гамильтониан в этой калибровке не зависит от у,
а значит,
[ру) А]=0 => ру = const.
Поэтому полный набор наблюдаемых можно выбрать в виде квантовых чи¬
сел — спектральных параметров кинетического импульса pz, обобщенного
импульса ру и дискретного номера уровня Ландау п:
ln.Py.Pz) - базис.
Если смысл спектрального параметра pz совершенно очевиден (он определя¬
ет скорость движения частицы вдоль оси z), то для выяснения физического
смысла параметра обобщенного импульса ру запишем гамильтониан
t е.,_Л2 Pf.Pl. »*£
Й=Ь+ш+ш{ъ~» =ш+ш+,1г<-*-<*»2-
W = -
где
РуС
еН'
В этой записи гамильтониана можно легко сразу заключить, что трехмер¬
ная задача движения заряженной частицы в постоянном магнитном поле
сводится к двумерной задаче: одномерного свободного движения по оси
поля и одномерного осциллятора. Параметр ру определяет среднее значение
координаты х, возле которого происходят гармонические колебания. Базис
стационарных волновых функций имеет вид
^п,ру,р2(г) = <г|п, Ру, pz) = eKpyy+p*z)/hxpn(x-(x)),
где 'фпМ — волновая функция n-го уровня осциллятора с частотой SlH. Под¬
черкнем, что энергия не зависит от ру.
Литература
[1] Л а н д а у Л. Д., Л и ф ш и ц Е. М. Квантовая механика. Нереляти¬
вистская теория. М.: Наука, 1974.
[2] М е с с и а А. Квантовая механика. Т. 1, 2. М.: Наука, 1978,1979.
[3] Б о у м А. Квантовая механика: основы и приложения. М.: Мир, 1990.
[4] Ш и ф ф Л. Квантовая механика. М.: ИЛ, 1967.
[5] Фок В. А. Начала квантовой механики. М.: Наука, 1976.
[6] Дирак П. А. М. Принципы квантовой механики. М.: Наука, 1979.
[7] Б л о х и н ц е в Д. И. Основы квантовой механики. М.: Наука, 1976.
[8] Давыдов А. С. Квантовая механика. М.: Наука, 1973.
[9] Соколов А. А., Тернов И. М., Жуковский В. Ч. Квантовая
механика. М.: Наука, 1979.
[10] Зелевинский В. Г. Лекции по квантовой механике. Новосибирск:
Сибирское университетское издательство, 2002.
[11] Белоусов Ю. М. Курс квантовой механики. Нерелятивистская тео¬
рия: Учебное пособие. М.: МФТИ, 2006.
[12] Елютин П. В., Кривченков В. Д. Квантовая механика. М.:
Наука, 1976.
[13] Галицкий В. М., К а р н а к о в Б. М., Коган В. И. Задачи по
квантовой механике. М.: Наука, 1981.
[14] Балашов В. В., Долинов В. К. Курс квантовой механики. М.;
Ижевск: РХД, 2001.
[15] Барабанов А. Л. Лекции по квантовой механике: Учебное пособие
в 2 частях. М.: МФТИ, 2005.
http: //theorphys. mipt. ru/biblio/qm-barabanov. html.
[16] Аллилуев С. П. Квантовая теория сложного атома и квантовая
теория излучения: Учебное пособие. М.: МФТИ, 1984.
[17] Белоусов Ю. М. Избранные главы квантовой механики: Учебное
пособие. М.: МФТИ, 1996.
[18] Белоусов Ю. М., Кузнецов В. П., Смилга В. П. Катехи¬
зис / Руководство по математике для начинающих изучать теоретиче¬
скую физику.—-М.: МФТИ, 2005.
[19] Ирошников Г. С. Континуальный интеграл и когерентные состоя¬
ния в квантовой механике и теории поля: Учебное пособие. М.: МФТИ,
1997.
542
Литература
[20] Тернов А. И. Основы релятивистской квантовой механики: Учебное
пособие. М.: МФТИ, 2002.
[21] Арнольд В. И. Математические методы классической механики. М.:
УРСС, 2003.
[22] Вергелес С. Н. Лекции по квантовой электродинамике. М.: Физмат-
лит, 2005.
[23] Вайнберг С. Квантовая теория поля. Т. 1. М.: Физматлит, 2003.
Литература к дополнению
[24] Додонов В. В., Манько В. И. Инварианты и эволюция нестаци¬
онарных квантовых систем // Труды ФИАН. Т. 183. М.: Наука, 1987.
[25] Белоусов Ю. М., Манько В. И. Матрица плотности. Представ¬
ления и применения в статистической физике. Ч. I, II. М.: МФТИ, 2004.
[26] Schwinger J. Coulomb Green’s Functions // Journal of Mathematical
Physics. 1964. Vol. 5,1606.
Предметный указатель
а-распад 185
Р -распад 237, 275
3-мерное пространство 521
4-вектор 268, 274, 277, 284, 289, 295,
300, 309, 318
4-импульс 270, 271, 277, 298, 306, 314
4-скорость 317
40-вектор 518, 521, 524, 527, 530
40-вращение 520
4В-пространство 516, 521
С-сопряжение 292
СР-преобразование 293
СР-четность 292
Е1-переход 378
g-фактор 327, 338
in-состояние 389,408, 510, 511
J-терм 354
;-терм 323
jj-связь 365
LS-связъ 365
out-состояние 390, 408, 510, 512
Р-сопряжение 292
Р-четность 70, 82,142,146,150,156, 321
— сферических гармоник 124
R-четность 75
^-матрица 211, 216, 218, 391,401
Т-инвариантность 60, 70, 79
^-матрица 401
— стационарная 402
Т-произведение 206, 207, 211, 215
Г-четность 61, 263, 274
Т-экспонента 41,191, 230, 396
5^-матрица 512, 519
абсолютно черный шар 427
адрон 338
алгебра 157, 327
— генераторов 129
группы Лоренца 265
— Грассмана 136, 299
— SU(2) 258
— коммутаторов 371
— Ли 108
— матриц Паули 296
— момента импульса 520
— сигма-матриц 301
амплитуда борновская 535
— Брейта—Вигнера 89
— вероятности 15, 20, 45, 313, 391,486,
496
— волны 426
— перехода 195, 216, 230, 231
— плотности вероятности 30
— рассеяния 398-400,403, 404,411,
412, 414,423, 425, 506-508, 512, 531
парциальная 412, 413,424, 536
кулоновская 537
упругого 401,402, 505, 508, 510
ангармоничность 201
антикоммутатор 126,134, 291, 302, 311,
482
антикоммутационное соотношение
291, 295, 312
для матриц Паули 126
антисимметризация 131
антисимметрия 31
античастица 215, 276, 285, 288, 291,
292, 299, 302, 313, 314
— дираковская 303
асимптотика 79,152,410,413, 513, 534
— волновой функции 423
асимптотическая свобода 339
асимптотическое поведение 350,422,
532
544
Предметный указатель
асимптотическое поведение волновой
функции
в задаче рассеяния, 398
в кулоновском поле, 510
радиальной волновой функции
144,410
рассеянной волны 423
ассоциативность 108
атом 19, 355, 377, 382
— азота 366
— водорода 19,149, 318, 322, 331, 349,
350, 378, 382
— гелия 341, 348, 354, 359
— кислорода 374
— многоэлектронный 357
— сложный 357
— углерода 360, 365
базис 16,19, 21, 34, 42, 44, 75, 95,134,
149, 210, 238, 245, 246, 256, 265, 272,
283, 289, 297, 303, 309, 313, 314, 316,
322, 332, 349, 358, 394, 405, 408, 411,
425, 486, 491, 495, 501, 517, 519, 520,
523, 540
— генераторов 108
— искаженных волн 390
— релятивистских полей 270
— сепарабельный 25, 30
— собственных векторов 485
— стационарных состояний
осциллятора 100
— счетный 25, 484
барион 336
барьер потенциальный 183,186,414
бета-функция 179, 531, 536
билинейная комбинация 296
биспинор 294, 305, 321, 322, 327, 335
— безмассовый 294
бозон 129, 281, 312, 313, 422
бра-вектор 22, 208, 251
буст 129, 255, 259, 261, 297, 301
вакуум 47, 96,133,135,186,188, 211,
213, 271, 272, 286, 287, 312, 378, 379,
385, 490
— инвариантный 285
вариация действия 196, 289, 300, 327,
346,347
— функционала 217
вариация Эйлера 198
вектор волновой 35, 277, 280, 283, 378,
379, 382, 385, 389, 399, 408, 409, 411,
414, 505, 506, 510, 530
переданный 507, 510
— младший 117,133, 273, 521
— набла в полярных координатах 119
— поляризации 301, 311, 380
фотона 384
— прицельного параметра 510
— Рунге—Ленца 155
— собственный 29, 58,107, 246, 248,
256, 272, 485, 501
унитарного оператора 73
— старший 117,121,133, 246, 248, 273,
421, 521
вектор-потенциал 369, 538, 539
вероятностная интерпретация 45, 390
вероятность 16, 20, 485, 498
— излучения 386
— перехода 231
в единицу времени 234, 380,400
интегральная 234
— распада 380
— рассеяния 399
в единицу времени 401
вершина 202, 212, 514
— «голая» 204
взаимодействие аномальное 335
— дальнодействующее 510
— дипольное 378, 379, 383
— калибровочное 327, 335, 336
— контактное 331
— кулоновское 369, 510
— минимальное 317, 327, 335
— обменное 130, 344, 347, 359, 422
— осцилляторов 219
— парное 369
— сильное 69, 306
— слабое 69,132, 237, 293, 306
— спин-орбитальное 330, 333, 354,
361, 370, 374
— спинов 323
— электромагнитное 69, 306
— электрослабое 275
вклад дарвиновский 331, 333
— диамагнитный 370, 372
возбуждение 60, 489
Предметный указатель
545
возмущение 174,177, 331, 332, 349, 353,
355, 361, 370, 378
— адиабатическое 237
— мгновенное 235
— периодическое 233
— постоянное 231
волна 35
— де Бройля 53, 80, 389, 390, 399, 401,
404, 405, 408, 412, 423, 505, 510, 511,
513
— искаженная 534
— материальная 390
— отраженная 83, 85,171
— падающая 83, 85,171,181, 398, 400,
404, 408, 507, 512
— парциальная 408, 412-416
— плоская 277, 289, 308
— прошедшая 83,182, 507
— рассеянная 398, 408, 512
стационарная 390
— свободная 199
— сферическая 405, 408, 410, 411
свободной частицы 405,409
волновая функция 25, 55, 65,112,130,
164,167, 269, 282, 313, 328, 390, 394,
408, 492, 505, 513, 529, 539
антисимметричная по
перестановкам тождественных
частиц 132, 311, 345, 347, 358
асимптотическая 408
осциллятора 97
правильная ведущего
приближения 227, 349, 354, 361, 365,
374
пространственная 357
радиальная 142,149,160, 406,
409, 413
рассеяния 403
свободной частицы 53, 403
связанного состояния в нуле 160,
333
симметричная по
перестановкам тождественных
частиц 132, 311, 350
скалярная 60, 70
спиновая 357,421,495
стационарная 397
волновой пакет 55, 56, 70, 99, 389, 390
вращение 105, 255, 261, 269
вращение бесконечно малое 109, 255
— конечное 136
— поляризации света в световолокне
243
— спина 243, 330
— спинора 126
время евклидово 196
— жизни 59,185, 234, 380, 382
резонанса 88, 426
— распада 383
вронскиан 77, 81, 83
вырождение 320, 334, 371,484, 487
— в атоме водорода 154
двукратное, 323
— кулоновское 154
— терма 372
вычисления на решетке 339
газ инертный 372
гамильтониан 34, 36, 38, 44,141,174,
185,192, 205, 223, 236, 278, 284, 287,
289, 291, 293, 310, 311, 327, 329, 330,
342, 343, 357, 377, 389, 396, 487, 492,
538-540
— атома во внешнем поле 369, 370
водорода 156
гелия 343, 349
— инвариантный 292
— квантованного поля 282
— осциллятора 91
— положительно определенный 270,
290
— поля Дирака 300
— свободной частицы 52
— спинора 290
гамма-матрицы 295, 302, 321, 325
гамма-функция 179, 534, 537
генератор 108,133,137, 269, 270, 274,
276, 277, 520
— бустов 259, 265, 271, 272
— вращений 111,114, 245, 246, 258,
265, 521
— группы Лоренца 263
Пуанкаре 275, 314
— симметрии 115
— спина 271, 272, 295
— трансляций 109, 271, 277
геометрическая оптика 35, 36,112,
163,165, 505
546
Предметный указатель
гиперзаряд 294
гиперон 338
гиперповорот 259
глюон 338
«головастик» 204
граничное условие 167,194,199, 208,
210, 212, 490, 512
грассманова переменная 136, 219, 290,
305
группа 67,129, 255, 261
— SO(3) 111, 129, 265
— SL(2, С) 266, 268, 288, 294
— SO(3,1) 265
— SU(2) 129,132, 258, 265, 294
калибровочная 132
— SU(2)®SU(2) 265
— U(l) 69, 294,313
— вращений 265, 520
спиноров 128, 266
— калибровочной симметрии 69,132
— Ли 108
— Лоренца 263-265, 268, 270, 295, 297
неоднородная 270
ортохронная собственная 275,
277
собственная ортохронная 261
— неабелева 338
— Пуанкаре 270, 274, 314
— ренормализационная 281
— симметрии 314
внутренней 133
— трансляций 270
— унитарная 69
дальнодействие 517
— кулоновское 390
движение вращательное 330
— инфинитное 79
— нерелятивистское 377
— обратно по времени 215, 264
— одномерное 77, 95,144,165
— орбитальное 322
— относительное 492
— поперечное 506
— радиальное 414
— свободное 414, 506
— финитное 79,168
действие 35, 57, 65,112,166,186,195,
209, 275, 276, 292-294, 310, 313, 317,
326, 328, 335, 506
— для спинора 297, 327
— инвариантное 284, 294, 314, 315
— квантованное 286
— эффективное 202, 220, 325, 329
дельта-функция Дирака 25, 29, 37,193,
234, 283, 531
детерминант 111,268, 271
— единичный 266
детерминизм 20
диаграмма Аргана 424-426
— лестничная 514, 528
— Фейнмана 200, 205, 514, 515
диамагнетизм 370, 372
дипольный момент 377, 380
дискретность 45
дисперсия 18, 29, 39,163, 481
— нулевая 29
диссипация 60
дифракция 317
длина вектора 109
— волны 35,165,168,184, 377, 403
комптоновская 327, 331
— рассеяния 414
дублет 294
«духи» 132
«дырка» 359, 363
единицы атомные 150, 343
— осцилляторные 93
задача двух тел 389
— двух тел 140
— Кеплера 155
— Коши 180
— рассеяния 397, 398, 400, 405, 407,
408, 517
нестационарная 390
стационарная 390
— с двумя уровнями 227
закон дисперсии 55, 391
— Ньютона 330
— преобразования тензорного
оператора 251
— сохранения вероятности 68
импульса 515
проекции спина 495
Предметный указатель
547
закон дисперсии тока 68, 315
энергии 235
запаздывание по времени 88
запутанность (entanglement) 485
заряд 275, 286, 289, 294, 300, 313, 314,
323, 332, 377, 539
— квантованный 285, 291
— поля 287, 292
— сохраняющийся 69, 284
— электрический 68, 310
— ядра 319
затухание 213
«золотое правило Ферми» 234
излучение абсолютно черного тела 15,
36,188
— вынужденное 233
— дипольное 378
— индуцированное 233, 234, 385
— спонтанное 377, 382, 385, 490
измерение 46
— единичное 496
— многократное 496
— совместное точное 33, 42
изоспин слабый 294
импульс 18, 34, 71, 91, 300, 327, 331,
385, 493, 505
— канонически сопряженный 18,44,
58, 65,109,111, 279
— обобщенный 38, 317, 325, 335, 538,
540
— переданный 403
инвариант 105, 245, 268, 276, 520, 524
— группы вращений 522
спиноров 128
— относительно вращений 126
— релятивистский 270, 272, 289
инвариантное подпространство 245
инвариантность 286, 321
— гамильтониана 57, 286
— действия 288
— калибровочная 241, 284, 317, 335
глобальная 68, 313
локальная 68
— матричного элемента 106
— метрики 129
— относительно обращения времени
60, 490
инвариантность относительно
зеркальных отражений 70
— релятивистская 261
— трансляционная 75, 395
инверсия ОРТ 277
— времени 60, 286, 287, 304, 314
— пространства 70, 71, 261, 274, 287,
292-294, 296, 297, 299, 303, 314, 321,
384
зеркальная 274
индекс верхний 126,128, 257, 267, 295
— нижний 126, 257, 295
— с точкой 129, 268, 295
— спинорный 126
интеграл гауссов 66
— движения 57, 60, 71, 75,155, 310, 313,
538
аддитивный 487, 494
— континуальный 191,194,196, 206,
339
— Коши 214
— по траекториям 191,194
— фейнмановский 191,194, 339
— функциональный 197
— Фурье 25
интенсивность излучения 381, 383, 386
— электромагнитногоп поля 386
интервал 255, 258, 261
интерференция 18, 35,118,130,163,
316, 422
— деструктивная 415
ионизация атома 371
искажение асимптотического
состояния 510
— фронта волны 423
источник 197, 200, 201, 210, 318, 397,
492, 514
калибровка 318, 369
— «чистая» 316
квадруполь 377
квазиимпульс 73
квазиклассика 163
квант 19, 45, 96,133, 215, 219, 300, 312,
327, 378, 385, 391
— поля 386
— с отрицательной энергией 215
квантование 19, 38, 63,119
— атома водорода 153
548
Предметный указатель
квантование вторичное 132, 283, 291,
300, 311, 366, 378
— каноническое 38, 40, 42, 44, 54, 91,
120,156, 280, 311
— момента импульса 115
— осциллятора 95
— свободных полей 314
— спектра 179
квантовая нелокальность 492, 498
— теория поля 281, 311, 335, 366
— хромодинамика 338
квантовое число 21, 44, 70,130,173,
312, 314, 321, 348, 349, 355, 371, 394,
484, 487, 520, 540
главное 146,153, 323, 332, 334,
349, 357, 529
магнитное 146, 357
орбитальное 146, 319, 357
радиальное 146,153, 323
терма 362
цвета 336
квантовый переход 59, 230, 377, 381,
385, 490
спонтанный 489, 490
кварк 336
— конституэнтный 336
— токовый 338
кет-вектор 21
кет-вектор 133, 208, 251, 313
киральность 291, 292, 295, 309
классическая механика 19, 34, 44, 57,
94,109,111,112,155,165, 209, 263,
278
классический предел 35, 36,159,163,
165,167,195
количество информации 491
коллапс волновой функции 497
коммутативность 43
коммутатор 31, 39, 62, 63,185, 256,
265, 310, 311, 315, 341, 482, 538, 539
— генераторов 108
бустов 260
— ковариантных производных 241,
317
— координата-импульс 37, 54,109
— момента импульса 111,112
— орбитального момента со спином
115
— тензорного оператора 251
коммутационное соотношение 44,
312, 520, 539
для генераторов трансляций и
бустов 270
для матриц Паули 126
для момента импульса 112, 258
для операторов рождения и
уничтожения поля 284
для осциллятора 94
конденсат кварк-глюонный 338
консервативная система 46
константа спин-орбитального
взаимодействия 362, 374
континуум 194
конфайнмент 338
конфигурация электронная 349, 350,
357, 367, 373, 384
координата 18, 34, 71, 91,493
— обобщенная 38, 44, 57,109,191, 279
— относительная 140
— центра масс 140
координаты декартовы 257, 270, 275
— полярные 120,142, 399, 511, 518, 522
— сферические 119
копенгагенская интерпретация 15
короткодействие 390
корпускулярно-волновой дуализм 15,
35, 391
коррелятор 499, 501
корреляция 481,496, 500, 502
— спиновая 495, 502
— статистическая 498
коэффициент Клебша—Гордана 249,
252, 253, 358, 372
— корреляции 482
— отражения 83,184
— прохождения 83,182,186
— разложения по базису 21
кратность вырождения 118,146,154,
226, 247
критерий применимости
адиабатического приближения 239
борновского приближения 403,
404, 505
для быстрых частиц 405
для медленных частиц 405
дипольного приближения 377
квазиклассики 168,186
теории возмущений 175, 226, 233
Предметный указатель
549
критерий применимости теории
возмущений нестационарной 234
лагранжиан 68, 69, 276
лазер 386, 490
лапласиан 522, 526
линейность 31
локальный реализм 492-494,498-500,
504
луч 35,112
— состояния 18, 20
магнетон Бора 370
магнитная восприимчивость 373
магнитный момент 330, 369, 370, 372,
373, 377, 495
аномальный 335
затравочный 335
кварка 337
наведенный 370, 374
протона 337
масса майорановская 305
— покоя 326
— приведенная 140,149, 389
— эффективная 338
массовая поверхность 531-533
матрица вращений 110,138, 246
— диагональная 28
— корреляций 482
— обратная 111
— ортогональная 111
— плотности 483-487,489-491,497
— рассеяния 514, 517, 528, 530
кулоновская 535
— транспонированная 111
— эрмитова 110, 295, 485
матрицы Дирака 294, 295, 301
— Паули 125,137, 266, 296, 327
матричная механика 63
матричный элемент 28, 62,106,194,
313, 348, 512, 513, 531
возмущения 231, 332
гамильтониана 193, 208
оператора векторного 383
неприводимого тензорного
252, 253
повышающего 118
понижающего 118
рождения 385
матричный элемент оператора
уничтожения 385
эволюции 393
перехода 378
приведенный 252, 372
мера интегрирования 194,197
метастабильность 382, 385
метод JWKB 165
— индукции 49
— итераций 166, 396, 514, 528
— Штерна—Герлаха 495
метрика 126, 255
— евклидова 119, 245
— Минковского 259, 262, 264
— обратная 259
— спинорная 126-128, 267
обратная 128
мишень 389
мода 290
— поперечная 310
— спиновая 314
— спинорная 290
модель конституэнтных кварков 336
— составная 336
момент импульса 142, 251
орбитальный 111,118,121,149,
246, 263, 320, 321, 323, 329, 332, 334,
342, 349, 384, 405, 408, 414, 509, 521
полный 114, 258, 332, 334, 349,
355
суммарный 247, 358
— распределения 57
мультиполь 377
мюон 336
наблюдаемая величина 15, 27, 44, 206,
313, 481
векторная 112
скалярная 111
набор наблюдаемых 58
напряженность поля 316, 317, 370
калибровочного 316
нарушение пространственной
четности 384
начальные данные 494
независимость статистического
ансамбля 486
нейтрино 293
— правое 306
550
Предметный указатель
нейтрино «стерильное» 306
нейтрон 243, 336
некоммутативность 494
неопределенность статистическая 494
— частоты перехода 59
непрерывность волновой функции 52
неприводимость 245
неравенство Белла 498, 500, 504
в форме CHSH 500, 502
номер зоны 76
норма 18, 21, 95,117, 224, 288, 312
— евклидова 20
— релятивистского состояния 280
нормальный символ 218, 281, 282, 285
нормировка 45, 53, 54, 70,173,196,
240, 285, 290, 313, 328, 343, 399, 484,
485, 497, 500, 506
— единичная 101
— нерелятивистская 279
— релятивистская 282, 311
— релятивистски инвариантная 283,
299
нормируемость 17, 20
нуклон 336
область асмиптотическая 407
— доступная для классической
частицы 167,170,185
— недоступная для классической
частицы 167,170,186
оболочка электронная 358
внешняя 361
заполненная 358, 361, 363, 372
оболочка электронная 349
обращение времени 60, 84, 215, 255,
261, 263, 274, 286, 293, 490
объем пространства 283
— фазовый 39,173
оператор 23, 26
— 4-импульса 299
— антилинейный 26, 61, 263, 286, 293,
304
— антиунитарный 275, 286
— вращений 138
спинора 138
— Гамильтона 63
— гамильтониана 36
— грассманов 292
— единичного измерения 496
оператор единичный 24, 28, 62,192
— заряда 314
— импульса 36, 53,106,107
радиального 143
эрмитов 37
— инфинитезимальный 108
— координаты 107
— Лапласа 521, 525, 537
— линейный 26, 44, 263, 285, 287
— момента импульса орбитального
257
повышающий 117,121,123,
125, 249, 359
понижающий 117, 246, 249,
421
— обратный 27
— перестановки тождественных
частиц 131, 312
— повышающий 95
— поля 300
— понижающий 95
— проецирования 23
— рождения 96,133, 208, 212, 218,
280-285, 291-293, 300, 303, 311, 312,
314, 378, 379, 539
античастицы 285
в голоморфном представлении
103
— скорости 52, 538
— тензорный неприводимый 251
— трансляций 105
— унитарный 27, 61, 73,106,107, 207,
401
— уничтожения 96, 99,102,133, 208,
218, 280-282, 284, 291-293, 300, 303,
311, 312, 314, 315, 378, 379, 539
в голоморфном представлении
103
— эволюции 26, 40, 62,191,195, 206,
210, 217, 229, 230, 281, 390, 392, 394,
396, 400, 401
в первом приближении 236
— эрмитов 23, 28, 44, 73,100,120,156,
246, 313, 384, 482
— эрмитово сопряженный 26
к антиунитарному 287
определитель Слетера 358
орбита замкнутая 156
ортогелий 343, 344, 348, 349
Предметный указатель
551
ортогональность 44,101, 224, 250
ортонормальность 22
ортонормированность 25, 311
осциллятор 63, 66, 91,133, 200, 208,
210, 212, 279, 379, 540
— гармонический 91,198, 539
трехмерный изотропный 145
— фермионный 133, 219, 291
— элементарный 280, 281
ось вращения 109,118,127, 246, 255
отражение 170,182
— зеркальное 97,105,111,124,156, 287
— многократное 88
— пространства 255, 320
зеркальное 384
— пространства-времени 264, 275
отталкивание электронов 341, 348,
351, 359
падение частицы на центр 144
парагелий 343, 344, 348, 349
парадокс ЭПР 491,494,496
в формулировке Бома 494,497,
501
парамагнетизм ван Флека 373
параметр глобальный 313
— локальный 313
— прицельный 506, 508, 510, 511
— скрытый 492, 494,496,498-500, 504
— спектральный 21, 24, 25, 44, 54, 394,
539, 540
парциально-волновой анализ 405,
408, 411, 425
переменные действие-угол 57
перенормировка 281, 531
пересечение уровней 228
перестановка 269, 281, 343, 345, 409,
526
— тождественных частиц 131, 283, 311,
313, 421
периодическая система элементов
Менделеева 360, 365
петля 204, 515
плотность вероятности 16, 25, 45, 68,
81,164, 353, 499
перехода 231, 391
— заряда 326
— квантов 285
— потока вероятности 386
плотность состояний 279, 283
дифференциальная 234
— спектра 173,177
— тока 326, 328
поверхностная гравитация 188,189
поворот бесконечно малый 246
— Вика 196, 213, 515, 516, 535
— на угол 2 я 118,127,130
поглощение 215
— вынужденное 233, 489
— индуцированное 233, 234, 385
подсистема 485
позитрон 326
поле 19, 45, 65
— адиабатического возмущения 238
— безмассовое 288, 294, 309
— векторное 257, 270, 306, 308
безмассовое 306, 311, 315-317, 335
калибровочное 68, 310, 311, 315
массивное 311
— вещественное 309
— внешнее 326, 330, 331, 370
— гравитационное 188
— Дирака 299, 317
безмассовое 297
массивное 297, 300
— зарядово сопряженное 276
— калибровочное 311,316-318
— квантованное 282, 284, 287,
291-293, 310, 313, 314
— киральное 273, 275, 288, 289, 292,
314
— классическое 282, 289, 300, 314
— компонентное 265
— кулоновское 320, 333, 510
— левое 273, 275
— магнитное 242, 307, 316, 330, 335,
369-371, 374
постоянное 538
сильное 374, 375
слабое 372, 374
— майорановское 305
— нейтральное 304
— неоднородное 495
— отрицательно частотное 278, 290
— положительно частотное 278
— поперечное 307, 311
— правое 273, 275, 288, 289
— продольное 309, 315
552
Предметный указатель
поле релятивистское 132, 269, 275, 313,
314
— самосогласованное 343, 348, 350,
354, 357, 359, 366, 373, 384
— свободное 292, 294
— скалярное 132, 264, 277, 293, 303,
310, 318
вещественное 277
комплексное 284, 318
— сопряженное 292
— спинорное 275, 294
— сферически симметричное 348
— центральное 405
— электрическое 186, 307, 310, 330,
345, 377
— электромагнитное 69,112, 308, 334
квантованное 377, 378, 385
— электростатическое 318
полином Гегенбауэра 521
— Лагерра 153
— Лежандра 123, 409, 411, 509, 536
присоединенный 124,154
— Чебышева 526, 527, 529
второго рода 517, 519, 525, 532
— Эрмита 97
полнота базиса 28, 69,135, 250, 295,
394, 537
полный набор наблюдаемых 34,
42-44,115,130, 297, 310, 539
в задаче с центральным
потенциалом 142
полюс 89, 213, 392, 425, 516, 529
поляризация 112,126,130, 275, 300,
308-310, 378, 381, 382, 385
— поперечная 308
поправка 333, 334
— борновская 403
— ведущая 369
— второго порядка 352
— высшего порядка 323
— к состоянию 224
— к энергии 175, 224, 349, 350
— квантовая 204, 482
— неперенормируемая 335
— первого порядка 239, 373
— петлевая 335, 396
— релятивистская 320, 328, 329, 331,
332, 334, 341, 354, 361, 369, 370, 373
— эйкональная 512
постоянная Больцмана 489,490
— Планка 32, 36,164
— тонкой структуры 150, 318, 334, 511
постулат 24
— квантовой механики 44,496
— полноты базиса 24
потенциал 38, 70, 78, 93,115,141,198,
230, 402, 412, 506, 514, 529
— короткодействующий 389, 398, 504,
507
— кулоновский 149,155,157, 318, 334,
423, 511, 512, 529
— парного взаимодействия 359
— периодический 74
— статический 328-330, 345, 390, 510
— сферически симметричный 343,
354, 389, 399
— термодинамический 489
— центрально-симметричный 329,
509
— центральный 141,145,149
— центробежный 143,150, 414
— ядра 346, 348, 349
потенциальная яма 86
поток вероятности 52, 68, 81, 82,164,
182, 392, 399, 423, 426, 506, 511
падающий 386, 422
парциальный 408
правило запрета 254, 372, 373, 383
— интервалов Ланде 363, 365, 373
— квантования Бора—Зоммерфельда
173,179
— отбора 253, 383
по моменту импульса 254
орбитальному 383
по полному спину 383
по проекции момента импульса
253
по четности 384
— Хунда 360, 367
второе 364
первое 360
предел больших квантовых чисел 19
— нерелятивистский 330
представление 44
— взаимодействия 230, 232
— волнового вектора 409
— Гейзенберга 62, 206, 232
— голоморфное 103,134, 208, 210, 212
Предметный указатель
553
представление Дирака 302, 325, 335
— импульсное 55, 69,192, 212, 289,
307, 309, 409, 512-515, 535, 537
— интегральное 530
для сдвига фазы 413
— киральное 294, 299, 302, 305, 321
— комплексно сопряженное 128
— координатное 35, 37, 46, 53, 67, 70,
119,192, 396, 408
— неунитарное 265
— прицельного параметра 509
— спектральное 381
— тензорного оператора стандартное
252
— транспонированное 128
— Шрёдингера 44, 62, 206
преобразование 313
— активное 74, 256
— антиортохронное несобственное
264
собственное 262
— бесконечно малое 281
— вектора 114
— внутреннее 314
— градиентное 68
— дискретное 255, 262, 297, 314
— дуальности 308
— инфинитезимальное 108, 257, 269
— калибровочное 68, 276, 284, 294,
314, 315
глобальное 67, 79, 289
локальное 68, 316
поля адиабатического
возмущения 240
— Лежандра 201
— Лоренца 129, 259, 298, 301, 302, 309,
330
— масштабное 521
— непрерывное 108, 255
— обратимое 107
— обратное 107, 265
— операторов 107
при вращениях 111
— ортохронное несобственное 262
собственное 262
— пассивное 74, 256
— поляризации 113
— спинора 138
— тождественное 118,130, 261, 264
преобразование унитарное 269, 302,
313, 314
— Фолди—Ваутхойзена 329
— Фурье 54, 56, 70,192,193, 214, 217,
392
прецессия Томаса 330
приближение адиабатическое 238
— асимптотическое 389
— борновское 403,404, 413, 414, 423,
505, 511
— ведущее 227, 230, 320, 326, 328, 343,
349, 354, 357, 371
— геометрической оптики 505
— дипольное 377, 384, 385
— квазиклассическое 168,182, 417
— нерелятивистское 325-327, 330, 331,
334, 335, 343
— одночастичное 327, 331
— первое 377
— эйкональное 506-510
принцип вариационный 65, 270, 311
— Гюйгенса 35,195
— детерминизма 45
— дополнительности Бора 45
— запрета Паули 131,133, 312, 337,
349, 357-359, 362
— калибровочный 69
— локального реализма 493
— наименьшего действия 35, 65, 69,
299
— причинности локальный 491,493,
494, 496, 498
— соответствия 19, 35, 42, 45,163, 282
— стационарности 35
— суперотбора 16
— суперпозиции 16,19,44, 309, 390
— Ферма 165
притяжение кулоновское 319
— ядра 341
прицельное расстояние 414, 423
пробой вакуума 188
проектор 23, 26, 295, 300, 302, 310, 401,
483-486, 497
проекция 21
— момента вращения 109
импульса 247, 332, 349, 358, 378,
408
— орбитального момента 332
— спина 495, 497, 501
554
Предметный указатель
произведение векторное 109,120, 245,
255, 257, 272, 327
— прямое 295, 302
— скалярное 21, 31, 245, 398, 503, 527
когерентных состояний 102
— тензорное 245, 246, 358
производная вариационная 199, 216
— ковариантная 68, 241, 315, 317, 335,
369, 522
— оператора по времени 41
пропагатор 213, 215, 218, 535
пространство векторное 108
комплексное 16, 21, 26
— волнового вектора 279, 285
— гильбертово 21, 30, 42, 44, 74, 79,
153, 269, 394, 484, 485
оснащенное 31, 37
— дуальное 22
— евклидово 105,109,126,129,136,
516, 517, 520, 523, 525, 537
3-мерное 245
— импульсное 290, 492
— квадратично интегрируемых
функций 37
— координатное 393, 492, 515
— Минковского 255, 259, 261, 270, 275,
393, 520
— параметров 240
— «с дыркой» 316
— состояний 30
асимптотическое 210, 389, 401,
426
— фазовое 194, 209
— фоковское 283, 286, 292, 314, 316,
378, 382, 385
пространство-время 255
протон 320, 331, 336
процесс необратимый 490
— обратимый 490
псевдовектор 142,156, 245, 255, 263,
274, 308, 320
— Паули—Любанского 271, 273, 277
псевдоскаляр 308
пси-функция 16, 35-37, 55, 78,167, 391
пучок 390
радиус боровский 151, 350
— взаимодействия 389, 390
— гравитационный 189
радиус действия 398, 414, 504
радиус-вектор 372, 378, 399,409, 506
разложение асимптотическое 411
— волны де Бройля по парциальным
волнам 408
— нерелятивистское 327
— по орбиталям 408
распад спонтанный 386
распределение Гаусса 96, 99
— Гиббса 188
— по числу квантов 101
— Пуассона 101,102
— термодинамическое 488
рассеяние 82,195, 389, 398, 504
— вперед 537
— кулоновское 390, 423, 510, 512, 517,
519, 537
— надбарьерное 414
— неупругое 185, 508, 509
— тождественных частиц 421
— упругое 185, 408, 412, 426, 508
расщепление 360, 374
— сверхтонкое 323, 334
— терма 355, 361, 363, 372, 375
спин-орбитальное 364, 374, 382
— тонкое 323, 334
— уровней 323, 334, 373
регуляризация 196
редукционные формулы 217
редукция волновой функции 497
резольвента 393, 516
резонанс 84, 87,185, 213, 233, 235, 413,
417, 423, 425
рекуррентные соотношения Крамерса
157, 333
ренормгруппа 281
ридберг 151, 343, 354
рождение кванта 215
— фотонов 188
— электрон-позитронных пар 186
ряд итерационный 515
— Тейлора 30,40, 49, 72, 319,407
— теории возмущений 224
самосопряженность зарядовая 305
свертка 212, 311
свободная энергия Гельмгольца 489
связность 316
Предметный указатель
555
связь спина со статистикой 132, 311,
313
сдвиг 57, 75, 314, 522
— бесконечно малый 316
— зонный 76
— лэмбовский 323, 334
— фазовый 408,411-413, 415, 507-509
парциальный 408, 424
сепарабельность 17,484
серия Бальмера 385
— Лаймана 385
сечение рассеяния 403, 417, 509
Брейта—Вигнера 425
геометрическое 404,417
дифференциальное 391, 399,402,
411,414, 422, 423, 536
неупругого 426
парциальное 411,412, 417, 423
полное 390, 402,404,411,424,
426, 508
упругого 426
сигма-гиперон 336
сигма-матрицы 289, 295, 327
сила дальнодействующая 423
— короткодействующая 423
— кулоновская 423
— центральная 115
символ Кристоффеля 522
— Кронекера 29, 54, 245
симметризация 132
симметрия 70, 294
— бозонных и фермионных мод 281
— дискретная 58, 60,105, 262, 292,
297, 303
— непрерывная 58,105
— перестановок 283, 313, 421
— сферическая 318
синглет 350
система декартовых координат 255
— инерциальная 255
— консервативная 58, 63,141, 390, 392
— покоя 300
— СГСЭ 380
— со связями 38
— термодинамическая 488, 490
— Хевисайда 310, 380
скаляр 115,128,129,142, 269, 275, 314,
332, 362, 372
скачок производной 90
скобка Пуассона 39, 44, 57,156
скорость 35,150,173,193, 208, 327, 330,
399, 511
— групповая 56, 87, 390
— света 151, 511
— фазовая 55, 390
след 245, 266
— матрицы плотности 488
смешивание состояний 232, 322
— уровней 228
собственная функция 37
собственное значение 29, 42,107, 208,
257, 273, 483
квадрата момента импульса 116
оператора инверсии времени 61
уничтожения 99
проекции момента импульса 116
— колебание 239
соотношение взаимности 84
— де Бройля 36
— неопределенностей 32, 39,163, 327,
331, 481, 494, 496, 498, 538
Гейзенберга 33, 45
координата-импульс 37, 99,150,
493
в матричной механике 64
минимизация 98
минимизированное 34
при наличии корреляций 483
энергия-время 59, 231, 235
— полноты базиса 102
— унитарности для «^-матрицы 401
— Фейнмана—Хеллманна 91,159
сопряжение 22
— зарядово 255, 264, 285, 287, 292,
297, 303, 305
— комплексное 22, 61, 255, 264, 275,
277, 287, 293, 303, 304, 409
— спинора 290
— эрмитово 22, 286, 293, 303, 312
состояние 15, 24, 34, 44, 300, 483,496,
498
— in 211, 389
— out 211, 390
— адиабатическое 237, 240
— антисимметричное по
перестановкам 342
по цвету 336
556
Предметный указатель
состояние асимптотическое 216, 389,
390, 394, 397, 400, 405, 423, 510, 512,
531
кулоновское 513
— вакуумное 96, 99, 271, 280
— возбужденное 349, 386
— вырожденное 59, 80,116
— запутанное 497
— квазистационарное 59,185
— киральное 295
— когерентное 34, 98,102, 208, 218,
280, 282, 291, 300, 385
фермионного осциллятора 134
— конечное 378, 382, 385, 387, 390,
400, 490, 512, 530
— метастабильное 386, 426
— многчастичное 283
— начальное 40, 378, 382, 387, 389,
400, 411, 490, 511, 512, 530
— невырожденное 95
— однофотонное 384
— одночастичное 280, 282, 283, 286,
288, 314, 328
— одноэлектронное 357
— основное 350
— по цвету 336
— связанное 81,152,157, 332, 333, 342,
350, 404, 425, 513, 517, 529
— сепарабельное 485, 486, 491,497
— симметричное по перестановкам
342, 359
— смешанное 20, 485
— собственное 46,119, 384, 496
вырожденное 43
невырожденное 43
— спиновое 342, 422
— стационарное 46, 55, 65, 69, 92, 93,
160,165, 231, 342, 344, 394, 484, 490
— триплетное 343
— фоковское 313
— частицы 313
— чистое 20, 483-486, 491,497
сохранение заряда 132
спектр 21, 46,179, 332, 366, 385, 484,
498, 538, 539
— атома водорода 153,154, 322, 331,
334
— вырожденный 80, 226
спектр дискретный 21, 29, 44, 64, 82,
96,163, 231, 377, 425, 513
невырожденный 223
— момента импульса 117
— невырожденный 64, 81, 237
— непрерывный 21, 24, 25, 29, 30, 44,
80, 231, 280, 380, 391, 425, 513, 515
— орбитального момента 119
— осциллятора 64, 96
фермионного 133
— трехмерного изотропного
гармонического осциллятора 146
спектральная задача 44, 46, 78
для осциллятора 94
— линия 385
спин 60,118,125, 246, 258, 272, 274,
277, 297-300, 303, 306, 320, 327, 329,
330, 332-335, 349, 350, 354, 362, 378,
421, 486, 495, 501, 503, 539
— векторной частицы 114
— полный 342, 383, 421
— полуцелый 273, 311
— суммарный 349, 358
— целый 273, 311
— электрона 323
— ядра 323
спинор 126,133, 266, 269, 300, 301, 321,
322
— СР-сопряженный 291
— абсолютно нейтральный 304, 305
— вейлевский 292, 296, 297, 305
левый 292, 293
правый 291
сопряженный 305
— двухкомпонентный 321, 325, 326
— дираковский 294, 295, 298, 305, 326,
335
— киральный 293
— левый 290, 292, 294, 297, 298, 305
— майорановский 304, 305
— нерелятивистский 327, 328, 335
— Паули 126
— правый 290, 292, 294, 297, 298, 305
— релятивистский 265, 275
— сопряженный зарядово 129
по Дираку 296
спиральность 273-276, 288, 291-294,
296, 297, 308, 310
Предметный указатель
557
среднее значение 18, 27,157, 484-486,
499
— число квантов 100
стабильность вакуума 213
стандартная модель 132, 275
статистика Бозе—Эйнштейна 132, 311
— Ферми—Дирака 132, 311, 342, 347,
357
статистическая сумма 488, 489
статистический ансамбль 486, 491
термодинамический 486, 489
— вес 487, 490, 491
стационарность статистического
ансамбля 486
столкновение неупругое 401,423, 426
— упругое 401,408
сумма моментов импульса 246
— по поляризациям 302
— прямая 245, 294
суперпозиция 16, 47, 59, 80,118,195,
247, 283, 284, 299, 321, 342, 386, 406,
407, 496
суперсимметрия 281
сфера Шварцшильда 188
сферическая гармоника 121,142,149,
154, 252, 318, 409, 521, 524, 526, 527,
529, 537
тахион 271
твердая сфера 415, 417
температура 489
— отрицательная 490
— черной дыры 188
тензор антисимметричный 335
— генераторов бустов
антисимметричный 259
спиновый 260
— дуальный 308
— Леви-Чивита 110,120, 257
— момента импульса 258
— напряженности 241, 307, 309, 335
— неприводимый 245, 371
— полностью антисимметричный
второго ранга 128
— симметричный бесследовый 245
— спина 258, 272, 335
— углов вращений 258
теорема Белла 498, 501, 502, 504
— Бора—Пайерса—Плачека 402
теорема Виета 483
— вириала 91,150,157
— Гаусса—Остроградского 67, 525
— Нётер 57, 67, 284, 313
— о телесном угле 242
— оптическая 398, 402, 412, 426, 508
— осцилляторная 82
— Паули—Людерса—Вигнера 277
— Стокса 241
— Эккарта—Вигнера 251-253, 371, 383
— Эренфеста 41,45,102
теория возмущений 205, 323, 335, 339,
343, 344, 348, 365, 373, 396, 402, 403
для осциллятора 214
нестационарная 229, 378
стационарная 223, 233
вырожденного спектра 226
невырожненного спектра 224
— информации 491
— перенормировок 396
— перенормируемая 335
— рассеяния 506
фазовая 426
— релятивистская 314
— со скрытыми параметрами 492,
498-500
— струн 281
тепловое равновесие 486, 489,490
терм 349, 355, 359, 360, 365, 366, 371,
375, 382
термостат 486, 487,490
тождественные частицы 130,131, 311,
312, 342, 421
тождество Бейкера—Хаусдорфа 51,193
— Якоби 31,108
ток 68, 275, 276, 300, 318
— сохраняющийся 284, 289, 313
— электрический 305
точка поворота 167,170,180,181,184
— стационарная 55,195
траектория 35, 38, 55,155,163,194,
196, 208, 316, 498, 499, 505, 507, 511
— осциллятора 94
трансляция 58, 72,105, 255, 269, 270,
275, 281, 315
— бесконечно малая 108
— инфинитезимальная 72
— конечная 76
транспонирование 22
558
Предметный указатель
тройка правая 109,120
углы Эйлера 136,138
угол вращения 109
— рассения 399
— телесный 242, 399, 412, 518, 521, 527
узел 81, 97,124,146,154
универсальность статистического
ансамбля 486, 488
унитарность 408
упорядочивание нормальное 208, 281
— операторов 38,192
— по Вейлю 192
— по времени 41,191, 207, 396
— хронологическое 207
уравнение волновое 277
— Гейзенберга 40, 57, 59, 62, 92, 97,
281, 330, 538
— движения 270, 279, 292, 294, 309,
311
— динамическое 15, 308
— Дирака 299, 323, 325, 330, 331, 334,
369
стационарное 320
— для ^-матрицы 513
— для замкнутых систем 487
— для матрицы рассеяния 528
— для радиальной волновой функции
143
— для резольвенты 393, 396
— для релятивистского электрона 302
— для спинора 289
— для функции Грина 393, 396, 527,
531
— интегральное 396, 397,400,402,
403, 412, 514
для функции Грина 397
— Клейна—Гордона—Фока 277, 318,
333
— Липпмана—Швингера 397
— Лиувилля 484, 487
— массовой поверхности 307, 310
— на собственное значение 29, 30,46,
92, 94, 99,100,116,121,124,131,139,
142, 227, 228, 239, 272, 277, 300, 301,
305, 320, 521, 524
— непрерывности 52, 68,165
— Паули 327
— Пуассона 345
уравнение радиальное 318, 349,406
— релятивистское 327
— секулярное 227, 332, 483
— функциональное с источником 198
— Шрёдингера 16, 20, 36, 40,44, 60,
65, 70, 75,141,164,195, 238, 289, 332,
342, 346, 394, 397,416, 484
для осциллятора 93
радиальное 412
стационарное 46,141,149, 389,
393, 394, 396, 400, 408, 425, 513
для радиальной волновой
функции 144
одномерное 77
уравнения Гамильтона 38,102, 280
— Гамильтона—Якоби 35, 36,165
— Лагранжа—Эйлера 65
квантовые 198
— Максвелла 308
— Прока 311
— Хартри 346
— Хартри—Фока 347, 348
— Швингера—Дайсона 198,201, 204
уровень 5-волновой 323
— атома водорода 343
— возбужденный 382, 490
— Ландау 538, 539
— невырожденный 79
— стационарный 93, 318, 517
усечение внешних линий 218
условие асимптотическое 412
— вырождения 59, 71, 76,116,156
— гармоничности 526
— полноты базиса 26, 527
— применимости борновского
приближения 404
фаза 166,174,176, 240, 285, 303, 304,
315, 316, 506
— Берри 240, 242
— волновой функции 130,131
— волны 35
— геометрическая 241
тривиальная 241
— комплексная 47, 55, 99,102,165,167,
276, 294, 303, 306, 313, 314, 412
глобальная 66, 284
относительная 18,171
— относительная 313, 386
Предметный указатель
559
фаза преобразования 296
— рассеяния 85, 412, 417, 423, 510
кулоновская 536, 537
парциальная 424
— спинора 321
— стационарная 87
фактор Ланде 327, 335, 372, 375
факторизация волновой функции 343,
346, 347, 357
фермион 127,129,130,133, 275, 281,
289, 291, 312, 313, 318, 336, 357, 422
флуктуация 35, 39, 58,163,185,186,
236, 282, 319, 327, 331, 334
— минимизированная 102
— числа квантов 300
— электромагнитного поля 323
— энергии 239
формализм гамильтонов 35
— Дирака 20, 483
формула Коши 392, 395
— Резерфорда 423, 536
— Стирлинга 413
фотон 19, 338, 378, 380, 382, 385, 496,
504, 510, 514
фотоумножитель 496
фотоэффект 36
фронт волны 55,165, 423
— сферический 408
функционал 197, 275
— У -матрицы 216
— производящий 200, 205, 214
функция Бесселя 509
— Блоха 74
— Ганкеля 407
— гармоническая 524, 526
— Грина 195, 200, 218, 392, 393, 396,
404, 425, 513, 525, 529, 531, 537
двухточечная 199, 215
усеченная 204
запаздывающая 195, 393, 394,
396
многоточечная 199
обратная 202
причинная 213
свободной частицы 394, 398, 514,
515, 534
связная 200, 211
стационарная 514
усеченная 203
функция Грина четырехточечная 200
— Лагранжа 278
— Неймана 407
— обобщенная 25, 31, 54
— оператора 40
— Хевисайда 195, 393, 394, 525
— Эйри 170
фурье-компонента 291
фурье-образ 279, 403
цикл 240, 241
частица 35, 45
— безмассовая 510
— быстрая 404, 416, 427
— векторная 113
— виртуальная 185,186
— заряженная 215
— майорановская 306
— массивная 303
— медленная 404,414
— нерелятивистская 329
— релятивистская 132, 255, 269
безмассовая 272, 275, 288
массивная 272
свободная 313
— свободная 36, 52, 56,115, 408, 505,
516
— скалярная 113, 292
— элементарная 281
частота 35, 277
— вращения 539
— ларморовская 372
— перехода 231
— прецессии 330
— угловая 111
— фазовая 35, 91
черная дыра 188
четность 321, 332
— зарядовая 294
— комбинированная 292
— пространственная 97,124,142, 263,
294, 298, 303, 320, 384, 385
число заполнения 349
— квантов 210
— состояний 491
ширина перехода 235
— резонанса 89, 425
— уровня 235, 381
560
Предметный указатель
эволюция 15
— вакуума 211
— волновой функции 36
— когерентного состояния 101
— матрицы плотности 487
— осциллятора 97
— состояния 44,191,195
эйконал 504, 506, 509, 510, 534
экранировка ядра 343, 346, 348, 350,
353, 361
электродинамика квантовая 281
— классическая 377
электрон 151, 294, 302, 317, 318, 320,
323, 326, 330, 331
— эквивалентный 349
элемент -матрицы 211, 392, 394, 399
— длины 119
— единичный 108
— обратный 108, 296
энергия вакуума 281
— ионизации 347, 348
— кинетическая 70,111,140,141,156,
169,185, 329, 341, 346, 398
энергия отрицательная 290
— покоя 325
— положительно определенная 292
— поля 280
— потенциальная 70,185, 370, 377, 530
— связи 318, 319, 323, 359, 371
— собственная 204
энтропия 489-491
— Шеннона 491
эффект Ааронова—Бома 316
— Зеемана 371, 374
аномальный 371, 374
— Пашена—Бака 374
— Рамзауэра 415
— релятивистский 323
— туннельный 183,184,186,188
— Хокинга 189
ядро нормального символа
голоморфное 218
— оператора 210, 218
голоморфное 210, 211, 217
якобиан 276