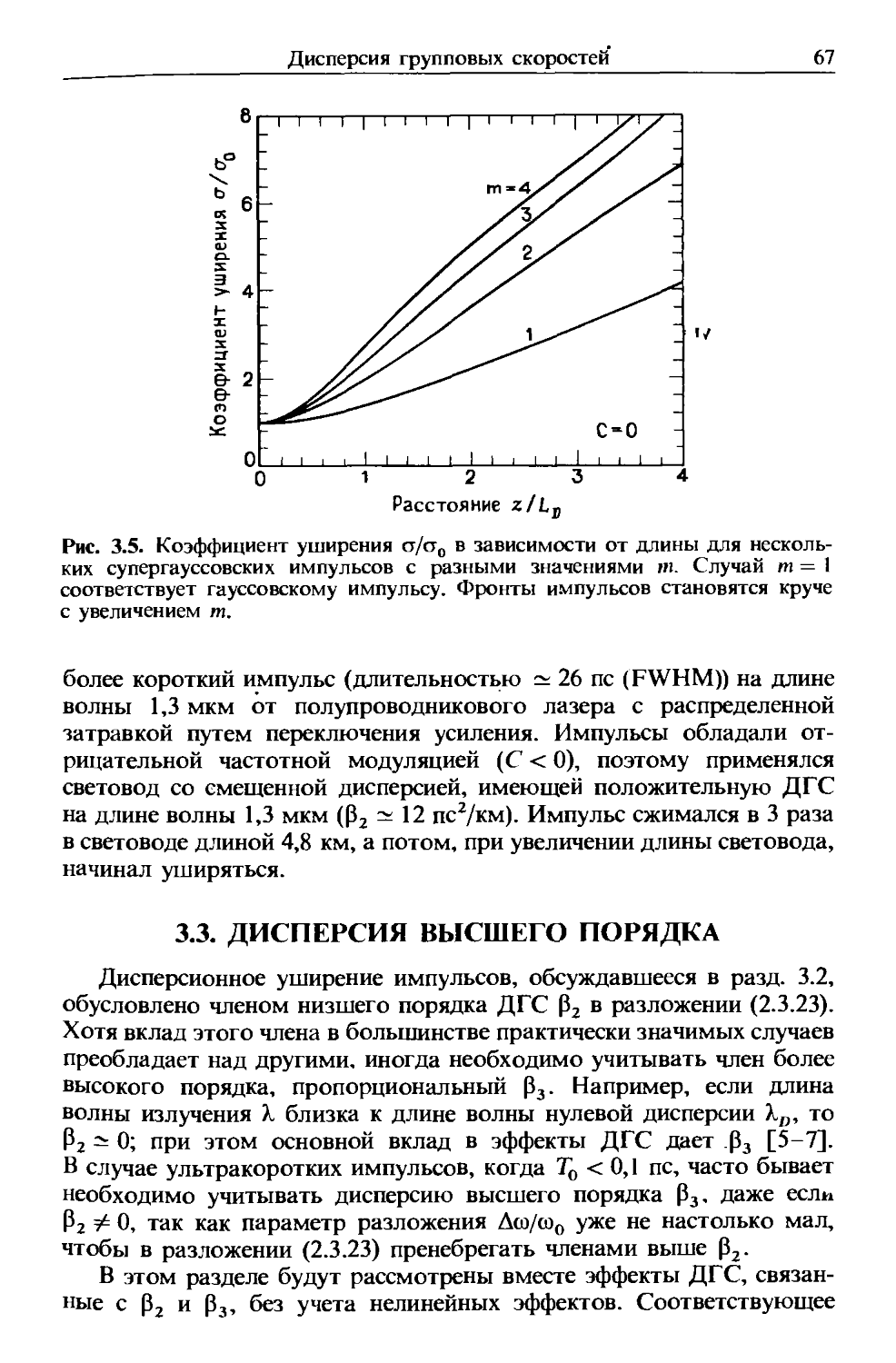
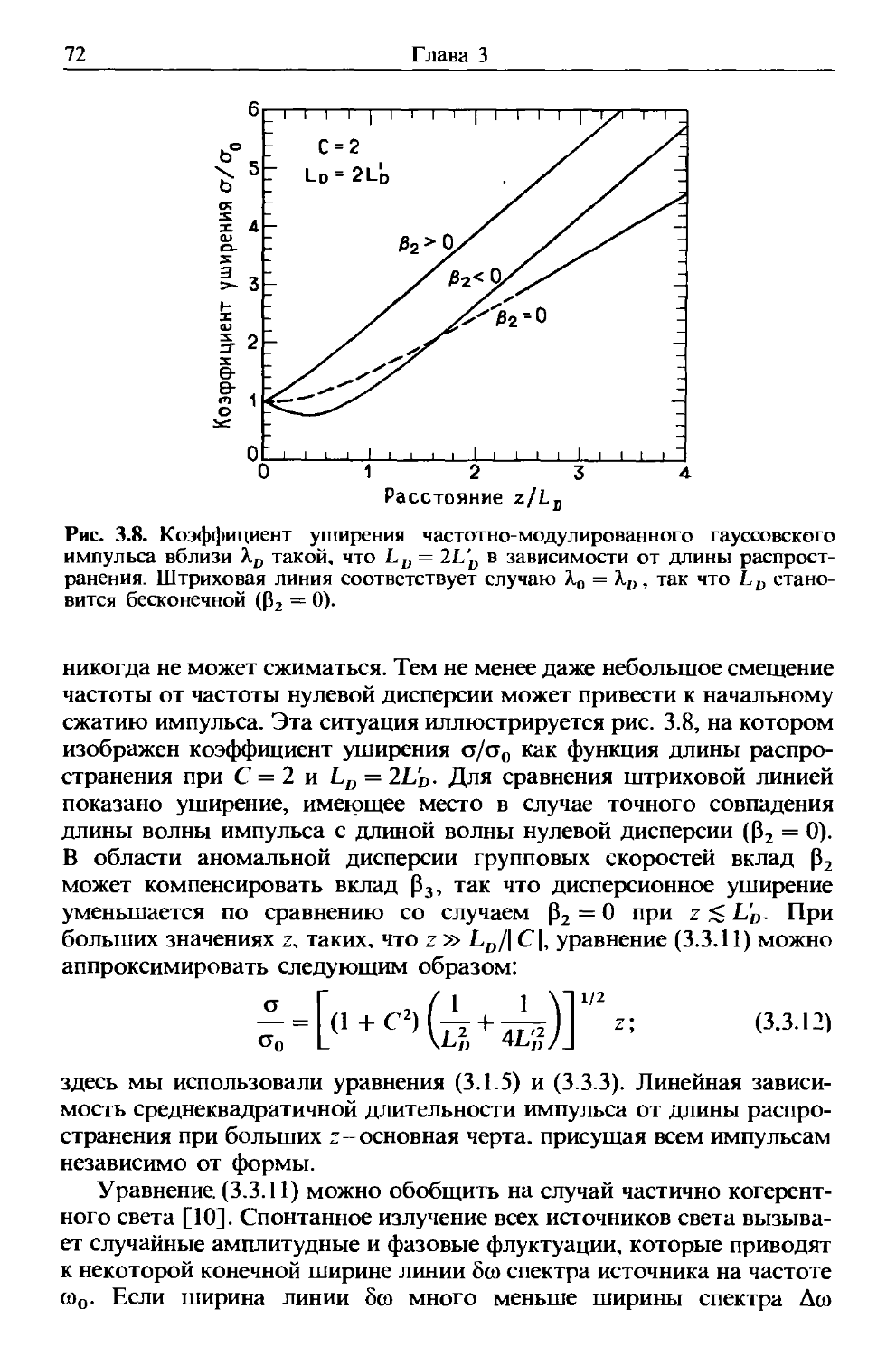
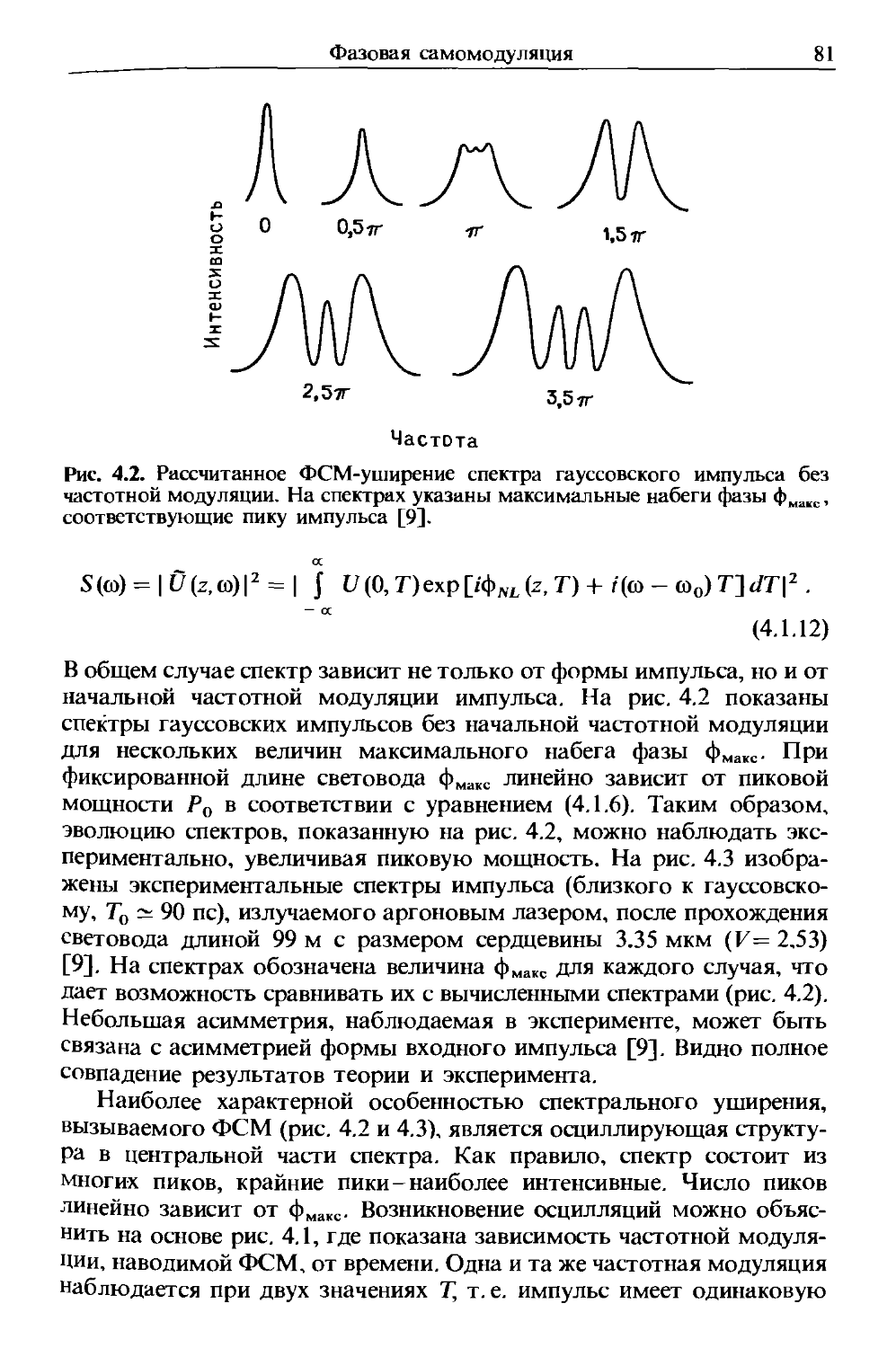
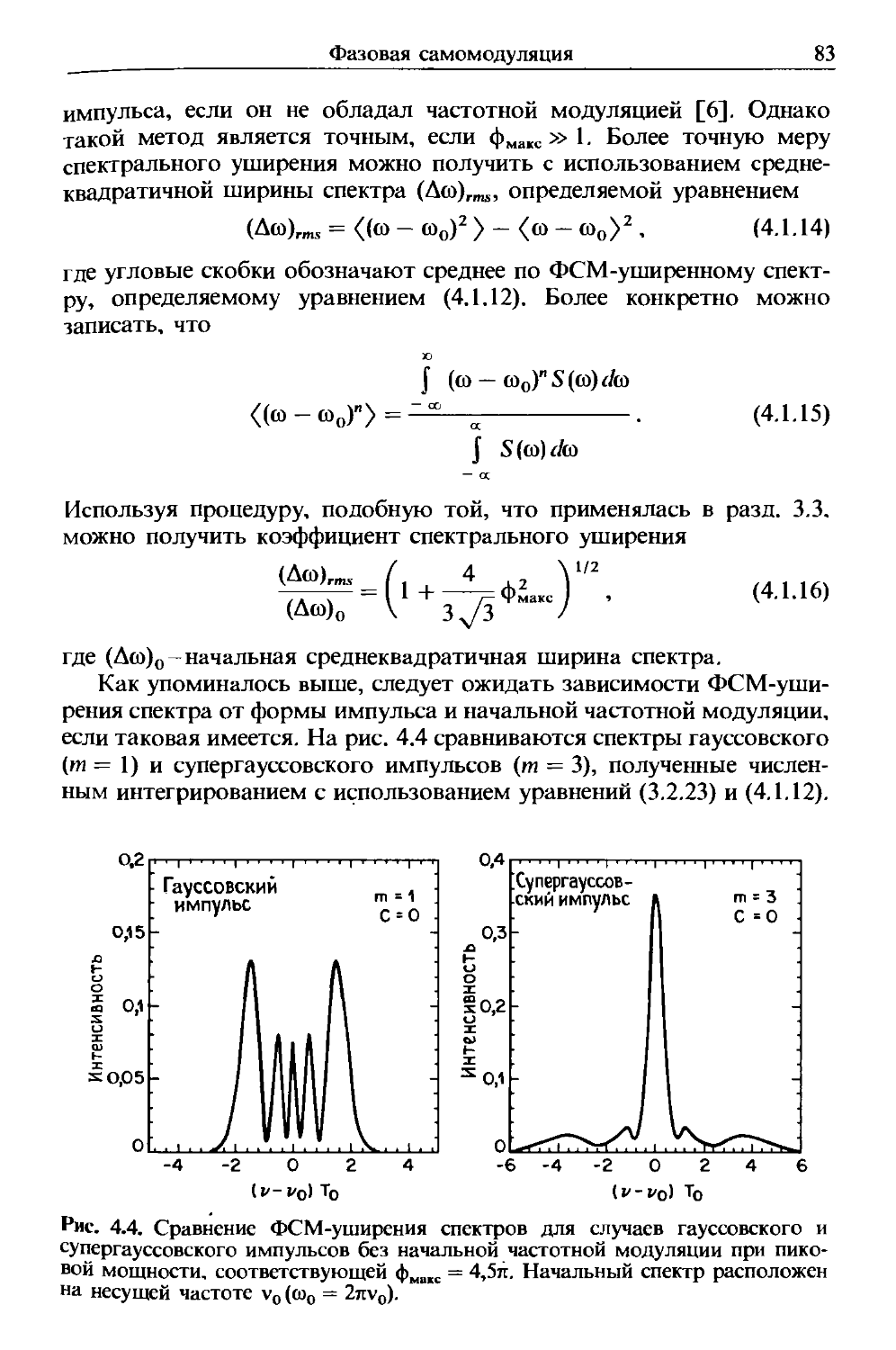
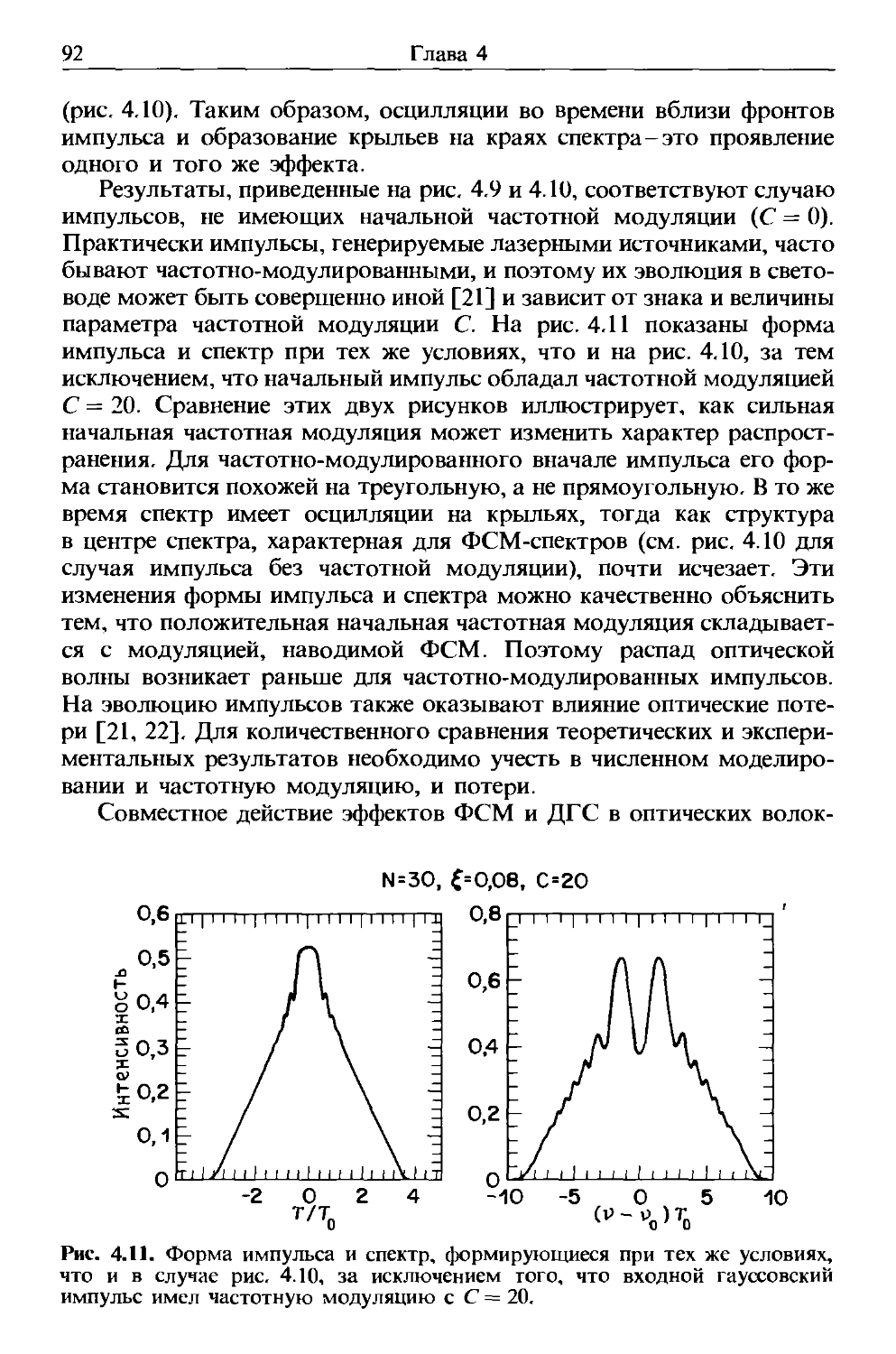
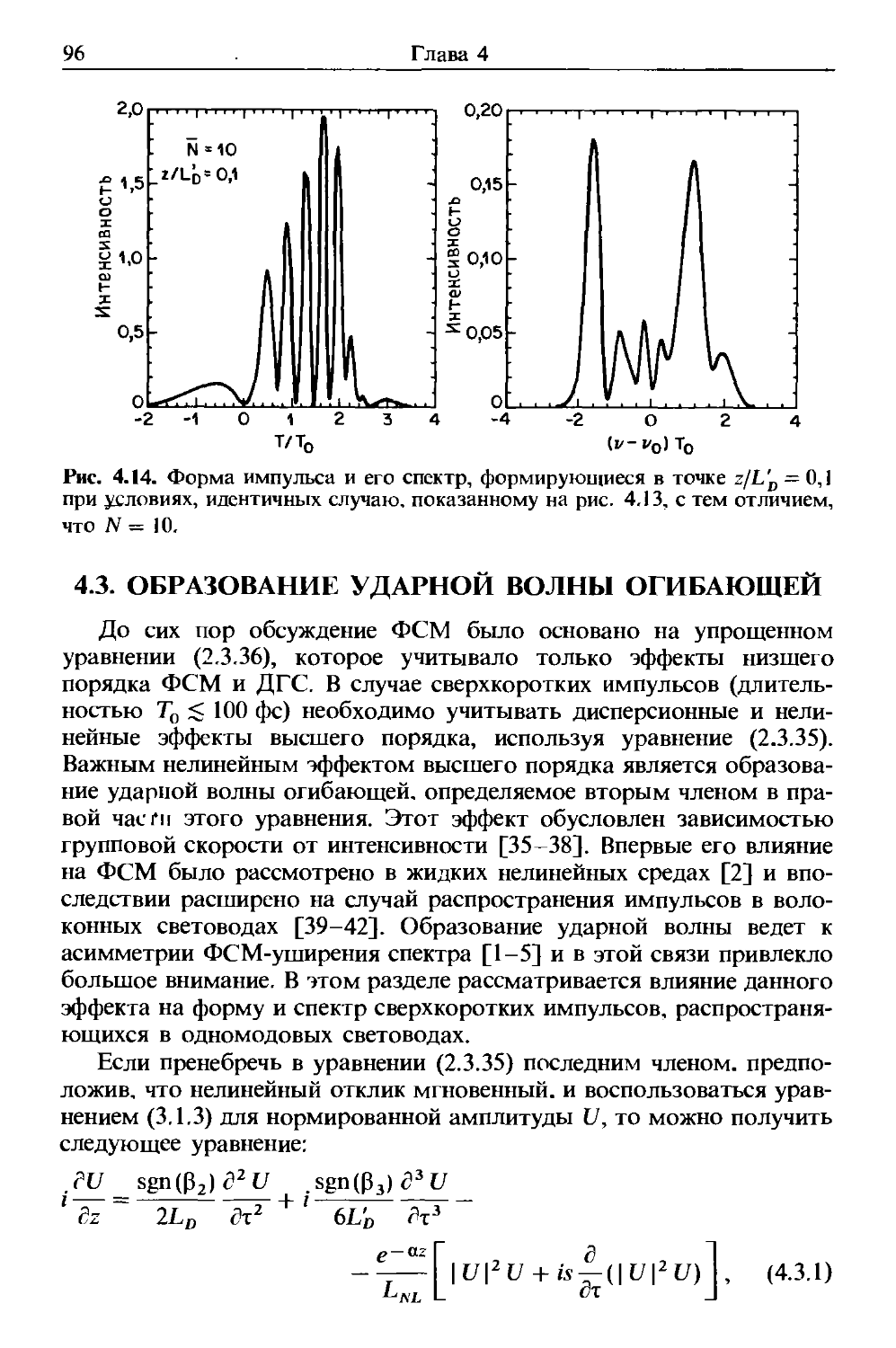
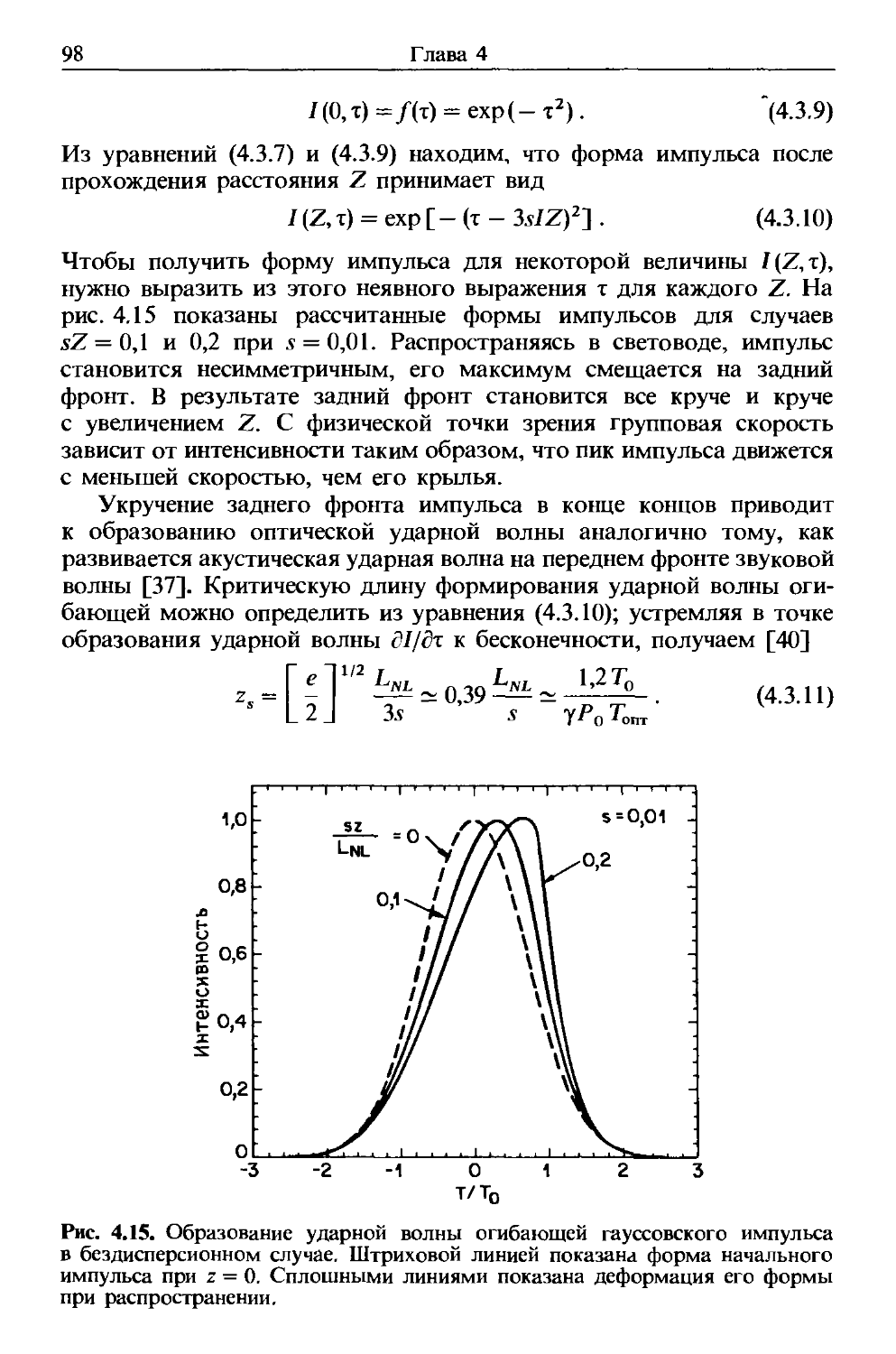
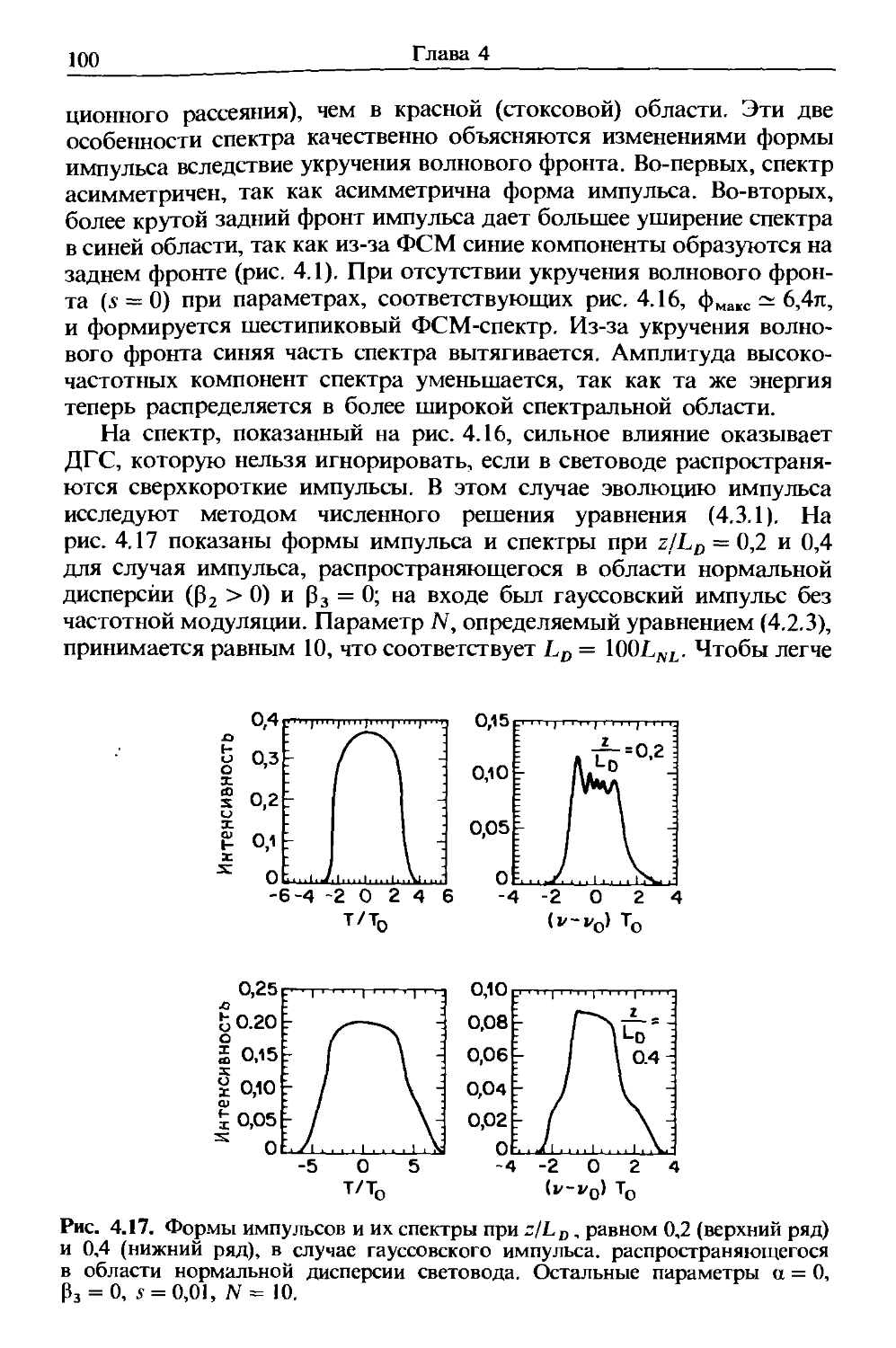
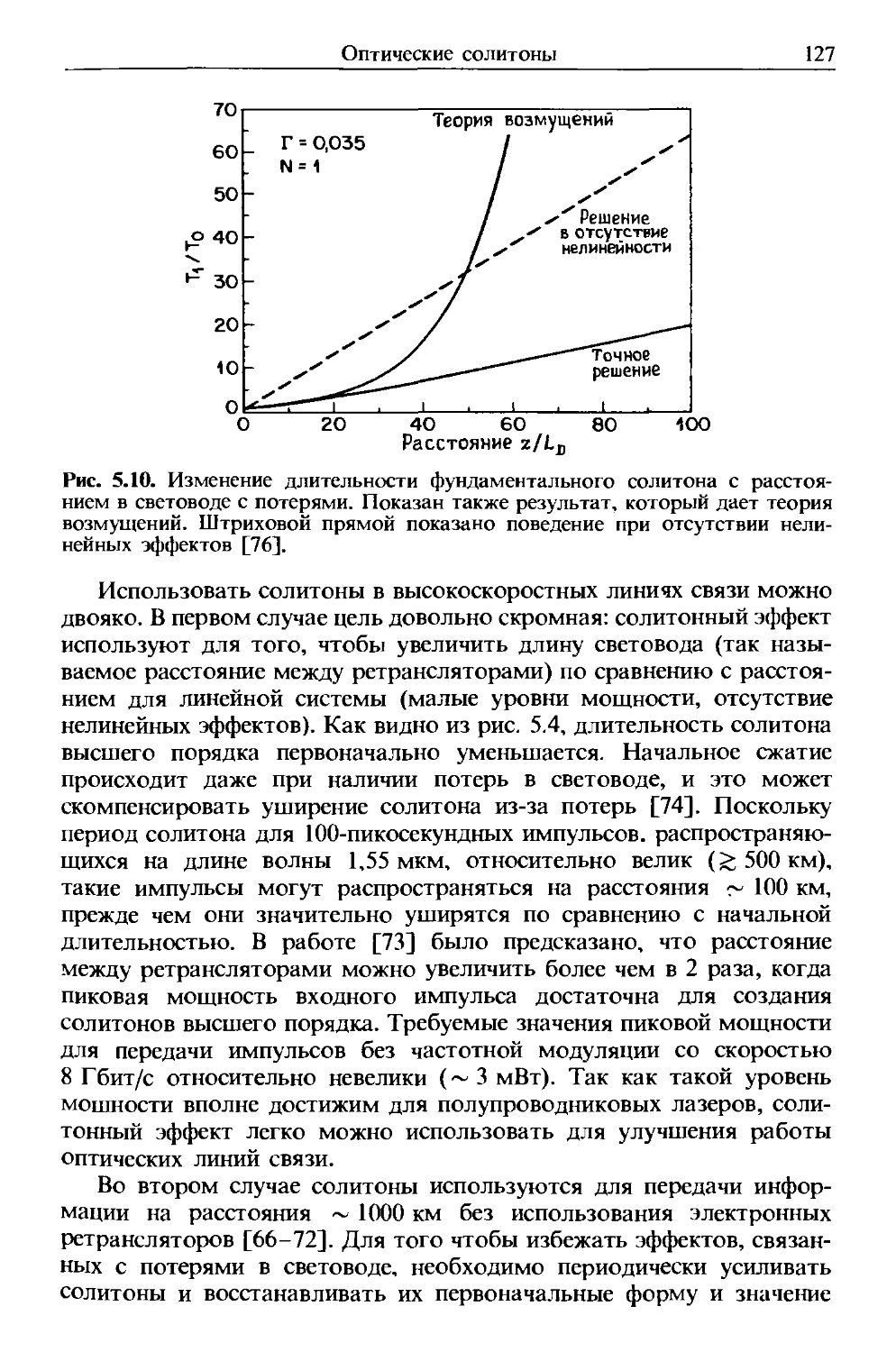
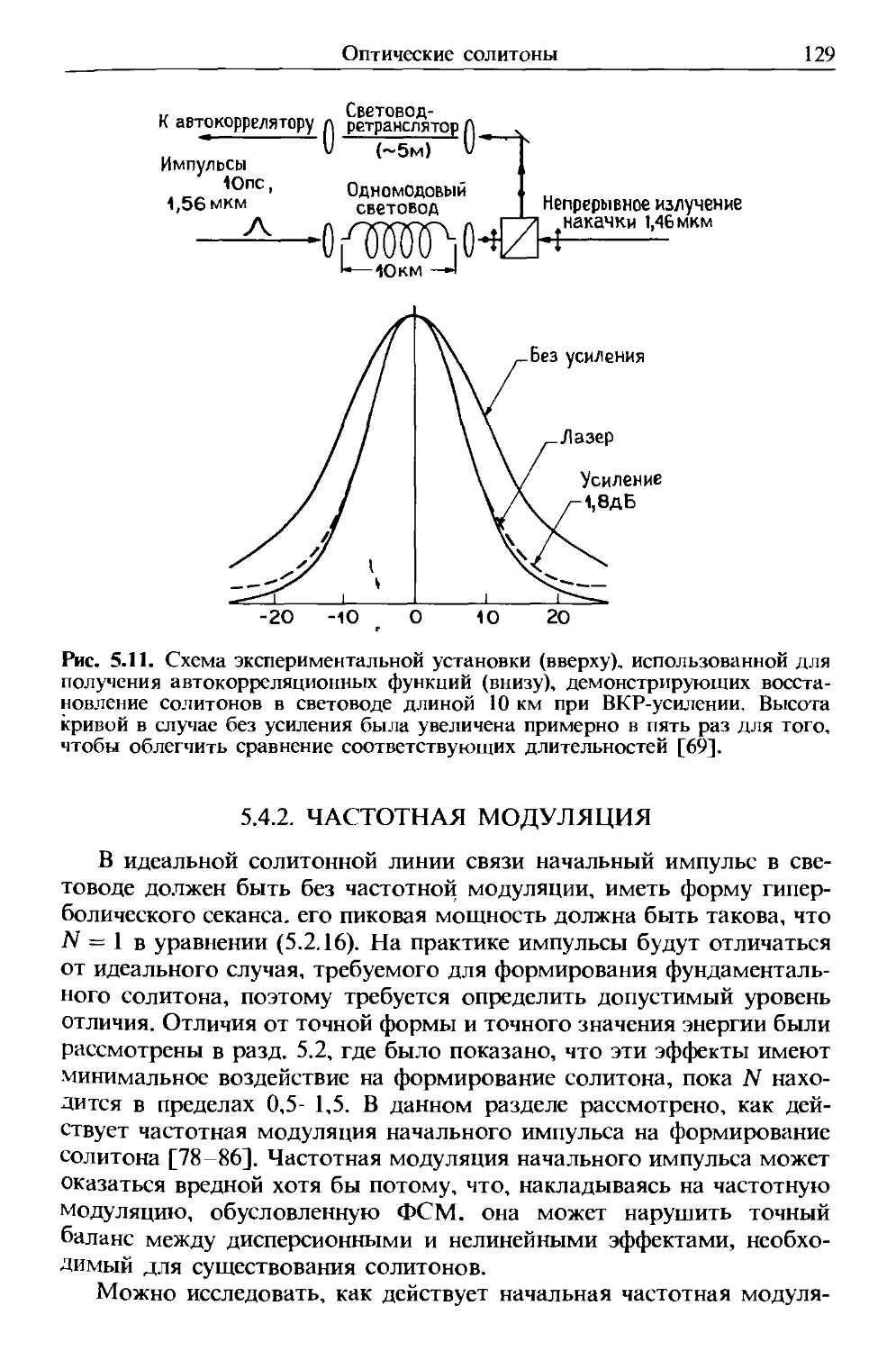
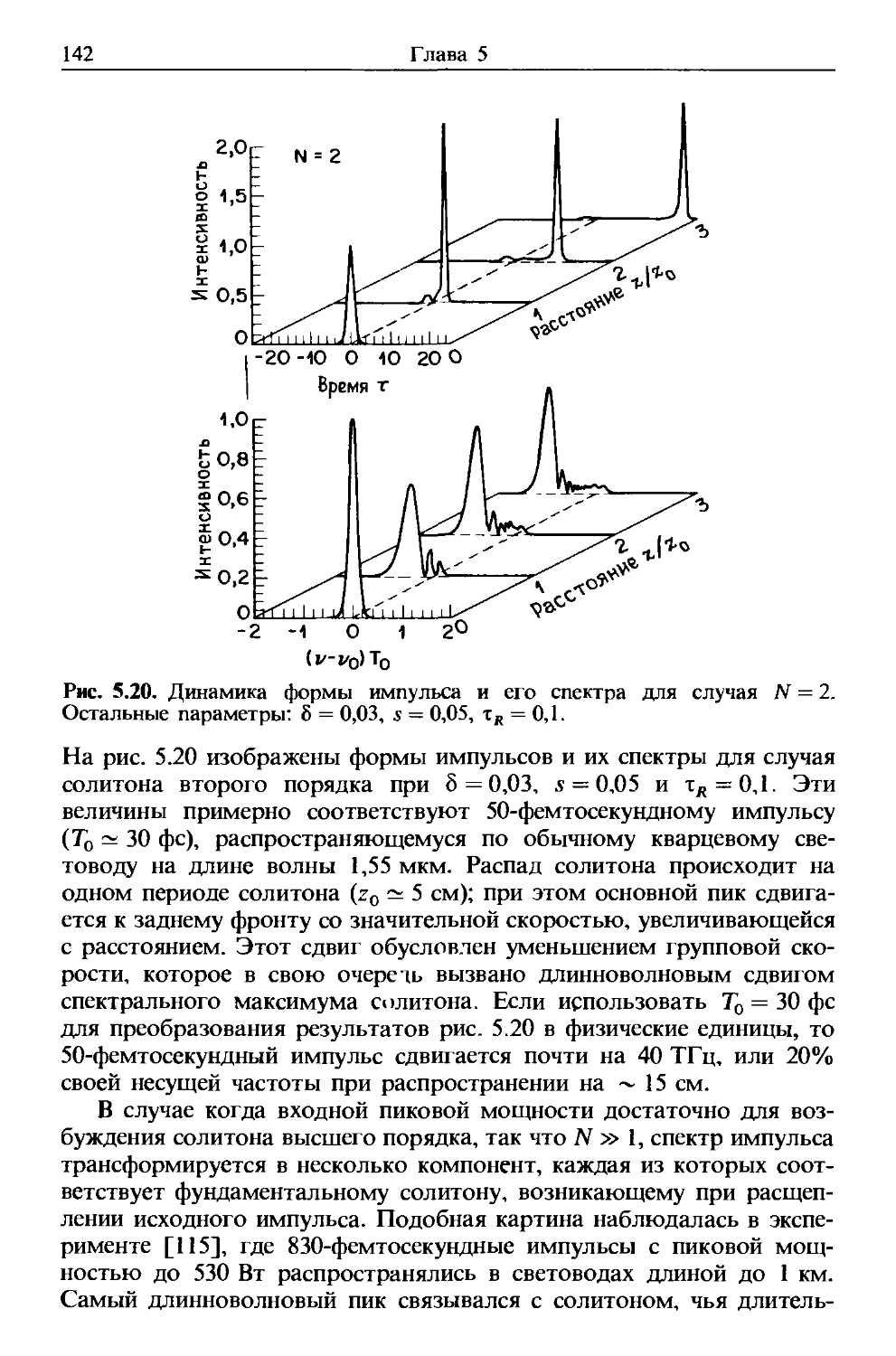
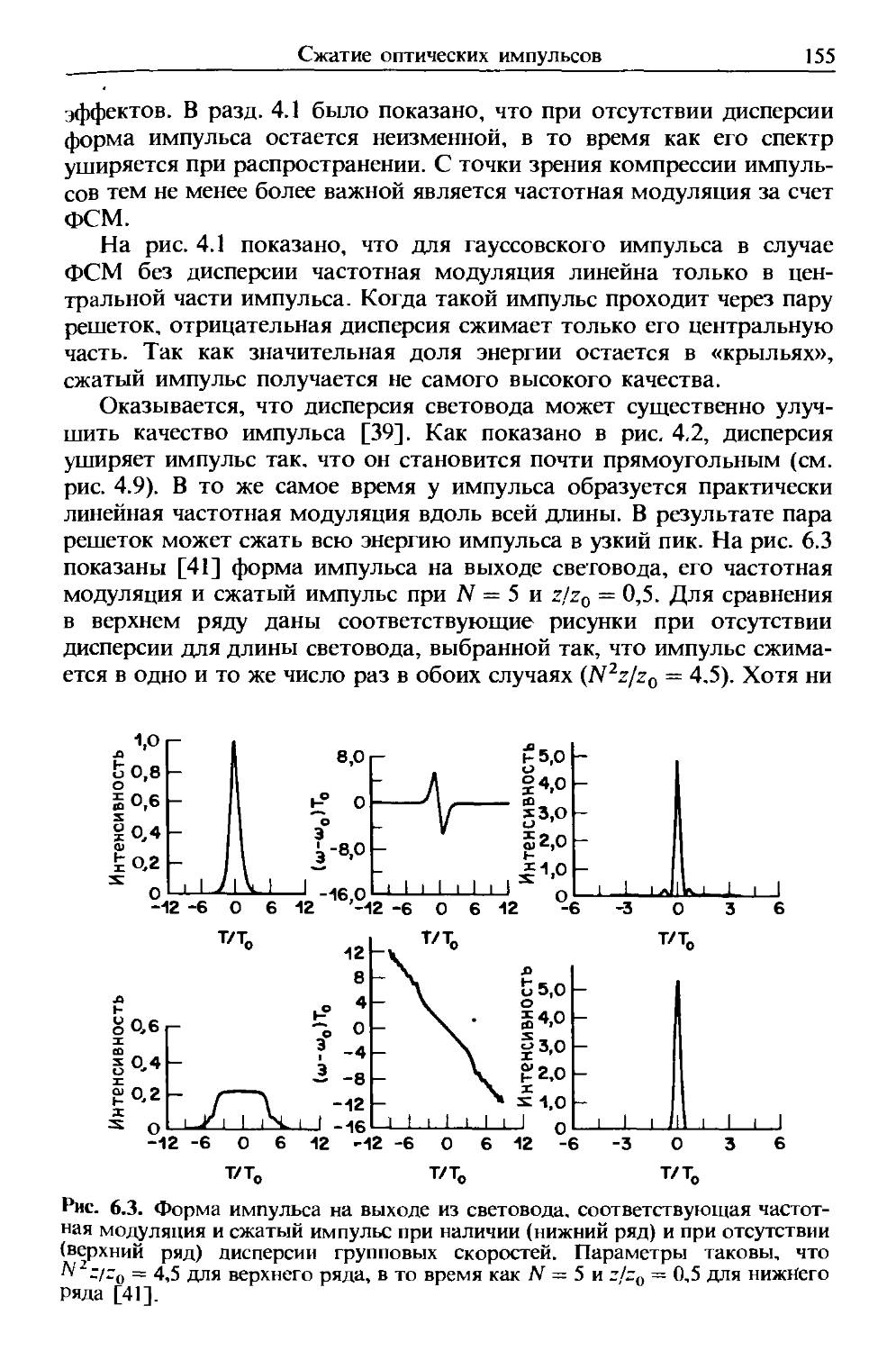
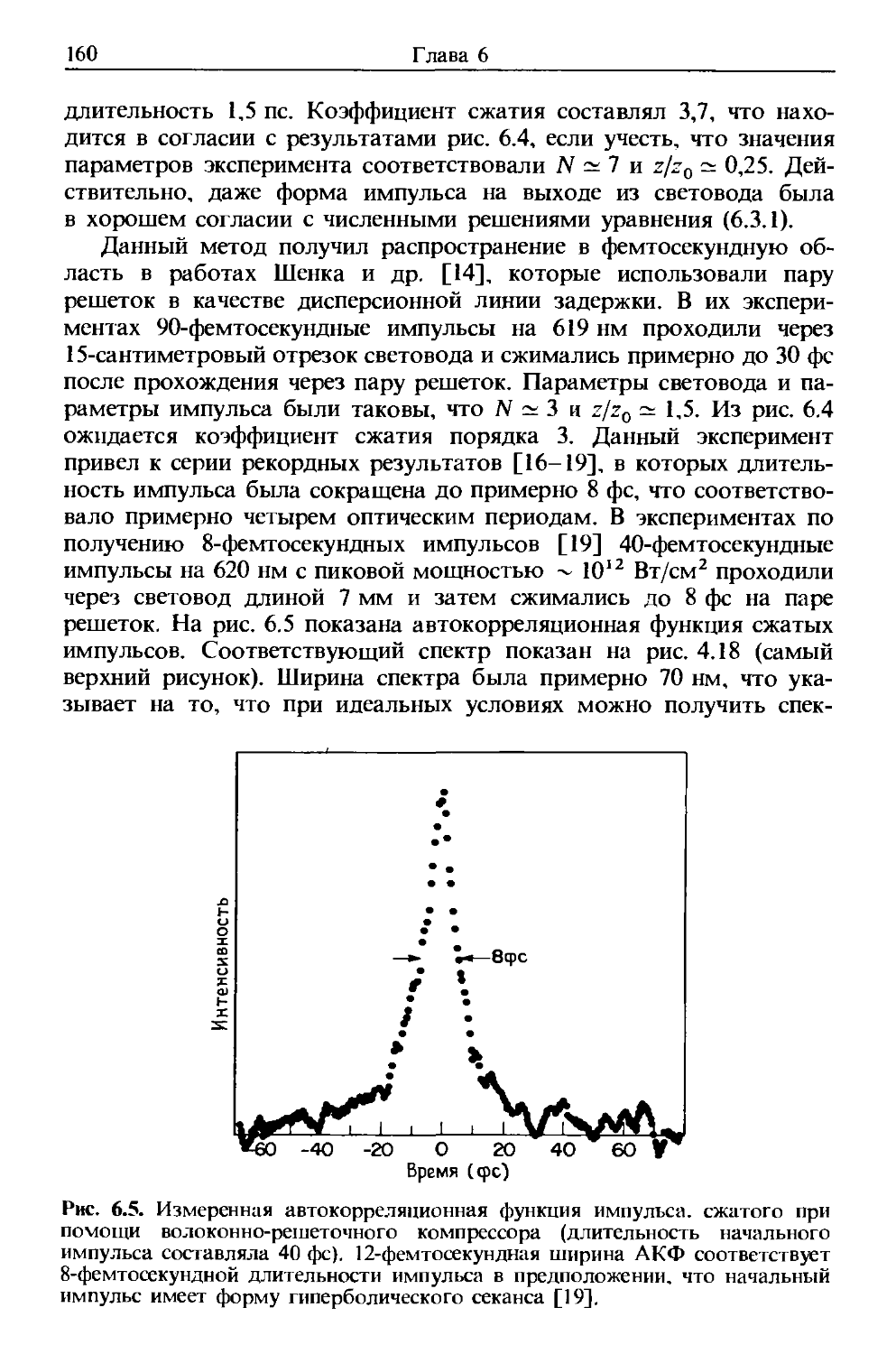
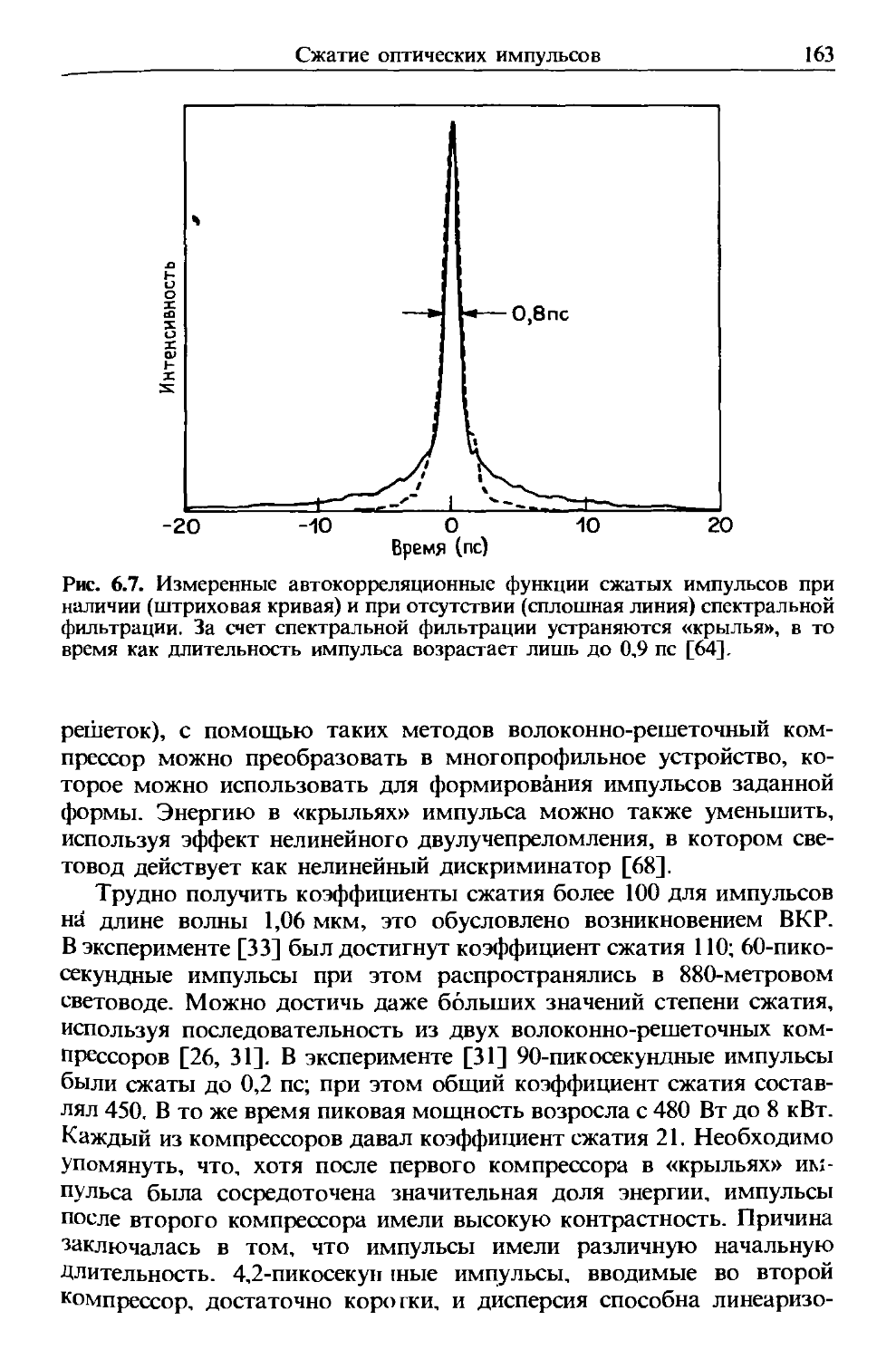
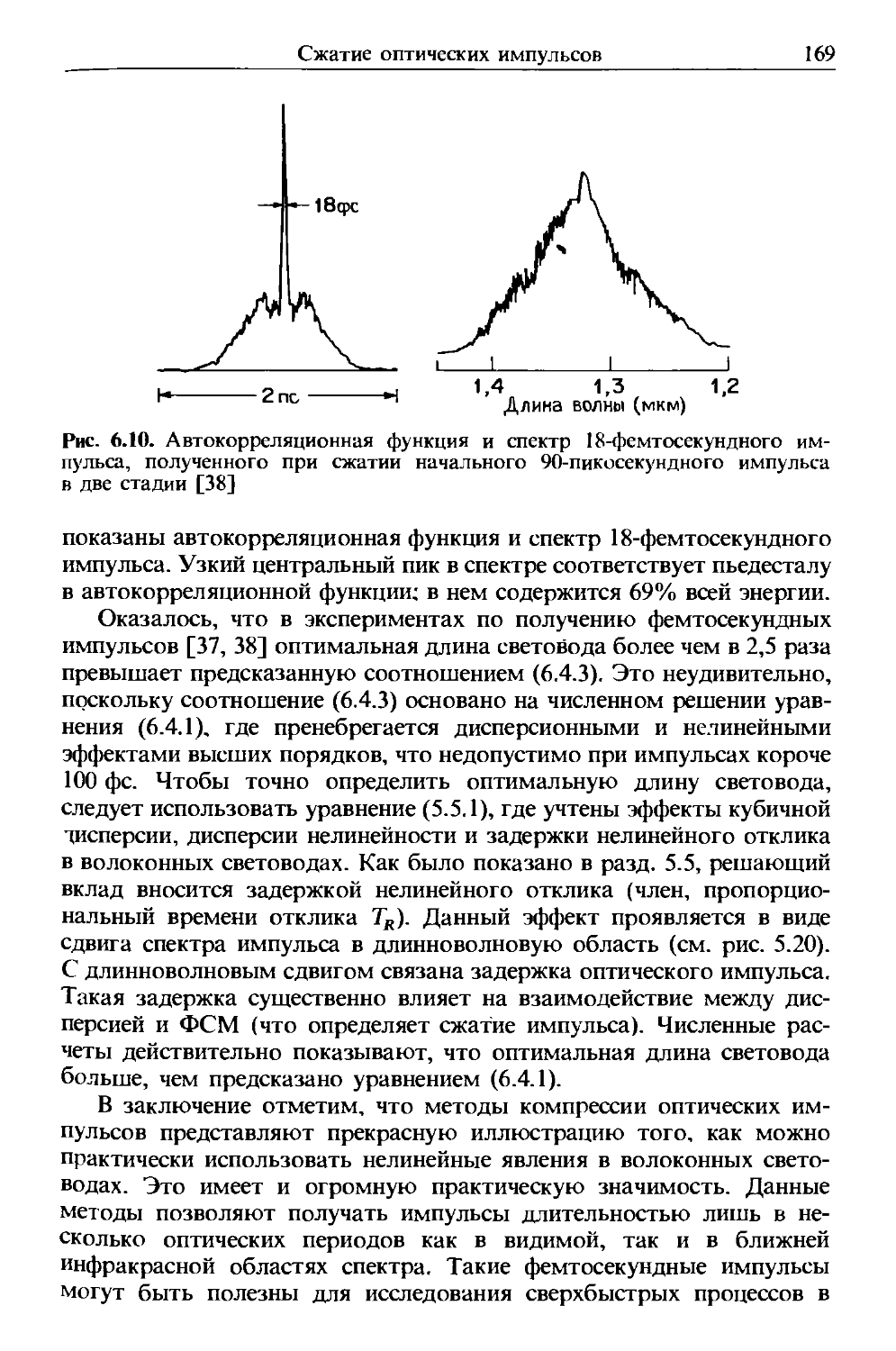
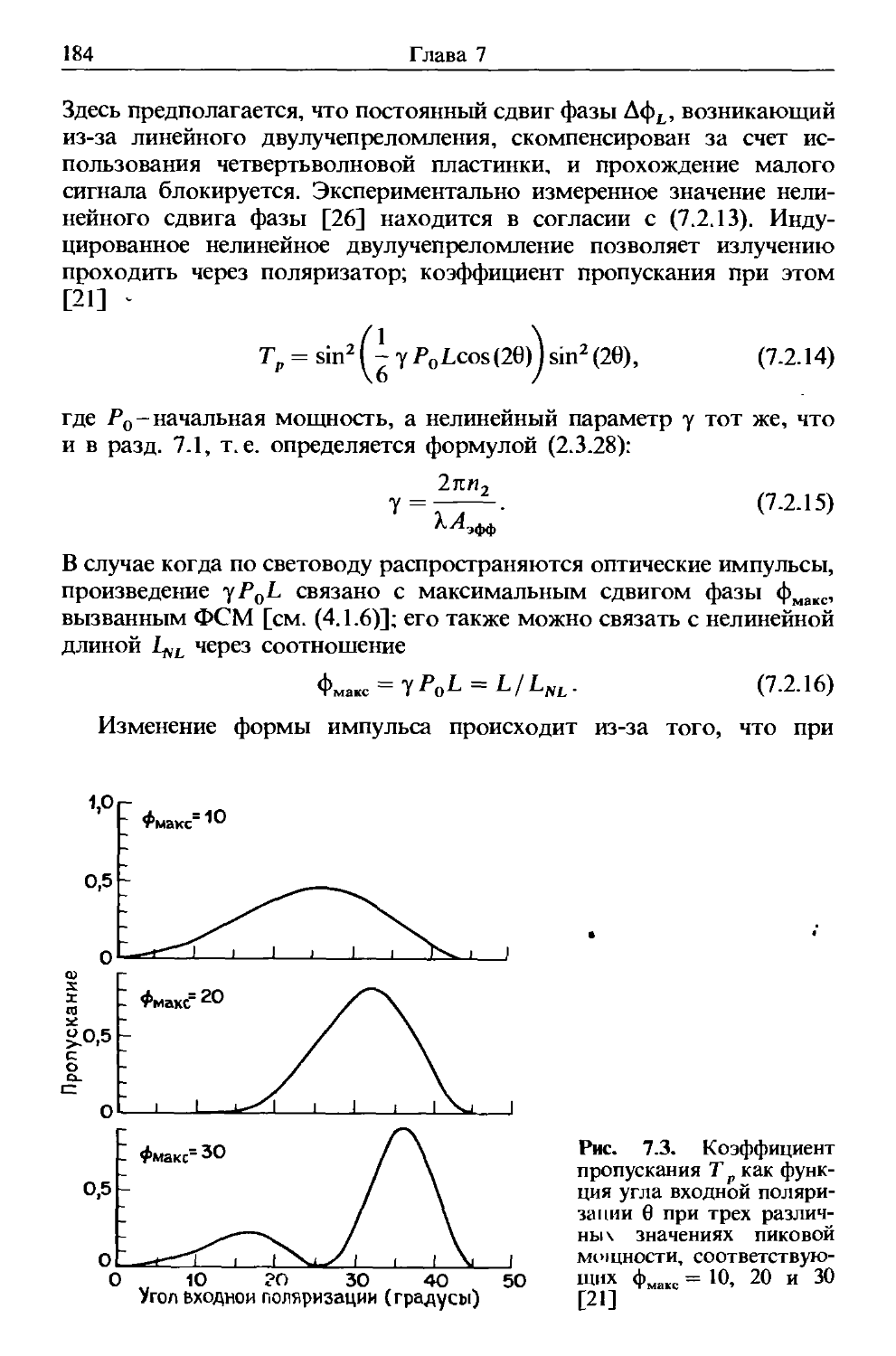
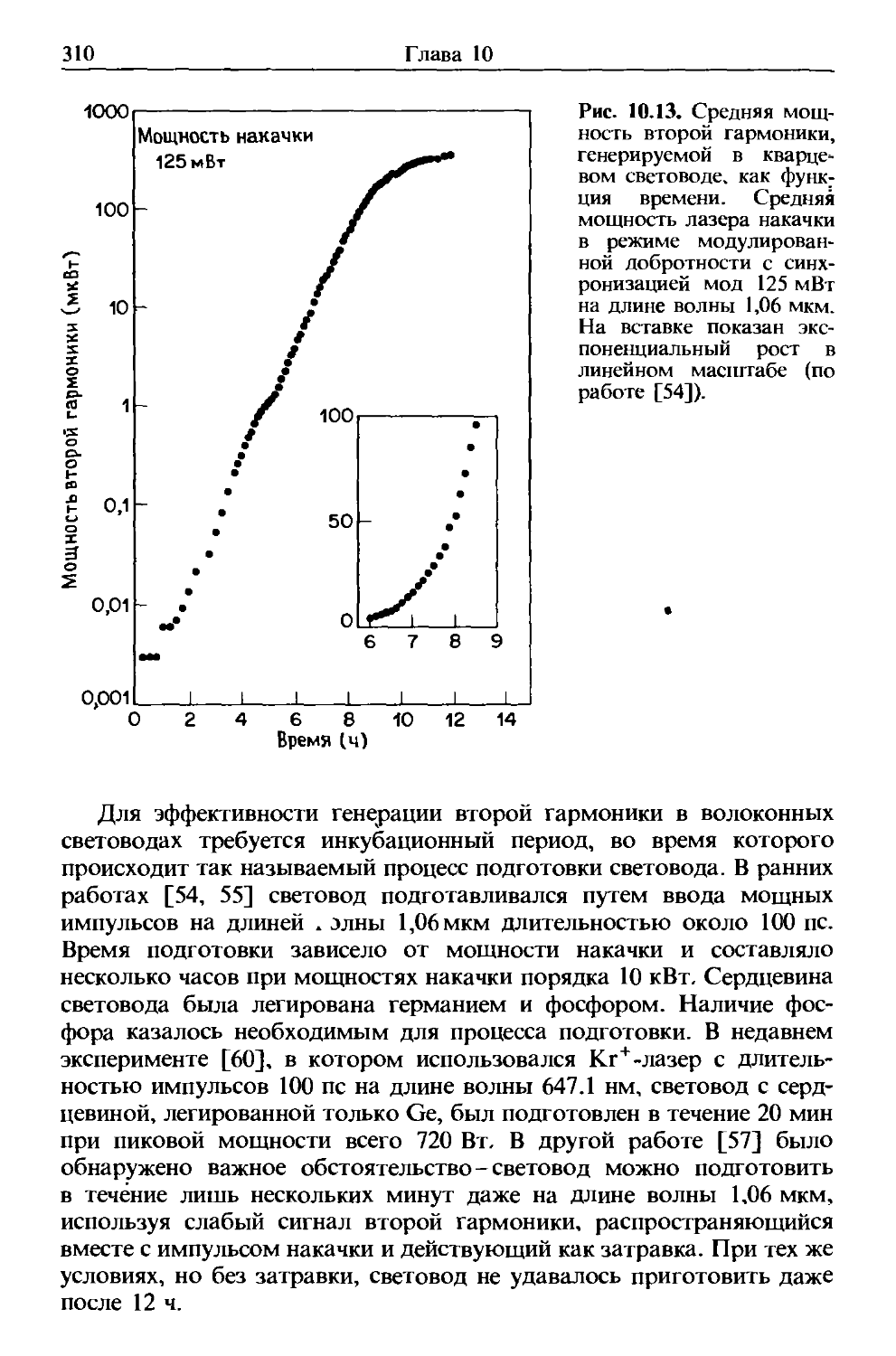
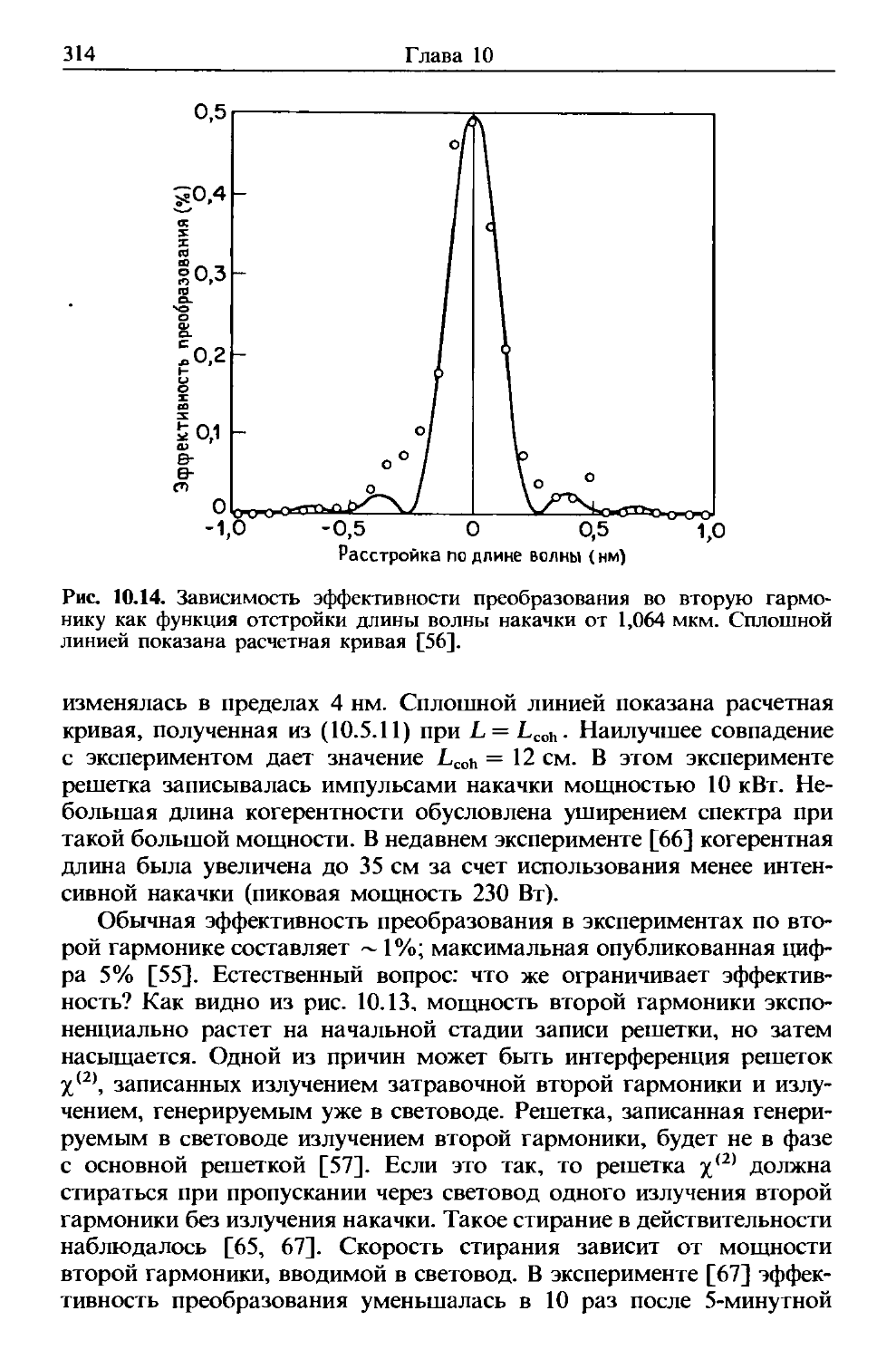
Author: Агравал Г.
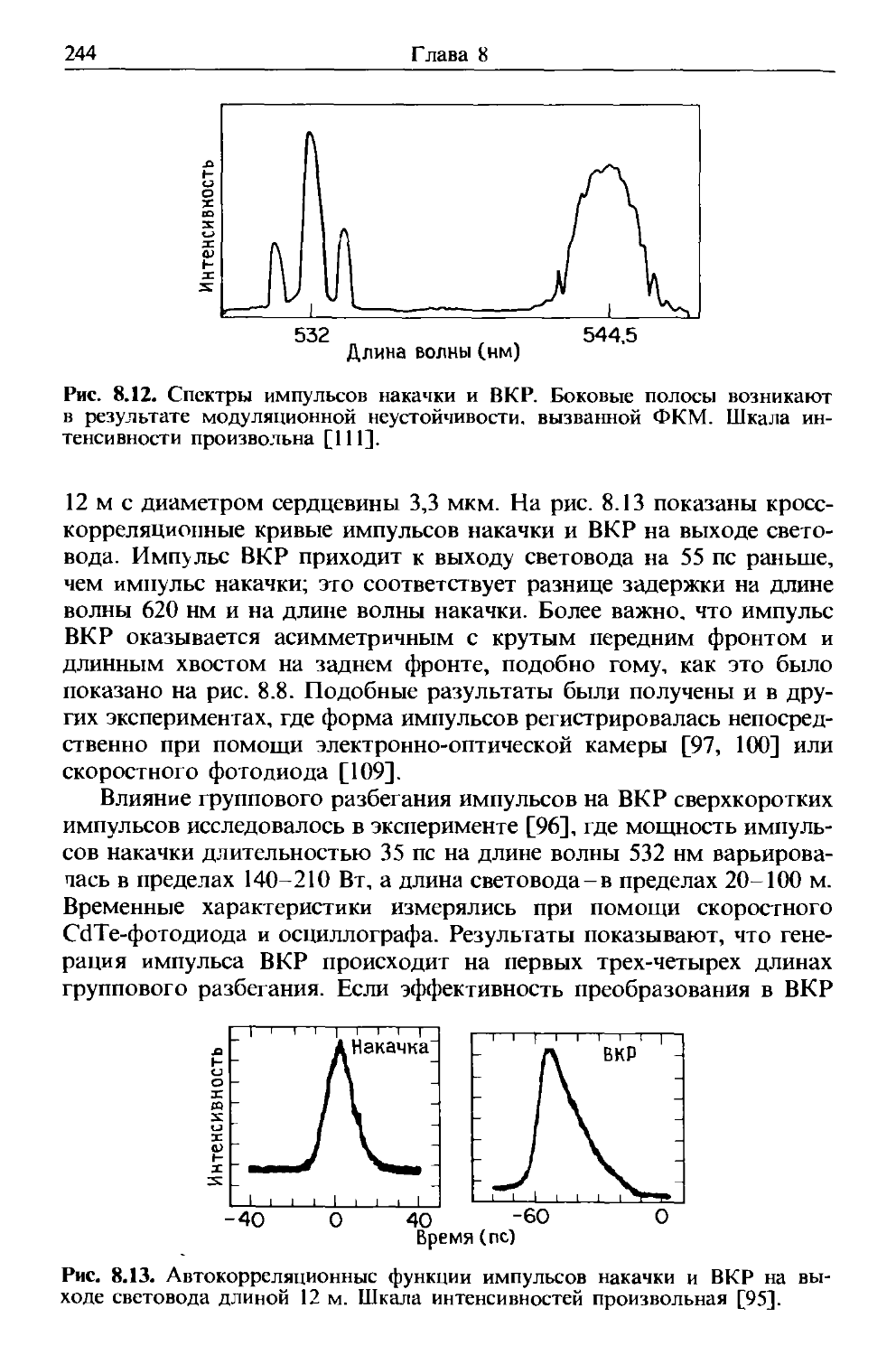
Tags: оптические приборы и аппаратура физика оптика нелинейная оптика
ISBN: 5-03-002418-2
Year: 1996
Text
NONLINEAR FIBER OPTICS
Govind P. Agrawal
The Institue of Optics University of Rochester
Rochester, New York
ACADEMIC PRESS, INC
Harcourt Brace Jovanovich, Publishers
Boston Snn Diego New York
London Sydney Tokyo Toronto
Published by arrangement with AT&T
ГАгравал
НЕЛИНЕЙНАЯ
ВОЛОКОННАЯ
ОПТИКА
Перевод с английского
С. В. Черникова, И. Ю. Хрущева,
Д. В. Коробкина
Под редакцией канд. физ.-мат. наук
П. В. Мамышева
Москва «Мир» 1996
ББК 22.336
А25
УДК 681.7.068
Агравал Г.
А25 Нелинейная волоконная оптика: Пер. с англ.-М.:
Мир, 1996.-323 с, ил.
ISBN 5-03-002418-2
В книге специалиста из США систематизированы результаты по нелинейной
волоконной оптике за первые 20 лет ее развития, с единых позиций рассмотрены
вопросы формирования оптических солитонов, компрессия лазерных импульсов,
параметрические процессы, а также различные приложения указанных эффектов
в разных информационных системах. Большое внимание уделено хроматической
дисперсии из-за ее важности в изучении нелинейных эффектов, возникающих при
распространении ультракоротких оптических импульсов.
Для специалистов в области нелинейной оптики, исследователей и инже-
инженеров, работающих в области волоконно-оптической связи, студентов и аспи-
аспирантов.
ББК 22.336
Редакция литературы по физике и астрономии
Издание выпущено в свет при содействии Комитета РФ по печати
ISBN 5 03 002418 2 (русск.) © 1989, by AT&T Bell Laboratories
ISBN 0 12 045140 9 (англ.) © Перевод на русский язык, Черников С, В.,
Хрущев И.Ю., Коробкин Д. В., 1996.
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Нелинейная волоконная оптика как направление нелинейной
оптики возникла в начале 70-х годов с появлением стеклянных
волоконных световодов с низкими потерями. Первоначально воло-
волоконные световоды разрабатывались как пассивная линейная среда для
передачи оптического излучения (в основном для целей связи,) но
очень скоро стало ясно, что они представляют собой качественно
новый уникальный материал для нелинейной оптики. Исключитель-
Исключительная перспективность волоконных световодов определяется их свойст-
свойствами, а они такие: неизменность поперечного размера лазерного
излучения на больших длинах распространения по световоду и низкие
потери лазерного излучения, уникальные дисперсионные характе-
характеристики и возможность как одномодового, так и многомодового
режимов распространения лазерного излучения по световоду.
За 20 лет существования нелинейной волоконной оптики были
достигнуты большие успехи как в решении прикладных задач кван-
квантовой электроники, так и в изучении фундаментальных физических
явлений. Такие нелинейные процессы, как параметрическое усиление,
вынужденное комбинационное рассеяние и вынужденное рассеяние
Мандельштама-Бриллюэна, успешно используются в создании и
разработке волоконных лазеров, усилителей и преобразователей па-
параметров излучения. В волоконных световодах изучаются сжатые
состояния света, генерация и распространение оптических солитонов,
явление фоточувствительности стекла.
Особую роль играют нелинейные эффекты в волоконнооптических
линиях связи. С одной стороны, нелинейные эффекты в световодах
ограничивают возможную скорость и дальность передачи информа-
информации по световодам и их необходимо учитывать при создании линий
связи. С другой стороны, при определенных условиях нелинейные
эффекты могут быть использованы для увеличения скорости и даль-
дальности передачи информации. Особо здесь следует упомянуть передачу
информации оптическими солитонами-лазерными импульсами, ко-
которые за счет совместного действия нелинейных и дисперсионных
эффектов распространяются по световоду без дисперсионного уши-
рения.
Предисловие редактора перевода
Из сказанного выше следует, что область применений нелинейных
явлений в волоконных световодах очень широка и не ограничивается
лишь одной оптической связью. В связи с этим наблюдается все
возрастающий интерес к нелинейной волоконной оптике со стороны
ученых и специалистов, работающих в различных областях физики.
Однако долгое время информация по нелинейной волоконной оптике
оставалась рассредоточенной в научных статьях, а количество об-
обзоров было невелико. Книга проф. Агравала-это первая и на
сегодняшний день наиболее полная монография, в которой сделана
довольно удачная попытка систематизировать результаты по нели-
нелинейной волоконной оптике за первые 20 лет ее развития. Автору
удалось найти такую форму изложения, что книга интересна и по-
полезна как для специалистов (которые найдут в ней богатый спра-
справочный материал), так и для лиц, лишь начинающих изучать предмет.
Отметим, что на Западе книга проф. Агравала пользуется неизменной
популярностью среди студентов, аспирантов и специалистов, рабо-
работающих в различных областях квантовой электроники и нелинейной
птики.
Книга вышла в свет на английском языке в 1989 г. С того времени
прошел немалый срок для такой бурно развивающейся области, как
нелинейная волоконная оптика, но книга не устарела, поскольку в ней
изложены основы нелинейной волоконной оптики.
Перевод выполнили: канд. физ.-мат. наук С. В. Черников (пре-
(предисловие и гл. 1-4), Д.В. Коробкин (гл. 5-7) и И.Ю.Хрущев
(гл. 8-10).
П. Мамышев
Анне, Сипре и Каролине
ПРЕДИСЛОВИЕ
За последние 15 лет изучение нелинейных эффектов в оптических
волокнах привело к созданию новой области нелинейной оптики,
получившей название нелинейной волоконной оптики. Результаты
интенсивных исследований в этой области важны как для фундамен-
фундаментальной науки, так и для технических приложений. Использование
волоконных световодов для сжатия импульсов позволило получить
оптические импульсы длительностью ~ 6 фс. Были разработаны но-
новые типы лазеров: волоконные ВКР-лазеры и солитонные лазеры,
в которых используются нелинейные эффекты в волоконных свето-
световодах. Тем не менее, несмотря на то, что нелинейная волоконная
оптика уже достигла определенного уровня зрелости, в научной
литературе есть лишь несколько обзоров, а большинство материалов
осталось рассредоточенным в оригинальных статьях. Цель данной
книги-дать общий обзор различных нелинейных явлений в воло-
волоконных световодах. Это современная монография, и, возможно, она
стимулирует дальнейшие работы в области нелинейной волоконной
оптики, поскольку в ней сконцентрирован материал, рассеянный по
многим источникам.
Книга предназначена как для тех, кто уже занимается нелинейной
волоконной оптикой, так и для тех, кто желает ознакомиться с ней.
Книга, наверное, будет полезна ученым и инженерам, интересую-
интересующимся волоконно-оптической связью, поскольку применению раз-
различных нелинейных эффектов в работе оптических систем в ней
уделено особое внимание. Некоторые главы книги могут также быть
полезны для университетских курсов, в которых изучаются нелиней-
нелинейная оптика, волоконная оптика или оптическая связь. В ней для этого
есть вся необходимая информация, так что студенту, знакомому
с теорией электромагнетизма, текст будет понятен. Кроме того,
каждая глава содержит много ссылок на соответствующие ориги-
оригинальные статьи, которые нужны для углубленного изучения вопроса.
Прямо или косвенно свой вклад в написание этой книги внесли
многие,. и все имена здесь перечислить невозможно. Я особенно
благодарен Р. Альфано, П. Балдэку, М. Лаксу и М. Потасеку за
плодотворную совместную работу и многочисленные обсуждения.
Хочется также поблагодарить Р. Альфано, П. Балдэка, Г. Хасегаву,
Предисловие
Р. Смита и Р. Столена за полезные обсуждения рукописи этой книги.
Автор признателен руководству AT&T Bell Laboratories за поддержку
проекта этой книги. Я особенно благодарен Р. Смиту, Дж. Геусику,
П. Энтони и А. Бобеку за поддержку. Текст был написан в AT&T Bell
Laboratories; набран с использованием операционной системы
UNIX®. Автор отмечает работников Центра обработки текстов за
хорошо выполненную работу.
Г. Агравал
Глава 1
ВВЕДЕНИЕ
В данной главе будет дан самый общий обзор тех характеристик
волоконных световодов, которые важны для понимания нелинейных
эффектов, обсуждаемых в последующих главах. В разд. 1.1 кратко
дается ретроспектива развития волоконной оптики. В разд. 1.2 об-
обсуждаются оптические потери, хроматическая дисперсия и двулуче-
преломление волоконных световодов. Особое внимание уделено' хро-
хроматической дисперсии из-за ее важности в изучении нелинейных
эффектов, возникающих при распространении ультракоротких опти-
оптических импульсов. В разд. 1.3 кратко описаны различные нелинейные
эффекты, которые обусловлены нелинейным преломлением и вы-
вынужденным неупругим рассеянием света. Среди нелинейных эффек-
эффектов, широко изученных при использовании волоконных световодов
в качестве нелинейной среды,- фазовая самомодуляция, фазовая кросс-
модуляция, четырехволновое взаимодействие, вынужденное комби-
комбинационное рассеяние и вынужденное рассеяние Мандельштама-
Бриллюэна. Каждый из этих эффектов подробно рассматривается
в отдельных главах. В разд. 1.4 рассказывается о структуре обсуж-
обсуждения в книге большого разнообразия нелинейных эффектов в воло-
волоконных световодах.
1.1. РЕТРОСПЕКТИВА
Явление полного внутреннего отражения, управляющее распрост-
распространением света в оптических волокнах, было известно еще в XIX в.
[1]. Первые стеклянные волокна без оболочки [2-4] были изготов-
изготовлены в 20-х годах нашего столетия, тем не менее развитие волоконной
оптики начинается только в 50-е годы, когда использование оболо-
чечного слоя [5-7] привело к значительному улучшению характе-
характеристик световодов. Волоконная оптика тогда быстро развивалась
главным образом с целью использования оптических кабелей из
стеклянных волокон для передачи изображений. В книге Капани [8],
изданной в 1967 г., дан обзор успехов, достигнутых к тому времени
в области волоконной оптики. Первые волоконные световоды по
современным меркам имели очень большие потери (типичные потери
составляли ~ 1000 дБ/км). Однако ситуация резко изменилась в
10 Глава 1
1970 г., когда благодаря высказанным ранее идеям [9] потери квар-
кварцевых световодов были уменьшены до ~20 дБ/км [10]. Дальнейший
прогресс в технологии изготовления [11, 12] привел к появлению
в 1979 г. волоконного световода с потерями около 0,2 дБ/км вблизи
длины волны 1,55 мкм [13]. Этот уровень потерь ограничен в основ-
основном фундаментальным процессом рэлеевского рассеяния.
Возможности таких волоконных световодов с низкими потерями
привели не только к революции в области волоконно-оптической
связи [14-17], но и к возникновению новой области науки-нелиней-
науки-нелинейной волоконной оптики. Первые нелинейные явления (вынужденное
комбинационное рассеяние и рассеяние Мандельштама-Бриллюэна)
были экспериментально [18, 19] и теоретически [20] исследованы
в одномодовых волоконных световодах еще в 1972 г. Эти работы
стимулировали изучение других нелинейных явлений-оптически
индуцированного двулучепреломления [21], параметрического четы-
рехфотонного смешения [22, 23], фазовой самомодуляции [24, 25].
Важный результат был получен в 1973 г., когда было теоретически
показано, что в оптических волокнах могут существовать солитоно-
подобные импульсы, которые обусловлены совместным действием
эффектов дисперсии и нелинейности [26]. Оптические солитоны позже
наблюдались в эксперименте [27]. Их использование привело к
большим успехам в области генерации и управления параметрами
ультракоротких оптических импульсов [28-32]. В равной степени
важное развитие получило использование оптических волокон для
сжатия импульсов [33-36]. Были получены импульсы длительностью
6 фс при использовании волоконных нелинейно-оптических методов
сжатия [37]. Недавно большое внимание привлекла фазовая кросс-
модуляция, возникающая, когда два импульса совместно и одновре-
одновременно распространяются в волоконном световоде [38-42]. Нели-
Нелинейная волоконная оптика очень быстро развивалась последние 15
лет. Многие результаты, полученные в этой области, важны как для
фундаментальной науки, так и для технологии. Некоторые из них
обсуждались в недавних обзорных статьях [43-50]. Как ожидается,
нелинейная волоконная оптика будет интересна в связи с развитием
оптической обработки информации.
1.2. ХАРАКТЕРИСТИКИ ВОЛОКОННЫХ СВЕТОВОДОВ
В самом простом случае волоконный световод состоит из сердце-
сердцевины и оболочки. Показатель преломления оболочки немного
меньше показателя преломления сердцевины. Такие световоды
обычно называют световодами со ступенчатым профилем показателя
преломления, чтобы отличать их от градиентных волоконных све-
световодов, у которых показатель преломления сердцевины плавно
уменьшается от ее центра к границе. На рис. 1.1 схематически
Введение
11
Показатель
преломления
Внешнее покрытие
Оболочка
Сердцевина
Радиус
Рис. 1.1. Схема поперечного сечения и профиля показателя преломления
волоконного световода со ступенчатым профилем показателя преломления.
показаны поперечное сечение и профиль показателя преломления
волоконного световода со ступенчатым профилем показателя пре-
преломления. Такой волоконный световод характеризуется двумя пара-
параметрами - относительной разностью показателей преломления серд-
сердцевины и оболочки:
/_1 — I 1,^.1 I
и нормированной частотой (параметром V):
V=koa(n\-nlI12, A.2.2)
где к0 = 2п/Х, а-радиус сердцевины. Я.-длина волны света [51-53].
Параметр V определяет число мод, которые могут распростра-
распространяться в волоконном световоде. Моды волоконного световода об-
обсуждаются в разд. 2.2, где показано, что световоды со ступенчатым
профилем показателя преломления поддерживают только одну моду,
когда V < 2,405. Световоды, удовлетворяющие этому условию, на-
называются одномодовыми. Главное различие между одномодовыми
и многомодовыми световодами состоит в том, что они имеют разные
радиусы сердцевины. Для обычных многомодовых световодов радиус
сердцевины а = 25-30 мкм, тогда как для одномодовых световодов
с типичным значением Д ~ 30-10 ~3 требуется, чтобы а было равно
2-4 мкм. Величина внешнего радиуса Ъ менее критична. Просто онг
должна быть достаточно велика, чтобы удерживать в себе полностью
поле излучения моды волоконного световода. Обычно Ь = 50-60 мкм
как для одномодовых, так и для многомодовых волоконных свето-
световодов. Поскольку нелинейные эффекты главным образом изучаются
в одномодовых световодах, термин оптический волоконный свето-
12 Глава 1
вод далее в тексте будет относиться к одномодовым световодам, если
не оговорено другое. В следующих подразделах мы обсудим: 1) про-
процесс изготовления, 2) оптические потери, 3) хроматическую диспер-
дисперсию и 4) двулучепреломление одномодовых волоконных световодов.
1.2.1. МАТЕРИАЛЫ И ИЗГОТОВЛЕНИЕ
Волоконные световоды с низкими потерями изготавливают из
кварцевого стекла, состоящего из плавленого (аморфного) кварца
SiO2. Чтобы получить разные показатели преломления сердцевины
и оболочки, в процессе изготовления применяют различные примеси.
Такие добавки, как GeO2 и Р2О5, увеличивают показатель прелом-
преломления чистого кварца и пригодны для сердцевины. В оболочке
в качестве добавок преимущественно используют фториды, так как
они уменьшают показатель преломления кварца.
Изготовление кварцевых волокон происходит в два этапа. На
первом этапе методом осаждения из газообразной фазы [54-56]
изготавливается цилиндрическая заготовка с заданными профилем
показателя преломления и соотношением размеров сердцевины и
оболочки. Обычно заготовка имеет длину 1 м и диаметр 2 см. На
второй стадии заготовку вытягивают в волокно, используя преци-
прецизионный механизм подачи заготовки в печь с некоторой определен-
определенной скоростью [57, 58]. Во время вытяжки соотношение размеров
оболочки и сердцевины сохраняется. Оба этапа (заготовка и вытяжка
волокна) технологически очень сложны [54-58], так как размер
сердцевины и профиль показателя преломления необходимо под-
поддерживать строго постоянными.
Для изготовления заготовки можно применять несколько мето-
методов. Обычно используют три: модифицированный метод химического
осаждения из газовой фазы (MCVD) [54], метод внешнего осаждения
из газовой фазы (OVD) [55], метод аксиального осаждения из газовой
фазы (VAD) [56]. Наиболее широко применяется метод MCVD. На
рис. 1.2 представлена схема соответствующего процесса. На внут-
внутреннюю поверхность трубки из кварцевого стекла последовательно
осаждают слои SiO2 при пропускании сквозь трубку пара SiCl4 и О2
при температуре около 1800сС. Чтобы обеспечить однородность,
многофакельная горелка должна перемещаться взад-вперед вдоль
вращающейся трубки. Величиной показателя преломления слоев
оболочки при этом управляют, добавляя в трубку фториды. Когда
после многократных прохождений факела осажденная оболочка
достигает достаточной толщины, к смеси паров добавляют пары
GeCl4 либо РОС13, чтобы сформировать сердцевину. После осажде-
осаждения всех слоев температуру факела увеличивают так, чтобы трубка
схлопнулась в твердую цилиндрическую заготовку.
Введение
13
Регулятор
расхода
газов
Г
Опорная трубка из
кварцевого стекла
гу-ку =* С?г
гНМногофакепьная
горелка
02
Сосуды с
хлоридами
Перемещение
Рис. 1.2. Схематическая диаграмма модифицированного метода химического
осаждения из газовой фазы (MCVD), широко применяемого для изготовления
волоконных световодов [54].
Изложенное выше описание очень краткое и дает только общее
представление. При изготовлении волоконных световодов необхо-
необходимо принимать во внимание много технологических особенностей.
Интересующийся читатель может обратиться к обширной литературе
по этому вопросу [54-58].
1.2.2. ОПТИЧЕСКИЕ ПОТЕРИ
Важным параметром волоконного световода является мера по-
потери мощности при распространении оптических сигналов внутри
волокна. Если Ро-мощность, вводимая в волоконный световод
длиной L, прошедшая мощность Рт дается выражением
Рт = Роехр(-aL), A.2.3)
где а-постоянная затухания, обычно называемая потерями свето-
световода. Потери в световоде удобно выражать в единицах дБ/км.
используя соотношение
= 4.343а:
A.2.4)
здесь для связи адБ и а использовано уравнение A.2.3).
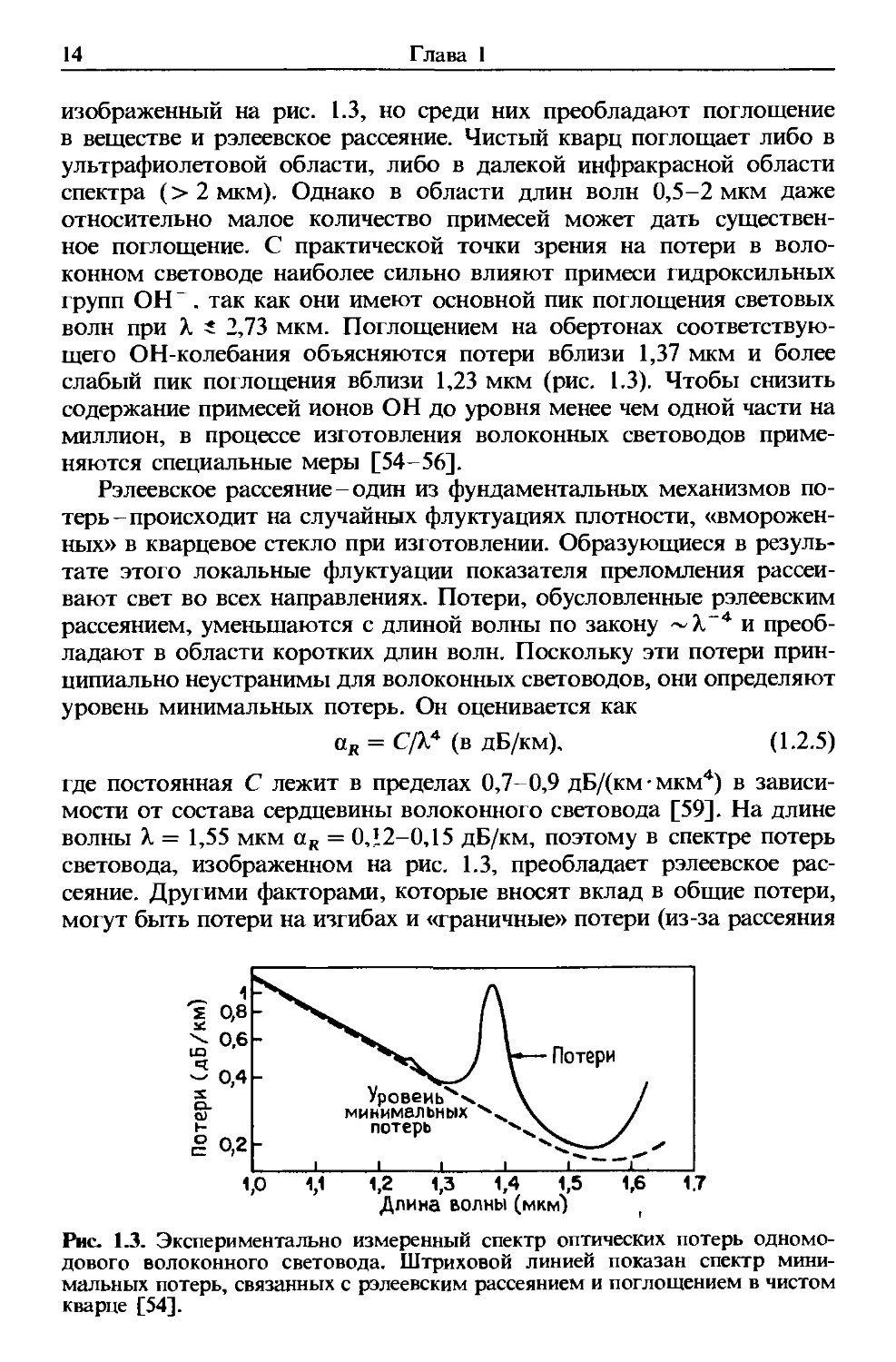
Потери в световоде зависят от длины волны света. На рис. 1.3
представлен спектр потерь в современном одномодовом волоконном
световоде, изготовленном по MCVD-методу [54]. Волокно имеет
минимальные потери 0,2 дБ/км вблизи длины волны 1,55 мкм. По-
Потери значительно возрастают с уменьшением длины волны, достигая
уровня 1-10дБ/км в видимой области спектра. Отметим, однако,
что даже при потерях 10 дБ/км постоянная затухания не выше
а«2-10~5см~1. По сравнению с большинством других материалов
это чрезвычайно низкая величина.
Несколько факторов вносят свой вклад в спектр потерь световода,
14
Глава 1
изображенный на рис. 1.3, но среди них преобладают поглощение
в веществе и рэлеевское рассеяние. Чистый кварц поглощает либо в
ультрафиолетовой области, либо в далекой инфракрасной области
спектра (> 2 мкм). Однако в области длин волн 0,5-2 мкм даже
относительно малое количество примесей может дать существен-
существенное поглощение. С практической точки зрения на потери в воло-
волоконном световоде наиболее сильно влияют примеси гидроксильных
групп ОН ~. так как они имеют основной пик поглощения световых
волн при X z 2,73 мкм. Поглощением на обертонах соответствую-
соответствующего ОН-колебания объясняются потери вблизи 1,37 мкм и более
слабый пик поглощения вблизи 1,23 мкм (рис. 1.3). Чтобы снизить
содержание примесей ионов ОН до уровня менее чем одной части на
миллион, в процессе изготовления волоконных световодов приме-
применяются специальные меры [54-56].
Рэлеевское рассеяние - один из фундаментальных механизмов по-
потерь-происходит на случайных флуктуациях плотности, «вморожен-
«вмороженных» в кварцевое стекло при изготовлении. Образующиеся в резуль-
результате этого локальные флуктуации показателя преломления рассеи-
рассеивают свет во всех направлениях. Потери, обусловленные рэлеевским
рассеянием, уменьшаются с длиной волны по закону ~\~л и преоб-
преобладают в области коротких длин волн. Поскольку эти потери прин-
принципиально неустранимы для волоконных световодов, они определяют
уровень минимальных потерь. Он оценивается как
aR = С/Хл (в дБ/км). A.2.5)
где постоянная С лежит в пределах 0,7-0,9 дБ/(км-мкм4) в зависи-
зависимости от состава сердцевины волоконного световода [59]. На длине
волны X = 1,55 мкм ак = 0,12-0,15 дБ/км, поэтому в спектре потерь
световода, изображенном на рис. 1.3, преобладает рэлеевское рас-
рассеяние. Другими факторами, которые вносят вклад в общие потери,
могут быть потери на изгибах и «граничные» потери (из-за рассеяния
1,0 1,1
1,2 1,3 1,4 1,5
Длина волны (мкм)
1,6 1.7
Рис. 1.3. Экспериментально измеренный спектр оптических потерь одномо-
дового волоконного световода. Штриховой линией показан спектр мини-
минимальных потерь, связанных с рэлеевским рассеянием и поглощением в чистом
кварце [54].
Введение 15
на гранте между сердцевиной и оболочкой) [51] Общие потери для
волокна в оптических линиях связи включают также потери на
соединениях двух концов световода друг с другом. Успехи в совре-
современной технологии позволили уменьшить эти потери до уровня
~0,01 дБ/км.
1.2.3. ХРОМАТИЧЕСКАЯ ДИСПЕРСИЯ
При взаимодействии электромагнитной волны со связанными
электронами диэлектрика отклик среды зависит от оптической ча-
частоты со. Это свойство, называемое хроматической дисперсией, про-
проявляется как частотная зависимость показателя преломления и (со).
Возникновение хроматической дисперсии связано с характерными
частотами, на которых среда поглощает электромагнитное излучение
вследствие осцилляции связанных электронов. Вдали от резонансных
частот среды поведение показателя среды хорошо описывается урав-
уравнением Селлмейера [51]
где cOj-резонансная частота и Bj—величина /-го резонанса. Суммиро-
Суммирование в уравнении A.2.6) производится по всем резонансным часто-
частотам вещества, которые вносят вклад в интересующей нас области
спектра. В случае оптических волокон параметры В} и ю,- опреде-
определяются путем подгонки измеренных дисперсионных критериев [60]
к уравнению A.2.6) при т = 3; они зависят от состава сердцеви-
сердцевины [53]. Для объемного кварцевого стекла эти параметры такие:
Ву = 0,696163, В2 = 0,4079426, Въ = 0,8974794, Ху = 0,0684043 мкм,
Х2 = 0.1162414 мкм. Хъ = 9.896161 мкм, где Xj = 2nc/a>j и с-скорость
света в вакууме [61].
Дисперсия в волоконном световоде имеет определяющее значение
при распространении коротких оптических импульсов, так как раз-
различные спектральные компоненты спектра импульса распростра-
распространяются с разными скоростями с/п (со). Даже в тех случаях, когда
нелинейные эффекты не важны, дисперсионное уширение импульса
может быть вредным для оптических линий связи. В нелинейном
режиме сочетание дисперсии и нелинейности может привести к ка-
качественно другой картине, которая обсуждается в следующих главах.
При математическом описании эффекты дисперсии в световоде учи-
учитываются разложением постоянной распространения моды р в ряд
Тейлора вблизи несущей частоты соо:
р(со) = и(со)^ = р0 + р, (со - соо) + -Р2(со - сооJ + ... , A.2.7)
с 2
16
Глава 1
где
Ida]
(т = 0,1,2,3...)-
A.2.8)
ш=ш0
Как показано в разд. 2.3, огибающая импульса движется с групповой
скоростью (f9 = 1/pj), а параметр р2 определяет уширение импульса.
С показателем преломления п и его производными параметры pt и р2
связаны соотношениями
= - 2
drc d2n\ a>d2n
со— )=-« = -
ясо / с vg
co-
t/co t/co
d2n
с da2 2nc2dX2'
A.2.9)
A.2.10)
где пд-групповой показатель преломления.
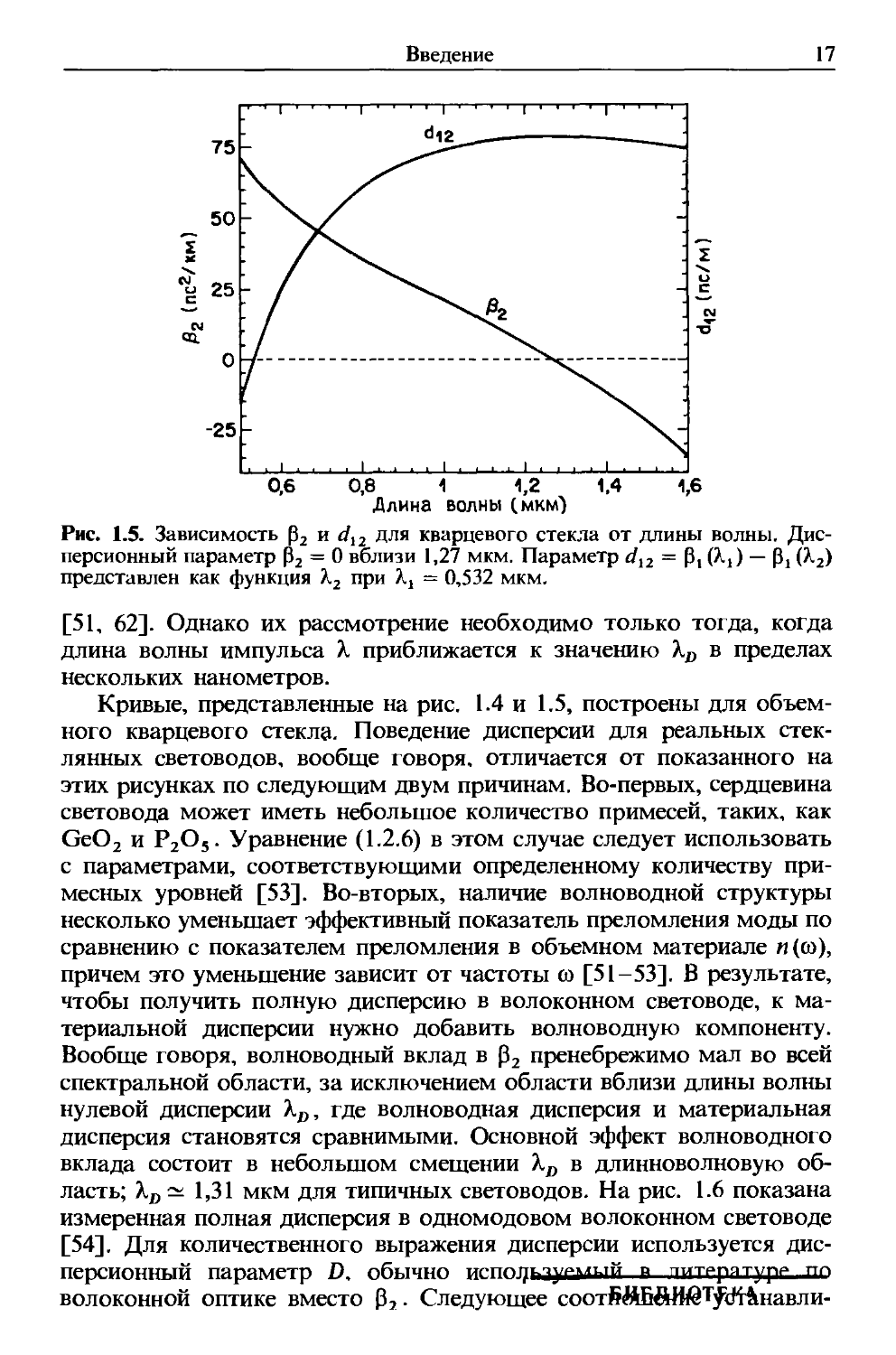
На рис. 1.4 и 1.5 показаны зависимости п, пд, р2 от длины волны
X для кварцевого стекла, полученные с использованием уравнений
A.2.6), A.2.9), A.2.10). Замечательно то. что р2 стремится к нулю на
длине волны приблизительно 1,27 мкм и становится отрицательным
для больших длин волн. Длина волны, на которой р2 = 0, часто
называется длиной волны нулевой дисперсии XD. Тем не менее
следует отметить, что при X = XD дисперсия не равна нулю. Описа-
Описание распространения импульсов вблизи X = XD требует включения в
разложение A.2.7) кубического слагаемого. Такие дисперсионные
эффекты более высокого порядка могут искажать сверхкороткие
оптические импульсы как в линейном, так и в нелинейном режимах
1,49
О.8 1 1,2
Ллина волны (мкм)
1,4
1,6
Рис. 1.4. Зависимость показателя преломления п и группового показателя
преломления п кварцевого стекла от длины волны.
Введение
17
00.
-25-
0,8 1 1,2
Длина волны (мкм)
Рис. 1.5. Зависимость р2 и di2 для кварцевого стекла от длины волны. Дис-
Дисперсионный параметр Р2 = 0 вблизи 1,27 мкм. Параметр dl2 = P, (Xj) — Pj (k2)
представлен как функция Х2 при Xj = 0,532 мкм.
[51, 62]. Однако их рассмотрение необходимо только тогда, когда
длина волны импульса X приближается к значению XD в пределах
нескольких нанометров.
Кривые, представленные на рис. 1.4 и 1.5, построены для объем-
объемного кварцевого стекла. Поведение дисперсии для реальных стек-
стеклянных световодов, вообще говоря, отличается от показанного на
этих рисунках по следующим двум причинам. Во-первых, сердцевина
световода может иметь небольшое количество примесей, таких, как
GeO2 и Р2О5. Уравнение A.2.6) в этом случае следует использовать
с параметрами, соответствующими определенному количеству при-
примесных уровней [53]. Во-вторых, наличие волноводной структуры
несколько уменьшает эффективный показатель преломления моды по
сравнению с показателем преломления в объемном материале и (со),
причем это уменьшение зависит от частоты со [51-53]. В результате,
чтобы получить полную дисперсию в волоконном световоде, к ма-
материальной дисперсии нужно добавить волноводную компоненту.
Вообще говоря, волноводный вклад в р2 пренебрежимо мал во всей
спектральной области, за исключением области вблизи длины волны
нулевой дисперсии Хв, где волноводная дисперсия и материальная
дисперсия становятся сравнимыми. Основной эффект волноводного
вклада состоит в небольшом смещении XD в длинноволновую об-
область; XD ^ 1,31 мкм для типичных световодов. На рис. 1.6 показана
измеренная полная дисперсия в одномодовом волоконном световоде
[54]. Для количественного выражения дисперсии используется дис-
дисперсионный параметр D. обычно
волоконной оптике вместо 3,. Следующее
18
Глава 1
1,3 1,4 1,5 1,6
Длина волны (мкм)
Рис. 1.6. Измеренная зависимость дисперсионного параметра D одномодо-
вого световода от длины волны. Длина волны нулевой дисперсии "kD смещена
к длине волны 1,312 мкм вследствие вклада волноводной дисперсии в полную
дисперсию световода [54].
вает связь между р2 и
d%
A.2.11)
Интересный чертой волноводной дисперсии является то, что ее
вклад в D (или р2) зависит от параметров волокна: радиуса сердце-
сердцевины а и разности показателей преломления сердцевины и оболочки
Ли. Этот факт может использоваться для смещения длины волны
нулевой дисперсии ~кв к 1,55 мкм, где световоды имеют минимальные
потери. Такие световоды со смещенной дисперсией [63] могут в
перспективе применяться в оптических системах связи. Можно созда-
создавать волоконные световоды с весьма пологой дисперсионной кривой,
имеющие малую дисперсию в широком спектральном диапазоне
1,3-1,6 мкм. Это достигается путем использования многих слоев
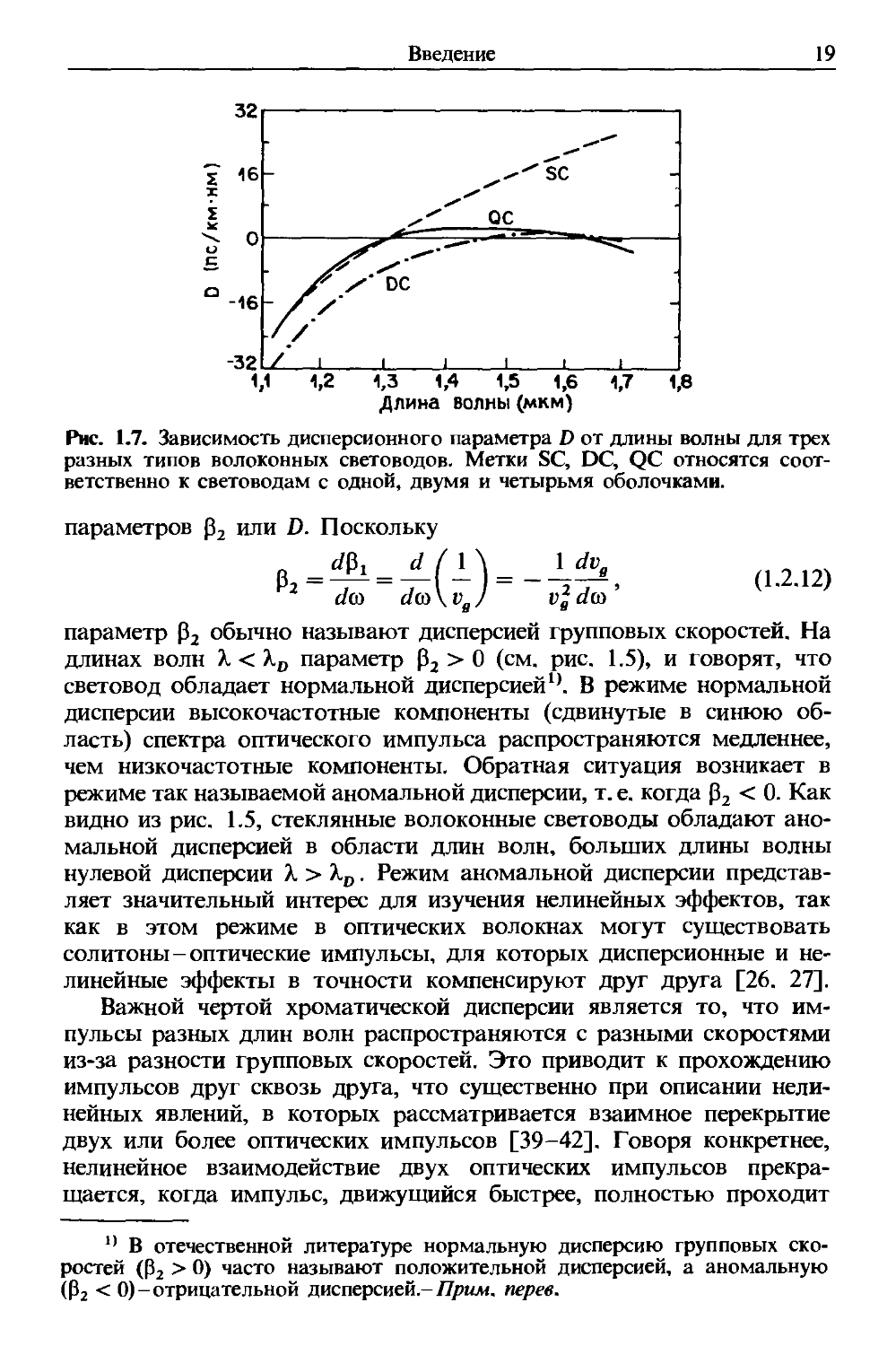
оболочки. На рис. 1.7 показаны измеренные дисперсионные кривые
[64] для двух таких световодов с несколькими оболочками, имеющих
двух- или трехслойные оболочки вокруг сердцевины. Для сравнения
дисперсионная кривая для световода с однослойной оболочкой также
показана (штриховой линией). Световод с четырехслойной оболочкой
характеризуется низкой дисперсией (| D \ < 1 пс/км • нм) в широкой
спектральной области от 1,25 до 1,65 мкм. Световоды с модифици-
модифицированными дисперсионными характеристиками полезны для изучения
нелинейных эффектов, когда в эксперименте требуются специаль-
специальные дисперсионные свойства.
Нелинейные эффекты в оптических волокнах могут быть качест-
качественно совершенно разными в зависимости от знака дисперсионных
Введение
19
ОС
16
0
-16
-з?
/ |
^_
s' DC
i i
QC
.—•
i
^&C
" ^
-
1 I
1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8
Длина волны (мкм)
Рис. 1.7. Зависимость дисперсионного параметра D от длины волны для трех
разных типов волоконных световодов. Метки SC, DC, QC относятся соот-
соответственно к световодам с одной, двумя и четырьмя оболочками.
параметров р2 или D. Поскольку
(
da daKv
2 da daKvJ vj; da
vj; da'
A.2.12)
параметр p2 обычно называют дисперсией групповых скоростей. На
длинах волн Х<ХВ параметр р2 > 0 (см. рис. 1.5), и говорят, что
световод обладает нормальной дисперсией1'. В режиме нормальной
дисперсии высокочастотные компоненты (сдвинутые в синюю об-
область) спектра оптического импульса распространяются медленнее,
чем низкочастотные компоненты. Обратная ситуация возникает в
режиме так называемой аномальной дисперсии, т. е. когда р2 < 0. Как
видно из рис. 1.5, стеклянные волоконные световоды обладают ано-
аномальной дисперсией в области длин волн, больших длины волны
нулевой дисперсии Х>ХВ. Режим аномальной дисперсии представ-
представляет значительный интерес для изучения нелинейных эффектов, так
как в этом режиме в оптических волокнах могут существовать
солитоны - оптические импульсы, для которых дисперсионные и не-
нелинейные эффекты в точности компенсируют друг друга [26. 27].
Важной чертой хроматической дисперсии является то, что им-
импульсы разных длин волн распространяются с разными скоростями
из-за разности групповых скоростей. Это приводит к прохождению
импульсов друг сквозь друга, что существенно при описании нели-
нелинейных явлений, в которых рассматривается взаимное перекрытие
двух или более оптических импульсов [39-42]. Говоря конкретнее,
нелинейное взаимодействие двух оптических импульсов прекра-
прекращается, когда импульс, движущийся быстрее, полностью проходит
" В отечественной литературе нормальную дисперсию групповых ско-
скоростей (Р2 > 0) часто называют положительной дисперсией, а аномальную
(Р2 < 0)-отрицательной дисперсией.- Прим. перев.
20 Глава 1
сквозь импульс, движущийся более медленно. Расстояние между
двумя импульсами определяется параметром расстройки групповых
скоростей dl2:
d12 = Pi(*i) - Pi (К) = ^ЧК) ~ v'HK), A-2-13)
где Х1 и Х2-длины волн, соответствующие несущим частотам двух
импульсов; pt на этих длинах волн оценивается с помощью уравнения
A.2.9). Для импульсов длительностью То можно определить длину
дисперсионного разбегания двух импульсов Lw следующим отно-
отношением:
Lw=TJ\dl2\. A.2.14)
На рис. 1.5 показана зависимость d12 от ~к2 для плавленого кварца
(использовано уравнение A.2.13) при Xj = 0,532 мкм). В режиме
нормальной дисперсии импульс с большей длиной волны движется
быстрее, тогда как обратный случай имеет место в режиме ано-
аномальной дисперсии. Например, если импульс на длине волны
Х2 = 1,06 мкм распространяется совместно с импульсом на длине
волны Х1 = 0,532 мкм, то они будут разбегаться со скоростью около
80 пс/м. Это соответствует длине разбегания Lw около 25 см при
То = 20 пс. Разность групповых скоростей играет важную роль в слу-
случае нелинейных эффектов, в которых имеет место фазовая кросс-мо-
кросс-модуляция [39-42].
1.2.4. МОДОВОЕ ДВУЛУЧЕПРЕЛОМЛЕНИЕ
Даже одномодовый волоконный световод, строго говоря, не
является одномодовым, так как может поддерживать две вырожден-
вырожденные моды, которые преимущественно поляризованы в двух ортого-
ортогональных направлениях. При идеальных условиях совершенной ци-
цилиндрической геометрии и изотропии вещества та мода, которая
возбуждена с поляризацией в х-направлении, не будет возбуждать
ортогональную у-поляризованную моду. Однако в реальных усло-
условиях малые отклонения от цилиндрической геометрии или малые
флуктуации в анизотропии вещества приводят к смешиванию двух
поляризационных состояний, снимая вырождение мод. Постоянные
распространения р становятся несколько различными для мод, по-
поляризованных в лг- и ^-направлениях. Это свойство называется дву-
лучепреломлением мод. Степень модового двулучепреломления В
определяется как [65, 66]
в = 1Р»-РУ1 = |Их_Иу|> A.2.15)
где пх и пу-эффективные показатели преломления мод в двух орто-
ортогональных поляризационных состояниях. Можно показать [66], что
при распространении в волоконном световоде происходит периоди-
Введение 21
ческий обмен мощностью между этими двумя модами; при данном
значении В соответствующий период LB равен
LB называется длиной биений. Ось, вдоль которой эффективный
показатель преломления моды меньше, называют быстрой осью,
потому что для света, поляризованного в этом направлении, группо-
групповая скорость больше. По той же причине ось с большим модовым
показателем преломления называют медленной осью.
В обычных одномодовых волоконных световодах величина В не
постоянна вдоль световода, а изменяется случайным образом из-за
флуктуации в форме сердцевины и анизотропии, вызываемой стати-
статическими напряжениями. Поэтому линейно-поляризованный свет, вво-
вводимый в волоконный световод, быстро теряет первоначальное со-
состояние поляризации. Для некоторых применений желательно, чтобы
свет проходил через волоконный световод, не изменяя своего со-
состояния поляризации. Такие световоды называют световодами, со-
сохраняющими состояние поляризации [65-69]. В них преднамеренно
создается сильное двулучепреломление, так что малые случайные
флуктуации двулучепреломления существенно не влияют на поляри-
поляризацию света. Один из способов создания двулучепреломления состоит
в нарушении цилиндрической симметрии и создании световодов с
эллиптической формой либо сердцевины, либо оболочки. Дости-
Достигаемая таким способом величина двулучепреломления довольно мала
(В ~ 10). В другом методе двулучепреломление вызывается ста-
статическими упругими напряжениями, что позволяет достичь В ~ 10~4.
Часто при изготовлении световода в заготовку с двух противопо-
противоположных сторон от сердцевины вводятся два стержня из боросили-
катного стекла. Модовое двулучепреломление В, вносимое этими
элементами, вызывающими статические напряжения, зависит от их
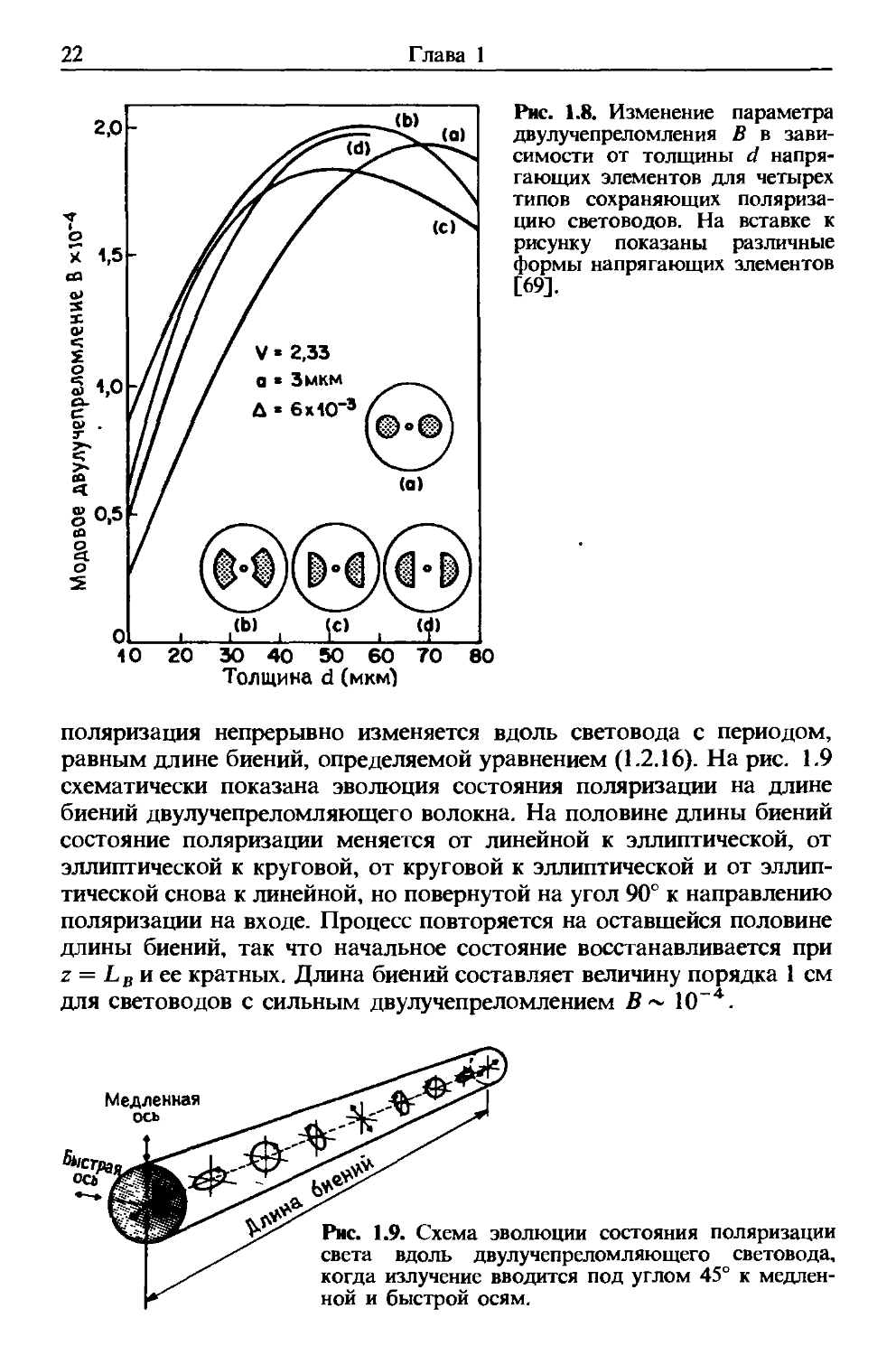
положения и толщины. На рис. 1.8 показана зависимость В от
толщины d для четырех форм элементов, вызывающих напряжения,
расположенных на расстоянии, равном пяти радиусам сердцевины
[69]. Величина В = 2-10 ~4 может быть достигнута при с1ъ диапазоне
50-60 мкм. Волоконные световоды такого типа часто имеют назва-
название «панда» или «галстук-бабочка», указывающее на форму попе-
поперечного сечения волокна. Существуют и другие подходы [68], в ко-
которых двулучепреломление создается деформированием заготовки.
Использование волоконных световодов, сохраняющих состояния
поляризации, требует идентификации медленной и быстрой осей,
прежде чем линейно-поляризованный свет будет введен в световод.
Если на входе направление поляризации излучения совпадает с
быстрой или медленной осями, поляризация при распространении не
изменяется. Если же поляризация направлена под углом к этим осям,
22
Глава 1
(а)
Рис. 1.8. Изменение параметра
двулучепреломления В в зави-
зависимости от толщины d напря-
напрягающих элементов для четырех
типов сохраняющих поляриза-
поляризацию световодов. На вставке к
рисунку показаны различные
формы напрягающих элементов
[69].
20 30 40 50 60 70 80
Толщина d (mkm)
поляризация непрерывно изменяется вдоль световода с периодом,
равным длине биений, определяемой уравнением A.2.16). На рис. 1.9
схематически показана эволюция состояния поляризации на длине
биений двулучепреломляющего волокна. На половине длины биений
состояние поляризации меняется от линейной к эллиптической, от
эллиптической к круговой, от круговой к эллиптической и от эллип-
эллиптической снова к линейной, но повернутой на угол 90е к направлению
поляризации на входе. Процесс повторяется на оставшейся половине
длины биений, так что начальное состояние восстанавливается при
z = LB и ее кратных. Длина биений составляет величину порядка 1 см
для световодов с сильным двулучепреломлением /?~ 10~4.
Медленная
ось
Рис. 1.9. Схема эволюции состояния поляризации
света вдоль двулучепреломляющего световода,
когда излучение вводится под углом 45° к медлен-
медленной и быстрой осям.
Введение 23
1.3. НЕЛИНЕЙНЫЕ ЭФФЕКТЫ В ВОЛОКОННЫХ
СВЕТОВОДАХ
Отклик любого диэлектрика на световое воздействие становится
нелинейным в сильном электромагнитном поле, и оптические воло-
волоконные световоды не составляют исключения. С теоретической точки
зрения возникновение нелинейного отклика связано с ангармониче-
ангармоническим движением связанных электронов при воздействии приложен-
приложенного поля Е. В результате индуцированная поляризация Р электри-
электрических диполей уже не является линейной, а удовлетворяет более
общему соотношению [70]
+ ...), (, 3.1)
где е0-диэлектрическая проницаемость вакуума, i' {J = 1, 2, ...)-
восприимчивость /-го порядка, xJ- тензор ранга у + 1, вводимый для
учета поляризационных эффектов. Главный вклад в Р вносит линей-
линейная восприимчивость хA)- Она определяет показатель преломления
и и постоянную затухания а, обсуждавшиеся в разд. 1.2. С воспри-
восприимчивостью второго порядка х<2) связаны такие эффекты, как гене-
генерация второй гармоники и генерация суммарной частоты [71].
Однако эта восприимчиость ненулевая только для сред, в которых на
молекулярном уровне отсутствует симметрия инверсии. Так как в
кварцевых стеклах молекула SiO2 обладает центром симметрии,
Х<2) = 0. Поэтому в оптических световодах не могут иметь место
эффекты второго порядка. Тем не менее слабые нелинейные эффекты
второго порядка могут возникать из-за электрических квадрупольных
и магнитных дипольных моментов. Примеси внутри сердцевины
волокна могут также при определенных условиях приводить к гене-
генерации второй гармоники (см. гл. 10).
1.3.1. НЕЛИНЕЙНОЕ ПРЕЛОМЛЕНИЕ
Нелинейные эффекты низшего порядка в оптических световодах
возникают из-за восприимчивости третьего порядка, которая от-
ответственна за такие явления, как генерация третьей гармоники,
четырехфотонное смешение,' нелинейное преломление [71]. Однако,
если не созданы специальные условия фазового синхронизма, нели-
нелинейные процессы, связанные с генерацией новых частот (например,
генерация третьей гармоники или четырехволновое смещение), в
светоодах не эффективны. Большинство нелинейных эффектов в во-
волоконных световодах возникают из-за нелинейного преломления
(зависимости показателя преломления от интенсивности) как ре-
результат ВКЛЕ
вится равен
зультат вклада %{3), т.е. показатель преломления световода стано-
A.3.2)
24 Глава 1
где и (со)-линейная часть, определяемая уравнением A.2.6), |?| ^ин-
^интенсивность поля внутри волокна и и2 - нелинейный показатель пре-
преломления, связанный с х<3) следующим отношением (см. разд. 2.3):
При получении уравнения A.3.3) предполагалось, что электрическое
поле линейно поляризовано, так что только одна компонента хйхх
тензора четвертого ранга вносит вклад в показатель преломления. То,
что х<3)~ тензор, может влиять на поляризационные свойства опти-
оптического пучка через нелинейное двулучепреломление [21, 45]. Такие
нелинейные эффекты рассматриваются в гл. 7.
Зависимость показателя преломления от интенсивности приводит
к множеству интересных нелинейных эффектов. Два наиболее широко
изученных эффекта-это фазовая самомодуляция (ФСМ) и фазовая
кросс-модуляция (ФКМ). ФСМ обусловлена самонаведенным набе-
набегом фазы, который оптическое поле приобретает при распростране-
распространении в волоконном световоде. Его величину можно получить, заметив,
что фаза оптического поля изменяется как
4> = nk0L=(n + n2\E\2)k0L, A.3.4)
*
где к0 = 2п/Х и L—длина световода. Зависящий от интенсивности
набег фазы фЛЬ = n2k0L\E\2 возникает вследствие ФСМ. Помимо
всего прочего, ФСМ приводит к спектральному уширению коротких
импульсов [25] и к существованию оптических солитонов в области
аномальной дисперсии групповых скоростей световода [26, 27]. Эти
вопросы обсуждаются в гл. 4 и 5.
ФКМ обусловлена нелинейным набегом фазы оптического поля,
который наведен другим полем на другой длине волны, распро-
распространяющимся совместно [38-42]. Его появление можно понять,
представив полное электрическое поле Е в уравнении A.3.1) как
Е = - \ Е1 ехр(— ico, 0 + ?2ехр(— /со21) + компл. сопр. , A.3.5)
когда два оптических поля на разных частотах со, и со2, поляризован-
поляризованных вдоль оси х, вместе и одновременно распространяются в волокне.
Нелинейный набег фазы поля на частоте cot тогда будет (см. разд. 7.1)
равен
2), A.3.6)
где мы пренебрегли всеми членами, возбуждающими поляризацию не
на частотах со, и со2, потому что для них отсутствует фазовый
синхронизм. Два члена в правой части уравнения A.3.6)-это ФСМ
и ФКМ соответственно.
Введение 25
Важной характерной чертой ФКМ является то, что для двух полей
одинаковой интенсивности вклад ФКМ в нелинейный набег фазы
в 2 раза больше чем вклад ФСМ. Помимо всего прочего ФКМ
вызывает асимметричное спектральное уширение совместно распро-
распространяющихся импульсов. В гл. 7 обсуждаются связанные с ФКМ
нелинейные эффекты.
1.3.2. ВЫНУЖДЕННОЕ НЕУПРУГОЕ РАССЕЯНИЕ
Вышеупомянутые нелинейные эффекты, связанные с восприимчи-
восприимчивостью третьего порядка %3, можно назвать упругим рассеянием
света в том смысле, что не происходит обмена энергией между
электромагнитным полем и диэлектрической средой. Второй класс
нелинейных эффектов вызван вынужденным неупругим рассеянием,
при котором оптическое поле передает часть своей энергии не-
нелинейной среде. В эту категорию попадают два важных нелинейных
эффекта; оба они связаны с возникновением колебательных мод
кварца. Это эффекты вынужденного комбинационного рассеяния
(ВКР) и рассеяния Мандельштама -Бриллюэна (ВРМБ); они были
среди первых нелинейных эффектов, обнаруженных в оптических
волокнах [18 -20]. Основное различие между этими эффектами со-
состоит в том, что в ВКР принимают участие оптические фононы, тогда
как в ВРМБ-акустические. В простой квантовомеханической модели,
применимой и к ВКР, и к ВРМБ, фотон падающего поля (часто
называемый накачкой) распадается на фотон меньшей (стоксовой)
частоты и фонон, имеющий такие энергию и количество движения,
которые соответствуют законам сохранения энергии и количества
движения. Конечно, фотон с большей энергией (на так называемой
антистоксовой частоте) может возникнуть, если может быть погло-
поглощен фонон с надлежащими энергией и количеством движения. Вместе
с тем, хотя ВКР и ВРМБ по своей природе очень похожи, различие
дисперсионных свойств акустических и оптических фононов приводит
к некоторым принципиальным различиям между ними. Основное
различие заключается в том, что ВРМБ в волоконных световодах
происходят только в обратном направлении, а ВКР преимуществен-
преимущественно по направлению распространения.
Полное описание ВКР и ВРМБ в волоконных световодах довольно
сложное, но для начального роста стоксовой волны существует
простое соотношение. Для ВКР оно дается уравнением
-f = 9Rlp1*' (L3-7)
az
где /s- интенсивность стоксовой волны, 1р - интенсивность накачки
и gR-коэффициент ВКР-усиления. Такое же уравнение имеет место
и для ВРМБ, если заменить gR на коэффициент ВРМБ-усиления дв.
26 Глава 1
Величины gR и дв в кварцевых световодах измерены эксперименталь-
экспериментально. Спектр ВКР-усиления очень широкий, ~ 30 ТГц [18]. Максимум
усиления при длине волны накачки 1 мкм gR =* 1 ¦ 10"ll см/Вт и
находится на стоксовом частотном сдвиге около 13 ТГц. Наоборот,
спектр ВРМБ-усиления очень узкий ~ 10 МГц. Максимум ВРМБ-
усиления находится на стоксовом сдвиге ~ 10 ГГц и составляет
величину около 6-10 ~9 см/Вт для узкой линии накачки [19]. Эта
величина уменьшается в Avp/AvB раз в случае, когда накачка имеет
широкий спектр; здесь Avp ширина линии накачки и AvB-ширина
линии ВРМБ-усиления.
Важная особенность ВКР и ВРМБ в гом, что эти эффекты
пороговые, т.е. существенное преобразование энергии накачки в
энергию стоксовой волны происходит, только когда интенсивность
накачки превышает некоторый пороговый уровень. Для ВКР в одно-
модовом световоде с oL » 1 пороговая интенсивность накачки равна
[20]
lf^l6(a/gR). A.3.8)
Обычно lXp ~ 10 МВт/см2 и ВКР может наблюдаться при мощности
накачки ~ 1 Вт. Подобные вычисления для ВРМБ показывают, что
пороговая интенсивность накачки равна
1* = 2Ца/дв). A.3.9)
Коэффициент ВРМБ-усиления дв более чем на 2 порядка величины
больше gR, поэтому обычная величина порога ВРМБ < 10 мВт.
Нелинейные явления ВКР и ВРМБ и их применение к оптической
волоконной связи рассматриваются в книге в гл. 8 и 9 соответственно.
1.3.3. ВАЖНОСТЬ НЕЛИНЕЙНЫХ ЭФФЕКТОВ
Измерения нелинейного показателя преломления в кварцевых
световодах [25] дают величину около 1,1-10~13ед. СГСЭ или
2,3-10~22 м2/В2 ед. МКС. В более привычных единицах п2 =
= 3,2-106 см2/Вт. Эта величина в кварце по сравнению с другими
нелинейными средами по крайней мере на 2 порядка величины
меньше. Точно так же и измерения коэффициентов ВКР- и ВРМБ-
усилений показывают, что их значения по порядку величины на 2 или
более порядка меньше, чем в других обычных нелинейных средах
[43]. Несмотря на малые величины нелинейных коэффициентов в
кварцевом стекле, нелинейные эффекты могут наблюдаться при
относительно низких мощностях. Это возможно благодаря двум
важным характеристикам одномодового волоконного световода-
малому размеру моды (~ 2-4 мкм) и чрезвычайно низким потерям
(< 1 дБ/км). Характерный параметр эффективности нелинейного
Введение 27
процесса в объемных средах-это произведение И^фф, где /-оптичес-
/-оптическая интенсивность и Ьэфф-эффективная длина взаимодействия [72].
Если излучение фокусируется в пятно радиуса w0, то / = P/nwo, где
Р—оптическая мощность. Ясно, что / можно увеличить, сильнее
фокусируя излучение, уменьшив тем самым и>0. Однако это ведет
к уменьшению Ьэфф, так как длина области фокусировки уменьшается
при увеличении фокусировки. Для гауссовского пучка Ьэфф ~ nwlfk
и произведение
не зависит от размера пятна и>0. В одномодовых световодах размер
пятна w0 определяется радиусом сердцевины а. Кроме того, диэлект-
диэлектрическим волноводам свойственно то, что постоянный размер пятна
сохраняется вдоль всей длины световода L. В этом случае длина
взаимодействия Ьэфф ограничивается потерями световода а. Исполь-
Используя уравнение l(z) = /оехр(— az), где 10 = Р/пн>о и Р—введенная
в волокно мощность, для произведения /Ьэфф получаем
Сравнение уравнений A.3.10) и A.3.11) показывает, что эффектив-
эффективность нелинейного процесса в волоконных световодах (ВС) может
быть увеличена во много раз [72]:
(IT \ 1
A.3.12)
где предполагается, что aL» 1. В видимой области спектра, обычно
при X = 0,53 мкм и и'о = 2,5¦ 10~5 см"' A0 дБ/км), этот коэффициент
составляет ~ 107. Увеличение эффективности может быть и в ~ 109
раз на длине волны вблизи 1,55 мкм, где световод имеет минималь-
минимальные потери a = 5-10~7 см @,2 дБ/км). Именно это огромное
увеличение эффективности нелинейных процессов делает оптические
волноводы пригодной нелинейной средой для наблюдения большого
разнообразия нелинейных эффектов при относительно низких мощ-
мощностях.
1.4. СТРУКТУРА КНИГИ
Цель этой книги-дать всесторонний обзор нелинейных явлений
в оптических волокнах. Расположение материала не соответствует
хронологическому порядку, в котором разные нелинейные эффекты
были впервые изучены в волоконных световодах. Главы расположены
так, чтобы по возможности сделать минимальными повторения.
28 Глава 1
В частности, в гл. 1-3 даются обзорный материал и математический
аппарат, необходимый для понимания разных нелинейных эффектов.
В гл. 4 7 обсуждаются нелинейные эффекты, приводящие к спект-
спектральному и временным изменениям оптической волны, не изменяя ее
энергии. В гл. 8-10 рассматриваются нелинейные эффекты генерации
новых оптических волн по средствам передачи им энергии волн
накачки. Ниже следует краткий обзор каждой главы, дающий пред-
представление о содержании книги.
В гл. 2 развит математический аппарат, необходимый для теоре-
теоретического понимания нелинейных явлений в волоконных световодах.
Начинается теоретическое описание уравнениями Максвелла: далее
при обсуждении мод световода и получении основного уравнения для
распространения амплитуды огибающей импульса используется
волновое уравнение в нелинейной среде с дисперсией. При выводе
уравнения отмечаются производимые приближения. Затем обсуж-
обсуждаются численные методы, используемые при решении основного
уравнения распространения; особенно выделяется фурье-метод с раз-
разделением по физическим факторам.
Глава 3 посвящена дисперсионным эффектам, которые возникают,
когда вводимая мощность и длина световода таковы, что нелиней-
нелинейными эффектами можно пренебречь. Главным образом действие
дисперсии групповых скоростей (ДГС) состоит в уширении оптичес-
оптического импульса при его распространении в волокне. Такое вызванное
дисперсией уширение рассматривается для нескольких форм им-
импульса; уделяется особое внимание действию частотной модуляции,
наведенной на входном импульсе. Обсуждаются также дисперсион-
дисперсионные эффекты высших порядков, важные вблизи длины волны нулевой
дисперсии световода.
В гл. 4 рассматривается нелинейное явление фазовой самомодуля-
самомодуляции ФСМ, являющееся результатом зависимости показателя прелом-
преломления от интенсивности. Главным образом действие ФСМ состоит
в уширении спектров оптических импульсов, распространяющихся
в световоде. Если ФСМ и ДГС действуют совместно в оптическом
волокне, то их действие сказывается также и на форме импульса.
Особенности спектрального уширения наводимого ФСМ без эффекта
ДГС и с ним обсуждаются в отдельных разделах. Также рассматри-
рассматриваются нелинейные и дисперсионные эффекты высших порядков,
важность которых нарастает, когда импульсы становятся короче 1 пс.
Глава 5 посвящена оптическим солитонам, привлекающим особое
внимание благодаря их фундаментальным свойствам, а также, в
перспективе, применениям в волоконно-оптической связи. В начале
главы рассматривается эффект модуляционной неустойчивости, что-
чтобы подчеркнуть важность взаимного влияния дисперсионных и не-
нелинейных эффектов, которое может иметь место в области аномаль-
аномальной ДГС оптических волокон. Затем вводится понятие фундаменталь-
Введение 29
ного солитона и солитонов высших порядков; для решения основного
уравнения распространения, известного как нелинейное уравнение
Шредингера, используется метод обратной задачи рассеяния. При-
Применениям солитонов в солитонных лазерах и в оптических солитон-
ных системах связи посвящаются два раздела. В заключение рас-
рассматриваются нелинейные и дисперсионные эффекты высшего поряд-
порядка, приводящие к распаду солитонов.
В гл. 6 рассматривается сжатие импульсов, важное с техно-
технологической точки зрения, так как это нелинейное явление было
использовано для получения импульсов длительностью 6 фс. Ис-
Используются два типа оптических компрессоров в зависимости от
того, длина волны X больше или меньше длины волны нулевой
дисперсии волокна. В видимой и ближней инфракрасной областях
(к < 1,3 мкм) оптические импульсы можно сжимать в волоконно-
решеточном компрессоре до 100 раз. Подробно обсуждаются теория
и конструкция таких компрессоров. В области длин волн 1,3-1,6 мкм
в компрессорах, основанных на солитонном эффекте, можно сжимать
оптические импульсы в ~ 100 раз, используя фундаментальное свой-
свойство солитонов высших порядков. Сочетая эти два метода сжатия
в области длин волн вблизи 1,3 мкм и используя световод со
смещенной дисперсией, можно получить сжатие в ~ 5000 раз. Дается
обзор экспериментальных достижений в этой области, а также теория
компрессоров, основанных на солитонном эффекте.
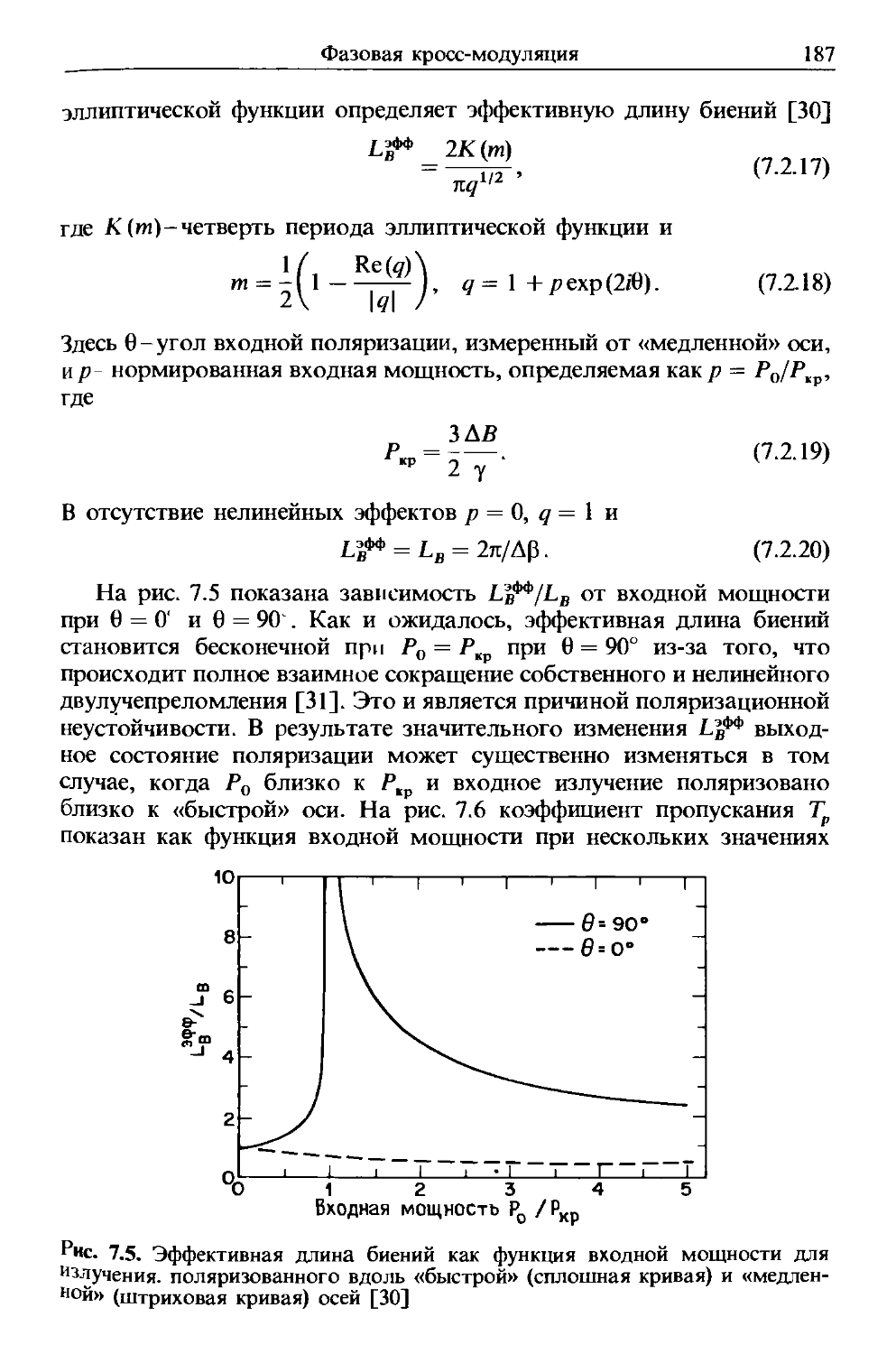
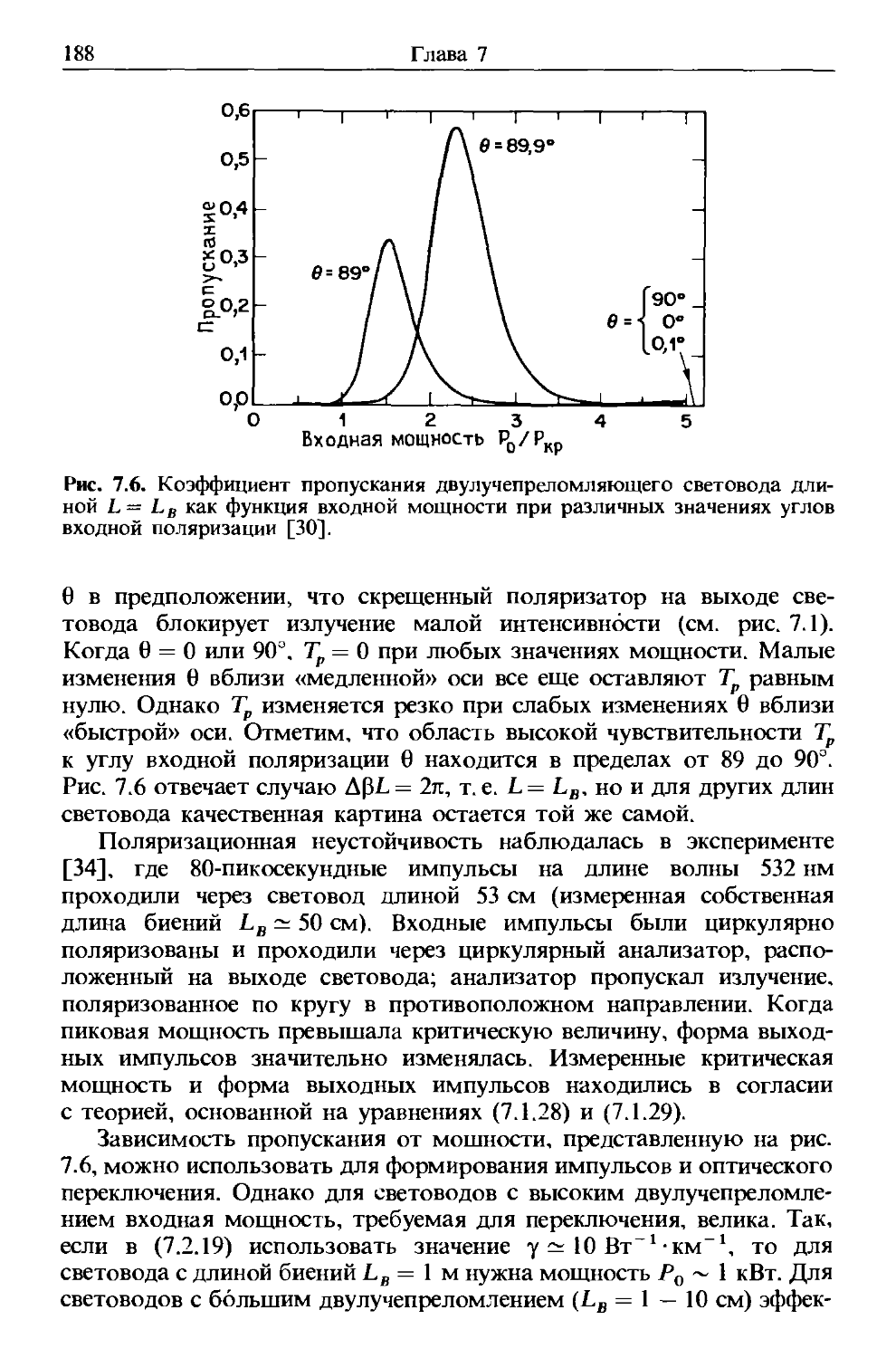
В гл. 7 сосредоточено внимание на эффекте фазовой кросс-
модуляции ФКМ, которое возникает, когда два оптических поля
распространяются одновременно и действуют друг на друга по-
посредством зависимости показателя преломления от интенсивности.
Нелинейная связь, вызванная ФКМ, может иметь место, не только
когда два излучения на разных длинах волн вводятся в волокно, но
также и вследствие взаимодействия между ортогонально поляризо-
поляризованными компонентами одного излучения в двулучепреломляющем
световоде. Рассмотрению последнего случая предшествует рассмотре-
рассмотрение таких нелинейных эффектов, как оптический эффект Керра и
вызванное двулучепреломлением изменение формы импульса. Не-
Нелинейное двулучепреломление ведет к поляризационной неустойчи-
неустойчивости, так как длина биений в световоде становится зависимой от
интенсивности. Обсуждается также его воздействие на оптические
солитоны. В следующих двух разделах рассмотрен случай, когда
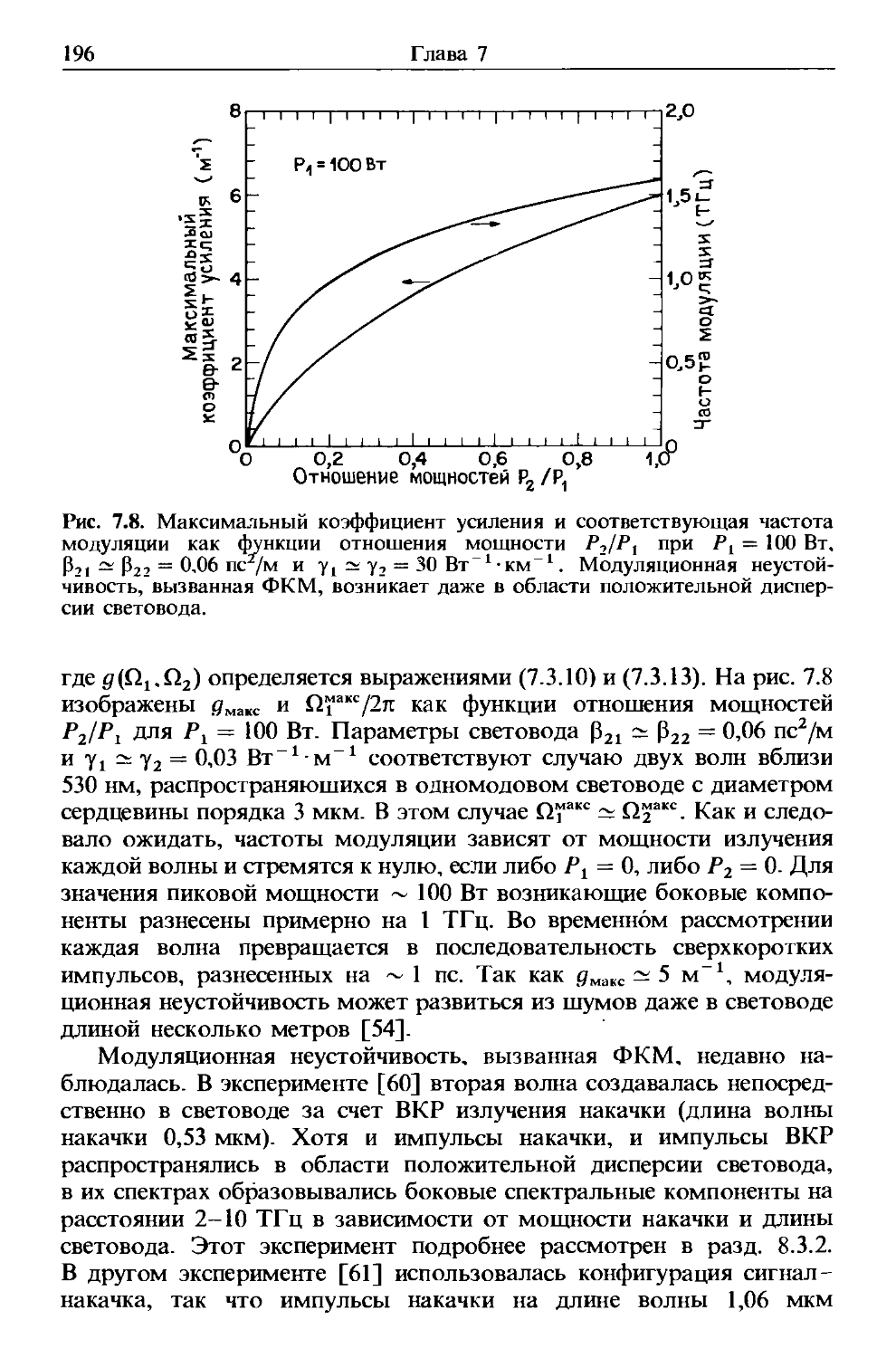
в световод вводится излучение на двух разных длинах волн. Инду-
Индуцируемая ФКМ-связь этих двух излучений может вызвать модуля-
модуляционную неустойчивость в области нормальной дисперсии групповых
скоростей световода. Эффект ФКМ, рассматриваемый в комбинации
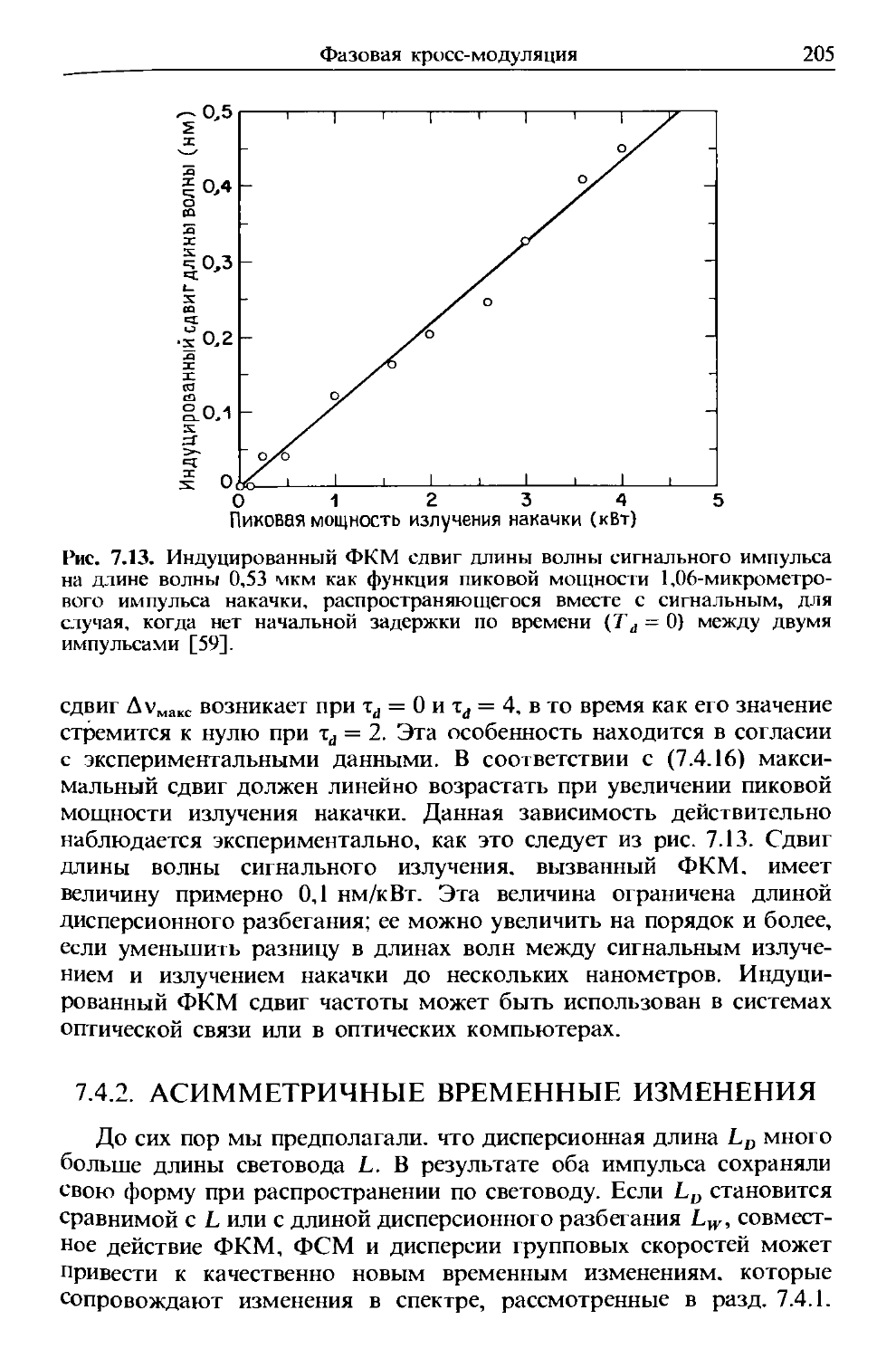
с эффектами ФСМ и ДГС. может привести к несимметричным
спектральным и временным изменениям. Вслед за этим рассматрива-
рассматривается взаимодействие между волнами, распространяющимися навстре-
30 Глава 1
чу друг другу, появляющееся вследствие ФКМ, и отмечается в этой
связи важность ФКМ для оптического волоконного гироскопа.
В последней части обсуждаются применения ФКМ для волоконно-
оптической связи.
В гл. 8 рассмотрено вынужденное комбинационное рассеяние
ВКР-явление генерации стоксовой волны (смещенной на 13 ТГЦ)
в поле волны накачки при распространении накачки в световоде. Это
происходит, только когда мощность накачки превышает пороговый
уровень. Сначала обсуждаются усиление и порог вынужденного
комбинационного рассеяния. Затем в двух отдельных разделах
описывается ВКР для случая непрерывной или квазинепрерывной
накачки и для случая сверхкоротких импульсов накачки. В последнем
случае сочетание ФСМ, ФКМ и ДГС приводит к качественно новым
особенностям. Эти особенности могут быть совершенно разными
в зависимости от того, находится накачка в области нормальной или
аномальной ДГС. Случай аномальной ДГС рассматривается в
последнем разделе, особенно выделены волоконно-оптические ВКР-
лазеры. Также обсуждаются применения ВКР-усилителей в волокон-
волоконно-оптической связи.
Глава 9 посвящена ВРМБ, которое проявляется в волоконных
световодах подобно ВКР, но с важными отличиями. ВРМБ пре-
преобразует часть энергии накачки в стоксовых волнах, распространяю-
распространяющуюся во встречном направлении и смещенную по частоте всего на
~ 10 ГГц. Из-за малой ширины линии ВРМБ-усиления (~ 10 МГц)
ВРМБ возникает эффективно только при непрерывной накачке или
накачке импульсами, имеющими спектральную ширину меньше
ширины линии усиления. Сначала описаны характеристики ВРМБ-
усиления в кварцевых световодах. Затем изложена теория ВРМБ,
рассматривающая такие вопросы, как порог ВРМБ, истощение
накачки и насыщение усиления. Обсуждаются также связанные с
ВРМБ неустойчивости. В обсуждении экспериментальных результа-
результатов особое внимание уделено волоконным ВРМБ-лазерам и усили-
усилителям. Последний раздел посвящается применениям ВРМБ для
волоконно-оптической связи.
В гл. 10 рассмотрены параметрические процессы, при которых
происходит обмен энергиями между несколькими оптическими вол-
волнами без активного участия нелинейной среды. Параметрические
процессы эффективно происходят, только когда выполнено условие
фазового синхронизма. Эти условия относительно легко выполнить
для нелинейного процесса четырехволнового смешения. И ему
посвящена основная часть главы. Теория параметрического усиления
следует из рассмотрения нелинейного взаимодействия четырех волн.
Подробно обсуждаются экспериментальные результаты и способы
получения фазового синхррнизма. Вслед за этим рассматриваются
параметрическое усиление и его применения. Последний раздел
Введение 31
посвящен генерации второй гармоники в световодах-явлению, кото-
которое привлекло недавно большое внимание из-за его важных техно-
технологических применений.
ЛИТЕРАТУРА
1. Tyndall J. Proc. Roy. Inst., 1, 446, A854).
2. Baird J. L., British Patent, 285, 738 A927).
3. HansellC. W., U. S. Patent, 1, 751, 584 A930).
4. Lamm H.. Z. Instrumentenk, 50, 579 A930).
5. van Hell A.C.S., Nature, 173, 39 A954).
6. Hirschowitz B.I. et al, Gastroenterology, 35, 50 A958).
7. Kapany N.S., J. Opt. Soc. Am., 49, 779 A959).
8. Kapany N.S., Fiber Optics: Principles and Applications, Academic, New York,
1967.
9. Kao K.C., Hockham G.H., Proc. IEE, 113, 1151 A966).
10. Kapron F.P., Keck D.B., Maurer R.D., Appl. Phys. Lett., 17, 423 A970).
11. Payne D.N., Gambling W.A., Electron. Lett., 10, 289 A974).
12. French W.G. et al., Bell Sys. Tech. J. 53, 951 A974).
13. Miya T. et al, Electron. Lett., 15, 106 A979).
14. Suemastu Y., Proc. IEEE, 71, 692 A983).
15. Li T, IEEE J. Sel. Areas Commun., SAC 1, 356 A983).
16. Basch E.E., ed., Optical Fiber Transmission, Sams, Indianapolis, 1986.
17. Miller S.E., Kaminow I.P., eds., Optical Fiber Telecommunications II, Aca-
Academic, Boston, 1988.
18. Stolen R.H., Ippen E.P., Tynes A. R., Appl. Phys. Lett., 20, 62 A972).
19. Ippen E.P., Stolen R.H., Appl. Phys. Lett, 21, 539 A972).
20. Smith R.G., Appl. Opt., 11, 2489 A972).
21. Stolen R.H., Ashkin A., Appl. Phys. Lett., 22, 294. A973).
22. Stolen R. H., Bjokholm J. E., Ashkin A., Appl. Phys. Lett, 24, 308 A974).
23. Stolen R. H., IEEE J. Quantum Electr, QE 11, 100 A975).
24. Ippen E.P., Shank С V., Gustafson Т.К., Appl. Phys. Lett, 24, 190 A974).
25. Stolen R.H., Lin C, Phys. Rev., A17, 1448 A978).
26. Hasegawa A.. Tappert F., Appl. Phys. Lett., 23, 142 A973).
27. Mollenauer L.F., Stolen R.H., Gordon J.P., Phys. Rev. Lett, 45, 1095 A980).
28. Mollenauer L.F., Stolen R.H., Opt. Lett, 9, 13 A984).
29. Mollenauer L.F., Gordon J.P., Islam M.N., IEEE J. Quantum Electr, QE-22,
157 A986).
30. Kafka J.D., Baer T, Opt. Lett., 12, 181 A987).
31. Islam M.N. et al.. Opt. Lett, 12, 814 A987).
32. Gouveia-Neto A.S., Gomes A.S.L., Taylor J.R., Opt. Quantum Electr, 20. 165
A988).
33. Nakatsuka H., Grischkowsky D,, Balant A.C., Phys. Rev. Lett., 47, 910 A981).
34. Shank C.V.et al., Appl. Phys. Lett, 40, 761 A982).
35. Nikolaus В., Grischkowskv D., Appl. Phys. Lett., 42, 1 A983).
36. Gomes A.S.L., Gouveia-Neto A.S., Taylor J.R., Opt. Quantum. Electr., 20, 95
A988).
37. Fork R.L. et al, Opt. Lett, 12, 483 A987).
38. Alfano R.R. et al. Opt. Lett., 14, 626 A986).
39. Alfano R.R. et al, Appl. Opt.. 26, 3491 A987).
40. Islam M.N. et al. Opt. Lett., 12, 625 A987).
41. Agrawal G. P., Phys. Rev. Lett., 59, 880 A987).
42. Schadt D., Jaskorzynska В., J. Opt. Soc. Am, B4, 856 A987).
43. Stolen R.H., Proc. IEEE, 68, 1232 A980).
44. Сисакян И.Н., Шварцбург А. В. Квант, электрон., 1984, т. 11, с. 1703.
32 Глава 1
45. Winful H. G., in: Optical Fiber Transmission, ed. by E. E. Basch, Sams,
Indianapolis, 1986.
46. Ахманов С. А., Выслоух В. А., Чиркни А.С. УФН, 1986, т. 99, с. 169.
47. Cotter D., Opt. Quant. Electr, 19, 1 A987).
48. Blow K.J., Doran N.J., IEE Proa, 134, Pt. J, 138 A987).
49. Marcuse D., in: Optical Fiber Telecommunications [I, ed. by S. E. Miller,
I. P. Kaminow, Academic, Boston, 1988.
50. Дианое Е.М., Мамышее П.В., Прохоров A.M. Квант, электрон., 1988,
т. 15, с. 5.
51. Marcuse D., Light Transmission Optics, van Nostrand Reinhold, New York,
1982, Ch. 8, 12.
52. Snyder A.W., LoveJ.D., Optical Waveguide Theory, Chapman and Hall,
London, 1983. [Имеется перевод: Снайдер А. В.. Лав Д. Д. Теория опти-
оптических волноводов. М.: Мир, 1987.]
53. Adams M.J., An Introduction to Optical Waveguides, Wiley, New York, 1981,
Ch. 7.
54. Nagel S. R., MucChesnev J. В.. Walker K. L., in: Optical Fiber Communications,
voL 1, ed. by T. Li, Academic, Orlando, 1985, Ch. 1.
55. Morrow A.J., Sarkar A., Schultz P. C, in: Optical Fiber Communications, vol. 1,
ed. by T. Li, Academic, Orlando, 1985, Ch. 2.
56. Niizeki N.. Inagaki N.. Edahiro Т., in: Optical Fiber Communications, vol. 1, ed.
by T. Li, Academic, Orlando, 1985, Ch. 3.
57. DiMarcello F. K, Kurkjian С R., Williams J. C, in: Optical Fiber Communi-
Communications, vol. 1, ed. by T. Li, Academic, Orlando, 1985, Ch. 4.
58. Paek U. C, J. Lightwave TechnoL, LT 4, 1048 A986).
59. Kanamori H. et al, J. Lightwave Technol., LT 4, 1144 A986).
60. Cohen L.G., J. Lightwave Technol., LT 3, 958 A985).
61. Malitson I.H., J. Opt. Soc. Am., 55, 1205 A965).
62. AgrawalG.P., Potasek M.J., Phys. Rev., A33, 1765 A986).
63. Ainslie B.J., Day C.R., J. Lightwave Technol., LT 4. 967 A986).
64. Cohen L.G., Mammel W.L., Jang S.J., Electron. Lett., 18, 1023 A982).
65. Stolen R.H. et al., Appl. Phys. Lett., 33, 699 A978).
66. Kaminow I. P., IEEE J. Quantum Electr., QE 17, 15 A981).
67. Payne D.N., Barlow A. J., Hanscn J.J.R., IEEE J. Quantum Electr., QE 18,
477 A982).
68. Stolen R. H.. Pleibel W, Simpson J. R., J. Lightwave Technol., LT 2, 639 A984).
69. Noda J., Okamoto K., Sasaki Y, J. Lightwave Technol., LT 4, 1071 A986).
70. Bloembergen N.. Nonlinear Optics, Benjamin, Reading, Mass., 1977, Ch. 1.
71. Shen Y.R., Principles of Nonlinear Optics, Wiley, New York, 1984. [Имеется
перевод: Шеи И. Р. Принципы нелинейной оптики. М.: Наука. 1989.]
72. Ippen E. P., in: Laser Applications to Optics and Spectroscopy, vol. 2, ed. by
S. F. Jacobs, M. Sargent III, J. F. Scott, M. O. Scully, Addison-Wesley, Reading,
Mass., 1975, Ch. 6.
Глава 2
РАСПРОСТРАНЕНИЕ ВОЛН В ВОЛОКОННЫХ
СВЕТОВОДАХ
Для понимания нелинейных явлений в волоконных световодах
необходимо рассмотреть теорию распространения электромагнитных
волн в нелинейной среде с дисперсией. Цель этой главы-получить
основное уравнение распространения оптических импульсов в одно-
модовых световодах. В разд. 2.1 вводятся уравнения Максвелла
и основные понятия, такие, как линейная и нелинейная индуцирован-
индуцированная поляризация и диэлектрическая проницаемость, зависящая от
частоты. Понятие мод волоконного световода вводится в разд. 2.2,
в котором обсуждается также, при каком условии световод будет
одномодовым. В разд. 2.3 рассматривается теория распространения
импульсов в нелинейной среде с дисперсией в приближении медленно
меняющихся амплитуд в предположении, что ширина спектра им-
импульса много меньше частоты электромагнитного поля. В разд. 2.4
обсуждаются численные методы, используемые для решения уравне-
уравнения распространения. Особое внимание уделено методу расщепления
по физическим факторам с использованием быстрого преобразования
Фурье на дисперсионном шаге (SSFM): он отличается большей
скоростью счета по сравнению с большинством разностных схем.
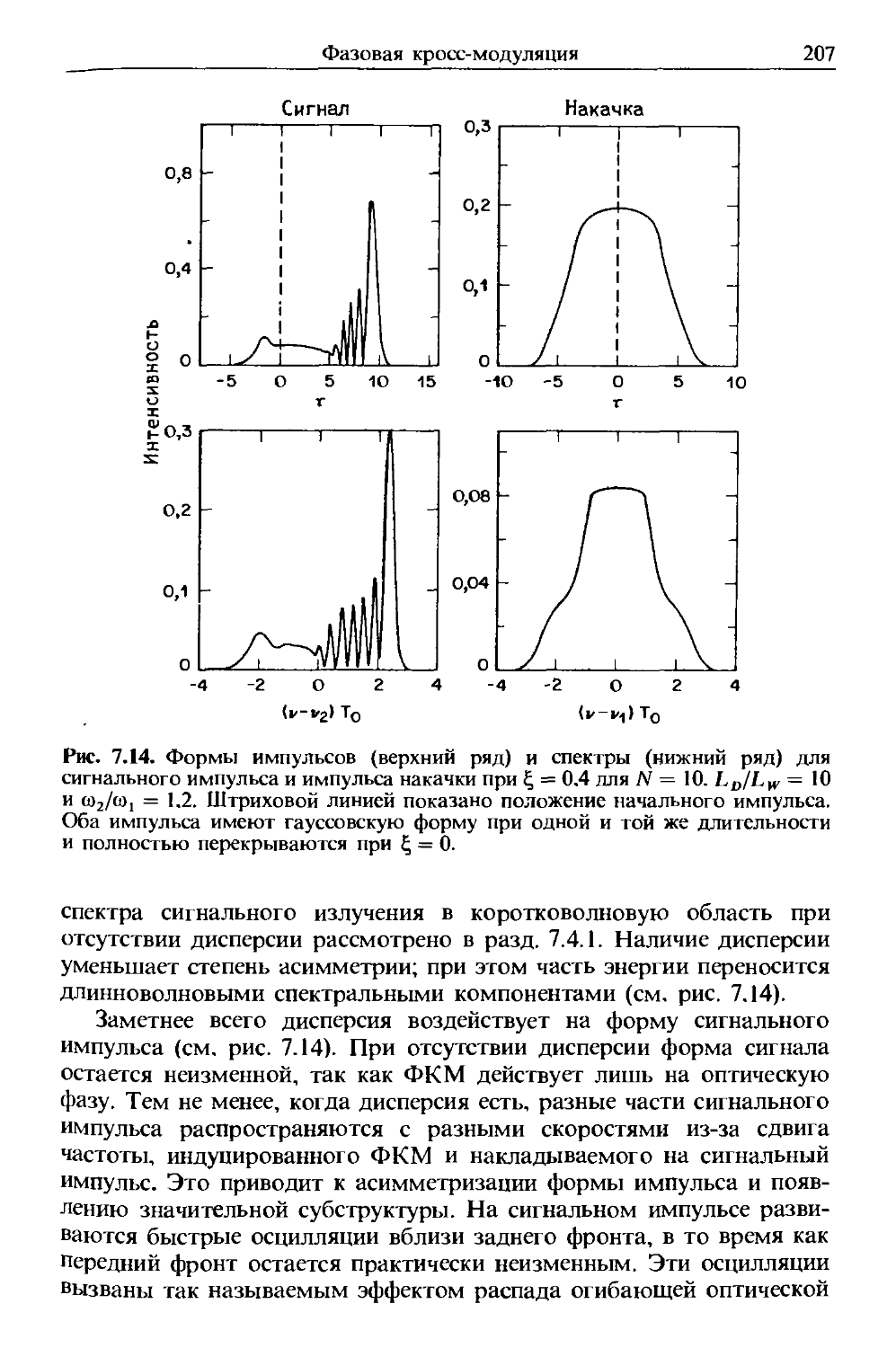
2.1. УРАВНЕНИЯ МАКСВЕЛЛА
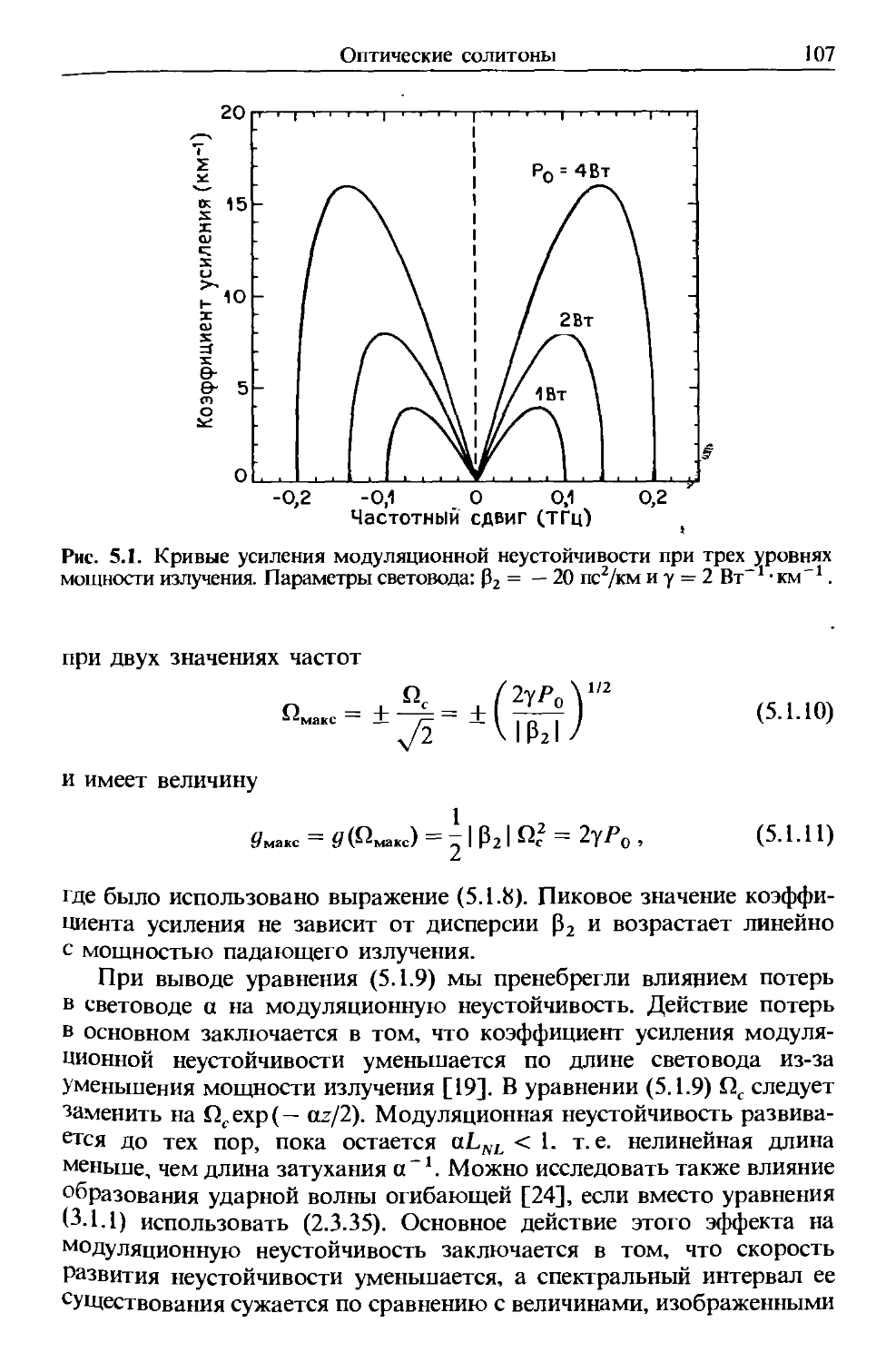
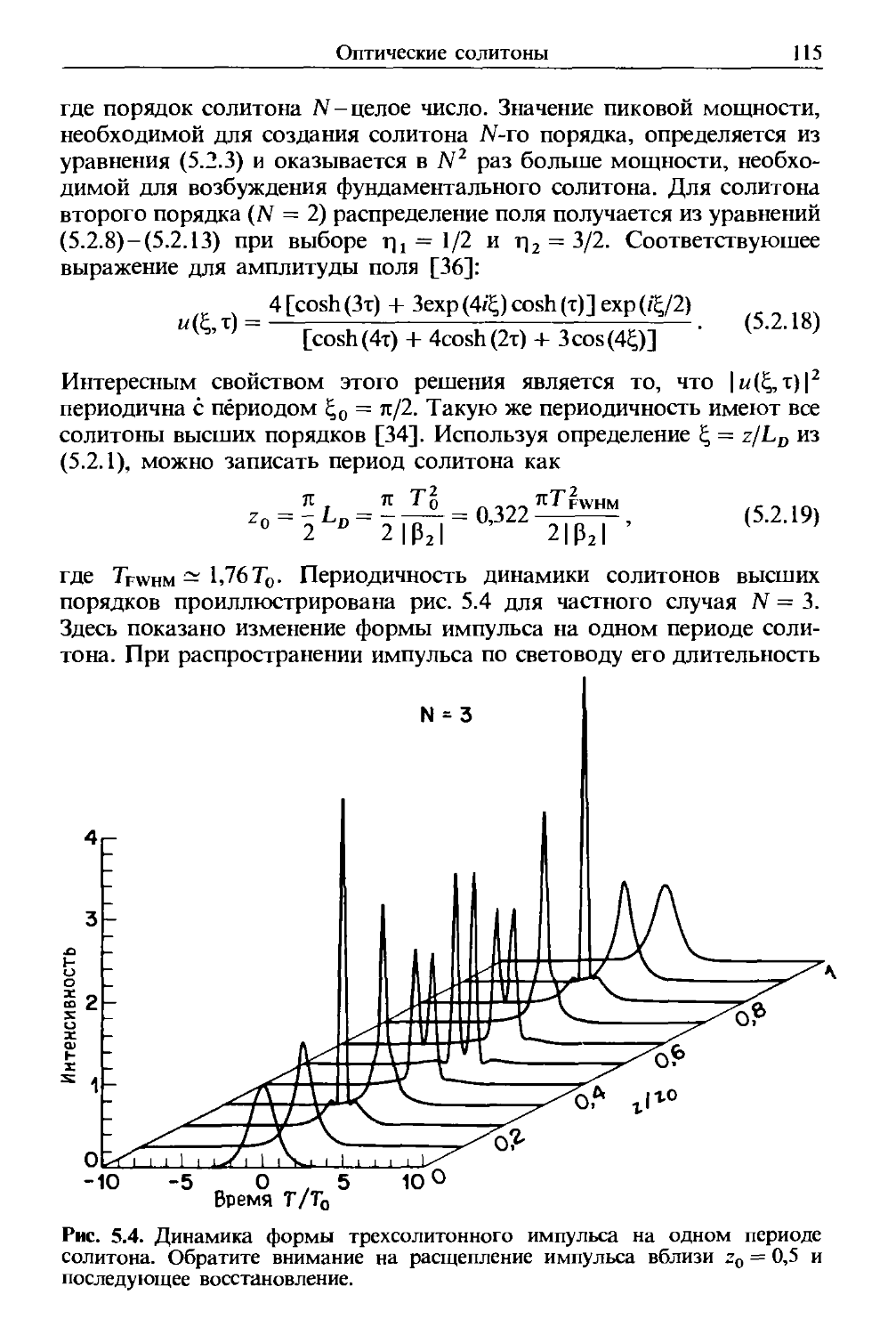
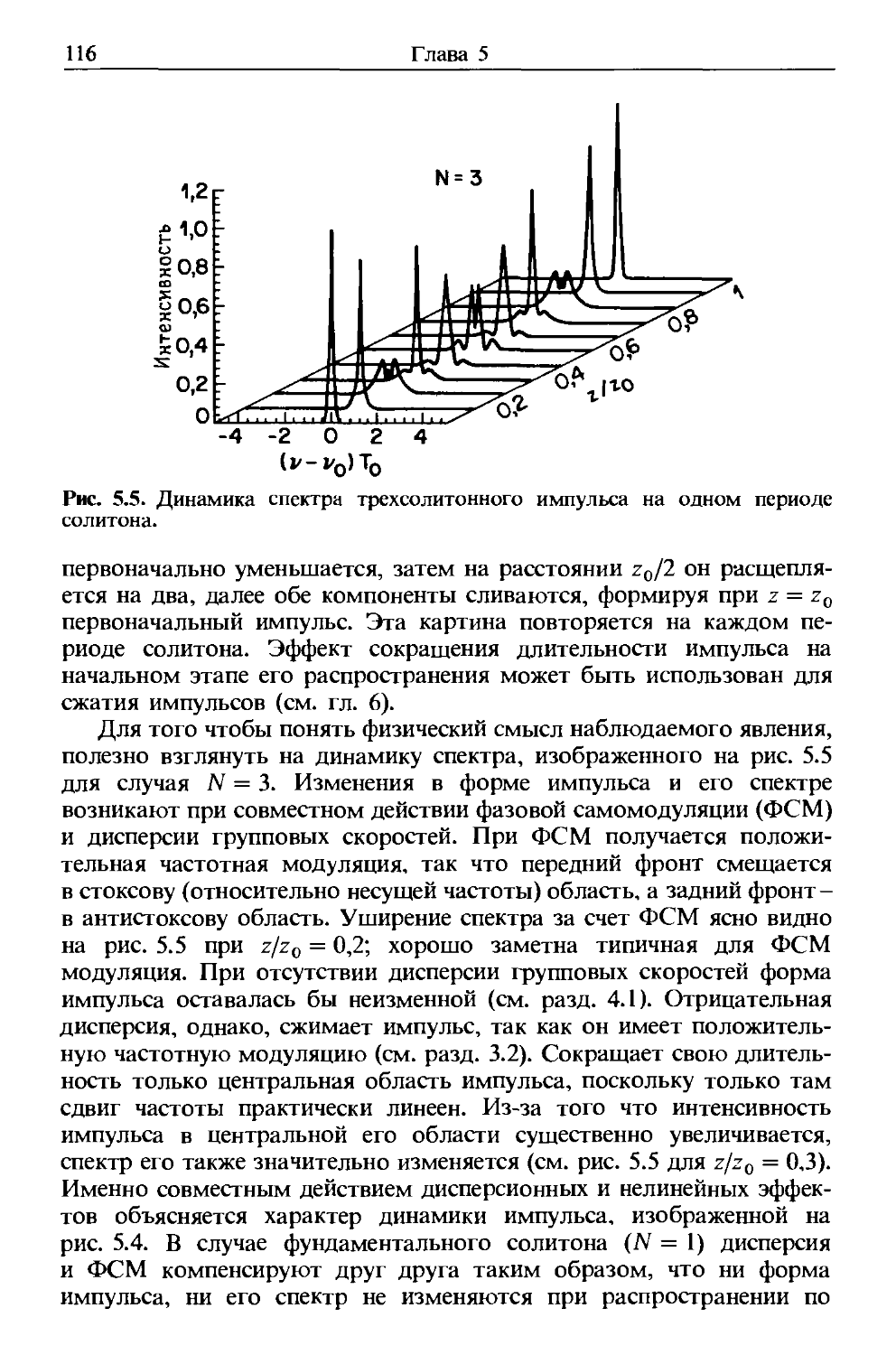
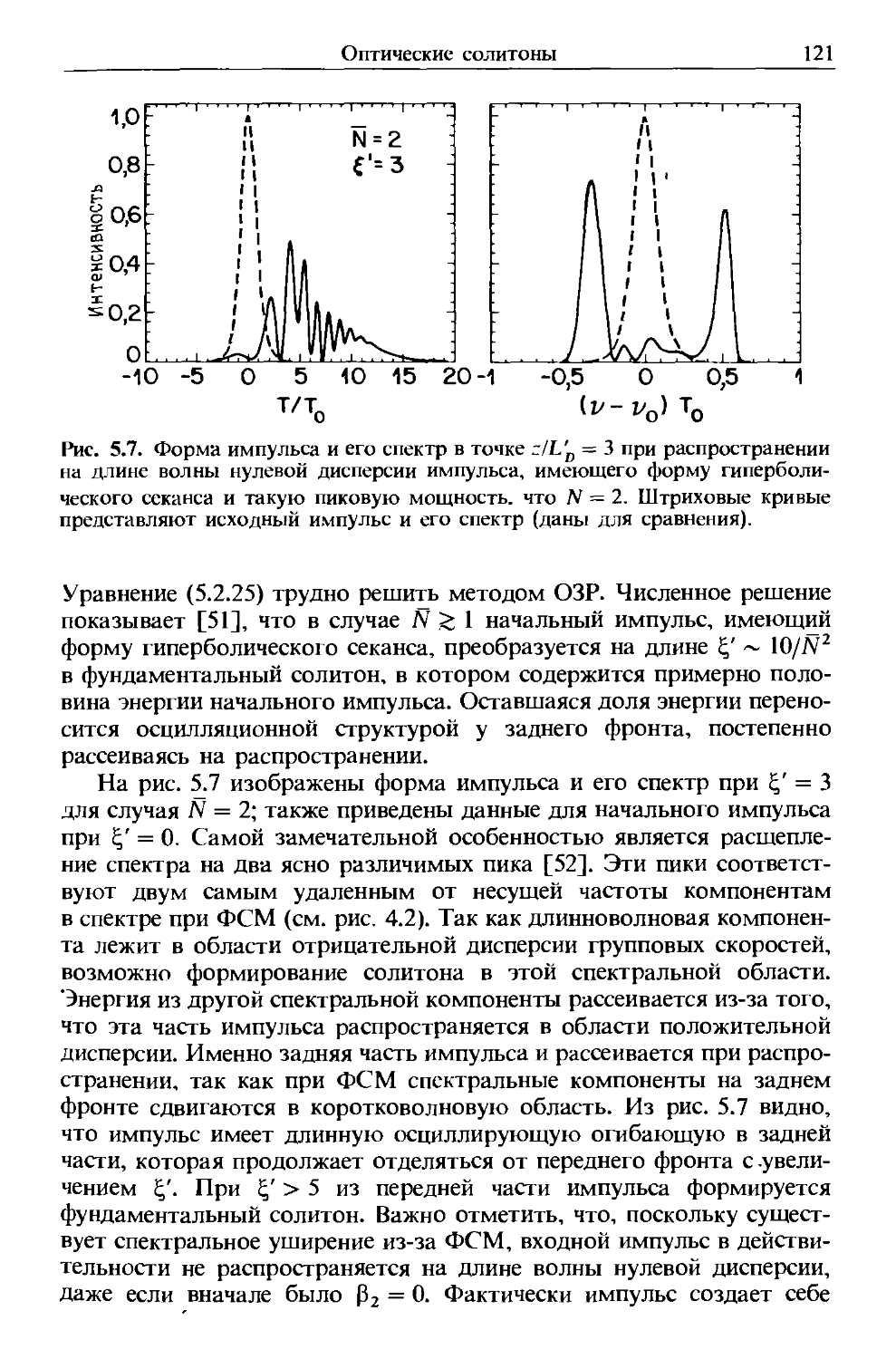
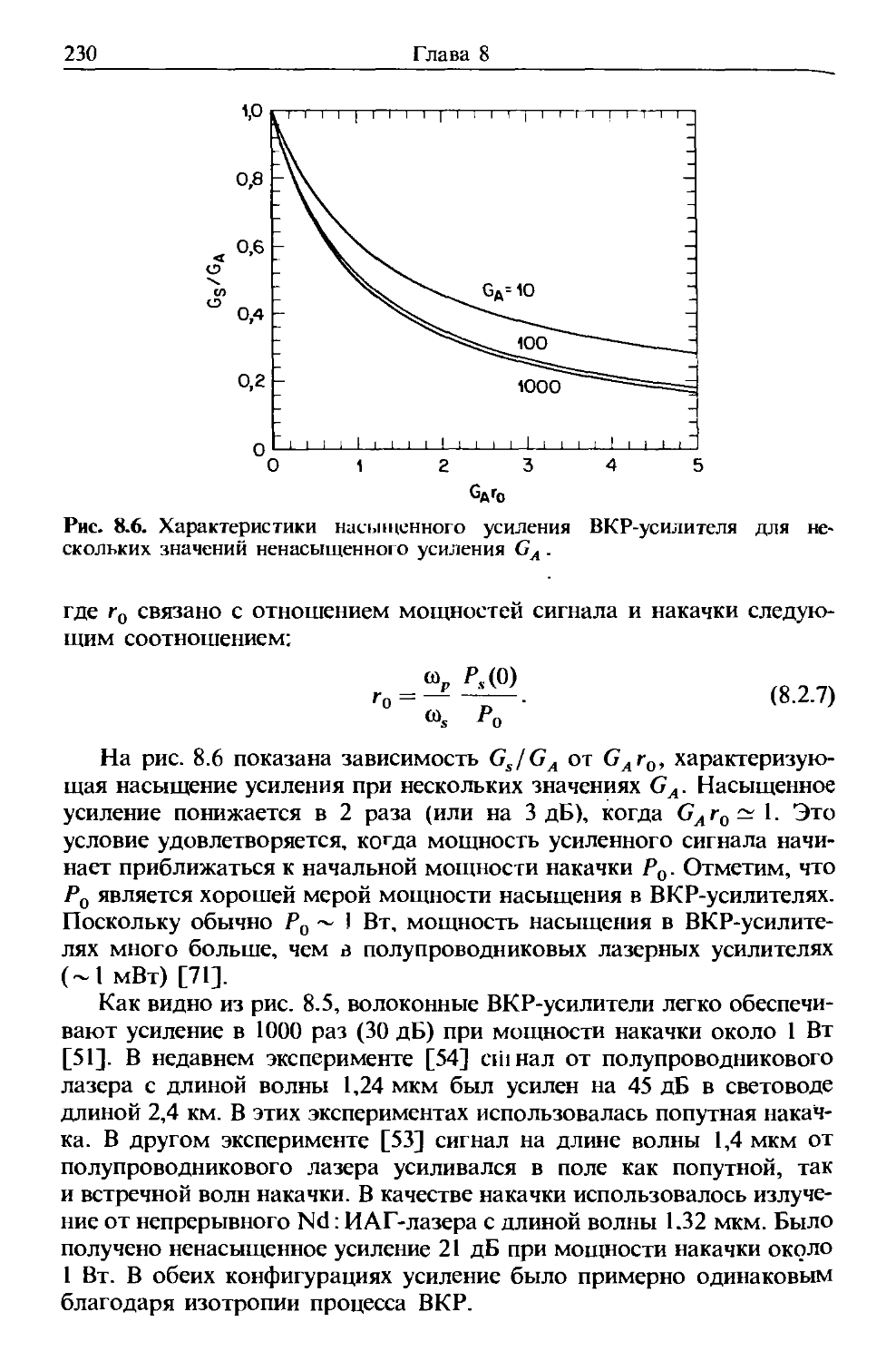
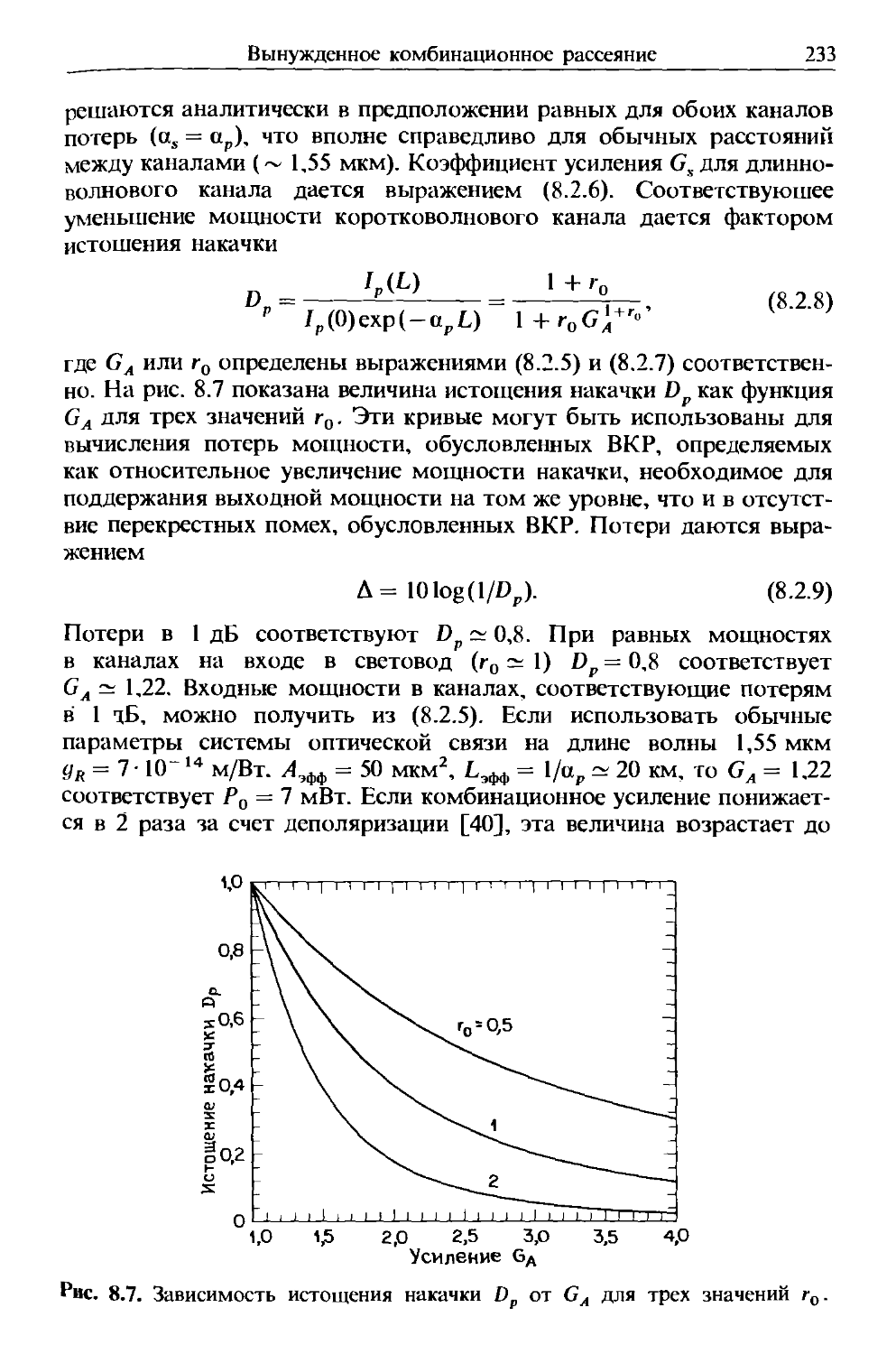
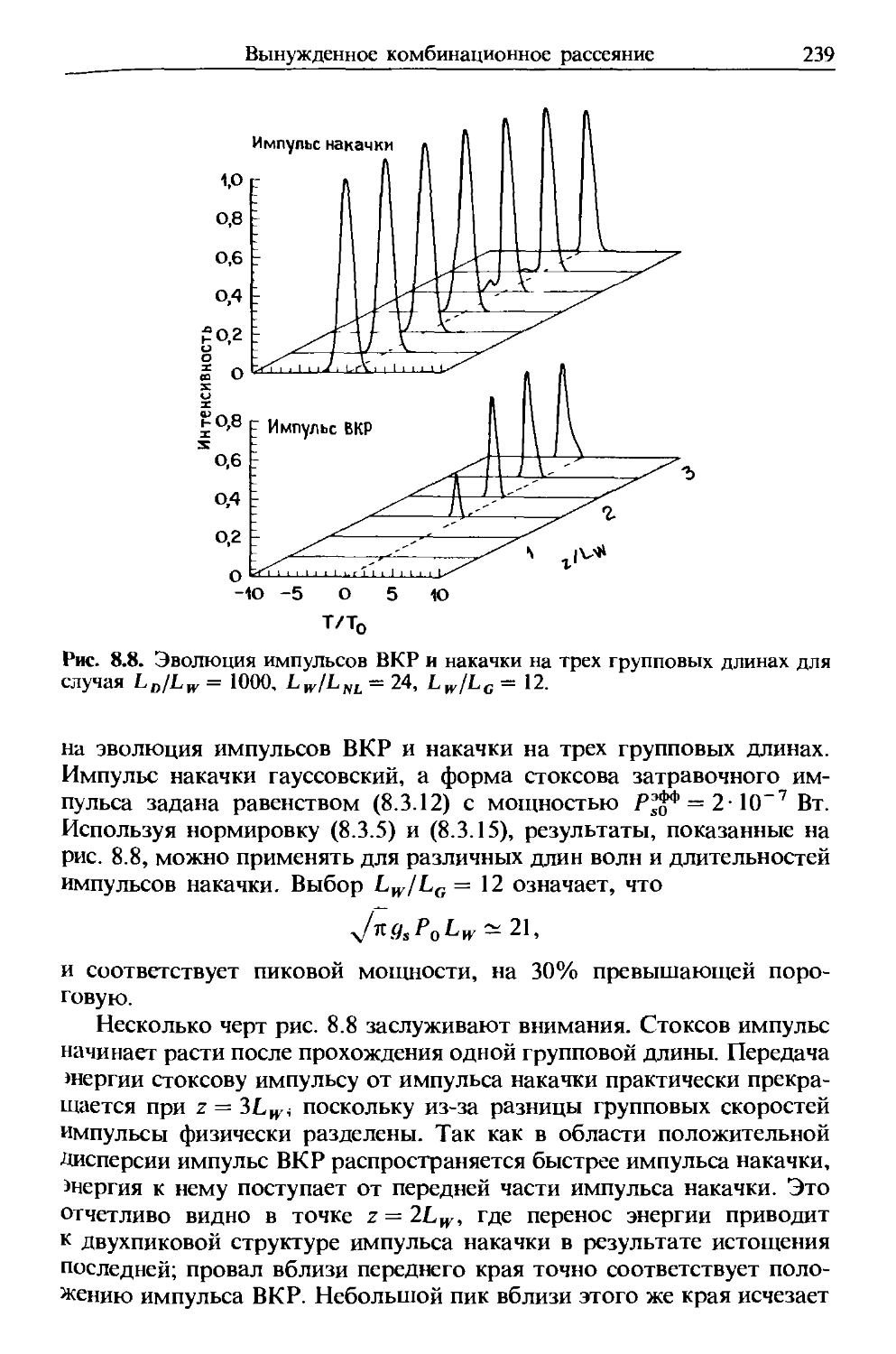
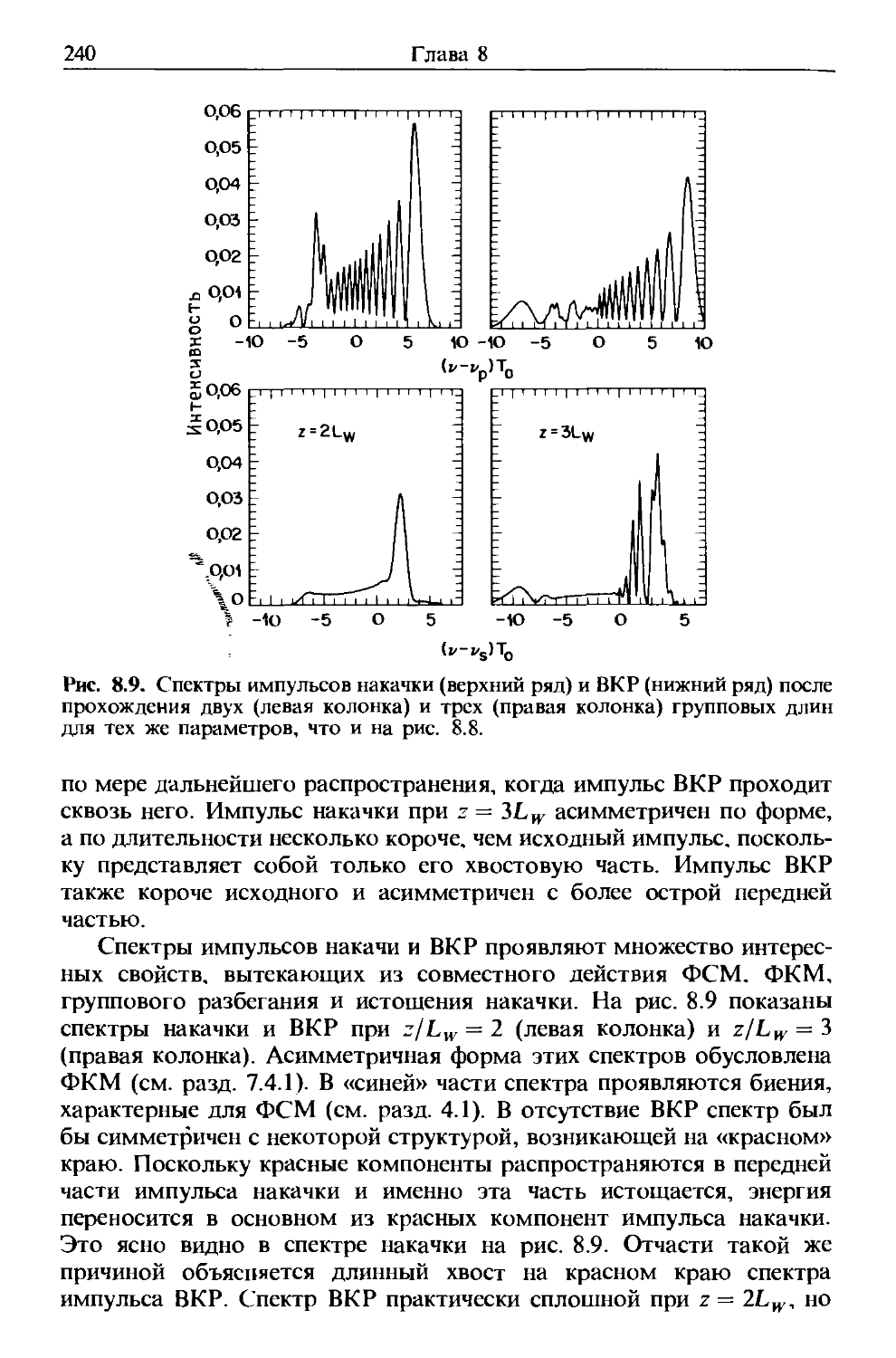
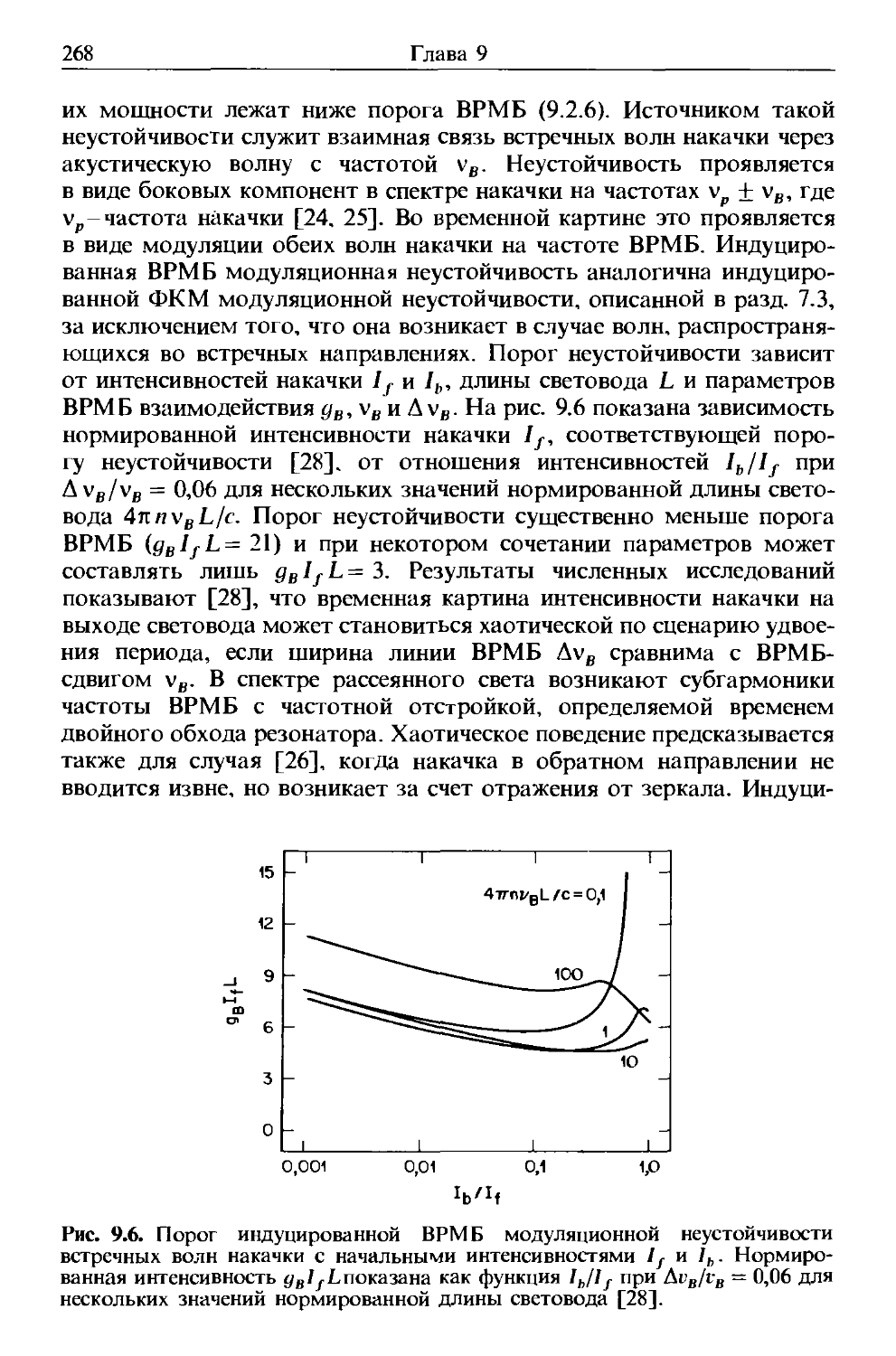
Как и все электромагнитные явления, распространение оптичес-
оптического поля в волокне описывается уравнением Максвелла. В системе
СИ эти уравнения имеют вид [1]
VxE= , B.1.1)
dt
VxH = J; + p B.1.2)
V-D=P/, B.1.3)
V-B=O, B.1.4)
где Е и Н-векторы электрического и магнитного полей, a D и В-
векторы электрической и магнитной индукции соответственно. Источ-
Источниками электромагнитного поля являются вектор плотности тока Jf
34 Глава 2
и плотности заряда pf. При отсутствии свободных зарядов в среде,
например, как в волоконном световоде, Jf = 0 и pf = 0.
Векторы электрической и магнитной индукции D и В возникают
как отклик среды'на электрическое и магнитное поля Е и Н,
распространяющиеся в среде, и связаны с ними следующими соотно-
соотношениями:
D = e0E + P, B.1.5)
В=ц0Н + М, B.1.6)
где е0 и ц0- диэлектрическая и магнитная постоянные вакуума,
Р и М - электрическая и магнитная поляризации. В случае волокон-
волоконного световода, являющегося немагнитным веществом, М = 0.
Уравнения Максвелла могут быть использованы для получения
уравнения, описывающего распространение света в волоконных
световодах:
„ _ „ 1 д2Е д2Р
где используется соотношение цоео = 1/с2, с-скорость света в
вакууме. Чтобы завершить описание, нужно ввести связь между
индуцированной поляризацией Р и электрическим полем Е. Вообще
говоря, чтобы определить Р, нужно использовать квантовомехани-
ческую теорию. Однако такой подход часто бывает необходим только
тогда, когда частота оптического поля близка к резонансным часто-
частотам среды. В противном же случае, вдали от резонансных частот, для
связи Р и Е можно использовать феноменологическое соотношение
A.3.1), которое справедливо в волоконных световодах в области длин
волн 0,5-2 мкм. представляющей интерес для изучения нелинейно-
оптических эффектов. Рассмотрим нелинейные эффекты только
третьего порядка, определяемые х<3>- Индуцированная поляризация
состоит из двух частей;
P(r, t) = PL(r, t) + P»L(r, t), B.1.8)
где PL-линейная и PNL-нелинейная части, связанные с электрическим
полем в самом общем случае соотношениями [2. 3]
PL(r,t) = E0 J x{1)U-f)-E{T,t')dt', B.1.9)
(X, t) = e0 J J f XC>(' - f,, f - f2, f - h): E(r, *,) E(r, t2)
x
xE{r.t3)dtidt2dt3. B.1.10)
Эти соотношения справедливы в дипольном приближении, когда
предполагается, что отклик среды является локальным.
Распространение волн в волоконных световодах 35
Уравнения B.1.7)—B.1.10) составляют общий формализм описа-
описания нелинейных эффектов низшего порядка в волоконных световодах.
Ввиду их сложности необходимо сделать несколько упрощающих
приближений. Наиболее общее упрощение состоит в том, что
нелинейная поляризация PNL в B.1.8) считается малым возмущением
полной индуцированной поляризации. Такое предположение оправ-
оправданно, так как в волоконных световодах |PwlI<<:IPlI- Поэтому
первым шагом будет решение уравнения B.1.7) при PNL = 0. Так как
уравнение B.1.7) линейно по Е, оно имеет простой вид в спектраль-
спектральном представлении:
V х V х Ё(г, co) + e(coW Ё(г, со) = О, B.1.11)
с2
где Ё (г, со) - фурье-компоненты Е(г, i), определяемые как
Ё(г, со)= J Е(М)ехр(гсог)<Л, • B.1.12)
— 00
а е(со)-диэлектрическая проницаемость, зависящая от частоты сле-
следующим образом:
е(со)= 1 + хA)(со); B.1.13)
здесь Х(П(Ю) фурье-преобразование функции хA'(')- Вообше хA)(юХ
а следовательно, и ? (со) комплексные величины. Используя опре-
определение
? = (и + ш.с/2соJ, B.1.14)
показатель преломления п и коэффициент поглощения а можно
выразить через действительную и мнимую части Х(П(Ю) как
«(co)=l+^Re[xA»], B.1.15)
а(со) = — Im[xA>(co)]; B.1.16)
здесь Re и Im обозначают соответственно действительную и мнимую
части. Частотная зависимость и и а в волоконных световодах
обсуждалась в разд. 1.2.
Прежде чем решать уравнение B.1.11), сделаем еще два упроще-
упрощения. Во-первых, пренебрежем мнимой частью е(со), так как ввиду
низких потерь в световодах мнимая часть мала по сравнению с
действительной. Тогда е(со) можно заменить на и2 (со). Во-вторых,
полагая и (со) независимым от пространственных координат в оболоч-
оболочке и сердцевине (для световода со ступенчатым профилем показателя
преломления), можно считать, что
Vx VxE = V(V-E)- V2E= - V2E; B.1.17)
36 Глава 2
здесь используются равенства V • D = eV ¦ Е = 0. При таких упроще-
упрощениях уравнение B.1.11) принимает вид
V2E + w2(co)^-E = O. B.1.18)
В следующем разделе уравнение B.1.18) решается в случае световода
со ступенчатым профилем показателя преломления; находятся моды
такого световода.
2.2. МОДЫ ВОЛОКОННОГО СВЕТОВОДА
При любой частоте со волоконный световод может иметь конечное
число направляемых мод, пространственные распределения полей
Ё(г,со) которых являются решениями волнового уравнения B.1.18)
при соответствующих граничных условиях. Кроме того, световод
может иметь континуум (счетное число) ненаправляемых излучатель-
ных мод. Излучательные моды не играют важной роли в обсуждении
нелинейных эффектов, поскольку предполагается, что световод имеет
совершенную (идеальную) цилиндрическую геометрию, хотя излуча-
излучательные моды важны в задачах, рассматривающих передачу энер-
энергии между связанными и излучательными модами [4]. В этом раз-
разделе кратко обсуждаются направляемые моды волоконных светово-
световодов [4, 5].
Принимая во внимание цилиндрическую симметрию волоконного
световода, удобно записать волновое уравнение B.1.18) в цилиндри-
цилиндрических координатах р, ф и z:
д2Ё let
dp2 р dp р2 дф2 dz2
где к0 = со/с = 2п/Х и Ё-фурье-компоненты электрического поля Е,
т.е.
1 °°
Е(г,0 = — f Ё(г,со)ехр(-/си)Ло. B.2.2)
2я -„о
Аналогичные соотношения выполняются и для магнитного поля
Н(г, t). Так как Е и Н удовлетворяют уравнениям Максвелла B.1.1)-
B.1.4), только две компоненты из шести независимы. Удобно вы-
выбрать Ez и Н. как независимые компоненты и выразить остальные Ёр,
?ф, Яр и #ф через Ezu H,. удовлетворяющие уравнению B.2.1). Для
решения волнового уравнения относительно Ez используется под-
подстановка
(i'Pz), B.2.3)
где А—нормировочная постоянная, р- постоянная распространения
Распространение волн в волоконных световодах 37
и т — целое число. Подставляя B.2.3) в B,2.1), для функции F(p)
получаем следующее уравнение:
d2F
idF Г , т2 \
--+ к1--j f = 0, B,2,4)
pdp L P2J
У +
dp2 pdp
где
к = п2к1-р2. B.2,5)
Показатель преломления и волокна с радиусом сердцевины а имеет
вид
2, р > а.
Уравнение B,2,4)-хорошо известное дифференциальное уравне-
уравнение, решением которого являются функции Бесселя, Общее решение
в сердцевине можно выразить как линейную комбинацию функции
Бесселя Jm(Kp) и функции Неймана Nm(Kp), Функция Nm{Kp) имеет
сингулярность при р = 0, поэтому физический смысл имеет только
решение
F(p) = JjKP), р<«, B,2,6)
где к получается из уравнения B,2,5) заменой и на пх; это показатель
преломления сердцевины, В оболочке (р > а) решение F (р) должно
экспоненциально убывать с увеличением р. Таким решением являют-
являются модифицированные функции Бесселя Кт:
F(p) = Km(yp), p>a, B.2.7)
где
y = (p2-Ǥ/cgI/2. B,2,8)
Следуя такой же процедуре, можно получить компоненту магнит-
магнитного поля Я?. Граничное условие требует, чтобы тангенциальные
компоненты Е и Н были непрерывны на поверхности, разделяющей
сердцевину и оболочку, т. е, Ez, Hz, ?ф и //ф при р = а должны быть
непрерывными функциями.
Непрерывность этих компонент поля на границе сердцевины
и оболочки (р = а) приводит к характеристическому уравнению,
решение которого определяет постоянную распространения Р для
моды световода. Так как процедура получения характеристического
уравнения хорошо известна [4, 5], сразу выпишем его:
J'm(Kd) К'т(уа)ЛУ Гт(ка) п\К'т(уа)
K()||J()
1 _ Гтр/со(и2 - я2)"!2
] |_ «к2у2И1 J '
n2yKJya)
B,2,9)
где штрих означает дифференцирование по аргументу. Уравнение
38 Глава 2
B.2.9) получено с использованием важного соотношения
к2 + у2 = (и?-и!)kg, B.2.10)
которое может быть получено из уравнений B.2.5) и B.2.8).
Характеристическое уравнение B.2.9) в общем случае может иметь
несколько решений для каждого целого значения т. Удобно выра-
выражать эти решения как Ртп, где т и и-целые числа. Каждое собствен-
собственное значение Р^, соответствует моде волоконного световода. Со-
Соответствующее решение уравнения B.2.1) дает распределение поля
моды. Оказывается [4, 5], что существуют два типа мод световода,
обозначаемые Н Етп и Е Нтп. При т = 0 эти моды аналогичны
поперечной электрической (ТЕ) и поперечной магнитной (ТН) модам
планарного волновода, так как аксиальные компоненты электричес-
электрического и магнитного полей равны нулю. Однако при т > 0 моды
волоконного световода гибридные, т. е. все шесть компонент электро-
электромагнитного поля отличны от нуля.
Число мод, поддерживаемых световодом на данной длине волны,
зависит от его параметров-радиуса сердцевины а и разности
показателей преломления для сердцевины и оболочки nl—n2.
Важным параметром каждой моды является ее частота отсечки. Эта
частота определяется условием у = 0. Величина к, для которой у = 0,
для данной моды определяет частоту отсечки из уравнения B.2.10).
Полезно определить нормализованную частоту V соотношением
V=Kca = koa(n2-n22I'2, B.2.11)
где у.с находится из уравнения B.2.10) при подстановке у = 0.
Параметр V был введен в разд. 1.2; изложенное выше показывает,
откуда он возникает и какор его физический смысл.
Характеристическое уравнение B.2.9) позволяет определить вели-
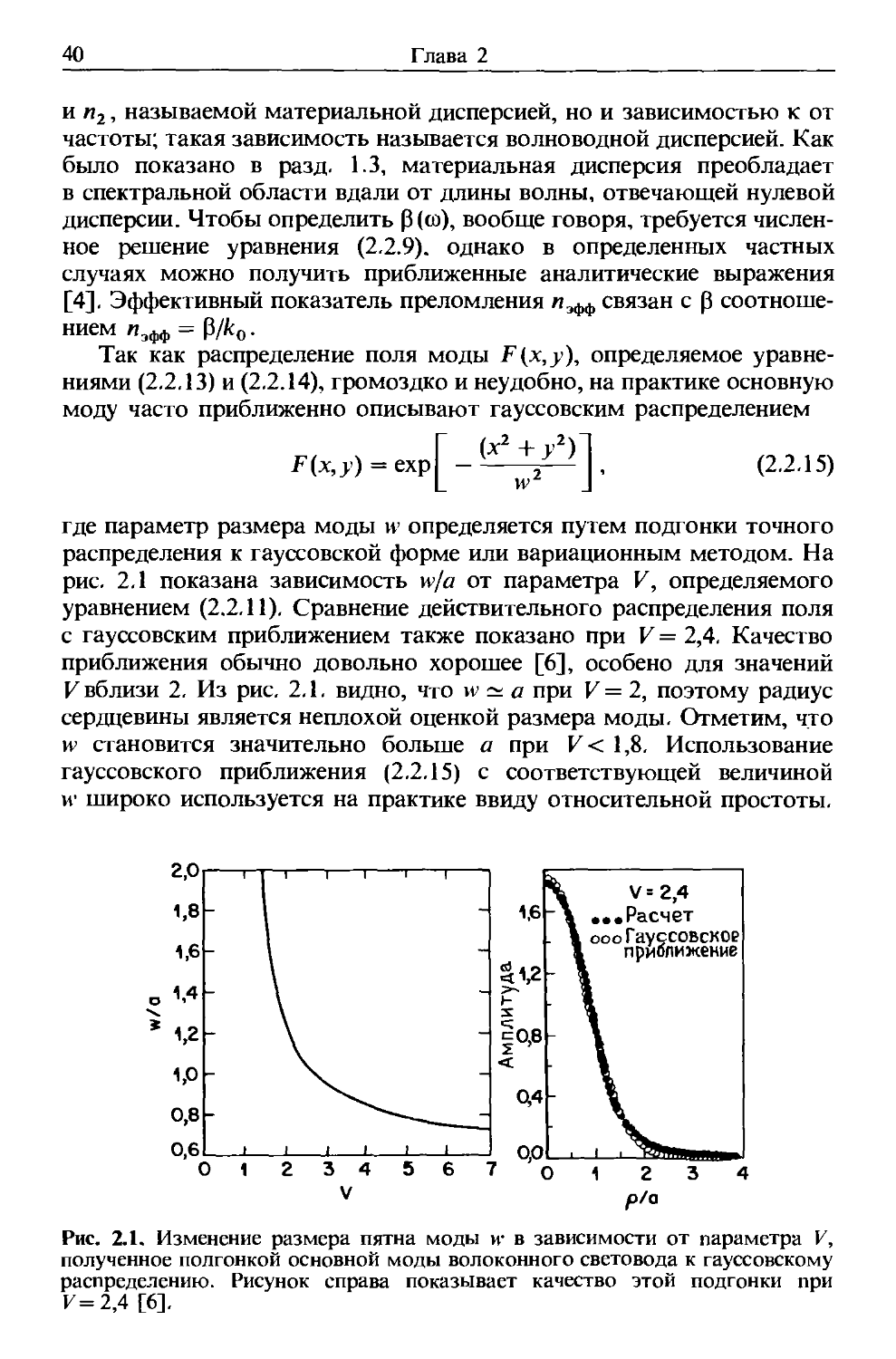
величины F-параметра отсечки разных мод. Эта довольно сложная
процедура описана во многих работах [4. 5]. Мы будем главным
образом рассматривать одномодовые световоды, поэтому ограни-
ограничимся обсуждением только условия отсечки, при котором волокно
может поддерживать только одну моду. В одномодовых световодах
поддерживается только //?\,-мода, называемая основной модой. Все
другие находятся за пределами отсечки, если параметр V< Vc, где
Кс-наименьший корень уравнения Jo(Fc) = 0 или Vc ^ 2,405. При
изготовлении волокон значение Fявляется критическим параметром.
Если V/Vc становится малым, то увеличиваются потери на микро-
микроизгибах в волокне. Поэтому на практике обычно делают волокна так.
чтобы параметр V был вблизи Vc. Длину волны отсечки Хс для
одномодового волоконного световода получаем, подставляя в
уравнение B.2.11) к0 = 2nfkc и V= 2,405. Для обычных значений
разности показателей преломления сердцевин и оболочки п1 — п2 =
= 0,005, Хс= 1,2 мкм при а = 4 мкм. Такое волокно поддерживает
Распространение волн в волоконных световодах 39
только одну моду для X > 1,2 мкм. Для того чтобы получить одно-
модовое волокно в видимой области, нужно, чтобы радиус сердце-
сердцевины был менее 2 мкм.
Поле Е(г, t), соответствующее моде НЕХХ, имеет три ненулевые
компоненты Ер, Е$ и Ez, или, в декартовых координатах, Ех, Еу и Ez,
среди которых либо Ех, либо Еу преобладает. Таким образом,
с большой точностью основную моду можно считать линейно-
поляризованной в х- или v-направлении в зависимости от того, Ех или
Еу преобладает. В этом отношении даже одномодовые волокна,
вообще говоря, не являются одномодовыми, так как они могут
поддерживать две ортогонально-поляризованные моды. Иногда
используют обозначение hPtm для линейно-поляризованных мод,
являющихся приближенным решением уравнения B.2.1). В этих
обозначениях основная //.?,,-мода соответствует L.P01-моде [5].
При идеальных условиях две ортогонально-поляризованные моды
вырожденны (т.е. они имеют одинаковые постоянные распростране-
распространения). На практике нерегулярности, такие, как случайные изменения
диаметра сердцевины вдоль длины волокна, снимают вырождение
мод, приводят к случайному смешиванию двух поляризационных
компонент и к изменению поляризации вводимого излучения при
распространении его вдоль волоконного световода. Как было сказано
в разд. 1.2.4, световоды, сохраняющие состояние поляризации,
получаются путем создания сильного двулучепреломления, снимаю-
снимающего вырождение мод. Такие волокна могут сохранять линейное
состояние поляризации, если излучение вводится поляризованным
в направлении одной из главных осей световода. Предполагая, что
вводимое излучение поляризовано вдоль главной оси (например,
а-оси). электрическое поле основной моды НЕХХ приближенно можно
представить как
Ё(г,со)= x{,4(co)F(x,v)exp(/p(co)z)}. B.2.12)
где А (со) - нормировочная постоянная. Поперечное распределение
поля в сердцевине следует из уравнения B.2.6):
р^а. B.2.13)
где р = (х2 + у2I/2-радиальное расстояние. Снаружи сердцевины
световода поле экспоненциально спадает, как [4]
F(*,>¦) = (a/pI/2Jo(Ka)exp[-y(p-<7)], p > а, B.2.14)
где Кт(ур) в уравнении B.2.7) приближено первым членом асимпто-
асимптотического разложения и добавлен постоянный множитель, чтобы
выполнялось условие равенства F(x,y) при р = яв уравнении B.2.13)
и B.2.14). Постоянная распространения Р(со) в уравнении B.2.12)
является решением характеристического уравнения B.2.9). Частотная
зависимость Р(со) определяется не только частотной зависимостью и.
40
Глава 2
и п2, называемой материальной дисперсией, но и зависимостью к от
частоты; такая зависимость называется волноводной дисперсией. Как
было показано в разд. 1.3, материальная дисперсия преобладает
в спектральной области вдали от длины волны, отвечающей нулевой
дисперсии. Чтобы определить р (со), вообще говоря, требуется числен-
численное решение уравнения B.2.9). однако в определенных частных
случаях можно получить приближенные аналитические выражения
[4]. Эффективный показатель преломления иэфф связан с р соотноше-
соотношением иэфф = РА0.
Так как распределение поля моды F(x,y), определяемое уравне-
уравнениями B.2.13) и B.2.14), громоздко и неудобно, на практике основную
моду часто приближенно описывают гауссовским распределением
B.2.15)
где параметр размера моды w определяется путем подгонки точного
распределения к гауссовскои форме или вариационным методом. На
рис. 2.1 показана зависимость w/a от параметра V, определяемого
уравнением B.2.11). Сравнение действительного распределения поля
с гауссовским приближением также показано при V = 2,4. Качество
приближения обычно довольно хорошее [6], особено для значений
V вблизи 2. Из рис. 2.1. видно, что w ~ а при V = 2, поэтому радиус
сердцевины является неплохой оценкой размера моды. Отметим, что
w становится значительно больше а при V < 1,8. Использование
гауссовского приближения B.2.15) с соответствующей величиной
и1 широко используется на практике ввиду относительной простоты.
Рис. 2.1. Изменение размера пятна моды и* в зависимости от параметра V,
полученное подгонкой основной моды волоконного световода к гауссовскому
распределению. Рисунок справа показывает качество этой подгонки при
К=2,4 [6].
Распространение волн в волоконных световодах 41
2.3. ОСНОВНОЕ УРАВНЕНИЕ РАСПРОСТРАНЕНИЯ
Большинство нелинейных эффектов в волоконных световодах
изучаются с использованием импульсов длительностью от ~ 10 не до
~ 10 фс. Когда такие импульсы распространяются в световоде, на их
форму и спектр влияют как дисперсионные, так и нелинейные
эффекты. В этом разделе мы выведем основное уравнение, описываю-
описывающее распространение оптических импульсов в волоконных свето-
световодах, как в нелинейной среде с дисперсией. Начнем вывод с волно-
волнового уравнения B.1.7). Используя уравнения B.1.8) и B.1.17), его
можно записать в виде
с2 dt2 " dt2 ™ dt2 '
где линейная PL и нелинейная PNL части индуцированной поляризации
связаны с электрическим полем Е соотношениями B.1.9) и B.1.10).
Для того чтобы решить уравнение B.3.1), нужно сделать не-
несколько упрощающих предположений. Во-первых, PNL будем считать
малым возмущением по отношению к PL . Во-вторых, предположим,
что состояние поляризации оптического поля сохраняется вдоль
длины волокна, так что справедлив скалярный подход. В-третьих,
будем считать оптическое поле квазимонохроматическим, т. е. спектр
с центром на частоте со0 имеет ширину Дсо, такую, что Дсо/со0 « 1. Так
как со0 ~ 1015 с, последнее допущение верно для импульсов дли-
длительностью > 0,1 пс (Дсо < 1013 с).
Используя приближение медленно меняющихся амплитуд, можно
выделить быстро изменяющуюся часть электрического поля, записав
Е(г,/) = -х[?(г,t)exp(— ia>oi) + компл. сопр.], B.3.2)
где «компл. сопр.» обозначает комплексно-сопряженное выражение,
х-единичный вектор в направлении поляризации электрического
поля, которое предполагается линейно-поляризованным в направле-
направлении оси х. Е(г, t)-медленно изменяющаяся функция времени (по
отношению к периоду оптической волны). Поляризации PL и PNL
также можно выразить подобным же образом, записав
PL (г, t) = -х [Д(г, 0ехр(- /со0 0 + компл. сопр.]. B.3.3)
^ i(i)ot) + компл. сопр.]. B.3.4)
Лнейную часть поляризации PL можно получить, подставляя уравне-
уравнение B.3.3) в уравнение B.1.9). В результае имеем
42 Глава 2
PL(T,t) = E0 f x?(t - t')E(r.Oexp[_iw0(t - t'
— CO
cc
= e0 I Xxlx (coJ?(r,co-cOo)exp[-/(co-co0)r]</co, B.3.5)
— OD
где ?(r, со) фурье-преобразование ^(г, г), определяемое так же, как
в уравнении B.1.12).-
Подставив уравнение B.3.4) в уравнение B.1.10), получаем уравне-
уравнение для нелинейной поляризации PVL(r, t), которое существенно
упрощается, если предположить, что нелинейный отклик мгновенный.
Тогда зависимость х<3> от времени в уравнении B.1.10) будет в виде
трех дельта-функций 5 (t — ty). В результате получаем, что
Р^(^') = еоХC>;Е(г,ОЕ(г,0е(г,0. B.3.6)
Приближение мгновенного нелинейного отклика означает пренебре-
пренебрежение дисперсией х<3)- Оно допустимо для импульсов длительностью
> 0,1 пс, так как электронный вклад в х<3> проявляется в волоконных
световодах во временном масштабе 1 —10 фс. Подставив уравнение
B.3.2) в уравнение B.3.6), находим, что PNL(r, t) состоит из одной
части, осциллирующей на частоте со0, и другой, осциллирующей на
частоте третьей гармоники Зсо0, которой обычно пренебрегают в
световодах (см. гл. 10). Используя уравнение B.3.4), для P(r, t)
получаем
^L{T,t) = E0ENLE(r,t), B.3.7)
где eNL~нелинейный вклад в диэлектрическую проницаемость,
определяемый как
е№=^х??**|?(г,0|2. B.3.8)
Чтобы получить волновое уравнение для медленно меняющейся
амплитуды E(r,t). более удобно использовать спектральное пред-
представление. В общем случае это невозможно, так как уравнение B.3.1)
нелинейное ввиду зависимости eNL от интенсивности. Поэтому
приближенно eNL считается постоянной при выводе уравнения распро-
распространения для ?(г, t) [7, 8]. Это приближение" оправдано с точки
зрения приближения медленно меняющихся амплитуд и того, что PNL
считается малым возмущением. Подставляя уравнения B.3.2)-B.3.4)
в уравнение B.3.1), находим, что фурье-компоненты Ё(т, со — со0),
определяемые как
¦ ?(r,co-co0)= f !(г,Оехр[/(со-со0H<Л, B.3.9)
— 00
удовлетворяют уравнению
V2?4-e(co)fcg?=O, B.3.10)
Распространение волн в волоконных световодах 43
где к0 = со/с, а
е(ш)=1+хЙИ + е^ B.3.11)
есть диэлектрическая проницаемость, нелинейная часть которой enl
определяется уравнением B.3.8). Так же как и в уравнении B.1.14),
можно из диэлектрической проницаемости определить показатель
преломления п и коэффициент поглощения а. Величина п получается
зависимой от интенсивности из-за eNL, поэтому удобно использовать
определение
w(co) = w(co) + w2|?|2. B.3.12)
Используя выражение е = (й + ia/2k0J и уравнения B.3.8), B.3.11)
и B.3.12), получаем нелинейный показатель преломления
и2=^Х&*- B.3.13)
Линейный показатель. преломления п и коэффициент поглощения
а связаны с действительной и мнимой частями х» »как и в уравнениях
B.1.15) и B.1.16).
Уравнение B.3.10) можно решить, используя метод разделения
переменных. Будем искать решение в виде
?(г,со - со0) = F(x,j) Л(г,со - co0)exp(/poz), B.3.14)
где A(z,со)-медленно меняющаяся функция z, po-волновое число,
которое будет определено позднее. Уравнение B.3.10) сводится к
двум следующим уравнениям для F(x,y) и A(z,(o):
B.3.15)
^ B.3.16)
Получая уравнение B.3.16), мы пренебрегли второй производной
д2 A/dz2, используя предположение, что A(z,со)-медленно меняющая-
меняющаяся функция z. Волновое число Р определяем как решение уравнения
B.3.15) для мод волоконного световода, следуя тому же способу,
который использовался в разд. 2.2. Диэлектрическую проницаемость
е(со) в уравнении B.3.15) можно приближенно выразить так:
B.3.17)
где Ди-малое возмущение:
^. B.3.18)
44 Глава 2
Уравнение B,3,15) решается с использованием теории возмущений
первого порядка [9]. Сначала находятся распределение поля моды
F(x,y) и соответствующая постоянная распространения р (to) при
е = и2. Для одномодового световода F(x,y) соответствует основной
моде НЕ11, определяемой уравнениями B,2,13) и B,2,14) или. в
гауссовском приближении, уравнением B,2,15), Затем в уравнении
B.3.15) учитывается эффект An. В первом приближении Ди не влияет
на распределение поля моды F(x,y), но изменяет собственное значе-
значение Р:
р(со) = р(со) + Др, B,3,19)
где
fcof ] An\F(x,y)\2dxdy
Др = ~-f , B,3,20)
f f \F(x,y)\2dxdy
— GO
На этом завершается формальное решение уравнения B,3.1) в
низшем порядке возмущений PNL. Используя уравнения B,3,2) и
B,3,12), электрическое поле Е можно записать в виде
Е(гл) = x-{F(x,y)A(z,t)exp[i(fioz - to0r)] + компл, сопр,} ,
B,3,21)
Фурье-преобразование A(z,a — со0) медленно меняющейся амплиту-
амплитуды A(z,t) удовлетворяет уравнению B,3,16). которое может быть
записано как
дА
— =/[р(ю) + Др-ро]Л, B,3,22)
где было использовано уравнение B,3,19) и приближения р2 — Ро —
=;2ро(Р —ро). Обратное фурье-преобразование уравнения B,3,22)
дает уравнение распространения для A (z, t). С этой целью разложим
Р(со) в ряд Тейлора в окрестности со0:
р(со) = р0 + (со - со0) pt + -(со - со0J р2 + -(со - со0K р3 + ,,, ,
2 о
B,3,23)
где
[?]
Кубическим слагаемым и слагаемыми более высокого порядка в этом
Распространение волн в волоконных световодах 45
разложении обычно пренебрегают, если ширина спектра Дсо «со0.
Это соответствует квазимонохроматическому приближению, исполь-
использованному при выводе уравнения B.3.22), и справедливо для им-
импульсов длительностью > 0,1 пс. Если Р2 — 0 для некоторого значе-
значения со0 (вблизи длины волны нулевой дисперсии световода, как
отмечалось в разд. 1.3.3), может возникнуть необходимость включить
в рассмотрение кубический член. Подставим уравнение B.3.23) в
уравнение B.3.22) и сделаем обратное фурье-преобразование:
A(z,t) = — | A(z,w — юо)ехр[ — /(со — co0)f]</co. B.3.25)
Фурье-преобразование оператора со — со0 заменяется оператором
дифференцирования i(d/dt). В результате получаем
дА -***-**-¦ B.з.26)
Член с Др описывает эффект оптических потерь и нелинейные
эффекты. Использовав уравнения B.3.18) и B.3.20) для Др, после
подстановки их в уравнение B.3.26) получаем
дА „ д2А i д2А
где нелинейный коэффициент у определяется выражением
ф
Параметр ^эфф называется эффективной площадью моды; он равен
\F(x,y)\2dxdyY
-¦ B-3-29)
f f \F(x,y)\*dxdy
— ao
Для определения эффективной площади моды в основном исполь-
используют распределения поля основной моды F(x,y) из уравнений B.2.13)
и B.2.14). Ясно, что Лэфф зависит от параметром волокна: радиуса
сердцевины и разности показателей преломления сердцевины и
оболочки. Ее можно без труда оценить, используя гауссовское
приближение основной моды B.2.15):
Лэфф = тш-2. B.3.30)
Параметр гауссовской моды w зависит от параметров световода
и может быть определен из рис. 2.1 и уравнения B.2.11). Обычно
46 Глава 2
у4эфф = 10-20 мкм2 в видимой области спектра и в диапазоне
50-80 мкм2 в области 1,5 мкм. Поэтому у может изменяться в диапа-
диапазоне 2-30 Вт -км в зависимости от длины волны, если положить
и2 = 3,2-106см7Вт.
Уравнение B.3.27) описывает распространение оптических им-
импульсов в одномодовых световодах. Оно описывает эффекты опти-
оптических потерь (а), хроматической дисперсии (Р, и Р2) и нелинейности
(у). Физический смысл параметров pt и Р2 рассматривается в разд.
1.2.3. В частности, огибающая импульса распространяется с группо-
групповой скоростью i>g = l/pt, a P2 характеризует дисперсию групповых
скоростей (ДГС). ДГС может быть положительной или отрицатель-
отрицательной в зависимости от того, длина волны X больше или меньше длины
волны нулевой дисперсии XD световода (см. рис. 1.5). В области
аномальной дисперсии (X > XD) величина Р2 отрицательная, и в
волоконном световоде могут распространяться оптические солитоны
(гл. 5). Обычно параметр р2 с* 60 пс2/км в видимой области спектра
и равен — 20 пс2/км на длине волны 1,55 мкм; смена знака происходит
около 1,3 мкм.
Уравнение распространения B.3.27) хорошо описывает многие
нелинейные эффекты, тем не менее его в некоторых случаях в зависи-
зависимости от условий эксперимента следует модифицировать. Например,
уравнение B.3.27) не учитывает эффектов вынужденного неупругого
рассеяния ВРМБ и ВКР, обсуждавшихся в разд. 1.3.2. Если пиковая
мощность импульса больше некоторого порогового уровня, под
действием ВКР и ВРМБ энергия этого импульса накачки может быть
передана стоксову импульсу, распространяющемуся совместно с
импульсом накачки (в прямом или противоположном направлении).
Эти два импульса взаимодействуют друг с другом посредством ВКР
или ВРМБ усиления и фазовой кросс-модуляции. Похожая ситуация
возникает, когда два импульса на разных длинах волн (спектральное
расстояние между ними больше, чем их ширины спектров) вводятся
в световод. Распространение нескольких импульсов описывается
системой уравнений, подобных уравнению B.3.27), модифицирован-
модифицированных так, чтобы учесть эффекты ФКМ и ВКР или ВРМБ-усиления.
Нлинейные эффекты, связанные с распространением одновременно
в волокне многих импульсов, обсуждаются в гл. 7-9.
Уравнение B.3.27) также следует модифицировать, если рас-
рассматривается распространение сверхкоротких импульсов длитель-
длительностью < 100 фс. Ширина спектра таких импульсов Дсо становится
сравнимой с несущей частотой со0, и некоторые приближения, сделан-
сделанные при выводе уравнения B.3.27), становятся необоснованными.
Кроме того, спектр таких коротких импульсов достаточно широкий
(> 5 ТГц), так что под действием ВКР низкочастотные компоненты
спектра могут усиливаться, получая энергию от высокочастотных
компонент спектра того же импульса. В результате спектр короткого
Распространение волн в волоконных световодах 47
импульса смещается в длинноволновую область спектра при распро-
распространении в световоде. Это явление называется вынужденным комби-
комбинационным саморассеянием [10]. Физически этот эффект объясняется
запаздывающим нелинейным откликом среды [11]. При выводе
уравнения B.3.27) в этом случае нельзя использовать уравнение
B.3.6), нужно использовать более общую форму записи нелинейной
поляризации B.1.10).'Включение в рассмотрение этих эффектов в
приближении малых возмущений [12] дает три дополнительных
члена в уравнении B.3.27). Обобщенное уравнение распространения
принимает вид
дА о дА i д2 А а , , 1 д* А
Легко объяснить смысл последних трех членов более высокого
порядка малости в уравнении B.3.31). Член, пропорциональный Р3>
характеризует кубическое слагаемое в разложении постоянной рас-
распространения в уравнении B.3.23). Этот член описывает дисперсион-
дисперсионные эффекты высшего порядка, которые становятся важными для
сверхкоротких импульсов с их широкими спектрами, даже когда
длина волны X находится далеко от длины волны нулевой дисперсии
[13, 14]. Член, пропорциональный «j, характеризует первую произ-
производную медленно меняющейся части PNL нелинейной поляризации
в уравнении B.3.1). Этот член вызывает самоукручение крыла им-
импульса (образование ударной волны огибающей), явление, привлек-
привлекшее большое внимание [15-23]. Параметр ау приближенно равен
<*!=—, B.3.32)
где у определяется в уравнении B.3.38).
Последний член уравнения B.3.31), пропорциональный а2, возни-
возникает как результат запаздывающего нелинейного отклика и описы-
описывает эффект самосмещения частоты (вынужденного комбинационного
саморассеяния) [10, 11]. В общем выражении B.1.10) для нелинейной
поляризации фурье-преобразование восприимчивости третьего по-
порядка %т- комплексная, зависящая от частоты функция. Мнимая
часть iiy> связана с ВКР-усилением и вносит вклад в мнимую часть а2,
а действительная часть х<3> вносит вклад в действительную часть а2 ¦
Моделируя этот эффект, часто пренебрегают действительной частью
я2 [22-26], записав а2 в виде
a2 = iyTR, B.3.33)
где у-параметр нелинейности, определенный в уравнении B.3.28),
48 Глава 2
и TR связано с наклоном линии ВКР-усиления [11], если предполо-
предположить, что оно линейно изменяется вблизи несущей частоты (см. разд.
8.1). Величина TR порядка ~5 фс.
Прежде чем решать уравнение B.3.31), полезно перейти в систему
координат, движущуюся с групповой скоростью vg импульса (так
называемые бегущие координаты). Выполним преобразование
T=t-zfva=t-faz B.3.34)
и, использовав уравнения B.3.31)—B.3.33), получим
ЗА a i д2 А 1 д3 А
+A^
B-з-35>
Это уравнение можно использовать для изучения распространения
импульсов длительностью до ~ 10 фс. В случае импульсов длитель-
длительностью Го < 100 фс, такой, что со0То » 1 и TR/T0 « 1, можно ис-
использовать более простое уравнение
г) A i \ ?} А
'4 |3
которое также можно получить из уравнения B.3.27), используя
преобразование B.3.34). В особом случае а = 0 уравнение B.3.36)
называется нелинейным уравнением Шредингера, подробно изучен-
изученным в связи с солитонами [27-30]. Проводя аналогию, уравнение
B.3.35) иногда называют обобщенным нелинейным уравнением
Шредингера. v
Важно отметить, что уравнение B.3.35) описывает эффект за-
задержанного нелинейного отклика среды приближенно. В более общем
случае нелинейная часть Аи показателя преломления рассматривается
зависящей от времени. Тогда уравнение B.3.35) заменяется на уравне-
уравнение [26]
дА a i д2А 1 д3 А
А ^^
| B.3.37)
где Аи удовлетворяет уравнению
TR^+An = n2\A\2. B.3.38)
Время отклика TR оценивается величиной 2-4 фс путем сопоставле-
Распространение волн в волоконных световодах 49
ния результатов эксперимента [26] и предсказаний уравнений B.3.37).
Уравнение B.3.38) предполагает экспоненциальный спад нелинейного
отклика, и его решение имеет вид
Tr о
Уравнение B.3.35) можно получить, разлагая \А{Т— Т')\2 в ряд
Тейлора в окрестности Г и сохраняя только член первого порядка.
В обшем случае экспонента в уравнении B.3.39) заменяется на
функцию отклика h(T'), которая находится на основании спектра
ВКР-усиления.
2.4. ЧИСЛЕННЫЕ МЕТОДЫ
Уравнение распространения B.3.35)-нелинейное дифференциаль-
дифференциальное уравнение с частными производными, которое, вообще говоря,
нельзя решить аналитически, за исключением некоторых частных
случаев, когда для решения применим метод обратной задачи рассея-
рассеяния [27]. Поэтому часто для изучения нелинейных эффектов в свето-
световодах необходимо численное моделирование. Для этой цели можно
использовать множество численных методов [31-38], которые
можно отнести к одному из двух классов: 1) разностные методы и 2)
псевдоспектральные методы. Вообще говоря, псевдоспектральные
методы на порядок или даже более быстрее при той же точности
счета [39]. Одним из наиболее широко используемых методов реше-
решения задачи распространения импульсов в нелинейной среде с диспер-
дисперсией является фурье-метод расщепления по физическим факторам
(SSFM) [33, 34]. Относительно большая скорость счета этим методом
по сравнению с большинством методов конечных разностей достига-
достигается благодаря использованию алгоритма быстрого фурье-преобра-
зования [40]. В этом разделе кратко описывается фурье-метод с
расщеплением по физическим факторам, а также его применение для
задачи распространения импульсов в волоконном световоде.
Чтобы понять принцип метода SSFM, удобно формально
записать уравнение B.3.35) в виде
ЗА . .
— =(D + N)A, B.4.1)
cz
где б-дифференциальный оператор, учитывающий дисперсию и
поглощение в линейной среде, а N нелинейный оператор, описываю-
описывающий действие нелинейностей световода на распространение импульса.
Эти операторы записываются следующим образом:
id2 1 ёъ а
50Глава 2
Вообще говоря, дисперсия и нелинейность действуют в световоде
совместно. В методе SSFM приближенное решение получают, пред-
предполагая, что при распространении оптического поля на малое рас-
расстояние А в световоде нелинейные и дисперсионные эффекты дейст-
действуют независимо, а именно распространение от точки z к z + А
описывается в два уже последовательных шага. На первом действует
только нелинейность и /5 = 0 в уравнении B.4.1). На втором шаге
действует только дисперсия и N = 0 в уравнении B.4.1). Математи-
Математически
A (z + А, Г) ^ exp (A D) exp (A N) A (z, Г). B.4.4.)
Действие экспоненциального оператора ехр(А/5) можно выполнить
в фурье-представлении, следуя формуле
exp(AZ))#(z, Г) = {F~Jexp[AD(/со)]F} B(z, Г), B.4.5)
где F обозначает оператор фурье-преобразования, /5 (ко) можно
получить из уравнения B.4.2), заменяя дифференциальный оператор
ё/et на /со, где со-частота в спектральном представлении. Так как
D (/со) в фурье-пространстве есть просто число, уравнение B.4.5)
решается непосредственно. Использование алгоритма БПФ [40]
делает решение уравнения B.4.5) относительно быстрым. Именно по
этой причине данный метод быстрее (вплоть до двух порядков
величины) для большинства разностных методов [39].
Чтобы оценить точность SSFM-метода, заметим, что формально
точное решение уравнения B.4.1) дается уравнением
ч
A{z + h,T) = exp [A0 + N) A(z, T), B.4.6)
если предположить N независимым от z. Здесь полезно вспомнить
формулу Бейкера Хаусдорфа [41] для двух некоммутирующих
операторов й и В:
+ ?+-[46] +—
B.4.7)
где [а, В] = аВ — Ва. Сравнение уравнений B.4.4) и B.4.6) показывает,
что БПФ игнорирует некоммутативность операторов D и N. Под-
Подставляя в уравнение B.4.7) а — hD и В = AN, находим, что слагаемое,
содержащее наибольшую ошибку, происходит из одинарного ком-
коммутатора 1/2 А2 [Д ft\. Таким образом, SSFM имеет точность до
второго порядка по шагу А.
Точность метода может улучшить, применив другую процедуру
Распространение волн в волоконных световодах 51
прохождения оптическим импульсом одного шага (от г до г + А).
В этой процедуре уравнение B.4.4) заменяется следующим уравне-
уравнением:
А (г + А, Т) ~ ехр Г^ б] ехрП JV (z') <fe'l exp Г^ б] А (г, Г).
B.4.8)
Главное отличие состоит в том, что действие нелинейности учиты-
учитывается в середине, а не на краю шага. Из-за симметричной формы
экспоненциального оператора в уравнении B.4.8) этот метод назы-
называют симметричным [42]. В интеграле в центральной экспоненте
полезно включить зависимость от z нелинейного оператора N.
Если шаг А достаточно мал, интеграл можно приближенно записать
как ехр (AN) так же, как в уравнении B.4.4). Наибольшее преиму-
преимущество этой симметризованной формы уравнения B.4.8) состоит
в том, что ошибка в этом случае будет третьего порядка малости по
Л, так как она будет определяться двойным коммутатором в уравне-
уравнении B.4.7). Это можно доказать, применив уравнение B.4.7) дважды
к уравнению B.4.8).
Точность метода можно еще улучшить, если приблизить интеграл
в уравнении B.4.8) более того, нежели величиной hN(z). Самый
простой способ-это применение для вычисления интеграла правила
трапеций:
АГ I
г') dz' ~ - \N (z) + N (z + A) . B.4.9)
Однако применить уравнение B.4.9) не просто, так как N{z + А)
неизвестно в центре сегмента в точке z + А/2. Нужно воспользоваться
методом итераций, который начинается заменой N (г + А) на N (:).
Затем находится A (z + А, Г) из уравнения B.4.8), которое в свою
очередь используется для нахождения величины N {z + А). Итерацион-
Итерационная процедура требует дополнительных затрат времени, тем не менее
полное время расчета можно сократить, увеличив размер шага
А благодаря увеличению точности численного алгоритма. На прак-
практике достаточно всего двух итераций.
Применять SSFM-метод относительно просто. Как показано на
Рис. 2.2, длина световода делится на множество сегментов, которые
не обязательно должны быть одинаковой длины. Оптический им-
импульс преобразуется от сегмента к сегменту в соответствии с уравне-
уравнением B.4.8). А именно, оптическое поле A (z, Г) сначала проходит
расстояние А/2, на котором действует только дисперсия групповых
скоростей; при этом используются алгоритм БПФ и уравнение B.4.5).
В точке z + А/2 поле умножается на нелинейный фактор, который
характеризует действие нелинейности на полной длине сегмента А, и,
N (
52
Глава 2
Только дисперсия Только нелинейность
АB,Т)
z=0
Рис. 2.2. Схема симметризованного SSF-метода, используемого для числен-
численного моделирования. Длина световода разбивается на большое количество
сегментов длины А. Внутри сегмента действие нелинейности учитывается
в центральной точке, указанной штриховой линией.
наконец, поле проходит оставшееся расстояние А/2, где действует
только дисперсия; в результате получается A (z + h, Г). Таким обра-
образом, предполагается, что нелинейность действует только в средней
точке каждого сегмента (штриховые линии на рис. 2.2).
SSFM-метод применялся для решения многих разнообразных
задач оптики, таких, как распространение волн в атмосфере [42, 43],
в световодах с градиентным профилем показателя преломления [44,
45], в полупроводниковых лазерах [46-48], в неустойчивых резона-
резонаторах [49, 50] и в волноводных ответвителях [51, 52]. Этот метод
часто называют методом распространения пучка [44-52], если его
применяют для описания стационарного распространения, когда
дисперсия заменяется дифракцией. В частном случае опирания
распространения импульсов в волоконных световодах он впервые
применялся в 1973 г. [28]. В настоящее время SSFM-метод широко
распространен [53-64] ввиду его большей скорости по сравнению
с разностными методами [39]. Он относительно прост в применении,
но требует осторожности в выборе размеров шагов по г и Г, чтобы
сохранить нужную точность. В частности, нужно проверять точность,
вычисляя сохраняющиеся величины, такие, как энергия импульса (в
отсутствие поглощения), вдоль длины волокна. Оптимальный выбор
размера шага зависит от степени сложности задачи. Существует
несколько рекомендаций в выборе шага; иногда необходимо повто-
повторять вычисления, уменьшив шаг, чтобы быть уверенным в точности
численного моделирования.
ЛИТЕРАТУРА
1. Magid L. M., Electromagnetic Fields, Energy and Waves Wiley, New York.
1972, Ch. 9.
2. Shen Y.R., Principles of Nonlinear Optics, Wiley, New York, 1984. [Имеется
Распространение волн в волоконных световодах 53
перевод: Шен И. Р. Принципы нелинейной оптики. М.: Наука, 1989.]
3. Schubert М., Wilhebni В., Nonlinear Optics and Quantum Electronics, Wiley,
New York, 1986, Ch. 1.
4 Marcuse D., Light Transmission Optics, van Nostrand Reinhold, New York,
1982, Ch. 8.
5. Snyder A. W., Love J. D., Optical Waveguide Theory, Chapman and Hall,
London, 1983, Ch. 12 15. [Имеется перевод: Снапдер А.В., Лав Д.Д. Тео-
Теория оптических волноводов.-М.: Мир, 1987.]
6. Marcuse D., J. Opt. Soc. Am. 68, 103 A978).
7. Agrawal G. P.. in: Supercontinuum Laser Source, ed. by R. R. Alfano,
Springer-Verlag, Heidelberg, 1989, Ch. 3.
8 Haus H. A., Waves and Fields in Optoelectronics, Prentice-Hall, Englewood
Cliffs, 1984, Ch. 10.
9. Morse P. M., Feshbach H.. Methods of Theoretical Physics, McGraw-Hill, New
York, 1953, Ch. 9.
10. Mitschke F.M., Mollenauer L.F., Opt. Lett., 11, 659 A986).
11. Gordon J.P., Opt. Lett., 11, 662 A986).
12. Kodama Y., Hasegawa A., IEEE J. Quantum Electron., QE-23, 510 A987).
13. BourkoffE.. Opt. Lett., 12, 272 A987).
14. Головченко Е.А. и <)р.-Письма в ЖЭТФ, 1987, т. 45, с. 73.
15. DeMartiniF. et al.. Phys. Rev., 164, 312 A967).
16. Grischkowsky D., Courtens E.. Armstrong J.A.. Phys. Rev. Lett, 31, 422 A973).
17. Tzoar N.. Jain M., Phys. Rev., A23, 1266 A981).
18. Anderson D.. Lisak M., Phys. Rev. A27, 1393 A983).
19. Yang G., Shen Y.P., Opt. Lett., 9, 510 A984).
20. Manassah J. T. et al., IEEE J. Quantum Electron., QE-22, 197 A986).
21. Головченко Е.А. и др.-ДАН СССР, 1986, т. 288, с. 851-856.
22. Ohkuma К., Ichikawa Y.H., Abe У., Opt. Lett., 22, 516 A987).
23. Kodama У., Nozaki К., Opt. Lett., 12, 1038 A987).
24. Beaud'P. et al.. IEEE J. Quantum Electron., QE-23, 1938 A987).
25. Tai K., Hasegawa A., Bekki N.. Opt. Lett., 13, 392 A988).
26. Гр\-динин А.Б. и др. Письма в ЖЭТФ, 1987, т. 45, с. 211.
27. Захаров В.Е., Шабот А. Б. ЖЭТФ, 1971, т. 61, с. 118.
28. Hasegawa A.. Tappert F., Appl. Phys. Lett., 23. 142 A973).
29. Satsuma J.. Yajima N.. Prog. Theor. Phys. Supply 55, 284 A974).
30. Dodd R. K. et al., Solitons and Nonlinear Wave Equations, Academic, New
York A982).
31. Карпман В.И., Крушкаль Е.М-ЖЭТФ, 1969, т. 55, с. 530.
32. Yajima N.. Outi A.. Prog. Theor. Phys, 45, 1997 A971).
33. Hardin R.H., Tappert F.D.. SIAM Rev. Chronicle, 15, 423 A973).
34. Fisher R.A., Bischel W.K., Appl. Phys. Lett, 23, 661 A973), J. Appl. Phys, 46,
4921 A975).
35. Ablowitz M.J., Ladik J.f\ Stud. Appl. Math., 55, 213 A976).
36. Greig I.S.. Morris J.L., J. \:omp. Phys., 20, 60 A976).
yi-Fomberg В., Whitham G.B.. Phil. Trans. Roy. Soc, 289, 373 A978).
38. Delfour M., Fortin M.. Payre G., J. Сотр. Phys., 44, 277 A981).
39. Taiia T.R., Ablowitz M.J.. J. Сотр. Phys., 55, 203 A984).
40. Coolev J. W.. Tukey J. W.. Math. Comput., 19, 297 A965).
41. Weiss G.H., Maradudin A. A., J. Math. Phys., 3, 771 A962).
42. Fleck J.A.. Morris J.R., Feit M.D., Apl. Phys., 10, 129 A976).
43. Lax M., Batteh J.H., Agrawal G. P.. J. Apl. Phys., 52, 109 A981).
44. Feit M.D.. Fleck J.A., Appl. Opt., 17, 3990 A978).
45. Feit M.D.. Fleck J.A., Appl. Opt., 18, 2843 A979).
46. Agrawal G. P., J. Appl. Phys., 56, 3100 A984).
47. Meissner P., Patzak E, Yevick D., IEEE J, Quantum Electron,, QE-20, 899
A984),
54 Глава 2
48. Agrawal G. P., J. Lightwave Technol., LT-2, 537 A984).
49. Sziklas E.A., Siegman A.E., Appl. Opt., 14, 1874 A975).
50. Lax M. et al, J. Opt. Soc. Am., A2, 732 A985).
51. Hermansson В., Yevick D., Danielsen P., IEEE J, Quantum Electron, QE-19,
1246 A983).
52. Thylen L, et al. Opt. Lett., 11, 739 A986),
53. Yevick D,, Hermansson В.. Opt. Commun., 47, 101 A983).
54. Выслоух В. А,, Матвеева Т, А,-Квант, электрон,, 1983, т. 10, с. 1688.
55. Blow K.J., Doran N.J., Cummins Е., Opt, Commun,, 48, 181 A983),
56. Hasegawa A.. Opt. Lett,, 9, 288 A984),
57. Lassen H.E. et al. Opt. Lett,, 10, 34 A985),
58. PotasekM.J., Agrawal G. P., Pinault S.C., J, Opt, Soc, Am,, B3, 205 A986),
59. Agrawal G. P., Potasek M.J.. Phys, Rev,, A33, 1765 A986),
60. Dianov E.M.. Prokhorov A.M.. Serkin V.N., Opt, Lett,, 11, 168 A986),
61. WaiP.K. et al, Opt. Lett,, 11, 464 A986),
62. Menyuk C.R., Opt. Lett., 12, 614 A987).
63. Выслоух В, А,, Матвеева Т. А, Квант, электрон,, 1987, т. 14, с. 792,
64. Krokel D,. Phys. Rev, Lett., 60, 29 A988).
65. van Roex J.. van der Donk J,. Lagasse P.E., J. Opt. Soc. Am. 71, 803 A981).
66. Thylen L, Opt. Quantum Electron,, 15, 433 A983),
Глава 3
ДИСПЕРСИЯ ГРУППОВЫХ СКОРОСТЕЙ
В предыдущей главе было показано, что совместное действие
эффектов дисперсии групповых скоростей (ДГС) и фазовой само-
самомодуляции (ФСМ) на оптический импульс, распространяющийся
внутри световода, можно изучать, решая основное уравнение рас-
распространения. Прежде чем рассматривать общий случай, будет
поучительно сначала рассмотреть действие только ДГС на эволюцию
импульса в световоде. В этой главе мы исследуем задачу о распро-
распространении импульса в световоде, считая его линейной средой. В разд.
3.1 обсуждаются условия, при которых эффекты ДГС преобладают
над нелинейными эффектами. С этой целью вводятся две характерные
длины, связанные с ДГС и ФСМ. Дисперсионное уширение опти-
оптических импульсов рассматривается в разд. 3,2 для импульсов разных
форм, В разд. 3.2 также обсуждается, как влияет начальная частотная
модуляция импульса на действие ДГС. В разд. 3,3 результаты
распространяются на случай уширения импульсов из-за дисперсии
высшего порядка. В заключение в разд. 3,4 показано, что эффекты
ДГС ограничивают функционирование оптических систем связи при
скорости передачи информации порядка нескольких Гбит/с.
3.1. РАЗНЫЕ РЕЖИМЫ РАСПРОСТРАНЕНИЯ
В разд. 2,3 было получено основное уравнение, описывающее
распространение оптических импульсов в одномодовом волоконном
световоде. Если длительность импульсов > 0.1 пс, можно воспользо-
воспользоваться уравнением B.3.36), имеющим (зид
ЗА i 1 ё2 л"-
i—=--aA+~^2—i-y\A\2A, C.1.1)
где А -медленно изменяющаяся амплитуда огибающей импульса,
Г-время, измеряемое в системе отсчета, движущейся с импульсом
с его групповой скоростью vg{T= t — z/vg). Три члена в правой части
уравнения C,1.1) описывают соответственно действие поглощения,
Дисперсии и нелинейности на распространение импульсов в световоде,
В зависимости от начальной длительности Го и пиковой мощности Ро
начального импульса либо дисперсионные, либо нелинейные эффекты
56 Глава 3
преобладают в эволюции импульса вдоль световода Полезно ввести
две характерные длины [1-3]: дисперсионную длину LD и нелинейную
длину LNL . В зависимости от соотношения между LD , LNL и длиной
световода L можно различать четыре различных режима эволюции
импульсов.
Введем нормировку времени на начальную длительность им-
импульса:
'о 1 о
Одновременно можно ввести нормированную амплитуду U, исполь-
используя определение
A(z,x)= 4/^exp(-az/2)[/(z,T), C.1.3)
где Ро-пиковая мощность начального импульса. Экспонента в
уравнении C.1,3) учитывает оптические потери в световоде. Из
уравнений C.1.1) C.1,3) следует, что нормированная амплитуда
G(г,т) удовлетворяет следующему уравнению распространения:
,
где sgh(p2) = + 1 в зависимости от знака ДГС р2 и
Дисперсионная длина LD и нелинейная длина LNL характеризуют
длину, на которой дисперсионные или нелинейные эффекты становят-
становятся важными для эволюции импульса вдоль длины L световода.
В зависимости от соотношения величин L, LD и LNL характер
распространения можно отнести к одной из следующих четырех
категорий.
Если L<kLnl и L<zLd, to ни дисперсионные, ни нелинейные
эффекты не играют существенной роли в процессе распространения
импульсов. Это можно понять из того, что обоими членами в правой
части уравнения C.1.4) можно пренебречь в этом случае (предполага-
(предполагается, что импульс достаточно гладкий, так что д2 V/дх2 ~ 1), В
результате U (z, т) = U @, т), т. е, импульс сохраняет свою форму при
распространении. В этом режиме волокно играет пассивную роль
и просто передает оптические импульсы (за исключением уменьшения
энергии импульса из-за оптических потерь). Этот режим пригоден для
оптических систем связи. Длина L обычно ~ 50 км в таких системах,
поэтому LD и LNL должны быть > 500 км для хорошей передачи
импульсов. Из уравнения C.1.5) можно оценить Го и Ро для
некоторых определенных параметров Р2 и У- На длине волны
Дисперсия групповых скоростей 57
X = 1,55 мкм, | Р2 I — 20 пс2/км и у ~ 20 Вт км. Используя эти
значения в уравнении C.1.5), получаем, что нелинейные и дисперсион-
дисперсионные эффекты пренебрежимо малы при L< 50 км, если То > 100 пс
и Ро < 0,1 мВт. LD и LNL становятся тем меньше, чем короче и
интенсивнее импульсы. Например, LD и LNL порядка ~ 50 м при
Го = 1 пс и Ро = 1 Вт. В случае пикосекундных импульсов нужно
учитывать и нелинейные, и дисперсионные эффекты, если длина
световода превышает длину в несколько метров.
Если L« L^L и L> LD, то в уравнении C.1.4) можно пренебречь
последним членом по сравнению с двумя другими. Тогда эволюция
импульса определяется эффектом ДГС и нелинейные эффекты играют
относительно малую роль. В этой главе будет обсуждено влияние
эффекта ДГС на распространение импульса. Режим, при котором
дисперсия преобладает, имеет место всегда, когда параметры свето-
световода и импульса такие, что
В грубом приближении Ро должно быть « 1 Вт для импульса
длительностью 1 пс при типичных значениях параметров световода
у и | Р2 I на длине волны Х= 1,55 мкм.
Если L« LD , но L> LNL , в уравнении C.1.4) дисперсионный член
пренебрежимо мал по сравнению с нелинейным членом (пока им-
импульс имеет гладкую временную огибающую, чтобы e2U/дт2 ~ 1).
В этом случае эффект ФСМ определяет эволюцию импульса в
волокне, приводя к спектральному уширению импульса. Это явление
будет рассмотрено в гл. 4. Режим, при котором нелинейность доми-
доминирует, имеет место всегда, когда
Этого условия просто достичь для относительно широких импульсов
(То> 100 пс) с пиковой мощностью 1 Вт. Отметим, что ФСМ может
приводить к изменению формы импульса даже в присутствии слабого
эффекта ДГС. Если импульс имеет крутой передний или задний
фронты, то дисперсионный член может стать важным, даже если
вначале удовлетворяется условие C.1.7).
Если длина световода L больше или порядка LD и LNL, то
дисперсия и нелинейность вместе действуют при распространении
импульса вдоль световода. Совместное влияние эффектов ДГС и
ФСМ может приводить к качественно другому поведению в сравне-
сравнении с тем, если только ДГС или. ФСМ действуют. В области
аномальной дисперсии групповых скоростей (Р2 < 0) в световоде
могут существовать солитоны; в гл. 5 обсуждаются свойства и
58 Глава 3
применения оптических солитонов. В области нормальной дисперсии
(р2 > 0) можно использовать эффекты ФСМ и ДГС для сжатия
импульсов. Этот вопрос обсуждается в гл. 6. Уравнение C.1.4)
исключительно полезно для изучения эволюции импульсов в свето-
световодах, когда нужно учитывать и дисперсионные, и нелинейные
эффекты. Часто бывает необходимо решать это уравнение численно,
используя те методы, которые обсуждались в разд. 2,4, чтобы
смоделировать полученные экспериментально результаты.
3.2. ДИСПЕРСИОННОЕ УШИРЕНИЕ ИМПУЛЬСОВ
В этом разделе мы рассматриваем действие ДГС на распростране-
распространение импульсов в линейной дисперсионной среде [4-18], полагая
в уравнении C.1.1) у = 0. Если определить нормированную амплиту-
амплитуду U(z, T) в соответствии с уравнением C.1,3), то U (г, Г) будет
удовлетворять следующему дифференциальному уравнению в част-
частных производных:
dU I d2U
i — = -Р2—г- (Ъ2Л)
Это уравнение совпадает с уравнением, которое описывает дифрак-
дифракцию света в поперечном направлении в одномерном случае. В самом
деле, эффекты во времени, связанные с дисперсией, имеют близкие
аналогии с пространственными дифракционными эффектами [2].
Уравнение C.2.1) легко решить, используя фурье-метод. Если V (z, со) -
фурье-преобразование U (z, T), такое, что
U(z,T)=— J ??(г,со)ехр(-/соГ)Ло, C.2.2)
то оно удовлетворяет простому дифференциальному уравнению
. дС 1 „ _,
решение которого записывается в виде
С (z, со) = С (О, со) ехр - р2 со2 г . C.2.4)
Уравнение C.2.4) показывает, что ДГС изменяет фазу в каждой
спектральной компоненте импульса на величину, зависящую от
частоты и длины распространения. Хотя такие изменения не влияют
на спектр импульса, они могут изменить форму импульса. Подстав-
Подставляя уравнение C.2.4) в уравнение C.2.2), получаем общее решение
уравнения C.2.1).
Дисперсия групповых скоростей 59
U (г, Г) = — ] С @,со)ехр - р2и2 z - /со Г Ло. C.2.5)
где 0 @, со) есть фурье-преобразование начального импульса при
z = 0:
t?@,co)= J G@,Г)ехр(/соТ)</Г. C.2.6)
— ос
Для простоты рассмотрим случай гауссовского импульса, имею-
имеющего вначале вид [9]
[^у C.2.7)
где Го-полуширина импульса (по уровню интенсивности 1/е от
максимальной), введенная в разд. 3.1. На практике вместо 7^, удобно
использовать полную длительность по уровню половины максималь-
максимальной интенсивности (FWHM). Для гауссовского импульса эти две
величины связаны соотношением
Tfwhm = 2(ln 2I'2 Го ~ 1,665ГО. C.2.8)
Используя уравнения C.2.5)-C.2.7) и выполнив интегрирование,
амплитуду на любой длине z световода можно записать в виде
U (z, Г) = П ехр Г - /2 1 • C.2.9)
Таким образом, гауссовские импульсы сохраняют свою форму, но его
длительность увеличивается:
T1 = r0[l+(z/LDJ]1/2, C.2.10)
где дисперсионная длина LD=To/|P2|. Уравнение C.2.10) показы-
показывает, что ДГС уширяет импульс. Степень уширения определяется
дисперсионной длиной LD. При определенной длине световода более
короткий импульс уширится больше, так как его дисперсиЬнная\
длина меньше. При z = LD гауссовский импульс уширяется в Jl раз.
На рис. 3.1 показаны | U (z, T) \2 при трех длинах z = 0,2 LD и 4 LD, что
демонстрирует степень дисперсионного уширения гауссовского им-
импульса.
Сравнение уравнений C.2.7) и C.2.9) показывает, что импульс,
вначале не имеющий частотной модуляции, приобретает частотную
модуляцию, проходя через световод. Это можно ясно увидеть,
записав U (z, T) в форме
U(z, T) = | U(z. Г)ехр [/ф(г, Г)], C.2.11)
60
Глава 3
Рис. 3.1. Дисперсионное уширение гауссовского илтульса в световоде при
: = 2LD и z = 4LD. Дисперсионная длина LD = Tg/\fi2\, где Р2 параметр
ДГС Штриховая линия показывает начальный импульс при z = 0.
где
ф(г.Т)=-
sgh(P2)(z/LD) Г
f-г + tan"
C.2.12)
Зависимость фазы ф (-, Т) от времени означает, что мгновенная
частота вдоль импульса отлична от несущей частоты <в0. Эта разница
частот 5<в равна производной —д$/дТ (знак «минус» появляется
вследствие выбора зависимости ехр( — /co0f) в уравнении B.3.2))
и выражается уравнением
?ф 2sgh(P2)(r/LD) Г
8со = — ——, =
РТ l+(=/LD)
C.2.13)
Уравнение C.2.13) показывает, что частота изменяется линейно по
импульсу. Этот случай называется линейной частотной модуляцией.
Частотная модуляция 5<в зависит от знака Р2. Разница частот 5<в
отрицательна на переднем фронте импульса (Г< 0) и линейно
увеличивается по импульсу в области нормальной дисперсии (Р2 > 0);
в области аномальной дисперсии (Р2 < 0) наблюдается противо-
противоположное поведение.
Процесс дисперсионного уширения импульса состоит в том, что,
как отмечалось в разд. 1.2.3, из-за ДГС разные частотные компонен-
компоненты импульса распространяются по световоду с несколько различны-
различными скоростями. А именно, длинноволновые компоненты движутся
быстрее, чем коротковолновые в области нормальной дисперсии
(Р2 > 0); в области аномальной дисперсии (fS2 < 0) наблюдается
Дисперсия групповых скоростей 61
обратное. Длительность импульса может оставаться неизменной,
если только все спектральные компоненты распространяются с одной
скоростью или, что то же самое, если C2 = 0. Любые временные
задержки разных спектральных компонент приводят к уширению
импульса.
Из уравнения C.2.10) следует, что уширение гауссовского им-
импульса, на входе не обладавшего частотной модуляцией, не зависит
от знака параметра дисперсии Р2. Таким образом, при определенной
величине дисперсионной длины LD импульс уширяется одинаково
в области как нормальной, так и аномальной дисперсии в световоде.
Поведение изменяется, однако, если гауссовский импульс вначале
имеет некоторую частотную модуляцию [10]. В случае линейной
частотной модуляции гауссовского импульса начальное поле записы-
записывается в виде (ср. уравнение C.2.7))
Г 1 + /С Г21
U @, Г) = ехр [ — —Л, C.2.14)
где С-параметр модуляции. Используя уравнение C.2.11), находим.
что частота увеличивается линейно от переднего фронта импульса
к заднему, если С > 0, и уменьшается, если С < 0. Будем называть
частотную модуляцию положительной и отрицательной в зависи-
зависимости от того, положителен или отрицателен параметр С. Величину
С можно оценить, исходя из ширины спектра гауссовского импульса.
Подставляя уравнение C.2.14) в уравнение C.2.6), получаем для
С{0,ю) выражение
Полуширину спектра (по уровню интенсивности 1/е от максималь-
максимальной) находим из уравнения C.2.15):
Аш = A +С2I2/Т0. C.2.16)
В отсутствие частотной модуляции (С = 0) импульс спектрально-
ограниченный и выполняется соотношение Дсо7^ = 1. Ширина спектра
увеличивается в A + С2I'2 раз, если есть линейная частотная модуля-
модуляция. Из измерений Лео и 7^,, используя уравнение C.2.16), можно
получить | С |.
Прошедшее через световод поле находится, если подставить
t'@,co) из уравнения C.2.15) в уравнение C.2.5). Уравнение можно
проинтегрировать аналитически и получить выражение
U(ZT) СХР
Г
U(Z'T) П - Ф,гA + Ю СХР Г 2Щ ~ Ф,*A + /О]
Таким образом, даже частотно-модулированный гауссовский им-
62
Глава 3
пульс сохраняет гауссовскую форму при распространении. Длитель-
Длительность импульса Гх после прохождения длины z световода связана
с начальной длительностью То соотношением [10]
Из этого уравнения видно, что уширение зависит от знаков параметра
ДГС Р2 и параметра частотной модуляции С. Гауссовский импульс
монотонно уширяется с увеличением z, если Р2С > 0. Если же Р2С < 0,
то импульс сначала снимается. Рис. 3.2 иллюстрирует это зави-
зависимостью коэффициента уширения импульса TJT0 от z/LD (при
С = 2). Дисперсионная длина LD определена в уравнении C.1.5). В
случае Р2 С < 0 длительность импульса становится минимальной при
zm = j^LD- C.2.19)
Минимальная величина длительностью импульса при z = zMHH равна
Гмии
1 —
A+С2I'2'
C.2.20)
Используя уравнения C.2.16) и C.2.10), находим, что при г = гмин
импульс спектрально ограничен, так как ЛсоТ!" = 1.
Начальное сжатие импульса в случае Р2 С < 0 можно объяснить на
0,5 1
Расстояние z/L
1.5
D-
Рис. 3.2. Коэффициент уширения импульса в зависимости от расстояния для
частотно-модулированного гауссовского импульса. Штриховая линия соот-
соответствует гауссовскому импульсу без частотной модуляции. В случае Р2 < 0
имеют место точно такие же кривые, если поменять знак коэффициента
частотной модуляции С.
Дисперсия групповых скоростей 63
основании уравнения C.2.13), описывающего наводимую дисперсией
частотную модуляцию на гауссовский импульс, сначала модуляцией
не обладавший. Когда импульс имеет вначале частотную модуляцию
при условии Р2 С < О, наводимая дисперсией частотная модуляция
противоположна по знаку по сравнению с начальной частотной
модуляцией. В результате частотная модуляция импульса при
распространении в световоде уменьшается, а импульс сжимается.
Минимальной длительность импульса становится в точке, где две
частотные модуляции компенсируют друг друга. При последующем
увеличении длины распространения частотная модуляция из-за
дисперсии начинает преобладать над начальной частотной модуля-
модуляцией и импульс начинает уширяться. Результирующую частотную
модуляцию как функцию z можно получить из уравнения C.2.17),
используя определение C.2.11) и C.2.13). Это решение подтверждает
качественную картину, описанную выше.
Импульсы, излучаемые многими лазерами, можно приближенно
считать гауссовскими, тем не менее часто бывает необходимо
рассмотреть другие формы импульсов. Обобщенный интерес пред-
представляют импульсы, имеющие форму гиперболического секанса,
которые естественно возникают в связи с оптическими солитонами
(см. гл. 5). Амплитуда поля таких импульсов на входе в световод
имеет форму
[|][§^] C.2.21)
где коэффициент частотной модуляции С определяет начальную
частотную модуляцию, аналогичную той, что описывается уравне-
уравнением C.2.14). Поле U(z,T) находится из уравнений C.2.5), C.2.6)
и C.2.21). К сожалению, для негауссовских импульсов не всегда
можно вычислить интеграл в уравнении C.2.5) аналитически. По-
Поэтому на рис. 3.3 показаны результаты численных вычислений формы
импульсов, прошедших расстояния z = 2LD и 4LD при отсутствии
частотной модуляции в начале световода (С = 0). Сравнение рис. 3.1
и 3.3 показывает, что качественные черты дисперсионного уширения
почти одинаковы для гауссовского импульса и импульса формы
гиперболического секанса. Отметим, что То, появляющееся в уравне-
уравнении C.2.21), с полной длительностью на уровне половины максималь-
максимальной интенсивности FWHM связано соотношением
Ffwhm = 21п A + v 2) Го ~ 1,763 Го. C.2.22)
Этим выражением следует пользоваться, если при сравнении ис-
используется FWHM. Аналогичное выражение для гауссовского им-
импульса дается уравнением C.2.8).
До сих пор рассматривались импульсы с относительно широкими
64
Глава 3
1,0
0,8
J
"~0,4
0,2
0
-
-
-
¦-- S
*—D
2/
и
I ¦ • ¦ ¦ I
л :
'» с = о
i \
1 \
1 \
D| \
I 1 :
1 \
-5
0
т/то
Рис. 3.3. Формы импульсов при : = 2LD и z = 4LD, возникающие в процессе
дисперсионного уширения импульса, у которого при z = 0 была форма
гиперболического секанса (штриховая линия). Сравните рис. 3.1, где показан
случай гауссовского импульса.
передним и задним фронтами. Но, как и можно было ожидать,
дисперсионное уширение оказалось чувствительным к крутизне фрон-
фронтов импульса. Вообще говоря, импульс с более крутыми передним
и задним фронтами уширяется быстрее просто потому, что такой
импульс имеет более широкий начальный спектр. Импульсы, излу-
излучаемые полупроводниковыми лазерами, попадают в эту категорию
и не могут, вообще говоря, быть аппроксимированы гауссовским
импульсом. При моделировании влияния крутизны фронтов им-
импульса на дисперсионное уширение можно использовать импульсы
супергауссовской формы. В случае супергауссовского импульса
уравнение C.2.14) принимает обобщенную форму [17]
1 ¦•-¦¦ " (з.2.23)
1
J,
где параметр т определяет степень крутизны фронта. Случай т = 1
соответствует случаю гауссовских импульсов с частотной модуля-
модуляцией. При больших т форма импульса приближается к прямо-
прямоугольной с резким передним и задним фронтами. Если определить
время нарастания импульса Тг как длительность увеличения интен-
интенсивности с 10 до 90% от пикового значения, то из уравнения C.2.23)
можно получить, что
2m
m
C.2.24)
Дисперсия групповых скоростей
65
Следовательно, параметр т можно определить из измерений Гг и Го.
На рис. 3.4 показаны формы импульсов в точках i = О, LD и 1LD
в случае супергауссовского импульса без частотной модуляции
(С = 0) с т = 3. Его нужно сравнить с рис. 3.1, где показан случай
гауссовского импульса (т = 1). Различие между этими случаями
можно отнести к более крутым переднему и заднему фронтам
супергауссовского импульса. При распространении гауссовский им-
импульс сохраняет свою форму, а супергауссовский импульс, кроме того
что уширяется с большей скоростью, еще и искажает свою форму.
Дальше уширение супергауссовского импульса можно объяснить его
более широким спектром по сравнению с гауссовским импульсом
вследствие большей крутизны фронтов. Задержка каждой спектраль-
спектральной компоненты, вызываемая ДГС, непосредственно связана с раз-
разностью ее частоты и средней частоты <в0, поэтому, чем больше
спектр, тем больше скорость уширения импульса.
Для импульсов сложной формы, подобной той, которая показана
на рис. 3.4, не совсем правильно измерять длительность импульса
по уровню половины максимальной интенсивности. Точнее будет
описывать длительность таких импульсов среднеквадратичной шири-
шириной о, определяемой уравнением [8, 9]
11/2
о = | <7 *>-<i-H , C.2.25)
Рис. 3.4. Формы импульсов, получающиеся в точках z = LDn z = 2LD, когда
начальный импульс при z = 0 имеет супергауссовскую форму (штриховая
линия). Сравните рис. 3.1, где показан случай гауссовского импульса.
66 Глава 3
00
ГДС
J Tn\U(z,T)\2dT
^ • C.2.26)
J \U(z,T)\2dT
— oo
С целью показать, как уширение импульса зависит от крутизны
фронтов импульса, на рис. 3.5 представлен коэффициент уширения
ст/ст0 для супергауссовских импульсов как функция длины распро-
распространения для т в диапазоне от 1 до 4. Здесь ст0-это начальная
среднеквадратичная длительность импульса при 2 = 0. Случай т = 1
соответствует гауссовскому импульсу; с увеличением т фронты
импульса становятся более крутыми. Как следует из уравнения
C.2.24), время нарастания импульса обратно пропорционально т,
поэтому ясно, что импульс, время нарастания которого короче,
уширяется быстрее. Кривые на рис. 3.5 представлены для случая
начального импульса, не имеющего частотной модуляции (С = 0).
Если в начале импульсы частотно модулированы, то величина их
уширения зависит от знака произведения Р2 С. Качественное поведе-
поведение подобно случаю гауссовского импульса (т = 1), показанному на
рис. 3.2. В частности, даже супергауссовский импульс сначала сжима-
сжимается, если Р2 С < 0. Можно аналитически определить коэффициент
уширения импульса. Используя уравнения C.2.5) и C.2.23)-C.2.26),
получаем [18]
Г A/2т) СР2 z Г B - 1/2т) A + С2) (т Р2 zJ
JT
J
ГC/2т) Г2, ГC/2т) ТЪ
C.2.27)
где Г-гамма-функция. Для гауссовского импульса (т = 1) это
уравнение переходит в уравнение C.2.18).
Начальное сжатие импульсов, обладающих частотной модуля-
модуляцией, наблюдалось в экспериментах [11, 12] по распространению
в световоде оптических импульсов, излучаемых полупроводниковым
лазером с непосредственной прямой модуляцией. В первом экспери-
эксперименте [11] входной импульс на длине волны 1,54 мкм имел положи-
положительную частотную модуляцию (С > 0). После 104 км распростране-
распространения в световоде в области аномальной дисперсии (Р2 — — 20 пс2/км)
импульс уширился почти в 5 раз. Во втором эксперименте [12]
полупроводниковый лазер излучал импульсы на длине волны
1,21 мкм, обладающие отрицательной частотной модуляцией (С < 0).
После 1,5 км распространения в световоде при нормальной дисперсии
(Р2 = 15 пс2/км) импульс сжался от 190 до 150 пс. Когда длина
световода была увеличена до 6 км, длительность импульса увеличи-
увеличилась до 300 пс в соответствии с показанным на рис. 3.2 качественным
поведением. В другом эксперименте [16] был получен значительно
Дисперсия групповых скоростей
67
2 3
Расстояние z/LB
Рис. 3.5. Коэффициент уширения ст/а0 в зависимости от длины для несколь-
нескольких супергауссовских импульсов с разными значениями ш. Случай m = 1
соответствует гауссовскому импульсу. Фронты импульсов становятся круче
с увеличением т.
более короткий импульс (длительностью ~ 26 пс (FWHM)) на длине
волны 1,3 мкм от полупроводникового лазера с распределенной
затравкой путем переключения усиления. Импульсы обладали от-
отрицательной частотной модуляцией (С < 0), поэтому применялся
световод со смещенной дисперсией, имеющей положительную ДГС
на длине волны 1,3 мкм (Р2 ^12 пс2/км). Импульс сжимался в 3 раза
в световоде длиной 4,8 км, а потом, при увеличении длины световода,
начинал уширяться.
3.3. ДИСПЕРСИЯ ВЫСШЕГО ПОРЯДКА
Дисперсионное уширение импульсов, обсуждавшееся в разд. 3.2,
обусловлено членом низшего порядка ДГС Р2 в разложении B.3.23).
Хотя вклад этого члена в большинстве практически значимых случаев
преобладает над другими, иногда необходимо учитывать член более
высокого порядка, пропорциональный Р3. Например, если длина
волны излучения X близка к длине волны нулевой дисперсии XD, то
Рг — 0; при этом основной вклад в эффекты ДГС дает рз [5-7].
В случае ультракоротких импульсов, когда 7^, < 0,1 пс, часто бывает
необходимо учитывать дисперсию высшего порядка Р3, даже если
Рг Ф 0, так как параметр разложения Асо/со0 уже не настолько мал,
чтобы в разложении B.3.23) пренебрегать членами выше Р2.
В этом разделе будут рассмотрены вместе эффекты ДГС, связан-
связанные с Р2 и рз, без учета нелинейных эффектов. Соответствующее
68 Глава 3
уравнение распространения для амплитуды A (z, Т) получается из
уравнения B.3.35) в пренебрежении нелинейными членами. Из уравне-
уравнения C.1.3) следует, что нормализованная амплитуда (У (z, Т) удовлет-
удовлетворяет уравнению
/^ = ^20 + ^РзЙ- C-3.1)
Это уравнение можно решить, используя метод Фурье (разд. 3.2).
Вместо уравнения C.2.5) получается следующее уравнение для про-
прошедшего поля:
U(z,T) = — J
C.3.2)
где фурье-преобразование (У @, со) входного поля определяется в
уравнении C.2.6). Если определено начальное поле U (О, Т), то на
основании уравнения C.3.2) можно изучить дисперсионные эффекты
высшего порядка. В частности, можно рассмотреть гауссовский,
супергауссовский импульсы или импульс формы гиперболического
секанса аналогичным образом, как в разд. 3.2. Для гауссовского
импульса можно получить аналитическое решение в виде функций
Эйри [6].
Как и следует ожидать, эволюция импульса в световоде зависит от
относительных величин Р2 и рз, которые в свою очередь зависят от
соотношения между ^.0 и XD. Если ^-0 = XD, то Р2 = 0 и обычно
Рз =0,1 пс3/км. Однако | Р21 ~ 1 пс2/км, даже когда 10 отличается от
XD всего на 10 нм. Для того чтобы сравнивать относительную
важность Р2 и Рз в уравнении C.3.1), удобно ввести дисперсионную
длину, связанную с дисперсионным членом высшего порядка, которая
определяется уравнением
Lb=Tg/|P3|, C.3.3)
где 7^, характеризует длительность импульса. Дисперсионная длина
LD, связанная с Р2, определяется как LD = Го/1Р2|. Дисперсионные
эффекты высшего порядка играют существенную роль, только когда
L'D<LD или 7о|Р2/Р3|<1. Для 100-пикосекундного импульса это
условие означает, что Р2 < 10 ~3 пс2/км при типичном значении
Рз = 0,1 пс3/км. Такие величины Р2 принимает, только когда ^-0
отличается от XD не более чем на 10 нм! На практике фиксировать
1,0 и 1„ с такой точностью очень трудно, поэтому вклад Р3 обычно
пренебрежимо мал по сравнению с Р2. Это на самом деле имеет место
в эксперименте [19, 20], где пикосекундные импульсы на длине волны
~к = 1,32 мкм распространяются на несколько километров. Ситуация
коренным образом изменяется для сверхкоротких импульсов с дли-
Дисперсия групповых скоростей
69
10
Рис. 3.6. Формы импульсов при z = SL'D в присутствии дисперсии высшего
порядка, имевших при z = О гауссовскую форму (штриховая линия). Сплошная
линия соответствует случаю Ко =KD . Пунктирной линией показан эффект
малых Р2, когда Хо и XD точно не совпадают и LD = L'D.
тельностью в фемтосекундном диапазоне. Например, Р2 может быть
порядка ~ 1 пс2/км при То = 0,1 пс, пока вклад Р3 еще существен. Так
как L'D ~ 10 м для таких величин Го, то влияние дисперсии высшего
порядка можно экспериментально увидеть при распространении
100-фемтосекундных импульсов на несколько метров в световоде
вблизи \D, так чтобы |^0 — %в\ < 10 нм.
На рис. 3.6 показаны формы импульсов при z = 5L'D для началь-
начального гауссовского импульса без частотной модуляции [С = 0 в
уравнении C.2.14)] для двух случаев Р2 = 0 (сплошная линия) и
величины Р2, такой, что LD = L'D (штриховая линия). Гауссовский
импульс остается гауссовским, когда в уравнении C.3.1) ДГС опре-
определяется только вкладом Р2; действие дисперсии высшего порядка,
определяемое вкладом Р3, искажает форму импульса. Он становится
асимметричным и имеет осциллирующую структуру на одном из
своих фронтов. В случае положительной величины Р3 (он показан на
рис. 3.6) осцилляции появляются на заднем фронте импульса. Когда
Рз отрицательно, осцилляции развиваются на переднем фронте
импульса. В случае Р2 = 0 возрастает глубина осцилляции, так что
интенсивность спадает до нуля между соседними периодами. Однако
даже относительно малая величина Р2 существенно сглаживает эти
осцилляции. В случае LD = L'D (P2 = Р3/То),
показанном на рис. 3.6, осцилляции почти исчезают и импульс имеет
Длинный хвост на заднем фронте. Для больших величин Р2, таких,
70
Глава 3
-20
Рис. 3.7. Эволюция супергауссовского импульса при m = 3 вдоль световода
в случаях р2 = 0 и Р3 > 0. Осцилляции на заднем фронте импульса появляются
под действием дисперсии высшего порядка.
что LD«L'D, форма импульса становится близкой к гауссовской
и дисперсия высшего порядка играет относительно малую роль.
Уравнение C.3.2) можно использовать для анализа эволюции
импульсов с другими формами огибающей и начальной частотной
модуляцией. В качестве примера на рис. 3.7 показана эволюция
супергауссовского импульса без начальной частотной модуляции на
длине волны нулевой дисперсии (Р2 = 0) при С = 0ит = Зв уравне-
уравнении C.2.23). Ясно, что формы импульсов могут сильно меняться
в зависимости от начальных условий. На практике чаще представляет
интерес не детальная структура импульса, а степень его дисперсион-
дисперсионного уширения. Так как длительность импульсов, показанных на
рис. 3.6, 3.7, измерять на уровне половины максимальной интенсив-
интенсивности не совсем правильно,будем использовать среднеквадратичную
длительность, определяемую уравнением C.2.25). В случае входного
гауссовского импульса можно получить простое аналитическое выра-
выражение для о, которое учитывает действие Р2, Р3 и начальной частот-
частотной модуляции С на дисперсионное уширение [10].
Чтобы вычислить а из уравнения C.2.25), нужно определить (Т"),
используя уравнение C.2.26). Так как фурье-преобразование U(z,a)
функции U (z, Т) определяется в уравнении C.3.2), удобно вычислять
(Т"У в спектральном представлении. Используя фурье-преобразова-
фурье-преобразование T(z, ю) интенсивности импульса | U (г, Т) |2
= J \U(z,T)\2exp{i(oT)dT
C.3.4)
и дифференцируя его п раз, получаем
lim A; f (z, ю) = (О" J Г" | U (z, T) |2 dT. C.3.5)
Используя уравнение C.3.5), из уравнения C.2.26) найдем, что
Дисперсия групповых скоростей 71
д" ~
lim 7Г* '(z'ш)' (ЗЛ6)
где нормировочная постоянная определяется как
JV= J \U{z,T)\2dT= J | [/(О, Г)|2 Л\ C.3.7)
— 00 — 00
Из теоремы о свертке следует, что
00
J(z,oo) = J t/U,ro-ro')i/*(z,ro')^ra'. C.3.8)
Выполняя дифференцирование и переходя к пределу в уравнении
C.3.6), получаем
<т"> = 77 J ° *(z-ш> ^ ^ (z-ю>J@ • <3-3-9)
В случае гауссовского импульса частотной модуляцией для U (z, ю)
из уравнений C.2.15) и C.3.2) можно получить следующее уравнение:
C.3.10)
Один или два раза дифференцируя это уравнение и подставляя
результат в уравнение C.391, находим, что интегрирование по ю
можно выполнить аналитически- Таким способом можно получить
и (Г), и (Т2). Подставляя получающиеся выражения в уравнение
C.2.25), находим [10], что
где ст0-начальная среднеквадратичная длительность гауссовского
импульса (ст0 = Tg/yj'l), обладающего частотной модуляцией. Как
и должно быть, уравнение C.3.11) сводится к уравнению C.2.18) при
Рз = 0. Похожее уравнение для ст/ст0 можно получить и в случае
супергауссовского импульса [18]. Полученное выражение обобщает
уравнение C.2.27) на случай дисперсии высшего порядка.
Из уравнения C.3.11) следует несколько интересных выводов.
Вообще говоря, свой вклад в уширение импульса вносят и Р2, и рз, но
зависимость их относительно вклада от параметра частотной
модуляции С качественно разная. Вклад Р2 зависит от знака Р2 С,
тогда как вклад рз не зависит ни от знака рз, ни от знака С. Таким
образом, в сравнении с поведением, показанным на рис. 3.2, частот-
частотно-модулированный импульс на длине волны нулевой дисперсии
72
Глава 3
5-
i Л -
2-
: С =
~ Ld"
-
1 1 '
2
/
i i I
У
1 1
/
i i i
-0
1 i
1 1 1 1 1
3-
8-
m
О
О 1 2 3 4
Расстояние z/LB
Рис. 3.8. Коэффициент уширения частотно-модулированного гауссовского
импульса вблизи XD такой, что LD = 2L'D в зависимости от длины распрост-
распространения. Штриховая линия соответствует случаю Хо = Х„, так что LD стано-
становится бесконечной (Р2 = 0).
никогда не может сжиматься. Тем не менее даже небольшое смещение
частоты от частоты нулевой дисперсии может привести к начальному
сжатию импульса. Эта ситуация иллюстрируется рис. 3.8, на котором
изображен коэффициент уширения ст/ст0 как функция длины распро-
распространения при С = 2 и LD = 2L'D. Для сравнения штриховой линией
показано уширение, имеющее место в случае точного совпадения
длины волны импульса с длиной волны нулевой дисперсии (Р2 = 0).
В области аномальной дисперсии групповых скоростей вклад Р2
может компенсировать вклад рз, так что дисперсионное уширение
уменьшается по сравнению со случаем Р2 = 0 при z < L'D. При
больших значениях z, таких, что z » LD/\ C\, уравнение C.3.11) можно
аппроксимировать следующим образом:
| 1/2
z; C.3.12)
здесь мы использовали уравнения C.1.5) и C.3.3). Линейная зависи-
зависимость среднеквадратичной длительности импульса от длины распро-
распространения при больших z-основная черта, присущая всем импульсам
независимо от формы.
Уравнение. C.3.11) можно обобщить на случай частично когерент-
когерентного света [10]. Спонтанное излучение всех источников света вызыва-
вызывает случайные амплитудные и фазовые флуктуации, которые приводят
к некоторой конечной ширине линии 5ю спектра источника на частоте
ю0. Если ширина линии 5ю много меньше ширины спектра Аю
Дисперсия групповых скоростей 73
(определяемой уравнением C.2.16) для частотно-модулированного
гауссовского импульса), ее влиянием на уширение импульса можно
пренебречь. Однако многие источники света, используемые в опти-
оптической связи (такие, как светодиоды и многомодовые полупроводни-
полупроводниковые лазеры), не удовлетворяют этому условию; становится необхо-
необходимым учитывать действие ширины линии источника. В случае
гауссовского спектра уравнение C.3.11) принимает обобщенную фор-
форму [10]
C.3.13)
где V= 5юТ0 и 5ю - полуширина на уровне 1/е гауссовского спектра.
Это уравнение описывает уширение частотно-модулированного гаус-
гауссовского импульса в линейной среде с дисперсией в наиболее общем
случае. В следующем разделе с помощью этого уравнения обсуждает-
обсуждается влияние эффекта ДГС на работу волоконно-оптических систем
связи.
3.4. ПРИМЕНЕНИЯ В ОПТИЧЕСКИХ СИСТЕМАХ СВЯЗИ
В волоконно-оптических системах связи информация передается
по-волокну в виде закодированной последовательности оптических
импульсов, длительность которых определяется скоростью передачи
В (бит/с) системы. Дисперсионное уширение импульсов нежелатель-
нежелательно, так как оно мешает приему сигналов, приводя к ошибкам при
передаче информации. Ясно, что ДГС будет ограничивать скорость
передачи В и длину линии передачи L волоконно-оптической системы
связи. Удобной мерой, характеризующей информационную емкость
линии связи, является произведение скорости передачи на длину
линии передачи информации BL. В этом разделе рассматривается, как
ДГС ограничивает величину BL.
Сначала рассмотрим случай, когда уширение импульса определя-
определяется главным образом большой спектральной шириной 5ю источника
EюТ0 » 1). Для гауссовского импульса без частотной модуляции
коэффициент уширения можно получить на основании уравнения
C.3.13). Предполагая вклад Р3 пренебрежимо малым и считая V» 1,
получаем
HWr-
где L-длина световода. Если В = BТ0) 1, то благодаря ДГС произ-
произведение BL ограничено величиной
Bn\V2\W), C.4.2)
74 Глава 3
где W= 5ю/л- полная спектральная ширина и к0- максимально до-
допустимый коэффициент уширения. В качестве иллюстрации рассмот-
рассмотрим случай, когда источником является многомодовыи полупровод-
полупроводниковый лазер [21], для которого И^ 1 ТГц. Если система работает
на длине волны, соответствующей минимальным потерям в светово-
световоде, то Р2 ^ —20 пс2/км. Предположим, что конструкция системы
требует, чтобы импульс уширялся не более чем на 20% от начальной
длительности при распространении в световоде, т.е. к0 = 1,2. Для
таких значений из уравнения C.4.2) следует, что BL< 5 Гбит/(с-км).
Для световода длиной 50 км ДГС ограничивает скорость передачи
относительно низкой величиной, около 100 Мбит/с. Однако если
многомодовыи полупроводниковый лазер работает на длине волны
вблизи нуля дисперсии A,3 мкм), то можно добиться величины
дисперсии | рг | < 1 пс2/км, что позволит увеличить предел произведе-
произведения BL до 100 ГбитДскм). Тогда многомодовые лазеры можно
использовать вплоть до скоростей передачи 2 Гбит/с на 50 км.
В волоконно-оптических системах связи, работающих на длине
волны 1,55 мкм. чтобы уменьшить действие ДГС, можно идти двумя
путями. Во-первых, использовать световоды со смещенной диспер-
дисперсией (см. разд. 1.2.3), в которых длина волны минимальной дисперсии
совпадает с длиной волны минимальных потерь. И, во-вторых,
использовать полупроводниковые лазеры, работающие преимущест-
преимущественно на одной продольной моде, так чтобы спектральная ширина
источника в непрерывной генерации была ниже 100 МГц [21]. Для
таких лазеров в уравнении C.4.2) под W понимается уже ширина
спектра импульса. Если гауссовский импульс не имеет частот-
частотной модуляции, то И^~ В. Тогда из уравнения C.4.2) следует,
что при L = 50 км ДГС некритична вплоть до скоростей передачи
10 Гбит/с.
Таких впечатляющих параметров, вообще говоря, трудно достичь,
если для получения закодированной последовательности битов полу-
полупроводниковый лазер модулируется непосредственно. Дело в том,
что импульсы, излучаемые лазером с прямой модуляцией током,
обладают частотной модуляцией, поэтому при рассмотрении диспер-
дисперсионного уширения импульсов необходимо учитывать влияние час-
частотной модуляции. В случае частотно-модулированного гауссовского
импульса выходная длительность импульса Тх связана с начальной
длительностью То уравнением C.2.18). В разд. 3.2 было показано, что
такие импульсы сначала могут сжиматься в зависимости от соотно-
соотношения знаков параметра ДГС Р2 и параметра частотной модуляции
С. Произведение BL можно получить из уравнения C.2.18) при данной
величине максимально допустимого уширения. На рис. 3.9 показан
предел произведения как функция параметра частотной модуляции
С при Р2 = — 20 пс2/км. Для сравнения также приведена кривая,
полученная для частотно-модулированных супергауссовских импуль-
Дисперсия групповых скоростей
75
1000
500
100
50
02
-
-
-
= -20пс2/км
/
У/
I 1 I 1
/
f 1
1
1
i.i,
-6-4 -2.0 2 4 6
Параметр частотной модуляции
Рис. 3.9. Ограниченное дисперсией произведение скорости передачи на длину
передачи для случаев частотно-модулированного гауссовского импульса
(сплошная линия) и супергауссовского импульса (штриховая линия) в зави-
зависимости от параметра частотной модуляции С.
сов при,т = 3 в уравнении C.2.23). В обоих случаях длина L, на
который импульс уширяется на 20%, получается при То = 125 пс
(длительности импульса, соответствующей скорости передачи 4 Гбит/с).
Как и следует ожидать, произведение BL меньше для супергауссов-
супергауссовского импульса, поскольку при распространении в световоде такие
импульсы уширяются быстрее, чем гауссовские (см. рис. 3.5).
На рис. 3.9 особенно заметно, что величина произведения BL при
отрицательных значениях частотной модуляции С резко падает. Это
происходит из-за того, что уширение импульса растет, когда Р2 С
положительно (см. рис. 3.2). К сожалению, для полупроводниковых
лазеров с непосредственной модуляцией, работающих на длине
волны 1,55 мкм, С обычно отрицательно и имеет типичную величину
около 5-6 [21]. Из рис. 3.9 видно, что для таких значений С BL
ограничено величиной < 100 Гбит/(с-км). Поэтому оптические сис-
системы связи на длине волны 1,55 мкм часто ограничены дисперсией,
даже если в качестве источников используются одномодовые полу-
полупроводниковые лазеры. При L = 50 км такие системы могут работать
со скоростью В < 2 Гбит/с. Дальнейшее увеличение скорости воз-
возможно на пути использования либо лазеров без частотной модуля-
модуляции, либо световодов со смещенной дисперсией. Отметим, что произ-
произведение BL максимально при положительном значении С ~ 1, по-
поскольку, когда Р2 С отрицательно, импульс сначала несколько сни-
снижается (см. рис. 3.2). Так как С в полупроводниковых лазерах
главным образом отрицательно, наилучшее функционирование
76 Глава 3
достигается при использовании световодов, имеющих небольшую
положительную величину ДГС.
ЛИТЕРАТУРА
1. Сисакян И.Н.. Шварцбург А. Б. Квант, электрон., 1984, т. 11, с. 1703.
2. Ахмапов С. А., Выслоу'х В. А., Чиркин А. С.-УФН, 1986, т. 149, с. 450.
3. Agrawal G.P., in: Supercontinuum Laser Source, ed. by R. R. Alfano. Springer-
Verlag, Heidelberg, 1989.
4. Garrett C.G.B.. McCumber D.E., Phys. Rev., Al, 305 A970).
5. Unger H.G., Arch. Electron. Uebertragungstech., 31, 518 A977).
6. Mivagi M.. Nishida S., Appl. Opt., 18, 678 A979).
7. Mivagi M., Nishida S., Appl. Opt., 18, 2237 A979).
8. Gloge D., Electron. Lett., 15, 686 A979).
9. MarcuseD.. Appl. Opt., 19, 1653 A980).
10. Marcuse D., Appl. Opt., 20, 3573 A981).
11. Iwashita K. et al.. Electron. Lett., 18, 873 A982).
12. Lin C, Tomita A.. Electron. Lett., 19, 837 A983).
13. Anderson D., Lisak M., Anderson P., Opt. Lett., 10, 134 A985).
14. Koyama F., Suematsu Y, IEEE J. Quantum Electron.. QE-21, 292 A985).
15. Tajima K., Washio K., Opt. Lett., 10, 460 A985).
16. Takada A., Sugie Т.. Sanwatari M., Electron. Lett., 21, 969 A985).
17. AgrawalG.P., Potasek M.J., Opt. Lett., 11, 318 A986).
18. Anderson D., Lisak M., Opt. Lett., 11, 569 A986).
19. Bloom D. M. et al.. Opt. Lett., 4, 297 A979).
20. Lin С et al., Electron. Lett., 18, 882 A982).
21. Agrawal G. P.. Dutta N.K., Long-Wavelength Semicondustor Lasers, Van
Nostrand Reinhold, New York, 1986.
Глава 4
ФАЗОВАЯ САМОМОДУЛЯЦИЯ (ФСМ)
Интересным проявлением зависимости показателя преломления
нелинейной среды от интенсивности является фазовая самомодуляция
(ФСМ)-явление, которое ведет к спектральному уширению опти-
оптических импульсов [1-9]. ФСМ эго аналог самофокусировки, но
развивающийся во времени. В самом деле, он впервые наблюдался
в связи с изучением нестационарной самофокусировки оптических
импульсов, распространяющихся в ячейке, заполненной CS2. Исполь-
Используя пикосекундные импульсы, Альфано и Шапиро наблюдали ФСМ
в твердых телах и стеклах [4]. Самые первые наблюдения ФСМ
в волоконных световодах были проведены с использованием волокон,
сердцевина которых была заполнена CS2. Систематическое изучение
ФСМ в кварцевых световодах было проведено Столеном и Лином
[9]. В этой главе ФСМ обсуждается применительно к оптическим
волокнам, в которых значительную роль играет дисперсия групповых
скоростей (ДГС). В разд. 4.1 мы рассматриваем случай чистого
}ффекта ФСМ, пренебрегая влиянием ДГС. Совместное действие
ДГС и ФСМ рассматривается в разд. 4.2; особенно подчеркивается
возникновение частотной модуляции из-за ФСМ. В разд. 4.3 обсуж-
обсуждаются нелинейные эффекты высших порядков, такие, как эффект
самоукручения волнового фронта импульса, возникающий из-за зави-
зависимости групповой скорости от интенсивности [2].
4.1. СПЕКТРАЛЬНОЕ УШИРЕНИЕ
ПОД ДЕЙСТВИЕМ ФСМ
Полное описание ФСМ в световодах требует численного решения
уравнения распространения B.3.31). полученного в разд. 2.3. Для
импульсов длительностью > 0,1 пс можно использовать более прос-
простое уравнение B.3.36). Если пренебречь влиянием ДГС на ФСМ,
можно еще более упростить уравнение B.3.36), положив Р2 равным
нулю. Условия, при которых можно пренебречь ДГС, были получены
в разд. 3.1, где для импульса вводятся нелинейная LNL и дисперсион-
дисперсионная LD длины (см. уравнение C.1.5)). Длительность импульса и пико-
пиковая мощность должны быть такими, чтобы LD»LNL < L, где
L- длина световода. Из уравнения C.1.7) следует, что ДГС можно
78 Глава 4
пренебречь для относительно широких импульсов (То > 100 пс) с
большой пиковой мощностью (Ро > 1 Вт).
Если использовать нормализованную амплитуду U(z, Т), опреде-
определенную в уравнении C.1.3), то уравнение распространения C.1.4)
в приближении Р2 = 0 принимает вид
BU i
— = —-exp(-az)|l/|2l/, D.1.1)
dz LNL
где а учитывает оптические потери в световоде. Нелинейная длина
LNL=(yP0)-\ D.1.2)
где Ро- пиковая мощность и у-параметр, связанный с нелинейным
показателем преломления п2 уравнением B.3.28). Решение уравнения
D.1.1) имеет вид
U(z, T)=U @, Г)ехр [|фЛ1.B. Л] . D.1.3)
где [/@, Т)~ амплитуда поля при z = 0 и
4>wt (z.T) = \U @, Т) |2 (z^/LNL ), D.1.4)
где
2эфф = - [1 - ехр(- az)] . D.1.5)
Из уравнения D.1.3) следует, что ФСМ вызывает набег фазы,
зависящий от интенсивности, тогда как форма импульса, определя-
определяемая \U(z,T)\2, остается неизменной. Нелинейный набег фазы
§nl = §nl (z- T). согласно уравнению D.1.4), увеличивается с увеличе-
увеличением длины распространения г. Величина z3<M) играет роль эффективной
длины, которая из-за потерь меньше z. В световоде без потерь a = 0
и 2зфф = z. Максимальный набег фазы возникает в -центре импульса
при Т= 0. Ввиду того что U нормирована так, что | G@,0) | = 1,
Фма«с = 2эффД^ = УРО 2,фф . D.1.6)
Физический смысл нелинейной длины LNL ясен из уравнения D.1.6):
это эффективная длина распространения, на которой фма1[с = 1. Для
типичного значения нелинейного параметра у = 20В~1-км~1 в ви-
видимом диапазоне LNL = 50 м при мощности Ро = 1 Вт и уменьшается
обратно пропорционально с увеличением мощности.
Уширение спектра из-за ФСМ возникает вследствие зависимости
ф,^ (z, T) от времени, так как изменение фазы импульса во времени
означает сдвиг мгновенной оптической частоты от основной частоты
ю0 при перемещении вдоль импульса. Изменение частоты 5ю опреде-
определяется уравнением
>?>ШЫ>е.!±. DЛ.7)
L
Фазовая самомодуляция
79
где знак минус возникает вследствие выбора ехр(— i(o0t) в уравне-
уравнении B.3.2). Как отмечалось в разд. 3.2, изменение 5ю во времени
можно рассматривать как частотную модуляцию импульса. Частот-
Частотная модуляция наводится ФСМ и растет по величине с длиной
распространения. Другими словами, генерация новых частотных
компонент происходит непрерывно по мере распространения по
световоду, вызывая уширение спектра по отношению к его начальной
ширине при z = 0.
Степень спектрального уширения зависит от формы импульса.
Рассмотрим, например, случай супергауссовского импульса, началь-
начальное поле G@, Т) которого задается уравнением C.2.23). Частотная
модуляция 6а (Т) вследствие ФСМ для такого импульса будет тогда
Параметр m для гауссовского импульса равен 1. Для больших
величин m начальный импульс приближается к прямоугольной фор-
форме, увеличивая крутизну своих переднего и заднего фронтов. На
рис. 4.1 показаны изменения нелинейного набега фазы и частоты 5ю
вдоль импульса при z3<M> = LNL в случаях гауссова (т = 1) и супер-
супергауссова (т = 3) импульсов. Так как фмь прямо пропорционален
\U@, T)\2 в уравнении D.1.4), то его изменение во времени точно
совпадает с формой интенсивности импульса. Изменение во времени
Рис. 4.1. Изменение во времени
набега фазы фЛЬ и частотной
модуляции 8ш, наводимой ФСМ
Для гауссовского (штриховая
линия) и супергауссовского
(сплошная линия) импульсов.
80 Глава 4
частотной модуляции 5ю имеет несколько интересных особенностей.
Во-первых, 5ю отрицательно на переднем фронте (красное смещение)
и становится положительным на заднем фронте (синее смещение).
Во-вторых, частотная модуляция линейна и положительна в большой
центральной части гауссовского импульса. В-третьих, частотная мо-
модуляция значительно больше для импульсов с более крутыми фрон-
фронтами. В-четвертых, поведение супергауссовского импульса отличается
от поведения гауссовского, так как частотная модуляция на нем
появляется только на склонах импульса и не имеет линейного
участка.
Оценить величину спектрального уширения, вызываемого ФСМ,
можно на основе пиковых величин 5ю (см. рис. 4.1). Количественно
эти пиковые значения можно найти, вычисляя максимумы 5ю(Т)
в уравнении D.1.8). Полагая первую производную 5ю(Г) по времени
равной нулю, находим максимальное значение 5юмакс:
ЙЮмакс = — Фмакс , D.1.9)
'О
где фмакс определено в уравнении D.1.6), константа / равна
Значение / слабо зависит от wi;/=0,86 при т = 1и уменьшается до
0,74 при увеличении т. Чтобы получить коэффициент уширения
спектра, нужно связать начальную ширину спектра Аю и длитель-
длительность То. В случае гауссовского импульса без частотной модуляции
Аю = Tq1 (уравнение C.2.16)). где Аю-полуширина по уровню 1/е.
Уравнение D.1.9) тогда принимает вид
йюмакс = 0,86Дюфмакс. D.1.11)
Из этого уравнения следует, что коэффициент уширения спектра
приблизительно равен величине максимального набега фазы фМа«с-
В случае супергауссовского импульса оценить Аю трудно из-за того,
что его спектр негауссовский. Тем не менее если предположить, что
Аю приблизительно равно Т~1, где Tr = TJm-время нарастания
импульса, определяемое уравнением C.2.24), то из уравнения D.1.9)
следует, что коэффициент уширения также равен максимальному
фазовому набегу фмакс- ФСМ может значительно уширить спектр, так
как можно достичь фмакс ~ 100. В случае интенсивных сверхкоротких
импульсов уширенный спектр может иметь ширину 100 ТГц и более
[4]; это явление иногда называют генерацией суперконтинуума.
Действительную форму спектра импульса можно получить, вы-
выполнив обратное преобразование Фурье уравнения D.1.3) следующим
образом:
Фазовая самомодуляция 81
2'57Г 3.5 тг
Частота
Рис. 4.2. Рассчитанное ФСМ-уширение спектра гауссовского импульса без
частотной модуляции. На спектрах указаны максимальные набеги фазы фма.с,
соответствующие пику импульса [9].
S(co) = |l/(z,co)|2 = | ] 1/@,Г)ехр[/ф^B,Г)+г(ш-шо)Г]^Г|2.
D.1.12)
В общем случае спектр зависит не только от формы импульса, но и от
начальной частотной модуляции импульса. На рис. 4.2 показаны
спектры гауссовских импульсов без начальной частотной модуляции
для нескольких величин максимального набега фазы фмаКс- При
фиксированной длине световода фмакс линейно зависит от пиковой
мощности Ро в соответствии с уравнением D.1.6). Таким образом,
эволюцию спектров, показанную на рис. 4.2, можно наблюдать экс-
экспериментально, увеличивая пиковую мощность. На рис. 4.3 изобра-
изображены экспериментальные спектры импульса (близкого к гауссовско-
му, То ~ 90 пс), излучаемого аргоновым лазером, после прохождения
световода длиной 99 м с размером сердцевины 3.35 мкм (F= 2,53)
[9]. На спектрах обозначена величина фмакс для каждого случая, что
дает возможность сравнивать их с вычисленными спектрами (рис. 4.2).
Небольшая асимметрия, наблюдаемая в эксперименте, может быть
связана с асимметрией формы входного импульса [9]. Видно полное
совпадение результатов теории и эксперимента.
Наиболее характерной особенностью спектрального уширения,
вызываемого ФСМ (рис. 4.2 и 4.3), является осциллирующая структу-
структура в центральной части спектра. Как правило, спектр состоит из
многих пиков, крайние пики-наиболее интенсивные. Число пиков
линейно зависит от фмакс- Возникновение осцилляции можно объяс-
объяснить на основе рис. 4.1, где показана зависимость частотной модуля-
модуляции, наводимой ФСМ, от времени. Одна и та же частотная модуляция
наблюдается при двух значениях Т, т. е. импульс имеет одинаковую
82
Глава 4
0,5 тг
тг
1,5 тг
о
I
2,5 тг
3,5 тг
50,0ГГц
4.5-7Г
Частотный спектр
Рис. 4.3. Экспериментальные спектры импульса, близкого по форме к гаус-
совскому, на выходе из 99-метрового световода. На спектрах указаны макси-
максимальные набеги фазы фма1К, линейно зависящие от пиковой мощности им-
импульса [9].
мгновенную частоту в двух разных точках импульса. На качествен-
качественном уровне эти две точки можно представить как две волны на одной
частоте, но с разными фазами, которые могут интерферировать
конструктивно или деструктивно в зависимости от их относительной
разности фаз. Многопиковая структура спектра импульса - результат
такой интерференции []]. Математически в фурье-интеграл (уравне-
(уравнение D.1.12)) наибольший вклад вносят именно те два значения
времени, при которых мгновенная частота одна и та же. Эти вклады,
будучи комплексными величинами, могут складываться в фазе или
в противофазе. На самом деле, можно воспользоваться методом
стационарной фазы, чтобы получить аналитическое выражение для
S(co), верное при больших значениях фма«с- Из этого выражения
следует, что число пиков М на ФСМ-уширенном спектре импульса
приближенно можно выразить следующим соотношением [3]:
Фма.с -
D.1.13)
Уравнение D.1.13) вместе с уравнением D.1.11) можно использо-
использовать для оценки начальной ширины спектра Асо или длительности То
Фазовая самомодуляция
83
импульса, если он не обладал частотной модуляцией [6]. Однако
такой метод является точным, если фма1[С» 1. Более точную меру
спектрального уширения можно получить с использованием средне-
среднеквадратичной ширины спектра (Aco)rms, определяемой уравнением
(Aco)rms = <(ш - со0J > - <со - шо>2 , D.1.14)
где угловые скобки обозначают среднее по ФСМ-уширенному спект-
спектру, определяемому уравнением D.1.12). Более конкретно можно
записать, что
(со-
ОС
J
D.1.15)
Используя процедуру, подобную той, что применялась в разд. 3.3,
можно получить коэффициент спектрального уширения
(Ato)m
(ДюH
= 1 +
D.1.16)
где (АсоH - начальная среднеквадратичная ширина спектра.
Как упоминалось выше, следует ожидать зависимости ФСМ-уши-
рения спектра от формы импульса и начальной частотной модуляции,
если таковая имеется. На рис. 4.4 сравниваются спектры гауссовского
(т = 1) и супергауссовского импульсов (т = 3), полученные числен-
численным интегрированием с использованием уравнений C.2.23) и D.1.12).
0,15
0,1
О.05
0
Гауссовский
импульс
Л
¦ I lift
J V V V V
m
С
А
= 1
= 0 ¦
-
-
0,4
-2
0 2
Vq) То
0,3
0,2
0,1
Супергауссов-
скии импульс
-6 -4
С =0
-2 0 2
lv-vo) То
Рис. 4.4. Сравнение ФСМ-уширения спектров для случаев гауссовского и
супергауссовского импульсов без начальной частотной модуляции при пико-
пиковой мощности, соответствующей фмо„. = 4,5л. Начальный спектр расположен
на несущей частоте v0 (ш0 = 2jtv0).
84
Глава 4
-4
о
а*
*0,2
0
С = -5
1
II II
-
1 II
, у , Л,
-6 -4 -2
0 2
Vq) То
Рис. 4.5. Влияние начальной частотной модуляции на ФСМ-уширение спект-
спектров гауссовского импульса при С = 5 (положительная частотная модуляция)
и С = — 5 (отрицательная частотная модуляция). Эти спектры следует срав-
сравнить с левым спектром на рис. 4.4. где С = 0. Во всех случаях фма1!С = 4,5л.
В обоих случаях предполагается, что начальный импульс не имеет
частотной модуляции (С = 0). Длина волокна и пиковая мощность
подбираются таким образом, чтобы фтах = 4,5л. Качественное разли-
различие между двумя спектрами можно пояснить на основании рис. 4.1,
где была показана частотная модуляция, наводимая ФСМ, для
гауссовского и супергауссовского импульсов. Область частот, где
расположен спектр супергауссовского импульса, почти в три раза
шире из-за того, что максимальная частотная модуляция, определя-
определяемая уравнением D.1.9), в случае супергауссовского импульса почти
в три раза больше. Несмотря на то, что каждый из спектров на
рис. 4.4 имеет 5 максимумов в соответствии с уравнением D.1.13),
в случае супергауссовского импульса большая часть энергии остается
в центральном пике. Это происходит потому, что частотная модуля-
модуляция почти равна нулю в центральной части супергауссовского им-
импульса (рис. 4.1) вследствие того, что его интенсивность почти од-
однородна при | Т\ < То. Частотная модуляция возникает главным
образом вблизи переднего и заднего фронтов. С увеличением крутиз-
крутизны фронтов хвосты спектра на рис. 4.4 расширяются на больший
частотный диапазон, но в то же время они несут меньше энергии, так
как частотное модулирование будет возникать в меньшей временной
области.
Начальная частотная модуляция также может приводить к су-
существенным изменениям спектров импульсов, уширенных вследствие
ФСМ. Это иллюстрируется рис. 4.5, где показаны спектры гауссовско-
гауссовского импульса с положительной и отрицательной частотными модуля-
модуляциями (С = + 5 в уравнении C.2.23)) при таких же условиях, что и на
Фазовая самомодуляния 85
рис. 4.4, т. е. фмакс = 4,5л. Сравнение этих спектров со спектром
гауссовского импульса без частотной модуляции (левая часть
рис. 4.4) показывает, что начальная частотная модуляция может
привести к качественным изменениям в спектральном уширении,
вызываемом ФСМ. Положительная частотная модуляция увеличива-
увеличивает число максимумов на спектре, тогда как в случае отрицательной
частотной модуляции (ЧМ) имеет место обратное. Это объясняется
тем, что частотная модуляция, наводимая ФСМ, линейна и положи-
положительна (частота увеличивается с увеличением Т) в центральной части
импульса (см. рис. 4.1). Таким образом, она складывается с началь-
начальной частотной модуляцией при С > 0, приводя к увеличению осцил-
осцилляции. В случае С < 0 два вклада в частотную модуляцию имеют
разные знаки в центре импульса. Крайние максимумы на рис. 4.5 для
С = — 5 возникают вследствие остаточной частотной модуляции на
переднем и заднем фронтах.
4.2. ВЛИЯНИЕ ДИСПЕРСИИ ГРУППОВЫХ СКОРОСТЕЙ
Эффекты ФСМ, обсуждавшиеся в разд. 4.1, реально описывают
распространение только относительно длинных импульсов (То >
> 100 пс), для которых дисперсионная длина LD много больше длины
световода L и нелинейной длины LNL. С укорочением импульсов
дисперсионная длина становится сравнимой с длиной световода,
и теперь необходимо рассмотреть совместное действие эффектов ДГС
и ФСМ [8]. В области аномальной дисперсии световода под дейст-
действием этих двух эффектов в совокупности в световоде могут существо-
существовать оптические солитоны [11, 12], которые будут обсуждаться в
гл. 5. В области нормальной дисперсии [13-15] совместное действие
эффектов ФСМ и ДГС нашло применение в компрессии оптических
импульсов. Эта тема обсуждена в гл. 6. В этом разделе рассматрива-
рассматриваются спектральные и временные изменения, которые происходят,
когда эффект ДГС учитывается при описании ФСМ [13-28].
Отправной точкой будет уравнение распространения C.1.4), кото-
которое можно переписать в следующей нормализованной форме;
j—-s п В )l — -N2e-*-\U\2U D 2 1)
где \ и т—нормированные переменные длины и времени
% = z/Lo, т = Т'Т0 , D.2.2)
параметр N вводится следующим образом;
L уР Tl
^v2=TJL = I7^-^- D-2-3)
86
Глава 4
Физический смысл N станет ясен в гл. 5, где показывается, что целые
величины N связаны с порядком солитона. Практическое значение
параметра N состоит в том, что решения уравнения D.2.1), получен-
полученные для определенной величины N, можно применить во многих
практических ситуациях, используя изменение масштаба в соответст-
соответствии с уравнением D.2.3). Например, если N = 1 при То = 1 пс,
Ро = 1 Вт, то вычисленные результаты также хорошо применимы для
То = 10 пс и Ро = 10 мВт или То = 0,1 пс и Ро = 100 Вт. Как следует
из уравнения D.2.3), N определяет относительное влияние эффектов
ФСМ и ДГС на эволюцию импульсов в волоконном световоде. При
N « 1 преобладает дисперсия, тогда как ФСМ доминирует при N » 1.
Если N ~ 1, то и ФСМ, и ДГС играют одинаково важную роль
в процессе эволюции импульса. В уравнении D.2.1) sgn(C2)= + 1
в зависимости от того, нормальна (Р2 > 0) или аномальна (р2 < 0)
ДГС. Для численного решения уравнения D.2.1) можно воспользо-
воспользоваться методом SSFM, описанным в разд. 2.4.
На рис. 4.6 показана эволюция формы импульса и его спектра
в случае начального гауссовского импульса без частотной модуляции
в области нормальной дисперсии световода при N = 1 и а = 0.
-10 -5 0 5
т/То
1.0 г
Рис. 4.6. Эволюция формы импульса (верхний график) и спектра импульса
(нижний график) на расстоянии z = 5LD гауссовского импульса без начальной
частотной модуляции, распространяющегося в области нормальной дисперсии
световода (Р2 > 0) при N = 1.
Фазовая самомодуляция
87
Качественное поведение в этом случае сильно отличается от случаев,
когда либо ДГС, либо ФСМ доминируют. В частности, импульс
уширяется значительно быстрее, чем в случае N = 0 (в отсутствие
ФСМ). Это объясняется тем, что ФСМ приводит к генерации новых
частотных компонент, смещенных в длинноволновую (красную) об-
область на переднем фронте и в коротковолновую (синюю) область на
заднем фронте импульса. Так как красные компоненты движутся
быстрее, чем синие в области нормальной дисперсии, ФСМ ведет
к увеличению скорости уширения импульса по сравнению с диспер-
дисперсионным уширением. Это в свою очередь влияет на спектральное
уширение, так как фазовый набег <frNL из-за ФСМ уменьшается в
сравнении со случаем, когда форма импульса остается неизменной.
В самом деле, фмакс = 5 при z = 5LD, и в отсутствие ДГС возникает
«двугорбый» спектр. То, что спектр импульса при z/D D = 5 на рис. 4.6
имеет один максимум, означает, что эффективный фма1Сс меньше
л из-за уширения импульса.
Ситуация изменяется, если импульс распространяется в области
аномальной дисперсии световода. На рис. 4.7 показаны формы им-
N= 1, /Зг<0
-3-2-1 0 1 2
lv-v0) To
Рис. 4.7. Эволюция формы импульса (верхний рисунок) и спектра (нижний
рисунок) при тех же условиях, что и на рис. 4,6, за исключением того, что
гауссовский импульс распространяется в области аномальной дисперсии
<Р2 < 0).
Глава 4
Рис. 4.8. Коэффициент уширения гауссовского импульса для случаев нор-
нормальной (Р2 > 0) и аномальной (р, < 0) ДГС. N = 1 для обоих случаев. Для
сравнения штриховой линией показано уширение в случае отсутствия ФСМ
(N = 0).
пульсов и спектры при тех же условиях, что и на рис. 4.6, за
исключением того что знак ДГС меняется на противоположный
(Р2 < 0). Импульс сначала несколько уширяется со скоростью много
меньшей, чем при дисперсионном уширении (без ФСМ), и затем
приходит к стационарному состоянию при z > 4LB. В то же время
спектр сужается, а не уширяется, как в случае только ФСМ без ДГС.
Такое поведение объясняется тем, что частотная модуляция, наводи-
наводимая ФСМ (уравнение D.1.8)), положительна, тогда как частотная
модуляция, наводимая дисперсионным уширением (уравнение C.2.13)),
отрицательна при Р2 < 0. Эти две частотные модуляции почти ком-
компенсируют друг друга в центральной части гауссовского импульса,
когда LD = LNL (N = 1). Форма импульса перестраивается при рас-
распространении таким образом, чтобы эта компенсация была как
можно более полной. Таким образом, совместное действие ДГС
и ФСМ приводит к возникновению импульса без частотной модуля-
модуляции. Описанная ситуация соответствует эволюции солитона; началь-
начальное уширение гауссовского импульса обусловлено тем, что солитон
имеет негауссовскую форму. Если же начальный импульс имеет
форму гиперболического секанса (уравнение C.2.21), С = 0), то ни
форма импульса, ни его спектр не изменяются при распространении.
Подробно этот вопрос будет рассмотрен в гл. 5.
Из рис. 4.6 и 4.7 следует, что основной эффект ФСМ-это измене-
изменение скорости уширения импульса, вызванного ДГС. На рис. 4.8
показана зависимость коэффициента уширения а/а0 от z/LD при
Фазовая самомодуляция 89
N = 1, когда в световод вводится гауссовский импульс без частотной
модуляции. Величина а-среднеквадратичная длительность, опреде-
определяемая уравнением C.2.25), и со-ее начальная величина. Для сравне-
сравнения штриховой прямой показан коэффициент уширения в отсутствие
ФСМ (N = 0). ФСМ приводит к увеличению скорости уширения
в области нормальной дисперсии и уменьшает ее в области аномаль-
аномальной дисперсии. Меньшая скорость уширения при Р2 < 0 может быть
использована в оптических системах связи, работающих на длине
волны 1,55 мкм, где Р2 — — 20 пс2/км. Как отмечалось в разд. 3.4,
возможности таких систем ограничиваются дисперсией такой степе-
степени, что произведение скорости передачи на длину BL обычно ниже
100 Гбит/скм для частотно-модулированных импульсов с С = —5.
Было показано [25], что BL можно увеличить почти в 2 раза,
увеличив пиковую мощность до 20-30 мВт, что обусловливается
действием ФСМ, проиллюстрированным на рис. 4.8 (случай Р2 < 0).
Обычно, чтобы изучить совместное действие эффектов ДГС и
ФСМ, бывает необходимо численно решить уравнение D.2.1). Тем не
менее было бы полезно даже приближенное аналитическое выражение
для длительности импульса, чтобы понять, как скорость уширения
функционально зависит от физических параметров. Для приближен-
приближенного решения уравнения D.2.1) использовалось несколько методов.
В одном из методов уравнение сначала решают, пренебрегая ДГС.
Затем результат используется как начальное условие и уравнение
D.2.1) снова решается, но на этот раз пренебрегают ФСМ. Этот
метод аналогичен фурье-методу с расщеплением по физическим
факторам (разд. 2.4) с той лишь разницей, что размер дисперсионного
шага равен длине световода. Таким образом можно аналитически
вычислить среднеквадратичную длительность импульса, следуя про-
процедуре, обсуждавшейся в разд. 3.3. В случае гауссовского импульса
без частотной модуляции при z = 0 коэффициент уширения выра-
выражается как [23]
зуз
где фмакс, т.е. максимальный ФСМ,-набег фаз, определяемый урав-
уравнением D.1.6). Это выражение довольно точно при фмакс < 1.
В другом методе уравнение D.2.1) решается в спектральном
представлении [16, 24]. В этом спектральном методе ФСМ рассмат-
рассматривается как четырехфотонный процесс [16], в котором из двух
фотонов на частоте накачки образуются два фотона: один на частоте,
смещенной в коротковолновую область, а другой-в длинноволно-
длинноволновую. Осциллирующая структура ФСМ-спектра обусловлена требова-
требованиями фазового синхронизма (см. разд. 10.1). Вообще говоря, уравне-
уравнение, описывающее эволюцию спектральных компонент, следует ре-
90
Глава 4
шать численно, тем не менее в некоторых случаях, если предполо-
предположить, что форма импульса меняется незначительно, его можно
решить и аналитически [24].
Третий метод основан на предположении, что импульс сохраняет
свою форму при распространении, но его длительность и частотная
модуляция могут изменяться при движении вдоль оси z. В случае
гауссовского импульса в форме уравнения C.2.14) параметры То
и С могут меняться по z. Их изменение с координатой z можно
определить, используя вариационный метод [18] или через интеграл
по траекториям [20]. Этот метод довольно мощный, так как он
позволяет физически описать эволюцию импульса даже в случае
частотно-модулированного импульса. Однако его применение огра-
ограничивается величиной N ;$ 1, когда форма импульса сильно не изме-
изменяется.
Если N » 1, то в уравнении D.2.1) ФСМ преобладает над ДГС по
крайней мере на начальной стадии эволюции импульса в световоде.
Однако оказывается, что ДГС нельзя рассматривать как возмущение.
Дело в том, что из-за большой частотной модуляции, наводимой
ФСМ, даже слабое влияние дисперсии ведет к существенному измене-
изменению формы импульса. В случае нормальной дисперсии (р2 > 0)
импульс становится близким к прямоугольному с относительно
резкими фронтами. Он имеет линейную частотную модуляцию на
всей своей ширине [14]. Именно эта линейная частотная модуляция
способствует сжатию импульсов в дисперсионных линиях задержки.
Этому вопросу посвящена гл. 6. Влияние ДГС имеет еще один аспект.
Изменение формы импульса ведет к тому, что эффективность ДГС
возрастает, так как вторая производная по Тв уравнении D.2.1) на
фронтах импульса увеличивается. Как следствие, на импульсе вблизи
Рис. 4.9. Эволюция гауссовского импульса без начальной частотной модуля-
модуляции на расстоянии z = O,1LD в области нормальной дисперсии световода при
N = 30.
Фазовая самомодуляция
91
N = 30, f = 0,08, C=0
-п0,04г
-2 0 2
Время т/т0
Рис. 4.10. Форма и спектр импульса на длине z/LD — 0.08; вначале импульс
был гауссовской формы и не имел частотной модуляции (С = 0). Все пара-
параметры идентичны тем, которые соответствуют рис. 4.9. Крылья на спектре
и тонкая структура на импульсе вблизи его фронтов вызваны эффектом
распада огибающей оптической волны.
его краев развивается тонкая структура. На рис. 4.9 показана эволю-
эволюция импульса при N = 30: вначале импульс был гауссовским и не
имел частотной модуляции. Осцилляции на импульсе вблизи его
краев существуют уже при z/LD = 0,06. Дальнейшее увеличение z ве-
ведет к уширению пьедестала импульса. На рис. 4.10 показаны форма
импульса и его спектр в точке zlLD = 0,08. Особенностью, заслужи-
заслуживающей внимания, является то, что быстрые осцилляции фронтов
импульса всегда сопровождаются образованием дополнительных
компонент на краях спектра. Центральная часть спектра, состоящая
из многих пиков, существенно модифицируется ДГС. В частности,
минимумы оказываются не столь глубокие, как те, что вызываются
лишь одним эффектом ФСМ.
Физические причины возникновения временных осцилляции вбли-
вблизи фронтов импульса связаны с волновой неустойчивостью-новым
явлением, называемым распадом оптической волны [22]. Смещенный
в длинноволновую область свет вблизи переднего фронта движется
быстрее (при р2 > 0) несмещенного света на переднем крае импульса
и обгоняет его. Обратное происходит для света, смещенного в корот-
коротковолновую область, на заднем фронте импульса. В обоих случаях на
переднем и заднем фронтах импульса волны на разных частотах
интерферируют. В результате этой интерференции формируются
осцилляции вблизи фронтов импульса на рис. 4.9. Это явление можно
интерпретировать и как четырехволновой процесс (см. разд. 10.1).
Нелинейное смещение двух разных частот cox и со2 на краях импульса
приводит к генерации новых частот; 2т ^ — со2 и 2со2 — сох. Эти новые
частотные компоненты формируют «крылья» на краях спектра
92
Глава 4
(рис. 4.10). Таким образом, осцилляции во времени вблизи фронтов
импульса и образование крыльев на краях спектра-это проявление
одного и того же эффекта.
Результаты, приведенные на рис. 4.9 и 4.10, соответствуют случаю
импульсов, не имеющих начальной частотной модуляции (С = 0).
Практически импульсы, генерируемые лазерными источниками, часто
бывают частотно-модулированными, и поэтому их эволюция в свето-
световоде может быть совершенно иной [21] и зависит от знака и величины
параметра частотной модуляции С. На рис. 4.11 показаны форма
импульса и спектр при тех же условиях, что и на рис. 4.10, за тем
исключением, что начальный импульс обладал частотной модуляцией
С =20. Сравнение этих двух рисунков иллюстрирует, как сильная
начальная частотная модуляция может изменить характер распрост-
распространения. Для частотно-модулированного вначале импульса его фор-
форма становится похожей на треугольную, а не прямоугольную. В то же
время спектр имеет осцилляции на крыльях, тогда как структура
в центре спектра, характерная для ФСМ-спектров (см. рис. 4.10 для
случая импульса без частотной модуляции), почти исчезает. Эти
изменения формы импульса и спектра можно качественно объяснить
тем, что положительная начальная частотная модуляция складывает-
складывается с модуляцией, наводимой ФСМ. Поэтому распад оптической
волны возникает раньше для частотно-модулированных импульсов.
На эволюцию импульсов также оказывают влияние оптические поте-
потери [21, 22]. Для количественного сравнения теоретических и экспери-
экспериментальных результатов необходимо учесть в численном моделиро-
моделировании и частотную модуляцию, и потери.
Совместное действие эффектов ФСМ и ДГС в оптических волок-
N=30, ?=0,08, с=20
0,8
Рис. 4.11. Форма импульса и спектр, формирующиеся при тех же условиях,
что и в случае рис. 4.10, за исключением того, что входной гауссовский
импульс имел частотную модуляцию с С = 20.
Фазовая самомодуляция
93
— 1,72нм
Длина волны
Рис. 4.12. Экспериментально наблюдавшийся спектр импульса на выходе из
93,5-метрового световода, когда в него вводился 35-пикосекундный импульс.
Этот спектр иллюстрирует спектральное уширение, вызываемое ФСМ. Для
сравнения на рисунке также приведен начальный спектр. Крылья на краях
спектра объясняются эффектом распада огибающей оптической волны. Вход-
Входная пиковая мощность 235 Вт соответствует N =; 173 [27].
нах впервые исследовалось в эксперименте [13] по распространению
5,5-пикосекундных (FWHM) импульсов (на длине волны 587 нм)
излучения лазера на красителе с синхронизацией мод в 70-метровом
световоде. При входной мощности 10 Вт (N ~ 7) выходной импульс
имел близкую к прямоугольной форму и положительную линейную
частотную модуляцию. Форма импульса определялась из измере-
измерений автокорреляционной функции, так как импульс был слишком
короткий, чтобы его форму можно было измерить непосредст-
непосредственно. В более позднем эксперименте [17] более широкие импульсы
длительностью ~ 150 пс от Nd: YAG-лазера, работающего на длине
волны 1.06 мкм, пропускались через 20-километровый световод. По
мере увеличения пиковой мощности импульсов, вводимых в световод
от 1 до 40 Вт (что соответствует изменению N в диапазоне от 20 до
150), выходные импульсы уширялись, становились почти прямоуголь-
прямоугольными, и затем на них появлялась структура на краях,-картина
эволюпии была подобна представленной на рис. 4.9. Для столь
больших длин световода необходимо учитывать потери в световоде;
экспериментальные результаты оказались в хорошем соответствии
с результатами численного моделирования уравнения D.2.1) [17, 21].
Доказательство существования явления распада оптической волны
оыло получено в эксперименте [27], где 35-пикосекундные (FWHM)
импульсы на длине волны 532 нм (излучение Nd; YAG-лазера на
Удвоенной частоте) с пиковой мощностью 235 Вт распространялись
94 Глава 4
в 93,5-метровом световоде с сохранением поляризации. На рис. 4.12
приведен спектр, наблюдавшийся в этом эксперименте. Несмотря на
то что в этом эксперименте N ^ 173, очевидно его принципиальное
совпадение со спектром, изображенным на рис. 4.10. Фактически
эффект распада оптической волны был открыт Томлинсоном и др.
[22] при попытке объяснить наличие крыльев на рис. 4.12. При
прямых измерениях распада волны [28] было обнаружено, что
крылья спектра в самом деле связаны с генерацией новых частотных
компонент вблизи краев импульса.
В заключение этого раздела вкратце рассмотрим случай распрост-
распространения импульса вблизи длины волны нулевой дисперсии (kD ^
= 1,3 мкм) световода [29-34]. Если оптическая длина волны Хо почти
совпадает с XD, P2~0 и дисперсионные эффекты низшего порядка
будут определяться членом рз в разложении B.3.23). Соответству-
Соответствующее уравнение распространения следует из уравнения B.3.35), если
положить Р2 = 0 и пренебречь нелинейными членами высшего поряд-
порядка. Если ввести дисперсионную длину L'd из уравнения C.3.3) и опре-
определить ^' = zjL'D как нормированную длину, получим
eu i гъи _
ф^-^-- N2e~^\U\2U, D.2.5)
где
AP=i^ = l?ll?. D26)
Так же как и в уравнении D.2.1), параметр N определяет соотношение
между эффектами ДГС и ФСН в процессе эволюции импульса: ДГС
преобладает, если N « 1, тогда как если N » 1, то доминирует ФСМ.
Уравнение D.2.5) можно решить .численно, используя фурье-метод
с разделением по физическим факторам, описанный в разд. 2.4.
В последующих рассуждениях предполагается, что р3 > 0. и пренеб-
регается влиянием оптических потерь (а = 0).
На рис. 4.13 показаны форма и спектр импульса на длине Ъ,' = 5
для случая N = 1, если начальный импульс был гауссовским без
частотной модуляции. Сравним получающиеся формы импульсов
в этом случае со случаем, когда отсутствует ФСМ (N = 0), показан-
показанным на рис. 3.6. Действие ФСМ состоит в увеличении числа осцилля-
осцилляции на заднем фронте импульса. В то же время интенсивность не
спадает до нуля в минимумах. Влияние ДГС также ясно видно на
рис. 4.13. В отсутствие ДГС формируется симметричный двухпико-
вый спектр, похожий на тот, что показан на рис. 4.2 для случая
Фма«с = 1>5я, так как фма1СС = 5 для параметров, использованных на
рис. 4.13. Действие ДГС приводит к асимметрии спектра, не изменяя
двухпиковую структуру. Эта ситуация резко отличается от той, что
показана на рис. 4.6 для случая нормальной дисперсии, в котором
Фазовая самомодуляция
95
0,6 г-
Рис. 4.13. Форма импульса и спектр, формирующиеся_из гауссовского им-
импульса без частотной модуляции на длине z = 5L'D при N = 1, если его длина
волны была точно равна длине волне нулевой дисперсии, а значит, при р2 = О
и рз > 0.
ДГС препятствует расщеплению спектра.
Эволюция импульса принимает качественно иные черты для
больших величин N. В качестве примера на рис. 4.14 показаны форма
и спектр импульса при Ъ,' = 0.1. сначала имевшего гауссовскую форму
без частотной модуляции, для случая N — 10. На импульсе формиру-
формируется осциллирующая структура с глубокой модуляцией. Из-за быст-
быстрых изменений огибающей во времени третья производная в уравне-
уравнении D.2.5) локально становится большой и возрастает роль ДГС при
распространении импульса в волокне. Самой примечательной осо-
особенностью спектра является то, что энергия концентрируется в двух
спектральных областях. Эта черта общая для всех значений N > 1.
Так как одна из частей спектра лежит в области аномальной диспер-
дисперсии, в этой области могут формироваться солитоны [34]. Энергия
в другой спектральной области, находящейся в области нормальной
дисперсии световода, рассеивается в процессе распространения. Осо-
Особенности, связанные с солитонами, в дальнейшем будут обсуждены
в гл. 5. Важно отметить, что вследствие спектрального уширения
в действительности импульс не распространяется при нулевой дис-
дисперсии, даже если сначала Р2 cz 0. На самом деле импульс создает
свою собственную р2 посредством ФСМ. Грубо говоря, эффектив-
эффективную величину Р2 можно определить как
кс/2я|, D.2.7)
где 8сома1[С-максимальное смешение частоты, определяемое из урав-
уравнения D.1.9). Параметр Р2 определяется положением доминирующих
крайних пиков в спектре, уширенном под действием ФСМ.
96
Глава 4
0,15
.о
?
g 0,10
^0,05
0
-
-
-
^ J
Л
-
-
VI. Л
-2
-2
О 2
Wo) То
Рис. 4.14. Форма импульса и его спектр, формирующиеся в точке z/L'D = 0,1
при условиях, идентичных случаю, показанному на рис. 4.13, с тем отличием,
что N = 10.
4.3. ОБРАЗОВАНИЕ УДАРНОЙ ВОЛНЫ ОГИБАЮЩЕЙ
До сих пор обсуждение ФСМ было основано на упрощенном
уравнении B.3.36), которое учитывало только эффекты низшего
порядка ФСМ и ДГС. В случае сверхкоротких импульсов (длитель-
(длительностью То < 100 фс) необходимо учитывать дисперсионные и нели-
нелинейные эффекты высшего порядка, используя уравнение B.3.35).
Важным нелинейным эффектом высшего порядка является образова-
образование ударной волны огибающей, определяемое вторым членом в пра-
правой час t и этого уравнения. Этот эффект обусловлен зависимостью
групповой скорости от интенсивности [35-38]. Впервые его влияние
на ФСМ было рассмотрено в жидких нелинейных средах [2] и впо-
впоследствии расширено на случай распространения импульсов в воло-
волоконных световодах [39-42]. Образование ударной волны ведет к
асимметрии ФСМ-уширения спектра [1-5] и в этой связи привлекло
большое внимание. В этом разделе рассматривается влияние данного
эффекта на форму и спектр сверхкоротких импульсов, распространя-
распространяющихся в одномодовых световодах.
Если пренебречь в уравнении B.3.35) последним членом, предпо-
предположив, что нелинейный отклик мгновенный, и воспользоваться урав-
уравнением C.1.3) для нормированной амплитуды U, то можно получить
следующее уравнение:
,r'C/sgn(p2M2C/
' +
2LD
6L'D
д
'Л1
D.3.1)
Фазовая самомодуляция 97
где LD, L'D и Ljy^-три характерные длины, которые были введены
в гл. 3; они определяются как
D ~ I R I" D ~ I R I' NL ~ vP ' ( '
IP2I 1Рз1 Y*o
Образование ударной волны описывается последним членом уравне-
уравнения D.3.1). параметр s определяется как
4 %, D.3.3)
* 4 %,
<°о 'о п'о
i де Топт период оптической волны 2л/соо. В видимой области спектра
Гопт ^ 2 фс, поэтому s-малая величина, превышающая 0,01 только
при Го < 60 фс.
Прежде чем рассматривать численные решения уравнения D.3.1),
поучительно рассмотреть сначала бездисперсионный случай, положив
Р2 = Р3 = 0. В этом частном случае уравнение D.3.1) можно решить
аналитически [37, 40]. Для простоты мы пренебрежем потерями
в световоде (а = 0). Если определить нормированную длину как
Z = z/LNL, уравнение D.3.1) принимает вид
^ + s^(\U\2U) = i\U\2U. D.3.4)
cZ ex
Подставив в уравнение D.3.4) U = ^//ехрО'ф) и разделив действи-
действительную и мнимую части, получим
^ + 3.7^ = 0, D.3.5)
Так как уравнение для интенсивности D.3.5) оказывается не связан-
связанным с уравнением для фазы D.3.6), его можно легко решить методом
характеристик. Общее решение имеет вид [37, 39]
/(Z, т) =/(т - 3sIZ), D.3.7)
где используется начальное условие
Д0,т)=/(т) D.3.8)
описывает начальную форму импульса при z = 0. Из уравнения
D-3.7) следует, что каждая точка т движется вдоль прямой линии от
начального значения и наклон этой линии зависит от интенсивности.
Это ведет к искажению формы импульса. Например, рассмотрим
случай гауссовского импульса
98
Глава 4
т2). D.3.9)
Из уравнений D.3.7) и D.3.9) находим, что форма импульса после
прохождения расстояния Z принимает вид
/ (Z, т) = ехр [ - (т - 3.S/ZJ] .
D.3.10)
Чтобы получить форму импульса для некоторой величины l(Z, т),
нужно выразить из этого неявного выражения т для каждого Z. На
рис. 4.15 показаны рассчитанные формы импульсов для случаев
sZ = 0,1 и 0,2 при s = 0,01. Распространяясь в световоде, импульс
становится несимметричным, его максимум смещается на задний
фронт. В результате задний фронт становится все круче и круче
с увеличением Z. С физической точки зрения групповая скорость
зависит от интенсивности таким образом, что пик импульса движется
с меньшей скоростью, чем его крылья.
Укручение заднего фронта импульса в конце концов приводит
к образованию оптической ударной волны аналогично тому, как
развивается акустическая ударная волна на переднем фронте звуковой
волны [37]. Критическую длину формирования ударной волны оги-
огибающей можно определить из уравнения D.3.10); устремляя в точке
образования ударной волны dl/dz к бесконечности, получаем [40]
1/2 г I I IT
z. = \ -
1,0-
0,8-
(О
X
О
|0,4
0,2-
-3
1111,1,,
SZ
(
-
¦ i > > ' ¦
-п /
11
11
1
, , , , 1 1
\
\\\
\
S
-0.2
I т-г-гт .
= 0,01 -
-
-2
-1
О
т/т0
Рис. 4.15. Образование ударной волны огибающей гауссовского импульса
в бездисперсионном случае. Штриховой линией показана форма начального
импульса при 7 = 0. Сплошными линиями показана деформация его формы
при распространении.
Фазовая самомодуляция
99
Рис. 4.16. Спектр гауссовского импульса на расстоянии z = 0.2L NL/s, где
s = 0.01 и LNL- нелинейная длина. Дисперсия нелинейности вызывает асим-
асимметрию спектра, уширенного ФСМ. Пренебрегается эффектом ДГС.
Подобное соотношение остается справедливым и для импульса в
форме гиперболического секанса с той лишь разницей, что численный
коэффициент 0,39 следует заменить на 0,43. Для пикосекундных
импульсов с То = 1 пс и Ро ~ 1 Вт длина zs ~ 100 км. Однако для
фемтосекундных импульсов То < 100 фс и Ро > 1 кВт zs обычно ста-
становится < 1 м. В результате значительное укручение волнового
фронта импульса может иметь место уже на длине в несколько
сантиметров. Оптическая ударная волна, соответствующая бесконеч-
бесконечно резкому заднему фронту, никогда не формируется на практике
из-за ДГС; чем круче становится волновой фронт импульса, тем
большее значение имеет дисперсионный член в уравнении D.3.1), и его
нельзя игнорировать. Влияние ДГС на укручение волнового фронта
будет рассмотрено в этом разделе несколько ниже. На длину форми-
формирования zs ударной волны также оказывают влияние и потери.
В бездисперсионном случае потери световода а задерживают образо-
образование оптической ударной волны, а если azs > 1, то ударная волна
вообще не формируется [40].
Укручение волнового фронта также оказывает воздействие на
спектральное уширение, вызываемое ФСМ. В бездисперсионном слу-
случае фазу ф(г,т) можно получить аналитически, решая уравнение
D.3.6). Спектр можно получить, взяв фурье-преобразование функции
?- (-, т) или воспользовавшись соотношением
S(fl» = | J
. D.3.12)
На рис. 4.16 показан спектр, вычисленный для случая sz/LNL = 0,2
и * = 0,01. Самая примечательная черта этого спектра его асим-
асимметрия: пиковая интенсивность больше для красных компонент
спектра, чем для синих. Другая особенность - это большее уширение
спектра в синей области (часто говорят «в антистоксовой области»,
используя терминологию, принятую для вынужденного комбина-
100
Глава 4
ционного рассеяния), чем в красной (стоксовой) области. Эти две
особенности спектра качественно объясняются изменениями формы
импульса вследствие укручения волнового фронта. Во-первых, спектр
асимметричен, так как асимметрична форма импульса. Во-вторых,
более крутой задний фронт импульса дает большее уширение спектра
в синей области, так как из-за ФСМ синие компоненты образуются на
заднем фронте (рис. 4.1). При отсутствии укручения волнового фрон-
фронта (s — 0) при параметрах, соответствующих рис. 4.16, фма1[С ^ 6,4л,
и формируется шестипиковый ФСМ-спектр. Из-за укручения волно-
волнового фронта синяя часть спектра вытягивается. Амплитуда высоко-
высокочастотных компонент спектра уменьшается, так как та же энергия
теперь распределяется в более широкой спектральной области.
На спектр, показанный на рис. 4.16, сильное влияние оказывает
ДГС, которую нельзя игнорировать, если в световоде распространя-
распространяются сверхкороткие импульсы. В этом случае эволюцию импульса
исследуют методом численного решения уравнения D.3.1). На
рис. 4.17 показаны формы импульса и спектры при z/LD = 0,2 и 0,4
для случая импульса, распространяющегося в области нормальной
дисперсии (р2 > 0) и рз = 0; на входе был гауссовский импульс без
частотной модуляции. Параметр N, определяемый уравнением D.2.3),
принимается равным 10, что соответствует LD = l00LNL. Чтобы легче
0,4
0,3
0.2 г
t 0.1
х.
и I I
П
-6-4-2 0 2 4 6
Т/Тп
i 0,05 -
Рис. 4.17. Формы импульсов и их спектры при z/LD, равном 0,2 (верхний ряд)
и 0,4 (нижний ряд), в случае гауссовского импульса, распространяющегося
в области нормальной дисперсии световода. Остальные параметры а = 0,
Р3 = 0, jr = 0,01, N= 10.
Фазовая самомодуляция 10)
было сравнивать результат с бездисперсионным случаем, параметр
ч принимается равным 0,01. Форма импульса и его спектр на верхней
части рис. 4.17 при sz/LNL = 0,2 в бездисперсионном случае (Р2 = 0)
соответствуют рис. 4.15 и 4.16. Из непосредственного сравнения
хорошо видно, что ДГС сильно влияет на форму импульса и спектр
даже при длине распространения меньше дисперсионной длины
(z>LD = 0,2). В нижней части рис. 4.17 показаны форма импульса
и спектр при z/LD = 0,4; налицо качественные изменения, вызываемые
ДГС. Для этих величин z/LD длина распространения z превышает
критическую длину формирования ударной волны zs, определяемую
уравнением D.3.11). Именно ДГС ослабляет ударную волну, уширяя
крутой задний фронт, что ясно видно из асимметрии формы импульса
на рис. 4.17. Хотя на спектре нет глубоких осцилляции (см. рис. 4.16
для бездисперсионного случая), удлиненный хвост в синей области
означает укручение волнового фронта. При увеличении длины рас-
распространения z импульс продолжает уширяться, а спектр почти не
изменяется.
Эффект образования ударной волны огибающей наблюдался экс-
экспериментально [2, 4] в жидкостях и твердых телах как большее
уширение спектра в синей области по сравнению с красной. В этих
ранних экспериментах ДГС играет относительно малую роль и
структура спектра похожа на ту, что показана на рис. 4.16. В случае
световодов эффект ДГС достаточно сильный, так что в эксперименте
о
о
I
у-
х 1,25
0,625
500 550 600 650 700 750
Длина волны (нм)
Рис. 4,18. Экспериментально наблюдаемые спектры 40-фемтосекундных
входных импульсов на выходе из 7-миллиметрового световода Указаны
пиковые значения интенсивностей входных импульсов. Верхний спектр соот-
соответствует значению N ^ 7,7 для параметров эксперимента [47].
102 Глава 4
должен наблюдаться спектр, как на рис. 4.17. В экспериментах по
сжатию импульсов [47] 40-фемтосекундные оптические импульсы на
длине волны 620 нм проходили через световод длиной 7 мм. На
рис. 4.18 показаны экспериментальные спектры на выходе из светово-
световода при разных величинах пиковых интенсивностей. Спектр асиммет-
асимметрично уширяется, и хвост спектра в синей области длиннее, чем
в красной, что объясняется укручением волнового фронта. В экспери-
эксперименте параметр s ^ 0,026 и дисперсионная длина была LD ~ 1 см,
если считать То = 24 фс (соответствующее FWHM 40 фс) для гауссов-
ского импульса. Полагая эффективную площадь сердцевины равной
10 мкм2, найдем, что пиковая мощность, соответствующая верхней
кривой на рис. 4.18. равна 200 кВт. Поэтому нелинейная длина
LNL ~ 0,16 мм и N ~ 7,7. Уравнение D.3.1) можно использовать для
численного моделирования эксперимента, используя приведенные
выше параметры. Учет Р3> вообще говоря, необходим [42], чтобы
воспроизвести детальную структуру наблюдавшихся в эксперименте
спектров на рис. 4.18.
Уравнение D.3.1) предполагает мгновенность нелинейного откли-
отклика и справедливо, только если время отклика TR много меньше
длительности импульса То. Влияние конечного времени отклика на
ФСМ было исследовано, в частности, для жидких нелинейных сред,
таких, как CS2, где TR = 8 10 пс, и может быть больше длительности
пикосекундных импульсов То [2, 5]. В случае волоконных световодов
TR ~ 5 фс из-за электронной природы нелинейности. Если длитель-
длительности оптических импульсов То < 100 фс, необходимо учитывать
конечность времени нелинейного отклика. В самой простой модели
предполагается, что нелинейный отклик спадает экспоненциально,
и эволюция импульса изучается на основе уравнений B.3.37) и B.3.39)
[48]. Несколько другой подход использовать вместо уравнения
D.3.39) уравнение B.3.35) [49]. Связь и справедливость двух подходов
обсуждались в разд. 2.3. Влияние конечного времени отклика наибо-
наиболее примечательно в сь 1зи с солитонами; оно приводит к распаду
солитонов [48, 49] и смещению частоты [50, 51]. Эти эффекты будут
рассмотрены в гл. 5.
ЛИТЕРАТУРА
1. ShimizuF.. Phys. Rev. Lett., 19, 1097 A967).
2. Gustafson Т.К. el al.. Phys. Rev., 177, 306 A969).
3. Cubeddu R. et al.. Phys. Rev., A2, 1955 A970).
4. Alfano R. Я, Shapiro S.L.,, Phys. Rev. Lett., 24. 592 A970); 24, 1217 A970).
5. Slien Y.R., Lov M. M. T. Phys. Rev., A3, 2099 A971).
6. Lin C.H., Gustafson Т.К., IEEE J. Quantum Electron., QE-8, 429 A972).
7. Ippen EP., Shank C. V.. Gustafson Т.К.. Appl. Phys. Lett., 24, 190 A974).
8. Fisher R.A.. Bischel W.K.. J. Appl. Phys., 46, 4921 A975).
9. Stolen R.H.. Lin C, Phys. Rev., A17, 1448 A978).
Фазовая самомодуляция 103
10 Pinault S.C., Potasek M.J., J. Opt. Soc. Am., B2, 1318 A985).
11. Hasegawa A., Tappert F.. Appl. Phys. Lett., 23, 142 A973); 23, 171 A973).
p Mollenauer L.F., Stolen R.H.. Gordon J.P., Phys. Rev. Lett., 45, 1095 A980).
13 Sakatsuka #., Grischkowsky D., Balant A.C., Phys. Rev. Lett., 47, 910 A981).
14 Grischkowsky D., Balant A.C., Appl. Phys. Lett., 41, 1 A982).
15. Tomlinson W.J., Stolen R.H., Shank С V., J. Opt. Soc. Am., 1, 139 A984).
16 BotineauJ., Stolen R.H.. i. Opt. Soc. Am., 72, 1592 A982).
17 Nelson B. P., Cotter D., Blow K.J.. Doran N. J., Opt. Commun., 48, 292 A983).
18. Anderson D., Phys. Rev., A27, 3135 A983).
19. Сиеакян И. #., Шварцбург А. В. Квант, электрон., 1984, т. 11, с. 1703.
70 Фаттахов A.M., Чиркин Л.С-Квант, электрон., 1984, т. 11, с. 2349.
21. Lassen Н.Е. et al.. Opt. Lett., 10, 34 A985).
22. Tomlinson W.J., Stolen R.H., Johnson A.M., Opt., Lett., 10, 457 A985).
23. Potasek M.J., AgrawalG.P., Pinault S. C, J. Opt. Soc. Am., B3, 205 A986).
24. Pask C, Vatarescu A.. J. Opt. Soc. Am., B3, 1018 A986).
25. Potasek M.J.. AgrawalG.P., Electron. Lett., 22, 759 A986).
26. Potasek M.J.. AgrawalG.P., Phys. Rev., A36, 3862 A987).
27. Johnson A.M., Simpson W.M.. J. Opt. Soc. Am., B2, 619 A985).
28. Hamaide J.-P., Emplit P., Electron. Lett., 24, 818 A988).
29. Blow K.J.. Doran N.J., Cumins E., Opt. Commun., 48, 181 A983).
30. Выслоух В. А- Квант, электрон., 1983, т. 10, с. 1688.
31. AgrawalG.P.. Potasek M.J., Phys. Rev., A33, 1765 A986).
32. Wai P. К. A., Menyuk C.R., Lee Y.C., Chen H.H.. Opt. Lett., 11, 464 A986).
33. BoverG.R., Carlotti X.F., Opt. Commun., 60, 18 A986).
34. WaiP.K.A., Menyuk C.R., Chen H.H., Lee Y.C., Opt. Lett., 12, 628 A987).
35. Островский Л. Л.-ЖЭТФ, 1966, т. 51, с. 1189.
36. Jonek RJ., Landauer R., Phys. Lett., A24, 228 A967).
37. DeMartini F., TownesC.H., Gustafson Т.К., Kelley P.L.. Phys. Rev., 164, 312
A-967).
38. Grischkowsky D., Courtens E., Armstrong J.A., Phys. Rev. Lett., 31, 422 A973).
39. Tzoar N.. Jain M., Phys. Rev., A23, 1266 A981).
40. Anderson D., LisakM.. Phys. Rev., A27, 1393 A983).
41. Гомвченко Е. А. и dp.-Письма в ЖЭТФ, 1985, т. 42, с. 74; ДАН СССР,
1986, т. 288, с. 851.
42. BourkoffE, Zhao Ж, Joseph R.L.. Christodoulides D.N., Opt. Lett., 12, 272
A987).
43. Fork R.L. et al. Opt. Lett., 8, 1 A983).
44. Yang G., Shen Y.R.. Opt. Lett., 9, 510 A984).
45. ManassahJ.T, Mustafa M. A., AlfanoR.R., Ho P.P., Phys. Lett., A113, 242
A985); IEEE J. Quantum Electron., QE-22, 197 A986).
46. Mestdagh D., Haelterman M., Opt. Commun., 61, 291 A987).
47. Kno.x W.H., et al., Appl. Phys. Lett., 46, 1120 A985).
48. Грудинин А.Б. и <)/v-Письма в ЖЭТФ, 1987, т. 45, с. 211.
49. Hodel W, Weber H.P., Opt. Lett., 12, 924 A987).
50. Mitschke F.M., Mollenauer L.F., Opt. Lett., 11, 659 A986).
51. Gordon J.P., Opt. Lett., 11, 662 A986).
Глава 5
ОПТИЧЕСКИЕ СОЛИТОНЫ
Нелинейные свойства оптических световодов самым ярким обра-
образом проявляются в области аномальной (отрицательной) дисперсии.
Здесь могут существовать так называемые солитоны-образования,
обусловленные совместным действием дисперсионных и нелинейных
эффектов. Сам термин «солитон» относится к специальному типу
волновых пакетов, которые могут распространяться на значительные
расстояния без искажения своей формы и сохраняются при столкно-
столкновениях друг с другом. Солитоны изучаются также во многих других
разделах физики [1-5]. Солитонный режим распространения в воло-
волоконных световодах интересен не только как фундаментальное явле-
явление, возможно практическое применение солитонов в волоконно-оп-
волоконно-оптических линиях связи. В данной главе изучается распространение
импульсов в области отрицательной дисперсии групповых скоростей,
особое внимание уделяется солитонному режиму распространения.
В разд. 5.1 рассматривается явление модуляционной неустойчивости.
Показано, что при наличии нелинейной фазовой самомодуляции
(ФСМ) стационарная гармоническая волна неустойчива относительно
малых возмущений амплитуды и фазы. В разд. 5.2 обсуждается метод
обратной задачи рассеяния (ОЗР), который может быть использован
для нахождения солитонных решений уравнения распространения.
Здесь же рассматриваются свойства так называемого фундаменталь-
фундаментального солитона и солитонов высших порядков. Следующие две главы
посвящены применению солитонов в некоторых системах. В разд. 5.3
рассматривается солитонный лазер; разд. 5.4 посвящен использова-
использованию солитонов в волоконно-оптических линиях связи. Нелинейные
эффекты высших порядков, такие, как дисперсия нелинейности и
задержка по времени нелинейного отклика, рассматриваются в
разд. 5.5.
5.1. Модуляционная неустойчивость
Во многих нелинейных системах стационарное волновое состояние
оказывается неустойчивым: совместное действие нелинейных и дис-
дисперсионных эффектов приводит к его модуляции [6-31]. Такое
явление, называемое модуляционной неустойчивостью, исследова-
Оптические солитоны 105
лось в самых разных областях физики: гидродинамике [7, 8], нели-
нелинейной оптике [9-11], физике плазмы [12 15]. Что касается волокон-
волоконной оптики, то для наблюдения модуляционной неустойчивости
требуется отрицательная дисперсия; сам эффект проявляется как
распад непрерывной или квазинепрерывной периодической волны на
последовательность сверхкоротких импульсов [16-23]. Отрицатель-
Отрицательная дисперсия необходима и для существования оптических солито-
нов. В действительности оба этих явления тесно связаны, что было
отмечено уже в ранних работах [6-11]. В данном разделе явление
модуляционной неустойчивости рассматривается как введение в тео-
теорию солитонов.
Вначале рассмотрим упрощенное уравнение распространения
B.3.36). Если пренебречь потерями, уравнение приобретает вид
и в литературе, посвященной солитонному режиму распространения,
называется нелинейным уравнением Шредингера [1-5]. Как уже
обсуждалось в разд. 2.3, A(z,T)-амплитуда огибающей волнового
пакета. Р2- величина дисперсии групповых скоростей, у параметр
нелинейности при ФСМ. В случае непрерывного излучения амплитуда
А в начале световода (z = 0) не зависит от Т. Предполагая, что
функция A (z, T) продолжает оставаться независимой от времени
Т при распространении по световоду, мы можем получить ста-
стационарное решение уравнения E.1.1)
^), E.1.2)
где fp-мощность излучения при z = 0 и ф^ фазовый сдвиг, опреде-
определяемый выражением
Фм.=УЛ>*- E.1.3)
Выражение E.1.2) показывает, что непрерывное излучение должно
распространяться по световоду без изменения, за исключением до-
дополнительного фазового сдвига, зависящего от интенсивности. (При
наличии потерь в световоде мощность излучения, естественно,
уменьшается.)
Выясним вопрос об устойчивости стационарного решения E.1.2).
Для этого рассмотрим малое возмущение стационарного решения
А = (^ГР~0 + а) ехр (/фи.) E.1.4)
и исследуем динамику малого возмущения а (г, Т). Подставляя E.1.4)
в E.1.1) и линеаризуя по а. получаем
/ЩР20-У/>О(« + «*Ь E-1.5)
106 Глава 5
Представим общее решение в виде
a(z, Т) = «1 cos(Kz - QT) + ia2sm(Kz - ПТ), E.1.6)
где К и Q-волновое число и частота возмущения Уравнение E.1.5)
переходит в систему двух однородных уравнений для «i и а2. Эта
система имеет нетривиальное решение только в том случае, если
К и Q удовлетворяют дисперсионному соотношению
^ 2, E.1.7)
где
Нелинейная длина LNL определена в уравнении C.1.5). Из диспер-
дисперсионного соотношения E.1.7) видно, что устойчивость стационарного
состояния существенно зависит от того, в области положительной
(нормальной) или отрицательной дисперсии световода распространя-
распространяется излучение. В случае положительной дисперсии групповых ско-
скоростей (Р2 > 0) волновое число К действительно при всех значениях
Q и стационарное состояние устойчиво относительно малых возму-
возмущений. С другой стороны, в случае отрицательной дисперсии группо-
групповых скоростей (р2 < 0) К становится мнимым при Q < Пс и возмуще-
возмущение a(z, T) экспоненциально нарастает по z. В результате непрерывное
решение E.1.2) является неустойчивым в случае р2 < 0. Данный вид
неустойчивости называется модуляционной неустойчивостью, так как
при этом возникает спонтанная модуляция стационарного состояния.
Похожие виды неустойчивости встречаются во многих других нели-
нелинейных системах. Их часто называют неустойчивостями, вызванными
самовоздействием [32, 33].
Рассмотрим частотную зависимость коэффициента усиления для
модуляционной неустойчивости. Значение коэффициента усиления (по
мощности) на частоте Q можно получить из E.1.7). используя условие
sgn(P2) = — 1. Соответствуюшее выражение для коэффициента уси-
усиления
0(П)=21т(К)=|Р2|П(Пс2-П2I/2, E.1.9)
где д(О) значение коэффициента усиления (на частоте со0 + П) для
возмущения, сдвинутого на частоту Q относительно частоты пада-
падающего излучения со0. Усиление отлично от нуля для случая |П| ^ Пс.
На рис. 5.1 изображены кривые усиления при трех различных
уровнях мощности. Величины р2 = - 20 пс2/км и у = 2 Вт км
соответствуют обычным световодам кварцевого стекла на длине
волны 1,55 мкм. Кривая усиления симметрична относительно Q = 0,
так что усиление исчезает при Q = 0. Максимум усиления достигается
Оптические солитоны
107
-0,2
-0,1 0 0,1
Частотный сдвиг (ТГц)
0,2
Рис. 5.1. Кривые усиления модуляционной неустойчивости при трех уровнях
мощности излучения. Параметры световода: Р2 = — 20 пс2/км и у = 2 Вт -км.
при двух значениях частот
и имеет величину
E.1.11)
где было использовано выражение E.1.8). Пиковое значение коэффи-
коэффициента усиления не зависит от дисперсии р2 и возрастает линейно
с мощностью падающего излучения.
При выводе уравнения E.1.9) мы пренебрегли влиянием потерь
в световоде а на модуляционную неустойчивость. Действие потерь
в основном заключается в том, что коэффициент усиления модуля-
модуляционной неустойчивости уменьшается по длине световода из-за
Уменьшения мощности излучения [19]. В уравнении E.1.9) Пс следует
¦заменить на Qc.exp(— az/2). Модуляционная неустойчивость развива-
развивайся до тех пор, пока остается aLNL < 1. т.е. нелинейная длина
меньше, чем длина затухания а. Можно исследовать также влияние
образования ударной волны огибающей [24], если вместо уравнения
C.1.1) использовать B.3.35). Основное действие этого эффекта на
модуляционную неустойчивость заключается в том, что скорость
Развития неустойчивости уменьшается, а спектральный интервал ее
существования сужается по сравнению с величинами, изображенными
108 Глава 5
на рис. 5.1. В работах [28, 30] рассматривались эффекты, обусловлен-
обусловленные учетом дисперсионных членов высших порядков и нелинейных
членов. Уравнение E.1.9) позволяет оценить коэффициент усиления
для модуляционной неустойчивости лишь в первом приближении,
чего, однако, достаточно для большинства практически значимых
случаев.
Как будет показано в разд. 10.3.2, модуляционная неустойчивость
может трактоваться как четырехволновое смешение с синхронизмом
за счет ФСМ. Если сигнал с частотой tOj = со0 + Q распространяется
совместно с непрерывным излучением накачки с частотой со0, го
сигнал должен усиливаться (коэффициет усиления определяется из
уравнения E.1.9)), если |Q|<QC. С физической точки зрения два
фотона интенсивного излучения накачки с частотой со0 преобразуют-
преобразуются в два различных фотона: один на частоте сигнала coj. а другой на
холостой частоте 2со0 — tOj. Случай, когда сигнал вводится одновре-
одновременно с излучением накачки, иногда называют индуцированной
модуляционной неустойчивостью [18, 23] в отличие от случаев одной
волны излучения.
Даже когда в световоде распространяется лишь одно излучение
накачки, модуляционная неустойчивость может привести к спонтан-
спонтанному распаду стационарной гармонической волны на периодическую
последовательность импульсов. Спонтанно испущенные или тепло-
тепловые фотоны действуют в этой ситуации в качестве сигнального
излучения, усиливающегося за счет модуляционной неустойчивости.
Поскольку наибольшее значение коэффициента усиления наблюдает-
наблюдается для частот со0 + Пмакс (где Пыякс определяется выражением E.1.10)),
эти частотные компоненты усиливаются больше всего Поэтому
прямым доказательством спонтанной модуляционной неустойчивос-
неустойчивости может служить наличие двух дополнительных спектральных ком-
компонент, расположенных симметрично по обе стороны от центральной
частоты со0 со спектральной отстройкой + Пмакс- В° временном
представлении стационарная гармоническая волна преобразуется в
периодическую последовательность импульсов с периодом Тт =/„а1кс>
ГДе /макс = П.макс/2п.
Модуляционная неустойчивость в области отрицательной диспер-
дисперсии волоконных световодов наблюдалась в эксперименте [22]. когда
100-пикосекундные (FWHM) импульсы Nd: YAG-лазера (длины вол-
волны генерации 1,319 мкм) проходили через световод длиной 1 км
с дисперсией р2 ^ — 3 пс2/км. На рис. 5.2 изображены автокорреля-
автокорреляционная функция (АКФ) и спектр излучения на выходе из световода
при пиковой мощности излучения Ро = 7,1 Вт. Расположение боковых
спектральных компонент находится в согласии с предсказанным
уравнением E.1.10). Расстояние между максимумами в АКФ обратно
пропорционально /макс в соответствии с теорией. Боковые спектраль-
спектральные компоненты второго порядка, которые видны на рис. 5.2, также
Оптические солитоны
109
2 пс
Временная задержка
1313 1315 1317 13191321 1323 1325
Длина волны (нм)
Рис. 5.2. Автокорреляционная функция АКФ и спектр излучения на выходе из
световода длиной I км (длительность начальных импульсов 100 пс. пиковая
мощность излучения 7,1 Вт). Модуляция в АКФ и наличие боковых спект-
спектральных компонент обусловлены модуляционной неустойчивостью [22].
описываются теорией [16]. В данном эксперименте для того, чтобы
избежать ВРМБ, используются 100-пикосекундные импульсы, а не
непрерывное излучение. Тем не менее, поскольку период модуля-
модуляционной неустойчивости ~ I пс. относительно широкие 100-пико-
100-пикосекундные импульсы обеспечивают условие квазинепрерывности для
наблюдения этого явления.
В аналогичных экспериментах [23] модуляционная неустойчи-
неустойчивость индуцировалась введением сигнала наряду с импульсами
YAG-лазера. Сигналом служило излучение InGaAsP-лазера, работа-
работающего в режиме одной продольной моды. Данный лазер мог пере-
перестраиваться в диапазоне нескольких нанометров вблизи длины волны
генерации YAG-лазера. Мощность сигнала 0,5 мВт была много
меньше пиковой мощности излучения импульсов YAG-лазера Ро =
= 3 Вт. Тем не менее наличие сигнала приводило к распаду импуль-
импульсов YAG-лазера на периодическую последовательность импульсов,
период которой составлял величину, обратную разности частот
сигнала и излучения накачки. Более того, данный период можно было
регулировать перестройкой длины волны lnGaAsP-лазера. На
рис. 5.3 изображены АКФ для двух различных длин волн сигнала.
Поскольку длительность наблюдаемых импульсов менее 1 пс. данный
метод позволяет генерировать субпикосекундные импульсы, частотой
следования которых можно управлять, перестраивая длину волны
сигнала.
Когда длительность импульсов излучения накачки менее 100 пс,
возможно возникновение модуляционной неустойчивости при дейст-
действии других механизмов, при этом отпадает необходимость в спон-
спонтанной эмиссии или в сигнальном излучении. Одним из таких меха-
механизмов является ФСМ. Если уширение спектра за счет ФСМ прибли-
приближается к П„акс, то спектральные компоненты в окрестности Пма11С на-
начинают действовать в качестве сигнального излучения, усиливаясь за
счет модуляционной неустойчивости. Можно оценить длину светово-
световода, на которой ширина спектра приближается к ПМа«с, используя
по
Глава 5
АЛЛАЛЛ
Рис. 5.3. АКФ, демонстрирующие индуцированную модуляционную не-
неустойчивость при двух различных длинах волн сигнального излучения. Период
модуляций можно регулировать перестройкой полупроводникового лазера,
работающего в качестве источника сигнала [23].
ScoMaIlc из уравнения D.1.9) и приравнивая Пмакс == 5сомакс. В случае
импульса гауссовской формы это условие удовлетворяется, когда
/ 2Т2 \1/2
z*QLDLNL)"* = (—-?-) , E.1.12)
где LD-дисперсионная длина, введенная в разд. 3.1. Численное
решение уравнения E.1.1) подтверждает, что модуляционная неустой-
неустойчивость оптических импульсов, вызванная ФСМ, существует [29].
В частности, на входном импульсе развивается глубокая модуляция
с частотой Пмакс/2п, и в спектре излучения появляются боковые
компоненты с той же частотой отстройки. Чтобы подтвердить, что
модуляционная неустойчивость может возникать подобным образом,
были также проведены эксперименты [29].
Анализ устойчивости стационарного решения уравнения E.1.1)
в линейном приближении показывает, что малые возмущения перво-
первоначально будут нарастать по экспоненциальному закону, определя-
определяемому уравнением E.1.9). Ясно, что экспоненциальный рост не может
продолжаться до бесконечности, поскольку спектральные компонен-
компоненты на частотах со0 + Q растут за счет излучения накачки на частоте
со0; истощение накачки в конце концов замедляет скорость роста [26].
Динамика модулированного состояния определяется уравнением
E.1.1). Численное решение этого уравнения для начального условия
в виде синусоидальной модуляции, наложенной на стационарное
состояние, показывает [18], что синусоидальная модуляция преобра-
преобразуется в последовательность узких импульсов, разделенных периодом
начальной модуляции. Расстояние, необходимое для образования
Оптические солитоны 111
гакой последовательности, зависит от начальной глубины модуляции
и обычно составляет величину ~ 1 5LD. При дальнейшем распрост-
распространении пиковая структура деформируется и в конце концов воз-
возвращается к первоначальному состоянию. Аналитическое решение
уравнения E.1.1) показывает, что данное поведение является общим
для произвольной периодической модуляции стационарного состоя-
состояния [21]. При соответствующем выборе длины световода можно
использовать явление индуцированной модуляционной неустойчи-
неустойчивости для генерации последовательности коротких оптических им-
импульсов, частотой повторения которых можно управлять. Также
было предложено использовать данное явление для полностью воло-
волоконного оптического переключателя [31]. Однако данное явление
имеет и свою отрицательную сторону. Модуляционная неустойчи-
неустойчивость может оказаться ограничивающим фактором для когерентных
систем связи [19, 20, 25], поскольку она приводии к нежелательной
амплитудной модуляции сигнала.
Существование модуляционной неустойчивости в области отрица-
отрицательной дисперсии групповых скоростей указывает на то, что харак-
характер решения уравнения E.1.1) существенно отличается в случае
Р2 < 0. Оказывается, что это уравнение имеет особые решения,
которые либо не меняются по z, либо являются периодичными
[34-36]. Что же касается волоконных световодов, то данные решения
известны как оптические солитоны, которые возникают благодаря
совместному действию дисперсионных и нелинейных эффектов. Сле-
Следующий раздел посвящен свойствам оптических солитонов.
5.2. ФУНДАМЕНТАЛЬНЫЕ СОЛИТОНЫ И СОЛИТОНЫ
ВЫСШИХ ПОРЯДКОВ
Нелинейное уравнение Шредингера (НУШ) E.1.1) принадлежит
к специальному классу уравнений, которые можно точно решить,
используя метод обратной задачи рассеяния (ОЗР). Этот метод был
открыт Гарднером и др. [37]. Захаров и Шабат [34] использовали его
для решения НУШ; данный метод стал важным инструментом
в математической физике [1-5]. Метод ОЗР по духу похож на метод
преобразования Фурье, который обычно используют для решения
нелинейных уравнений в частных производных. Этот подход состоит
в определении подходящей задачи рассеяния, потенциал которой
и есть искомое решение. Значение поля входного излучения (z = 0)
используется для получения начальных данных рассеяния, динамика
которых вдоль оси z легко находится из решения линейной задачи
рассеяния. Поскольку метод ОЗР в деталях изложен во многих книгах
[1 -5], мы лишь кратко опишем, как он используется для решения
Уравнения E.1.1).
112 Глава 5
Используя в уравнении E.1.1) замены
" = -Й = г-, т = ^> E-2Л)
мы получаем
dU le2U .
i— = sgn($2)-—T-N2\U\2U, E.2.2)
д?, 2 ёт2
где Ро — значение пиковой мошности, То-длительность начального
импульса, параметр N определяется как
-(
Дисперсионная длина LD и нелинейная длина LNL были определены
формулами C.1.5). Уравнение E.2.2) идентично уравнению D.2.1)
с той лишь разницей, что здесь мы пренебрегли потерями в световоде
(а = 0). В области отрицательной дисперсии групповых скоростей
sgn(p2)= — 1. Параметр N можно исключить из уравнения E.2.2)
заменой
yj2 \ 1/2
В этом случае уравнение E.2.2) принимает стандартную форму
нелинейного уравнения Шредингера:
*^ + ^^ + M2" = 0. E.2.5)
Для уравнения E.2.5) справедливо следующее соотношение подобия.
Если м(?, т)-решение этого уравнения, то ем(е2?, ет) также является
решением: е-произвольный нормировочный множитель.
В методе ОЗР прямая задача рассеяния, связанная с уравнением
E.2.5), сводится к системе [34]
V+^,=«v2, E.2.6)
^-X,V2=-u*Vl, E.2.7)
где v, и v2-амплитуды волн, рассеянных на потенциале «(?,, т),
^-собственное значение. Уравнения E.2.6) и E.2.7) используются,
чтобы для данного начального условия w@, т) получить начальные
данные рассеяния. Прямая задача рассеяния характеризуется коэффи-
коэффициентом отражения г (Q, который играет роль, аналогичную коэффи-
Оптические солитоны ИЗ
циенту Фурье в фурье-анализе. Он также характеризуется наличием
связанных состояний, которые соответствуют полюсам г (Q на комп-
комплексной ^-плоскости. Таким образом, начальные данные рассеяния
состоят из коэффициента отражения, г (Q комплексных полюсов ?^
и их вычетов Ср где / = 1, ..., N, если существует N таких полюсов.
Хотя параметр N в E.2.3) не обязательно является целым числом,
такое же обозначение используется для числа полюсов для того,
чтобы подчеркнуть, что целые величины определяют количество
полюсов. Динамику данных рассеяния по длине световода получают
из E.2.6) и E.2.7), используя хорошо известные методы [3, 34].
Потенциал «(?,, т) восстанавливается из данных рассеяния при
использовании метода ОЗР. В общем случае для этого требуется
решить сложное линейное интегральное уравнение. Однако в частном
случае, когда для начального потенциала w@, т) r(Q обращается
в нуль, «(?,, т) может быть определено при решении системы алгеб-
алгебраических уравнений. Данный случай и соответствует солитонам.
Порядок солитона характеризуется числом полюсов N или собствен-
собственных значений ?,- (/= 1 N)- Обшее решение имеет вид [34]
ий,т)=-2 X ЦуЪ, E.2.8)
где
^=^ехр(/дт + ^Ч) E.2.9)
и \i2j получаются из решения следующей системы линейных уравне-
уравнений:
V,,+ I ^7iV& = 0, E.2.10)
ь = l Sy — Sfc
V?,- I ^V« = V- E-2.11)
В общем случае собственные значения C,j комплексны (^- = ^. + ir\j).
Действительная часть \-s определяет изменение скорости солитона по
сравнению с групповой скоростью ve. Для того чтобы TV-солитонное
состояние оставалось связанным, необходимо, чтобы все компоненты
распространялись с одинаковыми скоростями. Математически это
означает, что все полюса Х,-} должны лежать на прямой, параллельной
мнимой оси. Не нарушая общности, можно предположить, что они
лежат на мнимой оси, так что \-} = 0. Подставляя ?,- = п\-} в уравнение
E.2.9), для Xj получаем
Xj = y/7iexp(-T]jT-iT]jZl). E.2.12)
Из E.2.8) —E.2.12) видно, что солитон JV-ro порядка определяется ц}
и cj(/ = U ¦¦¦. JV), где Cj в общем случае комплексны. Тем не менее 3JV
И4 Глава 5
действительных постоянных не являются независимыми. В частности,
если предполагается, что солитон симметричен относительно т = О,
то вычеты связаны с собственными значениями соотношениями [38]
л
П (Л; + Л»)
с} = ^ ¦ E.2.13)
п 1л,--л»1
k + j
Фундаментальный солитон соответствует случаю единственного
собственного значения r\1 (N = 1). Как это следует из E.2.8) E.2.12),
фундаментальный солитон имеет вид
и&т) = 2л, sechBr|, T)expBiTi?S) • E.2.14)
Собственное значение г\1 определяет амплитуду солитона. Канони-
Канонический вид фундаментального солитона получается при выборе
и @,0) = 1, так что 2r)j = 1. Уравнение E.2.14) соответственно приоб-
приобретает вид
и (?, т) = sech (т) exp (itjl). E.2.15)
Для волоконных световодов решение E.2.15) означает, что импульс
в форме гиперболического секанса с длительностью Го и пиковой
мощностью Ро выбраны такими, что в уравнении E.2.3) N = 1 будет
распространяться в идеальном световоде (без потерь) без искажения
своей формы на произвольно большие расстояния. Именно это
свойство фундаментальных солитонов делает их привлекательными
для передачи информации в системах оптической связи [35]. Значение
пиковой мощности фундаментального солитона Рх определяется из
формулы E.2.3) при подстановке N = 1:
1Р,| з,щр2|
У' О У' FWHM
где TFWhm — 1,76 То определяется из C.2.22); Xfwhm-длительность
импульса на полувысоте по интенсивности, величина, обычно исполь-
используемая на практике. Для значений параметров р2 и Y, типичных для
световодов из кварцевого стекла на длине волны 1,55 мкм, пиковая
мощность Рх - 5 Вт при То = 1 пс, а при То = 10 пс она уменьшается
до 50 мВт. При использовании световодов со смещенной дисперсией
с р2 =: — 2 пс2/км значение Рх уменьшается в 10 раз.
Солитоны высших порядков также описываются общим решением
E.2.8). Различные комбинации собственных значений r\j и вычетов с-;
дают бесконечное множество форм солитонов. Среди них особую
роль играют солитоны, имеющие начальную форму при ?, = 0
w@,t) = JVsech(T), E.2.17)
Оптические солитоны
115
где порядок солитона N — целое число. Значение пиковой мощности,
необходимой для создания солитона JV-ro порядка, определяется из
уравнения E.2.3) и оказывается в N2 раз больше мощности, необхо-
необходимой для возбуждения фундаментального солитона. Для солитона
второго порядка (N = 2) распределение поля получается из уравнений
E.2.8) —E.2.13) при выборе r)i = 1/2 и гJ = 3/2. Соответствующее
выражение для амплитуды поля [36]:
4 [cosh (Зт) + Зехр D%) cosh (т)] exp (SJ2)
[coshDx) + 4coshBT) + 3coD^)] ' ' '
Интересным свойством этого решения является то, что | и (?,, т) |2
периодична с периодом ?,0 = л/2. Такую же периодичность имеют все
солитоны высших порядков [34]. Используя определение ?, = z/LD из
E.2.1), можно записать период солитона как
т2
1 о
— - / — —-
=°'322
2
FWHM
E.2.19)
где Tfwhm — 1,76 То. Периодичность динамики солитонов высших
порядков проиллюстрирована рис. 5.4 для частного случая N = 3.
Здесь показано изменение формы импульса на одном периоде соли-
солитона. При распространении импульса по световоду его длительность
N = 3
4,-
О . 5
Время Т/То
Рис. 5.4. Динамика формы трехсолитонного импульса на одном периоде
солитона. Обратите внимание на расщепление импульса вблизи z0 = 0,5 и
последующее восстановление.
116
Глава 5
-4
iv-V0)T0
Рис. 5.5. Динамика спектра трехсолитонного импульса на одном периоде
солитона.
первоначально уменьшается, затем на расстоянии zo/2 он расщепля-
расщепляется на два, далее обе компоненты сливаются, формируя при z = z0
первоначальный импульс. Эта картина повторяется на каждом пе-
периоде солитона. Эффект сокращения длительности импульса на
начальном этапе его распространения может быть использован для
сжатия импульсов (см. гл. 6).
Для того чтобы понять физический смысл наблюдаемого явления,
полезно взглянуть на динамику спектра, изображенного на рис. 5.5
для случая N = 3. Изменения в форме импульса и его спектре
возникают при совместном действии фазовой самомодуляции (ФСМ)
и дисперсии групповых скоростей. При ФСМ получается положи-
положительная частотная модуляция, так что передний фронт смещается
в стоксову (относительно несущей частоты) область, а задний фронт -
в антистоксову область. Уширение спектра за счет ФСМ ясно видно
на рис. 5.5 при z/z0 = 0,2; хорошо заметна типичная для ФСМ
модуляция. При отсутствии дисперсии групповых скоростей форма
импульса оставалась бы неизменной (см. разд. 4.1). Отрицательная
дисперсия, однако, сжимает импульс, так как он имеет положитель-
положительную частотную модуляцию (см. разд. 3.2). Сокращает свою длитель-
длительность только центральная область импульса, поскольку только там
сдвиг частоты практически линеен. Из-за того что интенсивность
импульса в центральной его области существенно увеличивается,
спектр его также значительно изменяется (см. рис. 5.5 для z/z0 = 0,3).
Именно совместным действием дисперсионных и нелинейных эффек-
эффектов объясняется характер динамики импульса, изображенной на
рис. 5.4. В случае фундаментального солитона (N = 1) дисперсия
и ФСМ компенсируют друг друга таким образом, что ни форма
импульса, ни его спектр не изменяются при распространении по
Оптические солитоны 117
световоду. В случае солитонов высших порядков на начальном этапе
доминируют эффекты, связанные с ФСМ, но вскоре дисперсионные
эффекты «наверстывают упущенное», что приводит к сжатию им-
импульса (см. рис. 5.4). Теория солитонов показывает, что для импуль-
импульсов с формой в виде гиперболического секанса, имеющих пиковую
мощность, определяемую формулой E.2.3), совместное действие этих
эффектов приводит к тому, что динамика импульса оказывается
периодичной; первоначальная форма восстанавливается на расстоя-
расстояниях, кратных периоду солитона z0, определенному согласно E.2.19).
Для обычных световодов на основе, плавленого кварца Р2 =
= — 20 пс2/км на длине волны 1,55 мкм. Период солитона составляет
величину порядка 80 м для То = 1 пс и изменяется как Т2,, становясь
равным 8 км при То = 10 пс. Для световодов со смещенной диспер-
дисперсией Р2 — — 2 пс2/км, и z0 возрастает на порядок при тех же значе-
значениях То.
Возникает естественный вопрос: что случится, если начальная
форма импульса или значение пиковой мощности отличаются от тех,
которые требуются по соотношению E.2.17). Вначале рассмотрим
случай, когда значение пиковой мощности не точно соответствует
мощности солитона и величина N, полученная из E.2.3), не является
целым числом. Сапума и Яджима [36] использовали теорию возму-
возмущений для решения уравнений E.2.6) и E.2.7). Оказывается, что
импульс в процессе распространения по световоду «подстраивает»
свою длительность, становясь солитоном. При этом часть его энер-
энергии рассеивается. Импульс асимптотически преобразуется в солитон,
порядок которого есть целое число N, ближайшее к начальному
значению N. Если записать
N = N + e/ |б|<1/2, E.2.20)
то солитонная часть соответствует форме начального импульса
w@,т) = (N + 2е) sech[A + 2е/ЛГ)т] . E.2.21)
Длительность импульса в уравнении E.2.21)
Т'° = ЯТТгТ°- E'2-22)
Для фундаментального солитона (N = 1) длительность возрастает,
если е < 0; в случае N < 1/2 солитон вообще не образуется. С другой
стороны, если е > 0, то импульс сужается.
Влияние начальной формы импульса на формирование солитона
может быть исследовано при численном решении уравнения E.2.5).
На рис. 4.7 из гл. 4 изображена динамика гауссовского импульса,
имеющего начальное распределение поля в виде
ы@,т) = ехр(-т2/2). E.2.23)
118
Глава 5
Хотя N = 1, форма импульса изменяется при его распространении,
поскольку вначале она отличается от гиперболического секанса фун-
фундаментального солитона. Интересной особенностью рис. 4.7 является
то, что гауссовский импульс здесь асимптотически стремится к фун-
фундаментальному солитону. Эволюция фактически заканчивается при
z/LD = 5, что соответствует примерно трем периодам солитона.
Похожая картина имеет место и для импульсов с другими начальны-
начальными формами, например с супергауссовской. Длительность солитона
в конечном состоянии и расстояние, необходимое для эволюции
импульса в солитон, зависит от начальной формы, но качественно
поведение остается одним и тем же. Ясно, что солитон может быть
сформирован в том случае, если пиковая мощность начального
импульса превышает пороговую величину.
Хасэгава и Тапперт первыми указали на возможность солитонно-
го режима распространения в волоконных световодах [35]. Впервые
в экспериментах солитоны наблюдались Молленауэром и др. [39].
В этом эксперименте использовался лазер на центрах окраски, рабо-
работающий в режиме синхронизации мод (длительность импульсов
Tfwhm — 1 пс); длина волны генерации 1,55 мкм, что находится в об-
области минимальных потерь световода. Импульсы распространялись
по одномодовому световоду длиной 700 м, диаметр сердцевины
световода 9,3 мкм. Параметры световода, использованного в экспе-
эксперименте: Р2 — — 20,4 пс /км, у =г 1,3 Вт
•км
Подставляя То =
= 4 пс в выражение E.2.16), получаем значение пиковой мощности
фундаментального солитона порядка 1 Вт. В эксперименте значение
пиковой мощности изменялось в пределах 0,3-25 Вт, форма импуль-
импульсов и спектр измерялись на выходе световода. Поскольку прямое
измерение формы пикосекундных импульсов затруднительно, обычно
пользуются измерением автокорреляционной функции (АКФ). На
Лазер -10°1Опс
\
-Л- гз ггц /\ -JL-юоггц JLioon-ц уУ-юоггц
-1ОО1ОПС -1ОО1ОПС -lOOWnc -1ОО1ОПС
Ро-О,ЭВт Р0Ч,2Вт Ро,ОВт
-У 1*4. _Л I К У I I I V _
-lOOWnc -1ОО1ОПС -1ОО4ОПС
РО,ОВТ Р0И1,4Вт Р02,ЗВт
Рис. 5.6. Автокорреляционные функции (нижний ряд) и соответствующие
спектры (верхний ряд) на выходе световода при различных значениях пиковой
мощности Ро на входе. Спектр и АКФ начального импульса показаны
в прямоугольной рамке. Масштаб интенсивностей произвольный, так как все
кривые были приведены к одной и той же высоте [39].
Оптические солит оны И 9
рис. 5.6 изображены автокорреляционные функции и спектры им-
импульсов при разных уровнях входной мощности. Для сравнения там
же показаны АКФ и спектр лазерных импульсов (без световода).
Ширина спектра начальных импульсов 25 ГГц соответствует практи-
практически спектрально-ограниченным импульсам без частотной moj\ ih-
ции.
При малых уровнях вводимой мощности @.3 Вт) импульсы при
распространении испытывают дисперсионное уширение, что находит-
находится в согласии с результатами разд. 3.2. При возрастании вводимой
мощности импульсы на выходе сужались; конечная длительность
совпадала с начальной при значении вводимой мощности в Ро =
= 1,2 Вт. Этот уровень мощности соответствует формированию фун-
фундаментального солитона; теоретически рассчитано значение 1 Вт.
Налицо достаточно хорошее согласие, если учесть наличие ряда не
очень хорошо известных отклонений от идеального случая. В част-
частности, форма импульса на входе в световод не является точным
гиперболическим секансом.
При более высоких уровнях вводимой мощности в форме импуль-
импульса на выходе световода обнаруживается многопичковая структура.
Например, при 11,4 Вт АКФ представляет собой трехпичковую
структуру, которая соответствует расщеплению самого импульса на
два, что аналогично поведению трехсолитонного импульса вблизи
точки z/z0 = 0,5 (см. рис. 5.4). Наблюдаемый спектр также имеет
характерные особенности (рис. 5.5) вблизи z/z0 = 0,5. Период солитона
для экспериментальных параметров составляет 1,26 км. Таким обра-
образом, для использованного в эксперименте 700-метрового отрезка
световода z/z0 = 0,55. Поскольку уровень мощности 11,4 Вт также
практически в 9 раз превышает мощность фундамента чьного солито-
солитона, то данные на рис. 5.6 действительно соответствуют случаю N = 3.
Этот вывод подтверждается автокорреляционной функцией при
Ро = 22,5 Вт. Наблюдаемая пятипичковая структура соответствует
расщеплению лазерного импульса на три, что соответствует предска-
предсказаниям солитонной теории для солитона четвертого порядка (N = 4).
Периодичность солитонов высших порядков означает, что такие
импульсы должны восстанавливать первоначальную форму и спектр
на расстояниях, кратных периоду солитона. Такое восстановление
наблюдалось для солитонов второго и третьего порядков в экспери-
экспериментах [40], где длина световода 1,3 км соответствовала примерно
одному периоду солитона. В другом эксперименте [41] эффект сжатия
солитонов высших порядков на начальном этапе распространения,
изображенный на рис. 5.4 для случая N = 3. наблюдался для значений
N вплоть до 13. Подробнее это обсуждается в гл. 6. Солитоны
высших порядков также наблюдались на выходе лазера на красителе
с синхронизацией мод на сталкивающихся пучках, работающего
в видимом диапазоне (длина волны генерации 620 нм), посредством
120 Глава 5
внесения в лазерный резонатор оптических элементов с отрицатель-
отрицательной дисперсией групповых скоростей [42]. В этой системе также
наблюдались асимметричные солитоны второго порядка [43]. Про-
Пространственные моды нелинейного планарного волновода тоже могут
быть интерпретированы как солитоны высших порядков [44].
Поскольку для формирования солитонов требуется отрицательное
значение дисперсии групповых скоростей, солитоны не могут сущест-
существовать в волоконных световодах на длинах волн, меньших длины
волны нулевой дисперсии (~ 1,3 мкм). Тем не менее существование
другого типа солитона, известного как «темный» солитон, было
предсказано в [45] как решение уравнения E.2.2) при условии Р2 > 0.
Данный факт привлек значительное внимание [46-50]. Решение имеет
вид отдельного провала на однородном фоне. Если наложить гранич-
граничное условие, что | и (?,, т) | стремится к конечной величине для больших
значений | т |, то для нахождения солитонных решений первого и выс-
высших порядков можно пользоваться методом ОЗР [46]. Фундамен-
Фундаментальный солитон (N = 1) имеет вид
и (?, т) = tanh (т) ехр (К,). E.2.24)
Поведение солитонов высших порядков в случае положительной
дисперсии групповых скоростей коренным образом отличается от
случая отрицательной [48]. Существование темных солитонов было
подтверждено в экспериментах [49, 50]. В эксперименте [49] 26-пико-
секундные импульсы (на 595 нм) с провалом в центре шириной 5 пс
распространялись по световоду длиной 52 м. В другом эксперименте
[50] на вход 10-метрового световода поступали относительно длин-
длинные 100-пикосекундные импульсы с провалом шириной 0,3 пс, слу-
служащим темным импульсом. Импульсы на выходе имели параметры,
предсказанные уравнением E.2.2).
Интересной задачей также является исследование распространения
импульса вблизи длины волны нулевой хроматической дисперсии, так
что Р2 — 0. Тогда дисперсионные эффекты низшего порядка опреде-
определяются членом с Р3 в разложении B.3.23). Данный случай рассматри-
рассматривался в разд. 4.2. Динамика импульса определяется уравнением
D.2.5). Если пренебречь потерями в световоде (а = 0) и считать, что
коэффициент рз положителен, это уравнение приобретает вид
'¦1И^+м2"=0- E-2-25)
где ?,' = z/L'D, и = NU, N определяется как
N* = ^ = Щ?1. E.2.26)
LHL I Рз I
Дисперсионная длина L'D= Tq/IP3I определена в формуле C.3.3).
Оптические солитоны
121
1,0
0,8 Ь
|о,б
-0,2^
0
1 ' ' ' I ' ' ' ' I ' ' ' ' I ' ' ' ¦
д
II
II
II
11
1 1
! i
1 i
! к
< ил
i Л У и,
' Л 1 Лл
\...,.JJH..W
i ¦ i i i i ¦ i ¦ ¦_.
N = 2 :
f'=3 :
:
-10 -5
5 10 15 20-1 -0,5
—1—1 Г 1 1 I "I 1 Г-
Л i
1 1 '
1 \'
Ik
А
i
т i—1—i Г ' г~1 •—¦
t "
1
\ 1
1 1
1 I
-
0,5
Т/Т„
(z/-z/0) т0
Рис. 5.7. Форма импульса и его спектр в точке :/L'D = 3 при распространении
на длине волны нулевой дисперсии импульса, имеющего форму гиперболи-
гиперболического секанса и такую пиковую мощность, что N = 2. Штриховые кривые
представляют исходный импульс и его спектр (даны для сравнения).
Уравнение E.2.25) трудно решить методом ОЗР. Численное решение
показывает [51], что в случае N > 1 начальный импульс, имеющий
форму гиперболического секанса, преобразуется на длине ?,' ~ 10/N2
в фундаментальный солитон, в котором содержится примерно поло-
половина энергии начального импульса. Оставшаяся доля энергии перено-
переносится осцилляционной структурой у заднего фронта, постепенно
рассеиваясь на распространении.
На рис. 5.7 изображены форма импульса и его спектр при ?,' = 3
для случая N = 2; также приведены данные для начального импульса
при ?,' = 0. Самой замечательной особенностью является расщепле-
расщепление спектра на два ясно различимых пика [52]. Эти пики соответст-
соответствуют двум самым удаленным от несущей частоты компонентам
в спектре при ФСМ (см. рис. 4.2). Так как длинноволновая компонен-
компонента лежит в области отрицательной дисперсии групповых скоростей,
возможно формирование солитона в этой спектральной области.
Энергия из другой спектральной компоненты рассеивается из-за того,
что эта часть импульса распространяется в области положительной
дисперсии. Именно задняя часть импульса и рассеивается при распро-
распространении, так как при ФСМ спектральные компоненты на заднем
фронте сдвигаются в коротковолновую область. Из рис. 5.7 видно,
что импульс имеет длинную осциллирующую огибающую в задней
части, которая продолжает отделяться от переднего фронта с .увели-
.увеличением ?,'. При ?,' > 5 из передней части импульса формируется
фундаментальный солитон. Важно отметить, что, поскольку сущест-
существует спектральное уширение из-за ФСМ, входной импульс в действи-
действительности не распространяется на длине волны нулевой дисперсии,
Даже если вначале было Р2 = 0. Фактически импульс создает себе
122 Глава 5
свою собственную |Р2| через ФСМ. Эффективная величина |Р2|
определяется уравнением D.2.7) и больше для импульсов с большими
значениями пиковой мощности. Вообще говоря, солитонам на длине
волны нулевой дисперсии требуется меньшая мощность, чем тем,
которые распространяются в области отрицательной дисперсии груп-
групповых скоростей. Это видно из сравнения уравнений E.2.3) и E.2.26).
Для достижения одинаковых значений N и N для случая длины волны
нулевой дисперсии требуется мощность в То | Р2/Рз I Раз меньше.
В обычном световоде для формирования 1-пикосекундного солитона
на 1,3 мкм требуется в 100 раз меньшая мощность, чем на 1.55 мкм,
если длина волны излучения в первом случае хорошо совпадает
с длиной волны нулевой дисперсии [51].
В данном разделе были рассмотрены эффекты, связанные с куби-
кубическим членом нелинейной поляризации, записанным в виде B.3.6).
При очень больших уровнях мощности нелинейный отклик начинает
насыщаться, поэтому необходимо включать члены высших порядков.
Каплан [53] обобщил нелинейное уравнение Шредингера E.2.5),
заменив | U\2 в нелинейном члене на произвольную функцию/(| U\2).
Оказывается, что при определенных условиях поведение солитона
становится бистабильным. При заданном значении энергии импульса
бистабильные солитоны могут распространяться в двух состояниях;
при этом можно осуществлять переключение из одного состояния
в другое [54]. Вопросы устойчивости бистабильных состояний при-
привлекли большое внимание [55]. В волоконных световодах бистабиль-
ное поведение пока не наблюдали, поскольку для этого необходимы
чрезвычайно высокие значения мощности. Для этой цели более
подходящими могут быть среды с легко насыщающейся нелиней-
нелинейностью. В заключение отметим, что солитоны могут существовать
в волноводах с пространственно-периодичной величиной показателя
преломления, так как волна, распространяющаяся в такой среде, также
описывается нелинейным уравнением Шредингера [56].
5.3. СОЛИТОННЫЕ ЛАЗЕРЫ
Интересным и полезным использованием возможности волокон-
волоконных световодов формировать солитоны является разработка соли-
тонных лазеров [57 59]. Основная идея-использование волоконного
световода для осуществления синхронной подачи части энергии об-
обратно в резонатор лазера, работающего в режиме синхронизации
мод. Поскольку световод изменяет форму импульса, формируя в за-
зависимости от пиковой мощности фундаментальный солитон или
солитон высшего порядка, инжектируемый импульс отличается по
форме от импульса, генерируемого самим лазером. После нескольких
циклов формируется стационарное состояние, в котором импульсы
являются солитонами данного световода. Длительностью импульсов
Оптические солитоны
123
Лазер на центрах
окраски
Волоконный
световод
1,5мкм
Рис. 5.8. Схема солитонного лазера. М,, М2 и М3-зеркала со 100%-ным
отражением. М0-зеркало с отражением ~70%. Пластинка S служит для
деления пучка и имеет пропускание ~50%. Двулучепреломляющие пластинки
В используются для перестройки длины волны лазера. Микроскопические
объективы Lt и L2 используются для ввода излучения в отрезок одномодо-
вого поддерживающего поляризацию световода [57].
можно управлять, изменяя длину световода. При этом их длитель-
длительность может быть гораздо меньше, чем в случае одного лазера без
световода. Используя данный метод, можно получить импульсы
длительностью 50 фс [59].
В первой экспериментальной реализации солитонного лазера
Молленауэр и Столен [57] связали резонатор синхронно накачива-
накачиваемого лазера на центрах окраски с синхронизацией мод с другим
резонатором, содержащим отрезок одномодового световода, под-
поддерживающего поляризацию. На рис. 5.8 изображена схема экспери-
экспериментальной установки. При отсутствии волоконного резонатора сам
лазер на центрах окраски генерирует импульсы длительностью > 8 пс
(длительность на полувысоте по интенсивности), перестраиваемые
в диапазоне 1,4-1,6 мкм. Тем не менее, когда для обеспечения
синхронной обратной связи используется волоконный световод, дли-
длительность лазерных импульсов сокращается в зависимости от длины
световода до 0,2-2 пс. Автокорреляционные измерения показывают,
что импульсы имеют форму, близкую к гиперболическому секансу;
это подтверждает, что в световоде импульсы являются солитонами.
Дальнейшие измерения показали, что солитонный лазер работает
так, что в световоде распространялись солитоны второго порядка
(N = 2), а не фундаментальные солитоны. Длина световода составля-
составляла примерно го/2, так что входной импульс восстанавливается после
одного полного обхода по световоду. На рис. 5.9 показано измерен-
измеренное изменение длительности импульсов TFWHM (кружки) в зависимос-
зависимости от длины световода. Сплошная линия-показывает зависимость zo/2
из уравнения E.2.19); использовано значение р2 — — 20 пс2/км.
Штриховой линией показано значение пиковой мощности двухсоли-
тонного импульса (N = 2; Р2 = 4PJ, рассчитанное по формуле
124
Глава 5
30
10
3
1
0.3
¦ °\
У
/1 I
/p
\
/.
1
1
1
1
'•
\
1 1 \
3,0 Zp 1,0 0,5 Q3 Q2
Длительность импульса (.пс)
3000
- 1000
300 о
о
о
ГС
го
100 |
- 30
0.1
Рис. 5.9. Зависимость длительности импульса TFVVHM от длины волны све-
световода (кружки). Сплошная линия швисимость zo/2 от TFWHM (теория).
Штриховая линия зависимость пиковой мощности Р2 двухсолитонного
импульса (N = 2) от его длительности. Точки полученные из эксперимента
значения Р2 [57].
E.2.16). Экспериментальные значения Р2 (точки) находятся в хоро-
хорошем согласии с предсказанием теории солитонов.
Для теоретического описания работы солитонного лазера ис-
используют теорию синхронизации мод и теорию солитонов. В при-
приближении [38] солитонныи лазер (см. рис. 5.8) рассматривался как
однорезонаторное устройство. Хотя эта модель смогла объяснить
многие особенности эксперимента, она оказалась не полностью удов-
удовлетворительной. В частности, эта модель требовала, чтобы длина
световода L была равна периоду солитона z0, в то время как
экспериментально было найдено [58], что L может быть в целое
число раз меньше z0. По-видимому, для теоретического моделиро-
моделирования работы солитонного лазера необходимо использовать прибли-
приближение связанных резонаторов, хотя данный метод требует значи-
значительных численных расчетов [60-62]. В другом приближении [63]
солитонныи лазер рассматривался как лазер с синхронизацией мод за
счет инжектируемой затравки.
Что же касается экспериментов, то стабильность работы солитон-
Оптические солитоны 125
ного лазера была значительно улучшена благодаря использованию
петли обратной связи с сервоуправлением, при помощи которой
осуществлялась динамическая подстройка длины резонатора. При
этом поддерживалась постоянной фаза излучения, направляемого
обратно в лазерный резонатор [58]. Такая схема стабилизации
сделала солитонный лазер надежным лабораторным устройством.
Длительность импульсов солитонного лазера зависит от таких
параметров световода, как его длина и значение дисперсии групповых
скоростей Р2 на рабочей длине волны. Для обычных световодов,
имеющих Р2 ^ — 20 пс2/км в области 1,55 мкм, период солитона для
0,1-пикосекундных импульсов составляет величину z0 ~ 20 см, и по-
поэтому трудно получить импульсы короче. Тем не менее при исполь-
использовании световода с плоской дисперсионной характеристикой Р2 ~
~ — 2,5 пс2/км в диапазоне длин волн 1,4 1,6 мкм длительность
импульсов, генерируемых солитонным лазером, составила 50 фс [59].
5.4. СОЛИТОННЫЕ ЛИНИИ СВЯЗИ
Как ранее обсуждалось в разд. 3.4, работа высокоскоростных
линий связи обычно ограничена эффектом .дисперсии групповых
скоростей, из-за которого импульс уширяется, теряя энергию в би-
битовом промежутке. Поскольку солитоны могут сохранять свою
форму благодаря балансу между нелинейными и дисперсионными
эффектами, их использование могло бы улучшить работу таких
систем связи. Хотя использовать солитоны для оптической связи
было предложено еще в 1973 г. [35], только после экспериментально-
экспериментального наблюдения оптических солитонов в 1980 г. [39] эта идея при-
привлекла широкое внимание [64-75]. Однако, прежде чем создавать
солитонные линии связи, необходимо рассмотреть эффекты, способ-
способные наложить ограничения на конструкцию подобных систем. На-
Наиболее важными из них являются: I) потери в световоде, 2) наличие
частотной модуляции в начальном импульсе, 3) взаимодействие
соседние импульсов. В этом разделе обсуждаются ограничения,
накладываемые этими явлениями, а также рассматриваются вопросы,
связанные с конструированием реальных солитонных линий связи.
5.4.1. Потери в световоде
Поскольку солитон существует благодаря балансу нелинейных
и дисперсионных эффектов, для того чтобы сохранить солитонные
свойства импульса, необходимо поддерживать его пиковую мощ-
мощность. Поэтому потери в световоде вредны, так как из-за 4*их пиковая
мощность экспоненциально убывает по длине световода [см. A.2.3)].
В результате длительность фундаментального солитона также воз-
возрастает при распространении. Математически потери в световоде
126 Глава 5
можно описать, включив дополнительный член, описывающий зату-
затухание, в уравнение E.1.1), так что оно принимает форму уравнения
B.3.36). Если использовать безразмерную амплитуду м(^, т), введен-
введенную в разд. 5.2, уравнение E.2.5) принимает вид
/? + i? + |.|".--m,. E.4.,,
где
Уравнение E.4.1) можно решить, используя метод ОЗР, если рас-
рассматривать Г как малое возмущение [36]. Для начального импульса
в форме и @, т) = sech (т) приближенное в первом порядке по Г реше-
решение имеет вид [64]
и(?, т) = Mj sech(M!T)exp(/a), E.4.3)
где
E.4.4)
^ E.4.5)
Как и следовало ожидать, возмущенное решение E.4.3) сводится
к невозмущенному E.2.15) при Г = 0. Если записать MjT как T/7J
и использовать условие т = Т/То, то можно получить зависимость
длительности импульса Ti от длины световода
Т, = То ехрBГ?) = То exp(az). E.4.6)
Однако не следует ожидать, что экспоненциальное увеличение дли-
длительности фундаментального солитона по z будет иметь место для
произвольно больших расстояний. Это можно увидеть, исследуя
уравнение C.3.12), которое предсказывает линейное увеличение дли-
длительности по z в том случае, когда нелинейными эффектами можно
пренебречь. Численное решение уравнения E.4.1) показывает [76], что
возмущенное решение E.4.3) является достаточно точным только для
тех значений z, для которых выполняется условие az « 1. На рис. 5.10
изображен коэффициент уширения 7j/7^ как функция от ^ в случае,
когда фундаментальный солитон возбужден в световоде с потерями
Г = 0.035. Результат теории возмущений справедлив вплоть до
Г?, ш 0,7. В асимптотике (^ » 1) длительность импульса увеличивается
линейно более медленно, чем в линейной среде [77]. Похожее пове-
поведение наблюдается и у солитонов высших порядков [76]. Однако их
длительность претерпевает несколько колебаний, прежде чем начи-
начинает монотонно расти. Этот факт можно понять, если вспомнить
о периодичности эволюции солитонов высших порядков.
Оптические солитоны
127
60
50
40
30
20
10
0
1 Г = 0,035
-
'-
Теория возмущений
/
/ /
/ у Решение
/ ' ь отсутствие
/ s нелинейности
У ^ ' Точное
"^____^-— решение
i.i.i.
20
40 60 80
Расстояние z/LD
100
Рис. 5.10. Изменение длительности фундаментального солитона с расстоя-
расстоянием в световоде с потерями. Показан также результат, который дает теория
возмущений. Штриховой прямой показано поведение при отсутствии нели-
нелинейных эффектов [76].
Использовать солитоны в высокоскоростных линиях связи можно
двояко. В первом случае цель довольно скромная: солитонный эффект
используют для того, чтобы увеличить длину световода (так назы-
называемое расстояние между ретрансляторами) по сравнению с расстоя-
расстоянием для линейной системы (малые уровни мощности, отсутствие
нелинейных эффектов). Как видно из рис. 5.4, длительность солитона
высшего порядка первоначально уменьшается. Начальное сжатие
происходит даже при наличии потерь в световоде, и это может
скомпенсировать уширение солитона из-за потерь [74]. Поскольку
период солитона для 100-пикосекундных импульсов, распространяю-
распространяющихся на длине волны 1,55 мкм, относительно велик (>500км),
такие импульсы могут распространяться на расстояния ~ 100 км,
прежде чем они значительно уширятся по сравнению с начальной
длительностью. В работе [73] было предсказано, что расстояние
между ретрансляторами можно увеличить более чем в 2 раза, когда
пиковая мощность входного импульса достаточна для создания
солитонов высшего порядка. Требуемые значения пиковой мощности
для передачи импульсов без частотной модуляции со скоростью
8 Гбит/с относительно невелики (~ 3 мВт). Так как такой уровень
мощности вполне достижим для полупроводниковых лазеров, соли-
солитонный эффект легко можно использовать для улучшения работы
оптических линий связи.
Во втором случае солитоны используются для передачи инфор-
информации на расстояния ~ 1000 км без использования электронных
ретрансляторов [66-72]. Для того чтобы избежать эффектов, связан-
связанных с потерями в световоде, необходимо периодически усиливать
солитоны и восстанавливать их первоначальные форму и значение
128 Глава 5
пиковой мощности. В простой схеме [66] оптический усилитель
приводит энергию солитона к первоначальному уровню. Затем со-
литон сам приводи г свою длительность к начальному значению. Тем
не менее во время этой фазы сжатия теряется часть энергии в виде
дисперсионной волны. Появление такой рассеянной волны нежела-
нежелательно, поскольку при большом числе каскадов усиления в этой волне
может скопиться значительная энергия. Она может быть уменьшена
за счет сокращения расстояния между усилителями, так что Г^ « 1
или L« l,ct. Практически это условие ограничивает величину L рас-
расстояниями порядка 10 км или менее для а = 0,2 дБ/км [66].
Альтернативная схема [67] использует эффект ВКР (см. гл. 8) для
усиления солитонов; при этом используется излучение накачки, сдви-
сдвинутое выше по частоте на 13 ТГц (оно периодически инжектируется
в световод). Поскольку ВКР-усиление распределено по всей длине
световода, можно адиабатически усилить солитон, приблизительно
поддерживая N = 1: выполнение данного условия значительно умень-
уменьшает рассеянную долю энергии. С этой точки зрения схема, исполь-
использующая ВКР-усиление, наиболее перспективна в реальных системах
[68, 72].
Возможность данной схемы была продемонстрирована в экспе-
эксперименте [69], где солитонные импульсы длительностью 10 пс рас-
распространялись по 10-километровому световоду с ВКР-усилением
и без него. На рис. 5.11 изображена схема экспериментальной уста-
установки. Там также показаны АКФ лазерного импульса (без световода)
в сравнении с АКФ. полученной на выходе световода. При отсутствии
ВКР-усиления солитонный импульс уширяется примерно на 50%
из-за наличия потерь. Это находится в согласии с формулой E.4.6),
которая предсказывает 7~i/T0 =1,51 для параметров световода, ис-
использованного в эксперименте, а именно z-— 10 км и а = 0,0414 км
@,18 дБ/км). ВКР-усиление осуществлялось за счет инжектирования
непрерывного излучения накачки на 1,46 мкм от лазера на центрах
окраски в направлении, противоположном распространению соли-
солитонов. Мощность излучения накачки составляла 125 мВт. Как видно
из рис. 5.11, импульс на выходе практически идентичен по форме и по
энергии входному импульсу, что указыв.- т на практически полное
восстановление солитона. Малоинтенсив1 ле «крылья» в восстанов-
восстановленном солитоне приписаны рассеянной доле энергии, возникающей
из-за отличия формы входного импульса от гиперболического се-
секанса. Возможности схемы с ВКР-усиление i были продемонстриро-
продемонстрированы Молленауэром и Смитом в эксперименте [75], где 55-пико-
секундные импульсы могли 96 раз обращаться по 42-километровой
волоконной петле без значительного изменения своей длительности.
Это соответствовало эффективной длине распространения более чем
4000 км. Конструктивная сторона таких солитонных линий связи,
использующих ВКР-усиление, будет рассмотрена далее в этом раз-
разделе.
Оптические солитоны
129
Световод-
К автокоррелятору л ретранслятор (\
Импульсы
Юпс,
1,56 мкм
А
(~5м) \1
Одномодовый
световод
10км
Непрерывное излучение
накачки 1,46 мкм
Без усиления
Лазер
Усиление
1,8дБ
-20 -10
10
Рис. 5.11. Схема экспериментальной установки (вверху), использованной для
получения автокорреляционных функций (внизу), демонстрирующих восста-
восстановление солитонов в световоде длиной 10 км при ВКР-усилении. Высота
кривой в случае без усиления была увеличена примерно в пять раз для того,
чтобы облегчить сравнение соответствующих длительностей [69].
5.4.2. ЧАСТОТНАЯ МОДУЛЯЦИЯ
В идеальной солитонной линии связи начальный импульс в све-
световоде должен быть без частотной модуляции, иметь форму гипер-
гиперболического секанса, его пиковая мощность должна быть такова, что
N = 1 в уравнении E.2.16). На практике импульсы будут отличаться
от идеального случая, требуемого для формирования фундаменталь-
фундаментального солитона, поэтому требуется определить допустимый уровень
отличия. Отличия от точной формы и точного значения энергии были
рассмотрены в разд. 5.2, где было показано, что эти эффекты имеют
минимальное воздействие на формирование солитона, пока N нахо-
находится в пределах 0,5- 1,5. В данном разделе рассмотрено, как дей-
действует частотная модуляция начального импульса на формирование
солитона [78-86]. Частотная модуляция начального импульса может
оказаться вредной хотя бы потому, что, накладываясь на частотную
модуляцию, обусловленную ФСМ. она может нарушить точный
баланс между дисперсионными и нелинейными эффектами, необхо-
необходимый для существования солитонов.
Можно исследовать, как действует начальная частотная модуля-
130
Глава 5
-10 „О 10
Бремя г
Рис. 5.12. Формирование солитона при наличии начальной линейной частот-
частотной модуляции для случая N = 1 и С = 0,5.
ция, численно решая уравнение E.2.5) при начальной амплитуде
и (О, т) = N sech (т) ехр (- /Ст2/2), E.4.7)
где С-параметр частотной модуляции, введенный в разд. 3.2. Квад-
Квадратичное изменение фазы соответствует линейной частотной моду-
модуляции, такой, что оптическая частота нарастает со временем (поло-
(положительная частотная модуляция) для положительных значений С. На
рис. 5.12 изображена динамика фундаментального солитона (N = 1)
в случае относительно небольшой частотной модуляции С = 0,5.
Первоначально импульс сжимается главным образом из-за положи-
положительной частотной модуляции; начальное сжатие происходит даже
при отсутствии нелинейных эффектов. Далее импульс уширяется, но
в конце концов он сжимается второй раз; при этом за главным пиком
образуется второй, менее интенсивный и постепенно отдаляющийся
от основного. Главный пик преобразуется в солитон на расстояниях
Ь, > 15. Похожее поведение имеет место и для отрицательных значе-
значений С. Предполагается, что солитоны формируются при малых
значениях \С\, поскольку они обычно стабильны к слабым возму-
возмущениям. Однако солитон может разрушиться, если | С | превышает
некоторую критическую величину С.р. В случае N = 1 солитон,
изображенный на рис. 5.12, не образуется, если увеличить С от 0,5
до 2.
Критическое значение параметра частотной модуляции может
быть получено, если воспользоваться методом ОЗР [82-84]. Точнее,
решают уравнения E.2.6) и E.2.7) и получают собственное значение ?,
используя и из начального условия E.4.7). Солитоны существуют до
тех пор, пока мнимая часть L, положительна. Критическое значение
зависит от N; оказалось, что в случае N = 1 Сжр = 1,64 [82]. Оно
также зависит от вида фазового коэффициента в условии E.4.7) [84].
Оптические солитоны 131
Что же касается систем связи, то здесь начальную частотную моду-
модуляцию следует уменьшить, насколько это возможно. Сделать это
необходимо потому, что, хотя частотная модуляция и не приносит
вреда при | С | < С.р, часть энергии теряется в дисперсионном «хво-
«хвосте» во время формирования солитона [82]. Например, только 83%
начальной энергии преобразуется в солитон в случае С = 0,5 (изо-
(изображен на рис. 5.12), и эта доля уменьшается до 62% при С = 0,8.
5.4.3. ВЗАИМОДЕЙСТВИЕ СОЛИТОНОВ
Интервал времени Тв между соседними информационными бита-
битами или импульсами определяет скорость передачи информации В в
системе связи (В=\'ТВ). Поэтому необходимо определить, на-
насколько близко два солитона могут находиться друг относительно
друга, чтобы между ними не было взаимодействия [87-99]. Та же
самая нелинейность, которая необходима для существования одного
солитона, приводит к взаимодействию между соседними солитонами.
В этом разделе кратко рассматриваются те аспекты взаимодействия
солитонов, которые имеют отношение к созданию солитонных линий
связи.
Амплитуда пары солитонов на входе в световод может быть
записана в безразмерном виде
и@, т) = sech (т - д0) + гsech [г(т + qoj] eB, E.4.8)
где г-относительная амплитуда, 6 - относительная фаза, а начальное
расстояние между солитонами q0 связано со скоростью передачи
информации соотношением
E.4.9)
Можно исследовать взаимодейтвие солитонов, численно решая урав-
уравнение E.2.5) при начальных условиях, определяемых условием E.4.8).
Однако для прояснения физического смысла полезно воспользоваться
методом ОЗР, используя его для решения уравнений E.2.6) и E.2.7)
с начальным условием и@, т) в виде E.4.8). Такие исследования
показывают [88, 98], что взаимодействие зависит не только от
расстояния между солитонами q0, но и от относительной фазы
6 и относительной амплитуды г. Для частного случая 6 = 0, г = 1
и q0 » 1 расстояние q между солитонами на трассе распространения
S равно [88]
ехр[2(? - ft)] = 2[1 + cosD^"«o)] . E.4.10)
Из данного соотношения видно, что q (^) периодически изменяется по
132 Глава 5
длине световода с периодом
4Р = |ехр(9о). E.4.11)
Теория возмущений приводит к тому же результату [87]. Более
точное выражение, справедливое для произвольных величин q0, най-
найдено в [98]
_KsinhBgo)cosh(g0) rS4 121
2q0 + sinhB^0)
Соотношение E.4.11) является достаточно точным при q0 > 3, что
также найдено численно [89]. На рис. 5.13 изображена динамика
взаимодействия, демонстрирующая периодический коллапс пары со-
литонов при q0 = 3.5. 6 = 0 и г = 1 [97].
Периодический коллапс соседних солитонов нежелателен с точки
зрения системы связи. Можно решить данную проблему, увеличивая
расстояние между солитонами так, что zp» LT, где LT- расстояние,
на которое перс щется информация, zp = zoexp(go)- расстояние, на
котором происходит коллапс, z0- период солитона, определяемый
соотношением E.2.19). Поскольку 2^0^22000 при q0 = 10, такое
расстояние более чем достаточно для большинства систем связи.
Скорость передачи информации в этом случае ограничена уравнением
E.4.1' I.' но может достигать 45 Гбит/с, если использовать для передачи
информации 2-пикосекундные солитоны.
Можно значительно сократить расстояние между солитонами,
используя несколько различных схем. Оказывается, что сила притя-
притяжения между солитонами очень чувствительна к относительной фазе
6 и относительной амплитуде г. Фактически сила притяжения стано-
становится силой отталкивания при 6 # 0, так что в конце концов солитоны
-5
Рис. 5.13. Динамика пары солитонов, демонстрирующая периодический кол-
коллапс, обусловленный взаимодействием. Значение параметров: N — I, 6 = 0,
r=l,qo = 3.5 [98].
Оптические солитоны 133
Рис. 5.14. Динамика пары солитонов при 6 = я/4, так что солитоны при 4 = 0
находятся не в фазе [98]. Остальные условия идентичны условиям рис. 5.13.
удаляются друг от друга даже при относительно малом значении 6.
На рис. 5.14 изображена динамика пары солитонов при условиях,
идентичных условиям на рис. 5.13, за исключением того, что 6 = я/4,
а не нулю. Для предельного случая 6 = я расстояние между соли-
тонами q(?,) определяется выражением, получаемым из уравнения
E.4.10) заменой косинуса на гиперболический косинус [88]. Если пара
солитонов имеет одну и ту же фазу F = 0), но различные амплитуды,
то взаимодействие по-прежнему периодично, но уже без коллапса
[98]. Даже при г = 1,1 расстояние между солитонами не изменяется
более чем на 10% на каждом периоде, если q0 ^ 4. Ясно, что этот
метод может быть полезен для увеличения скорости передачи ин-
информации или пропускной способности. Взаимодействие между со-
солитонами может быть также видоизменено многими другими фак-
факторами, такими, как начальная частотная модуляция [95. 97], дис-
дисперсионные эффекты высших порядков [91] и нелинейные эффекты
высших порядков [96. 99]. Другой фактор, который следует учесть,—
это влияние потерь и периодического усиления на взаимодействие
между солитонами. Оказывается [97], что можно достичь надежной
передачи информации, если амплитуды соседних солитонов неодина-
неодинаковы.
5.4.4. ВОПРОСЫ, СВЯЗАННЫЕ С КОНСТРУИРОВАНИЕМ
КОНКРЕТНЫХ СОЛИТОННЫХ ЛИНИЙ СВЯЗИ
Солитонные линии связи способны передать информацию на
расстояния ~ 1000 км со скоростью, приближающейся к 100 Гбит/с,
при условии, что потери в световоде скомпенсированы за счет
134 Глава 5
Солитон
Рис. 5.15. Схема солитонной линии связи. Солитоны вводятся в «цепочку»
световодов, состоящую из многих сегментов длиной L. На конце каждого
сегмента через частотно-зависимый направленный ответвитель в обоих на-
направлениях вводится излучение накачки от непрерывного лазера.
должного усиления солитонов. Наиболее перспективной, по-видимо-
по-видимому, является схема с ВКР-усилением [67], схематично изображенная
на рис. 5.15. Передача информации осуществляется вблизи длины
волны минимальных потерь в световоде (~ 1,56 мкм). Периодически
с интервалом L, используя частотно-зависимый направленный от-
ответвитель, в световод по обоим направлениям вводят непрерывное
излучение лазера на длине волны 1,46 мкм. Важными параметрами
системы являются скорость передачи информации В, длительность
импульса 7^WHM. период усиления L и полная длина системы LT,
которая определяется числом каскадов усиления, при превышении
которого распространение солитонов становится неустойчивым. В
данном разделе рассматриваются те основные аспекты конструиро-
конструирования, которые определяют параметры системы.
Сначала рассмотрим, существует ли фундаментальное ограниче-
ограничение, накладываемое на систему схемой ВКР-усиления. Когерентное
усиление всегда сопровождается спонтанным шумом. Этот шум
может приводить к флуктуации времени прихода импульса на детек-
детектор. Физически это происходит из-за случайного изменения группо-
групповой скорости, возникающего из-за малого случайного сдвига несущей
частоты на каждой стад!" • усиления [100]. Если импульс не поступает
в промежуток времени, предназначенный для его (импульса) обна-
обнаружения, происходит ошибка. Если вероятность ошибки поддержи-
поддерживается на уровне ниже 10~9, то оказывается [72, 100], что произве-
произведение скорости передачи информации на длину системы BLT для
световода со смещенной дисперсией (Р2 ^ — 2 пс2/км) ограничена
величиной
BLT < 3 • 104 (Гбит/с) км. E.4.13)
Эта величина примерно на два порядка больше предела, ограничи-
ограничивающего работу линейных систем (см. разд. 3.4). Неравенство E.4.13)
показывает, что по солитонной линии связи можно передавать
информацию в пределах 3000 км со скоростью 10 Гбит/с или в пре-
пределах 300 км со скоростью 100 Гбит/с; при этом временные флук-
флуктуации еще не приведут к ошибке.
Оптические солитоны' 135
Выбор скорости передачи информации определяет расстояние
L между каскадами усиления, и обычно L изменяется как В~2. Это
ясно из того, что увеличение В, согласно E.4.9), приводит к умень-
уменьшению длительности импульса TFWhm (или То), что в свою очередь
уменьшает период солитона z0, определяемый соотношением E.2.19).
Более точные численные расчеты многокаскадного усиления показы-
показывают [68, 72], что распространение солитонов на большие расстояния
становится неустойчивым при L~ 8z0. На практике следует ограни-
ограничить L до величин L< 6z0. Используя E.2.19) и E.4.9), можно связать
L со скоростью передачи информации соотношением
EA14)
где q0 относительное расстояние между солитонами. Для сведения
к минимуму взаимодействия между солитонами обычно берут
q0 = 10. Если использовать световод со смещенной дисперсией
(Р2 = — 2 пс2/км на длине волны X = 1,55 мкм) и использовать зна-
значение q0 = 10, то произведение ВгЬ из неравенства E.4.14) ограничено
величиной
B2L<\-104 (Гбит/с2)км. E.4.15)
Величина L ограничена потерями в световоде cts и ар на сигналь-
сигнальной длине волны и на длине волны излучения накачки соответствен-
соответственно. Поскольку мощность излучения накачки непостоянна вдоль све-
световода, энергия солитона может значительно изменяться по длине
световода, даже если она и полностью восстанавливается в конце
каждого каскада усиления. Численные исследования указывают [68,
72], что для стабильной передачи солитона на большие расстояния
вариации в его энергии должны быть менее 20%. При cts = 0,18 дБ/км
и ар = 0,29 дБ/км (наименьшие значения, достигнутые к настоящему
времени) данные требования ограничивают L значениями меньше
50 км. Из экономических соображений L должна быть как можно
больше. Таким образом, ожидается, что в большинстве случаев
L находится в пределах 30-50 км.
Рассмотрим пример конкретной конструкции. Для обычного све-
световода с р2 ~ — 20 пс2/км как величина BLT, так и B2LT умень-
уменьшаются в 10 раз по сравнению с соотношениями E.4.13) и E.4.15).
В результате необходимо будет использовать более низкие скорости
передачи информации. Если выбрать рабочее значение периода уси-
усиления L = 40 км, го скорость передачи информации В = 5 Гбит/с.
Выбирая q0 = 10, из уравнения E.4.9) получаем длительность им-
пУльса 7^Whm = 17,6 пс. Значение пиковой мощности, требуемой для
возбуждения фундаментального солитона, оценивается из уравнения
E.2.16). Если использовать типичные значения у = 5Вт~1-км~1 (со-
(соответствующие эффективной площади сердцевины порядка 25 мкм2),
136 Глава 5
то Pl = 40 мВт. Полная длина системы ограничена величиной около
600 км из-за шумовых флуктуации.
Работа солитонной линии связи может быть значительно улуч-
улучшена за счет использования световодов со смещенной дисперсией
(Р2 — — 2 пс2/км). Если принять значение скорости передачи инфор-
информации равной 15 Гбит'с, то из неравенства E.4.15) следует, что
период усиления L=44km, в то время как из неравенства E.4.13)
видно, что полная длина системы LT= 2000 км. Необходимые дли-
длительность импульса и значение пиковой мощности для такой системы
Tfwhm = 5,87 пс и Ру = 36 мВт соответственно. Полная длина си-
системы может быть увеличина до 6000 км за счет уменьшения ско-
скорости передачи информации до 6 Гбит/с. Если необходимы более
высокие скорости, В можно увеличить до 20 30 Гбит/с, но только за
счет уменьшения и L, и LT. Солитонные линии связи, очевидно,
способны обеспечить передачу информации на расстояния ~ 1000 км
со скоростями ~ 10 Гбит/с. Практической демонстрацией такой воз-
возможности явился эксперимент [75], в котором 55-пикосекундные
импульсы могли циркулировать по 42-километровой волоконной
петле до 96 раз без значительного увеличения своей деятельности. Во
время каждого цикла ВКР-усиление практически компенсировало
потери в световоде. В этом эксперименте было показано, что соли-
тоны можно передавать на расстояние более 4000 км. Реализация
солитонных систем связи потребует тем не менее дальнейшей раз-
разработки частотно-зависимых ответвителей и лазеров накачки.
5.5. НЕЛИНЕЙНЫЕ ЭФФЕКТЫ ВЫСШИХ ПОРЯДКОВ
Свойства оптических солитонов, рассмотренные до сих пор в этой
главе, основаны на упрощенном уравнении распространения E.1.1).
Как показано в разд. 2.3, в случае когда длительность импульса
короче 100 фс, необходимо учитывать нелинейные и дисперсионные
члены высших порядков и использовать уравнение B.3.35). Необхо-
Необходимость учета дисперсии нелинейности (второй член в правой части)
была осознана довольно давно [101-106]. Необходимость учесть
эффект, связанный с конечным временем отклика нелинейности (по-
(последний член в правой части), стала очевидной, когда было открыто
новое явление, известное как вынужденное комбинационное саморас-
саморассеяние [107]. С тех пор нелинейным эффектам высшего порядка,
возникающим из-за задержки нелинейного от клика в световоде, стали
уделять значительное внимание [108-117]. В данном разделе рас-
рассмотрено влияние нелинейностей высших порядков на свойства со-
солитонов.
В терминах безразмерных переменных U, ^ и т, определенных
соотношениями E.2.1), уравнение B.3.35) приобретает следующий
Оптические солитоны 137
вид:
pu \е2и
= -7V2 \U\2U + is^-[\U\2U)-xRU^-^-(\U\2)\, E.5.1)
где предполагается, что импульс распространяется в области отри-
отрицательной дисперсии групповых скоростей (Р2 < 0); полагая а = 0, мы
пренебрегаем потерями в световоде. Параметр N определен в фор-
формуле E.2.3). Параметры 8, s и zR определяют соответственно эффекты
дисперсии высшего порядка, дисперсии нелинейности и задержки
нелинейного отклика. Их явное выражение:
В 2 Т
д = v = x = t E52)
Все три параметра изменяются обратно пропорционально длитель-
длительности импульса; ими можно пренебречь при То^ I пс. Они становят-
становятся заметными для фемтосекундных импульсов. Например, 8 ^ 0,03,
.v ~ 0.05 и тк~0,1 для 50-фемтосекундного импульса G^, ~ 30 фс),
распространяющегося на 1.55 мкм в обычном световоде из кварцево-
кварцевого стекла, если принять TR = 3 фс.
Рассмотрим сначала влияние дисперсии нелинейности, опреде-
определяемое параметром .v. При условии 6 = 0итк = 0в уравнении E.5.1)
динамика импульса определяется следующим уравнением:
+ j^ + N[\U\U + is(\U\U)^ 0. E.5.3)
Как было показано в разд. 4.3, действие дисперсии нелинейности при
отсутствии дисперсии групповых скоростей приводит к образованию
ударной волны на заднем фронте импульса. Это обусловлено зави-
зависимостью групповой скорости от интенсивности: вершина импульса
начинает двигаться медленнее, чем его края. Дисперсия групповых
скоростей ослабляет укручение фронта волны, но из-за дисперсии
нелинейности центр импульса все равно сдвигается. Это свойство
проиллюстрировано рис. 5.16, где изображена форма импульса при
4 = 0, 5 и 10 для л = 0,2 и N = 1; результат получен численным
решением уравнения E.5.3) при начальном условии {7@, т) = sech(T).
Поскольку при * # 0 вершина импульса движется медленнее, чем
края, она сдвигается к заднему фронту. Задержка хорошо аппрокси-
аппроксимируется выражением \й = .v^ при .v < 0,3. Хотя при распространении
импульс немного уширяется (примерно на 20% при Ь, = 10), он тем не
менее сохраняет солитонную природу. Это позволяет предположить,
что уравнение E.5.3) имеет солитонное решение, к которому импульс
асимптотически эволюционирует. Такое решение действительно су-
138
Глава 5
-4
-2 0 2
Время т
Рис. 5.16. Формы импульсов при ^ = 5 и ^ = Ю для фундаментального соли-
тона при учете дисперсии нелинейности (s = 0,2). Для сравнения штриховой
кривой показана начальная форма импульса. Сплошные кривые совпадают
с штриховой в том случае, когда s = 0.
ществует и имеет вид [102]
t/ft, х) = V(x - MQ exp [i
- Aft)] ,
E.5.4)
где М связано со сдвигом несущей частоты. В результате этого сдвига
изменяется групповая скорость. Сдвиг вершины на рис. 5.16 как раз
и обусловлен изменением групповой скорости. Явная форма К(т)
зависит от М и других параметров: N и s. В пределе л- = 0 она
переходит в гиперболический секанс E.2.15). Следует также отметить,
что уравнение E.5.3) может быть преобразовано в так называемое
модифицированное нелинейное уравнение Шредингера (аналогичное
E.5.3), но без третьего члена), чьи солитоноподобные решения ши-
широко изучались в физике плазмы [118-121].
Действие дисперсии нелинейности на солитоны высших порядков
знаменательно тем, что оно приводит к развалу таких солитонов на
составные части; это явление называется распадом связанного со-
состояния солитонов [104]. На рис. 5.17 изображен распад солитона
второго порядка (JV = 2) при л- = 0,2. При таком большом значении
параметра * два солитона полностью разделяются на расстоянии
в два периода солитона и продолжают удаляться друг от друга при
дальнейшем распространении по световоду. Качественно похожее
поведение имеет место и при меньших значениях *, за исключением
того, что для распада требуется большее расстояние. Понять физику
распада можно, используя метод ОЗР с дисперсией нелинейности,
действующей как возмущение [36]. В отсутствие дисперсии нелиней-
нелинейности (s = 0) два солитона образуют связанное состояние, поскольку
они распространяются с одинаковой скоростью (собственные значе-
Оптические солитоны
139
О
О 10
ремя г
Рис. 5.17. Распад солитона второго порядка (N = 2), вызванный дисперсией
нелинейности (s = 0.2). Показана динамика импульса на пяти периодах соли-
тона.
ния имеют одинаковые действительные части). Эффект дисперсии
нелинейности снимает вырождение так, что два солитона распро-
распространяются с различными скоростями. В результате они простран-
пространственно разделяются, и это разделение увеличивается практически
линейно с расстоянием [106]. Отношение высот на рис. 5.17 практи-
практически равно 9, что находится в согласии с ожидаемым отношением
ОЪЛЬJ' гДе ^1 и Л2-мнимые части собственных значений, опре-
определенных в разд. 5.2. Солитоны третьего и высших порядков демон-
демонстрируют похожую картину распада. В частности, солитон третьего
порядка (N = 3) распадается на три солитона [106]; высота их вершин
также находится в согласии с теорией ОЗР.
Действие дисперсии высшего порядка на распад солитона может
быть учтено включением члена с третьей производной в уравнение
E.5.1). Качественно поведение остается тем же самым. Фактически
дисперсия высшего порядка сама может приводить к распаду связан-
связанного состояния даже при отсутствии нелинейных эффектов высшего
порядка при условии, что параметр 8 превышает пороговую величину
[122]. Для солитона второго порядка (N = 2) пороговая величина
5 = 0,022, но она уменьшается до 0,006 для N = 3. Для обычных
кварцевых световодов на длине волны 1,55 мкм 8 превышает 0,022
Для импульсов короче 70 фс. Тем не менее этот порог может быть
достигнут для импульсов длиннее в 10 раз, если использовать
световод со смещенной дисперсией.
Эффект задержки нелинейного отклика описывается последним,
пропорциональным тк членом в уравнении E.5.1). На качественном
Уровне влияние этого члена на распад аналогично действию дис-
дисперсии нелинейности. В частности, даже относительно небольшое
140
Глава 5
•я
сивность
X
0
=
jj-
r
; -
-20
TR=O,O1
N = 2
A
i i I i i l7 I-Vtm i i
-10 0 10
Время т
1
JJ
20° ^
Рис. 5.18. Распад солитона второго порядка (N = 2). вызванный задержкой
нелинейного отклика световода (тк = 0.01).
значение zR приводит к распаду солитонов высших порядков [114,
117]. На рис. 5.18 изображен распад солитона второго порядка
(N = 2) при tr = 0,01. Чтобы выделить особенности, связанные с за-
задержкой нелинейного отклика, остальными эффектами высшего по-
порядка пренебрегли, положив б = 0 и .у = 0. Сравнение рис. 5.17 и 5.18
показывает сходство и различие в картине распада, обусловленного
двумя различными механизмами. Важное отличие заключается в том,
что относительно меньшие по сравнению с ,v значения тк могут
вызвать распад связанного состояния на данном расстоянии. На-
Например, если на рис. 5.17 взять .v = 0,01, то солитон не расщепляется
в пределах г = 5~0. Эта особенность указывает на то, что эффект tr на
практике доминирует над дисперсией нелинейности.
Еще одно важное отличие рис. 5.17 от 5.18 заключается в том, что
в случае дисперсии нелинейности оба солитона задерживаются, в то
время как в другом случае малоинтенсивный солитон ускоряется
и оказывается на переднем фронте начального импульса. Физический
смысл такого поведения можно понять из рис. 5.19, где дано срав-
сравнение спектра импульса при г = 5;0 с исходным спектром солитона
второго порядка, динамика которого представлена на рис. 5.18.
Сдвинутый в длинноволновую область спектральный пик соответ-
соответствует интенсивному солитону, сдвинутому вправо на рис. 5.18, в то
время как спектральная компонента, сдвинутая в коротковолновую
область, соответствует другому пику, сдвинутому влево на рис. 5.18.
Поскольку коротковолновые компоненты распространяются быстрее
чем длинноволновые, они сдвигаются вперед, в то время как осталь-
остальные задерживаются по сравнению с начальным импульсом. Именно
это и видно на рис. 5.18.
Наиболее важная особенность на рис. 5.19 значительный сдвиг
солитонного спектра в длинноволновую область, примерно в 4 раза
Оптические солитоны
141
превышающий начальную ширину спектра при zR = 0,01 и z/z0 = 5.
Такой длинноволновый сдвиг действительно наблюдался в экспери-
эксперименте [107], где 500-фемтосекундные импульсы распространялись по
392-метровому отрезку одномодового световода. Этот эффект на-
называют самосдвигом частоты солитона (вынужденным комбинаци-
комбинационным саморассеянием), поскольку он вызван самим импульсом.
Попытка объяснить наблюдаемый длинноволновый сдвш как воз-
воздействие задержки нелинейного отклика на распространение субпи-
косекундных импульсов была дана в [108]. С физической точки
зрения сдвиг в длинноволновую область можно объяснить, исходя из
эффекта ВКР. Для импульсов короче 1 пс начальная ширина их
спектра достаточно велика для того, чтобы комбинационное усиление
могло эффективно усиливать длинноволновые компоненты за счет
коротковолновых, действующих в качестве накачки (см. гл. 8). Этот
процесс продолжается по длине световода так, что энергия из длин-
длинноволновых компонент передается к коротковолновым. Такая пере-
перекачка энергии проявляется в виде длинноволнового сдвига солитон-
ного спектра, увеличивающегося с расстоянием. Простая модель
[108] показывает, что длинноволновый сдвиг зависит от длитель-
длительности импульса как TqA. Такой вывод также можно сделать, исходя
из рис. 5.18, где задержка солитона \л возрастает как (z/z0J. Так как
период солитона z0 пропорционален То [см. E.2.19)], \d изменяется
как Т^4. Поскольку \d прямо пропорционально длинноволновому
сдвигу, то последний изменяется гак же как Г^4.
В общем случае для импульсов короче 100 фс в уравнение E.5.1)
необходимо включать все три члена высшего порядка, поскольку
здесь уже нельзя пренебречь всеми тремя параметрами 8, л- и zR [114].
1,0
0,8
Ь
?0,6
ш
5
|0,4
0,2 -
-2
1 1 1 1 1 1 1 1
: z
-
-
_
-
'- /\
:, , ^/ , . ..
1 {
= 0l|
li
ii
и
I
I
I
I
!
ll
•I
i i i i
rR
N
1
I
\
1 i i i i
= o.oi :
= 2 -
-
-
_
-
-
'-
-
I i i i i "
-1 О 1
Частота (*-*>0)Т0
Рис. 5.19. Спектр импульса при z/z0 = 5 для тех же параметров, что и на
Рис. 5.18. Штриховой кривой показан спектр начального импульса
142
Глава 5
О 1
v-V0U0
Рис. 5.20. Динамика формы импульса и его спектра для случая N = 2.
Остальные параметры: 6 = 0,03, j = 0,05, т„ = 0,1.
На рис. 5.20 изображены формы импульсов и их спектры для случая
солитона второго порядка при 8=0,03, 5 = 0,05 и тЛ = 0,1. Эти
величины примерно соответствуют 50-фемтосекундному импульсу
(Го ~ 30 фс), распространяющемуся по обычному кварцевому све-
световоду на длине волны 1,55 мкм. Распад солитона происходит на
одном периоде солитона (z0 ~ 5 см); при этом основной пик сдвига-
сдвигается к заднему фронту со значительной скоростью, увеличивающейся
с расстоянием. Этот сдвиг обусловлен уменьшением групповой ско-
скорости, которое в свою очеречь вызвано длинноволновым сдвигом
спектрального максимума счлитона. Если использовать То = 30 фс
для преобразования результатов рис. 5.20 в физические единицы, то
50-фемтосекундный импульс сдвигается почти на 40 ТГц, или 20%
своей несущей частоты при распространении на ~ 15 см.
В случае когда входной пиковой мощности достаточно для воз-
возбуждения солитона высшего порядка, так что N » 1, спектр импульса
трансформируется в несколько компонент, каждая из которых соот-
соответствует фундаментальному солитону, возникающему при расщеп-
расщеплении исходного импульса. Подобная картина наблюдалась в экспе-
эксперименте [115], где 830-фемтосекундные импульсы с пиковой мощ-
мощностью до 530 Вт распространялись в световодах длиной до 1 км.
Самый длинноволновый пик связывался с солитоном, чья длитель-
Оптические солитоны 143
ность была наименьшей (~ 55 фс) после 12 м. а затем нарастала при
увеличении длины световода. Экспериментальные результаты нахо-
находились в согласии с предсказаниями уравнения E.5.1). Данный случай
рассмотрен в разд. 8.4 в контексте солитонных эффектов при вынуж-
вынужденном комбинационном рассеянии. Там также описываются комби-
комбинационные солитонные лазеры.
Хотя уравнение E.5.1) и описывает успешно распространение
фемтосекундных импульсов в волоконных световодах, оно является
лишь приближенным. Как показано в разд. 2.3, при более точном
подходе необходимо использовать уравнение B.3.27), где в Аи учи-
учитывают зависящий от времени отклик нелинейности световода. В
простом приближении предполагают, что Ал подчиняется уравнению
B.3.38), соответствующему экспоненциальному затуханию нелиней-
нелинейного отклика со временем релаксации TR. Численные расчеты пока-
показывают [112], что картина динамики качественно похожа на изобра-
изображенную на рис. 5.20. В частности, найдено, что длинноволновый
сдвиг солитона возрастает линейно по TR. Численная модель исполь-
использовалась для подгонки результатов эксперимента [113], где 70-фемто-
секундные импульсы распространялись в световоде со смещенной
дисперсией. Эксперимент позволил оценить время релаксации вели-
величиной 2-4 фс. Однако понимание того, как ведет себя солитон в
фемтосекундном диапазоне длительностей, еще далеко от полного.
ЛИТЕРАТУРА
1. Lamb G. L.. Jr.. Elements of Soliton Theory, Wiley, New York, 1980. [Имеется
перевод: Лэм Дж.Л. Введение в теорию солитонов. М: Мир. 1983.]
2. Bullough R.K.. Caudrey P.J.. eds., Solitons, Springer-Verlag, Heidelberg, 1980.
[Имеется перевод: Солитоны/под ред. Р. Буллаф, Ф. Кодри.-М.: Мир,
1983.]
3. Ablowitz M.J., Segur H., Solitons and the Inverse Scattering Transform,
Society for Industrial and Applied Mathematics, Philadelphia, 1981. [Имеется
перевод: Абловщ М., Сегур X. Солитоны и метод обратной задачи.-М.:
Мир, 1987.]
4. Dodd R. К, et я/., Solutons and Nonlinear Wave Equations, Academic, New
York, 1984. [Имеется перевод: Додд P. и др. Солитоны и нелинейные
волновые уравнения.-М.: Мир. 1988.]
5. Ablowitz М.. Fuchssteiner В., Kruskal М.. eds.. Topics in Soliton Theory and
Exactly Solvable Nonlinear Equations, World Scientific, Singapore, 1987.
6. Островский Л. /1.-ЖТФ, 1963, т. 33, с. 905; ЖЭТФ. 1966, т. 51, с. 1189.
7. Whitham СВ.. Proc. Roy. Soc 283, 238 A965); J. Fluid Mech.. 27, 399 A967).
8. Benjamin T.B., FeirJ.E.. J. Fluid Mech., 27, 417 A967).
9- Беспалов В.И., Таланов В.И. Письма в ЖЭТФ, 1966, т. 3, с. 471.
Ю. Карпман В. Я.-Письма в ЖЭТФ. 1967, т. 6, с. 829.
Ч. Карпман В. И., Крхшкаль Е.М. ЖЭТФ, 1969, т. 55, с. 530.
12. Taniuti Т., Washimi Я., Phys. Rev. Lett., 21, 209 A968).
13. Тат C.K.W., Phys. Fluids. 12, 1028 A969).
4. Hasegawa A., Phys. Rev. Lett., 24. 1165 A970); Phys. Fluids, 15. 870 A971).
15- Hasegawa A., Plasma Instabilities and Nonlinear Effects, Springer-Verlag,
Heidelberg, 1975.
144 Глава 5
16. Hasegawa A., Brinkman W.F., IEEE J. Quantum Electron., QE-16, 694 A980).
17. Anderson D.R., Dutta S., Gunshor R.L., J. Appl. Phys., 54, 5608 A983).
18. Hasegawa A,, Opt. Lett., 9, 288 A984).
19. Anderson D., Lisak M., Opt. Lett.. 9, 468 A984).
20. Hermansson В., Yeviek D., Opt. Commun., 52, 99 A984).
21. Ахмедиев Н.Н., Е.геонскип В.М., Кулагин Н.Е.- ЖЭТФ, 1985, т. 89,
с. 1542.
22. 7а/К., Hasegawa A,. Tomita A., Phys. Rev. Leti., 56, 135 A986).
23. Tai К. et al.. Appl. Phys. Lett., 49, 236 A986).
24. SlmkhiP.K.. Rasmussen J.J.. Opt. Lett., 11. 171 A986).
25. Tajima K., J. Lightwave Technol.. LT-4, 900 A986).
26. Kothari N.C., Opt. Commun.. 62. 247 A987).
27. Agrawal G.P., Phys. Rev. Lett., 59, 880 A987).
28. Potasek M.J., Opt. Lett., 12, 921 A987).
29. Potasek M.J.. Agniwal G.P.. Phys. Rev.. A36. 3862 A987).
30. Выс.юг.х В. А., Сухотскова Н.А. Квант, электрон., 1987, т. 14, с. 2371.
31. Islam M.N., Dijaili S.P., Gordon J.P., Opt. Lett., 13, 518 A988).
32. Boyd R. W., Raymer M. G., Narducci L. M., eels.. Optical Instabilities, Cambrid-
Cambridge University Press. London. 1986.
33. Arecchi F. Т., Harrison R. G., eds., Instabilities and Chaos in Quantum Optics.
Springer-Verlag, Heidelberg, 1987.
34. Захаров В.Е.. Шабат А,Б. ЖЭТФ. 1971, г. 61, с. 118.
35. Hasegawa A.. Tappert F., Appl. Phys. Lett., 23, 142 A973).
36. SaisumaJ.. Ya/ima N.. Prog. Theor. Phys. Suppl.. 55. 284 A974).
37. Gardner C.S., et a!.. Phys. Rev. Lett., 19, 1095 A967); Commun. Pure Appl.
Math., 27. 97 A974).
38. Haus H.A., Islam M.N., IEEE J. Quantum Electron.. QE-21, 1172 A985).
39. Mollenauer L.F., Stolen R.H.. Gordon J.P., Phys. Rev. Lett., 45, 1095 A980).
40. Stolen R.H., Mollenauer L.F., Tomlinson W.J., Opt. Lett.. 8. 186 A983).
41. Mollenauer L.F.. et al.. Opt. Lett., 8, 289 A983).
42. Salin F. et al., Phys. Rev. Lett., 56. 1132 A986).
43. Salin F. et al.. Phys. Rev. Lett., 60. 569 A988).
44. ManenfS.. Desailly R.. Froehlv C, Opt. Commun., 65, 193 A988).
45. Hasegawa A., Tappert F., Appl. Phys. Lett., 23, 171 A973).
46. Захаров В.Е.. Шабат А. Б, ЖЭТФ. 1973. т. 64. с. 1627.
47. Bendow В, et al,, J. Opt. Soc. Am., 70. 539 A980).
48. Blow K.J., Doran N.J., Phys. Lett.. 107A. 55 A985).
49. Emplit P. et al.. Opt. Commun., 62, 374 A987).
50. Kriikel D. et al.. Phys. Rev. Lett., 60, 29 A988).
51. Wai P. K. A. et al.. Opt. Lett., 12. 628 A987); IEEE J. Quantum Electron.,
QE-24. 373 A988).
52. Agrawal G.P.. Potasek M.J., Phys. Rev., A3. 1765 A986).
53. Kaplan A. E., Phys. Rev. Lett., 55, 1291 A985); IEEE J. Quantum Electron.,
QE-21, 1538 A985).
54. EnnsR.H.. Rangnekar S.S., Opt. I ctt., 12. 108 A987); IEEE J. Quantum
Electron., QE-23. 1199 A987).
55. Enns R. H., Rangnekar S. E., Kaplan I. E., Phys. Rev., A35, 446 A987); 36, 1270
A987).
56. Sipe J.E.. Winful H.G., Opt. Lett., 13. 132 A988).
57. Mollenauer L.F., Stolen R.H.. Opt. Lett.. 9. 13 A984).
58. Mitschke F.M., Mollenauer L.F., IEEE J. Quantum Electron., QE-22, 2242
A986).
59. Mitschke F.M.. Mollenauer L.F.. Opt. Lett., 12, 407 A987).
60. Blow K.J.. Wood D.. IEEE J. Quantum Electron., QE-22, 1109 A986); J. Opt.
Soc. Am., B5, 629 A988).
61. // F. et al.. Opt. Commun., 57, 350 A986); Physica, 320, 362 A986).
Оптические солитоны 145
62. Berg P. et al., Phys. Rev., A35, 4167 A987).
63. Bellinger P. A., J. Opt. Soc. Am., B5, 793 A988).
64 Hasegawa A.. Kodama У., Proc. IEEE, 69 1145 A981). [Имеется перевод:
Хшэгава А,. Кодами Ю- ГИИЭР. 1981, т. 69 (9), с. 57.]; Opt. Lett., 7, 285
A982).
65. Doran N.J.. Blow K.J., 1EEF J. Quantum Eleciron., QE-19, 1883 A983); Opt.
Commun. 42, 403 A982).
66. Kodcima Y, Hasegawa A,. Opt. Lett., 7, 339 A982); 8, 342 A983).
67. Huscyawa A., Opt. Lett., 8, 650 A983).
68. Hasegmra A,. Appl. Opt.. 23, 3302 A984).
69. Mollenauer L.F., Stolen R.H.. Islam M.N., Opt. Lett., 10, 229 A985).
70. Menvnk C.R.. Chen H.H., Lee Y.C.. Opt. Lett.. 10. 451 A985).
71. пиана» E.M. и др.-ДАН СССР, 1985, т. 283, с. 1342.
72. Mollenauer L.F.. Gordon J. P., Islam M.N., IEEE J. Quantum Electron.,
QE-22. 157 A986).
73. Potasek M.J.. Aarawal G.P., Electron. Lett., 22, 759 A986).
74. Tajima K,. Opt. Lett., 12, 54 A987).
75. Mollenauer L.F.Smith K.. Opt. Lett., 13, 675 A988).
76. Blow K.J.. Doran N.J., Opt. Commun., 52, 367 A985).
77. Anderson D,. Lisak M., Opt. Lett., 10, 390 A985).
78. Meinel R.. Opt. Commun., 47, 343 A983).
79. Дштов Е.М.. Прохоров A.M., СеркинВ.Н, ДАН СССР, 1983, т. 273,
с. 1112.
80. Фаттахов A.M.. Чиркни А. С. Квант, электрон., 1984, т. 11, с. 2349.
81. Lassen Н.Е. et al.. Opt. Lett., 10, 34 A985).
82. Desem С. Chu P.L., Opt. Lett., 11, 248 A986).
83. Blow K.J.. WoodD,. Opt. Commun., 58, 349 A986).
84. Маймиетов А. И., Склнроп Ю. М. Квант, электрон.. 1987. т. 14. с. 796.
85. Бе.юв М.Н, Квант, электрон.. 1987. т. 14, с. 1627.
86. Gouveia-Neto A.S.. Gomes A.S.L., Tailor J.R.. Opt. Commun., 64, 383 A987).
87. Karpman V.I.. Solobev V. V.. Physica, 3D. 487 A981).
88. Gordon J.P., Opt.. Lett., 8, 596 A983).
89. Blow K.J., Doran N.J., Electron. Lett., 19, 429 A983).
90. Hennansson В.. Yevick D.. Electron. Lett., 19. 570 A983).
91. dm P.L., Desem C, Technical Digest IOOC'83, Tokyo, 52 A983); Electron
Lett., 21, 228 A985).
92. SMojiri ?.. Fujii Y. Appl. Opt., 24, 358 A985).
93. Chu P.L., Desem C, Electron. Lett., 21, 1133 A985).
94. Anderson D.. Lisak M.. Phys. Rev., A32, 2270 A985); Opt. Lett., 11, 174 A986).
95. пиано» Е.М., Никонова З.С.. Серкии В. И. Квант, электрон., 1986, т. 13,
с. 1740.
96. Mitschke F.M.. Mollenauer L.F.. Opt. Lett., 12. 355 A987).
97. Chu P. L., Desem C. Opt. Lett., 12, 349 A987); Electron. Lett., 23, 260 A987).
98. dm P.L., Desem C. FEE Proc. 134. Pt. J. 145 A87).
99. Kodama Y, Nozaki K.. Opt. Lett., 12, 1038 A987).
100. Gordon J.P.. Haum H.A., Opt. Lett., 11, 665 A986).
101. Tzoar N.. Jain M.. Phys. Rev.. A23, 1266 A981).
Ю2. Anderson D.. Lisak M.. Phys. Rev., A27, 1393 A983).
103. Clmsrodoulides D.N.. Joseph R.I.. Appl. Phys. Lett.. 47, 76 A985).
104. Го.ювченко Е. А. и др.-Письма в ЖЭТФ. 1985, т. 42, с. 74; ДАН СССР,
1986, т. 288. с. 851.
№5. Го.ювченко Е.А. и др. Письма в ЖЭТФ, 1987, т. 45, с. 73.
¦06. Ohkuma К.. Ichikawa Y.H.. Abe Y, Opt. Lett., 12, 516 A987).
¦07. Mitschke F.M., Mollenauer L.F., Opt. Lett., 11, 659 A986).
108. Gordon J. P., Opt. Lett., 11, 662 A986).
Ю9. Kodtigm Y.. Hasegawa A., IEEE J. Quantum Electron., QE-23, 510 A987).
146 Глава 5
ПО. Zysset В.. BeaudP.. Hodel W., Appl. Phys. Lett., 50, 1027 A987).
111. Выслоух В.А., Матвеева Т. А. Квант, электрон., 1987, т. 14, с. 792.
112. Серкин В. Я.-Письма в ЖТФ, 1987, т. 13, с. 772; 1987, т. 13, с. 878.
113. Грудинин А. Б. и др. Письма в ЖЭТФ, 1987. т. 46, с. 175.
114. Hodel W., Weber И. P.. Opt. Lett., 12, 924 A987).
115. Beaud P. el al., IEEE J. Quantum Electron., QE-23, 1938 A987).
116. Gouveia-Neto A.S.. Gomes A.S.L.. Taylor J.R.. IEEE J. Quantum Electron.,
QE-24, 332 A988).
117. TaiK. Hasegawa A.. Bekki N.. Opt. Lett., 13, 392 A988).
118. Mjolhus E., J. Plasma Phys., 16, 321 A976); 19, 437 A978).
119. Mio K. et al.. J. Phys. Soc. Jpn, 41, 265 A976).
120. Wadati M., Konno K., lchikawa F.H., J. Phys. Soc. Jpn., 46, 1965 A979).
121. lchikawa Y.H. et at.. J. Phys. Soc. Jpn., 48, 279 A980).
122. Wai P. K. A. et al.. Opt. Lett., 11, 464 A986).
Глава 6
СЖАТИЕ ОПТИЧЕСКИХ ИМПУЛЬСОВ
Одним из важнейших применений нелинейных эффектов в воло-
волоконных световодах является сжатие оптических импульсов; экспери-
экспериментально были получены импульсы длительностью вплоть до 6 фс.
В данной главе рассмотрены методы компрессии импульсов, их
теоретические и экспериментальные аспекты. В разд. 6.1 изложена
основная идея, представлены два вида компрессоров, обычно исполь-
используемых для сжатия импульсов,- волоконно-решеточные компрессоры
и компрессоры, основанные на эффекте многосолитонного сжатия.
В волоконно-решеточном компрессоре используется отрезок воло-
волоконного световода с положительной дисперсией групповых скоро-
скоростей, за которым следует дисперсионная линия задержки с отрица-
отрицательной дисперсией групповых скоростей, представляющая собой
пару дифракционных решеток. Дисперсионная линия задержки рас-
рассмотрена в разд. 6.2, в то время как в разд. 6.3 представлены теория
и обзор экспериментальных результатов. В компрессорах, основан-
основанных на эффекте многосолитонного сжатия, используются солитоны
высших порядков, которые существуют в световоде благодаря сов-
совместному действию фазовой самомодуляции (ФСМ) и отрицательной
дисперсии. Теория такого компрессора представлена в разд. 6.4, далее
следуют экспериментальные результаты. Следует отметить, что в од-
одном из экспериментов по компрессии оптические импульсы были
сжаты в 5000 раз; при этом была использована двухкаскадная схема
сжатия, в которой за волоконно-решеточным компрессором следовал
оптимизированный компрессор, основанный на эффекте многосоли-
многосолитонного сжатия.
6.1. ВВЕДЕНИЕ
Идея, лежащая в основе компрессии оптических импульсов, заим-
заимствована из физики сканирующих радаров, где импульсы на микро-
микроволновых частотах, имевшие частотную модуляцию, сжимались,
проходя через дисперсионную линию задержки [1]. Физический меха-
механизм компрессии можно понять, обратившись к разд. 3.2, где рас-
рассматривается распространение импульсов с частотной модуляцией
в линейной диспергирующей среде.
148 Глава 6
Такая среда при распространении по ней импульса вызывает
свипирование его частоты, обусловленное дисперсией. Если началь-
начальная частотная модуляция противоположна по знаку частотной мо-
модуляции за счет дисперсии групповых скоростей, возможно их взаим-
взаимное сокращение, что приводит к тому, что конечный импульс стано-
становится короче начального. Так как частотная модуляция, вызванная
дисперсией, линейна [см. уравнение C.2.13)], то для максимального
сжатия начальный импульс должен иметь линейную частотную мо-
модуляцию. Более того, точная компенсация частотной модуляции
происходит только на определенной длине [см. уравнение C.2.19)].
Во временном представлении процесс сжатия можно представить
следующим образом. При наличии дисперсии групповых скоростей
различные частотные компоненты распространяются с разными ско-
скоростями. Если передний фронт импульса задержать должным обра-
образом (так, чтобы он приходил одновременно с задним фронтом),
выходной импульс сжимается. Для сжатия импульса с положитель-
положительной частотной модуляцией (частота нарастает к заднему фронту)
требуется отрицательная дисперсия групповых скоростей; при этом
длинноволновый передний фронт замедляется. С другой стороны, для
импульса с отрицательной частотной модуляцией требуется поло-
положительная дисперсия, для того чтобы замедлить коротковолновый
передний фронт.
В ранних работах по сжатию оптических импульсов [2 10] ис-
использовались как положительная, так и отрицательная дисперсии
в зависимости от того, как на импульс накладывалась начальная
частотная модуляция. В случае отрицательной частотной модуляции
[3] средой с положительной дисперсией служили жидкости или газы.
В случае положительной частотной модуляции оказалось, что наибо-
наиболее подходящим устройством с отрицательной дисперсией является
пара дифракционных решеток [4, 7]. В этих экспериментах при
сжатии импульсов не использовались нелинейные эффекты. Хотя
использовать ФСМ для компрессии импульсов было предложено еще
в 1969 г. [11, 12], эксперименты по сжатию импульсов при помощи
ФСМ начали проводиться лишь в 80-х годах, когда одномодовые
световоды из кварцевого стекла нашли широкое применение в ка-
качестве нелинейной среды [13-38]. Были получены импульсы длитель-
длительностью 6 фс на длине волны 620 нм [20], а также достигнут коэф-
коэффициент сжатия 5000 на длине волны 1,32 мкм [38]. Такой прогресс
был достигнут только благодаря детальному описанию динамики
импульса в волоконном световоде и оптимизации параметров све-
световода при помощи численного моделирования [39-47].
Компрессоры, основанные на нелинейных эффектах в волоконных
световодах, можно разделить на две категории, называемые здесь
волоконно-решеточными компрессорами и компрессорами, основан-
основанными на эффекте многосолитонного сжатия. В волоконно-решеточ-
Сжатие оптических импульсов 149
ном компрессоре импульс сначала распространяется в световоде
в области положительной дисперсии групповых скоростей, а затем
происходит его сжатие при помощи пары дифракционных решеток.
Задача световода - наложить практически линейную частотную мо-
модуляцию за счет комбинации нелинейных и дисперсионных эффектов
[39]. Пара дифракционных решеток создает отрицательную диспер-
дисперсию групповых скоростей, необходимую для сжатия импульсов с
положительной частотной модуляцией [4, 7]. С другой стороны,
компрессор, основанный на эффекте многосолитонного сжатия, со-
состоит только из отрезка световода специально подобранной длины.
Начальный импульс распространяется в области отрицательной дис-
дисперсии световода и сжимается за счет совместного действия ФСМ
и дисперсии. Компрессия здесь обусловлен:! фазой начального сжа-
сжатия, через которую проходят все солитоны высших порядков до того,
как их начальная форма восстановится после одного периода соли-
тона (см. разд. 5.2). Коэффициент сжатия зависит от пиковой мощ-
мощности импульса, определяющей порядок солитона N. Оба типа
компрессоров взаимно дополняют друг друга, работая обычно в раз-
разных областях спектра; граница определяется длиной волны нулевой
дисперсии (~ 1,3 мкм для кварцевых световодов). Таким образом,
волоконно-решеточный компрессор используется для сжатия импуль-
импульсов в видимой и ближней инфракрасной областях спектра, в то время
как компрессоры, основанные на эффекте многосолитонного сжатия,
используются в области 1,3-1,6 мкм. В области 1,3 мкм за счет
использования световодов со смещенной дисперсией можно приме-
применять компрессоры обоих типов. Двухкаскадная схема сжатия, где
использовались оба типа компрессоров, позволила получить коэф-
коэффициент сжатия 5000 в области 1,32 мкм [38].
6.2. ПАРА ДИФРАКЦИОННЫХ РЕШЕТОК
В видимой и ближней инфракрасных областях спектра
(к < 1,3 мкм) для сжатия импульсов обычно используют волоконно-
решеточный компрессор [14 33]. Задача пары дифракционных ре-
решеток создавать отрицательную дисперсию групповых скоростей [4.
7] для импульсов, имеющих положительную частотную модуляцию
после прохождения через световод. В данном разделе кратко описан
принцип действия пары дифракционных решеток [48 51]. На рис. 6.1
показана схема дисперсионной линии задержки, состояшей из пары
решеток; представлены соответствующие обозначения. Импульс па-
лает на первую из двух параллельных дифракционных решеток.
Различным частотным компонентам в спектре импульса соответ-
соответствуют разные углы дифракции. В результате разные частотные
компоненты испытывают различную временную задержку при про-
прохождении через пару решеток. Оказывается, что оптический путь
150 Глава 6
Рис. 6.1. Схема дисперсионной линии задержки, состоящей из пары решеток
и обозначения для пары решеток.
коротковолновых компонент меньше, чем длинноволновых. В им-
импульсе с положительной частотной модуляцией коротковолновые
компоненты находятся у заднего фронта, в то время как передний
фронт состоит из длинноволновых. Таким образом, проходя через
пару решеток, передний фронт «встречается» с задним и происходит
сжатие импульса.
Частотная зависимость угла дифракции 0Г определяется уравне-
уравнением дифракционной решетки. В случае дифракции первого порядка
0Г определяется уравнением
2пс
sin0r = sin0;, F.2.1)
соЛ
где 0.-угол падения и Л-период решетки (расстояние между штри-
штрихами). Предполагается, что как 0Г. так и 0; находятся по одну сторону
от нормали к решетке.
Временная задержка определяется [7, 51]
^, F-2.2)
С ЯСО
где /(со) -оптический путь и фс(со) фазовый сдвиг. Оптический путь
можно определить из рис. 6.1, используя простые геометрические
соотношения [50],
cos@ -0.)
/(со) = ll + l2 = d0 ' . F.2.3)
cos@r)
Для дальнейшего анализа в разд. 6.3 получим выражения для
фазового сдвига, приобретаемого спектральной компонентой с ча-
частотой со. Полезно разложить это выражение в ряд в окрестности
несущей частоты соо:
фс(со) = ф0 + /дсо - соо) - яс(со - сооJ + Ьс(а> - сооK + ..., F.2.4)
где ф0 - постоянная, tc — постоянная задержка, ас и Ьс принимают
Сжатие оптических импульсов 151
в расчет дисперсионные эффекты в паре решеток. Параметры ас и Ьс
можно получить, используя F.2.1)-F.2.4) и разлагая /(со) в ряд
Тейлора. В результате
4п2сЬ0
ас = -Т~2 1—' <6-2-5)
4n2cb0{\ + sin 0; sin 0rO)
г -, F-2.6)
где 8r0 определяется из F.2.1) при условии to = соо, b0 - расстояние
между центрами решеток (b0 = dosec(QrO)). Для большинства прак-
практически значимых случаев ширина спектра Асо «соо, кубичным чле-
членом и членами высших порядков в разложении F.2.4) можно пре-
пренебречь. Если пренебречь постоянным и линейным членами, фазовый
сдвиг приобретает вид
фс(со)^-яс(со-сооJ. F.2.7)
Поскольку ас в F.2.5) есть положительная величина, фс(со)-отри-
цателен. Отрицательное значение фазового сдвига соответствует
отрицательной дисперсии групповых скоростей. Это легко понять,
рассмотрев поле на выходе после пары решеток. Если Gвх(Г)-поле
на входе, поле на выходе имеет вид
f/вых СО = — ? #вх (со - соо) ехр рф,(со) - тГ\ Jco, F.2.8)
где 17ВЬ1Х(со)-фурье-образ (УВХ(Т), который определяется способом,
аналогичным уравнению C.2.2). Сравнивая уравнения F.2.8) и C.2.5),
мы видим, что пара дифракционных решеток создает отрицательную
дисперсию групповых скоростей с эффективным дисперсионным па-
параметром:
-2ac/V F.2.9)
Можно также определить эффективную дисперсионную длину,
используя при этом соотношение L^f* = ТЦ\ Р^ФФ I -> гДе Го-длитель-
Го-длительность начального импульса. Оценим порядок величины Р211*, исполь-
используя уравнения F.2.5) и F.2.9). В видимой области (Хо = 2пс!щ ^
— 0,5 мкм) Р|фф ~ 1 пс2/м, если принять Л ~ 1 мкм. Это соответ-
соответствует LJ,** ~ 1 м при Го ~ 1 пс. Расстояние между решетками, необ-
необходимое для сжатия импульсов, зависит от величины частотной
модуляции; обычно Ьо составляет какую-то долю Lff* [см. уравнение
C.2.19)]. Для субпикосекундных импульсов b0 ~ 10 см. Тем не менее
оно становится значительным (~ 10 м) при 7^, > 10 пс. Можно уве-
увеличить р^фф, используя в уравнении F.2.5) углы падения 8г0, близкие
к я/2. Однако, как видно из уравнения F.2.6), в такой схеме возрастает
вклад дисперсионных членов высших порядков; необходимо поэтому
152 Глава 6
в уравнении F.2.4) учитывать кубический член [48]. Также необходи-
необходимо учитывать кубический член для ультракоротких импульсов
(То < 10 фс), когда ширина спектра Асо становится сравнимой с 0)и
[49].
Недостатком пары решеток является то, что спектральные ком-
компоненты импульса диспергируют не только во времени, но и в про-
пространстве. В результате оптический пучок расходится между двумя
решетками; поперечное сечение его напоминает вытянутый эллипс,
а не круг. Такая деформация пучка явно нежелательна и становится
просто недопустимой при больших расстояниях между решетками.
Самое простое решение - отразить пучок обратно на решетки [52].
Такая двухпроходная схема не только восстанавливает исходное
поперечное сечение пучка, но и удваивает величину дисперсии груп-
групповых скоростей, тем самым уменьшая расстояние между решетками
в 2 раза [21]. Небольшой наклон отражаюшего зеркала позволяет
разделить траектории сжатого и входного импульсов. На практике
почти повсеместно применяется двухпроходная схема.
Другой недостаток пары решеток-это ее дифракционные потери.
При дифракции первого порядка в импульсе обычно остается 60 80%
всей энергии. Это приводит к тому, что за один проход энергия
в импульсе уменьшается в 2 раза, а в двухкаскадной схеме - в 4 раза.
Существуют две альтернативные схемы, которые могут создавать
отрицательную дисперсию при относительно меньших потерях; в не-
некоторых случаях они могут служить достойной заменой. Первая
схема использует интерферометр Жира Турнуа [2], предложенный
в 1964 г. для сжатия импульсов. Такой интерферометр может отра-
отражать почти всю энергию импульса, при этом различные спектральные
компоненты приобретают дисперсионный фазовый сдвиг в виде
F.2.7). Недавно было показано, что пара призм может создавать
отрицательную дисперсию при отражении [53]. Тем не менее тре-
требуемое расстояние между призмами обычно на два порядка больше,
чем между решетками, из-за относительно малого значения диспер-
дисперсии в кварцевом стекле. Это расстояние можно уменьшить, используя
такие материалы, как стекло из тяжелого флинта [54] или кристалл
ТеО2 [55]. Для призм из кристалла ТеО-, расстояние между ними
становится сравнимым с расстоянием между дифракционными ре-
решетками. В эксперименте [55] 800-фемтосекундные импульсы были
сжаты до 120 фс; при этом использовалась пара призм на расстоянии
25 см друг от jnyra. Поскольку потери энергии в паре призм можно
сократить до 2% и менее, их использование, вероятно, станет обще-
общепринятым. В качестве альтернативы паре решеток в работе [56] было
предложено использовать фазовую решетку, индуцированную в крис-
кристалле ультразвуковой волной со свипированной частотой. Если све-
световод обладает фоторефракцией, то, пользуясь стандартными мето-
методами голографии, внутри его сердцевины можно создать постоянную
Сжатие оптических импульсов 153
дифракционную решетку [57]. Такая фазовая решетка может со-
чдавать отрицательную дисперсию в том же самом световоде, кото-
который используется для создания линейной положительной частотной
модуляции в оптическом импульсе. При этом необходимость в паре
решеток отпадает [57].
6.3. ВОЛОКОННО-РЕШЕТОЧНЫЕ КОМПРЕССОРЫ
В данном разделе изложена теория волоконно-решеточного ком-
компрессора,, а гакже приведен обзор экспериментальных результатов по
сжатию сверхкоротких импульсов в видимой и ближней инфракрас-
инфракрасной областях спектра. Так как обычные кварцевые световоды имеют
положительную дисперсию только при длинах волн X <, 1,3 мкм,
такие компрессоры используются до длин волн порядка 1,32 мкм. На
рис. 6.2 показана схема волоконно-решеточного компрессора в двух-
проходной конфигурации [21]. Исходный импульс вводится в одно-
модовый, сохраняющий поляризацию волоконный световод через
микрообъектив; здесь импульс спектрально уширяется и приобретает
положительную частотную модуляцию по всей своей длине. Выход-
Выходной импульс попадает на пару решеток, где он сжимается благодаря
ее отрицательной дисперсии. Проходя пару решеток в противопо-
противоположном направлении, импульс восстанавливает свое первоначальное
поперечное сечение. Зеркало М[ слегка наклонено для того," чтобы
разделить входной и выходной пучки. Зеркало М2 выводит сжатый
импульс из компрессора без внесения каких-либо дополнительных
потерь.
6.3.1. ТЕОРИЯ
Хотя идея данной схемы довольно проста для того, чтобы
добиться оптимальной работы волоконно-решеточного компрессора,
необходимо ответить на несколько вопросов. Самыми основными
Сжатый
.импульс
Входной волооннй N
импульс
Рис. 6.2. Схема волоконно-решеточного компрессора, действующего по двух-
проходной схеме. Зеркало М2 (показано штриховой линией) находится выше
плоскости чертежа. Зеркало М, слегка наклонено для того, чтобы отделить
отраженный луч от падающего.
154 Глава 6
являются: 1) существует ли оптимальная длина световода, соответ-
соответствующая данным значениям параметров импульса? 2) существует ли
оптимальное расстояние между решетками для получения высокока-
высококачественных импульсов с максимальной степенью сжатия? Чтобы
ответить на эти вопросы, следует рассмотреть, как исходный импульс
с определенными длительностью и пиковой мощностью распро-
распространяется по световоду при наличии фазовой самомодуляции и дис-
дисперсии групповых скоростей. Динамика импульса при данных усло-
условиях была рассмотрена в разд. 4.2. Полезно использовать безразмер-
безразмерный вид D.2.1) уравнения распространения. При положительной
дисперсии (Р2 > 0) это уравнение приобретает вид
^\^Т + ^2е-аг\и\2и = 0, F.3.1)
2 ох2
nd(z/z0) 2 ох2
где т = 7JT0,
'-
а параметр N, с учетом уравнения D.2.3), определяется следующим
выражением:
N F33)
Lnl I P2 I
В F.3.1)-F.3.3) (У-безразмерная амплитуда, ,Р0-пиковая мощ-
мощность исходного импульса длительностью То, у-нелинейный пара-
параметр. Величины LD и LNL определены формулой C.1.5). Параметр
z0 — период солитона, введенный в разд. 5.2. Данное понятие оказы-
оказывается полезным и в области положительной дисперсии в том смысле,
что длительность импульса практически удваивается на этой длине
(г = z0) при отсутствии ФСМ [41].
Работа волоконно-решеточного компрессора может быть промо-
промоделирована следующим образом. Численно решается уравнение
F.3.1) и получается U(z, т) на выходе световода. Далее данное
значение используется в качестве начального поля в преобразовании
F.2.8), и получается сжатый импульс. Значение параметра ас в фор-
формуле F.2.7) можно изменять для того, чтобы оптимизировать работу
компрессора. Оптимальным компрессором является тот, у которого
расстояние между решетками соответствует оптимальной величине ас
так, что пиковая мощность сжатого импульса является наибольшей.
На практике волоконно-решеточный компрессор оптимизируется
именно таким способом. В дальнейшем мы пренебрегаем потерями
в световоде, поскольку необходимые длины световодов обычно малы
по сравнению с длиной поглощения (aL« 1).
Сначала рассмотрим случай чистой ФСМ без дисперсионных
Сжатие оптических импульсов
155
эффектов. В разд. 4.1 было показано, что при отсутствии дисперсии
форма импульса остается неизменной, в то время как его спектр
уширяется при распространении. С точки зрения компрессии импуль-
импульсов тем не менее более важной является частотная модуляция за счет
ФСМ.
На рис. 4.1 показано, что для гауссовского импульса в случае
ФСМ без дисперсии частотная модуляция линейна только в цен-
центральной части импульса. Когда такой импульс проходит через пару
решеток, отрицательная дисперсия сжимает только его центральную
часть. Так как значительная доля энергии остается в «крыльях»,
сжатый импульс получается не самого высокого качества.
Оказывается, что дисперсия световода может существенно улуч-
улучшить качество импульса [39]. Как показано в рис. 4.2, дисперсия
уширяет импульс так, что он становится почти прямоугольным (см.
рис. 4.9). В то же самое время у импульса образуется практически
линейная частотная модуляция вдоль всей длины. В результате пара
решеток может сжать всю энергию импульса в узкий пик. На рис. 6.3
показаны [41] форма импульса на выходе световода, его частотная
модуляция и сжатый импульс при N = 5 и z/z0 — 0,5. Для сравнения
в верхнем ряду даны соответствующие рисунки при отсутствии
дисперсии для длины световода, выбранной так, что импульс сжима-
сжимается в одно и то же число раз в обоих случаях (N2z/z0 = 4,5). Хотя ни
-з
-3
Рис. 6.3. Форма импульса на выходе из световода, соответствующая частот-
частотная модуляция и сжатый импульс при наличии (нижний ряд) и при отсутствии
(верхний ряд) дисперсии групповых скоростей. Параметры таковы, что
N~:/:o = 4,5 для верхнего ряда, в то время как N = 5 и z/z0 = 0,5 для нижнего
Ряда [41].
156 Глава 6
N2. ни z0 не являются величинами, ограниченными в пределе р2 = О,
их отношение остается конечным и его можно использовать для
сравнения обоих случаев. При сравнении двух рядов.на рис. 6.3 видно
благотворное воздействие дисперсии на качество сжатого импульса,
что определяется линейностью его частотной модуляции. Данное
преимущество тем не менее достигается только за счет уменьшения
степени сжатия при данном значении начальной пиковой мощности
[41].
Для количественного описания работы волоконно-решеточного
компрессора полезно ввести два параметра
сжат, Qc = | UBMX @) 12/Fc, F.3.4)
где 7^.жат-длительность сжатого импульса на полувысоте (по интен-
интенсивности), 7JrWHM-аналогичная величина для исходного импульса.
Ясно, что /^-коэффициент сжатия. Параметр Qc является мерой
качества сжатых импульсов. На входе в световод данная величина
равна 1, и для сжатого импульса желательно Qc ^ 1, чтобы практи-
практически вся энергия была сосредоточена в центральном пике. Численное
моделирование показывает [41], что существует оптимальная длина
световода, для которой как Fc, так и Qc максимальны. На рис. 6.4
показана зависимость Fc и Qc от z/z0 при значениях N в диапазоне
1-20; предполагается, что начальный импульс имеет форму гипер-
гиперболического секанса. Для относительно больших значений N(N ^ 5)
максимумы для Fc и Qe очевидны, так что необходимо оптимизиро-
оптимизировать длину световода. Качественно наличие такой оптимальной
длины zopt можно понять следующим образом. При z < zopi частотная
модуляция за счет ФСМ еще не линеаризуется, в то время как при
- > -opt дисперсионные эффекты настолько уширяют импульс, что
ФСМ теряет свою эффективность. Действительно, гор| хорошо ап-
аппроксимируется FLDLNty 2, что указывает на важность как дис-
дисперсионных, так и нелинейных эффектов для сжатия импульса.
Для практического создания компрессоров полезно выписать ряд
простых правил, которыми и определяются длина световода и опти-
оптимальное расстояние между решетками; при выполнении этих правил
достигается максимальная степень сжатия при заданных значениях
параметров световода и параметров импульса. Можно использовать
численные результаты рис. 6.4 для получения следующих соотноше-
соотношений, справедливых при N » 1 [41]:
F.3.5)
c F.3.6)
1FC-1,6/N, F.3.7)
где параметр решеток ас связан с оптимальным расстоянием между
ними соотношением F.2.5). Численный коэффициент зависит от
Сжатие оптических импульсов
157
Рио. 6.4. Коэффициент сжатия Fc и параметр качества Qc как функции длины
световода при значениях N в диапазоне 1 20. Расстояние между решетками
в каждом случае оптимизировано гак, что пиковая мощность сжатого им-
импульса максимальна [41].
формы входного импульса, при этом он будет немного отличаться от
1.6. если форма импульса отличается от гиперболического секанса.
Тем не менее уравнения F.3.5)—F.3.7) дают хорошее приближение
для любых форм импульса при N ^ 10. Похожие соотношения были
получены при аналитическом решении F.3.1); был использован метод
ОЗР и сделаны определенные предположения о форме импульса и его
частотной модуляции [40]. Когда уравнения F.3.5)-F.3.7) приме-
применяют на практике, сначала оценивают параметр N для данных
значений пиковой мощности Ро и длительности (TFWIIM ~ 1,76ТО для
гиперболического секанса). Затем, используя F.3.2) и F.3.5), находят
Длину световода zopl, в то время как из F.2.5) и F.3.6) находят
расстояние между решетками. В конце концов из соотношения F.3.7)
оценивают коэффициент сжатия.
Вышеизложенную теорию сжатия импульсов можно применять
в большинстве практически важных случаев, но не следует забывать
° ее ограничениях. Начнем с того, что предполагается отсутствие
частотной модуляции в исходном импульсе. В противном случае
158 Глава 6
эффект линейной частотной модуляции легко учесть, если решать
уравнение F.3.1) численно при начальном условии вида C.2.21), где
С-параметр частотной модуляции [47]. Для импульсов с отрица-
отрицательной частотной модуляцией (С < 0) оптимальная длина световода
возрастает, поскольку положительная частотная модуляция, созда-
создаваемая световодом, должна скомпенсировать начальную отрицатель-
отрицательную. В то же время коэффициент сжатия немного уменьшается
потому, что такая компенсация не является полной по всей длине
импульса. Обратное происходит в случае с положительной частотной
модуляцией (С > 0). Тем не менее для больших значений N(N > 10)
изменения в zop, и Fc относительно малы (< 10%) для импульсов,
ширина спектра которых не более чем в 2 раза превышает ширину
спектра импульса при отсутствии частотной модуляции. С этим
также связан вопрос о том, как будет влиять на сжатие импульсов
случайная частотная модуляция, возникающая из-за флуктуации
амплитуды и фазы начальных импульсов. Моделирование по методу
Монте-Карло показывает [45], что среднее значение коэффициента
сжатия уменьшается на величину, зависящую от изменения шума, но
оптимальная длина световода остается практически неизменной.
Кроме того, теория ограничена также тем, что ее результаты (см.
рис. 6.4) следуют из уравнения F.3.1), в котором пренебрегается
нелинейными и дисперсионными эффектами высших порядков. Это
оправданно, пока ширина спектра Асо «соо и результаты достаточно
точны для длительностей То > 0,1 пс. Для более коротких импульсов
следует использовать более общее уравнение распространения B.3.35)
из разд. 2.3. Действие дисперсии нелинейности на динамику импульса
было рассмотрено в разд. 4.3. В общем случае как форма импульса,
так и его спектр становятся несимметричными (см. рис. 4.17 и 4.18).
Большее уширение спектра в коротковолновой части на рис. 4.18
обусловлено большей частотной модуляцией у заднего фронта по
сравнению с передним. Поэтому частотная модуляция перестает быть
линейной, как это было бы без дисперсии нелинейности; в общем
случае для фемтосекундных импульсов коэффициент сжатия умень-
уменьшается по сравнению с предсказаниями рис. 6.4.
При 7^, < 50 фс на работу волоконно-решеточного компрессора
накладывается еще более жесткое ограничение, связанное с тем, что
пара решеток уже не действует как квадратичный компрессор. Для
таких коротких импульсов ширина спектра настолько велика, что
кубичный член в разложении F.2.4) становится сравнимым с квадра-
квадратичным, и его следует включить в уравнение F.2.8). Численные
результаты показывают [46], что значительная часть энергии в сжа-
сжатых импульсах распространяются в форме осциллирующего заднего
фронта (аналогично рис. 3.7). В результате коэффициент сжатия
уменьшается по сравнению с рис. 6.4. Это ограничение является
фундаментальным, и его можно обойти [20], лишь найдя способ
Сжатие оптических импульсов 159
преодолеть действие кубичного члена в уравнении F.2.4). Но, с дру-
другой стороны, можно использовать кубичный член для частичной
компенсации нелинейной частотной модуляции, вызванной диспер-
дисперсией нелинейности [58].
Максимальное ограничение на работу волоконно-решеточных
компрессоров накладывается вынужденным комбинационным рас-
рассеянием [59-62] (см. гл. 8). Хотя в соответствии с соотношением
F.3.7) коэффициент сжатия Fc ~ N и его можно увеличивать, повы-
повышай пиковую мощность начального импульса, на практике степень
сжатия ограничена. Это обусловлено тем, что пиковую мощность
импульса необходимо поддерживать ниже порога ВКР для того,
чтобы избежать перекачки энергии в стоксову компоненту. Более
того, даже если допустимы некоторые потери энергии, импульс,
соответствующий стоксовой компоненте, может взаимодействовать
с импульсом накачки через фазовую кросс-модуляцию; при этом
деформируется линейность частотной модуляции. Можно достичь
значительных коэффициентов сжатия даже в присутствии ВКР, оп-
оптимизируя параметры конструкции [62]. Численные расчеты пока-
показывают [59, 60], что из-за взаимодействия стоксова импульса и им-
импульса накачки значительная доля энергии в импульсе остается вне
компрессии.
Работу компрессора можно усовершенствовать, используя метод
спектральной фильтрации [24], в котором для селектирования спект-
спектра импульса рядом с зеркалом М, на рис. 6.2 помещается соответ-
соответствующая диафрагма. Метод спектральной фильтрации достаточно
мощен [63-65], его можно использовать не только для того, чтобы
улучшить работу волоконно-решеточных компрессоров, но и для
того, чтобы управлять формой импульса, модифицируя спектр вну-
внутри компрессора. Это возможно, так как пара решеток простран-
пространственно разделяет спектральные компоненты, и их можно модифи-
модифицировать (как по амплитуде, так и по фазе), используя маски,
расположенные у зеркала М, на рис. 6.2. Метод спектральной фильт-
фильтрации рассмотрен в следующем подразделе.
6.3.2. ЭКСПЕРИМЕНТЫ
В первом эксперименте по сжатию импульсов в оптических све-
световодах [13] 5,5-пикосекундные (FWHM) начальные импульсы на
587 нм с пиковой мощностью 10 Вт распространялись через световод
•Миной 70 м. 20-пикосекундные выходные импульсы были почти
прямоугольны по форме и имели уширенный за счет ФСМ спектр
с практически линейной частотной модуляцией. Это свойство пред-
предполагалось [39] из совместного действия дисперсии и нелинейности
(см. рис. 6.3). В качестве дисперсионной линии задержки вместо пары
Решеток использовался газ атомов натрия. Сжатые импульсы имели
160
Глава 6
длительность 1,5 пс. Коэффициент сжатия составлял 3,7, что нахо-
находится в согласии с результатами рис. 6.4, если учесть, что значения
параметров эксперимента соответствовали N =* 7 и z/z0 =: 0,25. Дей-
Действительно, даже форма импульса на выходе из световода была
в хорошем согласии с численными решениями уравнения F.3.1).
Данный метод получил распространение в фемтосекундную об-
область в работах Шенка и др. [14], которые использовали пару
решеток в качестве дисперсионной линии задержки. В их экспери-
экспериментах 90-фемтосекундные импульсы на 619 нм проходили через
15-сантиметровый отрезок световода и сжимались примерно до 30 фс
после прохождения через пару решеток. Параметры световода и па-
параметры импульса были таковы, что N ~ 3 и z/z0 = 1,5. Из рис. 6.4
ожидается коэффициент сжатия порядка 3. Данный эксперимент
привел к серии рекордных результатов [16-19], в которых длитель-
длительность импульса была сокращена до примерно 8 фс, что соответство-
соответствовало примерно четырем оптическим периодам. В экспериментах по
получению 8-фемтосекундных импульсов [19] 40-фемтосекундные
импульсы на 620 нм с пиковой мощностью ~ 1012 Вт/см2 проходили
через световод длиной 7 мм и затем сжимались до 8 фс на паре
решеток. На рис. 6.5 показана автокорреляционная функция сжатых
импульсов. Соответствующий спектр показан на рис. 4.18 (самый
верхний рисунок). Ширина спектра была примерно 70 нм, что ука-
указывает на то, что при идеальных условиях можно получить спек-
-20 О 20
Бремя (срс)
Рис. 6.5. Измеренная автокорреляционная функция импульса, сжатого при
помощи волоконно-решеточного компрессора (длительность начального
импульса составляла 40 фс). 12-фемтосекундная ширина АКФ соответствует
8-фемтосекундной длительности импульса в предположении, что начальный
импульс имеет форму гиперболического секанса [19].
Сжатие оптических импульсов
161
трально-ограниченные импульсы длительностью 6 фс. Оказывается,
что наиболее важным фактором, ограничивающим компрессию, яв-
является кубичное искажение фазы, возникающее из последнего члена
в разложении F.2.4). В более позднем эксперименте [20] кубическая
фаза пары решеток была скомпенсирована за счет использования
последовательности призм, и импульс был действительно сжат до
6 фс. Такой импульс на 620 нм состоит только из трех оптических
периодов; в настоящее время это рекордно короткая длительность
импульса света!
Целью других экспериментов было достижение максимального
коэффициента сжатия. Коэффициент сжатия 12 был достигнут в экс-
эксперименте [15], где 5,4-пикосекундные начальные импульсы лазера на
красителе сжимались до 0,45 пс; при этом использовался световод
длиной 30 м. Большее значение коэффициента сжатия 65 было полу-
получено в двухкаскадной схеме компрессии, где импульсы последова-
последовательно сжимались в двух волоконно-решеточных компрессорах. В
другом эксперименте [21] было осуществлено сжатие 33-пикосекунд-
ных импульсов второй гармоники Nd: YAG-лазера на 532 нм в од-
нокаскадной схеме: получен коэффициент сжатия 80. Данные импуль-
импульсы проходили через световод длиной 105 м, за ним следовала пара
решеток (оптимальное расстояние между ними Ьо = 7,24 м); в резуль-
результате сжатые импульсы имели длительность 0,41 пс. В этом экспери-
эксперименте использовалась двухпроходная схема сжатия (см. рис. 6.2);
сейчас она общепринята. На рис. 6.6 показан сжатый импульс в срав-
сравнении с начальным. Соответствующие спектры аналогичны изобра-
изображенным на рис. 4.12. Входная пиковая мощность 240 Вт соответст-
33 пс
-40
-20
О
Бремя (пс)
40
"ис. 6.6. Измеренные автокорреляционные функции исходного и сжатого
импульсов; коэффициент сжатия на одной стадии составляет значение 80 [21]
162 Глава 6
вует N ~ 145. Из формулы F.3.7) следует коэффициент сжатия 90. что
находится в разумнбм согласии с экспериментальным значением 80.
Хотя в принципе возможны большие значения коэффициента сжатия,
на практике нельзя сильно увеличивать пиковую мощность, посколь-
поскольку возникает ВКР.
Эксперименты, описанные выше, были осуществлены в видимой
области спектра. Метод волоконно-решеточного сжатия получил
распространение и в ближнюю инфракрасную область спектра, где
были получены сверхкороткие импульсы на длинах волн 1,06 и
1,32 мкм [22—34]. Генерация исходных импульсов на этих длинах
волн обычно осуществляется Nd: YAG-лазером в режиме синхрони-
синхронизации мод, при этом типичные значения длительности составляют
100 пс. В результате дисперсионная длина или параметр z0 относи-
относительно велики (~ 100 км). Из формулы F.3.5) следует, что даже для
значений N ~ 100 оптимальная длина световода превышает 1 км
Оптимальное расстояние между решетками так же относительно
велико (Ьо > 1 м), как это видно из F.2.5) и F.3.6).
'В первом эксперименте на длине волны 1,06 мкм [22] 60-пикосе-
кундные импульсы были сжаты в 15 раз после прохождения 10-мет-
10-метрового световода и пары решеток (b0 ~ 2,5 м). В другом эксперименте
[23] был достигнут коэффициент сжатия 45; использовались световод
длиной 300 м и компактная дисперсионная линия задержки из пары
решеток. Обычно в сжатых импульсах на 1,06 мкм значительная доля
энергии переносится в несжатых «крыльях» импульса, поскольку для
уменьшения оптических потерь обычно используют меньшие длины
световодов, чем те, которые предписаны уравнением F.3.5). Когда
дисперсионные эффекты не проявляются до конца, только централь-
центральная часть импульса имеет линейную частотную модуляцию и энергия
в «крыльях» остается несжатой. Для устранения этих «крыльев»
применяется метод спектральной фильтрации [24]. При этом исполь-
используется тот факт, что «крылья» содержат спектральные компоненты
крайних частот спектра импульса; их можно устранить, помещая
диафрагму (или фильтр) рядом с зеркалом М, на рис. 6.2. На рис. 6.7
сравниваются автокорреляционные функции сжатых импульсов, по-
полученные со спектральной фильтрацией и без нее [64]. Начальные
75-пикосекундные импульсы были сжаты до ~ 0,8 пс в обычном
волоконно-решеточном компрессоре; при этом коэффициент сжатия
был более 90. При использовании метода спектральной фильтрации
«крылья» в сжатом импульсе были устранены, при этом длительность
импульса увеличилась лишь до 0,9 пс. Данный метод был исполь-
использован для генерации импульсов заданной фопмы за счет использо-
использования специального амплитудно-фазового экрана вместо обычной
диафрагмы [63-65]. Кроме того, для этих целей можно также
использовать [66] модуляцию по времени импульсов с частотной
модуляцией сразу на выходе из световода (до прохождения пары
Сжатие оптических импульсов
163
О
Время (пс)
Рис. 6.7. Измеренные автокорреляционные функции сжатых импульсов при
наличии (штриховая кривая) и при отсутствии (сплошная линия) спектральной
фильтрации. За счет спектральной фильтрации устраняются «крылья», в то
время как длительность импульса возрастает лишь до 0,9 пс [64].
решеток), с помощью таких методов волоконно-решеточный ком-
компрессор можно преобразовать в многопрофильное устройство, ко-
которое можно использовать для формирования импульсов заданной
формы. Энергию в «крыльях» импульса можно также уменьшить,
используя эффект нелинейного двулучепреломления, в котором све-
световод действует как нелинейный дискриминатор [68].
Трудно получить коэффициенты сжатия более 100 для импульсов
на длине волны 1,06 мкм, это обусловлено возникновением ВКР.
В эксперименте [33] был достигнут коэффициент сжатия 110; 60-пико-
секундные импульсы при этом распространялись в 880-метровом
световоде. Можно достичь даже больших значений степени сжатия,
используя последовательность из двух волоконно-решеточных ком-
компрессоров [26, 31]. В эксперименте [31] 90-пикосекундные импульсы
были сжаты до 0,2 пс; при этом общий коэффициент сжатия состав-
составлял 450. В то же время пиковая мощность возросла с 480 Вт до 8 кВт.
Каждый из компрессоров давал коэффициент сжатия 21. Необходимо
упомянуть, что, хотя после первого компрессора в «крыльях» им-
импульса была сосредоточена значительная доля энергии, импульсы
после второго компрессора имели высокую контрастность. Причина
заключалась в том, что импульсы имели различную начальную
Длительность. 4,2-пикосекун шые импульсы, вводимые во второй
компрессор, достаточно коротки, и дисперсия способна линеаризо-
164 Глава 6
вать частотную модуляцию вдоль всего импульса. Результаты экс-
эксперимента находятся в хорошем согласии с теорией.
Метод волоконно-решеточного сжатия был распространен на
1,32 мкм, длину волны, на которой Nd: YAG-лазер с синхронизацией
мод способен генерировать мощные импульсы примерно 100-пико-
секундной длительности [27, 30]. Тем не менее, так как обычные
кварцевые световоды имеют положительную дисперсию только при
X < 1.3 мкм. необходимо использовать световоды со смещенной дис-
дисперсией (см. разд. 1.2) с длиной волны нулевой дисперсии вблизи
1,55 мкм. Оптимальная длина световода в формуле F.3.5) обычно
превышает 2 км. Тем не менее из-за малых потерь в световоде на
1,32 мкм (~ 0,4 дБ/км) данная величина не накладывает ограничений
на длину световода. В эксперименте [30] был реализован коэффици-
коэффициент сжатия 50; 100-пикосекундные импульсы сначала распространя-
распространялись через 2-километровый световод со смещенной дисперсией (нуле-
(нулевая дисперсия на 1,59 мкм). Для того чтобы уменьшить расстояние
между решетками до разумных величин, длина световода была
выбрана меньше оптимальной (ropl ~ 3,3 км). Уравнение F.3.7) пред-
предсказывает коэффициент сжатия 80, если длина световода и расстояние
между решетками являются оптимальными (N ~ 130 для параметров
эксперимента).
Использование длины волны 1,32 мкм имеет то преимущество,
что пару решеток можно заменить отрезком световода, так что
возможно реализовать полностью волоконный компрессор [27]. Два
световода с положительным и отрицательным коэффициентами дис-
дисперсии р, свариваются вместе и образуют компрессор. Световод
с положительным |32 создает линейную частотную модуляцию, в то
время как световод с отрицательным р2 сжимает этот импульс.
Необходимо оптимизировать длину обоих световодов согласно урав-
уравнениям F.3.5) и F.3.6). Параметр at заменяется на — p2L2/2 согласно
F.2.9). где L2 оптимальная длина второго световода с отрицатель-
отрицательным р2. При экспериментальном осуществлении этой концепции [27]
130-пикосекундные имп>льсы были сжаты до ~ 50 пс; использовался
2-километровый световод с р2 ~ 18,4 пс2/км и 8-километровый свето-
световод с р2 — — 4,6пс2'км. В экспериментах [36 38] использовался
метод двухкаскадного сжатия, в котором за волоконно-решеточным
компрессором следует световод с о грицательной дисперсией; получен
общий коэффициент сжатия 5000. В этих экспериментах сокращение
длительности импульса во втором каскаде происходило из-за эффек-
эффекта многосолитонного сжатия; данный вопрос рассматривается в сле-
следующем разделе.
Сжатие оптических импульсов 165
6.4. КОМПРЕССОРЫ, ОСНОВАННЫЕ
НА ЭФФЕКТЕ МНОГОСОЛИТОННОГО СЖАТИЯ
Когда импульсы с длиной волны более 1,3 мкм распространяются
в световодах, изготовленных из кварцевого стекла, на их динамику
обычно оказывают влияние ФСМ и отрицательная дисперсия. Такой
световод может сам действовать как компрессор; при этом исчезает
необходимость в паре решеток. Механизм компрессии связан с фун-
фундаментальным свойством солитонов высших порядков. Как показано
в разд. 5.2, эти солитоны имеют периодичную картину эволюции, при
этом в начале каждого периода происходит сжатие (см. рис. 5.4).
Соответствующим выбором длины световода можно сжать началь-
начальные импульсы; коэффициент сжатия при этом зависит от порядка
соли гона Лг. Такой компрессор называется компрессором, основан-
основанным на эффекте многосолитонного сжатия (или просто солитонным
компрессором), чтобы подчеркнуть роль солитонов. В данном раз-
разделе изложены теория и экспериментальные результаты, полученные
при использовании солитонных компрессоров.
6.4.1. ТЕОРИЯ
Если для простоты пренебречь потерями в световоде, то динамика
солитона порядка Лг описывается уравнением E.2.2). Пренебрежение
потерями оправдано тем, что рабочие длины световодов обычно
составляют малую долю длины поглощения (aL« 1). Вводя период
солитона г0 из уравнения F.3.2) и используя условие р2 < 0, можно
привести уравнение E.2.2) к виду
2 8U \i2U 7
/-——--—+ ЛГ2|1/|21/ = 0, F.4.1)
пс(ф0) 2 гт2
где параметр ./V определен в F.3.3). Хотя солитоны высших порядков
имеют периодичное поведение лишь при целых значениях N. для того
чтобы описать динамику импульса, можно решать уравнение F.4.1)
при любых значениях N. Вобщем случае исходный импульс испы-
испытывает сжатие на начальном этапе распространения при всех значе-
значениях Лг > 1. Оптимальная длина световода гор1 соответствует точке,
в которой длительность центрального пика минимальна. Коэффици-
Коэффициент сжатия есть отношение длительностей исходного и сжатого
импульсов.
Чтобы найти коэффициент сжатия Fc и оптимальную длину
световода гор1 как функции N. использовались численные методы [34].
Чтобы получить данные величины при целых N, можно использовать
метод ОЗР. На рис. 6.8 показаны зависимости F~l и 2ор1/г0 от ./V для
величин N в диапазоне 1 15. На рисунке также изображен параметр
качества Qc, определенный как доля энергии начального импульса.
166
Глава 6
-1,0,03
- 0,01
0,03 -
0,01
3 ' 5 7 9 11
Порядок солитона N
Рис. 6.8. Зависимость коэффициента сжатия Fc, оптимальной длины свето-
световода гопт и параметра качества Qc от параметра N. Светлые кружки соот-
соответствуют целым значениям N. Данные соответствуют экспериментам, вы-
выполненным с 320-метровым (крестики) и 100-метровым (темный кружок)
световодами [34].
сосредоточенная в сжатом пике. В противоположность волоконно-
решеточному компрессору, Qc здесь значительно меньше, чем идеаль-
идеальная величина 1, и монотонно уменьшается с ростом N. Данный
недостаток присущ солитонным компрессорам. Оставшаяся доля
энергии оказывается в . крыльях» импульса в форме широкого пье-
пьедестала вокруг сжатого пика. Можно следующим .образом пояснить
происхождение такого пьедестала. В начальной стадии многосоли-
тонного сжатия доминирующее воздействие оказывает ФСМ. По-
Поскольку частотная модуляция, вызванная ФСМ, линейна только
в центральной части импульса, только центральная область его
сжимается за счет отрицательной дисперсии. Энергия в «крыльях»
импульса остается несжатой и проявляется в виде широкого пье-
пьедестала.
Результаты рис. 6.8 и численное моделирование до N = 50 пока-
показывают, что коэффициент сжатия Fc и оптимальная длина световода
для солитонного компрессора хорошо аппроксимируются эмпири-
эмпирическими соотношениями [43]
FC~4,1N, F.4.2)
Сжатие оптических импульсов
167
-ор|
0,32 1,1
N N2
F.4.3)
Данные зависимости справедливы с точностью до нескольких про-
процентов при N > 10 и могут служить простыми правилами, анало-
аналогичными уравнениям F.3.5)-F.3.7) для волоконно-решеточных ком-
компрессоров. Непосредственное сравнение показывает, что при одних
и тех же значениях N и z0 солитонный компрессор дает коэффициент
сжатия в 6,5 раз больше; при этом длина световода короче в 5 раз.
При этом, однако, качество сжатого импульса ниже, так как в нем
находится лишь доля начальной шергии. Оставшаяся энергия со-
содержится в широком пьедестале.
6.4.2. ЭКСПЕРИМЕНТЫ
В первом эксперименте [34] 7-пикосекундные исходные импульсы
от лазера на центрах окраски с синхронизацией мод, работающего
вблизи 1,5 мкм, распространялись через 320-метровый световод
(-/-о ^ 0,25). Когда пиковая мощность начальных импульсов пре-
превышала 1,2 Вт (уровень мощности, соответствующий фундаменталь-
фундаментальному солитону), выходные импульсы становились короче начальных
на величину, которая возрастала при увеличении N. Наблюдаемые
значения коэффициента сжатия показаны на рис. 6.8 (крестики) для
трех значений N. Коэффициент сжатия был близок к теоретическому
Без подавления
17- ¦
100-метровый
световод
При самом эффектив-
эффективном подавлении
О
Время (пс)
Рис. 6.9. Автокорреляционная функция импульса, сжатого до 0,26 пс (дли-
(длительность исходного импульса составляла 7 пс); использовался эффект мно-
госолитонного сжатия. Штриховая и сплошная кривые даны для сравнения
пьедестала при наличии и при отсутствии нелинейного двулучепреломлсния
[34].
168 Глава 6
(~ 8) при N = 3, но становился существенно меньше теоретического
при больших значениях N. Это можно понять, вспомнив, что длина
световода 320 м близка к оптимальной при N = 3, но становится
слишком большой при больших значениях N. Действительно, умень-
уменьшив длину световода до 100 м (z/z0 ^ 0,077), коэффициент сжатия
увеличили до 27 при N = 13. Автокорреляционная функция 0,26-пико-
секундного сжатого импульса показана на рис. 6.9.
Оказалось, что при наилучших условиях эксперимента можно
подавить широкий пьедестал, характерный для сжатого импульса.
Такое подавление приписано нелинейному двулучепреломлению све-
световода, которое заставляет его работать в качестве нелинейного
дискриминатора [68, 69].
Данный механизм в принципе может полностью устранить пье-
пьедестал [68]. Можно также устранить пьедестал, отфильтровав низко-
низкочастотные компоненты сжатого импульса, которые и связаны с пье-
пьедесталом. Численные расчеты показывают [70], что полоса про-
пропускания Av^- такого фильтра связана с параметром N и длитель-
длительностью начального импульса TFViHM соотношением
F.4.4)
где численный коэффициент несущественно зависит от формы на-
начального импульса.
Солитонные компрессоры можно использовать для получения
очень больших коэффициентов сжатия. В эксперименте [35] был
продемонстрирован коэффициент сжатия ПО, когда 30-пикосекунд-
ные импульсы от параметрического генератора света (длина волны
генерации около 1,6 мкм) были сжаты до 275 фс при распространении
через световод длиной 250 м. Длина световода была близка к опти-
оптимальной, если предположить N ~ 28 (соответствует пиковой мощно-
мощности 0,6 кВт) и учесть, что z0 ~ 20 км для 30-пикосекундных начальных
импульсов. Наблюдаемое сжатие также находится в близком со-
согласии с F.4.2).
В экспериментах [36-38] были получены коэффициенты сжатия
~ 1000; при этом использовалось сжатие в две стадии, когда за
волоконно-решеточным компрессором следовал солитонный ком-
компрессор. В этих экспериментах использовались 100-пикосекундные
импульсы Nd: YAG-лазера с синхронизацией мод, работающего на
длине волны 1,32 мкм. На первой стадии использовался волоконно-
решеточный компрессор; здесь получены импульсы длительности
порядка 1-2 пс. Затем эти импульсы направлялись в солитонный
компрессор; длина световода при этом была тщательно подобрана,
что позволило получить коэффициент сжатия порядка 50. В экспе-
эксперименте [38] исходные 90-пикосекундные импульсы были сжаты до
18 фс (содержат только четыре оптических периода) при компрессии
в две стадии, общий коэффициент сжатия составлял 5000. На рис. 6.10
Сжатие оптических импульсов
169
-18фс
К-
-2пс
1,4 1,3
Длина волны (мкм)
1,2
Рис. 6.10. Автокорреляционная функция и спектр 18-фемтосекундного им-
импульса, полученного при сжатии начального 90-пикосекундного импульса
в две стадии [38]
показаны автокорреляционная функция и спектр 18-фемтосекундного
импульса. Узкий центральный пик в спектре соответствует пьедесталу
в автокорреляционной функции; в нем содержится 69% всей энергии.
Оказалось, что в экспериментах по получению фемтосекундных
импульсов [37, 38] оптимальная длина световода более чем в 2,5 раза
превышает предсказанную соотношением F.4.3). Это неудивительно,
поскольку соотношение F.4.3) основано на численном решении урав-
уравнения F.4.1), где пренебрегается дисперсионными и нелинейными
эффектами высших порядков, что недопустимо при импульсах короче
100 фс. Чтобы точно определить оптимальную длину световода,
следует использовать уравнение E.5.1), где учтены эффекты кубичной
•щсперсии, дисперсии нелинейности и задержки нелинейного отклика
в волоконных световодах. Как было показано в разд. 5.5, решающий
вклад вносится задержкой нелинейного отклика (член, пропорцио-
пропорциональный времени отклика TR). Данный эффект проявляется в виде
сдвига спектра импульса в длинноволновую область (см. рис. 5.20).
С длинноволновым сдвигом связана задержка оптического импульса.
Такая задержка существенно влияет на взаимодействие между дис-
дисперсией и ФСМ (что определяет сжатие импульса). Численные рас-
расчеты действительно показывают, что оптимальная длина световода
больше, чем предсказано уравнением F.4.1).
В заключение отметим, что методы компрессии оптических им-
импульсов представляют прекрасную иллюстрацию того, как можно
практически использовать нелинейные явления в волоконных свето-
световодах. Это имеет и огромную практическую значимость. Данные
методы позволяют получать импульсы длительностью лишь в не-
несколько оптических периодов как в видимой, так и в ближней
инфракрасной областях спектра. Такие фемтосекундные импульсы
могут быть полезны для исследования сверхбыстрых процессов в
170 Глава 6
атомах, молекулах и кристаллах. С практической точки зрения
волоконно-решеточные компрессоры разработаны настолько хоро-
хорошо, что производятся в промышленных условиях.
ЛИТЕРАТУРА
1. Klauder J.R. et al.. Bell. Syst. Tech. J., 39, 745 A960).
2. Gires F., Tournois P., Compt. Rend. Acad. Sci., 258 6112 A964).
3. Giordmaine J.A.. Duguav M.A., Hansen J.W., IEEE J. Quantum Electron.,
QE-4, 252 A968).
4. Treacv E.B.. Phys. Lett., A28, 34 A968).
5. Duguav M.A., Hansen J. W., Appl. Phys. Lett., 14, 14 A969).
6. Laubereau A., Phys. Lett., A29, 539 A969).
7. Treacy E.B.. IEEE J. Quantum Electron., QE-5, 454 A969).
8. Laubereau A., von der Linde D.. Z. Naturforsch., A25. 1626 A970).
9. Grischkowsky D., Appl. Phys. Lett., 25, 566 A974).
10. Wigmore J. K., Grischkowsky D., IEEE J. Quantum Electron., QE-14, 310 A978).
11. Fisher R.A.. Kelley P.L., Gustqfson Т.К.. Appl. Phys. Lett., 14, 140 A969).
12. Зельдович Б. Я., Собелъмап И. И-Письма в ЖЭТФ, 1971, т. 13, с. 182.
13. Nakatsuka Н.. Grischkowskv D., Balcmt A.C., Phys. Rev. Lett., 47, 910 A981).
14. Shank С V. et al, Appl. Phys. Lett., 40, 761 A982).
15. Nikolaus В.. Grischkowsky D., Appl. Phys. lett., 42, I A983); Appl. Phys. Lett., 43,
228 A983).
16. FujimotoJ.G., Weiner A.M., Ippen К P., Appl. Phys. Lett., 44, 832 A984):
17. Halbout J.-M., Grischkowsky d., Appl. Phys. Lett., 45, 1281 A984).
18. Palfrey S.L., Grischkowsky D., Opt. Lett., 10, 562 A985).
19. Knox W.H. et al, Appl. Phys. Lett., 46, 1120 A985).
20. Fork R.L. et a!.. Opt. Lett., 12, 483 A987).
21. Johnson A.M.. Stolen R.H., Simpson W.M., Appl. Phys. Lett., 44, 729 A984).
22. Диаиов Е.М. и dp. Квант, электрон., 1984, т. 11, с. 1078.
23. Kafka J.D. et al.. Opt. Lett., 9, 505 A984).
24. Heritage J.P. et al., Appl. Phys. Lett., 47, 87 A985).
25. Damm T. et al. Opt. Lett., 10, 176 A985).
26. Gomes A.S.L., Sibbett W., Taylor J.R.. Opt. Lett., 10, 338 A985).
27. Blow K.J.. Doran N.J.. Nelson B.P., Opt. Lett., 10, 393 A985).
28. Gomes A.S.L. et al. Opt. Commun., 53, 377 A985).
29. Strickland В.. Mourou G.. Opt. Commun., 55, 447 A985).
30. Tui K., Tomita A., Appl. Phys. Lett., 48, 309 A986).
31. Zvssct B. et al. Opt. Lett., 11, 156 A986).
32. Valk В.. Vilhelmsson K., Salour M.M., Appl. Phys. Lett., 50, 656 A987).
33. Диаиов Е.М. и др.-Квант, электрон., 1987, т. 14, с. 662.
34. Mollenauer L.F. et al. Opt. Lett., 8, 289 A983).
35. Диаиов Е.М. и Эр.-Письма в ЖЭТФ, 1984, т. 40, с. 148.
36. Tai К., Tomita A.. Appl. Phys. Lett., 48, 1033 A986).
37. Gouveia-Neto A.S., Gomes A.S.L.. Taylor J.R.. Opt. Lett., 12, 395 A987).
38. Gouveia-Neto A.S., Gomes A.S.L., Taylor J.R., J. Mod. Opt., 35, 7 A988).
39. Grischkowsky D.. Balant A.C., Appl. Phys. Lett., 41, 1 A982).
40. Meinel R.. Opt. Commun., 47, 343 A983).
41. Tomlinson W.J.. Stolen R.H., Shank С V.. J. Opt. Soc. Am., Bl, 139 A984).
42. Выслоух В. А. и Эр. Изв. АН СССР, сер. физ., 1985, т. 49 C), с. 573.
43. Дианов Е.М. и Эр.-Письма в ЖТФ, 1986, т. 12, с. 756.
44. Ахмапов С. А., Выслоух В. А., Чиркин А. С. УФН, 1986, т. 149. с. 449.
45. Выслоух В. А., Мурадян Л. А".-Квант, электрон., 1987, т. 14, с. 1437.
46. Tomlinson W.J., Knox W.H., J. Opt. Soc. Am., B4, 1404 A987).
47. Mestdagh D., Appl. Opt., 26, 5234 A987).
Сжатие оптических импульсов 171
48. McMullen J.M.. Appl. Opt., 18, 737 A979).
49. Cristov J.P.. Tomov I. V., Opt. Commun., 58, 338 A986).
50. Brorson S.D., Haus H.A., Appl. Opt., 27, 23 A988).
51. Brorson S.D., Haus H.A., J. Opt. Soc. Am., B5. 247 A988).
52. Debois J., Gires F., Tournois P., IEEE J. Quantum Electron., QE-9, 213 A973).
53. Martinez O.E., Gordon G.P., Fork R.L., J. Opt. Soc. Am., Al, 1003 A984).
54. Kafka J.D., Baer T, Opt. Lett., 12, 401 A987).
55. Nakazawa M. et al. J. Opt. Soc. Am., B5, 215 A988). *
56. Пожар В.Е., Пуаповошп В. И. Квант, электрон., 1987, т. 14, с. 811.
57. Winful H.G., Appl. Phys. Lett., 46, 527 A985).
58. Kubota H, Nakazawa M., Opt. Commun. 66, 79 A988).
59. Nakashima T. et al.. Opt. Lett., 12, 404 A987).
60. Weiner A.M., Heristage J.P.. Stolen R.H.. J. Opt. Soc. Am., B5, 364 A988).
61. Gomes A.S. L.. Gouveia-Neto A.S., Taylor J. R., Opt. Quantum Ecectron., 20, 95
A988).
62. Kuckartz M., Schulz R., Harde H.. J. Opt. Soc. Am., B5, 1353 A988).
63. Heritage J.P., Weiner A.M., Thurston R.N.. Opt. Lett., 10, 609 A985).
64. Weiner A.M., Heritage J.P., Thurston R.N., Opt. Lett., 11, 153 A986).
65. Thurston R.N. et al.. IEEE J. Quantum Electron., QE-22, 682 A986).
66. Haner M., Warren W.S., Appl. Phys. Lett., 52, 1458 A988).
67. Halas N.J., Grischkowsky D.. Appl. Phys. Lett., 48, 823 A986).
68. Stolen R.H.. Botineau J., Ashkin A., Opt. Lett., 7, 512 A982).
69. Nikolaus В., Grischkowsky D., Balant A.C., Opt. Lett., 8, 189 A983).
70. Дианов Е.М. и Эр.-Письма в ЖТФ, 1986, т. 12, с. 752.
Глава 7
ФАЗОВАЯ КРОСС-МОДУЛЯЦИЯ (ФКМ)
Когда две и более оптические волны вместе распространяются по
световоду, из-за нелинейности световода они могут взаимодейство-
взаимодействовать друг с другом. Вообще, в результате этого за счет таких
эффектов, как вынужденное комбинационное рассеяние, вынужденное
рассеяние Мандельштама Бриллюэна, генерация гармоник, четырех-
волновое смешение, при определенных условиях могут возникать
новые волны; все эти процессы рассматриваются в гл. 8-10. В то же
время нелинейность световода вызывает взаимодействие между
распространяющимися волнами за счет эффекта, называемого фа-
фазовой кросс-модуляцией (ФКМ). ФКМ всегда сопровождается фа-
фазовой самомодуляцией (ФСМ) и возникает из-за того, что эффектив-
эффективный показатель преломления какой-либо волны зависит не только от
интенсивности самой этой волны, но и от интенсивности других волн,
распространяющихся с ней совместно [1, 2].
Взаимодействие оптических волн в световоде за счет ФКМ при-
приводит к интересным нелинейным эффектам. В разд. 7.1 рассматри-
рассматривается подобная связь между двумя волнами с одинаковыми поля-
поляризациями, но с разными частотами, а также между волнами с одной
и той же частотой, но с различными состояниями поляризации.
В последнем случае нелинейное двулучепреломление за счет ФКМ
находит свое практическое применение в керровских затворах и
нелинейных дискриминаторах. В то же время оно является причи-
причиной поляризационной неустойчивости. Это явление рассмотрено
в разд. 7.2. В разд. 7.3 рассматривается модуляционная неустойчи-
неустойчивость, вызванная ФКМ; примечательно, что она может возникать
даже в области положительной дисперсии световода. В разд. 7.4
рассматривается влияние ФКМ на форму и спектр попутно рас-
распространяющихся сверхкоротких импульсов. В разд. 7.5 рассмотрены
взаимодействие встречно распространяющихся волн за счет ФКМ,
а также его воздействие на работу лазерных гироскопов. В разд. 7.6
рассказано о значении ФКМ для систем волоконной связи.
Фазовая кросс-модуляция 173
7.1. НЕЛИНЕЙНОЕ ВЗАИМОДЕЙСТВИЕ,
ОБУСЛОВЛЕННОЕ ФКМ
В данном разделе развита теория из разд. 2.3 применительно
к случаю двух оптических импульсов, распространяющихся вместе
в одномодовом световоде. Будет рассмотрено происхождение ФКМ.
В общем случае два оптических поля могут отличаться не только
своими длинами волн, но и состояниями поляризации. Далее,
поляризация каждого поля может при распространении изменяться
в результате оптически индуцированного нелинейного двулучепре-
ломления. Такие самоиндуцированные поляризационные эффекты
наблюдались еще в 1964 г. [3, 4], и с тех пор они широко исследуются
применительно к оптическому эффекту Керра [5 11]. В данном
разделе оба случая рассмотрены отдельно. Сначала мы рассмотрим
случай, когда две оптические волны с разными длинами волн линейно
поляризованы вдоль одной из главных осей световода, поддержи-
поддерживающего поляризацию, так что они могут сохранять свою поля-
поляризацию при распространении. Ниже рассмотрена связь между ком-
компонентами вектора поляризации одной и той же оптической волны,
вызванная ФКМ; при этом учитывается действие как собственного
межмодового двулучепреломления, так и оптически индуцированного
нелинейного двулучепреломления.
7.1.1. ВЗАИМОДЕЙСТВИЕ ВОЛН,
ИМЕЮЩИХ РАЗЛИЧНЫЕ ЧАСТОТЫ
В квазимонохроматнческом приближении полезно отделить быст-
быстроменяющуюся часть вектора электрического поля, записав его
в виде
F. (г, /) = - д- [?¦, ехр (— /со, I) + ?2ехр I — /со,/)] + компл. сопр., G.1.1)
1де л единичный вектор п тяризации, coL и из2 несущие частоты
iBjx импульсов; предполагается, чго соответствующие амплитуды Е1
и Е2 являются медленно меняющимися функциями времени в
масштабе времени со," l (J' -- 1 или 2). Данное предположение экви-
эквивалентно предположению ^соукшу. где Асоу- ширина спектра: это
справедливо для импульив длительностью 5= 0,1 пс. Динамика
медленно меняющихся амалитуд Е1 и Е2 определяется волновым
уравнением B.3.1) с линейной и нелинейной поляризациями, опре-
определяемыми B.3.5) и B.3.6).
Для того чтобы понять причину ФКМ, подставим уравнение
G.1.1) в B.3.6); в результате получим
PNL(r, i) = -x{PNl,(ы,)ехр(-/ы1/) + PVL(co,)exp(-;co2/) +
174
Глава 7
ZPcOi - co2)/] +
+ PNtBco2 — со^ехрЦ —/Bco2 — cot)/]} + компл. сопр.,
G.1.2)
где
12 + 21 ?t |
Bco2 - cot) = Хэфф ?2 ?*
или
G.1.3)
G.1.4)
G.1.5)
G.1.6)
G-1.7)
Явная зависимость тензора %^хх от частоты не показана, по-
поскольку его дисперсией мы пренебрегли.
Индуцированная нелинейная поляризация в G.1.2) имеет члены,
осциллирующие с новыми частотами 2cot — со2 и 2со2 — coL. Эти члены
возникают из-за четырехволнового смешения, что будет рассмотрено
в гл. 10. Для эффективной генерации новых частотных компонент
необходимо удовлетворить условию фазового синхронизма, чего на
практике обычно не происходит, если не принять специальных мер.
Предполагая, что фазовый синхронизм отсутствует, мы пренебрежем
в данной главе четырехволновым смешением. Оставшихся два члена
создают вклад в показатель преломления. Определить его можно,
записав Pnl(<uj) в виде (/= 1,2)
PNLl<Oj) = Вое?1-Ej G.1.8)
и комбинируя ее с линейной частью так, что полная поляризация
записывается в виде
P(aj) = e&jEJ, G.1.9)
где
- ?/ = ?;+ EjL = (nj + Аи;J, G.1.10)
Иу- линейная часть показателя преломления и Аиу-его изменение,
вызванное нелинейными эффектами третьего порядка. При условии
A«y« «у нелинейная часть показателя преломления определяется как
А«у ~ ef /2лу * n2(\Ej\2 + 2\E3_j\2), G.1.11)
где нелинейный коэффициент показателя преломления
= -~x%L; G-1-12)
здесь предполагается, что показатели преломления сердцевины
Фазовая кросс-модуляция 175
и оболочки световода практически совпадают и равны п. Параметр п2
тот же самый, что и в B.3.13).
Формула G.1.11) показывает, что показатель преломления оп-
оптической волны зависит не только от интенсивности самой волны, но
также и от интенсивности других волн, распространяющихся вместе
с данной. Так как волна распространяется по световоду, она
приобретает зависящую от интенсивности нелинейную фазу
G-1.13)
где j — 1 или 2. Первое слагаемое отвечает за ФСМ (см. гл. 4). Второе
возникает из-за фазовой модуляции одной волны другой волной,
распространяющейся вместе с ней, и отвечает за ФКМ. Коэффициент
2 в правой части G.1.13) показывает, что ФКМ в 2 раза эффективнее
ФСМ при той же интенсивности [2]. Причину этого можно просле-
проследить по числу слагаемых, которые приводят к утроенной сумме,
означающей в B.3.6) нелинейную поляризацию. Грубо говоря, когда
оптические частоты двух волн различны, число слагаемых удваивает-
удваивается по сравнению с вырожденным случаем.
Можно получить уравнение распространения для двух оптических
волн, следуя методу из разд. 2.3. Предполагая, что нелинейные
эффекты существенно не воздействуют на модовое распределение,
можно выделить поперечную зависимость, записав ?}(г, /) в виде
Ej(r, t) = Fj(x, y)Aj{z, /)exp(/p0/z), G.1.14)
где Fj(x, у) - модовое распределение для j-то поля (_/= 1,2), Aj(z, i)—
медленно меняющаяся амплитуда, pOj-соответствующая постоянная
распространения на частоте coy. Дисперсионные эффекты учитывают
при разложении частотно-зависимой постоянной распространения
Р;(со) для каждой волны таким же образом, как и в B.3.23), но
ограничиваются только квадратичными членами.
При этом возникает уравнение распространения для Aj(z,t)
ёА; дА, i д2А-, а, ш,со.- , , \
f + ^^ + iA ^1^1 + 2fW)Ai-GЛЛ5)
где к Ф j, filj=l/vgj, ги--групповая скорость, р2;~диспеРСИОННЬ1й
коэффициент, ау-коэффициент затухания. Интеграл перекрытия
fJk определяется (j, к = 1 или 2)
j? \Fj(x,y)\2\Fk{x.y)\2dxdy
Д= „ "°° z • <7ЛЛ6>
(И \Fiix,y)\2dxd?)(l J \Fk(x,y)\2dxdy)
176 ' Глава 7
Разница между интегралами перекрытия может быть значитель-
значительной в многомодовом световоде, где две волны могут распростра-
распространяться в разных модах. В случае одномодового световода flu
/22 и /12 обычно отличаются друг от друга из-за частотной за-
зависимости распределения моды Fj(x, у). Однако эта разница мала,
и на практике ею можно пренебречь. В этом случае уравнение G.1.15)
может быть записано в виде системы связанных уравнений
дА, 1 ЗА. i д2А. а.
-^- + —~ + ~P21-^ + jAl = iyl(\Al\2
G.1.17)
г + Р22^ + ~Л2 = П2(\А2\2 + 2\АУ\2)А
ci 2 дг
ёА7 1 дА7 i д2А7 а, , ,
^Г + г1 + -Р^ + ~Л2 = П2(\А2\2 + 2\АУ\2)А
2
ё: vg2
G.1.18)
где нелинейный коэффициент 7; введен аналогично B.3.28), именно
и, со.-
7; = -у^ G=U), G.1.19)
и предполагается, что эффективная площадь сердцевины АУфф(А3фф =
= 1//и) для обеих волн одинакова. В видимом диапазоне обычно
,4Эфф = 10- 2) мкм2. Соответствующие значения 7i и 72 лежат в об-
области 20-30 Вт ¦ км~1 в зависимости от частот а1 и со2. Обычно два
импульса не только имеют разные коэффициенты дисперсии, но
и скорости их распространения не совпадают из-за разницы в
групповых скоростях. Неравенство групповых скоростей играет
важную роль, поскольку оно ограничивает взаимодействие при ФКМ,
так как импульсы «разбегаются». Используя A.2.14), можно опре-
определить длину разбегания Lw; это длина световода, на которой два
первоначально совпадающих по времени импульса разделяются
полностью из-за разницы в групповых скоростях.
7.1.2. СВЯЗЬ МЕЖДУ КОМПОНЕНТАМИ ВЕКТОРА
ПОЛЯРИЗАЦИИ ОДНОЙ ВОЛНЫ
Электрическое поле эллиптически поляризованной волны может
быть записано в виде
Е(г, /) = -{.\ЕХ + vЕ )ехр(— /со0/) + компл. сопр., G.1.20)
2
где Ех и Еу комплексные амплитуды компонент вектора поляри-
поляризации волны с несущей частотой со0. Как и прежде, получим выраже-
выражение для нелинейной поляризации P,VL, подставляя выражение G.1.20)
Фазовая кросс-модуляция 177
в уравнение B.3.6). В изотропной среде PNt можно записать в общем
виде:
1
IVfo 0 = -(хРх + yPy)exp( — iv>ot) + компл. сопр., G.1.21)
где Рх и Ру определяются [11] как
2 _ »w . J J 4-х, J . J xy,x j , . >
где i, j = x или _y.
Три независимые компоненты x<3) связаны с %(хххх соотношением
ХC) ^ у C) _|_ ^C) , ,„C) ^-7 1 ^-i\
jcjcxjc Кххуу ' Кхуху ' Кхуух' yi.l.^J)
Относительная величина трех компонент зависит от конкретных
физических механизмов, вносящих вклад в хC)- В кварцевых свето-
световодах, где х'3) имеет в основном электронное происхождение [6], эти
три компоненты почти одинаковы по величине. Если для простоты
предположить, что они одинаковы, «поляризационные компоненты»
Рх и Ру из выражения G.1.22) приобретают вид
1- (Е*Еу)ЕА, G.1.24)
Зео
4
Р -~2v<3> \l\E \2 + -\Е I2 ? +-{Е*Е\Е \ П 1 25^
Последнее слагаемое G.1.24) и G.1.25) аналогично тому, что G.1.2)
возникает из-за четырехволнового смешения, но из-за вырождения
поляризационных компонент (ш1 = со2 = со0) дает вклад на одной
частоте. Его влияние на динамику поляризационных компонент
зависит от степени фазового согласования между ортогонально-по-
ортогонально-поляризованными модами, определяемой длиной биений LB;LB вводит-
вводится согласно A.2.16). Если длина световода L » LB, что имеет место
в сильно двулучепреломляющих световодах, то из-за большого
фазового рассогласования последние члены в выражениях G.1.24)
и G.1.25) вносят пренебрежимо малый вклад. С другой стороны, для
слабо двулучепреломляюших световодов этот член необходимо
включать, если L « LB.
Нелинейный вклад в показатель преломления Апх определяется
членом, пропорциональным Ех в G.1.24). Используя соотношения,
аналогичные уравнениям G.1.9) и G.1.10). можно вывести выражения
Для Апх и Апу. Они такие:
пу.
G.1.26)
178Глава 7
G.1.27)
здесь п2 определяется согласно G.1.12). Сравнение с G.1.11) по-
показывает, что формально оба случая схожи. Нелинейный фазовый
сдвиг получается при использовании соотношения, аналогичного
выражению G.1.13). Оказывается, что ФКМ между двумя поляри-
поляризационными компонентами менее эффективна, чем между двумя
волнами на различных частотах, так как она включает коэффициент
2/3, а не 2. Качественная картина тем не менее остается той же самой.
В частности, нелинейная связь между компонентами поля Ех и Еу,
индуцированная ФКМ, создает нелинейное двулучепреломление,
которое изменяет состояние поляризации, если входное излучение
эллиптически поляризовано. Это явление называется вращением
эллипса поляризации [3].
Можно вывести уравнение распространения, определяющее ди-
динамику двух поляризационных компонент, используя метод из разд.
2.3. Медленно меняющиеся амплитуды Ах и Ау, определенные
в G.1.14), удовлетворяют следующей системе связанных уравнений:
дАх дАх i д2Ах а
^^2B/Ар), G.1.28)
1У
''-''> ,-,. ar, ^ (~1 \ 29)
где Ар = pL* — р1)(-расстройка синхронизма из-за линейного или
модового двулучепреломления световода (см. разд. 1.2.4). Следует
отметить, что то же самое линейное двулучепреломление также
приводит к расстройке групповых скоростей между двумя поляри-
поляризационными компонентами. Уравнения G.1.28) и G.1.29) аналогичны
уравнениям G.1.17) и G.1.18), за исключением последнего члена.
И следует подчеркнуть, что из-за вырождения по частоте нелинейный
параметр у одинаков для обеих поляризационных компонент.
7.2. ЭФФЕКТЫ, СВЯЗАННЫЕ
С НЕЛИНЕЙНЫМ ДВУЛУЧЕПРЕЛОМЛЕНИЕМ
Как следует из результатов разд. 7.1, нелинейная связь между
двумя ортогональными компонентами вектора поляризации опти-
Фазовая кросс-модуляция 179
ческой волны изменяет соответствующие компоненты показателя
преломления на различные величины Апх и Апу. Это явление
называется самоиндуцированным, или нелинейным, двулучепрелом-
лением; оно имеет множество приложений. В данном разделе
рассмотрены эффекты нелинейного двулучепреломления в волокон-
волоконных световодах и их практическое использование.
7.2.1. ОПТИЧЕСКИЙ ЭФФЕКТ КЕРРА '"'
В оптическом эффекте Керра двулучепреломление, индуцирован-
индуцированное мощным излучением накачки, используется для того, чтобы
изменить состояние поляризации слабого сигнала при прохождении
через изотропный нелинейный диэлектрик [5, 6]. Данный эффект
можно применять в оптических затворах с пикосекундными врем&-
нами срабатывания [8]. В световодах его впервые наблюдали в 1973 г.
[12]; с тех пор этот эффект привлекает большое внимание [13-20].
Принцип действия керровского затвора показан на рис. 7.1. На входе
в световод излучения накачки и сигнальное излучение поляризованы
линейно: угол между направлениями их поляризаций равен 45 °.
Скрещенный поляризатор на выходе световода блокирует прохожде-
прохождение сигнала в отсутствие накачки. Когда накачка включается, разница
показателей преломления для параллельных и перпендикулярных
поляризационных компонент сигнала (по отношению к направлению
поляризации накачки) становится другой из-за двулучепреломления,
вызванного излучением накачки. Дополнительная разность фаз для
двух компонент на выходе из световода проявляется в виде изменения
состояния поляризации сигнального излучения, и часть сигнала про-
проходит через поляризатор. Коэффициент прохождения сигнала зависит
от интенсивности излучения накачки, и им можно управлять, просто
изменяя эту интенсивность. Поскольку сигнал на одной длине волны
может быть промодулирован накачкой на другой длине волны, этот
прибор называется также керровским модулятором, и его можно
применять в системах оптической связи и в оптических переключа-
переключателях.
Разность фаз между х- и ^'-компонентами сигнального излучения
Накачка
х
Поляризатор ПрИемнмк
— \ —¦<
Рис. 7.1. Керровский затвор. На входе в световод излучение накачки и сиг-
сигнальное излучение линейно-поляризованы под 45° друг отноапс.и.по друт.
Поляризатор блокирует прохождение сигнала в отсутствие накачки.
180 Глава 7
на выходе из световода длиной L определяется
2л L
Дф= —(й,-й,), G.2.1)
К
где X длина волны сигнального излучения и
пх = пх + Аих, пу = пу + Апу. G.2.2)
Линейные части показателей преломления пх и пу обычно раз-
различны из-за внутримодового двулученреломления в световодах,
поддерживающих поляризацию (см. разд. 1.2.4). Нелинейные части
Апх и Апу различны из-за двулучепреломления„ обусловленного
излучением накачки.
Рассмотрим случай накачки, линейно поляризованной вдоль оси х.
Компонента х сигнала поляризована параллельно вектору поля-
поляризации накачки. Соответствующее изменение Апх находим из вы-
выражения G.1.11). Если пренебречь вкладом сигнала, то
Апх = 2п2\Е/, G.2.3)
1де |?р|2 интенсивность излучения накачки. Когда накачка и сигнал
поляризованы ортогонально друг огносительно друга, только первый
член в выражении G.1.22) дает вклад Апу из-за разницы в длинах волн
сигнала и накачки [11]. Снова пренебрегая самовоздействием, по-
получаем для Апу
Апу=2п2Ь\Ер\\ G.2.4)
где
•»,_7C) 7о) /7 1 5)
' ~ KxxyylК.хххх У' V
Если хC) имеет чисто электронную основу, то b=l,3. Комби-
Комбинируя G.2.1 )-G.2.4). получаем для разности фаз
2л L
Аф = -y(A«L + п2в\Ер\2) = Дф^ + ДфЛ1, G.2.6)
где AnL = пх — и. определяется линейным двулучепреломлением,
а керровский ко:ффициент п2В определяется выражением
п2в=2и2A-Ь). G.2.7)
Коэффициент пропускания сигнала Тр связан с Аф простым
соотношением
Тр = 8т2(Аф,2). G.2.8)
Пропускание керровского затвора становится равным 100%. когда
Аф = л или нечетному числу л. С другой стороны, сдвш фазы на
четное число л полностью блокирует сигнал.
Для наблюдения оптического эффекта Керра обычно используют
Фазовая кросс-модуляция 181
световод, поддерживающий поляризацию, чюоы сохранять состоя-
состояние поляризации излучения накачки. Постоянный сдвиг фазы Дфь,
возникающий из-за линейного двулучепреломления, можно ском-
скомпенсировать [13], поместив четвертьволновую пластинку перед
поляризатором (рис. 7.1). На практике, однако, из-за изменения
температуры и давления Афь флуктуирует, поэтому четвертьвол-
четвертьволновую пластинку необходимо постоянно подстраивать. Альтерна-
Альтернативным подходом является использование двух одинаковых отрезков
световода, поддерживающего поляризацию, соединенных вместе так,
что их «быстрые» (или «медленные») оси находятся под прямым
углом друг к другу [17]. Так как AnL меняет знак во втором
световоде, суммарный сдвиг фазы Афь, обусловленный линейным
двулучепреломлением, компенсируется.
При идеальных условиях постоянная времени керровского затвора
ограничена временем отклика нелинейности ~ 2-4 фс. На практике
тем не менее дисперсия в световоде ограничивает постоянную
времени до величин от ~ 1 пс до ~ 1 не в зависимости от значения
рабочих параметров [13]. Ограничивающий фактор-расстройка
групповых скоростей сигнального излучения и излучения накачки.
Относительная групповая задержка определяется как
Atg = \L/vgl-L/vg2\ G.2.9)
и может превысить 1 не для 100-метрового световода, если не принять
специальных мер предосторожности для уменьшения данной рас-
расстройки. Первая возможность-выбрать длину волны сигнала и
длину волны накачки с противоположных сторон от длины волны
минимальной дисперсии (вблизи 1,3 мкм). Линейное двулучепрелом-
ление световода накладывает другое ограничение на постоянную
времени затвора. Из-за разницы AnL ортогональные поляризацион-
поляризационные компоненты сигнала распространяются с различными скорос-
скоростями. Относительная задержка между ними
Atp = LAnL/c. G.2.10)
Для 100-метрового световода с A«L=5-10~5, Atp = 17 пс. Ее
можно уменьшить, используя световод с меньшим двулучепреломле-
двулучепреломлением. Использование двух световодов, соединенных так, что их
«быстрые» оси оказываются под прямым углом друг к другу,
позволяет почти полностью устранить Atp. Фундаментальное огра-
ограничение на постоянную времени затвора накладывается дисперсией
групповых скоростей, которая уширяет импульс накачки при рас-
распространении по световоду. Уширение импульса можно свести
До 1 пс и менее, либо уменьшая длину световода, либо исполь-
используя накачку с длиной волны, близкой к длине волны нулевой
Дисперсии.
Можно оценить мощность накачки, необходимую для 100%-ного
182 Глава 7
пропускания сигнала, из формул G.2.6) и G.2.8):
^Г' G.2.11)
где ЛЭ(М)- эффективная площадь сердцевины. Потери в световоде
можно учесть, заменив L на эффективную длину
L,* = i[l-exp(-aL)]. G.2.12)
Используя п2в = 4,5-106 см2/Вт, -4Э(М) = Ю мкм2, X = 1,06 мкм,
получаем мощность излучения накачки Рр ~ 1 Вт для 100-метрового
световода. Мощность можно уменьшить, увеличивая длину свето-
световода, но при этом увеличится постоянная времени затвора G.2.9).
В эксперименте [14] Рр ~ 0,39 Вт при L = 580 м и Аэфф = 22 мкм2.
В другом эксперименте эффективная площадь сердцевины была
уменьшена до 2 мкм2 и в качестве накачки использовалось излучение
полупроводникового лазера на 1,3 мкм. Был получен сдвиг фазы
в 17° при мощности накачки только 27 мВт. Оценка PpL= 11 Вт-м,
сделанная в этом эксперименте, указывает на то, что мощности
накачки ~ 50 мВт может оказаться достаточно для 100%-ного
пропускания сигнала, если в каждом плече интерферометра Маха^
Цандера использовать 200-метровые отрезки световода.
Уравнение G.2.11) можно использовать для оценки постоян-
постоянной Керра п2в. Большинство измерений указывает [12-20],
что п2в = 4 — 6-10~16 см2/Вт с погрешностью порядка 20%. Данная
величина находится в согласии с G.2.7), если использовать п2 ~
^ 3,2-106 см2/Вт и Ъ ^ 1/3. Параметр В был измерен в экспери-
эксперименте [19], что позволило независимо определить отношение вос-
приимчивостей, указанное в G.2.5). Исходя из того что измеренное
значение b равно 0,34, -южно полагать, что в кварцевых световодах
доминирует электронный вклад в JCC)- Это находится в согласии
с измерениями, сделанными в объемных стеклах [7].
Полностью оптический керровский затвор использовался для
экспериментальной демонстрации оптического стробирования [15].
На рис. 7.2 схематично изображена экспериментальная установка.
Для компенсации линейного двулучепреломления световода исполь-
использовался компенсатор Бабине-Солейля. В качестве поляризатора
использовался отрезок световода с большим двулучепреломлением
(коэффициент экстинкции около 20 дБ). Он также служил в качестве
фильтра, поскольку этот световод имел высокие потери на длине
волны накачки 1.06 мкм. В качестве сигнала служило излучение
лазерного диода на длине волны 0,84 мкм. Стробируемый сигнал на
выходе имел форму последовательности импульсов, расстояние меж-
между которыми и длительность определялись импульсами накачки.
Фазовая кросс-модуляция 183
Накачка на
*" р Полупрозрачное Волоконный поляризатор
зеркало Линза и фильтр
л Световод ¦ ¦
Сигнал на ' ~^_гУ 3ерка/1° Приемник
^-As Компенсатор . .Гч
Бабине-Солейля Стробированныи ,' Г\-t-s
выход на л.=а5 I I II I t
Рис. 7.2. Полностью оптический керровский затвор, использованный для
оптического стробирования [15].
В этом эксперименте стробирующие импульсы накачки были до-
довольно длинными (примерно 300 пс). В другом эксперименте [17]
30-пикосекундные сигнальные импульсы с частотой следования 1,97
ГГЦ (полученные при использовании полупроводникового лазера
с распределенной обратной связью и модуляцией усиления, рабо-
работающего в области 1,3 мкм) демультиплексировались при исполь-
использовании 85-пикосекундных импульсов накачки от Nd: YAG-лазера
с синхронизацией мод.
7.2.2. ИЗМЕНЕНИЕ ФОРМЫ ИМПУЛЬСОВ
Нелинейное двулучепреломление, вызванное каким-либо импуль-
импульсом, может быть использовано для изменения его же формы,
поскольку пропускание через световод и поляризатор становится
зависящим от интенсивности. Например, световод может работать
как нелинейный дискриминатор [21]. В разд. 6.4.2 отмечалось, что
данное явление можно использовать для устранения пьедестала,
связанного с импульсом, сжатым в компрессоре [21-23]. Его также
можно использовать, для создания волоконно-оптических логических
ячеек [24, 25].
В работе нелинейного дискриминатора используется по существу
тот же принцип, что и для керровского затвора, показанного на рис.
7.1. Основное отличие заключается в том, что сигнал сам создает
нелинейное двулучепреломление и изменяет собственное состояние
Поляризации. Рассмотрим случай, когда входное излучение линейно-
поляризовано под углом 9 по отношению к одной из главных осей
(оси х) световода. Его компоненты Ех и Еу изменяют показатели
преломления пх и пу на величины Апх и Апу, определяемые вы-
выражениями G.1.26) и G.1.27) соответственно. Результирующий сдвиг
фазы между двумя компонентами на выходе световода равен
(|?*12-|?/). G-2.13)
184
Глава 7
Здесь предполагается, что постоянный сдвиг фазы A<j>L, возникающий
из-за линейного двулучепреломления, скомпенсирован за счет ис-
использования четвертьволновой пластинки, и прохождение малого
сигнала блокируется. Экспериментально измеренное значение нели-
нелинейного сдвига фазы [26] находится в согласии с G.2.13). Инду-
Индуцированное нелинейное двулучепреломление позволяет излучению
проходить через поляризатор; коэффициент пропускания при этом
[21] -
Т = sin2( - yP0LcosBe))sin2Be), G.2.14)
где Ро — начальная мощность, а нелинейный параметр у тот же, что
и в разд. 7.1, т.е. определяется формулой B.3.28):
2пп2
1 =
G.2.15)
Ьфф
В случае когда по световоду распространяются оптические импульсы,
произведение yP0L связано с максимальным сдвигом фазы фмакс,
вызванным ФСМ [см. D.1.6)]; его также можно связать с нелинейной
длиной lf/L через соотношение
. G.2.16)
Изменение формы импульса происходит из-за того, что при
1,0
0,5
- *макс=10
w
X
X
га
Р,5
0,5
О 10 ?О 30 40 50
Угол входной поляризации (градусы)
Рис. 7.3. Коэффициент
пропускания Т р как функ-
функция угла входной поляри-
поляризации в при трех различ-
различных значениях пиковой
мощности, соответствую-
Щ»Х Фмакс = 10> 20 И 30
[21]
Фазовая кросс-модуляция
185
данном значении угла 9 пропускание Тр зависит от мощности. Если
выбрать угол 9 так, чтобы максимизировать пропускание вершины
импульса, его «крылья» блокируются из-за относительно меньшего
уровня мощности; при этом выходной импульс оказывается короче
начального. Такое поведение наблюдалось экспериментально [22].
Оптимальное значение 9 зависит от пиковой мощности Ро. На рис. 7.3
представлен коэффициент пропускания Тр как функция 9 при трех
значениях фмакс. Пропускание может достичь 90% для 9 = 36,2° при
Экспериментальные результаты по изменению формы импульсов
указывают [22, 24], что наблюдаемое поведение не всегда согласуется
с тем, что следует из G.2.14). В частности, это уравнение предска-
предсказывает, что Тр = 0 при 9 = 45', т.е. входное излучение блокируется
поляризатором, когда компоненты Ех и Еу возбуждены с равными
амплитудами. На самом деле это не так. Подобное несоответствие
объясняется тем, что мы пренебрегли последним членом в уравнениях
G.1.28) и G.1.29). В более точной теории его следует учесть. Для
случая непрерывного или квазинепрерывного излучения, когда дис-
дисперсионными эффектами можно пренебречь, уравнения G.1.8) и
G.1.29) можно решить аналитически [27], пренебрегая производными
по времени и потерями. Результаты показывают, что, исключая
область 9% 45°, формула G.2.14) является достаточно точной в
случае световодов с сильным двулучепреломлением (APL » 1). В слу-
случае же слабого двулучепреломления формула G.2.14) неприменима.
На рис. 7.4 представлен коэффициент пропускания Тр как функция
6 при ApL = 2тг и фмакс = 7,5тг. Сравнивая соответствующий график
с выражением G.2.14). мы видим, как важно учитывать линейное
двулучепреломление. Физически это означает, что линейный и не-
1,0
0,8
ш 0,6
i
¦=,2
1 0 10 20 30 40
Угол входной поляризации (градусы)
Рис. 7.4. Коэффициент пропускания Тр как функция угла входной поляри-
поляризации 6, когда учтен эффект линейного двулучепреломления при Ар/, = 2л
и Фма«с = 7,5л. Штриховой кривой показано пропускание в случае Ар = 0 [27].
1 1 ' 1
-
—
1 1
1
1
1 .
. /
1/
/
/
, 1
'Y -
/ \
/ ^
' \
\
\
\
\
\
i i \
186 Глава 7
линейный вклады в показатель преломления конкурируют друг
с другом и их необходимо учитывать вместе.
7.2.3. ПОЛЯРИЗАЦИОННАЯ НЕУСТОЙЧИВОСТЬ
Как показано выше, точное описание нелинейных поляризацион-
поляризационных эффектов требует одновременного учета как собственного
линейного двулучепреломления, так и индуцированного нелинейного
двулучепреломления. В общем случае динамика состояния поля-
поляризации излучения при распространении по световоду определяется
уравнениями G.1.28) и G.1.29) и их решения широко исследуются
[27-44]. В случае непрерывного излучения была обнаружена неустой-
неустойчивость, известная как поляризационная [29-31]. Данная неустой-
неустойчивость проявляется в виде значительного изменения выходного
состояния поляризации, когда входные мощность или состояние
поляризации изменяются незначительно. В частности, явление поля-
поляризационной неустойчивости показывает, что «медленная» и «быст-
«быстрая» оси световода, поддерживающего состояние поляризации, не
полностью эквивалентны.
Происхождение поляризационной неустойчивости можно понять
исходя из следующих качественных соображений [30]. Когда входное
излучение поляризовано близко к «медленной» оси световода (оси х,
если пх > пу), нелинейное двулучепреломление добавляется к собст-
собственному линейному, что делает световод более двулучепреломляю-
щим. С другой стороны, когда входное излучение поляризовано
вблизи «быстрой» оси, нелинейное двулучепреломление уменьшает
собственное двулучепреломление на величину, зависящую от входной
мощности. В результате световод становится менее двулучепрелом-
ляющим и эффективная длина биений L^** возрастает. При кри-
критическом значении входной мощности нелинейное двулучепрелом-
двулучепреломление может полностью скомпенсировать собственное и L^** ста-
становится бесконечной. При дальнейшем увеличении входной мощ-
мощности световод снова становится двулучепреломляющим, но «мед-
«медленная» и «быстрая» оси меняются местами. Ясно, что большие
изменения выходного состояния поляризации могут возникать, когда
входная мощность близка к критической мощности, необходимой для
баланса линейного и нелинейного двулучепреломления. Грубо гово-
говоря, поляризационная неустойчивость возникает, когда входная пи-
пиковая мощность достаточно велика для того, чтобы сделать нели-
нелинейную длину LNL сравнимой с собственной длиной биений L.B.
Точное значение критической мощности получается при решении
уравнений G.1.28) и G.1.29). В случае непрерывного излучения
производные по времени можно положить равными нулю. Если для
простоты пренебречь потерями в световоде, эти уравнения можно
решить аналитически в виде эллиптических функций Якоби. Период
Фазовая кросс-модуляция
187
эллиптической функции определяет эффективную длину биений [30]
G.2.17)
где К (ж)-четверть периода эллиптической функции и
ж = -И ГГ)> 9= 1+^ехрB/9).
G.2.18)
Здесь 9-угол входной поляризации, измеренный от «медленной» оси,
ар- нормированная входная мощность, определяемая какр = Ро/Р ,
где
ЗАВ
В отсутствие нелинейных эффектов р = 0, q = 1 и
= LB = 2тг/Др.
G.2.20)
На рис. 7.5 показана зависимость L|**/LB от входной мощности
при 9 = 0' и 9 = 90\ Как и ожидалось, эффективная длина биений
становится бесконечной при Ро = Ркр при 9 = 90° из-за того, что
происходит полное взаимное сокращение собственного и нелинейного
двулучепреломления [31]. Это и является причиной поляризационной
неустойчивости. В результате значительного изменения L|** выход-
выходное состояние поляризации может существенно изменяться в том
случае, когда Ро близко к Р и входное излучение поляризовано
близко к «быстрой» оси. На рис. 7.6 коэффициент пропускания Тр
показан как функция входной мощности при нескольких значениях
12 3 4 5
Входная мощность Ро /Ркр
Рис. 7.5. Эффективная длина биений как функция входной мощности для
излучения, поляризованного вдоль «быстрой» (сплошная кривая) и «медлен-
«медленной» (штриховая кривая) осей [30]
188
Глава 7
0,5
X
n)
?0,3
= 02
В- '
0,1
0,0
1 1 '
-
e=89°/ \
/ V
1 ' 1 '
A 0 = 89,9°
/ \
/ \
\
/ \
' \
1 1
-
-
Гэо-
e = \ o-
lo,i°
I ' all
0 1 2 3 4 5
Входная мощность Р0/Ркр
Рис. 7.6. Коэффициент пропускания двулучепреломляющего световода дли-
длиной L = LB как функция входной мощности при различных значениях углов
входной поляризации [30].
9 в предположении, что скрещенный поляризатор на выходе све-
световода блокирует излучение малой интенсивности (см. рис. 7.1).
Когда 9 = 0 или 90°, Тр = 0 при любых значениях мощности. Малые
изменения 9 вблизи «медленной» оси все еще оставляют Тр равным
нулю. Однако Тр изменяется резко при слабых изменениях 9 вблизи
«быстрой» оси. Отметим, что область высокой чувствительности Тр
к углу входной поляризации 9 находится в пределах от 89 до 90°.
Рис. 7.6 отвечает случаю Ap\L = 2тг, т. e. L = LB, но и для других длин
световода качественная картина остается той же самой.
Поляризационная неустойчивость наблюдалась в эксперименте
[34], где 80-пикосекундные импульсы на длине волны 532 нм
проходили через световод длиной 53 см (измеренная собственная
длина биений LB ~ 50 см). Входные импульсы были циркулярно
поляризованы и проходили через циркулярный анализатор, распо-
расположенный на выходе световода; анализатор пропускал излучение,
поляризованное по кругу в противоположном направлении. Когда
пиковая мощность превышала критическую величину, форма выход-
выходных импульсов значительно изменялась. Измеренные критическая
мощность и форма выходных импульсов находились в согласии
с теорией, основанной на уравнениях G.1.28) и G.1.29).
Зависимость пропускания от мощности, представленную на рис.
7.6, можно использовать для формирования импульсов и оптического
переключения. Однако для световодов с высоким двулучепреломле-
нием входная мощность, требуемая для переключения, велика. Так,
если в G.2.19) использовать значение у ~ 10 Вт^1-км~1, то для
световода с длиной биений L, = 1 м нужна мощность Ро ~ 1 кВт. Для
световодов с большим двулучепреломлением (LB = 1—10 см) эффек-
Фазовая кросс-модуляция 189
ты, связанные с поляризационной неустойчивостью, становятся
несущественными, так как в большинстве экспериментов Ро не
превышает 1 кВт.
Если собственное двулучепреломление промодулировано вдоль
длины световода, то поляризационная неустойчивость может при-
привести к хаосу в выходном состоянии поляризации [38]. Модули-
Модулированное двулучепреломление может возникать, если световод од-
однородно скручен при намотке на барабан. Его также можно специаль-
специально внести в процессе производства, периодически раскачивая за-
заготовку или периодически создавая напряжения. Можно исследовать
действие модулированного линейного двулучепреломления на ди-
динамику состояния поляризации излучения в световоде, полагая Ар
в уравнениях G.1.28) и G.1.29) периодической функцией z. Это
полезно проделать для того, чтобы оценить область, в которой
должны находиться параметры, при которых удается избежать
хаотического переключения, если световод используется в качестве
оптического переключателя [36-39].
7.2.4. ДЕЙСТВИЕ ДВУЛУЧЕПРЕЛОМЛЕНИЯ
НА СОЛИТОНЫ
Когда оптические солитоны рассматривались в гл. 5, предпо-
предполагалось, что входной импульс линейно-поляризован вдоль одной из
главных осей световода, поддерживающего поляризацию. В данном
разделе мы рассмотрим, что происходит с солитонами, когда
идеальные условия (угол входной поляризации 9 = 0 или 90°) не
выполняются. Существуют два важных вопроса. Во-первых, в све-
световоде со слабым двулучепреломлением пиковая мощность может
превысить критическую, необходимую для поляризационной не-
неустойчивости [см. G.2.19)], что может в свою очередь воздействовать
на солитоны, поляризованные вдоль «быстрой» оси. Во-вторых,
в световоде с сильным двулучепреломлением расстройка групповых
скоростей между ортогонально-поляризованными компонентами
излучения может привести к расщеплению импульса, что также
может воздействовать на характеристики солитона. Оба этих вопроса
рассмотрены ниже.
Сначала рассмотрим эффект поляризационной неустойчивости
солитонов в световодах со слабым двулучепреломлением [40]. Если
пренебречь расстройкой групповых скоростей, то в уравнениях
G.1.28).и G.1.29) можно положить f>lx = fiiy. Аналогично Р2* — Рг? =
Р?- Два связанных уравнения можно переписать, используя без-
безразмерные переменные из E.2.1); можно ввести параметры соли-
тонной теории N и z0 (см. разд. 5.2), используя определения
N2-— z --I L -— П 2 21)
LNL L IP2l
190 Глава 7
где LD - дисперсионная длина и 7^,-длительность импульса. Получен-
Полученные связанные нелинейные уравнения Шредингера решаются числен-
численно; при этом используется метод SSFM (см. разд. 2.4).
Численные результаты показывают [40], что поляризационная
неустойчивость воздействует на устойчивость солитона так же, как
и в случае непрерывного излучения, описанного в разд. 7.2.3. Если
входная мощность не превышает пороговую величину или, что
эквивалентно, нелинейная длина LNL больше длины биений LB,
солитон остается устойчивым, будучи возбужденным как вдоль
«медленной», так и вдоль «быстрой» осей. С другой стороны, если
LNL<c LB, солитоны остаются устойчивыми вдоль «медленной», но
неустойчивыми вдоль «быстрой» оси. Фундаментальный солитон
(N = 1), возбужденный вблизи «быстрой» оси с LNL « LB, следует
следующему сценарию [40]. Начинается поляризационная неустой-
неустойчивость, и большая часть энергии импульса из «быстрой» моды
переходит в «медленную» на трассе в несколько периодов солитона,
в то время как часть энергии рассеивается. Энергия импульса
несколько раз «переключается» из одной поляризационной моды
в другую; этот процесс аналогичен релаксационным колебаниям.
Большая часть энергии в конце концов оказывается в солитоно-
подобном импульсе, распространяющемся вдоль «медленной» оси.
Солитоны высших порядков следуют несколько иному сценарию.
Пройдя через фазу начального сжатия, они распадаются на от-
отдельные компоненты, данный распад аналогичен описанному в разд.
5.5. Затем часть энергии передается в «медленную» моду. В конце
концов вдоль «медленной» моды появляется фундаментальный
солитон с длительностью меньше начальной. Связанные нелинейные
уравнения Шредингера также имеют точное решение, соответствую-
соответствующее фундаментальному солитону, чьи «медленные» и «быстрые»
поляризационные компоненты распространяются без изменения
формы [44]. Обе компоненты обычно имеют асимметричную форму,
а «медленная» компонента к тому же имеет структуру с двойной
вершиной.
Для того чтобы получить условие для поляризационной неустой-
неустойчивости солитона, можно использовать условие неустойчивости
непрерывного излучения. Если использовать формулу G.2.19), то
условие Ро > Рхр может быть записано в виде
APLWL<2,3. G.2.22)
Используя условие Ар = 2щЬв и формулу G.2.21), можно записать
это условие в виде
=0<l-N2LB. G.2.23)
Численные результаты в основном согласуются с неравенством
Фазовая кросс-модуляция 191
G.2.23) [40]. Обычно LB < 1 м даже для световодов со слабым
двулучепреломлением. Если использовать значение р2 = ~ 20 пс2/км
для фундаментального солитона (N = I), распространяющегося на
длине волны 1,55 мкм, z0 становится меньше 1 м только для
фемтосекундных импульсов G^, < 100 фс). Таким образом, поляри-
поляризационная неустойчивость не должна быть существенной для соли-
тонных линий связи (см. разд. 5.4), где предполагаемая длительность
импульса То ~ 10 пс и z0 ~ 1 км.
В световодах с сильным двулучепреломлением нельзя пренебречь
расстройкой групповых скоростей между «быстрой» и «медленной»
поляризационными компонентами входного импульса. Такая рас-
расстройка должна расщепить солитон на отдельные компоненты вдоль
обеих осей при условии, что угол входной поляризации 9 не совпадает
с 0 или 90°. Продолжают ли эти компоненты удаляться друг от друга
или остаются «поблизости», зависит от начальных параметров.
Эффект расстройки групповых скоростей исследовался при числен-
численном решении уравнений G.1.28) и G.1.29). Если предположить
$2х = $1У = Рг и использовать безразмерные переменные из разд. 5.2,
эти уравнения приобретают вид [42]
где и и v-безразмерные амплитуды вдоль осей х ну соответственно и
. G.2.26)
Последним членом в уравнениях G.1.28) и G.1.29) мы пренебрегли
в предположении относительно большого двулучепреломления, так
что пиковая мощность значительно ниже порога поляризационной
неустойчивости. Для простоты мы также пренебрегли потерями
в световоде. Для начального импульса, возбужденного с углом
входной поляризации 9, уравнения G.2.24) и G.2.25) решались
с начальными условиями
и @, т) = N cos 9 sech (т), v @, x) = N sin 9 sech (т). G.2.27)
Можно следующим образом обобщить численные результаты
[43]. Когда обе моды возбуждены одинаково (9 = 45"), две поля-
поляризационные компоненты остаются связанными, если N превышает
Пороговое значение Nlh, зависящее от 6; Nlh = 0,7 при 6 = 0,15; Nlh = 1
При 6 = 0,5. Когда обе моды возбуждены неодинаково и N превышает
кр, то динамика имеет' качественно иной характер и зависит от
вВДичины 6. На рис. 7.7 показаны амплитуды импульсов в обеих
^ для 9 = 30° при С, = 5тг и Ютг. Левая колонка соответствует
192
Глава 7
-40 -20
20
40 -40 -20
Время т
:. 7.7. Амплитуды импульсов | и | (сплошная линия) и | v | (штриховая линия)
при Ё, — 5л: (верхний ряд) и Ё, = 10л: (нижний ряд) при В = 30'. Значения
параметров N = 0,8 и 6 = 0,15 в левой колонке JV = 1.1 и 6 = 0.5 в правой
колонке [43].
Рис
при
6 = 0.15 и N = 0,8, в то время как 6 = 0,5 и N = 1,1 соответствуют
правой колонке. Для случая 6 = 0,15 оказывается, что меньший
импульс захватывается большим и они распространяются вместе.
В случае 6 = 0,5 только часть энергии меньшего импульса захва-
захватывается большим, оставшаяся доля энергии рассеивается при
распространении. Более сложное поведение имеет место при больших
значениях 6 и N.
Ясно, что нелинейное двулучепреломление в волоконных све-
световодах может воздействовать на динамику солитонов различными
способами. С практической точки зрения интересно, как расстройка
групповых скоростей будет воздействовать на работу солитонной
линии связи. Для световодов, поддерживающих поляризацию, необ-
необходимо возбуждать солитоны с состоянием поляризации вдоль
главных осей. Результаты данного раздела говорят о том, что малые
отклонения от идеальных условий не будут сильно воздействовать на
характеристики солитонов, поскольку поляризационная мода с
большей амплитудой способна захватить другую поляризационную
моду, так что они могут распространяться вместе, несмотря на
разницу в групповых скоростях. Воздействие случайных флуктуации
двулучепреломления на распространение солитонов в обычных
световодах, не поддерживающих поляризацию, еще не до конца
понято.
Фазовая кросс-модуляция 193
7.3. МОДУЛЯЦИОННАЯ НЕУСТОЙЧИВОСТЬ,
ВЫЗВАННАЯ ФКМ
Рассмотрим взаимодействие при фазовой кросс-модуляции двух
оптических волн с одинаковыми поляризациями, но с неперекры-
неперекрывающимися спектрами [46 61]. Следует особо выделить два случая.
В первом случае излучение лишь одной длины волны вводится
в световод, а остальные возникают внутри при вынужденном
комбинационном рассеянии; этот случай рассмотрен в гл. 8. В другом
случае оба луча вводятся в световод, распространяясь без обмена
энергией друг с другом. Во втором случае ФКМ иногда называют
индуцированной фазовой модуляцией [57, 58]. Поскольку два опти-
оптических луча или импульса распространяются по световоду совместно,
ФКМ вызывает взаимодействие между ними, что может привести
к временным и спектральным изменениям. Эффекты, вызванные
ФКМ, описываются уравнениями G.1.17) и G.1.18). В данном разделе
рассмотрено стационарное решение в виде непрерывной волны, в то
время как разд. 7.4 посвящен зависящим от времени решениям,
соответствующим сверхкоротким импульсам.
В случае двух непрерывных волн производные по времени в урав-
уравнениях G.1.17) и G.1.18) можно положить равными нулю. Если для
простоты пренебречь потерями в световоде, то эти уравнения имеют
следующее стационарное решение:
Aj = V^j-exp (/ф j), G.3.1)
где j = 1 или 2, Pj— значение входной мощности, а фу-нелинейный
фазовый сдвиг, определяемый соотношением
ф; = у.^р. + 2P3-j)z. G.3.2)
Сдвш фазы зависит от мощности обеих волн. Уравнение G.3.1)
показывает, что обе волны распространяются без изменения, за
исключением сдвига фазы, линейно нарастающего с расстоянием.
Прежде чем сделать такой вывод, следует рассмотреть устойчивость
стационарного решения к малым возмущениям. Воспользуемся
методом, аналогичным описанному в разд. 5.1. Напомним, что там
было показано, что одна непрерывная волна становится неустойчивой
в области отрицательной дисперсии световода из-за модуляционной
неустойчивости. Оказывается, что при совместном распространении
двух непрерывных волн модуляционная неустойчивость может раз-
развиться не только в области отрицательной дисперсии, но так же
и в области положительной дисперсии из-за взаимодействия двух
волн при ФКМ [54].
Следует методу из разд.5.1, исследуем устойчивость стационар-
стационарного состояния, представив зависящее от времени решение в виде
Aj = (y/Pj + «у) ехр (/фу), G.3.3)
194 Глава 7
где uj(z,t)-слабое возмущение. Подставляя выражение G.3.3) в
уравнения G.1.17) и G.1.18) и линеаризуя их по а1 и о2, получаем
систему из двух уравнений для возмущений а1 и а2:
dz T vgl dt T2H21 dt2 ~
= iylPl(al + of) + 2iyl(PlP2)l/2(a2 + of), G.3.4)
da2 1 da2 i d2a2
dz fs2 d< 2 22 dt2
где последний член обусловлен ФКМ. Ищем общее решение в виде
а, = Mj-cos \Kz - Qj(t - z/vgj)-] + ivjsin \Kz - П/r - z/rj], G.3.6)
где К-волновое число, Пу-частота возмущения (/=1 или 2).
Уравнения G.3.4)-G.3.6) дают систему из четырех однородных
уравнений для и1, и2, \1, \2. Эта система имеет нетривиальное
решение только тогда, когда возмущения удовлетворяют следую-
следующему дисперсионному соотношению:
(К2-/1)(К2-/2)=СФКМ, G.3.7)
где
1 /l \
f = - р П? I - р П? + 2уjP-1 G.3.8)
2 \2 /
при 7=1 или 2: параметр связи Сф(<м
°2^i^2- G-3.9)
Стационарное решение становится неустойчивым, если при неко-
некоторых значениях Q.l и П2 волновое число К имеет мнимую часть.
Тогда возмущения ot и а2 экспоненциально нарастают по длине
световода.
Уравнение G.3.7) легко решается для К2 [54]:
К2 = \ {(Л + /2) + [(Л + /2J + 4 (СФКМ - Л/2)]1/2}. G.3.10)
Данное решение показывает, что К2 становится отрицательным,
когда Сфкм >f\fi- Это-необходимое условие для модуляционной
неустойчивости. Используя уравнения G.3.8) и G.3.9), можно записать
это условие в виде
2! + 1)(П2/П22 + 1) < 4, G.3.11)
где знаки «плюс» или «минус» выбираются в зависимости от того,
положительной или отрицательной дисперсии групповых скоростей
Фазовая кросс-модуляция 195
это соответствует. Значения частот Пс1 и Пс2 определяются соот-
соотношением
lI'2, G.3.12)
где 7= 1 или 2. Когда условие G.3.11) удовлетворяется для частот
модуляции С11 и П2, коэффициент усиления возмущения по мощности
имеет вид
д(П1,П2)=21т(К). G.3.13)
Условие G.3.11) показывает, что существует область параметров
fit и П2, где коэффициент g(Q.l,Q.2) существует. Стационарное ре-
решение G.3.3.) неустойчиво к слабым возмущениям на этих частотах.
Самый важный вывод, вытекающий из условия G.3.11), заключается
в том, что модуляционная неустойчивость может возникать не-
независимо от знака коэффициента дисперсии. Таким образом, в то
время как для модуляционной неустойчивости одной волны требуется
отрицательная дисперсия групповых скоростей (см. разд. 5.1), в
случае двух волн она может возникать, даже если обе волны рас-
распространяются в области положительной дисперсии. Диапазон
частот зависит от того, являются ли Р21 и Р22 положительными,
отрицательными или имеют разные знаки. Наименьший диапазон
частот соответствует случаю, когда обе волны распространяются
в области положительной дисперсии световода [оба знака в условии
G.3..11) положительны]. Поскольку в этом случае модуляционная
неустойчивость обусловлена лишь ФКМ, его мы и будем рассмат-
рассматривать ниже.
Следует различать два случая. В случае индуцированной моду-
модуляционной неустойчивости на непрерывную волну накладывается
внешнее возмущение при возбуждении, например, сигнальной волны
с частотой cot + С11. Эта модуляция создает модуляцию второй волны
с частотой П2, такую, что g(Qt,Q2) максимально, и условие G.3.11)
удовлетворяется. В результате в спектрах этих волн появляются
модуляционные компоненты с частотами cot + С11 и со2+П2. Во
временном представлении непрерывные волны испытывают глубо-
глубокую модуляцию с периодом 2тг/П^. В целом процесс можно рас-
рассматривать как четырехволновое смешение с фазовым синхронизмом
за счет ФКМ.
В случае спонтанной модуляционной неустойчивости возмущение
возникает из шума. Спонтанно испущенный или тепловой фотон
Действует в качестве сигнала и усиливается за счет модуляционной
неустойчивости. Модуляция с частотами Q™aKC и П2а"с, соответст-
соответствующими максимуму д, нарастает наиболее быстро. Максимальный
коэффициент усиления дмвжс и частота Qy*KC (/= 1 или 2) можно
определить, решая
1Ь0' 1- = °' G314)
196
Глава 7
0,2 0,4 0,6
Отношение мощностей Р2
0,8
Рис. 7.8. Максимальный коэффициент усиления и соответствующая частота
модуляции как функции отношения мощности Р-,/Р, при Р1 = 100 Вт,
Р21 =а Р22 = 0,06 пс /м и Yj si у2 — 30 Вт-км. Модуляционная неустой-
неустойчивость, вызванная ФКМ, возникает даже в области положительной диспер-
дисперсии световода.
где д(О.1,О.2) определяется выражениями G.3.10) и G.3.13). На рис. 7.8
изображены fifMaKC и П"акс/2тг как функции отношения мощностей
P2/Pi Для Р1 = 100 Вт. Параметры световода Р21 ~ Р22 = 0,06 пс2/м
и Yi — Y2 = 0,03 Вт~1м~1 соответствуют случаю двух волн вблизи
530 нм, распространяюшихся в одномодовом световоде с диаметром
сердцевины порядка 3 мкм. В этом случае Q"aicc ~ П2акс- Как и следо-
следовало ожидать, частоты модуляции зависят от мощности излучения
каждой волны и стремятся к нулю, если либо Р1 = 0, либо Р2 = 0. Для
значения пиковой мощности ~ 100 Вт возникающие боковые компо-
компоненты разнесены примерно на I ТГц. Во временном рассмотрении
каждая волна превращается в последовательность сверхкоротких
импульсов, разнесенных на ~ 1 пс. Так как gfMaKC ~ 5 м, модуля-
модуляционная неустойчивость может развиться из шумов даже в световоде
длиной несколько метров [54].
Модуляционная неустойчивость, вызванная ФКМ, недавно на-
наблюдалась. В эксперименте [60] вторая волна создавалась непосред-
непосредственно в световоде за счет ВКР излучения накачки (длина волны
накачки 0,53 мкм). Хотя и импульсы накачки, и импульсы ВКР
распространялись в области положительной дисперсии световода,
в их спектрах образовывались боковые спектральные компоненты на
расстоянии 2-10 ТГц в зависимости от мощности накачки и длины
световода. Этот эксперимент подробнее рассмотрен в разд. 8.3.2.
В другом эксперименте [61] использовалась конфигурация сигнал-
накачка, так что импульсы накачки на длине волны 1,06 мкм
Фазовая кросс-модуляция
197
распространялись в области положительной дисперсии, в то время
как сигнальные импульсы на длине волны 1,32 мкм распространялись
в области отрицательной дисперсии групповых скоростей световода.
Когда сигнальные импульсы и импульсы накачки вводились в
световод одновременно, в спектре сигнального излучения развивают-
развиваются боковые компоненты на расстоянии 290 ГГц, что является
результатом модуляционной неустойчивости, индуцированной ФКМ.
В конце этого раздела рассмотрим воздействие ФКМ на мо-
модуляционную неустойчивость одной непрерывной волны в двулу-
чепреломляющем световоде. Нелинейное двулучепреломление, вы-
вызванное ФКМ, связывает две компоненты вектора поляризации,
динамика которых определяется уравнениями G.1.28) и G.1.29).
Устойчивость их стационарного решения (обсуждалась в разд. 7.2.3)
можно исследовать, пользуясь вышеупомянутым методом при
Qt = Q2 = Q в выражении G.3.6). Результаты сильно зависят от
соотношения между входной пиковой мощностью и порогом по-
поляризационной неустойчивости Ркр, определяемым выражением
G.2.19). При Р < Ркр модуляционная неустойчивость возникает
только в области отрицательной дисперсии, а результаты аналогичны
результатам разд. 5.1. Действие ФКМ заключается в уменьшении
коэффициента усиления [41] по сравнению с E.1.9), но максимальное
усиление возникает на той же частоте Q (см. рис. 5.1).
При Ро > PYp спектр усиления модуляционной неустойчивости
зависит от того, поляризовано ли излучение вдоль «медленной» или
«быстрой» осей [62]. Модуляционная неустойчивость может возни-
возникать даже в области положительной дисперсии световода. В отличие
от кривой усиления на рис. 5.1 мы видим, что коэффициент усиления
-15
1 -10 -
?
I 5
e-
i-
1 1
¦ -
-
r
-
1 1
-1
1 1
-*'
1 I i
..
N
\2,0
\
i I i
1 1
-\
\
43,0
\
1
1 1
\ Po
\
\
i i i 1 i i i i
/5г>0 "
/Ркр=4 ~:
-
-
-
0,5 1,0 -1,5 2,0 2,5
Частота модуляции (ТТц)
3,0
Рис. 7.9. Спектр усиления модуляционной неустойчивости для непрерыв-
непрерывного излучения, распространяющегося в двулучепреломляющем световоде
с длиной биений LB = 2 м. Входная поляризация вдоль «быстрой» оси
Р2 = 0,06 пс2/м, а у = 38 Вт"
[62].
198 Глава 7
не обращается в нуль вблизи Q = 0 в том случае, когда излучение
поляризовано вдоль «быстрой» оси. Эта зависимость изображена на
рис. 7.9 при LB = 2 м, р2 = 0,06 пс2/м и у = 0,038 Вт м. Относи-
Относительно большое значение коэффициента усиления при Q = 0 указыва-
указывает на то, что низкочастотные или постоянные флуктуации могут
быстро нарастать. Так здесь проявляется поляризационная неустой-
неустойчивость, рассмотренная в разд. 7.2.3. При Р'Р^, > 3 максимальный
коэффициент усиления возникает при П/2тг ~ 1 ТГц. В этом случае
непрерывная волна испытает глубокие модуляции, возникнут боко-
боковые спектральные компоненты аналогично случаю в разд. 5.1.
7.4. СПЕКТРАЛЬНЫЕ И ВРЕМЕННЫЕ ЭФФЕКТЫ
В данном разделе рассматриваются спектральные и временные
изменения, возникающие при взаимодействии за счет ФКМ между
двумя -импульсами с неперекрывающимися спектрами, которые
распространяются вместе. В уравнения G.1.17) и G.1.18), описываю-
описывающие их динамику в световоде, включены эффекты расстройки груп-
групповых скоростей, дисперсии групповых скоростей ФСМ и ФКМ. Если
для простоты пренебречь потерями в световоде, эти уравнения
приобретают вид
д2А1
i „ д2А
= iyl<\Al\2 + 2\A2\2)Al, G-4.1)
G.4.2)
Sz дТ 2 ^
где
Г=г-—, ^=V9l~Vs2 G.4.3)
V91 V91 V92
и Г- время, измеряемо • в системе отсчета, движущейся с импуль-
импульсом 1.
Для импульса длительностью То можно ввести длину диспер-
дисперсионного разбегания Lw и дисперсионную длину LD, а именно
Lw = -j, LD=—. G.4.4)
В зависимости от относительных величин Lw, LD и длины
световода L динамика обоих импульсов может значительно разли-
различаться. Если L мало по сравнению как с Lw, так и с LD, дис-
дисперсионные эффекты несущественны и ими можно пренебречь. Это
может иметь место при 7J,>1hchL<10m, если длины волн двух
импульсов находятся ближе 10 нм друг к другу (| d\ < 10 пс/м). В этом
квазинепрерывном случае стационарное решение из разд. 7.3 прием-
Фазовая кросс-модуляция 199
лемо. Если Lw < L, но LD » L, вторыми производными в уравнених
G.4.1) и G.4.2) можно пренебречь, но первые производные следует
оставить. Хотя форма импульса не меняется, комбинация расстройки
групповых скоростей и частотной модуляции, обусловленной нели-
нелинейностью, может значительно воздействовать на спектр. Это обыч-
обычно имеет место при 7^~100 пс, L~ 10 м и rf< 10 пс/м. Для
сверхкоротких импульсов (То < 10 пс) дисперсионные члены также
следует включить: ФКМ в этом случае воздействует как на форму
импульса, так и на его спектр. Оба этих случая рассмотрены ниже.
7.4.1. АСИММЕТРИЧНОЕ УШИРЕНИЕ СПЕКТРА
Этот раздел посвящен важному случаю, когда членами со
вторыми производными в уравнениях G.4.1) и G.4.2) можно пре-
пренебречь в предположении, что L«LD. Расстройка групповых ско-
скоростей учитывается через параметр d(Lw < L). Поскольку форма
импульсов не меняется, уравнения G.4.1) и G.4.2) можно решить
аналитически. Общее решение имеет вид
At (L, Т) = Ау @, DexpOV^). G.4.5)
A2(L, T) = А2ф, Т- Ы)ехр(/ф2), G.4.6)
где
L
0,T)\2 + 2l\A2@,T-zd)\2dz), G.4.7)
о
0,Т)\2 + 2$\А1@,Т+ zd)\2dz). G.4.8)
о
Физический смысл данных выражений ясен. По мере того как импульс
распространяется по световоду, его фаза модулируется из-за зави-
зависимости показателя преломления от интенсивности. Промодулиро-
ванная фаза имеет два слагаемых. Первое слагаемое в уравнениях
G.4.7) и G.4.8) обусловлено ФСМ (см. разд. 4.1). Второе происходит
из-за ФКМ. Его вклад изменяется вдоль длины световода из-за
расстройки групповых скоростей [52]. Полный вклад ФКМ в фазу
получается при интегрировании по длине световода.
Интеграл в выражениях G.4.7) и G.4.8) можно взять для им-
импульсов специальной формы. В качестве иллюстрации рассмотрим
случай двух гауссовских импульсов одинаковой длительности 7^, без
частотной модуляции. Начальные амплитуды имеют вид
А, @, Т) = Ул"ехр(- ~ J, G.4.9а)
А2 @, Т) = У^ехр (GJrIdJ), G-4.96)
200 Глава 7
где Pl и Р2-значения пиковой мощности иГг начальная задержка по
времени между двумя импульсами. Подставив систему G.4.9) в G.4.7),
получим явные выражения для нелинейной фазы ф^
<Ых) = Yi ДЛехр(- х2) + P2^[erf(x - т„) - erf(x - т„ - 6)]), G.4.10)
о
где erf-функция ошибок и
т=? ^ 6 = ^. G.4.11)
'о *о *о
Аналогичное выражение получается для ф2(Т).
Как показано в разд. 4.1, зависимость фазы от времени прояв-
проявляется в виде уширения спектра. Таким образом, спектр каждого
импульса будет уширяться, в нем будет наблюдаться многопичковая
структура, форма которой определяется относительным вкладом
ФСМ и ФКМ. На рис. 7.10 показаны спектры двух импульсов для
конкретного случая ylPlL = 40, PJP^ - 0,5, Y2/Y1 = 1,2, хй = 0, 6 = 5.
•Эти параметры соответствуют случаю, когда импульс мощностью
100 Вт на длине волны 630 нм возбужден вместе с 50-ваттным
импульсом на длине волны 530 нм с Та = 0. То = 10 пс и L= 5 м.
Наиболее заслуживающая внимания особенность рис. 7.10-асим-
7.10-асимметрия спектра, обусловленная исключительно ФКМ. При отсутст-
отсутствии взаимодействия за счет ФКМ обе спектра должны быть сим-
симметричными и испытывать меньшее уширение. Спектр импульса
2 более асимметричен, поскольку вклад ФКМ больше именно для
этого импульса (Р1 = 2Р2). Можно на качественном уровне понять
особенности спектра на рис. 7.10, рассмотрев нелинейный сдвиг
частоты. Для импульса 1 он имеет вид
- х2> - у [ехр(- (х - х„J) - ехр(- (т - т„ - бJ)] J,
G.4.12)
где использовалось выражение G.4.10). При хй = 0 и 1611 « 1 (L« Lw)
сдвиг частоты определяется простым соотношением
Avt (х) = ^ехр(- х2)^! + Р2Bх - 6)]. G.4.13)
Сдвиг частоты для импульса 2 можно получить, следуя похожей
процедуре:
Av2 (х) = ^ехр(- т2) [Р2т + Р1 Bт + S)]. G.4.14)
тгТ0
Фазовая кросс-модуляция
201
о,в
0,6
0,4
0,2
О
1
-
-
1
-5
I i
Импульс 2
У
1 щц
О 5
(l/-I/2)Tn
-
-
-
Рис. 7.10. Оптические спектры двух импульсов, распространяющихся вместе
и испытывающих асимметричное уширсние спектра, вызванное ФКМ. Зна-
Значения параметров: yvPvL = 40. P2/Pl = 0.5. у,/"^ = 1.2. xd = 0. L/Lw = 5.
Асимметрия в спектре возникает, поскольку AVy( — т) / Ау|-(т)(/= 1
или 2 до тех пор, пока 6/0). Для положительных значений 6 сдвш
частоты больше вблизи переднего фронта для импульса 1, в то время
как обратное имеет место для импульса 2. Поскольку передний
и задний фронты переносят соответственно длинноволновые и
коротковолновые компоненты, спектр импульса 1 сдвинут в длин-
длинноволновую область. Это и видно на рис. 7.10. Спектр импульса
2 испытывает больший сдвиг потому, что вклад ФКМ больше из-за
того, что Pt> Р2. Когда Р1 = Р2 и yt ~ у2, спектры обоих импульсов
будут зеркальным отображением друг друга.
Картина спектрального уширения может быть качественно иной,
если оба импульса в начальный момент не перекрываются, а разде-
разделены (что соответствует некоторой временной задержке). Для того
чтобы выделить эффект ФКМ. полезно рассмотреть случай, когда
Р1 « Р2. Сдвиг частоты, индуцированный накачкой и накладываемый
на сигнальный импульс, вычисляется из выражения G.4.12); вкладом
ФСМ пренебрегаем.
= sgnE)AvMaKC{exp[- (т -
- ехр[- (т - ха -
G.4.15)
где AvMaKC-максимальное значение сдвига частоты за счет ФКМ:
AvMaKC =
тгГ0|5| пТ0
G-4.16)
Отметим, что AvMaKC определяется длиной дисперсионного раз-
бегания Lw, а не фактической длиной световода L. Этого и следовало
ожидать, так как взаимодействие за счет ФКМ возникает только
тогда, когда импульсы перекрываются.
202
Глава 7
1,0
0.8
0,6
0,4
0,2
0
i
-
-
-
i
i i i i
s0 II
I ~
I I "
ill I "
ill I "
i Jiilllf Vi
-4 -2 0
1,0
XI
?0,8
о
?o,6
s
?0,4
О)
?0,2
0
i I
-
-
-
-
J
I ^-Г
I I
I
-
-
1
1
1
V
1 Т ^ 1
-4 -2 0
1,0
0,8
0,6
0,4
0,2
0
_
-
J
fill
Та s4
-
Ill
ill , ,"
-4 -2
1.0
0,5
0.0
-0,5
1,0
1
/\
/
/
/ '
1)
1
л
/1
1
\|
\|
Л|
1
1
_
1
_ я)
CO
CO
¦е-
0,0
-0,5
1,0
0,5
0,0
-0,5
-5
0,5 -
-5
-5
Т/Тп
- 1
1
_
<
1
/
/ 1
//
и
V
1 1
м\
|\
1 \
|1
|Д
i i
- 1
S
¦я
к
с
о
0|
о
-1 н
1
1
1
1
1
и
1 \
1
• л -
1 A
i \
] !
Рис. 7.11. Оптические спектры (левая колонка) и индуцированные ФКМ фаза
и сдвиг частоты (правая колонка) для сигнального импульса, распростра-
распространяющегося вместе с импульсом накачки, движущимся быстрее сигнального.
Форма сигнального импульса показана штриховой линией. Три ряда соот-
соответствуют начальной задержке импульса: Td = 0, 2 и 4 соответственно. Другие
параметры: y1P2L = 40. L'LW = 4.
Из уравнения G.4.15) следует, что индуцированный ФКМ сдвиг
частоты сигнала может значительно варьироваться, если хл и 5 имеют
противоположные знаки. В результате спектр сигнального излучения
может иметь качественно различные особенности в зависимости от
относительной величины ха и 5. Рассмотрим случай, когда импульс
накачки распространяется быстрее сигнала E < 0), но вначале он
задержан (хй ^ 0). На рис. 7.11 показаны спектр сигнального из-
излучения, фаза ф1 и сдвиг частоты Avt при 5 = — 4 и хй = 0, 2 и 4.
Длина световода L и пиковая мощность излучения накачки Р2
выбраны так, что yl P2L= 40 и L/Lw = 4. Для примера 10-пико-
Фазовая кросс-модуляция 203
секундный импульс накачки с расстройкой групповых скоростей
d= 10 пс/м имеет Lw = 1 м. Спектр сигнального излучения на рис.
7.11 при хл = 0 сдвинут в длинноволновую область и сильно асиммет-
асимметричен. При хй = 2 он становится опять симметричным, в то время как
при хл = 4 он снова асимметричен и сдвинут в коротковолновую
область. Фактически спектры при хл = 0 и хл = 4 зеркально симмет-
симметричны относительно центральной частоты vt = tOj/in.
Можно понять физический смысл особенностей спектров сигналь-
сигнального излучения, рассмотрев сдвиг частоты, вызванный ФКМ (что
изображено в правой колонке на рис. 7.11). При хл = 0. сдвиг частоты
положителен вдоль всего сигнального импульса, и максимальное его
значение возникает в центре импульса. В случае ФСМ, в отличие от
этого (см. рис. 4.1), сдвиг частоты отрицателен вблизи переднего
фронта, нулевой у центра импульса и положителен у заднего фронта.
Разница для случаев ФСМ и ФКМ обусловлена расстройкой груп-
групповых скоростей. При ха = 0 медленно движущийся сигнальный
импульс взаимодействует в основном с задним фронтом импульса
накачки. В результате индуцированный ФКМ сдвиг частоты поло-
положителен, спектр сигнального излучения имеет только компоненты,
сдвинутые в коротковолновую область. При хй — 4 импульс накачки
«догоняет» сигнальный импульс только в конце световода. Передний
фронт импульса накачки взаимодействует с сигнальным импульсом;
поэтому сдвиг частоты отрицателен и спектр сдвигается в длинно-
длинноволновую область. При ха = 2 у импульса накачки есть время не
только догнать сигнальный импульс, но и пройти сквозь него
симметричным образом. Сдвиг частоты равен нулю в центре им-
импульса. Его величина мала и внутри всего импульса. В результате
спектр сигнала симметрично уширяется, но в «крыльях» заключена
относительно малая доля энергии. В этом симметричном случае
спектр сигнала сильно зависит от отношения L/Lw. При хй = 1, если
L/Lw = 2, спектр сигнального излучения шире и имеет более сложную
структуру. С другой стороны, если L» Lw, спектр сигнального
излучения остается практически неизменным.
Уширение спектра, вызванное ФКМ, наблюдалось эксперимен-
экспериментально в конфигурации «накачка-сигнал». В эксперименте [52]
Ю-пикосекундные импульсы накачки были полуены от лазера на
центрах окраски, работающего на длине волны 1,51 мкм, в то время
как сигнальные импульсы на длине волны 1,61 мкм генерировались
в волоконном ВКР-лазере (см. разд. 8.2.2). Длина дисперсионного
разбегания составляла 80 м, в то время как дисперсионная длина
превышала 10 км. Наблюдались как симметричные, так и асим-
асимметричные спектры сигнального излучения, по мере того как длина
световода возрастала с 50 до 400 м. Эффективная задержка между
импульсами изменялась за счет расстройки резонатора волоконного
ВКР-лазера.
204
Глава 7
В другом эксперименте [59] Nd: YAG-лазер использовался для
генерации 33-пикосекундных импульсов накачки на длине волны
1.06 мкм и 25-пикосекундных сигнальных импульсов на длине волны
0,53 мкм. Первоначальная задержка между сигнальными импульсами
и импульсами накачки осуществлялась при помощи интерферометра
Маха - Цандера. Из-за относительно большой расстройки групповых
скоростей (d ~ 80 пс/м) длина дисперсионного разбегания составляла
лишь 25 см. Для световода длиной 1 м, используемого в экспери-
эксперименте, L/ Lw = 4. Спектры сигнального излучения измерялись при
изменении задержки Td и пиковой мощности излучения накачки.
Спектр сигнального излучения испытывал сдвиг как в длинновол-
длинноволновую, так и в коротковолновую области при некотором уширении.
Отметим, что спектральное разрешение не позволяло наблюдать
многопичковую структуру спектра. Такой вызванный ФКМ сдвиг
был назван индуцированным сдвигом частоты [59]. На рис. 7.12
изображен индуцированный сдвиг как функция задержки по времени
Тй. Сплошная линия теоретическая зависимость из выражения
G.4.15). Сдвиг частоты при данной временной задержке получается
при максимализации Av^t). Максимум находится вблизи т = 0,
и сдвиг частоты определяется выражением
Av, = AvMaKC{exp(-T2) - exp [- (т„ + 5J]}, G.4.17)
где 5^—4 для экспериментальных значений параметров и хй = TJ То
при 7^, ^ 20 пс. Уравнение G.4.17) показывает, что максимальный
-80 -40 О 40 80 120
Временная задержка (пс)
160
Рис. 7.12. Индуцированный ФКМ сдвиг длины волны сигнального импульса
на 0,53 мкм как функция начальной задержки 1.06-микрометрового импульса
накачки. Кружки представляют экспериментальные данные, в то время как
сплошная линия представляет теоретическую зависимость [59].
Фазовая кросс-модуляция
205
0 1 2 3 4 5
Пиковая мощность излучения накачки (кВт)
Рис. 7.13. Индуцированный ФКМ сдвиг длины волны сигнального импульса
на длине волны 0,53 мкм как функция пиковой мощности 1,06-микрометро-
вого импульса накачки, распространяющегося вместе с сигнальным, для
случая, когда нет начальной задержки по времени (Td = 0) между двумя
импульсами [59].
сдвиг AvMaKC возникает при хй = 0 и хл = 4, в то время как его значение
стремится к нулю при хл = 2. Эта особенность находится в согласии
с экспериментальными данными. В соответствии с G.4.16) макси-
максимальный сдвиг должен линейно возрастать при увеличении пиковой
мощности излучения накачки. Данная зависимость действительно
наблюдается экспериментально, как это следует из рис. 7.13. Сдвиг
длины волны сигнального излучения, вызванный ФКМ. имеет
величину примерно 0,1 нм/кВт. Эта величина ограничена длиной
дисперсионного разбегания; ее можно увеличить на порядок и более,
если уменьшить разницу в длинах волн между сигнальным излуче-
излучением и излучением накачки до нескольких нанометров. Индуци-
Индуцированный ФКМ сдвиг частоты может быть использован в системах
оптической связи или в оптических компьютерах.
7.4.2. АСИММЕТРИЧНЫЕ ВРЕМЕННЫЕ ИЗМЕНЕНИЯ
До сих пор мы предполагали, что дисперсионная длина LD много
больше длины световода L. В результате оба импульса сохраняли
свою форму при распространении по световоду. Если LD становится
сравнимой с L или с длиной дисперсионного разбегания Lw, совмест-
совместное действие ФКМ, ФСМ и дисперсии групповых скоростей может
привести к качественно новым временным изменениям, которые
сопровождают изменения в спектре, рассмотренные в разд. 7.4.1.
206 Глава 7
Можно исследовать эти временные изменения, численно решая урав-
уравнения G.1.17) и G.1.18). Здесь полезно ввести безразмерные перемен-
переменные, как в разд. 4.2.
f ^ .^ G.4.18)
и записать связанные уравнения для амплитуд в виде
^ ^^i , G.4.19)
где LD и Lw определены выражениями G.4.4), а параметр N введен
так же, как и в разд. 4.2,
N2 = TL = '4t?- <7А21>
L II
Потерями в световоде мы пренебрегли, полагая a,L« 1 (/= 1 или 2).
Второй член в уравнении G.4.20) описывает расстройку групповых
скоростей обоих импульсов. Выбор плюса или минуса зависит от
знака параметра d, определенного в G.4.3).
Для того чтобы выделить эффекты, связанные с ФКМ, полезно пе-
перейти к конфигурации «накачка-сигнал». Предполагая |С/2|2 « |t/J2,
в уравнениях G.4.19) и G.4.20) можно пренебречь членами, содержа-
содержащими |1/212- Тогда сигнал не воздействует на динамику импульса
накачки, определяемую уравнением G.4.19). Тем не менее импульс
накачки значительно воздействует на динамику сигнала за счет ФКМ.
Уравнение G.4.20) описывает совместное действие эффектов ФКМ
и дисперсии групповых скоростей на форму и спектр сигнального
импульса. Эти уравнения можно решить численно, используя частич-
частично видоизмененный метод SSFM, описанный в разд. 2.4.
На рис. 7.14 показаны форма импульсов и спектры для сигналь-
сигнального излучения и излучения накачки при ? = 0,4 в случае N = 10,
LD/LW= 10, Ю2/Ю! = 1.2 и Р22 — Ри > 0. Предполагается, что оба
импульса на входе в световод имеют гауссовскую форму при
одинаковой длительности, между ними нет временной задержки,
и импульс накачки распространяется быстрее сигнала (d > 0). Форма
и спектр импульса накачки обладают свойствами, возникающими из
совместного действия ФСМ и дисперсии групповых скоростей (см.
разд. 4.2). С другой стороны, форма и спектр сигнального импульса
определяются совместным действием ФКМ и дисперсии. Для срав-
сравнения на рис. 7.15 изображены спектры сигнала и накачки при
отсутствии дисперсии групповых скоростей; асимметричное уширение
Фазовая кросс-модуляция
207
Сигнал
0,3
0,2
0
Накачка
|
i
-
V-
-10 -5
0,08 -
_ 0,04 -
10
0,1 -
-4
Рис. 7.14. Формы импульсов (верхний ряд) и спектры (нижний ряд) для
сигнального импульса и импульса накачки при ?, = 0.4 для N = 10. LD/LW = 10
и а>2/а>1 = 1.2. Штриховой линией показано положение начального импульса.
Оба импульса имеют гауссовскую форму при одной и той же длительности
и полностью перекрываются при t, = 0.
спектра сигнального излучения в коротковолновую область при
отсутствии дисперсии рассмотрено в разд. 7.4.1. Наличие дисперсии
уменьшает степень асимметрии; при этом часть энергии переносится
длинноволновыми спектральными компонентами (см. рис. 7.14).
Заметнее всего дисперсия воздействует на форму сигнального
импульса (см. рис. 7.14). При отсутствии дисперсии форма сигнала
остается неизменной, так как ФКМ действует лишь на оптическую
фазу. Тем не менее, когда дисперсия есть, разные части сигнального
импульса распространяются с разными скоростями из-за сдвига
частоты, индуцированного ФКМ и накладываемого на сигнальный
импульс. Это приводит к асимметризации формы импульса и появ-
появлению значительной субструктуры. На сигнальном импульсе разви-
развиваются быстрые осцилляции вблизи заднего фронта, в то время как
передний фронт остается практически неизменным. Эти осцилляции
вызваны так называемым эффектом распада огибающей оптической
208
Глава 7
0,08
Рис. 7.15. Спектры сигнального импульса и импульса накачки при условиях,
идентичных указанным на рис. 7.14, за исключением того, что дисперсион-
дисперсионными эффектами пренебрегается. Форма импульсов не показана, так как она
остается неизменной.
волны, рассмотрены в разд. 4.2. Осцилляция на «крыльях» импульса
обусловлены там комбинацией ФСМ и дисперсии (см. рис. 4.10).
В данном случае именно комбинация ФКМ и дисперсии приводит
к осцилляциям по всему заднему фронту сигнального импульса.
С физической точки зрения данные процессы образования осцилляции
обусловлены следующим. Сдвиг частоты, индуцированный ФКМ,
максимален в центре импульса, как это следует из рис. 7.11 (верхний
ряд). Из-за положительной дисперсии вершина сигнального импульса
замедляется по отношению к его «крыльям». Распад огибающей
оптической волны возникает из-за того, что вершина отстает
и начинает интерферировать с задним фронтом. В данном случае
импульс накачки, двигаясь быстрее сигнала, взаимодействует с его
задним фронтом. Если же длины волн излучения накачки и сигнала
поменять местами так, что более медленный импульс накачки
взаимодействовал в основном с передним фронтом сигнального
импульса, то осцилляции возникнут вблизи переднего фронта, так как
индуцированный ФКМ сдвиг частоты ускорит вершину сигнального
импульса по отношению к его «крыльям». Наличие начальной
задержки между импульсом накачки и сигнальным импульсом может
привести к возникновению особенностей, качественно отличающих
дисперсионную ФКМ от случая, изображенного на рис. 7.11. На-
Например, можно значительно сжать сиг нальный импульс, оптимизируя
начальную задержку. Механизм компрессии аналогичен многосо-
литонному сжатию (см. разд. 6.4), за исключением того, что
индуцированное ФКМ-сжатие может происходить даже в области
положительной дисперсии световода.
Для экспериментального наблюдения асимметричных временных
эффектов, вызванных ФКМ, потребуется использовать фемтосекунд-
Фазовая кросс-модуляция 209
ные импульсы. Это происходит из-за того, что LD > 1 км для
То > 5 пс, в то время как длина дисперсионного разбегания Lw ~ 1 м
для типичных значений \d\ ~ 10 пс/м. Поскольку ФКМ возникает
только на трассах порядка нескольких длин дисперсионного разбега-
разбегания, взаимодействие между ФКМ и дисперсионными эффектами
может происходить, если LD и Lw становятся сравнимыми. Напри-
Например, если То = 100 фс, LD и Lw становятся ~ 10 см, и временные
эффекты, описанные выше, могут возникать в световоде длиной менее
метра. Для таких коротких импульсов необходимо учитывать нели-
нелинейные эффекты высших порядков, такие, как дисперсия нелиней-
нелинейности или задержка нелинейного отклика (см. разд. 2.3). Воздействие
ФКМ на динамику фемтосекундных импульсов находится в ранней
стадии исследований и заслуживает дальнейшего внимания.
7.5. НЕВЗАИМНОСТЬ, ВЫЗВАННАЯ ФКМ
До сих пор в тгой главе мы рассматривали ФКМ двух волн,
распространяющихся в одном и том же направлении; эти волны
отличались друг от друга длинами волн или состояниями поля-
поляризации. Третий возможный случай когда две волны с одинаковыми
частотами и состояниями поляризации распространяются по све-
световоду в противоположных направлениях. Прямая и обратная волны
будут взаимодействовать друг с другом за счет ФКМ. Такое
взаимодействие может привести к качественно новым свойствам,
проявляющимся в виде оптической бистабильности [63 66], когда
волоконный световод используется для создания нелинейного коль-
кольцевого резонатора. Также это может привести к оптическим
неустойчивостям и хаосу [67, 68]. Особый интерес представляет
невзаимность, вызванная ФКМ; она может воздействовать на работу
волоконных гироскопов [69-74] и волоконных ВКР-лазеров [75].
Чтобы понять причину невзаимности между волнами, распрост-
распространяющимися навстречу друг другу, воспользуемся методом из
разд. 7.1. Если А^ и А,— амплитуды прямой и обратной волн, то они
УДовлятворяют уравнениям связанных амплитуд, аналогичным урав-
уравнениям G.1.17) и G.1.18). В частности. А} удовлетворяет уравнению
G.5.1)
!Де «плюс» или «минус» соответствует j!= 1 или 2 соответственно.
^ случае непрерывного излучения эти уравнения легко решаются,
для простоты пренебречь потерями в световоде, решение имеет
вид
Aj(z) = JFjexp(± /ф,), G.5.2)
210
Глава 7
Лазер
Ответви тель
Приемник
Многовитковая
волоконная петля
Рис. 7.16. Схема волоконного гироскопа. Излучение лазера вводится через
50%-ный ответвитель, возбуждая встречные волны в многовитковой воло-
волоконной петле. Сдвиг фазы, вызванный вращением, измеряется фазочувстви-
тельным детектором.
где Pj- значение пиковой мощности, нелинейный сдвиг фазы опре-
определяется выражением
). G.5.3)
Если Р1 ф Р2, то для двух волн, распространяющихся навстречу
друг другу, сдвиги фазы ф1 и ф2 неодинаковы. Эта невзаимность
вызвана наличием коэффициента 2 в члене с ФКМ в выражении
G.5.3).
Невзаимность, обусловленная ФКМ, может оказаться вредной
для высокоточных волоконных гироскопов [76], используемых для
измерения скоростей вращения меньше 0,01 с/ч. На рис. 7.16 показана
схема конструкции волоконного гироскопа. Его действие основано на
эффекте Саньяка [77], при котором между волнами, распространя-
распространяющимися навстречу друг другу, возникает зависящий от скорости
вращения сдвиг фазы. Суммарный сдвиг фазы определяется вы-
выражением
G.5.4)
где L-полная длина световода, П-скорость вращения и S-масштаб-
ный коэффициент, зависящий от длины световода и радиуса во-
волоконной петли [76]. Если мощности Ру и Р2 постоянны, то член
с ФКМ в выражении G.5.4) несуществен. Но на практике уровень
мощности может флуктуировать. Даже при разнице в мощности
между встречными волнами в 1 мкВт сдвиг фазы Дф может
измениться на ~1-10~6рад, если принять у ~ 10 Вт -км и
L ~ 100 м. Эта величина обычно соответствует эквивалентной
скорости вращения ~0,1 °/ч, что указывает на то, что ФКМ может
значительно ограничить чувствительность волоконного гироскопа,
если не контролировать уровень мощности с точностью до 10 нВт.
Для того чтобы уменьшить эффект ФКМ и улучшить работу
гироскопа, можно воспользоваться рядом схем. В первой схеме [70]
Фазовая кросс-модуляция 211
лазерное излучение модулируется до того, как в волоконной петле
будут возбуждены встречные волны. Так как возникает явная за-
зависимость от времени, анализ этого случая осуществляется решением
уравнения G.5.1) с соответствующими граничными условиями [70.
74]. Результаты показывают, что эффект невзаимности можно
значительно уменьшить, если должным образом выбрать частоту
модуляции. Это понятно, так как ФКМ возникает только тогда, когда
два импульса перекрываются по времени. Невзаимность, вызванная
ФКМ, возникает из-за интерференции между встречными волнами.
Модуляция уменьшает связь между ними, тем самым уменьшая
эффективность такой интерференции. Действительно, тот же самый
результат можно получить, используя широкополосные источники
с ограниченным временем когерентности [71 -73]. Для этих целей
использовались тепловые источники или светодиоды [76].
Кратко рассмотрим воздействие ФКМ на оптическую бистабиль-
ность. Любая нелинейная среда, помещенная внутрь резонатора,
может проявлять бистабильность [78, 79], и волоконные световоды
не являются исключением. Если для этой цели использовать воло-
волоконный кольцевой резонатор, оптическая бистабильность может воз-
возникать вне зависимости от того, распространяется ли излучение по
или против часовой стрелки. Интересная ситуация возникает, когда
оптические волны возбуждаются в обоих направлениях. Из-за вза-
взаимодействия между встречными волнами за счет ФКМ устройство
действует как две связанные бистабильные системы, и оно может
обладать качественно новыми свойствами [63 66]. Хотя оптическую
бистабильность наблюдали [68] для случая однонаправленного
распространения в волоконном кольцевом резонаторе, исследование
двунаправленного случая не привлекло большого внимания. Воз-
Возможно, оптическая бистабильность в одномодовых волоконных
световодах будет использоваться для быстрых оптических переклю-
переключений.
7.6. ЗНАЧЕНИЕ ДЛЯ СИСТЕМ ОПТИЧЕСКОЙ СВЯЗИ
Поскольку волоконные световоды обычно используются для
передачи каких-либо данных и телефонных разговоров, важно понять,
как ФКМ воздействует на работу систем оптической связи [47, 48].
В многоканальной (с частотным уплотнением информации) системе
как ФКМ, так и ФСМ будут изменять фазу оптической волны
в каждом из каналов. В случаях когда информация передается за сче.'
амплитудной модуляции и некогерентно демодулируется. а также
в системах связи с прямым детектированием нелинейные изменения
Фазы малосущественны. Однако, если используются методы коге-
Рентной демодуляции, такие изменения фазы могут сильно ограни-
ограничить работу системы. Для того чтобы лучше поня гь это ограничение,
212 Глава 7
рассмотрим JW-канальную систему связи. Амплитуда Aj излучения
в каждом канале (/ = 1 — М) подчиняется уравнению распростра-
распространения, аналогичному G.1.17). Для типичных скоростей передачи
информации ~ 1 Гбит/с импульс, соответствующий битовому про-
промежутку, достаточно широк, и при рассмотрении нелинейных эф-
эффектов дисперсионные эффекты оказываются несущественными.
В этом случае уравнение G.1.17) может быть записано в виде
?А а м
-31 + - А, = /у(И/ + 2 ? \Am\*)Aj, G.6.1)
CZ L т ф]
где предполагается, что потери в световоде а и нелинейный параметр
у одинаковы для всех каналов. Вклад ФКМ от всех каналов включен
в уравнение G.6.1). Возникающая система М связанных уравнений
может быть решена аналитически; результат решения
^jj), G.6.2)
где Pj-мощность излучения, распространяющегося в 7-м канале.
ф, = у^фф(/>, + 2 ?/>„,), G.6.3)
тф'1
^эфф определяется выражением G.2.12). Обычно длина световода
L превышает длину поглощения (L» 1/а), и можно считать, что
эффективная длина /,эфф « 1/а.
В зависимости от того, осуществлялась для передачи информации
модуляция амплитудная или фазовая, следует различать два случая.
Сначала рассмотрим случай фазовой модуляции. Поскольку мощ-
мощность в каждом канале остается постоянной, нелинейное изменение
фазы одинаково для всех битовых импульсов. Вообще говоря,
фундаментальное ограничение для системы с фазовой модуляцией
возникает из-за флуктуации фазы. Но поскольку ф7-, согласно G.6.3),
зависит от мощности, флуктуации мощности приводят к флуктуа-
циям фазы, а это уменьшает отношение сигнал/шум на выходе
световода. Если для простоты предположить, что средняя мощность
во всех каналах одинакова, одинаково и стандартное отклонение ар.
Тогда стандартное отклонение флуктуации фазы принимает вид [47]
Y^P + 2yap I/2 G64)
а а
если в G.6.3) подставить /,эфф ~ 1/а. Два слагаемых представляют
вклады ФСМ и ФКМ в стф. Оценивая порядок величины, получаем
устР/а~0.02 при у ~ 1 Вт км ', а = 0,046 км @,2 дБ/км) и
Стр = 0,1 мВт (это обычные значения для оптических систем связи
в диапазоне 1,55 мкм). Вклад ФСМ в Стф пренебрежимо мал. Вклад
Фазовая кросс-модуляция 213
ФКМ может стать значительным в зависимости от числа каналов.
Оценки показывают, что Стф = 0,15 соотве гствует ухудшению чув-
чувствительности примерно на 0,5 дБ [80]. Из выражения G.6.4) видно,
что действие ФКМ на работу системы связи становится угрожающим
только при М > 20.
Теперь рассмотрим случай когерентной системы связи с ампли-
амплитудной модуляцией. Если используется фазочувствительное (гомо-
динное) детектирование, фаза ф; будет изменяться от одного би-
битового импульса к другому в зависимости от битовой структуры
соседних каналов. В худшем случае сдвиг фазы, вызванный ФКМ,
принимает вид
Дф = 2{у/а){М - \)Р, G.6.5)
где предполагается, что мощность Р одинакова во всех каналах. Если
в качестве приемлемой величины принять Аф ^ 0,1, мощность
в каждом канале будет ограничена величиной
Р< °'°5а . G.6.6)
Y(M-l) }
Это ограничение означает Р < 1 мВт даже при М = 5.
Эффекты ФКМ наблюдались в эксперименте с двумя каналами
[48]. Излучение от двух полупроводниковых лазеров, работающих на
длинах волн вблизи 1,3 и 1,5 мкм, вводилось в 15-километровый
отрезок одномодового световода. Сдвиг фазы излучения на длине
волны 1,5 мкм, вызванный излучением на 1,3 мкм, измерялся при
помощи интерферометра. При Р = 1 мВт был экспериментально
зарегистрирован сдвиг фазы Дф = 0,024. Это значение находится
в хорошем согласии с величиной 0,022, которая следует из G.6.5).
ЛИТЕРАТУРА
1. Лхманов С. Л., Сухорукое А. П.. Чиркин А. С. ЖЭТФ, 1968, т. 55, с. 1430.
2. Akhmanov S. A., Khokhlov R. К, Sukhorukov A. P.. in: Laser Handbook, vol. 2,
ed. by F.T. Arecchi, E.O. Schulz-Dubois, North-Holland, Amsterdam. 1972,
Ch. E3.
3. Maker P.D., Terhune R.W., Savage CM. Phys. Rev. Lett., 12, 507 A964).
4. Maker P.D., Terhune R.W., Phys. Rev., A137, A801 A965).
5. Mayer G., Gires F.. Compt. Rend. Acad. Sci., 258, 2039 A964).
6. Duguctv M.A.. Harisen J. W., Appl. Phys. Lett., 15, 192 A969).
7- Owyoung A., Hellwarth R.W.. George N.. Phys. Rev., B5, 628 A972).
8. Duguav M.A., in: Progress in Optics, vol. 14, ed. by E. Wolf, North-Holland,
Amsterdam, 1976, p. 163.
9. Hellwarth R. W., Prog. Quantum Electron., 5, 1 A977).
JO. Phu-Xuan N.G.. Rivoire G., Opt. Acta, 25, 233 A978).
"• Shen Y.R, The Principles of Nonlinear Optics, Wiley, New York, 1984. Ch. 16
[Имеется перевод: Шен И. Р. Принципы нелинейной оптики.-М.: Наука,
1989].
'2. Stolen R.H., Ashkin A., Appl. Phys. Lett., 22, 294 A973).
214 Глава 7
13. Dzledzk-J.M.. Stolen R.H., Aslikin A.. Appl. Opt.. 20. 1403 A981). .
14. Anal J.L., et ah. Opt. Commun.. 49, 405 A984).
15. Kitayama K., Kimura Y, Seikai S., Appl. Phys. Lett. 46, 623 A985).
16. Дианов E. M. и др.- Квант, электрон., 1987, т. 14. с. 822.
17. Morioka Т.. Samwatari М., Takada A., Elektron. Lett., 23, 453 A987).
18. Byron КС, Electron. Lett., 23, 1324 A987).
19. Morioka Т., Samwatari M.. Electron. Lett., 23, 1330 A987).
20. White I.H.. Pent у R.V.. Epwarth RE., Electron. Lett., 24, 340 A988).
21. Stolen R.H.. Rotinetm J., Ashkin A., Opt. Lett.. 7, 512 A982).
22. \'ikolnus В.. Grischkowskv D., Balani A.C., Opt. Lett., 8, 189 A983).
23. Halas N.J., Grischkowskv D.. Appl. Phys. Lett., 48, 823 A986).
24. Kitavama K., Kimura Y. Seikai S., Appl. Phys. Lett., 46, 317 A985); 46, 623
A985).
25. Kimura Y. et ai. Electron. Lett., 22, 277 A986).
26. Crosignani B. et ah. Opt. Lett.. 10, 89 A985).
27. Winful H.G., Appl. Phys. Lett., 47, 213 A985).
28. Crosignani В.. Di Porto P., Opt. Acta, 32, 1251 A985).
29. Daino В.. Gregori G.. Wabnitz S.. J. Appl. Phys. 58, 4512 A985); Opt. Lett., 11,42
A986).
30. Winful H.G.. Opt. Lett., 11, 33 A9&6).
31. Gregori G.. Wabnitz S.. Phys. Rev. Lett., 56, 600 A986).
32. Matera ?.. Wabnitz S.. Opt, Lett., 11, 467 A986).
33. Winftd H.G.. Ни A., Opt. Lett., 11. 668 A986).
34. Trillo S. et ah. Appl. Phys., 49, 1224 A986).
35. Vatarescu A., Appl. Phys. Lett., 49, 61 A986).
36. Wabnitz S.. Phys. Rev. Lett., 58. 1415 A987).
37. Mecozzi A. et ah. Opt. Lett.. 12, 275 A987).
38. Kimura Y.. Makazawa M.. Jpn. J. Appl. Phys., 26. 1503 A987).
39. Caglioti E., Trillo S.. Wabnitz S.. Opt. LetU 12, 1044 A987).
40. Blow K.J.. Doran N.J., Wood D.. Opt. Lett., 12, 202 A987).
41. Menruk C.R., IEEE J. Quantum Electron., QE 23, 174 A987).
42. Men'vuk C.R., Opt. Lett., 12, 614 A987).
43. Meiivuk C.R.. Opt. Soc. Am., B5, 392 A988).
44. Chri'stodotilidvs D.N.. Joseph R.I., Opt. Lett., 13, 53 A988).
45. Boardman A.D.. Cooper G.S.. J. Opt. Soc. Am., B5, 403 A988); J. Mod. Opt., 35,
407 A988).
46. GerstenJ.L. Alfano R. R.. Belie M., Phys. Rev., A21, 1222 A980).
47. Chraplyvy A.R.. Marcuse П.. Henry PS.. J. Lightwave Technol., LT-2, 6 A984).
48. Chraphr'y A.R.. Sione J Electron. Lett., 20. 996 A984).
49. Manassah J.T. et ah. Phys. Lett., A133, 242 A985).
50. Alfano R.R. et ah. Opt. Lett., 14, 626 A986).
51. Schadt D.. Jaskorzynska В.. Osterberg V.. J. Opt. Soc. Am., B3, 1257 A986).
52. Warn M.N. et «/..Opt. Lett.. 12, 625 A987).
53. Alfano R.R. et ah. Appl. Opt., 26, 3491 A987).
54. Agrawal G.P.. Phys. Rev. Lett., 59, 880 A987).
55. Schadt D.. Jaskorzynska В.. Electron. Lett., 23. 1090 A987); J. Opt. Soc. Am., B4,
856A987); 5, 2374 A988).
56. Manassah J.T.. Appl. Opt.. 26, 3747 A987); Opt. Lett.. 13. 755 A988).
57. Baldeck PL.. Ho P.P.. Alfano R. R.. Rev. Phys. Appl, 22. 1677 A987).
58. Alfano R.R., Ho P.P.. IEEE J. Quantum Electron., QE-24, 351 A988).
59. Baldeck PL.. Alfano R.R.. AgramilG.P.. Appl. Phys. Lett., 52, 1939 A988).
60. Baldeck P. L., Alfano R. R.. Agrawol G. P.. Int. Conf. Ultrafast Phenomena,
Paper PD2, July 12 15 A988).
61. Gouveia-Neto A.S. et ah. Opt. Lett., 13, 901 AУ88).
62. Wabnitz S., Phys. Rev., A38, 2018 A988).
63. AgnnvalG.P.. Appl. Phys. Lett, 38, 505 A981).
Фазовая кросс-модуляция 215
64. Kaplan A.E., IEEE J. Quantum Electron., QE-17, 118/A981); Opt. Lett., 6, 360
A981).
65. Kaplan A.E., Mevstre P.. Opt. Lett., 6, 590 A981); Opt. Commun. 40, 229 A982).
66 Agrawal G. P.. IEEE J. Quantum Electron., QE-18, 214 A982).
67. Silberberg Y.. Bar-Joseph I., Phys. Rev. Lett., 48, 1541 A982); J.Opt. Soc. Am.,
Bl, 662 A984).
68 Nakatsuka H. et a!.. Phys. Rev. Lett., 50, 109 A983).
69 Ezekiel S. Davis J.L.. Hellwarth R. W.. Opt. Lett., 7, 457 A982).
70 Bergh R.A.. Lefevre H.C.. Shaw H.J., Opt. Lett., 7, 282 A982).
71 Bergh R.A., et a!.. Opt. Lett., 7, 563 A982).
72. Peiermann K., Opt. Lett., 7, 623 A982).
73. Frigo N.J. et al. Opt. Lett., 8, 119 A983).
74. Crosignani В., Yariv A., J. Lightwave Technol., LT-3, 914 A985).
75. Кравцов Н.В.. Серкин В.Н. Квант, электрон., 1983, т. 10, с. 182.
76. Bergh R.A.. Lefevre Н.С.. Shaw H.J.. J. Lightwave Technol.. LT-2, 91 A984).
77. Sagnac G., Compt. Rend. Acad. Sci., 95, 708 A913).
78. Lugiaw L.A.. in: Progress in Optics, vol. 21, ed. by. E. Wolf, North-Holland,
Amsterdam, 1984.
79. Gibbs H. M.. Optical Bistability: Controlling Light with Light, Academic,
Orlando, 1985. [Имеется перевод: Гиббс X. Оптическая бистабильность:
Управление светом с помощью света,-М.: Мир, 1988].
80. Prabhu V. К., IEEE Trans. Aero. Elect. Syst., AES-12, 275 A976).
Глава 8
ВЫНУЖДЕННОЕ КОМБИНАЦИОННОЕ
РАССЕЯНИЕ (ВКР)
Вынужденное комбинационное рассеяние (ВКР)-нелинейный
процесс, который позволяет использовать световоды в качестве
широкополосных ВКР-усилителей и перестраиваемых ВКР-лазеров.
Но, с другой стороны, этот же процесс может резко ограничить
характеристики многоканальных оптических линий связи из-за пе-
переноса энергии из одного канала в соседние каналы. В этой главе
рассматриваются как применения ВКР, так и паразитные эффекты,
связанные с ним. В разд. 8.1 представлены основы теории ком-
комбинационного рассеяния, причем подробно обсуждается понятие
порога ВКР. В разд. 8.2 рассмотрено ВКР непрерывного или
квазинепрерывного излучения. Там же обсуждаются характеристики
волоконных ВКР-лазеров и усилителей и рассматриваются пере-
перекрестные помехи в многоканальных оптических линиях связи, обус-
обусловленные ВКР. ВКР сверхкоротких импульсов (СКИ), возникающее
при импульсах накачки длительностью менее 100 пс, рассмотрено
в разд. 8.3 и 8.4. В разд. 8.3 рассматривается случай положительной
дисперсии групповых скоростей, а разд. 8.4 посвящен изучению
солитонных эффектов при ВКР, возникающем в области отрица-
отрицательной дисперсии групповых скоростей волоконного световода.
Особое внимание уделено совместному действию дисперсионного
уширения импульса с фазовой самомодуляцией (ФСМ) и фазовой
кросс-модуляцией (ФКМ).
8.1. КОМБИНАЦИОННОЕ (РАМАНОВСКОЕ) УСИЛЕНИЕ
И ПОРОГ ВКР
При спонтанном комбинационном рассеянии во многих средах
небольшая часть (обычно ~10 6) мощности излучения накачки
преобразуется в излучение с более низкой частотой, причем величина
частотного сдвига определяется колебательными модами среды.
Этот процесс, называемый также эффектом Рамана [1], в квантовой
механике описывается как рассеяние фогона на молекуле, в процессе
которого молекула совершает переход между колебательными со-
состояниями, а частота фотона уменьшается. Исходное излучение
служит накачкой для генерации излучения на смещенной частоте.
Вынужденное комбинационное рассеяние
217
6 12 18 24 30
Частотный сдвиг (ТГц)
36
42
Рис. 8.1. Измеренный спектр комбинационного усиления для плавленого
кварца при накачке с длиной волны Хр = 1 мкм. Максимальное значение
усиления уменьшается с ростом X [11].
называемого также стоксовым излучением. В 1962 г. было замечено
[2], что при очень интенсивной накачке может возникать новое
явление-ВКР, при котором интенсивность стоксовой волны воз-
возрастает внутри среды так быстро, что в эту волну переходит большая
часть энергии накачки. После опубликования данного результата
ВКР широко исследовалось [3-8]. В случае непрерывной накачки
начальный рост интенсивности стоксовой волны описывается соот-
соотношением
!¦-'•'¦•
(8.1.1)
где ^-интенсивность стоксовой волны, 1р-интенсивность волны
накачки, a gR —коэффициент комбинационного усиления (рамановский
коэффициент). Последний связан с сечением спонтанного КР [3, 7],
которое можно измерить экспериментально. Из общей теории сле-
следует, что gR связан с мнимой частью нелинейной восприимчивости
[8]. которая может быть вычислена в. квантовомеханическом при-
приближении.
Коэффициент комбинационного усиления gR в одномодовых
световодах из кварцевого стекла был измерен Столеном и др. [9, 10]
в ранних экспериментах по ВКР. В общем случае gR зависит от
состава сердцевины световода и может существенно меняться в
218 Глава 8
зависимости от использования различных добавок. На рис. 8.1
показана зависимость yR плавленого кварца от частотной отстройки
при накачке на длине волны 1 мкм. Величину дк для других длин волн
накачки можно получить, используя обратную зависимость д1{ от Хр.
Спектр на рис. 8.1 был получен из измерений сечения спонтанного
КР. Измерение gR с использованием рамановского усиления в схеме
с накачкой и затравочным сигналом дает примерно те же значения
[Ю].
Самое существенное свойство комбинационного усиления в све-
световодах из плавленого кварца - большой частотный диапазон gR (до
40 ТГц) с широким максимумом усиления возле 13 ТГц. Такое
поведение связано с некристаллической природой стекла. В аморфных
материалах, таких, как плавленый кварц, полосы частот молеку-
молекулярных колебаний перекрываются и создают континуум [12]. В ре-
результате комбинационное усиление в кварцевых световодах существует
в широком диапазоне частот в отличие от большинства сред, где оно
возникает на специфических, вполне определенных частотах. Благо-
Благодаря этому свойству световоды могут действовать как широкополос-
широкополосные усилители, о чем будет сказано ниже.
Чтобы увидеть, как возникает процесс ВКР, рассмотрим непре-
непрерывное излучение накачки на частоте юр, распространяющееся
в световоде. Если пробное излучение на частоте tos перекрывается
с накачкой на входе световода, оно будет усиливаться за счет ВКР,
пока разница частот юр — cos лежит внутри комбинационной полосы
усиления (см. рис. 8.1). Если в световод вводится только излучение
накачки, спонтанное КР дает слабый сигнал, который действует как
пробный и усиливается по мере распространения. Поскольку КР
генерирует фотоны на всех частотах внутри полосы усиления,
усиливаются все частотные компоненты. Однако частотная компо-
компонента, для которой коэффициент gR максимален, возрастает быстрее
всего. В случае чистого плавленого кварца yR максимален для
частоты, смещенной от частоты накачки приблизительно на 13.2 ТГц
D40 см). Оказывается, когда мощность накачки превышает по-
пороговое значение [13], эта компонента усиливается почти экспо-
экспоненциально. Таким образом, ВКР приводит к генерации стоксовой
волны, частота которой определяется пиком комбинационного
усиления. Соответствующее смещение частоты называют иногда
стоксовым (или рамановским) частотным сдвигом.
Для нахождения порога ВКР следует рассмотреть взаимодействие
между волной накачки и стоксовой волной. В случае непрерывного
излучения это взаимодействие подчиняется системе двух связанных
уравнений:
^ s-as/,, (8.1.2)
Вынужденное комбинационное рассеяние 219
f =-%,/,/.-«,/,. (8-1.3)
где коэффициенты as и ар относятся к потерям в световоде на
стоксовой частоте и на частоте накачки. Эти уравнения могут быгь
строго выведены из уравнений Максвелла (разд. 2.1). Их также
можно получить, рассмотрев процессы рождения и уничтожения
фотонов в каждой волне. Легко проверить, что в отсутствие потерь
Это уравнение означает, что общее число фотонов при ВКР остается
постоянным.
Хотя для полного описания процесса ВКР уменьшение интенсив-
интенсивности волны накачки за счет оттока энергии в стоксову волну
(истощение накачки) должно быть учтено, при оценке порога ВКР им
можно пренебречь [13]. Если в уравнении (8.1.3) отбросить первый
член, ответственный за истощение накачки, оно легко решается.
Подставив решение в уравнение (8.1.2), получаем
где /0 - исходная интенсивность накачки при г = 0. Результатом
интегрирования (8.1.5) является
/s (L) = /s @) exp (GR Io ?эфф - as L), (8.1.6)
где
г г 1 ехп ( cit/^T /о | *7\
Из-за поглощения волны накачки в (8.1.6) вместо действительной
длины световода L входит эффективная длина ?эфф из (8.1.7).
Для использования (8.1.6) требуется значение Is @) при 2 = 0. На
практике ВКР вырастает из спонтанного КР, возникающего на всем
протяжении световода. Смитом [13] было показано, что это эквива-
эквивалентно наличию на входе в световод одного фотона на моду. Можно
рассчитать мощность стоксовой волны, рассмотрев усиление каждой
частотной компоненты с энергией Тгю в соответствии с (8.1.6) и затем
выполнив интегрирование по всему спектру комбинационного уси-
усиления, т.е.
X)
/)S(L)= J 7ноехр[0кAо)/оЬэфф-а5?]Ло, (8.1.8)
220 Глава 8
где световод предполагается одномодовым. Частотная зависимость
gR(u>) показана на рис. 8.1. Несмотря на то что функциональная
форма gR неизвестна, интеграл в (8.1.8) можно оценить методом
наискорейшего спуска, поскольку главный вклад в интеграл дает
узкая область вблизи пика усиления на частоте ю = ios. В результате
P.(L) = /»3*exp [0КК)/О?эфф - O.L]; (8.1.9)
здесь эффективная входная мощность при z = 0
Йсо5Яэфф, (8.1.10)
где
( * )"' №f) ¦ (8.1.11)
По физическому смыслу Бэфф-эффективная ширина полосы стоксова
излучения с центром в пике усиления при to = tos. Хотя Вэфф зависит
от интенсивности накачки и длины световода, спектральная ширина
пика максимального усиления (рис. 8.1) позволяет оценить ее по
порядку величины.
Порог ВКР определяется как такая мощность накачки в начале
световода, при которой на выходе световода мощность стоксовой
волны становится равной мощности накачки [13], или
PS(L) = Pp(L) = Poexp(-apL), (8.1.12)
где
Л>='оЛэфф, (8.1.13)
Ро -входная мощность накачки и /4эфф - эффективная площадь сердце-
сердцевины. Более строгая оценка показывает, что /4эфф приблизительно
дается соотношением B.3.29), если предположить, что волна накачки
(стоксова волна) распространяются в одной моде. В случае мно-
гомодового световода 1/Лэфф равняется интегралу перекрытия
G.1.16). Используя (8.1.9) и (8.1.12) и подстановку ао =: ар, получаем
условие порога в виде
РТехр{дкР0Ьэфф/Аэфф) = Ро, (8.1.14)
где />$¦ зависит от Ро также и через (8.1.10) и (8.1.11). Решение (8.1.14)
дает критическую мощность накачки, требуемую для достижения
порога ВКР. В предположении лоренцевой формы спектра усиления
критическая мощность накачки с хорошей точностью дается вы-
выражением [13]
Ьэфф/Лэфф^16. (8-1-15)
Аналогичный образ можно провести для случая, когда стоксова
волна распространяется навстречу волне накачки. Пороговое условие
в этом случае также дается выражением (8.1.15), но с числовым
Вынужденное комбинационное рассеяние 221
фактором 20 вместо 16. Поскольку при заданной мощности накачки
первым достигается порог для ВКР в прямом направлении. ВКР
в обратном направлении в световодах обычно не наблюдается.
Конечно, комбинационное усиление можно использовать для уси-
усиления встречного сигнала. Отметим также, что при выводе (8.1.15)
поляризация стоксовой волны и волны накачки в световоде пред-
предполагается неизменной. Если поляризация не сохраняется, порог ВКР
возрастает в 1-2 раза. В частности, для полностью деполяризо-
деполяризованного излучения он возрастает в 2 раза.
Несмотря на различные приближения, сделанные при выводе
условия (8.1.15), оно позволяет предсказать порог ВКР довольно
точно. Для длинных световодов, таких, что apL» 1, ?эфф ~ 1 ар. На
длине волны 1,55 мкм, в области минимальных оптических потерь
световодов (около 0,2 дБ/км), L3<t)<t) ~ 20 км. Если принять типичное
значение Лэфф = 50 мкм2, предсказанный порог ВКР составит около
600 мВт. В одноканальнмх системах оптической связи возникновение
ВКР маловероятно, поскольку типичная мощность, вводимая в све-
световод, составляет ~ 1 мВт. Для солитонных систем оптической связи
требуется более высокая мощность-около 40-50 мВт (см. разд. 5.4).
Эта величина все еще ниже критической. В видимом и ближнем
ИК-диапазонах типичные значения Лэфф 10-20 мкм2. Для такого
световода длиной 1 м формула (8.1.15) дает Pqp ~ 100 Вт. Поскольку
такие мощности легкодостижимы (например, от MAr-Nd-лазеров),
ВКР можно наблюдать в световодах длиной всего несколько метров.
В рамках изложенного рассмотрения нельзя объяснить рост
стоксовой волны выше порога ВКР, поскольку до сих пор мы
пренебрегали эффектом истощения накачки. Для учета этого эффекта
следует решить систему уравнений (8.1.2), (8.1.3). Эти уравнения
могут быть решены аналитически [14] в спепиальном случае as = ар.
Результаты показывают, что в этом случае пороговое условие (8.1.15)
остается довольно точным. Но когда порог ВКР достигнут, энергия
из волны накачки быстро перекачивается в стоксову волну. Теория
предсказывает полное перекачивание мощности накачки в стоксову
волну (исключая потери в световоде). На практике, однако, стоксова
волна, если ее мощность становится достаточной для того, чтобы
Удовлетворить (8.1.15), служит накачкой для генерации стоксовой
волны второго порядка. Такой процесс каскадного ВКР может
приводить к генерации многих порядков стоксовых волн, число
которых зависит от входной мощности накачки.
Изложенная теория ВКР непрерывного излучения (накачка по-
постоянной интенсивности) требует модификации, когда в качестве
накачки используются оптические импульсы. Почти всегда в све-
световодах используется именно импульсная накачка, поскольку при
накачке непрерывным излучением доминируют вынужденное рассея-
рассеяние Мандельштама-Бриллюэна (ВРМБ), которое благодаря более
222 Глава 8
низкому порогу подавляет ВКР (сМ- гл. 9). ВРМБ может быть
уменьшено или подавлено при использовании импульсов накачки
длительностью < 10 не. Если порог ВКР достигнут, каждый импульс
накачки генерирует стоксов импульс с центральной частотой tos,
смещенной вниз от частоты накачки примерно на 13 ТГц. Дина-
Динамическое описание ВКР в световодах заметно упрощается, если
считать отклик среды мгновенным. Справедливость такого допу-
допущения подтверждается тем, что широкий спектр усиления на рис. 8.1
предполагает время отклика, лежащее в фемтосекундном диапазоне.
Для импульсов накачки длительностью более 100 фс время отклика
мною меньше длительности импульса. Тогда взаимодействие между
стоксовым импульсом и импульсом накачки подчиняется системе
связанных уравнений, учитывающих эффекты комбинационного
усиления, истощения накачки, ФСМ, ФКМ и дисперсии. Эти уравне-
уравнения можно вывести из соответствующих уравнений разд. 2.3 в пред-
предположении хC) комплексной, в которой мнимая часть отвечает за
комбинационное усиление. Процедура аналогична той, что исполь-
использовалась в разд. 7.1.1 для получения G.1.17) и G.1.18). Действительно,
те же уравнения получаются, если коэффициенты поглощения а1 и а2
рассматривать как полные коэффициенты поглощения и заменить на
al=ap + gp\As\2Ap, (8.1.16)
а2 = ар-gs\Ap\2As. (8.1.17)
Если вместо индексов 1 и 2 мы будем использовать индексы pus для
обозначения соответственно полей стоксовой волны и волны накачки
и подставим (8.1.16) и (8.1.17) в G.1.17) и G.1.18), уравнения связанных
амплитуд примут вид
-JA'=
(8.1.18)
Ap\2As, (8.1.19)
где vgJ-групповая скорость, p2j— дисперсия групповых скоростей,
у,-коэффициент нелинейности (определенный в G.1.19)) и / = р или л.
Коэффициенты усиления gs и др связаны с пиковым значением дк:
Яш = 9r/A^, g,~(<apf<atHt. (8.1.20)
Решенияуравнений (8.1.18) и (8.1.19) обсуждаются в разд. 8.3, где
Вынужденное комбинационное рассеяние 223
мы рассмотрим ВКР пикосекундной накачки. Важная новая деталь
здесь-разница групповых скоростей, которая ограничивает процесс
ВКР временем, в течение которого стоксов импульс к импульс
накачки перекрываются. Новый масштаб длины-длина группового
разбегания-может быть введена выражением A.2.14) или
Lw=T0/\v;,l-v-l\, (8.1.21)
где То-длительность импульса накачки. Характерна Lw ~ 1 м в види-
видимой области для То ~ 5 пс. Для импульсов накачки длительностью
Гп ^ 1 не Lw превышает 200 м и обычно больше длины световодов,
используемых для наблюдения ВКР. Для таких импульсов дисперси-
дисперсионные эффекты пренебрежимо малы, и в таком квазинепрерывиом
режиме работает теория, развитая для непрерывного излучения на-
накачки. Действительно, уравнения (8.1.2) и (8.1.3) можно получить из
(8.1.18) и (8.1.19), если пренебречь производными по времени и при-
принять Ij = МуР/^эфф 0' = Р или s)- Экспериментальные результаты по
ВКР квазипостоянной накачки обсуждаются в следующем разделе,
а в разд. 8.3 рассматривается ВКР пикосекундных импульсов накачки.
Следует подчеркнуть, что уравнения (8.1.18) и (8.1.19) неприменимы
для накачки фемтосекундными импульсами, ширина спектра которых
превышает величину комбинационного сдвига. В таком случае следует
использовать обобщенное уравнение распространения B.3.35).
8.2. КВАЗИНЕПРЕРЫВНОЕ ВКР
После первого наблюдения ВКР [9] в световодах широко прово-
проводились исследования ВКР при накачке импульсами длительностью
~1 100 нс, что соответствует квазинепрерывному режиму [15-30].
Параллельно проводились работы по многопроходному ВКР, когда
световод, помещенный внут рь резонатора, образует перестраиваемый
ВКР-лазер [31 49]. Третье направление-использование ВКР для
усиления сигналов и создание в итоге волоконных ВКР-усилителей
[50 70]. В этом разделе обсуждаются все три направления исследова-
исследований ВКР в световодах. В отдельном подразделе рассматривается
также применение ВКР-усиления для многоканальных систем оптиче-
оптической связи.
8.2.1. ОДНОПРОХОДНАЯ ГЕНЕРАЦИЯ СТОКСОВЫХ
КОМПОНЕНТ
Первая экспериментальная демонстрация [9] ВКР в световодах
была проведена в видимой области при накачке импульсами второй
гармоники Nd: ИАГ-лазера на длине волны 532 нм. Для генерации
стоксова излучения на 545 нм в одномодовом световоде длиной 9 м
с Диаметром сердцевины 4 мкм требовалась накачка мощностью
224
Глава 8
около 75 Вт. В последующих экспериментах [16, 18] для генерации
ВКР использовались импульсы ИК-излучения ИАГ-лазера длитель-
длительностью 150 не на длине волны 1.06 мкм. В одном из экспериментов
[18] стоксова линия первого порядка на 1,12 мкм наблюдалась при
мощности накачки 70 Вт. Стоксовы линии высших порядков возника-
возникали при более высоких мощностях накачки, когда мощность стоксовой
компоненты становилась достаточной для накачки компоненты сле-
следующего порядка. На рис. 8.2 показан спектр при накачке мощ-
мощностью 1 кВт с отчетливо различными пятью стоксовыми линиями.
Каждая следующая стоксова линия шире предыдущей. Такое ушире-
ние, обусловленное конкурирующими нелинейными процессами, пре-
препятствует генерации стоксовых линий высших порядков. Недавние
эксперименты показали, что в видимой области возможна генерация
стокеовых линий вплоть до 15-го порядка [21, 22].
В этих экспериментах не делалось попыток измерить спектр
каждой стоксовой линии с высоким разрешением. В недавней работе
[27] для. изучения развития процесса ВКР в кварцевых световодах
изучалась форма стоксовой компоненты первого порядка, получен-
полученной при распространении по световоду длиной 100 м импульсов
накачки длительностью 1 не от аргонового лазера с синхронизацией
мод (кр = 514,5 км). На рис. 8.3 показаны спектры, наблюдавшиеся
при трех уровнях мощности накачки. На всех спектрах заметны два
пика-широкий на 440 см"* A3,2 ТГц) и узкий на 490 см^1 A4,7 ТГц).
При увеличении мощности накачки пиковая мощность широкой
линии достигает насыщения, в то время как узкий пик продолжает
15О
'1,5:
¦§100
л
\-
u
|75
О
2
ю
О
"=25
n
. 840мВт
-
-
-
s, s2 s3
•
(I
III
\\J\
I I I I I
1,O 1,1
1,2 1,3 1,4 1,5
Длина волны ImknT)
1,6
Рис. 8.2. Спектр ВКР с
пятью стоксовыми компо-
компонентами Sj — S5 при накачке
импульсами на длине волны
1,06 мкм. Вертикальная ли-
линия показывает выходную
мощность излучения накач-
накачки. Пиковая мощность из-
измерялась после монохрома-
тора с разрещением 1,5 нм
[18].
Вынужденное комбинационное рассеяние
225
в
S7
S6
§5
о-
?4
?3
э
I2
п
1 ' 1 1 1 1 J '
- \р=514,5нм
н- L= ЮОм
Рду=1,5 -
-
-
1
' "Мм
— ? —
35О 400 450 500
Частотный сдвиг (см)
О,9 1,1 1,3 1,5 1,7 1,9 2,1 2,3
Средняя мощность накачки
СВт)
Рис. 8.3. Зависимость спектра стоксовой линии первого порядка от средней
мощности накачки. Пиковая мощность накачки приблизительно в 12 раз
превышает среднюю, а-стоксовы спектры при трех мощностях накачки;
б- зависимость мощностей пиков спектра стоксовой линии от мощности
накачки [27].
возрастать. Эти изменения также показаны на рис. 8.3.
Двухпиковая структура спектра ВКР становится понятной, если
обратить внимание на то, что основной пик спектра комбинационного
усиления на рис. 8.1 в действительности состоит из двух пиков,
положение которых точно соответствует пикам спектра ВКР на
рис. 8.3. Подробная численная модель (в которой учитывается форма
спектра комбинационного усиления и эффекты как вынужденного, так
и спонтанного КР) предсказывает форму линии, соответствующую
результатам эксперимента [27]. Качественно описать процесс можно
следующим образом. За счет спонтанного КР происходит генерация
излучения во всей полосе комбинационного усиления. После прохож-
прохождения отрезка световода эти слабые сигналы усиливаются с соответ-
соответствующими коэффициентами усиления и к ним добавляется спонтан-
спонтанное излучение на данном отрезке. При небольших мощностях накачки
спектр стоксова излучения s (со) выгладит как спектр КР, искаженный
процессом экспоненциального усиления, т.е.
Пю)~ехр@к(ш)). (8.2.1)
При увеличении мощности накачки компонента с отстройкой
440 см, как более высокочастотная, может служить накачкой
Для ВКР-усиления низкочастотной компоненты, отстроенной на
490 см. Это в точности соответствует картине рис. 8.3. В конце
концов мощность стоксова излучения становится достаточной для
накачки стоксовой компоненты второго порядка. Данная модель
построена в приближении постоянной накачки, однако она достаточ-
достаточно точна для качественного объяснения графиков на рис. 8.3, посколь-
поскольку для импульсов длительностью > 1 не дисперсионные эффекты
226 Глава 8
незначительны. Когда используются импульсы накачки короче 1 не.
становится необходимым учет дисперсионных эффектов, в частности
группового запаздывания, приводящего к разбеганию импульсов.
Эти эффекты рассмотрены в разд. 8.3.
8.2.2. ВОЛОКОННЫЕ ВКР-ЛАЗЕРЫ
Важным применением явления ВКР в световодах стало развитие
волоконных ВКР-лазеров [31-49]. Такие лазеры не только
имеют более низкий порог, чем однопроходное ВКР, но и могут
перестраиваться в широком частотном диапазоне (~10ТГц). На
рис. 8.4 схематически показан волоконный ВКР-лазер. Отрезок одно-
модового световода помещен внутрь резонатора Фабри-Перо, обра-
образованного частично отражающими зеркалами Mt и М2. Резонатор
обеспечивает резонансную частотно-избирательную обратную связь
для стоксова излучения, возникающего в световоде благодаря ВКР.
Внутрирезонаторная призма позволяет перестраивать длину волны
лазерного излучения путем поворота зеркала М2. Порог генерации
лазера соответствует мощности накачки, при которой комбинацион-
комбинационное усиление за обход резонатора компенсирует потери в резонаторе,
состоящие из потерь на зеркалах и потерь при переводе отраженного
от зеркал излучения обратно в световод. Если принять потери за
обход резонатора равными обычному значению 10 дБ, то пороговым
условием будет
G = ехрB.9к />0Ьэфф/Лэфф) = 10, (8.2.2)
гДе ^эфф Л1151 световода длиной L дается уравнением (8.1.7). Если
световод не поддерживает поляризацию, то gR в (8.2.2) понижается
вдвое из-за относительной деполяризации волны накачки и стоксовои
волны вдоль световода [40]. Сравнение условий (8.1.15) и (8.2.2)
показывает, что пороговая мощность накачки в волоконном ВКР-
лазере по крайней мере на порядок меньше, чем при однопро-
однопроходном ВКР.
При первой демонстрации [9] волоконного ВКР-лазера использо-
использовался короткий световод A= 1,9 м) и пороговая мощность была
Накачка
Рис. 8.4. Схема перестраиваемого ВКР-лазера. Зеркала М, и М2 образуют
резонатор Фабри Перо. Микролинзы служат для ввода и вывода излучения из
световода. Внутрирезонаторная призма обеспечивает перестройку лазера при
вращении зеркала М2 [34].
Вынужденное комбинационное рассеяние 227
относительно высока (около 500 Вт). В недавних экспериментах [31,
32] использовались световоды большей длины (L ~ 10 м) и порог был
понижен до уровня 1 Вт. Это позволило получить непрерывный
режим работы волоконных ВКР-лазеров в области 0.50-0.53 мкм при
постоянной накачке от аргонового лазера. ВРМБ подавлялось благо-
благодаря тому, что спектральная ширина многомодовой накачки была
много больше ширины линии ВРМБ-усиления (см. разд. 9.1). Исполь-
Использование призмы позволяло перестраивать длину волны лазерного
излучения в диапазоне около 10 нм (^ 10 ТГц) [32, 33]. При высоких
мощностях накачки в световоде генерировались стоксовы компонен-
компоненты высших порядков, которые отклонялись призмой. При добавле-
добавлении в схему отдельных зеркал для каждой стоксовой компоненты
можно получить одновременную генерацию на нескольких длинах
волн, каждая из которых может перестраиваться поворотом соот-
соответствующего зеркала [37]. В другой работе [38] в кольцевом
резонаторе были получены пять порядков стоксовых компонент. При
накачке от Nd: ИАГ-лазеров волоконные ВКР-лазеры работали в
ИК-диапазоне 1,0-1,6 мкм, наиболее подходящем для оптической
связи [35, 39]. Была получена также генерация в УФ при накачке
эксимерными лазерами [45, 46].
Когда ВКР-лазер накачивается цугом импульсов, каждый стоксов
импульс после обхода резонатора должен быть достаточно точно
синхронизован с одним из следующих импульсов накачки. Однако
добиться такой синхронизации относительно легко. Из множества
длин волн, лежащих в широкой полосе ВКР-усиления, в лазере может
генерироваться излучение на некоторой длине волны, удовлетворяю-
удовлетворяющей требованию синхронности накачки. Кроме того, длину волны
генерации можно подстраивать простым изменением длины резона-
резонатора. Этот метод можно считать основанным на временной диспер-
дисперсии [34], чтобы отличить его от призменной подстройки (см. рис. 8.4),
основанной на пространственной дисперсии в призме. Метод времен-
временной дисперсии весьма эффективен при перестройке импульсных воло-
волоконных ВКР-лазеров в широком диапазоне длин волн. Скорость
перестройки можно получить следующим образом. Если длина ре-
резонатора меняется на AL, временная задержка А/ должна компенси-
компенсироваться таким изменением длины волны АХ, чтобы выполнялось
Условие
(8.2.3)
гДе L- длина световода и D — параметр дисперсии, введенный р
Разд. 1.2.3. Таким образом, скорость перестройки
**: = _!_—?_, (8.2.4)
AL cL\D(K)\ 2nc2L$2
1 л.' связь D с р2 взята из выражения A.2.11). Хотя скорость перестрой-
228 Глава 8
ки зависит от длины световода L и длины волны X, обычно она равна
~ 1 нм/см. В эксперименте [35] была получена скорость перестройки
1,8 нм/см в диапазоне 24 нм при генерации на длине волны 1,12 мкм
в световоде длиной 600 м.
Синхронно-накачиваемые волоконные ВКР-лазеры привлекатель-
привлекательны для генерации сверхкоротких световых импульсов [47]. Когда
такие лазеры накачиваются импульсами длительностью < 100 пс, то,
вообще говоря, необходимо учитывать эффекты дисперсии групповых
скоростей, групповое запаздывание импульсов, ФСМ и ФКМ. Эти
эффекты обсуждаются в разд. 8.3, где синхронно накачиваемые воло-
волоконные лазеры рассматриваются более подробно в отдельном под-
подразделе. Если импульс ВКР попадает в область отрицательной
дисперсии групповых скоростей световода, то солитонные эффекты
могут формировать импульсы длительностью 100 фс и менее. Такие
волоконные лазеры иногда называют солитонными ВКР-лазерами,
подробно они рассматриваются в разд. 8.4. Другое направление
развития волоконных лазеров-создание компактных устройств
с зеркалами, интегрированными в волоконный резонатор. Один из
способов добиться этого [49] замена зеркал на волоконные решеточ-
решеточные отражатели, изготовленные путем травления решетки на сердце-
сердцевине короткого отрезка световода. Другой путь-использование коль-
кольцевой конфигурации резонатора [48] на основе волоконной петли со
связью через волоконный ответвитель - позволяет получить цельно-
волоконный кольцевой ВКР-лазер с низким порогом.
8.2.3. ВОЛОКОННЫЕ ВКР-УСИЛИТЕЛИ
Волоконные световоды можно использовать для усиления сигна-
сигнала, если он распространяется вместе ? интенсивной волной накачки
и если его длина волны лежит внутри полосы комбинационного
усиления. (Поскольку в основе действия таких усилителей лежит
эффект ВКР, или эффект Рамана, их называют волоконными комби-
комбинационными (или рамановскими) усилителями.) Такие системы рас-
рассматривались вскоре после демонстрации ВКР в световодах [50],
однако большое внимание им стало уделяться в 80-е годы благодаря
их возможному применению в оптической связи [51-70]. Эксперимен-
Экспериментальная установка подобна изображенной на рис. 8.4, но без зеркал.
Возможны конфигурации, в которых накачка и сигнал распространя-
распространяются либо в одном, либо во встречных направлениях.
Величина усиления за один проход по ВКР-усилителю в непрерыв-
непрерывном или квазинепрерывном режиме может быть получена из выраже-
выражений (8.1.2) и (8.1.3). Если интенсивность сигнала остается много
меньше интенсивности накачки, то истощением накачки можно пре-
пренебречь. Тогда интенсивность сигнала на выходе усилителя при z = L
дается равенством (8.1.6). Поскольку в отсутствие накачки IS(L) =
Вынужденное комбинационное рассеяние
229
= /Д0)ехр(—asL), усиление дается выражением
/s(O)exp(-asL)
(8.2.5)
где Ро = 10АЭфф-моищостъ накачки на входе в усилитель, а эффектив-
эффективная длина усиления дается выражением (8.1.7). При типичных пара-
параметрах gR= 1 ¦ 1(Г13 м/Вт, ?эфф = 100 м, Аэфф = 10 мкм2 усиление
сигнала будет значительным при Ро > 1 Вт. На рис. 8.5 показана
зависимость GA от Ро в эксперименте [51], где сигнал на длине волны
1,064 мкм усиливался в поле накачки на 1,017 мкм в световоде длиной
1,3 км. Коэффициент усиления GA с ростом Ро возрастает сначала
экспоненциально, но затем, при Ро > 1 Вт, отклоняется от экспонен-
экспоненты. Это связано с насыщением усиления, обусловленным истощением
накачки. Сплошные кривые на рис. 8.5 получены численным решени-
решением уравнений (8.1.2) и (8.1.3) с учетом истощения накачки. Результаты
отлично согласуются с экспериментальными данными.
Приближенное выражение для насыщенного усиления ВКР-усили-
теля можно получить, аналитически решая уравнения (8.1.2) и (8.1.3)
в предположении равенства потерь для накачки и сигнала (as = ap).
В результате получим
Рис. 8.5. Зависимость коэффи-
коэффициента усиления GA от мощ-
мощности накачки Ро. Различные
значки показывают результаты
-•ксперимента для трех зна-
значений начальной мощности
сВДнала. Сплошные кривые по-
получены теоретически при
0« = 9,2-1О14м/Вт [51].
10"
Ю3
ю1
10°
L-1,3 км
Хр = 1.О17 мкм
Xs=1,064 мкм
о 0,91мВт
л 0,36 мВт
о 0,18мВт
— Теория
0,5 1,0 1,5
Мощность накачки (Вт)
2,0
230
Глава 8
Рис. 8.6. Характеристики huli.iiценного усиления ВКР-усилителя для не-
нескольких значений ненасыщенного усиления GA .
где г0 связано с отношением мощностей сигнала и накачки следую-
следующим соотношением;
Р.@)
(8.2.7)
На рис. 8.6 показана зависимость GS/GA от GAr0, характеризую-
характеризующая насыщение усиления при нескольких значениях GA. Насыщенное
усиление понижается в 2 раза (или на 3 дБ), когда GA r0 ~ 1. Это
условие удовлетворяется, когда мощность усиленного сигнала начи-
начинает приближаться к начальной мощности накачки Ро. Отметим, что
Ро является хорошей мерой мощности насыщения в ВКР-усилителях.
Поскольку обычно Ро ~ I Вт, мощность насыщения в ВКР-усилите-
ВКР-усилителях много больше, чем в полупроводниковых лазерных усилителях
(~1 мВт) [71].
Как видно из рис. 8.5, волоконные ВКР-усилители легко обеспечи-
обеспечивают усиление в 1000 раз C0 дБ) при мощности накачки около 1 Вт
[51]. В недавнем эксперименте [54] сшнал от полупроводникового
лазера с длиной волны 1,24 мкм был усилен на 45 дБ в световоде
длиной 2,4 км. В этих экспериментах использовалась попутная накач-
накачка. В другом эксперименте [53] сигнал на длине волны 1,4 мкм от
полупроводникового лазера усиливался в поле как попутной, так
и встречной волн накачки. В качестве накачки использовалось излуче-
излучение от непрерывного Nd: И АГ-лазера с длиной волны 1.32 мкм. Было
получено ненасыщенное усиление 21 дБ при мощности накачки около
1 Вт. В обеих конфигурациях усиление было примерно одинаковым
благодаря изотропии процесса ВКР.
Вынужденное комбинационное рассеяние 231
Для оптимального режима работы ВКР-усилителей на основе
световодов из кварцевого стекла разность частот накачки и сигнала
должна соответствовать пику комбинационного усиления на рис. 8.1
(~ 13 ТГц). В ближнем ИК-диапазоне наиболее практичный источник
накачки-Nd: И АГ-лазер, работающий на 1,06 или 1,32 мкм. Для
этого лазера максимальное усиление возникает на длинах волн
сигнала 1,12 и 1,40 мкм соответственно. Однако с точки зрения
оптической связи наиболее интересны длины волн 1.3 и 1,5 мкм.
Nd: ИАГ-лазер в этом случае можно использовать, если накачкой для
сигнала служат стоксовы компоненты высших порядков. Например,
стоксова компонента третьего порядка с длиной волны 1,24 мкм от
лазера на длине волны 1,06 мкм может служить накачкой для
усиления сигнала на длине волны 1,3 мкм. Действительно, в такой
схеме было получено усиление 20 дБ [56]. Таким же образом первая
стоксова компонента на длине волны 1,4 мкм ВКР от лазера с длиной
волны 1,32 мкм может служить накачкой для сигнала на длине волны
1,5 мкм. Усиление 24 дБ в такой схеме также было получено экспери-
экспериментально [57]. Эти эксперименты показали также необходимость
согласования направлений поляризации волн сигнала и накачки,
поскольку ВКР почти не проявляется в случае ортогональных поля-
поляризаций. Использование световода с высоким содержанием германия
в сердцевине, сохраняющего поляризацию, позволило получить уси-
усиление 20 дБ на длине волны 1,25 мкм при входной мощности накачки
лишь 3,7 Вт от лазера с модуляцией добротности и генерацией на
длине волны 1,34 мкм [58].
Возможное применение волоконных ВКР-усилителей предвари-
предварительное усиление сигнала перед его регистрацией на приемнике
системы оптической связи [72]. Измерения в эксперименте показали
[63], что отношение сигнал/шум на приемнике определяется усилен-
усиленным спонтанным КР, которое неизменно сопутствует процессу уси-
усиления. Часть энергии накачки преобразуется в спонтанное стоксо-
во излучение и усиливается вместе с сигналом. Таким образом,
выходное излучение состоит не только из желаемого сигнала, но
также из широкополосного шума с шириной спектра ~ 10 ТГц или
более. В приближении неистощенной накачки можно получить анали-
аналитическое выражение для мощности усиленного спонтанного излуче-
излучения [60]. С практической точки зрения представляет интерес отноше-
отношение мощностей сигнала при включенной и выключенной накачках.
"Это отношение можно измерить экспериментально. Эксперимент
с накачкой на длине волны 1,34 мкм показал, что это отношение
составляет около 24 дБ для первой стоксовой компоненты на длине
волны 1,42 мкм. но падает до 8 дБ, когда первая стоксова компонента
используется для усиления сигнала на длине волны 1.52 мкм. Это
отношение в схеме со встречными волнами сигнала и накачки
меньше, чем в схеме, где они распространяются в одном направлении
232 Глава 8
[73]. Отношение усиленного сигнала к неусиленному возрастает, если
излучение после световода проходит сквозь фильтр, пропускающий
сигнал, но уменьшающий ширину спектра усиленного спонтанного
шума.
Привлекательным свойством волоконных ВКР-усилителей являет-
является широкая полоса усиления (> 5 ТГц). Они могут использоваться
для усиления одновременно нескольких каналов в многоканальной
системе оптической связи. Это было продемонстрировано в экспери-
эксперименте [74], где сигналы от трех полупроводниковых лазеров с распре-
распределенной обратной связью в диапазоне 1,57-1,58 мкм одновременно
усиливались в поле накачки с длиной волны 1,47 мкм. В этом
эксперименте излучение накачки было получено от многомодового
полупроводникового лазера, что делает данную схему практически
применимой для систем оптической связи. При мощности накачки
всего 60 мВт было получено усиление 5 дБ. Теоретический анализ
двухканального комбинационного усиления показывает, что в общем
случае существует взаимодействие между каналами [75]. Широкая
полоса усиления волоконных ВКР-усилителей делает их пригодными
для усиления коротких оптических импульсов. Усовершенствованию
систем оптической связи с помощью комбинационного усиления
уделено значительное внимание [76-81]. Наиболее многообещаю-
многообещающим кажется использование комбинационного усиления для передачи
сверхкоротких солитоноподобных импульсов по световодам длиной
несколько тысяч километров [78, 80] (см. разд. 5.4). В эксперименте
[79] импульсы длительностью 10 пс на длине волны 1,56 мкм усили-
усиливались при накачке непрерывным лазером на центрах окраски с дли-
длиной волны 1,46 мкм. Усиление таких коротких импульсов возможно
только благодаря широкой полосе ВКР. Недавно в такой схеме было
продемонстрировано прохождение солитонов длительностью 55 пс
по световоду эффективной длиной 4000 км [81].
8.2.4. ПЕРЕКРЕСТНЫЕ ПОМЕХИ,
ОБУСЛОВЛЕННЫЕ ВКР
Тот же эффект ВКР, который применим для усиления сигналов
в системах оптической связи, вреден для многоканальных систем
оптической связи, использующих спектральное уплотнение. Причина
в том, что сигнал в коротковолновом канале может служить накачкой
для сигнала в длинноволновом канале и передавать ему; часть
энергии. Это приводит к перекрестным помехам между каналами,
которые могут значительно влиять на характеристики системы [82-
89].
Рассмотрим сначала двухканальную систему с коротковолновым
каналом, сигнал в котором служит накачкой. Перенос энергии между
каналами подчиняется уравнениям (8.1.3) и (8.1.2). Эти уравнения
Вынужденное комбинационное рассеяние
233
решаются аналитически в предположении равных для обоих каналов
потерь (as = ap), что вполне справедливо для обычных расстояний
между каналами (~ 1,55 мкм). Коэффициент усиления Gs для длинно-
длинноволнового канала дается выражением (8.2.6). Соответствующее
уменьшение мощности коротковолнового канала дается фактором
истощения накачки
D
/p@)exp(-apL) l+r0GlA
l+r°
(8.2.8)
где GA или г0 определены выражениями (8.2.5) и (8.2.7) соответствен-
соответственно. На рис. 8.7 показана величина истощения накачки Dp как функция
GA для трех значений г0. Эти кривые могут быть использованы для
вычисления потерь мощности, обусловленных ВКР, определяемых
как относительное увеличение мощности накачки, необходимое для
поддержания выходной мощности на том же уровне, что и в отсутст-
отсутствие перекрестных помех, обусловленных ВКР. Потери даются выра-
выражением
A=101og(l/D_).
(8.2.9)
Потери в 1 дБ соответствуют Dp ~ 0,8. При равных мощностях
в каналах на входе в световод (г0 ~ 1) Dp = 0,8 соответствует
GA ~ 1,22. Входные мощности в каналах, соответствующие потерям
в 1 чБ, можно получить из (8.2.5). Если использовать обычные
параметры системы оптической связи на длине волны 1,55 мкм
yR = 7 • 104 м/Вт. Л,фф = 50 мкм2, ?эфф = 1/ар ^ 20 км, то GA = 1.22
соответствует Ро = 7 мВт. Если комбинационное усиление понижает-
понижается в 2 раза за счет деполяризации [40], эта величина возрастает до
1,0 1,5 2,0 2,5 3,О 3,5 4,0
Усиление GA
Рис. 8.7. Зависимость истощения накачки D от GA для трех значений г0.
234 Глава 8
Ро = 14 мВт. Измерения потерь энергии в эксперименте с двумя
каналами [88] согласуются с уравнениями (8.2.8) и (8.2.9).
В многоканальных системах ситуация более сложная. Промежу-
Промежуточные каналы не только передают энергию в более длинноволновые
каналы, но в то же самое время получают энергию из более
коротковолновых каналов. Для М-канальной системы можно полу-
получить мощность на выходе каждого канала, решив М связанных
уравнений, подобных уравнениям (8.1.2) и (8.1.3). Коротковолновые
каналы наиболее подвержены перекрестным помехам, поскольку они
передают часть энергии во все каналы, лежащие внутри полосы
комбинационного усиления. Величина передаваемой энергии, однако,
различна для разных каналов, поскольку она определяется величиной
комбинационного усиления, соответствующей разнице длин волн.
Один из способов оценить эту величину - аппроксимация спектра
комбинационного рассеяния на рис. 8.1 треугольным профилем [84].
Результаты показывают, что для 10-канальной системы с расстояни-
расстоянием между каналами 10 нм входная мощность в каждом канале не
должна превышать 3 мВт, чтобы потери мощности оставались менее
0,5 дБ. Действительно, в эксперименте с 10 каналами [89] с расстоя-
расстоянием между каналами 3 нм при входной мощности в каждом канале
менее 1 мВт не наблюдалось потерь мощности, обусловленных ВКР.
8.3 ВКР СВЕРХКОРОТКИХ ИМПУЛЬСОВ
Режим ВКР может считаться непрерывным для импульсов накач-
накачки длительностью То :> 1 не, поскольку длина группового разбегания
Lw, определенная выражением (8.1.21), обычно превышает длину
световода L. Однако для сверхкоротких импульсов длительностью
То < 100 пс обычно Lw < L. ВКР, таким образом, ограничивается
разницей групповых скоростей и возникает только на расстояниях
z ~ Lw, даже если действительная длина световода L значительно
больше Lw. В то же время благодаря относительно высоким пиковым
мощностям становятся важными такие нелинейные эффекты, как
ФСМ и ФКМ: они могут существенно влиять на эволюцию импуль-
импульсов накачки и ВКР. В данном разделе обсуждаются эксперименталь-
экспериментальные и теоретические аспекты ВКР сверхкоротких импульсов в области
положительной дисперсии групповых скоростей световодов [90 112].
Следующий раздел посвящен случаю отрицательной дисперсии, где
действуют солитонные эффекты, использование которых привело
к появлению волоконных солитонных лазеров.
8.3.1. ТЕОРИЯ
В общем случае, когда эффекты дисперсии, ФСМ, ФКМ, группово-
группового разбегания и истощения накачки важны, уравнения (8.1.18) и
Вынужденное комбинационное рассеяние 235
(8.1.19) решаются численно [94, 99]. Если пренебречь потерями
в световоде в силу относительно малых длин, используемых в экспе-
экспериментах, и если время отсчитывать в бегущей системе координат,
связанной с импульсом накачки, эти уравнения принимают вид
дА i S2 А а
^ P(MI2 2\A\2)Ap-^\As\2Ap, (8.3.1)
2)As + -\Ap\2As, (8.3.2)
где
T= t - z/vgp, d = vgpl - v-l. (8.3.3)
Параметр группового разбегания d отвечает за разницу групповых
скоростей импульсов накачки и ВКР и составляет обычно 2-6 пс/м.
Дисперсия групповой скорости P2j-, параметр нелинейности 7у и рама-
новский коэффициент gj (j = р или s) несколько различаются для
импульсов накачки и ВКР из-за стоксова сдвига величиной 13 'ГГц
между длинами волн; разница связана с отношением длин волн ^PAS.
С учетом выражений A.2.10), B.3.28) и (8.1.20) эти параметры отно-
относятся как
п р а », Р. *, „ р „ /Q 1 л\
Для определения относительной важности различных слагаемых
в уравнениях (8.3.1) и (8.3.2) можно ввести четыре характерные длины.
Для импульсов накачки длительностью То и пиковой мощностью Ро
они определяются следующим образом:
Т2 Т 1 1
^ ^w — T~T,-> LNL= —, LG = —. (8.3.5)
1^1 Ур вР
^D To r ^w TT,-> LNL
IP2pl 1^1 Урро врР0
Дисперсионная длина LD, длина группового разбегания Lw, нелиней-
нелинейная длина LNL и длина комбинационного усиления LG задают масш-
масштабы длин, на которых становятся важными эффекты дисперсии
групповых скоростей, разбегания импульсов, нелинейности (ФСМ
и ФКМ) и комбинационного усиления соответственно. Доминирует
эффект, характерная длина которого минимальна. Типичное значение
Lw составляет 1 м (при То < 10 пс), в то время как LNL и LG
становятся меньше или сравнимыми с Lw при Ро > 10 Вт. Напротив,
LD ~ 1 км при Го = 10 пс. Таким образом, дисперсионные эффекты,
которые в уравнениях (8.3.1) и (8.3.2) описываются членами с произ-
производными второго порядка, пренебрежимо малы для импульсов дли-
длительностью 10 пс. Ситуация меняется для импульсов длительностью
^о ^ 1 пс, поскольку с уменьшением длительности импульса LD убы-
236 Глава 8
вает быстрее, чем Lw. Тогда дисперсионные эффекты заметно воздей-
воздействуют на эволюцию ВКР, в частности в области отрицательной
дисперсии (см. разд. 8.4).
Даже если пренебречь слагаемыми с производными второго по-
порядка в уравнениях (8.3.1) и (8.3.2). для их "решения необходимы
численные методы. Аналитическое решение можно получить в при-
приближении неистощенной накачки. Поскольку это приближение спра-
справедливо на ранней стадии ВКР и позволяет понять физику явления,
рассмотрим его более детально. Полученное аналитическое решение
включает эффекты ФКМ и разбегания импульсов. Эффекты группо-
группового разбегания без ФКМ [19, 85] и ФКМ без разбегания [91] были
рассмотрены относительно давно. Позднее в решения уравнений
(8.3.1) и (8.3.2) были включены оба эффекта при Р2р = P2s = О и др = 0.
Уравнение (8.3.1) для импульса накачки дает решение
Ap(z, Т) = Ар@, Т)ехр[/7р|Лр@, Т)\2z], (8.3.6)
где ФКМ не учитывается, поскольку | As\2 « \ Ар\2. По той же причине
в уравнении (8.3.2) не учитывается ФСМ стоксовой волны. Решением
уравнения (8.3.2) является [102]
At{z, Т) = AM T+ zd)exp[(fl,/2 + iyM)y{z, Г)], (8.3.7)
где
V(z, T) = ]\Ap{0, T+zd-z'd)\2dz'. (8.3.8)
о
Выражение (8.3.6) показывает, что импульс накачки начальной
амплитуды Ар@, Т) распространяется без изменения своей формы.
Фазовый сдвиг, обусловленный ФСМ, модулирует частоту импульса
накачки, что уширяет его спектр; уширение спектра при ФСМ
обсуждается в разд. 4.1. При распространении же по световоду
стоксова импульса меняются и его форма, и спектр; изменения формы
обусловлены комбинационным усилением, в то время как спектраль-
спектральные изменения связаны с ФКМ. Что касается группового разбегания,
то оно вызывает как спектральные, так и временные изменения,
которые зависят от фактора перекрытия V|/(r, T), учитывающего
разделение импульсов при распространении вдоль световода. Этот
фактор зависит от формы импульса. Для гауссовского импульса
накачки с начальной амплитудой
Ар@, Т)= J7ozxv(-T2I2TD (8.3.9)
интеграл в уравнении (8.3.8) может быть представлен с использовани-
использованием функции ошибок с результатом
у(z, т) = /V^T terf(T + 5>
о
Вынужденное комбинационное рассеяние 237
где т = Т/Тпи 5 длина распространения в единицах длин разбегания,
т.е.
z'Lw. (8.3.11)
Выражение (8.3.7), где у задано выражением (8.3.10), описывает
эволюцию стоксова импульса в случае гауссовского импульса накач-
накачки с начальными мощностью Ро и длительностью То CTFWHM =
= 1,66 Го). Амплитуда затравочного стоксова импульса Л5@, Г)-это
фиктивная амплитуда, введенная для учета спонтанного КР, возни-
возникающего на протяжении всего световода. Чтобы обойтись без введе-
введения фиктивного затравочного стоксова импульса в начале световода,
необходимо квантовомеханическое рассмотрение [113]. В квазиклас-
квазиклассическом приближении можно использовать результат, полученный
в разд. 8.1, где эффективная стоксова мощность в начале световода
была получена в предположении: один фотон на одну моду на всех
частотах внутри спектра комбинационного усиления. Выражение
(8.1.10), полученное для непрерывного режима, дает начальную пико-
пиковую мощность стоксова импульса, в то время как его форма остается
неопределенной. Численное решение уравнений (8.3.1) и (8.3.2) пока-
показывает, что форма и спектр импульса на выходе световода не очень
сильно зависят от выбора формы затравочного импульса. В простей-
простейшем случае можно предположить, что
, (8.3.12)
1де Р^Ф дается выражением (8.1.10). Альтернативой может служить
гауссовская форма затравочного импульса с пиковой мощностью
рчфф
В качестве простого применения аналитического решения (8.3.7)
рассмотрим порог ВКР [96] сверхкоротких импульсов. Пиковая
мощность стоксова импульса на выходе световода (; = L) дается
выражением _
Р,(L) = | A,(L, 0)|2 = FJ**ехр(д„ Ро Jn Lw), (8.3.13)
где использовалось выражение (8.3.10) при т = 0 и L/Lw» 1. Если
определить пороговое условие ВКР так же, как для непрерывного
режима, то порог достигается при PS(L) = Ро. Сравнение выражений
(8.1.14) и (8.3.13) показывает, что можно использовать условие порога
Для непрерывного режима, если принять
L^ = xnLw^TFWHM/\d\. (8.3.14)
В частности, для расчета критической пиковой мощности импульса
накачки можно использовать (8.1.15), если ?)фф взять из (8.3.14). Это
изменение естественно, поскольку эффективная длина взаимодействия
Между импульсами накачки и ВКР определяется длиной группового
Разбегания Lw; ВКР прекращается, когда дн.. импульса разбегаются
238 Глава 8
настолько, что перестают перекрываться. Выражения (8.1.15) и
(8.3.14) показывают, что порог ВКР зависит от длительности импуль-
импульса и снижается с возрастанием TFWHM. Для импульсов длительностью
~ 10 пс (Lw ~ 1 м) пороговая мощность накачки равна ~ 10 Вт.
На начальной стадии ВКР аналитическое решение (8.3.7) можно
использовать для получения как формы, так и спектра импульса ВКР
[102]. Эволюция спектра определяется модуляцией частоты за ФКМ.
Динамика частотной модуляции обсуждалась в разд. 7.4.1 в связи
с асимметричным уширением спектра, обусловленным ФКМ (см.
рис. 7.11). Модуляция частоты, вызванная ФКМ при ВКР, идентична
приведенной на рисунке, пока накачка остается неистощенной. Заме-
Заметим, что в области положительной дисперсии стоксов импульс
распространяется быстрее импульса накачки. В результате частотная
модуляция наиболее сильна в задней части стоксова импульса.
Следует подчеркнуть, что форма и спектр импульса существенно
изменяются, когда в рассмотрение включается истощение накачки
[94, 99]. Возрастающий импульс ВКР воздействует сам на себя через
ФСМ и на импульс накачки через ФКМ. Эти эффекты нельзя описать
простым аналитическим решением, и для понимания эволюции ВКР
необходимо численное решение уравнений (8.3.1) и (8.3.2). Для этой
цели можно использовать обобщение метода Фурье из разд. 2.4.
Метод требует определения стоксова импульса на входе в световод
согласно (8.1.10).
Для численного решения полезно ввести нормированные перемен-
переменные. Соответствующую шкалу расстояний вдоль световода можно
задать с помощью длины группового разбегания Lw. Вводя опреде-
определения
Z T А;
*' = —, т=-, и, = -$-г (8.3.15)
и используя (8.3.4), получаем уравнения (8.3.1) и (8.3.2) в виде
dUp i Lwd2Up_
dz' 2 LD дх2
dUs dUs irLwd2Us
dz' дх + 2 LD дх2
= ir — (\Us\2 +2\Up\2)Us + -—-\Up\2Us, (8.3.17)
Lnl 2 LG
где длины LD, Lw, LNL и LG заданы выражениями (8.3.5). Параметр
г = Kp/Ks при Кр = 1,06 мкм составляет около 0,95. На рис. 8.8 показа-
Вынужденное комбинационное рассеяние
239
Импульс накачки
Рис. 8.8. Эволюция импульсов ВКР и накачки на трех групповых длинах для
случая LD/LW= 1000, LW/LNL = 24, LW/LG = 12.
на эволюция импульсов ВКР и накачки на трех групповых длинах.
Импульс накачки гауссовский, а форма стоксова затравочного им-
импульса задана равенством (8.3.12) с мощностью Р^* = 2-10~7 Вт.
Используя нормировку (8.3.5) и (8.3.15), результаты, показанные на
рис. 8.8, можно применять для различных длин волн и длительностей
импульсов накачки. Выбор LW/LG = 12 означает, что
и соответствует пиковой мощности, на 30% превышающей поро-
пороговую.
Несколько черт рис. 8.8 заслуживают внимания. Стоксов импульс
начинает расти после прохождения одной групповой длины. Передача
энергии стоксову импульсу от импульса накачки практически прекра-
прекращается при z = ~SLWi поскольку из-за разницы групповых скоростей
импульсы физически разделены. Так как в области положительной
Дисперсии импульс ВКР распространяется быстрее импульса накачки,
энергия к нему поступает от передней части импульса накачки. Это
отчетливо видно в точке z = 2LW, где перенос энергии приводит
к двухпиковой структуре импульса накачки в результате истощения
последней; провал вблизи переднего края точно соответствует поло-
положению импульса ВКР. Небольшой пик вблизи этого же края исчезает
240
Глава 8
\JJUX3
О,О5
О,04
О,ОЗ
О,О2
X.QO1
к о
_i i i i ] i i i i i i i i i i
\
\
[ JilllJ
1 ' ':
\
11111
'-
и
X
CJ
-1О -5
1О -1О -5
О,О5
О,04
О,ОЗ
О.О2
QO1
\о
_| 1 i i н i i м i i i i i i i i 1.
f Z=2LW i
\ Л i
^ i 1 ^
-Ю -5
-1O -5
"-"s>To
Рис. 8.9. Спектры импульсов накачки (верхний ряд) и ВКР (нижний ряд) после
прохождения двух (левая колонка) и трех (правая колонка) групповых длин
для тех же параметров, что и на рис. 8.8.
по мере дальнейшего распространения, когда импульс ВКР проходит
сквозь него. Импульс накачки при z = ~SLW асимметричен по форме,
а по длительности несколько короче, чем исходный импульс, посколь-
поскольку представляет собой только его хвостовую часть. Импульс ВКР
также короче исходного и асимметричен с более острой передней
частью.
Спектры импульсов накачп и ВКР проявляют множество интерес-
интересных свойств, вытекающих из совместного действия ФСМ. ФКМ,
группового разбегания и истощения накачки. На рис. 8.9 показаны
спектры накачки и ВКР при z/Lw = 2 (левая колонка) и z/Lw = 3
(правая колонка). Асимметричная форма этих спектров обусловлена
ФКМ (см. разд. 7.4.1). В «синей» части спектра проявляются биения,
характерные для ФСМ (см. разд. 4.1). В отсутствие ВКР спектр был
бы симметричен с некоторой структурой, возникающей на «красном»
краю. Поскольку красные компоненты распространяются в передней
части импульса накачки и именно эта часть истощается, энергия
переносится в основном из красных компонент импульса накачки.
Это ясно видно в спектре накачки на рис. 8.9. Отчасти такой же
причиной объясняется длинный хвост на красном краю спектра
импульса ВКР. Спектр ВКР практически сплошной при z = 2LW, но
Вынужденное комбинационное рассеяние 241
приобретает заметную внутреннюю структуру при z=3Lw. Это
связано с совместным действием ФКМ и истощения накачки; частот-
частотная модуляция импульса ВКР может быстро менять величину и знак
и приводит к сложной форме спектра [94. 99].
Временная и спектральная структуры на рис. 8.8 и 8.9 зависят от
пиковой мощности исходных импульсов накачки через длины LG
и LNL в.уравнениях (8.3.16) и (8.3.17). Когда пиковая мощность
возрастает, LG и LNL уменьшаются в одинаковой пропорции. Числен-
Численные расчеты показывают, что при увеличении мощности накачки
импульс ВКР растет быстрее и переносит больше энергии, чем это
показано на рис. 8.8. Еще более важно, что с уменьшением LNL
возрастает частотная модуляция за счет как ФСМ, так и ФКМ
и спектры импульсов становятся шире, чем на рис. 8.9. Интересно,
что спектр импульса ВКР становится заметно шире, чем импульс
накачки. Это связано с эффектом ФКМ, более сильным для импульса
ВКР, чем для накачки. Частотная модуляция импульса ВКР, вызван-
вызванная ФКМ, была предсказана в 1976 г. [90]. Теоретически было
показано [91], что если пренебречь групповым разбеганием и истоще-
истощением накачки, то за счет ФКМ спектр импульса ВКР уширяется
в 2 раза больше, чем спектр импульса накачки. Результаты численных
расчетов, включающих эти эффосты, показывают, что уширение
импульса ВКР может превышать уширение импульса накачки в 3 ра-
раза. Это согласуется с экспериментом [101], о котором будет сказано
ниже. Прямые измерения частотной модуляции [96, ПО] также
показали ее возрастание в импульсе ВКР по сравнению с импульсом
накачки.
8.3.2. ЭКСПЕРИМЕНТЫ
Спектральные и временные свойства ВКР сверхкоротких импульсов
исследовались в многочисленных экспериментах в видимом и ближ-
ближнем ИК-диапазонах спектра. В эксперименте [92] импульсы длитель-
длительностью 60 пс на длине волны 1,06 мкм от Nd; ИАГ-лазера с синхро-
синхронизацией мод распространялись по световоду длиной 10 м. Когда
мощность накачки превышала порог ВКР (~ 1 кВт), генерировались
импульсы ВКР. Импульсы и накачки, на ВКР на выходе световода
были короче входного импульса, как и следовало ожидать на основа-
основании результатов, представленных на рис. 8.8. Спектр импульса ВКР
(ширина ~ 2 ТГц) был намного шире, чем спектр импульса накачки.
Величина спектрального уширения импульса ВКР при ФКМ по
сравнению со спектральным уширением импульса накачки была
определена в эксперименте [101], где импульсы длительностью 25 пс
на длине волны 532 нм распространялись по световоду длиной 10 м.
На рис. 8.10 показаны спектры, наблюдавшиеся при четырех различ-
различных значениях энергии импульса накачки. Ширина спектра крыла
242
Глава 8
CJ
о
I
X
s
\г,г
A
532
2,1 -
12 E0
544,5 532
X (нм)
544,5
Рис. 8.10. Спектры, полученные в эксперименте с 25-пикосекундными им-
импульсами на длине волны 532 мкм, распространявшимися в световоде длиной
10 м. Четыре спектра соответствуют различным энергиям импульса накачки,
нормированым на Ео, где Ео соответствует порогу ВКР [101].
ВКР, расположенного на длине волны 544,5 нм, втрое превосходила
ширину спектра импульса накачки. Это ожидалось из теории и связа-
связано с модуляцией частоты импульса ВКР за счет ФКМ [90, 91].
Из-за ограниченного разрешения спектрометра нельзя было раз-
разрешить тонкую структуру спектров на рис. 8.10. Детальный спектр
накачки был получен в эксперименте [100], где импульсы длитель-
длительностью 140 пс на длине волны 1,06 мкм распространялись по свето-
световоду длиной 150 м. На рис. 8.11 показаны наблюдавшиеся спектры
накачки при нескольких значениях пиковой входной мощности. По-
Порог ВКР составлял около 100 Вт. При Ро < 100 Вт в спектре прояв-
проявляется многопиковая структура, характерная для ФСМ (см. разд. 4.1).
Однако при Ро> 100 Вт спектр накачки уширяется и становится
асимметричным. Действительно, два спектра на рис. 8.11 (средний
ряд) качественно подобны спектрам на рис. 8.9 (верхний ряд). Асим-
Асимметрия спектров связана с совместным действием ФКМ и истощени-
истощением накачки.
Другое явление, могущее привести к качественно новым свойст-
свойствам спектра накачки, это модуляционная неустойчивость, вызванная
ФКМ. Она обсуждалась в разд. 7.3 для случая, когда оба импульса
вводятся в световод извне. Однако это явление должно иметь место
и в случае, когда второй импульс генерируется внутри световода.
Подобно случаю модуляционной неустойчивости, возникающей в об-
области отрицательной дисперсии (см. разд. 5.1), модуляционная не-
Вынужденное комбинационное рассеяние
243
устойчивость, вызываемая ФКМ, обнаруживает себя появлением
в спектре импульса боковых полос. На рис. 8.12 показаны спектры
импульсов накачки и ВКР, полученные в эксперименте [111] по
распространению импульсов длительностью 25 пс на длине волны
532 нм в отрезке световода длиной 3 м. Диаметр сердцевины свето-
световода был выбран равным лишь 3 мкм для того, чтобы исключить
возможность многомодового четырехволнового смешения (см.
гл. Ю). Центральный пик в спектре накачки (рис. 8.11) имеет сущест-
существенную внутреннюю структуру, которая в этом эксперименте оста-
осталась неразрешенной. Боковые полосы указывают на очевидное суще-
существование модуляционной неустойчивости, индуцированной ФКМ.
Положение боковых полос меняется с изменением длины световода
и пиковой мощности накачки. Было установлено, что это изменение
соответствует теории, изложенной в разд. 7.3. В спектре ВКР также
проявляются боковые компоненты, существование которых следует
из теории, хотя из-за ФКМ-уширения спектра они едва разрешены.
Измерения временных характеристик ВКР сверхкоротких импуль-
импульсов [94-97] показывают, что они подобны приведенным на рис. 8.8.
В эксперименте [95] импульсы от лазера на красителе длительностью
5 пс на длине волны 615 нм распространялись по световоду длиной
3Вт Л 8Вт . (I
ХоО5 j|L08 "Л
II I I им /
12 Вт
25 Вт.
53 Вт
0,26нм
0,49нм
106 Вт
1,2нм
Рис. 8.11. Экспериментальные спектры импульсов накачки после прохож-
прохождения 140-пик осеку ндных импульсов на длине волны 1,06 мкм через световод
Длиной 150 м при различных значеиях входной мощности. ВКР достигалось
пРи мощности около 100 Вт [100].
244
Глава 8
532
Длина волны (нм)
544.5
Рис. 8.12. Спектры импульсов накачки и ВКР. Боковые полосы возникают
в результате модуляционной неустойчивости, вызванной ФКМ. Шкала ин-
интенсивности произвольна [111].
12 м с диаметром сердцевины 3,3 мкм. На рис. 8.13 показаны кросс-
корреляционные кривые импульсов накачки и ВКР на выходе свето-
световода. Импульс ВКР приходит к выходу световода на 55 пс раньше,
чем импульс накачки; это соответствует разнице задержки на длине
волны 620 нм и на длине волны накачки. Более важно, что импульс
ВКР оказывается асимметричным с крутым передним фронтом и
длинным хвостом на заднем фронте, подобно гому, как это было
показано на рис. 8.8. Подобные разультаты были получены и в дру-
других экспериментах, где форма импульсов регистрировалась непосред-
непосредственно при помощи электронно-оптической камеры [97, 100] или
скоростного фотодиода [109].
Влияние группового разбегания импульсов на ВКР сверхкоротких
импульсов исследовалось в эксперименте [96], где мощность импуль-
импульсов накачки длительностью 35 пс на длине волны 532 нм варьирова-
аась в пределах 140-210 Вт, а длина световода-в пределах 20-100 м.
Временные характеристики измерялись при помощи скоростного
CdTe-фотодиода и осциллографа. Результаты показывают, что гене-
генерация импульса ВКР происходит на первых трех-четырех длинах
группового разбегания. Если эффективность преобразования в ВКР
-40
40 -60
Время (пс)
Рис. 8.13. Автокорреляционные функции импульсов накачки и ВКР на вы-
выходе световода длиной 12 м. Шкала интенсивностей произвольная [95].
Вынужденное комбинационное рассеяние 245
составляет 20%. то пик ВКР появляется приблизительно на двух
длинах группового разбегания, а при большей мощности накачки-на
меньшей длине. Эти выводы согласуются с результатами вычислений,
представленными на рис. 8.8. Длина группового разбегания в этих
экспериментах определялась согласно (8.3.5). где вместо То использо-
использовалась TFWHM.
До сих пор рассматривалось ВКР только первого порядка. Такое
ВКР наблюдалось в эксперименте с импульсами накачки длитель-
длительностью 5 пс на длине волны 615 нм пиковой мощностью 1,5 кВт [95].
В ближнем ИК-диапазоне генерация стоксовых компонент высших
порядков может происходить при накачке импульсами на длине
волны 1,06 мкм. Эффективность ВКР может существенно возрасти,
если использовать световоды с сердцевиной, легированной Р2О5, что
обусловлено относительно высоким рамановским коэффициентом
усиления в стеклах, содержащих Р2О5. Возможность использования
таких световодов при ВКР привлекает к ним большое внимание [114,
115].
С практической гочки зрения ВКР сверхкоротких импульсов
является фактором, ограничивающим характеристики волоконно-ре-
шеточных компрессоров (см. разд. 6.3), для оптимальной работы
которых пиковая мощность входных импульсов должна быть ниже
порога ВКР. ВКР действует не только как источник потерь, оно
ограничивает качество сжатия импульса [116, 117], поскольку ФКМ
между накачкой и стоксовой волной искажает линейность чирпа. Для
улучшения качества сжатых импульсов при наличии ВКР использова-
использовалась спектральная фильтрация [109]. При этом был выбран фильтр
с такой асимметричной полосой пропускания, что прошедший через
него импульс имел чирп, близкий к линейному. В недавней работе
[112] было показано, что сжатые импульсы хорошего качества можно
получить и в режиме сильного ВКР. но только ценой значительной
потери энергии.
8.3.3. ВОЛОКОННЫЕ ВКР-ЛАЗЕРЫ С СИНХРОННОЙ
НАКАЧКОЙ
Предыдущие подразделы были посвящены однопроходному ВКР.
Если поместить световод в резонатор (см. рис. 8.4), то однопроход-
однопроходный усилитель превращается в волоконный ВКР-лазер. Такие лазеры
обсуждались в разд. 8.2.2 в случаях непрерывного или квазинепрерыв-
квазинепрерывного режимов (То > 1 не). Здесь рассматриваются синхронно накачи-
накачиваемые волоконные ВКР-лазеры, испускающие импульсы длитель-
длительностью ~ 100 пс. В обычной схеме используются импульсы накачки
Длительностью около 100 пс на длине волны 1,06 мкм от Ш:ИАГ-
лазера с синхронизацией мод.
На рис. 8.14 временные и спектральные характеристики излучения
246
Глава 8
1 1 Oj
II ' *
II ' '
JrfJvR
Si
i
i
p
0 n -500
Время (.пс)
1,15 1,10
Дпикаволны (мкм)
1,05
Рис. 8.14. Временные и спектральные характеристики излучения волоконного
ВКР-лазера (штриховые линии) и в режиме однопроходной генерации (сплош-
(сплошные линии). Шкала интенсивностей произвольная [104].
на выходе однопроходного усилителя сравниваются с аналогичными
характеристиками ВКР-лазера. В этом эксперименте [104] длина
световода составляла 150 м, а длительность импульсов накачки-око-
накачки-около 120 пс (То = 80 пс). В случае однопроходного усиления в спектре
виден пик вблизи 1,12 мкм. Соответствующий стоксов импульс про-
проявляется на 300 пс раньше, чем импульс накачки, что обусловлено
групповым запаздыванием. В режиме лазера основной спектральный
пик возникает на длине волны 1,093 мкм, для которой накачка
действует синхронно. Кроме того, длина волны может перестраивать-
перестраиваться более чем на 50 нм посредством изменения длины резонатора на
10 см. Второй пик в спектре на рис. 8.14 соответствует несинхрони-
зованной с накачкой стоксовой компоненте второго порядка. Во
временной структуре излучения видны три пика, соответствующих
импульсу накачки и д^-м стоксовым импульсам первой и второй
стоксовых компонент. Импульс первой стоксовой компоненты доми-
доминирует благодаря тому, что для него выполнено условие синхронно-
синхронности накачки.
Длительность импульсов излучения волоконного ВКР-лазера при-
примерно такая же, как у импульсов накачки (~ 100 пс). Однако из-за
эффектов ФСМ и ФКМ эти импульсы частотно-модулированны, и,
если в достаточно большой части импульса чирп линеен, они могут
быть сжаты в волоконно-решеточном компрессоре (см. разд. 6.3).
Важным достижением было получение импульсов длительностью
0,8 пс при помещении компрессора внутрь резонатора волоконного
ВКР-лазера [47]. Расстояние между решетками регулировалось для
получения слегка отрицательной дисперсии при полном обходе резо-
резонатора лазера, т. е. пара решеток не только компенсировала положи-
положительную дисперсию световода, но и обеспечивала для импульсов,
Вынужденное комбинационное рассеяние 247
циркулирующих внутри резонатора, отрицательную общую диспер-
дисперсию трассы. С использованием такой методики недавно были получе-
получены импульсы длительностью 0,4 пс [103]. Кроме того, лазер был
перестраиваемым в диапазоне 1,076-1,12 мкм при длительности им-
импульсов 0,4-0,5 пс во всем интервале. Для перестройки длины волны
использовалась диафрагма, помещенная внутрь решеточного ком-
компрессора (см. разд. 6.3.2).
Перестраиваемый волоконный ВКР-лазер использовался и для
демонстрации усиления фемтосекундных оптических импульсов в во-
волоконном ВКР-усилителе в условиях как попутной, так и встреч-
встречной волн накачки [105]. Попутная накачка использовалась в схеме,
где 500-фемтосекундные импульсы сначала проходили через отрезок
световода длиной 100 м, где в результате действия дисперсии они
уширялись до 23 пс. Уширенные импульсы вместе с импульсами
накачки длительностью 50 пс на длине волны 1,06 мкм вводились
в усилитель, состоявший из 1-метрового световода. Усиленные им-
импульсы сжимались в решеточном компрессоре. Сжатые импульсы
были несколько шире F00-700 фс) исходных, но усилены по энергии
в 15 000 раз, когда мощность импульсов накачки составляла 150 кВт.
Эксперимент показал, что частотная модуляция 23-пикосекундных
исходных импульсов мало изменяется при усилении. Это указывает
на возможность использования ВКР сверхкоротких импульсов в
световодах не только для генерации фемтосекундных импульсов, но
и для получения высоких пиковых мощностей.
8.4. СОЛИТОННЫЕ ЭФФЕКТЫ ПРИ ВКР
Когда длина волны накачки лежит в области отрицательной
дисперсии световода, в импульсах накачки и ВКР могут появляться
солитонные эффекты, возникающие в результате совместного дейст-
действия нелинейности и дисперсии (см. гл. 5). Этот случай, в силу его
большой научной и практической важности, широко исследовался как
теоретически, так и экспериментально [118-138].
Интересная возможность состоит в том, что при некоторых
условиях почти вся энергия импульса передается в стоксов импульс,
который, как фундаментальный солитон, распространяется без иска-
искажений. Численный анализ показывает [118], что это действительно
возможно, если стоксов импульс формируется на расстоянии, где
импульс накачки, распространяющийся как солитон высшего поряд-
порядка, достигает минимальной длительности во время начальной фазы
сжатия. Для N > 10 это расстояние дается формулой F.4.3). Напро-
Напротив, если передача энергии в стоксов импульс задерживается и проис-
происходит, когда импульс накачки уже расщеплен (см. рис. 5.4 для случая
N = 3), то стоксов импульс не становится солитоном и его энергия
быстро рассеивается.
248 Глава 8
Уравнения (8.3.16) и (8.3.17) можно использовать в случае отрица-
отрицательной дисперсии, если просто изменить знак второй производной.
Как и в случае положительной дисперсии, показанном на рис. 8.8,
передача энергии в стоксов импульс происходит вблизи г — Lw.
Чтобы из импульса ВКР сформировать солитон, необходимо, чтобы
zopt =i Lw, где copt - оптимальная длина-световода для компрессора,
обсуждавшегося в разд. 6.4. Это условие подразумевает, что Lw не
должно быть слишком малым по сравнению с дисперсионной длиной
LD. Например, Lw = (ir/8)LD для солитона третьего порядка, если
учесть, что zopt = zo/4 при N = 3, где z0 = (л/2) LD- период солитона.
В разд. 6.4 было показано, что Lw я LD становятся сравнимыми для
фемтосекундных импульсов длительностью То < 100 фс. Для таких
сверхкоротких импульсов различие между импульсами накачки и
ВКР смазывается, поскольку их спектры начинают заметно перекры-
перекрываться. Это видно, например, из того факта, что пик усиления на
рис. 8.1 соответствует отстройке частоты величиной 13 ТГц, в то
время как ширина спектра 100-фемтосекундного импульса составляет
~ 10 ТГц. Уравнения (8.3.16) и (8.3.17) не дают реалистического
описания ВКР фемтосекундных импульсов, в частности для отрица-
отрицательной дисперсии, где исходный импульс может заметно укорачи-
укорачиваться в начале распространения.
Альтернативное описание дается обобщенным уравнением рас-
распространения B.3.35) и разд. 2.3, последний член которого, пропор-
пропорциональный времени нелинейного отклика TR. отвечает за ВКР. Как
обсуждалось выше, для небольших частотных отстроек TR связан
с наклоном кривой комбинационного усиления (см. рис. 8.1). Влияние
члена, отвечающего за комбинационное усиление, на эволюцию
фемтосекундных импульсов внутри световода уже обсуждалось в
разд. 5.5 после рассмотрения других нелинейных эффектов высших
порядков. На рис. 5.20 были показаны форма и спектр импульса,
пиковая мощность которого соответствует солитону второго поряд-
порядка. В таком случае исходный импульс расщепляется на два фрагмента
на длине одного периода солитона, явление, названное в разд. 5.5
распадом солитона. Это явление может быть интерпретировано как
вынужденное комбинационное (ВК) саморассеяние импульса [119],
которое может возникать, даже если порог ВКР с уровня шумовой
затравки еще не достигается. Основная идея состоит в следующем.
Входной импульс, являющийся солитоном высшего порядка, в на-
начальной фазе распространения укорачивается с одновременным уши-
рением спектра. Спектральное уширение красного крыла обеспечива-
обеспечивает затравку для комбинационного усиления, т. е. через ВКР синие
компоненты импульса служат накачкой для красных компонент. Это
ясно видно на рис. 5.20. где основной"' пик спекгра непрерывно
смещается в красную сторону. Такое смещение называют самосдви-
самосдвигом частоты солитона [121]. Во временном рассмотрении энергия
Вынужденное комбинационное рассеяние
249
в области красных компонент проявляется в виде импульса, запазды-
запаздывающего относительно начального. Это импульс ВКР.
Явление ВК-саморассеяния может возникать даже для пикосе-
кундных импульсов, если порядок солитона TV достаточно велик,
чтобы исходный спектр уширился (из-за ФСМ) до ~ 1 ТГц. Действи-
Действительно, в первом эксперименте, где наблюдалось данное явление
[119], входные импульсы длительностью 30 пс на длине волны
1,54 мкм распространялись по световоду длиной 250 м. На рис. 8.15
показаны спектры, наблюдавшиеся для четырех значений входной
пиковой мощности Ро в пределах 50-900 Вт. При Ро > 100 Вт на
красной стороне спектра появляется длинное крыло. Это значение
соответствует N = 30 при данных параметрах системы. Уравнения
F.4.3) и F.4.2) предсказывают сжатие выходного импульса приблизи-
приблизительно в 120 раз после прохождения 300-метровой трассы, если
принять период солитона г0 равным 27 км (То ~ 17 пс). Ширина
спектра такого сжатого импульса составляет ~ 2 ТГц. На рис. 8.15
приведена также автокорреляционная функция излучения, соответст-
соответствующая стоксову крылу верхнего спектра, смещенному по частоте на
1,6 ТГц от частоты накачки. Она соответствует стоксову импульсу
длительностью 200 фс.
Эффект ВК-саморассеяния привлек к себе значительное внимание
[119-130], так как он дает удобный способ генерации солитонов,
несущая частота которых может перестраиваться путем изменения
либо длины световода, либо входной мощности накачки. В экспери-
эксперименте [127] использование лазера на красителе позволило перестраи-
перестраивать входную длину волны в пределах 1,25-1,35 мкм так, что входной
импульс мог распространяться в областях как положительной, так
и отрицательной дисперсии световода (длина волны нулевой диспер-
дисперсии 1,317 мкм). На рис. 8.16 показаны спектры импульсов при измене-
изменении длины волны Хр от 1,28 до 1,317 мкм. Входной импульс длитель-
длительностью 0,83 пс мощностью 530 Вт распространялся по одномодово-
му световоду длиной 150 м. Стоксово крыло не появлялось в случае
Хр = 1,28 мкм из-за положительной дисперсии световода, хотя отчет-
Рис. 8.15. Спектры импульса
с исходной длительностью
30 пс на длине волны
1.54 мкм после распростра-
распространения по световоду с отри-
отрицательной дисперсией дли-
длиной 250 м для четырех раз-
различных значений начальной
мощности в пределах 50
900 Вт. Справа автокорре-
i J i V. i ляционная функция стоксова
крыла верхнего спектра
[П9].
1,60 1,58 1,56 1,54 1,52
Длина волны (мкм)
-2-1012
Время Inc)
250
Глава 8
i
трои:
(ОСТЬ
ш
43НЭ1Н1/
1 1
Р0 = 530Вт 1
Л
л/\
п
11
/ V
1 1 1
1,317мкм Д
1,3 мкм
д.
Х_= 1,28мкм
I l l
1.2
1,25
1,3 1,35 1,4
Длина волны (мкм)
1,45
Рис. 8.16. Спектры импульса на выходе световода длиной 150 м. когда в него
вводится импульс длительностью 0,83 пс, мощностью Ро = 530 Вт. Входная
длина волны менялась от 1,28 до 1,317 мкм. Длина волны нулевой дисперсии
световода 1,317 мкм [127].
ливо видно уширение спектра из-за ФСМ. При ^.р = 1,3 мкм форми-
формируются две стоксовы полосы, несмотря на то что эта длина волны
лежит в области положительной дисперсии, поскольку из-за ушире-
ния спектра, обусловленного ФСМ, значительная часть энергии им-
импульса накачки оказывается в области отрицательной дисперсии. При
Хр= 1,317 мкм стоксовы полосы более интенсивны благодаря более
интенсивному переносу энергии в сторону меньших частот при ВКР.
Изменения спектра импульса, начальная частота коъйрого лежит
в области отрицательной дисперсии, показаны на рис. 8.17 для случая
Хр = 1,341 мкм и длина световода L = 1 км. Спектр импульса сущест-
существенно меняется при увеличении пиковой мощности. При Ро = 530 Вт
появляются три стоксовы полосы (верхний спектр). Возникает также
антистоксова полоса, несущая 5-10% от начальной энергии. Во
временном представлении с каждой стоксовои линией связан отдель-
отдельный импульс. Автокорреляционные измерения показали [127], что
длительность этих стоксовых импульсов составляет ~ 300-400 фс.
Длительность существенно зависит от длины световода; наименьшая
длительность составляла около 55 фс при длине световода 12 м.
Большинство экспериментальных результатов можно объяснить, ис-
исходя из уравнения B.3.35).
Вынужденное комбинационное рассеяние
251
Поскольку генерация стоксовых компонент ВКР высших порядков
происходит даже в области положительной дисперсии, возможна
генерация солитонов ВКР даже тогда, когда начальная длина волны
намного меньше длины волны нулевой дисперсии. Это было проде-
продемонстрировано в эксперименте [122], где импульс с длиной волны
1,06 мкм создавал импульсы длительностью 70 фс на длине волны
1,5 мкм, хотя его длительность составляла 150 пс. Входной пиковой
мощности 5 кВт было достаточно для генерации многих стоксовых
компонент в световоде длиной 20 м. Стоксова компонента ВКР
четвертого порядка вблизи длины волны 1,3 мкм служила накачкой
для генерации континуума, который простирался до 1,7 мкм. В двух-
двухступенчатой схеме, где вторая ступень состояла из световода со
смещенной дисперсией длиной 2 м, длительность импульса была
сокращена до 18 фс, т.е. лишь до трех световых периодов.
Солитоны ВКР были также получены при накачке 100-пикосекунд-
ными импульсами от Nd: ИАГ-лазера с синхронизацией мод, рабо-
работавшего на длине волны 1,32 мкм. В эксперименте [129] в обычном
световоде с нулем дисперсии вблизи 1,3 мкм были получены 100-фем-
тосекундные импульсы ВКР на длине волны 1,4 мкм. В другом
1.2
1,3 1,4 1,5
Длина волны 1мкм)
Рис. 8.17. Спектры импульсов на выходе световода длиной 1 км для не-
нескольких значений пиковой мощности входного импульса длиной 0,83 пс.
Начальная длина волны 1,341 мкм лежит в области отрицательной дисперсии
[127].
252
Глава 8
Рис. 8.18. Схема солитонного ВКР-лазера с кольцевым резонатором.
BS-дихроичная пластинка; М] и М2 зеркала со 100%-ным отражением; Ъ1
и L2-микролинзы.
эксперименте [128] с тем же лазером использовался световод с нулем
дисперсии, смещенным на 1,46 мкм. Первая стоксова компонента на
длине волны 1,407 мкм служила накачкой для генерации стоксовой
компоненты второго порядка (на 1,516 мкм) в области отрицательной
дисперсии световода. Длительность импульса ВКР, связанного со
второй стоксовой компонентой, составила 130 фс. У импульса был
широкий пьедестал, и лишь около 30% энергии распространялось
в виде солитона.
Солитонные эффекты ВКР нашли применение в солитонных ВКР-
лазерах [132-138]. Подобно солитонным лазерам, обсуждавшимся
в разд. 5.3, такие лазеры дают выходное излучение в виде солитонов
длительностью ~ 100 фс, но на длине волны, соответствующей сток-
стоксовой компоненте первого порядка. Кроме того, длина волны может
перестраиваться в довольно больших пределах (~ 10 нм) с помощью
метода временной дисперсии, о котором говорилось в разд. 8.2.2.
Обычно используется кольцевая схема, показанная на рис. 8.18. Ди-
хроичная пластинка с высоким отражением на длине волн"ы накачки
и с частичным на стоксовой длине волны ^.s используется для ввода
излучения накачки и вывода лазерного излучения.
В первой экспериментальной демонстрации волоконного солитон-
солитонного ВКР-лазера [132] накачкой служили 10-пикосекундные импуль-
импульсы от лазера на центрах окраски на длине волны 1,48 мкм. Кольцевой
резонатор включал 500 м сохраняющего поляризацию одномодового
световода со смещенной дисперсией, длина волны нулевой дисперсии
XD которого находилась около 1,536 мкм. Это позволяло импульсам
ВКР и накачки перекрываться на значительной части световода, так
как их длины волн располагались по разные стороны от XD на
примерно равном расстоянии (ks ~ 1,58 мкм). Генерировались им-
импульсы длительностью 300 фс с малоинтенсивным, но широким
пьедесталом. Делались попытки удалить пьедестал, для чего схема на
рис. 8.18 была модифицирована: один отрезок световода был заменен
двумя с изменяемым коэффициентом связи между ними. Световод
Вынужденное комбинационное рассеяние 253
длиной 100 м обеспечивал комбинационное усиление, в то время как
другой световод длиной 500 м служил для сжатия импульса (ВКР
в нем не возникало, поскольку при переводе излучения из одного
световода в другой мощность накачки опускалась ниже порога.).
Удавалось получить импульсы без пьедестала длительностью 284 фс,
когда разница длин соответствовала 380 см или 11,4 ТГц. Однако,
когда длины волн отстояли друг от друга на 440 см (что соответст-
соответствует пику комбинационного усиления), значительная часть энергии
импульса содержалась в широком пьедестале. Такое сложное поведе-
поведение связано с эффектом ФКМ [133].
В недавних экспериментах [134 136] для накачки солитонных
ВКР-лазеров использовались импульсы длительностью 100 пс от
Nd: ИАГ-лазера с длиной волны генерации 1,32 мкм. Такой выбор
длины волны интересен возможностью использовать обычные свето-
световоды с XD ~ 1,3 мкм. К тому же импульсы и накачки, и ВКР близки
к длине волны нулевой дисперсии и могут перекрываться в световоде
достаточно долго, чтобы обеспечить нужное усиление (длина группо-
группового разбегания ~ 300 м). В эксперименте [134] были получены
импульсы длительностью 160 фс; при этом использовался световод,
не сохраняющий поляризацию, длиной 1.1 км. Импульсы имели
широкий пьедестал, и в солитонной составляющей содержалось лишь
около 20% энергии импульса. В другом эксперименте [136] использо-
использовался световод со смещенной дисперсией (kD ъ 1,46 мкм). При генера-
генерации второй и третьей стоксовых компонент вблизи длин волн 1,5
и 1,6 мкм соответственно наблюдались солитоны длительностью
около 200 фс. Этот процесс каскадного ВКР использовался также для
генерации солитонов вблизи длины волны 1,5 мкм при накачке
импульсами на длине волны 1,06 мкм [137]. При этом три первые
стоксовы компоненты расположены в области положительной дис-
дисперсии световода (XD =* 1.3 мкм). Четвертая и пятая стоксовы полосы
образуют в спектре широкое крыло в области длин волн 1,3-1,5 мкм,
которое содержит около половины входной энергии. Автокорреля-
Автокорреляционные функции импульсов на длинах волн 1,35; 1,4; 1,45 и 1,5 мкм
показали, что энергия в пьедестале уменьшается с увеличением длины
волны. Действительно, импульсы вблизи 1,5 мкм почти не имели
пьедестала.
Подводя итоги данной главы, отметим, что ВКР сверхкоротких
импульсов в области отрицательной дисперсии световодов - это нели-
нелинейное явление, при котором могут генерироваться сверхкороткие
солитоноподобные импульсы длительностью менее ~ 100 фс. Эти
солитоны нужно отличать от солитонов ВКР, возникающих в молеку-
молекулярных газах [139]. Там время отклика среды больше длительности
солитона, и необходимо учитывать динамику колебательных мод,
участвующих в процессе ВКР [139- 141]. В случае еветоводов время
комбинационного отклика много меньше длительности солитона.
254 Глава 8
Теоретическое описание солитонов, возникающих при ВКР в светово-
световодах, не завершено, и продолжается работа над новыми моделями
[123].
ЛИТЕРАТУРА
1. Raman С. К. Indian J. Phys., 2, 387 A928).
2. Woodbury E.J.. Ng W.K.. Proc. IRE., 50, 2347 A962).
3. Hellwarth R.W.. Phys. Rev., 130, 1850 A963); Appl. Opt., 2, 847 A963).
4. Garmire E. Pandarese E.. Townes C.H., Phys. Rev. Lett., 11, 160 A963).
5. Slien Y.R.. Bhembergen N.. Phys. Rev., 137, A1786 A965).
6. Bhembergen N.. Ani. J. Phys., 35, 989 A967).
7. Kaiser W., Maier M.. in: Laser Handbook, vol. 2, ed. by F. T. Arecchi,
E.O. Schulz-Dubois, North-Holland, Amsterdam, 1972, Ch. E2.
8. Shen Y. R., The Principles of Nonlinear Optics, Wiley, New York, 1984, Ch. 10.
[Имеется перевод: ШенИ.Р. Принципы нелинейной оптики.-М.: Мир,
1989.]
9. Stolen R.H.. Ippen E.P.. Tynes A.R.. Appl. Phys. Lett., 20, 62 A972).
10. Stolen R.H.. Ippen E.P.. Appl. Phys. Lett., 22, 276 A973).
11. Stolen R.H.. Proc. IEEE, 68, 1232 A980).
12. Shuker R.. Gammon R. W.. Phys. Rev. Lett., 25, 222 A970).
13. Smith R.G.. Appl. Opt., 11, 2489 A972).
14. AuYeung J., Yariv A., IEEE J. Quantum Electron., QE-14, 347 A978).
15. Lin C. Stolen R.H.. Appl. Phys. Lett., 28, 216 A976).
16. Lin С et al. Opt. Commun., 20, 426 A977).
17. Grigoryants V. V. et al.. Opt. Quantum Electron., 9, 351 A977).
18. Cohen L.G.. Lin C. IEEE Quantum Electron., QE-14. 855 A978).
19. Butylkin V.S., Grigoryants V.V.. Smirnov V.I., Opt. Quantum Electron., 11, 141
A979).
20. Stolen R. H.. in: Optical Fiber Communications, ed. by S. E. Miller, A. G. Chy-
noweth. Academic, New York, 1979, Ch. 5.
21. Gao P.-J. et al.. Appl. Phys., 24, 303 A981).
22. Rosman G.. Opt. Quantum Electron., 14, 92 A982).
23. Ohmori Y. Sesaki Y. Edahiro Т.. Trans. 1ECE Japan, E66, 146 A983).
24. Pint R. et al. Appl. Phys. Lett., 43, 6 A983).
25. Rothschild M.. Abad H.. Opt. Lett., 8, 653 A983).
26. Barbosa F.R.. Appl. Opt. Lett., 22, 3859 A983).
27. Stolen R.H.. Lee C. Jain R.K.. J. Opt. Soc. Am., Bl, 652 A984).
28. Suuki K.. Noguchi K.. Vesugi N.. Opt. Lett., 11, 656 A986).
29. Lin C, J. Lightwave Technol., LT-4, 1103 A986).
30. Gomes A.S.L. et al., Opt. Commun., 64, 373 A987).
31. Hill K.O.. Kawasaki B.S.. Johnson D.C., Appl. Phys. Lett., 28, 608 A976); 29,
181 A976).
32. Jain R.K. et al., Appl. Phys. Lett., 30, 162 A977).
33. Johnson D.C. et al.. Electron. Lett., 13, 53 A977).
34. Stolen R.H.. Lin C. Jain R.K.. Appl. Phys. Lett., 30, 340 A977).
35. Lin C, Stolen R.H.. Cohen L.G.. Appl. Phys. Lett., 31, 97 A977).
36. Lin С et al.. Opt. Lett., 1, 96 A977).
37. Jain R.K. et al.. Appl. Phys. Lett., 31, 89 A977).
38. Stolen R.H. et al.. IEEE J. Quantum Electron., QE-14, 860 A978).
39. Lin C. French W.G., Appl. Phys. Lett., 34, 10 A979).
40. Stolen R.H.. IEEE J. Quantum Electron., QE-15, 1157 A979).
41. Lin C. Glodis P.F.. Electron. Lett., 18, 696 A982).
42. Kakazawa M.. Masamitsu Т.. Ichida N.. J. Opt. Soc. Am., Bl, 86 A984).
43. Chraplyvy A.R.. Stone J.. Opt. Lett., 9, 241 A984).
44. Nakazawa M.. Opt. Lett., 10, 193 A985).
Вынужденное комбинационное рассеяние 255
45. РЫ R. et al, Appl. Opt., 25, 1048 A986).
46. Mizunami Т., Miyazaki Т.. Takagi K., J. Opt. Soc. Am., B4, 498 A987).
47. Kafka J. D., Head D. F., Baer Т.. in: Ultrafast Phenomena V, ed. by G. R.
Fleming, A. E. Siegman, Springer-Verlag, Berlin, 1986, p. 51.
48 Desurvire E., Imamoglu A., Shaw H.J., J. Lightwave, Technol., LT-5, 89 A987).
49. Kean P.N. et al., J. Mod. Opt. 35, 397 A988).
50. Lin C. Stolen R.H., Appl. Phys. Lett., 29, 428 A976).
51. Ikeda M.. Opt. Comraun, 39, 148 A981).
52. Koep G.A.. Kalen D.M.. Greene K.H., Electron. Lett., 18, 942 A982).
53. Aoki Y et al.. Electron. Lett., 19, 620 A983).
54. Desurvire E. et al.. Electron. Lett., 19, 751 A983).
55. Chraphvy A.R., Stone J., Burrus С A., Opt. Lett., 8, 415 A983).
56. Nakazawa M. et al. J. Opt. Soc. Am., Bl, 80 A984).
57. Nakamura K. et al., J. Lightwave Technol., LT-2. 379 A984).
58. Nakazawa M.. Appl. Phys. Lett., 46, 628 A985).
59. Nakazawa M., Nakashima Т., Seikai S., J. Opt. Soc. Am., B2, 215 A985).
60. Dakss M.L., Melmcin P., J. Lightwave Technol., LT-3, 806 A985).
61. Pocholle J.P. et al.. Opt. Eng., 24, 600 A985).
62. Durteste Y. Monerie M., Lamouler P.. Electron Lett., 21, 723 A985).
63. Olsson N.A., Hegarty J., J. Lightwave Technol., LT-4, 391 A986).
64. Vilhelmsson K.. J. Lightwave Technol., LT-4, 400 A986).
65. Desurvire E, Digonnet M. J. F., Shan- H. J., J. Lightwave Technol., LT-4, 426
A986).
66. Aoki Y. Kishida S., Washio K., Appl. Opt., 25, 1056 A986).
67. Seikai S.. Nakashima Т., Shibata N.. J. Lightwave Technol., LT-4, 583 A986).
68. Mochizuki K., Edagawa N.. Iwamoto Y, J. Lightwave Technol., LT-4, 1328
A986).
69. Davies R. W. et al, J. Lightwave Technol., LT-5, 1068 A987).
70. Davison A.S.. White J.H.. Electron. Lett., 23, 1344 A987).
71. O'Mahony M.J., J. Lightwave Technol., LT-6, 531 A988).
72. Hegarty J.. Olsson N.A.. Goldner L., Electron. Lett., 21, 290 A985).
73. Mochizuki K.. Edagawa N.. Ы-amoto Y, J. Lightwave Technol., LT-4, 1328
A986).
74. Edagawa N.. Mochizuki K., Iwamoto Y, Electron. Lett., 23, 196 A987). "
75. Dakss M.L., Melmann P., IEE Proa, 135, Pt. J. 96 A988).
76. Mochizuki K.. J. Lightwave Technol., LT-3, 688 A985).
77. Aoki Y, J. Lightwave Technol., LT-6, 1225 A988).
78. Hasegawa A., Appl. Opt., 23, 3302 A984).
79. Mollenauer L.F., Stolen R.H., Islam M.N., Opt. Lett., 10, 229 A985).
80. Mollenauer L. F., Gordon J. P.. Islam M. N.. IEEE J. Quantum Electron.,
QE-22, 157 A986).
81. Mollenauer L.F., Smith K.. Opt. Lett., 13, 675 A988).
82. Chraplyvy A.R., Henry P.S., Electron. Lett., 19, 641 A983).
83. Tomita A.. Opt. b>tt., 8, 412 A983).
84. Chraplyvy A. R., Electron. Lett., 20, 58 A984).
85. Cotter D.. Hill A.M.. Electron. Lett., 20, 185 A984).
86. Hill A.M.. Cotter D., Wright J. V., Electron. Lett., 20, 247 A984).
87. Mahlein H.F.. Opt. Quantum Electron., 16, 409 A984).
88. Hegartv J.. Olsson N.A., McGlashan-Powell M.. Electron. Lett., 21, 395 A985).
89. Olsson N. A. et al, Electron. Lett., 21, 105 A985).
90. Луговой В.Н. ЖЭТФ, 1976, т. 71, с 1307.
91. Gersten J.I., Alfano R.R., Belie M.. Phys. Rev., A21, 1222 A980).
92. Циинов ЕМ. и др.- Письма в ЖЭТФ, 1984, т. 39, с. 564.
93. Lu J.-H. Li Y.-L.. Jiang J.-L.. Opt. Quantum Electron., 17, 187 A985).
94. Дианов Е.М. и Эр-ЖЭТФ, 1985, т. 89, с. 781.
256 Глава 8
95. Vulk В.. Hodel W. Weber И. P.. Opt. Commun., 54, 363 A985).
96. Stolen R.H., Johnson A.M.. IEEE J. Quantum Electron., QE-22, 2154 A986).
97. French P.M.W. et al. IEEE J. Quantum Electron., QE-22, 2230 A986).
98. Schadt D.. Jaskorzynska В.. Osterberg U.. J. Opt. Soc. Am., B3, 1257 A986).
99. Schadt D.. Jaxkorzvnska В., J. Opt. Soc. Am., B4, 856 A987).
100. Keun P.N.. Smith K.. Sibbett W. IEE Proc, 134, Pt. J, 163 A987).
101. Alfano R.R. et al. Appl. Opt., 26, 3492 A987).
102. Manassah J.T., Appl. Opt., 26, 3747 A987).
103. Дианов Е.М. и др.- Письма в ЖЭТФ. 1987, т. 45. с. 469.
104. Smith К. et al, J. Mod. Opt., 34, 1227 A987).
105. Дианов Е. М. и др. Письма в ЖЭТФ, 1987, т. 46, с. 383.
106. Nakazawa М. et al. J. Opt. Soc. Am., B4, 1412 A987).
107. Buldeck P.L.. Ho P.P.. Alfano R.R.. Rev. Phys. Appl., 22, 1677 A987).
108. Alfano R.R.. Ho P.P.. IEEE J. Quantum Electron., QE-24, 351 A988).
109. Werner A.M.. Heritage J.P.. Stolen R.H.. J. Opt. Soc. Am., B5, 364 A988).
110. Gomes A.S.L.. da Si'lva V.L.. Taylor J.R.. J. Opt. Soc. Am., B5, 373 A988).
111. BaldeckP.L.. Alfano R.R.. AgrawalG.P.. Int. Conf. Ultrafast Phenomena,
Paper PD2, July 12 15 A988).
112. Kuckartz M., Schulz R.. Horde A.. Opt. Quantum Electron., 19, 237 A987); J.
Opt. Soc. Am., B5, 1353 A988).
113. Raymer M.G. et al. Phys. Rev., A32, 332 A985).
114. Suzuki K.. Noguchi K.. Uesugi N.. Opt. Lett, 11, 656 A986); J. Lightwave
Technol, LT-6, 94 A988).
115. Gomes A.S.L. et al.. Opt. Commun., 64, 373 A987).
116. Nakaxhima T. et al. Opt. Lett., 12, 404 A987).
117. Gomes A. S. L.. Gouveia-Neto A. S.. Taylor J. R.. Opt. Quantum Electron.. 20, 95
A988).
118. Bbicwvx В. А.. Серкии В. Н. Письма в ЖЭТФ, 1983, т. 38, с. 170. Изв. АН
СССР', сер. физ., 1984, т. 48, № 19, с. 1777.
119. Дианов Е.М. и Эр.-Письма в ЖЭТФ, 1985, т. 41. с. 242.
120. Dianov E.M.. Prokhorov A.M.. Serkin V.N.. Opt. Lett., 11, 168 A986).
121. Mitschke F.M.. Mollenaucr L.F.. Opt. Lett, 11, 659 A986).
122. Гргдшшн А. Б. и др. Письма в ЖЭТФ, 1987, т. 45, с. 211.
123. Се'ркин В.Н. Письма в ЖЭТФ, 1987, т. 13, с. 878.
124. Водопьчнов К.Л. и Эр.-Квант, электрон., 1987, т. 14, с. 2053.
125. Zysset В.. Beaud P.. Hodel W.. Appl. Phys. Lett., 50, 1027 A987).
126. Hodel W. Weber HP.. Opt. Lett., 12, 924 A987).
127. Beaud P. et al. IEEE J. Quantum Electron., QE-23, 1938 A987).
128. Gouveia-Neto A.S. et al. Electron. Lett., 23. 1034 A987).
129. Gouveia-Neto A.S.. Gomes A.S.L.. Tavlor J.R.. Opt. Lett, 12, 1035 A987).
130. Blow K.J.. Doran N.J.. WoodD.. J. Opt. Soc. Am, B5, 381 A988).
131. Gmweia-Neto A.S., Gomes A.S.L., Taylor J.R.. IEEE J. Quantum Electron.,
QE-24, 332 A988).
132. Islam M.N.. Mollenauer L.F., Stolen R.H., in: Ultrafast Phenomena V, ed. by
G. R. Fleming, A.E. Siegman, Springer-Verlag, Berlin, 1986, p. 46.
133. Islam M.N. et al. Opt. Lett, 12, 814 A987).
134. Kafka J.D.. Baer T. Opt. Lett., 12, 181 A967).
135. Gouveia-Neto A.S., Gomes A.S.L.. Taylor J.R., Electron. Lett, 23, 537 A987);
Opt. Quant, Electron.. 20, 165 A988).
136. Gouveia-Neto A.S. et al. Opt. Lett, 12, 927 A987).
137. da Silva V.L.. Gomes A.S.L.. Taylor J.R.. Opt. Commun, 66, 231 A988).
138. Haus H.A.. Nakazawa M., J. Opt. Soc. Am, B4, 652 A988).
139. Druhl K.. Wenzel R.G.. Carlsten J.L.. Phys. Rev. Lett., 51, 1171 A983); J. Stat.
Phys, 39, 615 A985).
140. EnglundJ.C. Bowden СМ.. Phys. Rev. Lett., 57, 2661 A986).
141. MacPherson D. C. Carlsten J.L.. Druhl K.J.. J. Opt. Soc. Am, B4, 1853 A987).
Глава 9
ВЫНУЖДЕННОЕ РАССЕЯНИЕ
МАНДЕЛЬШТАМА - БРИЛЛЮЭНА (ВРМБ)
Вынужденное рассеяние Мандельштама-Бриллюэна (ВРМБ)
представляет собой нелинейный процесс, который может возникать
в световодах при мощности излучения много меньшей, чем требуется
для вынужденного комбинационного рассеяния (ВКР). Оно проявля-
проявляется в виде генерации стоксовой волны, распространяющейся в обрат-
обратном направлении и содержащей наибольшую часть начальной энер-
энергии. В системах оптической связи ВРМБ может быть вредным
эффектом. В то же время оно может использоваться в ВРМБ-лазерах
и усилителях. В данной главе будут рассмотрены и применения
ВРМБ, и паразитные эффекты, связанные с ним. В разд. 9.1 представ-
представлены основные сведения о ВРМБ, в частности о ВРМБ-усилении.
В разд. 9.2 рассмотрены теоретические аспекты ВРМБ-пороговые
условия, истощение накачки и насыщение усиления. Там же рас-
рассматривается динамическое взаимодействие между волной накачки
и стоксовой волной, которое может приводить к неустойчивостям.
Экспериментальные результаты по ВРМБ описаны в разд. 9.3, под-
подразделы которого посвящены однопроходному ВРМБ, волокон-
волоконным ВРМБ-лазерам и волоконным ВРМБ-усилителям. Наконец,
в разд. 9.4 ВРМБ рассматривается с точки зрения оптической связи.
9.1. ВРМБ-УСИЛЕНИЕ
ВРМБ впервые наблюдалось в 1964 г. и широко исследовалось
в последующие годы [1-8]. Как и ВКР, оно проявляется в виде
генерации стоксова излучения с меньшей, чем у накачки, частотой,
причем величина частотного сдвига определяется нелинейной средой.
Однако между ВРМБ и ВКР существуют важные различия. Напри-
Например, стоксова волна при ВРМБ распространяется навстречу волне
накачки, а при ВКР в обоих направлениях. Стоксово смещение при
ВРМБ (~ 10 ТГц) на три порядка меньше, чем при ВКР. Пороговая
мощность накачки при ВРМБ зависит от ширины ее спектра. При
относительно длинных импульсах накачки (длительностью не менее
1 мкс) или при непрерывном излучении она может составлять всего
1 мВт. При коротких импульсах накачки длительностью менее 10 не
258 Глава 9
ВРМБ не возникает. Все эти различия обусловлены одним обстоя-
обстоятельством: при ВКР действуют оптические фононы, а при ВРМБ -
акустические.
Процесс ВРМБ можно описать классически как параметрическое
взаимодействие между волнами накачки, стоксовой и акустической.
Благодаря электрострикции накачка генерирует акустическую волну,
приводящую к периодической модуляции показателя преломления.
Индуцированная решетка показателя преломления рассеивает излуче-
излучение накачки в результате брэгговской дифракции. Поскольку решетка
движется со звуковой скоростью vA, частота рассеянного излучения
испытывает доплеровский сдвиг в длинноволновую область. В кван-
квантовой механике такое рассеяние описывается как уничтожение фотона
накачки и одновременное появление стоксова фотона и акустического
фонона. Из законов сохранения энергии и импульса при рассеянии
вытекают соотношения для частот и волновых векторов трех волн:
юх = юр-ю5, (9.1.1)
k^kp-k,, (9.1.2)
где юр и tos-частоты и кр и ks-волновые векторы накачки и стоксовой
волны соответственно. Частота а>д и волновой вектор кд акустиче-
акустической волны удовлетворяют дисперсионному уравнению
(oA = \kA\vA = 2vA\kp\ sin F/2), (9.1.3)
где 9-угол между направлениями распространения волн накачки
и стоксовой, а в векторном уравнении (9.1.2) было сделано приближе-
приближение |kp| ~ |kj. Уравнение (9.1.3) показывает, что смещение частоты
стоксовой волны зависит от угла рассеяния. В частности, оно макси-
максимально для обратного направления (9 = п) и исчезает для направле-
направления, совпадающего с вектором накачки (9 = 0). Для обратного на-
направления смещение частоты дается выражением
съ 2nvA
vb = t^ = ^A (9.1.4)
2л Ар
где использовалось (9.1.3) с подстановкой |кр| = 2пп/Хр, и показа-
показатель преломления и Хр-длина волны накачки.
В одномодовом световоде возможны только прямое и обратное
направления распространения. Хотя уравнение (9.1.3) предсказывает
отсутствие ВРМБ в прямом направлении (9 = 0), в световодах в этом
направлении может возникать спонтанное тепловое рассеяние Ман-
Мандельштама- Бриллюэна (РМБ). Это обусловлено тем. что в световоде
существуют направляемые акустические волны, в силу чего правило
отбора для волновых векторов может нарушаться. В результате
происходит генерация слабого стоксова излучения в прямом направ-
направлении [9]. Это явление называют спонтанным РМБ на направляемых
акустических волнах. На спектре стоксова излучения видно множе-
Вынужденное рассеяние Мандельштама - Бриллюэна 259
ство линий со сдвигом ~ 10-1000 МГц от частоты накачки. Они
исключительно слабы и далее не рассматриваются. В световодах
спонтанное РМБ с частотным смещением, данным формулой (9.1.4),
возникает только в обратном направлении. Если принять типичные
для световодов из кварцевого стекла значения vA = 5,96 км/с и
п = 1,45, то на длине волны Хр = 1,55 мкм vB = 11,1 ГГц.
Рост интенсивности стоксовой волны характеризуется коэффи-
коэффициентом усиления при ВРМБ 0B(v). максимальным при v = vB.
Однако в отличие от ВКР спектральная ширина ВРМБ-усиления AvB
очень мала (~ 10 МГц против ~ 5 ТГц). Ширина спектра связана
с временем затухания акустической волны или временем жизни
фотона Тв. Действительно, если принять затухание акустической
волны экспоненциальным (ехр(— t/TB)), то спектр ВРМБ-усиления
будет иметь лоренцеву форму
!/ <> (915)
(v - vBJ + (AvB/2J
где AvB — ширина спектра на полувысоте, связанная с временем
жизни фонона AvB = (жТв)~1. Максимальный коэффициент ВРМБ-
усиления при v = vB дается выражением [4]
(9,1.6)
где />j2-продольный акустооптический коэффициент, ро- плотность
материала и Хр-длина волны накачки.
Исследования рассеяния Мандельштама - Бриллюэна в объемных
образцах плавленого кварца были проделаны [10] уже в 1950 г. Более
поздние измерения [11], выполненные с одночастотным аргоновым
лазером, показали, что vB = 34,7 ГГц и A vB = 54 МГц на длине
волны Хр = 486 нм. Эти эксперименты также показывают, что A vB
зависит от величины смещения при РМБ и меняется несколько
быстрее, чем vB (квадратичная зависимость следует из теории).
С учетом обратной зависимости vB от Хр в (9.1.4) величина AvB
должна быть пропорциональна ^2. Это сужение спектральной поло-
полосы с возрастанием Хр компенсирует уменьшение коэффициента
ВРМБ-усиления, следующего из (9.1.6). В результате коэффициент
ВРМБ-усиления почти не зависит от длины волны накачки. Если
подставить в (9.1.6) типичные для плавленого кварца значения пара-
параметров, получится дв ~ 5-Ю1 м/Вт. Это почти на три порядка
больше комбинационного коэффициента усиления на длине волны
\ = 1,55 мкм (см. 8.1).
Спектр ВРМБ-усиления в кварцевых световодах может суще-
существенно отличаться от того, что наблюдается в объемных образ-
образцах, что обусловлено направляющими свойствами световода и при-
260
Глава 9
1 'l 1
Л в)
у, V
1 'i
i
6)
i ' i
и)
10,6
10,8
11,0 11,2
Частота (ГГц)
11,4
Рис. 9.1. Спектры ВРМБ-усиления в трех световодах при Хр = 1,525 мкм.
а световод с сердцевиной из плавленого кварца; б-световод с депрессиро-
ванной оболочкой; е- световод со смещенной дисперсией. Вертикальная шкала
произвольна [14].
сутствием добавок в сердцевине [12 16]. На рис. 9.1 показаны спект-
спектры, измеренные в трех различных световодах с различными структу-
структурами и различными концентрациями германия в сердцевине. Источ-
Источником служил полупроводниковый лазер с внешним резонатором
с длиной волны генерации 1,525 мкм, а в измерениях использовалось
гетеродинное детектирование с разрешением 3 МГц [14]. Световод
(я) имел сердцевину из почти чистого плавленого кварца (концентра-
(концентрация германия около 0,3 мол.%). Измеренный сдвиг частоты vB =
= 11,25 ГГц соответствует формуле (9.1.4) для этого световода, если
принять скорость звука такой же. как в объемном образце плавленого
кварца. ВРМБ-смещение в световодах уменьшается с ростом концент-
концентрации германия, что видно на спектрах (б) и (в). ВРМБ-спектр
световода (б) имеет двухпиковую структуру, обусловленную, видимо,
неоднородным распределением германия в сердцевине [14]. В другом
эксперименте [16] наблюдался ВРМБ-спектр с тремя пиками, что
объяснялось разницей скоростей звука в сердцевине и оболочке
световода.
Ширина линии ВРМБ-усиления на рис. 9.1 намного больше, чем
в объемном плавленом кварце (Лу„~17МГц на длине волны
"кр = 1,525 мкм). В других экспериментах также обнаружена линия,
в 2 раза более широкая, чем в объемных образцах [15, 16]. Отчасти
такое уширение связано с тем, что в световодах распространяются
направляемые акустические волны [12]. Однако в основном уширение
обусловлено неоднородностями сечения световода по длине. По-
Поскольку такие неоднородности различны в различных световодах,
ширина линии бриллюэновского усиления в них также различается
и может достигать 100 МГц на длине волны 1,55 мкм.
Уравнение (9.1.5) для ВРМБ-усиления получено при стационарных
условиях и действительно для непрерывной или квазинепрерывной
Вынужденное рассеяние Мандельштама - Бриллюэна 261
накачки (То » Т„), ширина спектра которой много меньше ширины
линии ВРМБ-усиления AvB. В случае импульсов накачки длитель-
длительностью То < Тв теория нестационарного ВРМБ [3-5] показывает, что
ВРМБ-усиление существенно понижается по сравнению с тем, что
дает уравнение (9.1.6). Действительно, если длительность импульса
становится меньше времени жизни фонона (То < 1 не), то ВРМБ-
усиление становится меньше комбинационного, такой импульс накач-
накачки посредством ВКР генерирует ВКР-импульс, что обсуждалось
в разд. 8.4.
Даже в случае непрерывной или квазинепрерывной накачки ВРМБ-
усиление существенно понижается, если Avp превышает AvB. Это
может происходить также с одномодовой накачкой, фаза которой
быстро меняется за время, меньшее чем время жизни фонона Тв.
Детальные вычисления показывают [17-20], что ВРМБ-усиление
в случае широкополосной накачки зависит от относительных величин
длины когерентности накачки Lcoh = c/(n A vp) и длины ВРМБ-взаимо-
действия Linl, определяемой как расстояние, на котором существенно
меняется амплитуда стоксовой волны. Если Lcoh » Linl, то процесс
ВРМБ не зависит от модовой структуры накачки, так как расстояние
между модами превышает A vB и ВРМБ-усиление почти такое же, как
для одномодового лазера на нескольких длинах взаимодействия [18].
Если же, Lcoh«Linl, то ВРМБ-усиление существенно понижается.
Последняя ситуация обычно реализуется в световодах, где длина
взаимодействия сравнима с длиной световода L. Если спектр накачки
имеет лоренцев профиль с шириной на полувысоте Avp, то форма
спектра ВРМБ-усиления по-прежнему описывается уравнением (9.1.5),
но пиковое усиление дается выражением [20]
AvB
(v), (9.1.7)
где 0B(vB) дается формулой (9.1.6). Таким образом, в случае Avp»
» A vB ВРМБ-усиление уменьшается в A vp/A vB раз.
9.2. ТЕОРИЯ
Как и в случае ВКР, рассмотрение ВРМБ в световодах требует
учета взаимодействия между стоксовой волной и волной накачки.
В стационарных условиях такое взаимодействие подчиняется системе
связанных уравнений, подобных уравнениям (8.1.2) и (8,1.3) из
разд. 8.1. Единственное отличие-другой знак при dljdz в соответ-
соответствии с направлением распространения стоксовой волны навстречу
волне накачки. Можно сделать два упрощения. Благодаря относи-
относительно небольшим значениям ВРМБ частотного сдвига можно при-
262 Глава 9
нять юр =: со„. По той же причине потери в световоде для волны
накачки и стоксовой волны практически одинаковы, т.е. ар ^ as = a.
С учетом этих приближений (8.1.2) и (8.1.3) превращаются в следую-
следующую систему:
— = -gBlDIs + a/s, (9.2.1)
dz
^=-вв/,/,-«/,, (9.2.2)
где дв коэффициент усиления при ВРМБ из разд. 9.1. Легко прове-
проверить, что в отсутствие потерь (а = 0)
d_
~dz
— (Is - Ip) = 0, (9.2.3)
как и должно быть в силу сохранения энергии при ВРМБ.
9.2.1. ПОРОГ ВРМБ
Систему связанных уравнений для интенсивностей (9.2.1), (9.2.2)
можно решить аналитически [4, 21]. Хотя такое решение пригодно
для полного описания ВРМБ, для понимания физики явления полезно
рассмотреть случай без истощения накачки, что позволяет оценить
величину порога ВРМБ. В таком случае стоксова волна, распрост-
распространяясь навстречу волне накачки, экспоненциально усиливается в со-
соответствии с уравнением
/ДО) = Is(L)txp(gBP0L3^/A3M - aL), (9.2.4)
где Ро = 1р@)Аэфф. Здесь Лэфф-эффективная площадь сечения, а эф-
эффективная длина взаимодействия дается выражением
L,** = -[l-exp(-aL)]. (9.2.5)
Уравнение (9.2.4) показывает, как стоксов сигнал, возникающий
в точке z = L, усиливается благодаря ВРМБ. На практике такой
сигнал обычно отсутствует (если только световод не используется как
ВРМБ-усилитель) и стоксова волна возникает из шумов спонтанного
МБ-рассеяния, возникающего в световоде. Как и в случае ВКР, это
эквивалентно инжекции одного эффективного фотона на одну моду
в точке, где усиление компенсирует потери световода [7]. Методом,
подобным использованному в разд. 8.1, получаем, что порог ВРМБ
достигается при критической мощности накачки Р1Т [7], получаемой
из выражения
ф^21, (9.2.6)
Вынужденное рассеяние Мандельштама Бриллюэна 263
где дв-пиковое значение ВРМБ-усиления, даваемого формулой
(9.1.6). Сравним отношения (9.2.6) с выражением (8.1.15), полученным
для случая ВКР. Численное значение 21 величина приблизительная,
поскольку она зависит от точного значения ширины линии ВРМБ-
усиления. Она может возрастать в 1- 2 раза в зависимости от того,
сохраняют ли стоксова волна и волна накачки поляризацию в свето-
световоде или нет. Случаю полной деполяризации соответствует увеличе-
увеличение численного фактора в 2 раза. Тем не менее выражение (9.2.6)
вполне применимо для оценки порога ВРМБ. Если взять обычные
значения параметров световода для оптической связи на 1.55 мкм:
Л,фф = 50 мкм2. Ьэфф =i 20 км, дв = 5-10" п м/Вт, то (9.2.6) дает кри-
критическую мощность накачки Р" = 1 мВт. Такой низкий порог делает
ВРМБ доминирующим нелинейным процессом в световодах. Приме-
Применения ВРМБ в волоконных системах оптической связи рассматри-
рассматриваются в разд. 9.4.
9.2.2. ИСТОЩЕНИЕ НАКАЧКИ И НАСЫЩЕНИЕ
УСИЛЕНИЯ
При достижении порога ВРМБ значительная часть энергии накач-
накачки преобразуется в энергию стоксовой волны. Для учета истощения
накачки необходимо точно решить уравнения (9.1.1) и (9.1.2). Общее
решение имеет вид [4, 21]
G(z)-b0
(l~bo)G(z)
/„(O)exp(-az), (9.2.7)
/_(O)exp(-ar), (9.2.8)
pv G(z)-b0
где
G(z) = exp{(l - bo)(go/a)\_l - exp(-az)]}, (9.2.9)
0). (9.2.10)
Здесь b0 (параметр эффективности ВРМБ) показывает, какая часть
исходной мощности накачки преобразуется в мощность стоксовой
волны, д0 - коэффициент усиления слабого сшнала.
Уравнения (9.2.7) и (9.2.8) описывают изменение интенсивное гей
стоксовой волны и волны накачки по длине световода в случае ВРМБ-
усиления сигнала, вводимого в световод в точке z = L поля накачки,
вводимой в точке z = 0. На рис. 9.2 показано изменение интенсивно-
стей стоксовой волны и волны накачки для двух значений входного
сигнала, соответствующих Ьы = Is(L)/Ip@) = 0,001 и 0,01. Потери
в световоде таковы, что aL=0,l. Коэффициент ВРМБ-усиления
e0L= 10 соответствует однопроходному усилению ехрA0) ^ 2,2-104.
264
Глава 9
0,2 0,4 0,6 0,8
Расстояние % /L
1,0
Рис. 9.2. Изменение интенсивностей волны накачки и стоксовой волны (нор-
(нормированных на входную интенсивность накачки) по длине световода для
входных (z = L) интенсивностей стоксовой волны 0,001 (сплошные линии)
и 0,01 (штриховые линии).
Рис. 9.3. Характеристики насыщения волоконных ВРМБ-усилителей при не-
нескольких значениях коэффициента ненасыщенного усиления Gл. Параметр
Ь1п~мощность входного сигнала, отнесенная к мощности накачки.
Вынужденное рассеяние Мандельштама Бриллюэна 265
Из-за истощения накачки усиление значительно меньше Тем не менее
50 и 70% энергии накачки переходят в стоксово излучение при
/,.п = 0,001 и 0,01 соответственно. Отметим также, что передача
основной части энергии происходит на первых 20% длины световода.
Характеристики насыщения волоконных ВРМБ-усилителей можно
получить из уравнения (9.2.7), если определить насыщенное и ненасы-
ненасыщенное усиление следующим образом:
/s(L)exp(-aL)
(9.2.11)
На рис. 9.3 показана зависимость GS/GA от GAbin для нескольких
значений GА. Сравним этот рисунок с рис. 8.6, где показаны характе-
характеристики насыщения ВКР-усилителя. Насыщенное усиление понижает-
понижается вдвое (или на 3 дБ), когда GAbln = 0,5 для GА в пределах 20-30 дБ.
Эти условия выполняются при мощности усиленного сигнала, состав-
составляющей 50% от входной мощности накачки. Типичная мощность
накачки при ВРМБ-усилении ~ 1 мВт, и, следовательно, мощность
насыщения составляет ~ 1 мВт в отличие от волоконных ВКР-усили-
телей, для которых мощность насыщения ~ 1 Вт.
9.2.3. ДИНАМИКА ВРМБ
Динамика ВРМБ зависит от соотношения длительности импульса
накачки То и времени жизни фонона 7^. При То < Тв необходимо
учитывать динамику акустической волны, так как ВРМБ-усиление
в этом случае зависит от времени [3, 5]. Однако даже при длительно-
длительности импульсов накачки больше Тв в динамическом поведении ВРМБ
проявляется множество интересных свойств. В частности, интенсив-
интенсивность стоксовых компонент испытывает релаксационные колебания
с периодом 27^. где 7^ время прохода по трассе [22]. В присутствии
внешней обратной связи эти релаксационные колебания становятся
устойчивыми [23], т.е. стоксова волна и волна накачки испытывают
самоиндуцированную модуляцию интенсивности. Эти эффекты хоро-
хорошо описываются уравнениями связанных амплитуд, подобными урав-
уравнениям (8.1.18) и (8.1.19). Однако эти уравнения существенно упроща-
упрощаются, если заметить, чго дисперсионные эффекты пренебрежимо
малы из-за относительно больших длительностей импульсов, а эф-
эффекты ФСМ и ФКМ также пренебрежимо малы из-за относительно
низких пиковых -мощностей импульсов стоксовой волны и волны
накачки. Определив /у = | Aj\2 (где / = р или s) и пренебрегая P2j- и уу
в уравнениях (8.1.18) и (8.1.19), получим уравнения, описывающие
временную эволюцию ВРМБ, в виде
02 V,, С Г
266
Глава 9
dt
(9.2.13)
где ^-групповая скорость. В стационарном случае эти уравнения
сводятся к уравнениям (9.2.1) и (9.2.2).
Хотя групповая скорость одинакова для волны накачки и стоксо-
вой волны, их относительная скорость равна 2vs, так как они
распространяются навстречу друг другу. Релаксационные колебания
возникают как следствие этой эффективной расстройки групповых
скоростей. Частоту и скорость затухания релаксационных колебаний
можно получить, анализируя устойчивость стационарного решения
уравнений (9.2.7) и (9.2.8) аналогично тому, как это делалось в
разд. 5.1 в случае модуляционной неустойчивости. Действие внешней
обратной связи можно учесть, взяв соответствующие граничные
условия на концах световода [23]. Такой линейный анализ устойчиво-
устойчивости дает также условия, при которых непрерывный сигнал становится
неустойчивым. Рассмотрим небольшое возмущение уровня непрерыв-
непрерывного сигнала, затухающее как ехр( — ht), где комплексный параметр
h можно определить, линеаризуя уравнения (9.2.12) и (9.2.13). Если
действительная часть h положительна, возмущение затухает экспо-
экспоненциально с релаксационными колебаниями частотой vr = 1т(Л)/2л.
Если же действительная часть h отрицательна, возмущение возраста-
возрастает со временем и непрерывный сигнал становится неустойчивым.
В этом случае ВРМБ ведет к модуляции интенсивностей накачки
и стоксова излучения даже в случае непрерывной накачки. На рис. 9.4
показаны области устойчивости и неустойчивости при наличии обрат-
обратной связи в зависимости от фактора усиления g0L, определенного
1,0
0,8
0,6
0,4
Устойчивость
Неустойчивость
i i i i i i i
10
20
30
Рис. 9.4. Устойчивая и неустойчивая области ВРМБ при натачии обратной
связи. Сплошной линией показано критическое значение относительной интен-
интенсивности стоксовой волны (b0 = /s@)//p@)), ниже которого непрерывный
сигнал неустойчив как функция фактора усиления g0L [23].
Вынужденное рассеяние Мандельштама - Бриллюэна
267
Стоксовы компоненты
Накачка
Рис. 9.5. Временная эволюция интенсивностей стоксовой волны (левая ко-
колонка) и волны накачки (правая колонка) с обратной связью (внизу) и без
обратной связи (вверху). Потери в световоде таковы, что aL = 0,15 [23].
выражением (9.2.10). Там же определен параметр Ьо.
На рис. 9.5 показана эволюция со временем интенсивностей сток-
совой волны и волны накачки, полученная из численного решения
уравнений (9.2.12) и (9.2.13). На верхних рисунках для g0L= 30
показаны релаксационные колебания в отсутствие обратной связи.
Период колебаний 2ТГ, где Тг-время прохода. Источником релакса-
релаксационных колебаний может служить следующий физический механизм
[22]. Быстрый рост стоксовой волны в начале световода истощает
накачку, что приводит к понижению усиления. Затем усиление восста-
восстанавливается, и процесс повторяется.
Нижний ряд на рис. 9.5 соответствует слабой обратной связи
RY R2 = 5- Ю'5, где Rt и R2- коэффициенты отражения от торцов
световода. Усиление g0L= 13 меньше порогового значения. Тем не
менее в результате действия обратной связи порог ВРМБ понижается
и происходит генерация стоксовой волны. Однако процесс не стано-
становится стационарным из-за неустойчивости, показанной на рис. 9.4.
Вместо этого выходные интенсивности волны накачки (г = L) и сток-
стоксовой волны (г = 0) осциллируют. Интересно, что картина становится
стационарной, если обратная связь усиливается так, что RYR2^
$s 2-10, поскольку для этого значения параметр Ьо лежит в области
устойчивости (см. рис. 9.4). Все указанные динамические свойства
ВРМБ наблюдались экспериментально [23].
Другая неустойчивость может возникать [24-28], когда в светово-
световоде одновременно распространяются две встречные волны, даже если
268
Глава 9
их мощности лежат ниже порога ВРМБ (9.2.6). Источником такой
неустойчивости служит взаимная связь встречных волн накачки через
акустическую волну с частотой vB. Неустойчивость проявляется
в виде боковых компонент в спектре накачки на частотах vp + vB, где
vp частота накачки [24, 25]. Во временной картине это проявляется
в виде модуляции обеих волн накачки на частоте ВРМБ. Индуциро-
Индуцированная ВРМБ модуляционная неустойчивость аналогична индуциро-
индуцированной ФКМ модуляционной неустойчивости, описанной в разд. 7.3,
за исключением того, что она возникает в случае волн, распространя-
распространяющихся во встречных направлениях. Порог неустойчивости зависит
от интенсивностей накачки Ifnlb, длины световода L и параметров
ВРМБ взаимодействия дв, vB и Л vB. На рис. 9.6 показана зависимость
нормированной интенсивности накачки If, соответствующей поро-
порогу неустойчивости [28]. от отношения интенсивностей Ib/If при
Avj/vj = 0,06 для нескольких значений нормированной длины свето-
световода 4nnvBL/c. Порог неустойчивости существенно меньше порога
ВРМБ (gBIfL= 21) и при некотором сочетании параметров может
составлять лишь gBIfL = 3. Результаты численных исследований
показывают [28], что временная картина интенсивности накачки на
выходе световода может становиться хаотической по сценарию удвое-
удвоения периода, если ширина линии ВРМБ AvB сравнима с ВРМБ-
сдвигом vB. В спектре рассеянного света возникают субгармоники
частоты ВРМБ с частотной отстройкой, определяемой временем
двойного обхода резонатора. Хаотическое поведение предсказывается
также для случая [26], когда накачка в обратном направлении не
вводится извне, но возникает за счет отражения от зеркала. Индуци-
15
12
9
3
0
I
I
I I
4тгм/в1_/с =
^_ 100
¦
I I
0,1
¦I
/
1
-
-
10
1
0,001
0,01
0,1
1,0
Рис. 9.6. Порог индуцированной ВРМБ модуляционной неустойчивости
встречных волн накачки с начальными интенсивностями lf и 1Ь. Нормиро-
Нормированная интенсивность gBlfL показана как функция /,,/// при AvB/vB = 0,06 для
нескольких значений нормированной длины световода [28].
Вынужденное рассеяние Мандельштама Бриллюэна
269
рованный ВРМБ хаос в световодах пока не наблюдался эксперимен-
экспериментально.
9.3. ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
Результаты экспериментов по ВРМБ можно классифицировать
так же, как это делалось в разд. 8.2 для ВКР, разбив их на три
категории: а) однопроходное ВРМБ, б) ВРМБ-лазеры и в) волокон-
волоконные ВРМБ-усилители. Они будут рассмотрены в трех соответствую-
соответствующих подразделах.
9.3.1. ОДНОПРОХОДНЫЕ ВРМБ
В первом эксперименте, где наблюдалось ВРМБ в световодах,
Иппен и Столен [6] использовали в качестве накачки излучение
импульсного ксенонового лазера с длиной волны 535,5 нм. Использо-
Использование внутрирезонаторного эталона позволило получить спектраль-
спектральную ширину накачки меньше ширины линии ВРМБ-усиления (около
100 МГц). Из-за больших потерь (около 1300 дБ'км) в эксперименте
использовались только короткие отрезки световода (L = 5-20 м).
Измеренный порог ВРМБ составил 2,3 Вт для световода длиной 5,8 м
и около 1 Вт для L = 20 м. что хорошо согласуется с (9.2.6) при
Л,фф= 13.5 мкм2. ВРМБ-смещение vB = 32,2 ГГц также согласуется
с уравнением (9.1.4).
На рис. 9.7 показаны типичные формы импульсов начального
С
¦—-~
(a)
4.
F)
Рис. 9.7. Форма импульса
накачки на входе и выходе
световода (а) и стоксова им-
импульса (б) при ВРМБ в све-
световоде длиной 5.8 м. Гори-
Горизонтальная шкала-200 не на
деление, вертикальная шка-
шкала произвольная [6].
270
Глава 9
и прошедшего через световод импульсов накачки и стоксова импульса
при ВРМБ в световоде длиной 5,8 м. Периодическая структура
связана с релаксационными колебаниями, природа которых обсужда-
обсуждалась в разд. 9.2.3. Период колебаний около 60 не соответствует
двойному времени распространения по световоду, как и предсказыва-
предсказывает теория [22]. Стоксов импульс короче импульса накачки, так как
ВРМБ преобразует энергию только центральной части импульса
накачки, где пиковая мощность превышает порог ВРМБ. В результа-
результате пиковая мощность стоксова импульса может превышать началь-
начальную пиковую мощность импульса накачки. Если пиковая мощность
стоксова импульса значительно превышает начальную мощность
накачки, то ВРМБ может привести к разрушению световода [6].
В большинстве ранних экспериментов порог ВРМБ был относи-
относительно высоким (> 100 мВт) из-за больших потерь. Как уже говори-
говорилось в разд. 9.2.1, при использовании световодов большой длины
с малыми потерями порог ВРМБ может составить лишь 1 мВт.
В эксперименте [29] со световодом длиной 4 км с потерями 4 дБ/км
порог ВРМБ при накачке с длиной волны 0,71 мкм от одночастотного
кольцевого лазера на красителе составил 30 мВт. В недавнем экспери-
эксперименте [30] при накачке непрерывным Nd: ИАГ-лазером на длине
волны 1,32 мкм порог ВРМБ был понижен до 5 мВт. Ширина спектра
натсачки A,6 МГц) была существенно меньше ширины линии ВРМБ-
усиления. В эксперименте использовался световод длиной 13,6 км
с потерями 0,41 дБ/км, что соответствует эффективной длине 7,66 км.
На рис. 9.8 показана схема эксперимента. Изолятор предохраняет
лазер от попадания в него стоксова излучения. В эксперименте
измерялись зависимости прошедшей и отраженной мощностей от
мощности накачки. На рис. 9.9 представлены данные эксперимента.
При небольшой мощности накачки отраженный сигнал обусловлен
просто 4%-ным отражением от торца световода. Порог ВРМБ
достигается при 5 мВт накачки, что проявляется в виде существенно-
существенного возрастания интенсивности отраженного сигнала, в котором те-
теперь доминирует стоксово излучение. В то же" время проходящая
мощность уменьшается в результате истощения накачки. Она пони-
понижается до уровня насыщения (около 2 мВт) при входной мощности
Изолятор
Ослабитель
Рис. 9.8. Схема экспериментальной установки для наблюдения ВРМБ в све-
световодах. ФД фото детекторы [30].
Вынужденное рассеяние Мандельштама -Вриллюэна
271
10
о
3 0,1
>
Z
со
0,01
Преобразование ^s'/
65% ^ *
Линейные
потери 5,6дБ
•g P обратном
направлении
1 10
Вводимая мощность (мВт)
Рис. 9.9. Зависимость мощности прошедшего и отраженного излучения от
мощности накачки, вводимой в одномодовый световод длиной 13,6 км [30].
более 10 мВт. Эффективность ВРМБ при этом составляет около 65%.
Еще в одном из недавних экспериментов [31] наблюдалось ВРМБ
с накачкой на длине волны 1,3 мкм и шириной полосы излучения
около 10 МГц от одночастотного полупроводникового лазера с рас-
распределенной обратной связью. Непрерывное излучение накачки вво-
вводилось в 30-километровый световод с потерями 0,46 дБ/км. Эффек-
Эффективная длина такого световода 9 км. Порог ВРМБ 9 мВт. Проводи-
Проводились измерения и с накачкой от Nd: ИАГ-лазера с шириной линии
20 кГц. Результаты были практически идентичными с теми, что были
получены с полупроводниковой накачкой, из чего можно заключить,
что ширина линии ВРМБ-усиления была заметно больше 15 МГц-
наибольшей измеренной ширины линии полупроводникового лазера
Avp. Оценка ширины ВРМБ-линии при помощи (9.1.7) дает AvB =
= 100 МГц. Как упоминалось в разд. 9.1, линия ВРМБ-усиления
в световодах заметно шире, чем в объемных образцах плавленого
кварца (^ 22 МГц на длине волны 1.3 мкм) из-за неоднородностей
световода. Эксперимент показал, что ВРМБ может легко возникать
в когерентных линиях связи, где обычно используются полупроводни-
полупроводниковые лазеры с Avp < 10 МГц. На длине волны 1,55 мкм пороговая
мощность минимальна (~ 1 мВт) из-за малых потерь в световодах
@,2 дБ/км) и, следовательно, большой эффективной длины (~ 20 км).
В большинстве экспериментов по ВРМБ существенно наличие
изолятора между лазером и световодом, что помогает избежать
отражения стоксова излучения от зеркала лазера. В отсутствие
272
Глава 9
Накачка
Ст
из
—
оксо
луче
во II
we |
1 1 |1|Антистоксово
A Ц ||[ излучение
Л ы
|нак
|
сачк
к—
Рис. 9.10. Спектры излучения в прямом (верхний рисунок) и обратном (ниж-
(нижний рисунок) направлениях со стоксовыми и антистоксовыми линиями не-
нескольких порядков, генерируемыми без оптической изоляции между лазером
и световодом. Разность частот между соседними линиями 34 ГГц [32].
изолятора заметная часть мощности стоксовой волны может снова
вводиться в световод. В эксперименте [32] в световод возвращалось
около 30% мощности стоксовой компоненты. В результате действия
обратной связи наблюдалась генерация нескольких порядков стоксо-
вых и антистоксовых линий. На рис. 9.10 показаны спектры излуче-
излучения, выходящего из световода длиной 53 м в прямом и обратном
направлениях. Расстояние между линиями 34 ГГц точно соответству-
соответствует величине ВРМБ-смещения при Хр = 514,5 нм. Антистоксовы ком-
компоненты генерируются в результате четырехволнового смещения
накачки и стоксовой волны, распространяющихся в одном направ-
направлении (см. разд. 10.1). Стоксовы компоненты высшего порядка гене-
генерируются, когда мощность компоненты более низкого порядка до-
достигает порога ВРМБ (9.2.6). Каскадное ВРМБ может возникать
и в ВРМБ-лазерах, которые будут обсуждаться в следующем подраз-
подразделе.
9.3.2. ВОЛОКОННЫЕ ВРМБ-ЛАЗЕРЫ
ВРМБ-усиление, как и комбинационное, можно использовать
в волоконных лазерах, если поместить световод в резонатор [33-38].
Для этой цели использовались и резонаторы Фабри Перо, и кольце-
кольцевые,-у тех и у других есть свои преимущества. Благодаря обратной
связи пороговая мощность накачки лазера существенно ниже того,
что дает выражение (9.2.6). Для типичного лазера вместо фактора 21
в выражении (9.2.6) нужно подставить 0,1-1 в зависимости от потерь
в резонаторе.
В первом непрерывном волоконном ВРМБ-лазере [33] кольцевой
резонатор состоял из световода длиной 9,5 м с потерями на длине
волны накачки Хр = 514,5 нм около 100 дБ/км. Из-за относительно
Вынужденное рассеяние Мандельштама- Бриллюэна
273
высоких потерь в резонаторе (около 70% за обход) пороговая
мощность составляла ~ 100 мВт. В недавнем эксперименте [38]
использование кольцевого волоконного резонатора, схема которого
приведена на рис. 9.11, позволило снизить пороговую мощность до
0,56 мВт. Благодаря использованию направленного ответвителя по-
потери в резонаторе за один обход составляли.лишь 3,5%. При таких
низких потерях мощность накачки внутри кольцевого резонатора
была в 30 раз больше входной мощности. Низкий порог лазера
позволял использовать в качестве накачки излучение гелий-неонового
лазера на длине волны 632.8 нм. Возможным применением таких
лазеров могут стать волоконные гироскопы [39].
Волоконные ВРМБ-лазеры с резонаторами Фабри-Перо качест-
качественно отличаются от кольцевых лазеров. Разница в том, что в резона-
резонаторах Фабри- Перо в обоих направлениях распространяются и сток-
совы волны, и волны накачки. Генерация стоксовых волн высших
порядков происходит посредством каскадного ВРМБ, когда каждая
стоксова компонента после того, как ее мощность становится больше
порога ВРМБ, служит накачкой для компоненты следующего поряд-
порядка. В то же время четырехволновое взаимодействие попутных стоксо-
стоксовых волн и волн накачки приводит к генерации антистоксовых
компонент. Спектр излучения такого лазера похож на спектр, пред-
представленный на рис. 9.10. Число стоксовых и антистоксовых компо-
компонент зависит от мощности накачки. В эксперименте [34], когда
20-метровый световод в резонаторе Фабри-Перо накачивался арго-
аргоновым лазером на длине волны 514,5 нм, наблюдались 14 линий
спектра, из которых 10 располагались со стоксовой стороны. Расстоя-
Расстояние между соседними линиями 34 ГГц. что соответствует ВРМБ-
смешению.
Одновременная генерация многих эквидистантных спектральных
линий в ВРМБ-лазере указывает на возможность получения сверхко-
сверхкоротких оптических импульсов при условии, что моды лазера удастся
засинхронизировать [40]. В эксперименте [35] для синхронизации
Отводящая
пластинка
Сканирующий
оптический
спектроанализатор
Направленный
ответвитесь
4 Стоксова
волна
оо
. Накачка
Контроллер
поляризации
Рис. 9.11. Схема волоконного ВРМБ кольцевого лазера с низким порогом
[38]
274 Глава 9
мод использовался внутрирезонаторный модулятор. Излучение лазе-
лазера представляло собой последовательность 7-8-наносекундных им-
импульсов с частотой повторения 8 МГц, соответствующей длине резо-
резонатора. Эти импульсы соответствуют синхронизации не многих
стоксовых компонент (что дало бы импульсы длительностью короче
30 пс), а нескольких продольных мод резонатора Фабри-Перо внут-
внутри стоксовой компоненты первого порядка. Релаксационные колеба-
колебания могут обеспечить активный механизм такой синхронизации мод,
поскольку их период равен времени обхода внутри световода. Наблю-
Наблюдалась частичная самосинхронизация мод волоконного ВРМБ-лазера
[35], но этот процесс не очень усто,йчив.
9.3.3. ВОЛОКОННЫЕ ВРМБ-УСИЛИТЕЛИ
ВРМБ-усиление в световодах можно использовать для усиления
слабых сигналов, частота которых смещена от частоты накачки на
величину ВРМБ-сдвига vB. Однако из-за исключительно узкой полосы
ВРМБ-усиления (A vB < 100 МГц) полоса пропускания такого усили-
усилителя обычно меньше 100 МГц, в то время как у ВКР-усилителей
полоса пропускания составляет приблизительно 5 ТГц. По этой
причине, несмотря на возможность заметного усиления при мощно-
мощности накачки лишь в несколько милливатт, ВРМБ-усилители до
недавнего времени не привлекали большого внимания. Активность,
заметная в этой области в последнее время, объясняется в основном
потенциальной возможностью применения таких усилителей в си-
системах оптической связи [41-48].
Теория волоконных ВРМБ-усилителей основывается на уравнени-
уравнениях (9.2.1) и (9.2.2), решение которых приводилось в разд. 9.2.2.
Ненасыщенное усиление за один проход GА задается выражениями
(9.2.10) и (9.2.11) и получается в виде
(9.3.1)
Экспоненциальный рост наблюдается, только если мощность сигнала
остается ниже уровня насыщения. Характеристики насыщения воло-
волоконных ВРМБ усилителей показаны на рис. 9.3. Насыщенное усиле-
усиление Gs понижается на 3 дБ, когда
GA(PJPO)^ 0,5, (9.3.2)
для GA в диапазоне 20-30 дБ и aL = 0,1. Здесь /^„-входная мощность
усиливаемого сигнала. Поскольку Ро ~ 1 мВт, мощность насыщения
также составляет около 1 мВт.
Полупроводниковый лазер накачки для ВРМБ-усилителя должен
работать в одночастотном режиме, чтобы ширина его спектральной
Вынужденное рассеяние Мандельштама Бриллюэна
275
Лагер
накачки
Сигнальный
лазер
Рис. 9.12. Схема волоконного ВРМБ-усилителя. ПЛ, И и ФД означают
соответственно полупроводниковый лазер с внешним резонатором, изолятор
и фотодетектор. Сплошные и штриховые линии показывают оптические пути
излучения накачки и сигнала соответственно [41].
линии была меньше ширины линии ВРМБ-усиления. В эксперименте
[41] источниками накачки и сигнального излучения служили два
полупроводниковых лазера с внешними резонаторами и с шириной
линий < 10 кГц. Оба лазера работали в непрерывном режиме и пере-
перестраивались в широком диапазоне вблизи 1,5 мкм. На рис. 9.12
представлена схема эксперимента. Излучение накачки вводилось в
световод длиной 37,5 км через симметричный ответвитель. С проти-
противоположной стороны в световод вводилось слабое (~10мкВт) сиг-
сигнальное излучение. Его длина волны перестраивалась, что позволило
измерить спектр ВРМБ-усиления. Его форма оказалась двухпиковой
с общей шириной около 150 МГц. Измеренное усиление в максимуме
экспоненциально зависело от мощности накачки, как и следует из
уравнения (9.3.1). При мощности накачки 3,7 мВт усиление составило
16 дБ (GA = 40).
Волоконные ВРМБ-усилители могут обеспечивать усиление на
уровне 20-40 дБ при мощности накачки лишь несколько милливатт.
Их узкая полоса усиления (обычно менее 100 МГц) может оказаться
преимуществом для тех применений, где требуется усиление неболь-
небольшой части спектра сигнала [43, 45]. Эти применения обсуждаются
в следующем разделе. Для получения постоянного усиления в относи-
относительно широком частотном диапазоне (более 100 МГц) можно ис-
использовать модуляцию лйзера накачки с помощью внешнего модуля-
модулятора [42]. Конечно, увеличение полосы усиления достигается за счет
понижения пикового усиления. Следовательно, для компенсации та-
такого понижения требуется дополнительная мощность накачки.
276 Глава 9
9.4. ПРИМЕНЕНИЯ В СИСТЕМАХ ОПТИЧЕСКОЙ СВЯЗИ
Поскольку порог ВРМБ в системах оптической связи может быть
довольно низким (~ 1 мВт в световоде с потерями а ~ 0,2 дБ'км),
важно представлять, как действует ВРМБ в таких системах. Эффект
ВРМБ может использоваться в системах связи для усиления, но
может являться и паразитным. Оба случая будут рассмотрены в дан-
данном разделе.
Начнем с нежелательных эффектов, обусловленных ВРМБ: Если
мощность излучения в световоде превышает порог ВРМБ, заметная
часть мощности преобразуется в стоксово излучение, распростра-
распространяющееся в обратном направлении. Это нежелательно по двум
причинам. Во-первых, в результате истощения накачки мощность
сигнала на приемнике может оказаться намного меньше, чем ожи-
ожидается в отсутствие ВРМБ. Во-вторых, стоксово излучение создает
обратную связь с передатчиком, которая может дестабилизировать
его работу [49. 50]. Таким образом, важно поддерживать мощность
в световоде ниже порога ВРМБ. Для увеличения уровня сигнала
можно повысить порог ВРМБ, для чего предлагалось несколько схем
[51-53]. Все эти схемы связаны с увеличением эффективной ширины
спектра сигнального излучения, что ведет к падению ВРМБ-усиления
(см. (9.1.7)).
Пороговое условие (9.2.6) было получено для непрерывной накач-
накачки, спектральная ширина которой Avp много меньше ширины линии
ВРМБ-усиления AvB. В системах оптической связи ширина спектра
Avp существенно возрастает с возрастанием скорости передачи инфор-
информации В, с которой модулируется несущее излучение. В этом случае
следует ожидать более высокого порога ВРМБ, чем при непрерывном
излучении. Величина, на которую возрастает порог, зависит от типа
модуляции при передаче данных [54. 55]. Используются три типа
модуляции: амплитудная (AM), частотная (ЧМ). фазовая (ФМ).
Вычисление порога ВРМБ в общем случае довольно сложное, по-
поскольку требует учета временных зависимостей [54]. Ситуация замет-
заметно упрощается, если предположить, что скорость передачи информа-
информации В много больше полосы ВРМБ-усиления AvB. Правда, и в этом
случае остается трудность, состоящая в том, что в реальной системе
связи последовательность нулей и единиц не задана раз и навсегда, а,
естественно, меняется от передачи к передаче. Чтобы учесть это
обстоятельство, вместо спектра непрерывной накачки можно рас-
рассмотреть спектр случайной последовательности нулей и единиц.
Такая замена корректна, поскольку ВРМБ, развиваясь навстречу
волне накачки, усредняет флуктуации, зависящие от времени [54, 55].
Неожиданным результатом такого упрощенного анализа является
то, что порог ВРМБ для AM и ФМ возрастает лишь в 2-4 раза
Вынужденное рассеяние Мандельштама-Бриллюэна
277
*10
й 5
о Эксперимент
— Теория
i I i
Лг 1 10 100 1000
Скорость передачи (МБит/с)
Рис. 9.13. Зависимость пикового ВРМБ-усиления от частоты следования
импульсов в псевдослучайной ФМ последовательности. Сплошной линией
показана расчетная зависимость для полосы усиления шириной 100 МГц
[55].
независимо от частоты модуляции. Для ФМ же, напротив, ВРМБ
усиление уменьшается с возрастанием скорости передачи В как [55]
Av.
вивпр-
(9.4.1)
и, следовательно, пороговая мощность должна возрастать с увели-
увеличением скорости передачи почти линейно. Экспериментальные ре-
результаты подтверждают этот вывод [55]. На рис. 9.13 показана
измеренная зависимость максимального ВРМБ-усиления от скорости
передачи в случае ФМ псевдослучайной последовательности. Кри-
Кривая, полученная из выражения (9.4.1) при AvB = 100 МГц, показана
сплошной линией. Видно, что порог ВРМБ для скоростей передачи
В > 1 Гбит'с может возрастать более чем на порядок. При таких
высоких скоростях передачи даже для AM и ЧМ пороговая мощность
может существенно возрастать в результате уширения спектра полу-
полупроводникового лазера при прямой модуляции [49]. Неоднородность
модуляции также может повышать пороговую мощность, что и на-
наблюдалось экспериментально в случае частотной модуляции [55].
Таким образом, оказывается, что мощность вплоть до 10 мВт может
вводиться в световод без ухудшения характеристик системы, вызван-
вызванного ВРМБ.
Предыдущие рассуждения относились к одноканальной системе
связи. В случае многоканальной системы мощность в каждом канале
также должна быть ниже порога ВРМБ. Однако ВРМБ в много-
многоканальных системах может приводить и к перекрестным помехам
между каналами, если связь осуществляется в обоих направлениях
и если разность частот излучения во встречных направлениях близка
к величине ВРМБ-смещения (vB « 11 ГГц на длине волны 1,55 мкм).
278 Глава 9
ВРМБ приводит к усилению сигнала в одном канале за счет другого
[56]. Экспериментально наблюдалось 10%-ное возрастание мощно-
мощности сигнала в одном канале при мощности во встречном канале всего
0,3 мВт. Однако в отличие от обусловленных ВКР перекрестных
помех, обсуждавшихся в разд. 8.2.4, от обусловленных ВРМБ пере-
перекрестных помех легко избавиться благодаря малой ширине полосы
ВРМБ-усиления (~ 100 МГц), в пределах которой такие перекрестные
помехи могут возникать.
Обратимся теперь к возможным применениям ВРМБ в системах
оптической связи. Все эти применения связаны с использованием
ВРМБ-усиления, которое может действовать при мощностях накачки
~ 1 мВт. Например, можно увеличить длину линии связи (или рас-
расстояние между ретрансляторами), если непрерывную накачку вводить
в световод навстречу сигналу. Можно также использовать ВРМБ-
усиление для увеличения чувствительности приемника. В эксперимен-
эксперименте [46] чувствительность приемника была улучшена на 16 дБ, когда
сигнал с частотой 90 Мбит/с передавался по световоду длиной 30 км
и одновременно усиливался в поле накачки мощностью 2,9 мВт,
вводившейся навстречу сигналу. Увеличение чувствительности прием-
приемника почти совпадало с величиной ВРМБ-усиления за один проход,
которое составляло 16,5 дБ. Это было возможно, поскольку мощ-
мощность сигнала (~ 1 мкВт) значительно превышала мощность шума
спонтанного МБ-рассеяния в световоде. Если ВРМБ-усиление исполь-
используется в предусилителе перед приемником, то характеристики усили-
усилителя будут ограничиваться спонтанным МБ-рассеянием. Шумовой
фактор волоконных ВРМБ-усилителей довольно велик (~ 100) из-за
большой населенности (^-kT/h vB) акустических фононов при комна-
комнатной температуре [46]. Этот фактор может ограничивать их примене-
применение в качестве предусилителей.
Узкая полоса ВРМБ-усиления может быть полезной для селектив-
селективного усиления небольшой порции спектра сигнала. Это свойство
было использовано в сх -ме [57], в которой чувствительность прием-
приемника увеличивалась за счет усиления несущей частоты, в то время как
боковые полосы не усиливались. По принципу работы схема подобна
гомодинному детектору, за исключением того, что усиленная несущая
выступает в качестве опорного сигнала. Это позволяет обойтись без
осциллятора, сфазированного с передатчиком, что непросто проде-
проделать без использования ВРМБ-усиления. При достаточном усилении
несущей можно поднять уровень сигнала по сравнению с шумами
приемника и достичь чувствительности, ограниченной только кванто-
квантовым шумом. При идеальных условиях максимальное увеличение
чувствительности пропорционально v GA, где GA-усиление за один
проход, даваемое выражением (9.3.1). При демонстрации описанной
выше схемы [43] несущая была усилена на 30 дБ больше, чем
боковые полосы, даже при частоте модуляции всего 80 МГц. Таким
Вынужденное рассеяние Мандельштама Бриллюэна 279
образом, представляется вполне достижимым улучшение чувстви-
чувствительности на 15 дБ или более при скорости передачи не менее
100 МБит/с. Основным фактором, ограничивающим скорость пере-
передачи в данной схеме, является фазовая кросс-модуляция, поскольку
разница между частотами накачки и несущей не равна величине
ВРМБ-смещения. Согласно вычислениям [44], для того чтобы флук-
1уации фазы не превышали 0,1 рад, необходимо, чтобы отклонение
частоты несущей от пика усиления составляло не более чем 100 кГц.
Нелинейный сдвиг фазы может также приводить к нежелательной
амплитудной модуляции частотно-модулированного сигнала [47].
Другое применение узкой линии ВРМБ-усиления связано с его
использованием в качестве перестраиваемого узкополосного оптиче-
оптического фильтра для селекции каналов в многоканальных системах
связи [45]. Если разность частот соседних каналов больше, а скорость
передачи меньше, чем ширина полосы усиления AvB, то, перестраивая
лазер накачки, можно избирательно усиливать данный канал. Эта
схема была экспериментально продемонстрирована с накачкой от
перестраиваемого лазера на центрах окраски [45]. По световоду
длиной 10 км осуществлялась передача по двум каналам со ско-
скоростью 45 Мбит/с. Каждый канал можно было усилить на 20 25 дБ
при мощности накачки 14 мВт. Важно, что каждый канал можно
было детектировать без ошибок (вероятность ошибки < 10" 8), когда
разность частот каналов превышала 140 МГц. В световоде, использо-
использовавшемся в данном эксперименте, AvB составляла ~ 100 МГц, т.е.
разность несущих частот соседних каналов, при которой еще не
возникают перекрестные помехи, может составлять лишь l,5AvB.
Недавно ВРМБ-усиление с накачкой от серийных полупроводнико-
полупроводниковых лазеров было использовано для одновременного усиления и де-
демодуляции частотно-модулированных сигналов со скоростью пере-
передачи около 250 Мбит/с [48]. Демодуляция была возможной благода-
благодаря узкой линии ВРМБ-усиления. Данные примеры показывают, что
ВРМБ, кроме негативного действия на системы связи, может быть
использовано и для их улучшения.
ЛИТЕРАТУРА
1. Chiuo R. К. Townes C.H.. Stoicheff В. P.. Phys. Rev. Lett., 12. 592 A964).
2. Garmire ?.. Tonnes C.H.. Appl. Phys. Lett., 5, 84 A964).
3. Kroll N.M.. J. Appl. Phys., 36, 34 A965).
4. Tung C.L.. J. Appl. Phys., 37, 2945 A966).
5. Kaiser W.. Maier M.. in: Laser Handbook, vol. 2, ed. by F. T. Arccchi,
E.O. Schub-Dubois (North-Holland, Amsterdam, 1972) Chap. E2.
6. Ippen E.P.. Stolen R.H.. Appl. Phys. Lett., 21, 539 A972).
7. Smith R.G., Appl. Opt., 11, 2489 A972).
8. Cotter D., J. Opt. Commun., 4, 10 A983).
9. Shelby R. M., Lcvenson M. D., Baver P. W., Phys. Rev. Lett, 54, 939 A985); Phys.
Rev., B31, 5244 A985).
280 Глава 9
10. Krishnan R.S., Nature, 165, 933 A950).
11. Heiman D, Hamilton D.S.. Helhvarth R.W., Phys. Rev., B19, 6583 A979).
12. Thomas P.J. et al., Phys. Rev., В19, 4986 A979).
13. Stone J.. Chraplyvy А. Л, Electron. Lett.. 19. 275 A983).
14. Tkach R.W., Chraplvvv A. R., Derosier R.M., Electron, Lett., 22, 1011 A986).
15. Shibata N.. Waarts R.G.. Bruun R.P., Opt. Lett., 12, 269 A987).
16. Azvma Y. et al.. Electron. Lett., 24, 250 A988).
17. VallerG.C, IEEE J. Quantum Electron., QE-22, 704 A986).
18. Narum P.. Sheldon M.D.. Boyd R. W., IEEE J. Quantum Electron., QE-22, 2161
A986).
19. Lichtman E. et al., J. Opt. Soc. Am., B4, 1397 A987).
20. Lichtman E. Friesem A. A.. Opt. Commun., 64, 544 A987).
21. Inns R.H.. Batra I. P., Phys. Lett., A28, 591 A969).
22. Johnson R.V.. Marburger J.H., Phys. Rev., A4, 1175 A971).
23. Bar-Joseph I. et al., J. Opt. Soc. Am., B2, 1606 A985).
24. Zel'dovich Ya.B.. Shkunov V.V., Sov. J. Quantum Electron., 12, 223 A982).
25. Andreev N.F., Besapalov V.I., Kiselev A.M.. Pasmanik G.A., Shilov A.A., Sov.
Phys. JETP 55, 612 A982).
26. Randall С J., Albritton J.R., Phys. Rev. Lett., 52, 1887 A984).
27. Narum P.. Boyd R.W., IEEE J. Quantum Electron., QE-23, 1216 A987).
28. Narum P. el al., J. Opt. Soc. Am., B5, 623 A988).
29. Uesugi N.. Ikeda M., Sasaki Y., Electron. Lett., 17, 379 A981).
30. Cotter D.. Electron. Lett, 18, 495 A982).
31. Aoki Y, Tajima K., Mito I.. Opt. Quantum Electron., 19, 141 A987).
32. Labudde P.. Anliker P.. Weber H.P., Opt. Commun.. 32. 385 A980).
33. Hill K.O., Kawasaki B.S.. Johnson D.C., Appl. Phys. Lett., 28, 608 A976).
34. Hill K.O.. Johnson D.C., Kawasaki B.S., Appl. Phys. Lett., 29, 185 A976).
35. Kawasaki B.S. et al., Appl. Phys. Lett., 32, 429 A978).
36. Stolen R.H., IEEE J. Quantum Electron., QE-15, 1157 A979).
37. Ponikvar D. R.. Ezekiel S, Opt. Lett, 6, 398, A981).
38. Stokes L.F., Chodorow M, Shaw H.J., Opt. Lett, 7, 509 A982).
39. Thomas P.J., Driel H.M., Stegeman G.I. A., Appl. Opt. 19, 1906 A980).
40. Lugovov V.N.. Streltsov V.N., Opt. Acta, 20. 165 A973).
41. Olsson'N.A., tan der Ziel J.P., Appl. Phys. Lett, 48, 1329 A986).
42. Olsson N.A.. van der Ziel J.P., Electron. Lett., 22, 488 A986).
43. Atkins C.G. et al.. Electron. Lett, 22, 556 A986).
44. Cotter D. et al.. Electron. Lett, 22. 671 A986).
45. Chraplvvv A. R.. Tkach R. W. Electron. Lett, 22, 1084 A986).
46. Olsson'N.A.. van der Ziel J.P.. J. Lightwave Technol, LT-5, 147 A987).
47. Waarts R.G., Friesem A. A.. Hefet: Y. Opt. Lett., 13, 152 A988).
48. Tkach R. W. et al.. Electron. Lett.. 24, 260 A988).
49. Agrawal G. P., Dutta N. K.. Long-Wavelength Semiconductor Lasers, Van
Nostrand Reinhold, New York, 1986, Ch. 6.
50. Tkach R. W, Chraplvvv A.R.. J. Lightwava Technol. LT-4, 1655 A9$6).
51. Cotter D.. Electron. Lett, 18, 638 A982).
52. Tsubokawa M. et al.. Electronc Lett., 22, 473 A986).
53. Hadjifotiou A., Hill G.A.. IEE Proc, 133, Pt. J. 256 A986).
54. Colter D.. Electron. Lett, 18, 504 A982).
55. Aoki Y. Tajima K.. Mho I.. J. Lightwave Technol. LT-6, 710 A988).
56. Waarts R.G.. Braun R.P.. Electron. Lett, 21, 1114 A985).
57. Arnaud J.A.. IEEE J. Quantum Electron. QE-4, 893 A968).
Глава 10
ПАРАМЕТРИЧЕСКИЕ ПРОЦЕССЫ
В процессах ВКР и ВРМБ волоконный световод, являясь нелиней-
нелинейной средой, играет активную роль в том смысле, что в этих процессах
участвуют колебания его молекул. Во многих других нелинейных
явлениях световод играет пассивную роль среды, в которой несколько
оптических волн взаимодействуют через нелинейный отклик электро-
электронов внешних оболочек. Такие процессы называют параметрическими,
поскольку они обусловлены светоиндуцированным изменением пара-
параметров среды, например изменением показателя преломления. К па-
параметрическим процессам относятся генерация гармоник, четырех-
волновое смешение и параметрическое усиление. В разд. 10.1 рас-
рассматривается физический механизм четырех волнового смешения, в то
время как в разд. 10.2 обсуждается его теория. Результаты экспери-
экспериментов и способы достижения фазового синхронизма рассмотрены
в разд. 10.3. Практические аспекты параметрического усиления и его
применения обсуждаются в разд. 10.4. Наконец, разд. 10.5 посвящен
генерации суммарных и кратных частот, в частности генерации
второй гармоники процессу, который становится неожиданно эф-
эффективным в световоде, подютовленном определенным образом.
10.1. ЧЕТЫРЕХВОЛНОВОЕ СМЕШЕНИЕ
Параметрические процессы обусловлены нелинейным откликом
электронов среды в электромагнитном поле. Зависимость наведенной
поляризации среды от величины приложенного поля содержит как
линейные, так и нелинейные члены, величина которых зависит от
нелинейных восприимчивостей [1-4] (см. выражение A.3.1)). Воз-
Возможны параметрические процессы различных порядков, причем по-
порядок процесса совпадает с порядком восприимчивости, ответст-
ответственной за него. Восприимчивость второго порядка 5СB) в изотропной
среде равна нулю (в дипольном приближении) [2 4]. По этой причине
параметрические процессы второго порядка, такие, как генерация
второй гармоники или генерация суммарных частот, в световодах из
плавленого кварца не должны иметь место. В действительности эти
процессы все же наблюдаются благодаря квадрупольному или маг-
нитно-дипольному эффектам, но их эффективность довольно низ-
282 Глава 10
ка. Недавно при определенных условиях в волоконных световодах
наблюдалась генерация второй гармоники с неожиданно большой
эффективностью преобразования (~1%). Более подробно парамет-
параметрические процессы второго порядка будут рассмотрены в разд. 10.5.
Параметрические процессы третьего порядка обусловлены взаи-
взаимодействием четырех оптических волн и включают в себя явления
генерации третьей гармоники, четырехволнового смешения и пара-
параметрического усиления [1-5]. Четырехволновое смешение достаточ-
достаточно интенсивно исследовалось [6-29], поскольку это довольно эффек-
эффективный способ генерации новых частот. Его основные свойства
следуют из рассмотрения нелинейной поляризации третьего порядка:
C) A0.1.1)
где Е-электрическое поле, PNL-наведенная нелинейная поляризация,
а е0-диэлектрическая проницаемость вакуума. Рассмотрим четыре
оптические волны с частотами со,, ю2, ю3 и ю4, линейно-поляризо-
линейно-поляризованные вдоль оси х. Суммарное электрическое поле гогда можно
представить в виде
1 4
Е = ? - ? ?jexp [i(kjz - u>}t)~\ + компл. сопр., A0.1.2)
где
kj = n}(oj/c, A0.1.3)
rij-показатель преломления, и все четыре волны распространяются
вдоль направления z. Если подставить A0.1.2) в A0.1.1) и выразить
PNL в виде
1 4
Pjvl = * - Yj PjexP [i(kjZ — ю7г)] + компл. сопр., A0.1.4)
2j=i
то выяснится, что Pj для 7 = 1, .... 4 состоит из большого числа
членов, включающих произведения трех напряженностей электри-
электрических полей. Например. Р4 можно выразить как
2 +1?2|2 + |?3
?2?fexp(/G_) + ...}, A0.1.5)
где
6+ =(/с, +к2 + к3 -kA)z-(ial + со2 + to3 — со4)/, A0.1.6)
6_ = (/ct + к2 - к3 - kA)z - (со, + ю2 - ю3 - ю4)Л A0.1.7)
Член, пропорциональный ?4 в A0.1.5), отвечает за эффекты ФСМ
и ФКМ. Остальные члены отвечают за четырехволновое смешение.
Какие из них эффективно осуществляют параметрическую связь волн,
Параметрические процессы 283
зависит от относительной фазы между ?4 и Р4, равной 6+, 6_ или
другому аналогичному углу. Четырехволновое смешение становится
значительным, только когда относительная фаза близка к нулю. Для
этого требуется согласование как частот, так и волновых векторов.
Последнее называют также согласованием фаз или фазовым синхро-
синхронизмом. В терминах квантовой механики четырехволновое смешение
описывается как уничтожение фотонов одной частоты и рождение
фотонов другой частоты, причем сохраняются энергия и импульс.
Основное отличие параметрического взаимодействия от ВКР и ВРМБ
состоит в том. что при процессах рассеяния согласование фаз дости-
достигается автоматически. Что же касается согласования фаз при пара-
параметрических процессах, то для этого требуется выполнение опре-
определенных условий, налагаемых на частоты и показатели преломления
среды.
В уравнении A0.1.5) можно выделить два типа четырехволнового
смешения. Второй член в правой части соответствует случаю пере-
передачи энергии трех фотонов одному фотону частоты со4 = со, + со2 +
+ ю3. Этот член отвечает за генерацию третьей гармоники (когда
Ю1 = Ю2 = юз) или за преобразование частоты в новую частоту
2ю, + ю3 (когда а1 = ю2 ф со3). Однако при таких процессах довольно
трудно обеспечить фазовый синхронизм и, следовательно, получить
высокую эффективность преобразования. Последний член в A0.1.5)
соответствует случаю уничтожения двух фотонов с частотами а>1 и со2
и одновременного рождения двух фотонов с такими частотами со3
и ю4. что
со3 + ю4 = со, + ю2. A0.1.8)
Условие фазового синхронизма в этом случае выполняется при
А/с = 0, где
А/с = к3 + /с4 — /с, — к2 = (и3со3 + и4ю4 — и, tot — и2ю2)/с A0.1.9)
и использовано выражение A0.1.3).
Относительно легко обеспечить выполнение условия Ак = 0 при
со, = со2. Этот случай частично вырожденного четырехволнового
смешения в волоконных световодах хорошо изучен [6-29]. Прояв-
Проявляется оно подобно ВКР. Мощная волна накачки с частотой C0j
генерирует две симметрично расположенные боковые полосы с часто-
частотами со3 и со4, сдвинутыми от частоты накачки на величину
fis = co, -to3 = co4-coj, A0.1.10)
где для определенности взято со3 < со4. По аналогии с ВКР низко-
и высокочастотная спектральные полосы (ю3 и со4) называются
соответственно стоксовой и антистоксовой компонентами. Частично
вырожденное четырехволновое смешение иногда называют трехвол-
новым смешением [6, 8], поскольку только три различные волны
284 Глава 10
участвуют в этом взаимодействии. Однако мы будем относить его
к четырехволновому смешению, оставляя термин «трехволновое сме-
смешение» за процессами, обусловленными восприимчивостью 5С<2). От-
Отметим также, что стоксову и антистоксову волны часто называют
сигнальной и холостой волнами, заимствуя терминологию из физики
СВЧ; при этом входной сигнал на частоте ю3 усиливается за счет
четырехволнового смешения.
10.2. ПАРАМЕТРИЧЕСКОЕ УСИЛЕНИЕ
Частично вырожденное четырехволновое смешение (а1 = со2) при-
приводит к переносу энергии из волны накачки в две волны с частотами,
смещенными от частоты накачки а1 в стоксову и антистоксову
области на величину fis, даваемую выражением A0.1.10). Если в све-
световод вводится только излучение накачки и выполняется условие
согласования фаз, то генерация стоксовой и антистоксовой волн
с частотами ю3 и со4 может инициироваться шумами подобно тому,
как это происходит при ВКР и ВРМБ. С другой стороны, если
в световод вместе с накачкой вводится слабый сигнал частоты ю3, то
он усиливается, причем одновременно генерируется новая волна
частоты ю4. Этот процесс называют параметрическим усилением.
В данном разделе выводится выражение для параметрического уси-
усиления, причем рассматривается нелинейное взаимодействие четырех
волн. Рассматривается общий случай (ai1 Ф со2).
В качестве исходного берется волновое уравнение B.3.1) для пол-
полного электрического поля E(r, t), где PNL дается выражением A0.1.1).
Подставим в волновое уравнение выражения A0.1.2) и A0.1.4) вместе
с аналогичным выражением для линейной части поляризации. Предпо-
Предположим, что излучение непрерывно или квазинепрерывно, тогда зависи-
зависимостью компонент поля Е} (J = 1, ... , 4), от времени можно пренеб-
пренебречь. Пространственная структура поля учитывается выражением
Ej(r) = FJ.(.x.y)Aj(=), A0.2.1)
где Fj(x, у) -пространственное распределение поля по сечению све-
световода [12]. Эволюция амплитуд Aj(z) подчиняется системе четырех
связанных уравнений, которые в параксиальном приближении запи-
записываются следующим образом [30]:
dAl in2 щ
~(Р = ~~ [(AiMJ+2 2. /ltMtl Mi +
+ 2/1234Л2Л3Л ехр(/Д/сг)]. A0.2.2)
^='^Ш22\Аг\2 + 2?Ьк\Ак\2)А2 +
+ 2/2134Л1 A3AA exp (iAfc:)], A0.2.3)
Параметрические процессы 285
+ 2f3412AlA2A% ехр(-/АЬ)], A0.2.4)
+ 2/4312 А1А2А% ехр (-гД/сг)], A0.2.5)
где расстройка волновых векторов А/с дается выражением
А/с = (й3н>3 + й4ю4 — nl (Bj — Л2ю2)/с; A0.2.6)
величины от й] до /?4-это эффективные показатели преломления для
соответствующих четырех мод световода. Заметим, что й1 и п2 могут
не совпадать, если волны накачки А1 и А2, даже совпадающие по
частоте, распространяются в разных модах. Интеграл перекрытия
fjk дается выражением A.7.16), а новый интеграл перекрытия /^(-вы-
/^(-выражением [12]
г (FrFfFkFl)
JlJkl [<1^12><1^12><1^12><1^|2>]1/2' ( }
где угловые скобки означают усреднение по поперечным коорди-
координатам д- и у. При выводе уравнений A0.2.2)-A0.2.5) мы пренебрегли
зависимостью 5СC) от частоты. Параметр й2-это нелинейный пока-
показатель преломления, определенный выражением B.3.13), где п со-
соответствует эффективному показателю преломления данной моды.
(Черта сверху введена для отличия п2 от п2, возникающего
в A0.1.9)).
Уравнения A0.2.2) A0.2.5) являются обидами в том смысле, что
они включают эффекты ФСМ, ФКМ, истощение накачки и четы-
рехволновое смешение; решаются они, вообще говоря, только чис-
численно. Однако для понимания физики описываемых данными урав-
уравнениями процессов полезно рассмотреть упрощенную ситуацию
когда волны накачки значительно интенсивнее стоксовой и антисток-
антистоксовой волн и остаются неистощенными в процессе взаимодействия.
Для дальнейшего упрощения предположим, что все интегралы пере-
перекрытия приблизительно одинаковы, т.е.
fIJU ^ftJ - 1/Лэфф (/,./ = 1. 2. 3, 4), A0.2.8)
Гле ^.фф-лффективная площадь сердцевины, введенная в разд. 2.3.
Это приближение справедливо для одномодовых световодов. Легко
расширить анализ на случай несовпадающих интегралов перекрытия
[1-]. Введем коэффициент нелинейности у^, используя определение
286 Глава 10
где у-некоторое среднее значение. (Последнее равенство справед-
справедливо, если пренебречь разницей оптических частот.) Решения урав-
уравнений A0.2.2) и A0.2.3) можно записать в виде
A^z) = УЛ ехр \t/(Pl + 2P2)z], A0.2.10)
Л2(-) = J~P~2 ехр [/у(/>2 + 2P1)z~\. A0.2.11)
где Pj = |/4j-@)|2 и Pl и Р2 — исходные мощности волн накачки в точке
z = 0. Это решение идентично тому, что было получено в разд. 7.3,
и показывает, что в отсутствие истощения волны накачки распростра-
распространяются без искажений, если не считать возмущений фазы, возни-
возникающих в результате ФСМ и ФКМ. Подставляя A0.2.10) и A0.2.11)
в A0.2.4) и A0.2.5), получаем
^А3 _ -,- г/Г) , 1
dz
dA%
A0.2.12)
= -2гу [(Л + P2) A% + (Л Р2)Ч2 ехр (-Й)Л3],A0.2.13)
dz
где
Q = [Ak-3y(Pl + P2)]z. A0.2.14)
Теперь введем
В} = A]expl-2iy(Pl + P2)z] A0.2.15)
для 7 = 3 и 4. Используя соотношения A0.2.12) —A0.2.15), получаем
—^ = 2/у (/>! PJ1'2 ехр (-«г) BJ , A0.2.16)
dz
^-2гу 1(Р,Р2)Ш ехр(-псг)Яз]. A0.2.17)
где
+ />2). A0.2.18)
Уравнения A0.2.16) и A0.2.17) определяют рост стоксовой и анти-
антистоксовой волн, возникающих в результате четырехволнового сме-
смешения. Их общее решение записывается в виде [12]
Въ{2) = (a3eaz + Ь3е~аг) ехр(-iv.z/2), A0.2.19)
B%(z) = (аАедг + ЬАе-дг) exp(ntz/2), A0.2.20)
где а3, Ь3, я4 и Л4 определяются из граничных условий, а коэффициент
параметрического усиления д дается в виде
2JУ'2. A0.2.21)
Параметрические процессы
287
Здесь введены параметры г и Ро:
-pi + P2; A0.2.22)
p0-суммарная начальная мощность накачки.
При выводе выражения для параметрического усиления предпола-
предполагалось, что две волны накачки различимы. Если же они неразличимы
ни по частоте, ни по поляризации и пространственной структуре,
в сумме A0.1.2) нужно рассматривать только три члена. Коэффициент
параметрического усиления будет по-прежнему даваться выражением
A0.2.21), только в этом случае Р1 = Рг, г — 1, а и заменяется на
A0.2.23)
На рис. 10.1 показана зависимость д от А/с для нескольких значений
уР0. Усиление максимально (дма11С = уР0) при и = 0 или Д/с = — 2уР0.
Область, в которой существует усиление, определяется неравенством
0>А/с> —4уРо. Все эти свойства следуют из выражений A0.2.21)
и A0.2.23). Смещение максимума усиления от точки Д/с = 0 вызвано
вкладом ФСМ и ФКМ в разницу фаз в уравнении A0.2.23). Это
смещение меньше, если в процессе участвуют две различные волны
накачки.
Интересно сравнить коэффициенты параметрического и ВКР-
усиления [7]. Из A0.2.21), взяв г=1, можно получить выраже-
выражение для максимального коэффициента параметрического усиления:
A0.2.24)
Ак (м-1)
Рис. 10.1. Зависимость параметрического усиления от расстройки волновых
векторов Ак для нескольких значений мощности накачки Ро. Смешение
максимума усиления от точки Ак = 0 обусловлено эффектами ФСМ и ФКМ.
288 Глава 10
где у взято из выражения A0.2.9), дР определяется выражением
'¦ 0Р = 2яй2/>ч. A0.2.25)
а длина волны накачки Xt = 2кс/а1. Приняв Х1 = 1 мкм и й2 =
= 3,2-10~20 м2/Вт, получим дР^2-103 м/Вт. Это приблизительно
в 2 раза больше, чем максимальное значение gR (см. рис. 8.1). Таким
образом, пороговая мощность четырехволнового смешения меньше
пороговой мощности ВКР, но только если выполняется условие
фазового синхронизма. На практике, однако, в длинных световодах
доминирует ВКР. Это происходит из-за того, что в длинном све-
световоде условие синхронизма трудно выполнить по всей длине из-за
вариаций диаметра сердцевины. Длина когерентности определяется
как
Lcoh = 2я/Дх. A0.2.26)
где Ах- максимальная допустимая расстройка волновых векторов.
Заметное четырехволновое смешение происходит на длине L < Lcoh.
Полоса параметрического усиления обсуждается в разд. 10.4.1.
10.3. СПОСОБЫ ПОЛУЧЕНИЯ ФАЗОВОГО
СИНХРОНИЗМА И ЭКСПЕРИМЕНТАЛЬНЫЕ
РЕЗУЛЬТАТЫ
Параметрическое усиление максимально, когда расстройка волно-
волновых векторов (определяемая выражением A0.2.18)) х = 0. Это можно
записать в виде
х = AkM + Akw + AkNL = 0, A0.3.1)
где Акм, Akw и AkNL соответствуют расстройкам, возникающим
в результате действия материальной дисперсии, волноводной диспер-
дисперсии и нелинейных эффектов соответственно. Вклад Акм и Akw можно
получить из уравнения A0.2.6), если записать эффективный пока-
показатель преломления как
fij = Hj + Anj, A0.3.2)
где Arij -изменение показателя преломления материала пг обуслов-
обусловленное структурой волновода. В случае частичного вырождения
(coj = ю2 ) три слагаемых в равенстве A0.3.1) выражаются следующим
образом:
Акм = (п3(о3 + и4ю4 — 2«! а>1 )/с, A0.3.3)
&kw = [Аи3(о3 + АП4Ы4 —(А»! + Ап2)а1~\/с, A0.3.4)
+P2). A0.3.5)
Параметрические процессы 289
Для выполнения условия фазового синхронизма необходимо, чтобы
хотя бы один из этих членов был отрицательным. Материальную
составляющую в A0.3.1) Акм можно выразить через частотный сдвиг
Qs (см. A0.1.10)), если использовать тождество fij = «jtOj/f 0 = 1-4)
и выражение B.3.23). В итоге получим
Акм^$2П?. A0.3.6)
где Р2-коэффициент дисперсии групповых скоростей на частоте
накачки а1. Равенство A0.3.6) справедливо, если длина волны накач-
накачки (к! = 2пс/а1) не слишком близка к длине волны нулевой дисперсии
XD. Поскольку при ki < kD ~ 1,3 мкм Р2 > 0, расстройка Акм по-
положительна в видимой и ближней ИК-областях спектра. При
Х1 < 1.3 мкм фазового синхронизма можно достичь, сделав Akw
отрицательной, что возможно при распространении взаимодейст-
взаимодействующих волн в различных модах многомодового световода. В боль-
большинстве ранних экспериментов использовался это г метод согласова-
согласования фаз [6-11].
В случае одномодового световода Akw = 0, поскольку Аи почти
одинаково для всех волн. В этом случае существуют три способа
получения фазового синхронизма. Если длина волны накачки близка
к XD, то Акм становится малой. Это позволяет получить фазовый
синхронизм для Х1 вблизи XD. Для Х1 > XD фазового синхронизма
можно также добиться, изменяя AkNL посредством изменения мощ-
мощности накачки. При Х1 <XD получить фазовый синхронизм можно
в двулучепреломляюших световодах, если взаимодействующие волны
имеют различные поляризации. Все эти способы обсуждаются ниже
в соответствующих подразделах.
10.3.1. ФАЗОВЫЙ СИНХРОНИЗМ В МНОГОМОДОВЫХ
СВЕТОВОДАХ
Как уже упоминалось выше, многомодовые световоды позволяют
получить фазовый синхронизм, когда Akw отрицательна и в точности
компенсирует положительный вклад Акм + AkNL в выражении
A0.3.1). Величина Akw зависит от выбора мод световода, в которых
распространяются волны, участвующие в четырехволновом взаимо-
взаимодействии. Для вычисления A/ij (/ = 1-4) каждой моды можно исполь-
использовать характеристическое уравнение B.2.9). Затем при помощи
уравнения A0.3.4) вычисляется Акц.. На рис. 10.2 показана расчетная
тависимость Akw от сдвига частоты (vs ~ П5/2я) для световода
с сердцевиной радиусом 5 мкм и разностью показателей преломления
0,006 [7]. Штриховой линией показана квадратичная зависимость
Акм, вытекающая из выражения A0.3.6). Частотный сдвиг vs, для
которого выполняется условие фазового синхронизма, определяется
абсциссой точки пересечения сплошной и штриховой кривых (A/cNL
290
Глава 10
9 12 0 30
Сдвиг частоты СТГц)
60 90 120
Рис. 10.2. Диаграммы фазового согласования для многомодовой (а) и одно-
модовой (б) накачки. Сплошные и штриховые линии соответствуют зависи-
зависимостям lAk^l и Дкм от частотного сдвига vs. Их пересечение определяет vs.
Точечные линии соответствуют радиусу сердцевины, увеличенному на 10%.
Кривые обозначены в терминах LPmn-Mop,- Над кривыми Akw даны значения
тип для четырех волн [7].
при этом предполагается пренебрежимо малым). На рис. 10.2 пока-
показаны два случая-когда накачка распространяется в одной моде или
в двух различных модах. В первом случае сдвиг частоты составляет
около 100 ТГц, а во втором vs ~ 1-10 ТГц. Вообще говоря, условию
фазового синхронизма могут удовлетворять несколько комбинаций
мод световода.
В первой экспериментальной демонстрации [6] четырехволнового
смешения с согласованием фаз импульсы накачки на длине волны
532 нм пиковой мощностью ~ 100 Вт вводились в световод длиной
9 см вместе с непрерывным излучением (мощностью ~ 10 мВт) ла-
Длина волны сигнального излучения (нм)
с 596 598 600 602 604 606 608 610
^ 480 478 476 474 472
Алина волны холостого излучения (.нм)
Рис. 10.3. Мощность и длина холостой волны как функция сигнальной длины
волны (верхняя шкала). На вставке показаны распределения интенсивности
в дальнем поле излучения, соответствующие двум основным пикам [6]
Параметрические процессы 291
зера на красителе, перестраиваемого в диапазоне 565 640 нм. Четы-
рехволновое смешение в таком параметрическом усилителе приво-
приводило к генерации новой волны в голубой области (ю4 = 2а t — со3),
которую называют холостой. На рис. 10.3 показаны наблюдавшиеся
спектры холостой волны, полученные при изменении сигнальной
частоты со3. Пять различных пиков соответствуют различным ком-
комбинациям мод световода, для которых выполняется условие синхро-
синхронизма. Картина в дальнем поле, наблюдаемая визуально, ясно
указывает на то, что холостая волна генерируется в разных модах.
В этом эксперименте волна накачки распространялась в одной моде.
Как и ожидалось (см. рис. 10.2), фазовый синхронизм возникал для
относительно больших сдвигов частоты в диапазоне 50 60 ТГц.
В другом эксперименте [11] наблюдался сдвиг частоты 130 ТГц, что
составило 23% от частоты накачки.
Четырехволновое смешение с малыми сдвигами частоты (~ 1-
10 ТГц) может возникать, если мощность накачки разделяется между
двумя различными модами световода (см. рис. 10.2). Такое взаимо-
взаимодействие относительно нечувствительно к вариациям диаметра серд-
певины [7]. и длины когерентности составляют ~ 10 м. Для vs ~
~ 10 ТГц четырехволновое смешение может накладываться на ком-
комбинационное усиление, поскольку генерируемая стоксова линия попа-
попадает в полосу комбинационного усиления. В эксперименте [7], где
импульсы накачки мощностью ~ 100-500 Вт на длине волны 532 нм
распространялись по световоду, в результате комбинационного уси-
усиления стоксовы линии были обычно более интенсивными, чем анти-
стоксовы.
Когда пикосекундные импульсы распространяются по многомо-
довому световоду, на протекание четырехволновых процессов дейст-
действует не только ВКР, но и ФСМ, ФКМ и дисперсия групповых
скоростей. В недавнем эксперименте [28] импульсы накачки длитель-
длительностью 25 пс на длине волны 532 нм распространялись по световоду
длиной 15 м, поддерживавшему четыре моды на длине волны накач-
накачки. На рис. 10.4 показаны спектры излучения на выходе световода.
При мощности накачки ниже пороговой наблюдалась только линия
накачки (спектр а). Три пары стоксовых и антистоксовых линий со
сдвигом частот 1-8 ТГц наблюдались при мощности накачки не-
несколько выше пороговой (спектр б). Стоксовы и антистоксовы линии
примерно одной амплитуды, что говорит об отсутствии заметного
ВКР в этом случае. Однако при увеличении мощности накачки из-за
комбинационного усиления стоксовы линии становятся намного более
интенсивными, чем антистоксовы (спектр в). При дальнейшем увели-
увеличении мощности накачки стоксовы линии, близкие к пику комбинаци-
комбинационного усиления, сравниваются по интенсивности с накачкой, а анти-
антистоксовы остаются слабыми (спектр г). В то же время наб подается
уширение и расщепление накачки и стоксовой линии, характ :рное для
292
Глава 10
а)
1
522
532
542 522 532 542
522 532 542 522
Длина волны (нм)
3)
532
542
Рис. 10.4. Спектры 25-пикосекундного импульса накачки на выходе свето-
световода. Мощность накачки, начиная от порога четырехволнового смешения
(~500 МВтсм2), прогрессивно возрастает от а к г [28].
ФСМ и ФКМ. Увеличение мощности накачки приводит к генерации
стоксовых линий высших порядков в результате каскадного ВКР. При
мощности накачки 1,5 ГВт/см2 уширенные стоксовы линии сливают-
сливаются в результате совместного действия ФСМ, ФКМ и ВКР, образуя
спектральный континуум в области 530-580 нм. На рис. 10.5 показан
спектр на выходе световода, полученный при таких условиях. Гене-
Генерация континуума в области 400 700 нм в объемных образцах стекол
впервые наблюдалась в 1970 г. [5] и в последние годы получила
множество применений [31].
522 532 542 552 562
Длина волны (км)
572 582
Рис. 10.5. Генерация континуума при условиях, идентичных рис. 10.4, когда
интенсивность накачки составила 1,5 ГВт/см2 [28].
Параметрические процессы 293
10.3.2. ФАЗОВЫЙ СИНХРОНИЗМ В ОДНОМОДОВЫХ
СВЕТОВОДАХ
В одномодовых световодах для волн одной поляризапии вклад
волноводной дисперсии Akw в расстройку волновых векторов очень
мал по сравнению с вкладом материальной дисперсии Акм, за
исключением окрестности длины волны нулевой дисперсии XD, где
они сравнимы по величине. Существуют три возможности прибли-
приблизительного согласования фаз в одномодовых световодах: 1) исполь-
использовать взаимодействие волн с небольшими частотами отстройки
и небольшую мощность накачки, с тем чтобы уменьшить Акм и AkNL;
2) работать вблизи нуля дисперсии световода, где Akw приблизитель-
приблизительно компенсирует Акм + AkNL, и 3) использовать взаимодействие
в области отрицательной дисперсии групповых скоростей, где Акм
отрицательно и может скомпенсировать A/cNL + Akw. Эти три случая
обсуждаются в данном разделе. Четвертый способ состоит в исполь-
использовании двулучепреломления световодов, сохраняющих поляриза-
поляризацию, и обсуждается в следующем разделе.
Четырехволновое смешение с неточным согласованием фаз
Из формы спектра усиления, показанного на рис. 10.1, следует, что
четырехволновое смешение возникает и в том случае, когда условие
х = 0 в выражении A0.3.1) выполняется не строго. Величина до-
допустимой расстройки волновых векторов зависит от длины световода
L и когерентности длины Lcoh. Предполагая, что материальный вклад
Акм доминирует в A0.3.1), можно связать Lcoh с частотным сдвигом
?2S, используя выражения A0.2.26) и A0.3.6). В результате имеем
^coh = 7-^-7 = Г?П7^- <1О-3-7>
\Акм\ |P2|fis2
В видимой области типичное значение Р2 = 50 60 пс2/км, что дает
f-coh > 1 км для частотных сдвигов vs = fis/2n < 100 ГГц. При такой
большой длине когерентности в одномодовых световодах может
возникать четырехволновое смешение с таким сдвигом частоты vs,
что L < Lcoh.
В раннем эксперименте [8] три непрерывные волны с разностями
частот в диапазоне 1-10 ГГц распространялись по световоду с таа-
метром сердцевины 4 мкм длиной 150 м, одномодовому на длине
волны аргонового лазера 514,5 нм. Четырехволновое смешение при-
приводило к генерации десяти новых частот так, что
со4 = со, + СО; — ю,., A0.3.8)
где /, J, к — 1, 2 или 3 и J ф к. Эксперимент показал также, что
четырехволновое смешение может приводить к уширению спектра,
величина которого возрастает с увеличением мощности излучения.
294
Глава 10
Линия непрерывного аргонового лазера шириной 3,9 ГГц уширялась
в световоде до 15,8 ГГц при мощности накачки 1,63 Вт. О таком
уширении спектра говорилось в разд. 4.1, где оно объяснялось про-
процессом ФСМ, но его можно интерпретировать и в терминах четырех-
четырехволнового смешения [32].
С практической точки зрения четырехволновое смешение может
приводить к перекрестным помехам в многоканальных когерентных
системах связи [26], где разность несущих частот каналов лежит
в диапазоне 0,1-100 ГГц. В недавнем эксперименте [27] три непре-
непрерывные волны с частотами, отстоящими друг от друга на ~ 10 ГГц,
распространялись по световоду длиной 3,5 км и мощность девяти
компонент четырехволнового смешения измерялась в зависимости от
мощности и разности частот волн накачки. На рис. 10.6 показаны
измеренные зависимости для волн с частотами/332 и/2з1, где введены
обозначения
U=fi+fj-fk- /7 =
A0.3.9)
В случае, показанном на рис. 10.6, а, /3 —/х = 11 ГГц, /2 —/t =
= 17,2 ГГц, Р1 = 0,43 и Р2 = 0,14 мВт, в то время как Р3 изменялась
от 0,15 до 0,60 мВт. В случае б Р3 = 0,55 мВт, а/3 —/2 менялась от 10
до 25 ГГц. Мощность генерируемого излучения РА зависела от Р3
линейно для компоненты /23i и квадратично для /332 ¦ Это объяс-
объясняется в рамках теории, изложенной в разд. 10.2, поскольку/23i гене-
генерируется в результате невырожденного, а /332 - вырожденного по
накачке четырехволнового смешения. Мощность излучения на часто-
частоте /23i больше, чем на частотах /23i и /321, также в результате
0.05 0,1 0,2 0,5 1 2 5
Входная мощность Р3 (мВт)
10
15 20
25
Рис. 10.6. Зависимость мощности генерируемого при четырехволновом сме-
смешении излучения от а) входной мощности Р3 и б) разности частот /3 —f г ¦
Длина световода 3,5 км [27].
Параметрические процессы
295
30
60 О 30 60 О
Сдвмг частоты (тгц1
30
60
Рис. 10.7. Диаграммы согласования фаз вблизи нуля дисперсии для трех
значений длины волны накачки А.,. Точечные, штриховые и сплошные линии
соответствуют Акм, М„,и их сумме [15].
вырождения, но несколько иного рода, а именно в силу того, что
к генерации одной и той же частоты могут приводить четырехвол-
новые процессы с различными комбинациями взаимодействующих
волн. Наконец, мощность Р4 падает с увеличением разности частот
из-за расстройки фазовых скоростей. Следует заметить, что при
мощностях накачки менее 1 мВт мощность генерируемого излучения
составляла 500 пВт. Такое преобразование может заметно ухудшать
характеристики когерентных линий связи, где чувствительность при-
приемника может быть ~ 1 нВт или менее в зависимости от скорости
передачи.
Согласование фаз вблизи длины волны нулевой дисперсии
Вклад материальной дисперсии в расстройку волновых векторов
вблизи длины волны нулевой дисперсии, равной в обычных свето-
световодах 1,28 мкм, становится малым и меняет свой знак. Волноводный
вклад Акц зависит от конструкции световода, но обычно положи-
положителен для длин волн близи 1,3 мкм. В ограниченной области длин
волн накачки и для определенных значений частотного сдвига vs
расстройка Акм может компенсировать величину Akw + Ak^L. На
рис. 10.7 показано поведение Акм и Akw (без учета AkNL) для
световода с диаметром сердцевины 7 мкм и с разностью показателей
преломления 0,006 [15]. Сердцевина легирована германием (мол
6%). Сдвиг частоты зависел от мощности накачки на длине волны A,t
и менялся в широком диапазоне ~ 1 -100 ТГц. Он также чувствителен
к вариациям диаметра сердцевины и разницы показателей прелом-
преломления. Эти два параметра могут использоваться для подбора частот-
частотного сдвига при заданной длине волны накачки [16].
В первом эксперименте [14] по четырехволновому смешению
вблизи длин волн 1,3 мкм использовался световод длиной 30 м
296 Глава 10
и импульсы ИАГ-лазера с модулированной добротностью на длине
волны 1,319 мкм в качестве накачки. Сигнал на длине волны
1,338 мкм (vs = 3,3 ТГц) был усилен на величину до 46 дБ, в то время
как на выходе световода наблюдались три пары стоксовых и анти-
антистоксовых линий. Эти равноудаленные линии (vs -¦ 3,3 ТГц) возни-
возникали в результате каскадного четырехволнового процесса, в котором
уже сгенерированные частоты взаимодействовали одна с другой,
генерируя новые частоты. В недавнем эксперименте [15] четырех-
волновое излучение возникало без сигнала из спонтанного излучения.
Импульсы от лазера с синхронизацией мод на длине волны 1,319 мкм
пиковой мощностью ~ 1 кВт распространялись по световоду длиной
50 м. Пиковая мощность превышала порог ВКР. На рис. 10.8 показан
полученный при этом спектр выходного излучения. В результате
четырехволнового смешения генерируются стоксовы и антистоксовы
линии на 1,67 и 1,09 мкм соответственно. Большой частотный сдвиг
(vs = 48 ТГц) сравним с тем, что наблюдается в многомодовых
световодах. Подобные эксперименты [16] показывают, что vs может
варьировать в пределах 3- 50 ТГц при изменении диаметра сердце-
сердцевины в пределах 7,2 -8,2 мкм. Таким образом, фазовый синхронизм
вблизи нуля дисперсии световодов позволяет использовать удобные
источники новых длин волн, накачиваемые ИАГ-лазером с длиной
волны 1,319 мкм.
Фазовый синхронизм, обусловленный ФСМ
Когда длина волны накачки лежит в области отрицательной
дисперсии групповых скоростей и значительно отстоит от XD, Акм
существенно превышает Akw и условие согласования фаз не выпол-
выполняется. Однако если Акм + Kkw отрицательно, то его может скомпен-
скомпенсировать нелинейный вклад AkNL. Сдвиг частоты Qs в этом случае
зависит от входной мощности накачки. Действительно, если взять
выражение A0.2.23) с подставленным в него Ак » Акм = Р2 fis2. то
Антмстоксова Стоксова
г- волна . Накачка . волна
A,09мкм) A,319мкм) / A,67мкм)
- 48 ТГц Т" 48 ТГц
Рамановский сдвиг
&
i Л
1,0 1,1 1.2 1,3 1,4 1,5 1,6 1,7
Длина волны С)
Рис. 10.8. Спектр стоксовых и антистоксовых линий четырехволнового сме-
смешения в одномодовом световоде. Видна также полоса ВКР [15].
Параметрические процессы 297
согласование фаз наступает в случае
fis = BY/y|p2|I/2, A0.3.10)
где Ро - входная мощность накачки. Таким образом, в среде с отрица-
отрицательной дисперсией синхронизм при четырехволновом смешении
достигается за счет процесса ФСМ; при этом генерируются боковые
спектральные полосы с частотами а1 + ?ls. Этот случай обсуждался
в разд. 5.1, где говорилось о модуляционной неустойчивости. Как уже
упоминалось, модуляционная неустойчивость в частотном представ-
представлении может рассматриваться в терминах четырехволнового смеше-
смешения, в то время как во временном представлении она возникает
в результате роста слабых возмущений из непрерывной волны.
В самом деле, частота модуляционной неустойчивости E.1.10) равна
сдвигу частоты fis A0.3.10), что говорит об эквивалентности этих двух
подходов.
10.3.3. ФАЗОВОЕ СОГЛАСОВАНИЕ
В ДВУЛУЧЕПРЕЛОМЛЯЮЩИХ СВЕТОВОДАХ
В одномодовых световодах, сохраняющих поляризацию, возмож-
возможно использование двулучепреломления световода для согласования
фаз волн с разными поляризациями. Разнипа показателей преломле-
преломления для различных поляризаций
Ьп = Апх-Апу A0.3.11)
(где Апх и Ди„- разности показателей преломления сердцевины и обо-
оболочки для мод, поляризованных вдоль медленной и вдоль быстрой
осей) определяет частотный сдвиг при четырехфотонном смешении
[17]. Полное описание параметрического усиления в двулучепре-
ломляющих световодах требует обобщения формализма, развитого
в разд. 10.2, путем решения волнового уравнения в векторной форме
в приближении, подобном тому, что использовалось в разд. 7.1.2.
Предполагая каждую из четырех волн поляризационной вдоль быст-
быстрой или медленной оси, получаем выражение для параметрического
усиления в таком же виде, как в A0.2.21), с небольшими изменениями
в определении параметров у и и. В частности, если в уравнении
G.1.23) в 5С<3) доминирует электронный вклад, то у уменьшается
в 3 раза по сравнению с величиной, полученной в A0.2.9). Расстройка
волновых векторов к также имеет три составляющих, как и в A0.3.1).
Однако волноводная составляющая Akw теперь уступает модовому
двулучепреломлению Ьп. Нелинейная составляющая AkNL также отли-
отличается от того, что дает A0.3.5). В дальнейшем AkNL будет предпола-
предполагаться пренебрежимо малой по сравнению с Акм и Akw.
Как и в предыдущем рассмотрении, фазовый синхронизм возни-
возникает, когда Акм и Akw компенсируют друг друга. Каждый из них
298 Глава 10
может быть как положительным, так и отрицательным. При Xl < XD
положительна Акм, поскольку Р2 положительна A0.3.6). Волноводная
составляющая Akw может быть сделана отрицательной, если волна
накачки поляризована вдоль медленной оси, в то время как стоксова
и антистоксова волны поляризованы вдоль быстрой оси. Это видно
из выражения A0.3.4). Поскольку Ди3 = Аи4 = &пу и A"i = Аи2 = А"*,
волноводная составляющая записывается в виде
Akw = [Аи^Юз + ю4) - 2Дихю,]/с = -гю^б^/с, A0.3.12)
где использовалось A0.3.11) и предполагалось, что со3 + ю4 = 2ю,. Из
выражений A0.3.6) и A0.3.12) следует, что Акм и Akw взаимно
компенсируются при отстройке Qs
6и\ 1/2
¦ <ш-313)
где А,! = 2яс/ю, [17]. При длине волны накачки к1 = 0,532 мкм,
Р2 « 60 пс2/км и 6и = 1 • 10 частотный сдви1 (vs = O.J2n) составляет
около 10 ТГц. В первом эксперименте [17] по четырехволновому
смешению в двулучепреломляющих световодах сдвиг частоты состав-
составлял 10-30 ТГц. Измеренные значения v5 хорошо совпадали с вычис-
вычисленными по формуле A0.3.13).
Выражение A0.3.13) выведено для случая, когда волны накачки А1
и А2 поляризованы вдоль медленной оси, а А3и Л4-вдоль быстрой
оси. Существует множество других комбинаций, для которых Akw
отрицательно и, следовательно, возможно согласование фаз. Соот-
Соответствующий частотный сдвиг Qs можно получить из A0.3.6), взяв
Akw из A0.3.4), где Ап} (/ = 1 -4) заменено на Апх или Апу в зави-
зависимости от поляризации волны. В табл. 10.1 приведены пять комби-
комбинаций взаимодействующих волн, для которых в двулучепреломляю-
двулучепреломляющих световодах может выполняться условие фазового синхронизма
[20]. В последней колонке приведены величины сдвига частоты для
Таблица 10.1. Пять типов фазового синхронизма в двулучепреломляющих
световодах и соответствующие сдвиги частоты. Символы s и / обозначают
поляризацию вдоль медленной и быстрой осей соответственно
Тип
процесса
I
II
III
IV
V
л,
s
s
s
S
S
Поляризация
волны
Лг А3
f *
f f
s f
s s
* /
A^
f
f
s
f
Сдвиг частоты
п.
П, = 6и/(Р2с)
Ъ2 - C1J2
П2 + П,/2
x/2fi2
/, = О„2п(ТГц,
4,0
47,5
43,5
51,5
67,2
Параметрические процессы 299
накачки на длине волны Xt = 532 нм и при р2 = 66 пс2/км, 5и =
= 5-10~4. Сдвиг частоты в случае I меньше, чем в остальных случаях,
более чем на порядок. Это обстоятельство было использовано для
упрощенной записи для ?25 в случаях III и IV: точное значение можно
получить, заменив ?22 на ?1'2 = (?2| + fli/4I 2. Величины частотных
сдвигов также приблизительны, поскольку при их вычислении не
учитывалась дисперсия двулучепреломления 5и. Учет дисперсии дву-
лучепреломления дает поправку к величине частотного сдвига при-
приблизительно в 10% в сторону уменьшения [20].
С практической точки зрения пять типов взаимодействия, при-
приведенные в табл. 10.1, можно разбить на две категории. Первые два
процесса соответствуют случаю, когда мощность накачки разде-
разделяется между быстрой и медленной модами. В остальных случаях
накачка поляризована вдоль медленной оси. В первой категории
процессов параметрическое усиление максимально, когда мощность
накачки в двух поляризационных модах равна, т.е. 9 = 45', где
9-угол между направлением поляризации накачки и медленной осью.
Даже в этом случае различные процессы конкурируют между собой,
поскольку значения коэффициентов параметрического усиления для
всех этих процессов приблизительно одинаковы. В эксперименте [21]
наблюдалось четырехволновое смешение с синхронизмом типа I при
накачке импульсами длительностью 15 пс на длине волны 585,3 нм от
лазера на красителе с синхронизацией мод. Доминировал пара-
параметрический процесс типа I, поскольку в этом случае расстройка
групповых скоростей различных волн относительно мала.
На рис. 10.9 показан спектр, наблюдавшийся на выходе световода
длиной 20 м при накачке пиковой мощностью ~ 1 кВт, поляри-
поляризованной под углом 9 ^ 44е [21]. Наличие в спектре стоксовой
и антистоксовой полос с частотной отстройкой +4 ТГц обусловлено
четырехволновым смешением типа I. Стоксова волна поляризована
вдоль медленной оси, в то время как актистоксова-вдоль быстрой
оси световода. Асимметричное уширение стоксовой линии и линии
накачки вызвано совместным действием эффектов ФКМ и ФСМ (см.
разд. 7.4). Относительное увеличение стоксовой компоненты обус-
обусловлено комбинационным усилением. Линия с частотной отстройкой
13 ТГц является стоксовой компонентой ВКР. Она поляризована
вдоль медленной оси, поскольку мощность накачки в медленной
поляризационной моде несколько больше, чем в быстрой (9 ^ 44е).
Увеличение 9 на 2-Зг приводит к изменению поляризации излучения
ВКР. Небольшой пик вблизи 10 ТГц возникает в результате невы-
невырожденного четырехволнового смешения (со, Ф ю2), в процессе кото-
которого слабая стоксова волна ВКР усиливается в поле накачки и сток-
стоксовой волны вырожденного четырехволнового смешения. Фазовый
синхронизм может возникать только при поляризации излучения ВКР
вдоль медленной оси. Пик вблизи 10 ТГц исчезает при увеличении
300
Глава 10
I ^.Накачка
Антисток-
сова вол на
*^ (s,f)
Стоксова волна
.»>,! II 1. (»> . . О
i
н
_ н-^
в = 44°
Крыло ВКР
. (s) .
6 3 0-3-6-9 -12 -15 -18
Сдвиг частоты (ТГц)
Рис. 10.9. Спектр излучения на выходе двулучепреломляющего световода
длиной 20 м при накачке импульсами длительностью 15 пс и пиковой мощ-
мощностью ~ 1 кВт. Угол между поляризацией накачки и медленной осью
световода составлял 44 . Индексы / и s соответствуют быстрой и медленной
поляризационным модам. Видна также линия ВКР. Небольшой пик вблизи
10 ТГц обусловлен невырожденным четырехволновым смешением [21].
9 до величины, превышающей 45 , так как при этом поляризация
излучения ВКР переключается в быструю поляризационную моду.
Использование двулучепреломления для согласования фаз при
четырехволновом смешении имеет то дополнительное преимущество,
что позволяет перестраивать частотный сдвиг vs в пределах 3-4 ТГц.
Такая подстройка возможна при изменении внешних факторов, таких,
как давление и температура. В эксперименте [18] волокно прижима-
прижималось к плоской пластине. При давлении 0,3 кг/см2 частотный сдвиг
изменялся на 4 ТГц. В похожем эксперименте [19] дополнительное
напряжение в световоде создавалось путем наматывания его на
цилиндрический стержень. При изменении диаметра стержня частот-
частотный сдвиг изменялся в пределах 3 ТГц. Возможна подстройка час-
частотного сдвига и путем изменения температуры, поскольку внутрен-
внутренние напряжения в двулучепреломляющих световодах зависят от
температуры. При нагревании световода до 700 °С была получена
перестройка в диапазоне 2,4 ТГц [22]. Наличие четырехволновых
процессов дает возможность измерять усредненное по длине светово-
световода двулучепреломление, поскольку сдвиг частоты зависит от 5и [23].
Частотный сдвиг, связанный с четырехволновыми процессами,
зависит также от мощности накачки, о чем говорит наличие нелиней-
Параметрические процессы 301
ной составляющей AkNL в выражении A0.3.1). При выводе выражения
A0.3.13) и других выражений для Qs в табл. 10.1 нелинейный вклад не
учитывался, хотя в общем случае его учет необходим. Обычно D.s
уменьшается с ростом мощности накачки. В эксперименте [24]
с возрастанием накачки Qs уменьшалось на 1,4%/Вт. Нелинейный
член A/cNL также можно использовать для согласования фаз. Это
связано с модуляционной неустойчивостью в двулучепреломляющих
световодах, о которой говорилось в разд. 7.4.
10.4. ПАРАМЕТРИЧЕСКОЕ УСИЛЕНИЕ
И ЕГО ПРИМЕНЕНИЯ
Четырехволновое смешение так же. как ВКР и ВРМБ, может
использоваться в усилителях и генераторах. Такие устройства при-
привлекают внимание в контексте явлений, связанных со сжатыми
состояниями [33-43]. В данном подразделе речь пойдет о таких
важных характеристиках параметрических усилителей, как коэффи-
коэффициент усиления и ширина полосы. Обсуждаются также вопросы
применения параметрических усилителей для получения сжатых со-
состояний и в оптической волоконной связи.
10.4.1. КОЭФФИЦИЕНТ УСИЛЕНИЯ И ШИРИНА
ПОЛОСЫ
Для полного описания параметрического усиления требуется чис-
численное решение систем A0.2.2) A0.2.5) с учетом эффекта истощения
накачки [37]. Однако заметно продвинуться в понимании физики
данного явления можно, рассмотрев приближенное решение A0.2.19)
и A0.2.20), которое не учитывает истощения накачки. Константы а3,
Ь3, с3 и d3 в этих решениях определяются из граничных условий. Если
в волокно вводятся волны накачки и сигнала, то мощности сигналь-
сигнальной и холостой волн на выходе световода (z = L) даются выра-
выражениями [12]
P3(L) = Р3@) [1 + A + x2/V) sinh2 (gLj]. A0.4.1)
P4(L) = P3@) A + x2f4g2) sinh2 (gL), A0.4.2)
где параметрическое усиление д дается выражением A0.2.21) и it-
суммарная расстройка волновых векторов, даваемая выражением
A0.2.18). Как и следовало ожидать, сигнал усиливается и генери-
генерируется холостая волна.
Ненасыщенное усиление за один проход по параметрическому
усилителю дается выражением
775 sinh2 @L). (Ю.4.3)
302 Глава 10
Сравним это выражение с (8.2.5), полученным для ВКР-усилителя.
Основное отличие в том, что параметрическое усиление зависит от
х и может быть довольно малым, если отсутствует фазовый синхро-
синхронизм. В пределе v.»yPor из выражений A0.2.21) и A0.4.3) получим
С другой стороны, при точном синхронизме (х = 0) и gL » 1 усиление
выражается в виде
GA^-exp(yPorL). A0.4.5)
Параметр г дается выражением A0.2.22); г = 1 соответствует случаю
вырождения по накачке, т.е. случаю, когда мощности двух волн
накачки равны.
Ширина полосы усиления М1А может быть определена из выра-
выражения A0.4.3) и в общем случае зависит от длины световода Lu мощ-
мощности накачки Ро. Рассмотрим сначала предел х » уР0, при котором
GA определяется выражением A0.4.4). При xL = +я усиление умень-
уменьшается в я2/4 раз. Определение величины Ml соответствует расстрой-
расстройке волновых векторов Дх = 2n/L; благодаря этому ширина полосы
усиления Q.s несколько больше, чем полная ширина на полувысоте
[12]. Поскольку в к доминирует материальная составляющая, Дх к
« 21Р21 Q.s M1A, выражение для ширины полосы записывается в виде
где Q.s-разность частот накачки и сигнала, соответствующая случаю
точного фазового синхронизма х = 0. С возрастанием мощности
накачки полоса усиления уширяется. Если использовать выражение
A0.4.3), то ширина полосы усиления &С1А будет определяться сле-
следующим образом [12]:
1 Y/n\2 I1'2
1{1) +{уР°гJ\ ¦ A0А7)
При больших мощностях накачки можно записать приближенное
выражение
AnA*iyPor)/\V2n2\K(\V2\nsLNL)-\ A0.4.8)
где предполагается г = 1 и LNL = (уР0)-1. Выражение A0.4.8) право-
правомерно при LNL« L. Грубая оценка ширины полосы усиления при
| Р21 = 20-60 пс2/км дает значение ~ 10-100 ГГц. При этом Ц./2я =
= 10 100 ТГц и LNL ~ 1 м. Данная величина является промежу-
промежуточной между аналогичными величинами ВКР-усилителей (~ 5 ТГц)
и ВРМБ-усилителей (~ 100 МГц).
Параметрические процессы 303
Ширина полосы усиления параметрических волоконных усили-
усилителей зависит от того, вводятся в световод вместе с накачкой
сигнальная и холостая волны или нет. В частности, сигнальная
и холостая волны могут как усиливаться, так и ослабляться в зави-
зависимости от относительной разности фаз. Эта зависимость от фазовых
соотношений наблюдалась в эксперименте [35], где сигнальная и хо-
холостая волны, смещенные по частоте от накачки на 130 МГц, рас-
распространялись по световоду длиной 350 м и относительная разность
фаз на входе в световод изменялась при помощи линии задержки.
Мощность сигнальной волны была минимальной и максимальной
при относительной фазе Лф = я/2 и Зя/2 соответственно и оставалась
постоянной при Лф = 0 и я. Коэффициент усиления при таких
условиях обычно линейно зависит от мощности накачки и длины
световода.
Учет истощения накачки также может привести к изменению
характеристик параметрических волоконных усилителей. В общем
случае систему уравнений A0.2.2) —A0.2.5) нужно решать численно
[37], хотя при специальных условиях возможны аналитические реше-
решения в эллиптических функциях [1]. Будут ли сигнальная и холостая
волны усиливаться или ослабляться, зависит от относительной фазы
9, определяемой выражением
9 = ф1+ф2-ф3-ф4, A0.4.9)
где ф;-фаза амплитуды А} (/=1-4). Усиление максимально при
9 = —я/2. Однако относительная фаза 9 изменяется в процессе пара-
параметрического взаимодействия. Поэтому, даже если 9 = — я/2 на входе
в световод, при распространении по световоду 9 меняется от 0 до я/2,
где сигнальная и холостая волны испытывают уже ослабление. Это
поведение показано на рис. 10.10, где представлена эволюция относи-
относительной фазы 9, мощности холостой волны />4 и мощности волны
накачки Р1 при распространении вдоль световода, причем предпола-
предполагалось, что на входе в световод выполняется условие фазового
синхронизма, мощность накачки составляет 70 Вт, Рх = Р2 и 9 =
= —я/2. Сплошные и штриховые линии соответствуют случаям
/>3@) = />4@) = 0,1 мкВт и />3@) = 6 мВт при />4@) = 0,1 мкВт соот-
соответственно. Последний случай соответствует собственно парамет-
параметрическому усилению, в то время как в первом случае обе волны
вырастают из шума. В обоих случаях холостая и сигнальная волны
периодически усиливаются и затухают. Это связано с тем, что
истощение накачки приводит к изменению величины 9, которая
в начале составляет —я/2. Таким образом, для параметрического
усиления требуется жесткий контроль длины световода даже при
точном фазовом синхронизме.
Предыдущее обсуждение касалось случая четырехволнового сме-
смешения непрерывных волн. При накачке световода короткими импуль-
304
Глава 10
50 100 150 200
z(n)
20
70
50-
30-
50
100 150 200
z(m)
50 100 150 200
Рис. 10.10. Зависимость от длины световода относительной фазы 6, мощности
холостой волны РА и мощности накачки Р1 при Pt = P2, Pt @) = 70 Вт,
6@) = л/2 и к = 0. Сплошные и штриховые линии соответствуют
/•3@) = Р4@) = 0,1 мкВт и Р3@) = 6мВт ПРИ />4@) = 0,1 мкВт соответст-
соответственно [37].
сами возможны два эффекта, ослабляющих параметрическое взаимо-
взаимодействие между волнами. Во-первых, спектр накачки уширяется
вследствие ФСМ. Если ширина спектра накачки превышает ширину
полосы усиления QA, то параметрическое усиление понижается по-
подобно тому, как это происходит с ВРМБ-усилением, о чем гово-
говорилось в разд. 9.1. Во-вторых, разница групповых скоростей им-
импульса накачки, сигнального и холостого импульсов приводит к их
разбеганию. Оба этих эффекта приводят к уменьшению эффективной
длины четырехволнового смешения. В случае пикосекундных импуль-
импульсов необходимо также учитывать дисперсию групповых скоростей
различных спектральных компонент внутри импульса. Для учета
данных эффектов необходимо включать в левую часть уравнений
A0.2.2) —A0.2.5) первые и вторые производные амплитуд А-} по вре-
времени.
10.4.2. ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
При параметрическом усилении использовались все способы полу-
получения фазового синхронизма, указанные в разд. 10.3. Основное отли-
отличие четырехволнового смешения от параметрического усиления со-
состоит в наличии либо отсутствии в световоде введенной извне
сигнальной волны на частоте, для которой выполняется условие
фазового синхронизма. В отсутгизие такой затравки вместо нее
выступают шумы.
Параметрические процессы
305
В первом эксперименте [6] по параметрическому усилению в све-
световодах фазовый синхронизм был обусловлен использованием мно-
гомодового световода. Пиковая мощность импульсов накачки на
длине волны 532 нм составляла ~ 100 Вт, а длина волны непрерыв-
непрерывного сигнал;! мощностью ~ 10 мВт перестраивалась вблизи 600 нм.
Усиление было небольшим из-за малой длины световода (9 см).
В недавнем эксперименте [14] использовалась накачка на длине
волны 1,319 мкм, лежащей недалеко от длины волны нулевой диспер-
дисперсии, что и обусловило выполнение условия синхронизма (см.
рис. 10.7). При пиковой мощности импульсов накачки в пределах
30-70 Вт измерялась мощность усиленного непрерывного сигнала
на длине волны 1,338 мкм на выходе световода длиной 30 м. На
рис. 10.11 показано усиление GA как функция мощности накачки Ро
при трех значениях входной мощности сигнала Ръ. Отклонение от
экспоненциальной формы кривой обусловлено насыщением усиления
вследствие истощения накачки. Отметим также, что GA существенно
падает при увеличении мощности сигнала от 0,26 до 6,2 мВт. При
мощности накачки Ро = 70 Вт усиление сигнала мощностью 0.26 мВт
составило 46 дБ. Эта цифра говорит о потенциальной возможности
использования волоконных световодов в качестве параметрических
усилителей при выполнении условия фазового синхронизма. Контро-
Контролировать выполнение этого условия при заданных частотах накачки
и сигнала удобно с помощью двулучепреломляющего световода,
в котором двулучепреломление меняется при воздействии внешнего
5хЮ4
20
30 40 50 60
Мощность накачки (Вт)
Рис. 10.11. Коэффициент
усиления СА параметри-
параметрического усилителя в за-
зависимости от мощности
накачки при трех различ-
различных значениях входной
мощности сигнала [14].
306 Глава 10
давления или изгиба. Параметрические усилители с такими схемами
были продемонстрированы. В эксперименте [33] усиление сигнала на
длине волны Ь292 мкм составило 38 дБ, причем для согласования
фаз к световоду прикладывалось внешнее давление. В другом экспе-
эксперименте [34] сигнал на длине волны 1,57 мкм от полупроводникового
лазера с распределенной обратной связью усиливался на 37 дБ в поле
накачки с длиной волны 1,319 мкм.
Параметрическое усиление можно использовать для создания
лазеров, помещая световод в резонатор Фабри-Перо. Такой четы-
рехфотонный волоконный лазер недавно был продемонстрирован
в эксперименте [36]. При накачке импульсами длительностью 100 пс
на длине волны 1,06 мкм от Nd: ИАГ-лазера с модуляцией доброт-
добротности и синхронизацией мод на выходе волоконного четырехфо-
тонного лазера наблюдались импульсы длительностью 65 пс на
длине волны 1,15 мкм. Длина резонатора подстраивалась таким
образом, чтобы накачка была синхронной. Ширина спектра генерации
составляла — 100 ГГц в соответствии с формулой A0.4.7).
10.4.3. ПРИМЕНЕНИЯ
Так же как и волоконные ВКР-усилители, параметрические усили-
усилители могут оказаться полезными в системах оптической связи. Эти
два типа усилителей отличаются друг от друга по ширине полосы
и по требованиям, предъявляемым к накачке. ВКР-усилители обла-
обладают широкой полосой (~ 5 ТГц). но требуют отстройки частоты
сигнала от частоты накачки около 13 ТГц. Параметрические уси-
усилители, напротив, имеют меньшую ширину полосы усиления
(~ 100 ГГц), но отстройка частоты сигнала от частоты накачки может
составлять ~ 100 ТГц. Такие параметры дают известную свободу
в выборе накачки, в то время как ширина полосы достаточно велика
для многих применений. Для обеспечения фазового согласования
можно использовать большое двулучепреломление световодов, под-
поддерживающих поляризацию.
Как и процессы ВКР и ВРМБ, параметрическое усиление может
приводить к перекрестным помехам в многоканальных системах
оптической связи [26]. Перекрестные помехи могут сказываться
в системах с разделением каналов ^ 10 ГГц. При таких небольших
частотных сдвигах четырехволновое смешение может возникать
в длинных световодах (~10км) даже при отсутствии фазового
синхронизма. Расчеты показывают [44], что в 100-канальной линии
оптической связи с разностью частот соседних каналов 5 ГГц для
того, чтобы уровень перекрестных помех составлял менее 1%, тре-
требуется, чтобы входная мощность в каждом канале была существенно
меньше 1 мВт.
Важным применением четырехволнового смешения стала демон-
Параметрические процессы 307
страция сжатых состояний в световодах [38-41]. Под этим термином
понимают состояния электромагнитного поля, при котором шумовые
флуктуации в одной из квадрупольных компонент понижаются до
уровня ниже уровня квантового шума. Для точного описания сжатых
состояний требуется квантовомеханическое рассмотрение, при кото-
котором амплитуды сигнальной и холостой волн В3 и ВА заменяются
соответствующими операторами уничтожения [38]. Далее, в рассмот-
рассмотрение включается квантовый шум, для чего в правую часть уравнений
A0.2.16) и A0.2.17) вводится флуктуационный член, известный как
сила Ланжевена [41]. Должны быть учтены и потери в световоде.
Сжатые состояния могут наблюдаться при ослаблении сигнальной
или холостой волны в поле накачки, фаза которой отличается от фазы
ослабляемой волны на определенную величину [35]. О возможности
такого ослабления говорилось в разд. 10.4.1. Спонтанное излучение
на сигнальной и холостой частотах генерирует фотоны со случайны-
случайными фазами. Четырехволновое смешение приводит к увеличению или
уменьшению числа пар фотонов на сигнальной и холостой частотах
в зависимости от их фазы. Когда фаза осциллятора при гомодинном
или гетеродинном детектировании соответствует относительной фазе
между волнами, ведущей к уменьшению числа фотонов в сигнальной
или холостой волне, наблюдается уменьшение шума ниже квантового
уровня.
Наблюдение сжатых состояний в волоконных световодах затруд-
затрудняется наличием конкурирующих процессов, таких, как спонтанное
или вынужденное МБ-рассеяние. Сжатые состояния наблюдаются,
только если уровень шумов этих процессов не превышает величины,
на которую уровень шумов понижается при четырехфотонном сме-
смешении. Несмотря на указанные затруднения, в эксперименте [39]
наблюдалось уменьшение уровня шумов на 12,5% ниже квантового
предела при распространении накачки на длине волны 647 нм в свето-
световоде длиной 114 м. Для подавления ВРМБ накачка модулировалась
с частотой 748 МГц, что намного больше ширины полосы ВРМБ-уси-
ления. Для подавления теплового МБ-рассеяния на направляемых
акустических волнах световод приходилось охлаждать в жидком
гелии, однако такое рассеяние все же ограничивало характеристики
системы. На рис. 10.12 показан спектр шумов, наблюдавшийся, когда
фаза локального осциллятора соответствовала минимуму шума.
Большие пики обусловлены МБ-рассеянием на радиальных акусти-
акустических модах. Сжатые состояния генерируются в областях частот,
отстоящих на 45 и 55 МГц от частоты накачки. В другом экспе-
эксперименте [40] по тому же световоду распространялось излучение
накачки с длинами волн 647 и 676 нм. При помощи двухчастотной
гомодинной схемы было зарегистрировано уменьшение шума на 20%
ниже квантового предела. Такое явление называют четырехмодовой
308
Глава 10
л
32,0
о
ироваш
"о
i.0,9
О
= 0,8
-
-
A
35 40 45 50 55
Сдвиг частоты (МГц)
60
65
Рис. 10.12. Спектр шумов при генерации сжатых состояний. Горизон-
Горизонтальная линия соответствует уровню квантовых шумов. Наличие областей
минимума шумов вблизи 45 и 55 МГц указывает на генерацию сжатых
состояний при четырехфотонном смешении [39].
генерацией сжатых состояний, поскольку в процессе участвуют две
пары сигнальных и холостых волн, соответствующих каждая своей
волне накачки. При такой генерации важную роль играют ФСМ
и ФКМ. Использование нелинейностей световода для генерации
сжатых состояний привлекательно с точки зрения их применения
в оптической связи.
10.5. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ
Четырехволновое смешение, доминирующий параметрический
процесс в волоконных световодах, генерирует спектральные боковые
полосы, отстоящие от частоты накачки вплоть до 100 ТГц. Во многих
экспериментах [45-51] при накачке волоконного световода мощными
импульсами на длине волны 1,06 мкм спектр выходного излучения
простирался в видимую и ультрафиолетовую области. Генерация
спектральных компонент в этих областях обусловлена смешиванием
двух или нескольких волн с частотами, сумма которых равна частоте
генерируемой волны. Так, взаимодействие двух волн с частотами ю1
и со2 может приводить к генерации вторых гармоник 20^ и 2со2,
третьих гармоник 3cOj и Зсо2 и суммарных частот вида а1 + со2,
2cOj + со2 и 2со2 + coj. Генерация таких частот, как 3cOj, Зсо2, 20^ + со2
и 2со2 + coj, вызывается параметрическими процессами третьего по-
порядка, обусловленными хC)- Эффективность преобразования доволь-
довольно низка, поскольку обычно для таких параметрических процессов
трудно достичь фазового синхронизма. В эксперименте [50] частоты
Параметрические процессы 309
третьих гармоник и суммарные частоты 2а1 + ю2 и 2со2 + и>1 генери-
генерировались в результате смешивания входной волны накачки и стоксо-
вой волны ВКР с длинами волн соответственно 1,06 и 1,12 мкм.
Двухметровый отрезок световода имел эллиптическую сердцевину
и накачивался импульсами пиковой мощности 5 кВт.
Несколько ранних экспериментов [46-49] показали, что при рас-
распространении по волоконному световоду мощного импульса накачки
на длине волны 1,06 мкм от Nd: ИАГ-лазера с синхронизацией мод
и модуляцией добротности происходит генерация второй гармоники
и суммарной частоты вида со, + со2. Эффективность преобразования
составляла около 0,1% как для суммарной частоты [49], так и для
второй гармоники [52]. Такая высокая эффективность неожиданна
для параметрических процессов второго порядка, поскольку воспри-
имчивость второго порядка % связана с нелинейным откликом
электрических диполей, следовательно, близка к нулю в изотропных
материалах, каким является плавленый кварц. Существует несколько
нелинейностей высших порядков, которые могут создать эффектив-
эффективную хB) для таких процессов; наиболее важны среди них нели-
нелинейности на границе сердцевины и оболочки и нелинейности, свя-
связанные с квадрупольным и магнитным моментами. Однако деталь-
детальные расчеты показывают [53], что эти нелинейности могут дать
увеличение эффективности преобразования максимум до 10 5 даже
при условии фазового синхронизма. Видимо, более высокие эф-
эффективности параметрических процессов второго порядка связаны
с другим механизмом.
Ключ к природе такого механизма появился, когда было об-
обнаружено, что мощность второй гармоники значительно возрастает,
если излучение накачки действует на световод в течение нескольких
часов [54]. На рис. 10.13 показана зависимость средней мощности
второй гармоники от времени при распространении по световоду
длиной 1 м импульсов накачки на длине волны 1,06 мкм, с дли-
длительностью 100-130 пс и со средней мощностью 125 мВт, от
Nd; ИАГ-лазера с модуляцией добротности и синхронизацией мод.
Мощность второй гармоники со временем растет почти экспонен-
экспоненциально и начинает насыщаться после 10 ч. Максимальная эффек-
эффективность преобразования составляла около 3%. Импульсы на длине
волны 0,53 мкм на выходе световода имели длительность около 55 пс
и мощность, достаточную для накачки лазера на красителе [54]. Этот
эксперимент способствовал дальнейшему возрастанию интереса
к ГВГ в световодах, и в последнее время изучению процесса под-
подготовки и природы генерации второй гармоники в волоконных
световодах уделяется значительное внимание [55-72]. Уровень по-
понимания этих процессов пока далек от совершенства, и работа
продолжается. Остаток этой главы посвящен обзору состояния дел ко
времени написания.
310
Глава 10
1000
100 -
X
о
О-
о
10 -
1 -
f 0,1
о
0,01 -
0,001
Мощность
125 мВт
;
и.
I
накачк
j
/
и
/
•
t
f
100
50
0
I
Г'
f
-
6 7 8 9
I I I
Рис. 10.13. Средняя мощ-
мощность второй гармоники,
генерируемой в кварце-
кварцевом световоде, как функг
ция времени. Средняя
мощность лазера накачки
в режиме модулирован-
модулированной добротности с синх-
синхронизацией мод 125 мВт
на длине волны 1,06 мкм.
На вставке показан экс-
экспоненциальный рост в
линейном масштабе (по
работе [54]).
6 8
Время 1ч
10 12
14
Для эффективности генерации второй гармоники в волоконных
световодах требуется инкубационный период, во время которого
происходит так называемый процесс подготовки световода. В ранних
работах [54, 55] световод подготавливался путем ввода мощных
импульсов на длиней . элны 1,06 мкм длительностью около 100 пс.
Время подготовки зависело от мощности накачки и составляло
несколько часов при мощностях накачки порядка 10 кВт. Сердцевина
световода была легирована германием и фосфором. Наличие фос-
фосфора казалось необходимым для процесса подготовки. В недавнем
эксперименте [60], в котором использовался Кг+-лазер с длитель-
длительностью импульсов 100 пс на длине волны 647.1 нм, световод с серд-
сердцевиной, легированной только Ge, был подготовлен в течение 20 мин
при пиковой мощности всего 720 Вт. В другой работе [57] было
обнаружено важное обстоятельство-световод можно подготовить
в течение лишь нескольких минут даже на длине волны 1,06 мкм,
используя слабый сигнал второй гармоники, распространяющийся
вместе с импульсом накачки и действующий как затравка. При тех же
условиях, но без затравки, световод не удавалось приготовить даже
после 12 ч.
Параметрические процессы 311
Для объяснения генерации второй гармоники было предложено
несколько физических механизмов [56-59]. Все они связаны с пе-
периодическим выстраиванием неких объектов, таких, как центры
окраски [56] или дефекты [57] вдоль световода, таким образом, что
автоматически выполняется условие фазового синхронизма. В одной
модели [57] выстраивание возникает через параметрический процесс
третьего порядка, в котором смешиваются накачка и вторая гар-
гармоника (генерируемая внутри световода или введенная извне) и со-
создают статическую поляризацию (на нулевой частоте), задаваемую
следующим образом:
Рйс = ^ Re [хC) Е* Е* ESH exp (iAkpz) ], A0.5.1)
где Ер-поле накачки на частоте сор; ?5н-поле затравочной второй
гармоники на частоте 2сор; и Акр-разность волновых векторов:
Акр = [«Bир) - 2и(шр)]ир/С. A0.5.2)
Статическая поляризация индуцирует статическое электрическое
поле, полярность которого периодически меняется вдоль световода
с периодом согласования фаз 2п/Акр (~30-40мкм для накачки
1,06 мкм). Это электрическое поле перераспределяет электрические
заряды и создает периодические массивы диполей. В формировании
диполей могут участвовать дефекты ловушки или центры окраски,
природа которых не вполне понятна. Главное, что такое перерас-
перераспределение зарядов нарушает центральную симметрию и имеет
период, требуемый для фазового синхронизма. В сущности, волокно
самоорганизуется для генерации второй гармоники. Математически
диполи могут откликаться на приложенное оптическое поле с эффек-
эффективной восприимчивостью хB)- В простейшем случае хB) предпо-
предполагается пропорциональной Pdc, т.е.
ХB) = aSHPdc = \ aSHEoXC»|?p|2|?SH|cos(A/cpz + ф ), A0.5.3)
где aSH - константа, величина которой зависит от микроскопического
процесса, отвечающего хB\ а фр-фаза, зависящая от начальных фаз
накачки и затравочной второй гармоники. В силу периодической
природы хB) говорят о создании в процессе подготовки решетки у}2)-
Для рассмотрения генерации второй гармоники на %т из A0.5.3)
можно проделать стандартную процедуру [1—4]. Предположим, что
накачка на частоте (лх вводится в подготовленное волокно. Частота
cot может, вообще говоря, отличаться от сор. Тогда поля накачки ?t
и второй гармоники Е2 удовлетворяют уравнениям связанных ампли-
амплитуд [56], именно
dA i
^iy{\A\2 + 2\A\2)A+^AAXc^(mz), A0.5.4)
312 Глава 10
dA
-^ = iy(\A2\2 + 2\А1\2)А2 + iySH Alexplha), A0.5.5)
где
^^i2XC)\Ep\2\ESH\^ (Ю.5.6)
/112-интеграл перекрытия (см. разд. 10.2) и
у. = Акр - Ак; A0.5.7)
Ак задано уравнением A0.5.2) после замены юр на ю1. Параметр
х-это остаточная расстройка волновых векторов, возникающая при
coj #сор. Члены, пропорциональные у, связаны с процессами ФСМ
и ФКМ и, вообще говоря, должны учитываться.
Для решения уравнений A0.5.4) и A0.5.5) можно использовать
метод из разд. 10.2. В приближении неистощенной накачки (|Л2|2 «
«l^il2) уравнение A0.5.4) имеет решение
Ау (z) = v^ exp {iyPi z), A0.5.8)
где Р1- вводная мощность накачки. Подставляя
В2 = А2ехр (-2гуЛ z) A0.5.9)
в уравнение A0.5.5), получаем
dB,
-j^ = iySHP1exP(iyz). A0.5.10)
Эффектами ФСМ и ФКМ в отличие от процесса четырехволнового
смешения можно пренебречь. Это означает, что в приближении
неистощенной накачки нелинейная составляющая расстройки волно-
волновых векторов отсутствует. Уравнение A0.5.10) легко решается, что
позволяет получить выражение для мощности второй гармоники
A0-5Л1)
При выводе A0.5.11) предполагалось, что решетка хB) записана на
всей длине световода L. Так было бы, если бы при записи ис-
использовалась непрерывная накачка с узким спектром. На практике же
используются импульсы длительностью ~ 100 пс. Использование та-
таких коротких импульсов влияет на процесс формирования решетки
нелинейности по двум причинам. Во-первых, групповое разбегание
импульсов накачки и второй гармоники ведет к тому, что после
прохождения нескольких длин Lw они уже не перекрываются. Для
импульсов накачки длительностью То«80 пс на длине волны
1,06 мкм длина группового разбегания Lw составляет «1м при
Параметрические процессы 313
дисперсии \dl2\ ~ 80 пс/м. Таким образом, решетка %т формируется
на длине не более 1 м при импульсах накачки длительностью
~ 100 пс. Во-вторых, уширение спектра, обусловленное ФСМ, ведет
к уменьшению длины когерентности накачки и, следовательно.
к уменьшению длины, на которой решетка хB) генерирует вторую
гармонику когерентно. Оказывается, что именно Lcoh является фак-
фактором, ограничивающим длину взаимодействия накачки и второй
гармоники, поскольку на практике Lcoh<Lw. На каждой частоте
накачки записывается, вообще говоря, своя решетка с периодом
2п/Акр, где Акр дается выражением A0.5.2). Для учета вклада всех
решеток выражение A0.5.1) для Рас следует проинтегрировать по
всему спектру накачки. Для гауссовой формы спектров накачки
и второй гармоники эффективная постоянная поляризация представ-
представляется в виде [66]
Р№ = Л.сехр [-(z/LcohJ], A0.5.12)
где
Lcoh = 2/|</I25cop|, A0.5.13)
d12 дается выражением A.2.13) и 5сор-полуширина спектра (на высоте
1/е) [66]. При \d12\ = 80 пс/м и ширине спектра на полувысоте 10 Гц
^-*coh ^ ^^ СМ.
В большинстве экспериментов с накачкой на длине волны
1,06 мкм спектральная ширина на входе в световод составляет
~ 10 ГГц. Однако вследствие ФСМ спектр накачки в световоде
уширяется (см. D.1.6) и D.1.11)). Это уширение заметно уменьшает
длину когерентности до величины порядка 10 см. При Lcoh < L
выражение A0.5.11) должно быть модифицировано. В простейшем
приближении [56] L просто заменяется на Lcoh в выражении A0.5.11).
Это предполагает, что Р?$Р = Рас при z ^ Lcoh и Р^ = 0 при z > Lcoh .
Это приближение можно уточнить, используя A0.5.12). Для этого ySH
в A0.5.10) нужно домножить на exp [-(r/LcohJ]. При интегрирова-
интегрировании выражение A0.5.10) дает результат [66]:
Р2М = \УбиР1 LCBb\2^ exp (-i^U*) . A0.5.14)
Следует подчеркнуть, что выражение A0.5.14) также является при-
приближенным; оно следует из уравнений A0.5.4) и A0.5.5), которые
справедливы только для непрерывного или квазинепрерывного излу-
излучения. Эти уравнения можно обобщить на случай нестационарной
накачки, введя первую и вторую производные амплитуд по времени
в левые части уравнений [73, 74].
В нескольких экспериментах была измерена зависимость мош-
ности второй гармоники от частоты. На рис. 10.14 показаны ре-
результаты такого измерения [56], в котором длина волны накачки
314
Глава 10
-0,5 0 0,5
Расстройка по длине волны (нм)
1,0
Рис. 10.14. Зависимость эффективности преобразования во вторую гармо-
гармонику как функция отстройки длины волны накачки от 1,064 мкм. Сплошной
линией показана расчетная кривая [56].
изменялась в пределах 4 нм. Сплошной линией показана расчетная
кривая, полученная из A0.5.11) при L = Lcoh. Наилучшее совпадение
с экспериментом дает значение Lcoh =12 см. В этом эксперименте
решетка записывалась импульсами накачки мощностью 10 кВт. Не-
Небольшая длина когерентности обусловлена уширением спектра при
такой большой мощности. В недавнем эксперименте [66] когерентная
длина была увеличена до 35 см за счет использования менее интен-
интенсивной накачки (пиковая мощность 230 Вт).
Обычная эффективность преобразования в экспериментах по вто-
второй гармонике составляет ~ 1%; максимальная опубликованная циф-
цифра 5% [55]. Естественный вопрос: что же ограничивает эффектив-
эффективность? Как видно из рис. 10.13, мощность второй гармоники экспо-
экспоненциально растет на начальной стадии записи решетки, но затем
насыщается. Одной из причин может быть интерференция решеток
у}2\ записанных излучением затравочной второй гармоники и излу-
излучением, генерируемым уже в световоде. Решетка, записанная генери-
генерируемым в световоде излучением второй гармоники, будет не в фазе
с основной решеткой [57]. Если это так, то решетка хB) должна
стираться при пропускании через световод одного излучения второй
гармоники без излучения накачки. Такое стирание в действительности
наблюдалось [65, 67]. Скорость стирания зависит от мощности
второй гармоники, вводимой в световод. В эксперименте [67] эффек-
эффективность преобразования уменьшалась в 10 раз после 5-минутной
Параметрические процессы 3^5
засветки излучением второй гармоники средней мощностью ~ 2 мВт.
Процесс стирания не был экспоненциальным, но зависел от времени
как A + Cf), где С-константа. Однако стирание было обратимым,
т. е. световод снова мог быть подготовлен до прежней эффективности.
Эти наблюдения согласуются с моделью [56, 57]. в которой появле-
появление нелинейности второго порядка объясняется ориентацией зарядов,
носителями которых могут быть центры окраски или различные типы
дефектов. Однако до конца микроскопическая картина явления пока
не ясна. Генерация второй гармоники в световодах продолжает
привлекать большое внимание в силу своей как научной, так, воз-
возможно, и технологической значимости.
ЛИТЕРАТУРА
1. Armstrong J.A. et al., Phys. Rev., 127, 1918 A962).
2. Bloembergen N., Nonlinear Optics, Benjamin, Reading, Mass., 1965. [Имеется
перевод: Бломберген Н. Нелинейная оптика.-М.: Мир, 1966.]
3. Shen Y.R.. The Principles of Nonlinear Optics, Wiley, New York, 1984.
[Имеется перевод: ШенИ.Р. Принципы нелинейной оптики.-М.: Мир,
1989.]
4. Schubert М., Wilhelmi В., Nonlinear Optics and Quantum Electronics, Wiley,
New York. 1986.
5. Alfano R.R., Shapiro S.L., Phys. Rev. Lett., 24, 584, A970).
6. Stolen R.H., Bjorkholm J.E., Ashkin A., Appl. Phys. Lett., 24, 308 A974).
7. Stolen R.H., IEEE J. Quantum Electron., QE-11. 100 A975).
8. Hill K.O. et al, J. Appl. Phys. 49, 5098 A978).
9. Saisy A. et al., Appl. Opt., 19, 1639 A980).
10. Hill K.O., Johnson D.C.. Kawasaki B.S., Appl. Opt., 20, 1075 A981).
11. Lin C, Bosch M.A., Appl. Phys. Lett., 38, 479 A981).
12. Stolen R.H., Bjorkholm J.E., IEEE J. Quantum Electron., QE-18, 1062 A982).
13. Lin C, J. Opt. Commun., 4, 2 A983).
14. Washio K.. Inoue K.. Kishida S., Electron. Lett, 16, 658 A980).
15. Lin С et al.. Opt. Lett., 6, 493 A981).
16. Lin С et al.. Electron. Lett., 18, 87 A982).
17. Stolen КН., Bosch M.A., Lin C, Opt. Lett., 6, 213 A981).
18. Kitavama K., Seikai S., Uchida N.. Appl. Phys. Lett., 41, 322 A982).
19. Kitavama K., Ohashi M.. Appl. Phys. Lett., 41, 619 A982).
20. JainR.K., Stenersen K., Appl. Phys. B35, 49 A984).
21. Stenersen K., Jain R.K., Opt. Commun., 51, 121 A984).
22. Ohashi M. et al.. Opt. Lett., 10, 77 A985).
23. Shibata N. et al.. Opt. Lett., 10, 154 A985).
24. Park H.G., Park J.D., Lee S.S.. Appl. Opt., 26, 2974 A987).
25. Garth S.J.. Pask C. Opt. Lett., 11, 380 A986).
26. Shibata N.. Braun R.P., Waarts R.G.. Electron. Lett., 22, 675 A986).
27. Shibata N.. Braun R.P., Waarts R.G., IEEE J. Quantum Electron., QE-23, 1205
A987)
28. Baldeck PL., Alfano R.R., J. Lightwave Technol., LT-5, 1712 A987).
29. Wang Q., Yang Т., Shen W, Chin. Phys. Lasers., 15, 46 A988)-
30. Pepper D. M., Yariv A., in: Optical Phase Conjugation, ed. by K. A. Usher,
Academic, New York, 1983, Ch. 2.
31. Alfano R.R. ed. Supercontinuum Laser Source, Sprmger-Verlag, Heidelberg,
1989.
316 Глава 14
32. Botineau J., Stolen R.H.. J. Opt. Soc. Am., 72, 1592 A982).
33. OhashiM. et al.. Appl. Phys. Lett., 41, 1111 A982).
34. PocholleJ.P. et al.. Opt. Eng., 24, 600 A985).
35. Bar-Joseph I. et al.. Opt. Lett., 11, 534 A986).
36. Margulis W., Osterberg V., Opt. Lett, 12, 519 A987).
37. Vatarescu A., J. Lightwave Technol., LT-5, 1652 A987).
38. Levenson M.D. et al., Phys. Rev., A32, 1550 A985).
39. Shelbv R.M. et al., Phys. Rev., Lett., 57, 691 A986).
40. Schumaker B.L. et al., Phys. Rev. Lett., 58, 357 A987).
41. Milburn G.J. et al., J. Opt. Soc. Am., B4, 1476 A987).
42. Savage СМ., Walls D.F., J. Opt. Soc. Am., B4, 1514 A987).
43. Reid M.D., Drummond P.D.. Phys. Rev. Lett., 60, 2731 A988).
44. Waarts R.G., Braim R-P.. Electron. Lett., 22, 873 A986).
45. Lin C, Nguyen V.T., French W.G.. Electron. Lett., 14, 822 A978).
46. Fujii Y. et al.. Opt. Lett., 5, 48 A980).
47. Sasaki Y. Ohmori Y. Appl. Phys. Lett., 39, 466 A981).
48. Ohmori Y., Sasaki Y, IEEE J. Quantum Electron., QE-18, 758 A982).
49. Sasaki Y, Ohmori Y, i. Opt. Commun., 4, 83, A983).
50. GabriaguesJ.M.. Opt. Lett, 8, 183 A983).
51. Nakazawa M.. Nakashima T. Seikai S., Appl. Phys. Lett, 45, 823 A984).
52. Gabriagues J. G., Fersing L., in: Digest of Conference on Lasers and Electro-
Optics, Optical Society of America, Washington, D.C., 1984, p. 176.
53. Terhune Я W, Weinberger D.A.. J. Opt Soc. Am., B4, 661 A987).
54. Osterberg U.. Margulis W., Opt. Lett, 11, 516 A986).
55. Osterberg U., Margulis W., Opt Lett, 12, 57 A987).
56. Farries M.C et al.. Electron. Lett, 23, 322 A987).
57. Stolen R.H.. Tom H.W.K., Opt Lett, 12, 585 A987).
58. Gabriagues J.M., Fevrier H.. Opt Lett, 12, 720 A987).
59. Баранова Н.Б., Зельдович В. Я. Письма в ЖЭТФ, 1987. т. 45, с. 562.
60. Valk В.. Kim E.M., Salour M.M., Appl. Phys. Lett, 51, 722 A987).
61. Payne F.P.. Electron. Lett, 23, 1215 A987).
62. Farries M.C, Fermann M.E., Electron. Lett, 24, 294 A988).
63. Mizrahi V. et al.. Opt Lett, 13, 279 A988).
64. Fermann M.E. et al.. Opt. Lett, 13, 282 A988).
65. Krotkus A., Margulis W., Appl. Phys. Lett, 52, 1942 A988).
66. Tom H.W.K. et al., Opt Lett, 13.'42 A988).
67. Ouellette F., Hill K.O., Johnson D.L.. Opt Lett, 13, 515 A988).
68. Bergot M.-V. et al.. Opt. Lett, 13, 592 A988).
69. Fermann M.E. et al., Electron. Lett, 24, 894 AОД8).
70. Chmela P., Opt. Lett, 13, 669 A988).
71. Mizrahi V. et al., Appl. Phys. Lett, 53, 557 A988).
72. Saifi M.A., Andrejco M.J., Opt. Lett, 13, 773 A988).
73. Manassah J.T., Cockfngs O.R., Opt. Lett, 12, 1005 A987).
74. Kothari N.C., Carlotti X., J. Opt. Soc. Am, B5, 756 A988).
ЗАКЛЮЧЕНИЕ
В предыдущих главах рассмотрены недавние достижения в об-
области нелинейной оптики волоконных световодов. Включить в книгу
самые последние результаты было сложно, во-первых, из-за разум-
разумных ограничений на размер текста и, во-вторых, из-за того, что
активно проводимые исследования в этой области дают новую
информацию практически ежедневно. Некоторые важные результаты,
не вошедшие в основной текст, для большей полноты картины
приведены ниже.
В последнее время значительное внимание уделяется исследо-
исследованиям нелинейных процессов в планарных световодах [1-3], что
обусловлено их возможными применениями в интегральной оптике
[4] и в оптическом переключении [5]. Важные результаты получены
с направленными нелинейными ответвителями [6-9], в которых
зависимость показателя преломления от частоты приводит к пере-
переключению света между двумя модами волновода. Нелинейность
световода позволяет создавать цельноволоконные нелинейные на-
направленные ответвители [10-12]. В разд. 7.2 обсуждалось нелинейное
переключение в двулучепреломляющих световодах. Недавно нелиней-
нелинейный направленный ответвитель с субпикосекундными временами
переключения был реализован на основе световода с двумя сердце-
сердцевинами [11]. В другой работе [13, 14] оптический эффект Керра был
использован для оптического переключения в световоде с одной
сердцевиной, поддерживающем две моды на рабочей длине волны.
Интерферометрическое переключение, обусловленное модуляцион-
модуляционной неустойчивостью в одномодовых световодах (см. разд. 5.1),
наблюдалось в интерферометре Маха-Цандера [15]. Интерес к пере-
переключению в волоконно-оптических системах будет, вероятно, сохра-
сохраняться в силу больших надежд, возлагаемых на оптические пере-
переключения вообще [5].
Использование световодов для создания лазеров и усилителей
представляет значительный практический интерес. В гл. 8 и 9 гово-
говорилось о том, как такие нелинейные эффекты, как ВКР и ВРМБ.
могут быть использованы для этой цели. Другая возможность со-
состоит в использовании световодов, легированных ионами редко-
редкоземельных элементов [16-38]. Оптическая накачка позволяет по-
318 Заключение
лучить инверсную населенность уровней редкоземельных ионов и,
следовательно, оптическое усиление на длине волны соответствующе-
соответствующего перехода. Легированный световод служит в качестве усилителя
или, при помещении его в резонатор, в качестве лазера. Нелинейности
в таких устройствах в основном связаны с населенностью уровней
легирующего элемента. Световод играет в некотором смысле пас-
пассивную роль, выступая лишь в качестве матрицы для легирующих
ионов. Однако спектр усиления редкоземельных ионов в световодах
существенно уширен, что позволяет использовать их в перестраи-
перестраиваемых лазерах и широкополосных усилителях.
Непрерывная генерация в волоконном неодимовом лазере при
комнатной температуре была продемонстрирована в 1974 г. [16].
С тех пор волоконные лазеры заметно усовершенствовались [17-25].
В таких лазерах возможна генерация одной продольной моды с ши-
шириной дриии ~ 1 МГц [23]. При синхронизации мод в волоконном
лазере генерируются импульсы ~100пс [25]. Особенно большим
интересом в последнее время пользуются лазеры и усилители на
основе световодов, легированных ионами эрбия [26-32], поскольку
их рабочая длина волны (вблизи 1,55 мкм) представляет большой
интерес для волоконно-оптической связи. В волоконных лазерах
использовались и другие редкоземельные элементы, такие, как са-
самарий и иттербий [33, 34]. Недавно вместо световодов из плавленого
кварца стали использоваться световоды на основе фтороцирконатных
стекол. Такие световоды, легированные неодимом, позволяют полу-
получать усиление и лазерную генерацию в области 1,3 мкм [35, 36]. Они
также применяются для работы в дальнем ИК-диапазоне вблизи
2-2,5 мкм, для чего используется легирование гольмием или тулием
[37, 38].
Некоторые световоды меняют свои оптические свойства под
действием интенсивного светового излучения в течение периода от
нескольких минут до нескольких. часов. В разд. 10.5 обсуждалась
генерация второй гармоники в световодах, подвергшихся воздей-
воздействию импульсов излучения на длине волны 1,06 мкм. Другой фото-
индуцированный эффект в световодах проявляется в появлении по-
постоянной решетки показателя преломления в световодах, легиро-
легированных германием, после воздействия на них непрерывного излучения
аргонового лазера вблизи 0,5 мкм. Этот эффект впервые наблюдался
Хиллом с соавторами [39] и затем интенсивно изучался [40-50]. Его
механизм, однако, не вполне ясен. Этот эффект фоточувствитель-
фоточувствительности световода представляет практический интерес, поскольку све-
световод с наведенной в нем решеткой действует как низкополосный
брэгговский фильтр [40]. Кроме того, его дисперсия вблизи длин
волн, на которых формируются решетки показателя преломления,
аномальна (Р2 < 0). Это свойство можно использовать для ком-
компенсации материальной дисперсии световодов в системах оптической
Заключение 319
связи [46]. Более того, световоды с аномальной-дисперсией в ви-
видимой области должны в принципе поддерживать в этой области
солитонный режим распространения импульсов. Они могут также
применяться для сжатия импульсов без внешней пары решеток [48].
Однако измерения показали, что аномальная дисперсия существует
только в узком спектральном диапазоне (~ 500 МГц) [50]. Для
сжатия пикосекундных импульсов этот диапазон необходимо уве-
увеличить.
Нелинейные эффекты в одномодовых световодах не должны
приводить к изменению пространственного распределения опти-
оптического поля. Иная ситуация в многомодовых световодах. Недавно
экспериментально наблюдалась самофокусировка импульса ВКР при
распространении импульса накачки длительностью 25 пс по све-
световоду с диаметром сердцевины 100 мкм [51]. В другом эксперименте
[52] распространение импульса ВКР в области аномальной дисперсии
многомодового световода приводило к формированию фемтосекунд-
ных солитонов (длительностью 70-100 фс), которые распространя-
распространялись в основной моде, хотя импульсами накачки (длительностью
150 пс) возбуждалось множество мод. Интересные результаты были
получены в эксперименте [53] по фазовой самомодуляции в гра-
градиентных многомодовых световодах, где она проявляет качественно
новые черты по сравнению с тем, что наблюдалось в одномодовых
световодах (см. гл. 4). Все эти результаты указывают на то, что
систематическое изучение нелинейных эффектов в многомодовых
световодах представляет несомненный интерес. Данные исследования
находятся в начальной стадии и ждут своего продолжения.
ЛИТЕРАТУРА
1. Stegeman G.I. et al., J. Lightwave Technol., 6, 953 A988).
2. Thvlen L., J. Lightwave Technol., 6, 847 A988).
3. ChemlaD.S., Schmitt-Rink S.. Miller D. А. В.. in: Optical Nonlinearities and
Instabilities in Semiconductors, ed. by H. Haug, Academic, Boston, 1988.
4. Tumir Т., ed., Guided-Wave Optoelectronics, Springer-Verlag, Heidelberg, 1988.
5. Gustafson T. K., Smith P. W.. eds., Photonic Switching, Springer-Verlag, Heidel-
Heidelberg, 1988.
6. Jensen S.M., IEEE J. Quantum Electron., QE-18, 1580 A982).
7. Майер А.А-Квант, электрон., т. 11, с. 157, 1984.
8. Lalles A. et al., IEEE J. Quantum Electron., QE-19, 1718 A983).
9. Wabnitz S. et al.. Appl. Phys. Lett., 49, 838 A986).
10. Silberberg S.R., Stegeman G.I.. Appl. Phys. Lett., 50, 801 A987).
11. Friberg S. R. et al., Appl. Phys. Lett., 5, 1135, A987).
12. Trillo S. et al.. Opt. Lett., 13, 672 A988).
13. Park H. G.. Pohalski С. С. Kim В. Y., Opt. Lett., 13, 776 A988).
14. Penty R.V., White I.H., Travis А. Я L., Electron. Lett., 24, 1338 A988).
15. Islam M.N.. Dijali S.P.. Gordon J.P., Opt. Lett., 13, 518 A988).
320 Заключение
16. Stone J., Burns C.A.. Appl. Opt., 13, 1256 A974).
17. \lears R.J. et al., Electron. Lett., 21, 738 A985).
18. Alcock I. P. et al.. Electron. Lett., 22, 84 A986).
19. Jawicev l.M. et al.. Electron. Lett., 22, 198 A986).
20. Alcock I. P. et al.. Electron. Lett., 22, 268 A986).
21. Reekie L. et al.. J. Lightwave Technol., LT-4, 956 A986).
22. Ziim M. et al.. Opt. Lett., 12, 316 A987).
23. Jauncey l.M. et al.. Electron. Lett., 24, 24 A988).
24. Liu K. et al.. Electron. Lett., 24, 838 A988).
25. Duling I.N.. Goldberg L.. WellerJ.F.. Electron. Lett., 24, 1334 A988).
26. Mears R.J. et al.. Electron. Lett., 22, 159 A986).
27. Reekie L. et al.. Electron. Lett.. 23, 1076 A987).
28. HannaD.C, Kcizer A., ShepherdD.P., Opt. Commun., 63, 417 A987); 65, 355
A988).
29. HannaD.C. et al.. Electron. Lett., 24, 1068 A988).
30. Fermann M.E. et al.. Electron. Lett., 24, 1135 A988).
31. Mears R.J. et al.. Electron. Lett, 23, 1026 A987).
32. Desurvire ?.. Simpson J.R.. Becker P.C., Opt. Lett., 12, 888 A987).
33. Fames M.C.. Morkel P.R.. Tow-mend J. E.. Electron. Lett., 24, 709 A988).
34. HannaD.C. et al.. Electron. Lett., 24, 1111 A988).
35. Brierlev M.C., Millar С A.. Electron. Lett., 23, 816 A987); 24, 438 A988).
36. Miniscalco W.J. et al.. Electron. Lett., 24, 28 A988).
37. Brierlev M.C., France P. Ш. Millar C.A., Electron. Lett., 24, 539 A988).
38. Esterow-itz ?., Allen R.. Aagurwal /.. Electron, Lett., 24. 1104 A988).
39. НШК.0. et al.. Appl. Phys. Lett., 32, 647 A978).
40. Kawasaki B.S. et al.. Opt. Lett., 3, 66 A978).
41. BuresJ., LapierreJ., Pascale D., Appl. Phys. Lett., 37, 860 A980).
42. LapierreJ., BuresJ.. Pascale D.. Opt. Commun., 40, 95 A981).
43. Lam D.K.W., Garside B.K., Appl. Phys. Opt.. 20, 440 A981).
44. Lapierre J., Bures J., Chevalier G., Opt. Lett., 7, 37 A982).
45. Bures J., Lacroix S.. Lapierre J.. Appl. Opt., 21, 3502 A982).
46. Lam D.K. W.. Garside B.K.. Hill K.O.. Opt. Lett., 7, 291 A982).
47. Parent M. et al., Appl. Opt., 24, 354 A985).
48. Winful H.G.. Appl. Phys. Lett., 46, 527 A985).
49. Stone J., J. Appl. Phys., 62. 4371 A987).
50. Kuo C.P. el al., Opt. Lett, 13, 1032 A988).
51. Baldeck P.L., Raccali F., Alfano R. R.. Opt. Lett., 12, 588 A987).
52. Грхдитт А.Б. и др. Письма в ЖЭТФ, т. 47, с. 297.
53. Manassah J. Т.. Baldeck P.L., Alfano R.R., Opt. Lett., 13, 589 A988).
ОГЛАВЛЕНИЕ
Предисловие редактора перевода ... ..... 5
Предисловие . . . 7
Глава 1. ВВЕДЕНИЕ ... 9
1.1. Ретроспектива ... ..... 9
1.2. Характеристики волоконных световщов . . . .10
1.2.1. Материалы и изготовление . 12
1.2.2. Оптические потери ..... . 13
1.2.3. Хроматическая дисперсия . ... . .15
1.2.4. Модовое двулучепреломление . . . . . .20
1.3.
Нелинейные эффекты в волоконных световодах . . .23
1.3.1. Нелинейное преломление .... 23
1.3.2. Вынужденное неупругое рассеяние. . 25
1.3.3. Важность нелинейных эффектов .... 26
1.4. Структура книги . ... . . 27
Литература . . . . 31
Глава 2. РАСПРОСТРАНЕНИЕ ВОЛН В ВОЛОКОННЫХ СВЕТО-
СВЕТОВОДАХ . . 33
2.1. Уравнения Максвелла ... . 33
2.2. Моды волоконного световода .... 36
2.3. Основное уравнение распространения . 41
2.4. Численные методы ....... . . 49
Литература . . 52
Глава 3. ДИСПЕРСИЯ ГРУППОВЫХ СКОРОСТЕЙ . .55
3.1. Разные режимы распространения 55
3.2. Дисперсионное уширение импульсов . . 58
3.3. Дисперсия высшего порядка .67
3.4. Применения в оптических системах связи . 73
Литература .... .76
Глава 4. ФАЗОВАЯ САМОМОДУЛЯЦИЯ (ФСМ) . . 77
4.1. Спектральное уширение под действием ФСМ . 77
4.2. Влияние дисперсии групповых скоростей . . 85
4.3. Образование ударной волны огибающей . . 96
Литература . . - 102
Глава 5. ОПТИЧЕСКИЕ СОЛИТОНЫ. . ... 104
5.1. Модуляционная неустойчивость ... 104
5.2. Фундаментальные' солитоны и солитоны высших порядков 111
322 Оглавление
5.3. Солитонные лазерьР = "".-."..... .... . . 122
5.4. Солитонные линии связи ... .125
5.4.1. Потери в световоде .... . . 125
5.4.2. Частотная модуляция ... . . 129
5.4.3. Взаимодействие солитонов 131
5.4.4. Вопросы, связанные с конструированием конкретных со-
литонных линий связи ... 133
5.5 Нелинейные эффекты высших порядков .... . . 136
Литература . 143
Глава 6- СЖАТИЕ ОПТИЧЕСКИХ ИМПУЛЬСОВ 147
6.1. Введение 147
6.2. Пара дифракционных решеток ... . . . . 149
6.3. Волоконно-решеточные компрессоры 153
6.3.1. Теория . . 153
6.3.2. Эксперименты 159
6.4. Компрессоры, основанные на эффекте многосолитонного сжа-
сжатия . 165
6.4.1. Теория 165
6.4.2. Эксперименты 167
Литература 170
Глава 7. ФАЗОВАЯ КРОСС-МОДУЛЯЦИЯ (ФКМ) 172
7.1. Нелинейное взаимодействие, обусловленное ФКМ 173
7.1.1. Взаимодействие волн, имеющих различные частоты 173
7.1.2. Связь между компонентами вектора поляризации одной
волны 176
7.2. Эффекты, связанные с нелинейным двулучепреломлением 178
7.2.1. Оптический эффект Керра 179
7.2.2. Изменение формы импульсов . ... 183
7.2.3. Поляризационная неустойчивость 186
7.2.4. Действие двулучепреломления на солитоны 189
7.3. Модуляционная неустойчивость, вызванная ФКМ . '. . . . 193
7.4. Спектральные и временные эффекты ... . 198
7.4.1. Асимметричное ущирение спектра 199
7.4.2. Асимметричные временные изменения . . .... 205
7.5. Невзаимность, вызванная ФКМ .... 209
7.6. Значение для систем оптической связи . . 211
Литература 213
Глава 8. ВЫНУЖДЕННОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ
(ВКР) 216
8.1. Комбинационное (рамановское) усиление и порог ВКР . . . 216
8.2. Квазинепрерывное ВКР 223
8.2.1. Однопроходная генерация стоксовых компонент . 223
8.2.2. Волоконные ВКР-лазеры 226
8.2.3. Волоконные ВКР-усилители 228
8.2.4. Перекрестные помехи, обусловленные ВКР .... 232
8.3. ВКР сверхкоротких импульсов 234
8.3.1. Теория . . . . 234
8.3.2. Эксперименты 241
8.3.3. Волоконные ВКР-лазеры с синхронной накачкой . . 245
8.4. Солитонные эффекты при ВКР . 247
Литература 254
Оглавление 323
Глава 9. ВЫНУЖДЕННОЕ РАССЕЯНИЕ МАНДЕЛЬШТАМА
БРИЛЛЮЭНА (ВРМБ) 257
9.1. ВРМБ-усиление . . 257
9.2. Теория ... 261
9.2.1. Порог ВРМБ 262
9.2.2. Истощение накачки и насыщение усиления . . . . 263
9.2.3. Динамика ВРМБ . . 265
9.3. Экспериментальные результаты . 269
9.3.1. Однопроходные ВРМБ. . . 269
9.3.2. Волоконные ВРМБ-лазеры ... . j.\ 272
9.3.3. Волоконные ВРМБ-усилители .... . . 274
9.4. Применения в системах оптической связи . . . . . . 276
Литература .... ... . . 279
Глава 10. ПАРАМЕТРИЧЕСКИЕ ПРОЦЕССЫ . . . . . 281
10.1. Четырехволновое смешение . .... . . 281
10.2. Параметрическое усиление 284
10.3. Способы получения фазового синхронизма и эксперименталь-
экспериментальные результаты . . . ' 288
10.3.1. Фазовый синхронизм в многомодовых световодах 289
10.3.2. Фазовый синхронизм в одномодовых световодах 293
10.3.3. Фазовое согласование в двулучепреломляющих свето-
световодах . 297
10.4. Параметрическое усиление и его применения ... . 301
10.4.1. Коэффициент усиления и ширина полосы . .301
10.4.2. Экспериментальные результаты. . . 304
10.4.3. Применения 306
10.5. Генерация второй гармоники . . 308
Литература ... . . •. . 315
Заключение ... . . . . 317
Литература 319
Учебное издание
Говинд П.Агравал
НЕЛИНЕЙНАЯ ВОЛОКОННАЯ ОПТИКА
Лицензия Л Р № 010174 от 22.01.92
Заведующий редакцией проф. |А. Н. Матвеев!
Зам. зав редакцией В. В. Герасимовский
Ведущий редактор Л. И. Третьякова
Редакторы Г. Г. Сорокина, И. А. Зиновьева
Художник А. В. Захаров
Художественный редактор О. Н. Адаскина
Технический редактор Н.И. Борисова
Корректор В. И. Киселева
ИБ № 7827
Сдано в набор 1.02.95. Подписано к нечаш 25.12.95 г. Форма! 60x88'',,,. Бумага кп.-журнальная.
Печать офсетная. Гарнитура тайме. Обьем 10Л5 бум. л. Усл. печ.л. 20,04. Усл.кр.-отт. 20.29. Уч.-изд. л.
21.89. Изд. !Ъ 2/8099. Тираж 1000 экз. Зак. G3?
ИЗДАТЕЛЬСТВО «МИР» Комитета Российской Федерации по печати. 129820. ГСП, Москва, И-110.
1-й Рижский пер.. 2.
Московская типография № 9 Комитета РФ по печати.
109033, Москва. Волочаевцкая ул. 40.
В издательстве «Мир»
в 1994 году вышла книга
Рамм А. Многомерные обратные задачи рассеяния. Пер. с англ.,
31 л., ил.
Книга известного американского специалиста посвящена изложе-
изложению методов решения многомерных обратных задач математической
физики. Она может служить также введением в теорию обратных
задач, в ней сформулирован широкий спектр обратных задач для
дифференциальных уравнений и проведено их замкнутое исследова-
исследование. Книга удачно дополняет вышедшие в нашей стране монографии
по этому предмету, пересекаясь с ними лишь незначительно. В ней
проводится новый метод исследования многомерных обратных задач,
развитый автором и основанный на новом понятии: полноте мно-
множества произведений решений дифференциальных уравнений с част-
частными производными. Излагаются также связанные с ними проблемы
обработки сигналов. Дана оценка устойчивости трехмерной обратной
задачи рассеяния на потенциале по данным при фиксированной
энергии.
Для математиков, физиков, инженеров, а также аспирантов и сту-
студентов старших курсов, интересующихся теорией обратных задач и их
приложениями.
Обращаться в отдел реализации издательства «Мир»: 129820,
Москва, И-110, ГСП, 1-й Рижский пер., 2. Телефоны:
286-83-88, 286-84-55 (оптовая продажа);
286-82-33 (розничная продажа).