Text
Н. БЛОМБЕРГЕН
NONLINEAR OPTICS
A LECTURE NOTE
Нелинейная оптика
N. BLOEMBERGEN
Harvard University
W. A. Benjamin, Inc.
New York — Amsterdam
1965
ПЕРЕВОД С АНГЛИЙСКОГО
ПОД РЕДАКЦИЕЙ
С. А. АХМАНОВА и Р. В. ХОХЛОВА
Издательство «Мир*
Москва 1966
УДК 535.1
Нелинейная оптика — одна из наиболее интересных новых обла-
областей физики. Особое значение она приобрела после изобретения оп-
оптических квантовых генераторов — лазеров. В интенсивных полях
современных лазеров возникают новые явления, а хорошо известные
оптические явления приобретают новые черты. Все эти новые эф-
эффекты объединяет нелинейная зависимость их протекания от интен-
интенсивности света.
Нелинейной оптикой активно занимаются исследователи мно-
многих стран. Уже первые результаты имеют большую научную и прак-
практическую ценность. Именно средствами нелинейной оптики удалось,
например, создать мощные генераторы ультрафиолетового излучения
и совершенно новые для оптики — перестраиваемые генераторы коге-
когерентного оптического излучения.
Предлагаемая книга — первая книга по нелинейной оптике, опу-
опубликованная в США, — написана крупным американским физиком
Н. Бломбергеном, широко известным своими работами по квантовой
электронике и нелинейной оптике. Ее*характеризует высокий научный
уровень и широкий охват современных проблем.
Во вступительной статье редакторов перевода кратко освещено
современное состояние нелинейной оптики и дан критический обзор
содержания книги.
Книга будет полезна как специалистам — физикам, так и лицам,
приступающим к изучению нелинейной оптики: инженерам по кван-
квантовой электронике, физикам смежных с оптикой специальностей, ас-
аспирантам и студентам старших курсов.
Редакция литературы по физике
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
I
Термин нелинейная оптика прочно вошел в научную
литературу в последние 3—4 года, прошедшие после
создания лазеров; нелинейными оптическими эффекта-
эффектами называют эффекты, характер протекания которых
зависит от интенсивности излучения.
Хорошо известно, что материальные уравнения
линейной электродинамики, которая описывает гармони-
гармонические волны, распространяющиеся в среде без искаже-
искажений, и где имеет место принцип суперпозиции, являются
приближенными. Так, линейное соотношение между
поляризацией и напряженностью электрического поля
Р = хЕ получается при простейшем классическом расче-
расчете на основе идеализированной модели гармонического
осциллятора; при более общем квантовом рассмотрении
линейная связь между поляризацией и полем соответ-
соответствует первому приближению теории возмущений. Сте-
Степень пригодности указанных приближений зависит в пер-
первую очередь от соотношения между амплитудой поля
световой волны и характерным внутренним полем Ео,
определяющим силы связи, действующие на оптический
электрон в среде. Поле Ео связано с потенциалом иони-
ионизации / и характерным расстоянием а (на котором поле
обеспечивает связь) соотношением еЕоа = /. Для атома
водорода это поле Ео = 5 • 109 в/см. Для конденсирован-
конденсированных сред величина Ео меньше, и, в частности, для полу-
полупроводников с относительно небольшой шириной запре-
запрещенной зоны Ео « Ю7 в/см; сравнимую с последней ве-
величиной напряженность поля нетрудно получить при
фокусировке пучка современного мощного лазера. По-
Поэтому для описания оптических эффектов в таких полях
линейное материальное уравнение должно быть замене-
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
но уравнением более сложного вида Р = Р(Е), где
Р(Е) в общем случае — функционал. Однако во всяком
случае для описания оптических явлений в нерезонанс-
нерезонансных условиях можно использовать разложение поляри-
поляризации в ряд по параметру Е/Ео < 1:
P=PL-fPNL, A)
где (с учетом запаздывания)
Ba)
оо со
PNL = j df j" У. (Г, t") Е (t — t') E(t — t' — f) df +
о о
j j
о о
Х(Г, t",t'")E(t — t')E (t-t'-f) X
°X E°(t — t'-t" — t'")dt"' + ... . B6)
Выражение B6) является естественным обобщением хо-
хорошо известного соотношения Bа) на нелинейный слу-
случай. Применяя к B6) преобразование Фурье и переходя
к записи по компонентам, имеем
P?L Ю = lijk К- «V «О Ej (ш?) Ек (со,) +
+ ХЩ1 К, «V ®r, ®s\Ej i®q) Ek W El W + • • • • Bв)
Спектральная компонента поляризации на частоте а>р
образуется за счет комбинации двух полей при учете
младшего нелинейного члена в разложении Р = Р(Е)
или трех и более полей при учете членов более высокого
порядка (в зависимости от соотношения между частота-
частотами Bв) содержат либо сами поля Е, либо комплексно
сопряженные величины). Нелинейные восприимчивости
различных порядков %цк, %цы и т. п., как и линейная вос-
восприимчивость к, определяются физическими свойствами
материальной среды и содержат, вообще говоря, более
полную информацию об электронных энергетических
уровнях, нежели к.
Следует иметь в виду, однако, что нелинейные эф-
эффекты при распространении световых волн в материаль-
материальной среде могут быть связаны не только с особенностями
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
поведения оптических электронов в сильном поле свето-
световой волны, но также и с взаимодействием света с
другими движениями среды: акустическими и оптиче-
оптическими фононами, спиновыми волнами, плазменными ко-
колебаниями и т. п.
Чтобы убедиться в этом, обратимся, например, к
задаче о распространении интенсивной гармонической
световой волны в жидкости. Помимо нелинейных эффек-
эффектов, связанных с поведением оптических электронов
отдельных молекул в сильном световом поле (назовем
их, для краткости, фотон-фотонными взаимодействия-
взаимодействиями), могут возникать также нелинейные эффекты, свя-
связанные с механическим воздействием поля на среду.
Хорошо известно, в частности, что в электромагнитной
волне возникают электрострикционные эффекты; соот-
соответствующее давление равно
?2 де „.
8л ^ dp у '
(здесь р — плотность и е — диэлектрическая проницае-
проницаемость). В монохроматической волне E~expi (at — k-r)
электрострикция приводит, в частности, к появлению
статического давления, пропорционального интенсивно-
интенсивности поля, а следовательно, от интенсивности зависит и
показатель преломления
п = ло + /*2?2+... . D)
В силу D) возникает «самовоздействие» волны, до-
достаточно заметное при потоках мощности ~108—109
вт/см2. В некоторых жидкостях, например сероугле-
сероуглероде, «2 достигает значений ~10~12 ед. CGSE и учет не-
нелинейной добавки к показателю преломления становится
существенным при полях, достижимых с помощью мощ-
мощных лазеров. В бигармоническом световом поле
Е = A/@)''-k> r)+ А2е/(И2'-к'г)
будет возникать давление на комбинационных часто-
частотах и, следовательно, такое поле будет генерировать, в
частности, акустическую волну на частоте Q = coi — ©2.
Последняя в свою очередь модулирует диэлектрическую
проницаемость среды и оказывает обратное воздействие
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
на электромагнитное поле, т. е. и здесь поведение све-
световой волны начинает зависеть от ее интенсивности.
Процессы указанного типа, при которых само поле све-
световой волны возбуждает движения, приводящие к его
рассеянию (фотон-фононные, фотон-магнонные, фотон-
плазмонные и т. п.), получили название вынужденного
рассеяния. Хотя в принципе и для их описания удается
вводить нелинейные восприимчивости типа восприимчи-
востей, определенных в B), важно иметь в виду их фи-
физическое отличие от процессов, в которых участвуют
только электромагнитные волны. [Нетрудно видеть, в
частности из C), что вынужденное рассеяние на акусти-
акустических фононах, как, впрочем, и самовоздействие све-
световой волны, связанное с электрострикцией, может быть
описано членом, кубичным по полю в формуле B6)].
Таким образом, физические причины, приводящие к по-
появлению нелинейных оптических эффектов, достаточно
многообразны.
Классификацию различных нелинейных оптических
эффектов можно дать, рассматривая усредненную по
времени свободную энергию F элемента объема среды.
В соответствии с вышесказанным при рассмотрении
энергетических соотношений будем учитывать не только
световые волны в среде (их напряженности обозначим
через ? и Я), но и низкочастотные электромагнитные
поля Ео, #о (включающие кек частный случай статиче-
статическое поле), акустические Лаф и оптические Лоф фононы.
Тогда в усредненную свободную энергию входят члены,
квадратичные по однородным переменным (оптическую
активность и линейный пьезоэффект мы здесь рассма-
рассматривать не будем), и члены более высокого порядка, со-
содержащие как однородные "переменные, так и перекрест-
перекрестные члены. Считая все поля близкими к монохромати-
монохроматическим, выражение для свободной энергии можно
представить в виде
+
1F3)ЕЕ'Ео + ...
E)
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
В выражении E) записаны, разумеется, не все члены
даже в рассматриваемых порядках; «роме того, наряду
с фигурирующими в E) членами должны быть включе-
включены и их комплексно сопряженные. Напомним также, что
частоты различных сомножителей членов, входящих в
(б), должны быть подобраны таким образом, чтобы
«быстрая» зависимость слагаемых от времени отсутст-
отсутствовала. Коэффициенты в E) являются, вообще говоря,
тензорами, порядо-к которых указан в верхнем индексе.
Поскольку поляризация, (Намагниченность, механические
силы получаются из E) путем дифференцирования по
соответствующим переменным (Р—*dF/dE*; M -у
-+д~Р/дН*; f—+dF/dAlb и т. п.), нетрудно видеть, что
нелинейные оптические эффекты могут быть связаны
только с кубичными членами и членами более высокого
порядка в E). Действительно, первые два члена в нели-
нелинейной поляризации Bв) определяются членами при 7C>
и xi4 B E); процесс возбуждения акустических фононов
световыми волнами [ср. C)] описывается членом при х'з3>
и т. п. В линейном же приближении (описываемом квад-
квадратичными членами в выражении для свободной энер-
энергии) ни волны одинаковой природы, ни волны разной
природы не взаимодействуют.
Не следует думать, что экспериментальное наблюде-
наблюдение взаимодействий, связанных с кубичными членами и
членами более высокого порядка в E), дело лишь по-
последних лет. Часть указанных членов соответствует эф-
эффектам, экспериментальное изучение которых было на-
начато еще в прошлом веке. Действительно, член с %63> по-
после дифференцирования по Е* дает Р = %(^ЕЕ0 — поля-
поляризацию, пропорциональную напряженности статическо-
статического электрического поля — хорошо известный линейный
электрооптический эффект, или эффект Поккельса.
Аналогичный член при %D> описывает квадратичный
эффект Керра; член при Xs3> Дает поляризацию Р =
= х^ЕНо и описывает вращение плоскости поляриза-
поляризации в магнитном поле, т. е. эффект Фарадея. Наконец,
члены с %з3> -и %(^} наряду с возбуждением фононов све-
световыми волнами описывают и рассеяние света на аку-
10
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
стических и оптических фононах (Р = %(^4ЕАф), т.е.
хорошо изученные в 20-х и 30-х годах эффекты обыч-
обычного (или, как теперь принято говорить, спонтанного)
релеевского и комбинационного рассеяния первого по-
порядка.
Перечисленные только что эффекты не относятся
к нелинейной оптике в смысле данного выше опреде-
определения; они имеют место и в весьма слабых световых
полях, где их протекание не зависит от интенсивности
света. Их можно назвать параметрическими оптически-
оптическими эффектами, т. е. эффектами, протекающими в сре-
средах, параметры которых заданным образом меняются
с помощью внешних сил. Вместе с тем то обстоятель-
обстоятельство, что параметрические эффекты определяются теми
же физическими свойствами среды, как и оптические
эффекты, зависящие от интенсивности световой волны,.
и, следовательно, всегда проявляются как обратное воз-
воздействие среды на поле, методическая общность в тео-
теоретическом рассмотрении задач о «воздействии поля на
среду и среды с переменными параметрами на поле де-
делает целесообразным включение «параметрической оп-
оптики» в качестве одного из разделов в нелинейную оп-
оптику, рассматриваемую в более широком смысле1). При
таком более общем подходе к разряду нелинейных опти-
оптических явлений следует отнести вообще все явления,
описываемые кубичными членами и членами более вы-
высокого порядка в E), содержащими световые поля, т. е.
все взаимодействия электромагнитных волн между со-
собой и с волнами иной природы. С таким широким опре-
определением понятия нелинейной оптики приходится часто
сталкиваться в литературе.
Период наиболее интенсивного развития параметри-
параметрической оптики относится к 20-м и 30-м годам; именно
в это время были проведены весьма важные исследо-
исследования спонтанного комбинационного рассеяния и спон-
спонтанного релеевского рассеяния; обстоятельное изложе-
! Дополнительным аргументом к этому может служить и то об-
обстоятельство, что иногда параметры среды для слабой световой
волны изменяются с помощью интенсивной световой волны; этот
случай в равной мере относится и к параметрической оптике и к не-
нелинейной оптике, понимаемой в узком смысле.
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
11
ние результатов, достигнутых параметрической оптикой
до изобретения лазеров, можно найти в многочислен-
многочисленных обзорах и монографиях (см., например, [1—3]).
Следует отметить, что весьма четкая трактовка явления
спонтанного комбинационного рассеяния, базирующаяся
на общем «колебательном» подходе, была дана
Л. И. Мандельштамом [4], указавшим, что это явление
можно трактовать как модуляцию световой волны, т. е.
как параметрический процесс.
Важную главу параметрической оптики составляют
классические работы по дифракции света на ультразву-
ультразвуке; их обзор и библиографию можно найти, например,
в книге Борна и Вольфа [5]. В достаточно общей форме
вопросы, связанные с распространением электромагнит-
электромагнитных волн в средах с переменными параметрами, рас-
рассматривались Бриллюэном (см. [6]); этому же вопросу
посвящена монография Рытова [7], опубликованная в
1940 г. Наконец, в сравнительно недавнее время вопро-
вопросы параметрической оптики рассматривались в обзоре
Слэтера [8].
Основной причиной относительно медленного разви-
развития собственно нелинейной оптики до изобретения лазе-
лазеров было отсутствие подходящих источников света. Вме-
Вместе с тем и здесь еще в годы, предшествовавшие бурно-
бурному развитию квантовой электроники, был выполнен ряд
важных исследований. В первую очередь к ним относятся
исследования С. И. Вавилова и его сотрудников, целе-
целеустремленно занимавшихся поисками нелинейных опти-
оптических эффектов. С. И. Вавиловым было отмечено, что
минимальные световые поля, при которых могут наблю-
наблюдаться нелинейные эффекты, соответствуют резонанс-
резонансным условиям; поэтому основное внимание было сосре-
сосредоточено на наблюдении нелинейных эффектов вблизи
линий поглощения. С. И. Вавилову и его сотрудникам
принадлежат первые наблюдения эффекта «просветле-
«просветления» непрозрачной среды в поле интенсивной волны, эф-
эффекта, широко используемого теперь в лазерной технике.
Чрезвычайно ясное и четкое рассмотрение причин появ-
появления оптических нелинейностей и качественной карти-
картины протекания нелинейных оптических эффектов содер-
содержится в монографии С. И. Вавилова «Микроструктура
12
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
света» [9]; там же им, по-видимому, впервые был вве-
введен и термин «нелинейная оптика».
Фактором, существенно стимулировавшим работы по
нелинейной оптике еще на раннем этапе, было интенсив-
вое развитие -нелинейной радиофизики <и> в особенности
ее теоретического раздела — нелинейной теории колеба-
колебаний. Действительно, .поскольку .и радиофизика и опти-
оптика имеют дело с колебаниями и волнами одной приро-
природы, представляется вполне естественным перенесение
идей и методов (нелинейной теории колебаний на оптику.
Именно под таким углом зрения обсуждались возмож-
возможности постановки опытов по нелинейным взаимодейст-
взаимодействиям световых волн в серии работ Горелика [10—12], вы-
выполненных еще в 1947—1950 гг. Один из предлагавшихся
опытов — весьма тонкий опыт по смешению оптическо-
оптического дублета (использовались зеемановские компонен-
компоненты зеленой линии ртути) на фотокатоде — был выполнен
Фор;рестером и сотрудниками в 1955 г. [13]. Следует
отметить, что, хотя с современными экспериментальны-
экспериментальными средствами опыты типа опыта Форрестера доступны
любой физической лаборатории, результаты анализа
влияния пространственной и временной когерентности
пучков на оптическое смешение, проведенного в рабо-
работах [10—13], представляют 'несомненный интерес и для
современной (нелинейной оптики.
Началом современного этапа развития нелинейной
оптики с полным основанием можно считать опыты
Фр'анкена и сотрудников [14], впервые наблюдавших
в середине 1961 г. генерацию второй гармоники рубино-
рубинового лазера в оптически прозрачных кристаллах. Инте-
Интересно, что уже в этом же году наблюдался и нелиней-
нелинейный оптический эффект более высокого порядка — само-
самовоздействие световой волны, обусловленное двухфотон-
ным поглощением (опыты Кайзера и Гарретта [15]). Эти
работы вызвали бурный поток теоретических и экспери-
экспериментальных исследований; успеху последних немало
способствовал и одновременный прогресс лазерной тех-
техники, позволивший от мощностей 1 квт/см2, использо-
использовавшихся в опытах Франкена и Гарретта, перейти к
мощностям 1000 Мет/см2 в нефокусированных пучках.
Наряду с исследованием «фотон-фотонных» взаимодей-
ЬСТУПИТЕЛЬНАЯ СТАТЬЯ
13
ствий в различных средах, при различных геометриях
опыта и т.п. уже в 1962 г. начались работы по исследо-
исследованию взаимодействий других типов, описываемых
перекрестными членами в E).
Одним из первых был зарегистрирован эффект, об-
обратный эффекту По.ккельса — оптическое детектирова-
детектирование. В 1962 г. был обнаружен эффект генерации коге-
когерентных оптических фононов в поле интенсивной свето-
световой волны [16] — эффект, приводящий в комбинации с
рассеянием света на этих фононах ¦ к так называемому
вынужденному комбинационному рассеянию, а в
1963 г. — и эффект генерации акустических фононов и
вынужденное рассеяние Мандельштама — Бриллюэна
(Таунс с сотрудниками [17]). Наконец, совсем недавно
былц экспериментально зарегистрировано вынужденное
рассеяние в области крыла линии Релея [18]. Регистра-
Регистрация нелинейных оптических эффектов, связанных с чле-
членами в E), содержащими магнитное поле, до последнего
времени вызывала значительные трудности; однако в
июне 1965 г. появилось сообщение [19] о наблюдении од-
одного из таких эффектов —обратного эффекта Фарадея;
последнее позволяет надеяться на успешное наблюдение
вынужденного рассеяния на спиновых волнах. Таким
образом, и в магнитооптике становится возможным на-
наблюдение не только параметрических, но и нелинейных
эффектов.
Хотя прогресс нелинейной оптики после изобретения
лазеров связан в первую очередь с возможностью полу-
получения значительных напряженвостей световых полей,
следует иметь в виду и другое немаловажное обстоя-
обстоятельство. Нелинейные оптические эффекты являются,
как правило, волновыми эффектами (протяженность
нелинейной среды в опыте составляет 103—104 длин
волн); поэтому на протекание нелинейного эффекта
существенно влияет временная и пространственная ко-
когерентность излучения. При высокой степени когерент-
когерентности возможно накопление даже весьма слабых нели-
нелинейных оптических эффектов на больших расстояниях.
Именно последним обстоятельством объясняется все
возрастающая роль газовых лазеров в нелинейной опти-
оптике (см., например, [20, 21, 44]). Можно думать, что в бли-
14
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
жайшее время опыты с газовыми лазерами будут одним
из интереснейших направлений в нелинейной оптике.
Результаты, полученные современной нелинейной оп-
оптикой, несколько схематично можно разбить на две
группы. К первой из них следует отнести новые данные
о микроскопических характеристиках вещества, полу-
полученные при изучении нелинейных оптических эффектов.
Только с появлением лазеров удалось измерить спек-
спектральные компоненты тензоров %(,3), %[4> на оптических
частотах; знание последних, вообще -говоря, дает инфор-
информацию об электронных энергетических полосах, не со-
содержащуюся в линейной восприимчивости. Новые воз-
возможности изучения энергетических уровней открывает
многофотонное поглощение (при двухфотонных процес-
процессах в центросимметричных средах возможны, в частно-
частности, переходы между уровнями с одинаковой чет-
четностью) ; соответствующую область спектроскопии на-
называют многофотонной спектроскопией. Вместе с тем
заметим, что эффекты вынужденного рассеяния опреде-
определяются теми же спектральными компонентами тензоров
Х(з3)> %з4) и т- Д-> чт0 и соответствующее спонтанное рас-
рассеяние, детально изученное ib параметрической оптике.
Однако в вынужденном рассеянии совершенно иной ха-
характер носит развитие волнового процесса в простран-
пространстве (имеет место экспоненциальное нарастание компо-
компонент рассеянного излучения). Наблюдение широкого
класса новых волновых взаимодействий представляет
собой вторую группу результатов нелинейной оптики.
Последние тесно связаны с практическими приложения-
приложениями нелинейной оптики. Уже сейчас нелинейная оптика
располагает и значительным количеством практических
достижений. К числу важнейшие из них следует отнести
следующие:
1. Создание мощных генераторов гармоник и комби-
комбинационных частот, перекрывающих (набором дискрет-
дискретных линий) диапазон длин волн от 0,2 до 1 мк. Значи-
Значительные мощности этих генераторов, достигающие еди-
единиц и десятков мегаватт (см. [22, 23]), позволяют рас-
расширить и экспериментальные возможности самой нели-
нелинейной оптики (они открывают возможности наблюде-
наблюдения вынужденного рассеяния в резонансных условиях,
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
15
двухфотонного поглощения в диэлектриках, многофотон-
многофотонной ионизации газов и т. п.). Именно средствами нели-
нелинейной оптики, возможно, удастся получить когерентное
излучение в области мягких рентгеновских лучей.
2. Создание параметрических усилителей и пере-
перестраиваемых параметрических генераторов света [24, 25].
Перспективы, открывающиеся в оптике в связи с созда-
созданием перестраиваемых генераторов света, трудно пере-
переоценить. Такие генераторы во многом расширят воз-
возможности изучения вещества, воздействия на вещество,
связи и т. п.
3. Ряд результатов, полученных нелинейной оптикой,
имеет непосредственное отношение к развитию самой
лазерной техники. В этой области следует отметить ра-
работы по модуляции добротности лазеров с помощью
насыщающихся фильтров [26] ,и работы по двухфотонной
накачке полупроводниковых лазеров, проведенные Ба-
Басовым с сотрудниками [27]. Интересно, что многофотон-
многофотонное поглощение ограничивает, по-видимому, предельные
мощности лазеров; «а это обстоятельство обратили вни-
внимание Бункин и Прохоров [28]. С другой стороны, ис-
использование двухфотонных переходов в инвертирован-
инвертированных системах, как впервые отметили Прохоров и Селива-
ненко [29], может привести, так же, как и указанный
выше метод параметрической генерации, к созданию ла-
лазеров с перестраиваемой частотой. Заметим, что в этой
области есть уже определенные практические успехи:
недавно наблюдался двухквантовый переход в инверти-
инвертированной системе, в котором участвовали фонон и фо-
фотон [30].
II
Предлагаемая книга принадлежит перу крупного
американского физика Бломбергена, хорошо известного
своими работами в области магнитного резонанса и
квантовой электроники. В области нелинейной оптики
Бломбергену и его сотрудникам принадлежит серия
весьма важных теоретических и экспериментальных ра-
работ (часть их включена в эту книгу в качестве лрило-
16
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
жений). Здесь следует упомянуть прежде всего работы
по теории нелинейной поляризации, в которых были
установлены чрезвычайно существенные пространствен-
пространственно-частотные перестановочные соотношения для тензо-
тензоров нелинейной восприимчивости, пионерские и в зна-
значительной мере исчерпывающие вопрос теоретические
и экспериментальные работы, посвященные волновым
явлениям на границе нелинейной среды, работы по тео-
теории нелинейных волновых процессов и теории вынуж-
вынужденного комбинационного рассеяния. Наиболее сущест-
существенными результатами последних является детальное
изучение поведения комбинационных восприимчивостей
и условий нарастания антистоксовых компонент в вы-
вынужденном рассеянии. Наконец, должны быть отмече-
отмечены работы Бломбергена и его сотрудников, посвященные
исследованию влияния многомодовой структуры лазер-
лазерного излучения на характер протекания процессов гене-
генерации оптических гармоник и вынужденного комбинаци-
комбинационного рассеяния. Все это делает книгу Бломбергена,
первую книгу по нелинейной оптике, изданную в США,
особенно интересной для советского читателя; написан-
написанная на высоком научном уровне, она содержит изложе-
изложение фундаментальных результатов, знакомство с кото-
которыми совершенно необходимо как для работающих в
области нелинейной оптики, так и для приступающих к
ее изучению.
Вместе с тем следует иметь в виду, что для нелиней-
нелинейной оптики, переживающей и по сей день период бурно-
бурного экстенсивного и интенсивного развития, почти полто-
полтора года, прошедшие между написанием книги автором
и завершением работы над русским переводом, яв-
являются большим сроком. Поэтому целесообразно дать
краткий обзор содержания предлагаемой книги под уг-
углом зрения современных достижений нелинейной опти-
оптики. Цель этого обзора (как и первого раздела настоя-
настоящей вводной статьи и многих подстрочных редакторских
примечаний) заключается также и в том, чтобы по воз-
возможности облегчить изучение книги читателям, впервые
знакомящимся с нелинейной оптикой (а такими чита-
читателями в силу современного интереса к лазерной техни
ке и связанными с ней научными достижениями будут
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
17
и радиоинженеры, и физики, работающие в смежных
областях, и студенты старших курсов).
Следует иметь в виду, что изучение материала книги
может потребовать от читателя затраты некоторого тру-
труда, поскольку научный уровень книги достаточно высок,
а изложение в ряде случаев носит конспективный харак-
характер. Определенные трудности могут возникать также
в связи с тем, что в этой бурно развивающейся области
физики еще не установилась стандартная терминология;
кроме того, и автор не всегда был последователен в ис-
использовании применяемых в книге терминов; некоторые
разъяснения на этот счет содержатся в редакторских
примечаниях.
III
При теоретическом рассмотрении все нелинейные оп-
оптические процессы естественным образом можно разде-
разделить на две группы. Характер протекания процессов
первого типа существенно определяется фазовыми соот-
соотношениями между взаимодействующими электромагнит-
электромагнитными полями, а следовательно, их описание невозможно
в терминах населенностей, характеризуемых заданными
числами фотонов. К процессам этого типа относятся оп-
оптическое умножение и смешение частот, параметриче-
параметрическое усиление и преобразование и т. п. Для процессов
второго типа, связанных с реальным изменением состоя-
состояния материальной системы, фазовые соотношения меж-
между электромагнитными полями не играют такой опреде-
определяющей роли; важными примерами последних являются
стоксово комбинационное рассеяние и многофотонное
поглощение.
Отмеченное разграничение нелинейных процессов по-
последовательно проводится в предлагаемой книге; оно
базируется на детальном исследовании поведения нели-
нелинейной восприимчивости среды, проведенном в прило-
приложении III (в конце книги). Процессы первого типа ав-
автор называет параметрическими, а второго — комбина-
комбинационными, или многоквантовыми. Следует отметить, что
такая терминология не всегда согласуется с терминоло-
терминологией, принятой в других работах (например, в [31] для
обозначения указанных процессов используются термины
2 Н. Бтомберген
18
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
когерентный, некогерентный, представляющиеся, во-
вообще говоря, более удачными); термин параметрический
в отечественной литературе, а иногда и в работах са-
самого автора (см., например, приложение I) -понимается
в более узком смысле, в котором он обычно исполь-
используется в теории колебаний.
Гл. 1 является введением, призванным очертить круг
рассматриваемых проблем и сообщить предварительные
сведения об экспериментальных основаниях нелинейной
оптики. Читателю, впервые знакомящемуся с этой об-
областью, она может показаться чрезмерно конспектив-
конспективной; в связи с этим наряду с литературой, приводимой
автором, можно рекомендовать обзоры [32, 33], а также
книгу [34], предназначенную для менее подготовленных
читателей.
Гл. 2 содержит сжатое, но вместе с тем разносторон-
разностороннее изложение квантовой теории нелинейной восприим-
восприимчивости. Ее содержание сильно связано с содержанием
приложения III. Основное внимание в гл. 2 уделено
применению метода 'матрицы плотности для расчета не-
нелинейных восприимчивостей. Для ознакомления с мето-
методом матрицы плотности под углом зрения задач, воз-
возникающих в нелинейной оптике, можно рекомендовать
также книгу Файна и Ханина [35]. Заметим, кстати, что
в ней детально разбираются и многие вопросы, являю-
являющиеся предметом гл. 2.
Микроскопическая теория нелинейной восприимчиво-
восприимчивости интенсивно развивается и в настоящее время. Из ра-
работ, опубликованных в этой области и. не отраженных
в книге, укажем на работу Л. В. Келдыша [36], посвя-
посвященную теории М'ногофотонной фотоионизации и много-
многофотонного поглощения, работу Батчера [37], посвящен-
посвященную последовательному изложению теории нелинейной
восприимчивости, обзор Овандера [38], посвященный
микроскопической теории нелинейных оптических эффек-
эффектов в кристаллах, и обзор Бонч-Бруевича и Ходового
[33].
В настоящее время намечаются определенные успе-
успехи в теории нелинейной восприимчивости конденсиро-
конденсированной среды, уже не ограничивающейся рассмотрением
самых элементарных моделей. Заслуживает внимания
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
19
обсуждение вопроса о связи атомной и макроскопиче-
макроскопической нелинейных восприимчивостей, поскольку здесь, по-
видимому, удается хотя бы грубо указать «ласе кристал-
кристаллов обладающих значительной нелинейной восприимчи-
восприимчивостью [39].
Недавно Терхьюн и его сотрудники [40] наблюдали
нелинейные оптические эффекты, связанные не с нели-
нелинейными свойствами среды как целого, а с нелинейными
свойствами отдельных молекул—так называемое трехфо-
тонное молекулярное рассеяние. Последнее открывает
важные перспективы изучения микроструктуры оптиче-
оптических нелинейностей и, несомненно, явится фактором,
стимулирующим дальнейшие теоретические исследова-
исследования. Интересно, что измеренная в работе [40] нелинейная
восприимчивость молекулы ССЦ соответствует воспри-
восприимчивости типичных пьезоэлектрических кристаллов.
Опыты такого рода могут способствовать выяснению
вопроса о влиянии межмолекулярного взаимодействия
на нелинейную восприимчивость.
Гл. 3 и 4 посвящены изложению основ теории волн
в нелинейных диспергирующих средах и ее приложениям
к различным задачам, возникающим в нелинейной оп-
оптике. Разумеется, число конкретных задач, решенных к
настоящему времени, существенно .превышает количест-
количество примеров, рассмотренных в книге. В 'частности, более
подробно, чем в основном тексте и приложении I, иссле-
исследована задача о генерации третьей гармоники, генера-
генерации суммарных и разностных частот, параметрическом
усилении при высокочастотной и низкочастотной накач-
накачке и т. п.; соответствующие ссылки даны в списке допол-
дополнительной литературы. Здесь же нам представляется
уместным обратить внимание на обстоятельства более
принципиального .порядка.
Отметим прежде всего, что переход от нелинейного
волнового уравнения к приближенным уравнениям пер-
первого порядка (так называемым уравнениям связанных
волн, или, как их еще называют, укороченным уравне-
уравнениям) выполнен в гл. 4 даже для случая плоских немо-
Аудированных волн не в общем виде. Действительно, в
книге ©сюду фигурируют уравнения для скалярных мед-
медленно меняющихся амплитуд, т. е. по существу предпо-
2*
20
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
лагается, . что -поляризация взаимодействующих волн
остается неизменной.
Более детальный анализ показывает, что это 'предпо-
'предположение обосновано для анизотропной среды (нормаль-
(нормальные волны которой имеют определенные направления
поляризаций), но для изотропной среды выполняется
лишь в частных случаях, поскольку здесь поляризации
нормальных волн произвольны. В общем же случае не-
нелинейного взаимодействия в оптически изотропной среде
(например, генерации второй гармоники в кристалле
типа GaAs, вынужденном комбинационном рассеянии
или вынужденном рассеянии Мандельштама — Бриллю-
эна в жидкостях) уравнения первого порядка являются
векторными и описывают одновременно изменение ам-
амплитуд и поляризаций взаимодействующих волн. Более
детально этот вопрос рассмотрен в работе [41]. Заметим,
кстати, что в теории нелинейных волновых явлений
в диспергирующих средах плодотворным оказывается
использование идей, а в ряде случаев и конкретных ме-
методов нелинейной теории колебаний (например, лри ана-
анализе системы уравнений для связанных волн полезным
оказывается метод фазовой плоскости и т. п.). Эта сто-
сторона нелинейной оптики подробно обсуждается в рабо-
работе [41]; там же можно 'найти и соответствующую библио-
библиографию.
Весьма существенным для современной нелинейной
оптики является распространение теории взаимодейст-
взаимодействия и самовоздействия волн на реальные пучки, обла-
обладающие конечной шириной спектральной линии (моду-
(модулированные, в частности импульсно-модулированные
волны) и конечным поперечным сечением. Задачи тако-
такого типа вообще не рассматриваются в настоящей книге.
Поэтому представляется целесообразным хотя бы крат-
кратко дать их конкретную формулировку. Это удобно сде-
сделать на примере стандартной задачи о генерации второй
оптической гармоники, рассмотренной в гл. 4 и в прило-
приложении I для плоских «емодулированных волн.
Если спектральная линия основного излучения имеет
конечную ширину Дш, малую по сравнению со средней
частотой со, Аш/ш <С 1, для полей основного излуче-
излучения и гармоники вместо формул D.23) из гл. 4 следует
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
21
писать, очевидно,
E1(w)=e1A1(t,z)ei(at~)Cl-T), F)
где Аи А2 — медленно меняющиеся функции теперь уже
и 'координаты и времени.
Подставляя F) >и G) в волновое уравнение ,и учиты-
учитывая лишь групповое запаздывание (что соответствует
первому приближению в учете дисперсионных эффектов
для (квазимонохроматических волн), приходим в случае
М:алой нелинейности к уравнениям первого порядка для
комплексных амплитуд [ср. с уравнениями D.24), D.25)]
dz
dz
¦ +
I dAt
и,, dt
1 dA2
щ dt
(8)
(9)
Здесь «i, «2 — групповые скорости волн основной часто-
частоты и волны гармоники; через Pi>2 для краткости обозна-
обозначены коэффициенты, фигурирующие в D.24) и D.25);
Ak = 2klz — k2z- Решение уравнений в частных произ-
производных (8), (9) представляет, вообще говоря, сущест-
существенно более сложную задачу, «ежели решение соответ-
соответствующих обыкновенных уравнений для немодулирован-
ных волн. Имеется, однако, важный частный случай,
для которого учет производных комплексных амплитуд
по времени тривиален. Это случай равенства групповых
скоростей U\ = «2 = и. При этом заменой переменных
| = t-\-z/u, г] = t — г/и система (8), (9) приводится
к системе уравнений в обыкновенных производных
dAl
A0)
(И)
имеющих тот же вид, что и для немодулированных волн.
Поэтому случай щ — и2 может быть назван квазистати-
22
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
ческим; характер изменения комплексных амплитуд
с координатой остается таким же, как и в немодулиро-
ванной волне, однако вид спектра в процессе нелиней-
нелинейного взаимодействия несколько модифицируется. Новые
обстоятельства возникают в случае щф и2, когда суще-
существует групповое запаздывание взаимодействующих
волн. На протяжении нелинейной среды / групповое за-
запаздывание Т == 1(и^х—и\-х ). Здесь характер изменения
комплексных амплитуд в пространстве определяется со-
соотношением между запаздыванием Т я характерным
временем т, определяющим ширину спектра волны ос-
основного излучения т «* (Лео) (таким образом, для слу-
чайно-модулирб'ванной волны т имеет порядок времени
корреляции, а для импульсно-модулированной— дли-
длительности импульса). Нетрудно убедиться путем непо-
непосредственного вычисления (это, впрочем, представляется
ясным и из физических соображений), что при
т>Г = /|«Г1—иГ'| A2)
процесс генерации гармоники происходит, как и в немо-
дулированной волне (т. е. справедливо квазистатиче-
квазистатическое приближение), а при т < Т возникают существен-
существенные отличия.
При Л] > А2 и Ak = 0 из (8) и (9) следует, что
A3)
A4)
|412~/2 при
| А, |2 ~ / при] т < Т.
Таким образом, если при т > Г интенсивность гармои»-
ки изменяется как квадрат числа частиц N среды, уча-
участвующих в нелинейном процессе, |Л2|2 ~ N2, то при
х<Т |/42|2~./V; зависимость интенсивности от N име-
имеет такой же вид, как и соответствующая зависимость
для типичного процесса некогерентного рассеяния (на-
(например, спонтанного комбинационного или спонтанного
рассеяния Мандельштама — Бриллюэна). Поэтому
длина
/,ш = (Дсо)~'Iwr1-Mi"'I"'' A5)
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
23
для которой т = Т, может быть названа когерентной
длиной. С зависимостью типа A4) приходится сталки-
сталкиваться и в задаче о генерации второй гармоники в стати-
статистически неоднородной среде. Наиболее ярким примером
такой ситуации является задача о нелинейном рассея-
рассеянии в среде с центром инверсии, в которой отдельные
молекулы обладают отличным от нуля тензором хщ
(см. [40]) '>. Следует иметь в виду вместе с тем, что тер-
термин «когерентная длина» широко используется в совре-
современной нелинейной оптике и для определения простран-
пространственных масштабов нелинейного взаимодействия, не
связанных со статистическими эффектами, в частности
пространственных масштабов, определяемых только
дисперсионными свойствами нелинейной среды.
• Уравнения в частных производных, типа уравнений
(8) и (9), должны, строго говоря, использоваться и при
исследовании других нелинейных процессов: смешения,
параметрического усиления, вынужденного рассеяния.
К счастью, в большинстве практически интересных слу-
случаев можно ограничиться квазистатическим приближе-
приближением, полагая (dAi/dt) — 0. Действительно, даже для
т« 10~8 сек (характерная длина импульса лазера с мо-
модулируемой добротностью) в задачах о генерации гар-
гармоник, о смешении частот, вынужденном комбинацион-
комбинационном рассеянии т «г Г при /« 102 см, что заметно превы-
превышает длины нелинейных сред, используемых в экспери-
эксперименте. Важным исключением, однако, оказывается вы-
вынужденное рассеяние Мандельштама — Бриллюэна; в
этом случае Г ^ Ifv, где v — скорость звука. Подставляя
v zz 105 см/сек ях= 10~8 сек, убеждаемся, что квазиста-
квазистатическое приближение становится неприменимым уже
при I ж Ю~3 см. Особенности рассеяния, связанные с
этим обстоятельством, подробно обсуждаются в рабо-
работе [42].
Обратимся теперь к вопросу об учете конечного по-
перечного сечения и расходимости волновых пучков в
нелинейной среде. В предлагаемой книге для анализа
11 Интересно, что при больших Ak некогерентный процесс генера-
генерации гармоники оказывается более эффективным, нежели когерент-
когерентный процесс.
24
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
явлений в ограниченных пучках (см. гл. 5, § 1) исполь-
используются результаты теории, развитой для плоских волн.
Нетрудно видеть, что такой подход соответствует по су-
существу приближению геометрической оптики — учиты-
учитывается лишь изменение комплексных амплитуд взаимо-
взаимодействующих волн вдоль лучей. Для учета же дифрак-
дифракционных эффектов в пучке конечного сечения (весьма
важных в таких задачах, как задачи о генерации гар-
гармоник и вынужденном рассеянии в фокусированных
пучках, задачи о нелинейных взаимодействиях на боль-
больших длинах, реализуемых в лучах газовых лазеров)
следует ввести в рассмотрение производные амплитуды
не только вдоль, но и поперек лучей.
Поэтому для ограниченных пучков решение нелиней-
нелинейных уравнений следует искать в виде (временные изме-
изменения здесь не записываем)
E=eA(r-s,rxs)eiiat'k'r). A6)
Здесь s — лучевой вектор; поскольку в направлениях,
перпендикулярных лучу, происходит переход в область
тени, изменения амплитуды вдоль луча следует считать
более медленными, нежели поперек луча. С учетом A6)
уравнения для амплитуд связанных волн, описывающие
процесс генерации второй гармоники в анизотропной
среде в двумерном пучке конечного поперечного сечения,
принимают вид
дА1 _ 1 d*Ai ;гз я«'Bк1-к,).г . „•
дг
дА2
дг
A7)
2*. &• ' Зх -"¦* k2)'M'- <18)
Здесь координата г отсчитывается вдоль луча, а х— по-
поперек луча. Уравнения записаны для наиболее интерес-
интересного случая, когда волна основной частоты обыкновен-
обыкновенная, а волна гармоники необыкновенная; у— угол ани-
анизотропии. При р, = р2 = 0 (линейная среда) уравнения
A7) и A8) переходят в уравнения параболического ти-
типа с мнимым коэффициентом диффузии, широко исполь-
используемым в современной теории дифракции [43]. Пользуясь
(w) и A8), удается построить последовательную тео-
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
25
пию генерации второй гармоники в фокусе, позволяю-
позволяющую удовлетворительно объяснить экспериментальные
ДаНЭффе«ты, связанные с конечным сечением световых
пучков, активно обсуждаются в последнее время в свя-
связи с опытами по генерации гармоник в двоякопрелом-
ляющих кристаллах (при больших длинах предел нара-
нарастанию мощности гармоники в пучке конечной апертуры
кладет различие направлений волнового и лучевого век-
векторов [21]), а также опытами по вынужденному комби-
комбинационному рассеянию (см. [45, 46]).
Однако, пожалуй, одной из наиболее интересных за-
задач современной нелинейной оптики'в которой принци-
принципиальную роль играет конечное сечение светового пучка,
является задача о самофокусировке и самоканализации
интенсивного светового пучка. В среде, показатель пре-
преломления которой зависит от интенсивности световой
волны [появление такой зависимости, как нетрудно ви-
видеть, связано с членами при 5СA4>'И х'з' в E)]> показатель
преломления внутри пучка может превышать показатель
преломления вне пучка и, следовательно, лучи будут
стремиться собраться к оси пучка [47]. Последнее долж-
должно, очевидно, приводить (при фокусировке в нелинейной
среде) к изменению фокусного расстояния линзы и к из-
изменению (как нетрудно показать, уменьшению) разме-
размеров фокальной области (эти явления могут быть назва-
названы самофокусировкой), а при определенных условиях
к режиму волноводного распространения пучка (само-
(самоканализация). Эффекты самофокусировки и самокана-
самоканализации можно проанализировать в том же «квазиопти-
«квазиоптическом» приближении, используя которое мы получили
уравнения A7) и A8). Рассматривая среду, для кото-
которой показатель преломления п = п0 + я2 \А |2, и подстав-
подставляя A6) в соответствующее волновое уравнение, полу-
получаем
dz
2ik
±^\А\*А,
2i
A9)
где А± —поперечный лапласиан (в двумерном случае
Aj. = dPjdx2). Анализ уравнения A9) показывает, что,
26
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
хотя режим самоканализации в экспериментальных ус-
условиях получить трудно (для этого необходим специаль-
специальный подбор «раевых условий), эффект самовоздействия
обязательно следует учитывать три анализе эксперимен-
экспериментов по нелинейной оптике, проводимых в фокусирован-
фокусированных (а иногда и нефокусированных) пучках. Эффект
уменьшения величины фокальной области, особенно для
сферических линз, может быть значительным (соответ-
(соответствующую библиографию см. в гл. 5).
Среди других задач, не затронутых в гл. 3—5, следует
указать на задачи, связанные с исследованием нелиней-
нелинейных явлений в оптических резонаторах. Первоочередный
интерес они предст'авляют в связи с исследованием про-
процессов в параметрических генераторах света, комбина-
комбинационных лазерах, резонаторных умножителях частоты.
Некоторые результаты, относящиеся к указанному кру-
кругу вопросов, можно найти в [41, 48—50], однако в целом
теория таких процессов еще далека от завершения.
В области экспериментальной нелинейной оптики
наиболее интересные исследования за время, прошедшее
после написания книги Бломбергена, выполнены в обла-
области параметрического усиления и генерации света и вы-
вынужденного рассеяния. Особый интерес здесь представ-
представляют работы, имеющие целью создание плавно пере-
перестраиваемых параметрических генераторов непрерывно-
непрерывного действия, использующих в качестве генераторов на-
накачки газовые лазеры [51]. Широкий круг исследований
по вынужденному комбинационному рассеянию ¦>, выпол-
выполненных в разных странах, показал, что, хотя многие
важные черты наблюдаемых здесь явлений согласуются
с теорией типа теории, развитой в гл. 4 настоящей кни-
книги, имеются и явления, не укладывающиеся в эту тео-
теоретическую схему. К последним относятся существен-
существенные отличия в диаграмме направленности антистоксово-
антистоксового излучения (иногда оно становится диффузным), ано-
аномально большие коэффициенты усиления стоксовых ком-
компонент, в несколько раз превосходящие теоретические,
резкое утирание линий и т. п. Эти явления обсужда-
обсуждались на состоявшихся летом 1965 г. конференциях по
Первый обзор по этому вопросу дан в работе [55].
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
27
нелинейной оптике в Минске [52] и в Сан-Хуане (Пуэрто-
Рико) [53]. В качестве одной из возможных причин этих
аномалий называлась многомодовая структура лазер-
лазерного излучения; имеются и данные, свидетельствующие
о важном вкладе эффектов самофокусировки.
Значительное количество невыясненных вопросов
имеется и в области изучения вынужденного рассеяния
Мандельштама — Бриллюэна. Так, не выяснен до конца
вопрос о существовании антистоксовых компонент в вы-
вынужденном рассеянии; результаты первых опытов,
в которых такие компоненты как будто бы наблюдались,
по-видимому, не подтвердились (см. [53]). Интересные
результаты получены при исследовании гармоник звука,
возникающего в процессе вынужденного рассеяния [54];
есть основание считать, что они могут быть достаточно
сильными. Наконец, весьма интересной задачей яв-
является наблюдение вынужденного рассеяния Мандель-
Мандельштама— Бриллюэна в кристаллах при низких темпера-
температурах, что может позволить вывести из среды гиперзву-
гиперзвуковые колебания, возникающие в процессе рассеяния.
Следует отметить, что эта область быстро расши-
расширяется; обсуждаются возможности наблюдения вынуж-
вынужденного рассеяния на плазмонах в твердых телах и маг-
нонах (см. [53]).
В заключение заметим, что в последнее время обна-
обнаруживается все более тесная связь между нелинейными
оптическими явлениями и разрушением оптически про-
прозрачных сред в интенсивных лазерных полях. С одной
стороны, такие эффекты, как многофотонное поглощение
и вынужденное рассеяние, могут стать причиной разру-
разрушения среды. С другой — разрушение сред ограничивает
предельные потоки мощности, которые могут быть про-
пропущены через среду, и, следовательно, ограничивает воз-
возможности наблюдения взаимодействий высоких поряд-
порядков и эффективность практических устройств, исполь-
использующих нелинейные оптические явления.
IV
При переводе и редактировании предлагаемой кни-
книги встретились определенные трудности, связанные пре-
28
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
жде всего с весьма лаконичным характером изложения.
Поэтому помимо подстрочных редакционных примеча-
примечаний не имеющие принципиального характера поправки
и разъяснения вносились непосредственно в текст; точ-
точно так же были исправлены и замеченные опечатки.
Однако т° обстоятельство, что ряд формул автор при-
приводит без вывода, не позволяет считать, что работа по
выявлению опечаток выполнена полностью. Следует
указать также, что терминология и обозначения в ори-
оригинале не всегда унифицированы; при редактировании
этот недостаток устранялся лишь в наиболее очевидных
случаях. Обозначения для векторных операций полно-
полностью соответствуют оригиналу. При транскрибировании
фамилий мы, где возможно, исходили из прецедентов,
основываясь на статьях и книгах, имеющихся на русском
языке, хотя распространенные транскрипции, возможно,
и не всегда правильны (в частности, фамилию автора,
по-видимому, правильнее произносить Блумберхен).
Отметим, наконец, что примечания редакторов и пе-
переводчиков сделаны лишь в основном тексте книги;
приложения, призванные служить справочным материа-
материалом, никак не комментируются, хотя, разумеется, целый
ряд вопросов, затронутых в них, детально изучался и в
последующие годы.
С. Ахманов, Р. Хохлов
Сентябрь 1965 г.
ЛИТЕРАТУРА
1. ВолькенштейнМ. В., Молекулярная оптика М 1951
2. Брандмюллер И., Мозер Г., Введение в спектроскопию
комбинационного рассеяния света, изд-во «Мир» 1964
3. Фабелинский И. Л., Молекулярное рассеяние света, М,
1965.
4- ^Дде,п.пШТаМ Л- И- СобРание трудов', т. I, II, Изд-во АН
СССР, 1Уои.
5. Born M-, Wolf E., Principles of Optics, London 1959
6. Б р и л л ю э н Л., Пароди М„ Распространение волн в перио-
периодически* структурах, ИЛ, 1959. р
7' ФИАНВ1940М' МоДулиР°ванные колебания и волны, Труды
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
29
8. Slater J., Rev. Mod. Phys., 30, 197 A958).
9 Вавилов С, И., Микроструктура света, Изд-во АН СССР, 1950.
10. Горелик Г. С, ДАН СССР, 43, 46 A947).
11. Горелик Г. С, Усп. физич. наук, 34, 321 A948).
12. Б о р о в и ц к и й С. И., Горелик Г. С, Усп. физич. наук, 59,
553 A956).
13 Forrester А. Т., Gudmunsen R. A., Johnson P. О.,
Phys. Rev., 99, 1691 A955).
14. F г а п к е п P., H i 1 1 А., Р е t е г s С, W e i п г е с h G., Phys. Rev.
Lett., 7, 118 A961).
15. Kaiser W., Qarre 11 G. C, Phys. Rev. Lett., 7, 229 A961).
16. Eckhardt G., Hellwarth R., McClung F., Schwa rz
S., W e i n e r D., W о о d b u г у Е., Phys. Rev. Lett., 9, 455 A962).
17. Chi а о R., Townes C, Stoicheff В., Phys. Rev. Lett., 12,
592 A964).
18. M а ш Д. И., Морозов В. В., С т а р у н о в В. С, Фабелин-
Фабелинский И. Л., ЖЭТФ, письма в редакцию, 2, № 1, 41 A965).
19. Pershan P., Van der Ziel J., Malmstrom L., Optically
induced magnetization resulting from the inverse Faraday effect
(см. [53]).
'20. Ash kin A., Boyd G., Dziedzic J., Phys. Rev. Lett., U, 14
A963).
-21. Ashkin A., Boyd G., Dziedzic J., Klein man D., Phys.
Rev., 137, № 4A, 1305 A965).
22. Terhune R., Maker P., Savage C, Appl. Phys. Lett., 2, 54
A963).
23. A x м а н о в С. А., К о в р и г и н А. И., Пискарскас А. С,
Хохлов Р. В., ЖЭТФ, письма в редакцию, 2, № 5, 223 A965).
24. Miller R., Giordma ine J., Phys. Rev. Lett., 14, 973 A965).
25. A x м а н о в С. А., Ковригин А. И., Пискарскас А. С,
Фадеев В. В. Хохлов Р. В., ЖЭТФ, письма в редакцию,
2, № 7, 3 A965).
26. S о г о k i n P., L u z z i J., L a n к а г d J., P e 11 i t G., IBM Journ.
Res., 8, 182 A964).
27. Басов Н. Г., Грасюк А. 3., Зубарев И. Г., Кат у ли н
В. А., ЖЭТФ, письма в редакцию, 1, № 4, 29 A965).
28. Бункин Ф. В., Прохоров А. М., ЖЭТФ, 48, №4, 1084
A965).
29. П рохоров А. М., Усгг. физич. наук, 85, № 4, 599 A965).
30. Shier en N., Stimulated phonon-photon doubie quantum emissi-
emission. (Cm. [53].)
31. P.ershan, Nat. Bur. Stand. Journ., 671 A964).
32. Terhune R.,. Solid State Design, 4, 38 A963).
(Имеется перевод в сборнике «Зарубежная радиоэлектроника»,
№ 6, М„ 1964.)
33. Б о н ч-Б р у е в и ч А. М., Ходовой В. И., Усп. физич. наук,
85, 3 A965).
34. Климонтович Ю. Л., Квантовые генераторы света и нели-
нелинейная оптика, М., 1966.
35. Ф айн В. М„ X анин Я. И., Квантовая радиофизика, М., 1965.
36. Келдыш Л. В., ЖЭТФ, 47, 1945 A964).
30
ВСТУПИТЕЛЬНАЯ СТАТЬЯ
Stale Univ..
14.
41.
42.
43.
44.
45.
46.
37. Butcher P. N., Bull. Eng. Experim. Stal., Ohio
1965, p. 143.
38. Овандер Л. Н., Усп. физич. наук, 86, № 1, 3 A965).
39. Miller R., Appl. Phys. Lett., 5, № 1, 17 A964).
40. T e r h u n e R., Maker P., Savage C, Phys. Rev. Lett.,
681 A965).
A x м а н о в С. А., Хохлов Р. В., Проблемы нелинейной опти-
кн, М„ 1964.
Кг oil N.. Journ. Appl. Phys, 36, № 1, 34 A965).
Малюжинец Г. Д., Усп. физич. наук, 69, 321 A959).
Francois G., Siegman A., Phys. Rev., 139, А4 A965).
Луговой В. Н, ЖЭТФ, 48, 1216 A965).
Haus Н., К е 1 ley П., Zeiger П., Phys. Rev., 138, А960
A965).
47. С h i а о R, Garmire E., Townes С, Phys. Rev. Lett., 13, 479
A964).
48. Kingston R., Me Whorter A., Proc. IEEE, 53, №1, 4
A965)
49. A x м а н о в С. А., Дмитриев В. Г., Моденов В. П., Фа-
Фадеев В. В., Радиотехника и электроника, 10, № 12 A965).
50. Gulver W., Seppi E, Journ. Appl. Phys, 35, 3421 A964).
51. As hk in A, Boyd G, Optical nonlinear parametric and har-
harmonic interactions in LiNbO3 (см. [53]),
52. А п а н а с е в и ч П. А, Журнал прикл. спектр, 3, № 2,
A965); Изв. АН БССР, серия физ.-математич. наук, № 4,
53. Physics of Quantum Electronics Conference Proceedings,
P. Kelley, B. Lax, P. Tannenwald, New York. 1965.
54. Brewer R., Appl. Phys. Lett, 6, № 8, 165 A965).
55. Зубов В. А., С у щи некий М. М, Шувалов И. К-,
физич. наук, 83, № 2, 197 A964).
196
1965.
ed.
Усп.
ПРЕДИСЛОВИЕ
Эта монография основана на лекциях, подготовлен-
подготовленных для курса квантовой электроники в Гарвардском
университете весной 1963 г. и для летней школы в Ле-
зуш в 1964 г. Нелинейная оптика — еще совсем молодая
область физики, предметом которой является изучение
эффектов, возникающих при очень высоких интенсивно-
стях света, достижимых в лазерных пучках. Нелинейная
оптика — одна из наиболее интересных областей иссле-
исследования, ставших доступными после разработки мощных
лазеров.
Писать монографию по нелинейной оптике в настоя-
настоящее время, когда она еще переживает период бурного
развития, по-видимому, безрассудная храбрость. Могут
сказать, что такая монография в лучшем случае'будет
способствовать тому, что она сама скоро окажется уста-
устаревшей. Тем не менее можно надеяться, что она сможет
иметь некоторую не столь быстро преходящую ценность.
Общие принципы электромагнитной теории Максвелла и
квантовой механики хорошо установлены. Они примени-
применимы и к описанию взаимодействий высшего порядка
между светом и материальной средой; свойства среды
описываются при этом с помощью нелинейных восприим-
чивостей.
Нелинейные свойства элементов цепей с сосредото-
сосредоточенными постоянными на радиочастотах и микроволно-
микроволновых систем хорошо известны радиоинженерам. В настоя-
настоящей монографии обсуждаются нелинейные явления на
оптических частотах. Оказывается, что генерация гар-
гармоник, параметрическое усиление, модуляция и вы-
выпрямление имеют свои аналоги и в видимой области
электромагнитного спектра. В настоящей книге изложе-
32
ПРЕДИСЛОВИЕ
Л
В
ние построено таким образом, что читатели, знакомые с
теорией электромагнитных волн, но незнакомые с кван-
квантовой механикой, могут ограничиться изучением чисто
классического описания нелинейных оптических явлений.
Эти читатели могут опустить гл. 2, в которой рассмат-
рассматривается квантовая теория линейной и нелинейной вос-
приимчивостей материальной среды.
Эта книга предназначена для всех тех, кто активно
интересуется квантовой электроникой, — для физиков,
исследующих нелинейные электромагнитные свой-
свойства материи, для радиоинженеров, работающих над
проблемами связи и другими применениями оптического
излучения высокой мощности, для оптиков, которым
важно знать поведение световых лучей при очень боль-
больших интенсивностях.
Так как нелинейная оптика находится еще в стадии
быстрого развития, не делалось попыток охватить все
экспериментальные данные и дать полную библиогра-
библиографию. Подчеркиваются фундаментальные теоретические
идеи и основные экспериментальные результаты.
Автор благодарен докторам Дюкуэнгу, Шену и Фор-
Форстеру, которые внимательно прочитали рукопись и внес-
внесли много поправок. За все оставшиеся ошибки полно-
полностью ответствен автор. Автор признателен редакторам
журнала Physical Review и соответствующим соавторам
за разрешение воспроизвести три приложения. Автор
благодарен докторам Першану и Терхьюну за предо-
предоставление некоторых материалов до их опубликования.
Автор выражает благодарность Элизабет Диксон, кото-
которая напечатала рукопись в сжатый срок.
Монография посвящается Дели Бломберген, чья под-
поддержка и сочувственное отношение сыграли решающую
роль в своевременном завершении этого труда.
Кембридж, Массачусетс,
июль 1964 г.
Н. Бломберген
КЛАССИЧЕСКОЕ ВВЕДЕНИЕ
§ 1. Нелинейные восприимчивости
Нелинейные свойства максвелловских материальных
уравнений
= e(E)E, B =
A.1)
известны достаточно давно; диэлектрическая и магнит-
магнитная проницаемости могут быть функциями ' напряжен-
ностей полей. При конструировании электрических ма-
машин в девятнадцатом столетии нелинейности проницае-
проницаемости ферромагнитной среды уделялось большое вни-
внимание. Причиной этой нелинейности является движение
границ и вращение доменов. Она может быть источни-
источником гармонических искажений в усилителях звуковой
частоты, в которых используются индуктивности с
ферромагнитными сердечниками. Парамагнитное насы-
насыщение, описанное Ланжевеном и Бриллюэном, может
рассматриваться как нелинейность на нулевой частоте.
Действие магнитных л диэлектрических усилителей ос-
основано на нелинейности ферромагнетиков и сегнето-
электриков на сравнительно низких частотах. Нелиней-
Нелинейные свойства плазмы тоже хорошо известны и являются
причиной Люксембург-Горьковского эффекта, возни-
возникающего при распространении радиоволн в ионосфере.
В последнее время нелинейные свойства плазмы и дру-
других материалов были исследованы в диапазоне СВЧ.
Нелинейность при ферромагнитном резонансе исполь-
использовалась, например, для генерации второй и более вы-
высоких гармоник в СВЧ диапазоне.
Нелинейные свойства вещества в оптическом диапа-
диапазоне были ярко продемонстрированы в опытах по гене-
генерации гармоник света. Франкен и др. [1] обнаружили
о
ультрафиолетовое излучение (X = 3470 А) с частотой,
3 Н. Бломберген
34
ГЛАВА 1
равной удвоенной частоте рубинового лазера, при про-
прохождении его луча через кристалл кварца. Схема экспе-
эксперимента показана на фиг. 1. Этот эксперимент, выпол-
выполненный в 1961 г., положил начало большому циклу
теоретических и экспериментальных исследований нели-
нелинейных оптических свойств различных сред. По этой
тематике имеется несколько обзоров [2—4], в которых
можно найти довольно полную библиографию. В настоя-
настоящей книге не делается попытки дать исчерпывающий
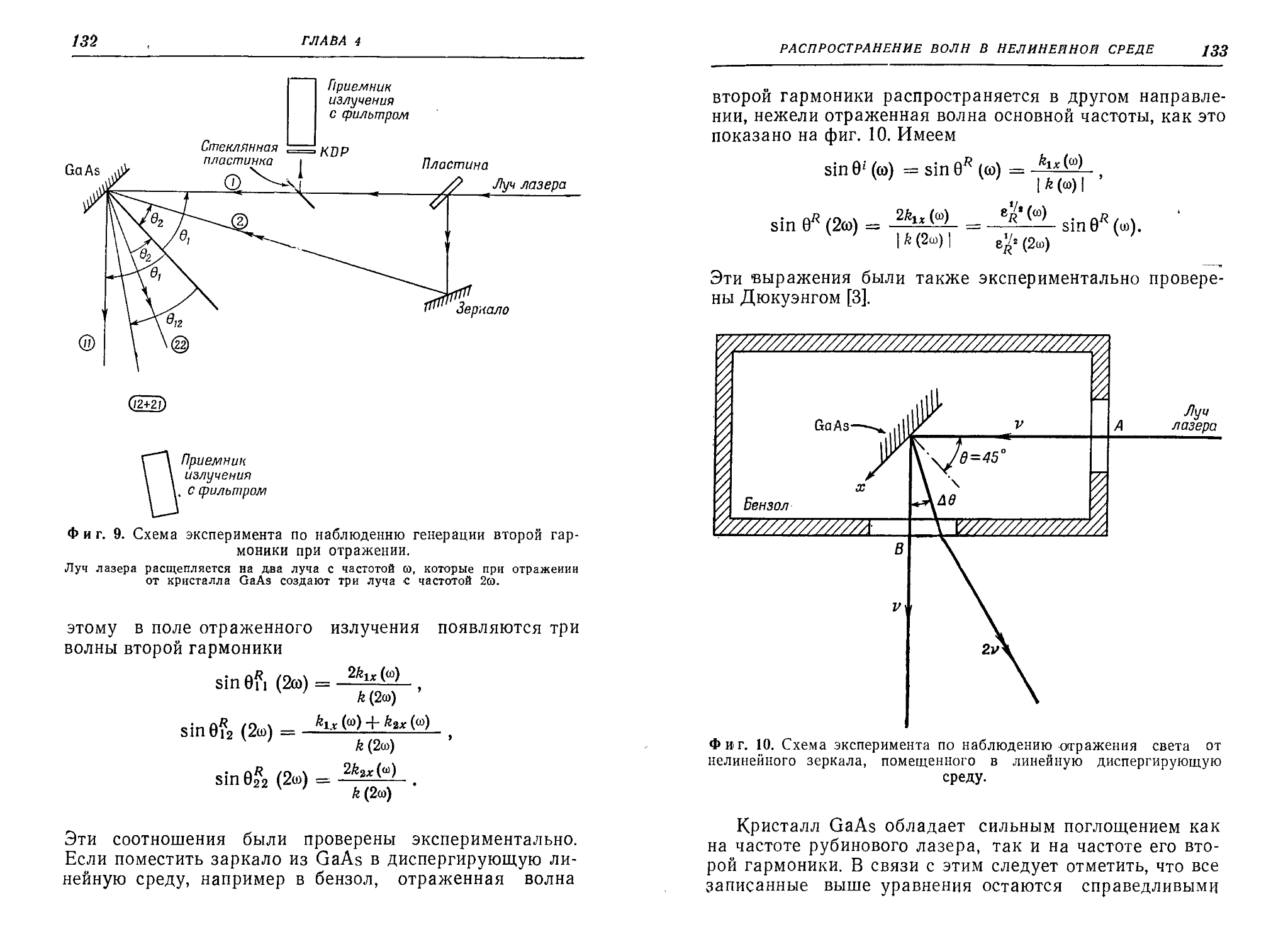
Нелинейный
кристалл
Рубиновый
мазер
Щ и 2ш,
Фотоэпемент
Нрасныб
фильтр
Ультрофиоле/ровый
филылр
Фиг. 1. Схема эксперимента по генерации второй гармоники света.
обзор всех работ в этой области исследования; основное
внимание уделяется обсуждению различных явлений с
единой точки зрения.
Нелинейные свойства материальной среды описы-
описываются с помощью разложения поляризации в ряд по
степеням напряженности поля. Например, в чисто ди-
польном случае имеем
XIEEE+... ,
A.2)
Первый член определяет обычную нелинейную воспри-
восприимчивость, второй ¦— нелинейную восприимчивость
низшего порядка и т. д. Такое разложение поляризации
по 'полю применимо вследствие (Малости оптических яе-
линейностей. Именно из-за «алой величины эффекта
оптические нелинейности были экспериментально обна-
обнаружены только .недавно, .после появления мощных лазе-
лазеров. С помощью лазеров с модуляцией добротности [5]
теперь удается получать электрические поля с макси-
максимальными амплитудами порядка 106 в/см, что соответ-
соответствует потоку мощности порядка 109 вт/см2. Вместе , с
КЛАССИЧЕСКОЕ ВВЕДЕНИЕ
3S
тем при благоприятных условиях можно обнаружить
нелинейные оптические эффекты ,и с потоком мощности
порядка 0,1 — 10 мет/см2.
Теория распространения волн в нелинейной среде
может 'быть развита чисто классически; при этом не-
нелинейные -оптические свойства среды могут анализиро-
анализироваться таким же образом, как анализировались линей-
линейные оптические свойства материальных сред в начале
прошлого столетия. Для развития теории нелинейных
свойств сред во времена Максвелла, Герца, Лоренца и"
Друде не хватало движущей силы экспериментальных
открытий. Экспериментальная реализация вынужденно-
вынужденного излучения света внезапно изменила обстановку;
началось энергичное исследование поведения световых
лучей высокой интенсивности. Уже сделано много об-
обобщений классических законов оптик» на случаи,
когда существенны нелинейности. В то же время сами
нелинейности представляют значительный интерес с
точки зрения изучения строения вещества. Подобная же
ситуация имеет место, разумеется, и в линейном случае.
Линейный показатель преломления определяет пути све-
световых лучей, и, наоборот, изучая их поведение, мы полу-
получаем данные о природе вещества.
§ 2. Классические атомные модели нелинейности
ГАЗ СВОБОДНЫХ ЭЛЕКТРОНОВ
Рассмотрим движение одного электрона в плазме
Под действием Линейно поляризованной световой вол-
волны, компоненты поля которой равны
Ex~Ee
= 2Re\Ее
ikz—iat]
A.3)
Где k = сое '. Заметим, что действительная амплитуда
волны равна 2|?|, т. е. наша- амплитуда \Е\ вдвое
меньше общепринятой. При использовании этого
нового определения, введенного Лершаном [4], линей-
линейная восприимчивость не изменяется, «о нелинейная
восприимчивость низшего порядка увеличивается вдвое;
дополнительные множители, равные двум, появляются
и в восприимчивостях высших порядков. Новое опреде-
определение обладает известным -преимуществом при рассмот-
рассмотрении свойств симметрии тензоров нелинейных воспри-
имчивостей. В предельном случае равенства двух ча-
частот, от которых зависит нелинейная восприимчивость,
или в случае, когда одна -частота становится равной
нулю, возможно (возникновение путаницы [6]. Новое оп-
определение позволяет .почти полностью избежать трудно-
трудностей, связанных с множителем два. В конце расчета
можно вернуться к старому определению. Фурье-ком-
Фурье-компонента какой-либо физической величины на частоте
+ со имеет временную зависимость вида ехр (—Ш), а
на частоте —со — вида exp(-HW).
Уравнения движения одного электрона в плазме
имеют вид
= еЕк -zBv
с у
тх
Феноменологическое время между столкновениями т
описывает затухание движения; наличие конечного т
обеспечивает существование стационарного состояния,
не зависящего от начальных условий. Нелинейные эф-
эффекты в A.4) связаны с лоренцевой силой; она приво-
приводит к возникновению гармоник. Стационарное решение
уравнений A.3) и A.4) может быть найдено в виде
ряда Фурье методом последовательных приближений.
В первом, линейном приближении имеем известный
результат:
т (со2 + (сот-1)
Если подставить это линейное решение в последнее
уравнение A.4), то в нелинейном приближении низшего
КЛАССИЧЕСКОЕ ВВЕДЕНИЕ
37
порядка получим
ехр Bikz — 2Ш)
Dсо + 2ix~') (со2 + /сот"')
A.6)
Линейный дипольный момент ех(а>) приводит к извест-
известной формуле Томсона, описывающей релеевское рас-
рассеяние овета свободными электронами. Аналогично ди-
дипольный момент ezBco) излучает и а частоте второй
гармоники. Этот нелинейный процесс рассеяния молено
грубо представить -как поглощение двух квантов из па-
падающего луча и излучение одного ,кванта удвоенной
частоты, причем диаграмма излучения соответствует
диполю, ориентированному вдоль направления падаю-
падающего луча.
Некогерентное нелинейное рассеяние отдельными
электронами не имеет, однако, практического значения.
Нелинейные явления настолько слабы, что обнаружить
можно лишь когерентное излучение большого ансамбля
частиц. Аналогичное различие между когерентным и
некогерентным рассеянием имеет место и для линейного
случая. Поэтому основное внимание должно быть скон-
сконцентрировано на средней поляризации небольшого объ-
объема и показателе преломления плазмы, а не на некоге-
некогерентном релеевском рассеянии за счет флуктуации плот-
плотности. В жидкостях и кристаллах относительные флук-
флуктуации .плотности еще меньше, и основной интерес пред-
представляет средняя поляризация среды '>.
Если средняя плотность электронов в плазме равна
No cm'3, то линейная поляризация равна
Р,И=*Х»?*И = #ое*(<в). A.7)
Так как на оптических частотах сот <С 1, то из A.5) и
A.7) непосредственно следует известное выражение для
1; Вместе с тем нелинейное рассеяние света конденсированной
Средой или газом несет информацию об индивидуальных нелинейных
свойствах отдельных молекул или иомов. Поэтому, несмотря па зна-
значительные экспериментальные трудности, наблюдение нелинейного
рассеяния представляет несомненный интерес. Теоретические оценки
некоторых характеристик нелинейного рассеяния даны в работах
[31*—33*]; об успешных опытах по наблюдению нелинейного рассея-
рассеяния излучения рубинового лазера в твердых телах и жидкостях сооб-
сообщалось в работе [34*]. — Прим. ред.
38
ГЛАВЛ 1
восприимчивости плазмы:
е — 1 = 4тг)( —
отсо2
Аналогично нелинейная поляризация с частотой второй
гармоники равна
PzBa) = N0ezBa).
В бесконечной плазме нет когерентного излучения с ча-
частотой 2со, так как .вектор нелинейной поляризации па-
параллелен направлению распространения. Однако коге-
когерентное излучение второй гармоники возможно на гра-
границе плазмы.
В этом же приближении имеется также небольшой
продольный постоянный ток, соответствующий члену
Плотность тока равна
Jt@) = N0ei@)
ОТ2с(со2 ¦
-кот-')
A.8)
В аналогичном классическом случае эго выражение
описывает передачу импульса при комптоновском рас-
рассеянии.
Описанная процедура может быть, конечно, исполь-
использована и для вычисления более высоких гармоник.
Имеется, в частности, компонента поляризации РхCа>),
которая может привести к излучению третьей гармо-
гармоники.
Нелинейности в плазме в диапазоне СВЧ могут
быть довольно большими, особенно в присутствии по-
постоянного магнитного поля, при котором может возник-
возникнуть циклотронный резонанс [7]. Помимо лоренцевой
силы в реальной плазме на более низких частотах
имеются . н другие источники (Нелинейности!. Следует
учитывать градиенты гидродинамического давления и
индуцированные вариации электронной плотности. До-
Довольно полное обсуждение всех этих эффектов дано
У'итмером и Барреттом [8].
КЛАССИЧЕСКОЕ ВВЕДЕНИЕ
39
АНГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
В очень полезной модели, использованной Друде и
Лоренцем (см. [9]) для расчета линейной поляризации
среды, электроны рассматриваются как гармонические
осцилляторы. Резонансные частоты осцилляторов вы-
выбирают при этом такими, чтобы они соответствовали
наблюдаемым атомным спектральным линиям. В дей-
действительности движение валентных электронов происхо-
происходит в кулоновском поле ионов. При очень больших от-
отклонениях от положения равновесия следует учитывать
ангармоничность электронных осцилляторов. Модель
ангармонического осциллятора уже использовалась
Релеем для объяснения нелинейностей в акустических
резонаторах [10].
Рассмотрим движение одномерного ангармоническо-
ангармонического осциллятора с затуханием, на который воздействует
электрическое поле с фурье-компонентами на частотах
± coi и ± со2:
х + Тх -f coo* + vx2 = — Re (?|1е'*«г-'''М 4-
tn
A.9)
Линейное приближение непосредственно дает известный
результат
ж (mi) =
A.10)
т( — i
В нелинейном приближении низшего порядка появ-
появляются слагаемые с частотами вторых гармоник 2соь
2со2, слагаемое с нулевой частотой, соответствующее
«выпрямлению» света за счет квадратичной нелинейно-
нелинейности vx2, и слагаемые с суммарной и разностной частота-
частотами coi + СО2 и coi — со2, соответствующие биениям между
двумя световыми волнами. Мы приведем только две фу-
рье-компоненты: вторую гармонику
i vE2 exp i
A.11)
40
ГЛАВА 1
и компоненту с разностной частотой
X КО, — С02) =
1
D (сох) ?>* (со2)
— со2)
A.12)
где в знаменателях введено обозначение
D (со) = соо — «2 —г'Гсо = D* (— со).
И; A.11) непосредственно следуют выражения для не-
нелинейной поляризации и нелинейной восприимчивости,
описывающих генерацию второй гармоники:
Р'х ' Bсо) = хххх Bсо, со, со) ?2 (со),
в, со, со) =
?>2 (со) D Bш)
A.13)
A.14)
Индексы ххх, конечно, излишни в одномерном примере.
Они лишь напоминают, что нелинейная восприимчи-
восприимчивость обычно связывает три вектора и имеет трансфор-
трансформационные свойства тензора третьего ранга. Обобщение
на случай трехмерного ангармонического осциллятора
очевидно. Аналогичное выражение может быть получе-
получено для нелинейной восприимчивости
Хххх((О!~ СО2, COi — С02).
Заметим, что дисперсия нелинейной восприимчивости
низшего порядка определяется значениями трех частот,
а не одной. Зависимость от частоты усиливается при
приближении к резонансу одного из знаменателей. Ес-
Если, например, разностная частота равна резонансной
частоте, D(ai —со2) = г'сооГ при coi — со2 = соо, то нели-
нелинейная восприимчивость л а разностной частоте больше,
чем на всех-других частотах.
Если разность со, — со2 равна или достаточно близка
к резонансной частоте соо, то при расчете нелинейных
эффектов следующего порядка можно удержать только
фурье-компшенту A.12). За счет члена их2 эта компо-
компонента вместе с линейными слагаемыми приводит к по-
появлению компонент с частотами 2щ—со2, щ—2со2 (по-
КЛАССИЧЕСКОЕ ВВЕДЕНИЕ
41
мимо компонент с первона-чальными частотами
и —со2). Так, например,
(e»/m3) V2E | El ,t
( Ш)
* =
ИЛИ
Ххххх (Щ - СО2 + COj — Щ) =
„ (е*/т3) v*
-.A.15)
К-(О,)
При резонансе, со, — со2 = соо, и при условии, что
со, ^> ю0, Z)(coi — со2) является чисто мнимой величиной;
другие множители в знаменателе действительны, по-
поэтому , ' ¦ *
Аналогично можно найти
Ххххх (Mi = СО! + С02 — С03) = ухххх (С02 = С02 -f COi —
и
Ххххх BC0j — С02 =
Oi — С02) =
?>2 (сох) D* (со2) D B@! — со2) D (сох — со2)
A.16)
COi)
A.17)
A.18)
Сравнение A.10), A.12) и A.16) показывает, что
между нелинейной поляризацией первого порядка и ли-
линейной поляризацией, а также между нелинейными по-
поляризациями смежных порядков имеют место следую-
следующие соотношения: ;
pL
pNL
nNL
е\'Е\ v
mD
На основе рассмотрения физической орироды связи
электрона в атоме можно считать, что если отклонение
х по порядку величины равно радиусу а равновесной
орбиты электрона, то нелинейная сила тих2 имеет ве-
величину того же порядка, что и линейная сила m<s>\a =
= е|?пт|, где Е?Т — внутриатомное электрическое поле,
42
ГЛАВА 1
связывающее электрон. Поэтому v/D » у/ю^ «а1 и
отношение поляризаций смежных порядков равно
е\Е\1тщ\а = \Е\ / \ЕаТ\. Амплитуда электрического
поля световой волны должна сравниваться с электриче-
электрическим полем внутри атома, типичная 'величина которого
порядка 3 - 10s в/см. Поэтому даже для предельных по-
потоков энергии 1010 вт/см2, имеющих место в фокусе ла-
лазера с модулированной добротностью, нелинейность
можно рассматривать как малое возмущение, посколь-
поскольку даже в этом предельном случае |?У?ат1 ~3-10-3.
Следует заметить, что это отношение увеличивается в
Q = ©о/Г раз, если один из сомножителей в знаменателе
становится резонансным ¦>. Вместе с тем даже малые не-
нелинейные эффекты могут быть обнаружены благодаря
высокой чувствительности оптических индикаторов.
Терхьюн [11], например, обнаружил эффект генерации в
кальците третьей гармоники излучения рубинового лазе-
лазера (работавшего в режиме свободной генерации), не-
несмотря на то, что в нелинейном .процессе участвовал
лишь один из 1015 фотонов основного излучения. В ти-
типичном импульсе рубинового лазера содержится 4 • 1018
фотонов A дж), поэтому сравнительно нетрудно обнару-
жить 1000 фотонов (за импульс) с % = 2313 А. Нели-
Нелинейная восприимчивость, описывающая процесс генера-
генерации третьей гармоники За, дается выражением, анало-
аналогичным A.15), но содержащим в этом случае в знаме-
знаменателе произведение ZK(o)i)Z)B«I)/)Ccoi).
МАГНИТНЫЕ ВОЛЧКИ
Значительное число нелинейных эффектов впервые
исследовалось в связи с магнитным резонансом [12—
15р. Это явление можно описать классически как дви-
движение безынерционного магнитного волчка с постоян-
постоянным отношением у его углового и магнитного моментов.
Уравнения движения Блоха для компонент вектора на-
') При наличии резонанса следует, вообще говоря, учитывать
эффект насыщения; это соответствует учету всех членов п разложе-
разложении Р = Р(Е) (см. гл. 2, § 6 и приложение III). — Прим. ред.
2) См. также ссылки в приложении IIJ.
КЛАССИЧЕСКОЕ ВВЕДЕНИЕ
43
магниченное™ с феноменологическими константами за-
затухания имеют вид
м
М(МНЬ'bJL
2
A.19)
Предположим, что «а систему одновременно действуют
сильное постоянное поле Яо, направленное вдоль оси z,
слабое переменное поле, осциллирующее с частотой юг
и также направленное вдоль оси z, и переменное поле
с частотой соь прецессирующее вокруг оси z:
eto'(
Hx
iHy =
Частота магнитного резонанса равна щ = уН0.
Опять можно найти решения для фурье-компонент
каждой из составляющих магнитного момента Мх, Му и
Mz. При разложении решения в ряд по возрастающим
степеням амплитуд полей Н\ и Н2 получаются следую-
следующие выражения для фурье-компонент, связанных с не-
нелинейным взаимодействием низшего порядка:
Л?ь(д)д_-2У1Я.1'Г1Г,М. , A.21)
[1 + К)^!]2
—2у2Н1Н*2М0 ехр [—i ((»! — с
A.22)
Формула A.21) описывает начальный этап известного
эффекта насыщения, а A.22) — генерацию разностной
частоты.' При замене со2 на —со2 получается аналогичное
выражение для суммарной частоты.
В следующем нелинейном приближении эти фурье-
компоненты опять взаимодействуют с исходными ноля-
нолями. Соответствующие члены здесь не приводятся; они
аналогичны выражениям, полученным в этом же при-
приближении для ангармонического осциллятора. Кроме
44
ГЛАВА I
того, они идентичны квантовомеханическим выражени-
выражениям, полученным в следующей главе и примененным для
случая, когда система обладает только двумя энергети-
энергетическими уровнями.
0,АА?сй'Чёск6ё
45
нелинейной
§ 3. Феноменологическая интерпретация
поляризации
Физическая интерпретация введенных выше комплекс-
комплексных 'нелинейных восприимчивостей требует анализа ле-
лежащих в их основе элементарных квантовых шроцеооов
и ие может быть дана в рамках настоящего классиче-
классического введения. Возможна, однако, феноменологическая
интерпретация. Рассмотрим сначала нелинейную поля-
поляризацию низшего порядка
pJJ.L - хК = Щ + «2) Е1Еяе'(к'+к')"-/ №'+Ш2)'. A.23)
В общем случае х является тензором третьего ранга.
В системах с центром инверсии он равен нулю. В кри-
кристаллах без центра инверсии ие равны нулю те же ком-
компоненты %ijh, что и у пьезоэлектрического тензора ¦>. Вид
этого тензора для различных точечных групп симметрии
рассматривался многими авторами (ом., например, [16,
17, 35*, 38*]).
Если одно из приложенных электрических полей 'По-
'Постоянно, например ©2 = 0, то A.23) описывает линей-
линейный электрооптический эффект в среде, 'которая может
быть поглощающей. Известно, что средняя по времени
работа, совершаемая гармоническим полем частоты ю
!) При coi = ш2 свойства симметрии тензора % (а>з = Wi + со2)
и пьезоэлектрического тензора идентичны. Оба тензора симметричны
по последним двум индексам. При coi ф а>2 тензор восприимчивости
не обязательно симметричен по этим индексам.
(Несимметричная по двум последним индексам часть тензора
Хак, отличная от нуля при йI=И=а>2, играет существенную роль в про-
процессе генерации суммарных и разностных частот в ряде жидкостей,
газов и поликристаллов. Антисимметричная часть является домини-
доминирующей нелинейностью в оптически активных жидкостях. Таблица
отличных от нуля антисимметричных компонент тензора %аь., для
всех кристаллических классов дана в обстоятельной работе Джорд-
мэйна [36*]; там же методом возмущений выполнена и оценка ве-
величины нелинейной поляризуемости для жидкостей. — Прим. ред.)
¦о
-л
над единицей объема диэлектрической среды, в случае,
когда Т много больше периода колебания, равна
г
dt ±= — 2ю Im Е • Р* = + 2со Im E* • Р.
A.24)
dt
В линейном случае W = 2a%" (<o) |E|2.
Заметим, что положительное поглощение имеет место
при положительных значениях %" (%L = %' + i%"), с уче-
учетом того, что по нашему определению волна с положи-
положительной частотой характеризуется временной зависимо-
зависимостью ехр (—Ш). В случае линейного электрооптического
эффекта имеется дополнительное поглощение энергия:
Однако в случае генерации второй гармоники мнимая
часть спектральной компоненты нелинейной восприим-
восприимчивости хBо) = о + о) не связана с поглощением. Ком-
Комплексное значение этой «нелинейной восприимчивости
определяет фазу поляризации с удвоенной частотой от-
относительно фазы светового поля с исходной частотой.
Средние по времени поглощаемая мощность и запасен-
запасенная анергия равны нулю в случае, когда поляризация
изменяется с частотой 2со при поле, имеющем частоту ©.
Заметим, что пространственное изменение фазы поляри-
поляризации с удвоенной частотой определяется волновым
вектором первичной волны и имеет, согласно A-23), вид
ехр Bikj • г).
При феноменологическом рассмотрении удобно ис-
использовать термодинамическую потенциальную функ-
функцию F, из которой путем дифференцирования можно
получить поляризацию. Эта функция идентична свобод-
свободной энергии и характеризует способность среды совер-
совершать работу над генераторами поля при постоянной
энтропии. Если среда не имеет потерь, то тепло не вы-
вырабатывается и энтропия среды постоянна. Имеет
смысл рассматривать только усредненную по времени
функцию, полный дифференциал которой равен
< dF > , = - ]ГР М • <*е;-? Р* (-Щ) - dS.,. A.25)
46
Глава t
В случае линейной среды получаем известное выраже-
выражение, квадратичное по амплитудам полей:
< Fh > = - Re 2 Е* (-со,) • XL (о),) • Е (со,). A. 26)
Нелинейность низшего порядка1 соответствует члену,
кубическому по амплитудам Фурье. Рассмотрим, напри-
например, случай трех волн с частотами coi, сог и юз = «h -f-
+ ©г- Усредненный по времени термодинамический по-
потенциал будет иметь слагаемое
< FHL > - - 2Re[E*3 (co3) XNL (co3 = щ + со2) Е (щ) Е2 (©,)].
A.27)
Отсюда получаем выражение для /-й компоненты поля-
поляризации с частотой о)з, обусловленной /-й компонентой
поля с частотой o)i и k-й компонентой поля с часто-
частотой ©г:
Pi К) = — —г- = bjk К = «1 + е>2) EjiEw
dEi3
Далее, так как в случае среды без потерь восприимчи-
восприимчивость 5С действительна, то
= Xijk (шз = «1 + «г) ?/з?*2.
Отсюда получаем условия симметрии ПО отношению к
перестановке индексов ').
Xi/k К = «1 +ч»з) = Xjik К = соа — со2) =
= Х*/;(<»* = ©а —©j). A.28)
Если нелинейные восприимчивости действительны, то
можно переставлять индексы при соответствующей пе-
перестановке частот. Если, кроме того, дисперсия во
всей области частот, содержащей оч, щ и юз, пренебре-
'' Далее в тексте эти соотношения Называются также простран-
пространственно-частотными перестановочными соотношениями. Этим подчер-
подчеркивается, что изменение частотных аргументов восприимчивостей
связано, вообще говоря, с изменением порядка координатных индек-
индексов. — Прим. ред.
К.ЛАССИЧЕСКОЕ ВВЕДЕНИЕ
47
LO
жимо мала, то частоты можно переставлять произволь-
произвольным образом. В этом случае тензор нелинейной воспри-
восприимчивости становится симметричным по всем индексам,
которые можно переставлять произвольно. Эти соотно-
соотношения для недиспергирующей среды впервые сформу-
сформулировал Клейнман [18], а общие соотношения симметрии
по индексам A.28) были получены Армстронгом, Блом-
бергеном, Дюкуэнгом и Першаном [19]">. Они могут
быть проверены в каждом конкретном случае непосред-
непосредственным расчетом. В частности, они имеют место для
ангармонического осциллятора без затухания.
Наличие компоненты нелинейной поляризации с ча-
частотой ©г, сдвинутой по фазе на 90° относительно поля с
той же частотой, обусловливает поглощение или усиле-
усиление на этой частоте. Например, средняя по времени ра-
работа, совершаемая волной Е3, имеющей частоту соз,
равна
W (со3) = — гсо3 (Е3 • Рз — Е; • Р3) = 2со3 Im E*3 • Р3.
Суммарная работа над средой, совершаемая в единицу
времени всеми тремя волнами и представляющая ско-
скорость нагревания среды, равна
W = — 2 Im ^ [Шик («з = Щ + со2) —
— ЩЩк К = со3 — со2) — щхкп К = «з — «i)J Е*чЕ'2кЕ31.
A.29)
В случае среды без потерь, когда восприимчивость %
действительна и удовлетворяет соотношениям симмет-
симметрии A.28), это выражение, естественно, равно нулю.
В этом приближении поглощаемая на частоте соз мощ-
мощность излучается на частотах оч и о>2, а мощность, по-
поглощаемая на частотах coi и оJ, излучается на часто*
те соз.
Если первоначально существовали только волны с
частотами cot и со2, то образуется фазированная решетка
диполей, осциллирующих с частотой «з = coi -f- co2. Излу-
Излучаемое этой решеткой поле с частотой ю3 будет рассчита-
') См. также [20].
48
ГЛАЁА 1
КЛАССИЧЕСКОЕ ВВЕДЕНИЕ
49
но в одной из последующих глав. В настоящей главе по-
поля считаются заданными и рассчитываются индуциро-
индуцированные поляризации, линейные и нелинейные. В даль-
дальнейшем мы будем рассматривать эти поляризации, в
свою очередь, как источники полей, и найдем самосогла-
самосогласованные решения с помощью уравнений Максвелла.
Рассмотрим генерацию второй гармоники волной не-
нелинейной поляризации
pNL /г) \ /п , \ р2 2ik,-r—2Ш
в присутствии электромагнитной волны частоты 2со,
?2exp(ik2>r—2iwt). Вследствие обычной частотной дис-
дисперсии фазовые скорости распространения электромаг-
электромагнитной волны частоты 2со и волны нелинейной поляриза-
поляризации будут отличны (к2 Ф 2к]). Фазы этих волн «разой-
«разойдутся» на я на расстоянии 1КОг, определяемом равенст-
равенством (k2 — 2ki)-iKOr = tt. Поэтому знак поглощаемой из
поля второй гармоники мощности
— W (со) = W Bсо) = 2со Im ?2PNL Bco)
будет периодически изменяться с расстоянием. После то-
того как волна второй гармоники нарастет до определенной
величины (это сопровождается соответствующим умень-
уменьшением мощности первичной волны) она снова начнет
поглощаться, а мощность первичной волны возрастать
и т. д. Этот «интерференционный» эффект можно на-
наглядно продемонстрировать, если в экспериментальной
установке, изображенной на фиг. 1, изменять оптиче-
оптическую толщину нелинейного кристалла путем вращения
его или изменения температуры. Характерная зависи-
зависимость мощности второй гармоники от толщины кри-
кристалла, полученная Терхьюном и др. [21], представлена
на фиг. 2. Расстояние между двумя смежными максиму-
максимумами соответствует изменению оптического пути -на
2/кор- Джордмейн [22] и Терхьюн [21] показали, что это
рассогласование фазовых скоростей, связанное с частот-
частотной дисперсией, можно скомпенсировать, используя взаи-
взаимодействие обыкновенной и необыкновенной волн в од-
одноосных кристаллах. Фиг. 3 демонстрирует чрезвычайно
большой рост интенсивности второй гармоники при
второй гармоники со скоростью обыкновенного луча пер-
первичной волны (при ki || k2 согласование фазовых скоро-
скоростей в этих опытах сводится к их уравниванию).
Если coi — оптическая частота, а со2 лежит в диапазоне
СВЧ, то поляризация на частотах ©i ± со2 приводит к по-
появлению боковых частот у оптической несущей. Эта СВЧ
40
30
20
Ю 0 10
Угол поворота, град
20
30
40
Фиг. 2, Зависимость интенсивности гармоники от оптической тол-
толщины пьезоэлектрического кристалла для случая, когда фазовые ско-
скорости исходной волны и волны второй гармоники не согласованы
(по данным работы [21]).
модуляция света имеет большое значение для связи [23,
24]. Согласование скоростей здесь также существенно в
случаях, когда протяженность устройства больше одной
длины волны модулирующего сигнала '>. Эксперимен-
!) Для модулированных волн, с которыми мы имеем дело в этом
примере, должны быть согласованы уже не фазовые скорости, а
групповая скорость модулированной волны и фазовая скорость мо-
модулирующей волны. В так называемом модуляторе бегущей волны
модуляция эффективна, если проекция групповой скорости света на
направление распространения модулирующей волны равна фазовой
4 Н. Бломбсрген
50
ГЛАВА 1
тально наблюдался также обратный процесс, при кото-
котором биения двух световых лучей приводили к генера-
генерации СВЧ мощности на разностной частоте.
Угол, град
Фиг. 3. Графики, характеризующие зависимость интенсивности вто-
второй гармоники в кристалле КН2РО4 от углов 6 и ф, образованных
волновым вектором основного излучения с осями кристалла (по дан-
данным работы B1]).
Ось z—оптическая ось кристалла. Резкое возрастание интенсивности гармо-
гармоники при 0 = 0о соответствует согласованию фазовых скоростей необыкновен-
необыкновенной волны частоты 2га и обыкновенной волны частоты ш.
Возможно также наблюдение суммарной частоты при
взаимодействии двух различных световых пучков. Нако-
Наконец, при 0J = —«ч и Е2 = Е\ -соотношение A.23) опи-
описывает также появление статической нелинейной поля-
поляризации («выпрямление» света). В этом случае на про-
продольных гранях кристалла появляется постоянное напря-
напряжение, которое наблюдалось Фраикеном и др. [25]. Этот
Классическое ЬвеДенйе
51
эффект можно рассматривать как обратный линейный
электрооптический эффект.
Обратимся теперь к рассмотрению нелинейной поля-
поляризации следующего порядка малости:
Pnl {щ + Ш2 + щ) = хЕ1Е2Е3е1 <k'+k*+k')-r-<- <">+"*+"'>'.
Отметим сразу же, что входящий сюда тензор восприим-
восприимчивости четвертого ранга отличен от нуля для всех групп
точечной симметрии !). В изотропных жидкостях также
возможен целый ряд явлений, связанных с нелиней-
нелинейностью подобного типа.
При o)i = 0J = «>з записанная выше нелинейная поля-
поляризация обусловливает генерацию третьей гармоники,
что впервые наблюдалось Терхьюном и др. [11]. При
о), = со2 = —оK и Ег=-Е2 = Е* нелинейная поляриза-
поляризация содержит компоненту
К) =
К = — ©1
1— шг) х
хЕ](~Ф1)Ек(щ)Е1(+а1). A.30)
Действительная часть входящей сюда спектральной ком-
компоненты восприимчивости описывает изменение показа-
показателя преломления, пропорциональное интенсивности све-
светового луча, мнимая же часть описывает зависимость
коэффициента поглощения света от интенсивности.
В частности, она описывает начальную стадию эффекта
насыщения, хорошо известного в области магнитного ре-
резонанса. Эта компонента велика, когда частота wi близ-
близка к резонансной. Этот эффект используется в так назы-
называемых насыщающихся фильтрах, которые становятся
прозрачными при больших потоках мощности [26]. Ком-
Компонента мнимой нелинейной восприимчивости, макси-
максимальная при резонансе среды на частоте 2o)i, описывает
двухквантовое поглощение, наблюдавшееся Гарреттом
и Кайзером [27]. В работе [27] была обнаружена голубая
флуоресценция ионов Еи2+ в CaF2 при облучении их
светом рубинового лазера. Красные кванты не могут воз-
возбудить ион путем независимых последовательных одно-
'' Таблицу отличных от нуля компонент %цы для всех кристал-
кристаллических классов можно найти в C7*]. — Прим.. ред.
4*
ГЛАВА i
квантовых процессов; подтверждением двухквантовой
природы наблюдавшейся флуоресценции была ее про-
пропорциональность квадрату интенсивности излучения ру-
рубинового лазера.
В изотропной жидкости тензор четвертого ранга име-
имеет только две независимые компоненты. В этом случае
соотношение A.30) может быть записано в векторной
форме
PNL И = Хм И Е И (Е (ю) • Е* (-со)) +
+ Xi2E*(-co)(E(co).E(o))), A.31)
где использованы обозначения Фойгта:
1 = хх, 2 = г/г/, 4 = ху.
Терхьюн продемонстрировал существование компоненты
%i2- Этот эксперимент будет более подробно обсуждаться
в гл. 5.
Если положить coi > со2 = — соз и считать для просто-
простоты, что поле Е2 линейно поляризовано в направлении х,
то нелинейная поляризация с частотой «м будет иметь
следующие компоненты:
Действительные части этих компонент поляризации опи-
описывают изменение показателя преломления на частоте
©I в присутствии поля с частотой со2- При о>г = О эти со-
соотношения просто описывают квадратичный электрооп-
электрооптический эффект (эффект Керра), т. е. двулучепрелом-
ление, возникающее в электрическом поле.
Мнимая часть %" > 0 представляет положительное
поглощение, пропорциональное интенсивности поля на
частоте оJ- Заметим, что фаза этой нелинейной поляри-
поляризации фиксирована относительно фазы поля этой же ча-
частоты.
Изменение средней по времени плотности свободной
энергии, обусловленное одновременным присутствием
КЛАССИЧЕСКОЕ ВВЕДЕНИЕ
53
полей с частотами ©i и со2 и биквадратное по амплитудам
этих полей, можно представить в следующем виде:
Средняя по времени суммарная мощность, поглощае-
поглощаемая средой, равна
W = 2 (со, -»г) [Jm "Ai К = «1 + со2 -со2) | Е1х\* ?2д|2 +
Здесь было использовано соотношение симметрии для
тензора комплексной восприимчивости типа A.17). Это
соотношение имеет место, если существенна только одна
резонансная частота среды, близкая к сог — о>ь а зату-
затухание Г можно удержать только в одном из знаменате-
знаменателей. Такое условие удовлетворяется в модели ангармо-
ангармонического осциллятора.
Согласно A.17), при резонансе («ч — сог = соо)
Im%n(co2 = ©г + wi — coi) < 0; на меньшей частоте юг
поглощение отрицательно, а на большей частоте о)]
положительно. При достаточно большом значении
|?(o>i) |2 отрицательное поглощение, связанное с %ц, мо-
может превысить все потери на частоте оJ, и напряжен-
напряженность поля E2(a2) будет экспоненциально нарастать
в пространстве, причем постоянная нарастания пропор-
пропорциональна интенсивности поля на частоте ом. Если уси-
усиление достаточно велико и имеется обратная связь, то на
частоте сог может возникнуть генерация. Строгое рас-
рассмотрение процесса самовозбуждения колебаний воз-
возможно лишь на основе квантовой механики [здесь сущест-
существенно спонтанное излучение, поскольку при ?(о)г) = 0,
PNL @J) = 0]. Грубо спонтанное излучение можно рас-
рассматривать как шум, вызванный нулевыми колебаниями
осцилляторов. Этот шум усиливается и приводит к са-
самовозбуждению автоколебаний.
Рассмотренный эффект соответствует процессу вы-
вынужденного комбинационного рассеяния, при котором
поглощается квант ha и излучается квант Лю2 (стоксова
частота), а энергия системы увеличивается на Йсоо =
54
ГЛАВА 1
= Л(о)] — оJ). Эффект вынужденного комбинационного
рассеяния был открыт Вудбери и др. {28]. Они обнару-
обнаружили, что при определенных условиях рубиновый лагер,
Полупрозрачное
зеркало
to,
Модулятор
Зеркало с ячейкой
Керра ру6цн
Бензол
Вращаю-
Вращающееся Частично
зеркало отрашоющее
покрытие
Линза
Бензол
Рубин
и т.д.
Фотопленка
Ф и r. 4. a — схема генератора, использующего эффект вынужденно-
ного комбинационного рассеяния; б — схема эксперимента по наблю-
наблюдению вынужденного излучения со стоксовой и антистоксовой часто-
частотами вне оптического резонатора (лазерный луч фокусируется в
объем рассеивающей среды).
в котором между зеркалами резонатора помещена ячей-
ячейка с жидкостью, помимо основного излучения с X =
о
= 6943 А излучает дополнительную частоту. Разность
основной и дополнительной частот оказывается равной
частоте колебательного перехода молекул соответствую-
соответствующей жидкости. Дополнительное излучение возникает при
превышении определенного порогового уровня мощности
основного излучения лазера '>.
Эффект проявляется вполне четко, как только превы-
превышен порог. Он наблюдался в большом числе различных
') Таким образом, в опытах Вудбери и др. исследовался ггне-
ратор, использующий эффект вынужденного комбинационного рас-
рассеяния; обратная связь на частоте оJ осуществлялась за счет от-
отражений от зеркал лазерного резонатора. Такой генератор в лите-
литературе называют также раман-лазером или комбинационным лазе-
лазером. — Прим. ред.
КЛАССИЧЕСКОЕ ВВЕДЕНИЕ
55
жидкостей, а также в твердых телах и газах. В последу-
последующих работах было выяснено, что эффект возможен
также и вне лазерного резонатора, если луч лазера фо-
фокусируется внутри кристалла или ячейки с исследуемой
жидкостью. Если имеется излучение и на лазерной часто-
частоте coi и на стоксовой частоте со2, то возникает нелинейная
поляризация на антистоксовой частоте 2coi — сог- Эта
компонента определяется восприимчивостью, данной
выражением A.18) с тем же резонансным знаменате-
знаменателем D{iA\ — со2). Терхьюн [29] первый обнаружил излу-
излучение на антистоксовой частоте. Это излучение имеет
характерную коническую диаграмму направленности.
Естественно, будут существовать и компоненты поляри-
поляризации с другими комбинационными частотами ©i +
+ л(со[—сог), o)i—n(coi — 0J) и т. д. Явление вынуж-
вынужденного комбинационного рассеяния будет обсуждаться
более подробно в гл. 5. Типичные схемы экспериментов
показаны на фиг. 4.
§ 4. План дальнейшего изложения
В этой главе мы ввели нелинейную поляризацию и
выразили ее через приложенные поля, которые предпо-
предполагались заданными. Следующий логический шаг заклю-
заключается в рассмотрении этой нелинейной поляризации
как дополнительного источника полей. Этот второй шаг
будет сделан в гл. 3. Читатель, не желающий прерывать
изучение классической трактовки нелинейных оптиче-
оптических эффектов, может опустить следующую главу, в ко-
которой нелинейная восприимчивость рассчитывается кван-
товомеханически с целью дальнейшего выяснения атом-
атомного механизма нелинейности. В гл. 2 мы не будем огра-
ограничиваться рассмотрением чисто дипольного взаимодей-
взаимодействия. В ней установлены некоторые общие соотношения,
связывающие действительные и мнимые части нелиней-
нелинейных восприимчивостей и основные квантовые процессы;
кратко обсуждаются также пределы применимости полу-
полуклассического рассмотрения полей.
В гл. 3 нелинейные материальные уравнения включа-
включаются в систему уравнений Максвелла. Взаимодействие
между световыми волнами в нелинейной среде рассмат-
56
ГЛАВА 1
ривается в гл. 4. Даны решения связанных волновых
уравнений для параметрических эффектов и эффектов
типа комбинационного рассеяния '). Рассмотрено также
взаимодействие световых и упругих волн. На основании
анализа граничных условий для нелинейной среды обоб-
обобщены оптические законы отражения, преломления и т. д.
Краткий обзор экспериментальных результатов и их
интерпретация даны в гл. 5. Обсуждаются величины не-
нелинейных восприимчивостей различных материалов.
Особое внимание уделяется анализу эксперименталь-
экспериментальных данных по комбинационному рассеянию. Некоторые
частные вопросы, включающие задачу о нелинейности
в лазерных генераторах, упомянуты в гл. 6. В качестве
приложения в книгу для удобства читателей включены
три ранее опубликованные статьи, что позволило опус-
опустить в основном тексте некоторые довольно сложные
расчеты.
ЛИТЕРАТУРА
1. Frank en P. A., Hill A. E., Peters С. W. Weinreich
G., Phys. Rev. Lett., 7, 118 A961).
2 Fr an ken P. A., Ward J. F., Rev. Mod. Phys. 35, 23 A963).
3. Bloembergen N., Proc. IEEE, 51, 124 A963).
4. Pershan P. S., Progress in Optics, Amsterdam (в печати).
'> Здесь и далее автор пользуется введенной им ранее класси-
классификацией нелинейных волновых взаимодействий (см., например,
приложение III к книге). Параметрическими он называет волновые
взаимодействия, характер протекания которых существенно зависит
от фазовых соотношений между взаимодействующими волнами (та-
(такие, как генерация гармоник, смешение, собственно параметрическое
усиление и т. п.), а комбинационными — взаимодействия типа сток-
сова комбинационного рассеяния, которые зависят от квадратов ам-
амплитуд (чисел фотонов) и не зависят от фаз. Подробную мотиви-
мотивировку такой классификации можно найти также в [39*]. Определен-
Определенным неудобством указанной терминологии является то обстоятель-
обстоятельство, что часто термин «параметрическое взаимодействие» понимает-
понимается в более узком смысле (см., в частности, приложение I). Поэтому
далее, там, где использование термина «параметрическое взаимодей-
взаимодействие» может вызвать неясности, сделаны примечания. Отметим так-
также, что более удачными представляются использующиеся также в
литературе для обозначения вышеуказанных типов взаимодействий
термины «когерентные» и «некогерентные» волновые взаимодейст-
взаимодействия. — Прим. ред.
КЛАССИЧЕСКОЕ ВВЕДЕНИЕ
57
5 .М. cClung F. J., Hellwarth R. W., Proc. IEEE, 51, 46
A963).
6. Wa rd J. F., Franken P. A., Phys. Rev., 133, AI83 A964).
7 Lax В Mavroides J. G., Edwards D. F., Phys. Rev.
Lett., 8, '166 A962).
8 Whitmer R. F., Barrett E. В., Phys. Rev., 121, 661 A961);
125, 1478 A962).
9. Becker R., Electronen Theorie, Leipzig, 1933. (Имеется пере-
перевод: P. Б е к к е р, Электронная теория, М., 1941.)
10. Rayleigh, Theory of Sound, vol. 1, New York, 1945, p. 76.
(Имеется перевод: Релей, Теория звука, т. I., M.—Л., 1940.1
П. Terhune R. W., Maker P. D., Savage С. М., Phys. Rev.
Lett., 8, 404 A962).
12 Brossel J., Cagnac В., Kastler A., Journ. Phys. Rad.,
15, 6 A954).
13. Kusch P., Phys. Rev., 93, 1022 A954).
14. В loch F. Phys. Rev., 102, 104 A956).
15. Ay res W. P., Vartanian P. H., Me Ichor J. L. Journ,
Appl. Phys., 27, 188 A956).
16. Nye J. F., Physical Properties of Crystals, Oxford, 1957.
(Имеется перевод: Дж. Най, Физические свойства кристаллов,
ИЛ, 1962.)
17. Smith С. S., Solid State Physics, vol. 5, ed. Seitz F.. Turn-
bull D., New York, 1958.
18. Kleinman D. A., Phys. Rev., 126, 1977 A962).
19. Armstrong J. A, Bloenibergen N.. Ducuing J.,
Pershan P. S., Phys. Rev., 127, 1918 A962). (См. приложе-
приложение I к настоящей книге).
20. Карпман В. И., ЖЭТФ, 44, 1307 A963).
21. Maker P. D., Terhune R. W., Nisenhoff M., Savage
С. М., Phys. Rev. Lett., 8, 21 A962).
22 Giordmaine J. A., Phys. Rev. Lett., 8, 19 A962).
23. 'Kaminow I. P., Liu J.. Proc. IEEE, 51, 132 A963).
24. Peters С J., Proc. IEEE, 51, 147 A963).
25. В ass M. Franken P. A., Ward J. F., Weinreich G.,
Phys! Rev. Lett.. 9, 446 A962).
26. Sorokin P. P., Luzzi J. J., La nkar d J. R., Pettit
G. D., IBM Journ. Res., 8, 182 A964).
27. Kaiser W., Garrett G. С. В., Phys. Rev. Lett., 7, 229
A961).
28. Eckhardt G, Hellwarth R. W., McClung F. J.,
Schwarz S. E., Weiner D., Wood bur у Е. J., Phys. Rev.
Lett. 9 455 П962).
29. Terhune R. W. Bull. Am. Phys. Soc, II (8), 359 A963).
30. Terhune R. W., Solid State Design, 4, 38 (November 1063).
(Имеется перевод в сборнике «Зарубежная радиоэлектроникой,
№ 6, М., 1964.)
31*. Li-Yin-Yunn, Acta Phys. Sinica, 20, 164 A964)".
¦> Здесь и далее звездочками отмечены работы, добавленные ре-
редакторами перевода. — Прим. ред.
58
ГЛАВА 1
32*. iKielich S., Bull. Acad. Polon. Sci., 12, 53 A964).
33*. Ахманов С. А., Клышко Д. Н., ЖЭТФ, письма в редак-
редакцию, 2, 15 A965).
34*. Terhune R. W., Maker P. D., Savage С M Phys Rev
Lett., 14, 681, 1965.
35*. Ахманов С. А., Хохлов Р. В., Проблемы нелинейной оп-
оптики, М., 1964, гл. V.
Giordmaine J. A., Phys. Rev., 138, А1599 A965).
Maker P. D., Terhune R. W., Savage С. М., Procee-
Proceedings Third Conference on Quantum Electronics, Paris, 1963, ed
P. Grivet, N. Bloembergen, New York, 1964, p. 1559.
Ландау Л. Д., Лифшиц Е. М., Электродинамика сплош-
сплошных сред, М., 1957.
Файн В. М., Ханин Я. И., Кванторяя радиофизика, М.,
1965.
36*
37*
38
39
Л
В
КВАНТОВАЯ ТЕОРИЯ
НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕЙ
§ 1. Уравнение Лиувилля для матрицы плотности ')
В отсутствие переменных внешних полей квантовоме-
ханическая система, описываемая гамильтонианом Жо,
имеет не зависящие от времени собственные состояния
ип с энергиями Wn, которые являются решениями урав-
уравнения Шредингера
WoUn = Wnun. B.1)
Функции ип образуют полную систему ортогональных
функций. Отклик рассматриваемой квантовомеханиче-
ской системы на зависящее от времени возмущение Ж\ (t)
описывается зависящей от времени волновой функцией,
которую можно представить в виде ряда по ип с коэффи-
коэффициентами, зависящими от времени.
B.2)
Коэффициенты с удовлетворяют дифференциальным
уравнениям
с — т~1У\с (k \Ж0 + Ж1 (t) In). B.3)
Среднее значение некоторого оператора О в момент вре-
времени /равно
= (ф* (О
@) ==
B.4)
к.т
¦' Прекрасное изложение метода матрицы плотности и его при-
применений см., например, в [1—3]. (См. также {33*, 34*]. — Прим. ред.)
60
ГЛАВА 2
где R — оператор с матричными элементами Rkm =
= ckc"m. Из уравнений B.3) следует, что R удовлетворяет
дифференциальному уравнению
R=ih
~1
B.5)
Эта операторная форма справедлива в любом представ-
представлении и особенно удобна в случае, когда имеется ан-
ансамбль систем, описываемых одним и тем же гамильто-
гамильтонианом Ж = Жь-\-Жх{г) . Среднее по ансамблю R = р
называется матрицей плотности; эта матрица удовлетво-
удовлетворяет уравнению движения
р = -т~1[Ж,р\. B.6)
Если известны средние начальные условия для ансамбля,
то решение этого уравнения позволяет найти среднее по
ансамблю любой физической величины, изображаемой
оператором О:
<O> = Sp(pO). B.7)
Так как ^оне зависит от времени, гЖ\(г) мы рассмат-
рассматриваем как малое возмущение, то решение можно найти
в виде ряда по степеням^. Перейдем к представлению
взаимодействия
р —
B.8)
В этом представлении р' удовлетворяет уравнению
dp'
dt
B.9)
которое можно решить методом последовательных при-
приближений:
р' (/) = р' @) - г/Г1 J [ж[ (П, р' @)] df -
t t
dt' $ dr [ж[ (t'),w'i (t"), p' @)]] +... . B.Ю)
о о
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕЙ 61
Можно, конечно, совершить обратный переход к гейзен-
гейзенберговскому представлению p(t), что завершает фор-
формальное решение с помощью теории возмущений для не-
нестационарных процессов.
§ 2. Случайные возмущения и затухание
Как следует из материала гл. 1, нас будет интересо-
интересовать в основном стационарный отклик на возмущение
периодическими электромагнитными полями. Однако все
рассматриваемые нами системы подвержены неизбеж-
неизбежным стохастическим возмущениям. Затухание, которое
было введено в классические уравнения движения фено-
феноменологическим образом, обусловлено усредненным дей-
действием этих возмущений. Физическое происхождение
этих случайных возмущений различно. Тепловое движе-
движение в жидкостях, колебания^решетки в кристаллах, спон-
спонтанное излучение, безызлучательный распад при спон-
спонтанной эмиссии фононов, столкновения с электронами
проводимости, ионные или молекулярные столкновения
в газе — все эти процессы могут быть причиной возму-
возмущений. При полуклассическом подходе случайное возму-
возмущение M\{t) —оператор, действующий только на рас-
рассматриваемую материальную систему. Изменения элек-
электромагнитных полей, колебания, движение частиц опи-
описываются классически стохастическим образом. Среднее
значение {3?{(t) > = 0, т. е. все матричные элементы
< (т\ Ж[\п) > исчезают при усреднении. Если имеется
неисчезающая часть, то ее можно включить ъЖ^. Стоха-
Стохастический процесс предполагается стационарным, так
что корреляционные функции типа < Ж \jii{tKt itmn(t +
+ т)> не зависят от t. Спектральные плотности могуг
быть определены путем фурье-преобразования этих
функций корреляции. Существенно, что спектры рас-
рассматриваемых стохастических процессов достаточно ши-
широки, вследствие чего может быть введено конечное вре-
время корреляции тс, такое, что
Ж\,ы @ afi.m/1 (t + т) = 0 при х > тс.
62
ГЛАВА
Рассмотрим решение B.10) уравнения B.9) при t ^> тс.
Возьмем среднее по всем процессам затухания. Корре-
Корреляцией между р'@) иЖ'(/) можно пренебречь. В прин-
принципе начальное значение р'@) определяется непосредст-
непосредственно предшествовавшими значениями Ж{?), которые
в свою очередь коррелируют с непосредственно следую-
следующими за ними значениями Ж(?). Однако корреляция
между Ж(?) и р'@) исчезает при ? > тс, и основной
вклад в интегралы в B.10) дают интервалы времени, для
которых ?' > тс, ? > тс, но ? — t" < те. Перейдем от пе-
переменной Г к т = ?—i". Предел интегрирования по т по
этой же причине может быть распространен до + оо. Ес-
Если члены высшего порядка в B.10) пренебрежимо малы,
то усредненное решение для t 3> тс при случайном воз-
возмущении равно
B.11)
Относительное изменение р'(^) составляет
Р'(О-Р'(О) ^ t dp' _ ,L-2-nL
Если среднее квадратичное возмущение достаточно ма-
мало и быстро изменяется, так что
/Г'№|2тс2<<1, B.13)
то можно выбрать время таким образом, чтобы выполня-
выполнялось условие / >тс и вместе с тем имело место неравен-
неравенство
Р'(О-Р'(О)
р'@)
«1.
При этих условиях члены высшего порядка в B.10)
действительно малы, поскольку отношение двух последу-
последующих приближений равно, очевидно, (Л-2 < | Жх | > Ч\ I/г.
Следовательно, условие B.13) позволяет записать B.11)
в виде
. B.14)
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОС.ТЕЙ 63
Если записать это операторное равенство в явном виде
в представлении, в котором гамильтониан Жо диагона-
диагоналей, то скорость изменения типичного матричного эле-
элемента выразится следующим образом:
dt
-^lr?l
Rkl.mnPmn,
где коэффициенты R не зависят от t вследствие стацио-
стационарности. Если пренебречь малыми секулярными возму-
возмущениями, т. е. оставить только непериодические члены,
для которых (Ohm = Щп, то можно получить не завися-
зависящую от времени характеристическую матрицу затухания
dt
, tnn Pmn.
B.15)
Если исключить возможность случайного вырождения и
не рассматривать равное или почти равное расстояние
между уровнями, то единственными несекулярными чле-
членами, вызванными стохастическим возмущением, будут
релаксационные члены
d ' " B.16)
at
pkk =
>тт = 2i WkmPmm ~ 2i Wmk )Ркк.
Последнее равенство соответствует скоростным уравне-
уравнениям, описывающим изменение населенностеи различных
энергетических уровней. Коэффициент whm может быть
идентифицирован с пропорциональной времени вероят'
ностью перехода между уровнями k и т. Расписывая
коммутаторы в B.14), получаем1'
Г2
wka=h-' \Mkm{t)Mmk(t-x)e km dx. B.17)
ктТ
'"> В B.15) и B.17) константы затухания выражены через воз-
возмущение в представлении Шредингера с явными экспоненциальны-
экспоненциальными временными факторами. Сама матрица плотности все еще рас-
рассматривается в представлении взаимодействия.
64
ГЛАВА 2
Таким образом, вероятность перехода пропорциональна
спектральной плотности матричного элемента, связы-
связывающего уровни, разность энергий которых соответству-
соответствует частоте aikm- Все диагональные элементы релаксируют
связанным образом, так что система с 31 энергетически-
энергетическими уровнями, удовлетворяющими соотношению 2р^ = 1,
имеет 3? — 1 характерных времен релаксации.
Затухание недиагональных элементов ры можно полу-
получить аналогичным образом, рассматривая различные
слагаемые в коммутаторах. Вклад иедиагональных эле-
элементов возмущения равен
= - 4- 2 («к +
B.18)
Адиабатическая часть затухания недиагональных эле-
элементов связана со случайными возмущениями энергети-
энергетических уровней диагональными элементами стохастиче-
стохастических процессов. В определенном смысле возмущения мо-
модулируют резонансную частоту и уширяют резонанс сле-
следующим образом:
R lf« = - Г2 J
- 9tkk @ % и V- т) - Ма
(t-x)}dx =
B.19)
где
(t) =*
(П \Щ-A\ЖХ @ |/).
Наиболее серьезным недостатком этой полуклассиче-
полуклассической теории релаксации является то, что система релак-
сирует согласно B.16) к конечному состоянию с равны-
равными друг другу диагональными элементами матрицы плот-
плотности. Это соответствует термодинамическому равнове-
равновесию при бесконечно большой температуре. Из общих фи-
физических соображений следует ожидать, что в конечном
состоянии система приобретает температуру резервуа-
резервуара, который обусловливает случайное движение, приво-
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕИ 65
дящее к затуханию. В действительности, как это будет
показано в § 8 настоящей главы, надлежащее квантова-
квантование резервуара устраняет этот недостаток, А пока на ос-
основании принципа детального равновесия примем, что
Wu = w ue~%0'k"lkT. B.201
Это условие обеспечивает больцмановское распределе-
распределение равновесных населенностей
П — Г. Р~йЮ?„/*Г /О О1\
Pkk— РппУ • (?.61)
Недиагональные элементы релаксируют к нулевым
значениям в соответствии с условием хаотичности фаз
волновых функций при термодинамическом равновесии.
Заметим также, что при воздействии стохастического
возмущения ') среднее значение р^п остается равным ну-
нулю. Случайный процесс не приводит в среднем к установ-
установлению определенных фазовых соотношений.
Следует заметить, что различные механизмы затуха-
затухания не обязательно должны быть связаны с одной и той
же температурой. Ярким примером этого является про-
процесс накачки лазера некогерентным излучением. В те-
телесном угле, охватываемом лампой-вспышкой, некоге-
некогерентные излучательные процессы имеют высокую темпе-
температуру, в других направлениях — много меньшую, а
безызлучательные переходы, связанные с решеткой, ха-
характеризуются температурой кристалла. В газовом ла-
лазере процессы столкновений с электронами описываются
одной температурой, столкновений со стенками — другой
и т. д.
Любые стохастические процессы, удовлетворяющие
основному условию B.13), и в том числе процессы неко-
некогерентной накачки, можно учесть с помощью соответст-
соответствующих феноменологических релаксационных членов.
Зависящее от времени когерентное возмущение со-
состоит из одного или нескольких периодических слагае-
слагаемых, имеющих очень большое или бесконечное время
корреляции тс- Спектральная плотность такого возмуще-
возмущения описывается б-функциями. Мы не будем рассматри-
рассматривать промежуточный случай, при котором п~11 Ж \ \хс~ 1.
'> С достаточно широким спектром. — Прим. перев.
.5 Н. Бломберген
66
ГЛАВА 2
После обратного перехода от представления взаимо-
взаимодействия к представлению Шредингера уравнение дви-
движения принимает вид
р = _^-" [Жо, р] ~ih~l [Жкот(t), р] + Яр, B.22)
где /? связано с не зависящим от времени затуханием,
определяемым равенствами B.16) и B.19) в представле-
представлении, в котором гамильтониан Жо диагоналей. Релаксаци-
Релаксационный член можно представить в операторной форме
только в определенных частных случаях. Если имеется
система энергетических уровней п, подверженных только
неадиабатическим возмущениям, и если стохастическое
возмущение связывает эти уровни только с уровнями ц,,
не принадлежащими системе, то релаксационный член
можно представить в виде — '^(Гр + рГ), где Г — диа-
диагональная матрица,
Кроме рассмотренного выше однородного уширения,
часто приходится иметь дело с неоднородным ушире-
нием, вызванным распределением резонансных частот.
Такое уширение могут вызвать, например, внутренние
напряжения в кристаллах. В некоторых случаях разум-
разумное приближение можно получить простым увеличением
констант затухания Rum, так чтобы они соответствовали
наблюдаемому уширению линии. Однако такой метод
может дать неправильные результаты. В принципе не-
неоднородное уширение следует учитывать усреднением
по распределению резонансных частот в конце расчета.
§ 3. Отклик на периодические возмущения
В то время как отклик на случайные возмущения
рассматривался на основе временного подхода, стацио-
стационарный отклик на периодические возмущения алгебраи-
алгебраически проще рассчитывать с помощью спектрального
подхода. Для получения решения в виде ряда по возра-
возрастающим степеням когерентного возмущения, так же
как и в § 2, будет использоваться метод матрицы плот-
плотности [4] (см. также [5]).
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕЙ 67
В случае стационарного отклика уравнения являются
алгебраическими. В первом приближении уравнения
для типичных диагонального и недиагонального элемен-
элементов имеют вид
kk
- г/Г1 [Жког (со) , р< V,
B.23)
= - /<о«р1кУ-
- ih~' [Жког (со),
где р@) — стационарное решение для матрицы плотности
в отсутствие когерентных возмущений. Диагональные
элементы не обязательно имеют больцмановское рас-
распределение. На систему могут действовать некогерент-
некогерентные источники накачки, изменяющие стационарные насе-
населенности настолько, что для некоторых уровней будет
иметь место инверсия. В обычных условиях р<°> имеет
распределение, соответствующее термодинамическому
равновесию. Недиагональные элементы р<°> всегда равны
нулю. При термодинамическом равновесии фазы распре-
распределены случайно; распределение фаз остается таковым и
в присутствии некогерентной накачки.
Решение уравнений B.23) в первом приближении оп-
определяет линейный отклик, который содержит те же фу-
рье-компоненты, что и возмущение Жкот(со). Второе при-
приближение получается при подстановке линейного при-
приближения в уравнение движения. В общем случае член
Ж (со) .pCtyjfe будет содержать комбинации частот исход-
исходного возмущения. Например, компоненты с частотой
второй гармоники определяются уравнениями
B.24)
Bи) = - fowpg> Bсо) -Г
Й~'1#ког И, РШ (©)]«.
Эта процедура может быть продолжена до бесконеч-
бесконечности. В самом общем случае фурье-компонента с часто-
5*
68
ГЛАВА 2
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕЙ
69
той а„ = соп-1 + со в /г-м приближении, пропорциональ-
пропорциональная л-й степени возмущения, может быть найдена по
фурье-компоненте с частотой con-i предыдущего прибли-
приближения:
К)=-г-соАгрЙ>„)-Г,
и B.25)
Таким образом, имеется система алгебраических опе-
операций для нахождения спектральных компонент элемен-
элементов матрицы плотности р в виде ряда по степеням воз-
возмущения. С помощью соотношения B.7) для среднего
значения физической величины О (которая сама может
явно зависеть от времени) можно найти фурье-компо-
фурье-компоненты стационарного отклика любой физической вели-
величины.
Проиллюстрируем эту процедуру с помощью просто-
простого физического примера. Рассчитаем фурье-компоненты
среднего значения электрического дипольного момента
ансамбля локализованных одноэлектронных систем на
частотах второй и третьей гармоник. Пусть когерентное
возмущение имеет вид
^ког (t) = —ex [Ехе~ш + Е*хеШ1
]
B.26)
и пусть оператор дипольного момента ех имеет только
действительные недиагональные элементы xng = xgn,
Xnn = 0.
Согласно уравнениям B.23), линейные фурье-компо-
фурье-компоненты матрицы плотности равны
\Pgg —
Pnn
(Z.Z/)
аналогичные выражения для компонент на частоте —со
получаются заменой со на —со и Ех на Ех. Среднее зна-
значение линейного электрического дипольного момента
равно
B.28)
n g
,— (со ¦
ю
см
Двойная сумма представляет комплексную воспри-
восприимчивость системы. Если не делать различия между
макроскопическим и действующим полями и прене-
пренебречь затуханием, то получим дисперсионную формулу
Крамерса— Гейзенберга
X' (со) = 2N0h
-1
2«>
ng
- со2)
2\— 1
где No — плотность числа частиц в состоянии \g > .
Заметим, что выражение B.28) действительно при
со ->- 0, т. е. в постоянном поле модель связанных зарядов
не приводит к стационарным потерям. Эта особенность
является следствием раздельного рассмотрения затуха-
затухания матричных элементов png(±co) и pgn(±u>). В дей-
действительном представлении, при котором не делается
различия между положительными и отрицательными ча-
частотами, приходится вносить- поправку в релаксацион-
релаксационные члены поперечных компонент (например, в уравне-
уравнениях Блоха), так что релаксация происходит
к термодинамическому равновесию, соответствующему
мгновенному значению гамильтониана ^о+^ког@-
Этот вопрос, детально разобранный Ван Флеком и Вай-
скопфом [6], для оптического диапазона имеет несколь-
несколько академический интерес, поскольку роль антирезонанс-
антирезонансного члена, у которого о и a>ng имеют одинаковый знак,
здесь пренебрежимо мала. Тем не менее с удовлетворе-
удовлетворением отмечаем, что наш подход дает правильные резуль-
результаты даже на очень низких частотах. Заметим также,
что мнимая часть изменяет знак при изменении знака со,
поэтому знак поглощаемой мощности одинаков для по-
положительных и отрицательных частот.
Рассмотрим далее нелинейную поляризацию низшего
порядка, которая будет иметь фурье-компоненты с ча-
частотами второй гармоники ±2м и с нулевой частотой.
Изменение населенности р(„^ @) соответствует эффекту
насыщения. Так как диагональные элементы хпп пред-
предполагаются равными нулю, то для расчета поляризации
на частоте второй гармоники нужно определить только
иедиэгональные элементы р^)п B©). Из уравнения
70
ГЛАВА 2
B.24) после подстановки в него B.27) непосредственно
получаем
?- ft«B(o-(on,f|
X
е хп„пхп,п„п е
Bа,-<о„.„ + /IV„) (со - »„,„„ + ,¦[¦„,„.
Л.<0) @) \
\Рп"п" — Рп'п') •
B.29)
Среднее значение дипольного момента на частоте вто-
второй гармоники равно
Bо>) > = Хххх Bо>) Е'
™ =
B.30)
В случае, когда затухание пренебрежимо мало, нели-
нелинейная восприимчивость может быть представлена в
другой форме, если в выражении B.29) сгруппировать
члены, содержащие pj?|,». Множитель 2со — ©n- n в зна-
знаменателе при этом сокращается (этого не происхо-
происходит при наличии затухания, так как в общем случае
Г„'П Ф Г„»„4- Г„'„»). В отсутствие затухания, изменив
индексы тройной суммы, получаем
(Щ
h~2 X
п + п1
X [Bсо - со^)-1 (со - co^.g)-1 + B@ + со^)-1 X
Xtm + ffl^)-1 —(ш+ю^)-1^-©^)-1]. B.31)
Отсюда следует, что эта нелинейная восприимчивость
равна нулю в системах с центром инверсии, не имеющих
случайного вырождения. В таких системах волновые
функции g, n, п' имеют определенную четность и х свя-
связывает только состояния с противоположными четностя-
ми. Так как выражение B.31) содержит нечетное число
матричных элементов оператора х, то оно равно нулю.
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕЯ 71
В соответствии с нашим определением комплексных ам-
амплитуд эта нелинейная восприимчивость в два раза
больше выражений, полученных в предыдущих работах
И.
Приведенные расчеты показывают, что метод матри-
матрицы плотности упрощает трудоемкие вычисления, свя-
связанные с использованием возмущенных волновых функ-
функций (такой подход применяется в приложении I) и в то
же время позволяет естественным образом ввести зату-
затухание. Применение метода матрицы плотности позволяет
описывать поглощение и дисперсию в одном порядке
теории возмущений, поэтому он используется здесь и в
приложении III. В приложении III приведены полные
выражения для нелинейной поляризации с суммарной
частотой ©з = ©1 + ©2 в случае, когда на систему дей-
действуют два периодических электрических поля. Симмет-
Симметричная форма тензора нелинейной восприимчивости тре-
третьего ранга [см. формулу B.23) приложения III] имеет
место только в случае среды без потерь. Соотношения
симметрии относительно перестановки индексов, полу-
полученные в гл. 1 из феноменологических энергетических со-
соображений, подтверждаются, таким образом, непосред-
непосредственными расчетами.
Аналогично, поляризация на частоте третьей гармо-
гармоники может быть получена из следующего выражения:
Ч2)„B») - РЙ,. B») eXn,nEf)
C©) =
B.32)
При суммировании индекс п' можно положить равным
п" или п, так что нам понадобятся фурье-компоненты
диагонального элемента р|г2п)B©), которые при пренебре-
пренебрежении малым диагональным затуханием равны
Рае
toft2
X
X
¦ +
"ng Т li ng
-]. B.33)
ГЛАВА 2
Подстановка B.33) и B.29) в B.32) дает выражение
для р$)п (Зсо), которое позволяет рассчитать поляриза-
поляризацию с частотой третьей гармоники:
Р (Зсо) = х (Зсо) Е3е~^ = No ^ ^ ех^Х (Зсо).
л" п
В пренебрежении затуханием и изменением населенио-
стей (что всегда оправдано практически) это выражение
должно свестись к формуле B.22) приложения I. Если
затухание пренебрежимо мало, то можно перегруппиро-
перегруппировать слагаемые и изменить индексы. Это дает
2
n"+g n' n+g g
B.34)
где
" Bсо — в>я.в)-' (со
-1 Bсо + ovg)-1 (со
= (Зсо - ш„.в)
— (Зсо + ovg
+ (со - ovg) Bсо - cort'g)-] (со +
— (© + GV'g) B© -f COn.g)-] (СО —
co,lg) -' —
<ong)-1 +
a>ng)~l —
Это выражение с точностью до множителя 4 совпадает
с формулой B.22) приложения I (расхождение в 4 раза
возникает вследствие нашего измененного определения
комплексных амплитуд поля).
Метод матрицы плотности использовался многими
авторами для расчета нелинейного отклика среды на
оптических частотах [8—13]. Мы рассмотрим нелиней-
нелинейность низшего порядка более систематически для слу-
случая, когда исходное поле содержит две частоты и учи-
учитываются все мультипольные моменты. Это описание
особенно полезно в случае нелокализованных электрон-
электронных волновых функций.
§ 4. Нелинейная проводимость низшего порядка
Рассмотрим твердое тело в одноэлектронном прибли-
приближении; будем использовать блоховские волновые функ-
функции. Поскольку «блоховские» электроны реагируют на
усредненные по пространству электрические и маглит-
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСГЕЙ 73
ные поля, проведение различия между действующим и
макроскопическим полями излишне. Разумеется, это
различие существенно для локализованных электронов
в плотной среде, поэтому для таких электронов наше
рассмотрение следует модифицировать. Это будет сде-
сделано в следующей главе. Как показывает более деталь-
детальное рассмотрение Нозьера и Пайнса [14] и Адлера [15],
для блоховских электронов действующее поле равно
макроскопическому.
Электромагнитное поле определяется векторным по-
потенциалом
А (г,t) = 2Re[A1e'4''r-'<e»' + А2е'ч«-г-'ш«(]. B.35)
В этом параграфе волновой вектор поля обозначается
через q, так как обозначение к мы оставляем для волно-
волнового вектора блоховского электрона. Ниже будет ис-
использоваться кулоновская калибровка, в которой ска-
скалярный потенциал равен нулю, ср = О
Е = LJ9*. H = VxA. B.36)
Гамильтониан взаимодействия в случае одного нереля-
нерелятивистского электрона равен
2mc
i -s-VxA-f
2тс2
A-A.
B.37)
Оператор плотности тока для электрона с зарядом +е
равен
j (г«) = +-^{[б(г-го) (Р ~ТА) + (Р ~Т АN (Г~Го)]+
+ 2i [б (г - г0) (р X s) — (р х s) 6 (г - г0)]}, B.38)
где оператор положения определяется следующим об-
образом:
б (г — г0) = |го> <го|.
В последующем изложении плотность спинового тока не
учитывается и член гамильтониана, зависящий от спина,
будет опущен. Цель расчета — найти компоненту плот-
плотности тока с частотой соз = coi + со2. Из формулы B.35)
следует, что пространственное изменение этой компо-
74
ГЛАВА 2
ненты описывается фактором expjfqi + Яг)-г. Наша
задача периодична не только во времени, но и в про-
пространстве, поэтому мы применим фурье-преобразова-
ние к пространству волновых чисел:
{,Oe-'4-r'dro. B.39)
Поскольку явная зависимость j от времени определяется
векторным потенциалом А(/), следует различать три ча-
частотные фурье-компоненты этого оператора:
j Di + q2>0) = + —
j (qx + q2, to,)=
me
B.40)
me
¦ Лае-'ч«-г.
Фурье-компонента плотности тока с частотой соз = coi +
+ 0J, квадратичная по амплитудам поля, дается выра-
выражением
n n'
+ qs.
>s)Jn-«i
W Un (
-q».o)
q2.
B.41)
Матричные элементы возмущения Ж КОг по блоховским
волновым функциям
равны
Э?пп' (©1. s) = б (к - к' - q, 2) X
B.42)
К) =
б (k-k'-qx -q2)X
где
X (nk\n'k')A1-A2,
(n'k'\O\nk) = —
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕИ 75
(интегрирование производится по единичной ячейке с
объемом V). Фурье-компоненты матрицы плотности,
входящие в B.41), можно рассчитать теперь с помощью
рекуррентного соотношения B.25). В нулевом порядке
матрица плотности определяется распределением Фер-
Ферми—-Дирака для термодинамического равновесия:
Pan =
e(Wn-EF)/kT+l ¦
B.43)
Подставляя все члены в B.41), получаем явное выраже-
выражение, идентичное формулам в работах Ченга и Миллера
[12], формула A3), и Дюкуэнга [16]:
г. <*>з) ) =
Е
(n,U\p
n'nk
,
; n'-k-q, -
Гп' .k - q. -
-- 2 (••
tn \
г,
X (п' ,к—i
\k-q,-q
p-Tft».n»'.k-a.|x
n", к — q
-„):
-7^-Т1
n,k
%'k - q,; «'. к - q, - q2 + ;Г«',п")
B.44)
76
ГЛАВА 2
где через 2' обозначен член, комплексно сопряженный
предыдущему члену с обратными знаками ©ь ©2, Я\ и #2
(Р — оператор перестановки).
Применим сначала это выражение к газу свободных
электронов. Эта система имеет только одну энергетиче-
энергетическую зону. Передача энергии при столкновении фотона
оптического диапазона с электроном ничтожна:
hvnk.nk' = ~ [k2- (к - q,,2J] « /ко, ,2.
Если затухание также мало, то знаменатели в B.44)
не зависят от к. В случае поперечных электромагнитных
волн, распространяющихся в направлении а, волновой
вектор q имеет только а-компоненты. Так как для сво-
свободного электрона unk постоянно, матричный элемент
Рр + hkp — '/2^1 р, входящий в первое слагаемое B.44),
равен Щ. После суммирования по всем kp слагаемые с
k$ и —&р взаимно уничтожаются. По той же причине
последнее слагаемое в формуле B.44) исчезает. В ре-
результате получаем следующее выражение:
/„
©2) -
V
8т
2
2т2ш1ю2
X
X
'2<x
2m2c<ai(a2
B.45)
где N—число электронов проводимости. При ы\ = ©о
это выражение идентично классическому
/ B©) = — Nez Bo>),
где 2B©) определяется формулой A.6) при Г = тг' = 0.
Вернемся к дипольному приближению, положив в
B.44) qi = q2 = 0. Ясно, что в этом приближении для
свободных электронов получается нулевой результат.
Матричный элемент типа
(п", к — цг — q21 ра
h (ka — — qи — -у
п, к)
КВАНТОВАЯ ТЕОРИЙ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕЙ 71
в B.44) можно заменить в этом приближении матрич-
матричным элементом для межзонного вертикального пере-
перехода
(Я", k | Ра | П, k) = p"n, n = j Un"kPaUnkdr. B. 46)
Плотность нелинейного тока принимает вид
( /« (®з) У = 0<iPv (юз == Ю1 "f" ^г) ^Р O^i) ^v (®a) > (^*
где тензор нелинейной проводимости равен
Pnn'Pn'n"Pn"n
Pnn'Pn'n"Pn"n
iVn'n (
Pnn'Pn'n"Pn"n
[(о, + «в, - «„.„, (*) + Кп.п. (*)] [Bl - «„.„ (*) + /Гя.„ (*)]
B.48)
Здесь суммирование по к заменено интегрированием.
Зависимость всех матричных элементов в выражении [ ]
от к подразумевается. Интегрирование по зонам можно
в определенном смысле рассматривать как учет неодно-
неоднородного уширения резонансных линий ©П'л"- Предпо-
Предполагается, что зоны п" не заселены.
Если среда имеет центр инверсии, то можно так опре-
определить функции и, что un.k (r) = un, -k (—г) и поэтому
Рп-п(к) = — P%i'(—k)- Следовательно, тензор аар1
глАвА i
равен нулю в дипольном приближении. Можно показать
обычным способом, что в этом же приближении (при по-
постоянстве векторного потенциала в пределах единичной
ячейки) имеют место следующие равенства:
тс
=m
~~lpnn'- B.49)
Поэтому недиагональные матричные элементы импульса
можно заменить соответствующими матричными элемен-
элементами дипольного момента. В этом же приближении про-
проводимость связана с восприимчивостью следующим об-
образом:
jNL((o3) = а: ЕЕ = -^- = - щ>зХ: ЕЕ. B.50)
Если выражение B.48) просуммировать по всем элек-
электронам заселенной зоны, то оно должно быть полностью
эквивалентно формулам B.21) и B,22) приложения III.
Эту эквивалентность можно доказать в общем виде,
что впервые было проделано Гепперт-Майер [17]. Рас-
Рассмотрим гамильтониан одноэлектронной системы, раз-
размеры которой малы по сравнению с длиной волны:
' = f- + V (г)
2т
тс
P-A(r,
2mc2
r,t). B.51)
Соответствующий лагранжиан равен
2 с '
Добавление к нему полной производной по времени не
изменит уравнений движения системы, поэтому лагран-
лагранжиан
—
с
dt
B.52)
эквивалентен первоначальному. Эквивалентный гамиль-
гамильтониан равен
^' = TL+l/C-) + -r-^^-. B.53)
lm с dt
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕЙ 79
Если пространственное изменение мало, то полную про-
производную по времени можно заменить частной производ-
производной, так что в дипольном приближении эквивалентный
гамильтониан равен
1m
(г) — е г • Е =
B.54)
Фьютак [18] (см. также [19]) обобщил это доказатель-
доказательство и показал, что в высшем приближении эквивалент-
эквивалентный гамильтониан действительно соответствует мульти-
польному разложению
^ког = — Р.Е — М.Н —Q:VE+..., B.55)
где Q — квадрупольный момент. Это выражение не учи-
учитывает полностью установление диамагнитной энергии в
системе, что, однако, не имеет значения для обсуждае-
обсуждаемых здесь нелинейных эффектов.
С физической точки зрения это разложение весьма
удобно в случае локализованных волновых функций. Та-
Такими функциями описываются валентные электроны мо-
молекул жидкостей и газов, групп молекул в твердых те-
телах и локализованных парамагнитных ионов. Матрицу
плотности можно разложить в комбинированный ряд
по степеням Е, Н и VE . Средние значения электриче-
электрического дипольного момента, магнитного дипольного мо-
момента и электрического квадрупольного момента можно
представить в виде суммы фурье-компонент, каждой из
которых соответствует комбинированный ряд по степе-
степеням амплитуд электрического и магнитного поля и их
градиентов. Эта процедура не представляет принци-
принципиальных трудностей, но довольно громоздка. Члены,
связанные с магнитным дипольным и электрическим
квадрупольным моментами, описывают генерацию второй
гармоники в кристаллах с центром инверсии; эксперимен-
экспериментально этот эффект наблюдался в кальците. Полный пе-
перечень всех квадратичных членов для электрического
диполя, магнитного диполя и электрического квадруполя
недавно был дан Адлером [13].
ГЛАВА 2
§ 5. Нелинейные восприимчивости, описывающие
процессы типа комбинационного рассеяния "
Плотность тока, пропорциональная третьей степени
амплитуды поля, может быть получена в принципе ана-
аналогичным образом. Ввиду сложности выражения, а так-
также ввиду того, что кубические члены имеют заметную
величину лишь для электродипольных матричных эле-
элементов, эти члены высшего порядка малости рассматри-
рассматриваются далее только в дипольном приближении. Выра-
Выражение для поляризации с частотой третьей гармоники
уже было получено в гл. 2, § 3. Если на систему дейст-
действует поле с двумя частотами, то возможно появление
большого числа членов с комбинационными частотами;
из них мы рассмотрим лишь те частоты, которые близки
к резонансу. Обозначим через wv колебательную резо-
резонансную частоту системы. Пусть к системе приложено
бигармоническое поле с частотами сод (например, излу-
излучение лазера) и cos, близкой к cot — av (индекс s соот-
соответствует стоксовой частоте). При вычислении воспри-
восприимчивости оставим только члены, имеющие знаменатель
вида
Д = coL — cos — a>v -f iVv
(предполагается, что все другие частоты ©L, соя, wL + cos
и т. д. далеки от резонансных частот системы). Эффекты
типа комбинационного рассеяния в случае систем с дву-
двумя и тремя квантовыми уровнями рассчитаны в прило-
приложении III.
Здесь мы рассмотрим предложенную Шеном упро-
упрощенную модель, отражающую основные физические осо-
особенности молекулярного комбинационного рассеяния.
Пусть \g > основное и \п > первое возбужденное
электронные состояния. Колебания ядер разложим по
нормальным типам колебаний. Будем рассматривать
основное |0> и первое возбужденное |1 > колебатель-
колебательные состояния только одного нормального типа. В га-
'> В литературе указанные восприимчивости называют также
восприимчивостями рамановского типа, или рамановскими воспри-
имчивостями. Далее в этой книге они также называются комбина-
комбинационными восприимчивостями. — Прим. ред.
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕП 81
Ьш,
Ьша
¦9'
Фиг. 5. Переходы комбинационного типа в модели с двумя элект-
электронными и двумя ядерными колебательными уровнями.
мильтониан взаимодействия входят когерентное возму-
возмущение за счет двух световых волн, действующих на элек-
электрон, и взаимодействие между орбитальным движением
электрона и колебаниями ядер:
= — exEL (coL) — exEs (cos)
B.56)
Четыре рассматриваемых уровня энергии показаны
на фиг. 5. Из-за орбитально-колебательного взаимодей-
взаимодействия частоты колебаний в состояниях \g) и \п) раз-
6 Н. Бломбергеи
82
ГЛАВА 2
личны. Пусть отличны от нуля только следующие мат-
матричные элементы:
Матричные элементы гамильтониана взаимодействия
имеют следующие фурье-компоненты:
„«»«>
lrig'
— ding — CXngCS*
V— exne)
(~ ex
ag)
%<0„
B.57;
аналогичные выражения имеют место и для частоты coL.
Эти равенства основаны на приближении Борна — Оп-
пенгеймера и на том факте, что среднее расстояние меж-
между колебательными уровнями
h®v=—h (cog-go -f ffln'n»)
много меньше расстояния между электронными уровня-
уровнями fr(x}ng. Равенства B.57) означают, что дипольный мо-
момент, а следовательно и электронная поляризуемость
зависят от ядерной колебательной координаты парамет-
параметрически (это подробно показано Плачеком [20]).
Если предположить, что первоначально молекула на-
находилась в основном колебательном состоянии, pgog» =
= I, то матрица плотности в первом, линейном прибли-
приближении равна
P
B.58)
ft (со
L,s'
Во втором приближении удерживаем только члены с ре-
резонансным знаменателем
Квантовая теория иелиньйных восприимчивостеи 83
ь-2
-f
un«g»
B.59)
Компонента p^2,^ (соь—cos) или находится не в резонан-
резонансе, или тождественно равна нулю. Из этого выражения
можно в свою очередь определить фурье-компоненты
Р$*(-со5)( p%((oL), pj&.
Имеем, например,
(- cos) = -
D- cos -f со
(СО/. — ffln-g
D-сос 4-со
. — cos) и p^go(coL—2cos).
у-1 V~V B) /
») ЛлГ Pg'g»(C0L~-C0s),
(«L —C0s),
B.60)
^
,)
pirn» (— C0s) = + h~l (CO/. — 0nog»)~' ^gonoL p^go (CO/. — C0s).
Наконец, находим спектральную компоненту нелинейной
поляризации с частотой cos:
< />NL (cos) > = < PNL (- cos) > •= N Sp {{ех)УЩ- cos)} =
-XsK^cot-cot+co,)!^!2^, B.6J)
где «стоксова» восприимчивость равна
X
6*
у — —
As
xngXgn
mL-'°n°go
WL — cos - ц
CO, U)
'g'g»
г
'go
g°
I
2
x
'"g'g»
•^reg-^g-n
4-
B.62)
84
ГЛАВА 2
{ц определяется соотношением B.57); N— число моле-
молекул в 1 см3). Заметим, что при точном резонансе, coj, —
— cos— cog-g» =0, Xs — чисто мнимая отрицательная ве-
величина, что соответствует отрицательному поглощению
(т. е. усилению) на частоте cos, пропорциональному ин-
интенсивности излучения с частотой (Ol\El\2. Аналогично
находим поляризацию на частоте u>l-
Р (<й?_) = ~/_ b^\hs\. (z. Do)
На частоте соь имеется положительное поглощение, про-
пропорциональное интенсивности поля с частотой cos. Если
бы первоначальные населенности колебательных уров-
уровней были инвертированы (p^'g' = 1 вместо р^„ = 1),
то знак Xs был бы обратным. В этом случае положитель-
положительное поглощение имело бы место на частоте cos, а усиле-
усиление— на частоте col. Однако в обычных условиях насе-
населенность возбужденного колебательного уровня незна-
незначительна.
Нелинейная поляризация с антистоксовой частотой
соа, вызванная полем с частотами cos и соь, равна
Теперь в гамильтониане B.56) нужно учесть еще поле
Еа с антистоксовой частотой. Можно рассчитать нелиней-
нелинейную поляризацию, обусловленную резонансными процес-
процессами типа комбинационного рассеяния на каждой из
трех частот cos, col и соа в присутствии трех полей Es, EL
и Еа. Обозначим через %*а «антистоксову» восприимчи-
восприимчивость, получаемую из формулы B.62) при замене соь на
©а и cos на col. Эта величина %а* будет отличаться от %s
только знаменателями слагаемых под знаком модуля
в B.62). Можно показать непосредственным расчетом,
что восприимчивость в равенстве B.64) можно выразить
как (Xs X«) '/г • ^ тех случаях, когда дисперсией можно
пренебречь, (%'s %a) v* = X*-
Следует упомянуть, что в нелинейных восприимчиво-
стях рассматриваемого типа имеются и другие, нерезо-
нерезонансные слагаемые. Несмотря на отсутствие резонанса,
они могут иметь заметную величину из-за того, что вхо-
-I
01
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕИ 85
дящие в них матричные элементы не обязательно связа-
связаны с энергетическими уровнями колебаний ядер, и поэ-
поэтому не содержат фактора приведения t\. Дисперсией
этой нерезонансной части восприимчивости можно пре-
пренебречь, поскольку расстояние до возбужденных элек-
электронных уровней много больше чем юо—cos. Соответст-
Соответствующую часть поляризации можно характеризовать
единственной нерезонансной действительной восприимчи-
восприимчивостью %NR.
Таким образом спектральные компоненты нелиней-
нелинейной поляризации можно представить следующими равен-
равенствами, которые проверяются непосредственным расче-
расчетом [аналогичным расчету, с помощью которого была по-
получена формула B.62)]:
(/.: + 7.NR) EL| Es
Е1Ра, B.65)
EL\Ea\* +
E'LEsEa, B.66)
?ш B.67)
P Ю = (X.
Отсюда следует комплексное соотношение симметрии
(xsXa)v= = 1 К - 2coL-co«) ^ 7;- (Шв = 2coL-cos). B.68)
Последнее соотношение является иллюстрацией сле-
следующего правила, выполняющегося в случае, когда
член, описывающий затухание, имеется только в одном
знаменателе. Когда перестановка частот в аргументе
нелинейной восприимчивости вызывает изменение знака
комбинации частот, близкой к резонансной, следуе1
брать комплексно сопряженное значение %. В аргументе
x(cos = 2col — <Ba) к резонансной частоте близка частота
соь — соа, а в %*((оа — 2о>ь — cos) — частота aL — cos = —
— (соь — toa). Поэтому производится операция комплекс-
комплексного сопряжения. Подробное рассмотрение вопроса о
том, как член затухания iTn'n соответствует резонансу
col — bis — bin'n, подтв?рждает это правило. Можно пред-
предположить, что это соо? ношение справедливо и для не-
86
ГЛАВА 2
диагональных элементов тензоров четвертого ранга при
одновременной перестановке индексов и частот:
По существу это является применением соотношений Он-
загера, которые можно обосновать, исходя из существо-
существования диссипативной функции, описывающей стационар-
стационарные потери. Першан [21] рассмотрел этот вопрос; при
этом он не устанавливал, однако, связи между запасен-
запасенной свободной энергией и диссипативной функцией так,
как это было сделано здесь с помощью действительной
и мнимой частей одной и той же комплексной восприим-
восприимчивости.
Фактически Першан, а также Батчер и Мак-Лин [22]
ввели комплексные восприимчивости или проводимости
для среды без потерь. Часть тензорной восприимчивости
с нечетным числом индексов, относящихся к магнитном>
полю или намагниченности, чисто мнимая. Часть, кото-
которая умножается на четное число компонент магнитного
поля, в случае отсутствия потерь действительна; послед-
последнее следует из рассмотрения симметрии по отношению
К изменению знака времени.
Поэтому чисто электродипольные восприимчивости
действительны при отсутствии потерь. Следовательно, со-
соотношения симметрии, подобные B.68), описывают связь
между свободной энергией и диссипативной функцией.
В линейном случае связь между действительной и мни-
мнимой частями восприимчивостей выражается в виде соот-
соотношений Крамерса — Кронига. Поскольку мы ограничи-
ограничиваемся рассмотрением только тех частей нелинейной вос-
восприимчивости, которые содержат лишь один комплекс-
комплексный знаменатель, они удовлетворяют соотношениям Кра-
Крамерса—Кронига, справедливым в линейном случае
(фиг. 6). Только для этих частей восприимчивости спра-
справедливы перестановочные соотношения симметрии B.68).
Восприимчивости, описывающие процессы типа комбина-
комбинационного рассеяния, и относятся к этой категории.
Мнимые части членов с %s и %а в B.67) описывают
процессы комбинационного рассеяния, показанные на
фиг. 5. Действительная часть %s описывает параметриче-
параметрический процесс — одновременное рассеяние квантов с ча-
КВАНТОВДЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕЙ
87
стотами соь и cos. Интерференция всех этих процессов
рассеяния высшего порядка в однородной среде приво-
приводит к изменению показателя преломления на частоте cos,
пропорциональному |?l|2. а на частоте соь — пропорцио-
пропорциональному \ES\2.
Фиг. 6. Дисперсия комплексной комбинационной восприимчивости.
Стоксова частота ш.=ш2—ш увеличивается справа налево. Выполняются
соотношения Крамерса — Кронига.
Действительные части членов, пропорциональных
(хд*)f/i, соответствуют процессу рассеяния, при кото-
котором 2 кванта с частотой col превращаются в квант и>8 и
квант Фа (или обратному процессу). Интерференция всех
процессов рассеяния приводит в однородной среде к гене-
генерации лазерным лучом частот cos и соа (или к обратному
процессу). Интересна физическая интерпретация мнимых
частей членов, содержащих (y.sX*)Vl и (хДо)>/2> Эти
члены соответствуют интерференции двух показанных на
фиг. 5 комбинационных процессов с одинаковыми началь-
начальными и одинаковыми конечными уровнями. Эти интер-
интерференционные члены могут или увеличить или уменьшить
суммарную скорость перехода между колебательными
уровнями. В первом случае интерференция приводит,
к увеличению усиления на частоте со., и поглощения на (оа,.
88
ГЛАВА 2
во втором — к уменьшению усилия на cos и поглощения
на (ла- Какой именно вариант реализуется — зависит от
относительных фаз EL, Es и Еа. Существенная роль фа-
фазовых соотношений между взаимодействующими волна-
волнами показывает, что к квантовой интерпретации рассмат-
рассматриваемых процессов следует подходить с осторожностью.
Если фазы заданы, число квантов определено неточно.
В частности, было бы ошибкой полагать, что не может
быть усиления па антистоксовой частоте. Корректное
квантовое описание в этом случае возможно лишь с при-
привлечением для осцилляторных состояний поля модели
связанных волновых пакетов. Вместе с тем очень хоро-
хорошим приближением является описание этих явлений
классическим методом связанных волн. Этот метод бу-
будет рассматриваться в гл. 4.
§ 6. Резонансные эффекты высших порядков
В большинстве случаев метод разложения в ряд по
возрастающим степеням амплитуд поля адекватен зада-
задачам, возникающим при изучении нелинейных эффектов
в оптическом диапазоне. Но иногда следует удерживать
все степени компонент поля, частоты которых близки
к резонансу. Такое положение возникает обычно при ис-
исследовании магнитного резонанса на радиочастотах и
СВЧ. Наиболее известным примером является эффект
насыщения двухуровневой системы при резонансе
i —Pu =
B.69)
Здесь фурье-компонента с нулевой частотой диагональ-
диагонального матричного элемента выражена через все степени
величины \Ж\% («12) |2.' При когерентном возмущении
всегда можно удержать все степени одной фурье-ком-
поненты с помощью перехода к вращающейся системе
координат. Этот метод подробно изложен в книгах по
магнитному резонансу.
Если из условий резонанса можно априори решить,
какие фурье-компоненты матрицы плотности будут мак-
максимальны, то всеми остальными фурье-компонентами в
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСП РИ ИМЧ И ВОСТЕИ 89
уравнении движения B.25) для матрицы плотности
можно будет пренебречь.
После этого стационарный отклик опишется системой
Ш линейных алгебраических уравнений относительно $1
оставшихся фурье-компонент. В случаях двух- и трех-
трехуровневых систем эта процедура иллюстрируется в при-
приложении III, § 3 и 4, где компоненты матрицы плотности
выражены через все степени возмущения.
§ 7. Соотношения Крамерса — Кронига
Дисперсионные соотношения, существующие для ли-
линейных восприимчивостей, имеют аналоги и в нелиней-
нелинейном случае. К сожалению, полезность их ограничивается,
по-видимому, случаем генерации второй гармоники. Это
было отмечено Прайсом [11]; мы в данном параграфе бу-
будем следовать изложению Касперса [23].
Нелинейный стационарный отклик низшего порядка
системы, на которую действует возмущение, определится
последним членом формулы B.10), если верхние пределы
интегрирования заменить в нем на бесконечности. Для
возмущения, равного
можно сразу найти стационарный отклик на суммарной
частоте, если провести статистическое усреднение по ан-
ансамблю и по различным процессам затухания:
со оо
= - ¦& J* J
J
e-l*tX
x{e-l*tXSp[[p0,&,(-t—c)], 9f(-
S>y(-f-T)],#n-O]$>*}. B.70)
Если ©2^- «i, то выражение для cog~ = со2 — coi получает-
получается заменой coi на —©ь Рассмотрим %(оа? ) = %(соз) как
одну функцию, определенную для положительных и отри-
90
ГЛАВА 2
дательных значений частоты соь Поскольку %(соз) имеет
вид
дисперсионные соотношения могут быть формально полу-
получены, исходя из следующего весьма общего условия: %
должна быть аналитической функцией в нижней полу-
полуплоскости комплексной плоскости соь
, так как yft//(oo,co2) =0
B.71)
(перечеркнутый знак интеграла означает, что интеграл
берется в смысле главного значения).
Полезность аналогичного соотношения для действи-
действительной и мнимых частей линейной восприимчивости обу-
обусловлена тем, что его правую часть можно разделить на
два интеграла с пределами 0, + оо, а также тем, что
действительная и мнимая части этих интегралов каждая
в отдельности представляет интерес. В нелинейном слу-
случае это не так. Функцию х(юз) следует разделить на ча-
части, имеющие физический смысл
X (со+ = со2 + со,' > 0), у (Щ = wi — w2 > 0) и
Х(—со--со2 —оз;>0).
Разбивая ось частот со,' на три соответствующих уча-
участка, приходим к трем интегральным соотношениям
р2
(О
B. 72)
КВАНТОВАН ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕЙ
91
(~М3 ="'2
[выражение для %(—coj ) получается из последнего со-
соотношения при перемене местами ©i и со2]. Эти равенства
связывают действительную часть восприимчивости на
суммарной частоте с мнимыми частями восприимчиво-
стей на суммарной и разностной частотах. В случае фик-
фиксированного соотношения между ©i и сог и в особенно-
особенности при со,' = оJ формулы упрощаются. Действительная
и мнимая части восприимчивости, описывающей генера-
генерацию второй гармоники, связаны следующим образом:
B.73)
Эти соотношения не имеют, однако, такой ценности, как
аналогичные соотношения для линейного случая, несмо-
несмотря на их формальную идентичность. Мнимая часть соот-
соответствует здесь не поглощению, а просто компоненте
второй гармоники, имеющей фазу 2cpi + л/2, где epi — фа-
фаза волны основного излучения. Генерация второй гармо-
гармоники осуществляется, как правило, лишь на нескольких
фиксированных частотах, на которых имеются достаточ-
достаточно мощные лазерные генераторы основного излучения.
Если бы измерения интенсивности второй гармоники,
пропорциональной |хBсо) |2, были проведены в широком
диапазоне частот, то дисперсионные соотношения позво-
позволили бы определить относительные фазы первой и второй
гармоники на каждой частоте. Следует отметить, одна-
однако, что эта информация не представляет большого инте-
интереса.
92
ГЛАВА 2
§ 8. Квантование полей
В предыдущем изложении восприимчивости были оп-
определены с помощью полуклассического подхода, при ко-
котором электромагнитные поля описываются классически.
Амплитуда и фаза волны описываются при этом как
с-числа. Этот подход очень полезен, так как позволяет
рассматривать явления, в которых существенны относи-
относительные фазы взаимодействующих волн. Число квантов
достаточно велико, так что фазы могут быть определены.
Нас не интересует переход из одного состояния электро-
электромагнитного поля с заданным числом квантов в каждом
осцилляторе поля в другое состояние, в котором число
квантов в одном или более осцилляторах изменилось на
1, 2 или 3. Такие процессы можно описывать с помощью
вероятностей перехода в единицу времени или сечений
рассеяния и поглощения.
Основной интерес представляет квазистационарное
состояние электромагнитных полей, которое образуется в
результате интерференции большого числа процессов
рассеяния. Обе ситуации, конечно, связаны, так как опи-
описываются с помощью одних и тех же матричных элемен-
элементов гамильтониана взаимодействия между электромаг-
электромагнитным полем и средой. Данная проблема присуща не
только нелинейной оптике. Она хорошо известна и в ли-
линейной оптике, где линейная восприимчивость (или пока-
показатель преломления) связана с сечениями релеевского
рассеяния и поглощения. Этот вопрос кратко обсуждал-
обсуждался Крамерсом [24] и Гайтлером [25]. Настоящий параграф
посвящен этой же проблеме в нелинейном случае.
ПРОЦЕССЫ НЕЛИНЕЙНОГО ПОГЛОЩЕНИЯ
И РАССЕЯНИЯ
Вероятность перехода для процесса двухквантового
поглощения была рассчитана Гепперт-Майер [17], а про-
процесс рассеяния с участием трех квантов рассматривался
Блзтоном [26] и Гуттингером [27]. Поле в вакууме пред-
представляется в виде линейной комбинации плоских моно-
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕЙ 93
хроматических бегущих волн:
А (г, t) = "V [<?! U) А. (г) + о* (Л А*
X
где
а динамическая переменная равна
B.74)
B.75)
B.76)
Переменные qx и q*x не эрмитовы и не сопряжены кано-
канонически, однако можно перейти к каноническим дейст-
действительным переменным:
Q + I
^х = Qx = -"°x (<7x-<?!)¦
Гамильтониан вакуумных осцилляторов равен
B.77)
B.78)
B.79)
Через <7Х и <7Х* обозначены соответственно операторы
рождения и уничтожения фотонов. Их единственные не-
неравные нулю матричные элементы равны
Волновые функции осцилляторов ортогональны:
2@,
и удовлетворяют соотношениям коммутации
4x41 — Я]Лх=-2^7 &&¦
B.80)
B.81)
Пусть \а) и \Ь) представляют два невырожденных
собственных состояния гамильтониана материальной си-
системы. Гамильтониан взаимодействия между материаль
94
глАЬл 2
ной системой и полем B.37) имеет следующие неравные
нулю матричные элементы:
(я, + 1) х
(а;лх + 1; Ь,пх) - —^
B.82)
х
Слагаемое в B.37), содержащее А2, где
+ Ч&К-К)'
имеет следующие матричные элементы:
Х(пх + 1I/2(«д+1)
и аналогичные выражения для
5Г(а,ях+1,я|1+1;6,ях,/1в) и
B.84)
Составной матричный элемент второго порядка, со-
соответствующий переходу кванта от осциллятора "К к ос-
осциллятору р. при одновременном переходе материальной
системы из состояния \а) в состояние \Ь), равен
У'(Ь,пх,п + 1; с,пх,пц,)Ж'(с,пх,п ; а,пх + 1,пц)
f_
X
X
Г B.85)
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТИ! 95
Если произвести интегрирование по распределению
конечных состояний материальной системы, то пропор-
пропорциональная времени вероятность вынужденного комби-
комбинационного рассеяния определится с помощью «золотого
правила»:
^ A2j^|2^(vx-v(i). B.86)
В силу затухания и из-за других случайных возмущений
материальной системы форма линии определяется нор-
нормированной лоренцевой кривой:
л- / \ 21 а{, Ш .« Q7\
?Г I V I = , V = . (Z. о/ I
Будем считать для простоты, что обе волны поляризо-
поляризованы в направлении х и выполнено условие резонанса
шЬо = сох—сод. При резонансе отнесенная к единице
времени вероятность вынужденного комбинационного
рассеяния в дипольном приближении равна
\\(п +nJL
B.88)
Сечение рассеяния можно определить следующим обра-
образом. Пусть число падающих квантов п\ -\- 1 заключено в
объеме V. Число квантов палающих в 1 сек на 1 см2 за-
заключено в объеме V = с. Вероятность перехода под дей-
действием потока, равного одному кванту на 1 см2 в 1 сек,
есть сечение рассеяния:
м =
B.89)
где Яд —поток квантов со стоксовой частотой мд, па-
падающих на 1 см2 в 1 сек.
Сечение рассеяния непосредственно связано с ослаб-
ослаблением интенсивности на единицу длины, которое в свою
очередь можно связать с мнимой частью восприимчиво-
восприимчивости. Рассмотрим разреженную среду с iV0 молекул в 1 см*
96
ГЛАВА 2
и показателем преломления, близким к единице (рас-
(рассмотрение легко обобщить и на плотные среды). Сечение
линейного поглощения аПОгл связано с ослаблением Ин-
Интенсивности соотношением
/ (z) = / @) Г"™1* = / @) е-4ма/с^г.
Аналогично ослабление луча с частотой сох (мы счи-
считаем ее частотой лазера), обусловленное вынужденным
комбинационным рассеянием, связано с активной частью
нелинейной поляризации,
-^~(~i:)\EJ- B-90)
Поток мощности на стоксовой частоте сод при
квантов Пд равен
числе
B.91)
Выражение для вектора Пойнтинга содержит множитель
'/гтг, а не УвЯ в силу нашего определения комплексных
амплитуд. Комбинируя B.89) — B.91), получаем, нако-
наконец, выражение для мнимой части комбинационной вос-
восприимчивости при резонансе
B.92)
Это выражение согласуется с формулой B.62), если сум-
суммирование по с проводить только по двум уровням п° и
п' (см. фиг. 5) и если в знаменателе B.62) учесть усло-
условие резонанса соь — cos = cog'g», которое идентично ус-
условию сох — сод = (Аъа- Предполагается, что уровни с не
находятся в резонансе ни с одной из рассматриваемых
частот. Это требование необходимо для справедливости
соотношений B.62), B.85), а следовательно и B.92)
Итак, между сечением когерентного комбинационного
рассеяния и мнимой частью комбинационной восприим
чивости имеется такое же соответствие, как и между
сечением однофотонного когерентного поглощения и мни-
мнимой частью линейной восприимчивости.
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕИ 97
Аналогичным образом можно рассмотреть случай
двухфотонного поглощения. В этом случае вместо B.88)
получаем почти идентичное выражение, в котором— а>д
заменено на +(°и • Условие регонанса теперь имеет вид:
«и + сод = соьа. Если Яд в B.89) опять равно потоку
квантов на частоте сод, то Пд + 1 в B.88) следует заме-
заменить на Пц . Сечение двухфотонного поглощения связано,
конечно, с мнимой частью восприимчивости, определяе-
мой из соотношений
P"L (%) = V (»д = % + «X - «О ЕД | Е, Г •
Заметим, что мнимые части, получаемые из обоих соот-
соотношений, равны, поскольку имеется одновременное по-
поглощение на обеих частотах. Так как резонансная часто-
частота сох. + сод имеет одинаковый знак для обеих восприим-
чивостей, это согласуется с правилом, сформулирован-
сформулированным в § 5.
Читатель должен был заметить, что при переходе от
B.88) к B.89) единица в (Яд+1) была опущена. Она
соответствует, конечно, спонтанному комбинационному
излучению при числе начальных стоксовых квантов п ц
равном нулю. Это излучение происходит во все типы ко-
колебаний [i с частотами сод, близкими к сох — а>ьа- В этом
случае плотность конечных состояний определяется не
g(v), а плотностью осцилляторов поля. Заменяя g( ч\ —
—"'и) в формуле B.86) на Vc~3v^d?2—плотность типов
колебаний, имеющих одинаковые поляризации, получаем
выражение для дифференциального сечения спонтанного
комбинационного рассеяния do/dQ, отнесенного к единич-
единичному телесному углу, к единице объема среды и к одной
поляризации излучения '>.
B.93)
dQ.
') Нормировка в этих расчетах представляет следующую труд-
трудность. Сечение рассеяния можно нормировать к одной молекуле.
Волновая функция молекулы, входящая в соотношения B.82), нор-
нормирована к единице. Если в единице объема имеется iV0 молекул,
7 Н. Бломберген
98
I ЛАВА i
Сравнение B.92) и B.89) с B.93) приводит к соотноше-
соотношению между сечением вынужденного рассеяния и сечени-
сечением некогерентного спонтанного рассеяния.
СЕЧЕНИЯ РАССЕЯНИЯ И НЕЛИНЕЙНЫЕ
ВОСПРИИМЧИВОСТИ
Связь между действительными частями нелинейных
восприимчивостей и сечением рассеяния сложнее. Сущ-
Сущность проблемы можно уяснить, рассматривая, например,
восприимчивость, определяемую соотношением
р KJ = х К = ®i + щ) EiEt>
или любую другую восприимчивость, являющуюся тен-
тензором нечетного ранга. Вероятность перехода (или сече-
сечение рассеяния) всегда содержит квадраты абсолютных
величин и поэтому всегда приводит к тензорам воспри-
восприимчивостей четного ранга. Возникающая трудность свя-
связана, очевидно, с тем, что полная определенность чисел
квантов в начальном и конечном состояниях поля пред-
предполагает полную неопределенность фаз.
Эта проблема возникает уже при определении дейст-
действительной части линейной восприимчивости в случае,
когда поле квантуется. Обычно делается попытка связать
линейную дисперсию с сечением релеевского рассеяния.
Это сечение получается из выражения для сечения ком-
комбинационного рассеяния заменой сод на «V = сох и кд
на кх'Фкх. Конечное состояние материальной системы
то сечение некогерентного рассеяния, отнесенное к единице объема,
в No раз больше. Однако волновая функция .потока первичных фо-
фотонов нормирована к объему V = с, так как нас интересует число
фотонов, проходящих через I см2 ,в 1 сек. Этот объем V и входит
в B.82) и B.88).
В электродипольном приближении сечение рассеяния проще все-
всего найти, конечно, исходя непосредственно из эквивалентного га-
гамильтониана B.54). Можно также преобразовать обычно приводи-
приводимое в учебниках выражение, содержащее оператор р,к виду B.88),
если учесть правила коммутации риг. Подробности этого преобра-
преобразования даны Крамерсом. . .
Предполагалось, что рассеяние происходит в плоскости, перпен-
перпендикулярной к направлению поляризации электрических полей.
Формулу B.88) нетрудно обобщить и на случай, когда векторы
электрических полей до и после рассеяния не параллельны.
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕЙ 90
совпадает теперь с исходным и должно обозначаться че-
через g, а не через а. Промежуточные состояния будем обо-
обозначать через п. Предполагается, что первоначальное
число квантов осциллятора поля кх< равно нулю. Диф-
Дифференциальное сечение релеевского рассеяния, отнесен-
отнесенное к одной молекуле в состоянии g и к единичному телес-
телесному углу при одной поляризации, согласно B.93), равно
+ <a\- <°ng
+ (r-**v)gn(f*\)ngl\\ B>94)
°>x + <W J I
Отсюда обычно делается заключение, что рассеянное
излучение соответствует полю излучения дипольного мо-
момента, индуцированного в молекуле исходным полем с
волновым вектором к\ и поляризацией ах . Поэтому
этот дипольный момент пропорционален сумме, стоящей
в B.94) под знаком модуля. Этот вывод, конечно, верен,
но он не позволяет определить фазу дипольного момента.
Имеется также другая причина, не позволяющая свя-
связать непосредственно линейную дисперсию с сечением
релеевского рассеяния. Рассмотрим сперва систему из
No молекул в единице объема, положение которых опре-
определяется векторами R*. Хотя фазы типов колебаний с за-
заданным числом квантов неопределенны, относительные
фазы в различных точках пространства определяются
формой соответствующих типов колебаний в B.75). Та-
Таким образом, сечение релеевского рассеяния этим еди-
единичным объемом равно
%*с*
N. I
2е
где в квадратных скобках должно стоять то же выраже-
выражение, что и в B.94). Если No молекул распределены рав-
равномерно в кристалле, то сумма по i в пределе большого
объема равна нулю для всех направлений вторичного из-
излучения, кроме тех, для которых удовлетворяется усло-
условие отражения Брэгга. На оптических частотах в случае
too
ГлАвА i
плотной среды это условие не может быть выполнено,
поскольку длина световых волн много больше расстоя-
расстояний между молекулами. В однородных кристаллах и
жидкостях релеевское рассеяние отсутствует; оно воз-
возможно лишь при наличии флуктуации плотности относи-
относительно среднего распределения, периодического или рав-
равномерного.
Может иметь место, конечно, эффективная интерфе-
интерференция излучения различных индуцированных диполей в
прямом направлении, для которого кх = кх'. Однако
именно для этого направления формула рассеяния све-
световых квантов B.95) неприменима. В этом случае конеч-
конечное состояние системы, состоящей из атомов и поля,
идентично исходному состоянию, так что вероятность пе-
перехода теряет смысл. Именно интерференция рассеян-
рассеянных вперед волн с падающей волной определяет показа-
показатель преломления среды, а тем самым и пути световых
лучей.
Эта же трудность возникает и при рассмотрении нели-
нелинейных восприимчивостей. Нелинейный дипольный мо-
момент системы без центра инверсии, определяемый соот-
соотношением
Р (газ) = 1 (Щ = «1 +
(щ) Ег (со2),
можно связать с сечением рассеяния процесса, в котором
участвуют три кванта и три типа колебаний вакуумного
поля кь к2 и к3. Начальное число квантов в этих трех ти-
типах колебаний равноя*,4~ U п*« + 1, 0. Можно рассчи-
рассчитать вероятность перехода в конечное состояние, в кото-
котором числа квантов равны л*,, я*„ tik, — 1. Далее, из-
излучение с частотой соз можно отождествить с излучением
дипольного момента, имеющего частоту соз. Рассматривая
элемент объема кристалла, содержащий большое число
элементарных ячеек, можно даже показать, что суммар-
суммарный матричный элемент рассеяния содержит [аналогично
B.95)] сумму вида
При достаточно большом объеме эта сумма не равна
нулю лишь при к3 = к] + к2. Последнее соотношение яв-
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕЙ JOJ
ляется условием сохранения импульса при столкновении
трех квантов. Решетка кристалла может поглотить толь-
только импульс, пропорциональный вектору обратной решет-
решетки, который соответствует по порядку величины импуль-
импульсу рентгеновских квантов. Итак, поскольку решетка
в отличие от изолированного атома не может сбалансиро-
сбалансировать импульсы квантов видимого света, то в случае до-
достаточно больших кристаллов импульс этих квантов дол-
должен сохраняться.
Если первоначально имеется также поле Е3 с часто-
частотой соз, то, как следует из полуклассического рассмотре-
рассмотрения, чрезвычайно важным является соотношение между
фазой поля Е3 и фазой нелинейной поляризации Р(щ),
определяемой фазами полей Ех и Е2. От этого соотноше-
соотношения зависит, будет ли волна Е3 расти, совершая отрица-
отрицательную работу над средой, или будет затухать, совер-
совершая положительную работу. Этот эффект, чувствитель-
чувствительный к относительным фазам падающих волн, не может
быть описан с помощью квантового рассмотрения, в ко-
котором числа квантов фиксированы.
Хотя рассмотрение процессов рассеяния, сечения ко-
которых содержат степени амплитуд полей, вдвое превы-
превышающие ранги искомых тензоров восприимчивостей, мо-
может дать большое количество информации, некоторые
явления, зависящие от фаговых соотношений между по-
полями, при этом безвозвратно теряются. Из полукласси-
полуклассического же рассмотрения тонкое соотношение между
действительными и мнимыми частями комплексных ли-
линейных или нелинейных восприимчивостей следует со-
совершенно естественно. Возникает вопрос, как можно
получить такую информацию из теории, в которой поле
квантуется?
КОГЕРЕНТНЫЕ КВАНТОВЫЕ СОСТОЯНИЯ. ПРЕДЕЛЫ
ПРИМЕНИМОСТИ ПОЛУКЛАССИЧЕСКОГО ПОДХОДА
Для этого необходимо, очевидно, включить фазовую
информацию относительно начальных состояний вакуум-
вакуумного поля в квантовое описание, которое должно воз-
возможно ближе следовать классическому описанию волн.
Это можно сделать, вводя волновые пакеты с минималь-
102
ГЛАВА 2
ной неопределенностью в смысле Эренфеста, являющиеся
подходящей суперпозицией состояний с заданными чис-
числами квантов. Этот метод позволяет получить наилуч-
наилучшее возможное в квантовой механике одновременное оп-
определение амплитуды и фазы. Можно показать, что для
состояния, являющегося суперпозицией состояний с раз-
различными п, распределенных по закону Пуассона, выпол-
выполняются следующие соотношения:
|л>
п=0
Г —гГ{—\п — 2'"ч>1
\е п(п) е
" L п\ J
оо
'= V
п=0
сп\*п, B.96)
Эти когерентные состояния, введенные еще Шрединге-
ром, недавно были подробно исследованы Глаубером
[28] и многими другими авторами. Мы не будем здесь
обсуждать связь восприимчивостей с этими состояниями.
Согласно принципу соответствия, в предельном случае
больших п получаемые с помощью B.96) результаты
должны совпадать с результатами полуклассической
теории. Следует иметь в виду, что почти все нелинейные
оптические явления наблюдаются при больших п. Типич-
Типичный импульс лазера с модулируемой добротностью со-
содержит около 1018 световых квантов, распределенных
примерно по 102—104 типам колебаний. Информация о
фазе может быть утрачена при прохождении луча лазе-
лазера через среду с потерями. По мере затухания волны
волновой пакет с минимальной неопределенностью, опи-
описываемый соотношением B.96), будет переходить в дру-
другие когерентные состояния с меньшими значениями п.
После того, как луч ослабится до значений п, меньших
10 или 5, значение фазы перестает быть точно опреде-
определенным.
В задаче о генерации гармоник квантовые флуктуа-
флуктуации надо учитывать лишь на начальной стадии процесса,
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕЙ JQ3
Нарастание интенсивности второй гармоники должно
начинаться с уровня нулевых колебаний. Вначале фаза
не определена, но, согласно принципу соответствия, лю-
любой волновой пакет с частотой 2со и заметным значением
< пBо) > будет иметь фазу <фBоо) > , близкую к
2<ф(со)>— я/2. При этом значении фазы отрицатель-
отрицательная работа, совершаемая полем над средой, имеющей
нелинейную поляризацию с фазой 2<ф(оо)>, будет
максимальна и будет происходить наиболее быстрое
нарастание волны гармоники. Далее, вследствие дис-
дисперсии согласование волновых пакетов будет нару-
нарушаться.
Все эти результаты, легко получаемые из полуклас-
полуклассической теории, должны следовать и из квантового опи-
описания, использующего когерентные состояния. Строгое
описание свойств квантовых шумов в нелинейных устрой-
устройствах и лазерах должно основываться на этих когерент-
когерентных состояниях. Большая работа в указанном направле-
направлении выполнена Люиселлом [29], а также Гордоном и др.
[30, 31].
Полуклассическая теория, используемая в настоящей
монографии, правильно и гораздо проще описывает не-
нелинейные оптические эффекты; исключением являются
случаи, соответствующие настолько низким уровням ин-
интенсивности, что становятся существенными квантовые
шумы. В этих случаях в полуклассической теории необ-
необходимо дополнительно учесть процессы спонтанного из-
излучения, описанные выше в этом параграфе. При этом
к когерентным полям добавляются поля со случайными
фазами и с амплитудами, характерными для спонтанно-
спонтанного излучения. Эти поля и являются «шумовыми источни-
источниками», которые добавляются к классическим полям.
Установление классического поля в лазере начинается с
уровня этого шума. Фаза поля в лазерном типе колеба-
колебаний априори неизвестна. По мере того как волна, распро-
распространяясь по образцу, нарастает и многократно возвра-
возвращается обратно за счет отражения от зеркал, устанавли-
устанавливается определенная (но заранее неизвестная) фаза. По
той же причине априори неизвестна и фага поля со сток-
совой частотой в лазере, использующем вынужденное
комбинационное рассеяние.
104
ГЛАВА 2
Можно полагать, что введение в полуклассическую
теорию некогерентных шумовых источников даст удов-
удовлетворительное (хотя и не строгое) описание всех явле
ний, имеющих практическое значение.
КВАНТОВАЯ ТЕОРИЯ ЗАТУХАНИЯ
В заключение рассмотрим в общих чертах теорию ре-
релаксации матрицы плотности при взаимодействиях систе-
системы с квантованными случайными полями. Однородное
уширение оптических линий часто обусловлено спонтан-
спонтанным излучением фотонов или фононов. Фононное поле
можно проквантовать таким же образом, как и электро-
электромагнитное поле. Для упрощения вычислений рассмотрим
только два энергетических уровня \а > и \Ь > гамильто-
гамильтониана Жо материальной системы. Гамильтониан поля
(электромагнитного или колебательного) обозначим че-
через Ж). Предположим, что взаимодействие между мате-
материальной системой и полем можно представить в виде
произведения оператора О, действующего на материаль-
материальную систему, и оператора F, действующего на полевые
переменные. Стохастическое возмущение, зависящее от
времени, равно
Ч 1
Жвз (t) = OF (t) = e+7L v Fe~l% f 0. B.97)
Случайная функция F(t) является теперь квантовым
оператором, действующим на полевые переменные. Если
в момент времени t = 0 система находилась в состоянии
\Ь) , а поле в состоянии |f>, то, согласно B.17), веро-
вероятность обнаружить в момент времени t систему в со-
состоянии |а> и поле в состоянии |f> равна
War.4 @ = ^-2 f df Г df < b, ?\ЖВЗ (f) | a, f > х
о о
t oo
X<a,nMB3(t")\b,f>=\Oab\2n-2idt\dr(f\F(t)\f'y x
X <f'\F(t-x)\f)e-ili>b°\
Отсюда, проводя статистическое усреднение по началь-
начальным состояниям поля / и суммируя по конечным состоя-
К.ВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕИ 105
/', получаем вероятность перехода, пропорциональ-
пропорциональную времени
Wb^a = '
с с/
x(f'\F(t-r)\f). B.98)
Вероятность найти систему первоначально в состоянии /
равна
r —EfjkT —Wf/kT
B.99)
Можно ввести квантовомеханический аналог функции
корреляции
{3ef) F(t+ •*)], B.100)
не зависящий от представления Ж/. Рассматривая соот-
соответствующую спектральную плотность
B.101)
B.102)
—00
вероятность перехода можно представить в виде
Для обратного перехода имеем
Wa.b^h-'lOj'Ji^). B.103)
Эти два выражения не равны, что легко показать, оце-
оценивая /(со) в представлении, в котором гамильтониан Ж^
диагоналей
/1 ^ I Г
х
xe'^'-^dx. B.104)
Поскольку распределение состояний резервуара являет-
является однородным, интеграл по т по существу представляет
106
ГЛАВА 2
собой б-функцию:
%\<f\F\f-
f
Отсюда
W ,-Wu P+%a>"b/kT n Шсч
wa-*b — Wb-t-ab • \Л. 1UO^
Таким образом, априорная вероятность того, что мате-
материальная система совершит переход вниз (с уменьше-
уменьшением ее энергии), больше вероятности перехода вверх —
в точном соответствии с равенством B.20), которое было
постулировано на основании принципа детального рав-
равновесия. Происхождение этого неравенства, конечно,
весьма просто. Переход материальной системы в со-
состояние с меньшей энергией требует соответствующего
возрастания энергии поля, которое служит тепловым
резервуаром. Поскольку состояния резервуара с мень-
меньшими энергиями имеют априори большую вероятность
быть занятыми, то переход вверх для данной пары уров-
уровней резервуара более вероятен.
В оптическом диапазоне На ^> kT, и температуру
резервуара можно считать равной нулю. Все оптиче-
оптические осцилляторы вакуума находятся в основном состоя
нии. Материальная система не совершает переходов
вверх. Пеоеходы вниз соответствуют спонтанному излу-
излучению. Равенство B.104) можно записать в виде
+°°
J (+ ®аь) — ]л I (. п\ — 0 \F\n\ = 1 ) la?x dx,
—оо X
B.106)
где суммирование по X проводится по всем вакуумным
осцилляторам. Интегрирование по т дает плотность ос-
осцилляторов на резонансной частоте, равную c~3Vv%b dvdQ.
Если подставить в B.103) соответствующее выражение
для матричного элемента Ощ„ то с помощью B.106)
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕИ Ю7
обычным образом получаем вероятность спонтанного из-
излучения. Все рассуждения § 2 настоящей главы можно
применить теперь к затуханию, обусловленному спонтан-
спонтанным излучением. Если учесть конечность температуры
теплового поля излучения, то из B.104) и B.106) полу-
получаем выражение для вероятности перехода вниз
и для вероятности перехода вверх
где
B.107)
B.108)
— функция Планка для среднего числа возбужденных
фотонов при тепловом равновесии.
Поперечная релаксация двухуровневой системы опи-
описывается константой Гаь. Если диагональные элементы
гамильтониана взаимодействия, дающие адиабатические
г.клады, равны нулю, то поперечное затухание равно
- i Раа +
i = -iBS + 0aCT
B-109)
Согласно результатам § 2 настоящей главы, частотная
зависимость отклика на гармонический сигнал имеет
лоренцеву форму, которая при низких температурах
(п < 1) имеет вид
= —. B.110)
2я v '
1
С-ТJ
Эта функция формы линии описывает также форму
самой линии спонтанного излучения. Спонтанное излу-
излучение имеет такую форму для всех направлений излуче-
излучения и для любой поляризации. Это можно показать с
помощью следующих рассуждений. Выделим один ва-
вакуумный осциллятор частоты со с заданными направле-
направлением и поляризацией. Все остальные осцилляторы обу-
обусловливают практически такое же случайное возмуще-
возмущение, как и раньше, следовательно, затухание и форма
108
ГЛАВА 2
линии g(v) остаются неизменными. Ясно, что такое рас-
рассмотрение спонтанного излучения основано на большой
плотности вакуумных осцилляторов. Поле излучения
действительно может служить тепловым резервуаром.
В случае, когда материальная система заключена в
объемный резонатор, имеющий только один или не-
несколько типов колебаний в интересующем нас диапазоне
частот, картина будет совершенно иной. Джейнс [32]
дал изящное квантовомеханическое рассмотрение взаи-
взаимодействия между двухуровневой материальной систе-
системой и одним осциллятором поля. В оптическом диапазо-
диапазоне с такими случаями не приходится иметь дела.
На этом мы заканчиваем главу, посвященную кван-
товомеханическому рассмотрению нелинейных воспри-
имчивостей. В ней было показано, как с помощью мето-
метода матрицы плотности и полуклассического приближе-
приближения можно рассчитать средние значения фурье-компо-
нент поляризации в виде ряда по возрастающим степе-
степеням амплитуд приложенных полей. Феноменологические
релаксационные члены были выражены через случайные
возмущения, включая затухание за счет спонтанного
излучения. При дальнейшем развитии теории, средние
значения нелинейной поляризации, определяемые задан-
заданными полями, должны в свою очередь рассматриваться
как дополнительные источники этих полей. Этот сле-
следующий шаг будет сделан в гл. 3. Поскольку фурье-ком-
поненты были рассчитаны с помощью полуклассическогс
метода, поля со случайными фазами, обусловленные
спонтанным излучением, должны добавляться к класси-
классическим полям.
ЛИТЕРАТУРА
1. Tolman R. С, Principles of Statistical Mechanics, New York,
1938.
2. Abragam A., Principles of Nuclear Magnetism, New York,
1961. (Имеется перевод: А. А бра гам, Ядерный магнетизм,
ИЛ, 1964.)
3. S I i с h t e г С. P., Principles of Magnetic Resonance, New York,
1962.
4. Bloembergen N.; S h e n Y. R., Phys. .Rev., 133, A37 A964)
(См. приложение III к настоящей книге.)
5. Фзйн В. М, Ящин Э. Г., ДЭТФ, 46, 695 A964).
КВАНТОВАЯ ТЕОРИЯ НЕЛИНЕЙНЫХ ВОСПРИИМЧИВОСТЕИ 109
6. VanVleckJ. H., WeisskopfV F, Rev. Mod. Phys., 17,
227 A945).
7. Armstrong J. A., Bloembergen N., Ducuing J.,
Pershan P. S.. Phys. Rev., 127, 1918 A962). (См. прило-
приложение I к настоящей книге.)
8. Butcher P. N.. McLean Т. Р., Proc. Phys. Soc, 81, 219
A963).
9. Lou don R., Proc. Phys. Soc, 80, 952 A962).
10. Kelley P. L., Journ. Chem. Phys. Sol., 24, 607 A963).
11. Price P. J., Phys. Rev., 130, 1792 A963).
12. Cheng H, Miller P. В., Phys. Rev., 134, A683 A964).
13. Adler E., Phys. iRev., 134, A728 A964).
14. Nozieres P., Pines D., Phys. Rev., 109, 762 A958).
15. Adler S., Phys. .Rev. 126, 413 A962).
16. D u с u i n g J., These, Universite de Paris, 1964.
17. Goeppert-iMayer M., Ann. Phys., 9, 273 A931).
18. Fiutak J., Canad. Journ. Phys., 41, 12 A963).
19. Power E. A., Zienau S., Phil. Trans. Roy. Soc, 251A, 54
A959).
20. Placzek G., Marx Handbuch der Radiologie, 2 Aufl., Bd VI,
Tl. II A934). (Имеется перевод: Г. П л а ч е к, Релеевское рас-
рассеяние и раман-эффект, Харьков, 1935.)
21. Р е г s h a n P. S., Phys. Rev., 130, 919 A963)
22. Butcher P. N.. McLean Т. Р., Proc. Phys. Soc, 83, 579
A964).
23. Casper s W. J., Phys. Rev., 133A, 1249 A964).
24. К r a m e r s H. A., Quantum Mechanics, Amsterdam, 1957,
p. 482.
25. H e i 11 e r W., Quantum Theory of .Radiation, 3 ed., New York,
1954. (Имеется перевод: В. Г а й т л е р, Квантовая теория из-
излучения, ИЛ, 1956.)
26. Blaton J., Zs. Phys, 69, 835 A931).
27. Guttinger P., Helv. Phys. Acta, 5, 237 A932).
28. Glauber R. J, Phys. Rev, 130, 2529 A963); 131, 2766 A963).
29. L о u i s e 11 W. H, Y a r i v A, S i e g m a n A. E, Phys. Rev,
124, 1646 A961).
30. Gordon J. P., L о u i s e 11 W. H., Walker L. R., Phys. Rev,
129, 481 A963).
31. Gordon J. P, Walker L. R., Louisell W. H, Phys. Rev,
130, 806 A963).
32. Jaynes E. Т, Cummings F. W, Proc. IEEE, 51, 89
A963).
33*. Б л о х и н ц е в Д. И, Основы квантовой механики, М, 1963,
стр. 167.
34* Ф а й н В. М, X а н и н Я. И, Квантовая радиофизика, М.,
1965, стр. 18.
л
УРАВНЕНИЯ МАКСВЕЛЛА
В НЕЛИНЕЙНОЙ СРЕДЕ
В гл. 1 и 2 нелинейная поляризация или нелинейная
плотность тока были выражены через поля; в свою
очередь эти величины сами служат источниками полей.
Обсуждение связанных с этим обстоятельств является
предметом настоящей главы. Нелинейная плотность то-
тока, вычисленная в гл. 1 классическими методами, а в
гл. 2 — как среднее значение квантовомеханического
оператора, теперь должна быть введена в уравнения
Максвелла.
Исходными являются, как известно, микроскопиче-
микроскопические уравнения Максвелла, записанные для полей в
вакууме и точечных зарядов. Они имеют вид (приняты
стандартные обозначения)
J_jte 4я ,
с ~dl с~"
_}_d±
с dt '
V-b=0.
C.1)
Здесь j — микроскопическая плотность тока, включаю-
включающая в соответствии с уравнением B.38) линейную и не-
нелинейную части и спиновую плотность тока. Макроскопи-
Макроскопические уравнения Максвелла получаются усреднением
уравнений C.1) по объему, много большему характер-
характерных атомных размеров, но малому по сравнению с дли-
длиной волны [1]. Для очень коротких волн (например, для
рентгеновских лучей) такой способ, очевидно, неприме-
неприменим. На оптических частотах такое усреднение дает
известные преимущества и подробно описано в литера-
литературе. В результате усреднения приходим к уравнениям
УРАВНЕНИЯ МАКСВЕЛЛА В НЕЛИНЕЙНОЙ СРЕДЕ
111
для макроскопических полей
с dt
Усредненную по объему плотность тока обычно раз-
разлагают в ряд по мультиполям, предварительно выделив
плотность тока проводимости:
f |.. C.3)
Такое разложение, вообще говоря, не является одно-
однозначным. Электрический дипольный момент определен
однозначно лишь в случае, когда единичный элемен!
объема в целом является нейтральным. Вектор М оп-
определен неоднозначно,если производная dP/dt отлична
от нуля, а квадрупольный момент определен неодно-
неоднозначно, если вектор Р отличен от нуля. Тем не менее
подобное разложение оказывается полезным, если рас-
рассматриваемый объем можно разделить на единичные
ячейки, для которых указанные моменты могут быть вы-
вычислены как последовательные приближения для вели-
величины J. Все они могут содержать, помимо линейных, и
нелинейные члены.
§ 1. Энергетические соотношения
Из уравнений Максвелла обычным образом (см., на-
например, [2]), нетрудно получить закон сохранения энер-
энергии (см. [3]):
Л-V -EXB+-S-B. — -j-J-E.—
4я 4я dt 4я dt
Е- J = 0. C.4)
Запишем материальные уравнения
Н = В — 4тгМ и D = Е + 4иР.
Последнее определение предполагает, что
V-D —
112
ГЛАВА 3
Подставляя C.3) в уравнение C.4), получаем
4л \ с dt j 4я dt
4я
dt
dt
C.5)
Отметим, что наличие в C.5) квадрупольного момен-
момента, зависящего от времени, приводит к необходимости
дать новое определение вектора Пойнтинга; в этом слу-
случае он определяется величиной, стоящей в скобках в
уравнении C.5). Из C.5) следует, что сумма потока
энергии из элемента объема и работы, совершенной
полем над единицей объема материальной среды, равна
уменьшению плотности энергии, запасенной электро-
электромагнитным полем,
8я
(
dt \8п
Для среды без потерь работа, произведенная над едини-
единицей объема, равна величине, на которую возрастает
плотность электромагнитной части внутренней энергии
среды U:
C.6)
dt
dt
dt
dt
Введем потенциальную функцию F (свободную энер-
энергию) с помощью соотношения
F=U — H- М — ЕР — VE:Q. C.7)
Эта энергия связана с работой, проделанной генератора-
генераторами для создания полей в среде; она имеет полный диф-
дифференциал
dF=— P-dE — M-dH — Q:dVE. C.8)
Если функция F выражена через напряженности полей,
то соответствующие поляризации могут быть получены
путем ее дифференцирования.
До сих пор рассмотрение носило общий характер.
Теперь мы ограничимся случаем слабо нелинейной сре-
среды, находящейся в квазистационарном состоянии. Пред-
Представляя поля в виде гармонических сигналов с ампли-
УРАВНЕНИЯ МАКСВЕЛЛА В НЕЛИНЕЙНОЙ СРЕДЕ
113
тудами, медленно изменяющимися во времени, для мед-
медленно меняющихся амплитуд можно записать
t+T
)
t-T
Время Т выбирается, с одной стороны, таким, чтобы
выполнялось условие аТ ^> 1, но вместе с тем таким,
чтобы величина Е(а, t) не зависела от Т. При значитель-
значительной нелинейности одновременное выполнение указанных
условий невозможно; к счастью, оптические нелинейно-
нелинейности можно всегда рассматривать как малые возмущения,
так что поля хорошо описываются с помощью конечного
числа фурье-компонент '>. Рассматривая спектральные
компоненты поляризации и полей, определенные соглас-
согласно C.9) «а Ш частотах, для усредненного по времени
полного дифференциала F имеем (в комплексной за-
записи)
< dF > = - 2Re 2 IP
(- ©,) + М (ш,)
¦dti*(—и,) + Q (и,-): VE* (—©,)] C.10)
[быстро флуктуирующие члены в C.8) отброшены]. Для
того чтобы в вакууме перейти от стационарного состоя-
состояния, описываемого амплитудами Фурье Е*(—©г) и т. д.,
к новому стационарному состоянию с амплитудами Фу-
Фурье Е*(—о)г) + dE*(—о,-), генераторы должны произ-
произвести определенную работу. При наличии среды с за-
заданными фурье-компонентами поляризации работа, ко-
которая должна быть проделана внешними генераторами,
оказывается меньшей на величину < dF > . Фурье-ком-
'' Представление C.9) соответствует полю, «недоразложенному»
в интеграл Фурье, и связано с возможностью выделения зависимости
поля от «быстрого» и «медленного» времени. Для поля в нелинейной
недиссипативной среде введение таких двух различных временных
масштабов возможно, если время, в течение которого спектральное
распределение поля существенно меняется за счет нелинейного вза-
взаимодействия, значительно превышает период колебаний.—Прим.
ped.
8 П. Бломберген
114
ГЛАВА 3
поненты поляризации получаются из F дифференциро-
дифференцированием:
<¦*>-- т?
dF
dF
Q (со,-) =
Для линейного случая эти соотношения хорошо извест-
известны; в линейной среде F является квадратичной функцией
амплитуд полей. Например, для электрического диполя
FL = -
(- «О • X М • Е (со,).
Если же изменение свободной энергии в непоглощаю-
щей среде выразить рядом по степеням амплитуд полей,
то можно будет вычислить фурье-компоненты нелиней-
нелинейной поляризации различного порядка. Нелинейная часть
усредненной по времени свободной энергии может быть
связана с нелинейной восприимчивостью. В гл. 1 было
показано, как пространственно-частотные перестановоч-
перестановочные соотношения для нелинейной восприимчивости сле-
следуют из того физического факта, что работа, затрачен-
затраченная при достижении стационарного состояния, не зави-
зависит от способа его достижения. При этом изменения счи-
считаются медленными в смысле соотношения C.9), так что
сохраняется смысл понятия «частота». Итак в общем
случае функцию F следует записать в виде ряда по ве-
величинам Е, Н и VE. Можно вывести таким образом
компоненты электрической поляризации, пропорциональ-
пропорциональные амплитуде магнитного поля, и т. д. В среде с цен-
центром инверсии младшие нелинейные члены в разложении
свободной энергии F по полю имеют вид
> = -
- ХаЕЕ*Н - XsEEVE* - х4 ЕЕ* VE -
сопр. C.11)
Сумма отрицательных частот, соответствующих величи-
величинам со звездочкой, и положительных частот, соответ-
соответствующих членам без звездочек, равна нулю.
УРАВНЕНИЯ МАКСВЕЛЛА В НЕЛИНЕЙНОЙ СРЕДЕ Ц5
Следует отметить, что при наличии дисперсии вы-
вычисление средней внутренней энергии среды U1) пред-
представляет определенные трудности. Поскольку в чисто
монохроматическом поле систематического изменения
энергии не происходит, мы рассмотрим квазимонохро-
квазимонохроматическое поле вида
Отсюда
dt
Рассмотрим линейную диспергирующую среду, для ко-
которой поляризация имеет вид
Разложим линейную восприимчивость в ряд вблизи ок
и, поскольку величина Е(иц) меняется достаточно мед-
медленно, удержим только члены первой степени по г\
Р @ = Х (со,.) Е @ + (|L)e| J
Среднее значение электромагнитной части внутренней
энергии среды равно
Е(е>.)
< U > = 2Re j E* . dP = 2ReE* (со,) . Р (со,) -
Я(и;)
— 2Re J P (t) • dE* (t) = 2Re Ге* (со,) • Р (со,-) —
о L
-уЕ* КО • X Ы • Е (<*>,) + JCO.E* (со,)- (^-)и_. Е (со,)].
'' Детальное обсуждение вопроса об энергии поля в дисперги-
диспергирующих линейных средах можно найти в [5*]. — Прим. ред.
116
ГЛАВА 3
Опустим индекс i у частот в фурье-компонентах. Исклю-
Исключая множитель 4, обусловленный нашим определением
амплитуд (см. гл. 1), получаем обычный результат
< U > = Е* (и) . -^Э. . е (и). C.12)
до ~v"''
Можно убедиться, что это выражение действительно
равно сумме кинетической и потенциальной энергии
находящегося под внешним воздействием гармониче-
гармонического осциллятора, который моделирует процессы в ли-
линейной диспергирующей среде.
При наличии дисперсии переход от формулы C.8) к
усредненному по времени соотношению C.10) нуждает-
нуждается в некоторых уточнениях. Дифференцируя функцию
Fb no E'lt получаем
Дифференцируя Fb также и по Ej, получаем следующее
соотношение:
Отсюда сразу следует соотношение симметрии для
тензора линейной восприимчивости, %ц((а) = %ц(а).
Полученные соотношения могут быть распростране-
распространены на случай нелинейной диспергирующей среды. Если
амплитуда поля с частотой о)[ медленно возрастает, в то
время как амплитуды полей с частотами оJ и юз = o>i +
+ «г остаются постоянными, то количество работы, про-
проделанной над средой и обусловленной нелинейностью,
равно
2Re
Е*з
+ (о2, t)
Еа
Изменение амплитуды E(u>i) является достаточно мед-
медленным; подынтегральные величины Е*3 и Е2 не зависят
от ?(@i, t). Обусловленный нелинейностью прирост ус-
усредненной по времени внутренней энергии среды равен
УРАВНЕНИЯ МАКСВЕЛЛА В НЕЛИНЕЙНОЙ СРЕДЕ
117
Для соответствующего изменения свободной энергии F
получаем
< ^L > = _ 2ReEr P*NL (й2 - щ) = - 2Re [xNLExE2E;].
В случае, когда все частоты различны, наличие диспер-
дисперсии не приводит к необходимости внесения 'каких-либо
поправок в эти формулы. При равенстве же двух частот
следует добавить производные нелинейной восприимчи-
восприимчивости по этим частотам, аналогично тому, как это было
сделано для линейной среды. Пространственно-частот-
Пространственно-частотные соотношения симметрии остаются справедливыми и
в этом случае. Более важное приложение пространствен-
пространственно-частотные соотношения симметрии находят в случае,
когда дисперсия в непосредственной окрестности частот
им, юг, 0K и т. д. очень слаба, однако имеются области
сильного поглощения и дисперсии в интервалах между
этими частотами. В этом случае тонкий анализ энерге-
энергетических соотношений при наличии дисперсии малоин-
малоинтересен.
В областях сильной дисперсии всегда существенны
потери. Для поглощающей среды оказывается возмож-
возможным выразить поглощение или скорость изменения эн-
энтропии в стационарном состоянии через диссипативную
функцию. Этот вопрос был рассмотрен Першаном [3],
который обратил внимание на связь в линейном случае
с соотношениями Онзагера. Поскольку наиболее полез-
полезные свойства симметрии для той части нелинейной вос-
восприимчивости, которая соответствует потерям, были уже
выведены в гл. 2, обсуждение этого вопроса заканчивает-
заканчивается. Некоторые свойства нелинейных членов в выраже-
выражении для свободной энергии C.11) обсуждаются в гл. 5.
§ 2. Действующие поля в оптически плотной среде
В гл. 1 и 2 дипольный момент молекулы (или группы
молекул) был выражен через действующее на нее элек-
электрическое поле. Это действующее (или локальное) поле
совпадает с макроскопическим полем, фигурирующим в
уравнениях Максвелла, только в разреженных газах.
118
ГЛАВА 3
В конденсированной же среде следует принять во вни-
внимание влияние соседних диполей. Однако различием
среднего действующего и макроскопического полей для
случая валентных электронов в полупроводниках и ме-
металлах можно пренебречь. Для локализованных ионов
или групп молекул различие между действующим и
макроскопи-ческим полями может быть рассчитано ме-
методом Лоренца.
Рассмотрим для простоты ион в среде с кубической
симметрией. Действующее поле равно
E,oc = E + ^P = E + ^PL-)-^PNL. C.13)
О о о
Здесь в поляризацию включены и линейное и нелиней
ное слагающие. Обозначим линейную поляризуемость
через а, нелинейную поляризуемость через %aJk (co3 =
= o)i + ©г)- Пусть в 1 см3 содержится N ионов; тогда
для линейной поляризации имеем
C.14)
C.15)
C.16)
Нелинейная поляризация равна
PNL = ^xaTE,.,oc-E2,,oc.
Для вектора электрической индукции имеем
D = Е + 4uPL + 4ttPnl.
Комбинируя выражения C.13) и C.14), получаем
pL =
_ J?L Na
4Я pNL\ 8-1
3 / 4я
¦ 4Я p
3
NL
Подставляя последнее выражение в C.16), находим
D = еЕ + 4u -i±i- PNL = еЕ
О
4uP
NLS
C.17)
Отсюда следует, что в плотной среде величина нелиней-
нелинейной поляризации, которая должна быть подставлена в
уравнения Максвелла, «нелинейный источник», в
(е + 2)/3 раз больше индуцированного нелинейного ди-
У РАВНЕНИЯ МАКСВЕЛЛА В НЕЛИНЕЙНОЙ СРЕДЕ
119
польного момента, умноженного на число ионов в 1 см3.
Комбинируя выражения C.15) — C.17), находим связь
между макроскопической нелинейной восприимчивостью
и нелинейной поляризуемостью изолированной молеку-
молекулы или атома:
+ 2
+ 2
3
X Л^хат (оK = и
= Хмакр К = '
3 3
+ ©.) Е К) Е (и,) -
1 + и») Е К) Е К).
X
C.18)
Так как поправочный коэффициент, стоящий перед %ат
(в 3.18), симметричен относительно перестановки частот,
(Oi, ©2. соз, перестановочные соотношения, выведенные
ранее для хат, остаются справедливыми для макроско-
макроскопической нелинейной восприимчивости %макР. Приведен-
Приведенные формулы приложимы, по-видимому, лишь к кри-
кристаллам типа CuCl (т.е. ионным класса 43 т). Это
тетраэдральные кубические кристаллы без центра инвер-
инверсии. Учет выведенных выше поправочных коэффициен-
коэффициентов, разумеется, весьма существен для сред с большими
диэлектрическими проницаемостями. При выводе соот-
соотношения C.18) предполагалось, что валентный электрон
локализован вблизи узла решетки с кубической симмет-
симметрией. Очевидно, что это предположение совершенно не
соответствует условиям, в которых находятся валентные
электроны в полупроводниках типа GaAs; в этом случае
поправочный коэффициент, учитывающий отличие дей-
действующего поля от макроскопического, следует поло-
положить, по-видимому, равным единице. Сомнительно, что-
чтобы и для CuCl соотношение C.18) являлось вполне
точным.
Соотношение C.17) остается справедливым для нели-
нейностей более высокого порядка. Так, в выражении
для макроскопической восприимчивости, описывающей
генерацию третьей гармоники в щелочно-галоидных кри-
кристаллах, необходимо учесть поправочный коэффициент
81
120
ГЛАВА 3
Аналогичный поправочный коэффициент необходим и в
случае жидкости. При расчете комбинационной воспри-
восприимчивости молекулярных неассоциированных жидкостей
величину хат (м« = 2й>1,—(os) следует умножить на по-
поправочный коэффициент
[е (соL) + 2]2 [е К) + 2] [е К) + 2]
81
Для сред, не обладающих кубической симметрией, фак-
фактор действующего поля Лоренца в отличие от C.13)
имеет, вообще говоря, тензорную структуру. Переста-
Перестановочные соотношения остаются справедливыми и здесь,
как это следует из общего энергетического рассмотре-
рассмотрения, проведенного в § 1. Более детальное рассмотрение
вопроса об учете отличия действующего поля от макро-
макроскопического в анизотропной среде проведено в прило-
приложении I.
Корректное же определение поправочных коэффици-
коэффициентов в анизотропных средах (как, например, в кри-
кристалле КН2РО4) оказывается затруднительным. По-
Поскольку этими поправками ни в коем случае нельзя
пренебречь, они вносят значительную неопределенность
ь количественные результаты теории.
§ 3. Уравнения связанных волн в нелинейной среде
После того как в принципе уточнено понятие макро-
макроскопической нелинейной восприимчивости, обратимся
вновь к уравнениям Максвелла. Полезно записать эти
уравнения для каждой фурье-компоненты, выделяя при
этом нелинейные члены. При таком способе записи четко
выявляются свойства «нелинейного источника» (nonline-
(nonlinear source— NLS). Для простоты будем рассматривать
немагнитную среду, ц,ь = 1.
VxEW = +iP-HW.
C.19)
V X Н (со,) = — / (~^-) е К) • Е («>|) +
7-
СРАВНЕНИЯ МАКСВЕЛЛА В НЕЛИНЕЙНОЙ СРЕДЕ
121
Комбинируя эти уравнения, приходим к нелинейному
волновому уравнению
V X VX Е К) -
Е (о),-) -
C.20)
Если величину JNLS (со3) выразить через фурье-компонен-
фурье-компоненты поля с другими частотами, получим систему связан-
связанных волновых уравнений. Естественно, что с ростом
числа учитываемых фурье-компонент трудности решения
этой системы быстро возрастают. Весьма важно из фи-
физических соображений выбрать такое число фурье-ком-
понет, которое необходимо для получения приближен-
приближенного решения.
В электродипольном приближении уравнения Мак-
Максвелла для каждой фурье-компоненты могут быть запи-
записаны следующим образом:
C.21)
?XH(fflj)=- / (-2L) г (щ) . Е (о),) - Аш l-^-\ P
\ с J \ с }
Волновое уравнение имеет вид
V X V X Е Ы - (-^-J -, К) • Е ((о,) = An ^
NLS
C.22)
Для определенности рассмотрим случай нелинейности
самого низкого порядка, приводящей к взаимодействию
трех волн с частотами <м3 = ©i + ©2, «ч и сог. В этом
случае получаем систему трех нелинейных векторных
волновых уравнений
V X V X Ех К) - (-5L j2 е К) . Е, К) =
= 4тс (-^-] х (щ = (о3 — и2) Е3 (и3) Е'2 (— и2),
V с /
V X V X Ег К) - (-Ш2- У г
122
ГЛАВА 3
- 4тг I—)* X К = «з — ©i) E3 К) Et (— «»i).
C.23)
V X Vx Ез(о)з)- {-^-f* (©a) • E, (©,) =
K
= ©i
Эти уравнения справедливы и для диссипативной
среды. В этом случае величины е и ^ являются комплек-
комплексными. Для слабо диссипативной среды величины г (о)]),
(юг) и е(соз) следует рассматривать как комплексные,
а мнимыми частями нелинейных восприимчивостей мож-
можно пренебречь. Нелинейная восприимчивость подчиняет-
подчиняется в этом случае перестановочным соотношениям сим-
симметрии A.28). Если имеется сильное затухание только
вблизи одной из частот, например, вблизи кц, то можно
записать
Xijk (<°i == «>з — Щ) = Ш {Щ = °>з — ©i) =
= Xjik (">» = °>i + »г)-
В более общих случаях простых соотношений симметрии
не существует.
Волновые уравнения типа уравнений C.23) должны
решаться с учетом соответствующих граничных условий
Тангенциальные компоненты векторов Е и Н должны
быть непрерывны на границе для каждой фурье-компо-
ненты в отдельности, поскольку общие граничные усло-
условия должны удовлетворяться в любой момент времени-
Точно так же должны быть непрерывны на границе нор-
нормальные компоненты векторов D и В для каждой фурье-
компоненты.
В принципе задачу нельзя ограничить тремя фурье-
компонентами, поскольку в силу нелинейности в среде
генерируются высшие комбинационные частоты
± /iCOx ± /аСО2 ± 13Щ-
Практически можно исключить большую часть комбина-
комбинаций частот, так как амплитуды соответствующих волн
будут пренебрежимо малыми. Однако существует по
УРАВНЕНИЯ МАКСВЕЛЛА В НЕЛИНЕЙНОЙ СРЕДЕ
123
крайней мере одна задача, а именно задача о вынуж-
вынужденном комбинационном рассеянии, где необходимо учи-
учитывать значительное число волн. Получение аналитиче-
аналитических решений в таких случаях обычно затруднительно.
В следующей главе мы обсудим целый ряд физически
интересных случаев. Используя физически обоснованные
приближения, можно получать решения с различной
степенью точности и сложности. Фундаментальной осно-
основой для получения таких решений остается, естественно,
малая величина нелинейности оптических свойств среды.
§ 4. Частное решение уравнений Максвелла
для недиспергирующей среды с нелинейностью
произвольного вида
Решение этой задачи было дано Броером D]. Он рас-
рассматривал электромагнитную волну с произвольной за-
зависимостью ее амплитуды от времени, падающую из
вакуума нормально к границе недиспергирующей среды
с нелинейностью произвольного вида. Здесь мы приве-
приведем решение, полученное Броером для отраженной вол-
волны; это позволяет выявить особенности случая, когда
нелинейность нельзя считать малой.
Рассмотрим немагнитную среду (В = Н), заполняю-
заполняющую пространство z > 0 и характеризуемую произ-
произвольной функциональной связью между!) (илиР1*1^) иЕ.
Уравнения Максвелла поля с Еу Ф 0 и Вх Ф 0 имеют вид
дЕу
дг
дВх
dt
дВх
дг
dt
C.24)
Опустим индексы х н у и введем функцию
3D
дЕ
-с-2.
Тогда уравнения запишутся в виде
дВ . дЕ дВ
ir- <3-25»
Решение может быть записано в дифференциальной
форме
124
ГЛАВА 3
для
—
dt
=v,
C.26)
— —dB для
с
—
at
= — v.
В нелинейной среде существуют решения, соответствую-
соответствующие волнам, бегущим от границы. Если изменение во
времени поля на границе описывается уравнением
то решение в среде имеет вид
Е
= e\t —-
L v(E
C.27)')
Естественно, что функция G(t) в свою очередь опре-
определяется падающей и отраженной волнами в вакууме,
2<0. Обозначим падающую волну через /пад(^ — z/c), a
отраженную через /0Тр (t + z/c). Тогда для полей в ваку-
вакууме получим
?„к(г<О) = Ц/ -
C.28)
Последнее решение при 2 = 0 должно быть согласовано
с магнитным полем внутри среды. Интегрируя уравнение
C.26), получаем
j
Git)
dD \T
dE
dE.
C.29)
Ч Таким образом уравнение C.27) описывает волну, каждая
точка профиля которой движется со скоростью, зависящей от на-
напряженности поля. Решения типа C.27) детально обсуждались в
работах Гапонова и Фрейдмана [6*, 7*] в связи с теорией ударных
электромагнитных волн. — Прим. ред.
00
УРАВНЕНИЯ МАКСВЕЛЛА В НЕЛИНЕЙНОЙ СРЕДЕ
125
Приравнивая тангенциальные компоненты при 2 = 0, на-
находим соотношение между падающей и отраженной вол-
волнами:
тр !
fna«-fOTp=
dE
C.30)
В гл. 4 для волны, отраженной от нелинейной среды, мы
получим ряд Фурье, содержащий гармоники и комбина-
комбинационные тона падающей квазимонохроматической волны.
Для малой нелинейности это решение быстро сходится к
точному решению C.30). Такое приближенное решение
удобно сравнивать с результатами экспериментов, в кото-
которых проводится спектральный анализ отраженного света;
оно легко может быть распространено на случай наклон-
наклонного падения, нелинейной анизотропной среды и т. д.
Точное решение C.30) должно напоминать о существе
приближений, сделанных в теории, в которой рассматри-
рассматривается конечное число фурье-компонент.
ЛИТЕРАТУРА
Rosenfeld L., Theory of Electrons, Amsterdam, 1949.
Born M., Wolf E., Principles of Optics, London, 1959, Ch. 1.
Pershan P. S., Phys. Rev., 130, 919 A963).
BroerL J. F, Phys. Lett., 4, 65 A963).
Ландау Л. Д., Лифшиц Е. М., Электродинамика сплош-
сплошных сред, М., 1957.
6*. Талонов А. В., Фрейдман Г. И., ЖЭТФ, 36, 3, 957 A959).
7*. Талонов А. В., Фрейдман Г. И., Изв. ВУЗ'ов, Радиофизи-
Радиофизика, 3, № 1, 79 A960).
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
8*. Коган Ш. М., ЖЭТФ„ 43, 7, 304 A962).
К электродинамике слабонелинейных сред.
9*. Терхьюн Р., Зарубежная радиоэлектроника, № 6, М., 1964.
л
в
РАСПРОСТРАНЕНИЕ ВОЛН
В НЕЛИНЕЙНОЙ СРЕДЕ
§ 1. Генерация волн на комбинационных частотах
заданными электромагнитными полями; граничные
условия на поверхности нелинейной среды
В этом параграфе мы проанализируем процесс гене-
генерации в нелинейной среде волн с комбинационными час-
частотами под действием заданных гармонических полей.
Рассмотрим нелинейную среду, в которой распространя-
распространяются волны с частотами coi,..., со*,..., волновыми векторами
kb..,kj,.. и векторами поляризации ei...,e{.... Эти волны
возбуждают волну нелинейной поляризации PNLS с ком-
комбинационной частотой cos = 2/гЮ,-, а последняя в свою
i
очередь излучает волну той же частоты cos. На начальных
стадиях процесса амплитуда волны с частотой cos весьма
мала, так что обратной реакции ее на основные волны
можно пренебречь; вследствие этого амплитуды полей ис-
исходных волн можно в этом случае рассматривать как за-
заданные функции. В таком приближении п достаточно рас-
рассмотреть только одно волновое уравнение, или, точнее,
два уравнения для двух направлений поляризации.
Волну нелинейной поляризации запишем в виде
D.1)
где
0)c =
') В литературе его называют также «приближением заданного
поля»; далее этот термин употребляется и в настоящей книге. —
Прим. ред.
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
127
XNL —тензор нелинейной восприимчивости ранга
S|/i| + 1. Для отрицательных индексов lt величины
еИг должны быть заменены на комплексно сопряжен-
сопряженные. (Здесь А{ — комплексные амплитуды волн, е» — еди-
единичные векторы вдоль направления поляризации.) Знак
произведения употреблен в целях сокращения записи для
повторяющихся векторов. Практическое значение имеют,
конечно, лишь случаи малого числа частот, т. е. случаи
малых U. В частности, задаче о генерации второй гармо-
гармоники соответствуют индексы i — 1 и / = 2.
Волновое уравнение для поля с комбинационной час-
частотой (os запишем в виде
V х V х Е («у _ -^- Es = ^± P$"-VV.-'».' .D.2)
с2 с2
Общее решение уравнения D.2) состоит из частного ре-
решения неоднородного уравнения и общего решения одно-
однородного уравнения. Последнее является линейной комби-
комбинацией всех плоских (или каких-либо других ортого-
ортогональных) волн, которые могут распространяться в ли-
линейной среде на частоте cos. Граничные условия опреде-
определяют, какая именно линейная комбинация должна быть
рассмотрена [1].
Пусть граница нелинейной среды расположена в пло-
плоскости z = 0, а падающие волны являются бесконечно
протяженными плоскими волнами (учет конечного попе-
поперечного сечения светового луча будет произведен в сле-
следующей главе). Такая модель соответствует большинству
экспериментов в нелинейной оптике. Направления пада-
падающих лучей непосредственно определяют тангенциальные
компоненты волнового вектора ksx , ksy волны нелиней-
нелинейной поляризации. При отражении и преломлении попе-
поперечные компоненты этих векторов сохраняются, посколь-
поскольку граничные условия должны удовлетворяться везде на
плоскости 2 = 0. Отсюда сразу получаем
В этих уравнениях величины k{X и kiV — тангенциаль-
тангенциальные компоненты волнового вектора падающей волны
частоты иг; их значения сохраняются и после ее прелом-
128
ГЛАВА 4
ления. Тангенциальные компоненты волнового вектора,
равные ksx , ?jj , имеют и электромагнитные волны часто-
частоты as, которые удовлетворяют граничным условиям. На-
Направление распространения волны нелинейной поляриза-
поляризации определяется z-компонентами волновых векторов
Кг —
(здесь kTlz есть z-компонента волнового вектора прелом-
преломленной волны частоты со»).
Целый ряд характерных особенностей процесса гене-
генерации волн комбинационных частот может быть выяснен
при рассмотрении оптически изотропной среды (кубичес-
(кубический кристалл или изотропная жидкость). Не ограничи-
ограничивая общности, выберем направление оси у так, чтобы
ksy = 0. Как и в линейной задаче о преломлении, здесь
можно по отдельности рассмотреть электромагнитную
волну с частотой cos, поляризованную нормально к пло-
плоскости падения и возбуждаемую компонентой P^LS =
) и В0ЛНу ,с электрическим вектором в плоско-
плоскости xz, возбуждаемую компонентой нелинейной поляри-
поляризации Р^8 , параллельной этой же плоскости.
Для первого случая общее решение уравнения D.2)
с учетом граничных условий имеет вид
Г,г
D.3)
где kT — волновой вектор прошедшей волны, являющей-
являющейся решением однородного уравнения. Его модуль равен
|kT| =coser'/c, тангенциальная компонента kTx равна
k*x. Второй член в D.3) соответствует частному реше-
решению неоднородного уравнения '). Амплитуда решения од-
однородного уравнения А^ должна быть определена из
условия непрерывности тангенциальных компонент век-
векторов Е и Н. Эти два условия требуют также присутствия
') В дальнейшем автор называет их также однородной и неод-
неоднородной волнами. — Прим. ред.
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
129
«отраженной» волны с частотой cos, распространяющейся
от границы обратно в линейную среду
D.4)
где
Факт присутствия в линейной среде поля с частотой cos
нетрудно понять из следующих соображений. Из уравне-
уравнений Максвелла C.2) следует, что магнитное поле про-
пропорционально величине dPNhS/dt. Поскольку имеется маг-
магнитное поле в нелинейной среде при z > 0, то должно
быть магнитное поле с той же частотой cos и в линейной
среде при z < 0. Условие непрерывности компоненты Еу
при z = 0 имеет вид
.
D.5)
а условие непрерывности компоненты Нх при z = 0
¦¦ - |к*!4я(
|k
D.6)
Здесь введены показанные на фиг. 7 угол отражения
Эя и углы преломления: Эт для электромагнитной волны
с частотой а и 0S для волны нелинейной поляризации. Их
можно найти из уравнений
sin 0Г =
1 sin QR = j ks | sin 9S = \ ltkl
D.7)
Направления распространения всех волн с комбинацион-
комбинационными частотами определяются углами падения и плос-
плоскостями падения исходных волн; этот факт иллюстри-
9 Н. Бломберген
130
ГЛАВА 4
Фиг. 7. Направления волновых векторов волны нелинейной поляри-
поляризации, а также «преломленной» и «отраженной» волн, генерируемых
этой поляризацией, для случая, когда электрический вектор норма-
нормален к плоскости отражения.
Показаны также и поляризации этих волн.
руется фиг. 8, построенной для случая сложения частот
двух волн. Уравнения D.5) и D.6) можно разрешить от-
относительно А^ и А7^. Вводя обозначение е^2 =
= с j ks j to~l, для амплитуды «отраженной» волны полу-
получаем
Ах = — 47rPxLS[ (er2 соs Qf -f- ед1 cos 0#) X
X (er2coser-f es"coses)] '.
D.8)
Впервые вторая гармоника в поле излучения, отраженно-
отраженного от нелинейного кристалла, наблюдалась Дюкуэнгом и
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
131
Фиг. 8. Геометрические соотношения между волновыми векторами
двух плоских волн, падающих на плоскую границу нелинейной среды,
и отраженной и прошедшей волн суммарной частоты.
Бломбергеном [2]. Они использовали кристалл GaAs,
принадлежащий к классу 43/тг. Поскольку кристаллы это-
этого класса оптически изотропны, приведенная здесь теория
непосредственно описывает этот эксперимент. На фиг. 9
изображена схема эксперимента. Здесь два луча основ-
основной частоты (использовался рубиновый лазер) падают на
нелинейный кристалл под разными углами падения
"IX
sin0»=-
k ¦ k
В кристалле эти лучи образуют три волны нелинейной
поляризации с частотами второй гармоники; благодаря
9*
/32
ГЛАВА 4
Стеклянная
пластинка
Г/риемник
излучения
с фильтром
Пластина
Зернало
Q Приемник
излучения
. с фильтром
Фиг. 9. Схема эксперимента по наблюдению генерации второй гар-
гармоники при отражении.
Луч лазера расщепляется на два луча с частотой и, которые при отражении
от кристалла GaAs создают три луча с частотой 2и.
этому в поле отраженного излучения появляются три
волны второй гармоники
sinef, Bи) = 2
= fti* И
Эти соотношения были проверены экспериментально.
Если поместить заркало из GaAs в диспергирующую ли-
линейную среду, например в бензол, отраженная волна
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
133
второй гармоники распространяется в другом направле-
направлении, нежели отраженная волна основной частоты, как это
показано на фиг. 10. Имеем
2klx (со)
sin QR B©) =
I k B@) | eV* Bu))
ft (») I '
sin9*(u)).
Эти выражения были также экспериментально провере-
проверены Дюкуэнгом [3].
У////////////////////77//////////////////7/7У/
¦Луч
лазера
V-
Фиг. 10. Схема эксперимента по наблюдению отражения света от
нелинейного зеркала, помещенного в линейную диспергирующую
среду.
Кристалл GaAs обладает сильным поглощением как
на частоте рубинового лазера, так и на частоте его вто-
второй гармоники. В связи с этим следует отметить, что все
записанные выше уравнения остаются справедливыми
134
ГЛАВА 4
и для комплексных значений ел, гт и es. В сильно погло-
поглощающей среде нелинейные эффекты легче наблюдать в
поле отраженных лучей. При этом следует иметь в виду,
что в этом случае нелинейная восприимчивость возраста-
возрастает, что обусловлено резонансными эффектами (см. гл. 1
и 2). Эффективный поверхностный слой, дающий сущест-
существенный вклад в «отраженный» луч второй гармоники,
имеет толщину порядка меньшей из длин затухания для
волн с частотами со и 2со, Это отражено в формуле D.8),
где в знаменателе присутствуют величины es и гт. Интен-
Интенсивность «отраженной» волны второй гармоники пропор-
пропорциональна квадрату нелинейной восприимчивости
|^nl|2 в гл 5 мы более подробно обсудим методику из-
измерения нелинейной восприимчивости среды по интенсив-
интенсивности «отраженной» гармоники, там же обсуждаются и
факторы, определяющие ее поляризацию. Амплитуда
А^ отраженной волны, поляризованной в плоскости от-
отражения, может быть найдена аналогичным образом; она
определяется компонентой нелинейного источника в этой
плоскости P^LS [см. формулу D.12) приложения II].
Здесь для «отражения» гармоники имеет место аналог
угла Брюстера: при определенном направлении волново-
волнового вектора амплитуда А* обращается в нуль. Более под-
подробное исследование проведено в приложении II.
Прошедшая волна с поляризацией, перпендикулярной
плоскости падения, описывается формулами D.3), D.5) и
D.8). Используя соотношения D.7), для амплитуды Ат
прошедшей волны находим
cos
cos
D.9)
Из рассмотрения фиг. 7 следует, что
(ks — kr) • г = сое" {el1' cos 0S~ zj* cos 0r) z.
Прошедшую волну можно представить как волну, фаза
которой изменяется по закону expt(kT-r — cos/), а ампли-
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
135
туда зависит от расстояния z (отсчет от границы). Из
формул D.3) и D.5) для прошедшей волны получаем
NLSexPtimc
X
X e
t—llAt
Для значений z, удовлетворяющих условию
ш~хг{г1г cos 0S — г^ cos 8Г) « 1,
прошедшая волна описывается выражением
= [Л? +
c~l
(ac~lг) (в?1 cos 9, +
D.10)
D.11)
D.12)
Таким образом, начальная амплитуда прошедшей волны
равна амплитуде отраженной волны; компонента, сдви-
сдвинутая по фазе относительно PNLS на 90°, возрастает про-
пропорционально расстоянию от границы. Волна совершает
отрицательную работу над нелинейной поляризацией.
Интенсивность растет как z2, пока сохраняются постоян-
постоянные фазовые соотношения между PNLS и электромагнит-
электромагнитной волной. Последнее имеет место для любых z, если
нормальные к границе компоненты фазовых скоростей
согласованы, т. е.
8s2 cos 0S == е^2 cos 0f.
Компоненты фазовых скоростей, параллельные границе,
согласованы всегда в силу граничных условий. Учитывая
определение es, убеждаемся, что согласование возможно,
если только es = ет, 0s = 0т и, следовательно, ks = kT.
Вследствие частотной дисперсии света в кубических кри-
кристаллах эти соотношения') не могут быть удовлетворены.
Однако в анизотропных кристаллах согласование фазо-
фазовых скоростей основной волны и гармоники (или, в об-
'' Их называют также «условиями пространственного синхро-
синхронизма» или сокращенно «условиями синхронизма». Направление в
нелинейной среде, в котором выполняется указанное условие, называ-
называют направлением синхронизма. — Прим. ред.
136
ГЛАВА 4
щем случае, волны с комбинационной частотой) оказы-
оказывается возможным за счет компенсации дисперсии света
с помощью явления двойного лучепреломления. В этом
случае в приближении заданного поля интенсивность
волны гармоники неограниченно возрастает с ростом г.
Однако в действительности, когда интенсивность гармо-
гармоники становится сравнимой с интенсивностью основной
волны, приближение заданного поля перестает быть
справедливым. Проблема обратной реакции волны гар-
гармоники на основную волну будет обсуждаться в § 2 на-
настоящей главы.
Если условие согласования фазовых скоростей не вы-
выполнено, интенсивность волны с частотой cos будет изме-
изменяться с расстоянием z по синусоидальному закону. Рас-
Расстояние между двумя соседними максимумами дается
выражением
(osc~l (e'/2 cos 0S — ет' cos 0r) z = 2тт.
Вообще говоря, прошедшая волна является неодно-
неоднородной плоской волной. Плоскости постоянной амплиту-
амплитуды (ими, очевидно, являются плоскости z = const) не сов-
совпадают с плоскостями постоянной фазы. Исключение со-
составляет случай распространения волн нормально к гра-
границе. В этом случае интенсивность волны определяется
уравнением D.10) (малый член Л ^ опущен)
iNLS
4 sin2 — asc
~l
— e^ г
D.13)
Сравнение формул D.13) и D.8) показывает, что макси-
максимальная интенсивность прошедшей волны примерно в
4e^/(es—8тJ раз больше, чем интенсивность отражен-
отраженной волны. Для обычного рассогласования фазовых ско-
скоростей, обусловленного частотной дисперсией, эта вели-
величина имеет порядок 104— 105. Тем самым пренебрежение
величиной Л^ в проходящей волне оправдано.
Периодическое изменение интенсивности второй гар-
гармоники при изменении оптической толщины нелинейной
среды впервые было продемонстрировано Мейкером и
Терхьюном; результаты их опытов представлены на
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
137
фиг. 2. По максимумам интенсивности гармоники из та-
таких кривых определяется величина нелинейной восприим-
восприимчивости, в то же время расстояние между максимумами
определяет когерентную длину или величину, обратную
величине рассогласования фазовых скоростей (е51/г —
— ej-/2)"'. Введя показатели преломления ns и пт и длину
волны в вакууме Яо, можно определить понятие когерент-
когерентной длины
'ког = 2п ±- (el'' - в?')-1 = Хо (ns ~ ПТУХ. D.14)
Когерентная длина —это расстояние, на котором волна
нелинейной поляризации и электромагнитная волна, со-
соответствующая решению однородного уравнения, идут в
фазе. Интенсивность отраженной волны оказывается
много слабее, так как вклад в эту волну дает лишь слой
атомов толщиной ~Х/2пт.
В экспериментах нелинейная среда представляет со-
собой обычно плоскопараллельную пластину. В этом случае
изложенные выше аналитические результаты можно не-
непосредственно сравнить с экспериментальными данными,
если задняя сторона пластины не отражает ни основную
волну, ни волну гармоники. Полный анализ случая плос-
плоскопараллельной пластины дается в приложении II, где
произведен учет граничных условий как на передней, так
и на задней границах. При малых френелевских коэффи-
коэффициентах отражения соответствующая поправка для про-
прошедшей волны гармоники обычно оказывается малой Ч.
Вместе с тем даже малых отражений от задней границы
оказывается достаточно для того, чтобы сильно изменить
значение амплитуды Е*1 ; влияние задней границы на
поведение нелинейных отраженных волн с частотой cos
можно не учитывать только в том случае, когда среда
сильно поглощает на частоте cos. Заметим, что в этом слу-
случае существует и прошедшая волна с частотой cos, выхо-
" Вместе с тем следует иметь в виду, что определенный инте-
интерес могут представить и случаи, когда отражения от границ нели-
нелинейного слоя значительны. В частности, такая ситуация имеет ме-
место, когда нелинейная среда помещена в резонатор типа Фабри —
Перо (см., например, [31*, 32*]).— Прим. ред.
138
ГЛАВА 4
дящая из кристалла, если только основные волны не за-
затухают (этот случай соответствует комплексному кт и
действительному ks). Волна с частотой ws излучается ис-
источником нелинейной поляризации, помещенным в среду.
Из уравнения D.3) непосредственно находим интенсив-
интенсивность прошедшей волны -для случая, когда волна часто-
частоты cos в среде затухает
В приложении II дается полное обсуждение случая дру-
другой поляризации; анализируются также явления полного
отражения и полного прохождения в нелинейном случае.
Даже если ел и ет являются действительными величина-
величинами, углы падения могут быть выбраны таким образом,
что один или более векторов кл, ks и кт окажутся комп-
комплексными.
Особый случай «отражения» второй гармоники, поля-
поляризованной в плоскости отражения, от свободных элек-
электронов проанализировали Крониг и Боукема [4] (нели-
(нелинейность этого типа обсуждалась также в гл. 1, § 2).
АНИЗОТРОПНАЯ СРЕДА
Подобные же, хотя и алгебраически более сложные,
расчеты можно провести для одноосных и двухосных кри-
кристаллов. Такие кристаллы представляют большой инте-
интерес, поскольку в ряде случае они допускают согласование
фазовых скоростей основной волны и волны гармоники;
этот случай обсуждался Клейнманом [33*]. В общем слу-
случае анизотропной среды падающая волна образует две
преломленные волны; они, вообще говоря, не подчиняют-
подчиняются закону преломления Снеллиуса, однако тангенциаль-
тангенциальные компоненты волновых векторов непрерывны на гра-
границе. Преломленные волны возбуждают волны нелиней-
нелинейной поляризации. Рассмотрим одну из них с волновым
вектором kg, направлением поляризации р и амплитудой
|PNLS|. В общем случае возникают две электромагнит-
электромагнитные волны, волновые векторы которых kv, v = I, 2, имеют
такие же, какиук8, тангенциальные компоненты. Допус-
Допустим, что эти компоненты исчезающе малы. Тогда векто-
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
139
ры кь к2 и ks направлены по нормали ns. Векторы, харак-
характеризующие направление поляризации волн, обозначим
через ei и е2. Однородное волновое уравнение имеет вид
D.16)
Можно ввести также три единичных вектора db d2 и d3,
таких, что векторы dj и е-е, так же, как и векторы d2 и
е-е2, параллельны, а вектор d3 ортогонален векторам
d, и d2(d3 = е3 = ns). Легко видеть, что
= d2 • е • ех = d3 • Vei= d3 .• 8 • е2 = 0.
Введя
А = «5^ +е2А2 + е3А3,
D.17)
запишем уравнение D.2) в виде
или, принимая во внимание D.16),
о
[ | ks |2 — | k* |2] [e, — ns (ns • eJJI X
ХЛ,-8.е3Л3-4тгрР0. D.18)
2
Поскольку d3 = ns = е3, произведение в скобках с
определяет величину Л3:
4я ( п3 • р) Ро
По • е • п.
D.19)
140
ГЛАВА 4
Исключая As из выражения D.19), получаем
2
v=l
D.20)
Далее, вводя в D.20) векторы d; и d2 [см. уравнение
D.16) для v = 1 или 2], получаем
. _ 4яРо(со/с)*1(с1,-р)-(а, .в.ЙО(п*-р)/(п*-е-п*)]
D.21)
Общее решение составляется из решения неоднородного
уравнения и двух волн, являющихся решениями однород-
однородного уравнения; их волновые векторы и векторы поляри-
поляризаций определяются линейными свойствами среды. Амп-
Амплитуды этих волн, так же как амплитуда и поляризация
нормально отраженной волны, должны быть определены
из условий непрерывности для Ех, Ev, Hx, Ну при 2 = 0.
§ 2. Взаимодействие двух связанных волн. Генерация
второй гармоники
Как уже указывалось, условие согласования фазовых
скоростей основной волны и волны гармоники может
быть выполнено в анизотропном кристалле; оно может
быть также выполнено в изотропных средах, когда в не-
небольших частотных интервалах, попадающих в рабочий
диапазон частот, существуют области аномальной диспер-
дисперсии. Это условие может быть выполнено в изотропных
средах с нормальной дисперсией, если число взаимодей-
взаимодействующих волн более трех. Наконец, оно может быть вы-
выполнено при взаимодействии оптической и акустической
волн. Для всех этих случаев важно проанализировать ре-
решение нелинейных волновых уравнений с учетом обрат-
обратной реакции волн гармоник и комбинационных частот на
порождающие их волны, т. е. выйти за рамки приближе-
приближения заданного поля,
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
141
Рассмотрим наиболее простой, но важный случай ге-
генерации второй гармоники. Обозначим частоты через
coi = со и иг = 2со, векторы поляризации через ei и е2 и
волновые векторы однородных волн через kt и кг. Пусть
вновь плоскость z = 0 является границей нелинейной
среды. Для тангенциальных компонент выполняются ус-
условия k2x = 2kxx, k2v — 2kly, однако вследствие дисперсии
k2z — 2ku = Ak. Для общности допустим, что Ak Ф 0, по-
поскольку случаи неточного согласования фазовых скоро-
скоростей также представляют интерес. Ранее мы учитывали
зависимость от координаты только для амплитуды гар-
гармоники. Однако если амплитуда гармоники A2(z) стано-
становится сравнимой по величине с амплитудой основной
волны Аь то из энергетических соображений следует
ожидать, что амплитуда А\ будет уменьшаться, и ее уже
нельзя будет рассматривать как заданную функцию. Да-
Далее волнами на всех других частотах, кроме со и 2со, мы
пренебрежем, так как им соответствуют большие рассог-
рассогласования фазовых скоростей, согласно D.13), они быст-
быстро осциллируют и амплитуды их невелики. Таким обра-
образом, рассмотрим только два волновых уравнения типа
C.23):
-!^ |2Е2 =
-^- J PNLS Bco),
D.22)
V X V X Е, - | kx j2^ = 4тг ^ PNLS (со).
\ с I
Ищем решения в виде
D.23)
Подстановка дает два дифференциальных уравнения вто-
второго порядка для А\ и А2. Если изменение амплитуды на
расстоянии порядка длины волны мало, \d2A/dz2\ <C
<Ck\dA/dz\, то производными второго порядка можно
142
ГЛАВА 4
пренебречь; в результате получаем уравнения первого
порядка для комплексных амплитуд связанных волн
— Ilk, COS Otx • COS (ОС, —Pi) L =
dz
tx • X (m = 2co — to): e2ex/42/4 Ге'ААг,
— 2ik2 cos a2 cos (a2 — [
дг
4яBш
с2
е2 •
- со + со) : ^х
D.24)
D.25)
Здесь а — угол между векторами D и Е в анизотропной
среде (он равен углу между волновым вектором к и век-
вектором Пойнтинга), а § — угол между волновым вектором
и нормалью к границе z (см. фиг. 11). Нелинейные вос-
восприимчивости определяются из свободной энергии
F = 2Re (x???j) D.26)
и удовлетворяют соотношениям симметрии
Нщ Bсо = со + со) = x/tj (со = 2со — со).
Нетрудно получить первый интеграл уравнений D.24) и
D.25). Умножим уравнениеD.25)на /4*с2/8ясо2, а уравне-
уравнение, комплексно-сопряженное D.24), на — /4,с2/4ясо2 и
сложим. В силу соотношений симметрии правые части
уравнений взаимно уничтожаются
kx cos 04 cos @4 —
дА\ i
рх) Ах ¦ -) k2 cos <х2 X
02 2
D.27)
Вектор Пойнтинга для волны в анизотропной среде имеет
величину
4я
D.28)
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
143
Следовательно, для первого интеграла уравнений имеем
ISjcosfa'-pj + 2Ц S3 |cos(ag— Cg) = W_ 4 ^
и> 2<а со "
Величина W есть полная мощность, протекающая через
единицу площади в направлении оси z нормально к гра-
границе. Для непоглощающей среды эта величина является,
Линейная
среда
Поверхность
постоянной
амплитуды
Поверхность
постоянной
/фазы
I
Анизотропная
нелинейная
среда
Фиг. 11. Диаграмма, показывающая направления векторов в анизо-
анизотропной среде.
Показаны углы между волновым вектором, вектором Пойнтиига и нормалью
к границе. Построение выполнено для положительного одноосного кристалла'
(а>0). В отрицательном одноосном кристалле (а<0), например в KDP, век-
вектор Е лежит между векторами D н к .
конечно, постоянной. Уравнение D.29) записано в фор-
форме, аналогичной известным соотношениям Мэнли — Роу,
широко используемым в теории колебаний систем с со-
144
ГЛАВА 4
средоточенными параметрами. Из D.29) следует, что ес-
если число квантов, проходящих через 1 см2 в 1 сек в на-
направлении оси z на частоте 2со, возрастает на единицу,
то число квантов на основной частоте уменьшается на
два. Следовательно, классическая теория сохраняет ха-
характерные черты процесса трехквантового рассеяния,
которое обсуждалось в гл. 2. Интегральные соотношения
Мэнли — Роу остаются справедливыми и для взаимодей-
взаимодействий трех или более волн; соответствующие примеры
приведены в приложении I. Соотношения Мэнли — Роу в
этих случаях несут даже больше информации, посколь-
поскольку они не идентичны условию постоянства полного потока
мощности.
Общее решение системы дифференциальных уравне-
уравнений D.24) — D.26) может быть получено только при
переходе к действительным переменным. В приложе-
приложении I дано такое общее решение системы уравнений двух
(§ 5) и трех (§ 6) связанных волн. Здесь мы рассмотрим
только частное решение для случая точного согласова-
согласования фазовых скоростей основной волны и волны гармо-
гармоники.
Исследование уравнений D.24) и D.25) показывает,
что для случая Ak = 0 можно выбрать величину А1 = р]
действительной, а величину А2 = гр2 чисто мнимой. Дей-
Действительные амплитуды при щ = а2 = О, Pi = Рг = О,
k2 = 2&i удовлетворяют дифференциальным уравнениям
dz
=-CPlp2,
dz
где
с =
V2
D.30)
D.31)
Пусть при z = 0 pi = pi @) и р2 = 0. В действительности,
как следует из уравнения D.10), граничные условия для
волны гармоники с амплитудой Рг@) оказываются не-
несколько иными; однако начальная амплитуда рг настоль-
настолько мала, что процесс генерации второй гармоники хорошо
соответствует условию рг(О) = 0. Первый интеграл имеет
вид
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
145
Подстановка этого соотношения в последнее из уравне-
уравнений D.30) дает
С[р»(О)-рЦ. D.32)
Производя элементарное интегрирование, получаем
p, = Pl(O)th[Cp1(O)z]. D.33)
Поскольку интенсивность второй гармоники растет, мощ-
мощность на основной частоте падает:
р1 = р1(О) sell [CPl @) г]. D.34)
Характеристическая длина нелинейного взаимодействия
может быть определена с помощью соотношения
/ = С-'рг' @) = Гйсе-'Лх (ш) Р, (О)]-1 •
к« w L av /Ki wj 8я2ХBсо)Р1@)
D. 35)
Нл этой длине около 60% мощности преобразуется в
мощность второй гармоники (здесь п—показатель пре-
преломления, X— длина волны в вакууме). При расчете чис-
численных значений следует помнить, что по нашему опре-
определению амплитуд величина %Bа) вдвое больше значе-
значения, обычно употребляемого в литературе, а амплитуда
pi @) для данного уровня мощности — вдвое меньше.
На величину когерентной длины это, конечно, не влияет.
При нашем определении хBо>) = 6-10~9 ед. CGSE для
кристалла КН2РО4 (сокращенно KDP). Для амплитуды
2pi @) = 2,7 • 105 в/см, соответствующей потоку плотно-
плотности мощности пер2 /2л = 100 Мет/см2, находим / = 0,5 см
при % = 6943 А.
Терхьюн и др. [5] получили 20%-ное преобразование
мощности излучения рубинового лазера в излучение вто-
второй гармоники. Луч был слегка сфокусирован и распро-
распространялся точно вдоль направления синхронизма в
KDP. Тот факт, что не вся мощность может быть преоб-
преобразована во вторую гармонику, связан, по-видимому, с
присутствием в лазерном пучке набора лучей, для кото-
которых условия синхронизма не могут быть выполнены одно-
одновременно. Существует довольно распространенное мне-
Ю Н. Бломберген
146
ГЛАВА 4
ние, что из-за необходимости «термодинамического рав-
равновесия» во вторую гармонику может быть преобразова-
преобразовано не более 50% мощности основной волны. Однако оно
основано на недоразумении; если фаза исходной волны
полностью определена, ее энтропия равна нулю; в коге-
когерентных процессах без флуктуации это остается справед-
справедливым. Термодинамика здесь к делу не относится.
а. е„
о
ю
20 30 40 50 60 10 80 90 100
Фиг. 12. Экспериментальная зависимость относительной амплитуды
акустической волны частоты 9,1 -109 гц в кристалле MgO от амплиту-
амплитуды на входной грани кристалла е0 (по данным Ширена).
Уменьшение амплитуды основной волны происходит вследствие перекачки ее
энергии во вторую гармонику. Сплошная кривая построена по формуле D.34).
Наиболее существенный вывод, следующий из D.33),
состоит в том, что в среде без потерь возможно полное
преобразование мощности основного излучения во вто-
вторую гармонику. Хотя в опытах по генерации световых
гармоник такое преобразование и не было достигнуто,
тем не менее оно было получено Ширеном [6] для акусти-
акустических волн. На фиг. 12 произведено сравнение получен-
полученных Ширеном экспериментальных результатов с теорети-
теоретической кривой [формула D.34)], описывающей уменьше-
уменьшение амплитуды основной волны в некотором сечении не-
нелинейной среды в функции амплитуды падающей волны
на границе нелинейной среды. В следующем параграфе
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
147
показано, что развитая теория действительно пригодна
для описания нелинейных взаимодействий акустических
волн.
§ 3. Взаимодействия электромагнитных волн
с акустическими волнами
АКУСТИЧЕСКИЕ НЕЛИНЕЙНОСТИ
Нелинейные свойства твердых тел, описываемые ан-
ангармоническими членами в уравнениях теории упругости,
известны достаточно давно. Ниже мы убедимся, что тео-
теория нелинейных взаимодействий акустических волн
может быть развита точно так же, как это было сделано
ранее для электромагнитных волн. Вместе с тем следует
отметить, что, поскольку для заданного направления рас-
распространения возможны три типа акустических волн, а
соотношения между деформацией и напряжением уже
для линейного случая описываются тензором четвертого
ранга, теория нелинейных взаимодействий акустических
волн оказывается более сложной, нежели соответствую-
соответствующая теория для электромагнитных волн.
Мы не будем здесь, однако, подробно рассматривать
акустические нелинейные эффекты, а проследим лишь
аналогию их с нелинейными электромагнитными взаи-
взаимодействиями. Для этой цели достаточно рассмотреть
случай чисто продольных акустических волн; пусть они
распространяются в направлении оси z. В области гипер-
гиперзвуковых частот акустические и оптические длины волн
оказываются сравнимыми. Частотная дисперсия для
акустических волн весьма мала, так что нетрудно осу-
осуществить точное согласование фазовых скоростей на рас-
расстояниях порядка 1 см. Кроме того, затухание акустиче-
акустических волн может быть весьма малым; в чистых кристал-
кристаллах при температуре жидкого гелия акустическая волна
затухает в е раз на расстояниях порядка 10 см. и более.
Не представляет труда возбудить акустические волны
с интенсивностями, при которых начинают проявляться
нелинейные свойства среды. В теории нелинейных взаи-
взаимодействий акустических волн роль использованных на-
нами ранее соотношений для векторов Р и Е должны иг-
10»
148
ГЛАВА 4
рать соотношения между величинами напряжения а и
деформации S. Обозначим линейный модуль упругости
через С, а самый младший нелинейный модуль упруго-
упругости через А. Запишем общее тензорное соотношение
в виде
о„ --= C\lkSkl + ASuSmn +... ¦ D. 36)
Для рассматриваемого случая продольных волн, распро-
распространяющихся вдоль оси z, имеем
згг = СS2; + CNLS2Z2, D.37)
где CNL означает АЩ , а С = Сгг\. В общем случае коэф-
коэффициенты С и CNL удовлетворяют неравенству
3C<CNL<16C.
Уравнение для продольной волны, распространяю-
распространяющейся в направлении оси z, выводится при рассмотрении
уравнения движения единицы объема с удельной плотно-
плотностью р. Учитывая, что Szz = du/dz (где и — смещение),
запишем линейное волновое уравнение в виде
дг
д2и
dz2
или для безразмерной величины деформации
Р I dz2
D.38)
D.39)
Данные по дисперсии величины С (со) можно найти в
книгах [7, 8]; заметим, что С (со) изменяется менее чем на
10~6 в диапазоне частот от 0 до 1010 гц. Решения линейно-
линейного волнового уравнения могут быть записаны в виде бегу-
щих волн 2Re[Sj exp(iq\Z — ia?t)] с фазовой скоростью
w\/q\ =(C/pI/s. Нелинейное волновое уравнение имеет
вид
— ) = •. D.40)
р J дг2 р дг2
Для деформаций 5 < 10~2 нелинейный член [правая часть
D.40)] можно рассматривать как малое возмущение.
Наличие в уравнении D.40) S2 показывает, что акустиче-
акустическая волна Sl частоты coi будет генерировать волну вто-
втоРАСПРОСТРЛНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
149
рой гармоники S2. Закон нарастания величины S2(z) опи-
описывается уравнениями связанных волн. Принимая во вни-
внимание, что
d2S
dS
dz
эти уравнения можно записать в виде
D.41)
D.42)
Эти уравнения по форме точно совпадают с уравнениями
D.24) и D.25) для связанных электромагнитных волн в
случае идеального согласования фазовых скоростей. Вме-
Вместе с тем имеется, конечно, и существенное различие.
В акустическом случае нельзя ограничиться двумя вол-
волнами, поскольку в силу слабой дисперсии волна третьей
гармоники, вообще говоря, тоже сильно взаимодействует
с волнами на частотах coi и 2соь Это приводит к сильному
усложнению задачи. Недостаточно просто добавить к
D.41) и D.42) уравнение для третьей гармоники:
D.43)
Необходимо еще включить в уравнение D.41) член, про-
пропорциональный S3S* , а в уравнение D.42) —член, про-
пропорциональный S3S* . Как только интенсивность волны
третьей гармоники достигнет заметной величины, начнет-
начнется генерация четвертой гармоники и т. д. К счастью, ока-
оказывается возможным изменить постоянную распростра-
распространения ультразвуковой волны путем использования ее
взаимодействия с парамагнитными ионами. Спиновые
уровни последних могут быть «настроены» на акустичес-
акустическую частоту с помощью внешнего магнитного поля; такая
«настройка» приводит к появлению поглощения и ано-
аномальной дисперсии для ультразвуковых волн. Соответст-
Соответствующие эксперименты были выполнены Ширеном в кри-
кристалле MgO с присадкой ионов Ni2+ или Fe2+; этим мето-
150
ГЛАВА 4
дом ему удалось подавить третью гармонику. Математи-
Математически влияние парамагнитных ионов может быть описано
добавлением к модулям упругости в волновом урав-
уравнении комплексной величины АСмагн. В упрощенных урав-
уравнениях первого порядка магнитное возмущение учиты-
учитывается добавлением к правой части уравнения D.43)
члена АСмагнР'Ч^з- Действительная часть величины
ЛСмагн вызывает рассогласование фазовых скоростей, а
мнимая часть — поглощение волны 53. Вблизи магнитно-
магнитного резонанса обе части дают вклад в подавление волны
третьей гармоники S3. Поэтому уравнения D.41) и D.42)
оказываются для этого случая хорошим приближением.
Описанным методом Ширен [6] получил эксперименталь-
экспериментальные точки (см. фиг. 12), удивительно хорошо совпадаю-
совпадающие с теоретической кривой, рассчитанной для случая
взаимодействия только двух волн. В случае когда третья
гармоника не подавлена, амплитуда основной волны как
функция начальной амплитуды спадает более медленно.
В этом случае, характеризуемом отсутствием дисперсии,
генерируются все гармоники, и решение дается формула-
формулами типа C.27) и C.29).
РАССЕЯНИЕ МАНДЕЛЬШТАМА — БРИЛЛЮЭНА
Теперь мы рассмотрим взаимодействие акустических
и оптических волн. При упругих деформациях среды ме-
меняется ее коэффициент преломления. Это явление хорошо
известно и используется для анализа напряжений опти-
оптическими методами. Давно известно и явление изменения
показателя преломления с изменением плотности при
гидростатическом сжатии. Распространение световых
волн в среде при наличии периодических упругих дефор-
деформаций, систематически исследовалось Бриллюэном''.
'> Напомним, что особый интерес эти исследования представля-
представляли в связи с выяснением природы тонкой структуры релеевского
рассеяния. В исследованиях, проведенных Бриллюэном и Мандель-
Мандельштамом, было установлено, что тонкая структура связана с рассея-
рассеянием света на тепловых акустических волнах, существующих в рас-
рассеивающей среде. Компоненты тонкой структуры со смещениями,
описываемыми формулой D.44), носят название дублета Мандель-
Мандельштама— Бриллюэна, а рассеяние света на акустических волнах —
рассеяния Мандельштама — Бриллюэна. В опытах по рассеянию с
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕПНОП СРЕДЕ
151
Влияние акустических волн на распространение света
можно трактовать как дифракцию световой волны на ре-
решетке с переменным коэффициентом преломления, обра-
образованной акустическими колебаниями; можно сказать
также, что световая волна с волновым вектором к, и
частотой ал, рассеиваясь на акустической волне с волно-
волновым вектором q2 и частотой а>2, образует световую волну
с волновым вектором к3 и частотой ю3. Законы сохране-
сохранения энергии и квазиимпульса требуют выполнения соот-
соотношений
«з = м1+«2 и k3 = k1-fq2.
Для акустических фононов с частотой ниже 1010 гц эти
условия всегда могут быть выполнены. Хотя импульс q%
может быть по порядку величины сравним с kx и k2 (по-
(поскольку фазовая скорость звука значительно ниже ско-
скорости света), акустическая частота а>2 <С coi, (o3. Поэтому
треугольники для импульсов, изображенные на фиг. 13,
можно рассматривать как равнобедренные, со сторонами
|kj| ~ |к3|. Отсюда сразу же следует соотношение для
угла рассеяния света
— = q
или для частоты акустической волны
рассеяние,
W sin
обусловливающей
D.44)
где v — фазовая скорость звука в среде, а щ — показа-
показатель преломления на частоте ац. Максимальная частота
использованием обычных источников света воздействием световых
волн на акустические волны можно пренебречь. При этом наблюда-
наблюдается так называемое спонтанное рассеяние Мандельштама — Брил-
Бриллюэна на тепловых акустических волнах. Подробное изложение со-
соответствующих теоретических и экспериментальных данных можно
найти в C4*, 35*]. В настоящей же книге основное внимание уделе-
уделено взаимодействию световых волн с когерентными акустическими
волнами, и в особенности когерентными акустическими волнами, вы-
вызываемыми светом эа счет эффекта электрострикции. Последний
эффект носит название вынужденного рассеяния Мандельштама —
Бриллюэна. — Прим. ред.
152
ГЛАВА 4
звука, участвующего в рассеянии Мандельштама —
Бриллюэна, соответствует рассеянию света в обратном
направлении, 9 = я. Интенсивность рассеянного света
для рассматриваемого случая можно вычислить таким
же способом, как и интенсивность волны суммарной час-
частоты, генерируемой двумя световыми волнами.
к3.(ш,-шг1
q2(w2)
kt(w,)
Фиг. 13. Направление волновых векторов при рассеянии Мандель-
Мандельштама — Бриллюэна.
а — в элементарном акте рассеяния акустический фоной излучается; рассеян-
рассеянный свет имеет частоту, меньшую, чем падающий свет частоты (fli (стоксово
рассеяние).
б — в элементарном акте фонон поглощается; рассеянный свет имеет часто-
частоту, большую, чем падающий свет частоты (Oi (антистоксово рассеяние).
Для усредненной по времени нелинейной части энер-
энергии в среде в присутствии двух световых и одной акусти-
акустической волн имеем
(F}=,2RepElS2El D.45)
Если частота звука w2 = 0 и амплитуда Е*ъ заменена на
Е\, то это соотношение описывает энергию фотоупругой
связи. Постоянная фотоупругости р является тензором
четвертого ранга, который связывает тензор деформаций
с векторами двух электрических полей. Фотоупругие
постоянные измерены для целого ряда материалов и име-
имеют обычно величину ~1, например 0,5.
Из соотношения D.45) непосредственно получаем вы-
выражение для волны поляризации с частотой со3:
Р (со3) =
D.46)
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
153
Процесс генерации световой волны с частотой w3 описы-
описывается формулой D.12), которая в случае полного согла-
согласования фазовых скоростей остается справедливой до
тех пор, пока интенсивность волны с частотой со3 не воз-
возрастет настолько, что станет заметной уменьшение ин-
интенсивности одной или обеих волн с частотами coi, co2.
Интересно, что недавно предложено применить рас-
рассеяние света на ультразвуковых волнах для модуляции
излучения лазера. Кристалл кварца помещается внутрь
Ш, + О),
Зеркало х~"
wL-w2
/Кварц
Уль тразвуковой
преобразо ват ель
Разряд в смеси He-Ne
¦ —
-*. из. —ш9
Фиг. 14. Схема установки для ультразвуковой модуляции излуче-
излучения газового лазера с полностью отражающими зеркалами. Отраже-
Отражение от внутренних граней кристалла отсутствует в силу условия
Брюстера (по данным работы [30]).
Ультразвуковая бегущая волна с волновым вектором q2 после прохождения
через кристалл кварца поглощается.
резонатора газового лазера, как это показано на фиг. 14.
Зеркала являются полностью отражающими, и если
кварц не возбужден, излучение лазера из резонатора не
выходит. Если же в кварце возбуждена бегущая в по-
поперечном направлении ультразвуковая волна с частотой,
удовлетворяющей условию D.44), то из резонатора будет
выходить свет со смещенной частотой. Величину связи
можно регулировать изменением амплитуды ультразву-
ультразвуковой волны.
Наличие связи между световыми и акустическими вол-
волнами D.45) может приводить к возбуждению света и на
разностной частоте, мз- = а>\ — сог- Соответствующая
волна поляризации с частотой (Оз- имеет вид
Р (со3_) =
D.47)
154
ГЛАВА 4
В этом случае закон сохранения импульса запишется в
виде
k3_= ki— q2.
Если это соотношение выполнено, интенсивности акусти-
акустической (со2) и рассеянной световой (соз-) волн будут воз-
возрастать с расстоянием, а интенсивность исходной свето-
световой волны (coi) —уменьшаться.
Если световая или акустическая волны являются
стоячими волнами, необходимо рассмотреть все возмож-
возможные комбинации прямой и обратной волн.
Пользуясь выражением для усредненной по времени
свободной энергии D.45), можно рассмотреть также за-
задачу о генерации акустической волны, возникающей в
результате смешения двух световых волн. Дифференци-
Дифференцируя D.45) по S2, для фурье-компоненты тензора напря-
напряжений с частотой (о2 = coi — со3, имеем
о&то = p?.?3-e'(k'~ki)'r~W. D.48)
При coi = соз получаем постоянное напряжение (электро-
стрикция в переменном поле). Периодически изменяю-
изменяющееся напряжение частоты со2 служит источником аку-
акустических волн, в полном соответствии с неоднородным
волновым уравнением [ср. с уравнением D.40)]:
d*s
- С
йгг
= -1 к, - к3
D.49)
Нетрудно видеть, что световая волна с частотой со3-
будет возрастать одновременно с акустической волной
частоты со2. В связи с этим возникает интересный вопрос,
что будет, если начальная амплитуда Е3- выбирается
весьма малой. Очевидно, что волны с частотами со2 и соз-
будут нарастать за счет энергии световой волны с боль-
большей частотой соь Наконец, величину ?3- можно положить
равной нулю. Могут ли волны с частотами соз- и со2 нара-
нарастать от уровня шумов? Эта задача сводится к задаче
о параметрической генерации и преобразовании часто-
частоты вниз; она будет рассмотрена в следующем параграфе.
Следует иметь в виду, что такие эффекты могут иметь
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
155
место не только при взаимодействии световых и акусти-
акустических волн, но и при взаимодействии только световых
волн.
§ 4. Параметрическое преобразование частоты вниз
и параметрическое возбуждение автоколебаний
Обратимся к уравнениям D.33) и D.34), описываю-
описывающим процесс генерации второй гармоники света в случае
полного согласования фазовых скоростей. Допустим, что
с помощью слоя диспергирующего материала фаза вол-
волны второй гармоники в какой-то точке сдвинута на 180°
относительно фазы основной волны, и после этого фазо-
фазовые скорости волн вновь согласованы. После этой опера-
операции производные амплитуд изменяют знак: теперь вторая
гармоника подавляется, в то время как основная волна
(субгармоника) регенерируется.
Процесс генерации субгармоники соответствует гра-
граничным условиям Л](со) = 0, Л2Bсо) = А2@). Однако при
таких граничных условиях, как следует из уравнений
при z = 0, dA\ldz = dA%jdz — 0, и, следовательно, волны
не взаимодействуют. В действительности А]@)Ф0, что
связано с неизбежным наличием шумов в среде. Поэтому
можно записать А\@) = Аш (со), где величина Аш (со)
определяется спектральной компонентой шума на часто-
частоте со. Ниже мы увидим, что при определенных условиях
нелинейная среда, возбуждаемая интенсивной волной с
частотой 2со, способна к усилению волн частоты со. Сле-
Следовательно, шум будет усилен и при введении соответст-
соответствующей обратной связи могут возбудиться автоколеба-
автоколебания. Это обстоятельство было отмечено Кингстоном [9].
Кролль [10] более подробно исследовал процесс парамет-
параметрического преобразования энергии световой волны с ча-
частотой coi вниз по частоте в энергию двух световых волн
с частотами а>2 и со3- = щ — сог.
Обратимся к анализу этого последнего случая '). Све-
1J Таким образом, энергия интенсивной волны частоты o)i (ее
называют также волной накачки) может передаваться либо волне
субгармоники частоты Wi/2 (такой режим называют режимом «вы-
«вырожденного параметрического усиления»), либо в более общем слу-
156
ГЛАВА 4
товое поле с частотой «я, которое можно назвать накач-
накачкой (обычно источником накачки является лазер с ча-
частотой wl), будем считать заданным. Два связанных вол-
волновых уравнения, описывающих поля с частотами юг
(далее, это поле будем называть также полем сигнала
@2 = o>s и Из (так называемая холостая частота со3 = ач),
имеют вид
в (k ) to2 4лга2 *
* "; Es = —^ х ((о, = coL — <т) Е JE,-,
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
V X V X Es
D.50)
с2
с2
ElEs
X X* (— Ш| = - «l + О ElEs D.51)
(индекс L относится к волне накачки, aL — cos + (о*).
Ищем решение в виде
Es = Л-^
E', = elA'lei^-kL)^+^i D.52)
(здесь As и Л{ считаются постоянными). Подстановка
этих выражений в уравнения D.50) и D.51) приводит к
двум однородным алгебраическим соотношениям для ам-
амплитуд Д. и А*. . Ненулевые решения имеют место в слу-
случае, когда определитель системы равен нулю. Если гра-
граничные условия поставлены при z = 0, амплитуды волн
могут изменяться только вдоль оси z. Поэтому проекции
волнового вектора kxs и kys являются действительными,
а проекция kzs — комплексной. Приравнивая нулю опре-
определитель системы, получаем
[kl + (kl + kl.) - (k?J] [(*„ - k2LJ + (kxs- kxLJ +
2\EL\\ D.53)
чае — двум волнам с частотами ш2, ш3, удовлетворяющим условию
оI = оJ+|Соз («невырожденное параметрическое усиление»). Оба
эти режима усиления световых волн наблюдались недавно экспери-
экспериментально '[36*, 37*]. Изложение теории вырожденного параметри-
параметрического усиления бегущих волн можно найти, например, в [38*1. —
Прим. ред.
157
где для сокращения записи введено обозначение
X = es/((os) : eLe,. Это — уравнение четвертой степени от-
относительно ksz при заданном значении тангенциальной
компоненты волнового вектора (k2xs + kyS)l/*- Корни
уравнения, имеющие отрицательные мнимые части, соот-
соответствуют экспоненциально нарастающим связанным
волнам. Величины k° и k° в D.53)—постоянные распро-
распространения собственных волн среды с частотами со.ч и со;,
являющихся решениями однородного уравнения (в отсут-
отсутствие накачки EL = 0). Если среда обладает потерями на
частоте ws или ьн, эти постоянные распространения явля-
являются комплексными; при этом величину (k°sJ для вол-
волны Es следует заменить на (&°JA + ie"s/e's ), а величину
(??J для волны ??—«a (k°J A — te^/e/).
Введем обозначения для г-компонент постоянных рас-
распространения собственных волн:
klJ-(k2xs + k2y5)]1'2,
0\2 /,2 , г.2 М 1/2
kzl =
и величины рассогласования фазовых скоростей в направ-
направлении оси z: Ak = kfs —kZL + kf., причем рассматривать
будем только те значения тангенциальных компонент,
для которых ДА: <^ к°г . Корни уравнения D.53) отлича-
отличаются от kfz на малую величину Дх. Уравнение четвертой
степени для среды без потерь принимает вид
[+ 2О* + (АхJ] [— 2kfi (Ak + Ax) + (Ak + ДхJ] =
4jI(o,-<os
с2
D.54)
Это уравнение имеет 2 корня Дх, величины которых ма-
малы, и два корня Дх вблизи значения —2А:8°г . Последние
два решения соответствуют обратным волнам, бегущим
в направлении, противоположном направлению распро-
распространения волны накачки. Первые два корня можно вы-
вычислить с достаточной точностью, если в уравнении
D.54) опустить члены (ДхJ и (Д/г + ДхJ, стоящие в
158
ГЛАВА 4
квадратных скобках. Тогда остается квадратное уравне-
уравнение с двумя корнями:
— J- Ak± Г
2 [
X
X
J
D.55)
Легко видеть, что один из корней будет иметь отрица-
отрицательную мнимую часть (т. е. будет возможно усиление)
в случае выполнения условия
Усиление максимально при Ak = 0. Возрастающая вол-
волна представляет собой линейную комбинацию волны сиг-
сигнала и волны с холостой частотой. Отношение их ампли-
амплитуд равно значению собственного вектора, соответствую-
соответствующего собственному значению Ах. Если усиление
превышает неизбежные потери, возникающие вследствие
рассеяния или потерь при отражении от зеркал, исполь-
используемых для создания обратной связи, в рассматриваемой
среде возникают колебания (параметрическая генера-
генерация). Следует подчеркнуть, что требование согласования
фазовых скоростей является весьма жестким; необходи-
необходимо поэтому, чтобы в эксперименте расходимость волны
накачки была минимальной и определялась только ди-
дифракцией.
Вышеуказанным способом рассмотрение можно рас-
распространить и на случай среды с потерями. Нетрудно
также показать, что переход от характеристического
уравнения четвертой степени D.53) к квадратному урав-
уравнению соответствует переходу от уравнений второго по-
порядка D.50) и D.51) к приближенным уравнениям пер-
первого порядка (см. § 2 настоящей главы); в этом прибли-
приближении также можно учесть и поглощение.
Аналогично тому как это было сделано при выводе
уравнений D.24) и D.25), можно получить уравнения
первого порядка для медленно меняющихся амплитуд;
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
159
обозначим их через Es и ?г-. Полагая углы ai = а% = 0,
имеем
dE]
dz
D.56)
= — i '- 7 t.Ltse —-—aiE]. D.57)
2ft™ c2
Здесь введены коэффициенты затухания по амплитуде as
и аг-; они непосредственно определяются величиной мни-
мнимой части диэлектрической проницаемости. Решение этих
уравнений дает две волны с постоянными распростране-
распространения k? + Ах, где
дх = _ _i_ Ak + ± i K + a.) ± j_L [Ak - i (a, - as)f -
|xl2|?Ll2 I1''2
D.58)
В отсутствие потерь это соотношение идентично форму-
формуле D.55). Для получения усиления необходимо, чтобы
коэффициент нарастания превосходил декремент затуха-
затухания; для случая полного согласования фазовых скоро-
скоростей и при равенстве потерь для обеих волн это условие
может быть записано в виде
r
Весьма интересный результат получается в случае, когда
потери для одной волны существенно превышают потери
для другой. Пусть
! /umym\l/2
\RziRzs)
'' Таким образом, при as, ,=^0 и Д&^0 усиление возникает
лишь при превышении некоторого порогового значения напряженно-
напряженности поля накачки. Уравнения вида D.56) и D.57) описывают так-
также процессы вынужденного рассеяния; в этом случае пороговое по-
поле называют «порогом» вынужденного рассеяния (см. ниже).—
Прим. ред.
160
ГЛАВА 4
В этом случае квадратный корень D.58) распадается
на два значения
. . , . / 4nra/cos \2 X2|?lI2 .. -„,
= + ««/ +И—^-L) —— ; D.59)
Ах
Ах = ias — i
с2
D.60)
Если величина as достаточно мала, то усиление для од-
одной из волн будет всегда иметь место, несмотря на то
что другая волна будет сильно поглощаться. Усиливае-
Усиливаемая волна практически содержит только поле с часто-
частотой ws; волна с частотой ац имеет существенно меньшую
амплитуду. Рассмотренное решение может быть получе-
получено более просто, если в уравнении D.57) пренебречь чле-
членом \dE*. ldz\ по сравнению с величиной щЕ*. Подстав-
Подставляя величину Е'. из уравнения D.57) в D.56), сразу же
получаем выражение для постоянной распространения
усиливаемой волны, соответствующей значению D.60).
При подстановке решения для Es в уравнение D.57) по-
получаем выражение для волны поляризации с частотой со,.
Отношение амплитуд взаимодействующих волн равно
Эти предельные случаи весьма поучительны. Итак, мни-
мнимая часть величины Ах в D.58), или более точно ко-
корень Ах уравнения четвертой степени типа D.53), где
учтено затухание, дает полное описание процессов уси-
усиления и затухания при параметрическом преобразовании
вниз по частоте. Для каждого собственного значения Ах
можно найти соответствующие собственные волны, т. е.
надлежащую линейную комбинацию волн с частотами cos
И (Hi.
Аналогичное рассмотрение может быть проведено для
случая, когда одна из волн, например волна с часто-
частотой (Ог, является акустической. Это — рассеяние Ман-
Мандельштама — Бриллюэна. В этом случае уравнение D.51)
нужно заменить акустическим волновым уравнением
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
161
D.49). Выведенные ранее формулы остаются справедли-
справедливыми; следует произвести лишь подстановки соответст-
соответствующих физических величин. В кристаллах и жидкостях
при комнатной температуре поглощение акустических
волн оказывается много большим, чем поглощение свето-
световой волны в прозрачной среде. Типичное значение коэф-
коэффициента поглощения для гиперзвуковой волны щ при
температуре 300° К на частоте 10ш гц составляет 400 см~1;
величина а* возрастает как квадрат частоты. Поглоще-
Поглощение же света характеризуется коэффициентом
as<0,l см~К Следовательно, можно ожидать усиления
рассеянной световой волны с частотой cos. Рассеяние Ман-
Мандельштама — Бриллюэна во многом похоже на комбина-
комбинационное рассеяние света. Действительно, в элементар-
элементарном акте рассеяния квант частоты лазера аь
поглощается, световой квант частоты cos = wL — соак из-
излучается, а акустический фонон /га>ак = h®i из-за силь-
сильного затухания звука в среде поглощается. Легко видеть,
что если величина щ постепенно уменьшается до значе-
значения, сравнимого с величиной as, характер процесса рас-
рассеяния изменяется. При больших щ это процесс типа
комбинационного рассеяния, где усиливается в основном
рассеянная световая волна, а при малых а; — процесс
параметрической генерации одновременно обеих волн —
акустической и световой. Экспериментально последний
режим можно реализовать путем охлаждения кристалла
до температуры жидкого гелия, при которой величины щ
и as оказываются сравнимыми.
В § 3 было показано, что луч рассеянного света может
идти в обратном направлении; это имеет место, когда ве-
величины kfz и^в уравнениях D.58) — D.60) отрицатель-
отрицательны. Для обратной волны коэффициент затухания as сле-
следует взять с обратным знаком. В предельном случае
большого затухания звуковой волны выведенные соотно-
соотношения остаются справедливыми при отрицательных зна-
значениях kzi и as. Мнимая часть величины Ах изменяет свой
знак. Поскольку взаимодействующие волны распростра-
распространяются теперь в противоположных направлениях, усиле-
усиление обратной волны определяется формулой D.60), если
затухание акустической волны велико. Более общая тео-
теория явления вынужденного рассеяния Мандельштама —
11 Н. Бломберген
162
ГЛАВА 4
Бриллюэна развита Кроллем [11]. Он детально проанали-
проанализировал режим рассеяния под углом 180° (рассеяния в
обратном направлении) для случая, когда акустическое
поглощение не слишком велико по сравнению с величи-
величиной параметрического усиления. Кролль обратил также
внимание на то обстоятельство, что при анализе рассея-
рассеяния Мандельштама — Бриллюэна весьма существенным
является учет нестационарных процессов. Действительно,
за время длительности импульса лазера (~10^8 сек)
акустическая волна может не успеть пройти расстояние,
обеспечивающее достаточное усиление. Поэтому в урав-
уравнениях D.56) и D.57) необходим учет производных ком-
комплексных амплитуд по времени; в работе [11] дано реше-
решение таких уравнений.
Ряд теоретических вопросов, связанных с эффектом
вынужденного рассеяния Мандельштама — Бриллюэна,
был рассмотрен Таунсом и др. [12]. Экспериментально
рассеяние в кварце и сапфире наблюдали Чао, Таунс и
Стойчев [12]. Схема их эксперимента представлена на
фиг. 15. При комнатной температуре пороговая мощность
лазера, соответствующая появлению вынужденного рас-
рассеяния, оказывается весьма высокой; пороговые плотно-
плотности потока мощности в сфокусированном лазерном луче
составляют по оценкам 1010 вт/см2. При этом в ультра-
ультразвук преобразуется доля мощности лазера ~соак/мь, ко-
которая из-за сильного поглощения звука за время, мень-
меньшее 10~7 сек, переходит в тепло. Кристаллы неизменно
повреждались, как только интенсивность лазерного излу-
излучения оказывалась достаточной для наблюдения эффекта
вынужденного рассеяния. В этих опытах в основном ре-
регистрировалось рассеяние в обратном направлении. Вы-
Вынужденное рассеяние в обратном направлении идет, по-
видимому, наиболее эффективно, поскольку длина вза-
взаимодействия рассеянного излучения с излучением лазера
в этом случае максимальна. Здесь уместно заметить, что
рассеяние Мандельштама — Бриллюэна в прямом на-
направлении (Э = 0, см. фиг. 13) возможно в анизотропных
кристаллах. Здесь падающая световая волна может быть
рассеяна с образованием волны стоксовой частоты, имею-
имеющей другую поляризацию и распространяющуюся в
том же направлении. Законы сохранения энергии и им-
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
163
пульса при Мак Ф 0 выполняются здесь в силу двойного
лучепреломления '>.
При превышении порога вынужденного рассеяния
вдоль луча лазера заметная часть мощности лазера пре-
преобразуется в мощность волны стоксовой частоты. При
этом мощность рассеиваемой волны уменьшается, и
вследствие этого другие нелинейные процессы, например
Зеркала
(R = 0l)
Кристалл
Матовал
стеклянная
пластинка
Интерферометр
Фабри- Перо
Линзы (f= 130 см)
Фотопластинка
Фиг. 15. Схема эксперимента по наблюдению вынужденного рассея-
рассеяния Мандельштама — Бриллюэна в обратном направлении (по дан-
данным работы A2]).
Расстояние между пластинами интерферометра Фабри —Перо 0,16 см.
вынужденное рассеяние в других направлениях, могут
быть подавлены. Подобное взаимовлияние различных не-
нелинейных процессов, связанных с определенным порогом,
имеет большое значение. Нелинейная природа явлений
'> Действительно, формула D.44), из которой следует, что
«ак = 0 при 9 = 0, относится к случаю изотропной среды. В анизо-
анизотропной среде, где падающая и рассеянная волны могут быть вол-
волнами разных поляризаций (соответствующие показатели прелом-
преломления я, и я2), вместо D.44) следует писать шак = со, (у/с){(я, —
— я2J + л,я2 X Bsin Q/2J]1!t , откуда следует, что при я, Ф п2
Мак ф 0 и при 9 = 0. Соответствующий эксперимент по наблюдению
вынужденного рассеяния в кварце описан в C9*]. — Прим. ред.
11*
164
ГЛАВА 4
такова, что реализуются лишь процессы с самыми низ-
низкими порогами. Вынужденное рассеяние Мандельшта-
Мандельштама — Бриллюэна может конкурировать с вынужденным
комбинационным рассеянием. Как уже указывалось, эти
процессы весьма схожи, только роль акустических фоно-
нов играют в последнем случае оптические фононы, на-
например молекулярные колебания. В этой связи примеча-
примечательным является тот факт, что кварц и сапфир не дают
эффекта вынужденного комбинационного рассеяния, в то
время как кальцит, в котором последний эффект имеет
место, не дает вынужденного рассеяния Мандельшта-
Мандельштама — Бриллюэна.
§ 5. Вынужденное комбинационное рассеяние
Теория этого эффекта обсуждалась многими автора-
авторами [14—24]. При классической трактовке вынужденного
комбинационного рассеяния как параметрического про-
процесса [25] его можно рассматривать как явление, в зна-
значительной мере аналогичное вынужденному рассеянию
Мандельштама — Бриллюэна; связь между световой вол-
волной стоксовой частоты cos и оптическими фононами с ча-
частотой сои возникает в поле волны накачки частоты
юх, = cos + fi>». Основное различие этих явлений состоит
в том, что дисперсионные характеристики среды для
оптических фононов существенно отличаются от таковых
для акустических фононов. Для колебаний типичной мо-
молекулярной группы, например СО3 в кальците или С — Н
в молекулярных органических жидкостях, ширина соот-
соответствующей фононной ветви весьма мала. Поскольку
интерес представляют лишь длинноволновые фононы с
длиной волны, соответствующей длине волны света,
ka < 10~3 (здесь а — характерный внутриатомный раз-
размер), частота оь постоянна при изменении волнового чис-
числа в довольно широких пределах. Поэтому закон сохра-
сохранения импульса при рассеянии на таких оптических фо-
нонах выполняется для произвольного направления
распространения электромагнитной волны с частотой cos.
Дисперсионные характеристики для электромагнитных
волн и оптических фононов представлены на фиг. 16.
Из-за колебательно-электронного взаимодействия дис-
РЛСПРОСТРЛПЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
166
персионные кривые не пересекаются, причем имеется
весьма узкая полоса частот, близких к частоте молеку-
молекулярных колебаний, соответствующая очень сильному
поглощению электромагнитных волн. Соотношения
ЕМ
Оптическая ветвь
Ю
2-ад-
Фиг. 16. Дисперсионные кривые для электромагнитных волн, опти-
оптических фононов и акустических фононов в случае больших длин
волн, X 3> а (масштаб не выдержан).
Комбинационное рассеяние на сильных колебательных модах при относитель
ио слабой связи с электромагнитным полем возможно и в прямом направ-
направлении.
Крамерса—Кронига показывают, что диэлектрическая
проницаемость для частоты со ^ со» несколько меньше,
чем для частоты со ^ со„. Наклон кривых пропорционален
величине е"'''1. Дальнейшее повышение частоты в сторо-
сторону видимой части спектра сопровождается уменьшением
166
ГЛАВА 4
наклона кривых, соответствующим естественной диспер-
дисперсии света. Для выполнения закона сохранения импульса
при рассеянии стоксовой компоненты света в прямом
направлении должно быть
kL — ks = 8I/2 (COL) С-' (<DL — CDs) = 8I/2 (<DL) c"'©, = C".
Оптические фоионы с таким значением волнового векто-
вектора существуют, если е'/г (со/,) > е1/г (со = со„ — б) (б —
малая величина, равная по порядку полосе частот силь-
сильного поглощения). Это возможно; см. пунктирную линию
с наклоном е'/* (соь) на фиг. 16. Для стоксовых компо-
компонент, распространяющихся в других направлениях, мож-
можно, очевидно, найти оптические фононы с согласованным
импульсом, большим по величине, чем &"ин . Дисперсион-
Дисперсионная кривая для акустических фононов также построена
на фиг. 16, однако масштаб для нее не соблюден. Заме-
Заметим, что все эти кривые относятся лишь к весьма малым
значениям величины ka, поскольку оптическая длина
волны много больше внутриатомных расстояний.
Лоудон {17, 18] рассмотрел случай очень сильной фо-
тон-фононной связи, возникающей при взаимодействии
света с колебаниями ионной решетки. В этом случае
e(w = иг, — б) = Bdc, тогда как в диапазоне частот, лежа-
лежащем выше частоты ионных колебаний, диэлектрическая
проницаемость оказывается много меньшей и равной
квадрату коэффициента преломления для инфракрасной
области. Дисперсионные эффекты здесь выражены более
резко и качественно иллюстрируются графиками фиг. 17.
Выполнение закона сохранения импульса для стоксовой
компоненты, распространяющейся в прямом направле-
направлении, в кубических или изотропных средах невозможно.
Лоудон показал, однако, что в анизотропных кристаллах
рассеяние в прямом направлении возможно.
Мы уделим основное внимание существенно более
узким фононным оптическим ветвям, связанным с моле-
молекулярными колебаниями '). Эффект вынужденного комби-
'> Обстоятельный обзор литературы по спонтанному и вынуж-
вынужденному комбинационному рассеянию в кристаллах дан Лоудоном
[40*]. — Прим. ред,
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
167
национного рассеяния наблюдался до сих пор только для
этих ветвей. Потери при этом существенно меньше, чем а
случае широких оптических ветвей. Наблюдение же
Полное отражение
Фиг. 17. Дисперсионные характеристики связанных электромагнит-
электромагнитных волн и оптически активных ионных колебаний.
А — световая волна; В и С — соответственно продольные и поперечные фо
ноны в отсутствие связи с электромагнитными волнами; D — низкочастотная
электромагнитная волна; Е — поперечные фононы ионной решетки, связанные
с низкочастотной электромагнитной волной; F — наклон днсперсиоииой ха-
характеристики, соответствующий согласованию фазовых скоростей при комби-
комбинационном рассеянии в прямом направлении. В случае очень сильной связи
рассеяние в прямом направлении в кубических ионных кристаллах невозмож-
невозможно. Лоудои [17, 18] показал, что согласование фазовых скоростей в прямом на-
направлении возможно в анизотропных кристаллах.
эффекта вынужденного комбинационного рассеяния на
оптических фононах в ионной решетке, например в NaCl,
может быть связано с большими трудностями из-за высо-
высокого порога.
168
ГЛАВА 4
Связь между ядерной колебательной координатой R
и полем описывается классически поляризуемостью, па-
параметрически зависящей от R:
<^ = %+~R+--- • D.61)
OK
Эта модель была введена Плачеком. Члены более высо-
высокого порядка в нашем случае пренебрежимо малы. Сво-
Свободная энергия молекулы в электрическом поле равна
F= La?«__L _*_#?*. D.62)
2 2 dR K '
Вместо локального колебания R введем волну оптических
фононов
где Q = RBpa2y^ означает нормальную координату
волны, нормированную на единицу объема; здесь р —
плотность, «г, — частота колебаний. В этом случае для
усредненной по времени свободной энергии единицы объ-
объема в присутствии одновременно двух световых волн и
одной волны оптических фононов имеем
1 + AlE[EL). D.63)
> = N
Это выражение имеет ту же форму, что и соотноше-
соотношение D.45) для энергии фотоупругой связи. Теперь можно
записать уравнения связанных волн, аналогичные урав-
уравнениям D.56) и D.57). Волновое уравнение для оптиче-
оптических фононов отличается, однако, от уравнения D.49)
для акустических фононов в силу различия дисперсион-
дисперсионных характеристик. Поэтому в уравнении для амплиту-
амплитуды молекулярных колебаний появляется групповая
скорость dajdkv
dz
'dz
da
dQ
— ко,
E*LES-
~v{kv)Al. D.65)
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
169
Характерной особенностью процесса является то, что за-
затухание оптических фононов намного превышает затуха-
затухание световых волн, поэтому последним мы пренебрегаем.
Коэффициент поглощения для волны оптических фононов
записывается в виде (dkv/dav) T(kv), где Г имеет раз-
размерность частоты и обратна по величине характеристиче-
характеристическому времени затухания для оптических фононов. Не
следует путать величину а в формуле D.65) для молеку-
молекулярной поляризуемости с декрементами затухания и;
и as в уравнениях D.56) и D.57).
Здесь мы снова имеем два экспоненциальных реше-
решения, в которых мы опустим величину exp (iAkz), так как
при cos = соь — ю„ для любого направления величину Ak
можно принять равной нулю. Эти волны распространя-
распространяются вдоль оси z и характеризуются постоянной распро-
распространения k™z + Ах, где
Ач = + ± ¦
2
¦г (*») + '" [-7
v dkv / da \2 .
dkv
C2km dw0 \ dQ
D.66)
Так как параметр поглощения Г„ всегда оказывается
весьма большой величиной, то, раскладывая квадратный
корень в ряд, для постоянной нарастания получаем
—— ' I '
kmc2
2р<о0Г (ka)
EL
D.67)
Волна, соответствующая этому собственному значению,
является чисто световой волной с частотой cos. Конечно,
присутствует и небольшая «примесь» волны оптических
фононов; она индуцируется при одновременном наличии
волн лазера и стоксовой компоненты. Амплитуда этой
волны может быть вычислена непосредственно из урав-
уравнения D.65), если пренебречь величиной dA'v /dz по срав-
сравнению с диссипативным членом.
Представляет интерес сравнить вышеприведенное
классическое описание эффекта вынужденного комбина-
комбинационного рассеяния с квантовомеханическим расчетом
170
ГЛАВА 4
восприимчивости при комбинационном рассеянии, в ре-
результате которого была получена формула B.62). Вкван-
товомеханической трактовке колебательные уровни явля-
являются частью квантованных энергетических уровней ло-
локализованной молекулы. При классическом же подходе
электронные квантованные уровни включают в поляри-
поляризуемость а, а молекулярные колебания трактуются как
классическая волна. Мнимая постоянная распростране-
распространения, соответствующая усилению, может быть выражена
через комбинационную восприимчивость
гпи>~
Ач=+ i ~ls\EL
или
t,m 2
Rszc
Г (kv
D.68)
D.69)
Теперь продемонстрируем эквивалентность формул B.62)
и D.69). С учетом известного выражения для линейной
поляризуемости ао [см. формулу Крамерса — Гейзенбер-
га B.28)] запишем выражение для мнимой части комби-
комбинационной восприимчивости B.62) в виде')
X' =
N
2 2
П а0
»ng
D.70)
Безразмерная постоянная [i\(uv/(ul— «ng)]2 является ко-
коэффициентом редукции для переходов, связывающих раз-
различные колебательные уровни. Отсюда имеем равенство
R\ I да
а„
dR }о
Классическая энергия осциллятора с амплитудой 2R свя-
связана с частотой соотношением
]a2vR2 = hav. D.71)
1J Следует отметить, что иерезонансный член в формуле B.62)
имеет знак, противоположный знаку члена, появляющегося в выра-
выражении для линейной восприимчивости <х0. Поэтому формула D.70) и
выражения, производные от нее, носят лишь приближенный харак-
характер.
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
171
Исключая h и т] из формулы D.70), приходим к соот-
соотношению D.69).
Параллель между квантовомеханической и классиче-
классической трактовками комбинационного рассеяния может
быть сделана даже более полной, если квантовать нор-
нормальные фононные моды, а не локализованные колеба-
колебательные уровни. Преимуществом такой «нелокальной»
трактовки является то, что она позволяет учесть зави-
зависимость поглощения от волнового вектора фонона. По-
Поглощение оптических фононов вызвано в основном вза-
взаимодействием с акустическими фононами, которое обус-
обусловлено ангармоническими упругими силами и несовер-
несовершенствами кристаллов. Проведение детального количе-
количественного расчета распада оптического фонона на
два или более акустических фонона затруднительно. На
основе общего рассмотрения в пространстве импульсов
для конечного состояния можно ожидать, что фонон с
волновым вектором kL + ks будет поглощаться несколько
сильнее, чем фонон с вектором kL — ks. Поэтому величи-
величина усиления на единицу длины для стоксовой волны в
прямом направлении, пропорциональная F~l(kL— ks),
должна быть на несколько процентов больше усиления
на единицу длины для стоксовой волны, рассеиваемой в
обратном направлении [последнее пропорционально
Г {kL + ks)]. Бломберген и Шен [25] предложили при-
привлечь эти рассуждения для объяснения наблюдаемой на
опыте асимметрии в интенсивности стоксовой компонен-
компоненты при рассеянии вперед и назад. При значительном экс-
экспоненциальном усилении разница в величине поглощения
в несколько процентов может привести к изменению ин-
интенсивности стоксовой компоненты на порядок.
Быстрое затухание фононной волны приводит к тому,
что усиление стоксовой компоненты не зависит от фазы
этой волны. Возрастание амплитуды стоксовой волны в
заданном поле EL описывается уравнением
dts
dz
j
Is
D.72)
В действительности амплитуда Es экспоненциально воз-
возрастает с расстоянием лишь до тех пор, пока она не ста-
норится сравнимой с Eh. После этого величина Eh уже
172
ГЛАВА 4
не может больше рассматриваться как фиксированный
параметр. Ее уменьшение описывается уравнением
dE,
dz
'C\eA2\el\.
D.73)
Следует отметить, что в отличие от опытов по смешению
и генерации гармоник, где обратной реакцией на порож-
порождающие волны во многих случаях можно пренебречь, в
экспериментах по вынужденному комбинационному рас-
рассеянию наблюдается, как правило, уменьшение мощно-
мощности накачки; оно неизбежно при высоком уровне мощно-
мощности или при использовании длинных кювет. Решение си-
системы двух связанных уравнений D.72) и D.73) было
дано Лоудоном [17, 18]Х). Поскольку, как уже указыва-
указывалось, фазовые соотношения несущественны, от этих урав-
уравнений можно перейти к уравнениям для интенсивностей.
Умножим уравнение D.72) на E*s , а уравнение D.73) на
E'L . Далее, используя соотношение между числом фото-
фотонов, проходящих через 1 см2 в 1 сек, и интенсивностью
|?s|2, nsh(os = (се'/'/2л) \ES\2, а также аналогичное соот-
соотношение для частоты ац, уравнения связанных волн мож-
можно записать в виде 2~>
= -W(ns+])nL, D.74)
где
5 L,
cV1/2e}/2
I/Л
D.75)
Уравнения для чисел фотонов, записанные в такой фор-
форме, могут быть получены и непосредственно при кванто-
вомеханическом подходе; это было проделано Хелвор-
сом [14] и Цайгером [15]. При высоких уровнях мощности
1; См. также работы [41*, 42*]; в последней аналогичное рассмо-
рассмотрение проведено для среды, состоящей из анизотропных моле-
молекул. — Прим. ред.
2) В уравнениях D.74) множители (п„ + 1) записаны вместо па
из соображений получения соответствия с квантовой теорией. —
Прим. ред.
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ 173
(«ьЗ>1) спонтанным излучением можно пренебречь; в
этом случае уравнения элементарно интегрируются. Пер-
Первым интегралом является, конечно, закон сохранения
полного числа фотонов, ns + nL = n°s + гс° (здесь п° и
n°L—числа квантов на границе 2 = 0). С учетом этого
первое уравнение системы D.74) можно записать в виде
D.76)
решение которого имеет вид
?2 [( )]
Область применимости этого решения, однако, ограни-
ограничена. Прежде всего, в действительности возбуждается не
одна стоксова волна, так как усиление на стоксовой ча-
частоте имеет место во всех направлениях. Определенное
направление может быть выделено с помощью внешних
зеркал, понижающих порог возбуждения вынужденного
рассеяния для определенной моды. Так делается в лазе-
лазерах, использующих эффект комбинационного рассеяния.
Как только интенсивность стоксовой компоненты в этой
моде возрастает, стоксова волна сама начинает служить
накачкой и генерирует волну с частотой coSs = cos — сои =
= oil — 2оь. Сообщения о генерации таких стоксовых
компонент второго порядка появились в первых публи-
публикациях по лазерам на комбинационном рассеянии [26];
эти компоненты были обнаружены и многими другими
экспериментаторами. В свою очередь излучение с часто-
частотой (Dss может служить накачкой и генерировать волну
с. частотой cusss = coz, — Зсо« и т. д. Волна с часто-
частотой coss не будет генерироваться, если начальное число
квантов с частотой лазера меньше числа квантов, соот-
соответствующего двойному порогу. В этом случае величи-
величина ns не может превысить порогового уровня, необходи-
необходимого для процесса генерации стоксовых компонент
второго порядка'). В модели рассеяния, описываемой
1( Помимо описанного механизма генерации стоксовых компо-
компонент высших порядков, возможен и другой механизм, при котором
порог их генерации равен порогу для первой стоксовой компоненты
(см. [20]). — Прим. оед.
174
ГЛАВА 4
уравнениями типа D.74), порог связан с поглощением на
стоксовой частоте; для его количественного описания
следует добавить в D.74) соответствующие члены.
Поскольку начальная мощность лазера легко может
превысить порог вынужденного рассеяния на частоте o)s
на один или два порядка, для полного исследования яв-
явления оказывается необходимым решать систему многих
связанных уравнений. Интенсивность волны лазера быст-
быстро падает до величины, превосходящей порог не более
чем в несколько раз; возрастание интенсивности сток-
совой волны также ограничено за счет процесса образо-
образования стоксовых компонент второго порядка. С увеличе-
увеличением интенсивности волны лазера в экспериментах по
комбинационному рассеянию появляются стоксовы линии
все более высокого порядка; однако интенсивность каж-
каждой из стоксовых линий более низкого порядка не может
возрасти выше определенного значения. В этом состоит
ограничивающее действие нелинейных процессов на ин-
интенсивности волн. Можно, конечно, искусственно повы-
повысить порог генерации на частоте coSs, вводя сильное по-
поглощение на частоте coSs (но не на частоте cos) ¦ Вслед-
Вследствие этого волна с частотой coss будет исключена из
системы связанных уравнений (точно так же сильное
поглощение может исключить из взаимодействия фонон-
ную волну с частотой av). Если волна частоты coss не воз-
возбуждается, не могут возникнуть и стоксовы компоненты
более высокого порядка. В этом случае применимо ре-
решение D.76) двух связанных уравнений для волн с часто-
частотами сох, и cos. Однако в описанных к настоящему времени
экспериментах такого подавления компонент не наблю-
наблюдалось. Более того, если нет резонатора, выделяющего
стоксовы волны определенного направления, то возмож-
возможно интенсивное излучение и на антистоксовых частотах
«о = ©ь + со»;. Это излучение, впервые наблюдавшееся
Терхыоном [27], имеет коническую диаграмму направлен-
направленности; экспериментально наблюдаются также и антисток-
совы компоненты более высокого порядка с частотами
сох, + /civ
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
175
§ 6. Связь между стоксовыми и антистоксовыми
волнами
При более полном теоретическом исследовании вы-
вынужденного комбинационного рассеяния следует рас-
рассмотреть систему уравнений для связанных волн с часто-
частотой иг,, частотой лазера сох, и со всеми комбинационными
частотами сох, ± lav. Эти волны могут распространяться
во многих направлениях. Чтобы сделать задачу разре-
разрешимой, следует ввести некоторые упрощающие предпо-
предположения. Во-первых, можно исключить уравнение для
волны с частотой сои, поскольку оптические фононы силь-
сильно поглощаются средой. Во-вторых, допустим, что имеет
место поглощение и для световых волн с частотами
сох, ± 2cLb. Это позволяет исключить волны стоксовых и
антистоксовых компонент с индексом I ^ 2. Хотя волна
нелинейной поляризации с частотой сох, + Заь может ге-
генерироваться при смешении антистоксовой и стоксовой
компонент, 2соа — cos, соответствующая нелинейная вос-
восприимчивость для этого процесса не будет резонансной.
По той же причине можно исключить из рассмотрения и
волны с частотами гармоник 2соь и т. д. Таким образом,
мы ограничимся рассмотрением уравнений связанных
волн с тремя частотами: сох,, cos и соа; однако даже и этот
случай не поддается аналитическому исследованию. По-
Поэтому мы будем считать поле накачки Еь заданным. Та-
Такое приближение достаточно хорошо соответствует (по
крайней мере на начальном этапе процесса рассеяния)
экспериментально реализуемым условиям, когда интен-
интенсивный луч лазера падает на плоскую границу (z => 0)
нелинейной среды — кристалла, жидкости или газа.
В этом приближении процесс генерации излучения с
частотами cos и соа описывается системой уравнений для
связанных волн с амплитудами Es и Е*а. Без существен-
существенного ограничения общности будем считать среду изотроп-
изотропной. Предположим далее, что все волны поляризованы
одинаково, так что можно использовать выражения для
скалярной комбинационной восприимчивости B.62) и
B.68). Точно так же можно, разумеется, рассмотреть и
случай, когда поляризации стоксовой и антистоксовой
компонент и поляризация излучения лазера перпендику-
176
ГЛАВА 4
лярны. Ко всем комбинационным восприимчивостям сле-
следует прибавить действительную нерезонансную компо-
компоненту %Nr; ее дисперсией можно пренебречь, поскольку
возбужденные электронные уровни сильно разнесены по
сравнению с величиной wa — cos. Соотношения между
комплексными величинами %а и Xs обсуждались в гл. 2.
Система двух уравнений для связанных волн может
быть теперь записана в виде
V2ES —
дР
~а " "а 4я З2
с2 а^2 с2 di*
D.77)
D.78)
Как и прежде, решения можно искать в виде плоских
волн, у которых плоскости постоянных амплитуд парал-
параллельны границе раздела линейной и нелинейной сред.
Поэтому решения записываем в виде (амплитуды счи-
считаются постоянными)
Поле накачки представим в виде
Es (г, f) =
(г, 0 = Ele
х g-'
D.79)
Подстановка этих решений в волновые уравнения D.77)
и D.78) сводит последние к двум однородным алгебраи-
алгебраическим уравнениям. Определитель этой системы должен
быть равен нулю. Для каждого набора значений kxs, kus
и (ds получается уравнение четвертой степени для kzs. От-
Отрицательная мнимая часть корня kzs соответствует уси-
усилению. Задача состоит в том, чтобы определить, как
величина этого усиления изменяется в функции танген-
РАСПРОСТРАМЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
177
циальных компонент, определяющих направление выхо-
выходящей волны, и частоты cos. Следует помнить, что пове-
поведение ВеЛИЧИН %s И %а Вблизи ЧаСТОТ COz, — CDs == COu И
«а — «ь = со« соответственно носит резонансный харак-
характер.
Введем волновые векторы для линейной среды в от-
отсутствие накачки EL = 0, тогда с учетом линейных потерь
в среде имеем
D.81)
D.82)
Определенные таким образом коэффициенты поглощения
оказываются соответственно в (cosGs) и (cos9a)~' раз
большими, чем измеренные вдоль направления распро-
I*:
-Ак
Фиг. 18. Геометрические соотношения между волновыми векторами
стоксовой и антистоксовой волн и волны лазера.
Величина Д& характеризует рассогласование фазовых скоростей в направлении
нормали к границе нелинейной среды.
12 Н. Бломберген
178
ГЛАВА 4
странения волны. Далее, введем z-компоненты для тан-
тангенциальных компонент волновых векторов в отсутствие
поля накачки:
D.83)
ьт - \(ь°J — ь2 —k2] 2 -\(k°J~Bkr —kY —
Kaz— \\%ка) ках Ray\ — \\ка) \^kLk ksxJ
1
-Vku-kJ*}*. D.84)
В отсутствие накачки величина рассогласования для вол-
волновых векторов в 2-направлении равна (см. фиг. 18)
— Ak^2kLz — k?z — C. D.85)
Имея в виду, что решения для ksz слабо отличаются от
величины k°zs, введем новую переменную
Д* = *в-*2. D.86)
Полагая определитель системы связанных уравнений
равным нулю, получаем для Ах уравнение четвертой сте-
степени
(А*-«
Г
X
(Ak
+
+ Уm\ El2}
= 0.
D-87)
Рассмотрим прежде всего случай Ak = 0, соответ-
соответствующий точному согласованию фазовых скоростей для
линейной среды, 2кх, — ks — ка = 0. В случае равных ли-
линейных потерь, аа = as = asa, пренебрегая дисперсией
комбинационной восприимчивости Ха ~ Xs> получаем
двойной корень Ах = iasa- Это означает, что в направле-
направлениях, для которых условия согласования точно выполне-
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
ны, не могут генерироваться ни стоксовы, ни антисток-
совы компоненты. Этот несколько неожиданный результат
объясняется тем, что положительная работа, произве-
произведенная нормальным колебанием вблизи частоты cos,
точно компенсируется отрицательной работой, произве-
произведенной вблизи частоты соа. Такая ситуация хорошо из-
известна в теории параметрических усилителей, где не мо-
может быть получено усиление на частоте cos = соь — со*,
если не подавлена боковая частота сох, + со,-.
Пренебрегая членами (АхJ и (,Ах+А&J, приводим
уравнение четвертой степени к квадратному уравнению.
Такое приближение оправдано, поскольку \Ak\ «С kaz и
поскольку интерес представляют лишь те решения, для
которых |Ах| «С &sz. Два отброшенных корня соответ-
соответствуют обратным бегущим волнам. Полученное квадрат-
квадратное уравнение можно записать в виде
(Ах - \„) (Дх- XJ - laslsa = О, D.88)
где
2ЯШ2.
*«, = ias + -J^T (Z, + У-Nr) I El I2,
ya + yNR) \El\>,
Лит
C Raz
Ksha =
s a
f(y*y
sz"~az
Точно такое же квадратное уравнение можно получить,
исходя из уравнений для связанных волн [25].
Корни уравнения D.88) можно, конечно, записать в
самом общем виде. В действительности же наибольший
интерес представляет случай равных коэффициентов по-
потерь, as = aa = aas, и пренебрежимой дисперсии комби-
комбинационного рассеяния, %s(?>2s/kmsz = X*aa2Jkmaz. В этом
случае после алгебраических упрощений для корней
уравнения имеем
1 г 1 2яш2
Ax = ;asa-TA*± -LAfe. ^
12*
D.89)
180
ГЛАВА 4
При Ak = 0 оба корня равны iasa; они описывают затуха-
затухание обеих волн. Если же величина Ak велика, квадрат-
квадратный корень в D.89) можно разложить в ряд; в этом слу-
случае имеем
D.90)
D.91)
Первый корень Axs соответствует, очевидно, стоксовой
волне. Мнимая часть величины Xs отрицательна, и волна
усиливается, если величина asa не слишком велика.
В пределе при
2я<о2
это совпадает с фактором нарастания стоксовой волны,
вычисленным ранее [см. D.68)]. Другой корень соответ-
соответствует почти чисто антистоксовой затухающей волне.
Подставляя выражение D.90) для собственного зна-
значения Axs в уравнения связанных волн, находим, что от-
отношение интенсивностей антистоксовой и стоксовой ком-
компонент равно
При малых Ak это приближение теряет силу. Вблизи на-
направления, на котором фазовые скорости согласованы,
связь стоксовой и антистоксовой компонент оказывается
весьма сильной. Эта связь характеризуется соотноше-
соотношением D.89). Так как оно содержит корень квадратный
из комплексной величины, проследить поведение усиле-
усиления, соответствующего мнимой части квадратного корня,
довольно затруднительно. Для каждого значения Ak, т. е.
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
181
для каждого значения поперечной компоненты (k2sx +
+ k2sy)'/*, можно найти зависимость коэффициента уси-
усиления от частоты cds. Резонансная часть восприимчиво-
восприимчивости Xs является, конечно, быстро изменяющейся функ-
функцией частоты cos. Ее действительная и мнимая части
показаны на фиг. 6.
т7,0
д5
Фиг. 19. Зависимость коэффициента нарастания для связанных
стоксовой и антистоксовой волн от рассогласования Ak в направ-
направлении оси г.
Кривые нормированы к величине gs — коэффициенту нарастания для сток
совой компоненты, направление распространения которой отлично от направ-
направления полного согласования.
Зависимость коэффициента нарастания от величины
Ak иллюстрируется фиг. 19; усиление резко падает до
нуля в области точного согласования фазовых скоростей
(Л& = 0). Асимметрия кривой вызвана нерезонансным
¦йш/Г = 0,25
Фиг. 20. Зависимость коэффициента усиления по мощности для ан-
антистоксовой волиы от нормированного рассогласования в направле-
направлении оси z, Ak/ga, где gs = 4я(о/с2й^) xs \^Л2-
Для каждого значения hk направление излучения на выходе кюветы с рас-
рассеивающей средой может быть найдено нз фиг. 18. Для каждого направления
наблюдения существует расстройка Аи — со — со^+со^, для которой усиление
максимально. Асимметрия кривых относительно значения Ak — 0 имеет место
из-за нерезонансной части восприимчивости,
s макс
^ "*
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
183
членом. При расчете кривых было принято %NR> 0 и
\%nrIis MaKC | = 0,1. Если принять в расчет распределение
мощности в волне между стоксовой и антистоксовой ком-
компонентами, то усиление антистоксовой компоненты как
функция рассогласования фазовых скоростей будет иметь
другой вид. На фиг. 20 приведены результаты расчета
этой функции на вычислительной машине. Для каждого
значения Ak смещение частоты Лео выбиралось так, чтобы
получить максимальное усиление. В этом примере для
максимума усиления антистоксовой волны находим
Лео—0,3 Г. Вообще говоря, можно ожидать, что усиление
будет иметь место в полосе порядка 0,5Г/2я.
На кривых фиг. 19 и 20 величина Ak нормирована на
величину коэффициента нарастания по мощности сток-
совой волны
4яш? , . _
" А- '
[см. формулу D.68)]. Максимум усиления на фиг. 20 со-
соответствует величине Ak/gs = 2. Направление распро-
распространения волны, соответствующее данному значению
Ak, находится из формул D.83) — D.85). Геометриче-
Геометрические соотношения представлены на фиг. 18. Геометриче-
Геометрическая диаграмма полностью определяется заданием тан-
тангенциальных компонент k°, &° и волнового вектора кь.
Заданное значение Ak может быть связано таким обра-
образом с поперечными компонентами импульса. Следова-
Следовательно, может быть определено и отклонение направ-
направления максимального усиления от направления 0О, соот-
соответствующего точному согласованию фазовых скоростей,
поскольку тангенциальные компоненты импульсов на
границе определяют направление луча вне нелинейной
среды.
Итак, порог вынужденного рассеяния является функ-
функцией направления. Правда, при наблюдении комбина-
комбинационного рассеяния в кюветах, длина которых много
больше диаметра луча, геометрические факторы играют
доминирующую роль. Однако даже для идеализирован-
идеализированного случая бесконечно протяженных плоских волн
имеет место резкое возрастание порога вблизи направ-
184
ГЛАВА 4
ления полного согласования фазовых скоростей. Точно
в этом направлении порог равен бесконечности; поэтому
в направленном интенсивном излучении стоксовой ком-
компоненты будет наблюдаться темное кольцо, определяе-
определяемое направлением точного согласования фазовых ско-
скоростей. Одновременно возникает яркое кольцо (воз-
(возможно два, если величина %NR весьма мала) для анти-
антистоксовой компоненты в направлениях, смещенных от
направления точного согласования. Лишь небольшая
часть интенсивности в других направлениях соответ-
соответствует антистоксовой компоненте. Отношение интенсив-
интенсивности антистоксовой и стоксовой компонент определяет-
определяется формулой D.92).
Подчеркнем, что все эги результаты получены для
случая, когда излучение на частотах соь ± /со„ при / ^ 2
подавлено, а поле накачки можно рассматривать как за-
заданное. Однако ни одно из этих условий в эксперимен-
экспериментах по вынужденному комбинационному рассеянию обыч-
обычно не выполняется; сравнение результатов теории с экс-
экспериментом мы отложим до следующей главы.
Представляет также интерес теория усилителя, ис-
использующего эффект вынужденного комбинационного
рассеяния. В этом случае, кроме луча лазера, на нели-
нелинейную среду падает внешнее излучение с частотой ли-
либо cos, либо соа. Направление падающего луча, например,
с частотой cos
Е™* exp(ikls-r~[iu>st)
определяется тангенциальными компонентами волнового
вектора. Следовательно, величина Ak определена. Теперь
следует взять подходящую линейную комбинацию волн,
соответствующих этому значению Ak и частоте cos, кото-
которая удовлетворяет граничным условиям.
Обозначим два корня через Ах\ и Ак2; соответствую-
соответствующие собственные функции равны
']. D.93)
D.94)
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ 185
Комплексные собственные векторы нормированы
где
= f(A4).
с\а *а,\ С2а ?а,2
Зависимости функций от х, у, z опущены, так как они
полностью определяются формулой D.80).
Амплитуды собственных мод определяются теперь
граничными условиями при z = 0, а полное решение бу-
будет дополнительно включать две отраженные волны с
частотами cos и соа соответственно. Это дает четыре амп-
амплитуды, определяемые из условия непрерывности танген-
тангенциальных компонент векторов Е и Н раздельно на часто-
частотах cos и соа. Из расчетов § 1 настоящей главы следует,
что амплитуды отраженных волн весьма малы, поэтому
для приближенного определения величин А\ и А2 можно
использовать следующие два уравнения:
с,Л + с«А = ?*Пад> CiA + CftA-O. D.95)
Второе граничное условие будет ниже несколько моди-
модифицировано. После подстановки амплитуд в D.93)
и D.94) находим, что решения для стоксовой и антисток-
антистоксовой компонент являются линейными комбинациями
двух экспонент. Исключая случай распространения в на-
направлении точного согласования, одна из этих волн будет
экспоненциально усиливаться. Для достаточно больших
расстояний z остается только это решение. Направление,
в котором энергия стоксовой компоненты выходит из
плоскопараллельной кюветы с рассеивающей средой, па-
параллельно конечно направлению падающего луча. Выхо-
Выходящее же из кюветы излучение антистоксовой компонен-
компоненты распространяется, вообще говоря, в другом направле-
направлении, определяемом тангенциальными компонентами его
волновых векторов.
Для весьма малых значений z амплитуда антистоксо-
антистоксовой компоненты пропорциональна z, что согласуется
с общими соотношениями § 1. Разлагая экспоненту в ряд
для случая |Ах8| <С 1, имеем
c2aA2Av.2) z ei
D.96)
186
ГЛАВА 4
Направлению точного согласования соответствуют два
корня с решениями, затухающими по экспоненциальному
закону. Для условий, при которых выведена формула
D.89), эти корни равны, Axi = Ахг = iasa. В этом вырож-
вырожденном случае уравнения D.93) и D.94) не являются ли-
линейно независимыми, и амплитуда Еа в соответствии
с уравнением D.96) тождественно равна нулю. Правиль-
Правильное решение принимает тогда следующую форму:
lim
= — Azze
,<S-«saZ
D.97)
Значение производной dEJdz для малых г в этом случае
лучше определить из соотношений § 1. Для малых z ре-
решение должно переходить в формулу D.12). В действи-
действительности, для случая Axi ф Ак2 оказывается возможным
заменить граничное условие с\аА\ + С2п^2 = 0 [см. урав-
уравнения D.95)] условием того, что выражение i(ciaA.\kx\ +
+ с2аЛ2Ак2)г соответствует нарастанию, описываемому
формулой D.12).
На этом мы заканчиваем изложение теории связан-
связанных волн. Возникающие здесь задачи не ограничивают-
ограничиваются, конечно, взаимодействиями световых или акустиче-
акустических волн. Подобным же образом могут быть рассмотре-
рассмотрены взаимодействия между световыми и спиновыми вол-
волнами. Заметим, что параметрическое взаимодействие свя-
связанных спиновых волн рассматривалось Сулом и Тьеном
еще до появления нелинейной оптики [28]. Во многом
аналогичные явления наблюдаются и при взаимодейст-
взаимодействии электромагнитных волн с волнами плотности и ско-
скорости электронов в лампе с бегущей волной [29]. Чита-
Читатель, знакомый с теорией параметрических усилителей,
встретился в этой главе с множеством знакомых ему
фактов. Наиболее интересными новыми аспектами, при-
присущими нелинейным взаимодействиям световых волн, яв-
являются трехмерный характер взаимодействий и специ-
специфические дисперсионные характеристики. В гл. 5 мы зай-
займемся сравнением теоретических результатов с экспери-
экспериментальными данными.
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
187
ЛИТЕРАТУРА
1. Bloembergen N, Pershan P. S., Phys. Rev., 128, 606
A962). (См. приложение II к настоящей книге.)
2. D u с u i n g J, Bloembergen N, Phys. Rev. Lett., 10, 474
A963).
3. Bloembergen N, Ducuing J., Phys. Lett., 6, 5 A963).
4. К г о n i g R., В о u k e m a J. I., Proc. Roy. Neth. Acad. (Amster*
dam), 66B, 8 A963).
5. Terhune'R. W., Maker P. D., Savage С. М., Appl Phys
Lett., 2, 54 A963).
6. Shir en N. S., Appl. Phys. Lett., 4, 82 A964).
7. Z i m a n J. M, Electrons and Phonons, Oxford, 1960, Ch. 3. (Име-
(Имеется перевод: Дж. 3 а й м а н, Электроны и фононы, ИЛ, 1962.)
8. Born M., Huang К., Dynamical Theory of Crystal Lattices,
Oxford. 1954. (Имеется перевод: М. Борн, Хуан Кунь, Дина-
Динамическая теория кристаллических решеток, ИЛ, 1958.)
9. Kingston R. Н„ Proc. IRE, 50, 472 A962).
10. -К г о 11 N. М, Phys. Rev., 127, 1207 A962).
11. Kroll N. М., Journ. Appl. Phys., 36, 34 A965).
12. Chiao iR., Townes С. Н., Stoicheff В., Phys. Rev. Lett.,
12, 592 A964).
13. Chi ao R, Garmire E, Townes С H, Rendiconti S. I. F.
Corso 22, August 1963, New York, 1964.
14. Hellwarth R. W, Phys. Rev., 130, 1850 A963).
15. Zeiger H. J., Tannenwald P. E., Proceedings 3rd Interna-
International Conference on Quantum Electronics, Paris, February 1963,
eds. P. Grivet, N. Bloembergen, New York, 1964, p. 1589.
16. В 1 oe m b er ge n N, Proceedings 3rd International Conference
on Quantum Electronics, Paris, February, 1963, eds. P. Grivet,'
N. Bloembergen, New York, 1964, p. 150.
17. Lou don R., Proc. Phys. Soc, A82, 393 A963).
18. Lou don R, Proc. Roy. Soc, A275, 218 A963).
19. Terhune R. W., Solid State Design, 4, 38 (November 1963).
20. Garmire E, Pandarese iE., Townes С. Н. Phys. Rev.
Lett, 11, 160 A963).
21. Javan A., Rendiconti S. I. F. Corso 22, August 1963, New York,
1964.
22. Hellwarth R. W., Appl. Optics, 2, 847 A963).
23. Hellwarth R. W., Current Sci. (India), 33, 129 A964).
24. Zeiger H. J., Tannenwald P. E, Kern S., Herendeen R..
Phys. Rev. Lett, 11, 419 A963).
25. Bloembergen N, Shen Y. R, Phys. Rev. Lett, 12, 504
A964).
26. Eckhardt G, Hellwarth R. W. McClung F. J.,
Schwa rz S. E, WeinerD, Phys. Rev. Lett., 9, 455 A962).
27. Terhune R. W, Bull. Am. Phys. Soc, II, 8, 359 A963).
28. Tien P. K, Suhl H., Proc. IRE, 46, 700 A958).
29. Pierce J. R, Traveling-Wave Tubes, New York, 1950. (Имеется
перевод: Д. Пирс, Лампа с бегущей волной, М, 1955.)
188
ГЛАВА 4
30 S i e g m a n A. E., Q u a t e C. F., В j о г к h о I m J., Francois
G. Appi. Phys. Lett., 5, 1 A964).
31*. Kingston R., McWhorter A, Proc. IEEE, 53, №1, 4
A965).
32*. АхмановС. А, Дмитриев В. Г., Моденов В. П., Ра-
Радиотехника и электроника, 10, 649 A965).
33*. Klein man D, Phys. Rev., 128, 1761 A962).
34*. Фабелинский И. Л., Усп. физич. наук, 63, № 2, 356 A957).
35*. Фабелинский И. Л., Молекулярное рассеяние света, М.,
1965.
36*. G i о г d m a i n e J. A., M i 11 е г R., Phys. Rev. Lett, 14, 973
A965).
37*. Ахманов С. А., Ковригин А. И., Пискарскас А. С,
Фадеев В. В., Хохлов Р. В., ЖЭГФ, письма в редакцию,
2, № 7 A965).
38*. Ахманов С. А., Хохлов Р. В., Проблемы нелинейной опти-
оптики, М., 1964.
39*. Hsu H., Kavage W., Phys. Lett., 15, 207 A965).
40*. Lou don R., Advances in Physics, October 1904.
41*. Платоненко В. Т., Хохлов Р. В., ЖЭТФ, 46, 555 A964).
42*. П л а то н ен ко В. Т., X о х л о в Р. В., Оптика и спектроско-
спектроскопия, 18, № 3, 369 A965).
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
43*. Луговой В. Н., Препринт ФИАН, А-60 A965).
Излучение стоксовых и антистоксовых компонент произ-
произвольных порядков при вынужденном комбинационном рас-
рассеянии.
44*. Луговой В. Н., ЖЭТФ, 48, 1216 A965).
О вынужденном комбинационном рассеянии в антистоксо-
антистоксовой области.
45*. Файн В. М., Ящин Э. Г., ЖЭТФ, 46, 695 A964).
К теории индуцированного комбинационного излучения.
46*. Зубов В. А., Сущи не кий М. М., Шувалов И. К-, Усп.
физич. наук, 83, № 2, 197 A964).
Стимулированное комбинационное рассеяние света.
47*. Степанов Б. И., АпанасевичП. А., Жури, прикл. спектр.,
2, № 1, 37 A965).
Вынужденное комбинационное грассеяние внутри резонато-
резонатора первичного ОКГ.
48*. Апанасевич П. А., Степанов Б. И., Журн. прикл. спектр.,
1, № 3 A964).
Влияние вынужденного комбинационного рассеяния на ин-
интенсивность и спектральный состав рассеянного излучения.
49*. Хромо пуло Ю. Г., Изв ВУЗ'ов, Радиофизика, 7, № 4, 674
A964).
К теории комбинационного излучения в сильных полях.
РАСПРОСТРАНЕНИЕ ВОЛН В НЕЛИНЕЙНОЙ СРЕДЕ
189
50*. Tang С, Deutsh Т., Phys. Rev., 138, № 1А, Al A965)
Generation of antistokes radiation in the higher order
coherent Raman processes.
51*" ™«i R> КеПеУ p-. Zeiger H, Phys. Rev., 138, A690
)
Generation of stokes and antistokes radiation in Raman
media.
52*. M a ip у ш к о И. А., Машке в ич В. С, Укр физич. жтои 10
№ 3, 321 A965). ' '
Генерация второй оптической гармоники в резонаторе ла-
лазера.
53*. Bioembergen N., Shen Y. R., Phys. Rev., 137, № 6A, 1787
AУоо).
Theory of stimulated Brillouin and Raman scattering.
л
в
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
§ 1. Экспериментальная проверка законов нелинейного
взаимодействия световых волн в объеме и на поверхности
нелинейной среды
Все эксперименты по параметрическим взаимодейст-
взаимодействиям световых волн, выполненные до настоящего време-
времени, достаточно хорошо описываются соотношениями, при-
приведенными в гл. 4, § 1 и 2. Наиболее тщательную провер-
проверку теории позволили осуществить эксперименты по гене-
генерации второй световой гармоники в пьезоэлектрических
кристаллах. Франкен в своем первом эксперименте [1]
фокусировал луч рубинового лазера с длиной волны
6943 А в кристалл кварца в пятно диаметром около 1 мм.
Энергия лазерного импульса равнялась приблизительно
3 дж, длительность составляла около 10~3 сек. Излучение,
выходившее из кварца, регистрировалось с помощью
кварцевого спектрографа на фотопленке, нечувствитель-
нечувствительной к красному свету. Оценки показали, что около 10~п
от общего числа фотонов, имевшихся в импульсе, преоб-
преобразовывалось в кванты ультрафиолетового излучения с
длиной волны 3471 А. Эксперименты, выполненные позже
с использованием дифракционных решеток, подтвердили,
что генерируемая частота равна удвоенной частоте излу-
излучения рубинового лазера с точностью до 10~5. В этих экс-
экспериментах производилось сравнение дифракционного
спектра первого порядка ультрафиолетового излучения с
дифракционным спектром второго порядка излучения ру-
рубина, причем оба спектра получались во время одной
и той же экспозиции :).
Результаты первых экспериментов, описанных в гл. 1,
хорошо согласуются с формулами D.12) и D.13).
В частности, результаты опытов по генерации второй гар-
¦> Более подробные данные, полученные в этих опытах, можно
найти в [53*. 54*]. — Прим. ред.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
191
моники света в плоскопараллельной пластинке с изме-
изменяющейся оптической толщиной, которые представлены
графически на фиг. 2, описываются формулой D.13). Ве-
Величина, характеризующая рассогласование фазовых ско-
скоростей, е 1/г Bсо)—e'/s(co), определяется из расстояния
между максимумами, а их высота позволяет найти вели-
величину нелинейной восприимчивости. Схема опыта, приве-
приведенная на фиг. 1, обычно используется при определении
нелинейных восприимчивостей; соответствующий расчет
выполняется по формуле D.13).
Джордмейн [2], а также Мейкер и др. [3] одновременно
указали на то, что в отрицательном одноосном кристалле
с достаточно большим двойным лучепреломлением фазо-
фазовая скорость обыкновенной волны основной частоты сов-
совпадает с фазовой скоростью необыкновенной волны
удвоенной частоты при условии, что световые волны идут
в некотором определенном направлении по отношению
к оптической оси. В дигидрофосфате калия КН2РО4
(KDP) это происходит тогда, когда луч рубинового ла-
О
зера, имеющий длину волны 6940 А и поляризованный
перпендикулярно к оптической оси, образует с ней угол
в 49,8 ± 0,5°. Использование этого обстоятельства позво-
позволяет увеличить интенсивность второй гармоники на много
порядков. При точном согласовании фазовых скоростей
интенсивность пропорциональна квадрату длины кри-
кристалла, как это следует из соотношения D.12). Однако
задача сохранения согласования фазовых скоростей на
больших длинах оказывается сложной в связи с тем, что
луч рубинового лазера обычно содержит много продоль-
продольных и поперечных мод. Поэтому для повышения интен-
интенсивности гармоники выгодно фокусировать лазерный
луч. Вследствие возрастания интенсивности в фокусе
уменьшается характеристическая длина нелинейного
взаимодействия, которая определяется выражением
D.35). Терхьюн, Мейкер и Сэвидж [4] использовали лин-
линзу с фокусным расстоянием 25 см для фокусировки излу-
излучения лазера с модулируемой добротностью, который да-
давал около 0,1 дж за 20-10~9 сек, в кристалл NH4H2PO4
(ADP). Они смогли преобразовать во вторую гармонику
более 20% излучения рубинового лазера и наблюдали
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
193
192
ГЛАВА 5
уменьшение интенсивности волны основного излучения,
описываемое соотношением D.34). Интересно заметить,
что в этом эксперименте не удавалось использовать KDP.
Край полосы ультрафиолетового поглощения находится
в KDP вблизи от частоты третьей гармоники рубинового
лазера, и поэтому трехфотонное поглощение разрушало
этот кристалл, тогда как в ADP, полоса поглощения кото-
которого смещена дальше в ультрафиолетовую область, излу-
излучение той же интенсивности не приводило к поврежде-
повреждениям.
ГЕОМЕТРИЧЕСКИЕ СООБРАЖЕНИЯ
Идеальный фокус луча, обладающего дифракционной
расходимостью, характеризуется величиной
г _ R-i _ nll
где // — фокусная длина в вакууме, d — диаметр луча,
п — показатель преломления среды, в которой находится
фокус, р — полный угол при вершине конуса света, выхо-
выходящего из фокуса. Дифракционная теория идеального
фокуса для / > 1 подробно изложена в книге [5]. Поле
излучения в зоне высокой интенсивности вблизи фокуса
можно приближенно описать с помощью плоской волны,
распространяющейся в цилиндрической области длиной
? = -&- E.1)
и диаметром
6 =
2Х„/
E.2)
Длина волны в этой области уменьшается в [1—D/)~2]
раз.
Плотность потока мощности в фокусе увеличивается
в (d/бJ раз. Ясно, что в реальных условиях такого уве-
увеличения не получается, так как расходимость луча лазе-
лазера превышает дифракционную. Примем, что расходи-
расходимость несфокусированного луча составляет 4- 10~3 рад.
В таком случае диаметр луча света в фокусе
при // = 25 см будет равен 0,1 см. Эта величина в десять
раз меньше диаметра поперечного сечения несфокусиро-
несфокусированного луча, равного примерно 1 см. Плотность потока
мощности в фокусе приблизительно в 100 раз больше, чем
в несфокусированном луче и составляет около
500 Мвт/см2. Тогда в соответствии с формулой D.35) ха-
характеристическая длина нелинейного взаимодействия бу-
будет порядка 2 мм. Это значение примерно вдвое превыша-
превышает длину фокальной области ?. Соотношение D.34) дает
при этом для коэффициента преобразования на длине ?
приблизительно ту величину, которая наблюдается экс-
экспериментально. Вместе с тем следует иметь в виду, что
формулы D.33) и D.34), вообще говоря, неприменимы
для оценки реальных экспериментальных ситуаций. По-
Подробная картина структуры мод в луче лазера и в фокусе
неизвестна. Интенсивность распределена неравномерно
по поперечному сечению луча. В сложной структуре ла-
лазерного луча существуют узкие пучки, которые преобра-
преобразуются в гармонику почти полностью; вместе с тем, осо-
особенно в периферических частях луча, существуют пучки,
которые слабо преобразуются или вообще, остаются не-
преобразованными. Эта ситуация осложняется анизотро-
анизотропией среды. Не для всех направлений в луче конечной
расходимости выполняется условие точного согласования
фазовых скоростей''.
Клейнман [6] теоретически исследовал генерацию вто-
второй гармоники в одноосных кристаллах, когда на них па-
падают пучки конечной расходимости, а не плоские волны
с бесконечно большим поперечным сечением. Примем, что
интенсивность излучения основной частоты равномерно
распределена по углам в малом интервале А0 вокруг на-
направления точного согласования фазовых скоростей 0о.
Угловое распределение интенсивности излучения второй
1J Теория генерации гармоник в фокусе, развитая с учетом
дифракционных эффектов, показывает, что учет явлений лишь в об-
области, описываемой формулами E.1) и E.2), достаточен только для
случая фокусировки длиннофокусной линзой (| > L, где L — длина
нелинейного кристалла). Энергетический выигрыш за счет фокуси-
фокусировки максимален при \~ L; однако если угол анизотропии в не-
нелинейном кристалле не слишком мал, имеет смысл фокусировать
лишь те пучки, расходимость которых превышает дифракционную.
При | < L определенный вклад в интенсивность гармоники дают
околофокальные области, где волна уже не может считаться пло-
плоской. Более подробное рассмотрение см. в [55*, 93*]. — Прим. ред.
13 П. Бломберген
194
ГЛАВА 5
гармоники, генерируемой в плоско-параллельной пла-
пластинке толщиной z, пропорционально значениям функции
sin2 {[я F) - я (в0)] (oc^z) [п F) - я F0)Г2.
Показатель преломления необыкновенного луча п яв-
является функцией угла 6. Полная интенсивность второй
гармоники, усредненная по всем направлениям, пропор-
пропорциональна интегралу
1
— f
Л6 J
E.3)
При (dn/dQ0)ac-lzAQ <C 1 этот интеграл можно аппрокси-
аппроксимировать выражением a2c~2z2. При (dn/dQ0)(>)C-]zAQ > 1
интеграл можно преобразовать к виду
+ 00
">
~2 sin2udu = nac-h
—
Пользуясь вышеприведенными формулами, можно
ввести понятие эффективной когерентной длины нелиней-
нелинейного взаимодействия для пучка с угловой расходимостью
Д6, распространяющегося вблизи направления точного
согласования фазовых скоростей
)\ E.4)
о
Для кристалла KDP при Я = 3470 А
пг2 = 1,534-2 cos2 6 + 1,487-2 sin2 0.
Угол, соответствующий точному согласованию фазовых
скоростей, равен 0О = 49,9°. Поэтому для дп/дв0 « 0,03
и типичной расходимости луча рубинового лазера А0 =
= 4-10~3 рад получаем, что эффективная длина 1'каг =
= 0,1 см. При z > 1'ког интенсивность второй гармоники
будет расти уже пропорционально z, а не z2. К счастью,
величина /к'ог оказывается такой же, как глубина фокуса
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
195
и характеристическая длина нелинейного взаимодейст-
взаимодействия, так что предыдущее рассмотрение остается спра-
справедливым х\
Джордмейн [2] исследовал также генерацию второй
гармоники в том случае, когда лучи основной частоты
идут не по одному направлению. В треугольнике, образо-
образованном волновыми векторами, возможно согласование
фазовых скоростей двух обыкновенных лучей основной
частоты и одного необыкновенного луча гармоники, иду-
идущих в направлениях, близких к Во. При этом наблюда-
наблюдаются интересные картины распределения интенсивности,
которые подтверждают выводы, полученные при теорети-
теоретическом рассмотрении вопроса о согласовании фазовых
скоростей.
ВОЗНИКНОВЕНИЕ ВОЛН ГАРМОНИК
ПРИ ОТРАЖЕНИИ
Некоторые исследователи наблюдали генерацию вто-
второй гармоники при прохождении света через пластину,
которая сильно поглощает гармонику, но пропускает вол-
волну основной частоты; этот эффект олисывается нелиней-
нелинейной поляризацией, входящей в соотношение D.15).
') Здесь уместно сделать некоторые пояснения. Понятие коге-
когерентной длины нелинейного взаимодействия для расходящегося
пучка, введенное в этом параграфе, не следует путать с понятием
длины когерентного взаимодействия для плоской волны, введенным
ранее [см., например, формулу D.14)]. При этом в обоих случаях
рассматриваются строго монохроматические волны, так что фазо-
фазовые соотношения между основной волной и гармоникой остаются
регулярными как для / < /Ког, так и для / > /Ког- Когерентная же
длина является пространственным масштабом нелинейного взаимо-
взаимодействия, на котором сохраняется определенный закон нарастания
интенсивности гармоники с расстоянием. Таким образом, использо-
использование термина «когерентный» представляется здесь не совсем удач-
ным, поскольку обычно его связывают оо статистикой. Когерентная
длина, имеющая статистическую природу, появляется в нелинейной
оптике при исследовании нелинейных взаимодействий в статистиче-
статистически неоднородной среде или же при исследовании нелинейных взаи-
взаимодействий волн с конечной шириной спектра; в этом случае при
I >'когТк°РРеляция между основным излучением и второй гармони-
гармоникой ослабляется. — Прим. ред.
13*
ГЛАВА S
Когда среда поглощает и излучение основной частоты
и гармонику, генерация второй гармоники возможна
только при отражении. Этот эффект впервые наблюдался
Дюкузнгом [7]. Факторы, определяющие направление
отраженных лучей гармоники, уже обсуждались в
гл. 4, § 1. Поляризация излучения второй гармоники,
Фото-
умножитель
~ 2ш
КНР Фото-
или кварц умножитель
2
Фильтр
Поляризатор
Лазер
Фиг. 21. Схема экспериментальной установки для измерения нели-
нелинейной восприимчивости кристалла GaAs методом отражения.
возникающей при отражении света от поверхности кри-
кристалла GaAs, измерялась с помощью экспериментальной
установки, схема которой приведена на фиг. 21. Тензор
третьего ранга %циB(о = со + со) в кристаллах класса
симметрии 43 т имеет следующие отличные от нуля ком-
компоненты:
Xxyz = Хгху = Хугх = ~ Хи- E- 5)
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЫАТЫ
197
Падающий луч лазера поляризован перпендикулярно
плоскости падения. Компоненты нелинейной поляризации
по прямоугольным кристаллографическим осям равны
E.6)
Ру B@) ^
Pz B@) = y_uExEr
Если кристалл, являющийся «нелинейным зеркалом»,
поворачивать вокруг нормали, совпадающей с кристал-
кристаллографическим направлением [011], то поляризацию из-
излучения основной частоты можно сделать параллельной
направлениям [100], [111] и [011] соответственно. В первом
случае Еу = Ez — 0 и поляризация на частоте второй
гармоники не возбуждается. При Е(со), параллельном па-
правлению [111], ?*(<») = Еу(ф) = Ег(ы) и из соотноше-
соотношений E.6) сразу же получается, что и вектор РBсо) па-
параллелен направлению [111]. Следовательно, поляриза-
поляризация гармоники, возникающей при отражении, также пер-
перпендикулярна плоскости падения. При Ех — 0, Еу = Ez
поляризация с частотой гармоники имеет только х-кои-
поненту. В этом случае вектор РBсо) составляет прямой
угол с поляризацией падающего луча лазера, поэтому по-
поляризация отраженного луча гармоники лежит в плоско-
плоскости отражения. Сказанное хорошо подтверждается экс-
экспериментальными данными, приведенными на фиг. 22 и
23. Экспериментальные значения интенсивности парал-
параллельной и перпендикулярной компоненты отраженного
излучения второй гармоники сравниваются с теоретичес-
теоретическими кривыми, дающими зависимость интенсивности гар-
гармоники от угла ф между направлением поляризации вол-
волны основной частоты и кристаллографической осью х.
Для геометрии фиг. 21 угловая зависимость интенсивно-
интенсивности отраженного излучения гармоники для двух поляри-
поляризаций дается следующими выражениями:
/х Bи) ~Р\ B.о)
Bm)
cos2
E.7)
198
ГЛАВА 5
90
Фиг. 22. Зависимость интенсивности луча второй гармоники, воз-
возникающей при отражении от поверхности кристалла GaAs, от угла
между плоскостью падения и кристаллографической осью {100].
Волны основной частоты и второй гармоники поляризованы перпендикулярно
плоскости падения. Интенсивность отраженного луча измеряется по отноше-
отношению к интенсивности излучения, возникающего в нелинейном процессе того
же порядка в KDP или кварце.
Пластина из GaAs прозрачна для излучения с длиной
волны Я = 1,06 мк, которое дает лазер на неодимовом
стекле. В этом случае можно определить отношение ин-
интенсивности отраженного излучения второй гармоники к
интенсивности излучения гармоники, прошедшего через
пластинку. Согласно D.8) и D.15), это отношение не
должно зависеть от нелинейной восприимчивости вещест-
вещества. Указанные выражения действительно дают правиль-
правильную величину этого отношения, которое эксперименталь-
экспериментально было определено Дюкуэнгом. Все сказанное можно
рассматривать как проверку правильности обобщенных
формул Френеля для интенсивности отраженного излуче-
излучения гармоники,
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
199
ф, град
Фиг. 23. Зависимость интенсивности луча второй гармоники, воз-
возникающей при отражении от поверхности кристалла GaAs, от угла
между плоскостью падения и кристаллографической осью [100].
Луч основной частоты поляризован перпендикулярно плоскости падения, а луч
второй гармоники — в плоскости падения.
ГЕНЕРАЦИЯ СУММАРНОЙ И РАЗНОСТНОЙ ЧАСТОТ
Франкен и др. [8] первыми получили суммарную час-
частоту при смешении двух лучей света с разными частота-
частотами. Они использовали два рубиновых лазера, работавших
при различных температурах, вследствие чего их длины
волн отличались на 10 А. В ультрафиолетовом излучении,
выходящем из нелинейного кристалла, они действительно
наблюдали три частоты: две вторые гармоники и суммар-
суммарную частоту. Смит и Браслау [9] получили разностную
частоту при смешении излучения рубинового лазера с
о
излучением линии 3115 А, испускаемой ртутным разря-
разрядом. Последний источник является «некогерентным», и
его излучение должно рассматриваться как суперпози-
200
ГЛАВА 5
ция большого числа плоских волн. Каждая из них сме-
смешивается с излучением лазера и создает излучение
разностной частоты с длиной волны вблизи Я = 5650 А.
Смит и Браслау наблюдали также линию суммарной
частоты с длиной волны 3056 А, получившуюся при сме-
смешении излучения рубинового лазера и ртутной линии
5470 А. В экспериментах других авторов были получены
также суммарная и разностная частота излучения руби-
рубинового и неодимового лазеров. Терхьюн получил частоту
Зсо, удвоив сначала частоту излучения рубинового лазера
в KDP, а затем смешав луч с частотой 2со и часть луча с
частотой со в другом нелинейном кристалле, ориентиро-
ориентированном так, чтобы обеспечить согласование фазовых ско-
скоростей.
Франкёп с сотрудниками [10] наблюдали выпрямление
света в KDP, которое можно рассматривать также как
биения с нулевой частотой. Соответствующая нелинейная
поляризация равна
@) = Izxy @ = СО - СО) [Ех (СО) Е'у (- СО)
+ ?(-©) ?,(©)].
E.8)
В связи с тем, что объем взаимодействия для светового
луча в нелинейной среде трудно определить, ошибка из-
измерения этой восприимчивости может достигать, по-види-
по-видимому, 200%. Указанный эксперимент позволяет осущест-
осуществить интересную проверку пространственно-частотных
перестановочных соотношений для тензора нелинейной
восприимчивости путем сравнения выпрямления с линей-
линейным электрооптическим эффектом в постоянном поле
рх И = Хгуг (со = со + 0) ?у (со) Ег @).
E.9)
Нелинейная восприимчивость связана с постоянной гзв,
которая обычно приводится в литературе, соотношением
+ Xxyz (и) ~ СО + 0) = —
4л
В пределах точности эксперимента было установлено
равенство
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
201
1хуг (со = со + 0) = у2„ @ = со — со) = 13 . 10~8 ед. CGSE'1.
Отношение величин, характеризующих выпрямление све-
света в КН2РО4 и KD2PO4, очень хорошо совпадает с соот-
соответствующим отношением для линейных электрооптиче-
электрооптических постоянных.
Когда постоянное поле в соотношении E.9) заменяет-
заменяется переменным полем, частота которого лежит в радио-
или СВЧ диапазоне, вблизи световой несущей возникают
боковые полосы
Ру К + <•>„) = X (со = coL + com) Ех (coL) Ег (шт),
E.10)
Ру К — сот) = z (с0 = u'i~ ш'т) Ех (coL) Е*г (— o)J.
Эти боковые полосы света были разрешены с помощью
дифракционного спектрографа для сот/2я = 15 Ггц. Ка-
Каминов [11, 12] и многие другие исследователи создали
практические модуляторы света, работающие в диапазо-
диапазоне СВЧ. Можно осуществить много вариантов устройств,
предназначенных для согласования фазовых скоростей
световых волн и сверхвысокочастотных радиоволн, рас-
распространяющихся в волноводе. Для исследования про-
процессов в таких системах теорию взаимодействия волн
следует распространить на другие типы волн, отличаю-
отличающихся от плоских. Обратный процесс, когда в результа-
результате смешения двух световых волн возникает волна нели-
нелинейной поляризации с частотой, лежащей в диапазоне
СВЧ, экспериментально наблюдался Нибуром [13]. Две
аксиальные моды рубинового лазера, отличающиеся по
частоте на 2,964 Ггц, были смешаны в кристалле кварца,
который одновременно являлся частью резонатора лазе-
лазера и частью СВЧ резонатора.
Таким образом, соотношения, приведенные в гл. 4, § 1
и 2, хорошо описывают широкий круг наблюдавшихся
экспериментально параметрических взаимодействий, свя-
'> Заметим, что при нашем определении амплитуд постоянного
поля величина х1Ху @ = ч>—м) в четыре раза больше того значе-
значения, которое дано Уордом и Франкеном [10]. В связи с тем что мы
делаем различие между положительными и отрицательными часто-
частотами, пространственно-частотное перестановочное соотношение не
содержит здесь множителя 4.
202
ГЛАВА 5
занных с оптическими нелинейностями низшего порядка.
И наоборот, эти соотношения можно использовать для
определения из экспериментальных данных численных
значений нелинейных восприимчивостей.
§ 2. Определение абсолютной величины нелинейной
восприимчивости
Трудность получения надежной величины нелинейной
восприимчивости по измеренной интенсивности второй
гармоники связана с многомодовой структурой излучения
твердотельных лазеров высокой мощности. Распределе-
Распределение интенсивности в произвольном поперечном сечении
луча точно не известно. Импульсный характер излучения
создает дополнительные трудности. Интенсивность второй
гармоники пропорциональна не квадрату интегральной
интенсивности излучения основной частоты, а интегралу
от квадрата этой интенсивности. Связанные с этим за-
затруднения подробно анализируются в следующем пара-
параграфе.
С другой стороны, газовые лазеры работают в непре-
непрерывном режиме и имеют четкую геометрию луча. Ашкин,
Бойд и Дзидзик [14] использовали для получения опти-
оптических гармоник гелий-неоновый лазер, генерировавший
излучение с длиной волны 1,1526 мк в основной моде
@0<7) с радиальным распределением интенсивности
h = /оехр (— 2г2/а2) при размере пятна а = 0,21 см. Луч
имел дифракционную расходимость с угловой полушири-
полушириной, равной всего 3- 10~5 рад. Для таких параметров ко-
когерентная длина /к'ог , определяемая выражением E.4),
составляет в кристалле KDP около 20 см. Используя
такой луч и кристалл длиной z = 1,23 см, можно добиться
точного согласования фазовых скоростей, при котором
интенсивность второй гармоники нарастает как г1.
Ашкин, Бойд и Дзидзик проверили эту зависимость на
кристаллах трех различных длин. Как показано на
фиг. 24, изменение интенсивности второй гармоники
вблизи направления точного согласования фазовых ско-
скоростей хорошо описывается соотношением D.13). Так
как мощность луча непрерывного газового лазера состав-
составляет всего 1.48 ¦ 10~3 вт, то, несмотря на точное согла-
ЭКСПЕРИМЕНТЛЛЬНЫЕ РЕЗУЛЬТАТЫ
203
сование фазовых скоростей, мощность второй гармоники
очень мала. Максимальная наблюдаемая мощность вто-
второй гармоники, генерируемой в кристалле KDP длиной
1,23 см, равнялась 8,1 • 10~14 вт. Поляризация падающего
луча лазера направлена вдоль [ПО]. Необыкновенный луч
второй гармоники поляризован в плоскости, содержащей
х8,1 х/О
-0,1
Фиг. 24. Экспериментальная зависимость интенсивности второй
гармоники в кристалле KDP от угла между лучом газового лазера и
направлением точного согласования фазовых скоростей (по дан-
данным работы A4]).
Газовый лазер работал в одномодовом режиме ТЕМ 00 . Кружками обозначе-
обозначены экспериментальные точки; сплошная кривая построена по формуле D 13).
Мощность основного излучения составляла Р, = 1,48 • Ю-3 вт, длина кристал-
кристалла I- 1,23 см.
кристаллографическую ось z и волновой вектор падаю-
падающей волны. Угол с осью г, при котором выполняется усло-
условие согласования фазовых скоростей для Я = 1,15 мк, ра-
равен Qm = 41°. Направление распространения энергии со-
составляет небольшой угол а с направлением волнового
вектора. Если диаметр луча равен а, то необыкновенный
луч второй гармоники, волновой вектор которого парал-
параллелен обыкновенному лучу основной частоты, пройдя
расстояние a/tg а, выйдет в сторону из сечения, занятого
лучом основной частоты. В рассматриваемом экспери-
эксперименте при а = 0,21 см и z = 1,25 см этот эффект, очевид-
204
ГЛАВА 5
но, не играет роли '). Эффективный нелинейный источник,
возбуждающий необыкновенную волну гармоники, пред-
представляет собой компоненту нелинейной поляризации, па-
параллельную вектору электрического поля ЕBсо) волны
pnLS (г) = P™hS sin @M -1- а) - хзв B(о = со -|-
-f ш) sin (QM + а) ЕХх (г) Е1у (г).
Это выражение для PNLS(r) подставляется в соотношение
D.13), после чего производится интегрирование по точно
известному радиальному распределению интенсивности
основной частоты. Используя такой метод, Ашкин, Бойд и
Дзидзик нашли, что Хз"<рР Bю = со + со) = F ± 2) X
X Ю~9 ед. CGSE для 2лсаГ' = 1,15 мк. Эта величина
вдвое превышает значение, приведенное в их оригиналь-
оригинальной статье, что связано с нашим определением амплитуд
ноля. Интенсивность излучения второй гармоники изме-
измерялась также и для других мод. Результаты наблюдений
хорошо согласуются с вычисленными распределениями
интенсивности в поперечном сечении луча.
§ 3. Многомодовая структура и флуктуационные
явления
Хотя газовый лазер может работать в режиме одной
поперечной моды, тем не менее при этом могут существо-
существовать еще несколько продольных мод с эквидистантными
частотами. Ниже будет показано, что это может вызвать
систематическую ошибку при определении величины не-
нелинейной восприимчивости из опытов по генерации вто-
второй гармоники: истинная_величина %зв может оказаться
меньше измеренной в ]/2 раз. Многомодовая структура
излучения реального лазера, который можно рассматри-
рассматривать как ряд параллельных когерентных генераторов, су-
существенно усложняет картину взаимодействия волн в
нелинейной среде; многомодовая структура вызывает, в
'> Подробное исследование влияния различия направлений лу-
лучевого и волнового векторов в нелинейной анизотропной среде на
проносе генерации второй гармоники выполнено в недавно опубли-
опубликованной работе [56*].-— Прим. ред.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
205
частности, флуктуации интенсивности второй гармоники.
В общем случае и задача о генерации гармоник и другие
нелинейные оптические задачи должны рассматриваться
как статистические, поскольку поле лазерного излучения
состоит из ряда волн, амплитуды и фазы которых явля-
являются случайными величинами. Вообще говоря, они не
обязательно статистически независимы; нелинейные про-
процессы связывают различные моды лазера и могут уста-
установить между ними частичную или полную корреляцию.
Однако в некоторых случаях обосновано рассмотрение
комплексных амплитуд как статистически независимых.
Примером может служить излучение рубинового лазера,
различные моды которого образованы различными воз-
возбужденными ионами.
Представим поле лазерного излучения для одного на-
направления поляризации в виде
Е (г л = Vfl и (хи) ?1кп1г~~1ШпР E 11)
Индекс / использован для обозначения поперечных мод, а
п — продольных. Интенсивность второй гармоники, воз-
возбужденной этим лазерным полем в пластине из нелиней-
нелинейного вещества толщиной г, дается соотношением D.13)
и может быть записана в виде четверной суммы
64n2)xNLl2sina — i
г^' — г1/)
X
X
x
x
У) u'i (*> У) "г (*• У) "/'"
E.12)
Экспериментально наблюдаемая величина обычно реги-
регистрируется через посредство квадратичного процесса,
проинтегрированного по определенному интервалу вре-
времени и определенной площади поперечного сечения.
Если, например, измеряется ток фотоумножителя,
2д6
ГЛАВА &
вызванный излучением с частотой второй гармоники, то
интегрирование производится по интервалу времени Т,
равному постоянной времени регистрирующей схемы,
и по поперечному сечению фотокатода. Хотя интервал Т
достаточно короток для того, чтобы считать амплитуды
не зависящими от времени, тем не менее это время обыч-
обычно превышает период биений любых двух различных
частотных компонент. Экспоненту в соотношении E.12),
проинтегрированную по Г, можно заменить б-функцией.
Так как различные моды щ ортогональны, интенсив-
интенсивность основной частоты, или фототок, равна просто
т
2
щ,п"\"
E.13)
Множитель t]i учитывает чувствительность фотоумножи-
фотоумножителя и другие параметры регистрирующей схемы.
Измеренную интенсивность второй гармоники, или со-
соответствующий фототок можно в общем случае получить
из выражения E.12). В простейшем случае, когда ампли-
амплитуды отдельных мод постоянны, а фазы фпу являются ста-
статистически независимыми переменными, равномерно рас-
распределенными по интервалу 0 — 2я, среднее значение
интенсивности второй гармоники можно записать в виде
7 .IV? L 9п. I vNL 2
X
E.14)
Здесь постоянная т]2 включает чувствительность фотоум-
фотоумножителя на частоте гармоники и геометрический множи-
множитель, входящий в выражение E.12). Постоянные С опре-
определяются соотношением
\iи)"*"*dxdy- E.15)
Если амплитуды постоянны, то интенсивность основной
частоты является регулярной, а интенсивность второй
гармоники — случайной величиной, так как различные
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
20?
пары мод основной частоты, имеющие случайные фазы,
дают вклад в одну и ту же моду второй гармоники.
Рассмотрим газовый лазер, излучающий большое ко-
количество эквидистантных продольных мод и только одну
поперечную моду ]. Амплитуды этих мод можно считать
постоянными, а фазы не обязательно статистически неза-
независимыми. В этих предположениях комбинация выраже-
выражений E.13) и E.14) дает для N мод равной амплитуды
41
X
2'|
п+п'
ЯпП«п
E.16)
Сумма со штрихом означает суммирование по N(N— 1)
паре мод. Если заданная интенсивность излучения основ-
основной частоты /] не сосредоточена в одной моде, а распре-
распределена по N модам, то средняя интенсивность второй
гармоники увеличивается в B + АН) раз. Нелинейная
восприимчивость, определенная по результатам такого
эксперимента без учета модовой структуры излучения,
может оказаться завышенной в ]/2 раз. Физическое
объяснение состоит в том, что наибольший вклад в вели-
величину нелинейного эффекта дают интерференционные чле-
члены, соответствующие возрастанию амплитуды. Неодно-
Неоднородное распределение во времени и пространстве при
заданной интегральной интенсивности излучения основ-
основной частоты будет приводить к увеличению мощности
гармоники. В литературе сообщалось о наблюдавшихся
иногда отклонениях от квадратичного соотношения
/2 ~ 1\. Объяснение, возможно, заключается в том, что
модовая структура излучения изменяется при возраста-
возрастании мощности лазера /].
Помимо возрастания средней мощности гармоники,
будут иметь место флуктуации ее мощности около сред-
среднего значения. Величину < 1\ > — < /2 > а можно вычис-
вычислить с помощью полинома восьмой степени по случайным
амплитудам мод основной частоты. Аналогичное рассмот-
ГЛАВА $
рение можно провести и для нелинейных процессов более
высокого порядка.
Дюкуэнг [15] наблюдал флуктуации коэффициента,
связывающего величины /2 и /? для различных импуль-
импульсов рубинового лазера с модулируемой добротностью.
Иногда импульс с меньшей интенсивностью излучения
основной частоты давал более мощную гармонику. Одна-
Однако между двумя нелинейными процессами одного поряд-
порядка, вызванными одним и тем же лазерным импульсом,
существует регулярное соответствие, не подверженное
флуктуациям (для их наблюдения излучение лазера раз-
разделяется на две части с помощью полупрозрачного зерка-
зеркала) . Этот метод позволяет получить надежные относи-
сительные величины нелинейной восприимчивости.
На фиг. 21 приведена схема экспериментальной установ-
установки, на которой измерялась нелинейная восприимчивость
GaAs; ее величина определялась по отношению к нели-
нелинейной восприимчивости, обусловливающей генерацию
второй гармоники в KDP или кварце. Если перед кварце-
кварцевым кристаллом помещалась рассеивающая пластинка
из матированного стекла, не обладающая поглощением,
то указанное регулярное соответствие нарушалось. Про-
Пространственное распределение мод в двух образцах нели-
нелинейного вещества переставало быть идентичным. Этот
эксперимент убедительно показывает, что в импульсе ру-
рубинового лазера генерируются одновременно несколько
мод ¦>.
Многомодовая структура лазерного излучения оказы-
оказывает также сильное влияние на генерацию малых раз-
разностных частот. Рассмотрим сначала эффекты, связанные
с наличием ряда продольных мод.
Пусть смешиваются два луча, содержащие соответст-
соответственно N\ и N2 частотных компонент, сгруппированных
около coi и ©г. Каждая частотная компонента первого лу-
луча будет смешиваться с каждой компонентой второго
') Флуктуации мощности гармоники могут быть связаны, вооб-
вообще говоря, не только с флуктуационным разбросом фаз в разных
модах основного излучения (см., например, [76*]). Заметим также,
что для ряда задач представляет интерес не только дисперсия мощ-'
ности гармоники, но и временные характеристики ее флуктуации
[77*]. — Прим. ред.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
209
луча и давать разностную частоту вблизи шг — &>ь Шири-
Ширина полосы регистрирующей системы, настроенной на час-
частоту юг — соь определит, какие из всех возможных комби-
комбинаций частотных компонент N{N2 дадут вклад в регист-
регистрируемый сигнал. Если ширина полосы детектора меньше
разности частот между N эквидистантными компонента-
компонентами каждого луча, то результирующий сигнал на частоте
0J — coi будет меньше сигнала, созданного двумя идеаль-
идеально монохроматичными лучами света такой же интенсив-
интенсивности в N раз, где N равно большему из чисел N\, N2.
Обратимся теперь к эффектам, обусловливаемым раз-
различием в пространственной когерентности смешиваемых
лучей. Предположим, что длина волны излучения раз-
разностной частоты равна или больше поперечного сечения
лучей или нелинейного кристалла. Тогда мощность, гене-
генерируемая на разностной частоте, пропорциональна квад-
квадрату средней по поперечному сечению поляризации с ча-
частотой 0J—о)ь Поляризация, в пространственном рас-
распределении которой по поперечному сечению имеются уз-
узлы, не может излучать, если размеры поперечного сече-
сечения малы по сравнению с длиной волны. В этом случае
интерференция гасит излучение. Поэтому излучение на
разностной частоте могут давать только те моды двух
лучей света, которые имеют одно и то же пространствен-
пространственное распределение, причем длина волны излучения долж-
должна быть больше диаметра пучков света. Если в каждом
пучке имеется соответственно J\ и J2 пространственных
мод, то интенсивность излучения разностной частоты
уменьшается в / раз, где / — большее из двух чисел J\, J2.
При получении из света излучения разностной частоты,
находящейся в диапазоне СВЧ, важно иметь лучи, обла-
обладающие только дифракционной расходимостью. Коэффи-
Коэффициент ослабления интенсивности обусловлен по существу
ограничениями конечных состояний в фазовом простран-
пространстве на низких частотах.
В обратном процессе СВЧ модуляции некогерентного
луча света коэффициент ослабления отсутствует. Свето-
Световые компоненты в боковых полосах всегда смогут найти
моду с соответствующей частотой o)nj ± шевч и с соот-
соответствующим распределением амплитуды Mnj«c*B4 п0 п0"
перечному сечению. Очевидно, что коэффициент ослабле-
14 Н. Бломберген
210
ГЛАВА S
пня отсутствует в экспериментах по смешению излучения
рубинового лазера с излучением неодимового лазера,
имеющим широкую полосу частот, или с некогерентным
излучением ртутного разряда.
Коэффициент ослабления отсутствует также при вы-
выпрямлении света. В этом случае каждая мода может
смешиваться сама с собой и создавать постоянное напря-
напряжение, пропорциональное интегральной интенсивности
основной частоты, безотносительно к распределению ин-
интенсивности по модам.
Приведенные соображения по существу аналогичны
соображениям, высказанным Форрестером [16], при ана-
анализе влияния пространственной когерентности, на фото-
фотоэлектрическое смешение. Фотоэлектрический эффект
также является нелинейным эффектом с квадратичной
характеристикой '>.
§ 4. Нелинейные восприимчивости пьезоэлектрических
кристаллов
Методы, изложенные в общих чертах в гл. 1 и 5, ис-
использовались для измерения компонент тензоров воспри-
восприимчивости третьего ранга, описывающих генерацию вто-
второй гармоники в ряде кристаллов. Измерения обычно
производятся по отношению к стандартной величине
компоненты %zxyBa = со + со) для KDP, равной при ком-
комнатной температуре 6,0- 10~9 ед. CGSE и принятой за еди-
единицу. Для получения точных относительных значений
важно избегать направления точного согласования фазо-
фазовых скоростей и близких к нему направлений. В этих слу-
случаях данные были бы чрезвычайно чувствительны к гео-
геометрии, и требовалось бы точно знать конфигурацию мод
и ориентацию кристалла. Кроме того, для получения
надежных данных необходимо провести измерения не-
нескольких максимумов и минимумов на кривых типа, при-
11 В последнее время весьма оживленно дискутируются также
вопросы, связанные с влиянием модовой структуры излучения лазе-
лазеров на протекание процессов вынужденного рассеяния (см. [78* —
83*]. Дискуссионным, в частности, является вопрос о влиянии мо-
модовой структуры на интенсивность линий вынужденного комбина-
комбинационного рассеяния (ср., например, [79*] и [82*]). — Прим. ред.
Таблица 1
Относительные величины компонент тензора нелинейной
восприимчивости yJjk Bсо = со + со)
Используются обозначения Фойгта- а- = 1 « = 9 г = 3
уг = гу = 4, хг = гх = 5, ху = ух = 6. Величина у,; для KDP
принята за единицу. Ее абсолютное значение ь, = 6 10-е ед
Кристалл
КН2РО4
(тетрагональ-
(тетрагональный)
КН2РО4
(орторомбиче-
ский)
KD2PO4
NH4H2PO4
KH2As04
Кварц
ВаТЮ3
CdS
;4*
Восприимчивость для генерации
второй гармоники <
Х = 6943А
7.3E = 1,00
Xi4 = 0,95 + 0,06
7-14 = 0,86 ±0,05
Хз; = 1,23 ±0,1
Х15 = 1,20 ± 0,1
=0.83 ±0,1
Х24 = 0,80± 0,1
7.за = 0.0
7.3S =0,75± 0 02
'-и = 0,76 ±0,04
Хи=0,85± 0,1
7.38=0,93+ 0,06
7.14= 0,89 ± 0,04
/.зв = 1,25 ±0,05
/и =1,07 ±0,05
7.зв = 1,0 ±0,1
7.14 = 0,86 ± 0,1
7.11 =
7.14 =
7as =
7.31 =
Хзз =
7.15 =
'-3! =
7зз —
А. = 1 ,06 мк
1,0
1,01 ±0,05
0,92 ± 0,04
0,91 ±0,03
0,99+ 0 05
0,98 ±0,05
0 82 ± 0,04
0,00 ±0,05
35,0± 3
37 0± 3
14,0 ± 1
35,0±3
32,0 + 2
63,0 ± 4
Литература
[17]
[18]
[18]
[18]
[18]
[18]
[18]
[17]
[17]
[18]
[17]
[17]
[18]
[18]
[18]
[18]
[19]
[19]
[19]
[19]
[19]
[21]
[21]
[21]
212
ГЛА6А S
Продолжение табл. 1
Кристалл
GaAs
InAs
InSb
GaSb
ZnO
AIPO4
Восприимчивость для генерации
второй гармоники
Х = 6943А
7u=570 ±100
"/.и = 370 ± 75
Хм = 820 ±150
Xi4 =865± 1Б0
Х24 = Xl5
Х32 = Хз1
Хзз — Хз1
Хп = Хз1
X = 1 ,06 мк
330 0± 100
210,0 + 75
324,0+ 100
224,0 ±75
4,7 ± 0,4
4,3±0,4
14,3 ±0,4
0,84 ±0,07
Литература
[22
[22
[22
[22
[23]
[23]
веденной на фиг. 2. Далее, для определения всех незави-
независимых компонент тензора восприимчивости можно ис-
использовать соотношение D.13) для различных ориента-
ориентации поляризации луча основной частоты и луча второй
гармоники по отношению к кристаллографическим осям.
Опубликованные к настоящему времени данные получены
почти исключительно с помощью рубиновых лазеров, у
о
которых ha — 1,79 эв (X = 6940 А), и неодимовых лазеров
на стекле или вольфрамате кальция (CaWO,j) с присад-
присадкой Nd3+, имеющих /гм= 1,17 эв (Я = 1,06 мк) '). В табл. 1
приведены только самые новые и, по-видимому, самые
надежные данные.
В связи с тем, что две частоты равны, спектральная
компонента тензора нелинейной восприимчивости
3C*yzBu>) симметрична по двум последним индексам:
Луг
Bю = со + ш) = Xizy Bю = © -f ш)=— du.
'> Только в последнее время появились сообщения об опытах,
в которых генерация гармоник происходила при возбуждении не-
нелинейной среды излучением с длинами волн X = 0,53 мк и с некото-
некоторыми другими [57*—59*] — Прим. ред.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
213
Здесь i принимает значения х = 1, у = 2, z = 3. Приня-
Приняты обозначения Фойгта, согласно которым
yz = zy = 4, xz = zx = 5, xy = ух — 6.
Первые четыре кристалла в табл. 1 имеют тетрагональ-
тетрагональную симметрию класса 42т или Vd, характерную для
KDP. Отличными от нуля компонентами являются
ofi4 = ^25 и с?зб- Тригональный кварц обладает симмет-
симметрией класса 32 или Рз, причем отличны от нуля компо-
компоненты dn = —с/22 = — ^26 и of 14=—й?25. Четыре кристалла
в таблице относятся к полупроводникам типа A111 BY
с решеткой типа ZnS, имеющей тетрагональную сим-
симметрию класса 43т или Td. Отличными от нуля ком-
компонентами являются d\i = е?25 = <^зб- О свойствах сим-
симметрии других кристаллов можно узнать в работах, на
которые даны ссылки в табл. 1. Тензор третьего ранга d
характеризуется такими же свойствами симметрии, как
и пьезоэлектрический тензор. Он часто используется в
литературе вместо %. Его компоненты с индексами 4,
5, 6 вдвое больше соответствующих компонент %.
Результаты экспериментов по определению нелиней-
нелинейных восприимчивостей согласуются с известным.и свой-
свойствами симметрии. Интересно отметить, что часто ока-
оказывается справедливым дополнительное свойство сим-
симметрии, известное как соотношение Клейнмана [24].
Частотная дисперсия нелинейной восприимчивости в
области прозрачности кристаллов настолько мала, что
часто можно менять местами 2со и со без соответствую-
соответствующей перестановки индексов. Это дает дополнительное
соотношение вида dH ^ d3e для кристаллов класса
KDP и du « o?25 для кварца. Так как из симметрии
кристалла кварца следует равенство dH — —d2$, то по-
получается, что в кварце в пределах точности эксперимен-
эксперимента d\4 = 0. В KDP указанное соотношение, вероятно, не
выполняется строго, так как Ван дер Зил нашел, что в
этом случае dH = @,86 ± 0,05)d s?> .
'' За время, прошедшее после написания этой книги, интенсив-
интенсивная работа по определению нелинейных восприимчивостей xnh в
различных кристаллах продолжалась. Пожалуй, одним из наиболее
интересных ее результатов следует признать открытие нового весь-
214
ГЛАВА 5
температурная зависимость и дисперсия
нелинейной восприимчивости в kdp
Ван дер Зил [18] подробно исследовал температурную
зависимость нелинейной восприимчивости в KDP и не-
некоторых других кристаллах с такой же структурой. При
температуре ниже 122° К кристалл KDP переходит в
сегнетоэлектрическую фазу с орторсмбической симмет-
симметрией (класс тт2). Если охладить кристалл до темпера-
температуры, меньшей температуры перехода, в достаточно
сильном электрическом поле, направленном по тетраго-
тетрагональной оси, то образуется один сегнетоэлектрический
домен с орторомбическими осями х', у', повернутыми на
45° по отношению к осям х, у исходной тетрагональной
структуры. Тензор нелинейной восприимчивости в сегне-
тоэлектриче.ской фазе имеет компоненты:
х'
у'
г \
х'х'
0
0
Хз1
у-у'
0
0
Х32
ZZ
0
0
Хзз
zx'
0
XI4
0
y'z
lib
0
0
x'y'
0
0
0
Величины измеренных восприимчивостей приведены на
фиг. 25. В каждой фазе они не зависят от температуры,
причем в орторомбической фазе оказалось невозможно
измерить %зз из-за его малости. Компоненты 5С з! и
Х,'5, вероятно, имеют противоположные знаки, то же
относится и к % 32 и % 24- Изменение абсолютной величи-
величины восприимчивости при переходе из одной фазы в дру-
другую мало. В соответствии с требованиями симметрии в
ма эффективного нелинейного кристалла 1ЛЫЬОз [60*, 61*]. Этот од-
одноосный пьезоэлектрический кристалл, относящийся к группе Ът и
имеющий й?31 = 3,6 • 10~3 ед. CGSE (при использовании обычной за-
записи для поля), допускает согласование фазовых скоростей. Исполь-
Используя этот кристалл, удается создать эффективные удвоители часто-
частоты и перестраиваемые параметрические генераторы света (см.
гл. 4). — Прим. ред.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
215
тетрагональной фазе с инверсионной поворотной осью
четвертого порядка те же самые величины, отнесенные к
орторомбическим осям, должны иметь противоположный
знак.
X
Т, °К
Фиг. 25. Температурная зависимость нелинейной восприимчивости
в KDP.
Фазовый переход происходит при температуре 122° К.
Если охлаждать кристалл, не прикладывая к нему
электрического поля, то образуется сегнетоэлектриче-
ская доменная структура, в которой орторомбические
оси соседних доменов образуют между собой угол в 90е.
Это приводит к изменению знака нелинейной восприим-
восприимчивости при переходе от одного домена к другому. Так
как величина доменов сравнима с длиной когерентного
взаимодействия, в многодоменном кристалле можно
получить сильное увеличение интенсивности гармоники.
Объясняется это тем, что, когда разность фаз между
волной гармоники и волной основной частоты должна
была бы стать слишком большой, происходит изменение
знака нелинейной поляризации на частоте второй гармо-
гармоники на обратный. В результате волна гармоники про-
продолжает нарастать. Интенсивность второй гармоники в
многодоменных кристаллах может увеличиться на два
216
ГЛАВА 5
порядка и зависит от конкретных особенностей доменной
структуры. Аналогичные эффекты наблюдались Милле-
Миллером [19, 20] в сегнетоэлектрике ВаТЮз. Этот же эффект
можно использовать для компенсации рассогласования
фазовых скоростей в кубических кристаллах: кристалли-
кристаллические пластинки набирают в стопу так, чтобы оси [011]
соседних пластинок оказались попеременно повернутыми
на 90е (см. приложение I).
Нелинейная восприимчивость %3в @ = со — со) в KDP
приблизительно в 40 раз больше величины 5(збBсо = со +
+ со). Такая большая дисперсия обусловливается в ос-
основном усилением действующих полей ионной поляриза-
поляризацией и подробно обсуждалась Франкеном [10]. На СВЧ
этот ионный вклад в нелинейную поляризацию все еще
существует, так что
Хзв (№свч = Ш2 — »i) = Хзв @ = «1 — Щ)-
Нелинейные восприимчивости орторомбической фазы
можно вывести из нелинейных восприимчивостей тетра-
тетрагональной фазы более высокого порядка, учитывая
внутреннее постоянное поле, вызванное спонтанной ста-
статической поляризацией. Имеем, например,
Xi is Bto = со + со) = xTfT Bсо = со -f со) +
+ уМ1% Bсо = со + со + 0) Р3 + /Г2ТзРззBсо=(й + со +0 +0)Р23,
Х223 Bсо = со + со) = — [хТ!тзР Bсо^= со -f со) —
— Хтрз;Bсо = со + со + 0) Р3 +
+ Xmss B@ = со + ш + 0 + 0) Pi].
Аналогичным образом учитывая линейный электроопти-
электрооптический эффект, вызванный действующим электрическим
полем, которое создано спонтанной статической поляри-
поляризацией, можно связать величину двойного лучепреломле-
лучепреломления орторомбической фазы с показателями преломления
тетрагональной фазы. Ван дер Зил [18] и Миллер [19,
20] исследовали связь между указанными тензорами и
пришли к некоторым интересным заключениям относи-
относительно действующего поля.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТЛТЫ
217
НЕЛИНЕЙНЫЕ ВОСПРИИМЧИВОСТИ ПОЛУПРОВОДНИКОВ
Дисперсия нелинейной восприимчивости становится
более резко выраженной, когда одна из частот попадает
в область поглощения вещества. Если начинает погло-
поглощаться излучение с частотой второй гармоники, то про-
происходит заметное увеличение нелинейной восприимчиво-
восприимчивости. Такой эффект наблюдали Зорев и Мус [21], которые
работали с твердыми растворами ZnS—CdS и CdS—
CdSe. Ширина запрещенной зоны Eg в этих кристаллах
в зависимости от концентрации систематически изме-
изменяется от 1,71 эв в CdSe до 2,36 эв в CdS и до 3,52 эв
в ZnS. Такой диапазон изменения Eg вдвое превышает
энергию фотонов, испускаемых лазером на неодимовом
стекле. При уменьшении ширины запрещенной зоны с
1,52 B/гсо) до 0,73 B/гсо), приводящему к попаданию вто-
второй гармоники в область сильного поглощения, нелиней-
нелинейная восприимчивость 5(ззз B@ = ш + (о) увеличивается на
порядок. Этот результат согласуется с теоретическим
расчетом по формуле B.48). Резонансный знаменатель
этого выражения, зависящий от частоты coi + со2 = 2со,
показывает, что, после того как 2/гсо станет больше Eg,
нелинейная восприимчивость должна расти по такому
же закону, как и комплексная линейная восприимчивость
на частоте 2со. Таким образом, существует во всяком
случае качественное согласие между теорией и экспе-
экспериментом. Заслуживает внимания то, что даже в обла-
области прозрачности, где Eg > 2/гсо, нелинейность CdS
много больше, чем KDP. Объяснение, по-видимому, за-
заключается в том, что отклонение от инверсионной сим-
симметрии в CdS и полупроводниках типа AinBv гораздо
сильнее. Поэтому значительно большая сила осциллято-
осциллятора связывается с волновыми функциями валентных элек-
электронов, не обладающими определенной четностью.
Указанные нелинейности были определены в экспе-
экспериментах по генерации второй гармоники в объеме;
нелинейная восприимчивость же полупроводников типа
АшВv измерялась методом отражения'), показанном
'> Некоторые новые данные о дисперсии нелинейной восприим-
восприимчивости в монокристаллах GaAs, InAs, InSb, ZnTe, полученные
методом отражения, сообщались в [58*]. — Прим. ред.
218
ГЛАВА 5
на фиг. 21. Так как излучение основной частоты (лазе-
(лазера) поглощается кристаллом, для предотвращения раз-
разрушения его поверхности вследствие избыточного нагре-
нагревания и испарения мощность потока падающего
излучения должна быть не слишком велика. К счастью,
значительная часть поглощенного лазерного света,
по-видимому, снова испускается в виде рекомбинацион-
ного излучения. Поверхность должна быть отполирована
и химически протравлена. Все отраженное излучение с
частотой гармоники возникает в слое толщиной около
400 А. равной глубине поглощения света на частоте
второй гармоники. Проверкой качества этого слоя яв-
является равенство нулю интенсивности отраженной гар-
гармоники для специальных ориентации, отмеченных на
фиг. 22 и 23. Это служит доказательством того, что по-
поверхностный слой имеет такую же симметрию, как и
остальная часть кристалла. Если луч лазера падает
под углом 45° и поляризация нормальна к плоскости
падения, параллельной кристаллографической оси [111],
то нелинейная поляризация равна
Bсо) =
I2 = 3-1
(со) |* X
EЛ7)
Последний множитель в этом выражении является фре-
нелевским коэффициентом пропускания, позволяющим
выразить поле внутри полупроводника через напряжен-
напряженность поля в падающем лазерном луче. Пользуясь соот-
соотношением D.8), для амплитуды гармоники в отражен-
отраженной волне получаем
er
JEM. | Епал (со) |2
Be(со)-
12
1 J
х
х
{[2еBсо)-1]'
E.18)
Наблюдаемая интенсивность второй гармоники пропор-
пропорциональна квадрату абсолютной величины этого выра-
ЖСПР.РИМЕИТАЛЬНЫЕ РЕЗУЛЬТАТЫ
219
жения. Необходимо подчеркнуть, что в экспериментах
по генерации второй гармоники измеряется только абсо-
абсолютная величина комплексной восприимчивости.
Ширина запрещенной зоны в GaAs, равная 1,35 эв,
больше энергии кванта излучения неодимового лазера,
равной 1,17 эв. В этом случае, воспользовавшись соот-
соотношением D.15), нелинейную восприимчивость можно
также измерить по генерации гармоники в объеме. Оба
метода дают согласующиеся результаты, но измерения
по методу отражения оказываются в 2—3 раза более
точными. Большая неопределенность результатов изме-
измерения восприимчивости по генерации гармоники в
объеме вызвана неопределенностью значений комплекс-
комплексного линейного показателя преломления. В выражение
D.15) для интенсивности гармоники входит разность
этих величин, взятых на частотах со и 2со. Указанное
обстоятельство ограничивает точность такого метода.
Существует значительная дисперсия величины
ХнBсо = со + со) в интервале от /гсо = 1,17 эв до /гсо =
= 1,79 эв. В InSb (Ей = 0,24 эв), InAs (Eg = 0,45 эв)
и GaSb (?g = 0,81 эв) всегда поглощаются и излучение
основной частоты и вторая гармоника. В GaAs с Ее =
= 1,35 Эб излучение неодимового лазера основной ча-
частоты не поглощается. Заметим, что в случае, когда
в дополнение к поглощению второй гармоники начинает-
начинается поглощение излучения основной частоты, существен-
существенных изменений нелинейной восприимчивости не про-
происходит. Когда частота гармоники попадает в область
поглощения, нелинейная восприимчивость возрастает на
порядок, однако дополнительное поглощение излучения
основной частоты может самое большее изменить наклон
дисперсионной кривой, но не порядок величины воспри-
восприимчивости. Такое поведение восприимчивости в общих
чертах согласуется с соотношением B.48). Так как ши-
ширина зон велика по сравнению с постоянной затухания Г,
то можно перейти к пределу при Г—>-0 и использовать
соотношение
1.1 1
lim • = Главное значение
Г-,а сог — и>п„п, -f /Г co2 - со..
un"n'
— Ш (CO2
E.19)
220
ГЛАВА S
при вычислении интеграла в выражении B.48). Таким
способом нелинейные восприимчивости можно выразить
через те же смешанные плотности состояний, которые
встречаются в теории линейной диэлектрической прони-
проницаемости [25]. Могут иметься критические точки, где
смешанная плотность состояний высока. Если окажется
возможным измерять нелинейность на более высоких
частотах, то можно попытаться отыскать такие макси-
максимумы комплексной нелинейной восприимчивости. Ис-
Исследование выражения B.48) показывает, что возможен
также другой тип сингулярности в поведении нелиней-
нелинейной восприимчивости, который не наблюдается в линей-
линейном случае. Два знаменателя могут одновременно ока-
оказаться вблизи от резонанса, когда со„'П (k) = 2соП'л" (k).
В этом случае, а также вблизи от края зоны следует
пользоваться выражением B.48), не переходя к пределу
при Г-+0 в соответствии с соотношением E.19). Хотя
нелинейности в указанных полупроводниковых соедине-
соединениях очень велики, вторая гармоника генерируется в
действительности слабо. Эффективный когерентный
объем излучающей поляризации, пропорциональный
глубине поглощения, уменьшается быстрее, чем растет
нелинейность '). Нелинейная восприимчивость дает боль-
больше информации о структуре электронных зон, чем толь-
только одни линейные оптические константы, потому что она
описывает свойства, характерные для волновых функций
зон смешанной четности.
Полупроводники Si и Ge, имеющие центры инверсии,
не дают заметной интенсивности второй гармоники. Их
нелинейность по крайней мере на три порядка меньше,
чем в GaAs, а интенсивность генерируемой ими второй
гармоники меньше в 106 раз. Эти эффекты не зависят от
легирующих примесей и удельного сопротивления мате-
материала, что указывает на то, что нелинейности электрон-
электронной плазмы ненаблюдаемы. Это не удивительно:
нелинейность плазмы в таком металле, как серебро, по
оценкам, которые можно сделать, пользуясь выражения-
выражениями A.6) или B.45), того же порядка, что и в KDP, или
приблизительно в 400 раз меньше, чем в GaAs. Однако
'» Эти вопросы обсуждаются также в [62*, 63*]. — Прим. ред.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
221
нелинейность трудно обнаружить, поскольку поглощение
в металле очень велико. Даже если использовать узкие
плазменные резонансы в серебре, для того чтобы умень-
уменьшить, насколько это возможно, некоторые из знаменате-
знаменателей, входящих в выражения, аналогичные соотношениям
E.17) или E.18), то и тогда эксперимент останется все
еще очень сложным. Нелинейность плазмы в полупро-
полупроводнике можно увеличить во много раз в далекой инфра-
инфракрасной области, где при малых эффективных массах
и сильных магнитных полях может возникать циклотрон-
циклотронный резонанс [26]. Очевидно, что существует много воз-
возможностей для проведения дальнейших экспериментов.
§ 5. Электрические квадрупольные эффекты
Терхьюн [27] наблюдал генерацию второй гармоники
в кристалле кальцита, который имеет центр инверсии.
Этот кристалл относится к группе симметрии 2>т или
D3d- Эффект очень мал и может наблюдаться лишь при
тщательном согласовании фазовых скоростей обыкно-
обыкновенной волны основной частоты и необыкновенной вол-
волны второй гармоники '>. Генерацию второй гармоники
можно сильно увеличить, если приложить к кристаллу
постоянное электрическое поле (фиг. 26). Это поле на-
нарушает инверсионную симметрию. В этом случае волна
нелинейной поляризации связана с восприимчивостью,
описываемой тензором четвертого ранга,
PNLS Bm) = х Bсо = со + со + 0) Е (со) Е (со) Edc @). E. 20)
Интенсивность второй гармоники действительно возра-
возрастает пропорционально Ejc. Однако в настоящем раз-
разделе мы будем интересоваться случаем Edc@) = 0.
В этом случае генерация второй гармоники обусловлена
'> Следует отметить, что выполнение закона сохранения им-
импульса в кальците возможно и в том случае, когда обыкновенная и
необыкновенная волны основного излучения взаимодействуют с не-
необыкновенной волной гармоники. Такие взаимодействия возможны
и в других кристаллах. — Прим. ред.
222
ГЛАВА 5
квадрупольным эффектом, который можно получить из
свободной энергии
— ^ im Ej (a) Et (со
у И V*?j (со) -
Bш) + компл. сопр. E. 21)
Входящий сюда тензор восприимчивости симметричен
по последним двум индексам. Першан [28] детально рас-
рассмотрел энергию, связанную с квадрупольными членами,
и показал, что без потери общности можно положить
у* = 0. В таком случае нелинейная плотность тока в
соответствии с выражением C.3) равна
Jt (йо) = 2&D
Так как для плоских волн градиент V* "отличен от нуля
только в направлении распространения волны и i = k,
то волна второй гармоники, фазовая скорость которой
согласована, вызывается продольной волной нелинейной
поляризации. В изотропной среде этот источник не мо-
может возбуждать электромагнитную волну, однако в
кальците угол а между векторами D и Е для направле-
направления, соответствующего согласованию фазовых скоростей,
равен приблизительно 7°. В результате эффективная
составляющая продольного тока, которая может возбу-
возбуждать электромагнитную волну, равна
В выражении E.22) имеется несколько компонент тен-
тензора, которые дают вклад в нелинейную поляризацию
при характерной для эксперимента геометрии. Измерен-
Измеренная Терхьюном интенсивность второй гармоники позво-
позволяет оценить порядок величины этих компонент:
|х" |sina~ Ю8 ед. CGSE или \%и \ - 10"!7 ед. CGSE.
Очевидно, что надежен только порядок величины, так как
трудности определения абсолютных значений оказыва-
оказываются даже более серьезными, чем в предыдущих слу-
случаях. *
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
223
В изотропной среде генерация второй гармоники мо-
может происходить в результате квадрупольного взаимо-
взаимодействия, если в области нелинейного взаимодействия
-200
-/00 0 100
Edc, кв/см
гоо
Фиг. 26. Зависимость интенсивности излучения второй гармоники
/2 (в относительных единицах), возникающей в кальците, от величины
приложенного к кристаллу постоянного электрического поля (по
данным работы D1]).
В отсутствие постоянного поля генерация гармоники обусловлена только квад-
квадрупольным эффектом.
идут два луча света, образующие между собой угол <р и
имеющие различные направления поляризации. Для
согласования фазовых скоростей все же желательно
использовать анизотропный кристалл, в котором волна
второй гармоники распространялась бы в направлени-
направлениях, образующих углы <pi и <рг = qp — <pi с направлением
лучей основной частоты. Нелинейный источник, опреде-
определяемый соотношением E.22), имеет в этом случае попе-
поперечные компоненты. Джордмейн [29] описал эксперимент
224
ГЛАВА 5
по генерации второй гармоники в кальците, в котором
используется указанная геометрия.
Магнитные дипольные эффекты также можно про-
проанализировать, пользуясь соответствующим выражением
для свободной энергии [одним из примеров является со-
соотношение C.11)]. Першан [28] провел детальное обсуж-
обсуждение свойств симметрии таких эффектов. В частности,
под действием импульса света с круговой поляризацией
должно наблюдаться индуцированное намагничение не-
поглощающей среды. Этот эффект обратен в термодина-
термодинамическом отношении фарадееву вращению, и его можно
вывести из того же члена выражения для свободной энер-
энергии, записанного через постоянную Верде. Сообщений о
наблюдении такого эффекта пока нет 1J.
Сильное намагничение можно возбудить излучением
рубинового лазера с круговой поляризацией при погло-
поглощении его в другом рубине. В этом случае происходит
перераспределение населенностей зеемановских уровней
ионов Сг3+, что в значительной мере аналогично опти-
оптической накачке в газах.
§ 6. Генерация третьей гармоники
Теперь мы обратимся к рассмотрению эффектов, ко-
которые можно получить из усредненной по времени сво-
свободной энергии, описываемой полиномом четвертой сте-
степени по напряженностям электрического поля. Терхьюн
и др. [30] наблюдали генерацию третьей гармоники в
изотропных жидкостях, кубических кристаллах и каль-
кальците. В последнем случае согласование фазовых скоро-
скоростей луча основной частоты и луча третьей гармоники
возможно для двух направлений. Для угла 57° по отно-
отношению к тригональной оси имеет 2&о(со) + ke((o) =
= &еCю), а для угла 47° выполняется соотношение
3^0 (со) = &вCсо). Здесь индексы о и е обозначают обык-
обыкновенную и необыкновенную волны. Генерации третьей
гармоники описываются тензором четвертого ранга; со-
'> Сообщение о наблюдении этого эффекта в монокристалле
CaF2 с ионами Еи2+ было сделано недавно на конференции по
квантовой электронике в Пуэрто-Рико F4*]. — Прим. ред.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
225
ю-6\-
Фиг. 27. Зависимость интенсивности излучения третьей гармоники
/3 возникающей в кальците, от падающей на кристалл мощности из-
излучения основной частоты Л (по данным работы {30]).
Все величины выражены в относительных единицах. Прямая соответствует
закону /» ~ It .
ответствующая нелинейная поляризация имеет вид
Pi (За) = 2 Х„« (Зсо = со + со + со) ?,- (со) Ek (со) Et (со).
iki
E.23)
Терхьюн и др. [30] указали отличные от нуля компонен-
компоненты тензора xmi для 32 точечных групп симметрии. Как
показано на фиг. 27, измеренная интенсивность излуче-
излучения на частоте Зсо действительно оказалась пропорцио-
15 Н. Бломберген
226
ГлАвА s
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
нальной кубу интенсивности излучения основной частоты.
Максимальное значение коэффициента преобразования
энергии составляет 3 • 10~6. Эта величина получена в
фокусированном луче лазера с модулируемой доброт-
добротностью, идущем в направлении согласования фазовых
скоростей. Следует отметить, что интенсивность поля в
фокусе лазера с модулируемой добротностью настолько
велика, что здесь можно разрушить почти любой кри-
кристалл. Поэтому при наблюдении генерации третьей гар-
гармоники интенсивность луча лазера уменьшалась до ве-
величины несколько меньшей критической. Разрушение
кристалла в лазерном луче может происходить вслед-
вследствие поглощения энергии примесями, многофотонного
поглощения или возбуждения колебаний среды, связан-
связанных с вынужденным комбинационным рассеянием или
вынужденным рассеянием Мандельштама — Бриллюэна.
При этом мгновенное выделение тепла в небольшом
объеме вызывает образование ударной волны.
Порядок величины |%(Зсо = со + со + со) | равен по
оценкам 10~15 ед. CG'SE. Для кубических кристаллов,
таких, как LiF, соотношение E.23) можно записать в
виде
E.24)
где А + В = хин и В = хпгг = Хпзз. Терхьюн обнару-
обнаружил, что опыты по генерации третьей гармоники указы-
указывают на некоторую анизотропию в этих кристаллах. Так
как в этом случае невозможно осуществить согласование
фазовых скоростей, эффект трудно наблюдать. Постоян-
Постоянная А определенно отлична от нуля.
§ 7. Многофотонное поглощение
Поперечное сечение процесса двухфотонного погло-
поглощения рассматривалось в гл. 2. Клейнман [31] и Брон-
Бронштейн [32] дали более подробный анализ этой задачи.
Если падающий луч света когерентен, то, как показано
в гл. 2, § 8, процесс можно также описать с помощью
мнимой нелинейной восприимчивости. Поглощение двух
квантов из одного и того же луча описывается соотноше-
соотношением
PfL (со) = ix"aki (со = — со + со + со) Е] (— со) Ek (to) El (со).
E. 25)
Свойства симметрии этого тензора, симметричного по
двум первым и двум последним индексам, идентичны
свойствам симметрии тензоров упругости, которые хоро-
хорошо известны для всех точечных групп.
Двухфотонное поглощение впервые наблюдалось
Кайзером и Гарреттом [33], которые освещали кристалл
CaF2, содержавший ионы Еи2+, лучом рубинового лазе-
лазера. При этом кристалл испускал характерное излучение
флуоресценции с длиной волны 4250 А, соответствующее
переходу Ей2+ из возбужденного состояния. Интенсив-
Интенсивность флуоресценции была пропорциональна квадрату
интенсивности луча лазера. Эта голубая флуоресценция
наблюдалась ранее только при возбуждении ультрафио-
ультрафиолетовой полосы поглощения Еи2+. В опытах же с руби-
рубиновым лазером два кванта красного света индуцируют
переход на этот возбужденный уровень, находящийся в
ультрафиолетовой области. Возможность двух последо-
последовательных процессов однофотонного поглощения исклю-
исключается, поскольку нет поддающегося измерению линей-
линейного поглощения на частоте излучения рубина, и не из-
известно уровней энергии, расположенных на «половине
пути» вверх. В опытах [33] приблизительно один из 107
падающих фотонов поглощался в кристалле толщиной
1 мм, в котором .плотность ионов Еи2+ составляла No =
= 2,4-1018 см'3, причем плотность потока фотонов равня-
равнялась 8- 1023 см~2 • сек~1. Напряженность поля, вычислен-
вычисленная с помощью соотношения B.91), равнялась |?х| =
= 9 ед. CGiSE — 2700 в-см~1. Нелинейная восприимчи-
восприимчивость, определенная из величины поглощения на длине
1 си, равного 4я(сох/с) { + %") \Е\ |2 = 10~6, составляет
%"{(?> = ¦—со + Ш+0)) « 10~14 ед. CGiSE. Это значение
можно существенно увеличить, если окажется возмож-
возможным уменьшить ширину полосы поглощения в ультра-
ультрафиолетовой области и увеличить концентрацию ионов
ШВА S
Eu2+. При остром резонансе восприимчивости могут
иметь значительно большую величину.
Хопфилд и др. [34] нашли важное для спектроскопии
применение многофотонного поглощения, Схема их эк-
экспериментальной установки приведена на фиг. 28. Обра-
Образец находится под воздействием двух лучей света, один
Кварцевое окно-
Ксеноновая
дуговвя
лампа ,----*
¦Кварцевое окно
Дифракционный
монохроматор
На верхнюю
развертку
осциллозрофа
Фото-
умножителе
осциллографе
Фиг. 28. Схема использования двухфотонного поглощения в спек-
спектроскопии.
Контролируется изменение поглощения света, испускаемого ксеноновой лампой
в кристалле KI во время прохождения через него импульса лазерного излу-
излучения (по данным работы [341).
из которых создан импульсом излучения рубинового ла-
лазера, другой образован непрерывным излучением дуго-
дуговой ксеноновой лампы. Двухфотонное поглощение об-
обнаруживается по изменению коэффициента поглощения
света ксеноновой лампы в образце (кристалл KI) при
прохождении через него импульса излучения рубинового
лазера. Этот метод позволял исследовать дисперсионные
характеристики процесса двухфотонного поглощения в
широком диапазоне частот. Результаты такого экспери-
эксперимента дополняют данные, полученные при исследовании
однофотонного поглощения, так как в двухфотонных
электрических дипольных переходах начальные и конеч-
конечные состояния имеют одинаковую четность.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
229
В связи с тем что второй источник света дает неко-
некогерентное излучение в широком спектре частот, нелиней-
нелинейную восприимчивость, определенную в гл. 2 для периоди-
периодических возмущений, нельзя непосредственно использо-
использовать для теоретических оценок. Коэффициент нелинейно-
нелинейного поглощения можно, конечно, выразить через попереч-
поперечное сечение поглощения, пропорциональное интенсивно-
интенсивности некогерентного луча, приходящейся на единичный ин-
интервал частот.
Недавно Синг и Брэдли [35] наблюдали трехфотонное
поглощение в кристаллах нафталина. Интенсивность
О
флуоресценции с длиной волны 3000 А, возбужденной
фокусированным лучом рубинового лазера, была про-
пропорциональна третьей степени интенсивности излучения
основной частоты. При плотности потока фотонов в фо-
фокусе 2- 1027 см~2-сек~] эффективность преобразования
составляла около 10~10. Процесс ступенчатого возбужде-
возбуждения, по-видимому, исключен ').
§ 8. Зависимость показателя преломления
от интенсивности света
Если в соотношении E.25) восприимчивость рассмат-
рассматривать как действительную величину, то мы получим
феноменологическое описание эффекта, заключающегося
'> В последнее время многофотонное поглощение является пред-
предметом интенсивных экспериментальных и теоретических исследова-
исследований. Укажем здесь иа экспериментальную работу Н. Делоне и Г. Во-
Воронова [65*], зарегистрировавших семифотонную фотоионизацию бла-
благородных газов в поле рубинового лазера; работу [66*], в которой
детально исследовалось двухфотонное поглощение в CdS; исследо-
исследования Н. Г. Басова и др. [67*], посвященные вкладу двухфотонных
процессов в возбуждение полупроводникового лазера; работу [58*],
где была сделана попытка зарегистрировать двухфотонное поглоще-
поглощение в диэлектриках. Из теоретических работ следует указать на об-
обстоятельную работу Л. В. Келдыша [68*], посвященную теории мно-
многофотонной ионизации газов и твердых тел; работу Голда и Бебба
[69*], связанную с той же проблемой; работу Ф. В. Бункина и
А. М. Прохорова [70*], обсуждавших роль миогофотонного поглоще-
поглощения в установлении предельной мощности лазера. Обстоятельный об-
обзор данных по многофотонному поглощению по уровню, достигнутому
к концу 1964 г., выполнен А. М Бонч-Бруевичсм и В. А Ходовым
[71*]. —Прим. ред,
230
ГЛАВА 5
в изменении показателя преломления в зависимости от
интенсивности. Для изотропной среды нелинейную поля-
поляризацию можно записать в виде
Т' (со) = АЕ, (со) [Е* (- со) . Е»] +
E.26)
Постоянные А и В связаны с компонентами симметрич-
симметричного тензора четвертого ранга следующими соотноше-
соотношениями:
= — СО
= А + — В,
E.27)
Ххуху — -Л,
в результате чего автоматически выполняется условие
изотропии '>
Хххуу = —- В =: Хлглглгл: — Хедад.
Терхьюн и др. [36] обнаружили существование члена В
простым способом. В непоглощающей среде А и В дей-
действительны. Когда компоненты линейно поляризованной
волны, входящие в выражение E.26), преобразуются к
виду
для зависящих от интенсивности изменений показателей
преломления, соответствующих двум круговым поляри-
поляризациям, можно найти следующие выражения:
= -f- [AE+E
+
E.28)
1 Иногда недиагональные компоненты берутся вдвое большей
величины. В таком случае в соотношении E.27) вместо нашей за-
записи х надо писать Ххуху + гхуух.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
231
Показатели преломления света с круговой и линейной
поляризациями различны. Использовался эллиптически
поляризованный свет рубинового лазера, который фоку-
фокусировался в жидкость через слюдяную пластинку в '/в Я.
Призма Рошона позволяла разделить две линейные по-
поляризации, соответствующие «быстрой» и «медленной»
осям пластинки в '/в Я. При малых интенсивностях лазер-
лазерного луча интенсивности этих двух поляризаций равны.
При больших интенсивностях наблюдается разбаланс,
вызванный поворотом эллипсоида поляризации, и описы-
Баемый соотношением E.28). Терхьюн с сотр. измерили
константу нелинейности В = 2(%'хххх —%хуху) для мно-
многих жидкостей. Полученные величины лежат в пределах
от 8-Ю5 ед. CGSE для воды до 10~13 ед. CGSE для
сероуглерода ') (используется введенное выше определе-
определение амплитуд). Большое значение последней величины
обусловлено близостью резонанса для двухфотонного
поглощения. Джордмейн [37] действительно наблюдал
поглощение излучения рубинового лазера в сероуглеро-
сероуглероде, зависящее от интенсивности и характеризующееся
величиной %//(оо = -—со + со + со). К сожалению, описан-
описанный выше метод трудно распространить на кубические
кристаллы. Камнем преткновения является двойное лу-
лучепреломление, связанное с напряжениями в твердых
телах.
'» Наличие таких нелинейных поправок к диэлектрической про-
проницаемости приводит к существенному изменению характера взаи-
взаимодействия и распространения интенсивных волн в нелинейной сре-
среде. При больших интенсивностях света условия согласования фа-
фазовых скоростей начинают зависеть от интенсивности; это обсто-
обстоятельство может влиять на характер параметрических взаимодейст-
взаимодействий (см. [72*]). Однако наибольший интерес здесь представляет
возможность появления эффектов самофокусировки и самоканали-
самоканализации мощных световых пучков [73*—75*]. В среде с показателем
преломления, возрастающим с ростом интенсивности света, диаметр
фокусного пятна уменьшается, а при определенных условиях воз-
возможна и самоканализация пучка. Различные аспекты этой проблемы
проанализированы в G3*—75*]. Заметим также, что зависимость по-
показателя преломления от интенсивности световой волны может быть
связана не только с нелинейной поляризацией, но и с электрострик-
цией, рассмотренной в гл. 4 этой книги в связи с вынужденным
рассеянием Мандельштама — Бриллюэна. — Прим. ред.
232
ГЛАВА 5
§ 9. Вынужденное комбинационное рассеяние
Вудбери и Нг [38] обнаружили, что рубиновый лазер,
показанный на фиг. 4, а, добротность которого модули-
модулировалась с помощью ячейки Керра на нитробензоле, в
дополнение к нормальному излучению рубина с длиной
о
волны 6943 А испускал интенсивное излучение с длиной
о
волны 7670 А. Правильное объяснение этого эффекта
было дано вскоре Хелворсрм и др. [39]. Когда между
зеркалами резонатора лазера помещаются различные
жидкости, то наблюдается дополнительное излучение
света на различных частотах. Все они смещены по отно-
отношению к частоте излучения рубина на величину, соот-
соответствующую колебательной частоте молекул жидкости •>.
Спектры вынужденного комбинационного рассеяния
для некоторых жидкостей [39] и твердых тел [40] приве-
приведены в табл. 2. В спектре вынужденного комбинационно-
комбинационного рассеяния появляются только те частоты, которые со-
соответствуют наиболее узкой и наиболее интенсивной
линии спонтанного комбинационного рассеяния. Иногда
появляются две линии. Обычно они принадлежат к пол-
полносимметричным колебаниям. Указанные выше особен-
особенности вынужденного рассеяния не являются неожидан-
неожиданными, поскольку процесс с самым низким порогом будет
стремиться ограничить мощность излучения лазера на
уровне, меньшем более высоких пороговых значений.
Дальнейшее возрастание мощности какачки увеличит
интенсивность этой стоксовой линии, но не приведет
к появлению других линий спектра комбинационного рас-
рассеяния. Однако когда стоксова линия достигнет доста-
достаточной интенсивности, она сама создаст новую стоксову
линию с частотой wL — 2cot, и т. д. Эти линии более высо-
высокого порядка, о существовании которых также говори-
'> Материал § 9—11 базируется иа результатах опытов, получа-
получаемых с рубиновым лазером. Следует отметить, что в последнее вре-
время были обнаружены возможности расширения средств экспери-
экспериментального изучения вынужденного комбинационного рассеяния.
Так, в {84*] сообщается о наблюдении вынужденного рассеяния на
X ~ 1,06 мк, а в [85*] — на X ~ 0,53 мк. Последнее открывает опре-
определенные возможности изучения вынужденного рассеяния в резо-
резонансных условиях. — Прим. ред.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
233
Таблица 2
Сравнение частотных смещений стоксовых линий,
излучаемых при вынужденном комбинационном рассеянии,
с частотными смещениями наиболее интенсивных линий,
испускаемых при спонтанном комбинационном рассеянии [39, 40]
Вещество
Зензол
Нитробензол
Толуол
1 -бромнафталин
Пиридин
Циклогексаи
Дейтерированный бензол
Алмаз
Кальцит
а-сера
Смещение когерент-
когерентных комбинационных
линий по отношению
к линии рубина, см
3064+2
990 ±2
1980±4
1344+2
2-A34б±2)
3-A340±5)
1004+4
1368
992 ±2
2-(992±5)
2852+1
944,3+1
2-944
1325
2661
1075
2171
216
472
946
Смещение двух
наиболее интенсивных
некогерентных сток-
стоксовых линий, см~~'
3064
991,6
1345 и 1004
1002 и 785
1363 и 3060
991 и 3054
801 и 2853
944,7 и 2292
1331,8
1085,6
216 и 468
лось в первом сообщении [37], имеют частоты, точно рав-
равные гармоникам частоты первого колебательного
перехода. Они не могут быть связаны с комбинационным
рассеянием второго порядка, возбуждаемым излучением
с частотой сох,, при котором молекула совершает переход,
сопровождающийся изменением колебательного кванто-
квантового числа на две единицы. Матричный элемент такого
перехода весьма мал, а ангармоничность колебаний до-
234
ГЛАВА 5
статочно велика для того, чтобы не наблюдалось совпа-
совпадения частоты спонтанного комбинационного рассеяния,
обусловленного переходом с изменением колебательного
квантового числа на два, равной a>L — (ib*=o-»-2 , с часто-
частотой (Оь — 2ю„=о-»ь
Теория, изложенная в гл. 4, § 5, непосредственно при-
ложима к рассматриваемым здесь явлениям. Нелиней-
Нелинейная восприимчивость, описывающая комбинационные
рассеяния (комбинационная восприимчивость), дается
выражением D.70), идентичным соотношению, которым
пользовались Терхьюн и др. [41]. Напомним, что наша
комбинационная восприимчивость в 4 раза больше, что
обусловлено измененным определением амплитуд поля.
Усиление стоксовых компонент дается выражением
D.68). При заданной мощности излучения лазера наша
величина \EL\2 в 4 раза меньше, в результате чего уси-
усиление стоксовой компоненты на длине в 1 см совпадает
со значением, вычисленным Терхьюном для того же
уровня мощности. Соотношение D.70) можно несколько
обобщить, если учесть, что в соответствии с распределе-
распределением Максвелла — Больцмана возбужденное колебатель-
колебательное состояние также может быть частично заселено. Вы-
Выражение для восприимчивости на стоксовой частоте
перепишем здесь в виде
(Y E.29)
Коэффициент нарастания мощности в 2 раза превышает
соответствующий амплитудный коэффициент, который
дается соотношением D.68) и равен
nl0
E.30)
В это выражение введены длина волны излучения в ва-
вакууме Яо и показатель преломления среды п. В выраже-
выражении E.30) не учтено различие между ksz и &s°. Плотность
потока мощности в луче лазера равна (пс/2п) \ЕЬ\2.
В качестве приемлемого значения комбинационной
восприимчивости свободной молекулы можно взять ве-
величину т)аыа0/(ооь — юп?) ~ Ю~25 ед. CGSE. Как покдза-
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
235
но в гл. 2, § 8, эта величина непосредственно связана
с поперечным сечением некогерентного комбинационного
рассеяния. Комбинационная восприимчивость на порядок
меньше восприимчивости, обусловленной чисто электрон-
электронным переходом, при котором не происходит изменения
колебательных координат ядер. Для типичного значения
ширины линии колебательного перехода 3 см~1 (отсчет
на уровне половины максимальной интенсивности), чему
соответствует Гг, = 2я • 10", и для N = 1022 получаем
\%"s I ~ 1,6'10~13 ед. CGSE. Если учесть поправочный
множитель Лоренца (eL + 2J(ss + 2J/81, то \x"s | ста-
станет равной 6,5-10~13 ед. CGSE. Эта величина \%"s\ при-
примерно на порядок больше нерезонансных восприимчи-
востей, рассмотренных в § 8 настоящей главы. Мы полу-
получаем выигрыш в со„/Г„ ~ 103 раз, вызванный колебатель-
колебательным резонансом, и проигрываем в 10—100 раз из-за су-
существования связи ' между колебаниями электронов
и ядер. Выражение E.30) дает для коэффициента нара-
нарастания по мощности на стоксовой частоте значение
Истоке = 1,4* Ю~3 см-1 при условии, что плотность потока
мощности излучения лазера равна 2 Мвт/см2, чему соот-
соответствует \ЕЬ\ =53 ед. CGSE. Усиление стоксовой
компоненты за один проход кюветы длиной 10 см равно
е0-014. Для того чтобы при такой величине усиления со-
создать условия, необходимые для генерации, следует ис-
использовать зеркала с коэффициентом отражения 99%.
Уровень мощности внутри резонатора лазера, вероятно,
на порядок выше и равен 20 Мет. В этом случае усиление
за один проход кюветы будет равно е0'14 и комбинацион-
комбинационный лазер легко возбудится.
Результаты вычислений находятся в удовлетворитель-
удовлетворительном согласии с цифрами, приведенными Хелворсом для
нитробензола [42]. По его оценке коэффициент нараста-
нарастания равен 0,3 см при уровне мощности накачки
100 Мет/см2, что соответствует плотности потока фото-
фотонов 3 • 1026 см~2 • сект1. Согласно измерениям, полное
поперечное сечение комбинационного рассеяния, полу-
полученное интегрированием по углу Q = 4л, равно
6-10~30 см2. Частота колебательного перехода равна
1345 см'1; полуширина линии составляет 4 см~]. В ре-
236
ГЛАВА 5
зультате величина |%*| для нитробензола оказывается
равной 2,4 -10~12 ед. CQSE. Точность определенного таким
способом значения \%"s | невелика. Все проблемы, об-
обсужденные в § 2 при рассмотрении нелинейности низше-
низшего порядка, возникают снова и в более сложном виде
при исследовании комбинационного рассеяния. Измере-
Измерения поперечного сечения комбинационного рассеяния
в бензоле, где (о„/2яс = 992 см~1 и Т„/2яс = 3,1 см~1,
дают для комбинационной восприимчивости величину
D,8 ± 1,2) • 10~12 ед. CGSE. Это значение удовлетвори-
удовлетворительно совпадает с результатами, полученными при из-
измерении порога генерации комбинационного лазера на
бензоле ¦>.
За исключением специфического провала (см.
фиг. 19) вблизи направления согласования фазовой ско-
скорости антистоксовой компоненты с фазовой скоростью
излучения основной частоты, коэффициент усиления вы-
вынужденного комбинационного рассеяния почти изотро-
изотропен. Действительно, оказывается возможным получить
вынужденное излучение со стоксовои частотой, идущее
под углом к лазерному лучу накачки [43]. Конечно, при
параллельном расположении лучей объем взаимодейст-
взаимодействия оказывается обычно намного больше. Так как эф-
эффективная длина взаимодействия для внеосевого на-
направления меньше, то для возбуждения рассеяния в этом
направлении величину отражений для излучения со сток-
совой частотой, идущего вперед, следует свести к мини-
минимуму, а на пути внеосевого луча установить зеркала
с высоким коэффициентом отражения. Если сфокусиро-
сфокусировать лазерный луч диаметром 1 см с помощью цилиндри-
цилиндрической линзы, то в фокусе ее перпендикулярно направ-
направлению исходного луча образуется линия длиной 1 см
с высокой плотностью мощности накачки. Создав обрат-
обратную связь с помощью зеркал, расположенных перпенди-
перпендикулярно этой линии. Танненвальд [44] осуществил гене-
генерацию стоксовои компоненты в направлении, образующем
прямой угол с накачкой.
'> Значительные трудности в сравнении экспериментальных н
теоретических данных связаны с многомодовой структурой лазер-
лазерного излучения (см. [78*—83*]). — Прим. ред.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
Начальные условия, необходимые' для самовозбуж-
самовозбуждения колебаний, определяются шумами. Проще всего
рассмотреть спонтанное комбинационное рассеяние, воз-
возникающее в слое вещества, перпендикулярном направ-
направлению распространения излучения со стоксовои частотой,
поскольку источником входного сигнала для усилителя
на стоксовои частоте является излучение, испускаемое
соседними слоями. Анализ процесса самовозбуждения
комбинационного лазера полностью аналогичен исследо-
исследованию процесса установления колебаний в лампах бегу-
бегущей волны. Условие существования стационарных коле-
колебаний можно в общем случае записать в «баркгаузенов-
ской» форме
""*.+*>'= 1. E.31)
Здесь Г\ и г2 — коэффициенты отражения двух зеркал
для комплексной амплитуды на частоте cos, d — длина
кюветы, Ак — комплексный корень, определяемый соот-
соотношением D.66) или D.67). Это условие является вы-
выражением того факта, что для незатухающих колебаний
усиление по амплитуде в замкнутом контуре равно еди-
единице. Мнимая часть выражения E.31) эквивалентна
условию возбуждения колебаний в лазере, выведенному
Таунсом и Шавловым. Она определяет пороговое зна-
значение |?х,|2. Если в начальный момент величина
\EL\2 больше порогового значения, то амплитуда коле-
колебаний со стоксовои частотой будет расти до тех пор,
пока дополнительные потери не уменьшат уровень на-
накачки до некоторого установившегося значения. Дейст-
Действительно, в стационарном состоянии должны удовлетво-
удовлетворяться одновременно два условия возбуждения
колебаний на частотах сох, и cos. Действительная
часть выражения E.31) определяет частоту ко:
лебаний. При достаточно большой естественной ширине
линий комбинационного рассеяния точное значение ча-
частоты определяется расстоянием между зеркалами d.
Если зеркала расположены не на концах кюветы, то ле-
левую часть выражения E.31) следует, конечно, умножить
еще на соответствующие экспоненты, описывающие рас-
распространение в других средах, находящихся в резона-
резонаторе.
t-ЛАвА Ь
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
23д
Интенсивность стоксовой компоненты может вырасти
до такой величины, что она сможет сама служить накач-
накачкой для второй стоксовой линии и т. д. Генерацию на
этих новых частотах можно подавить с помощью селек^
тивных просветляющих покрытий на окошках или спе-
специальных поглотителей в кювете для комбинационного
рассеяния. Без таких предосторожностей при возраста-
возрастании мощности лазерной накачки мощность выходного
излучения будет распределяться по все возрастающему
числу стоксовых компонент сравнимой интенсивности.
Наблюдались случаи, когда более 60% выходной мощ-
мощности излучалось на стоксовых частотах. Вероятно, ко-
коэффициент преобразования мог бы быть и выше '), если
бы этому не препятствовало то обстоятельство, что луч
лазера обычно далек от однородной плоской волны. Ча-
Части луча, где интенсивность невысока, преобразуются
только частично или вообще не преобразуются. С точки
зрения эффективности преобразования рубиновый лазер,
дающий излучение в виде немногих очень ярких нитей,
был бы лучше лазера, дающего луч с равномерным рас-
распределением интенсивности по поперечному сечению, при
условии, что полные потоки мощности в обоих случаях
одинаковы. Изменение интенсивности лазера во времени
также играет важную роль.
Экспериментально в нефокусированных лучах, уси-
усиленных в лазерном усилителе, можно получить пиковые
мощности, превышающие 500 Мет. В этом случае в ни-
нитробензоле на длине 10 см усиление на стоксовой частоте
равнялось бы e]S. Очевидно, что обратная связь, создан-
созданная случайным рассеянием всего лишь одной миллион-
миллионной доли излучения, была бы достаточна для того, чтобы
в системе возникла генерация. На пути в 30 см усиление
равнялось бы е45. Это означает, что один входной фотон
создавал бы в среднем 1020 фотонов. Однако это число
больше начального числа квантов лазерного излучения,
которое не превышает обычно 1018. Поэтому интенсив-
интенсивность лазерного луча уменьшается, прежде чем он до-
'» Для теоретического исследования вопроса о предельном
к. п. д. лазера, использующего эффект вынужденного комбинацион-
комбинационного рассеяния, надо решить систему D.72), D.73) в резонаторе.
Результаты такого анализа сообщаются в [87*, 88*]. — Прим. ред.
стигнет конца кюветы. Если диаметр луча равен 1 см, то
заметное усиление на стоксовой частоте существует
вплоть до углов в несколько градусов. Соответствующее
излучение со стоксовой частотой, идущее вперед под ма-
малыми углами к направлению основного луча, можно об-
обнаружить, если оно пройдет в кювете путь длиной око-
около 15 см. Из-за экспоненциального характера усиления
излучение представляется выходящим из определенного
места в кювете. Это излучение можно рассматривать
как усиленные шумы. Если кювета короче, то для полу-
получения заметной интенсивности необходима некоторая ми-
минимальная обратная связь. Даже в кюветах с
брюстеровскими окнами существует достаточное рассея-
рассеяние в обратном направлении, равное примерно 10~6.
В этом случае внеосевое излучение со стоксовой часто-
частотой кажется выходящим из области размером в несколь-
несколько миллиметров, расположенной в самом конце кюветы,
так как такие лучи усиливаются больше всего. В корот-
коротких кюветах, длина которых, например, меньше 10 см,
эффектами запаздывания можно пренебречь. Усиление
в обратном направлении должно быть таким же, как
в параллельном ему прямом направлении. Однако пред-
предварительные экспериментальные данные показали, что
интенсивность излучения, направленного назад, меньше
в 2—4 раза. Если, как предполагалось в гл. 4, § 5, по-
постоянная затухания изменяется в зависимости от направ-
направления на несколько процентов, то это приведет к умень-
уменьшению усиления от величины е20 для излучения,
направленного вперед, до величины е19 для излучения,
направленного назад, что достаточно для объяснения
указанного эффекта.
§ 10. Стоксовы и антистоксовы компоненты высших
порядков
Фокусируя луч лазера, нетрудно получить плотности
потока мощности, превышающие 1000 Мвт/см2. Терхьюн
[45] первый осуществил эксперимент, схема которого по-
показана на фиг. 4, б. Он обнаружил, что бензол, жидкий
азот и некоторые другие жидкости, кроме интенсивных
стоксовых компонент различных порядков, испускают еще
ГЛАВА S
свет, образующий цветные кольца. Вскоре после этого
об аналогичных наблюдениях сообщили и другие иссле-
исследователи [46, 47].
Типичное распределение интенсивности по частотам
и направлениям показано на фиг. 29. Частотный спектр,
проинтегрированный по всем направлениям, можно полу-
получить с помощью спектрального прибора высокой разре-
разрешающей силы, на щель которого проектируется изобра-
изображение матовой стеклянной пластинки, расположенной за
кюветой комбинационного рассеяния в непосредственной
близости от нее. Стойчев [46] указал на некоторые ха-
характерные особенности, относящиеся к ширине и струк-
структуре линий. При очень высоких уровнях мощности про-
происходит уширение линий, которое может достигать
50 см~1, что в 10 раз превышает ширину линии спонтан-
спонтанного комбинационного рассеяния ]). Вблизи от порога
антистоксовы линии могут быть значительно более узки-
узкими, чем Г, и иметь ширину 0,2 см~К
Терхьюн и др. [48] обнаружили очень сильное излуче-
излучение с антистоксовой частотой, испускаемое газами в пря-
прямом направлении. Полученный в этом эксперименте
спектр #2 приведен на фиг. 30. Свет, идущий в прямом
направлении, кажется белым, потому что все конусы
антистоксовых компонент перекрываются. Несмотря на
относительно малое число молекул в единице объема,
находящихся в данном колебательно-вращательном со-
состоянии, эффект, наблюдаемый в газах, оказывается
сильным из-за очень малой ширины линии Г. При давле-
давлениях выше одной атмосферы ширина линии обратно про-
пропорциональна давлению. В соответствии с выражением
E.29) это означает независимость усиления на единицу
длины от давления газа, что и наблюдается эксперимен-
экспериментально. При низких давлениях величина Г определяется
допплеровской шириной. Однако при приближении к та-
таким давлениям ширина спектра выходного излучения
лазера, равная обычно 0,1 см~1, становится сравнимой
с Г. В этом случае при заданной полной мощности излу-
излучения лазера усиление перестает быть независимым о г
') Возможные причины уширения линий вынужденного комби-
комбинационного рассеяния обсуждаются в [86*]. ~Лрим. ред.'
:¦•:¦, Зеленый
¦Красный -
Тежнсхраст'й
а ин(ррйжг)йймы.
¦—-ч
ICO А
Длина щолпы
6000
Фиг. 29. Распределение по направлениям и частотам интенсивно-
интенсивности стоксовых и антистоксовых компонент, возникающих в бензоле
при возбуждении фокусированным лучом рубинового лазера с моду-
модулируемой добротностью (по данным работы [18]).
¦ ваяны-.371
iОттхытельтш •¦
4482 А 5388 А ?$43 A 87S5A
7В%
Фиг. 30. Спектр излучения когерентного комбинационного рассея-
рассеяния, возникающего при фокусировке в газообразном водороде луча
рубинового лазера с модулируемой добротностью (по данным
работы [48]).
Снимок получен за один импульс, длительность которого равна 2 • 10-а сек.
15 Н. Бломберген
242
ГЛАВА S
давления. Не все моды лазерного луча могут возбуждать
данную моду излучения со стоксовой частотой. В таком
случае надо брать свертку лоренцевского контура коле-
колебательной линии и спектрального распределения излуче-
излучения лазера.
Терхьюн и др. [48] оценили, что за один проход через
фокус в газообразном водороде усиление должно состав-
составлять е500. Как показано в § 1, при фокусировке луча,
имеющего только дифракционную расходимость, интен-
интенсивность в области фокуса увеличивается в (d/8J ~
~ /~2 раз. Однако эффективная длина фокуса умень-
уменьшается в /+2 раза. Поэтому усиление стоксовой компо-
компоненты за один проход через фокус не зависит от / и в
соответствии с соотношениями E.1), E.2) и E.30) дает-
дается выражением
""" " ~ "' ""'"С\* 2nd*
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
243
пка
пк
Соответствующее усиление на 3 дб больше усиления,
которое получается в нефокусированном луче на длине,
необходимой для того, чтобы диаметр луча с дифрак-
дифракционной расходимостью увеличился в 2 раза.
Данные, полученные в самое последнее время, пока-
показали, что даже в жидкостях и твердых телах помимо
излучения, выходящего по образующей конуса, сущест-
существует интенсивное излучение с частотой соа = Wz, + со„,
идущее в прямом направлении. Углы конусов, измерен-
измеренные в жидкостях, а также спектральная ширина раз-
различных стоксовых и антистоксовых линий определяют-
определяются, по-видимому, особенностями экспериментальной
установки и свойствами фокуса.
Чао и Стойчев [49] точно измерили углы при вершине
конусов в кальците. В этом случае ввиду возможного
разрушения кристалла под действием излучения очень
высокой интенсивности лазерный луч фокусировался
в точку, расположенную вне его. Как указывалось выше,
все излучение комбинационного рассеяния представляет-
представляется выходящим из конца кристалла. Чао и Стойчев на-
наблюдали также темные кольца в угловом распределении
интенсивности стоксовых компонент различных поряд-
порядков и яркие кольца на антистоксовых частотах. Значе-
N0
СП
ния половинных углов, под которыми выходит излучение
различных антистоксовых компонент, приведены в
табл. 3, где даны также углы, соответствующие точному
согласованию фазовых скоростей, вычисленные с по-
помощью известных величин линейных показателей пре-
преломления.
Таблица 3
Экспериментальные углы испускания антистоксовых компонент
различных порядков, возбуждаемых лучом рубинового лазера
в кальците, и вычисленные направления
точного согласования фазовых скоростей [49]
Частота
@L+2<oo ¦
(OL +3<oo
Длина
волиы,
о
А
6456,0
6033,2
5662,3
5334,4
Угол испускания излучения, 10~2 рад
наблюдаемая
величина
2,89±0,03
5,42±0,08
7,80±0,2
10,64±0,4
величина, экстра-
экстраполированная
к линзе с беско-
бесконечно большим
фокусным
расстоянием
2,50±0,03
5,03±0,08
7,64±0,2
10,2±0,4
значение,
вычисленное
для точного
согласования
фазовых
скоростей
2,49
4,91
7,29
9,61
Можно дать следующее объяснение углового распре-
распределения интенсивности излучения на стоксовой частоте.
Хотя усиление на единицу длины почти изотропно, при
отклонениях от направления луча на несколько граду-
градусов интенсивность быстро падает из-за сокращения эф-
эффективной длины взаимодействия с лучом лазера.
Заметим, что в силу экспоненциального характера усг
ления даже очень небольшое изменение длины пути, из-
изменяющейся приблизительно как (cos б), может выз-
вызвать сильное изменение наблюдаемой интенсивности.
При угле 0о, соответствующем точному линейному !> со-
согласованию фазовых скоростей ks° + k^ = 2k° , имеет-
имеется показанный на фиг. 19 очень узкий провал, не связан-
¦> Термином «линейное» автор подчеркивает, что используются
значения волновых чисел, полученные из измерений в линейном ре-
режиме. — Прим. ред.
16*
244
ГЛАВА S
ный с указанным геометрическим эффектом. Этот про-
провал объясняет появление темного кольца на фоне
излучения стоксовой частоты в кальците. В других ве-
веществах такое кольцо также должно существовать, но,
по-видимому, его маскирует рассеянный свет.
В соответствии с изложенным в гл. 4, § 6 в усилен-
усиленной волне всегда присутствует излучение с антистоксо-
антистоксовой частотой. В прямом направлении усиление настоль-
настолько велико, что это излучение можно обнаружить. В со-
соответствии с выражениями D.92) и D.68) или E.30)
отношение интенсивностей антистоксовой и стоксовой
компонент составляет Gг gsJAk~2, что равно прибли-
приближенно квадрату усиления по амплитуде на длине коге-
когерентного взаимодейотвия. Для нитробензола Ak~l в пря-
прямом направлении равно приблизительно 10~2 см. При
усилении по мощности 10 дб/см отношение интенсивно-
интенсивностей было бы равно 0,01%, что дает, по-видимому, пра-
правильный порядок величины.
Около направления линейного согласования фазовых
скоростей постоянная нарастания уменьшается, а отно-
относительная интенсивность антистоксовой компоненты
растет. На фиг. 20 интенсивность антистоксовой компо-
компоненты дана как функция Ak для двух типичных значений
усиления в прямом направлении. Когда усиление равно
120 дб, антистоксовая компонента максимальна в том
направлении, для которого рассогласование фазовых
скоростей составляет Ak = 2 gs. Это рассогласование не
очень чувствительно к величине полного усиления. От-
Отклонение поперечной составляющей волнового вектора
от направления согласования фазовых скоростей можно
определить из соотношения
(k°x + Akf + [kl - -j- AkY = (k°x)* + (kl)* = (k°sJ.
Для малых относительных изменений kx получаем
1 k% *, • Afe
2tg90
где 0о —направление точного согласования фазовых
скоростей; для излучения рубина, идущего в нитробен-
ЭКСПЕРИМЕНТАЛЬПЫЕ РЕЗУЛЬТАТЫ
245
золе, 9о = 2,5°. Угол, под которым излучение с антисток-
антистоксовой частотой наблюдается вне кюветы, определяется
соотношением sin 9 = {k°x + Akx)/k*aK, где kfK —
волновой вектор в вакууме. Для малых углов и малых
изменений сразу же получаем
Д9 Ыгх hk
"u Kx ^«s l& Do
Направление, соответствующее максимуму интенсивно-
интенсивности антистоксовой компоненты, отклоняется от направ-
направления точного согласования на угол
А0 =
E.32)
Для gs = 4 см~\ соответствующего усилению
18 дб/см, находим, что в нитробензоле А0 = 0,1°. В об-
области фокуса усиление может даже превысить это зна-
значение; соответственно больше будет и величина А0.
Сообщалось, что экспериментальное значение угла, со-
соответствующего первому антистоксову кольцу в нитро-
нитробензоле, равно 3,1°, откуда А0 = 0,6°. Другие исследова-
исследователи дают иные значения для отклонения. Результаты,
по-видимому, очень чувствительны к изменению условий
эксперимента. Чао и Стойчев получили меньшие откло-
отклонения А0 в кальците, когда пользовались более длинно-
длиннофокусными линзами. Экспериментальное значение, экс-
экстраполированное к бесконечно большой фокусной длине,
А0~О,1°.
Так как предположения, на которых основана теория,
изложенная в гл. 4, § 6, не выполняются в условиях
реального эксперимента, то можно считать, что теория
не расходится с экспериментальными результатами.
Происходит уменьшение мощности излучения лазера, и
не подавляются высшие стоксовы и антистоксовы ком-
комбинационные частоты. Весьма важным фактором являет-
является, по-видимому, также то, что распределение интенсив-
интенсивности в луче лазера очень неравномерно.
Можно показать, что наблюдаемое излучение анти-
антистоксовой частоты должно идти преимущественно через
область максимальной интенсивности луча лазера. Как
следует из рассмотрения кривых фиг. 20, излучение, про-
246
ГЛАВА 5
ходящее через эту область под углом меньшим 9о +
+ Лбмакс, усилится незначительно. Излучение, идущее
под большим углом, будет получать, однако, достаточ-
достаточное усиление. Кривые усиления на фиг. 20 показывают,
что интенсивность антистоксовой компоненты быстро
уменьшается при углах, меньших 9о + А0Макс, где
Лбмакс равно угловому отклонению, соответствующему
области максимального усиления.
Для газов направление согласования фазовых скоро-
скоростей, совпадает по существу с прямым направлением
луча, k\ =0. В этом случае максимальное усиление
антистоксовой компоненты получается для угла
0ы
Akx
.V.
При gs = 4, соответствующему усилению 18 дб/см, этот
угол равен 8- 10~3 pad или приблизительно 0,5°. Он рас-
растет как квадратный корень из постоянной нарастания.
В газе излучение с антистоксовой частотой идет преиму-
преимущественно в прямом направлении, хотя и не совсем точ-
точно. Усиление на стоксовой частоте также должно иметь
провал вблизи прямого направления. Однако из-за рас-
рассеяния и влияния геометрических факторов он может
быть незаметен.
Генерация высших комбинационных частот может
быть связана с различными механизмами, обсуждавши-
обсуждавшимися Терхьюном [41], Гармайром, Пандарезе и Таун-
сом [50]. Направленные вперед высшие стоксовы линии
излучения coss = coz, — 2со„, <»sss = aL — Зи„ и т. д. можно
получить с помощью указанного ранее процесса каскад-
каскадного комбинационного рассеяния. В распределении по
углам интенсивности излучения с частотой coss также
имеется темное кольцо, характеризующееся волновым
вектором kss. Оно вызвано параметрической связью, су-
существующей между четырьмя волнами. К ним относят-
относятся волна антистоксовой частоты, волновый вектор кото-
которой к"акс совпадает с направлением яркого кольца,
волна излучения лазера с волновым вектором кь и вол-
волна со стоксовой частотой, выбранная из направленного
вперед конуса стоксовой компоненты так, чтобы удов-
ЖСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
247
летворялось соотношение ка — kL = ks — к.,.,. Величины,
находящиеся в левой части этого соотношения, полно-
полностью определены и' по величине и по направлению. Зна-
Значения волновых векторов в правой части определяются
линейной дисперсией вещества. Таким способом можно
найти направление kss. Появление соответствующего
кольца вызывается нелинейным источником
pNLs , ) _ Е*Е Е KkL+k-ka).^!(i>sst
Аналогичным образом появление яркого антистоксова
кольца второго порядка будет вызываться нелинейным
источником
Процесс можно повторить; например, кольцо на часто-
частоте coaaa = соь + Зсо„ будет создаваться источником
в направлении, определяемом векторами кааа и ks, для
которых выполняется соотношение согласования фазо-
фазовых скоростей кааа + ks = каа + kL. Экспериментально
наблюдалось 5—6 антистоксовых колец и столько же
стоксовых колец высшего порядка. Это указывает на то,
что волны достаточно интенсивны для того, чтобы сме-
смешиваться друг с другом много раз. Возможно этим же
обусловливается большая спектральная ширина компо-
компонент, которая в 5—10 раз превышает ширину спонтан-
спонтанных линий. Кривые усиления на фиг. 20, обсуждавшиеся
в гл. 4, § 6, показывают, что существует значительное
усиление в интервале частот, равном по порядку полови-
половине ширины линии. В дополнение к возбуждению поляри-
поляризации С ЧаСТОТОЙ СОааа фурЬе-КОМПОНеНТЫ С ЧаСТОТОЙ СОаа
могут снова смешиваться с излучением лазера aL и ком-
компонентами частоты cos, воссоздавая излучение частоты
соа. Однако ширина линии этого вновь созданного излу-
излучения будет определяться сверткой первоначального
контура линии с самим собой. Если такую свертку
повторить 5 раз, то ширина линий может достичь зна-
значения 5Г и более. Это рассуждение носит лишь качест-
качественный характер. Волны и их взаимодействия настолько
интенсивны, что для получения количественных резуль-
248
ГЛАВА 5
татов потребовалось бы решить полную систему уравне-
уравнений для всех связанных волн. Параметрическое описа-
описание может дать лишь качественную картину явления.
Точное положение темных и ярких колец высших поряд-
порядков можно определить, только используя метод связан-
связанных волн.
§ П. Комбинационные восприимчивости
Возбуждение волн со стоксовыми и антистоксовыми
частотами в фокусированном лазерном луче высокой
интенсивности является замечательным явлением, одна-
однако экспериментальные условия не обладают достаточ-
достаточной определенностью для того, чтобы проверить теорию
и выяснить природу различных физических механизмов
этого явления. Возникшую здесь ситуацию можно срав-
сравнить с изучением работы и характеристик электронной
лампы. В первую очередь лампа исследуется как усили-
усилитель слабых сигналов, а не как мощный генератор.
С этой точки зрения свойства веществ, использующихся
в комбинационном лазере, должны исследоваться в тон-
тонких кюветах такой толщины, при которой невозможно
самовозбуждение колебаний на комбинационных часто-
частотах под действием интенсивного лазерного излучения
с частотой соь- В этом случае можно измерить усиление,
если направить в кювету также излучение малой интен-
интенсивности с частотами as или ма. Экспериментально всег-
всегда можно поддерживать усиление на уровне меньшем
чем 2—3 раза. При этом не будет ни уменьшения интен-
интенсивности лазерного излучения, ни заметного возбужде-
возбуждения стоксовых и антистоксовых линий высших порядков.
При такой постановке опыта можно независимо контро-
контролировать интенсивность, поляризацию, направление и
частоту луча лазера и луча стоксовой частоты. В идеаль-
идеальном случае каждый из лучей состоял бы только из одной
моды, т. е. был бы монохроматичным и имел бы
только дифракционную расходимость. Такие экспери-
эксперименты могли бы дать надежные значения комбинацион-
комбинационных восприимчивостеи и обеспечить детальную проверку
теории, изложенной в гл. 2 и 4. Схема возможной экс-
экспериментальной установки приведена на Фиг. 31.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
249
Луч мощного лазера делится на две части, одна из
которых используется для генерации излучения со сток-
стоксовой частотой в кювете для комбинационного рассея-
рассеяния. После этого излучение лазера отфильтровывается,-
Лазер
с модулируемой
добротностью
Кювета 1
Спектрограф
\н
Кювета Z шг
Фиг. 31. Схема экспериментальной установки для измерения ком-
комбинационных восприимчивостеи.
Усиление иа стоксовой частоте определяется в тонкой кювете / в зависимо-
зависимости от интенсивности, направления и поляризации луча лазера и стоксовой
компоненты, получаемой в кювете 2.
и стоксова компонента после соответствующего ослаб-
ослабления и выставления поляризации смешивается с остав-
оставшейся частью луча лазера, причем направление стоксо-
стоксовой компоненты можно менять по отношению к направ-
направлению луча. Затем эти два луча пропускаются через
тонкую кювету, в которой находится образец исследу-
исследуемого вещества. Таким методом можно измерить усиле-
усиление как функцию направления, поляризации и интенсив-
интенсивности. Можно также исследовать генерацию антисток-
антистоксовой компоненты вблизи от направления согласования
фазовых скоростей.
Брет и Майер [51] провели такой эксперимент, хотя
угол между направлениями лучей со стоксовой и анти-
антистоксовой частотами у них не варьировался. В их случае
оба излучения с частотами coL и cos генерировались в
комбинационном лазере, после чего лучи по отдельности
ослаблялись селективными фильтрами. Направление по-
поляризации в лучах задавалось, причем угол между
направлениями поляризаций можно было изменять, про-
пропуская излучение через пластинку заданной толщины,
создававшей нужную разность фаз. Используя этот ме-
метод, они обнаружили, что усиление стоксовой компонен-
компоненты в бензоле с поляризацией, перпендикулярной поля-
поляризации лазера, исчезающе мало по сравнению с тем
250
ГЛАВА 5
случаем, когда обе поляризации параллельны. Это не
значит, что компонента тензора %ХХуу очень мала по
сравнению с %Хххх- Экспоненциальный характер усиле-
усиления приводит к тому, что различие между величинами
этих компонент в 1,5—2 раза достаточно для того, чтобы
отношение наблюдаемых интенсивностей стоксовых ком-
компонент с двумя возможными поляризациями было вели-
велико. Был обнаружен также важный эффект насыщения
усиления, заключающийся в том, что усиление зависит
от интенсивности усиливаемой стоксовой компоненты.
Терхьюн [52] исследовал параметрическое взаимодей-
взаимодействие, приводящее к появлению излучения с частотой
2соь— (соь — сов) = wi, + со0 в тонких образцах различ-
различных кубических кристаллов и жидкостей. Фокусирован-
Фокусированный луч комбинационного лазера на бензоле содержал
линейно поляризованный свет с частотами aL и aL — со„
с av/2nc = 992 смг1. Излучения со всеми другими часто-
частотами были отфильтрованы из луча. В пластинках, выре-
вырезанных из кубических кристаллов, свет распространялся
вдоль оси [001]. Угол между осью [100] и направлением
параллельных поляризаций излучений с частотами aL
и aL-—av обозначается через 0. При 0 = 45° интенсив-
интенсивность излучения с частотой coz, + av оказывается дру-
другой, чем при 6 = 0 и 90°, что указывает на анизотропию
тензора восприимчивости четвертого ранга в кубиче-
кубических кристаллах.
При изменении толщины кристаллов параметриче-
параметрическое взаимодействие обнаруживает типичные осцилля-
осцилляции. Длина когерентного взаимодействия для трех волн,
распространяющихся в направлении оси z, составляет
около 1 мм. Относительная интенсивность света с часто-
частотой соь + со„ определяет величину компонент тензора
восприимчивости четвертого ранга. Сигналом сравнения
служил сигнал, выходящий из бензола. Эффект, наблю-
наблюдаемый в бензоле, является, конечно, наиболее сильным,
что связано с резонансом для комбинационной воспри-
восприимчивости. В других веществах измеряется существен-
существенно нерезонансная компонента тензора нелинейной вос-
восприимчивости. Численные значения восприимчивостей
««
fW
= - К -
щ бензол
) + Ч +
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
251
для различых кристаллов и жидкостей приведены во
втором столбце табл. 4. В третьем столбце даны отно-
Таблица 4
Восприимчивость У.хххх различных кубических кристаллов
и жидкостей
Восприимчивость Ххххх соответствует формуле E.33). Ча-
Частота й?_ равна частоте излучения рубинового лазера;
ш„/2яе = 992 см-1."
Коэффициент анизотропии дан в третьем столбце.
Длина когерентного взаимодействия для параметрической
генерации излучения с частотой u>L + ш0 дана
в четвертом столбце (по данным Терхьюна).
Вещество
LiF
' KI
CaF2
MgO
KC1
NaCl
KBr
Плавл. SiO2
C6H5CH3
QH5Br
C6H6
1 гхххх 1 ¦ i о13
эрг—' см3
0,24
0,29
0,4
1,2
2,3
2,1
3,6
0,8
4,8
7,2
481)
I^xxxx
У-хуху ""г l-xxyy
+ 0,74 ±0,10
0,54
0,66
0,61
1,10
0,78
0,91
1
1
1
1
1 , MM
3,27
0,45
2,94
1,27
0,92
0,88
0,67
1,45
0,80
0,65
0,70
') Это резонансное значение вычислено по величине попереч-
поперечного сечения комбинационного рассеяния. Оно используется при
определении абсолютных иерезонансных значений восприимчиво-
восприимчивостей ххххх, приведенных в этом столбце для других веществ.
шения ххххх/(%хуху + %ххуУ), характеризующие анизотро-
анизотропию (ср. со сказанным в § 8). Длина когерентного вза-
взаимодействия, помещенная в последнем столбце, вычис-
вычислена по известной величине линейной дисперсии среды.
Комбинационная восприимчивость для бензола, опреде-
определенная по величине поперечного сечения комбинацион-
252
ГЛАВА 5
ного рассеяния, использовалась в качестве опорного
значения, так как абсолютные измерения сопряжены
с указанными ранее трудностями.
392
1010
woo
A -i
Znc ' CM
Фиг. 32. Зависимость комбинационной восприимчивости Ixj* Xg*\.
описывающей генерацию антистоксовой компоненты с частотой
Ыь + д = (ojr, + col — (о)ь —Д), от Д вблизи частоты колебательного
резонанса о, (по данным Терхьюна).
Терхьюн E2] сумел также получить резонансные
кривые комбинационной восприимчивости, используя
комбинационные лазеры с кюветами, в которые помеща-
помещались различные жидкости с почти равными колебатель-
колебательными резонансными частотами. Он использовал в гене-
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
233
раторе следующие жидкости: бензол (частота колеба-
колебаний А/2яс = 992,4 см'1), анилин (996,8 см'1), бромбензол
A000,3 см-1), бензонитрил A001,6 см~1), толуол
A003,8 см~1), фторбензол A009,1 см-1). Зависимость
величины сигнала от частоты шг, + А для бензола, бром-
бензола и толуола показана в виде кривых на фиг. 32.
Терхьюн использовал также дейтерированный бензол
с А/2яс = 945 см'1 для измерения нерезонансной части
тензора комбинационной восприимчивости. Он нашел,
что для бензола xNn/(XoXsI/l= 0,05, для бромбензола
0,25 и для толуола 0,16. Для согласования с результа-
результатами этих измерений кривые фиг. 32 должны иметь не-
несколько большую асимметрию.
Очевидно, что потребуется еще выполнить большую
работу по тщательному количественному определению
комплексных комбинационных восприимчивостей, их
симметрии и дисперсионных свойств твердых тел, жид-
жидкостей и газов. Однако начало этой работе положено,
и можно ожидать, что в ближайшем будущем она будет
успешно продолжаться.
ЛИТЕРАТУРА
1. F г а п k e n P. A., H i 11 А. Е., Р е t e r s С. W., W e i п г е i с h G.,
Phys. Rev. Lett, 7, .118 A961).
2. Q iordm a i ne J. A., Phys. Rev. Lett., 8, 19 A962).
3. Maker P. D., Terhune R. W., Nisenoff M., S a v a-
g e С. М., Phys. Rev. Lett., 8, 21 A962).
4. T e r h u n e R. W., Maker P. D., Savage С. М., Appl. Phys.
Lett., 2, 54 A963).
5. BornM, Wolf E., Principles of Optics, London, 1959, p. 434.
6. Klein man D. A., Phys. Rev., 128, 1761 A962).
7. Ducuing J., Bloembergen N., Phys. Rev. Lett., 1,0, 474
A963).
8. Bass M., F r a n к e n P. A., H i 11 A. E., Peters С W., W e i n-
reich G., Phys. Rev. Lett., 8, 18 A962).
9. S m i t h A. W., В r a s 1 a u N., IBM Journ. Res., 6, 361 A962).
10. Ward J. F., Fran ken P. A., Phys. Rev., 133, A183 {1964).
11. Kaminow I. P., Phys. Rev. Lett., 6, 528 A961).
12. R i g г о d W. W., К a m i n о w I. P., Proc. IEEE, 51, 137 A963).
13. Ni ebuhr К- Е., Appl. Phys. Lett., 2, 136 A963).
14. Ashkin A., Boyd G. D., Dziedzic J. M., Phys. Rev. Lett.,
11, 14 A963).
15. D u с u i n g J., В 1 о e m b e r g e n N., Phys. Rev., 133, 1493 A964).
16. Forrester А. Т., Gudmundsen R. A., Johnson P. O.,
Phys. Rev., 99. 1961 A955).
554
ГЛАВА S
17. Miller R. С, К 1 e i n ш a n D. A., S a v a g e A., Phys. Rev. Lett,
11, 146 A963).
18. Van der Ziel J. P., Bloembergen N., Phys. Rev., 135,
A1662 A964).
19. Miller R. C, Phys. Rev., 131, 95 A963); 134, A1313 A964).
20. (Miller R. C, Appl. Phys. Lett, 5, 17 A964).
21. Soref R. A., Moos H. W., Journ. Appl. Phys., 35, 2152 A964.).
22. Bloembergen N., Chang R. K-, D u с u i n g J., L a 11 e-
mand P., Proceedings International Conference on Semicondu-
Semiconductors, Paris, July 1964.
23. S a v a g e А. (в печати).
24. Kleinman D. A., Phys. Rev., 126, 1977 A962).
25. Phillip H. R., E h r e n r e i с h H., Phys. Rev., 129, 1550 A963).
26. Lax В., Mavroides J. G., Edwards D. F., Phys. Rev. Lett.,
8, 166 A962).
27. Terhune R. W., Maker P, Savage С. М., Phys. Rev. Lett.,
8, 21 A962).
28. Pershan P. S., Phys. Rev., 130, 919 A963).
29. Giordmaine J. A., Proceedings Third Conference on Quantum
Electronics, Paris, 1963; ed. P. Qrivet, N. Bloembergen, New
York, 1964, p. 1449.
30. Maker P. D. Terhune R. W., Savage С. M., Proceedings
Third Conference on Quantum Electronics, Paris, 1963; ed.
P. Grivet, N. Bloembergen, New York, 1964, p. 1559.
31. Kleinman D. A., Phys. Rev., 125, 87 A962). (Имеется пере-
перевод в сб. «Лазеры», ИЛ, 1963.)
32. Braunstein R., Phys. Rev., 125, 475 A962). (Имеется перевод
в сб «Лазеры», ИЛ, 1963.)
33. Kaiser W., Garret t С. G. В., Phys. Rev. Lett, 7, 229 A961).
34. H о p f i e 1 d J. J., W о r 1 о с к J. M., Park K-, Phys. Rev. Lett.,
П, 414 A953).
35. S i n g h S., В r a d 1 e у L. Т., Phys. Rev. Lett, 12, 612 A964).
36. Maker P. D., Terhune R. W., Sa v a g e С. M., Phys. Rev.
Lett., 12, 507 A964).
37. Giordmaine J. A., Howe J. A., Phys. Rev. Lett., II, 207
A963).
38. Woodbury E. J., N g W. K. Proc. IRE, 50, 2367 A962).
39. E с к h а г d t G., H e 11 w a r t h R. W., M с С 1 u n g F. J.,
S с h w a r z S. E., Weiner D., Woodbury E. J., Phys. Rev.
Lett, 9, 455 A962).
40. Eckhardt G., В or tf eld D. P, Geller M., Appl. Phys.
Lett, 3, 36 A963).
41. Terhune R. W., Solid State Design, 4, 38 (November 1963).
42. Hellwarth R. W., Appl. Optics, 2, 847 A963).
43. T а к u m a R, Jennings D. A, Appl. Phys. Lett, 4, 185 A964).
44. Dennis J. H, Tannenwald P E., Appl. Phys. Lett, 5, 58
A964).
45. Terhu ne R. W., Bull. Am. Phys. Soc, II, 8, 359 A963).
46. Stoicheff B. P., Phys. Lett., 7, 186 A963).
47. Z e i s e r H. J., Tannenwald P. E, Kern S, Heren-
deen R., Phys. Rev. Lett., 11, 419 A963).
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
253
48. M i п с к R. W., T e r h u n e R. W., R a d о W. G., Appl. Phys. Lett.,
3, 181 A963).
49. Chiao R., Stoicheff B. P., Phys. Rev. Lett., 12, 290 A964).
50. G a r m i r e E., Pandarese F., Townes С. Н Phys Rev.
Lett., 11, 160 A963).
51. Bret G, Mayer Q, Compt. iRend., 258, 3265 A964).
52. Maker P., Terhune R., Phys. Rev., 137, № ЗА, А801 A965).
53*. Boyne H. S., Martin W. C, Journ. Opt. Soc. Am.,
52, 880 A962).
54*. Abel la I. D., Proc. IRE, 50, 1824 A962).
55*. Ax м а нов С. А., Ковригин А. И., Кулакова Н. К.,
ЖЭТФ, 48, № 6, 1545 A965).
56*. В о у d G. D., A s h k i n A., D z i e d z i с J. M., Kleinman D.,
Phys. Rev., 137, A1305 A965).
57*. Johnson F., Nature, 204, 985 A964).
58*. Ахмадов С. А., Ковригин А. И., Пискарскас А. С,
Хохлов Р. В., ЖЭТФ, письма в редакцию, 2, № 5, 223 A965).
59*. Bloembergen N., С h a n g R. К., D u c'u i n g I., Quantum
Electronics Conference, 28—30 June, 1965, Puerto Rico, San Juan.
Dispersion of the nonlinear susceptibility in crystals with
zinc-blende symmetry.
60*. В о у d G. D., M i 11 e r R. C, Nassau K-, Bond W. L., Sa-
vage A., Appl. Phys. Lett., 5, 234 A965).
61*. Miller R. С, В о у d G. D., S a v a g e A., Appl. Phys. Lett., 6,
77 A965).
62*. Афанасьев А. М., Маныкин Э. А., ЖЭТФ, 48, № 2, 483
A965).
63*. Афанасьев А. М., Маныкин Э А., ЖЭТФ, 48, № 3, 931
A965).
64*. Pershan p. S., Van der Ziel J. P., M a 1 m s t г о m L. D.,
Quantum Electronics Conference, 28—30 June, 1965, Puerto Rico,
San Juan.
Optically induced magnetization resulting from the inverse
Faraday effect.
65*. Делоне Ff. Б., Воронов Г. С, ЖЭТФ, письма в редак-
редакцию, 1, № ,2, 42 01965).
66*. Braunstein R., Ockman N., Phys. .Rev., 134, A499 A965).
67*. Басов Н. Г., Грасюк А. 3., Зубарев И. Г., К а т у-
л и н В. А., ЖЭТФ, письма в редакцию, I, № 4, 29 A965).
68.*. Келдыш Л. В, ЖЭТФ, 47, 1945 A964).
69*. Gold А., В ebb В., Phys. Rev. Lett., 14, 60 A965).
70*. Бункин Ф. В., Прохоров А. М., ЖЭТФ, 48, № 4, 1084
A965).
71*. Бонч-Бруевич А М., Ходовой В. А., Усл. физич наук,
85, № 1, 3 (-1965).
72*. А х м а н о в С. А., X о х л о в Р. В., Проблемы нелинейной оп-
оптики, М., 1964
73*. Аекарьян Г. А., ЖЭТФ, 42, 1567 A962).
74* Таланов В. И., Изв. ВУЗ'ов, Радиофизика, 7, 564 A962).
75*. Chiao R., G a r m i r e E., Townes С. Н.. Phys. Rev. Lett,
13, 479 A964).
256
ГЛАВА 5
76* Ах м а нов С. А., Ковригин А. И., Хохлов Р. В., Ч у н а-
ев О. Н., ЖЭТФ, 45, 1336 A963).
77* Ахм ан Ob С. А., Чи р кип А. С, Изв. ВУЗ'ов, Радиофизика,
8, № 3, 569 A965).
78* Bloembergen N.. Shen Y., Phys. Rev., 137, № 6A, A1787
A965).
79*. Bloembergen N., Shen Y., Phys. Rev. Lett., 13, № 24, 720
A964).
80* Bloembergen N., Lallemand P., Appl. Phys. Lett, 6,
№ 10, 210 A965).
81*. Lallemand P., Bloembergen N., Appl. Phys. Lett., 6,
№ 10, 212 A965).
82*. McClu ng F. J., Wagner W. Q., Weiner D., Quantum
Electronics Conference, 28—30 June, 1965, Puerto Rico, San Juan.
Anomalies in stimulated Raman scattering conversion effi-
efficiencies.
83*. Wagner W. G., Yatsiv S., H e 11 w a r t h R., Quantum Ele-
Electronic Conference, 28—30 June, 1965, Puerto Rico, San Juan.
Effect of laser beats on the spectrum of stokes and anti-
stokes radiation in stimulated Raman scattering.
84*. Martin J., Thomas E., Phys. Lett, 16, № 2, 132 A965).
85* Ахманов С А., К о в ри г и н А. И., Р о м а н ю к А. К., Ку-
' лакюва Н. К, Хохлов Р, В., ЖЭТФ, 48, № 4, 1202 A965).
86* Л л а т о н е н к о В., Стаменов К. В., Хохлов Р. В., ЖЭТФ,
49, № 10 A965).
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
87* Степанов Б.И, Апанасевич П.А., Журн. прикл. спектр.,
2, № 1, 37 A965).
Вынужденное комбинационное рассеяние в резонаторе
первичного ОКГ.
88*. Quiver W., Seppi E., Journ. Appl. Phys., 35, 3421 A964).
Characteristics of an ideal Raman oscillator — amplifier.
89*. Маш Д. И., Морозов В. В., С тар умов В. С, Фа белии-
ский И. Л., ЖЭТФ, письма в редакцию, 2, № 1, A965).
Вынужденное рассеяние света крыла линии Рэлея.
90* Ashkin A., Boyd Q., Klein man D., Appl. Phys. Lett, 6,
№ 9, 179 A965).
Phase matched second-harmonic generation in KDP without
double refraction.
91* Kaiser W., M a i e r M.t G i о г d a m i n e, Appl. Phys. Lett., 6,
№ 2, 25 A965).
Vibrational interaction in mixed liquides during stimulated
Raman action.
92* 3 у б о в В. А., С у щ и н с к и и М. М., Ш у в а л о в И. К., ЖЭТФ,
48, № 1, 370 A965).
Исследование вынужденного комбинационного рассеяния
93*. А х м а н о в С. А., С у х о р у к о в А. П., X о х л о в Р. В., ЖЭТФ,
50, № 2 П966).
Л
В
ЗАКЛЮЧЕНИЕ
Существует много других вопросов, которые следо-
следовало бы рассмотреть в пределах широкого диапазона
тем, входящих в понятие нелинейной оптики. Краткость
настоящей главы позволяет лишь напомнить о них, хотя
это и несправедливо по отношению к ним.
Фотоэлектрический эффект представляет собой, по
существу, нелинейный процесс с квадратичной характе-
характеристикой: измеряемый фототок пропорционален квадра-
квадрату напряженности поля. Значительный интерес представ-
представляет нахождение частотной характеристики фотоэффек-
фотоэффекта. Если на светочувствительное вещество падают две
световые волны с частотами ац и со2, то возникает воп-
вопрос, какова будет компонента фототока на частоте
o)i — иг? Определяющим фактором в этом случае яв-
является однородное время затухания т возбужденного
электронного состояния, и частотная характеристика
большого класса явлений, связанных с фотоэлектриче-
фотоэлектричеством и фотопроводимостью, ведет себя как [1 + (со,—
-@2)V]-V.[l-3].
Не обсуждались эксперименты по взаимодействию
света с радиоволнами на СВЧ, хотя они привели к соз-
созданию многих важных устройств. Не рассматривались
также нелинейные эффекты в плазме [4, 5] в диапазоне
СВЧ и в далекой инфракрасной области.
Поглощение, зависящее от интенсивности, описыва-
описывается соотношением B.69). Решение волнового уравне-
уравнения, в котором учитывается наличие поглощения, зави-
зависящего от мощности, показало бы, как изменяется зату-
затухание при прохождении волны очень большой интенсив-
интенсивности через насыщающееся вещество. Это явление ис-
17 Н. Бломберген
258
ГЛАВА в
пользуется в так называемых насыщающихся фильтрах.
Такие фильтры становятся прозрачными при высоких
интенсивностях и могут использоваться в качестве эле-
элементов, модулирующих добротность в импульсных лазе-
лазерах |[6].
Другие явления, хорошо известные по опытам с маг-
магнитным резонансом в диапазонах радиочастот и СВЧ,
могут иметь свои аналогии в оптическом диапазоне.
Можно рассмотреть случаи, когда импульсы света очень
высокой интенсивности возбуждают достаточно узкие
уровни энергии. Тогда будут наблюдаться зависящие от
интенсивности смещения резонансной частоты и т. д.
Не обсуждались также важные теоретические вопро-
вопросы, касающиеся взаимодействия света со светом в ваку-
вакууме, нелинейного взаимодействия света с релятивистским
электроном, квантовых флуктуации и квантовых шумов
в параметрических устройствах и устройствах, исполь-
использующих явление комбинационного рассеяния. Единст-
Единственным оправданием этого может служить то, что рас-
рассмотрение указанных вопросов увело бы нас слишком
далеко от центральной темы настоящей монографии —
изучения нелинейных восприимчивостей вещества.
§ 1. Нелинейности в лазерах
Ссылка на указанную особенность монографии не
может служить оправданием того, что не рассматривает-
рассматривается роль нелинейностей в работе лазеров. Поведение лю-
любого генератора определяется нелинейностью его харак-
характеристики. Амплитуда колебаний ограничивается эффек-
эффектом насыщения населенностей уровней, между которыми
происходит лазерный переход. Скоростные уравнения,
определяющие изменение населенностей в лазерах раз-
различных типов, хорошо известны. Они соответствуют рас-
рассмотрению диагональных элементов матрицы плотности,
проведенному в общих чертах в гл. 2. Нет необходимо-
необходимости повторять их здесь. Однако проведенное там рас-
рассмотрение справедливо только для неподвижных атомов
или молекул. Качественно их можно применить к газо-
газовым лазерам, соответствующим образом учитывая каж-
каждый раз допплеровское уширение.
ЗАКЛЮЧЕНИЕ
Недавно Лэмб G] опубликовал теорию газового ла-
лазера, в которой матрица плотности зависит также от
скорости и положения атома. Тот же вопрос рассмот-
рассмотрели в серии статей также Хакен и Зауерманн [8]. Ког-
Когда лазер генерирует две моды, они могут конкурировать
между собой, в результате чего возникают интересные
явления затягивания. Если газовый лазер генерирует
одновременно три эквидистантные или почти эквиди-
эквидистантные продольные моды, то наблюдается эффект не-
нелинейной связи. Он заключается в том, что волны с час-
частотами toi и иг взаимодействуют и возбуждают волну
нелинейной поляризации с частотой соз = 2со2 — u>i. Если
несинхронизованная частота генератора со^ очень близка
к соз> то наблюдается затягивание и синхронизация ге-
генерируемых частот [9]. Лэмб развил детальную теорию
этих нелинейностей. Он рассмотрел также устойчивость
процесса генерации трех связанных мод.
В этой книге рассмотрены прежде всего бегущие
волны. Исключая случай кольцевых лазеров, картина
мод в генераторах обычно соответствует картине стоя-
стоячей волны. Конечно, каждую стоячую волну можно рас-
рассматривать как две бегущие волны, но вследствие удва-
удваивания количества волн сложность проблемы в значи-
значительной.степени увеличивается.
При существующих уровнях мощности процесс гене-
генерации гармоник или комбинационное рассеяние внутри
резонатора газового лазера малоэффективен, однако
это утверждение требует пересмотра, если излучение
внутри резонатора фокусируется. Явление генерации
гармоник в полупроводниковых лазерах (GaAs) доста-
достаточно известно [10, 11]. Его можно рассчитать с помощью
обычной теории, используя заданную волну нелинейной
поляризации.
§ 2. Другие нерешенные проблемы
В настоящей монографии рассматривались почти
исключительно плоские волны с бесконечно большим
поперечным сечением и плоские бесконечные границы.
Такой подход согласуется с духом геометрической опти-
оптики, в которой знание хода узких лучей света позволяет
17*
260
описать более сложные случаи. Например, правила об-
образования изображения линзами выводятся из закона
Снеллиуса, который получен в результате изучения пре-
преломления плоской волны на плоской границе раздела
двух сред. Аналогичным образом можно проанализиро-
проанализировать неоднородные волны источника и их интерферен-
интерференцию с однородными волнами в процессе прохождения
света через нелинейные линзы, призмы, многослойные
покрытия и т.д. Эффекты, обусловленные конечными
размерами пучка, можно объяснить дифракцией в со-
соответствии с принципами Кирхгофа и Гюйгенса.
Теорию дифракции необходимо распространить на
нелинейные среды. В частности, следует более точно рас-
рассмотреть нарастание волны в фокальной области линзы.
Наиболее простой способ (применимый в приближении
заданного поля) заключается в получении решения для
заданного распределения нелинейной поляризации. За-
Задача же излучения гармоник сферами и цилиндра-
цилиндрами малых размеров не представляет особых труд-
трудностей.
Все уравнения в этой книге были выведены для ста-
стационарного состояния (производные комплексных ам-
амплитуд по времени полагались равными нулю). Не вы-
вызывает сомнений, что стационарное состояние устанав-
устанавливается быстро и, вероятно, существует даже для
импульсов лазеров с модулируемой добротностью, дли-
длительность которых составляет всего 10~8 сек. Вместе
с тем, желательно провести дальнейшее тщательное ис-
исследование проблем, связанных с переходными процес-
процессами. Кролль [12] выполнил недавно исследование пере-
переходного процесса для вынужденного рассеяния Мандель-
Мандельштама—Бриллюэна. В этом случае из-за относительно
малой скорости звуковых волн длительность импульса
лазера с модулируемой добротностью может оказаться
недостаточной для того, чтобы успело установиться ста-
стационарное состояние. В случае процессов комбинацион-
комбинационного рассеяния и параметрических процессов, в которых
участвуют только световые волны, стационарные реше-
решения, по-видимому, являются хорошим приближением к
существующей в действительности физической ситуа-
ситуации.
ЗАКЛЮЧЕНИЕ
261
Весьма важной проблемой является вопрос о проч-
прочности веществ, подвергающихся действию предельно
больших световых полей. Имеется много указаний на то,
что это не столько оптическая проблема, сколько проб-
проблема, связанная с тепловыделением. При достаточно
высокой интенсивности возникают некоторые нелинейные
диссипативные процессы. Таковыми могут являться
комбинационное рассеяние или рассеяние Мандельшта-
Мандельштама— Бриллюэна, вызывающее выделение колебательной
энергии, или же это может быть многофотонное погло-
поглощение. В кристалле выделение тепла может легко на-
начаться в области дефекта решетки или примеси. Эта
энергия выделяется в объеме причудливой формы,
обусловленной распределением интенсивности в фокусе,
за очень короткий промежуток времени. В результате
все сводится к проблеме гидродинамической ударной
волны.
Список перечисленных выше вопросов, рассмотрение
которых незавершено, несомненно не является полным.
Однако были сформулированы основные методы, с по-
помощью которых можно найти решение этих и других
проблем:
1. Основные нелинейные оптические свойства веществ
можно описать, используя существующие классические
или квантовомеханические представления о структуре
вещества.
2. Эти нелинейные свойства можно описать с по-
помощью тензоров комплексной восприимчивости увеличи-
увеличивающихся рангов.
3. Даже при наивысших достижимых плотностях из-
излучения указанные нелинейности можно рассматривать
как малые возмущения и ввести их в уравнения Мак-
Максвелла, чтобы получить систему связанных волновых
уравнений.
4. Обобщая методы теории параметрических усили-
усилителей бегущей волны, можно найти приближенные реше-
решения связанных нелинейных уравнений.
262
ГЛАВА б
5. Эти решения приводят к обобщению на нелиней-
нелинейный случай хорошо известных законов оптического от-
отражения, закона Снеллиуса, формул Френеля и т. д.
6. Сферу использования развитого метода можно
расширить, включив в нее взаимодействие с фононами.
Тот же метод применим для рассмотрения вынужденно-
вынужденного рассеяния Мандельштама — Бриллюэна и комбина-
комбинационного рассеяния, которые можно описать, вводя со-
соответствующие восприимчивости.
7. Измерения нелинейных восприимчивостеи, их сим-
симметрии и дисперсионных свойств как функции несколь-
нескольких частот дают дополнительную информацию о струк-
структуре вещества.
Наконец, знание указанных свойств вещества приве-
приведет к созданию многих нелинейных устройств, которые
в ультрафиолетовой, видимой и инфракрасной частях
электромагнитного спектра будут выполнять те же
функции, которые, как известно, выполняют нелинейные
лампы и нелинейные элементы цепей на более низких
частотах.
ЛИТЕРАТУРА
1. Pershan P. S., Bloembergen N., Appl. Phys. Lett., 2, 117
A963).
2. LasherQ. J., N e t h e г с о 11 A. H., Journ. Appl. Phys., 34, 2122
A963).
3. Svelto O., Col em an P. D., Di Domenico M., Jr., Pan-
tell R. H., Journ. Appl. Phys., 34, 3182 A963).
4. P 1 a t z m a n P. M., T z о а г N., Phys. Rev. Lett., 12, 573 A964)
5. Kroll N. M., Rou A., Rostoker N., Phys. Rev. Lett, 13, 83
A964).
6. Bret G., Gires F., Compt. Rend., 258, 4702 A964).
7. Lamb W. E., Jr., Phys. Rev., 134, A 1420 A964).
8. H a k e n H., S a u e r m a n n H., Zs. Phys., 173, 261 A963); 176, 47 ¦
A963).
9. Witt em an W. J., Haisma J., Phys. Rev. Lett., 12, 617 A964).
10. Armstrong J. A., Nathan N. I., Smith A. W., Appl. Phys.
Lett., 3, 68 A963).
11. Malms trom L. D. Schlickman J. J., Kingston R. H.,
Journ. Appl. Phys., 35, 248 A964).
12. Kroll N. M, Journ. Appl Phys., 36, 34 A965).
П р и л о ж
н и я
Приложение 1
ВЗАИМОДЕЙСТВИЕ СВЕТОВЫХ ВОЛН
В НЕЛИНЕЙНОМ ДИЭЛЕКТРИКЕ
Цж. Армстронг, Н. Бломберген,
Ж. Дюкуэнг, П. Першан
.1, A. Arms tr on g*, N. Bloembergen*, J. Ducuing**,
P. S. Pershan*, Phys. Rev., 127, 1918 A962)
С помощью квантовомеханической теории возмущений вычисле-
вычислены индуцированный нелинейный электрический дипольный момент и
моменты более высоких порядков атомной системы, облучаемой
одновременно двумя или тремя световыми волнами. Учтены члены,
квадратичные и кубичные по полю. Выведено важное простран-
пространственно-частотное перестановочное соотношение для нелинейной
восприимчивости и проанализирована ее зависимость от частоты.
Установлено соотношение между нелинейными микроскопическими
свойствами и эффективной макроскопической нелинейной поляриза-
поляризацией, которую можно ввести в уравнения Максвелла для бесконеч-
бесконечной однородной анизотропной нелинейной диэлектрической среды.
Для нелинейного диэлектрика выведены соотношения для энергии
и мощности, соответствующие соотношениям Мэнли — Роу в теории
параметрических усилителей. Получены в явной форме решения си-
системы уравнений для комплексных амплитуд, описывающих взаимо-
взаимодействие плоской световой волны с ее второй гармоникой или
взаимодействие трех плоских электромагнитных волн, которые удов-
удовлетворяют энергетическому соотношению Шз = wi + w2 и соотноше-
соотношению для импульсов k3 = ki + k2 + Ак. Рассмотрена генерация треть-
третьей гармоники и взаимодействие между большим числом волн. Об-
Обсуждены возможности применения теории для исследования низко-
низкочастотного и высокочастотного эффекта Керра, модуляции света,
генерации гармоник и параметрического преобразования света.
§ 1. Введение
Взаимодействие электромагнитных волн с вещест-
веществом, состоящим из атомов, было рассмотрено с учетом
членов высших порядков в теории возмущений уже
в первые годы существования современной квантовой
механики [1—3]. В последнее время снова возрос инте-
* Division of Engineering and Applied Physics, Harvard Univer-
University, Cambridge, Massachusetts.
** Departament de Physique Appliquee, Cie Gle de Telegraphic
sans fil (Orsay), France.
266
ПРИЛОЖЕНИЕ I
pec к исследованию поглощения двух или большего
числа световых квантов и рассеяния с участием трех или
большего количества квантов [4—7]. Это связано с тем,
что лазеры позволяют получать интенсивные потоки све-
света, благодаря чему стало возможным экспериментальное
наблюдение указанных процессов высокого порядка
в лаборатории.
Франкен и др. [8] наблюдали возникновение второй
гармоники света, соответствующее элементарным про-
процессам аннигиляции двух световых квантов и рождения
одного нового кванта с удвоенной энергией. Гарретт
и Кайзер (9] наблюдали двухфотонное поглощение.
Грубая оценка интенсивности света, требуемой для
наблюдения этих эффектов, может быть получена сле-
следующим образом. Если рассеяние обусловлено электри-
электрическими дипольными переходами, то интенсивность про-
процесса рассеяния более высокого порядка меньше интен-
интенсивности рассеяния предыдущего порядка в (Ei/E^J ~
~[eEa/(W0—Wn)]2 раз. Здесь Ех— электрическое поле
световой волны; ?ат~3-108 в/см— среднее атомное
электрическое поле, действующее на валентные электро-
электроны; а — радиус атома; WQ—Wn — средняя энергия воз-
возбуждения атома. В тех случаях, когда данный процесс
рассеяния, вызванный электрическими дипольными пе-
переходами, оказывается запрещенным (что определяется
условиями четности), то в указанном соотношении по-
появляется дополнительный множитель (а/ЯJ ~ 10~7.
В связи с тем, что можно с высокой степенью точно-
точности экспериментально отличать многофотонные процес-
процессы от процессов более низкого порядка, нелинейные эф-
эффекты легко удается наблюдать при (Et/EMJ ~ 10~10,
или Ei = 3 • 103 в/см. Это соответствует интенсивности
света 0,25 Мвт/см2. Такие интенсивности можно получить
даже в несфокусированных лазерных пучках. Сообща-
Сообщалось, что короткий импульс рубинового лазера, работав-
работавшего с ячейкой Керра в качестве затвора A0, 11], имел
пиковую мощность 10 Мет в пучке с поперечным сече-
сечением около 0,5 см2. В сфокусированных пучках можно
получить более высокие интенсивности. Со временем
будут доступны гораздо большие пиковые плотности
мощности, чем те, о которых сообщалось до сих пор.
ПРИЛОЖЕНИЕ 1
267
В экспериментах Франкена' и других исследователей
[8, 12—15], изучавших процесс возникновения гармоник
светового излучения, первостепенную важность имели
когерентные эффекты. Интенсивность оптических гармо-
гармоник может возрастать как квадрат числа рассеивающих
центров. Даже в газовой среде представляет интерес не
столько некогерентное рассеяние отдельными молекула-
молекулами, сколько когерентные эффекты, создаваемые эквива-
эквивалентной сплошной средой с такой же средней плотно-
плотностью. То же различие возникает и в линейной теории
дисперсии. Некогерентное релеевское рассеяние обуслов-
обусловливает голубой цвет неба, а когерентное рассеяние
определяет показатель преломления воздуха.
В опубликованных теоретических работах [4—7] под-
подробно рассматривались некогерентные нелинейные про-
процессы, в частности многофотонное поглощение. При
обычном рассмотрении элементарных процессов рассея-
рассеяния на отдельных молекулах вопрос о когерентности
падающих и рассеянных фотонов остается нерешенным.
С другой стороны, оптический показатель преломления
лучше всего определяется полуклассическим методом
[16]. Вычислив с помощью квантовомеханических мето-
методов среднее значение индуцированного дипольного мо-
момента атомной системы, можно возвратиться к макро-
макроскопической поляризации и классической теории Мак-
Максвелла и Лоренца для сплошных сред [17, 18].
В настоящей статье мы выберем именно этот путь
для определения нелинейной части поляризации. В § 2
выводятся квантовомеханические выражения для нели-
нелинейных индуцированных электрических дипольных мо-
моментов с точностью до членов, квадратичных и кубичных
относительно напряженности поля. Эти выражения
иллюстрируются на примере ангармонического осцил-
осциллятора. В § 3 устанавливается связь между микроско-
микроскопическими нелинейными свойствами среды и величинами,
характеризующими макроскопическое поле. Обсуждает-
Обсуждается также запаздывание и моменты более высоких по-
порядков. В § 4 нелинейная поляризация вводится в урав-
уравнения Максвелла. Решения этих уравнений в явной
форме для бесконечного нелинейного анизотропного ди-
диэлектрика даны в § 5—7. Они описывают взаимодейст-
268
ПРИЛОЖЕНИЕ I
вие между основной волной и ее второй гармоникой, а
также между тремя плоскими электромагнитными вол-
волнами, частоты которых связаны соотношением соз =
= mi+ W2 (являющимся по существу законом сохранения
энергии), а волновые векторы — соотношением к3 =
= к\ + к2 + Лк, где /Дк|<С /к31 (сохранение импуль-
импульса). Эти решения могут рассматриваться как обобще-
обобщение теории параметрического усилителя бегущей волны
[19]. [Последняя относится к частому случаю, когда по-
поток мощности в одной из волн (накачке) значительно
больше, чем в двух других волнах.] В настоящей же
статье все три волны считаются равноправными. В § 7
полученные выводы распространены на случай генера-
генерации третьей гармоники и взаимодействия между че-
четырьмя волнами. Связь теории с экспериментом кратко
обсуждается в § 8.
Многоквантовое поглощение и генерация гармоник,
конечно, наблюдались и раньше в радиочастотном
и СВЧ диапазонах электромагнитного спектра. Там эф-
эффекты распространения обычно не играют важной роли,
за исключением случая параметрического усилителя бе-
бегущей волны. В оптической же области фазовые соот-
соотношения между волнами, распространяющимися в нели-
нелинейной среде, играют определяющую роль. Особый инте-
интерес представляет этот эффект на границе нелинейного
диэлектрика. Хорошо известные законы отражения и
преломления света в линейной среде можно распростра-
распространить на нелинейную среду. Модифицированные законы
Снеллиуса и Френеля для гармоник света будут рас-
рассмотрены в отдельной статье [20].
§ 2. Вывод квантовомеханических выражений
для нелинейных источников
В настоящем параграфе для описания нелинейного
взаимодействия нескольких монохроматических волн в
стационарном поле излучения будет использована полу-
полуклассическая теория взаимодействия излучения с веще-
веществом (Клейн [21]). Крамере [16] подробно рассмотрел
вопрос о том, как, пользуясь этим полуклассическим ме-
ПрилоЖёНие i
269
тодом, можно построить теорию когерентного рассеяния
и определить величину линейной диэлектрической прони-
проницаемости. Его метод будет распространен на более вы-
высокие порядки теории возмущений. Это естественным
образом приведет к описанию нелинейных диэлектриче-
диэлектрических свойств среды.
л. нелинейные источники, зависящие от е2
Влияние излучения на систему заключается в том, что
оно вызывает изменение средней величины плотности
электронного тока. Плотность этого индуцированного то-
тока рассматривается затем как источник рассеянного из-
излучения. Для определенности будем считать, что поле
представляет собой суперпозицию трех гармонических
волн, частоты которых удовлетворяют соотношению
coi + оJ = из- Векторный потенциал поля падающего из-
излучения в вакууме есть
Ь).
B-1)
A = ^ iiqi cos (k,- • r — со
(=1,2,3
где aj — единичный вектор поляризации. Гамильтониан
взаимодействий имеет вид
е « _ е2
тс
2/пс2
,], B.2)
причем суммирование производится по всем k электро-
электронам. Записывая Жвз в такой форме, мы приняли куло-
новскую калибровку
divA = 0, E=-Re^-^-], B.3)
которая подразумевает, что р и А коммутативны. Так
как р — эрмитов оператор, а А — действительная вели-
величина, то Ж вз является эрмитовым оператором. Заметим,
однако, что некоторые члены, например p-aexp(tk.r),
могут и не быть эрмитовыми.
Волновые функции невозмущенной системы обозна-
обозначим через фп, собственные значения энергии — через Wn-
Для простоты примем, что функции фп являются произ-
270
Приложение i
ведениями одноэлектронных волновых функций фге =
= П фп(/г). Если нет постоянного магнитного поля (и не
п
учитывается спин), то волновые функции <pn без потери
общности можно считать действительными. Обозначим
волновую функцию возмущенного основного состояния
через i|5g. Эти волновые функции используются для вы-
вычисления величины плотности индуцированного электрон-
электронного тока
=2
-4)
где сумма берется по k электронам. (Нелинейная часть
выражения этого типа называется в дальнейшем нели-
нелинейным источником.)
Члены выражения B.4), линейные по полю, детально
исследованы Крамерсом, который показал, каким обра-
образом можно использовать их для определения линейной
диэлектрической восприимчивости среды. В настоящей
статье нас интересуют члены, квадратичные (и кубич-
кубичные) по полям А,-. Для получения всех членов, квадра-
квадратичных по А{, возмущенные волновые функции должны
быть вычислены с точностью до второго порядка неста-
нестационарной теории возмущений [3]
% @ = 2 i8ng + G«" (P • А) + ««" (А • А) +
п
+ а{п2) (р • A)] qyf*"»'- B.5)
Из этого выражения видно, что среди коэффициен-
коэффициентов разложения первого порядка имеются члены как
линейные, так и квадратичные по А,- .
Члены в B.4), квадратичные по А,- , можно сгруппи-
сгруппировать в соответствии с их зависимостью от частоты. Так
как поле падающего излучения содержит три различные
частоты, то возмущенные волновые функции второго по-
порядка будут иметь зависимость от времени с де-
девятью различными частотами. Можно, например, рас-
рассмотреть нелинейный источник на частоте соь обуслов-
обусловленный взаимодействием полей с частотами ю3 и сог, или
источник на частоте 2соь обусловленный взаимодействи-
взаимодействиПРИЛОЖЕНИЕ 1
ем поля частоты coj с самим собой, и т. д. Продемонстри-
Продемонстрируем использование выражения B.4) на примере вычис-
вычисления нелинейного источника на частоте соз = wi + сог.
появляющегося в результате взаимодействия волн с ча-
частотами С01 И tt»2.
Мы будем интересоваться только той частью нелиней-
нелинейного источника на частоте со3, которая дает когерентный
вклад 'в падающую волну с частотой юз- Вычислим B.4),
сохраняя лишь те члены, которые зависят от времени как
ехр(±Шз^) и пропорциональны qiq2,
(Рv (®s)}gg = {рv (ю3)}+ е!ю>' + {рv (Шя)}й е ~ to«*. B.6)
Можно считать, что выражение B.6) определяет вели-
величину fpvJig. Выражение для плотности индуцированного
тока B.6) содержит вклады от производных по времени
всех мультипольных моментов возмущенного распределе-
распределения электронов. Однако если ввести соответствующее за-
запаздывание этой плотности тока, т. е. умножить член
выражения B.6), пропорциональный ехр (±ш30. на
ехр(± /к3"Г) и взять затем среднюю величину результи-
результирующего выражения, то источник с частотой со3 принима-
принимает форму производной по времени от эффективного ди-
польного момента
NL
(соз),
со3) = 2Re [^L (ю3)
B.7)
Выражение для $Р_ (со3)ехр(—/юзО в явной форме
имеет вид (для удобства мы опускаем суммирование по
электронам)
WlL К) е~ ^ - < g | {pv (со3)Г • e~ 'kl'r | g > е~ш =
где
B.8)
,» (k2-ks)-
ПРИЛОЖЕНИЕ 1 273
2J2 , ПРИЛОЖЕНИЕ 1 . ¦
B-10)
~2
(е'<ki~ks)'ra1)/-,g (е <к2'га2 • р),*.я Аналогичные выражения определяют эффективные
_| _ __ |~ нелинейные дипольные моменты на частотах coi и со2-
''ё 2 Правильность выражений B.7) — B.10) можно прове-
I" - w -;ksr ) / i(ki+k2)r\ рить, выписав не зависящую от времени часть энергии
_]- _..L__l^ P_^L! f — + возмущения третьего порядка (MB3)gg, которая кубична
<°,'g —тз по напряженности поля q. Эта энергия содержит в прин-
принципе вклады от всех мультипольных моментов системы,
/о п\ Каждый член в выражениях B.9) и B.10) содержит
\ ' ' по крайней мере один матричный элемент вида (А • ры).
Комплексные экспоненты в выражении B.1) для А мож-
можно разложить по матричным элементам всех мультиполь-
• р)-,• (е'к2'га -р)- ных моментов атомной системы. Если существует центр
—— f- симметрии, то волновые функции ф,- будут иметь опреде-
(СО ; - (О \ ,-, Л-2N L
,_,-. - - - Jg 2/ ленную четность. В этом случае члены в Ч»Эфф, соответ-
соответствующие электрическим диполям (т. е. члены нулевого
~ tk''rp)j'g (e~~ 'k'rai • pYj.j (e~ 'кг'г аг • pYjg порядка по к), исчезнут. Однако члены, соответствующие
TJ i ш wm. _Lm ) ' электрическим квадруполям (и магнитным диполям),
( l'g з) ( ;g ч.) \ линейные по к, дадут конечный результат.
( ~гк,-гр\ / ikrrj \ (е'к»-га • р)- i Предположим теперь, что атомная система не имеет
_f Ж- О 1 Ч. л- центра инверсии. В этом случае члены нулевого порядка
;'g~~ 3Н lg~ v по к в ^Рэфф будут доминировать над всеми остальны-
/ ~ ik г \ 1 —дк,-гл \* I -!к,гА \* ми> и мы можем положить все множители вида
(е ' p)/'g(e 2 Ч-Р)\'\\е ' ai' P);g . exp(±tk-r) равными единице. В результате выражение
(«W + »3) (w/g + mi) сильно упрощается, ибо, как показано Гепперт-Майер
[2], возмущение ^СВз теперь можно записать в виде
— (ё~~ ' З'гр);>; ( е^"' ''га! -p)i'g (е1 !'га2 • p)/g ^> 9J.E(rt f2.ll)
(mj'g + mi) (m/g"~ И2) где ^Р — оператор полного электрического дипольного
момента молекулы, а Е (t) — полное (действительное)
J_/ — jka-r *л ik,.rA \ i ~ik2-rA у локальное электрическое поле. Снова рассмотрим слу-
2 '' ai' P//'g <- 2 P^jg qaj» трех волн> частоты которых связаны прежним соот-
/ш.г _m wm. 4-о) ) ношением, и запишем электрическое поле в виде
1 _.кзг .kirA _.кгг. , ' Е@= 2 E,.cosK/ + <P,). B.12)
¦ f- Далее, так как А имеет теперь только диагональные ма-
(ш/'г + тг) (т/^""ш1) тричные элементы, мы можем написать (pv)op =
18 II. Бломберген
274
ПРИЛОЖЕНИЕ 1
= (дф/д()ор; теперь необходимо только вычислить
( ё\ Ф\§ > , сохраняя, как и раньше, лишь члены, про-
пропорциональные EiEj и зависящие от времени с частотой
coi, CO2 или соз- Используя те же волновые функции второ-
второго порядка, найдем для ( tya)eg следующее выраже-
выражение:
= cos
- Ъ)
cos
cos
-Е3)
Е0 (*/в-Е3)
ф2)
Е2) Af
B.13)
где
A,v =
2ft*
C,v =
1
, B.14)
Использован тот факт, что волновые функции предпола-
предполагаются действительными.
Заметим, что каждая фурье-компонента (tyab)#g
может быть записана в виде тензора третьего ранга (с
числом компонент 3x9), действующего на несимметрич-
несимметричный тензор второго ранга. Этот тензор второго ранга яв-
является произведением электрических полей двух разных
частот
= cos
ф3 — ф2)
(сох =
«2)
2
ПРИЛОЖЕНИЕ I
275
(«3) = cos
l B.15)
Фх + Ф2) ^ P
Сравнение B.13) и B.14) с B.15) позволяет получить
явные квантовомеханические выражения для Pijft(co).
Исследование этих формул приводит к следующим важ-
важным пространственно-частотным перестановочным соот-
соотношениям
Ру* («1 = «з — «г) = Рид («а = «з — «i) -
= P;«fo = ffll+«>2). B.16)
Частоты можно переставлять произвольно, если одновре-
одновременно координатные индексы I, j я k переставляются та-
таким образом, что данная частота всегда связана с одним
и тем же индексом. Благодаря этим соотношениям число
констант, требующихся для описания микроскопической
нелинейной поляризации, обусловленной существованием
трех волн в системе с симметрией класса Сь уменьшает-
уменьшается с 81 до 27.
Рассмотрим теперь частный случай — генерацию вто-
второй гармоники: coi = со2 = '/г^з- Так как теперь спра-
справедливы соотношения 2coi = 2со2 = соз, из — coi = coi и
из — и2 = иг, а также coi + to2 = @3, то при вычислении
волновой функции второго порядка нужно рассмотреть
большее число членов. Результат, однако, сводится
просто к умножению выражения B.13) для $« на 2.
Кроме того, поскольку величина Spa рассчитывалась
для поля ?icos(coi^ + Ф1) + ?'icos(coi^ + ф!) +
+ E3cos(o)St + ф3) = 2?1cos(coi^ + Ф1) + •?13cos(co3^ +
+ фз), то как Еи так и Е2 в выражении B.13) нужно
заменить на EJ2. Заменяя далее в B.14) со2 на coi и из на
к>2, получаем следующее выражение для нелинейной по-
поляризации в случае генерации второй гармоники;
= COS
А
иг
IS*
-f
276
ПРИЛОЖЕНИЕ I
cos
j.j'
где
B.17)
' '¦"'
Б. НЕЛИНЕЙНЫЕ ИСТОЧНИКИ, ЗАВИСЯЩИЕ ОТ ?3
Если включить в расчеты члены следующего порядка
теории возмущений, можно найти нелинейные источники
третьего порядка по электрическим полям. Например,
при взаимодействии с системой падающей волны, имею-
имеющей частоту соь возникает поляризация на частоте Зсоь
Это процесс генерации третьей гармоники. В общем
случае мы имеем дело с падающим излучением, являю-
являющимся суперпозицией четырех монохроматических волн,
частоты которых различны и удовлетворяют соотноше-
соотношению coi + юг + соз = М4. Для простоты снова ограничим-
ограничимся электродипольным приближением: exp(±fk-r) = 1.
Квантовомеханическое выражение для фурье-комионен-
ты $i4|L (с частотой м4), пропорциональной ЕгЕ2Ез, име-
имеет следующий вид:
V?L К) = —гг cos (°V + <Рх + ъ + <рз) х
х
((О kg ±
;±»1±0K)@,^±0K)
;
± ш4) (co.,g ± @х ± ш2) (<o;-g ± ю2)
{
,
4) @)/(g ±
. ± ш2)
ПРИЛОЖЕНИЕ I
277
(У/7 • Ез) (^/g • Ei)
± »х ± OK)(»/g ± 0,г)
,
,
• Ез)
± 0L)
0/г ±
j
Е2)
,\г ±
)
(»,.« ± »! ± @я) (O);e ± «з>
• Ез) (У/7 • Е0 (У/g • Е2)
з) (Ш/'« ± Ш1 ± W2) (»/« ± Ш2)
,
("/'в ± »2 ± •>„) (M/g ± »2)
• Е2) (У/7 • Ез) (У/g • Ei)
("Ag Т wa) (w/'g ± wl ± аз) (т/в ± COl)
•Е«)(У/7-Е«)(У/«-Е1)
,
¦ (Ш*в Т Шз) (M/'g ± ^l ± Ш2) (Ш/в ± ml)l '
где для краткости мы воспользовались обозначением
B.19)
± Ш2 ± аз) (шы ±
1
l) (Ш/'в + Ш2
И Т. Д.
Kg + wi) (ч - Ш2 - из) (m/e - и\
Выражение B.19) определяет ty?L (т) как
$L К) ="- cos (<d4* + Ф1 + Фг + Фз) X
X У. v№np К =«! + ©, + ш.) ElmEinEsp, B.20)
т,п,р
где все частоты различны. Компоненты тензора угтпр
не обращаются в нуль в том случае, когда система об-
278
ПРИЛОЖЕНИЕ I
ладает центром инверсии, а волновые функции — хо-
хорошо определенной четностью. В случае симметрии
класса Сг тензор ушпр имеет 3 X 27 компонент. Значения
Y для трех других компонент поляризации (как функции
трех различных полей) получаются из y(wi) с помощью
перестановок, подобных тем, которые используются для
трех волн
у1тпр D=1+2 + 3)= утпр A = 4 _ 2 - 3) =
= Упшр B = 4-1-3)= ур1тп C = 4-1- 2). B. 21)
Различные случаи, когда четыре частоты удовлетво-
удовлетворяют дополнительным соотношениям, удобнее рассмат-
рассматривать отдельно, а не как частные случаи выражения
B.19). Наиболее важное значение имеет случай, когда
(oi = со2 = соз = '/зам. Примем, что поле падающего из-
излучения имеет вид Е = ?'icos(co^ +<pi) + ?2cosCcoi^ +
+ ф2), и вычислим в 5PNLCcoj) член, пропорциональный
С?, а в $NL (coi)—член, пропорциональный Е\ Е2.
Соответствующие выражения имеют вид
NL ^^З^^Зф,) х
х У ,
($л \ Ы ± 3mi) (ft
±
х У
(Wftg T «l)(u/'e ± 2»!) (»/<t ± »!) /'
/_+ 2ф1 — ф2)
At?
X
B.22)
2u)i) (w/g± 3mi)
:±wi)(M/'
:**/- • Е2)
'ji 2
l) ,
)
ПРИЛОЖЕНИЕ 1
270
)
(M*g-wi)
{
,
23)
В. НЕЛИНЕЙНАЯ ИОННАЯ ПОЛЯРИЗАЦИЯ
В предыдущем рассмотрении мы имели дело с поля-
поляризацией SKNL, обусловленной только движением элек-
электронов внутри атомов или молекул. В общем случае
электрическая поляризация системы содержит также
ионный вклад, обусловленный вынужденными колебания-
колебаниями заряженных ионов. Если ионы колеблются в поле,
потенциал которого ангармоничен, они дают вклад в
В случае генерации второй гармоники нелинейная
ионная поляризация вычисляется следующим образом.
Используется упрощенная модель колебаний системы:
заданная молекула рассматривается как совокупность
трех независимых одномерных ангармонических осцил-
осцилляторов. В отсутствие излучения гамильтониан системы
имеет вид
pt
+ .
~2 (V?)—
B.24)
280
ПРИЛОЖЕНИЕ 1
В дипольном приближении взаимодействие системы с из-
излучением описывается гамильтонианом
2 e/iEtit),
где
Е ^^
i=x,y,z
qpi) -т-1
cp2).
Существует два способа вычисления < ф,- > . В од-
одном из них используется теория возмущений четвертого
порядка, в которой матричные элементы гамильтониана
Ж' учитываются один раз, а гамильтониана Жвз —три
раза. В другом способе сначала с помощью Ж' вычис-
вычисляются волновые функции ангармонических осциллято-
осцилляторов до первого порядка по А* [22]. Затем эти возмущен-
возмущенные волновые функции подставляются в выражение
B.17). В результате и в том и в другом случае получает-
получается следующее выражение для той части фх . которая
обусловлена действием Е\ХЕ\Х,
сох)
2ф1) =
тх
?^005B^+29!)
?)
B.25)
К этому выражению мы пришли квантовомеханическим
путем, но точно такой же результат для рассматриваемой
части ф*1" можно получить, пользуясь чисто классиче-
классическим методом вычислений.
Изложим теперь кратко классический расчет и при-
применим его для исследования генерации третьей гармони-
гармоники ангармоническим осциллятором. Квантовомеханиче-
ский расчет в явном виде не производился, но результа-
результаты его были бы почти наверняка идентичны с теми, ко-
которые приведены ниже. Рассмотрим ангармонический
осциллятор, совершающий колебания в направлении х,
описываемый лг-составляющей выражения B.24). Запи-
Запишем классические уравнения движения этого осциллято-
осциллятора в вынуждающем поле ?ixCos(co^ + ф[). Предполо-
Предположим, что решение для х можно представить в виде
х = хг cos (axt -f- фх) ~f- x2cos
-f- Зф
ПРИЛОЖЕНИЕ I
281
Легко найти, что
^LC«1) = e^3@ = ??cos
1
Зф1)
X
X
Так как
'"x
2m
11л-
1
B.26)
для
обычных
f
колебаний
отношение
BA2/mr])[l/(coo* — 4oif)] составляет 10~2— 10~3, если
(Oj — оптическая частота, то в выражении B.26) следует
удержать лишь второй член.
§ 3. Соотношения между величинами, связанными
с макроскопическими полями в нелинейных
диэлектриках
А. ГАЗЫ
Когда оптический показатель преломления близок к
единице, различие между микроскопическим полем, дей-
действующим на отдельную молекулу, и макроскопическим
полем пренебрежимо мало. Такая ситуация точно осу-
осуществляется только в газах. На молекулы действует
электромагнитное поле, описываемое соотношениям»
B.1) и B.3). Эффективная нелинейная поляризация в
элементе объема газа с центром в точке г0 получается п
результате усреднения эффективного дипольного момен-
момента молекулы, описываемого выражениями B.7)—B.10),
по всем заполненным состояниям g, взятым с соответ
ствующим статистическим весом, и умножения на число
молекул N в единице объема. Вводя Дк = kj + к2 — к3
и Дф = ф! + ф2 — фз, получаем для эффективной нели-
нелинейной поляризации в точке г0
7-1 #,<72e3 t (Дк-г„+ДФ)ег (к,.го-й,(+Фа)
C.1)
где Z—статистическая сумма, а [*Д + S8]gg определя-
определяется выражениями B.9) и B.10).
282
ПРИЛОЖЕНИЕ I
Нелинейная поляризация на частоте со3 будет, вообще
говоря, иметь компоненту, параллельную электрическому
полю
? _
C.2)
е
с J
и находящуюся с ним в фазе, и компоненту, параллель-
параллельную полю Е3, но отличающуюся от него по фазе на 90°.
Реактивная компонента поляризации, PNL (co3, реакт.),
находящаяся в фазе с полем, будет изменять эффектив-
эффективную диэлектрическую проницаемость для волны с ча-
частотой со3 на величину Ae^L = PNL (со3, реакт.) qj*^ c-
Активная компонента поляризации PNL (юз, акт.), отли-
отличающаяся по фазе от поля, приводит к нарастанию или
ослаблению интенсивности волны, имеющей частоту со3-
Этот факт имеет первостепенное практическое значение..
Он объясняет генерацию гармоник света, смешение и
т. д.
Выражения B.9) и B.10) учитывают влияние всех
мультипольных моментов молекулы. Так как газ явля-
является изотропной средой, то среднее значение нелинейно-
нелинейного источника окажется равным нулю, если сохранить
только электрические дипольные члены, т. е. если поло-
положить exp(ik-r) равными единице во всех матричных эле-
элементах. Заметим, что для электрических диполей [9f +
-f-89] является действительной величиной. Если, однако,
один из трех матричных элементов соответствует элек-
электрическому квадруполю (или магнитному диполю), а
другие два — электрическим диполям, то между Р^фф
и тремя векторами (аь а2 и линейной комбина-
комбинацией кь к2 и к3) существует связь, описываемая тензором
четвертого ранга. В этом случае [ 91+33] является чисто
мнимой величиной.
Компоненты РЭфф (соз), составляющие прямые углы
с аз, будут создавать (или ослаблять) либо волны с ча-
частотой юз, имеющие то же направление к3, но другую по-
поляризацию, либо волны с частотой соз, имеющие другое
направление к3. Кроме того, компоненты поляризации
с разностной частотой сог—«м будут создавать волны
этой же частоты, но другой поляризации. Эти новые вол-
волны интерферируют со старыми, порождают другие вол-
ПРИЛОЖЕНИЕ 1
283
ны и т. д. Вряд ли оправдано ограничиваться рассмотре-
рассмотрением трех или четырех волн. Тем не менее это можно
сделать, если существует только один набор волн, для
которых Ак = 0 или по крайней мере намного меньше,
чем для других возможных наборов. Хотя вначале могут
возникнуть несколько волн, продолжать нарастать будет
только одна волна, для которой Ак = 0. Для других
волн знак фазового множителя ехр(—iAk-r0) изменится
после того, как эти волны пройдут некоторое расстоя-
расстояние Аг.
В этой точке член PNL (акт.) в выражении B.8) из-
изменит знак, и нарастание сменится ослаблением. Ука-
Указанный процесс будет подробно проанализирован в сле-
следующих параграфах.
Два примера, приводимых ниже, иллюстрируют эти
замечания и показывают, каким образом такие ситуации
могут возникнуть даже в газовой среде. Примем, что
существенны только электродипольные матричные эле-
элементы. В этом случае необходимо учитывать члены до
четвертого порядка по амплитудам электрического поля
qa/c.
Рассмотрим сначала случай, когда на газ действует
сильное постоянное электрическое поле. Для РЭфф в
выражении B.19) можно ограничиться членами до чет-
четвертого порядка. Однако теперь одна из частот, напри-
например o>i, равна нулю. Введем новые обозначения для
частот и полей: Е\ -+EnOci, co2-»-coi, соз->-со2 и
0L-^-0K = СО 1 + 0J ¦
Примем, что все эти поля поляризованы в направле-
направлении х. Учитывая свойства симметрии тензора четвертого
ранга в изотропной среде (усреднение по всем ориента-
циям молекул), получаем из B.19) выражение для
х-компоненты индуцированной поляризации. При усло-
условии, что все три волны распространяются в направлении
г, для нелинейной поляризации находим
PNL (юз) =
[cos (ksz -
®st) cos (Akz -f Аф) — sin (ksz — щ() sin (Akz -f A<p)];
C.3)
2H4
ПРИЛОЖЕНИЕ 1
величина [ ]gg действительна и равна
ft,/'./
где {}hi'j дается соотношением B.19), в котором все
числители положены равными единице и введены новые
обозначения частот. Частоты coi и со2 можно выбрать по
отношению к известным резонансным частотам молекул
таким образом, чтобы за счет линейной дисперсии фазо-
фазовые скорости оказались согласованными
Для других комбинаций частот, например «i—со2, соэ, м2
или юз + соь юз. coi и т. д., фазовые скорости не согласо-
согласованы. В этом случае проблема фактически сводится к
рассмотрению трех линейно поляризованных волн, при-
приведенных выше. Можно выбрать частоты coi и со2 так,
чтобы они были несколько ниже колебательной
полосы поглощения молекулы, например НС1. За-
Затем нужно произвести суммирование в ¦ выражении
C.3) по состояниям ангармонического осциллятора.
Благодаря дисперсии, связанной с колебательным по-
поглощением, может выполняться условие согласования
фаз #i + k2 = ks. Экспериментально согласование мож-
можно облегчить, изменяя давление или вводя примеси
других молекул. Хотя величина нелинейной поляризации
в газе, очевидно, много меньше, чем в конденсированной
среде, линейная поляризация здесь также невелика.
В газе можно обеспечить согласование фазовых скоро-
скоростей на гораздо больших расстояниях. В газе отношение
нелинейной поляризации к линейной, как нетрудно по-
показать, может быть сделано более благоприятным, чем
в конденсированной среде, так как в последней обычно
имеется много атомов или ионов, которые не дают за-
заметного вклада в нелинейность, но обусловливают зна-
значительную часть линейного показателя преломления.
Пусть точка z и начальные фазы волн фЬ ф2 и
фз выбраны так, что Akz + Лф = 0. Тогда нелинейная
поляризация находится в фазе с электрическим полем,
и дает вклад в нелинейную, диэлектрическую проницае-
ПРИЛОЖЕНИЕ I
285
мость. Будем считать амплитуды Е] и Е2 двух световых
волн с частотами coi и со2 фиксированными. В этом случае
мы получим фиксированную амплитуду Pnl(cu3), времен-
временной множитель которой находится в фазе с волной,
имеющей частоту ю3 и амплитуду Е3. Если амплитуда
этой волны изменяется от 0 до Е3, то усредненная по
времени запасенная энергия изменяется из-за нелиней-
нелинейности среды на величину V2PNL(ro3)E3. Множитель '/2
появляется в результате усреднения cos2co3/ по времени.
Поэтому нелинейность вызовет изменение диэлектриче-
диэлектрической проницаемости для волны с частотой со3, если при-
присутствуют волны с частотами а>\ и со2.
Если Akz + Лф = л/2, то нелинейный вклад в диэлек-
диэлектрическую проницаемость отсутствует. В этом случае фа-
фаза нелинейной поляризации отличается точно на 90° от
фазы волны с частотой ю3. Нелинейная поляризация со-
совершает над волной положительную или отрицательную
работу. Работа, совершенная за единицу времени нели-
нелинейной поляризацией вещества над волной, может быть
записана в виде
.). C.4)
период
Вследствие этого амплитуда волны Е3 будет изменяться.
Если вначале имелись две волны и, и и2 и фазовые
скорости были полностью согласованы, Ak = 0, то нач-
начнет нарастать волна с частотой со3 и фазой ф3 = ф2 +
+ Ф1 + я/2. Пока эта фаза сохраняется, реактивная ком-
компонента нелинейной поляризации (равна нулю. Возраста-
Возрастание амплитуды в этом частном случае, а также в общем
случае произвольных начальных амшитуд и фаз и от-
отличных от нуля значений Ak будет рассмотрено в § 5—7.
Обсудим теперь другой пример, к которому легко при-
применить тот же формализм, — генерацию волны третьей
гармоники в газе. Пусть имеется линейно поляризован-
поляризованная волна ?'a:cos(A1z—(ui^). Возникающая гари этом по-
поляризация на частоте ю3 = 3coi дается выражени-
выражением B.26).
В отсутствие постоянного поля четные гармоники не
генерируются. Другие поляризации также отсутствуют.
286
ПРИЛОЖЕНИЕ I
Примем, что пятая гармоника имеет плохое согласова-
согласование фаз. В результате -проблема сводится к взаимодей-
взаимодействию двух электромагнитных волн. Подробные 1решения
для амплитуд и фаз будут даны ;в § 7. Энергетические
соотношения, подобные обсуждавшимся выше, выводят-
выводятся легко. В выражение для свободной энергии единич-
единичного объема газа, на который одновременно действует
волна основной частоты и третья гармоника, линейно по-
поляризованная в том же направлении, входит член, про-
пропорциональный Е\ Еъ. Согласования фаз в принципе
можно достигнуть, используя резонансную дисперсию
вблизи полос поглощения молекул. Если основная часто-
частота выбрана немного меньшей частоты полосы поглоще-
поглощения, то ангармонический осциллятор дает очень большой
резонансный знаменатель. Тогда в соответствии с выра-
выражением B.26) нелинейность будет пропорциональна
?
— @ ?)
~3
Б. ИЗОТРОПНЫЕ И КУБИЧЕСКИЕ
КОНДЕНСИРОВАННЫЕ СРЕДЫ
В конденсированной среде каждый атом или ион / на-
находится в действующем поле Еюс, которое отлично от
поля Е, входящего в уравнение Максвелла. Лоренц по-
показал, что в жидкости или в кристалле с кубической
симметрией действующее поле равно
юс— +"^и полн- +~JfU + ^fu • (
Вектор электрической индукции D, входящий в урав-
уравнения Максвелла, есть
D = Е -f 4uPL + 4dPNL. C.6)
Линейную поляризацию можно выразить с помощью
линейной поляризуемости а в виде
РЬ=Л/аЕ1ос. C.7)
Из выражений C.5) и C.7) следует, что
pL __ Na p , JVa 4я pNL __
~ 1 — */anNa ~3~ ~
4я
Е 4-
~1 PNL
ПРИЛОЖЕНИЕ 1
28?
Подстановка этого соотношения в выражение C.6) дает
D = eE + -^-?-47rPNL = eE-f 4ttPnls. C.8)
Отсюда следует важный результат, заключающийся
в том, что эффективный нелинейный источник в (е + 2)/3
раза превышает нелинейную поляризацию, которая оп-
определяется выражением
= ЛфЕ1осЕ1ос =
C.9)
Указанное различие обусловлено энергией взаимодейст-
взаимодействия между нелинейным дипольным моментом, располо-
расположенным в одном узле решетки, и линейным дипольным
моментом, находящимся в другом узле. Присутствие не-
нелинейного дипольного момента в одном узле изменяет
действующее поле и, следовательно, линейный дипольный
момент в других узлах решетки. Это в свою очередь вы-
вызывает изменение электрической индукции. Взаимодейст-
Взаимодействие между нелинейными дипольными моментами, распо-
расположенными в различных узлах, не учтено в выражении
C.9), что допустимо в рамках 'Настоящей статьи, в кото-
которой нелинейность рассматривается как малое возмуще-
возмущение. Как указано во введении, нелинейная часть
в eEia/(WQ—Wn) раз меньше линейной поляризации.
Комбинируя соотношения C.8) и C.9), получаем сле-
следующее выражение для макроскопической нелинейной
восприимчивости:
XNL (со3 = ©! + Щ) = Щ («з = ©1 + '
X
X
s К) 4- 2 еЫ-^2 б(«3) 4- 2
C.10)
Полученное выражение легко обобщить и получить соот-
соотношения более высоких порядков, справедливые для че-
четырех или большего числа волн. Заметим, что для макро-
макроскопических величин х справедливы те же пространствен-
но-'частотные соотношения, что и для микроскопических
величин § [см. B.16)]. Для конденсированных диэлектри-
диэлектриков полностью справедливы те соображения относительно
запасенной энергии и мощности, переданной между вол-
288
ПРИЛОЖЕНИЕ 1
ПРИЛОЖЕНИЕ 1
289
нами, которые были приведены в п. «а» для газов при
условии, что величина PNLS определяется выражением
C.8). С такой оговоркой обсуждение 'Примеров для газов
без изменений применимо к жидкостям и кубическим
кристаллам, обладающим центрами симметрии.
В кубических кристаллах со структурой ZnS, у кото-
которых отсутствует центр инверсии, конечное взаимодейст-
взаимодействие между тремя волнами будет иметь место даже в том
случае, когда сохраняются только электрические диполь-
ные матричные элементы, и на кристалл не действует
внешнее постоянное электрическое поле. Тензор третьего
ранга %ijk имеет отличные от нуля компоненты, если все
три индекса различны (например %Xyz)- В таких кристал-
кристаллах легко генерируется вторая световая гармоника, но
здесь трудно скорректировать линейную дисперсию так,
чтобы достигнуть согласования фазовых скоростей волны
основной частоты и волны на частоте гармоники. Джорд-
мейн [13], а также Мейкер, Терхьюн и др. [14] показали,
каким образом возможно осуществить такое согласова-
согласование для обыкновенного и необыкновенного луча в ани-
анизотропных кристаллах. Более сложные нелинейные связи,
существующие в этих кристаллах, будут рассмотрены
в следующем параграфе. Следует, однако, иметь в виду,
что основные физические идеи остаются при этом не-
неизменными.
В. АНИЗОТРОПНЫЕ КРИСТАЛЛЫ
Общий случай произвольного числа атомов в элемен-
элементарной ячейке кристалла произвольной симметрии можно
исследовать тем же методом. Вместо одной скалярной
поляризуемости и одного скалярного лоренцевского мно-
множителя, равного 4я/3, мы имеем теперь много различных
тензоров, которые обсуждаются в § 9. Приведем здесь вы-
выражения (9.11) и (9.13), которые понадобятся нам
в дальнейшем:
Макроскопическая нелинейная восприимчивость
C.11), очевидно, удовлетворяет тем же пространственно-
частотным перестановочным соотношениям B.16), кото-
которые справедливы для отдельных микроскопических не-
нелинейных поляризуемостей pW. Тензоры второго ранга N
определены в § 9.
Заметим, что тензор третьего ранга макроскопической
нелинейной восприимчивости обладает свойствами точеч-
точечной симметрии кристаллической решетки в целом, тогда
как индивидуальные нелинейные поляризуемости обла-
обладают свойствами симметрии отдельных узлов решетки.
Это относится и к тензорам более высокого ранга.
Пространственно-частотные перестановочные соотно-
соотношения позволяют найти нелинейную часть средней по
времени плотности свободной энергии диэлектрика
= ~ SdT — PdE.
Эту величину можно определить, тогда как мгновенная
величина свободной энергии не имеет смысла, посколь-
поскольку в среде с дисперсией полная поляризация не опреде-
определяется однозначно полным полем, взятым в данный мо-
момент времени. Нелинейная часть, пропорциональная
EiE2E3, дается интегралом, взятым в девятимерном про-
пространстве от начала координат до точки Еь Е2, Е3:
ЕЬЕ2,Е3
r,NL 1
dEs
(со3 = «1 + со2)
= со, —
Е3Е1
+ dEx • x(col = co3 — co2)
В силу пространственно-частотных
E3E2.
-f
C.14)
перестановочных
соотношений это выражение не зависит от пути интегри-
интегрирования [23]. Имеем
= со,
r,NLS
(ffl3) = X («з = ©i + Щ) ¦ EiE2.
C.11)
C.12)
xPNLS(co2)=
__J_Ei>pNLS(cOi)> C.15)
19 H Бломберген
290
ПРИЛОЖЕНИЕ I
Множитель '/г получается в результате усреднения по
времени. Все величины представляют собой амплитуды.
Нелинейную поляризацию на каждой из трех частот
можно получить, взяв от FNh частные производные по
компонентам Еь Е2 и Е3 соответственно. Для частного
случая, когда имеется только линейно поляризованная
волна основной частоты ?icoscoi/ и линейно поляризо-
поляризованная волна гармоники ?12cos2coi/, можно написать
cNL 1_ у
Г — — 1.
Амплитуды нелинейной поляризации имеют вид
pN
LS
У-Е\.
C.16)
C.17)
Множитель 2 снова введен для того, чтобы получать ам-
амплитуды из усредненной по времени свободной энергии.
Эти соотношения можно легко обобщить на случай, ког-
когда имеется зависимость от четвертой и более высоких
степеней Е.
Плотность энергии поля, обусловленного нелинейно-
нелинейностью среды,равна
= — У Е,.
Р,.^3(реакт.)—1
<=1,2,3
= — 3FNL -f F
•NL
¦ ~2Fm
C.18)
Такое же соотношение справедливо для волны основной
частоты и второй гармоники. Если учитываются члены,
кубические по амплитудам -поля, то усредненная по вре-
времени энергия поля равна взятой с минусом удвоенной
свободной энергии вещества. Для членов четвертого
порядка получается
UNL (Eu Е%, ?а, Et) = -3FNL(EU E2,E3, E4). C.19)
Активные компоненты нелинейной поляризации не дают
вклада в свободную энергию, но, как показывает соот-
прйлоЖеийе i
ношение C.4), они ответственны за произведенную рабо-
работу. Необходимо заметить, что знаки компонент Р с
частотами coi и сог, отличающихся по фазе на 90° от по-
полей Е на тех же частотах, противоположны знаку PNhS
(со3, акт.). Суммарная работа, произведенная недиоси-
пативным диэлектриком над электромагнитными волна-
волнами, равна нулю. То же относится к полной работе, вы-
выполненной волнами над средой,
j Pri|L ^0.C.20)
Период
Период
Эти рассуждения, касающиеся усредненной по време-
времени свободной энергии при наличии трех электромагнит-
электромагнитных волн, можно распространить на случаи, когда имеют
место эффекты, вызванные магнитными диполями и элек-
электрическими квадруполями. Например, для кристалла,
обладающего инверсионной симметрией, усредненная по
времени свободная энергия имеет вид [24]
= E3 • у,?нн (ю3 —
= «з — Щ) '¦ Н3Н2,
C.21)
причем выполняются следующие пространственно-частот-
пространственно-частотные перестановочные соотношения:
= Щ -f Щ) = 7~HjEiH
/E.HjHk
= С03 — С02) И Т. Д.
C.22)
Члены, линейные по Я, отсутствуют, если только опера-
операция обращения времени не является элементом симмет-
симметрии 'кристалла (как это имеет место в ферромагнетиках
и антиферромагнетиках).
В настоящей статье мы все время считаем, что типы
колебаний невырождены и линейно поляризованы. Слу-
Случай вырожденных, а также циркулярно поляризованных
типов колебаний, мы не рассматриваем. Когда через изо-
тропное вещество проходит циркулярно поляризованный
свет, то устанавливается направление времени и стано-
становятся важными члены, линейные по Н. Следует отметить.
19*
292
ПРИЛОЖЕНИЕ 1
что нелинейные эффекты, связанные с фарадеевым вра-
вращением, исключены из проводимого нами рассмотрения.
В анизотропных кристаллах с центром симметрии от-
отличные от нуля магнитоэлектрические дипольные члены
самого низкого порядка 'квадратичны по Ё и Н. Эти чле-
члены, вообще говоря, малы, но они могут оказаться важ-
важными при возникновении второй гармоники или взаимо-
взаимодействии между тремя волнами в присутствии большого
статического магнитного поля.
В отсутствие внешнего постоянного электрического и
магнитного поля в кристаллах с центром симметрии ос-
остается еще член, кубический по амплитудам поля. Он
относится « смешанному дипольно-квадрупольному ти-
типу и соответствует вкладу в усредненную по времени сво-
свободную энергию, равному
NL
FNL = k3E3: Q («з =
+ k,E2: Q (co2 =
щ):
: ЕзЕ1
C.23)
§ 4. Связь между электромагнитными волнами
Уравнения Максвелла в нелинейной диэлектрической
среде без потерь можно записать для каждой частотной
компонентЪ1 в виде
V
V
X
X
H
= —
— т
1
с
1
с
dB
dt '
dD
dt
1 de • E
1 с dt '
4л
с
apNLS
dt
D-
D.
1)
2)
Нелинейный источник был определен выше. Уравнение
энергетического баланса можно написать, приравнивая
поток энергии в элемент объема V, ограниченный поверх-
поверхностью а, к сумме изменения энергии, запасенной нели-
нелинейной средой, и работы, выполненной нелинейной поля-
поляризацией над линейной волной с частотой со3,
1 <
lit
Е, х Но • ndo —
8я dt
{Е3 • г (щ) ¦ Е3+
dV. D.3)
ПРИЛОЖЕНИЕ I
293
Все величины в этом выражении действительны и подоб-
подобны соответствующим величинам для частот &>i и сог- Если
уравнения, записанные для трех частот, усреднить по це-
целому числу периодов и сложить, то алгебраическая сум-
сумма последних членов справа обратится в нуль в соот-
соответствии с соотношением C.20). В результате получится
обычное уравнение баланса энергии для диэлектрика
без потерь. Слева имеем полный поток мощности через
поверхность а. Более интересно обсудить вектор Пойн-
тинга и баланс энергии для каждой частоты отдельно.
Рассмотрим волну
Е3 - Re
(z)
= а3р3 (z) cos [k3z
Фз (г)].
D.4)
В линейной среде комплексная амплитуда плоской вол-
волны постоянна. В нелинейной среде эта комплексная ам-
амплитуда будет изменяться из-за взаимодействия с други-
другими волнами с частотами ац и юг- Волновая нормаль взя-
взята в направлении оси г, которая ориентирована
совершенно произвольно по отношению к кристаллогра-
кристаллографическим осям. В анизотропных кристаллах вектор по-
поляризации а3 может составлять некоторый угол с направ-
направлением z. Энергия распространяется в напра-влении
г' в плоскости, определяемой векторами а3 и г, причем
вектор z перпендикулярен а3. Геометрические соотноше-
соотношения между макроскопическими параметрами поля подроб-
подробно рассмотрены Борном и Вольфом [25]. Угол между z' и
z обозначен ими через а.
Из выражения D,1) следует, что при ц = 1 магнит-
магнитное поле, перпендикулярное Е и z, равно по величине
1^1 = рз&зса>7 cos а.
Рассмотрим цилиндр, показанный на фиг. 1, ограни-
ограниченный плоскостями z и z + Az и имеющий поперечное
сечение 1 см2. Если выражение D.3) проинтегрировать по
времени по целому числу 'периодов и по пространству
в пределах указанного цилиндра, то получим
4пю.,
C0S2
г_ D _ 5)
294
ПРИЛОЖЕНИЕ 1
Подставляя сюда вместо PNLS выражение C.12), прихо-
приходим к дифференциальному уравнению для амплитуды
волны с частотой со3
2 /~ „М| ллч
cos2 a3
dz V2
Обозначение для разности фаз между тремя волнами да-
дано в § 3. Здесь сделано предположение, что результи-
результирующий вектор к! + к2 направ-
направлен по оси z. Далее мы будем
считать, что фазовые скорости
трех волн почти параллельны
друг другу, за исключением
случая точного согласования
ki -J- k2 = k3, когда волновые
векторы могут иметь произ-
произвольные направления. Эффек-
Эффекты, возникающие из-за неболь-
небольшого рассогласования фазовых
скоростей вдоль направлений х
и у, не будут учитываться.
В этом случае лучевые ско-
скорости будут, конечно, также
почти параллельны друг дру-
другу. Физическое взаимодейст-
взаимодействие между пучками света ко-
конечного поперечного сечения
происходит вдоль направления
потока энергии г'. Этот вывод
указывает на важность члена
с (cosa)~2 с физической точки зрения. Он также показы-
показывает, что истинным источником является компонента не-
нелинейной поляризации, параллельная вектору электри-
электрического толя. Существует, конечно, другая волна, также
распространяющаяся вдоль оси гя имеющая иной вектор
поляризации аз . Примем, что фазовая скорость этой вол-
волны сильно рассогласована, Ak'~^> Ak. Поэтому мы не бу-
будем учитывать эту волну, равно как и волны других
частот.
В уравнении D.6) не учитывается влияние реактивной
компоненты PNLS, -которая изменяет фазу <p(z). Пред-
Предz +Az
Фиг. 1. Распространение
света в анизотропном кри-
кристалле.
Нормаль к поверхности волно-
волнового фронта направлена по оси
г, поток энергии идет в на-
направлении распространения лу-
луча г'.
ПРИЛОЖЕНИЕ 1
295
ставляет интерес произвести полный учет влияния
несколько другим способом, исходя из волнового уравне-
уравнения. Для Е3 и P3NLs используем комплексные обозначе-
обозначения в соответствии с выражением D.4). Это, безусловно,
можно сделать после того, как выполнена нелинейная
операция нахождения действительных значений актив-
активной и реактивной компонент PNLS(w3). Комбинируя
уравнения Максвелла D.1) и D.2), получаем волновое
уравнение с нелинейным источником
VxVxE + -!-^==_i^^lS. D.7)
с2 Ж2 с дП У '
Если приравнять левую часть этого уравнения нулю,
то мы будем иметь однородное уравнение, которому в ли-
линейной среде удовлетворяет волна D.4), где A(z) —по-
—постоянная величина. Неоднородное уравнение может
быть удовлетворено, если A (z) удовлетворяет другой
системе дифференциальных уравнений, получающейся
в результате прямой подстановки. В физически реали-
реализуемых ситуациях относительное изменение амплитуды
на расстоянии, равном длине волны, мало, так как нели-
нелинейная восприимчивость очень мала по сравнению с ли-
линейной частью. Поэтому можно пренебречь членами
с второй производной от амплитуды d2A/dz2 <С kdAjdz.
Умножая уравнение D.7) скалярно на а3 и подставляя
вместо Е выражение D.4), получаем дифференциальное
уравнение для комплексной амплитуды
+ 2а3 • (VA,) X [V х
4яш,
<¦ (*¦+*•)г-М
Это уравнение можно преобразовать следующим об-
образом:
+ 2а3 х [V х aselk'z-^} . V4
X
с2
dz'
JAkz
D.8)
296
ПРИЛОЖЕНИЕ I
Компонента Е, взятая в направлении другого вектора
поляризации, подчиняется такому же уравнению, но с
большим значением Ak. Третью компоненту Е удобнее
всего найти из условия
V- D =- V- E-f 4ttV.
PNLS =
Если взять производную от уравнения D.8) по направле-
направлению волновой нормали и найти действительную часть, то
в результате снова получим уравнение D.6). Аналогич-
Аналогичные дифференциальные уравнения можно вывести для
Ai(z) и А2(г). Заметим, что для получения /^exp (ia>it)
надо скомбинировать А3ехр (i®3t) с А г ехр (—гсогО-
и т. д. Пространственно-частотные перестановочные соот-
соотношения позволяют ввести действительную постоянную
Л = — а3 • х (а>3): a,a2 = — а2 • х («г): а^ =
2л - , ч - -
и система уравнений для амплитуд принимает вид
dz
dA\
" dz'
dA9
dz
j
ki cos2 at
i cos2 a2
ka cos2 а3
Л'
D.9)
Аналогичным образом получаются уравнения, описываю-
описывающие изменения амплитуды и фазы второй гармоники,
взаимодействующей с основной волной
dA*
dz
dz
cos2
k2 cos2 a3
i B4,-A,) г
D.10)
Эти уравнения можно обобщить на более высокие
степени амплитуд поля. Например, амплитудные уравне-
ПРИЛОЖЕНИЕ I
297
ния, описывающие генерацию третьей гармоники, имеют
вид
dA]
dz
\ca\aV Cfti-
+ С'А\А1А\-\-С"А\АйА\],
dAs , Им2
dz
k3 cos2 a3
где постоянная С равна
2Я А / -Ч А А
х (юз =¦- «1 + «1 + «i): а1а]а1
с2
D.11)
= -^-3i ' X"К = шз — Ш1 — °>i) '¦ k^i- D.11а)
Входящий сюда тензор четвертого ранга х' выражается
через нелинейную поляризуемость у' более высокого по-
порядка, которая определяется из соотношения B.22). Ве-
Величины С, С" и С" можно связать с нелинейной поляри-
поляризуемостью аналогичным способом. Они входят в члены,
чисто реактивные по своей природе. Из обозначений яс-
ясно, что, например, член С"А\ А3Аз= dAi /dz соответст-
соответствует вкладу, вносимому в когерентное рассеяние кван-
квантовым процессом, в «отором фотоны с частотами coi и юз
рассеиваются одновременно. Поток мощности при этом
не изменяется. Действительно, эти реактивные члены опи-
описывают низкочастотный эффект Керра. Постоянная рас-
распространения волны с частотой юз изменяется под влия-
влиянием члена, пропорционального Споот?'пост аналогично
тому, как она изменяется под действием члена C"AxAi -f-
+ С'"А3А* Этот вопрос будет обсуждаться в §7.
Генерирование третьей гармоники является частным
случаем взаимодействия между четырьмя электромагнит-
электромагнитными волнами. Если, например, для них справедливы
следующие соотношения между частотами и волновыми
векторами:
Ak =
<! —к4,
298
ПРИЛОЖЕНИЕ I
то система амплитудных уравнений имеет вид
; Лп ;.,2 4
dAt _
dz ki cos2 a,
j л* -2/-.
a An (WnC.
dz
, cos2 a2
4
^4*2
dz
cos2 a3
-^U2^4e''Afe —
.-,,2
k3 cos2 a3 ?
dz
A
&4 cos2 a4
life , i»\
e -f
cos2 a4
Снова в правую часть входят чисто реактивные члены,
соответствующие эффекту Керра.
Некоторые интегралы этих комплексных амплитуд-
амплитудных уравнений можно пюлучить сразу же, умножая урав-
уравнения соответственно на А\, Л2, Аз и А а и добавляя ком-
комплексно сопряженные выражения. Правые части стано-
становятся (равными. Заметим, что составляющую вектора
Пойнтинга вдоль волновой нормали можно записать
в виде
ccosctl
l(E,x
D.13)
аналогичные соотношения получаются и для других час-
частот. Таким методом получаются соотношения Мэнли —
Роу [26], хорошо известные в теории параметрических
усилителей [19]. Величины
cos a
cos ai
г
cos аг
cosa3
D.14)
ПРИЛОЖЕНИЕ 1
299
I Si
cos ax
-IS,
cos a4
сохраняются в процессе взаимодействия. Физическая ин-
интерпретация заключается в следующем. Если число кван-
квантов, проходящих через 1 см2 волнового фронта в 1 сек
в волне с частотой соь увеличивается на некоторое коли-
количество, то число квантов .в волне с частотой ац также
увеличивается на то же количество, а в волнах с часто-
частотами со2 и юз уменьшается на ту же величину [27]. Соот-
Соотношения Мэнли — Роу, соответствующие уравнениям
D.9) — D.11), получаются с помощью такого же метода.
Для нахождения полного решения системы нелинейных
дифференциальных уравнений необходимо вернуться
к действительным величинам. Это будет выполнено в сле-
следующих параграфах.
§ 5. Генерация второй гармоники. Точное решение
Используя те же обозначения, что и в D.4), можно
записать комплексные уравнения D.10), описывающие
генерацию второй гармоники, в -виде уравнений для их
действительных и мнимых частей
dpi
dz
kx cos2 сц
dz
cos2 a2
•pip2sinl
pfsinG,
dz
= Ak —
Pf
p2fe2cos2a2
E.la)
E.16)
cose, E.1b)
где 0 = 2ф1 (z) — qJ(z) + Akz и Ak = 2/гг — k% Из пер-
первых двух уравнений получается соотношение Мэнли —
Роу, которое для случая двух волн эквивалентно усло-
условию сохранения потока мощности в диэлектрике без по-
потерь:
W =
E.2)
300
ПРИЛОЖЕНИЕ I
Подставляя уравнения E.1а) и E.16) в уравнение
E.1в), получаем
E.3)
dz ¦ sin 0 dz
Дальнейшее упрощение можно получить с помощью под-
становок
/ r2fe, rns2 ч, \*/г
Pi.
tl —
V —
cos2a2 \':
E.4)
Z.
Уравнения E.1) и E.3) принимают вид
du _
dl
dv о ¦ п
— trsmo,
dQ . cos 6 dln(u*v)
——- = AS -f-
где
sin 0
V,
E.5)
E.6)
1 cos2 ax / \ с2/га cos2
а соотношение E.2) записывается следующим образом:
1=«8 + Л E.7)
А. СОГЛАСОВАННЫЕ ФАЗОВЫЕ СКОРОСТИ .
Когда волны основной частоты и второй гармоники
имеют одинаковые фазовые скорости, т. е. 2&i = k2 и
А? = As = 0, то можно сразу проинтегрировать третье
из уравнений E.5) и получить вторую постоянную инте-
интегрирования
V? (°) Рг @) cos2 <*! cos я2 X
E.8)
ПРИЛОЖЕНИЕ I
301
Из соотношений E.5), E.7) и E.8) получается
— = ±2[у2A — v2J — Г2]'/г, E.9)
где выбор знака « + » или «—» определяется знаком
sin6 для z = 0. Общее решение уравнения E.9) можно
записать в виде эллиптического интеграла
; = -\- - Г ^^—г-. E. Ю)
2 J [v2 A —а2J — Г2] '»
Так как величина v действительна и равна или меньше 1,
то v2 может изменяться лишь между двумя наимень-
наименьшими положительными корнями уравнения у2A —
—и2J—Г2 = 0. Обозначим эти два корня через va и vb,
va =S^ ?>ь. Тогда v колеблется между иа и vb с периодом,
который дается выражением
[о2A — a2J — r2j'/!
E.11)
Типичное решение показано графически на фиг. 2. Част-
Частный случай краевого условия Г = 0 означает, что va =
= 0, vl = 1, Пс -у со. В этом случае интегрирование
выражения E.10) производится элементарно и дает
E.12)
Постоянная интегрирования ^о равна нулю, если при
2 = 0 амплитуда второй гармоники равна нулю, т. е.
р2@) =0. Такое краевое условие часто используется.
Соответствующее решение представлено на фиг. 3. Сле-
Следует иметь в виду, однако, что корректное рассмотрение
граничных условий иа поверхности диэлектрика приво-
приводит к отличному от нуля, но достаточно малому значе-
значению р2@). Для большинства кристаллов величины
cos2ai и cos2a2 близки к единице. Характеристическую
302
ПРИЛОЖЕНИЕ 1
I
g
Q
I
w
0,5
|
о
Q
I
Л,
Ф и г. 2. Изменение относительной мощности волны основной частоты
и волны второй гармоники для произвольных краевых условий.
о
Фиг. 3. Кривые, характеризующие нарастание нормированной амп-
амплитуды волны второй гармоники и уменьшение нормированной амп-
амплитуды волны основной частоты при точном согласовании фазовых
скоростей в случае, когда амплитуда волны второй гармоники на гра-
границе равна нулю.
длину нелинейного взаимодействия / можно
следующим выражением:
L—1 - /Л1
определить
I). E.13)
На этом расстоянии около 75% мощности основной ча-
частоты преобразуется во вторую гармонику.
ПРИЛОЖЕНИЕ I
ЗОВ
Если pi @), т. е. амплитуда волны основной частоты
при 2 = 0 стремится к нулю, то ?0-> °°- Интенсивность
субгармоники мала в системе с бегущей волной. Однако
она может быть существенно повышена за счет обрат-
обратной связи (амплитуда pi при 2 = 0 определяется шума-
шумами). Такой случай рассмотрен Кингстоном [28].
Выражения E.12) справедливы при Pi@)=^0,
Рг(О) ф 0, если выполняется условие фг@) — 2ф[@) =
= ±я/2. При точном согласовании эта разность фаз бу-
будет сохраняться.
Если sin 8@) = + 1, то будет усиливаться вторая
гармоника, если же sin0@) = — 1, то усиливается ос-
основная волна. Когда сначала усиливается основная вол-
волна (?о<0), вторая гармоника уменьшается до нуля, а
затем возрастает до тех пор, пока вся мощность не ока-
окажется сосредоточенной в ней. Когда сначала усиливает-
усиливается вторая гармоника (?о>О), она монотонно растет,
стремясь достигнуть уровня, соответствующего полному
преобразованию мощности.
Если ввести величину
9 9
8
и обозначить третий корень кубического
v2(l— v2J — Г2 = 0 через $ > v\ > vl ,
ние E.10) можно записать в виде
±1
(«*-?
dy
уравнения
то выраже-
E.14)
где
Величина у определяется как эллиптическая функция
Якоби от ?. Нормированные амплитуды и и v можно за-
записать в следующем виде [29]:
г.* —
м» = 1—и2 —
где Со определяется условием при z = 0 [т. е. значением
г/ (O)J и величиной у.
304
ПРИЛОЖЕНИЕ I
Результаты проведенного анализа суммированы на
фиг. 4. Площадь, ограниченная кривыми и2 и у2, опре-
определяет интервал изменения этих величин при разных
О 0,005 0,01 0,015 Г2
Фиг. 4. Зависимость диапазона изменения мощности Д/ в волне ос-
основной частоты и волне второй гармоники при точном согласовании
фазовых скоростей от параметра Г2 [см. выражение E.8)].
значениях Г2. Заметим, что соотношения E.7) и E.8)
дают для максимального значения Г макс =4/27 = 0,143.
Б. НЕТОЧНОЕ СОГЛАСОВАНИЕ ФАЗОВЫХ СКОРОСТЕЙ
Если фазовые скорости волны основной частоты и
второй гармоники согласованы неточно, т. е. Ak Ф 0 и
поэтому АвфО, то уравнения E.5) все же можно проин-
ПРИЛОЖЕНИЕ .'
305
тегрировать методом вариации параметра в решении
однородного уравнения. Таким способом находим более
общее решение
ш2 cos 6 + — Asv2 — IV
о
E.15)
где Гд5 можно выразить через величину Г, которая опрр-
делена соотношением E.8)
Гд, = Г+ ~&sv2@). E.16)
Обобщением выражения E.10) является выражение
o»(oJ»2(l —
О2J
Все сказанное ранее о соотношении E.10) и решениях
для Ak = 0 можно теперь перенести на выражение E.17).
Решения для Ak Ф 0 даются формулами E.13) и E.14)
с тем же определением у2. Три корня vc ^ v ь ^
^ »о ^0 являются теперь корнями уравнения
оаA — у2K — [Г — -As[f2 — у @
= 0. E. 18)
Для важного случая pi@)»p2@) при Akjk, < 1 и
cos a, = cos2a2 « 1 полезны следующие приближения:
Г^^с°Иф2@)-2ф1@)],
E.19)
2^ К/кг) pi @)
E.20)
где / определяется выражением E.13). Корни уравне-
уравнения E.18) можно, вообще говоря, найти графически. Для
простого случая р2@) =0[Г = 0 и и@) =0]
1
v; LAs/4 +
(As/4Jj'
E.21)
20 Н. Бломберген
306
ПРИЛОЖЕНИЕ I
а период дается эллиптическим интегралом
dt
1 sin2 /]
E.22)
Если условие согласования фазовых скоростей при-
приближенно выполнено, т. е.
As;=sA?Z<l, E.23)
то величины vb и Пс, определяемые соотношениями
E.21) и E.22), относительно мало зависят от As и про-
происходит существенное преобразование мощности. На
фиг. 5 приведены соответствующие примеры для не-
нескольких значений рассогласования фазовых скоростей.
При As 3> 1 наилучшее приближение к точному зна-
значению выражения E.17) можно получить, возвращаясь к
уравнениям E.1). Наиболее важным экспериментальным
случаем является неточное согласование, при котором
Р2 всегда остается малой величиной. В этом случае pj
можно рассматривать как интеграл движения.
Если амплитуда второй гармоники при 2 = 0 равна
нулю, то приближенные решения уравнений E.16) и
E.1в) имеют вид
(z) =
2
4Р1
sin
AW
Заметим, что изменение фазы с расстоянием определяет-
определяется величиной Ate/2, а не Д&2. Фазовая скорость волны
второй гармоники, возбуждаемой при 2 = 0 в процессе
нелинейного взаимодействия, не равна скорости одно-
однородной ') волны с частотой 2со. Если, однако, при 2 = 0
вторая гармоника достаточно велика, так что Д&р2@)>
^>pi@)//, то ее фазовая скорость равна фазовой скоро-
скорости волны с частотой 2со
E.246)
(*) = Р2 @) + ~ Рх @) [sin F0 + Ate) - sin 0O],
akl
'' Под однородными волнами понимаются волны, являющиеся
решениями однородного волнового уравнения.—¦ Прим. ред.
ПРИЛОЖЕНИЕ 1
307
Мощность р| (z) имеет период 1/А& независимо от зна-
значения рг@). При0<9<я мощность передается ог
волны с частотой со к волне с частотой 2со. Когда волны
пройдут вдоль 2 расстояние zi/Ak, мощность начинает
передаваться в обратном направлении от волны с часто-
частотой 2со к волне с частотой со. В любом случае мощность
второй гармоники не достигает больших значений. Имен-
Именно этим оправдывается пренебрежение более высокими
О
Фиг. 5. Кривые, характеризующие изменение нормированной ампли-
амплитуды волны второй гармоники р2 при различных величинах рассо-
рассогласования фазовых скоростей.
гармониками в системе амплитудных уравнений. Вообще
фазовые скорости этих гармоник и волны основной ча-
частоты рассогласованы сильнее, чем приблизительно со-
согласованные фазовые скорости волны основной частоты
и второй гармоники. Поэтому высшие гармоники будут
нарастать до амплитуд, много меньших амплитуды вол-
волны второй гармоники.
В. СРЕДА С ПОТЕРЯМИ
Затухание, или потери, можно, конечно, ввести в
уравнения Максвелла D.1) и D.2) и в волновое урав-
уравнение D.7) таким же способом, как это делается в слу-
случае линейной среды. При получении гармоник нужно
принимать в расчет даже очень малые потери, но тем не
20*
308
ПРИЛОЖЕНИЕ 1
менее представляет интерес рассмотреть случай, когда
длина поглощения сравнима или меньше определенной
ранее длины взаимодействия /.
Для диэлектрика с потерями амплитудные уравне-
уравнения E.1) должны быть заменены следующими:
dpi
dz
dz
COS2 <Xi
dz
/e2cos2a2 Pl
cos 6 dln(P?P2)
sin 0 dz
E.25)
Для частного случая Ь{ = b2 = b точное решение можно
найти с помощью подстановок
Для Ak = 0 получаем
E.26)
dy
dR2
dy
kx cos2 аг
cos2
E.27)
dy sin 0
dy
Далее решение ищется, как и в случае среды, без потерь.
Для того чтобы происходило заметное преобразование
мощности, необходимо выполнение условия b < l~l.
§ 6. Три связанные волны. Точное решение
Общие амплитудные уравнения D.9) можно записать
в виде уравнений для их действительных и мнимых ча-
частей, подобно тому, как это было сделано с уравнениями
ПРИЛОЖЕНИЕ I
309
E.1) для второй гармоники
kx cos2 %
dz
k2 cos2 a2
4>lK
p2p3sin8,
in 0,
dz &3cos2a3
1 = "+'
W2 РзР1
з cos2 a2 p2
pip2sin6,
F.1)
P1P2
P3
-^-i^)cose,
^cos2^ px I
где
9 = Akz + ф3 (z) — ф2 (z) — фх (z) и Mi=k3~k2 — kx.
Поток мощности через единицу площади в направле-
направлении, параллельном направлению распространения, равен
8я
p2
р2 ..f.
2
Сделаем следующие подстановки, которые значительно
упрощают дальнейшие расчеты:
COS2
cos2
с =
/ L м
P2>
Ps,
2, 2, 2
F.3)
cos2 aj cos2 a2 cos2 a3
Z.
310
ПРИЛОЖЕНИЕ 1
Уравнения F.1) принимают вид
du, . „
—±- = — UzllRSinV.
^ =-ад sin 9,
ал.
F.4)
du3
dl
= «1«2sin 0,
dl
где AS = Akz\l.
Условие сохранения потока мощности F.2) выража-
выражается соотношением
@,Ы2 + @2«2 + @3«з = L F-5)
Мы можем определить три другие константы ти т2, т3:
2
3'
?, F-6)
т, = м2
т3 = «2 —ы2,
которые представляют собой векторные соотношения
Мэнли — Роу, взятые в направлении распространения.
Последнее из уравнений F.4) можно сразу проинтег-
проинтегрировать; это дает
cos 6 =
Г + :
F.7)
Используя выражение F.7) для исключения sin 0 из
уравнений F.4), получаем
J..2
= ± 2
[(«,«,«,)«- (Г +
. F.8)
Пользуясь соотношениями Мэнли — Роу F.6), находим
4«\ dD)
ПРИЛОЖЕНИЕ 1
311
Уравнение
FЛ0)
имеет три корня для «|; обозначим их и\с ^ ы|
"за ^^- Вводя величину
\с ^ ы|б
4-4а
о о т
6-«за
F.11)
получаем эллиптический интеграл Якоби в стандартной
форме; теперь выражение F.9) можно записать в виде
где
..2
О О
4с-4а
вид
Общее решение для интенсивности трех волн имеет
. Y]
«I (С) = «22 @) + и\ @) - «^ - (и*» - и\а) sn» [(ц|, -
-«УЛ(С + С.),?], F-13)
«? (С) = «? @) +«! @) -«L,-(«326-«L)sn' [(«з2,-
А. ТОЧНОЕ СОГЛАСОВАНИЕ, Ak = 0
Простейший представляющий физический интерес
случай мы получаем, когда pi@) > рг(О) > 0 и рз(О) =
= 0. Это соответствует очень сильной накачке на часто-
частоте ©I, преобразующей сигнал с частотой сог в сигнал с
частотой ©з. Если воспользоваться величинами, входя-
Я12
ПРИЛОЖЕНИЕ I
щими в F.12) и F.13), то для рассматриваемого случая
получаем
,,2 _т ^т — Ы2 -.2 _ Q 2 // 1
«Зс —' ^- ' — "ЗЬ> иЗа ' V nn *¦
Соотношение F.12) можно проинтегрировать непосред-
непосредственно; это дает
u3(C) =m'/« sin (т',Ч). F.14)
Если положить cos2ai = cos2a2 = cos2cc3 = 1, то амплиту-
амплитуда электрического поля оказывается равной
p2@)sini^, F.15)
где длина взаимодействия / рассматриваемого процесса
дается выражением
Г1 = и /Ссо2со3 (AsA:8rVlpi @). F.16)
Для периода изменения энергии имеем в этом случае
Типичное решение представлено на фиг. 6.
При со3 > «г имеется усиление по мощности при пре-
преобразовании фотонов низкой частоты в фотоны более
высокой частоты. Расстояние, на котором достигается
максимальное усиление, обратно пропорционально ам-
амплитуде накачки на частоте coj. Этот случай обычно
встречается в параметрических преобразователях.
Если при 2 = 0 имеется одинаковое число фотонов с
частотой coi и со2 и отсутствуют фотоны с частотой а3, то
решение становится очень простым. Эти краевые условия
эквивалентны следующим равенствам: тх = т2, т3 = 0,
Г = 0. Пространственный масштаб взаимодействия бес-
бесконечен. Числа фотонов с частотой coi и (г>2 убывают с
одинаковыми скоростями
«х = и» = «г @) sch— ,
Таким образом, этот частный случай аналогичен генера-
генерации второй гармоники при точном согласовании.
ПРИЛОЖЕНИЕ 1
313
Если Ш\ ф т2, то передача энергии между волнами
происходит с периодом по ?, равным [ср. соотношения
E.11) и F.9)]
Пс= 2
du3
Когда в одной из волн фотоны исчерпываются, направ-
направление передачи энергии меняется на обратное.
Фиг. 6. Зависимость относительного числа фотонов в трех бегущих
волнах от z при точном согласовании фазовых скоростей ( ©2 = Мз +
+ й)ь k3 = k2 + kx).
Волна с частотой (Oi содержит очень большое число квантов и может рас-
рассматриваться как накачка в параметрическом преобразователе (преобразование
осуществляется либо вверх от еь к е>3, либо вниз от ю3 к (Ог). При г = 0 име-
имеем П3 =¦ 0, П\ = 100 П2.
Рассмотрим теперь другой случай, когда при 2 = 0
в волне с самой высокой частотой оэ3 содержится очень
большое число фотонов, много меньше фотонов имеется
в волне с частотой coi, а фотоны с частотой сог отсут-
отсутствуют, т.е. Ыз@)>«!@), ы2@) = 0. Соотношения
314
ПРИЛОЖЕНИЕ I
Мэнли — Роу [см. F.6)] принимают вид
Таким образом,
«32c = «3@)+"i(°). ":
Усиленный сигнал с частотой
жением F.13) равен
и\ (С) = и\ @) + и§ @)
«2@)
в соответствии с выра-
выра^ uf@)-fu?@) J
Если мы определим длину / соотношением
«з@)(С-С0),
F.17)
F.18)
то выражение F.17) можно переписать в виде
— р32(°) h-
pf @)
F.19)
@). Этот случай
2 », р2@)
где использовано неравенство рз@)
иллюстрируется кривыми на фиг. 7.
Чтобы удовлетворить краевому условию рг(О) = 0,
следует положить zo/l равным половине периода эллип-
эллиптической функции Якоби sn.
Для рз@) > pi@) полупериод можно аппроксимиро-
аппроксимировать выражением [30]
iL^-Lln ll^-l. F.20)
/ 2 ЮзР?@)
Таким образом, максимально возможное значение мощ-
мощности, переданной сигналу с частотой соь достигается на
длине г0, определяемой выражением
1 С п?- it\\
F.21)
f @)
ПРИЛОЖЕНИЕ I
315
а период изменения энергии равен
Интересно сравнить длину z0, необходимую для осу-
осуществления заметной передачи мощности от волны с
частотой соз к волне с частотой соь с длиной, нужной для
Фиг. 7. Зависимость относительного числа фотонов в трех бегущих
волнах от z при точном согласовании фазовых скоростей (»з = Ш2 +
+ а и k + k)
2 i)
Волна с частотой и3 содержит большое число квантов при z — 0 и может рас
сматриваться как накачка параметрического усилителя. При z — 0 имеем п2 —
¦=0, п3 — 20 щ.
получения значительной интенсивности второй гармони-
гармоники на частоте 2соз- Последняя длина приблизительно
равна величине, определяемой соотношением F.18), в
чем можно убедиться, сравнивая это соотношение с вы-
выражением E.13). Таким образом, формула F.20) не-
непосредственно дает отношение указанных пространствен-
пространственных масштабов. Если 16coip^ (О)/со3р2'@) = Ю6, то zo/l
равно приблизительно 7,5. Эффективное преобразование
частоты оказывается задачей, не намного более труд-
трудной, нежели эффективная генерация второй гармоники.
Соотношение F.17) описывает также параметриче-
параметрическое усиление с учетом конечной мощности накачки. Это
316
ПРИЛОЖЕНИЕ I
решение можно, например, использовать для оценки
степени нелинейности усиления.
Если при 2 = 0 числа фотонов в волнах с частотами
со3 и И1 являются величинами одного порядка, изменение
энергии волн с расстоянием снова имеет колебательный
Фиг. 8. Зависимость относительного числа фотонов в трех бегущих
волнах от г при точном согласовании фазовых скоростей.
Волиы с частотами ш, и ш3 содержат одинаковые ло порядку величины коли-
количества фотонов. При z = 0 имеем я2 = 0, П\ — 1,5 Яз.
характер. Когда число квантов в одной из волн значи-
значительно уменьшается, происходит изменение направления
передачи энергии. На фиг. 8 дано решение для краевого
условия м?@) = 1,5 «з2 @). "!(°) = 0.
В этом случае период изменения энергии равен
(т2)
I ,)
duo
где отношение zjt, определяется выражением F.3). Рас-
Рассмотренные случаи иллюстрируют обобщение теории
обычных параметрических усилителей.
ПРИЛОЖЕНИЕ 1
317
Б. НЕТОЧНОЕ СОГЛАСОВАНИЕ
Общее решение F.13) описывает также важный для
эксперимента случай, когда Ak Ф 0. При этом направле-
направление передачи энергии между волнами изменяется на
обратное, когда сдвиг фаз между волнами становится
ю
~As
Фиг. 9. Зависимость отношения максимального числа фотонов с час-
частотой Mi, равного tii макс, к полному числу падающих фотонов
rt@) от As.
При 2 = 0 имеем га3@)//г,@) = 20, л,,@) = 0.
равным 180°. Соображения, высказанные при обсужде-
обсуждении генерации второй гармоники в случае рассогласова-
рассогласования фазовых скоростей, можно полностью применить и
к рассмотрению взаимодействия между тремя волнами.
При сильном рассогласовании получается синусоиадаль-
ное изменение амплитуд, аналогичное описываемому
выражением E.24) и хорошо известное в теории обыч-
обычных параметрических преобразователей бегущей волны.
Влияние рассогласования на процесс с краевым услови-
условием «3@) ~> «i@), м2@) показано на фиг. 9. Максималь-
Максимальное число фотонов, которое можно получить в волне
с частотой СО], ограничивается степенью рассогласова-
рассогласования AS.
318
ПРИЛОЖЕНИЕ I
В. СРЕДА С ПОТЕРЯМИ
Влияние потерь можно учесть в уравнениях F.1) так
же, как они учитывались в § 5 при исследовании задачи
о двух, волнах. Результат заключается в том, что пара-
параметрические эффекты могут проявиться лишь в том слу-
случае, когда «длина затухания» мала по сравнению с ха-
характерной длиной взаимодействия волн с различными
частотами.
§ 7. Четыре взаимодействующие волны. Генерация
третьей гармоники
Уравнения D.12), описывающие общий случай взаи-
взаимодействия четырех волн, и уравнения D.11), относя-
относящиеся только к генерации третьей гармоники, можно ис-
исследовать тем же методом, который использовался в по-
последних двух параграфах для изучения взаимодействия
трех волн и исследования генерации второй гармоники.
Мы отметим только несколько важных особенностей, ко-
которые возникают при обобщении теории на случаи взаи-
взаимодействия более высоких порядков.
Действительные и мнимые части уравнений D.11),
описывающих процесс генерации третьей гармоники,
имеют вид
Эш2Ср,
dz
dpi
dz
dp3 __
dz k3 cos2 <
cos 6
sinfl
¦sin i
cos2
sin I
С
ki cos2 a.
dz
C"
3C"
k3cos2 a3
C"
\ k3 cos3 ct3 kx cos2
G.1a)
G.16)
G.1b)
Единственный эффект, обусловленный существованием в
уравнениях D.11) членов, в которые входят постоянные
С, С" и С", заключается в изменении фазовых скоро-
скоростей двух волн с частотами и и За по сравнению с их
значениями в случае малых сигналов. Это вызвано тем,
ПРИЛОЖЕНИЕ I
319
что средние по времени от Е\ и Е% приводят к эффекту
Керра, пропорциональному квадрату напряженности
электрического поля. Указанное обстоятельство верно
также и в том случае, когда имеется только одна волна,
например с частотой со, распространяющаяся в нелиней-
нелинейной среде. При достаточно больших интенсивностях фа-
фазовая скорость зависит от амплитуды волны.
Пусть фазовые скорости рассогласованы настолько,
что величина Ak больше любого из двух последних чле-
членов уравнения G.1 в). В этом случае можно принять, что
изменение фазы дается выражением
dz dz
Действительно, С имеет тот же порядок величины, что
и С, С" и С", a pi никогда не отличается слишком силь-
сильно от своего краевого значения и может приближенно
рассматриваться как интеграл движения.
Далее обсуждение будет идти точно так же, как оно
производилось при рассмотрении генерации второй гар-
гармоники [описываемой соотношением E.24)]. Если третья
гармоника генерируется при 2 = 0 вследствие нелиней-
нелинейного взаимодействия, то скорость распространения ее
отличается от скорости обычной волны с частотой Зсо.
Решения имеют вид
9~ Акг л JL
2 2
G.2)
rov/ /?3cos2a3 АЛ/2 " . G'3^
Если значение рз(О) достаточно велико, то 9 = Akz +
+ я/2 + 9о и рз определяется интегрированием уравне-
уравнения G.16). Сделаем следующие подстановки:
с2 ki ~ Wi
Pi,
и =
—— COS2 (
v =
- COS2 OCg
3»i(
G.4)
4)v
Я20
ПРИЛОЖЕНИЕ 1
где W — полный поток мощности, аналогичный тому,
который определяется соотношением E.2). Тогда урав-
уравнения G.1) сводятся к системе
du
dz
dv
dz
= и3 sin
As+ctg9
d In(v
аи1
bv2
G.5а)
G.56)
G.5в)
dz ' ' ' ° dz
где a, b, As можно получить непосредственно, если сде-
сделать соответствующие подстановки. Уравнение G.5в)
('.о)
у
можно проинтегрировать; при этом получим
ш3cos9 = Г-f-^ 2!—- 1 !—у2.
Закон сохранения энергии имеет вид
«2 + у2 = 1. G.7)
Подставляя выражения G.6) и G.7) в уравнение G.56),
получаем интегральное уравнение
о"(С)
X
— и2K — v2 Г- (As
G.8)
Если мощность третьей гармоники при 2 = 0 равна нулю,
то у@) = 0 и Г = lU (а—Ь). Решение для v2 будет ос-
осциллировать между двумя корнями уравнения
|\L(As + a)+l(&-a)u2]2) = 0. G.9)
Один из корней уравнения G.9) v2 = 0, что является
нижним пределом и2. Следующий корень будет меньше
единицы, если только не имеет места равенство а = b =
= As. Физически это означает, что нельзя согласовать
фазовые скорости двух волн, если не выполняется ука-
указанное равенство. Так как р? и р| изменяются, то под
влиянием квадратичного эффекта Керра меняются фазо-
ПРИЛОЖЕНИЕ I
321
вые скорости двух волн. Без точного согласования фазо-
фазовых скоростей нельзя осуществить полную передачу
мощности от волны с частотой со к волне с частотой За.
Однако эти соображения носят чисто академический ха-
характер, так как указанный процесс начинает играть су-
существенную роль лишь после того, как возникнет доста-
достаточно интенсивная волна на частоте гармоники. Для
любых взаимодействий, в которых участвует более трех
волн, имеет место такой же эффект.
§ 8. Применения теории к анализу экспериментальных
ситуаций
А. ГЕНЕРАЦИЯ ГАРМОНИК И СУБГАРМОНИК
В настоящее время наиболее изученным нелинейным
эффектом является генерация второй гармоники. Анализ,
проведенный в § 5, показывает, что в принципе можно
преобразовать всю падающую мощность во вторую гар-
гармонику. Так как для KDP величина %^z составляет
около 10~" ед. CGSE {14], то для амплитуды падающего
излучения pi@) =30 кв/см длина взаимодействия /
[см. E.13)] есть величина порядка 103 см. При согласо-
согласованных фазовых скоростях на пути z — 1 см преобра-
преобразуется только около 10~8 от мощности падающего излуче-
излучения. Конечно, можно значительно увеличить мощность в
импульсе и получить напряженности, достигающие
106 в/см. Но даже и в этом случае требуемое согла-
согласование фазовых скоростей на длине взаимодействия,
конечно, не будет достигнуто для всех лучей, находя-
находящихся в пределах телесного угла, занятого пучком.
Поэтому после того как волны прошли расстояние d =
= n(Ak)~l, необходимо применять схемы фазовой кор-
коррекции.
Сдвиг фаз на 180° в 9 = Akz + 2cpi — ф2 можно полу-
получить несколькими способами. Можно, например, пропус
тить волну сквозь фазовый корректор, изготовленный в
виде пластины из диспергирующего линейного диэлектри-
диэлектрика. С экспериментальной точки зрения более выгодно
пропустить световые волны сквозь другой кристалл KDP,
ориентация которого обратна ориентации первого кри-
21 Н. Бломберген
322
ПРИЛОЖЕНИЕ I
сталла (фиг. 10). В «перевернутом» кристалле знак тен-
тензора восприимчивости третьего ранга и вследствие этого
. ZnS
[по]
еии,)
X
о
X
h
X
X
у.
vwww
Фиг. 10. Три варианта схем, предназначенных для осуществления
фазовой коррекции в случае, когда фазовые скорости волны основной
частоты и второй гармоники согласованы неточно.
а — свет проходит через стопу кристаллических пластинок, каждая из кото-
которых имеет толщину б — 2i(k2 — 2&i)-' и повернута по отношению к предыду-
предыдущей так, что является ее инвертированным отображением. Нелинейная вос-
восприимчивость %Xyz ПРИ переходе ог одяой пластинки к другой меняет знак.
Линейные оптические свойства не изменяются. Эта схема может, конечно,
быть применима также к пьезоэлектрическим кристаллам, симметрия которых
отлична от кубической; б — волиы основной частоты и второй гармоники
испытывают многократные .полные отражения в кристалле толщиной d = (&2 —
—2?i)-'Boi —6j)cos в. При каждом отражении Е, и Е„ испытывают скачок
фазы на 180°, в результате чего произведение ЕаЕ, меняет знак; в — бегущая
волна на частоте (Oi возбуждает резонатор интерферометра, который содержит
нелинейный диэлектрик. Резонатор настроен на частоту оJ и имеет длину / =
¦= яА,2/2<(&2—2А|)~'я. Обратная волна гармоники ие взаимодействует с вол-
волной накачки. Однако при каждом прямом прохождении она имеет фазу, при
которой происходит усиление.
знак константы взаимодействия изменятся на обратный.
Такую фазовую коррекцию можно повторять всякий раз
после прохождения светом в кристалле пути длиной d.
ПРИЛОЖЕНИЕ I
323
Более простой способ получения того же результата за-
заключается в использовании отражения обеих световых
волн после прохождения ими расстояния d. Каждая из
них испытывает при отражении скачок фазы на 180°, в
результате чего АО = 2Аф1—Аф2 изменяется на 180°.
В этом случае меняется на обратное направление свето-
световых волн в пространстве, а не ориентация кристалла.
Другая схема фазовой коррекции заключается в ис-
использовании многократного отражения одного из лучей
света в резонаторе с высокой добротностью Q. Пусть,
например, вторая гармоника отражается, пройдя путь
d = я (Аи)-1, равный расстоянию между пластинами ин-
интерферометра Фабри — Перо. После того как вторая
гармоника вернется назад к передней пластине и снова
отразится от нее, она опять окажется в фазе сама с со-
собой и с падающей бегущей волной основной частоты.
Эффективная длина взаимодействия и к. п. д. преобра-
преобразования возрастают в Q раз. Если резонатор одновремен-
одновременно настроен на основную частоту и частоту второй гар-
гармоники, то его максимальная длина равна d =
= jtQ-'(A&)-'. Когда многократное отражение испыты-
испытывают обе волны, размер резонатора уменьшается, но
выигрыша в максимально достижимой величине коэф-
коэффициента преобразования не получается. Ясно, что очень
сильное увеличение коэффициента преобразования могло
бы привести к почти полному превращению излучения
основной частоты во вторую гармонику. Однако макси-
максимально достигнутая до настоящего времени величина
коэффициента преобразования, судя по опубликован-
опубликованным сообщениям, равна 10~6.
Кингстон [28] показал, каким образом лазерный пучок
может возбуждать резонатор, настроенный на ' частоту
субгармоники. В этом случае вторая гармоника отдает
мощность волне основной частоты. В соответствии с клас-
классическими уравнениями D.10) этот процесс не может на-
начать развиваться при А\ = 0. Колебания с основной ча-
частотой или с частотой субгармоники возникают из нуле-
нулевых колебаний или при спонтанном излучении двух кван-
квантов субгармоники, сопровождающем исчезновение одного
кванта в лазерном пучке. Этот процесс установления ко-
колебаний аналогичен такому же процессу в генераторе с
21*
324
ПРИЛОЖЕНИЕ 1
самовозбуждением, который начинает работать с уров-
уровня шумов. Классические уравнения для комплексных ам-
амплитуд D.9) — D.12) имеют форму, которая позволяет
легко проквантовать их. Важность нулевых колебаний
и квантовых шумов обсуждается в очень интересной
статье Люиселла, Ярива и Сигмена C1]. Их метод можно
применить к нашим уравнениям.
Б. ПРЕОБРАЗОВАНИЕ ЧАСТОТЫ
Аналогичным образом можно рассмотреть фазовую
коррекцию и эффективную длину взаимодействия между
тремя волнами. Важным применением могла бы явиться
генерация миллиметровых волн или далекого инфракрас-
инфракрасного излучения при смешении колебаний двух лазеров,
которое приводит к биениям. Такие биения можно полу-
получить, используя излучение двух рубиновых лазеров,
имеющих разные температуры, или две зеемановские
компоненты излучения одного лазера, находящегося в
сильном магнитном поле. Соотношения Мэнли — Роу
показывают, что при пиковой мощности в импульсе ру-
рубинового лазера, равной 10 Мет, и длительности им-
импульса 10~8 сек можно получить за время этого импульса
мощность порядка 10 кет на длине волны 0,7 мм при ус-
условии точного согласования фазовых скоростей. Коэф-
Коэффициент связи пропорционален %Xyz{®m = (оз — «2)- Эта
величина может значительно отличаться от соответствую-
соответствующей величины для удвоения, потому что в том случае,
когда одна из частот лежит ниже полосы инфракрасного
поглощения, смещения ионов играют более заметную
роль.
Интересная ситуация возникает в том случае, когда
необходимо обнаружить слабый когерентный световой
сигнал с частотой cos. При этом можно воспользоваться
преимуществами параметрического преобразования ча-
частоты вверх с помощью мощного лазерного пучка (на-
(накачки) с частотой Юр. Выходное излучение преобразова-
преобразователя имеет суммарную частоту щ = ios + сор. Если осу-
осуществлено точное согласование фазовых скоростей, то
вся мощность сигнала преобразуется в мощность волны
с частотой со/. Если частота cos находится в инфракрасной
ПРИЛОЖЕНИЕ I
325
области, а сор— в красной, то со/ может соответствовать
зеленой или даже голубой части, что позволяет с боль-
большой эффективностью регистрировать это излучение
с помощью фотоумножителя. Указанное устройство не
обладает шумами в том смысле, что в отсутствие сигнала
не будет и выходного излучения с частотой со/. Шум,
обусловленный спонтанным излучением, отсутствует, так
как кванты излучения накачки не могут самопроизволь-'
но создать квант с частотой со/, иначе будет нарушен
закон сохранения энергии. В указанном смысле такое
устройство лучше лазерного усилителя, у которого эф-
эффективная шумовая температура спонтанного излучения
равна ha Ik, т. е. всегда отлична от нуля. Эффективная
длина взаимодействия в данном случае определяется
соотношением F.16).
В. ЛИНЕЙНЫЙ ЭЛЕКТРООПТИЧЕСКИЙ ЭФФЕКТ
НА НУЛЕВОЙ ЧАСТОТЕ И НА СВЕРХВЫСОКИХ ЧАСТОТАХ
Теория электрооптического эффекта была создана
уже в первые годы существования квантовой механики
[32]. Она содержится в нашей теории как частный слу-
случай, когда одна из частот равна нулю: со3 = (о2 = ы, ац =
= 0. Рассмотрим, например, геометрию, используемую
в кристалле KDP. Постоянное электрическое поле ?Пост
прикладывается по направлению тетрагональной оси г.
Световая волна, линейно поляризованная по оси х, рас-
распространяется в направлении г. Наличие нелинейного ко-
коэффициента связи %Ухг{(лг = со2 + 0) будет приводить
к возбуждению волны той же частоты и с тем же волно-
волновым вектором, линейно поляризованной в направлении у.
Систему амплитудных уравнений можно записать для
этого случая в виде [ср. с уравнением E.1)]
= Кр И ? sin (<р ф)
=-Крх
sin
— Фу).
Они описывают изменение поляризации волны за счет
электрооптического эффекта, происходящее по мере того,
как волна перемещается в направлении г. При обычном
326
ПРИЛОЖЕНИЕ I
описании этого эффекта говорят, что одноосный кри-
кристалл при наложении постоянного поля становится дву-
осным. Нормальные типы поляризации для волны, рас-
распространяющейся вдоль оси z, соответствуют линейным
поляризациям вдоль новых осей х' и у', образующих уг-
углы 45° с кристаллическими осями хну. Постоянные
распространения этих волн отличаются друг от друга
на величину, пропорциональную ^ост-
Рассмотрение электрооптического эффекта представ-
представляет особый интерес в том случае, когда постоянное поле
заменено сверхвысокочастотным. Недавно был предло-
предложен вариант СВЧ модулятора света бегущей волны [33].
Хотя излагаемая теория, строго говоря, в данном случае
не вполне применима, тем не менее ею можно восполь-
воспользоваться для приближенного рассмотрения. В волноводе
может существовать продольная компонента поля СВЧ.
Кроме того, размеры волновода нетрудно подобрать та-
таким образом, чтобы фазовая скорость поля СВЧ Ezm ~
~Ег cos(d)mt¦—k\z), распространяющегося в нем, была
согласована с фазовой скоростью световой волны
?'xcos(co2^ — k2z). Эта волна все еще рассматривается,
конечно, как волна в свободном пространстве.
Развитую теорию нелинейного взаимодействия сво-
свободных волн можно распространить на случай взаимо-
взаимодействия волн в волноводе. Поле СВЧ в модуляторе све-
света можно с полным основанием рассматривать как за-
заданное, так как поток квантов СВЧ намного превышает
поток квантов света. Связь, обусловленная нелинейной
восприимчивостью %у2ж(ыз = ыт + ьъ), приводит к появ-
лению излучения света с суммарной частотой, поляризо-
поляризованного в направлении у (боковая полоса). Конечно,
существует также волна с разностной частотой со4 =
= — coj —(- @2- Поле СВЧ может в свою очередь взаимо-
взаимодействовать с этими боковыми полосами и создавать
дополнительные боковые полосы. Все эти световые вол-
волны приблизительно согласованы по фазовым скоростям,
так как они очень мало отличаются друг от друга по ча-
частоте. В этом случае теория, развитая в настоящей ра-
работе, неприменима. Однако здесь можно использовать
теорию Саймона [34], так как поле СВЧ можно рассмат-
рассматривать как фиксированный параметр.
ПРИЛОЖЕНИЕ I
327
Указанный случай иллюстрирует значение дисперсии
нелинейной восприимчивости. В случае квадратичных
нелинейностей эта величина определяется тремя часто-
частотами. Пространственно-частотные перестановочные соот-
соотношения показывают, что процессы СВЧ модуляции
света и генерации СВЧ в результате биений между дву-
двумя световыми волнами описываются одной и той же по-
постоянной
Хгух К? =
С0„
"/гул- К =
Необходимо, однако, чтобы направление поля СВЧ в том
и другом случаях было одинаковым. Линейные и нели-
нелинейные движения ионов участвуют в обоих процессах
в равной степени. Если все три частоты находятся в ви-
видимой области спектра, то величина X будет заметно от-
отличаться от рассмотренной выше, потому что в этом слу-
случае движение ионов совсем не будет участвовать в про-
процессе. Все это подробно описывается микроскопическими
уравнениями, приведенными в § 2.
Сделаем несколько заключительных замечаний, резю-
резюмирующих изложенную в настоящей работе теорию. Не-
Нелинейные свойства, присущие электронам и ионам, на-
находящимся в атомах, молекулах и конденсированных
средах, можно связать с макроскопическими свойствами
максвелловских полей в нелинейных диэлектриках. Это
позволяет в свою очередь дать подробное описание про-
процессов когерентного нелинейного рассеяния с помощью
макроскопических нелинейных восприимчивостей. Рас-
Рассмотрение взаимодействия между когерентными свето-
световыми волнами приводит к решению, которое указывает
на возможность полного преобразования мощности од-
одной частоты в другие в рассмотренных здесь идеали-
идеализированных случаях. Это решение получено путем обоб-
обобщения теории параметрического усиления. Оно может
использоваться при анализе случая большой мощности
сигнала и холостого излучения, либо большой мощности
одного холостого излучения и учитывает уменьшение в
обоих случаях мощности накачки. Весьма общим спо-
способом выведены соотношения Мэнли — Роу. В связи
с тем, что нелинейные материальные соотношения
328
ПРИЛОЖЕНИЕ I
введены в уравнения Максвелла, теорию можно легко
применить к большому числу различных эксперимен-
экспериментальных ситуаций, в которых существенны нелиней-
нелинейности.
§ 9. Об учете действующего поля в анизотропной среде
Действующее поле на месте г-го атома в элементар-
элементарной ячейке можно записать в виде
Е(/)/ = Е
(<7)
(P
L(/)
NL(/)
),
(9.1)
а поляризации г-го атома на частоте со3 связаны с дейст-
действующими полями на частотах ojj и со2 («з = ft>i + ыг) со-
соотношениями
PNL(/) (щ) = р<г> (ш3 = щ + щ) :Еа;;(ю2) Е(Ш(щ). (9.2)
Здесь U''"> и о"' представляют собой матрицы 3x3. Из
выражений (9.1) и (9.2) можно получить
)/ = а(п ¦ Е
(i) =о(/)
Когда соотношение записывается для одной частоты, то
мы будем опускать обозначение со. Определим теперь
тензор второго ранга
МШ) = 8G-а(г).Ь>. (9.3)
В результате выражение (9.2') примет вид
У М('7) • PL(/) = о(" • Е + PNL(;) - У МШ) • PNL(/). (9. 2")
/ i
Если бы мы записали М<'Л по компонентам, то можно
было бы видеть, что это матрица 3N X 3N, где Л^ есть
число атомов в элементарной ячейке. Ясно, что эта
«сверхматрица» имеет обратную матрицу. Это позволяет
определить новый ряд матриц 3X3 R(i:i), таких, что
R</*> = V
: Miik) =
(9. 4)
ПРИЛОЖЕНИЕ !
329
Теперь можно преобразовать выражение (9.2") и полу-
получить
pL(k) . pNL(ft) _ -^ n(ki) _ a(i) , ? , •yi p(A«) _ pNL(i)
i i
Суммируя по всем атомам в элементарной ячейке, полу-
получаем
ik
Исследование показывает, что
=¦¦= > R a
ik
(9.5)
(9.6)
D (to3) = e (oK) E (ю3)
где
ik
LS(co3),
(9.7)
Запишем PNL<-) (шз) в виде функции тензоров микро-
микроскопической нелинейной поляризуемости и макроскопиче-
макроскопических полей Максвелла с частотами ы\ и сог- Если PNb <C
<С Рь, то выражения (9.1) и (9.2) можно объединить в
виде соотношения
2
(9.8)
Энергетические соображения требуют симметрии тензо-
тензора поляризуемости и тензора Лоренца. При условии
Vi!)=L{ii} = (LUi))r,
где Аг означает тензор, транспонированный по отноше-
отношению к А , соотношение (9.8) можно переписать в виде
]>](М(/0)т-Е(/)'=--Е. (9.8')
330
ПРИЛОЖЕНИЕ 1
Транспонируя выражение (9.4), можно преобразовать
соотношение (9.8') к выражению следующего вида:
р(ЬI _ ^ /р('*)\г . р /Q ОЧ
Комбинируя соотношение (9.9) с (9.7) и (9.2), получаем
pNLS к) -2R (а»)Ш) ¦ р(" ^ = Ы2+Wi('"
X Е (со2)]- 2 [(R
('°
Определим
Тогда PNLS можно записать как
(9.10)
, (9.11)
где (а, 6, с)-компонента X равна
У-а,Ь.е (t°3 = «2+W1) =
=2 2$i,f (Шз = Шг+Wi) ^ю^ ы м." ю- (9-12)
/ rf.e.f
Пространственно-частотные перестановочные соотноше-
соотношения очевидны. Соотношение (9.12) можно записать в тен-
тензорных обозначениях в следующем виде:
X (щ=щ + щ) =2P")(«>8 = ffl2+ffli):N(')(<a3) N^KJN'V)-
(9.13)
§ 10. Заключение
Необходимо подчеркнуть три предположения, кото-
которые были сделаны в изложенной теории:
1. Рассматривались только строго монохроматические
волны, т. е. не принимались во внимание эффекты, обус-
обусловленные конечной шириной спектральных линий взаи-
взаимодействующих волн.
ПРИЛОЖЕНИЕ I
331
2. Рассматривались волны только с точно определен-
определенными волновыми векторами, т. е. не учитывалось влияние
конечной угловой расходимости реальных пучков света.
. 3. Принималось, что дисперсия среды позволяет пол-
полностью пренебречь всеми волнами, за исключением не-
небольшого числа волн с хорошо согласованными фазовы-
фазовыми скоростями. Иными словами, влияние волн с недо-
недостаточно хорошо согласованными фазовыми скоростями
не исследовалось. Эти волны будут слабо взаимодейст-
взаимодействовать с волнами, рассматривавшимися в теории.
Интересно заметить, что нелинейность в принципе по-
позволяет осуществить тепловой контакт между различны-
различными электромагнитными типа,ми колебаний. Нелинейный
диэлектрик без потерь может занять место угольной ча-
частички, введенной Больцманом для обеспечения тепло-
теплового равновесия электромагнитного поля, заключенного
в полость.
Наконец, следует подчеркнуть, что проведенное в на-
настоящей работе рассмотрение ограничено случаем бес-
бесконечной однородной нелинейной среды. Интересные эф-
эффекты, возникающие на границе нелинейного диэлек-
диэлектрика, будут рассмотрены в другой статье').
ЛИТЕРАТУРА
1. Dirac P. A. M., Proc. Roy. Soc., A114, 143, 710. A927).
2. Goepper t-M а у e r >M., Ann. Phys., 9, 273 A931).
3. Frenkel J., Wave Mechanics, Advanced General Theory, New
York, 1934, p. 226.
4. Neugebauer Th., Acta Phys. Acad. Sci. Hung., 10, 221 A959).
5. К 1 e i n m a n D. A., Phys. Rev., 125, 87 A962). (Имеется перевод
в сб. «Лазеры», ИЛ, 1963.)
6. Braunstein R., Phys. Rev., 125, 475 A962). (Имеется перевод
в сб. «Лазеры», ИЛ, 1963.)
7. Hennenberger W. С, Bull. Am. Phys. Soc, 7, 14 A962).
8. Frank en P., Hill A. E., iP e t e r s C. W., W e i n r e i с h G.,
Phys. Rev., Lett., 7, 118 A961).
9. KaiserW, GarrettC. G. В., Phys. Rev. Lett., 7, 229 A961).
10. Hellwarth R. W., в «лиге Advances in Quantum Electronics,
ed. J. R. Singer, New York, 1961, p. 335.
11. McCl ung F. J., Journ. Appl. Phys., 33, 828 A962).
12. Bass iM., Franken P. A., Hill A. E., Peters С W., W e i n-
reich G., Phys. Rev. Lett., 8, 18 A962).
'' См. приложение II.— Прим. ред,
334
ПРИЛОЖЕНИЕ II
приходим к обобщению давно известных законов отра-
отражения и преломления света. Закон зеркального отраже-
отражения света (равенство углов падения и отражения) был
известен еще в античной Греции и точно сформулирован
Героном Александрийским '[7] х\ Законы преломления
Снеллиуса относят к 1621 г.2)
В § 3 настоящей статьи дается обобщение этих зако-
законов для волн оптических гармоник и волн с суммарной
и разностной частотами (для случая, когда на границу
нелинейной среды падают два световых луча). Решение
уравнений Максвелла с надлежащими граничными усло-
условиями приводит к появлению гармоник как в отражен-
отраженном, так и в преломленном свете.
В § 4 определены интенсивность и поляризация воз-
возникающих на границе гармоник. Полученные результаты
можно считать обобщением законов Френеля [9], установ-
установленных в 1823 г. для линейного случая на основе упру-
упругой теории света. В нелинейной теории существует ана-
аналог угла Брюстера для волны гармоники: для этого угла
интенсивность отраженной волны гармоники равна нулю,
если ее электрический вектор Е лежит в плоскости, опре-
определяемой нормалью к границе и волновым вектором от-
отраженной волны.
В § 5 обсуждается нелинейный аналог явления пол-
полного отражение, имеющего место в линейном диэлектри-
диэлектрике. Круг нелинейных явлений, в том числе появление
экспоненциально затухающих волн, оказывается здесь
весьма широким. Ниже будет показано, что полностью
отраженная волна основной частоты может создавать
как отраженную, так и прошедшую волны гармоники,
в то время как две обычные преломленные волны могут
привести к появлению затухающей волны на разностной
частоте.
В § 6 рассматривается плоскопараллельная нелиней-
нелинейная диэлектрическая пластина. Получены выражения
для волн гармоник, возникающих на обеих сторонах пла-
пластины. Существует фундаментальное различие между
') Обширный исторический материал содержится, например, в
книге [8].
2) Теория отражения и преломления света излагается во многих
учебниках по оптике; см., например, [9].
ПРИЛОЖЕНИЕ II
335
случаями падения световых волн на границу со стороны
вакуума или нелинейной среды; напомним, что такого
различия для линейной среды нет.
В § 7 с помощью интегральных уравнений кратко рас-
рассматривается формулировка задачи о распространении
света в нелинейной среде.
Результаты работы обсуждаются в заключении (§ 8).
Теоретические результаты имеют непосредственное отно-
отношение к экспериментальным данным. В частности, реше-
решения, полученные в настоящей работе, характеризуют про-
процесс нарастания амплитуд гармоник, когда основная
волна попадает в нелинейный кристалл.
Прежде чем перейти к обсуждению общих решений,
в § 2 мы рассмотрим простой пример для иллюстрации
основных физических явлений, возникающих на границе
между линейной и нелинейной средами.
§ 2. Гармоники, возникающие на границе
(частный случай)
В качестве примера, позволяющего выявить все су-
существенные физические черты интересующего нас явле-
явления, рассмотрим случай генерации второй гармоники при
падении плоской монохроматической волны с частотой
coi на грань кристалла, не обладающего центром ин-
инверсии. Световая волна будет испытывать в кристалле
обычное преломление. В общем случае двупреломляю-
щих кристаллов возникает два преломленных луча. Во
избежание ненужных усложнений рассмотрим только
один преломленный луч. Такое рассмотрение справед-
справедливо в случае кубических кристаллов (например, ZnS)
или одноосных кристаллов, например дигидрофосфата
калия (KDP), если плоскость падения содержит оптиче-
оптическую ось к падающий луч поляризован в этой плоскости.
Систему координат выберем таким образом, чтобы гра-
граница совпадала с плоскостью z = О, а плоскость паде-
падения— с плоскостью у = 0. Волновые векторы падающей
и преломленной волн обозначим соответственно через
k'j и к[. Последний определяется законом Снеллиуса,
а амплитуда преломленной волны Е^ —законами Фре-
Френеля для линейной среды.
336
ПРИЛОЖЕНИЕ II
Нелинейная восприимчивость среды обусловливает
поляризацию па частотах гармоник, что в свою очередь
приводит к возникновению излучения на этих частотах.
Эффективный нелинейный источник на частоте второй
гармоники «а = 2coi характеризуется величиной
pPNLS = PNLS Bщ) = х К = 2Ш0 : ElElei(k* ги'(). B.1)
Волновой вектор в выражении B.1) равен удвоенно-
удвоенному волновому вектору основной преломленной волны,
ks = 2k[.
Нелинейный источник был введен в работе [6], где пока-
показано, как тензор восприимчивости может быть связан
с нелинейными атомными свойствами среды. Там пока-
показано также, что эффективный нелинейный источник лег-
легко может быть включен в уравнения Максвелла для не-
нелинейной среды:
1 Л..Ц
B.2)
с dt
~~ с ~dt с
дР
,NLS
dt
B.3)
В рассматриваемом случае кубического кристалла
или при специально выбранной пространственной гео-
геометрии величину е можно считать скаляром; кроме того,
будем считать |л = 1. Волны на частоте второй гармони-
гармоники удовлетворяют волновому уравнению
VxVxE2-f
4я
а/а
с2
B.4)
Подчеркнем, что B.4) представляет собой обычное ли-
линейное волновое уравнение, дополненное в правой части
нелинейным источником. Общее решение такого уравне-
уравнения содержит, как известно, решение однородного урав-
уравнения и частное решение неоднородного уравнения •>.
'• Для краткости соответствующие волны называются далее
однородными и неоднородными волнами.— Прим, ред.
ПРИЛОЖЕНИЕ II
337
Er2 = eTele
X p-
X
L (kTJ J
Нг2 = ^(к^хелг)Й2е
B.5)
2co,
p)e
В вакууме решения однородного волнового уравнения
в форме обычных плоских волн имеют вид
Е? -
B.6)
Направления волновых векторов отраженной волны
к% и однородной прошедшей волны к?, векторов по-
поляризации ет и eR и амплитуды отраженной и про-
прошедшей волн Щ и <d? определяются из граничных ус-
условий. Оказывается, что нелинейный источник излучает
в некотором нлправлении обратно в вакуум и в некото-
некотором направлении в среду (в более общем случае анизо-
анизотропной среды—в двух направлениях). Рассматривае-
Рассматриваемая задача очень похожа на задачу об отражении и пре-
преломлении на границе линейной среды, за исключением
того обстоятельства, что здесь роль падающей волны иг-
играет «неоднородная волна» с амплитудой, пропорцио-
пропорциональной PNLS _
Тангенциальные компоненты векторов Е и Н должны
быть непрерывны на всей границе в любой момент вре-
времени. Это требует непрерывности на границе компонент
с частотами coi и 2шь Чтобы эти требования одновремен-
одновременно выполнялись во всех точках границы, следует поло-
положить, что для основной частоты
klx = k\x = k\x.
22 И- Бломберген
338
ПРИЛОЖЕНИЕ 11
Из непрерывности тангенциальных компонент полей вол-
волны с частотой 2@] имеем
оьт t,s u% иг
/Л\х = К2х = К2х = «2л;-
Эти соотношения эквивалентны требованию сохранения
тангенциальных компонент импульсов. При нашем выбо-
выборе системы координат все у-компоненты волновых векто-
векторов равны нулю. Так как абсолютные значения волновых
векторов определяются диэлектрической проницаемостью
= —[е Bы)]1/2 и т. д.,
то из условия сохранения тангенциальных компонент не-
непосредственно получаем углы отражения и преломления
волны второй гармоники
sine? =
? =
i\x
KI
= sin
sin Иг =
sin6s =
-— = e-V. B(o) sinS'.
I
s"I/2 (ш) sin e''.
\ki\
B.7)
Поскольку вакуум не обладает дисперсией, отражен-
отраженная волна второй гармоники распространяется в том же
направлении, что и отраженная волна основной частоты.
В то время как волна нелинейной поляризации распро-
распространяется в том же направлении, что и основная прохо-
проходящая волна, однородная волна с частотой гармоники
будет распространяться,.вообще говоря, в ином направ-
направлении. Волновые векторы обеих волн параллельны либо
в предельном случае точного фазового согласования
e(w) = еB(о), либо в случае нормального падения. Ре-
Решение волнового уравнения B.4) требует дальнейшего
рассмотрения этих предельных случаев, что и будет
выполнено в § 4. Важный вопрос о рассогласовании
фазовых скоростей в направлении, нормальном к направ-
направлению распространения, в работе [6] остался невыяснен-
невыясненным. Этот вопрос будет здесь рассмотрен; рассогласо-
приложеиие и
339
вание определяется как ориентацией границы относи-
относительно осей кристалла, так и дисперсией среды. Гео-
Геометрические соотношения иллюстрируются на фиг. 1.
Вопрос об интенсивности и поляризации волн гармо-
гармоник в этом параграфе будет обсуждаться только для
kRLZw)
'Bш)
Фиг. 1. Падающая, отраженная и преломленная волны с основной
частотой и с частотой второй гармоники вблизи границы между
кристаллом KDP и вакуумом.
Фазовые скорости обыкновенного луча основной частоты и необыкновенного
луча второй гармоники не согласованы.
случая, когда нелинейная поляризация нормальна к пло-
плоскости падения, т. е. р—у. Более общее обсуждение от-
отложим до § 4. Рассматриваемый здесь случай реали-
реализуется в кристалле KDP, когда вектор Е падающей
волны с основной частотой лежит в плоскости падения,
содержащей оптическую ось кристалла. Это следует из
рассмотрения симметрии тензора X • Если прошедшая
волна с основной частотой является необыкновенным
22*
340
ПРИЛОЖЕНИЕ 11
ПРИЛОЖЕНИЕ II
341
лучом, поле Ef будет иметь в общем случае х'- и г'-ком-
поненты. Система координат (х', yf, г) фиксирована по
отношению к кристаллу. Направление оси z совпадает
с оптической осью, а ось у' совпадает с осью у. Так как
единственной отличной от нуля компонентой тензора вос-
восприимчивости является Хх'у'г-, нелинейный источник по-
поляризован в направлении у' = у в соответствии с соотно-
соотношением B.1).
Граничные условия, которые согласуют решения B.5)
и B.6), могут теперь быть удовлетворены выбором волн
гармоник с электрическим вектором, нормальным к пло-
плоскости падения, eT=eR — у. Для случая, которому со-
соответствует фиг. 1, эти волны представляют собой обык-
обыкновенные лучи. Требование непрерывности тангенциаль-
тангенциальных компонент Еу на границе z = 0 приводит к условию
5 2 =
8 Bco) — 8 (со)
B.8)
а непрерывность х-компонент магнитного поля обеспечи-
обеспечивается при выполнении условия
= е1/2 Bco)^cos6r —е1/2 (се) cos 6s X
X
s Bco) — е (со)
B.9)
Амплитуды электрических полей отраженной и прошед-
прошедшей волн гармоник можн*о вычислить, решая уравнения
B.8) и B.9):
sBco)-8(co)
Величина <&\ определяется непосредственно из B.8).
Следует помнить, что полное поле в диэлектрической сре-
среде определяется, конечно, интерференцией между одно-,
родной и неоднородной волнами в соответствии с соот-
соотношениями B.5); полное поле на границе равно ёв. Ум-
Умножая числитель и знаменатель выражения B.10) на
?1/z Bco)cos8r+ e'/2(co)cos 0s и используя законы пре-
преломления B.7), приходим к выражению
или
[81/2Bco)cos0r-j> cosQ^] [81/2Bco)cos0r-f81/2(co)cos9'S]
B.11a)
„,« __ - 4nPHLS sin2 9r sin Qs
sin (е'-ф- er) sin (er-f es) sm;e''
B.116)
Амплитуда отраженной волны оказывается, таким
образом, нечувствительной к рассогласованию фазовых
скоростей в среде; напомним в связи с этим, что в кри-
кристалле KDP обыкновенная волна гармоники и необык-
необыкновенная волна основной частоты не могут быть согла-
согласованы. Можно утверждать, что отраженный луч излу-
излучается слоем толщиной порядка длины волны. Более
глубокие слои полубесконечной среды не дают вклада
в отраженный луч. Это утверждение уточняется в § 6,
где строго рассмотрена диэлектрическая пластина конеч-
конечной толщины. Если величина Е&т ~ 3- 108 в/см соответ-
соответствует типичным межатомным полям, коэффициент пре-
преобразования (по мощности) в отраженную волну
гармоники приближенно характеризуется величиной
( Ет{ I ELr J. Для относительно небольшой плотности
мощности основного излучения, равной 105 вт/см2, эта
величина составляет около 4- 10~10. Поскольку экспери-
экспериментально удавалось зарегистрировать вторую гармони-
гармонику при коэффициенте преобразования, меньшем 1СН2,
отраженная гармоника в этом случае будет легко наблю-
наблюдаться. Отметим также, что сейчас достижимы плотно-
плотности мощности 107 вт/см2 в импульсе (для несфокусиро-
несфокусированного пучка лазера).
Чтобы вычислить угловое распределение отраженной
волны гармоники из соотношений B.11а) и B.116), не-
необходимо рассчитать угловую зависимость самой величи-
величины PNLs Последнее можно сделать, пользуясь форму-
формулами Френеля для линейной среды; они дают определен-'
ную угловую зависимость для амплитуды волны основ--
ной частоты и тем самым для PNLS.
342
ПРИЛОЖЕНИЕ II
Начальная амплитуда прошедшей волны гармоники
имеет почти ту же величину, что и для отраженной вол-
волны. Однако затем прошедшая волна будет нарастать. Де-
Детальный анализ прошедшей волны мы отложим до § 4,
где будет установлена ее связь с решениями, получен-
полученными ранее для бесконечной среды.
Полный поток мощности на границе недиссипативной
нелинейной среды, конечно, сохраняется, так как интен-
интенсивности отраженной и прошедшей волн на основной ча-
частоте будут несколько меньше, чем в случае строго ли-
линейного диэлектрика. Формально это следует из учета
поляризации PNLs (coi), возникающей в результате
взаимодействия между основной волной и волной гармо-
гармоники. Вместе с тем, поскольку преобразование энергии
на границе всегда мало, амплитуду волны основной ча-
частоты с достаточной степенью точности можно рассматри-
рассматривать как фиксированный параметр. Уменьшение энергии
основной волны внутри нелинейного диэлектрика деталь-
детально обсуждалось в работе [6]. Однако учет реакции волн
гармоник на основную волну, к счастью, не обязателен
при анализе явлений на границе нелинейной среды.
§ 3. Общие законы преломления и отражения
Рассмотрим границу (z = 0) между линейной средой,
где распространяются падающая и отраженная волны
(мы будем характеризовать их соответственно индексами
/ и R), и нелинейной средой, где распространяется про-
прошедшая волна (отмеченная индексом Т). Пусть на гра-
границу из линейной среды падают две плоские волны,
Еге V ' ' I и Е2е \ 2 2 >.
В общем случае от границы будут распространяться
волны со всеми суммарными и разностными частотами
m,coi ± т2а>2, где т,, т2 — целые числа. Мы подробно
рассмотрим случай генерации суммарной частоты со3 =
= coi + «г. Это рассмотрение нетрудно распространить
и на случаи генерации разностной и других комбинаци-
комбинационных частот, а также на случай падения на границу
трех или более волн.
ПРИЛОЖЕНИЕ II
343
Геометрические соотношения иллюстрируются на
фиг. 2. Здесь 6', и 02—углы падения двух волн; плоско-
плоскости падения составляют угол <р между собой. Выберем
направления осей х и у координатной системы так, что
<( — hi \
К\ v "v •
Ф и г. 2. Два падающих луча с частотами «i и «2, возбуждающие от-
отраженную волну и однородную и неоднородную прошедшие волны
с суммарной частотой а>з = &>i +a>2, распространяющиеся в глубь не-
нелинейной среды.
Для того чтобы граничные условия удовлетворялись
одновременно во всех точках плоскости z = 0, необходи-
необходимо и достаточно выполнения условия сохранения х- и у-
компонент волновых векторов. Для волны на суммарной
частоте условие сохранения компонент записывается
в виде
*
C.1)
344
ПРИЛОЖЕНИЕ II
Выражение C.1) непосредственно приводит к следующей
теореме: направления распространения неоднородной
волны источника, однородных прошедшей и отраженной
волн с суммарной частотой и нормаль к границе лежат
в одной плоскости. При нашем выборе системы коорди-
координат эта «плоскость отраженной волны с суммарной ча-
частотой» совпадает с плоскостью xz. Аналогичные теоремы
имеют место и для волн с разностной и другими комби-
комбинационными частотами, хотя их плоскости отражения
в общем случае будут различными.
Распространение неоднородной волны с суммарной ча-
частотой, амплитуда которой пропорциональна величине
PNLS (шз), описывается величиной exp[t(k[ -f- k?) -г —
— /((Oi + и2)^]- Угол 8^ между направлением ее распро-
распространения в нелинейной среде и нормалью определяется
выражением
sin Щ =
,s
з —
Волновые векторы к^ и кт2 определяются законами пре-
преломления Снеллиуса для обычного линейного случая.
Условимся, что все углы, составляемые с нормалью
к границе, изменяются в интервале от 0 до л/2, а угол ф
между плоскостями падения волн — в интервале от 0 до
я. Из простых тригонометрических соотношений имеем
kl21' sin2 B2 -+- 2 | k\ | \k\ | sin 6{ sin 62 cos ф. C.2)
Вводя диэлектрическую проницаемость е = &2(со2/с2)~',
перепишем C.2) в виде
sins673 ¦¦¦= F3©3 sin2 G? = efcoi sin2 G'i + efcoi sin2 62 +
+ 2(e?efI/2(Oi(O2sine'isine2- cos ф. C.3)
Верхние индексы R и T относятся соответственно к ли-
линейной и нелинейной средам, нижние индексы — к часто-
частотам. Полезно ввести эффективную диэлектрическую про-
ПРИЛОЖЕНИЕ II
345
ницаемость es для нелинейного источника, определяе-
определяемую соотношением
es sin2 ef = е'з sin2 63 - е? sin2 ef. C.4)
В частном случае совпадения плоскостей падения полу-
получается простое соотношение, весьма напоминающее за-
закон Снеллиуса
(eSI/2sine3r = ^.F?)sinei ±^(г^у1\ш1 C.5)
Знак « + » следует использовать в том случае, когда обе
волны падают по одну сторону от нормали, знак «—» —
в случае, когда они падают с противоположных сторон.
Если линейная среда является оптически более плотной,
чем нелинейная, е^ ~ s| > s[, то sin 63 может ока-
оказаться больше единицы. Этот случай полного отражения
мы подробно обсудим в § 5 после рассмотрения вопроса
об интенсивности и поляризации. Если нас интересует
волна с разностной частотой «в—з= кн — и2, нетрудно за-
записать соотношения, аналогичные C.1) — C.3). Для
краткости приведем лишь соотношение, аналогичное
C.5),
ш-3
sin e/
_б)
Знак « + » следует теперь использовать в том случае, ког-
когда волны падают с прютивоположных сторон от нормали.
Поскольку кч/ю-з > 1, здесь легко осуществляется слу-
случай sin 6^3> 1; при этом отраженная волна с разностной
частотой исчезает. Такая ситуация не имеет аналога
в линейной теории. При е^3 > е^3' Даже если sin б^3 >
т
> 1, существуют две возможности: sin в—3 > 1 и
sin 0^3 < 1- Легко видеть, что задачи, связанные с пол-
полным отражением и прохождением света, в нелинейном
случае более разнообразны; их обсуждение проводится
в§ 5.
Случай генерации второй гармоники, рассмотренный
в предыдущем параграфе, описывается соотношением
346
ПРИЛОЖЕНИЕ II
C.3), если в нем положить 6j = В'2, ф — 0 и s^ = s^ =.
= s^. Вообще говоря, волны с суммарной и разностной
частотами будут отражаться в том же направлении, что
и волны с частотами км и со2, если падающие лучи при-
приходят в одном направлении, а среда не обладает дис-
дисперсией.
Условия сохранения тангенциальных компонент вол-
волновых векторов [см. C.1)] носят общий характер. Они
легко могут быть использованы для определения направ-
направлений распространения волн с комбинационными часто-
частотами более высокого порядка. Эти условия остаются в
силе независимо от того, является ли излучение гармо-
гармоники дипольным (электрическим или магнитным) или
квадрупольным; они справедливы и для анизотропной
среды. В этом случае существуют два направления для
волнового вектора с заданными тангенциальными компо-
компонентами. В общем случае здесь возникнет четыре неодно-
неоднородные волны с суммарной частотой, соответствующие
смешению двух преломленных волн с частотой и, и двух
преломленных волн с частотой оо2. Если линейная среда
также является анизотропной, возникнут две однородные
прошедшие волны (угол преломления 6^) и две отра-
отраженные волны (угол отражения 6j^).
§ 4. Поляризация и интенсивность волн
с комбинационными частотами
В этом параграфе мы ограничимся обсуждением слу-
случая изотропной среды, хотя пример, рассмотренный
в § 2, показывает, что при определенной геометрии все
рассуждения применимы и к анизотропным кристаллам.
Обобщение вычислений на анизотропный случай не вы-
вызывает каких-либо принципиальных затруднений, но при-
приводит к такому усложнению алгебраических расчетов,
что проводить их вряд ли целесообразно.
При расчете поляризации и интенсивности волн с сум-
суммарной частотой соз = coi + и2 мы будем исходить из вы-
выражения для нелинейной поляризации, индуцируемой
в среде
Р К) = X К = ©х + Щ) ¦ ЕТе?<Л ' 2j 3 . D.1)
ПРИЛОЖЕНИЕ II
347
Преломленные волны с частотами ы1 и (о2 выражаются
через падающие волны с помощью формул Френеля и
Снеллиуса; тем самым определена нелинейная поляри-
поляризация на частоте и3- Угловая зависимость величины
Фиг. 3. Волны гармоники на границе нелинейной среды,
ванные нормально к плоскости отражения.
поляризо-
поляризоопределяется прошедшими линейными волнами,
которые можно найти с помощью обычных формул Фре-
Френеля. При анализе угловой зависимости генерации ком-
комбинационных волн следует брать соответствующую вели-
величину для PNLS. Как и в линейном случае, можно неза-
350
ПРИЛОЖЕНИЕ It
вильно отражает начальный этап процесса генерации
гармоники и позволяет корректно сформулировать гра-
граничные условия, используемые в [6] при решении систе-
системы приближенных уравнений первого порядка для ам-
илитуд связанных волн. Отметим, что на начальном эта-
этапе амплитуды волн с частотами И] и оJ постоянны (точ-
(точнее, уменьшаются пропорционально z2).
Следует иметь в виду, что для прошедшей волны по-
поверхности постоянной амплитуды и постоянной фазы не
совпадают. Исключение составляет случай, когда волны
распространяются нормально к границе. В этом частном
случае амплитуды отраженной и прошедшей волн опре-
определяются выражениями
^s (еУ2 + еГГ (ej/s + гТУ, D.9)
гт
Как амплитуда, так и фаза прошедшей волны, рас-
распространяющейся в нелинейной среде, изменяются с рас-
расстоянием.
Б.ПАРАЛЛЕЛЬНАЯ ПОЛЯРИЗАЦИЯ
Волны гармоник с параллельной поляризацией (Еу —
— PyLS = 0) генерируются х- и z-компонентами нели-
нелинейной поляризации. Удобно характеризовать нелиней-
нелинейную поляризацию в плоскости отражения ее величиной
PNls и уГЛОМ а между ее направлением и направле-
направлением волнового вектора ks.
Непрерывность тангенциальных компонент в плоско-
плоскости z = 0 имеет место, как следует из B.5) и B.6) и
фиг. 4, если
ех = —е1 cos eR = s\ cos er +
sin a cos
4kPiJlsoos a sin Qs
es —
у =¦ — eR' ?* = — ег ё ц — es
1/2
sin a
eS eT
¦ D.11)
ПРИЛОЖЕНИЕ It
351
Последний член в D.10) связан с продольной компонен-
компонентой вектора Е. Продольные компоненты векторов D или
Н в этом случае, конечно, равны нулю. Непрерывность
их нормальных компонент на границе автоматически
следует из соотношений C.3), D.10) и D.11). Исключая
из последних двух соотношений величину Ь"|[, для ам-
амплитуды отраженной волны получим
FR
С II =
АлР
-NLS
sin a
— 1
— Г
cos
- + 4 2 cos Q
4-
j/2
cos 6Г -\г г\!2 cos Qs
cos a sin 6S
cos
. cos
D.12)
Используя C.3), преобразуем выражение D.12) к виду
F4 - 4jtf|?LS sin 9s sin 2 6r sin (a + 0r \ Qs)
sin
sin F7
sin
+ 9R) cos F7. - 0R)
D.13)
При точном согласовании фазовых скоростей @s = 6т)
не наблюдается каких-либо аномалий в поведении ин-
интенсивности отраженной волны. В пределе при нормаль-
нормальном отражении (Bs = QT = 9д = 0) выражение D.12)
имеет ту же форму, что и D.9), за исключением отрица-
отрицательного знака. Это различие тривиально и является
следствием условий, принятых на фиг. 3 и 4. В случае
нормального отражения нет различия между параллель-
параллельной и перпендикулярной поляризациями.
Соотношение D.13) указывает на существование угла
Брюстера для комбинационных волн, соответствующего
обращению амплитуды отраженной волны в нуль, ?^ =
= 0. При 0г = я — a — Bs отраженная гармоника пол-
полностью поляризована перпендикулярно плоскости отра-
отражения. Это условие означает, что нелинейная поляриза-
поляризация параллельна тому направлению в нелинейной среде,
для которого распространяющаяся вдоль него волна при
преломлении в линейную среду дает отраженную волну
в направлении 6Д. Физический смысл угла Брюстера со-
352
ПРИЛОЖЕНИЕ II
ПРИЛОЖЕНИЕ II
353
NIS
стоит в том, что нелинейная поляризация не может излу-
излучать внутри среды в направлении, в котором мог бы су-
существовать отраженный луч. Эта интерпретация на пер-
первый взгляд противоречит простому объяснению угла
Брюстера в линейном случае, согласно которому поля-
поляризация не может излу-
излучать в вакуум парал-
параллельно своему собствен-
собственному направлению, что
приводит к условию
9д + 9г = л/2.
Фиг. 5 показывает, как
можно примирить эти две
интерпретации. Поляри-
Поляризацию, индуцированную
падающей из вакуума
волной, мож!но рассмат-
рассматривать как линейный ис-
источник PLS. Этот источ-
источник излучает внутри сре-
среды. Именно таким обра-
образом мы учитываем ди-
пюльное взаимодействие в
решетке и тем самым
вводим в рассмотрение
нелинейную поляриза-
поляризацию. Вместе с тем мы мо-
можем рассматривать пол-
полную поляризацию решет-
решетки, включающую как ли-
линейную, та.к и нелиней-
нелинейную части. Тогда следует
считать, что эта полная поляризация излучает в вакуум;
в результате мы приходим к обычной интерпретации угла
Брюстера: полная поляризация параллельна направле-
направлению отражения.
Резюмируем сказанное. Дипольное взаимодействие,
т. е. лоренцева поправка к действующему полю, должно
учитываться только один раз. Это можно сделать двумя
способами: либо вычислять полную поляризацию и счи-
считать, что она излучает в вакуум, либо рассматривать
Фиг. 4. Волны гармоники на гра-
границе нелинейной среды, поляризо-
поляризованные в плоскости отражения.
Нелинейная поляризация и электриче-
электрическое поле могут иметь .продольные ком-
компоненты.
поле излучения в среде, созданное поляризацией, кото-
которая индуцирована волной в вакууме. Затронутые.вопро-
сы носят чисто семантический характер. Уравнения Мак-
Максвелла, конечно, правильно учитывают дипольное взаи-
взаимодействие в среде. Амплитуду прошедшей волны, по-
поляризованной в плоскости падения, можно получить,
Фиг. 5. Угол Брюстера для линейного и нелинейного отражения.
Полная поляризация ие может излучать в вакуум в направлении отраженного
луча. Источник поляризации не может излучать в среду в направлении векто-
вектора я_т, вследствие чего может существовать луч, отраженный в вакуум.
подставляя pyLS и g^ в B.5); последняя величина
определяется из уравнений D.11) и D.12). С помощью
соотношения D.7) можно опять записать поле, прошед-
прошедшее в нелинейную среду, в виде одной волны, распрост-
распространяющейся в направлении вектора кг, но с амплитудой,
зависящей от расстояния z от границы. Амплитуда элек-
электрического поля прошедшей волны Ет.. будет в общем
случае иметь как продольную, так и поперечную компо-
компоненты. Вводя угол р между полем ?[ и направлением
распространения кг, для поперечной компоненты элек-
электрического поля полной прошедшей волны после некото-
23 Н. Бломберген
354
ПРИЛОЖЕНИЕ II
рых преобразований получаем
ls sin 0s sin 9r sin (a -f 9r + 9S)
E я sin
er sin (9r + 9S) sin (8r + QR) cos Fr - QR)
'sin a sin 9 s cos 9 s Nlq .
1 "NLScosasin F7.-65)
X
er sin (9r 4- 9S)
X ef1 exp UumT'z^s'2 cos 0s — e7-/2cos67-)} +
+ 4KPt]jLS sin a cos (QT — Qs) X
exp j(i»c-l z(&s
cos 6s _ ei/2 cos e^j _
es-er
Первые три члена дают постоянную величину, соответст-
соответствующую граничному значению амплитуды прошедшей
волны; последний член изменяется с расстоянием z
вследствие интерференции между волнами, являющими-
являющимися решениями однородного и неоднородного волновых
уравнений. Для расстояний z, настолько малых, что не
появляется сколь-нибудь заметного рассогласования фа-
фазовых скоростей, интенсивность волны растет пропорцио-
пропорционально г2. Амплитуда волны имеет компоненту, сдвину-
сдвинутую по фазе на 90°:
NLs sinacos(97--95)
'tTZr || .
Для продольной компоненты вектора электрического
поля, параллельной вектору кт, имеем
9s) s'n (вг ~ 9s)}
sin a sin? 8S_ cos a cos^t
ersin(e7.4-es) X
{^eec~lz(eV2coses —e^acoser)). D.15)
Из-за присутствия этой продольной компоненты энергия
в прошедшем луче распространяется в направлении, от-
отличном от направления вектора кт. При точном согласо-
согласовании фазовых скоростей продольная компонента яв-
является постоянной величиной. Электрическое поле в не-
нелинейной среде полностью определяется формулами
ПРИЛОЖЕНИЕ II
3.55
D.14) и D.15) как для случая точного согласования фа-
фазовых скоростей @s = '9г). так и для рассогласования.
Следует помнить, разумеется, что они получены в при-
приближении заданных полей падающих волн. Это прибли-
приближение хорошо удовлетворяется, поскольку вблизи гра-
границы относительные амплитуды комбинационных волн
весьма малы. Вместе с тем полученные результаты мо-
могут быть согласованы с более общими решениями для
бесконечной среды, в которых учитывается обратная
реакция волн с комбинационными частотами на падаю-
падающие волны.
Интересно отметить, что даже в случае чисто продоль-
продольной нелинейной поляризации (а = 0) и точного согласо-
согласования фазовых скоростей Fs = 8г) в среде имеется по-
поперечная волна, однако эта волна не возрастает с рас-
расстоянием. Ее источником является продольная волна
вблизи границы; эта же волна создает и отраженный
луч. Можно также сказать, что нелинейная поляризация
индуцирует линейную поляризацию, которая не является
чисто продольной и может излучать. В случае нормаль-
нормального падения (QT = 6s = 0) излучение от продольной
компоненты нелинейной поляризации полностью отсут-
отсутствует.
В. ДАЛЬНЕЙШИЕ ОБОБЩЕНИЯ И ПРИМЕРЫ
Рассуждения, проведенные в этом параграфе, можно
непосредственно обобщить на случай высших гармоник.
Для этого достаточно определить величину поляризации
pNLs на интересующей нас частоте, появление которой
связано с волнами, падающими из линейной среды.
Уравнения этого параграфа остаются справедливыми,
если углы 6s, бг и бл в каждом отдельном случае опреде-
определены надлежащим образом, как описано в § 3.
Уравнения остаются справедливыми и для поглощаю-
поглощающей среды. В этом случае величины ег и es являются
комплексными: углы 0Г и 6s, вообще говоря, тоже яв-
являются комплексными величинами. Угол отражения, оп-
определяемый формулой C.3), остается действительной
величиной. Темп затухания основной волны и волны гар-
гармоники в среде определяется характеристическими дли-
23*
SSfi
ПРИЛОЖЕНИЕ It
)'/2j
нами, затухания Kj1 и K~
Ks.t = Im [шГ1 (es,r + ies,r)'/j-
В том случае, когда потери в нелинейной среде на рас-
расстоянии длины волны малы (Kh <С 1 или е" -С е'), интен-
интенсивность отраженной волны не изменяется по порядку
величины. Общие выражения D.5) и D.13) могут быть
записаны в отдельности для действительной и мнимой
частей. Из-за потерь в среде амплитуда отраженной вол-
волны гармоники будет сдвинута по фазе относительно ве-
величины fNLS Сама величина f»NLS определяется
световыми волнами внутри среды, которые в свою оче-
очередь сдвинуты по фазе относительно падающей волны.
В качестве примера приведем выражение для амплитуды
отраженной волны с суммарной частотой в случае нор-
нормального падения
ER (Вн = 0) = — 4ttPnls
[е'т (со3)
(ш3)]
т (Щ) + 1гт (щ)]!/2 +
+ -^ [ег ((»!) + ге'г («,)]+ — Wt («2) + teT (©2)]
D.16)
Соотношения такого типа описывают процесс генерации
гармоники вблизи поверхности металла. Если рассмат-
рассматривать плазму, то ее линейная проводимость может
быть выражена через комплексную диэлектрическую
проницаемость, а нелинейные свойства можно описать
с помощью величины PNLS. Эта величина определяется
формулой B.1), в которую должны теперь входить, ко-
конечно, поля внутри металла.
Нетрудно провести обобщение теории на случай, когда
на границу нелинейной среды, кроме волн с частотами
«1 и иг, падает также и волна с частотой и3. Такая за-
задача представляет интерес при рассмотрении усиления
сигнала с частотой юз-
Выведенные уравнения остаются справедливыми, ес-
если ен = гт, т. е. на границе изменяются только нелиней-
нелинейные свойства среды. Экспериментально такая ситуация
имеет место, например, в случае, когда к части кристал-
ПРИЛОЖЕНИЕ II
357
ла, находящейся в области z > 0, приложено сильное по-
постоянное электрическое поле ?ПОСт, тогда как в области
z < 0 это поле отсутствует. Предположим для простоты,
что свет падает нормально к границе. Этот случай, про-
проиллюстрированный на фиг. 6, соответствует идеализиро-
идеализированной геометрии весьма интересного эксперимента по
генерации второй гармоники в кальците, проведенного
Терхыоном и др. [5].
Вакуум
Z = -d
2=0
Фиг. 0. Идеализированная геометрия для случая возбуждения вто-
второй гармоники в кристалле кальцита.
В отсутствие постоянного электрического поля в области г < 0 волна гармо-
гармоники генерируется за счет квадрупольного эффекта; при наложении поля
^поств области 2>0 преобладает дипольное излучение. На границе B = 0)
волны интерферируют.
Основная волна с частотой (оь поляризованная в на-
направлении оси х, возбуждает в кальците волну нели-
нелинейной поляризации. Поскольку этот кристалл обладает
центром инверсии, величина pNLs> описывающая про-
процесс генерации второй гармоники, содержит два члена
PNLS = Q • Ei V Е, + х • Е^Е^. D.17)
Из ненулевых компонент тензоров четвертого ранга
Q и X Для нашего случая представляют интерес компо-
компоненты х'х'х'х', x'x'z'z' и z'z'z'z'. Они приводят к появле-
появлению нелинейной поляризации в плоскости xz. В случае
нормального падения продольная компонента P^ls пе
представляет особого интереса. Для .v-компонепты пели-
358
ПРИЛОЖЕНИЕ II
нейной поляризации имеем
PNxL^iPfs для
Множитель i учитывает тот факт, что оператор гради-
градиента дает сдвиг по фазе на 90°. Нелинейная поляризация
на частоте второй гармоники, индуцированная постоян-
постоянным электрическим полем, сдвинута по фазе на 90° от-
относительно поляризации, индуцированной квадруполь-
пым эффектом. С последним эффектом связана генерация
гармоники в области—d < z < 0. Если на расстояни-
расстояниях ~ d приближенно удовлетворяется условие согласова-
согласования фазовых скоростей, то для амплитуды волны второй
гармоники, падающей на границу z = 0, имеем
Е' Bсо) =
Это выражение содержит волну гармоники, возбужден-
возбужденную при 2 = —d, и нарастающую с координатой волну,
связанную с квадрупольным взаимодействием. Условия
непрерывности для величин Ех и #„ при z — 0, где те-
теперь имеет место скачок нелинейной поляризации PNLS
= p
NLS
_ p
NLS
= _ 0)
приводят к следующему выражению для
электрического поля прошедшей волны:
(.'-'пост/'
амплитуды
El (z > 0)
\4nPf\d-
{ЕПОСТ)}
81/2BM)[81/2BM)+81/2HJ
D.19)
Выражение D.19) показывает, каким образом граничная
волна, индуцированная постоянным электрическим по-
полем, может интерферировать с волной, обусловленной
квадрупольным эффектом в области, где постоянное
электрическое поле отсутствует. С указанной интерфе-
интерференцией, по-видимому, связано то, что в экспериментах
ПРИЛОЖЕНИЕ II
359
Терхьюна и др. [5] минимум интенсивности второй гармо-
гармоники в кальците наблюдался при Епост Ф 0. Вместе с тем
нельзя с полной уверенностью утверждать, что этот ми-
минимум имеет место при взаимной компенсации квадру-
польного эффекта и эффекта, обусловленного постоянным
электрическим полем. Такая компенсация возможна
лишь в том случае, когда однородное поле ?пост действу-
действует на весь объем кристалла. При такой идеальной гео-
геометрии минимум интенсивности гармоники действитель-
действительно должен наблюдаться при ?пост = 0. Наши рассужде-
рассуждения относятся лишь к тому случаю, когда поле ?цост на
границе терпит разрыв, однако подобные же интерфе-
интерференционные явления будут наблюдаться и в тех областях,
где существует градиент постоянного электрического
поля. В § 6 мы проанализируем более сложную модель,
представляющую собой набор плоскопараллельных пла-
пластин с различными нелинейными и линейными свойст-
свойствами.
§ 5. Полное отражение и прохождение
Экспоненциальное затухание (или исчезновение) волн
может иметь место и в недиссипативных средах. Это яв-
явление в линейных диэлектриках называют полным вну-
внутренним отражением [8]. Оно имеет место, если значение
sin 8Г, полученное из закона преломления, оказывается
больше единицы. В целом ряде случаев для нелинейной
среды один или более из углов 9Н, 9s и 9Г можно рас-
рассматривать как комплексные величины, несмотря на то
что диэлектрическая проницаемость является действи-
действительной величиной. В этом параграфе мы рассмотрим
поведение волн с суммарной (оK = o)i + со2) и разност-
разностной (и-з = й1 — оJ) частотами.
Случай А. Углы б[ и б? действительны. Обе па-
падающие волны проходят в нелинейную среду. Нелиней-
Нелинейная поляризация в среде будет возникать обычным об-
образом. Неоднородная волна имеет действительный вол-
волновой вектор, sin 9S < 1. Исследование соотношения C.3)
показывает, что в случае нормальной дисперсии (гз>
> ?1,2 и е3 > 61,г) углы 9'3 и 93 всегда дейст-"
360
ПРИЛОЖЕНИЯ II
вительны. Совершенно иная ситуация возникает для вол-
волны с разностной частотой. Для углов имеем общее выра-
выражение
coi3e-3 sin2 8* 3 - ©i3er 3 sin B7^ = «2e? sin2 В{ +
? sin2 Ql2 — 2co,co2 (e?)!/2 (e?I/2 sin B'i sin '2 cos q>. E.1)
Чем меньше разностная частота <о-з, тем больше вероят-
вероятность того, что волны на этой частоте не будут излу-
излучаться. Эта вероятность особенно велика, если cos ср < О,
т. е. если две падающие волны попадают на границу с
противоположных сторон от нормали и если углы паде-
падения близки к 90°.
Из выражения E.1) следует, что всякий раз, когда
sin 8r или sin 8г больше единицы, волны будут затухать
по экспоненциальному закону (соответственно в линей-
линейной или нелинейной среде). Затухание отраженной
или прошедшей волны с частотой ш-3 характеризуется
следующей зависимостью:
exp [i (k\x — k'2x) x + i (k\y — kl2y) y] X
X exp [
1)
1/2
<в_8С {г%
г].
Зависимость от координат х и у носит колебательный
характер, однако волны затухают в направлении оси
z и существуют лишь вблизи границы в области с разме-
размерами порядка нескольких длин волн. Здесь можно раз-
различать четыре возможности:
1. sin 8s < 1, sin 8т < 1, sin 8H < 1. Это обычная си-
ситуация, которая подробно обсуждалась в предыдущих
параграфах. Все волны распространяются.
2. sin 6s < 1, sin 8г < 1, но sin 8Й > 1. Этот случай мо-
может иметь место для волны с разностной частотой <о-3,
если е_з<е—з . Отраженная волна с частотой (о-3 от-
отсутствует; волна с разностной частотой полностью про-
проходит в среду. Амплитуда прошедшей волны определяет-
определяется соотношениями D.8), D.14) и D.15). Так как
sin20H > 1, величина cos8j( = i(sin20H— 1)'/2является чи-
ПРИЛОЖЕНИЕ II
36/
сто мнимой. Соотношение D.5) можно переписать в
виде
?*=.
sin
sin 9д [ sin'0R'"cosj6rr_+ i (sin2 QR — lI''2 sin 6r
E.2)
Амплитуда отраженной волны сама по себе не пред-
представляет большого интереса, поскольку она быстро за-
затухает при удалении от границы. Комбинируя E.2) и
D.8), получаем, что прошедшая волна сдвинута по фазе
относительно волны нелинейной поляризации. Отсут-
Отсутствие отраженной волны не влияет на нарастающую
часть прошедшей волны.
Подобные же результаты можно получить для случая,
когда прошедшая волна поляризована в плоскости паде-
падения; амплитуды по-прежнему определяются соотноше-
соотношениями D.14) и D.15). Подставляя в знаменатель перво-
первого члена правой части D.14) величину
sin
cos (87-—
sinercoser
убеждаемся, что прошедшая волна сдвинута по фазе от-
относительно величины P^LS. Отсутствие отраженной
волны не влияет на нарастающую часть прошедшей вол-
волны и на продольную компоненту [см. D.15)].
3. sin8s<l, 81п8д<1, sin0r>l. Такая ситуация
имеет место для волны с разностной частотой если
е-з > ?-з . В этом случае величина cos0_3 = t"(sin26—з—
— 1) 1/г является чисто мнимой. Амплитуда отраженной
волны для перпендикулярной поляризации по-прежиему
определяется формулами D.5) и D.13). Эти выражения
легко разложить на действительную и мнимую части,
однако результаты мы не приводим. Здесь имеет место
сдвиг по фазе, так как амплитуда отраженной волны яв-
является теперь комплексной величиной. Отсутствие про-
прошедшей однородной волны не влияет на порядок вели-
величины этой амплитуды.
При этих условиях прошедшая волна все же сущест-
существует, поскольку неоднородная волна распространяется
362
ПРИЛОЖЕНИЕ II
На расстоянии от границы, превышающем несколько
длин волн, прошедшая волна определяется выражением
4яР
,NLS
E.4)
Подобным же выражением описывается волна с парал-
параллельной поляризацией. Здесь не существует согласова-
согласования фазовых скоростей, поскольку при sin8s<l и
sin 0г > 1 должно выполняться условие es — ет > 0. Мы
не получим особой выгоды в том случае, когда es-^-бт,
поскольку при этом неоднородное решение E.4) затуха-
затухает все медленнее и медленнее, если sin 8s < 1.
4. sin 8s < 1, sin бд > 1, sin 8Г > 1 • Здесь не исчезает
лишь неоднородная прошедшая волна. Амплитуда про-
прошедшей волны при удалении от границы снова опреде-
определяется формулой E.4).
Случай Б. Обе падающие волны испытывают пол-
полное отражение, sin8f>l и sin 8 2 > 1 - В этом случае,
который имеет место, когда линейная среда является оп-
оптически более плотной, чем нелинейная, неоднородная
волна всегда исчезает, sinus > 1- Волна нелинейной по-
поляризации экспоненциально затухает при удалении от
границы; однако поляризация на суммарной или раз-
разностной частотах, существующая лишь в поверхностном
слое толщиной порядка одной длины волны, может ге-
генерировать как отраженные, так и прошедшие бегущие
волны. Мы рассмотрим несколько вариантов:
1. sin 8s > 1, sin8T > 1, sin 8д < 1. При этих услови-
условиях волны с суммарной и разностной частотами также
полностью отражаются. Такой случай обычно имеет ме-
место, когда единственная падающая волна с основной ча-
частотой полностью отражается. Для второй гармоники,
например, существует угол 8Г, для которого величина
sin 6гBсо) = [ет'(сп)/ет* Bo))]sin8s больше единицы,
если только нет аномальной дисперсии. Интенсивность
отраженной гармоники вновь определяется формулами
D.5) или D.13), где теперь обе величины cos 8s и cos 6т
являются чисто мнимыми. Здесь будут иметь место фа-
фазовые сдвиги относительно величины pNLS; однако су-
существенно то, что интенсивность отраженной гармоники
ПРИЛОЖЕНИЕ II
363
оказывается величиной одного и того же порядка незави-
независимо от того, испытывает ли падающая волна полное
отражение или проходит в среду. Это дает возможность
генерировать вторую гармонику или гармоники более
высокого порядка при повторных полных отражениях от
поверхностей нелинейного диэлектрика.
2. sin 8S > 1, но sin8r < 1, sin Вд <: 1. Этот случай
имеет место, например, если волна с суммарной часто-
частотой возбуждается двумя полностью отражающимися па-
падающими волнами, попадающими на гр-аницу с противо-
противоположных сторон. Поскольку неоднородная волна бы-
быстро затухает, амплитуды поля отраженной и прошед-
прошедшей волн определяются соответственно выражениями
D.5) и D.2), где величина cos 6s является чисто мнимой.
Точно так же могут быть рассмотрены волны, поляризо-
поляризованные в плоскости отражения.
3. sin 8s > 1, sin 6г < 1, sin 6« > 1. Поскольку из пер-
первого условия следует, что eH(wi и ©г) > er(coi и и2), а из
двух последних — что ед(и3) < ет(ю3), эта ситуация ред-
редко встречается в изотропных средах; она может иметь
место при специальном подборе обыкновенного и не-
необыкновенного лучей в анизотропной среде.
4. sin 8S > 1, sin8r > 1, sin Эн > 1. Этот случай не
представляет большого интереса, поскольку здесь все
волны гармоник являются исчезающими.
Случай В. Величина sin 8s комплексна. Рассмотрим
такие условия, когда одна из падающих волн (напри-
(например, с частотой o)i) проходит, а волна с частотой и2 пол-
полностью отражается. Волна нелинейной поляризации,
возбужденная на суммарной частоте, вновь будет экспо-
экспоненциально затухать при удалении от границы. Прост-
Пространственная зависимость величины ^nls (Из) опреде-
определяется выражением
exp [i(k\x + k'2x)x + i (k\y + k2y)y]
[!(fI/2([)]
X
X exp
X exp
co<
<r'
] x
I)'4
В показателе экспоненциальной функции комплекс-
комплексный множитель стоит теперь и перед координатой г.
36 i
приложение ;i
Можно снова рассмотреть четыре возможности:
1. sin 0Г > 1, sin0« < 1;
2. sin0r<l, sinB«< 1;
3. sin0r< 1, sm0tf> 1;
4. sin0r> 1, sin0«> 1.
Оценка интенсивности отраженной и прошедшей волн
проводится совершенно так же, как в соответствующем
варианте случая Б. Интенсивность прошедшей волны
снова определяется однородной волной, поскольку неод-
неоднородная волна экспоненциально затухает. Для ER и <ЕТ
можно снова использовать обобщенные формулы
Френеля, где величины sin0s и cos 0s теперь являются
комплексными:
cos0s = i<fic~'e2/2(sin20? — lI;2 +(oc"'e!
В более подробных расчетах нет необходимости.
§ 6. Нелинейная плоскопараллельная пластина
Рассмотрим бесконечно широкую пластину М из не-
нелинейного диэлектрика, ограниченную плоскостями z =
= о и z = d и помещенную между двумя линейными ди-
диэлектриками R и Т. Пусть две волны с частотами ю.
и (о2 падают из среды R, z < 0, как схематически изо-
изображено на фиг. 7. Они возбуждают в нелинейной среде
две прямые волны {Еим и Е2,м) и Две обратные волны
(ЕиМ' и Е2,м>). Эти волны, которые могут быть рассчи-
рассчитаны с помощью обычной линейной теории, возбуждают
волну нелинейной поляризации с суммарной часто-
частотой Из-
В общем случае этой волне нелинейной поляризации
соответствуют четыре неоднородные волны
= x exP U (kn + k*x) x + l (ku + hy) У\ X
X
Ei,ME?,A,exp \i(k^
X exp \i (kf,z -
X
(
ПРИЛОЖЕНИЕ II
365
X exp fi (- kt + kt) z] +E,,ME,
.AC
X
-i(k^z + k2,z)z\). F.1)
Следует отметить, что приведенные неоднородные волны
имеют одну и ту же зависимость от координат хну. Гра-
Граничные условия при z = 0 и z = d выполняются для сум-
суммы четырех однородных волн с частотой и3, имеющих
Нелинейная
среда
2=
Волны основной частоты Неоднородные
однородные волны
с частотой ш3
Фиг. 7. Волны в нелинейной плоскопараллельной пластине.
Основные волны Я™ и ЕМ с частотой со, и Е^ и Е^' с частотой и2 возбуж-
возбуждают неоднородные волны с частотой со3 = C0i + a2. В число четырех однород-
однородных волн на частоте со3 входят отраженная ER и прошедшая Е? волны с сум-
суммарной частотой соз.
одинаковую зависимость от х и у. Все эти волны, на-
направления распространения которых лежат в одной пло-
плоскости с нормалью к границе пластины, также показа-
показаны на фиг. 7. Можно снова рассмотреть по отдельности
случаи, когда вектор Е(со3) и нелинейная поляризация
перпендикулярны и параллельны этой плоскости.
Заметим, что существующая в линейном случае сим-
симметрия волн, идущих из среды А в среду В и из среды В
в среду А, в нелинейных средах отсутствует. Если свет
падает на границу со стороны нелинейной среды, он
всегда содержит однородную и неоднородную падаю-
падающие волны, тогда как свет, падающий со стороны ли-
линейной среды, содержит только однородную волну.
Исследование нелинейной пластины представляет
очевидный интерес для множества экспериментальных
задач. Генерация гармоник обычно происходит в пласти-
пластинах из нелинейного вещества. Аналогичная ситуация
366
ПРИЛОЖЕНИЕ It
возникает при возбуждении волн гармоник внутри кри-
кристалла лазера или в интерферометре Фабри—Перо. Хотя
мы подробно рассмотрим лишь волны с суммарной ча-
частотой, описанный метод можно использовать и для рас-
расчета волн гармоник более высокого порядка, волн с раз-
разностной частотой и т. Д. Во всех этих случаях требуется
исследовать только компоненты нелинейной поляризации
[см. F.1)] с соответствующими частотами. Однако дан-
данный здесь метод расчета применим лишь в предположе-
предположении о малости амплитуд генерируемых гармоник. Ампли-
Амплитуды падающих волн с частотами coj и со2 рассматри-
рассматриваются в пластине как фиксированные параметры,
определяемые линейной теорией; нелинейные явления не
приводят к сколь-нибудь заметному их ослаблению.
Нас интересуют в основном волны ?з и ?з , выхо-
выходящие из противоположных сторон пластины. Чтобы не
усложнять без необходимости алгебраические выкладки,
будем рассматривать только одну неоднородную волну,
соответствующую первому члену в правой части выра-
выражения F.1). Такое приближение представляется доста-
достаточно корректным, если линейный коэффициент отраже-
отражения диэлектрика мал, Е\,м<Е\,м, Еъм' <Е2,м- Не
представляет труда обобщить уравнения и на случай
высоких коэффициентов отражения. Этим же методом
может быть исследован случай, когда в среде R имеется
падающая волна с частотой со3. Постоянная распростра-
распространения неоднородной волны опять равна ©зС es/2
Ниже мы опустим индекс 3, так как будем рассматри-
рассматривать лишь величины, относящиеся к суммарной частоте.
При сделанных предположениях граничные условия
для случая перпендикулярной поляризации можно запи-
записать в виде
Еу (г = 0) = Ея = Ем + Ем. + 4uPNLS (es - гм)~\ F. 2)
s {es~EMrle^s, F.3)
= 0)= — еЦ2cosQRER = еЦ2cos9^ (Ем — Ем-) +
+ 4Trsi/2cosesPNLS(8s— ел,), f F.4)
ПРИЛОЖЕНИЕ U
Н
cos
= вд,2 cos QM
2 cos esP
F.5)
где ф8 и фм—фазовые сдвиги соответственно для неод-
неоднородной и однородной волн:
cos 6s;
<ос~
dcos 6^. F.6)
Мы получили систему четырех линейных уравнений, ко-
которая может быть разрешена относительно четырех ам-
амплитуд и фаз.
Комплексные амплитуды отраженной и прошедшей
волн с суммарной частотой определяются выражениями
х
X (cos срм — cos <ps) (eM — es)~l -f
-f ier cos 67- (e]i cos Э^)~ (ем cos Qm sin cps
(
+ / (em2 cos Qm sin (fM — es2 cos 0S sin tps) {eM — es)~l],
F.7)
El = 4t:PnlsD- ' [_ (e^2 cos QR + гУ2 cos Qs) X
X (cosqjjn—cos<ps) (ем—ss)-1 — ier'2cosQr (e1m2cosQm)~1 X
X [e1m2 cos Qm sin фг — exJ2 cos 8s sin ц>м) {&м — ss)~' +
+ / (em2 cos 6msin фл, — es/2 cos 0s sin cps) (ем — es)~v\,
F.8)
где
D — cos срм (8r/2 cos Эг -f eR cos B^J —
— /sin фл* [e«/2sr/2 cos QR cos 8r (s^2 cos 6^)-' -f
]. F.9)
Члены в числителях выражений F.7) и F.8) сгруппиро-
сгруппированы таким образом, что каждый из них остается конеч-
368
ПРИЛОЖЕНИЕ II
{sin
ным при ем-ves (случай полного согласования). Для
этого предельного случая получаем
Е* (ЕМ = г3) = i2nPNLSD~l {code'1 [l ~-e}/2coser X
X (eAi2 cos QM)~l] ehM + sin ум (sr/2 cos QT +
+ eM!2cosQM)(^cosQMy2}, F.10)
ET± (8M==8S) =j27rPNLSn""l"~''PM{sinmMCp.i;2coseJM>)-1 X
X[l-e?
+ «>dc-1[H-ei!/2coseR(eJli2coseJM)-1]}. F.11)
Как прошедшая, так и отраженная волны содержат
члены, пропорциональные толщине нелинейного диэлек-
диэлектрика. В отраженной волне этот член обусловлен прямой
нарастающей волной, отраженной от второй поверхно-
поверхности, где имеет место скачок диэлектрической проницае-
проницаемости. При 8т = 8м скачок отсутствует и этот член ис-
исчезает. В этом случае амплитуда отраженной волны за-
зависит от толщины слоя как sin фм, а фаза определяется
знаменателем D [см. F.9)]. При отражении от полубес-
полубесконечной среды амплитуда отраженной волны меняется
в пределах от нуля до удвоенного значения, определяе-
определяемого выражением D.5). Это нетрудно понять, так как
по мере возрастания толщины диэлектрика все новые
слои диполей начинают играть активную роль и в ре-
результате интерференция приводит как к усилению, так
и к ослаблению волны. Среднее значение амплитуды
для бесконечной толщины составляет ровно половину
амплитуды для оптимальной толщины.
Как и следовало ожидать, амплитуда прошедшей
волны содержит член, пропорциональный толщине слоя;
кроме того, в нее входит граничная волна от первой по-
поверхности. При ел = ем эта волна, естественно, исчезает.
В предельном случае, когда толщина пластины срав-
сравнима с длиной волны, общие выражения F.7) и F.8)
упрощаются
^Е{ ^ ?« « i47:PNLS (codf-1)(8''2cos 6r + гЦ* cos б*).
S F,12)
ПРИЛОЖЕНИЕ II
369
Для тонкой пластины амплитуды волн, распространяю-
' щихся в прямом (прошедшая волна) и в обратном (от-
(отраженная волна) направлениях, оказываются равными.
Интенсивности обеих волн пропорциональны квадрату
толщины пластины, так как все атомы излучают коге-
когерентно. Можно сказать также, что волны гармоник, ге-
генерируемых на передней и задней поверхностях, гасят
друг друга в результате интерференции, обусловленной
скачком нелинейной части восприимчивости %(©з = «м 4-
+ ©г)- Этот эффект аналогичен интерференции в тонких
линейных пленках, обусловленной скачком величины е.
Если коэффициент отражения для основных волн ве-
велик, как, например, в итерферометре Фабри—Перо, то
следует учесть и другое неоднородное решение в F.1).
Алгебраически это сводится к суммированию по индексу
S в F.7), F.8) и в выражениях, описывающих предель-
предельные случаи.
Случай параллельной поляризации может быть рас-
рассмотрен точно таким же образом. Граничные условия
имеют вид
Ех (г = 0) = - ER cos QR = (Ем - Ем-)
— 4tiPnls sin a cos 0s (e* — es) — 4ttPnls cos a sin 0se^',
F.13)
Ez(z = d)=ETcos QT = [EMet9M - Ем-е-*"] cos 6^ -
— 4^" sin a cos 9S (EM — es)~l e"s —
F.14)
F.15)
F.16)
Hy B = 0) = eR'* ER = eM> [EM + EM) -
-l
' sin ass'2 (гм — es) ,
Hy (z = d) = 8r2 ET =
"'e'*s
sin ae1^ (eM - es)"'e'*s.
Для амплитуд отраженной и прошедшей волн полу-
получаем
sin
^ cos 9S — е^г cos 8Г) X
24 II- Бломберген
370
Приложение п
X
(coscpAf — cos<ps) (ем — es) ~Н
X
X (es2 sin фл! cos 9м - eM2 cos 0s sin <ps) (ем — es) +
еУ* sin ws cos 0m — ем cos 0S sin фм) X
.
X (ед,
sin
sin
— cos ro,s) — i
r2 sin
u 1
cos 0m + zm sin фмСОэОт) ,
F.17)
E\ = 4ttPnls'sin airVs [-(eR/2 cos 0s + eK' cos9R) X
Х(со5фЛ1— соэфз) (ем — esj +м i л
X (es2 sin фм cos 6M — ел
_ fcos9R (8s* sin ф5 cos 9^ — eM2 cos 9S sin фл) X
cosOM
)"ig^s [_.8^'2 sin 9S X
X (ем-—
X
где
(Sill
JM
F. 18),
D =-. cos Фм (е^г cos QT -f er/2 cos 9R) - i sin Фм X
X Тем2 cos 9м)-' [ем cos 9R cos QT + (eRer)''2 cos^ 9M
F.19)
Числители в выражениях F.17) и F.18), как и -раньше,
с^рунпированы в члены, которые остаются конечными
при едАея. Для случая точного согласования имеем:
—1 . I/ "Г
¦ ' sin a
Приложение и
371
cos 07
cos 0,
sin
F.20)
(es == гм)
cosO
sin а
(г м2
cos
COS On "I
?L sj
cos9mJ
sin B0m + а) е'*м\ .
F.21)
В пределе, когда толщина пластины сравиима с дли-
длиной волны, соотношения F.17) и F.18) имеют вид
' г
sin 9M cos (9S + a) +
+ cos 9r sin (9S + a)j (s^2 cos QR +er2 cos 0r)~', F.22)
—— sin QM cos (9s + a) —
— cos 9д sin (9S + a) (e^2 cos 9r + s^'2 cos 0R)~'. F. 23)
Обсуждение случая перпендикулярной поляризации,
описываемого «формулами F.10) — F.12), можно прове-
провести аналогично. При параллельной поляризации симмет-
симметрия прямой и обратной волн нарушается.
Отметим также появление угла Брюстера в случае
точного согласования, гм = es. При 29М + a = я отсут-
отсутствует обратная волна, генерируемая в среде. Если, кро-
кроме того, мы подавим отражение прямой волны на второй
гармонике, выбрав ет = ем, то интенсивность отражен-
отраженной волны будет равна нулю. В случае линейной плоско-
плоскопараллельной пластины полное прохождение имеет ме-
место как через переднюю, так и через заднюю границы,
если соблюдены условия Брюстера. В нелинейном же
случае такая симметрия отсутствует.
24*
372
ПРИЛОЖЕНИЕ 11
Физический смысл угла Брюстера можно объяснить
точно так же, как и при рассмотрении полубесконечной
среды. Если направление вектора полной поляризации
(линейной + нелинейной) в среде параллельно направ-
направлению распространения отраженного луча, его амплиту-
амплитуда обращается в нуль. Это можно проиллюстрировать,
рассматривая очень тонкую пленку в вакууме. Если от-
отраженная волна должна отсутствовать, то из условия
непрерывности величин D и Е можно определить полную
поляризацию внутри среды, (D — Е)/4л.
Компоненты этой полной поляризации можно выра-
выразить через PNLS:
pNLS
* = -L—. F.24)
_ pNLS
х,у — г х,у >
Поскольку поляризация PNLS составляет угол 8s + a
с нормалью к границе (нормаль направлена внутрь не-
нелинейной среды М), полная поляризация образует с нор-
нормалью угол ?, тангенс которого в ем раз больше. Условие
Брюстера записываетя как 'Q + 6Д = я, или
tgei? = -tgC = -e^Itg(es + a). F.25)
Для ет = er = 1 имеем {&т1^м)'г sin0M = s^1 sin6r. Сле-
Следовательно, F.25) эквивалентно условию, что амплитуда
отраженной волны, определяемая формулой F.22), об-
обращается в нуль.
§ 7. Метод интегральных уравнений в задачах
о распространении волн в нелинейных средах
С микроскопической точки зрения существует только
поле падающего излучения в вакууме и микроскопиче-
микроскопические поля в вакууме, излучаемые атомными диполями.
Эвальд и Цсин показали, что для случая линейного ди-
диэлектрика рассмотрение запаздывающих полей атомных
диполей приводит после интегрирования к тем же ре-
результатам, что и комбинация уравнений Максвелла с ло-
ренцевой моделью квазистатических действующих полей.
Точно так же результаты, полученные в работе [6] пу-
путем применения уравнений Максвелла (с учетом лорен-
ПРИЛОЖЕНИЕ II
373
цевой поправки) к нелинейному диэлектрику, можно обо-
обосновать, обобщая метод Эвальда и Осина. В последую-
последующем изложении мы будем придерживаться подхода и
обозначений, используемых в книге Борна и Вольфа [9]
при исследовании линейного случая. Как и в линейной
задаче, отраженная и преломленная волны на границе
нелинейной среды точно определяются с помощью мето-
метода интегральных уравнений.
Пусть полубесконечный диэлектрик в области z ^ О,
соприкасающийся с вакуумом, существующим в области
z > 0, характеризуется плотностью поляризации P(r, t),
содержащей как линейную, так и нелинейную части. Не-
Нелинейная поляризация определяется нелинейной поля-
поляризуемостью единичной ячейки (см. [6]). Пусть нелиней-
нелинейная поляризация i-я ячейки равна 5aNL(^, /-,-). Если мы
имеем N ячеек в единице объема, то плотность нелиней-
нелинейной поляризации равна PNL(/-, t) = iV5SNL(f, г). В самом
общем случае при наличии падающего поля Ег(г, t) пол-
полное электрическое поле в какой-либо точке г среды мо-
может быть записано в виде
Е'(г, t)--=EU) + V X V Ж"
R
dV, G.1)
где о — малая поверхность, окружающая точку г, а 2 —
наружная поверхность диэлектрика. Рассмотрим компо-
компоненту поля G.1) с частотой со, для которой PNL Ф О
В качестве пробных решений примем выражения
G.2)
PNL(r, (o)=F(r),
где поля в правой части удовлетворяют уравнениям
0й = О,
(О \2
" + «,lfl!
2Q*
V2Q
е/— I Q* =0,
с
374
ПРИЛОЖЕНИЕ II
Q;=0,
G.3)
Скорость волны источника в среде, характеризуемая ве-
величиной 8s, может быть определена из решения линейной
задачи для исходных волн с частотами, отличными от
частоты со. Линейная диэлектрическая проницаемость на
частоте © равна е. Входящая в интеграл G.1) амплитуда
полной'поляризации единицы объема равна
Р(г', a>) = Mx[Q« + Q*] + F, G.4)
где а — поляризуемость единичной ячейки на частоте со,
N — число единичных ячеек в 1 см3.
Подстановка выражений G.2) и G.4) в G.1) приво-
приводит, с использованием методики Борна и Вольфа [9], к
выражению
Qa (г) + Q» (г) = Q' (г) + А
3
"АМе
8—1
Q* (Г)
A/aQa(r')-f F(r')
es-l
8S —
G.5)
= (l/R) exp[i(a/c)R]. Учет четвертого члена
в правой части необходим, так как, вообще говоря, чле-
ны V ¦ F и V • Qa не равны нулю.
Уравнение G.5) содержит компоненты, распростра-
распространяющиеся со скоростями с, c(s)~1/2 hc(ss)~I/2. Если
уравнение должно выполняться для всех точек среды, то
каждый из этих членов по отдельности должен быть ра-
ПРИЛОЖЕНИЕ II
375
вен нулю. Соответственно для компонент, распростра-
распространяющихся со скоростью с, получаем
O = Q'-+f—Г ? X Vx [dS'.{ }; G.6a)
\ « / J
для -компонент, распространяющихся со скоростью
с(е)~Ч* , имеем
Qb=*!LNal±LQib. G.66)
3 8-1
для компонент, распространяющихся со скоростью
Qa =
3 6,-1
F(r)]
8.-1
—) V [V • (NaQa (г) + F (г))} . G.6в)
Выражение G.66) дает обычное решение однородного
уравнения для линейной среды
4зх яг в — 1 /*7 *7\
Л/а = . - . ('•';
Выражение G.6в) является решением неоднородного
уравнения. Можно показать, что величина Qa эквива-
эквивалентна действующему полю, связанному с неоднородной
частью решений B.5). В этом нетрудно убедиться, рас-
рассматривая два разных случая: 1) векторы F и ks парал-
параллельны; 2) векторы F и ks перпендикулярны. В первом
случае G.6в) приводится к виду
Qa==_i!L?±lF.
9 8
Неоднородная часть поляризации G.4) может быть
выражена через линейную и нелинейную поляризации и
эффективный нелинейный источник (см. [6])
фф
PL
PNL
F =
1. G.8)
Это выражение согласуется с макроскопическим опреде-
определением величины PNLS для продольной компоненты
в том случае, когда величина D равна нулю,
D = Е + AnPL + 4ttPnl = е? + АпР-3 = 0, G,9)
376
ПРИЛОЖЕНИЕ II
Подобное же соответствие имеет место для поперечной
компоненты.
Соотношение G.6а) дает граничные условия для не-
нелинейной среды. Амплитуда вектора Q6 однозначно оп-
определяется величинами Qa, F и Q\ Таким образом, уста-
устанавливается соответствие между интегральными и диф-
дифференциальными уравнениями. Здесь также имеются од-
однородные и.неоднородные решения; амплитуда 'последних
определяется граничными условиями.
Поле отраженной волны вне среды получается значи-
значительно более 'просто, поскольку дифференциальный опе-
оператор в этом случае можно вынести за знак интеграла
E*(r, t) = V XV X
¦("•'-т)
dV.
G.10)
Величина P(r', t) известна из решений уравнений G.4)
и G.6). Интегрирование уравнения G.10) довольно тру-
трудоемко, «о зато оно представляет собой прямой метод; он
приводит к результатам, согласующимся с .решениями бо-
более простых уравнений § 4.
§ 8. Обсуждение и выводы
Теоретические результаты, полученные в § 3 и 4, при-
применимы ко многим экспериментальным ситуациям.
В опытах по генерации гармоник обычно используется
пластина из нелинейного кристалла. Результаты, полу-
полученные в § 6, позволяют определить интенсивность гар-
гармоники, излучаемой в прямом и обратном 'Направлениях.
При этом детально рассмотрены как общий случай про-
произвольной толщины 'пластины и рассогласования фазовых
скоростей, так и предельный случай полного согласова-
согласования на всей толщине пластины. Выведенные здесь соот-
соотношения описывают и генерацию гармоник внутри кри-
кристалла лазера. Поскольку в последнем случае основной
является стоячая волна, нужно учитывать не одну волну,
а сумму неоднородных волн внутри кристалла. В общем
случае фазовые скорости не согласованы. Интенсивность
гармоники является периодической функцией длины ин-
ПРИЛОЖЕНИЕ II
377
терферометра Фабри — Перо, однако она не превышает
интенсивность, получаемую в тонком слое толщиной
/ = coc-1(ss/2 — ем2 ).
Сильная зависимость интенсивности гармоники от
рассогласования фазовых скоростей, т. е. от величины
?м — ss и от толщины d затрудняет точное количествен-
количественное определение нелинейной восприимчивости с помощью
выражений F.7) или F.8) и F.17) или F.18) и экспери-
экспериментального наблюдения генерации гармоники в пла-
пластине. Эту трудность можно обойти, если наблюдать
гармонику, отраженную от одной границы нелинейной
среды. Примем в соотношениях, приведенных в § 6,
?т = ем, что соответствует согласованию показателей
преломления нелинейной пластины и линейной среды.
Для экспериментальной реализации условий, эквива-
эквивалентных идеализированной задаче об отражении от по-
полубесконечной среды, можно применить простой метод —
сделать вторую поверхность диффузной и поглощающей
или вырезать ее под углом к передней поверхности. Мож-
Можно использовать также полностью отраженный луч с ос-
основной частотой, 'который генерирует гармоники на рас-
расстоянии, равном глубине проникновения, т. е. порядка
нескольких длин волн, как показано § 5. В любом случае
нужно еще совершенно точно знать распределение интен-
интенсивности падающего лазерного луча во времени и в по-
поперечном сечении. После проведения абсолютной калиб-
калибровки можно таким образом измерить нелинейную
восприимчивость любого образца, если сравнить интен-
интенсивность отраженной от него гармоники с интенсивно-
интенсивностью гармоники, генерируемой нелинейным стандартным
образцом, через который проходит тот же луч лазера.
В кристаллах, обладающих центром инверсии, нели-
нелинейная поляризация на частоте второй гармоники, как
следует вд D.18), может возникнуть только из-за элек-
электрического квадрупольного эффекта. Поэтому нелиней-
нелинейная поляризация и амплитуда волны второй гармоники,
распространяющейся от границы, уменьшается для кри-
кристаллов этого типа в (ia/Xi\)~l раз по сравнению с кри-
кристаллами, у которых центр инверсии отсутствует, где a —
характеристический атомный размер. Множитель т) < 1
учитывает то обстоятельство, что нечетная часть «ристал-
378
ПРИЛОЖЕНИЕ U
лического потенциала меньше, чем четная часть. Экспе-
Эксперименты Терхьюна по генерации второй гармоники в кри-
кристаллах KDP и кальците показали, что в KDP величина
•Л <~ 0,1. Все выводы настоящей работы в равной степени
справедливы как для кристаллов, обладающих инверси-
инверсионной симметрией, так и для кристаллов, не обладаю-
обладающих ею.
Можно предположить, что поверхностные слои кри-
кристалла, обладающего в целом центром инверсии, не име-
имеют инверсионной симметрии, а генерация второй гармо-
гармоники осуществляется пограничным атомным слоем. Для
описания процесса генерации гармоник в поверхностных
слоях толщиной а непосредственно приложимы соотно-
соотношения F.12), F.22) и F.23). Амплитуда отраженной
волны гармоники, определяемая этим слоем, будет
в ti~' раз меньше, чем амплитуда отраженной волны, воз-
возникающей в граничном слое толщиной к из-за квадру^
польного эффекта. Поэтому можно полагать, что в про-
процессе генерации гармоники поверхностные атомные слои
играют несущественную роль. В принципе их влияние
можно оценить, наблюдая прошедшую « отраженную
волны гармоник в пластинах с разными толщиной и кри-
кристаллографической ориентацией.
Факт генерации гармоник в граничном слое толщи-
толщиной (порядка А. даже в том случае, когда основная волна
полностью отражается, наводит на мысль о новой схеме
генератора оптических гармоник, показанной на фиг. 8.
Основная волна с частотой со распространяется в плотной
линейной среде (например, жидкости) между двумя
стенками из нелинейного диэлектрика. При этом имеет
место многократное полное внутреннее отражение. При
каждом отражении генерируется вторая гармоника. Рас-
Расстояние между нелинейными стенками и дисперсия ли-
линейной среды могут быть выбраны таким образом, что
при каждом отражении вторая гармоника генерирова-
генерировалась с фазой, необходимой для нарастания интенсивно-
интенсивности гармоники. Фазовые сдвиги, возникающие при пол-
полном отражении основной и второй гармоник, могут быть
вычислены с помощью метода, изложенного в § 5. Про-
Проблема согласования фазовых скоростей теперь перено-
переносится на линейную изотропную среду. Если расстояние
ПРИЛОЖЕНИЕ II
379
между нелинейными стенками сделать очень малым, мы
приходим к линейному оптическому волокну (световоду)
с нелинейным покрытием. Очевидно, что методы, ис-
использованные для анализа нелинейного взаимодействия
' Линейная
среда
Нелинейная среда
Фиг. 8. Генерация гармоники при многократном полном отражении
от нелинейного диэлектрика.
Изображенная схема может соответствовать жидкости, находящейся между
двумя нелинейными кристаллами, или оптическому волокну с нелинейным
покрытием.
Фиг. 9. Разделение основного луча, однородного и неоднородного
лучей гармоники с помощью призмы.
Вследствие рассогласования фазовых скоростей и дифракции пучков конечного
диаметра мощность гармоники в разделенных лучах ограничена величиной
которая равна или меньше мощности, получаемой при использовании плоско-
плоскопараллельного слоя.
волн в свободном пространстве, могут быть применены и
при исследовании распространения основной волны и
волны гармоники в оптических волноводах [10].
До сих пор мы ограничивались плоскими волнами и
плоскими 'бесконечными границами. Можно обобщить
расчеты на случай пучков конечного диаметра d, призм и
380
ПРИЛОЛХЕНИЕ II
даже изогнутых границ. При обобщении понятий одно-
однородной и неоднородной волн в нелинейной среде на пучки
конечного диаметра следует соблюдать известную осто-
осторожность. Эти пучки разделяются 'призмой, как схемати-
схематически токазано на фиг. 9. Неоднородный луч выходит из
призмы в направлении, промежуточном между направ-
направлениями основного луча и однородного луча гармоники.
Разумеется, не следует думать, что таким образом мож-
можно устранить взаимное гашение однородной и неодно-
неоднородной волн гармоники и что в разделенных лучах мож-
можно получить большую интенсивность гармоники. Ампли-
Амплитуда каждого луча в отдельности пропорциональна вели-
величине (ем — ss) и становится весьма большой, когда до-
достигается полное согласование фазовых скоростей. Одна-
Однако при этом угловая дисперсия призмы уменьшается.
Если угловая дисперсия призмы меньше дифракционно-
дифракционного угла, определяемого конечным диаметром пучка, то
пучки не будут разделены.
Используя обозначения § 6 и фиг. 9, выразлм угол
отклонения однородного луча через угол падения 6^ и
угол при вершине призмы if:
где
sin 9(- sin гр ctg B^ — cos tpsin вг-, , (8.1)
sin 6^ = sin 6,-.
(8.2)
Дифференцируя (8.1) и (8.2), приходим к выражению
для угла между однородным и неоднородным лучами,
выраженного через малую величину рассогласования
фазовых скоростей
(8.3)
Для разрешения лучей да выходе призмы должно выпол-
выполняться условие
(8.4)
где D — диаметр пучка на выходе. Минимальная дли-
длина /, которую должен пройти в призме центр пучка диа-
приложение и
381
метром D, равна
1>
Dsin
B cos QM cos 0r)
Комбинируя соотношения (8.3) — (8.5), получаем
C.5)
(8.6)
Итак, для того чтобы однородный и неоднородный лучи
разделились, луч должен пройти в нелинейной призме
в среднем по меньшей мере «когерентную длину». Этого
следовало ожидать из энергетических соображений.
На когерентной длине нелинейная среда производит
максимальную работу, и мощность гармоники достигает
максимума. Эта мощность содержится либо в неразде-
неразделенном пучке, прошедшем сквозь плоскопараллельную
пластину, либо в разделенных пучках, прошедших через
призму. С таким же положением мы сталкиваемся при
попытке разделить однородную и неоднородную волны
в фокусе хроматической линзы.
Итак, включение нелинейных материальных уравне-
уравнений в систему уравнений Максвелла позволило решить
ряд простых граничных задач. [Выяснение закономерно-
закономерностей отражения и преломления света на поверхностях
нелинейного диэлектрика позволяет полностью проана-
проанализировать процессы генерации световых гармоник и
смешения световых волн в ограниченной нелинейной
среде. Такой анализ весьма важен для понимания осо-
особенностей поведения оптических приборов и систем при
очень высоких уровнях плотности мощности света, дости-
достижимых в лучах лазеров.
ЛИТЕРАТУРА
1. Fran ken P., Hill A. E., Peters С. W., Weinreich G,
Phys. Rev. Lett., 7, 118 A961).
2. Bass M., Franken P. A, Hill A. E., Peters С W, Wein-
Weinreich G., Phys. Rev. Lett., 8, 18 A962).
3. Giordmaine J. A., Phys. Rev Lett., 8, 19 A962).
ПРИЛОЖЕНИЕ II
4. Maker P. D., TcrhuneR. W., NisenoffM, Savage
С. М., Phys. Rev. Lett., 8, 21 A962).
5. Terhune R. W., Maker P. D., Savage С. М., Phvs Rev
Lett., 8, 404 A962).
6. Armstrong J. A., Bloembergen N., Ducuing J Per-
shan P. S., Phys. Rev., 127, 1918 A962).
7. Heronus Alexandrinus, Катояпха. (Имеется перевод на
латинский и немецкий языки, Лейпциг, 1899.)
8. W h i 11 a k e г Е. Т., A History of the Theories of the Aether and
Electricity, vol. 1, London, 1952.
9. Born M., Wolf E., Principles of Optics, London, 1959, Ch. I, II.
10. S n i t z e г Е., в книге Advances in Quantum Electronics, ed J. R.
Singer, New York, 1961, p. 348.
Приложение III
КВАНТОВОМЕХАНИЧЕСКОЕ СРАВНЕНИЕ НЕЛИНЕЙНЫХ
ВОСПРИИМЧИВОСТЕИ ПАРАМЕТРИЧЕСКИХ СРЕД,
ЛАЗЕРОВ И КОМБИНАЦИОННЫХ ЛАЗЕРОВ
Н. Бломберген, И. Шен
N. Bloembergen*, Y. R. S h е п *, Phys. Rev., 133, А37 A964).
С помощью метода матрицы плотности описывается стационар-
стационарный отклик нелинейной среды на несколько одновременно приложен-
приложенных монохроматических электромагнитных полей. Разложение в ряд
Фурье по степеням амплитуд приложенных полей особенно удобно
для описания параметрического отклика в спектральных областях,
в которых поглощение мало. По мере приближения к резонансам
материальной системы общий формализм позволяет выявить связь
между параметрическими процессами и одно- и многофотонными
поглощательными и излучательными процессами. Обобщено прове-
проведенное ранее рассмотрение двух- и трехуровневых систем. Обсуж-
Обсуждается также реакция произвольной нелинейной среды на электро-
электромагнитные поля.
§ 1. Введение
В идеальной среде без потерь имеют место только па-
параметрические процессы, так «ак зависимость вероятно-
вероятности переходов между энергетическими уровнями мате-
материальной системы от частоты фотонов имеет особенности
типа б-функции и суммарная энергия фотонов остается
постоянной. Нелинейные процессы рассеяния с участием
трех или большего числа фотонов были рассмотрены
Блэтоном [1] и Гуттингером B]. Соответствующая нели-
нелинейная часть поляризации, обусловленная интерференци-
интерференцией всех 'процессов рассеяния такого типа на атомах кри-
кристаллической решетки, была рассчитана Армстронгом и
др. i[3] для случая среды без потерь.
Если обобщить эту теорию, учтя эффекты затухания,
то оказывается, что параметрические процессы перепле-
переплетаются с процессами, при которых поглощается или из-
излучается один или большее число фотонов. Так как про-
* Division of Engineering and Applied Physics, Harvard Univer-
University, Cambridge, Massachusetts.
384
ПРИЛОЖЕНИЕ III
цеосы затухания являются статистическими по своей .при-
.природе 'И обусловлены взаимодействием со случайными
фотонными и фононными полями, относительно которых
мы располагаем далеко не полной информацией, то впол-
вполне уместно воспользоваться методом матрицы плотности.
Карплюс и Швингер [4] применили его для описания эф-
эффекта насыщения в радиоспектроскопии. Этот эффект
можно рассматривать как разновидность нелинейного
процесса, при котором происходит 'последовательное по-
поглощение и излучение фотонов одной частоты.
Метод матрицы плотности в дальнейшем усиленно
развивался, в особенности при изучении ядерной магнит-
магнитной релаксации [5—10]. Мы ограничимся рассмотрением
разбавленных систем, <в 'которых энергия взаимодейст-
взаимодействия между частицами значительно меньше расстояний
между энергетическими уровнями, а также гораздо мень-
меньше разностей между этими расстояниями для одной ча-
частицы. Случай эквидистантных уровней рассматриваться
не будет. Эти предположения обычно выполняются
в оптической области спектра, а иногда и в СВЧ области
для разбавленных парамагнитных материалов. Широта
области, в которой гамильтониан случайных взаимодей-
взаимодействий имеет постоянную спектральную плотность, обыч-
обычно превышает ширину линий отдельных переходов. Эти
переходы связаны с излучательными и безызлучательны-
ми процессами, при которых происходит поглощение
или излучение фотонов и (или) фононов. Взаимодейст-
Взаимодействие со случайными (тепловыми) полями излучения и ко-
колебаниями решетки включает эффект спонтанной эмис-
эмиссии. Если воспользоваться терминологией теории маг-
нитной релаксации, то рассматриваемый случай относит-
относится к модели «быстрого движения в изотропной среде».
В этом случае влияние гамильтониана случайных взаи-
взаимодействий на движение матрицы плотности описывает-
описывается феноменологическими параметрами затухания.
Фаа
dt /случ
, WanPnn — 2l WnaPaa
n
dt
случ
— ~ RababPab * abPab-
A.1)
A.2)
!
ПРИЛОЖЕНИЕ III
385
\
Имеется 31 — 1 времен продольной релаксации, так как
ЭД диагональных элементов релаксируют 'комбинирован-
'комбинированно. Обратные им величины равны собственным значени-
значениям матрицы Wnn'. Каждый яедиагональный элемент за-
затухает с характеристическим временем поперечной ре-
релаксации Г аь , которое имеет в общем случае как адиа-
адиабатическую, так и неадиабатическую части. Последняя
обусловлена конечным временем жизни, связанным с ве-
вероятностями переходов wan, ^Ьп- В том случае, когда
ИМееТСЯ ТОЛЬКО Два урОВНЯ, Гнеадиаб = Xli Тх = Wab + Wba.
Адиабатическая часть обусловлена случайной модуляци-
модуляцией расщепления hvba за счет диагональных элементов
гамильтониана случайных взаимодействий, что может
быть вызвано, например, колебаниями решетки. В част-
частном случае, когда единственное случайное возмущение
неадиабатично и вызвано спонтанным излучением фото-
фотонов с уровней а и Ь на другие ниже .расположенные
уровни, релаксационные члены можно выразить через
антикоммутатор
~г\ =-(Гр + рП. A.3)
ОТ /затух
где Г—диагональная матрица. В области магнитного
резонанса теория релаксации была разработана для
случая, когда взаимодействие между индивидуальными
спинами может сильно влиять на релаксационное пове-
поведение (см., например, [9]). Если же не учитывать взаимо-
взаимодействие между отдельными атомами или ионами, то
форма релаксационных членов >не изменяется и при воз-
воздействии периодических полей. (Правда, строго говоря,
имеется небольшое изменение, так как в приближении
релаксации за счет быстрого движения система релакси-
рует к термодинамическому равновесному состоянию, со-
соответствующему мгновенному значению приложенных
полей.) Однако предположение о том, что релаксацион-
релаксационные члены всегда описываются выражениями вида A.1)
и A.2), является очень хорошим приближением для фи-
физических условий, встречающихся в лазерах и в нели-
нелинейных оптических приборах. Неоднородное уширение,
уширение оптических линий механическими напряжения-
напряжениями и т. д. всегда можно учесть, интегрируя конечные ре-
25 Н. Бломберген
386
ПРИЛОЖЕНИЕ 111
зультаты, (полученные в настоящей работе, по распреде-
распределению резонансных частот атомной системы.
Полный гамильтониан состоит из трех слагаемых:
й^а. Жког и Жслуч- Член Ж а определяет невозмущенные
энергетические уровни атомной системы, Ж кот— взаимо-
взаимодействие этой системы с одним или с большим числом
приложенных монохроматических полей, а Жслуч пред-
представляет собой гамильтониан случайных взаимодействий,
который включает не только уже обсуждавшиеся фотон-
фотонные и фононные релаксационные процессы, но и 'прило-
'приложенные случайные поля накачки. Бели, найример, лазер-
лазерный кристалл освещается импульсной лампой, то на него
действуют случайные поля, характеризуемые различны-
различными температурами в зависимости от характера освеще-
освещения. В этом случае вероятности 'перехода и1од действием
случайных полей удовлетворяют следующим соотноше-
соотношениям:
Wab = Z ®аЬ
где
s a -htb /kT2
Wba = Wabe
Таким образом, получаем следующее уравнение движе-
движения для матрицы плотности:
ihp = [ЖА, Р] + [Жкот, Р] + ih (-J-) , A.4)
\ Of /случ
где последнее слагаемое определяется соотношениями
A.1) и A.2). Исходя из этого уравнения, различные ав-
авторы обсуждали отклик материальной системы на два
приложенных одновременно периодических поля. Особое
внимание уделялось двух- и трехуровневым мазерным
системам. Джаван, Винтер и Ятсив [12—14] подчеркива-
подчеркивают важность двухквантовых комбинационных процессов,
которые могут происходить в таких системах. Андерсон
[15] подробно описал основной параметрический процесс
в трехуровневой системе. Клогстон [16] получил форму-
формулу, описывающую все эти процессы. Хотя он рассматри-
рассматривал в основном трехуровневый мазер, он не опустил, как
утверждает Файн [17], параметрический член. Файн так-
ПРИЛОЖЕНИЕ lit
3St
же использовал метод матрицы плотности для рассмот-
рассмотрения действия мазерных генераторов [18]. Кастлер [19]
и его сотрудники [20, 21], а также Уилкокс и Лэмю [22, 23]
широко использовали этот формализм для описания од-
одновременного действия радиочастотных и оптических по-
полей. В случае двухуровневой системы формализм матри-
матрицы плотности эквивалентен классическим уравнениям
Блоха для магнитного резонанса [24]. Генерация гармо-
гармоник при ферромагнитном резонансе теоретически и экс-
экспериментально исследовалась Эйрсом, Вартаняном и
А^лхором [25].
,; Во всех этих работах основное внимание уделяется
различным сторонам одной и той же общей задачи — оп-
рёЦеления стационарното отклика атомной системы на
одновременное воздействие нескольких периодических
возмущений. Обычно рассматриваются такие случаи,
когда частота возмущения близка к резонансной часто-
частоте системы. В настоящей работе особое внимание уделя-
уделяется параметрическому случаю, когда все частоты дале-
далеки от резонансных частот системы. Общая процедура
расчета описана в § 2. Применяя этот расчет, можно по-
получить все известные результаты, если в каждой задаче
воспользоваться соответствующими приближениями. Не-
Нелинейный стационарный отклик двухуровневой системы
рассмотрен в § 3, где обсуждаются как параметрические,
так и комбинационные процессы. В § 4 рассмотрена из-
известная модель трехуровневой системы, на которую дейст-
действуют три монохроматических ноля; обобщены результа-
результаты Клогстона [16] и Джавана''. В § 5 описана реакция
нелинейной среды на электромагнитные поля (это общее
определение охватывает мазерные, индуцированные ком-
комбинационные и параметрические эффекты).
§ 2. Общий расчет нелинейных проводимостей
и восприимчивостей
Стационарное решение для матрицы плотности, пред-
представленной в виде ряда по степеням когерентных перио-
периодических возмущений, можно найти из следующей носле-
'¦' Основные результаты, полученные в § 4, были доложены на
Парижской конференции по квантовой радиофизике; см. [20].
25*
ПРИЛОЖЕНИЕ 111
довательности уравнении:
@I
= K,p@>]+m-
ihp —
гзатух
dt '
, B.1)
A,
+
01
+
(n-l)
Pl '
l
J •
Первое уравнение описывает матрицу -плотности при
термодинамическом равновесии. Линейный отклик систе-
системы определяется вторым уравнением: рО зависит от тех
же частот, что и Ж КОг- Во втором приближении стацио-
стационарный отклик р<2) содержит члены с суммарной, разност-
разностной и двойной частотами, а также не зависящие от вре-
времени члены. Последние описывают начальную стадию
процесса насыщения и обусловлены биениями между
компонентами Жког и р*1) с положительными и отрица-
отрицательными частотами. Подстановка р<2> в уравнение для
рC) дает фурье-компоненты следующего приближения
и т. д. Отметим, что в стационарном случае дифферен-
дифференцирование в левых частях уравнений сводится к умноже-
умножению на — С2(± п,-(Ог), где t%i—целое число, ( + Шг) -компо-
-компонента зависит от времени как ехр(—ia>it), а (—ц>г) -ком-
-компонента— как ехр( + йог^). Таким образом, каждый по-
последующий шаг соответствует очень простой алгебраи-
алгебраической операции, связывающей фурье-комтюненты данно-
данного приближения с компонентами предыдущего прибли-
приближения. Прайс [27] (см. также [28]) использовал времен-
временной подход и рассматривал общий нелинейный отклик
как результат интегрирования функции отклика на еди-
единичное ступенчатое возмущение, однако стационарный
отклик на периодические силы легче определить с по-
помощью спектрального подхода.
Хотя этот формализм применим не только к случаю
электромагнитных возмущений, но пригоден, например,
и для описания отклика системы на периодическое меха-
механическое внешнее воздействие, использованная в даль-
дальнейшем форма Жког соответствует полуклассическому
ПРИЛОЖЕНИИ 111
389
нерелятивистскому взаимодействию связанного электро-
электрона, имеющего заряд — е, с конечным числом электромаг-
электромагнитных типов колебаний:
Л
2mc
(Р • А + А • р) + JL s . у х А + Л А • А,
me
B.2)
где векторный потенциал электромагнитной волны равен
А (г, 0 = — У [Ат (г) e-to«' -f Al (г) е ША B 3)
B.4)
Оператор плотности тока имеет вид [29]
j(ro) = -
2/и
где
r0) (PXS)—(pxsN(r—г0)] ,
B.5)
б (г — г0) = | г0 > <го|.
Фурье-компоненты плотности тока в пространстве волно-
волновых чисел записываются следующим образом:
v ' J lK >' B-o)
их матричные элементы равны
jn'n— ( п' | j (k) | n у =
__ rft.r/. , e
2/n
~2ihs х
B.7)
| ()
Среднее значение плотности тока как функции вре-
времени определяется соотношением
п а'
B.8)
390
ПРИЛОЖЕНИЕ III
Это среднее значение можно снова разложить на фурье-
компоненты последовательных высших приближений [30].
В п-'Ы приближении можно написать
< j<»> (k, t) > - 2 2 (Ь (lOWpi"» @ +
B.9)
где ji(k)—линейная по полю часть оператора плотно-
плотности тока.
Тензор линейной проводимости определяется как от-
отношение полученного в первом приближении среднего
значения плотности тока с частотой со и волновым векто-
вектором k iK амплитуде электрического поля с теми же часто-
частотой и волновым вектором:
<р>(к,ю)> =0(со, к)Е(к,ю). B.10)
Аналогично определяются тензоры проводимости высше-
высшего порядка
aNL
(k1...k/J,
п, ©„). B.11)
Заметим, что какая-либо частота ±ып может повто-
повторяться несколько раз. Поэтому, например, плотность то-
тока в третьем приближении будет содержать компоненту
с частотой (Оь пропорциональную E(oji)E*(—a»i)E(a»i),
которую можно рассматривать как поправку к j(I'(a»i),
учитывающую насыщение.
Средние значения и линейной и нелинейной частей
плотности тока можно считать источниками и подставить
в уравнения Максвелла
„ . 1 db
dt
at
<Иг,о> ,
B.12)
где е и b — поля в вакууме.
ПРИЛОЖЕНИЕ III
391
Подробное рассмотрение влияния нелинейных источ-
источников на распространение электромагнитных волн в не-
нелинейной среде 'было проведено в другой работе [3].
Здесь дается только общее описание квантовомеханиче-
окого расчета этих источников.
Во многих практических случаях, например для ре-
решетки с небольшой примесью ионов переходных метал-
металлов, интересно выделить в более явной форме различные
мультипольные моменты, содержащиеся в матричных
элементах B.7). Фьютак [31] показал в общем виде, что
возмущение ЖКОт, описываемое выражением B.2), мож-
можно канонически преобразовать к эквивалентному виду')
Ж'КОГ = ~Ф-Е — 2Я • H-Q:VE+... . B.13)
С помощью этого эквивалентного гамильтониана
получаются такие же средние значения всех физических
величин, как и с помощью первоначального гамильто-
гамильтониана. Среднее значение плотности тока теперь опреде-
определяется следующим выражением:
dt
B.14)
где N— число атомных систем в единице объема.
Разложения B.13) и B.14) по мультипольным мо-
моментам не однозначны и зависят or выбора начала коор-
координат. Этот выбор часто можно сделать, исходя из физи-
физических соображений; например, начало можно поместить
в центр примесного парамагнитного иона в решетке.
Если удержать только дипольные матричные элементы,
то дипольные источники можно включить в уравнения
Максвелла обычным образом:
дН 4п д!Л B.15)
V х Е = - -H?L — —
dt
dt
!) Выражение B.13) не вполне корректно описывает установле-
установление диамагнитной энергии. Правильный результат получается при
использовании члена с Л2 в B.2). Это расхождение не имеет, одна-
однако, значения для рассматриваемых здесь нелинейиостей.
392
ПРИЛОЖЕНИЕ III
vxh = —L^l
с dt
с dt
P(r,t)=NSp(Vp(r,t)).
M(r, t) = N Sp CRp (r, 0).
B.17)
B-18)
Поправки для случая оптически плотной среды об-
обсуждались в другой работе [3].
Преимущество трансформированного гамильтониа-
гамильтониана B.13) заключается в том, что некоммутирующие опе-
операторы р и г не фигурируют одновременно. При расчете
линейной электрической восприимчивости с помощью
гамильтониана, содержащего операторы момента, необ-
необходима большая тщательность [32, 33]. При переходе
к нелинейным членам высших порядков среднее значение
электрического дипольного момента Sp( Фр ) можно сра-
сразу оценить с помощью гамильтониана B.13). При рас-
расчете по теории возмущений получается ряд по степеням
амплитуд электрических и магнитных полей.
В системе, не обладающей центром инверсии, нели-
нелинейным членом низшего порядка является дипольный мо-
момент, пропорциональный квадратичной функции ампли-
амплитуд электрического ноля. Рассмотрим фурье-компоненту
дипольного момента с суммарной частотой юз = coi + к>2,
индуцированную электрическим полем с частотами coi
и со2- Гамильтониан в данном случае равен
Предположим, что оператор электрического диполь-
дипольного момента имеет только недиагональные матричные
элементы (случай, когда существенны диагональные
элементы, будет рассмотрен в § 3). Типичный недиаго-
недиагональный элемент матрицы плотности удовлетворяет
уравнению
itipnn'= (+GW — П\п')рпп> +У (Жпп"рП"п' —рап'Жп-п-).
B.19)
ПРИЛОЖЕНИЕ III
393
В первом (т. е. линейном) приближении для этих не-
недиагональных элементов имеем
J_ • •
I A) Km,) 2
<> 1(Ч)_
п"п'\ —
l — wn"n'+iVn"n'
№>•-№•). B.20)
и аналогичные выражения для компонент с часто-
частотами — COi И ±СО2-
Во втором приближении получаем
х
"п'п'
_|_
¦tin Гц"п"
X
п" 4 п,п'
п(°) —о'0)
"п'п' Уп"п'
X
,@) „@)
. B.21)
Можно рассчитать среднее значение дипольного мо-
момента на частоте шз, пропорциональное произведению
амплитуд полей с частотами a>i и щ, и найти тензор не-
нелинейной поляризации третьего ранга. Его компоненты
Pijft определяются следующим соотношением:
< ^2) К = «>! + »я) > = -у hk iEj Ы Ek Ы +
+ Ek (ш2) Ej К)} = 22 C°/)»»'{Р»2'»}(Ш1+011)- B.22)
п п'
Множитель 'Д добавлен для того, чтобы при действи-
действительном значении р и при действительных по-
полях Ei cos ant и ?2 cos co2^ поляризация была равна
SPiCOs ыз^. Это выражение симметрично относительно
компонент ?j(o)i) и ?ft(a>2), что непосредственно следует
из B.21),
394
ПРИЛОЖЕНИЕ 111
Если затухание мало, слагаемые i Г „„» в знаменате-
знаменателях выражения B.21) можно опустить. Это обстоятель-
обстоятельство важно при генерации гармоник в оптической об-
области, когда все частоты далеки от резонансных. Если
знаменатели действительны и содержат только разности
частот, то слагаемые в выражении B.21) можно пере-
перегруппировать. Компоненту тензора поляризации третьего
ранга в отсутствие затухания можно выразить следую-
следующим образом:
ЦФп, п'
X (?>ft)n'«iC' -f {Sfi)n'
B.23)
где
Ann'
В
„„.
=B/г2)~' [(со3 — <x>ng)~l (a>i— GVg)"'],
= B/г2) [(cos — a>ng)'1 (©2— ©„'«)"'],
= B/г2)-1 [((оз + ©„.«)-' ((o2 + ©„g)-1],
= [2h2)-1 [((оз +(о„'ё)~' ((oi + (o^)-1],
= -BЙ2)^' [(©i + ©n'g) (©2 -©„«)"
При дополнительном предположении, что матричные
элементы ^„„' действительны, равенство B.23) иден-
идентично равенствам B.13) и B.14) работы Армстронга
и др. C].
Аналогичным образом можно определить нелинейные
электрические и магнитные восприимчивости в высших
приближениях. Эти нелинейные комплексные восприим-
восприимчивости описывают не только параметрические эффекты,
но также и эффекты насыщения, мазерные и индуциро-
индуцированные комбинационные эффекты. В области частот,
ПРИЛОЖЕНИЕ 111
395
далеких от частот резонансных переходов, доминируют
параметрические эффекты. В этом случае разложение по
степеням амплитуд поля особенно удобно. В случае же
резонанса часто желательно удержать все члены в раз-
разложении фурье-компоненты матрицы плотности по степе-
степеням поля, чтобы полностью описать эффект насыщения.
В этом случае необходимо априори решить, какие компо-
компоненты каждого матричного элемента следует удержать
и какие можно отбросить как малые несекулярные сла-
слагаемые. Приравнивая в левых и правых частях уравне-
уравнений движения A.4) члены с одинаковой частотной зави-
зависимостью, мы получаем систему линейных алгебраи-
алгебраических уравнений. В принципе фурье-компоненты матри-
матрицы плотности и, следовательно, средние значения
дипольных моментов могут быть найдены с помощью
алгебраических операций. Практически же число неиз-
неизвестных велико даже в относительно простых случаях
двух или трех энергетических уровней. Можно воспользо-
воспользоваться вычислительными машинами, но при этом труднее
представить себе все физические явления при интерфе-
интерференции параметрических, мазерных, индуцированных
комбинационных и других многофотонных процессов.
Ниже мы применим описанные здесь общие методы
к двух- и трехуровневым системам. В этих случаях могут
быть выявлены основные нелинейные механизмы.
В результате анализа мы увидим, в каких случаях до-
доминируют параметрические и в каких — мазерные эф-
эффекты и каким образом они интерферируют.
Если приложенные электрические или магнитные
поля содержат постоянную составляющую, т. е. если одна
частота равна нулю, то из развитого формализма следу-
следуют в качестве частных случаев эффект Покельса и квад-
квадратичный электрооптический эффект, а также эффект
Фарадея и квадратичные магнитные эффекты. В случае
постоянных полей необходимо внести поправки в релак-
релаксационные члены. Парамагнитная составляющая в эф-
эффекте Фарадея, «апример, является следствием измене-
изменения населенностей состояний при приложении постоян-
постоянного магнитного поля. Как уже упоминалось, релаксация
происходит к равновесному состоянию, соответствующе-
соответствующему мгновенным значениям приложенных полей,
396
ПРИЛОЖЕНИЕ 111
§ 3. Нелинейные восприимчивости двухуровневой
системы
Рассмотрим систему с двумя энергетическими уровня-
уровнями | а > и | b > , расстояние между которыми равно
<
C.1)
А. ДВА ВРАЩАЮЩИХСЯ ПОЛЯ
Пусть два периодических возмущения с частотами ом
и со2 имеют только недиагональные матричные элементы.
Если говорить о магнитном резонансе, то это означает,
что на систему действуют два вращающихся высоко-
высокочастотных поля. Если иг = —соь то имеем высокочастот-
высокочастотное линейно поляризованное поле. Мы воспользуемся
обозначениями, принятыми для магнитодипольных пере-
переходов, хотя результаты остаются в силе для любой двух-
двухуровневой системы A0, 23].
Пусть
«л ко г*
= ОЬаЬ
и Таь = Тч; тогда уравнения движения имеют вид
%а6 = - К<*Ьа + П71)раЬ + ffib (Pbb~Paa)' C-2a)
( l) pbb ~ Раа) . C.26)
X {ръь ~ Раа ~ Pbb + Раа) , C • 2в)
Pan + pbb = У. I-J.^rj
В первом порядке получаем известное линейное при-
приближение
= "а .i_i (р™' ~ Pw)
A)
и аналогичные выражения для р^' (ы2), pal' (mi)
ПРИЛОЖЕНИЕ 111
397
и раь} (а>2)- Заметим, что в случае затухания pba( + <ai) —
~ +раь {—ом). Во втором приближении разность между
диагональными элементами матрицы плотности имеет
фурье-компоненты с частотами coi — (о2, ©2—coi и посто-
постоянную составляющую:
о*—2 | |2 гг и*
ГB) B)Yro'-M2» ' ^1 ' 2
— со2 -\-iTY
X
C.3)
\Pbb — Раа) — [КРЬЬ Раа ) \ ¦
Из C.2г) следует, что в общем случае при ю ф О
Рьь И +PaaN =--0.
Эти составляющие дают продольную компоненту на-
намагниченности на разностной частоте
е-( (ш,—со,)
/ jgj \ (Mi
_. ,. fnB) Г1BI(со,-со!1) _»(
— — (-10 \Pbb — Раа I S
(о.
где
При (oi = —@2 эта компонента описывает генерацию
второй гармоники при магнитном резонансе, обуслов-
обусловленном линейно поляризованным высокочастотным по-
полем.
Очевидно, что возникновение поляризации на раз-
разностной частоте ± (a»2 — wi) является параметрическим
процессом. Заметим, что фаза намагниченности на этой
частоте зависит от разности фаз приложенных полей
с частотами coi и <в2. Будет ли поглощение на частоте
©2 — a»i положительным или отрицательным, зависит от
фазы продольного магнитного поля на этой частоте.
Приложение т
Постоянная составляющая второго приближения опи-
описывает начало насыщения при наличии двух вращаю-
вращающихся полей:
и |2
Г B) B) (пост \—2Т1Тг% \1аЬ
\Pbb-Paa) = 7 s^Z
[ (®\ — юЬа) Т
J°H
C.5)
Ясно, что это только первое приближение к описанию
эффекта насыщения, которое можно получить разложе-
разложением обычного знаменателя, описывающего насыщение,
в степенной ряд.
Если разность рьь — раа (в 3.2а) заменить на
B) B) * C)
Рьь —Раа , то получим третье приближение pW , кото-
которое имеет новые частотные компоненты 2o>i — а>2
и 2©2 — «м- Это параметрические члены. При ©i = —002
они описывают генерацию третьей гармоники.
Кроме того, оказывается, что намагниченность на
частоте со] имеет слагаемые, пропорциональные |#i|2#i
и | //г |2//1 - Первое слагаемое всегда уменьшает получен-
полученное в первом приближении поглощение на частоте шь
Оно соответствует процессам поглощения и излучения
фотонов с энергией Ami и описывает начинающееся насы-
насыщение сигнала на частоте шь Второе слагаемое соответ-
соответствует поглощению (излучению) кванта Acoi и излучению
(поглощению) кванта Асо2. Разность энергии фотонов
±А(со2 — coi) поглощается за счет механизма затухания.
Это слагаемое соответствует комбинационному процессу
и может или увеличить или уменьшить поглощение на
частоте ом. Описанная процедура может быть продолже-
^ C) C) „ D) D)
на бесконечно; из рьа и раь можно найти рьь —Раа
и т. д. В результате получаются приближения по воз-
возрастающим степеням #i и Я2.
Можно также получить решение в виде ряда по степе-
степеням Я2> верное в любом порядке по Н\. Это решение уже
обсуждалось Блохом [7], который воспользовался систе-
системой координат, вращающейся с частотой И|. В этой
системе большое возмущение Н\ не зависит от времени.
В настоящей работе решение для матрицы плотности
ПРИЛОЖЕНИЕ 111
ЗФв
определяется в лабораторной системе координат. Ста-
Стационарное решение в приближении, не зависящем от Н2,
является, конечно, не чем иным, как известным решением
уравнения Блоха, учитывающим насыщение
пост пост / @) @)\
Pbb ~Paa ={Pbb ~раа')Х
X
Г,Г
C.6)
,Г2
Pba =
пост пост\
во — Pbb ).
Найдем теперь линейные по Н2 слагаемые элементов
матрицы плотности. Выражение C.6) все еще справедли-
справедливо в этом приближении. Рассмотрим одновременно урав-
уравнения для [рьь — раа}(ш*-ш'>, pW и pi?101':
(@2 -ща + ЯТОРЙ1* = - h'^baHz (рТа™ ~ РГь") +
+ И ynJIi (pbb - раа)(Ш2-ш'», C.7)
— 2П цйоЯфЙ1 J<Ol), C.8)
(«г — 2@] — С006 + tT~2~l) plab~2mt) = — ft~l\labHl {pbb —
— раа}(Ш2-Ш1). C.9)
Явному решению этой системы уравнений легко дать
физическую интерпретацию, обращаясь к системе коор-
координат, вращающейся с частотой чц. Аналитическое реше-
решение для рйа2' имеет вид
Рба2' = — Й~Уйа#2 (Раа —Рбй)П0СТ «2 —(Оба + /77' —
2К~2\ \JLab\ 2|#, | 2 ' —'
ю2 — coj+fT, — 2% \у,аЬ\ \Н{\ /(ю2—2ш,—о)а6-(
C.10)
Предположим, что две приложенные частоты сущест-
существенно различны, так что их можно различить физически,
400
ПРИЛОЖЕНИЕ 111
|C02 — K>i|>rj-'. Тогда выражение C.10) можно преоб-
преобразовать к следующему виду:
р^2>= —D-y?r\labH2 [(@2-©!) ((О2— 2С0! — С0а6 +
- 2/
Г21
(раа - Р66)ПОСТ,
D = (@2 — «1 ) [(@2 —
. —Г,1,"|2_
-—2
2 | тт 2
#1
-2|
~T'2 J -t
2 I it i 2
(@6a — «I Г— C.11)
i[2(@2—(OiJ —
i 2 •
Рассмотрение знаменателя показывает, что действи-
действительная часть исчезает при
©2-со, = ± {(@1-@6аJ + 4й-2|цй6|2#2 + 7Г2}+1/2.
C.12)
Это соответствует резонансу относительно эффектив-
эффективного поля во вращающейся системе координат. Послед-
Последнее слагаемое в числителе соответствует комбинационно-
комбинационному процессу; первое слагаемое дает линейную дисперсию.
Оба эффекта изменяются под действием знаменателя,
который учитывает поглощение и последующее излуче-
излучение произвольного числа квантов ha>\, так как в степен-
степенном разложении удержаны все степени |#i|2. Парамет-
Параметрические процессы проявляются в соответствующих вы-
выражениях для рьъ — раа, которые могут быть получены
подстановкой C.10) или C.11) в уравнение C.8).
В высших приближениях члены, пропорциональ-
пропорциональные Яг и |Я2|2, можно было бы рассчитать аналогич-
аналогичным образом, однако при этом быстро возрастает трудо-
трудоемкость алгебраических выкладок; кроме того, различ-
различные квантовые процессы настолько переплетаются, что
не могут быть разделены.
Б. ОДНО ВРАЩАЮЩЕЕСЯ ПОЛЕ И ОДНО
ПРОДОЛЬНОЕ ОСЦИЛЛИРУЮЩЕЕ ПОЛЕ
В том случае, когда на образец действует одно вра-
вращающееся и одно продольное осциллирующее поле, отри-
отрицательное поглощение, связанное с комбинационными
ПРИЛОЖЕНИЕ 111
401
процессами, выявляется очень четко. Гамильтониан коге-
когерентных возмущений имеет вид
jufKOT TT —tusxt rufKOT*
Obba '— \*-ba ** l" ¦— olab »
'aa — '— Xbb — — f
—im.t
+ Иф )¦
Уравнения движения записываются теперь следую-
следующим образом:
*"*Рбв = — Vba Hie-'OJ (paa — pbb) — h (@6fl + tTt) pba ~
~^(Н3е-!^ + Н1е+'ю'1)рЬа, C.13)
%Я~1 (Vba Hie~'ait Pab ~ ЦаЬ Нle+"'ht Qba) ~~
Pbb — Paa = ~
( @) . @|\
\Pbb~-Paa-—Pbb+Paa)
Мы считаем, что kT > \i0H3 — условие, всегда выпол-
выполняющееся на практике. Последним слагаемым можно
пренебречь в соответствии с приближениями, принятыми
для механизма затухания и обсуждавшимися в начале
настоящей работы. Это слагаемое учитывает то обстоя-
обстоятельство, что система релаксирует к состоянию теплового
равновесия, соответствующему мгновенному гамильто-
гамильтониану ЖА + ЖТ @. а непросто Ж а, это приводит
к небольшой продольной восприимчивости
bb —Раа!
sh
1Ю31
/0 о Л
\РЬЬ—Раа)-
C.15)
Рассматриваемое слагаемое будет удержано в следу-
следующем приближении, чтобы показать, что его вклад пре-
пренебрежимо мал.
Нелинейный отклик в низшем приближении состоит
из поправки на насыщение {рьь — р аа }пост, пропорцио-
пропорциональной |Я]|2, и параметрической компоненты для по-
поперечной составляющей намагниченности с частотами
26 Н. Бломберген
402
ПРИЛОЖЕНИЕ HI
(Oi ± Юз- Эту компоненту можно получить из недиаго-
недиагональных фурье-компонент, например,
|(ш1-ш3) _
Ч- — 2
X
"Ьа'
sh (haba/kT)
X
X
i<03T
C.16)
Последнее слагаемое возникает из первого члена
в правой части равенства C.13) после подстановки вы-
выражения C.15). Оно, очевидно, отличается от первого
слагаемого множителем
sh
поэтому в дальнейшем мы будем им пренебрегать.
В следующем приближении появляются поправки
к компонентам с первоначальными частотами wi и ±со3,
пропорциональные интенсивностям приложенных полей
X
X
+Члены, пропорциональные Н1\Н1\2,
гТ~1
C.17)
C.18)
ПРИЛОЖЕНИЕ 1П_
403
Рассмотрим случай wi — соз = Ыба. Между уровнями
| а > и | Ь > возможен двухквантовыи комбинационный
переход, как показано на фиг. \,а. Исключим однокван-
товые переходы, | —a>i + к>ьа\ 3>7Т , откуда следует, что
«з ~л>Т~21 :^ Т Г'1. В этом случае первые члены в правых
w3-w,=wba
Sz(w2)
Sz(w3)
и s в г
Фиг. 1. Нелинейные процессы в двухуровневой системе.
а — комбинационный процесс с излучением «поперечного» кванта и поглоще-
поглощением «продольного» кванта; б — двухквантовое поглощение; в — комбинаци-
комбинационный процесс с поглощением «поперечного» кванта и излучением «продоль-
«продольного» кванта; г — схематическое представление параметрического процесса.
частях равенств C.17) и C.18) преобладают и нелиней-
нелинейная восприимчивость становится чисто мнимой.
C.19)
= — ш.к
Who !ц* I21
C.20)
(ьь
При нормальных населенностях, piV —р(ьь > 0, знак
восприимчивости таков, что на частоте a>i имеется поло-
положительное поглощение, пропорциональное интенсив-
интенсивности \Н3\2, а на частоте из —отрицательное поглоще-
поглощение, пропорциональное интенсивности |Я]|2, «аки следо-
следовало ожидать при комбинационном эффекте.
Если (oi + из = (Оба, то доминируют последние чле-
члены в C.17) и C.18). При этом знак C.19) сохраняется,
26*
404
ПРИЛОЖЕНИЕ 111
но знак C.20) изменяется на обратный. Теперь имеет
место положительное поглощение на обеих частотах, со-
соответствующее процессу двухквантового поглощения,
показанному на фиг. 1,6.
Фиг. 1, в иллюстрирует случай, когда coi < 0, а»з =
= Шба — соь Хотя знак мнимой восприимчивости C.19)
остается формально неизменным, он теперь соответствует
отрицательному поглощению на частоте | coi |, так как
знак coi отрицателен. Переход с уровня \а ) на уро-
уровень \Ь > совершается с излучением кванта Йом и погло-
поглощением большого кванта Й(оз. Если начальные населен-
населенности инвертированы р!,"'—р'аа > 0, все знаки изме-
изменяются на обратные и все процессы происходят в обрат-
обратном направлении.
Эту задачу также можно решать с учетом^ всех степе-
степеней Ну. При этом опять можно идентифицировать основ-
основные физические'процессы — параметрические и комбина-
комбинационные. В полуклассической теории комбинационные
процессы описываются нелинейными комплексными вос-
приимчивостями, которые четко отличаются от восприим-
чивостей для параметрических процессов. Квантовый
процесс, которому соответствует параметрическая вос-
восприимчивость C.16), представлен на фиг. 1,г. Атомная
система чисто реактивна и не совершает действительного
перехода на уровень с другой энергией. Хотя параметри-
параметрический процесс изображается как трехфотонное рассея-
рассеяние, он описывается более низким приближением теории
возмущения по сравнению с комбинационным процессом.
Причина этого состоит в том, что это когерентный дис-
дисперсионный эффект, а не процесс некогерентного рассея-
рассеяния. (В последнем случае вероятность перехода пропор-
пропорциональна квадрату матричного элемента, так что фазо-
фазовая информация теряется.) Аналогично линейная дис-
дисперсия соответствует когерентному рассеянию. Хотя
последнее часто представляют как процесс рассеяния,
в котором первичный и вторичный фотоны имеют одина-
одинаковую частоту, оно появляется в том же порядке теории
возмущения для матрицы плотности, что и однофотон-
ный ноглощательный процесс. Строго говоря, некоррект-
некорректно представлять линейную дисперсионную поляризацию
ПРИЛОЖЕНИЕ Ш
406
и нелинейную поляризацию как процессы рассеяния фо-
фотонов, в которых фазовая информация не имеет значе-
значения. Фаза индуцированной поляризации на частотах
coi ± юз определяется фазами приложенных полей с ча-
частотами (Oi и (оз и число квантов известно неточно. Вопрос
о том, будет ли происходить поглощение на комбина-
комбинационных частотах, нельзя решить, не зная фаз полей на
этих частотах. Конечно, неправильно было бы полагать,
что поле с частотами (Oi ± (о3 отсутствует. Если даже
первоначально поле с этими комбинационными частота-
частотами не было приложено, такое поле появится вследствие
нелинейной поляризации. Чтобы получить самосогласо-
самосогласованное решение, необходимо учесть реакцию поляриза-
поляризации на электромагнитные типы колебаний. Это будет сде-
сделано в § 5.
В. ДВА ВРАЩАЮЩИХСЯ ПОЛЯ И ОДНО ПРОДОЛЬНОЕ ПОЛЕ
Пусть два вращающихся поля имеют частоты а,[ и а»2,
а частота продольного поля равна ±а»з = ±((Oi — сог).
Если применить метод разложения в ряд по возрастаю-
возрастающим степеням амплитуд поля, то рассматриваемый слу-
случай будет описываться комбинацией результатов, полу-
полученных в п. «а» и «б». Такой метод представляет собой
наилучший систематический подход к задаче. В том слу-
случае, когда как а»ь так и (Ог близки к резонансной частоте
и разность | соi — (Ог| мала, не существует удовлетвори-
удовлетворительной процедуры укорочения. При этом следует удер-
удерживать следующие диагональные фурье-компоненты:
(р66-раа)ПОСТ- (Р66-Ра«)(±°Ч (РьЬ-?аа)(±Ыг)
«Почти резонансными» оказываются
нальные компоненты:
И Т. Д.
такие недиаго-
недиаго(со,) (со2) (ffli—@2) {2со
Pba > Pba - Pba > Pba
(Зсо2—2и
Pba
Bco2-co,) Cco,-2co2)
Pba > Pba >
И Т. Д.
Если к трехуровневой системе приложены три поля
с частотами (Оь а>2 и юз = «и + ©2, то можно однозначно
идентифицировать конечное число «почти резонансных»
членов. Этот случай, представляющий значительный
практический интерес, будет рассмотрен в § 4.
406
ПРИЛОЖЕНИЕ III
§ 4. Нелинейная восприимчивость трехуровневой
системы
Стационарный отклик системы с нижним энергети-
энергетическим состоянием \а >, средним состоянием \Ь) и верх-
верхним состоянием \с > на три приложенных поля с часто-
частотами соь а>2 и соз = coi + CO2 можно рассчитать с помощью
общего метода разложения в ряд Фурье и по степеням
поля. Если три приложенные частоты близки к резонанс-
резонансным частотам, например, j соi — сог,а| <С а>ьа, | сог — шсь| <С
<С (Ось и, следовательно, |со3 — wca| <C coca, то ряд может
быть оборван однозначным образом. Удерживаются
только определенные матричные элементы периоди-
периодических возмущений, так что укороченный гамильтониан
становится равным
0
Ун
0
D.1)
В случае электродипольных переходов имеем, напри-
например, Vab = —Я~'Я* - Ei и т.д. Заметим, что укороченный
гамильтониан можно сделать не зависящим от времени
с помощью диагонального унитарного преобразования
и =,
О 1
о о
о
о
D.2)
^Уилкокс и Лэмб [22] решили задачу для трехуровне-
трехуровневой системы при наличии двух приложенных полей
в этом представлении. Однако стационарное решение
легче получить в лабораторной системе координат. То
обстоятельство, что задача может быть преобразована
к проблеме, в которой каждый матричный элемент в ста-
стационарном состоянии не зависит от времени, позволяет
предположить, что в лабораторной системе координат
каждый элемент матрицы плотности имеет только одну
фурье-компоненту. Это предположение оправдывается.
Удерживаются лишь постоянные составляющие диаго-
диагональных элементов матрицы плотности и следующие
приложение in
407
шесть недиагональных фурье-компонент: P'^1' и рай',
Рса И рас , РсЬ и Pbc
Уравнения движения сводятся к девяти линейным
алгебраическим уравнениям с девятью неизвестными.
Одно «з этих уравнений — неоднородное условие норми-
нормировки р"аСТ + рбГг + р ™ст = 1. При введении обозна-
обозначений
CD 1 — Cuba + i^ba ~~ — Дай .
. G>2 — COc6 + il\b = — Aftc ,
CD-3 — COca + H\a = — Aac
D.3)
получается следующее выражение для уравнений движе-
движения в матричной форме (см. стр. 408).
Решение этой системы линейных уравнений дает зави-
зависимость элементов матрицы плотности от всех степеней
амплитуд трех приложенных полей. Следовательно, ре-
решение содержит все возможные интерференционные эф-
эффекты между одно- и многоквантовыми поглощательны-
ми и излучательными процессами и параметрическими
процессами рассеяния, а также эффекты насыщения,
связанные с последовательными поглощением и излуче-
излучением квантов.
Известны методы упрощения задач с матрицами,
имеющими размерность 9X10. Полезно исключить внача-
вначале раЬ, рьс и рса и представить оставшиеся шесть перемен-
переменных в виде двух векторов р = (paa, р6б, рсс) и ц = (р6а,
Рсь, рас) ¦ Шесть оставшихся уравнений можно предста-
представить как двухвекторные уравнения, умноженные н«
матрицы 3x3. Этот метод использовался Уилкоксом
и Лэмбом [22], а также Ятсивом [14], которые решили
проблему для случая двух больших приложенных полей.
Он позволяет расположить различные слагаемые соот-
соответственно степеням амплитуд поля. Получающиеся вы-
выражения слишком громоздки и мало поучительны, поэто-
поэтому они здесь не приводятся. Если все три поля очень
велики, \V/T\ S> 1, то наступит «тепловая смерть» систе-
системы, рай = pbb = pcc = 7з- В промежуточном случае, когда
несколько отношений- V/Г и ш/Г имеют величину порядка
единицы, возможны специфические инверсионные эффек-.
Q.
о*
S
Q.
о.
3 ~
I ^ 3 *3
Q. Q.
о
5
ПРИЛОЖЕНИЕ III
409
ты; может даже оказаться, что при ограниченном интер-
интервале значений амплитуд поля и параметров релаксации
Рсс — Раа > 0. Следует отметить, однако, что общее реше-
решение системы D.4) является очень громоздким и не пред-
представляет поэтому практической ценности.
Полезнее рассмотреть более частный случай, когда
удерживаются все степени амплитуды одного сильного
поля, скажем, с частотой к>з и используется разложение
в ряд по степеням амплитуд двух слабых полей с часто-
частотами Mi и ш2- Этот подход уже использовался Клогсто-
ном [16]; мы будем следовать его расчету. Мы не будем
делать предположения, что юз = мСа, и сгруппируем раз-
различные члены так, чтобы им можно было дать физи-
физическую интерпретацию. Рассмотрим сначала решение
нулевого приближения, не зависящее от амплитуд полей
с частотами а>\ и юг- Для этого следует взять первую,
вторую, третью и последнюю строки матричного уравне-
уравнения D.4) я опустить в них Vab, Vba, Vbe и VCb- В резуль-
результате получаются члены, не зависящие от полей с частота-
частотами mi и ш2- Решение состоит из известных населенностей
трехуровневого мазера, р <о°> , р[°> и р(с°} и отклика
недиагональных элементов на частоте накачки:
(n(O)i(oK) г (om-ш,)* = д-1 у /р@)_р@)\
\Рса I (Рас I са уса\Уаа Vcc)
Далее рассмотрим совместно два уравнения для рЬа
и рьс, т. е. пятую и шестую строки матрицы D.4)
- Vcapi'J + Vbcpi'J = 0, D. 4a)
Vba (PaJ - р$ )
Vbc (P(c°c ~ pi*') +
~ Vacpti +Vba9ac = 0. D.46)
Решение этой системы дает нам первое приближение
для рьа и рьс, линейное по амплитудам полей с частота-
частотами О)) И Ы2-
РЬа I —
-l
f@) @)\ ,
ba \Раа ~ Pbb ) ~\
1>сс)
Г
D.5)
27
Бломберген
410
ПРИЛОЖЕНИЕ 111
Это выражение содержит те же члены, что и равенст-
равенство B5) работы Клогстона [16]. Аналогичное выражение
имеет место для р <.{,> = р^'*. Члены перегруппированы
для облегчения их идентификации.
Если частоты выбраны так, что отклик максимален
для данного значения амплитуды накачки, то множи-
множитель, стоящий вне квадратных скобок, всегда имеет вели-
величину порядка единицы. Если расширение линий из-за
поля накачки меньше их естественной ширины | УОс/Г| <С
<С 1, то этот множитель можно, очевидно, заменить на
единицу. Однако при |^ас/Г|>1. рассматриваемый
множитель имеет провал при резонансных частотах
со! = шЬЯ) 02 = (лъс, что приводит к характерному расщеп-
расщеплению резонанса. Это непосредственно видно из резо-
резонансных условий C.12), записанных во вращающейся
системе координат. Когда частота установлена вне про-
провала в центре так, что отклик максимален, то множи-
множитель опять имеет значение порядка единицы.
Первое слагаемое в квадратных скобках равенст-
равенства D.5) имеет вид линейного отклика. Разность населен-
ностей р (?? — pb°b' не определяется только температурой,
а является функцией мощности накачки |^ас|2. Это сла-
слагаемое в случае р$—р^°» >0 описывает мазерное
действие.
Второе слагаемое соответствует индуцированному
комбинационному эффекту. Вероятность перехода
с уровня \Ь > на \с > с поглощением кванта Йюз и излу-
излучением кванта tuo^ должна быть пропорциональна
Ръъ — Рсс- Второе слагаемое отражает также процесс с ве-
вероятностью, пропорциональной раа — Рьь, который дол-
должен быть добавлен к индуцированному комбинационно-
комбинационному переходу. Он представляет собой одноквантовое
поглощение, связанное с переходом \а >-> \Ь > и сопро-
сопровождаемое одновременным рассеянием одного или более
квантов Ны3.
Третье и четвертое слагаемые в квадратных скобках
имеют вид параметрических членов. Приложенные поля
с частотой юз и ш2 создают поляризацию с частотой юь
Однако эти слагаемые представляют не только процесс
рассеяния с участием трех квантов. Они описывают так-
ПРИЛОЖЕНИЕ III
411
же интерференцию между однофотонными и комбина-
комбинационными процессами в выражении для вероятности
перехода между уровнями \а > и \Ь >, которые связаны
матричным элементом вида с Vab + c'VacVcb. Это приво-
приводит к поглощению, пропорциональному VabVbcVca. Полу-
Полученным в этом приближении выражениям уже очень
трудно дать наглядную физическую интерпретацию
и связать их с элементарными квантовыми процессами.
a
в
Ф и г. 2. Нелинейные процессы в трехуровневой системе.
а — комбинационный процесс; б — параметрический процесс; в — комбинация
процессов насыщения, мазериых, индуцированных комбинационных и пара-
параметрических процессов (все схемы не следует понимать слишком буквально).
Схему на фиг. 2 не следует понимать слишком букваль-
буквально. Макроскопическое поведение описывается комплекс-
комплексными восприимчивостями параметрического или комби-
комбинационного типа. Первые соответствуют поляризации на
комбинационной частоте, индуцированной полями, при-
приложенными на других частотах. Комплексное значение
восприимчивости определяет фазу поляризации по отно-
отношению к этим приложенным полям. Не зная фазы на
комбинационной частоте, нельзя решить, происходит ли
поглощение. Восприимчивость комбинационного типа
описывает комплексное изменение линейного показателя
преломления, пропорциональное интенсивности поля
27*
412
ПРИЛОЖЕНИЕ 111
с другой частотой. Его мнимая часть соответствует поло-
положительному или отрицательному поглощению.
Решение D.5) для р<,{,>= р^'/я р^> = р<{,>*можно сно-
снова подставить в уравнения для населенностей и для
р = р* , что определит второе приближение, квадра-
квадратичное по амплитудам слабых полей |Уаь|
VabVbc я VcbVba. В третьем приближении можно вос-
воспользоваться уравнениями D.4а) и D.46), чтобы полу-
получить соотношение между р^1 и р?2)—р^2) и т. д. Эта
процедура трудоемка, и в случае, когда поля с частотами
Mi и ш2 сравнимы с параметрами затухания,
I Vab, bJTab, be | ~ 1, можно с тем же успехом решать пол-
полную матрицу D.4).
Обсудим теперь несколько подробнее относительную
роль различных членов в D.5). Если расширение линии
из-за поля накачки мало по сравнению с ее естественной
шириной и все частоты близки к резонансным, то первый
член доминирует, и мы получим известный случай трех-
трехуровневого мазера на твердом теле.
При очень больших |Vac| второй, комбинационный,
член не обязательно будет больше первого, так как при
этом разность населенностей p{a°J — р^°> стремится к ну-
нулю. Следует помнить, что индекс @) относится к нулевой
степени амплитуд только малых полей. Фактически оп-
оптимальный отклик, т. е. максимальное значение р^>, бу-
будет иметь место при |У2С/Д2| — 1, как уже пояснялось
выше. В этом случае комбинационный член имеет тот же
порядок величины, что и мазерный член, и для подробно-
подробного сравнения необходимо знать точные значения
I Vca/Aoc| и \VcJAbc\-
Существует, однако, ситуация, в которой комбинаци-
комбинационный член всегда доминирует. Так будет обстоять дело
в том случае, когда только одна частота юг = (ось явля-
является резонансной и приложенное на этой частоте поле
очень мало, Уьс = 0. В силу последнего условия пара-
параметрические члены обращаются в нуль. Поскольку ни
частота mi, ни частота накачки юз не резонансны, т. е.
|©1 — (i>ba\ > Тьа Я | СО 1 — CD&a| = | ©3 — «еа | >
> | Vca | > Тса, мнимая часть первого члена, соот-
ПРИЛОЖЕ11ИЕ III
413
ветствующая линейному поглощению, равна
Гьа|Аьа|1/ьа(р^°) — Р*°}) ¦ Отношение комбинационного
члена к линейному поглощению легко может быть сде-
сделано больше единицы:
Рю - р?})
г6сгй
> — п'°>
о@)\
Так как поле накачки нерезонансно, населенности факти-
фактически имеют равновесные значения. Если расширение
линии, обусловленное полем накачки, больше естествен-
естественных ширин Гьс и Гьа, то доминирует комбинационный
процесс. Перечисленные условия, конечно, в точности со-
соответствуют условиям, при которых наблюдалось дейст-
действие комбинационного лазера [34].
Если все три частоты достаточно далеки от резонан-
резонанса, то параметрические члены в D.5) могут всегда быть
сделаны преобладающими. Отношение параметрическо-
параметрического члена к линейному поглощению в этом случае больше
единицы, если
Это условие может быть выполнено даже в случае, -когда
уширение линий из-за накачки меньше ее естественной
ширины. Если первоначально амплитуда Vba очень мала,
то большие приложенные поля с частотами ш3 и ш2 соз-
создадут поляризацию на частоте «м. Этот «чисто парамет-
параметрический» случай иллюстрируется на фиг. 2, б, хотя сле-
следует помнить, как отмечалось выше, ограниченность та-
такого наглядного представления. Если приложенные час-
частоты далеки от резонансных, то процедура укорочения,
которая поивела к равенству D.5), уже неприменима.
Очевидно, что в этом случае следует вернуться к общему
методу, описанному в § 2.
До сих пор предполагалось, что амплитуды полей за-
заданы. Это предположение выполняется при расчете мак-
макроскопических восприимчивостей. Если приложенное
поле с частотой ю, исчезает, Vab = 0, то в D.5) остаются
только параметрические члены. Они создадут поляриза-
поляризацию с частотой (oi, которая в свою очередь приведет
414
ПРИЛОЖЕНИЕ 111
к появлению поля с частотой а\. Предположение, что
Vab = 0, не самосогласовано. На примере этого крайнего
случая ясно видна важность вопроса о связи амплитуд
полей с реакцией материальной системы на поля.
§ 5. Связь между нелинейной средой
и электромагнитными типами колебаний
Вопрос об обратной реакции материальной системы
на электромагнитные типы колебаний давно анализиро-
анализировался Бломбергеном и Паундом [35]. Они рассматривали
прецессирующую намагниченность при магнитном резо-
резонансе как источник электромагнитных типов колебаний.
Этот способ применялся в дальнейшем многими автора-
авторами [15—17, 36, 37]. Математически уравнения движения
классического гармонического осциллятора (или осцил-
осцилляторов), соответствующего электромагнитному типу
(или типам) колебаний, добавляются к уравнениям дви-
движения для элементов матрицы плотности. Мы ограни-
ограничимся случаем электрического дипольного взаимодейст-
взаимодействия и разложим электрическое поле по нормальным ти-
типам колебаний с динамическими переменными px(t):
Е(г, 0 = -D^2^@Ех(г), E.1)
х
где действительные функции Ех образуют нормирован-
нормированную ортогональную систему
x(r).E(i(r)dr = 6x!i. E.2)
Джейнс [36] дал изящное рассмотрение связи между
полуклассическим подходом и строгой теорией с кванто-
квантованными гармоническими осцилляторами. Классическое
уравнение движения для К-го гармонического осцилля-
осциллятора можно представить в виде
X
.(r)rfr + -L<
dt*
~T~ ¦* внешн^ / *
X
E.3)
Затухание типа колебаний, которое обусловлено на-
наведенными токами и потерями за счет связи, описывает-
ПРИЛОЖЕНИЕ III
415
ся феноменологическим членом, содержащим доброт-
добротность Q\; через е и jx обозначены линейные электриче-
электрическая и магнитная восприимчивости среды, не содержа-
содержащие членов, которые явно входят в среднее значение
поляризации;
<Р(Г,
t).
E.4)
nn'
Последний член в E.3) представляет внешнюю вынуж-
вынуждающую силу, которой является, например, входной ко-
когерентный сигнал или мощность, поступающая от внеш-
внешнего генератора накачки.
Уравнения E.3) после подстановки выражения E.4)
нужно решить совместно с уравнениями движения B.1)
для элементов матрицы плотности. Заметим, что Ж Ког —
линейная функция динамических переменных р\ (t). Те-
Теперь также возможно найти стационарное решение, раз-
разложив в ряды все элементы pnn- (t) и все переменные
pi(t). Эта процедура, которая быстро становится гро-
громоздкой, будет проиллюстрирована на нескольких при-
примерах.
В случае СВЧ или оптического квантового генерато-
генератора с некогерентной накачкой мы имеем двухуровневую
атомную систему и один электромагнитный тип колеба-
колебаний, который создает осциллирующее поле в месте распо-
расположения активных частиц (с плотностью jV см~3). Сле-
Следует рассматривать совместно четыре уравнения: урав-
уравнения для постоянной составляющей разности населен-
ностей р"°ст—р™ст для двух недиагональных фурье-
компонент матрицы плотности р$= р^ш)* и р^> = р^ю)*
и для фурье-компоненты (для частоты ш) динамической
переменной р <ш), соответствующей единственному типу
колебаний с резонансной частотой ©х, близкой к ©. Урав-
Уравнение E.3) для этой стационарной компоненты можно
написать в явной форме
Рх
X
ец (—
X [ J *ta ¦ Е, (г) р$ (г)
(г) РЙ> (г) dr] ¦ E.5)
416
ПРИЛОЖЕНИЕ III
Здесь были использованы свойства ортонормироваино-
сти действительных функций Fx. Решение уравнения
E.5) совместно с уравнениями для элементов матрицы
плотности детально описано Файном [18] и Дэкисом [37].
Ими получено условие возбуждения стационарных коле-
колебаний в мазере.
В качестве следующего примера рассмотрим пара-
параметрический случай низшего порядка, обсуждавшийся
в § 2. Предположим, что имеются три типа колебаний
резонатора с резонансными частотами сох, ~ «и, «н2 ~
~ ©2 и шх, ~ wi + ©г- После того как уравнения для
матричных элементов плотности решены и элементы вы-
выражены через полевые динамические переменные /?х„
Р\2 и P),s, из уравнений B.22) и E.1) получаются выра-
выражения для среднего значения поляризации в функции
этих полевых переменных. Они могут быть представлены
с помощью линейной и нелинейной восприимчивостей
< Р<»'> (г) > =
+ D*JXNL К =
< ро.» (г) > = -
Dt^xnlK = (Oe
< Pto'> (r) > = -
) D*)'/. .Ех,(г) /
соз - <о8) : ЕХз (г)ЕХз (г) pi
х К) (W' ¦ ЕХ2 (г) р[У
-fflx) :EX3(r)EXl (Ор^
'2 ¦ Ex, (r) />1?!
E-6)
Эти выражения следует подставить в уравнения E.3)
для удерживаемых фурье-кймпонент динамических пере-
переменных р{у= pi-^)', p[y=p[-^f, p{y^pi-^\ Все дру-
другие фурье-комяоненты отбрасываются как нерезонанс-
нерезонансные. Таким образом получается система уравнений, опи-
описывающих нелинейную связь низшего порядка между
электромагнитными типами колебаний
ПРИЛОЖЕНИЕ III
417
Wr-) fЕ>.(г)
J
xNL
= ©з — Щ) ¦¦ Ex. (Г) ЕХ, (Г) df + 4- ^в
E.7)
и два аналогичных равенства для /?(.Ш2> и px(a>s). Интеграл
в первом члене правой части берется по всему объему
резонатора. Он равен произведению «фактора заполне-
заполнения» на линейную часть восприимчивости, не включен-
включенную в е. Второй член соответствует нелинейной связи
низшего порядка. С помощью аналогичных методов Лэмб
[38] (см. также [39]). рассмотрел нелинейную связь меж-
между типами колебаний в газовом оптическом квантовом
генераторе.
Уравнения E.7) аналогичны, конечно, связанным
уравнениям для амплитуд, полученным в работе Арм-
Армстронга и др. [3] (см. в особенности уравнение D.9)
работы [3]). Это скорее алгебраические, а не дифферен-
дифференциальные уравнения, так как они описывают стационар-
стационарный отклик системы на периодические вынуждающие
силы и колебательные нелинейные эффекты, а не эффек-
эффекты для бегущих волн. Уравнения E.7) являются не-
несколько более общими, чем соответствующие уравнения
Армстронга, поскольку в них учитывается механизм за-
затухания и в нелинейной среде, и в стенках резонатора.
Интегралы по объему образца в нелинейном члене соот-
соответствуют условию сохранения момента, или согласова-
согласования фазовых скоростей в случае бесконечной однородной
среды без потерь и однородных плоских волн. При ©i =
= (о2 уравнения E.7) удобно применять для описания
генерации второй СВЧ гармоники в ферритах или гене-
генерации гармоник в резонаторах лазеров.
Эту процедуру легко, конечно, обобщить на случай,
когда учитываются нелинейные эффекты высших поряд-
порядков, включая комбинационные эффекты. При равной ну-
нулю вынуждающей силе система нелинейных однородных
уравнений может иметь отличное от нуля решение в том
случае, когда случайное иоле накачки создает некоторую
инверсию населенностей. Если на одной частоте, скажем
юз, имеется большой входной сигнал, то на двух других,
418
ПРИЛОЖЕНИЕ 111
меньших частотах могут одновременно возникнуть коле-
колебания из-за параметрических членов, смешанных с ма-
зерными и индуцированными комбинационными члена-
членами. Чтобы показать, что все нелинейности в принципе
включены в этот формализм, рассмотрим снова трехуров-
трехуровневую систему. Предположим, что три поля с частотами
©1, (о2 и юз возникают вследствие возбуждения трех элек-
электромагнитных типов колебаний с резонансными частота-
частотами сох, ~ (Оь сох, ~ юг, он, ~ со3. Сохраним только ре-
резонансные фурье-компоненты динамических переменных,
соответствующих этим типам колебаний. Следовательно,
реакция материальной системы на поля будет учтена,
если к девяти уравнениям для матричных элементов
плотности D.4) прибавить следующие три уравнения
для типов колебаний:
X
X
DлI''
X
X
E),2(r))p(Cb2)(r)dr + JF(m2).
Dл)'
E.8)
^ + m
X
полученные из
степеней р (±m»»f
Недиагональные матричные элементы,
уравнений D.4) и зависящие от всех
p(±m^ и Р^'К можно представить в E.8). Этот метод
описания соответствует эксперименту Келлингтона [40].
Полученные алгебраические уравнения могут быть
в принципе решены относительно компонент р'х±а>). Вслед-
ПРИЛОЖЕНИЕ III
419
ствие сложных нелинейностей в правой части необходи-
необходимо применять приближенные методы. Представляется,
однако, маловероятным, что способ, использованный
Клогстоном [16], который в выражении для поля реакции
удерживал линейные по /?(xmi) и р[Шг) члены, позволит по-
получить удовлетворительное описание квантовых генера-
генераторов.
§ 6. Заключение
Получены общие выражения для комплексных нели-
нелинейных восприимчивостей при наличии затухания, кото-
которые одновременно описывают параметрические, мазер-
ные и индуцированные комбинационные эффекты. Если
приложенные поля близки к резонансам атомной систе-
системы и их амплитуды соответствуют расширениям линий,
превышающим их естественную ширину, разделить эти
эффекты невозможно. При этом следует рассматривать
общую поляризацию, которая является смесью линей-
линейных и нелинейных эффектов, и считать ее источником,
взаимодействующим с электромагнитными полями. По-
Получены связанные уравнения для динамических пере-
переменных поля и матрицы плотности произвольной нели-
нелинейной среды; однако для нахождения стационарных
решений в явном виде необходимо удерживать только
малое число членов в степенном разложении, отбрасы-
отбрасывать нерезонансные члены и применять другие прибли-
приближения,
ЛИТЕРАТУРА
1. Blaton J., Zs. Phys., 69, 835 A931).
2. Guttinger P., Helv. Phys. Ada, 5, 237 A932).
3. Armstrong J., BloembergenN., DucuingJ., Per-
shan P. S., Phys. iRev., 127, 1918 A962). (См. приложение I
к настоящей книге.)
4. К а г р 1 u s R., S с h w i n g e r J., Phys. Rev., 73, 1020 0948).
5. Kubo R., Tomi ta K-, Journ. Phys. Soc. Japan, 9, 888 A954).
6. WangsnessR. K, Bloch iF., Phys. iRev., 89, 278 A953).
7. Bloch R, Phys. Rev., 102, 104 A956).
8. Redfield A. G., IBM Journ., 1, 19 A957).
9. Abragam A., Principles of Nuclear Magnetism, Oxford, 1961.
(Имеется перевод: А, Абрагам, Ядерный магнетизм, ИЛ,
1964.)
420
ПРИЛОЖЕНИЕ III
10. Hubb a rd P. S., Rev. Mod. Phys., 33, 249 A961).
11. Javan A., Phys. Rev., 107, 1579 <1957).
12. Winter J. M., Journ. Phys. Rad., 19, 802 A958).
13. Javan A., Journ. Phys. Rad., 19, 806 A959).
14. Yatsiv S., Phys. Rev., 113, 1538 A959).
15. Anderson P. W., Journ. Appl. Phys., 28, 1049 A957).
16. Clogston A. M., Journ. Chem. Phys. Sol, 4, 271 A958). (Име-
(Имеется перевод в сб. «Квантовые парамагнитные усилители», ИЛ,
1960.)
17. Файн В. М, Ханин Я. И,. Яшин Э. Г., ЖЭТФ, 41, 986 A961).
18. Ф айн В М„ Ханин Я. И„ ЖЭТФ, 41, 1498 A961).
19. Kastler A., Rendiconti S. I. F. XVII Corso, New York, 1962,
p. 167.
20. Barrat J. P. Journ. Phys. Rad., 20, 541, 633, 657 A959).
21. Cohen -Tannoudj i C, Rendiconti S. I. F. XVII Corso, New
York, 1962, p. 240.
22. Wilcox L. R., Lamb W. E., Phys. Rev., 119, 1915 A960).
23. Lamb W. E., Sanders Т. M., Phys. Rev., 119, 1901 A960).
24. Feynman R. P., Vernon F. L., Hellwarth R. W., Journ.
Appl. Phys., 28, 49 A957).
25. А у r e s W. P., V a r t a n i a n P. H., M e 1 с h о r J. L., Journ.
Appl. Phys., 27, 188 A956).
26. Bloembergen N., Proceeding of the Third International Con-
Conference on Quantum Electronics, New York, 1963.
27. P r i с e P. J., Phys. Rev, 130, 1792 A963).
28. Kelley P. L, Journ. Phys. Chem. Sol, 24, 607 A963).
29. Me s s i ah A, Quantum Mechanics, New York, 1961.
30. S h e n Y. R, Phys. Rev. (в печати).
31. Fiutak J, Canad. Journ. Phys., 41, 12 A963).
32. Dirac P. A. M, Proc. Roy. Soc, A114, 143, 720 A927).
33. Kramers H. A, Quantum Mechanics, Amsterdam, 1959, p. 482.
34. E с к a r d Q., H e 11 w a r t h R. W, McClung F. J., Schwarz
J. E, Weiner D., Woodbury E. J, Phys. Rev. Lett., 9, 455
A962).
35. Bloembergen N, Pound R. V, Phys. Rev, 95, 8 A954).
36. Jaynes E. T, Cummings F. W, Proc. IEEE, 51, 89 A963).
37. Davis L. W., Proc. IEEE, 51, 76 A963).
38. Lamb W. E, Phys, Rev, 134, A1429 A964).
39. Haken H, Sauerman H, Zs. Phys.. 173, 261 A963).
40. Kellington С. М, Phys, Rev. Lett, 9, 57 A962).
СОДЕРЖАНИЕ
Вступительная статья 5
Литература 28
Предисловие 31
Глава 1. Классическое введение. (Перевод Д. Н. Клышко) 33
§ 1. Нелинейные восприимчивости 33
§ 2. Классические атомные модели нелинейности 35
Газ свободных электронов C5). Ангармоничес-
Ангармонический осциллятор C9). Магнитные волчки D2).
§ 3. Феноменологическая интерпретация нелинейной
поляризации 44
§ 4. План дальнейшего изложения 55
Литература 56
Глава 2. Квантовая теория нелинейных восприимчивостей.
(Перевод Д. Н. Клышко) 59
§ 1. Уравнение Лиувилля для матрицы плотности 59
§ 2. Случайные возмущения и затухание 61
§ 3. Отклик на периодические возмущения 66
§ 4. Нелинейная проводимость низшего порядка 72
§ 5. Нелинейные восприимчивости, описывающие про-
процессы типа комбинационного рассеяния 80
§ 6. Резонансные эффекты высших порядков 88
§ 7. Соотношения Крамерса—Кронига 89
§ 8. Квантование полей , 92
Процессы нелинейного поглощения и рассеяния
(92). Сечения рассеяния и нелинейные воспри-
восприимчивости (98). Когерентные квантовые со-
состояния. Пределы применимости полуклассиче-
полуклассического подхода A01). Квантовая теория зату-
затухания A04).
Литература 108
Глава 3. Уравнения Максвелла в нелинейной среде. (Пере-
(Перевод В. Г. Дмитриева) ПО
§ 1. Энергетические соотношения 111
§ 2. Действующие поля в оптически плотной среде ... 117
§ 3. Уравнения связанных волн в нелинейной среде ... 120
§ 4. Частное решение уравнений Максвелла для недис-
пергируюшей среды с нелинейностью произвольно-
произвольного вида 123
Литература 125
422
СОДЕРЖАНИЕ
СОДЕРЖАНИЕ
423
Глава 4. Распространение волн в нелинейной среде. (Пере-
(Перевод В. Г. Дмитриева) 126
§ 1. Генерация волн на комбинационных частотах
заданными электромагнитными полями; граничные
условия на поверхности нелинейной среды 126
Анизотропная среда A38).
§ 2. Взаимодействие двух связанных волн. Генерация
второй гармоники • 140
§ 3. Взаимодействия электромагнитных волн с акусти-
акустическими волнами 147
Акустические нелинейности A47). Рассеяние
Мандельштама — Бриллюэна A50).
§ 4. Параметрическое преобразование частоты вниз и
параметрическое возбуждение автоколебаний 155
§ 5. Вынужденное комбинационное рассеяние » 164
§ 6. Связь между стоксовыми и антистоксовыми вол-
волнами « 1^5
Литература 187
Глава 5. Экспериментальные результаты. (Перевод А. Г. Ер-
Ершова) 190
§ 1. Экспериментальная проверка законов нелинейного
взаимодействия световых волн в объеме и на по-
поверхности нелинейной среды 190
Геометрические соображения A92). Возникно-
Возникновение волн гармоник при отражении A95). Ге-
Генерация суммарной и разностной частот A99).
§ 2. Определение абсолютной величины нелинейной
восприимчивости * 202
§ 3. Многомодовая структура и флуктуационные явле-
явления 204
§ 4. Нелинейные восприимчивости пьезоэлектрических
кристаллов 210
Температурная зависимость и дисперсия не-
нелинейной восприимчивости в KDP B14). Нели-
Нелинейные восприимчивости полупроводников
B17).
§ 5. Электрические квадрупольные эффекты 221
§ 6. Генерация третьей гармоники 224
§ 7. Многофотонное поглощение * 226
§ 8. Зависимость показателя преломления от интен-
интенсивности света 229
§ 9. Вынужденное комбинационное рассеяние 232
§ 10. Стоксовы и антистоксовы компоненты высших
порядков w 239
§ 11. Комбинационные восприимчивости 248
Литература 253
Глава 6. Заключение. (Перевод А. Г. Ершова) 257
§ 1. Нелинейности в лазерах 258
§ 2. Другие нерешенные проблемы 259
Литература 262
Приложения
I- Дж. Армстронг, Н. Бломберген, Ж. Дюкуэнг,
П. Перша в. Взаимодействие световых воли в нелинейном
диэлектрике. (Перевод А. Г. Ершова) „ » 265
§ 1. Введение 265
§ 2. Вывод квантовомеханических выражений для не-
нелинейных источников к.-... 268
А. Нелинейные источники, зависящие от Е2
B69). Б. Нелинейные источники, зависящие от
Е3 B76). В. Нелинейная ионная поляризация
B79).
§ 3. Соотношения между величинами, связанными с
макроскопическими полями в нелинейных диэлек-
диэлектриках 281
А. Газы B81). Б. Изотропные и кубические
конденсированные среды B86). В. Анизотроп-
Анизотропные кристаллы B88).
§ 4. Связь между электромагнитными волнами 292
§ 5. Генерация второй гармоники. Точное решение ... 299
А. Согласованные фазовые скорости C00).
Б. Неточное согласование фазовых скоростей
C04). В. Среда с потерями C07).
§ 6. Три связанные волны. Точное решение 308
А. Точное согласование, Д&=0 C11). Б. Неточ-
Неточное согласование C17). В. Среда с потерями
C18).
§ 7. Четыре взаимодействующие волны. Генерация
третьей гармоники 318
§ 8. Применения теории к анализу экспериментальных
ситуаций 321
А. Генерация гармоник и субгармоник C21).
Б. Преобразование частоты C24). В. Линей-
Линейный электрооптическнй эффект на нулевой ча-
частоте и на сверхвысоких частотах C251.
§ 9. Об учете действующего поля в анизотропной
среде , 328
§ 10. Заключение 330
Литература '331
II. Н. Б л о м б е р г е н, П. П е р ш а н. Световые волны на
границе нелинейной среды. (Перевод В. Г. Дмитриева) ... 333
§ 1. Введение 333
§ 2. Гармоники, возникающие на границе (частный
случай) „ , 335
§ 3. Общие законы преломления и отражения 342
§ 4. Поляризация и интенсивность волн с комбина-
комбинационными частотами » 346
А. Перпендикулярная поляризация C48).
Б. Параллельная поляризация C50). В. Даль-
Дальнейшие обобщения и примеры C55).
§ 5. Полное отражение п прохождение 359
I
424 СОДЕРЖАНИЕ
§ 6. Нелинейная плоско параллельная пластина 364
§ 7. Метод интегральных уравнений в задачах о рас-
распространении волн в нелинейных средах 372
§ 8. Обсуждение н выводы , 376
Литература 381
III. Н. Б л о м б е р г е н, И. Ш е н. Квантовомеханическое срав-
сравнение нелинейных восприимчивостей параметрических сред,
лазеров и комбинационных лазеров. (Перевод
Д. И. Клышко) ..,.,, , 383
§ 1. Введение 383
§ 2. Общий расчет нелинейных проводимостей и вос-
восприимчивостей 387
§ 3. Нелинейные восприимчивости двухуровневой си-
системы 396
А. Два вращающихся поля C96). Б. Одно вра-
вращающееся поле и одно продольное осциллиру-
осциллирующее поле D00). В. Два вращающихся поля
и одно продольное поле D05).
§ 4. Нелинейная восприимчивость трехуровневой си-
системы 406
§ 5. Связь между нелинейной средой и электромагнит-
электромагнитными типами колебаний 414
6. Заключение 419
: и те р а ту р а 419
Н. Бломберген
Нелинейная оптика
Редакторы В. В. Рабин и И. Г. Нахимсон
Художник В. И. Заикин
Художественный редактор Е. И. Бескова
Технический редактор Л. М. Харьковская
Корректор С. Г. Троцкая
Слано в производство 28/Х 1965 г. Подписано к печати 2/VI 1966 г.
Бумага 84 X 108</з2 - 6,62 бум. л. 22,26 усл. печ. л. Уч.-нзд. л. 20,22
Изд. № 2/3384 Цена 1 р. 68 к. Зак. 1691
Темплан 1966 г. Изд-ва «Мир» пор. № 54
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2
Экспериментальная типография ВНИИПП Комитета по печати при Совете
Министров СССР, Москва, И-51, Цветной бульвар, 39.