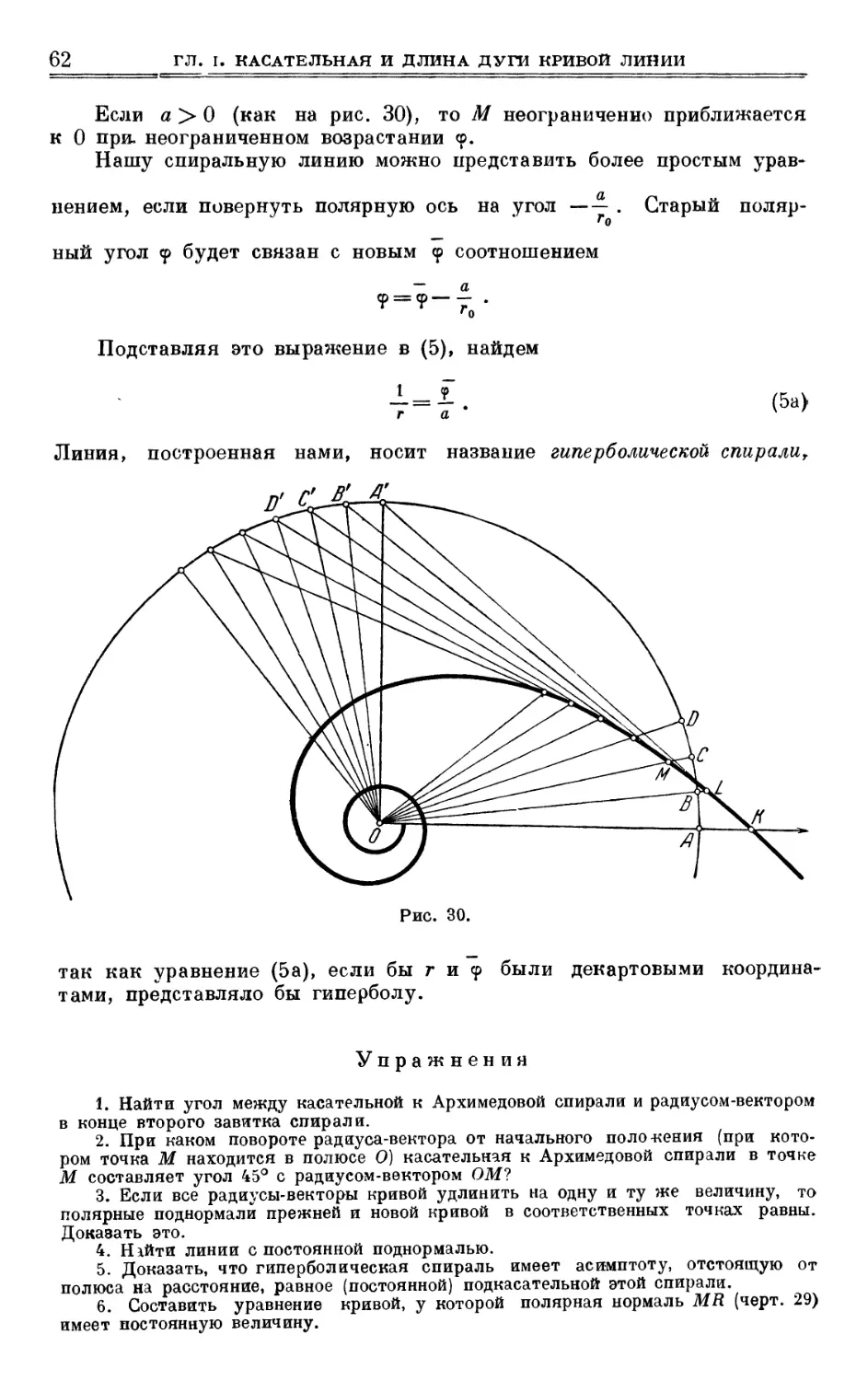
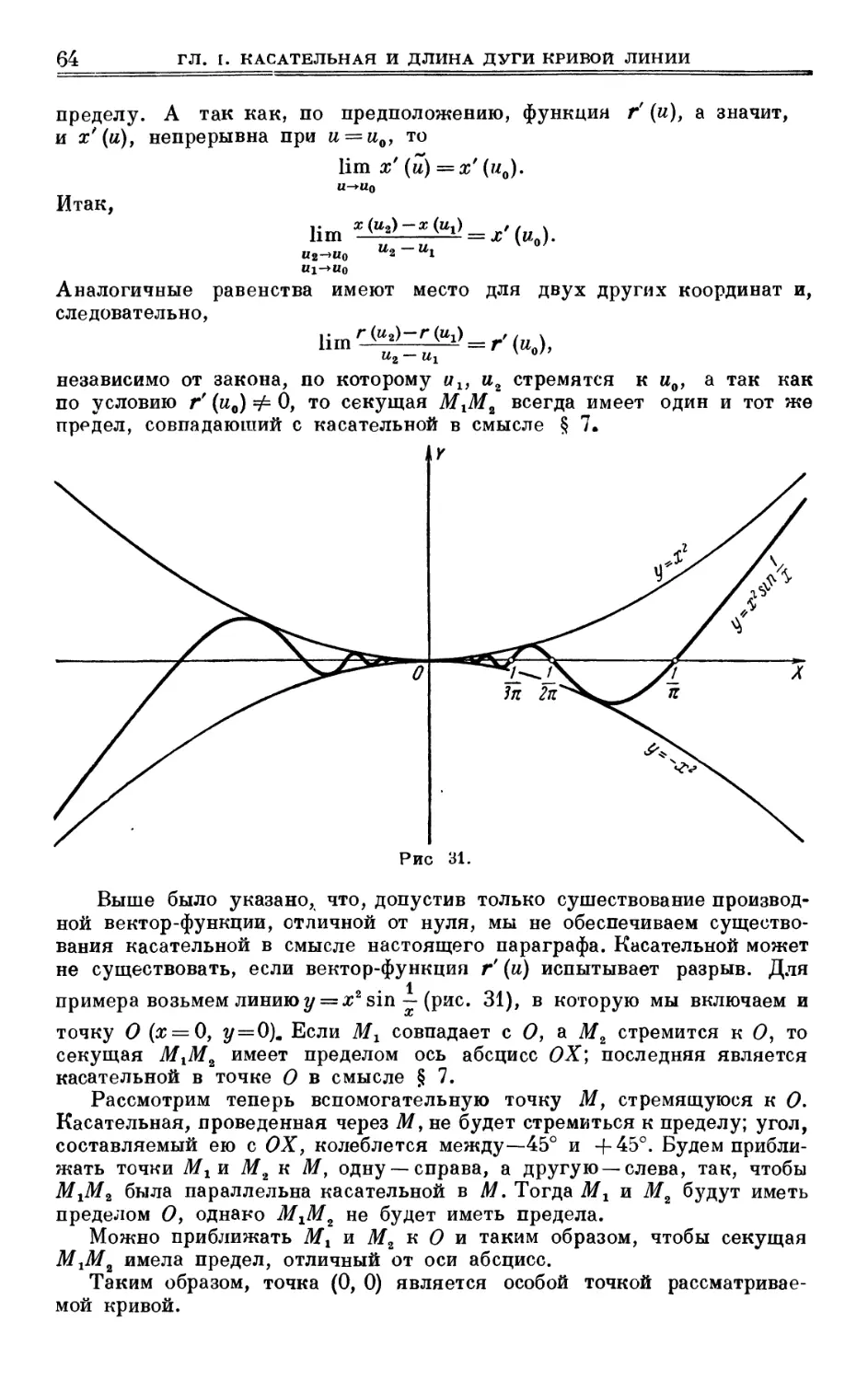
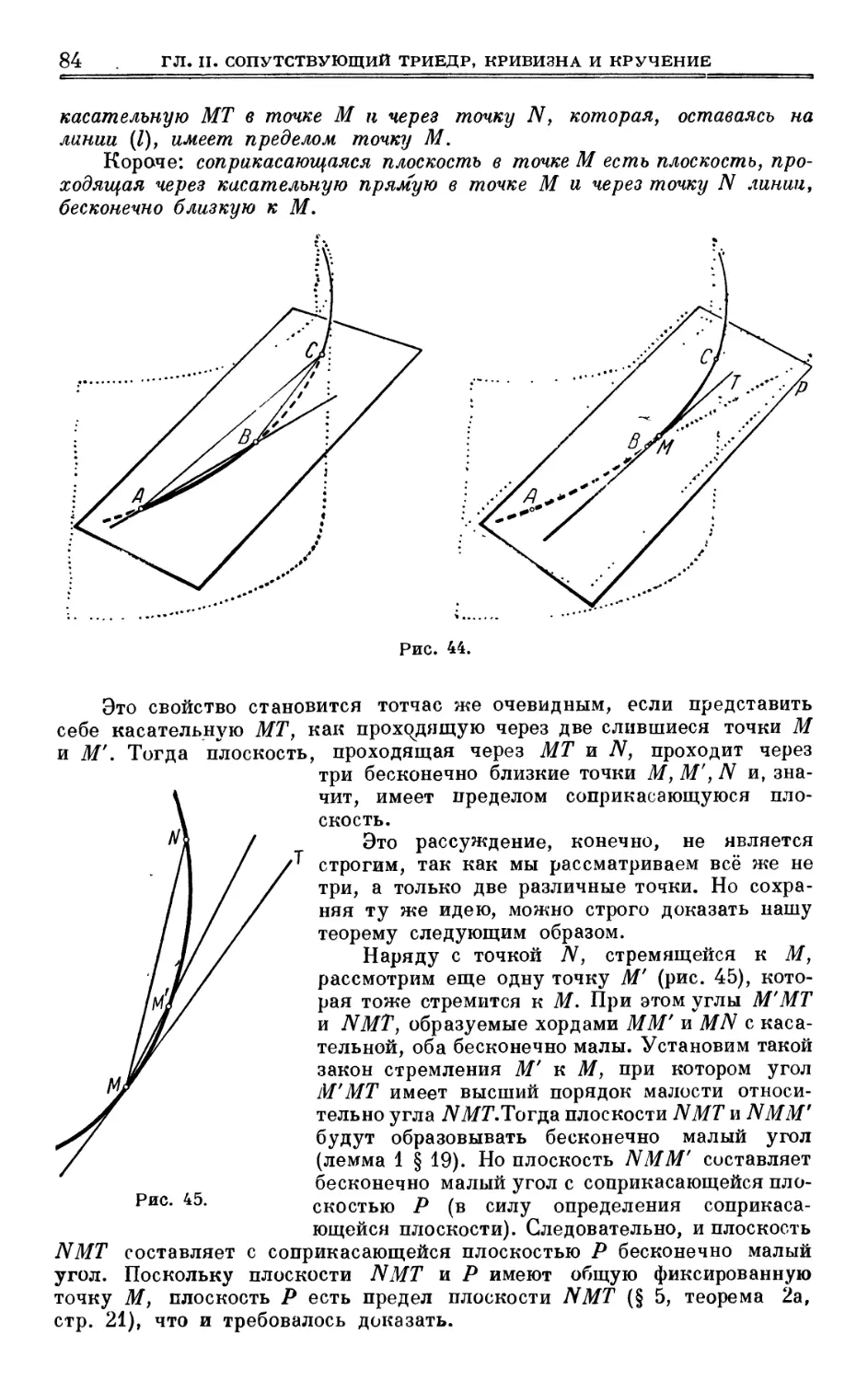
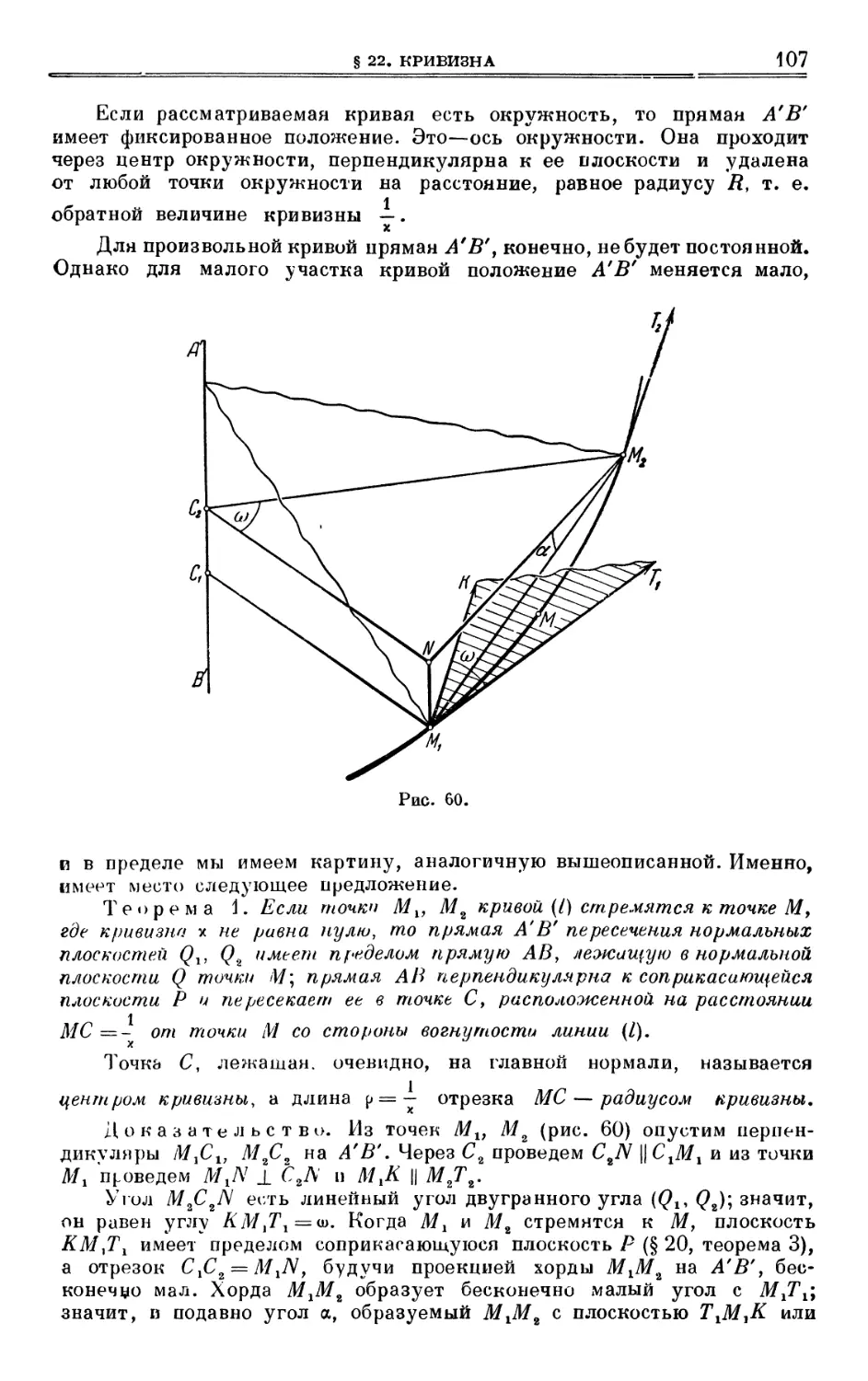
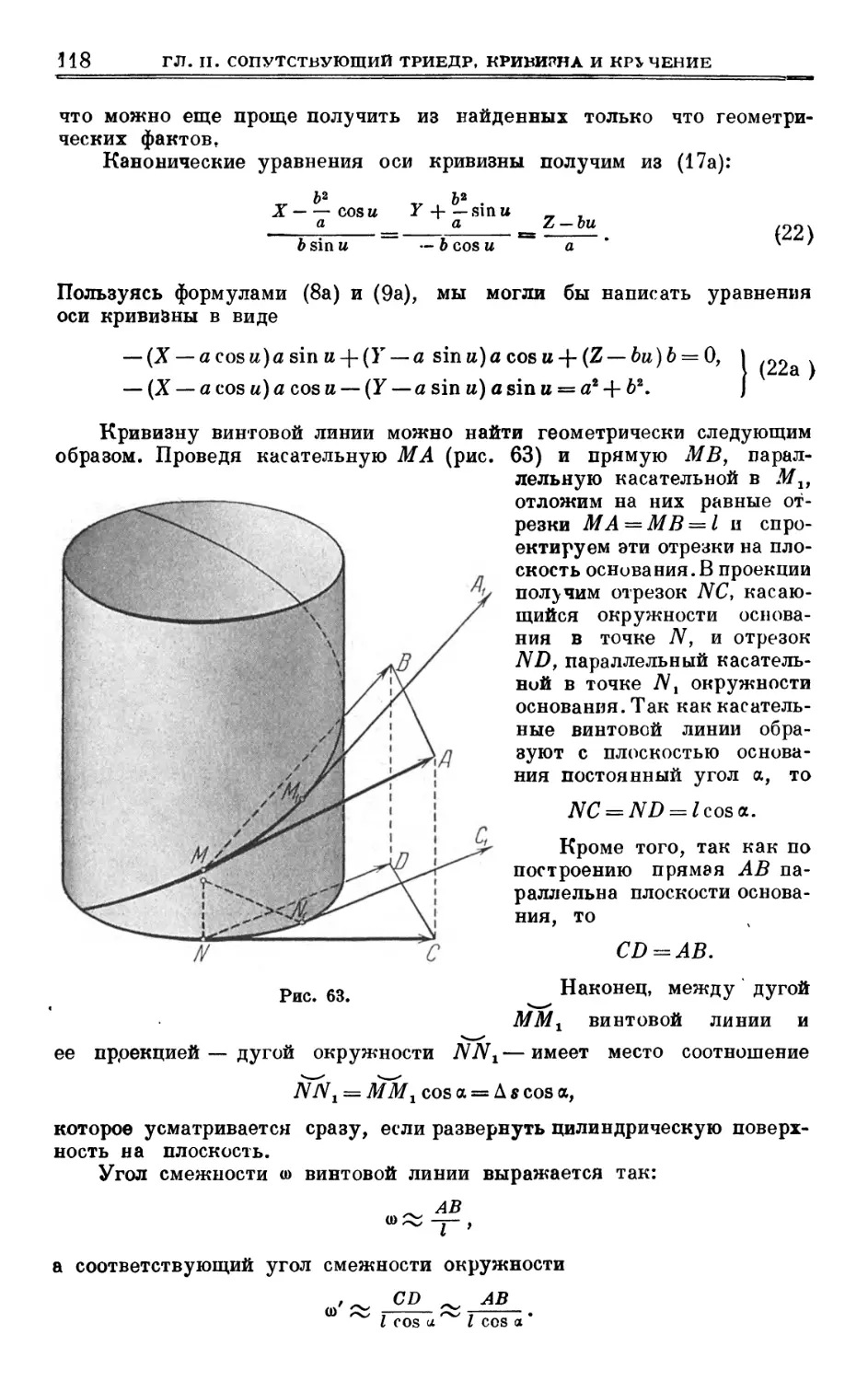
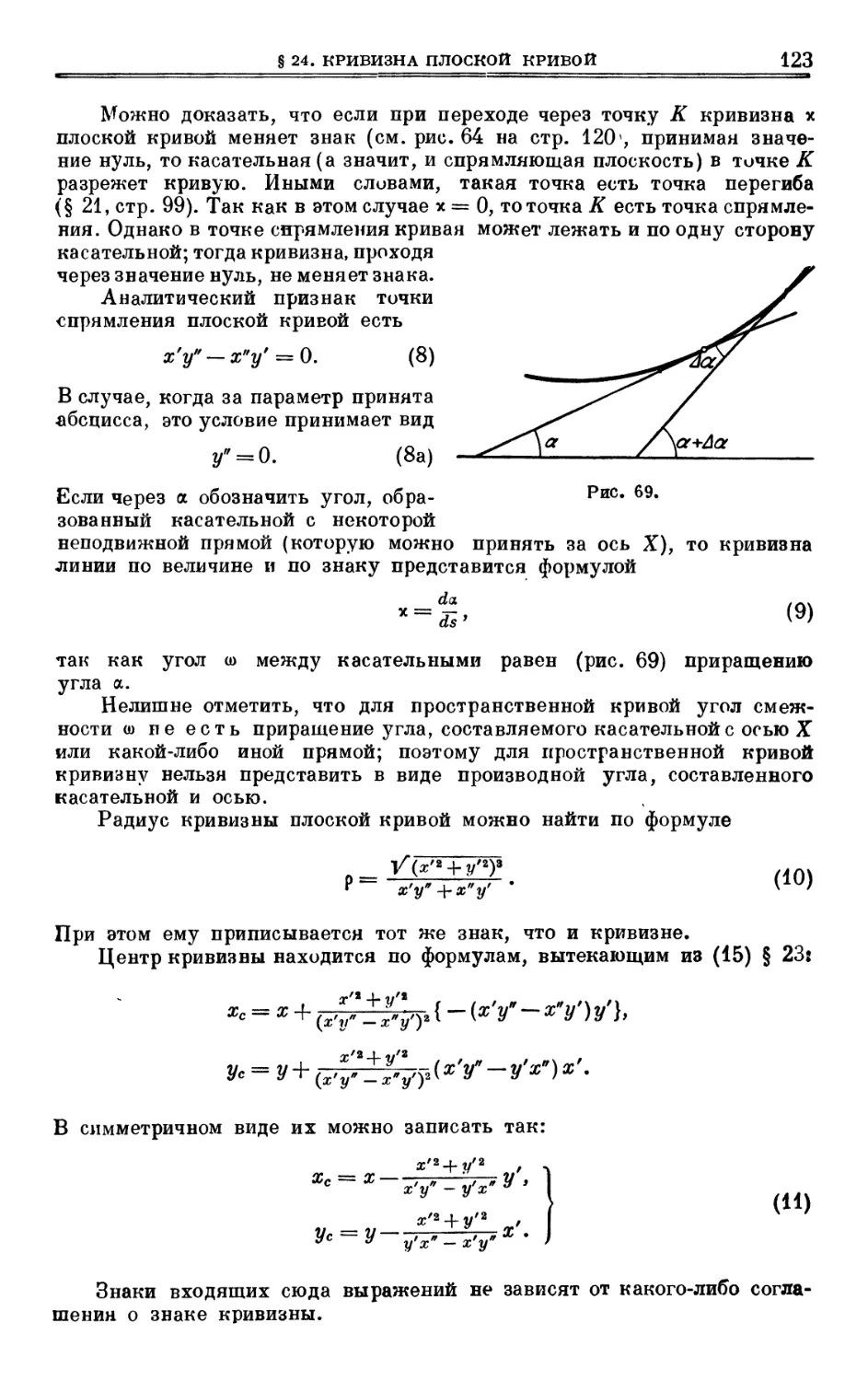
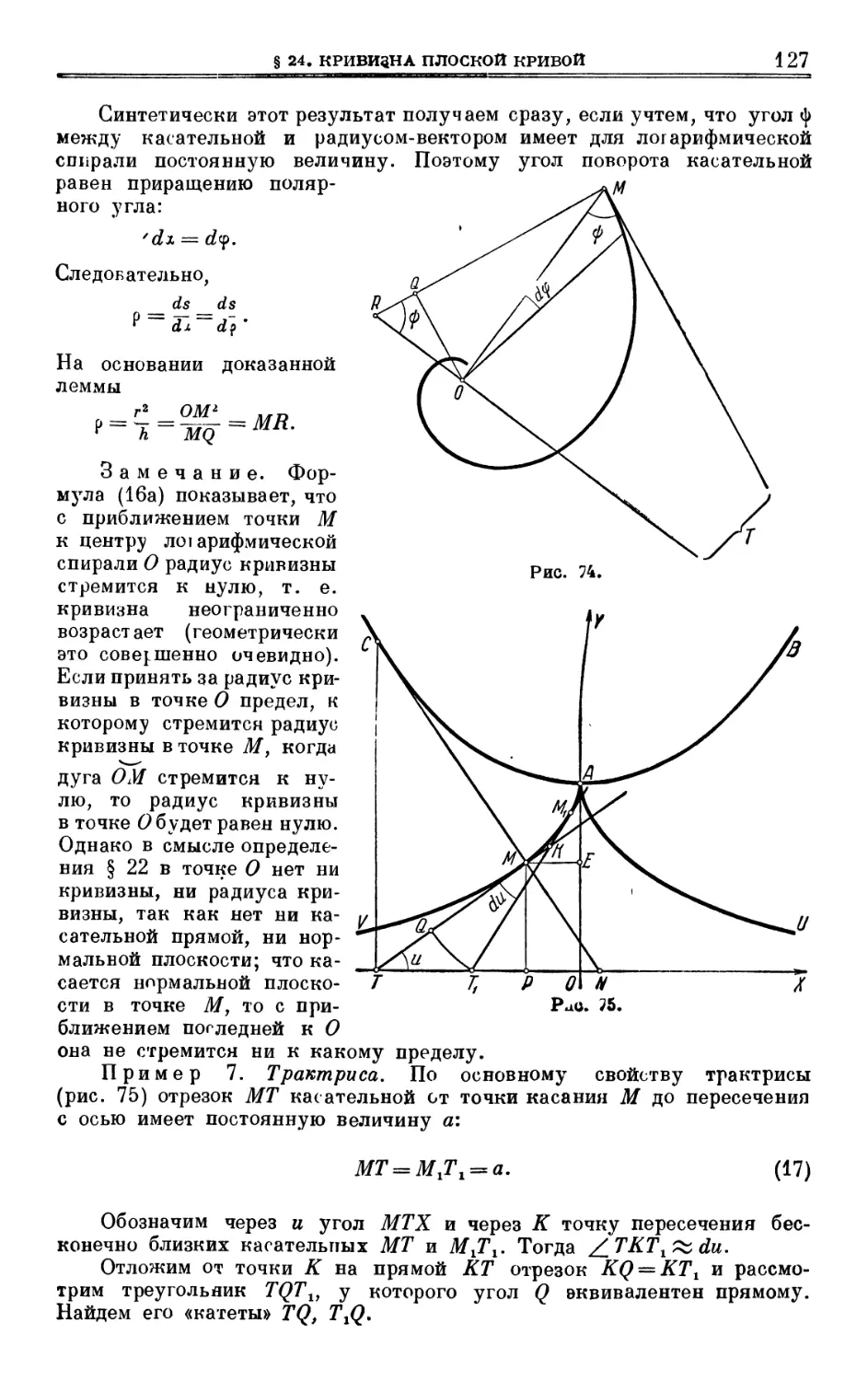
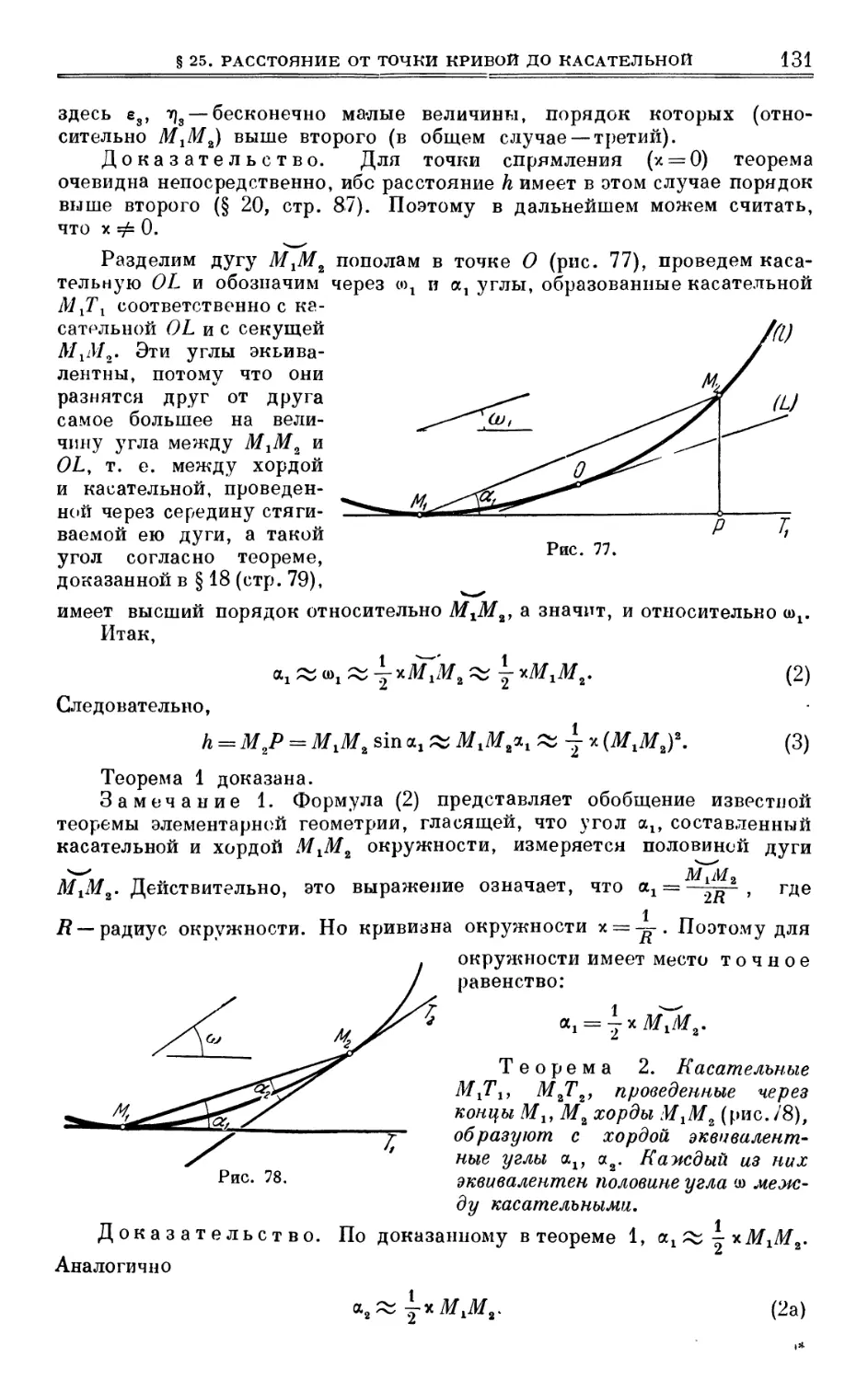
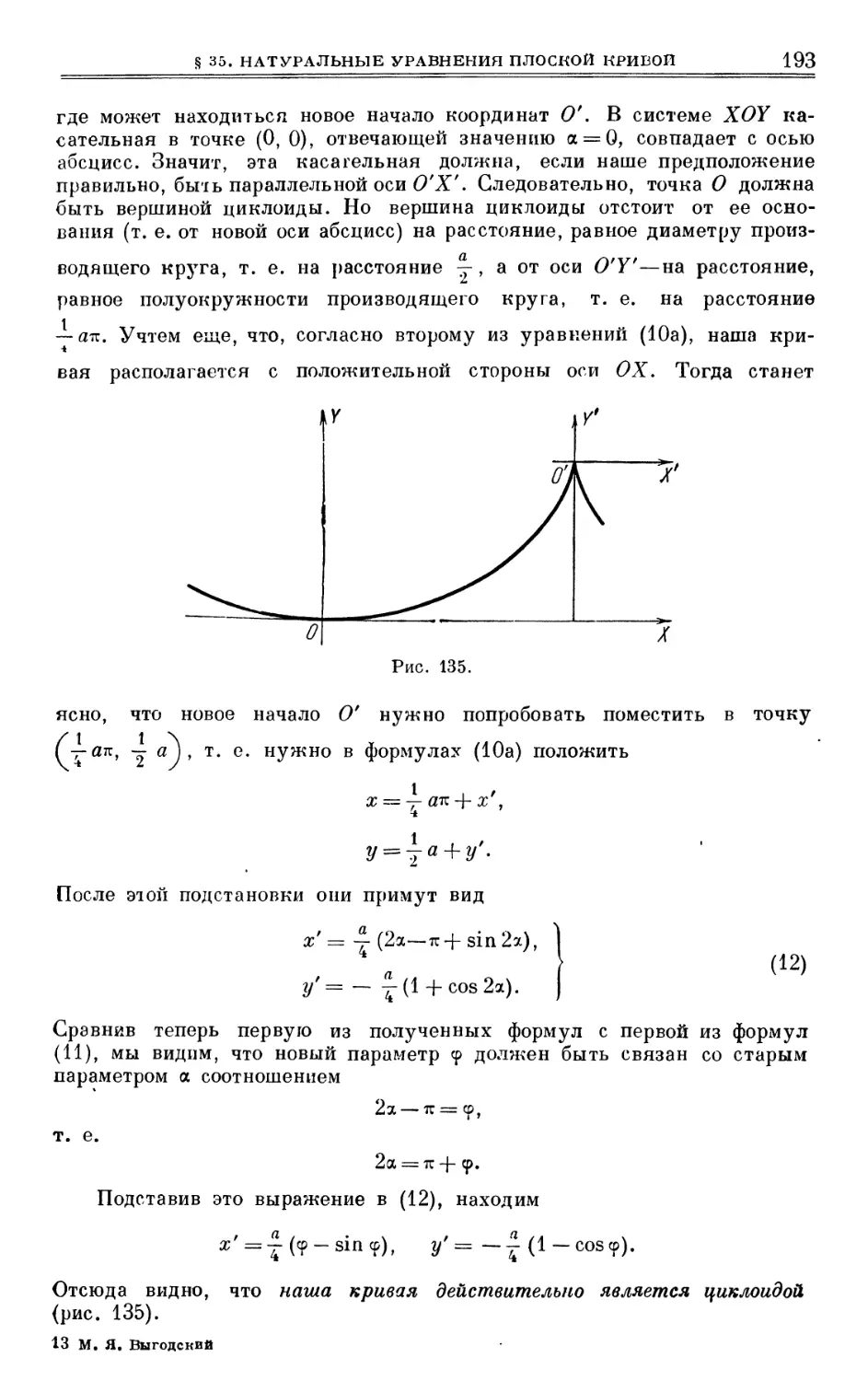
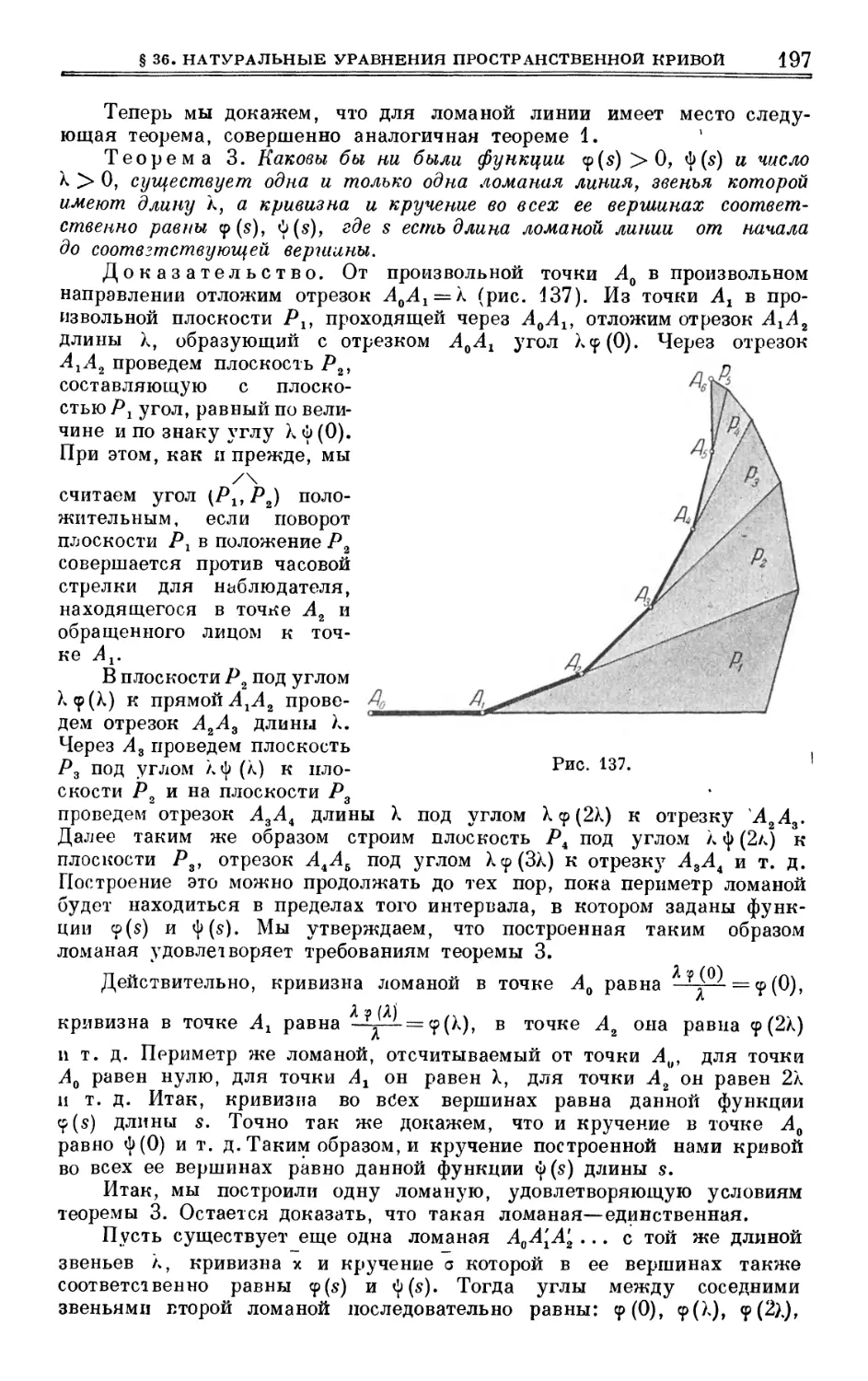
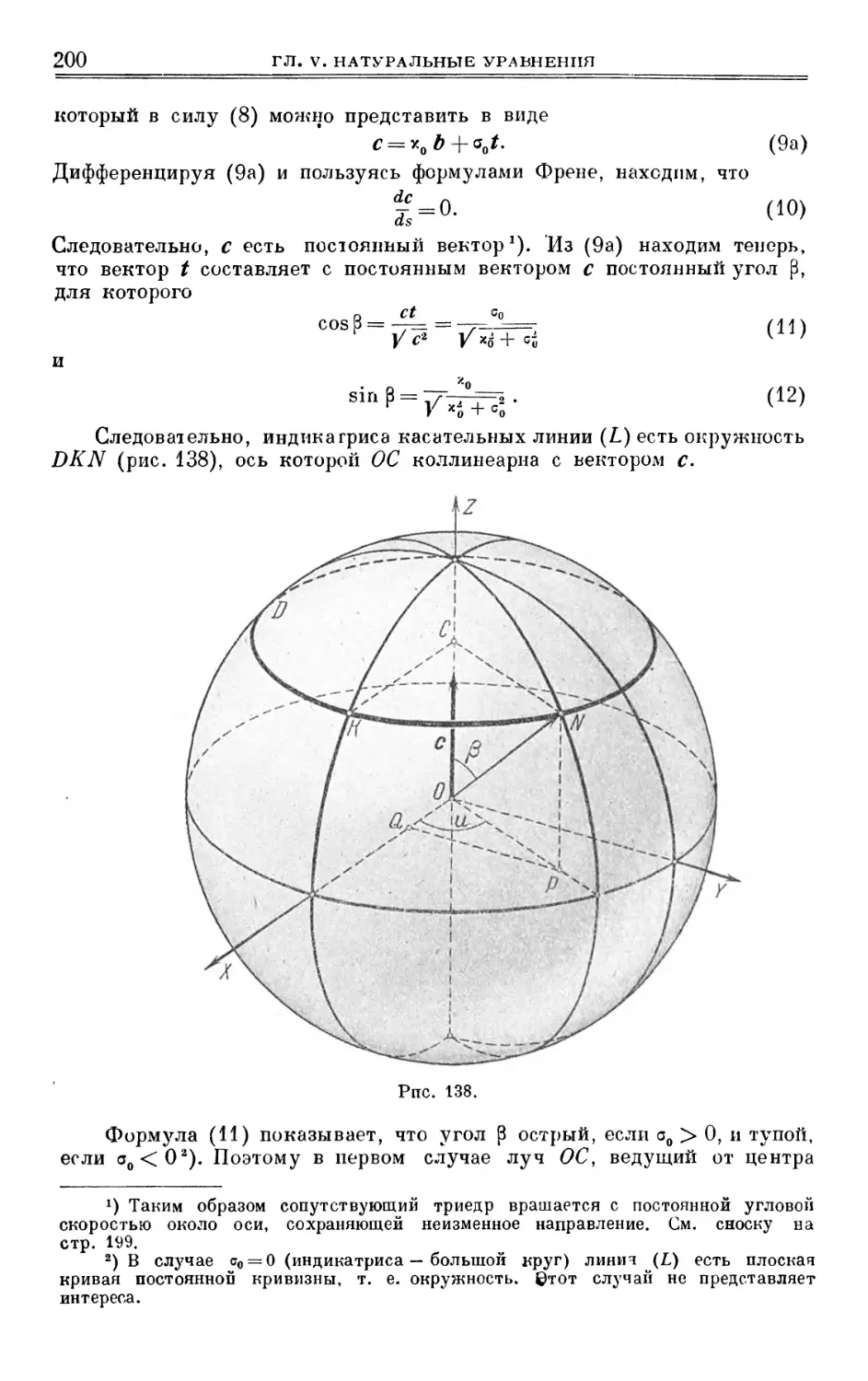
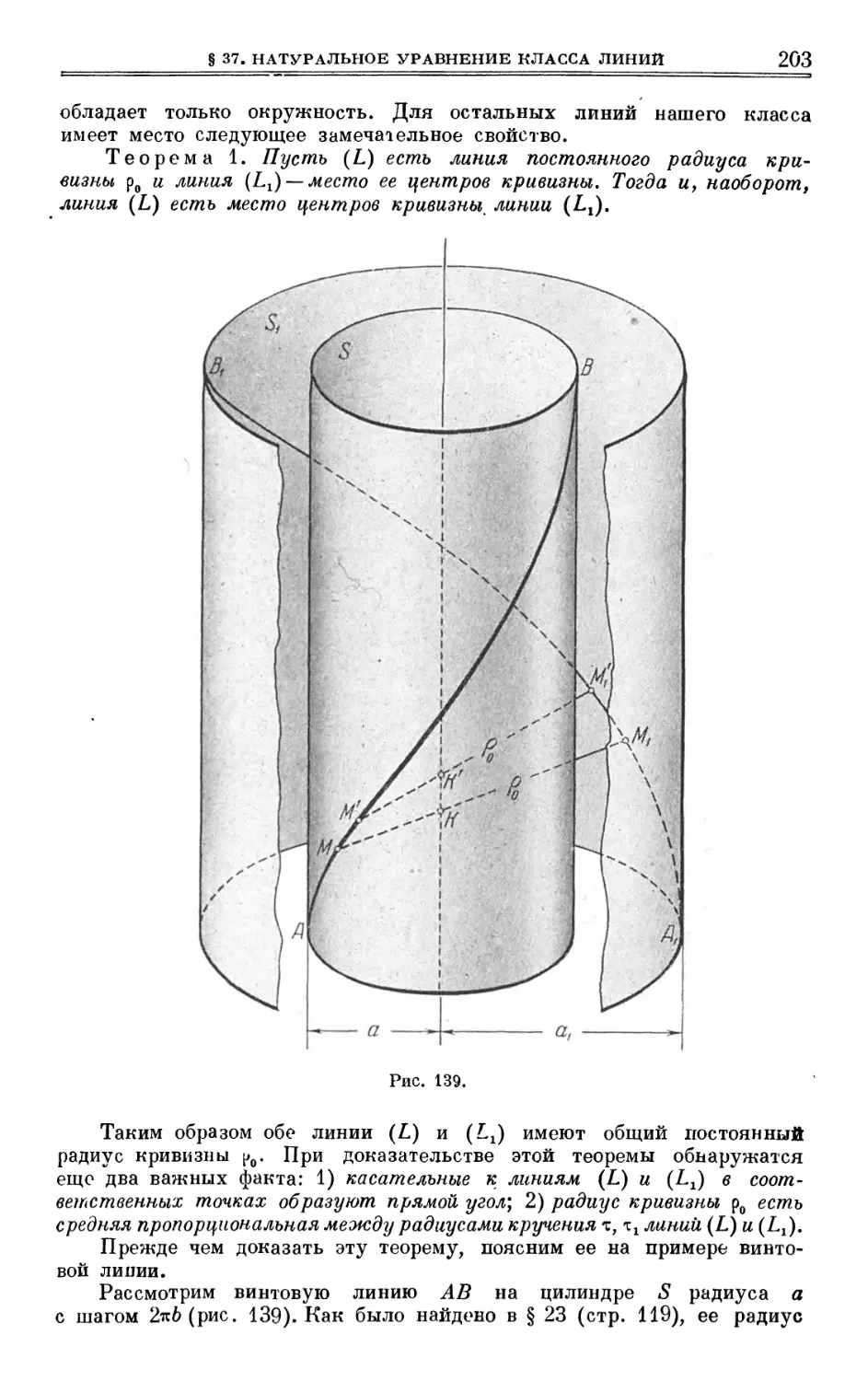
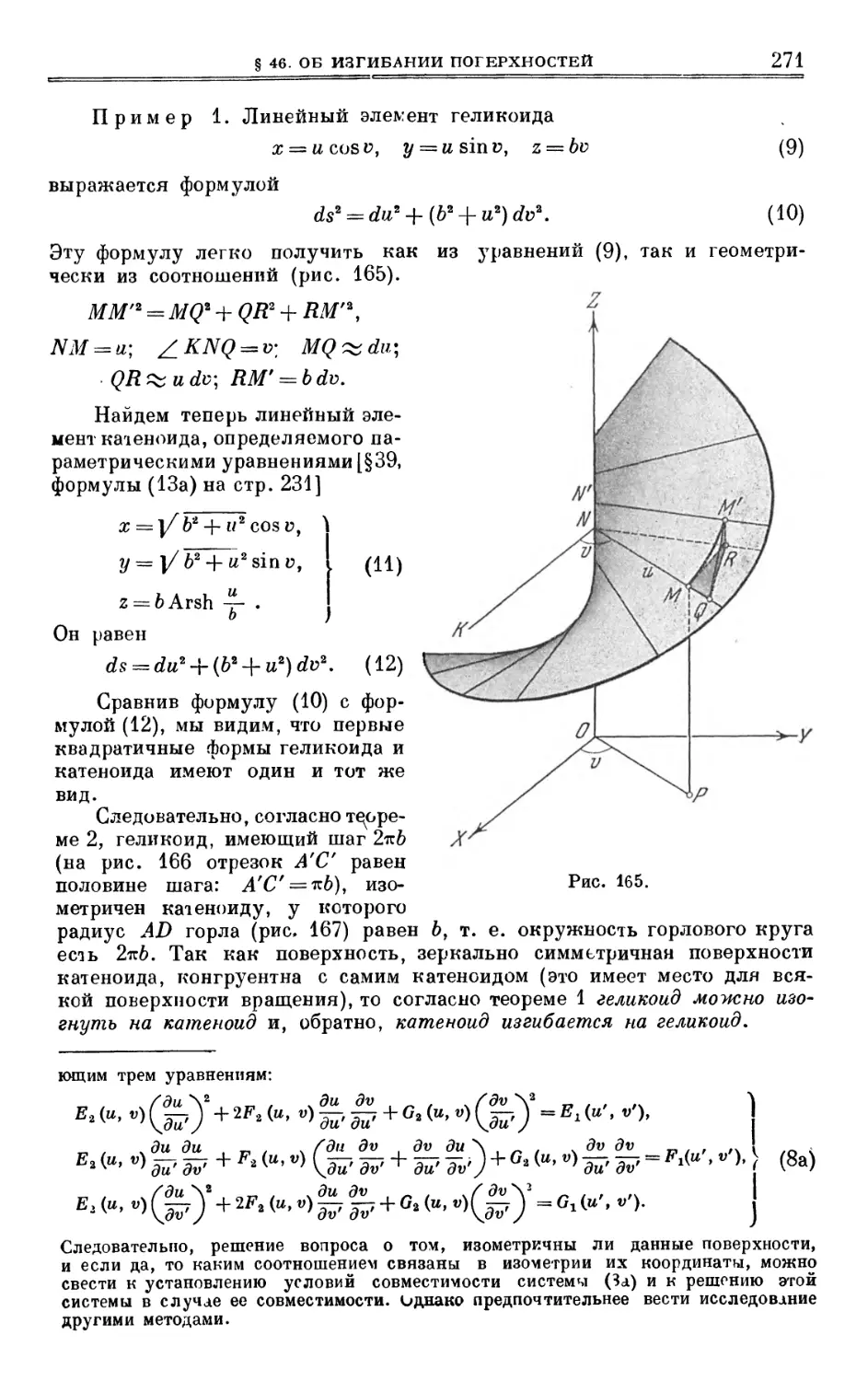
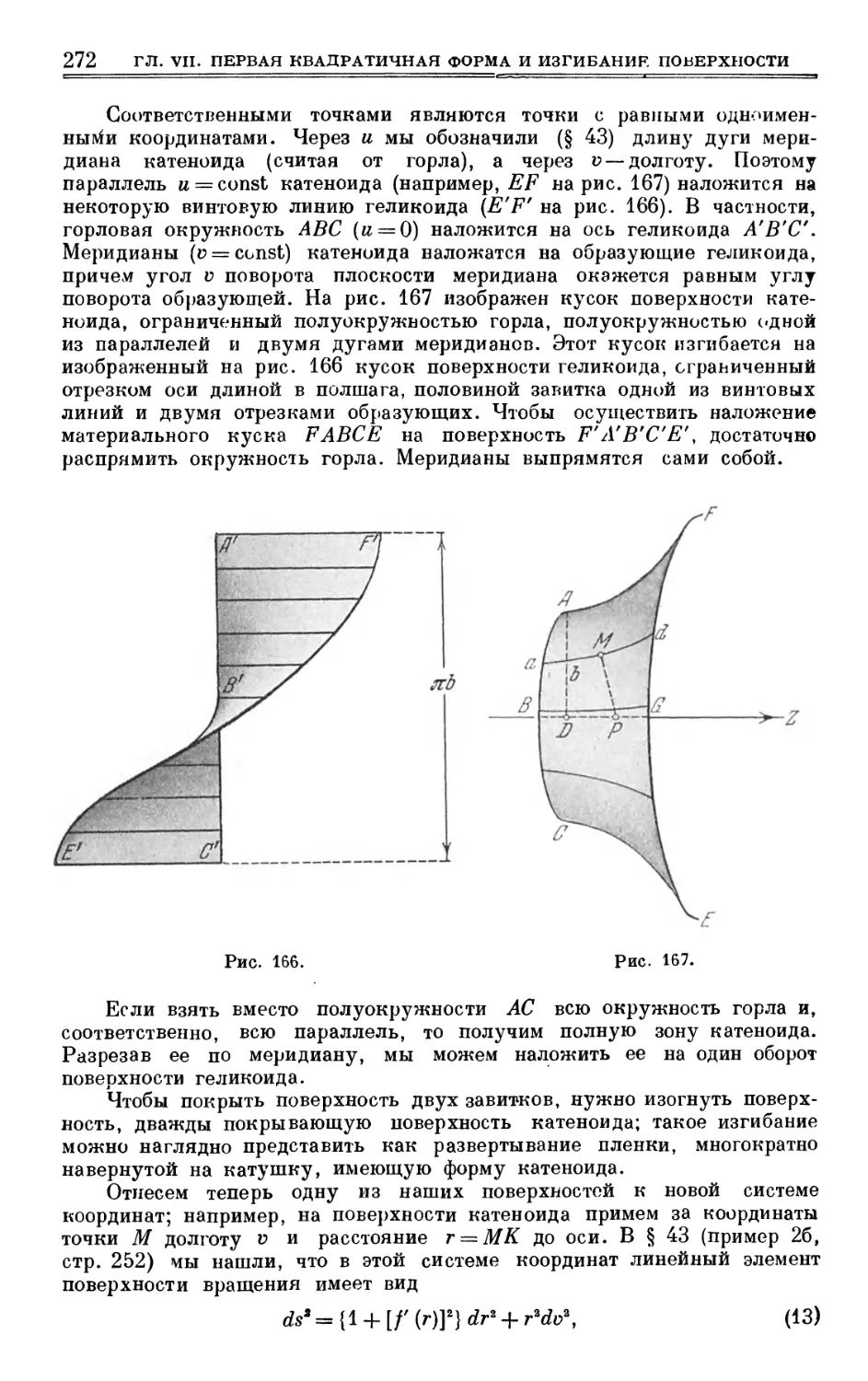
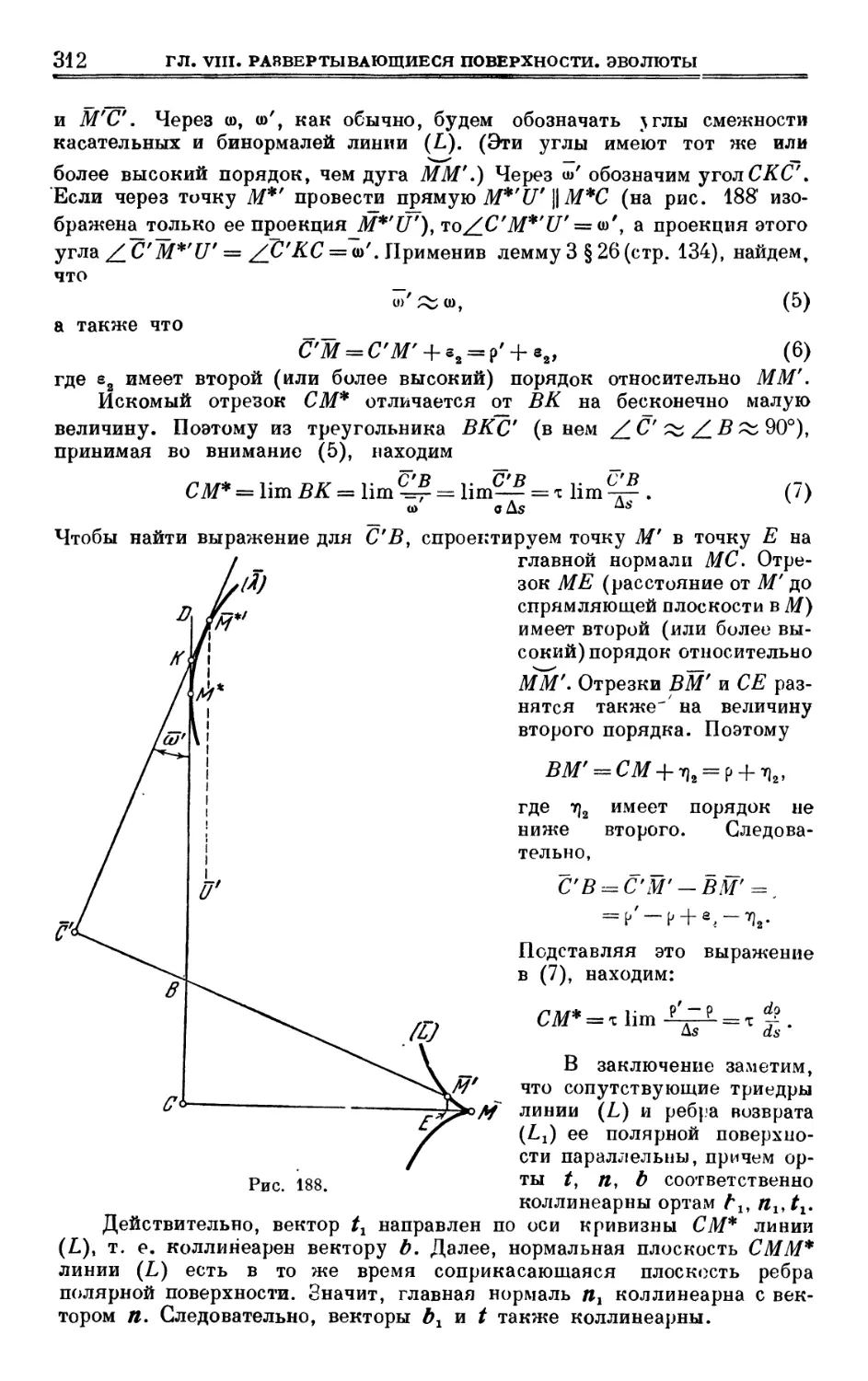
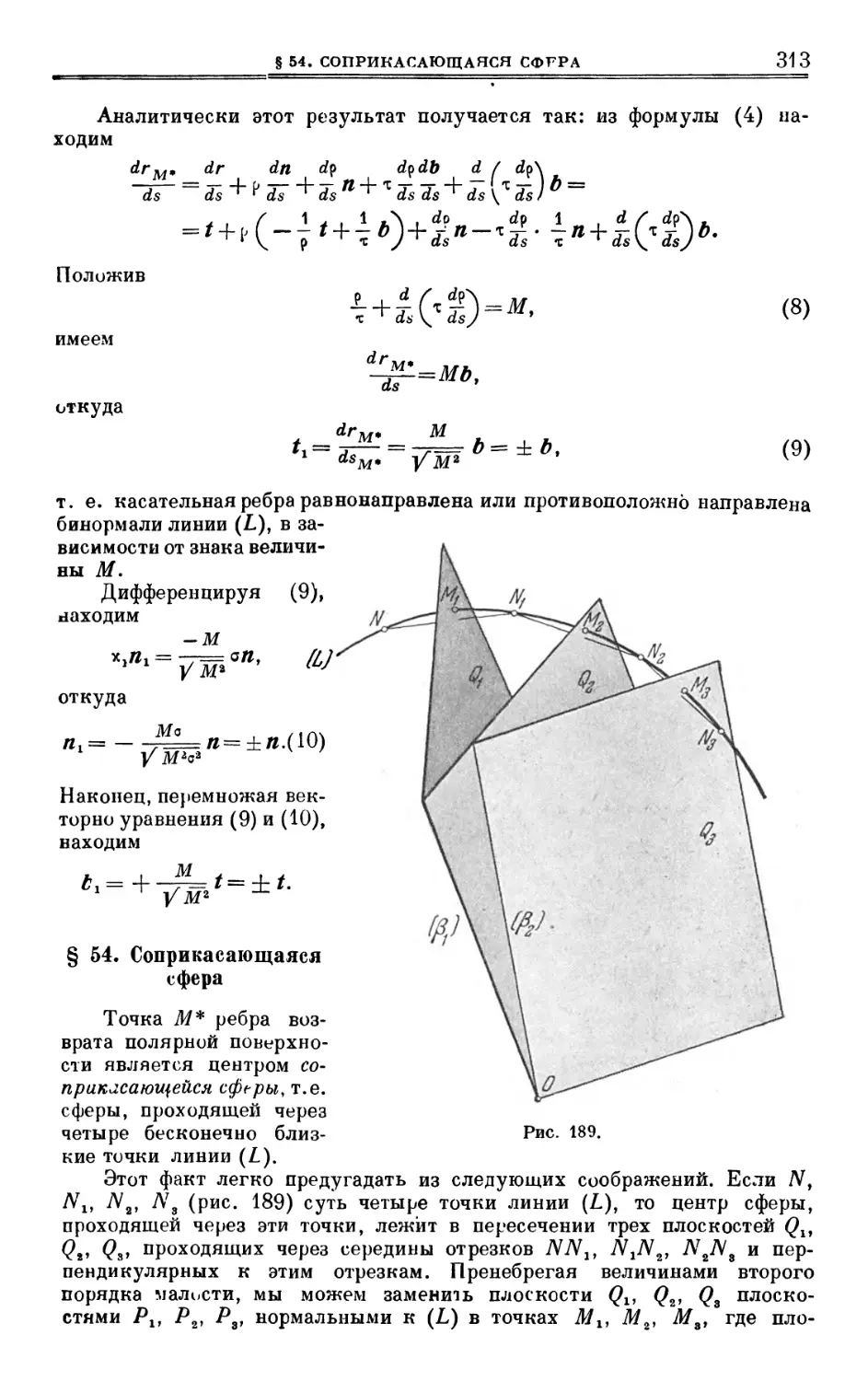
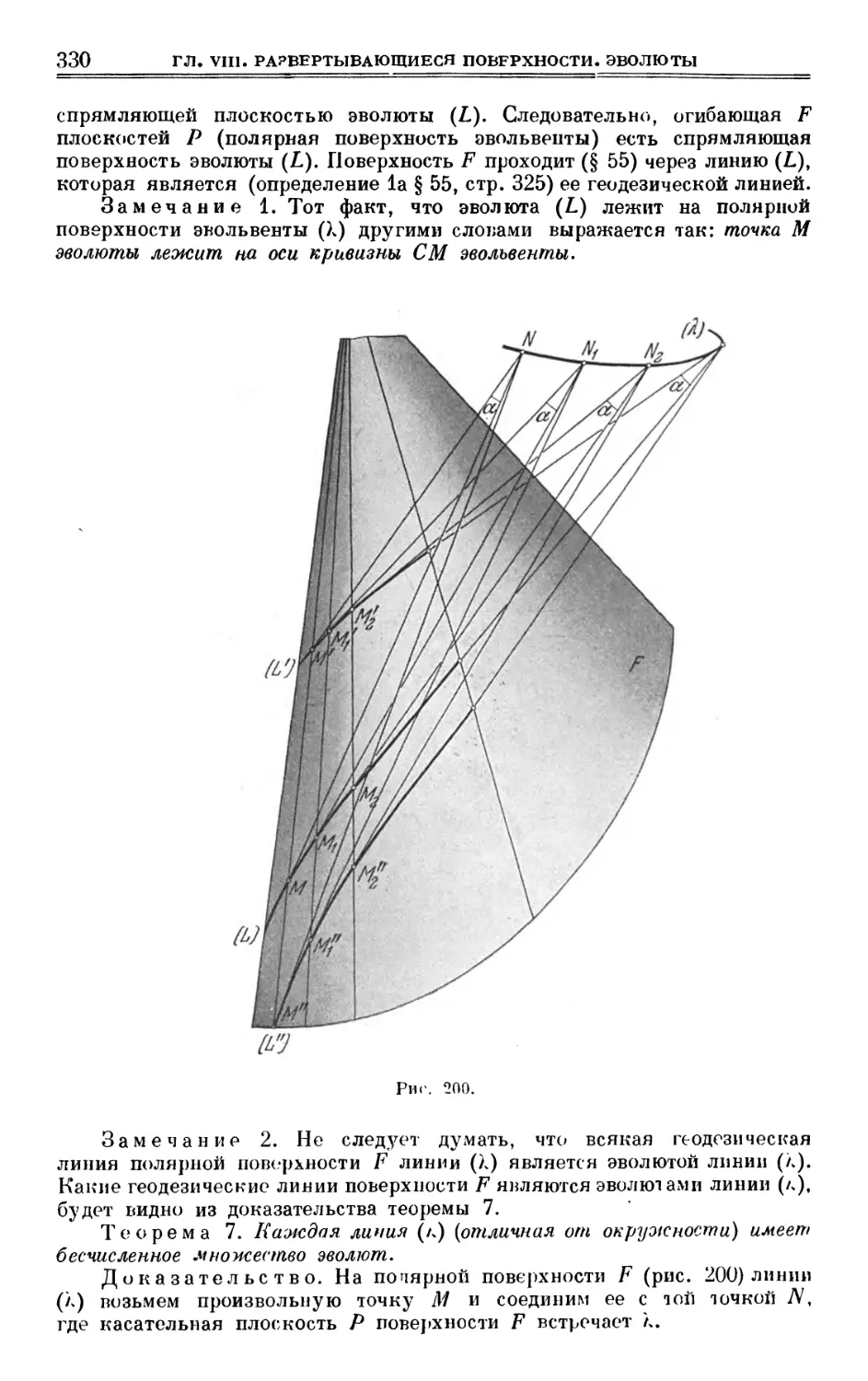
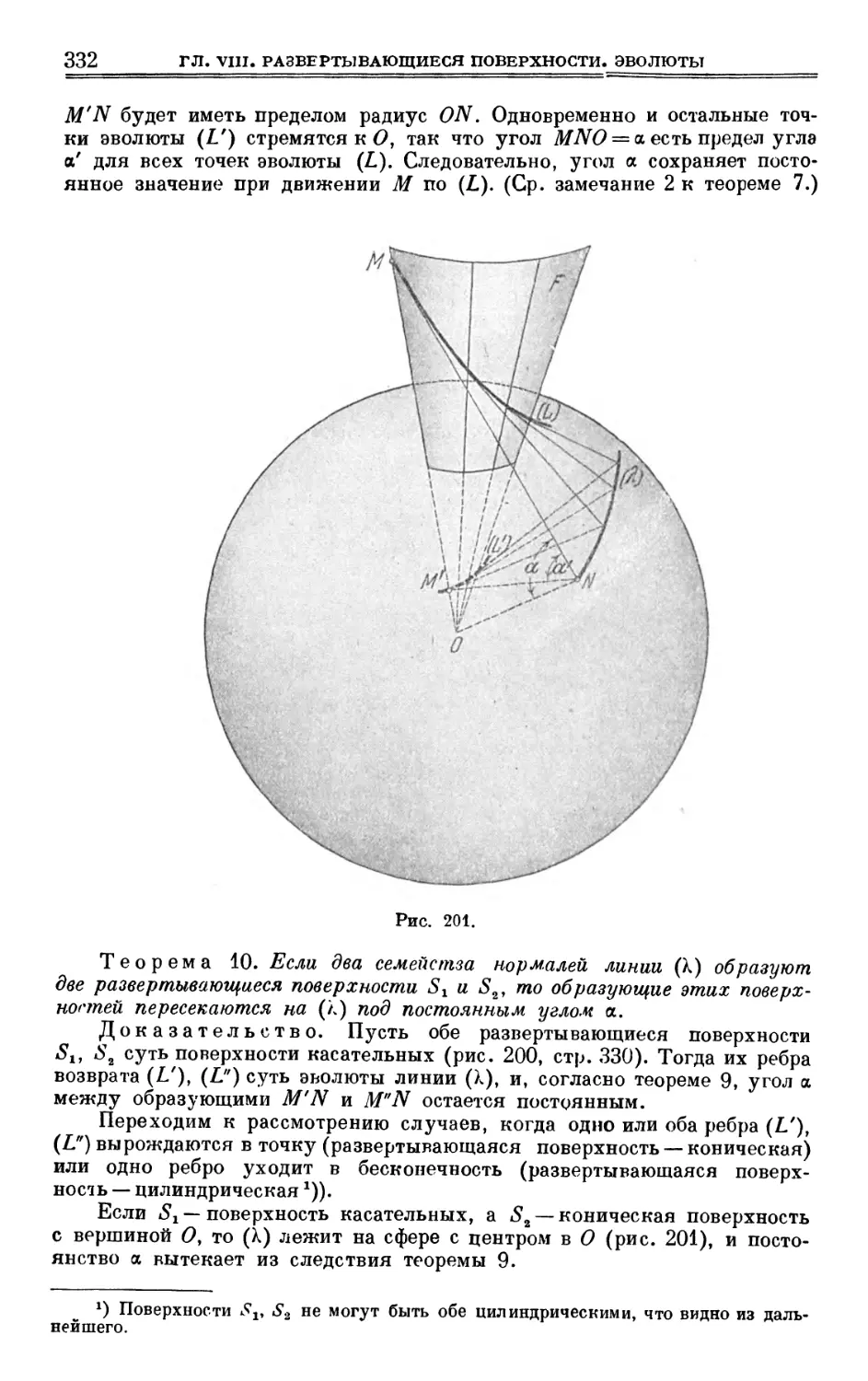
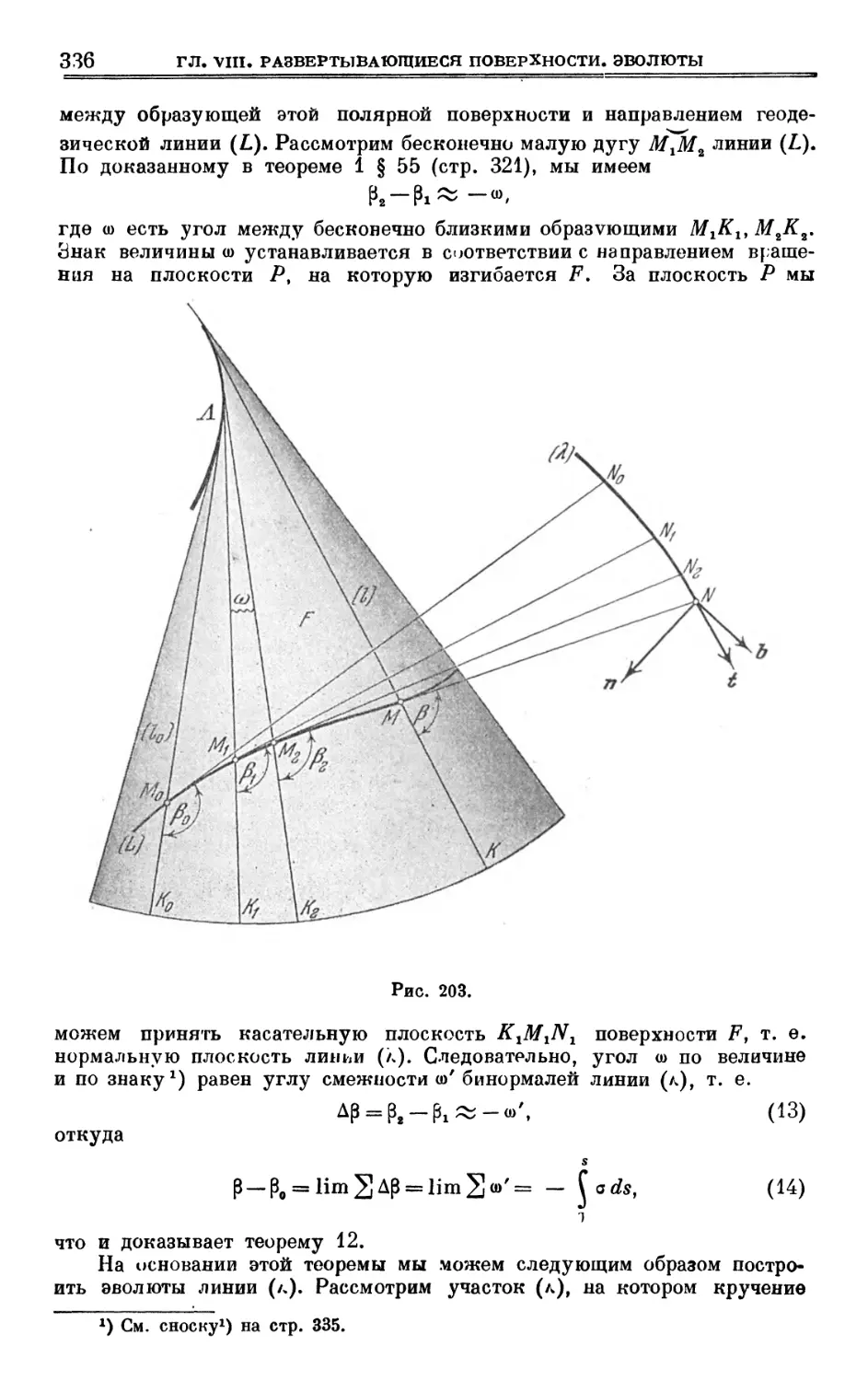
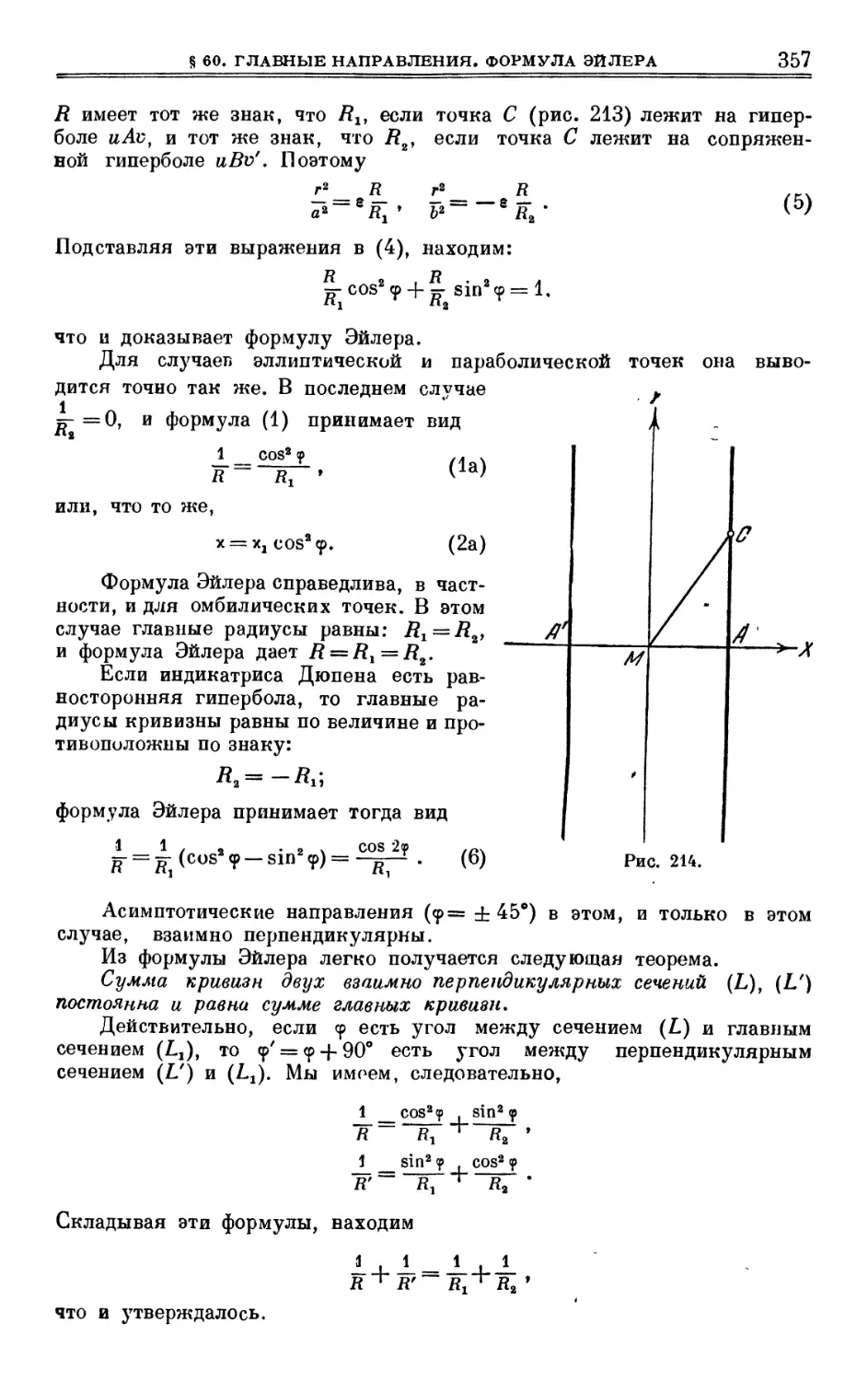
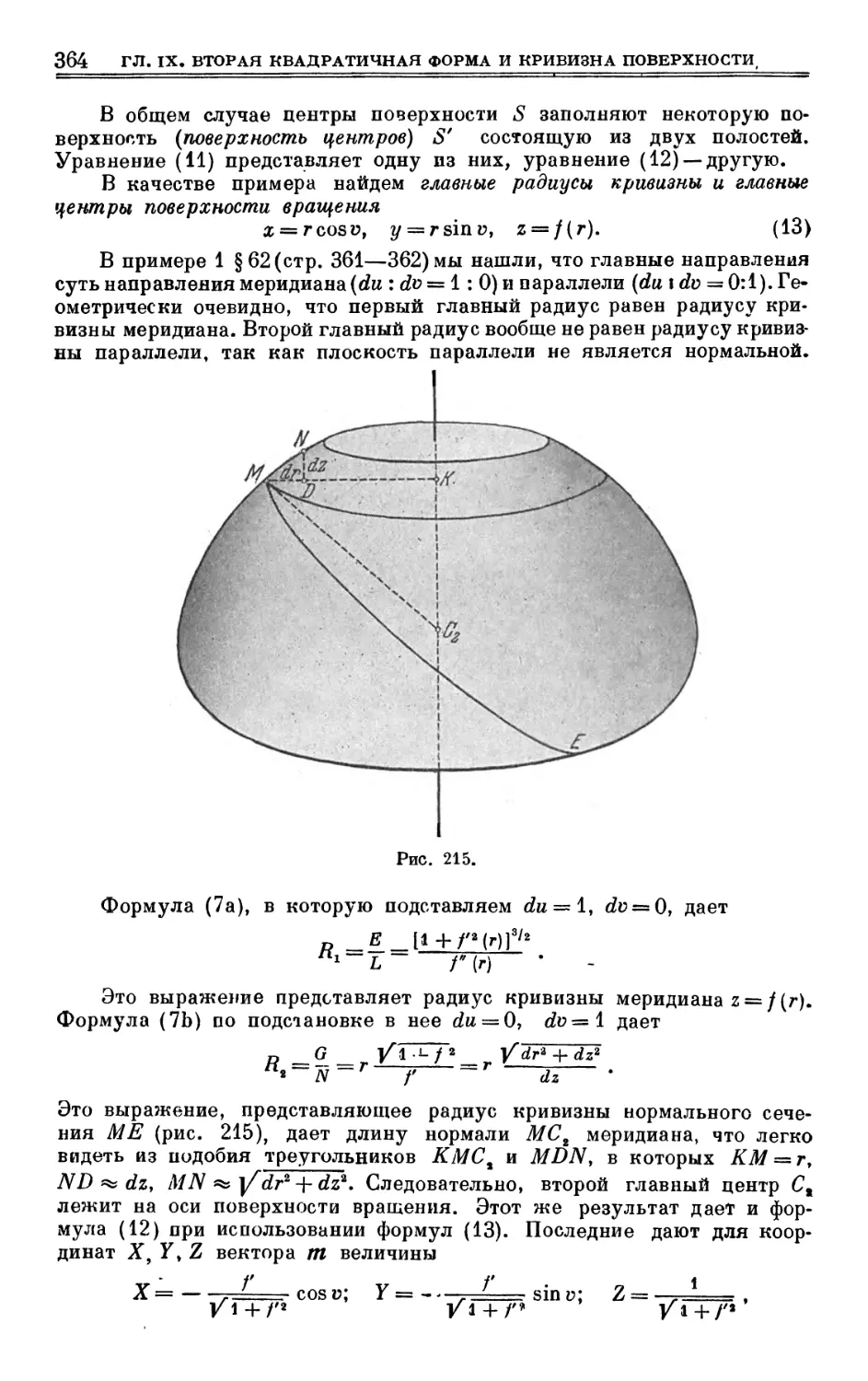
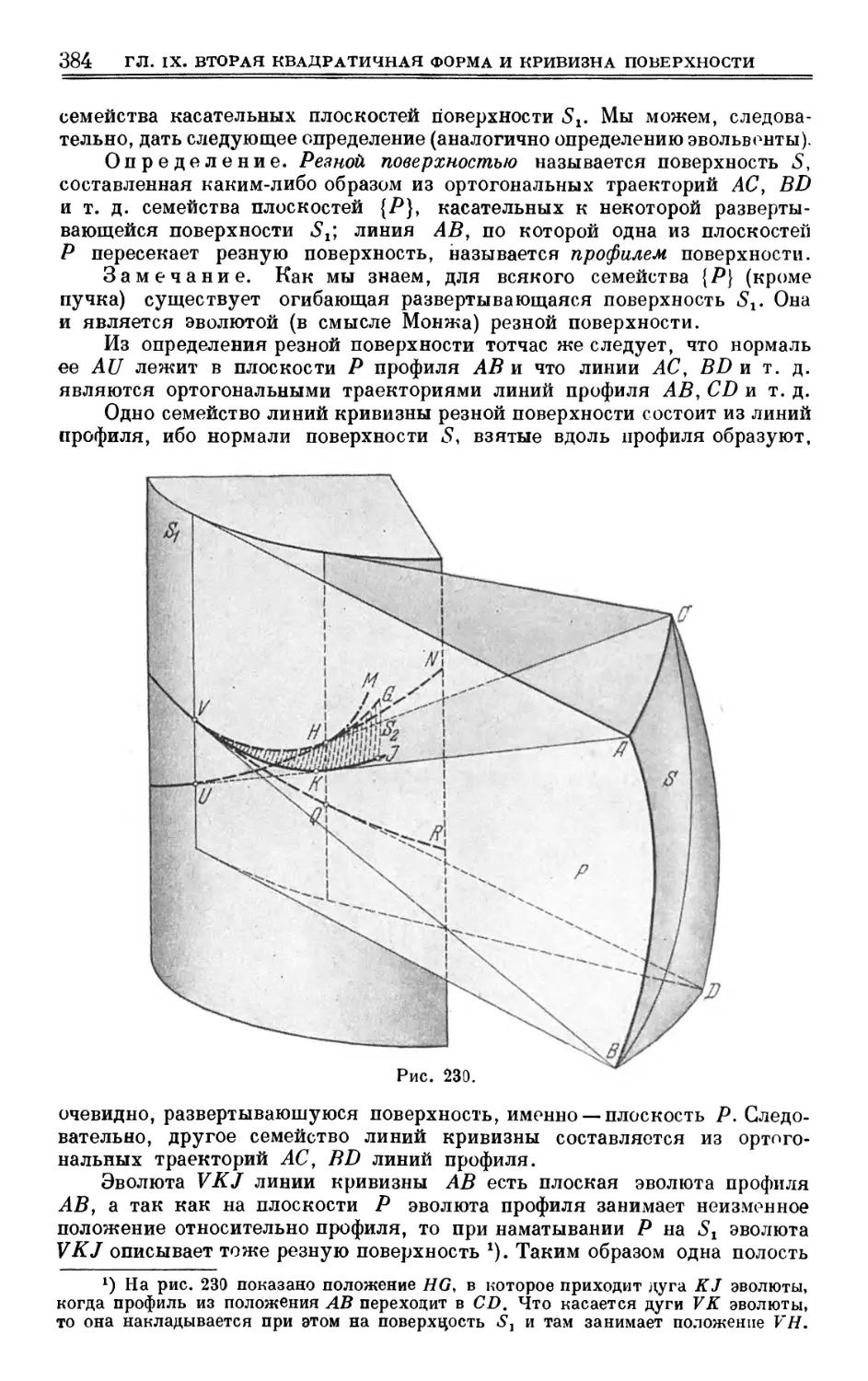
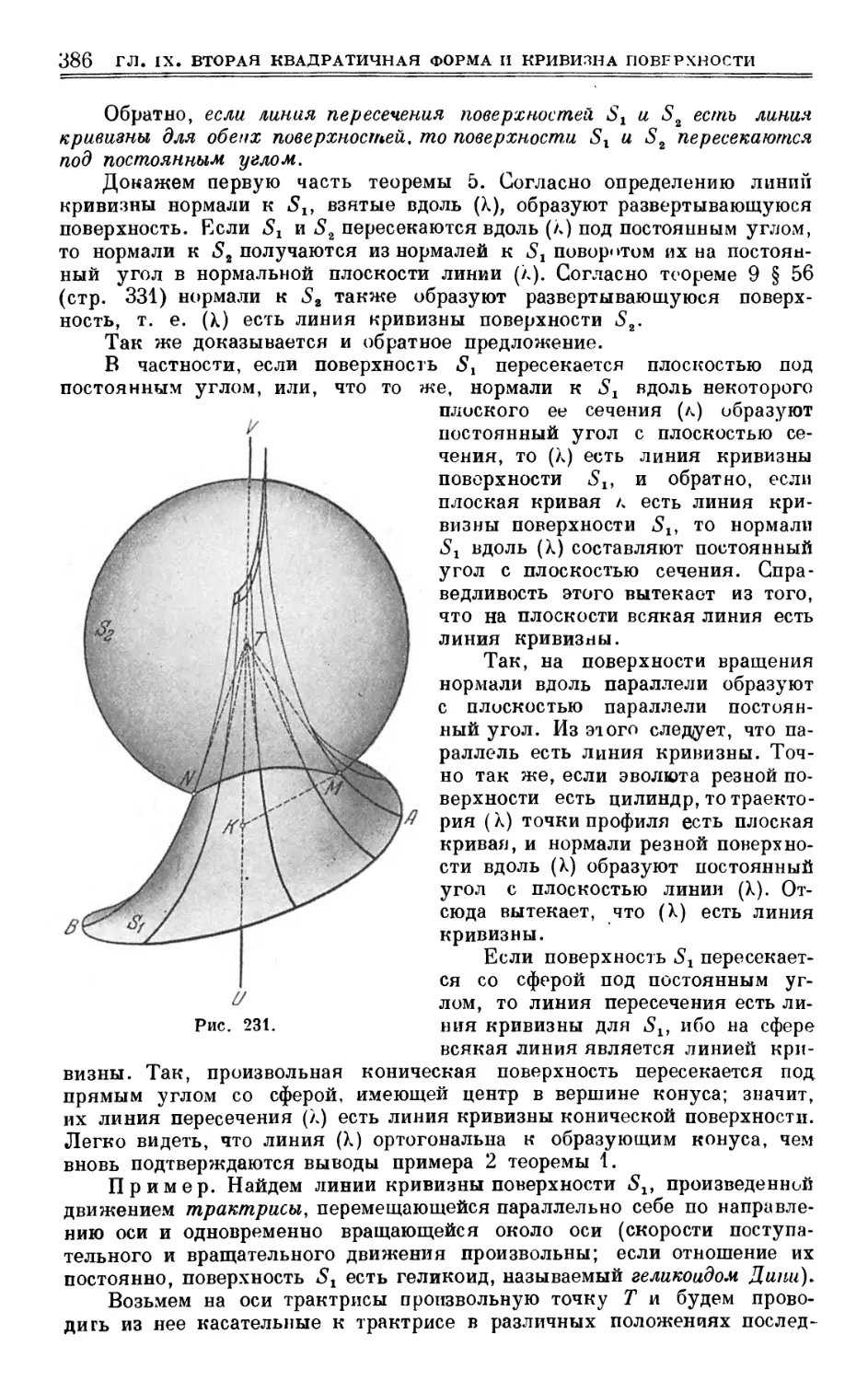
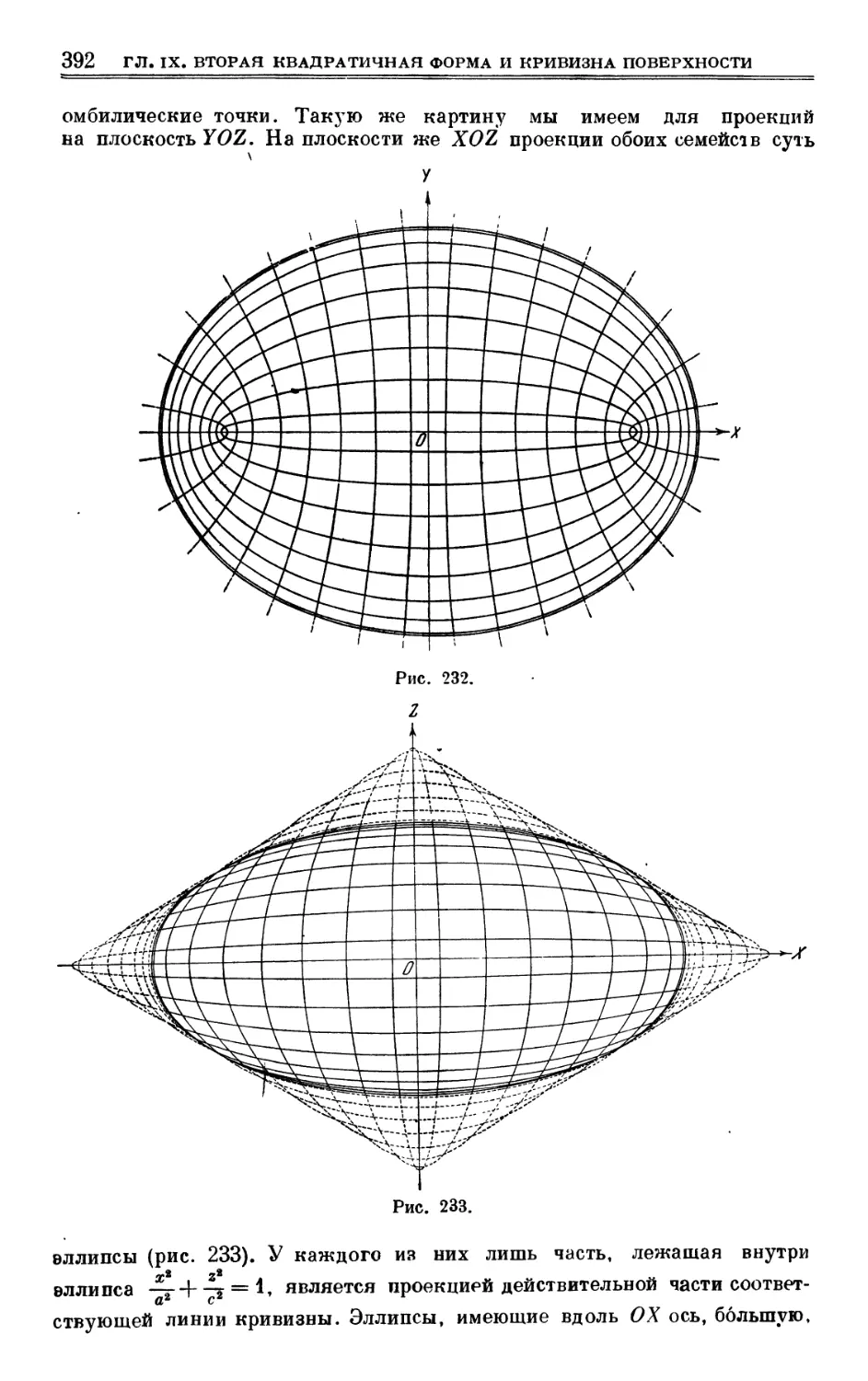
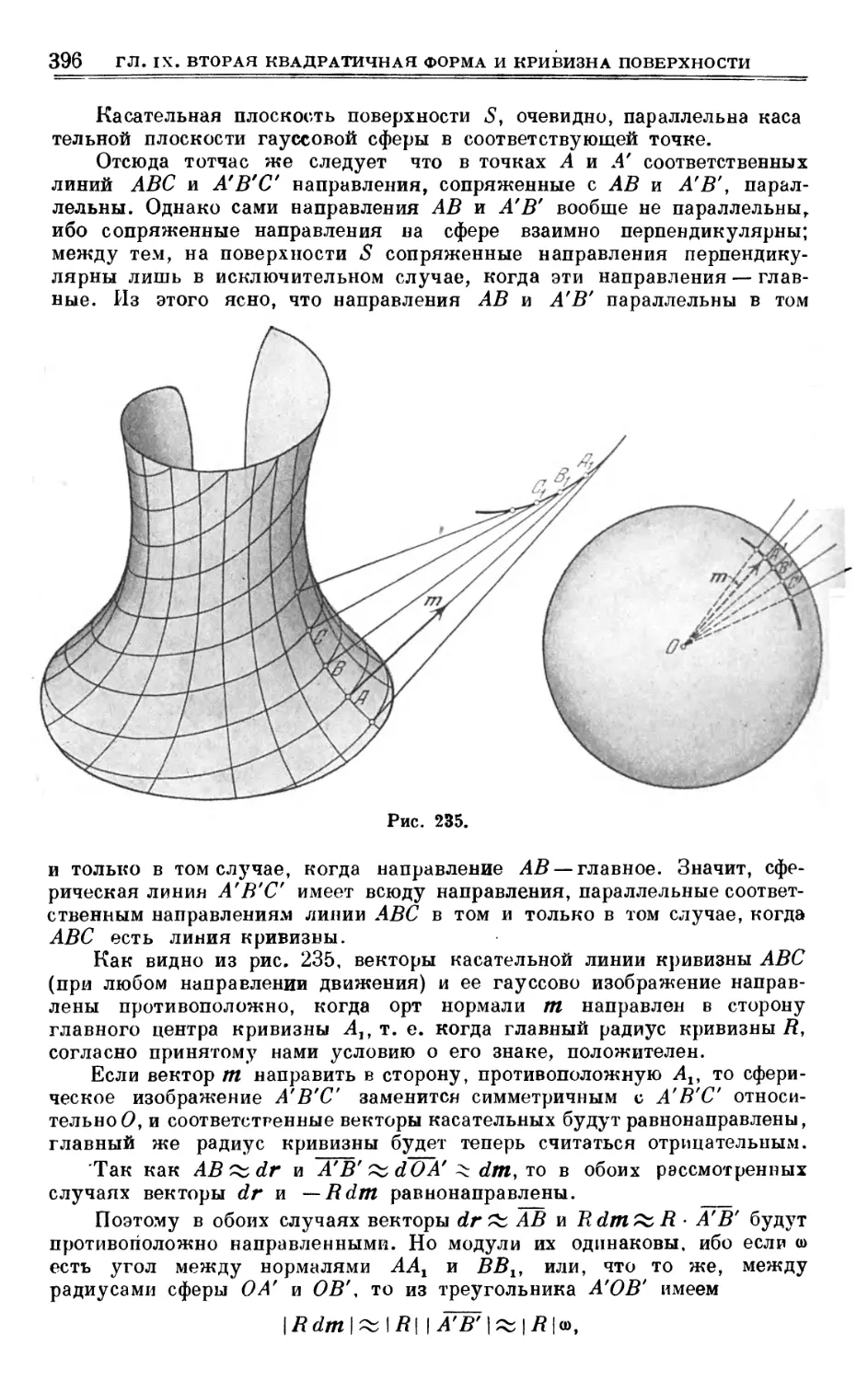
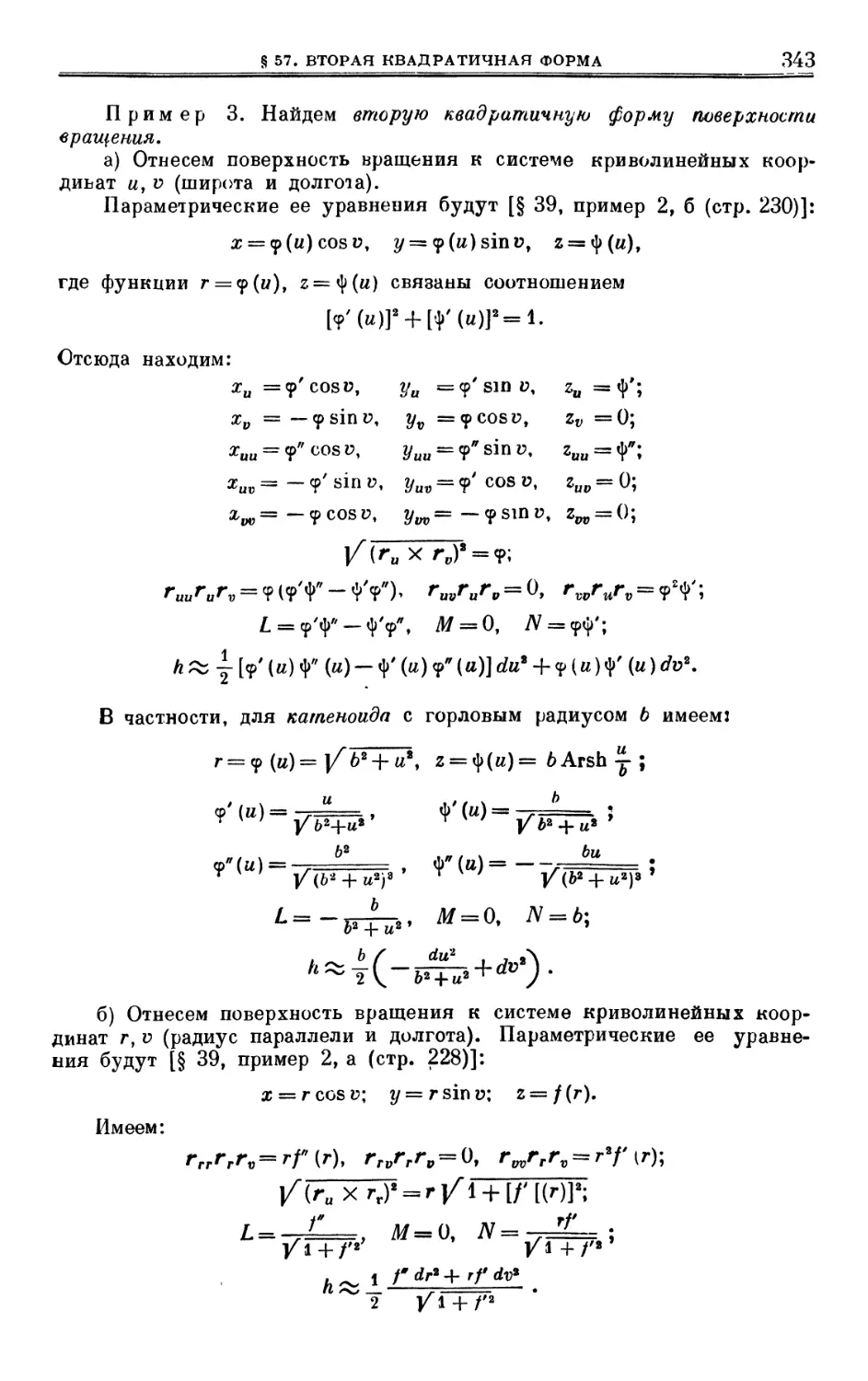Author: Выгодский М.Я.
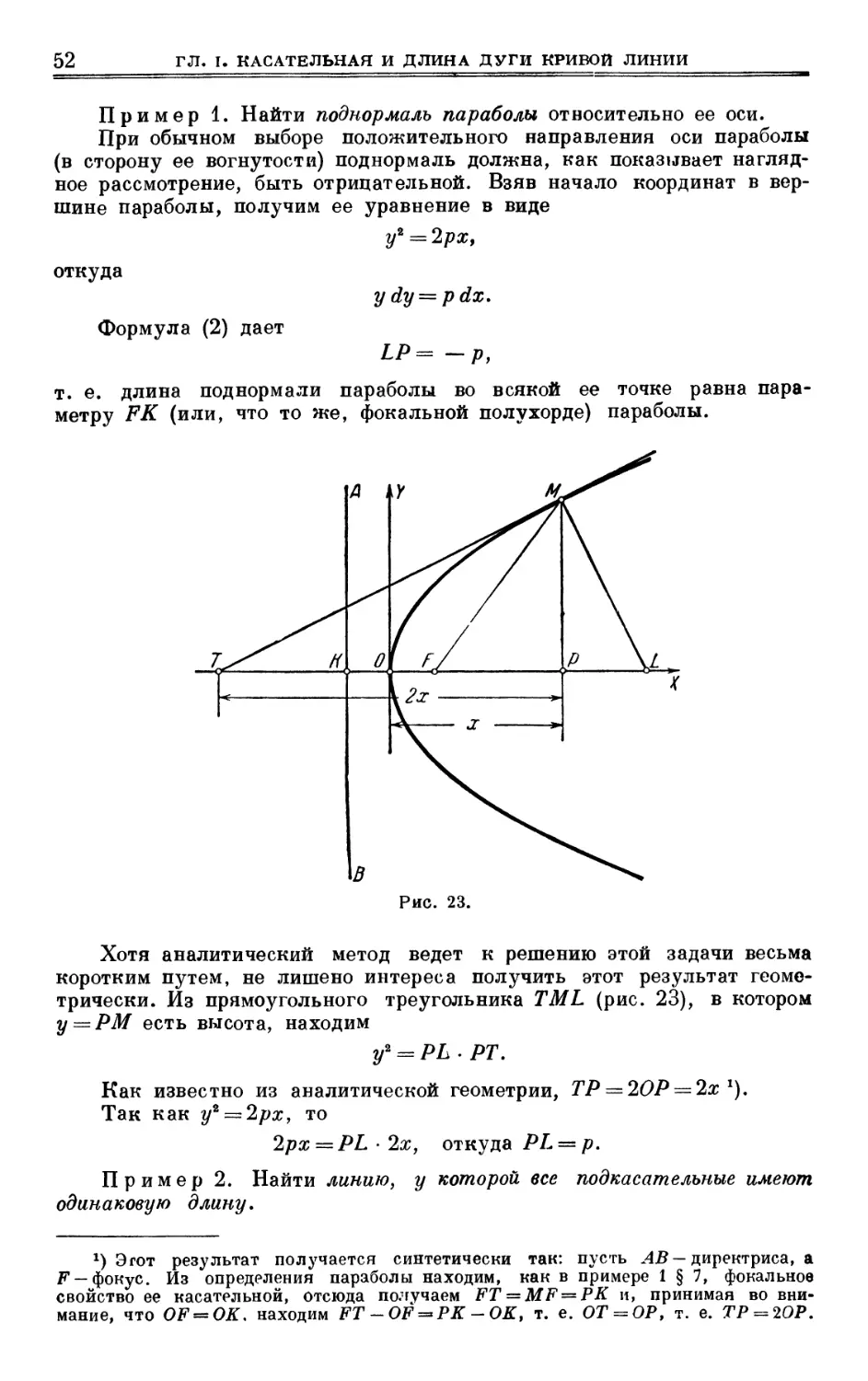
Tags: дифференциальная геометрия государственное издательство технико-теоретической литературы
Year: 1949
Text
М. Я. ВЫГОДСКИЙ
Г1
ДИФФЕРЕНЦИАЛЬНАЯ
ГЕОМЕТРИЯ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1949 ЛЕНИНГРАД
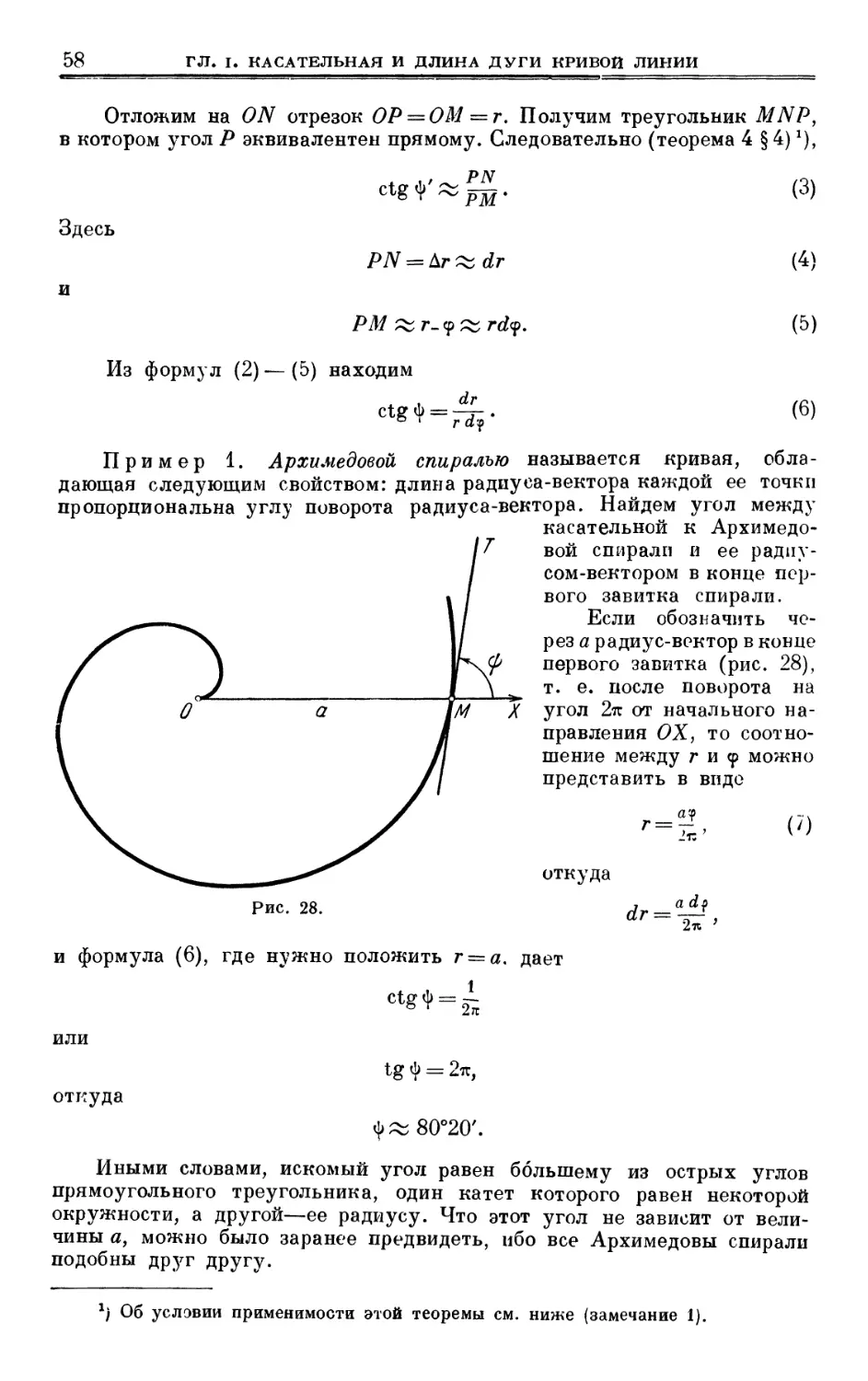
11-5-4
Посвящаю памяти моего сына
Льва Марковича ВЫГОДСКОГО,
погибшего в бою
с немецко-фашистскими захватчиками
при селе Угляны Витебского района
20 января 1944 года.
ОГЛАВЛЕНИЕ
Предисловие 8
ВВЕДЕНИЕ
§ 1. Предмет дифференциальной геометрии 11
§ 2. О линиях . . . . 12
§ 3. Порядок малости. Эквивалентность 14
§ 4. Эквивалентные соотношения в треугольнике 17
§ 5. Пределы геометрических образов 20
глава j
КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
§ 6. Аналитическое представление кривой линии 26
§ 7. Каоательная 35
§ 8. Уравнения касательной 41
§ 9. Касательные и нормали плоских кривых 47
§ 10. Подкасательная и поднормаль 51
§ И. Трактриса 54
§ 12. Касательная к линии, заданной полярным свойством 56
§ 13. Полярные подкасательная и поднормаль 60
§ 14. Об определении касательной 63
§ 15. Длина дуги 65
§ 16. Определение понятия «длина дуги» 72
§ 17. Цепная линия 74
§ 18. Длина дуги как параметр 77
глава и
СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
§ 19. Три леммы ♦ . . . 81
§ 20. Соприкасающаяся плоскость 83
§ 21. Сопутствующий триедр 96
§ 22. Кривизна Ю4
§ 23. Формулы для вычисления кривизны. Аналитический вывод теорем § 22 111
§ 24. Кривизна плоской кривой .... ... . 119
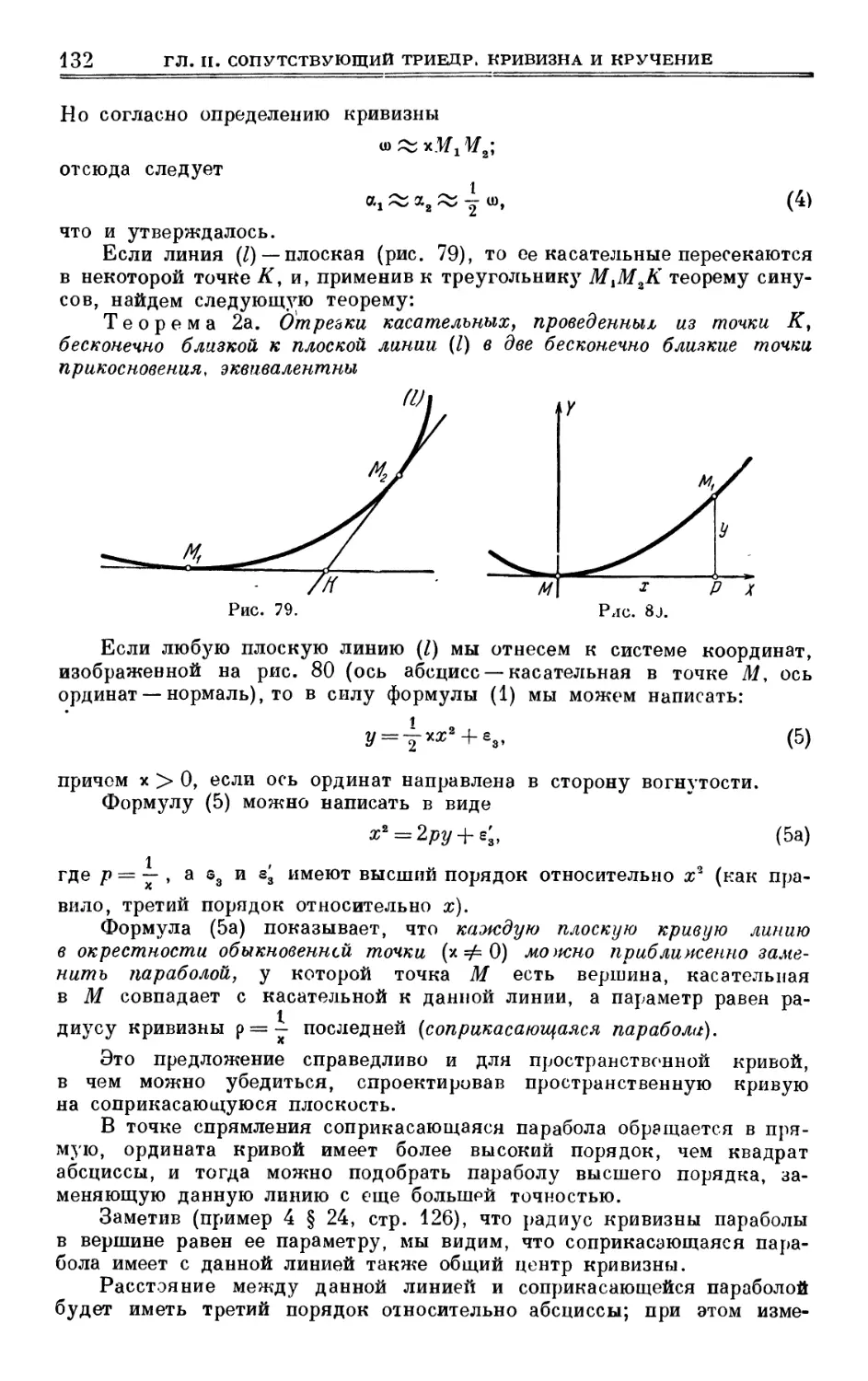
§ 25. Расстояние от точки кривой до бесконечно близкой касательной 130
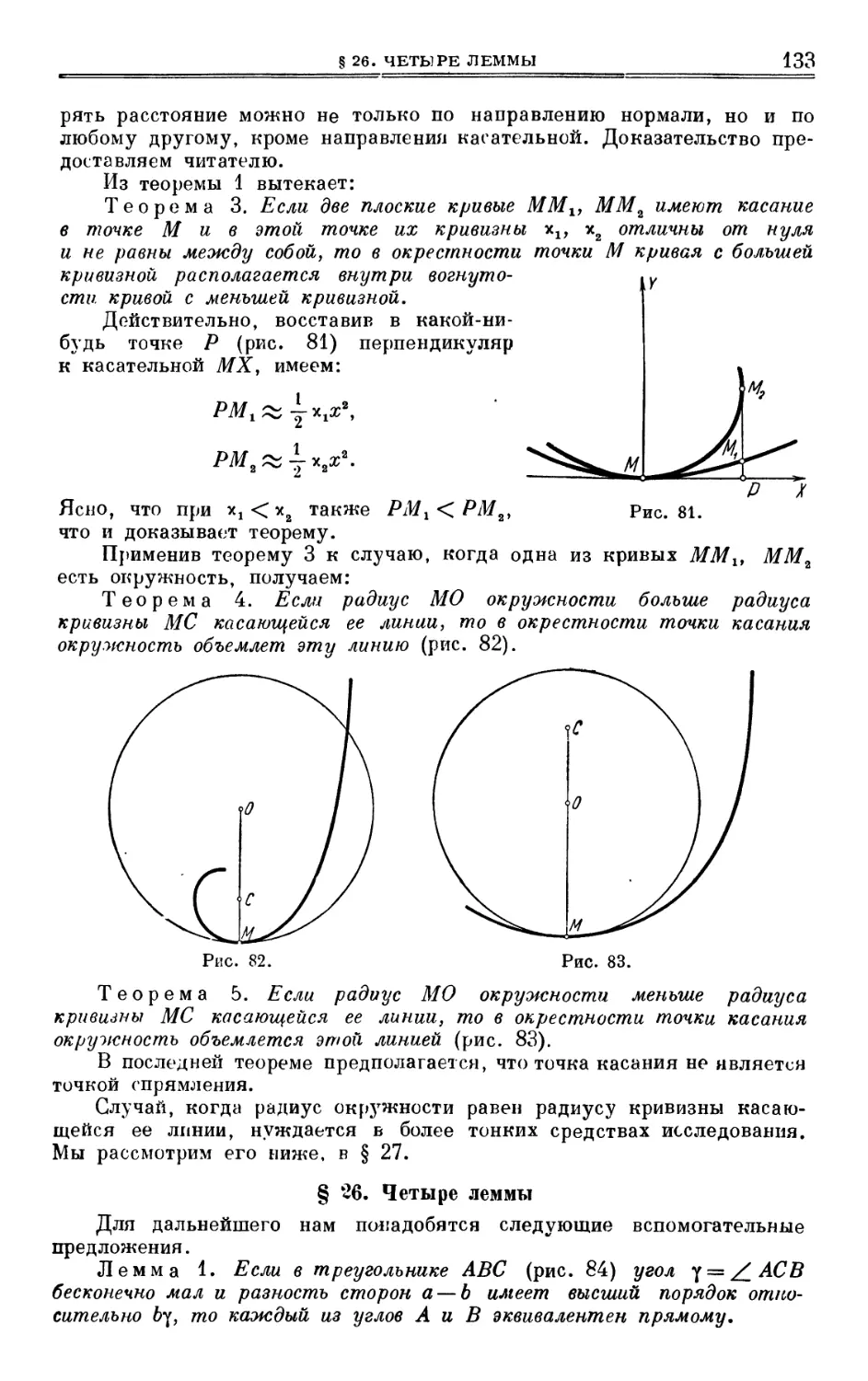
§ 26. Четыре леммы . . *33
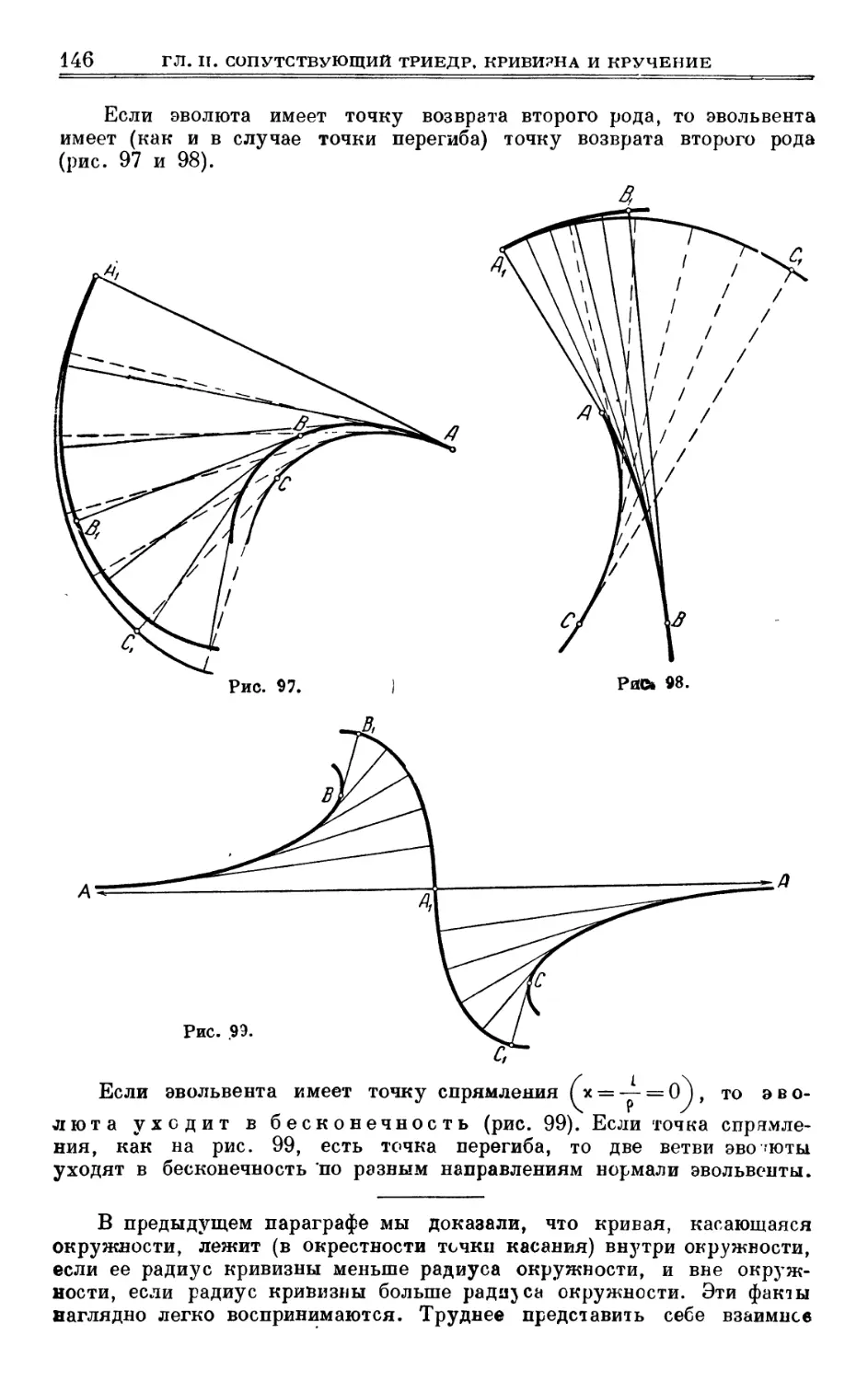
§ 27. Эвольвента и эволюта плоской кривой 136
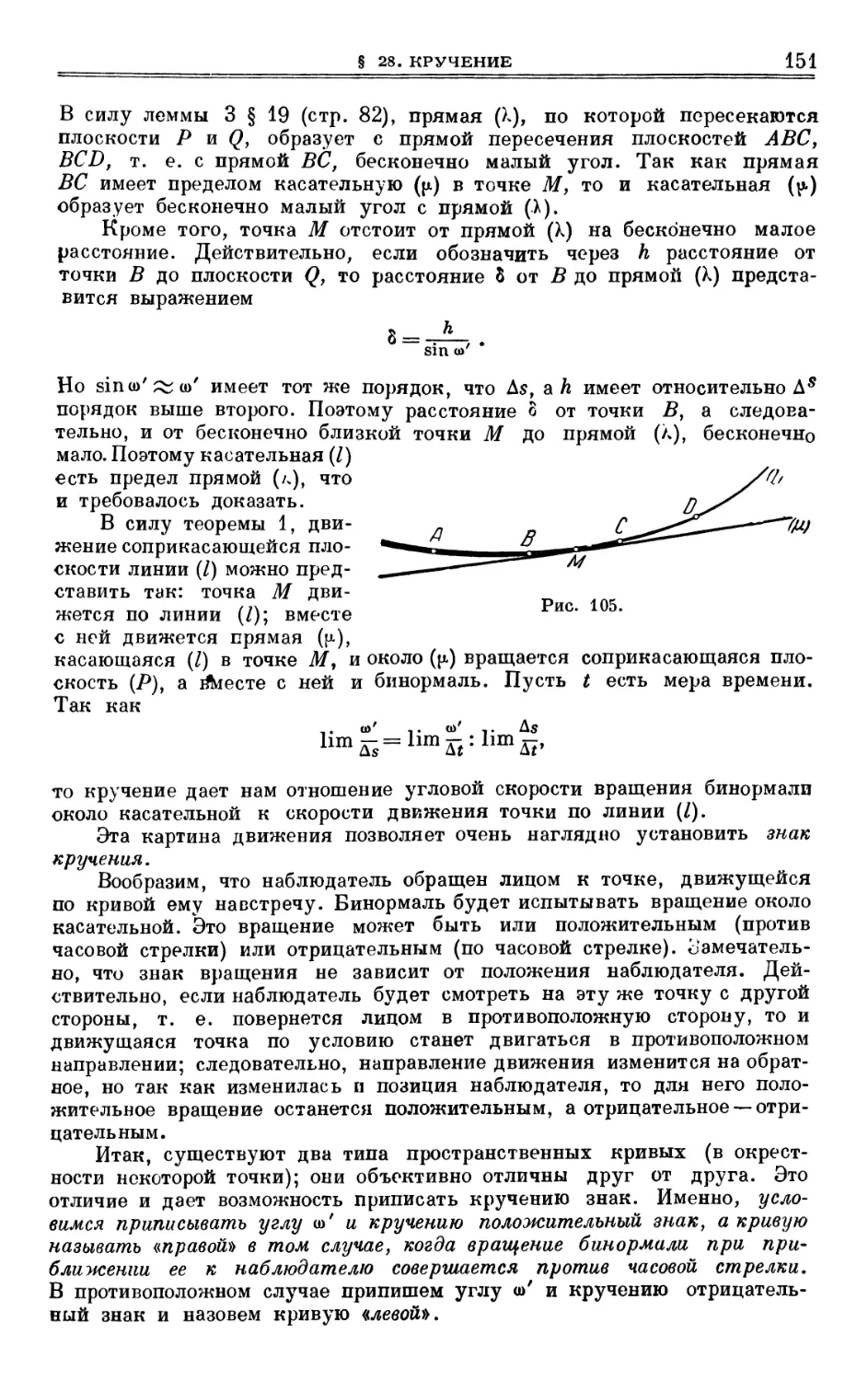
§ 28. Кручение 15°
ОГЛАВЛЕНИЕ
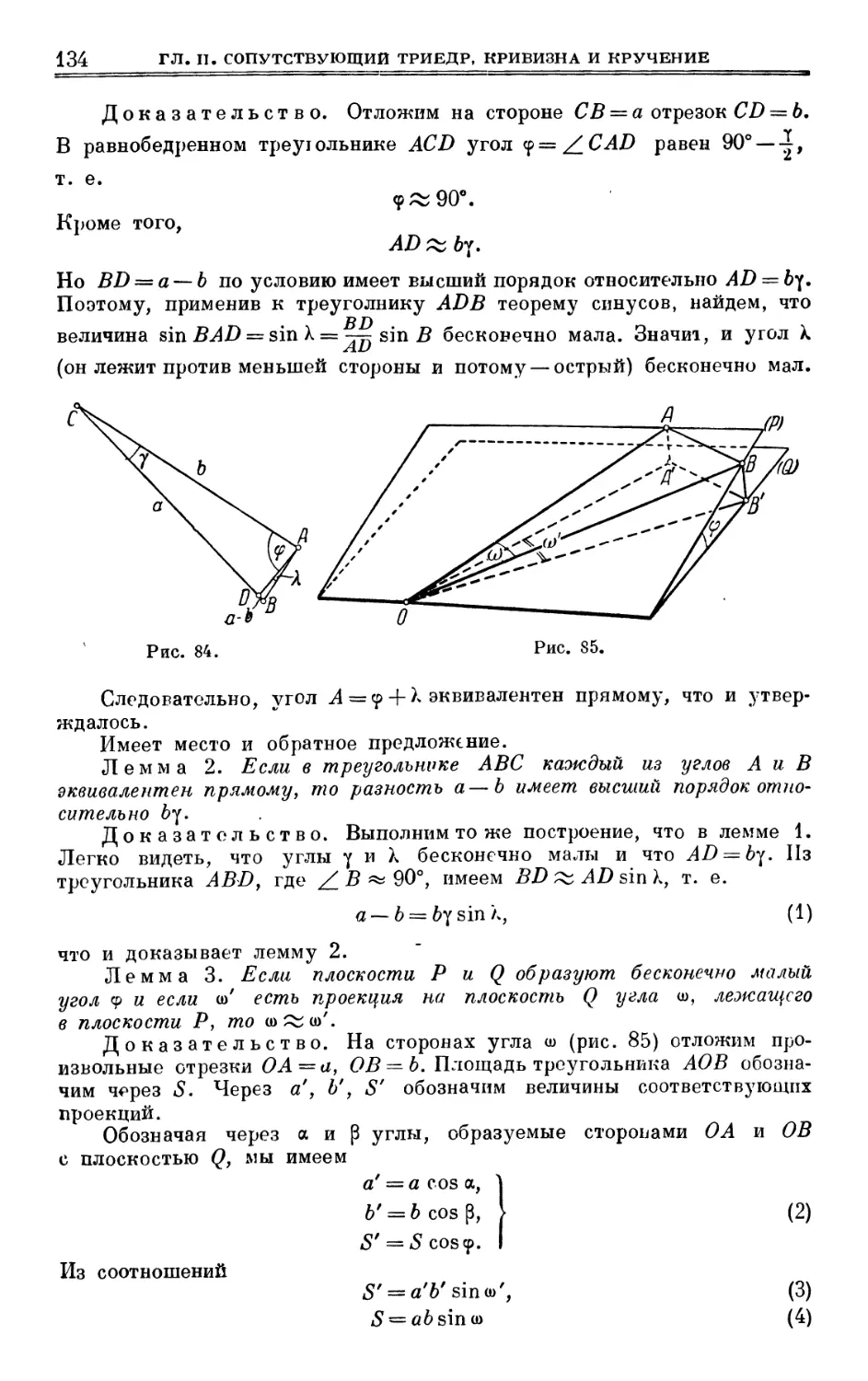
ГЛАВА III
ФОРМУЛЫ ФРЕНЕ
§ 29. Формулы Френе 157
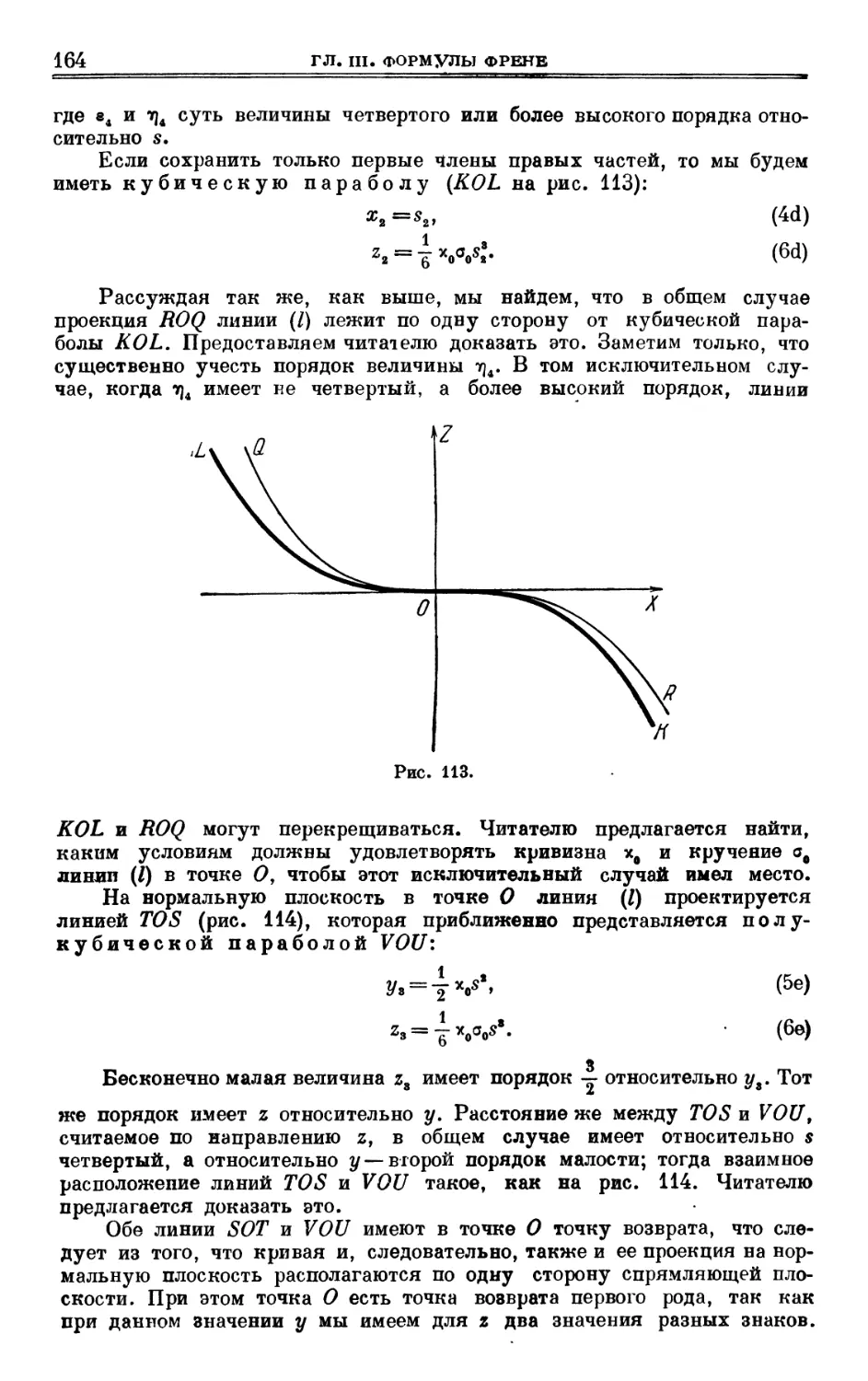
§ 30. Каноническое представление кривой 161
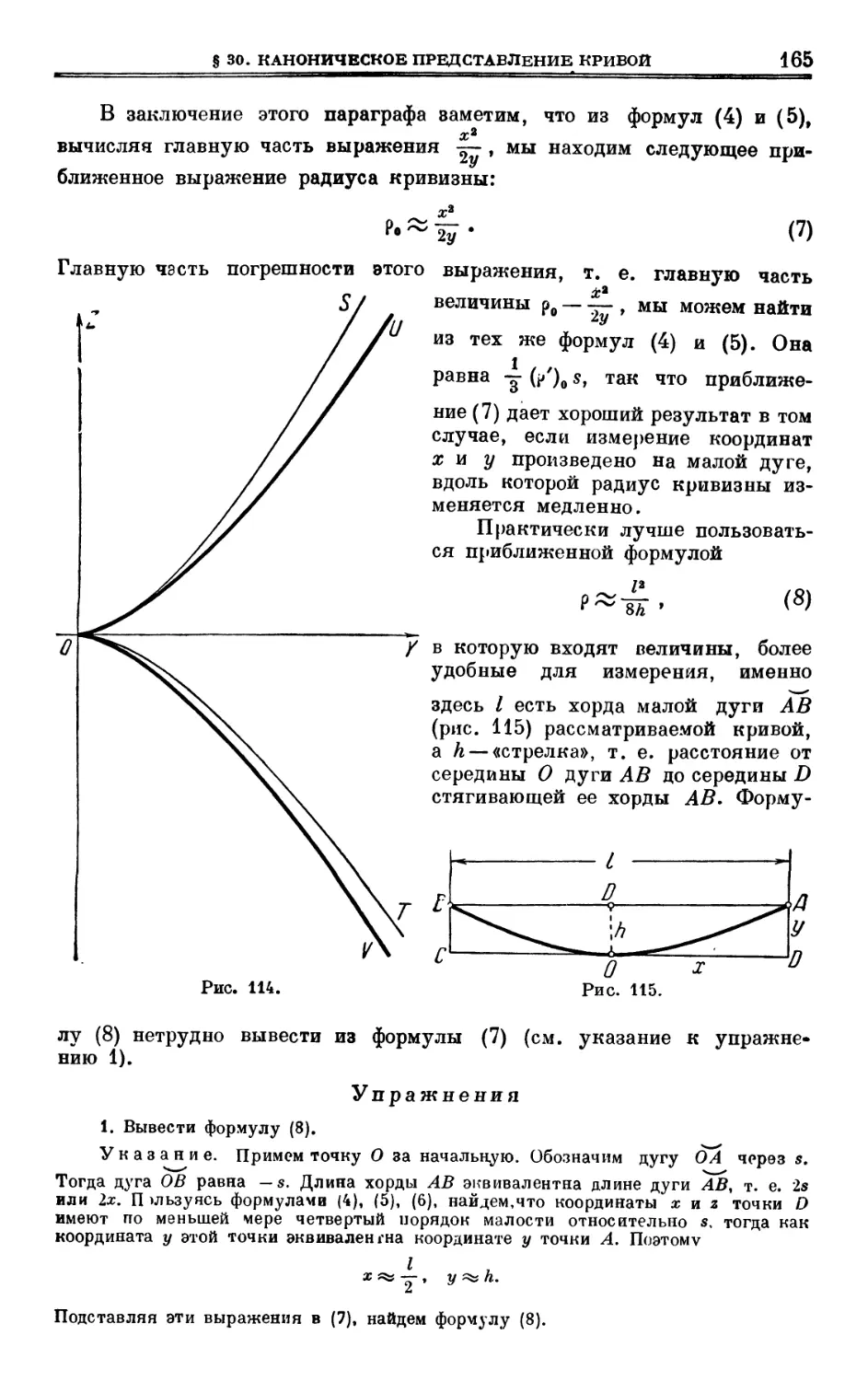
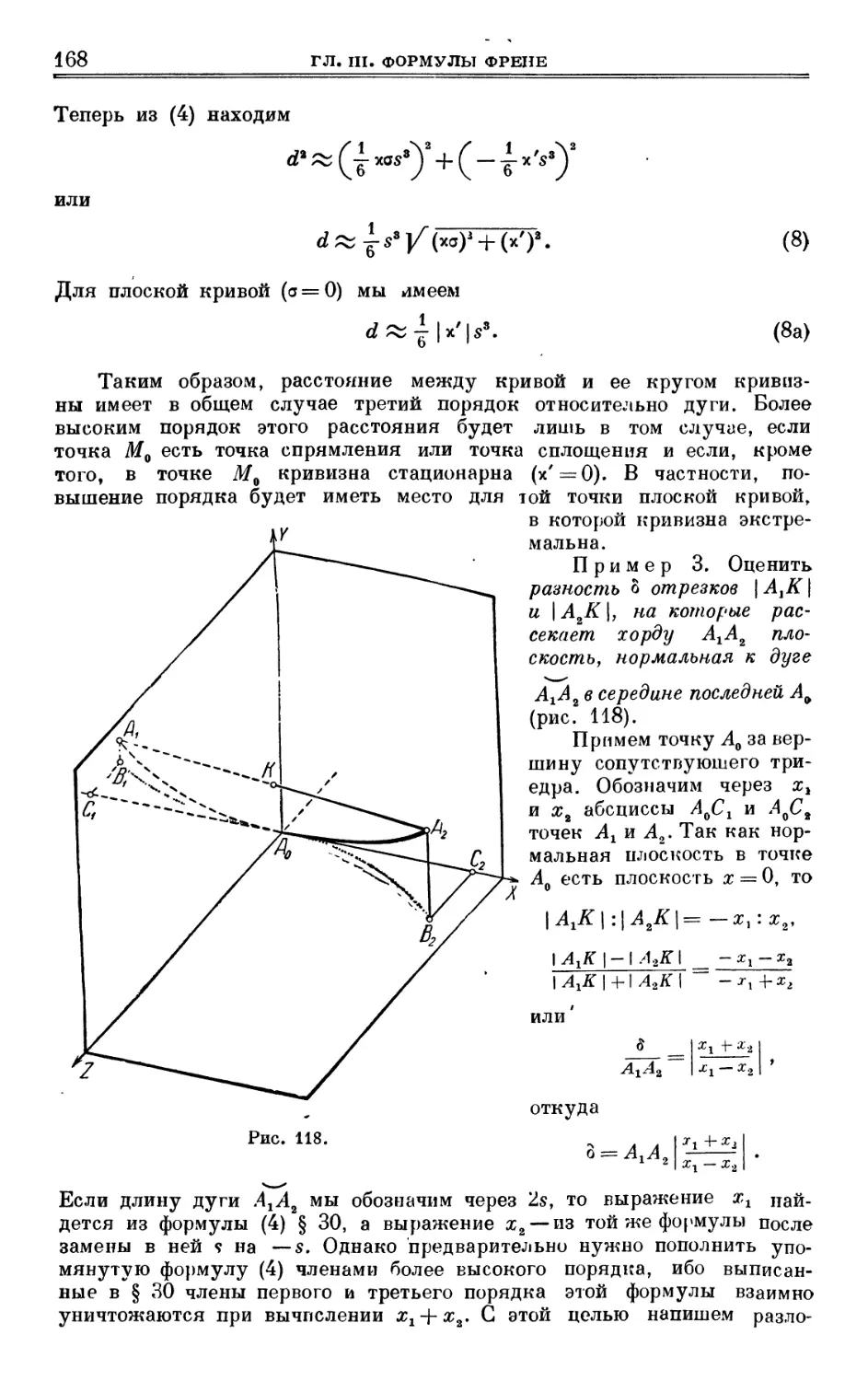
§ 31. Оценка некоторых геометрических величин 166
ГЛАВА IV
НЕКОТОРЫЕ СВОЙСТВА СФЕРИЧЕСКИХ ФИГУР
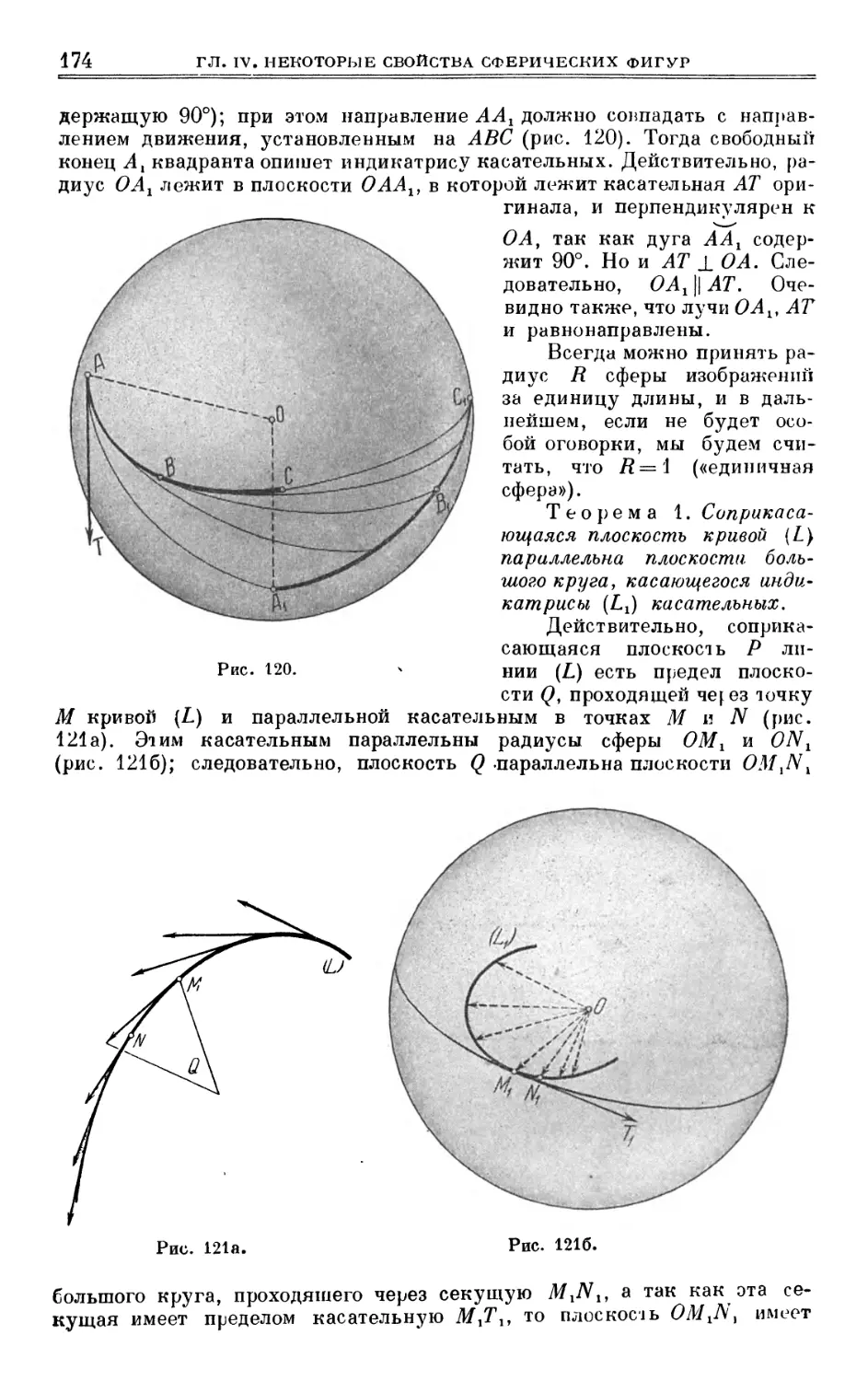
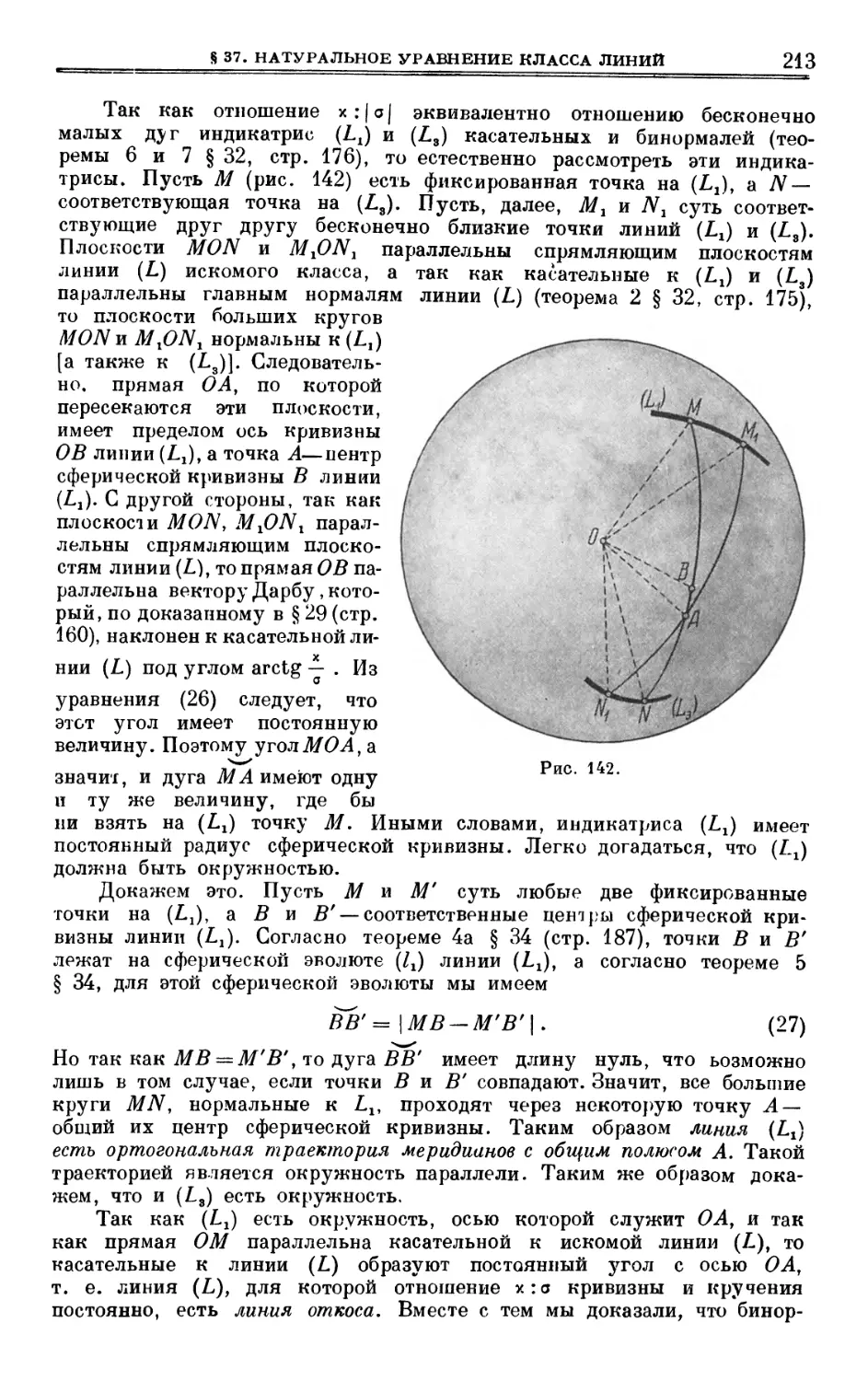
§ 32. Сферические индикатрисы 173
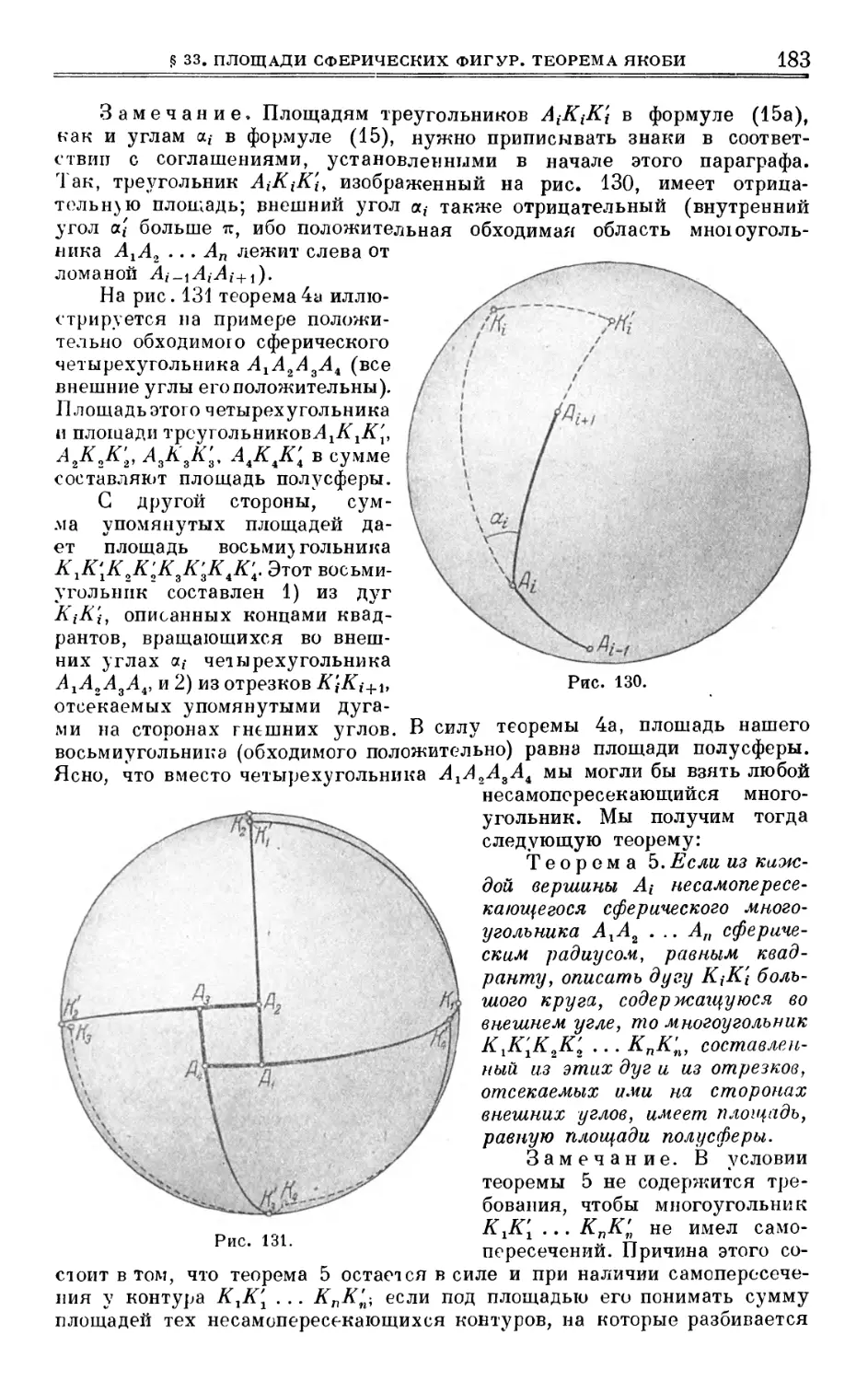
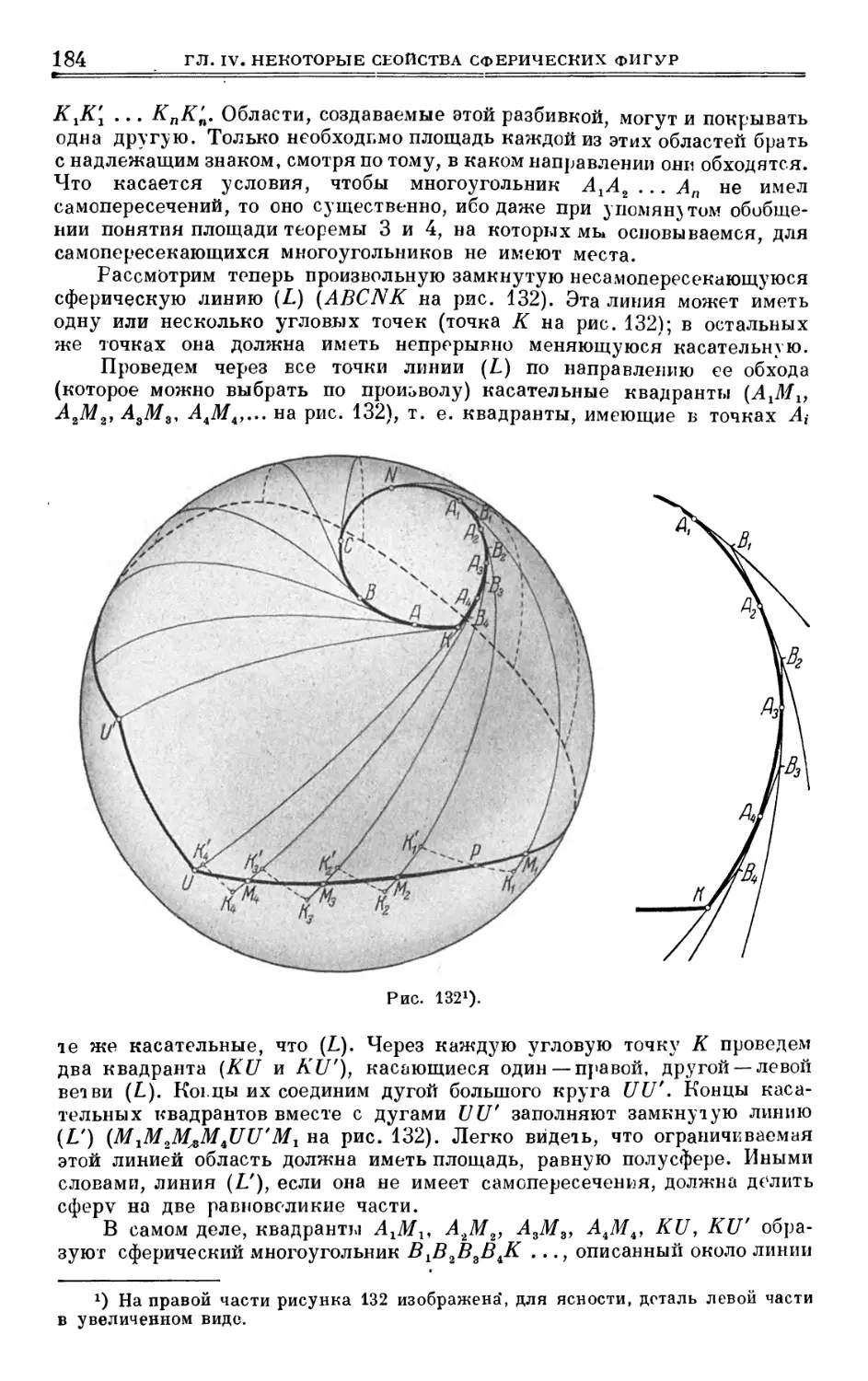
§ 33. Площади сферических фигур. Теорема Якоби 176
§ 34. Сферические эвольвенты и эволюты 186
глава v
НАТУРАЛЬНЫЕ УРАВНЕНИЯ
§ 35. Натуральные уравнения плоской кривой 189
§ 36. Натуральные уравнения пространственной кривой 194
§ 37. Натуральное уравнение класса линий 202
ГЛАВА VI
КРИВАЯ ПОВЕРХНОСТЬ И ЕЕ КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
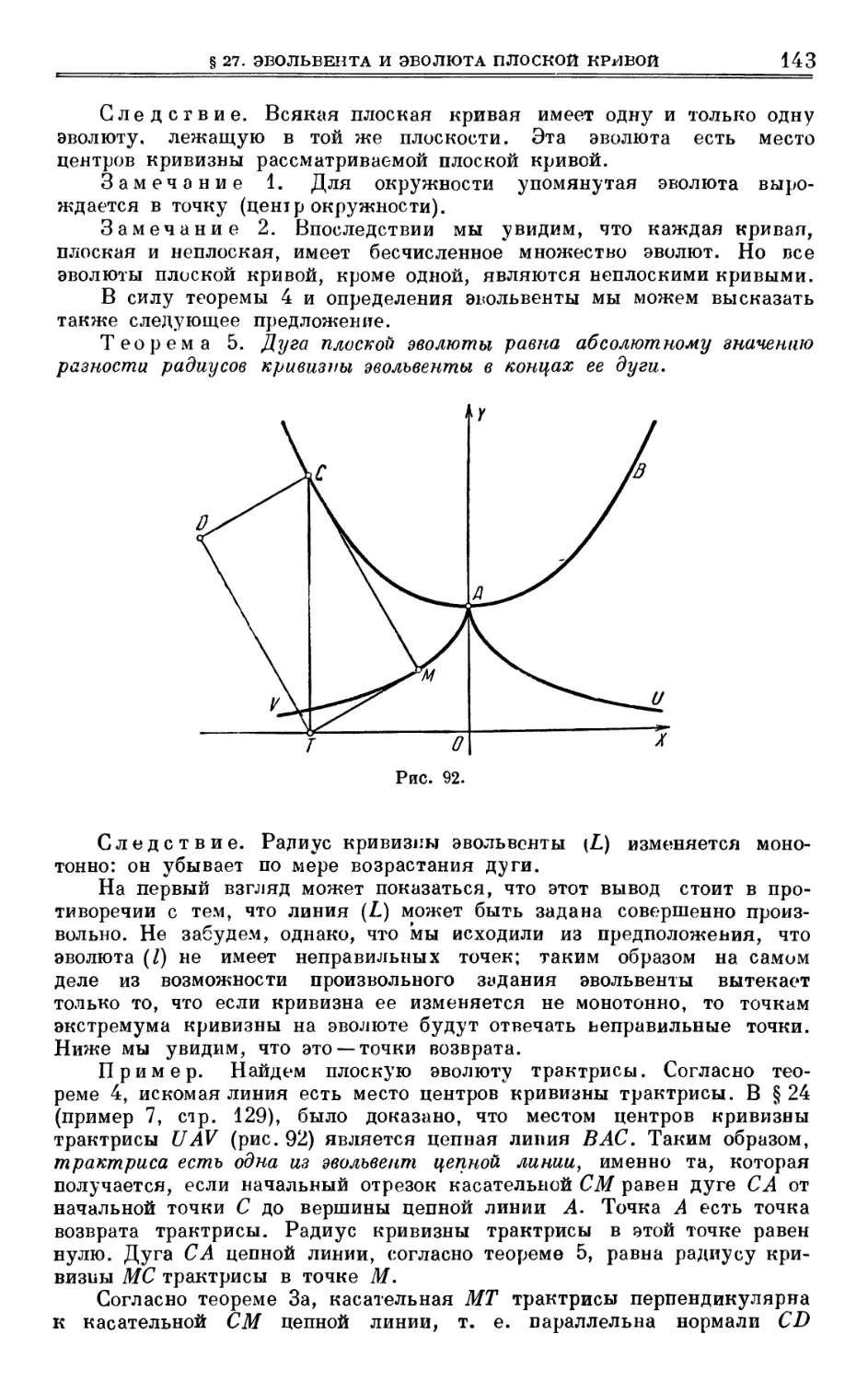
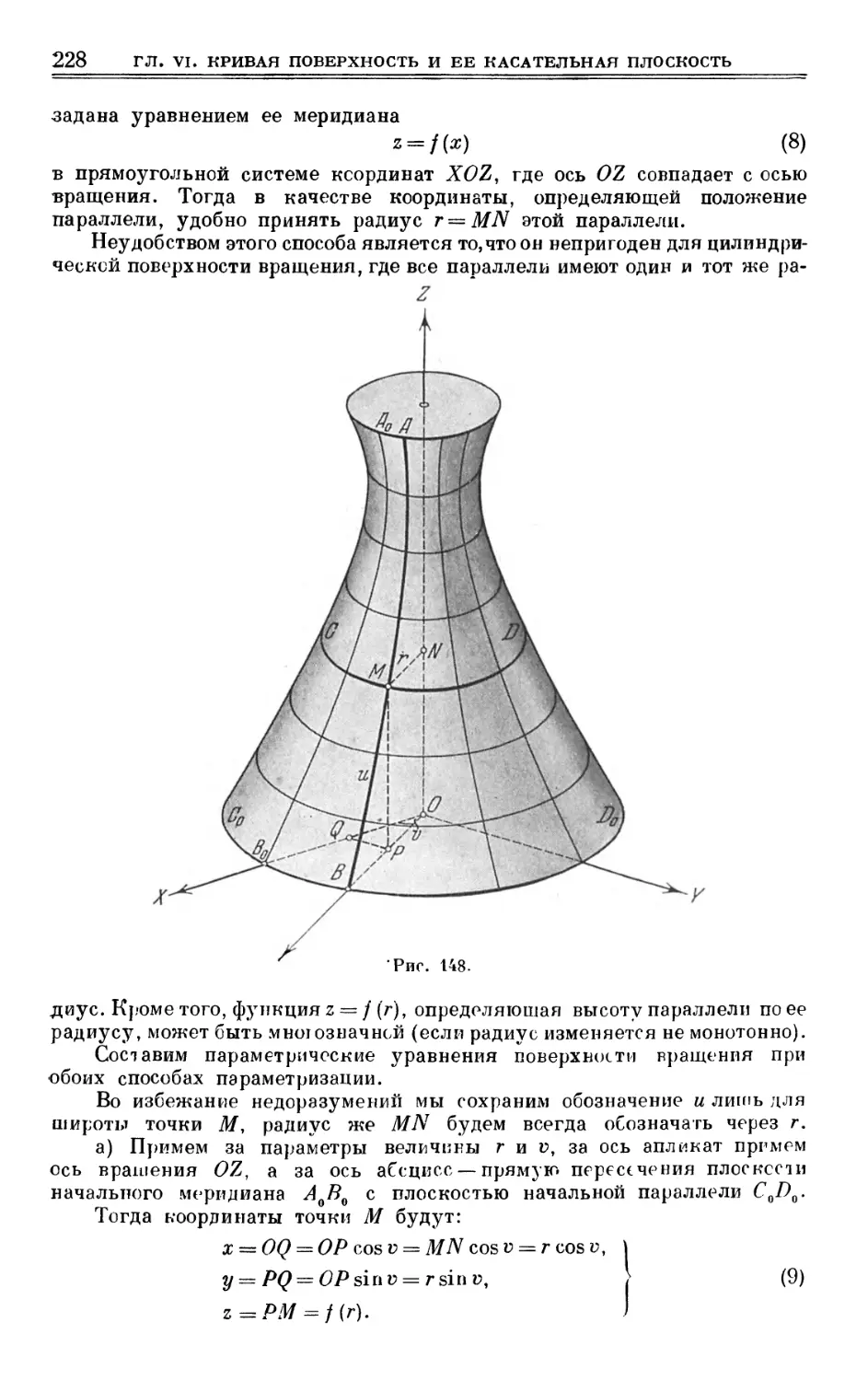
§ 38. О поверхностях 222
§ 39. Аналитическое представление поверхности 223
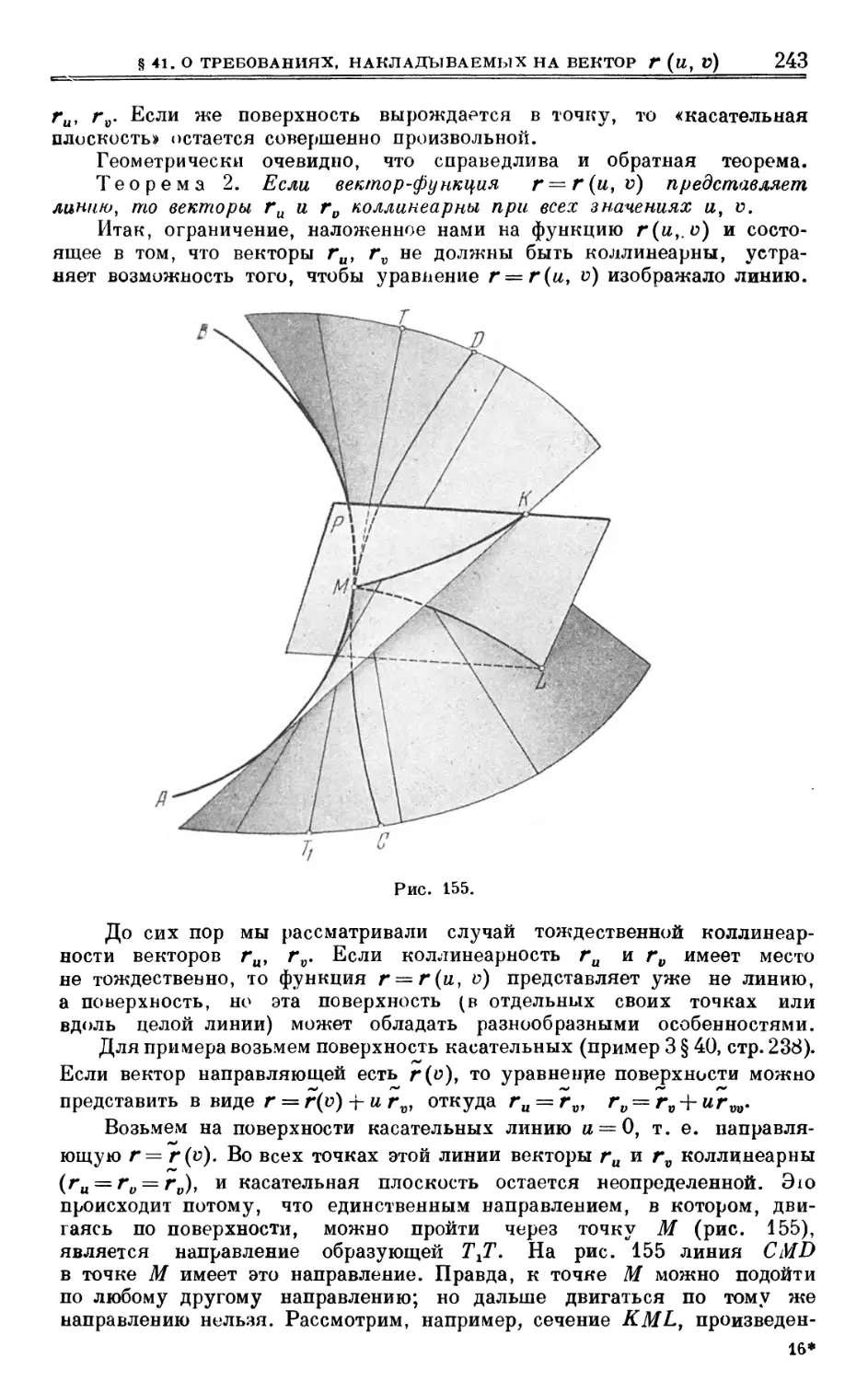
§ 40. Карательная плоскость и нормаль 235
§ 41. О требованиях, накладываемых на функцию г (u, v) 240
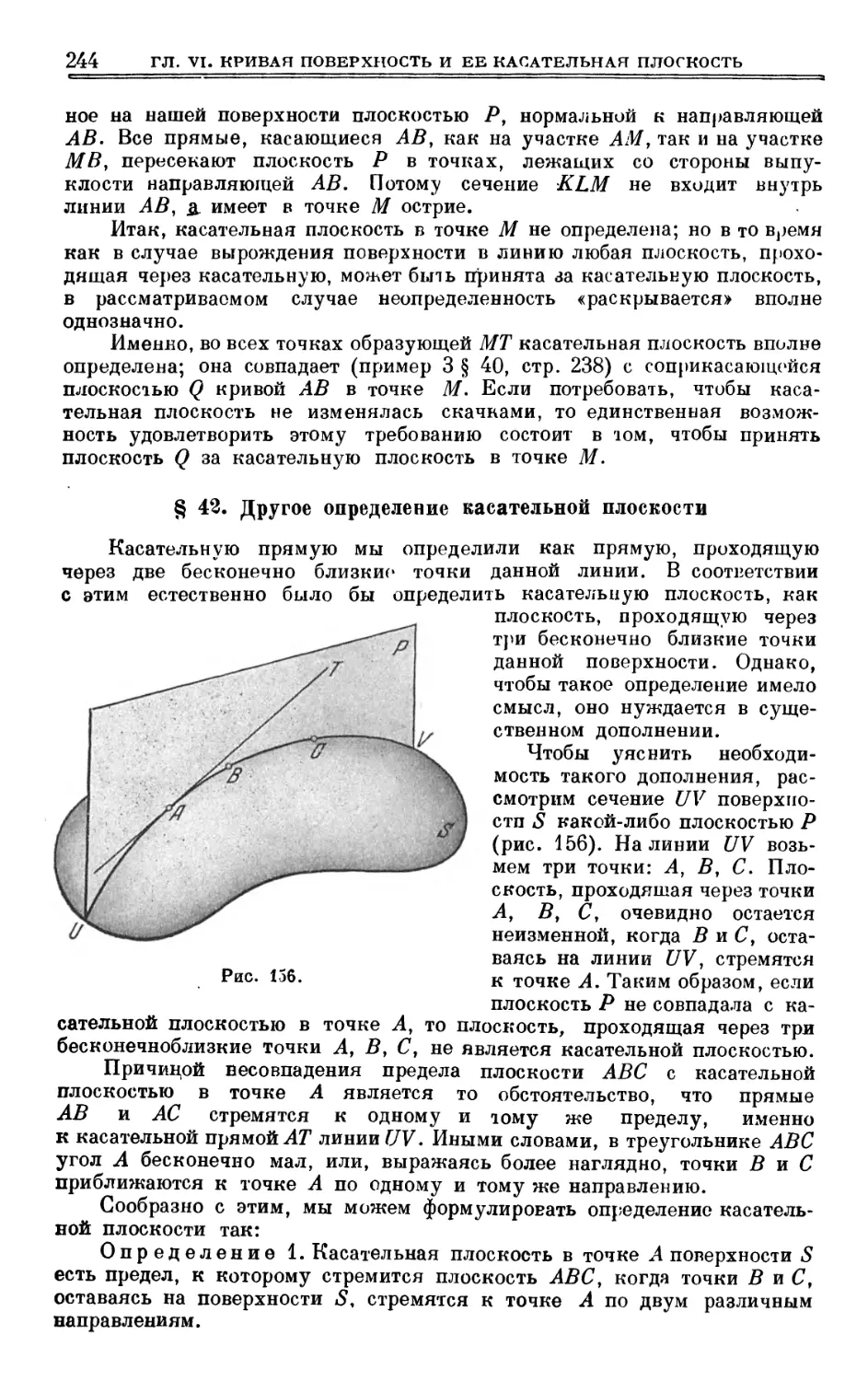
§ 42. Другое определение касательной плоскости 244
ГЛАВА VII
ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИЗГИБАНИЕ ПОВЕРХНОСТИ
§ 43. Линейный элемент и первая квадратичная форма 247
§ 44. Направления на поверхности и углы между ними 254
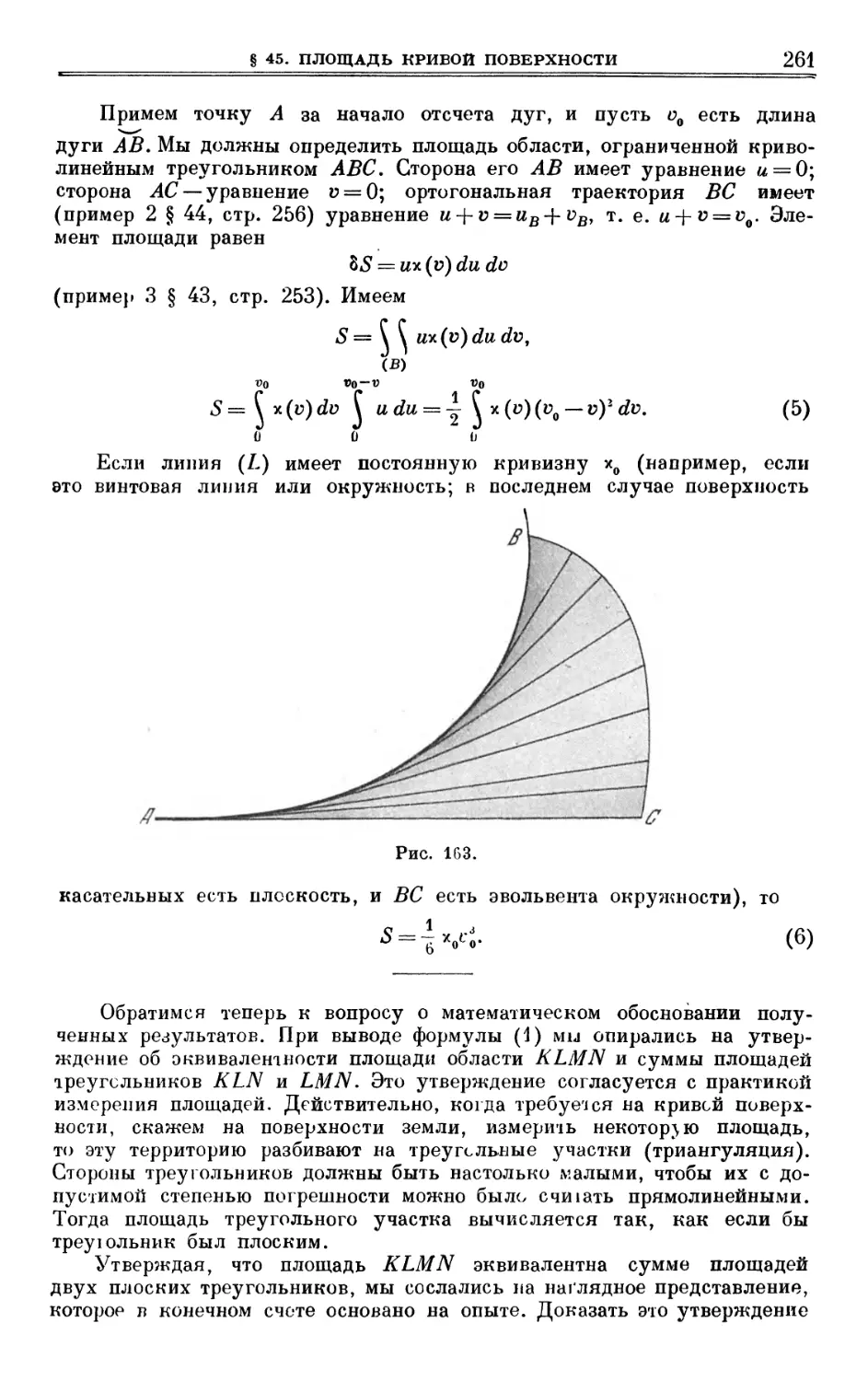
§ 45. Площадь кривой поверхности 258
§ 46. Об изгибании поверхностей 266
§ 47. Внутренняя геометрия поверхности 278
ГЛАВА VIII
РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
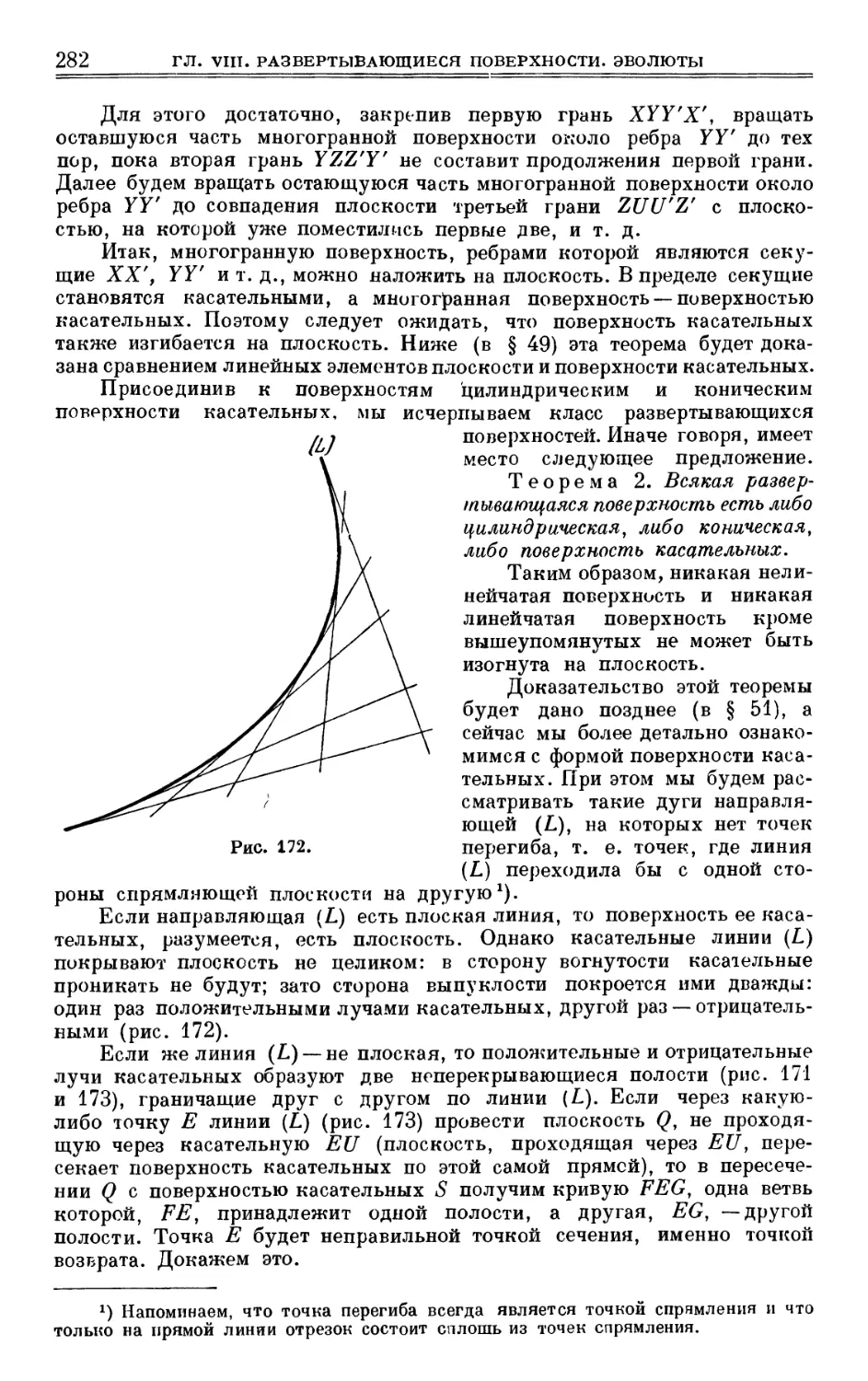
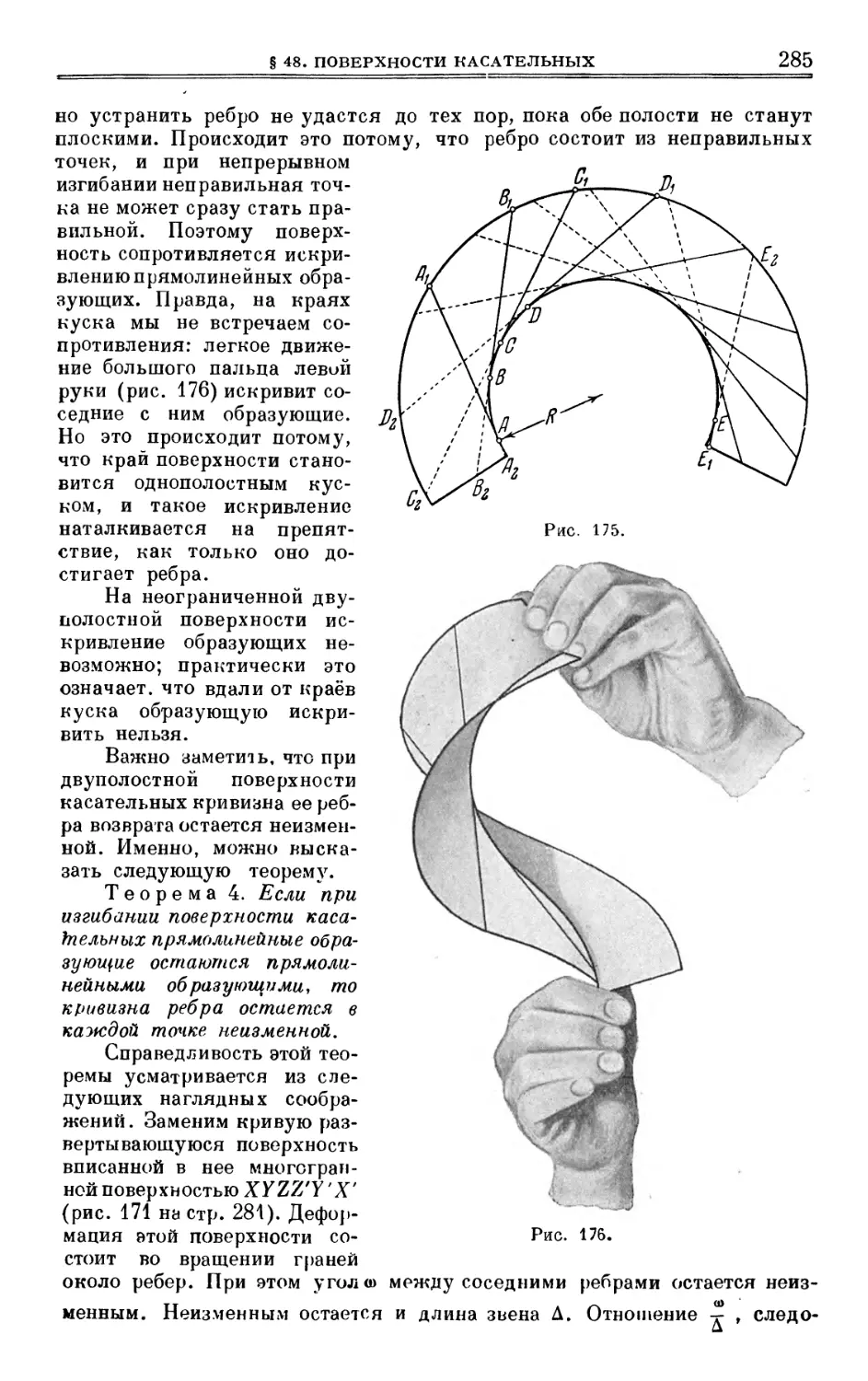
§ 48. Поверхности касательных ... 281
§ 49. Доказательство теорем 1 и 4 § 48 286
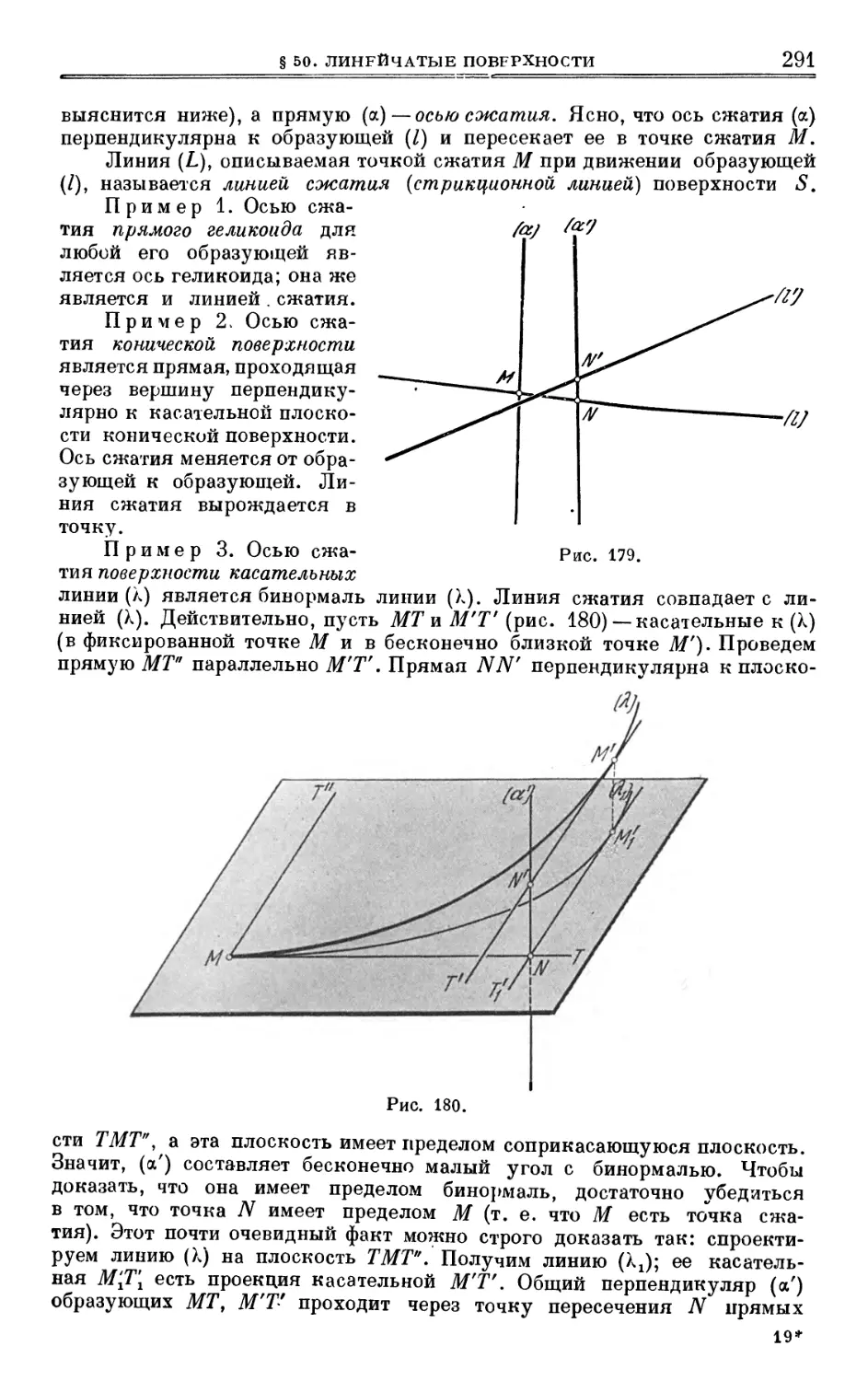
§ 50. Линейчатые поверхности 287
§ 51. Доказательство теоремы 2 § 48 298
§ 52. Огибаюшая однопараметрического семейства плоскостей 300
§ 53. Полярная поверхность . ... 307
§ 54. Соприкасающаяся сфера 313
§ 55. Спрямляющая плоскость и геодезическая линия 317
§ 56. Эволюты и эвольвенты пространственных кривых 326
ОГЛАВЛЕНИЕ
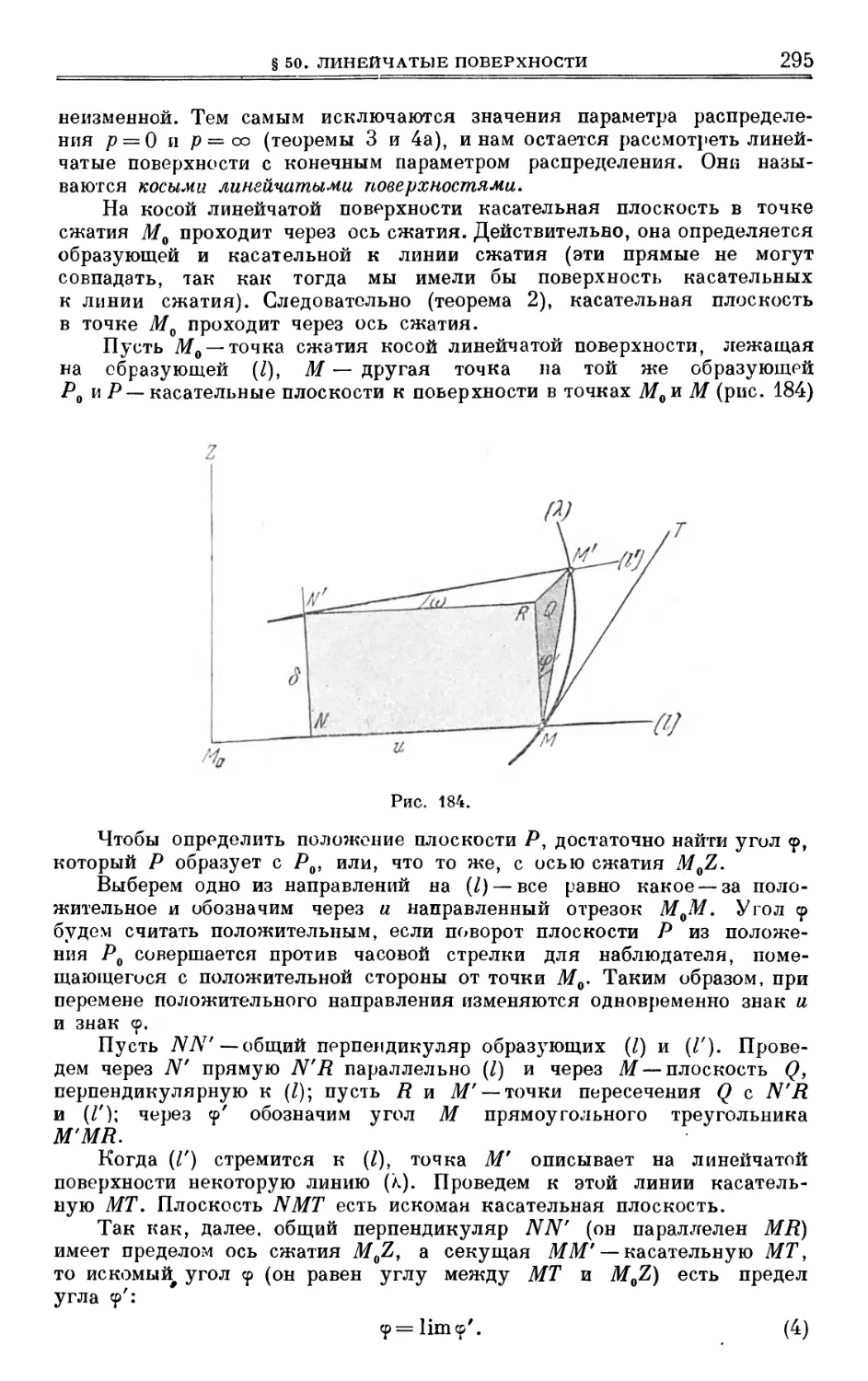
ГЛАВА IX
ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
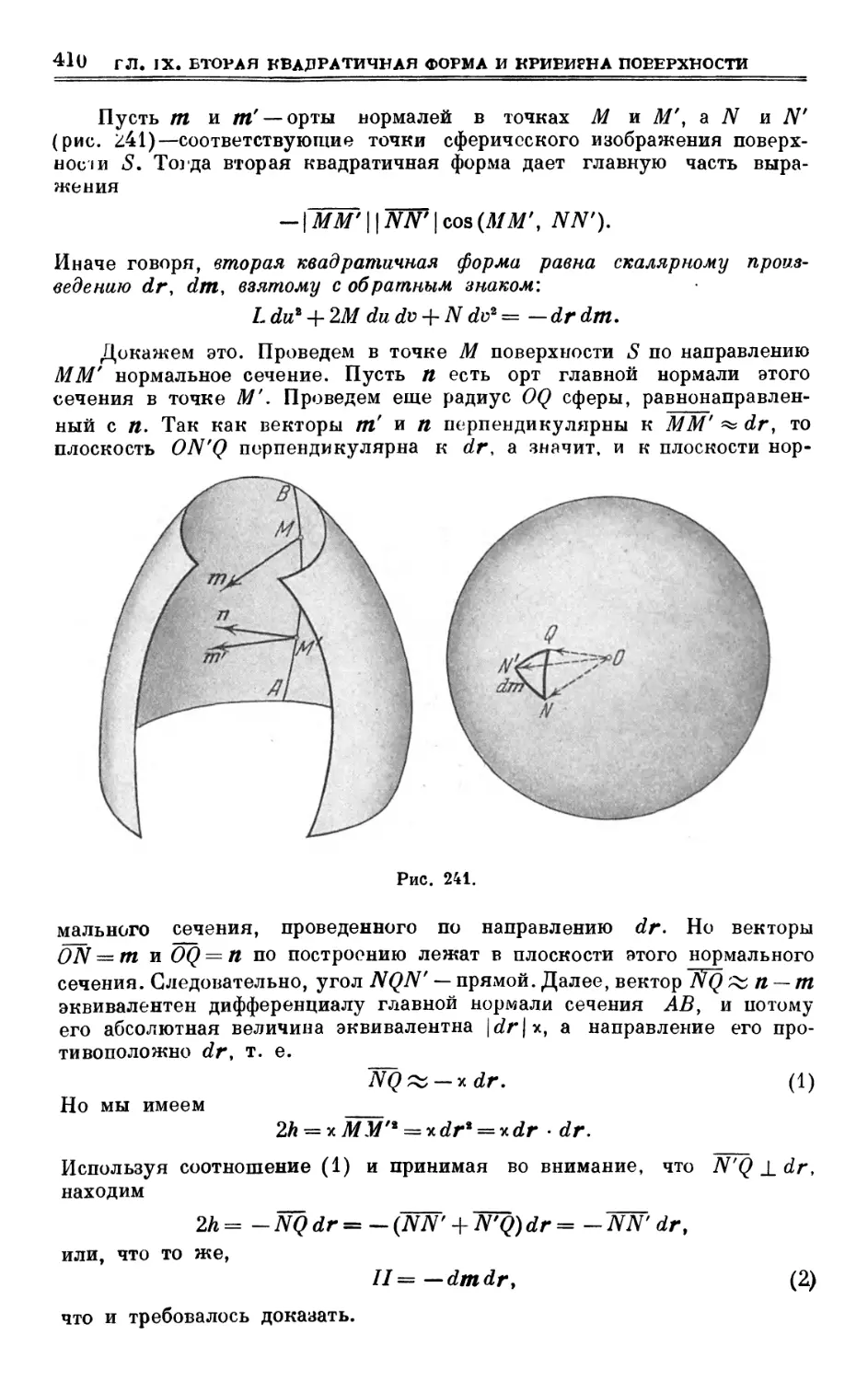
§ 57. Расстояние от точки поверхности до касательной плоскости и вторая
квадратичная форма 338
§ 58. Соприкасающийся параболоид. Три типа точек поверхности ... 344
§ 59. Индикатриса Дюпена. Кривизна нормальных сечений 350
§ 60. Главные направления. Формула Эйлера • 355
§ 61. О предпосылках эйлерова закона распределения кривизн 358
§ 62. Аналитическое разыскание главных направлений 360
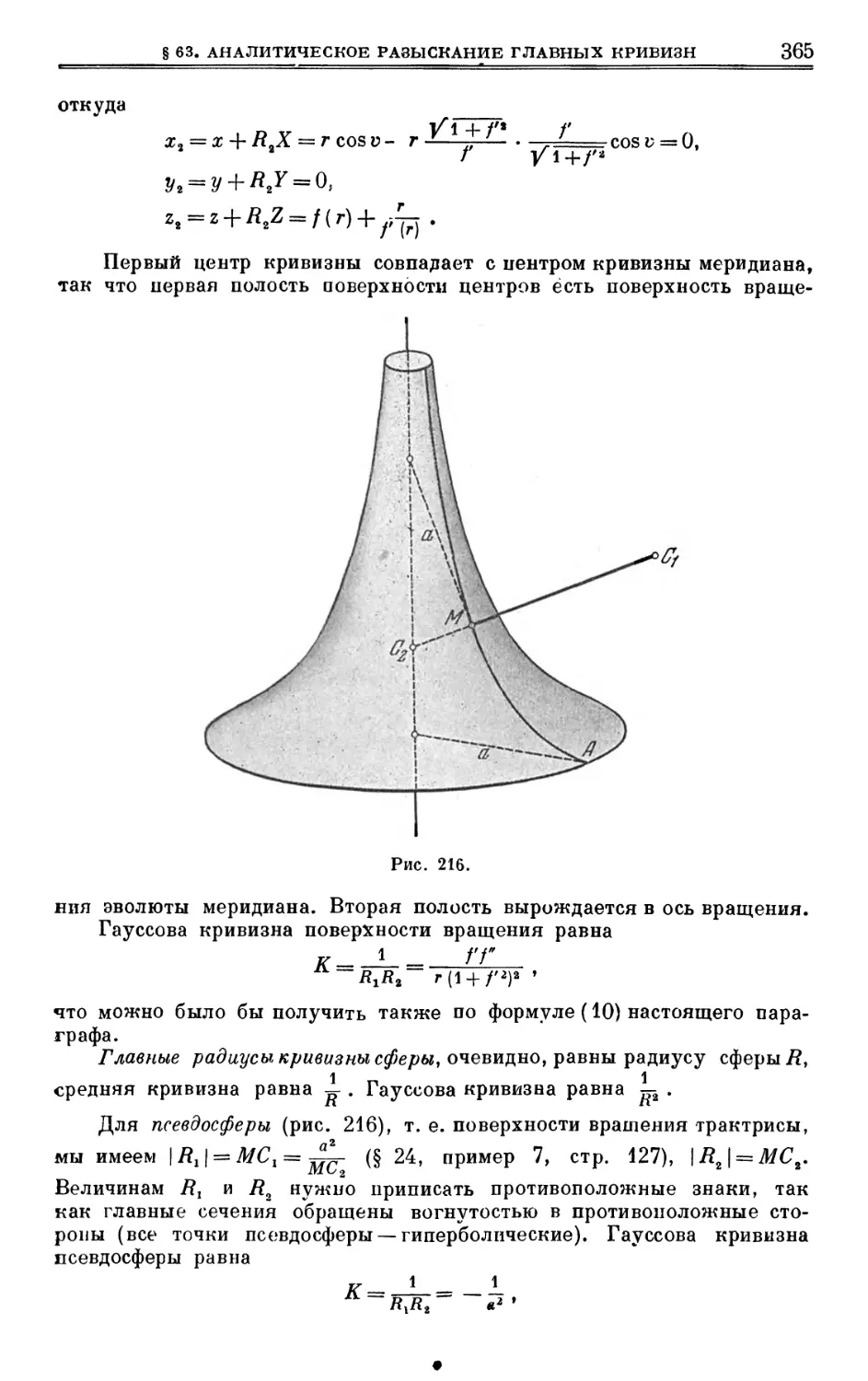
§ 63. Аналитическое разыскание главных кривизн 362
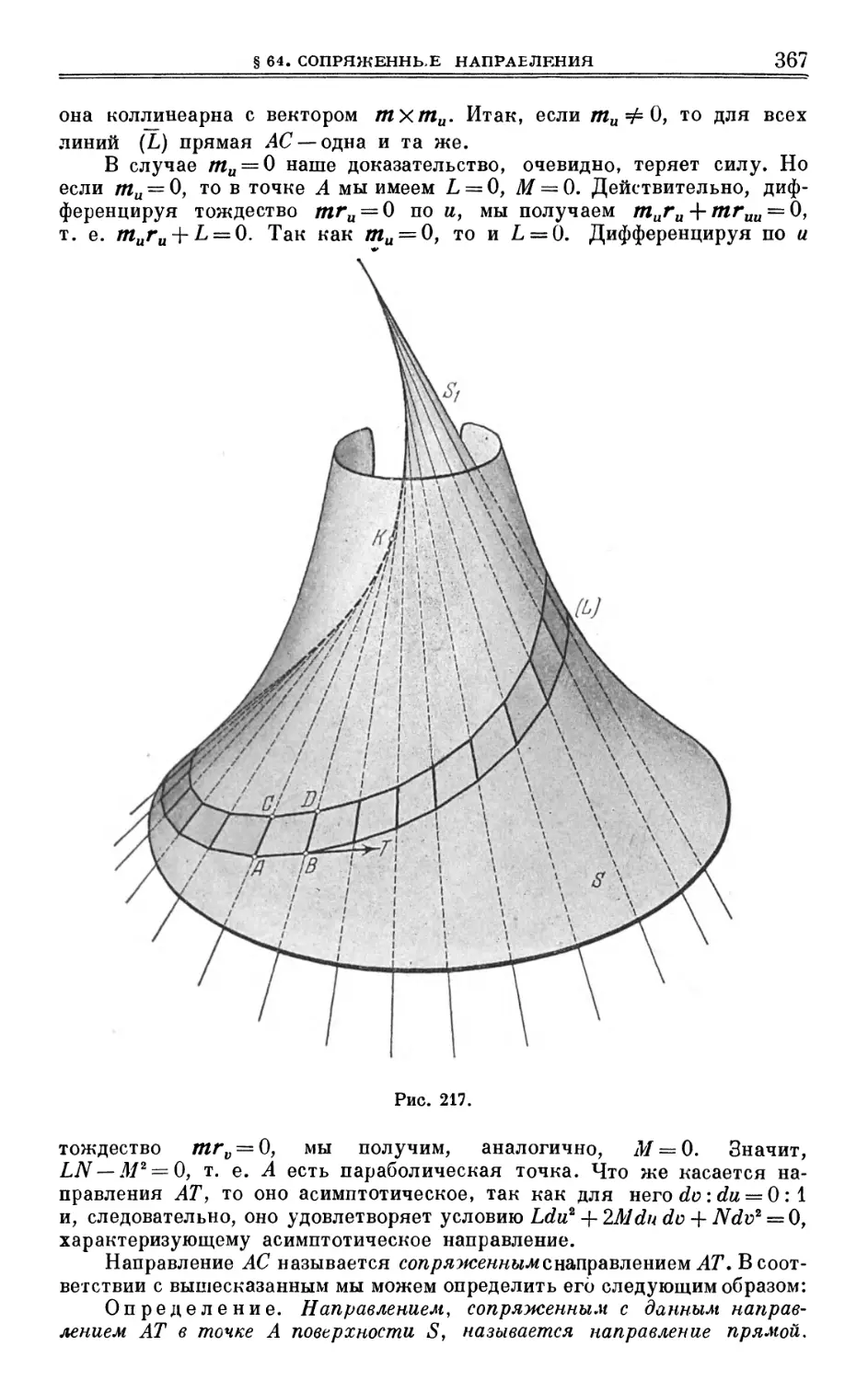
§ 64. Сопряженные направления 366
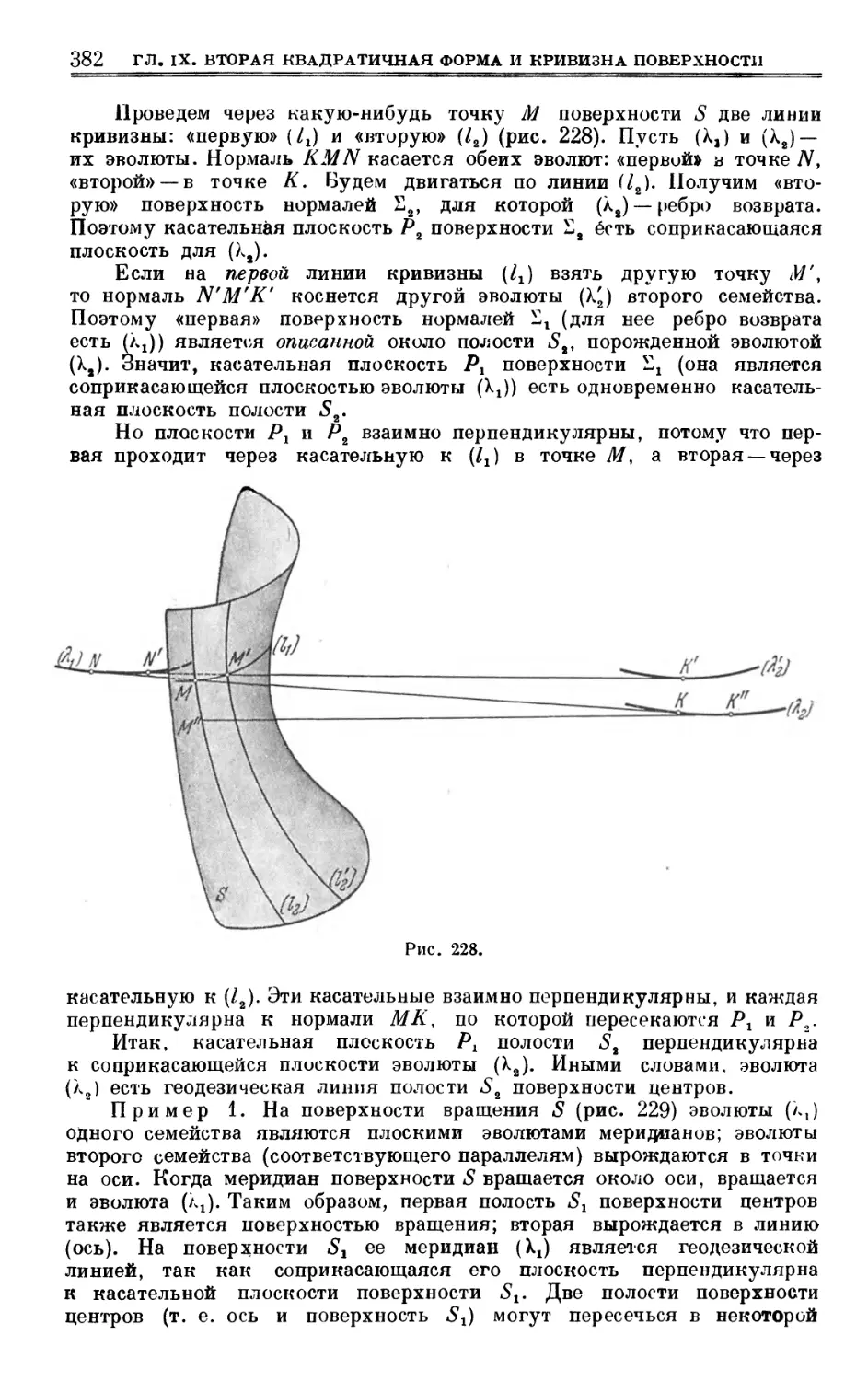
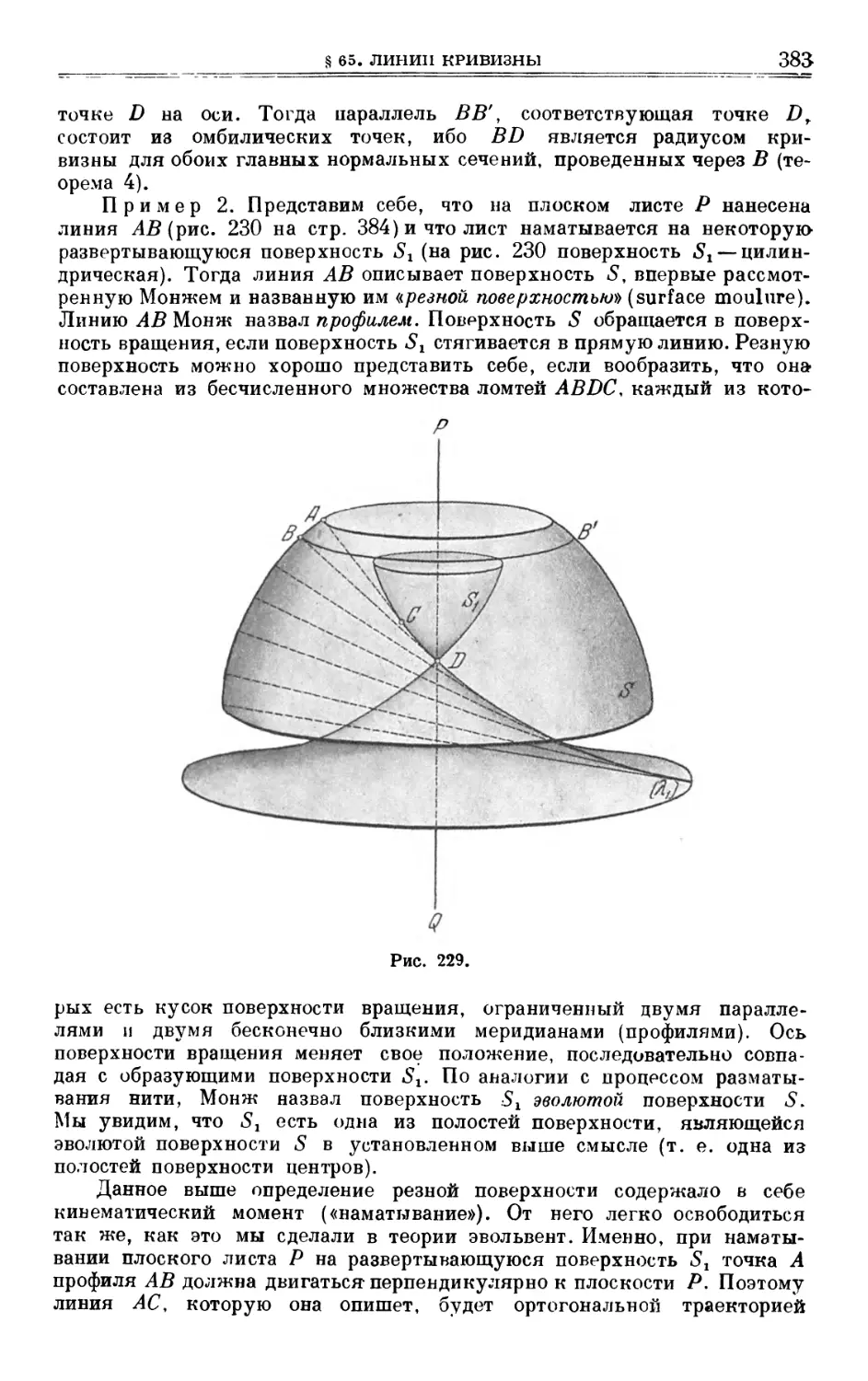
§ 65. Линии кривизны 374
§ 66. Аналитическое разыскание линий кривизны 387
§ 67. Аналитический вывод уравнения линий кривизны 394
§ 68. Сферическое изображение поверхности 395
§ 69. Асимптотические линии 401
§ 70. Новая интерпретация второй квадратичной формы 409
§ 71. Третья квадратичная форма 411
ГЛАВА X
ОСНОВНЫЕ ФОРМУЛЫ ТЕОРИИ ПОВЕРХНОСТЕЙ
И ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
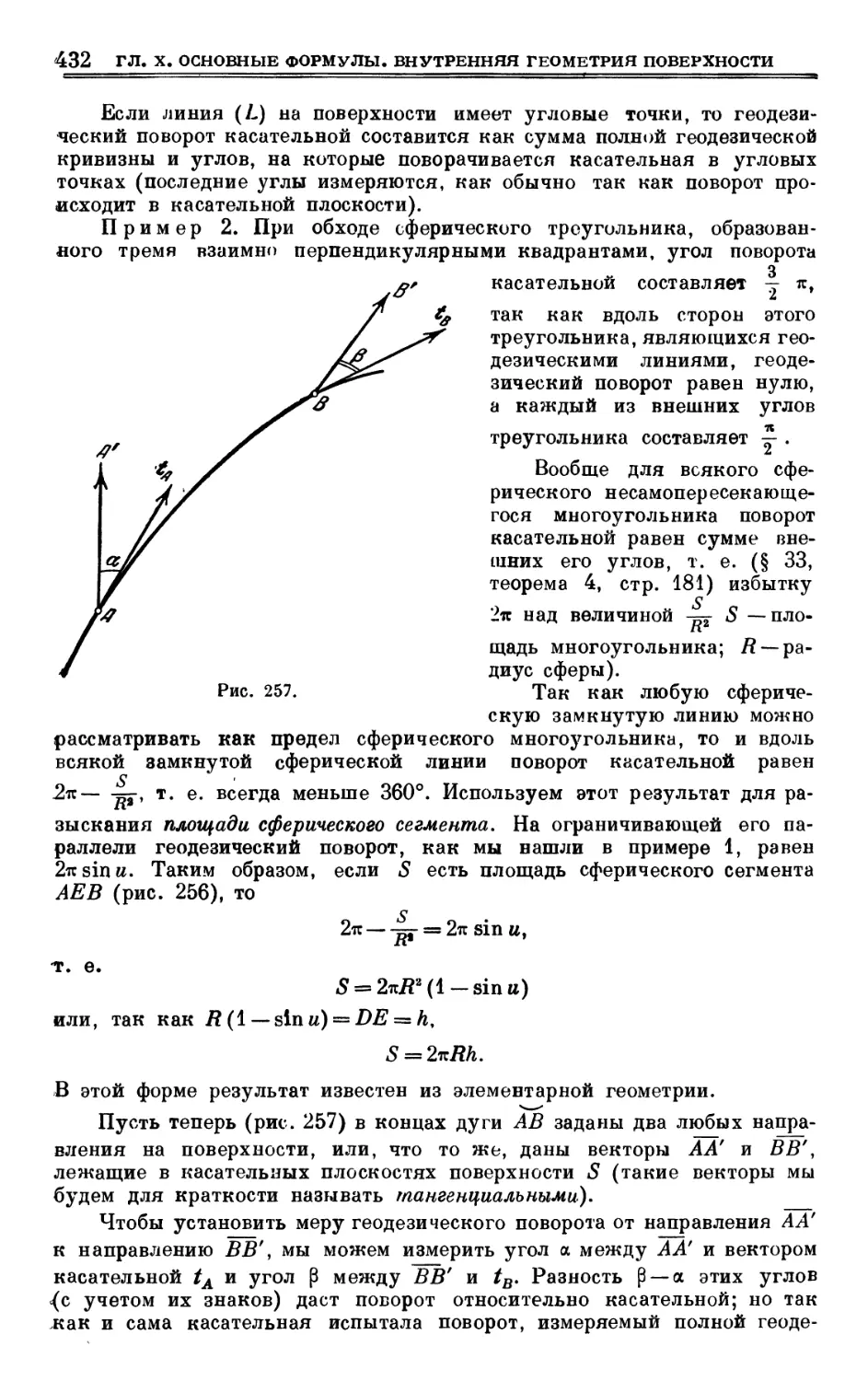
§ 72. Формула и теорема Менье 414
§ 73. Геодезические линии 421
§ 74. Геодезическая кривизна 426
§ 75. Изгибание полосы. Геодезические окружности Дарбу 428
§ 76. Геодезический поворот и параллельное перенесение 430
§ 77. Теоремы Гаусса и Бонне 439
§ 78 Основные формулы теории поверхностей 447
§ 79 Уравнение Гаусса 453
§ 80. Уравнения Петерсона-Майнарди 455
§ 81. Формула для геодезической кривизны 458
§ 82. Аналитическое доказательство теоремы Гаусса-Бонне ... 463
§ 83. Уравнение геодезической линии 465
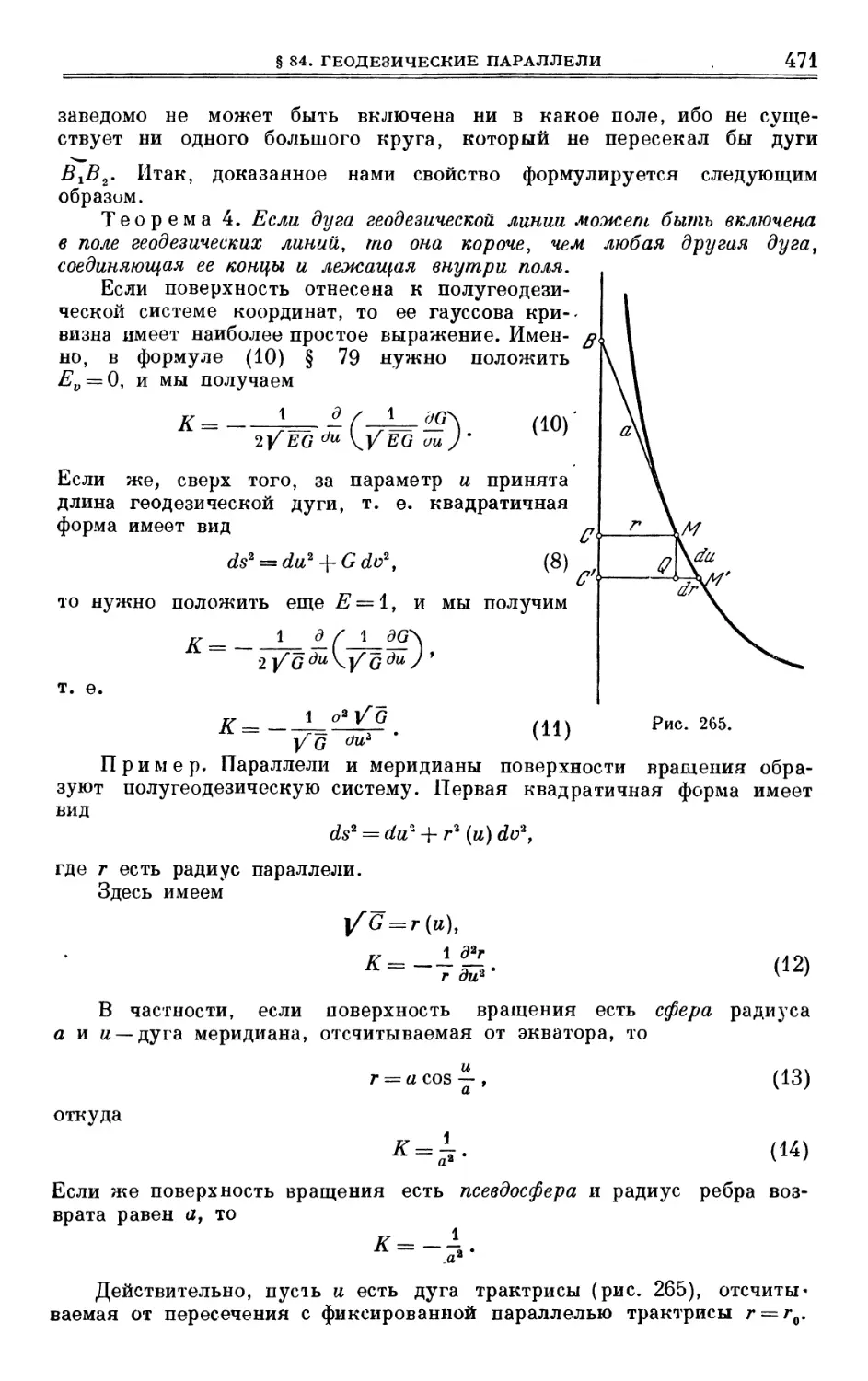
§ 84. Геодезические параллели • 468
§ 85. Поверхности постоянной гауссовой крививны. Движения поверхности
по самой себе 472
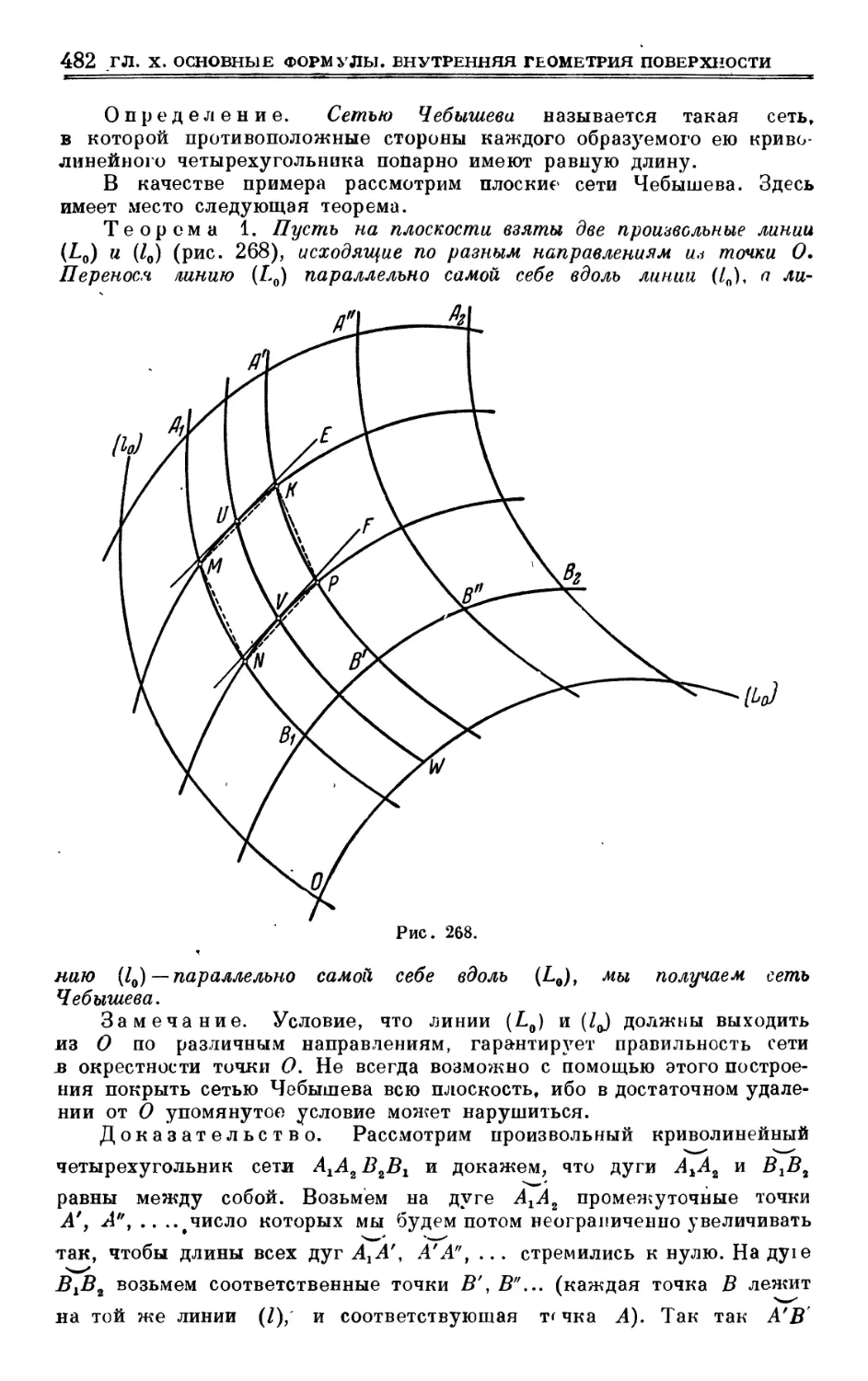
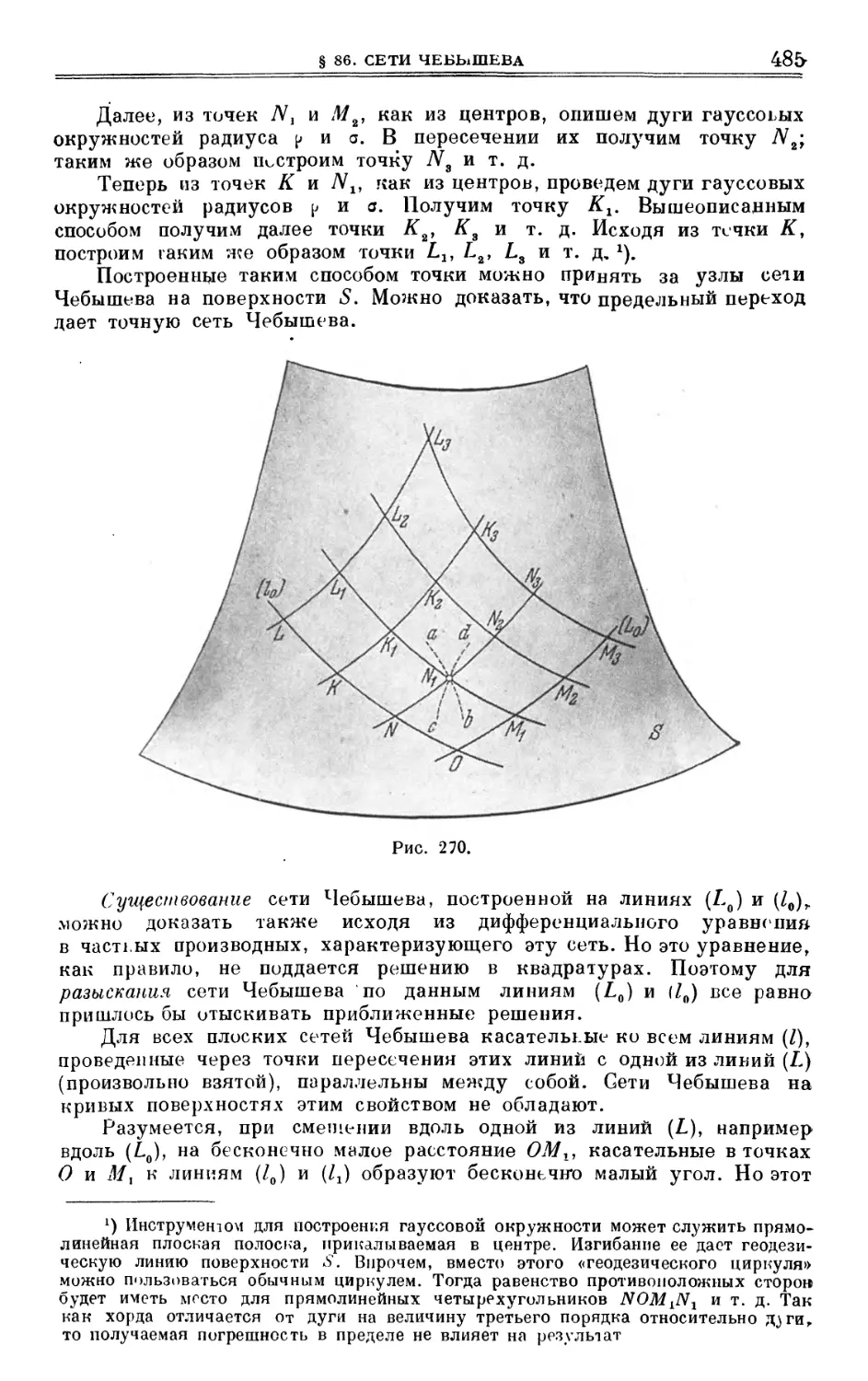
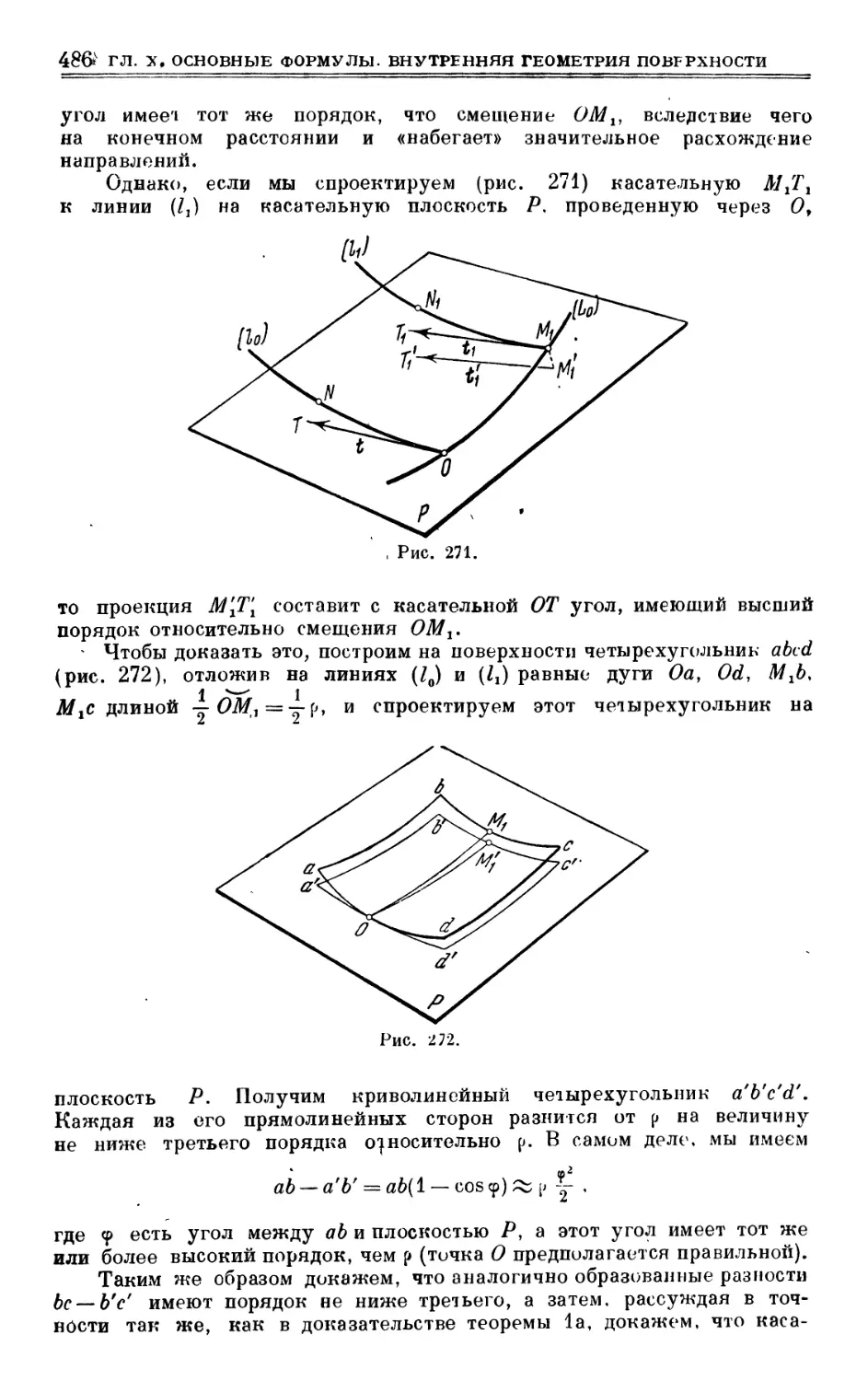
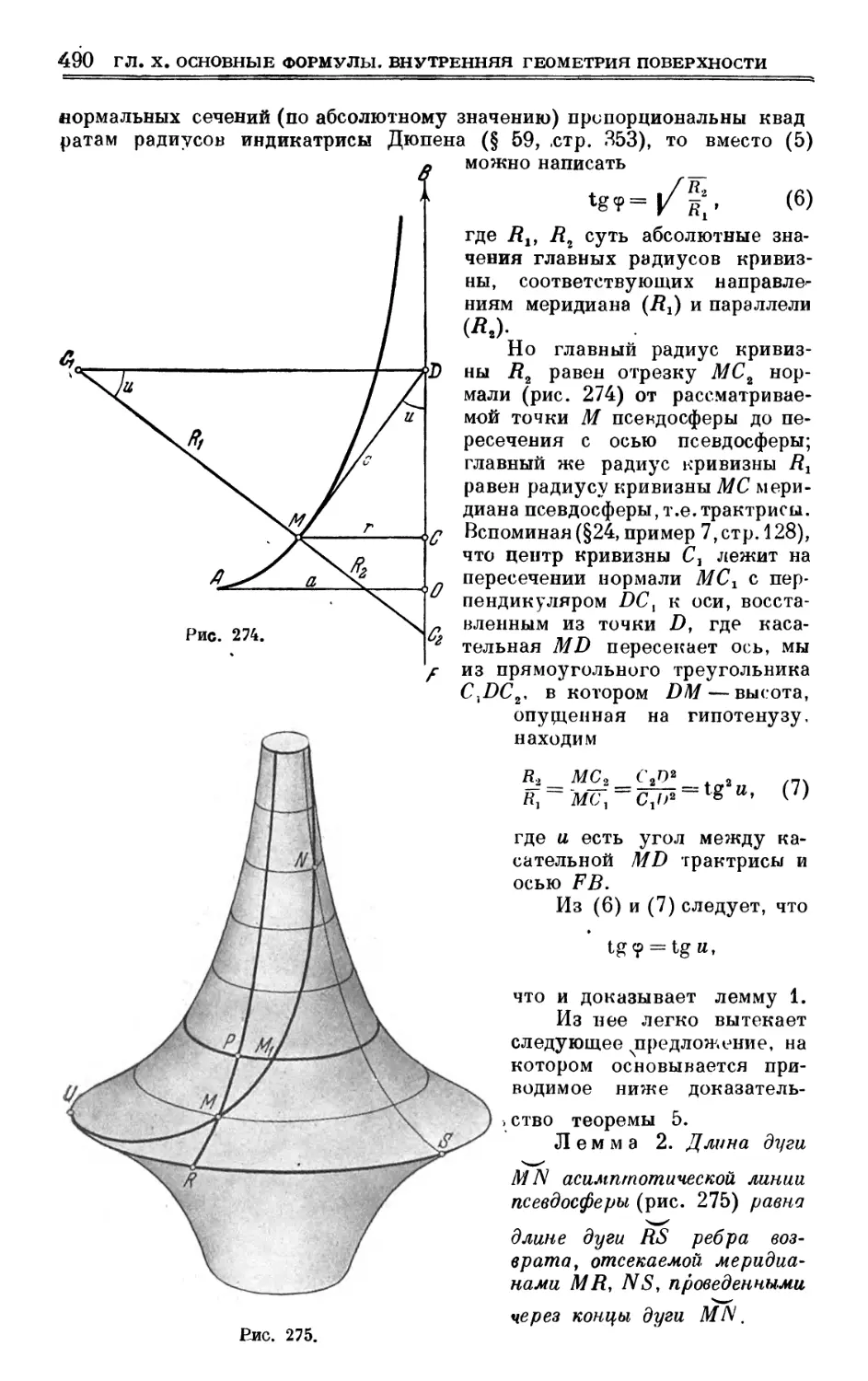
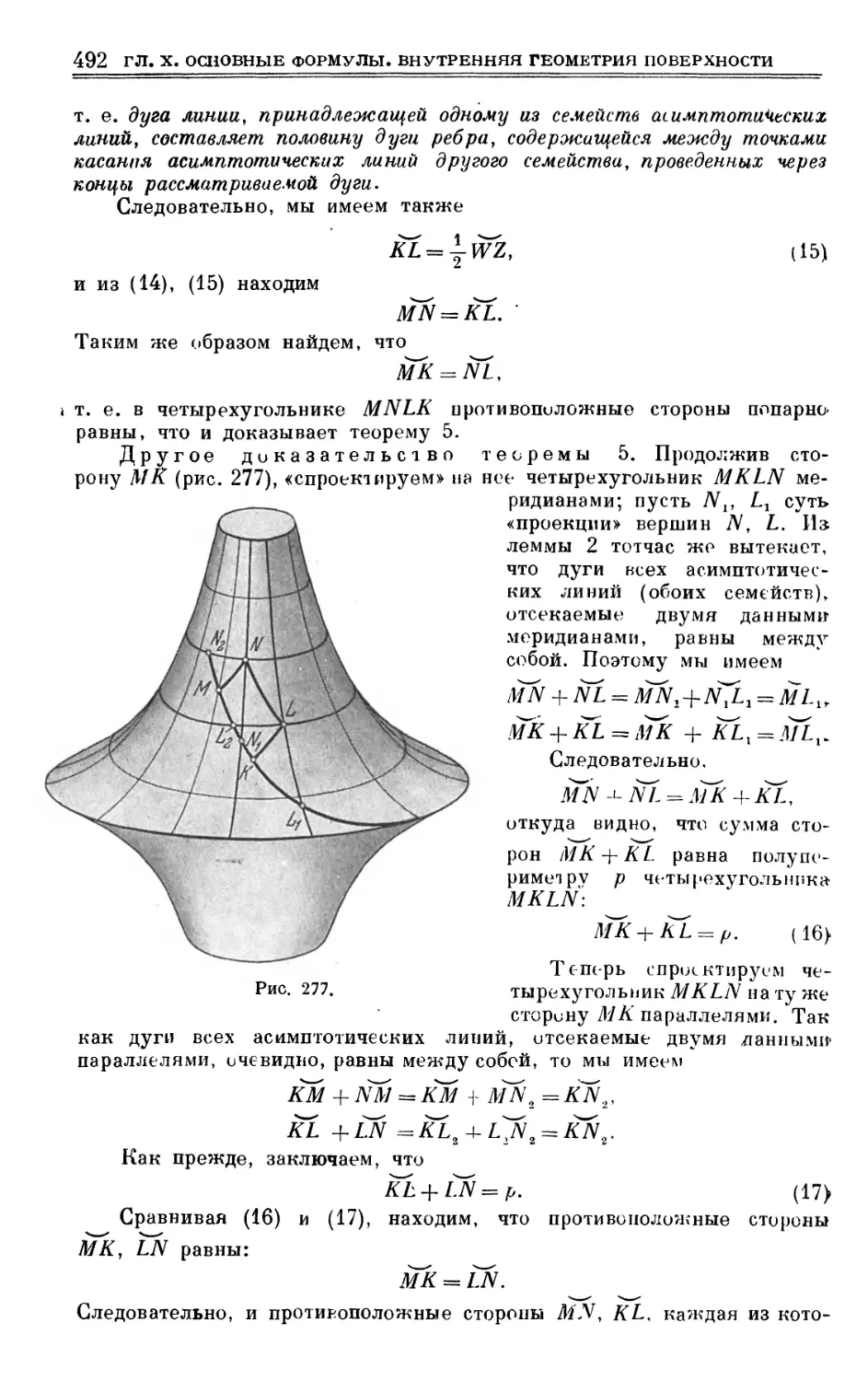
§ 86. Сети Чебышева 481
Заключительное слово автора 496
Приложение. Основные сведения по векторному анализу 498
Алфавитный указатель 507
ПРЕДИСЛОВИЕ
В этой книге читатель найдет материал, в основном совпадающий
с материалом других руководств по дифференциальной геометрии
и отвечающий программам университетов и педагогических институтов.
Но по методу изложения эта книга существенно отличается от
упомянутых руководств.
Обычно дифференциальная геометрия излагается аналитически;
это значит, что исследуемые геометрические объекты относятся к
некоторой системе координат, в результате чего решение геометрического
вопроса сводится к исследованию уравнений, связывающих координаты.
Плодотворность этого метода общеизвестна. Однако он имеет и свою
оборотную сторону. Именно, в течение всего процесса исследования
геометрические объекты и, что важнее всего, их внутренние связи
оттесняются на задний план и остаются в тени. Вследствие этого
утрачивается наглядность, а вместе с тем и психологическая
убедительность.
В этой книге преобладает синтетический метод; это значит, что
от условия вопроса к его решению мы идем прямым путем, выполняя
геометрические построения и вычисления, внутренне связанные с
исследуемыми объектами. Таким образом, геометрическая фигура все время
находится в поле зрения читателя.
Синтетический метод исследования применялся в дифференциальной
геометрии с самого момента ее возникновения. Но в учебной литературе
он, насколько мне известно, систематически использовался лишь при
изложении теории кривых. В русской же литературе до сих пор не было
ни одного руководства, где хотя бы теория кривых излагалась
синтетически.
Принято думать, что доставляемое синтетическим методом
преимущество наглядности покупается ценой пренебрежения строгостью. Это
мнение основывается на том, что обычно при пользовании синтетическим
методом одни величины заменяют другими, им эквивалентными, без
достаточного обоснования такой замены. Наглядные представления
делают ее довольно правдоподобной; с другой стороны, правильность
полученного результата может быть строго доказана аналитически.
Может быть, именно поэтому и не было сделано попытки внести
в синтетические методы дифференциальной геометрии ту степень
строгости, которая характеризует ее аналитические методы.
ПРЕДИСЛОВИЕ 9
Между гем оказывается, что и синтетические доказательства
в дифференциальной геометрии можно обосновать с полной
строгостью. С этой целью здесь введены понятия предела геометрического
образа (точки, прямой, плоскости) и доказаны основные теоремы об этих
пределах. Последние играют в синтетическом методе ту же роль, что
в аналитическом методе теоремы о пределе функции. Как ни странно,
но факт, что хотя сплошь и рядом пользуются такими выражениями,
как «касательная есть предельное положение секущей», но нигде не
определяется, что такое «предельное положение». Я предпочитаю
выражение «касательная есть предел секущей прямой», и в § 5 читатель
найдет точное определение понятия предела прямой линии.
Стремление достигнуть наибольшей яркости геометрических
представлений выражается в этой книге не только преобладанием
синтетического метода исследования, но и подбором большого числа примеров,
выясняющих индивидуальные особенности разнообразных линий и
поверхностей. Этой же цели служат многочисленные рисунки. Нелишне
также отметить, что, прежде чем ввести какое-нибудь новое понятие,
я стараюсь выявить те физические факты, которые лежат в его основе.
Как сказано, синтетический метод в этой книге является
преобладающим. Однако и аналитическому методу уделено должное внимание,
так как эта книга является прежде всего руководством для учащихся.
И я думаю, что усвоение аналитических рассуждений только
выигрывает при их сопоставлении с рассуждениями синтетическими. С другой
стороны, я не видел необходимости в том, чтобы для каждого
предложения давать как аналитическое, так и синтетическое доказательство.
После того как оба метода достаточно усвоены, предпочтительно
пользоваться в каждом отдельном случае тем, который ведет к цели быстрее.
Отмечу еще одну особенность этой книги. В тех случаях, когда
проведение строгого доказательства связано со вспомогательными
построениями, могущими утомить внимание читателя, я часто привожу сначала
наводящее рассуждение, дающее основную идею доказательства. И я
рекомендую учащемуся при первом чтении именно на это наводящее
рассуждение обратить особое внимание. Пусть он также старается
в других случаях, где это наводящее рассуждение не выделено, извлечь
из полного доказательства его «скелет», т. е. усвоить прежде всего его
идею. При повторном чтении можно будет в деталях разобрать все те
вспомогательные построения и вычисления, которые имеют задачей
придать рассуждениям полную строгость.
В работе над этой книгой большую помощь оказали мне
нижеперечисленные лица.
Проф. Г. Б. Гуревич, прочитавший чрезвычайно внимательно
рукопись, обратил мое внимание на ряд существенных пробелов в
доказательствах, а также отметил стилистические недочеты и вычислительные
ошибки. За это я приношу ему глубочайшую признательность.
10 ПРЕДИСЛОВИЕ
Я с благодарностью воспользовался также критическими
замечаниями проф. Я. С. Дубнова и проф. Н. В. Ефимова.
Моему ученику Э. Г. Позняку я обязан указанием некоторых
недостатков изложения, а главным образом—тщательным и любовным
выполнением рисунков. Художники В. А. Сапожников и Е. П. Яковлев
хорошо воспроизвели эти рисунки для клише, за что, я приношу им
глубокую признательность.
Моей ученице Е. И. Кологрив я обязан помощью в технической
работе. За помощь в технической работе, а также в чтении авторской
корректуры я очень признателен В. А. Гуковской.
В заключение считаю долгом отметить, что ряд глав я подверг
коренной переработке, учитывая советы И. Н. Бронштейна.
Эта книга писалась в годы Великой Отечественной войны. В то
время, когда я работал над книгой, пришла весть о гибели на фронте
моего сына Льва Марковича Выгодского (28/IV-1919—20/1-1944). Его
памяти я посвящаю эту книгу.
М. Выгодский
7 апреля 1949 г.
ВВЕДЕНИЕ
§ 1. Предмет дифференциальной геометрии
Приступая к изложению специальной научной дисциплины,
невозможно дать точное определение ее предмета и очертить границы,
отделяющие ее от смежных областей. Тем не менее всегда желательно, чтобы
учащийся получил в начале занятий хотя бы общее представление
о предмете изучении, в данном случае —о предмете дифференциальной
геометрии.
Можно сказать, что дифференциальная геометрия есть учение
об общих свойствах кривых линий и кривых поверхностей. Этим мы
проводим границу между дифференциальной геометрией г элементарной
геометрией, в которой по преимуществу изучаются прямые линии,
плоские поверхности и образованные ими фигуры. Впрочем, в
элементарной геометрии рассматриваются также простейшие кривые линии
и поверхности (окружность, сферическая, цилиндрическая и коническая
поверхности), так что проведенная нами граница, конечно, несколько
расплывчата. Сверх того, элементарная геометрия является необходимой
основой для дифференциальной геометрии.
В аналитической геометрии также изучаются некоторые кривые
линии и поверхности. В особенности подробно рассматриваются там
свойства кривых второго порядка и поверхностей второго порядка.
Но почти все эти свойства носят частный характер, т. е. они относятся
к изучаемому классу линий или поверхностей, а не к линиям или
поверхностям вообще. В дифференциальной же геометрии изучаются
по преимуществу общие свойства линий и поверхностей. Для
аналитической геометрии характерно применение координатного метода. В
дифференциальной геометрии координатный метод также широко
применяется, однако в ней можно с успехом пользоваться и чист©
геометрическими («синтетическими») приемами, характерными для элементарной
геометрии, т. е. построениями и вычислениями, непосредственно
связанными с изучаемым геометрическим объектом. В этой книге читатель
найдет много примеров применения синтетических методов.
Чтобы пояснить, какие свойства могут бьиь общими для всех линий
или для всех поверхностей, мы можем указать, например, что всякая
кривая линия обладает большей или меньшей степенью искривленности.
Эту искривленность можно у охарактеризовать некоторым числом,
называемым кривизной линии. Кривизна линии, вообще говоря, меняется oi
точки к точке. Так, у дуги АВ (рис. 1) кривизна становится все
больше и больше по мере продвижения из точки А в точку В. При
этом существенно, что кривизна линии АВ в некоторой ее точке М
не зависит от того, как далеко в обе стороны от нее простирается дуга
АВ: если укоротить эту дугу, отрезав от нее дуги ААг и ВВ1У не сод ер-
12 ВВЕДЕНИЕ
жащие точки М, то остающаяся дуга AXBX в точке М будет иметь ту
же кривизну, что раньше имела дуга АВ. Как бы мала ни была дуга
AXBX, кривизна в точке М остается одной и той же. Поэтому можно
сказать, что кривизна линии характеризует ее «локальное» (т. е. местное)
свойство или, иначе, что это свойство принадлежит бесконечно малой
части лиции, составляющей
окрестность точки М.
Дифференциальная гео-
метрия занимается
преимущественно изучением таких
локальных свойств линий и
поверхностей.
Имея дело с бесконечно
малыми частями
геометрических объектов,
дифференциальная геометрия,
естественно, использует исчисление
бесконечно малых, в первую
очередь — дифференциальное
Рис. 1. исчисление; отсюда и
название «дифференциальная
геометрия». Более того, своим возникновением дифференциальное
исчисление в значительной мере обязано вопросам, ныне изучаемым в
дифференциальной геометрии.
Итак, дифференциальную геометрию мы можем определить как
учение об общих (преимущественно—-локальных) свойствах кривых линий
и кривых поверхностей.
§ 2. О линиях
Первоначальное понятие о точке, линии и поверхности мы
приобретаем из повседневного опыта, и в основу всякого определения этих
геометрических объектов должны быть положены некоторые свойства
тех материальных объектов, которые порождают наши геометрические
представления.
Одно из таких свойств состоит в том, что линия является границей
поверхности; другое — в том, что линия является следом
движущейся точки. Каждое из них можно положить в основу определения
понятия линии. Для дифференциальной геометрии второе свойство
является более важным. Точно так же поверхность предпочтительно
рассматривать, как след движущейся линии (последняя при движении
может менять свою форму).
Этим наглядным пояснениям можно придать форму точных
математических определений, но ввиду ряда трудностей мы не будем этого
делать. Заметим только следующее.
Точка, движущаяся вдоль линии, непрерывно меняет свое
положение с течением времени; время же, протекшее от некоторого
начального момента, можно охарактеризовать заданием одного числа (например,
числа секунд). Иными словами, положение точки на линии
определяется одной непрерывно меняющейся величиной и (одним параметром).
Нет необходимости в качестве параметра рассматривать именно время;
можно, например, взять расстояние движущейся точки от неподвижной.
Однако во многих случаях привлечение времени в качестве величины,
определяющей положение точки на линии, придает геометрической
картине большую наглядность.
§ 2. О ЛИНИЯХ 13
Если мы желаем определить положение точки на поверхности
и характеризовать непрерывное движение по поверхности, мы не можем
обойтись одним параметром: нужны уже два. Так, на плоскости
положение точки можно определить заданием абсциссы и ординаты. Если
поверхность описывается движением линии, то за один из параметров
(и) можно принять время —этот параметр характеризует положение
движущейся линии. За другой параметр (v) можно принять, скажем,
расстояние, которое н^жно пройти по движущейся линии, чтобы попасть
в какую-либо ее точку, отправляясь от некоторой, раз навсегда
отмеченной ее точки.
Таким образом, лини^ является однопараметричесшм (одномерным),
а поверхность — дог/параметрическим (двумерным) множеством точек.
Так как линия рассматривается нами как след движущейся точки,
то она должна быть непрерывной. Таким образом, не всякое одномерное
множество точек мы можем назвать линией. Ограничение, которое
накладывается наглядным представлением непрерывности линии, можно
сформулировать кратк© следующим образом: в однопараметрическом
множестве точек, составляющих линии, двум бесконечно близким
значениям параметра отвечают две бесконечно близкие точки1).
Этим, однако, не исчерпываются все те ограничения, которые
накладываются наглядным представлением о линии, как следе
движущейся точки. Так, движущаяся точка в каждом своем положении
должна иметь определенное направление движения. Прямая линия,,
проходящая через рассматриваемую точку и указывающая это
направление, есть касательная прямая. Ниже будет дано точное определение
касательной; здесь же заметим, что существование касательной прямой,
столь очевидное для наглядного представления, не является логическим
следствием непрерывности линии и поэтому должно быть оговорено как
новое требование, предъявляемое к нашему однопараметрическому
множеству точек.
Дальнейшее требование, которое мы должны выставить в целях
соответствия геометрических объектов их прообразам в действительности,
состоит в том, чтобы положение касательной прямой менялось также
непрерывно. Это значит, что угол ср между касательными в точках
Мг и М2 должен стремиться к нулю при стремлении к нулю дуги МгМ2.
Далее мы потребуем, чтобы отношение —^— при приближении
точек Мj и М2 к неподвижной точке М стремилось к пределу,
зависящему только от положения точки М, но не от способа приближения
Мг и М2 к М.
Вообще мы будем требовать, чтобы вводимые в рассмотрение
переменные величины были непрерывны и чтобы отношения их бесконечно
малых изменений стремились к пределам.
Впрочем, мы будем допускать отступления от этого требования,
если речь будет итти об отдельной точке рассматриваемой линии или
об отдельной линии рассматриваемой поверхности. Такие отступления
диктуются опять-таки наглядными представлениями.
Так, изображенная на рис. 2 линия ABC всюду имеет определенное
направление, за исключением точки 5, в которой она не имеет напра-
1) Более подробно: если М' и М" суть две точки нащего точечного
множества и если и' и и" суть соответствующие им значения параметра и, то длина
отрезка М'М" стремится к нулю всякий раз, как к нулю стремится разность и" —и'
ВВЕДЕНИЕ
вления или, что то же, не имеет касательной прямой. Можно было бы
сказать, что в точке В линия ABC имеет две различные касательные: одна
(tfi^i) указывает направление от А к В, другая (u2v2)—направление от В к С.
Но во всяком случае в точке В нарушается непрерывность поворота
РИС. 2.
касательной: бесконечно малому смещению из точки Л/, в точку М%
отвечает конечный угол поворота касательной.
Точки, в которых нарушаются те или иные требования,
накладываемые на линию или поверхность, называются неправильными или
особыми.
§ 3. Порядок малости. Эквивалентность
При изучении кривых линий и поверхностей нам постоянно придется
иметь дело с бесконечно малыми величинами—как скалярными, так и
векторными. При этом мы будем предполагать, что читатель знаком
с элементами анализа скалярного и векторного х). Всё же мы должны
здесь остановиться на двух вопросах анализа ввиду их особой важности
для дальнейшего. Это —вопрос о порядке малости и вопрос об
эквивалентности величин.
Прежде всего оговоримся, что в отличие от общепринятой
терминологии мы будем называть величину конечной, если она имеет предел,
отличный от нуля и бесконечности. Таким образом, каждая величина,
если она имеет предел, является либо бесконечно малой, либо
конечной, либо бесконечно большой.
Пусть теперь мы имеем две величины: а и 6. Они могут быть обе
скалярные, обе векторные или одна скалярная, а другая векторная;
каждая из них может быть бесконечно малой, конечной или даже
бесконечно большой. Если отношение |а| : |6| их модулей имеет предел
(только такие случаи и будут нам встречаться в этой книге), то мы
1) Для удобства читателей, в конце книги (стр. 438—506) вкратце изложены все
те сведения по векторному анализу, которые могут потребоваться при изучении
этого руководства. Более подробные сведения читатель может найти в книге
Я. С. Дубнова «Основы векторного исчисления», §§ 51—58.
Для изучения тех разделов этой книги, где изложение ведется синтетическим
методом (эти разделы играют ведущую роль), знание векторного анализа не
требуется вовсе, а по скалярному анализу нужно иметь только самые начальные
сведения, изложенные, например, в книге М. Я. Выгодского «Краткий учебник
высшей математики», глава 5; глава 6, §§ 1—8; глава 7; глава 9, §§ I—12.
§ 3. ПОРЯДОК МАЛОСТИ. ЭКВИВАЛЕНТНОСТЬ 15
хможем распространить на них то сравнение по их «порядку», которое
устанавливается обычно в анализе для скалярных бесконечно малых
величин. Именно, мы скажем, что величина а имеет высший (более
высокий) порядок, чем величина 6, если отношение |а|:|6| бесконечно
мало; мы скажем, что а имеет тот лее (одинаковый) порядок, что Ьг
если отношение |а|:|6| конечно; наконец, мы скажем, что а имеет
низший порядок, чем 6, если отношение |а|:|6| бесконечно велико.
Мы будем в том же смысле употреблять выражения: «порядок
величины а выше порядка величины 6», «порядок а равен порядку 6» и т. п.
При этом нет необходимости предполагать, что порядок величины
*может быть выражен числом. Однако во всех тех вопросах, которые
мы будем рассматривать в этой кнше, будет возможно и числовое
выражение порядка. Именно, можно будет взять некоторую
бесконечно малую величину а, такую, что все рассматриваемые величины
будут иметь одинаковые порядки с какими-либо степенями величины а.
Показатель степени п, при котором ал имеет тот же порядок, что
величина а, мы и можем взять в качестве числовой меры порядка
величины а (относительно а). Величина, порядок которой выражается
положительным числом, б^дет бесконечно малой; величина, порядок
которой равен нулю, будет конечной; величина, порядок которой
выражается отрицательным числом, будет бесконечно большой. Нелишне
заметить, что и в том случае, когда порядок нельзя выразить числом,
закон упорядоченного расположения сохраняет силу, т. е. если
порядок а выше, чем порядок ft, и порядок b выше, чем порядок с, то
порядок а выше порядка с; точно так же ясно, что если порядок а равен
порядку ft, а порядок ft равен порядку с, то порядок а равен порядку с,
и что если порядок а выше порядка 6, то порядок Ь ниже порядка а.
Переходя к определению эквивалентности величин, заметим, что
в анализе эквивалентными называют обычно такие бесконечно малые
величины, предел отношения которых равен единице. Это определение
непосредственно распространяется и на конечные и на бесконечно
большие скалярные величины, но для векторных величин оно непригодно,
так как отношение векторов в векторном исчислении не
рассматривается; что же касается отношения модулей, то в том случае, когда
оно имеет пределом единицу, нет всё же основания считать
соответствующие векторы эквивалентными, ибо их направления при этом
могут образовывать конечный угол.
Поэтому мы будем исходить из иного определения
эквивалентности. Именно, величины а и b (они могут быть или обе скалярными
или обе векторными) мы назовем эквивалентными (a^ft), если их
разность а — Ь имеет более высокий порядок, чем одна из них, например,
чехм а. Нетрудно доказать, что тогда порядок разности а — Ь также
выше, чем порядок ft. Как известно, для скалярных величин это
определение эквивалентности равносильно предыдущему.
В этой книге соотношение эквивалентности будет играть гораздо
более активную роль, чем в обычном изложении. Это стоит в связи
с тем, что мы будем систематически находить зависимости между
различными переменными геометрическими величинами из
геометрических построений. При этом эквивалентным величинам будут отвечать
на чертеже приближенно равные отрезки, угды и т. д.
Эквивалентности обладают многими свойствами равенств; однако
полной аналогии между ними нет. Последнее обстоятельство и является,
повидимому, причиной малого к ним внимания. Но даже при
необходимости вводить некоторые дополнительные условии, при которых
16 ВВЕДЕНИЕ
с эквивалентности ми можно оперировать так же, как с равенствами,
применение эквивалентностей в выкладках оказывается весьма полезным.
В этом мы не раз будем яметь случай убеждаться.
Укажем здесь те свойства эквивалентностей, которыми нам придется
пользоваться.
1) Если а^Ь и Ь^с, то а^с.
1а) Если а^Ь, то kazzkb (кфО).
2) Если для скалярных величин а и Ь имеют место
эквивалентности azza' и b^b\ то
в последнем соотношении п есть любое число; первое соотношение
распространяется на любое (постоянное) число скалярных сомножителей.
Для векторного и для скалярного произведения векторов замена
сомножителей другими, им эквивалентными, может оказаться
неправомерной: новое произведение может оказаться неэквивалентным прежнему.
Это видно из такого примера. Пусть а и b суть два постоянных взаимно
перпендикулярных вектора (не равных нулю), а и есть бесконечно
малый вектор. Мы имеем (a-\~u)b = ub. Сомножитель a + tt нельзя
заменить эквивалентным ему сомножителем а + 2ц, так как после
такой замены скалярное произведение будет равняться 2ub, а эта
величина не эквивалентна ub. Однако легко доказать, что упомянутая
замена может для скалярного произведения оказаться неправомерной
только тогда, когда, как в рассмотренном примере, векторы а и 6
образуют угол, эквивалентный (в частности равный) прямому. Таким
образом, можем сказать, что
3) Если угол между векторами а и b не эквивалентен прямому
и если а^аг и bz^b', то
Точно так же имеет место следующее свойство:
4) Если угол между векторами а и b имеет конечную величину
и если а&а' -и bzzb', то
axbzza' xb'1).
Неправомерной может оказаться и замена слагаемых некоторой
скалярной или векторной суммы другими соответственно
эквивалентными слагаемыми. Так, если а = 1 -j- s и 6=—1, где е есть бесконечно
малая величина, то сумма а + b равна е. Если же слагаемое а
заменить эквивалентным ему слагаемым 1 + 2е, то сумма а + Ь даст
величину 2е, которая не эквивалентна величине е. Легко доказать однако,
что замена слагаемых эквивалентными величинами может оказаться
неправомерной лишь тогда, когда сумма а + Ь имеет более высокий
порядок, чем одно из слагаемых. Таким образом, можно сказать, что
5) Если сумма (скалярная или векторная) ах + а2 + . .. +ап (число
слагаемых п постоянно) имеет тот же или более низкий порядок, чем
порядок каждого слагаемого, и если
то
ах + а2 + . .. + ап & а[ + а'2 + ... + а'п.
l) axb обозначает векторное произведение.
8 4. ЭКВИВАЛЕНТНЫЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ 17
В частности, если а19 а2, ..., ап суть скалярные величины одного знака,
то сумма, будучи больше по абсолютному значению каждого из
слагаемых, заведомо не имеет более высокого порядка. Поэтому
5а) Если в сумме ах + а2 + ... + ап все слагаемые суть скалярные
чины одного знака и если at ^a'i(i = l, 2, ..., п), mos
величины
Замечание. Последнее свойство можно распространить и на
случай, когда число слагаемых п неограниченно возрастает. Нужно только
допустить, что эквивалентность
#i ^ а\
является равномерной. Это означает, что всем неравенствам -• —
где е есть заданное число, можно удовлетворить одновременно, если
число слагаемых п взять достаточно большим. Допущение это носит
настолько широкий характер, что на первый взгляд может показаться
даже излишним1).
§ 4. Эквивалентные соотношения в треугольнике
Как отмечено выше, в этой книге важную роль играют
синтетические доказательства. Отличие проводимых здесь доказательств от
доказательств, употребляемых в элементарной геометрии, состоит лишь
в том, что мы пренебрегаем величинами высшего порядка, т. е.
заменяем одни величины другими, им эквивалентными. Что от такой замены
результат не страдает, это при небольшом навыке можно видеть, так
сказать, на-глаз. Но для строгости доказательства необходимо всякий
раз, как мы пренебрегаем какой-нибудь величиной, доказать законность
эюго приема, потому что, как мы видели в предыдущем параграфе,
безоговорочно отбрасывать величины высшего порядка нельзя.
Чтобы эти вспомогательные рассуждения не заслоняли идею
доказательства, полезно установить некоторые основные предложения,
на которые в дальнейшем мы будем неоднократно ссылаться при замене
одних величин другими, им эквивалентными.
Теорема 1. Если е есть бесконечно малая величина, то
Slfl S /-^, £, £ — Sin S /-\^ -— ,
^ , „ ,£2
COS ~ s^Z 1 1 " С04 £ /^-'
' ^ 2 '
tgs^£, tg s — е^-.
Для доказательства этих эквивалентностей достаточно написать
известные из анализа разложения тригонометрических функций в
степенные ряды.
Следующие три теоремы устанавливают эквивалентные соотношения
в треугольнике ABC, в котором один угол эквивалентен прямому.
Мы рекомендуем читателю обратить особое внимание на наглядное
содержание этих основных теорем; заучивать же их нет никакой необ-
1) Доказательство можно найти в книге Н. Н. Лузина «Интегральное
исчисление», 1946 г., § 55.
2 М. Я. Выгодский
18 ВВЕДЕНИЕ
ходимости. Не будет вреда, если при первом чтении читатель опустит
приводимые здесь доказательства этих предложений.
Теорема 2. Если в треугольнике ABC угол А эквивалентен
прямому, то
а2^Ь2+с2 (1)
и
sin В ^ - . (2)
а х '
Доказательство.
1. Для всякого треугольника имеет место соотношение
a2 = b2 + c2 — 2bc cos А.
В данном же случае 2совЛ есть бесконечно малая величина. Поэтому
26с cos А имеет высший порядок относительно 6с. He нарушая общности,
можем считать, что с<!6.. Тогда 26с cos А имеет высший порядок
относительно б2, а значит, и подавно относительно 62 + с2. Этим доказано,
что
2. Так как по условию sin.4^1, то, применив теорему синусов,
находим
sini?= -sin A ^ -.
а а
Теорема 3. Если в треугольнике ABC угол А эквивалентен
прямому и угол В стремится к некоторому пределу, то имеют место
следующие соотношения:
lim sin В = lim - , (2а)
lim cos В = lim -, (За)
lim tg5 = lim*, (4a)
limctg# = lim*-. (5a)
Доказательство. Формула (2а) непосредственно следует из (2).
Наряду с (2а) имеет место формула
lim sin С = lim - , (2а')
отличающаяся от (2а) только обозначениями.
Далее, так как по условию lim /_A = 90° и так как
ZC =*180°-Z A-Z В,
то
lim Z С-90° — limZB.
Так как функции sin я, cos# всюду непрерывны, то
lim sin С = sin lim С и cos lim B = lim cos В.
С помощью этих соотношений мы получаем из последнего равенства
lim sin С = J im cos В,
§ 4. ЭКВИВАЛЕНТНЫЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ 19
и сравнение с (2а') дает
lim cos В = lim - .
a
Деля равенство (2а) на (За).и применяя основные теоремы о
пределах, мы получаем
limtgi? = lim-, (4а)
с
а деля (За) на (2а), аналогично
lim ctg5 = lim^-.
Теорема 3 доказана.
Замечание. Может быть, у читателя возник вопрос: почему
соотношения
cos В ZZ с- , (3)
*\> (4)
аналогичные соотношениям (За), (4а), (5а), не были упомянуты в
заключении теоремы 2? Ответим: потому что эти соотношения могут оказаться
неверными. Правда, это может произойти лишь в исключительном
случае; из следующего предложения будет видно, в каком именно.
Теорема 4. Если в треугольнике ABC угол А эквивалентен
прямому, то соотношения (3), (4) и (5) имеют место при добавочном
условии, чтобы угол В не был эквивалентен прямому или, что то же, чтобы
угол С был конечным.
Доказательство. Наряду с (2) имеет место формула
«in С ~ с (9'\
отличающаяся от (2) только обозначениями.
По условию Z А % 90° и
имеет конечную величину, так что порядок этой величины не выше
порядка каждого из слагаемых правой части. Поэтому (§ 3, свойство 5)
мы можем, рассматривая равенство (а) как эквивалентность, заменить
в нем величину /i на 90°. Тогда получим
ZC^90°-ZB, (P)
откуда, в силу теоремы 1 и свойства 1 § 3,
sin Czz sin (90°-В),
т. е.
sin С s^z cos и.
Сравнив с (2'), имеем
Деля эквивалентность
-. (3)
а х '
sinS^ (2)
2*
20 ВВЕДЕНИЕ
на (3), получаем
tg£^*. (4)
Деля (3) на (2), получаем
ctg В ^у. (5)
о
Замечание 1. Если угол В эквивалентен прямому или, что
то же, если угол С бесконечно мал, то замена величины /_ А в (ос)
величиной 90° незаконна. Так, если е есть бесконечно малая величина
и если /_А = 90° — sh/B = 90° — е, то /_ С = 2е, между тем как по
формуле (р) мы получили бы /^С^г.
Замечание 2. Как мы видели, применение формул (3), (4), (5)
к случаю, когда limC = 0, может привести к ошибочным результатам.
Однако благодари тем требованиям, которые мы накладываем на
изучаемые геометрические образы, мы Схможем с безопасностью применять
эти формулы при решении всякой задачи «в общем виде», т. е. при
выводе таких соотношений, где относительно угла С не делается никаких
предположений. При первом же случае такого использования формул
(3), (4), (5) этот вопрос будет освещен обстоятельно х\.
§ 5. Пределы геометрических образов
Понятие предела, которое вводится в анализе, по существу
заимствовано из геометрии или, лучше сказать, из кинематики. Поэтому
нижеприводимое определение не содержит для читателя, знакомого
с анализом, ничего нового.
Определение 1. Постоянная точка А называется пределом
переменной точки А\ если расстояние ААГ бесконечно мало.
Нам нужно теперь ввести понятия предела прямой и предела
плоскости, которое математически характеризовало бы механический процесс
«стремления» прямой а' к прямой а или плоскости Р' к плоскости Р.
При этом нежелательно вводить в рассмотрение какой-либо посторонний
объект, каким является, скажем, система координат.
Следующие определения удовлетворяют этим требованиям и вместе
с определением 1 составляют однотипную группу.
Определение 2. Постоянная прямая а называется пределом
переменной прямой а', если расстояние любой фиксированной точки А
прямой а до прямой а' бесконечно мало.
Определение 3. Постоянная плоскость Р называется пределом
переменной плоскости Р', если расстояние любой фиксированной точки А
плоскости Р до плоскости Р' бесконечно мало.
Наглядное представление показывает, что угол между прямой а
и «стремящейся» к ней пряхмой а' должен быть бесконечно мал.
Докажем это.
Теорема 1. Если прямая а есть предел прямой а', то острый
угол <р между этими прямыми бесконечно мал.
Доказательство. Возьмем на а две фиксированные точки
А, В (рис. 3) и проведем через них плоскости Р, Q перпендикулярно
к а'. Пусть А', Z?' — точки пересечения этих плоскостей с прямой л\
См. стр. 59—60.
5. ПРЕДЕЛЫ ГЕОМЕТРИЧЕСКИХ ОБРАЗОВ
21
Через точку В проведем прямую ВС, параллельную а', до пересечения
в точке С с плоскостью Р.
Согласно определению 2, отрезки А А' и ВВ' = С А' бесконечно
малы. Следовательно, отрезок АС, не превосходящий АА' + СА',
тоже бесконечно мал. Из треугольника АСВ, в котором сторона АВ
имеет постоянную величину, находим sin<p = -jD. Следовательно,
величина sincp, а значит, и ф, бесконечно мала. Теорема 1 доказана.
Разумеется, одной бесконечной малости
угла ср недостаточно для утверждения, что &'
постоянная прямая а есть предел прямой а';
например, если а' проходит через постоянную
точку К, то при ф—^0 прямая будет иметь
пределом прямую, проведенную через К
параллельно а.
Следующая теорема дает одно из
достаточных условий для того, чтобы прямая а была
пределом прямой а'.
Теорема 1а. Если фиксированная точка А
постоянной прямой а отстоит на бесконечно
малое расстояние от прямой а' и если угол ф между
а и а' бесконечно мал, то а есть предел а'.
Доказательство. Возьмем на а
произвольную фиксированную точку В, отличную
от Л, и выполним то же построение, что и
в предыдущей теореме (рис. 3). Так как по
условию угол ф бесконечно мал, то бесконечно
мал и отрезок АС = АВ вшф. Но по условию
и отрезок АА' бесконечно мал. Следовательно,
бесконечно мал и отрезок ВВ' = СА', не
превосходящий СА+АС. Но ВВ' дает расстояние
от В до а', и В— произвольная точка прямой а.
Следовательно, прямая а, согласно
определению 2, есть предел прямой а'.
Аналогично теоремам 1 и 1а можно
высказать следующие столь же очевидные
предложения:
Теорема 2. Если плоскость Р есть
предел плоскости Р', то острый угол ф между Рис- ^*
этими плоскостями бесконечно мал.
Теорема 2а. Если фиксированная точка А постоянной
плоскости Р отстоит на бесконечно малое расстояние от плоскости Р'
и если угол ф между Р и Р' бесконечно мал, то плоскость Р есть
предел плоскости Р'.
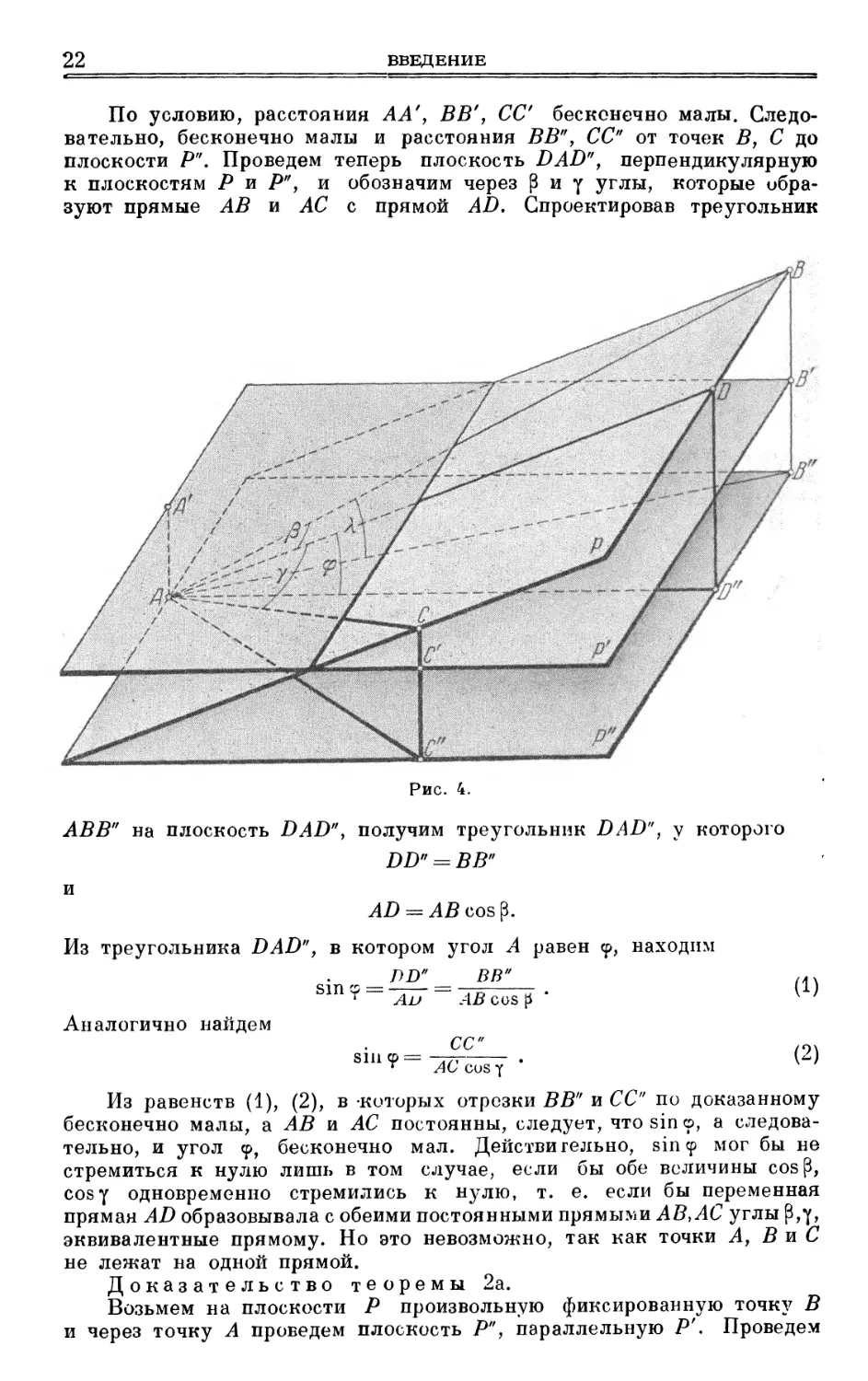
Доказательство теоремы 2.
Возьмем на плоскости Р три фиксированные точки (рис. 4)
А, В, С, не лежащие на одной прямой. Проведем через точку А
плоскость Р", параллельную Р', и проведем через А, В, С
перпендикуляры АА'\ ВВ'у СС к плоскости Р'. Пусть прямые ВВ', СС встречают
плоскость Р" в точках В", С"'. Тогда направленные отрезки ВВ', ВВГ
и т. д. связаны соотношениями:
ВВ" = ВВ' + В'В" = ВВ' + А'А,
Г*Г*п ПП* _1_ Р'Пп ПО* _J_ А* Л
^^ \у т \у \s ' I * \s ^^ ■ \^ \s ■ j £\ Х\.%
22 ВВЕДЕНИЕ
По условию, расстояния АА', ВВ', СС бесконечно малы.
Следовательно, бесконечно малы и расстояния BBff, СС" от точек В, С до
плоскости Р". Проведем теперь плоскость DAD", перпендикулярную
к плоскостям Р и Р", и обозначим через р и у углы, которые
образуют прямые АВ и АС с прямой AD. Спроектировав треугольник
Рис. 4.
ABB" на плоскость DAD", получим треугольник DAD", у которого
DD" = В В"
и
Из треугольника DAD", в котором угол ^4 равен <р, находим
ВВ"
_ ЛД _
Sin ? ~ ~л17 ~\-Ш cos p ' ^
Аналогично найдем
СС /г)\
т AC cus f
Из равенств (1), (2), в-которых отрезки ВВ" и СС" по доказанному
бесконечно малы, а АВ и АС постоянны, следует, что sin о, а
следовательно, и угол у, бесконечно мал. Действительно, sincp мог бы не
стремиться к нулю лишь в том случае, если бы обе величины cos[3,
cosy одновременно стремились к нулю, т. е. если бы переменная
прямая AD образовывала с обеими постоянными прямыми АВ,АС углы р,у,
эквивалентные прямому. Но это невозможно, так как точки А, В и С
не лежат на одной прямой.
Доказательство теоремы 2а.
Возьмем на плоскости Р произвольную фиксированную точку В
и через точку А проведем плоскость Р", параллельную Р'. Проведем
§ 5. ПРЕДЕЛЫ ГЕОМЕТРИЧЕСКИХ ОБР АРОВ
23
ВВ' перпендикулярно к Р' и обозначим через В" точку пересечения
ВВ' с Р". Тогда будем иметь (рис. 4) для направленных отрезков
равенство
В В' = В В" + В" В' = АВ sin X + АА', (3)
где X —угол между АВ и плоскостью Р' (или, что то же,
плоскостью Р"). Этот угол не превосходит угла <р, который по условию
бесконечно мал. Расстояние АА' тоже бесконечно мало. Поэтому из
(3) следует, что и расстояние ВВ' бесконечно мало, что и доказывает
теорему 2а.
Переменная прямая может быть задана двумя переменными
точками: А\ В', через которые она должна проходить, а также двумя
переменными
плоскостями Р', Q'y пересечением
которых она должна
являться.
Нам чаще придется
иметь дело со вторым
способом задания. Поэтому
мы докажем здесь
следующее почти очевидное
предложение.
Теорема 3. Если
плоскость Р есть предел
плоскости Р*', а плоскотъ Q
{отличная от Р)'—
предел плоскости Q', и если
Р и Q пересекаются по
прямой а, то плоскости
Р' и Q' пересекаются по прямой а', имеющей пределом прямую а.
Доказательство. Что плоскости Р' и Q', начиная с
некоторого момента, должны пересечься и оставаться пересекающимися, это
ясно из того, что угол (Р'9 Q')1) отличается от постоянного и не
равного нулю угла (Р, Q) самое большее на сумму углов (Р, Р')9 (Q, Q'),
а эти углы бесконечно малы. Значит, угол (/>', Q') имеет конечную
величину, м плоскости Р', Q' , с определенного момента не могут быть
параллельными.
Заметив это, возьмем на прямой а произвольную фиксированную
точку К (рис. 5). Так как точка К лежит на плоскости2) Р, то,
согласно определению 2, ее расстояние р до плоскости Р' бесконечно
мало. Аналогично устанавливается, что расстояние q точки К до
плоскости Q' тоже бесконечно мало.
Проведем через К плоскость АОВ, перпендикулярную к а'. Она
пересечет а' в некоторой точке О; отрезок KO = d дает расстояние
от К до а', а угол АОВ = и измеряет угол (P',Q') и по доказанному
имеет конечную величину. Проведя прямые КМ и KL, соответственно
параллельные О А и ОВ, находим, что отрезки
Рис. 5.
Sinu>
Sl.l
2) Здесь всюду речь идет об острых углах.
2) Плоскости Р и Q не показаны на рис. 5, чтобы не усложнять чертежа.
24 ВВЕДЕНИЕ
бесконечно малы. Следовательно, расстояние КО, не превосходящее
ОМ + МК, тоже бесконечно мало. Этим теорема 3 доказана.
Нам остается установить признаки пределов геометрических
образов, заданных аналитически. Они просты и единообразны.
Теорема 4. Если г0 и r(t) суть радиусы-векторы постоянной
точки Мо и переменной точки М и если
ru, (4)
то точка Мо есть предел точки М (при t—>t0).
Действительно, из (4) следует
lim(r — ro) = O,
т. е. расстояние М0М = ]/(г •— г0)* бесконечно мало.
В координатной форме этот признак формулируется так:
Если х0, г/0, z0 — координаты постоянной точки Л/о, а величины
x(t)>y{t)> z(t) — координаты переменной точки М, и если
= x%, limу(t) = y0
то точка Мо есть предел точки М.
Теорема 5. Если переменная плоскость представляется
уравнением
N(t)r + D(t) = 0 (5)
и если
ЛГв=£О; lim D(t) = D0, (6)
то плоскость
Nor + Do = O (7)
есть предел плоскости (5) (при t—>tQ).
Доказательство. Возьмем на плоскости (7) произвольную
фиксированную точку г = а, так что имеем
, = 0. (8)
Расстояние d от этой точки до плоскости (5) (по абсолютной величине
и по знаку) представляется выражением
Принимая во внимание (6), имеем
и в силу (8)
что и доказывает теорему 5.
В координатной форме теорема 5 формулируется так:
Если переменная плоскость представляется уравнением
O (9)
§ 5. ПРЕДЕЛЫ ГЕОМЕТРИЧЕСКИХ ОБРАЗОВ 25
и если
lim A (t) = A0; UmB{t) = B0; limC(t) = Cj lim
t-+t0 t-+t0 t-+t0 t-+t0
то плоскость
есть предел плоскости (9).
Замечание. Аналогичный признак имеет место и для других
форм уравнения плоскости. Так, если переменная плоскость
представляется уравнением
N(t)(r-s(t)) + D(t) = 0 (10)
и если
lim N(t) = N0, Um s(t) = s0, lim D(t) = D0,
t-+t0 t->t0 t-+t0
то плоскость
есть предел плоскости (10).
Теорема 6. Если переменная прямая представляется уравнениями
= 0, N(t)r+D{t) = 0 (11)
и если при t—»£0
lim N (t) = No] lim N(t) = ЛГ0
и
lim D (t) = Do; lim D(t) - D$f
причем векторы Л^о и Л^о не коллинеарны, то прямая (11) имеет
пределом прямую
Nor-tDo = O; Ns+D^O. (12)
Эта теорема непосредственно следует из предыдущей и из теоремы 3.
Замечание. Условие, чтобы векторы No и ЛГ0 не были
коллинеарны, существенно. В случае коллинеарности этих векторов
уравнения (12) представляют либо пару параллельных плоскостей, либо
две совпадающие илоскости. В обоих случаях условие теоремы 3
нарушается. В первом случае прямая (11) заведомо не имеет предела.
Во втором случае переменные плоскости, представляемые уравнениями
(11), образуют бесконечно малый угол, и предел прямой (11) может
существовать; тогда он является прямой, лежащей в плоскости
Nor-\- D0 = 0. Но для разыскания этой прямой уравнения (12)
недостаточны. В дальнейшем мы встретился с подобными случаями и тогда
увидим, как при этих обстоятельствах можно отыскать предел прямой
(11).
Читателю предлагается сформулировать теорему 6 в
координатной форме.
ГЛАВА I
КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
§ 6. Аналитическое представление кривой линии
Если отнести линию к прямоугольной или иной системе координат,
то каждая точка этой линии приобретает три координаты, т. е. три
числа х, у, z, определяющие ее положение относительно избранной
нами системы координат. Эти числа меняются при движении точки
М вдоль линии, т. е.при изменении параметра и, определяющего
положение точки М на рассматриваемой линии. Иными словами,
координаты х, у, z являются функциями от и:
х = х(и), y = tj(u), z = z(u). (1)
Так как, согласно сказанному в § 2, рассматриваемая линия
должна быть непрерывной, то и функции х(и), у (и), z(u) должны быть
непрерывными1). Уравнения (1) называются параметрическими
уравнениями рассматриваемой линии.
За параметр и мы можем, в частности, принять расстояние точки М
до плоскости XOY, т. е. координату z. Тогда уравнения (1) будут
иметь вид:
ij = <?(z) (2)
(третье уравнение обратится в тождество z = z).
Заметим, что могут встретиться случаи, когда уравнения линии
нельзя представить в виде (2). Так, если рассматриваемая линия лежит
в плоскости XOY, то для всех ее точек z = 0 и потому координаты
х, у нельзя рассматривать как функции z. В этом случае за параметр
и можно принять координату х или координату у. Заметим также,
что функции /(z) и <p(z) могут оказаться и не однозначными. Это будет
в том случае, если кривая пересекает какую-либо плоскость,
параллельную плоскости XOY, два или несколько раз. В двух таких точках
пересечения одному и тому же значению z соответствуют различные пары
значений х, у. Если взять не всю рассматриваемую линию, а лишь
такую ее часть, чтобы каждая из «горизонтальных» плоскостей z = const
1) В противном случае бесконечно близким значениям и', и" параметра и
не соответствовали бы бесконечно близкие значения, по крайней мере, одной
из функций х (и), у (и), z (и), а тогда расстояние между соответствующими
точками М', М" не было бы бесконечно малым. Чтобы обеспечить существование
касательной прямой, мы в дальнейшем потребуем, чтобы функции ж (u), y(u)> z(u)
были не только непрерывны, но и дифференцируемы (см. ниже, § 8).
§ 6. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВОЙ ЛИНИИ 27
имела с ней не более одной точки, то за счет такого укорочения линии
можно избавиться от многозначности.
Как известно, первое из уравнений (2) представляет уравнение
параллельной проекции рассматриваемой линии на координатную
плоскость XOZ; проектирование производится по направлению оси у\ точно
так же второе уравнение (2) есть уравнение проекции на плоскость
YOZ; проектирование производится по направлению оси х.
Уравнение x = f(z) можно также рассматривать как уравнение
цилиндрической поверхности, проектирующей рассматриваемую линию
на плоскость XOZ, и точно так же уравнение 2/ = <p(z) представляет
цилиндрическую поверхность, проектирующую рассматриваемую линию
на плоскость YOZ.
Таким образом рассматриваемая линия оказывается линией
пересечения двух цилиндрических поверхностей:
Через рассматриваемую линию можно провести бесчисленное
множество других поверхностей; если уравнения двух таких поверхностей
суть
F{x, у, z)=0, Ф(х, у, z) = 0, (3)
то координаты любой точки рассматриваемой линии должны
удовлетворять обоим этим уравнениям. Значит, если функции х (и), y(u)f z(u),
задаваемые уравнением (1), подставить в уравнения (3), последние
должны обратиться в тождества. Уравнения (2) являются, очевидно,
частным видом уравнений (3).
Уравнения (3) также называются уравнениями рассматриваемой
линии. С помощью преобразований можно перейти от одного вида
уравнений линии к другому. Так, если мы имеем уравнения вида (3), то
к уравнениям вида (1) можно перейти таким образом: положим z = <]> (и),
где 6 (и) есть какая-нибудь (непрерывная и дифференцируемая)
функция. Подставим в уравнения (3) вместо z функцию ф (и). Если удастся
разрешить полученную систему уравнений относительно х и у, мы
получим выражения х = f (и), у = у (и), которые вместе с выражением z = <Ь (и)
дадут три уравнения вида (1). Ясно, что это преобразование, равно
как и другие, можно произвести не единственным способом.
Для изучения пространственных линий наиболее удобным
средством аналитического представления являются уравнения вида (1).
Уравнения вида (2) можно рассматривать как% частный их случай
(х = /(и), 2/ = ? (и), г = и).
При изучении плоских кривых часто является более удобным,
приняв плоскость кривой за плоскость z = 0, пользоваться уравнением
вида F(x, у)=0, в частности, вида y^f(x). Впрочем и ^дось
параметрический способ представления во многих случаях предпочтительнее.
Пример 1. Плоскость (рис. 6) с начерченной на ней прямой
линией наворачивается на круглую цилиндрическую поверхность. После
навертывания прямая линия становится кривой {винтовая линия).
Составим ее уравнение.
Обозначим через а радиус цилиндра и через а угол, составляемый
данной прямой АВ с прямой AD, которая наворачивается на окружность
основания.
Оси координат Еыберем так: за ось Z примем ось цилиндра; за
ось X —радиус основания, проходящий через ту точку А окружности,
через которую проходит винтовая линия.
28 ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
Примем за параметр и центральный угол u — AON дуги AN, на
которую наложилась в рассматриваемый момент прямая AD. Точка N,
следовательно, есть проекция точки М винтовой линии на плоскость XOY*
Проектируя ее на ОХ, находим точку Р и имеем
ОР = х, PN = y, NM = z.
Из треугольника PON находим выражения координат х, у через
параметр: x = acosu; y = asinu. Так как при наворачивании плоскости на
цилиндр координаты z всех ее
точек не меняют величины, то
z = KL, и из треугольника ALK
имеем z — AL- tg а. Но AL после
наворачивания накладывается на
дугу AN. Поэтому AL = AN = аи.
Итак, имеем следующие
уравнения винтовой линии, их полезно
запомнить:
х = a cos u\ у = а sin и;
z = a tg а . и = Ьи, (4)
где через Ь обозначена величина
atga.
Геометрический смысл
величины b выясняется из следующих
соображений. Если точку L
отодвинуть от точки А на расстояние
AL = 2tzu, равное длине
окружности основания цилиндра, то
после наворачивания плоскости
на цилиндр точка К займет
положение С на той же образующей,
на которой находится А, т. е.
винтован линия сделает один
виток. Расстояние АС = h
называется шагом винтовой линьи.
Очевидно,
h = AL tg a = 2iza tg а = 2тг6.
Таким образом, Ь есть радиус
ис* * окружности, длина которой равна
шагу винтовой линии. Нетрудно видеть, что b ecib также та высота, на
которую поднимается точка М, когда проходящая через нее плоскость
осевого сечения поворачивается на угол, равный одному радиану.
Если исключить и из первых двух уравнений (4), получим
уравнение
а*, (5)
представляющее проекцию винтовой линии на основание цилиндра.
Это —окружность, что очевидно и непосредственно. Если же
исключить и из двух последних уравнений (4), то получим уравнение
у = a sin ^-,
§ 6. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВОЙ ЛИНИИ 29
представляющее проекцию винтовой линии на плоскость осевого
сечения YOZ. Как мы видим, эта проекция есть синусоида. Проекция
винтовой линии на плоскость осевого сечения XOZ представляется
уравнением
Z
х = a cos -г-.
о
По форме своей она ничем не отличается от предыдущей линии, но
расположена она относительно осей иначе.
Таким образом, винтовую линию можно рассматривать как
пересечение круглого цилиндра х2 + у2 = а2 с синусоидальным цилиндром
» = flsin~.
Кроме этих поверхностей, через винтовую линию проходит
бесчисленное множество других. Если, например, мы разделим второе из
уравнений (4) на первое и затем исключим и с помощью третьего
уравнения (4), то получим
z = 6Arctg-~- (5a)
Ясно, что это уравнение обратится в тождество после подстановки
в него выражений (4), так что оно представляет одну из поверхностей,
проходящих через винтовую линию1). Взятые совместно, уравнения (5)
и (5а) также являются уравнениями винтовой линии.
Уравнения винтовой линии можно также преобразовать к виду
=±\/га2-х2, z = bArctg^a2~x* , (6)
у
где роль параметра играет х. Здесь мы получаем многозначные
функции параметра, ибо винтовая линия пересекает плоскости х = const
бесчисленное множество раз.
*) Форму этой поверхности легко установить следующим образом. Пересечем
ее какой-нибудь плоскостью Р, параллельной плоскости XOY. Уравнение этой
плоскости имеет вид
z = c,
где с есть некоторая постоянная величина. Линия пересечения плоскости Р и нашей
поверхности представляется двумя уравнениями:
z = b Arctg — , z = c;
преобразуя их, находим уравнения
которые представляют прямую линию, пересекающую ось Z и образующую с осью
X угол а=— , пропорциональный расстоянию с плоскости Р до плоскости XOY.
Таким образом, наша поверхность может быть образована движением прямой линии,
которая все время остается параллельной плоскости XOY и все время пересекает
ось Z, причем смещение ее вдоль оси Z пропорционально углу поворота около
той же оси. Эта поверхность называется прямым геликоидом. Если сгладить
поверхность винтовой лестницы, она будет иметь форму прямого геликоида. На рис. 150
(стр. 231) дано, изображение этой поверхности. Прямой геликоид, на котором
лежит рассматриваемая винтовая линия, образован прямыми, проходящими через
винтовую линию и ось цилиндра, на котором она нанесена, параллельно плоскости
'основания цилиндра.
30 ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
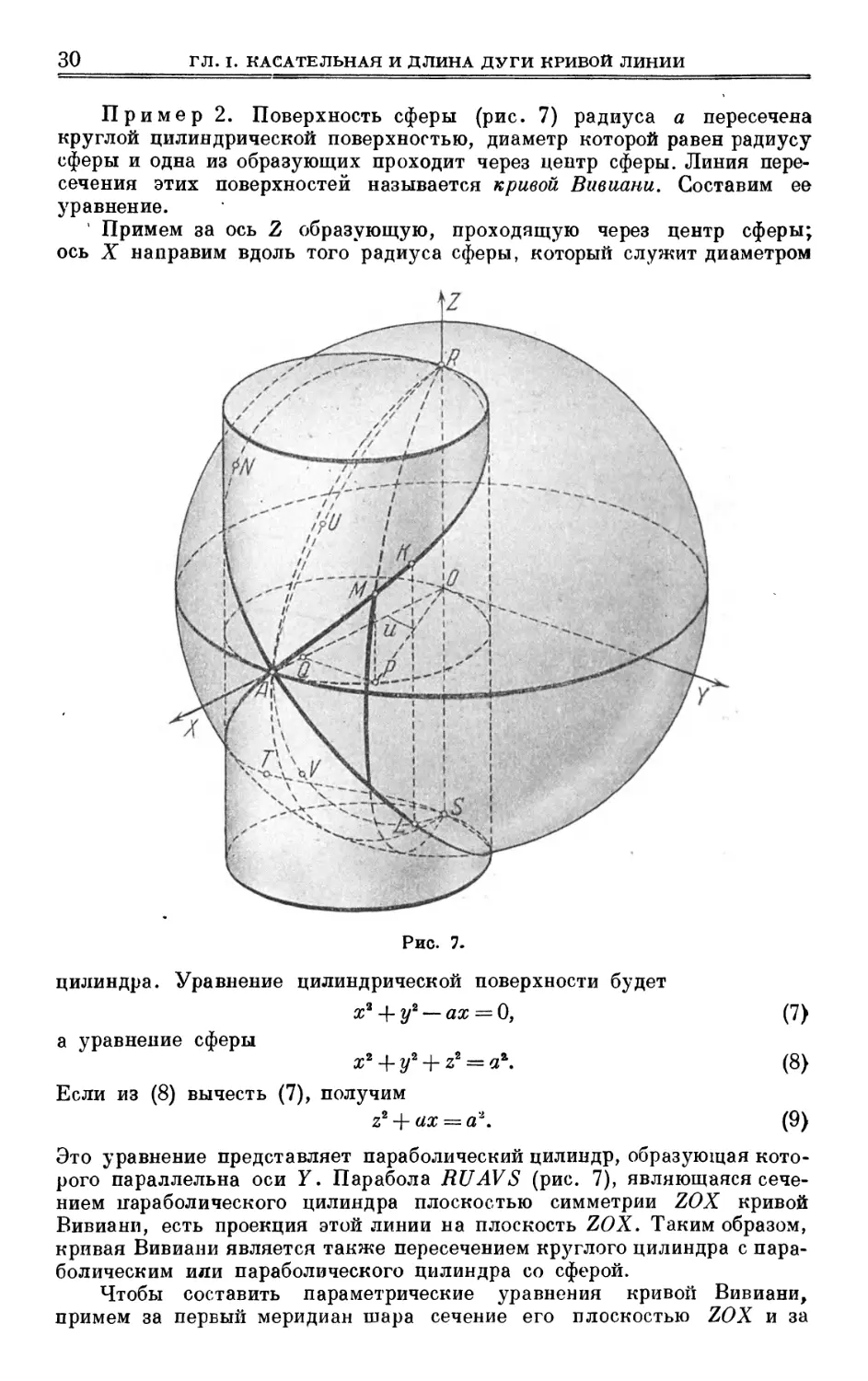
Пример 2. Поверхность сферы (рис. 7) радиуса а пересечена
круглой цилиндрической поверхностью, диаметр которой равен радиусу
сферы и одна из образующих проходит через центр сферы. Линия
пересечения этих поверхностей называется кривой Внешни. Составим ее
уравнение.
1 Примем за ось 2 образующую, проходящую через центр сферы;
ось X направим вдоль того радиуса сферы, который служит диаметром
Рис. 7.
цилиндра. Уравнение цилиндрической поверхности будет
ах = 0, (7)
а уравнение сферы
x* + y* + z* = a\ (8)
Если из (8) вычесть (7), получим
z% + ax = a\ (9)
Это уравнение представляет параболический цилиндр, образующая
которого параллельна оси У. Парабола RUAVS (рис. 7), являющаяся
сечением параболического цилиндра плоскостью симметрии ZOX кривой
Вивиани, есть проекция этой линии на плоскость ZOX. Таким образом,
кривая Вивиани является также пересечением круглого цилиндра с
параболическим или параболического цилиндра со сферой.
Чтобы составить параметрические уравнения кривой Вивиани,
примем за первый меридиан шара сечение его плоскостью ZOX и за
§ 6. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВОЙ ЛИНИИ 3J.
ось шара —ось Z; за параметр и примем долготу точки М на сфере.
Угол АОР на рис. 7 равен и.
В треугольнике АОР угол Р, вписанный в окружность диаметра
АО = а и опирающийся на этот диаметр, равен 90°. Поэтому
OP = a cos и.
В треугольнике ОРМ угол Р прямой и М0 = а; следовательно,
МР2 = а2 — а2 cos2 и = a2 sin2 и.
z = MP = ± asm и.
Наконец, из треугольника OPQ находим
х = OQ = О& cos и — a cos2 и,
у = QP = OP sin a = a cos и sin и.
Итак, параметрические уравнения кривой Вивиани можно написать
в виде
uf y = aGOsusinu, z= ± asinu. (10)
Из чертежа ясно, что долгота точки, лежащей на кривой Вивиани,
принимает значения от м= —90° до и= +90°. Двойной знак
последнего из уравнений (10) об}7словливается тем, что на одной и той же
долготе мы имеем две точки кривой Вивиани (точки L и К на рис. 7),
симметричные относительно экватора. Положив z = + я sin и и изменяя
и от —90° до +90°, мы заставим точку М пройти путь STAKR.
Полагая z — —a sin и и снова изменяя а от —90° до +90°, мы заставим
точку описать остающуюся часть кривой Вивиани, не меняя
направления движения.
Таким образом, чтобы описать всю кривую Вивиани, мы вносим
разрыв в изменение параметра и, который в точке R скачком переходит
от значения и= +90° к значению и==—90°. Этого можно избежать
следующим образом. Введем параметр и', равный долготе и на участке
STAKR и равный 180° + и на участке RNALS. Очевидно, и' будет
изменяться непрерывно от —90° до +270°, когда точка М будет
описывать путь STAKRNALS. Посмотрим, как будут выражаться х, у, z
через новый параметр. Так как на участке STAKR мы имеем и = и'
и в формуле (10) следует брать знак +, то на этом участке
ж = я cos2»', у = cos и' sin и, z = as\nu'.
На участке RNALS следует положить и~и' —180° и в формуле (10)
взять знак минус. Получим
х = а cos2 («' —180°) = a cos2 и', }
y = acos(u—180°) sin (м' —180°) = я cos и'sin и', ^ (Юа)
z = — a sin (и' —180°) = a sin и . )
Мы видим, что через новый параметр и координаты выражаются на
обеих половинах кривой Вивиани одними и теми же формулами (10а).
Нетрудно видеть, что если параметр и' непрерывно заменять от 270°
до 630°, точка (х, уу z), определенная формулами (10а), опишет
кривую Вивиани в том же направлении еще один раз и т. д. Значит, если
в формулах (Юа) изменять величину и' от любого значения и[ до
значения и'0-\-360°у то точка (х, уу z) опишет один раз кривую Вивиани
целиком. В частности, можно изменять и' от 0° до 360°.
32
ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
Пример 3. Прямая OL (рис. 8) вращается в плоскости около
точки О с постоянной угловой скоростью со. Точка М движется по
прямой OL со скоростью, пропорциональной расстоянию ОМ.
Описываемая точкой Л/ линия называется логарифмической спиралью.
По характеру условия видно, что удобнее всего ввести полярную
систему координат. За полюс принимаем О, за полярную ось
—произвольный луч ОХ. Взяв точку А,
соответствующую полярному углу 9 = 0,
обозначим через г0 ее расстояние
до центра. За параметр естественно
принять время t\ отсчитывать его
будем от момента прохождения М
через А. Из условия, задачи имеем
9 = «>* (11)
dr
(12)
Рис. 8.
где т есть постоянная величина.
В случае т = 0
логарифмическая спираль обращается в окруж-
dr
ность, так как тогда скорость т-
движения точки М по прямой OL
равна нулю, и точка М остается на
постоянном расстоянии от О. В
случае т > 0 точка М удаляется от О;
в случае т < 0 течка М прибли-
dr
жается к О. Переписав (12) в виде — = mdt и интегрируя
£ = т\А,
/о
находим
или
In — = mt
= roemt.
(13)
(13а)
Уравнения (11) и (13а) дают параметрическое представление
кривой в полярных координатах. Исключая t и полагая
находим полярное уравнение логарифмической спирали:
lnf = *?
(14)
или
г =
\ (14а)
Уравнение (14) выражает, что полярный угол пропорционален
логарифму радиуса вектора, измеренного с помощью г§, как единицы
масштаба; отсюда название «логарифмическая спираль».
§ в. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВОЙ ЛИНИИ 33
Уравнение (14а) показывает, что при к > 0 точка М неограниченно
удаляется от начала по мере роста угла 9- Когда же угол 9
неограниченно уменьшается (9—* — со)7 расстояние г стремится к нулю. При
к < 0, наоборот, имеем limr = 0 при <р^°° и limr= со при 9—>—со.
Следовательно, логарифмическая спираль, если она не обращается
в окружность, имеет бесчисленное множество завитков как при
удалении от полюса, так и при приближении к нему.
Форма логарифмической спирали существенно зависит от
абсолютной величины коэффициента к: чем больше (к), тем больше расстояние
между завитками.
Знак величины к существенного значения не имеет: при перемене
его на обратный значение г, прежде соответствовавшее углу 9> будет
соответствовать углу — 9> т. е. мы полечим линию, симметричную
первоначальной относительно полярной оси. Такие две спирали, правда,
нельзя наложить друг на друга, если смещать их в их плоскости.
Однако, если перевернуть наизнанку плоскость чертежа вместе с одной
из начерченных на ней спиралей, то эту спираль можно будет
совместить с другой, оставленной на лицевой стороне плоскости чертежа.
В заключение заметим, что, перейдя от полярной системы
координат к прямоугольной, мы получим следующие параметрические
уравнения логарифмической спирали:
х = r0ekvcos<p,
где полярный угол ф играет роль параметра.
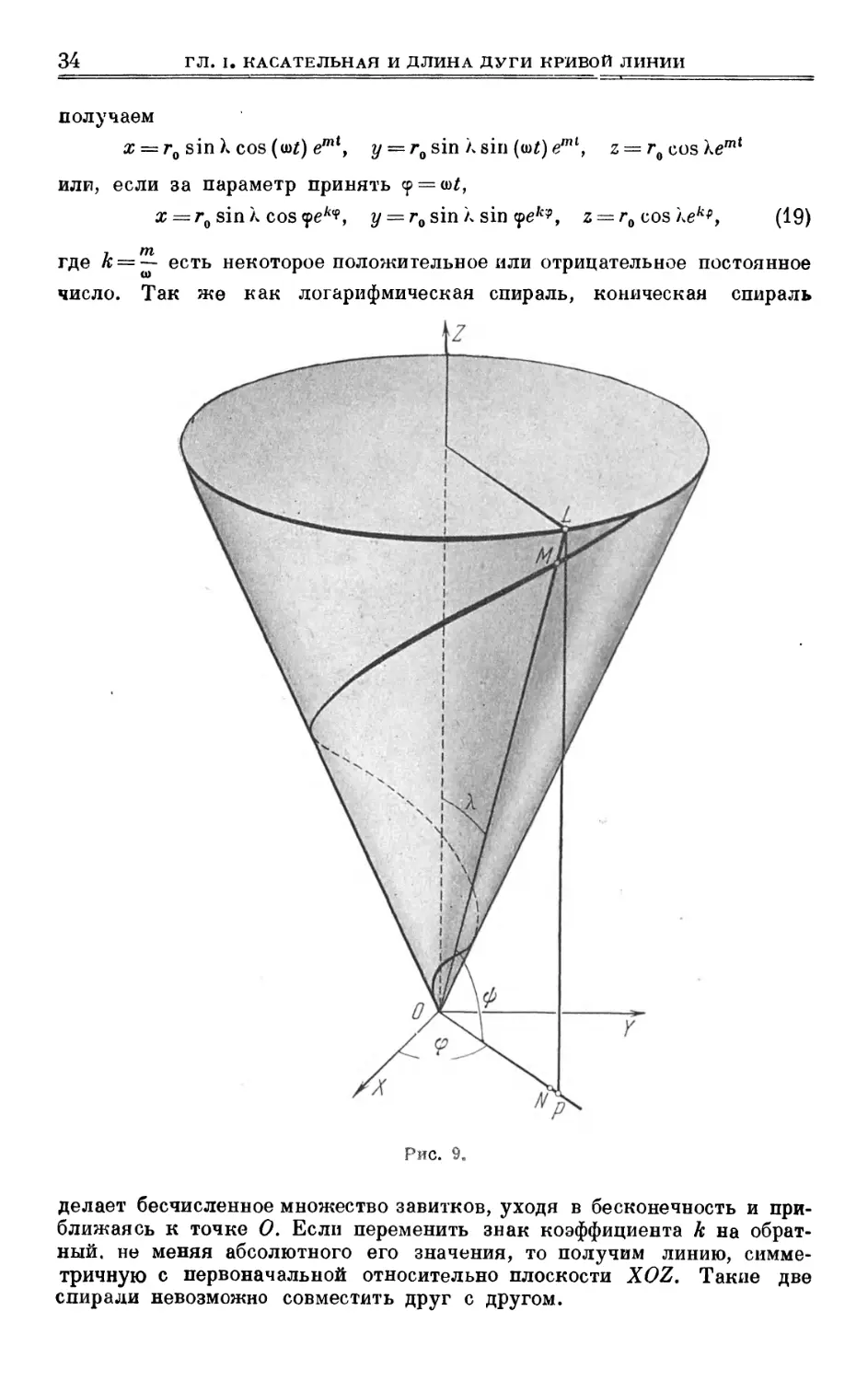
При-мер 4. Прямая OL (рис. 9) вращается около оси OZ,
описывая круглую коническую поверхность. При этом плоскость осевого
сечения ZOL вращается с постоянной угловой скоростью ш. Точка М
движется по прямой 0L со скоростью, пропорциональной расстоянию
ОМ подвижной точки до вершины конуса. Описываемая точкой М
линия называется конической спиралью.
Введем полярную систему координат в пространстве. В ней
положение точки М определяется радиусом-вектором г —ОМ, широтой^ = /_POL
и долготой Ф = Z.XOP.
По условию задачи широта точки М остается постоянной:
os 9, \
in 9, I
где л—угол между осью OZ и образующей конуса OL. Долгота 9 есть
двугранный угол между плоскостью XOZ и подвижной плоскостью
осевого сечения; согласно условию имеем
9 = в>/. (17)
Рассуждая, как в предыдущей задаче, найдем еще
r = roemt, (18)
где т есть некоторая положительная или отрицательная постоянная
величина, а г0 есть радиус-вектор в начальный момент. Уравнения
(16), (17), (18) дают параметрическое представление конической спирали
в полярной системе координат.
Переходя к прямоугольной системе с помощью формул
х = rccs<}>cos9> г/= г cos ф sin 9? z
3 М. Я. Выгодский
34 ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
получаем
x = r0 sin X cos (u)J) emi, y = r0 sin к sin (Ы) eml> z = r0 cos
или, если за параметр принять ср = ш^,
х = r0 sin л. cos <$екч, У = г0 sin л sin <pe/c?J, z = r0 cos лел^, (19)
где /t = — есть некоторое положительное или отрицательное постоянное
число. Так же как логарифмическая спираль, коническая спираль
Рже. 9,
делает бесчисленное множество завитков, уходя в бесконечность и
приближаясь к точке О. Если переменить знак коэффициента к на
обратный, не меняя абсолютного его значения, то получим линию,
симметричную с первоначальной относительно плоскости XOZ. Такие две
спирали невозможно совместить друг с другом.
§ 7. КАСАТЕЛЬНАЯ 35
Уравнения проекции конической спирали на плоскость основания
конуса мы получим, взяв первые два уравнения (19). Сравнение с
уравнением (15) показывает, что коническая спираль проектируется на
основание конуса логарифмической спиралью. Геометрически это ясно
из того, что проекция прямой OL на плоскости XOY вращается
с постоянной угловой скоростью (о, и проекция точки М движется
по ОР со скоростью, пропорциональной ОР.
§ 7. Касательная
Касательной прямой в данной точке М линии (I) мы называем
предел, к которому стремится секущая ММг, когда точка Мх, оставаясь
на линии (Z), стремится к точке М. Короче (но менее точно):
касательная есть прямая, соединяющая две бесконечно близкие точки кривой.
Замечание. В силу основного соглашения (§ 2) мы
рассматриваем только те линии, для которых упомянутый предел, в соответствии
с наглядными представлениями, существует. Напомним, что в
отдельных точках мы можем допускать исключение из этого положения, так
что в отдельных точках касательная может и не существовать. Ниже
будет указано, какие аналитические свойства вектор-функции г (и),
имеющей годографом рассматриваемую кривую, могут обеспечить
осуществление нашего требования.
Рис. 10.
Касательная к прямой линии согласно этому определению есть
сама прямая. Если линия (/) —кривая, то задача разыскания
касательной состоит в разыскании каких-либо ее свойств, определяющих
положение касательной относительно данной линии. Такими свойствами могут
служить уравнения касательной в какой-либо системе координат,
к которой отнесена данная линия (ниже будет показано, как составить
уравнения касательной по данным уравнениям кривой). Если линия
задается каким-либо ее геометрическим свойством, мы можем составить
ее уравнения, из них получить уравнения касательной, а из последних
найти такое свойство, которое наиболее удобно для построения
касательной или для иных целей. Первый из этих этапов требует
некоторой инициативы, второй совершается автоматически, третий требует
большей или меньшей изобретательности. В ряде случаев эту
изобретательность проще проявить непосредственно, исходя из геометрического
свойства, которым эта линия определена.
Пример 1. Эллипс есть место точек М, сумма расстояний
которых от фокусов Fx и F2 постоянна. Рассмотрим две бесконечно близкие
точки эллипса И и /V "(рис. 10). Согласно определению эллипса имеем
1 1 2 2* V /
3*
36 ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
Проведя дуги NP и NQ с центрами F1 и F2, получим отрезки
PM^NF.-MF, и QM
В силу формулы (1) эти отрезки равны:
В прямолинейных треугольниках PNM и NQM углы Ру Q эквивалентны
прямому, так как они лежат при основаниях равнобедренных треуголь-
Рис. 11.
ников NPFt и NQF2 с бесконечно малыми углами при вершинах
Ft и Ftf. По теореме 2 § 4 (стр. 18) имеем
sin
Так как PM = MQ, то
sin Z. PNM ?z sin Z MNQ.
Следовательно,
ZPNM^ Z.MNQ,
и, значит,
т. е. хорда NM образует с радиусом-вектором F2M и с продолжением
радиуса-вектора FXM эквивалентные углы. Если точку М закрепить
неподвижно, то с приближением к ней точки N хорд^ MN будет иметь
пределом касательную к эллипсу в точке Му радиусы же векторы
FХМ и F%М остаются неподвижными. Поэтому касательная в точке М
эллипса должна делить пополам угол между одним из
радиусов-векторов и продолжением другого.
Это чрезвычайно удобное для построения свойство касательной
можно получить и из уравнения касательной. Однако в последнем
случае нужно предварительно вывести уравнение эллипса, что требует,
как известно, довольно громоздких выкладок. Сверх того, указанным
выше способом это свойство обнаруживается проще и доказывается
легче. Таким именно образом оно и было установлено Торричелли
и Робервалем в 30-х годах XVII века.
Пример 2. Циклоида (рис. 11) есть линия, описываемая точкой
окружности круга, катящегося без скольжения по прямой; эта прямая
называется основанием циклоиды.
§ 7. КАСАТЕЛЬНАЯ
37
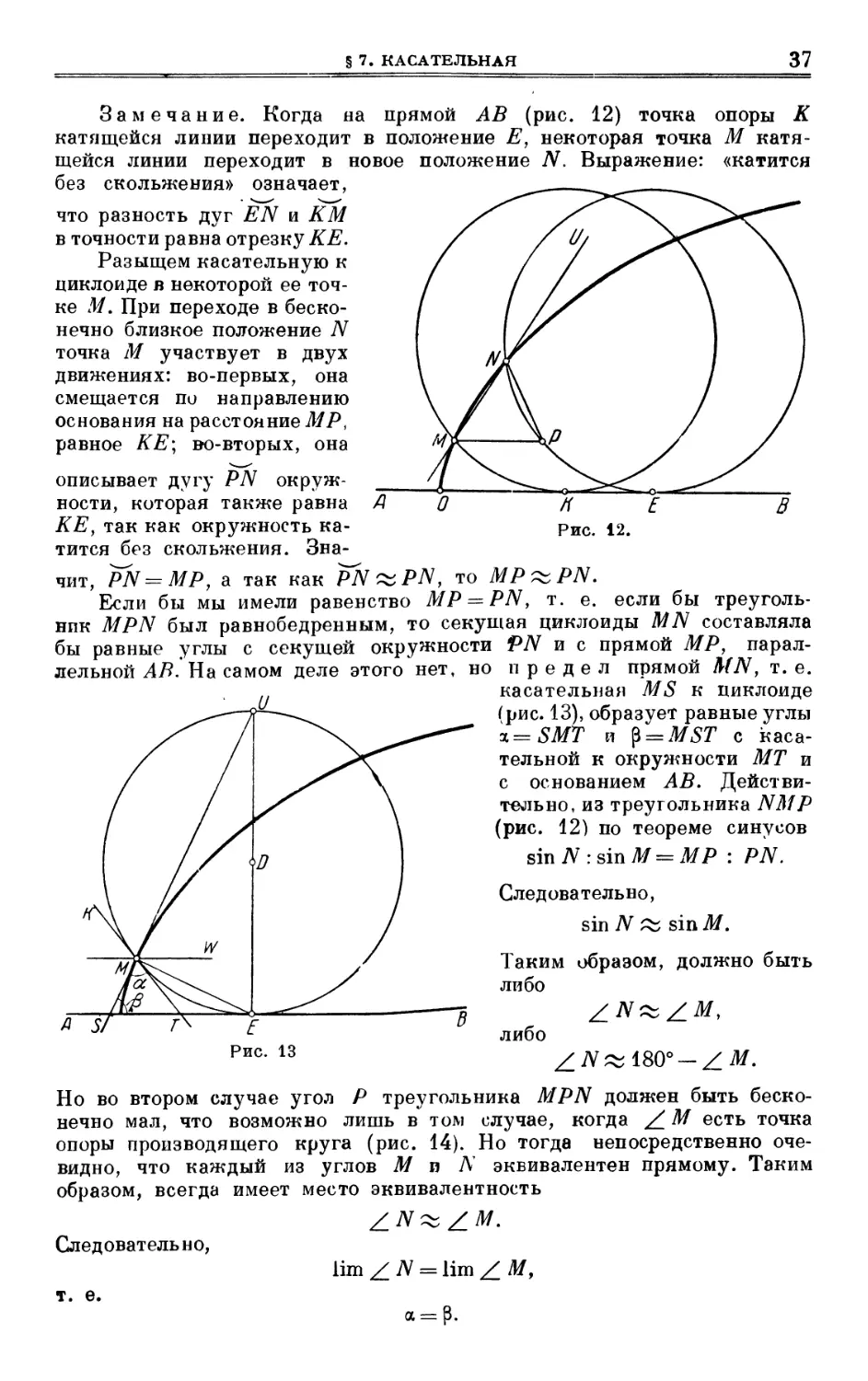
Замечание. Когда на прямой АВ (рис. 12) точка опоры К
катящейся линии переходит в положение Е, некоторая точка М
катящейся линии переходит в новое положение N. Выражение: «катится
без скольжения» означает,
что разность дуг EN и КМ
в точности равна отрезку КЕ.
Разыщем касательную к
циклоиде в некоторой ее
точке М. При переходе в
бесконечно близкое положение N
точка М участвует в двух
движениях: во-первых, она
смещается пи направлению
основания на расстояние МР,
равное КЕ; во-вторых, она
описывает дугу PN окруж- __^
ности, которая также равна А 'О /Т Е ~В
КЕ, так как окружность ка- Рис. 12.
тится без скольжения.
Значит, PN=MP, а так как PNzzPN, то
Если бы мы имели равенство MP = PN9 т. е. если бы
треугольник MPN был равнобедренным, то секущая циклоиды MN составляла
бы равные углы с секущей окружности PN и с прямой МР,
параллельной АВ. На самом деле этого нет, но предел прямой MN, т.е.
касательная MS к циклоиде
(рис. 13), образует равные углы
%=SMT и р = ЛШ7 с
касательной к окружности МТ и
с основанием АВ.
Действительно, из треугольника NMP
(рис. 12) по теореме синусов
sin N : sin М = МР : PN.
Следовательно,
sin N ^ sin M.
Таким образом, должно быть
либо
A~S/
либо
Но во втором случае угол Р треугольника MPN должен быть
бесконечно мал, что возможно лишь в том случае, когда /_ М есть точка
опоры производящего круга (рис. 14). Но тогда непосредственно
очевидно, что каждый из углов М и Л эквивалентен прямому. Таким
образом, всегда имеет место эквивалентность
Следовательно,
т. е.
lim Z N = I
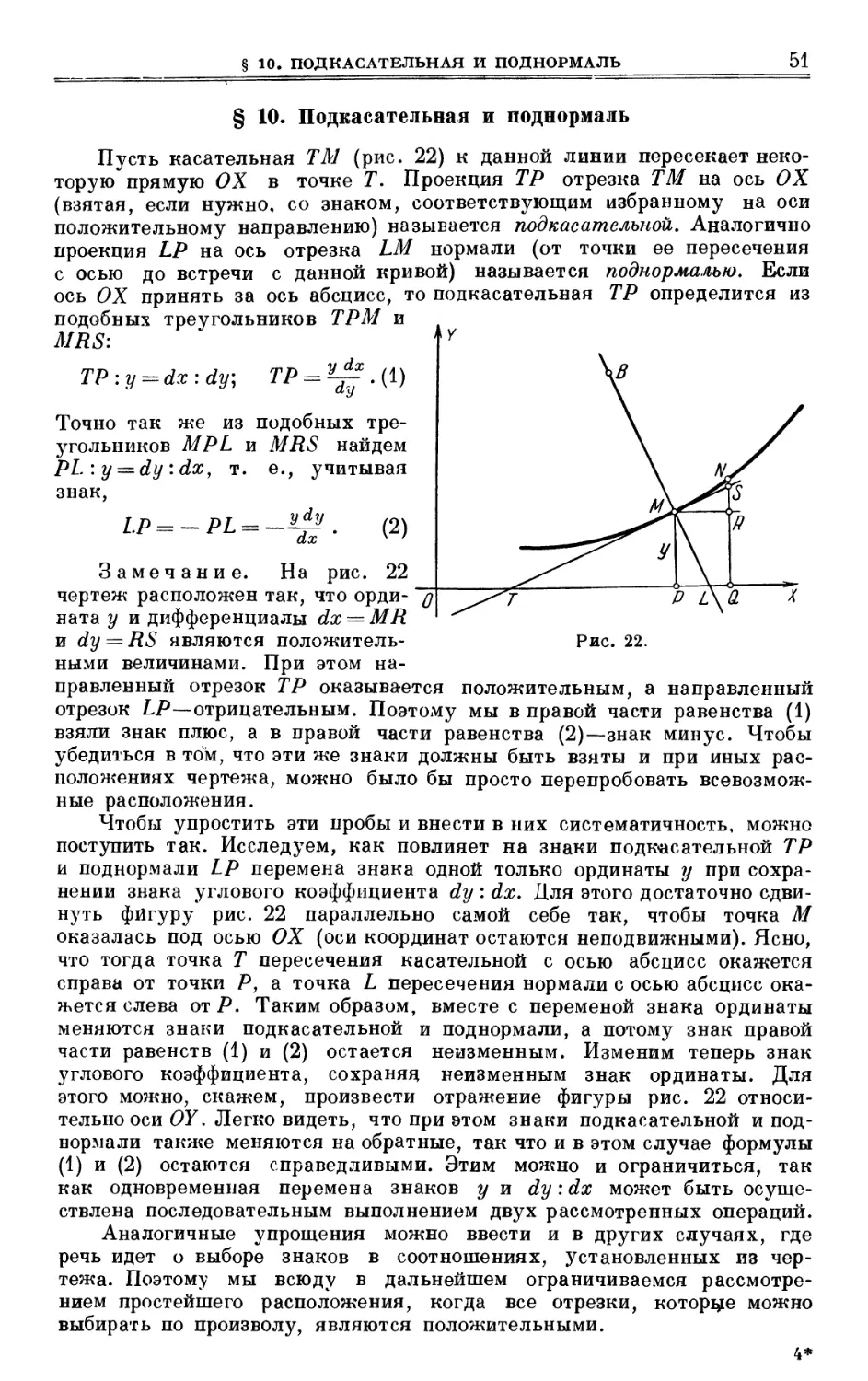
38
ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
м
в
Рис. 14.
Замечание. В случае, когда М совпадает, как на рис. 14,
с точкой опоры окружности, точка N может стремиться к М только
с одной стороны (сверху). Поэтому в начальной точке циклоида имеет
только одностороннюю
касательную. Эта точка
циклоиды является (см. рис. 14)
неправильной.
Итак, мы установили
следующее свойство
касательной к циклоиде.
Касательная к циклоиде
составляет равные углы с
направлением основания и
направлением касательной к
окружности.
Из этого свойства легко
получить следующие два
свойства касательной к
циклоиде.
Касательная MU
циклоиды делит, согласно
доказанному, пополам угол KMW (рис. 13), а прямая ME, соединяющая М
с точкой опоры, делит пополам смежный угол TMW (ибо треугольник
МЕТ—равнобедренный, а углы WME и МЕТ — внутренние* накрест
лежащие при параллельных MW и ТЕ). Следовательно, ЕМ j_ Ml]y
т. е. касательная к циклоиде
перпендикулярна к прямой,
соединяющей точку касания с точкой
опоры производящего круга.
Так как прямой угол EMU —
вписанный, то EU — диаметр.
Следовательно: касательная к
циклоиде проходит через точку U
производящей окружности,
диаметрально противоположную
точке опоры.
Еще проще, но менее строго,
можно получить эти свойства так.
Будем рассматривать окружность
как многоугольник с бесконечным
числом сторон, а точку опоры Е —
как вершину многоугольника.
Тогда точка М описывает дугу
окружности с центром в точке Е
и радиусом ЕМ, т. е.
касательная к циклоиде в точке М
перпендикулярна к ЕМ. Это
рассуждение было применено Декартом.
Пример 3. Найдем касательную к логарифмической спирали
(пример 3 § 6, стр. 32). Точка М (рис. 15), переходя в бесконечно близкое
положение N, участвует в двух движениях. Во-первых, она описывает
дугу MQ окружности радиуса ОМ = г. При обозначениях § 6 имеем
MQ = rd<p = ru>dt. Во-вторых, точка М удаляется по вращающейся
прямой 01 центра на расстояние QN = ON — OMd d
Рис. 15.
§ 7. КАСАТЕЛЬНАЯ 39
Если т = О, то логарифмическая спираль обращается в окружность,
так что она пересекает все радиусы-векторы под постоянным углом,
равным прямому. Если же тфО, то точка М движется по
направлению, отличному от перпендикулярного к радиусу-вектору, и,
следовательно, угол NMQ — конечный. Поэтому из треугольника NMQ, в
котором угол Q эквивалентен прямому, а прилежащие стороны эквивалентны
Рис. 16.
и mrdt, находим (теорема 4 § 4):
ON mrdt m
Следовательно, обозначая через ф угол между касательной МТ и
радиусом-вектором ОМ, имеем
Итак, касательная логарифмической спирали образует постоянный
угол с радиусом-вектором. Входивший в уравнения спирали коэффициент
к есть не что иное как котангенс этого угла.
Пример 4. Найдем касательную к конической спирала. В примере
4 § 6 мы видели, что эта спираль проектируется на плоскость
основания конуса логарифмической спиралью UCD (рис. 16). Основываясь
40 ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
на этом, легко доказать, что касательная к конической спирали
составляет с образующей конуса постоянный угол <]>'. Действительно, возьмем
две бесконечно близкие точки конической спирали М и N. Отложим
на образующей SM отрезок SR = SN. Получим треугольник MRN,
в котором угол R эквивалентен прямому. Угол N мы можем считать
конечным, так как, если бы он был бесконечно малым, то
направление конической спирали совпало бы с направлением параллели конз^са,
т. е. коническая спираль обратилась бы в окружность. В силу теоремы
4 § 4 имеем
Рассмотрим проекции DK, КС прямолинейных отрезков NR, RM. Имеем
РТС
-—
sin /.
РТС
NR — DK, RM = -— , где X — угол между осью и образующей конуса,
sin /
Следовательно,
Так как к и К суть постоянные величины, то
Ctgf =^ = 0
что и доказывает наше утверждение.
Наглядное представление показывает, что касательная в точке М
прилегает к кривой теснее, чем всякая другая прямая, проведенная
через точку М. Это свойство точно
формулируется следующим
образом.
Теорема. Расстояние d = М'Р
(рис. 17) от точки М' кривой до
касательной в бесконечно близкой
точке М есть бесконечно малая
величина высшего (в общем случае —
второго) порядка относительно рас-
стояния ММ'.
Рис. 17. Действительно, в треугольнике
ММ'Р угол М'МР = а бесконечно
мал, так как касательная МТ есть предел секущей ММ'. Поэтому
sin a ^ а и, следовательно,
d = М'Р = MM' sin a ^ М'а.
Таким образом d = M'P имеет высший порядок относительно ММ'.
Точка М предполагается правильной; поэтому отношение ^^>
стремится к некоторому пределу. Случаи, когда он равен нулю или
бесконечности, являются исключительными (и не только потому, что их
только два, но и потому, что они могут иметь место лишь в отдельных
точках кривой). В общем случае щ^, имеет конечный предел и, значит,
d имеет второй порядок относительно ММ'.
Обратно, если расстояние точки М' данной кривой до некоторой
фиксированной прямой МТ, проведенной через точку М этой кривой.
§ 8. УРАВНЕНИЯ КАСАТЕЛЬНОЙ
41
есть бесконечно малая величина высшего порядка относительно ММ',
то МТ есть касательная в точке Af. Действительно, из треугольника
ММ'Р находим
М'Р
sin a =
ММ'
так как порядок М'Р выше порядка ММ'У то sin a, a следовательно,
и а есть бесконечно малая величина. Значит, фиксированная прямая
МТ есть предел секущей ММ' > т. е. касательная.
Таким образом можно дать еще такое определение касательной:
касательная к кривой в ее точке М есть прямая, проходящая через М
и отстоящая от бесконечно близкой точки М' этой кривой на
расстояние высшего порядка малости относительно ММ'.
§ 8. Уравнения касательной
Введем теперь формулы для аналитического определения
касательной в декартовой системе координат. Будем впредь обозначать
буквой М точку данной кривой и через г —ее радиус-вектор ОМ
(рис. 18). Координаты вектора ОМ
суть декартовы координаты точки М%
Будем считать, что уравнения
кривой известны, т. е. что вектор г дан
в функции г(и) параметра и. Чтобы
составить уравнение касательной,
проходящей через точку М,
достаточно найти еще одну точку этой
касательной, т. е. какой-нибудь
отличный от нуля вектор MN, ведущий
от точки М к этой второй точке.
Так как искомая касательная есть
предел секущей ММ1У то естественно
взять на этой секущей какой-нибудь
вектор и искать предел, к
которому он стремится при
приближении секущей к своему пределу. Из векторов, коллинеарных с
секущей, казалось бы, проще всего взять вектор MMi=*kr = r1 — r.
Но этот вектор не годится, так как его предел есть нуль-
вектор.
О
Рис. 18.
Возьмем поэтому вектор МК
= ~ . Пусть он стремится к
пределу MNy отличному от нуля; тогда прямая MN есть искомая
касательная. Действительно, угол между переменным вектором МК и его
пределом MN бесконечно мал. Но этот угол есть не что иное, как
угол между прямой MN и переменной прямой ММ'. Так как у этих
прямых точка М общая, то (§ 5, теорема 1а, стр. 21) прямая MN есть
предел секущей ММ', т. е. касательная в точке Л/.
Но вектор MN, будучи пределом вектора МК — -^, есть не что
иное, как производная вектор-функция или, другими словами, вектор
скорости г' (и) в точке М. Поэтому, если через R обозначить текущий
42 ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
радиус-вектор касательной ON, то вектор R—r(u) коллинеарен
с вектором скорости г'(и), т. е.
R-r{n) = cr'(u), (1)
где v есть число, дающее отношение модуля вектора R— r= MN
к модулю вектора скорости. Уравнение (1) можно представить также
в виде
Я = г (и)+ »/"(»)• (1а)
Уравнение (1) или (1а) и есть уравнение искомой касательной в
векторной форме. Параметр и рассматривается здесь как постоянная
величина, так как точка М фиксирована. От переменного параметра v
зависит положение точки N на касательной прямой.
Если через X, У, Z обозначить текущие координаты точки N
(и вектора /?), то уравнения касательной в координатной форме будут:
X = x(u) + vx'(u), )
Y = y{u) + vy'(u), j> (2)
Z = z{u) + vz'(u). j
Исключая и, получим канонические уравнения касательной:
X -х Y-у Z- z
у' z
(2а)
За направляющие коэффициенты касательной можно взять х', у',
%' или величины dxy dy, dz, им пропорциональные. Если система
координат прямоугольная, то углы а, р, у> образуемые касательной
с осями, определяются по «направляющим косинусам»:
х' dx
cos a = -
V + t/"+;
z' dz
COS Y = .. = —
* yv* + }/* + 2/2 "/a
косинусы суть координаты вектора = —=, коллинеарного
у г'1 у drl
с касательной и имеющего модуль 1. Вектор -£= мы назовем
единичным вектором касательной и будем обозначать через /, так что
*=-4= = -4L= (4)
У r'z Ydr1 '
Предыдущие формулы были выведены в предположении, что
вектор-функция г {и) имеет в рассматриваемой точке производную,
отличную от нуля. Из хода рассуждения ясно, что если
вектор-функция г {и) имеет при и = и0 отличную от нуля производную, то
годограф этой вектор-функции имеет в соответствующей точке М (и0)
касательную. Так как мы условились, что рассматриваемые нами
линии в согласии с наглядным представлением о линии должны иметь
касательные всюду, за исключением, быть может, отдельных (особых)
точек, то естественно при аналитическом задании линии потребовать,
чтобы вектор-функция г (и) имела для всех значений и кроме, может
§ 8. УРАВНЕНИЯ КАСАТЕЛЬНОЙ
43
А/
Рис. 19.
быть, некоторых изолированных значений, отличную от нуля
производную.
Посмотрим, какие последствия может повлечь невыполнение
этого требования. Если вектор-функция г(и) имела бы при всех
значениях и производную, равную нулю, то она была бы постоянным
вектором, и годограф вектор-функции г (и) оказался бы неподвижной
точкой. Эту точку можно рассматривать как «вырожденную» линию.
Если, например, точка М (и) описывает окружность около центра
М0(и0) с данной угловой скоростью «), то модуль вектора скорости
г' (а) имеет тем меь-ыпую величину, чем меньше радиус окружности.
Если точку Мо рассматривать как вырожденную окружность с
радиусом, равным нулю, то
вектору скорости г' (и) нужно
приписать модуль нуль;
направление егонеопределенно.
Итак, в случае, когда
г' (и) = О тождественно,
линия вырождается в точку.
Обращение же вектора г' (и)
в нуль при изолированном
значении и и, тем более,
несуществование производной
от г (и) могут сопровождаться
несуществованием
касательной в соответствующей точке1). Так, например, линия АМВ,
изображенная на рис. 19, может быть описана непрерывным движением с
мгновенной остановкой в точке У1#. Тогда вектор-функция г {и) при
соответствующем значении аргумента и будет иметь производную, равную ,нулю.
В течке же TV линия CND, изображенная на том же рисунке, не имеет
касательной, так как секущая NNX с приближением точки TV, к точке N
по ветви CN стремится к одному проделу, а секущая NN2 при
приближении N2 к N по ветви DN стремится к другому пределу («левая»
и «правая» касательные NT1 и NTt). Такая точка называется, угловой
или точкой излома. Угловые точки являются неправильными (§ 2).
Для линии AM В секущие ММХ и ММ2 имеют пределом одну и ту же
прямую МТ, которую, следовательно, можно назвать касательной
в точке М. Однако в точке Л/ все же имеет место нарушение
правильности: описывая линию АМВ, мы должны в точке М направление
движения переменить на обратное. Следовательно, в точке М вектор
скорости должен либо равняться нулю, либо вовсе не существовать
(если скорость меняется скачком). Такая точка, в которой направление
движения меняется на обратное, называется точкой возврата. Ее тоже
нужно считать неправильной. Точками возврата являются, например, те
точки циклоиды, которые лежат на ее основании (рис. 11 на стр. 36).
В дальнейшем, если не будет сделано особых оговорок, мы будем
считать, что вектор-функция г (и), задающая линию, имеет в
рассматриваемой точке отличную от нуля производную. Этим мы исключаем
г) Но этого может и не быть. Так, окружность во всех своих точках имеет,
конечно, касательную прямую. Однако ее можно описать таким непрерывным
движением, при котором в отдельных точках скорость будет равна нулю, tf таких
точках вектор г (и) будет иметь производную, равную нулю. Более того, ту же
окружность можно представить описанной таким непрерывным движением, при
котором в отдельных точках скорость изменяется скачком; в таких точках скорость в
обычном смысле слова не существует, и вектор-функция г (и) не имеет производной
44
ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
из рассмотрения случай вырождения линии в точку, а также случай точек
перегиба и излома, и обеспечиваем существование касательной прямий.
Если линия задана пересечением поверхностей F(x, у, z)=0
и Ф(х, у, z) = О, то касательную в точке (х, у, z) можно представить
уравнениями (2а), в которых отношения dx :dy: dz определяются из
уравнений.
Fxdx + Fydy + Fzdz = O и Фхdx + Фу dy + Фгdz = 0. (5)
Они дают
Т? К ГР ТР Т? 7?
(6)
(7)
Чтобы не загромождать память, достаточно запомнить уравнение (2а)
и в каждом отдельном случае, дифференцируя данные уравнения,
определять dx : dy :dz.
Плоскость, проходящая через точку М данной линии
перпендикулярно к касательной в этой точке, называется нормальной пло
скостью. Вектор касательной г' является нормалью этой плоскости.
Поэтому ее уравнение есть
(/?-г)г' = 0 (8)
или
(R — r)dr = 0, (8a)
dx:
так что уравнения
dy : dz =
Фу
касательной
Х-х _
:
суть
ф!
F F
Г 2 Г X
Ф2 Фх
Fx
Ф
X
ф! ф
Z — z
Фх Фу
т. е. в прямоугольных координатах
или
(9)
= 0. (9а)
Если линия задана пересечением поверхностей F(x, у, z) = 0,
Ф {х, у, z) = 0, то отношения dx:dy:dz определяются уравнением (6).
Если в (9а) подставить выражения (6), получим уравнение нормальной
плоскости в виде
Х-х Y-y Z-z
F,
Ф,
.0.
(Ю)
Замечание. Если условиться, что в формулах (3) и (4) этого
параграфа квадратные корни берутся всегда со знаком «плюс», то
углы касательной с осями определяются однозначно. Однако эта
однозначность обусловлена выбором параметризации, т. е.
направлением движения по кривой, порождаемого возрастанием параметра и.
Стоит переменить направление движения (для чего достаточно ввести
новый параметр «1,= —и), как направляющие косинусы переменят
знаки. Действительно,
dx dx
du ~~ du^
И Т. д.
§ 8. УРАВНЕНИЯ КАСАТЕЛЬНОЙ 45
Направление движения, соответствующее возрастанию параметра,
называют «положительным» направлением. Из сказанного ясно, что
выбор положительного направления на кривой, пока параметризация
на ней не установлена, всецело зависит от нашего произвола.
Пример 1. Найдем уравнения касательной к винтовой
линии (§6). Имеем
x = acosu, y = asinu, z — bu\
х'= — a sin а, у' = a cos и, ъ' = Ь.
Уравнения касательной будут:
X — a cos и Y — a sin и Z — Ьи
— a sin и a cos и Ь
Направляющие косинусы будут:
— a sin и a sin и
cos a =
V sin2 и + a2 oos2 и 4 Ь* У а* + Ь* '
a cos и Ъ
COSY
Третья формула показывает, что касательная образует с осью z угол у
постоянной величины. Так как (§ 6) 6 = atga, то
a tff a
cos у = — * —- = sin a,
}/fl2fl2tgja
так что у= у —ос.
Этот результат станет геометрически очевидным, если мы учтем,
что при навертывании плоскости на вертикальный цилиндр угол
-—а, который начерченная на плоскости прямая составляет с
вертикалью, остается неизменным.
Нормальная плоскость винтовой линии имеет уравнение
(X — a cos и) (— a sin и) + (Y — a sin и) {a cos и) + (Z —• Ьи) 6 = 0,
т. е.
— аХ sin и + aY cos и + Zb — 62и = 0.
Пример 2. Найдем уравнения касательной прямой и нормальной
плоскости к кривой Вивиани (§ 6, стр. 30).
Если уравнения кривой Вивиани написать в виде
х* + У2 + z2 = а2, хг + у2 — ах = 0,
то, дифференцируя, получим
х dx + г/с?2/ + z dz = 0; 2г/йг/ + (2x-—a)dx = Q,
откуда
dx: dy :dz = 2yz : z(a — 2x) : — ay.
Уравнения касательной будут:
X-x = Y-y = z--<s
2t/2 ~~ z(a — 2.c) ~~ —ay '
а уравнение нормальной плоскости:
(X - х) 2yz -r (Y — у) z {a — 2х) — (Z - z) ay = 0.
46 ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
Если использовать параметрические уравнения (10а) § 6 (в
которых мы можем вместо и' написать и), то направляющие коэффициенты
dx :dy : dz найдем в виде
dx: dy :dz = — sin 2u : cos 2u : cos u.
Пусть требуется определить наименьший угол, образуемый кривой
Вивиани с осью цилиндрической поверхности, на которой она взята.
Согласно формуле (3), для кривой Вивиани имеем
о COS2 U
COS2 Y=
1
Наименьшее абсолютное значение угла у соответствует наибольшему
гаименынему а
1 + COS2 U 1
COS2M
значению -л ъ—, т. е. наименьшему значению величины
1 + COS2 U ' J
COS2 U COS2 U
+1.
Эю наименьшее значение достигается при cos2«=l, т. е. при м = 0
и при и = 180°.
Оба эти значения и дают, согласно уравнениям 10 § 6, одну и ту
же точку А (а, 0, 0). Однако кривая Вивиани проходит через эту точку
дважды. При и = 0 мы имеем
cosw ___
Y'2 '
откуда у=+45°. Точно так же найдем, что при к = тг угол
равен —45°.
В заключение подтвердим аналитически доказанное в § 7 свойство
касательной.
Как известно, расстояние d от точки М' с радиусом-вектором г + Аг
до прямой, проходящей через М (г) по направлению вектора
касательной г', выражается формулой
а =
V(r'y
Знаменатель этого выражения есть конечная величина, так как по
предположению г' Ф 0; поэтому порядок малости равен порядку
малости вектора Агхг'. Но Дг:=г/Дм + г, где в есть бесконечно малая
векторная величина высшего порядка относительно ~и. Поэтому
ДГ х г' = (Г'Аи + а) х г' =Л х г\
Таким образом, порядок малости d во всяком случае выше порядка Дм-
Если же допустить, что вектор г имеет и вторую производную, та
Дг
х г' = (г'Дв + -f Г"А"2 + • *') х г' = -т(г" хГ') А"2 + '' '>
так что d имеет второй порядок малости, если векторы г', г" некол-
линеарны, и более высокий, если эти векторы коллинеарны.
8 9. КАСАТЕЛЬНЫЕ И НОРМАЛИ ПЛОСКИХ КРИВЫХ 47
Упражнения
1 В каких точках линия
параллельна координатным плоскостям?
2. В каких точках линия предыдущей задачи параллельна плоскости
З ?
3. В каких точках эта же линяя перпендикулярна к прямой
X -~ у = 2?
4. Составить уравнение касательной прямой и нормальной плоскости к линии
х = а (и — sin и), y = a(l —cosu), z = 4asin —
в точке и = —. Какой угол касательная образует с осью Z?
5. Оси цилиндрических круглых поверхностей радиусов а и 2а пересекаются
под прямым углом.^ Найти углы, образуемые с осями координат линией
пересечения поверхностей в тех ее точках, где ее встречает плоскость, проходящая
через ось меньшего цилиндра под углом '*5° к оси большего цилиндра.
6. Найти угол, образуемый касательной к конической спирали с осью конуса.
Уравнения стирали см. § 6 Сравнить результат с полученным в примере 4 § 7.
1 Доказать, что если радиус-вектор г (и) имеет при и — и0 равные нулю
производные первых а — 1 порядков и не обращающуюся в нуль производную га-го
порядка, то линия г = г(и) имеет в соответствующей точке касательной прямую,
уравнение которой есть
Х-х(щ) = Y-y (щ) = Z-z(uQ)
§ 9. Касательные и нормали плоских кривых
Все то, что выше сказано о касательных к кривым линиям,
относится, в частности, и к кривым плоским. Однако здесь можно,
во-первых, внести некоторые упрощения и, во-вторых, установить ряд
специальных свойств, не распространяющихся на пространственные
кривые.
Если принять плоскость данной линии за плоскость XOY, то
кривая представится параметрически уравнениями
х=*х(и), у = у(и). (1)
Третье ее уравнение Z—0, как само собой разумеющееся, можно не
выписывать. Параметрические уравнения касательной [ср. формулы (2)
§ 8] можно записать так:
(2)
Исключая v, получим
■ ^-^. , (2а)
или
37" • (2b)
Если линия задана уравнением F (х, у) = 0, то,
продифференцировав это уравнение, найдем
(3)
48
ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
Исключив dx: dy из (3) и (2Ь), найдем уравнение касательной
в виде х)
Y-y) = 0. (4)
В частности, если линия задана уравнением y = j(x), то
уравнение касательной будет
Прямая, проведенная через течку М данной линии и
перпендикулярная к касательной в этой точке, называется нормалью.
Уравнение нормали (лежащей в данной плоскости) если линия
дана уравнениями (1), можно записать в виде
(X-x)x' + {Y-y)y' = Q (5)
или
(X — х) dx + (Y — у) dy = 0. (5а)
Действительно, црямая (5) проходит через точку М (х, у) и
перпендикулярна к касательной, ибо ее направляющие коэффициенты
суть —dy:dx. Уравнение (5) можно получить также из уравнения (9)
§ 8, рассматривая нормаль как пересечение нормальной плоскости (9) с
плоскостью кривой z = 0.
Если линия дана уравнением F (х, у) = 07 то из уравнения (5а) и
уравнения Fxdx + Fydy = 0, исключая dx : dy, найдем
Х — х Y-y
= 0.
(6)
Это уравнение аналогично уравнению (10) § 8, из которого оно
получается, если положить Ф = £. Уравнение (6) можно переписать
также в виде
-^ = -^. (6a)
В частности, если линия задана уравнением y = f(x), то
уравнение нормали есть
(X - х) + f (x) (Y — у) = 0. (6Ь)
Из приведенных здесь уравнений достаточно удержать в памяти
(2Ь) п (5а) •).
Пример 1. Найдем уравнения касательной и нормали к циклоиде
и получим аналитически их свойства.
Прежде всего нужно иметь уравнение циклоиды. За ось X
примем прямую, по которой катится окружность. За начало координат
примем ту точку оси, в которой находилась течка М, описывающая
циклоиду. За параметр примем центральный угол и = ^/_ ЕСМ (рис. 21)
дуги ЕМ окружности между точкой опоры Е и точкой М',
описывающей циклоиду. Угол и отсчитывается в направлении, указанном
1) Это уравнение можно было бы получить из
уравнения (7) § 8, полагая там 2 = 0 и Ф-[х, у, z) = z.
а) Уравнение (2b) непосредственно
«прочитывается» ия треугольников МАК и MNR (рис. 20\
которые в пределе подобны (MR ъ dx, NR ъ dy; МК = X — х,
AK-Y-y).
м
р\к
Рис. 20.
§ 9. КАСАТЕЛЬНЫЕ И НОРМАЛИ ПЛОСКИХ КРИВЫХ
49
стрелкой. Если а есть радиус окружности, то дуга ЕМ равна аи,
а так как качение происходит без скольжения, то
или
= аи.
Из рис. 21 находим:
х = ОР = ОЕ- РЕ = ОЕ - MQ,
х = а(и —-sin и),
у = а(1 — cos и).
= РМ = ЕС - QC,
^ '
Эти уравнения полезно помнить. Нелишне также заметить, что их
вывод имеет совершенно общий характер, так что уравнения (7)
справедливы для любого
значения параметра и. Из этих
уравнений находим
х' = а (1 — cos и), у'= а sin и
и уравнение касательной (2а)
напишем в виде
X — а (и — sin и) Y — а (1 — cos и) ,^v
1 — cos и sin и '' '
а уравнение нормали (5)—в виде
[X — а (а — sin и)] (1 — cos и) +
+ [Y — а (1 — cos и)] sin и = 0. (9)
Чтобы доказать, что нормаль
проходит через точку опоры Е,
достаточно удостовериться, что
уравнение (9) удовлетворяется
значениями х — аи, у = 0. Чтобы доказать, что касательная проходит
через диаметрально противоположную точку U', достаточно убедиться
в том, что уравнение (8) удовлетворяется при
х = аи, у —2а.
Пример 2. Найдем уравнения касательной и нормали эллипса.
Отнеся эллипс к его осям, получим уравнение
По формуле (4) найдем уравнение касательной:
(Х-х)х (Г-у)у п
а* "*" б2 *
По формуле (6а) найдем уравнения нормали:
Если взять параметрические уравнения эллипса
# = acosM, y = 6 sin и,
то уравнение касательной согласно формуле (2а) будет
X — a cos и Y — Ъ sin и
bcosu
(10)
(И)
(12)
(13)
(14)
М. Я. Выгодский
50 ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
и уравнение нормали [формула (5)]:
—(X — a cos и) a sin и + (Y — b sin и) Ь cos a = 0. (15)
Докажем теперь аналитически свойство касательной к эллипсу,
выведенное в § 7. Выкладки будут проще, если взять
параметрические уравнения эллипса. За направляющие коэффициенты касательной
согласно уравнению (14) примем величины
%' =—asintt, y' = bcosu. (16.)
Направляющие коэффициенты радиуса-вектора, ведущего из Fx (с, 0)
к М(х, у), будут
х — с = a cos и — с, у = Ь sin и, (17)
причем величины а, Ь, с связаны соотношением
а2 = Ь2 + с2. (18)
Угол <рх ^между вектором касательной (16) и вектором FiiJ/ (рис. 10
на стр. 35) определится из формулы
— a sin и (a cos и — с) + Ь2 cos и sin ц # ,*-.
C0S Cf>1 = /a2 sin2 u + б2 cos^ и /(а cos и - с)2 + 62sin2 и ' '
аналогично найдем угол ср2 между вектором (16) и вектором F2M:
— a sin и (a cosм -he) -\-b2 cos a sin м /у1/_ v
cos ф2 = - > — • (19а)
у a2 sin2 u + b2 cos2 м |/ (a cos w -f c)2+62 sin2 и
Радикалы в знаменателях формул (19), (19а) представляют
арифметические значения корней. В формуле (19) числитель можно
преобразовать, заменяя Ь2 на а2—с2, так:
— a sin и (a cos и — с) + Ь2 cos и sin u = ac sin и — с2 sin и cos и =
= с sin и (а — с cos и).
Второе подкоренное выражение формулы (19) преобразуем так:
(a cos и — с)2 + &2 sin2 н = a2 cos2 а — 2ас cos и + с2 + a2 sin2 гг — с2 sin2 u=
= а2 — 2ас cos а + с2 cos2 и = (а — с cos м)2.
Так как а > с, то а—ccos&>0 при всяком гг; следовательно,
арифметическое значение второго корня есть + (а—-с cos и), и формула (19) дает
cos 9i = г . (20)
T yV sin2 wh&2 cos2 w
Из формулы (19а) таким же образом найдем:
— с sin и /Гк/Ч .
спя у, = . (20а)
72 /a2sin2u + &2cos2M v
Сравнение формул (20) и (20а) показывает, что вектор касательной
образует равные углы с вектором FXM и вектором MF2, т. е. с
направлением одного из радиусов-векторов и направлением,
противоположным другому.
Сравнение с выводом § 7 показывает, что в этом, как и во
многих других случаях, синтетическое рассуждение дает результат быстрее
и нагляднее, чем аналитическое. Не забудем также, что мы
воспользовались известными уравнениями эллипса, вывод которых также
потребовал бы некоторого труда. В иных случаях, напротив,
аналитический метод ведет к цели быстрее.
§ 10. ПОДКАСАТЕЛЬНАЯ И ПОДНОРМАЛЬ
51
§ 10. Подкасательная и поднормаль
Пусть касательная ТМ (рис. 22) к данной линии пересекает
некоторую прямую ОХ в точке Т. Проекция ТР отрезка ТМ на ось ОХ
(взятая, если нужно, со знаком, соответствующим избранному на оси
положительному направлению) называется подкасапгелъной. Аналогично
проекция LP на ось отрезка LM нормали (от точки ее пересечения
с осью до встречи с данной кривой) называется поднормалью. Если
ось ОХ принять за ось абсцисс, то подкасательная ТР определится из
подобных треугольников ТРМ и
MRS:
В
Точно так же из подобных
треугольников MPL и MRS найдем
PL:y = dy:dx, т. е., учитывая
знак,
dx '
Замечание. На рис. 22
чертеж расположен так, что
ордината у и дифференциалы dx = MR
и dy = RS являются положитель- Рис. 22.
ными величинами. При этом
направленный отрезок ТР оказывается положительным, а направленный
отрезок LP—отрицательным. Поэтому мы в правой части равенства (1)
взяли знак плюс, а в правой части равенства (2)—знак минус. Чтобы
убедиться в том, что эти же знаки должны быть взяты и при иных
расположениях чертежа, можно было бы просто перепробовать
всевозможные расположения.
Чтобы упростить эти пробы и внести в них систематичность, можно
поступить так. Исследуем, как повлияет на знаки подк-асательной ТР
и поднормали LP перемена знака одной только ординаты у при
сохранении знака углового коэффициента dy : dx. Для этого достаточно
сдвинуть фигуру рис. 22 параллельно самой себе так, чтобы точка М
оказалась под осью ОХ (оси координат остаются неподвижными). Ясно,
что тогда точка Т пересечения касательной с осью абсцисс окажется
справа от точки Р, а точка L пересечения нормали с осью абсцисс
окажется слева от Р. Таким образом, вместе с переменой знака ординаты
меняются знаки подкасательной и поднормали, а потому знак правой
части равенств (1) и (2) остается неизменным. Изменим теперь знак
углового коэффициента, сохраняя неизменным знак ординаты. Для
этого можно, скажем, произвести отражение фигуры рис. 22
относительно оси OY. Легко видеть, что при этом знаки подкасательной и
поднормали также меняются на обратные, так что и в этом случае формулы
(1) и (2) остаются справедливыми. Этим можно и ограничиться, так
как одновременная перемена знаков у и dy: dx может быть
осуществлена последовательным выполнением двух рассмотренных операций.
Аналогичные упрощения можно ввести и в других случаях, где
речь идет о выборе знаков в соотношениях, установленных из
чертежа. Поэтому мы всюду в дальнейшем ограничиваемся
рассмотрением простейшего расположения, когда все отрезки, которое можно
выбирать по произволу, являются положительными.
4*
52
ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
Пример 1. Найти поднормаль параболы относительно ее оси.
При обычном выборе положительного направления оси параболы
(в сторону ее вогнутости) поднормаль должна, как показывает
наглядное рассмотрение, быть отрицательной. Взяв начало координат в
вершине параболы, получим ее уравнение в виде
откуда
Формула (2) дает
y' = zpx,
ydy = pdx.
LP= -p,
т. е. длина поднормали параболы во всякой ее точке равна
параметру FK (или, что то же, фокальной полу хорде) параболы.
Рис. 23.
Хотя аналитический метод ведет к решению этой задачи весьма
коротким путем, не лишено интереса получить этот результат
геометрически. Из прямоугольного треугольника TML (рис. 23), в котором
у = РМ есть высота, находим
Как известно из аналитической геометрии, ТР = 2ОР = 2х *).
Так как у* = 2рх, то
2рх = PL - 2х, откуда PL = p.
Пример 2. Найти линию, у которой все подкасателъные имеют
одинаковую длину.
х) Этот результат получается синтетически так: пусть АВ — директриса, а
F — фокус. Из определения параболы находим, как в примере 1 § 7, фокальное
свойство ее касательной, отсюда получаем FT = MF = PK и, принимая во
внимание, что OF —ОК. находим FT — OF=*PK — ОК, т. е. ОТ = ОР, т. е. ТР = 2ОР
10. ПОД К АСА ТЕЛЬНАЯ И ПОДНОРМАЛЬ
53
Обозначив эту длину через а, из уравнения (1) получаем:
у dx
dy
= а
или
Отсюда
, dy
dx = a — .
У
2/о
(3)
Выбор начальной ординаты 2/0 не имеет никакого влияния на
форму линии, так как на данной оси мы можем начало координат
Рис. 24.
выбрать произвольно, а следовательно, за начальную ординату можно
принять любую ординату искомой линии.
Найденная линии называется логарифмиаощ уравнение (3),
разрешенное относительно у, дает
У = Уое<Г, (4)
т. е. логарифмика есть график показательной функции. Так как под-
касательная логарифмики имеет постоянную длр;ну, то ее можно
(приближенно) построить так. Из точки Р (рис. 24), произвольно взятой на
оси, проводим ординату РМ произвольной длины и откладываем отрезок
ТР = а. Соединяем точки Т и М; на прямой ТМ или ее продолжении
54
ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
берем вблизи М точку Мг. Проводим ординату МХРХ\ откладываем
отрезок Т1Р1 = а, соединяем Тг и Мг. На продолжении ТгМг берем
точку М% и т. д. Проводим через точки М, М19 М2 и т. д. плавную
линию. Прямые МТ, М1Т1, М2Т2 и т. д. соединяют близкие точки этой
линии и потому практически служат касательными; равные отрезки
ТР = Т1Р1—Т2Р2 = ...практически служат подкасательными. Величина
у0 в уравнении (4) есть ордината OR в точке О, принятой за начало.
Ось ОХ логарифмики служит ее асимптотой.
§ 11. Трактриса
Пусть к материальной точке (т. е. к тяжелому телу малых
размеров) М, лежащей на горизонтальной плоскости, прикреплена
нерастяжимая нить МТ (рис. 25), и пусть конец Т этой нити движется
по некоторой прямой ОТ, лежащей в этой же плоскости. Тогда
точка Му увлекаемая натянутой нитью, опишет линию, называемую
трактрисой.
Чтобы дать геометрическое определение трактрисы, заметим, что
точка М движется по направлению МТ и что отрезок МТ сохраняет
постоянную длину, так как нить предполагается нерастяжимой.
Следовательно, отрезок касательной от точки касания до пересечения
с осью должен иметь постоянную длину.
Поэтому дадим такое определение: трактрисой называется линия,
у которой отрезок касательной между точкой касания и некоторой
прямой (осью) имеет постоянную величину а.
Приближенное построение трактрисы можно выполнить так: взяв
точку М так, чтобы расстояние ее от оси не превосходило а, засекаем
д^гой радиуса МТ = а точку Т на оси. На отрезке МТ или его
продолжении берем точку М19 близкую к М. Засекаем дугой радиуса а
точку Тг на оси. Таким же образом строим точки М29 М3 и т. д.
Соединяя точки М, М19 М2, ... плавной линией (если точки М, М1}
М2, ... близки друг к другу, то линия видна и без того), получаем
кривую, которая близка по форме к трактрисе. В самом деле,
касательные к этой кривой мало отличаются от прямых МТ, МгТ19
М2Т2, .. . , а отрезки МТ, М,Т19 М2Т29 ... по построению имеют
постоянную длину а.
§11. ТРАКТРИСА 55
Если все отрезки МТ, M1Tlf М2Т2, ... взять равными между собой:
то ординаты МР, MxPlf M2P2,... образуют, как легко видеть,
убывающую геометрическою прогрессию:
MtPt = (\ —\)MP.
Отсюда видно, что при движении точки М по трактрисе в
направлении МТ ординаты ее должны неограниченно убывать по длине, так
что ось трактрисы должна быть ее асимптотой.
Так как расстояние oi точки трактрисы до ее оси никогда не
превосходит величины а, то наивысшая точка А трактрисы должна
отстоять от оси на расстояние, равное а. Эта точка называется вершиной
трактрисы. Касательная в вершине должна совпадать с
перпендикуляром АО к оси, так как в противном случае касательная имела бы
длину, большую а. Исходя из точки А, можно построить две
симметричные относительно высоты АО ветви трактрисы. Обе они
касаются прямой АО в точке А. При прохождении через точку А
направление движения по трактрисе меняется на обратное, т. е. А есть
течка возврата (§ 8).
Найдем параметрические уравнения трактрисы. Ось ее примем за
ось абсцисс. Ось ординат проведем через вершину. За параметр
примем угол и = Z_ XTM между положительным направлением оси и
направлением касательной. При этом касательную условимся направлять
всегда в сторону вершины (см. рис. 25). Тогда при изменении абсциссы
от —со до +оо параметр непрерывно изменяется от и = 0 до и=к.
При любом положении точки М имеем:
РМ = y = asinu, (1)
ТР = a cos и. (2)
Но подкасательная ТР, согласно формуле (1) § 10, равна у -р ;
поэтому
. (3)
Подставляя сюда из (1) выражения y = asinu, dy = a cos и du, находим:
7 a cos2 и 7 //ч
dx = — du. (4)
sin и v ;
При избранной нами системе координат значению х = 0 отвечает
значение и — y . Поэтому
и и
2 и I' (1 — sin2 и) du
sin и
-г 2
Итак, параметрические уравнения трактрисы имеют вид:
х = а ( In tg — + cos и J, I
г/ = a sin u. j
tt dc a cos2 u rfV /~ r ^
Производные т- ——: , j^=a cos и обе обращаются в нуль в точке Л,
ttl£ Sin U CtU **
56 Г Л, I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
т. е. при и = ^-. Следовательно, через вершину А точка М проходит
со скоростью нуль. Это обусловлено тем, что вершина есть точка
возврата трактрисы.
Из параметрических уравнений (5) можно исключить параметр и,
но уравнение, которое мы получим, громоздко и для практических
целей мало пригодно.
Поверхность, образованная вращением трактрисы около оси, назы-
вает'ся псевдосферой. Она играет очень важную роль в теории поверхностей.
Упражнения
1. Составить уравнения касательной и нормали к гиперболе. Доказать
аналитически и синтетически, что ьасатсльная делит пополам угол между радиусами-
векторами, проведенными в точку касания.
2. Доказать аналитически и синтетически, что касательная к параболе
образует равные углы с осью и радиусом-вектором, исходящим из фокуса. При
синтетическом доказательстве использовать
директрису.
3. Доказать, что если отрезок
нормали линии (Z), заключенной между (I)
и кшой-нибудь осью, имеет постоянную
длину, то линия (I) есть прямая,
параллельная оси, или окружность с центром
на оси.
4г. Найти на эллипсе такую точку,
чтобы отрезки касательной, заключенные
между этой точкой и осями эллипса, были
равны.
Указание (для синтетического
решения). Рассматривать эллипс как
окружность, рлвномерно сжатую к одному из
диаметров. Показать, что при таьом
сжатии середина отрезка остается серединой.
5. Под каким углом циклоида пере-
р 2~ секает производящий круг, когда подвиж-
°* ная точка отстоит от точки опоры по дуге
окружности на 60°?
Замечание. Угол между кривыми линиями измеряется углом между их
касатрльными.
6. Доказать аналитически и синтетически, что параболы, имеющие общий фок^с
и противоположно направленные осп, пересеюются под прямым углом.
Замечание. При синтетическом доказательстве можно использовать
свойство, изложенное в упражнении 2.
7. Доказать аналитически и синтетически, что софокусные (т. е. имеющие
общие фокусы) эллипс и гипербола пересекаются под прямым углом.
8. Доказать, что трактриса высоты а пересекает под прямым углом
окружность радиуса а с центром на оси трактрисы.
9. Геометрическое место оснований перпендикуляров, опущенных из точки А
на касательные к линии (Z), называется подэрой линии II) относительно полюса Л.
Доказ1ть что подэра окружности есть улитка Паскаля. Синтетически задача
решается элементарно.
Замечание. Улитка Паскаля определяется так. На окружности АСВ
(рис. 26) выбираем точку А. Остальные точки С окружности соединяем с А
и откладываем на АС отрезки CD — CE постоянной длины. Геометрическое место
точек Е и D есть улитка Паскаля. Мо»но откладывать отрезок постоянной длины
лишь в одну сторону; тогда точка С должна описать окружность дважды.
§ 12, Касательная к линии, заданной полярным свойством
Многие плоские линии (например, спираль Архимеда,
логарифмическая спираль и другие спиральные линии) лучше всего определяются
«полярными» их свойствами, т. е. зависимостью между расстоянием
М (рис. 27) переменной точки М линии (/) от некоторой постояп-
§ 12. КАСАТЕЛЬНАЯ К ЛИНИИ, РАД АННОЙ ПОЛЯРНЫМ СВОЙСТВОМ 57
ной точки О («пол/оса») и углом поворота ср = /_ ХОМ луча ОМ,
отсчитываемым от фиксированного направлении ОХ («полярная ось»).
Уравнение
г = г{у), (1)
выражающее аналитически это свойство, называется полярным
уравнением линии (/) (или уравнением в полярной системе координат
с полюсом О и полярной осью ОХ).
Величину угла <р нецелесообразно ограничивать какими-нибудь
значениями (например, полаять 0<<p<2ir): ведь спиральные линии
характеризуются именно тем, что луч ОМ
совершает множество оборотов около О.
Отказываясь от ограничения величины 9»
мы, в сущности, теряем «систему координат»,
ибо отдельной точке М, взятой на плоскости,
отвечает не одно, а бесчисленное множество
значений у, отличающихся друг от друта на
числа, кратные 2тс. Но об этой потере не
приходится сожалеть, если нашей целью является
изучение свойств определенной линии (/), так
как угол поворота луча ОМ при движении М
вдоль (/) имеет вполне определенную
величину, а величина «начального» угла не играет
существенной роли хотя бы потому, что «по- О Л
лярная ось» может быть взята по произволу.
Лишь одна точка—полюс—оказывается в ис. - .
неблагоприятном положении (но для нее и
ограничение 0<<р< 2тг не спасает положения): в этой точке угол 9 остается
совершенно неопределенным. И если линия (/) проходит через полюс
(как, например, Архимедова спираль—см. ниже, пример 1), то за
значение 9 в полюсе остается принять предел, к которому стремится
величина 9> когда точка М стремится к О (если таковой предел
существует) .
Поэтому там, где не будет сделано особой оговорки, мы будем
рассматривать только такие дуги линии (/), которые не
содержат полюса; иначе говоря, случай г = 0 мы будем считать
исключенным.
В соответствии с этим величину г мы можем считать
положительной.
После этих предварительных замечаний мы перейдем к вопросу
о разыскании касательной к линии (/), заданной ее полярным
свойством.
Положение касательной МТ вполне определяется величиной угла
& = ^КМТ, который эта касательная образует с радиусом-векто
ром ОМ К. Этот угол мы условимся отсчитывать от луча МК к лучу МТ,
направленному в сторону возрастания угла 9- При этом условии угол <Ь
всегда лежит в пределах от 0 до тс и, следовательно, вполне
определяется величиной tg<]> или ctgu.
Возьмем на (I) точку N, бесконечно близкую к фиксированной
точке Л/. Прямая МТ согласно определению касательной есть предел
прямой MN; прямая же ОМ есть предел прямой ON. Поэтому,
обозначив через ф' угол MNO, мы имеем
Ф^Ф'. (2)
58
ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
Отложим на ON отрезок ОР = ОМ = г. Получим треугольник MNP,
в котором угол Р эквивалентен прямому. Следовательно (теорема 4 § 4) *),
Здесь
PN = Аг ^ dr
(3)
(4)
PM 2Z
Из формул (2) — (5) находим
rdy.
(6)
Пример 1. Архимедовой спиралью называется кривая,
обладающая следующим свойством: длина радиуса-вектора каждой ее точки
пропорциональна углу поворота радиуса-вектора. Найдем угол между
касательной к Архимедо-
\Т вой спирали и ее
радиусом-вектором в конце
первого завитка спирали.
Если обозначить
через а радиус-вектор в конце
первого завитка (рис. 28),
т. е. после поворота на
угол 2тг от начального
направления ОХ, то
соотношение между г и 9 можно
представить в виде
откуда
Рис. 28.
ad?
и формула (6), где нужно положить г = а, дает
1
ИЛИ
откуда
<1>«80°20'.
Иными словами, искомый угол равен большему из острых углов
прямоугольного треугольника, один катет которого равен некоторой
окружности, а другой—ее радиусу. Что этот угол не зависит от
величины а, можно было заранее предвидеть, ибо все Архимедовы спирали
подобны друг другу.
х) Об условии применимости этой теоремы см. ниже (замечание 1).
§ 12. КАСАТЕЛЬНАЯ К ЛИНИИ, ЗАДАННОЙ ПОЛЯРНЫМ СВОЙСТВОМ 59
Пример 2. Найти линии, пересекающие все лучи, исходящие
из полюса, под постоянным углом.
В формуле (6) мы можем по условию положить
ctg ф = к,
где к есть постоянная величина. Уравнение (6) принимает вид
Интегрируя, имеем
откуда
1п ■£ = *?> (8)
т. е. только логарифмические спирали обладают требуемым свойством
(ср. § 6, пример 3).
Замечание 1. При выводе формулы (6) мы воспользовались
теоремой 4 § 4. Эта теорема, как было показано в разъяснявшем ее
замечании 1 (стр. 20), может быть неверной, если угол ф'
эквивалентен прямому, т. е. если угол ф— прямой.
Однако формула (6) верна при любом значении ф; в самом деле,
мы могли бы вывести ее, опираясь не на теорему 4 § 4, а на теорему 3
того же параграфа, которая верна всегда. Идея вывода осталась бы
неизменной. Именно, вместо (2) мы напишем
ф ф'. (2')
Согласно теореме 3 § 4, имеем (рис. 27):
- lim ctg f = lira ~. (3')
Далее, вместо эквивалентности (4) напишем
PN = Ar (4')
(эквивалентность Дг ^ dr нам теперь не нужна1)).
Согласно (5), можем написать соотношение
РМ^гАср, (5')
выражающее эквивалентность дуги МР = г^у окружности радиуса г
и стягивающей ее хорды РМ, Теперь из формул (2') — (5') находим:
PN Аг
ctg ф = ctg lim ф' = lim ctg f = lim -^ = lim ^,
а так как по определению производной
.. Дл dr
lim г- = т-,
Д? dy'
то
^- (6)
1) Заметим, что в исключительном случае, когда ф = —, эта эквивалентность
не имеет места, ибо тогда dr = 0.
60
ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
Как мы видим из сопоставления двух вышеприведенных выводов,
каждому шагу в первом выводе соответствует аналогичный шаг во
втором. Поэтому они по существу тождественны. Мы предпочли первый
по соображениям простоты и нагляднее™.
По' тем же соображениям мы будем и впредь пользоваться
теоремой 4 § 4 при решении различных задач «в общем случае», т. е. при
выводе таких соотношений, где относительно угла В (в нашем случае—
относительно угла ф') не делается никаких предположений.
Если бы у читателя возникли опасения относительно правильности
результата в исключительном случае, когда /_ В ^ *'■ , то он всегда
может, опираясь на теорему 3 § 4, провести доказательство, шаг за
шагом соответствующее доказательству, основанному на теореме 4 § ±.
Но эти сомнения можно устранить и заранее. Дело в том, что мы
накладываем на рассматриваемые нами линии требование
непрерывности. Поэтому, если некоторое соотношение (например, форм}ла (6))
доказано для всех значений величины <]>, кроме Ф = £•, то в силу
непрерывности это соотношение будет заведомо справедливо и при ^ = —л
Замечание 2. Интересно заметить, что соотношение
как вытекает из формулы (6), служит необходимым и достаточным
условием для перпендикулярности касательной МТ к
радиусу-вектору ОМ. Это условие аналогично условию перпендикулярности
касательной к ординате, которое выражается соотношением ^ = 0.
§ 13. Полярные подкасательная и поднормаль
Пусть М есть какая-либо точка плоской линии (/), отнесенной
к некоторому полюсу О. Проведем через этот полюс прямую АВ,
перпендикулярную к радиусу-вектору ОМ. Примем за положительное то
Ш
д
я о
Рис. 29.
направление на прямой АВ, которое укажет вектор ОМ после
поворота его на угол + ^- (на рис. 29 положительное направление имеет
луч О В).
Проведем через точку М касательную МТ и нормаль MR к линии (/).
Пусть Т и R суть точки их пересечения с АВ. Направленный
отрезок ОТ называется полярной подкасателъной (для точки Л/);
направленный отрезок OR—полярной поднормалью.
§ 13. ПОЛЯРНЫЕ ПОД КАСАТЕЛЬНАЯ И ПОДНОРМАЛЬ 61
Легко видеть, что подкасательная ОТ отрицательна, когда угол ф
острый, и положительна, когда угол ф тупой. В соответствии с этим,
в обоих случаях из треугольника ОМТ, где ^Л/ = ф, находим
OT=-rtgty. (1)
Знаки ОТ и OR, как нетрудно видеть, всегда противоположны;
в соответствии с этим, из треугольника MOR, где /^М = ~ — ф, находим
OR = rctgt}. (2)
Подставляя выражение для ctg<]> из формулы (6) предыдущего
параграфа, получаем:
от =-*-£, (3)
Эти формулы приобретают большую наглядность и легко
восстанавливаются в памяти, если сопоставить треугольники ОМТ и OMR с
бесконечно малым треугольником MPN (в котором PN = Ar и ОМ Z^r&y).
Так, приняв треугольники OMR, MPN за подобные и заменив в
пропорции
PN:OR = PM:OM
(которая верна лить приближенно) величины PN и РМ выражениями
dr и rdy, мы получаем пропорцию
d r : OR = rd<p : г
(которая является точной) и из нее находим
Заметим, что отрезок МТ часто называют полярной касательной,
а отрезок MR—полярной нормалью. Этим отрезкам знака приписать
нельзя.
Пример. Найти линию, имеющую постоянную полярную подка-
сательную.
Полагая в формуле (3) ОТ = а, находим
ч dr dy
~r7 = ~a '
Интегрируя, получаем полярное уравнение искомой линии:
О форме этой линии можно получить представление с помощью
следующего приближенного построения (сравни пример 2 § 10).
Проведем (рис. 30) окружность радиуса ОА = а. На ней возьмем
ряд близких точек А, В, С,... и построим точки А', В', С, ... так,
чтобы дуги АА', ВВ\ СС',*... содержали по 90°. Отложив на одном
из лучей, принимаемом за полярную ось, например, на ОА, отрезок ОК
длины г0, соединим прямой линией точку К с А'. Точку L, в которой
А 'К пересекает ОВ, соединим с В'; точку 71/, в которой B'L
пересекает ОС, соединим с С" и т. д. Получим спиральную линию KLM...
62
ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
Если а > О (как на рис. 30), то М неограниченно приближается
к 0 при» неограниченном возрастании ср.
Нашу спиральную линию можно представить более простым
уравнением, если повернуть полярную ось на угол —- . Старый
полярный угол ср будет связан с новым ср соотношением
Подставляя это выражение в (5), найдем
(5а>
Линия, построенная нами, носит название гиперболической спиралит
Рис. 30.
так как уравнение (5а), если бы г и ср были декартовыми
координатами, представляло бы гиперболу.
Упражнения
1. Найти угол между касательной к Архимедовой спирали и радиусом-вектором
в конце второго завитка спирали.
2. При каком повороте радиуса-вектора от начального положения (при
котором точка М находится в полюсе О) касательная к Архимедовой спирали в точке
М составляет угол 45° с радиусом-вектором ОМ?
3. Если все радиусы-векторы кривой удлинить на одну и ту же величину, то
полярные поднормали прежней и новой кривой в соответственных точках равны.
Доказать это.
4. Н*йти линии с постоянной поднормалью.
5. Доказать, что гиперболическая спираль имеет асимптоту, отстоящую от
полюса на расстояние, равное (постоянной) подкасательной этой спирали.
6. Составить уравнение кривой, у которой полярная нормаль MR (черт. 2У)
имеет постоянную величину.
§ 14. ОБ ОПРЕДЕЛЕНИИ КАСАТЕЛЬНОЙ 63
§ 14. Об определении касательной
Если через данную точку М начерченной на бумаге кривой (/)
нам нужно провести касательную, мы обычно поступаем таким
образом: помещаем линейку так, чтобы ее ребро пересекло (/) в двух
точках М19 М2, близких к М. Затем смещаем линейку по Направлению
к М так, чтобы точки Мг и М2 слились с М. Тогда ребро линейка
сольется с искомой касательной.
В соответствии с этим способом построения, мы можем установить
такое определение касательной.
Касательная прямая в точке М линии (I) есть предел, к которому
стремится секущая МХМ2, когда две переменные точки МЛ и М'2,
оставаясь на линии (/), имеют общим пределом точку М.
В § 7 (на стр. 35) мы исходили из иного определения касательной,
так как оно является общелринятым. Но с той точки зрения, которую
мы проводим в настоящей книге, следует предпочесть определение,
данное только что, так как оно в большей степени согласуется с
наглядными представлениями (см. пример, приведенный в конце этого
параграфа).
Ясно, что прямая, являющаяся касательной в смысле определения
§ 7, является касательной и в установленном здесь смысле.
В самом деле, точка М является пределом точки М2 и в том
случае, когда последняя покоится в М. Но тогда секущая МгМ2
обращается в секущую MMlt которая при стремлении Мх к М имеет
пределом касательную в смысле § 7.
Но будет ли секущая MJ\12 иметь один и тот же предел,
независимо от закона, по которому Мг и М2 стремятся к Ml Наглядное
представление, как мы видели, дает на этот вопрос положительный
ответ. Поэтому естественно отнести такие точки, где это свойство на
будет иметь места (если такие существуют) к числу особых. Итак,
мы будем требовать, чтобы для обыкновенной точки М секущая МгМ2
имела единственный предел при стремлении Мг и М2 к М по
произвольному закону.
Этому требованию соответствует некоторое требование,
накладывающееся на вектор-функцию г (и), представляющую радиус-вектор
рассматриваемой линии. Для того чтобы линия г=г(и) имела
касательную в смысле § 7, достаточно, как мы видели, допустить
существование отличной от нуля производной вектор-функции г' (и). Этого
допущения, однако, недостаточно для того, чтобы линия г=г(и)
имела в точке и = и0 касательную в смысле настоящего параграфа.
Теперь достаточным условием существования касательной является
требование,4 чтобы производная г' (и) была в точке и = и0 непрерывна.
Действительно, секущая МгМ2 коллинеарна с вектором
г(и2)-г(иг)
и2 - их
где их и и2 суть значения параметра, отвечающие точкам Мх и М2.
Рассмотрим одну из координат этого вектора, например, его абсциссу
По теореме Лаграижа эта координата равна х (м), где и есть
некоторое число, заключенное между иг и и2. По какому бы закону иг и и^
нп стремились к и, промежуточное значение и стремится к тому же
64
ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
пределу. А так как, по предположению, функция г' (и), а значит,
и я'(и), непрерывна при и = и0, то
Итак,
lim
Аналогичные равенства имеют место для двух других координат и,
следовательно,
независимо от закона, по которому их, и2 стремятся к и0, а так как
по условию г' (гг0) Ф 0, то секущая МХМ2 всегда имеет один и тот же
предел, совпадающий с касательной в смысле § 7.
Рис 31.
Выше было указано, что, допустив только существование
производной вектор-функции, отличной от нуля, мы не обеспечиваем
существования касательной в смысле настоящего параграфа. Касательной может
не существовать, если вектор-функция г' (и) испытывает разрыв. Для
примера возьмем линию у ==х2 sin — (рис. 31), в которую мы включаем и
точку О (х = 0, у=0)т Если Мх совпадает с Оу а Л/2 стремится к О, то
секущая МХМ2 имеет пределом ось абсцисс ОХ; последняя является
касательной в точке О в смысле § 7.
Рассмотрим теперь вспомогательную точку М, стремящуюся к О.
Касательная, проведенная через М, не будет стремиться к пределу; угол,
составляемый ею с ОХ, колеблется между—45° и +45°. Будем
приближать точки Мг и М2 к Л/, одну —справа, а другую —слева, так, чтобы
МХМ2 была параллельна касательной в М. Тогда Мх и М2 будут иметь
пределом О, однако М1М2 не будет иметь предела.
Можно приближать Мх и М2 к О и таким образом, чтобы секущая
МгМ2 имела предел, отличный от оси абсцисс.
Таким образом, точка (0, 0) является особой точкой
рассматриваемой кривой.
§ 15. ДЛИНА ДУГИ
65
Замечание. С точки зрения данного здесь определения
касательной линия у = хг sin — в точке (0, 0) не имеет Е^асательной; с
точки зрения общепринятого определения (§ 7) касательная существует.
Таким образом, определение § 7 носит более общий характер. Эта
общность представляет несомненное его преимущество, если под «линией»
понимать геометрический образ некоторого уравнения. * Тогда
необычное для наглядного представления поведение «линий» приобретает
большой интерес. Если же, как мы это делаем, под «линией» понимать
такой геометрический объект, прообразом которого являются известные
физические объекты, то предпочтительно считать, что точка (0, 0)
линии, заданной уравнением у = х2 sin — , является особой.
§ 15. Длина дуги
Понятие о длине кривой линии наравне с понятием о длине
прямой линии принадлежит к числу первейших представлений человека.
Как мы знаем из элементарной геометрии, понятие о длине
прямолинейного 01 резка вводится в геометрию как
начальное, без всякого определения. Сравнительно
недавно выяснилось, что понятие длины дуги
кривой линии требует определения, и мы
ниже выясним, почему возникает такая
потребность; пока же мы выведем формулу для
определения длины дуги, опираясь на наглядные
представления, которые нам дает
повседневный опыт и в истинности которых у
непредубежденного читателя вряд ли возникнут какие-
либо сомнения.
Прежде всего, представляется ясным, что
если криволинейную дугу АВ, длину которой
мы ищем, разбить на п частей AAlf АгА2,
А2А3, .. ., А^гВ (рис. 32), то длина дуги АВ
окажется равной сумме длин п дуг AAlf АХА2,
и т. д.
Будем неограниченно увеличивать число п
частей, на которые мы разбиваем дугу АВ. Закон выбора точек деления
может быть каким угодно, лишь бы только длины всех частей А^11+1
(А0 = А) стремились к нулю (т. е. длина наибольшей части должна быть
бесконечно малой). Наглядное представление показывает, что при этом
длина какой-либо частичной дуги A(AiJrl становится приближенно
равной длине ]/ Arf хорды этой дуги и что степень точности этого
приближения тем больше, чем дуга меньше. В самом деле, исходя именно
из этого убеждения, мы измеряем шагами длину криволинейной
тропинки, промеряем с помощью масштаба длину нанесенной на карту реки
и т. д. С другой стороны, выражение ]/Дг| приближенно равно
выражению
\д
А2АЯ,
Б
Рис. 32.
так что
М. Я. Выгодский
i/i,
(1)
66 ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
Значит, длина дуги АВ должна приближенно выражаться суммой
п-1
1=0
и степень точности этого выражения должна быть тем большей, чем
меньше д^ги AiAi+1. Если это так, то длина дуги АВ есть предел
выражения (1а), а этот предел есть не что иное, как интеграл
"в
\{/[ГЩЫп, (2)
"А
нижним пределом которого является значение иА параметра иу
соответствующее началу А дуги АВ, а верхним—значение ив,
соответствующее концу В этой дуги. Если фиксировать начало дуги, т. е.
значение параметра иА = и0, а конец дуги непрерывно изменять, т. е.
в качестве верхнего предела взять переменную величину параметра и,
то, обозначая переменную длину дуги через s, мы найдем
(3)
«о
Согласно основной теореме исчисления бесконечно малых,
дифференциал функции s (и) равен подинтегральному выражению, т. е.
ds=\/'[r7Ju)'Ydu. (4)
Сравнив этот результат с формулой (1), мы видим, что бесконечно
малая хорда, а значит, и бесконечно малая дуга кривой линии,
эквивалентна дифференциалу длины дуги. Поэтому величину ds называют
также «элементом дуги».
В прямоугольных координатах формулы (3) и (4) принимают вид
*'(и)]1 da, (За)
«О
ds = f/[x' (u)Y + [y' (u)l + [z' (и)]Ча = Ydx* + dy* + dz*. (4a)
Сравнение формулы (4а) с формулой (3) § 8 (стр. 42) показывает, что
косинусы углов, образуемых линией ds с осями координат,
представляются формулами
dr, о dy dz
cosp ^ сову а. (5)
Они выражают тот очевидный геометрический факт, что проекции
элемента дуги на координатные оси суть дифференциалы
соответствующих координат.
Мы видим, что определение длины дуги сводится к нахождению
элемента дуги, после чего остается выполнить интегрирование. Как
показывают нижеприводимые примеры, элемент дуги можно находить
как аналитически (если исходить из уравнения линии), так
синтетически (если исходить из внутренних геометрических свойств линии).
§ 15. ДЛИНА ДУГИ
67
Пример 1. Найдем длииу дуги винтовой линии. Запишем ее
уравнение в виде
# = acosw, г/= a sin w, z — Ьи
и за начало отсчета примем точку А(и = 0)\ тогда имеем
ds =
s =
= Ya^V du,
du = J/V
Геометрически этот результат вытекает из того, что искомая
длина дуги равна длине отрезка АВ (рис. 6 на стр. 28), наложившего^я
на дугу винтовой линии при
навертывании плоскости на цилиндр.
Но АВ = \/ AD^DB'; AD = аи
(так как AD навертывается на
дугу окружности с центральным
углом u); DB—bUj так что
Пример 2. Эвольвентой (рао-
верткой) окружности называется
линия, описываемая концом М
натянутой нити, сматываемой с
круглой катушки (или
наматываемой на катушку; в последнем
случае точка М движется по той
же линии в обратном
направлении). Нить предполагается
нерастяжимой.
Если освободи1ь это
определение от содержащихся в нем
механических условий, то
эвольвенту окружности можно
определить следующим построением: йа
окружности радиуса а выбираем
начальную точку А (рис. Зо); из
всех точек В окружности
проводим касательные ВМ; на
касательных откладываем в
направлении дуги ВА отрезки ВМ,
равные дугам В А. Место точек М есть эвольвента окружности. Она
имеет форму спирали, выходящей из точки А по направлению
продолжения радиуса ОА.
Приняв за параметр угол и = /_АОВ и за начало отсчета дуг
точку А, найдем длину дуги s эвольвенты окружности.
Пусть В и В1 — бесконечно близкие точки окружности, М и Мг —
соответствующие точки ее эвольвенты и С —точка пересечения ВМ и
и ВХМХ. Чтобы найти ds^MMl7 используем треугольник СММХ, в
котором, как усматривается из чертежа, /^Мх эквивалентен прямому.
Докажем это.
5*
Рис. 33.
68 ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
Найдем разность сторон СМ — СМХ. Мы имеем
: С В + ВМ,
Г1 = В1МХ-В1С.
Следовательно,
СМ—СМХ = (СВ + ВХС) - {BXMX - ВМ) =
== СВ + ВХС — (АВХ — АВ) = С В + ВХС — ВВХ =
du i
или (теорема 1 § 4, стр. 17)
СМ-СМ^ « 2а • { (у)' - ^
Отложив на СЛ/ отрезок CD = CM1 и соединив Z> и Л/х, получим
треугольник MXMD, в котором
и
/)М1 = 2СЖ! sin ^ « CM, du.
Следовательно, отношение г-— ^ jz ^- du2 бесконечно мало, а так
как
sin MMJ) __ DM
sin MxMZ) "~ Щ '
то величина 81пЛ/Л/х1) бесконечно мала. Значит, острый угол MMYD
также бесконечно мал.
Но мы имеем
ZCM1M= Z.CM.D+ /_MMXD = 90° -J±+/_MMJ).
Следовательно,
Z. CMXM % 90°,
что и утверждалось.
Теперь находим (теорема 4 § 4)
MM, ^ CMX tg dw ^ (5^^! — 5ХС) tg du.
Но отрезок Z?jC бесконечно мал, tgdu^du и ВХМХ = АВХ~
= а (м + ^w) ^ а«. Поэтому
так что
ds = aw du,
откуда
s = \ awc?M = у «'t'2. (6)
о
Геометрический смысл этой формулы, как легко видеть, состоит
в том, что прямоугольник, построенный на спрямленной дуге AM
эвольвенты и на диаметре 2а окружности, равновелик квадрату,
построенному на спрямленной дуге АВ окружности.
§ 15. ДЛИНА ДУГИ
69
Замечание. Формулу (6) мы вывели со всей строгостью, чом
я вызваны были некоторые длинноты рассуждения. Притти к этой
формуле можно гораздо про-
ще, если, пренебрегая малыми
высшего порядка, рассмотреть
вместо треугольника СММг
треугольник ВХММХ и
считать, что МВ1 = МВ + ВВ1, а
также что </В1 = /_С.
Формула (6) получается тогда
сразу.
При некотором навыке в
подобных случаях заранее
видно, законно ли заменить одну
фигуру другой; а после того
как результат получен, его уже
нетрудно строго обосновать.
Чтобы получить длину ду-
^ " Рис. 34.
ги AM аналитически, намнун--
но будет составить уравнение эвольвенты окружности. Взяв систему
координат, показанную на рис. 34,
получим
■ a cos и 4- ВМ cos (~ — и j ,
::} <7>
= a sin и — ВМ cos и '
или
х = a cos и + аи sin и,
у = а sin и —аи cos
откуда
dx = аи cos и du, dy = бш sin и d«,
ds=\/r dx2 -t- d?/2 = <ш dw,
s = l^2. (7a)
Пример З. Найдем дг/гг/ циклоиды, описываемую при полном
обороте окружности радиуса а.
Обозначим через <р УГ0Л> на который поворачивается окружность,
когда точка, описывающая циклоиду, переходит из начального
положения О в некоторое положение И (рис.35). Пусть TV ее гь точка
циклоиды, бесконечно близкая к М. Проведем через М прямую,
параллельную основанию циклоиды до пересечения в точке Р с окружностью,
проходящей через N. Легко видеть, что j/ECP = <p,Z.PLN = dy и
NP^adv. n/TATrk М AT
' Как мы доказали в примере 2 § 7, в треугольнике MNP углы М и /V
эквивалентны. Значит,
(8)
70
ГЛ» I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
Что касается угла Р, то он в точности равен углу ECR = <р + -4 >
ибо стороны этих углов взаимно перпендикулярны. Следовательно,
ZP*i<f. (9)
Теперь для MN^ds, применяя теорему синусов и учитывая (8) и (9),
имеем *)
:2asinjrd?. (10)
smM
Следовательно,
cos 2
= 2а sin -|-
При полном обороте производящей окружности <р меняется от 0
до 2тг. Следовательно,
2
? = \ 2a sin -| dp = 8a,
(И)
т.е. длина одной ветви циклоиды равна учетверенному диаметру
производящей окружности.
Аналитически этот результат получим так: в системе координат,
показанной на рис. 35, уравнения
циклоиды будут (пример 2 § 7):
ft^V х — а(у — sin <p), y = a(l — cos<p);
dx = a(l — cos<f)c?9> dy = a sin <
ds2 = a2dy2 [(1 — cos cp)2
= 2a2(l-(
2n
= tf \ ]/2(l —
0
= 2a ^ sin |- dcp-
Рис. 36.
Найдем теперь выражение
элемента дуги плоской линии в полярных
координатах. Проведем в концы бесконечно малой дуги ММХ (рис. 36)
радиусы-векторы ОМ', ОМХ и отложим на ОМХ отрезок OQ = OM = r.
Элемент
Тогда QMt = Ar^dr. Дуга окружности MQ равна
дуги ММ! находим из треугольника MQMх. Прямолинейный отрезок MQ
эквивалентен дуге MQ\ следовательно, MQ z^rdy. Угол MQM1
эквивалентен прямому, так как хорда QM составляет бесконечно малый
угол с касательной в точке Q к дуге QM. Следовательно,
+ dr\
Зна
чит,
(12)
l) Соотношение (10) получается сразу, если рассматривать треугольник MNP
с эквивалентными сторонами МР и NP как равнобедренный.
§ 15. ДЛИНА ДУГИ
71
Эту формулу можно получить аналитически из (4а), подставляя
вместо прямоугольных координат их выражения через полярные:
х = г ccs ср» dx = dr cos 9 — f sin 9 d9,
у = r sin 9, dy = sin 9 dr + r cos 9 a 9,
ds= \/ dx2 ~\-dy2 = }/" (cos 9 dr — r sih 9 dcp)2-i- (sin 9dr + \
Синтетический метод вывода формулы (12) имеет перед аналитическим
то преимущество, что позво- ^^Be^e^
ляет восстановить формулу — —— ^
(12) почти мгновенно,
вообразив соответст вующий чертеж.
Пример 4. Найти дли- ^,
ну дуги логарифмической
спирали по ее поляриому
уравнению г = roek<p.
Имеем
dr = kroek* d9,
\<&№dtf% =
¥2
—e*'i).(13)
Рис. 37.
Используя данное уравнение спирали, можно переписать этот
результат еще так:
s = V±^:(T.2_ri)t (14)
т. е. длина дуги логарифмической спирали пропорциональна разности
радиусов-векторов, проведенных к концам этой дуги.
Синтетически эту задачу можно решить так: из треугольника MNQ
(рис. 37) находим:
' cos ф ^ cos ф "
Но угол 6 между радиусом-вектором логарифмической спирали и ее
касательной имеет (иример 3 § 7) постоянную величину. Поэтому
/2
/2
J СОвф СО8ф ^2 *"*
Эта формула тождественна с (14), так как (§ 7, стр. 39)cti>0 = £
откуда
cos ф = ,. .
72 ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
Фор1^ула (14) показывает, что если один из концов дуги
логарифмической спирали стремится к полюсу (гх —>0), то длина дуги
стремится к конечному пределу -—i— г2 = -^-г . Между тем, спираль
делает бесконечное число завитков около полюса. Таким образом, может
случиться, что линия имеет бесконечное число завитков, а длина ее
остается конечной. Читатель докажет, что длины последовательных
завитков логарифмической спирали образуют геометрическую
прогрессию. Величина —-^г есть сумма этой (бесконечной) прогрессии.
§ 16. Определение понятия «длина дуги»
При выводе формулы (3) § 15, выражающей длину дуги кривой
линии, мы опирались на следующие два свойства, основанных на
наглядном представлении:
1) длина дуги равна сумме длин ее частей,
' 2) длина дуги и длина стягивающей ее хорды эквивалентны.
Если первое свойство обладает столь большой очевидностью, что
оно может показаться не требующим доказательства, то второе, не
столь очевидное, представляется желательным доказать. Однако
всякое доказательство должно опираться или на некоторые предложения,
принятые за аксиомы, или на предложения, прежде выведенные из
аксиом. Но среди аксиом, обычно принимаемых в элементарной
геометрии, ни одна не говорит ничего о длине кривой линии. Поэтому
необходимо либо ввести одну или несколько новых аксиом,
высказывающих некоторые свойства длины дуги, либо ввести такое
определение понятия длины дуги, которое свело бы это понятие к понятиям
более элементарным (для которых аксиомы уже были установлены).
Так, можно принять в качестве аксиом два вышеприведенных
свойства. Опираясь на них, можно, например, доказать (что мы и
сделали в § 15) следующее свойство длины д>ги:
3) Длина дуги есть предел, к которому стремится периметр
вписанной в нее ломаной линии, когда число звеньев неограниченно
возрастает так, что длина наибольшего из звеньев стремится к нулю.
Можно, однако, именно это третье свойство принять за
определение, и тогда свойства 1) и 2) могут быть доказаны.
Обычно свойство 3) вводится не в качестве аксиомы, а в качестве
определения. Различие между этими двумя способами состоит лишь
в том, что в первом случае мы рассматриваем понятие длины кривой
линии как первоначальное, и выражение «длина дуги есть предел...»
понимаем в том смысле, что между двумя величинами, о каждой из
которых мы имеем предварительное понятие, существует определенная
связь. Во втором же случае мы ограничиваемся меньшим числом
первоначальных понятий, и выражение «длина дуги есть предел»
приобретает смысл: «длиной дуги мы условимся называть предел...»
Но, как бы ни вводить третье свойство, в качестве ли определения
или в качестве аксиомы, необходимо еще доказать, что упоминаемый
в этом свойстве предел действительно существует и не зависит от
закона, по которому строится ломаная линия с растущим числом звеньев.
Мы докажем это следующим образом.
Длина звена А{А^± ломаной линии ААХЛ2 ... Ап^ В (рис. 38)
представляется выражением |/(г/+1 — г,)2 = \^(&г()2, так что периметр
§ 16. ОПРЕДЕЛЕНИЕ ПОНЯТИЯ «ДЛИНА ДУГИ»
73
рп равен сумме таких выражений:
Рп=
i=0
Стоящая под знаком суммы величина ]/"(Аг)2 эквивалентна
выражению j/(rfr)2 или, что то же, выражению ]/"г'2 Аи:
Т^ЛГДи,. (1а)
Так как в сумме (1) все слагаемые положительны, то согласно
свойству 5 § 3 из эквивалентности (i а) вытекает эквивалентность1)
Рп^ 2 V\r9 (и,)]1 Аи,.
1=0
Но последняя сумма имеет, как известно, предел, не зависящий от способа
разбиения числового интервала (иАомв)^ т. е. независима от способа
построения ломаной с растущим числом
звеньев. Этот предел есть интеграл
"в
(2)
Следовательно, и сумма (1), дающая
периметр ломаной, при всяком законе ее
построения, имеет один и тот же предел. Он
равен интегралу (2).
Так как предел периметра ломаной есть
длина s дуги АВ, то
(3)
Рис. 38.
иА
Таким образом, мы снова получили формулу (3) § 15. Приняв
свойство 3) за определение длины дуги, мы можем доказать все
остальные свойства длины дуги.
Дадим доказательство свойства 2), т. е. докажем эквивалентность
дуги и хорды. Рассмотрим какую-нибудь дугу АВ. Чтобы упростить
доказательство, предположим (хотя в этом нет необходимости), что
все вписанные ломаные линии, последовательные вершины которых
берутся в направлении возрастания параметра дуги АВ, выпуклы.
Проведем (рис. 38) касательные АС и ВС в концах дуги АВ.
Как видно из чертежа и как нетрудно доказать, исходя из
принятой нами выпуклости вписанных ломаных, ломаная АСВ будет
объемлющей для венкой вписанной ломаной ААХА2 ... 5. Поэтому
периметр рп меньше суммы АС + ВС. С другой стороны, этот
периметр больше длины хорды АВ. Итак, периметр рп содержится в гра-
х) Мы допускаем равномерность эквивалентности (1а) (см. замечание к
свойству 5) § 3).
74
ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
ницах между АВ и АС + СВ. Значит, между этими же границами
содержится и предел вписанной ломаной, т. е. длина s дуги АВ.
Если дуга А В бесконечно мала, то бесконечно малы также углы
С5Л р П CD
CAB=zol и
Следовательно,
р. Проводя высоту CD, имеем
AD = AC cosaczz АС,
BD = ВС совр» ВС.
АВ = AD + BD ^ АС
Итак, сумма АС+ВС эквивалентна хорде ЛЯ. Тем более
эквивалентна хорде АВ дуга АВ, которая по доказанному разнится от хорды
АВ меньше, чем сумма АС + ВС.
Исходя из принятого нами определения, легко доказать и
свойство 1). Предоставляем это читателю.
§ 17. Цепная линия
Цепной линией называется линия провеса однородной нити (или
цепи), подвешенной за оба ее конца.
Исходя из этого определения, найдем уравнение цепной линии
и длину ее дуги. Обозначим через А (рис. 39) низшую точку нити
(вершину цепной линии).
Проходящую через нее
вертикаль, которая, очевидно,
должна служить осью
симметрии цепной линии,
примем за ось ординат.
Направим эту ось вверх. С выбором
начала координат мы
повременим, ибо, как будет видно,
его целесообразнее взять не
в вершине, а на некотором
расстоянии 01 нее снизу.
Рассмотрим
произвольную точку М цепной линии.
Дуга AM — s находится в
равновесии под действием
следующих сил: 1) веса цеп-
ной линии ms, где через т
Рис. 39. обозначается вес единицы
длины нити; 2) натяжении q,
испытываемого нитью в начале дуги А; сила q направлена
горизонтально, а величина ее зависит от длины нити»и расположения
точек подвеса; 3) натяжения р, испытываемого нитью в точке М\
сила направлена по ка< ательной к цепной нити.
Что касается сил натяжения, действующих в других точках
дуги AM, мы их можем не рассматривать, так как в каждой точке
действуют взаимно уравновешивающиеся натяжения, противоположно
направленные. Силу р мы можем разложить на составляющие: вертикальную и
горизонтальную. Горизонтальная составляющая равна р cos а или, в силу
формулы (5) § 15, р -^ ; вертикальная составляющая равна р sin а = р ^
17. ЦЕПНАЯ ЛИНИЯ * 75
Так как дуга AM должна находиться в равновесии, то
горизонтальная составляющая должна уничтожаться силой q, а
вертикальная—силой ms, так что
dx /л.
р-ъ-ъ (1)
/»аг = т«. (2)
Уравнение (1) определит /?, когда будет найдено уравнение
цепной линии. Чтобы найти это уравнение, исключим р из уравнений (1)
и (2). Получим
dy — s a\
где через а обозначена величина — , т. е. длина нити, вес которой
равен натяжению в вершине. Нам остается решить уравнение (3),
в котором величины s, x, у связаны соотношением
ds2 = dx2 + dy2. (4)
Исключив из уравнений (3) и (4) dx, получим
(4а)
■С.
Полагая С—О, мы этим фиксируем выбор начала координат;
именно, из уравнения
3, = /?"+? (5)
мы находим, что вершина А (для нее s — О) должна иметь ординату у = а,
т. е. за ось абсцисс мы берем прямую, лежащую на расстояние а от
вершины книзу (физический смысл длины а мы выше выяснили).
Эта прямая называется директрисой цепной линии.
Уравнение (5) дает выражение длины дуги цепной линии через
ее ординату:
s=}fy2-a2. (6)
Чтобы найти уравнение цепной линии, остается подставить это
выражение в (3). Находим
dy _ У у* - а*
dx a
Интегрируя при выше введенных начальных условиях (в точке
А мы имеем х = 0, у = а), находим
X (* Си XI а 1 V
- = \ J = Arch — ,
а } Vv- — а2 а
О Y у
т. е.
х х
„ а. | Л а
Таково уравнение цепной линии.
76 ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
Теперь, если желательно найти s как функцию абсциссы, достаточно
подставить найденное выражение у в уравнение (6), и мы найдем
х_ _ х_
х е а — е а
s=ashT = a . (8)
Цепная линия обладает следующими замечательными свойствами:
1) Проекция ML ее ординаты на нормаль имеет постоянную
величину, равную расстоянию вершины от директрисы.
Действительно, il/L = г/cos a = у -j-\ согласно (8) и (7) ds = ch — dx =
= — dx. Поэтому
а
МТ — У п (Q\
2-dx
а
2) Проекция МК ординаты на касательную равна длине дуги.
Проще всего это усматривается из треугольника МРК. Принимая
во внимание соотношение (5), имеем
МК2 = МРг - ML2 = у2- а1 = s2.
Это свийство позволяет легко находить дугу цепной линии графически.
Поверхность вращения цепной линии около ее директрисы
называется катеноидом (catena-г-цепь). Она играет важную роль в теории
поверхностей.
Упражнения
1. Найти длину дуги линии
г3 t*
приняв за начало отсчета точку t = l.
2. Доказать, что длина дуги линии х2 = 3у; 2xy = Zzy отсчитываемая от точки
(О, 0, 0), равна с + tj- %3-
3. Найти длину дуги Архимедовой спирали, отсчитываемой от полюса.
4. Найти длину дуги параболы, приняв вершину за начало отсчета.
5. То же для полу кубической параболы.
6. Показать, что кардиоида имеет длину, вчетверо превосходящую диаметр
производящей окружности.
Замечание. Кардиоида есть траектория точки окружности, катящейся
без скольжения по другой окружности того же радиуса. Таким образом она
является частным видом эпициклоиды. Ее можно также рассматривать как улитьу
Паскаля при условии (см. упражнение 9 § И, стр. 50), что постоянный стрезок*
откладываемый на секущей, равен диаметру окружности. Докажите синтетически
тождественность этих определений.
7. Доказать, что дуга циклоиды, отсчитываемая от ее вершины (наивысшая
точка циклоиды), равна* удвоенной хорде, соединяющей точку циклоиды с
наивысшей точкой катящейся окружности.
8. Доказать, что длина дуги конической спирали (пример * § 6)
пропорциональна разности расстояний концов дуги до вершины ьоиуса. Найти длину дуги,
один из концов которой находится в вершине конуса (ср. тот же пример).
9. Прямая линия скользит по винтовой линии с шагом 2nb и по ее оси,
Ь
оставаясь перпендикулярной к оси. Параболоид вращения с параметром — имеет
ту же ось, что винтовая линия. Подвижная прямая пересекает параболоид и
образует на нем линию, проходящую через вершину А. Приняв А за начало отсчета,
§ 18. ДЛИНА ДУГИ КАК ПАРАМЕТР 77
'- ■ — > •=
2 г3
найти длину дуги этой линии. Доказать, что она равна г ■+■ — -^ , где г есть
расстояние конца дуги до оси.
10. Показать, что длина дуги трактрисы, отсчитываемая от вершины, равна
a In — (при обозначениях § 11). Синтетически выражение дифференциала дуги
легко находится из рассмотрения треугольника МРТ и подобного ему бесконечно
малого треугольника со сторонами dx, dy, ds.
§ 18. Длина дуги как параметр
Положение точки на линии, как мы знаем, определяется
значением некоторого параметра. При этом параметр можно выбирать с очень
большой степенью произвола. Так, в примере 2 § 6 мы приняли
за параметр кривой Вивиани долготу ее точки, а могли бы выбрать
за параметр ее широту или ее расстояние до плоскости экватора. Каждый
из выбираемых таким образом параметров будет являться функцией
другого. Обратно, если величина t' связана с параметром t взаимно
однозначной функциональной зависимостью, то и t' можно принять
за параметр, так как заданием значения t' определяется значение t,
а "следовательно, и положение точки на линии.
Среди бесчисленного множества параметров, определяющих
положение точки на некоторой линии, особо важную роль играет длина дуги
этой линии, отсчитываемая от некоторой ее точки, ибо при этом выборе
параметра многие формулы теории кривых значительно упрощаются.
Начало отсчета дуги можно выбрать как угодно, благодаря чему этот
параметр определен в каждой точке линии лишь с точностью до
произвольного постоянного слагаемого. Кроме того, можно откладывать
положительные дуги либо в одну, либо в другую сторону от начала
отсчета, благодаря чему появляется неопределенность в знаке.
Заметим, что, будучи наиболее удобным параметром для общей
теории кривых, длина дуги часто, напротив, оказывается мало удобной,
когда речь идет об исследовании линий частного типа, так как
координаты точки могут не выражаться через длину дуги с помощью
элементарных функций или иметь очень сложное выражение, тогда как
через другие параметры их выражения будут проще.
Для того чтобы найги выражения координат через длину дуги,
когда известны выражения их через иной параметр и:
х = х(и), у = у(и), z = z(u), , (1)
нужно найти дугу s из формулы
s = ^ /*'2 + 2/'2 + *'2 du (2)
«о
и исключить и из формул (1), (2). После этого будем иметь
выражения вида
* = x(s)9 y = y(s), z = z{s). j (3)
В формуле (2) остаются произвольными значения и0 и знак
радикала. Условимся брать его положительным; благодаря этому при
заранее данной параметризации устанавливается положительное
направление дуг; именно оно совпадает тогда с направлением возрастания
параметра и. Но, очевидно, это условие не вносит объективного кри
78 ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
терия, так как при иной параметризации (например, при и = —и)
положительное направление дуг изменится на обратное.
Выбор дуги s в качестве параметра не мешает нам
рассматривать величину s как время, но закон движения теперь перестает быть
произвольным, именно криволинейный путь от начала отсчета до
произвольной точки теперь численно равен времени, т. е. точка движется
по линии с постоянной по абсолютной величине скоростью, численно
равной единице.
Аналитически это легко проверяется такой выкладкой: модуль
скорости равен у (~т~^) =—f=_--, но согласно (3) § 15 \/ds>j = \/ dr\
так что
Итак, вектор скорости (вектор -касательной) теперь является
единичным вектором. Обозначая единичный вектор касательной через t,
имеем
Координатами вектора t являются величины
dx dif n dz //x
-j—= cosa, -t- = cos3, -j—= cosy. (4)
ds ' ds ' ' ds » v '
Из постоянства модуля вектора скорости вытекает1), что вектор
ускорения ~тт = т перпендикулярен к вектору скорости t, т. е.
dr d2r .dt л „ d'-r dt ~
j- -fj = *-J- ={). Вектор -t~y = -г- называется вектором кривизны.
Основание для этого наименования вскоре выяснится.
Пример 1. Уравнения винтовой линии мы нашли (§ 6) в виде
а: = a cos и, у = а&\пи, z = bu. (5)
Длина дуги выражается через параметр и (§ 15, пример 1)
уравнением
s = \/a2-\- Ъ2и.
Если принять з за параметр, уравнения (5) заменятся следующими:
s s bs
х = а cos ~7~ у У = а sin — , z = —z .
Вектор касательной имеет координаты
— а . s , -Х- a s ,
_______ g ЦП ——————;——-; "И _ПГ - COS Ъ Z^
Вектор кривизны имеет координаты
Как легко проверить,
г'2 = х'2-\-у'2 + г'* = 1, r'r" = x'x"-\ y'y"-\ z'z" = 0.
См. стр. 503.
§ 18. ДЛИНА ДУГИ КАК ПАРАМЕТР
79
Пример 2. Если за параметр цепной линии
1 X
(С)
принять дугу, отсчитываемую от вершины в сторону положительных
абсцисс, то получим уравнения
= a Arsh — , у = \/ а2 -\- s2.
(7)
Эти выражения непосредственно даны формулами (8 и (5) § 17. Их
можно получить из формулы (6), если вы-
числить
s=
\
= \ ch — dx = a sh — .
.) а а
(8)
Это дает первое уравнение (7). Второе
получим, исключая х из уравнений (8) и (6).
Вектор скорости имеет координаты
Вектор ускорения имеет координаты
X" = — ■
У =.
Соотношения f = г'2 = 1, W = г'г" = О
очевидны.
Длину дуги особенно удобно принимать за параметр в тех случаях,
когда условие вопроса содержит какие-либо соотношения между
дугами кривой. Рассмотрим, например, следующее важное свойство
пространственных кривых.
На дуге АВ пространственной кривей, как правило, не существует
такой точки, в которой касательная была бы параллельна хорде АВ1),
тогда как для дуги плоской кривой, по крайней мере, одна такая точка
всегда существует. Но для бесконечно малей дуги пространственной
кривой имеет место теорема, распространяющая, хотя и в ослабленной форме,
упомянутое свойство плоских дуг.
Теорема. Касательная, проведенная через середину С бесконечно
малой дуги АВ (рис. 40), образует с секущей АВ бесконечно малый
угол высшего (в общем случае второго) порядка относительно дуги АВ
(и} следовательно, относительно хорды АВ).
Для доказательства обозначим через г, г^, Гв радиусы-векторы
точек С, А и В. Пусть приращение параметра (дуги), соответствующее
переходу из точки С в точку В, есть As. Тогда приращение параметра,
соответствующее переходу из точки С в точку В, есть — As.
J) См., например, рис. 6 на стр. 28. Хорда АС дуги АМС винтовой линии
вертикальна, но на дуге АМС нет ни одной точки с вертикальной касательной.
80 ГЛ. I. КАСАТЕЛЬНАЯ И ДЛИНА ДУГИ КРИВОЙ ЛИНИИ
Предполагая существование третьей производной вектора г (и), имеем
rB = r+ г'As +1 rwAs2 +1 г"As8 + ... (9)
и
rA = r-r'As + ±rnAs*-\r'"Asz+... (10)
Многоточия означают, что опущенное слагаемое имеет порядок,
превышающий порядок последнего члена.
Вектор OL = ГвГ£А, коллинеарный с секущей АВ, выразится с
помощью этих формул следующим образом:
Этот вектор разнится от вектора касательной ОК = г', проведенной
через точку С, на вектор ifZ = -£-r"'Asa + ..., который # общем случае имеет
второй порядок относительно As; порядок будет более высокий только
в том случае, если г"' = 0. Из треугольника LOK находим, что угол
между векторами OL и ОК, т. е. угол между секущей АВ и касательной
в точке С, имеет второй или более высокий порядок,- что и требовалось
доказать.
Доказывается это так же, как выше; только вместо членов
— г"'As* в формулах (9) и (10) берутся члены, порядок которых
-1- 6
выше второго
Упражнения
Приняв дугу за параметр, написать уравнения линий:
1) x = t-{-—- , y = t—^-, s = t2 (начало отсчета взять в точке
О О
2) циклоиды,
3) конической спирали,
4) трактрисы.
ГЛАВА II
СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
§ 19. Три леммы
Эту главу мы начнем с рассмотрения трех лемм, необходимых
для дальнейшего. В них речь идет об условиях, обеспечивающих
бесконечную малость угла между двумя плоскостями и двумя прямыми.
Лемма 1. Если угол <р между прямыми OBlfOB2 (рис. 41) имеет
высший порядок относительно угла (3 между прямыми ОАХ, ОВХ ф<90°),
то угол а между
плоскостями ОАгВх и ОАгВ2 бесконечно
мал.
Доказательство.
Отложим на прямых ОВ1У
ОВ2 равные отрезки
постоянной длины ЦОВ1=ОВ2 = 1)
и спроектируем треугольник
ОВгВ2 на плоскость Р,
перпендикулярную к ОАХ и
проходящую через О. Получим
треугольник ОКгК2, у
которого угол при вершине О
равен а. Сторона ОКХ этого
треугольника равна I sin jj и,
следовательно, имеет тот же
порядок, что угол р.
Сторона же КХК2 не
превосходит отрезка BJB^ эквива- / р
лентного /<р« Так как по
условию ср имеет высший порядок Рис. 41.
относительно (3, то КгК2
имеет высший порядок относительно ОКХ. По теореме синусов имеем
Отсюда видно, что sin а есть бесконечно малая величина. Но угол а
острый, так как лежит против наименьшей стороны
треугольника ОКгК2. Поэтому а имеет пределом нуль (а не 180°).
Доказанная лемма устанавливает, что если сторону ОВХ угла А1ОВ1 = (3
повернуть на угол <р высшего порядка относительно р, то плоскость
угла AfiBx повернется на бесконечно малый угол а. Заметим еще,
что углы АхОВг и АхОВг разнятся на величину, не превосходящую
угла <р, т. е. эти углы эквивалентны.
6 М. Я. Выгодский
82
ГЛ. И. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
Пусть теперь после поворота прямой ОВХ в положение 0В2
происходит еще поворот прямой ОАг в положение ОА2 (рис. 42),
причем угол поворота 9' имеет высший порядок относительно угла
А1ОВ11 а значит, и относительно А1ОВ2. Применяя снова лемму 1,
мы можем утверждать, что плоскость А2ОВ2 составляет бесконечно
малый угол с плоскостью АгОВ2, а значит, и с
плоскостью А1ОВ1. Этим мы доказали следующую
лемму:
Лемма 2. Если прямые ОА2УОВ2 образуют
"* с прямыми ОА19 0Вг соответственно углы высшего
порядка относительно угла между прямыми
ОА1У ОВ1У . то угол между плоскостями АгОВъ
и А2ОВ2 бесконечно мал.
Наконец, по аналогии с этой леммой можно
сформулировать следующее предложение:
Лемма 3. Если плоскости P2fQ2 (рис.43)
образуют с плоскостями Р1У Qx соответственно
углы <р, <р' высшего порядка относительно острого
угла между плоскостями Pi,Qlf то угол между
прямыми Рх X Qxu P2xQ2 (no которым
пересекаются плоскости Р1У Qx и, соответственно, плоско-
сти Р2} Q2) бесконечно мал.
Доказательство. Проведем из какой-
нибудь точки О прямые ОА1У ОВ1У ОА2У ОВ2У соот-
перпендикулярные плоскостям Р1У Qly P2,Q2* Плоскости
будут соответственно перпендикулярны к прямым
X Q2, и лемма 3 непосредственно следует из леммы 2.
ветственно
АхОВи
РгХО
AfiB2
Рис. 43.
Лемма 3 устанавливает, что если две пересекающиеся плоскости Pl,QJ
заменить плоскостями Р2, Q2 образующими с Рг, Qx соответственно углы
высшего порядка относительно угла между Рг и Qly то новые плоскости
пересекутся по прямой, образующей бесконечно малый угол с прежней
линией пересечения.
Установив эти три леммы, мы перейдем к основной теме
настоящей главы.
§ 20. СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ 83
§ 20. Соприкасающаяся плоскость
Всякая материальная линия обладает тем свойством, что
достаточно малый ее кусок можно приближенно принять за прямолинейный
отрезок в юм смысле, что все хорды этого куска практически
сливаются в одну прямую линию. Отвлеченный образ этой прямой линии
есть касательная, которую мы определили (§ 14) как предел секущей,
проходящей через две сближающиеся точки кривой.
Аналогичным образом можно небольшой кусок материальной
пространственной линии принять за кусок плоской кривой. Именно, даже
тогда, когда кусок рассматриваемой линии недостаточно мал для
того, чтобы все его хорды практически умещались на одной прямой,
он может оказаться достаточно малым, чтобы все его хорды
практически умещались в одной плоскости.
Наглядное представление об этом дает следующий опыт. Возьмем
проволочную модель какой-либо пространственной кривой и небольшой
листок бумаги. Прикладывая этот листок к различным участкам
проволочной модели, мы увидим, что его можно уложить на такой участок
модели, который весьма значительно уклоняется от прямолинейной
формы.
Отвлеченный образ такого листка называется соприкасающейся
плоскостью пространственной кривой. В полном соответствии с
вышеуказанным определением касательной прямой, соприкасающуюся
плоскость можно определить следующим образом.
Определение. Соприкасающейся плоскостью Р кривой линии (I)
в данной ее точке М называется предел, к которому стремится
плоскость Р', проведенная через три точки А, В, С, когда эти три точки,
оставаясь на линии (I), имеют общим пределом точку М.
Короче, но менее точно: соприкасающаяся плоскость есть
плоскость, проходящая через три бесконечно близкие точки линии.
Замечание. В соответствии с установленным выше опытным
фактом, мы будем считать правильными точками линии (I) лишь
такие точки, в которых упомянутый предел существует, и притом
независимо от закона стремления точек А, В, С к точке М. Мы
будем рассматривать лишь такие линии, все точки которых, за
исключением, может быть, отдельных (изолированных), являются правильными
в этом смысле. Ниже будет показано, какие требования достаточно
предъявить к вектор-функции г (и) при'аналитическом задании кривой
для того, чтобы было обеспечено существование соприкасающейся
плоскости.
Теорема 1. Соприкасающаяся плоскость в точке М проходит
через касательную в точке М.
Действительно, если три точки А, В, С (рис. 44) стремятся к
точке М, то прямая АВ имеет пределом касательную МТ в точке М,
а плоскость ABC, в которой лежит прямая АВ, имеет пределом
соприкасающуюся плоскость Р в точке М. Следовательно, МТ лежит
в плоскости Р.
Через касательную МТ проходит, кроме соприкасающейся
плоскости, бесчисленное множество плоскостей. Каждую из них можно
назвать касательной плоскостью к кривой (/). Соприкасающуюся
плоскость можно выделить из числа всех касательных плоскостей
следующим определяющим ее свойством:
Теорема 2. Соприкасающаяся плоскость в точке М линии. (/)
есть предел, к которому стремится плоскость, проходящая через
84
ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
касательную МТ в точке М и черев точку N, которая, оставаясь на
линии (I), имеет пределом точку М.
Короче: соприкасающаяся плоскость в точке М есть плоскость,
проходящая через касательную прямую в точке М и через точку N линии,
бесконечно близкую к М.
Рис. 44.
Это свойство становится тотчас же очевидным, если представить
себе касательную МТ, как проходящую через две слившиеся точки М
и М'. Тогда плоскость, проходящая через МТ и N, проходит через
три бесконечно близкие точки М, М', N и,
значит, имеет пределом соприкасающуюся
плоскость.
Это рассуждение, конечно, не является
строгим, так как мы рассматриваем всё же не
три, а только две различные точки. Но
сохраняя ту же идею, можно строго доказать нашу
теорему следующим образом.
Наряду с точкой N, стремящейся к М,
рассмотрим еще одну точку М' (рис. 45),
которая тоже стремится к М. При этом углы М'МТ
и NMT, образуемые хордами ММ' и MN с
касательной, оба бесконечно малы. Установим такой
закон стремления М' к М, при котором угол
М'МТ имеет высший порядок малости
относительно угла NMT.Тогда плоскости NMT и NMM'
будут образовывать бесконечно малый угол
(лемма 1 § 19). Но плоскость NMM' составляет
бесконечно малый угол с соприкасающейся
плоскостью Р (в силу определения
соприкасающейся плоскости). Следовательно, и плоскость
NMT составляет с соприкасающейся плоскостью Р бесконечно малый
угол. Поскольку плоскости NMT и Р имеют общую фиксированную
точку М, плоскость Р есть предел плоскости NMT (§ 5, теорема 2а,
стр. 21), что и требовалось доказать.
Рис. 45.
§ 20. СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ
85
Замечание 1. В нашем нестрогом рассуждении точки М и М'
рассматривались как слившиеся. Рассуждая строго, мы
рассматриваем их раздельно, но берем М' так, что расстояние ММ' имеет
высший порядок относительно расстояния MN.
Замечание 2. Доказанное свойство соприкасающейся плоскости
часто принимается за ее определение. Часто также за определение
соприкасающейся плоскости принимается следующее ее свойство.
Теорема 3. Соприкасающаяся плоскость в точке М линии (/)
есть предел, к которому стремится плоскость, проходящая через
Рис. 4о.
касательную МТ в точке М и параллельная касательной М'Т' в
бесконечно близкой точке М' линии (/).
Доказательство. ПроведехМ через точку М (рис. 46)
нормальную плоскость.(? и спроектируем на нее линию (/). Пусть точка N
кривой (I) спроектируется в точку К проекции (/'). Касательная NU
линии (/) должна спроектироваться в касательную KR линии (/'), ибо
бесконечно близкие точки линии (I) проектируются в бесконечно
близкие точки линии (Г). Соприкасающаяся плоскость в точке М есть,
согласно теореме 2, предел плоскости TMN, следом которой на
плоскости (Q) является секущая МК кривой (/').
Рассмотрим теперь плоскость TMS, проходящую через
касательную МТ и параллельную касательной NU. Ее следом на плоскости (Q)
является некоторая прямая MS, параллельная проекции KR
касательной NV. Так как KR есть касательная, а МК — секущая линии (V),
то угол между KR и МК бесконечно мал. Следовательно, бесконечно
мал и равный ему угол KMS, а значит, и угол между
плоскостями ТМК и TMS (для которого угол KMS является линейным
углом). Следовательно, плоскость TMS имеет тот же предел, что
86 ГЛ. II, СОПУТСТВУЮЩИЙ ТРИЕДР, КРИРИЗНА И КРУЧЕНИЕ
и плоскость ТМК (т. е. плоскость TMN), что и доказывает
теорему.
Для вывода уравнения соприкасающейся плоскости линии (Z),
заданной уравнением г—г (и), нам будет полезна следующая теорема.
Теорема 4. Соприкасающаяся плоскость содержит векторы /(и)
(вектор скорости) и Г" (и) (вектор ускорения).
Доказательство. Что соприкасающаяся плоскость содержит
вектор скорости г' (и), непосредственно следует из теоремы 1. Что
касается вектора ускорения, то он определяется как предел вектора
г'(и+Аи)-г'(и)
Аи
при Аи—>0. Вектор г' (и) коллинеарен с касательной МТ в точке М
(рис. 46), и точно так же вектор г' (и -j- Аи) коллинеарен с
касательной NU в точке N. Значит, вектор г (м + ц)~ г кц) компланарен
с касательными МТ и NU, т. е. лежит в плоскости TMS.
Следовательно, предел этого вектора, т. е. вектор г" (и)> лежит в
соприкасающейся плоскости (которая, как доказано, есть предел плоскости TMS).
Теорема 4, таким образом, доказана.
Предположим теперь, что вектор г" (и) не коллинеарен с
вектором г'(и). Тогда соприкасающаяся плоскость в точке и вполне
определена, так как, согласно теореме 4, она должна содержать векто| ы
г', г". Если R есть радиус-вектор произвольной точки соприкасающейся
плоскости, то векторы R — г, г', г" компланарны, т. е.
(R-r)r'r" = 0. (1)
Это и есть уравнение соприкасающейся плоскости в векторной форме.
В координатной форме оно имеет вид
Х-х Y — y Z-;
х' у' z'
х" у" z"
В случае коллинеарности векторов г', г"', это уравнение обращается
в тождество и потому становится непригодным. Коллинеарность
векторов г', г" имеет место прежде всего тогда, когда рассматриваемая
линия — прямая. Но для прямой линии соприкасающаяся плоскость
и должна по самому определению оставаться неопределенной. Для
кривых же линий коллинеарность векторов скорости и ускорения
может иметь место лишь в исключительных точках.
В самом деле, представляется очевидным, что движение,
ускорение которого всегда имеет то же направление, что скорость (или
противоположное), является прямолинейным. Это подтверждается и
следующим вычислением. Пусть г' и г" всегда коллинеарны. Тогда
г" — \г', где к—некоторая скалярная функция аргумента и. Возьмем
г'
единичный вектор касательной t= _ и найдем производную
= 0. (2)
Подставляя сюда г" = \г^у находим, что /'=0, т. е. направление
линии постоянно. Отсюда ясно, что наша линия —прямая, что
подтверждается и аналитически, ибо из^г = 0 следует t=a, где а —посто-
§ 20. СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ 87
янный вектор; далее, из -^ = t = a следует r=as-\-b, что
представляет параметрическое уравнение прямой линии.
Исключительные точки, в которых векторы г', г" коллинеарны,
называются точками спрямления, так как в окрестности таких точек
кривая в меньшей степени, чем обычно, уклоняется от
прямолинейности. Этому описательному признаку можно придать различные точные
формулировки, например такую: как мы знаем, расстояние от точки N
кривой линии до касательной в бесконечно близкой точке М имеет
(§ 7, стр. 40) в общем случае второй порядок относительно дуги Ля TV; более
высокий порядок (как правило, третий) это расстояние имеет в том
и только в том случае, когда г'хг" = 0, т. е. когда векторы г', г"
коллинеарны. Таким образом, точка спрямления характеризуется тем,
что в ее окрестности кривая, прилегает к своей касательной теснее,
чем обычно. Ниже мы увидим, что и в других отношениях кривая
в точке спрямления уподобляется прямой линии.
Точки спрямления мы должны считать правильными хотя бы
потому, что в противном случае нужно было бы считать, что все
точки прямой линии —неправильные.
Замечание 1. Не следует думать, что в точке спрямления
кривая линия не имеет соприкасающейся плоскости. Но уравнение
соприкасающейся плоскости будет иметь иной вид (см. ниже
упражнение 7 на стр. 96).
Совершенно очевидно, что для любой точки плоской линии
соприкасающаяся плоскость совпадает с плоскостью, в которой эта
линия лежит. Обратно, кривая, соприкасающаяся плоскость которой
постоянна, непременно является плоской. Это следует из того, что
всякая точка М кривой линии лежит в своей соприкасающейся
плоскости, так что если все соприкасающиеся плоскости совпадают с
некоторой постоянной плоскостью Р, то и все точки М принадлежат
этой плоскости.
Замечание 2. Можно доказать, что постоянство плоскости Р
вытекает уже из постоянства ее направления, т. е. что если все
соприкасающиеся плоскости параллельны, то они совпадают, и
данная линия — плоская. Действительно, приведем уравнение (1) к
нормальном)^ виду:
R(r'xr')
/(г'х г")2 l/(r'xr7
По условию, единичный вектор г * г — = а имеет постоянное
значение. Представим свободный член в виде га. Производная от га равна
г'а = —r r r ■ = 0. Следовательно, и свободный член уравнения (3)
У (г' х г")2
имеет постоянную величину, и мы имеем Ra = const, т. е. все точки
кривой (Z) лежат в одной плоскости.
Прежде чем перейти к рассмотрению примеров, установим, какие
требования в случае аналитического задания линии нужно предъявить
к вектор-функции г (и), чтобы обеспечить существование
соприкасающейся плоскости в данной точке М рассматриваемой линии.
Если желательно, чтобы уравнение соприкасающейся плоскости
имело вид (1), то нужно, очевидно, потребовать существования первой
и второй производной вектор-функции и неколлинеарности этих вектор-
88 ГЛ. И. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
функций1). Если дополнительно потребовать еще и непрерывности
вектор-функции г"2), то существование соприкасающейся плоскости
(в смысле принятого нами определения) будет обеспечено.
Действительно, возьмем на линии г=г(и) какие-либо три
последовательные точки А1у А2,А3. Соответствующие значения параметра и
обозначим через и1у и29и3 (н1<гг2<и3), а радиусы-векторы riii^, r(w2),
г(и3) будем для крдткости обозначать через rly r2, г3.
Оставляя пока точки А1У А2У А3 фиксированными, заставим
переменную точку А описывать линию г = г(и). При этом смешанное
произведение {АгА, АХА2У АХА3) должно обращаться в нуль, когда точка А
проходит через точки А1У А2У А3. Иными словами, скалярная функция
? (и) = (г (и) - гг) (г, - гг) (г, - г,) (4)
обращается в нуль при значениях и==и1у и = и2У и = и3 (и1<и2<и3).
По теореме Ролля производная функция <р' (н) должна обращаться в нуль
при некотором значении и, промежуточном между иг и и2 (мы
обозначим это промежуточное значение через ul2)y а также при некотором
значении и = а23У промежуточном между и = и2 и и = и3. Так как
то
r/(tti,)(r,-r1)(r,-r1) = O (5)
и
r*(*t9)(rt-rl)(r9-rl) = Q. (5a)
Геометрически уравнения (5) и (5а) означают, что в некоторой точке
А12У лежащей на ду1е АгА2У и в некоторой точке А23У лежащей на
дуге А2АЗУ касательная параллельна плоскости А1А2А3.
Рассмотрим теперь скалярную функцию
В силу уравнений (5) и (5а) эта функция обращается в нуль при
значениях и = и12 и и = и23. Следовательно, ее производная
f (в) = г* (и) (г,-г,)(г,-г,)
обращается в нуль при некотором значении и = и123У промежуточном
между и = и12 и и = и23:
r"(ul23)(r2-n)(r,-r1) = 0. (6)
Геометрически это означает, что некоторой то^ке А1с>3, принадлежащей
ду1е АХА2АН, вектор ускорения параллелен плоскости А1А2А3 (сравнить
с теоремой 4).
Пусть /? есть радиус-вектор произвольной точки плоскости АХА2А3.
Тогда вектор R—rx лежит в плоскости АгА2А3. Векторы г'12, г[03
1) Это требование вовсе не является необходимым. Так, соприкасающаяся
плоскость безусловно существует в каждой точке плоской линии, между тем как
в неправильных точках этой линии может не существовать не только г"', но
даже г'.
2) Ото требование существенно: без него существование соприкасающейся
плоскости не обеспечено.
§ 20. СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ 89
по доказанному также компланарны с этой плоскостью.
Компланарность векторов R — rl} r'12, r'123 аналитически выражается уравнением
(Я-rj/•;,/•;„ = 0, (6а)
которое, таким образом, представляет уравнение плоскости АгАгА9.
Теперь будем приближать точки АгА2А9 к фиксированной точке М
рассматриваемой линии. Вместе с ними и точки А12, А12з будут
стремиться к точке М'. Вследствие предположенной непрерывности векторов
г\ г" в точке Л/, будем иметь
г' х г" = lim г'12 X г123
(здесь через г', г" мы
обозначаем векторы скорости и
ускорения в фиксированной
точке М). Значит, плоскость
(J?-r)rV = 0 (7)
будет пределом плоскости
АгА2Аа [теорема 5 § 5]. Таким
образом, мы доказали, что
соприкасающаяся плоскость в
точке М существует, и вновь
получили ее з7равнение (1) — (7).
В заключение заметим, что
если за определение
соприкасающейся плоскости взять
свойство, доказанное в теореме 2,
или свойство, доказанное в
теореме 3, то для существования
соприкасающейся плоскости
достаточно допустить
существование векторов г', г" в
рассматриваемой точке М, не
предполагая непрерывности века о- Рис. 47.
pa г".
Пример 1. Найдем соприкасающуюся плоскость винтовой линии.
Соприкасающаяся плоскость в точке М (рис. 47) проходит через
касательную МТ к винтовой линии в точке М и через прямую МТг,
параллельную касательной МХТХ в бесконечно близкой точке Мг. Но
так как все касательные винтовой линии образуют один и тот же
угол y(tgY = —J с плоскостью основания цилиндра, то МТ2 и МТ
суть бесконечно близкие образующие круглого конуса, осью
которого служит образующая MB цилиндра. Искомая соприкасающаяся
плоскость есть касательная плоскость конуса. Значит, она составляет
угол у с плоскостью основания цилиндра и пересекает последнюю
по прямой Л/С, перпендикулярной к образующей конуса МТ и к оси
конуса MB (она же —образующая цилиндра). Значит, прямая МС
направлена по радиусу цилиндрической поверхности. Итак,
соприкасающаяся плоскость Р винтовой линии проходит через касательную МТ
и радиус цилиндрической поверхности МС.
Так как соприкасающаяся плоскость проходит через прямую МС,
перпендикулярную к прямым МТ и MB, то соприкасающаяся
90 ГЛ. П. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
плоскость перпендикулярна к плоскости ТМВ, которая является
касательной плоскостью цилиндрической поверхности.
Подтвердим это аналитически. Из уравнений винтовой линии
# = acosw, y = asinu, z — bu
находим
х'— — a sin и, у' = a cos и, z' = by
х" = — a cos и, у" = a sin и, z" = 0,
и уравнение (2), где теперь можно вместо X, Yy Z ввести обозначения
х, у, z, принимает вид
(х — a cos и) (b sin и) + (у — a sin и) (— b cos и) + (z — bu) а — О,
т. е.
(b sin и • х) — (Ьсо$а • y)-\-az = abu. (8)
Из него видно, что с плоскостью XOY соприкасающаяся плоскость
образует угол а, определяемый из уравнения
а . а
cos а = - -\ -г
YЪ2 sin2 и + б2 cos2 и + а2 ]/ а* + Ь*
Значит, а —постоянная величина, и tga = —. Так как
координаты точки С суть х = 0, 2/ = 0, z = bu, то они удовлетворяют уравнению
(8), и, знач1 т,
соприкасающаяся плоскость
проходит через МС.
Пример 2.
Бинтовой линией общего типа
или линией откоса
называется всякая кривая,
образующая с данной
примой (g) постоянный угол р.
Если через линию
откоса (/) провести
цилиндрическую поверхность S
(рис. 48) с образующими,
параллельными (g), то
линия откоса, как и
обыкновенная винтовая линия,
будет пересекать
образующие под постоянным
углом. Обыкновенная
винтовая линия выделяется
из винтовых линий общего
типа тем, что для нее
цилиндр S — круглый.
Буквально повторив
геометрические
рассуждении предыдущего при-
Рис. 48. мера, найдем, что
соприкасающаяся плоскость Р
линии откоса образует постоянный угол у = 90° — [J (рис. 48) с
перпендикулярным сечением Q поверхности S, и также—что она
перпендикулярна к плоскости ТМВ у проходящей через образующую MB цилин-
§ 20, СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ 91[
дрической поверхности и через касательную МТ к линии откоса. Эта
плоскость есть касательная плоскость цилиндрической поверхности *).
Пример 3. Оси ОХ и OY двух цилиндров с радиусами Ь и а
пересекаются под прямым углом (рис. 49). В пересечении образуются две
замкнутые линии ABCD и A'B'C'D'*). Совокупность этих линий мы
назовем бицилиндрами. Она пересекает плоскость XOY осей
цилиндров в точках А, С, А', С — вершинах бицилиндрики.
Найти угол ф, образуемый соприкасающейся плоскостью линии
ABC в точке А с осью ОХ.
Рис. 49.
Приняв ОХ и OY за оси координат, напишем уравнения
цилиндрических поверхностей
}
Система этих уравнений представляет бицилиндрику. Точка А
бицилилдрики имеет координаты х = а, y = b, z = 0. Систему
уравнений (9) можио представить в параметрической форме бесчисленными
способами; например, ей можно придать вид
х = a cos t, г/ = + j/ Ь2 — а2 sin21, z = a sin t,
x) Общее определение касательной плоскости к произвольной кривой
поверхности будет дано позднее. Здесь можно ограничиться замечанием, что касательная
плоскость цилиндрической поверхности общего вида проходит через ее
образующую и через касательную прямую к какой-либо линии, проведенной на
цилиндрической поверхности через рассматриваемую точку.
а) В случае равенства радиусов а и Ь эти две линии смыкаются (точка В
сливается с точкой D', а точка D с точкой В'\ рис. 49). Дуга BAD вместе с
дугой B'A'D' дает один эллипс; дуга DCB вместе с дугой D'C'B' дает другой эллипс.
Читателю предлагается доказать это.
92 гл. и. сопутствующий триедр, кривизна и кручение
где перед радикалом взят знак плюс, потому что нам нужна только
та ветвь Оицилиндрики, которая проходит через точку А; этой точке
соответствует значение параметра £ = 0.
Теперь остается найти выражения первых и вторых производных
по ty положить в них t = 0 и подставить полученные значения в общее
уравнение (2) соприкасающейся плоскости.
Вычисления будут довольно громоздкими. Чтобы облегчить их,
желательно иметь наиболее симметричные уравнения бицилиндрики.
Но такими являются сами уравнения (9). Поэтому целесообразно
поступить следующим образом.
Представим себе, что координаты токушей точки бицилиндрики
являются функциями времени, но какими именно функциями, мы
не будем фиксировать. Другими словами, не будем наперед
усматривать, по какому закону движется по бицилиндрике ее точка.
Обозначая штрихами дифференцирование по времени, мы получим из (9)
следующие уравнения:
yy'J{ zz' = 0, xx' + zz' = 0,
откуда найдем
х : у' : z1 = yz : zx : — ху.
Величины х', у', z', как и следовало ожидать, определяются лишь
с точностью до множителя, который зависит от закона движения
по линии ABC. Полагая этот множитель равным единице, мы
фиксируем зокон движения и имеем
*' = У*> У' = я*> z'=—xy. (10)
Отсюда
x" = y'z + yz'; y" = z'x + zx'; z"= —x'y — xy',
и, снова используя формулы (10),
x" = z2x — xif; у" = — x2y-\-z2y\ z" = —yzz — x2z.
Уравнение соприкасающейся плоскости в точке А будет
-я У-6 Z
0 - 0 -аЪ
— аЪ2 —a2b 0
т. е.
-0,
-a2 = 0. (11)
Уравнение (11) показывает, что соприкасающаяся плоскость в А
перпендикулярна к вектору (а, —6, 0) и, значит, к прямой СОС, что
дает простой способ построения этой плоскости.
Искомый угол ф найдется из соотношения
sin 6 = —JL=r или
у
В § 7 (стр. 40) было доказано, что если точка М не является
точкой спрямления, то расстояние от точки М' линии, бесконечно близкой
к точке М (рис. 50), до касательной МТ имеет второй порядок
малости относительно хорды ММ', а значит, и относительно дуги ММ'.
Отсюда сейчас же следует, что расстояние Ь от точки М' до любой
плоскости R, проходящей через касательную МТ, имеет второй или
более высокий порядок малости.
20. СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ
93
Действительно, опустив из точки М' перпендикуляр M'Q = Z на
плоскость R и перпендикуляр M'P = d на касательную, имеем
Q где u. = Q
Таким образом, если при приближении точки М' к М угол а не
стремится к нулю, то 8 имеет тот же порядок малости, что и d, т. е.
второй.
Более высокий порядок малости величина S будет иметь в том
« только в том случае, когда угол M'PQ будет бесконечно мал. Но
угол а = M'PQ есть линейный угол двугранного угла, образованного
плоскостью R с плоскостью /?', проходящей через касательную МТ
и бесконечно близкую точку М'. Он стремится к нулю, если R есть
предел плоскости /?', т. е. если R есть соприкасающаяся плоскость.
Рис. 50.
Обратно, если некоторая фиксированная плоскость R, проходящая
через касательную МТ, обладает тем свойством, что бесконечно
близкая точка М' отстоит от нее на расстояние 8, имеющее порядок
малости выше второго, то плоскость R есть соприкасающаяся. Действительно,
д
из равенства sin а =-у заключаем, что sin a, a следовательно, и а есть
бесконечно малая величина, т. е. R есть предел Я' или, что то же,
R есть соприкасающаяся плоскость.
Таким образом получаем следующую теорему:
Теорема 5. Расстояние о точки М' кривой до соприкасающейся
плоскости в бесконечно близкой точке М есть бесконечно малая
величина, имеющая относительно дуги ММ' порядок малости выше второго
(в общем случае третий).
Аналитически эту теорему докажем так.
Как известно из аналитической геометрии, расстояние о от точки
Л/'(г + Аг) до плоскости (/? — г)г'г" = 0 по величине и по знаку
представляется формулой
Y(r'xr"f
Так как по предположению М не есть точка спрямления, то
знаменатель не равен нулю и порядок о равен порядку числителя. И
(Лг)г'г" = (г'&м + -* г" Аи2 + V" ±и3 + ...) /"г" =
94 ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
Таким образом, в общем случае 8 имеет третий порядок малости,
и лишь в случае компланарности векторов г', г" и г"' порядок будет
выше.
Мы получаем теперь следующую картину: плоскость, проходящая
через точку М и не содержащая касательной, отстоит от соседних с М
точек на расстояние первого порядка малости; плоскость, проходящая
через касательную и не совпадающая с соприкасающейся, прилегает
к кривой теснее (Ь имеет второй порядок). Из всех плоскостей,
проходящих через М, теснее всего прилегает к кривой соприкасающаяся
плоскость (8 имеет порядок выше второго). Следовательно, это заме-
Рис. 51.
чательное свойство можно было бы принять за определение
соприкасающейся плоскости.
Посмотрим, как располагается кривая линия относительно
плоскостей указанных трех типов.
Если расстояние 6 имеет первый порядок малости, т. е. главная
его часть пропорциональна Аи, то оно меняет знак при переходе от
Аи < 0 к Аи > 0, т. е. при прохождении через точку М. Следовательно,
вблизи точки М кривая переходит с одной стороны плоскости на
другую; таким образом, плоскость, не проходящая через касательную,
«разрезает» кривую на две части. Если расстояние о имеет второй порядок
малости, то главная часть Ь пропорциональна Аи2 и, следовательно,
сохраняет знак при переходе от отрицательных Aw к положительным.
Значит, плоскость, проходящая через касательную и не совпадающая
с соприкасающейся, не разрезает кривую надвое; кривая располагается
с одной ее стороны (сторона вогнутости), аналогично тому, как
плоская кривая в окрестности ее точки М в общем случае лежит по одну
сторону касательной прямой МТ.
Если же через точку М провести соприкасающуюся плоскость,
то в общем случае (когда г'г"г'" Ф 0) она разрезает кривую надвое, ибо
теперь главная часть 8 пропорциональна Дм3. Чтобы лучше
представить себе расположение кривой относительно соприкасающейся пло-
§ 20. СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ 95
скости, нанесем на круглом цилиндре (рис. 51) винтовую линию и
наклоним цилиндр так, чтобы касательная МТ в рассматриваемой точко
оказалась горизонтально расположенной на уровне глаз, а касательная
плоскость цилиндра в точке М (она на рисунке не изображена)
оказалась вертикальной. Тогда (пример 1 этого параграфа)
соприкасающаяся плоскость (L) будет горизонтальной, и мы увидим, что часть
ВМ винтовой линии лежит выше, а часть МА—ниже плоскости (L).
Так как зрительный образ даст нам (при достаточном удалении
модели от глаз) вертикальную проекцию, то нам покажется, что кривая
AM В переходит с одной стороны касательной прямой на другую,
перегибаясь в точке М. Этого перегиба в точке М мы не будем видеть при
другом расположении цилиндра (перегиб появится в других точках).
Теперь мы можем следующим образом подытожить полученные
нами результаты.
Теорема 6. Пусть точка М линии (I) не является точкой
спрямления (г' X г" Ф 0) и пусть через М проведена плоскость Р.
Если эта плоскость не проходит через касательную МТ, проведенную
через М, то в окрестности точки М линия (I) располагается по обе
стороны от плоскости Р.
Если плоскость Р проходит через касательную МТ, но не является
соприкасающейся плоскостью, то линия (I) располагается по одну сторону
от плоскости Р [сторона вогнутости линии (/)].
Если же плоскость Р является соприкасающейся, то в общем случае
(когда r'r"r"' Ф0) линия (I) располагается по обе стороны плоскости.
В начале этого параграфа мы провели аналогию между
касательной прямой и соприкасающейся плоскостью. Эту аналогию можно
продолжить. Мы доказали (§ 18), что касательная, проведенная через
середину С дуги АВ, составляет бесконечно малый угол высшего
(второго) порядка с секущей АВ. Докажем для соприкасающейся
плоскости аналогичную теорему.
Теорема 7. Соприкасающаяся плоскость, проведенная через
середину С дуги АВ, составляет бесконечно малый угол второго
порядка (относительно АВ) с плоскостью, проведенной через точки А, В, С.
Доказательство проводится тем же методом. Сохраняя обозначения
§ 18 (стр. 79—80), имеем
гв-г = r'As +1 r"As2 + 1 r'"As3 + ±
r-rA = r'As - -J- r"As2 + i r'" As3 - I rIVAs4 + .. -.
Вектор нормали плоскости ABC коллинеарен вектору
Член, содержащий As4, обращается в нуль, так как, во-первых,
взаимно уничтожаются члены — (r'xr'")As4 и j (г'" X г') As* и,
во-вторых, член — (r"xr") As4 равен нулю.
Следовательно, вектор нормали плоскости ABC коллинеарен также
вектору
96 ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
который разнится от вектора нормали г' X г" соприкасающейся
плоскости в точке С на бесконечно малый вектор второго или более
высокого порядка. Отсюда, как в § 18, вытекает, что угол нормали
плоскости ABC и нормали соприкасающейся плоскости в С, т. е. угол
между плоскостью ABC и соприкасающейся плоскостью имеет в общем
случае второй порядок малости.
Уп ражнения
1. Найти уравнение соприкасающейся плоскости линии
2. Найти уравнение солрикасающейся плоскости конической слирали.
3. Найти уравнение соприкасающейся плоскости линии
у2 = 2рх, x'2*=2pz в точке (2р, 2р, 2р).
4. Найти уравнение соприкасающейся плоскости линии пересечения
трехосного эллипсоида с концентрической сферой.
5. Найти угол между соприкасающимися плоскостями кривой Вивиани в двух
ее точках, наиболее удаленных друг от друга.
6. Вывести уравнение соприкасающейся плоскости, исходя из второго ее
определения, т. е. рассматривая ее как предел плоскости, проходящей
через касательную МТ в фиксированной точке М и через точку N, стремядую-
ся к М.
Указание. Уравнение плоскости TMN есть (R-r) г' Дг = 0. Выразить Дг
через векторы г', г", пользуясь формулой Тейлора.
7. Если М есть точка спрямления и если вектор г' не коллинеарен с
вектором г"', то соприкасающаяся плоскость представляется уравнением {R — г) г'г'" =0.
Если же вектор г' коллинеарен с вектором г"', но не коллинеарен с
вектором rlv, то уравнение соприкасающейся плоскости имеет вид (R — /*)r'rlv = 0.
Доказать это,' исходя из второго или третьего определения соприкасаюдейся
плоскости.
Указание. Воспользоваться разложением в строку Тейлора.
§ 21. Сопутствующий триедр
Всякая линия имеет в данной ее точке бесчисленное множество
нормалей, т. е. прямых, перпендикулярных к касательной. Очевидно,
все они лежат в нормальной плоскости. Среди них естественно
выделяются две, именно: нормаль, лежащая в соприкасающейся
плоскости, и нормаль, перпендикулярная к соприкасающейся
плоскости. Первая называется главной нормалью, вторая — бинормалью.
Очевидно, что главную нормаль можно определить так же, как прямую
пересечения соприкасающейся и нормальной плоскостей.
Чтобы эти образы получили полную наглядность, необходимо на
модели (скрученная проволока) научиться находить их «на-глаз».
Следующие примеры также помогут усвоению.
Пример 1. Для плоской кривой главной нормалью является <га,
которая лежит в данной плоскости (в планиметрии она именуется
просто нормалью). Бинормаль есть перпендикуляр к плоскости кривой.
Пример 2. У линии откоса главная нормаль перпендикулярна
к поверхности несущего ее цилиндра1). Это вытекает из того, что
*) Выражение «прямая (I) перпендикулярна к поверхности S» означает, что
в точке пересечения с поверхностью S прямая (Z) перлендикулярна к
касательной плоскости поверхности S.
§ 21. СОПУТСТВУЮЩИЙ ТРИЕДР 97
соприкасающаяся плоскость винтовой линии общего типа (пример 2 § 15)
перпендикулярна к поверхности цилиндра1).
В частности, у винтовой линии (обыкновенной) главная нормаль
(МК на рис. 52) пересекает ось цилиндра ib точке А') под прямым
углом, что дает простое построение главной нормали. Ребра винтовой
лестницы дают наглядный образ главных нормалей винтовой линии.
Бинормаль MR винтовой линии лежит в касательной плоскости
цилиндра, ибо как бинормаль, так и касательная плоскость проходят
через точку М и перпендикулярны к соприкасающейся плоскости.
Бинормаль MR образует с
образующей ЛВ цилиндра постоянный
угол, равный углу у между
касательной и плоскостью основания
цилиндра. Действительно, угол
между MR и АВ равен углу
между соприкасающейся плоскостью
(перпендикулярной к MR) и
плоскостью основания цилиндра
(перпендикулярной к АВ), Но в
примере 1 §20(стр.89) мы видели,
что упомянутые плоскости об] а-
з\ют постоянный угол, равный
углу у между касательной и
плоскостью основания цилиндра.
Касательная, главная
нормаль и бинормаль опред* ляют,
попарно взятые, три взаимно
перпендикулярные плоскости.
Плоскость, проходящая через
касательную и главную нормаль,
есть соприкасающаяся плоскость
(по определению главной
нормали). Плоскость, проходяшая че- Рис. 52.
рез главную нормаль и бинормаль,
есть нормальная плоскость. Плоскость, проходяшая через
касательную и бинормаль, называется спрямляющей плоскостью. Почему она
получила такое название, выяснится в дальнейшем. Для винтовой
линии и вообтце для линии откоса спрямляющая плоскость, очевидно,
совпадает с касательной плоскостью цилиндра.
Схематическое изображение всех упомянутых прямых и плоскостей
дано га рис. 53. *
Трехгранный угол, образованный соприкасающейся, нормальной
и спрямляющей плоскостями, называется сопутствующим (или
подвижным) триедром (трехгранником).
Найдем направления ребер сопутствующего триедра. Мы уже
знаем, что касательная коллинеариа с вектором J*' = j-« Бинормаль по
определению перпендикулярна к соприкасающейся плоскости, а эта
') Это выражение нужно понимать в том же смысле, как предыдущее:
соприкасающаяся плоскость iep шндикулярна к касательной плоскости цилиндрической
поверхности, проведенной через рассматриваемую точку линии откоса.
7 М. Я. Выгодский
98
ГЛ. И. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
плоскость содержит векторы г' и г". Поэтому бинормаль коллинеарна
с вектором г' хг", что видно и из уравнения (1) § 20 (стр. 86). Наконец,
главная нормаль перпендикулярна к касательной и к бинормали.
Поэтому она коллинеарна с вектором (г' хг")хг'. Раскрывая двойное
векторное произведение, находим
(г/хГ)хг"-(г'2)г"-(гУ)г'- (1)
Соответственно с этим, наряду с известными уже уравнениями
нормальной плоскости
(Я_Г)Г' = О (2)
и соприкасающейся плоскости
мы можем написать уравнение спрямляющей плоскости:
(3)
Выражение (1) показывает, что главная нормаль компланарна
с векторами скорости и ускорения, что очевидно и непосредственно,
Рис. 53.
ибо векторы г', г" лежат в соприкасающейся плоскости, в которой
по определению расположена и главная нормаль.
Замечание. Для точек спрямления (§ 20) эти результаты
теряют силу, ибо соприкасающаяся плоскость не определяется
вектором г'хг"(он обращается в нуль). Для изолированных точек
спрямления можно получить иные выражения векторов бинормали и главной
нормали. Если же линия сплошь состоит из точек спрямления, то она—
прямая, и тогда бинормаль и главная нормаль вообще неопределенны.
Согласно теореме 6 § 20 нормальная плоскость в точке Л/, не
являющейся точкой спрямления, разрезает кривую на две части. То же
имеет место в общем случае для соприкасающейся плоскости.
Спрямляющая же плоскость, согласно той же теореме, не разрезает кривую.
Кривая располагается по одну сторону спрямляющей плоскости. Эта
сторона называется стороной вогнутости кривой; противоположная
сторона — стороной выпуклости.
21. СОПУТСТВУЮЩИЙ ТРИЕДР
Однако такое расположение кривой относительно спрямляющей
плоскости необходимо имеет место лишь в том случае, когда
рассматриваемая точка не является точкой спрямления. В случае же
точки спрямления кривая, как правило, располагается по обе стороны
спрямляющей плоскости. Такой исключительный случай изображен
на рис. 54. Здесь мы имеем плоскую линию (L), лежащую в
горизонт альной плоскости Р и имеющую в точке М точку
спрямления. Вертикальная плоскость Q является спрямляющей плоскостью
Рис. 54.
в точке Л/, вертикальная плоскость Л—нормальной плоскостью. Мы
видим, что спрямляющая плоскость разрезает линию (L) в точке М.
Точка кривой, в которой спрямляющаяся плоскость разрезает
ее надвое, называется точкой перегиба. Так как точка перегиба
непременно является точкой спрямления, а кривая линия не может сплошь
состоять из точек спрямления (§ 20), то точки перегиба являются
исключительными. Однако мы не должны их считать
неправильными.
Мы сейчас увидим) что, как правило, точка перегиба является
точкой спрямления, и обратно, точка спрямления будет точкой
перегиба, но и здесь возможны исключения.
Разложив вектор ММ1 = /? — г в ряд
и подставив это разложение в левую часть уравнения (4)
спрямляющей плоскости, мы найдем, что коэффициент при Аи обращается
в нуль:
г' {г" (г'2) - r'(r'r")} = (г'г") (г'2) - г'2 (г'г") = 0,
так что имеем
(5)
7*
100
ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
Теперь видно, что если коэффициент у (г" X г')2 главного члена
разложения (5) не равен нулю, то знак левой части уравнения (4)
остается постояшшм, и линия располагается по одну сторону от
спрямляющей плоскости.
Спрямляющая плоскость может разрезать линию надвое лишь
тогда, когда модуль вектора г" х г' равен нулю, то-есть в точках
спрямления. Если в этом исключительном случае член третьего
порядка в разложении (5) — мы не выписали его — не обращается
в нуль, то рассматриваемая точка спрямления является в то же время
и точкой перегиба. В исключительном случае, когда
разложение (5) начинается с члена четвертого, шестого и т. д. порядка,
рассматриваемая точка, будучи точкой спрямления, не будет точкой
перегиба. Простейшим примером такой точки является точка (0, 0)
плоской кривой г/ = #4.
Выше мы нашли выражения векторов, направленных вдоль ребер
сопутствующего триедра, и уравнения граней сопутствующего триедра
в векторной форме. Дадим теперь уравнения этих ребер и граней
в координатном виде.
Направляющие коэффициенты бинормали суть координаты вектора
В = г' х г" (6)
и имеют вид
(6а)
У'
У
z'
z"
У
и. =
z'
z"
х'
х"
у V =
%'
х"
У'
У"
Уравнения бинормали можно записать в виде
Х- х Y-y Z-z
(6Ь)
Я JJL V
Уравнение соприкасающейся плоскости было дано в § 20.
Направляющие коэффициенты главной нормали суть координаты вектора
N = B xr' = (r' xr") xr' = r'2r" — {r'r")r'y (7)
так что они выражаются формулами
= (х/2 + г/2 + z'2) х" - (х'х" + у'у" + z'z") x',
= (х'2 + у'2 + z'2) у" - (х'х" + у'у" + z'z") y\ } (7а)
L =
и.
У'
V
z'
я
х'
V
z'
Я
х'
|1
У'
I
= (х'2 + у'2 + z'2) z" — {х'х" + у'у" + z'z") z'. J
Если за параметр принята дуга кривой линии, то
г" = х'2 + yt2 + zf2 = l, r'r' = х'х" + у'у" + z'tT = 0
d*x
d*z
Уравнения главной нормали можно записать в виде
Х-х _ Y-y _ Z-z
% ~ -ч ~ с '
а уравнение спрямляющей плоскости — в виде
(7Ь)
(7с)
21. СОПУТСТВУЮЩИЙ ТРИЕДР 101
в частности, если за параметр принять дуг}, имеем
Пример 3. Найдем векторы главной нормали и бинормали
винтовой линии
x = acosu, г/= a sin и, z=bu.
Имеем
%' = —a sin uf у* = а cos uy г' = 6,
х" = — а cos м, г/" = — a sin w, z" = 0.
Вектор бинормали г' X г" имеет координаты
Этот вектор коллинеарен с бинормалью (ср. пример 1 § 20,
стр. 89). Уравнение бинормали можно записать в виде
X — a cos и Y — a sin и Z — Ъи
Ь sin и — Ь cos и а
С осью винтовой линии, т. е. с осью Z, бинормаль образует
угол <р» определяемый из уравнения
1ШИ
т. е. угол <р имеет постоянную величину и равен углу, образуемому
касательной с плоскостью основания цилиндра, что мы уже знаем
из геометрических соображений (пример 2).
Вектор главной нормали N=В X г' имеет координаты
с
) sin и, С =
Z X
Уравнения главной нормали можно записать в виде
X - a cos и У — a sin и Z—hu
cos u "~" sin a ~ О
Этим уравнениям удовлетворяют координаты х = 0, у = 0, z = buf т. е.
главная нормаль пересекает ось винтовой линии; сверх того (так как
С = 0)* она перпендикулярна к оси.
Уравнение спрямляющей плоскости будет
(X — a cos и) cos и + (У — a sin и) sin а = О,
т. е.
X cos и + Y sin и = аг.
Эта плоскость параллельна оси цилиндра и отстоит от центра
основания на расстояние а, равное радиусу цилиндра. Следовательно,
спрямляющая плоскость совпадает с касательной плоскостью цилиндра.
Ребра сопутствующего триедра мы можем принять за оси
координат. Эта система координат, будучи внутренне связана с кривой
линией, является удобнейшей при изучении свойств кривой в
окрестности данной ее точки. Принято в качестве первой оси ^оси абсцисс)
102 ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
брать касательную-, в качестве второй (оси ординат) — главную
нормаль; в качестве третьей (оси апликат) — бинормаль.
Положительное направление на касательной устанавливается по
произволу. Если кривая задана параметрическими уравнениями,
естественно принять за положительное направление то, в котором точка
движется при возрастании параметра (если параметр рассматривать как
время, это будет направление движения). Это соглашение не
обладает, конечно, объективным характером для кривой, взятой
безотносительно к закону движения. В противоположность этому на главной
нормали положительное направление можно выбрать с помощью
объективного признака. Именно, положительное направление главной
нормали выбирается так, чтобы оно указывало сторону вогнутости
кривой. В силу этого соглашения главная нормаль окружности
направляется внутрь окружности; главная нормаль винтовой линии
направлена к ее оси (от М к К на рис. 52).
Наконец, для бинормали положительное направление мы
установим так, чтобы оси подвижного триедра, взятые в указанном порядке
(касательная, главная нормаль, бинормаль), образовывали тройку той же
ориентации, которая принята за ориентацию всех вообще декартовых
систем координат, т. е. той же ориентации, что тройка векторов
a, by ах Ь. Если, как мы будем для определенности предполагать,
эти векторы по определению векторного произведения образуют
правую тройку, то и оси сопутствующего триедра должны будут образов
вывать правую тройку.
Эти соглашения позволяют нам найти выражения для единичных
векторов, указывающих направления ребер сопутствующего триедра.
Так как г' есть вектор касательной, то единичный вектор
касательной— мы будем впредь обозначать его через t—есть
здесь и в дальнейшем перед радикалом подразумевается знак + .
Так как вектор г' указывает направление возрастания параметра,
то, в силу наших соглашений, в формуле (9) нужно взять знак плюс,
и мы имеем
* = -£=. <9а)
Единичный вектор, указывающий положительное направление
главной нормали, обозначается через #. Мы имеем
Формула (7) дает для N* следующее выражение:
др = |Г/2Г„ __ {Г'г»)г'у = (Г'*у г»*_2r/a(r'r")2 + (r'r")2 г'2 =
= (г/2)2 г"2- r/2 (r'r")2 = г/2 {г'2г"2- (гУ)1} - г/2 (г' х г")2.
Отсюда
r'y-(ry-)/- т
/г'2/(/"хг')«
Остается выбрать знак так, чтобы вектор п указывал сторону
вогнутости. Так как в этом случае вектор п и вектор ММ' = /?— г (рис. 55)
§ 21. СОПУТСТВУЮЩИЙ ТРИЕДР
103
указывают одну и ту же сторону (именно сторону вогнутости)
данной кривой, то угол между ними должен быть острый и, следовательно,
n{R-r)>0,
т. е.
±(/?-r){r'V-(r'r")r'}>0
или (ср. формулу (5))
± y (г" х г')2 Аи2 > 0.
Очевидно, это неравенство может иметь место только в том
случае, если в формуле (10) взять знак плюс.
Итак,
г'2г" — (г'г") г'
У^У х г7*)2
(10а)
Мы видим, что вектор N, определённый формулой (7), равнонаправлен
с вектором п.
А
¥
Рис. 55.
Рис. 56.
Заметим, что вектор ускорения г" (который может иметь
различные направления в зависимости от закона движения) всегда
направлен в сторону вогнутости. Геометрически это видно из того, что
Агг = ТТГ (рис. 56) указывает в сторону вогнутости, если Дм > 0, и в
сторону выпуклости, если Дм < 0. Поэтому вектор д- , а значит» и
Л г'
r" = liiii-r—, направлен в сторону вогнутости.
Аналитически это видно из того, что скалярное произведение
r"N= г'~г"2 — (r'r")2 = (г' X г")2 всегда положительно.
Единичный вектор, указывающий положительное направление
бинормали, обозначается через Ь. Мы имеем
~ YB>~~
г' х г"
V (V х г")2
(11)
Выбрать знак нужно так, чтобы тройка t, n, b была правой. Но
вместо вектора t можно взять равпонаправленный с ним вектор г',
а вместо п — вектор г", который, согласно доказанному, указывает
в сторону вогнутости, т. е. лежит в соприкасающейся плоскости
по ту же сторону от касательной прямой, что вектор п. Векторы
г'уг", /? = /•'X г" образуют правую тройку. Поэтому в формуле (11)
104 гл. и. сопутствующий триедр, кривизна и кручение
берем знак плюс и получаем
. г' х г"
Можно было бы найти вектор b и непосредственно, вычисляя
векторное произведение
n-\ ' r'*r>-(r>r*)r'l
Если за параметр принять дугу, то выражение (10а) для п
принимает особенно простой вид:
n=f^- (1Ob)
Мы еще раз убеждаемся, что вектор кривизны г" равнонаправлен
с положительной главной нормалью.
Координаты векторов t, пу Ь суть не что иное, как направляющие
косинусы касательной, главной нормали и бинормали.
Упражнения
1. Найти уравнения бинормали и главной нормали кривой ж = м, у = и*, z = a3
в точке и s=l.
2. То же для кривой ж = * -н — , г/ = г —^- , z = t2 при t = 1.
о о
3. Найти уравнения главной нормали кривой
х* + у* = Юа2, уа + za = 25а2
в точке (а, За, 4а).
4. В каждой точке кривой
х=а(и — sin а), у = а (1 — cos и), z = 4asin —
на главной ее нормали отложен отрезок длины а 1/ 14- sin2 — . Доказать, что
геометрическое место концов этих отрезков есть синусоида.
5. На бинормалях винтовой линии отложены отрезки равной длины; доказать
(аналитически и синтетически), что концы этих отрезков лежат на другой винтовой
линии.
6. Найти выражение вектора бинормали в точке спрямления.
§ 22. Кривизна
Направление кривой линии меняется от точки к точке, тогда как
направление прямой остается постоянным. Чем более резко меняется
направление кривой, тем больше ее «кривизна». Таково содержание
наглядного представления о кривизне, которое мы приобретаем
из повседневного опыта. Оро, повидимому, не поддается более точному
описанию, так как само не является достаточно отчетливым и носит
скорее качественный, чем количественный характер. Чтобы с пользой
ввести это понятие в геометрию, нужно дагь такое определение
кривизны, которое, будучи точным, вместе с тем по возможности
лучше отвечало бы наглядному представлению.
При переходе из точки М1 в бесконечно близкую точку М%
кривой (I) касательная Л/,7\ получает новое направление М2Т2 (рис. 57),
бесконечно мало отличающееся от первоначального. Угол ш,
составляемый касательными МХТХ и М2Т2, называется углом смежности
§ 22. КРИВИГНА 105
касательной. Величина этого угла не может, однако, служить мерой
кривизны линии в точке М, так как если у двух кривых один
и тот же угол смежности соответствует различным длинам дуги ММ1У
то мы не можем приписать им одинаковую кривизну. Естественно
принять за меру кривизны угол смежности, рассчитанный на единицу
длины дуги, т. е. частное -^ . Предел этой величины при As—>0
и принимается за меру кривизны линии.
Мы приходим к следующему определению.
Определение. Кривизна линии (I)
в данной ее точке М есть предел, к
которому стремится отношение углам немеду
касательными в точках Мг, М2 к дуге /п
М1М2, когда точки Мlf M2, оставаясь на
линии (/), стремятся к точке М.
Короче: кривизна есть предел
отношения угла смелености касательных к Рис. 57.
соответствующей дуге.
Кривизну мы будем обозначать через х, так что по определению
x = lim-£-. (1)
Величины As и о> мы считаем положительными, так что кривизна
будет величиной положительной. Можно и нужно ли видоизменить
это определение так, чтобы кривизне приписывать и знак
(положительный или отрицательный)—этот вопрос мы рассмотрим ниже.
Согласно данному выше определению, кривизна прямой линии
во всякой ее точке равна нулю.
Во всякой точке окружности радиуса R кривизна равна 1:Д,
т. е. обратной величине радиуса. В самом деле, угол между
касательными в точках Мх, М2 равен углу Д/1ОМ2 = о) между радиусами,
проведенными к концам дуги МХМ2 окружности. Так как дуга МгМ2
окружности измеряется произведением R&, то -^-= — и, следо-
МХМ%
О) 1 .
вательно, hm „ = -5-»
Замечание 1. Наглядное представление о линии, основанное
на повседневном опыте и наблюдении, показывает, что на не слишком
большом участке линии кривизна ее меняется мало; иными словами,
угол ш приблизительно пропорционален дуге As. В соответствии с этим
в дифференциальной геометрии мы допускаем, что предел отношения
-^- , т. е. кривизна, существует для всех точек линии, за исключением,
может быть, отдельных изолированных ее точек, которые мы будем
считать неправильными. Какие требования, предъявляемые к вектор-
функции r(w), аналитически определяющей линию, обеспечивают
существование кривизны, будет показано в следующем параграфе.
Замечание 2. Отношение -£- может иметь несобственный предел
(lim -£- = 00 J. Мы будем говорить, что в соответствующей точке
кривизна линии бесконечно велика. Нам придется
встречаться с точками такого рода, и тогда мы выясним, как выглядит
106
ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИРНА И КРУЧЕНИЕ
линия в окрестности такой точки. Здесь же заметим, что никакая
линия (имеющая кривизну во всех точках) не может сплошь состоять
из точек, в которых кривизна бесконечно велика. Докажем это для
случаи плоской кривой (гля пространственной кривой доказательство
несколько усложняется, но идею его
можно сохранить).
Пусть О есть начало отсчета дуг
на линии (Z) (рис. 58), ОК—касательная
в точке О, ср — угол между ОК и
касательной МТ в произвольной точке М,
s—длина дуги ОМ.
Так как угол ср не остается
постоянным ни на одном участке кривой линии,
то s является функцией от ср:
Рис. 58. , ч
/Г
Пусть в точке М19 бесконечно близкой к М, величина 9
принимает значение cpt. Из рис. 58 видно, что со = грх—ср = Дер, так что
Если бы для всех точек
линии (I) отношение -г1- имело
бесконечный предел, т. е. если
" As
бы отношение д— стремилось к
нулю, то мы имели бы
тождественно
откуда
s = const.
Это означало бы, что дуга
M^lM2=s2—s1 между любыми
двумя точками линии (I) равна
нулю, что, очевидно, невоз-
можно.
Кривизну линии можно
определить иначе следующим
образом.
Проведем через точки Мх
и М2 (рис. 59) нормальные
плоскости^! и Q2. Они пересекутся
по некоторой прямой А'В',
лежащей в стороне вогнутости
линии (/), и образуют двугран- Рис. 59.
ный угол, равный углу ш.
Поэтому кривизну можно определить также, как предел отношения угла
между бесконечно близкими нормальными плоскостями к
соответствующей дуге кривой.
§ 22. КРИВИЗНА
107
Если рассматриваемая кривая есть окружность, то прямая А'В'
имеет фиксированное положение. Это—ось окружности. Она проходит
через центр окружности, перпендикулярна к ее плоскости и удалена
от любой точки окружности на расстояние, равное радиусу R, т. е.
обратной величине кривизны —.
Для произвольной кривой прямая А'В', конечно, не будет постоянной.
Однако для малого участка кривой положение А'В' меняется мало,
и в пределе мы имеем картину, аналогичную вышеописанной. Именно,
имеет место следующее предложение.
Теорема 1. Если точки Мх, М2 кривой (/) стремятся к точке М,
где кривизна у не равна нулю, то прямая А'В' пересечения нормальных
плоскостей Qlf Q2 имеет пределом прямую АВ, лежащую в нормальной
плоскости Q точки М\ прямая АИ перпендикулярна к соприкасающейся
плоскости Р и пересекает ее в точке С, расположенной на расстоянии
МС =- от точки М со стороны вогнутости линии (/).
Точка С, лежащая, очевидно, на главной нормали, называется
центром кривизны, а длина р = — отрезка МС— радиусом кривизны.
Доказательств о. Из точек Ми М2 (рис. 60) опустим
перпендикуляры MjC1} М2С„ на А'В'. Через С2 проведем C2N \\C1Ml и из точки
М, проведем MXN ± С2А и МХК \\ М2Т2.
Угол М2С21\! есть линейный угол двугранного угла (Ql4 Q2); значит,
он равен углу К М1Т1 = ш. Когда Мх и М2 стремятся к М, плоскость
КМЛТХ имеет пределом соприкасающуюся плоскость Р (§ 20, теорема 3),
а отрезок ClC2 = M1N, будучи проекцией хорды МгМ2 на А'В',
бесконечно мал. Хорда М1М2 образует бесконечно малый угол с МгТх\
значит, и подавно угол а, образуемый МгМ2 с плоскостью ТгМлК или
108 ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
с параллельной ей плоскостью M2NC2, бесконечно мал. Следовательно,
M2N = МХМ2 cos а « МгМ2. (2)
Далее, так как прямые M2N и МгТг образуют бесконечно малые
углы с М1М2, то и между собой они образуют бесконечно малый угол.
Но угол между C2N и M1Tlf равный углу С1М1Т1У равен 90°.
Следовательно, в треугольнике C2NM2 угол N эквивалентен прямому.
Принимая во внимание (2), получаем
т. е.
limNCt=± = f (4)
или
lim MlCl = f. (5)
Проследим теперь, к какому пределу стремятся А'В' и точка Сг.
Для этого заметим, что прямая М1Сг лежит в пересечении плоскостей
Qx и TXMXK. Первая имеет пределом нормальную плоскость Q в точке М>
а вторая—соприкасающуюся плоскость Р.
Значит, прямая МхСг имеет пределом пересечение Р и Q, т. е.
главную нормаль в точке М (теорема 6 § 5). Так как ИтД/1С1 = —,
то точка Сх имеет пределом точку С, лежащую на главной нормали
на расстоянии р = — от М, т. е. Сг стремится к центру кривизны.
Наконец, прямая А'В', перпендикулярная к плоскости МгКгТг и
пересекающая ее в Сг, имеет пределом прямую АВ, перпендикулярную
к Я и пересекающую ее в С, т. е. ось кривизны. Этим теорема 1
доказана.
Замечание 1. Доказательство сохраняет силу для точек,
в которых кривизна х бесконечна. Величина ^ тогда равна нулю, т. е.
центр кривизны С совпадает с точкой М лашии (/).
Замечание 2. К случаю х = 0 теорема 1 неприменима без
дополнительных оговорок. Это видно хотя бы из того, что нормальные
плоскости прямой линии (для всех ее точек х = 0) вовсе не пересекаются
друг с другом. Но представляется очевидным (ниже это будет доказано),
что прямая есть единственная линия, всюду имеющая нулевую
кривизну. Кривые же линии, как мы ниже покажем, могут иметь
нулевою кривизну лишь в точках спрямления. В окрестности такой
точки нормальные плоскости, как правило, пересекаются, и линия
их пересечения А'В', как и в обшем случае, образует бесконечно
малый угол с бинормалью (это доказывается так же, как для общего
случая), но расстояние от точки М до прямой А'В' стремится к
бесконечности, что видно из формулы (3). Таким образом, прямая А'В'
не имеет предела в собственном смысле слова. В этом случае говорит,
что радиус кривизны р «равен бесконечности», и пишут р=оо.
Таким образом, в случае х ф 0 мы имеем
p ^ = oo, (6)
где символ lim обозначает несобственный предел.
§ 22. КРИВИРНА
109
В обоих случаях мы можем теперь пользоваться записью
1
(7)
которая при *Ф 0 имеет точный смысл, а при х = 0 условный.
Итак, достаточно малый участок всякой линии уподобляется
в известном смысле окружности, причем роль оси окружности играет
ось кривизны, а центра окружности—центр кривизны. Эту аналогию
можно продолжить. Проведем через три близкие точки М1У М2, Мг
линии (I) окружность. Поскольку линия (/) в указанном смысле сходна
с окружностью, можно ожидать, что ось и центр этой окружности
D
Рис. 61.
М1М2М3 будут практически совпадать соответственно с осью и
центром кривизны линии (7). Действительно, имеет место следующая
теорема.
Теорема 2. Ось окружности, проходящей через три точки
Mlf М2, М3 линии (/), при стремлении этих точек к фиксированной
точке М, где х Ф 0, имеет пределом ось кривизны АВ, принадлежащую
точке М\ центр окружности М1М2М3 имеет пределом центр
кривизны С 1).
Доказательство. Пусть М19 М2, М3—три последовательные
точки линии (Z), лежащие в плоскости Р'. Проведем (рис. 61) через
середины К, L хорд МХМ2, М2М3 плоскости Q' и Н\ соответственно
перпендикулярные к хордам МХМ2, М2М3. Прямая А'В', по которой
пересекаются плоскости Q' и R', есть ось окружности МгМ2Мъ.
1) ^сли кривизна х в точке М равна нулю, то радиус окружности МхМ^Мг
неограниченно возрастает, когда точки Mlt Mit М3 стремятся к М. Ин ами
словами, центр С окружности М1МгМя удаляется в бесконечность. Читателю
предлагается доказать это vxoa рассуждения остается тот же, что приведен ниже
для общего случая фО)
НО ГЛ. П. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
Точка С" пересечения А'В' с плоскостью Р', проведенной через точки
М19 М2, Л/3, есть центр окружности МхМ2Мг.
Соединим точки К и L. Прямая KL как средняя линия
треугольника МгМгМ9 иараллельна МгМ3 и равна — М1М3, а значит,
эквивалентна ~2 МгМ3. Итак,
^-^МгМ3. (8)
Разделим дуги МХМ29 М2М3 в точках D, Е пополам. Тогда
и в силу (8)
KLzzDE. (10)
Проведем в точках D, Е касательные DT, ES. Угол между ним»
обозначим через о>. Пусть эти касательные образуют с хордами МхМг9
М2М8 соответственно углы а19 а2. Так как D n E суть середины дуг
МгМ2 и M2M8i то по аеореме § 18 (стр. 79) углы ах и а2 имеют
соответственно высший порядок относительно МгМ2 и М2М8.
Следовательно, как а19 так и <х2 имеют высший порядок относительно МгМзГ
а в силу (9)—также относительно DE. Но по условию х Ф 0; поэтому
DE имеет тот же или более высокий порядок, чем о>. Следовательно,
углы ах и а2 имеют высший порядок относительно а>.
Пусть теперь о' есть бесконечно малый угол между
секущими МхМг и М2М3. Тогда угол KCL, который является
линейным углом двугранного угла (Q', R'), также равен о/. Углы о> и со'
разнятся друг от друга, самое большее, на сумму углов ск.1 + а%, т, е*
на величину высшего порядка относительно а>. Таклм образом.
Рассмотрим треугольник CKL. В нем угол L (а также угол К)
эквивалентен прямому, ибо CL перпендикулярна к М2М9, а МгМ%
образует с KL бесконечно малый угол (этот угол равен углу между
секущими M2MS и MXMZ, имеющими общий предел). Поэтому
Следовательно,
с9 к « Ц- (13>
(О
и в силу (10) и (И)
О)
Так как правая часть имеет пределом радиус кривизны р, то
\imC'K = v. (14>
При стремлении точек Ми М2 к пределу М точка К стремится
к тому же пределу, секущая МгМ2 имеет пределом касательную ъМ и,
8 23. ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ КРИВИЗНЫ 111
значит, плоскость Q' имеет пределом нормальную плоскость Q в точке
М. Плоскость же Р' имеет пределом соприкасающуюся плоскость Р1).
Следова1ельно, прямая С К, по которой пересекаются Q' и Р',
имеет пределом пересечение Q и Р, т. е. главную нормаль в точке А/,
а так как WmKC = $, то точка С" имеет пределом точку С на главной
нормали, отстоящую от М на расстояние \>9 т. е. центр кривизны.
Наконец, прямая А'В', которая проходит через точку С" и
перпендикулярна к плоскости Р', будет иметь пределом прямую АВ,
проходящую через центр кривизны С и перпендикулярную к
соприкасающейся плоскости Р, т. е. ось кривизны.
Следствие 1. Радиус окружности, проведенной через точки
Д/\Л/2Л/3 линии (/), стремящиеся к фиксированной точке М, имеет
пределом радиус кривизны \> в точке М.
Действительно, радиус окружности М1М2М3 равен отрезку МгС.
Так как предел М\ есть М, а предел С" есть С, то lim МгС =
=л/с = ?.
Определение 1. Окружность (К) называется пределом
окружности {К'), если плоскость, в которой лежит (К), есть предел
плоскости, в которой лежит (К'), центр окружности (К) есть предел
центра окружности (К') и радиус окружности (К) есть предел радиуса
окружности (К ) 2).
Определение 2. Окружность, проведенная из центра кривизны,
соответствующего точке М радиусом р, равным радиусу кривизны
и лежащая в соприкасающейся плоскости точки М, называется
окружностью (кругом) кривизны в точке М.
Согласно этим определениям и в силу теоремы 2, а также
следствия 1, мы имеем:
'Следствие 2. Круг кривизны линии (I) в точке М есть предел
окружности, которая проводится через три точки Mlf M2, М3 линии (/),
стремящиеся к точке М 3).
Очевидно, круг кривизны имеет в точке М ту же касательную,
что линия (/).
§ 23. Формулы для вычисления кривизны.
Аналитический вывод теорем § 22
В этом и следующем параграфе мы дадим ряд примеров, в
которых кривизна линии может быть легко найдена синтетическим
методом, исходя из заданного способа построения линии. Чтобы
сопоставить синтетический метод с аналитическим, мы параллельно дадим
и аналитическое решение. Для этого выведем предварительно общие
формулы.
Пусть линия (I) определена заданием вектор-функции
1) Эта плоскость, так же как центр и ось кривизны, не изображена на рис. 61
во избежание чрезмерного усложнения чертежа.
2) Можно дать этому определению такую равносильную форму: окружность (К)
называется пределом окружности (#'), если кратчайшее расстояние от любой
фиксированной точки окружности (К) до окружности (К') стремится к нулю. В этой
форме определение сохраняет смысл и для случая, когда (-ЙГ)—прямая линия.
3) Если кривизна линии (I) в точке М равна нулю, то центр С окружности
MLM2MZ при стремлении Mv Мы М3 к М неограниченно удаляется от точки М.
Пределом окружности МХМ2МЪ (см. предыдущее примечание) является тогда
касательная прямая линии (/) в точке М. Эту прямую мы будем рассматривать как
(вырожденный) круг кривизны.
112
ГЛ. И. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИРИГЯА И КРУЧЕНИЕ
Пусть а — иг, и = и2 суть переменные значения параметра и, которые
соответствуют точкам М1у М2, стремящимся к точке Л/; постоянное
значение параметра, соответствующее точке Ы, будем обозначать
просто через и. Согласно определению § 22 (стр. 105) кривизна х
в точке М предс!авляется выражением
= lim
"1-»" М,М*
и2-и 1 &
(1)
Здесь со есть угол Т1М1Т/2 (рис. 62) между Еектором касательной
М1Т1 = г'1 и вектором МгТ'2У равным вектору касательной Л/2712 = г'1).
Для вычисления предела (1) заменим величины ш и As
эквивалентными им выражениями.
Так как дуга M1M2 = As эквивалентна хорде МгМ2, то
Если функция г (и) имеет в
точке М непрерывную производную, то
это состжшение можно (см. § 15,
стр. 65) записать так:
r'2 (и) Аи2,
(2)
1'* 1 где Аи = и2 — иг.
Рис 62. Чтобы составить выражение,
эквивалентное о), рассмотрим
параллелограмм, построенный на векторах М1Т1 = г'г и М2Т'2 = г2. Площадь его S
представляется выражением
где Ar' = r'2 — r'1, а так как S = | М1Г11 | М2Т21 sin ш, то
V г? V г?
Так как при стремлении Мг и М2 к М
о) ^ sin о),
и вследствие предполагаемой непрерывности г1 (и)
V ri ^ V Г2 ^ V г >
то из (3) получаем
(3)
(За)
Пользуясь (2) и (За), формулу (1) можно написать в виде
1) Для сокращения мы будем писать, как прежде, г\ вместо г'
г' (w2) и т. п.
), r2 вместо
§ 23. ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ КРИВИЗНЫ ИЗ
Предполагая, что функция г (и) имеет непрерывную вторую
производную, т. е. что г' (и) обладает непрерывной первой производной, получим
отсюда:
У[г'(и)хг*(и)]* (..
W^W * ()
Это и есть искомая формула для кривизны линии (Z).
Эту важную формулу можно упростить, если за параметр взять
дугу. Тогда г'* = (£У = 1, г'г" = 0 и
(г' х г")2 = r'V"2 — (r'r"Y = г"2,
и формула (4) дает
/^ lSl- (5)
d2r
Теперь ясно, почему вектор -г^ называется вектором кривизны:
модуль этого вектора дает кривизну линии.
В координатной форме кривизна выражается формулой
- х"у'У + (y'z" - z'u'Y + <z'x* -
или, если за параметр взята дуга,
0+Сз?)+Сг0 • (5a)
Так как величина х по условию положительна, то перед радикалами
будем подразумевать знак плюс.
Согласно формуле (4) кривизна обращается в нуль в том и только
в том случае, когда г'хг" = 0, т. е. только в точках спрямления.
Следовательно (§ 20), единственная линия, кривизна которой всюду
равна нулю, есть прямая. Это мы уже отмечали в § 22.
Найдем теперь уравнения оси кривизны. Согласно определению,
(теорема 1 § 22) ось кривизны есть предел прямой А'В' пересечения
нормальных плоскостей, проведенных через точки Мх и Мг, которые
стремятся к точке М.
Сохраняя предыдущие обозначения, мы можем представить
уравнения прямой А'В' в виде
(Я-г)/•' = <), (6)
(Я-г-Дг)(г/+Аг') = 0. (6а)
Если бы плоскости (6) и (6а) имели пределами две различные
плоскости, то линия пересечения последних была бы пределом прямой А'В'
(§ 5, теорема 6).
Но плоскости (6) и (6а) имеют один и тот же предел —
нормальную плоскость в точке М, уравнение которой (/?— r)r' = 0. Поэтому
постараемся заменить нормальную плоскость (6а) какой-либо
плоскостью, тоже принадлежащей пучку с осью А'В', но имеющей другой
предел.
Вычтем из уравнения (6а) уравнение (6) и разность разделим
на Дм. Получим
М. Я. Выгодский
114
ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
Прямая А* В' есть пересечение плоскостей (6) и (7). Так как lim д—=г" (м),
lim ~ = г' (и), lim Дг' = 0, то ось кривизны будет пересечением плоскостей
(Я_Г)Г' = 0, (8)
(tf-r)r"-r'2 = 0, (9)
если, конечно, эти плоскости не параллельны, т. е. если векторы г',
г" не коллинеарны. А в этом случае линия (/) имеет в точке М
соприкасающуюся плоскость, уравнение которой есть
(Л-г)гУ = 0. (10)
Из уравнений (8), (9), (10) мы можем найти центр кривизны С.
Действительно, он является по определению точкой пересечения оси
кривизны и соприкасающейся плоскости. Поэтому его радиус-вектор
R~rc удовлетворяет всем трем уравнениям (8), (9), (10), которые
в координатной форме имеют вид
(X — х) х' + (У — у) у' + (Z — z) z = 0, (8а)
0, (9а)
0. (10а)
(Х-х)
xfz*
Р-У)
z"x"
+ (Z-z)
x'y'
x"y"
Из этих уравнений можно найти X — х, Y—yf Z — z, а затем X, Y, Z.
Вектор /?—г, определяемый из уравнений (8), (9), (10), имеет
началом точку М, а концом — точку С. Согласно определению, радиус
кривизны равен модулю этого вектора, так что мы найдем радиус
кривизны р из формулы
? = V(R- r)\ ' (И)
где /?-—г удовлетворяет уравнениям (8), (9), (10).
Намеченные здесь вычисления мы выполним легче всего, если
привлечем геометрические соображения. Именно, уравнения (8) и (10)
показывают, что вектор R — г перпендикулярен к векторам
касательной г' и бинормали г' X г". Следовательно, он лежит на главной
нормали, т. е. коллинеарен с двойным векторным произведением
(г' X г") X г':
If —г = р(г'хг")хг'. (12)
или
Я-г^Нг'1/-*-(/•>")/•'}. (13)
Неизвестный числовой множитель р определим из уравнения (9),
которое по подстановке вместо R—r его выражения (12) или (13) дает
г'2 = p. {r1 V"2-(r'r")2}=l* (г' х г")\
откуда
Следовательно,
R~r = {р£ру (г' х г") хг'= jpg-.-p {г'V - (г'г") г'} (14)
S 23. ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ КРИВИЗНЫ 115
или
rc = /?=r+F^]I{r'V-(rV')r'}. (15)
Формулы (11) и (14) дают для радиуса кривизны выражение
т. e.
fl/"/172)3
Сравнив эту формулу с формулой (4), находим
(16а)
т. е. радиус кривизны имеет величину, обратную кривизне, что было
геометрически доказано в § 22.
Формула (16) и формула (10а) § 21
r'*r"-(r'r")r'
п-
V г'* /(/-' х /-V
позволяют придать формуле (15) простой вид:
гс = г + \>п. (15а)
Геометрический смысл формулы (15а) состоит в том, что центр
кривизны С лежит на главной нормали на расстоянии р = — от
точки М со стороны вогнутости линии (/) (в эту сторону по нашему
соглашению направлен единичный вектор п). Этот резулыат вместе
с формулами (Ь) и (9) исчерпывает содержание теоремы 1 § 22.
Аналитическое доказательство теоремы 2 § 22 мы предла'аем
провести читателю, пользуясь указаниями, данными в упражнении 6
(стр. 119).
Если за параметр принята дуга, то имеем
Имея выражение (15) для центра кривизны и зная, что ось
кривизны коллинеарна с вектором г' X г", можем написать канонические
уравнения оси кривизны в виде
R-rc =v(r' х г"), (17)
где v — переменный параметр. В координатной форме имеем
где хс, ус, zc определены формулой (15).
Замечание 1. Отметим, что существование кривизны (в смысле
определения § 22) в точке М обеспечивается существованием и
непрерывностью второй производной г" (а) в точке М, но не
обеспечивается, если г" (и) в точке М разрывна. М^кно понятие кривизны
определить в более узком смысле, заставив точку М% совпадать с фиксиро-
8*
116 ГЛ. И. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
ванной точкой Л/. Тогда переменной остается только точка М19
стремящаяся к Му и тогда существование кривизны не требует
непрерывности г" (и) (ср. § 14).
Замечание 2. Формула (16) для радиуса кривизны была
выведена в предположении, что векторы г' и г" не коллинеарны. В случае,
когда векторы г' и г" коллинеарны, т. е. когда М есть точка
спрямления, наш вывод теряет силу, а в формуле (16) появляется нуль в
знаменателе, так что формально мы приходим к соотношению
р = оо. (1бЬ)
Это соотношение, если его понимать в смысле, установленном в
замечании 2 к теореме 1 § 22 (стр. 108), верно.
В самом деле, при коллинеарности векторов г' и г" мы, в силу
формулы (4), имеем х = 0, а в этом случае, как мы видели в § 22,
расстояние от точки М до прямой А'В' бесконечно велико.
С другой стороны, если точка М' имеет пределом точку
спрямления М, то кривизна х' бесконечно мала и, значит, согласно формуле (16а),
радиус кривизны р' бесконечно велик. Таким образом, соотношение (16Ь)
верно и в том смысле, что при стремлении точки М' к точке
спрямления М радиус кривизны неограниченно возрастает.
(Vr'2)3
Замечание 3. Формула о = ;_ . показывает, что радиус
у(г'хг"У
кривизны в правильной точке М (в ней г' ф 0) не может равняться
нулю, т. е. центр кривизны линии не может лежать на этой линии.
Но если в (неправильной) точке мы имеем г' = 0, то равенство р =0
возможно. Только, конечно, формула (16) становится непригодной как
потому, что в нуль обращаются и числитель и знаменатель, так и
потому, что в неправильной точке не существует вторая производная
Г". Но при весьма общих предположениях можно показать, что если
[t = 0, то имеет место также соотношение
0=lim I/ г7*^8: /[/" (и,) х г" (а,)]2,
так что радиус кривизны в точке Мх стремится к нулю, когда
точка Мх приближается к (неправильной) точке М, для которой р —0.
Поэтому целесообразно условиться, что в такой неправильной
точке кривизна у. бесконечна, и писать
1
X = — = ОО .
р
Примеры таких неправильных точек мы встретим в дальнейшем
(см. пример 7 § 24, стр. 127).
Замечание 4. Обратим внимание на то, что формула (15),
дающая радиус-вектор центра кривизны, не содержит радикалов.
Геометрически этому соответствует тот факт, что центр кривизны имеет
вполне определенное положение, не зависящее от каких-либо
соглашений относительно знаков. Напротив, величина кривизны определена
была только по абсолютному значению. Мы согласились приписывать
ей положительные значения, но ничто не мешало бы приписать
кривизне раз навсегда отрицательное значение.
Возникает вопрос, нельзя ли ввести такое соглашение, которое
приписало бы одним точкам кривой положительную, а другим
отрицательную кривизну. Такое соглашение имело бы смысл, если можно
было бы объективно различать «положительное» и «отрицательное»
8 23. ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ КРИВИЗНЫ 11 7
вращение вектора касательной при переходе от точки М к точке Мг.
Это вращение происходит, как мы знаем, в соприкасающейся плоскости
точки М. Чтобы определить, вращается ли вектор касательной по
часовой стрелке или против нее, нужно непременно указать, с
какой стороны соприкасающейся плоскости должен поместиться
наблюдатель. Но этого нельзя сделать, так как положительное и
отрицательное направления бинормали определяются лишь после того, как
выбрано положительное направление касательной, а это последнее выби-
гается по произволу. Таким образом, геометрически ясно, что
различение двух знаков кривизны для пространственной кривой смысла
иметь не может. Аналитически этому соответствует тот факт, что ни
от одного из двух радикалов, входящих в (4а) или в (5а),
освободиться нельзя.
Пример. Рассмотрим винтовую линию
x = acosu, у = a sin и, z = bu.
Подставляя в выражения (г' X г")2 и г'2 значения координат
векторов г' и г" (пример 3 § 21, стр. 101), находим
г'2 = а2 + Ь\ (г' X г")2 = а2 (а* + б2), (18)
так что
(20)
Эти формулы полезно запомнить. Обратим внимание на то, что
кривизна винтовой линии постоянна, что геометрически очевидно.
Из формулы (20) вытекает р = я-)—> а. Таким образом, центр
кривизны винтовой линии лежит на главной нормали за точкой ее
б2
пересечения с осью цилиндра на расстоянии р—а = — от оси
цилиндра. Ясно, что центр кривизны описывает новую винтовую линию
с тем же ходом 6, -лежащую на цилиндре радиуса — ; в случае о== а
центры кривизны располагаются на том же цилиндре, что и данная
линия, и заполняют винтовую линию, симметричную с данной. Ее
можно пол\чить из данной, повернув цилиндр около оси на 180°.
Обозначив в обшем случае через а' радиус цилиндра, на котором
располагаются центры кривизны, имеем
Симметрия этой формулы показывает, что каждая из двух винтовых
линий является местом центров кривизны для другой.
Координаты центра кривизны найдем по формуле (15):
(21)
хс = a cos и + fl2 (a^+b*) (g2 + Ь2) (~ а CQS u )=
= a cos и ( 1 — ^--t— Л = cos и = a' cos (к-j-u),
b2
- s
zc = bu = z,
ус— — -
И8 ГЛ. И. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУ ЧЕНИЕ
что можно еще проще получить из найденных только что
геометрических фактов,
Канонические уравнения оси кривизны получим из (17а):
Ь2 Ъ2
X cosw Y-\—sin u
a a Zj — ou
Ъ sin и — Ъ cos и а
Пользуясь формулами (8а) и (9а), мы могли бы написать уравнения
оси кривизны в виде
— (X — acostt)esina + (r — a smu)acosu-\-(Z — bu)b = O, \ ^o \
— (Х — а cos и) a cos и — (У — a sin и) a sin и = а2 + b2. J
Кривизну винтовой линии можно найти геометрически следующим
образом. Проведя касательную МА (рис. 63) и прямую MB,
параллельную касательной в МХУ
отложим на них равные
отрезки MA = MB = I и
спроектируем эти отрезки на
плоскость основания. В проекции
получим отрезок NC,
касающийся окружности
основания в точке N, и отрезок
ND, параллельный
касательной в точке TV, окружности
основания. Так как
касательные винтовой линии
образуют с плоскостью
основания постоянный угол а, то
Кроме того, так как по
построению прямая АВ
параллельна плоскости
основания, то
CD^AB.
Рис# 63. Наконец, между дугой
ММг винтовой линии и
ее проекцией — дугой окружности NNX — имеет место соотношение
NNX = ММг cos a = A s cos а,
которое усматривается сразу, если развернуть цилиндрическую
поверхность на плоскость.
Угол смежности со винтовой линии выражается так:
а соответствующий угол смежности окружности
CD _ АВ
(О
I cos a'4'/ cos а #
§ 24. КРИВИЗНА ПЛОСКОЙ КРИЕОЙ 119
Для кривизны винтовой линии находим
_АВ
для кривизны окружности имеем
АВ
I cos Jt As cos a
Следовательно,
x cos2a =
Ho x' = — . Поэтому
Упра жн ения
Найти радиус, центр и ось кривизны следующих линий:
1. x = acos3u, г/= a sin3 u, z = acos2^.
2. х* = 2pz, y2 = 2qz.
3. x2- у2 -f z2 = a2, г/2-(2ж + 2)я = 0 в точке (a, a, a).
4. Доказать, что радиус кривизны конической спирали пропорционален
расстоянию точки спирали до оси конуса.
5. Найти радиус кривизны бицилиндрики в ее вершине (пример 3 § 20, стр. 91).
6. Доказать аналитически, что центр С окружности, проходящей через
три точки Мlf M2, М3 линии (/), стремящиеся к точке М, имеет пределом центр
кривизны С линии (I) в точке М, а радиус р' окружности МЛМЛМ9 имеет
пределом радиус кривизны р.
Указание. Так как центр С лежит в одной плоскости с М19 М2, ikf3, то
его радиус-вектор />' удовлетворяет уравнению (7) § 20, т. е
Так как точки Н„ М2, Мг отстоят от С на расстояние р', то функция
<гс,-г(|0У-рч (Ь)
обращается в нуль при u~ult m = w2, m = w3. Рассуждая так, как в § 20 при выводе
формулы (7), найдем, что
(гс->-ш) ri2 = 0' (с>
г'^ = 0, (d)
где Г(12у г' суть значения г (и), г'(и), соответствующие некоторому значению
<* = м12, промежуточному между и — щ и и = и2 (вообще и^у Ф и12). Аналогичный
смысл имеют значения r(lfl), г[тУ r'(l2s). "
Обозначив через Ct предел С, а через pj- предел р', находим из (а), (с), (а)
три уравнения, отличающиеся от (8), (9), (10) лишь заменой R и р на гС1 и р1#
Поэтому rCj=rc. Из уравнения (Ь) находим pi = p.
§ 24. Кривизна плоской кривой
Все выводы предыдущих параграфов, разумеется, сохраняют силу
и для плоских кривых; однако для последних имеют место важные
специальные свойства. Так, для плоской кривой можно ввести
соглашение относительно знака кривизны, чего, как мы видели, для
пространственной кривой сделать нельзя. Пространство делится плоскостью
кривой на две части, и можно считать, что наблюдатель постоянно
пребывает в одной из них; для пространственной кривой вследствие
переменности ее соприкасающейся плоскости этого сделать нельзя.
1.20
ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
Пусть на некоторой плоскости дана кривая А В (рис. 64).
Установим на ней направление движения, например от А к В; тогда вектор
скорости на участке АК вращается в одном направлении (по часовой
стрелке), а на участке KB —в противоположном. При перемене
направления движения или при переходе наблюдателя на другую сторону
плоскости направление вращения касательной меняется на обратное.
Однако указанная противоположность между участками АК и KB
Рис. 64.
сохраняется. Это позволяет приписать кривизне на одном из участков
положительный, на другом —отрицательный знак. Ясно, что объктив-
ного смысла каждый из этих знаков сам но себе иметь не может. Но
различие знаков имеет объективный характер. Так, между линией
Рис. 65.
Рис. 66.
на рис. 64 и линией на рис. 65 существует объективное различие,
состоящее в том, что в первом случае знак кривизны меняется, а во
втором он остается неизменным.
Условимся считать кривизну положительной, если вращение
вектора касательной (при заданном направлении движения и заданном
положении наблюдателя) происходит против часовой стрелки, и
отрицательной, если вращение происходит по часовой стрелке. Тогда для
§ 24. КРИВИЗНА ПЛОСКОЙ КРИВОЙ
121
точки, в которой кривизна положительна, вектор г' X Дг' (рис. 66)
указывает сторону наблюдателя; если кривизна отрицательна, он
указывает противоположную сторону.
Если векторы г' и г" неколлинеарны, то вектор
г' xdr' = (r' х rn)du
составляет главную часть вектора г' X А/*'; значит, векторы г' X Дг'
и г' X г" указывают одну и ту же сторону той плоскости, в
которой расположена данная кривая. Поэтому кривизна плоской кривой
выразится формулой
± Vjr'xr")2
ур*
(1)
где нужно взять знак плюс, если вектор г' X г" направлен в сторону
наблюдателя, и знак минус —в противном случае.
Если ввести (правую) декартову систему координат и условиться,
что наблюдатель помещается всегда со стороны положительных апли-
кат, то кривизна положительна в
случае, когда х' у" — х" у' > 0, а так как для
плоской кривой (лежащей в плоскости
. = 0)
(г' х г")2 = (х'у" — х"у')*, г'1 = х'2 + у'\
то формула (1) принимает вид
x= -J-
(2)
и в силу соглашения о знаке кривизны
имеем
(3)
Рис. 67.
Деиствительно, по абсолютной величине выражения (2) и (3) равны,
а знак левой части формулы (3) соответствует нашему соглашению
о знаке кривизны.
Пример 1. Зададим окружность параметрическими уравнениями
х = a cos и, у —a sin и.
Возрастанию аргумента и = /_ АОМ соответствует движение
точки М против часовой стрелки (рис. 67). Касательная при этом вращается
также против часовой стролки. Следовательно, кривизна, вычисленная
по формуле (3), должна быть положительной. Действительно,
*x' = —'jsinu, у' — auosu, я" =—a cos и, у" = — a sin и,
и формула (3) дает
a2 sin2 и 4- a* cos2 a a2 I
Если уравнение окружности взять в виде
x = asmv, y=acosv,
122
ГЛ. П. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
то возрастанию аргумента v = ^/ YOM соответствует вращение по
часовой стрелке, и формула (3) даст
х= •
а
Если в уравнении произвольной плоской кривой за аргумент
принять абсциссу х, то имеем х' = 1, х" = 0, и формула (3) принимает вид
(4)
Знак кривизны совпадает со знаком второй производной.
Кривизна, вычисленная по формуле (4), положительна в том
случае, когда при движении в сторону положительных абсцисс
касательная вращается против часовой
стрелки, т. е. когда кривая обращена
вогнутостью вверх. Вследствие этого
для кривой АВ на рис. 68 кривизна
в точках Мг и М2, вычисленная по
формуле (4), будет положительной,
а кривизна в точках Мл,
М4—отрицательной. Между тем при
непрерывном движении вдоль АВ
кривизна, очевидно, не должна менять
знака. Видимое несоответствие
происходит оттого, что возрастанию х
соответств}ют в точках Мх (на уча-
стке AU) и М2 (на участке UВ)
противоположные направления обхода
линии АВ.
Пример 2. Возьмем уравнение окружности в виде х2 + у2=аг
и примем за параметр х. Имеем х + уу' = 0, откуда
Далее 1 + у'2 + уу" = О, откуда
(5)
(6)
Подставляя (6) в (4), имеем х= — -
Так как
символ \fy2 обозначает положительное число, то мы не можем
написать ]fyz = у, а должны положить \/ уг = \ у |, откуда
х= —
ы
ау '
(7)
При у > 0 имеем х= — i , при у < 0 имеем х = + — . При
формула (7) становится неопределенной1).
х) Разумеется, и в точке у = 0 кривизна окружности х2 + у2=аа равна — по
абсолютной величине. Неопределенность же формулы (7) объясняется тем, что
формула (4) непригодна для точки у « 0; вдесь не существует (конечных)
производных у\ у".
§ 24. КРИВИЗНА ПЛОСКОЙ КРИВОЙ
123
Можно доказать, что если при переходе через точку К кривизна х
плоской кривой меняет знак (см. рис.64 на стр. 120, принимая
значение нуль, то касательная (а значит, и спрямляющая плоскость) в точке К
разрежет кривую. Иными сливами, такая точка есть точка перегиба
(§21, стр. 99). Так как в этом случае х = 0, то точка К есть точка
спрямления. Однако в точке спрямления кривая может лежать и по одну сторону
касательной; тогда кривизна, проходя
через значение нуль, не меняет знака.
Аналитический признак точки
спрямления плоской кривой есть
х'у" — х"у' =
(8)
В случае, когда за параметр принята
абсцисса, это условие принимает вид
У" = 0. (8а)
Рис. 69.
Если через а обозначить угол,
образованный касательной с некоторой
неподвижной прямой (которую можно принять за ось X), то кривиэна
линии по величине и по знаку представится формулой
da
(9)
так как угол w между касательными равен (рис. 69) приращению
угла а.
Нелишне отметить, что для пространственной кривой угол
смежности (о пе есть приращение угла, составляемого касательной с осью X
или какой-либо иной прямой; поэтому для пространственной кривой
кривизну нельзя представить в виде производной угла, составленного
касательной и осью.
Радиус кривизны плоской кривой можно найти по формуле
х'у" -\-х"у'
(10)
При этом ему приписывается тот же знак, что и кривизне.
Центр кривизны находится по формулам, вытекающим из (15) § 23:
Хс=Х-\-
(х'у" -х"
В симметричном виде их можно записать так:
__ s'2-f-У'2 ,
Хс-Х-~х'у"-у'х"У
(11)
Знаки входящих сюда выражений не зависят от какого-либо
соглашения о знаке кривизны.
124
ГЛ. П. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
Пример 3. Кубическая парабола а2у = х* (рис. 70). Имеем
Зх2
йа*х
У ~ а* > У -Р"' Х-
Кривизна меняет знак при переходе через начало координат. В начале
координат х = 0. Линия имеет
здесь точку спрямления,
являющуюся также течкой
перегиба.
Пример 4.
Биквадратная парабола а*у = х* (рис 71).
К
Рис. 70.
0
Рис. 71.
Кривизна ее
(12)
В начале координат
имеем точку спрямления х=0.
Она не является точкой
перегиба, так как знак кривизны
не меняется.
Пример 5. Парабола
у2 = 2рх. Если за
независимую переменную принять у,
имеем
х' = —,
р '
х"
х = — ;
Р*
(13)
Следовательно, парабола
всюду обращена вогыутослыо
в положительную сторону
оси X.
Если за независимую
переменную принять х,имеем
,/ _ Р ,/< — РУ' _ _ t
У --, У -- уъ- уг>
- Р1\У\А
У*
ур
(14)
верхней половины (?/>0)
имеем
г'2
дли нижней половины
(14а»
(14Ь)
В верхней половине выпуклость параболы обращеьа вниз, в
нижней— вверх. При непрерывном движении по параболе знак кривизны
§ 24. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 125
не меняется. В вершине {у — О) кривизна равна — , т. е. радиус
кривизны равен параметру. Наши формулы, в согласии с наглядным
представлением, показывают, что кривизна в вершине имеет наибольшую
величину; при удалении от вершины кривизна стремится к нулю.
При всей простоте вычисления, найденные результаты не обладают
достаточной наглядностью и в силу этого не дают простых
способов построения. Чтобы разыскать такие способы, полезно прибегнуть к
синтетическим приемам. Предварительно установим лемму, полезную
при отыскании радиуса кривизны многих линий.
М
Рис. 72.
Лемма. Если ср (рис. 72) есть полярный угол, ОМ = г —
радиус-вектор кривой, a h = OP — перпендикуляр, опущенный из полюса
на касательную, то дифференциал дуги ds ^ ММг представляется
формулой
ds = r^. (15)
Эта формула вытекает из сравнения двух выражений для площади F
треугольника МОМХ\
F = 1 г (г + Дг) sin Д<р & -1 г2 d<f9
F^
Ее можно также получить из подобных (в пределе) треугольников MMXQ
п МОР.
С помощью этой леммы найдем радиус кривизны р параболы.
Обозначим через а угол MKF между касательной к параболе
в точке М и осью параболы (рис. 73). По известному свойству
параболы угол KMF между касательной и фокальным
радиусом-вектором MF также равен а.
Примем фокус F параболы за полюс, а ось параболы—-за
полярную ось. Тогда полярный угол ср, как внешний угол треугольника KFM,
равен 2а. Поэтому радиус кривизны параболы р = з- равен -jr , и по
формуле (15) находим
126
ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
Отрезки г и h можно построить следующим образом: из точки М
опускаем перпендикуляр MS на директрису параболы TR. Очевидно,
касательная б) дет биссектрисой
угла SMF. Поэтому из
равнобедренного треугольника SMF
находим
= MF = MS.
Итак,
2MS*
(15a>
Чтобы построить отрезок,
равный {,, опустим перпен-
дик)ляр SU на нормаль;
имеем Mlf = SP, и в силу
известной теоремы
планиметрии
IMS*
MU
= 2MR.
Мы получаем: радиус
кривизны параболы равен
удвоенному отрезку нормали от тон-
ки на параболе до
пересечения с ди/ектрисой1).
Аналитическую проверку предоставляем читателю.
В частности, радиус кривизны в вершине параболы равен параметру
Рис. 73.
Пример 6. Логарифмическая спираль (рис. 74). Имеем
х = гоел* cos ср, у = rQek* sin ср,
х' = гоек- (к cos ср — sin ср),
у' = г9ек* (к sin ср + cos ср),
хп = гоеАф (к2 cos ср — 2к sin ср — cos ср),
у" = roe*f (к2 sin ср + 2к cos cp—sin ср),
Г»е У К +
х'у» - х'у'
(16)
Чтобы построить р, проведем нормаль MR. Из прямоугольного
треугольника OMR находим
ОМ ,А» v
(16а)
т. е. радиус кривизны логарифмической спирали равен полярной
нормали (§ 13).
г) На рис. 73 точка С, в которой пересекаются нормали МС, МХС%
проведенные через близкие точки Mlt M, практически может быть принята за центр
кривизны. Мы видим, что МС = 2MR.
§ 24. КРИВИЗНА ПЛОСКОЙ КРИВОЙ
127
Синтетически этот результат получаем сразу, если учтем, что угол ф
между касательной и радиусом-вектором имеет для логарифмической
спирали постоянную величину. Поэтому угол поворота касательной
равен приращению
полярного угла:
Следовательно,
ds ds
На основании доказанной
леммы
_г> _ОМ_*_
р ~~ h ~ MQ"=
Замечание.
Формула (16а) показывает, что
с приближением точки М
к центру ло!арифмической
спирали О радиус кривизны
стремится к нулю, т. е.
кривизна неограниченно
возраст ает (геометрически
это совершенно очевидно).
Если принять за радиус
кривизны в точке О предел, к
которому стремится радиус
кривизны в точке 71/, когда
дуга ОМ стремится к
нулю, то радиус кривизны
в точке Сбудет равен нулю.
Однако в смысле
определения § 22 в точке О нет ни
кривизны, ни радиуса
кривизны, так как нет ни
касательной прямой, ни
нормальной плоскости; что ка- __
сается нормальной плоско- 7
сти в точке М, то с при- Рас. 75.
ближением последней к О
она не стремится ни к какому пределу.
Пример 7. Трактриса. По основному свойству трактрисы
(рис. 75) отрезок МТ касательной от точки касания М до пересечения
с осью имеет постоянную величину а:
MT = MxTx = a. (17)
Обозначим через и угол МТХ и через К точку пересечения
бесконечно близких касательных МТ и М1Т1. Тогда /^ТКТг^ du.
Отложим от точки К на прямой КТ отрезок KQ = KTt и
рассмотрим треугольяик TQTlf у которого угол Q эквивалентен прямому.
Найдем его «катеты» TQ, TXQ.
128 ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
Мы имеем
КТг = МгТх - МгК =а- МХКУ
КТ =
Следовательно,
Но периметр МК + МХК описанной ломаной МгКМ эквивалентен длине
us дуги МХМ (§ 16), так что
TQ&ds. (18)
Далее из треугольника KTXQ находим
TXQ 2z KTxdu,
и так как КТХ = а — МХК ^ а, то
T&zzadu (19)
Наконец, из треугольника TQTX находим
TQ&T&agu,
т. е. в силу (18) и (19)
ds — a ctgudu.
След овательн о,
^ (20)
Читателю предлагается проверить эту формулу аналитически с
помощью формул (5) § 11 (стр. 55).
Если провести нормаль MN, то из треугольника TMN находим
ctgu
и, следовательно,
т. е. радиус кривизны трактрисы обратно пропорционален отрезку
нормали от точки на кривой на оси трактрисы.
Для построения центра кривизны проводим ТС перпендикулярно
к оси. Точка С пересечения этой прямой с нормалью есть центр
кривизны. Действительно, из прямоугольного треугольника NTC,
в котором ТМ есть высота, находим
TM' а'
Найдем место центров кривизны трактрисы.
Расположим систему координат, как на рис. 39 (стр. 74). Из
треугольника ТМС на рис. 75 имеем (§ 11):
хс = ОТ + РТ = х — и cos и,
т. е. в силу формулы (5) § 11
хс = a In tg y .
§ 24. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 129
Место центров кривизны представляется параметрическими
уравнениями:
*c = alntgf; Ус = а^. (22)
Исключая параметр и, находим
»
g 2
2/c = 7Utt +е 2 J. (23)
Итак, место центров кривизны трактрисы есть цепная линия (§ 17).
Читателю предлагается проверить и этот результат аналитически
с помощью формул (11).
Замечание. Формула (20) дает для вершины А трактрисы (и = 90°)
значение р = 0. Как было отмечено в § 23 (стр. 116), радиус кривизны
не может равняться нулю в правильной точке. Но точка А и не
является правильной. Она является точкой возврата. Вектор г'(и) такой
точки равен нулю и остается равным нулю при всякой параметризации.
Поэтому радиус кривизны не может быть определен по формуле (10),
т/(х'г 4- и'2)3 0
которая дает \> = z^m—-?„-!- = — . Правда, по формуле (10) можно
снова получить формулу (20): [> = actgu, но она будет, таким образом,
доказана для всех точек, кроме точки и=—. Самое большее, что мы
можем утверждать, — это то, что при приближении М к А величина
[> стремится к нулю, т. е. что
lim (j (и) = 0.
В противоположность эгому, изложенный выщ}е синтетический вывод
сохраняет силу и для случая и = £ . Аналитический вывод указан
в упражнении 8.
Упражнения
1. Вычислить радиус кривизны пперболической спирали.
2. Найти аналитически и синтетически радиус кривизны эвольвенты
окружности (§ 12).
3. Доказать аналитически и синтетически, что радиус кривизны цепной линии
равен отрезку нормали (от точки на цепной линии до ее основания).
4. Доказать аналитически и синтетически, что радиус кривизны циклоиды
вдвое больше отрезка нормали от точки циклоиды до прямой, по которой катится
производящий круг.
5. Вычислить кривизну эллипза и показать, что она пропорциональна кубу
расстояния от центра до касательной.
6. Доказать (синтетически), что радиус окружности, описанный около
треугольника, составленного тремя бесконечно близкими касательными плоской кривой,
вчетверо меньше радиуса кривизны.
7. Вывести выражение радиуса кривизны в полярных координатах
8. Доказать, что в ючке возврата А трактрисы радаус кривизны (в смысле
определения § 22) существует и равен нулю.
Указание. Возьмем на трактрисе
a( cos и -Ь In tg ~ J,
j/ = a sinii
М. Я. Выгодский
130 ГЛ. П. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
две точки Mlt М2, соответствующие значениям параметра и — щ, и = и2. Проведем
нормали MtD, M2D, которые пересекаются в точке D, и найдем предел, к которому
тс тс
стремится D при щ—>— , и2—> — . Это можно сделать, составляя уравнения
нормалей MXD, M2D. Менее громоздким будет такой путь. Дуги МгА, Ма<4 можно
представить выражениями
МА а\п
М2А а\п
^ sina2
или, введя величины
— выражениями
МА \
М-,А = а\п, M2A a]n.
1 cos vx cos v2
Дуга МхМг по величине и по знаку равна
М^М> = а (in—— qp In—— Y
- V cost;2 costly'
где верхний знак берется, когда Мх и М2 лежат по одну сторону от А,
и нижний, — когда точка А лежит между Мг и М2. Внешний угол при вершине D
треугольника MXMZD равен
u2-u1 = v2 — v1.
Сторона M-J) этого треугольника равна —.—^—-—^ sin M% Поэтому
х sin (v2 — Vj) sm (v2 — vx)
Нужно доказать, что последняя величина стремится к нулю при иг —* 0,
v2—^0. Тогда, поскольку точка Мх стремится к А, должна стремиться к А
и точка £, т. е. центр кривизны совпадает с точкой Л, и мы будем иметь р = 0.
- 9. К какому пределу стремится радиус кривизны полукубической параболы
Zay2 — 2xz в точке М при стремлении М к точке (0,0)? Существует ли радиус
кривизны в самой точке (0,0)? ,
См. замечание к примеру 7 и указание к предыдущему упражнению.
§ 25. Расстояние от точки кривой до бесконечно близкой касательной
Мы знаем, что расстояние М2Р (рис. 76) от точки М2 кривой (/)
до касательной в бесконечно близкой точке Мх имеет высший (в общем
случае — второй) порядок относительно дуги МгМ2 или хорды МгМг
или ее проекции МгР на касатель-
ную М1Т1. Наглядное представление
показывает, что расстояние М2Р
_ увеличится, если дугу М1М2 искри-
'' вить еше сильнее. В соответствии
Рис. 76. с этим ИМеет место следующая
теорема.
Теорема 1. Если точки М19 М2 линии (I) (рис. 77) стремятся
к точке М, то расстояние h от точки М2 до касательной МХТХ
в точке Мх с точностью до бесконечно малых второго порядка равно
половине произведения кривизны х в точке М на квадрат хорды МхМг
(или ее проекции х = МгР на касательную МгТг):
1 4 (1)
§ 25. РАССТОЯНИЕ ОТ ТОЧКИ КРИВОЙ ДО КАСАТЕЛЬНОЙ
131
здесь е3, т)3 — бесконечно малые величины, порядок которых
(относительно МХМ2) выше второго (в общем случае —третий).
Доказательство. Для точки спряхмления (* = 0) теорема
очевидна непосредственно, ибо расстояние h имеет в этом случае порядок
выше второго (§ 20, стр. 87). Поэтому в дальнейшем можем считать,
что у. Ф 0.
Разделим дугу МХМ2 пополам в точке О (рис. 77), проведем
касательную OL и обозначим через со1 и а, углы, образованные касательной
МХТХ соответственно с
касательной OL и с секущей
МХМ2. Эти углы
эквивалентны, потому что они
разнятся друг от друга
самое большее на
величину угла между МХМ2 и
OL, т. е. между хордой
и касательной,
проведенной через середину
стягиваемой ею дуги, а такой
угол согласно теореме, с*
доказанной в § 18 (стр. 79),
имеет высший порядок относительно МгМ2, а значит, и относительно
Итак,
;«), ^—1
Следовательно,
h = MJP = МХМ2 sin ах « МхМ2ъх %|х (МХМ2)\ (3)
Теорема 1 доказана.
Замечание 1. Формула (2) представляет обобщение известной
теоремы элементарной геометрии, гласящей, что угол а19 составленный
касательной и хордой МХМ2 окружности, измеряется половиной дуги
MXM2. Действительно, это выражение означает, что аг =
где
Л —радиус окружности. Но кривизна окружности х~ — . Поэтому для
окружности имеет место точное
равенство:
Рис. 78.
Теорема 2. Касательные
М1ТХУ М2Т2У проведенные через
концы Мх, Мг хорды МХМ2 (рис./8),
образуют с хордой
эквивалентные углы ах, а2. Каждый из них
эквивалентен половине угла а>
мемеду касательными.
Доказательство. По доказанному в теореме 1, olx£z - v.MxM2.
Аналогично
a2^lxil/xM2. (2a)
132
ГЛ. И. СОПУТСТВУЮЩИЙ ТРИЕДР. КРИВИЗНА И КРУЧЕНИЕ
Но согласно определению кривизны
отсюда следует
ах ^ а2 ^ - со, (4)
что и утверждалось.
Если линия (/) —плоская (рис. 79), то ее касательные пересекаются
в некоторой точке К, и, применив к треугольник у МкМ2К теорему
синусов, найдем следующею теорему:
Теорема 2а. Отрезки касательных, проведенных, из точки К,
бесконечно близкой к плоской линии (I) в две бесконечно близкие точки
прикосновения, эквивалентны
Ш\
Рис. 79.
Р X
Если любую плоскую линию (I) мы отнесем к системе координат,
изображенной на рис. 80 (ось абсцисс — касательная в точке МУ ось
ординат —нормаль), то в силу формулы (1) мы можем написать:
причем у. > 0, если ось ординат направлена в сторону вогнутости.
Формулу (5) можно написать в виде
(5)
„ (5а)
где р = — , а ©3 и Sg имеют высший порядок относительно я2 (как
правило, третий порядок относительно х).
Формула (5а) показывает, что каждую плоскую кривую линию
в окрестности обыкновеннсй точки (*ф0) можно приближенно
заменить параболой, у которой точка М есть вершина, касательная
в М совпадает с касательной к данной линии, а параметр равен
радиусу кривизны р = — последней (соприкасающаяся парабола).
Это предложение справедливо и для пространственной кривой,
в чем можно убедиться, спроектировав пространственную кривую
на соприкасающуюся плоскость.
В точке спрямления соприкасающаяся парабола обращается в
прямую, ордината кривой имеет более высокий порядок, чем квадрат
абсциссы, и тогда можно подобрать параболу высшего порядка,
заменяющую данную линию с еще большрй точностью.
Заметив (пример 4 § 24, стр. 126), что радиус кривизны параболы
в вершине равен ее параметру, мы видим, что соприкасающаяся
парабола имеет с данной линией также общий центр кривизны.
Расстояние между данной линией и соприкасающейся параболой
будет иметь третий порядок относительно абсциссы; при этом изме-
§ 26. ЧЕТЫРЕ ЛЕММЫ
133
рять расстояние можно не только по направлению нормали, но и по
любому другому, кроме направлении касательной. Доказательство
предоставляем читателю.
Из теоремы 1 вытекает:
Теорема 3. Если две плоские кривые ММХ, ММ2 имеют касание
в точке М и в этой точке их кривизны %19 х2 отличны от нуля
и не равны между собой, то в окрестности точки М кривая с большей
кривизной располагается внутри вогнуто-
сти кривой с меньшей кривизной.
Действительно, восставив в
какой-нибудь точке Р (рис. 81) перпендикуляр
к касательной MX, имеем:
РМ ^ -— У Г2
Р X
Ясно, что при ^ < х2 также РМХ<РМ2, Рис.81,
что и доказывает теорему.
Применив теорему 3 к случаю, когда одна из кривых ММи ММ2
есть окружность, получаем:
Теорема 4. Если радиус МО окружности больше радиуса
кривизны МС касающейся ее линии, то в окрестности точки касания
окружность объемлет эту линию (рис. 82).
Рис. 82.
Рис. 83.
Теорема 5. Если радиус МО окружности меньше радиуса
кривизны МС касающейся ее линии, то в окрестности точки касания
окружность объемлется этой линией (рис. 83).
В последней теореме предполагается, что точка касания не является
точкой спрямления.
Случай, когда радиус окружности равен радиусу кривизны
касающейся ее линии, нуждается в более тонких средствах исследования.
Мы рассмотрим его ниже, в § 27.
§ 26. Четыре леммы
Для дальнейшего нам понадобятся следующие вспомогательные
предложения.
Лемма 1. Если в треугольнике ABC (рис. 84) угол у = /_АСВ
бесконечно мал и разность сторон а — Ь имеет высший порядок
относительно 6у, то каждый из углов А и В эквивалентен прямому.
134
ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
Доказательство. Отложим на стороне С В = а отрезок CD = 6.
В равнобедренном треугольнике ACD угол <f = ^/CAD равен 90° —-|,
т. е.
9^90°.
Кроме того,
Но BD=a—b по условию имеет высший порядок относительно AD = 6у.
Поэтому, применив к треуголнику ADB теорему синусов, найдем, что
7? Г)
величина sin BAD = sin ^ = jn s^n В бесконечно мала. Значи!, и угол >.
(он лежит против меньшей стороны и потому— острый) бесконечно мал.
Рис. 84.
Рис. 85.
Следовательно, угол А = 9 + X эквивалентен прямому, что и
утверждалось.
Имеет место и обратное предложение.
Лемма 2. Если в треугольнике ABC каждый из углов А и В
эквивалентен прямому, то разность а—b имеет высший порядок
относительно 6у.
Доказательство. Выполним то же построение, что в лемме 1.
Легко видеть, что углы у и X бесконечно малы и что AD — by* Из
треугольника ABD, где ^/#^90°, имеем BD ^ AD sin X, т. е.
a — 6 = 6ysin>4, (1)
что и доказывает лемму 2.
Лемма 3. Если плоскости Р и Q образуют бесконечно малый
угол ф и если а/ есть проекция на плоскость Q угла ш, лежащего
в плоскости Р, то ш^а/.
Доказательство. На сторонах угла со (рис. 85) отложим
произвольные отрезки ОА = а, ОВ — b. Площадь треугольника АОВ
обозначим через S. Через a', b', S' обозначим величины соответствующих
проекций.
Обозначая через а и р углы, образуемые стороиами О А и ОВ
с плоскостью Q, мы имеем
а' = а cos а, Л
b' = b cos p, i (2)
S' = S COS9. I
Из соотношений
(3)
(4)
§ 26. ЧЕТЫРЕ ЛЕММЫ
135
находим:
и в силу (2)
sin со'
Sin (О
sin <•>'
S'ab
Sa'V
cos 9
(5)
sin ш
COS л COS {J * ' '
Так как углы ос и р не превосходят угла у, а последний бесконечно
мел, то из (6) находим
sin а/ ^ sin о. (7)
Если угол о) (а значит, и а>') бесконечно мал,
то соотношение
ш'»со (8)
следует из (7).
Если же угол о>— конечный, то
эквивалентность (8) вытекает уже из того, что угол о/
получается из ш поворотом его сторон на углы
а и р, так что | ш — a/ | не может превосходить
Лемма 4. Пусть ABC (рис. 86)—
трехгранный угол с бесконечно малыми плоскими
углами a = /_BSC, §±= /_ASC, у= / Л52?
« пусть внешний угол <р двугранного угла,
противолежащего
Тогда
углу 1, бесконечно мал.
(9)
Рис. 86.
Доказательство. Заметим прежде
всего, что двугранный угол при робре £.#
(а также и при ребре 5Л) бесконечно мал.
Чтобы доказать это, проведем сечение ABC,
перпендикулярное к ребру SC. Тогда внешний
угол треугольника ABC при вершине С равен <р
и, значит, бесконечно мал. Следовательно, бесконечно мал и угол ABC.
Этот угол, провда, не является линейным углом двугранного угла
при ребре SB. Однако разность упомянутых углов бесконечно мала.
Действительно, SB составляет бесконечно малый угол а с SC;
следовательно, угол между SB и плоскостью ABC эквивалентен прямому.
Значит, ВС и В А образуют бесконечно малые углы со сторонами
линейного угла, измеряющего двугранный угол при SB. Значит,
последний угол бесконечно мал.
Заметив это, спроектируем ребро SA на плоскость BSC. Пусть
проекция есть SD. Тогда угол BSD есть проекция угла BSA—y
и, согласно предыдущей лемме,
5 Y- (Ю)
(И)
(12)
Точно так же угол CSD есть проекция угла CSA = р, так что
Мы имеем также
138 гл. п. сопутствующий триедр, кривизна и кручение
Сложив (11) и (12) и сменив с (10), имеем
что и утверждалось.
§ 27. Эвольвента и эволюта плоской кривой
Теория кривизны плоской линии замечательным образом связана
с другим вопросом теории кривых, именно с теорией эволют и эвольвент.
Если гибкая и нерастяжимая нить M0MN (рис. 87), будучи
закреплена в некоторой точке Мо линии АВ (катушки) и натянута в свободной
точке N, наматывается на кривую АВ или разматывается с нее, то
В
точка N описывает кривую линию CD, называемую эвольвентой липии
АВ, Линия же АВ называется эволютой линии CD1).
Этому механическому определению легко придать чисто
геометрическую форму. Для этого заметим, что, в то время как наматываемая
нить накладывается на какую-либо часть катушки, например на дугу
М2А1Я, ее свободный отрезок M2N9_ укорачивается на величину
M2N2 — M^N3, равную дуге М2М9. Поэтому геометрическое построение
эволюты можно выполнить следующим образом.
Возьмем дугу АВ произвольной плоской или пространственной
кривой. Предположим пока, что на дуге АВ все точки правильные;
тогда при надлежаще выбранном законе движения направление
движения меняется непрерывно. Это направление примем за направление
отсчета положительных дуг.
В этом направлении отложим на касательной в начальной
точке Мо отрезок lo = MoNo произвольной длины.
На остальных касательных откладываем отрезки, длина которых /
равна разности /0 — s между начальным отрезком и длиной дуги
х) «Эвольвента» в переводе означает — развертывающая: «эволюта» — раз-
вернутая.
§ 27. ЭВОЛЬВЕНТА И ЭВОЛЮТА ПЛОСКОЙ КРИЕОЙ 1 37
= M0M от начальной точки до течки касания М:
Место CD концов этих отрезков и есть эвольвента линии АВ.
Итак, мы приходим к следующему определению.
Определение. Эвольвентой кривой АВ называется место концов
отрезков ее касательных, длины которых убывают на величину, равную
приращению дуги линии АВ. Если CD есть эвольвента линии АВ,
то АВ называется эволютой линии CD.
D
Рис. 88.
Из определения эвольвенты непосредственно ^вытекают следующие
два предложения. v
Теорема 1. Длина дуги эволюты равноправности отрезков
касательных эволюты в концах дуги (отрезки откладываются от точки
касания до ьстрсчи с эвольвентой).
Теорема 2. Всякая кривая, пространственная или плоская, имеет
бесчисленное множество эвольвент. Через каждую точку какой-либо
касательной к эволюте проходит одна и только одна эвольвента. Если
эволюта лежит в плоскости (<р), то все ее эвольвенты лежат в той
же плоскости.
Теорема 3. Касательные эволюты являются нормалями эвольвенты.
На эту теорему нас наводят следующие соображения: представим
себе, что вместо кривой АВ мы имеем ломанию линию; тогда конец
нити описывает дугу окружности с центром в вершине М ломаной
линии, и касательная к эволюте служит радиусом этой дуги, т. е. ее
нормалью.
Докажем эту теорему геометрически. Пусть точки Mlf M2 эволюты
АВ (рис. 88) имеют пределом точку М, где кривизна x = lim^;— от-
MtMt
лична от нуля (теорема верна и для случая х = 0, но доказательство
потребует более тонких средств). Предположим сначала, что длина
нити MN не равна нулю (случай A/7V=O будет рассмотрен ниже).
138 гл. и. сопутствующий триедр, кривизна и кручение
Заметим прежде всего, что хорда МгМ2 образует с касательными
MxNly M2N2 углы р = /^mN1M1M2 и y = J/_M1M%K, каждый из которых
эквивалентен половине угла ш между MxNXi M2N2 (§ 25, теорема 2):
?«|. (2)
Далее, угол 9 является внешним углом треугольника MtM2N2t в
котором угол X при вершине 7V2 имеет высший порядок относительно <р.
Действительно, по теореме синусов
МлМо sin Я А /О\
MXN2 smy <p v '
Левая часть (3) бесконечно мала, потому что величина МгМг —
бесконечно малая, a MXN2—конечная (по предположению M2N2 — конечная
величина, a MXN2>M2N2 — МгМ2). Значит, X имеет высший порядок
относительно <р> т« е« ? — Х^9в
С другой стороны, угол а = Z N2MXM2, очевидно, равен у — к, так
что, в силу (2),
а«|. (4)
Теперь докажем, что угол N1M1N2 эквивалентен о. В случае,
когда АВ есть плоская кривая, это само собой ясно, так как тогда
MlN1 и M2N2 лежат в одной плоскости и о есть внешний угол
треугольника, внутренние углы которого суть X и / N2МгМ2.
Если же кривая АВ — не плоская, то доказательство можно вести
так: плоскость M2MXN2, проходящая через касательную M2N2 и точку
Ми бесконечно близкую к М2, имеет пределом соприкасающуюся
плоскость в точке М. Тот же предел имеет плоскость M2MxNXi
проходящая через касательную MXNX и точку М9. Следовательно,
плоскости M2MXN2 и M2M1N1 образуют бесконечно малый угол. Плоские же
углы аир бесконечно малы. Следовательно (лемма 4 § 26),
и в силу (\) и (4)
^_ 1 1 2 /1^*' * \ /
Рассмотрим теперь треугольник MXM2N2 и докажем, что сторона
его MXN2 разнится от суммы двух других его сторон на величину
M2N2 + М1М2 - MXN2 = e> (6)
имеющую высший порядок относительно ш. Проектируя MXM2N2 на
MXN21 находим
MXN2 = M2N2 cos X + МгМ2 cos a, (7)
откуда
s = M2N2 + МХМ2 — MXN2 = M2N2 (1 — cos X) + MXN2 (1 — cos a)^
% I (M2N2 . X2 -f- Л/ХЛ/2 • a2). (8)
Так как a имеет тот же порядок, что ш, а к — высший, то из (8)
следует, что г имеет высший порядок относительно ш.
Эти предварительные рассуждения, в которых мы пока еще вовсе не
учитывали специфического свойства эвольвенты, нужны были для того,
чтобы сделать строгим нижеприводимое доказательство.
§ 27. ЭВОЛЬВЕНТА И ЭВОЛЮТА ПЛОСКОЙ КРИВОЙ 139
Согласно определению эвольвенты имеем
~2. (9)
Следовательно,
где е' имеет высший порядок относительно МХМ2 а так как по
предположению у. Ф 0, то е' имеет высший порядок также и относительно а).
Рассмотрим треугольник NXMXN2, у которого угол Мг по
доказанному эквивалентен <о, и оценим разность его сторон:
т| = MXNX — MXN2. (11)
Подставляя в (11) вместо Л/^ выражение (10) и принимая во
внимание (6), находим
Ч = в + е'. (12)
Итак, разность M1NJ — M1N2 имеет высший порядок относительно
бесконечно малого угла &2zZ_Mu а значит, и относительно MxNx(d.
Следовательно (лемма 1 § 26), угол M1N1N2 эквивалентен прямому.
Следовательно, касательная MxNx эволюты АВ есть нормаль
эвольвенты CD.
Углом между пересекающимися линиями называют угол между
касательными этих линий в точке пересечения. Пользуясь этим
наименованием, мы можем сказать, что согласно теореме 3 эвольвента пересекает
все касательные ортогонально (т. е. под прямым углом), или иначе:
Теорема За. Эвольвента есть ортогональная траектория
касательных эволюты.
Это свойство может быть принято за определение эвольвенты, так
как справедливо также обратное предложение.
Теорема 36. Всякая ортогональная траектория касательных
к кривой АВ есть эвольвента этой кривой.
Если считать очевидным, что через данную точку фиксированной
касательной к АВ проходит только одна ортогональная траектория
касательных, то теорема 36 непосредственно следует из За.
Если же поставить этот факт под сомнение, то теорему 36 можно
доказать, обращая доказательство теоремы 3.
Именно, из того, что MXNX пересекает CD под прямым углом,
следует, что в треугольнике N1M1N2 угол Nx эквивалентен прямому
(угол N2 также эквивалентен прямому, ибо /_МХ бесконечно мал).
Согласно лемме 2 § 26, величина
M1N1 — M1N2 = o (13)
имеет высший порядок относительно угла N1M1N2. Но (по доказанному
в теореме 3) /_МХ^^. Там же было доказано, что величина
МХМ2 + M2N2 — MXN2 = е (6)
имеет высший порядок относительно ш.
Вычитая (6) из (13), находим
М jTV\—М 2N 2 — МгМ2 — Ъ — е, (14)
т. е.
140
ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
Разность отрезков M^/V^ — M2N2J будучи эквивалентна хорде MtM2,
эквивалентна, конечно, и дуге МхМг. Но здесь имеет место не только
эквивалентность, но и точное равенство. Это можно доказать так.
Возьмем на эволюте АВ две произвольные, но фиксированные
точки (рис. 89) Мо и М1 и вставим между ними промежуточные точки
Mv М2, М3, ..., Мк, которые потом
мы будем уплотнять, увеличивая
их число. Написав для хорд М0М17
МХМ2, М2М3... ряд эквивалент-
ностей, аналогичных (15) и
сложив их, получим
M0N9-M'N'&
« момг + мгмш + ... + мкм\
(16)
Правая часть (16) представляет
периметр ломансй, вписанной в
дугу М0М'. Переходя к пределу,
получим
MQN9 — M'N' = M^M'.
Рис* 89* Вспоминая определение
эвольвенты, мы видим, что линия N0N'
есть эвольвента линии М0М', что и доказывает теорему 36.
Замечание. Из сопоставления теорем За и 36 тотчас же
вытекает единственность ортогональной траектории касательных,
проходящей через фиксированную точку 7V0
касательной MaNQ.
При доказательстве теорем За, 36
мы исключили случай MN = Q;
рассмотрим его сейчас.
Этот случай наступает в тот
момент, когда нить, закрепленная в
точке Мо (рис. 90), целикомналожилась
на эволюту АВ, покрыв дугу М0Л/,
равную начальной длине нити M0N0.
Представим себе, что точка Мх
движется по эволюте, стремясь к
точке М, как к пределу. Так как по
предположению на эволюте нет
неправильных точек, то касательная
MXNX эволюты будет иметь преде-
.лом касательную ST в точке М,
а так как при этом MXNX остается
все время перпендикулярной к
касательной NXTX эвольвенты, то и в
точке М, общей для эволюты и
эвольвенты, касательная к эвольвенте должна быть перпендикулярной к ST,
если касательная в М существует.
Последнее условие нельзя заранее считать выполненным: ведь
в точке М построение эвольвенты как будто заканчивается, ибо
механическое построение с помощью нити M0N0 дальше продолжать
Рис. 90.
§ 27. ЭВОЛЬВЕНТА И ЭВОЛЮТА ПЛОСКОЙ КРИВОЙ 141
заведомо нельзя. Во всяком случае эвольвенту нельзя продолжать
б прежнем направлении, ибо мы перешли бы со сюроны эволюты
в сторону вогнутости, а туда не может проникнуть точка Nt.
Всё, что мы можем утверждать на основании вышесказанного,— это
то, что «правая касательная» эвольвенты в точке М перпендикулярна
к касательной ST эволюты в той же точке1).
Чтобы ответить на вопрос, существует ли в точке М касательная
в прямом смысле, нужно прежде всего установить, можем ли мы
продолжить построение эвольвенты, сохранив ее геометрическое
определение, данное в начале параграфа. Оказывается, что это возможно.
Ведь на касательной эволюты А В мы различаем два направления:
положительное и отрицательное, причем первое совпадает с
направлением отсчета дуг на эволюте, т. е. на нашем рисунке — с
направлением М0М. Поэтому, если мы возьмем какую-нибудь точку М2 ниже
точки My то на соответствующей касательной мы должны будем
отложить отрицательный отрезок
M2N2 = M0N0 - М\М, = М^М - М^М2 = - ММ2.
Мы получим таким образом, наряду с прежней ветвью UM
эвольвенты, вторую ее ветвь MV. Нетрудно видеть, что эту ветвь тоже
можно получить механически. Именно, если в какой-нибудь точке М9,
расположенной ниже М, укрепить один конец нити M3N3, длина
которой равна длине дуги М3М, то при наматывании этой нити на
дугу МгМ (или при разматывании от точки М) конец нити опишет
вторую ветвь эвольвенты.
Рассуждая, как выше, мы убедимся, что и вторая ветвь
эвольвенты пересекает касательные эволюты под прямым углом и приходит
в точку М с правосторонней касательной, перпендикулярной к ST.
9 Таким образом, обе ветви в точке М имеют общую правостороннюю
касательную. Ясно, что точка М и после присоединения второй ветви
остается неправильной, ибо направление движения по эвольвенте
меняется в этой точке на противоположное, т. е. М есть точка
возврата эвольвенты. При этом ветвь UM обращена вогнутостью в
сторону точки S, а ветвь VM—в противоположную сторону. Течка возврата,
в которой ветви обращены вогнутостью в противоположные стороны,
называется точкой возврата первого рода, в отличие от точек возврата
второго рода, в которых ветви обращены вогнутостью в одну и ту же
сторону. С такими точками мы вскоре встретимся.
Возвращаясь к поставленному выше вопросу: существует ли
в точке М касательная в прямом смысле, мы должны ответить на
него отрицательно, ибо если г, а эвольвенте взяты две точки Nx и N2,
принадлежащие разным ветвям и имеющие общим пределом точку М,
то секущая N\N2 может иметь пределом любую прямую, проходящую
через М. Она может и вовсе не иметь предела.
Теперь ясно, что теоремы За, 36 остаются в силе и для случая
MN = 0 с той, однако, оговоркой, что под направлением эвольвенты
в точке М мы должны понимать направление односторонней
касательной.
1) Это можно доказать также и по тому плану, как была доказана теорема 3.
Придется тольчо уточнить оценки. Именно, нужно будет доказать, что величина ij
имеет относительно о> порядок не ниже третьего, ибо величина МXNX • ш будет
иметь теперь не первый, а второй порядок относительно о>.
142
ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
Связь теории эволют и эвольвент с теорией кривизны плоских
кривых обнаруживается из следующего предложения:
Теорема 4. Всякая плоская линия (I) есть место центров
кривизны своей эвольвенты (Z.).
Доказательство. Пусть Мг есть фиксированная точка
линии (I) (рис. 91) и пусть точка М2 этой линии стремится к Ми как
к пределу. Тогда точка пересечения Е фиксированной касательной
MlNl и переменной касательной M2N2 также имеет пределом Мх.
В самом деле, в треугольнике МХЕМ2 внешний угол при вершине Е
бесконечно мал и, следовательно, внутренний угол М2 также
бесконечно мал, а внутренний угол при вершине Е — тупой. Значит,
сторона МХЕ меньше бесконечно малой стороны МХМ21 т. е. \\т МХЕ = 0.
Итак, Мх есть предел точки Е. Но прямые MlNly M2N2 согласно
теореме 3 суть бесконечно близкие нормали эвольвенты (L). Поэтому
точка их пересечения имеет пределом
центр кривизны эвольвенты (для точки
А\). Следовательно, точка Мг эволюты (/)
есть центр кривизны эвольвенты (L).
Следствие. В точке М, общей для
эволюты и эвольвенты, радиус кривизны
эвольвенты равен нулю. Как мы знаем,
эта точка есть неправильная точка
эвольвенты (точка возврата); тем не менее,
здесь кривизна эвольвенты существует в
обычном смысле слова, т. е. точки TV, и
N\ (рис. 90 на стр. 140) могут
стремиться к М и по разным ветвям эвольвенты;
точка пересечения нормалей всегда будет
иметь один и тот же предел, именно,
точку М. Ведь нормали эвольвенты являются
касательными эволюты, а касательные
в бесконечно близких точках Ми М2
эволюты пересекаются в точке, которая имеет тот же предел, что и точки
касания
Наряду с теоремой 4 имеет место и обратное предложение.
Теорема 4а. Место центров кривизны плоской линии (L)
является ее эволютой.
Это предложение тотчас же следует из теоремы 4, если принять,
что для всякой плоской линии существует плоская эволюта. Так как
этого мы еще не Еправе утверждать, то мы должны непосредственно
убедиться, чю упомянутое геометрическое место действительно
является эволютой линии (L).
Пусть Мх есть центр кривизны фиксированной нормали NlF1
(рис. 91) данной линии (Z.), а Л/2 — центр кривизны переменной
нормали N2F2. Когда N2 стремится к NL9 центр кривизны Л/2, стремясь
к нешру кривизны М1У как к пределу, описывает дугу М2МХ
некоторой линии (/). Докажем, что эта линия в точке Мх касается прямой
N\Ft. В самом деле, в треугольнике MLEM2 внешний угол при
вершине Е бесконечно мал. Поэтому угол между секущей MtM2 и
фиксированной прямой N^! бесконечно мал; следовательно, Л^/<\ ость
предел секущей МХМ2У т. е. касательная к линии (/) в точке Мг.
Итак, нормали к линии (L) служат касательными к линии (Z);
значит (теорема 36), (L) есть эвольвента линии (/), т. е. (/) есть эволюта
линии (Z.), что и требовалось доказать.
Рис. 91.
§ 27. ЭВОЛЬВЕНТА И ЭВОЛЮТА ПЛОСКОЙ КРИВОЙ
143
Следствие. Всякая плоская кривая имеет одну и только одну
эволюту, лежащую в той же плоскости. Эта эволюта есть место
центров кривизны рассматриваемой плоской кривой.
Замечание 1. Для окружности упомянутая эволюта
вырождается в точку (центр окружности).
Замечание 2. Впоследствии мы увидим, что каждая кривая,
плоская и неплоская, имеет бесчисленное множество эволют. Но все
эволюты плоской кривой, кроме одной, являются неплоскими кривыми.
В силу теоремы 4 и определения эвольвенты мы можем высказать
также следующее предложение.
Теорема 5. Дуга плоской эволюты равна абсолютному значению
разности радиусов кривизны эвольвенты в концах ее дуги.
D
Следствие. Радиус кривизны эвольвенты (L) изменяется
монотонно: он убывает по мере возрастания дуги.
На первый взгляд может показаться, что этот вывод стоит в
противоречии с тем, что линия (L) может быть задана совершенно
произвольно. Не забудем, однако, что мы исходили из предположения, что
эволюта (/) не имеет неправильных точек; таким образом на самом
деле из возможности произвольного задания эвольвенты вытекает
только то, что если кривизна ее изменяется не монотонно, то точкам
экстремума кривизны на эволюте будут отвечать ьеправильные точки.
Ниже мы увидим, что это —точки возврата.
Пример. Найдем плоскую эволюту трактрисы. Согласно
теореме 4, искомая линия есть место центров кривизны трактрисы. В § 24
(пример 7, стр. 129), было доказано, что местом центров кривизны
трактрисы UAV (рис. 92) является цепная линия ВАС. Таким образом,
трактриса есть одна из эвольвент цепной линии, именно та, которая
получается, если начальный отрезок касательной СМ равен дуге С А от
начальной точки С до вершины цепной линии А, Точка А есть точка
возврата трактрисы. Радиус кривизны трактрисы в этой точке равен
нулю. Дуга С А цепной линии, согласно теореме 5, равна радиусу
кривизны МС трактрисы в точке М.
Согласно теореме За, касательная МТ трактрисы перпендикулярна
к касательной СМ цепной линии, т. е. параллельна нормали CD
144 ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
Рис. 95. . Л
§ 27. ЭВОЛЬВЕНТА И ЭВОЛЮТА ПЛОСКОЙ КРИЕОЙ
145
цепной линии. Приняв во внимание, что отрезок МТ имеет, по основному
свойству тракарисы, постоянную длину а, мы можем вновь получить
следующие свойства цепной линии, найденные уже в § 17.
1. Проекция CD ординаты СТ цепной линли на ее нормаль имеет
постоянную длину.
2. Проекция СМ ординаты СТ цепной линии на ее касательную
имеет длину, равную длине ее дуги СА, отсчитываемой от вершины.
Мы видели, что эвольвента правильной линии всегда имеет одну
неправильную точку (при MN = 0); но помимо этого она может иметь
и другие неправильности. Так, имеет несто следующая теорема:
Теорема 6. Точке перегиба эволюты соответствует на эвольвенте
точка возврата второго рода (т. е. такая точка возврата, в которой
ветви обращены вогнутостью в одну сторону).
Действительно, при прохождении через точку перегиба А (рис. 93)
кривизна эволюты меняет знак, т. е. вектор касательной меняет
направление вращения на обратное. Если на участке В А вектор касательной
вращался по часовой стрелке, то на участке АС он вращается против
часовой стрелки, так что точка эвольвенты проходит участок FD п
одном направлении, a DE — в противоположном. Две ветви эвольвенты
касаются друг друга, так как обе перпендикулярны к AD Обе ветви
обращены вогнутостью в сторону общего их центра кривизны А.
Откажемся теперь от предположения о правильности эволюты
и рассмотрим случай, когда сама эволюта имеет точку возврата.
Пусть точка А эволюты CAB (рис. 94, 95) есть точка возврата первого
рода. Так как на дуге, содержащей
А, нельзя установить непрерывно
меняющегося направления движения,
нам придется построить для каждой
из ветвей С А, АВ эволюты свою
эвольвенту, причем, чтобы не было
разрыва, от точки А в обоих случаях
должен быть отложен один и тот же
отрезок ААХ. Так как отрезок ААг
является нормалью для обеих
эвольвент (теорема 3), то совокупность
Э1их эвольвент образует линию с
непрерывно меняющейся касательной.
Согласно теореме 5, радиус
кривизны эвольвенты на участке В1А1
изменяется монотонно; на участке
С1А1 он изменяется также монотонно;
при этом, если вдоль 51Л1 радиус
кривизны убывает (рис. 94), то он
убывает и вдоль СгАг, так что в
точке AY мы имеем минимум радиуса
кривизны; если же вдоль ВгАг радиус
кривизны возрастает (рис. 95), то он возрастает и вдоль СгА19 так что
в точке Ах мы имеем максимум радиуса кривизны.
Итак, имеет место теорема:
Теорема 7. Экстремуму кривизны эвольвенты соответствует на
эволюте точка возврата первого рода.
Эта теорема хорошо иллюстрируется на примере эволюты эллипса
(рис. 96), имеющей 4 точки возврата Л, В, С, D, соответствующие
четырем вершинам эллипса.
Ю М. Я. Вкгодский
146
ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИРНА И КРУЧЕНИЕ
Если эволюта имеет точку возврата второго рода, то эвольвента
имеет (как и в случае точки перегиба) точку возврата второго рода
(рис. 97 и 98).
д
Рис. .99.
Если эвольвента имеет точку спрямления (* = — = 0}, то
эволюта уходит в бесконечность (рис. 99). Если точка
спрямления, как на рис. 99, есть точка перегиба, то две ветви эвопоты
уходят в бесконечность по разным направлениям нормали эвольвенты.
В предыдущем параграфе мы доказали, что кривая, касающаяся
окружности, лежит (в окрестности точки касания) внутри окружвости,
если ее радиус кривизны меньше радиуса окружности, и вне
окружности, если радиус кривизны больше paflajca окружности. Эти факты
наглядно легко воспринимаются. Труднее представить себе взаимное
§ 27. ЭВОЛЬВЕНТА И ЭВОЛЮТА ПЛОСКОЙ КРИВОЙ
147
расположение кривой и касающейся ее окружности- в том случае,
кот да радиус кривизны равен радиусу окружности, т. е. когда центр
окружности совпадает с пентром кривизны, или, что то же, когда
окружность является слфужностью кривизны.
Рис. 100.
Рис. 101.
Рас.
Рис. 103.
Может случиться, что кривая в окрестное!и некоторой ее точки .4
располагается внутри круга ее кривизны, проведенного через А (это
имеет место, например, в конце малой оси эллипса (рис. 100); может
также случиться, что кривая распола1ается вне круга кривизны. Это
имеет место в конце большой сси эллипса (рис. 101). Однако в общем
сл\чае кривая, как мы сейчас докажем, лежит частью внутри, частью
вне своего круга кривизны (рис. 102).
Теорема 8. Если в окрестности точки А кривизна линии
меняется монотонно, то в направлении возрастания радиуса
кривизны кривая выходит из круга кривизны, а в направлении убывания
радиуса кривизны — входит в него (на рис. 102 дуга В А, на
которой радиус кривизны меньше, чем в точке А, лежит внутри, а дуга
АС, на которой он больше, чем в точке А, — вне круга кривизны
точки А).
Ю*
148 гл. и. сопутствующий триедр, кривирна и кручение
Пусть в точке В (рис. 103) радиус кривизны линии ВАС меньше,
а в точке С больше, чем в точке А. Построим центры кривизны В1У
А1У Сг точек В, А, С. Они лежат на эволюте В1А1С1 данной линии ВАС.
Окружность, описанная из центра Ах радиусом АгА, есть круг
кривизны для точки А. Соединим центр ее Ах с точкой С Имеем
а значит, и подавно,
С1С<с7А1 + А1С. (17)
Но, согласно теореме 5,
С1С = С?А1 + А1А. (18)
Сравнение равенства (18) с неравенством (17) дает
АгА < АХС,
т. е. точка С лежит вне круга кривизны точки А.
Соединим теперь точку Аг с точкой В. Имеем
г (19)
и, согласно теореме 5,
BJB^A^ — AJi^ (20)
Сравнение (19) и (20) дает
АгВ<АхА,
т. е. точка В лежит внуари круга кривизны точки Аг. Теорема
доказана.
Теорема 9. Если в точке А радиус кривизны имеет максимум
(рис. 101), то кривая в окрестности точки А лежит внутри круга
кривизны.
Теорема 10. Если в точке А радиус кривизны имеет минимум,
то кривая в окрестности точки А лежит вне круга кривизны (рис. 100).
Эти теоремы доказываются так же, как теорема 8.
Взаимное расположение кривой и круга ее кривизны в обшем
случае усматривается весьма просто еще следующим образом.
Возьмем на кривой QS (рис. 104) три точки В, А, Си через них
проведем окружность. Если эта окружность не имеет, кроме А, В, С,
дрЗ^гих общих точек с кривой и не касается ее в точке А, В или С,
то кривая ровно три раза пересечет окружность. Если точка Q лежит
внутри окружности, то точка Р (между В и А) лежит вне
окружности, точка R (между А и С) —внутри и, наконец, точка S (за С) —
вне окружности. Если точка Q лежала бы вне окружности, то таким же
образом убедились бы, что S лежит внутри. Следовательно, линия QS
переходит изнутри окружности вовне. Если упомянутые условия
соблюдаются все время при стремлении точек В, А, С к общему
пределу, то и относительно предельной окружности, т. е. круга кривизны,
кривая QS расположится таким же образом. Но в исключительных
случаях (теоремы 9 и 10 уточняют, в каких именно) окружность может
касаться кривой в одной из точек А, В, С или пересекать кривую QS
§ 27. ЭВОЛЬВЕНТА И ЭВОЛЮТА ПЛОСКОЙ КРИВОЙ
149
еще один или несколько раз. В этих случаях кривая может
располагаться внутри или вне круга кривизны.
Можно сказать, что в общем случае круг кривизны имеет с
кривой три слившиеся общие точки, в исключительном же случае — четыре
или больше.
У пражнения
1. Доказать, что эволюта обыкновенной параболы есть полукубическая
парабола. Начертить эволюту приближенным построением.
2. Составить параметрические уравнения эволюты циклоиды; начертить
эволюту приближенным построением. Доказать, что эта эволюта конгруентна с
эвольвентой.
3. Найти эвольвенты полукубической параболы с помощью приближенного
построения (использовать теорему 3); составить их уравнения. Какая из этих
эвольвент есть парабола?
4. Найти все эвольвенты циклоиды.
5. Доказать синтетически, что эволюта логарифмической спирали есть
логарифмическая спираль (ср. пример 6 § 24, стр. 127).
6. Плоская кривая проектируется на ее круг кривизны из центра, не
лежащего на общей касательной. Какой порядок малости отрезка проектирующей
прямой между кривой и кругом кривизны?
7. Доказать, что если кривизна плоской линии изменяется монотонно, то
круги кривизны последовательно вкладываются друг в друга, причем ни один из
кругов не касается другого (ср. теорему 8 настоящего параграфа).
8. Доказать, что фиксированная точка прямой, катящейся без скольжения по
кривой линии, описывает одну из эвольвент этой линии.
9. Доказать (синтетически), что радиус кривизны эволюты можно представить
выражением
dl d(f)
где р и 5—радиус кривизны и дуга для соответствующей точки эвольвенты.
10. Второй эволютой линии называется эволюта ее эволюты. Вывести
выражение радиуса кривизны р2 второй эволюты
150 ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
§ 28. Кручение
Развивая дальше намеченную в § 20 аналогию между касательной
прямой и соприкасающейся плоскостью, мы введем понятие кручения
линии, аналогичное понятию кривизны. Кривизна характеризовала
отклонение линии (I) от прямолинейной формы. Кручение характеризует
отклонение линии от плоской формы. За меру кривизны линии (/)
в точке М мы приняли предел отношения ^- угла смежности го
касательных прямых к соответствующей дуге As. За меру кручения линии
(I) в точке М мы по аналогии примем предел отношения ^- угла
смежности а>' соприкасающихся плоскостей (или, что то же, бинормалей)
к соответствующей дуге As. Ясно, что для плоской кривой кручение
всюду равно нулю. Те точки, для которых упомянутый предел не
существует, мы будем считать неправильными и допускать их в
качестве исключения лишь в отдельных изолированных точках
рассматриваемой линии,
В отличие от кривизны, кручению можно приписать не только
абсолютную величину, но и знак, и притом по признаку, не зависящему
ни от положения наблюдателя, ни от выбора направления движения
на линии.
Чтобы обнаружить этот признак, заметим предваршельно, что две
бесконечно близкие соприкасающиеся плоскости пересекаются по
касательной (точную формулировку см. ниже). Этот факт не сразу
усматривается наглядно, и потому необходимо закрепить его в воображении
с помощью модели: взяв проволочную модель кривой и плоский к\сок
жести или бумаги и наложив возможно плотнее этот кусок на кривую,
получим соприкасающуюся плоскость. Придавая соприкасающейся
плоскости малые смещения, увидим, что, смещаясь, наша плоскость
получает вращательное движение около касательной.
Дадим теперь точную формулировку упомянутого факта.
Теорема 1. Если кручение линии (I) в точке М не равно нулю,
то прямая пересечения соприкасающихся плоскостей Р и Q,
проведенных через точки В и С, стремящиеся к М, имеет пределом
касательную в точке М.
Замечание. Теорема остается верной и в том случае, если
кручение в точке М равно нулю; достаточно допустить, что существует
не равная нулю производная —■^ какого-либо порядка к. Однако дока-
ds
зательство теоремы для сличая <з = 0 требует более сильных средств.
Если о = 0 тождественно, то теорема 1 не имеет силы, ибо тогда, как
мы вскоре докажем (теорема 2), линия (/) — плоская, и ее
соприкасающаяся плоскость неподвижна.
Доказательство. Возьмем на линии (/) дугу AD,
содержащую дугу ЯС так, чтобы AB = BC = CD (рис. 105). По теореме 7 § 20
(стр. 95) плоскости Р, Q образуют с плоскостями ABC, BCD
соответственно углы а, [3, имеющие второй (или более высокий) порядок
относительно Z?C = As. Так как кручение в точке М отлично от нуля, то
угол го' между соприкасающимися плоскостями Р, Q имеет первый
(или более низкий) порядок относительно As. Следовательно, углы а
и р имеют второй (или более высокий) порядок относительно угла го'.
§ 28. КРУЧЕНИЕ 151
В силу леммы 3 § 19 (стр. 82), прямая ().), по которой пересекаются
плоскости Р и Q, образует с прямой пересечения плоскостей ABC,
BCD, т. е. с прямой ВС, бесконечно малый угол. Так как прямая
ВС имеет пределом касательную (|х) в точке М, то и касательная (у.)
образует бесконечно малый угол с прямой (X).
Кроме того, точка М отстоит от прямой (I) на бесконечно малое
расстояние. Действительно, если обозначить через h расстояние от
точки В до плоскости Q, то расстояние 8 от В до прямой (к)
представится выражением
Sin о)'
Но sinew'^ о/ имеет тот же порядок, что As, aft имеет относительно As
порядок выше второго. Поэтому расстояние о от точки В, а
следовательно, и от бесконечно близкой точки М до прямой (л), бесконечно
мало. Поэтому касательная (/)
есть предел прямой (л.), что
и требовалось доказать.
В силу теоремы 1, дви-
жение соприкасающейся пло-
скости линии (/) можно пред-
ставить так: точка М дви-
жется по линии (/); вместе ис*
с ней движется прямая (^),
касающаяся (/) в точке М, и около (р.) вращается соприкасающаяся
плоскость (/>), а имеете с ней и бинормаль. Пусть t есть мера времени.
Так как
As
то кручение дает нам отношение угловой скорости вращения бинормали
около касательной к скорости движения точки по линии (I).
Эта картина движения позволяет очень наглядно установить знак
кручения.
Вообразим, что наблюдатель обращен лицом к точке, движущейся
по кривой ему навстречу. Бинормаль будет испытывать вращение около
касательной. Это вращение может быть или положительным (против
часовой стрелки) или отрицательным (по часовой стрелке), оамечатель-
но, что знак вращения не зависит от положения наблюдателя.
Действительно, если наблюдатель будет смотреть на эту же точку с другой
стороны, т. е. повернется лицом в противоположную сторону, то и
движущаяся точка по условию станет двигаться в противоположном
направлении; следовательно, направление движения изменится на
обратное, но так как изменилась и позиция наблюдателя, то для него
положительное вращение останется положительным, а отрицательное —
отрицательным.
Итак, существуют два типа пространственных кривых (в
окрестности некоторой точки); они объективно отличны друг от друга. Это
отличие и дает возможность приписать кручению знак. Именно,
условимся приписывать углу о/ и кручению положительный знак, а кривую
называть «правой» в том случае, когда вращение бинормали при при-
ближении ее к наблюдателю совершается против часовой стрелки.
В противоположном случае припишем углу со' и кручению
отрицательный знак и назовем кривую «левой».
152 ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
Примерами правой и левой кривой могут служить две винтовые
линии, изображенные на рис. 106, а (правая) и 106, б (левая). Нарезки
гаек и болтов обычно представляют правые винтовые линии.
Отмеченная нами независимость «правизны» и «левизны» от положения
наблюдателя выражается в том, что гайку можно навинчивать на болт как
с одной, так и с другой стороны. Но правую гайку нельзя навинтить
на левый болт. Для лучшего усвоения необходимо поупражняться в
различении правых и левых кривых на проволочных моделях, а также
вычертить правые и левые линии на кривых поверхностях (шаре,
конусе и др.)-
Пусть г (и) есть радиус-вектор переменной точки М линии (/).
Направление движения по линии (I) можно задать вектором скорости г'(и).
Направление бинормали определяется коллинеарным с ней вектором В,
а) б)
Рис. 106.
который, если М не является точкой спрямления (т. е. если х^Ов точке
М), можно представить выражением г' ХГ" *). Если вращение бинормали
совершается против часовой стрелки относительно наблюдателя,
расположенного со стороны вектору г' (и), то векторы
B(a),B'{u) = d-l, г'(и),
взятые в указанном порядке, образуют правую тройку. Если же бинормаль
вращается по часовой стрелке, то векторы В, В\ г' образуют лев)Ю
тройку. Поэтому наше соглашение о знаке кручения равносильно
следующему: кручение считается положительным, если векторы В, В'
О случае х=0 см. ниже, стр. 155.
§ 28. КРУЧЕНИЕ
153
и г', взятые в указанном порядке, образуют правую тройку, и
отрицательным, если тройка векторов В, В', г' —левая1) (вектор Весть любой
вектор, направленный по бинормали).
Теперь определение кручения можно сформулировать так:
Определение. Кручением называется величина, абсолютное
значение которой равно пределу отношения угла смежности о/
соприкасающейся плоскости к длине соответствующей дуги As; знак угла ш' и
кручения считается положительным, если векторы В, В' и г' образуют
правую тройку, и отрицательным, если эта тройка векторов — левая.
Кручение мы будем обозначать всегда через а. Обратная величина
— ==т, по аналогии с радиусом кривизны у, называется радиусом
кручения. Кручение называется также «второй кривизной».
При вычислении кривизны мы определяли угол смежности
касательных с помощью площади параллелограмма, построенного на
векторах касательных. Если мы для вычисления кручения будем
определять угол смежности бинормалей с помощью площади параллелограмма,
построенного на векторах бинормали, то найдем лишь ею абсолютную
величину, ибо площадь есть величина,которую в пространстве
ориентировать нельзя. Чтобы учесть знак угла
смежности и>' между бинормалями В и
В -f- А/?, определим этот угол с помощью
(ориентированного) объема V
параллелепипеда, построенного на Еекторах В,В-\-±В
и г' (рис. 107). Этот объем по абсолютной
величине и по знаку равен
V^B{B + AB)r' = BABr'. (1)
С другой стороны, его абсолютная
величина равна
|K|-5.}/P2|cos?|, (2)
где S есть площадь параллелограмма, pkic. Ю7.
построенного на векторах В, В-\-АВ, и
9 —угол между вектором Вх(В+ А/?), перпендикулярным к основанию
параллелепипеда, и вектором касательной г'. Так как векторы В и В + АВ
соответственно перпендикулярны к соприкасающимся плоскостям в двух
бесконечно близких точках, то вектор Вх(В+ АВ) коллинеарен с
прямой (л), по которой пересекаются эти соприкасающиеся плоскости.
Положим сначала, что кручение не равно нулю. Тогда согласно теореме 1
прямая (а) имеет пределом касательную. Поэтому lim <р = 0 im \i
так что |coscp|^l. Площадь S выражается формулой
так что формула (2) принимает вид
х) В этом определении устраняется «наблюдатель». Однако для определения
правой тройки мы нуждаемся, если не в одушевленном наблюдателе, то в его
правой руке или в изготовленном его руками штопоре и т. п. Таким образом,
хотя правая кривая отличается от левой объективно, однако, чтобы пояснить,
какую кривую мы называем правой, а какую — левой, необходимо привлечь
известный" из опыта объект, аналогично тому, как различие правой и левой руки можно
характеризовать без ссылки на образец, но, чтобы объяснить, какая именно из
двух рук—правая, необходимо показать хотя бы один раз эту руку.
154 ГЛ. II. СОПУТСТВУЮЩИЙ ТРИЕДР, КРИВИЗНА И КРУЧЕНИЕ
а так как, вследствие принятого нами соглашения, знаки величин V
и а/ совпадают, величины же В2 и \/*г" положительны, то из
сравнения формул (1) и (3) мы получаем
ВЬВг '^В2ш '/г*",
откуда
, ^ ВЬВг'
В* V г"1
Теперь находим кручение
' ВВ'г'
(4)
Остаётся выразить векторы В, В' через производные вектора г.
Ограничиваясь случаем, когда М не есть точка спрямления, можем положить
В=г'хг". (5)
Отсюда находим
B' = {r'xr")' = r'xr'". (6)
Подставляя в ВхВ' выражение В' из (6), находим
Подставим выражение В из (5); скалярное произведение Вг' обращается
в нуль, и мы получаем: fix В' = г' (г' г" г'"), откуда
##'/•' = г'2 (rVV"), (7)
и окончательно, подставляя выражения (7) и (5) в формулу (4). находим
0=
(r'xr")"
или в координатной форме
f f f
х- у z-
x" y" z"
: [(x'y - x-y'Y + (y'zT - y"z'Y + (z'x" - zTx')1]. (8a)
Если за параметр принять дугу, то r'2 = l, r'r" = O и знаменатель
в формуле (8) можно представить в виде
(Г' х r"f = r'V2 — (г'г'У = г"\
так что
dr d2r d*r
Js ~d? ds* 2 fdr d*r d*r \
0== ^^Y =[> \Jl*dFj
При выводе формулы (8) мы предполагали, что кручение не равно
нулю. Нетрудно видеть, что и в случае а = 0 формула (8) верна,
т. е. что при о = 0 также r'r"r"' = 0.
В самом деле, если о = 0, то угол о>' имеет высший порядок
относительно As. Следовательно, высший порядок имеет и объем В &В г'
параллелепипеда, построенного на векторах В, B + lB, r'. Поэтому
ё**1
цюё**£1 = о, т. е. ВВ'г' = 0.
As '
Так как для правильной точки г'2 Ф 0, то формула (7) (при выводе
ее условие о^О не играло никакой роли) дает
r'rV'-O. (10)
§ 28. КРУЧЕНИЕ 155
Таким образом, формула (10) дает необходимое и достаточное
условие того, чтобы в точке М, где х Ф 0, кручение равнялось нулю.
При выводе формулы (4) существенно предполагалось, что
производная /?' (и) существует и непрерывна в рассматриваемой точке М
(непрерывность требуется для того, чтобы точки М19 Мг могли
стремиться к М по произвольному закону; ср. § 14). Как видно из
выкладок, это требование обеспечивается существованием и непрерывностью
третьей производной г'" (и) вектор-функции г (и).
Замечание. Формула (4) остается, конечно, в силе и тогда,
когда в точке М кривизна равна нулю, т. е. когда М есть точка
спрямления. Но формула (5) и все дальнейшие выкладки теряют силу
для этого исключительного случая. Это, однако, не означает, что
в точке спрямлеьия кривая не может иметь кручения или что
кручение ее в такой точке непременно равно нулю. Но только кручение
в этом сл\чае выражается другой формулой (см. упражнение 5
на стр. 156), и существование его не обеспечивается существованием
первых трех производных вектора г (и).
Выше было сказано, что кручение плоской линии всюду равно
нулю. Справедливо и обратное предложение.
Теорема 2. Если вдоль линии (I) кручение всюду равно нулю, то
линия (I) — плоская.
Доказательство. Согласно определению кручения, равенство
о = 0 означает, что угол смежности «>' бинормалей имеет высший
порядок относительно As, а так как а)'^|Д#|, то соотношение о = 0
равносильно условию
т. е. вектор Ь есть величина постоянная. Таким образом, бинормаль Ьу
а значит, и соприкасающаяся плоскость сохраняют постоянное
направление. Отсюда следует (§ 20, замечание 2), что соприкасающаяся
плоскость сохраняет и постоянное положение, т. е. линия (/) — плоская,
что и требовалось доказать.
Итак, необходимым и достаточным условием того, чтобы линия (I)
была плоской, является тождественное обращение кручения в нуль.
Однако в отдельных точках неплоской кривой кручение может
обращаться в нуль. Такие точки характеризуются (при у. Ф 0, т. е.
при г' X г" Ф 0) соотношением
выражающим компланарность векторов г', г", г'"; они называются
точками сплощения. В них линия имеет «более плоский» вид. Точнее:
расстояние точки сплощения М до соприкасающейся плоскости
в бесконечно близкой точке Мг имеет не третий, как в общем случае,
а более высокий порядок малости.
Пример 1. Найдем кручение винтовой линии
х — а cos и, у = а sin и, z = bu.
(г'г"г'"):
— a si пи a cos и b
— a cos и —a sin и О
a sin и — a cos и О
= a2b, (г' X г"У =
156 ГЛ. II. СОПУТСТЕУКШШЙ ТРИРДР, КРИВИЗНА И КРУЧЕНИЕ
Этот результат можно получить синтетически так же, как в § 23
(стр. 117) мы нашли кривизну винтовой линии. Только равные отрезки
МА и MB нужно отложить не на касательных, а на бинормалях,
которые составляют с плоскостью основания постоянный угол
тс f Ъ a
Y = «—а ( cos Y = -. sin у = .
При Ь > О кручение о > О, т. е. винтовая линия —правая; при Ъ < О
винтовая линия —левая; при 6 = 0 она обращается в окружность, для
которой, как и для всякой плоской кривой, кручение равно нулю.
Как кручение, так и кривизна винтовой линии постоянны. Мы
увидим, что только винтовая линия совмещает эти два свойства.
Напротив, существует бесчисленное множество линий, у которых
постоянна только кривизна или только кручение.
Пример 2. Найдем кручение линии
х = аги2 + 2Ьги + сг, у = а2и2 + 2b2u + с2, z = a3a* + 2bsu + c3. (12)
Вычисление проще всего вести в векторной форме, положив
г = аи2 + 2Ьи + Су
где вектор а имеет координаты alf a2, аг и т. д.
Находим г'= 2 (aw+ 6), r" = 2a, г'" = 0. Кручение а всюду равш>
нулю. Значит, линия — плоская. Ее плоскость находится как
соприкасающаяся плоскость в какой-нибудь точке; например, в точке
а = 0 (т. е. г — С) соприкасающаяся плоскость имеет уравнение
(/? — с) (аи + Ь) а = 0, или (R — с)Ьа = 0.
Итак, за вектор нормали плоскости можно принять вектор Ь X п.
Читателю предлагается доказать, что линия (12) есть кривая
2-го порядка.
Упражнения
1. Найти кручение линии x* = 2az, y2 = 2bz.
2. Найти кручение конической спирали.
3. Найти кручение бицилиндрики в ее вершине. Имеет ли эта кривая точки
сплощения?
4. Доказать, что если соприкасающаяся плоскость любой точки кривой
проходит через фиксированную точку Р, то она постоянна, т. е. кривая—плоская.
Указание: а) Построить ряд равноотстоящих точек Л, В, С, D, . . . , про-
вестп через точки А, В, С; В, С, 1) и т. д. плоскости, оценить порядок малости
расстояния этих плоскостей до точки Р и отсюда — порядок малости угла
смежности соприкасающихся плоскостей, б) Исходя из компланарности векторов
гР — г, г', г", доказать компланарность векторов г', г", г"'.
5. Доказать, что в точке М, где векторы г' и г" коллинеарны, но векторы
г' и г'" не коллинеарны, кручение представляется формулой
r,r,>.r\v
С = -
(г' х г'")2
ГЛАВА III
ФОРМУЛЫ ФРЕНЕ
§ 29. Формулы Френе
С заданной пространственной кривой связано множество
геометрических объектов, изучение которых представляет большой интерес.
Исследование этих объектов чрезвычайно облегчается, если отнести
их к система координат, которую мы назовем натуральной: в ней за
координатные оси принимаются ребра сопутствующею триедра. Но
тогда недостаточно знать, как меняются координаты изучаемого объекта;
необходимо еще учесть, что меняется система координат, т. е. ее
основные орты /, п, Ь. Поэтому в исследование входя! производные
этих векторов. Эти производные сами могут быть отнесены к
сопутствующему триедру. Поэтому важно знать выражения производных
от Бекторов t, П, Ь, через самые векторы t, It, Ь. Эти выражения
даются формулами, найденными (в координатной форме) французским
математиком Френе (Frenet) в 1847 г. 1).
Первая формула Френе дает выражение вектора -г-. Этот вектор,
который есть не что иное, как вектор кривизны -jr2f ибо t= -т J , имеет
согласно формуле (5) § 23 (стр. ИЗ) модуль, равный кривизне:
\/ ( -гЧ ) = х.
_
ds2
Кроме того, согласно формуле (10а) § 21 (стр. 103), мы имеем
п = -djz
Сопоставление этих формул дает
7^Y
или, что то же,
(первая формула Френе).
1) Так как работа Френе была напечатана в провинции (Тулуза) в виде
брошюры, она осталась неизвестной, и в 1851 г. другой французский магеяатш
Серре ( erret) олубляковал те же результаты в парижском математическом
журнале Nouvelles Annales des Maihematiques. Статья Френе б^ла напечатана в to\i
же журнале в 1864 г. Поэтому некоторые авторы называют формулы Френз
формулами Серре, другие —формулами Френе-Серре, третьа — фэрмулами Серре-Френе.
158 гл. in. формулы френе
Напомним, что п есть единичный вектор, направленный по
главной нормали в сторону вогнутости кривой.
Приведенный вывод не оставляет желать лучшего в смысле
краткости. Однако, чтобы лучше выяснить геометрический смысл
формулы (1), мы выведем ее непосредственно геометрически.
Пусть OA~t (рис. 108) есть единичный вектор касательной
в точке М, a OB = t -f- Af— единичный вектор касательной в бесконечно
близкой точке М1У перенесенный параллельно самому себе так, что
его начало совпадает с точкой М. Вектор At=AB эквивалентен dt.
Из равнобедренного треугольника ЛОВ, у которого бесконечно малый
- угол О равен углу смежности о> касатель-
"У~\ ных, находим
\ut
Так как угол А эквивалентен прямому,.
а плоскость АОВ имеет пределом
соприкасающуюся плоскость (теорема 3 § 20, стр. 85), то прямая АВ имеет
пределом главную нормаль. При этом вектор dt^AB направлен в
сторону вогнутости (так как он указывает направление вращения
касательной). Итак, вектор dt равнонаправлен с вектором п, а модуль его
эквивалентен (о. Следовательно,
dt ^ <!)#•
Отсюда
т. е.
Так как все входящие в эту формулу величины постоянны для
фиксированной точки, то
Вторая формула Френе дает выражение для -т , третья — для -,- .
Выведем сначала третью формулу Френе, которая получается арало-
гично первой.
Как мы видели в начале § 28 (стр. 150) соприкасающаяся плоскость,
а значит, и единичный вектор бинормали Ь, вращается около
касательной, так что db лежит в нормальной плоскости Q (рис. 109);
будучи перпендикулярен к Ь, он направлен по главной нормали. Если
кривая — правая, то вращение b происходит против часовой стрелки
(при наблюдении со стороны t), т. е. вектор db (рис. 109) направлен
в сторону (— п). Модуль же этого вектора равен углу смежности
бинормалей <*>'• Таким образом,
dbzz — w'n,
^-~ — — п
(третья формула Френе).
§ 29. ФОРМУЛЫ ФРЕНЕ
159
Если кривая —левая, то вектор db направлен в сторону п, но
модуль этого вектора (как величина положительная) равен —а/, ибо
угол а>' теперь, когда бинормаль вращается по часовой стрелке,
отрицателен. Таким образом предыдущие формулы сохраняют силу.
Вторая формула Френе сразу получается из соотношения
n = bxt.
Дифференцируя его и принимая во внимание (1) и (3), находим
dn
ds
(2)
(вторая формула Френе).
Несмотря на крайнюю простоту этого аналитического вывода,
не лишне рассмотреть вопрос и геометрически. Положение
сопутствующего триедра вполне определяется
заданием касательной и бинормали,
Поэтому, когда известны смещения
An
п
в
Qh-*^
й
Рис. 109.
f ис. 110.
касательной -и бинормали, определяется также смещение главной
нормали. Произведем сначала смещение только касательной, оставляя на месте
бинормаль. Тогда вектор dn^^n (рис. НО) направлен в сторону—tf,
а модуль его, т. е. длина отрезка А'В', равен «>; таким образом, от этого
вращения вектор п получает приращение, эквивалентное
— ш*.
Затем будем вращать бинормаль, оставляя касательную неподвижной
(при этом безразлично, исходить ли из первоначального положения
сопутствующего триедра или из того, в которое он приведен
предыдущим вращением, так как соответствующие значения An будут
эквивалентны друг другу). Тогда вектор п получит приращение Д|»,
эквивалентное (о'6. Читателю предлагается построить чертеж, рассмотрев
отдельно случаи правой и левой кривой. Полное приращение вектора п
является суммой рассмотренных двух. Поэтому
dn
(2)
160 ГЛ. III. ФОРМУЛЫ ФРЕНЕ
В механике доказывается, что два бесконечно малых вращения
твердого тела около двух пересекающихся осей равносильны одному
вращению; вектор угловой скорости этого движения равен сумме
векторов угловой скорости, представляющих два произведенных вращения.
Будем рассматривать сопутствующий триедр как твердую систему
и считать, что дуга данной линии численно равна времени. Тогда вектор
угловой скорости первого из рассмотренных выше вращений ecib j^&,
а второго, 'jjgt. Таким образом, вектор угловой скорости
сопутствующего триедра есть
\&+Ж- (За)
Ось мгновенного вращения триедра имеет направление этого вектора,
так что точки, лежащие в спрямляющей плоскости (b, t) на прямой,
проходящей через вершину триедра и наклоненной к касательной под
углом
fe (ЗЬ)
fe
остаются неподвижными. Иными словами, эт^« прямая есть пересечение
двух бесконечно близких спрямляющих плоскостей. Вектор r.b-\-at
называется вектором Дарбу,
Сопоставим три формулы Френе, записав их в виде1):
ds ~
dn t '
db _ П
1s~~ * — —
•J
или
(4а)
Звездочки обозначают отсутствующие члены.
Формулы Френе дают выражения первых производных векторов t, n, Ь.
Но с их помощью можно найти выражения высших производных.
Вычислим, например, вторую производную вектора t:
1_ ^
p2 dsn^ p ds '
Вместо -г- вставляем его выражение из (2) и находим
й=—W-4-?»+-*. (5)
а*-2 р2 р2 ds р*
Таким же образом найдем производные третьего и более высокого
порядка.
Формулы Френе являются основным аналитическим аппаратом
дифференциальной 1еоме1рии; их нужно твердо запомнить.
х) Если считать, как это делают некоторые авторы, кручение положительным
в том случае, когда бинормаль вращается по часовой стрелке, то в формулах (4)
придэтся заменить ^ на — z.
§ 30. КАНОНИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВОЙ 161
§ 30. Каноническое представление кривой
В качестве первого примера применения формул Френе рассмотрим
вопрос о приближенном представлении кривой в окрестности ее точки.
Результаты, которые мы полечим, oiчасти уже известны из
предшествующего, что позволит нам выявить преимущества, доставляемые
формулами Френе.
Возьмем в качестве координатных осей X,Y, Z ребра
сопутствующего триедра в некоторой точке О кривой (/). За параметр примем
длину дуги, отсчитываемой от точки О, так что для точки О имеем
s = 0. Радиус-вектор г{х, у, z} точки М, бесконечно близкой к О,
можно представить выражением
r = r'as+±ry+±r'a"s*+..., (1)
где через г'о, г\, г'" обозначены производные вектора г в начале
координат, а многоточием обозначена погрешность е4, имеющая более
высокий порядок, чем s3.
В это разложение подставим выражения векторов r'ot r'o, ... через
/, д, П из формул (1), (2), (3) и (5) § 29:
(2)
к
0
dt
""ds
dH
ds*
n
Po
7
t
Й
Получим
Выражения, стоящие в скобках, суть координаты х, у, z точки М,
так что, пренебрегая членами порядка выше третьего, имеем
у =* +W/-{$S* = * +^ va+f Ю.Л (5)
1 1
г — * * -—s3 = * * +Txn5fts8. (6)
bpo;o 6 • *
Итак, с точностью до бесконечно малых третьего порядка всякая
линия в окрестности некоторой ее точки может быть представлена
уравнениями (4), (5), (6).
Уравнение (4) показывает, что расстояние х от точки М до
нормальной плоскости х = 0 есть бесконечно малая величина первого
порядка, эквивалентная длине дуги, что геометрически легко
подтвердить. Та же формула показывает, что дуга s превосходит расстояние х
ее конца до нормальной плоскости на величину третьего порядка
малости, эквивалентную t-*os3-
Если наша линия есть окружность (рис. 111), то s = poa, z = posina,
и формула (6) дает
sina = a —~a3+ ..., (7)
11 М. Я. Выгодский
162
ГЛ. III. ФОРМУЛЫ ФРЕНЕ
т. е. известное разложение в ряд функции sin а. Если бы мы в
формуле (4) не ограничились членами третьего порядка, а пошли бы
дальше, то мы получили бы и дальнейшие члены разложения (7).
Уравнение (5) показывает, что расстояние у точки М до
спрямляющей плоскос1и у = О, в случае, если точка М не является точкой
спрямления (■— фО), есть бесконечно малая величина второго порядка
(ср. § 21, стр. 99—100), вследствие чего кривая лежит по одну
сторону спрямляющей плоскости (р0 есть положительная величина). В
случае же точки спрямления (— = 0), если величина
не обращается в н}ль, у имеет третий порядок малости, и кривая
переходит с одной стороны спрямляющейся плоскости на другую.
Формула (6) показывает, что расстояние точки М линии (/) до
соприкасающейся плоскости в общем случае (т. е. если М не является
ни точкой спрямления, ни точкой спло-
щения) есть бесконечно малая величина
третьего порядка; значит, кривая (I)
переходит с одной стороны
соприкасающейся плоскости на другую (s меняет
знак при переходе через 5 = 0).
Расстояние d= у у2 4- ъ1 от точки М
до касательной в точке О имеет главной
частью yttsy-s~ или в силу (4)
0
* г2
— и,
Zp
(8)
Рис. Ш.
что мы знаем из § 25 (стр. 130). Так же
докажем, что расстояние от точки М до
бинормали и до главной нормали имеет
первый порядок малости.
На соприкасающуюся плоскость z = 0 точки О кривая (/)
проектируется кривой АОВ (рис. 112), уравнения которой имеют вид
4v+4 (*')•*■
(4а)
(5а)
Если и этих уравнениях сохранить только первые члены правых
частей, то мы получим параболу (COD на рис. 112):
*i = *i, (4b)
2/i = у V% (5b)
Она представляет приближенно линию АОВ и вместе с тем линию (l)t
к которой, как мы знаем, соприкасающаяся плоскость прилегает теснее,
чем всякая другая плоскость. Парабола COD называется
соприкасающейся параболой линии (/) в точке О. Параметр соприкасающейся
параболы равен — =(v Следовательно (пример 5 § 24, стр. 124), радиусы
кривизны линии (I) и ее соприкасающейся параболы равны.
§ 30. КАНОНИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВОЙ
163
Посмотрим, каково взаимное расположение проекции АОВ и
соприкасающейся параболы COD линии (/).' Возьмем на них соответственно
точки М и Mlf имеющие равные абсциссы х=хх. Как видно из
уравнений (4а) и (4Ь), разность s — s1 = г3 параметров s и s2 будет иметь
в общем случае (х^ Ф 0) третий порядок относительно s, а значит,
и относительно х. Уравнение (5а) мы можем представить в виде
У = \ *. (*, + •,)* + | (*')« (*1 + *,)3 + • • •
Вычитая последнее уравнение из (5Ь), находим, что отрезок Д/71/т
по абсолютной величине и по знаку эквивалентен — (х')0 s].
Следовательно, в общем случае, когда (х')0 Ф 0, т. е. когда в точке О
кривизна линии (/) меняется монотонно, отрезок ММЛ имеет третий
Рис. 112.
порядок относительно х и, значит, меняет знак при переходе через
точку О. Поэтому проекция линии (/) на соприкасающуюся плоскость
переходит со стороны выпуклости соприкасающейся параболы в сторону
ее вогнутости (рис. 112), т. е. извне внутрь.
Так же ведет себя проекция АОВ по отношению к кругу кривизны
линии (Z). Действительно, согласно теореме 8 § 27 (стр. 147), линия АОВ,
если кривизна ее в окрестности О изменяется монотонно, выходит из своего
круга кривизны в направлении возрастания ее радиуса кривизны и
входит в свой круг кривизны в направлении убывании радиуса кривизны.
Но круг кривизны линии АОВ совпадает с круюм кривизны линии (/).
Действительно, оба эти круга лежат в соприкасающейся плоскости XOY
и касают'ся прямой ОХ. Радиусы же этих кругов равны, в чем проще
всего убедиться, вычислив кривизну х линии АОВ в точке s=0,
воспользовавшись параметрическими уравнениями (4а), (5а). Мы найдем,
что х=х0. Итак, круг кривизны линии АОВ является вместе с тем
кругом кривизны линии (Z), и, значит, линия АОВ в общем случае
переходит со стороны выпуклости круга кривизны линии (/) на
сторону его вогнутости, т. е. извне внутрь.
* На спрямляющую плоскость XOZ линия (I) проектируется
кривой ROQ (рис. ИЗ), уравнении которой имеют вид:
x = s — — xfca + e4t (4c)
(6с)
11
164
ГЛ. III. ФОРМУЛЫ ФРЕНВ
где е4 и т)4 суть величины четвертого или более высокого порядка
относительно s.
Если сохранить только первые члены правых частей, то мы будем
иметь кубическую параболу (KOL на рис. 113):
*2=*2, (4d)
Рассуждая так же, как выше, мы найдем, что в общем случае
проекция ROQ линии (/) лежит по одну сторону от кубической
параболы KOL. Предоставляем читааелю доказать это. Заметим только, что
существенно учесть порядок величины т]4. В том исключительном
случае, когда Y)4 имеет ие четвертый, а более высокий порядок, линии
Z
О
Рис. 113.
KOL и ROQ могут перекрещиваться. Читателю предлагается найти,
каким условиям должны удовлетворять кривизна хв и кручение а9
линип (/) в точке О, чтобы этот исключительный случай имел место.
На нормальную плоскость в точке О линия (I) проектируется
линией TOS (рис. 114), которая приближенно представляется
полукубической параболой VOU:
2/8=4vf, (5e)
^з — Т^ хоао* * \и*?/
Бесконечно малая величина z8 имеет порядок — относительно yz. Тот
же порядок имеет z относительно у. Расстояние же между TOS и VOUt
считаемое по направлению z, в общем случае имеет относительно $
четвертый, а относительно у — второй порядок малости; тогда взаимное
расположение линий TOS и VOU такое, как на рис. 114. Читателю
предлагается доказать это.
Обе линии SOT и VOU имеют в точке О точку возврата, что
следует из того, что кривая и, следовательно, также и ее проекция на
нормальную плоскость располагаются по одну сторону спрямляющей
плоскости. При этом точка О есть точка возврата первого рода, так как
при данном значении у мы имеем для z два значения разных знаков.
§ 30. КАНОНИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КРИВОЙ
165
В заключение этого параграфа заметим, что из формул (4) и (5),
вычисляя главную часть выражения -|- , мы находим следующее
приближенное выражение радиуса кривизны:
Po-fJ- (7)
Главную часть погрешности этого выражения, т. е. главную часть
S/ величины р0 — — , мы можем найти
из тех же формул (4) и (5). Она
равна -£• (/)0 s, так что
приближение (7) дает хороший результат в том
случае, если измерение координат
х и у произведено на малой дуге,
вдоль которой радиус кривизны
изменяется медленно.
Практически лучше
пользоваться приближенной формулой
/ в которую входят величины, более
удобные для измерения, именно
здесь / есть хорда малой дуги АВ
(рис. 115) рассматриваемой кривой,
a h — «стрелка», т. е. расстояние от
середины О дуги АВ до середины D
стягивающей ее хорды АВ.
Форму- L
D
\h
Рис. 114.
О
Рис. 115.
а
у
лу (8) нетрудно вывести из формулы (7) (см. указание к
упражнению 1).
Упражнения
1. Вывести формулу (8).
Указание. Примем точку О за начальную. Обозначим дугу О А через 5.
Тогда дуга ОБ равна — s. Длина хорды АВ эквивалентна длине дуги АВ, т. е. 2s
или 1х. П шъзуясь формулами (4), (5), (6), найдем,что координаты х и ъ точки О
имеют по меньшей мере четвертый порядок малости относительно s, тогда как
координата у этой точки эквивалентна координате у точки А. Поэтому
х я& —, у z& h.
Подставляя эти выражения в (7), найдем формулу (8).
166 ГЛ. III. ФОРМУЛЫ ФРЕНЕ
_ 1 хи
2. Показать, что радиус кручения т = — эквивалентен величине .--- . где
a oz
я, ?/, z суть координаты точки рассматриваемой линии относительно системы
координат, начало которой взято в бесконечно близкой точке. Оценить
погрешность соответствующей приближенной формулы.
§ 31. Оценка некоторых геометрических величин
Значение формул Френе хорошо иллюстрируется также при оценке
геометрических величин. С помощью формул Фроне мы не только
определяем порядок их малости, но и находим эквивалентные им
выражения, зависящие от кривизны, кручения и их производных.
Пример 1. Оценим разность между дугой и стягивающей ее
хордой. По самому определению дуги, она эквивалентна хорде, т. е.
разность между ними имеет порядок малости выше первого.
Оказывается, что эта разность в общехМ
случае имеет третий порядок отно-
м -^^ сительно дуги и эквивалентна тг—> ,
где s — длина дуги, а р —радиус
Рис. 116. кривизны в какой-либо ее точке.
Если за начало координат принять конец А дуги АВ и другой
ее конец В считать «текущей» точкой, то вектор АВ (рис. 116)
равен г. Длина АВ есть }/~г2, и мы должны оценить разность d =
Чтобы избежать извлечений корня, преобразуем это выражение:
d = —r= ^ —-г— . (1)
Из формул (4), (5) и (6) § 30 имеем, опуская ненужные теперь
индексы начальной точки:
или*)
-2 ^ Я2 * С4 | * «4 ^ „2 1_ 4 /9\
Зр "^ip1 ^ 12P3 " ^'
Из (1) и (2) получаем
~ 12р"2 -Z5^24p"25# W
Так как на бесконечно малой дуге радиусы кривизны всех точек
эквивалентны, то под р можно понимать радиус кривизны в любой
точке дуги.
*) В выполненных преобразованиях мы отбрасываем все члены порядна выше
четвертого. Если бы случилось, что учитываемые нами члены в конечном итоге
взаимно уничтожились, это значило бы, что нужно было учесть также члены
пятого, а может быть, и более высокого порядка. На всякий случай не мешало бы
проявить некоторую осторожность в самом начале и учитывать члены, скажем,
до шестого порядка. Однако, это сильно усложнило бы вычисления. При
некотором навыке в подобного рода вычислениях вырабатывается умение предугадывать
то количество членов, которое заведомо достаточно для того, чтобы не потерять
главную часть результата.
§ 31. ОЦЕНКА НЕКОТОРЫХ ГЕОМЕТРИЧЕСКИХ ВЕЛИЧИН
167
В окрестности ючки спрямления, где — =0, формула (3) теряет
силу. Там d им-еет более высокий (как правило—четвертый) порядок.
Пример 2. Оценить кратчайшее расстояние d от точки М
линии (I) до круга кривизны, проведенного через точку Мо.
Проведем через точку М плоскость Q, перпендикулярную к
соприкасающейся плоскости Р в точке Мо и проходящую через центр С
окружности кривизны в Мо (рис. 117). Пусть /V — точка пересечения
Рис. 117.
Q с этой окружностью и В — проекция М на плоскость Р. Тогда
d = \MN\ есть искомое кратчайшее расстояние. Мы имеем
d2 = ВМ2 + BN2 = ВМ2 + (ВС - CN)2.
В системе координат, отнесенной к сопутствующему триедру
точки /1/0, три точки Мч В, С имеют координаты: М(х, у, z), B(x, у, 0),
С (0, р, 0). Поэтому
BM—z, ВС = ]/х1 + (р—г/)2, СЛ^ = р,
так что
Прежде чем подставить выражения
% = IXS2 , J_XV +
полезно упростить вюрое слагаемое в (4), учитывая, что р есть
постоянная величина и что х имеет первый, а у — второй порядок
относительно s. Мы имеем
(5)
(6)
(7)
1
"2 **" ~ У
Подставляя сюда выражения (5) и (6) и отбрасывая величины выше
третьего порядка, имеем
х*2 + "в" х
168
ГЛ. III. ФОРМУЛЫ ФРЕНЕ
Теперь из (4) находим
или
Для плоской кривой (<з = 0) мы имеем
, _ 1
(8)
(8а)
Таким образом, расстояние между кривой и ее кругом
кривизны имеет в общем случае третий порядок относительно дуги. Более
высоким порядок этого расстояния будет лишь в том случае, если
точка Мо есть точка спрямления или точка сплощения и если, кроме
того, в точке Мй кривизна стационарна (х' = 0). В частности,
повышение порядка будет иметь место для той точки плоской кривой,
в которой кривизна
экстремальна.
Пример 3. Оценить
разность о отрезков \AtK\
и | А2К |, на которые
рассекает хорду АгА2
плоскость, нормальная к дуге
АХА2 в середине последней А^
(рис. 118).
Примем точку Ао за
вершину сопутствующего три-
едра. Обозначим через хъ
и х% абсциссы А0Сг и А0С2
точек Ах и А2. Так как
нормальная плоскость в точке
Ао есть плоскость х = 0, то
\АгК |-| А2К\ __ -хг-
\АгК\+\А%К\ ~~ -^i+
или
откуда
Рис. 118.
Если длину дуги АгА2 мы обозначим через 2s, то выражение хх
найдется из формулы (4) § 30, а выражение х2 — из той же формулы после
замены в ней 9 на —s. Однако предварительно нужно пополнить
упомянутую формулу (4) членами более высокого порядка, ибо
выписанные в § 30 члены первого и третьего порядка этой формулы взаимно
уничтожаются при вычислении хг-{-х2. С этой целью напишем разло-
§ 31. ОЦЕНКА НЕКОТОРЫХ ГЕОМЕТРИЧЕСКИХ ВЕЛИЧИН 169
жение вектора r(s) в виде
Г (8) = (Г')„ * + 4
и учтем влияние четвертого члена (влияние первых трех уже учтено
в формуле (4) § 30).
Мы уже нашли [формула (2) § 30] с помощью формул Френе
выражение
р2 р2 ' рт
Эту формулу мы должны продифференцировать еще разт причем для
нашей цели достаточно вайти те члены, которые содержат t. Снова
применив формулы Френе, найдем
Пополнив теперь формулу (4) членом четвертой степени (на нем можно
остановиться, ибо он не уничтожается в выражении хг + х2), получим
и, следовательно,
о = А2А,
или
^ 4
25 * 4р3* ~"4р35 '
(9)
Пример 4. Оценить кратчайшее расстояние между двумя
бесконечно близкими касательными кривой линии.
За начало отсчета примем одну из точек касания Мо.
Координатные с;рты в этой точке обозначим t0, п0У &0У Вектор М0М = г, ведущий
в бесконечно близкую точку касания М, представится в виде
г = xt0 + уп0 + zt0, (10)
где координаты ж, г/, z, согласии формулам (4), (5), (6) § 30,
выражаются через дугу s = M0M следующим образом:
Ь J
Если t есть орт касательной в точке М, то кратчайшее расстояние d
между касательными в Мо и М выражается извесаной из
аналитической геометрии формулой
, rUt
170
ГЛ. III. ФОРМУЛЫ ФРЕНЕ
которая дает не только абсолютную величину, но и знак расстояния:
для правой пары касательных формз^ла (12) дает положительный, а для
левой —отрицательный знак *).
Так как
то числитель формулы (12) равен
rtot - (xt0 4- уп0 + zb0) t0 (x
а знаменатель равен
у'п0 + z'bQ) = zif - yz\
(13)
так что
zy'-yz'
и — —,— ' •
Для оценки величины d мы в эту точную формулу подставим
приближенные выражения у, ъ из формул (11) и выражения
)
(14)
получаемые дифференцированием (11). Главная часть числителя имеет
четвертый порядок, а знаменателя—первый. Пренебрегая членами
высших порядков, находим
"4.+ .... (15)
т. е.
(16)
Формула (16) показывает, что расстояние между двумя бесконечно
близкими касательными по абсолютной величине вдвое меньше, чем
расстояние z от точки на кривой до бесконечно близкой
соприкасающейся плоскости. Для дальнейшего важно подчеркнуть, что d имеет
высший порядок малости относительно дуги М0М. Мы видим также,
что касательные правой кривой образуют левую пару, что
рекомендуется представить себе наглядно.
Замечание 1. Обратим внимание читателя на ошибку,
которую можно допустить, если вести вычисление следующим образом.
!) Пара неперпендикулярных скрещивающихся прямых
(*i)» U2) (Рис 119) называется правой, если для
наблюдателя, находящегося в точке С2 (на продолжении общего
перпендикуляра К1К2 в сторону второй прямой), вращение от
(1г) к (Z2) на острый угол происходит против часовой стрелки.
Устанавливаемая таким образом ориентация не зависит
от того, какая прямая взята за первую, потому что
если считать первой прямую (Z2), а второй — прямую (Zx), то
наблюдателю придется переместиться из точки Сг в какую-
либо точку Сг на продолжении К^К2^ сторону прямой Цх).
Формула (12) подтверждает факт этой независимости
аналитически: одновременно с перестановкой векторов t0 и t мы
должны заменить в ней г на —г. Вследствие этого
величина rtQt сохранит прежний знак.
Рис. 119.
§ 3 1. ОЦЕНКА НЕКОТОРЫХ ГЕОМЕТРИЧЕСКИХ ВЕЛИЧИН 171
Мы имеем t = ttt-\- &ta, и следовательно, формула (12) дает
rf= , *** = , "As . (17)
V«*"-)% /(их*)*
Кроме того,
Заменив в (17) величину ^ эквивалентной величиной хояо,
найдем
или, принимая во внимание (10) и (11),
^{w3' (20)
что не согласуется с формулой (16). Источником ошибки послужило
ю, что мы заменили в смешанном произведении (17) сомножитель —
эквивалентным сомножителем у0П0. Такая замена может дать
произведение, не эквивалентное прежнему. Эквивалентность нарушается от
того, что смешанное произведение может обращаться в нуль и тогда,
когда ни один сомножитель нулю не равен, вследствие чего порядок
произведения может не равняться сумме порядков сомножителей.
В самом деле, в нашем примере мы имеем
где в—бесконечно малый вектор (первого порядка). Если мы им
пренебрегаем, то теряем произведение rtoe, которое, невидимому,
имеет порядок более высокий, чем rtono\ на самом же деле порядки этих
величин одинаковы.
. Действительно, в произведении rtono сомножитель г имеет первый
порядок. Два остальных—конечны. Однако произведение имеет не
первый, а третий порядок, ибо член первого порядка коллинеарен
•с сомножителем^, а член второго порядка—-с сомножителем я0.
Произведение же rtQz = y(notQz), в котором у имеет второй, а в—первый
порядок, может иметь также третий порядок (если главная часть s не
компланарна с векгорами п0, /0). В нашем случае оно, действительно,
имеет третий порядок, в чем и содержится источник ошибки.
Замечание 2. Формулу (16) можно получить также
следующим образом. Краачайшее расстояние между прямыми / и 1г можно
измерить так: через какую-либо точку А прямой (/) проводим
плоскость Q, перпендикулярную к (/). На эту плоскость проектируем
ортогонально прямую (1г) и получаем прямую (/'). Расстояние между
{/) и (1г) равно расстоянию от точки А до прямой (/'). Если (/) есть
касательная в точке Мо, то, взяв эту точку за точку А, проектируем
касательную (1Х) в точке М на нормальную плоскость точки АГ0.
Проекция (Г) есть не что иное, как касательная к проекции данной линии..
Но последняя проекция может быть принята за полукубическую парабо-
1 72 ГЛ. III. ФОРМУЛЫ ФРЕНЕ
лу г/ = -г-х5а, z =-г-хо58 (см. стр. 164). Остается составить уравнение
касательной в точке (у, z) и найти расстояние до этой касательной от
точки (у = 0, 2 = 0).
У п ражн.ен жк
1. Разность d = | AD | — | DB | отрезков, на которые нормальная плоскость
в точке О разбивает хорду АВ — 1, параллельную спрямляющей плоскости в точ-
Z2 dp
кв О, эквивалентна выражению — — j-, где s есть дуга, для которой
положительное направление отсчета совпадает с направлением АВ.
2. Оценить разность | О А \ — | OB | дуг, на которые разбивается дуга АВ
плоскостью, перпендикулярной к хорде АВ и проходящей через середину D этой
хорды.
3. Оценить угол между плоскостью, проходящей через равноотстоящие точки
А, В, С и соприкасающейся плоскостью в средней точке В (ср. § 20, теорема 7).
4. Оценить разность между половиной угла смежности касательных и углом,
составляемым одной из касательных с хордой, соединяющей точки касания.
5. Доказать, что угол смежности касательных ю эквивалентен сумме л -f $ углов,
образуемых касательными с хордой, соединяющей точки касания (для плоских
кривых имеем точное равенство). Оценить разность между о> и а ■+- р.
6^ Точка пересечения прямой I с перпендикуляром, общим для / и другой
прямой 1\ называется точкой сжатия, прямой / (относительно данной пары).
Доказать, что точка сжатия касательной (относительно бесконечно близкой
касательной) в пределе совпадает с точкой касания. Оценить расстояние от точки
сжааия до хорды, соединяющей точки касания.
7. Оценить разность между углом, составленным бесконечно близкими
соприкасающимися плоскостями в точках Мъ М2, и удвоенным углом, составляемым
соприкасающейся плоскостью в точке Mj с плоскостью, параллельной
касательным в точках Мх и Mi%
8. Доказать, что расстояние d' от точки М линии {I) до круга кривизны в
бесконечно близкой точке Мо, измеряемое по направлению, параллельному
нормальной плоскости в точке Мо, эквивалентно кратчайшему расстоянию d от точки
М до круга кривизны в Мо. Найти оценку величины d' из точного значения этой
величины и сравнить результат с результатом примера 2.
ГЛАВА IV
НЕКОТОРЫЕ СВОЙСТВА СФЕРИЧЕСКИХ ФИГУР
§ 32. Сферические индикатрисы
При исследовании ряда геометрических вопросов бывает полезно
прибегать к изображению линий и поверхностей па сфере. Эти
изображения могут иметь очень разнообразный характер. Можно, например,
проектировать точки данной линии или поверхности из центра сферы;
точки пересечения проектирующих лучей со сферой будут
изображениями соответствующих точек оригинала. Такой характер носит,
например, изображение звездного неба на сфере планетария. В
дифференциальной геометрии применяются иные изображения. С каждой точкой М
изучаемого объекта связывается некоторое направление (например,
если изучается линия, — направление касательной или бинормали, или
вектора Дарбу и т. д.). По этому направлению из центра сферы
проводится радиус. Точка М1 пересечения последнего со сферой
изображает точку. Такие изображения называются сферическими
индикатрисами *).
Так, сферическая индикатриса касательных есть сферическая
линия, радиусы точек которой равнонаправлены с касательными
данной линии, на которой установлено некоторое направление движения.
Если изменить направление движения ьэ обратное, то получим другую
сферическую индикатрису касательных, симметричную с первой
относительно центра сферы.
Примеры: сферическая индикатриса касательных плоской кривой
есть дуга большого круга сферы, параллельного плоскости кривой.
Если плоская кривая имеет точку перегиба А, то на индикатрисе ей
соответствует конец Ах дуги большого круга. При прохождении через
точку А движущаяся точка индикатрисы возрашается назад по той
дуге, которую только что прошла. Если замкнутая плоская кривая (С)
не имеет течек перегиба, сферическая индикатриса ее касательных (Сх)
есть окружность большого круга. Для прямой линии индикатриса
касательных вырождается в точку. Сферическая индикатриса главных
нормалей плоской криЕой АВ есть дуга А2В2 той же окружности,
на которой лежит сферическая индикатриса касательных АХВХ. Дуга
А2В2 получается поворотом дуги АХВХ на 90°. Сферическая
индикатриса бинормалей плоской линии вырождается в точку.
Сферическую индикатрису А1В1СХ касательных сферической
кривой ABC можно построить так: через точку А проведем большой
круг, касающийся ABC, и на нем отложим квадрант ААх(т. е. дугу, со-
*) Слово «индикатриса», заимствованное из французской терминологии, означает
в буквальном переводе «указательница».
174 ГЛ. IV. НЕКОТОРЫЕ СВОЙСТВА СФЕРИЧЕСКИХ ФИГУР
держащую 90°); при этм направление ААХ должно совпадать с
направлением движения, установленным на ABC (рис. 120). Тогда свободный
конец Ах квадранта опишет индикатрису касательных. Действительно,
радиус ОАХ лежит в плоскости OAAlf в которой лежит касательная AT
оригинала, и перпендикулярен к
ОА, так как дуга ААХ
содержит 90°. Но и AT ±ОА.
Следовательно, ОА1 || AT.
Очевидно также, что лучи ОА1У AT
и равнонаправлены.
Всегда можно принять
радиус R сферы изображений
за единицу длины, и в
дальнейшем, если не будет
особой оговорки, мы будем
считать, что R=\ («единичная
сфера»).
Теорема 1.
Соприкасающаяся плоскость кривой (L)
параллельна плоскости
большого круга, касающегося
индикатрисы (Lx) касательных.
Действительно,
соприкасающаяся плоскость Р ли-
Рис. 120. * нии (L) есть предел
плоскости (?, проходящей че^ез точку
М кривой (L) и параллельной касательным в точках М а N (рис.
121а). Этим касательным параллельны радиусы сферы ОМХ и ONl
(рис. 1216); следовательно, плоскость Q параллельна плоскости 0MlNl
Рис. 121а. Рис. 1216.
большого круга, проходящего через секущую MYNU а так как эта
секущая имеет пределом касательную МгТх, то плоскость ОМХА\ имеет
§ 32, СФЕРИЧЕСКИЕ ИНДИКАТРИСЫ 175
пределом плоскость Рх большого круга, касающегося индикатрисы (Lx).
Следовательно, плоскости Р и Рх параллельны. Теорема доказана.
Можно сказать, что плоскость касательного к индикатрисе (Lx)
большого круга изображает соприкасающуюся плоскость линии (L).
Теорема 2. Вектор касательной МХТХ сферической индикатрисы
{Lx) касательных линии (L) равнонаправлеи с ортом п главной нормали
линии (L).
Действительно, так как вектор ОМХ есть не что иное, как орт
касательной t линии (L), то вектор MjNt равен вектор}' Atf; и, значит,
луч MXNX разнонаправлен с вектором -^ , а так как касательная МхТг
есть предел секущей MxNXy
то она равнонаправлена с
,. At
вектором lim -д- = #.
Теорема 3.
Сферическая индикатриса (Lo)
главных нормалей есть место
концов квадрантов,
касающихся индикатрисы (Lx)
касательных.
Действительно, согласно
теореме '2 главная нормаль
исходной линии (L)
параллельна касательной
индикатрисы (Lx), т. е.
индикатриса (L2) главных нормалей
кривой (L) является вместе
с тем индикатрисой
касательных сферической кривой (Lx).
Следовательно, линия (L2)
описывается концом квадран- Рис- 122#
та, касающегося (Lx) (если линия ABC на рис. 120 на стр. 174 есть
индикатриса касательных, то АХВХСХ есть индикатриса главных
нормалей).
Теорема 4. Сферическая индикатриса (L3) бинормалей
описывается одним из полюсов большого круга, касающегося индикатрисы
касательных (£J; именно — тем полюсом М3, который лежит по левую
руку наблюдателя, движущегося по поверхности сферы вдоль (Lx).
Действительно, направление ОМХ (рис. 122) от ног наблюдателя
к его голове есть направление вектора t линии (I), а направление
движения вдоль (Lx) есть, по доказанному в теореме 2, направление
вектора я. Следовательно, направление вектора Ь совпадает с
направлением луча ОМЪ.
Теорема 5. Индикатриса касательных (Lx) и индикатриса
бинормалей (Lz) имеют в соответственных точках Мх и М3
параллельные касательные (обе они параллельны главной нормали линии (L)).
При этом, если линия (L) левая, то касательные МХТХ и М3Т3 равно-
направлены; если же линия (L) правая, то они направлены в
противоположные стороны.
Действительно, векторы ОМХ, ОМ3 (рис. 122) соответственно равны
векторам tub линии (L). Поэтому векторы скорости в точках Мх и Ms
равнонаправлены соответственно с векторами dt = vnds и dt = —ends,
176 ГЛ. IV. НЕКОТОРЫЕ СВОЙСТВА СФЕРИЧЕСКИХ ФИГУР
а так как величина х всегда положительна, то векторы dt и db равно-
направлены, когда о < 0, и противоположно направлены, когда а > 0.
Теорема 6. Радиус кривизны линии (L) равен отношению
дифференциала ее дуги к дифференциалу соответствующей дуги
индикатрисы касательные.
Действительно, мы имеем
^ А$
! '^-' _____
Г '"^S 9
где (о—угол между бесконечно близкими касательными линии (L) или,
что то же, угол между бесконечно близкими радиусами ОМ17 ONt
сферы (рис. 1216 на стр. 174). Так как радиус сферы мы принимаем
за единицу длины, то
где As1 = M1N1 есть дуга индикатрисы (L^). Следовательно,
или
ds
Теорема 7. Абсолютная величина радиуса кручения линии (L)
равна отношению дифференциала ее дуги к дифференциалу
соответствующей дуги индикатрисы (Lz) бинормалей:
i i ds
Доказывается, как предыдущая теорема.
Упражнения
1. Индикатриса главных нормалей есть место концов квадрантов, касающихся
индикатрисы бинормалей.
2. Доказать, что индикатриса касательных есть место полюсов больших
кругов, касающихся индикатрисы бинормалей.
3. Все линии, имеющие данную индикатрису касательных, имеют в точках
с соответственно параллельными касательными одно и то же отношение кривизны
к кручению.
4. Построить индикатрису главных нормалей сферической кривой.
5. Построить сферическую индикатрису касательных по индикатрисе
главных нормалей (существует бесчисленное множество решений, зависящих от
произвольной постов иной).
6. Меяду углами смежности касательной со, бинормали со' и главной нормали
о" существует соотношение
а>"<^и>2-Но'*.
7. Какой вид имеет кривая, если ее индикатриса бинормалей имеет точку
возврата.
8. Доказать, что сферическая линия, пересекающая под прямым углом
большие круги, касающиеся индикатрисы (L3) бинормалей линии (L), имеет ту же
индикатрису касательных, что (L).
§ 33. Площади сферических фигур. Теорема Якоби
Учение о площадях сферических фигур принадлежит, по сути дела,
элементарной геометрии. Но так как в наш школьный курс оно не
входит, то мы не можем предполагать его известным. Поэтому мы
изложим здесь некоторые свойства сферических фигур и их площадей,
на которые в дальнейшем мы будем опираться. Они представляют
и сами по себе большой интерес.
§ 33. ПЛОЩАДИ СФЕРИЧЕСКИХ ФИГУР. ТЕОРЕМА ЯКОБИ 177
Всякая замкнутая сферическая линия (L), не имеющая
самопересечения, разделяет сферу на две обласаи. ПлощадяхМ *) этих областей
мы можем приписать знаки. Для
этого предварительно
установим на линии (L) направление
обхода — его можно выбрать по
произволу.. Область (i?j),
которая остается по левую руку
человека, идущего вдоль (L) по
внешней поверхности сферы,
мы назовем «положительно
обходимой^ и площадь ее 5Х будем
считать положительной
величиной. Другая область (В2) будет
оставаться при этом по правую
руку; ее площадь S2 мы будем
считать величиной
отрицательной.
В силу этого условия мы
будем иметь
51-51 = 4«Д1. (1)
Сферическим многоугольны,- Рис. 123.
ком (A1A2A3AiA5 на рис. 123)
называется замкнутая линия, составленная рядом дуг больших кругов.
Дуги эти (стороны сферического многоугольника) не должны
превосходить полуокружности
большого круга. Нумерация вершин
устанавливается в
соответствии с принятым направлением
обхода.
Плоский многоугольник
имеет не менее трех сторон.
Сферический же многоугольник
может иметь только две стороны
(двуугольник). Вершинами
всякого двуугольника служат
диаметрально противоположные
точки сферы (Лийна рис. 124).
Стороны двуугольника суть
полуокружности больших
кругов (ALB и АКБ). Углы при
вершинах двуугольника равны
между собой.
Сферический
многоугольник называется выпуклым, если
Рис. 124. он целиком лежит на одной из
двух полусфер, образованных
большим кругом, которому принадлежит какая-либо сторона
многоугольника. Выпуклый многоугольник не может иметь самопересечения.
х) Общее определение площади кривой поверхности будет дано ниже (§ 45).
Здесь мы опираемся на наглядное представление о площади и на те сведения,
который даются в элементарной геометрии о площади сферы и ее частей.
12 М. Я. Выгодский
178 ГЛ. IV. НЕКОТОРЫЕ СВОЙСТВА СФЕРИЧЕСКИХ ФИГУР
Сферический треугольник всегда является выпуклым. Под
площадью сферического треугольника, если не сделано особой оюворки,
понимают ту из величин Su S2, которая по абсолютному значению
меньше, чем площадь полусферы, т.е. чем 2т,П2. Что касается площади
других многоугольников (в том числе и выпуклых), то для нашей цели
выгоднее сохранить произвол выбора между величинами Sl n S2.
Относительно углов многоугольника, внешних и внутренних, мы
установим следующие соглашения.
Положительным направлением вращения мы считаем направление,
противоположное направлению вращения часовой стрелки. При этом
предполагается, что наблюдатель находится с внешней стороны сферы.
Внешним углом а, сферического многоугольника АХА2А3 ... Аа
(рис. 125) при вершине At мы назовем угол, на который нужно
повернуть продолжение AiCi сюроны
Ai-iA} до совмещения со
стороной AtAi+x. При этом абсолютное
значение а7- должно быть меньше,
чем тт. У четырехугольника
Ах А2 А3 Л4, изображенного на
рис. 125, внешний угол а3 при
вершине А3 — отрицательный;
остальные внешние углы
—положительные. Если переменить
направление обхода на
противоположное (нумерацию вершин
придется изменить), то знаки всех
внешних углов переменятся на
обратные.
Внутренним углом а\
сферического (несамопересекаюгцегося)
многоугольника А1А2А3...Ап при
вершине А( мы назовем тот
угол, на который нужно повер-
Рис. 125. путь сторону А(А(+1 до
совмещения со стороной AtAi-\. При этом
поворот должен производиться в таком направлении, чтобы вращающаяся
дуга вступала в ту из областей (By), (B2), которую мы отнесли к
многоугольнику. Это отнесение произвольно, но оно должно быть одним
и тем же для всех вершин. Так, если к чеаырехугольнику АгА2А?АА,
изображенному на рис. 125, отнести положительно обходимую область
(В^, то внутренний угол ol'z образуется вращением стороны ASA4
в положительном направлении, причем угол си'3 оказывается большим,
чем два прямых («входящий угол»). Если же к четырехугольнику
АгА2А8АА мы отнесем отрицательно обходимую область (В2), то
внутренний угол будет отрицательным, а по абсолютному значению —
меньше двух прямых. Вообще при нашем соглашении все внутренние
углы а\ имеют один и тот же знак, совпадающий со знаком площади
многоугольника, а сумма внешнего и внутреннего углов при любой
вершине по абсолютной величине равна двум прямым:
а, + *;='±*. (2)
Знак правой части—тот же,что знак площади рассматриваемой области.
Переходя к определению площадей сферических фигур, условимся
за единицу площади принимать квадрат радиуса сферы. Тогда поверх-
§ 33. ПЛОЩАДИ СФЕРИЧЕСКИХ ФИГУР. ТЕОРЕМА ЯКОБИ 179
ность всей сферы будет равна 4тг. Для площади двуугольника имеет
место следующая теорема.
Теорема 1. Площадь S положительно обходимого сферического
двуугольника, внутренний угол которого есть у, равна 2<р.
Действительно, площадь двуугольника, очевидно, пропорциональна
углу ф. Но при ср = 2тс двуугольник покроет всю сферу, так что его
площадь будет равна 4тг. Из пропорции
S : 4гс = ср : 2тс .
получаем
S = 2?, (3)
что и утверждалось.
Теорема 2. Площадь положительно обходимого сферического
треугольника равна избытку суммы его внутренних углов над тт.
Рассмотрим сферический треугольник ABC (рис. 126). Обозначим
внутренние углы при вершинах А, В, С соответственно через а', р', у'.
Продолжим стороны этих
внутренних углов до пересечения их
соответственно в точках А1}
Вх, С1} диаметрально
противоположных вершинам А, В, С.
Получим три двуугольника:
АВАгС, ВСВгА, САСгВ (второй
из них на рис. 126 располагается
по обе стороны от плоскости
видимого контура сферы).
Двуугольник АВАХС покрывается
данным треугольником ABC и
дополнительным к нему
треугольником АХСВ, так что,
согласно 1еореме 1, имеем
пл. ABC + ил. АХС В = 2а'. (4)
Точно так же найдем, что
пл. ABC + пл. ВгАС = 2(3', (5)
пл. ЛВС + пл. СХВА = 2у'. (6) РиС* 126*
Так как треугольники ВХАС и ВАХСХ симметричны, то их площади равны.
Поэтому формулу (5) можно переписать в виде:
пл. ABC + пл. А1ВС1 = 2р\ (7)
Сложим равенства (4), (6) и (7). Получим
3 пл. ABC + пл. АХСВ + пл. СХВА + ил. АхВСг = 2 (а' + р' + у'). (8)
Но треугольники ABC, ЛХСВ, СХВАУ АХВСХ покрывают полусферу
(обращенную на рис. 126 к зрителю); поэтому
пл. ABC + пл. АХСВ + пл. СХВА + пл. АгВСг ■= 2тг. (9)
Вычитая (9) из (8) и деля пополам, получаем
пл. ABC = а' + р' + у' — тс, (10)
что и требовалось доказать.
12*
180 ГЛ. IV. НЕКОТОРЫЕ СВОЙСТВА СФЕРИЧЕСКИХ ФИГУР
Следствие. Сумма внутренних углов сферического треугольника
по абсолютной величине всегда больше 180°. Чем меньше плошадь
сферического треугольника, тем ближе к 180° сумма его внутренних
углов. Так как за единицу площади мы принимаем квадрат радиуса
сферы, то с увеличением этого радиуса площадь треугольника с
данными вершинами А, В, С стремится к нулю. Таким образом, в
предельном случае, когда треугольник ABC плоский, сумма ею
внутренних углов составляет 180°.
Теорема 3. Площадь положительно обходимой области (В)}
ограничиваемой несамопересекающимся многоугольником АгА2 ... Ап,
равна избытку суммы его внутренних углов над (лг — 2) тт.
Замечание. За. область (В) можно принять любую из двух
областей (Вх), (В2), на которые многоугольник АХА2 ... Ап делит сферу.
Конечно, соответственно
должны быть взяты и внутренние
углы.
Теорема 3 обычно
формулируется короче следующим
образом,
Площадь сферического
многоугольника равна избытку
суммы внутренних его углов над
(п-2) к.
Доказательство проводится
особенно просто для того
случая, когда в области (В) можно
выбрать точку О так, чтобы п
треугольников OAXAV OA2A3,...,
ОАпАг, не перекрыгаясь друг
с другом, покрыли область (В).
Такой случай имеет место, в
частности, для выпуклого
многоугольника (рис. 127): если
Рис. 127. точку О выбрать где-либо
внутри области (В\), меньшей
полусферы, то упомянутые треугольники покроют область (fij; если О выбрать
где-либо внутри области (B[)t симметричной с (В^, то покроется
область (В2).
В рассматриваемом случае площадь области (В) равна сумме
площадей треугольников OAtAi+\, т. е., в силу теоремы 2, она равна избытку
суммы всех внутренних углов этих треугольников над пк. Но сумма
всех внутренних углов треугольников OAtAi+i9 очевидно, равна сумме
всех внутренних углов многоугольника АХА2 . .. Ап и углов А(дА(+х
при вершине О. Последние же составляют вместе 2тг. Поэтому площадь
(В) равна избытку суммы внутренних углов многоугольника над (тг — 2) т:,
что и требовалось доказать.
В случае, если область (В) не разбивается на треугольники
рассмотренного типа, ее все же можно «триангулировать», т. е. покрыть
сетью неперекрывающихся треугольников. Только к вершинам
многоугольника придется добавить не один «узел триангуляции» О, а
большее их число. Положим, что это число равно р. Мы можем считать,
что ни один из этих узлов йе принадлежит стороне какого-либо
треугольника нашей сети (если бы такой случай имел место, можно его
устранить за счет смещения узла и присоединения к сети нового тре-
§ 33. ПЛОЩАДИ СФЕРИЧЕСКИХ ФИГУР. ТЕОРЕМА ЯКОБИ 181
угольника). Теперь мы можем вести доказательство так же, как в
рассмотренном частном случае. Мы найдем, что площадь многоугольника
равна избытку суммы его внутренних углов над (х — 2р)п, где жесть
число треугольников сети:
пл. АХА%... Ап = а'1 + *'2+...+ап-(х-2р)п. (И)
Остается только доказать, что
х-2р = п-2. (12)
Формулу (12) проще всего выьести из теоремы Эйлера о
многогранниках; эта теорема утверждает, что сумма числа граней и числа
вершин многогранника на 2 больше, чем число ребер. Проведем из центра
сферы С радиусы САТ к вершинам многоугольника и построим хорды,
стягивающие дуги сферических треугольников, составляющих
триангуляционную сеть. Мы получим многогранник, все грани которого —
треугольники. Число граней этого многогранника, очевидно, равно х-\-пу
число гершин равно я + Р+1 (вершины многоугольника, добавочные
узлы и центр сферы). Что же касается числа ребер, то оно в полтора
раза больше числа граней, так как каждая грань имеет три ребра
и каждое ребро принадлежит двум граням. Итак, число ребер равно
— (х-{-п). Согласно теореме Эйлера, имеем
(x + n) + (n+p + l) = j(x+n) + 2. (13)
После упрощений отсюда получается формула (12), и тем самым теорема 3
доказана для общего случая. Формула (11) принимает вид
п
пл. АгА2 ... Ап= 2 <z'i — (n — 2) ic. (14)
Следствие. Сумма внутренних углов положительно обходимого
сферического многоугольника всегда больше, чем (л —2) я.
Теорема 4. Площадь несамопересекающегося (положительно
обходимого) сферического многоугольника равна избытку 2тт: над суммой его
внешних углов.
Действительно, согласно формуле (2), мы имеем
где а,- есть внешний угол многоугольника АгА2 ... Ап при вершине At.
Подставляя это выражение в формулу (14), находим
пл. АХА2 ... Ап = пп— 2 а, —(л —2)те,
откуда
пл. АХАШ ... Ап = 2к— 2«£. . (15)
Пример 1. Проведем на сфере три взаимно перпендикулярных
больших круга; пусть AxAtA9 (рис. 128) есть один из восьми
.сферических треугольников, образованных этими кругами. Область (J5),
которая обходится положительно при данной нумерации вершин, есть
большая из областей {Вх), (В2). Площадь ее, очевидно, равна 7/8 площади
сферы, т. е. у те. Применим для вычисления этой площади теорему 3.
182 ГЛ. IV. НЕКОТОРЫЕ СВОЙСТВА СФЕРИЧЕСКИХ ФИГУР
Каждый из трех внутренних углов области (В) равен утг; значит, избы-
ток суммы внутренних углов над (п — 2) тс, т. е. над тс, равен -^ тс. Тот
же результат мы получим из
теоремы 4, если учтем, что
внешние углы нашего треугольника
отрицательны.
Пример 2. Рассмотрим
шестиугольник AxA2AzAAAbAt
(рис. 129), образованный дугахми
тех же больших кругов, и
найдем площадь положительно
обходимой области (В)
(большая часть ее, затемненная на
рис. 129, лежит на видимой
полусфере). Каждый из
внешних углов при вершинах А^,
Aiy AQ равен —, а каждый из
внешних углов при вершинах
Ах, Ая, Аъ равен — -^-. Таким
образом, сумма всех внешних
Рис 128. углов равна нулю, и, согласно
теореме 4, площадь (В) равна 2л,
т. е. наш шестиугольник делит сферу на две равные части. Тот же
результат получатся и по теореме 3.
Теорему 4 можно высказать в более наглядной форме, если принять
во внимание, что входящая в формулу (15) величина аг- есть, согласно
теореме 1, площадь половины
двуугольника с внутренним
углом af. Опишем из вершины At
(рис. 130) сферическим радиусом
AtKi9 равным квадранту (т. е.
четверти большого круга), дугу
К^, содержащуюся во
внешнем угле аг. Треугольник^ (К9К'Ь
очевидно, составляет половину
двуугольника с внутренним
углом <xit и, значит, площадь
его равна а,-. Поэтому
формулу (15) мы можем записать
в виде
пл. АгА2 ... Ап +
+ 2 m.AtKiKi = 2nf (15а)
что на словах можно высказать
так:
Теорема 4а. Площадь Рис Шв
положительно обходимого не-
самопересекающегося сферического многоугольника AtA2 ... Ап и площади
треугольников АгК{К\, описываемых квадрантами AtKi, которые
вращаются во внегиних углах а,-, в сумме еоставлякт площадь полусферы.
§ 33. ПЛОЩАДИ СФЕРИЧЕСКИХ ФИГУР. ТЕОРЕМА ЯКОБИ 183
Замечание, Площадям треугольников Л(К(К\ в формуле (15а),
как и углам а,- в формуле (15), нужно приписывать знаки в
соответствии с соглашениями, установленными в начале этого параграфа.
Так, треугольник А(К(К\У изображенный на рис. 130, имеет
отрицательною площадь; внешний угол az- также отрицательный (внутренний
угол а\ больше тг, ибо положительная обходимая область мноюуголь-
нпка АгА2 ... Ап лежит слева от
ломаной Ai-\AiAi+\).
На рис. 131 теорема 4а
иллюстрируется на примере
положительно обходимого сферического
четырехугольника A1A2A3Ai (все
внешние углы его положительны).
Площадь этого четырехугольника
и площади треугольниковЛ^!^,
А2К2К'2, АаК9К'3, ААК4К'А в сумме
составляют площадь полусферы.
С другой стороны,
сумма упомянутых площадей
дает площадь восьми} голышка
K^K\K2K'2K3K'3KJ£\. Этот
восьмиугольник составлен 1) из дуг
KiK'i, описанных концами
квадрантов, вращающихся во
внешних углах а,- четырехугольника
AYA2A3AV и2)изотрезков#;/£1+1, Рис. 130.
отсекаемых упомянутыми
дугами на сторонах гнешних углов. В силу теоремы 4а, плошадь нашего
восьмиугольника (обходимого положительно) равна площади полусферы.
Ясно, что вместо четырехугольника АхАгАъА^ мы могли бы взять любой
несамопересекающийся
многоугольник. Мы получим тогда
следующую теорему:
Теорема 5. Если из киж-
дой вершины Ai несамопересе-
кающегося сферического
многоугольника АХА2 . .. Ап
сферическим радиусом, равным
квадранту, описать дугу К\К\
большого круги, содермсагцуюся во
внешнем угле, то многоугольник
КхК'гК2К'2 ... КпК'п,
составленный из этих дуг и из отрезков,
отсекаемых ими на сторонах
внешних углов, имеет площадь,
равную площади полусферы.
Замечание. В условии
теоремы 5 не содержится
требования, чтобы многоугольник
КгК[ ... К„К'п не имел
самопересечений. Причина этого
состоит втом, что теорема 5 остается в силе и при наличии
самопересечения у контура КгК[ . .. КпК'п, если под площадью его понимать сумму
площадей тех несамопересекающихся контуров, на которые разбивается
184 ГЛ. IV. НЕКОТОРЫЕ СВОЙСТВА СФЕРИЧЕСКИХ ФИГУР
КХК[ ... КпК'п. Области, создаваемые этой разбивкой, могут и покрывать
одна другую. Только необходимо площадь каждой из этих областей брать
с надлежащим знаком, смотря по тому, в каком направлении они обходятся.
Что касается условия, чтобы многоугольник АХА А не имел
самопересечений, то оно существенно, ибо даже при упомянутом
обобщении понятия площади теоремы 3 и 4, на которых мы основываемся, для
самопересекающихся многоугольников не имеют места.
Рассмотрим теперь произвольную замкнутую несамопересекающуюся
сферическую линию (L) (ABCNK на рис. 132). Эта линия может иметь
одну или несколько угловых точек (точка К на рис. 132); в остальных
же точках она должна иметь непрерывно меняющуюся касательную.
Проведем через все точки линии (L) по направлению ее обхода
(которое можно выбрать по произволу) касательные квадранты (АХМ1У
А2М2, 43М3, А^М4,... на рис. 132), т. е. квадранты, имеющие в точках At
Рис. 1321).
те же касательные, что (L). Через каждую угловую точку К проведем
два квадранта (KU и KU'), касающиеся один — правой, другой —левой
веави (L). Когцы их соединим дугой большого круга UU'. Концы
касательных квадрантов вместе с дугами UU' заполняют замкнутую линию
(U) (МгМ2МЛМJJU'Мг на рис. 132). Легко видеть, что ограничиваемая
этой линией область должна иметь площадь, равную полусфере. Иными
словами, линия (Z/), если она не имеет самопересечения, должна делить
сферу на две равновеликие части.
В самом деле, квадранты АхМ1ч А2М2, AZMZ, ААМ^ KU, KU'
образуют сферический хмногоугольник B1B2B3BiK ..., описанный около линии
х) На правой части рисунка 132 изображена', для ясности, деталь левой части
в увеличенном виде.
§ 33. ПЛОЩАДИ СФЕРИЧЕСКИХ ФИГУР. ТЕОГЕМА ЯКОБИ 185
(I). Описав из вершин Blf В2, ... этого многоугольника радиусом,
равным квадранту, дуги КХК[, К2К21 ..., получим многоугольник
КХК'ХК2К'2 ..., который, согласно теореме 5, имеет площадь 27г. Но
площадь £', ограничиваемая линией (/-'), есть предел площади
многоугольника КХК[К2К2 ... г). Поэтому 5' = 2тг, и мы получаем
следующую теорему:
Теорема 6. Линия (U), описываемая концом квадранта,
касающегося замкнутой не самопересекающейся сферической линии (L),
ограничивает площадь, равную полусфере. При этом, если линия (L) имеет
угловые точки, то в состав (U) включаются также содержащиеся
в соответствующих внешних углах дуги, описываемые концом квадранта,
вращающегося около угловой точки.
Эта теорема сослужит нам службу в теории поверхностей (§ 77).
Здесь же мы применим ее к доказательству замечательной теоремы,
установленной Якоби в 1842 году.
Теорема 7 (Якоби). Сферическая индикатриса главных
нормалей замкнутой кривой (L) (при нижеупомянутых предположениях) делит
сферу на две равные части.
Доказательство. Положим, что линия (7-) имеет непрерывно
изменяющуюся касательную. Тогда ее индикатриса касательных есть
непрерывная замкнутая линия; обозначим эту линию через (L). Если
линия (L) не имеет самопересечения, то линия (Z/), описываемая концом
квадранта, касающегося (L), ограничивает площадь, равную полусфере.
Значит, если линия (Z/) также не имеет самопересечения, то она делит
сферу на равные части. Но (//) есть индикатриса главных нормалей
лрнии (/.) (теорема 3 § 32), что и доказывает теорему Якоби.
Замечание. Таким образом, теорема Якоби имеет место при
следующих предположениях:
1) индикатриса касательных линии (L) непрерывна и не имеет
самопересечений; последнее условие заведомо выполняется, если (L) не имеет
равнонаправленных касательных; 2) индикатриса главных нормалей
линии (L) непрерывна и не ИхМеет самопересечения. Первое из условий
(2) равнозначно предположению о непрерывном изменении касательной
сферической линии (L); это предположение можно ослабить, но тогда
индикатрису (L') главных нормалей нужно дополнить надлежаще взятыми
дугами больших кругов (как в теореме 6). Что касается второго из
условий (2), то его можно отбросить при надлежащем обобщении понятия
площади сферической кривей (см. замечание к теореАме 5).
1) В самом деле, по построению, дуги МХК}, М2К[, ... соответственно равны
дугам АХВХ, ВХА^ . . ., не превосходящим максимальной длины I стороны описан
ного многоугольника. Площади треугольников МхКгР, РК{М2 соответственно
эквивалентны площадям одноименных прямолинейных треугольников, а сумма
абсолютных величин этих последних площадей не превосходит величины
т. е. величины 1(КХК[ + КгК\А-. . .). Стоящая в скобках сумма есть сумма
внешних углов описанного многоугольника и потому не превосходит 2*. Таким образом,
площадь б' могла бы разниться от площади фигуры К^К'^КуК^ ... не более чем
на 2nl (на самом деле они в точности равны, так как треугольники РКХМ^
РК\М% имеют одинаковые площади). При неограниченном уменьшении всех дуг
AiAi^ величина I стремится к нулю, так что S* есть предел площади КхК'хКгК1>...
486 ГЛ. IV. НЕКОТОРЫЕ СВОЙСТВА СФЕРИЧЕСКИХ ФИГУР
§ 34. Сферические эвольвенты и эволюты
Теории эвольвент и эволют плоских кривых, с которой мы
познакомились в § 27, отвечает в сферической геометрии теория сферических
эвольвент и эволют. Аналогия между этими теориями простирается очень
далеко, хотя она и не является полной.
Так как прямым линиям плоскости отвечают на сфере большие
круги, то мы, в соответствии с § 27, можем сформулировать следующее
определение.
Сферической эвольвентой сферической линии (I) (рис. 133) называется
место концов дуг, откладываемых на касательных к (/) больших кругах
Рис. 133.
так, чтобы длины этих дуг убывали на величину, равную приращению дуги
линии (Z)1). Если (L) есть сферическая эвольвента линии (/), то (/)
называется сферической эволютой линии (L). Эвольвенту (/) мы будем считать
состоящей из правильных точек.
Тогда для сферических эвольвент и эволют имеют место следующие
предложения, аналогичные теоремам 1, 2 и 3 § 27.
Теорема 1. Длина дуги МгМ2 эволюты равна разности M1N1 —
— M2N2 дуг, отложенных от точек М1У М2 па касательных болыиих
кругах до встречи в точках Nly N2 с эвольвентой.
Теорема 2. Всякая сферическая линия имеет бесчисленное
множество сферических эвольвент. Через каждую точку какого-либо боль-
гиого круга, касательного к эволюте, проходит одна и только одна
эвольвента.
Теорема 3. Сферическая эвольвента есть ортогональная
траектория больших кругов, касающихся эволюты; обратно, всякая
ортогональная траектория болыиих кругов, касающихся линии (I), есть
эвольвента линии (I).
1) Дуги на касательных кругах линии (I) можно откладывать как в
направлении возрастания дуги (I), так и в противоположном. В последнем случае нужно
считать эти дуги отрицательными. Ср. § 27, стр. 141.
§ 34. СФЕРИЧЕСКИЕ ЭВОЛЬВЕНТЫ И ЭВОЛЮТЫ 187
Теорехмы 1 и 2 непосредственно вытекают из определения
эвольвенты. Что касается теоремы 3, то ее можно доказать по тому же плану,
как теорему 3 § 27 (стр. 137).
Теоремы 4 и 4а § 27 (стр. 142) могут быть перенесены в сферическую
геометрию только при некотором изменении их формулировок. В самом
деле, центр кривизны сферической линии не лежит на рассматриваемой
сфере, так что место центров кривизны линии (L) заведомо не может
быть ее сферической эволютой. Но мы можем ввести понятие
«сферического центра кривизны», аналогичное понятию центра кривизны плоской
кривой. Для этого проведем через две близкие точки N1, N2 линии (L)
(рис. 133) нормальные большие круги NiM11 NXM2. Они пересекутся
в двух симметричных точках Е, Е'. Пусть точки Nl7 N2 стремятся
к общему пределу TV; тогда прямая ЕЕ' имеет пределом ось кривизны
линии (L) (для точки N). Следовательно, точки Е, Е' имеют пределами
те две точки М, М'', в которых ось кривизны пересекает сферу. Точки
М, М' мы и назовем сферическими центрами кривизны линии (L) (для
точки N). Дугу NM или NМ' (смотря по тому, какой из центров
кривизны мы рассматриваем) мы назовем сферическим радиусом кривизны.
Теперь мы можем следующим образом сформулировать
предложения, аналогичные теоремам 4 и 4а § 27.
Теорема 4. Всякая сферическая линия (I) вместе с симметричной
ей линией (Г) есть место сферических центров кривизны своей
сферической эвольвенты (L).
Теорема 4а. Место сферических центров кривизны линии (L)
является ее сферической эволютой.
Эти теоремы можно доказать совершенно так же, как в § 27.
Из них следует, что всякая сферическая линия имеет одну и только
одну эволюту (состоящую из двух симметричных ветвей).
Из теоремы 4 и определения сферической эвольвенты тотчас же
вытекает
Теорема 5. Дуга сферической эволюты (все точки которой
правильные) равна абсолютной величине разности радиусов сферической
кривизны эвольвенты в концах ее дуги.
Теорию сферических эволют и эвольвент можно связать с теорией
сферических индикатрис и с успехом применить к решению ряда задач
теории пространственных кривых. Две такие задачи будут рассмотрены
ниже в § 37 (случаи 3 и 4). Там нам придется использовать следующие
предложения.
Теорема 6. Сферическая эвольвента (L) индикатрисы (Г)
бинормалей произвольной линии (L) и сама линия (L) имеют в
соответственных точках соответственно параллельные касательные, главные нормали
и бинормали.
Доказательство. Большой круг, касающийся линии (/) в
некоторой точке Mj, параллелен нормальной плоской линии (L) в
соответственной точке A/j, ибо радиус сферы ОМг параллелен бинормали
к (L), а касательная к (/) параллельна главной нормали линии (L)
(теорема 5 §32, стр. 175). Сферическая эвольвента (L) линии(I) есть
ортогональная траектория больших кругов, касающихся (/), и потому ее касательная
перпендикулярна к нормальной плоскости линии (L) в соответствующей
точке. Значит, касательные к (L) и (L) в соответственных точках
параллельны. В силу теорем 3 и 4 § 32, соответственно параллельны также
главные нормали и бинормали.
188 ГЛ. IV. НЕКОТОРЫЕ СВОЙСТВА СФЕРИЧЕСКИХ ФИГУР
. Если точки двух каких-либо линий можно поставить в такое
соответствие, при котором соответственные касательные (а значит, также
соответственные главные нормали и соответственные бинормали)
параллельны, то мы будем говорить, что рассматриваемые линии находятся
в параллельном соответствии *). Пользуясь этим названием, >ш можем
сформулировать теорему 6 еще и так:
Сферическая эвольвента индикатрисы бинормалей линии (L)
находится в параллельном соответствии с линией (L).
Справедливо и обратное предложение:
Теорема 6а. Если сферическая линия (L) находится в
параллельном соответствии с линией (L), то индикатриса бинормалей линии
(L) есть одна из ветвей сферической эволюты (/) линии (L).
Доказательство. Сферические центры кривизны линии (Z.)
лежат на оси кривизны этой линии, а эта ось по условию параллельна
бинормали линии (L). Поэтому один из центров сферической кривизны
принадлежит индикатрисе бинормалей линии (L).
Следствие. Индикатриса бинормалей сферической линии (L) есть
одна из ветвей ее эволюты (/).
*) Такое соответствие называется таьже соответствием Комбескюра (Combes-
cure).
В
ГЛАВА V
НАТУРАЛЬНЫЕ УРАВНЕНИЯ
§ 35. Натуральные уравнения плоской кривой
После того как на данной линии (Z) выбрана некоторая
начальная точка А и установлено положительное направление для дуг,
отсчитываемых от точки А, положение любой точки М линии (/)
определяется заданием длины дуги s = AM, а так как в каждой своей точке
линия (/) имеет вполне
определенную кривизну и
и кручение о, то как
кривизна, так и кручение
данной линии становятся
вполне определенными
функциями длины дуги.
Уравнения
*=?(*); * = ф(0, (1)
выражающие кривизну и
кручение кривой через ее
дугу, называются
«натуральными» или
«внутренними» уравнениями этой
кривой. Такое название
оправдывается тем, что
уравнения (1) не содержат
координат, так что они
характеризуют форму
линии без привлечения посторонних геометрических объектов (системы
координат).
Пример 1. Найдем натуральные уравнения эвольвенты
окружности, приняв за начало отсчета д^г s точку А (рис. 134), общую для
окружности и ее эвольвенты. Положительное направление дуг s выберем
так, чтобы оно отвечало положительному повороту радиуса окружности.
Тогда длила дуги s=AM, как было найдено в примере 2 § 15 (стр. 69,,
равна
. 1 •
где а есть радиус окружности, а и—-угол поворота радиуса ОБ.
С другой стороны, из теории эволют (§ 27, теорема 5, стр. 143),
мы знаем, что радиус кривизны р эвольвенты равен отрезку ВМ, а этот
190 ГЛ. V. НАТУРАЛЬНЫЕ УРАВНЕНИЯ
последний имеет ту же длину, что и дуга АВ = аи. Итак, имеем
р = аи.
Исключая и из обоих уравнений, находим
Это уравнение, или, что то же, уравнение
представляет кривизну эвольвенты окружности в функции ее дуги.
Кручение же эвольвенты окружности, как и всякой плоской кривой,
всюду равно нулю:
о = 0.
1
Уравнения х = у— и а = 0 суть натуральные уравнения эвольвенты
окружности.
Возникает вопрос—в какой степени натуральные уравнения
определяют кривую линию, т. е. не могут ли две различные линии иметь
одни и те же натуральные уравнения? В связи с этим возникает также
вопрос: можно ли задать функции ср (s) и Ф($) по произволу, т. е.
всегда ли существует хотя бы одна линия, кривизна и кручение
которой выражались бы заранее данными функциями дуги. В согласии
с нашими исходными установками мы, конечно, предполагаем, чю эти
функции непрерывны.
Прежде всего, ясно, что две конгруентные линии, т. е. две линии,
отличающиеся друг от друга лишь положением в пространстве и
могущие быть наложенными друг на друга, должны иметь одни и те же
натуральные уравнения, если в обеих кривых длина дуги отсчиты-
вается от точек, совмещающихся при наложении. Таким образом, одной
и той же паре натуральных уравнений отвечает бесчисленное
множество конгруентных линий. Однако по существу мы имеем здесь одну
линию, только взятую в различных положениях. Поэтому мы
условимся рассматривать все эти линии как одну, и тогда на
поставленные выше вопросы можно ответить следующим образом:
Теорема. Каковы бы ни были непрерывные функции ср (s) > 0 и
u(s), существует одна и только одна линия, натуральные уравнения
которой суть
(1)
Ввиду того что доказательство этой теоремы представляет
значительные трудности, мы рассмотрим сначала менее общую, но
практически весьма важную теорему. Именно, сохраняя за первым из
уравнений (1) полный произвол, мы предположим, что второе уравнение
имеет вид с = 0, и докажем, что в этом случае существует одна и
только одна кривая, натуральные уравнения которой суть
x = 9(s), o = 0. (1')
Прежде всего, ясно, что если искомая кривая существует, то она
должна непременно быть плоской, так как только для плоской
кривой кручение тождественно равно нулю. Итак, задача сводится к
отысканию такой плоской кривой, для которой кривизна х является
данной функцией длины дуги.
§ 35. НАТУРАЛЬНЫЕ УРАВНЕНИЯ ПЛОСКОЙ КРИВОЙ 191
Возьмем на плоскости прямоугольную систему координат XOY.
Всегда можно считать, что искомая кривая проходи! через начало
координат О и что точка О является вместе с тем началом отсчета дуг на
искомой кривой; можно также принять, что в начальной точке О
касательная к искомой кривой совпадает с осью абсцисс. Действительно,
какова бы ни была линия (/), всегда можно построить конгруентную
ей линию (/'), удовлетворяющую указанным условиям.
Обозначим через а угол, который касательная в произвольной
точке искомой линии образует с касательной в начальной точке. Как
мы знаем, для плоской кривой имеет место соотношение
т. е.
da = y.ds. (3)
Так как, согласно (1), для искомой кривой x = cp(s) и так как по
условию значению s = 0 соответствует значение а = 0, то для искомой
кривой должно иметь место соотношение
а=^ <?(s)ds. (4)
и
Таким образом, угол, а, образуемый касательной к искомой кривой
с осью абсцисс, а вместе с тем и его тригонометрические функции
должны быть определенными функциями дуги.
Поэтому из известных соотношений
dx __ dy .
ds ' ds ^ '
мы находим
dx = cos a ds, dy = sin a ds, (6)
а так как по условию при s = 0 мы имеем х = 0 и г/ = 0, то для
искомой кривой должно иметь место соотношение
S S
х= \ cos ads, У=\ sin cuds. (7)
о • о
В этих формулах мы можем с помощью соотношения (4) выразит ь
одну из величин a, s через другую; таким образом, если выполнить
интегрирования, требуемые формулами (4) и (7), мы получим
параметрические уравнения, которые должны иметь место для искомой кривой.
Эти уравнения можно записать в общем виде так:
S S S S
х = \ cos С \ х (я) ds ) ds, у = \ sin С \ х (s) dsj ds. (7а)
оо оо
Значит, искомая кривая, если она существует, является
единственной и представляется уравнениями (7а). Чтобы доказать теперь
существование искомой кривой, достаточно рассмотреть линию,
заданную параметрическими уравнениями (7), в которых а есть функция от s,
определяемая уравнением (4). При этом параметру s мы не должны
пока приписывать определенного геометрического смысла. Но из фор-
192 ГЛ. V. НАТУРАЛЬНЫЕ УРАВНЕНИЯ
мул (7) мы тотчас же выводим формулы (6), а из них получим, что
dx2 + dy^ = ds\
откуда следует, что ds есть элемент дуги кривой. Из соотношений (6),
или, что то же, из соотношений (5) мы, кроме того, заключаем, что
а есть угол, образуемый касательной с осью абсцисс. Следовательно,
кривизна х рассматриваемой линии равна ^; но в силу соотношения
(4) мы имеем doc = <p (s) ds, т. е. x = -r- = <p(s). Следовательно, кривизна
рассматриваемой линии равна той функции длины дуги, которая
требуется уравнением (1). Итак, искомая кривая действительно
существует, и она единственна (с точностью до движения).
Пример 2. Найдем кривую, натуральные уравнения коюрой
имеют вид
Здесь мы имеем
<р (s) =
Формула (4) дает
(р=4)-
а
откуда, интегрируя, находим
= arcsin - , (10)
или
s =z a sin a; ds — a cos a da.
Формулы (7) дают
S a
x = \ cos a ds ■=- a \ cos2 a da = |- (2a + sin 2x),
. 2/= \ sinarfs' = a \ sinacosarfa = -|- sin2 a= -^- (1 — cos 2a).
oo J
Можно было бы выразить здесь а через 5 с помощью уравнения (10),
но в этом нет необходимости.
Уравнения (10а) дают полное решение нашей задачи. Интересно,
однако, исследовать эти уравнения, чтобы составить себе представление
о форме найденной линии. Легко заметить, что уравнения (10а) сходны
по виду с уравнениями циклоиды
*/ = Т (? —sin<p), у' = т(1 -coscp), (И)
произведенной качением круга радиуса у- .
Возникает вопрос, не представляют ли уравнения (Юа) циклоиду,
отнесенную к непривычному параметру и к смещенному (без поворота
осей) началу координат. Чтобы ответить на этот вопрос, сообразим,
§ 35. НАТУРАЛЬНЫЕ УРАВНЕНИЯ ПЛОСКОЙ КРИВОЙ
193
где может находиться новое начало координат О''. В системе XOY
касательная в точке (0, 0), отвечающей значению а = 0, совпадает с осью
абсцисс. Значит, эта касательная должна, если наше предположение
правильно, быть параллельной оси О'Х'. Следовательно, точка О должна
быть вершиной циклоиды. Но вершина циклоиды отстоит от ее
основания (т. е. от новой оси абсцисс) на расстояние, равное диаметру
производящего круга, т. е. на расстояние — , а от оси O'Y'—на расстояние,
равное полуокружности производящего круга, т. е. на расстояние
— атг. Учтем еще, что, согласно второму из уравнений (10а), наша
кривая располагается с положительной стороны оси ОХ. Тогда станет
О
Рис. 135.
ясно, что новое начало О' нужно попробовать поместить в точку
уйяг, ■- aj, т. о. нужно в формулах (10а) положить
X = —
После этой подстановки они примут вид
х' = — (2а—it+ sin 2а),
у'=— £ (1 +cos 2а).
(12)
Сравнив теперь первую из полученных формул с первой из формул
(И), мы видим, что новый параметр <р должен быть связан со старым
параметром а соотношением
2а-тг = ср,
т. е.
Подставив это выражение в (12), находим
Отсюда видно, что наша кривая действительно является циклоидой
(рис. 135).
13 М. Я. Выгодский
194 ГЛ. V. НАТУРАЛЬНЫЕ УРАВНЕНИЯ
Упр аж не ния
1. Доказать, что натуральное уравнение
представляет эвольвенту окружности (ср. пример 1).
2. Найти натуральное уравнение цепной линии.
3. Исходя из найденного в предыдущем упражнении натурального уравнения,
доказать, что оно представляет цепную линию.
4. Найти линию, представляемую натуральным уравнением
р = rns (m = const).
5. В предыдущих двух задачах функция х (s) в точке 5 = 0 не была
непрерывной. Какие особенности явились результатом этого?
6. Доказать, что натуральное уравнение
аЪ
представляет линию, описываемую точкой окружности радиуса г=^- ,
катящейся без скольжения по наружной стороне другой окружности радиуса
Эта линия называется эпициклоидой.
§ 36. Натуральные уравнения пространственной кривой
В предыдущем параграфе мы высказали общую теорему, которую
можно сформулировать так:
Теорема 1. Каковы бы ни были непрерывные функции <р (s) > 0
и ty(s), существует одна и только одна линия, для которой кривизна
и кручение в каждой ее точке соответственно равны ср (s), <]>($), где
s есть дуга кривой, отсчитываемая от начальной ее точки до
некоторой ее точки М.
Эта общая теорема не была доказана; мы доказали только частный
ее случай, где произвольной предполагалась только функция <p(s),
функция же <J> (s) предполагалась тождественно равной нулю. Для этого
случая мы нашли выражения (7а) § 35 координат искомой линии через
длину ее дуги. Эти выражения довольно просты: они содержат лишь
элементарные (тригонометрические) функции и знаки интегралов
(«квадратуры»).
Трудность доказательства общей теоремы обусловливается тем, что
при сохранении произвола функций <p(s) и <f(s) подобные выражения
получить не удается. Можно даже доказать, что таких выражений и
не существует. Тем не менее, всякий раз как функции <p(s), fy(s)
заданы, координаты искомой линии, приведенной в надлежащее
положение, оказываются однозначно определенными функциями ее дуги.
Аналитическое доказательство теоремы 1 и сводится к доказательству
этого последнего утверждения.
При проведении доказательства обычно привлекается на помощь
одна общая теорема теории дифференциальных уравнений. Мы не
предполагаем у читателя знакомства с этой теоремой. Кроме того, мы
хотели бы уяснить геометрическую сторону вопроса, показав, как можно
построить искомую кривую. Поэтому мы здесь покажем, как можно
доказать теорему 1 геометрически. Так как полное проведение
доказательства было бы слишком громоздким, то мы доведем его лишь до
такого пункта, где наглядные соображения сделают справедливость
теоремы 1 очевидной.
§ 36. НАТУРАЛЬНЫЕ УРАВНЕНИЯ ПРОСТРАНСТВЕННОЙ КРИВОЙ
195
Рассмотрим дугу АВ какой-либо кривой линии и впишем в нее,
начиная от точки Л, ломаную линию ALMNPQR (рис. 136) так, чтобы
все ее звенья (кроме, может быть, последнею) имели равную
длину к. На линии -АВ возьмем какую-либо точку С и отметим четыре
вершины ломаной М, N, Р, Q, непосредственно предшествующие точке С.
Если сама точка С окажется вершиной, условимся брать ее в качестве'
четвертой точки.
Докажем, что если длина звена к стремится к нулю, то,
отношение угла со между соседними звеньями MN и NP (или NP и PQ)
к длине звена к имеет пределом
кривизну *с линии АВ в
точке С.
В самом деле, звено MN
образует с касательной EU в
середине Е дуги MN угол
высшего порядка малости
относительно дуги MN (теорема 7 § 20,
стр. 95) и, значит, относительно
звена MN = к. Точно так же
звено NP образует угол высшего
порядка малости относительно к
с касательной FV в середине F Рис. 136.
дуги NP. Поэтому угол ш между
звеньями MN и NP эквивалентен углу о между касательными EU, FV:
Ш^Ф, (J)
С другой стороны, обозначая через р длину дуги EF, имеем
а так как дуги MN и NP соответственно эквивалентны хордам MN
и NP, равным л, то (§ 3, свойство 5а, стр. 17)
11»4>.+ £х = Х. (2)
Из соотношений (1) и (2) находим т ' = -^-^ —^у , где через
А А (1 Е
у. обозначена кривизна линии АВ в точке Е, а так как точка Е
имеет пределом точку С, то
lim -j- = ус,
что и требовалось доказать.
Таким же образом докажем, что отношение угла о> между
плоскостями MNP и NPQ к длине звена к имеет пределом кручение
линии сс в точке С. Действительно, упомянутые плоскости образуют
углы аир высшего порядка соответственно с соприкасающимися
плоскостями линии АВ в точках Nx и Р19 являющихся серединами
дуг МР и 7V() (§ 20, теорема 7). Следовательно, угол между
плоскостями MNP и NPQ эквивалентен углу о/ между соприкасающимися
плоскостями линии АВ в точках Nx и Р1У ибо они разнятся друг
13*
196 ГЛ. V. НАТУРАЛЬНЫЕ УРАВНЕНИЯ
от друга самое большее на а + р, а так как дуга N1P1 = v, как легко
^ (MNP,NPQ) ш' о/ tJ лт
видеть, эквивалентна Л, то j — = j ^ — ^ a Vi. Но точка /V,
имеет пределом точку С. Поэтому
lim 7 = °с'
что и требовалось доказать.
Доказанным только что теоремам можно придать более яркую
формулировку, если ввести понятие кривизны и кручения ломаной линии
с равными звеньями. Именно, кривизной такой линии в ее вершине Л,
мы назовем отношение угла ш между звеньями AiAi+\ и Ai+\Ai+z
к длине звена к. 0с1альным точкам ломаной можно приписать
кривизну, равную кривизне в ближайшей предшествующей вершине. При
этом соглашении кривизна ломаной линии с равными звеньями в точке К
будет функцией «длины дуги», т. е. периметра ломаной от начальной
ее точки до точки К. Функция эта, конечно, будет разрывной в
вершинах. Она определена- для Есех точек ломаной, вплоть до
предпоследней вершины (в ней она уже не определена).
Аналогично определяется кручение ломаной с равными звеньями.
В вершине At мы будем считать кручение равным отношению угла о/
между плоскостями AtAt+i Af+2 и Ai+i Ai+2Ai+s к длине звена X.
Кручению мы припишем положительный знак, если поворот плоскости
At Ai+iAi+ъ в положение Ai+\At+2 ^i+з совершается в направлении,
противоположном вращению часовой стрелки для наблюдателя,
находящегося в точке А(+2 и обращенного лицом к точке Л,-+1. В
остальных точках ломаной кручение можно считать равным кручению в
ближайшей предшествующей вершине, и тогда кручение будет функцией
длины дуги ломаной, определенной для всех ее точек, вплоть до
второй от конца вершины.
Если С есть некоторая точка кривой АВ, а С — ближайшая
предыдущая вершина ломаной с равными звеньями, вписанной в эту кривлю,
то, как легко вытекает из определения длины дуги кривой линии,
длина F ломаной линии ALM ... С, вписываемой по указанному выше
закону в кривую АВ, при неограниченном уменьшении длины звена \
имеет пределом длину дуги АС. Поэтому доказанные выше теоремы
мы можем теперь сформулировать следующим образом.
Теорема 2. Если s есть длина дуги АС кривой АВ, то кривизна
x(s) и кручение a(s) кривой АВ в точке С суть пределы, к которым
стремятся соответственно кривизна к($, X) и кручение c(s,\) вписан-
ной ломаной линии с началом в точке А и длиной звеньев X, когда к
стремится к нулю г):
x(s) = Hmx(s, \)f (3)
(s,X). (4)
х) Кривизна x(s, А) и кручение o(s, Я) берутся в той точке С ломаной, для
которой периметр AMN .. .С равен дуге АС = $, так что С не обязательно
является вершиной ломаной.
§ 36. НАТУРАЛЬНЫЕ УРАВНЕНИЯ ПРОСТРАНСТВЕННОЙ КРИВОЙ 197
Теперь мы докажем, что для ломаной линии имеет место
следующая теорема, совершенно аналогичная теореме 1.
Теорема 3. Каковы бы ни были функции <p(s)>0, ty(s) и число
X > О, существует одна и только одна ломаная линия, звенья которой
имеют длину X, а кривизна и кручение во всех ее вершинах
соответственно равны <р(*)> ty(s)> г^е s есть длина ломаной линии от начала
до соотвзтствующей вершины.
Доказательство. От произвольной точки Ао в произвольном
направлении отложим отрезок А0А1 = к (рис. 137). Из точки Ах в
произвольной плоскости Р17 проходящей через A0Alt отложим отрезок АХА%
длины X, образующий с отрезком А0А± угол Хср(О). Через отрезок
АХА2 проведем плоскость Р21
составляющую с
плоскостью Рх угол, равный по
величине и по знаку углу X ф (0).
При этом, как и прежде, мы
/\
считаем угол (Р1УР2)
положительным, если поворот
плоскости Рх в положение Р2
совершается против часовой
стрелки для наблюдателя,
находящегося в точке А2 и
обращенного лицом к
точке Аг.
В плоскости Р2 под углом
Хср(Х) к прямой АХА2
проведем отрезок А2А3 длины X.
Через Az проведем плоскость
Р3 под углом X ф (X) к нло- Рис- 137-
скости Р2 и на плоскости Р3
проведем отрезок А3А4 длины X под углом X <р (2Х) к отрезку %А2А3.
Далее таким же образом строим плоскость РА под углом X ф (2к) к
плоскости Р3, отрезок А^А5 под углом Х<р(ЗХ) к отрезк}7 AZA^ и т. д.
Построение это можно продолжать до тех пор, пока периметр ломаной
будет находиться в пределах того интервала, в котором заданы
функции <р(5) и Ф(5)- Мы утверждаем, что построенная таким образом
ломаная удовлетворяет требованиям теоремы 3.
Действительно, кривизна ломаной в точке Ао равна у| У =
кривизна в точке Аг равна —LLL==<p(>4)> B точке А2 она равна <р(2Х)
и т. д. Периметр же ломаной, отсчитываемый от точки A{t, для точки
Ао равен нулю, для точки Ах он равен X, для точки А2 он равен 2Х
и т. д. Итак, кривизна во всех вершинах равна данной функции
cp(s) длины s. Точно так же докажем, что и кручение в точке Ао
равно ф(0) и т. д. Таким образом, и кручение построенной нами кривой
во всех ее вершинах равно данной функции fy(s) длины s.
Итак, мы построили одну ломаную, удовлетворяющую условиям
теоремы 3. Остается доказать, что такая ломаная—единственная.
Пусть существует еще одна ломаная А0А[А'2 ... с той же длиной
звеньев X, кривизна х и кручение о которой в ее вершинах также
соответсавенно равны y(s) и ty(s). Тогда углы между соседними
звеньями кторой ломаной последовательно равны: <р(0) (^) (2)
198 ГЛ. V. НАТУРАЛЬНЫЕ УРАВНЕНИЯ
р(), ... и т. д. Углы между соседними ее плоскостями Р'о, Р[, -Р2\...
и т. д. равны ф (0), ф (X), ф (2л) и т. д., т. е. линейные углы второй
ломаной соответственно равны линейным углам первой, а двугранные —
двугранным. Наложим вторую ломаную на первую так, чтобы вершины
A'Q, A'lt А[ упали в вершины AQy А1У А2. Очевидно, это возможно. При
эюм плоскости Ри Р[ совпадут, а вследствие равенства двугранных
углов (Р[Р'2) и (PiP2) плоскость Р'2 совпадет с плоскостью Р'г. Вслед-
/\ /\
ствие равенства линейных углов (АХА2, А2А3) и (А[А'21 A[A'Z) совпадут
также прямые А2А[ и А2А3, а значит, и отрезки А'гА'г, А2А3, ибо они
равны. Продолжая это рассуждение, убедимся, что ломаные Л^А^...
и А0АгА2 ... конгруентны, а две конгруентные линии мы условились
рассматривать как одну и ту же линию.
Теорема 3, таким образом, строго доказана, и теорема 1,
высказывающая совершенно аналогичное утверждение относительно кривой
линии, становится весьма правдоподобной. Рассмотрим этот вопрос
несколько подробнее.
Построим ломаную линию фиксированной длины sen равными
звеньями так, чтобы ее кривизна и кручение в вершинах равнялись
ср($), ty(s), где s есть периметр лодоаной, отсчитываемый от начальной
точки Ао до соответствующей вершины. Затем будем неограниченно
увеличивать число звеньев гг. Для определенности можно предположить,
что при этом фиксируется начальная точка Ао, направление первого
звена А0Аг и положение плоскости Рг первых двух звеньев. Мы будем
получать ломаные линии, звенья которых будут неограниченно
уменьшаться. Вместе с тем будут неограниченно уменьшаться и углы
между соседними звеньями, а также и углы между соседними
гранями ломаной. Представляется весьма правдоподобным, что с
некоторого момента ломаные линии, которые мы строим, будут практически
неотличимы друг от друга и сольются в одну кривую линию,
кривизна и кручение которой будут практически выражаться теми
функциями длины дуги, которыми тыражались они для всех ломаных линий.
Чтобы придать этому наглядному рассуждению силу
доказательства, нужно было бы рассмотреть множество тех положений, которые
будет занимать точка М ломаной, отстоящая от начала на некотором
определенном расстоянии s. Нужно было бы доказать, что эта точка
при неограниченном увеличении числа звеньев стремится к
определенному пределу К. Совокупность таких «предельных точек К даст
некоторую линию. Нз^жно будет теперь доказать, что кривизна и кручение
этой линии действительно представляются теми же функциями дуги,
которыми представлялись кривизна и кручение всех рассмотренных
ломаных. Наконец, останется доказать, что такая линия единственна.
Как мы видим, наше доказательство будет совершенно строгим, если
мы докажем правомерность обрисованного нами предельного перехода.
Это, однако, потребовало бы больших усилий, и потому мы
ограничиваемся ссылкой на наглядные представления. Для читателей, знакомых
с теорией дифференциальных уравнений, заметим, что намеченное здесь
доказательство может быть проведено в геометрической форме по тому
же методу, который в общей теории дифференциальных уравнений
называется методом Коши-Липшица.
Соображения, подобные вышеприведенным, делают очень наглядным
также следующий интересный факт.
§ 36. НАТУРАЛЬНЫЕ УРАВНЕНИЯ ПРОСТРАНСТВЕННОЙ КРИВОЙ 199
Рассмотрим две пары натуральных уравнений:
* = ?(*), * = ф(*) (5)
{ср (s) > 0}, отличающиеся лишь знаком функции, дающей кручение. Если
при построении ломаных линий с теми же натуральными уравнениями
мы будем исходить из одной и той же точки А17 одного й того же
направления начального звена АгА2 и одного и того же положения
начальной плоскости АгА2А31 то последовательно строящиеся прямые
AiAt+i и плоскости AtAt+iAt+2 будут для двух линий всегда
симметричны относительно плоскости АгА2А^. Следовательно, ломаные линии
будут попарно зеркально симметричны. Значит, и кривые линии (5) и
(6) зеркально симметричны. Обратно, натуральные уравнения всяких
двух зеркально симметричных линий (L) и (Lx) отличаются только
знаком функции a (s). Действительно, ввиду симметрии (L) и (Ьг)
в соответственных точках углы смежности касательных, а также
бинормалей, соответственно равны по абсолютной величине; но при
зеркальном отражении вращение против часовой стрелки переходит
во врашение по часовой стрелке, так чю кривые (L) и (Ьг) имеют
равные по абсолютной величине кривизну и кручение, а знаки
кручения у них противоположны.
Так как конгруентные линии имеют одинаковые натуральные
уравнения, то неплоские зеркально симметричные линии (а Ф 0) никогда
нельзя наложить друг на друга так, чтобы в совмещение пришли
соответственные (по симметрии) точки оригинала и зеркального
изображения.
Выше было отмечено, что натуральные уравнения
(7)
в обшем случае не могут быть решены в квадратурах. Это, конечно,
не значит, что для уравнений (7) нельзя найти элементарное решение
при частных видах функций <р($) и <М5)-
Пример. Найти линию (L), кривизна и кручение которой
постоянны.
Уравнения (7) принимают вид
* = *о (*о>°) ° = <V (8)
Чтобы найти линию (L), введем в рассмотрение вектор *)
(9)
*) Ятот прием может показаться весьма искусственным. Но поскольку
не существует общего метода для элементарного решения системы натуральных
уравнений, поиски такого решения в частном случае неизбежно требуют
некоторых ухищрений. С другой стороны, вектор *b + at взят не без оснований.
Не только в данном, но и в других случаях рассмотрение его может содействовать
решению. Дело в том, что этот вектор («вектор Дарбу») представляет вектор
угловой скорости вращения сопутствующего триедра (относительно дуги s). Это
было показано в § 29 (стр. 160).
200 ГЛ. V. НАТУРАЛЬНЫЕ УРАВНЕНИЯ
который в силу (8) можно представить в виде
c = *0b + o0t. (9a)
Дифференцируя (9а) и пользуясь формулами Френе, находим, что
d£=o. (Ю)
Следовательно, с есть постоянный вектор1). Из (9а) находим теперь,
что вектор t составляет с постоянным вектором с постоянный угол р,
для которого
И
7$т.
Следовательно, индикатриса касательных линии (L) есть окружность
DKN (рис. 138), ось которой ОС коллинеарна с вектором с.
Рпс. 138.
Формула (11) показывает, что угол р острый, если о0 > 0, и тупой,
если о0<02). Поэтому в первом случае луч ОС, ведущий от центра
*) Таким образом сопутствующий триедр врашается с постоянной угловой
скоростью около оси, сохраняющей неизменное направление. См. сноску на
стр. 199.
2) В случае с0 = 0 (индикатриса — большой круг) линия (L) есть плоская
кривая постоянной кривизны, т. е. окружность, ©тот случай не представляет
интереса.
§ 36. НАТУРАЛЬНЫЕ УРАВНЕНИЯ ПРОСТРАНСТВЕННОЙ КРИВОЙ 201
сферы О к центру индикатрисы С, равнонаправлен с вектором с,
во втором — противоположно направлен.
Пусть точка К индикатрисы касательных соответствует началу
отсчета дуг s на (Z.), а течка N-— переменной точке М линии (L).
Обозначим через sx дугу KN, описанную точкой .Л^согласно теореме 6
§ 32 (стр. 176), имеем
Интегрируя, получаем
Чтобы найти уравнения линии (L), введем прямоугольную систему
координат, связав ее с индикатрисой DKN следующим образом: начало
возьмем в центре сферы (9; за положительное направление оси OZ
примем направление вектора с, а за положительное направление оси
ОХ примем направление СК. При таком выборе осей точка N будет
описывать индикатрису касательных в направлении от ОХ к OY*),
так что, обозначив через и угол поворота радиуса СК в положение СЛТ,
мы будем иметь (напоминаем, что мы приняли радиус сферы за единицу
длины)
#W __ _£i_ jvs. М5)
~~ CN sin p sin ф ' V
Теперь мы можем выразить координаты орта ON — t— -£ через
дугу s линии (L) следующим образом:
d* =OQ = OPco$u = sin В cos-^£L )
as Sin p ,
(16)
j
Проинтегрируем уравнения (16), выбрав подходящим образом
координаты х0, у0, z0 начальной точки линии (L):
сое
sin |
z = s cos В.
Если подставить сюда выражения (11) и (12), то получим следующие
уравнения искомой линии:
х =
*п
у=-^а сое(]/xj+ ,;*), > (is)
5.
x) Действительно, движение точки N происходит по направлению орта п
линии (L) (теорема 2 § 32, стр. 175), а векторы с, ON = t и п образуют всегда
правую тройку, ибо в силу (9) ctn = x(btn)>0.
202 ГЛ. V. НАТУРАЛЬНЫЕ УРАВНЕНИЯ
Эти уравнения представляют винтовую линию радиуса а с шагом 2тс&,
где
в=т5т, *=-^; (19)
если ввести параметр v = у +|/^ + Oq s, to уравнения (17а) примут
знакомый нам вид
х = a cos v,
y = asinvt
Z = bv — у
(20)
(постоянное слагаемое в третьем уравнении можно устранить переносом
начала).
§ 37* Натуральное уравнение класса линий
Как мы видели, существует одна и только одна линия, кривизна и
кручение которой выражаются данными непрерывными функциями длины
Дуги:
*=?(*), (1)
* = Ф(*). (2)
Поэтому, если нам задано только одно из этих соотношений, например
уравнение (1), то этому соотношению удовлетворяет бесчисленное
множество линий. Именно, можно еще по произволу задать
соотношение (2). Таким образом, уравнение вида (1), взятое отдельно,
представляет очень широкий класс линий, зависящий от произвольной
функции ty(s). Уравнение (1) называется натуральным у равнением этого класса.
Вообще всякое соотношение вида
/(*, х, о) = 0 (3)
представляет столь же широкий класс линий, ибо к нему можно
по произволу добавить уравнение вида (2). v
Можно задать класс кривых соотношением более общего вида
dx do d2x d2a
или, что то же, соотношением вида
dx d2o d4 \ n ,,4
d ;0 (4a)
Геометрические свойства таких классов могут быть весьма различны.
Рассмотрим здесь несколько интересных случаев.
Случай 1. Кривые постоянной кривизны.
Этот класс линий представляется натуральным уравнением
Р = Ро, (5)
где р0 — произвольная постоянная величина, или равносильным ему
уравнением
не содержащим никаких величин, кроме р и s.
Все окружности и все винтовые линии входят в этот класс.
Окружность выделяется в этом классе тем, что для нее место центров
кривизны есть точка. Как будет видно из дальнейшего, этим свойсавом
§ 37. НАТУРАЛЬНОЕ УРАВНЕНИЕ КЛАССА ЛИНИЙ 203
обладает только окружность. Для остальных линий нашего класса
имеет место следующее замечааельное свойство.
Теорема 1. Пусть (L) есть линия постоянного радиуса
кривизны р0 и линия (Li) —место ее центров кривизны. Тогда и, наоборот,
линия (L) есть место центров кривизны^ линии {Lx).
Рис. 139.
Таким образом обе линии (L) и (Ьх) имеют общий постоянный
радиус кривизны р0. При доказательстве этой теоремы обнаружатся
еще два важных факта: 1) касательные к линиям (L) и (Lx) в
соответственных точках образуют прямой угол) 2) радиус кривизны р0 есть
средняя пропорциональная между радиусами кручения т, тх ланий (L) и (/.j).
Прежде чем доказать эту теорему, поясним ее на примере
винтовой линии.
Рассмотрим винтовую линию АВ на цилиндре S радиуса а
с шагом 2тс6(рис. 139). Как было найдено в § 23 (стр. 119), ее радиус
204 ГЛ. V. НАТУРАЛЬНЫЕ УРАВНЕНИЯ
кривизны равен
~т~ а '
Следовательно, центр кривизны Мг точки М лежит на продолжении
радиуса МК^=а на расстоянии аг=^~ от оси, что мы уже получили
раньше, в § 23 (стр. И 7).
Касательные к линиям АВ, А1В1 в соответственных точках М и Мъ
лежат в параллельных вертикальных плоскостях, касающихся
цилиндров S, 51# Эти касательные составляют с направлением оси цилиндров
углы <р, cpi> для которых (§ 8, пример 1, стр. 45)
и так как по горизонтальному направлению точки М и Мг движутся
в противоположные стороны, а по вертикальному направлению — в одну
и ту же сторону, ю знаки величин tgcp и tg<pi противоположны, и,
следовательно, касательные в точках М и Мх взаимно перпендикулярны.
Заметим еще, что в случае, когда а = 6, обе винтовые линии
располагаются на одном цилиндре симметрично относи!ельно его оси.
В этом случае линии АВ и А1В1 конгруентны; они имеют равные
кручения и образуют с осью углы в 45°. В остальных случаях радиусы
кручения т, т, линий А В и АХВХ различны по абсолютной величине,
но одинаковы по знаку:
_а'1+Ь2 __ Ь(а2-\-Ь2)
Tl~~"~5 "" ^ '
Отсюда видно, что произведение радиусов кручения равно квадрату
общего радиуса кривизны:
Вернемся теперь к общему случаю линии постоянной кривизны.
Доказательство теоремы 1. Пусть точка Мх (рис. 140)
есть центр кривизны линии (L) в точке М и пусть радиус кривизны,
т. е. отрезок ММ19 сохраняет постоянную величину р0. Отрезок ММХ
лежит на главной нормали линии (L), а один из его концов, точка М,
движется по направлению орта t. Поэтому вектор скорости этого конца
перпендикулярен к ММг\ значит, отрезок ММХ может сохранять свою
длину в том и юлько в том случае, если другой его конец Мх
движется тоже перпендикулярно к ММг. Иными словами, орт tx линии (Lx)
перпендикулярен к вектору М~МХ.
Докажем, что орт tx перпендикулярен также к орту t, т. е. что
орт tx коллинеарен с ортом 6.
Возьмем на (L) точку М', бесконечно близкую к М\ пусть
/Несоответствующая точка линии (Lx). Перенеся начало М' вектора М'М[
в точку М, мы получим вектор MR и будем иметь
^bds (6)
(на рис. 140 первое слагаемое изображено вектором MXS, второе —
вектором SR).
§ 37. НАТУРАЛЬНОЕ УРАВНЕНИЕ КЛАССА ЛИНИЙ
205
Первое слагаемое в правой части (6) эквивалентно вектору М'М,
т. е. по направлению касательной в М точка Mv смещается на
отрезок MXS, эквивалентный дуге ММ'', в сторону, противоположную
смещению ММ' течки Л/. Если учесть, что и точка R, чюбы
совместиться с М[, должна сместиться на вектор RM[, равный ММ' щ
то окажется, что
составляющая смещения М^М^ по
направлению t имеет высший
порядок относительно ds,так
что *
^ (7)
Следовательно, центр.
кривизны Мх движется по
направлению бинормали в
точке Л/, что и утверждалось.
Формула (7) показывает,
что место точек (Мх)
представляет течку только в том
случае, когда—= 0, т. е.
когда линия (L) —плоская,
а длоская линия постоянною радиуса кривизны есть окружность. Для
всякой другой линии (/.) постоянной кривизны точка М1 описывает
некоторую линию (LJ. Та же формула (7) показывает, что длина
дуги МХМ[ эквивалентна величине —^ ds, а так как угол смежности о>1
касательных линии (Ly) есть ке что иное, как угол смежности а/
бинормалей линии (Z.), то для радиуса кривизны р2 линии (Lx) мы имеем
Рис. 140.
Po
(8)
т. е. линия (Lt) имеет" постоянный радиус кривизны р0.
Остается доказать, что центром кривизны линии (Lt) в точке Мг
является точка М. Для этого достаточно убедиться в том, что орт пх
главной нормали линии (Lx) равнонаправлен с вектором М,М, т. е.
с ортом —п (а не с ортом /г).
Геометрически это почти очевидно: ведь соприкасающаяся плоскость
линии (L), в'которой лежит отрезок ММи вращается около касательной
прямой в точке М (§ 28, теорема 1, стр. 150). Таким образом, линия (IJ,
описцваемая концом Mlt должна быть обращена вогнутостью в сторону
точки М.
С помощью вычисления мы получим тот же результат следующим
образом. Формула (7), которую можно записать в виде
дает
(9)
206 ГЛ. V. НАТУРАЛЬНЫЕ УРАВНЕНИЯ
так что
Учитывая, что — есть постоянная величина (равная +1 при
х > 0 и — 1 при t < 0) г) и принимая во внимание (9), находим
dst «с ds dsx т
а так как, с другой стороны,
то
JI^-JI. (И)
Теперь нетрудно найти радиус кручения линии (LJ. Перемножая
векторно (10) и (11), находим
Отсюда, принимая во внимание (9), получаем
rffti_M^_di_i_xiJLni4_
i dSl - t ds dsx - x р„ и р„ -
а так как, с другой стороны,
ТО
или
т. е. радиус кривизны р0 есть средняя пропорциональная между z и т1#
Обратим внимание на то, что знаки кручения линий (L) и (Lj)
всегда одинаковы.
В заключение найдем общее уравнение линии (L) постоянной
кривизны, иными словами,—общее решение дифференциального уравнения
d2r d2x , d2y, . d2z \ , АЧ //|ОЧ
a?-a?+a?+j?-« (с-const). (12)
Так как к этому уравнению можно присоединить еще уравнение
c = ty(s), где <]>($) — совершенно произвольная непрерывная функция
аргумента s, то естественно предположить, что в искомом классе линий
х) Если величина с= — меняет знак на обратный, проходя через нуль,
то (L,) имеет точку возврата. Случай * = 0 невозможен, так как предполагается,
что точка М — правильная.
fi 37. НАТУРАЛЬНОЕ УРАВНЕНИЕ КЛАССА ЛИНИЙ 207
имеется такая, для которой индикатриса касательных является любой
наперед заданной сферической линией *).
Проверим это предположение. Построим произвольную сферическую
линию (Lj) и будем искать линию (L), для которой (Ьг) есть
индикатриса касательных и для которой в то же время имеет место
соотношение (> = р0.
Обозначим через гх радиус-вектор ОМХ индикатрисы (Lx) и через
sx — ее дугу. Задание индикатрисы определяет гх как
вектор-функцию от sx:
г, = М',) (rj = l). (13)
Величины s и slt в силу теоремы 6 § 32 (стр. 176), связаны
соотношением
игр»- (14>
Поэтому из формулы (13), которую можно переписать в виде
/ = —= (s )
находим
откуда
\i(s1)ds1. (16)
Легко проверить, что линия (L), определяемая уравнением (16),
действительно, удовлетворяет предъявленным к ней требованиям,
т. е. ее индикатриса касательных представляется уравнением (13),
а радиус кривизны р равен р0.
Действительно, обращая предыдущий вывод, мы, возводя (15) ска-
лярно в квадрат, найдем
откуда получаем (14).
Разделив (15) на (14), находим
£=мо. (17)
т. е. (Lj) есть индикатриса касательных линии (L).
Далее, дифференцируя (17) и принимая во внимание (14), находим
d*r _ drx
d ~" d
ds* ~" dsx ds£ — dsx
Согласно формуле (5) § 23 (стр. ИЗ) имеем
г) Сферическую линию можно определить, например, заданием широты и
в функции долготы v. Поэтому можно сказать, что вид сферической линии задается
функцией ц=/(г>).
208ГЛ. У. НАТУРАЛЬНЫЕ УРАВНЕНИЯ
Следовательно,
т. е. радиус кривизны р линии (L) равен р0.
Значит, индикатриса касательных действительно может быть задана
совершенно произвольно, и класс линий постоянной кривизны
полностью представляется *) уравнением (16) или, в координатной форме,
уравнениями
где xl(s1), 2/1 (^i), z1(sl)—~произвольные функции аргумента slt
удовлетворяющие соотношению
Случай 2. Кривые постоянного кручения.
Этот класс линий представляется натуральным уравнением
t = v (18)
где т0 — произвольная постоянная величина.
Для линий рассматриваемого класса не найдено свойств,
аналогичных свойству предыдущего класса. Но представляется интересным
разыскать общее уравнение 'линий постоянного кручения, так как при
этом обнаруживается замечательное свойство индикатрисы бинормалей
любой пространственной линии.
Привлечение индикатрисы бинормалей напрашивается естественно:
ведь величина т0 по абсолютному значению равна т- (теорема 7 § 32,
стр. 176):
где sB — длина дуги индикатрисы бинормалей (L3). В связи с этим
нам заранее придется исключить случай т0 = оо . В этом случае
уравнение (18), как мы знаем, представляет класс плоских кривых,
а индикатриса бинормалей вырождается в точку.
Итак, зададим сферическую линию (Z.3) уравнением
где rz(s3) — произвольная единичная вектор-функция:
и будем искать линию (L), для которой (L3) является индикатрисой
бинормалей.
Орт -т^ должен быть параллелен (теорема 5 § 32) орту п главной
3
нормали искомой линии (L), т. е.
1) Мы, конечно, ищем только такие линии (I), для которых касательные всюду
существуют и изменяются непрерывно.
§ 37. НАТУРАЛЬНОЕ УРАВНЕНИЕ КЛАССА ЛИНИЙ 209
Сопоставляя теоремы 2 и b § 32 (стр.175), мы можем сказать, что знак
«плюс» в формуле (20) берется в том случае, когда т0 < 0, а знак
«минус»—когда т0 > 0. Таким образом, вместо (20) можно написать
По векторам
Ь = Г« И П = — -~ -т-2-
8 |тв| ds9
находим орт касательной искомой кривой:
X*g). (22)
Отсюда, принимая во внимание, что-^- = |т |, находим
8
Сокращая на | т01 и интегрируя, находим
s" (23)
о
или, что то же,
г8
r = 4.)(r,xdr,). (23а)
Итак, линия (L), если она существует, представляется
уравнением (23). Остается найти индикатрису бинормалей (L9) и радиус
кручения т линии (23). Если окажется, что (L9) тождественна (с Ls)
и * = %, то (23), действительно, представляет искомую линию.
Найдем орт t линии (23).
Отнесем для удобства расчета линию (23) к параметру s3. Вектор
касательной будет
Отсюда
Уже сейчас видно, что линию (£8) нельзя задать совершенно
произвольно. Именно, она не должна включать дуги большого круга,
ибо если (Ьъ) есть большой круг, то вектор кривизны -~ будет
dsz
направлен от точки М3 к центру сферы, т. е. г8 и —~ тождественно
коллинеарны, а тогда, в силу (24) и (25), были бы тождественно
коллинеарны и векторы -^- , -f , i\ е. линия (L) была бы црямой.
asz ds3
Но для прямой линии кручение неопределенно.
14 М. Я. Выгодский
210 ГЛ. V. НАТУРАЛЬНЫЕ УРАВНЕНИЯ
Случай, когда векторы г3, —^- коллинеарны нетождественна
(тогда линия (23) имеет точку спрямления), не представляет опасности,
но тогда кручение нельзя вычислять по обычной формуле [§ 28, (8).
стр. 154], и потому мы будем рассматривать линию (L3) на таком ее
участке, на котором ее соприкасающаяся плоскость не проходит через
центр сферы; тогда векторы г3 и —£- нигде не коллинеарны.
ds3
Продолжая вычисление, найдем векторное произведение
dr х *L
которое раввонаправлено (а не только коллинеарно) с ортом Ь.
Пользуясь (24), (25) и формулой двойного векторного произведения, находим
dr v d*r - ** ft- dr* *1гЛ t-
Отсюда видно, что
в том и только в том случае, когда
В случае же *), когда
мы имеем
Ь=-гш.
Иными словами, (L3) является индикатрисой бинормалей линии (23)
в том и только в том случае, если выполнено условие (28); в
противном случае индикатрисой бинормалей служит сферическая линия,
симметричная с (L3).
Пусть теперь условие (28) выполнено; тогда, как показывает
вычисление, приведенное рижо, радиус кручения х = — имеет постоян-
0
ную величину, равную т0.
В самом деле, мы имеем теперь
* = >%, • (29)
г=Р (30)
ast as3
и ранее найденное соотношение:
*) Так как мы исключили случай, когда соприкасающаязя плоскость проходит
rfr, d2r3 dr% dV,
через центр сферы, то векторы г8, т— , -j-* не кэмпланарны, т. е. r3 -j— —~ Ф 0.
ass я^з S3 ds3
§ 37. НАТУРАЛЬНОЕ УРАВНЕНИЕ КЛАССА ЛИНИЙ 211
В силу (29) и (30) его можно переписать в виде
откуда
. db I dr /ОЛ ч
ds9 xods3 v '
Кручение а= — линии (23) мы вычислим по формуле
. db dr
ds ds
0
'C&J
получаемой из формулы (4) § 28 (стр. 154) заменой произвольного
вектора В, равнонаправленного с ортом Ь бинормали, самим этим ортом.
Принимая во внимание формулу (31а) и учитывая, что Ь2 = г1г = 1,
мы можем преобразовать (32) следующим образом:
Таким образом,
Итак, кручение линии (23) имеет требуемую величину, и,
следовательно, искомый класс линий представляется уравнением
где г3 (53) есть любая единичная вектор-функция, удовлетворяющая
условию
(в отдельных точках выражение (28) может обращаться в нуль).
Посмотрим, каков iеометричоский смысл этого условия.
Представим себе наблюдателя, движущеюся на сфере вдоль
линии (Z-з) в направлении возрастания дуги s8. Вектор г8 указывает
направление от ног его к голове, вектор -/^ — направление его дви-
жения, а вектор -— — направление к центру кривизны линии (Lz).
dss
Условие (28) означает, что центр кривизны линии (18) остается
по левую руку наблюдателя, или, что то же, сторона сферический
вогнутости лежит слева от него. В случае Гя-р1—3 = 0 центр кри-
dss dst,
визны (он совпадает тогда с центром сферы) лежит под ногами. Это,
однако, может случиться лишь на один момент, так как тождесткен-
g> dr» d2r&
ное обращение г3 -т— —у в нуль возможно лишь на дуге большого
круга, а она не может быть индикатрисой бинормалей кривой линии.
14*
212 ГЛ. V. НАТУРАЛЬНЫЕ УРАВНЕНИЯ
Таким образом, можно сказать, что наблюдатель всегда будет видеть
линию (L8) слева от себя.
Заметим, что условие (28) имеет силу не только для кривых
постоянного кручения, но и для любых линий. Именно, сферическая
линия (L8) может быть индикатрисой бинормалей какой бы то ни было
кривой в том и только в том случае, если 1) она отлична от большого
круга и 2) направление движения по ней задано так, что сферическая
вогнутость остается по левую руку движущегося по сфере
наблюдателя.
В этом можно убедиться аналогичной выкладкой. Однако, чтобы
геометрически осмыслить этот удивительный факт, лучше
воспользоваться геометрическими соображениями, которые мы здесь вкратце
изложим.
Пусть ААг (рис. 141) есть индикатриса бинормалей некоторой
линии (L), и направление от А к Ах есть положительное направление на ААХ.
Отложим от точки А в
положительном направлении какую-
нибудь дугу AM касательного
большого круга, меньшую
полуокружности, и через точку М
проведем сферическую
эвольвенту (L) линии ААг, Линии (L)
a(L) будут находиться в
параллельном соответствии. Поэтому
векторы t = MTf n = MN линии
(L) и векторы f, n линии (L)
связаны соотношениями
1= ± t; n= ±п.
При этом знаки правых
частей должны быть
одинаковыми. Значит, векторы д = МВ
и Ь = ОА бинормалей равны
между собой:
[ Рис. 141. Ъ^Ш
Вектор п = MW направлен в сторону вогнутости линии (L). Поэтому
он совпадает с отрицательным направлением AU линии ААг в точке М.
Вектор t = MT направлен в сторону сферической вогнутости линии ААХ
в точке А, а так как векторы t, ny b образуют правую тройку, то
направление сферической вогнутости лшши_ ААХ, отрицательное
направление на ней и направление вектора О А образуют правую тройку х).
Случай 3. Линии, для которых отношение кривизны и круче-
Ния —величина постоянная. Найдем класс линий, представляемый
натуральным уравнением
х:а = const. (26)
х) Отмеченный здесь интересный факт в известной автору литературе нигде
не упомянут. Более того, в некоторых сочинениях утверждается, что индикатриса
бинормалей может быть задана произвольно. См., например, O.K.
Житомирский, В. Д. Львовский, В. И. Мил и не к ий- «Задачи по высшей
геометрии^, ч. II, ОНТИ, 1937 г., стр. 86; решение задачи № 65 (ошибочно
помеченное № 64).
§ 37. НАТУРАЛЬНОЕ УРАВНЕНИЕ КЛАССА ЛИНИЙ 213
Так как отношение х:|о| эквивалентно отношению бесконечно
малых дуг индикатрис (Lx) и (L3) касательных и бинормалей
(теоремы 6 и 7 § 32, стр. 176), то естественно рассмотреть эти
индикатрисы. Пусть М (рис. 142) есть фиксированная точка на (L,), a TV —
соответствующая точка на (Z.8). Пусть, далее, Мг и Nx суть
соответствующие друг другу бесконечно близкие точки линий (Lx) и (Z8).
Плоскости MON и MxONj параллельны спрямляющим плоскостям
линии (L) искомого класса, а так как касательные к (Lr) и (L9)
параллельны главным нормалям линии (L) (теорема 2 § 32, стр. 175),
то плоскости больших кругов
MONn MXONX нормальны к (Z.,)
[а также к (Ls)].
Следовательно, прямая О А, по которой
пересекаются эти плоскости,
имеет пределом ось кривизны
ОВ линии (LJ, а точка А—центр
сферической кривизны В линии
(Li). С другой стороны, так как
плоскос1и MON, M1ONl
параллельны спрямляющим
плоскостям линии (L), то прямая ОВ
параллельна вектору Дарбу,
который, по доказанному в § 29 (стр.
160), наклонен к касательной
линии (L) под углом arctg -^ . Из
уравнения (26) следует, что
этот угол имеет постоянную
величину. Поэтому угол МО А, а
ч/ Рис 142
значит, и дуга МА имеют одну
и ту же величину, где бы
ни взять на (Lx) точку М. Иными словами, индикатриса (Lx) имеет
постоянный радиус сферической кривизны. Легко догадаться, что (Lx)
должна быть окружностью.
Докажем это. Пусть М и М' суть любые две фиксированные
точки на (Z.j), а В и В' — соответственные центры сферической
кривизны линии (Lx). Согласно теореме 4а § 34 (стр. 187), точки В и В'
лежат на сферической эволюте (1г) линии (Ьг), а согласно теореме 5
§ 34, для этой сферической эволюты мы имеем
ВВ'= \МВ — М'В'\. (27)
Но так как МВ = М'В\ то дуга ВВ' имеет длину нуль, что возможно
лишь в том случае, если точки В и В' совпадают. Значит, все большие
круги MN, нормальные к Ll4 проходят через некоторую точку А —
общий их центр сферической кривизны. Таким образом линия (Lx)
есть ортогональная траектория меридианов с общим полюсом А. Такой
траекторией является окружность параллели. Таким же образом
докажем, что и (Л8) ^ть окружность.
Так как {Ьг) есть окружность, осью которой служит ОА, и так
как прямая ОМ параллельна касательной к искомой линии (А), то
касательные к линии (L) образуют постоянный угол с осью ОА,
т. е. линия (L), для которой отношение и:с? кривизны и кручения
постоянно, есть линия откоса. Вместе с тем мы доказали, что бинор-
214 Г Л, V, НАТУРАЛЬНЫЕ УРАВНЕНИЯ
мали линии откоса также составляют постоянный угол с ее осью.
Легко также убедиться в том, что главные нормали линии откоса
перпендикулярны к ее оси, что мы уже доказали иным путем в § 21
(пример 2, стр. 96—97).
Обратно, для всякой линии откоса отношение х:о постоянно.
Для доказательства достаточно обратить предшествующее рассуждение,
что предлагается сделать читателю.
Итак, класс линий', для которых имеет место уравнение (26),
представляет множество всех линий откоса.
Аналитически полученные результаты можно найти так:
рассмотрим единичный вектор
(он равнонаправлен с вектором Дарбу з£+х#). Согласно
уравнению (26), величины и —у=== постоянны; можно положить
— = cos р, — = sin р,
откуда
tgp=~=/rc. (29*
о
Уравнение (28) примет вид
npfl. (30)
Дифференцируем это уравнение. Пользуясь формулами Френе и
соотношениями (29), мы найдем
т. е. а есть постоянный вектор. Из уравнения (29) находим также,
что вектор касательной t образует с вектором а постоянный угол р.
Следовательно, искомая линия есть линия откоса.
Обратное предложение докажем так: пусть линия (L) составляет
постоянный угол р с постоянным единичным вектором а\ тогда
at = cos p. (31)
Дифференцируя, находим
ал = 0, (32)
т, е, вектор а перпендикулярен к главной нормали; значит, он
компланарен с векторами t, b, я так как с вектором t он составляет угол р,
то с вектором Ь он составляет угол ~— р. Значит, имеем
a = *cosp + *sin£. (33)
Теперь продифференцируем уравнение (33); с помощью формул Френе
находим:
(у cos р — о sin р) п = 0,
и так как п Ф 0, то
х cos p — о sin p = 0,
т. е. х и о связаны соотношением
y = a tgp= та.
§ 37. НАТУРАЛЬНОЕ УРАВНЕНИЕ КЛАССА ЛИНИЙ 215
Итак, для того чтобы кривая была линией откоса, необходимо и
достаточно, чтобы ее кривизна я кручение были пропорциональны.
Постоянное отношение — дает тангенс угла, образуемого линией откоса
-с образующей цилиндра, на который она нанесена.
Случай 4. Сферические линии. Поставим задачу: найти
натуральное уравнение класса сферических линий.
Рассмотрим сначала сферические линий, расположенные на сфере
данного радиуса R.
В этот класс входят в качестве тривиального случая окружности
«больших и малых кругов. Как и для всяких плоских линий, для них
удовлетворяется уравнение
а = 0 (х = оо), (34)
-а радиус кривизны имеет постоянную величину:
Р = Р0<Д. (35)
Исключим временно этот тривиальный случай; кроме того,
предположим пока, что на рассматриваемой дуге сферической линии (L) нет
точек, для которых соприкасающаяся плоскость проходит через центр
сферы О. Следовательно, радиус кривизны il/C = p (рис. 143) на
рассматриваемой дуге всегда меньше радиуса сферы R=OM:
Р < Л. (36)
Тогда на линии (L) можно установить такое направление
движения, чтобы центр кривизны С оставался по левую сторону
наблюдателя, перемещающегося на сфере вдоль (L). При этом выборе
положительного направления орт бинормали b линии (L) направлен по лучу
ОС, и точка N, где ОС пересекает сферу, описывает индикатрису
•бинормалей (/) линии (L). Вместе с тем, линия (I) является
[теорема 6а § 34, следствие (стр. 188)] одной из ветвей эволюты линии (Z.),
именно той ветвью, для которой дуга MN большого круга, нормального
к (L), меньше 90°, или, что то же, для которой /_ M0N = ? меньше
прямого:
?<|. (37)
Считая величину 9 положительной, мы находим из
треугольника МОС:
ср = arcsin -~, (38)
так что, обозначая через рСф сферический радиус линии (Z.), имеем
рСф = MN = Д? = R arcsin -|. (39)
Пусть Мо есть начало отсчета дуг на (L), 7V0 — соответствующая
точка линии (/), s — длина дуги М0М и .93 — длина соответствуюшей
дуги N0N. Возьмем точку М', бесконечно близкую к М, и
соответствующую ей точку N' на (I). Так как радиусы ON, ON' равнона-
правлены с бинормалями, то
т. е.
ds, = R\o\ds. (40)
216 ГЛ. V. НАТУРАЛЬНЫЕ УРАВНЕНИЯ
Рис. 143.
Рис. 144.
§ 37. НАТУРАЛЬНОЕ УРАВНЕНИЕ КЛАССА ЛИНИЙ 217
С другой стороны, по теореме 5 § 34 (стр. 187)
так что
| с?рсф \ = R\a\ds. (42}
Это равенство можно переписать также в виде
так как величины -j^ и а имеют противоположные знаки. Действи-
тельно, если о > О, то вектор NK= -^=—сп направлен от точки N
по касательной к (I) в сторону, противоположную вектору л, т. е.
в направлении от N к А/. Но тогда при движении oi М к М' в пфю-
жительном направлении дуга рСф = |Л/7У| уменьшается, т. е. —^- < 0.
Этот случай и изображен на рис. 143. Если же о<0 (рис. 144), то»
Из (39) и (42а) находим
ds
(43>
Если бы установили на (L) противоположное направление
движения, то величина ~ изменила бы знак на обратный, и вместо (43) мы
имели бы *
(44 \
Таким образом, знак в правой части не имеет существенного
значения; поэтому, освободившись от радикала, мы представим
уравнение (43) в виде
(45)
или
Очевидно, что в обоих случаях, исключенных нами из
рассмотрении, уравнение (45) тоже удовлетворяется. В самом деле, при
р = const мы имеем одновременно а = 0, а при р = Д мы имеем ^ = 0,
так как R есть максимальное значение для р х).
Итак, для всех сферических линий удовлетворяется уравнение (45).
Но без дополнительных оговорок нельзя утверждать, что (45) есть
натуральное уравнение класса линий, принадлежащих сфере радиуса R.
1) Предполагается, что производная-^ существует.
218 ГЛ. У. НАТУРАЛЬНЫЕ УРАВНЕНИЯ
ибо этому уравнению удовлетворяют во всяком случае и все линии
постоянного радиуса кривизны \> = R, например все винтовые линии,
у которых радиус а и шаг 2тс6 связаны соотношением
Естественно возникает вопрос, ьет ли еще каких-либо линий,
удовлетворяющих уравнению (45).
Ответ на него дает следующая теорема.
Теорема. Всякая линия непостоянной кривизны, для
которой удовлетворяется натуральное уравнение (45), лежит на сфере
радиуса R.
Доказательство. Пусть радиус кривизны р и кр}чение с ли-
аии (L) удовлетворяют уравнению
= оЧЯ'-Р3). (45а)
Из уравнения (45а) следует, прежде всего, что всюду на линии (L)
иричем по условию тождественное равенство р=Я не имеет места;
изолированные же точки, для которых р = Д, мы можем устранить,
рассматривая достаточно малую дугу линии (Z.). Поэтому
уравнение (45а) можно представить в виде
= ± а. (47)
Если на линии (L) тождественно с=0, то в силу (47) -г- = 0 в,
•следовательно, р = const: значит, (L) есть плоская линия постоянного
радиуса кривизны R, т. е. окружность радиуса р<Я. Такую
окружность можно поместить на сферу радиуса Д, и значит, этот случай мы
в дальнейшем можем исключить.
Если же а = 0 в изолированных точках линии (L), то мы
исключим эти точки, взяв достаточно малую дугу линии (L). Теперь, не
нарушая общности, мы можем переписать уравнение (47) в виде
V
-—=-= -•: (48)
У Д2 - с2
•это означает, что если линия (L) — правая, то направление отсчета
дуг s совпадает с направлением убывания радиуса кривизны р, а если
линия (L) — левая, то — с направлением возрастания р1).
Построим на сфере радиуса R индикатрису бинормалей (I) линии (L)
(NQNN' на рис. 143) и возьмем на ней какую-нибудь точку 7V0. Пусть
1) Ничто не мешало бы, впрочем, взять в правой части (48) знак плюс
вместо минуса: только в построении, которое ниже выюлняется, пришл^ь бы
дуги NM откладывать в противоположную сторону от N.
§ 57. НАТУРАЛЬНОЕ УРАВНЕНИЕ КЛАССА ЛИНИЙ 219
е соответственной точке Мо линял (L) радиус кривизны р имеет
значение р = р0. На большом круге, касающемся (I) в точке NQ1 отложим
дугу N0M0, меньшую квадранта, длиной R arc sin ~. При этом, если
а>0, то дугу N0M0 будем, как на рис. 143, откладывать в
направлении возрастания дуги (I) (соответствующем направлению отсчета дуг
«а (I), если же з<0, то —в противоположном направлении (как на
рис. 144).
Через точку Мо проведем сферическую эвольвенту (L) линии (I).
Через s, р, о = — мы будем обозначать дугу, радиус кривизны
и кручение линии (L). Мы докажем, что линии (L) и (L) конгруентны.
Для этого достаточно доказать, что в соответственных точках М и М
линий (L) и (L) имеют место равенства:
ибо тогда обе линии имеют одни и те же натуральные уравнения.
Согласно теореме 6 § 34 линии (L) и (L) находятся в параллельном
соответствии, т. е. орты t, n, b линии (L) коллинеарны ортам t, n> Ь
линии (L). Мы докажем, прежде всего,, что эти орты соответственно
равны.
Начнем с орта п. Он равнонаправлен с вектором МС, ведущим цт
точки М к центру кривизны С и, значит, противоположно
направлен сортом NK, касающимся (I) в точке N и направленным от N к М,
NK=-n. (49)
С"другой стороны, орт NK коллинеарен с ортом л (теорема 5 § 32,
•стр. 175); при этом, согласно построению, он всегда равен —л.
Действительно, положительное направление на индикатрисе бинормалей (/) есть
направление вектора -г- = —an. По построению NK равнонаправлен с
вектором — <зп при а > 0 и противоположно направлен при о < 0.
Следовательно, в обоих случаях он равнонаправлен с вектором — п:
~ -п.
Лз обоих последних равенств следует, что
л = л. (49а)
Возьмем теперь орт t. В силу параллельного соответствия между
{L) и (L), мы имеем
t = ei, (50)
где е = + 1 или — 1.
Дифференцируя (50) по s и применяя первую формулу Френе, имеем:
^ (51)
(52)
- ds
так как величины х, х, -у- положительны, то
220 Г Л, V. НАТУРАЛЬНЫЕ УРАВНЕНИЯ
Сравнивая с (50), находим, что е = 1 и, значит,
* = *, (53)
а из (49а) и (53) следует, что
Ь = Ъ. (54>
Таким образом, (I) является индикатрисой бинормалей также и для (£)►
Далее, обе линии (L) и (L) имеют кручение одинакового знака.
Это ясно как из геометрических соображений, так и из соотношений
_____ db9 - - db dbds_
dsy ds ds dfe *
Наконец, относительно линии (L) следует заметить, что для
наблюдателя, движущегося по сфере в положительном направлении
[соответствующем положительному направлению л а (£)], центр кривизны С
будет оставаться слева. В самом деле, по построению дуга MN
меньше квадранта, т. е. угол между векторами ОМ, ON = tR острый.
Значит, тройка векторов t, n, ОМ (последний направлен от ног
наблюдателя к голове) имеет ту же ориентацию, что /, я, д.
При таком направлении обхода для сферической линии (L) имеет
место уравнение
S_,= -o. (55>
С другой стороны, для линии (L) имеет место уравнение
do
ds
:=-а. (56)
Перепишем (55), (56) в виде -, _р = — odsy ___=== —ads.
Правые части этих уравнений равны как по абсолютной величине,
так и по знаку, ибо (I) есть общая индикатриса бинормалей линии (L)
и (I), и, значит (теорема 7 § 32, стр. 176),
Сверх того, по доказанному о и о имеют одинаковые знаки. Следовательно,
dp __ dp
j/i?2 - f j/i?a - pa "
Интегрируя, находим
( *_..{-*. (58>
J У Д2 _ p2 J У Я2 - p2
Po Po
Выполняя интегрирование и учитывая, что M0N0 = R arcsin |, апо
построению M0N0 = R arcsin^- , имеем
P = p. (59)
Теперь сопоставим соотношения
ds^top и ds ^ ю p.
§ 37. НАТУРАЛЬНОЕ УРАВНЕНИЕ КЛАССА ЛИНИЙ 221
Здесь со и (о — углы смежности касательных линий (L) и (L); так как
последние находятся в параллельном соответствии, то
со=ш. (60)
Из (59) и (60) получаем
ds^ds. (61)
Беря начала отсчета в каких-нибудь соответственных точках
линий (L) и (/,), получим
s = s. (62)
Наконец, из соотношения (57) находим
|о| = |а|.
а так как по доказанному знаки а и с одинаковы, то
"а = а. (63)
Равенства (59), (62) и (63) устанавливают конгруентность линий (L)
и (L), и наша теорема доказана.
Итак, класс линий, представляемых натуральным уравнением
содержит 1) все линии, проведенные на сфере радиуса Д, и 2) все
линии постоянного радиуса кривизны R.
Но из уравнения (46) легко получить такое натуральное
уравнение, которое будет охватывать только сферические линии.
Именно, дифференцируя (46), мы получаем
Это уравнение равносильно уравнению (46), в котором постоянная
величина R произвольна. Следовательно, оно охватывает все сферические
линии и все линии постоянной кривизны. Но, с другой стороны, уравнение
2-° (63>
равносильное уравнению р = Я, где R — произвольная постоянная
величина, охватывает все линии постоянной кривизны, и только их.
Поэтому, устранив в (46а) множитель j-, мы получаем уравнение
которое охватывает все сферические линии, и только их.
Итак, (64) или равносильное ему уравнение
есть натуральное уравнение класса всех сферических линий.
ГЛАВА VI
КРИВАЯ ПОВЕРХНОСТЬ И ЕЕ КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
§ 38. О поверхностях
Как было разъяснено в § 2, поверхность является двупараметри-
ческим (двумерным) множеством точек. Однако, подобно тому как
не. всякое одномерное множество точек целесообразно называть линией,
так и не всякое двумерное множество точек целесообразно именовать
поверхностью. Чтобы обеспечить соответствие с нашим наглядным
представлением о поверхности, мы должны наложить на двумерное
множество точек, которое будем
называть . поверхностью,
некоторые дополнительные
требования.
Прежде всего нужно обес-
П€Ч!1ть непрерывность
поверхности. Для этого нужно
потребовать, чтобы при бесконечно
малом изменении параметров
и и v точка поверхности
смещалась на бесконечно малое
расстояние.
Далее, мы должны обеспе-
Рис. 145. чить существование касательной
плоскости.
Взяв на поверхности точку М (рис. 145), проведем через нее на
поверхности линии ММ1у ММ2, ММ31 ... Эти линии будут в ючке М иметь
касательные МТ1У МТ2, МГ3.
Мы требуем, чтобы все эти касательные лежали в одной плоскости;
эту плоскость мы называем касательной плоскостью в точке М. Наше
требование выражает в отвлеченной форме тот опытный факт, что
у физического тела малую часть его поверхности мы обычно можем
представлять себе плосксй. Так, находясь в открытом море, мы
принимаем поверхность воды за плоскость, тогда как на самом деле
поверхность воды кривая. Так же мы можем поступать со всякой «гладкой»
погерхностью, если выделяемая ее часть достаточно мала.
Но на опыте мы встречаемся и с такими поверхностями, которые
в некоторых своих частях несходны с плоскостью. Такова, например,
коническая поверхность вблизи ее вершины. Через вершину S
конической поверхности можно провести бесчисленное множество линей,
обладающих касательными в точке S (односторонними, если
рассматривается одна полость, и двусторонними, если рассматриваются обе
полости конической поверхности). При этом любая образующая конической
§ 39. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПОВЕРХНОСТИ 22Х
поверхности может служить касательной. Ясно, что в одной плоскости*
эти касательные не лежат.
Нетрудно представить себе поверхность, на которой имеется
множество заострений, иодобных вершине конической поверхности. Поэтому
от требования существования касательной плоскости мы будем
допускать отступления, если речь будет итти об отдельных (изолированных)
точках поверхности и даже о целых линиях (линиях излома
поверхности). Но такие точки и линии мы будем называть особыми или
неправильными.
Как мы увидим далее, в соответствии с наглядными
представлениями нам придется ввести еще некоторые дополнительные требования;,
о них будет сказано в свое время.
§ 39. Аналитическое представление поверхности
В аналитической геометрии положение точки М на плоскости
определяется двумя числами х и у — координатами точки М. Эти числа
могут иметь бесконечно многообразные геометрические истолкования.
Так, в полярной системе
координат координата <р дает
величину угла между полярной
осью и лучом, который исходит
из начала координат О и
проходит через точку Л/; в
биполярной системе обе координаты
дают расстояния точки М до
полюсов. Но, какова бы ни
была система координат, всегда
можно рассматривать каждую
из координат как число,
выделяющее из некоторого одно-
параметрического множества
линий одну из этих линий.
Координата является как бы
номером этой линии. Так, в Рис. 146.
полярной системе координат
значение г0 радиуса-вектора г выделяет из всех окружностей, имеющих:
центр в начале координат О, ту, радиус которой равен г0; значение же <р*
координаты <р выделяет из всех лучей, имеющих начало в О, тот,
который составляет с полярнсй осью угол ср0*
Этот способ определения положения ючки на плоскости можно
применить и к люСой кривей поверхности. Для этого возьмем на
поверхности S какое-нибудь однопараметрическсе множество или (как иначе
говорят) какое-нибудь семейство линий (I) (рис. 146), которое
покрывало бы поверхность S. Это семейство может состоять из каких yi одно
линий; единственное условие, которое должно быть обязательно
соблюдено, сосюит в том, чтобы никакие две линии (1Х) и (12) этою
семейства не имели общих точек. В противном случае общая точка носила бы
не один, а два «номера», т. е. одну из ее координат нельзя было бы
однозначно определить. Указанное условие будет соблюдено, например,
в том случае, если мы возьмем на поверхности S совершенно
произвольную линию (/0) п отнесем этой линии значение параметра и' = 0;
затем по одну сторону от этой линии нанесем на поверхности S те точки,
кратчайшее расстояние которых от линии (/0) равно d (это расстояние-
224 ГЛ. VI. КРИВАЯ ПОВЕРХНОСТЬ И ЕЕ КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
можно измерять на самой поверхности). Геометрическое место таких
точек есть некоторая линия, которой мы отнесем значение параметра
и' =d.
Построив семейство линий (Z), мы можем отнести каждой из них
определенное значение первой координаты и. За это значение можно
принять либо само значение параметра и', либо какую-нибудь
функцию от и'. Так, в нашем примере за координату и линии (I) можно
принять либо кратчаййРее расстояние d между линиями (Zo) и (I), либо
какую-нибудь функцию этого расстояния, например его квадрат.
Разумеется, нужно позаботиться о том, чтобы с непрерывным
перемещением линии (I) по поверхности и координата и менялась непрерывно,
а также чтобы каждому значению координаты и отвечала только одна
линия (Z).
Теперь возьмем на поверхности какое-нибудь другое семейство
линий (Л). При построении его нужно соблюсти те же условия, что при
построении первого семейства. Сверх того, позаботимся о том, чтобы
каждая линия второго семейства пересекала все линии первого
семейства. При этом пересекающиеся линии должны иметь различные
направления (т. е. касательные не должны совпадать). Если,
например, мы проведем линии (Л) так, чтобы каждая из них пересекала все
линии (I) под углом 45° или под прямым углом, то мы получим
семейство, удовлетворяющее всем упомянутым требованиям. Построив второе
семейство, мы можем отнести каждой из его линий определенное
значение второй координаты v. После этого положение каждой точки
на поверхности можно определить двумя числами, именно значениями
координат и, v тех линий (Z), (Л), которые проходят через эту точку.
Сообразно с этим координаты и и v казываются криволинейными
координатами точки М на поверхности 8. Ясно, что для всех точек
линии (I) криволинейная координата и имеет одно и то же значение,
тогда как для всех точек линии (Л) одно и то же значение имеет
координата v. Сообразно с этим линии (I) и (Л) называются координатными
(или параметрическими) линиями, причем линии (I) (для которых
координата и сохраняет постоянную величину) называются «линиями v»,
а линии (Л) (для которых v = const) называются «линиями и».
Аналогия между криволинейными координатами точки на
поверхности и координатами точки плоскости идет очень далеко.
Так, уравнения
и = и (t); v = v (t)
представляют некоторую линию, лежащую на поверхности 8.
В самом деле, каждому значению параметра t отвечает пара
значений и, v, т. е. определенная точка М поверхности 8. При изменении /
точка М пробегает одномерное множество, т. е. описывает (оставаясь
на поверхности) линию.
Точно так же уравнение вида и = <р (v) или v = яр (и) и вообще
J (и, v) = 0 представляет некоторую линию поверхности 8. Чтобы узнать,
имеют ли две линии/х (и, v) =0и/2 (и, v) = 0 общие точки и если имеют,
то—какие, достаточно исследовать и решить систему уравнений
Л(«,»)=0; /»(«,«)=0. (1)
Предположим теперь, что поверхность 8 с установленной на ней
•системой криволинейных координат отнесена к какой-нибудь
пространственной координатной системе, например к декартовой. Тогда
пространственные координаты х, у, г точки М нашей поверхности будут, оче-
§ 39. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПОВЕРХНОСТИ 225
видно, функциями криволинейных координат и, v:
(2)
z = z(u, v).
Уравнения (2) называются параметрическими уравнениями
поверхности. Если какие-либо два уравнения системы (2), например первое и вю-
рое, удастся разрешить относительно и и и, то, подставив найденные
выражения в третье из уравнений (2), мы получим уравнение вида
z = z{x,y), (3)
выражающее одну из координат поверхности S через две другие. Это
уравнение можно рассматривать как частный вид уравнений (2); именно,
если за параметры и и v принять координаты х и у, то первые два
уравнения системы (2) принимают вид
х = х, у = у,
третье же будет иметь вид (3). В общем случае функция z (и, v) будет
мноючначной.
Уравнение (3) является результатом исключения параметров и и v из
уравнений (2). Однако исключение можно выполнять различными
способами, и в тех случаях, когда функция z(u, v) оказывается многозначной,
бывает предпочтительно искать результат исключения в виде уравнения
F(x,y,z) = 0, (4)
в котором функция F(x, у у z) была бы однозначной.
Уравнение вида (3) является частным видом уравнения (4).
Пример 1. Положение точки на сфере можно определить следующим
образом. За «первое» семейство координатных линий примем «параллели»
сферы, т. е. сечения сферы параллельными плоскостями (рис. 147).
За параметр и* этою семейства можно принять, скажем, сферическое
расстояние AJK какой-либо параллели от «экватора», т. е. от большого
круга, уходящего в наше семейство. Если приписать параметру и' знак
плюс, когда параллель лежит в одном из полушарий, на которые
экватор делит сферу («сеьерном»), к знак минус, когда параллель лежит
в другом полушарии («южном»), то каждому значению параметра и' будет
отвечать только одна параллель (/).
За «первую» координату а можно принять либо само значение и',
т. е. сферическое расстояние параллели от экватора, либо какую-нибудь
функш ю величины и'. Так, можно принять за координату гг угол МОК
(широта), который радиус ОМ сферы образует с плоскостью экватора:
u = ZMOK. (5)
Зависимость и от и! выражается при этом формулой
м = 4' (5а)
где R есть радиус сферы. Величина и меняется от —90° до -1-90°.
За второе семейство координатных линий примем сечения сферы
пол; плоскостями, проходящими через ось О А, перпендикулярную к эк-
ватсру. Все линии (л) этого семейства суть полуокружности больших
Kj.yioB {«меридианы»)', они пересекают параллели подуглом 90°.
Каждый меридиан пересекает все параллели. Чтобы отнести каждому
меридиану определенное значение второй координаты v, примем какой-либо
15 М. Я. Вьгодский
226 ГЛ. VI. КРИВАЯ ПОВЕРХНОСТЬ И ЕЕ КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
меридиан AL за начальный. Тогда за вторую координату можно
принять угол v между плоскостью какого-либо меридиана ЛК и
плоскостью меридиана AL. Эюч угол (долгота) изменяется в пределах от 0°
до 360° и отсчитывается обычно в том направлении, при котором
точка К движется по экватору, вращаясь против часовой стрелки, если ее
наблюдать из «северного» полушария. Таким образом, мы имеем
(5b)
Широта и и долгота v являются криволинейными координатами точки
на поверхности сферы. Линиями и являются меридианы (v = const),
линиями и —параллели (и = const).
Рис. 147.
Заметим, что при построении второго семейства координатных линий
отчасти нарушены условия, которым должна удовлетворять
координатная сеть, а именно: все линии (к) имеют две обшче точки—
«полюсы» сферы. Вследствие этого для каждого из полюсов нельзя
однозначно определить долготу v. Но, если рассматривать любую
область сферы, не содержащую полюсов, то положение каждой ее
точки однозначно определяется значениями координат и и v.
Отнесем теперь сферу к прямоугольной системе координат, приняв
диаметр О А за ось Z; диаметр же OL, лежащий в плоскости
начального меридиааа и перпендикулярный к ОА, примем за ось X. Тогда
плоскость XOY совпадает с плоскостью экватора. Чтобы выразить
координаты х, у, z точки М в функции широты и долготы, опустим
из М перпендикуляр МР на плоскость XOY и из точки Р —
перпендикуляр PQ на ось ОХ.
Из треугольника МОР находим
= R sin Z. МОК = Rsinu
OP ==R cos и.
§ 39. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПОВЕРХНОСТИ 227
Из треугольника же OQP имеем
x==0Q = OP cos Z. LOP = R cos и cos »,
y = QP = OP sin Z LOP = Rcosu sin o.
Уравнения
x = R cos и cos y, y = R cos м sin u, z = R sin и (6)
суть параметрические уравнения сферы.
Всякое уравнение <р(и,у)=0, связывающее и и у, представляет
некоторую сферическую линию. Действительно, зададим широте и
некоторое значение а. Мы получим одну из параллелей сферы. Из
уравнения ср(#,<;) = 0 найдем соответствующее значение (одно или несколько)
долготы о. Получим один из меридианов. Пересечение найденного
меридиана с взяюй параллелью дает некоторую точку М. На других
параллелях аналогично найдутся точки; совокупность их составит линию,
форма которой определяется видом функции <р(и, v)=Q. Так, полагая
и — у, получаем линию, вдоль которой широта равна долготе. Декартовы
координаты точек этой линии можно выразить через параметр о,
полагая в формулах (6) u = v. Найдем
x = Rcos2v, у = R cos v sin v, z = Rsinv. (7)
Сравнив эти уравнения с уравнениями (10) § 6 (стр. 31), мы видим,
что наша линия есть кривая Вивиани.
Пример 2. Поверхность вращения.
Всякая поверхность вращения геометрически характеризуется тем,
что все плоскости, перпендикулярные к некоторой оси OZ (ось
вращения), пересекают поверхность по окружностям («параллелям»), центры
которых лежат на оси.
Естественно за первое семейство координатных линий поверхности
вращения S принять ее параллели, а за второе семейство — меридианы,
т. е. сечения поверхности S полуплоскостями, проходящими через ось;
такова, например, линия АВ на рис. 148. Поверхность S может быть
образована вращением ее меридиана около оси; впрочем, та же
поверхность может быть образована вращением любой лежащей на ней линии
(кроме параллели). Таким образом, выбранная нами координатная сеть
состоит из семейства параллелей и семейства меридианов. Нам остается
еще установить, каким числовым значением и характеризуется
произвольно взятая параллель CD и каким значением v характеризуется
произвольно взятый меридиар АВ. Тогда точка М, лежащая в
пересечении CD и АВ, будет иметь криволинейные координаты и и v.
В качестве параметра и, характеризующего положение меридиана АВ,
удобнее всею взять «долготу» этого меридиана, т. е. угол, составляемый
плоскостью данного меридиана с плоскостью некоторого начального
меридиана А0В0. Этот угол мы будем измерять радианами.
В качестве параметра и, определяющего положение параллели CD,
можно взять величину, аналогичную географической широте, а именно —
расстояние параллели CD до некоторой начальной параллели C0D0,
измеряемое дугой меридиана С0С = BM = D^D.
Такая система координат представляет естественное обобщение
1 еографлческой системы и для многих целей является удобнейшей.
Она пригодна для любой поверхности вращения.
Но часто бывает удобнее пользоваться другой параметризацией
нашей координатной сети. Именно, поверхность вращения может быть
15*
228 ГЛ. VI. КРИВАЯ ПОВЕРХНОСТЬ И ЕЕ КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
задана уравнением ее меридиана
z = f(x) (8)
в прямоугольной системе координат XOZ, где ось OZ совпадает с осью
вращения. Тогда в качестве координаты, определяющей положение
параллели, удобно принять радиус r—MN этой параллели.
Неудобством этого способа является то,что он непригоден для
цилиндрической повефхности вращения, где все параллели имеют один и тот же ра-
Рис. 148.
диус. Кроме того, функцияz = /(>), определяющая высоту параллели по ее
радиусу, может быть многозначней (если радиус изменяется не монотонно).
Составим параметрические уравнения поверхности вращения при
обоих способах параметризации.
Во избежание недоразумений мы сохраним обозначение и лишь для
широты точки М, радиус же MN будем всегда обозначать через г.
а) Примем за параметры величины гиг;, за ось апликат пррмем
ось врашения OZ, а за ось абсцисс — прямую пересечения плоскости
начального меридиана А0Б0 с плоскостью начальной параллели C0D0.
Тогда координаты точки М будут:
х = OQ = OP cos v = MN cos v = r cos v, \
(9)
§ 39. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПОВЕРХНОСТИ 229
Если положить г = const, то уравнения (9) представят параллель,,
а если v = const, то —меридиан. Уравнение
r = r(v) (10)
представляет некоторую линию (Z) на поверхности S. Нетрудно видеть,
что (10) вместе с тем представляет уравнение проекции линии (/)
на плоскость какой-либо параллели в полярных координатах (г — радиус-
вектор, и —полярный угол). Параметрические уравнения линии (/) суть
х= г (с) cosy,
у =r(c) sinv, \ (11)
Пусть, например, поверхность S есть параболоид вращения. Приняв
его вершину за начало координат (начальная параллель вырождается
при этом в точку), имеем уравнение меридиана
так что
Уравнения (9) принимают вид
х = г cos v,
y = r sin v,
(9а)
Потребовав, чтобы радиус точки М был пропорционален ее долготе,
т. е. чтобы было
r = av, (10а)
мы получим спиральную линию на параболоиде (она проектируется
на плоскость XOY архимедовой спиралью); ее параметрические
уравнения суть
, z = -^-, (Ha)
б) Примем теперь за параметры величины а и и. Тогда радиус г
параллели будет некоторой функцией (однозначной) ее «широты» и:
г = ? (и). (12)
Заданием этой функции определяется форма поверхности вращения
и ее меридиана.
Высота z параллели также будет однозначной функцией от и:
*=Ф(в); (13)
при этом функции г = ф(и) и z = <!>(«) связаны соотношением
du2 = dr2 + dz\ (14)
выражающим дифференциал дуги меридиана через дифференциалы
прямоугольных координат г и z.
230 ГЛ. VI. КРИВАЯ ПОВЕРХНОСТЬ И ЕЕ КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
Из (14) находим
dz = |/dtt2 — dr2 = \f ! — [<?'(и)]2 du,
т. е.
}f du2-dr2 = [ if l-W(*)¥**- (15)
D 0
Таким же образом можно получить соотношение
^)fl-W(u)Ydu. (15а)
Параметрические уравнения поверхности вращения теперь принимают вид
х = <p(w)cosu
где следует заменить ф(м) выражением (15) или <р(и)
выражением (15а).
Замечание. Зная
уравнение меридиана
можно считать известными
функции г = у(и) и z = <b(u).
Именно, из (14) находим *)
(17)
Уравнение (17) определяет и
как функцию от г. Функция
(18)
есть обратная фз
Из (18) и (12) находим
Ф (и) = /[?(*)]■ (19)
Для иллюстрации
сказанного рассмотрим катеноид,
т. е. поверхность враи.ения
цепной линии (§ 17, стр. 74)
Ретс. 149 около ее директрисы. Примем
за начальную параллель
горловую окружность CD катеноида (рис. 149) и обозначим через 6 ее радиус,
т. е. высоту цепной линии. Тогда, согласно формулам (5) и (8) § 17
(стр. 75—76), мы имеем (при измененных обозначениях) уравнения
г =»/б1 4-а1 = <р (и) (12а)
*) Если / (г) есть многозначная функция, то правую часть (17) нужно
рассматривать как криволинейный интеграл.
§ 39, АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПОВЕРХНОСТИ 231
откуда
Z=6Arshf- = 6 1nu-±J^^=<K«). (13а)
Параметрические уравнения катеноида в этой системе координат
будут:
х = j/б2 + и2 cos t>, у = |/б2 + u2sinv, z = 6Arsh-r-. (16a)
Пример 3. Прямым геликоидом (или просто геликоидом)
называется поверхность, образовавшая движением прямой АВ, которая,
пересекая неподвижную прямую ОЪ (ось геликоида) под прямым углом,
Рис. 150.
вращается около этой оси и в то же время смещается вдоль нее на
расстояние, пропорциональное углу поворота (рис. 150). За
криволинейные координаты точки М геликоида мы можем принять 1) ее
расстояние и = МА до оси и 2) угол v поворота образующей AM,
отсчитываемый от некоторого начального положения.
Отнесем геликоид к прямоугольной системе координат, приняв
его ось за ось Z, а начальное положение образующей — за ось X. Тогда
х = OQ = OP cos v = MA cos v = и cos v,
у = QP = a sin v.
Согласно условию, путь О А, пройденный точкой А по оси,
пропорционален угл\ v, и мы можем положить z = OA = bv, где b («ход
геликоида») есть смещение образующей при поророте ее на один радиан.
Итак, параметрические уравнения геликоида суть
y = usmv, z — bv. (20)
232 ГЛ. VI. КРИВАЯ ПО1ЕРХНОСТЬ И ЕЕ КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
Если задать постоянное значение v0 углу v и изменять и, то точка М
опишет образующую АВ, которая будет «линией ш>. Это видно и из
уравнений (20),, которые при v = v0 принимают вид
x = ucosv0, y = usinv0, z = bo0 (20a)
и изображают прямую, параллельную плоскости XOY.
Если задать постоянное значение а параметру и и изменять v,
то точка М будет оставаться на поверхности цилиндра радиуса а;
по условию ее смещение вдоль оси будет пропорционально ду«е
окружности, описанной ее проекцией Р на основание цилиндра. Поэтому
после развертывания цилиндра путь точки М станет прямолинейным,
т. е. точка М описывает винтовую линию. Это видно и из уравнений (20),
которые при и = а принимают вид
х = a cos у, 2/ = a sin v, z = bv. (21)
Пример 4. Линейчатой поверхностью называется поверхность,
порождаемая произвольно движущейся прямой линией («образующей»).
Взяв на линейчатой поверхности любую линию АВ (рис. 151),
отличную от прямолинейной образующей, примем ее за «направляющую».
Обозначим радиус-вектор точки N направляющей через г, а длину
дуги линии АВ, отсчитываемой от некоторого начала, — через s.
Имеем r = r(s). Параметр s
определяет положение
образующей. Положение точки М
на образующей можно задать
длиной и отрезка MN.
Обозначим через / единичный
вектор образующей:
и через г — радиус-вектор
точки М. Тогда
r=?(s) + ul(s) (22)
есть уравнение линейчатой
Рис. 151. поверхности. Координатные
линии .9 суть линии,
получаемые из АВ смещением ее точек вдоль образующих на одно и то же
расстояние. Линии и суть прямолинейные образующие.
Прямой геликоид есть частный вид линейчатой поверхности; его
уравнения (20) можно получить из (22).
Для этого отнесем прямой геликоид к той же системе координат, что
в предыдущем примере (рис. 150). За направляющую примем ось прямого
геликоида (ось Z), а за начало отсчета дуг на направляющей — начало
координат О, Тогда вектор-функция r(s) представится уравнениями
Найдем теперь выражения координат 7, (3, у единичного вектора
l(s). Так как смещению образующей вдоль оси на расстояние 6 отвечает
поворот образующей на один радиан, то угол между вектором / (s)
и начальным его положением (когда он был направлен по оси х)
§ 39. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПОВЕРХНОСТИ 233
равен у . А так как образующая все время перпендикулярна к оси zf
то с осью у она составляет угол -— =- . Поэтому имеем
По формуле (22) находим
х = х + uol = и cos -г , )
, > (22а)
у = у + и$ = и sin j , J
Вместо дуги s можно было бы взять любой параметр и, задающий
положение N на направляющей. В частности, для прямого геликоида
можем взять за параметр угол поворота v\ он связан с s соотношением
s = z — bv.
Подставляя это выражение в (22а), получаем уравнения (20).
Пример 5. Важным классом линейчатых поверхностей являются
поверхности касательных. Они порождаются прямой, которая во всех
своих положениях касается некоторой пространственной линии. Приняв
эту линию за направляющую, мы имеем /(s) = r7(s). Уравнение (22)
принимает вид
г\ (23)
ИЛИ
r = r + uf. (23а)
Уравнение (23) сохраняет силу и тогда, когда за параметр
направляющей вместо s взята иная переменная. Однако модуль г' не будет
тогда равен 1; поэтому и будет выражать не длину отрезка
касательной, а величину, пропорциональную длине (коэффициент
пропорциональности в общем случае меняется при переходе от одной образующей
к другой).
Составим уравнение поверхности касательных винтовой линии. Век-
юр г задается уравнениями (§ 18, стр. 78):
s s bs
х = a cos —r===—i , у = a sin == ,
Уравнения искомой поверхности будут:
s аи
х = а cos , . sin -у-.
s , аи
у — a sin , -1 . cos
* /a2f 62 Vaa + b2
_ 65
~~ /2 + 62
(25)
Линии s = const суть касательные винтовой линии. Линии H=const
суть винтовые линии, нанесенные на цилиндрах радиуса а = ау 1+
и имеюшие тот же шаг 2тс6, что данная винтовая линия.
234 ГЛ. VI. КРИВАЯ ПОВЕРХНОСТЬ И ЕЕ КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
Геометрически это видно из рис. 152, где отрезок касательной и = NM
спроектирован на плоскость, перпендикулярную к оси винтовой линии.
В треугольнике NPM угол при вершине М равен углу у между
касательной винтовой линии и ее осью. Следовательно (§ 8, пример 1)
(стр. 45):
cos ZPMN h
откуда
из треугольника же LNP имеем
Мы видим, что проекция конца М отрезка NM постоянной длины
описывает окружность радиуса а у 1 + 2^/2\ с другой стороны, сме-
Рис. 152.
щение точки М по направлению оси равно смещению точки N. Наше
утверждение доказано.
Аналитически можно убедиться в его справедливости так.
Положив
представим уравнения (25) в виде
) (26)
§ 40. КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ 235
Будем считать и постоянной величиной; положив a — ayi+-
а2 + Ь2 '
перенесем начало координат в точку (0; 0; z= J!i==.) и дере-
пишем (26) в виде
a); y=flsin( * Н~ ОС ) ; Z = /-—- .
х = а гпя ( --fa
Сравнение (26) с (24) показывает, что линия 5 есть винтовая
линия радиуса я, повернутая относительно данной на угол а, и
имеющая тот же шаг 2тг6.
Упражнения
Составить уравнения:
1. Псевдосферы (поверхность вращения трактрисы около ее оси).
*2. Поверхности вращения прямой линии около скрещивающейся с ней оси.
Показать, что меридиан поверхности есть гипербола.
3. Поверхности касательных к конической спирали.
'*. Поверхности касательных к кривой Вивиани.
5. Показать аналитически и синтетически, что поверхность касательных
винтовой линии пересекается плоскостью, перепендикулярной к оси винтовой
линии по эвольвенте круга.
Указание (для синтетического доказательства): найти длину проекции
•отрезка касательной винтовой линии на секущую плоскость.
6. Составить уравнение конической поверхности, направляющей которой служит
мзинтован линия, а вершина лежит на оси винтовой линии. Показать, что сечение
поверхности плоскостью, перпендикулярной к оси, есть гиперболическая спираль.
§ 40. Касательная плоскость в нормаль
В § 38 (стр. 222) мы потребовали, чтобы касательные ко всем линиям,
проврденным на поверхности S через точку М, лежали в одной плоскости,
и назвали последнюю касательной плоскостью в точке М. Пусть
поверхность отнесена к криволинейным координатам (и, v). Тогда
касательные к координатной линии г; и к координатной линии а,
проходящие через точку М, лежат в касательной плоскости точки М. Вектор г
на линии и зависит от одного параметра и (для него v = const). По-
эюму касательная к линии и коллинеарна с частной производной ^
(т. е. с производной функцией вектора г, взятой в предположении
?;=--const). Точно так же касательная к линии v коллинеарна с
вектором — . Векторы ^ и д£ , которые мы для краткости будем
обозначать ru, rv, не коллинеарьы между собой, так как пересекающиеся в
точке М линия и и линия v должны иметь различные направления.
Поэтому векторы ru,rv вполне определяют касательную плоскость.
Еелии через /? обозначить радиус-вектор произвольной точки касательной
плоскости, то уравнение касательной плоскости (выражающее, что
вектор /?— г компланарен с векторами ru,rv) будет
(R-r)rurD = 0. (1)
В декартовых координатах оно имеет ьид
Х-х Y — y Z-z
*и Уи Zu
*v Уи Zv
= 0. (la)
236 ГЛ. VI. КРИВАЯ ПОВЕРХНОСТЬ И ЕЕ КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
Перпендикуляр к касательной плоскости, проведенный через точку
касания, называется нормалью поверхности, а всякий вектор, колли-
неарный с нормалью, называется вектором нормали. Так как нормаль
перпендикулярна к векторам ги и rv, то векторное произведение ruxrv.
является вектором нормали. Если начало этого вектора поместить
в соответствующей точке поверхности, то направление его укажет одну
из двух сторон поверхности в рассматриваемой точке. Вектор нормали
ri>x ru= —(ru><rv) укажет другую сторону поверхности. Условимся
считать сторону, в которую направлен вектор ruxrv, положительной
стороной поверхности, а сторону, в которую направлен вектор rvxrur
отрицательной стороной. Ясно, что согласно этому условию любая
сторона поверхности может быть принята за положительную, ибо от
нас .зависит, какие координатные линии принять за линии w, a
какие — за линии у1).
Единичный вектор нормали, направленный в положительную
сторону, будем обозначать через ш, так что
Заметим, что, в силу определения вектора т, тройка векторов
rwm всегДа является правой.
Уравнения нормали можно записать в виде
Х-х __ Г-у _ Z-z
yuzv-zuyv ~~ zuxv-xuzv ~~ xuyv *
Координаты вектора т суть косинусы углов а, (3, у, образованных
положительно направленной нормалью с осями прямоугольных
координат, так что имеем
и две аналогичные формулы для cos(3, cosy.
Пример 1. Касательная плоскость к поверхности вращения
проходит через касательные прямые к меридиану и к параллели. Так как
направление параллели всегда перпендикулярно к плоскости меридиана,
то касательная плоскость перпендикулярна к плоскости меридиана.
Поэтому нормаль поверхности вращения лежит в плоскости меридиана
и совпадает с (главной) нормалью меридиана.
Если параметрические уравнения поверхности вращения взять в виде
x = rcosv, y = rsinv, z = f(r)y
то вектор rw{cosu, sin и, f'(r)} дает направление меридиана v = const,
а вектор rv{—г sin v, r cos v; 0}—направление параллели. Вектор
нормали ruxrv имеет координаты
— rf (r) cos v; — rf (r) sin и; г.
*) Может показаться, что положительную сторону поверхности подобно
положительной стороне спрямляющей плоскости можно определить объективно, как.
сторону вогнутости поверхности. Однако это возможно только для таких
поверхностей, которые, подобно сфере, располагаются по одну сторону от
касательной плоскости. Для поверхностей, которые, подобно гиперболическому
параболоиду или псевдосфере, разрезаются надвое касательной плоскостью, такое»
различение невозможно.
§ 40 КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ 237
Если &{0;0;1} есть вектор оси 2, то
О 0 1
kr\
г cos v r sin и /(г)
— rf cos v — rf sin v г
= 0,
т. е. вектор нормали компланарен с векюром точки М и вектором оси.
Это показывает, что нормаль лежит в плоскости меридиана—чю ранее
было показано геометрически.
Уравнение касательной плоскости имеет вид
(X — г cos v) f (r) cos v + (У — г sin v) f (r) sin v = Z — f (r),
или
Z = f (r) cosv . X + f (r)sinvY + rf (r)+ f(r).
Уравнения нормали суть
X — r cos v __ Г — г sin v__Z—/ (г)
/' (г) cos v ~~ /' (г) sin v ~~ —1 *
Угол у, составляемый положительным направлением нормали
с осью Z, находим по формуле
-1
из которой видно, что вдоль параллели (?= const) нормали образуют
с осью вращения один и тот же jtoji; геометрически это очевидно.
Пример 2. Касательная плоскость Р прямого геликоида в точке Л/,
лежащей на оси (рис. 153), проходит через ось и образующую MN.
Рис. 153.
Действительно, обе эти линии лежат на геликоиде, и их
касательными ярляк-тся они сами, b точке N, не лежашей на оси, касательная
плоскость Q проходит через образ\ющ>ю МN и через каса1ельа>ю NL
238 ГЛ. VI, КРИВАЯ ПОВЕРХНОСТЬ И ЕЕ КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
к винтовой линии NN'. Таким образом, плоскости Р и Q не совпадаю!»
Найдем угол между ними. Проведя прямую NK, параллельную оси,
получаем угол /_KNM ==у, который является линейным углом
искомого двугранного угла, ибо MN есть главная нормаль винтовой
линии NN' (§ 21, пример 3, стр. 101). Пусть 2пЬ есть шаг геликоида
и, значит, также шаг винтовой линии NN'. Так как а есть радиус
цилиндра, несущего эту винтовую линию, ю (§ 8, пример 1, стр. 45)
Мы видим, чао при движении точки N по прямолинейной образующей
касательная плоскость Q геликоида вращается около образующей,
причем тангенс угла поворота, отсчитываемого от плоскости Р,
проходящей через ось, пропорционален расстоянию MN = a точки N от оси.
При изменении и от — оо до + °о касательная плоскость делает
поворот от угла —90° до +90°.
Тот же результат найдем аналитически. Согласно уравнениям (17)
§ 39 (стр. 231), радиус-вектор геликоида есть
г {u cos и, ttsini;, bv}.
Отсюда
ru {cosy, sin г?, 0},
rv { — Msintf, м cost;, 6},
(ruxrv) { +6 sinvy — 6 cos*;, и},
b sin v Q b cos v и
cos a = - , cosp= , cosy = - ,.
Yb*+u* j/>+a2 ]/>M'2
Обозначая через ао,Во,уо направляющие косинусы нормали в точке
М(и = 0), имеем
cosa0 = sinw, cos(30=— cos и, cosy0=0.
Следовательно,
cos 9 = cos a cos a0 + cos j3 cos Po + cos у cos у0 = ,
Пример З. Рассмотрим поверхность касателышх к произвольной
кривой Л#(рис. 154) и будем искааь касательную плоскость Р в точке Л',
лежащей на фиксированной образующей MN (M — точка касания).
Касательная плоскость пройдет через MN. Чюбы полностью определить
ее положение, поступим следующим образом.
Из произвольной точки Мг линии АВ проводим MXL\\MN и через
ючку N — плоскость, перпендикулярную к MtL. Она пересечет MXL
и образующую MlN1 в некоторых точках /- и N1. Местом точек TVj
будет некоторая линия л, лежашая на поверхности касательных.
Когда Мг стремится к М, точка Nt имеет пределом 7V, а плоскосп
M1N1L (проходящая через касательную M{NX и прямую MXL\
параллельную бесконечно близкой касательной MN) имеет пределом
соприкасающуюся плоскость линии АВ в асчке М. Плсскость MJNM
(проходящая через касательную MN и бесконечно близкую точку М) имеет
тот же предел; поэтому угол между упомянутыми плоскостями и
измеряющий его линейный угол а бесконечно малы. Но а есть внешний
угол треугольника NYLN при вершине L. Следсвательно. бесконечно
мал и внутренний угол NXNL, т. е. угол между секущей NN1 линии (к)
и плоскостью i\fxLNM. Значит, касательная к X в точке TV (предел
секущей NNt) принадлежит соприкасющейся плоскости лмнии АН
§ 40. КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ 239
в точке М (пределу плоскости MXLNM). Искомая касательная
плоскость Р проходит через касательную к (л) в точке N и образующую A/7V;
обе эти прямые лежат в соприкасающейся плоскости линии АВ*
Следовательно, плоскость Р есть соприкасающаяся плоскость линии ЛВ.
Мы приходим к выводу:
Касательная плоскость поверхности касательных остается
неизменной вдоль образующей; она совпадает с соприкасающейся плоскостью
направляющей (в точке ее касания с образующей).
Этот вывод можно было предвидеть из менее строгих соображений
Именно, мы знаем, что расстояние между касательными MN и MlNi
Рис. 15'*.
имеет высший (третий) порядок малости; пренебрегая этой величиной,,
мы можем считать, что MN и MXNX лежат и одной плоскости. Ясно,
что эта плоскость в пределе есть соприкасающаяся.
Подтвердим наш вывод аналитически. Уравнение поверхности
касательных есть [формула (21) § 39, стр. 233)]
Отсюда *и=^, *. = £ + «£. *„Х*.-«(£х £).
Это уравнение показывает, что вектор нормали поверхности колли-
dr d*r
неарен с вектором оинормали -^— x -т-у направляющей, так что
касательная плоскость в точке N(s, и) совпадает с соприкасающейся
плоскостью направляющей в точке М (s).
Касательная плоскость остается неизменной также на.образующей
конуса (который можно считать вырождением поверхности касательных:
направляющая вырождается в точку) и на образующей цилиндра
(которую можно рассматривать как вырождение конуса: вершина уходит
в бесконечность).
Из примера 2 видно, что не всякая линейчатая поверхность имеет
вдоль образующей одну и ту же касательную плоскость. Ниже
будет показано, что у всех других линейчатых поверхностей (кроме
цилиндрических, конических и поверхностей касательных) касательная
плоскость вдоль образуюшей не остается одной и той же.
240 ГЛ. VI. КРИВАЯ ПОВЕРХНОСТЬ И ЕЕ КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
§ 41. О требованиях, накладываемых на функцию г (и, v)
В § 39 мы видели, что на поверхности S, заданной каким-либо
геометрическим ее свойством, можно ввести криволинейные координаты
и, v, после чего, если ее отнести к декартовой системе координат
с началом в некоторой точке О, координаты я, у, z будут
определенными функциями параметров и, v. Вместе с тем вектор г = ОМ,
ведущий из начала О в точку М поверхности S, будет вектор-функцией
тех же скалярных параметров и, о.
Пусть теперь, обратно, задана вектор-функция r = r(u, v) двух
скалярных аргументов и, v. Возьмем в пространстве некоторою точку О
и будем откладывать от нее всевозможные значения ОМ
вектор-функции г (и, v). Точки М, являющиеся концами этих векторов, образуют
двупараметрическое множество. В общем случае это дьупараметриче-
ское множесттзо представляет некоторую поверхность. Однако для этого
необходимо, чтобы вектор-функция r(w, v) удовлетворяла некоторым
требованиям, которые мы сейчас выясним.
Согласно требованию, высказанному в § 38 (стр. 222), всякая по-
верхюзть должна быть непрерывной, а это значит, что вектор г = ОМ
должен быть непрерывной функцией аргументов и, v. Далее, если
множество точек М есть некоторая поверхность, то через каждую точку М
должны проходить две координатные линии (и = const, v = const); они
должны иметь в точке М две (несовпадающие друг с другом)
касательные (§ 39, стр. 224); эти касательные коллинеарны с векторами ru, rv
{§ 40, стр. 235). Поэтому вектор-функция г {и, v) должна иметь частные
производные по обоим аргументам, и эти частные производные ru, rv
не должны быть коллинеарны между собой, т. е. должно быть
гиХГиф 0.
Наконец, согласно требованию § 38, поверхность должна иметь
(в правильной точнее М) касательную плоскость, т. е. касательные
ко всем линиям, проходяшим через М, должны быть компланарны
с векторами ru, /V Как будет ниже показано, существование
производных гы, rv и их неколлинеарность еще не обеспечивают выполнения
этого требования. Но если мы предположим, что вектор-функция г (й, v),
кроме того, дифференцируема, т. е. что приращенге r(u-Ldu, v-L-dc) —
— г (и, v) при любых значениях du, do эквивалентно выражению
rudu4~ rvdo [полному дифференциалу функции г (и, v)], то
существование касательной плоскости будет заведомо обеспечено.
^ ействительно, проведем на поверхности S через точку М какую-
либо линию (L). Вдоль нее координаты и, v и, значит, вектор г (а, с)
будут функциями некоторого параметра /; касательная к L будет кол-
линеарна с вектором —т— , а этот последний, в силу дифференцируемо-
сти функции г (и, у), равен
т. е. компланарен с векторами ru, rv, что и требовалось доказать.
Итак, в случае дифференцируемое™ функции г (и, v)
существование касательной плоскости обеспечено. Если же функция г (и, с)
не дифференцируема, то соотношение (1) может не выполняться; то]да,
несмотря на существование касательных прямых ко всем линиям,
£ 41. О ТРЕБОВАНИЯХ, НАКЛАДЫВАЕМЫХ НА ВЕКТОР Г (п, V) 241
проведенным на поверхности черея точку Л/, касательная плоскость
в точке М может не существовать.
Простейший пример такой точки дает вершина О любой
конической поверхности. Рассмотрим для простоты случай круглого котса
z =}/" х2 + у2. Через точку О можно провести на конической
поверхности множество линий, переходящих с одной полости конуса на
Другую. Касательными к этим линиям блдут образующие, а они не
лежат в одной плоскости. Итак, в вершине конуса касательной
плоскости не существует. Между тем, если положить х — и,
y = vy то z= ]/ы2 4-и2, и функция г (и, v) в вершине (0, 0) непрерывна
и имеет частные производные ги{1; 0; 1}; rv {0; 1; 1} 1). Однако
полного диффегенпиала функция ]/«/2 + и2 в вершине (0, 0) не имеет, т. е»
величина j/' dx* + dy* вообще неэквивалентна dx-\-dy.
Посмотрим теперь, что произойдет, если мы, сохранив требование
дифс|егенппруемости функции г (и, и), откая емся от требования ьекол-
линеа{ности векторов ru, rv. Рассмотрим сначала пример. Пусть
координаты х, г/, z вектора г выражаются через параметры и, v уравнениями
x = 2u + v, у = 4и8 + 4/л? + в1? z=e2Uev; (2)
тогда векторы
коллинеарны для любой точки (м, v)f и плоскость, проходящая через
них, остается неопределенной. Эта неопределенность вызывается в
данном случае тем, что уравнения (2) представляю! линию.
Действительно, положив 2м + v = w, мы можем представлять уравнения (2)
в виде
z = w9 2/=cv2f * = <?*, (3)
т. е. вектор г окажется функцией одного параметра w.
Рассмотренный пример показывает, что функция (скалярная или
векторная) одного аргумента может рассматриваться как частный вид
функции двух (или большего числа) переменных, аналогично tomv как
постоянную величину можно рассматривать как частный вид переменней.
Сообразно с этим, можно рассматривать линию как частный вид
поверхности. В самом деле, в общем случае поверхность описывается движением
dz
х) Частная производная — при u = 0, w = 0 не может быть вычислена по (fop*
dz и
муле — = ; она находится непосредственно:
dz ,. г(А 0)-z(0<» h
-^— = Jim
д
-^— = Jim 7— = lim-r e !•
ди ft_0 h -0 hmMjh
В окрестности точки (0, 0) частная производная — равна . Когда и и v
аи -у и 2 ц_ V2
стремятся к нулю, ^ может стремиться к любому пределу (р зависимости
от связи между и и v ) и даже может вовсе не иметь предела. Иными словами,
-—- , равно как и -=— , в точке (0, 0) разрывна» что является следствием недиф*
ференцируемости функции z (и, v) в точке (0, 0).
16 М. Я. Выгодский
242 ГЛ. VI. КРИВАЯ ПОВЕРХНОСТЬ И ЕЕ КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
линии (меняющей свою форму), так что различным постоянным значениям
v соответствуют различные положения движущейся координатной линии
v = const. R исключительных же случаях линия v = const, движется сама
по себе. Так, в нашем примере значению параметра v = 0
соответствует линия х = 2и, у = 4w2, z = е2и; значению же параметра v = 1
отвечает та же линия, только иначе параметризованная. Именью, точка,
отвечающая значению и = и0, смещается в положение, которое прежде
занимала точка и = и0 + - .
В общем случае уравнение w(u, v)=c представляет некоторое
семейство линий на поверхности. В рассматриваемом же
исключительном случае каждая линия такого семейства может вырождаться в точку.
В нашем примере, положив w = 2u4-v, мы имеем, что уравнение
2и + v = с представляет точку (с, с2, ес).
Итак, в рассмотренном примере коллинеарность векторов ru, г„
была вызвана тем, что поверхность выродилась в линию. Этот пример
является типичным. Именно, имеет место следующее предложение.
Теорема 1. Если векторы ru, rv коллинеарны при любых
значениях параметров м, и, то уравнение
r = r(w, у) (4)
представляет линию или (в случае г„==0, г„ = 0) точку.
Доказательство. В случае коллинеарности векторов ru, rD эти
векторы связаны соотношением
^«1 + ^ = 0, (5)
где а и р суть некоторые скалярные функции от и и у, не обращающиеся
в нуль одновременно.
Составим дифференциальное уравнение:
du:dv = <x (и, v) : p (и, v). (6)
Как известно из анализа, это уравнение имеет общее решение:
9 (и, v) = С. (7)
Докажем, что вектор-функция (4) может рассматриваться как функция
одного параметра: w—y(u, v).
Действительно, при постоянном значении С параметра w
удовлетворяется уравнение (6) и, значит, в силу (5), также и уравнение
rudu + rvdv = 0, (8)
dr = 0, (9)
откуда
a nst (10)
Итак, определенному значению параметра w = cp(ttt v)
соответствует определенное значение вектора г {и, v)y а это и значит, что вектор
г (и, v) есть функция одного аргумента w=y(u, v):
г (»f v) = г [9 (и, v)] = r (w). (11)
Значит, уравнение r = r(u, v) представляет линию r = r(w)\ в случае,
когда r(w) есть постоянная величина, эта линия обращается в точку.
Естественно, что когда поверхность вырождается в линию (и, тем более,
в точку), она и не может иметь определенной касательной плоскости.
За ее касательную плоскость можно принять любую плоскость,
проходящую через касательную прямую, с которой коллинеарны векторы
§ 41. О ТРЕБОВАНИЯХ, НАКЛАДЬ!БАЕМЫХ НА ВЕКТОР Г (н, V) 243
ru, ru. Если же поверхность вырождается в точку, то «касательная
плоскость» остается совершенно произвольной.
Геометрически очевидно, что справедлива и обратная теорема.
Теорема 2. Если вектор-функция r = r(u,v) представляет
линию, то векторы ги и г0 коллинеарны при всех значениях и, v.
Итак, ограничение, наложенное нами на функцию г {и,, о) и
состоящее в том, что векторы гы, rv не должны быть коллинеарны,
устраняет возможность того, чтобы уравнение r = r(uf v) изображало линию.
Рис. 155.
До сих пор мы рассматривали случай тождественной
коллинеарности векторов ru, rv. Если коллинеарность ги и rv имеет место
не тождественно, то функция r = r(u, v) представляет уже не линию,
а поверхность, но эта поверхность (в отдельных своих точках или
вдоль целой линии) может обладать разнообразными особенностями.
Для примера возьмем поверхность касательных (пример 3 § 40, стр. 238).
Если вектор направляющей есть г (о), то уравнение поверхности можно
представить в виде r = r(v) + urv7 откуда ru = rv, rv = rv + urm.
Возьмем на поверхности касательных линию а = 0, т. е.
направляющую г = r(v). Во всех точках этой линии векторы ги и rv коллщнеарны
{fu = ru = rv)i и касательная плоскость остается неопределенной. Эю
происходит потому, что единственным направлением, в котором,
двигаясь по поверхности, можно пройти через точку М (рис. 155),
является направление образующей 7\7\ На рис. 155 линия CMD
в точке М имеет это направление. Правда, к точке М можно подойти
по любому другому направлению; но дальше двигаться по тому же
направлению нельзя. Рассмотрим, например, сечение KML, произведен-
16*
244 ГЛ. VI. КРИВАЯ ПОВЕРХНОСТЬ И ЕЕ КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
ное на нашей поверхности плоскостью Ру нормальной к направляющей
АВ. Все прямые, касающиеся АВ, как на участке АМУ так и на участке
MB, пересекают плоскость Р в точках, лежащих со стороны
выпуклости направляющей АВ. Потому сечение KLM не входит внутрь
линии АВ, & имеет в точке М острие.
Итак, касательная плоскость в точке М не определена; но в то время
как в случае вырождения поверхности в линию любая плоскость,
проходящая через касательную, может быть принята за касательную плоскость,
в рассматриваемом случае неопределенность «раскрывается» вполне
однозначно.
Именно, во всех точках образующей МТ касательная плоскость вполне
определена; она совпадает (пример 3 § 40, стр. 238) с соприкасающейся
плоскосаью Q кривой АВ в точке М. Если потребовать, чтобы
касательная плоскость не изменялась скачками, то единственная
возможность удовлетворить этому требованию состоит в юм, чтобы принять
плоскость Q за касательную плоскость в точке М.
§ 42. Другое определение касательной плоскости
Касательную прямую мы определили как прямую, проходящую
через две бесконечно близкие точки данной линии. В соответствии
с этим естественно было бы определить касательную плоскость, как
плоскость, проходящую через
три бесконечно близкие точки
данной поверхности. Однако,
чтобы такое определение имело
смысл, оно нуждается в
существенном дополнении.
Чтобы уяснить
необходимость такого дополнения,
рассмотрим сечение UV поверхпо-
стп S какой-либо плоскостью Р
(рис. 156). На линии UV
возьмем три точки: А, В, С.
Плоскость, проходящая через точки
А, В, С, очевидно остается
неизменной, когда В и С,
оставаясь на линии С/У, стремятся
Рис. 156. к точке А. Таким образом, если
плоскость Р не совпадала с
касательной плоскостью в точке А, то плоскость, проходящая через три
бесконечноблизкие точки А, В, С, не является касательной плоскостью.
Причиной несовпадения предела плоскости ABC с касательной
плоскостью в точке А является то обстоятельство, что прямые
АВ и АС стремятся к одному и юму же пределу, именно
к касательной прямой AT линии UV. Иными словами, в треугольнике ABC
угол А бесконечно мал, или, выражаясь более наглядно, точки В и С
приближаются к точке А по одному и тому же направлению.
Сообразно с этим, мы можем формулировать определение
касательной плоскости так:
Определение 1. Касательная плоскость в точке Л поверхности S
есть предел, к которому стремится плоскость ABC, когда точки В и С,
оставаясь на поверхности S, стремятся к точке А по двум различным
направлениям.
§ 42. ДРУГОЕ ОПРЕДЕЛЕНИЕ КАСАТЕЛЬНОЙ ПЛОСКОСТИ 245
Докажем, что это определение равносильно определению § 38
(стр. 222). Действительно, пусть точка В стремится к А, двигаясь вдоль
линии Llt а точка С — вдоль линии L2 (рис. 157). Тогда прямая АВ имеет
пределом касательную АТ1 линии Lly а прямая АС — касательную
АТ2 линии L2. Следовательно, плоскость ABC в пределе проходит
через касательные АТг и АТ9. По условию эти касательные различны
между собой;
следовательно, проходяшая через них
плоскость есть касательная
плоскость в точке А.
Аналитически этот же
результат получается так:
если г есть вектор точки А7
а гв и гс—лекторы точек
В и С, то плоскость ABC
представляется уравнением
(Д-г)(гв-г)(гс-г) = 0.
Обозначим через da,
dv дифференциалы
координат и, v, соответствующие
смещению из точки А в
точку В, а через Ъи, <&>
—дифференциалы координат, соот- ^ис- ^7.
ветствующие смещению из
точки А в точку С. Так как направления, по которым В и С
стремятся к А, различны, то отношения du:dv и luiov не равны между
собой. Имеем:
rB — r = rudu + rvv + ... ,
rc — r = rum + rvbv + ... ,
(rB — r) X (rc — r) = (rH X rv) (dulv — Zudv) + ...
Члены, обозначенные в этих формулах многоточием, имеют высший
порядок малости относительно выписанных членов.
Так как du : do ф Ьи : 8и, то dulv iudo^O
Уравнение (1) можно переписать в виде
((R-r)rurv)(duiv-budv)+...=O
или в виде
(R-r)rurv+...=0, (2)
где многоточие обозначает бесконечно малую величину. В пределе
уравнение (2) дает
(R-r)rurv = 0,
т. е. уравнение касательной плоскости (§ 40, стр. 235).
В данном выше определении мы полаяли, что из трех бесконечно
близких точек Л, В, С одна фиксирована. Это ограничение
несущественно. Можно высказать более общее определение.
246 ГЛ. VI. КРИВАЯ ПОВЕРХНОСТЬ И ЕЕ КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
Определение 2. Касательная плоскость в точке А
поверхности S есть предел, к которому стремится плоскость BCD, когда точки
В, С, D, ос!аваясь на поверхности S, стремятся к точке А так, что
треугольник ВВС не имеет бесконечно малых углов.
Чтобы упомянутый предел существовал, достаточно потребовать
непрерывности производных гы, rv\ доказательство предоставляем пре-
вести читателю *).
*) Как известно, из непрерывности функций ru, rv вытекает дифференцируе-
мость функции г (и, v). Но функция г (м, v) может быть дифференцируемой и при
разрывности функций г„, /у, тогда плоскость В( D, при надлежаще выбранном
законе стремления точек В, С, D к А, может стремиться к пределу, отличному
от касательной плоскости в точке А в смысле определения 1 (ср. § 14, стр. 63).
ГЛАВА VII
ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИЗГИБАНИЕ ПОВЕРХНОСТИ
§ 43. Линейный элемент и первая квадратичная форма
Расстояние между любыми двумя точками на плоскости М(х, у)
и M'(#-fA#, у + &у), если эта плоскость отнесена к декарювой
системе координат, выражается, как известно, формулой
ММ'2 = Д#2 + 2 cos (о Дж Ау + Дг/2, (1)
где «> есть угол между положительными направлениями осей координат.
Расстояние между
двумя точками М (и, v) и
М'(и + Аи, у + Ду) на
поверхности S (рис. 158),
отнесенной к
криволинейным координатам и, v, —
будем ли мы измерять его
по прямой линии или по
кратчайшей линии,
соединяющей на поверхности S
точки М и М', — не
удается ныразить через Да, Ди
столь же простой
формулой. Однако, если точки М Рис- 158.
и М' бесконечно близки,
то главная часть расстояния ММ' выражается формулой, сходной с (1)
и представляющей ее обобщение.
Для определенности будем считать, что точка М(и, v) фиксирована,
а точка М' стремится к М по произвольной линии.
Проведем через М координатные линии МА (линия и) и MB
(линия v) и обозначим через ш угол между ними 1). Через точку М'
проведем линию v. Она пересечет МА в некоторой точке Q, причем
угол о' при вершине Q будет эквивалентен углу а>:
со' % а), (2)
так как при стремлении М' к М угол о/ стремится к углу а>.
Рассмотрим теперь прямолинейный треугольник MQM' (он не
начерчен на рис. 158). Его внешний угол ш" при вершине Q образован
секущими MQ и M'Q, а эти секущие образуют бесконечно малые углы
с касательными координатных линий в точке Q. Так как угол а/
1) Так как направления координатных ланий различны, то
248 ГЛ. VII. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИЗГИБАНИЕ ПОВЕРХНОСТИ
имеет конечную величину, то а>" ^ а/, и вследствие (2)
а>"^а>. (2а)
Рассматривая соотношение
ММ" = MQl + 2MQ • QM' cos а>" + QM'2 (3)
как эквивалентность, мы можем заменить в нем отдельные слагаемые
правой части эквивалентными величинами *).
Обозначив через гиг соответственно векторы точек М и Q и
помня, что вдоль MQ меняется только и, а вдоль QM' — только у»
найдем:
M£2=br2zxr^du\ (4)
QM'2 = Дг2 % ?% Л2 с^ г* <to2 a), (4a)
cos а>" ^ |/*Гы с?й j/r\do - cos со ^ rurudu do. (5)
Подставляя эти выражения в формулу (3), найдем
Л/М'2 % rJ42 + 2rurw du do + г^о1. (6)
Формула (6) еще проще получается аналитически. Именно,
ММ'2 = Ага % rfr2 ^ (гн (2а + rv rfi?)a % r^ du2 + 2гыгр ^ dy + r? cfo2.
Мы дали геометрический ее вывод потому, что на этом пути станет
особенно наглядным геометрический смысл входящих в нее величии.
Если через s обозначить дугу линии, по которой движется точка М\
направляясь к точке М, то MM'2 z^ds* и ds2=dr2. Поэтому формуле
(6) можно придать вид
ds2 = Eda* + 2F dudo + G do\ (7)
где мы, следуя Гауссу, положили
rl = E, rurv = F, r\ = G. (8)
Величина ds, определяемая формулой (7), называется линейным
элементом поверхности. Она дает дифференциал дуги для всевозможных
линий, проходящих через точку М(и, v). Правая часть формулы (7)
является относительно du, do однородным полиномом (формой) второй
степени. Она называется первой гауссовой квадратичной
дифференциальной формой или, короче, первой квадрагпиччой формой.
Коэффициенты Е, F, G этой формы суть функции от и, о, так что для данной
точки М (и, v) они являются величинами постоянными (не зависящими
от du, do).
Геометрический смысл этих коэффициентов выясняется из формул
(4), (4а), (5). Если мы обозначим через dsu и dsv дифференциалы дуг
линий и л о, проходящих через Q, то
J) Мы имеем на это право (§ 3, свойство 5, стр. 16), так как сторона ММ' не
может иметь высшего порядка ни относительно М^, ни относительно QM'. Чтобы
убедиться в этом, достаточно применить теорему синусов и учесть, что sin и/' не
может быть бесконечно малой величиной.
2) Мы предполагаем, что производная /%, непрерывна. Из этого следует, что
Г (и, v) есть дифференцируемая функция (см. В а л л е-П у с с е н, Курс анализа
бесконечно малых, т. 1, § Ii8, ГТТИ, 1933 г.). Как ниже будет видно, можно было
бы ограничиться требованием дифференцируемости г (и, г>).
8 43. ЛИНЕЙНЫЙ ЭЛЕМЕНТ И ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА 249
и формула (4) дает
Ф)\ (9)
т. е. коэффициент Е есть квадрат производной дуги линии и по ее
парамеару. Аналогично находи*м из (4а)
dsl = Gdo>; С = фу, (10)
т. е. коэффициент G есть квадрат производной дуги линии v по ее
параметру.
Наконец, формула (5) дает
dsu dsv cos со = F du dv; Р — т^' i-^cosio, (11)
что в силу (9) и (10) можно также записать в виде
(12)
Таким образом, при данных скоростях движения по координатным
линиям величина F пропорциональна косинусу угла между этими
линиями.
Так как вектор ги неравен нулю (§ 8, стр. 43) и так как величина
rl^zf-plj не может быть отрицательной, то при любых значениях «, о
мы имеем
E(u,v)>0. (13)
Аналогично
G(u,v)>0. (14)
Что касается F, то формула (12) показывает, что эта величина
положительна, если угол ш — острый^ отрицательна, если он тупой, и равна
нулю, если он прямой. Если координатные линии всюду пересекаются
под прямым углом, то F тождественно равно нулю, и обратно, если
F = 0, то координатная сеть—ортогональная.
Важно также отметить, что величина EG — F1 {дискриминант
первой квадратичной формы) всегда положительна. Действительно, мы
имеем
£G-P! = rW-(Vt)8 = (roxrX (15)
Так как векторы ги и rv не коллинеарны (§ 41, стр. 240), то вектор
Ги X rv (это—вектор нормали к поверхности) нулю не равен; поэтому
EG-F*>0. (16)
Выясним геометрический смысл дискриминанта EG — F1. Обозначим
через с площадь прямолинейного треугольника MQM*'. Тогда
оа = 1 MQ2 • QM'2 sin2 аз = \ (MQ x QM')\
Заменяя согласно (4) и (4а) векторы MQ и QjI эквивалентными
им векторами rudo и r0do и учитывая, что угол со между ги и г
отличен от нуля, мы можем (§ 3, свойство 4,) написать
250 ГЛ. VII. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИЗГИБАНИЕ ПОВЕРХНОСТИ
или, в силу (15),
F2)?, (17)
где а есть площадь прямоугольного треугольника с катетами du, do.
Итак, дискриминант EG— F2 есть предел, к которому стремится
отношение квадрата площади прямолинейного треугольника MQM'
к квадрату площади прямоугольного треугольника, стороны которого
суть приращения координат
и у о, соответствующие
сторонам MQ, MQ'.
Если ввести обозначения
то имеем
W = ]im2r. (18)
О
Если на линии и параметр
и равен ее дуге sut то,
согласно формуле (9), будем иметь
Е = 19 (19)
причем если равенство su = и
имеет место вдоль всех линий
иу то Е = 1 тождественно; если
Рис* 159. же яи = и только вдоль одной
из линий и, скажем, на линии
v = vOf то имеем Е (и, оо) = 1 при всех значениях и. Обратно, если
Е — \ (тождественно или при o = v0)y то дуга su линии и с точностью
до произвольного постоянного слагаемого равна параметру и (на всех
линиях и или вдоль линии о = и0). Точно так же, соотношение G = l
означает, что вдоль линии о дуга ее 9Ы равна параметру у.
Пример 1. Обозначив через и и о широту и долготу сферы,
найдем линейный элемент <'феры радиуса а.
Проведем через точку сферы М параллель MQ, а через другую ее
точку М' — меридиан M'Q (рис. 159). В треугольнике MQM'
MQ ^ CMdo ^ a cos
M'Q = d (BQ) = d (аи) = adu. (20)
Так как Z<?=90°, то
Следовательно,
ds2 = a1 du2 + a2 cos2u dv2. (21)
Таким образом,
E \ /7 0 G 22, (22)
W = /£G-F2 = a2 cos и х). (22a)
l) В правой части (22а) мы написали a2 cos a, a не — a2 cos и, так как широта и
меняется от - 90° до 4-90°, a W есть положительное число.
8 43. ЛИНЕЙНЫЙ ЭЛЕМЕНТ И ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА 251
Тот же результат получим аналитически из уравнений сферы:
г = a cos и cos v, y = a cos и sin v, z = a sin и.
Имеем:
ds2 = dr2 = dx2 + dy2 + dz2 =
= a2 [(sin и cos vdu — cos и sin и di;)2 +
-f ( — sin и sin v du + cos м cos и cfo)2 + coslv им2.
Члены, содержащие б?мс?у, уничтожаются, и мы получаем снова
формулу (21).
Замечание. Формулы (22) показывают, что величины Е, С и W
вообще положительны; но б и W при м = ±90° обращаются в нуль. Между
тем, выше было доказано, что эти
величины не могут быть равны
нулю.
Кажущееся противоречие
объясняется тем, что наша
координатная сеть, как было отмечено в
примере 1 § 39 (стр. 226), не полностью
удовлетворяет требованиям,
установленным в § 38. И именно для
пслюсов сферы (гг=±9О°), где
эти требования нарушены,
оказываются неверными формулы (14)
и (15) настоящего параграфа.
Линии v (параллели) вырождаются
здесь к точки, так что вектор
скорости rv оказывается равным
нулю, вследствие чего мы и
имеем
Пример 2. Линейный эле-
мент поверхности вращения.
а) Отнесем поверхность
вращения к системе криволинейных
координат и, v («широта» и «дол- Рис- 1б°-
гота»). Приняв АВ за начальную
параллель и АЕ — за начальный меридиан, найдем из рис. 160:
QM'^du; MQ^rdv.
Как в предыдущем примере, находим
(23)
ds2 = du2 + [<р (u)]2dv\ (24)
Здесь Е=\\ это соотношение вытекает из того, что за параметр и
принята дуга линии и (меридиана). Далее, F = 0; это вытекает из того,
что координатная сеть параллелей и меридианов ортогональна.
252 ГЛ. VII. ПИРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИЗГИБАНИЕ ПОВЕРХНОСТИ
Формулу (24) мы можем получить аналитически из уравнений,
найденных в примере 2 § 39 (стр. 230):
х = г (и) cos v, 1
чад. I
J
Они дают:
= (coso dr — r sin v dr)2 -f (sin и dr + r cos v dv)2 -f du2 — dr2 = du2 + r2 (u) dv2.
Так, для катеноида (г = j/ 63 + м2) мы имеем
dei = dtti + (6t + at)rf»f-
б) Отнесем поверхность вращения к системе криволинейных
координат г, у. Из того же рисунка 160, где ОС = z = f(z),QK zzdz, KM'^dr,
MQ^rdo находим
M'Q2»KM'2 + QK2 ^dr2 + dz2 = {l + [/' (r)]2} dr2. (26)
Подставляя в (23), находим:
ds2 = {1 + [/'(г)]2} dr2 + rW. (27)
Эту формулу можно получить аналитически из уравнений
х = г cos v, \
y = rsinv, 1 (28)
z = f(r). ]
р 2
В качестве иллюстрации рассмотрим параболоид вращения z=f (г) = 2р *
Согласно (27), мы имеем
ds2=(l+~)dr2 + r4o2. (29)
Пример 3. Найдем линейный элемент поверхности касательных
к линии АВ: r = r(v), где через v обозначена длина дуги AN этой
линии, отсчитываемая от некоторой ее начальной точки А (рис. 161).
Величину v примем за одну из координат любой точки М
касательной NT; за другою координату и точки М примем длину дуги Лл/,
взятую со знаком плюс, если направление от N к М совпадает с
положительным направлением отсчета дуг, и со знаком минус —в противном
случае.
§ 43. ЛИНЕЙНЫЙ ЭЛЕМЕНТ И ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА 253
Проведем через М ортогональную траекторию МК касательных
(т. е. эвольвенту линии АВ). Тогда в треугольнике МКМ' угол К
эквивалентен прямому, и мы имеем
ds2« MM'2» МК2 + КМ'2. (30)
Выразим МК,КМ' через du, do.
В треугольнике MNK угол N эквивалентен углу со между
касательными МТУ М'Т1 (это было доказано в теореме 3 § 27, стр. 138),
а угол М эквивалентен прямому по построению. Поэтому
КМ % NM tg со ^ шо ^ и х (у) cfo. (30а)
Далее, по свойству эвольвенты
NM-N'K = NN' = ±o. (30b)
С другой стороны, мы имеем
N'M'-NM=*u. (30с)
Складывая (ЗОЬ) и (30с), находим
N'M' — N'K = Am + Аи » da + rfw. (31)
Из (30), (30a) и (31) находим
ds2 = a2xW + (du + do)2 = du2 + 2du do + (l + uV) do2. (32)
Аналитически формулу (32) можно получить так. Уравнение
поверхности касательных г (иу о) можно записать (§ 39, стр. 233) в виде
. (33)
Параметры и, v имеют прежнее значение; t есть орт касательной
t=rv. (34)
Дифференцируем (33) и, принимая во внимание (34), находим
или согласно первой формуле Френе
dr = (t-\-um) do -\- tdu.
Отсюда
ds2 = dr2 = (t + urn)2 do2 + 2t{t + am) da do + du*,
или
ds2 = (1 + uV) do2 + Uu do + da2,
т. e.
£=l,F=l,(;=l-f и2х2,Т^=|м|х. (35)
Замечание 1. Равенство /? = 1 свидетельствз^ет о том, что и есть
длина дуги линии а, что согласно с нашим выбором системы
криволинейных координат.
Замечание 2. Как показывают формулы (35), величины E,FtG
всегда положительны. Величина же W положительна для всех точек,
за исключением: 1) точек, для которых н = 0, т. е. точек, лежащих
на направляющей АВ, и 2) точек, принадлежащих касательным в точках
спрямления АВ (для этих точек х(г) = 0).
254 ГЛ. VII. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИЗГИБАНИЕ ПОВЕРХНОСТИ
Это объяснятся следующим образом. Координатными линиями и
являются у нас касательные к АВ; координатной же линией о является
всякая линия А'В'', представляющая собою место точек, находящихся
от АВ на постоянном расстоянии (ес^и это расстояние отсчитывать
по касательным). Согласно требованиям, высказанным в § 39 (стр. 2*_;4),
две координатные линии, исходящие из некоторой точки, должны иметь
различные направления. Однако в упомянутых случаях это требование
нарушается: координатные линии касаются друг друга. Это совершенно
очевидна для точек линии АВ, ибо направление этс й линии есть не что
иное, как направление ее касательной. Читателю предлагается убедиться
в том, что дело обстоит так же в случае x(u) = 0.
Упражнения
1. Найти аналитичзски и синтетически линейный элемент прямого геликоида.
2. Показать, что первая квадратичная форма поверхности, заданной в
прямоугольной системе уравнением
*=»*(*, У),
имеет аид
(1 + />а) dx* + 2Pq dx dy + (1 + g") dy\
где
dz dz
3. Найти линейный элемент гиперболического параболоида.
§ 44. Направления на поверхности и углы между ними
В предыдущем параграфе мы вывели формулу
= /£ du2 + 2Fdudo + J do\ (1)
которая дает главную часть расстояния между точкой М поверхности
*S и другой ее точкой М' * стремящейся к первой по некоторой линии.
Таким образом, величины du, do бесконечно малы; их отношение
зависит от того, по какой линии точка М' приближается к М. Что же
касается величин Е, F, G, то для фиксированной точки М они
имеют одну и ту же величину, как бы ни приближалась точка М'
к точке Д/.
Если мы теперь из всевозможных линий, проходящих через М
на поверхности S, выберем какую-нибудь одну определенную линию (I),
то коирдинаты и, v станут функциями одного параметра, и отношение
du : do будет иметь в данной точке М вполне определенную величину.
Эта величина будет характеризовать направление линии (L) в точке М,
иными словами—направление касательной к (L) в точке М. Для нсех
линий, проведенных через М на поверхности S по этому направлению,
величина duido будет иметь одно и то же значение; обратно, если для
двух линий, проведенных через М на поверхности 5, отношение da : do
имеет одно и то же значение, то эти линии будут иметь одно и то же
направление, т. е. общую касательную.
Действительно, направление линии (L) в точке М определяется
ортом t:
tdr
44. НАПРАВЛЕНИЯ НА ПОВЕРХНОСТИ И УГЛЫ МЕЖДУ НИМИ 255
Заменяя величину ds ее выражением (1), находим
j__ Г и du + Г г dv
У Е du* -f "IFdu dv^G dv2- #
Так как лекторы ru, rv — это векторы касательных в точке/I/ к
координатным линиям, то они имеют для данной точки (iif и данном выборе
системы криволинейных координат) определенные значения, и мы гидим
из формулы (1а), что направление t всецело зависит от отношения du : do.
Пусть в точке М заданы на поверхности 5 два различных
направления. Дифференциалы, отвечающие одному из них, обозначим du, dv;
дифференциалы, отвечающие другому, пусть будут Ьи, bv Обозначая
через t и tfj орты этих направлений, имеем наряду с (1а) формулу
t = rbu + r$v
1
Е ди* + 2F dudv
Так как косинус угла между ортами / и tx равен их скалярному
произведению, то для угла 9 между направлениями zr ™ jr находим из (la) в (lb)
cos9 = —■ Jr^du^rrdv^rju 4-гr bv)
У Е du2 -\-2F dudv^-G dv2 \ E Ы1 + 2Fdu dv -f G dv2 #
Раскрывая скобки в числителе и принимая во внимание формулы (8)
предыдущего параграфа, находим:
__ Edudu + F(du$u + dvdu) + Gdvdv ,~\
^ ~~ УЕ du* -h 2F du dv -b G dv* Уе ди2 + 2F ди $v + G dv2 *
Мы видим, что для разыскания угла между двумя направлениями
du $u
заданными отношениями -г- и ^-, достаточно знать первую
квадратичную форму поверхности.
Выражение
Edubu+F (dubv + dv8и) + Gdvbv=(EЬи + F bv)du + (Fbu + GZv)dv (3)
есть билинейная форма, полярная относительно первой квадратичной
формы. Если положить du = ou, dv = bv, выражение (3) обращается
в первую квадратичную форму.
Положительное направление координатной линии и мы получим,
положив du = l, dv = 0, положительное направление линии v — положив
Ьи = 0, 8у=1. Подставив эти значения в формулу (2)^ найдем д^я угла
<р = о) между координатными линиями выражение
уже полученное нами в § 43 (стр. 249).
Согласно формуле (2) условие перпендикулярности двух
направлений имеет вид
Е du Ьи + F (du bv + dv си) + Gdvbv = O, (5)
или
(Edu + F dv) Ы + (F du + G dv) bv = 0. (5a)
Пример 1. Линейный элемент плоскости, отнесенной к декартовой
системе координат с координатным углом ш, имеет вид [ем. формулу (1)
§ 43, стр. 247]
dsz = dxl + 2cos udxdy + dy2. (6)
Здесь
256 ГЛ. VII. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИРГИБАНИЕ ПОВЕРХНОСТИ
тт dx fix y
Угол <р между направлениями т- и т- находится по формуле
da; ## 4- COS to (d# Si/ 4- dy or) 4- dt/ by /Пх
COS Ф = — —y • (I)
у dz2 4- 2 cos a» da: rfy + cfr/2 у дх2 + 2 cos to 6\г o</ 4- fy2
Условие перпендикулярности имеет вид
<£r Sa + cos u> (rfa; by + с??/ 8ж) + dy Zy = 0 (8)
к, в частности, для прямоугольной системы координат (ш = 90°)
O. (8a)
Если через А; и кг обозначить угловые коэффициенты касательных
к двум плоским линиям, проведенным через точку А/, то
К — dx' Kl"Yx '
и условие перпендикулярности (8) принимает вид
ккг + cos о (к + кг) + 1 = 0, (8')
а формулу (7) можно переписать в виде
у/с2 4-2 cos о/с 4-1 V ^
Преимущество формул (7) и (8), содержащих дифференциалы,
состоит в их симметричности.
Все три коэффициента первой формы в нашем примере постоянны.
Поэтому формулы (6), (7), (8) остаются верными и в том случае, если
входящие в них дифференциалы заменить конечными приращениями или,
что то же, направляющими коэффициентами соответствующих прямых
линий. Мы получим тогда известные основные формулы аналитической
геометрии.
Пример 2. Найти ортогональные траектории прямолинейных
образующих поверхности касательных.
Еслр* v есть дуга линии (L) и и — длина отрезка, отложенного
на касательной к (L), то для поверхности, касательных к линии (L)
имеем (пример 3 § 43, стр. 252):
Е= 1, F= I, G = I + и2
Условие (5а) ортогональности двух направлений для поверхности
касательных имеет вид
(du + dv) Ъи + [du + (1 + [и (х)]2) dv) lv = 0. (9)
Направление образующей мы зададим, положив 8н = 1,8и = О. Тогда
уравнение (9) примет вид
O. (10)
Вдоль ортогональной траектории образующих, т. е. вдоль линии,
пересекающей все образующие под прямым углом, координаты и, i суть
функции одного параметра. Дифференциалы этих функций связаны
соотношением (10). Следовательно, сами координаты к, v связаны
соотношением
« + »=/.. (Юа)
где /0 есть некоторая постоянная величина. Меняя значение этой
постоянной, будем пол\чать различные ортогональные траектории образующих.
§ 44. НАПРАВЛЕНИЯ НА ПОВЕРХНОСТИ И УГЛЫ МЕЖДУ НИМИ 257
Уравнение (Юа) выражает следующий геометрический факт: отрезок
прямолинейной образующей от точки касания до ортогональной
траектории убывает на величину, равную приращению дуги линии (L). Иными
словами, ортогональная траектория касательных линий (L) есть
эвольвента этой линии. Это было доказано геометрически в теореме 36 § 27
(стр. 139).
Пример 3. Линия, пересекающая все меридианы сферы под
постоянным углом, называется локсодромой. Эта линия играет важную роль
в мореплавании: двигаясь по локсодроме, корабль сохраняет один и тот
же курс (при этом, однако, он совершает не кратчайший путь).
Связь между широтой и долготой точки локсодромы можно найти
так: коэффициенты первой формы сферической поверхности (пример
1 § 43, стр. 250) суть
E = a2,F = 0,G = a2 cos2'*;
угол <р между двумя направлениями выражается, следовательно,
формулой
du Ъи 4- cos2w dv dv
cos о = г .
у du* + cos2h dv* \Ыг +- cos2u dv2
Направление меридиана задается значениями Ьи = 1, 8i? = 0. Для направле-
du
ния локсодромы j- получаем уравнение
du
COS CD =
У du2+cos*udv*
где ср —постоянная величина. Разделяя переменные, находим
^^сЦ<р. (11)
Два знака в прагой части (11) соответствуют двум возможным
направлениям движения (западному и восточному). Через каждую точку
сферы проходят две локсодромы; одна из них — правая кривая, а другая—
левая. Выбрав знак плюс, найдем уравнение одного из двух семейств
локсодром
где и0 есть широта точки пересечения локсодромы с первым меридианом.
Дифференциальное уравнение (11) можно получить весьма легко
из геомеарических соображений. Именно, в треугольнике MQM' (рис. 159
на стр. 250) можно положить M'Q 2z adu\ MQ 2z a cos и dv\ /_ MM'Q 2z 9;
следовательно,
^ M'Q du
ctg 9 ^ -~r ^ 3- .
° T MQ cos и dv
Упражнения
1. Найти угол между образующей поверхности касательных и линией на этой
поверхности, точки которой находятся на постоянном расстоянии от направляющей.
Показать, что вблизи направляющей этот угол близок к нулю» а на большом
удалении близок к 90э.
2. Иаогоналъной (т. е. «равноугольной») траекторией семейства линий
называется линия, пересекающая все линии этого семейства под одним и тем же углом.
Найти уравнение изогональных траекторий образующих прямого геликоида.
17 М. Я. ВыгодскиС
258 ГЛ. VII. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИРГИБАНИЕ ПОВЕРХНОСТИ
3. Найти дифференциальное уравнение изогональных траекторий меридианов
поверхности вращения. Проинтегрировать это уравнение для случая, когда
поверхность вращения есть катеншд.
4. 11айти ортогональные траектории образующих геликоида, профилем
которого (см. ниже, стр. 273) язляется прямая, пересекающая ось под постоянным
углом сх = 45° (косой геликоид).
5. Найти ортогональные траектории винтовых линий, проведенных на
поверхности косого геликоида.
6. Доказать, что линии, делящие пополам на всем своем протяжении углы
между координатными линиями, определяются дифференциальным уравнением
YEdu ± yr~Gdv = Q.
Ъ ьазание. При сгнтетическом выводе полезно учесть, что треугольник,
стороны которого суть 1) биссектриса данного угла, 2) одна из его сторон, 3)
прямая, параллельная другой стороне, является равнобедренным.
7. Проверить аналитически, что направления линий У Е du -f- YGdv = O
и YE du — У G dv = 0 (см. предыдущее упражнение) взаимно перпендикулярны.
8. Найти линии, делящие пополам угол между прямыми и винтовыми линиями
поверхности касательных винтовой линии.
§ 45. Площадь кривой поверхности
Понятие о площади кривой поверхности, как и понятие о длине
кривой линии, мы приобретаем из опыта. Опираясь на заимствованные
из опыта наглядные представления, мы можем вывести формулу для
вычисления площади поверхности, подобно тому как в § 15 (стр.65) мы нашли
выражение длины дуги кривей линии. Но, как было показано в§ 16 (стр. 72),
для доказательства найденной формулы необходимо какое-либо свойство
длины кривой линии принять за основу в качестве аксиомы или
определения понятия «длина дуги». Так же, конечно, обстоит дело и в
вопросе о площади кривой поверхности. Однако, кок мы увидим ниже,
при формулировке такого определения встречаются трудности, которых
не было в случае длины кривой линии. Тем более естественно будет
и здесь сначала довериться наглядным представлениям, получить из них
формулу для площади поверхности и лишь тогда рассмотреть вопрос
об определении понятия «площадь поверхности».
Пусть на кривой поверхности S дана некоторая область (В),
ограниченная замкнутой линией PQRT1) (рис. 162). Требуется найт:?
площадь, занимаемую этой областью.
Чтобы разыскать площадь нашей области, мы можем разбить ее
ка части; искомая площадь найдется суммированием их % площадей.
Разбивку на части можно осуществить с помощью некоторой
координатной сети. Область (В) разобьется на криволинейные
четырехугольники KLMN («криволинейные параллелограммы») и прилегающие к
границе части таких четырехугольников. При измельчении разбивки
части, прилегающие к границе, можно заключить внутрь безгранично
суживающейся полосы. Общая их площадь поэтому будет стремиться
к нулю.
Чтобы оценить площадь четырехугольникаKLMN, построим
прямолинейные треугольники KLN и LMN. При измельчении разбивки
плоскости их бесконечно мало отличны от касательной плоскости
в точке N. Площадь каждого из них эквивалентна (§ 43, стр. 250) вели-
*) Мы ограничиваемся рассмотрением односеявных областей, но все
рассуждения применимы и к областям многосвязным, например, к области, заключений
между замкнутой несамонересекаюшейся линией PQRT и какой-либо несамопере-
секающейся замкнутой линией, лежащей внутри PQRT.
§ 45, ПЛОЩАДЬ КРИВОЙ ПОВЕРХНОСТИ 259
чине *) - Wdu do, где через W обозначенЪ выражение ^EG — F2, так
что площадь вместе взятых прямолинейных треугольников KLN и LMN
эквивалентна величине Wdu do. Если довериться наглядному
представлению, то плошадь, ограничиваемую на кривей поверхности
криволинейным четырехугольником KLMN', мы можем считать также
эквивалентной величине Wdu do
пл. KLMNzz Wdu do.
Величина Wdu do называется «элементом площади» кривой
поверхности и обозначается символом о5. Площадь S всей области (В) экви-
Рис. 162.
валентна сумме величин Ъ — Wdudo, вычисленных для всех
четырехугольников, лежащих внутри (В). Эта сумма имеет пределом интеграл
\ \ Wdu do, распространенный на то множество значений и, и, которое
соответствует области (В). Поэтому
(В) (В)
г) Эквивалентность площади о треугольника LMN выражению ~ Wdu dv
была док\зана в § 43 для случая, когда переменные и, v зависят от одного
параметра. Но доказательство остается тем же и для случая, котда и, v суть
независимые переменные. Также и в этом случае эквивалентность аъ* — Wdudv
можно понимать как в том смысле, что НтГ о : — Wdudv J== 1, так и в том
смысле, что с Wdudv имеет высший порядок малости относительно
произведения dudv, когда du и dv стремятся к нулю по произвольному закону.
Заметим, что в рассматриваемом случае, когда переменные a, v независимы,
нецелесообразно обозначать их дифференциалы одним и тем же символом d\ лучше
было бы различать их, обозначая дифференциалы и, скажем, через dxu, а
дифференциалы V —через d2v. Сохраняя здесь общепринятые обозначения duy dv, мы
отметим, что указанный дефект обозначения является одной из причин (другая
будет указана ниже), почему при замене переменных
м = (р (и\ v'), и = ф(аг, v') (a)
новое выражение интеграла (1) не получается простой подстановкой вместо du, dv
их выражений, найденных из (л).
17*
260 ГЛ. VII. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИРГИБАНИЕ ПОВЕРХНОСТИ
Пример 1. Если отнести плоскость к косоугольной системе
координат (и — ху v = 7j; пример 1 § 44), то элемент площади SS будет
bS = Wdu do = sin o> dx dy.
В этом примере oS есть точное значение площади
четырехугольника KLMN (который является точным параллелограммом). Площадь 5
области (В) выражается интегралом
S = sin со \ \ dxdy. (2)
(В)
Пример 2. Если отнести сферу к географическим координатам
(и — широта, v — долгота), то (пример 1 § 43, стр. 250)
dS = a2 cos и du dv,
^ cos и dudv. (3)
(В)
Найдем по этой формуле площадь сферического двуугольника
с углом v0 при вершине. Примем одну из сторон двуугольника за
линию у = 0; другая будет иметь уравнение v = v0. Область В можно
определить неравенствами
Из формулы (3) находим
S — а2 V du cos и \ dv =!
+#
те
"1
что очевидно и из синтетических соображений (см. § 33, стр. 179).
Пример 3. Найти площадь выпуклой сферической области,
ограниченной петлей линии В ив чачи (см. рис. 7 на стр. 30).
Отнесем сферу к географическим координатам. При надлежащем
выборе полюса и первого меридиана одна половина границы области
имеет уравнение v = u; другая у=—и. Площадь S петли равна
2 +и 2"
S = a2 [du sin и \ dv = 2а* \ м sin м rfw = 2а2
или
S = а2 К dv \ sin и du = a2 \ cos vdv = 2a2. (4)
те
"2"
Общая площадь двух петель кривой Вивиани составляет 4а*,
т. е. равна площади квадрата, описанного около большого круга.
Пример 4. Найти площадь S поверхности касательных к линии (L),
ограниченную дугой АВ линии (Z.), прямолинейной образующей,
проходящей через А и ортогональной траекторией ВС образующих,
исходящей из точки В (рис. 163).
§ 45. ПЛОЩАДЬ КРИВОЙ ПОВЕРХНОСТИ 261
Примем точку А за начало отсчета дуг, и пусть о0 есть длина
дуги АВ. Мы должны определить площадь области, ограниченной
криволинейным треугольником ABC. Сторона его АВ имеет уравнение и = 0;
сторона АС — уравнение и = 0; ортогональная траектория ВС имеет
(пример 2 § 44, стр. 256) уравнение u + v = uB+vB, т. е. u+v = v0.
Элемент площади равен
85 = их (v) du do
(приме}» 3 § 43, стр. 253). Имеем
£=4 4 u*(v)dudv,
(В)
о vo—v vq
= { x(v)dv \ udu = ± i *(v)(vo — vydv. (5)
0 0 U
0 U
Если линия (L) имеет постоянную кривизну х0 (например, если
это винтовая лииия или окружность; в последнем случае поверхность
Рис. 163.
касательных есть плоскость, и ВС есть эвольвента окружности), то
s=4 vs- (6)
Обратимся теперь к вопросу о математическом обосновании
полученных результатов. При выводе формулы (1) мы опирались на
утверждение об эквивалетности площади области KLMN и суммы площадей
треугольников KLN и LMN. Это утверждение согласуется с практикой
измерения площадей. Действительно, когда требуется на кривей
поверхности, скажем на поверхности земли, измерить некоторою площадь,
то эту территорию разбивают на треугольные участки (триангуляция).
Стороны треугольников должны быть настолько малыми, чтобы их с
допустимой степенью погрешности можно было счшать прямолинейными.
Тогда площадь треугольного участка вычисляется так, как если бы
треуюльник был плоским.
Утверждая, что площадь KLMN эквивалентна сумме площадей
двух плоских треугольников, мы сослались на наглядное представление,
которое в конечном счете основано на опыте. Доказать это утверждение
262 ГЛ. VII. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИГ ГИБАНИЕ ПОВЕРХНОСТИ
мы можем лишь1 в том случае, если предварительно определим, что
такое площадь кривой поверхности.
Определение площади кривой поверхности можно сформулировать
по-разному. Но как.бы его ни построить, нужно обеспечшь, чтобы из
него вытекала упомянутая эквивалентность. В противном случае
определенное нами понятие площади не соответствовало бы тому
представлению о площади, которое помимо всяких определений имеет каждый.
Из определения площади должно также вытекать, что при любом
разделении области на части площадь области равна сумме площадей
ее частей. Это свойство, кратко именуемое аддитивностью, также лежит
в основе техники измерения площадей. При выводе формулы (1) мы
использовали и его.
Очевидность упомянутых свойств была причиной того, что
математики долгое время считали их само собой разумеющимися и потому
не испытывали потребности в определении площади. Коши указал на
необходимость подобных определений. Остановившись перед
трудностями, с которыми оказалось связанным чисто геометрическое
определение площади поверхности, он наметил (а для длины дуги кривой
линии и провел) следующее наиболее простое решение вопроса.
Установим определение: площадью области (В) называется число,
равное двойному интегралу1)
Wdu dv. (7)
(В)
При таком определении необходимо прежде всего доказать, что
величина \ \ Wdu dv не зависит от выбора криволинейных координат.
(В)
Пусть и, v суть координаты точки М в одной системе, а и, v —
координаты той же точки в другой системе. Очевидно, что и, v суть
функции от и, у, и обратно.
Дискриминант W2 = FG — F2, вычисленный для новой системы
координат, вообще не равен дискриминанту W2. Он не только выражается
иной функцией от и, £>, чем W2 ьт и, vf но и пссле подстановки Еме-
сто и, v их выражений через и, v не совпадает с функцией W(u, v).
Однако между W и W существует простое соотношение. Согласно
формуле (15) § 43 (стр. 249)
W = Y(ruxrv)2. (8)
Аналогично имеем
ГХГ;)'. (8а)
Вычислим векторное произведение г- X
ди dv\
х) Идея Коши состоит, следовательно, в том, чтобы менее очевидное и
исторически позже открытое свойство принять за определение и из него вывести те
свойства, из которых оно было фактически получено. Эта идея была широко
использована позднейшими математиками; к ней часто прибегают и в настоящее
время. В лпрек ей можно поставить «неестественность» построения. Однако эта
неестественность проистекает не от упот{ ебления идеи Коши, а от злоупотребления
ею. Если определение высказывается не догматически, как плод произвола, а
предваряется анализом тех предпосылок, которые приводят к этому определению, оно
теряет искусственный характер.
§ 45. ПЛОЩАДЬ КРИЕОЙ ПОВЕРХНОСТИ
263
Раскрывая скобки и учитывая соотношения rux ru = rvX rv = 0;
rpXru=-rnX rv, находим
/ du dv du dv \ . . /q\
" u ^ du dv dv du У
выражение в скобках есть определитель Якоби — „ j . Из (8) и (9) следует
D (и, v)
(10)
(u, v)
Таково соотношение между W и W.
Отнеся поверхность к системе координат (и, v), мы должны вместо
интеграла \ \ Wdudv взять
(В)
\Ydu do.
(И)
(В)
Докажем, что этот интеграл имеет ту же величину, что\ \Wdudo.
Действительно, согласно (10), имеем
(В)
\ Wdado =
(В) (В)
, v)
D(u, v)
dado.
(12)
Согласно известной формуле преобразования переменных в кратном
интеграле1) имеем
(В)
(В)
D (и, г;)
dudo.
(13)
*) Эта формула обычно доказывается в курсах анализа (см., например, Гурса,
Курс математического анализа, т. 1, ч. 1, стр. 289, ГТТИ, 1933 г.) с помоцью
теоремы Остроградского-Грина, что делает доказательство мало наглядным.
Учащемуся, кроме того, представляется странным, что для кратного интеграла
переход к новым переменным нельзя совершить так, как это делается для интеграла
функции одного переменного, т. е. подстановкой вместо du, dv их выражений
через du, dv. Поэтому здесь нелишне разъяснить этот вопрос геометрически.
Нижеприводимое пояснение не претендует на строгость и имеет целью лишь уяснить
суть дела.
Введем прежде всего целесообразные (см. сноску на стр. 259) обозначения;
именно, будем обозначать дифференциалы, относящиеся к смещению вдоль линий
NM, NK (рис. 162 на стр. 2">9), соответственно символами dud. Будем, далее,
рассматривать общий случа^, когда линии NM, NK не должн-j быть
координатными. Тогда для площади S четырехугольника KNML получаем выражение:
£2 ^ (NM х NK)2 = [(ru du + rv dv) x
du dv
ъ W* (du dv - dv duy = W*
8u dv
(*)
это
выражеВ частном случае, когда линии и и v — координатные (du = 0, dv =
ние принимает вид W1du2dvi.
Если исходить из этого выражения, то выражение площади того же
четырехугольника в новых переменных получается из (л) подстановкой вместо du, dv, du, dv
их выражений через du, dv, du, dv. Именно, мы находим;
= W
du dv
du dv
--W
du j* . du ~ dv ,~ dv -
-zr йл-\—— dv —Ы du -\ — dv
du
dv
du
dv
du ~ du .~ dv ~ dv ~
—-z du H ^r dv —zr du -{ ^r dv
du dv du dv
Это выражение, на основании теоремы об умножении определителей, можно
264 ГЛ. VII. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИЗГИБАНИЕ ПОВЕРХНОСТИ
Из (12) и (13) получаем
[ [ Wdu do=\\ Wdu do,
(В) (В)
что и требовалось доказать.
Теперь определение площади как числа, равного \ \ Wdu dv, с логи-
(В)
ческой стороны полностью оправдано, и тем самым формула (7) не
нуждается вовсе в доказательстве. Напротив, из нее могут быть выведены те
два свойства, на которые мы прежде ссылались при выводе
формулы (7).
Докажем, во-первых, эквивалентность плошади четырехугольной
области KNML и суммы площадей треугольников NML и NLK.
Пусть Ws есть значение W в точке Л; обозначим через ч\ разность
W(и, v)—Wn Для произвольной точки области KNML:
H = W(u, и) — WV . (14)
В силу предполагаехмой (равномерной) непрерывности функции W (и, v)
максимальное абсолютное значение е величины ч\ стремится к нулю
при неограниченном измельчении координатной сети.
Площадь четырехугольника KNML по определению равна
(15)
(В)
(В)
Обозначим через Ди, Аи приращения координат на сторонах NM, NK.
В первом из интегралов правой части (15) мы можем рынести
постоянную величину Wn за знак интеграла, так что упомянутый интеграл
представить в следующем виде:
D (и, v)
D (и, v)
du dv
du dv
du dv
du dv
OU QV
du dv
$u dv
^ «w , входящие в (а) и (р), суть площади плоских
Величины
параллелограммов, стороны которых проектируются на прямоугольные оси
координат отрезками du, dv, du, dv и, соответственно, du, dv, du, dv, если обозначить
их через da, da, то из (£i) поллчим формулу преобразования двойного интеграла:
(В)
(В)
b (и, v)
Итак, то обстоятельство, что в двойном интеграле нельзя производить
преобразование дифференциалов, имеет в основе нецелесообразное обозначение эле-
du dv
мента площади через dudv\ его правильнее было бы обозначить через $и $v
В самом деле, если при старых переменных элемент плогаади ограничивался
координатными линиями и мог быть представлен произведением du <Ь, то в новых
переменных тот же элемент ограничен линиями, которые, вообще говоря, не являются
координатными. Поэтому и нельзя преобразовать двойной интеграл,
представленный в виде \ \ Wdudv, подстановкой выражений для du> dv. Все сказанное выше
(В)
относится и к двойному интегралу любой функции F(u, v).
§ 45. ПЛОЩАДЬ КРИВОЙ ПОВЕРХНОСТИ 265
u-f-Ди
равен W\r \ du \ di? = FF/xrAtt Ai?. Формула (15) принимает вид
ы и
пл. KNML = WNAuAv+{{ y\du dv.
(В)
Первое слагаемое правой части, как мы знаем, эквивалентно сумме
площадей прямолинейных треугольников NML, NLK, а второе
слагаемое, абсолютная величина которого не превосходит еДаДи, имеет
высший порядок относительно произведения. Этим наше утверждение
доказано.
Что касается аддитивного свойства площади, то оно непосредственно
вытекает из определения кратного интеграла.
Итак, данное нами определение площади согласуеися с основными
двумя свойствами плсшади, известными нам из опыта. Мы можем
теперь, опираясь на определение (7), без труда доказать, что площадь
области (В) есть предел суммы площадей треугольников NML, NKL
и остальных треугольников, аналогичным образом построенных на
вершинах сгущающейся сети.
Эти треугольники образуют многогранник (точнее, многогранную,
в общем случае не замкнутою, поверхность), вйисанный в область (/?).
Можно, следовательно, утверждать, что площадь области (В) есть
предел плошади многогранника, вписанного в область так, что
вершинами его (треугольных) граней служат вершины сгущающейся
координатной сети.
Представляется поэтому естественным вместо аналитического
определения площади поверхности дать другое, чисто геометрическое и притом
аналогичное определению длины дуги как предела вписанной ломаной
линии. Именно, естественно определить площадь поверхности как
предел, к которому стремится площадь вписанного многогранника с
треугольными гранями, когда длина наибольшего ребра этого
многогранника стремится к нулю.
Однако есть основания заранее опасаться, что без некоторого
дополнительного требования такое определение окажется несостоятельным.
Действительно, прямая, соединяющая бесконечно близкие точки А и В
кривой, составляет бесконечно малый угол с касательной в какой-либо
точке дуги АВ, так что направления сторон ломаной близки к
направлениям кривой. Между тем, мы видели (§ 42, стр. 244), что плоскость,
проходящая через три бесконечно близкие точки А, В9 С кривой
поверхности, может составлять какой угодно угол с касательной плоскостью
в точке А, Поэтому нормали граней вписанного многогранника не
обязаны иметь направления, близкие к направлениям нормалей поверхностей.
Не может ли случиться, что поверхности некоторых многогранников
окажутся столь шероховатыми, что их площади смогут стремиться
к пределу, отличному от площади поверхности, и даже неограниченно
возрастать*)? Оказывается, что при соответствующем законе выбора
1) Вспомним аналогичный «парадокс» для плоских „
линий: зигзагообразная ломаная линия ABGD...N А Л Л а а Л /V
(рис. 164), звенья которой составляют угол а с пря- ^у УV mAv ^
AN в F
мой AN у имеет всегда длину и не стремится к
' cos a Рис. 164.
пределу AN, хотя бы вершины ее стремились к AN.
266 ГЛ. VII. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИЗГИБАНИЕ ПОВЕРХНОСТИ
вершин всегда можно добиться того, чтобы поверхность многогранника
стремилась к любому, заранее заданному пределу, превосходящему
площадь области *).
Таким образом, без дополнительных условий мы не можем
определить площадь кривой поверхности как предел площади вписанного
многогранника. Впрочем, необходимые дополнительные условия догюльно
естественны. Достаточно, например, потребовать, чтобы грани
вписанного многогранника составляли бесконечно малые углы с
касательными плоскостями или, взамен этого, чтобы треугольники, служащие
гранями, имели конечные углы. Можно доказать, что при любом
из этих условий площади вписанных многогранников стремятся к одному
и тому же пределу. Этот предел (он совпадает с величиной \ \ Wdu dv)
(В)
можно по определению принять за площадь области (В).
Можно также определить площадь поверхности следующим образом.
Разобьем область (В) иа части (Вг)у (В2), ... , (Вп) каким угодно
образом, например с помощью сети кривых. Внутри каждой части (Bt)
возьмем некоторую точку ut и спроектируем часть (В{) на касательную
плоскость Qt в точке щ лучами, параллельными постоянному
направлению. Можно доказать, что сумма площадей проекций при
измельчении разбивки стремится к пределу \ \ Wdu do, каков бы ни был
(В)
закон измельчения и каково бы ни было направление проектирования.
Таким образом, можно дать такое определение: площадью области (В)
называется предел, к которому стремится сумма площпдей проекций
(Bf) на касательные плоскости Qt. Это определение и связанные с ним
доказательства приводятся в большинстве курсов анализа.
Упражнения
1. Найти площадь поверхности касательных к винтовой линии, если область
ограничена двумя винтовыми линиями и двумя образующими.
2. На той же поверхности найти площадь, ограниченную двумя винтовыми
линиями и двумя ортогональными их траекториями.
3. На поверхности косого геликоида, образующие которого составляют угол
45° с осью, найти площадь, ограниченную двумя образующими и двумя
ортогональными траекториями.
4. Та же задача для прямого геликоида.
5. На образующей прямого геликоида отложен от оси отрезок постоянной длины
—■ Ь с шагом 2теЬ. Найти площадь, описываемую этим отрезком при полном обороте
о
около оси.
6 Найти полную поверхность тора, описанного окружностью радиуса а,
вращающейся около оси, отстоящей от ее центра на расстояние &(&>а).
§ 46. Об изгибании поверхностей
Гибкую нерастяжимую нить можно наложить на любую линию.
В противоположность этому, гибкую нерастяжимую пленку на любую
поверхность наложить нельзя. Так, плоский лист можно наложить на
поверхность цилиндра, но нельзя наложить на поверхность шара.
Если мы попытаемся обернуть шар бумагой, бумага сомнется или
порвется.
*) Простой пример такого построения приводится во многих курсах анализа;
см., например, Курант, Курс дифференциального и интегрального исчисления,
ч. 2, ГТТИ, 1931 г., стр. 2i8-249.
§ 46. ОБ ИЗГИБАНИИ ПОВЕРХНОСТЕЙ 267
Наложимость или неналожимость пленки на поверхность тела
совершенно не зависит от материала, из коюрого сделаны пленка и тело,
т. е. наложимость есть чисто геометрическое взаимное свойство пары
поверхностей. Чтобы ею изучить, мы должны прежде всею дать
геометрическое определение наложимости; оно, конечно, должно быть
согласовано с физическим процессом наложения.
Процесс наложения можно представить себе следующим образом.
Некоторая нерастяжимая материальная пленка имеет первоначально
форму поверхности 5Х; зааем она деформируется и принимает форму
поверхности S2. В процессе дефорхмации она принимает непрерывный
ряд промежуточных положений. При этом всякая материальная линия
пленки все время сохраняет свою длину — в этом проявляется
нерастяжимость пленки. Между точками поверхности aS2 и S2, таким образом,
естественно устанавливается однозначное соответствие. Именно,
соответствующими являются те точки, в которых побывала одна и та же
материальная точка пленки. Такое же соответствие устанавливается
между любой парой промежуточных положений пленки, а также между
каким-нибудь промежуточным ее положением и одним из положений
Sly S2. Нам остается описать это соответствие чисто геометрически,
не прибегая к посредству физического образа пленки.
Рассмотрим множество поверхностей St; здесь числовой индекс t
принимает все значения в некотором промежутке, например от t = 1
до t = 2, и каждому значению t отвечает определенная поверхность
(геометрический образ пленки). Такое множество называется однопара-
метрическим семейством поверхностей.
На одной из поверхностей семейства, скажем, на Slt возьмем
какую-либо точку Мг и поставим ей в однозначное соответствие на
каждой из поверхностей St точку Mv Множество точек Mt'(l<*<2)
образует линию Lt (геометрический образ линии, по которой движется
материальная точка пленки).
Для того чтобы эта геометрическая картина соответствовала
физическому процессу деформации пленки, мы должны наложить на
семейство St некоторые требования.
Прежде всего, мы предполагаем, конечно, что каждая из
поверхностей St обладает своиетъами, идеализирующими свойства
материальной пленки, т. е. что она непрерывна и имеет всюду касательную
плоскость или, чю то же, имеет всюду нормаль; мы предполагаем также,
что орт нормали обладает непрерывностью и дифференцируемостыо.
Но, кроме того, мы должны потребовать также, чтобы изменение
самой поверхности St и ее касательных плоскостей при изменении
параметра t происходило "непрерывно. Это требование можно
сформулировать в точных терминах следующим образом. Пусть Mt есть
произвольная точка на поверхности St\ Mt+bt — соответствующая ей точка
на поверхности St+м] /^ — касательная плоскость в точке Mt иЯ*+Д*~~
касательная плоскость в точке Mt+u- Тогда при Дг-->0 точка Mt должна
быть пределом точки Л/{+д*, а плоскость Pt — пределом плоскости Р/+д*.
Удовлетворяющее этому условию семейство поверхностей с
установленным на нем соответствием точек дает нам геометрическую картину
деформации пленки. Но эта картина схватывает всевозможные
деформации, в том числе и такие, которые сопровождаются растяжением
пленки (если она, скажем, резиновая).
Чтобы охарактеризовать деформацию нерастяжимой пленки,
нужно учесть, что при такой деформации длина всякой материальной
линии остается неизменной.
268 ГЛ. VII. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИЗГИБАНИЕ ПОВЕРХНОСТИ
В согласии с этим дадим следующие определения.
Определение 1. Две поверхности Sx и S2 называются
изометрическими (т. е. «равноизмеримыми»), если между их точками можно
установить такое соответствие, при котором все соответственные
их линии имели бы равную длину.
Определение 2. Две поверхности St и S2 называются
изгибаемыми (или наложимыми) друг на друга, если можно построить такое
семейство поверхностей, которое содержало бы St и S2 и в котором
все поверхности изометричны с поверхностью Sx (и, следовательно,
друг с другом).
Ясно, что поверхности, изгибаемые друг на друга, непременно
изометричны. На первый взгляд может показаться, что и, обратно,
всякие изометричные поверхности изгибаемы друг на друга.
Простой пример убеждает, что это не так: перчатка с левой руки
изометрична с поверхностью правой руки, но не надевается на правую
руку. Правда, ее можно вывернуть наизнанку, но при этом в процессе
выворачивания на перчатке непременно появится, по крайней мере,
вдоль одной линии складка. Между тем, все поверхности семейства,
о котором говорится в определении 1, предполагаются, конечно,
гладкими, т. е. касательная плоскость на каждой из них должна
изменяться непрерывно. Вдоль складки эта непрерывность нарушается.
Итак, существуют поверхности, которые изометричны, но не
изгибаемы друг на друга. Тем более замечательно, что рассмотренный
сейчас случай зеркально симметричных поверхностей является по
существу единственным случаем, когда изометрия поверхностей
не влечет за собой их изгибаемости друг на друга. Именно, с
некоторыми оговорками, о которых сейчас будет сказано, имеет место
следующая теорема.
Теорема 1. Если поверхность St изометрична с поверхностью S2,
но не изгибаема па нее, то она изгибается на зеркальное изображение
поверхности S2.
Оговорки, о которых мы упомянули, состоят в следующем.
Во-первых, в этой теореме, как и всегда в дифференциальной геометрии,
подразумевается, что речь идет о достаточно малых кусках поверхностей.
Во-вторых, на поверхности могут оказаться исключительные точки,
в окрестности которых нельзя осуществить изгибание ее на
изометрическую поверхность. Впрочем, этот случай можно считать
«патологическим»; во всяком случае ни на одной из тех поверхностей, которые
обычно рассматриваются в дифференциальной геометрии, таких точек
не существует
Доказательство теоремы 1 выходит за рамки элементарного курса.
Мы привели ее для того, чтобы стало ясным, что разлртчие между
изгибаемостью и изометрией не столь у?к гелико. Поэтому часто
термин «изгибаемые поверхности* употребляют в расширительном
смысле, понимая под ним поверхности изометричиые.
Как мы сейчас докажем, изгибаемость поверхности теснейшим
образом связана с ее первой квадратичной формой. Именно, имеют
место след}ющие теоремы.
Теорема 2. Если две поверхности St a S2 имеют одну и ту же
первую квадратичную форму, то они изометричны.
Пусть поверхность Sx отнесена к некоторой системе
криволинейных координат а, и, а поверхность 52 — к некоторой системе
криволинейных координат, для которых мы сохраним те же
обозначения м, и, хотя координатные линии одной поверхности могут быть не кон-
§46. ОБ ИЗГИБАНИИ ПОВЕРХНОСТЕЙ 269
груентны с координатными линиями другой. По условию теоремы
первая квадратичная форма для обеих поверхностей имеет один и тот
же вид:
Е (и, v) du2 + 2F (и, v) dudv + G (a, v) dv\
где Е, F, G суть заданные функции от н, у.
Возьмем на поверхности iSx какую-нибудь линию
^ » = ?(0; (1)
длина дуги Л1В1 этой линии между точками Аг и В1 выражается
интегралом
2Fdu do + Gdo% = J \fE[f'{t)Y + 2Ff'(t)<t'(t) + G[<f'{t)]*dt, (2)
где величины E, F, G cyib теперь функции от t\ именно, Е =E[f (t)y <p(t)]
и т. д.
Подставим в соответствие каждой точке Мг (uY vt) поверхности St
ту точку M2(ii2, v2) поверхности S2, координаты которой имеют те же
значения, что одноименные координаты точки Mlt т. е.
Тогда дуга А2В2 поверхности S2, определяемая уравнениями
концам которой А2, В2 соответствуют значения t = tA, t = tBi будет
соответствовать дуге А1В1 поверхности Sx. Длина дуги А2В2,
очевидно, представится тем же интегралом (2). Следовательно,
соответственные дуги поверхностей St и 6^ имеют равные длины, т. е. поверхности
Sx и S2 изометричны.
Теорема 3. Если поверхности Sx и S2 изометричны, то при
надлежащем выборе криволинейных координат они имеют одну и ту
же первую квадратичную форму.
Действительно, введем на поверхности St произвольную систему
криволинейных координат. Пусть точка Мх в этой системе имеет
координаты и, v. Припишем точке М2, соответствующей точке Мх в изо-
метрии, те же значения координат. Этим на поверхности б^
определится система криволинейных координат, т. е. ее радиус-вектор г станет
заданной функцией от и, v. Значит, определяется и первая квадратичная
форма
ds\ = Et(u, v)du2 + 2F2(ut v)dudv+G2(u, v)dv\ (3)
Докажем, что эта квадратичная форма тождественна с первой
квадратичной формой
ds\ =E1(u9 v) du2 + 2F1 {и, v) du dv + Gx (и, v) do2 . (4)
поверхности Slf т. е. что E1(u, tf) = j?2 (в, v) и т. д.
Дадим координатам и, v значения
270 ГЛ. VII. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИЗГИБАНИЕ ПОВЕРХНОСТИ
Этим на поверхности S, будет задана пара точек Мг и Л/j, а на
поверхности S2— пара точек М2 и М'2, соответствующая первой паре в силу
данного изометрического соответствии. Длина всякой дуги Мг Ч[,
ограниченней точками М17 М[, равна длине соответственной дуги Мо\Ц.
Следовательно, дифференциал dst всякой дуги, проходящей через М\,
равен дифференциалу ds2 соответственной дуги, проходящей через Мо.
Из (3) и (4) следует, что при фиксированных значениях а, Ь и любых
значениях du, do мы должны, иметь
Et{a,
= Е2(а, b)du2 + 2F2{a, b)dudv + Gt(a, b)do\ (5)
Как известно из алгебры, уравнение (5) может иметь относительно
-it бесчисленное множество решений в том и только в том случае,
когда
E1(a,b) = E2(a,b), F^a, b) = FM(a, Ь), Gx (a, b) = G2 (a, 6),
а так как а и b суть произвольно выбранные значения и, и, то
функции Ег (и, v) и Е2(и, v) тождественны; точно так же F1{u, v) = F2(uy у),
Gx (и, v) = G2 (uy v)y что и требовалось доказать.
Заметим, что изометрические поверхности 6^ и S2 могут быть
параметризованы так, вто соответственные их точки будут иметь
неранные одноименные координаты. Тогда они будут иметь различные
выражения для первой квадратичной формы:
ds\ - Е1 {и, v) du* + 2F1 {и, v) du dv + Gl{u, v) do2 (6)
и
G2(u,v)dv\ (6')
Однако на поверхности S2, по доказанному, можно ввести другую
сисаему координат и\ i/, так, чтобы
ds\ = Е, (и\ v') du'2 + 2F, (и\ v') du'dv' + G2 (н', v')dc'2. (7>
Тогда старые координаты (и, v) поверхности S2 будут функциями
новых координат и\ v':
в = ф(в/,о/), » = Х«*>'). (8)
Если эти выражения подставить в формулу (6), то она должна принять
вид (7). Мы получаем следующую теорему.
Теорема 4. Если поверхности Si и S2 изометричны, то первой
квадратичной форме поверхности S2 после подстановки вместо и, о
надлежаще выбранных выражений их через новые параметры п', */
мочено придать тот же вид, который имеет первая квадратичная
форма поверхности St.
Обратная теорема, очевидно, тоже справедлива. Поэтому вопрос
о том, изометричны ли две данные поверхности, можно свести к вопросу:
существуют ли функции (8), которые приводят данную форму (6)
к виду данной формы (7)1).
*) Подставив вместо и и v их выражения (8) в формулу (6) и сравнив
полученное выражение с формой (7)
Ег (u', v') du'* + 2^! (u't v') du' dv' + GL (u', v') dv'2,
мы видим, что функции ы=ф(м', v') и v = X(u'f v') должны удовлетворять следу-
§ 46. ОБ ИЗГИБАНИИ ПОГЕРХНОСТЕЙ 271
Пример 1. Линейный элемент геликоида
x = ucosv, 2/ = Hsiny, z — bv (9)
выражается формулой
ds2 = du2 + (b2 + u2)dv\ (10)
Эту формулу легко получить как из уравнений (9), так и
геометрически из соотношений (рис. 165).
ММ'2 = MQ2 + QR2 + RMny
QRZzudv; RM' = bdv.
Найдем теперь линейный
элемент кааеноида, определяемого
параметрическими уравнениями [§39,
формулы (13а) на стр. 231]
x = \/rb* + и2 cos и,
у= j/ Ь2 + и2 sin v,
(И)
Он равен
\-u*)dv\ (12)
Сравнив формулу (10) с
формулой (12), мы видим, что первые
квадратичные формы геликоида и
катеноида имеют один и тот же
вид.
Следовательно, согласно
теореме 2, геликоид, имеющий шаг 2ти6
(на рис. 166 отрезок А'С равен
половине шага: -4'С/ = тг6), изо- Рис. 165.
метричен ка1еноиду, у которого
радиус AD горла (рис, 167) равен 6, т. е. окружность горлового круга
есть 2тс6. Так как поверхность, зеркально симметричная поверхности
катеноида, конгруентна с самим катеноидом (это имеет место для
всякой поверхности вращения), то согласно теореме 1 геликоид можно
изогнуть на катеноид и, обратно, катеноид изгибается на геликоид.
ющим трем уравнениям:
(8a)
Следовательно, решение вопроса о том, изометркчны ли данные поверхности,
и если да, то каким соотношением связаны в изометрии их координаты, можно
свести к установлению условий совместимости системы (За) и к решению этой
системы в случае ее совместимости. Однако предпочтительнее вести исследование
другими методами.
272 ГЛ. VII. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИЗГИБАНИЕ ПОВЕРХНОСТИ
Соответственными точками являются точки с равными
одноименными координатами. Через и мы обозначили (§ 43) длину дуги
меридиана катеноида (считая от горла), а через tf —долготу. Поэтому
параллель и = const катеноида (например, £7? на рис. 167) наложится на
некоторую винтовую линию геликоида (E'F' на рис. 166). В частности,
горловая окружность ABC (и — О) наложится на ось геликоида А'В'С.
Меридианы (v = const) катеноида наложатся на образующие геликоида,
причем угол о поворота плоскости меридиана окажется равным углу
поворота образующей. На рис. 167 изображен кусок поверхности
катеноида, ограниченный полуокружностью горла, полуокружностью одной
из параллелей и двумя дугами меридианов. Этот кусок изгибается на
изображенный на рис. 166 кусок поверхности геликоида, ограниченный
отрезком оси длиной в полшага, половиной завитка одной из винтовых
линий и двумя отрезками образующих. Чтобы осуществить наложение
материального куска FABCE на поверхность Fr A'B'C'E' y достаточно
распрямить окружность горла. Меридианы выпрямятся сами собой.
Рис. 166. Рис. 167.
Если взять вместо полуокружности АС всю окружность горла и,
соответственно, всю параллель, то получим полную зону катеноида.
Разрезав ее по меридиану, мы можем наложить ее на один оборот
поверхности геликоида.
Чтобы покрыть поверхность двух завитков, нужно изогнуть
поверхность, дважды покрывающую поверхность катеноида; такое изгибание
можно наглядно представить как развертывание пленки, многократно
навернутой на катушку, имеющую форму катеноида.
Отнесем теперь одну из наших поверхностей к новой системе
координат; например, на поверхности катеноида примем за координаты
точки М долготу v и расстояние г = МК до оси. В § 43 (пример 26,
стр. 252) мы нашли, что в этой системе координат линейный элемент
поверхности вращения имеет вид
ds* = {1 + [/' (г)]2} dr* + rW, (13)
§ 46. ОБ ИЗГИБАНИИ ПОВЕРХНОСТЕЙ 273
где /(г) есть функция, выражающая расстояние DK = z точки М до
плоскости начальной параллели (z = 0)> т. е. z — f(r) есть уравнение
меридиана. В нашем примере меридиан есть цепная линия и,
следовательно,
аак что
& = ££+№. (14)
Если мы для согласования обозначений с обозначениями теоремы 3
заменим букву г буквой и, то линейный элемент катеноида примет
вид
7 о
ds =
отличный от вида линейного элемента геликоида
ds% = du* + (u% + b%)do\ (10)
Несмотря на это различие, мы могли бы из формул (10) и (14') для
линейных элементов заключить, что поверхности, обладающие этими
линейными элементами (мы можем совсем не интересоваться вопросом
о виде этих поверхностей), изгибаемы друг на друга. Для этого
достаточно показать, что при надлежащей замене переменных одна из форм
(10), (14') становится тождественной с другой. Действительно, если
в формуле (10) положить
и = /и/а-6', v = v"9 (15)
то она примет вид
аь ~ и'2 —&2 ' »
тождественный с видом формулы (14'). Как видно из формул
преобразования координат (15), в новой системе координатными линиями
геликоида попрежнему служат образующие и винтовые линии.
Действительно, винтовая линия и = и0 в новой системе имеет уравнение
}/м'2. — Ь2 = и0, т. е. й' = |/и£+6а = const. В старой системе и
обозначало расстояние точки геликоида до оси. В новой системе и' есть некоторая
функция эюго расстояния; ее можно геометрически истолковать как
длину гипотенузы треугольника, катетами которого служат отрезки и и 6;
можно также сказать, что и' есть ордината цепной линии, длина дуги
которой есть и. Из последнего истолкования видно, что при наложении
геликоида на катеноид, когда образующая изгибается на цепную линию,
величина и' равна радиусу параллели.
Замечание. Вообще, если преобразование координат выполняется
по формулам
в = /(«'). v = 9(v'), (16)
то координатные линии остаются прежними, и обратно, если при
преобразовании координат координатные линии сохраняются, то
преобразование имеет вид (16).
Пример 2. Геликоидом общего вида (рис. 168) называется всякая
поверхность, образованная некоторой линией (профилем), вращающейся
около оси и одновременно поступательно движущейся по направлению
этой оси, причем скорости этих движений пропорциональны..
18 М. Я. Выгодский
274 ГЛ. VII. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИЗГИБАНИЕ ПОВЕРХНОСТИ
Прямой геликоид есть частный вид этой поверхности; профилем
его является прямая, пересекающая ось под прямым углом. Всякая
поверхность вращения также есть частный вид геликоида: именно,
если скорость поступательного движения равна нулю, профиль
описывает поверхность вращения.
Примем ось геликоида за ось Z; пусть уравнение профиля имеет
вид z=(p(^); тогда уравнения геликоида, как легко видеть, можно
записать в виде
x = ucosv, y = usinv, z = y(u) + bo, (17)
где и есть расстояние МК точки М 1еликоида до оси; v — угол поворота
плоскости профиля, отсчитываемый от плоскости ZOX; 6 есть
постоянная величина — отношение
скорости поступательного движения к
угловой скорости.
Из формул (17) находим
линейный элемент геликоида:
ds2 = [! + (<?'(и))2] du2 +
+ 26 ?' (и) dudo + {Ъ1 + и2) do2. (18)
Для прямого геликоида можно
положить <р (и) = 0, и мы
получаем формулу (10); для
поверхности вращения имеем 6 = 0, и
формула (18) принимает вид (13).
Прямой геликоид, как было
показано в предыдущем примере,
изгибается на поверхность
вращения цепной линии.
Это свойство можно обобщить.
Именно, имеет место следующее
предложение (теорема Бура):
Всякий геликоид изгибается
на некоторую поверхность
вращения. При этом винтовые линии
и = const накладываются на
параллели, а их ортогональные
траектории — на меридианы.
Заметим, что профиль
геликоида является ортогональной
траекторией только для прямого
геликоида. Действительно,
координатные линии v и и геликоида
суть винтовые линии и = const
рис !£3 и профили v = const; они
перпендикулярны в том и только в том
случае, когда F = O(§44), т. е. когда <р'(г) = О. Таким образом
профиль геликоида в общем случае не накладывается на меридиан.
Чтобы доказать теорему Бура, введем на геликоиде новую систему
координат так, чтобы координатными линиями были винтовые линии
и их ортогональные траектории. Для этого найдем дифференциальные
уравнения ортогональных траекторий линий и = const в старых коор-
§ 46. ОБ ИЗГИБАНИИ ПОВЕРХНОСТЕЙ 275
динатах. Они определяются из условия перпендикулярности (5а) § 44
(стр. 255), в которых нужно положить 8м:8ю = О:1.
Мы получаем
Ь 9' (и) du + (и2 + Ь2) do = О, (19)
откуда
6 \ Ц2 , fr2 + У = С- (20)
Так как в новой системе координат линии (20) должны быть
координатными линиями, то в новой системе криволинейных координат
и1, vx их уравнение должно иметь вид v1 = c1. С изменением с мы
переходим от одной траектории к другой, т. е. меняется и с1. При
фиксированном с остается постоянным и сх. Следовательно, сх есть
функция от с, т. е. v1 есть функция от Ь \ У 2" ," + в- Обратно, если vx
есть какая-лиоо функция от 6 \ - 2 ' /2 -\-v, например, если
то из уравнения (20) следует, что вдоль ортогональной траектории
величина ъг остается постоянной. Значит, положив
мы относим 1еликоид к такси сисаеме, в которой координатные линии
ux — const остаются прежними, т. е. являются винювыми линиями,
а координатные линии vx= const cj'ib орюгональьые араскюрии
винтовых линий.
Формулы
«-й1, - = ^-6 5(f^ (22)
даю1 выражения старых координат через новые. Подставляя эти
выражения и их дифференциалы в (18), находим
ul)do\. (23)
С другой стороны, элемент длины поверхности вращения можно
представить (§ 43, стр. 252) в ьиде
ds2 = [1 + (/'(«))'] d? + й2 <й2, (24)
где а есть радиус параллели, a f{u) есть функция, дающая уравнение
меридиану
Из сравнения квадратичных форм (23) и (24) легко усмотреть, что
между координатами и, v и иг, ъг можно установить соотношения, в силу
которых одна из <}°РМ станет тождественна с другсй. В самом деле,
если положить в формуле (23)
vt = ho (25)
И
*+«:=£. (26)
13*
276 ГЛ. VII. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИЗГИБАНИЕ ПОВЕРХНОСТИ
где А;— любая постоянная величина, то член (bl + u\)do\ примет вид
u2do*, как в формуле (24). Что касается первого члена формулы (23),
то в силу соотношения (26) он примет вид Udu2y где U есть
определенная функция от и. Чтобы получить квадратичную форму (24), нужно
иметь £/ = 1+/'2(м)- Этим определяется вид функции /' (и)= '_ ,
du
именно _ = \^и — 1, и мы
du г
найдем уравнение мерпдиана:
z=\ л/U-idu.
Так как U содержит
произвольную постоянную к, то
существует бесчисленное множество
поверхностей вращения, изоме-
тричных с данным геликоидом.
В силу теоремы 1 все они
изгибаются на геликоид. Ясно, что
они изгибаются также друг на
друга.
В качестве иллюстрации
рассмотрим косой геликоид, т. е.
геликоид, профилем которого
служит прямая, пересекающая
ось (рис. 169). Если через а
обозначить угол между
профилем (образующей) и осью, то
функция cp(w)> определяющая
форму профиля, будет иметь вид
у(и) = и ctg a,
откуда
Уравнение (20)
ортогональных траекторий принимает вид
Рис. 169. ,
6сЦа$^~+v = c (27)
или, в конечном виде, fcctgaarctg т- + у = с.
Формулы (22) преобразования координат будут теперь
U = ttj,
или в дифференциалах
§ 46. ОБ И8ГИБАНИИ ПОВЕРХНОСТЕЙ 277
Формула (18) для линейного элемента геликоида в нашем примере
имеет вид
' ds2 = csc2 atftt2 + 2b ctg a dudo + (b2 + u2) do2. (29)
После преобразования координат линейный элемент косого
геликоида выразится следующим образом:
( ^^ u\)dv\. (30)
Положив
Vl = kv,_ (31)
Ь* + и\ = ^, (32')
мы приведем линейный элемент к виду
и'2 CSC2 a — к2 Cts:2 а Ь2 ,—2 -„ .-„ /ооч
du2 -f w2 do". (33)
/с2 (w2 -
Положив коэффициент при du1 равным 1 + [/' (м)]2, найдем
/' Ги\ = 1 1 /^2
7 ^ ^ к у
a)
Меридиан поверхности вращения, на которую можно наложить косой
геликоид, определяется уравнением
и2 (CSC2 a - к2) + Ь2к2 (к* - Ctg2 a) ,-
2 = т-
Интеграл (35) в общем случае не выражается в элементарных функциях
(он принадлежит к числу так называемых эллиптических интегралов).
Но, как сразу бросается в глаза, в случаях
A2 = csc2a (36)
и
&2 = ctg2a (37)
мы получаем элементарные интегралы; именно, в первом случае имеем
= I U = h arch -—~— /Qfi'i
• I / — и csc л V /
I I/ W2 ~~- CSC2 (X&2
(постоянная интегрирования не имеет существенного значения, так как
она лишь смещает начало координат).
Уравнение (38), где и рассматривается как абсцисса, или, что
то же,
и= fccscach -r (39)
представляет «удлиненную цепную линию» (АВ на рис. 170), получаемую
из обыкновенной цепной линии А'В' пропорциональным увеличением
ординат в отношении csca:l. Искомая поверхносаь вращения есть
«удлиненный катеноид». В случае прямого геликоида л —90°, csca = l,
так что прямой геликоид накладывается на обыкновенный катеноид,
как мы нашли выше.
278 ГЛ. VII. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИЗГИБАНИЕ ПОВЕРХНОСТИ
Если же мы положим
или
. С in
Jv*-
2 = ctg2<x, то формула (35) дает
= tg а V и2 - б2 <
Ь2 Ctg2 а
!ctg2a,
(40)
--=1.
ft2 Ctg2 л bl
Меридиан представляет гиперболу, для которой ось вращения
служит мнимой осью. Таким образом, косой геликоид можно наложить на
однополостный гиперболоид. Мы знаем, что на меридианы его
накладываются ортогональные траектории винтовых линий. Интересно
отметить, что на его прямолинейные образующие накладываются
прямолинейные образующие косого геликоида.
Чиаателю предлагается доказать это.
Легко также доказать, что ось
геликоида накладывается на горло
гиперболоида. Примой геликоид (а = 90°) нельзя
наложить на однополостный
гиперболоид, или, лучше сказать, гиперболоид,
на который он изгибается,
стягивается в прямую (ось вращения). Чтобы
уяснить себе картину, заметим, что
один завиток геликоида с увеличением
угла а должен обертывать
соответствующий гиперболоид неограниченно много
раз и свертываться в суживающуюся
трубочку.
Упражнения
1. Сравнив первые квадратичные формы
цилиндрической поверхности и плоскости,
убедиться в изгибаемости их друг на друга.
2. Та же задача для конической
поверхности .
3. Найти обшее уравнение меридианов всех поверхностей вращения, изгибаемых
на поверхность вращения с данным меридианом.
4. Найти уравнение меридиана поверхности вращения, изгибаемой на шар
(см. предыдущую задачу).
5. Найти профиль геликоида, на который можно изогнуть поверхность
вращения укороченного катеноида (меридианом последнего служит линия, полученная
пропорциональным укорочением ординат цепной линии).
§ 47. Внутренняя геометрия поверхности
При изгибании поверхности свойства связанных с ней
геометрических объектов, вообще говоря, меняются; меняются и значения величин,
характеризующих эти объекты. Так, пря изгибании линейчатой
поверхности прямолинейные образующие могут искривляться (пример 1 § 46,
стр. 271). Вообще, линия, проведенная на любой поверхности при
изгибаниях последней, меняет кривизну, а также кручение. Расстояние d
точки М от касательной плоскости в точке Мг тоже меняется. Например,
кусок круглой цилиндрической поверхности можно изогнуть на круглую
цилиндрическую поверхность с большим радиусом основания. При этом
величина d уменьшается.
Однако ряд свойств и величин, связанных с поверхностью и се
фигурами, остаются неизменными или, как говорят, инвариантными при
О
Рис. 170.
§ 47. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ 279
любых ее изгибаниях. По самому определению изгибания,
инвариантными являются длины всех дуг. Но из неизменности этих длин
вытекает также неизменность углов между любыми пересекающимися
на поверхности линиями. Действительно, линии (Lt) и (L2) пересекаются
в точке А под углом а. Взяв на этих линиях точки Вг и В2, бесконечно
близкие к точке А, построим треугольник АВХВ2. После изгибания
поверхности точки Л, В1у В2 займут положения А', В[, В'2У причем
расстояния А'В'Х, В[В[ В2А' будут эквивалентны соответственным
расстояниям АВ1У ВхВ2, В2А. Следовательно, угол при А' эквивалентен а,
а так как а есть постоянная величина, то он равен а.
В частности, перпендикулярность линий есть инвариантное их
свойство относительно любого изгибания.
Плсшадь области также есть инвариант изгибания. Это очевидное
предложение можно доказать, сравнив два соответственных элемента
площади, т. е. площади двух прямолинейных треугольников АВгВ2
и AfB[B'2 с соответственно эквивалентными сторонами. Их илощади
эквивалентны; следовательно (§ 45), площади двух соответственных
областей уаввы.
Свойства поверхности, инвариантные относительно изгибания,
называют внутренними свойствами поверхности, а раздел геометрии,
занимающейся этими свойствами, —внутренней геометрией поверхности.
В общей теории поверхностей поверхность рассматривается как твердое
тело, и помимо внутренних свойств изучаются те ее свойства, которые
необходимо требуют выхода во внешнее пространство. Внутренняя
же геометрия исследует те факты, которые могут быть установлены
измерениями на самой поверхности; для изучения их нет необходимости
даже предполагать существование трехмерного пространства. Вообразим
себе мыслящее «двумерное» существо, лишенное всяких сведений
об окружающем его пространстве. Имея возможность измерять длины
линий и углы между ними, это существо может создать геометрию,
аналогичную нашей планиметрии, но во многом отличную от нее. Так,
в этой геометрии сумма углов треугольника не будет р>авна 180°
и вообще не будет постоянной величиной. Все факты геометрии этого
воображаемого двумерного геометра будем наблюдать и мы. И мы
сможем констатировать, что эти факты имеют место и при изгибании,
которого наш воображаемый геометр вовсе не заметит. Если же мы
подвергнем поверхность деформации, связанной с растяжением, то
двумерный геометр, хотя он ничего не знает о движении, связанном
с деформацией, сможет констатировать нарушение законов геометрии.
Мы не будем останавливаться на не лишенном интереса вопросе, как
объяснит эти изменения наше воображаемое существо.
Наш рассказ о двумерном геометре не столь фантастичен, как может
с первого взгляда показаться. В положении, сходном с вышеописанным,
находимся мы сами, когда производим измерения на поверхности земли.
Именно в связи с этими измерениями Гаусс около 100 лет назад
заложил фундамент внутренней геометрии, выделив ее из общей теории
поверхностей и получив ряд замечательных теорем, с которыми мы
в дальнейшем ознакомимся.
В основу внутренней геометрии Гаусс положил введенную им же
первую квадратичную форму. Значение ее для внутренней геометрии
состоит в том, что задание ее полностью определяет все внутренние
свойства поверхности.
Объясним это подробнее. Пусть нам удалось выразить какую-либо
геометрическую величину через коэффициенты первой квадратичной
280 ГЛ. VII. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА И ИЗГИБАНИЕ ПОВЕРХНОСТИ
формы. В это выражение могут входить также дифференциалы
криволинейных координат, характеризующие рассматриваемую фигуру. Так,
угол между двумя пересекающимися кривыми выражается формулой:
Е dubu + Fjdudv -f dv$u) + Gdvdv
COS <p —
в которую входят коэффициенты Е, F, G первой квадратичной формы
и дифференциалы du, do, 6w, bv, характеризующие направления
пересекающихся линий. Тогда мы можем утверждать, что рассматриваемая
геометрическая величина (в нашем примере—угол между двумя линиями)
остаётся неизменной при любом изгибании поверхностей. Иными словами,
все свойства, относящиеся к рассматриваемой величине <р (скажем,
перпендикулярность двух линий) являются внутренними свойствами
поверхности.
Обратно, пусть какая-либо геометрическая величина (например,
площадь куска поверхности) остаётся неизменной при всевозможных
изгибаниях поверхности. Тогда эта величина должна выражаться через
коэффициенты первой квадратичной формы. Точнее: пусть на любых
двух изометрических поверхностях рассматриваемая геометрическая
величина имеет для соответственных фигур одно и то же значение. Тогда эта
величина имеет одно и тоже значение для соответственных фигур на всяких
двух поверхностях с одинаковыми первыми квадратичными формами.
Это непосредственно следует из теоремы 2 §46 (стр. 268). В нашем
примере значение площади куска поверхности представляется выражением
r-F2dudv.
IB)
В эту формулу, кроме дифференциалов координат, входят лишь
коэффициенты первой квадратичной формы.
Итак, всякая связанная с поверхностью геометрическая величина,
которая выражается через коэффициенты первой квадратичной формы,
принадлежит внутренней геометрии поверхности, и обратно, всякая
внутренняя геометрическая величина может быть выражена через
коэффициенты первой квадратичной формы.
Поясним сказанное следующим примером. Кривизна х линии (I)
на поверхности S заведомо не является внутренней геометрической
величиной. Значит, величина х не может быть выражена через
дифференциалы координат и коэффициенты первой квадратичной формы. Точно
так же, угол <р между соприкасающейся плоскостью линии (/) и
касательной плоскостью Р к поверхности S не является
внутренне-геометрической величиной.
Однако произведение х cos <р (оно выражает кривизну х' проекции
линии (I) на плоскость Р) остается неизменным при всевозможных
изгибаниях поверхностей, т. е. принадлежит внутренней геометрии
поверхности1).
Отсюда видно, что первая квадратичная форма играет для
внутренней геометрии фундаментальную роль.
*) Двумерному геометру недоступно измерение величин х и ср. Но величину х' он
может измерить, не сходя с поверхности. Только он даст ей иное истолкование.
Он, как увидим нише, будет считать ее мерой кривизны линии (Z).
ГЛАВА VIII
РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
§ 48. Поверхности касательных
В этой главе мы изучим очень важный и для геометрии и для
техники класс поверхностей, а, именно—поверхности, изгибаемые на
плоскость. Такие поверхности называются развертывающимися.
К классу развертывающихся поверхностей принадлежат, прежде всего,
все цилиндрические и конические поверхности. Однако они не
исчерпывают упомянутого класса, как явствует из следующей теоремы:
Рис. 171.
Теорема 1. Всякая поверхность касательных есть развертывав
югцаяся поверхность.
К этой теореме легко прийти из следующих наглядных
соображений. Впишем в кривую (L) (рис. 171) ломаную линию ABCDE...
Продолжил в обе стороны хорды АВ, ВС, CD, DEy ..., мы получим
многогранную поверхность XYZU ... U'Z'Y'X'. Эту поверхность можно
наложить на плоскость.
282
ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
Для этого достаточно, закрепив первую грань XYY'X', вращать
оставшуюся часть многогранной поверхности около ребра YY' до тех
пор, пока вторая грань Y7jZ'Y' не составит продолжения первой грани.
Далее будем вращать остающуюся часть многогранной поверхности около
ребра YY' до совпадения плоскости третьей грани ZUU'Z' с
плоскостью, на которой уже поместились первые две, и т. д.
Итак, многогранную поверхность, ребрами которой являются
секущие XX', YY' и т. д., можно наложить на плоскость. В пределе секущие
становятся касательными, а многогранная поверхность — поверхностью
касательных. Поэтому следует ожидать, что поверхность касательных
также изгибается на плоскость. Ниже (в § 49) эта теорема будет
доказана сравнением линейных элементов плоскости и поверхности касательных.
Присоединив к поверхностям цилиндрическим и коническим
поверхности касательных, мы исчерпываем класс развертывающихся
поверхностей. Иначе говоря, имеет
место следующее предложение.
Теорема 2. Всякая
развертывающаяся поверхность есть либо
цилиндрическая, либо коническая,
либо поверхность касательных.
Таким образом, никакая
нелинейчатая поверхность и никакая
линейчатая поверхность кроме
вышеупомянутых не может быть
изогнута на плоскость.
Доказательство этой теоремы
будет дано позднее (в § 51), а
сейчас мы более детально
ознакомимся с формой поверхности
касательных. При этом мы будем
рассматривать такие дуги
направляющей (L), на которых нет точек
перегиба, т. е. точек, где линия
(L) переходила бы с одной
стороны спрямляющей плоскости на другую1).
Если направляющая (L) есть плоская линия, то поверхность ее
касательных, разумеется, есть плоскость. Однако касательные линии (L)
покрывают плоскость не целиком: в сторону вогнутости касаюльные
проникать не будут; зато сторона выпуклости покроется ими дважды:
один раз положительными лучами касательных, другой раз —
отрицательными (рис. 172).
Если же линия (L) —не плоская, то положительные и отрицательные
лучи касательных образуют две неперекрывающиеся полости (рис. 171
и 173), граничащие друг с другом по линии (L). Если через какую-
либо точку Е линии (L) (рис. 173) провести плоскость Q, не
проходящую через касательную EU (плоскость, проходящая через EU,
пересекает поверхность касательных по этой самой прямей), то в
пересечении Q с поверхностью касательных S получим кривую FEG, одна ветвь
которой, FE, принадлежит одной полости, а другая, EG, —другой
полости. Точка Е будет неправильной точкой сечения, именно точкой
возврата. Докажем это.
Рис. 172.
г) Напоминаем, что точка перегиба всегда является точкой спрямления и что
только на прямой линяй отрезок состоит сплошь из точек спрямления.
§ 48. ПОВЕРХНОСТИ КАСАТЕЛЬНЫХ 283
Для определенности предположим, что плоскость Q есть
нормальная плоскость линии (L) (в общем случае ход доказательства останется
тем же). Так как касательные к линии (L) целиком лежат со сторсны
выпуклости (Z.), то сечение FEG целиком лежит по одну сторону
от спрямляющей плоскости Р кривой (L). Значит, сечение FEG лежит
по одну сторону от прямой EN, по которой пересекаются спрямляющая
плоскость и плоскость сечения. В рассматриваемом случае, когда
плоскость сечения— нормальная, прямая EN есть бинормаль. Кроме того,
в точку Е обе ветви приходят по одному и тому же направлению,
Рис. 173.
именно—по прямой пересечения соприкасающейся плоскости с плоскостью
сечения (в рассматриваемом случае по направлению главной нормали).
Действительно, пусть К есть точка касания той образующей,
на которой лежит некоторая точка F сечения. Тогда секущая EF
линии FEG есть пересечение плоскости Q с плоскостью EKF, проходящей
через касательную KF линии (L) и точку Е. Когда точка К стремится
к точке Е, точка F также стремится к Е, плоскость же EKF имеет
пределом соприкасающуюся плоскость линии (L) в точке Е.
Следовательно, секущая EF имеет пределом (теорема 3 § 5, стр. 23) прямую
пересечения нормальной плоскости Q и соприкасающейся плоскости
в точке Е, т. е. главную нормаль линии (L).
Ясно, что секущая EG будет иметь тот же предел. Таким образом
обе ветви, FE и GE линии FEG будут иметь в точке Е общую
одностороннюю касательную, т. е. точка Е есть точка возврата сечения FEG.
Линия (L), принадлежащая поверхности S и обладающая тем
свойством, что все плоские сечения (кроме тех, плоскости которых проходят
через касательные к линии (Л)), имеют на (L) точки возврата, называется
284
ГЛ. VIII, РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
ребром возврата поверхности S. Таким образом, на основании
доказанного мы получаем следующее предложение.
Теорема 3. Направляющая поверхности касательных является
ее ребром возврата.
Прежде чем перейти к доказательству теоремы 1, полезно составить
себе некоторое представление о процессе изгибания поверхности
касательных.
Одпополостный кусок поверхности касательных можно изгибать
двояким образом: сохраняя или не сохраняя прямолинейные
образующие. Если мы возьмем кусок бумаги (рис. 174, а), начертим на нем
ряд прямых XX', YY\ ZZ\ ... , касающихся некоторой плоской линии
(она не изображена на рисунке), произведем по этим прямым сгибы,
а затем снова расправим листок, то на нем останутся легкие следы
сгибов, которые помешают искривлению начерченных прямых. После
этого легко будет изгибать листок непрерывно, не допуская, однако,
искривления прямых (рис. 174, б). Применив же. небольшое усилие,
можно будет и искривить прямо-
/ линейные образующие. Однако при
этом непременно появятся новые
прямолинейные образующие, что
Рис. 174.
и должно быть в силу теоремы 2. Если же мы имеем двуполостный кусок
поверхности касательных S неплоской кривой (£), то даже при
отсутствии сгибов поверхность окажет сопротивление попытке искривить
образующие вдали от краев куска. Чтобы уяснить себе все это,
сделайте такую модель.
Наложив друг на друга два листа плотной бумаги, вырежьте в двух
экземплярах «воротничок», изображенный на рис. 175, и склейте (а еще
лучше сшейте частой строчкой) два таких воротничка по линии
ABCDE ... В ряде точек А, В, С, D и т. д. начертите на обоих
экземплярах касательные к линии ABCDE ... , продолжив их в обе
стороны. Затем, раздвинув листы, деформируйте нашу модель (рис. 176). Линия
ABCDE ... станет ребром возврата некоторой развертывающейся
поверхности. Полукасательные AAV ВВ1У ССг и т. д. станут образующими одной
из полостей, полукасательные АА2, ВВ2, СС2 и т. д. —образующими
другой полости (на первой полости эти полукасательные искривляются,
так же как искривятся полукаса!ельные ААХ, ВВг на второй полости).
На рис. 176 показано, как удобнее всего держать модель.
Небольшого движения рук достаточно, чтобы поверхность без
всякого сопротивления изогнулась. Ребро возврата при этом меняет форму,
§ 48. ПОВЕРХНОСТИ КАСАТЕЛЬНЫХ
285
но устранить ребро не удастся до тех пор, пока обе полости не станут
плоскими. Происходит это потому, что ребро состоит из неправильных
точек, и при непрерывном
изгибании неправильная
точка не может сразу стать
правильной. Поэтому
поверхность сопротивляется
искривлению прямолинейных
образующих. Правда, на краях
куска мы не встречаем
сопротивления: легкое
движение большого пальца левой
руки (рис. 176) искривит
соседние с ним образующие.
Но это происходит потому,
что край поверхности
становится однополостным
куском, и такое искривление
наталкивается на препят- Ряс. 175.
ствие, как только оно
достигает ребра.
На неограниченной
двуполостной поверхности
искривление образующих
невозможно; практически это
означает, что вдали от краёв
куска образующую
искривить нельзя.
Важно заметить, что при
двуполостной поверхности
касательных кривизна ее
ребра возврата остается
неизменной. Именно, можно
высказать следующую теорему.
Теорема 4. Если при
изгибании поверхности каса-
Ыельных прямолинейные
образующие остаются
прямолинейными образующими у то
кривизна ребра остается в
каждой точке неизменной.
Справедливость этой
теоремы усматривается из
следующих наглядных
соображений. Заменим кривую
развертывающуюся поверхность
вписанной в нее
многогранной поверхностью XYZZ'Y 'X'
(рис. 171 на стр. 281).
Деформация этой поверхности со- Рис. 176.
стоит во вращении граней
около ребер. При этом уголш между соседними ребрами остается
неизменным. Неизменным остается и длина звена А. Отношение ^ , следо-
286 ГЛ. VIII. РАЗВЕРТЫВАЮ ДИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
вательно, также неизменно. В пределе многогранная поверхность
становится развертывающейся, ребра—касательными ребра возврата, а
отношение ^—кривизной ребра возврата.
Строгое доказательство этой теоремы мы дадим ниже в § 49.
Пример. Если ребро возврата поверхности касательных S имеет
постоянную кривизну — , то при изгибании двуполостного куска
поверхности S ребро возврата, деформируясь, остается кривой постоянной
кривизны тг • При наложении S на плоскость линия (L) сохранит свою
кривизну и, следовательно, станет окружностью радиуса R.
Это дает нам возможность механически осуществить построение
кривых постоянной кривизны, которое мы выполнили аналитически
в § 37. Для этого достаточно сделать «воротничок» (рис. 175), у
которого линия ABCDE была бы дугой окружности радиуса R. При
описанном выше изгибании воротничка кривизна будет оставаться
неизменной, а кручение будет меняться. В общем случае оно будет
различным в различных точках ребра. Но если ребро возврата
растягивать за концы, оставив свободной остальную часть поверхности,
натяжение будет примерно одинаковым по всему ребру, вследствие чего
кручение ребра будет повсюду примерно одинаковым. Получится,
следовательно, ребро, имеющее постоянную кривизну и постоянное
кручение, т. е. винтовая линия.
Уяснив себе факт, выражаемый теоремой 4, мы легко усвоим идею
доказательства теоремы 1, которое дано в следующем параграфе.
§ 49. Доказательство теорем 1 и 4 § 48
В теореме 1 предыдущего параграфа утверждалось, что всякая
поверхность касательных изгибается на плоскость. Докажем это.
Пусть мы имеем поверхность S касательных данной линии (L).
Функция х = ср($) нам, следовательно, известна. Возьмем плоскую
линию (Ад), кривизна *! которой выражается той же функцией дуги
y^rzrcp^) (такая линия, как доказано в § 35, всегда существует и
единственна). Будем рассматривать плоскость как поверхность
касательных линии (L2) и отнесем ее к криволинейным координатам а, и,
где, как прежде, и есть отрезок касательной, отсчитываемый от точки
касания до точки Мх{а, v), а и = ^ есть длина дуги линии (Lx) от
некоторой начальной точки. Поверхность S отнесем к такой же системе
координат и каждой ее точке М поставим в соответствие точку Мх
плоскости с теми же значениями координат и, и. Согласно § 43
(пример 3, стр. 252) линейный элемент как для плоскости, так и для
поверхности S будет иметь вид
ds2 = da2 + 2du do + [1 + (<p (v))V] do\
Следовательно, поверхность S изометрична с плоскостью. В этой
мзометрии ребру возврата (L) поверхности S соответствует вполне
определенная по форме плоская линия (LJ, кривизна которой выражается
той же функцией дуги, что кривизна ребра (L). Если точка М
поверхности лежит на касательной NM, проведенной через точку N ребра (Z.),
то по изометрии ей отвечает на плоскости точка Д/а, лежащая на
касательной, проведенной в точке Nl9 соответствующей N, причем
NMN
§ 50. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ 287
Очевидно, такая же изометрия существует между плоскостью и
поверхностью касательных любой линии (Z/), кривизна которой
выражается той же функцией <р($). Таких линий существует бесчисленное
множесаво, так как кручение <s = a(s) линии (Z/) можно задать по
произволу, после чего линия (U) по форме вполне определяется (§ 36).
Пусть кручение линии (L) выражается через дугу функцией ф (s).
Рассмотрим семейство кривых, заданных на1уральными уравнениями
-х = ср (5), a = aty(s), где параметр а может иметь любое значение между
нулем и единицей. При а = 1 мы получаем линию (L), а при а = 0 —
плоскую линию {Ьг). Непрерывному изменению а от 1 до 0
соответствует непрерывное изменение ребра возврата (L) в плоскую кривую (Lx)
и, следовательно, непрерывное изменение поверхности S в плоскость.
Таким образом поверхность S не только изометрична с плоскостью,
но и изгибаема на нее. Этим доказана теорема 1 1).
Докажем теперь теорему 4; в ней утверждалось, чю если при
изгибании поверхности касательных прямолинейные образующие
остаются прямолинейными образующими и, значит, ребро возврата остается
ребром, то кривизна ребра в каждой точке остается неизменной.
Пусть две поверхности касательных S и St изгибаются одна на
другую так, что ребра их (Z.) и (Lx) совмещаются. Примем за
начальные точки ребер две точки, совмещающиеся при наложении. Тогда
при прежних обозначениях мы имеем для линейных элементов
поверхностей б1 и б1! выражения
ds2 = du2 + Ыа do + [1 + (х (o))hi2] do2, (1)
ds\ = du2 + Ida do + [1 -j- (xx (o))2u2\ do\ (2)
где у. и хх суть кривизны ребер в налагающихся точках. Эти ъыраже-
ния согласно теореме 3 § 46 (стр. 269) должны быть тождественны, а для
этого необходимо, чтобы х (у) = х1 (у).
Таким образом, если поверхности S и б^ изгибаются одна на
другую с сохранением ребра прямолинейных образующих, то кривизна
ребра остается неизменной. Этим доказана теорема 4 § 48.
§ 50. Линейчатые поверхности
Нам осталось доказать теорему 2 § 48, утверждающую, что всякая
развертывающаяся поверхность есть либо цилиндрическая, либо
коническая, либо поверхность касательных. Мы докажем это в следующем
параграфе, где будет установлено, что на всякой развертывающейся
поверхности существует такое семейство линий, что вдоль каждой из
них касательная плоскость остается неизменной. Этим свойством
обладает, как мы знаем (пример 3 § 40, стр. 238), поверхность касательных,
а также цилиндрическая и коническая. Теорема будет доказана, если
будет установлено, что кроме поверхностей касательных,
цилиндрических и конических никакие другие не обладают этим свойством.
В настоящем параграфе мы и установим это характерное свойство.
Попутно мы познакомимся с некоторыми свойствами линейчатых
поверхностей, которые и сами по себе представляют большой интерес для
геометрии и для механики.
1) Читатель без труда докажет, что цилиндрическая и коническая
поверхности также являются развертывающимися. Эти поверхности удобно отнести к
образующим и к их ортогональным траекториям.
288 ГЛ. VIIT. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
Прежде всего установим две леммы.
Лемма 1. Пусть на линейчатой поверхности S проведена
линия (L), имеющая с каждой из образующих по одной общей точке М,
и пусть ш есть угол между двумя прямолинейными образующими М'Т'
и М"Т" (рис. 177), имеющими общим пределом образующую МТ. Если
для всех точек М величина о> имеет высший порядок относительно дуги
М'М", то (о есть точный нуль, т. е. все образующие параллельны
друг другу (поверхность S —цилиндрическая).
Доказательство. Построим сферическую индикатрису (Z.J
прямолинейных образующих (для случая поверхности касательных это —
индикатриса касательных линии (£)). Пусть точки М\, М\, Мг
соответствуют точкам М', М"\ М. Через s и s1 обозначим длины соответ-
Рас. 177.
ственных дуг линий (I), (Z.J. Тогда
т. to ds.
Если ш имеет высший порядок относительно МЧИ", то -^ = 0. Пи
as
условию, это равенство имеет место тождественно. Значит, точка Мх
постоянна, т. е. все образующие параллельны друг другу.
Замечание 1. Когда S есть поверхность касательных линии (L),
то лемма 1 утверждает, что если кривизна (L) всюду равна нулю,'
(£) — прямая линия. Когда S есть поверхность бинормалей, то лемма
утверждает, что если кручение (Z.) всюду равно нулю, то ее
бинормали параллельны (т. е. линия L — плоская).
Замечание 2. Для нецилиндрических поверхностей о> тоже может
иметь высший порядок относительно ДГМ", но лишь для отдельных
образующих («цилиндрических» образующих), подобно тому как кривая
§ 50. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ 289
линия в отдельных точках может иметь нулевую кривизну (или
неплоская линия в отдельных точках — нулевое кручение).
Пример. Представим себе поверхность S, образованную
движением прямой (/), пересекающей постоянную прямую (Z.) и образующую
с ней постоянный угол, как это имеет место у косого или прямого
геликоида. Пусть точка М пересечения (Z) с (L) движется по оси (L)
с постоянной скоростью, но осевая плоскость вращается с переменной
угловой скоростью. Если в некоторый момент угловая скорость равна
нулю, то с» имеет высший порядок относительно ММ', и в ;*тот момент
поверхность S сходна с цилиндрической.
Замечание 3. Низший порядок относительно М'М" угол со может
иметь всюду лишь в том случае, когда линия (L) вырождается
в точку М, т. е. когда поверхность S коническая, а М — ее вершина.
Действительно, мы должны иметь теперь -=—=0, т. е. точка М по-
стоянна. Для отдельных же образующих («конических») ш может иметь
низший порядок относительно М' М" и на поверхностях, отличных от
конических.
Пример. Представим себе поверхность, образованную движением
прямой (/), пересекающей ось (L) в точке М и образующей" с (L)
постоянный угол. Пусть угловая скорость вращения осевой плоскости
постоянна, а скорость движения точки М по оси переменна. Если эта
скорость в некоторый момент равна нулю, то ш имеет низший
порядок относительно М'М", и в этот момент поверхность S сходна
с конической.
Лемма 2. Пусть линия (L) имеет по одной общей точке М с
каждой из плоскостей Ри, в совокупности составляющих непрерывное одно-
параметрическое семейство плоскостей (и~ параметр, задающий
отдельную плоскость) *), и пусть и> есть угол между плоскостями Р', Р",
имеющими общим пределом плоскость Рц. Если для всех точек М
величина о) имеет высший порядок относительно дуги М'М" (М' и Й"—-точки
линии (Z.), принадлежащие Р' и Р"), то все плоскости семейства
параллельны друг другу.
Доказательство—то же, что для леммы 1; только вместо
индикатрисы образующих строится индикатриса нормалей плоскостей Ри.
Теперь мы можем сделать первый шаг к установлению
интересующего нас характерного свойства поверхностей касательных,
цилиндрических и конических.
Теорема 1. Пусть неплоская поверхность S образована
непрерывным семейством линий (Lu) (и — параметр, задающий линию
семейства) и пусть вдоль каждой из линий Lu касательная плоскость Ри
к S остается неизменной. Тогда S есть линейчатая поверхность и
Lu — ее прямолинейные образующие.
Замечание. Касательная плоскосиь может оставаться неизменной
вдоль некоторой кривой линии и на нелинейчатой поверхности, но это
может иметь место лишь для изолированных кривых. Например, на
поверхности баранки или спасательного круга (такая поверхность
называется тором) имеются две такие линии — верхняя и нижняя
окружности.
г) Непрерывность семейства плоскостей характеризуется тем, что плоскость
Ри является пределом плоскости Ри+Дц пра Дм -+ 0.
19 М. Я. Выгодский
290 ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
Доказательство. Очевидно, каждая линия Lu сама лежит
в соответствующей плоскости Ри. Так как поверхность 5 —не плоская;
то на ней можно провести линию (/), которая пересекла бы все линии
Lu и не лежала бы в плоскости одной из них,—скажем, линии АВ.
Пусть точка М' линии £и+ды (рис. 178), двигаясь по (/), стремится
к точке М линии Lu. Тогда прямая а, по которой пересекаются *)
плоскости Ри и Ры+ди, неограниченно приближается к точке М. В самом
деле, пусть Ь есть расстояние от М до а, ш —угол между плоскостями
Р \\ Рц+ьи и d — расстояние от М до плоскости Ри+ди. Эти величины,
очевидно, связаны соотношением
Но d имеет высший порядок относительно ММ', а угол ш —тот же
порядок, что ММ' (лемма 2)2). Поэтому величина 8
бесконечно мала.
Но за точку М можно взять любую точку на Lu.
Следовательно, все точки линии Lu бесконечно
близки к прямой а, а это возможно ,/Лишь в том
случае, если Lu есть прямая линия, которая является
пределом прямой а. Этим теорема 1 доказана.
Мы можем сформулировать ее еще таким
образом: если касательные плоскости поверхности S
образуют однопараметрическое семейство, то S есть
линейчатая поверхность.
Теперь нам предстоит доказать, что из всех
линейчатых поверхностей только поверхности
касательных, цилиндрические и конические имеют одно-
параметрическое семейство касательных плоскостей.
Для этого ознакомимся ближе со строением линейчатых поверхностей.
Пусть S есть некоторая линейчатая поверхность. Возьмем на ней
две прямолинейные образующие (/) и (V) (рис. 179), имеющие общий
предел. Для определенности предположим, что одна из них (I) постоянна
(нетрудно распространить всё последующее на случай, когда обе
переменны). Если S не является цилиндрической поверхностью (этот
обыденный случай мы оставим пока в стороне), то существует
единственная прямая а', перпендикулярная к образующим (I) и (Г) и
пересекающая обе эти образующие (в точках Л7 uiV'). Пусть точка М есть
предел точки N и прямая а — предел прямой а'. Мы назовем М точкой
сжатия (ее называют также центральной точкой по причине, которая
х) Плоскость -Ры+ди не может оставаться параллельной плоскости PUi ибо
это означало бы, что на целом куске поверхности S все касательные плоскости Ри
параллельны, а это возможно только в том случае, если S есть плоскость. Если
последний факт не представляется очевидным, его можно доказать так. Пусть
т0 есть (постоянный) орт нормали поверхности S. Тогда для всех точек и для
всех направлений на S должно быть m0dr = 0, откуда m0r = p (p — const); это
уравнение представляет плоскость.
2) Мы можем считать, что в точке М не имеет места исключительный
случай, когда lim ^ =0, ибо такие точки заранее можно исключить; доказатель-
ММ'
отво от этого не пострадает.
§ 50. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
291
выяснится ниже), а прямую (а) — осью сжатия. Ясно, что ось сжатия (а)
перпендикулярна к образующей (/) и пересекает ее в точке сжатия М.
Линия (L), описываемая точкой сжатия М при движении образующей
(/), называется линией сжатия {стрикционной линией) поверхности S.
Пример 1. Осью
сжатия прямого геликоида для
любой его образующей
является ось геликоида; она же
является и линией . сжатия.
Пример 2, Осью
сжатия конической поверхности
является прямая, проходящая
через вершину
перпендикулярно к касательной
плоскости конической поверхности.
Ось сжатия меняется от
образующей к образующей.
Линия сжатия вырождается в
точку.
Пример 3. Осью ежа- РИС# 179.
тия поверхности касательных
линии (а) является бинормаль линии (к). Линия сжатия совпадаете
линией (к). Действительно, пусть МТ и М'Т' (рис. 180) — касательные к (к)
(в фиксированной точке М и в бесконечно близкой точке Д/'). Проведем
прямую МТ" параллельно М'Т'. Прямая NN' перпендикулярна к плоско-
Рис. 180.
сти ТМТ", а эта плоскость имеет пределом соприкасающуюся плоскость.
Значит, (а') составляет бесконечно малый угол с бинормалью. Чтобы
доказать, что она имеет пределом бинормаль, достаточно убедиться
в том, что точка N имеет пределом М (т. е. что М есть точка
сжатия). Этот почти очевидный факт можно строго доказать так:
спроектируем линию (к) на плоскость ТМТ". Получим линию (к,); ее
касательная М'^ есть проекция касательной МТ. Общий перпендикуляр (а')
образующих МТ, М'Т' проходит через точку пересечения N прямых
19*
292 ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
М[Т[ и МТ; последние же являются касательными в концах дуги ММ[
плоской кривой (>ч). Поэтому точка N бесконечно близка к М.
Замечание. Цилиндрическая поверхность не имеет линии
сжатия; условно можно сказать, что эта линия бесконечно удалена.
В первом примере линия сжатия была перпендикулярна к
образующим; в третьем примере она касалась образующих. В общем случае
линия сурсатпия пересекает образующие
под углом, отличным от прямого,
Пример 4. На однополостном
гиперболоиде вращения (рис. 181) линией
сжатия является горловая окружность
(L), пересекающая образующие под
острым углом.
Этот, на первый взгляд странный
факт обусловливается тем, что, хотя
точки N и N' образующих (/) и (/')
при неограниченном сближении
последних неограниченно сближаются с
точками сжатия М и Мг, однако
направления ММг и NN' не должны
стремиться к одному и тому же пределу; ведь в
общем случае бесконечно малые
отрезки NM и N'MX имеют тот же
порядок, что NN', и потому пренебрегать
ими нельзя.
Ось сжатия однополостного
гиперболоида лежит в касательной
плоскости соответствующей горловой точки,
т. е. в плоскости, проведенной через
образующую и касательную к горловой
*J|4C 181 окружности. Вообще имеет место
следующая теорема.
Теорема 2. Касательная МТ к линии сжатия лежит в
плоскости Р, проведенной через ось сжатия MZ и образующую (/).
Рис. 182.
Доказательство. Проведем через общий перпендикуляр NN'
бесконечно близких образующих (/) и (Г) и через образующую (I) пло-
§ 50. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ 293
скостьР' (рис 182). Спроектируем на эту плоскость хорду ММ' линии
сжатия; пусть Л есть проекция точки М'. Докажем, что угол ф= / M'MR
между ММ' и плоскостью Р' бесконечно мал. Из треугольника MM'R
находим
M'R ^ N'M' • «>
где ш—угол между (/) и (/'). Но ш имеет тот же порядок, что ММ'
(лемма 1), а отрезок N'M' бесконечно мал, так как обе точки М' и N'
имеют пределом точку М. Следовательно, угол ф бесконечно мал.
С другой стороны, угол ср между плоскостями Р и Р' тоже
бесконечно мал, так как NN' имеет пределом MZ. Следовательно, хорда ММ'
составляет бесконечно малый угол с плоскостью Р. Значит, касатель-4
ная МТ лежит в плоскости Р.
Определение. Пусть 8 есть кратчайшее расстояние между
фиксированной образующей (I) линейчатой поверхности S и бесконечно
близкой образующей (/'), а (о — угол между (/) и (/'). Предел р
отношения о : (о называется параметром распределения поверхности S [для
данной образующей (/)]:
р = lim — .
Можно сказать, что р есть рассчитанное на один радиан
«повышение» образующей по направлению оси сжатия, так что 2пр есть шаг
винтовой поверхности (прямого геликоида), которую описала бы образующая,
если ось и угловая скорость вращения оставались бы неизменными.
Параметру распределения можно приписать и знак, именно, можем
считать р положительной величиной, если упомянутый геликоид
—правый, и отрицательной, если он — левый; иными словами, р
положительно, если бесконечно близкие образующие составляют правую пару,
и отрицательно, если эта пара —левая (см. стр. 170).
Параметр распределения может быть бесконечно большой величиной
(ур = оо). Однако лишь для цилиндрических поверхностей соотношение
р = оо имеет место тождественно.
Действительно, пусть As есть дуга какой-либо линии (L),
содержащейся между бесконечно близкими образующими линейчатой
поверхности 5. Очевидно, As> 8. Поэтому, если р = оо, т. е. если о> имеет
высший порядок относительно As, то тем более ш имеет высший
порядок относительно As. Следовательно (лемма 1), соотношение р=оо
имеет место только для цилиндрических поверхностей. Ясно, что для
цилиндрических поверхностей оно имеет место всегда. Мы получаем
следующую теорему.
Теорема 3. Для того чтобы линейчатая поверхность была
цилиндрической, необходимо и достаточно, чтобы параметр распределения
повсюду был бесконечно большим.
Другим крайним случаем является тождественное обращение
параметра распределения в нуль. Ясно, что это имеет место для
конической поверхности. Но конус — не единственная линейчатая поверхность с
нулевым параметром распределения. Тем же свойством обладает всякая
поверхность касательных. Однако этим исчерпывается упомянутый
класс поверхностей. Таким образом, имеют место следующие теоремы.
Теорема 4. Параметр распределения всякой поверхности
касательных тождественно равен нулю.
Теорема 4а. Если для линейчатой поверхности S с
невырожденной линией сжатия (L) параметр распределения тождественно равен
нулю, то S есть поверхность касательных линии (L).
294
ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ, ЭВОЛЮТЫ
Доказательство. Отрезок NN' (рис. 183), дающий
кратчайшее расстояние между касательными (/) и (Г) линии (Z.), есть
проекция хорды ММ' на общий перпендикуляр (а') образующих (/), (Г).
Поэтому, обозначая через X угол между ММ' и (а'), имеем
b = NN'=MM'cask, (1)
откуда
ММ1
U 1V± IVX \
— — COS Л.
(2)
Пусть (Г) имеет пределом (Z). Тогда угол между (/) и ММ'
бесконечно мал. Значит, угол к между (а') и ММ' эквивалентен прямому,
и lim cos д. ;= 0. Что касает-
2 ММ'
| ся отношения , то оно
со
имеет пределом кривизну х
линии (L), которая (в
правильной точке) не может
быть бесконечной. Поэтому
из (2) находим
/? = limA = 0, (3)
•/I? чт0 Доказывает теорему 4.
Пусть теперь имеет
место соотношение (3).
Докажем, что тогда линия
сжатия поверхности S
касается ее образующих.
Пусть МиМ'-точки
сжатия образующих (I) и
(Г) и пусть (/') имеет
пределом (Z). Получив, как
выше, соотношение (2),
заметим, что в силу леммы 1
(замечание 3, стр. 289) величина не может быть бесконечно малой.
Поэтому из (2) и (3) следует, что limcosX = 0, т. е.
С другой стороны, общий перпендикуляр (а') имеет пределом ось
сжатия MZ, а секущая ММ' —касательную к линии сжатия в точке М.
Следовательно, ось сжатия MZ перпендикулярна к касательной к линии
сжатия в точке М, а так как эта касательная, ось сжатия MZ и
образующая (I) лежат в одной плоскости (теорема 2), то касательная к линии
сжатия совпадает с образующей (Z), что доказывает теорему 4а.
Рис. 183.
Мы займемся теперь вопросом о поведении касательной плоскости
к линейчатой поверхности при движении точки касания вдоль
образующей.
Цилиндрические и конические поверхности, а также поверхности
касательных мы можем исключить из рассмотрения, так как для них,
как мы уже знаем, касательная плоскость остается вдоль образующей
§ 50. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ 295
неизменной. Тем самым исключаются значения параметра
распределения р = 0 и р = оо (теоремы 3 и 4а), и нам остается рассмотреть
линейчатые поверхности с конечным параметром распределения. Они
называются косыми линейчатыми поверхностями.
На косой линейчатой поверхности касательная плоскость в точке
сжатия Мо проходит через ось сжатия. Действительно, она определяется
образующей и касательной к линии сжатия (эти прямые не могут
совпадать, так как тогда мы имели бы поверхность касательных
к линии сжатия). Следовательно (теорема 2), касательная плоскость
в точке Мо проходит через ось сжатия.
Пусть Мо— точка сжатия косой линейчатой поверхности, лежащая
на образующей (/), М — другая точка на той же образующей
Ро и Р — касательные плоскости к поверхности в точках Д/Ои М (рис. 184)
Рис. 184.
Чтобы определить положение плоскости Р, достаточно найти угол ср,
который Р образует с Ро, или, что то же, с осью сжатия M0Z.
Выберем одно из направлений на (/) —все равно какое —за
положительное и обозначим через и направленный отрезок М0М. Угол ср
будем считать положительным, если поворот плоскости Р из
положения Ро совершается против часовой стрелки для наблюдателя,
помещающегося с положительной стороны от точки Мо. Таким образом, при
перемене положительного направления изменяются одновременно знак и
и знак ср.
Пусть NN'— общий перпендикуляр образующих (I) и (/').
Проведем через N' прямую N'R параллельно (I) и через М — плоскость Q,
перпендикулярную к (/); пусть R и М'— точки пересечения Q с N'R
и (Г); через ср' обозначим угол М прямоугольного треугольника
M'MR.
Когда (Г) стремится к (/), точка М' описывает на линейчатой
поверхности некоторую линию (к). Проведем к этой линии
касательную МТ. Плоскость NMT есть искомая касательная плоскость.
Так как, далее, общий перпендикуляр NN' (он параллелен MR)
имеет пределом ось сжатия M0Z, а секущая ММ' — касательную МТ,
то искомый^ угол ср (он равен углу между МТ и M0Z) есть предел
угла ср':
9=limcp/. (4)
296 ГЛ. VIII. РАЗВЕРТ БАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
Из треугольника MRM' находнм
RM'
Но
b (6)
RM' = N'R tgu = NMtgu. (7)
Точка N имеет пределом точку сжатия Мо. Поэтому
NM2zM0M=u (8)
и, значит, в силу (7)
RM'teuu. (9)
Из формул (5), (6), (9) находим
и в силу (4)
t£ 9 = и lim 4г = и : lim — = — . (10)
с * О со р
Мы приходим к следующей теореме Шаля (Chasle):
Теорема 5. Если S есть косая линейчатая поверхность, то
касательная плоскость Р вдоль образующей не остается неизменной, и
тангенс угла <р, образуемого плоскостью Р с осью сжатия, пропорционален
расстоянию и = М0М от точки сжатия Мо до точки касания М.
Замечание 1. В формуле (10) параметр распределения р может
иметь как положительное, так и отрицательное значение. В первом
случае касательная плоскость при приближении точки касания к
наблюдателю вращается против часовой стрелки (независимо от положения
наблюдателя); яо втором —по часовой стрелке. Первый случай имеет
место, в частности, для правой винтовой поверхности, второй —для левой.
Замечание 2. Формула (10) показывает, что при неограниченном
удалении точки М касательная плоскость имеет пределом плоское!ь,
перпендикулярную к оси сжатия. Эта плоскость называется
касательной плоскостью в бесконечно удаленной точке. На равных расстояниях
справа и слева от оси сжатия касательные плоскости образуют равные
углы с плоскостью ZM0M. Поэтому точка сжатия Мо называется
центральной точкой, а плоскость ZM0M— центральной плоскостью
образующей (Z). Когда точка М пробегает всю образующую, касательная
плоскость совершает поворот на 180°.
Замечание 3. Если и = р, то формула (10) дает ^=-£.
Следовательно, параметр распределения есть не что иное, как такое
расстояние, которое нужно отложить по образующей от точки сжатия
для того, чтобы касательная плоскость повернулась на угол в 45°. Конечно,
исключаются случаи р=оэ и р = 0; о них сказано ниже.
Замечание 4. Случаи р = оо (цилиндрическая поверхность)
и /? = 0 (поверхность касательных и коническая) можно рассматривать
как предельные. Если р—оо, то мы имеем, в соответствии с (10),
соотношение
т. е.
§ 50. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ 297
II в самом деле, для цилиндрической поверхности касательная плоскость
неизменна на образующей. Правда, для цилиндрической поверхности
ось сжатия неопределенна, но направление общею перпендикуляра
имеет предел: это ьаправление перпендикулярно к образующей и
параллельно касательной плоскости.
Если р = 0, то для всех точек образующей, кроме точки сжатия
(и = 0)у формула (10) дает
tg<p= со
или
те
? 2 '
т. е. касательная плоскость перпендикулярна к оси сжатия. Как мы
знаем, это и имеет место для конической поверхности и поверхности
касательных (р=^.О).
Но для точки сжатия (гг = 0) формула (10) при р = 0 дает
неопределенность. И в самом деле, для конической поверхности касательная
плоскость в точке сжатия остается неопределенной. Касательная
плоскость в прямом смысле не определена и в точке сжатия Мо
поверхности касательных, потому что Мо — неправильная точка (сечения
поверхности касательных имеют в Мо точку возврата). Можно (стр. 244)
определить «по непрерывности» касательную плоскость в точке Мо
как соприкасающуюся плоскость линии сжатия. При этом, однаки,
мы вступим в противоречие с теоремой 5, ибо тогда «касательная»
плоскость не пройдет через ось. Пожалуй, целесообразнее условиться
принять за касательную плоскость в точке Мо спрямляющую плоскость
линии сжатия. Тогда в точке Мо касательная плоскость при движении
точки касания вдоль образующей изменится скачком.
Чтобы лучше уяснить себе поведение касательной плоскости
в точке сжатия при р = 0, рассмотрим пример, где параметр
распределения обращается в нуль не тождественно.
Представим себе винтообразную поверхность, порожденную
движением прямой (Z), которая пересекает ось (£.) под прямым углом
и вращается около нее с постоянной угловой скоростью; пусть точка
пересечения образующей с осью движется в одном направлении с
переменной скоростью, которая в некоторый момент обращается в нуль.
Очевидно, параметр распределения в этот момент обращается в нуль.
Во всех точках соответствующей образующей, кроме точки сжатия Мо,
касательная плоскость перпендикулярна к оси (L). В самой же точке Мо
касательная плоскость Ро (она существует) проходит через ось. Значит,
касательная плоскость в точке М0У если к этой точке приближаться
по образующей, меняется скачком.
Рассмотрим теперь поведение касательной плоскости на соседних
образующих, где параметр распределения мал, но не равен нулю.
Для них поворот касательной плоскости от центрального положения
на определенный угол (например на 45°) будет совершаться на
небольшом расстоянии (в нашем случае—на расстоянии р). По мере
приближения образующей к критическому положению, где р = 0, это
расстояние будет все более уменьшаться. Из этого ясно, что в любой
окрестности точки Мо (на образующих, отличных от рассмотренной)
найдутся точки, в которых касательные плоскости составляют
с плоскостью Ро любой наперед заданный угол.
Из теоремы 5 тотчас же вытекает, что касательная плоскость
может оставаться неизменной вдоль образующей линейчатой поверх-
298 ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
ности только тогда, если на этой образующей параметр распределения
равен нулю или бесконечности. Мы знаем также, что если р = 0 для
всех образующих, то линейчатая поверхность является либо конической,
либо поверхностью касательных, а если р = ор для всех образующих,
то поверхность —цилиндрическая.
Сопоставляя это с теоремой 1 настоящего параграфа, мы приходим
к следующему важному результату.
Теорема 5. Если поверхность S образована непрерывным
семейством линий, вдоль каждой из которых касательная плоскость остается
неизменной, то S является либо цилиндром, либо конусом, либо
поверхностью касательных, а каждая из упомянутых линий есть прямо-
линейная образующая.
Опираясь на эту теорему, мы сможем доказать теорему 2 § 48,
оставшуюся там недоказанной.
§ 51. Доказательство теоремы 2 § 48
В теореме 2 § 48 утверждалось, что всякая развертывающаяся
поверхность является либо цилиндром, либо конусом, либо поверхностью
касательных. Докажем это1).
Обозначим через и, v прямоугольные координаты той точки плоскости
Р, на которую попадает точка развертывающейся поверхности S при
изгибании последней на Р, и отнесем поверхность S к криволинейным
координатам иу v. Координатными линиями ыа S будут, таким образом,
изогнутые линии абсцисс и ординат.
Коэффициенты первой квадратичной формы поверхности 5 будут
равны
# = r£ = l, F = rurv = 0, G = r* = l, (1)
так что
EG-F* = (ruxroy = l. (la)
Дифференцируя уравнения (1J и (13) по и и v, найдем
rurUu = °> ruruv = Oy rvruv = 0, rvrvv = O. (2)
Дифференцируя второе из уравнений (1) и принимая во внимание
(28) и (23), найдем
rvruu = 0, rurvv = O. (3)
Составим выражение
которое в силу (2) и (3) равно нулю. Раскрывая его, находим
ГииГии — rbv = 0. (4)
Из (2J и (Зх) видно, что вектор гии либо равен нулю, либо
перпендикулярен к векторам ru, rv. В обоих сл}гчаях можно написать
гии = ат, (5,)
где т = гих rv есть орт нормали поверхности S (в силу (1а) т2 = 1).
Таким же образом, из (22) и (23) найдем
'_ гии = $т (5.)
х) По причинам, объясненным в конце этого параграфа, мы ограничиваемся
здесь аналитическим доказательством. Синтетическое доказательство будет дано
позднее.
§ 51. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 2 § 48 299
и из (2J и (32)
гю = чт- (5з)
Числа а,[3,у в силу (4) связаны соотношением
ау-р2 = 0. (6)
Если все три числа а, р, у равны нулю, то из (5J и (52) следует, что
орт ru на всей поверхности S является постоянным; из (52) и (53)
следует, что орт rv также остается всюду постоянным. Значит, на всей
поверхности S остаеася постоянным орт нормали, т. е. S есть
плоскость *).
Пусть теперь не все числа a, J3, у равны нулю; тогда, в силу (6),
по крайней мере одно из чисел а, у отлично от нуля. Не нарушая
общности, можем сиитать, что у Ф 0.
Если при этом а = 0, то в силу (6) также (3 = 0. Тогда из (Ьг) и (52)
снова следует, что на всей поверхности орт ги является постоянным.
Это значит^ чго всякая линия v = const (для нее ги
есть орт касательной) является прямой. При этом
все прямые v = const параллельны).
Следовательно, S есть цилиндрическая поверхность2).
Наконец, в случае а Ф 0, у Ф 0 мы имеем
в силу (6) также В Ф 0, и соотношение (6) можно
переписать в виде
а:р = р:Т. (7)
Покажем, что в этом случае поверхность
имеет семейство линий (X), вдоль каждой из
которых касательная плоскость остается неизменной.
Это семейство определяется одним из
уравнений
а (и, v) du + $ (u} v) do = 0, (8)
р (и, v) du 4- у (и, v) dv = 0, (9) рис ш
из которых одно является следствием другого
в силу (7). Существование (и единственность) такого семейства
обеспечивается основным предложением теории дифференциальных уравнений.
Геометрически оно совершенно очевидно, ибо, например, условие (8)
задает в каждой точке поверхности S вполне определенное направление
(рис. 185), и можно, выйдя из любой точки поверхности, смещаться
таким образом, чтобы направление движения в каждой точке пути
совпадало с направлением, заданным в этой точке уравнением (8).
Умножая (8) и (9) на орт нормали т и принимая во внимание
(5i)i (52)» (^з)> мы получаем соотношения
Они должны удовлетворяться при смещении вдоль каждой из линий X,
а так как их можно переписать в виде
:£}
х) Если ги = a, rv = b, то г = аи + bv -f- с, где с — постоянный вектор.
Последнее уравнение представляет плоскость.
*) В силу (12) линии и = const суть ортогональные траектории образующих.
300 ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
то вдоль каждой из линий (к) остаются постоянными как орт гы, так
и орт rv, а следовательно, и орт нормали т=ги хгв. Значит, вдоль
линии (а) касательная плоскосиь остается неизменной1).
Из теоремы 5 § 50 (стр. 296) вытекает, что поверхность S является
либо цилиндрической, либо конической, либо поверхностью
касательных, а линии (к) суть прямолинейные образующие поверхности S.
Этим полностью доказана теорема 2 § 48.
Замечание. В нашем доказательстве мы предполагали не только
существование первого дифференциала вектор-функции г (и, v), но также
и наличие высших (вторых и третьих) производных.
Геометрически это означает, что, кроме существования касательной
плоскости, предполагаются выполненными еще некоторые требования,
предъявляемые к поверхности. Лишь в следующей главе (§ 61, стр. 358)
эти требования будут выяснены и оправданы физическими
соображениями. Поэтому мы здесь не имеем возможности провести
геометрическое доказательство; оно будет дано в § 77 (теорема 6, замечание, стр. 446)*
В связи с Э1им интересно заметить, что при менее жестких
требованиях, предъявляемых к функции г (а, и>), доказанная здесь теорема
заведомо неверна: как показал в 1899 г. Лебег, тогда можно задать
(аналитически) такие поверхности, которые изгибаемы на плоскость,
но не имеют прямолинейных образующих. Однако такие поверхности
непременно имеют бесчисленное множество неизолированных
неправильных точек, и осуществить их материально нет возможности.
§ 52. Огибающая однопараметрического семейства плоскостей
На основании теоремы 5 § 50 мы можем утверждать, что только
развертывающиеся поверхности (т.е. цилиндрические, конические и
поверхности касательных) имеют однопараметрическое семейство касательных
плоскостей; все прочие поверхности (как линейчатые, так и
нелинейчатые) имеют двупараметрическое семейство касательных плоскостей.
Но семейство плоскостей Р (однопараметрическое или
двупараметрическое) можно задать и независимо от поверхности, которой
касаются плоскости Р. Например, можно взять множество нормальных
плоскостей некоторой линии L (однопараметрическое семейство) или
множество плоскостей, находящихся на заданном расстоянии от данной
точки (двупараметрическое семейство).
Определение. Поверхность S, у которой множество
касательных плоскостей совпадает с множеством плоскостей семейства {Р},
называется огибающей семейства {Р}.
Пример 1. Для однопараметрического семейства плоскостей,
проходящих через данную точку О и составляющих постоянный угол а
с прямой О А, огибающей является круглая коническая поверхность
с осью ОА, вершиной О и углом а между осью и образующей.
Пример 2. Для двупараметрического семейства плоскостей,
находящихся на одном vl том же расстоянии а от данной точки, огибающей
является поверхность сферы радиуса а.
) Вдоль всякой линии па любой поверхности удовлетворяется соотношение
= 0. При постоянстве т оно дает mr = /> (/> = const). Это уравнение
представляет некоторую плоскость 2, в которой лежит линия (А).
Плоскость (2), будучи перпендикулярной к т и преходя через все точки
линии (Я), должна для всех этих точек совпадать с касательными плоскостями
поверхности S. Таким образом, вдоль каждой линии (Я) касательная плоскость
остается неизменной.
§ 52. ОГИБАЮЩАЯ ОДНОПАРАМ£ТРИЧЕСКОГО СЕМЕЙСТВА ПЛОСКОСТЕЙ 301
Данное здесь определение не затрагивает вопроса о том, существует
ли для данного семейства плоскостей огибающая поверхность или нет.
Этот вопрос мы сейчас и решим для однопараметрического семейства.
Геометрически очевидно, что пучок плоскостей, проходящих через
некоторую ось (этот пучок представляет однопараметрическое семейство),
огибающей не может иметь. Точно так же не может иметь огибающей
пучок параллельных плоскостей. Однако эти два случая (из которых
второй является вырождением первого) —исключительные. Именно,
имеет место следующая теорема:
Теорема 1. Всякое однопараметрическое семейство плоскостей
{за исключением пучка плоскостей, проходящих через некоторую ось или
параллельных между собою) имеет огибающую поверхность {она,
конечно, является развертывающейся).
Как и всегда, мы предполагаем, что все рассматриваемые
переменные геометрические объекты имеют пределы.
Пусть т есть орт нормали плоскости Pt, а р — расстояние этой
плоскости до начальной точки О. Обе величины тир являются,
таким образом, данными функциями параметра t:
m = m(t); p = p{t),
которые мы будем считать дважды дифференцируемыми.
При этом мы можем считать, что орт m(t) tie является
постоянным, так как в случае постоянства т мы имели бы семейство
параллельных плоскостей, заведомо не имеющее огибающей. Тем самым
исключается возможность тождественного соотношения
m'(t) = 0.
Случай нетождественного соотношения т' (t) = 0 мы тоже можем
исключить, рассматривая достаточно малый промежуток изменения
параметра t. Итак, впредь будем считать, что
т'МФО. (1)
Всё семейство {Р\ можно охватить уравнением
m(t)r-.p{t) = 0. (2)
Для разыскания огибающей этого семейс!ва мы поступим так. Сначала
мы предположим, что искомая огибающая существует, и найдем
на каждой плоскости Pt такую прялхую (Zt), которая одна только
и может быть образующей искомой поверхности. Затем мы докажем,
что поверхность 5, порожденная прямыми (/,), действительно является
огибающей семейства плоскостей Pt.
У всякой развертывающейся поверхности образующая является
пределом пересечения двух бесконечно близких касательных плоскостей.
Поэтому для разыскания образующей (Zt) нужно найти предел, к
которому стремится прямая (Г), представляемая двумя уравнениями:
m(t)r-p(t) = 0, (2)
m{t + M)r -p{t + ±t) = O (3)
при М—*0.
Теорема 6 § 5 (стр. 25), которой мы пользовались для разыскания
предела переменной прямой, здесь непосредственно неприменима, так как
302 ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
lim m (t +At) = m(t) и lim p(t +At) = p(t), т. е. плоскость (З) в пределе
совпадает с плоскостью (2).
Но ту же прямую (/') мы можем представить системой уравнений
m(t)r-p(t) = 0 (2)
и
Уравнение (За) получено вычитанием (2) из (3) и делением на At.
Пределом плоскости (За) при Д£—>0 является плоскость
m'(t)r-p'(t) = 0. (4)
В силу теоремы 6 § 5, уравнения
m(t)r-p(t)=0, (2)
m'(t)r-p'{t) = 0 (4)
дают искомую прямую (/,), если только векторы m(t) и ni'(t) не кол-
линеарны.
Но коллинеарными они быть не могут, так как в силу
соотношения [m(t)]2 = 0 мы имеем m(t)m''(J) = 0, т. е. векторы m{t) и т'(t)
(оба они отличны от нуля) перпендикулярны.
Система (2), (4) при фиксированном значении t дает одну прямую,
принадлежащую фиксированной плоскости Pt; при переменном значении
t — семейство прямых lt. В исключительном случае все прямые
семейства могут совпасть; тогда все плоскости Pt проходят через эту прямую,
и наше семейство Pt есть пучок. В этом случае огибающей заведомо
не существует.
Пусть теперь прямая (lt) не остается постоянной. Докажем, что
касательная плоскость поверхности 5, описываемой прямой (Zt),
совпадает во всякой точке Mt этой прямой с плоскостью Pt.
Для этого проведем на S какую-нибудь линию (X), имеющую
с каждой из образующих (lt) no одной общей точке Mt. Когда точка М{
описывает линию (X), ее радиус-вектор г является функцией параметра t:
Так как каждая точка Mt лежит на соответствующей образующей (/(),
то функция r{t) должна тождественно удовлетворять уравнениям (2) и (4),
т. е. имеют место тождества:
(t)-p(t) = O, (2a)
m'(t)r(t)-p'(t)==0. (4a)
Дифференцируя (2а) и принимая во внимание (4а), находим
m(t)?'(t) = 0. (5)
Так как г' (t) есть вектор касательной линии (X), то уравнение (5)
выражает, что касательная к линии (X) в точке Mt перпендикулярна
к нормали m(t) плоскости Р%у а так как линию X на поверхности S
можно провести произвольно, то в каждсй точке поверхности S
ее касательная плоскость совпадает с некоторой плоскостью Рх.
Этим мы доказали, что всякое однопараметрическое семейство
плоскостей, отличное от пучка (осевого или параллельного), имеет
§ 52. ОГИБАЮЩАЯ ОДНОПАРАМЕТРИЧЕСКОГО СЕМЕЙСТВА ПЛОСКОСТЕЙ 303
огибающую поверхность S. Эта поверхность представляется парой
уравнений (2) и (4), где t есть переменная величина, подлежащая
исключению. При постоянном t те же уравнения представляют
прямолинейную образующую (lt) поверхности S.
Если вектор т (t) x tnf (t) сохраняет постоянное направление,
т. е. если орт
m(t) xm'Jt)_ = a .jv
/[«(О xW (011
является постоянным, то все образующие поверхности (S) параллелььы
и S есть цилиндрическая поверхность.
Если же орт a(t) не постоянный, то, как мы прежде доказали
геометрически, образующие (lt) касаются некоторой линии —ребра
возврата поверхности S. Подтвердим это аналитически и вместе с тем
покажем, как аналитически найти это ребро -по заданным функциям
m(t), p(t)y определяющим семейство {Р}-
Как и при разыскании образующих, мы сначала предположим, что
искомое ребро найдено. Тогда на каждой образующей lt есть одна
точка Л/*, в которой она касается ребра. Пусть г* есть ее радиус-
вектор. Когда точка Л/* описывает ребро, г* является функцией
параметра t:
r* = r*(t).
Эта функция тождественно удовлетворяет уравнениям (2) и (4), т. е.
имеют место соотношения
09 (2b)
m'(t)r*(t)-p'(t) = 0, (4b)
которые независимы вследствие неколлинеарности т и т'.
Чтобы найти функцию r*(t), нам нужно найти третье соотношение,
независимое от (2Ь) и (4Ь). Проще всего получить его, исходя из того
геометрического факта, что, какова бы ни была линия (А), касательная
во всякой ее точке К (не являющейся ни ючкой спрямления, ни точкой
сплощения) и соприкасающаяся плоскость в бесконечно близкой точке К
пересекаются в точке К', бесконечно близкой к К г).
Но соприкасающаяся плоскость ребра возврата является
касательной плоскостью поверхности, образованной касательными ребра. Поэтому
возьмем плоскость Pt+u данного семейства. Ее уравнение есть
) = O. (6)
Будем искать предел, к которому, при At—>0 стремится точка
пересечения плоскости Pi + м с фиксированной прямой (Zt), уравнения
которой суть
m(t)r-p(t) = 0, (2)
m'W-j/(0 = 0. (4)
х) Здесь нет нужды доказывать этот доьольно очевидный факт, так как
последующая проверка подтвердит, что найденная линия г* (t), действительно,
является ребром. Впрочем, доказательство не составляет большого труда. Мы знаем,
что точка К отстоит от соприкасающейся плоскости в точке Кх на расстоянии fl,
имеющем (при хфО; афО) третий порядок относительно ККХ. Пользуясь
формулами Френе, легко доказать, что угол <р между касательной в точке К и
соприкасающейся плоскостью в точке Кг имеет второй порядок, а так как .0^= -—
sin у у
то ККХ бесконечно мало (вычисление дает К К' = ~- ККХ ) .
sin
304 - ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
Иными словами, мы ищем предел точки пересечения трех плоскостей
(2), (4), (6) при фиксированном t и бесконечно малом At.
Так как плоскость (6) имеет при At —->0 пределом плоскость (2),
то мы должны прибегнуть к преобразованию системы (2), (4), (6).
Но теперь недостаточно, как мы делали прежде, вычесть (2) из (6)
и разделить на At> ибо тогда в пределе мы получим плоскость (4).
Однако мы можем поступить следующим образом: помножим уравнение (4)
на (—At), уравнение (2) на —1 и после этого сложим (6), (2) и (4).
Разделив затем на — At2, получим:
/rc(Q-m'(0 At
I r
Точка К\ принадлежащая плоскостям (2), (4), (6), принадлежит
также и плоскости (7). Значит, искомый предел К точки К'
принадлежит пределу плоскости (7), а он представляется (теорема 5 § 5,
стр. 24) уравнением
m"{t)r-p"{t) = 0. (8)
В системе уравнений
' m(t)r-p(t) = 0, (2)
m'(t)r-p'{t) = 0, (4)
m"{t)r-p"{t) = 0 (8)
первые два уравнения по доказанному независимы и совместны.
Третье же независимо от первых двух и совместно с ними.
Действительно, в противном случае мы имели бы соотношение
у '
где а (г), р (t) — некоторые скалярные функции от t.
Но в этом случае орт
Y(m х ту
был бы постоянным [в чем можно удостовериться, дифференцируя (10)
и принимая во внимание (9) *)], а тогда мы имели бы случай
цилиндрической поверхности, который уже рассмотрен выше.
Итак, система (2), (4), (8) на каждой образующей (lt) определяет
точку Mf с радиусом-вектором г*(*), так что вектор-функция
тождественно удовлетворяет уравнениям
т'(О г* (')-/>'(0 = 0, (4а)
m'(t)r*(t) — p"(t)=0. (8a)
Может оказаться, что г*(£) есть постоянная величина. В этом слхчао
все плоскости Pt проходят через постоянную точку, и поверхность
S — коническая. Если же г*(г) не постоянно, то точка М* описывает
линию Z.*, которая должна быть ребром возврата.
2) Случай, когда (9) удовлетворяется нетождественно, нас не интересует,
потому что мы можем взять достаточно малый промежуток изменения t, где (9)
не удовлетворяется.
§ 52. ОГИБАЮЩАЯ ОДНОПАРАМЕТРИЧЕСКОГО СЕМЕЙСТВА ПЛОСКОСТЕЙ 305
Проверим это. Дифференцируем (2а), учитывая (4а); затем
дифференцируем (4а), учитывая (8а). Получим
|»(Ог'*(О-р(О = о, (И)
m'(t)r'(t)-p'(t) = O. (12)
Так как r*'(t) есть вектор касательной линии L*, то уравнение (11)
выражает, что касательная к L* лежит в плоскости
т (t)r-p (0 = 0, (2)
а уравнение (12) —что касательная к L* лежит в плоскости
m'(t)r-P'(t) = 0. (4)
Значит, она совпадает с прямой пересечения плоскостей (2), (4),
т. е. с образующей (Zt). Итак, S есть поверхность касательных линии (£*)•
Уравнения этой линии мы получим, решая систему (2), (4), (8).
Пример. Пусть семейство плоскостей Pt задано уравнением
b sin t • х — b cos t • у + az — abt = 0. (2')
Дифференцируя его по t, находим
b cos t - x + b sin t • у — «6 = 0. (4')
Система (2'), (4') определяет при фиксированном t образующую (/()
поверхности S — огибающей семейства Pt\ при переменном t она дает
огибающую поверхность. Уравнение последней можно получить
исключением t из уравнений (2') и (4'). Это исключение можно
осуществить так: перенесем члены, не содержащие тригонометрических
функций, в правые части уравнений (2') и (4'). Возводя в квадрат
полученные уравнения и складывая их, находим
Ь2 (х2 + у2) = а2 (Ы - zf + а*Ь\
откуда
. z Ух2 -Н у' - ^
t==~b ±
~b ± а •
Это выражение подставляем в (4') и находим уравнение огибающей
z Ух jy
т± -—г
Предпочтительнее иметь параметрические уравнения этой поверхности;
их удобно взять таким образом: образующая (Zf), как видно из
уравнений (2') и (4'), проходит через точку (acos£, asint, bt), так что ее
уравнения можно написать в виде
# = acos£ — wasintf, у = a sin t + иа cos t, z= bt + bu.
При постоянном t и переменном и эти уравнения дают образующую /е;
при переменных и и t оки представляют огибающую семейства.
Сравнение их с уравнениями (22) § 39 (стр. 233) показало бы, что образующие
суть касательные к винтовой линии. Этот результат мы получим и
непосредственно. Именно, ребро возврата (Z.*) огибающей 5, согласно
доказанному, представляется системой уравнений
b sin t-x — b cos t-y + az — abt = 0, (2')
b cos t- x + b sin t»y —ab =0, (4')
— 6sin*.rc + 6cos*.y *=0. (8')
20 M. Я. Выгодский
306 ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
Разрешая ее относительно я, у, z, находим
ty z = 6/.
В связи с вышеизложенным интересно отметить еще одно важное
предложение.
Теорема 2. Точка М* ребра возврата поверхности касательных
есть предел точки пересечения трех бесконечно близких касательных
плоскостей развертывающейся поверхности.
Иными словами: точка пересечения трех бесконечно близких
соприкасающихся плоскостей всякой неплоской линии (I*) в пределе
совпадает с точкой линии (£*).
Это свойство представляется очевидным из следующих
соображений: если вместо развертывающейся поверхности взять многогранную
поверхность XYZU. ..U'Z'Y'X' (рис. 171 на стр. 280), то точка
пересечения трех последовательных граней XYY'X' (ABC), YZZ'Y' (BCD)
и ZUU'Z' (CDE) есть вершина С ломаной ABCDE. В пределе
ломаная ABCDE становится ребром возврата, а грани XYY'X' ит.'д.-
касательными плоскостями развертывающейся поверхности.
Ясно, что теорема 2 распространяется и на коническую
поверхность (ребро возврата вырождается в точку — вершину конуса).
Чтобы строго доказать эту теорему, отыщем предел точки
пересечения трех плоскостей Р, Р*+д*, Pt+zt при Д£—>0, ot —>0. Чтобы
не усложнять выкладок, предположим, что величины At, It и At — bt
имеют одинаковый порядок (например, Д£ = г, Ы =—г).
Плоскости Р, Pt+м и Pt+ы представляются уравнениями
~p(t) = 0, (13)
т (t + Дг) г — р (t + At) = 0, (14)
т (t + Ы) г — р (t + Щ = 0. (15)
Второе и третье уравнения можно представить в виде
*(0^ + ]=0, (16)
[т (t) + т' (t) 8* + {т' (t) Ы3 +72] г +
+ [p(t) + P' (t)tt + ± p" (t)U* + rl2] = 0y (17)
где гх у\1у eg, т)2 имеют высший порядок относительно каждой из
величин Дг2, U2.
Вычтем (13) из (16) и разность разделим на А*. Аналогично
поступим с уравнениями (13) и (17). Тогда получим:
' (t) + ±p"(t)/u + v\t] = O, (18)
[(0+ у(О4][/ (t)+ ~pff(t)ot + yi,]=^Oy (19)
где г3, т)8, г4, т}4 имеют высший порядок относительно каждой из
величин Дг, 8г и о^ — Д^.
§ 53. ПОЛЯРНАЯ ПОВЕРХНОСТЬ 307
Наконец, вычтем (18) из (19) и разность разделим на у (Ы — М).
Получим:
[ 2^#][^#]0. (20)
Здесь вторые слагаемые в каждой скобке бесконечно малы.
Так как система уравнений (13), (18), (20) равносильна
системе (13), (14), (15), то точка Л/', принадлежащая трем плоскостям
Pty Pt+м, Pt+ы, принадлежит также плоскостям Р'г и Р'2У
представляемым уравнениями (18) и (20). Значит, точка М, которую точка М'
имеет пределом, принадлежит плоскостям Рх и Р2, которые являются
пределами соответственно для Р[ и Р'2.
Уравнения плоскостей Рх и Р2 мы получим (теорема 5 § 5, стр. 24)
из (18) и (20); именно, уравнение плоскости Рх будет
m'(t)r-p'(t) = 0, (21)
а уравнение плоскости Р2
m"(t)r-p"{t) = 0. (22)
Точка М определяется, следовательно, уравнениями (13), (21), (22),
а они совпадают с уравнениями (2), (4), (8), которыми определялась
точка М* ребра возврата. Этим теорема 2 доказана.
§ 53. Полярная поверхность
Как мы видели, поверхность касательных любой линии (L)
является развертывающейся. В противоположность этому, поверхность
главных нормалей и поверхность бинормалей ни для какой неплоской
линии не могут быть развертывающимися.
Рассмотрим сначала поверхность Sn главных нормалей
пространственной кривой. Если бы она была развертывающейся, то вдоль
главной нормали касательная плоскость была бы неизменной;
следовательно, она совпадала бы с касательной плоскостью, проведенной в точке М
линии (L). Последняя проходит через главную нормаль (образующую)
и касательную к линии (L) (направляющей), т. е. является
соприкасающейся плоскостью линии (L).
Но бесконечно близкие соприкасающиеся плоскости пересекаются
по прямой, пределом которой является касательная к (L).
Следовательно, поверхность Sn имела бы образующими не только главные
нормали, но также и касательные. Но всякая развертывающаяся
поверхность (кроме плоскости) имеет только одно семейство образующих.
Вот еще одно доказательство. Найдем параметр распределения
р поверхности Sn. Кратчайшее расстояние 8 между главными
нормалями п и п 4- An есть, очевидно, проекция вектора Аг на какую-либо
прямую, перпендикулярную к п и п+кп> или, что то же, к п и А/г.
Орт этой прямой будет п Х п- , так что
Угол о) между п и # + А# эквивалентен дуге индикатрисы главных
нормалей, т. е.
20*
308 ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
Значит, цараметр распределения будет
dr dn
ds ds
= fdn\2 *
Подставляя сюда
dr __ t dn — -^
находим
л tn(-xt+ob)
P~ (-xt+аЬУ
Как видим, для неплоской линии (L) (в правильной ее точке)
параметр распределения поверхности Sn не может быть равен ни нулю,
ни бесконечности. Значит, Sn — косая линейчатая поверхность.
Вычисление, аналогичное вышеприведенному, покажет, что
параметр распределения поверхности Sb бинормалей есть
dr db
ds ds
P
jsj
Подставляя сюда
dr , db
найдем
Таким образом, для неплоской кривой (L) (в правильной ее точке)
параметр распределения не может равняться ни нулю, ни бесконечности.
Значит, Sb —косая линейчатая поверхность. Если же (L) — плоская
линря, то р= оо; следовательно, поверхность Sb —цилиндрическая,
что очевидно и непосредственно.
Итак, из ребер сопутствующего триедра только касательная
описывает развертывающуюся поверхность. Что касается граней
триедра, то каждая из них огибается развертывающейся поверхностью (§ 52,
теорема 1, стр. 301).
Соприкасающиеся плоскости огибаются, как мы знаем,
поверхностью касательных.
Огибающая S нормальных плоскостей линии (L) (рис. 186)
называется полярной поверхностью этой линии. Образующая (/)
полярной поверхности есть предел прямой пересечения бесконечно близких
нормальных плоскостей Р линии (L), т. е. ось кривизны этой линии.
Следоваельно, эта образующая направлена параллельно бинормали
линии (L) и пересекает главную нормаль в центре кривизны. Иными
словами, место центров кривизны линии (L) принадлежит полярной
поверхности. Ребро возврата к полярной поверхности образовано
точками пересечения трех бесконечно близких нормальных
плоскостей (§ 52, теорема 2, стр. 306).
Согласно определению полярной поверхности всякая кривая (L)
пересекает все касательные плоскости своей полярной поверхности
под прямым углом.
Поэтому, если требуется по данной развертывающейся
поверхности S найти линию (L), для которой S есть полярная поверхность,
§ 53. ПОЛЯРНАЯ ПОВЕРХНОСТЬ 309
то для этого нужно найти ортогональную траекторию касательных
плоскостей поверхности S.
Если на одной из касательных плоскостей задать по произволу
точку М, то через эту точку можно будет провести одну ортогональную
траекторию, так что всякая развертывающаяся поверхность S является
полярной поверхностью для оо2 различных линий (L).
Ортогональность линии (L) и касательных плоскостей поверхности
(5) ставит (L) и S в то же взаимоотношение, в котором находятся
эвольвента с эволютой. Ниже (§ 56) мы увидим, что в теории эволют
пространственных линий полярные поверхности этих линий играют
важную роль. Здесь же отметим, что линию (L) можно получить из поверх-
Рис. 186.
ности тем же механическим процессом, которым эвольвента
получалась из эволюты. Только вместо того, чтобы обертывать эволюту
натянутой нитью, мы будем обераывать развертывающуюся
поверхность S плоскостью Р. Тогда фиксированная точка М этой
плоскости опишет ортогональную траекторию касательных плоскостей, т. е.
искомую линию (L).
Пример 1. Полярная поверхность плоской кривой (L) есть
цилиндрическая поверхность. Ее образующие перпендикулярны к
плоскости кривей, а за ее направляющую можно принять эволюту линии
(L). Обратно, если полярная поверхность есть цилиндр, то исходная
линия (L) лежит в одной плоскости, перпендикулярной к образующим
цилиндра. Это легко усмотреть из описанного выше механического
построения.
Пример 2. Полярная поверхность 5 всякой сферической линии
(I) есть коническая поверхность; вершина ее совпадает с центром
сферы О. Действительно, все нормальные плоскости линии (L)
проходят через центр О\ следовательно, прямая пересечения бесконечно
310 ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
близких нормальных плоскостей, т. е. ось кривизны, также проходит
через центр.
Обратно, если S есть коническая поверхность с вершиной в О, то
(L) есть линия, принадлежащая сфере с центром в О. Действительно,
точка М, двигаясь вдоль (L), перемещается перпендикулярно к
касательной плоскости Р и, следовательно, к црямой ОМ. Легко видеть,
что при этом дифференциал dp расстояния р = ОМ равен нулю, так
что величина р остается постоянной, и линия (L) лежит на сфере
радиуса р с центром в О. Также и из механического построения
линии (L) ясно, что изгибаемая плоскость Р все время проходит через
точку Оу так что отрезок ОМ сохраняет постоянную длину.
Следуя общему методу, изложенному в § 52, мы можем
аналитически найти полярную поверхность данной линии (L) следующим
образом. Если s есть дуга линии (L), г —ее радиус-вектор и /? — радиус-
вектор точки нормальной плоскости Р, то уравнение семейства
нормальных плоскостей есть 1)
(R-r)t = 0. (1)
Дифференцируя это уравнение по дуге s, от которой зависят г и t, n
dr . dt I
принимая во внимание, что-т-=Г, j- = *п— — п, находим
(Я-г)1я-1=0, (2)
ИЛИ
(R-r n = ?. (2а)
Уравнения (1) и (2а) представляют ось кривизны (/) — образующую
полярной поверхности. Из них видно, что направление оси кривизны
перпендикулярно к векторам t и п, т. е. параллельно бинормали Ьу
а также что проекция вектора /?—г, идущего от точки М(г) линии
(L) к какой-либо точке N оси кривизны, на главную нормаль имеет
алгебраическое значение +р, т. е. что ось кривизны пересекает
главную нормаль в центре кривизны С кривой (L).
Чтобы найти ребро возврата полярной поверхности, можно
дифференцировать систему уравнений (1) и (2) или эквивалентную ей
систему (1), (2а). Дифференцируя (1), находим снова уравнение (2а).
Дифференцируя (2а), находим
«-»•>£-*-£■
Итак, принимая во внимание соотношения tn = 0, -^s= —*t-\-<sb, а также
уравнение (1), получаем
%
ИЛИ
(*-r)* = *g. (3)
Уравнения (1), (2а), (3) позволяют определить положение точки М*
ребра полярной поверхности. Уравнение (1) показывает, что вектор
1) Не лишним будет отметить, что при этих обозначениях г есть радиус-вектор
не текущей точки плоскости Р, а точки линии (L), т. е. заданная вектор
функция дуги 5, которую мы здесь берем в качестве параметра £.
§ 53. ПОЛЯРНАЯ ПОВЕРХНОСТЬ 311
MM* ~R—r перпендикулярен к вектору t (рис. 187), т. е. лежит
в нормальной плоскости; уравнение (2а) выражает, что проекция МС
вектора ММ* на вектор п равна р, т. е. что М* лежит на оси
кривизны. Наконец, уравнение (3) говорит, что алгебраическое значение
проекции СМ* вектора ММ* на ось кривизны равно т -£. Таким образом,
координаты точки М* относительно сопутствующего триедра суть
(£)
ds ч ^ ;
Форм)-ла (4) показывает, что для построения ребра полярной
поверхности линии (L) нужно на образующих отложить от центров
кривизны линии (L) отрезки
длины т ~ .
Ребро полярной
поверхности может совпадать с местом
центров кривизны только в том
случае, если т ^=0, а так как
для неплоской кривой не может
иметь места тождество t^=0,
то должно быть ^ = 0, т. е.
Р = const: для кривых постоян-
пойкривизны, и только для них,
ребро полярной поверхности
неплоской линии совпадает с
местом центров кривизны.
Далее, формула (4)
показывает, что если на кривой с
переменным радиусом кривизны
движение происходит по
направлению возрастания
радиуса кривизны (в этом случае
то ребро полярной по-
s Рис. 187.
верхности смещено от места
центров кривизны по положительному направлению бинормали для
правой кривой (т > 0) и по отрицательному—для левой (х < 0). Если кривая
из правой становится левой, или наоборот, переходя через точку спло-
щения ( — = 0 J , то ребро переходит по другую сторону места центров
(через бесконечность).
Положение точки ребра возврата можно синтетически найти
следующим образом. Обозначим через Си С центры кривизны для бесконечно
близких точек М и М' данной линии (Z.), через М* и М*' —
соответствующие точки ребра возврата (X) полярной поверхности и спроектируем
линию (Z.), ребро возврата (X) и отрезки М'С" = р/ и СМ*' на
нормальную плоскость МСМ*. В проекции получим (рис. 188) линии
(L), (к) и отрезки М'С, СМ*' (на рис. 188 изображены только
упомянутые проекции). Пусть К и В суть точки пересечения СМ* с СМ*'
312
ГЛ. VIII. РА8ВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
и М'С. Через со, со', как обычно, будем обозначать \глы смежности
касательных и бинормалей линии (L). (Эти углы имеют тот же или
более высокий порядок, чем дуга ММ'.) Через о/ обозначим уголСКС.
Если через точку М*' провести прямую M*'U' || М*С (на рис. 1881
изображена только ее проекция M*'U'), to^C'M*'U' = &', а проекция этого
угла Z.C'M*'U' = /С'КС = ш'. Применив лемму 3 §26(стр. 134), найдем,
что
»'%», (5)
а также что
где е2 имеет второй (или более высокий) порядок относительно ММ'.
Искомый отрезок СМ* отличается от ВК на бесконечно малую
величину. Поэтому из треугольника ВКС' (в нем Z_ С' ^ Z- В Zz 90°),
принимая во внимание (5), находим
С В -«-<-* (7)
СМ*-
с As
Чтобы найти выражение для С В, спроектируем точку М' в точку Е на
главной нормали МС.
Отрезок ME (расстояние от М' до
д у^ спрямляющей плоскости в М)
*** имеет второй (или более
высокий) порядок относительно
ММ'. Отрезки ВМ' и СЕ
разнятся также' на величину
второго порядка. Поэтому
где т\2 имеет порядок не
ниже второго.
Следовательно,
Подставляя это выражение
в (7), находим:
ртцг* 1- р' — р do
As ds *
В заключение заметим,
что сопутствующие триедры
линии (L) и ребра возврата
(Z.x) ее полярной
поверхности параллельны, причем ор-
Рис. 188. ты *> л' ^ соответственно
коллинеарны ортам Лх, nlit1.
Действительно, вектор tx направлен по оси кривизны СМ* линии
(L), т. е. коллинеарен вектору Ь. Далее, нормальная плоскость СММ*
линии (L) есть в то же время соприкасающаяся плоскость ребра
полярной поверхности. Значит, главная нормаль пг коллинеарна с
вектором п. Следовательно, векторы Ьх и t также коллинеарны.
§ 54. СОПРИКАСАЮЩАЯСЯ СФГРА 313
Аналитически этот результат получается так: из формулы (4)
находим
drM* dr dn
Положив
имеем
откуда
т. е. касательная ребра равнонаправлена или противоположно направлена
бинормали линии (L), в
зависимости от знака
величины М.
Дифференцируя (9),
заходим
откуда
Наконец, перемножая век-
торно уравнения (9) и (10),
находим
§ 54. Соприкасающаяся
сфера
Точка Л/* ребра
возврата полярной
поверхности является центром
соприкасающейся сферы, т.е.
сферы, проходящей через
четыре бесконечно близ- Рис. 189.
кие точки линии (L).
Этот факт легко предугадать из следующих соображений. Если /V,
Nlf N2, Ns (рис. 189) суть четыре точки линии (L), то центр сферы,
проходящей через эти точки, лежит в пересечении трех плоскостей Qlt
QiJ Qs> проходящих через середины отрезков NNlf 7V17V2, N2N9 и
перпендикулярных к этим отрезкам. Пренебрегая величинами второго
порядка малости, мы можем заменить плоскости Qlf Q2, Qz
плоскостями Plf Р2, Р3, нормальными к (L) в точках М19 М2, М8, где пло-
314 ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
скости Ql9 Q2, Q3 пересекают дуги NN19 NXN2, N2N3. Точка
пересечения плоскостей Р1У Р2, Р3 в пределе лежит на ребре возврата
полярной поверхности. Но для того, чтобы заключить, что точка
пересечения плоскостей Qly Q21 Q3 имеет тот же предел, что точка пересечения
плоскостей Plt Р2У Р8, нужно доказать, что прямая (ах) пересечения
плоскостей Рх и Р2 разнится от прямой (f^) пересечения плоскостей
Q1 и Q2 бесконечно малыми величинами второго порядка, и то же —
относительно прямой (а2) пересечения плоскостей Р2, Р3 и прямой (j32)
пересечения плоскостей Q2, Q3, ибо в общем случае замена двух
плоскостей двумя другими, соответственно разнящимися ог первых на
величины второго порядка, дает прямую пересечения, разнящуюся от
первой прямой величинами первого порядка, а этого недостаточно для
утверждения, что точка пересечения («х), (а2) имеет тот же предел, что
и точка пересечения (рх), (|38). Во избежание громоздких выкладок мы
пойдем по другому пути.
Уравнение сферы радиуса R с центром в точке С имеет вид
(r-rcf = R\ (1)
Если сфера должна проходить через точки N1(s1)f ^2(s2)y N3(s3), N4(si)
линии (L) r=r(s) (s — длина дуги), то уравнение
должно удовлетворяться значениями s = su s = s2, s = s3, s = s4, т.е. имеют
место соотношения
Эти соотношения позволяют найти радиус-вектор гс центра сферы
NtN2N9NA и ее радиус Л. Чтобы найти пределы, к которым
стремятся гс и Л, когда четыре точки Nly N2, N3, iV4 стремятся к точке N (.<?),
вычтем первое уравнение (2) из второго. Получим уравнение
kOO-rcr-[r(Sl)-rcr=o, (3)
которому должен удовлетворять вектор гс центра сферы N1N2N3I\\.
Применяя к левой части формулу конечных приращений Лагранжа1),
находим
[r(8t)-rc]r'(st) = 0, (4)
где s5 заключено между sx и s2, т. е. точка iV5 лежит между iVx и N2 .
Проделаем те же действия со вторым и третьим, а затем—с третьим
и четвертым уравнениями (4). Получим три уравнения:
[r(sg)-rc]t(s§) = 0, [r(se)-rc]*(s6) = 0, [r(s7)-rc]*(s,) = Of (5)
выражающие, что центр сферы iV^iV^iVgiV^ лежит в пересечении трех
плоскостей, нормальных к линии (L) в точках N5, 7V6, N7. Эти
точки стремятся к тому же пределу, что точки Nly N2, N3, iV4. Но
предел точки пересечения трех бесконечно близких нормальных
х) Эта формула имеет место, так как [г (s) — r#]2 есть скалярная функция
параметра s.
§ 54. СОПРИКАСАЮЩАЯСЯ СФЕРА 315
■■ • ' ' ' '
плоскостей лежит на ребре полярной поверхности, что и требовалось
доказать х).
Таким образом, центр соприкасающейся сферы имеет
относительно сопутствующего триедра кривой (L) координаты 0; р; т •£:
гс = г + 1>п + *^Ь. (9)
Радиус MC = R соприкасающейся сферы определяется из
уравнений (1), (9) или из рисунка 188 на стр. 312 (где обозначения иные:
R2M* M2 + СМ*2):
Соприкасающаяся сфера проходит через круг кривизны линии (L),
так как последний есть предел окружности, проходящей через точки
Nlt N9, 7V3, а эта окружность принадлежит сфере NtN2N3NA. В общем
случае круг кривизны есть малый круг соприкасающейся сферы; он
становится большим кругом лишь в случае, когда j- = 0, т. е. лишь для
тех точек линии (L), в которых кривизна стационарна. Совпадение
круга кривизны с большим кругом соприкасающейся сферы на всем
протяжении линии (L) имеет место только для кривых постоянной кривизны.
Расстояние d от точки Мг линии (L) до соприкасающейся сферы
в бесконечно близкой точке М имеет четвертый (или высший) порядок
малости, т. е. линия (L) весьма тесно прилегает к своей
соприкасающейся сфере. Действительно, мы имеем
^^ (11)
Порядок малости d равен порядку малости МХС2 — МС2 (так как
знаменатель выражения (11) стремится к 2R). Мы имеем:
MJ? _ Л2 = (г, - rcf - (г - rcf = А (г - rc)\ ^
Разложим приращение Д(г — гс)2 в ряд по степеням b,s = MMx\ так
как три первые производные согласно формулам (1), (2а), (3) § 53 или
(8) настоящего параграфа обращаются в нуль, то разложение начинается
с члена четвертого или высшего порядка, что и требовалось доказать
х) Если бы мы хотели найти положение центра соприкасающейся сферы, не
опираясь на предшествующие сведения, то можем поступать далее так: вычтем
(5j) из (52) и (5о) из (53) и снова применим 1еорему Лагранжа. Используя формулу
dt 1
— = — п> получим два уравнения:
[Г (Sa) - Г с] П (S8) = p (S8), [Г (59) ~ Г С] П (59) = р (59) (6)
выражающие, что на дуге iV1yV2yV3iV4 имеются две точки N8,N9, обладающие тем
свойством, что центр сферы N1N2N3Ni проектируется на главные нормали ns> /iq
в соответствующие центры кривизны. Наконец, из уравнений (6), пользуясь тем
же приемом, получаем
выражающее, что па дуге NiN2NsN4 имеется точка iV10, обладающая тем
свойством, что на ее ось кривизны центр сферы iVliV27V3iV4 проектируется в точку
ребра. Уравнения (2), (5), (6) и (7) при переходе к пределу s$ -*> s дают для центра
и радиуса соприкасающейся сферы уравнения
(Г-.г<7)2 = /?2; (г_Г(7)/в0; (г~г£7)п = р; (г-Гс)Ь = ^9 (8)
из которых три последние совпадают с уравнениями (1), (2а), (3) предыдущее
параграфа.
316 ГЛ. VIII, РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
Вычисление показывает, что производная четвертого порядка равна
и, следовательно, в общем случае отлична от нуля. Поэтому в общем
случае главная часть разности МХС — R имеет четвертый порядок, и,
следовательно, в окрестности точки М линия (L) располагается либо
целиком внутри, либо целиком вне соприкасающейся сферы. Какой
из этих случаев имеет место, зависит, от знака величины
К тому же выводу приводит такое рассуждение: предположим, что
линия (L) б окрестности точки М пересекает сферу, проходящую через
точки N19 N2, N9, NA, только в этих четырех точках. Тогда, если дуга
NtN2 лежит внутри сферы, то дуга N2NS лежит вне сферы, а дуга
JS/ iV4 — снова внутри сферы. Значит, по обе стороны от дуги NtNA
линия (L) выходит из сферы. В пределе точки Nl9 N2, N3, iV4 сливаются
в одну точку М, и по обе стороны этой точки линия (L) лежит вне
соприкасающейся сферы. Подобное же рассуждение покажет, что если
дуга NtN2 лежит вне сферы, то линия (L) по обе стороны от М лежит
внутри соприкасающейся сферы.
Из формулы (12) легко вытекает, что кривая постоянной кривизны
(._£- = 0 )вблизи М лежит вне своей соприкасающейся сферы.
ds J
Выражение М = ~^ + т.(х ~т~\ стоящее в фигурных скобках формулы
(12), есть не что иное, как [формула (8) § 53, стр. 313] отношение ^- , где $с
есть длина дуги геометрршеского места центров соприкасающихся сфер
(т. е. ребра полярной поверхности). Иными словами, М есть скорость
движения центра соприкасающейся плоскости относительно дуги линии (L).
Если линия (L) есть сферическая кривая (сфера, на которой она
лежит, служит соприкасающейся сферой для всех точек (L)), то ребро
полярной поверхности стягивается в точку; поэтому для того, чтобы
линия (L) была сферическая, необходимо следующее условие:
Это условие также и достаточно, ибо оно означает, что для ребра
полярной поверхности -р = 0 и, следовательно, rc = const, т. е. ребро
стягивается в точку.
Из механических соображений предыдущего параграфа вытекает,
что (L) есть сферическая кривая. Геометрически это очевидно из того,
что соприкасающаяся сфера при неподвижном центре ие может менять
величины радиуса, ибо тогда линия (L) пересекала бы сферу, тогда
как она должна касаться ее. Аналитически постоянство радиуса
соприкасающейся сферы вытекает из формулы (10), которая дает
Итак, (13) есть натуральное уравнение сферических линий, что
прежде (§ 37, стр. 221) мы нашли на другом пути.
§ 55 . СПРЯМЛЯЮЩАЯ ПОВЕРХНОСТЬ И ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ 317
§ 55. Спрямляющая поверхность и геодезическая линия
Определение 1. Развертывающаяся поверхность F, огибающая
семейство спрямляющих плоскостей линии (L), называется спрямляющей
поверхностью линии (1Л
Пример 1. Спрямляюи^ая поверхность плоской линии (L) есть
цилиндрическая поверхность, образующие которой проходят через (L)
перпендикулярно к ее плоскости. Таким образом, образующая
спрямляющей поверхности есть в этом случае бинормаль (L).
Пример 2. Спрямляющая поверхность винтовой линии (L) есть
цилиндрическая поверхность F, на которой располагается линия (L).
Действительно, касательная плоскость поверхности F есть спрямляющая
плоскость винтовой линии, ибо главная нормаль совпадает с радиусом
цилиндра. В этом примере образующая спрямдяющей поверхности
не совпадает с бинормалью (L).
В противоположность полярной поверхности, спрямляющая
поверхность F всегда проходит через линию (L).
Действительно, уравнение спрямляющей плоскости есть
(J?-r)» = O. (1)
Слодуя общему методу § 52, мы найдем уравнение образующей
спрямляющей поверхности, присоединив к уравнению (1) уравнение
(Я-г)(-х*+с*) = 0, (2)
которое получено дифференцированием (1) по дуге линии (L). Мы видим,
что прямая (1), (2) проходит через точку М (г) линии (L). Направление
образующей определяется векторным произведениемг)
nx(-*t+ab)=xb + Gt. (3)
Если через а обозначить угол между образующей спрямляющей
поверхности и бинормалью линии (Z.), то
cos ос =
(За)
Название спрямляющей поверхность F и плоскость Р получили
благодаря следующему важному свойству поверхности F.
Теорема l.Mpu изгибании спрямляющей поверхности F линии
(L) на плоскости кривая (L) становится прямой линией.
Для доказательства этой теореАмы и обратной ей установим
предварительно следующие леммы.
Лемма 1. Пусть прямые ОАг, 0А21 составляющие бесконечно
малый угол о>, наклонены к оси OL под конечными углами у1? у2,
а плоскости А1ОА2У AXOL в пределе перпендикулярны. Тогда разность
у, — Yi имеет высший порядок относительно <о.
х) Этот вектор есть не чтю иное, как вектор Дарбу [формула (За) § 29, стр. 160].
Что образующая счрямляюцей юверхыостл коллинеарна с вектором Дарбу, видно и из
механических сооэражзний. Действительно, мы знаем, что вектор Дарбу (который
на фавлен по оси мгновенного вращения сопутствующего триедра) л^жит в с 1рям-
ляющей плоскости. Таким образом, спрямляющая плоскость ис 1ытывает вращение
около вектора Дарбу. Значит, этот вектор коллинеарен с пересечением бесконечно
близких С1фямляющих плоскостей.
318 ГЛ. VIII. РАЗВЕРТЫВМОЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
Доказательство. Отложим иа ОА1У ОА2 (рис. 190) равные
отрезки OAls=OAi = а и спроектируем их на OL. Проекции ОСХ, ОСi
разнятся на величину
С1С2 = a (cos у2 — cos yJ. (4)
С другой стороны, обозначая через ty угол между АХА2 и осью
OL{b =Z.AAiDi)> имеем
СХС2 = АХА2 cos <]> ^ аш cos <!>. (5)
Из (4) и (5) находим
cos у2 — cos Yi ^ «> cos ф. (6)
По условию, плоскость ОАХА2 в пределе перпендикулярна к плоскости
AXOL. Кроме того, прямая АХА2, лежащая в плоскости ОАХА2, в
пределе перпендикулярна к прямой ОАХ (лежащей
в плоскости AOL), ибо в равнобедренном
треугольнике АХОА2 угол (о бесконечно мал.
Следовательно, АХА2 в пределе перпендикулярна
к плоскости AXOL. Значит, угол ф
эквивалентен прямому. В силу (6) величина cosy2 —
— cosYi имеет высший порядок
относительно to, а так как угол Yi конечный, то из
соотношения
cos y2 - cos Yi ^ sin yx (yx - y2)
(выражающего, что приращение функции co*y
эквивалентно ое дифференциалу) видно, что
и Yi~~ Y2 имеет высший порядок относительное!).
Имеет место и обратное предложение.
Лемма 1а. Если при обозначениях
леммы 1 разность у2 — Yi имеет высший порядок
относительно со, то плоскость Ах0Ао в
пределе перпендикулярна к плоскости AXOL.
Для доказательства достаточно обратить
рассуждение предыдущей леммы.
Лемма 2. Пусть {к} (рис. 191) есть
семейство прямых X, лежащих в одной пло-
Рис. 190. скости, и $ — угол, образуемый прямой )<
с прямой UV, лежащей в той же
плоскости. Тогда имеет место соотношение
где индексами 1, 2 обозначены величины, относящиеся к двум
произвольным прямым семейства {X}.
Замечание. Начальный луч угла ji направлен по X,
конечный—по UV. Направление того и другого луча на соответствующей
прямой безразлично, лишь бы направление луча на X менялось
непрерывно.
• Для доказательства достаточно провести через произвольную точку О
(рис. 192) лучи ([xj, (|*2), соответственно параллельные лучам (XJ, и
(д2), и луч OW, параллельный UV.
Имеет место и обратное предложение.
§ 55. СПРЯМЛЯЮЩАЯ ПОВЕРХНОСТЬ И ГЕОДЕЕИЧЕСКАЯ ЛИНИЯ
319
Лемма 2а. Пусть {X} есть семейство прямых, лежащих водной
плоскости, и $—угол, образуемый при пересечении прямой (X)
с некоторой линией UV, лежащей в той же плоскости. Если всегда
имеет место соотношение
P,-Pi=-(Cb,), (8)
то линия UV — прямая.
Доказательство. Проведем (рис. 193) лучи 0Slt OS^,
параллельные касательным Л/ijT,, М2Т2 в точках встречи прямых (/.,), (>,2) с UV;
Рис. 193.
проведем также лучи OLX, OL21 параллельные (Хх), (Х2). Мы имеем:
32 - Рх - Z SXOS2 - Z LXOL2 = Z(MJly MJ2) - (О.)- (9)
Сравнение (8) и (9) дает
т. е. все касательные к UV имеют одно и то же направление. Значит,
линия UV — прямая.
320 ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
Переходим теперь к доказательству теоремы 1.
Сперва рассмотрим случай, когда спрямляющая поверхность F
линии (L) — ци л ин дри чес к аи (как у винтовой линии). Проведем
через бесконечно близкие точки М17 М2 линии (L) (рис. 194) образующие
(лх), (Х2) и обозначим через ух, у2 углы, которые Э1и образующие
составляют с касательными М1Т11 М2Т2. Докажем, что углы ух и у2 равны.
Проведем через Ми М2 касательные плоскости Рк, Р2 к
поверхности F, т. е. спрямляющие плоскости линии (L). Пусть СЕ —
прямая их пересечения. Через
какую-либо точку О прямой
СЕ проведем ОА1\\М1Т1 и
ОА21| М2Т2. Плоскость АХОА%
в пределе параллельна
соприкасающейся плоскости
линии (L), т. е. в пределе
перпендикулярна к
спрямляющей плоскости Рг. Прямые
ОА1У ОА2 по построению
составляют с СЕ углы Yi» Y2*
Эти углы —конечные, ибо
образующая спрямляющей
поверхности линии (L) не
может совпадать с касательной
к (/-), как легко видеть из
формулы (3).
Согласно лемме 1, углы
Yi и у2 [»азннтся на
величину высшего порядка
относительно угла со = АгОА2,
который есть не что иное,
как угол смежности
касательных (L). Значит, y2—Ti
имеет высший порядок и
относительно дуги МХМ2, т. е.
-~- = 0, откуда y = const,
Рис. 194. т. е. разность у2 — уа есть
точный нуль.
Мы видим, что линия (L) есть линия откоса цилиндрической
поверхности F.
Развернем теперь поверхность F на плоскость. При этом семейство
образующих (л) перейдет в семейство параллельных прямых на
плоскости, а угол y сохранит свою величину, т. е. останется постоянным.
Значит, линия откоса (L) перейдет в прямую, что и доказывает
теорехму 1 для случая цилиндрической поверхности.
В случае, когда F является конической поверхностью или
поверхностью касательных, доказательство несколько усложняется.
Пусть, например, F есть конус (рис. 195). Выполнив то же построение
с теми же обозначениями, мы, как в первом случае, докажем, что
Y2 — Yi имеет высший порядок относительно дуги МХМ2. Однако
теперь углы Yi, Y2 составлены касательными М1Т11 М2Т2 не с
образующими (>чХ), (>ч2), а с прямой СЕ, по которой пересекаются
касательные плоскости Р1} Р2.
§ 55, СПРЯМЛЯЮЩАЯ ПОВЕРХНОСТЬ И ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ 321
Что касается углов рх, [32, которые составлены касательной М1Т1
с образующей (Xj) и касательной М2Т2 с (Х2), то они разнятся от углов
у2 соответственно на величины того же порядка, что сами утлы
у2- Именно, обозначив через Rly R2 точки пересечения М1Т1, М2Т.
Е мы из треугольников
^С, MtR2C найдем
уи у2
с СЕ,
x = Ti + ?i. \
откуда
Р2 —Pi=Y2 —Yx —(Т2 + Тх). (11)
Обозначив через ш1 угол
между образующими (Хх), (к2), мы
в силу леммы 4 § 26 (стр. 135)
имеем
«>1^?1 + <Р2. (12)
С другой стороны, разность
у2 — ух имеет по доказанному
высший порядок относительно
М1М2) а значит, и относительно
<ох (теорема синусов,
примененная к треугольнику МХСМ2).
Поэтому (11) можно записать
в виде
Развернем теперь
поверхность F (коническую или
поверхность касательных) на
плоскость.
Семейство образующих (X)
перейдет в семейство прямых (к)
на плоскости (в случае конуса
это —пучок): углы [S сохранятся
в точности:
Докажем, что угол ш^ образованный прямыми (>ч) и (Х2), будет
эквивалентен углу о)1:
о^^а)^ (15)
Пусть сначала F есть коническая поверхность (рис. 195). Проведем
дугу GXG2, ортогональную к образующим; она сохранит свою длину
и наложится на дугу окружности радиуса CGX. Таким образом, будем
иметь
а из треугольника CG1G2 имеем
откуда и следует (15).
21 М. Я. Выгодский
322 ГЛ. VIII. PAF BE РТЫ БАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
Для поверхности касательных (рис. 196) эквивалентность (15) можно
доказать так1). Рассмотрим бесконечно малую дугу NXN2 ребра
возврата (/). Обозначим через х кривизну ребра (/) и через Nly /V2 —точки
Рис. 196.
касания (XJ, (X2) с ребром; тогда
ш1^х • NJV2. (16)
Аналогичное соотношение имеем для а^:
u^x-N^N^. (16а)
Но как кривизна, так и дуга ребра остаются при изгибании на
плоскость неизменными (теорема 4 § 48, стр. 285), т. е.
Следовательно, ш, =<й1.
Сопоставляя, (13), (14) и (15), мы имеем как для конуса, так и для
поверхности касательных
Докажем, что эта эквивалентность есть точное равенство.
Действительно, угол (о равен приращению Д[* угла р, который прямая (а)
образует с каким-либо направлением на рассматриваемой плоскости. Поэтому
') Соотношение (12) доказывается так же, как для конической поверхности;
то, что Ах и А2 пересекают СЕ в двух разных точках С и D, не играет никакой
роли.
$ 55. СПРЯМЛЯЮЩАЯ ПОВЕРХНОСТЬ И ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ 323
(17) можно написать в виде
Значит,
dl- 1
откуда
Pa-Pi=-(l*,-^i)=-(/^>M). (18)
Следовательно (лемма 2а), линия (Z), в которую превращается (L) после
наложения на плоскость, —-прямая. Этим теорема 1 полностью доказана.
Имеет место также и обратное предложение:
Теорема 2. Если при изгибании развертывающейся поверхности F
на плоскость линия (L) становится прямой, то F есть спрямляющая
поверхность линии (L).
Доказательство. По условию линия (L) (мы сохраняем
обозначения теоремы 1) —прямая. Поэтому (лемма 2)
?.-?i=-(>u,S)= -п. (19)
Если угол (о всегда равен нулю, то семейство прямых (X) есть
параллельный пучок; прямая (L) пересекает все прямые (/,) под одним
и тем же углом. Значит, поверхность F — цилиндрическая, линия (L)
есть линия откоса, а для линии откоса соприкасающаяся плоскость
перпендикулярна к касательной плоскости поверхности F (§ 20,
пример 2, стр. 90), т. е. касательная плоскость Р поверхности F есть
спрямляющая плоскость линии (L).
Если же угол о> не равен нулю, го F будет конусом или
поверхностью касательных, и для доказательства теоремы 2 достаточно обратить
рассуждение теоремы 1, применив леммы 1а и 2 вместо лемм 1 и 2а.
Читателю рекомендуется провести это доказательство.
Аналитическое доказательство теорем 1 и 2. Пусть
t, я, Ъ суть орты касательной, главной нормали и бинормали ребра
возврата поверхности F, t1 — орт касательной линии (L) и а —угол
между линией (L) и образующей поверхности S. Тогда вектор tx
выражается через векторы /, п формулой
tx = cos a t + sin а п. (20)
П\сть известно, что F есть спрямляющая поверхность линии (Z.), т. е.
что" касательная плоскость F является спрямляющей плоскостью (L).
Заметив, что касательная плоскость к F есть соприкасающаяся
плоскость ребра (/), мы видим, что орт бинормали b ребра (/) коллинеарен
с главней нормалью линии (Z.); эта главная нормаль коллинеарна с век-
dtx dtx ds dt
тором -3—= -^r jf и, следовательно, с вектором -~ .
Дифференцируя (20), находим
(21)
Коллинеарность ~- и Ь имеет место в том и только в том случае,
если
(22)
21*
324 ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
Согласно лемме 2а, линия, в которую обратится кривая (L) при
развертываний F на плоскость, будет прямой. Этим доказана
теорема 1.
Обратно, пусть известно, что линия (L) при развертывании F на
плоскость делается прямой. Тогда, согласно лемме 2, имеет место
уравнение (22); из уравнений (22) и (21) вытекает коллинеарность векторов
-г-1 и Ь; значит, главная нормаль линии (L) совпадает с нормалью к
поверхности F, т. е. спрямляющая плоскость линии (L) —с касательной пло-
cKOCTbto F. Этим доказана теорема 2.
Из теоремы 2 тотчас же вытекают следующие предложения:
Теорема 3. На каждой развертывающейся поверхности F через
любую ее точку К по любому заданному в этой точке направлению (не
совпадающему с направлением образующей)
можно провести линию (L), для которой F
будет спрямляющей поверхностью.
Для доказательства достаточно
изогнуть F на плоскость, затем провести через К
прямую по заданному направлению и,
наконец, снива изогнуть поверхность в прежнее
положение. Подобным же образом докажем
и другое важное предложение:
Теорема 4. Если дуга АВ кривой
линии (L) есть кратчайший (на
поверхности) путь между точками А и В
развертывающейся поверхности F, то F есть
спрямляющая поверхность линии (L).
Обратное предложение также
справедливо, но с существенной оговоркой.
Теорема 5. Если развертывающаяся
поверхность F есть спрямляющая
поверхность линии (L) и если кусок S этой
поверхности можно целиком наложить на
плоскость, не производя на нем разрезов, то
любая дуга АВ линии (L) есть кратчайший
(на куске S) путь между точками А и В.
Действительно, согласно теореме 1 при
р 197 изгибании S на плоскость дуга АВ станет
отрезком прямой линии, и путь АВ = 1 будет
кратчайшим как на плоскости, так и на поверхности S.
Замечание. Оговорка, содержащаяся в условии теоремы 5 и
требующая, чтобы кусок S развертывающейся поверхности F можно было
наложить на плоскость, не производя разрезов, является существенной.
Если это требование не соблюдается, то наше доказательство теряет
силу, так как, производя разрезы, мы можем разорвать сплошную линию
поверхности F на разрозненные части.,
Так, например, цилиндрическая поверхность F (рис. 197) есть
спрямляющая поверхность для винтовой линии AUVBH. Дуга AU этой
линии есть кратчайший путь между её концами А и U; но дуга AUVB
этой линии уже не даёт кратчайшего расстояния между точками А и В
на цилиндрической поверхности, ибо точки А и В можно соединить
дугой винтовой линии АСВ, которая и служит кратчайшим путём.
§ 55. СПРЯМЛЯЮЩАЯ ПОРЕРХНОСТЬ И ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ 325
Наше доказательство здесь нельзя провести потому, что всякий
разрез, позволяющий изогнуть цилиндрическую поверхность F на
плоскость, непременно рассечет линию AUVB надвое или на большее
число частей.
Дуга AUV винтовой линии AUVBH также не даёт кратчайшего
расстояния между её концами А и У. В этом случае можно произвести
разрез, не рассекающий линии AUV, так что после изгибания
поверхности F на плоскость линия AUV станет прямой. Но при этом порвется
связь между точками А и V вдоль образующей, в то время как именно
отрезок AV образующей и даёт кратчайшее расстояние между А и V.
Оговорку, содержащуюся в теореме 5, можно видоизменить,
сформулировав следующее предложение.
Теорема 5а Если развертывающаяся поверхность F есть
спрямляющая поверхность линии (/.), то достаточно малая дуга АВ
линии (L) есть кратчайший путь между А и В.
В начале этого параграфа мы определили спрямляющую
поверхность Е как огибающую спрямляющих плоскостей данной линии (L).
Чаше приходится итти обратным пз^тем: исходить из данной
поверхности F и на ней строить линию (L). Тогда линия (L) называется
геодезической линией поверхности F. В связи с этим определение 1
(на сгр. 317) можно сформулировать в иной форме следующим образом.
Определение 1а. Линия (Z.) на (развертывающейся)
поверхности F называется геодезической линией этой поверхности, если ее
спрямляюшан плоскость совпадает с касательной плоскостью этой
поверхности.
Мы взяли слово «развертывающейся» в скобки, потому что
определение 1а можно, очевидно, распространить на случай любой
поверхности, а так как спрямляющая и соприкасающаяся плоскости всякой
линии (L) взаимно перпендикулярны, то определение 1а (отнеся его
к любой поверхности) можно высказать в следующей форме.
Определение 2. Линия (L) на поверхности S называется
геодезической линией этой поверхности, если в любой ее точке М
соприкасающаяся плоскость линей (Z.) перпендикулярна к касательной плоскости
поверхности S в той же точке.
Так, на поверхности сферы всякий большой круг является
геодезической линией; ьа поверхности вращения всякий меридиан есть
геодезическая линия.
К числу геодезических линий относят также всякую
прямолинейную образующую. Так как спрямляющая плоскость для прямой линии
остается неопределенной, то ее можно считать совпадающей с
касательной плоскостью поверхности 5, и тогда определение геодезической
линии остается в силе для прямой линии. Так, образующая геликоида
есть его геодезическая линия. «Спрямляющая плоскость» ее не остается
постоянной, но вращается около образующей.
Теперь мы можем сформулировать доказанные выше теоремы
следующим образом.
Теорема 1. При изгибании развертывающейся поверхности F на*
плоскость все геодезические линии становятся прямыми.
Теорема 2. Если при изгибании развертывающейся поверхности
на плоскость линия (L) становится прямой, то она есть геодезическая
линия поверхности.
326 ГЛ. VIII. РАЯВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
Теорема 3. На каждой развертывающейся поверхности через
любую ее точку в любом направлении можно провести геодезическую линию.
Теорема 4. Если дуга АВ линии (L) есть кратчайший путь
между точками А и В развертывающейся поверхности, то (L) есть
геодезическая линия.
Теорема 5. Достаточно малая дуга АВ геодезической линии
развертывающейся поверхности есть кратчайший путь между А и В.
Теоремы 3, 4 и 5 ос!аются в силе и для неразвертывающихся
поверхностей, что будет позднее (§ 73) доказано.
Упражнения
1. Доказать аналитически теоремы 1 и 2 для цилиндрических и конических
поверхностей.
2. Доказать, что спрямляющая поверхность всякой линии откоса есть
цилиндрическая поверхность.
3. Доказать, что все геодезические линии цилиндрической поверхности суть
ее образующие и линии откоса.
4. Найти общее уравнение геодезической линии на поверхности круглого
конуса.
5. Доказать, что если развернутый угол круглого конуса больше или равен
180°, то его геодезические линии не имеют самопересечения.
6. Доказать, что если развернутый угол круглой конической поверхности
равен 90°, то всякая геодезическая линия имеет одну точку самопересечения
7. Сколько точек самопересечения имеет геодезическая линия круглой
конической поверхности, у которой угол осевого сечения равен 15°?
8. Найти общее уравнение геодезической линии на поверхности касательных
винтовой линии.
§ 56. Эволюты и эвольвенты пространственных кривых
В § 27 мы изучили свойства эвольвенты и эволюты плоской
кривой. Часть этих свойств (например, теоремы 4 и 4а § 27, стр. 142)
теряют свою силу при рассмотрении пространственных кривых. Однако
некоторые свойства уже в § 27 были доказаны для любой линии, как
плоской, так и пространственной. Перечислим эти предложения и заодно
напомним определение эвольвенты и эволюты.
Определение. Эвольвента (к) линии (L) (рис. 198) есть место
концов отрезков ее касательных, длины которых убывают па величину,
равную приращению дуги линии (L). Если (к) есть эвольвента линии (/-),
то (L) называется эволютой линии (к).
Механически эвольвента (д) получается из эволюты (L)
наматыванием или разматыванием па (L) гибкой норастяжимой нити, один
конец которой закреплен; другой конец описывает линию (к).
Теорема 1. Длина дуги эволюты равна разности отрезков
касательных эволюты в концах дуга (AM = AB — MN).
Теорема 2. Всякая линия имеет бесчисленное множество
эвольвент.
Теорема 3. Касательные эволюты (MN на рис. 198) являются
нормалями эвольвенты (к); иными словами:
Теорема За. Эвольвента (к) есть ортогональная траектория
^касательных эволюты (L).
Теорема 36. Всякая ортогональная траектория (к) касательных
кривой (L) есть эвольвента этой кривой.
Для пространственных линий теорему За можно высказать еще
следующим образом.
§ 56. ЭВОЛЮТЫ И ЭВОЛЬВЕНТЫ ПРОСТРАНСТВЕННЫХ КРИВЫХ 327
Теорема Зв. Эволюта (L) есть ребро возврата развертывающейся
поверхности S нормалей эвольвенты (>ч).
Замечание. Следует предостеречь читателя от возможной ошибки:
нормали неплоской эвольвенты (к), порождающие развертывающуюся
поверхность касательных эволюты (L), ни в каком случае не являются
главными нормалями линии (к). Действительно, в § 53 (стр. 307) было
доказано, что поверхность главных нормалей неплоской кривой —косая.
Разумеется, вполне возможно, что одна из касательных MN эволюты
служит главной нормалью эвольвенты ().). Но тогда остальные нормали
в окрестности точки N — не главные.
В § 27 теорема За и обратная ей теорема 36 были доказаны
синтетически. Приведем здесь аналитическое их доказательство.
Рис. 198.
Доказательство теоремы За. Пусть г есть вектор точки
эволюты, /-J —вектор эвольвенты, / —длиш отрезка MN, /0 — длина
начального отрезка АВ. Приняв за начало дуг эвольвенты точку ^4(5 = 0),
мы имеем, согласно определению эвольвенты, следующее уравнение:
r.-r + tfo-*)*. " (1)
откуда
что выражает равнонаправлепность касательной эвольвенты и главной
328 ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
нормали эволюты, т. е. перпендикулярность эвольвенты и касательной
к эволюте.
Доказательство теоремы 36. Всякая точка линии (X)
принадлежит некоторой касательной линии (Z.); значит, мы имеем
rx = r + lt. (3)
Далее, во условию касательная к линии (X) перпендикулярна к
касательной кривой (Z.), т. е.
Уравнения (3) и (4) дают
откуда
4 + ;г!=0- (5)
Интегрируя при начальных условиях 5 = 0, 1=10, находим
l = l.-s, (6)
т. е. длина отрезка касательной кривой (Z.) убывает на величину,
равную приращению её дуги. Значит, (X) есть эвольвента линии (I).
Формула (1), где 10 рассматривается как произвольная величина,
дает в векторной форме уравнение всех эвольвент данной линии r = r (s).
Пример 1. Найдем уравнения эвольвенты окружности
, z = 0.
За начало отсчета дуг возьмем точку (1; 0), тогда s — au.
Согласно формуле (1), эвольвента окружности представляется
уравнениями
хг = acosM — (lo — au)sinu, ух = я sin м + (/0 — aa)cos и, z1 = 0. . (7)
Так как окружность может, вращаясь около центра Оу двигаться
сама по себе, то все ее эвольвенты конгруентны между собой и
отличаются только положением точки возврата К. Если ось х направить по
лучу ОК1 то в уравнениях (7) нужно будет положить /0 = 0, и они
примут тот вид
хг — а (cosm + m sin к), ух = a (sin а — и cos и), ^^О,
в котором мы их получили в примере 2 § 15 (стр. 169).
Пример 2. Найдем уравнения эвольвенты винтовой линии
x=acosu, y = i b
Можно положить s=|/ a2 + b2 и. Формула (1) даег
хх = а cos и — (10 — 1/ а2 + 6J м; -^
= a cos и + аи sin и °а sin и,
a cos и
= a sin u — au cos и -\—> °g cos w,
§ 56. ЭВОЛЮТЫ И ЭВОЛЬВЕНТЫ ПРОСТРАНСТВЕННЫХ КРИВЫХ 329
Сравнив эти уравнения с уравнениями (7), мы видим, что эвольвенты
любой винтовой линии, нанесенной на цилиндр радиуса я, тождественны
с эвольвентами окружности, лежащей в основании цилиндра.
Впрочем, это сразу видно геометрически. Действительно,
проектируя винтовую линию с ее касательными на плоскость основания
цилиндра, мы получаем окружность с ее касательными. При этом длина всех
дуг и отрезков уменьшается в постоянном отношении, а потому
эвольвента винтовой линии проектируется эвольвентой окружности.
Касательная к эвольвенте (д) {ВТ на рис. 198), как явстьу т из
теоремы За, параллельна некоторой нормали ^45 эволюты (L) в
соответственной точке А. Важно
заметить, что эта
нормаль— главная, т. е.
имеет место следующая
теорема.
Теорема 4.
Касательная к
эвольвенте параллельна главной
нормали эволюты.
Действительно,
эвольвента (/,) .иежит на
поверхности S
касательных эволюты (Z.);
значит, касательная
эвольвенты ВТ (рис. 198)
лежит в касательной
плоскости поверхности 5,
т. е. в
соприкасающейся плоскости эволюты.
Сверх того, (X)
перпендикулярна к
касательной АВ эволюты.
Значит, она параллельна
главной нормали
эволюты [что видно и из
формулы (2) настоящего Рис> 199.
параграфа].
Из теоремы 4 тотчас же следует, что для всякой кривой имеет
место следующее предложение, которое в § 27 (стр. 140) было
доказано только для плоской кривой.
Теорема 5. Точка К, общая эволюте и эвольвенте, есть точка
возврата эвольвенты.
Действительно, эвольвента располагается в окрестности К со
стороны выпуклости эволюты, и при приближении к точке К с обеих
сторон касательная эвольвенты, согласно теореме 4, стремится к главной
нормали в точке К. Таким образом, в точке К направление эвольвенты
меняется на противоположное.
Теорема 6. Эволюта (L) лежит на полярной поверхности F
эвольвенты (к) и является геодезической линией полярной поверхности F.
Доказательство. Так как касательная MN (рис. 199) эволюты
(L) есть нормаль эвольвенты (X), то MN лежит в нормальной плоскости Р
эвольвенты. Так как главная нормаль MR эволюты параллельна
касательной NT эвольвенты (теорема 4), то плоскость Р, сверх того,
перпендикулярна к главной нормали MR. Значит, плоскость Р является
330 ГЛ* VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
спрямляющей плоскостью эволюты (L). Следовательно, огибающая F
плоскостей Р (полярная поверхность эвольвенты) есть спрямляющая
поверхность эволюты (L). Поверхность F проходит (§ 55) через линию (L),
которая является (определение 1а § 55, стр. 325) ее геодезической линией.
Замечание 1. Тот факт, что эволюта (L) лежит на полярной
поверхности эвольвенты (X) другими словами выражается так: точка М
эволюты лежит на оси кривизны СМ эвольвенты.
Риг. 200.
Замечание 2. Не следует думать, что всякая геодезическая
линия полярной поверхности F линии ().) является эволютой линии (/*).
Какие геодезические линии поверхности F являются эволют ами линии (а),
будет видно из доказательства теоремы 7.
Теорема 7. Каждая линия (к) (отличная от окружности) имеет
бесчисленное множество эволют.
Доказательство. На попярной поверхности F (рис. 200) линии
()ч) возьмем произвольную точку М и соединим ее с той точкой N,
где касательная плоскость Р поверхности F встречает /,.
§ 56. ЭВОЛЮТЫ И ЭВОЛЬВЕНТЫ ПРОСТРАНСТВЕННЫХ КРИВЫХ 331
Это построение определяет для каждой точки М поверхности
единственное направление, по которому может проходить через М эволюта
линии (л). Этим на поверхности определяется целое семейство линий (L),
каждая из которых во всех своих точках имеет установленное
направление (ср. § 51 и рис. 185 на стр. 299). Легко видеть, что все линии (L),
построенные таким образом, действительно являются эволютами линии
(а). В самом деле, так как плоскости Р суть нормальные плоскости линии
(а), то касательные MN линий (Z.) суть нормали линии (а), и, согласно
теореме 36, (а)есть эвольвента линии (Z.), т. е. (L) есть эволюта линии (л).
Замечание 1. Окружность не имеет эволют, потому что ее
полярная поверхность вырождается в прямую линию—ось окружности. Можно
сказать, что все эволюты окружности вырождаются в точки. С другой
стороны, окружность—единственная линия, у которой полярная
поверхность вырождается.
Замечание 2. Если полярная поверхность F есть произвольный
конус с вершиной О, что имеет место в том и только в том случае,
когда (а) лежит (§ 53, стр. 310) на сфере с центром О, то вершину О
можно рассматривать как выродившуюся эволюту линии (а). Остальные
же эволюты суть (невыродившиеся) геодезические линии конуса.
Замечание 3. Как мы знаем (теорема 4 § 27, стр. 142), всякая
плоская линия (\) (отличная от окружности) имеет единственную
эволюту, лежащую в ее плоскости. Это —место центров кривизны линии
(а). Из теоремы 6 следует, что все остальные эволюты линии ()) —
неплоские. Они являются геодезическими линиями цилиндрической
полярной поверхности, т. о. линиями откоса (§ 55, теорема 1, стр. 320,
случай цилиндрической поверхности).
Теорема 8. После развертывания полярной поверхности F линии (к)
на плоскость, эволюты линии (X) образуют пучок прямых.
Доказательство. Будем изгибать F (рис. 200) таким образом,
чтобы одна ее образующая М'ММ" и касательная плоскость MM'N,
проходящая через эту образующую, оставались неподвижными. Тогда
при изгибании F эволюты (£), (£'), (L") и т. д. линии (X), деформируясь,
продолжают касаться прямых /1/7V, M'N, M"N и т. д., сходящихся
и точке Л7. После того как F и а ложится на плоскость MM'N, эволюты
(L), (U) (£"), которые по доказанному в теореме 6 являются
геодезическими линиями, станут прямыми (§ 55, теорема 1, стр. 317).
Следовательно, они совпадут с прямыми MN, M'N, M"N, образующими
пучок с центром в N.
Теорема 9. Касательные MN и M'N к двум эволютам (L) п (/.')
(рис. 200), проходящие через одну и ту 'же точку N эвольвенты X,
пересекаются в ней под постоянным углом а.
Доказательство. Угол & между касательными MN и M'N
(рис. 200) есть ничто иное, как угол между теми двумя прямыми,
на которые согласно предыдущей теореме наложатся эволюты (L) и (£'),
если поверхность F изогнуть на плоскость. Поэтому тот же уюл а
составят касательные М^г и M[Nly M.,N2 и M'2N2 и т. д.
Следствие. Если (X) есть сферическая линия, то касательная MN
к какой-либо ее эволюте (L) (рис. 201) образует постоянный угол с
радиусом сферы N0.
Для доказательства проведем на полярной поверхности F (это —
коническая погерхность с вершиной в центре сферы О) эволюту (//)
черег* точку М\ близкую к центру О. Касательная M'N составляет
с MN некоторый угол а', который остается по доказанному неизменным
для данной пары эволют. Теперь заставим М' приближаться к центру О.
332 гл. уш. развертывающиеся поверхности, эволюты
M'N будет иметь пределом радиус ON. Одновременно и остальные
точки эволюты (L') стремятся к О, так что угол MNO = а есть предел угла
а' для всех точек эволюты (Z.). Следовательно, угол а сохраняет
постоянное значение при движении М по (£). (Ср. замечание 2 к теореме 7.)
Рис. 201.
Теорема 10. Если два семепстза нормалей линии (X) образуют
две развертывающиеся поверхности Sx и S21 то образующие этих поверх-
ногтей пересекаются на (л) под постоянным углом а.
Доказательство. Пусть обе развертывающиеся поверхности
$1> $2 суть поверхности касательных (рис. 200, стр. 330). Тогда их ребра
возврата (I'), (£") суть эволюты линии (X), и, согласно теореме 9, угол а
между образующими M'N и M"N остается постоянным.
Переходим к рассмотрению случаев, когда одно или оба ребра (L')t
(£") вырождаются в точку (развертывающаяся поверхность — коническая)
или одно ребро уходит в бесконечность (развертывающаяся
поверхность — цилиндрическая *)).
Если #! —поверхность касательных, a S2 — коническая поверхность
с вершиной О, то (к) лежит на сфере с центром в О (рис. 201), и
постоянство а вытекает из следствия теоремы 9.
2) Поверхности Slt S2 не могут быть обе цилиндрическими, что видно из
дальнейшего.
§ 56. ЭВОЛЮТЫ И ЭВОЛЬВЕНТЫ ПРОСТРАНСТВЕННЫХ КРИВЫХ 333
Если как а?!, так и 32 суть конические поверхности с вершинами
0г, 02, то все нормальные плоскости линии (д) проходят через
прямую ОгО2. Значит, (д) должна быть ортогональной траекторией пучка
плоскостей с осью 0102, т. е. окружностью (ось ОгО2 есть ее
вырожденная полярная поверхность *)). В этом случае одна из развертывающихся
поверхностей нормалей будет круглым цилиндром с осью ОХО2У а все
остальные (в том числе Sx и S2) — круглыми коническими поверхностями
Рис. 292.
с вершинами, лежащими на оси ОХО2. Очевидно, теорема 8 и в этом
случае справедлива.
Пусчь, наконец, St есть цилиндрическая поверхность. Тогда (д)
есть плоская линия (перпендикулярное сечение поверхности Sx). Случай,
когда (д) есть окружность, уже рассмотрен. Если же (д) не является
окружностью, то полярная поверхность есть (невырожденная)
цилиндрическая поверхность F (рис. 202); ее сечение плоскостью линии (д)
есть плоская эволюта (L) линии (д).
Так как все нормали линии (X), кроме образующих поверхности Sly
пересекают каждая свою ось кривизны, то поверхность S2 не может
быть ни цилиндрической, ни конической. Ее ребро (£') (это— линия
откоса) лежит на полярной поверхности F и является эволютой линии (к).
Согласно теореме 9, образующие NM2 поверхности S2 составляют
постоянный угол р с образующими NM> касающимися плоской эволюты.
Следовательно, они составляют постоянный угол а = 90° с образующими
поверхности St.
Итак, теорема 10 справедлива для всякой линии д. Имеет место
и обратное предложение:
Таким образом, если Sx и £а—конические поверхности, то обе—круглые.
334 , ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
Теорема 11. Если все образующие развертывающейся
поверхности S нормалей линии (X) повернуть в соответствующих нормальных
плоскостях на постоянный угол а, то новая поверхность нормалей S'
также будет развертывающейся.
Доказательство. В общем случае развертывающаяся
поверхность S имеет невырожденное ребро возврата (£) — одну из эволют
линии (X) (рис. 200, на cip. 330). Повернем одну образующую iV/l/
поверхности S на угол а в положение NM'. Пусть М' есть точка
касания NM с полярной поверхностью F линии (/,) [М' лежит на оси
кривизны л:инии (к)]. Через точку М' проведем эволюту (U) (теорема 7).
Каждая касательная эволюты (Z/) пересечет соответствующую
касательную эволюты (L) под одним и тем же углом а (теорема 9) и,
следовательно, сорпадет с образующей поверхности нормалей S'.
Следовательно, S' есть развертывающаяся поверхность касательных к (Z/), что
и утверждается в теореме 11.
В исключительном случае одна из эволют (L), (Z/) может
выродиться в точку [тогда (X)— сферическая линия] или уйти в
бесконечность [тогда (X) —плоская кривая]. Читателю предлагается
соответствующим образом видоизменить доказательство.
В следующей теореме мы встретимся с терминами «полная
кривизна» и «полнее кручение»; объясним их.
Для характеристики искривленности линии в данной ее точке мы
ввели величину x = lim~, которую мы назвали кривизной. Для
характеристики искривленности линии на данном ее участке нужно ввести
в рассмотрение другую величин}7.
Для плоской выпуклой кривой в качестве гакой величины
можно взять просто угол между касательными в концах дуги. Но
для неплоской линии эта мера искривленности является мало
подходящей, потому что, например, угол между касательными к
винтовой линии в концах одного ее завитка равен нулю. Поэтому за меру
искривленности дуги пространственной кривой в целом лучше принять
сумму поворотов, которые совершает касательная на малых участках
рассматриваемой дуги. Сообразно с этим мы можем установить
следующее определение.
Определение 1. Полной (или интегральной) кривизной К дуги АВ
называется предел, к которому стремится сумма углов смежности о>
касательных, когда наибольший из участков, на которые разбита дуга АВ,
стремится к нулю:
2 (9)
As-M)
Так как cd^xAs, to формула (9) дает
т. е.
в
(*. (10)
§ 56. ЭВОЛЮТЫ И ЭВОЛЬВЕНТЫ ПРОСТРАНСТВЕННЫХ КРИВЫХ 335
Так как бесконечно малый угол поворота касательной эквивалентен
соответствующей дуге индикатрисы касательной, то полную кривизн\г
дуги АВ можно определить так же, как длину соответствующей дуги
А1В1 индикатрисы касательных.
Совершенно аналогично определяется полное кручение.
Определение 2. Полным (или интегральным) кручением )±
дуги АВ называется предел, к которому стремится алгебраическая
сумма углов смежности а/ бинормалей1), когда наибольший из
участков, на которые разбита дуга АВ, стремится к нулю:
As-И)
откуда
ь
V
2=Л ads.
А
Если кручение не меняет знака на дуге АВ, то абсолютная
величина полного кручения равна длине соответствующей дуги А3В3
индикатрисы бинормалей.
После этих объяснений вернемся к эволютам и эвольвентам и
поставим задачу о разыскании всех эволют данной линии (X).
Эту задачу мы уже рассматривали в теореме 7, где было доказано
существование искомых эволют. Но для построения их мы еше не имеем
удобного способа2). Ниже дан такой способ.
Возьмем на (X) некоторую точку No (рис. 203) и проведем через
нее произвольную нормаль NJM^> встречающую соответствующую ось
кривизны (Zo) в точке Л/о. Чтобы отыскать эволюту (L), проходящую
через Л/о, мы должны для каждой точки N линии (X) найти такую
нормаль, которая в пересечении с соответствующей осью кривизны (/)
дала бы точку М искомой эволюты. Для этого достаточно знать угол р
между (/) и NM, а этот угол можно определить, опираясь на следующую
теорему.
Теорема 12. Приращение угли В = /^KMN\ на который нужно
повернуть ось кривизны NK линии (X) до совмещения с касательной МN
фиксированной эволюты (L) линии (X), равно взятому с обратным знаком
полному кручению соответствующей дуги эвольвенты (К):
ds. (12)
При этом вращение оси кривизны считается положительным, если оно
совершается от орта b линии (X) к ее орту п.
Доказательство. Эволюта (L) линии (X) есть геодезическая
линия ее полярной поверхности F (теорема 6), а р== /^KMN есть угол
1) Угол <«/ считается положительным, если бинормаль в точке М вращается
около касательной против часовой стрелки при приближении точки М к
наблюдателю (с какой стороны от точки М он находится—безразлично). Иными словами,
углу о/ приписывается тот же знак, что и кручению с.
2) Следуя методу, изложенному в теореме 7, мы должны построить на
полярной поверхности семейство эволют по заданному «полю направлений», что
аналитически равносильно заданию дифференциального уравнения. Излагаемое здесь
решение позволяет построить эволюту «по точкам», что аналитически равносильно
решению упомянутого дифференциального уравнения.
336 ГЛ. VIII. РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ. ЭВОЛЮТЫ
между образующей этой полярной поверхности и направлением
геодезической линии (L). Рассмотрим бесконечно малую дугу МгМ2 линии (L).
По доказанному в теореме 1 § 55 (стр. 321), мы имеем
где ш есть угол между бесконечно близкими образующими M1KltM2K2.
йнак величины о) устанавливается в соответствии с направлением
вращения на плоскости Р, на которую изгибается F. За плоскость Р мы
Рис. 203.
можем принять касательную плоскость K1MlN1 поверхности F, т. е.
нормальную плоскость лиыьи (/„). Следовательно, угол ш по величине
и по знаку1) равен углу смежности со'бинормалей линии (л), т. е.
Др = р,-р1«-ш'1 (13)
откуда
ads, (14)
1
что и доказывает теорему 12.
На основании этой теоремы мы можем следующим образом
построить эволюты линии (л). Рассмотрим участок (л), на котором кручение
*) См. сноску1) на стр. 335.
§ 56. ЭВОЛЮТЫ И ЭВОЛЬВЕНТЫ ПРОСТРАНСТВЕННЫХ КРИВЫХ 337
не меняет знака, например о > 0. В начальной точке No проводим
нормаль N0M0 под произвольным углом [30 к бинормали. Во всякой
другой точке N нормаль нужно провести под углом р0 — р., где угол [х
численно равен дуге индикатрисы бинормалей, соответствующей дуге N0N.
Место точек пересечения нормали NM с соответствующей осью
кривизны ecib одна из эволют линии (>.). Остальные эволюты получаются
поворотом всех нормалей на постоянный угол.
Замечание. Так как угол ю (в случае, когда F является
поверхностью касательных) по абсолютной величине равен углу смежности
касательных ребра возврата (А) (рис. 203) поверхности F, то вместо (14)
можно написать формулу |{3-— |30| = \ хл^л, справедливую для всякого
о
участка, где кручение не меняет знака. Таким образом, приращение
угла р по абсолютной величине равно полной кривизне ребра возврата
полной поверхнссти, т. е. полной кривизне места центров
соприкасающихся сфер линии (к).
В заключение решим задачу о разыскании эволют аналитически.
Пусть эвольвента (к) дана уравнением r = r (s). Так как точка М
эволюты лежит на оси кривизны точки N, то
гх = г + ^п \- р ctg р Ь. (15)
Чтобы по данному уравнению r = r(s) найти выражение Г1 = г1(&),
нужно найти выражение угла р в функции s. Но касательная эволюты
должна совпадать с прямой MN, т. е. векторы -г^ и гх — Г =
должны быть коллинеарны. Из (15) находим
Для коллинеарности гг — г и ^необходимо и достаточно выполнение
условия
p:pctgp = (g-paetgp): [^(pctgp) +pa] . (17)
После упрощений находим: ^=о, что снова доказывает теорему 12.
Искомое уравнение эволюты будет
гх = г+ [>п +[>ctg f\ads +const j b. (18)
Упражнения
1. Доказать, что эволюта не может быть ребром возврата полярной поверхности,
2. Если эволюта есть место центров кривизны эвольвенты, то эвольвента —
плоская линия.
3 При развертывании полярной поверхности на плоскость место центров
кривизны становится подэрой ребра относительно центра пучка прямых, в
которые обращаются эволюты.
4. Найти все эволюты винтовой линии.
5. Найти выражения кривизны и кручения эволюты по данным кривизне
и кручению эвольвенты.
22 М. Я. Выготский
ГЛАВА IX
ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА
ПОВЕРХНОСТИ
§ 57. Расстояние от точки поверхности до касательной плоскости
и вторая квадратичная форма
Расстояние h от точки М' поверхности S (рис. 204) до касательной
плоскости Р в бесконечно близкой точке М имеет высший порядок
относительно отрезка ММ' или относительно проекции MQ отрезка ММ'
на плоскость Р.
Действительно, если точка М' приближается к М по любому
пути М'М, то расстояние M'Q от М' до касательной MQ имеет, согласно
Рис. 204.
теореме § 7 (стр. 40), высший порядок малости, а так как MQ лежит в
касательной плоскости Р, то величина h и подавно имеет высший
порядок. Аналитически в этом убеждаемся так: если т есть орт
нормали в точке Му то
h = MM'm = Arm. (1)
Так как вектор г предполагается дифференцируемым, то
где вектор е имеет высший порядок относительно
J) Это выражение означает, что отношение модуля s к величине р = \/rdu2+dv*
бесконечно мало вместе с р. В аналогичном смысле нужно понимать выражение
«е имеет второй, третий и т. д. порядок относительно du,dv».
§ 57. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА 339
Вектор
перпендикулярен к ги и rv\ поэтому
т= /цХГ* : (2)
ё/я, (3)
так что Л имеет тот же порядок, что з.
Положим, что вектор г имеет и второй дифференциал, т. е. что
(rd2 + 2r
где у\ имеет порядок выше второго относительно duydo. Тогда главная
часть расстояния h есть квадратичная функция от duy do. , Именно,
согласно (1) имеем
h = ^ [(>\,и /я) ^2 + 2 (ruv m) dudo + (rVD m) do2] + ^mt (4)
т. e.1)
h « i (Ым2 + 2Ши<*<; + Mfo1], (4')
где коэффициенты L,M,N, постоянные для данной точки Mf являются
функциями u,v и выражаются формулами
и аналогично
L = гиит = "" ц = = ии и щ^ j
l^(r,,xr.,V VEG-F*
(5)
Выражение Ldu2 + 2Mdudo -{- Ndo2 называется второй гауссовой
квадратичной формой. Если первая квадратичная форма дает элемент
дуги, определяющий внутреннюю геометрию поверхности, то вторая
квадратичная форма характеризует внешний вид поверхности и, как
видно из простейших примеров (например, для случая цилиндрической
поверхности), численно меняется при изгибании поверхности.
В противоположность первой квадратичной форме, которая при
всех значениях du,do имеет положительную величину, вторая
квадратичная форма может иметь как положительную, так и отрицательную
величину. Если она положительна, то точка М' поверхности £ лежит
по ту же сторону от касательной плоскости Р, куда указывает орт ш,
исходящий из точки М. Если вторая квадратичная форма отрицательна,
то М' лежит по ту сторону от Р, куда указывает орт « — /я».
Вторая квадратичная форма может равняться нулю либо
тождественно (тогда L = M = N = 0), либо при некоторых значениях du,dv
(являющихся корнями уравнения Ldu2 -\-2Mdado + Ndo2 = 0).
Равенство нулю второй квадратичной формы означает, что
расстояние h имеет высший порядок относительно Аг2 (либо по всевозможным
направлениям, либо по тем направлениям du: dvf для которых
удовлетворяется уравнение Ldu2 + IMdudv + Ndv2 = 0).
1) Разумеется, эта эквивалентность имеет место при условии, что правая ее
часть не обращается в нуль.
22*
340 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Замечание. Какой знак имеет вторая квадратичная форма при
данном направлении du:dv — это не имеет существенного значения, так
как положительное направление нормали зависит (§ 40, стр. 236) от
параметризации поверхности. Но весьма существенно, остается ли знак
второй квадратичной формы одним и тем же для всех значений du: do
или для одних значений он положителен, для других — отрицателен.
В первом случае поверхность 5 в окрестности точки М располагается
по одну сторону касательной плоскости Р (как, например, поверхность
сферы); во втором случае S лежит частью по одну, а частью —по
другую сторону (как, например, поверхность гиперболического
параболоида). Об этом подробнее будет сказано ниже (§ 58).
Пример 1. Найдем вторую квадратичную форму поверхности
касательных линии r = r(s).
Для вектора г поверхности касательных имеем выражение
r = r(v) + t(v)u, (6)
где v = s есть длина дуги ребра возврата, а а —отрезок касательной.
Из (6) находим:
( £^ — х/)и.
Отсюда
Следовательно,
h % j xa | и | do2 % -i coo)' | и |, (7)
где ад и о)' — углы смежности касательных и бинормалей ребра
возврата 1).
Замечание. Знак h не зависит от направления du : dv. Значит,
в окрестности любой точки М (у-мФ 0, а Ф 0) поверхность касательных
лежит по одну сторону соприкасающейся плоскости ребра.
Однако, при переходе точки М фиксированной образующей с одной
стороны полости на другую, поверхность касательных переходит на
противоположную сторону плоскости Р. Между тем, знак h при этом
не меняется. Но не забудем, что теперь меняется положительное
направление нормали: орт т=—~ v нормали, равный -~ Ь, совпадаете Ь
V(rxry \и\
при и > 0 и с « — д» при и < 0.
Формулу (7) можно синтетически получить следующим образом.
Из точки М' (рис. 205) опустим перпендикуляр M'Q на касательную
плоскость Р, проведенную через М. Опустим также перпендикуляр М'А
на прямую ABB', по которой пересекаются касательные плоскости Р
и Р' (В — точка пересечения прямой ABB' с касагельной ребра КМ;
В' — точка пересечения прямой ABB' с касательной К'М').
Углы ИВА, М'В'А эквивалентны, а сумма их эквивалентна
(лемма 4 § 26, стр. 135) углу смежности ш между КМ и К'М'. Таким
образом,
Z MB A » Z М'В'А » у .
Угол ш' берется со знаком плюс или минус, соответственно знаку кручения.
§ 57. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА 341
Из треугольника АК'М' находим
Из треугольника AM'Q находим
где о)' есть угол между касательными плоскостями Р и Р', т. е.
Рис. 205.
между соприкасающимися плоскостями ребра в аочках К и К\
Окончательно имеем
^ 2 ' '
Пример 2. Найдем вторую квадратичную форму прямого
геликоида:
я = и cos у, y = Hsiny, z=fcy.
Из этих уравнений находим:
ru = cos у, уи = sin у, z u = 0;
хо = — и sin у, yD =u cos у, zv = 6;
хии = °» У«о = 0, г„ы = 0;
жи1) = — sin у, уии = cos у, zuo = (Jj
аот = — a cos у, yrv = — м sin у, zw == 0;
— sin у cos у 0
cosy sin у 0
« cos у Ь
342 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
— U COS V
cos и
— и sin у
— и sin v
sin г?
и cos у
0
0
b
= 0;
—
(8)
Этот результат тоже легко получить синтетически. Соединим точку
M'(u+du> v + dv) с точкой V(u + du, v) (рис. 206). Плоскость MVM',
проведенная через главную
нормаль MV винтовой
линии L'VM' и хорду VM\
составляет с
соприкасающейся плоскостью/*' линии
L'VM' в точке V (плоскость
Р'не изображена на рис.206)
угол высшего (второго)
порядка относительно VM'.
Но плоскость Р' является
касательной плоскостью
геликоида в точке Т7. Uo-
этому угол р между
плоскостью AJVQ, касающейся
геликоида в точке Му и
плоскостью MVM'
эквивалентен углу между
касательными плоскостями в
точках М и V, т. е. он
эквивалентен дифференциалу
cfo, где 9 есть угол между
касательной плоскостью Ро
и касательной плоскостью Р в точке М.
Рис. 206.
в точке сжатия Л/о
о
Так как (§ 40, пример 2, стр. 237) мы имеем
то
fx^tf?'
Следовательно,
bdu
u*+ b2 *
где s есть дуга винтовой линии L'V и, значит,
ds^Yu2 + b2dv.
Из формул (9) и (10) находим
(9)
(10)
(И)
V
Это выражение отличается от формулы (8) знаком; но знак расстояния
h зависит от выбора положительного направления нормали геликоида,
т. е. по существу произволен.
§ 57. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА 343
Пример 3. Найдем вторую квадратичную форму поверхности
вращения.
а) Отнесем поверхность вращения к системе криволинейных коор-
диьат и, v (широта и долгота).
Параметрические ее уравнения будут [§ 39, пример 2, б (стр. 230)]:
где функции г = <р(и), z=ty(u) связаны соотношением
[?'(в)]1+ [f <«)]•= 1.
Отсюда находим:
хи =<р'cos», уи = <p'sine, г„ =ф';
х„ =— <р sin», yv =<pcosu, Zy = 0;
zuu = 9"cos», yuu = <p" sin ю, гоо = ф";
жио = - <p' sin d, yuv = 9' cos v, zuo = 0;
u X ro)8 = <p;
rUttrurB = 0, rvvrurv = <?*<!?';
Z. = 9'<l>e — <1»'9*. Л/=0, Л^ = 9ф';
В частности, для катеноида с горловым радиусом 6 имеем:
;
ь
ф'(н)=_^=, ф'(и) = -т===~ ;
62 .„_ бгг
б) Отнесем поверхность вращения к системе криволинейных
координат г, v (радиус параллели и долгота). Параметрические ее
уравнения будут [§ 39, пример 2, а (стр. 228)]:
х = г cos v; у —г sin и; z = / (г).
Имеем:
rrrrrrv = rf (г), rrvrrrv = 0, rmrrrv = r'f'(r);
/(ruxrr)a = rj/l + [/'[(r)]8;
^6 м=0 "=;
rl 7^
2 /1 + /'*
344 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА nOBFPXHOCTH
В частности, для катеноида с горловым радиусом b имеем:
/(?•) = Ь Arch -£-, /'(r) = -=L==, f(r)= bT ;
Если в эту формулу подставить выражение
то мы получим найденную выше формулу
Пример 4. Если поверхность задана уравнением z= z(x, у), то,
положив х = и, y = vy будем иметь
(гн X rv)2=l + p2 + q2; ruururv=r; ruvrurv = s; rvvrurv = t:
здесь через р, а7 г, s, t обозначены по Монжу частные производные от
функции z (х, у):
— d*z t — —
s ~ д^Гду ? !hp' f
так что
9h
Упражнения
1. Найти вторую квадратичную форму для цилиндрической и конической
поверхности.
2. Найти вторую квадратичную форму для псевдосферы.
3. То же для шара.
4. То же для косого геликоида
§ 58. Соприкасающийся параболоид. Три типа точек поверхности
Отнесем кривую поверхность S к прямоугольной системе
координат, приняи за начало точку М поверхности 5 и за оси X, Y — любые
две взаимно перпендикулярные прямые, лежащие в касательной
плоскости Р точки Л/. Пусть z= f{xf/y) есть уравнение поверхности S
в этой системе координат. Обозначим через p,q,r,s,t частные
производные от функции f(x, у):
dx~pi ду Ъ дх* г' dxdy-~S' ду2 *
В точке М величины р и q равны нулю, так как векторы гХУ гу
касательных к координатным линиям х = 0 и у = 0 имеют координаты
(1; 0; р) и (0; 1; q), а в принятой нами системе координат эти векторы
в точке М перпендикулярны к оси z.
Расстояние z = A от точки М* (х, у), бесконечно близкой к М (0, 0),
до касательной плоскости Р представляется выражением
± *) + \, (1)
g 58. СОПРИКАСАЮЩИЙСЯ ПАРАБОЛОИД. ТРИ ТИПА ТОЧЕК ПОВЕРХНОСТИ 345
где т]8 есть бесконечно малая величина порядка выше второго
относительно х, у. В общем случае v\s имеет третий порядок.
Сравнение формулы (1) с формулой (4') § 57 (стр. 339) показывает, что
величиьы г, s, t суть коэффициенты L, Л/, N второй квадратичной формы
поверхности S в точке М относительно введенной координатной системы.
Это легко проверить по формулам (5) § 57 (ср. пример 4 § 57).
Если пренебречь величиной т)3, то вместо поверхности S мы полу*
чим поверхность Slt определяемую уравнением
z=±(rx* + 2sxy + ty2). (2)
Расстояние т]8 между поверхностями S и 5t по направлению обшей
их нормали в точке М имеет порядок выше второго относительно х, у.
Поверхность Sx, приближенно заменяющая поверхность 5, есть
поверхность второго порядка; при rt— s2 > 0 она является
эллиптическим параболоидом; при rt — s2 < 0— гиперболическим параболоидом;
npnrt — s2 = 0—параболическим цилиндром, который можно
рассматривать как вырождение параболоида. Поэтому поверхность St мы
назовем соприкасающимся параболоидом поверхности S в точке М.
Вследствие высокого порядка близости поверхностей S и St,
форма поверхности S в окрестности точки М сходна с формой
соприкасающегося параболоида, и так как последняя поверхность изучена
нами в аналитической геометрии, то мы можем сразу составить себе
представление о поведении поверхности S. В соответствии с тремя
типами соприкасающегося параболоида мы должны будем различать
три типа точек М поверхности S.
1) Если соприкасающийся параболоид является эллиптическим,
т. е. если в данной точке r£ — s*>0, мы назовем точку М
эллиптической точкой; в частности, если соприкасающийся параболоид окажется
параболоидом вращения, точка М называется омбилической.
2) Если ссприкасаюшийся параболоид является гиперболическим,
т. е. rt — s2 < 0, мы назовем Ы гиперболической точкой.
3) Если соприкасающийся параболоид вырождается п
параболический цилиндр, т. е. rt — s2 = 0, мы назовем М параболической точкой.
Как известно (§ 57), расстояние от точки М' поверхности до
касательной плоскости Р в бесконечно близкой точке М имеет высший
порядок малости относительно ММ', т. е. относительно ж, у.
Формула (1) показывает, что в общем случае этот порядок равен двум.
Но если направляющие коэффициенты dx:dy^x:y удовлетворяют
уравнению
г dx2 +2sdxdy+t dy2 = 0, (3)
то в формуле (1) первое слагаемое обращается в нуль, и в
соответствующем направлении поверхность S отстоит от касательной плоскости Р
на расстояние, порядок которого выше второго относительно dx, dy
(в общем случае — третий).
Направление, в котором расстояние точки М' поверхности от
касательной плоскости в точке М имеет порядок выше второго
относительно А/Л/', мы назовем асимптотическим. Основание для такого
наименования сейчас выяснится. Так как уравнение (3) имеет
действительные решения лишь при rt— s2<0, то в эллиптической точке
не существует (действительных) асимптотических направлений, в
гиперболической точке их два; в параболической точке — одно.
346 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Сечение соприкасающегося параболоида Sx плоскостью z = с,
параллельной касательной плоскости Р, есть центральная кривая
второго,порядка
rx2 + 2sxy+ty2 = 2c. _ (4)
Сечение поверхности S тою же плоскостью имеет уравнение
гх2 + 2sxy + ty2 + 2-цДху) ;= 2с. (5)
Чем меньше величина с, тем ближе подходят обе кривые (4) и (5)
к точке (0, 0) и тем более сходную форму они имеют вблизи этой точки.
1) В случае эллиптической точки {rt — s2 > 0) сечения (4) суть
элл и псы — действительные, если с имеет тот же знак, что г и /,
и мнимые в противном случае. Соприкасающийся параболоид Sx лежит
Рис. 207.
по одну сторону от касательной плоскости и во всех направлениях
удаляется от касательной плоскости Р на расстояние второго порядка
относительно х, у. Значит, поверхность S, отстоящая от Sx на
расстояние порядка выше второго, также располагается по одну сторону от Р.
О форме поверхности в окрестности эллиптической точкиr M дает
представление рис. 204 на стр. 338.
2) В случае гиперболической точки (r£ —s2<0) сечения (4)
соприкасающегося параболоида суть гиперболы; пара асимптот каждой
из гипербол имеет уравнение
гх2 + 2sxy + ty* = 0. (6)
Как видно из сравнения формул (6) и (3), направления асимптот
совпадают с теми, в которых S отстоит от касательной плоскости на
расстояние порядка выше второго относительно dx, dy4 почему эти
последние направления и называются асимптотическими.
Соприкасающийся параболоид Sx пересекает касательную
плоскость Р по двум прямолинейным образующим: аа' и ЭДГ (рис. 207);
пара этих прямых представляется уравнением (6). Внутри углов
Л/р, а'Л/(3' параболоид Sx располагается по одну сторону от плоско-
§ 58. СОПРИКАСАЮЩИЙСЯ ПАРАБОЛОИД. ТРИ ТИПА ТОЧЕК ПОВЕРХНОСТИ 347
сти Р, скажем, сверху от нее; внутри же углов a/i/p, аЛ/р'— по другую
(снизу). Рассуждая, как в случае эллиптической точки, придем к выводу,
что и поверхность S внутри углов аЛ/р, а'Л/р' располагается сверху,
а внутри углов а'Л/р, аЛ/р' — снизу от плоскости Р и, следовательно,
пересекает плоскость Р. Линия пересечения состоит из двух (вообще
криволинейных) ветвей; одна (AMА') касается в точке М
образующей aa'; другая (БМВ') касается образующей рр'.
3) В случае параболической точки (rt — s2 = 0) сечения
соприкасающегося параболоида (цилиндра) S± (рис. 208) суть пары
параллельных прямых, представляемых уравнением (6), т. е. имеющих
асимптотическое направление. Соприкасающийся цилиндр лежит по одну
сторону от плоскости Р;
поэтому во всех неасимп-
тотических направлениях
и поверхность S
располагается по oahj сторону от
плоскости Р, скажем,
снизу. Но по
асимптотическому направлению, в
котором цилиндр Sx имеет
с плоскостью Р общую
образующую, поверхность
S, как правило,
располагается частью снизу, а
частью сверху касательной
плоскости, именно,в одну
сторону от точки касания
поверхность опускается
под касательную
плоскость, а в
противоположную
сторон}'—поднимается над касательной
плоскостью. Действительно, Рис. 208.
в общем случае величина
т)3 в формуле (1) имеет
третий порядок относительно смещения ММ', и тогда знак тг)8 меняется
на обратный при переходе через точку М по какому-либо направлению. При
перемещении в неасимптотическом направлении эта перемена знака
несущественна, так как решающую роль играет знак величины rx2 + 2sxy+ ty2.
Но при перемещении в асимптотическом направлении (rx2 + 2sxy + ty2 = 0)
знак у\8 имеет решающее значение для знака z. Поэтому в общем
случае в окрестности параболической точки поверхность S в окрестности М
по всем направлениям располагается «снизу» от Р, за исключением
одного асимптотического луча Л/р. По направлению этого луча
поверхность 5 в общем случае располагается сверху от Р. Плоскость Р
пересекает S по линии UMV, имеющей в М точку возврата. Поверхность S
лежит сверху от Р внутри «угла» UMV (имеющего меру нуль!)
и снизу —во всей остальной части Р.
Замечание. В случае, когда т]3 имеет четвертый или вообще
четный порядок относительно смещения MMf по асимптотическому
направлению, поверхность S в окрестности параболической точки М
будет располагаться по одну сторону от касательной плоскости.
Пример такого расположения будет приведен в дальнейшем (§ 65, теорема 4,
пример 2, стр. 380).
348 ГЛ. IX. ВТОРАЯ КЕАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Поверхность S отнюдь не должна сплошь состоять из однотипных
точек. Она может иметь как эллиптические точки (Z. на рис. 209), так
и гиперболические (К на рис. 209). Граница между областями
эллиптических и гиперболических точек будет состоять из параболических
точек (М на рис. 209).
Чтобы определить, к какому из трех типов принадлежит данная
точка поверхности S, нет необходимости относить эту поверхность
к прямоугольной системе координат. Задание второй квадратичной формы
поверхности S в какой угодно криволинейной системе позволяет
определить тип точек, а также
асимптотические направления.
Действительно, вторая
квадратичная форма
L du2 + 2AJdu dv + Ndv2
дает(§ 57, стр.339) удвоенное расстояние
поверхности до касательной плоскости
с точностью до величин второго
порядка. Так как в асимптотическом
направлении это расстояние должно иметь
высший порядок относительно du, do,
то асимптотическое направление
характеризуется уравнением
L du2 + 2Mdu dv + AW = 0, (7)
частным видом которого (при du = x\
dv = y) служит уравнение (3). Если
это уравнение не имеет действительных
корней, т. е. если для данных
значений и, v
LN-M2>0, (8a)
Рис. 209. то точка (и, v) принадлежит к
эллиптическому типу. Если уравнение (7)
дает для da : dv два действительных корня, то эти корни определяют
два асимптотических направления, и точка (и, v) принадлежит к
гиперболическому типу. Таким образом, для гиперболических точек
LN — M2<Q. (8b)
Наконец, если уравнение (7) имеет один действительный корень, он
определяет единственное асимптотическое направление, и точка (и, v) —
параболическая. Для такой точки
LN-M2 = Q. (8c)
Пример 1. Очевидно, что все точки сферы—эллиптические и что
соприкасающиеся параболоиды суть поверхности вращения, т. е. все
точки сферы—омбилические. Так как расстояние между сферой и
соприкасающимся параболоидом имеет порядок выше второго относительно
смещения от точки касания, то большой круг сферы есть круг кривизны
для меридиана параболоида. Значит, параметр меридиана равен радиусу
сферы.
Вычисление подтверждает эти выводы. Уравнение шара,
касающегося плоскости XOY, имеет вид
§ 58. СОПРИКАСАЮЩИЙСЯ ПАРАБОЛОИД. ТРИ ТИПА ТОЧЕК ПОВЕРХНОСТИ 349
Дифференцируя, находим
x + (z-R)p = 0, y + (z-R)q = O, (9)
так что при х = 0, у —0, z = 0 имеем
p = q = O.
Дифференцируя (9), находим
1 + />2 + (2-Я)г = 0, pq+(z-R)s = 0, l + q* + {z-R)t = O, (10)
так что при ъ = р = q = 0 имеем
r=*=l, S=0
и для соприкасающегося параболоида получаем уравнение
Это уравнение представляет поверхность вращения параболы
Пример 2. Каждая точка М развертывающейся поверхности S
(не принадлежащая ребру возврата) является параболической точкой.
Действительно, в общем случае, как мы видели в примере 1 § 57
(стр. 340), в окрестности точки М поверхность S лежит по одну
сторону от касательной плоскости Р\ таким образом, точка М не
является гиперболической. Но она не может быть и эллиптической, тай как
направление образующей, очевидно, является асимптотическим.
Аналитически этот результат находим так. Вторая квадратичная
форма развертывающейся поверхности (пример 1 § 57) имеет вид
ха | и | do2. Уравнение
хз | и | do2 = 0
имеет двойной корень do = 0, т. е. единственное асимптотическое
направление совпадает с направлением образующей.
Если ребро возврата имеет точку сплощения (а = 0), то во всех
направлениях расстояние развертывающейся поверхности до
касательной плоскости имеет малость высшего порядка. В этом случае все
направления—асимптотические. Такое положение может иметь место
и для неразвертывающихся поверхностей, если на них есть точки, где
Можно, однако, доказать, что поверхность, где в каждой точке все
направления асимптотические, непременно плоская.
Пример 3. Каждая точка М прямого геликоида является
гиперболической. Действительно, мы имеем здесь два асимптотических
направления. Одним из них является, очевидно, направление
прямолинейной образующей; докажеАм, что другое есть направление винтовой
линии. Действительно, касательная плоскость геликоида совпадает
с соприкасающейся плоскостью винтовой линии. Следовательно, точка М'
винтовой линии, бесконечно близкая к точке М, отстоит от
соприкасающейся плоскости в М на расстояние третьего порядка относительно
ММ' (§ 20, теорема 5, стр. 93). Этим наше утверждение доказано.
350 ГЛ. IX. ВТОРАЯ7КБАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Аналитически мы получим этот результат так. Вторая
квадратичная форма геликоида (§ 57, пример 2, стр. 342) имеет вид
dudv
/V = O, M= , "Ъ V
Дискриминант ее равен — М2 = —ГХТГ2 и* слеД°вательно» всегда
отрицателен. Асимптотические направления находятся как корни уравнения
и, следовательно, совпадают с направлениями координатных линий
du = 0 и dv = 0.
В заключение заметим, что данная поверхность S в точке М
имеет ту же вторую квадратичную форму, что и соответствующий
соприкасающийся параболоид.
Эго следует непосредственно из того, что упомянутые квадратичные
формы представляют удвоенное расстояние поверхности до касательной
плоскости с точностью до величин второго порядка, а эти расстояния
для обеих поверхностей с точностью до величин второго порядка равны.
Поэтому, если за координаты и> v точки М\ параболоида принять
координаты той точки М' поверхности, которая лежит на прямой MfQ,
параллельной нормали в М, то численные значения
коэффициентов Z., М, N будут для обеих поверхностей в их точке касания
одинаковы.
Упражнения
Определить тип точек и асимптотические направления на следующих
поверхностях:
1. Однополостного гиперболоида.
2. Двуполостного гиперболоида.
3. Катеноида.
4. Косого геликоида.
§ 59. Индикатриса Дюпена. Кривизна нормальных сечений
Сечение поверхности S плоскостью, проходящей через нормаль МК
(рис. 210), называется нормальным ее сечением (в точке М). Поставим
себе задачу: определить кривизну нормального сечения (а),
проведенного через данную точку М в произвольном направлении du:dv.
Опустим из точки М', лежащей на нормальном сечении (k)r
перпендикуляр M'Q на касательную МТ к этому сечению в точке М\
Очевидно, M'Q является также перпендикуляром к касательной
плоскости, так что с точностью до величин второго порядка имеем:
2Л = 2M'Q = Ldu2 + 2Mdu do + Ndo\ (1)
Но кривизна x линии (\) равна (§ 25, теорема 1, стр. 130)
x = hm ,,,,;, = lim -r-z . (2)
MM * As2
С точностью до бесконечно малых второго порядка относительно du, dv,
имеем:
As2 = Е du2 + 2F du dv + G do2 и 2h = Ldu2 + 2Mdu dv + Ndv2. (3)
Из формул (2) и (3) находим:
_ L du2 + 2M du dv + N dv* _ П ,,,
* - E du* + 2F du do + G dv* ~" / ' [ '
5 59. ИНДИКАТРИСА ДЮПЕНА. КРИВИЗНА НОРМАЛЬНЫХ СЕЧЕНИЙ 351
т. е. кривизна нормального сечения равна отношению второй
квадратичной формы к первой.
Величина х может быть положительной или отрицательной, смотря
по знаку второй квадратичной формы (первая квадратичная форма всегда
положительна). Но вторая квадратичная форма положительна в том
случае, когда точка М' лежит по ту сторону от касательной плоскости,
куда указывает орт т, исходящий из точки М. Поэтому формула (4)
приписывает кривизне нормального сечения положительный знак, когда нор-
Рис. 210.
мальное сечение обращено вогнутостью по направлению т, и
отрицательный, когда оно обращено вогнутостью в сторону—т. Хотя выбор
положительного направления нормали остается совершенно произвольным и,
значит, знак кривизны сам по себе геометрического смысла не имеет,'
однако постоянство или непостоянство знака х позволяет судшь о том',
обращены ли все нормальные сечения вогнутостью в одну сторону или
имеются сечения, вогнутости которых противоположно направлены.
Геометрически очевидно, что в эллиптической точке все нормальные
сечения вогнуты в одну сторону; в гиперболической же точке сечения,
идущие внутри пары вертикальных углов ai¥p, a'AffJ' (рис. 207
на стр. 346) вогнуты в одну сторону, а сечения, идущие внутри пары
смежных углов a'il/j3, аЛ/р', — в противоположную.
Этот результат дает и формула (4). Действительно, при LN—M2> 0
форма // имеет при любом значении duidv знак величины L (или N)t
ибо
Ldu2 + 2Mdudv + Ndo* = V-d* + MdvY+^LN-M*)d* $ (5)
а при LN — M2 < 0 форма 77 дважды меняет знак, принимая нулевые
значения для значений du: dv, являющихся корнями квадратного
уравнения
L du2 + 2Mdu do + Ndo* = 0,
т. е. дающих асимптотические направления.
352 ГЛ. ТХ. ВТОРАЯ КРАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Итак, в асимптотических направлениях нормальные сечения имеют
кривизну х = 0, 1. е. точка М для каждого из этих сечений есть точка
спрямления. В общем случае (когда h имеет третий или иной нечетный
порядок) мы имеем здесь ючку перегиба.
В параболической точке (LN — М2 = 0) форма // обращается в нуль
для единственного асимптотического направления; согласно формуле (5),
era можно определить из
уравнения
Ldu + Mdv = 0.
В этом направлении
нормальное сечение имеет в М точку
спрямления (в общем случае —
точку перегиба; рис.208 на стр. 347);
в остальных направлениях все
нормальные сечения обращены
вогнутостью в одну сторону.
Формула (4) позволяет найти
кривизны всех нормальных
сечений, но она мало удобна для
обозрения закона распределения этих
крияизн. Этот закон становится
чрезвычайно наглядным, если
прибегнуть к графическому
изображению, предложенному в 1823 году
французским инженером и
геометром Дюпеном (Gh. Dupin),
учеником Монжа.
Рис. 211. Рассмотрим соприкасающийся
параболоид Sx (рис. 211)
поверхности S (эта поверхность не изображена на рисунке, чтобы не загромождать
чертежа) и на нем точку М[, лежащую на том же перпендикуляре
к касательной плоскости Р, что и точка Л/'.
Так как расстояния M[Q и M'Q равны с точностью до величин
второго порядка относительно du, dv, а отрезки ММ\ и ММ'
эквивалентны между собой, то кривизна нормального сечения поверхности S
равна кривизне соответствующего нормального сечения
соприкасающегося параболоида St. Но нормальное сечение параболоида Sx есть
парабола с вершиной в точке М (M[MU на рис. 211), и, как мы знаем
(§ 24, пример 5, стр. 126), радиус кривизны параболы в ее вершине
равен параметру р параболы.
Опустим из точки М\ перпендикуляр М[К = г на ось параболы
МК, т. е. на общую нормаль поверхностей S и Sx. В силу
канонического уравнения параболы имеем
т. е.
Отсюда естественно возникает следующее построение. На каком-либо
расстоянии hx от исследуемой точки М пересекаем соприкасающийся
§ 59, ИНДИКАТРИСА ДЮПЕНА. КРИВИЗНА НОРМАЛЬНЫХ СЕЧЕНИЙ 353
параболоид плоскостью, параллельной касательной плоскости Р в
точке М. Получаем центральную кривую второго порядка АВ (рис. 211);
эта кривая есть эллипс для эллиптической точки, гипербола — для
гиперболической и пара параллельных прямых — для параболической.
Спроектируем кривую АВ на плоскость Р. Получим кривую второго
порядка EF с центром в точке М. Проведем теперь через точку М
какое-либо нормальное сечение, обращенное вогнутостью в сторону
кривой АВ] тогда радиус кривизны Л = — этого сечения в точке Д/,
согласно формуле (6), будет равен
R = lL49L m
2hl~~2MK' Ki)
т. е. радиус кривизны нормального сечения поверхности 5
пропорционален квадрату полудиаметра кривой EF, проведенного в
направлении нормального сечения.
Если точка М — эллиптическая или параболическая, то для
наглядного суждения о распределении кривизн нормальных сечений
поверхности S достаточно взять проекцию одного из сечений
соприкасающегося параболоида Sx. Если же точка М — гиперболическая, то не все
диаметры линии EF (гиперболы) будут пересекать ее в
действительных точках. В этом случае придется взять проекции двух сечений
параболоида Slf расположенных на расстоянии ± hx от точки М. Эти
проекции будут сопряженными гиперболами; общая пара их асимптот
даст асимптотические направления в точке М.
Индикатрисой Дюпена называется проекция (на касательную
плоскость Р точки М) пары сечений соприкасающегося параболоида 51?
проведенных на расстоянии ± Л от плоскости Р.
Индикатриса Дюпена для гиперболической точки есть пара
сопряженных гипербол; для эллиптической точки — пара эллипсов, из
которых один — действительный, а другой — мнимый; для параболической—
две пары параллельных прямых: одна — действительная, другая —
мнимая. Ясно, что практическое значение имеет только действительная
часть индикатрисы.
Индикатриса Дюпена дает полную картину распределения кривизн
нормальных сечений; именно, радиус кривизны какого-либо нормального
сечения поверхности S пропорционален квадрату соответствующего
полудиаметра г индикатрисы.
При этом радиус кривизны нормального сечения в гиперболической
точке нужно считать положительным, когда диаметр индикатрисы
пересекает одну из составляющих ее гипербол, и отрицательным,
когда он пересекает другую. Диаметру, взятому в асимптотическом
направлении, нужно приписать бесконечную длину.
Размеры индикатрисы Дюпена остаются, очевидно,
неопределенными. Чтобы по индикатрисе Дюпена определить не только величины,
пропорциональные радиусам кривизны нормальных сечений, но и сами
радиусы кривизны, нужно, кроме индикатрисы, задать еще величину
hL = МКУ и тогда радиус кривизны R можно найти простым
построением, показанным на рис. 212 (где радиус окружности равен 2АХ).
Можно сказать, что индикатриса Дюпена в пределе подобна
сечению поверхности S, проведенному на бесконечно малом расстоянии от
точки М параллельно касательной плоскости Р. Это выражение имеет
следующий точный смысл. Проведем плоскость Q, параллельную Р,
на фиксированном расстоянии h -ht от точки М и спроектируем сече-
23 м. Я. Выгодский
354 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
ния поверхностей ^ и 5 на плоскость Р. Получим фиксированную
индикатрису Дюпена (Ьг) и некоторую линию (L). При достаточной
малости кг всякий неасимптотический луч, исходящий из М, пересечет
не только индикатрису (Z.i), но и линию (L). Пусть Nt и N —
соответствующие точки пересечения. Теперь будем приближать плоскость Q
к точке М и одновременно увеличивать в одном и том же отношении
отрезки MNX и MN так, чтобы переменная индикатриса Дюпена
преобразовывалась в фиксированную индикатрису (La). Пусть точка N
преобразуется при этом в точку TV, а линия (L) — в линию (L). Тогда точка N
имеет пределом точку Nl9 а касательная к (L) в точке N имеет
пределом касательную к (Lx) в
точке Nx.
У \ Докажем зто. Согласно
формуле (1) § 58 (стр. 344) координаты х, у
точки М связаны соотношением
При бесконечно малом h
величины ху у бесконечно малы, и h
имеет второй порядок относительно
р = l/V 4- у2; функция т/з (я, у)
(предполагается, что она имеет второй
дифференциал) имеет высший
порядок относительно р2, или, что то
же, относительно hx. Переменная
индикатриса Дюпена имеет уравне-
ние
* = 2h. (8)
Рис 212
Чтобы преобразовать ее в линию (L2), нужно увеличить ее в
масштабе \/~кг: |/ Л, т. е. положить
'-01. -Э)
Тогда уравнение (8) примет вид:
(10)
Подвергнув тому же преобразованию линию (L), получим линию (L),
координаты которой связаны соотношением
= 2hl9 (H)
Где г\ = г\—- бесконечно мало вместе с h.
Пусть а есть угол, образуемый лучом MN с осью х, а р, и р-
длиш/ отрезков ONX и ON. Из (11) найдем:
р2 (г cos2 а + 2s cos а sin а +1 sin2 а) -t- 2tj = 2А1# (12)
Из (10) найдем аналогичное соотношение, но без члена 2г\, для р1# Так
как у\ бесконечно мало, то limp = p1 и, значит, точка Л^ есть предел
точки N.
§ 60. ГЛАВНЫЕ НАПРАВЛЕНИЯ. ФОРМУЛА ЭЙЛЕРА 355
Далее, из (11) следует, что касательная в точке М имеет угловой
коэффициент
^ ( U)( g) (13,
Докажем, что при бесконечно малом h обе функции -2, -? бесконечно
дх ду
малы. Учитывая равенство t\ = f\z-± и первое из равенств (9), имеем:
дх дхК1* hJ-dx[yl*.hJ V hi~dx V h*
Так как yj3 обладает вторым дифференциалом и имеет высший
порядок относительно (>2, то — имеет высший порядок относительно р,
т. е. относительно |/h. Из (14) следует, что -^ бесконечно мало.
Написав выражение углового коэффициента касательной к линии
(LJ, аналогичное (13), но без последних членов в каждой из скобок
и сравнив его с (13), убедимся, что касательная к (L) в точке N имеет
пределом касательную к (Lx) в точке Nx.
§ 60. Главные направления. Формула Эйлера
С помощью индикатрисы Дюпена мы можем не только обозреть
закон распределения кривизн нормальных сечений, но и установить
ряд важных предложений теории поверхностей.
Рхли индикатриса Дюпена является окружностью, т. е.
рассматриваемая точка М поверхности S — омбилическая, то кривизны всех
нормальных сечений равны. Во всех остальных случаях кривизна
нормального сечения имеет два экстремальных значения; направления,
в которых кривизна нормального сечения имеет минимум и максимум,
суть направления главных диаметров индикатрисы Дюпена и,
следовательно, они взаимно перпендикулярны. Эти направления называются
главными направлениями на поверхности S в точке М.
В случае, если точка М — омбилическая, мы будем считать все
направления главными. Нормальные сечения (Lx)y (L2), проведенные
в главных направлениях, называются главными сечениями; кривизны
главных сечений называются главными кривизнами поверхности 5
в точке М.
Главные кривизны в эллиптической точке (см. рис. 212) имеют
одинаковые знаки, а в гиперболической (рис. 213) —противоположные.
В параболической точке (рис. 214) одна из главных кривизн (в
направлении MY) равна нулю. В гиперболической точке имеем два
асимптотических направления (Ми, Мо на рис. 213) с нулевой кривизной
нормального сечения. Эти направления было бы ошибочно считать
главными: кривизны нормальных сечений имеют здесь значения,
наименьшие по абсолютной величине; однако эти значения не минимальны,
так как кривизна переходит здесь от положительных значений к
отрицательным.
23*
356 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Радиус кривизны Д = — любого нормального сечения (L)
выражается через главные радиусы кривизны {{формулой Эйлера)):г)
1 cos2 f sin2 ?
или, что то же,
х = Xj cos2 cp + х8 sin2 9,
где через <р обозначен угол между плоскостью сечений (L) и (Z.J.
(1)
(2)
и'-
Р,ис. 213.
Эта формула легко выводится из рассмотрения индикатрисы Дюпена.
Пусть, например, точка М является гиперболической. Приняв за оси
координат главные диаметры индикатрисы, мы можем представить ее
уравнение в виде
?-й=8 (3)
(где s=+l для гиперболы с действительной полуосью МА = а и
s = — 1 для сопряженной гиперболы с действительной полуосью MB = 6).
Так как
то уравнение (3) дает
—9 cos 9 — г,
а2 т Ь2
г,
(4)
Но радиусы кривизны R, R17 R2 по абсолютной величине
пропорциональны квадратам полудиаметров г2, а2, Ь2 (§ 59, стр. 353), причем
2R,R2
•. Формула (1)
г) Эйлер дал в 1760 году формулу Я = £—-„ т R . 91Л
дана Дюпеном. Нелишне отметить, что Дюпен дал легко обозримый вывод
формулы Эйлера; сам Эйлер получил ее с помощью весьма громоздких вычислений
(см. вводную статью «Возникновение дифференциальной геометрии» к книге Монжа
«Приложение анализа к геометрии», ОНТИ, 1936 г., стр. 18—20).
§ 60. ГЛАВНЫЕ НАПРАВЛЕНИЯ. ФОРМУЛА ЭЙЛЕРА
357
R имеет тот же знак, что Rlf если точка С (рис. 213) лежит на
гиперболе uAv1 и тот же знак, что Д2, если точка С лежит на
сопряженной гиперболе uBv\ Поэтому
г2 R г2 R ,,ч
Подставляя эти выражения в (4), находим:
R 9 , R . о л
w COS2 Ф + 5" Sin Ф = 1,
"1 «2
что и доказывает формулу Эйлера.
Для случаев эллиптической и параболической точек она
выводится точно так же. В последнем случае >
£-=0, и формула (1) принимает вид
1 cos2 <р
или, что то же,
(1а)
x = x1cos1<p. (2a)
Формула Эйлера справедлива, в
частности, и для омбилических точек. В этом
случае главные радиусы равны: R1 = R2,
и формула Эйлера дает R = R1=R2.
Если индикатриса Дюпена есть
равносторонняя гипербола, то главные
радиусы кривизны равны по величине и
противоположны по знаку:
Л2= —Ri\
формула Эйлера принимает тогда вид
cos 2<p /ЛЧ
W
• 2 \
~~ sin *)=
Рис. 214.
Асимптотические направления (<р= ±45°) в этом, и только в этом
случае, взаимно перпендикулярны.
Из формулы Эйлера легко получается следующая теорема.
Сумма кривизн двух взаимно перпендикулярных сечений (L), (U)
постоянна и равна сумме главных кривизн.
Действительно, если ср есть угол между сечением (L) и главным
сечением (L,), то ср/==? + 90° есть угол между перпендикулярным
сечением (L) и (L2). Мы имоем, следовательно,
cos2? , sin2?
1
7f R
J___sin
cos2
Складывая эти формулы, находим
R
что и утверждалось.
358 Г Л, IX, ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Величина Y\R^~w)> К0Т0Рая по Доказанному равна полусумме
главных кривизн, называется средней кривизной поверхности в точке М.
Если индикатриса есть равносторонняя гипербола, то средняя кривизна
равна нулю, и обратно,
Поверхности, для которых средняя кривизна в любой точке равна
нулю, или, что то же, главные радиусы кривизны равны по величине
и обратны по знаку (7?х = — Д2), составляют очень важный и
интересный класс; они называются минимальными поверхностями.
Из числа изученных нами поверхностей минимальными являются
геликоид (прямой) и катеноид. Действительно, асимптотические
направления геликоида суть (§ 58, пример 3, стр. 349) направления
образующей и винтовой линии. Они, очевидно, взаимно перпендикулярны,
и индикатриса Дюпена есть равносторонняя гипербола, оси которой
служат биссектрисами асимптотических направлений. Чтобы убедиться
в том, что катеноид есть также минимальная поверхность^ возьмем его
вторую квадратичную форму (§ 57, пример 3, стр. 344):
и найдем асимптотические направления:
dr:dv=+ |//:
С помощью первой квадратичной формы убедимся, что эти направления
взаимно перпендикулярны.
Упражнения
1. Вывести формулу Д = (Д1 + Д.)^(дГ-Д«) cos 2? (см' сноску на Стр* 35б)'
2. Вычислить кривизну нормального сечения круглого цилиндра,
составляющего с окружностью основания угол 43°.
3. Какую форму имеет индикатриса Дюпена для точек косого геликоида?
4. Тот же вопрос для точек, принадлежащих наружному экватору тора, и для
точек, лежащих на внутреннем экваторе.
5. Через точку М поверхности S проведены в ее касательной плоскости
т прямых, каждая из которых образует с соседней один и тот же угол — .
Доказать, что средняя арифметическая
т \Rt R2 "' RmJ
кривизн соответствующих нормальных сечений равна средней кривизне
поверхности £ в точке М.
6. Может ли развертывающаяся поверхность быть минимальной; может ли
она иметь омбилические точки?
7. Доказать, что для нормальных сечений, проведенных в двух сопряженных
направлениях индикатрисы Дюпена, сумма радиусов кривизны постоянна.
§ 61. О предпосылках эйлерова закона распределения кривизн
Формула Эйлера позволяет определить кривизны всех нормальных
сечений через кривизны двух главных сечений. Между тем, мы легко
можем построить поверхность, у которой в данной точке М кривизны
нормальных сечений распределяются по любому закону. Мы можем,
например, взять параболу с вершиной в точке М и, вращая плоскость
§ 61. О ПРЕДПОСЫЛКАХ ЭЙЛЕРОВА ЗАКОНА РАСПРЕДЕЛЕНИЯ КРИВИЗН 359
параболы около оси последней, изменять параметр последней по
произвольному закону. Ясно, что в точке М для нормальных сечений
поверхности, полученной таким образом, формула Эйлера вообще не
будет справедлива.
Кажущаяся парадоксальность этого факта объясняется следующим
образом: при выводе формулы Эйлера мы опирались на доказанное
в § 59 (стр. 352) предложение, что кривизна нормального сечения
поверхности равна кривизне соответствующего сечения соприкасающегося
параболоида. Но самое существование соприкасающегося параболоида
было доказано в предположении [§ 58, формула (1) на стр. 344], что
вектор r(u,v) поверхности S имеет в точке М второй дифференциал.
Если же функция г (и, v) имеет в точке M(u,v) первый дифференциал,
но не имеет второго, то поверхность S в этой точке имеет касательную
плоскость (§ 41, стр. 240), но не имеет соприкасающегося параболоида.
Легкость, с которой мы строим поверхность, не подчиняющуюся
закону Эйлера, может навести на мысль, что требование
существования второго дифференциала является очень жестким и не соответствует
основанным на опыте геометрическим представлениям, а так как
второй дифференциал функции заведомо существует, если эта функция
имеет третьи производные, то может показаться, что предположение
о существовании производных любого порядка плохо соответствует
действительности.
Такое заключение было бы неправильным, как неправильно было бы,
опираясь на реальную осуществимость поверхности с конической
точкой, считать, что требование существования первого дифференциала
является неестественным. Действительно, подобно коническим точкам,
где поверхность не имеет касательной плоскости, точки, где
поверхность не имеет соприкасающегося параболоида, на реально
осуществимых поверхностях могут существовать лишь изолированно. Можно легко
реализовать непрерывную поверхность, имеющую в точке М любое
распределение кривизн, но в окрестности точки М все точки будут
«эйлеровыми».
Эгот эмпирический факт можно характеризовать еще тем, что в
сечении поверхности S плоскостью, параллельной касательной плоскости
и бесконечно близкой к ней, получается линия, в пределе подобная
центральной кривой второго порядка. Требование, чтобы это подобие
имело место для поверхности S, равносильно требованию
существования второго дифференциала функции г (и, v).
Поясним сказанное примером. Будем вращать параболу x2 = 2pz
около ее оси (оси z), одновременно изменяя параметр р обратно про
порционально четвертой степени косинуса угла <р> образуемого
плоскостью вращающейся параболы с начальным ее положением. Мы
получим поверхность, уравнение которой в прямоугольной системе
координат есть
(1)
при дополнительном условии, что при ж = 0, у = 0 также и 2 = 0.
В точке (0, 0, 0) кривизны нормальных сечений пропорциональны
cos4 9; максимальное значение кривизны есть x,=i- (при <p = OV мини
Ро 1 "
мальное х2 = 0 (<р = 90°). Таким образом, направления ж==0 и у = 0
являются главными, и если бы формула Эйлера была верна для точки
360 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
(0, 0, 0), то мы имели бы x = x1cos2<p, тогда как по построению
x = x1cos4cp. (2)
Несоблюдение эйлерова закона распределения кривизн обусловливается
здесь тем, что функция z — - 2 ц » хотя она и имеет в точке М
вторые производные *):
г = -, 5 = 0, г = 0,
Ро
однако не имеет второго дифференциала. Действительно, разность между
£и U^+^y+'y'^Wo**равна -У
р. у)WoРоУ+^
второй (а не более высокий порядок малости относительно х, у). Третьей
производной ^ функция z=-—* . в точке (0; 0) вовсе не имеет.
Между тем в любой другой точке эта функция имеет производные
всех порядков, и, следовательно, во всех остальных точках
поверхности теорема Эйлера имеет место.
§ 62. Аналитическое разыскание главных направлений
В § 59 (стр. 350) мы получили для кривизны нормального сечения
следующее выражение:
dudy + Ndv2 _II /.v
~ 7 " ^ '
Определяемая им величина х в общем случае зависит от du: dvy
единственным исключением является случай, когда в данной точке
первая и вторая квадратичные формы пропорциональны, т. е. когда
*) Эти значения находим таким образом. Уравнение (1) при дополнительном
условии z (0, 0) == 0 дает при любом х
так что zxx(x, 0) = — и, в частности,
*хх(0,0)=у.
Далее, из уравнения (1) находим, что при любом у и хфО
Но и при ж = 0 это соотношение также имеет место, ибо z (0, у) = 0. Поэтому,
в частности, имеем
zy(x,0) = 0, (4)
«у(0, у)==0. (5)
Из (4) находим, что \
1„я(0,0)-0,
а из (5) получаем
§ 62. АНАЛИТИЧЕСКОЕ РАЗЫСКАНИЕ ГЛАВНЫХ НАПРАВЛЕНИИ 361
В этом случае все нормальные сечения имеют одну и ту же кривизну,
и, следовательно, индикатриса Дюпена есть окружность. Таким
образом, условия (2) необходимы и достаточны, чтобы точка (м, v) была
омбилической (§ 58, стр. 345). В остальных случаях в главном
направлении (§ 60, стр. 355) величина х должна иметь экстремальное значение;
следовательно, производная от к по аргументу da: dv$ от которого
зависит отношение -j , должна равняться нулю. Для соблюдения
симметрии в выкладках будем считать один из дифференциалов, например
do, постоянной величиной. Дифференцируя (1) по du и приравнивая
производную нулю, находим
(Е du2 + 2Fdudv + G dv2) (Ldu + M dv)—
Это уравнение сразу упрощается, если использовать тождества:
I = E du2 + 2F du dv-\-G dv2 = (E du + F dv) du + (F du -f G dv) dv, (3)
// = Ldu2 + 2Mdudv+Ndv2 = (Ldu+Mdv)du+(Mdu + Ndv)dv, (4)
и мы получаем для главных направлений уравнение
Edu + Fdv Fdu + Gdv
Ldu + Mdv Mdu + Ndv
его можно также представить в виде
dv2 — du dv du2
-0; (5)
E F G
= 0. (6)
L M N
Основываясь на вышеизложенных геометрических рассуждениях,
мы можем заранее утверждать, что это уравнение всегда имеет два
действительных и притом различных корня, что соответствующие два
направления взаимно перпендикулярны и что найденные значения
du:dv, действительно, дают экстремумы величины х.
Аналитическое доказательство этих фактов потребовало бы
громоздких преобразований1).
Пример 1. Найдем главные направления поверхности вращения
Для нее имеем
E = l + U'(r)Y, F = 0, G = r\ (9)
Т t" Л TV
пьства действительности корней }
искриминант
(EN — GL)2 - 4 (ЕМ — FL) (FN — GM) (7)
в виде
{[Е (EN - GL) - 2F(EM - FL)]2 + 4 (EG--F2) (ЕМ — FL)2^ : E2.
Эта величина ие может быть отрицательной, ибо EG — F2 > 0. Нулю же она
может равняться лишь в том случае, если одновременно
EN - GL = 0, ЕМ - FL = 0, (8)
что равносильно условию (2), которое соответствует случаю омбилической
точки. В этом случае определитель (6) равен нулю тождественно, так что любое
направление можно считать главным (§ 60). В остальных случаях дискриминант (7)
всегда положителен и, значит, корни уравнения (6) действительны и различны.
1) Так, для доказательства действительности корней уравнения (6) можно
было бы представить его дискриминант
362 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Уравнение (6) принимает вид
drdo = 0
и, следовательно, одно главное направление (dv = Q) есть направление
меридиана, а другое (dr = 0) — направление параллели.
Пример 2. Найдем главные направления прямого геликоида
x = ucosv, y = usinv, z = bo.
Имеем
E = lf F = 0, G = u2 + b\
L-0, M= ~b , 7V = 0.
Уравнение (6) дает
du:do=±\/(u2-j-b2). (10)
Каждое из этих направлений составляет с образующей dv = 0 угол 45°.
Действительно, в общем случае направление du : do составляет с
направлением dv = Q угол <р, для которого
Edu + Fdv du
COS Ф
У Е du* + 2F du dv + G d»J ]/ dwa + (u2 ■+- b*) dv2
В случае, когда имеет место уравнение (10), мы получаем
du 1
= —=—=, ,
V 2du* V 2
т. е. 9= ±45°.
Итак, главные направления геликоида делят пополам углы между
направлениями образующей и винтовой линии.
Тот же результат сразу получается геометрически: направления
образующей и винтовой линии суть асимптотические направления (§ 60,
стр. 358), и потому направления осей индикатрисы Дюпена делят
пополам углы между ними.'
§ 63. Аналитическое разыскание главных кривизн
Для нахождения главных кривизн мы могли бы определить из
уравнения (5) § 62 два значения du :dv и подставить их в уравнения (1).
Чтобы избежать громоздких выкладок, лучше поступать так.
Уравнение (5) можно представить в виде пропорции
Ldu + Mdv Mdu + Ndv
Edu + Fdv ~~ Fdu + Gdv ' ' '
Обозначив через X общую величину этих двух отношений, найдем
Ldu + M dv = l(E du + F do), (2)
Mdu + Ndo = \(Fdu + Gdv), (3)
откуда по формулам (3) и (4) § 62
L du2 + 2М dudv + N dv* = I (E du2 + IF du do + Gdv2).
Формула (1) § 62 дает тогда
§ 63. АНАЛИТИЧЕСКОЕ РАЗЫСКАНИЕ ГЛАВНЫХ КРИВИЗН
363
и остается найти величину X из уравнений (2) и (3); представив их
с виде
(I — \E)du + (M —
— lF)dv = 0, \
-W)dv = O, J
мы находим для А = — следующее уравнение:
~"RE М~~Ж
R R
или
(EG-F2) ±2-(LG-
±
(6)
а 1 1 1 1
ото уравнение дает две главные кривизны: g = б~ и 7^ == я" #
их, можно вычислить соответствующие значения du : dv по одной из
формул (4). Если же, напротив, главные направления ранее найдены,
то главные кривизны найдем по одной из формул (2), (3), т. е.
1 Ldu + М dv ,n ч
R~"Edu + Fdv ( '
или
^
R Fdu + Gdv e
Уравнение (6) дает для средней кривизны Н (§ 60, стр. 358)
следующее выражение:
1/1 , IN I LG-2MF + EN ,Q,
В теории поверхностей очень важную роль играет величина К,
равная произведению главных кривизн
Эта величина называется гауссовой кривизной (или просто
кривизной) поверхности (в данной ее точке). Уравнение (6) дает для этой
величины выражение
к LN-M*
т. е. гауссова кривизна равна частному от деления дискриминанта
второй квадратичной формы на дискриминант первой квадратичной
формы.
В эллиптических точках кривизна поверхности положительна,
в гиперболических —отрицательна; в параболических — равна нулю.
Эю сразу вытекает как из геометрических соображений, так и из
формулы (10).
Центры кривизны главных нормальных сечений поверхности
называются центрами поверхности (в данной ее точке). Оба центра
лежат на нормали к поверхности, и их векторы г19 г2 суть
г, (и, v) = г (н, v)+Rt (и, v)m (и, v),
r2 (u, v) = r (и, v) + R2(u.v)m In, v).
(11)
(12)
364 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ,
В общем случае центры поверхности S заполняют некоторую
поверхность (поверхность центров) S' состоящую из двух полостей.
Уравнение (11) представляет одну из них, уравнение (12) —другую.
В качестве примера найдем главные радиусы кривизны и главные
центры поверхности вращения
x = rcosv, y = r sin v, z = f(r). (13)
В примере 1 §62 (стр. 361—362) мы нашли, что главные направления
суть направления меридиана (du : do = 1: 0) и параллели (du \ dv = 0:1). Ге«
ометрически очевидно, что первый главный радиус равен радиусу
кривизны меридиана. Второй главный радиус вообще не равен радиусу
кривизны параллели, так как плоскость параллели не является нормальной.
Рис. 215.
Формула (7а), в которую подставляем с?гг = 1, dy = O, дает
о _g_[H-//2(r)]3/2
ni~L /"(г)
Это выражение представляет радиус кривизны меридиана z = /(/•).
Формула (7Ь) по подстановке в нее du = 0, efo=l дает
2 ~~ N ~Г f —Г dz
Это выражение, представляющее радиус кривизны нормального
сечения ME (рис. 215), дает длину нормали МС2 меридиана, что легко
видеть из подобия треугольников KMCt и MDN, в которых KM = rf
ND^dz, MN «ь ]/dr2 + dz2. Следовательно, второй главный центр С%
лежит на оси поверхности вращения. Этот же результат дает и
формула (12) при использовании формул (13). Последние дают для
координат Х9 Y, Z вектора т величины
У= ' sinn; Z =
§ 63. АНАЛИТИЧЕСКОЕ РАЗЫСКАНИЕ ГЛАВНЫХ КРИВИЗН 365
откуда
г» тг 1/14- /'* /'
xi = x + R2X = r cosv- r
-г-^— - —
Первый центр кривизны совпадает с центром кривизны меридиана,
так что первая полость поверхности центров есть поверхность враще-
Рис. 216.
ния эволюты меридиана. Вторая полость вырождается в ось вращения.
Гауссова кривизна поверхности вращения равна
к 1 _ ГГ
ДА"
что можно было бы получить также по формуле (10) настоящего
параграфа.
Главные радиусы кривизны сферы, очевидно, равны радиусу сферы/?,
1 1
средняя кривизна равна ^-. Гауссова кривизна равна т™ •
Для псевдосферы (рис. 216), т. е. поверхности врашения трактрисы,
мы имеем |/?, \ = МСг = ^ (§ 24, пример 7, стр. 127), \R2\ = MC2.
Величинам Rx и Ro нужно приписать противоположные знаки, так
как главные сечения обращены вогнутостью в противоположные
стороны (все точки псевдосферы —гиперболические). Гауссова кривизна
псевдосферы равна
366 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
т. е. псевдосфера, как и шар, имеет постоянную кривизну, откуда
и ее название («лжесфера»). Но кривизна шара положительна, а
кривизна псевдосферы — отрицательна.
Упражнен ия
1. Найти аналитически главные радиусы кривизны псевдосферы
х = a sin и cos и, у = a sin и sin v, z = a cos и -j- a In tg — .
2. Найти главные радиусы кривизны гатеноида и доказать, что его средняя
кривизн а равна нулю. , , >-
3. Та же задача для геликолда.
4. Доказать, что гауссова кривизна геликоида и катеноида в точках,
совмещающихся при наложении одной из этих поверхностей на другую, равны.
§ 64. Сопряженные направления
Возьмем на поверхности S какую-нибудь линию (L) (рис. 217).
Касательные плоскости поверхности S, проведенные через точки,
лежащие на (L), огибаются некоторой развертывающейся поверхностью 5Х.
Поверхность Sx проходит через (L) и во всех точках линии
(L) имеет с поверхностью S общие касательные плоскости, т. е.
поверхности S и St касаются друг друга вдоль (L). Говорят также,
что развертывающаяся поверхность S^ описана около S вдоль (L).
Так, развертывающаяся поверхность, описанная около шара вдоль
экватора, есть цилиндр, а вдоль всякой другой параллели —конус.
Мы знаем, что в общем случае поверхность S не может быть
изогнута на плоскость. Но узкую ее полосу, прилегающую к линии (L)
(рис. 217), практически можно наложить на плоскость за счет
растяжений, составляющих ничтожно малую часть деформируемых дуг.
Это объясняется тем, что прилегающая к (L) полоса описанной
развертывающейся поверхности Sx изгибается на плоскость без всяких
растяжений, а отрезок АС образующей АК разнится от той дуги
поверхности S, которая проектируется на/нее по направлению
нормали в точке А, на величину третьего порядка относительно АС.
Обратно, неразвертывающуюся поверхность S можно практически
получить из плоских полос склеиванием или сшиванием их.
Важно заметить, что в общем случае направление АС остается
тем же, если вместо (L) мы возьмем любую другую линию, касающуюся
(L) в точке А, т. е. имеющую то же направление AT. Именно,
направление АС может измениться лишь в том случае, если А —
параболическая точка и притом AT — асимптотическое направление.
Докажем это.
Примем (L) за координатную линию v=0. В остальном
координатная сеть произвольна. Тогда для всякой линии (L), касающейся (L),
мы в точке касания А будем иметь do :du=-0: 1.
Пусть в точке А орт нормали т имеет ненулевую производную
ти(ти ф 0). Прямая (/), по которой касательная плоскость в А
пересекается с касательной плоскостью в бесконечно близкой точке А'
линии (L), коллинеарна с вектором тх(т + &т) =тх&т. Но
вектор Д/# эквивалентен вектору ти&и + mvkvy а так как Дг; имеет
высший порядок относительно Дм, то Am ъ ти&и. Так как, далее,
векторы nty ти не коллинеарны (они перпендикулярны), то тх&т^
ku. Прямая АС является пределом прямой (/), а поэтому
§ 64. СОПРЯЖЕННЕЕ НАПРАЕЛЕНИЯ 367
она коллинеарна с вектором тхти. Итак, если тиФ0, то для всех
линий (L) прямая АС — одна и та же.
В случае ти = 0 наше доказательство, очевидно, теряет силу. Но
если ти = 0, то в точке А мы имеем L = 0, M = 0. Действительно,
дифференцируя тождество тги = 0 по и, мы получаем тиги + тгии = 0,
т. е. muru + L = 0. Так как ти = 0, то и L = 0. Дифференцируя по и
Рис. 217.
тождество mrv = 0, мы получим, аналогично, М = 0. Значит,
LN — Л/2 = 0, т. е. А есть параболическая точка. Что же касается
направления AT у то оно асимптотическое, так как для него do : du = 0 : 1
и, следовательно, оно удовлетворяет условию Ldu2 + 2Mdu do + Ndv2 = 0,
характеризующему асимптотическое направление.
Направление АС называется со7г/>я:>/се«/шл* с направлением AT. В
соответствии с вышесказанным мы можем определить его следующим образом:
Определение. Направлением, сопряженным с данным
направлением AT в точке А поверхности 5, называется направление прямой.
368 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
являющейся пределом линии пересечения касательной плоскости в точке А
с касательной плоскостью в точке В, когда В стремится к А по
направлению AT.
Сопряженные направления обладают свойством взаимности, т. е.
если направление АС сопряжено с направлением АВ, то и обратно,
направление АВ сопряжено с АС. Это замечательное свойство тотчас
же вытекает из следующей теоремы:
Теорема 1. Во всякой эллиптической или гиперболической точке А
направление АВ и сопряурсенное с ним направление АС суть направления
взаимно сопряженных диаметров индикатрисы Дюпена.
Доказательство. Предположим сначала, что направление АВ —
не асимптотическое.
Проведем через него
нормальное сечение АА* (рис. 218).
Пусть плоское сечение
DA\ параллельное
касательной плоскости Ру
пересекает это нормальное
сечение в точке А'. Про-
) ведем через А'
касательную плоскость Р'. Пусть
BU есть прямая
пересечения плоскостей Р и Р'.
По доказанному она имеет
пределом прямую,
исходящую из А по
направлению, сопряженному с АВ.
Касательная А'С к
Рис. 218. сечению DA' лежит в
касательной плоскости Р'. А
так как плоскость сечения DA' параллельна плоскости Р, то прямые
А'С и BU, по которым Р' пересекает плоскость сечения и плоскость Р,
параллельны.
Будем теперь приближать сечение DA' к плоскости Р. Тогда
точка А' будет иметь пределом точку А, прямая ОА' — параллельную
ей прямую АВ, а касательная А'С, параллельная BU> — прямую АС.
Если при этом мы будем подвергать сечение DA' подобному
увеличению в масштабе j/^i: \fh, где h = AO, а /гх — фиксированный отрезок,
то касательная А'С' преобразуется в некоторую прямую А"С,
параллельную А'С. По доказанному в § 59, прямая Л"С"будет иметь
проделом касательную к индикатрисе Дюпена, проведенную через конец
полудиаметра, исходящего из А по направлению АВ. Следовательно,
прямая АС параллельна касательной индикатрисе Дюпена в конце
полудиаметра, направленного по АВ. По известной теореме
аналитической геометрии отсюда следует, что АС и АВ суть взаимно
сопряженные диаметры. Этим теорема 1 доказана для случая, когда
направление АВ — не асимптотическое.
В случае, когда направление АВ— асимптотическое (и, значит,
точка А — гиперболическая), нужно провести нормальное сечение,
составляющее с сечением АА' бесконечно малый угол, и совершить переход
к пределу. Сопряженный диаметр индикатрисы будет в этом случае
иметь пределом ту жЪ асимптоту индикатрисы Дюпена. Таким образом,
в гиперболической точке для каждого из асимптотических
направлений сопряженным является оно само.
§ 64. СОПРЯЖЕННЫЕ НАПРАВЛЕНИЯ 369
Возьмем для примера точку 4 на поверхности прямого геликоида.
Если точка А' взята на той же образующей, что А, то касательные
плоскости Р и Р' пересекаются по прямой АА', так что асимптотическое
направление АА' само себе сопряжено. Если же точка А' взята на
винтовой линии, проходящей через Л, то касательные плоскости Р
и Р' суть' соприкасающиеся плоскости винтовой линии, и пределом
их пересечения является касательная к винтовой линии. Таким образом,
и в этом случае направление АА' само себе сопряжено.
Замечание. В параболической точке для всякого
неасимптотического направления сопряженным является асимптотическое направление
(докажите это); асимптотическое же направление в общем случае не
имеет сопряженного.
Следствие 1. Главные направления являются взаимно
сопряженными.
Следствие 2. В
омбилической точке всякие два
взаимно сопряженных
направления перпендикулярны.
Следствие 3. Во
всякой неомбилической точке
имеется только одна пара
взаимно сопряженные
направлений,
перпендикулярных друг к другу, —
главные направления.
Два семейства линий на
поверхности образуют
«сопряженную сетъъ, если каждая
линия первого семейства
пересекает каждую линию
второго и в точке пересечения
направления этих двух линий
сопряжены.
Примером сопряженной
сети может служить сеть
меридианов и параллелей на
поверхности вращения. На
всякой поверхности существует
бесчисленное множество
сопряженных сетей. При этом
одно из семейств, образующих
сеть, можно выбрать
произвольно. Тогда в каждой точке
поверхности определяется со- Рис. 219.
пряженное направление и
«поле» этих направлений определяет второе семейство. Приближенно
построить это семейство можно так: возьмем на линии (Lj) первого
семейства какую-нибудь точку Ах и перейдем по сопряженному направлению
в точку А2 бесконечно близкой линии (L2) первого семейства; в точке А2
имеем новое сопряженное направление: перейдем по этому направлению
в точку А3 линии (L8) и т. д. То же построение проделаем для точек
Blf Сг и т. д. линии (L2). Линии АгА%Аг, BXB2BZ и т. д. в пределе (при
2i М. Я* Выгодский
370 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
сгущении линий первого семейства) дадут линии второго семейства. Ниже
будет дано аналитическое решение этой задачи.
Интересный и важный тип сопряженной сети был указан Кёнигсом
(Konigs).
Теорема 2. На любой поверхности все «линии тени» от точек,
лежащих на прямой (g), и сечения поверхности пучком плоскостей
с осью (g) образуют сопряженную сеть (рис. 219).
Линчей тени точки V на поверхности 5 мы называем линию
касания (L) поверхности S с описанной конической поверхностью,
имеющей вершину в точке V. Эта линия отделяет освещенную часть
поверхности от неосвещенной, если V — светящаяся точка.
Для доказательства теоремы Кёнигса достаточно заметить, что
развертывающаяся поверхность, описанная вдоль (L) около S, есть
коническая поверхность с вершиной V. Образующая AV этой поверхности
дает направление, сопряженное с направлением АВ линии (L).
Проведем теперь плоскость VOA через прямую (g) и точку А.
В сечении полечим линию АО, для которой прямая AV будет
касательной, ибо она принадлежит: 1) плоскости линии АО и 2) касательной
плоскости поверхности конуса, а значит, и касательной плоскости
поверхности S. Итак, линия АО в гочке А имеет направление,
сопряженное с (L). Так же докажем, что при пересечении АО с линией
тени от любой другой точки U прямой (g) направления этих линий
сопряжены. Этим теорема Кёнигса доказана.
Если прямая (g), оставаясь параллельной некоторой плоскости Р,
удаляется в бесконечность, то пучок плоскостей с осью (g) переходит
в пучок плоскостей, параллельных плоскости Р, а конусы тени
переходят в цилиндры, образующие которых параллельны плоскости Р.
Поэтому в качестве предельного случая теоремы Кёнигоа получаем
следующее предложение.
Теорема 3. На любой поверхности S линии касания с
описанными цилиндрическими поверхностями, образующие которых
параллельны плоскости Р (линии тени от параллельных пучков лучей)%
и сечения поверхности пучком плоскостей, параллельных плоскости Р>
образуют сопряженную сеть.
Эту теорему можно доказать и непосредственно, рассуждая так же,
как в теореме 2.
Пример 1. Возьмем произвольный эллипсоид (рис. 220) и
проведем любой его Диаметр (g). Линия тени А1В1 от точки U, взятой
на (g), есть не что иное, как селение эллипсоида плоскостью, полярной
относительно U. Перемещая точку U по прямой (g), будем получать
плоские сечения эллипсоида, параллельные диаметральной плоскости
АВ, сопряженной с диаметром PQ. Согласно теореме 2 эти плоские
сечения образуют сопряженную сеть о сечениями PA, PC
плоскостями, проходящими через (g).
Этот же пример может иллюстрировать и теорему 3.
Действительно, пусть прямая (а) параллельна диаметральной
плоскости АВ (рис. 221). Рассмотрим пучок лучей, параллельных (а).
Линия тени, образуемой этим пучком, есть сечение эллипсоида
диаметральной плоскостью PC, сопряженной с направлением (а).
Если (р) есть другая прямая, параллельная плоскости АВ, то пучок
лучей, параллельных (р), дает линию тени PD, являющуюся сечением
эллипсоида диаметральной плоскостью, сопряженной с направлением (Р).
Сечения PC, PD и все другие, построенные аналогичным образом
§ 64. СОПРЯЖЕННЫЕ НАПРАВЛЕНИЯ 371
(они теперь рассматриваются как линии тени), проходят через диаметр {g),
сопряженный с плоскостью АВ. Согласно теореме 3 сечения АгВ19 па-
Рис. 220.
раллельные АВ, образуют сопряженную сеть с сечениями PC, PD и т. д.
Рис. 221.
Аналитическое условие сопряженносш двух направлений du:do
и Ьи: to можно найти из следующих соображений. Прямая BU
пересечения плоскостей Р и Р' (рис. 218 на стр. 368) перпендикулярна
372 ГЛ« IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
к векторам нормали ru x rv в точках А и А', а значит, и к разности
этих векторов А(гы X rv) ^ d(ru x rv). Здесь буквой d обозначено
дифференцирование по направлению АВ. Будем обозначать через 8
дифференцирование по сопряженному направлению АС. Тогда вектор 8г,
коллинеарный с пределом АС прямой BU, должен быть
перпендикулярен к вектору d(ru X г„), т. е.
brd{ru х rv) = 0. (1)
Раскрывая это соотношение, получаем
(rutu + rvbv) {(ruu X rv)du + (ru х ruv)du +
+ (ruv X rv)dv +(ru X rjdv} = 0. (2)
Произведения члена rvbv на первое и третье слагаемые выражения (2)
в фигурных скобках равны нулю, так же как произведения члена rubu
на второе и четвертое слагаемые. Согласно (5) § 57 (стр. 339) имеем:
rv (ru X ruv) =-M
rv (ru X rvv) =-N
так что уравнение (2) принимает вид
Lduou + M (dubv + dvbu) + Ndvbv = O (3)
или
O, (За)
т. е. условием сопряженности двух направлений является обращение
в нуль билинейной формы, полярной относительно второй квадратичной
формы г).
Формула (За) позволяет по данному направлению ou:ov найти
сопряженное duidv. Если, в частности, ищется направление,
сопряженное с направлением координатной линии v = const, то, полагая
8м == 1, bv = 0, находим
0, (4)
и точно так же для направления, сопряженного с и = const, имеем
Mdu + Ndv = 0. (4a)
В случае, если Л/ = 0, направления координатных линий всюду
взаимно сопряжены, т. е. координатные линии образуют сопряженную
сеть. Обратно: если координатные линии образуют сопряженную сеть,
то уравнение (3) должно всегда удовлетворяться при du = 0, 8и = 0,
т. е. доджно быть А/=0.
*) Вспомним, что обращение в нуль билинейной формы, полярной
относительно первой квадратичной формы, есть условие перпендикулярности двух
направлений (§ 44, стр. 255).
§ 64. СОПРЯЖЕННЫЕ НАПРАВЛЕНИЯ 373
С помощью уравнения (За) можно также найти семейство линий,
образующих с данным семейством сопряженную сеть. Для этого
необходимо решить дифференциальное уравнение, получающееся из (За)
после подстановки вместо Ъи, bv их выражений, определяемых по
данному уравнению семейства.
Пример 2. На поверхности эллиптического параболоида
проведены сечения плоскостями
х + у = const. (6)
Найти семейство линий, образующих с этими сечениями сопряженную
сеть.
Примем ж, у за криволинейные координаты поверхности
параболоида. Коэффициенты!., М, N второй квадратичной формы (пример 4 § 57,
стр. 344) будут пропорциональны вторым производным функции —4-4- •
L-.M :7V=-:0:i
а о
и уравнение (3) принимает вид
dxbx dyby . п.
Величины Ъх, Ьу связаны, согласно (6), соотношением
так что можем положить в уравнении (7)
8а; = 1, 8г/= -1.
Получаем дифференциальное уравнение
dx dy n
а Ъ
общее решение которого есть
£-£ = const. (8)
Таким образом, искомое семейство состоит из сечений параболоида
параллельными плоскостями (8).
Этот результат можно было найти также геометрически с помощью
теоремы 3 (ср. пример 1).
Из определения сопряженного направления непосредственно
вытекает следующее предложение.
Теорема 4. Прямые, касающиеся поверхности вдоль линии (L)1)
и имеющие направления, сопряженные с направлениями
касательных к (L), образуют развертывающуюся поверхность.
Прямые, касающиеся поверхности вдоль (L) и имеющие
направления касательных к (L)t очевидно, также образуют развертывающуюся
поверхность. В случае, когда линия (L) всюду имеет асимптотическое
направление, эта развертывающаяся поверхность совпадает с первой.
На вопрос, не существуют ли, помимо упомянутых двух
поверхностей, иные развертывающиеся поверхности, составленные из прямых,
касающихся поверхности вдоль (L), дает отрицательный ответ
следующая теорема.
1) Это выражение означает, что точки линии (L) являются точками касания
рассматриваемых прямых с поверхностью.
374 Г Л. IX, ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Теорема 5. Если прямые (л), касающиеся поверхности S вдоль
линии (L), образуют развертывающуюся поверхность S' и не совпадают
с касательными к (L), то они имеют направления, сопряженные
с направлениями касательных к (L).
Действительно, развертывающаяся поверхность S' проходит через
линию (L); поэтому ее Касательная плоскость Р' проходит через
касательную к (L). Сверх того, плоскость Р' проходит через прямую (л),
касающуюся поверхности. Значит, касательная плоскость Р'
развертывающейся поверхности совпадает с касательной плоскостью Р
поверхности S, т. е. S' описана около S вдоль (L). Значит, образующая (к)
имеет направление, сопряженное с (L).
Доказательство потеряло бы силу, если бы направление (к)
совпадало с направлением касательной, так как плоскость Р' проходила бы
не через две, а лишь через одну прямую, касающуюся поверхности.
В этом случае касательная плоскость развертывающейся поверхности
совпадает с соприкасающейся плоскостью L.
Упражнения
1. В каком исключительном случае к семейству линий на поверхности нельзя
присоединить другое так, чтобы эти семейства покрыли поверхность
сопряженной осью?
2 На сфере проведены сечения плоскостями, проходящими через прямую g,
пересекающую сферу. Доказать, что сопряженное семейство состоит из сечений
сферы плоскостями, проходящими через прямую («?'), не пересекающую сферу
и перпендикулярную к плоскости большого круга, проведенного через (g).
3. Доказать, что сопряженная сеть сферических линий, построенная в
предыдущем упражнении, ортогональна.
4. Найти на гиперболическом параболоиде семейство, образующее
сопряженную сеть с плоскими сечениями, параллельными одному из главных сечений.
5. На поверхности геликоида
дано семейство линий м + ю = const. Составить дифференциальное уравнение
сопряженного семейства.
§ 65. Линии кривизны
Если на поверхности S проведена произвольная линия (L), то
нормали поверхности, взятые вдоль линии (Z.), образуют линейчатую
поверхность, которая в общем случае будет «косой», т. е. не будет
развертывающейся.
Так, поверхность S, образованная нормалями прямого геликоида,
взятыми вдоль его образующей (/), является косой, так как ее линия
сжатия, которая, очевидно, совпадает с (/), перпендикулярна к
образующим поверхности1) S.
Монж поставил и разрешил вопрос о разыскании на поверхности
таких линий, вдоль которых нормали образуют развертывающуюся
поверхность 2). Эти линии Монж назвал линиями кривизны. Важнейшее
свойство линий кривизны выражается следующей теоремой.
х) Эта поверхность является гиперболическим параболоидом.
•) Эту задачу Монж ставит в связь с задачей целесообразной конструкции
свода. Если требуется построить свод, поверхность которого имеет заданную
форму, то для разделения поверхности на плиты удобнее всего взять
развертывающиеся поверхности, образующие которых были бы нормальны к поверхности
свода. Такие швы сделать легче, чем швы иной формы. См. Монж, Приложение
анализа к геометрии, ОНТИ, 1936 г., стр. 232.
§ 65. линии кривизны ' 375
Теорема 1. Для того чтобы линия (L), проведенная на
поверхности S, была линией кривизны этой поверхности, необходимой
достаточно, чтобы ее направление всюду совпадало с главным
направлением.
Пусть линия (L) является линией кривизны, т. е. нормали к
поверхности S, взятые вдоль (L), образуют развертывающуюся поверхность.
Нормали поверхности S являются одновременно нормалями линии (/-).
Повернув каждую из этих нормалей на угол 90° около
касательной к (£), мы получим новую поверхность нормалей линии (/,). Эта
поверхность будет, согласно теореме 11 § 56 (стр. 334), также
развертывающейся. Но теперь она образована касательными поверхности S,
перпендикулярными к (L). Согласно теореме 5 § 64 эти касательные
имеют направления, сопряженные с (L).
Но два взаимно сопряженные и притом перпендикулярные
направления суть главные направления (следствия 2 и 3 теоремы 1 § 64).
Итак, наше условие необходимо.
Но оно и достаточно. Действительно, если линия (L) всюду имеет
главное направление, то сопряженные с (L) направления
перпендикулярны к (£). Значит (теорема 4 § 64), касательные прямые,
перпендикулярные к (L), образуют развертывающуюся поверхность. Повернув
эти прямые на угол 90°, получим снова развертывающуюся поверхность.
Эта поверхность образована нормалями к S, так что линия (L),
действительно, есть линия кривизны поверхности S.
Аналитическое доказательство теоремы 1 будет дано ниже (§ 67,
стр. 394).
Пример 1. На поверхности вращения все меридианы и все
параллели являются линиями кривизны. Действительно, нормаль поверхности
вращения лежит в плоскости меридиана, так что взятые вдоль
меридиана нормали образуют развертывающуюся поверхность (плоскосаь).
Нормали, взятые вдоль параллели, также образуют развертывающуюся
поверхность, именно, круглый конус с вершиной на оси вращения.
Согласно теореме 1 направления меридиана и параллели суть главные
направления.
Аналитически это было доказано в § 62 (стр. 362).
Пример 2. На развертывающейся поверхности образующие и их
ортогональные траектории суть линии кривизны. Действительно,
нормали, взятые вдоль образующей, образуют плоскость. Что касается
ортогональной траектории образующих (эвольвенты ребра возврата),
то нормали, взятые вдоль нее, получаются из образующих данной
развертывающейся поверхности поворотом на постоянный угол 90°
и потому также образуют развертывающуюся поверхность (ее ребро
возврата есть другая эволюта ортогональной траектории). Из теоремы 1
следует, что направления образуюшей и ее ортогональной
траектории суть главные направления развертывающейся поверхности. "Это
легко вытекает и непосредственно из определения главного
направления .
В самом деле, все точки развертывающейся поверхности —
параболические (§ 58, пример 2, стр. 349). Индикатриса Дюпена есть пара
прямых, параллельных образующей, так что главные диаметры
индикатрисы направлены по образующей и по перпендикуляру к ней.
Образующая косой линейчатой поверхности (все точки такой
поверхности— гиперболические) не может быть линией кривизны, ибо ее
направление есть одно из двух асимптотических направлений, а главные
направления служат биссектрисами асимптотических.
376 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Пример 3. На прямом геликоиде кривые, пересекающие
образующие под углом 45°, суть линии кривизны. Действительно, эти линии всюду
имеют главные направления (§ 62, пример 2, стр. 362). Два семейства
линий кривизны геликоида изображены на рис. 222.
Пример 4. На сфере всякая линия является линией кривизны,
ибо нормали сферы образуют вдоль всякой линии коническую
поверхность с вершиной ь центре сферы. Из теоремы 1 следует, что на сфере
все направления являются главными. Это непосредственно вытекает
из того, что любая точка сферы является омбилической (индикатриса
Дюпена — окружность). На плоскости также все линии суть линии
кривизны; впрочем, случай плоскости есть предельный случай сферы
(сфера бесконечно большого радиуса).
Возникает вопрос, существуют ли кроме сферы другие поверхности,
на которых все линии суть линии кривизны, или, что то же, для
Рис. 222.
которых все точки являются омбилическими. На этот вопрос отвечает
следующая теорема, установленная Менье, учеником Монжа.
Теорема 2. Сфера (и плоскость как предельный ее случай) есть
единственная поверхность^ на которой все линии суть линии кривизны.
Доказательство. Пусть поверхность 5 —такая, на которой
все линии суть линии кривизны. Проведем в некоторой точке А
поверхности S нормаль АА' (рис. 223) и через АА' проведем некоторую
плоскость Р. Пусть линия ABC есть сечение поверхности S этой
плоскостью. По условию линия ABC есть линия кривизны, т. е. нормали
поверхности АА', ВВ', СС образуют развертывающуюся поверхность S'.
Но главные нормали плоской линии ABC также образуют
развертывающуюся поверхность (плоскость Р). Согласно теореме 10 § 56 (стр. 332)
нормали АА', ВВ', СС образуют постоянный угол с соответствующими
главными нормалями линии ABC; а так как по построению АА' есть
§ 65. линии кривизны 377
главная нормаль этой линии, то и все нормали ВВ\ СС и т. д. лежат
в плоскости ABC. Значит, нормали в точках А и С пересекаются
в некоторой точке О (собственной или несобственной). Но точки Аи С
могут быть взяты совершенно произвольно. Поэтому, если мы возьмем
ка поверхности S точку D, не лежащую в плоскости Р, то нормаль DD'
должна пересечь как нормаль АА'', так и нормаль СС. При этом она
должна пройти через точку 0, ибо в противном случае она
пересекала бы АА' и СС' в двух различных точках и, следовательно,
лежала бы целиком в плоскости Р, между тем как точка D не лежит
в этой плоскости.
Так же докажем, что нормаль, взятая в любой другой точке
поверхности S (ь том числе и в любой точке линии ЛВС), пройдет,
через точку О. Итак, все
нормали поверхности S проходят
через одну точку О *). Ясно, что
поверхность S есть сфера (если
точка О несобственная, то —
плоскость).
Согласно доказанной
теореме на несферической
поверхности омбилические точки могут
либо быть изолированными,
либо в крайнем случае заполнять
некоторую линию. Последний
случай следует считать
исключительным, ибо, для того чтобы
точка была омбилической,
необходимо (§ 62, стр. 361)
удовлетворить двум уравнениям с
двумя неизвестными и, v:
Е "" F ~~ G #
Если эти уравнения
несовместны, омбилических точек
нет; если они совместны и неза- рис 223
висимы, имеем одну или
несколько омбилических точек; если одно из них есть следствие другого,
получаем линию омбилических точек.
Примером поверхности без омбилических точек может служить
любая поверхность гиперболического типа. Примером поверхности с
изолированными омбилическими точками может служить эллипсоид
вращения (вершины— омбилические точки). Пример поверхности, имеющей
линию омбилических точек, будет рассмотрен ниже.
Если мы пока исключим из рассмотрения омбилические точки,
то в каждой точке поверхности будем иметь пару взаимно
перпендикулярных главных направлений. Таким образом, мы получаем два поля
направлений на поверхности; они определяют два семейства линий
кривизны, составляющих ортогональную сеть. Эта сеть будет содержать
1) Если бы расстояние точек А поверхности S до О не было постоянным,
то касательная плоскость не была бы перпендикулярной к ОА и нормаль АА'
не проходила бы через О. Аналитически: если г есть вектор ОА, то из rrtt = Or
rrt = 0 вытекает — (г2) = 0, ^-(г2) = 0, т. е. г2 == const.
378 Г Л» IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
все линии кривизны поверхности. Примером такой сети служат
меридианы и параллели поверхности врашения.
Сеть линий кривизны является не только ортогональной, но и
сопряженной. Обратно, единственная сеть, являющаяся ортогональной и
сопряженной, есть сеть линий кривизны (§ 64, теорема 1, следствие 3).
Не лишне заметить, что нормаль к поверхности не является в общем
случае главной нормалью линий кривизны; иначе говоря,
соприкасающаяся плоскость линии кривизны вообще не совпадает с плоскостью
главного нормального сечения. Например, на круглом конусе с углом
в осевом сечении, равным 90°, круговые сечения являются линиями
кривизны, а соответствующие главные сечения —параболы. Точно так же
главный радиус кривизны вообще не равен радиусу кривизны линии
кривизны. Но между главным радиусом кривизны и линией кривизны
существует связь, установленная Монжем с помощью вычисления.,
Чтобы лучше уяснить эту связь геометрически, полезно
предварительно заметить следующее. Пусть через точку М поверхности S
(рис, 224) проведено какое-либо нормальное сечение (L). Нормаль MN
поверхности S лежит в плоскости Р этого сечения. Но нормаль M'N',
Рис. 224.
проведенная через другую точку М' того же сечения, в общем случае
не лежит в плоскости Р, даже в том случае, если (L) — главное сечение.
Так, на круглом конусе с углом 90° ь осевом сечении всякая
парабола является нормальным сечением в своей вершине, но во всех
остальных ее точках нормали к поверхности не лежат в плоскости сечения.
Разумеется, когда точка М' бесконечно близка к М, нормаль M'N'
составляет бесконечно малый угол а с плоскостью Р, или, что то же,
с главной нормалью М'К' сечения (L), которая является
проекцией M'N' на Р. Но если сечение (L) — не главное, то угол а имеет
тот же порядок, что угол 9 между нормалями MN, M'N'. Если же
(L) — главное сечение, то а имеет высший порядок относительно <р-
Чтобы доказать это, проведем через какую-либо точку О (правая
часть рисунка 224) прямые ON, ON'y OK, соответственно
параллельные MN, M'N', М'К'. Так как ON и ON' соответственно
перпендикулярны к плоскостям Q и Q\ касающимся 5 в точках М и М\
§ 65. линии кривизны 379
то плоскость NON' перпендикулярна к прямой UV, по которой
пересекаются плоскости Q и Q'. Но направление ММ' — главное. Поэтому UV
в пределе перпендикулярна к касательной МТ, а' значит, и к
плоскости Р. Следовательно, плоскость NON' составляет бесконечно малый
угол fi с плоскостью Р и, значит, с параллельной ей плоскостью
NOK'. Проведя сечение трехгранного угла ONN'K' плоскостью NK'N\
перпендикулярной к ON, из прямоугольного треугольника NK'N' находим
а так как
NN'ZzON-v и N'K'^ON' . az
то
т. е. а имеет высший порядок относительно ср. Учитывая, что угол
ty = Z.NOK' разнится от угла <р менее, чем на а, мы получаем
следующую теорему.
Рис. 225.
Теорема 3. Если (L) есть главное нормальное сечение поверхности S
в точке М, а М' — бесконечно близкая к М точка линии (Z.), то имеет
место эквивалентность
где о есть угол между нормалями MN, M'N' поверхности S, а Ц —
угол между главными нормалями MN, М'К' сечения (L).
Опираясь на это предложение, мы можем геометрически доказать
упомянутую выше теорему Монжа, которая гласит:
Теорема 4. Центр кривизны главного нормального сечения (L)
лежит на ребре возврата (X) поверхности нормалей, взятых вдоль линии
кримизны (/), касающейся (L).
Замечание. Теорема остается в силе и для случая вырождения
ребра возврата. Именно, если ребро вырождается в точку, т. е.
поверхность нормалей вдоль (I) — коническая, то центр кривизны (L) лежит
в вершине конуса; если нормали поверхности вдоль (/) параллельны, то
радиус кривизны (L) бесконечно велик (см. нижеприведенные примеры).
Доказательство. Так как нормаль CMN поверхности S в точке
М (рис. 225) является вместе с тем главной нормалью сечения (L),
380 ГЛ, IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
то центр кривизны линии (L) лежит на CMN. Чтобы убедиться, что
он совпадает с точкой С ребра возврата, достаточно доказать, что радиус
кривизны р линии (L) в точке М равен МС.
Отложим от точки М на линии кривизны (/) и на сечении (L)
равные бесконечно малые дуги
Так как (L) и (I) касаются друг друга, то угол М'ММг бесконечно
мал, и из треугольника М'ММХ находим, что М'МУ имеет высший
порядок относительно MM' —As.
Следовательно, угол р между нормалями MxNly M'N' имеет высший
порядок относительно угла <р между нормалями MN, M'N'. Значит,
угол <р эквивалентен углу <pi между
MN я М^г:
?i«<?, (2)
а согласно теореме 3 мы имеем
Ф«ф. (3)
Из (2) и (3) находим
?i«4>. (4)
Так как линия кривизны (/) есгь
ортогональная траектория нормалей,
то расстояние МС от точки М до
ребра возврата поверхности
нормалей равно
Ш (5)
а для радиуса кривизны р
нормального сечения мы имеем
p = lim-^-. (6)
Из (5) и (6) находим
что и утверждает теорема 4. Ясно,
что приведенное доказательство
применимо без всяких изменений и для
Рис. 226. упомянутых в замечании случаев
вырождения.
Пример 1. Главными нормальными сечениями эллипсоида
вращения (рис. 226) в точке М является меридиан AM В, обозначенный (Lt),
и эллипс ME, обозначенный (Z-2), плоскость которого перпендикулярна
к плоскости (Lx).
Главное сечение (Lt) одновременно является линией кривизны.
Поверхность нормалей, взятых вдоль (Z.J, имеет «ребром» нлоскую
эволюту DCX эллипса (Ьг)9 обозначенную (Х^. Центр кривизны С, линии {Lx)
лежит на ()ч). Линия кривизны (Z2), касающаяся главного сечения
(L2), есть параллель MN эллипсоида. Поверхность нормалей, взятых
вдоль (/2), есть конус с вершиной Сг на оси эллипсоида. Точка С2 есть
центр кривизны эллипса (L2) (для точки М).
§ 65. ЛИНИИ КРИВИЗНЫ 381
Пример 2. Возьмем на поверхности тора (рис. 227) точку М,
лежащую на верхней окружности. Здесь одно из главных нормальных
сечений тора (как и всякой поверхности вращения) есть меридиан NC,
который в данном случае является окружностью. Эта окружность
служит вместе с тем линией кривизны тора. Соответствующее ребро
возврата вырождается в точку С —центр окружности NC. Второе
нормальное сечение, перпендикулярное к первому, есть овальная линия МК.
Она касается в точке М верхней параллели тора МА, которая является
второй линией кривизны. Поверхность нормалей тора, взятых вдоль
МА, есть цилиндр, образующая которого параллельна оси тора. Согласно
теореме 4 радиус кривизны сечения МК бесконечно велик, т. е. в точке
TV кривизна овала МК равна нулю. Значит, второе главное
направление является одновременно
асимптотическим.
Следовательно, индикатриса Дюпена
должна быть парой прямых,
т. е. точка М —
параболическая. Заметим попутно, что
здесь мы имеем нетипичное
для параболической точки
расположение поверхности
относительно касательной
плоскости: поверхность не
переходит с одной стороны
этой плоскости на другую.
Это вызвано тем, что по
асимптотическому
направлению поверхность тора уда- Рис- 22?.
ляется от касательной
плоскости на расстояние, имеющее не третий, как в общем случае, а
четвертый порядок.
Точку С — центр кривизны главного нормального сечения — мы
назвали в § 63 (стр. 363) центром поверхности S. Таким образом, на
каждой нормали существуют два центра, соответствующие двум главным
сечениям. Положение этих центров аналитически можно найти по
формулам (6), (11), (12) § 63. В омбилической точке эти два центра
совпадают. В эллиптической точке они лежат по одну, в гиперболической —
по разные стороны от точки М. В параболической точке один центр
уходит в бесконечность.
По доказанному в теореме 4, нормали вдоль линии кривизны (/)
касаются линии (я) центров. Таким образом, эта линия является
одной из эволют линии (Z); для краткости ее называют просто эволютой
линии кривизны.
Каждое из двух семейств линий кривизны поверхности S
порождает семейство эволют, в совокупности образующих одну полость
{{поверхности центров». Поверхность центров, т. е. место центров кривизны
поверхности S, называется также поверхностью эволют или просто
эволютой поверхности S. Две полости, из которых состоит эволюта
поверхности 5, имеют общие точки лишь в том случае, если на поверхности
S имеются омбилические точки.
Следующая замечательная теорема также принадлежит Монжу.
Теорема 5. Эволюта линии кривизны есть геодезическая линия
на своей полости поверхности центров.
382 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Проведем через какую-нибудь точку М поверхности S две линии
кривизны: «первую» (1Х) и «вторую» (12) (рис. 228). Пусть (X,) и (^2) —
их эволюты. Нормаль KMN касается обеих эволют: «первой» а точке N,
«второй» —в точке К. Будем двигаться по линии (12). Получим
«вторую» поверхность нормалей 2а, для которой (л2) —ребро возврата.
Поэтому касательная плоскость Р2 поверхности Е2 есть соприкасающаяся
плоскость для (>ча).
Если на первой линии кривизны (1Х) взять другую точку М\
то нормаль N'M'K' коснется другой эволюты (\'2) второго семейства.
Поэтому «первая» поверхность нормалей £г (для нее ребро возврата
есть (f^)) является описанной около полости S2, порожденной эволютой
(Х2). Значит, касательная плоскость Рх поверхности И2 (она является
соприкасающейся плоскостью эволюты (кх)) есть одновременно
касательная плоскость полости 52.
Но плоскости Рх и Р2 взаимно перпендикулярны, потому что
первая проходит через касательную к (/J в точке У1/, а вторая —через
Рис. 228.
касательную к (/2). Эти касательные взаимно перпендикулярны, и каждая
перпендикулярна к нормали МК, по которой пересекаются Р1 и Р2.
Итак, касательная плоскость Рх полости S2 перпендикулярна
к соприкасающейся плоскости эволюты (Х2). Иными словами, эволюта
(л2) есть геодезическая линия полости S2 поверхности центров.
Пример 1. На поверхности вращения S (рис. 229) эволюты (ум)
одного семейства являются плоскими эволютами меридианов; эволюты
второго семейства (соответствующего параллелям) вырождаются в точки
на оси. Когда меридиан поверхности S вращается около оси, вращается
и эволюта (>n). Таким образом, первая полость Sx поверхности центров
также является поверхностью вращения; вторая вырождается в линию
(ось). На поверхности Sx ее меридиан (XJ является геодезической
линией, так как соприкасающаяся его плоскость перпендикулярна
к касательной плоскости поверхности Sx. Две полости поверхности
центров (т. е. ось и поверхность Sx) могут пересечься в некоторой
i 65, ЛИНИИ КРИВИЗНЫ 383
точке D на оси. Тогда параллель ВВ\ соответствующая точке Dr
состоит из омбилических точек, ибо BD является радиусом
кривизны для обоих главных нормальных сечений, проведенных через В
(теорема 4).
Пример 2. Представим себе, что на плоском листе Р нанесена
линия Л5(рис. 230 на стр. 384) и что лист наматывается на некоторую-
развертывающуюся поверхность Sx (на рис. 230 поверхность St —
цилиндрическая). Тогда линия АВ описывает поверхность 5, впервые
рассмотренную Монжем и названную им «резной поверхностью» (surface moulure).
Линию АВ Монж назвал профилем. Поверхность S обращается в
поверхность вращения, если поверхность Sx стягивается в прямую линию. Резную
поверхность можно хорошо представить себе, если вообразить, что она
составлена из бесчисленного множества ломтей ABDC, каждый из кото-
Рис. 229.
рых есть кусок поверхности вращения, ограниченный двумя
параллелями и двумя бесконечно близкими меридианами (профилями). Ось
поверхности вращения меняет свое положение, последовательно
совпадая с образующими поверхности 6\. По аналогии с процессом
разматывания нити, Монж назвал поверхность Sx эволютой поверхности S*
Мы увидим, что S, есть одна из полостей поверхности, являющейся
эволютой поверхности 5 в установленном выше смысле (т. е. одна из
полостей поверхности центров).
Данное выше определение резной поверхности содержало в себе
кинематический момент («наматывание»). От него легко освободиться
так же, как это мы сделали в теории эвольвент. Именно, при
наматывании плоского листа Р на развертывающуюся поверхность St точка А
профиля АВ должна двигаться перпендикулярно к плоскости Р. Поэтому
линия АС, которую она опишет, будет ортогональной траекторией
384 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
семейства касательных плоскостей поверхности Sx. Мы можем,
следовательно, дать следующее определение (аналогично определению эвольвенты).
Определение. Резной поверхностью называется поверхность S,
составленная каким-либо образом из ортогональных траекторий AC, BD
и т. д. семейства плоскостей {/*}, касательных к некоторой
развертывающейся поверхности Sx\ линия АВ, по которой одна из плоскостей
Р пересекает резную поверхность, называется профилем поверхности.
Замечание. Как мы знаем, для всякого семейства {Р} (кроме
пучка) существует огибающая развертывающаяся поверхность 5^ Она
и является эволютой (в смысле Монжа) резной поверхности.
Из определения резной поверхности тотчас же следует, что нормаль
ее AU лежит в плоскости Р профиля АВ и что линии AC, BD и т. д.
являются ортогональными траекториями линий профиля АВ, CD и т. д.
Одно семейство линий кривизны резной поверхности состоит из линий
профиля, ибо нормали поверхности S, взятые вдоль профиля образуют,
Рис. 230.
очевидно, развертывающуюся поверхность, именно —плоскость Р,
Следовательно, другое семейство линий кривизны составляется из
ортогональных траекторий AC, BD линий профиля.
Эволюта VKJ линии кривизны АВ есть плоская эволюта профиля
АВ, а так как на плоскости Р эволюта профиля занимает неизменное
положение относительно профиля, то при наматывании Р на Sx эволюта
VKJ описывает тоже резную поверхность г). Таким образом одна полость
1) На рис. 230 показано положение HG, в которое приходит дуга KJ эволюты,
когда профиль из положения АВ переходит в CD, Что касается дуги VK эволюты,
то она накладывается при этом на поверхность Sj и там занимает положение ГЯ.
65. ЛИНИИ КРИВИЗНЫ 385
Fx поверхности центров есть резная поверхность, профиль которой есть
эволюта профиля данной поверхности S.
Другой полостью поверхности центров является, как было
упомянуто выше, развертывающаяся поверхность Sx. Действительно, -так как
плоскости Р являются по определению нормальными плоскостями
для каждой из вторых линий кривизны AC, BD и т. д., то 5, есть
полярная поверхность линий кривизны АС> bD, . ••; значит, их
эволюты UHN', VQR согласно теореме 6 § 56 (стр. 329) лежат на Sx, что
и утверждалось.
Согласно той же теореме эволюты UHN, VQR должны быть
геодезическими линиями поверхности Sx (в частности, если Sx есть цилиндр,
то эти эволюты являются линиями откоса, а если Sx — круглый цилиндр,
то —обыкновенными винтовыми линиями).
Эволюты VJ, HG линий кривизны АВ, CD согласно теореме 6 тоже
являются геодезическими линиями на своей полости £а. И в самом деле,
касательная плоскость £2 к 32 в точке Н проходит через нормаль НС
поверхности S и через касательную к С А в точке С. Так как С А есть
ортогональная траектория плоскостей профиля, то £а перпендикулярна
к плоскости профиля CD, т. е. к соприкасающейся плоскости
эволюты HG.
Отыщем еше омбилические точки резной поверхности. В них оба
центра кривизны поверхности S должны совпасть. Так как первый
центр лежит на той образующей поверхности Sx, где плоскость профиля
касается Sx, а второй —на эволюте профиля, то оба центра совпадают
в том случае, когда эволюта VKJ пересекает упомянутую образующую
в некоторой точке V. Обе эволюты VKJ и VQR, проходящие .через
такую точку, касаются некоторой нормали VB поверхности 5, и эта
нормаль пересекает поверхность S в омбилической точке В. Таким
образом, в «общем» случае (т. е. в случае, когда первые эволюты
пересекают соответствующие образующие) на каждом профиле будет лежать
одна или несколько омбилических точек. На поверхности S существует,
таким образом, линия омбилических точек.
Эту линию можно построить следующим образом. Пусть VHM есть
та линия поверхности Slt на которую накладывается эволюта линии
профиля при наматывании плоскости Р на 5Г Очевидно, что эта линия
есть место точек пересечения первых эволют с соответствующими
образующими поверхности Sx (иными словами, пересечение двух полостей
поверхности центров). Очевидно также, что касательные первой эволюты
при изгибании Р на St становятся касательными к линии VHM. Поэтому
для разыскания линии омбилических точек поверхности S достаточно
провести поверхность касательных линии VHM. Она пересечет
поверхность S по искомой линии ВС, а так как касательные лини*: VHM суть
нормали поверхности 5, то линия омбилических точек есть эвольвента
линии VH, и ее можно механически построить с помощью обертывания
линии VHM натянутой нитью.
Замечание. Как мы знаем, через неомбилическую точку
проходят две линии кривизны. Через омбилическую же точку могут проходить
и три (ВA, BD и линия неомбилических точек ВС на рис. 223, стр. 377).
Из теоремы 4 тотчас же вытекает следующая важная теорема,
указанная Иоахимсталем.
Теорема 5. Если две поверхности St и S2 пересекаются под
постоянным углом и линия их пересечения (к) является линией кривизны
для поверхности S1} то она является линией кривизны и для
поверхности 58.
25 М. Я. Выгодский
386 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Обратно, если линия пересечения поверхностей S± и S2 есть линия
кривизны для обеих поверхностей, то поверхности St и S2 пересекаются
под постоянным углом.
Докажем первую часть теоремы 5. Согласно определению линий
кривизны нормали к Sly взятые вдоль (X), образуют развертывающуюся
поверхность. Если Sx и S2 пересекаются вдоль (X) под постоянным углохМ,
то нормали к S2 получаются из нормалей к Sj поворотом ох на
постоянный угол в нормальной плоскости линии (X). Согласно теореме 9 § 56
(стр. 331) нормали к S2 также образуют развертывающуюся
поверхность, т. е. (X) есть линия кривизны поверхности S2.
Так же доказывается и обратное предложение.
В частности, если поверхность St пересекается плоскостью под
постоянным углом, или, что то же, нормали к St вдоль некоторого
плоского ее сечения (д) образуют
постоянный угол с плоскостью
сечения, то (X) есть линия кривизны
поверхности SX1 и обратно, если
плоская кривая л. есть линия
кривизны поверхности SX1 то нормали
5Х вдоль (X) составляют постоянный
угол с плоскостью сечения.
Справедливость этого вытекает из того,
что на плоскости всякая линия есть
линия кривизны.
Так, на поверхности вращения
нормали вдоль параллели образуют
с плоскостью параллели
постоянный угол. Из этого следует, что
параллель есть линия кривизны.
Точно так же, если эволюта резной
поверхности есть цилиндр, то
траектория (X) точки профиля есть плоская
кривая, и нормали резной
поверхности вдоль (X) образуют постоянный
угол с плоскостью линии (X).
Отсюда вытекает, что (X) есть линия
кривизны.
Если поверхность Sx
пересекается со сферой под постоянным
углом, то линия пересечения есть ли-
Рис. 231. ния кривизны для Slt ибо на сфере
всякая линия является линией
кривизны. Так, произвольная коническая поверхность пересекается под
прямым углом со сферой, имеющей центр в вершине конуса; значит,
их линия пересечения (X) есть линия кривизны конической поверхности.
Легко видеть, что линия (X) ортогональна к образующим конуса, чем
вновь подтверждаются выводы примера 2 теоремы 1.
Пример. Найдем линии кривизны поверхности Slt произведенной
движением трактрисы, перемещающейся параллельно себе по
направлению оси и одновременно вращающейся около оси (скорости
поступательного и вращательного движения произвольны; если отношение их
постоянно, поверхность St есть геликоид, называемый геликоидом Лини).
Возьмем на оси трактрисы произвольную точку Т и будем
проводить из нее касательные к трактрисе в различных положениях послед-
§ 66. АНАЛИТИЧЕСКОЕ РАЗЫСКАНИЕ ЛИНИЙ КРИВИЗНЫ 387
ней. По основному свойству трактрисы длины этих касательных равны
высоте трактрисы: ТМ = TN = а.
Следовательно, точки касания образуют некоторую сферическую
линию MN (рис. 231). Сфера S2, пересекаясь с поверхностью S± по
линии MN, образует с ней вдоль MN прямой угол. Действительно,
нормаль МК к Sx в точке М перпендикулярна к касательной МТ
трактрисы МА. Но МТ есть нормаль сферы S2. По теореме Иоахим-
сталя, линия MN есть линия кривизны поверхности Sx. Следовательно,
одно семейство линий кривизны поверхности Sx состоит из
сферических линий. Так как трактрисы AM\ NB и т. д. входят в сферу S%
по направлениям радиусов МТ, NT, то направления трактрис
ортогональны к направлениям сферических линий кривизны. Следовательно,
трактрисы поверхности *S2 образуют второе семейство ее линий
кривизны. (К такому же выводу мы могли бы прийти, основываясь на
теореме Кёнигса, ибо MN есть линия тени на Sx от точки Т.) В силу
обратной теоремы Иоахимсталя поверхность St пересекается с
плоскостью трактрисы под постоянным углом. Этот угол может меняться,
переходя от одной трактрисы к другой. В частности, для поверхности
вращения (псевдосфера) этот угол равен прямому. Он становится тем
острее, чем больше отношение скорости поступательного движения
к скорости вращательного движения.
§ 6G. Аналитическое разыскание линий кривизны
Согласно теореме 1 § 65 (стр. 375) направление линии кривизны
всюду должно совпадать с главным направлением. Поэтому для
разыскания уравнения линий кривизны нужно решить дифференциальное
уравнение (§ 62, стр. 361).
dv2 — du do du2
E F G
L M N
= 0. (1)
Это уравнение удовлетворится, если коэффициенты 2?, F, G форАмы /
будут пропорциональны коэффициентам L, М, N формы //, что имеет
место в омбилических точках. Поэтому, если уравнения
JL — M- — J.L (2\
Е ~~ F ~~G * '
удовлетворяются вдоль некоторой линии f(u,v) = O, то эта линия,
состоящая из омбилических точек, является линией кривизны. Помимо
этой линии (если она существует), мы имеем два ортогональных
семейства линий кривизны, определяемых двумя дифференциальными уравне-
нпяхми первого порядка
du . ч du . .
на которые распадается уравнение (1).
В дальнейшем мы будем рассматривать только такие области
поверхности, которые не содержат омбилических точек. Тогда имеет место
следующее важное предложение.
Для того чтобы координатные линии и> v были линиями кривизны
поверхности 5, необходимо и достаточно, чтобы тождественно имели
место равенства
р = 0, Л/ = 0. (Э)
25*
388 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Геометрически это следует из того, что условие F = 0 есть
условие ортогональности сети, а М = 0— условие сопряженности (§ 64).
Но направления, которые одновременно ортогональны и сопряжены,
суть главные направления, которые в неомбилических точках
определены однозначно. Этим наше утверждение доказано.
Аналитически докажем это предложение так.
Если Р = 0 и Д/=0, то уравнение (1) принимает вид
(EN — LG)dudv = 0. (4)
Коэффициент EN — LG не может равняться нулю, так как в этом случае
удовлетворялись бы уравнения (2), т. е. поверхность имела бы
омбилические точки. Следовательно, уравнение (4) равносильно уравнению
du do = 0,
что дает du = 0 и dv = 0, т. е. координатные линии и = const, v = const
суть линии кривизны.
Обратно, если линии а = const, v = const суть линии кривизны,
то уравнение (1) должно удовлетворяться при du = l, dv=:0 и при
du — 0, dv=l. Следовательно, должны иметь
LF-EM = 0, NF-GM = Q. (5)
Система уравнений (5) допускает относительно F и М лишь одно
решение: F — M=Q, ибо если бы существовало ненулевое решение, то мы
могли бы исключить F, М\ мы имели бы
0; (6)
но тогда уравнение (1) удовлетворялось бы тождественно, т. е. на
поверхности были бы омбилические точки.
При исследовании общих свойств кривых поверхностей мы всегда
можем предполагать, что за координатные линии выбраны линии
кривизны. Ввиду того что формы I и II принимают тогда простейший вид
I = Edu* + G dv\ II =L du* + Ndv\
исследование этим чрезвычайно облегчается. Однако если поверхность
задана в иной системе параметров, то аналитическое определение линий
кривизны требует решения дифференциальных уравнений, которые
могут не приводиться к квадратурам или, если приводятся, не
интегрироваться в элементарных функциях. Поэтому фактическое
определение линий кривизны представляется во многих случаях весьма
затруднительным.
Когда поверхность отнесена к линиям кривизны, главные радиусы
кривизны определяются в силу уравнения (6) § 63 (стр. 363) и
уравнений (3) настоящего параграфа из соотношения
^ + LN 0. (7)
Гауссова кривизна К — ^-^ равна
Удвоенная средняя кривизна 2Н = -^- + -^- равна
(9)
§ 66. АНАЛИТИЧЕСКОЕ РАЗЫСКАНИЕ ЛИНИЙ КРИВИЗНЫ 389
Поэтому главные кривизны суть
±-± ±~*
Я, - Е • R2 """С ' (1U)
что можно найти и непосредственно, решая уравнение (7).
Пример 1. Для геликоида
x = ucosv4 y = usinvy z—bv (11)
имеем
2b du dv
Уравнение (1) распадается на следующие два уравнения:
du , ~
» + Ь2
du
(12)
Интегрируя их, находим
Аг sh -г = ± (v — v0)
или
м= ± 6sh(y-y0). (13)
Каждая линия кривизны образует угол 45° со всеми
образующими (§ 62, стр. 362). Форма этих линий видна на рис. 222 (стр. 375).
Главные кривизны найдем по формуле (7а) § 63 (стр. 363):
_!__ Ldu + Mdy
R ~ Edu + Fdv '
Подставляя сюда
= 0; du :dv= ]/ ¥Tb2 :(± 1),
V^a2 + Ь2
находим
it —1!ПТ= ^=+^Ь- <">
K-iAr =-,„.1\„, ■ (15)
Уравнение (16) показывает, что геликоид является минимальной
поверхностью. Уравнение (15) показывает, что величина у —К равна
кручению о винтовой линии, проходящей через данную точку геликоида.
Оба главных радиуса кривизны по абсолютной величине равны — = т.
Установим уравнения полостей поверхности центров. Если через
г2 и г„ обозначить векторы первого и второго центра и через т — орт
нормали, то
Найдем координаты X, У, Z вектора т= r" x Гг> - •
390 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Из (11) находим
v b sin v
Ь cost;
yu2 + b2 yu2-\-b2 yu2 + b2
Из уравнений (17) с помощью уравнений (14) находим:
b2 -f- и2 b sin v г —z г» •
хх = ч cos v j-— . = и cos v — 1/ w2 + б2 sin v,
-l/ U2'+ б2 COS У,
Эти уравнения дают первую полость поверхности центров.
Уравнения второй полости получаем, переменив на обратные знаки перед
радикалом.
Пример 2. Найдем линии кривизны трехосного эллипсоида
5- + fJ-+"S = l (<*>b>c). (19)
Примем за параметры координаты х> у. Тогда в общем случае
jj rdx2 + sdxdy+t dy*
У \ _f- р2 -f q2
Уравнение (1) принимает вид
dy2 — dx dy dx
i + p2 pq
r s t
= 0.
(20)
В нашем случае^ когда координаты х, г/, z связаны
соотношением (19), имеем
(21)
(22)
L* ~ с2
откуда
с2 х с2 у
Дифференцируем эти соотношения и, снова используя их, находим
a2
Но согласно (19) имеем
г/2
Поэтому выражению г можно придать вид
г4
Аналогично найдем
с*
t= —
так что
Я 66, АНАЛИТИЧЕСКОЕ РАЗЫСКАНИЕ ЛИНИЙ КРИВИЗНЫ 391
Уравнение (20) примет вид
dy2 — dxdy dx2
aAz2 + c4aa с4 xy u-z- -f u-y- n /9ov
62 — y* xy
Раскрыв определитель и подставив вместо za его выражение из (19),
найдем следующее уравнение,
Ь2$ху dx2 - {Ь2$х2 — a2az/2 +■ а262у) dx dy - а2<хху dy* = 0, (24)
где положено
Это на первый взгляд неприступное уравнение было решено Монжем
следующим остроумным приемом: порядок уравнения (24) Монж
повысил, продифференцировав его по х. Из полученного уравнения и
уравнения (24) оказалось возможным исключить постоянные величины,
и задача свелась к интегрированию уравнения второго порядка,
которое Монж представил в виде
у dy
T
Общий интеграл этого уравнения, как легко видеть, имеет вид
или
х2 и1
7^±7Г2=1< (25)
так что линия кривизны эллипсоида проектируется на главную
диаметральную плоскость XOY эллипсами или гиперболами.
Полуоси m, n этих конических сечений связаны одним соотноше-
нием, которое мы получим, подставляя в (24 выражения г/, -^,
найденные из (25). Мы получим
Таким образом, полуоси каждого эллипса суть координаты некоторой
точки определенной гиперболы, а полусси каждой !иперболы
—координаты некоторой точки определенного эллипса (рис. 232). Это дает
возможность легко построить проекции двух семейств линий кривизны
на плоскость XOY. Проекции одного из семейств, к которому нринад-
лежит эллипс ^-+^2=1, суть лежащие внутри него эллипсы. Проек-
ции второго семейслва, к которому принадлежит эллипс -^ -\- -$ = 1
(он проектируется прямой OQ), изображаются гиперболами. Части
х1 у2 л
этих гипербол, лежащие за пределами эллипса —2" + "тг = ^» служат
проекциями мнимых точек. Все действительные точки линий
кривизны проектируются, очевидно, внутрь этого эллипса. Две точки,
находящиеся во внутренней части всех эллипсов и гипербол, суть
проекции омбилических точек. В каждую из них проектируется по две
392 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
омбилические точки. Такую же картину мы имеем для проекций
на плоскость YOZ. На плоскости те XOZ проекции обоих еемейс!в суть
I
-\
Л
А
А
-
3
**=
1
у
SS3S
BSS
=s
r
r
F
1
u
с
... —-1
■r
П
em,
1 1 l?ii I 1 1 1 1 II ^ Y
Рис. 233.
эллипсы (рис. 233). У каждого из них лишь часть, лежащая внутри
эллипса ^т+-~2==1» является проекцией действительной части
соответствующей линии кривизны. Эллипсы, имеющие вдоль ОХ ось, бблыпую.
§ 66. АНАЛИТИЧЕСКОЕ РАЗЫСКАНИЕ ЛИНИЙ КРИВИЗНЫ 393
чем а, суть проекции первого семейства линий кривизны; эллипсы, име-
юшие вдоль ОХ ось, меньшую, чем а, суть проекции второго семейства.
На рис. 232 ясно видно, что через каждз^ю неомбилическую точку
эллипсоида проходит одна пара линий кривизны. Что касается
омбилической точки, то в ее бесконечно малой окрестности имеются линии
кривизны всевозможных направлений. Через самую же омбилическую
точку проходит только одна линия кривизны — эллипс —т + -^ = 1 ♦
лежащий в плоскости г/ = 0. Этот эллипс разбивается четырьмя
омбилическими точками на четыре части, из которых две симметричные
Рис. 234.
части примыкают к линиям кривизны одного семейства, а две другие —
к линиям кривизны второго семейства.
В случае эллипсоида вращения линии кривизны, примыкающие
к стягивающейся в точку дуге эллипса у = 0, обращаются в параллели,
а линии кривизны другого семейства обращаются в меридианы, и тогда
через каждую из двух омбилических точек проходит бесчисленное
множество линий кривизны.
Рис. 234 изображает линии кривизны трехосного эллипсоида.
У пра жн ени я
1. Найти уравнения линий кривизны на геликоиде Дини (§ 65, стр. 386):
х bs a sin и cos v; y=±a sin и sin v\ г = a cos и + In tg — 4- bv.
2. Доказать, что одна из полостей поверхности центров геликоида Дини
есть также геликоид, профиль которого есть параллельная проекция цепной линии.
3. Найти уравнения полостей поверхности центров для геликоида Дини.
4. Доказать, что все линии кривизны гиперболического параболоида az2*=xp
проектируются на плоскость ху гиперболами.
5. Найти вычислением линии кривизны развертывающейся поверхности.
6. Найти уравнение линий кривизны поверхности
394 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
§ 67. Аналитический вывод уравнения линий кривизны
Уравнение (1) предыдущего параграфа есть уравнение линий,
имеющих всюду главное направление. Тождественность этих линий с линиями
кривизны была доказана в § 65 (теорема 1, стр. 375) синтетически.
Выведем теперь уравнение (1) аналитически, опираясь на определение
лилий кривизны, данное в § 65. Тем самым будет аналитически
доказана теорема 1 § 65.
Пусть нормали вдоль некоторой линии (L) поверхности S образуют
развертывающуюся поверхность с ребром возврата (X). Если х есть
расстояние от точки М линии (L) до соответствующей точки N эволюты
(X), а г и г—соответственно векторы точек М и N, то
г=г + хт, (1)
где т есть орт нормали в точке М.
Мы должны теперь выразить требование, чтобы векюр касательной
к месту точек г и орт т были коллинеарны, и это требование
определит направление линии (L). а также величину х расстояния MN.
Эта величина будет положительной, если вектор MN равнонаправлон
с т и отрицательной — в противном случае. Ураьноние (1) дает
dr^dr + xdm + mdx. (2)
Так как по условию векторы dr и mdx коллинеарны, то и вектор
dr + xdm, равный их разности, должен быть коллинеарен с вектором т.
Но векторы dr и dm оба перпендикулярны к орту т. Значит, вектор
dr + xdm компланарен г касательной плоскостью. Поэтому он может
быть коллинеэрен с т лишь в случае
0 (3)
или
(ru + хти )du + (rv + xmv )dv = O. (4)
Помножим (4) скалярно на ги и на rv. Получим:
(rl + xru mu) du + (ru rv+xru mv) do = О,
Заметим, что
0 = 0' 1 (5)
(rurD + xrvmu)du + (r2v + xrvmv)dv = Q. J
Кроме того, вследствие тождеств тги = 0, mrv = 0, имеем
muru = —tnruu= — Z., murv= —mruv= — M,
mvru = — mruu = —M, mvrv = — mrvv = — N. l
Таким образом, уравнения (5) можно переписать в виде
(Е — xL) da + (F — хМ) dv = 0,
{F — zM)du + (G — zN)dv = Q. ( '
Если из этих уравнений исключить ж, найдем дифференциальное
уравнение линий кривизны:
Edu + Fdv Fdu + Gdv
Ldn + Mdv Mdn + Ndv ~ '
§ 68. СФЕРИЧЕСКОЕ ИЗОБРАЖЕНИЕ ПОВЕРХНОСТИ 395
которое совпадает с уравнением (5) § 62 для главных направлений
(стр. 361). Таким образом, теорема 1 § 65 доказана аналитически.
Если же из уравнений (5а) исключить du:dc, то найдем для
расстояния х от линии кривизны до ее эволюты уравнение
£ — xL F — xM
F-xM G-xN =
[которое совпадает с уравнением (5) § 63 (стр. 363), если величину х
заменить величиной + R]. Следовательно, расстояние MN по величине
и знаку равно главному радиусу кривизны, чем доказана аналитически
теорема 4 § 65.
Формула (3) принимает, следовательно, вид
dr + Rdm = 0. (7)
Дифференциалы относятся здесь к смещению по линии кривизны,
а величина R обозначает тот из двух главных радиусов, который отвечает
взятой линии кривизны. Формула (7) носит имя Родрига (О. Rodrigues),
давшего ее в 1816 году в координатной форме. Если линии кривизны
приняты за параметрические линии, то для одной из них формула
Родрига принимает вид
ru + R1ntu = Oy (8)
а для другой
ro==R2mv = 0. (8a)
Формула Родрига геометрически непосредственно следует из
теоремы 4 § 65; ее геометрический вывод удобно связать с построениями
на сфере, о которых будет речь в следующем параграфе.
§ 68. Сферическое изображение поверхности
Если из центра сферы Q мы будем проводить радиусы,
параллельные нормалям поверхности S, то каждая точка А этой поверхности
отобразится в некоторую точку А' сферы. Это отображение было впервые
применено Гауссом и называется его именем. Радиус сферы
принимается обычно за единицу длины.
Каждой линии ABC на поверхности S отвечает на гауссовой сфере
некоторая линия А'В'С. Последняя может выродиться в точку в том
и только в том случае, когда касательная плоскость вдоль ABC
остается неизменной, как это имеет, например, место на крайних
параллелях тора.
Каждой области поверхности S отвечает на гауссовой сфере некоторая
область. Последняя может выродиться в точку только тогда, если
поверхность S — плоская. Гауссово изображение области может
выродиться также в линию. Это будет в том и только в том случае, когда
на поверхности S имеется семейсаво линий, вдоль каждой из которых
касательная плоскость неизменна. Поверхность S должна быть,
следовательно, огибающей однопараметрического семейства плоскостей, т. е.
(§48, теорема 1, стр. 281) развертывающейся поверхностью. Тогда
образующей поверхности S отвечает на гауссовой сфере точка. В частности,
если S есть произвольная цилиндрическая поверхность, то ее
сферическое изображение есть дуга большого круга.
396 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Касательная плоскость поверхности 5, очевидно, параллельна каса
тельной плоскости гауссовой сферы в соответствующей точке.
Отсюда тотчас же следует что в точках А и А' соответственных
линий ABC и А'В'С направления, сопряженные с АВ и А 'В',
параллельны. Однако сами направления АВ и А'В' вообще не параллельны,,
ибо сопряженные направления на сфере взаимно перпендикулярны;
между тем, на поверхности S сопряженные направления
перпендикулярны лишь в исключительном случае, когда эти направления —
главные. Из этого ясно, что направления АВ и А'В' параллельны в том
Рис. 235.
и только в том случае, когда направление АВ — главное. Значит,
сферическая линия А'В'С имеет всюду направления, параллельные
соответственным направлениям линии ABC в том и только в том случае, когда
ABC есть линия кривизны.
Как видно из рис. 235, векторы касательной линии кривизны ABC
(при любом направлении движения) и ее гауссово изображение
направлены противоположно, когда орт нормали т направлен в сторону
главного центра кривизны Аи т. е. когда главный радиус кривизны/?,
согласно принятому нами условию о его знаке, положителен.
Если вектор т направить в сторону, противоположную А1ч то
сферическое изображение А'В'С заменится симметричным с А'В'С'
относительной, и соответстгенные векторы касательных будут равнонаправлены,
главный же радиус кривизны будет теперь считаться отрицательным.
Так как AB^dr и А'В' ^ dOA' ^ dm, то в обоих рассмотренных
случаях векторы dr и —Rdm равнонаправлены.
Поэтому в обоих случаях векторы dr ^ АВ и R dm ^ R • А'В' будут
противоположно направленными. Но модули их одинаковы, ибо если а>
есть угол между нормалями ААХ и ВВ1г или, что то же, между
радиусами сферы ОА' и ОВ\ то из треугольника А'ОВ' имеем
\Rdm\m\R\ \AFW\^\R\^,
3 68. СФЕРИЧЕСКОЕ ИЗОБРАЖЕНИЕ ПОВЕРХНОСТИ 397
а из треугольника АВВ1
Следовательно,
dr=-Rdm, (1)
и мы получаем формулу Родрига, выведенную аналитически в § 67.
Если элемент дуги AB = \dr\ вращать около точки А в касательной
плоскости поверхности S, тс соответственный элемент А'В' = \dm\
сферического изображения будет вообще вращаться около точки А'.
Вообразим наблюдателя, который смотрит на поверхность S с той
стороны, куда указывает вектор т, исходящий из точки А. Если он
посмотрит затем на поверхность сферы с той же стороны, т. е. извне,
то могут представиться два случая: 1) направления вращения элементов
АВ и А1 В' одинаковы; 2) Э1и направления противоположны.
Так как направления, сопряженные с АВ и А'В'', параллельны и,
следовательно, вращаются в одном и том же направлении, то первый
случай имеет место тогда, когда диаметр индикатрисы Дюпена и
сопряженный с ним диаметр вращаются в одном направлении. Это имеет
место в том и только в том случае, когда индикатриса есть эллипс,
т. е. когда точка .4 —эллиптическая, или, что то же, когда гауссова
кривизна К > 0. Второй случай имеет место в том и только в том
случае, когда точка А — гиперболическая, т. е. когда К < 0. В случае
параболической точки {К = 0) элемент А'В' вовсе не вращается, оставаясь
всегда перпендикулярным к асимптотическому направлению,
сопряженному со всеми направлениями в точке А.
Аналитически различие между этими случаями можно выразить
следующим образом. Возьмем векторы касательных гы, rv координатных
линий v = const и и = const. Соответствующие им векторы касательных
сферического изображения координатных линий будут ти, tnv{мы
предполагаем, что соответствующим точкам приписываются одни и те же
значения и, v).
Векторные произведения ru x fv и ти X tnv соответственно кол-
линеарны нормалям поверхности S и сферы, т. е. коллииеарны между
собой. Но если направления вращения вектора касательной на 5 и на
гауссовой сфере совпадают, то векторы ru x rv и ти X fltv равно-
направлены; если же они противоположны, то и векторы г„ х rv,
ти X mv имеют противоположные направления.
Итак, для эллиптической точки (if >0) коэффициент X в соотношении
ти xmv = l(rux rv) (2)
положителен, для гиперболической (К < 0) он отрицателен. Для
параболической точки /.= 0, т. е. векторы ти, mv коллинеарны.
Изображение координатной сети в окрестности такой точки не дает уже сети,
ибо изображения координатных линий, как и всех других линий,
проходящих через параболическую точку, касаются друг друга. В случае
развертывающейся поверхности (у нее все точки—параболические), все
линии отображаются на одну и ту же сферическую линию
(образующие отображаются в точки этой линии).
Вместо того чтобы рассматривать вращение элемента дуги в
касательной плоскости, можно поступить еще следующим образом. Окружив
точку А на поверхности S малым замкнутым контуром (/-), спроектируем
398 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА II КРИВИЗНА ПОВЕРХНОСТИ
последний на касательную плоскость в точке А. Мы получим плоский
замкнутый контур (L'); для каждого из направлений этого контура
можно в точке А указать параллельное направление, так что каждому
из двух направлений обхода контура (L) будет отвечать напрапление
вращения элемента дуги около точки А. Выполнив то же построение
для точки А' сферической поверхности S\ мы придем к такому
результату:
Если точка А эллиптическая, то направления обхода этой точки
и ее сферического изображения одинаковы; если точка А —
гиперболическая , то эти направления противоположны. Для параболической
точки могут иметь место как тот, так и другой случаи.
Полная кривизна J cods дуги М1М2 плоской линии равна углу
между касательными или, что то же, углу между нормалями в концах
дуги. Таким образом, мерой полной кривизны плоской кривой служит
длина дуги индикатрисы нормалей. По аналогии с этим Гаусс ввел
понятие полной кривизны области (Р) поверхности S. Именно, за ее меру
он принял площадь F' соответствующей области (Р') сферического
изображения. Так как площадь F' пропорциональна квадрату радиуса а
сферы, то полную кривизну следует положить равной —— ; она равна F',
если радиус хауссовой сферы принять за единицу длины. Кривизной
поверхности в данной точке А Гаусс назвал предел, к которому
стремится отношение F':F, когда область Р стягивается к точке А. Что
этот предел не зависит от формы области (Р), будет в дальнейшем
показано.
Кривизне поверхности можно приписать знак. Именно, мы будем
считать ее положительной, если направления обхода малых областей
(Р) и (Р') совпадают, и отрицательной, если эти направления
противоположны. По доказанному, кривизна поверхности в эллиптической точке
положительна, а в гиперболической—-отрицательна. Кривизна же
поверхности в параболической точке равна нулю. Действительно,
по доказанному различным направлен! ям в точке А отвечает только
одно направление А'В' в точке А/. По этому направлению размер
области (Р') имеет тот же порядок малости, что наибольшая хорда
области (Р), тогда как по перпендикулярному направления)
(параллельному асимптотическому в точке А) область (JP') должна иметь
порядок высший, чем все хорды области (Р). Таким образом, F' имеет
порядок выше, чем F, и кривизна в А равна нулю.
Следовательно, кривизна поверхности в точке А по знаку
совпадает с величиной К = , которую мы выше назвали гауссовой кривизной.
Но эти величины равны и по абсолютной величине.
В самом деле, построим на поверхности S четырехугольник BCDE
(рис. 236), охватывающий точку А и ограниченный дугами линии
кривизны ВС, CD, DE7 ЕВ. На сфере ему соответствует
четырехугольник B'C'D'E', ограниченный дугами больших кругов и имеющий
в соответственных точках те же направлении сторон. Так как углы
обоих четырехугольников прямые, то площади их эквивалентны
произведениям ВС- BE и В*С - В'Е'\
Р'ъВ'С'-В'Е' (3>
§ 68. СФЕРИЧЕСКОЕ ИЗОБРАЖЕНИЕ ПОВЕРХНОСТИ 399
Но если Rc и RE суть главные радиусы кривизны в точке В, то
по доказанному
ВСъ\Нс\- В'С, BEzz\RE\. В'Е'. (4)
Сопоставляя (3) и (4), находим
EL — х
F ~~\RC-RE\'
В пределе Rc и RE становятся главными радиусами кривизны в точке Аг
и мы имеем
£^ (5)
что и требовалось доказать.
Если мы припишем знаки площадям поверхности, считая их
положительными, когда они обходятся в направлении, противоположном
Рис. 236.
стрелке часов (при наблюдении с той стороны, куда указывает вектор т*
исходящий из точки поверхности), то можно высказать следующее
предложение:
Теорема 1. Предел отношения площади сферического
изображения поверхности S к площади соответствующей области
поверхности S по величине и по знаку равен гауссовой кривизне поверхности.
Эта теорема, позволяющая построить определение кривизны
поверхности, аналогичное определению кривизны линии, доказана нами в
предположении, что упомянутый в ней предел не зависит от формы
области (Р). В юм, что это предположение справедливо, мы можем
убедиться следующим образом.
Разобьем область (Р) на более мелкие области с помощью сети
линий кривизны. Пограничные с контуром четырехугольники можно
не принимать во внимание, аак как их общая плошадь имеет высший
порядок относительно площади всей области (Р). Для каждого же
четырехугольника, ограниченного линиями кривизны, по доказанному
FiZzKiFi, где Kt есть гауссова кривизна какой-либо точки *'-п>
400 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
четырехугольника, а так как вся область (Р) стягивается в точку А,
то можно также написать FJ ^ KFf, где К есть кривизна поверхности
в точке А. Суммируя эти эквивалентности, находим F'z&KF, что
и требовалось доказать.
Приведем еще аналитический вывод доказанной теоремы.
Элемент площади dF поверхности S равен (§ 45, стр. 263) модулю вектора
(^Х^)^^1)- Аналогично, элемент площади dF' сферического
изображения есть модуль вектора (muy,rnv)dxudjo. Согласно (2)
(пги х mv) dxu
к (ru x rv) dxu dtv.
Поэтому отношение -т=г по абсолютной величине равно к. Но в силу
соглашения о знаке площади эти величины равны и по знаку. Таким
образом,
.. F* dF9 ,
hm у = -ты = к.
Чтобы найти выражение X, помножим равенство
тихт0 = к (ги х г9)
скалярно на вектор гихг0. Получим
Принимая во внимание соотношения (6) § 67 (стр. 394), имеем
-L -М
= к
Е
F
откуда
(6)
что и требовалось доказать.
Формула (6) дает для полной кривизны области (Р) поверхности S
выражение
F'= ^ KdF= ^ \ K^EG-F'dadv.
О)
Из теоремы (1) тотчас же вытекает следующий важный результат. Мы
знаем, что все точки развертывающейся поверхности — параболические.
Оказывается, что имеет место и обратное предложение.
Теорема 2. Поверхность, все точки которой параболические, есть
развертывающаяся поверхность.
Действительно, если все точки поверхности S параболические,
то гауссова кривизна К тождественно равна нулю. Поэтому площадь
изображения любой области (Р) поверхности S равна нулю, а это может
быть лишь в том случае, если вся поверхность S изображается линией
(или точкой). Иными словами, поверхность S имеет оо1 (или только
одну) касательную плоскость. Следовательно (§ 50), S есть
развертывающаяся поверхность (или плоскость).
1) Дифференциалы, соответствующие смещениям вдоль двух координатных
линий, мы отмечаем индексами 1, 2. См. примечание в § 45 на стр. 263.
§ 69. АСИМПТОТИЧЕСКИЕ ЛИНИИ 401
В заключение рассмотрим вопрос о том, в каком случае сферическое
изображение поверхности S сохраняет величину углов между
произвольными направлениями, исходящими из точки А. Для этого, очевидно,
необходимо и достаточно, чтобы при любом повороте направления АВ
сопряженное направление АВХ поворачивалось на тот же угол. Если
А есть эллиптическая точка, то АВХ вращается в ту же сторону, что
АВ, и потому угол между АВ и АВг остается постоянным, а так как
для главных направлений этот угол—прямой, то все сопряженные
диаметры индикатрисы Дюпена перпендикулярны. Значит, точка А~
омби.гическая.
Пусть теперь А есть гиперболическая точка и пусть АВ имеет
асимптотическое направление. Тогда АВг совпадает с АВ. Если
АВ повернуть до совпадения с главным направлением, АВХ
повернется в противоположную сторону и совпадет с другим главным
направлением. Так как углы поворота должны быть равны, то
асимптота индикатрисы Дюпена делит пополам угол между главными
направлениями, т. е. является равносторонней гиперболой. Значит,
необходимо, чтобы средняя кривизна поверхности в точке А равнялась
нулю. Легко видеть, что этого и достаточно. Если мы потребуем, чтобы
сферическое изображение было конформным, т. е. чтобы оно повсюду
сохраняло все углы, то это по доказанному возможно только в двух
случаях: 1) если все точки поверхности S — омбилические; но тогда
поверхность S есть сфера (§ 65, теорема 2, стр. 376), и изображение носит
тривиальный характер; 2) если во всех точках поверхности S средняя
кривизна равна нулю, т. е. если поверхность S — минимальная. Мы
получаем следующую важную теорему.
Теорема 3. Сферическое изображение поверхности 5, отличной
от сферы, конформно в том и только в том случае, если S есть
минимальная поверхность.
§ 69. Асимптотические линии
Линии, рсюду имеющие асимптотические направления, называются
асимптотическими. Из определения асимптотического направления
следует, что кривизна нормальных сечений, касающихся асимптотической
линии, равна нулю (§ 59, стр. 352). Иными словами, эти нормальные
сечения имеют в местах касания точки спрямления (в общем случае-—
точки перегиба). Обратно, если кривизна нормальных сечений,
касающихся некоторой линии, равна нулю, то эта линия—асимптотическая.
На поверхности прямого геликоида все винтоЕые линии и все
прямолинейные образующие являются асимптотическими линиями
(пример 3 § 58, стр. 349). Вообще на всякой линейчатой поверхности
образующие являются асимптотическими линиями, ибо нормальное
сечение в направлении образующей совпадает с самой образующей.
Основное свойство асимптотических линий выражается следующей
теоремой.
Теорема 1. Если кривая (L) есть асимптотическая линия
поверхности S, то соприкасающаяся плоскость в любой ее точке М есть
касательная плоскость поверхности S.
Д( йавительно, согласно определению аегмчтотического направления
точка М' линии (L), бесконечно близкая к М, должна отстоять от
касательной плоскости Р в точке М на расстояние, порядок которого
выше второго (относительно ММ'). Но расстояние от точки М' до
плоскости Р, проходящей через точку М, имеет порядок выше второго
26 М. Я. Выгодский
402 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
в том и только в том случае (§ 20, теорема 5, стр. 9о), если плоскость Р
является соприкасающейся плоскостью. Этим наша теорема доказана.
Справедлива и обратная теорема.
Теорема 2. Если соприкасающаяся плоскость линии (L) на
поверхности S всюду совпадает с касательной плоскостью, то (L) есть
асимптотическая линия.
Для доказательства достаточно обратить предыдущее рассуждение
(ср. § 58, пример 3, стр. 349).
Если совпадение соприкасающейся и касательной плоскостей имеет
место лишь э одной точке кривой (L), то в этой точке линия (L) имеет
асимптотическое направление, т. е. касается асимптотической линии.
Пример 1. На поверхности S, образованной главными нормалями
произвольной линии (/.), сама линия (L) является асимптотической
линией. Действительно, касательная плоскость поверхности S проходит
через касательную к линии (L). и через прямолинейную образующую
поверхности S, т. е. через главную нормаль к (L). Таким образом,
касательная плоскость есть соприкасающаяся плоскость линии (L).
В силу теоремы 2 (L) есть асимптотическая линия поверхности S.
Если на поверхности S имеется прямая линия (к), то эта линия
по доказанному —асимптотическая. Теорема 1 тогда теряег смысл,
но ее можно распространить и на этот случай, ибо вследствие
неопределенности соприкасающейся плоскости ничто не мешает согласиться
отождествлять ее с касательной плоскостью поверхности S.
Сопряженные направления вдоль асимптотической линии совпадают
с направлениями самой асимптотической линии. Поэтому направления
сферического изображения асимптотической линии и самой
асимптотической линии в соответственных точках взаимно перпендикулярны.
По той же причине семейство асимптотических линий, и только такое
семейство, не может быть дополнено до сопряженной сети.
В § 58 [формула (7), стр. 348], мы получили уравнение
= 0, (1)
определяющее асимптотические направления в данной точке.
Это уравнение, если в нем считать L, М, N функциями и и v,
представляет дифференциальное уравнение асимптотических линий.
Уравнения
du:dv = 9i (u> v)> du: dv= <p2 (и, v), (2)
на которые распадается уравнение (1), определяют два семейства
асимптотических линий.
Для того чтобы семейство параметрических линий v = const состояло
из асимптотических линий, необходимо и достаточно, чтобы
тождественно обратился в нуль коэффициент L второй формы, т. е. чтобы
L = 0. (3)
Действительно, если v = const есть асимптотическая линия, то
уравнение (1) должно удовлетворяться при du = l, dv = 0; подставляя в него
эти значения, находим 1 = 0. Обратно, при L = 0 уравнение (1) имеет вид
0 (4)
и удовлетворяется при do = 0. Точно так же условие N = 0 необходимо
и достаточно, чтобы линии w = ccnst были асимптотическими. Чтобы
оба семейства координатных линий были асимптотическими, необходимо
и достаточно условие L = N = 0.
69. АСИМПТОТИЧЕСКИЕ ЛИНИИ
403
Пример 2. Если за координатные линии прямого геликоида
принять прямолинейные образующие и винтовые линии, то (пример 2
§ 57, стр. 342)
jj—2bdudv
Поэтому асимптотические линии прямого геликоида суть его образующие
и винтовые линии.
Так же докажем, что для того, чтобы одна из параметрических линий,
например v = 0, была асимптотической, необходимо и достаточно, чтобы
вдоль нее коэффициент L обращался
в нуль, т. е. чтобы
L(u, 0) = 0.
Пример 3. Найдем уравнения
асимптотических линий псевдосферы
х = а sin и cos v; y = a sin и sin v\
z = a cos и + a In tg |.
Вычисляя коэффициенты второй
квадратичной формы, находим
a cos u
.
sin и
= 0, N = я cos и sin и.
Уравнение (1) принимает вид
(5)
Оно распадается на два уравнения:
du 1 du
sin и
sum
-do.
(б)
Рассмотрим первое из них.
Интегрируя его, находим
v — vo = lntg^. (7)
Рис. 237.
Это уравнение устанавливает связь между долготой v точки М
асимптотической линии псевдосферы и углом и =MTZ, определяющим
положение точки М на меридиане (рис. 237). Чгобы наглядней сделать
эту связь, заметим, что в силу уравнений трактрисы
х ~ a sin ut z = a cos и
Intg^
мы имеем
Кроме того,
Следовательно,
= a cos и + a In tg ^ .
QT = — a cos и.
Таким образом, уравнение (7) выражает, что угол v — v0 поворота
плоскости меридиана от начального положения пропорционален отрезку
ОТ. Так как этот отрезок неограниченно увеличивается, то
асимптотическая линия делает бесчисленное множество завитков/ Первый
26*
404 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
завиток, начинающийся у ребра возврата UV (рис. 238), закапчивается,
когда точка Т поднимается на высоту 2iwj. Точка М винтовой линии
будет находиться на высоте (2тс 4- cos и) а, т. е. (угол и близок к 2тг)
несколько выше пятикратной величины а.
Угол, образуемый асимптотической линией с осью псевдосферы,
стремится к нулю по мере удаления от ребра возврата. Действительно,
диаметр индикатрисы Дюпена, направленный по меридиану, ори этом
растет, а диаметр, направленный по параллели, убывает. Индикатриса
Рис. 238.
вытягивается вдоль меридиана, и асимптоты ее стремятся совпасть
с меридианом. Напротив, при приближении к ребру возврата второй
диаметр индикатрисы стремится к бесконечности, так как второй радиус
кривизны (отрезок нормали псевдосферы), очевидно, бесконечен в
вершине А. Первый же радиус кривизны (радиус кривизны трактрисы)
в точке А равен нулю (пример 7 § 24, стр. 129). Следовательно,
вблизи ребра UV индикатриса вытягивается вдоль параллели, и
асимптотическая линия при встрече с ребром касается его.
Все асимптотические линии одного семейства получаются вращением
одной из них около оси псевдосферы. Асимптотические линии другого
семейства симметричны с первыми. Асимптотические линии одного
семейства — правые, другого —левые.
В § 86 (стр. 489—493) свойства асимптотических линий
псевдосферы будут исследованы геометрически.
§ 69. АСИМПТОТИЧЕСКИЕ ЛИНИИ 405
Через эллиптическую точку поверхности действительных
асимптотических линий провести, очевидно, нельзя. Через каждую
гиперболическую точку поверхности проходят две асимптотические линии.
В параболической точке два асимптотических направления сливаются
в одно, и в общем случае мы получаем картину, подобную изображенной
на рис. 239: на линии UV, состоящей из параболических точек и
отделяющей область гиперболических точек CDVU от области эллиптических
точек ABVU', сходятся, попарно касаясь друг друга, асимптотические
линии поверхности. Иными словами, асимптотические линии можно
объединить в одно семейство линий с
точками возврата на линии UV.
Бельтрами (1866 г.) и Эннепер (1870г.)
установили следующую связь между
кручением асимптотических линий и
гауссовой кривизной поверхности.
Теорема 3. Квадрат кручения
каждой из двух асимптотических линий (Ьг)
и (Z.,), проходящих чере» точку М
поверхности S, равен абсолютному
значению гауссовой кривизны поверхности
в этой точке. При этом линии (LJ и
(Lt) имеют кручения противоположных
8ников.
Мы дадим синтетическое
доказательство этой теоремы. Так как
соприкасающаяся плоскость асимптотической ли-
нид является касательной плоскостью по- Рис- 239«
верхности S, то квадрат кручения
асимптотической линии в точке М равен -т-2. Построим индикатрису Дюпена
и сферическое отображение поверхности S (рис. 240). Смещению
dr по асимптотическому направлению на поверхности S
отвечает смешение MiQl^dm на сфере, перпендикулярное к т.
Если мы придем в течку Q из точки М, сместившись сначала
по главному направлению в точку Р, а затем по второму главному
направлению в точку Q, то этому пути на сфере будет отвечать путь
М\P\Qn причем смешение МгРг, Pfii совершается также по главным
направлениям, соответственно параллельным МР и PQ. Имеем:
(8)
W^^-PQ*. (9)
Но так как MQ есть асимптота индикатрисы, то
или
МР'^Шг, PQ*=-lRt. (10)
С помощью соотношений (8), (9), (10) получаем:
АД,-АД,
406 ГЛ. IX, ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Итак, квадрат кручения каждой из двух асимпют^ческих линий,
проходящих через точку Д/, равен взятой с обратным знаком гауссовой
кривизне (которая, если асимптотические линии действительны, должна
быть отрицательной или в крайнем случае может равняться нулю).
Г
S
б)
Рис. 240.
Исследуем теперь вопрос о знаке кручения о. Для определенности
предположим, что вектор т нормали направлен от точки М к чвдателю.
Пусть движение вдоль асимптотической линии совершается по
направлению от М к Q. Вектор dm у который для любой линии нернендикулярен
к направлению, сопряженному с dr, для асимптотической линии будет
коллинеарен с прямой qq'', перпендикулярной к MQ. Вектор т колли-
неарен с бинормалью асимптотической линии (т= ±ft). Поэтому, если
кручение а положительно, тройка векторов t, dm, m должна быть левой,
если же о отрицательно, то эта тройка —правая. Эю знапит, что при
а > 0 вектор dm равнонаправлен с лучом Mq\ с которым луч MQ
совпадает после поворота на угол — 90°; при о < 0 вектор dm
равнонаправлен с лучом Mq, с которым MQ совпадает после поворота на
угол +90°.
Для определенности предположим, что имеет место второй случай
(о < 0), и докажем, что тогда для другого асимптотического направ-
§ 69. АСИМПТОТИЧЕСКИЕ ЛИНИИ 407
ления имеет место первый случай (а > 0). Иными словами, нужно
доказать, что если поворот от асимптотического направления MQ
к направлению Mq вектора dm совершается в положительном
направлении, то поворот от асимптотического направления MS к
соответствующему направлению dm совершается в отрицательном направлении,
т. е. что вектор dm равнонаправлен с Ms, а не с Ms'.
Для доказательства будем вращааь вектор dr из положения, кол-
линеарного с MQ, в положительном направлении до совпадения с
направлением MS. Диаметр индикатрисы, сопряженный с направлением
dr, будет тогда вращаться из положения MQ в положение MS'
в отрицательном направлении. Вектор dm, перпендикулярный к
сопряженному диаметру, будет вращаться также в отрицательном
направлении и потому в конце движения окажется направленным именно
по Ms, а не по Ms' (при прохождении вектора dr через главное
направление MY вектор dm пройдет тоже через это направление).
Этим доказано, что кривизны двух асимптотических линий имеют
противоположные знаки, что составляет вторую часть теоремы 3.
Доказанная теорема распространяется и на случай, когда
асимптотическая линия — прямая, если под кручением прямой понимать
скорость вращения касательной плоскости вдоль этой прямой (см.
замечание к примеру 1 на стр. 402).
Следующая теорема (Бельтрами, 1865 г.) дает замечательное
выражение для кривизны асимптотической линии. Как известно
(§ 58, стр. 346), касательная плоскость в точке М поверхности S
пересекает эту поверхность по линии, обе ветви которой имеют в точке М
асимптотические направления. Эта теорема устанавливает зависимость
между кривизной какой-либо из этих ветвей и кривизной касающейся
ее асимптотической линии.
Теорема 4. Каждая ветвь сеченая поверхности касательной
плоскостью в гиперболической точке М имеет в этой точке кривизну х,
в полтора раза меньшую, чем кривизна ха асимптотической линии,
касающейся рассматриваемой ветви.
Эта теорема выделяется среди всех других теорем настоящей
главы тем, что она требует существования не только второго, но
и третьего дифференциала вектора г. В тех точках поверхности, где
это требование не выполняется, теорема Бельтрами может оказаться
неверной.
Для доказательства примем за координатный триедр
сопутствующий триедр асимптотической линии в рассматриваемой точке..
Согласно теореме 1 плоскость XMY совпадает с касательной
плоскостью. Следовательно, уравнение поверхности должно иметь вид
где г0, 50, £0 - значения частных производных г, s, t в точке Л/(0, 0),
о ^ d3z dzz dzz d5z
a a, p, у» о —значения частных производных -г—;, т-тт-> -о—*-ъ» —^
1 г дх3 дхЮу дх ду2 0уъ
в той же точке. Из (11) находим
(12)
408 ГЛ. IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИВИЗНА ПОВЕРХНОСТИ
Вдоль рассматриваемой асимптотической линии должно
удовлетворяться дифференциальное уравнение
г dx2 + 2sdxdy + t dy2 = 0. (13)
При нашем выборе осей мы должны при я = 0, г/ = 0 иметь dy = O.
Поэтому мы должны иметь
го=О.
Далее, для асимптотической линии у имеет относительно х порядок
не ниже двух, а z—в точности третий порядок, ибо кручение
асимптотической линии, по теореме 3, не равно нулю. Поэтому для точек
асимптотической линии удовлетворяется \ равнение
z = soxy + -g- clxz + ... , (14)
где многоточие заменяет члены порядка выше третьего. Уравнения же
(12), если в них сохранить только главные члены, примут вид
г = аж+..., s = so+..., t = to+... (15)
Подставляя эти выражения в (13), мы видим, что вдоль
рассматриваемой асимптотической линии удовлетворяется уравнение
axdx2 + 2sodxdy+tody*+ ...=0. (16)
Но при нашем выборе осей мы должны иметь
2/ = у*а*2+..., (17)
откуда
(18)
Подставляем выражение (18) в (16); находим
аж + 2$0хая+...=0, (19)
где отброшенные члены Г в их числе -г t^lx2 J имеют порядок выше
первого. Уравнение (19) можно сократить на я, так как при нашем
выборе осей ь окрестности точки (0, 0) абсцисса не равна нулю.
Тогда получим
т. е.
*.«-4i- (20>
Таково выражение кривизны асимптотической линии. Оно зависит,
как мы видим, от третьей производной а = -^ .
Найдем теперь кривизну рассматриваемой ветви плоского сечения
z = 0. Так как оно имеет то же направление, что асимптотическая
линия, то уравнение поверхности (11) мъжно взять в усеченном виде
(14); полагая в этом уравнении z = 0, находим уравнение
8,ру + ±*х9+...=0, (21)
которому должно удовлетворять соотношение
г/=1хя2 + ... (22)
§ 70. НОВАЯ ИНТКРПГЕТАЦИЯ ВТОРОЙ КВАДРАТИЧНОЙ ФОРМЫ 409
Подставляя это выражение в (21), находим
х=—ij-. (23)
Сравнивая (20) и (23), находим
что и утверждает теорема 4.
Замечание. Пользуясь найденным выражением (20) кривизны
аеимшои ческих линьй, мы можем ле!ко проверить вычислением
теорему 3. Для этого перепишем уравнение (14) в виде
и подставим сюда канонические уравнения асимптотической линии!
г/ = 1*ая8, 2 = -£-сахая8.
По сокращении на *а#8 найдем
*a = V (24)
С другой стороны, вычислив гауссову кривизну поверхности в точке М,
найдем
LN-M*
Сравнение (24) и (25) дает
<4- -Л,
что и утверждает теорема 3.
Упражнения
1 Найти асимптотические линии гиперболического параболоида.
2 Имеются ли на развертывающейся поверхности асимптотические линии,,
отличные от прямолинейных образующих?
3. найти асимптотические лиш.и катеноида.
4. Проверит!, теорему 3 для геликоида.
5. Найти ьручение асимптотических линий псевдосферы.
6 Найти гауссов\ кривизну поверхности главных нормалей линии (L) в точке,
лежащей на (L).
1 Найти ьручение асимптотических линий поверхности бинормалей линии (L).
Является ли (/.) асимптотической линией этой поверхности?
8 Доказать, что асимптотическая линия, если она одновременно являете»
линией кривизны, состоит сплошь из параболических точек. Примером может
служить верхняя или нижняя параллель тора.
§ 70. Новая интерпретация второй квадратичной формы
Вторая квадратичная форма
была получена нами в § 57 (стр. 339) как выражение главной части
удвоенного расстояния 2А от точки М поверхности S до касательной
ело< ьости в бесконечно близкий точке М\ Но второй квадратичной
форме можно дать еще иное геометрическое истолкование.
410 Г Л, IX. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИБИРНА ПОВЕРХНОСТИ
Пусть т и т'— орты нормалей в точках М и М', а N и N'
(рис. 241)—соответствующие точки сферического изображения
поверхности S. Тогда вторая квадратичная форма дает главную часть
выражения
-1 ММ' 11NN' | cos (MM', NN').
Иначе говоря, вторая квадратичная форма равна скалярному
произведению dr, dm, взятому с обратным знаком:
L du2 + 2M dudv + N dv2 = —drdm.
Докажем это. Проведем в точке М поверхности S по направлению
ММ' нормальное сечение. Пусть п есть орт главной нормали этого
сечения в точке М\ Проведем еще радиус OQ сферы, равнонаправлен-
ный с п. Так как векторы т' и п перпендикулярны к ММ' ъ dr, то
плоскость ON'Q перпендикулярна к dr, а значит, и к плоскости нор-
Рис. 241.
мального сечения, проведенного по направлению dr. Но векторы
ON = т и OQ = п по построению лежат в плоскости этого нормального
сечения. Следовательно, угол NQN' — прямой. Далее, вектор NQ^ п~т
эквивалентен дифференциалу главной нормали сечения АВ, и потому
его абсолютная величина эквивалентна |dr|x, а направление его
противоположно dr, т. е.
lVQzz — *dr. (1)
Но мы имеем
Используя соотношение (1) и принимая во внимание, что 7V'(? J_ dr,
находим
2h= -Щdr=-(Ш' + WQ)dr=-Ш'dr,
или, что то же,
H=—dmdr9 (2)
что и требовалось доказать.
§ 71. ТРЕТЬЯ КВАДРАТИЧНАЯ ФОРМА 411
Очень коротким, но менее наглядным образом формулу (2) можно
получить следующим образом.
Величину 2h можно выразить (§ 57, стр. 339) в виде
2Л^2(Дг/ю)^ 2(dr + jd2r+ . ..^\m^d2rm. (3)
•Здесь мы воспользовались тождественным соотношением
= 0. (4)
Дифференцируя это соотношение, находим d2r ffl + dr dffl = 0. Поэтому
равенство (3) примет вид
II=~drdm. (5)
§ 71. Третья квадратичная форма
Отношение второй квадратичной формы к первой дает кривизны
нормальных сечений поверхности во всевозможных направлениях, так
что можно сказать, что это отношение дает меру искривления
поверхности. Однако мерой искривления могут служить и другие величины.
Еще в 1776 году Менье предложил измерять искривление поверхности
в данном направлении аналогично тому, как измеряется искривление
линии, именно, он назвал кривизной поверхности (в данном направлении)
отношение угла смежности касательных плоскостей к длине
соответствующей дуги поверхности. Так как упомянутый угол равен углу
между смежными нормалями, а последний измеряется дугой NN'
гауссова изображения, то квадрат меры Менье есть не что иное, как
отношение
NN'2 _ dm*
MM'2 ~~ dr2 '
Знаменатель этого отношения есть первая квадратичная форма;
числитель также можно представить квадратичной формой дифференциалов
du, dv:
dm2 =(mudu + mv dv)2 = e du2 + 2fdudv + g dv\ (1)
где
е = тъ, f = mumv, g = mi. (2)
Выражение edu2 + 2f dudv + gdv2 называется третьей
квадратичной дифференциальной формой. Оно представляет линейный элемент
гауссова изображения поверхности.
Если mfj имеем любые три величины, представляемые
квадратичными формами двух переменных, то мы можем, исключив эти
переменные, найти зависимость между вашими тремя величинами. Но
в общем случае мы получим уравнение второй степени. В нашем же
случае между квадратичными формами
dv +Gdv2,
II = L dn2 + 2М du dv + Ndv\ \ (3)
= edu2 +2fdudv +gdv2 J
существует линейная зависимость. Происходит это потому, что три
формы /, //, /// можно представить как скалярные произведения,
412 ГЛ. IX, ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА И КРИРИРНА ПОВЕРХНОСТИ
составленные из двух векторов dr, dm, именно:
I = dr\ \
II=-drdm, \ (4)
111 = dm2. J
Так как вектор dm вполне определяется заданием вектора dr,
то dr2, dm2у drdm зависят только от направления и длины dr, но
не зависят от выбранной на поверхности системы координат. Поэтому
мы ворьмем наиболее удобную систему, приняв за координатные лиш и
и = const, v = const лунии кривизны поверхности. То1да векторы ги>
rv будут взаимно перпендикулярны и, кроме того, селласно формулам
Родрига (§ 67, стр. 395)
Поэтому мы имеем
vdv, (5)
du—i-rvdv. (Q)
Формулы (5) и (6) позволяют выразить векторы rudu и rv dvчерез dr
и dm* Именно, помножая (5) на -„ и складывая с (6), находим
"2
и аналогично
а так как векторы, стояшие в левых частях (7) и (8), будучи колли-
неарны с направлениями линий кривизны, взаимно перпендикулярны,
то их скалярное произведение равно нулю, и мы находим
(kdr+dmXkdr+dm)=°-
Выполняя умножение и принимая во внимание (4), находим
Величина ^-о- есть гауссова кривизна поверхности, а я-+п- есть
удвоенная средняя кривизна, поэтому можем написать
^./-2Я//+/// = 0. . (10)
Этим устанавливается линейная зависимость между тремя основными
формами, причем выяснен и геометрический смысл коэффициентов
этой зависимости.
Но, как выше указано, значения /, //, /// совершенно не
зависят от выбора системы криволинейных координат на поверхности.
§ 71. ТРЕТЬЯ КВАДРАТИЧНАЯ ФОРМА 413
Поэтому теперь мы можем вернуться к произвольной системе
координат, т. е. для /, // и /// взять выражения (3), а для К и 2Я
—выражения
EG-F*
найденные в § 63.
Так как зависимость (10) должна иметь место при любых
значениях du, do, то коэффициенты при du*,dudv, do* в левой части (10)
должны по отдельности обращаться в нуль, т. е. имеем
(12)
Принимая во внимание формулы (11), мы видим, что
коэффициенты е, /, g выражаются рациональными функциями от коэффициентов
первых двух квадратичных форм.
ГЛАВА X
Основные формулы теории поверхностей и внутренняя
геометрия поверхности
§ 72. Формула в теорема Менье
Ближайшей нашей задачей является изучение кривизны
произвольной линии, проведенной на поверхности. Для этой цели нам будет
полезно следующее простое предложение.
Теорема 1. Если линия (L) ортогонально проектируется на
плоскость Р, проходящую через ее касательную в точке М, то кри-
Рис. 242.
визна х линии (L) и кривизна х' ее проекции (L') в рассматриваемой
точке связаны соотношением
х' =xcos ср,
где ср есть угол между плоскостью проекций Р и соприкасающейся
плоскостью Рх линии (L).
Для доказательства проведем через точку N линии (L) (рис. 242)
и проекцию N' этой точки плоскость NN'Q, nej пендикулярную
к касательной МТ. Пусть Q есть точка пересечения этой плоскости
с МТ. Так как прямые NQ и N'Q перпендикулярны к МТ, то
т х' = 2-^ (1)
§ 72. ФОРМУЛА И ТЕОРЕМА МЕНЬЕ 415
Из прямоугольного треугольника NN'Q мы имеем
N'Q = NQcosQ. (la)
По построению угол Q есть линейный угол плоскостей Р и TMN.
Последняя же имеет пределом соприкасающуюся плоскость Рх линии (L)
(§ 20, теорема 2, стр. 83—84). Поэтому
и из формул (1), (1а), (1Ь) мы получаем
x' = xcos<p, (1с)
что и требовалось доказать.
Формула (1с) показывает, что кривизна проекции в точке М не
может превосходить кривизны проектируемой линии в той же точке.
Рис. 243.
Теперь рассмотрим на поверхности S какую-либо линию (L).
Спроектируем ее на плоскость Рп нормального сечения (I),
касающегося (L) в точке М, и на касательную плоскость Р к поверхности
в той же точке. Обозначим проекции соответственно через (Ln) и (Lg)
(рис. 243); если через <р мы обозначим угол между соприкасающейся
плоскостью линии (L) и плоскостью Рп, то по теореме 1 будем иметь
для кривизн хл и ид линий (Ln) и (Lg) выражения
(2)
(3)
Величина хп называется нормальной кривизной линии (L); величина хд —
тангенциальной или геодезической кривизной. Центр кривизны линии (Lg)
называется центром геодезической кривизны; радиус кривизны ptf
линии (Lg) называется радиусом геодезической кривизны.
Что касается центра и радиуса кривизны линии (Ln), то они
совпадают с центром и радиусом кривизны нормального сечения (л),
касающегося (L) в точке М.
Докажем это. Проведем (рис. 244) через М' плоскость M'DEy
перпендикулярную к общей касательной МТ линий (L), (Ln) и (л).
Пусть В, С и D — течки пересечения этой плоскости соответственно
416 ГЛ. X, ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
с проекцией (Ln), нормальным сечением (к) и касательной МТ. Тогда
для кривизны хя нормального сечения и кривизны хл проекции (Ln)
мы имеем следующие выражении:
1С О ,. 2BD
Но отрезок CD есть расстояние точки С от касательной
плоскости Р в точке М\ отрезок же BD равен отрезку М'Е, дающему
расстояние точки М' от той же плоскости. Так как линии (/,) и (L)
имеют в точке М одно и то же направление и каждая из точек С
и М' удалена от М на расстояние, эквивалентное MD, то
расстояния CD и M'E = BD эквивалентны 1):
CDzzBD.
Значит, кривизны хд и хп равны.
Итак, нормальная кривизна хл есть не что иное, как кривизна
нормального сечения, и формула (2) устанавливает связь между
Рис. 244.
кривизной любой линии (£) поверхности S и кривизной касающегося
ее нормального сечения. Эта замечательная формула носит ими
Менье (Ch. Meusnier), которым она была найдена в 1/76 году через
шесть лет после опубликования эйлеровой формулы. Вместе с
последней она в общем случае дает возможность найти кривизну
линии (L) по данному ее направлению и по положению ее
соприкасающейся плоскости.
Предположим сначала, что направление линии (L) в точке М
не является асимптотическим; тогда хп Ф 0, и из формулы (2) мы
находим
* = —. (4)
cos v K ]
Мы видим, что все линии, проведенные на поверхности через
данную ее точку М по данному неасимптотическому направлению
и имеющие в М данную соприкасающуюся плоскость, имеют одну
*) Главная часть каждого ив этих расстояний естьу
§ 72. ФОРМУЛА И ТЕОРЕМА МЕНЬЕ 417
и ту же кривизну. В частности, эту кривизну имеет и плоское
сечение поверхности, образованное данной соприкасающейся плоскостью.
При этом все линии, имеющие4
данное направление, имеют не
меньшую кривизну, чем нормальное
сечение, идущее в том же
направлении.
Формулу (2) в рассматриваемом
случае (хл Ф 0) можно переписать
в виде
p = JU^=JRcos?. (5)
Здесь R = — есть радиус кривизны
хп
нормального сечения. Формула (5)
показывает, что проекция этого
радиуса на соприкасающуюся
плоскость линии (L) дает радиус
кривизны последней линии. Таким
образом, имеет место следующее пред- Рис- 245«
ложение.
Теорема 2. Центр кривизны О линии (L), имеющей чеасимпто-
тическое направление, есть проекция центра кривизны С нормального се-
чения, касающегося линии (L), на соприкасающуюся плоскость этой линии.
Теорема эта особенно очевидна
для плоских сечений шара (рис. 245).
Ее можно поэтому сформулировааь
еще так:
Геометрическое место кругов
кривизны всех линий, проходящих на
поверхности через данную точку М
в данном (неасимптотическом)
направлении, есть сфера, касающаяся
поверхности в точке М\ радиус
этой сферы равен радиусу кривизны
нормального сечения, проведенного в
рассматриваемом направлении.
В этом виде теорема и была
сформулирована Менье.
Если рассматривать линии,
проведенные на поверхности в
направлении, отличном от
первоначального, то место кругов кривизны
тоже будет сферой, но радиус этой
сферы в общем случае не будет
тем же.
Таким образом, поверхность в
общем случае нельзя приближенно за-
Рис 246. менить сферой, наподобие того, как
линию можно заменить
соприкасающейся окружностью. Это возможно лишь в омбилическей точке.
Замечание. Теорема 2 позволяет также построить центр
кривизны Сп нормального сечения по данному центру кривизны С
27 М. Я, Выгодский
418 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
линии (L). Для этого достаточно провести ось кривизны (к) линии (Z.)
(рис. 246). В пересечении с нормалью поверхности получим центр
кривизны Сп нормального сечения. Точно так же в пересечении (л)
с касательной плоскостью найдем центр геодезической кривизны Сг
Так, центр геодезической кривизны параллели поверхности вращения
лежит, как видно на рис. 246, на пересечении оси вращения с
касательной пряхМой меридиана в соответствующей точке. На оси
вращения лежит и центр кривизны нормального сечения, в чем мы
убедились еще раньше (§ 65, пример 1, стр. 382).
Из формулы (2) снова вытекает, что соприкасающаяся
плоскость линии (L) в точке М может совпадать с касательной плоскостью
поверхности лишь в том случае, когда направление (L) в
рассматриваемой точке —асимптотическое (ср. теорему 2 § 69, стр. 402).
Интересно посмотреть, чтб делается с плоским сечением, проведенным
в неасимптотическом направлении МТ,
когда плоскость сечения, вращаясь
около прямой МТ, стремится к
касательной плоскости поверхности 5.
Если точка М является
эллиптической (например, если поверхность
S — сфера), то сечение стягивается
в точку М. При этом кривизна
сечения в точке М стремится к
бесконечности. В гиперболической точке
кривизна сечения также стремится
к бесконечности, но сечение не
стягивается в точку, а напоминает ветвь
гиперболы с вершиной в М (рис. 247).
По мере увеличения кривизны
сечения к ветви AM В приближается
другая ветвь А'М'В1', не проходящая
через М. Когда секущая плоскость
совпадает с касатзльной плоскостью,
точка М' сливается с М, и на линии
АМВ в точке М появляется излом.
Полуветвь AM в точке М принимает
асимптотическое направление и
находит себе продолжение в полуветви
М'В'. Таким образом, хотя во всяком
допредельном положении сечение имело в точке М неасимптотическое
направление, в предельном положении оно имеет два направления, и оба
они — асимптотические.
Обращаемся теперь к рассмотрению случая, когда линия (L)
в точке М имеет асимптотическое направление, т. е. когда ее
нормальная кривизна хл = 0. Если соприкасающаяся плоскость линии (L)
не совпадает с касательной плоскостью f <p=£ y)> т0> согласно
формуле (4), мы должны иметь х = 0, т. е. все линии, идущие в
асимптотическом направлении и имеющие соприкасающуюся плоскость,
отличную от касательной плоскости, имеют в рассматриваемой точке
спрямление. Таких линий сущесавует бесчисленное множество (в том числе
все сечения поверхности плоскостями, отличными от касательной).
Если же для линии (L), обладающей в точке М асимптотическим
направлением, соприкасающаяся плоскость совпадает с касательной,
Рис. 247.
§ 72. ФОРМУЛА И ТЕОРЕМА МЕНЬЕ 419
то кривизна ее отнюдь не должна равняться нулю. Формула (4) дает
для нее неопределенное выражение —~- = -- 9 и она, действительно,
неопределенна, т. е. может в данной точке М иметь различные
значения. Так, одна из ветвей сечения поверхности касательной
плоскостью имеет кривизну, в полтора раза бдлыпую, чем кривизна
асимптотической линии, касающейся этой ветви (§ 69, теорема 4, стр. 407).
Более того, имеет место следующая теорема.
Теорема 3. Через любую гиперболическую или параболическую
точку М поверхности S молено провести в любом ее асимптотическом
направлении линию (L), соприкасающаяся плоскость которой совпадает
Рис. 248.
с касательной плоскостью и которая имеет в рассматриваемой точке
любую наперед заданную кривизну.
Для доказательства построим в касательной плоскости линию (L'),
касающуюся асимптоты МТ иидикатрисы Дюпена и имеющую в точке
касания заданную кривизну, Очевидно, таких линий можно построить
бесчисленное множество. Построим прямой цилиндр, имеющий
линию (Z/) основанием. Линия (L), по которой этот цилиндр
пересекает поверхность, будет искомой.
Действительно, пусть N есть точка линии (I), бесконечно
близкая к М, и N' — ее проекция на касательную плоскость, т. е.
соответствующая точка линии (Z/) (рис. 248). Проведем плоскость NN'Q,
перпендикулярную к МТ. Линия (L) в точке М, очевидно, имеет
ту же касательную МТ, что линия (!'), и так как направление МТ —
асимптотическое, то катет NN' в треугольнике NN'Q имеет порядок
выше второго относительно MQ. Пусть кривизна линии (Z/) в точке М
отлична от нуля. Тогда катет NQ имеет второй порядок
относительно MQ и, следовательно,
NQ^N'Q,
и из соотношений
27*
420 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
вытекает
x = V (6)
Если же кривизна линии (£') равна нулю, то N'Q имеет, так же1
как NN', порядок выше второго. Значит, и NQ имеет порядок выше
второго, т. е. кривизна х линии (L) также равна нулю. Этим наша
теорема доказана.
Теорему 3 можно дополнить следующим предложением.
Теорема 4. Кривизна всякой линии (Z.), имеющей в
рассматриваемой точке асимптотическое направление, равна ее геодезической
кривизне хд.
Действительно, если соприкасающаяся плоскость линии (L)
совпадает с касательной плоскостью (<р = ~V то формула (3) дает
х = хд. Если же <р Ф ~ , то по доказанному х = 0, и формула (3)
дает ъд = 0.
В частности, геодезическая кривизна асимптотической линии всюду
равна ее кривизне. Обратно, если вдоль всей линии (L) имеем *д = *,
то линия (L) — асимптотическая. Действительно, в силу формулы
Y.g = х sin <р
мы должны иметь либо <? = •£> либо х = 0. В обоих случаях формула
хп = х cos <р
дает
хп = 0,
т. е. во всех точках линии (L) кривизна нормального сечения,
имеющего то же направление, что (/.), равна нулю; иначе говоря,
направление линии (L) всюду совпадает с асимптотическим направлением
поверхности.
Не лишним будет заметить, что на плоскости геодезическая
кривизна всякой линии равна ее кривизне.
Из определения геодезической кривизны непосредственно
вытекает также следующая теорема.
Теорема 5. Если две поверхности Sx и S2 касаются друг друга
вдоль линии (L), то на обеих поверхностях линия (L) имеет одну и ту
«же геодезическую кривизну.
В заключение дадим аналитическое доказательство формулы Менье.
Согласно первой формуле Френе мы имеем
—в-
Помножив это равенство скалярно на т и принимая во внимание,
что mtl = cos cp, находим
_ L du2 4- 2Mdu dy + Ndy2 __Il
~ Edu1 f 2Fdл dv + Gdv2 ~" T "
Согласно формуле (4) § 59 (стр. 350), в которой при нынешних
наших обозначениях мы должны вместо х написать хп, находим
х cos 9 = х„.
§ 73. ГЕОДЕЗИЧЕСКИЕ ЛИНИИ 421
Упражнения
1. Если нормальная кривизна линии (L) всюду равна ее кривизне, то линия
(I) — геодезическая (§ 55, стр. 325).
2. Радиус геодезической кривизны для всех параллелей псевдосферы равен
радиусу кривизны а ребра возврата.
3. Геодезическая кривизна винтовой линии на поверхности прямого
геликоида ра^на кривизне этой винтовой линии, а на поверхности цилиндра—нулю.
4. Геодезическая кривизна меридиана поверхности вращения равна нулю.
5. Найти кривизну эллипса в его вершинах, рассматривая эллипс как
сечение круглого цилиндра.
§ 73. Геодезические линии
В § 55 (стр. 325) мы определили геодезическую линию поверхности
как такую линию, вдоль которой соприкасающаяся плоскость всюду
перпендикулярна к касательной плоскости поверхности, т. е. главная
нормаль совпадает с нормалью поверхности. К числу геодезических
линий хмы отнесли также прямолинейные образующие.
Таким образом, вдоль геодезической линии (L) либо х = 0 (если
(Ц—-прямая линия), либо угол <р между соприкасающейся плоскостью
и плоскостью нормального сечения равен нулю. В обоих случаях для
геодезической кривизны хд получаем
O, (1)
а для нормальной кривизны
хп = х cos <p = х. (2)
Очевидно, что и обратно, из условия (1) или (2) следует, что
линия L) — геодезическая. Поэтому мы можем сказать, что
геодезическая линия поверхности есть линия нулевой геодезической кривизны
или что геодезическая линия есть линия, для которой нормальная
кривизна всюду равна кривизне.
На плоскости геодезическими линиями являются прямые линии и
только они.
Геодезические линии обладают многими свойствами, очень важными
для практики и чрезвычайно интересными с теоретической стороны*
Поскольку прямые линии являются геодезическими линиями
плоскости, все эти свойства представляют обобщение свойств прямой линии.
При этом многие важные свойства прямых полностью сохраняются
для геодезических линий на любой поверхносш.
Подобно тому, как на плоскости из каждой точки исходит пучок
прямых, на кривой поверхности через каждую точку М проходит
пучок геодезических линий, и по каждому направлению проходит одна
и только одна геодезическая линия.
Чтобы наглядно убедиться в этом, выполним построение, которое
позволяет приближенно (с любой степенью точности) провести
геодезическую линию через данную точку М по заданному направлению МТ
(рис. 249).
Проведем через нормаль АМВ и прямую МТ плоскость Р. На
произведенном ею нормальном сечении возьмем малую дугу Л/Л/' = а.
В точкеМ'проведем нормаль А'М'В', ачерез эту нормаль —плоскость Р\
проходящую через Д/. Эта плоскость даст нормальное сечение, на
котором мы отложим малую дугу М'М" той же длины а (впрочем,
равенство дуг не существенно). Через М" проводим нормаль А!'М"В"\
422 гл. х, основные формулы, внутренняя геометрия поверхности
через эту нормаль и М' проводим нормальное сечение, на нем
откладываем М"М'" = а и т. д.
Мы получаем на поверхности линию (L,), состоящую из дуг ММ\
М'М"У М"М'",... Эту линию можно приближенно считать
геодезической; приближение будет тем лучшим, чем меньше длина о.
В самом деле, по построению ломаная ММ' М"М'" ...,
описанная в (Li), является ребром возврата многогранной поверхности Elf
образованной из кусков ММ'КК', М''М"К'Кп,.. . нормальных плоскостей
Р, Р\ Р", ... В пределе поверхность Ёх станет развертывающейся
поверхностью S, огибающей семейство нормальных плоскостей {Р}\
Рис. 249.
линия же (L) стаиет ребром возврата поверхности S. Значит, все
соприкасающееся плоскости линии (L) будут нормальными
плоскостями поверхности S, т. е. они будут перпендикулнриы к касательным
плоскостям поверхности S. Значит, линия (L) — геодезическая, так
что (Lt) представляет геодезическую линию приближенно.
Разумеется, для того чтобы сделать это доказательство строгим,
нужно оправдать законность предельного перехода. Это мощно сделать
следующим образомз 1) полагаем а = —, где <? есть фиксированная
длина, а п стремится к бесконечности; рассматривая точку М<п\
лежащую в конце л-го звена линии (Ьг), докажем, что Д/<») имеет
пределом некоторую точку Ms. 2) Рассмотрим место (L) точек Мь при
переменном s и докажем, что (L) всюду имеет соприкасающуюся
плоскость, которая совпадает с нормальной плоскостью поверхности S.
Рассужденяя, которые здесь намечены, равносильны
доказательству теоремы о существовании решения дифференциального уравнения
геодезической линии (по методу Коши-Липщица). Поэтому теоретически
§ 73. ГЕОДЕЗИЧЕСКИЕ ЛИНИИ 423
предпочтительно вывести это уравнение (что сделано ниже в § 83)
и опереться на упомянутую теорему.
Но предлагаемый здесь метод построения имеет практический
интерес как потому, что позволяет найти геодезическую линию
поверхности, не зная уравнения этой поверхности, так и потому, что
лишь в исключительных случаях уравнение геодезической линии
удается решить в квадратурах.
Геодезическая линия является «прямейшей» линией поверхности
в том смысле, что в каждой ее точке М по направлению
геодезической линии нельзя провести линии, которая имела бы здесь меньшую
кривизну. Это совершенно очевидно, если геодезическая линия
—прямая. Но это верно и
для криволинейных
геодезических линий, ибо для
них согласно формуле (2)
§ 72 х = хл, а для
всякой другой линии хп =
= х cos 9 <. х.
На плоскости
кратчайшее расстояние между
двумя точками дает прямая
линия. На кривой
поверхности кратчайшей линией,
соединяющей две данные
точки, является дуга
геодезической линии. В § 55
(стр. 325) это было
доказано для развертывающихся Рис. 250.
поверхностей. Теперь мы
установим это ее экстремальное свойство для любой поверхности.
Теорема 1. Для того чтобы линия (L), соединяющая точки
А и В поверхности S была кратчайшим (на поверхности) путем
между точками А и В, необходимо, чтобы линия (L) была геодезической.
Возьмем на дуге АВ линии (L) произвольную т< чку С и докажем,
что кривизна линии (L) в этой точке равна ее нормальной кривизне.
Идея приводимого ниже доказательства состоит в использовании
очевидного факта, что длина дуги CD, соединяющей две
фиксированные близкие точки С и D поверхности (рис. 250), тем меньше, чем
меньше кривизна дуги. Вследствие этого кратчайшая дуга должна
быть прямейшей, т. е. геодезической.
Доказательство. Возьмем на дуге АВ точку D в
окрестности точки С и проведем в точке С нормальное сечение (X),
проходящее через точку Z). Кривизну дуги (к) в точке С обозначим хд,
кривизну дуги (L) в той же точке — через у. и нормальную ее кривизну —
через хл.
Докажем, что дуга CD^) линии (L) не превосходит дуги СЪ{Х)
нормального сечения, т. е. что
(3)
Действительно, по условию путь по дуге АВ = AC -\~CD(L) + DB
короче, чем всякий другой путь из А в В. В частности, он короче,
424 гл. х, основные формулы» внутренняя геометрия поверхности
чем путь AC + CD(d +DB, если дуги (к) и (L) не совпадают. Если же
эти дуги совпадают, то оба пути равны. Отсюда тотчас же следует
неравенство (3).
Пусть теперь / есть длина хорды CD. По доказанному в § 31
(пример 1, стр. 166), главная часть разности между дугой CD(d и
хордой есть хт х2/8:
CD(L) = l+±rx4> + et, (4)
где е4 имеет порядок выше третьего относительно /. Точно так же
CZ>u)=/+^3+7)4, (5)
где т}4 имеет порядок выше третьего.
В силу неравенства (3) имеем
4'3(*2-^Н*4-14<0, (6)
а так как />0, то, разделив (6) на —^ /3, находим
** — *j + Т)< 0, (6а)
где т}= ^S4"")i4 есть бесконечно малая величина.
При приближении тички D к точке С вдоль линии (L) хорда CD
стремится к касательной к (L) в точке С, так что кривизна хя
нормального сечения С-О(л) в точке С стремится к нормальной кривизне хп
линии (L) в той же точке. При переходе к пределу неравенство (6а)
дает х2 — х*<0, т. е. х2<х£ или
Но кривизна х не может быть меньше, чем нормальная кривизна
, и потому должно быть
т. е. <р — 0, а так как точка С была взята на дуге ЛВ совершенно
произвольно, то равенство (7) имеет место вдоль всей линии (L). Следора-
тельно, линия (L)~геодезическая.
Итак, необходимость нашего условия экстремальности строго доказана.
Но бев дальнейших оговорок это условие не достаточно: не всякая
дуга геодезической линии дает кратчайшее расстояние между концами
этой дуги. В § 55 (стр. 324) мы уже приводили пример, показывающий, что
даже на развертывающихся поверхностях дуга геодезической линии
может не быть кратчайшей. В качестве другого примера приведем-
случай шаровой поверхности. Здесь геодезическими линиями являются
большие круги. Но дуга АВ большого круга является кратчайшей лишь
в том случае, если она не превосходит половины окружности. В
противном случае кратчайшее расстояние дает не она. а дополнительная
к ней дуга большого круга.
Рассмотренные примеры выдвигают вопрос: в каком случае дуга
АК геодезической линии (L) дает кратчайшее расстояние между точкам»
А и В. Чтобы ответить на него, рассмотрим пучок геодезических линий.
§ 73. ГЕОДЕЗИЧЕСКИЕ ЛИНИИ 425
выходящих из точки А (рис. 2Ъ1). Линии этого пучка при их
достаточном продолжении могут пересекаться друг с другом (как это имеет
место для шара и для цилиндра). Но мы будем откладывать на них
дуги, длины которых, отсчитываемые от Л, имели бы равные длины /,
и эту длину / выберем достаточно малой, чтобы устранить взаимные
пересечения линий нашего пучка. Представляется очевидным, что такой
выбор возможен. Во всяком случае мы будем рассматривать только те
поверхности, для которых это выполнимо1).
Построенные дуги должны заполнить некоторую область (Л); она
называется гауссовым геодезическим кругом радиуса /; точка А
называется центром геодезического круга. Мы утверждаем теперь следующее.
Теорема 2. Для того чтобы дуга АК геодезической линии была
кратчайшим на поверхности расстоянием между точками А и К.
достаточно, чтобы точка К лежала внутри
некоторого геодезического круга с центром У^1 / ^Ч g
в точке А.
Действительно, на поверхности должна
существовать кратчайшая дуга, соединяющая
точки i и В; это мы принимаем как
очевидный факт и во всяком случае ограничиваемся
рассмотрением тех поверхностей, которые
обладают этим свойством. Согласно теореме 1 эта
дуга должна принадлежать некоторой
геодезической линии. Если АК есть единственная
геодезическая линия, проходящая через А л В,
то она и дает кратчайшее расстояние. Если же существует еще некоторая
геодезическая дуга ACDK, то согласно определению геодезического
круга эта дуга должна выходить за пределы круга в некоторой точке С.
Длина дуги ACDK, следовательно, больше, чем АС = 1, тогда как длина
дуги АК меньше, чем I. Следовательно, и в этом случае АК есть
кратчайшая дуга.
Можно указать и другие, менее суровые условия, достаточные для
того, чтобы данная геодезическая дуга была кратчайшей. Во всяком
случае теорема 2 позволяет утверждать, что дуга АС геодезической
линии, исходящей из фиксированной точки А по фиксированному
направлению, дает кратчайшее расстояние между точками Л, С, по крайней
мере, до тех пор, пока С, удаляясь от А, не выйдет за пределы
некоторого геодезического круга с центром в А.
Пример. Пусть точка А лежит на сфере. Две геодезические линии,
исходящие из точки А, пересекаются всегда в диаметрально
противоположной точке А'. Поэтому мы можем отложить на больших кругах,
исходящих из А, дуги равной длины /, не превосходящей
полуокружности большого круга. Они заполнят поверхность некоторого
сферического сегмента с вершиной в А. Эта область есть гауссов
геодезический круг, и если точка, отправляясь от А, описывает какую-либо
геодезическую линию, то до тех пор пока С не достигнет А\ дуга АС
этой геодезической линии будет кратчайшим расстоянием между
Л и С.
1) Можно доказать, что для аналитических поверхностей это допущение всегда
справедливо.
426 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОГТИ
§ 74. Геодезическая кривизна
Как мы видели в предыдущем параграфе, геодезические линии
кривой поверхности играют роль, аналогичную прямым на плоскости. Эту
аналогию можно использовать для установления понятия «внутренней
кривизны» линии на поверхности. А именно, кривизна плоской кривой
^сть предел отношения -у , где As есть длина бесконечно малой дуги
МгМ21 а а) — угол при пересечении касательных прямых, проведенных
в концах дуги МХМ2. По аналогии с этим можно провести в концах
Mi и М2 дуги некоторой линии, лежащей на поверхности 5,
геодезические касательные, т. е. геодезические линии, касаюшиеся МХМ%
в точках Мх и М2. Пусть они
пересекутся в некоторой точке С. В2
Тогда они образуют между собой
некоторый угол ш; предел
отношения этого угла к длине бесш -
Рис. 252.
Рис. 253.
нечно малой дуги (мы предположим, что он существует)
естественно принять за определение «внутренней кривизны^ линии на
поверхности. Замечательно, что определенная таким образом «внутренняя
кривизна» оказывается равной геодезической кривизне. Именно, имеет
место следующая теорема.
Теорема 1. Если геодезические касательные MXN^ MtN'% (рис. 252)
линии (L) поверхности S пересекаются в точке С под углом ш, и точка
М1У М2У а вместе г ними и точка С, стремятся к точке М, то предел
•отношения Vw^— равен геодезической кривизне линии (L) в точке М.
М,М2
Доказательство. Проведем через точку пересечения С
геодезических касательных MXNY, M2N2 касательную плоскость Q и спроек-
тир5тем на нее точку Л/, линию (L) и геодезические касательные MtNlf
M2N2. В проекции (рис. 253) получим точку М' и линии (L'), M\N\,
M'2N'2. Последние, пересекаясь в точке С под углом ш, имеют в этой
точке кривизны, равные нулю (согласно определению геодезической
§ 74. ГЕОДЕЗИЧЕСКАЯ КРИВИЛИ А 427
линии). Когда Мг и М2 стремятся к М, точка С и касательная
плоскость Q имеют пределом точку М и касательную плоскость Р,
проведенную через М. В общем случае, рассмотрением которого мы
ограничимся, угол <р между плоскостями Р и Q, угол со и дуги МгМ2У
МХС, СМ2 имеют один и тот же порядок.
Кривизна •*! проекции (£.') в точке М' меняется вместе с тем, как
меняет положение плоскость проекции. Она имеет своим пределом
кривизну проекции линии (L) на касательную плоскость Р в точке М,
т. е. геодезическую кривизну ъд линии (L) в точке М', так что
**»*'; (1)
■с другой стороны,
*'«-£-, (2)
М[М'9
где со'' = /_BJ)B2 есть угол между касательными прямыми М[В1у
М\В%.
Этот угол разнится от угла со между касательными САг, СА2 к линиям
CN'V CN2 на величину а —13, где а есть угол между М[Вг и СА1У a ji —
угол между М'9В2 и СА2:
а)'=(о + р~а. (3)
Отсюда следует, что углы со' и со эквивалентны. Действительно,
угол а образован касательными в концах бесконечно малой дуги
М\СУ которая имеет в точке С кривизну, равную нулю. Значит, он
«меет высший порядок относительно Д/jC, а значит, и относительно
хорды М'гМ'%, которая эквивалентна (§ 26, лемма 3, стр. 134) хорде и дуге
МХМ2. Точно так же и угол {3 имеет высший порядок относительно
MJM^. Но си имеет тот же порядок, что МХМ\. Следовательно, из
тождества (3) вытекает эквивалентность
СО'^О). (4)
Принимая во внимание соотношения (1), (2), (4) и эквивалентность
M[M'2zzMjhti (5)
получаем
*»»-^-t (6)
МХМ2
что и доказывает теорему 1.
Замечание. До сих пор геодезическую кривизну xff мы считали
существенно положительной. Однако величине *д можно приписать знак
так же, как мы это сделали в § 24 (QTp. 120) для плоской кривой. Ихменно,
зсли поворот геодезической касательной совершается в положительном
направлении (против часовой стрелки), мы припишем величине хд
положительный знак; в противном же случае —отрицательный. Разумеется,
и теперь, и для плоской кривой, выбор знака будет зависеть от
произвола в выборе положительного направления движения и положительной
стороны самой поверхности. Как легко видеть, определенный таким
образом знак совпадает со знаком кривизны проекции (£') линии (L)
на касательную плоскость Р, если положительная сторона для
плоскости Р беретса та же, что для поверхности S и направление движения
оо (I/) — то жо, что по (L).
428 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ, ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
Из теоремы 1 тотчас же вытекает следующее весьма важное
предложение.
Теорема 2. Геодезическая кривизна линии (L) па поверхности S
остается неизменной при шгибапии поверхности.
Действительно, так как геодезические линии поверхности S и только
они дают кратчайшие расстояния на поверхности, то и после изгибания
они остаются геодезическими. Далее, как угол ш, так и дуга М^М%
при изгибании сохраняют свои величины. Значит, сохраняет свою
величину и геодезическая кривизна.
§ 75. Изгибание полосы. Геодезические окружности Дарбу
Из доказанной инвариантности геодезической кривизны относительно
изгибания вытекает еще одно определение геодезической кривизны и
геодезических линий, имеющее большое теоретическое и практическое значение.
Пусть на поверхности S дана некоторая линия (L). Опишем вдоль
нее около поверхности 5 развертывающуюся поверхность Sx.
По теореме 5 § 72 (стр. 420) линия (I) на поверхности Sx имеет ту
же геодезическую кривизну, что на 5. Изогнем развертывающуюся
поверхность Sx на плоскость.
Линия (L) превратится в некоторую
линию (Z,); при этом по теореме 2
§ 74 (стр. 428), ее геодезическая
кривизна всюду остается неизменной.
Но геодезическая кривизна кривой
на плоской поверхности есть не что
иное, как обыкновенная ее кривизна.
Поэтому геодезическая кривизна
линии (L) на поверхности S есть
кривизна той плоской линии (L), в
которую преобразуется (L) про
наложении описанной около S
развертывающейся поверхности на
плоскость.
Заметим, что для построения
Рис. 254. линии (L) на практике нет
необходимости строить развертывающуюся
поверхность, касающуюся линии (L). Достаточно вырезать узкую полосу
(iSl) вдоль линии (L) (рис. 254). Эту полосу можно будет приложить
к плоскости весьма плотно даже при довольно значительной ширине
полосы. _
Поясним это утверждение. Проведем через_каждую точку М
поверхности S нормаль. Если расстояние и от М до линии (L)
достаточно мало, то нормаль пересечет S в некоторой точке М.
Соответствие, устанавливаемое этим между S и s, не будет изометрическое;
однако отношение линейных элементов —, при любом направлении
ds
элемента ds> отличается от 1 на величину, которая не только
бесконечно мала вместе с а, но и имеет второй или высший порядок
относительно м.
Из этого факта, который мы доказывать не будем, следует, что
полосу (SL) ширины и можно наложить на развертывающуюся
поверхность 6^ (а значит, и на плоскость) после такого растяжения, для
§ 75. ИЗГИБАНИЕ ПОЛОСЫ, ГЕОДЕЗИЧЕСКИЕ ОКРУЖНОСТИ ДАРБУ 429
которого линейный коэффициент расширения всюду имеет второй или
более высокий порядок относительно и. Это растяжение можно
осуществить за счет эластичности материала.
Доказанное здесь предложение дает простой способ построения
геодезических линий в а любой поверхности. Вырежем прямолинейную
бумажную полоску и приложим ее к поверхности. Полоска примет
форму развертывающейся поверхности, касающейся данной поверхности,
и линия касания будет геодезической линией. Построение будет тем
более точным, чем более узка полоска, ибо если полоска имеет
значительную ширину, то касание может произойти ве вдоль изогнутой
прямой, а вдоль другой линии, помещающейся на полоске. Этим способом
можно построить геодезическую линию, проходящую через данную
точку по данному направлению, а также геодезическую линию,
соединяющую две данные точки. Вращая полоску около неподвижной точки,
мы заставим подвижные ее точки описывать геодезические круги Гаусса.
Возьмем теперь плоскую полоску, имеющую вид дуги окружности
радиуса R. Накладывая эту полоску на поверхность, найдем линии
сюстоянш й геодезической кривизны -^-. Дарбу предложил называть эти
линии геодезическими окружностями. Геодезические окружности Дарбу
вообще не тождественны с геодезическими окружностями Гаусса. Это
видно хотя бы из того, что окружности Гаусса всегда замкнуты, тогда
как окружности Дарбу в общем случае не замкнуты. Так, на
поверхности прямого геликоида винтовая линия имеет постоянную
геодезическую кривизну, равную ее обыкновенной кривизне (§ 72, теорема 4,
стр. 420). Значит, винтовые линии геликоида суть окружности Д&рбу.
Но они не замкнуты. На поверхности вращения параллели являются
геодезическими окружностями Дарбу, ибо их геодезическая кривизна
постоянна (§ 72, теорема 2, стр. 417). Однако они в общем случае не
являются окружностями Гаусса. На поверхности шара все
геодезические окружности Дарбу суть обычные окружности и совпадают с
окружностями Гаусса.
Геодезические линии также являются окружностями Дарбу (нулевой
геодезическсй кривизны). Как и другие окружности Дарбу, они в общем
случае незамкнуты (например, винтовые линии на цилиндре). Если
поверхность S замкнута, то геодезическая линия, как и всякая другая
геодезическая окружность, при достаточном продолжении в общем
случае пересечет сама себя и будет иметь бесчисленное множество
самопересечений. Лишь в исключительных случаях геодезическая линия,
возвратясь в исходную точку, снова пойдет по прежнему направлению.
Такие геодезические линии называются замкнутыми,
Пуанкаре в 1905 году доказал, что на выпуклой замкнутой
поверхности всегда существует, по крайней мере, одна замкнутая
геодезическая линия. С помощью физических соображений он пришел к выводу,
что найденная им геодезическая линия не имеет самопересечения. Он
высказал также предположение, что на всякой выпуклой замкнутой
поверхности имеется не только одна, но не менее трех замкнутых линий.
В 1926 году советскими математиками Л. А. Люстерником и
Л. Г. Шнирельманом было доказано, что, действительно, на всякой
выпуклой поверхности есть по меньшей мере три замкнутые и притом
несамопересекающиеся геодезические линии. Предполагать, что на
всякой выпуклой поверхности существует большее число замкнутых
геодезических линий, нельзя, так как, например, на поверхности трехосного
эллипсоида их существует только три (главные сечения эллипсоида).
430 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
§ 76. Геодезический поворот и параллельное
перенесение
Если точка движется по геодезической линии поверхности, то для
наблюдателя, могушего ориентироваться в окружающем поверхность
пространстве, направление движения точки, вообще говоря, меняется.
Но наблюдатель, не имеющий возможности ориентироваться во внешнем
пространстве (или не испытывающий в этом нужды) будет в этом случае
полагать, что направление движения остается неизменным.
Так, дорогу, которая поднимается на горный хребет из долины,
мы считаем «прямой», если она не отклоняется вправо или влево. Мы,
следовательно, считаем, что направление движения меняется лишь в том
случае, если искривлена проекция пути на плоскость дороги. Иными
словами, вместо кривизны линии мы учитываем ее
геодезическую кривизну. Поэтому геодезическая
линия (вдоль нее геодезическая кривизна равна
нулю) яьляется на поверхности линией «постоянного
направлениям.
Эти соображения приводят нас к установлению
понятий о геодезическом повороте и о
геодезическом параллелизме. На плоскости мерой поворота
направления дуги АВ служит угол а между каса-
тельными в концах дуги. Мы можем измерить его,
построив, скажем, в точке В вектор /#,
параллельный вектору касательной t& в точке А (рис. 255).
Если мы поступим так же для дуги АВ кривой
поверхности, то вектор г'в в общем случае не будет
лежать в касательной плоскости точки J5, и потому
угол между 1'в и tB не даст внутренне
геометрической меры поворота.
Но угол поворота касательной плоской кривой
в
мы можем получить еще как интеграл \ xc?s, где
А
х —кривизна линии АВ.. В согласии с вышеприведенными наглядными
соображениями, мы условимся теперь измерять искривленность линии АВ
на поверхности S в точке М ее геодезической кривизной ъд в этой точке.
Мы отметили в § 74 (стр. 426), что эта величина может быть найдена
измерениями на самой поверхности, например как предел отношения
•—- угла (Oj между геодезическими касательными к длине As дуги
между точками касания. Тогда за меру поворота касательной на поверх-
в
ности естественно взять интеграл \ y.gds, т. е. предел суммы бесконечно
л
малых поворотов o>^xffAs, измеряемых, скажем, углами между
геодезическими касательными.
Определение 1. Геодезический поворот касательной на дуге АВ
в
есть интеграл Vx^ds дуги АВ. Его называют полной геодезической
А
кривизной.
Рис. 255.
§ 76. ГЕОДЕЗИЧЕСКИЙ ПОВОРОТ И ПАРАЛЛЕЛЬНОЕ ПЕРЕНЕСЕНИЕ 431
Обратим внимание, что прежде мы определяли кривизну из
понятия угла, а сейчас обобщаем понятие угла, исходя из понятия
геодезической кривизны.
Впрочем, мы можем дать равносильное определение геодезического
поворота, обойдя упоминание о геодезической кривизне и не пользуясь
(в явном виде) интегрированием. Именно, опишем около данной
поверхности 5 вдоль дуги АВ развертывающуюся поверхность Sx и изогнем
последнюю на плоскость. По доказанному в § 75, кривизна х изогнутой
линии АВ равна прежней ее геодезической кривизне; следовательно,.
в
интеграл \ *gds дает также
А
в
полную кривизну \ х ds изогну-
А
той на плоскость линии, т. е. угол
между касательными
изогнутой линии в концах ее дуги.
Поэтому можно
определить угол геодезического
поворота касательной еще так.
Определение 2.
Геодезический поворот касательной
на дуге АВ есть угол между
касательными в концах той
дуги, в которую обратится АВ
после наложения ее полосы на
плоскость.
В частности,
геодезический поворот касательной
геодезической линии равен нулю,
так как геодезическая линия
после наложения ее полосы на
плоскость обратится в прямую.
Если линия (L) на
плоскости замкнута и выпукла, то при
обходе ее угол поворота каса- с*
тельной составляет 2тг.
Геодезический поворот касательной вдоль выпуклой замкнутой линии на
поверхности в общем случае отличен от 2к.
Пример 1. Найдем геодезический поворот касательной на
параллели АВ шара, имеющей широту и (рис. 256).
Как мы видели в § 72 (теорема 2, замечание, стр. 417), радиус
геодезической кривизны параллели рд = АС. Следовательно, поворот
касательной на. параллели равен
(6
*gds = -^ & ds = 2тс ^= 2тс sin и.
Тот же результат получим, если развернем на плоскость коническую
поверхность, касающуюся шара вдоль параллели. Параллель обратится
в дугу окружности радиуса АС. Длина дуги будет равна 2izAD\
следовательно, центральный угол равен 2тс-^-=2тсзп1 и.
432 ГЛ, X, ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
Если линия (А) на поверхности имеет угловые точки, то
геодезический поворот касательной составится как сумма подной геодезической
кривизны и углов, на которые поворачивается касательная в угловых
точках (последние углы измеряются, как обычно так как поворот
происходит в касательной плоскости).
Пример 2. При обходе сферического треугольника,
образованного тремя взаимно перпендикулярными квадрантами, угол поворота
3
касательной составляет -т к9
так как вдоль сторон этого
треугольника, являющихся
геодезическими линиями,
геодезический поворот равен нулю,
а каждый из внешних углов
треугольника составляет ~ .
Вообще для всякого
сферического несамопересекающе-
гося многоугольника поворот
касательной равен сумме
внешних его углов, т. е. (§ 33,
теорема 4, стр. 181) избытку
с»
/V 2гс над величиной -^ S
—площадь многоугольника; Л —
радиус сферы).
Рис. 257. Так как любую
сферическую замкнутую линию можно
рассматривать как предел сферического многоугольника, то и вдоль
всякой замкнутой сферической линии поворот касательной равен
с» ,
2iz— -™-, т. е. всегда меньше 360°. Используем этот результат для
разыскания площади сферического сегмента. На ограничивающей его
параллели геодезический поворот, как мы нашли в примере 1, равен
2tzs\x\u. Таким образом, если S есть площадь сферического сегмента
АЕВ (рис. 256), то
2*- ж
• 2тг sin и,
т. е.
или, так как R (1 —sin и)
В этой форме результат известен из элементарной геометрии.
Пусть теперь (рис. 257) в концах дуги АВ заданы два любых
направления на поверхности, или, что то же, даны векторы АА' и ВВ',
лежащие в касательных плоскостях поверхности S (такие векторы мы
будем для краткости называть тангенциальными).
Чтобы установить меру геодезического поворота от направления АА'
к направлению ВВ', мы можем измерить угол а между АА' и вектором
касательной tA и угол р между ВВ' и tB. Разность [3 — а этих углов
<{с учетом их знаков) даст поворот относительно касательной; но так
как и сама касательная испытала поворот, измеряемый полной геоде-
§ 76. ГЕОДЕЗИЧЕСКИЙ ПОВОРОТ И ПАРАЛЛЕЛЬНОЕ ПЕРЕНЕСЕНИЕ 433
зической кривизной, то геодезический поворот от АА' к ВВ' следует
положить равным
в
А
Мы примем формулу (1) за определение геодезического поворота
тангенциального вектора АА' в положение ВВ' вдоль дуги АВ.
Определение 3. Геодезическим поворотом тангенциального
вектора А А' в положение В В' вдоль линии А А' называется сумма
полной геодезической кривизны дуги АА' и приращения угла между
вектором касательной линии (L) и тангенциальным вектором.
Будем подвергать поверхность изгибанию, оставляя векторы АА'
и В В' неизменно связанными с касательными плоскостями в точках А
и В. При этом углы а и р не изменят своей величины, и
следовательно, геодезический поворот от АА' к ВВ' есть инвариант изгибания.
Если, как прежде, мы опишем около S вдоль АВ развертывающуюся
поверхнос!ь и наложим ее на плоскость, то величина \*gdb даст
обычно измеряемый угол между tA и tB, а величина р —а + \^о?г>*, как легко
видеть, даст обычно измеряемый угол между АА' и ВВ'. Итак, можно
дать еще такое определение геодезического поворота, равносильное
определению 3.
Определение 4. Геодезический поворот от тангенциального
вектора АА' к вектору ВВ' вдоль дуги АВ есть угол между теми
векторами, в которые обратятся А А' и В В' после наложения полосы АВ
на плоскость.
Следует подчеркнуть, что геодезический поворот от АА' к ВВ'
существенно зависит от выбора пути АВ. Так, если АВ есть
геодезическая линия, то геодезический поворот будет равен разности р — а.
Но между теми же точками А, В можно провести другие линии,
касающиеся геодезической АВ в точках А и В. Следовательно, величины а
в
и (3 останутся прежними, в то время как интеграл \xgds в общем
А
случае не будет равен нулю.
Если угол геодезического поворота от АА' к ВВ' вдоль АВ равен
нулю или 180°, то естественно назвать векторы АА' и В В'
геодезически параллельными (соответственно — рае но направленными или
противоположно направленными). Ясно, что при изгибании полосы на
плоскость геодезически параллельные векторы переходят в векторы,
параллельные в обычном смысле. Ясно также, что понятие о
геодезическом параллелизме двух векторов ^меет смысл только тогда, когда
оба вектора связаны с определенными точками поверхности и лежат
в касательных плоскостях, и когда при этом задан путь, ведущий от
начала одного вектора к началу другого.
Определение 5. Если векторы АА' и ВВ' геодезически равно-
направлены и, сверх того, имеют одинаковые длины, мы назовем их
28 М. Я. Выгодский
434 гл. х. основные формулы, внутренняя геометрия поверхности
геодезически равными (относительно пути АВ) и будем говорить, что
вектор АА' ипараллелъно перенесет в точку В. Формула (1),
принимающая теперь вид
gds = O, (2)
показывает, что для параллельного перенесения вектора А А' вдоль
пути АВ нужно от точки В в соответствующей касательной плоскости
в
повернуть вектор касательной tB на угол р, равный а—\ *gds, и иа
А
полученном луче отложить отрезок В В' той же длины, что АА'.
Пусть теперь на поверхности S задано тангенциальное векторное
поле, т. е. для каждой точки М (и, v) однозначно определен исходящий
из нее тангенциальный вектор p(u,v). Сместившись из точки М в
бесконечно близкую точку М' по некоторому направлению duidv, мы
находим здесь тангенциальный вектор р'. Дифференциал dp, т. е.
главная линейная часть разности р'—р, в обшем случае не является
тангенциальным вектором и поэтому не имеет внутренне
геометрического смысла. Но пользуясь обобщенным понятием параллельного
переноса, мы можем и разность векторов р' и р понимать в обобщенном
смысле. Именно, обычно мы для нахождения разности векторов
параллельно переносим, например, вектор р' так, чтобы его начало
совместилось с началом вектора р. Теперь же мы будем совершать вместо
обычного параллельного переноса геодезически параллельный переход
по заданному направлению. Перенеся вектор р' в точку М, мы
получим геодезически равный ему вектор р19 лежащий, так же как и рг
в касательной плоскости точки М (в новом ее положении).
Следовательно, разность рг—р, а значит, и ее главная часть (линейная
относительно ds) есть тангенциальный вектор. Эта главная часть называется
абсолютным дифференциалом вектора р и обозначается через Dp.
Отношение -?■ называется абсолютной производной вектора р (по данному
направлению).
Иными словами, абсолютная производная -£ вектора рм в данной
точке М (по данному направлению а) есть предел отношения д5 ,
еде As есть длина бесконечно малой дуги ММ' (имеющей в М
направление а), а рх есть вектор, полученный геодезическим параллельным
переносом вектора. рм> из тючки М' в точку М по дуге ММ'.
Если все векторы р, исходящие из точек некоторой линии (L)?
геодезически параллельны, то абсолютная производная -^ [взятая по
направлению (L)] тождественно равна нулю.
Обратно, если -^ = 0, то векторы р геодезически параллельны
[относительно линии (L)].
Имеет место следующее предложение.
Теорема 1. Абсолютный дифференциал Dp тангенциального
вектора р есть проекция дифференциала dp этого вектора на
касательную плоскость.
§ 76. ГЕОДЕВИЧЕСКИЙ ПОВОРОТ И ПАРАЛЛЕЛЬНОЕ ПЕРЕНЕСЕНИЕ 435
Доказательство. Проведем через рассматриваемую точку М
(рис. 258) бесконечно малую дугу MN геодезической линии. Пусть MQ
и NT— касательные векторы в концах этой дуги, a MJ = рм и NK=p^—
векторы данного поля, исходящие из М и N.
Пусть вектор р^ после геодезического переноса в точку М
обратился в вектор p1 = MJ1. Тогда абсолютный дифференциал Dp с
точностью до величин первого порядка (относительно ds) равен
Dp = p1-pM+-.-=MT1-MJ+... (3)
Обыкновенный же дифференциал dp с точностью до величин первого
порядка равен
dp = psf — рм + • • • =
а его проекция на
касательную плоскость в
точке М равна
пр. dp = пр. {pN —
+ . ..=iqb/to — пр. рм+
+ ...=N7K'-MT. (4)
Многоточием обозначены
величины высшего
порядка относительно ds.
Из (3) и (4) видно,
что для доказательства
соотношения
достаточно убедиться в
том, что перенесенный
вектор рх = MJY разнится
от проекции N К'
вектора рх на величину вые- Рис. 258.
шего порядка
относительно ds. Таким образом, теорема будет доказана, если мы
обнаружим: 1) что длины отрезков N'K' и MJX разнятся на величину высшего
порядка и 2) что угол между N'K' и MJX имеет высший порядок
(относительно ds). Докажем то и другое.
1) По определению геодезического перенесения, векторы рх и рн
имеют равные длины, т. е,
MJX = NK. (5)
Кроме того, по построению имеем
N'K'= NK cosy, (6)
где ср есть угол между касательными плоскостями в точках М и N.
В силу (5) и (6) имеем
MJX - N'K' = NK - N'K' = NK (1 - cos 9) *> NK £ ,
а так как <р имеет порядок не ниже, чем ds, то MJX—N'K' имеет
относительно ds высший порядок.
28*
436 гл. х. основные формулы, внутренняя геометрия поверхности
2) Углы ц.= /_QMJX и /ч'= /_T'N'K' лежат в одной плоскости;
поэтому
т. е. интересующий нас угол между N'K' и MJ1 представляется
выражением
(N'K^MJ,) = {N'TJMQ) + Ox - >/). (7а)
Каждое из слагаемых правой части (7а) имеет высший порядок
относительно ds. Действительно, N'T' и MQ — это касательные в
концах дуги MN'. Отношение угла между ними к MN имеет пределом
геодезическую кривизну, а эта последняя равна нулю, так как MN —
геодезическая линия. Значит, первое слагаемое в (7а) имеет высший
порядок относительно ds.
Что касается второго слагаемого fx — X', то оно равно к — к' (где
к~ Z.TNK), так как по определению геодезического перенесения
углы к и [л равны. Разность же к — У между углом к и его
проекцией к' имеет высший порядок относительно угла <р» а значит, и
относительно ds1). Этим теорема 1 доказана.
1) Это можно доказать так. Проведем через точку Л7 (рис 259) плоскость T"NK",
параллельную T'N'K', и спроектируем на нее угол Я = ^/ Т ' К. Получим угол
у : V^z. Т'Л'К". Пусть NU есть
прямая пересечения плоскостей TNK
и T"NK"\ Я^Я.-углы UNT, UNK
и Я;,Я1-углы UNT", UNK".
Очевидно, мы имеем
Х = Х2—11 и V = л'2 — Я(,
так что
Я — Я' = (Я» — Я2) — (Я, — Ях).
Докажем, что каждое из
слагаемых Л2—Х'г, Л\—К имеет
высший порядок относительно <р-
Проведем через точку Г и ее
проекцию Т" плоскость Tt"R,
перпендикулярную к NU; пусть Я —
точка пересечения этой плоскости
с NU. Из треугольников TNR, T"NR, TT"R находим
RT = RN • tg Я,; RT" = RN - tg Я[, RT" = RT - cos <p,
откуда
tg A'^tj^
Следовательно,
Рис. 259.
Если оставить в стороне случай
~ (для этого случая наше рассуждение
нуждается в некоторой модификации), то из последней формулы следует, что
разность Хг — Х[ бесконечно мала. Относительно <р она имеет второй порядок, потому
L - Я',
что, заменяя левую часть формулы эквивалентным выражением . , мы полу-
OS /j
чаем
*i — К
11
2
Так же докажем, что Хг — Х'г имеет второй порядок относительна
§ 76. ГЕОДЕЗИЧЕСКИЙ ПОВОРОТ И ПАРАЛЛЕЛЬНОЕ ПЕРЕНЕСЕНИЕ 437
Замечание. Вместо геодезической линии MN мы могли бы
взять любую другую, идущую ь том же направлении. Тогда \ xgds Ф О,
но зато и угол между MQ и N'T' равен \*gds+y\2. Читателю
предлагается провести доказательство полностью.
Для абсолютной производной имеет место аналогичное
предложение.
Теорема 2. Абсолютная производная -~ тангенциального
вектора р есть проекция производной -£ этого вектора на касательную
точно разделить соотношение
Dp=np.dp (8)
п лось ость.
Для доказательства достаточно разделить соотношение
на ds. Получим
Dp
что л утверждается в теореме 2.
Из теоремы 1 вытекает также следующее предложение.
Теорема 3. Разность
dp—Dp
между дифференциалом п абсолютным дифференциалом есть вектор,
коллинеарный с нормалью к поверхности.
Действительно, хчы имеем
pw — пр. рм.
Но разность между вектором и его проекцией на плоскость есть
вектор, перпендикулярный к плоскости проекций, т. е. к касательной
плоскости.
Итак, абсолютный дифференциал векюра р можно также
определить как главную часть тангенциальной компоненты обыкновенного
дифференциала вектора р\ иными словами, для получения Dp можно
разложить dp на два слагаемых вектора: тангенциальный и
нормальный и откинуть второе слагаемое.
Для абсолютной производной имеет место аналогичное
предложение.
Пример 1. Найдем абсолютную производную орта касательной
к лпнии АВ по направлению этой линии. Обыкновенная
производная равна у.п. Абсолютная производная равна проекции вектора ш
на касательную плоскость. Очевидно, эта проекция направлена по
главной нормали п' к проекции линии АВ на касательную плоскость,
и модуль ее равен xcos(#, п'). Итак, эта проекция равна xcos(/i, л')л/ =
= xfl/i'. Следовательно, обыкновенная производная ^ есть вектор
кривизны линии АВ, а абсолютная производная есть вектор кривизн**
438 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
N"—*' I Tit I
проекции линии АВ. Модуль \-т-\ абсолютной производной вектора
равен геодезической кривизне хд1 подобно тому как модуль
■т- обык-
as
новенной производной того же вектора равен кривизне х.
Мы видим, что абсолютная производная играет для внутренней
геометрии поверхности ту же роль, что производная для внешней
геометрии.
Пример 2. Если линия АВ является геодезической, то
абсолютная производная ее орта касательной, взятая по направлению АВ,
равна нулю.
Это предложение, вытекающее из предыдущего примера, можно
доказать еще так. Производная -т- = *п коллинеарна с нормалью т к
поверхности, ибо для геодезической линии главная нормаль совпадает
с т. Таким образом тангенциальная составляющая вектора -у-, т. е. абсо-
лютная производная -т- , равна нулю1).
Упр ажне ния
1. Если геодезическая линия является одновременно линией кривизны, то
она —плоская. Обратно, если геодезическая линия —плоская, то она есть линия
кривизны.
2. Может ли геодезическая линия быть одновременно асимптотической?
3. Доказать, что линия (L)—геодезическая на поверхности ее бинормалей.
4. Доказать, что геодезическая кривизна линии (L) на поверхности ее
главных нормалей раьна кривизне линии (L).
5. Могут ли существовать замкнутые геодезические линии на поверхности
касательных с незамкнутым ребром возврата?
6. Используя экстремальное свойство геодезической линии, доказать, что
если две бесконечно близкие геодезические линии О А и ОВ пересечены линией АВ
в точках А и В, лежащих внутри некоторого круга Гаусса, и если угол ОВА —
тупой, то О4> ОВ.
Указание. Провести через В дугу, перпендикулярную ОВ.
7. Опираясь на предыдущую теорему, доказать, что круг Гаусса ортогонален
ко всем геодезическим линиям, исходящим из его центра.
8. Доказать, что на всякой поверхности, изгибаемой на сферу или на
плоскость, имеются замкнутые окружности Дарбу.
9. Доказать, что геодезическая кривизна хд линии (L) на поверхности S
2h >*—'
есть предел отношения —2, где s есть длина бесконечно малой дуги Мikfx, a h —
измеряемое на поверхности S кратчайшее расстояние от точки Мх до геодезической
линии (I) касающейся (L) в точке М.
Указание. Спроектировать линию (L) на касательную плоскость Р в
точке М.
10. Основываясь на теореме 2 § 74 (стр. 428), доказать, что геодезическая кривизна
линии (L) на поверхности S есть предел отношения ■ ^ , где ш1 есть угол между
ММг
нормалями (Я) и (А^ линии (L), лежащими в касательных плоскостях,
проведенных через точки М, М, поверхности S.
Указание. Спроектировать линию (L) и нормаль (Ях) на касательную
плоскость в точке М и доказать эквивалентность угла между (главными)
нормалями проекции и угла «>!.
х) Понятие об абсолютном дифференциале было подготовлено в работах Римана,
Христоффеля и Липшица, Риччи на рубеже 19-го и 20-го веков разработал алгоритм
абсолютного дифференцирования и ввел самый термин «абсолютный дифференциал*
и «абсолютное дифференциальное исчисление». Понятие параллельного перенесения
введено сотрудником Риччи—Т. Леви Чивита. Поэтому оно называется
«параллелизмом Леви-Чивитаь.
$ 77. ТЕОРЕМЫ ГАУССА И БОННЕ 439
11. На касательных к винтовой линии отложены отрезки равной длины.
Найти геодезическую кривизну места концов этих отрезков.
Указание. Развернуть поверхность касательных на плоскость.
12. Найти геодезический поворот касательной кривой Вивиани вдоль одной её
петли на сфере и на цилиндре.
13. На бинормалях кривой (L) отложены в одну сторону отрезки постоянной
длины л. Доказать, что радиус геодезической кривизны места концов этих
отрезков на поверхности бинормалей равен lfa2-\-t2 (т— радиус кручения).
14. Доказать, что геодезический поворот той нормали линии (L), которая лежит
в касательной плоскости, равен - геодезической кривизне соответствующей дуги
линии (L).
15. Доказать, что при параллельном перенесении двух векторов, исходящих
из точки Л, в сдну и ту же точку, угол между векторами не изменяется.
16. Два вектора р и q исходят из одной точки А поверхности. Вектор р
параллельно перенесен вдоль линии ABC в точку В, а вектор q—вдоль той же
линии в точку С. Пусть рв, рс—векторы, возникшие после этого перенесения.
Равны ли между собой геодезический поворот от вектора рв к вектору рс (при
перенесении вдс;ль ВС) и угол между векторами р и q?
17. По какому направлению абсолютный дифференциал орта касательной t
равен обыкновенному?
§ 77. Теоремы Гаусса и Бонне
При положительном обходе всякого замкнутого плоского контура,
не имеющего самопересечений, касательная поворачивается на угол 2тс.
Если же такой контур проведен на кривой поверхности, то
касательная поворачивается в общем случае на угол, отличный от 2it, что мы
видели из примера 1 § 76.
Таким образом разность между 2тс и полной геодезической
кривизной линии (L), ограничивающей односвязную область (JS), можно
принять за меру искривленности области (В).
Оказывается, что эта мера совпадает с полной кривизной
области (В), т. е. с интегралом \ \ KdS гауссовой кривизны, т. е.
(В)
(1)
Если линия (L) имеет угловые точки, то в интеграл геодезической
кривизны w-Xgds нужно включить сумму углов поворота в этих точках.
Теорема, выражаемая формулой (1), была опубликована Бонне
в 1848 г. Она была еще раньше получена Гауссом. Но Гаусс
опубликовал (з* 1827 г.) лишь частный ее случай, в котором область (В)
является «геодезическим треугольником», т. е. односвязной областью,
ограниченной тремя геодезическими линиями АВ, ВСУ АС. В этом
случае у.д = 0, и полная геодезическая кривизна сводится к сумме
внешних углов а, р, у геодезического треугольника. Формула (1)
принимает вид
2те —(a + p + Y)^ \\ KdS- (2)
(В)
Пример 1. Рассмотрим положительно обходимый сферический
сегмент. Полная геодезическая кривизна контура равна (пример 2 § 76,
стр. 432).
s_
440 ГЛ, X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
Так как гауссова кривизна сферы равна -^, то полная кривизна
сферического сегмента равна
{В)
Эти значения (Dx^ds и \ \ KdS удовлетворяют соотношению (1).
(В)
Пример 2. Рассмотрим положительно обходимую область (В)
сферы, ограниченную тремя квадрантами и превосходящую полусферу.
Площадь этой области равна -^ полусферы, т. е. — -Д2; значит,
гауссова кривизна
(В)
Каждый внешний угол равен —-, значит, сумма их
Эти значения удовлетворяют соотношению (2).
В работах Гаусса и Бонне даны весьма громоздкие аналитические
доказательства. В настоящее время известны короткие аналитические
доказательства (одно из них мы приведем позднее, в § 82 (стр. 463), после
того как будет установлена формула геодезической кривизны) Однако
эти аналитические доказательства оставляют в тени геометрическую
картину. Поэтому мы дадим здесь, следуя Ж. Бертрану, синтетический
вывод теорем Гаусса и Бонне.
Теорема 1. Внешние углы а, р, у положительно обходимого
геодезического треугольника поверхности S и его полная кривизна
\\
KdS в сумме составляют 2тг.
(В)
Замечание 1. Углы а, р, у по условию всегда положительны,
величина же \ \ KdS может быть и отрицательной, ибо для гипербо-
(В)
личрских точек поверхности К < 0.
Замечание 2. В нижеприводимом доказательстве геодезический
треугольник предполагается не слишком большим, а именно, его
контур не должен иметь равнонаправленных касательных, а на
ограничиваемой им области поверхности S не должно быть равнонапраьлон-
иых нормалей. Тогда сферическая индикатриса касательных контура
ио будет иметь самопересечений, а гауссово сфсфическое изображение
треугольника не будет иметь самоперекрытий. Оба эти обстоятельства,
как нетрудно будет видеть, существенны для нижеприводимого
доказательства. Однако теорема 1 остается в силе и в общем случае, что
будет следовать из теоремы 3.
Замечание 3. При доказательстве мы ограничиваемся случаем,
когда орт п главной нормали контура треугольника меняется
непрерывно. Это имеет место всегда для поверхности положительной
кривизны. Если же на контуре треугольника имеются гиперболпчрские
§ 77. ТЕОРЕМЫ ГАУССА II БОННЕ 441
точки (К < 0), то вектор п может менять свое направление на
противоположное скачком *). Это может иметь место либо там, где контур
имеет асимптотическое направление, либо в вершине треугольника при
переходе с одной его стороны на другую. В этом случае
нижеприводимое доказательство нуждалось бы в некоторых дополнительных
построениях, но общий ход его можно сохранить.
Доказательство. Так как главные нормали геодезической
линии являются одновременно нормалями поверхности, то мы можем
установить положительное направление на нормалях так, чтобы на
контуре геодезического треугольника abc (рис. 260) оно совпадало
с направлением вогнутости сторон. В соответствии с этим выбором
однозначно определяется положительное направление обхода области
abc.
Теперь построим на сфэре S* (рис. 261) гауссово изображение ABC
треугольника abc. Наряду с этим построим для сторон ab, be, ca
геодезического треугольника abc индикатрисы касательных A2Blt B2CL,
СОА1. Эти три индикатрисы оторваны друг от друга, потому что
касательная к контуру треугольника abc изменяется скачком в вершинах
треугольника. Чтобы устранить этот разрыв, мы будем вращать около
вершины а луч, начальное положение которого совпадает с
направлением стороны са в точке а, а конечное — с направлением стороны ab
в той же точке. Вращение совершается в касательной плоскости,
проходящей через а, в направлении обхода контура. Тогда радиус сферы,
равнонаправленный с вращающимся лучом, вычертит своим концом
дугу А1А2 большого круга, соединяющую друг с другом индикатрисы
СпА1 и А„В1. Если такое же построение мы проделаем для двух
других вершин геодезического треугольника abc, то получим дуги
больших кругов fi,jB2, СхСг. Дуги АХА2, В1В2, СХС2 численно равны
внешним углам а, [3, у, имеют полюсами соответственные вершины А, В, С
гауссова изображения и описываются в положительном или
отрицательном направлении в зависимости от знака углов а, р, у. Мы
получаем, таким образом, замкнутую несамопересекающуюся сферическую
линию АЛВ1В.1С^С„А1, которую можно считать индикатрисой касательных
контура abc. Согласно теореме 6 § 33 (стр. 185), конец квадранта,
касающегося линии А2В1ВпС1С2А1ч описывает линию (Lf), которая
ограничивает площадь, равную 2ти. При этом в состав (//) должны быть
включены дуги, описываемые концом квадранта, вращающегося во
внешних углах при вершинах А2, Вх, В2, С1ч С2, А1.
Но по теореме 3 § 32 (стр. 175), касательный квадрант индикатрисы
касательных одной из сторон треугольника abc, например индикатрисы
А,В1 стороны ab, описывает индикатрису главных нормалей стороны ab,
а так как орт главной нормали линии ab по условию совпадает с ортом
нормали поверхности 5, то конец квадранта, касающегося сферической
дуги А2В1ч опишет сторону АВ гауссова изображения ABC (что и
показано на,рис. 261). Аналогично конец квадранта, касающегося дуг
В2СХ и СоАи опишет соответственно стороны ВС, С А гауссова
изображения (чтобы не загромождать чертежа, промежуточные положения
квадрантов на рис. 261 не изображены).
Таким образом, дугами АВ, ВС, СА линии (Z/)
ограничивается- площадь сферического изображения ABC треугольника abc, по
1) Впрочем, и на поверхности, сплошь состоящей из гиперболических точек,
можно построить такие геодезические треугольники, на контуре которых орт п
меняется непрерывно.
442 гл. х. основные формулы, внутренняя геометрия поверхности
§ 77. ТЕОРЕМЫ ГАУССА И БОННЕ 443
величине и по знаку равная \ \ KdS *). Но нужно еще учесть ту
часть линии (£'), которая описывается концом квадранта при
движении его начала по дугам А^А2, В1В2, СХС2 больших кругов и при
вращении около вершин А2У В1У В2, С1у Сг, Ах. Эта-то часть ч
ограничит площадь, равную сумме внешних углов треугольника аЬс.
В самом деле, после того как мы, пройдя индикатрису А2ВХ,
придем в точку 2?,, конец квадранта, описав дугу АВ, окажется в
полюсе В дуги В1В2. Теперь квадрант нужно будет повернуть около Вх
(на угол —90°) до совпадения его направления с направлением дуги
В1В2. При этом конец В опишет дугу BU (содержащую 90°). Теперь
будем двигать начало касательного квадранта по дуге ВгВ2, пока его
начало не совпадет с точкой В2\ так как дуга ВХВ2 принадлежит
большому кругу, то и касательный квадрант будет оставаться на том же
большом круге. Следовательно, его конец опишет дугу UV большого
круга, равную дуге ВХВ21 т. е, внешнему зтглу р. Наконец, нужно
совершить поворот квадранта около В2 из положения B2V до
совпадения его направления с направлением касательной к индикатрисе В2С1
(на угол +90°). При этом конец квадранта, описав дугу VB
(содержащую 90°), снова окажется на индикатрисе главных нормалей, т. е.
в точке В. В итоге он обойдет сферический треугольник BUV', причем
обход совершится в положительном направлении, если угол (3
положителен, ибо тогда дуга ВХВ2, а значит, и дуга UV, описывается в
положительном направлении относительно вершины В. Так как
треугольник BUV составляет половину двуугольника с углом В = $ при
вершине, то площадь BUV (§ 33, тоорема 1, стр. 179) равна (3.
Таким же образом мы найдем, что в состав площади,
ограниченной линией (Z/), входят еще два треугольника с вершинами в точках
С и А (они не изображены на рис. 261); их площади соответственно
равны у и а. Как было уже указано, по теореме 3 § 32 мы получаем
a + P + Y+ ^KdS = 2izy (3)
что и требовалось доказать 2).
В формулу (3) можно вместо внешних углов а, р, у ввести
внутренние углы а', р', у'; так как
то мы находим
что можно сформулировать следующим образом.
Теорема 2. Избыток суммы внутренних углов геодезического
треугольника над тс равен полной кривизне ограничиваемой им области.
х) Это значит, что треугольник ABC обходится положительно, если J J KdS > 0,
и отрицательно, если J J KdS < 0. На нашем рисунке треугольник ABC
обходится отрицательно, так как треугольник аЬс взят на поверхности отрицательной
кривизны.
2) Если условие, высказанное в замечании 3, не было бы соблюдено, то
индрикатрисы главных норм \лей сторон ab, be, ca лишь частично лежали бы на
контуре ABC, частично же принадлежали бы контуру А'В'С\ симметричному с ABC
относительно центра сферы, так что линия (L') имела бы разрывы. Для
устранения их нужно было бы ввести новые дуги больших кругов, что и обусловливало бы
усложнение доказательства.
444 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
На поверхности, всюду имеющей положительную кривизну, т. е.
состоящей из эллиптических точек, сумма внутренних углов
геодезического треугольника больше 180°; сумма же внешних углов
меньше 360°. На поверхности, всюду имеющей отрицательную
кривизну, сумма внутренних углов меньше 180°, а сумма внешних углов
больше 360°. Наконец, на поверхности нулевой кривизны эта сумма
равна 180°, как для прямолинейного треугольника. Последнее
вытекает также из того, что поверхность нулевой гауссовой кривизны
есть развертывающаяся поверхность (§ 68, стр. 400).
Теорема 3. Избыток суммы внутренних углов *[, а2, ... , а^
положительно обходимого геодезического многоугольника,
ограничивающего односвязную область (В) поверхности S над (п — 2)тг, равен
полной кривизне области (В):
&[ + *[ + ... +<»;; —(л —2)к= ^ KdS. (5)
(В)
Для доказательства достаточно покрыть область (В) сетью
неперекрывающихся геодезических треугольников и применить к каждому
из них теорему 2. Доказательство ведется совершенно так же, как
в теореме 3 § 33 (стр. 180), которая представляет частный случай
настоящей теоремы (поверхность S является сферой радиуса 1); тогда
А йо = \ \ йо
В)
есть площадь сферического многоугольника.
Важно отметить, что в условии теоремы 3 мы не требуем ни
того, чтобьт контур многоугольника не имел равионаправленных
касательных, ни того, чтобы в области (В) поверхность S не имела равно-
направленных нормалей. Действительно, хотя при доказательстве
теоремы 1, из которой мы вывели использованную здесь теорему 3, это
требование было существенно, однако треугольники, покрывающие
область (В), можно взять столь малыми, чтобы для каждого из них
в отдельности упомянутые требования удовлетворялись. Теперь мы
видим, что и теорема 1, которую можно рассматривать как частный
случай теоремы 3, справедлива для совершенно произвольного
геодезического треугольника.
Если заменить каждый внутренний угол а- его выражением
тг — а/ через внешний угол а,-, то формула (5) даст
(В)
т. е. получается следующая теорема:
Теорема 4. Внешние углы а3, а2,..., ал положительно
обходимого геодезического многоугольника, ограничивающего односвязную
область (В), и полная его кривизна \ \ KdS в сумме составляют 2-.
\в)
Рассмотрим теперь на поверхности S произвольную линию (X),
ограничивающую некоторую односвязную область (В). Линия (X) может
иметь угловые точки в конечном числе (как точка Аь на рис. 262).
Опишем около (а) геодезический многоугольник АХА%АЬАААЬ. Две
касательные е каждой угловой точке должны быть его сторонами.
§. 77. ТЕОРЕМЫ ГАУССА И БОННЕ 445
Остальные точки касания берем произвольно. Применим к
геодезическому многоугольнику теорему 4 и перейдем к пределу, неограниченно
уменьшая расстояния между точками касания. Предел полной
кривизны многоугольника ecib полная кривизна области (5), т. е.
KdS. В сумме а2 -\- ... + ап те слагаемые, которые соответствуют
угловым точкам, остаются неизменными. Число же остальных
бесконечно возрастает; каждое из них бесконечно мало и, согласно теореме 1
§ 74 (стр. 426), эквивалентно х^Д$, где As есть дуга (X) между точками
касания (например, между Мг и М2 на рис. 262), а кд — геодезическая
Рис. 262.
кривизна линии (л) в какой-либо точке дуги As. Величине ъд
надлежит приписать знак плюс, если поворот геодезической касательной
совершается против стрелки часов при наблюдении со стороны
нормали к поверхности; в противном случае ъд берется со знаком минус.
Сумма ^ *<А9 имеет пределом интеграл Ф *gds, и из теоремы (4) по-
U)
лучаем следующую теорему Гаусса-Бонне.
Теорема 5. Полная кривизна полоукительно обходимой одно-
связной области (В) поверхности S вместе с полной геодезической
кривизной ее контура (\) (в которую при наличии угловых точек входит
сумма соответствующих внешних углов) равна 2тс:
^ i (7)
(В)
Полная кривизна области была раньше определена как площадь
гауссова сферического изображения области. Формула (7) показывает,
что ее можно определить через такие величины, которые имеют
внутренне геометрический смысл, т. е. доступны измерениям,
производимым на самой поверхности. Следовательно, полная кривизна
оказывается инвариантом изгибания.
Гауссова кривизна К в точке М есть (теорема 1 § 68, стр. 399)
предел отношения F': F полной кривизны F' области (В) к ее площади
F, когда последняя стягивается в точку М. Следовательно, имеет место
следующая теорема на стр. 446.
446 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
Теорема 6. Гауссова кривизна есть инвариант изгибания.
Эта найденная Гауссом теорема явилась столь поразительной,
что современники назвали ее «theorema egregium» (превосходная
теорема).
Замечание. Как непосредственное следствие из теоремы 6 можно
геометрически вывести теорему 2 § 48 (стр. 282), которую мы
аналитически доказали в § 51 (стр. 298) и которая гласит, что всякая
поверхность, изгибаемая на плоскость, есть либо цилиндрическая, либо
коническая, либо поверхность касательных.
В самом деле, так как гауссова кривизна есть инвариант
изгибания, а для плоскости она тождественно равна нулю, то
развертывающиеся поверхности должны во всех своих точках иметь нулевую
гауссову кривизну; иными словами, все точки развертывающейся
поверхности должны быть параболическими, а такая поверхность
должна (теорема 2 § 68, стр. 400) иметь однопараметрическое семейство
касательных плоскостей, т. е. (теорема 2 § 48) она является либо
цилиндрической, либо конической, либо поверхностью касательных.
Чтобы найти измерением на поверхности ее гауссову кривизну,
достаточно построить малый геодезический треугольник и измерить
сумму «-1+а2 + аз его внутренних углов. Избыток этой суммы над 2тс
дает полную кривизну трез^гольника (эта величина, как и площадь
треугольника, имеет малость второго порядка). Измерив площадь
треугольника и поделив на нее полную кривизну, находим
приближенное значение гауссовой кривизны К для точек, лежащих внутри
геодезического треугольника. Степень точности растет, если треугольник
стягивается в точку и если относительная погрешность измерений не
увеличивается. В случае, когда гауссова кривизна К поверхности
постоянна, отношение F': F также постоянно и равно К. В этом случае
нет необходимости брать малые треугольники. Напротив, для
большего треугольника, где избыток суммы углов над тс велик, измерения
могут быть сделаны с большей относительной точностью. Обратно,
если измерения покажут, что для треугольников произвольного вида
избыток F' суммы углов над я (полная кривизна) пропорционален
площади F, то гауссова кривизна К постоянна и равна F': F. Такой
случай имеет место для геодезических треугольников на поверхности
земли и, значит, измерениями на поверхности земли можно найти
гауссову кривизну земной поверхности Ку а так как главные радиусы
кривизны здесь равны радиусу R земного шара, то последний может
быть определен по формуле1)
_4==|/ZZZ
г) Отметим, что никакие измерения, произведенные на ограниченном участке
вемной поверхности, не могут привести к заключению, что земля - шар, так как
при изгибании сферической поверхности все площади и углы оставались бы
неизменными. Однако, если известно, что поверхность земли замкнута и всюду имеет
одну и ту же кривизну, то можно утверждать, что она является сферой, ибо
можно доказать, что сфера есть единственная замкнутая поверхность постоянной
положительной кривизны. Иными словами, сферу в целом изогнуть нельзя. Стоит,
впрочем, вырезать из сферы сколь угодно малый кусок, чтобы изгибание стало
возможным.
§ 78. ОСНОВНЫЕ ФОРМУЛЫ ТЕОРИИ ПОВЕРХНОСТЕЙ 447
Эти факты, которые мы получили как следсгвие аеорем Гаусса,
были для самого Гаусса исходным пунктом его исследований по теории
поверхностей.
Упражнен ия
1. Доказать, что сумма внутренних углов геодезического треугольника на
поверхности псевдосферы меньше те, и недостаток до те (псевдосферический дефицит)
равен '— , где S — площадь треугольника и а — радиус ребра возврата (см. § 63,
примвр на стр. 365).
2. Доказать, что геодезический поворот касательной вдоль границы псевдо-
сферической области равен 2те -, где S — площадь области и а —радиус ребра
возврата.
3. Доказать, что на псевдосфере нет замкнутых геодезических линий.
4. Могут ли существовать замкнутые геодезические линии на поверхности,
не имеющей эллиптических точек?
5. Если поверхность может быть разбита на две области замкнутой несамо-
пересекающейся линией (L) (как поверхность сферы экватором, параллелью или
иным способом), то ее полная кривизна равна 4те (т. е. поверхности единичной
гауссовой сферы).
Указание. Применить теорему Гаусса-Вонне к каждой из двух областей
поверхности. Учесть, что, обхода линию (L) в определенном направлении, мы
оставляем одну из областей по правую, а другую—по левую руку, и что, вследствие
этого, геодезической кривизне линии (L) в одной и той же ее точке должны быть
приписаны противоположные знаки.
§ 78. Основные формулы теории поверхностей
В предыдущем параграфе мы, основываясь на ряде синтетически
установленных теорем, доказали, что гауссова кривизна К есть
инвариант изгибания. Между тем, выражение
K = EG-F* ' ^
которое мы прежде нашли для гауссовой кривизны, содержит
коэффициенты второй квадратичной формы, каждый из которых может
менять свою величину при изгибании; так, для геликоида (§ 57, пример
2, стр* 341) мы имеем
L iV = 0, (2)
а для катеноида, на который изгибается геликоид, мы имеем (§57,
пример 3, стр. 343)
причем накладывающиеся друг на друга точки этих поверхностей имеют
одни и те же криволинейные координаты, ибо первые квадратичные
формы для обеих поверхностей имеют коэффициенты
E = l, F = 0, G = u2 + b\ (4)
Понятно, что, раз величина К должна оставаться при изгибании
неизменной, дискриминант LN — M2 должен оставаться неизменным,
несмотря на изменение величин L, N, М в отдельности; это легко
проверить на нашем примере: как для геликоида, так и для катеноида
448 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
Значит (§ 47), для определения величины LN—M2, а вместе с ней
и величины К, дсстаточно знать коэффициенты Е> F, G первой
квадратичной формы; если мы в этом убедимся вычислением, то theorema
egregium будет доказана аналитически, и найденное выражение
величины К позволит вычислить гауссову кривизну поверхности по ее
квадратичной форме даже в том случае, если бы вид поверхности
оставался совершенно неизвестным. Опубликованное Гауссом
доказательство его «превосходной теоремы» именно в том и состояло, что
он дал выражение для дискриминанта LN — М2 через коэффициенты
Е, F, G и их производные по параметрам м, v.
Чтобы получить это выражение в наиболее симметричной форме
(у Гаусса оно было очень громоздким) и наиболее методическим образом,
мы предварительно установим основные уравнения теории поверхностей,
играющие в этой теории такую же роль, как формулы Френе в теории
кривых.
Именно, векторы ru, rv и т — —р1 Х Гг л можно принять за
координатные векторы; всякий вектор р, связанный с одной точкой
поверхности, выразится линейно через ru, rv, т:
p = xru + yrv + zm. (6)
Величины х, у, z суть координаты вектора р в системе ru, rv, т.
То обстоятельство, что координатные векторы Ги, rv в общем случае
не единичны, не играет существенной роли.
В частности, ми можем представить в виде (6) производные
векторов ru, rv, tn, подобно тому как в формулах Френе мы
представляем производные ортов t, n, b в виде линейных комбинаций самих
ортов.
Наша задача будет состоять в том, чтобы выразить координаты
х, у, z векторов гми, ruvi rvv, mu, mv через коэффициенты первой
и второй квадратичных форм, подобно тому как в формулах Френе
мы выражали координаты векторов tu. nu, Ьи через кривизну и
кручение. Начнем с вычисления координат х, у, z вектора ruu. Для этого
применим обычный прием векторной алгебры: помножим уравнение
rUu = яг и + yrv + zm (7)
скалярно на ru, rv и т. Получим три уравнения:
гицги = хг% +yrurv *, (8)
rUurv^xrurv + yrl *, (9)
ruum= * * z. (10)
Члены, стоявшие на месте звездочек, обратились в нуль; коэффициент
при z в уравнении (10) есть т2 = 1 Так как
Г г
то уравнение (10) прямо дает требуемое выражение для z:
z = L.
Величины х, у нужно найти из уравнений (8) и (9), где
коэффициенты при неизвестных суть
г*-#, rurv = F, rl = G. (И)
§ 78. ОСНОВНЫЕ ФОРМУЛЫ ТЕОРИИ ПОВЕРХНОСТЕЙ 449
Остается выразить свободные члены через коэффициенты основных
форм. Формулы (И) дают
/9 Я1 ЯР1 «9 ТР
Первое из этих соотношений дает
ГиГии = Т^ • (13)
Два последних дают
dF 1 дЕ //|/ч
>Vuli=--T^ . (14)
Теперь можно решить уравнения (8) и (9), после чего формула (7)
примет вид
дЕ dF дЕ дЕ dF дЕ
ди ди^ dv , du^ du dv _ j
Г""~ 2(EG-F2)
Аналогично можно найти выражения для ruv и г^.
^Е dG dG дЕ
(j _ /У _ /i /У
_ dv ди ди dv A1
ruv — 2 (EG - F2) u "*" 2 (EG - **) u ' '
и и dv du dv dv du дт .„.
rw= 2 (EG - F2) Гц^ 2 (EG - F2) rv+l\m. (11)
Принципиально задача наша в отношении векторов ruu) ruv и гт
решена. Но в составлении коэффициентов при ru, rv нельзя усмотреть
простой закон; причина этого кроется в видимом отсутствии симметрии
в формулах (13), (14) и им подобных. Чтобы выявить эту симметрию,
мы введем симметричные обозначения параметров и основных
квадратичных форм. Именно, параметры и, v мы будем теперь обозначать
через и1, и2, так что du1, du2 суть дифференциалы du, do.
Индексы 1, 2 мы ставим сверху, а не снизу, следуя принятому, обычаю,
целесообразность которого сказывается при дальнейшем развитии
теории дифференциальных квадратичных форм. Вместо (du1)* мы будем
писать drfdu1; вместо (du2)1 будем писать du2du2. Коэффициенты первой
и второй квадратичных форм мы будем обозначать
ft //* п — rt С i~*» IA ft\
Oil f б 12 *"~~ О 21 "~~~ I О 22 ~~~ ' V '
Таким образом, символами gl2 и g2l обозначается одна и та же
величина; мы будем брать, смотря по надобности, то ее обозначение,
которое обеспечит симметрию. То же самое можно сказать о
символах Ь1%, 621.
Буквой g (баз индекса) обозначим дискриминант первой формы
Е F
#21 #22
F G
(20)
Символом gik будем обозначать приведенный минор элемента
в определителе g, т. е.
\\_%гг 12 = ^21 _. _я £ia_ __ _ ^21 22 _ fu
£ * S £ * £
29 м. Я. Выгодский
450 гл. х. основные формулы, внутренняя геометрия поверхности
Для частных производных векторов гит введем обозначения
• 1 ^^ ' Ы» ' 2 == 'V* 11 ~= UU* * 12 2l 'IIU 'Ш*> * 22 W
^i- *яы, m2 = mv. (22)
Аналогично обозначаются и высшие производные.
Следовательно, при новых обозначениях имеем:
>Vi = gii, r1r2 = gl2, r22 = g22, (23)
r11m=—rlm1 = blJ; rl2rn = — r^m2 = b12\
r2lm= —r2m = b2l; r12rn = — r2m2 = b22t (24)
или, что то же,
(* = 1, 2; 4=1, 2), (23а)
Ь(к (*=1, 2; 4=1, 2). (24а)
Основные формы представятся теперь в виде
i1 + ёг^иЧи2 + g2ldu2dul + g22du2du2 = ^oin ,
(25)
1 + bl2da4u2 + b2Xdu2dux + b22du2du2 = %l
Символ 2 означает суммирование но обоим индексам i, кг
каждый из которых принимает значения 1, 2.
В новых обозначениях вычисления, проделанные нами для
определения коэффициентов х, у, z в разложениях ruu, rlw, rvv, могут
быть единообразно проведены для вектора rik(i = l,2\ 4=1,2)
следующим образом. Помножая уравнение
rik = xrx + yr2 + zm (26)
на rlf гг и т, находим
(27)
(28)
rikm = z. (29)
В силу (4а), имеем из (29) z = bik. Чтобы из уравнений (27), (28)
найти я, у, нужно выразить величины rikrx rikr2, через gllt gl2, g22.
Объединяя обе искомые величины, ищем единое выражение для шести
величин Ггкгх (/ = 1, 2; 4 = 1, 2;Z = 1, 2). Вместо формул (12) мы
ползучим из соотношений r(rk = giki riri = gn, rkt*i — gkl следующие три
симметричных уравнения:
(30)
-jj-f = Г,' 1Гк + Г{кГ{. J
Складывая два последних уравнения и вычитая первое, находим
Закон составления правой части теперь ярко выявляется: член,
входящий со знаком минус, имеет то же расположение индексов, что
искомое скалярное произведение, тогда как положительные члены
$ 78. ОСНОВНЫЕ ФОРМУЛЫ ТЕОРИИ ПОВЕРХНОСТЕЙ 451
содержат две остающиеся перестановки тех же индексов. Нарушение
симметрии в формулах (13)"и (14) и им аналогичных объясняется тем,
что в формуле (31) члены оказываются попарно подобными.
Правая часть формулы (31) сокращенно обозначается символом
или Г/,*,-; он называется символом Христоффеля первого рода:
L i J =! '•'*- 2 \£?
Итак, христоффелев символ первого рода Г/,** дает выражение
для скалярного произведения r,rik. Это выражение содержит первые
производные первой квадратичной формы. Следовательно, величины
rikri cyib инварианты изгибания.
Из формулы (32) видно, что величины \\jk симметричны
относительно индексов i, к, так что всего имеем шесть существенно
различных величин: ГМ1, Г1>12, Ti.22, Гг.и. 1*2,21, 1'2,22-
Уравнения (27) и (28) принимают теперь вид:
l\ik = xgu + !jgn, (33)
l\ik = xgit+ygtt. (34)
Неизвестные х, у, если воспользоваться обозначениями (21),
представятся выражениями
y g\ib + g\ikj
Так как величины х, у суть коэффициенты при г1у Г2 в разложении
вектора Пк, то выражения (35) обозначаются символами | 1 \, I \ \
или Г/Л, V(k- Эти символы называются символами Христоффеля второго
рода; они объединяются выражением
В силу симметрии индексов Христоффеля первого рода ирдексы
второго рода также симметричны, так что имеются шесть существенно
различных величин: Г}ь Г}2, Г22, Г?ь Г?2, Чг- Выражение Г]А зависит
через g0/ от коэффициентов первой формы, а через Г«,,а оно зависит
от первых производных этих коэффициентов. Поэтому величины Vlik
суть также инварианты изгибания.
Теперь три формулы (15), (16), (17) могут быть представлены
в едином и симметричном виде:
rik = ПаГ, + Vhrt + bikm, (37)
где в силу формул (36) и (32) христоффелевы символы второго рода
l'ik* Vfa можно заменить выражениями
^» (38)
«1|2
Чтобы усвоить полученные результаты, читателю предлагается
получить из формулы (37) прежде найденные выражения (15), (16), (17).
Формулы (15), (16), (17), или, что то же, формула (37), называются
деривационными формулами Гаусса (термин «деравацияъ означает
операцию нахождения производной функции). Гаусс получил эти формулы
29*
452 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
в 1826 году в несимметричном виде. Симметризация достигнута Хри-
стоффелем в 1869 году, развившим глубокие идеи, высказанные Рима-
ном в его диссертации 1848 года (опубликована в 1861 году).
Перейдем к выводу формул, дающих разложения векторов ntlt т%.
Напишем уравнение
тг = хгг + yr% + zm\ (39)
отсюда найдем:
т.Гг = хгггх + yrxr2 + zmrlf
\ (40)
= хтгг + ymr% + zmm.
Принимая во внимание формулы (23а) и (24а), а также
соотношения ^<^ = у-^- = 0 и тгг = 0, находим:
2 22 \ (41)
0==z. j
Последнее равенство легко было предвидеть, так как производная
единичного вектора нормали т перпендикулярна к т, т. е.
компланарна с векторами г19 г2, так что можно было с самого начала опустить
последнее слагаемое в (39). Первые две формулы (41) дают для х, у
значения
(42)
t - {gnblt + g-btt) rt = - 2 Въ-Къ. (43)
В развернутом виде эти формулы имеют вид
или в наших прежних обозначениях
— __ GL-FM r __ -zUL±.?M r 1
__ GM-FN - FM + EN \ ^ ^
mv— ~" EG- Fz Ги EG - F2 Г°* ]
Коэффициенты в разложениях векторов ти1 mv зависят от
коэффициентов обеих квадратичных форм.
Формулы (44а) называются формулами Вейнгартена. Они были
опубликованы Вейнгартеном в 1861 году. Вместе с формулами Гаусса
они вскоре стали основными формулами аналитической теории поверх-
востей.
Упражнения
Доказать тождества:
§ 79. УРАВНЕНИЕ ГАУССА . 453
§ 79. Уравнение Гаусса
С помощью деривационных формул Гаусса мы можем получить
выражение дискриминанта Ь1ХЬ22 — b\t = LN — М* через коэффициенты
первой квадратичной формы и тем доказать аналитически
инвариантность (относительно изгибания) гауссовой кривизны
Мм - Иг _ LN-M2
g — EG-F* '
Выпишем формулы Гаусса [§ 78, (37), стр. 451]:
т, (1)
т, (2)
т. (3)
Если мы составим выражение rxlr22 — rl2rl2J то коэффициенты второй
формы в силу соотношений г1т = 0, г2т = 0 войдут только в нужной
нам комбинации: bxlb22 — bl2bl2. Учитывая, что rtrk=gik, мы получим:
Гг,г22 - г12г12 = (ВД, - Г{,Г1,)gll + (Г^Г;, - Г}2Г212) gl2 +
+ (ВД, - вд.) g21 + (г^г;, - г;,!';,) gt2 + ъ1Хъ22 - 6l8&l2 f
или, в сокращенной записи,
ГггГ» - Г12Г12 = ^ (ПЛ, ~ Р^Г},) g«p + 61 А, - 6l26l2i (4)
Чтобы выразить дискриминант b11b22—bl2bl2 через коэффициенты
первой формы, остается представить левую часть (4) через gik (ибо
христоффелевы символы Г*х суть функции glfc и их производных). Но
величину rxir22 — rl2r12 можно представить в виде
riS*2 - rl2rl2 = ^ (rxlr%) - ^ (rl2ra) (5)
или
ГцГ.! - ^12Г12 = ^ (Г,,^) - ^| (Г12Гг), (6)
а величины rikri = Fltik выражаются через gik по формуле (31) § 78
(стр. 450). Подставляя в (5) вместо г1Хг2 и г12г2 выражения
dgl*
dgxi Л
да* ) '
находим
То же выражение получим из (6). Окончательно имеем из (4):
2
-J {""2 + X
Это уравнение называют уравнением Гаусса. Подставляя выражение (8)
454 гл. х. основные формулы, внутренняя геометрия поверхности
в формулу К = х1 12 ~ "» мы представляем гауссову кривизну через
ollo22 &12
коэффициенты первой квадратичной формы и их производные; тем
самым доказана инвариантность гауссовой кривизны относительно
изгибания.
Если уравнение Гаусса представить в раскрытом виде с помощью
формул (38) § 78, оно примет более сложный и лишенный симметрии
вид, в каком его получил сам Гаусс в результате громоздких
выкладок. Можно, однако, преобразовать выражение (8) к другим более
простым и все же симметричным формам. Так, Фробениус дал следующее
выражение для гауссовой кривизны:
EG
-Ml
- F*
Ь
g
ll"22
-*1
2
, 1
, \(EG-F*Y
У EG - F1 1 ox>
E
ge
Eu
Gv
ou
Ou 1
- F* J
r, r, r, g- OE dE dF
где через Ьи, Eo, Fu и т. д. обозначены величины — , —— , — и т. д.
Это выражение достаточно легко запоминается и может хорошо
служить для удобного вычисления гауссовой кривизны по заданной первой
квадратичной форме.
Однако для исследования конкретных геометрических вопросов
эта и другие общие формулы все же мало пригодны. Огромный выигрыш
здесь, как и в других геометрических задачах, дает
специализированный выбор системы координат. Так, если поверхность отнесена к
прямоугольной криволинейной сети, что обычно легко достигается и дает
еще широкий простор для дальнейшей специализации системы
координат, то формула (8) или равносильная ей формула (9) чрезвычайно
упрощается. Действительно, мы имеем тогда F = Q и. следовательно,
%FU = Fv = 0, и формула (9) принимает вид
Весьма полезным упражнением будет получить это выражение
непосредственно из формулы (8).
Пример. Пусть задана первая квадратичная форма поверхности
Эту первую форму, как мы знаем, имеют, в частности, геликоид
и катеноид.
Найдем гауссову кривизну поверхности по формуле (10). Имеем:
к== 1 Г <* 2и 1 = ft*
Сравните этот результат с формулой (5) § 78 (стр. 447).
§ 80. УРАВНЕНИЯ ПЕТЕРСОНА-МАЙНАРДИ 455
Упражнения
1. Найти гауссову кривизну поверхностей, изгибаемых на сферу радиуса а.
2. Найти гауссову кривизну поверхностей, изгибаемых на псевдосферу,
у которой радиус ребра возврата равен а.
3. Вычислить гауссову кривизну поверхностей, изгибаемых на поверхность
вращения.
4. Исходя из выражения линейного элемента развертывающейся поверхности
ds2 = du2 + 2du dv + [1 + (* (v))2 и2] dv2,
доказать, что ее гауссова кривизна равна нулю.
5. Линейный элемент всякой поверхности при соответствующем выборе
параметров можно привести к виду
ds* = b(u, v)(du*-{-dv'2).
Доказать, что гауссова кривизна представится тогда выражением
_ 1 Г<921пЯ
L <*и1 + dv2 J '
6. Доказать, чго гаусзову кривизну можно представить выражением
i «ten . dg1% i dg22 \
<ггК- ч 2 ди2 ди2 T ^u1 ow2 2 ^a1 di*V "
О
}2 gn g
£ glt gI
Указание. Преобразовать выражение (г1Хгггг) (r2Zrxr2) — (г12ггг2)2, дважды
применив теорему умножения смешанных произведений (теорема умножения опре-
1\е штрлей).
§ 80. Уравнения Петерсона-Майнарди
Когда поверхность подвергается изгибанию, ее первая
квадратичная форма, выражающая квадрат элемента длины ds2, остается
неизменней, тогда как вторая квадратичная форма, выражающая двойное
расстояние поверхности от касательной плоскости, подвергается
изменению. Уравнение Гаусса показывает, однако, что при всевозможных
изгибаниях поверхности некоторая функция коэффициентов второй
формы (LN — M2) остается неизменной в силу зависимости (8) § 79
между bik, gik и производными послед ник функций. Геометрически это
означает, что хотя и не все, но некоторые внешние свойстве
поверхности могут вполне определяться ее внутренними свойствами. В
данном случае внутренние свойства поверхности определяют площадь ее
сферического изображения или произведение ее главных кривизн.
Естественно возникает вопрос, не существуют ли и другие
зависимости между коэффициентами biky gik и их производными, т. е. не
подчинены ли внешние геометрические свойства поверхности еще
каким-либо ограничениям, вытекающим из внутренних ее свойств.
Мы обнаружим сейчас две такие зависимости, связывающие
коэффициенты bik и их первые производные (последние не входили в
уравнение Гаусса) с коэффициентами gik и их первыми производными.
Мы имеем следующие выражения коэффициентов второй формы
через основные векторы:
b11=—rlml1 bl2=—r1m2. (1)
Продифференцируем первое по и2, а второе по и1:
"^2L= —гхтхг — тгГ^; "^f= — rimn — ^2rn- (2)
Вычитая из псфвого уравнения второе, находим
^-тггх, = д-^--тхг1г. (3)
456 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
Остается подставить вместо гх1 и rl2 их выражения через
деривационные формулы Гаусса (1) и (2) § 79 (стр. 453):
Учитывая, что mtm = 0 и —т(гк = Ьгк, мы найдем
%■ + г; А, + ПА, - ^ + гг.6» + г; а,. (4)
Если вместо выражений (1) мы будем исходить из выражений b2l = — г2тх\
622=—г2ш2, то после аналогичных выкладок, которые читателю
предлагается выполнить, получим
Эти формулы объединяются в виде
г; а. = ^f + Ч.*и + ПА,-
Закон составления этой формулы таков: в каждой ее стороне нижние
индексы христоффелевых символов совпадают с индексами
дифференцируемой величины bik\ один из индексов величин 6, входящих линейно,
совпадает с индексом переменной, по которой берется частная
производная; другой индекс пробегает значения 1, 2 вместе с верхним
индексом символа Христоффеля. Если формулы (5) и (6) полностью
раскрыть с помощью формул (38) § 78, они потеряют обозримость.
Формулы, равносильные (6), были впервые найдены русским
математиком К. М. Петерсоном в его диссертации 1853 года. Эта
диссертация не была напечатана, и результаты К. М. Петерсона были
переоткрыты и опубликованы в 1856 году итальянским математиком
Майнарди (G. Mainardi). Однако значевие уравнений
Петерсона-Майнарди не было оценено, и они были забыты. В 1868 году их нашел
вновь итальянский математик Кодацци (D. Codazzi). Поэтому в
литературе их именовали уравнениями Кодацци.
Из уравнений Гаусса и Петерсона-Майнарди можно, конечно,
получить бесчисленное множество соотношений между gik, bik и их
производными; но существуют ли, кроме них, существенно новые
соотношения?
Если мы внимательнее всмотримся в те преобразования, которые
мы выполнили при выводе уравнений Гаусса и Петерсона-Майнарди,
то сможем заметить, что существенную роль в этих выводах играло
изменение порядка дифференцирования. Так, при вычитании второго
уравнения (2) из первого мы отождествили производную ^ц1 ди% с
производной АдУ* . Этот прием мы можем применять систематически
Oil ОН
к системе пяти деривационных формул Гаусса и Вейнгартена
!+«-*,.) Г„
(7)
§ 80. УРАВНЕНИЯ ПЕТЕРСОНА-МАЙНАРДИ 457
Именно, мы должны иметь
д/*ц д^*12 . ^f*l2 _ ^^*22 . дП%1 ^^ Ottli /O\
~дп* = "дп1 ' дй*" — -^1 » ^2" ~ диТ • I '
Вычислим ^-f1 по формуле (7); мы найдем выражение, содержащее
производные величин gik и 6/Л, а также векторы rlly rJ2, m. Последние
мы выразим с помощью (7Х), (72), (78) через основные векторы и через
величины gikf bik и производные величин gik. Поступив аналогично
с производной -~1 и подставив найденные выражения -^ и -^у в
первую из формул (8), мы получим векторное уравнение вида
ai^i + а2Г2 + asm = 0, (9)
где а19 а2, а8 будут функциями от gik, bik и их производных, причем,
как легко видеть, порядок производных от gik будет не выше второго,
а порядок производных от bik — не выше первого.
Используя остальные уравнения (8), мы получим еще два
векторных уравнения вида:
Piri + P1r1 + Pti» = Of (10)
Vi+Y/'. + T.'W-O. (11)
Уравнения (9), (Ю), (11) могут удовлетворяться в том и только
в том случае, если каждый из коэффициентов a/f (3f, yf- равен нулю.
Таким образом, мы получим девять соотношений между bik, gik и их
производными . Но вычисления показывают, что каждое из
соотношений ах = 0, а2=0, pj = 0, Р2 = 0 дает одно и то же уравнение, именно —
уравнение Гаусса. Каждое из соотношений а3 и у2 дает уравнение (4);
каждое из уравнений Р8 = 0 и Y2 = 0 дает зфавнение (5); наконец,
соотношение y3 = 0 удовлетворяется тождественно.
Таким образом, систематическое исследование основных уравнений
(7) не дает никаких новых соотношений между коэффициентами первой
и второй форм.
Но, может быть, из каких-нибудь иных соображений можно найти
соотношение вида
£ dgik dbik
которое не было бы следствием уравнений Гаусса и
Петерсона-Майнарди, однако удовлетворялось бы для всякой поверхности?
На этс т вопрос также следует ответить отрицательно, и вот почему.
Пусть некоторое соотношение (12) не является следствием уравнений
Гаусса и Петерсона-Майнарди. Это значит, что можно указать
(безотносительно к какой-либо поверхности) шесть функций gik{ux, a2), 6/fc(^1, и2),
которые обладают следующими свойствами: 1) они удовлетворяют
уравнениям Гаусса и Петерсона-Майнарди и 2) не удовлетворяют
соотношению (12). Нижеприводимая теорема устанавливает, что наличие первого
свойства обеспечивает существование такой поверхности г=г(г/\м2),
для которой коэффициенты gik, bik первой и второй квадратичной
формы тождественно равнялись бы функциям gik(ux, и2), bik(ux, и2). Для
этой поверхности функции gik, bik заведомо не удовлетворяют
соотношению (12). Итак, соотношение вида (12), которое удовлетворяется
для всякой поверхности, непременно является следствием уравнений
Гаусса и Петерсона-Майнарди.
458 ГЛ. X, ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
Теорема, на которую мы только что ссылались, формулируется
следующим образом:
Если задать любые две квадратичные формы:
f =rglldaldal + 2gl9du4u2 + g22du4u2 (13)
//
9 = b^du'du1 + 2bl2du4u2 + b22du2du2, (14)
коэффициенты которых удовлетворяют уравнениям Гаусса и Петерсона-
Майнарди, а также условию
то существует одна и — с точностью до движения — только одна
поверхность r = r(uly и2), для которой f есть первая, а <р — вторая
квадратичная форма.
Не проводя доказательства полностью, наметим его ход.
Если искомая поверхность, действительно, существует, то вектор-
функция г (и1, и2) должна удовлетворять уравнениям (/), где величины
gik (входящие в развернутые выражения символов Христоффеля) и bik
заменены выражениями gik(ul, a2), biK(ul, и2). Произведя эту замену,
будем искать решение системы дифференциальных уравнений (7), в
которой неизвестными являются векторы гг, г2, т. Для совместности
этой системы необходимо и достаточно выполнение условий (8), или,
что то же, уравнений (9), (Ю), (И). Но эти уравнения сводятся, как
сказано, к уравнениям Гаусса и Петерсона-Майнарди. Последние же-
по условию удовлетворяются. Поэтому условия интегрируемости для
системы (7) заведомо выполнены, так что существуют вектор-функции
г (а1, и2), т(и1, и2), удовлетворяющие уравнениям (7).
Более того, можно доказать, что среди решений уравнений (7)
имеются и такие, для которых
r,rk = glk{u\ и2), -rimk = b,k(u\u}). /
Возьмем одно из таких решений; функция г = г (и1, и2) дает
некоторую поверхность* у которой коэффициенты первой и второй
квадратичной формы, в силу (15), совпадут с функциями.
Взятое нами решение не будет с аналитической точки зрения
единственным. Однако бесчисленное множество других решений системы (7),
(15) дают ту же самую поверхность, но в другом положении. Это
можно доказать, пользуясь свободой выбора начала координат и
направления координатных осей.
Замечание. Пока вторая квадратичная форма не задана, первую
можно выбрать совершенно произвольно; уравнения Гаусса и Петерсона-
Майнарди оставляют еще очень широкий произвол в выборе второй
формы. Таким образом, существует бесчисленное множество (изометрич-
ных) поверхностей, имеющих совершенно произвольную наперед
заданную положительную форму.
§ 81. Формула для геодезической кривизны
В §§ 73 и 74 (стр. 421—428) были синтетически доказаны
основные предложения, относящиеся к теории геодезической кривизны и
геодезических линий. Мы не дали там аналитического выражения
геодезической кривизны, так как общая формула очень громоздка, и полу-
§ 81. ФОРМУЛА ДЛЯ ГЕОДЕЗИЧЕСКОЙ КРИВИЗНЫ 459
чение ее потребовало бы утомительных выкладок. Деривационные
формулы Гаусса позволяют упростить вычисления и дают
симметричный вид результату, причем непосредственно обнаруживается
инвариантность геодезической кривизны относительно изгибания.
Пусть на поверхности задана некоторая линия (L)
м1 = и1(0» u2=u2(t). (1)
Геодезическую кривизну линии (L) мы определили как кривизну
ое проекции (L) на касательную плоскость; как было доказано в § 76
(пример 1, стр. 437), вектор кривизны линии (Z/) есть проекция вектора
кривизны j-7 = j- линии (L) на касательную плоскость или, иными
словами, абсолютная производная ^- орта касательной линии (L) по
направлению самой линии (L). Геодезическая кривизна есть модуль этой
проекции
Но геодезической кривизне, как было указано в § 74 (теорема 1,
замечание, стр. 427), можно приписать и знак. Именно, согласно принятому
условию величина у.д считается положительной, если при наблюдении'
с положительной стороны поверхности (эта сторона указывается ортом
т = -1—-—2 , исходящим из рассматриваемой точки) центр геодезической
/ Dt\
кривизны ( ведущее к нему направление указывается вектором — J
располагается слева от наблюдателя, обращенного лицом в сторону
орта t. Таким образом, знак геодезической кривизны совпадает со
знаком смешанного произведения mt ,- . Но и по абсолютной величине
пто смешанное произведение, в силу (2), равно геодезической кривизне.
Поэтому геодезическая кривизна представляется следующей формулой:
Эту формулу можно также записать в виде
где абсолютная производная заменена обыкновенной производной -, ;
действительно, эти производные разнятся друг от друга на вектор,
коллинеарный с сомножителем т (теорема 3 § 76, стр. 437), так что
смешанное произведение от этой замены не меняет своей величины.
Читателю предлагается получить формулу (4), не пользуясь понятием
абсолютной производной. Этим лучше уяснится суть процесса
абсолютного дифференцирования.
Выражение (3) или (4) имеет очень протой вид, но в раскрытом
виде оно значительно усложняется. Именно, мы имеем
du1 du2 f (Г
1 ds 2 ds* '
dt du1 du1 o du1 du2 du2 du d^u1 d2u2 .^
При подстановке выражений (5) и (6) в формулу (4) мы получим
множество смешанных произведений вида rikri?n; чтобы выразить эти про-
460 г л, х. основные формулы» внутренняя геометрия поверхности
изведения через коэффициенты основных форм с наименьшей затратой
труда, применим деривационные формулы Гаусса
(7)
= r212n + IV2 + ^2^. ]
Формула (6) примет вид:
ds ~~ Гх L ds* ±Ll1 ds ds~t" ^ i2 ds ds "*" 22 ds ~3F J "*"
L " d5 rf5 "^ ^ " ^5 rf5 ~T X 22 rfs "5J J
или, в сокращенной форме,
Вектор, коллинеарный с т, не окажет влияния на величину
смешанного произведения (4); его можно отбросить. Остающиеся два
dt
слагаемых дают проекцию вектора -у- на касательную плоскость, т. е»
Dt
абсолютную производную -j :
Dt
Величины, стоящие в прямых скобках, суть координаты вектора
Dt r\r /Dt\l /DtX*
т- по направлениям rlt r2. Ооозначив их через ( -т- ) , ( -j ) , т. е^
положив
г ) в"й^> + 2j ^«P17 17 (1• = 1»2), (10>
мы можем переписать (9) в виде
Dt _
Остается подставить выражения (5) и (11) в формулу (3) или, что то
же, выражения (5) и (8) в формулу (4). При этом смешанное
произведение разобьется на четыре слагаемых, из которых два (тгхгх и
тг2гг) равны нулю. Два других (тг2гг и тггг2) можно выразить
через коэффициенты первой квадратичной формы. Действительно, мы
имеем
ггх г2 = т \/г(г1 х г2)2 = т j/~g,
так что
тгхгх = - тгггх = /J. (12)
81. ФОРМУЛА ДЛЯ ГЕОДЕЗИЧЕСКОЙ КРИВИЗНЫ
461
Заметив это, найдем из (3)
ds \ ds
ds {ds
(13)
Подставляя сюда вместо координат (-г) ; ( -г ) абсолютной
производной -т- их выра?кения (10), находим для геодезической кривизны
следующее симметричное выражение:
du* dW rJ du*
s ds2 + « ds
9 2 duj-du?
Zi I2 ds ds
d5 ^5 "^ Zi I2 d« rf5
• (14)
Чтобы перейти от параметра 5 к произвольному параметру t, через
который выражены и1, и2 в формулах (1), нужно подставить в (14)
выражения
du1 duldl dW Л*1/AN» , dutdH
du2 d2u2 г* du1 dH
и аналогичные выражения для -j- -т-j . При этом слагаемые -т- -^-г ,
du2 dH r
-j7 -T-g , пропорциональные элементам первого столбца определителя,
можно отбросить. За знак определителя выйдет величина
- Y ( dt
dsj
Г222 (и2)2
Формула (14) примет вид
__ VSll #22 — gl2
(gn (ui
и* и*
где точками обозначено дифференцирование по произвольному
параметру. В этом своем виде формула геодезической кривизны, несмотря
на ее длинноту, легко запоминается благодаря симметрии, которой она
обязана употреблению символов Христоффеля. Для вычислений
желательно иметь формулу, в которой символы Христоффеля были бы уже
заменены своими выражениями через Gik и их производные. Эти
выражения, как видно из формул (15), (16), (17) § 78 (стр. 449), принимают
после приведений несимметричный вид:
, _GEU-2FFU
1" 2 (EG - F2) f
! =GET-FGU
ll2~~ 2(EG-Fi)f
pl -FGV+2GFV-GGU
i22— 2(EG-F2)
2 -FEU-2EFU-EEV
" 2 (EG — F>)
2 EGU-FEV
12 2(EG-F2)9
\
2(EG-F2) |
^EGV-2FFV + FGU
2(EG-F2) ' )
> (17)
Чтобы придать окончательной формуле симметричный вид, нужно
подвергнуть результат подстановки этих выражений новым преобра-
462 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
зеваниям. Тогда можно получить, например, выражение
3
\fEG-F2 (Ей* + 2Fuv + Gv*)* xg =
=(EG-F*)(uv-№)4 (Ей + Fc)\(Fu-± E^u* + Gu iw + A Gv
- (Fa + Gb) {~ £u«2 + Evuv + (>„ - { GB) в« j- , (18)
данное Белътрами.
Отметим, что выражение геодезической кривизны зависит от
коэффициентов первой квадратичной формы и их первых частных
производных.
Для геодезической кривизны координатной линии и = const
формула (18), в которую нужно подставить и — и = 0, i?=l, у = 0, дает
2 G42
что можно также записать в виде
л f ~TFr* z?2 /„ \ ( \ \ (\fc\
у £L(jr — г (У.д)и= const = —dv\ / 7^ ) дп ^* '*
В частности, если система криволинейных координат
прямоугольна (F = 0), получаем
(20)
Замечание. Положив i?=l, мы установили на линии и = О
направление обхода, соответствующее возрастанию параметра v. Положив
1;= — 1, мы выбрали бы противоположное направление обхода,
вследствие чего величина xff должна изменить знак на обратный.
Упражнения
1. Вывести формулу (19) настоящего параграфа из формулы (16).
2. Вычислить геодезическую кривизну параллели поверхности вращения.
3. Вычислить геодезическую кривизну винтовой линии на геликоиде и на
круглом цилиндре.
4. Вычислить геодезическую кривизну координатных линий на поверхности
коноида: x = ucosv\ y~usinv, z = j(v). Здесь можно применить формулу (20).
Проверить результат по формуле (\).
5. На бинормалях кривой (L) отложены в одну сторону отрезки равной
длины а. Вычислить геодезическую кривизну места концов этих отрезков на
поверхности бинормалей.
Указание. Результат можно получить очень быстро, если учесть теорему,
сформулированную в упражнении 10 § 76 (стр. 438).
6. Доказать, что геодезическая кривизна изогональной траектории меридианов
сферы (локсооромы) равна sincptgu, где и — широта, а <р — постоянный угол между
локсодромой и меридианом.
7. Найти геодезическую кривизну кривой Вивпани 1) на сфере, 2) па круглом
цилиндре.
8. Вывести из формулы (16) формулу кривизны плоской кривой.
9. Доказать, что абсолютный дифференциал вектора р, данного разложением
р s xlrY Л- жаг2 (х1 и х2 суть функции от и1, и2), выражается формулой
• 2 2
3 82. АНАЛИТИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ГАУССА-БОННЕ 463
§ 82. Аналитическое доказательство теоремы Гаусса-Бонне
В § 77 (стр. 439) мы дали синтетитическое доказательство теоремы
Гаусса-Бонне; она }ттверждает, что полная кривизна односвязной
области (В) поверхности S вместе с полной геодезической кривизной ее ков-
тура (X) равна 2тг:
^KdS+S^ds^'Z'K. (1)
Теперь, имея формулы для т.д и для К, мы можем дать
аналитическое доказательство этой теоремы. Мы должны, следовательно,
выразить двойной интеграл \ \ jST rf.v через криволинейный £ ъд ds,
(В) J
взятый по контуру области.
Чтобы выполнить это преобразование возможно проще, выберем
удобную систему координат. Именно, замкнутый контур (X) мы примем
Рис. 263.
за одну из координатных линий и = const, положив для него, скажем,
и = 1. Приняв какую-либо точку С (рис. 263) на (X) за начало отсчета
дуг и обходя (X) в положительном направлении, будем приписывать
точке М линии (X) значение и, равное длине пройденной дуги. Таким
образом, в начале обхода в точке С имеем у = 0, а в конце обхода
в той же точке С имеем v = a, где а есть длина контура.
Возьмем теперь внутри области (В) какую-нибудь точку О.
Непрерывно деформируя контур X, будем стягивать его в точку О,
сохраняя его замкнутость. Так как область (В) односвязна, то
это возможно сделать бесчисленными способами. Мы выберем
один какой-либо процесс стягивания и припишем промежуточным
положениям контура в качестве координаты и значения, непрерывно
убывающие по произвольному закону от и=1 до и=0; при и = 0
контур вырождается в точку О. Наконец, построим ортогональные
траектории линий v = const и каждой из них припишем то значение у,
которое отвечает точке ее пересечения с контуром (X).
Таким образом, область (В) будет покрыта ортогональной
координатной сетью, которую можно считать правильной всюду, кроме точки О.
Правда, на линии ОС, принадлежащей семейству v = const, всякой
точке отвечают два значения и, именно v = 0 и v = a. Но это обстоя-
464 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
тельство не имеет существенного значения, так как мы сможем,
проведя линию АС, для которой v = a — а, изъять из области (В) ту ее
часть, которая содержится между ОС и ОС, и проведя вычисления
для оставшейся области, перейти к пределу при а—>0.
Построив указанным образом координатную сеть, напишем
выражения для гауссовой кривизны К и для геодезической кривизны у.д
линий и = const.
Согласно формуле (10) § 79 (стр. 454) мы имеем
2/eg iovKYeg J du \Yeg
а согласно формуле (20) § 81 (стр. 462),
9 YEG ди
Введя для краткости обозначения
^-JL-ZUL. (3)
мы можем переписать эти формулы так:
«.-*• (5)
Наконец, элемент площади dS в прямоугольной системе
криволинейных координат имеет вид
dS = \/'EG du do = АВ du dv. (6)
Исключим из области (В) ту ее часль, которая лежит внутри малого
контура (р.), соответствующего значению и = е, охватывающего точку О,
и найдем полную кривизну остальной области (В'). С помощью (4)
(6) получаем
{В')
Найдем отдельно два интеграла в правой части (7). Имеем
\ \ «*>*- \ * I
(В') е 0 е
Но так как значениям v = 0 и v = a отвечает одна и та же линия ОС
то
/АЛ Г АЛ _0
так что первый из интегралов правой части (7) равен нулю. Далее
имеем
{В') 0 s
а
§ 83. УРАВНЕНИЕ ГЕОДЕЗИЧЕСКОЙ ЛИНИИ 465
Учитывая, что элемент дуги координатной линии и = const имеет вид
ds=yrGdo = Bdvy (9)
мы можем переписать формулу (8) в виде
(Bf) 0
где а' есть длина контура (u).
■jD
Так как величина -щ , согласно формуле (5), есть не что иное,
как геодезическая кривизна *д контура a —const, то входящие
в правую часть (10) интегралы представляют полные кривизны линий
и = з и и = 1, и мы имеем
tgdS. (И)
(В') (В') * ' (jl) (Я)
Переходя к пределу при е—> О, получим в левой части полную
кривизну \ \ KdS области (В). В правой части второе слагаемое остается
(В)
постоянным, а первое, как мы сейчас докажем, имеет своим
пределом 2тс.
Действительно, если спроектировать линию (р.) на касательную
плоскость в точке О, то элемент дуги ds' проекции (р.') эквивалентен
элементу ds, а кривизна проекции эквивалентна х^. Поэтому полная
геодезическая кривизна линии (р.) эквивалентна полной кривизне плоской
замкнутой линии (р<'), т. е. углу полного поворота ее касательной. Итак,
lim \ у.д ds = 2тг,
(V-)
и формула (11) дает
С С С
\ \ л\. ofib === Atz — \ ул ds%
J J J 9
(В) Я
что и доказывает теорему Гаусса-Бонне.
§ 83. Уравнение геодезической линии
Так как геодезическая линия, как мы знаем, есть линия нулевой
геодезической кривизны, то ее уравнение мы получим, приравнивая
нулю выражение (16) § 81 (стр. 461). Возвращаясь к обозначениям
параметров через и и о, находим:
du d2o - do d2a + (1\\ da2 4- 2I\2, da do +1\?2 do2) da -
- (Гп da2 + 2Г{2 du do + Г^2 do2) do =-- 0. (1)
Здесь независимое переменное остается совершенно произвольным; если
принять за независимое переменное один из параметров, скажем и,
то искомой функцией будет v(a); она должна быть определена из
дифференциального уравнения
V + (Г;, + 21>' + Г;2 (v'f) - (Г;ж + 21>' + Г,», (»')>' = 0, (2)
в котором все величины Г суть данные функции переменных и и v.
Дифференциальное уравнение (2) имеет второй порядок, что можно
3J М. Я. Выгодский
466 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
было предвидеть заранее, так как через данную точку в данном
направлении должна проходить одна геодезическая линия. Из анализа
известно, что соответствующее решение уравнения (2) должно
существовать при весьма общих допущениях относительно его коэффициентов.
Однако фактическое интегрирование уравнения геодезической
линии представляет задачу, которая даже в простейших случаях не
получила удовлетворительного решения.
В ряде случаев оказывается выгодным ввести в качестве
независимого переменного дугу s. Ее связывает с параметрами и, v
соотношение
ds2 = Edu* + 2F dudo + G do2, (3)
V i or>2 du^ dv p3 Л^У 1 d_H __
ds ) "t" 12 ds ds^122 \ds ) J ds
которое совместно с уравнением
du d^o dv d2u ,[тм ^V i or>2 du dv
57 ds2 ~~ ds~ ds~> + L \ ) t
J ^Ll^ds ds^L*'\dsJ \ds U W
определяет две функции: и (s) и v (s).
Систему уравнений (3), (4) можно преобразовать к виду
£+г- От)"+*"-££
Эти уравнения можно объединить, записав их кратко так:
Вместо того, чтобы проделывать утомительное преобразование,
приводящее от уравнений (3), (4) к уравнениям (5), (6), лучше будет
воспользоваться следующими соображениями: согласно формуле (9) § 81
(стр. 460), левые части уравнений (5), (6) суть координаты вектора
геодезической кривизны -у- . Для геодезической линии этот вектор равен
нулю, что возможно в том и только в том случае, если каждая из
координат по отдельности равна нулю.
В качестве примера применения формул (7) найдем геодезические
линии поверхности вращения. Ее первая квадратичная форма имеет вид
du* + r2do2, (8)
где и — дуга меридиана, v — долгота, а г —радиус параллели, который
на данной поверхности есть определенная функция от п.
Возьмем уравнение (6); так как мы имеем E = l, F = 0, G = r*t
то по формулам (17) § 81 (стр. 461)
р2 _о г1 — — Г2 — 0
L 11 U» L 12 г » L 22 U#
Уравнение (6) принимает вид
dH 2rududv _n ,Q.
ds^~ ds~ds-U' <У>
Помножая это уравнение на г2, можем записать его в виде
d Г
*(.'£)-«■
§ 83. yPAJBHEHHE ГЕОДЕЗИЧЕСКОЙ ЛИНИИ 467
Следовательно,
,-g-c, (10)
где с —постоянная величина.
Это уравнение уже легко проинтегрировать. Но прежде выясним
его геометрический смысл. Величина г do есть дифференциал дуги
параллели; рассмотрев треугольник ABC (рис. 264), составленный
дугой геодезической линии ВС ^ ds, дугой параллели АВ ^ г do
и дугой АС меридиана, мы ви-
r dv
дим, что -j- = smcp, где© —угол >
между направлением
геодезической линии и направлением
меридиана. Уравнение (10),
записанное в виде
rsin9 = c, (11)
выражает следующую теорему,
впервые установленную Клеро
(Glairaut) в 1733 году.
Теорема. Для всякой
геодезической линии на поверхности
вращения произведение радиуса
параллели на синус угла,
составляемого геодезической линией с
меридианом, есть постоянная
величина.
Иными словами, синус угла,
составляемого геодезической
линией с меридианом, обратно
пропорционален радиусу параллели Рис. 264.
(см. рис. 264).
Возвращаясь к уравнению (10), которое ¥ы перепишем в виде
r2dv = cydu2 + r2do2,
мы после элементарных преобразований получаем:
*) v
Это уравнение представляет все геодезические линии поверхности
вращения.
Упражн ения
1 Найти уравнение геодезических линий на поверхности конуса.
Указание. Можно воспользоваться теоремой Клеро. Так как при
развертывании конуса на плоскость система меридианов и параллелей обращается в
координатные линии полярной системы, полезно проверить результат, составив
уравнение прямых линий в полярных координатах. Учесть соотношение между долготой
и амплитудой.
2. Написать уравнение геодезической линии на поверхности
* = /(*, у)-
30*
468 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ, ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
3. Преобразовать уравнения (5) и (6) к виду
Указание. Помножить (о) на Еу а (7) на F и сложить. Воспользоваться
уравнениями (33—35) § 78 (стр. 451) и ввести символы Христоффеля первого рода;
затем воспользоваться формулами (32) § 73.
§ 84. Геодезические параллели
Как было упомянуто, уравнение геодезических линий поддается
интегрированию лишь для некоторых классов поверхностей. Тем
не менее, опираясь на него, можно подлечить весьма важные общие
предложения, относящиеся к теории геодезических линий и вообще
к теории поверхностей.
Решающую роль в этих исследованиях играет надлежащий выбор
системы координат.
Возьмем какое-либо семейство геодезических линий. Единственное
требование, которое мы предъявим к нему, состоит в том, что через
каждую точку рассматриваемой области В должна проходить одна
и только одна линия семейства. За пределами области В наши
геодезические линии могут и пересекаться между собой. Говорят, что линии
такого семейства образуют поле геодезических линий* Примем эти
геодезические линии за координатные линии v = const (т. е. за «линии //»).
Ортогональные траектории взятого семейства примем за линии и = const.
Такая система координат называется полу геодезической. В этой системе
координат первая квадратичная форма поверхности принимает особенно
простой вид. В силу ортогональности координатных линий должно быть
F = 0, т. е. первая форма имеет вид
ds2 = Edu2 + Gdv\ (1)
Но так как линия v = const -— геодезическая, то уравнение (1) или (6)
§ 83 должно удовлетворяться при do = dlv = О, что возможно лишь в том
случае, если 1^ = 0; принимая во внимание, что при F = 0 согласно
(17) § 81 (стр. 461)
11 2G ' ^'
мы видим, что должно быть
Я, = 0, (3)
т. е. коэффициент Е может зависеть только от и, но не от и;
следовательно, мы имеем
ds'i=E(u)du2 + G(uy v)dv\ (4)
Рассмотрим две ортогональные траектории и = иг и и = и2 и найдем
длину дуги геодезической линии v = v0, заключенной между этими
двумя траекториями. Полагая в (4) dv = 0, имеем
)du. (5)
Если бы линии v~v0 пе бычи геодезическими, то подинтегратытая
функция зависела бы также от параметра ^0, i. e. имела бы вид
§ 84. ГЕОДЕЗИЧЕСКИЕ ПАРАЛЛЕЛИ 469
E(u,vQ), и длина (5) зависела бы от выбора линии v = v0. Но в нашем
случае величина s при данных иг, и2, т. е. при данных двух
траекториях, одна и та же для всех линий v = const. Так как семейство
геодезических линий было выбрано произвольно, то мы получаем
следующую теорему.
Теорема 1. Ортогональные траектории любого семейства
геодезических линий отсекают на геодезических линиях дуги равной длины.
Замечание. Теорема 1 доказана нами в предположении, что
геодезические линии семейства образуют поле (в противном случае
наша координатная система была бы неправильной). Можно, однако,
доказать, что теорема 1 (а также теоремы 2 и 3) сохраняет силу
и в том случае, когда рассматриваемые геодезические линии пересекают
друг друга. Но теорема 4 в этом случае неверна.
Обращением теоремы 1 является следующее предложение.
Теорема 2. Если любые две ортогональные траектории
некоторого семейства отсекают дуги равной длины на всех линиях этого
семейства, то семейство состоит из геодезических линий.
Для доказательства примем линии семейства за координатные линии
v = const, а ортогональные траектории—за линии и = const. Дуга линии
первого семейства, заключенная между двумя линиями второго, пред-
"2
ставится интегралом \ \/~Е (и, v0) du. Этот интеграл не должен зависеть
U2 "2
д
dv0
Так как это равенство имеет место при любых значениях иг и и2,
то —=0, т. е. Е зависит только от и. Но тогда уравнение геодези-
ческсй линии удовлетворяется при v = const, т. е. линия v = const
есть геодезическая.
Теорему 1 можно обратить еще следующим образом.
Теорема 3. Если на геодезических линиях, пересекающих
некоторую линию L под прямым углом, отложены дуги равной длины,
началом которых служит точка линии L, то место концов этих дуг есть
ортогональная траектория проведенных геодезических линий.
Эта теорема легко доказывается от противного.
Если геодезические линии образуют пучок с вершиной в точке Л,
то имеют место следующие теоремы, являющиеся предельными
случаями теорем 1, 2, 3.
Теорема 1а. Ортогональные траектории пучка геодезических
линий суть гауссовы окружности.
Теорема 2а. Если ортогональные траектории пучка линий,
проведенных через точку А, отсекают на линиях пучка дуги равной длины,
то пучок состоит из геодезических линий.
Теорема За. Окружность гауссова круга ортогональна к его
геодезическим радиусам *).
Если рассматриваемая поверхность является плоскостью, то все
геодезические линии суть прямые, и доказанные теоремы становятся
особенно наглядными.
Ср. упражнения 6 и 7 § 76, стр. 438.
4?0 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
Ортогональные траектории семейства геодезических линий
называются геодезическими параллелями. Нетрудно убедиться в том, что
касательная к геодезической параллели после геодезического
перенесения вдоль геодезической линии становится касательной к другой
геодезической параллели, так что в соответственных точках направления
геодезических параллелей являются параллельными в смысле Леви-
Чивита.
Задача разыскания геодезических параллелей эквивалентна задаче
о разыскании геодезических линий, но, как показали работы Якоби
и других математиков, следовавших по его пути, практически
сведение второй задачи к первой представляет ряд преимуществ.
Возвращаясь к квадратичной форме
ds2 = E(a)du2 + G(uy v)do\
характеризующей полугеодезическую систему, заметим, что ей можно
придать еще более простой вид, если вместо и ввести новый параметр
и\ связанный с и соотношением
E(u)du = du' (6)
или, что то же,
"2
^ E(u)du = u2-u[. (7)
hi
Уравнение (5) показывает, что новый параметр и есть не что
иное, как длина дуги геодезических линий о — const, отсчитываемой
от геодезической параллели и =и'г. Теперь первая квадратичная форма
принимает вид
ds* = du*+G(u,v)dv*. (8)
Формула (8) тотчас же доказывает экстремальное свойство
геодезических линий. Именно, рассмотрим на геодезической линии v = v0
две точки Лг(и1У v0) и А2(и2, v0). Длина дуги АгА2 геодезической линии
равна и2 — их. Соединим теперь точки А1 и А2 линией, вдоль которой
v не сохраняет постоянного значения; тогда дуга АХА2 имеет длину
5 / (^J (9)
"l "1
Так как G > 0 и т- не может быть тождественно нулем, то подинте-
грэльная функция всегда имеет значения, большие единицы. Поэтому
проведенная дуга имеет длину, большую, чем дуга АХА2 геодезической
линии.
На первый взгляд может показаться, что согласно нашему
рассуждению любая дуга геодезической линии дает кратчайшее расстояние
между двумя ее концами, что, конечно, неверно (см. § 73, стр. 424).
На самом деле в наших рассуждениях мы исходили из возможности
включения дуги АХА2 в геодезическое поле. Можно доказать, что
достаточно малую дугу геодезической линии действительно можно
включить в поле и притом бесчисленным числом способов. Но если дуга
АХА2 велика, то включение может оказаться невозможным, и тогда
не существует требующейся нам полугеодезической системы координат.
Например, дуга ВХВ2 большого круга сферы— большая полуокружности,
§ 84. ГЕОДЕЗИЧЕСКИЕ ПАРАЛЛЕЛИ
471
заведомо не может быть включена ни в какое поле, ибо не
существует ни одного большого круга, который не пересекал бы дуги
В1В2. Итак, доказанное нами свойство формулируется следующим
образом.
Теорема 4. Если дуга геодезической линии может быть включена
в поле геодезических линий, то она короче, чем любая другая дуга,
соединяющая ее концы и лежащая внутри поля.
Если поверхность отнесена к
полугеодезической системе координат, то ее гауссова
кривизна имеет наиболее простое выражение.
Именно, в формуле (10) § 79 нужно положить
Ev = 0, и мы получаем
VrE du YEG
auj
(10)'
Если же, сверх того, за параметр и принята
длина геодезической дуги, т. е. квадратичная
форма имеет вид п{
ds2 = du2 + G do2, (8)
C'\
то нужно положить еще Е = 1, и мы получим
т. е.
1 о2 Yg
7Ъ ""
(И)
Рис. 265.
YG
Пример. Параллели и меридианы поверхности вращения
образуют иолугеодезическую систему. Первая квадратичная форма имеет
вид
где г есть радиус параллели.
Здесь имеем
*=—;Г1- (12)
В частности, если поверхность вращения есть сфера радиуса
а и и — дуга меридиана, отсчитываемая от экватора, то
откуда
г = a cos — ,
(13)
(14)
Если же поверхность вращения есть псевдосфера и радиус ребра
возврата равен а, то
4
Действительно, nycib и есть дуга трактрисы (рис. 265), отсчиты*
ваемая от пересечения с фиксированной параллелью трактрисы г = г0.
472 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
Из подобия треугольников M'QM и МСВ находим
dr du
откуда
Г-Г.Д
Это выражение подставляем в (12); находим
§ 85. Поверхности постоянной гауссовой кривизны.
Движения поверхности по самой себе
Плоскость, сфера и псевдосфера имеют постоянную гауссову
кривизну К. В первом случае К = 0, во втором К = —^ (а — радиус с(}еры);
в третьем К= j (а—радиус ребра или радиус геодезической
кривизны любой параллели псевдосферы).
Мы уже знаем, что все поверхности нулевой гауссовой кривизны
изгибаются на плоскость. Оказывается, что все поверхности постоянной
положительной кривизны накладываются на сферу, а все поверхности
постоянной отрицательной кривизны —на псевдосферу *)• При этом
остается широкая степень произвола в способе накладывания.
Именно, любой «линейный элемент» (т. е. любую точку с
заданным при ней любым направлением), взятый, скажем, на поверхности
постоянной отрицательной гауссовой кривизны (К= —-V можно
совместить с любым линейным элементом псевдосферы той же кривизны.
Та же широта произвола имеет место и для поверхностей нулевой
и положительной кривизны, и для них это очевидно, так как всякий
линейный элемент плоскости или сферы, двигая его по поверхности,
можно совместить со всяким другим линейным ее элементом.
Рассмотрим сначала случай поверхности S постоянной
положительной кривизны К = — . Возьмем на S какую-либо точку А (рис. 266)
и зададим при ной направление а. На поверхности сферы S' радиуса R
возьмем какую-либо точку А' и при ней направление а'. Если, как
утверждалось, можно наложить S на S' так, чтобы элемент Ау а
совпал с элементом А' у а', то геодезическая линия (L), проходящая через
А по направлению а, должна совместиться с большим кругом (//)>
идушим через А' по направлению а'. Поэтому отнесем поверхности
S и S' к криволинейным координатам и, v следующим образом. Пусть
В и Б' — точки, лежащие соответственно на (L) и (U) па расстоянии
v от точек А и А' (расстояние измеряется по геодезическим линиям
(£), (£'))• Через точки В и В' проведем геодезические линии (л) и (>/),
соответственно перпендикулярные к L и U. (Линия (У) есть большей
круг.) На линиях (к) и (У) возьмем точки М и Л/', отстоящие
соответственно от В и В' на расстоянии и. Примем величины гг, v за
координаты точек М и М'. Очевидно, что на сфере величины ^ и ^ суть
1) Нелишним будет еще раз напомнить, что речь идет о достаточно малых
кусках поверхностей постоянной кривизны.
3 85. ПОВЕРХНОСТИ ПОСТОЯННОЙ ГАУССОВОЙ КРИВИЕНЫ 473
широта и долгота точки М'. На поверхности S получим
координатную сеть, в которой линии и = const соответствуют параллелям, а линии
v = const — меридианам сферы.
Отнесем поверхнос!и S и S' к координатам и, v и найдем элемент
длины поверхности S.
Согласно теореме 3 предыдущего параграфа (стр. 469) линии и = const
суть геодезические параллели, так что и, v суть полугеодезические
координаты; так как и есть длина геодезической линии (к) (v = const),
то первая форма имеет вид
,v)dv\ (1)
Но в нашем случае эта форма должна иметь еще более специальный
характер, а именно: 1) на линии а = 0 (т. е. на линии (L), которая должна
Рис. 266.
совместиться с «экватором»), параметр v есть длина дуги этой линии,
2) линия (L) является не только геодезической параллелью, но в то
же время и геодезической линией; 3) поверхность S имеет постоянную
кривизну К = -^ .
Из первого условия следует, что при и==0 функция G(0, v)
обращается в единицу при любом и. Действительно, формула (Г) дает при
d0
ds2 = G(0, v)dv\
а первое условие дает
ds* = dv2.
Сравнивая эти равенства, находим
G(0, i?)=l. (la)
Из второго условия следует, что при к=0 частная производная
—5—^-У обращается в нуль при любом v.
474 гл. х. основные формулы, внутренняя геометрия поверхности
Действительно, геодезическая кривизна линии и = const равна
(§ 81, формула 20)
/ ч 1 эУо (2)
(V"=const = yeg ди~ *
Подставляя сюда ег = О, JB=1 и G(0, v)=l, имеем
/у ч __ а/0(0, v)__ I dG{04v) (2)
а так как согласно второму условию линия а = 0 есть геодезическая,
то имеем *)
^-0. (3)
Из третьего условия вытекает, что функция G(u,v) должна всюду
удовлетворять уравнению
Действительно, в § 84 (стр. 471) мы нашли, что в полугеодезической
системе гауссова кривизна К выражается формулой
Согласно третьему условию К = --1^ приравнивая эти два
выражения, находим уравнение (4).
Формулы (2), (3) и (4) позволяют однозначно определить вид
функции G. Уравнение (4), как легко проверить, удовлетворяется при
/G = ?(!?)cos£ + *(i>)sin^f (5)
где 9 (и) и ф(у) суть произвольные функции от и. Из теории
дифференциальных уравнений известно, что формула (5) дает наиболее общее
решение уравнения (4). Поэтому остается выяснить, какой вид имеют
функции <р (v) и <|>(и) в нашем случае. Из (5) находим
o = ?H (6)
Сравнивая формулы (6) и (1а), находим
<p(i?)=l.
Сравнение формул (7) и (3) дает
ф(|?)==0.
Подставляя эти выражения в (5), находим
cos-g-f (8)
*) Формула (3) устанавливает равенство (с точностью до бесконечно малых
величин) дуги линии (L) и бесконечно близкой к ней дуги геодезической
параллели, отсекаемой теми же линиями (А> Это уяснится наглядно, если вспомнить,
что дуга параллели, заключенная между двумя фиксированными меридианами, имеет
экстремум, когда параллель совпадает с экватором.
§ 85. ПОВЕРХНОСТИ ПОСТОЯННОЙ ГАУССОВОЙ КРИВИЗНЫ 475
и следовательно, первая квадратичная форма поверхности S имеет вид
ds2 = du2 +cos*-д7do\ (9)
Все вышеприведенные рассуждения можно повторить и по
отношению к поверхности сферы, в чем, впрочем, нет нужды, так как мы
уже хорошо знаем, что первая форма для поверхности сферы имеет
вид (9). Итак, обе поверхности имеют одинаковую квадратичную форму.
Следовательно, поверхность S можно изогнуть на сферу; из построения
ясно, что при этом можно
любой линейный элемент
поверхности совместить с
любым элементом сферы.
Рассмотрим теперь
поверхность S постоянной
отрицательной кривизны
К = — -=£- и сопоставим ее
с псевдосферой £", у
которой радиус ребра равен Л.
Пусть те линейные
элементы этих
поверхностей, которые мы хотим
совместить, суть А, а и,
соответственно, А', а,'.
Пусть у' (рис. 267 *)) есть
угол, который
направление а' образует с
направлением р' параллели в
точке А'. Возьмем в
точке А направление р,
составляющее с а тот же
угол <р'« Если мы совместим
элементы i, p и А', р',
то, очевидно, совместятся
также элементы Л, аи рис 2б7
А', а'. Так как
геодезическая кривизна любой параллели псевдосферы равна — и при
изгибании геодезическая кривизна должна оставаться неизменной,
то параллели (Z/), проходящей через А', должна отвечать на S линия
(L) постоянной геодезической кривизны -~- (окружность Дарбу).
Заданием точки А и направления р такая окружность вполне опреде
ляется2).
В соответствии с этим построим на поверхностях S и S'
полугеодезические координатные системы аналогично тому, как мы сделали
это в предыдущем случае, а именно, построим на поверхностях S и. S'
х) На рис. 267 изображена только псевдосфера.
а) Это можно доказать исходя из уравнения хд = -— , которое в раскрытом виде
дает дифференциальное уравнение второго порядка. Геометрически это ясно из
того, что геодезическая окружность Дарбу получается наложением на поверхность
*S плоской полосы, взятой вдоль окружности радиуса Л.
476 ГЛ. X. ОСНОЕНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
линии (/-), (£.') постоянной геодезической кривизны -=- , проходящие
соответственно через точки А, А' по направлениям р, £Г (направление В
есть направление параллели, так что линия (Z/) есть параллель
псевдосферы). Пусть В и В' суть точки, лежащие соответственно на (L)
и (V) на расстоянии v от точек А, А' (расстояние отсчитывается по
линиям (L), (£') постоянной геодезической кривизны). Через точки В
и В' проведем геодезические линии (X), (X'), соответственно
перпендикулярные к (Z.), '//) (на псевдосфере линия (X') есть меридиан). На
линиях (л), (к') возьмем точки М, М\ отстоящие соответственно от В>
В' на расстоянии и. Величины и, v примем за координаты точек
М и М\
Найдем первую форму поверхности S. Она должна иметь вид
ds2 = du2 + G{uJv)dv\
причем специальные условия состоят в том, что 1) на линии L(u = 0)
параметр v есть дуга этой линии, 2) геодезическая кривизна линии (L)
1 1
равна -к-, 3) поверхность S имеет постоянную кривизну К=—-^.
Рассуждая, как в предыдущем случае, найдем, что первое условие
дает
G(O,!>) = 1. ч (2а)
Второе условие дает
J dG (0, t?)
(За)
2 ди ~~ R '
Из третьего вытекает, что G(u, v) удовлетворяет уравнению
Общее решение этого уравнения есть
/G = (p(u)eR + ^(y) e R, (5a)
откуда
(6a)
или
Сравнивая формулы (6а) и (2а), находим
<р(0) + Ф(&) = 1.
С помощью (2а) и (За) соотношение (7Ь) перепишется так:
<р(ю)—ф(ю) = 1.
Система уравнений (10) и (11) дает
9 00=1, ф(I?) = 0t
8 85. ПОВЕРХНОСТИ ПОСТОЯННОЙ ГАУССОВОЙ КРИВИЗНЫ 477
так что, согласно (5а), первая форма имеет вид
ds2 = du2 + eRdo\ (12)
Повторяя дословно все предшествующие рассуждения, найдем,
что тот же вид имеет первая форма псевдосферы. Следовательно, всякую
поверхность постоянной отрицательной кривизны можно наложить на
псевдосферу; из построения ясно, что при этом можно совместить
любую пару линейных элементов.
Так как две поверхности, налагающиеся на третью, налагаются
друг на друга, то мы можем сформулировать следующую теорему.
Теорема 1. Две любые поверхности с одной и той dice
постоянной кривизной можно изогнуть друг на друга так, чтобы любая точка
А первой поверхности с заданным при ней направлением а перешла
в любую точку А' второй поверхности с 'заданным при ней
направлением а'.
Очень важный частный случай этой теоремы представляется тогда,
когда одна и та же поверхность постоянной кривизны рассматривается
как две совмещенные поверхности. В этом случае теорема утверждает,
что поверхность постоянной кривизны можно изогнуть так, что любой
ее линейный элемент совместится с любым другим. В частности, можно
взять два линейных элемента, имеющих общую точку А и
отличающихся только направлениями а, а'. Переводя направление а в а'
непрерывным движением, мы сообщим поверхности такое изгибание, при
котором она будет непрерывно вращаться около точки А.
Для плоскости и сферы совмещение двух произвольных линейных
элементов может быть произведено и без изгибания с помощью
непрерывного движения поверхности по самой себе. Такое совмещение двух
произвольных элементов на других поверхностях постоянной кривизны
невозможно. Но с точки зрения внутренней геометрии непрерывное
изгибание поверхности на себя, переводящее любой элемент в любой
другой, можно рассматривать как движение поверхности по себе.
Говорят, что движение поверхности постоянной кривизны по себе
(т. е. ее непрерывное изгибание на себя) обладает тремя степенями
свободы. Это значит, что результат движения зависит от трех
параметров, каждому из которых можно давать произвольные значения.
Действительно, положение точки А', на которую должна на ложиться
точка А, задается двумя параметрами (значениями ее координат).
Направление же а', в которое должно перейти направление а, задается
одним параметром (например, углом между а' и координатной линией
v = const). Заданием этих трех параметров вполне определяется
окончательное положение поверхности и, следовательно, положение любой
ее фигуры.
«Движение» этой фигуры не меняет первоначальной длины всех ее
линий и первоначальной величины всех ее углов, т. е. фигура в
начальном положении с точки зрения внутренней геометрии «конгруентна»
с фигурой в ее конечном положении.
Это обстоятельство позволяет ожидать, что на поверхности
постоянной кривизнь1 можно построить геометрию, сходную с элементарной
планиметрией. И действительно, внутренняя геометрия поверхности
постоянной положительной кривизны есть не что иное, как
сферическая геометрия, известная уже более двух тысяч лет и
разрабатывавшаяся, главным образом, в связи с потребностями астрономии. Что
касается внутренней геометрии поверхности постоянной отрицательней
478 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
кривизны, то, как показал Бельтрами в 1868 году, эта геометрия
совпадает с геометрией Н. И. Лобачевского, которую великий русский
ученый создал в конце двадцатых годов 19-го века (первая публикация
в 1829 году, а устное сообщение в 1826 году). Именно, если мы будем
называть геодезические линии поверхности постоянной отрицательной
кривизны прямыми линиями, а углы на поверхности будем измерять
обычным образом, то все свойства фигур на плоскости Лобачевского
окажутся реализованными на поверхности постоянной отрицательной
кривизны (в частности, на псевдосфере). Так, в геометрии Лобачевского
сумма углов треугольника меньше двух прямых, и недостаток ее до
двух прямых пропорционален площади треугольника. Этим свойством
обладают и геодезические треугольники поверхности постоянной
отрицательной кривизны, что тотчас же следуег из теоремы Гаусса (§ 77,
теорема 1).
Необходимо, однако, заметить, что поверхность постоянной
кривизны обладает всеми свойствами плоскости Лобачевского лишь в
достаточно малых своих частях. Так, на псевдосфере геодезическую
линию нельзя продолжить за ребро возврата, тогда как прямую на
плоскости Лобачевского можно продолжать неограниченно.
Как мы установили выше, поверхность постоянной кривизны,
изгибаясь сама на себя, обладает тремя степенями свободы движения.
Возникает вопрос, существуют ли поверхности непостоянной кривизны,
обладающие этим же свойством. На этот вопрос нужно дать
отрицательный ответ.
Действительно, при изгибании поверхности ее гауссова кривизна
остается неизменной, а так как точку А должно-быть возможно
совместить с любой точкой А', то во всех точках поверхности ее газ^ссова
кривизна должна быть одной и той же.
Итак, поверхность, обладающая тремя степенями свободы <кдвижения>
по самой себе, необходимо имеет постоянную кривизну.
Но если так, то не существует ли поверхностей, допускающих
изгибание на себя с меньшим числом степеней свободы?
Оказывается, что поверхностей, допускающих самоизгибание только
с двумя степенями свободы, не существует. Действительно, если
изгибание поверхности имеет хотя бы две степени свободы, то и тогда
любую ее точку можно совместить с любой другой. Но тогда гауссова
кривизна во всех точках одна и та же, и по доказанному, изгибание
имеет три степени свободы. ч
Что касается поверхностей с одной степенью свободы
самоизгибания, то такие поверхности заведомо существуют. Действительно,
поверхность вращения непостоянной кривизны (скажем, катеноид) можно
двигать по себе даже без изгибания (вращением около оси). Ясно, что
и всякая поверхность, изгибаемая на поверхность вращения, допускает
«движение» по себе. При этом возможно даже движение без изгибания
(например, прямого геликоида). Спрашивается, существуют ли, помимо
поверхностей, изгибаемых на поверхность вращения, другие
поверхности, изгибаемые на себя с одной степенью свободы. Отрицательный
ответ на этот вопрос дает следующая теорема.
Теорема 2. Если поверхность S допускает непрерывное изгибание
на себя с одной степенью свободы, то она наложима на поверхность
вращения.
Доказательство. Так как поверхность 5, изгибаясь, может
двигаться по себе лишь с одной степенью свободы, то ее гауссова
кривизна не должна быть постоянней. Но если точку AQ поверх-
§ 85. ПОВЕРХНОСТИ ПОСТОЯННОЙ ГАУССОВОЙ КРИВИЗНЫ 479
ности S можно совместить с точкой А, то гауссова кривизна в этих
точках должна быть одинакова. Поэтому точка Ло (и0, v0) может
двигаться только по одной линии (Z.), именно но линии, вдоль
которой К (а, у) = К (и0, vQ). Любая другая точка линии (L) может,
очевидно, двигаться также только по этой линии. Поэтому линия (L)
при движении поверхности движется сама по себе. Так как, далее,
геодезическая кривизна линии (L) в точке Ао не меняется при изгибании,
ю во всех точках линии (L) геодезическая кривизна должна быть
одна и та же (т. е. (L) есть окружность Дарбу). Линии (L) образуют
на поверхности однопараметрическое семейство. Рассмотрим две линии
этого семейства (Lx) и (£2). Проведем геодезическую линию (/*),
перпендикулярную к (LJ, до пересечения с (L2). При движении
поверхности геодезическая дуга LXL2 движе1ся, оставаясь
перпендикулярной к (L2) и сохраняя неизменной длину. Следовательно, (L2) и (£х)
(теорема 3 § 84, стр. 469) суть геодезические параллели. Все это легко
проверяется для поверхностей вращения.
Остается доказать, что, в силу этих свойств, первая квадратичная
форма может быть приведена к тому же виду
(13)
который она имеет дня поверхностей вращения. Ясно, что геодезические
линии (X) мы должны принять за линии v = const; их ортогональные
траектории (L) — за линии и = const. При этом за параметр и примем
дугу геодезической линии (л), отсчитываемую от некоторой начальной
геодезической параллели (Lo)\ параметр v можно выбрать произвольно.
В этой иолугеодезической системе первая форма должна иметь вид
Геодезическая кривизна всякой линии и = const выражается
формулой (2) настоящего параграфа:
Подставляя сюда /?=1, находим
(14)
По доказанному, эта величина должна оставаться неизменной вдоль
линии и = const. Но при переходе с одной линии u = const на другую
геодезическая кривизна может и меняться. Поэтому в общем случае
она зависит от и (но не от v). В силу (14), мы имеем
^■1п/г = ф(и), (15)
где ф (и) есть некоторая функция от и.
Таково требование, накладываемое на функцию G(h, v)
специальным характером поверхности.
Из (15) находим
u + V19 (16)
где Vx есть некоторая функция аргумента и.
480 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
Эту формулу можно переписать в виде
= UV,
где U = e$G(u)du и У = еЪ.
Значит, первую квадратичную форму можно представить в виде
ds2=du2 + U2V4v\ (17)
Если функция V сводится к постоянной величине, -то эта форма уже
имеет вид (13). Если же V не является постоянной величиной, то мы
введем новый параметр vlt связанный с v соо!ношением dox = Vdo,
т. е. определяемый по формуле
После этой замены мы опять приходим к форме (13).
Этим наша теорема доказана.
Добавим, что согласно теореме Бура (§ 46, стр. 274) всякую
поверхность, могущую двигаться по себе с одной степенью свободы,
можно наложить также и на геликоид (в общем случае — косой).
Упражнения
1. Каждую поверхность можно отнести к геодезической полярной системе
координат. За полюс примем любую точку Л. Через и обозначим длину
геодезической дуги, ведущей от полюса к некоторой точке М. Через v обозначим угол,
составляемый линией AM с начальным налравлением, исходящим из полюса
Доказать, что первая квадратичная форма в полярной системе координат
имеет вид
ds2 = du2 + G (ut v) dv2,
причем }/"G(0, v) — 0;
2. Доказать, что гауссову кривизну поверхности можно определить как предел
3 L - 2пг
отношения —, где L есть длина окружности гауссова круга бесконечно
малого радиуса г.
Указание. Воспользоваться разложением функции
по степеням и и результатами предыдущего упражнения.
3. Доказать, что гауссова кривизна есть предел величины , где
S—площадь гауссова круга радиуса г.
4. На поверхности постоянной отрицательной кривизны — — вчбрана некоторая
геодезическая линия (L). Расстояние МР точки М от линии (L), считаемое по
геодезическому перпендикуляру, принято за параметр и. Расстояние точки Р ит начала
отсчета на линии (L) принято за параметр v. Доказать, что первая форма имеет
вид du2JrCh2 -TT-dv2. Сопоставить результат с формулой (9) .
5. На поверхности постоянной положительной кривизны ~ язтга некотор ш
1
линия (L) постоянной геодезической кривизны — . Расстояние МР точки М от этой
п
линии принято за параметр и. Расстояние Р от начала отсчета на (L) принято
за параметр v. Доказать, что первая форма имеет вид du1 \-(cos ~ \-sin — j dv1
\ li h у
Сопоставить результат с формулой (12)
§ 86. СЕТИ ЧЕБЫШЕВА 481
§ 86. Сети Чебышева
Среди вопросов внутренней геометрии теории поверхностей большой
интерес как в теоретическом, так и в практическом отношении
представляет теория сетей Чебышева, названных так по имени великого
русского математика П. Л. Чебышева, положившего основу этой
теории *).
В 1878 году П. Л. Чебышев выступил с докладом, тема которого —
«О кройке одежды» — на первый взгляд может показаться совсем
не математической. Но П. Л. Чебышев, обладавший замечательным
даро.м математической расшифровки задач практики, в этом докладе
высказал положения, имеющие наряду с большим практическим
интересом и важное теоретическое значение.
При кройке одежды, равно как при изготовлении матерчатых
оболочек для исевозможных изделий, начиная от аэростатов и кончая
футбольныхми мячами, необходимо из плоской ткани сделать покрытие
для кривой поверхности, возможно лучше прилегающее к этой
поверхности. На первый взгляд может показаться, что здесь мы имеем дело
с изгибанием поверхности и что прилегание плоской тканв к кривой
неразвертывающейся поверхности может быть достигнуто только за счет
растяжения матерки.
Однако простой опыт, который каждый может проделать со своим
носовым платком, показывает, что деформация ткани в общем случае не
является ее изгибанием. При продольном или поперечном растяжении
ткани она почти не поддается растяжению. Но при растяжении но
диагональному направлению можно достигнуть очень значительного
удлинения. Здесь мы имеем дело, таким образом, не с удлинением нитей
ткани, а с изменением углов между нитями. Вследствие этого в первом
приближении м( жно считать, что нити ткани нерастяжимы, т. е.
расстояние между двумя точками поверхности, отсчитываемое вдоль нити,
неизменно. Однако в ьротивоположность тому, что имеет место при
изгибании поверхности, расстояния между точками ткани, находящимися
на разных нитях, может изменяться. Мы имеем, следовательно,
деформацию более общего типа, чем изгибание; изгибание является лишь
частным случаем «одевания» поверхности.
Чтобы лучше представить себе геометричесьи деформацию одевания
поверхности, мы можем вместо ткани взять сетку, сделанную из
практически нерастяжимых нитей. В ткани переплетение нитей «сенсвы»
и «утка» создает трение между нитями, которое препятствует
деформации. В сетке же, где нити связаны только заузлениями, это трение
почти отсутствует.
Всякий знает, что сеткой можко очень хорошо обтягивать тела
самой различной формы. На поверхности тела образуется
геометрическая сеть, выделяющаяся среди других геометрических сетей
следующим признаком: две линии, принадлежащие одному семейству нитей,
отсекают на любой линии, принадлежащей другому семейству нитей,
дуги одной и той же длины.
Иными словами, в любом криволинейном четырехугольнике,
образованном линиями сети Чебышева, противоположные стороны равны.
Это свойство мы и примем за определение сети Чебышева*.
ССГ
31 М.
х) В дальнейшее развитие этой теории большой вклад внесли математики
"Р (Я. С. Дубнов, Н. В. Ефимов, Д. Д. Мордухай-Болтовской).
\1 £Т ТЗч 1|М
482 гл. х. основные формулы, внутренняя геометрия поверхности
Определение. Сетью Чебыгиева называется такая сеть,
в которой противоположные стороны каждого образуемого ею
криволинейного четырехугольника попарно имеют равную длину.
В качестве примера рассмотрим плоские сети Чебышева. Здесь
имеет место следующая теорема.
Теорема 1. Пусть на плоскости взяты две произвольные линии
(Lo) и (10) (рис. 268), исходящие по разным направлениям u.i точки О.
Перенося линию (Lo) параллельно самой себе вдоль линии (/0), а ли-
(U
Рис. 268.
нию (10) — параллельно самой себе вдоль (Lo), мы получаем сеть
Чебыгиева,
Замечание. Условие, что линии (Lo) и (ZJ должны выходить
из О по различным направлениям, гарантирует правильность сети
.в окрестности тички О. Не всегда возможно с помощью этого
построения покрыть сетью Чебышева всю плоскость, ибо в достаточном
удалении от О упомянутое условие может нарушиться.
Доказательство. Рассмотрим произвольный криволинейный
четырехугольник сети АХА2 В2Вг и докажем, что дуги АЪА2 и ВгВ2
равны между собой. Возьмем на дуге АХА2 промежуточные точки
А'у А", .. ..#число которых мы будем потом неограниченно увеличивать
так, чтобы длины всех дуг АгА\ А'А", ... стремились к нулю. На ду1е
BtB2 возьмем соответственные точки В', В".., (каждая точка В лежит
на той же линии (/), и соответствующая т< чка А). Так так А'В
§ 86. СЕТИ ЧЕБЫШЕВА 483
получена параллельным переносом АгВг то хорды АХА' и ВХВ' равны;
аналогично А'А"=В'В". Суммируя и переходя к пределу, заключаем,
что АХА2 — В1В2.Так же докажем, что AXBX = А2В2. Итак, в произвол^
ном криволинейном четырехугольнике нашей сети противоположные
стороны попарно равны, т. е. построенная сеть есть сеть Чебышева.
Сети параллельного переноса, которые мы сейчас рассмотрели,
исчерпывают весь класс чебышевских сетей на плоскости. Иными
словами, теорема 1 допускает следующее
обращение.
Теорема 1а. Если два семейства
плоских линий (L) и (I) образуют сеть
Чебышева, то в каждой паре линий одного
семейства одна линия получается
параллельным переносом другой.
Доказательство. Возьмем на пло- М\
скости фиксированную точку U (тот же
рис. 268) и проведем через нее линию МК
из семейства (L). Отиожим на ней равные
бесконечно малые дуги UМ = UK = ^.
Через точки Л/, Uу К проведем линии A/7V,
UW, К Риз семейства (/). На линии MN
отложим дугу MN того же порядка, что а;
для определенности можем положить
MN = o. Через N проведем линию NVP Рис. 269.
из семейства (/.), которая пересечет
линии UW, КР в точках У, Р. Получим четырехугольник MNPK сети
Чебышева, в котором каждая из криволинейных сторон равна а и
сторона NP разделена точкой V пополам. Все углы криволинейного
четырехугольника — конечные.
В прямолинейном же четырехугольнике MNPK (он изображен
в увеличенном виде на рис. 269) все стороны эквивалентны а и
разнятся друг от друга на величину не ниже третьего порядка
относительно а (на самом деле KMNP есть точный ромб, но это еще нужно
доказать). Проведем через N и if прямые, параллельные соответственно
прямым МК и MN. Они пересекутся в некоторой точке R. При
смещении точки Р в точку R расстояния ее до точек N и К меняются
на величину не ниже третьего порядка относительно а, а вместе с тем
и относительно диагонали NK, которая имеет тот же порядок, что о,
ибо угол NRK — конечный. Поэтому само смещение PR имеет тоже третий
или высший порядок *) относительно а.
Применив к треугольнику NRP теорему синусов, заключаем, что
угол RNP имеет второй или высший порядок2) относительно а.
Но угол RNP есть нечто иное, как угол между хордами МК и NP,
а эти хорды составляют соответственно с касательными UE и VF,
1) Если это не представляется очевядным, то, чтобы не выполнять громоздкой
выкладки, можно юити другим 1утем, указанным в следующей сноске.
2) Этот вывид можно сделать также из следующего расчета. Мы имеем
NK1 \-NP*- RP*_AK [NP + KP)(VP—KP)
2NK • NP ~2NP+ 2NK-NP
Ho NP-\-KPaz2]\P, a AP—КР имеет порядок по ниже третьего относительно KN,
484 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
проведенными через середины дуг MR, NP, углы высшего порядка
относительно а. Следовательно, касательные UE, VF образуют друг
■с другом угол высшего порядка относительно дуги UV. Так как это
имеет место для всех точек линии (/), проходящей через С/, то вс всех
точках линии UW касательные к линиям (L) параллельны между
собой1).
Теперь очевидно, что всякая дуга А2В2, принадлежащая какой-
либо линии из семейства (Z), получается из соответственной дуги АХВХ
любой другой линии того же семейства параллельным переносом, т. е. что
всякий прямолинейный четырехугольник АХА2 В2ВЛ сети Чебышева есть
параллелограмм.
Действительно, дуги АХА2 и ВгВ2 в соответственных точках имеют
параллельные касательные. Кроме того, любые соответственные дуги,
принадлежащие АгА2 и ВХВ2, равны по условию. Следовательно, в
соответственных точках дуги АХА2 и ВХВ2 имеют одинаковые кривизны;
значит, их натуральные уравнения одинаковы. Следовательно, дуги
АгА2, ВХВ2 конгруенаны, а хорды АХА2, ВХВ2 равны и параллельны.
Этим теорема 1а доказана.
Из теорем 1 и 1а следует, что на плоской поверхности существует
бесчисленное множество сетей Чебышева. Каждая такая сеть вполне
определяется заданием двух линий (L) и (/), исходящих из точки О
и принадлежащих одна первому, а другая — второму семейству нитей.
Линии (L) и (/) можно задать произвольно, лишь бы они имели
в точке О различные направления.
Естественно ожидать, что с той же степенью произвола можно
строить сети Чебышева и на любой поверхности. В этом можно
убедиться с помошью следующего построения.
Пусть на поверхности S (рис. 270) через (правильную) точку О
проведены линии (Lo), (/0). Отложим на (Lo) небольшие дуги ОМ19
М\М2, М2М и т. д. равной длины р, а на линии (/0)— небольшие дуги
ON, NK, RL и т. д. равной длины а. Из точки N, как из центра,
опишем дугу аЬ гауссовой окружности геодезического радиуса р; из
точки М', как из центра, опишем дугу cd гауссовой окружности
геодезического радиуса а. В пересечении дуг ab, cd получим точку iV,.
Значит,
■где е2 имеет порядок не ниже второго относительно о Точно так же найдем
где тг)2* тоже имеет порядок не ниже второго относительно а. Так как NP раз-
.нится от NM hi величину не ниже третьего порядка, то косинусы углов RNK,
РУК, и следовательно, и сами углы разнятся друг от друга на величину не ниже
второго порядка относительно с.
'1) Если л есть угол между касательной UE и фиксированным на плоскости
направлением, a s—дуга линии UW, то угол между UE и VF есть Да и по доказанному
-j- = Ит -г— = 0. Следовательно, а == const.
*ds As
§ 86. СЕТИ ЧЕБЫШЕВА 485"
Далее, из точек Nx и Л/2, как из центров, опишем дуги гауссоьых
окружностей радиуса р и а. В пересечении их получим точку N2;
таким же образом построим точку N3 и т. д.
Теперь из точек К и Nlt как из центров, проведем дуги гауссовых
окружностей радиусов [> и а. Получим точку Кх. Вышеописадным
способом получихМ далее точки К2, К3 и т. д. Исходя из течки К,
построим таким же образом точки Lly L2, L3 и т. д, г).
Построенное таким способом точки можно принять за узлы сети
Чебышева на поверхности 5. Можно доказать, что предельный переход
дает точную сеть Чебышева.
Рис. 270.
Существование сети Чебышева, построенной на линиях (LQ) и (10)г
можно доказать также исходя из дифференциального уравнения
в частных ороизводных, характеризующего эту сеть. Но это уравнение,
как правило, не поддается решению в квадратурах. Поэтому для
разыскания сети Чебышева по данным линиям (Lo) и (Zo) все равно
пришлось бы отыскивать приближенные решения.
Для всех плоских сетей Чебышева касателькые ко всем линиям (/),
проведенные через точки пересечения этих линий с одной из линий (L)
(произвольно взятой), параллельны между собой. Сети Чебышева на
кривых поверхностях этим свойством не обладают.
Разумеется, при смешении вдоль одной из линий (L), например
вдоль (Lo), на бесконечно малое расстояние ОМ1У касательные в точках
О и Мх к линиям (/0) и (1Х) образуют бесконечно малый угол. Но этот
1) Инструментом для построения гауссовой окружности может служить прямо-
линейная плоская полоска, прикалываемая в центре. Изгибание ее дает
геодезическую линяю поверхности S. Впрочем, вместо этого «геодезического циркуля»
можно пользоваться обычным циркулем. Тогда равенство противоположных сторов
будет иметь мосто для прямолинейных четырехугольников N0MlN1 и т. д. Так
как хорда отличается от дуги на величину третьего порядка относительно д
то получаемая погрешность в пределе не влияет на результат
486*4 гл. х, основные формулы, внутренняя геометрия поверхности
угол имеет тот же порядок, что смещение ОМг, вследствие чего
на конечном расстоянии и «набегает» значительное расхождение
направлений.
Однако, если мы спроектируем (рис. 271) касательную М1Т1
к линии (Zj) на касательную плоскость Р, проведенную через 0f
По)
, Рис. 271.
то проекция M'jTi составит с касательной ОТ угол, имеющий высший
порядок относительно смещения ОМг.
- Чтобы доказать это, построим на поверхности четырехугольник abed
(рис. 272), отложив на линиях (/0) и (1г) равные дуги Оау Od, Mxb,
Мгс длиной — OMi=-t-\j, и спроектируем этот четырехугольник на
Рис. 272.
плоскость Р. Получим криволинейный четырехугольник a'b'c'd'.
Каждая из его прямолинейных сторон разнится от р на величину
не ниже третьего порядка относительно р. В самом деле, мы имеем
ab — a'b' = ab(l — cos9)^ и у .
где <р есть угол между ab и плоскостью Р, а этот угол имеет тот же
или более высокий порядок, чем р (точка О предполагается правильной).
Таким же образом докажем, что аналогично образованные разности
bc — b'cf имеют порядок не ниже третьего, а затем, рассуждая в
точности так же, как в доказательстве теоремы 1а, докажем, что каса-
86. СЕТИ ЧЕБЫШЕВА 487
тельная к Ь'с' в точке М[ (а она является проекцией касательной М^х)
составляет с ОТ угол высшего порядка относительно ОМг, а отсюда
вытекает следующее свойство сетей Чебышева, представляющее
обобщение теоремы 1а.
Теорема 2. Если два семейства линий, взятых на произвольной
поверхности S, образуют сеть Чебышева, то касательная к переменной
линии (I) одного семейства, проведенная через точку пересечения линии (I)
с фиксированной линией (L) другого семейства, переносится вдоль
линии (L) геодезически параллельно.
Доказательство. Пусть t=OT (рис. 271) есть орт касательной
к линии (/0) в точке О\ tx = М1Т1 — орт касательной к линии (1г)
в бесконечно близкой точке М19 лежащей на ,той же линии (Lo), что О;
t\ = М[Т\ — проекция вектора tx на касательную плоскость Р,
проведенную через О. Через s обозначим дугу линии (Lo) и через а — угол
между векторами t v\ t\. Легко видеть, что
a«|*-*;i,
а так как
*-/; = пр. (/-/,) = пр. М
и по доказанному а имеет высший порядок относительно As, то
пр.^=Нтпр.^ = О. (1)
В силу теоремы 2 § 76 (стр. 437) проекция производной т- нэ касательную
плоскость есть абсолютная производная -т- . Следовательно,
соотношение (1) можно переписать в виде
Это равенство выполняется для всех точек линии (Z.o). Значит, все
орты t геодезически параллельны (относительно линии (Lo)), что
и утверждает теорема 2.
Теорема 2 допускает следующее обращение.
Теорема 2а. Если каждое из двух семейств линий, образующих
на поверхности S правильную сеть, обладает тем свойством, что
касательная к переменной линии (I) этого семейства при движении точки
касания по любой фиксированной линии (L) другого семейства
переносится геодезически параллельно, то сеть, образуемая линиями (I) и (L),
есть сеть Чебышева.
Доказательство мы опускаем; пользуясь указаниями, данными
р упражнении 8 (стр. 494), читатель проведет доказательство сам.
Из определения сети Чебышева тотчас же вытекает следующее
предложение.
Теорема 3. При всяком изгибании поверхности сеть Чебышева
остается сетью Чебышева.
Вследствие этого при аналитическом изучении сетей Чебышева
основное значение приобретают следующие теоремы относительно
вида первой квадратичной формы поверхности, отнесенной к сети
Чебышева.
Теорема 4. Если поверхность S отнесена к такой системе
криволинейных координат и, v, что ее первая квадратичная форма имеет вид
v)dudo + V(v)do2 (3)
488 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
(U не зависит от v; V не зависит от и) то координатная сеть является
сетью Чебышева.
Доказательство. Возьмем четырехугольник, образованный
линиями и = и,; и = к2; u = *V, v = v2..
U2
Его сторона, лежащая на линии v = v1% имеет длину y^U (u)du9
ui
Ту же длину имеет противоположная сторона, лежашая на линии v = v2*
Противоположные же стороны и = и^ и*=и2 имеют каждая дли-
ну \ \fV{v)dv. Следовательно, наша координатная сеть есть сеть
Чебышева.
Имеет место также обратная теорема.
Теорема 4а. Если какую-либо сеть Чебышева на поверхности
S принять за координатную сеть, то при любой параметризации этой
сети первая квадратичная форма Е du2 + 2F dudv -\-G do2 поверхности S
имеет вид
)dv2. (3)
Доказательство. В координатном четырехугольнике,
образованном линиями u = ult u = u2J v = vly v = v2, сторона, лежащая на линии
v = v1% имеет длину \\/~E(u,v1)duJ ь сторона, лежащая на линии
»2
v = v2, —длину \ |/ Е(и, v2)du. При любых значениях vx и v2 эти длин],'.
равны, так как соответственные линии по условию образуют сеть
Чебышева. А это возможно лишь в том случае, если величина E(u,v)
при любом фиксированном значении и остается неизменш й, когда t
меняется1), т. е. лишь в том случае, когда Е фактически не зависит
от v. Так .же докажем, что G не заяисит от гг.
Если вместо и и v ввести новые параметры р= \ Udu, <7=\ Vdv.
то форма (3) примет вид:
(4)
» Следующая выкладка доказывает это утверждение:
Г#(м, v)du~ fE(u<v)du
_ V" vwnr-^rdu=lim u_i_
dv J l u-V y _ <,
i
"2
Следовательно, \ -~-^-du = 0, а так как это соотношение имеет меечи для любо»х
значений м,, м2, то —^— =0, т. е. Е от v не зависит.
§ 86. СЬТИ ЧЕБЫШЕВА 489
Параметры р и q имеют тот же геометрический смысл, что
косоугольные декартовы координаты на плоскосли: это —длины координатных
линий, проходящих через рассматриваемую точку М (от точки М до
пересечения с начальными линиями р = 0, (7 = 0, играющими роль
декартовых сетей).
Величина w(p,q) сеть угол между координатными линиями. В де-
картовсй системе координат этот угол — постоянный. В чебышевской же
системе координат р, q он в общем случае меняется.
Следующая теорема дает замечательный пример сети Чебышева.
Теорема 5. Два семейства асимптотических линий псевдосферы
образуют сеть Чебышева.
В примере 3 § 69 (стр. 403) мы нашли аналитически уравнения
асимптотических линий псевдссферы, отш сенной к ее меридианам и параллелям.
Если принять асимптотические
линии за новые координатные
линии и совершить переход от
старых координат к новым, то
первая квадратичная форма
примет вид (3), и из теоремы 4а
будет следовать, чю
асимптотические линии псевдосферы об-
раяуют сеть Чебышева.
Предоставляя читателю
выполнить соответствующие
выкладки, мы дадим здесь гес-
метрический вывод теоремы 5
Прежде всего, мы должны вмс -
сто дифференциального л
равнения асимптотических линии
псевдссферы, полученного н
примере 3 § 69, установить
соответствующее
геометрическое их свойство. Оно
формулируется следующим образам.
Лемма 1. Угол <р>
образуемый асимптотической
линией псевдосферы с меридианом
{ на рис. 273), равен
углу MDC, образуемому
касательной MD к меридиану с осью
FB псевдосферы.
Другими словами, если
касательную плоскость псевдосфе- Рис. 273.
ры повернуть в надлежащем
направлении на 90° около касательной MD к меридиану, ю касательная
МТ к асимптотической линии совместится с прямой MS, параллельной
оси псевдосферы.
Доказательство. Угол ©, образуемый асимптотическим и
главным направлением меридиана, определяется соотношением
^, (5)
где гх есть полуось индикатрисы Дюпена, направленная по меридиану,
а г2 —полуось, направленная по параллели. Так как радиусы кривизны
490 ГЛ. X. ОСНОВНЫЕ ФОРМУЛЫ. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
нормальных сечений (по абсолютному значению) пропорциональны квад
ратам радиусов индикатрисы Дюпена (§ 59, .стр. 353), то вместо (5)
л можно написать
Рис. 274.
где R19 R2 суть абсолютные
значения главных радиусов
кривизны, соответствующих направлен
ниям меридиана (Rx) и параллели
(Л,).
Но главный радиус кривиз-
Ф ны Д2 равен отрезку МС2
нормали (рис. 274) от
рассматриваемой точки М псевдосферы до
пересечения с осью псевдосферы;
главный же радиус кривизны i?j
равен радиусу кривизны МС
меридиана псевдосферы, т.е. трактрисы.
.ff Вспоминая (§24, пример 7, стр. 128),
что центр кривизны С1 лежит на
пересечении нормали МСХ с пер-
пендикуляром DCt к оси,
восставленным из точки Z), где
касательная МD пересекает ось, мы
f из прямоугольного треугольника
CtDC2, в котором DM — высота,
опущенная на гипотенузу,
находим
R*
(7)
где и есть угол между
касательной MD трактрисы и
осью FB.
Из (6) и (7) следует, что
Вис. 275.
что и доказывает лемму 1.
Из нее легко вытекает
следующее ^предложение, на
котором основывается
приводимое ниже доказатель-
-, ство теоремы 5.
Лемма 2. Длина дуги
MN асимптотической линии
псевдосферы (рис. 275) равна
длине дуги RS ребра воз-
врата, отсекаемой
меридианами MR, NS, проведенными
через концы дуги MN.
§ 86. СЕТИ ЧЕБЫП1ЕВА 491
В частносаи, эта лемма утверждает, что длина асимптотической
дуги UN, отсчитываемая от точки U ее касания с ребром возврата,
равна дуге US ребра возврата.
Доказательство. Рассмотрим бесконечно малый треугольник,
МРМ1, образованный меридианом RMP, параллелью РМ л и дугой ММ\
асимптотической линии UN.
Обозначая через г радиус параллели, через v — долготу и через
<р —угол между асимптотической линией и меридианом, мы находим
Обращаясь к рис.274, где МС = ги угол и = Z. MDC по
доказанному в лемме 1 равен углу <р> мы находим, что
а согласно основному свойству трактрисы MD — AO—a, где а есть
радиус ребра возврата
псевдосферы. Таким образом,
из (8) и (9) следует
ММХ
так что, обозначая через s
длину асимптотической
дуги MN, имеем
откуда
s = a(vN — vM). (11)
Правая часть (11),
очевидно, есть длин • дуги ES
ребра возврата. Этим
лемма 2 доказана.
Теперь теорему 5
можно доказать следующим
образом.
Доказательство
теоремы 5. Рассмотрим рис 27б.
четырехугольник MNLK
(рис. 276), составленный дугами асимптотических линий UA1N,
VKL, WKM, ZLN (U, V, И7, Z —точки касания этих дуг с ребром
возврата псевдосферы).
Через вершины У(7, Л7 проведем меридианы MR, NS до встречи
в точках RS с ребром возврата.
Вследствие симметрии асимптотических линий МU, MW относи
тельно меридиана MR мы имеем:
\ (12)
и аналогично
US = SZ = \UZ. (13)
Из леммы 2 и соотношений (12), (13) следует, что
l b ±U \ (14)
492 гл. х. основные формулы, внутренняя геометрия поверхности
т. е. дуга линии, принадлежащей одному из семейств асимптотических
линий, составляет половину дуги ребра, содержащейся между точками
касания асимптотических линий другого семейства, проведенных через
концы рассматриваемой дуги.
Следовательно, мы имеем также
(15)
и из (14), (15) находим
MN^KL.
Таким же образом найдем, что
т. е. в четырехугольнике MNLK противоположные стороны попарно»
равны, что и доказывает теорему 5.
Другое доказательство теоремы 5. Продолжив
сторону МК (рис. 277), «спроектируем» на нее четырехугольник MKLN
меридианами; пусть Nt, L1 суть
«проекции» вершин N, L. Из
леммы 2 тотчас же вытекает,
что дуги всех
асимптотических линий (обоих семейств),
отсекаемые двумя данными-
меридианами, равны между
собой. Поэтому мы имеем
.1 = MLlr
KLl
Следовательно,
откуда видно, что сумма
сторон MK + KL равна
полупериметру р четырехугольника
MKLN:
Теперь спроектируем че-
Рис. 277. тырехугольник MKLN на ту же
сторину МК параллелями. Так
как дуги всех асимптотических линий, отсекаемые двумя данными1
параллелями, очевидно, равны между собой, то мы имеем
КМ T
KL +LN =9 J2 t
Как прежде, заключаем, что
KL + LN=p. (17)
Сравнивая (16) и (17), находим, что противоположные стороны
МК, LN равны:
МК = LN. ^
Следовательно, и противоположные стороны MN, KL, каждая из кото-
i 86. СЕТИ ЧЕБЫШЕВА 493
рых дополняет до полупериметра сторону МК (или LN)> равны друг
Теорема 5 допускает замечательное обобщение для любой
поверхности постоянной отрицательной кривизны. Именно, имеет место
следующая теорема.
Теорема 6. На всякой поверхности постоянной отрицательной
кривизны два семейства асимптотических линий образуют сеть Чебыгиева.
Доказательство читатель сможет провести сам, пользуясь
указаниями, данными в упражнениях 9 — 10 (стр. 495).
Замечание. Мы совершили бы ошибку, если бы стали
доказывать теорему 6, изгибая псевдосферу на рассматриваемую поверхность
постоянной отрицательной кривизны. Хотя при изгибании сеть
асимптотических линий псевдосферы и остается сетью Чебышева, но в общем
•случае асимптотические линии после изгибания становятся
неасимптотическими.
Упражнения
1. Можно ли на конической поверхности построить такую сеть Чебышева,
у которой одно семейство нитей состояло бы из образующих? Тот же вопрос для
чдилиндрических поверхностей.
Указание. Воспользоваться теоремой 1а.
2. Доказать, что только на развертывающихся поверхностях угол между
нитями сети Чебышева может быть постоянным.
Указание Исследовать первую квадратичную форму.
3. Доказать, что только на развертывающихся поверхностях оба семейства
шитей сети Чебышева могут быть геодезическими линиями.
Указание. Отнести поверхность к рассматриваемой сети Чебышева и
приравнять нулю выражения для геодезической кривизны координатных линий.
Воспользоваться выражением (t) для линейного элемелта.
4. Для подготовки к следующему упражнению доказать, что если первая
•квадратичная форма поверхности S имеет вид
du2 + 2 cos со du dv + dv2t (18)
тде о> есть функция только от и:
и) = и) (и),
-Т0 £_ развертывающаяся поверхность, и линии и = const являются геодезическими.
Указание. Вычислив гауссову кривизну поверхности и геодезическую
кривизну (х7)и линии и = const, найдем, что та и другая равны нулю. Другой
'Способ: представить (i) в виде
(sin со du)2 -f (cos о» du -f dv)2 (19)
iiv введя новые параметры ху уу привестя (4) к виду
dz*+dy*.
5. Если в сети Чебышева на поверхности -5" одно семейство нитей состоит из
геодезических линий, то поверхность £—развертывающаяся; после изгибания
поверхности S на плоскость упомянутое семейство обращается в семейство
параллель ibix прямых.
Указание. Аналитическое доказательство можно провеет i, опираясь
на результат предыдущего упражнения. (Элемент дуги поверхности S% отнесенлой
к сети Чебышева, можн.» представить в виде du2 + 2cos to du dv \-dv2. Приравняв нулю
dm
выражение для (*q)u, найдем» что —— = 0).
Синтетическое доказательство мо^но вести так: рассмотреть дугу
ортогональной траеьтории, заключенную между бесконечно близкими геодезическими нитями;
.доказать, что для всех траекторий эта дуга имеет одну и ту же длину.
Следовательно, рассматриваемые геодезические линии и их ортогональные траектории
«образуют сеть Чебыщева. Использовать результат упражнения 2.
494 гл. х, основные формулы, внутренняя геометрия поверхности
6. Доказать, что полные геодезические кривизны сторон четырехугольник»
сети Чебышева в сумме составляют 2 (л[ -f «а + аз +* а4 ~ 2те)> rj*e af ~~ внутренние
углы этого четырехугольника.
Указание. В силу теоремы 2 и результата примера 1 § 76 (стр. 431—i32), мы*
имеем -Ч— = х^, где <р — угол между касательной к стороне AiAL+1 четырехугольника
и пересекающей ее нитью другого семейства. Интегрируя это соотношение вдоль
стороны четырехугольника, находим, что разность упомянутых углов в вершинах
равна полной геодезической кривизне стороны Л|Л^+1.
7. Площадь асимптотического четырехугольника на поверхности псевдосферы
равна a2(aJ-f-a2 + a3 + a4-2TC)> где а —радиус ребра возврата й aj—внутренние углы.
Указание. Использовать теорему 5, теорему Гаусса-Бонне и результат
предыдущего упражнения.
8. Доказать теорему 2а настоящего параграфа.
Указание. Рассмотрим полосу, ограниченную фиксированной линией (L>
первого семейства (рис. 278), бесконечно близкой линией (£') и
фиксированными линиями аа\ ее9 второго семейства. На дуге ае откладываем дуги аЬу
be, cd и т. д., равные дуге аа' (или имеющие тот же порядок). Через точки &„
Рис. 278.
с, d и т. д. проведены линии второго семейства. Берем «центр»
четырехугольника abb'a', т. е. точку о, делящую пополам обе проходя цие через нее дуги
nlt km (nl принадлежит первому, km — второму семейству). Проектируем аЪЪ'а'
на касательную плоскость в точке о. Получаем четырехугольник a^&jaj. Из
условия теоремы 2а следует, что касательные в точках п[1\ к сторонам
четырехугольника образуют с касательной к линии тк в точке О углы высшего порядка
(за главную бесконечно малую принимаем аа'). Отсюда следует, что угол между
хордами ЪгЬ[, аха'х имеет малость высшего порядка. Аналогичное заключение делаем*
для другой пары хорд. Противоположные стороны четырехугольника abb'а'
разнятся на величину, порядок которой выше двух (разбить аг ЬхЬ[а[ диагональю на
два треугольника). Длины дуг ас и а'с' разнятся на величину высшего порядка
относительно аа'. Так как эю имеет место для любой линии (L), то дуги всех
линий (L), заключенные между аа' и ЬЬ\ равны
9. Для подготовки доказательства теоремы 6 настоящего параграфа доказать
следующую теорему, обобщающую лемму 2.
На всякой поверхности S постоянной отрицательной кривизны ^ дуги
всех асимптотических линий {обоих семейств), отсекаемые двумя данными
линиями кривизны одного и того же семейства, равны меоюду собой.
§ 86. СЕТИ ЧЕБЫШЕВА 49£>
Указание. Обозначим через dsv dsz линейные элементы линий кривизны
«первого» и «второго» семейств, через ds —элемент дуги асимптотической лини»
(ds2 = dsf -f dsf). Из рассмотрения индикатрисы Дюпена находим
ds*:dsl= l^ltlflj
(Rlt R2 — главные радиусы кривизны). Следовательно,
j) (20>
Приняв за линии и (v = const) первое семейство линий кривизны, а за линии
г-второе, найдем [формула (7Ь) § 63 (стр. 363), где полагаем du = O]
(22 >
Тогда (20) примет вид
ds* = G ( 1 + —^j- j dv2. (23)
Чтобы доказать нашу теорему, достаточно показать *), что G ( 1Н—-^- J не за-
висит от и, т. е. что
4-
ди
Для этого используем второе уравнение Петерсона-Майнарди (§ 80, формула (5),
стр. 456). Если подставить туда Ьгг = М = 0, ^22 == ср и заменить символы Христрф-
феля Г|! и Г\2 их выражениями (формулы (17) § 81, стр. 461), получим уравнение
2EGNU - (EN + GL) Gu = 0. (25>
Учитывая соотношение
LN 1_
EG ~ a2 '
нетрудно показать, что уравнения (24) и (25) равносильны 2).
10. Опираясь на результат предыдущего упражнения, доказать теорему 6„
Указание. Доказательство можно вести совершенно так же, как во втором
доказательстве теоремы 5.
*) Если в этом пункте рассуждение покажется нестрогим, можно искать
v2 _-
Г / / a2N*\
вариацию интеграла \ I/ Gf Н—7Ч~) dv по.параметру с, входящему в уравне-
ние a = cp(v, с) асимптотической линии. Получим снова уравнение (24).
*) Первое уравнение Петерсоыа-Майнарди дает тот же результат для другого*
семейства линий кривизны.
ЗАКЛЮЧИТЕЛЬНОЕ СЛОВО АВТОРА
Большая часть вопросов, рассмотренных в этой книге, была
освещена с двух точек зрения —синтетической и аналитической. Теперь
уместно сопоставить их друг с другом.
Не только в аналитической и дифференциальной, но и в
элементарной геометрии мы не обходимся без вычислений. Но в
элементарной геометрии вычисления играют вспомогательную роль; ведущая
роль принадлежит построению. В аналитической же геометрии
ведущую роль играют вычисления, а построениям принадлежит
вспомогательная роль. Притом вычисления, производимые в элементарной
геометрии, выполняются над отрезками, углами, площадями и т. д.,
непосредственно связанными с изучаемыми геометрическими
фигурами. В аналитической геометрии вычисления производятся, как
правило, над вспомогательными величинами (координатами). Таково
взаимоотношение синтетического и аналитического методов в геометрии.
Мы видим, что между ними нет резкой границы 1).
Азбучной истиной педагогики является положение, что всякая
наука усваивается тем прочнее, чем более многообразно она связана
•с конкретными представлениями. Поэтому при прочих равных
условиях синтетический метод изложения дифференциальной геометрии
должен быть более действенным с педагогической стороны. ' Из этсго
убеждения исходил автор этой книги, решаясь прибавить к
многочисленным руководствам по дифференциальной геометрии еще одно.
Объем книги уменьшился бы почти вдвое, если бы из нее
устранить аналитические выводы. Это можно было бы сделать без ущерба
для полноты материала. Но тогда читатель не овладел бы таким
мощным орудием исследования, каким является вычислительный аппарат
дифференциальной геометрии.
С другой стороны, можно было бы значительно уменьшить число
страниц в книге, если бы изменить количественное соотношение между
аналитическими и синтетическими рассуждениями в пользу первых.
Но в таком случае не была бы достигнута другая цель, которая
представляется автору не менее важной: научить читателя
синтетическим методам исследования.
Многие полагают, что эти методы мало эффективны в сравнении
с аналитическими. С этим суждением автору трз^дно согласиться.
Когда известный круг вопросов подвергся уже глубокому
исследованию, когда для него уже создан «универсальный» алгоритм, тогда
вычисление дает, если не самый короткий, то самый
механизированный путь решения задачи. Но для этого нужно, чтобы сама задача
х) Так, помещаемый в школьных учебниках вывод теоремы Герона следует
•считать скорее аналитическим, чем синтетическим (в противоположность выводу,
который излагает сам Герон и который оснопан на остроумном построении).
заключительное слово автора 497
принадлежала к хорошо разработанной области проблем. История
свидетельствует о том, что почти на каждом существенно новом этапе своего
развития геометрия вновь и вновь привлекала на помощь
синтетические методы. Так была создана, например, проективная геометрия,
в которой синтетическим методам и ныне принадлежит важная роль;
так была открыта Н. И. Лобачевским неевклидова геометрия; таким
путем шла топология.
В области дифференциальной геометрии поучительным примером
может служить теорема Гильберта о поверхностях постоянной
отрицательной кривизны {не существует поверхности постоянной
отрицательной кривизны, не имеющей нигде особенностей). Она была впервые
доказана (в 1901 году) с существенным использованием геометрических
построений. Чисто аналитического ее доказательства, насколько автору
известно, не дано и до сих пор.
Как было сказано, преимуществом аналитического метода перед
синтетическим является его «механизированность», которая может дать
экономию сил даже в том случае, когда идешь более длинным путем.
Преимуществом же синтетического метода является то, что его путь,
как правило, более прямой и потому лучше обозримый. Теорему
Кёнигса, например, можно вывести аналитически, но несравненно
проще ее можно доказать и, что еще важнее, обнаружить на
геометрическом пути. И даже в аналитических исследованиях отдельные
участки рассуждения бывает лсчче преодолеть синтетически.
Автотранспорт есть чудеснейшее средство сообщения, и по ровной
j^opore пешеход не угонится за автомобилем. Но автомобилю часто
трудно пройти там, где свободно проходит пешеход, а взобраться
на вершину горы он сможет лишь после того, как много пеших людей
проложат ему дорогу.
Сравнение—не доказательство, но оно иногда поясняет мысль лучше
длинного рассуждения. И если с появлением автотранспорта у людей
не исчезла необходимость учиться ходить, то следует ли думать, что
с созданием аналитического метода отпадает потребность в
синтетическом методе?
Нет, оба метода, аналитический и синтетический, имеют право
на существование. Они должны взаимно дополнять друг друга.
Вот почему синтетическому методу, мало представленному в
учебной" литературе, здесь уделено столько места.
2 М. Я. Выгодскив
ПРИЛОЖЕНИЕ
ОСНОВНЫЕ СВЕДЕНИЯ ПО ВЕКТОРНОМУ АНАЛИЗУ
1. Векторная функция
При изучении кривых линий и кривых поверхностей нам приходится иметь
дело с векторами, меняющимися в зависимости от выбора точки на изучаемой
линии или поверхности. Простейшим примером такого вектора может служить
вектор ОМ (рис. 279), тчало которого лежит в фиксированной точке О, а конец
совпадает с выбираемой по произволу точкой М
изучаемой линии АВ. Так как положение точки %М на
линии АВ о феделяется заданием зтчения параметра и,
то и вектор ОМ олределяечся заданием этого значения.
Естественно поэтому установить понятие
«векторной функции», аналогичное понятию функции,
вводимому в анализе бесконечно малых Имени.), вектор р мы
называем векторной функцией (или, короче, «вгктор-
функциейъ) скалярного аргумента и, если каждому
значению и соответствует одно опрсделе ное значение
вектора р Запись р\и) или p=f(u) или р = р(и) и т. д
выражает, что р есть ветор функция скаляра it.
Рассмотрим еще один пример. Пусть две.точки iV,
и N2 одновременно движутся по линиям ^^ и А2В>
(рис. 280). Тогда каждому значению меры времени t ce-
Рис. 279. ответствует определенное значение вектора # = /V1/V2
Вектор q есть вектор-функция скаляра t
В противоположность предыдущему примеру, здесь начало Nx переменного
вектора q является подвижным \1ы можем, однако, выбрать какую-либо фикси-
Рис. 280.
Рис. 281.
рованную точку О (рис. 281) и принять ее за начало векторов ОМ, равных
векторам ~N\N2. Подвижной конец М вектора ОМ опишет тогда неклторую линию PQ
Она называется годографом вектор-функции q
ОСНОВНЫЕ СВЕДЕНИЯ ПО ВЕКТОРНОМУ АНАЛИЗУ 499
Совершенно так же, как мы определили вектор-функцию одного скалярного
аргумента, можно очределить вектор-функцию двух скалярных аргументов, и
годограф этой вектор-функции (последний будет представлять собой в общем случае
некоторую поверхность).
На* вектор-функции можно распространить все основные понятия, вводимые
для обычных скалярнлх функций, в первую очередь понятие предела. Именно,
вектор а мы называем пределом вектор-функции р=р(и) при и~>и0:
а = limp (и),
и ->ыо
если для всякого положительного числа е можно указать такое положительное'
число tj, что при
\и—щ\<-г\ (1)
модуль разности векторов р и а будет меньше, чем е:
|/>(м)—а|<е. (2)
Чтобы сдела1ь это определение наглядным, представим себе, что аргумент и
есть мера времени. Пусть (рис. 282) а = ОА и р(и) = ОМ
Неравенство (1) выражает тогда, что подвижная точка М годиграфа PQ
рассматривается в момент времени и, отделенный от момента и0 промежутком
времени, не превышающим тц; неравенство (2)
выражает, что точка М удалена от
точки А на расстояние AM — \p(u) — a\t не
превышающее е. Приведенное выше
определение предела означает, таким образом,
что подвижной конец М вектора ОМ не
выйдет за пределы сферы («сколь \ годно
малого») радиуса е с центром в точке А
в течрние («достаточно малого»)
промежутка времени от и0—у](е) до uo-^-fi(e)
Наглядное представление о
непрерывности движения подсказывает, что при
указанных обстоятельствах точка М вмо
мент и = и0 должна совпадать с точкой Л
т е. что
Свойство, выражаемое этой форму- Pwq. 282.
лой, можно принять за определение
непрерывности вектор-функции Именно, вектор-функцию р (и) мы назовем
непрерывной при и = и0, если значение этой функции р (и0) равно пределу, к которому
стремится р(и) при и -> и0.
Теорема о пределе суммы остается верной и для вектор-функций; остается
справедливой и теорема о пределе произведения, причем можно рассматривать:
произведение скалярной функции на векторную, скалярное ipo 1зведение двух
вектор-функций, векторное произведение двух вектор-функций, а значит, и смешанное
произведение трех вектор-функций. Теорема о пределе частного остается в силе
для единственного вида деления, рассматриваемого в векторной алгебре, т. е для
деления вектора на число
Постоянный вектор можно рассматривать как вектор-функцию: пределом
этой вектор-функции ( ipn каком угодно значении скалярного аргумента) нужно
тогда считать ее самое.
Веьтор р(и) называется бесконечно малым, если при и -* и0 бесконечно мал
' и -* ц„
его модуль. Порядком малости вектора называется порядок малости его модуля1).
1) С введением понятия бесконечно м алого вектора мы можем дать еще
такое определелие неирер явности вектор-функции, равносильное в >1шеприведрн-
ному: веьтор-функция р(и) назыв1ется непрерывной при и0, если бесконечно малому
приращению Аи ее аргумента и соответствует бесконечно малое прлращеиие
ДР =Р (") — Р (и0) самой вектор-функции.
32*
600
ПРИЛОЖЕНИЕ
2. Производная вектор-функции
Совершенно так же, как в обычном анализе, определяется в векторном
анализе производная функция. Именно, производной вектор-функцией от
вектор-функции р(и) скалярного аргумента и называется предел, к которому стремится
отношение
р(и + Аи)-р{и)
Аи
при фиксированном значении и и бесконечно малом Аи. Эта производная функция
которая, разумеется, также является векторной функцией аргумента и,
обозначается через р' (и), так что
л *
Существование производной функции, так же, как это имеет место в обычном
анализе, не является логическим следствием непрерывности функции р(и). Но
мы рассматриваем только такие вектор-функции, для которых производная
функция существует. Это условле,
которое с формальной стороны
представляется ограничением
общности, вполне
оправдывается наглядными представлениями
о движении, и, таким образом, с
той точки зрения, на которую мы
встали в этой книге (§ 2, стр. 13),
на самом деле не суживает
круга изучаемых объектов
Действительно, пусть
вектор ОМ (рис. 283) представляет
значение р(и), вектор
ОМ'—значение р (и ■+• Аи) и линия АВ есть
годограф вектор-функции р (и).
Тогда вектор ММ' представляет
приращение р(и -\- Аи)—р (и)
вектор-функции р (и), отношение
этого приращения к скаляру Аи
(приращению аргумента) есть
некоторый вектор МК, коллинеар-
ный с вектором ММ', т е. с
секущей прямой. Наглядное
представление показывает, что с
приближением точки М' к точке
М, т. е. при Аи -* 0, секущая
Рис. 283 ' ' ММ\ вращаясь около точки М,
приближается к касательной пря-
s мой МТ.
Таким образом, совершенно естественно принять; что «направление вектора
МК = ^'ц~*~ "j—pW стремится к некоторому пределу»; точнее говоря,
что,существует такое направление (направление касательной годографа), с которым взк-
иор МК при Аи -► 0 образует бесконечно малый угол а.
• Покажем теперь, что столь же естественно принять, что и модуль вектора МК
стремится при и -► и0 к некоторому пределу. Тогда станет ясно, что и сам взк-
iop МК, у которого как направление, так и длина стремятся к пределу, имеет
при и -* «о определенный предел.
Для большей наглядности примем, что скалярный аргумент и есть мера
времени. Тогда модуль (абсолютное значение) приращения аргумента \Аи\ есть
мера промежутка времени, в течение которого точка годографа переходит из
положения М в положение М\ Модуль же приращения \р(и ^Аи)—р(и)\ в-к-
тор-функции р{и) есть длина хорды ММ' годографа. Значит, модуль вектора МК
«сть отношение расстояния между точками М и Мг к времени, в.течение которого
движущаяся точка переходит из I в М'. Иными словами, модуль вектора МК
есть та скорость, которую имела бы движущаяся на участке ММ' точка, если бы
ОСНОВНЫЕ СВЕДЕНИЯ ПО ВЕКТОРНОМУ АНАЛИЗУ
501
ее движение от М к М' было прямолинейным и равномерным. Назовем эту
величину «средней скоростью» точки М на участке ММ'.
Как показывает повседневное наблюдение над плавными движениями малых
материальных тел («материальных точек»), эта «средняя скорость» при
фиксированном начале М и достаточно малом промежутке времени Дм является
практически постоянной величиной. Это и дает нам основание принять, что «средняя
скорость» при фиксированном начале движения стремится к определенному
пределу, кигда Дм -♦ 0, т е\ когда точка М' приближается к точке М. Но это и
означает, что мы допускаем существование предела модуля вектора МК.
Как было выше сказано, из этого допущения и допущения о
существовании предела направления того же вектора вытекает, что и сам вектор
МйГ = — ~— имеет предел. Именно, этот предел есть вектор ML,
отложенный на касательной МТ в направлении от М к М' и имеющий длину,
равную пределу модуля вектора
р (и + Дм)-р (м) '
Аи
Вектор ML и представит производную вектор-функцию от вектор-функции
ОМ—р(и). Производная вектор-функция от р(и) называется также вектором
скорости; это наименование, вполне
оправданное для того случая, когда
скалярным аргументом является мера
времени, сохраняется и в тех случаях,
ьогда аргумент не является временем.
Производная функция от
производной р' (м) вектор-функции р (м)
называется второй производной вектор-
функции р(и), или вектором
ускорения, и обозначается р"(и). Аналогично
определяются производные высших
порядков.
Частные производные вектор-
функции многих переменных
определяются так же, как частные
производные в обычном анализе.
3. Дифференциал вектор-
функции
Дифференциал вентор-функции
можно определить так же, как
определяется дифференциал в обычном
анализе, т. е. как главную линейную часть
приращегия функции.Точнее,
дифференциал ее к тор-функции р (и) есть такая Рис. 284.
векторная величина, которая
^пропорциональна приращению независимого переменного и 2) отличается от приращения
Др=р(м + Дм) — р(и) вектор-функции р(и) на бесконечно малую величину
высшего порядка относительно бесконечно малого приращения независимого
переменного. Дифференциал вектор-функции р(и) обозначается через dp (и).
Можно доказать так же, как для случая скалярных функций, что обоим
требованиям, предъявленным к дифференциалу, удовлетворяет (для функций
одной переменной) выражение р' (м) du. Здесь через du обозначен дифференциал
скалярной величины м. При этом не предполагается, что скалярная величина и
принята за независимое переменное. За независимое переменное можно принять
любую функцию v от м, и все же выражение р' (м) du будет дифференциалом
функции. Однако в этом случае дифференциал du вообще (если новое независимое
переменное v i e есть линейная функция от м) не равен приращению Дм, тогда
как если за независимое переменное принимается аргумент м, дифференциал du и
приращение Дм равны между собой.
Поэтому дифференциал вектор-функции получает наиболее простое
геометрическое истолкование именно для случая, когда за независимое переменное принят
аргумент и. Пусть попрежкему и есть мера времени и ЛВ — годограф вектора
р{и) (рис. 284). Вектор скорости р' (м) коллинеарен с касательной МТ. Значит,
502 ПРИЛОЖЕНИЕ
и дифференциал dp — р' (и) du есть вектор, коллинеарный с касательной. Модуль | dp\
этого вектора равен произведению модуля вектора р' (и) на абсолютную
величину du, т. е. произвэдению скорости движения в точке М на время, в
течение которого подвижная точка годографа переходит из точки М в соседнюю
точку М'
Итак, вектор dp есть тот отрезок МК, который был бы пройден за время* Аи
движущейся точкой, если бы она двигалась из тички М по инерции в течение
промежутка времени, в который она приходит в М'. Приращение же
Ар=р (и + Аи)—р(и) вектор-функции р(и) представляется вектором ММ'.
Утверждая, что векчор МК —р' (и) du представляет дифференциал
вектор-функции р (и), мы опираемся на упомянутую выше теорему о том, что векторная
величина р' (и) du удовлетворяет обоим требованиям, которые составляют
определение дифференциала Таким образом, из этой теоремы, между прочим,
следует, что вектор М'К, представляющий разность между приращенлем ММ'
функции р (и) и ее дифференциалом МК, имеет относительно du высший
порядок малости. Так как вектор р' (и) du (мы предполагаем, что вентор
скорости р' (и) в точке М не равен нулю) имеет тот же порядок малости, что du, то
мы приходим к заключению, что отрезок М'К имеет малость высшего порядна
относительно отрезка МК. Иными словами, расстояние между действительным
положением точки на ее траектории и положением, которое она имела бы, если
бы столько же времени двигалась по инерции из положения М, имеет высший
порядок малости относительно этого предполагаемого смещения. Предоставляем
читателю дать чисто геометрическое доказательство этого предложения 1).
Не лишним будет заметить, что если не требовать, чтобы за независимое
переменное принимался аргумент и, то для одного и того же приращения аргумента и
дифференциал вектор-функции будет иметь различные значения, однако все они
будут коллинеарны и будут разниться друг от друга по модулю на бесконечно
малую величину высшего порядка относительно Аи.
4. Правила дифференцирования векторов
При выводе основных теорем о пределах и правил дифференцирования в
анализе бесконечно малых мы опираемся на законы алгебраических операций сложения
и умножения, а они сохраняют свою силу и в векторной алгебре, за
исключением закона переместительности сомножителей в векторном и смешанном
произведениях. Поэтому, повторяя слово в слово знакомые рассуждения, мы придем к
следующим формулам скалярного анализа.
1) da = Q, где а — постоянный вектор.
2) d(p + q-r) = dp+dq-dr.
3) d(/.p) = ?i dp-\-d"kpi где А — скалярная величина, если она равна постоянной
величине л, то
За) d(xp) = adp.
4) d(pq) = р dq 4 dp q\ в частности, если р есть постоянный векгор р = а, то
4а) d (aq) = a dq.
В формулах 3) и 4) можно переставлять сомножители.
5) d(p х q) = p x dq-\-dpx q; в частности, если р есть постоянный вектор
р = а, то
5а) d(a x q)~a x dq.
В формулах 5) и 5а) перестановка сомножителей допустима только при условии
перемены знака перед произведением.
6) d (pqr) —pq dr -\-p dq r a dp qr.
В формуле 6) допустимы (без перемены знака) лишь циклические
перестановки
Если мы имеем дело с функциями одного аргумента, то, разделив обе части
вышеприведенных формул на дифференциал скалярного аргумента, получим
соответствующие формулы для производных, например,
dq dp ч, ,
==р Ти+ £ q ПЛИ &д) =рд +рд и т-д
1) Нужно рассмотреть треугольник ММ'К, в котором угол М бесконечно мал.
Предполагая, что два других угла этого треугольника не являются бесконечно
малыми (что равносильно предположению, что Бектор р' (и) не равен пулю),
применим к треугольнику ММ'К теорему ;ин^сов.
ОСНОВНЫЕ СВЕДЕНИЯ ПО ВЕКТОРНОМУ АНАЛИЗУ
503
В качестве примера рассмотрим случай дифференцирования скалярного
квадрата р2. Формула (4) дает
или (если имеем вектор-функцию одного скалярного аргумента)
Пусть, в частности, переменный вектор р имеет постоянную длину (меняется
лишь его направление). Тогда р2 есть постоянное число (квадрат длины), и
следовательно, pdp = Q, т. е. векторы р и dp взаимно перпендикулярны: дифференциал
вектора постоянной длины перпендикулярен к этому вектору. Геометрический
смысл этого предложения таков: если р сохраняет постоянную длину, то конец
вектора (при фиксированном начале) лежит на сфере; бесконечно малое
смещение Д/? конца вектора направлено по секущей, соединяющей бесконечно близкие
точки сферы. Дифференциал dp, равный Дуо с точностью до бесконечно малых
высшего порядка, расположен в касательной плоскости сферы. Если р есть
функция одного аргумента, конец р описывает сферическую линию; дифференциал dp
11 производная -~- (вектор скорости движения) перпепдикуля; ны к радиусу сферы.
dP
Если производная ~- вектора р сохраняет постоянный модуль, то, повторив
d2p
аналогичные рассуждения, найдем, что вектор ускорения ^\ перпендикулярен
к вектору скорости. хМеханически^ смысл этого предложения таков: если
движение по кривой совершается с постоянной скоростью (равномерное криволинейное
движение), то ускорение направлено перпендикулярно к скорости.
Рассмотрим еще несколько примеров. х
2= d (р*2 = Р dP
iVp2 Yp2
3) (р' < Р"У =р" х р" л- р' х р"' = р' х р'" =± -р'" х р',
4) d(qq'q"):=dqqrq* + qdq'q" -f- qq'dq" = qq'dq".
Первые два слагаемых обращаются и нуль в силу коллинеарности векторов
= q'du и q'y а также векторов dq' и q".
5) d
' X q"Y =
Y(q'
x q"
6) Пусть р2 (и)=1 и требуется найти (рр'р")2.
Имеем
р* рр' рр"
(РР'Р'У- рр р> р'р'
Р'Р Р'Р' р"г
Но при р2=\ имеем рр' = 0 и рр" -f/?'2 = q, откуда рр" = — р'2 Поэтому
1 0 - pfi
(РР'Р")2== 0 р'2 р'р" =р'2р"2 — (р'р")2—(р'2У = (р'хр")2—(р'1
-р" р'р" р"2
В заключение заметим, что теорема Лагранжа о конечном «приращении
функции не может быть перенесена на вектор-функции, т. е. выражение
рщ
вообще говоря, не равно р'( и) ни при каком значении и параметра, заключенном
«между и и и -\г Дм. В самом деле> вектор — д-^—^ направлен по хорде
годографа, а вектор р'(и)—по касательной в некоторой точке годографа, лежащей
между концами хорды. Если кривая не лежит в одной плоскости, то среди ее
касательных может не найтись ни одной, которая была бы параллельна хо^де,
504
ПРИЛОЖЕНИЕ
соединяющей концы дуги. Так, если взять один завиток винтовой линии на
вертикальном цилиндре, то хорда этой дуги вертикальна, а все касательные—наклонны.
Хотя теорема Лагранжа о конечных приращениях в общем случае
оказывается для вектор-функций неверной, однако остается в силе важная теорема, которат
в анализе часто выводится из теоремы Лагранжа. Именно, если дифференциал
вектора р тождественно равен нулю, то вектор р имеет постоянное значение,
т. е. из dp = 0 вытекает р = а, где а—постоянный вектор. Доказать это можно,
например, так: представим вектор р в виде р=ж/+ yj -f zk, где /, / k— какие-либо
три некомпланарных постоянных вектора. По условию dx-l -\-dy.j -f- dzk = О,
откуда dx = dy = dz = 0. Три скаляра #, у, zy таким образом, постоянны, так что
ир — постоянный вектор.
5* Интегрирование вектор-функции
Определенный интеграл \ p(u)du вектор-функции р (и) есть предел суммы вида
где ult ua, ..., wn_! суть какие-либо значения и, содержащиеся между а и {*
и образующие монотонную последовательность, а через Wi,l+1 обозначено любое
Рис. 285.
промежуточное значение в интервале (щ, щ+1). Суммирование совершается
по индексу *.
Определенный интеграл вектор-функции можно геометрически построить так: на
дуге годографа АВ (рис 285) возьмем п последовательных точек: А (Ао), Alf A^ ...,
Ап (В), отвечающих значениям параметра: и0 = а, щ, щ, .., ип = (J. В какую-либо
точку дуги А0Аг проведем из некоторого фиксированного начала вектор р01, в какую-
либо точку дуги АХА2 — векторр12 и т. д Построим вектор ТМ =р01 • (щ - щ),
который параллелен вектору р01, вектор MN=plz • (^2 — ^1) и т- Д- Замыкающий вектор
LS равен сумме 2p*Mi'i+i) * (wi + i"" ui)- При неограниченном уменьшении Есех
дуг AiAi+1 замыкающий вектор стремится к пределу \ p(u)du. (Мы предполагаем
а
существование этого предела и его независимость от выбора точек на годографе.
Можно показать, что для этого достаточно, чтобы вектор-функция р (и) была
непрерывной.)
Неопределенный интеграл вектор-функции р (и) есть совокупность всех ер
«первообразных» функций, т. е. таких вектор-функций Р(и), для которых
dP(u)—p(u)du
ОСНОВНЫЕ СВЕДЕНИЯ ПО ВЕКТОРНОМУ АНАЛИЗУ
50&
Если Рг (и) есть одна из первообразных функций, то Рг (и) -fa (а — произвольный
постоянный вектор) также есть первообразная функция, ибо
(и) +а\= dPx (и)
dPx (и) =р (и) du.
Обратно, всякая первообразная вектор-функция разнится от одной из них Рг(и)
на постоянный вектор ибо, если dP(u)=p(u)du и dP1{u)=p(u)du, то
<*[/>(")-Л («)]= О,
откуда следует, что вектор Р(и) — ЯДи) имеет постоянное значение.
Неопределенный интеграл обозначается символом \ p(u)du, так что при указанных
обозначениях
Определенный интеграл вектор-
функции равен разности значений
первообразной функции:
Действительно, согласно определению
интеграл \ dP(u) есть предел суммы диф- Рис. 286.
а
ференциалов dP (u)=p(u)Au. Заменяя дифференциал вектор-функции ее
приращением АР(ч), мы допускаем погрешность на вектор высшего порядка малости;
можно доказать, что сумма этих погрешностей имеет пределом нуль-вектор, тан
что интеграл \ dP(u) равен пределу суммы приращений АР(и). Но эта сумма равна
а
-iP{ui) — P(ul)}+ ... +{Р(ип
Геометрический смысл этой теоремы таков: если АВ (рис. 286) есть годограф
вектора Р(и), то р (и) есть вектор скорости точки А годографа; величины р (и) Аи
суть векторыТЙ, АгМ, A2N и т. д., отличающиеся от векторов AAV АгА2, AZAZ и т. д.
на бесконечно малые высшего порядка. Сумма ^р{и)Аи отличается на бесконечно
малый вектор высшего порядка от суммы векторов ААХ + АхАг + А2Лг+ ..., т. е. от
веьтора АВ, замыкающего дугу годографа. Но
6. Приращение вектор-функции
Для нахождения пределов различных вектор-функций можно с успехом
применять приближенные выражения приращения вектор-функции с помощью
многочленов, расположенных по степеням приращенит Аи скалярного аргумента.
Простейшим выражением этого вида является .дифференциал вектор-функции. Именно,
приращение вектор-функции
mowho заменить эквивалентной ему величиной dp (м)=рг (и) Аи; согласно определению
дифференциала величины р (и + h) — р (и) и р'(и)Аи отличаются на векторную
величину высшего порядка малости относительно Аи; если обозначить ее через э2, то
sa. (1)
.506 ПРИЛОЖЕНИЕ
Погрешность более высокого порядка получается, если заменить Ар (и)
эквивалентной величиной
р' (и) Аи + ~- р" (и) (Дм)2 + -А- р'" (и) (Аи)* +...+-L р(п> (и) (Аи)" ,
аналогичной строке Тейлора. Именно, погрешность имеет по меньшей мере
\п + 1)-й порядок малости относительно Аи, так что
р (u±h)=p (u) + pf (и) Аи + -L р» (и) (Аи)* + . .. 4- ~^Р(П) (и) (Дм)" + еп+1, (2)
где еп+1 есть вектор высшего порядка малости по сравнению с (Аи)п, т е.
lim ^lli=O.
Аи^0 (Дм)"
Предполагая, что вектор-функция р(и) имеет также и (п + 1)-ую
производную, имеем
и вектор *еп+1 либо имеет тот же порядок, что (Аи)п+1 (если р<п + 1) (и) ф 0), либо
высший (если p<w+1> (u) = 0).
Таки^ образом, аналогия £ фактами скалярного анализа простирается очень
далеко. Однако «остаточный член» еп+1 нельзя представить в «лагранжеьой» форме,
нбо уже для частного случая (1), как было показано в конце п. 4, теорема Лагранжа
-не имеет места.
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
{Цифры обозначают страницы *)]
Абсолютная ироизнодна я 434
Абсолютный дифференциал 434
Анализ векторный 498
Аналитическое представление линии 26
— — поверхности 223
Аналитический метод 9, 496
Архимедова спираль 58
Асимптотические линии 401
Асимптотическое направление 345, 346
Бельтрами 405, 462, 478
— теорема 407
Бельтрами-Эннепера теорема 405
Бертран 440
Бесконечно малый вектор 499
Биквадратная парабола 124
Бинормаль 96.
Бидплиндрика 91
Бонне 439
— теорема 439, 440, 445, 463
Бура теорема 274
Вейнгартена формулы 452
Вектор бесконечно"малый 499
— Дарбу 160
— кривизны 78, 113
— скорости 501
— ускорения 501
Векторная функция (вектор-функция) 498
— — непрерывная 499
Векторное поле тангенциальное 434
Векторы геодезически параллельные 433
— — равнонаправленные,
противонаправленные 433
— — ранные 434
— тангенциальные 432
Векторный анализ 498
Величины, их порядок 15
— эквивалентные 15
Внвиани кривая 30, 31, 45, 227, 260
Винтовая линия 27, 28, 45, 67, 78, 89, 97,
101, 117, 155, 317, У>28
— — общего типа 90
Внешний, внутренний угол сферического
многоугольника 178
Внутреннее уравнение 189, 194, 202
Внутренние * свойства поверхности 279
Внутренняя геометрия поверхности 279
— кривизна линии 426
Вогнутость, сторона вогнутости 94, 98
Возврата ребро 284
— точка 1-го, 2-го рода 43, 141
Вращения параболоид '229
— поверхность 227, 236, 251, 274, 343,
361, 364, 375, 466, 471
— эллипсоид 380
Вторая квадратичная форма 339, 409
— кривизна 153
Входящий угол 178
Выпуклость, сторона выпуклости 98
Высший порядок 15
Гаусс 279, 395, 398, 439, 448
Гаусса теорема 439, 440, 445, 463
— уравнение 453
Гауссов геодезический круг 425
Гауссова квадратичная форма 248
— кривизна 363, 446
— сфера 395
Геликоид (прямой) 29, 231, 237, 271,
341, 349, 362, 376, 389, 403
— Дини 386, 393
— косой 276
— общего вида 273
Геодезическая кривизна 415, 426,
458
полная 430
— линия 325, 421, 423, 465', 468
— — замкнутая 429
— окружность Дарбу 429
— параллель 470
Геодезически параллельные векторы 433
— равные векторы 434
Геодезический круг (гауссов) 425
— поворот 430, 431, 433
Гильберт 497
Гиперболическая спираль 62
— точка 345
Гиперболоид однополостный 278
Главная нормаль 96, 100
Главные кривизны 355, 362
— направления 355, 361
— нормальные сечения 355
Годограф вектор-функции 498
х) Указывается та страница, где приводится определение понятия или нажней-
щие, относящиеся к нему формулы. Исключение сделано для названий крииых
«ли поверхностей, приводимых в качестве примеров—для них приведены все
страницы, на которых эти кривые и поверхности упоминаются.
508
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Дарбу вектор 160
— геодезическая окружность 429
Движение поверхности по себе 477
Двупараметрическое множество точек
13
Двуугольник 177, 260
Дини геликоид 386, 393
Директриса цепной линии 75
Дискриминант 1-й квадратичной формы
Дифференциал абсолютный 434
— вектор-функции 501
Дифференциальная геометрия 12
Дифференцирование векторов, правила
502
Длина дуги 66, 72, 77
Долгота 226, 227
"убнов Я. С. 481
уга (длина дуги, элемент дуги) 66, 72,
77
Дюпен 352, 356
Дюпена индикатриса 353
Ефимов Н. В. 481
Изгибание поверхности 266
— полосы 428
Изгибаемые поверхности 268
Излома точка 43
Изображение сферическое поверхности
395
Изогональная траектория 257
Изометрические поверхности 268
Индикатриса Дюпена 353
— сферическая 173, 175
И нтеграл вектор -функции определенный,
— — неопределенный 504
Интегральная кривизна 334
Интегральное кручение 335
Иоахимсталя теорема 385
Каноническое представление кривой
161
Квадратичная форма первая 248
вторая 339, 409
третья 411
Касательная (прямая) 13, 35, 42, 44, 48
— плоскость (кривой) 83
поверхности 222, 235, 244, 246
— полярная 61
Касательных поверхность 233, 238, 252,
260, 281, 298, 340
Катеноид 76, 230, 271, 343
Кёнигс 370
Кёнигса теорема 370
Клеро теорема 467
Класс-линий, натуральное уравнение 202
Кодацци 456
Комбескюра соответствие 188
Конечная величина 14
Коническая поверхность 282, 298
— спираль 33, 39
Координат система полу геодезическая
468
Координатные линии 224
Координатный метод И
Координаты криволинейные 224
Косая линейчатая поверхность 295
Коши 262
Кривая, см. название соотв. линии
Кривая линия, аналитическое
представление 26
, каноническое представление 161
правая, левая 151
Кривизна линии 104, 105, 111, ИЗ
внутренняя 426
вторая 153
геодезическая 415, 426, 458
— — нормальная 415
полная (интегральная) 334
— — — (геодезическая) 430
— ломаной линии 196
— нормального сечения 351
— поверхности 363, 398
в данном направлении 411
гауссова 363, 446
средняя 358
— постоянная, кривые пост, кривизны
202, 206, 311
— —, поверхности пост, кривизны 472
Кривизны вектор 78, ИЗ
— главные 355, 362
— линии 374, 387, 392
— окружность (круг) 111
— радиус 107, 123
сферический 187
— центр (для кривой) 107, 123
(для поверхности) 363
Криволинейные координаты 224
Круг геодезический (гауссов) 425
— кривизны 111
Кручение 150, 151, 152
— ломаной линии 196
— полное (интегральное) 335
— постоянное, линии пост, кручения 208
Кручения радиус 153
Кубическая парабола 124
Левая кривая 151
— пара прямых 170
Леви-Чивита 438
— параллелизм 438
Линейный элемент поверхности 248
Линейчатая поверхность 232, 287
косая 295
Линии, семейство линий 223
— координатные 224
Линия 12, 65, см. также название линии
—, аналитическое представление 26
—, уравнения 26, 27
— особая 223
— сжатия 291
— тени 370
Липшиц 438
Лобачевский Н. И. 478, 497
Логарифмика 53
Логарифмическая спираль 32, 33, 38,
59, 71, 126
Локальные свойства кривой 12
Локсодрома 257
Люстерник Л. А. 429
Майнарди 456
Менье 411
АЛФАВИТНЫЙ (УКАЗАТЕЛЬ
509
Менье теорема 414, 417
т- формула 415, 416, 420
Меридиан 226, 227
Минимальней поверхность 358
Многоугольник сферический 177
Множество точек однопараметрическое,
дву параметрическое 13
Монж 374, 383, 391
Монжа теорема 379, 381
Мордухай-Болтовской Д* Д. 481
Наложимые поверхности 268
Направление (на поверхности) 254
— асимптотическое 345, 346
Направления главные 355, 361
— сопряженные 367
Направляющая линейчатой поверхности
232
Натуральное уравнение 189, 194, 202
Неопределенный интеграл
вектор-функции 504
Неправильная точка 14, 223
— линия 223
Непрерывность вектор-функции 499
— линии 13
— поверхности 222
Низший порядок 15
Нормаль главная 96, 100
— к плоской кривой 48, 96
— к плоскости 44
— поверхности 236
— полярная 61
—, вектор нормали 236
Нормальная кривизна линии 415
— плоскость 44
Нормальное сечение 350
, кривизна 351
Область положительно обходимая 177
Образующая линейчатой поверхности 232
Огибающая семейства плоскостей 300
Однопараметрическое множество точек 13
— семейство поверхностей 267
Однополостный гиперболоид 278
Окружность 121, 122, 328
— геодезическая Дарбу 429
— кривизны 111
Омбилическая точка 345
Омбилических точек линия 385
Описанная (вдоль линии) поверхность 366
Определенный интеграл вектор-функции
504
Особая линия 223
— точка 14, 223
Остроградский М. В. 263
Остроградского-Грина теорема 263
Ось полярная 57
— сжатия 291
Ортогональная траектория 257
Откоса линия 90
Оценка геометрических величин 166
Пара прямых правая, левая 170
Парабола 52, 124
— биквадратная 124
— кубическая 124
— соприкасающаяся 132
Параболическая точка 345
Параболоид вращения 229
— соприкасающийся 345
— эллиптический 373
Параллелизм Леви-Чивита 438
Параллель 225, 227
— геодезическая 470
Параллельное соответствие' 188 *
Параллельные (геодезически) векторы 433
Параметр-12
— (длина дуги) 77
— распределения 293
—, симметричные обозначения 449
Параметрические уравнения линии 26
поверхности 225 *
Паскаля улитка 56
Первая квадратичная форма 248
Перегиба точка 99
Петерсон К. М. 456
Петерсона-Майнарди уравнения 456
Плоскость 255, 376
—, предел плоскости 20
— касательная к кривой 83
(поверхности) 222, 235, 244, 246
— нормальная 44
— соприкасающаяся 83—86
— спрямляющая 97, 100
— центральная 296
Площадь поверхности 258, 262, 266
Площадь, элемент площади 259
— сферического, многоугольника 180
сегмента 432
— сферических фигур 176
Поворот геодезический 430, 431
тангенциального вектора 433
Поверхность 12, см. также название
поверхности
—, аналитическое представление 223
—, параметрические уравнения 225
Подвижной триедр (трехгранник) 97
Подкасательная 51
— полярная 60
Поднормаль 51
— полярная 60
Подэра 56
Поле векторное тангенциальное 434
— геодезических линий 468
Полная кривизна дуги 334
геодезическая 430
области 398
Полное кручение дуги 335
Положительно обходимая область 177
Положительное направление вращения
178
— направление на касательной, главной
нормали, бинормали 102
Полугеодезическая система координат 468
Полюс 57
Полярная касательная 61
— нормаль 61
— ось 57
— поверхность 308
— подкасательная 60
— поднормаль 60
— форма 255
Полярное уравнение линии 57
Полярные координаты, элемент дуги 70
510
АЛФАВИТНЬ Й УКАЗАТЕЛЬ
Порядок высший, низший, одинаковый 15
— малости вектора 499
Постоянная кривизна, линии пост,
кривизны 202, 311
, поверхности пост, кривизны 472
Постоянное кручение, линии пост,
кручения 208
— направление, линии пост,
направления 430
Правая кривая 151
— пара прямых 170
Предел вектор -функции 499
— точки, прямой, плоскости 20
—, теоремы о пределах 20
Приращение вектор-функции 505
Производная абсолютная 434
Производная вектор-функции 500
вторая 501
— — частная 501
Профиль геликоида общего вида 273
— резной поверхности 383, 384
Прямая, предел прямой 20
Прямой геликоид 29, 231, 237, 271, 341,
349, 362, 376, 389, 403
Прямых пара правая, левая 170
Псевдосфера 56,235,365, 366, 403,471,
472, 489
Пуанкаре 429
Равные (геодезически) векторы 434
Радиус кривизны 107, 123
геодезической 415
— — сферический 187
— кручения 153
Развертка окружности 67
Развертывающаяся поверхность 281, 349,
375, 400
Распределения параметр 293
Ребро возврата 284
Резная поверхность 383
Риман 438
Риччи 438
Роберваль 36
Родрига формула 395
Сегмент, площадь сферического сегмента
432
Семейство линий 223
— поверхностен однопараметрическое 267
Серре 157
Сеть сопряженная 369
— Чебышева 481, 482
Сечение нормальное 350
— —, кривизна 351
Сечения главные 355
Сжатия линия 291
— ось 291
— точка 172, 290
Символ Христоффеля 1-го, 2-го рода 451
Симметричные обозначения параметров
Синтетические методы 9, И, 496
Система координат полугеодезическан
468
Смежности угол 104
Соответствие параллельное (Комбескюра)
188
Соприкасающаяся парабола 132
— плоскость 83—86
Соприкасающаяся сфера 313
Соприкасающийся параболоид 345
Сопряженные направления 367
Сопряженная сеть 369
Сопутствующий триедр (трехгранник) 97
Спираль Архимеда 58
— гиперболическая 62
— коническая 33, 39
— логарифмическая 32, 33, 38, 59, 71, 126.
Сплощения точка 155
Спрямления точка 87, 95
Спрямляющая поверхность 317
— плоскость 97, 100, 317
Средняя кривизна поверхности 358
Сфера (шар) 227, 250, 365, 376, 431, Ш
— гауссова 39">
— соприкасающаяся 313
Сферическая геометрия 477
— индикатриса 173—175
— линия 173, 188, 215, 221, 316
— фигура 176
— эвольгюнта 186
— эволюта 186
Сферический двуугольник 260
— многоугольник 177
— сегмент 432
— цен-ip кривизны 187
— радиус кривизны 187
Сферическое изображение поверхности»
395
Тангенциальная кривизна 415
Тангенциальное векторное поле 434
Тони линия 370
Теорема, см. соотв. название
Theorema egregium 446
Top 2<9, 380
Торрйчелли 36
Точка, предел точки 20
— возврата 1-го, 2-го рода 43, 141
— гиперболическая 345
— излома 43
— неправильная 14, 223
— омбилическая 345
— особая 14, 223
— параболическая 345
— перегиба 99
— сжатия 172, 290
— сплощения 155
— спрямления 87, 95
— угловая 43
— центральная 290, 296
— эллиптическая 345
Траектория ортогональная,изогональнагт
Трактриса 54, 127, 143
Третья квадратичная форма 411
Трехгранник (триедр) сон}тствуюшнй.
(подвижной) 97
Триангуляция 261
Угловая точка 43
Угол смежности 104
— между направлениями на поверхности
254
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
511
Улитка Паскаля 56
Уравнение, см соотв. название
Форма квадратичная первая 24&
вторая 339, 409
— — третья 411
— полярная 255
Формула, см. ссотв. название
Френе 157
— формулы 157, 158, 159, 160
Фробениуса формула 454
Христоффеля символы 1-го, 2-го рода
451
Христоффель 438
Центр кривизны 107, 108
— — геодезической 415
сферический 187
— поверхности 363
Центральная точка 290, 296
— плоскость 29^'
Центров поверхность 381
Цепная линия 74, 79, 129, 143
Циклоида 36, 3 8, 48, 09, 192, 193
Цилиндрическая поверхность 282, 298
Чебышев П. Л. 481
Чебышева сеть 481, 482
Шаля теорема 296
Шаг винтовой линии 28
Шар, см. Сфера
Широта 226
Шнирельман Л. Г. 429
Эвольвента 136—137, 326
— окружности 189
— сферическая 186
Эволют поверхность 381
Эволюта 136—137, 326
— поверхности 381
— сферическая 186
Эйлер 356 '
Эйлера формула 356, 357
Эквивалентные величины 15
— соотношения в треугольнике 17
Эквивалентность равномерная 17
—, свойства 16
Экстремум кривизны 145
Элемент дуги 66, 70
— линейный поверхности 248
— площади 259
Эллипс 35, 36, 49
Эллипсоид 370, 391
— вращения 380, 393
Эллиптическая точка 345
Эллиптический параболоид 373
Эпициклоида 194
Якоби 185
— определитель 263
— теорема 185
Ред. И И. Бронштейн
Тех. ред. Р. Я. Остроумова
Подписано к печати 26/VIII 1949 г. А 09696
31,75 печ. л. 46,91 уч.-изд. л. 59 552 тип. зн.
в печ. л. Заказ Л» 1369.
Цена 16 р. 40 к. Переплет 1 р.
Отпечатано в тип. Н-! с матриц
16 типографии Главполиграфиздата
при Совете Министров СССР,
Москва, Трехпрудный, пер., 9.