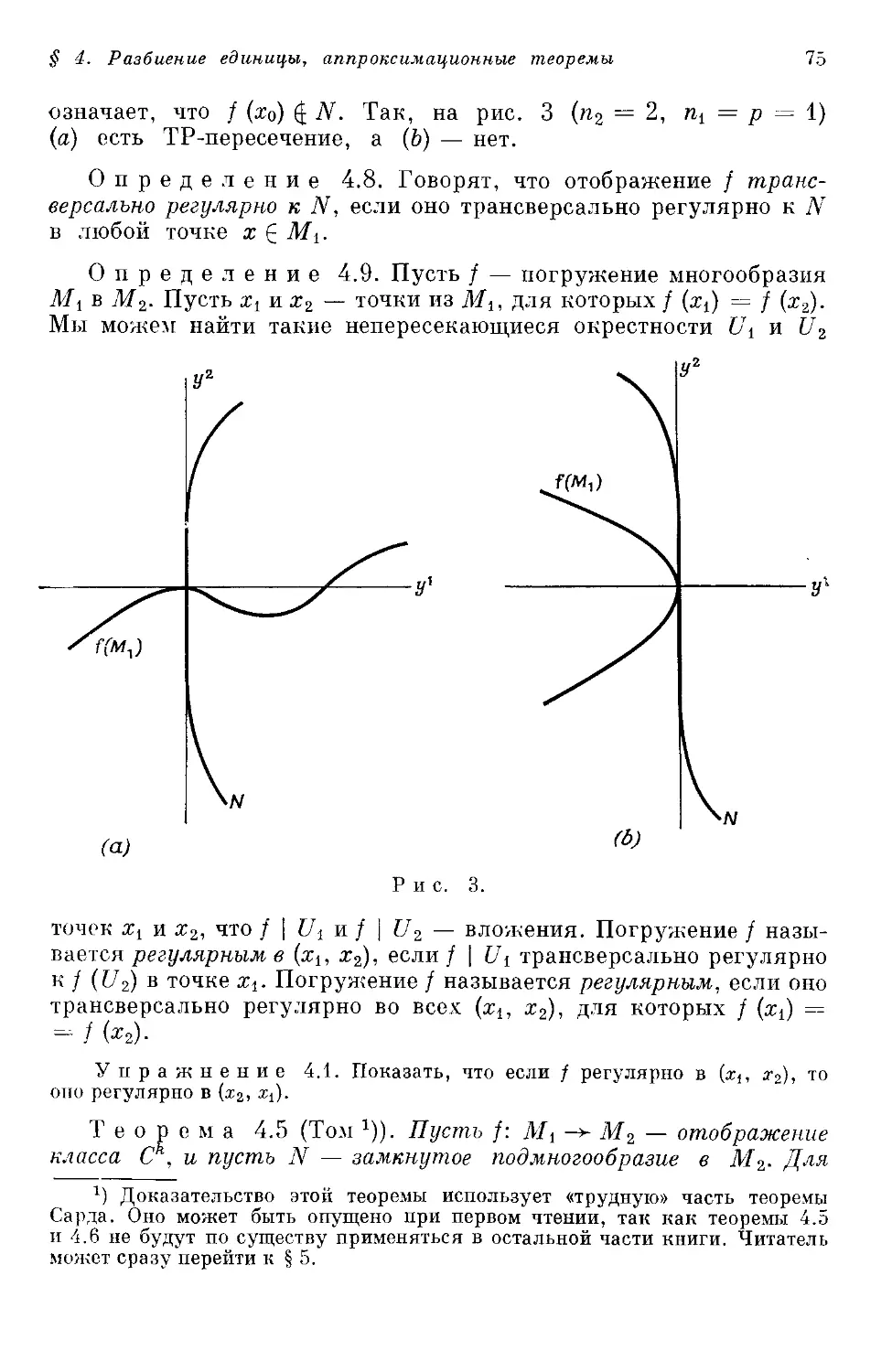
Author: Стернберг С.
Tags: математика геометрия высшая математика дифференциальная геометрия переводная литература издательство мир
Year: 1964
Text
ИЗДАТЕЛЬСТВО
«М И Р»
Shlomo Sternberg
Associate Professor of Mathematics,
Harvard University
LECTURES ON DIFFERENTIAL GEOMETRY
Prentice Hall, Inc. Englewood Cliffs, X.J.
1964
С. Стернберг
ЛЕКЦИИ
ПО ДИФФЕРЕНЦИАЛЬНОЙ
ГЕОМЕТРИИ
Перевод с ohiao некого
Д. Б. АЛЕКСЕЕВСКОГО
Под редакцией
А. Л. ОППЩИКА
ИЗДАТЕЛЬСТВО «МИР»
Москва 1970
Книга известного американского математика со-
держит современное изложение основ теории диф-
ференцируемых многообразий, вариационного исчис-
ления, дифференциальной геометрии, а также теории
групп Ли.
Для чтения ее достаточно знаний начального
университетского курса. Книга заинтересует мате-
матиков самых различных специальностей.
Редакция литературы по математическим наукам
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Как пишет сам автор в предисловии, эта книга не является
ни «основами», ни обзором современной дифференциальной гео-
метрии. Первые три ее главы следует рассматривать как введение
в дифференциальную геометрию, а остальные четыре дают далеко
продвинутое и подробное изложение отдельных вопросов, а именно
вариационного исчисления на многообразиях, теории групп Ли,
дифференциальной геометрии евклидова пространства и геоме-
трии G-структур (вместе с теорией связностей).
Особенностью книги является то, что в ней сочетается изложе-
ние некоторых замечательных результатов «классической» диффе-
ренциальной геометрии (например, результаты Гаусса по теории
поверхностей и новые исследования в этом направлении) с «совре-
менным» аспектом этой науки, который принято рассматривать
как изучение так называемых «инфинитезимальных структур»
на многообразиях. При этом показывается, как классическая
теория кривых и поверхностей в евклидовом пространстве может
быть выведена пз общих фактов теории групп Ли и расслоенных
пространств.
Большой интерес представляет последняя глава книги, в кото-
рой изложены идеи и результаты Э. Картана по проблеме экви-
валентности G-структур. Читатель получает полное представление
о той роли, которую играет в дифференциальной геометрии поня-
тие расслоенного пространства *). В частности, касательное и кока-
сательное расслоения служат в гл. IV естественными рамками
Г Как пишет Н. Бурбакп в своих «Очерках по истории математики»
(ИЛ, М., 1963, стр. 133), «дифференциальной геометрии после ее блестящего
расцвета... стала угрожать опасность впасть... в склеротическое состояние,
пока современные исследования (берущие свое начало особенно от идей Э. Кар-
тана) расслоенных пространств и «глобальных» проблем не вернули ей жизне-
способность».
6
Предисловие редактора перевода
для вариационного исчисления (в том числе вариационных прин-
ципов классической механики).
При переводе были исправлены некоторые неточности и опечат-
ки оригинала.
Книга написана активно работающим математиком, широко
известным своими исследованиями в теории псевдогрупп Ли
и других вопросах дифференциальной геометрии, и несет на себе
печать его индивидуальности. Она, несомненно, будет с интересом
встречена советскими читателями.
А. Л. Оиищик
ИЗ ПРЕДИСЛОВИЯ АВТОРА
Эта книга основана на лекциях, прочитанных в Гарварде
в течение 1960—61 учебного года. Она предполагает знакомство
читателя с элементами современной алгебры (группы, векторные
пространства и т. п.), теоретико-множественной топологии, а так-
же с некоторыми элементарными понятиями анализа. В остальном
изложение замкнуто в себе. Однако по охвату материала эту книгу
нельзя считать полной. Я не преследую цели дать «основы» с изло-
жением всех фундаментальных сведений о предмете или «обзор»,
затрагивающий любую тему. Скорее я излагаю интересующие меня
избранные вопросы дифференциальной геометрии с точки зрения,
которую, я надеюсь, читатель сочтет достаточно последова-
тельной.
Тот, кто хочет изучить дифференциальную геометрию, должен
прочесть также и другие книги, чтобы, с одной стороны, познако-
миться с иным подходом к изложенному здесь материалу, а с дру-
гой — найти изложение не рассмотренных здесь вопросов. В ана-
лизе содержания книги по главам, следующем ниже, я дам несколь-
ко советов по поводу дальнейшего чтения. Для общих справок
я рекомендую четыре книги. Это «Введение в теорию дифферен-
цируемых многообразий» Ленга [9], где содержится ясное изложе-
ние основ теории дифференцируемых многообразий, и «Группы
Ли и дифференциальная геометрия» Номидзу [13], содержащая
теорию связностей. Большая часть материала этих двух книг
приводится в той или иной форме и у нас, однако читателю поучи-
тельно было бы ознакомиться с изложением этих вопросов, кото-
рое не связано с другими рассматриваемыми нами темами. Изложе-
ние теорем де Рама и Ходжа и связанных с ними фактов римановой
геометрии читатель найдет в книге де Рама «Дифференцируемые
многообразия». Наконец, читатель должен изучить какую-нибудь
книгу по классической дифференциальной геометрии; здесь я
не могу отдать предпочтение ни одной из них.
Несколько слов о характере изложения. Местами оно сжато,
а местами подробно. В основном я старался быть кратким там, где
материал является «стандартным» (как, например, при изложении
теории связностей в § 1 гл. VII). Кроме того, книга писалась более
8
Из предисловия автора
двух лет, так что мой стиль менялся в зависимости от погоды,
настроения и т. и. На протяжении всей книги приводятся упраж-
нения. Их надо рассматривать как составную часть текста. Лишь
немногие из них являются трудными. По большей части эти упраж-
нения содержат дополнительные сведения, которые я счел более
уместным и поучительным представить в такой форме. Часто
доказательство теоремы опирается на предыдущее упражнение.
Надеюсь, что в книге нет серьезных логических ошибок.
Однако я не питаю подобных надежд относительно знаков, множи-
телей 2л и тому подобных вещей. Забота о том, чтобы все формулы
были в порядке, стоила мне немало сил, но, несмотря на все мои
старания, в текст, без сомнения, вкралось немало ошибок подоб-
ного сорта. Единственное, что я могу посоветовать,— тщательно
проверяйте все формулы. Чем сложнее формула или уравнение,
тем более восприимчива она к ошибке...
Теперь я дам более подробный анализ содержания. В гл. I
собран алгебраический аппарат, который используется на протя-
жении всей книги. Весь материал является стандартным. Справ-
ки — в книге Бурбаки «Полилинейная алгебра». Наши обозначе-
ния достаточно близки к обозначениям Бурбаки.
В гл. II приведены основные сведения о дифференцируемых
многообразиях и отображениях. Другая трактовка большей части
этого материала (за исключением теоремы Сарда и аппроксима-
ционных теорем) дана в упомянутой выше книге Ленга. Я включил
теорему Сарда по двум причинам. Во-первых, она имеет большой
самостоятельный интерес и находит многочисленные применения
(а вместе с тем отыскать ее доказательство в литературе довольно
трудно). Во-вторых, эта весьма нетривиальная теорема элемен-
тарна р том смысле, что в ней используется только понятие диф-
ференцируемого отображения. Как-то я обнаружил, что мне
трудно усвоить последовательность определений, если они не
подкреплены действительно серьезной теоремой, связывающей
их воедино. Для читателей с теми же склонностями я привожу
теорему Сарда и различные аппроксимационные теоремы даже
до того, как дано определение касательного пространства.
Моя трактовка «величин», состоящая в рассмотрении в каче-
стве первичного объекта расслоения реперов (или кореперов),
вероятно, не является самой прозрачной (см. снова книгу Ленга).
Я стремился мотивировать этим понятие главного расслоения,
а также показать, что тензоры и им подобные объекты являются
«объектами первого порядка» и что существуют аналогичные объек-
ты «высших порядков», хотя последние и не рассматриваются
в этой книге.
Глава III содержит стандартные сведения относительно инте-
грирования на многообразиях. Другой подход, а также доказа-
Из предисловия автора
9
тельство теоремы де Рама и теория гармонических форм содержат-
ся в книге де Рама «Дифференцируемые многообразия» [15]. Даль-
нейшее обсуждение материала § 4 и 5 с многочисленными краси-
выми применениями читатель найдет в книге Э. Картана «Инте-
гральные инварианты» [6]. Эта книга, подобно всем работам
Э. Картана, богата геометрическими идеями. Она становится
вполне доступной, как только читатель привыкнет к языку бес-
конечно малых. Что касается § 6, то существует много хороших
изложений теории преобразований в механике. Мне больше всего
нравятся последние две главы книги Леви-Чивита и Амальди
«Курс теоретической механики». Современное изложение см.
в книге Голдстейна «Классическая механика» 1).
В главе IV мы рассматриваем вариационное исчисление как
изучение некоторых геометрических структур. Наша точка зрения
в некотором смысле является промежуточной между точкой зре-
ния Картана, изложенной им в его «Интегральных инвариантах»,
и точкой зрения Каратеодори в его «Variationsrechnung» [5].
Влияние Каратеодори особенно сказывается в нашей трактовке
достаточных условий. Упор, который мы делаем на рассмотрение
геометрических объектов, связанных внутренним образом с каса-
тельным и кокасательным расслоениями, приводит к тому, что
некоторые идеи собственно вариационного исчисления остаются
в тени. В частности, мы не даем достаточно ясного изложения
второй вариации и не приводим теорему Морса об индексе и вообще
теорию Морса. Хорошее изложение теории Морса читатель найдет
в записях лекций Ботта, прочитанных им в Боннском универси-
тете (1960 г.), и принстонских лекций Милнора (1961 г.) 2).
Глава V содержит стандартные сведения из теории групп Ли.
Классическим руководством здесь является книга Шевалле «Тео-
рия групп Ли».
Глава VI — наименее связная часть этой книги. В ней я попы-
тался применить результаты предыдущих глав к дифференциаль-
ной геометрии евклидова пространства, в частности, показать, что
структурные уравнения группы евклидовых движений играют
решающую роль в этой теории. Я также стараюсь здесь мотивиро-
вать понятие связности, которое вводится в гл. VII. Из гл. VI
читатель получит исключительно однобокое представление
об евклидовой геометрии. Он должен дополнить его чтением учеб-
ника по классической дифференциальной геометрии. Хорошим
*) См. также книгу Ф. Р. Гантмахера «Лекции по аналитической меха-
нике» (М., 1966).— Прим. ред.
2) Bott R., Morse theory and its application to homotopy theory, Lec-
ture notes by A. van de Ven (mimeographed), University of Bonn, 1960; M и л-
н о p Дж., Теория Морса, «Мир», М., 1965.
10
Из предисловия автора
справочником с многочисленными ссылками является, по-види-
мому, книга Бляшке «Введение в дифференциальную геометрию»,
обозначения которой близки к нашим.
В гл. VII излагается теория G-структур. § 1 посвящен теории
связностей. Хорошим руководством здесь является упомянутая
выше книга Номидзу. В остальной части главы рассматривается
то, что Картан назвал общей проблемой эквивалентности. Значи-
тельная часть собрания работ Картана (все еще не вполне оценен-
ных) посвящена этому вопросу. Я попытался изложить несколько
его основных идей и методов. Данная здесь трактовка почти пол-
ностью основана на совместной с И. М. Сингером работе
по бесконечным группам Ли х). § 4 перекликается с толкованием
Гийемина, приведенным в его диссертации (Гарвард, 1964). Другой
подход к теории G-структур дал Бернар [3].
Не все главы зависят от всего предыдущего материала. Вот
примерная схема зависимости глав:
VII
Писать эту книгу было долгим и трудным делом, и многие
мне помогли в этом. Прежде всего я обязан моим учителям: влия-
ние покойного профессора Уинтнера сказывается прежде всего
в сильном тяготении к классической механике. Моим первым
знакомством с работами Эли Картана и, конечно, с современной
дифференциальной геометрией я обязан профессору Чжэню.
По рассматриваемым в книге вопросам я имел много полезных
бесед с профессорами Боттом, Глисоном, Херманом, Ленгом,
Макки и Пале. Я обязан профессорам Номидзу и Смейлу, указав-
шим мне ошибки, вкравшиеся в черновик книги. Как уже упоми-
налось, большая часть гл. VII основана на совместной работе
с профессором Сингером. Особую признательность я выражаю
доктору Хан Са за многостороннюю помощь при подготовке этой
книги — от упрощения доказательств и изложения до неблаго-
дарной работы исправления типографских опечаток.
С. Стернберг
1) Первая часть этой работы опубликована в J. Analyse Math., 15 (1965),
1-114.
Глава I
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ
Основная идея дифференциальной геометрии состоит в применении аппа-
рата анализа к решению геометрических задач. Важнейший метод анализа
предлагает для изучения объектов исследовать их «инфинитезимальные (беско-
нечно малые) части». Так, для изучения кривой исследуются ее касательные,
для изучения функции — ее дифференциалы п т. д. Основное преимущество
перехода к «бесконечно малым» заключается в том, что при этом все объекты
становятся линейными. Так, каждая кривая «инфинитезимально» есть пря-
мая линия (в том смысле, что мы можем заменить ее касательной), каждое
дифференцируемое отображение «инфинитезимально» является линейным
(заменяется своей матрицей Якоби). Поскольку нас будут интересовать в даль-
нейшем кривые, поверхности и вообще «дифференцируемые объекты» высших
размерностей, мы прежде всего изучим их «инфинитезимальные» аналоги.
Это приводит к рассмотрению ряда алгебраических вопросов, которые объ-
единяются в раздел, известный под названием «полилинейная алгебра».
В этой главе собраны необходимые для дальнейшего алгебраические
сведения (главным образом, из тензорной алгебры) и уточняется терминоло-
гия. Большая часть этого материала общеизвестна, поэтому изложение
здесь более краткое, чем обычно. Подробности читатель найдет в учебниках
по линейной алгебре.
Мы предполагаем, что читатель свободно владеет понятиями векторного
пространства, дуального пространства, линейного преобразования, группы
и т. п. [В большей части этой главы не важно, над каким основным полем
определены рассматриваемые векторные пространства. В некоторых случаях
поле характеристики 2 может вызвать обычные трудности. Однако нас будет
интересовать только поле вещественных чисел.]
§ 1. ТЕНЗОРНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРНЫХ ПРОСТРАНСТВ
Пусть V и W — векторные пространства размерностей т и п
соответственно. Отображение f прямого произведения Г X И7
в векторное пространство Z называется билинейным, если оно
линейно по каждому переменному в отдельности, т. е. если
f (aivi + a2v?,j bjWi -|- bgf/'a) =
= (yx, Wi) + dib2f (in, w2) + a2bif (v2, wt) + a2b2f (y2, w2)
для всех векторов Vx, v2 из V, u>lt w2 из W и любых чисел at, a2,
bx, b2. Заметим, что если vit . . ., vm — базис пространства V,
a Wx, . . wn — базис пространства W, то любое билинейное
отображение / однозначно определяется значениями / (vt, Wj).
12
Гл. I. Предварительные сведения из алгебры
Упражнение 1.1. Пусть / : V X W —> Z — билинейное отобра-
жение и g : У — линейное отображение векторного пространства Z
в векторное пространство Y. Показать, что gof: V X W-+Y есть билинейное
отображение.
Обозначим через Hom (V, W) множество линейных отображе-
ний пространства V в пространство W. Напомним, что Нот (У, W)
есть векторное пространство размерности тп. Обозначим через V*
пространство всех линейных функций на V, т. е. дуальное к V
пространство. Определим отображение <р: V X W -> Нот (У*, ТУ)
следующим образом: каждой паре (у, w) сопоставим линейное ото-
бражение ф (у, w) пространства У* в ТУ, задаваемое формулой
ф (у, w) V* = (у, V* ) w
[где v* £ V*, a (у, v* ) — значение линейной функции v* на век-
торе v; следовательно, (у, v*) есть число].
Упражнение 1.2. Показать, что ср: V X W -> Hom (У*,
есть билинейное отображение.
Упражнение 1.3. Пусть . . ., vm — базис пространства V,
а ид, . . ., wn — базис пространства W. Показать, что
{ф (иг, Wj}}, i = 1, . . ., гаг; ; = 1, . . ., га,
есть базис пространства Нот (У*, W).
Пусть f: У X ТУ -> Z — билинейное отображение. Определим
линейное отображение gf Hom (У*, ТУ) -> Z. Положим
(ф (щ, Wj)) = f (Vt, Wj),
где vt, . . ., vm — базис пространства У, а и\, . . ., wn — базис
пространства ТУ. Это определяет отображение gf на базисе
{ф (щ, Wj)} пространства Нот (У*, ТУ). На все пространство
Нот (У*, ТУ) отображение gf продолжается по линейности.
Упражнение 1.4. Показать, что для любых u g V и iv £ W мы
имеем gf (<р (v, w)) = f (и, iv). Вывести отсюда, что отображение gf не зависит
от выбора базисов . . ., i:m и гад, . . ., ivn.
Итак, мы сопоставили каждому билинейному отображению
/: У X ТУ -> Z такое линейное отображение gf Hom (У*, ТУ) -> Z.
что
/ = gf ° Ф- (1-1)
Ясно, что / немедленно определяется по gf.
Упражнение 1.5. Показать, что gf однозначно определяется фор-
мулой (1.1), т. е. если h о ср = h' о ср, то h = h'.
§ 1. Тензорные произведения векторных пространств
13
Более общо, пусть Vk — конечномерные векторные
пространства. Отображение /: Vi X . . . X Vh -> W называется
полилинейным, если оно линейно по каждому переменному
в отдельности, т. е. если
/ (щ, . . aui + bvi, ui+l, . . uh) =
= af (wi, . . ., m, . . ., uk) + bf (ih, . . Vi, . . uh).
Мы хотим найти векторное пространство, универсальное отно-
сительно полилинейных отображений произведения Vi X . . .
. . . X Vfc, т. е. построить векторное пространство U и такое
полилинейное отображение <р: Vi X ... X Vh -> U, что для любо-
го полилинейного отображения /: Vt X . . . X Vh -> W суще-
ствует единственное линейное отображение g: U W, для кото-
рого f = g о ср:
ViX ... хпЛс/
W
Короче говоря, мы хотим, чтобы каждое f можно было пропу-
стить через ф. Прежде всего ясно, что векторное пространство U
и отображение ф определяются с точностью до изоморфизма.
Действительно, если заданы два таких пространства и U2
и отображения ф] и ф2, то мы можем пропустить ф4 через ф2:
FiX ... хП-ЛЕ72
т. е. <Р1 = £1°ф2, где g'{ однозначно определено. Аналогично, ф2 =
= £а°Ф1, откуда Ф1 = Й°5'2°Фг По условию единственности g[°gg =
= id, и, значит, g[ осуществляет изоморфизм между U2 и Е7\.
Установим теперь существование пространства U. Пусть
U обозначает свободное векторное пространство, образующими
которого являются элементы из Vi X ... X Vk. Таким образом,
U есть множество всех конечных линейных комбинаций символов
вида (щ, . . ., vh), где Vj £ Vj. Пусть R — подпространство в U.
порожденное элементами вида
а (щ, • • ., vh) — (Vi, . . avt, vi+i, . . ., vk),
(щ. . . ., Vi + Wi, . . ., Vh) — (Vi, . . ., Щ, . . ., vh) —
— (щ, ., Vk).
14
Гл. I. Предварительные сведения из алгебры
Тогда пространство U = U/R обозначается символом Vi ® . -
. . . ® и называется тензорным произведением пространств Уг.
Определим полилинейное отображение <р: V] X . . . X Vh
-> Vi 0 . . . ® Vk, ставя в соответствие вектору (t’j, . . vh) £
£ Vi X . . . X Vh c U гго класс смежности по модулю R. Мы
будем писать
ф (ix'i, . . Vk) = Vi ® ® vk.
Пространство Vi ® . . . <8> Vh вместе с отображением ф универ-
сально относительно полилинейных отображений. Действительно,
пусть
/: П X . . . X Vh Z
— полилинейное отображение. Определим отображение g: U Z,
полагая g . ., vh) = / (щ, . . ., vh) и продолжая g по линей-
ности. Так как / полилинейно, g аннулирует R и, значит, опреде-
ляет такое отображение g: Vi ® . . . ® Vh -> Z, что f — g °
Поскольку ф отображает Vi X . . . X Vk на множество образую-
щих пространства Vi ® . . . ® Vh, из равенства h ° ф = 0 сле-
дует, что h = 0. Это доказывает единственность отображения g.
Итак, справедлива следующая
Теорема 1.1. Пусть Vi, . . ., Vh — векторные простран-
ства. Тогда существуют векторное пространство Vi ® . . . ® Vh
и полилинейное отображение
ф: Vi X . . . X Vh -> Vi ® . . . <8> Vk,
универсальные относительно полилинейных отображений. Любое
другое универсальное пространство U канонически изоморф-
но Vi ® . . . ® Vk. Положим ф (к1? . . ., vh) = Vi ® . . . ® Vh,
и пусть {eir, г) — базис пространства Vr (1 ir dim 7Г).
Тогда {е^, 4 0 . . . 0 <?i &} — базис пространства Vi ® . . .
. . .®Vk.
Доказательство последнего утверждения — единственного
непроверенного еще утверждения теоремы — мы оставляем чита-
телю в качестве упражнения.
Упражнение 1.6. Показать, что существует канонический изомор-
физм пространства (Vi ® . . . ® 7г) ® (V;+i ® . . . 0 УД на Щ ® ® Д
Мы будем обозначать этот изоморфизм через As (по первым буквам слова
associative).
Упражнение 1.7. Показать, что существует канонический изо-
морфизм пространства V\ ® V2 на V2 ® Vt-
Упражнение 1.8. Показать, что К ®> V = V, если К — основ-
ное поле.
§ 2. Тензорная алгебра векторного пространства
15
Пусть ТI. Vj -> Wt (i = 1, . . fc) — линейные отображения
векторных пространств. Тогда отображение ф: У1 X . . . X Уй ->
-> Wi 0 . . . 0 Wk, переводящее вектор (щ, . . vh) в вектор
(TiVi) 0 . . . 0 (Tkvk), очевидно, полилинейно и, значит, опре-
деляет линейное отображение
Л 0 . . . 0 Tk: Vi 0 . . . 0 Vk -> Wi 0 . . . 0 Wk.
Если Si'. (i = 1, . . к) — линейные отображения
векторных пространств, то
\Ti ® . 0 Тк) о (Si 0 . . . 0 Sk) =
= (TioSi) 0 . . . 0 (Tk°Sk).
В частности, если рг — представление 1) группы Gt в векторном
пространстве Vt (i = 1, . . ., к), то мы можем построить пред-
ставление р! <8> . . . <8> pft группы Gi X . . . X Gk в пространстве
Vi 0 . . . 0 Vk, полагая
(Р1 0 . . . 0 pft) (gi, . . gk) = pt (gi) 0 ... 0 pft (gk).
Пусть Gi = . . . = Gk = G. Рассматривая композицию диагональ-
ного отображения G —> G X ... X G, заданного формулой g —>
(g, с отображением pt 0 . . . 0 pft, мы получим пред-
ставление группы G в пространстве Vi 0 . . . 0 Vk, которое
переводит g в р, (g) 0 . . . 0 pft (g)- Это представление называется
тензорным произведением представлений р15 . . ., pft.
Упражнение 1.9. Пусть S: V -> V и Т: W —г W, причем матрица
линейного преобразования S в базисе {eit . . ., ет} пространства V равна
(sy), а матрица линейного преобразования Т в базисе {Л, . . ., про-
странства W равна (tki). Какова матрица преобразования S 0 Т в базисе
{«; 0 fk} пространства V 0 ТУ?
§ 2. ТЕНЗОРНАЯ АЛГЕБРА ВЕКТОРНОГО ПРОСТРАНСТВА
Пусть V — конечномерное векторное пространство, а У* —
пространство линейных форм на V. Если и g V и w* £ У*, то
значение формы w* на векторе v обозначим (и, w*). Особый инте-
рес представляют тензорные произведения нескольких экземпля-
ров пространств V и V*. Например, пространство V 0 У* может
быть отождествлено с пространством всех линейных преобразова-
ний пространства У (см. упражнение 1.4). Действительно, форму-
ла (f 0 g*) (v) = (и, g*) f позволяет отождествить любой элемент
х) Напомним, что представление группы G в векторном пространстве V
есть гомоморфизм р группы G в группу всех линейных преобразовании про-
странства V. Таким образом, р (g) есть линейное преобразование и р (gig->) =
= р (gi) ° Р fe)-
16
Гл. I. Предварителъные сведения из алгебры
вида f 0 g* из V 0 V* с некоторым линейным преобразованием.
Это отождествление продолжается по линейности на все V 0 V*.
С другой стороны, пусть {е^, . . ., еп} — базис пространства V,
а {е1*, . . еп*} — дуальный базис пространства V*, так что
<ег,?*) = б( =
1, если г = /,
О, если i Ф j.
Тогда линейное преобразование, имеющее в базисе {еь ...,еп}
матрицу (а)), отождествляется с 2 aiei 0 е3* £ V 0 V*. Подобным
же образом легко устанавливается, что пространство V* 0 V* можно
рассматривать как пространство билинейных форм на V.
Мы будем изучать пространства вида 71 0 . . . 0 Vk, где каж-
дое V} есть или V, или V*. Если пространство состоит из г экзем-
пляров пространства 7 и s экземпляров пространства V*, то оно
называется пространством тензоров типа (г, s); число г называет
ся контравариантной, а число s — ковариантной степенью.
Конечно, числа г, s не определяют пространство. Играет роль так-
же порядок расположения сомножителей: мы различаем про-
странства V 0 V* и V* 0 V. Если даны два пространства тензо-
ров U = Vt 0 . . . 0 Vh типа (г, s) и U' = 7( 0 . . . 0 Vk
типа (г', s'), то ассоциативность тензорного произведения позво-
ляет определить билинейное отображение произведения U X U'
в пространство Vi 0 ... 0 Vk 0 7' 0 ... 0 Vp тензоров типа
(г + r', s + s'). Это отображение определяет мультипликативную
структуру на (слабой) прямой сумме всех тензорных произведений
пространств V и 7*. Мы обозначим это пространство через Т (7):
Т (7) = К + 7 + 7* + 707+70 7* +
+ V* 0 7 + 7* 0 7* + . . . .
Рассматриваемое вместе с мультипликативной структурой, оно
называется тензорной алгеброй векторного пространства 7.
Существует другая важная операция — свертка, отображаю-
щая пространство тензоров типа (г, s) в пространство тензоров
типа (г — 1, s — 1) (если г, s>l). Она определяется следующим
образом. Пусть U = 71 0 . . . 0 Vk, где 7г = 7, Vj = 7*
(1 + i к, 1 j к). Пусть U' — тензорное произведение всех
сомножителей тензорного произведения U (в том же порядке),
за исключением 7, и Vj. Отображение 7f X . . X Vk -> U',
определенное формулой
(Vi, . . ., Vh) -> {Vi, Vj) Vi® . . . ® Vk
(тензорное произведение справа не содержит vt и vj), как легко
видеть, полилинейно. Оно определяет отображение U -> U',
называемое сверткой по индексам i и /.
§ 2. Тензорная алгебра векторного пространства
17
Для произвольного линейного преобразования S простран-
ства V обозначим через S* преобразование пространства V*,
определяемое формулой
(v, S*w*} = {Sv, w*} для всех v g V, iv* £ V*.
Пусть {ej, ...,еп}— базис V и {е1*, ...,еп*} — дуальный базис
V*. Невырожденное линейное преобразование А пространства V
переводит базис {еД в базис {/Д, где fi = Aet. Для дуального
базиса {f1*} имеем р* = (А~1)*ег*. Предположим, что базисы {еД
и {/Д связаны между собой следующим образом:
ei = 3 it = 2 Pte;,
так что
'Тогда
/’*==2а{е’*, «’* = 2
Таким образом, если v С V, v = 2 viei = 2 “’Vb то
wi = 2
а если v*QV*, v* = 2 = 2 т0
Hi — 2 fi&j-
Согласно теореме 1.1, базис {е17 ..., еп} вместе с дуальным
определяет базис в любом пространстве тензоров. Например, базис
пространства V ® V* ® V ® V, соответствующий базису {е{, .. ., е„},
состоит из тензоров {е^ ® е'12* ® ets ® ejj, 1Сц, i2, i3, i4<n.
Любой тензор t QV ® У* ® V ® V может быть записан в виде
t = 3 Л2’А?{1 ® ef2* ® ei3 ® е{4. (2.1)
Й, Й> «3. Й
Если t разлагается по базису, соответствующему другому базису
{Л,
t = 2 ® fis* ® fj3 ® /й,
то связь коэффициентов разложений дается формулой
^;23з34 = 2а»Ы:^йз{*- (2-2)
Тензорное произведение тензора t на тензор г = 2 rlli2’3eii ®
® е’2* ® Ci3 дается формулой
t ® г= 2 t\i3iir\i2eil ® ei2* ® б1з ® е.4 0 б{5 ® еч* 0 е.^
Так как положение индексов указывает, какое тензорное про-
изведение базисных векторов рассматривается, мы будем иногда
2 С. Стернберг
18
Гл. I. Предварительные сведения из алгебры
писать
* = (Л?'4) (2.1*)
вместо более длинного выражения (2.1). Таким образом, вышепри-
веденное равенство может быть переписано в виде
(^WVHW,i!)-
Аналогично в терминах координат может быть выражена свертка
тензоров.
У пражнение 2.1. Показать, что свертка тензора (i’1^3’4) по первым
двум индексам дает (^^г*34)-
г
Обозначение, введенное при замене формулы (2.1) на (2.1*),
можно рассмотреть с несколько другой точки зрения. Пусть!.-;
(р (У)—множество всех реперов (т. е. базисов) пространства У.*-?
Пусть GL (п) (полная линейная группа от п переменных) есть*»/
группа всех невырожденных матриц порядка п, причем произведе-
ние м ггриц (а)) и (а)г) задается формулой
k
Любая матрица А = (aj) С GL (п) определяет отображение мно-
жества Jp (У) на себя: если е=(е^ • . -, en) £ jp" (У), то eA = f =
= (fi, •••. fn), где
fj=2aJei- (2-3)
Если А' = (а)г) и М' = g, то
^г = 2а^=2 (2.4)
г h
Но (2а^а0 — АА'. Таким образом, мы можем переписать (2.4)
в виде
е (АА') = (еА) А'. (2.5)
Именно поэтому действие А на репер е мы записываем как еА
вместо того, чтобы, как обычно, писать функцию слева от аргу-
мента. Формула (2.5) показывает, что GL (п) действует справа
как группа преобразований множества JT (У). Заметим, что она
действует свободно: две различные матрицы переводят произволь-
ный репер в два различных репера, и, кроме того, транзитивно:
произвольный репер может быть переведен в любой другой репер
с помощью подходящей матрицы. Пусть теперь Q — произвольное
пространство, на котором GL (п) действует слева, т. е.
(AA')q = A(A'q). (2.6)
$ 2. Тензорная алгебра векторного пространства
19
На пространстве & (У) X Q введем следующее отношение экви-
валентности:
(е, р) ~ (f, q),
если существует такая матрица AQGL(n), что
f = еА и р = Aq.
Нетрудно проверить, что это действительно отношение эквива-
лентности. Классы эквивалентных элементов пространства JF (У) Х<2
называются величинами типа Q (над У). Приведем несколько
примеров.
1. Пусть Qv = Rn— пространство всех наборов п чисел X —
= (я1, ...,;г”). Если А=(а}), то положим А (х1, ...,хп) =
= (у1, ..уп), где уг = 2 ccjj:3. Построим отображение <р: д' (У) х
XQ —»У, полагая ф (в, х) = 2 x3ei- Тогда
Ф (еА, А~гХ) = 2 (о&й) = 2 x}ej-
~ *, 3, k
Таким образом, ф постоянно на классах эквивалентных элемен-
тов пространства д (У) X Qv. Следовательно, оно отображает вели-
чины типа Qv в У. С другой стороны, отображение, которое ставит
в соответствие любым v £ У, е £ д (У) координаты вектора и
в базисе е, и правило замены координат позволяют сопоставить
каждому v £ У единственную величину типа Qv.
2. Пусть Qv* = Rn — пространство всех наборов п чисел
(xit . . ., хп), а группа GL (п) действует на Qv* следующим образом:
A (Xi, . ,.,хп) = (у{, . . ., уп), уг = 2
где А = (а}) и 2аЖ=т &k- Определим отображение ф: jF (У) X
X Qv* —* У*, полагая
ф(е, (х^ .. хп))= 2^*-
Как и выше, это отображение постоянно на классах эквива-
лентных элементов и поэтому позволяет отождествить величины
типа Qv* с У*.
3. Если мы выберем в качестве Q тензорное произведение
нескольких различных пространств Qv и Qv*, то полученное про-
странство можно отождествить с соответствующим тензорным
произведением пространств У и У*. Именно это кроется за симво-
лизмом формулы (2.1*). Такая точка зрения удобна, поскольку
часто на практике мы встречаемся с наборами nh чисел (коорди-
нат), заданных для каждого репера, и законом преобразования
2*
20
Гл. I. Л редварительные сведения из алгебръ:
этих координат при замене репера, т. е. с величинами определен-
ного типа. Если координаты меняются по закону, определяемому
тензорным произведением представлений группы GL (п) на Qv
и Qv*, то соответствующая величина может быть отождествлена
с тензором.
4. Пусть = R и Ах — | х. Величины этого типа
называются (скалярными) плотностями веса р.
5. Пусть Qp = Rh и группа GL (п) действует на Qp согласно
fc-мерному линейному представлению р этой группы. Величины
типа Qp называются линейными величинами. Все величины четырех
предыдущих примеров линейны. Важность линейных величин
заключается в том, что любая линейная величина может быть
получена из своих неприводимых компонент при помощи простей-
ших операций (т. е. тензорного произведения и прямой суммы).
Упражнение 2.2. Предположим, что для каждого репера (еь ..,, еп)
задано множество чисел Показать, что эти числа определяют
тензор тогда и только тогда, когда для любого тензора eSjli2j3 выражение
У Z1......s . .
il> ’-2, ’з
определяет тензор. [Число и положение индексов, по которым производится
суммирование, не играют в критерии никакой роли.]
§ 3. КОНТРАВАРИАНТНАЯ И СИММЕТРИЧЕСКАЯ АЛГЕБРЫ
С тензорной алгеброй связаны некоторые другие алгебры,
представляющие значительный интерес. Прежде всего множество
С (У) всех тензоров ковариантной степени нуль является, очевид-
но, подалгеброй алгебры Т (V):
С(у) = #+ у + у®у+...=
= С° (У) у С1 (У) + С2 (У) + . . .,
где Ср (У) = У ® ® У (р раз). Она называется алгеброй
контравариантных тензоров.
Упражнение 3.1. Показать, что алгебра С (И) обладает следую-
щим свойством «универсальности»: для любого отображения f пространства
V в ассоциативную алгебру А существует единственный гомоморфизм
<р: С (И) А, такой, что / = <р о i, где i — вложение V в С (И).
Всякое линейное отображение /: У W индуцирует линейное
отображение (кото-
$ 3. Контравариантная и симметрическая алгебры 21
рое обозначается символом Ср (/)) и тем самым гомоморфизм С (/):
С (V) ->• С (17) х). Ясно, что С (f о g) = C (/) □ С (g).
Определим спаривание * 2) пространств С (V) и С (V* ) в К
следующим образом:
(х,у*) = 0, если xQCp(V), y*QCq(V*), p=£q,
и {х, у*) есть полная свертка тензора х ® у* по всем индексам
по порядку, если х£Ср(у), у* QCP (7*). В терминах координат,
если х=(хч.....О), а у* = (у^....ip), то
<£,*/*)= 2 ....ip.
il...ip
Легко видеть, что это спаривание позволяет отождествить Ср (7*)
с (Ср (7))*. Более того, это отождествление естественно в следую-
щем смысле: для любого отображения f: V—>W и элементов
x£C(V), у* QC (W*)
{С (/)z, у*} = {х, С (/*)£/*>, (3.1)
где /*: W*—>7* —дуальное отображение3). Поэтому мы будем
отождествлять Ср (7*) с (Ср (7))*.
Упражнение 3.2. Показать, что
... ®2р, У1*® ... ® уР*) = (Х1, yl*) ... {Хр, у?*}.
В пространстве Ср (7) действует группа лр подстановок из р эле-
ментов: пусть заданы подстановка о£лр и тензор вида ® ® хр\
мы полагаем
О (Zj ® ® Zp) = ^a(l) ® . . . ® ^сг(р)
и продолжаем отображение о по линейности на все CP(V). В тер-
минах координат
*0-1(1)..
Таким образом, мы имеем представление группы лр в простран-
стве Ср (7). Легко видеть, что это представление коммутирует
с тензорным произведением представлений группы GL (и), т. е. для
о г.....^) = а
J) Таким образом, правило, которое сопоставляет каждому векторному
пространству V алгебру С (7), является ковариантным функтором, и только
в силу несчастной исторической случайности алгебра С (7) называется
контравариантной.
2) То есть билинейное отображение произведения С (7) X С (7*) ъ К,—
Прим, перев.
3) Оно определяется формулой v£ 7, oj*£P7*.—
Прим, перев.
22
Гл. I. 1Jредварителъные сведения из алгебры
p(o) = sgno =
любых t £ Ср (7), о £ лр и g С GL (п) мы имеем
got = ogt, (3.2)
где gt = (g ® ® g) t (р сомножителей).
Из (3.2) следует, что любой общий собственный вектор пред-
ставления группы Пр, т. е. любой тензор, удовлетворяющий
условию
ot = р (a) t, (3.3)
где р — некоторая числовая функция на лр, переводится пре-
образованием g в тензор, удовлетворяющий тому же уравнению
ogt = got = gp (о) t = р (о) gt.
Два важных частных случая соответствуют функциям
р (о) = 1
и
4-1, если о четно,
— 1, если о нечетно.
Подпространство пространства Ср (7), состоящее из тензоров,
удовлетворяющих равенству ot = t, будет обозначаться Sp (7)
и называться пространством симметрических (контр авар иант-
ных) тензоров степени р. Существует естественная проекция of
пространства Ср (7) на Sp (7). Она задается формулой
«^(0 = 7г 2 °*-
Легко проверить, что <У>2 = <У’ и что (Ср (7)) = Sp (7). Пусть
5(7) = Я + 51аЭ + ^2(^)+--- •
Определим в S (7) произведение, полагая
а © b = if (а ® Ь).
Упражнение 3.3. Показать, что S (F) — коммутативная ассо-
циативная алгебра.
Упражнение 3.4. Показать, что алгебра S (V) универсальна
по отношению к отображениям пространства V в коммутативные алгебры,
т. е. если f: V -> А, то сушествует единственный гомоморфизм ср: S (У)-»-А,
такой, что f = ср о г, где i — вложение V в S (V).
Упражнение 3.5. Показать, что 5 (V*) можно отождествить
с кольцом полиноминальных функций на пространстве V.
Упражнение 3.6. Определим действие V на 5 (V*), полагая
v [ж] = 0, если
$ 3. Контравариантная и симметрическая алгебры
23
и v [ж] —тензор pvfjQx, свернутый по любым двум индексам, если х g Sp (7*).
Показать, что и [s © £] = г[з] © Z-j-s © v [£]-и, значит, v есть дифференциро-
вание алгебры S (V*). Показать, что при отождествлении, указанном в упраж-
нении 3.5, этому действию соответствует дифференцирование в направлении v.
У пражнение 3.7. Пусть f: V Показать, что о Ср (f)=CP (/) о ^Р,
так что / индуцирует отображение Sp (/): Sp (7) -> Sp (ТУ) и гомоморфизм
5(/): S (7) ->S (W).
Упражнение 3.8. Показать, что если х g Ср (V) и у*ССр(У*),
то {<fx, у*) = {х, <fy*}. Вывести из этого, что можно отождествить Sp (7*)
с (Sp (7))* и что это отождествление естественно.
Пространство S2 (V*) есть пространство всех симметрических
билинейных форм на V. Форму b g S2 (7*) называют иногда
индефинитной метрикой на V. Она сопоставляет каждому и £ V
«длину» Ъ (и, v). Благодаря изоморфизму пространства V* <8> V*
с Нот (7, 7*) форма Ъ индуцирует линейное отображение 7 ->
-> 7*. Это отображение является изоморфизмом тогда и только
тогда, когда при любом фиксированном и =^= 0 линейная функ-
ция Ъ (р, •) не равна тождественно нулю. Метрика Ь, обладающая
этим свойством, называется невырожденной. Выбор невырожден-
ной метрики (которая индуцирует изоморфизм 7 на 7*, а следо-
вательно, и 7* на 7) позволяет отображать тензоры контрава-
риантного типа в тензоры ковариантного типа, и обратно. Пусть
в некотором базисе невырожденная метрика b задается матрицей
(gu), а тензор из 7 ® 7, определяющий изоморфизм 7* -> 7,
обратный к индуцированному метрикой Ь,~— матрицей (gi3) х).
Тогда, например, мы имеем изоморфизм 7 ® 7* ® 7 —►
—> 7 ® 7 <8> 7*, определяемый формулой
Операции умножения на (g4) или (g;^) с последующей сверткой
иногда называют подниманием (или опусканием) индексов. По изве-
стной теореме алгебры каждая метрика над полем вещественных
чисел R в подходящей системе координат имеет вид
k г
b(v, v)= (^)2— 3 (7()2, где и = (у1).
г=1 г=й+1
Целые числа к иг являются инвариантами метрики Ь. Если г = п,
то Ъ невырожденна, и обратно. Если к = п, то Ъ (у, и) > 0 для
всех v Ф 0, и метрика называется положительно определенной,
или евклидовой. Если к = п — 1, то метрика называется лорен-
цевой.
т) Таким образом, матрицы )gl}) и (gb) взаимно обратны.— Прим, перев.
24
Гл. I. Предварительные сведения из алгебры
§ 4. ВНЕШНЯЯ АЛГЕБРА
Теперь мы рассмотрим подпространство пространства Ср (7),
соответствующее второму собственному значению р (о) в (3.3),
т. е. пространство антисимметрических тензоров Др (7). Как
и для пространства симметрических тензоров, существует очевид-
ная проекция С1' (V) на /\Р (7), задаваемая формулой
= 2 (sgno)o(i),
а
где sgn а = + 1 в соответствии с тем, четна а или нечетна. Как
и раньше, мы вводим умножение в
Л (Ю=Л° (F)+Л1 (Юг Л2 (Ю + • • •
(где Д° (7) = К, Д1 (7) = 7), полагая
sAt = ^(s8<), ^Л₽(7), *бД’(7)
Таким образом, s /\ t £ Др+9 (у). Знак подстановки из р + 1
элементов, передвигающей первые р элементов за последние q
элементов, равен (— 1)р? (подстановка получается, если переста-
вить каждый из первых р элементов, начиная с p-то, с последними
q элементами, т. е. в результате pq транспозиций соседних элемен-
тов). Следовательно, Л (t ® s) = (—I)”9 Л (s ® I) или
зд г = (-1)рЧДз. (4.1)
Упражнение 4.1. Показать, что Д (Г) — ассоциативная алгебра.
Упражнение 4.2. Охарактеризовать ДР (У) и Д (У) свойствами
универсальности.
Теорема 4.1. Размерность внешней алгебры Д (7) п-мерного
векторного пространства V равна 2п. Если eit ..., еп — базис 7,
то базис пространства Д (7) образуют элементы 1 и
ецД...Дец, Кч< . . . < ir<n, г=1, ...,п. (4.2)
Доказательство. Элементы (ец ® ® е3г) =
= ejiA .•. очевидно, порождают Дг(7). Из соотношений
антикоммутативности (4.1) следует, что ец Д . . . Д eir, где
.. . < 7, порождают Дг(7) и что Дг (7) = 0 при г > п.
Осталось показать, что элементы (4.2) линейно независимы. Можно
считать число г фиксированным, так как члены, соответствующие
различным значениям г, очевидно, независимы. Далее, при г = п
/\ • • • /\ = (^1 ® ® ^п)
$ 4. Внешняя алгебра 25
так как различные члены вида ® . ® ein независимы. Пред-
положим, что при г <^п существует линейное соотношение вида
S ......ireh Л • • • Л eir = °- (4-3)
Пусть /г+1, ..jn — множество индексов, дополнительное к фикси-
рованному множеству индексов ц, ..., ir. Умножим равенство
(4.3) на ец+1 Д ... Д ein- Все члены произведения, за исключением
члена с е»х Д ... Д е»г> содержат два одинаковых сомножителя
и, следовательно, равны нулю ввиду антикоммутативности. Поэтому
а11...Л • • • Л eir Л\+1Л • • • Л ein= ± аЯ...Д ... Д еп =
= 0, откуда »г = 0 и теорема доказана.
В зависимости от ситуации мы будем либо выражать анти-
симметрические тензоры в виде разложения по базисам (4.2),
либо задавать их координатами. Так, мы будем писать
i = 2 t4........Л • • • Л или * = (*11........tr)-
»1<.. .<ir
Рассмотрим теперь некоторые геометрические применения
внешней алгебры.
Теорема 4.2. Необходимое и достаточное условие линейной
зависимости векторов х1г . . ., хг состоит в том, что
хг Д . . . Д хг = 0. (4.4}
Доказательство. Если эти векторы зависимы, то мы
можем выразить один из них через другие, скажем
Г— 1
Тогда
Л . . . Л xr = Х1 Л ... Л (2 akxk) =
= S Л • • • Л Л = 0,
так как каждый член последней суммы содержит одинаковые-
сомножители. С другой стороны, если векторы Xi, . . ., хг линейно-
независимы, то мы можем всегда найти такие векторы xr+i, . . .
. . . , хп, что Xi, . . . , хп образуют базис V. Тогда Xi Д . . .
. . . Д хп 0, и тем более xt Д . . . Д хг 0.
Элементы из /\г (У) иногда называют r-векторами. Те г-векто-
ры, которые могут быть записаны как внешнее произведение век-
торов из V (всякий r-вектор представим в виде линейной комбина-
ции таких r-векторов), называют разложимыми r-векторами. Спра-
ведлива следующая
26
Гл. I. Предварителъные сведения из алгебры
Теорема 4.3. Каждому r-мерному линейному подпростран-
ству W в V соответствует разложимый r-вектор w 0, опреде-
ленный с точностью до (ненулевого) скалярного множителя, причем
х £ W тогда и только тогда, когда х /\ w = 0.
Пусть Wi и W2 — подпространства размерности ri и r2, a
и и>2 — соответствующие ггвектор и г2-вектор. Для того что-
бы Wi cz W2, необходимо и достаточно существование такого
(г2 — 1\)-вектора и, что w2 = Wi /\ и. Для выполнения условия
Wi п W2 = {0} необходимо и достаточно, чтобы гщ /\ w2^= О,
причем в этом случае /\ w2 есть (ri -j- г2)-вектор, соответствую-
щий Wi + W2.
Доказательство. Пусть Xi, . . ., хг — базис W; поло-
жим w = Xi /\ ... /\ хТ. Если yi, . . ., уГ — любой другой
базис и
Pi = S ^ijXj,
ТО У1 Л • • Л Уг = det (atj) xt Д . . . /\ xr,
так что r-вектор и> определен с точностью до скалярного множите-
ля. В силу предыдущей теоремы вектор х является линейной
комбинацией векторов xt, . . ., хг тогда и только тогда, когда
Zt Д . . . Дг. Д j - к /\ т = 0.
Необходимое и достаточное условие того, что Wt содержится
в W2, состоит в том, что любой базис xit ..., хп подпростран-
ства Wi может быть продолжен до базиса xlt . . ., хГ1, хГ1 + i, . . ., хГ2
подпространства W2. Тогда wx = xt Д ... Д zri, w2 = х{ Д . . . Д хГ2
и v = xri + i /\ . . . Д жГ2. Необходимое и достаточное условие того,
что И71ПИ72 = {О}, состоит в линейной независимости векторов
Xi, ..., Хп, Pi, ..., yrs, где yi, ..., рГ2— базис W2. Но если
Wi = Xi Д . . . Д хГ1, w2 = Pi/\ ... Д рГ2, то это условие эквивалентно
тому, что Wi/\w2=^0. Если «дДи^ДО, то цц Д w2 = Д . . .
... Д хГ1 /\ Pi /\ ... /\Рг2 есть, очевидно, r-вектор, соответствую-
щий Wi~)-W2. Теорема доказана.
Можно перефразировать результаты теоремы 4.3. сказав, что р-мерные
подпространства соответствуют классам эквивалентных разложимых р-векто-
ров, если два р-вектора считать эквивалентными, когда они отличаются
ненулевым множителем. Это, конечно, многомерный аналог того утверждения,
что прямая, проходящая через начало координат, определяет лежащий на ней
вектор с точностью до ненулевого множителя. В элементарной геометрии
изучается также понятие «направленной» прямой. Каждая прямая имеет два
направления. Не существует, конечно, способа выбора предпочтительного
направления, но можно сказать, что эти два направления различаются «зна-
ком». Для точной формулировки этих понятий введем более сильное отно-
шение эквивалентности между векторами: будем считать два вектора экви-
валентными, если они отличаются положительным множителем. Направлен-
$ 4. Внешняя алгебра
21
ная прямая — класс эквивалентности по этому отношению. Ясно, что каж-
дому старому классу эквивалентности (прямой линии) соответствуют два
новых, и становится прозрачным источник различия в знаке. Аналогично,
в высших размерностях мы можем говорить об ориентированных р-мерных
пространствах. Это классы эквивалентности р-векторов с более сильным
отношением эквивалентности: два р-вектора эквивалентны, если они отли-
чаются положительным множителем. Снова каждое р-мерное пространство
имеет две ориентации. [В двумерном случае, например, ориентация опре-
деляется заданием направления вращения: по или против часовой стрелки.
В трехмерном случае мы различаем правило правой и левой руки, как пока-
зано на рис. 1.]
Выбор р-вектора означает больше, чем выбор ориентированной р-мер-
ной плоскости. Два различных р-вектора, определяющих одну и ту же ориен-
тированную р-мерную плоскость, отличаются постоянным множителем. Этот
множитель есть пнвариант полной линейной группы. При этом мы имеем
в виду, что если х1 Л . . . Д хр = ку± Д . . . Д ур, то
Д₽(Д(®1Л ... /\хр')=к Др(Л (У1Л • Л уР)
для любого Т g GL (п) х). Таким образом (в том же интуитивном смысле, что
и предыдущее утверждение о знаке), p-вектор определяет, кроме ориенти-
рованной р-мерной плоскости, нечто еще; два различных р-вектора, соот-
ветствующих одной и той же р-мерной плоскости, отличаются некоторым
корректно определенным скаляром. В случае р — 1 это означает просто, что
х) Здесь Др (Т) — ограничение отображения Ср (Т) на Др (В).— Прим,
перев.
28
Гл. I. Предварительные сведения из алгебры
вектор определяет нечто большее, чем направленную прямую; два вектора х
и у, лежащие на одной и той же направленной прямой, имеют корректно
определенное положительное отношение к, где х = ку. Нельзя говорить
о длине вектора, пока не задана метрика. Если задана евклидова метрика,
то вектор х может быть определен на ориентированной прямой указанием его
длины || х || (метрика фиксирует произвольный масштаб). Тогда множитель к
есть отношение длины вектора х к длине вектора у. Интересно, что, хотя
длина вектора зависит от выбора метрики, отношение длин (двух векторов,.
лежащих на одной и той же прямой) от него не зависит. Позднее мы уви-
дим, что выбор евклидовой метрики на V индуцирует метрику на (Г)
и, значит, сопоставляет каждому p-вектору xt Д . . . Д Хр его величину
|| Xi Д . . . . Д хр ||. Эта величина есть объем параллелепипеда, натянутого
на xt, . . ., Хр. Снова, в то время как объем || xt Д . . . Д хр || зависит от выбо-
ра метрики, отношение двух объемов от него не зависит. В любом случае
при фиксированной евклидовой метрике выбор р-вектора Xt Д ... Д хр рав-
нозначен выбору p-мерной плоскости, ориентации этой p-мерной плоскости
и объема. Конечно, выбор xt Д . . . Д хр включает в себя меньше,
чем выбор векторов Xi, . . ., хр. Задание векторов xt, . . ., Хр определяет
дополнительно сам параллелепипед с объемом || Xi Д . . . Д хр ]| и порядок
его ребер.
Пока мы занимаемся вопросами линейной независимости,
сформулируем одну элементарную теорему, важные применения
которой будут даны позднее.
Теорема 4.4 (лемма Картана). Пусть векторы . . ., хр
линейно независимы и
ДЛУ1+---+^ЛУР = О. (4.5)
Тогда
р
= 2 Ац = Ар.
3=1
Доказательство. Выберем a?p+1, ..., хп так, чтобы век-
торы Xi, ..., хр, хр+1, ..., хп составляли базис V. Тогда мы
можем написать
3=1 3=р+1
Подставляя это выражение в (4.5), получим
3 (Ац — Aji)xi /\xj+ 2 BtjXi /\xj = 0. (4.6)
Кз'ёР i=£P> 3>P
Произведения Xt/\xj (i </) линейно независимы по теореме 4.1.
Значит, 5г; = 0, Atj = Aji, ч. т. д.
Пусть /: V—>W — линейное отображение. Тогда для любого
о g лр мы имеем оСр (/) = С'' (/) о, так что
^CP(/) = CJ’(/) Л. (4.7)
§ 4. Внешняя алгебра
29
Поэтому Ср (/) отображает /\р (V) в /\р (ТУ). Мы будем обозна-
чать ограничение Ср (/) на ДР (У) через ДР(/). Равенство (4.7)
показывает также, что если мы обозначим через /\ (/) отображе-
ние Д(У)->Д(1У), совпадающее на ДР (У) с ДР (/), то Д(/)
будет гомоморфизмом Д (У) в Д(ТУ). Далее, для xQCp(V),
у* £ Ср (У*) и а £ лр имеем
(о(х), у*) = (ж, о"1 (у*)).
Поэтому
(Лж, y*) = (z, Лу*).
Если теперь х^Др(У), то x = dx и
<х,у*) = (х,Лу*). (4.8)
Принимая во внимание предыдущее отождествление (Ср (У))*
с СР(У*), мы можем естественным образом отождествить (ДР(У))*
с ДР(У*), используя спаривание (,), ограниченное на ДР (У)
и ДР(У*). Однако удобнее использовать спаривание (|) (мы заме-
нили запятую'на |), определяемое формулой
{х | у*} = р\ {х, у*) (4.9)
для xQ/\v (У), У*СДР(У*). Это спаривание, конечно, тоже есте-
ственно (т. е. ведет себя должным образом при отображениях).
Чтобы сделать эту двойственность между ДР (У) и ДР (У*)
более ясной, вычислим (х | у*) для разложимых р-векторов. Если
x — xi Л • • • /\хр = с4 (xt ® . . . ® хр) и У-У1*/\ • /\ !/"*-
= <^(у1*® ... ® ур*), то, согласно упражнению 3.2, уравне-
нию (4.9) и равенству Лг = Л, имеем
(z I у*) = р! (Л (Xi ® . . . ® Хр), Л (у1* ® .. . ® ур*)) =
= р! (Л (^ ® ... ® хр), у1* ® ... ® ур*) =
= S Sgno(za(1) ® .. . ® za(p), у1* ® ... ® ур*) =
СТ ~ Лр
= 2 Sgno^ad), у1*) . . . (za(p), ур*),
или
{х | у*) = det {xi, у?*). (4.10)
Векторное пространство Д₽ (У*) = (Др (У))* называется про-
странством внешних р-форм над У. Алгебра Д (У*) называется
алгеброй внешних форм над У.
30
Гл. I. Предварительные сведения из алгебры
Определим спаривание (|) пространства Д (У) с Д (V*) фор-
мулой
(ж|у*) = 0, если а:€ЛР(У), г/*€Д9(У*), P^q,
и формулой (4.9), если p = q.
Упражнение 4.3. Пусть q, ..., еп—базис V и е1*, ..еп* — дуаль-
ный базис V*. Показать, что относительно спаривания { | ) дуальным
к базису
{«йЛ ••• Л е,г} (1<Н< ... <гг, г=0, ..., п)
является базис
{Л* д... л Л*}.
Это спаривание пространств Д (У) и Д (У*) позволяет для
любого линейного оператора на Д (У) определить сопряженный
оператор как линейный оператор на Д (У*). В частности, мы
можем определить оператор, сопряженный к оператору (левого)
внешнего умножения. Он называется оператором (правого) вну-
треннего умножения. Более точно, для любого и С Д (У) мы опре-
деляем линейный оператор и_\- на Д (У*), полагая
<x|uj у*) = (и Л х | у*) для всех х$/\ (У). (4.11)
Упражнение 4.4. Показать, что J (u2 J у*) = (u2 Л “i) J У*-
Из формулы (4.11) ясно, что если м^Д₽(У) и уСДг(У*)^
то и j у* Q/\r~v (У*) при г> р и =0 при г<р. В частности,
если г = р, то и j у* = (и | у*}. Таким образом,
енЛ ••• A%JeJ1*A ••• Ле’г* =
f 0, если {ij, . . ., ip} qt {/i, , /г},
= 1 (4.12)
I ± eai* A ... A e ar-P*,
где cq, ..., аг_р — множество индексов, дополнительное к q, ..., ip.
в ji, ..., jr, а знак есть знак подстановки (7’4, • • •, /г) —> (й, • • •, ip?
cq, ..., аг_р). В частности,
ег J е’1* Л • • • Л > =
( 0, если I =/= jk для любого к,
[ (—l)ft-V'i*A Л«’М*Л ejk+l* А<Д если г = Д.
(4-13)
$ 4. Внешняя алгебра
31
Формула (4.13) показывает, что внутреннее умножение на е;
во внешней алгебре можно рассматривать как аналог частного
дифференцирования по t-й переменной. Как и следовало ожидать,
последовательные «частные производные» зависят от порядка:
из упражнения 4.4 следует, что е, j (е, j у*) = — j (ег j ?/*).
Кроме того, если мы умножим (4.13) на ег и просуммируем по I,
то получим (сначала для базисных векторов, а затем по линейно-
сти) для любого у* £ Дг (V*) аналог теоремы Эйлера об однород-
ных функциях:
п
S е* Л (ег J у*) = гу*. (4.14)
i = 1
Упражнение 4.5. Показать, что внутреннее умножение на х с V
на самом деле есть антидифференцирование алгебры Д (V*), т. е. что
для любых x^v, у*е/\р (V*) и y*t/\q(V*)
(у!Лу?) = (* J у?)Лу!+(-1)ру?Л(* J у*}-
Внутреннее умножение часто используется для того, чтобы
следующим образом связать алгебру Д (У) с Д (У*):
Теорема 4.5. Пусть ей е* — дуальные базисы (одномерных)
пространств /\п (У) и /\п (У*) соответственно. Линейное ото-
бражение е±: ДГ(У)—>ДП"Г(У*)> определенное формулой
е± (х) — х J е*,
является изоморфизмом /\г (У) на /\п~г (У*), переводящим раз-
ложимые элементы в разложимые. Если w 0 есть разложимый
r-вектор, соответствующий линейному подпространству ТУ, то
e_L w соответствует подпространству W° (состоящему из всех
линейных функций, равных нулю на РУ).
Доказательство. Если мы выберем такие дуальные
базисы, что Д . . . Д еп = е и е1* Д . . . Д еп* = е*, то фор-
мула (4.13) показывает, что отображение есть изоморфизм. Раз-
ложимые элементы степени п отображаются в Д° (У*), так что здесь
доказывать нечего. Любой разложимый элемент степени г < п
записывается в виде е^ /\ ... /\ еТ, причем мы можем дополнить
векторы {ei, . . ., еТ) до базиса {е1; . . ., еп} так, чтобы в! Д . . .
. . . /\еп = е. Тогда формула (4.13) показывает, что
е± (qA ... Л ег) = ± е(г+1)* А ... Де"*.
Но элемент справа разложим и соответствует пространству,
порожденному п — г линейно независимыми формами е<г+1>* , . . .
. . ., е71*, которые обращаются в нуль на W. Теорема доказана.
:32
Гл. I. Предварительные сведения из алгебры
Упражнение 4.6. Показать, что всякий (п — 1)-вектор разложим.
Мы можем ввести правое внутреннее умножение в Д (V)
на элементы из Д (V*) по формуле
{х L и* ] у*} = (ж | и* Л У*)- (4.15)
.Для L справедливы аналоги вышеприведенных утверждений
относительно J. Предположим, что V снабжено евклидовой метри-
кой, т. е. на V определено скалярное произведение (,), удовлетво-
ряющее условиям
1) (ж, у) = (у, х),
2) (aiXt -j- azxz, у) = (х1; у) + а2 (х2, у),
3) (х, х) > 0, если х Ф 0.
'Тогда мы можем отождествить вектор у g V с вектором у* £ V*,
для которого (х, у*) = (х, у). Определим теперь скалярное про-
изведение в СР(У), полагая
(xi ® ® хТ, yi ® ® уг) = (хи у^ ... (хг, уг)
для разложимых элементов и продолжая по линейности. Если
мы будем считать, что Ср (У) ортогонально Cq (У), когда р q,
то получим скалярное произведение в С (У). Заметим, что <У>
и А — самосопряженные операторы относительно этого скаляр-
ного произведения.
Если мы ограничим скалярное произведение ( , ) на 5 (У) или
Д (У), то получим скалярное произведение в этих простран-
ствах. Как и раньше, определим скалярное произведение ( | )
в Др (У), умножая ( , ) на дополнительный множитель:
(ж | у) = р! (z, у) для х, у £ Др (У). (4.16)
Тогда
(Xi л • • • Л хр I У\ л • • • Л Ур) = (det (Xi, yj)); (4.17)
в частности,
|| Xi Л • • • Л Хр II = (Xi Л • • • Л хр IХ1 Л ... Л Хр)1/2 =
= (det (Xi, ^))1/2 (4.18)
есть объем параллелепипеда, натянутого на xt, . . ., хр.
Поскольку пространство Д71 (У) одномерно, в нем имеется
ровно два элемента е и —е, для которых || е || = 1. Выбор одного
из них определяет ориентацию в У.
По теореме 4.5 выбор (скажем) е определяет изоморфизм
<р: Дг (У) -> /\п~г (У*)- С другой стороны, скалярное произведение
§ 5. Внешние уравнения
33
определяет изоморфизм /\" r (V*) иа /\п r (У). Комбинируя эти
изоморфизмы, мы получим изоморфизм
*: ЛГ(П-^ЛП-Г(Ю. (4.19)
У п р а ж н е н и е 4.7. Пусть . ., еп — ортоцормированный базис
в V относительно ( | ). Показать, что Д . . . Д et } образуют ортонор-
мированпый базис в (У) относительно ( [ ).
У п р а ж н е п и е 4.8. Найти разложение по этому базису тензора
* (<Д Л • • • Л^р)-
Упражнение 4.9. Показать, что х /\ * х = е.
Упражнение 4.10. Показать, что * * х = (—1)г О1"1') х, если
х 6 /\ ' ОТ
Упражнение 4.11. Показать, что если хну — векторы трехмер-
ного евклидова пространства, то * (х Д у) есть «векторное произведение» х
и ;/.
У п р а ж н е н и е 4.12. Показать, что * есть изометрия, т. е. (*х | *у) =
= (х I У)-
Упражнение 4.13. Показать, что х Д * у = (х | у) е для х, у £
еЛР
§ 5. ВНЕШНИЕ УРАВНЕНИЯ
Прежде всего установим нормальный вид внешней 2-формы,
аналогичный (диагональному) каноническому виду симметриче-
ской квадратичной формы.
Теорема 5.1. Для любой формы 7*СД2(К*) существует
базис {у'1*, ..., /"*} пространства V*, в котором
q* = f1* Д уг* Д ... Д y(2p-D* Д у2Р*. (5.1)
Целое число р зависит только от q*.
Доказательство. Предположим, что в базисе {ег*} форма q*
имеет вид
i < i
Если г/* ДО, то мы можем (перенумеровав базис, если понадобится)
считать, что «12Д0. Тогда
\ а12 а12 /
Л (^12е2* + а1з^3* + • •. +amen*) + q1*,
34
Гл. I. Предварительные сведения из алгебры
где форма qr* не содержит е1* и е2*. Положим
-с _ gl*_ «23 ез*_ __ а2п еп*
Л «12 ’ ’ ‘ «12
Уг = я12е2* + я13е3* + ... + я1пе"*;
тогда у1*, У2*, е3*, . . е“* линейно независимы и
= Z1* /\ /2* -|- •
Если q1* = 0, то все доказано. В противном случае мы продолжаем
процесс, пока не получим требуемый нормальный вид.
Целое число р может быть описано внутренним образом. Дей-
ствительно, рассмотрим линейное подпространство Е (q*) cz V*,
порожденное элементами вида
х j q* (5.2)
для всех х С V. Это подпространство (называемое ассоциированной
системой формы q*), очевидно, порождается также элементами
gi_}q*. (5-3)
где gi, . . ., gn — базис V. Если взять gt = у;, где {Ув . . .. fn} —
базис, дуальный к базису {У1*, . . ., У”*}, то формы (5.3) равны
У1*, у2*, . . ., у2'1*. Значит, 2р = dim Е (?*), и теорема доказана.
Ассоциированная система может быть определена для q* £ Др (У*)
при любом р>1. Говорят, что подпространство W* cz V* оберты-
вает форму q*, если q* £ /\р (И7*) cz Др (7*). Покажем прежде
всего, что W* обертывает q* тогда и только тогда, когда
х J q* ^W* для всех я:£Др-1(У). (5-4)
Для этого выберем базис е1*, ..., es* подпространства W* и про-
должим его до базиса пространства V*. Пусть еь ..., еп — дуаль-
ный базис V. Как и раньше, выражение «для всех ^бДР-1(У)»
в (5.4) можно заменить выражением «для всех базисных элемен-
тов из ДР-1(У)». Если q*<z/\P(V), то
q* = 3 ац......Л ... Л Л*.
Форма q* лежит в Др (И7*) тогда и только тогда, когда Яц.t = О
для ip >s, что эквивалентно условию (5.4).
Условие (5.4) показывает также, что существует минимальное
подпространство Е (q*), обертывающее q*, а именно пространство,
порождаемое формами х J q* для всех х £ Др~1 (У) . Размерность
пространства Е (q*) называется рангом формы q*. Если форма q*
разложима, 7*-?/1* Л ••• Л//”*, то Е (д*) порождается элементами
у1*, ...,ур*. Отсюда следует
§ 5. Внешние уравнения
35
Теорема 5.2. р-форма разложима тогда и только тогда,
когда ее ранг равен р.
Упражнение 5.1. Показать, что 2-форма <4.]^* Л разложима
тогда и только тогда, когда
aiJakn aikajn а ina jk = О-
Упражнение 5.2. Показать, что 3-форма разложима тогда и только
тогда, когда
aijhanlm aijnaklm т aijlaknm aijmaknl — 0.
Какова общая теорема?
Следует заметить, что (Е (q*))° (множество векторов, на кото-
рых все формы из Е (q*) обращаются в нуль) допускает простую
характеризацию. Действительно, если х £ (Е (q*))°, то
х j <?* = 0. (5.5)
С другой стороны, размерность пространства решений уравне-
ния (5.5) не может превышать п — г (где г — ранг q*), иначе q*
можно было бы выразить меньше, чем через г, линейно независи-
мых векторов. Таким образом,
х £ (Е (<?*))° тогда и только тогда, когда х j q* = 0. (5.6)'
Пусть W — подпространство пространства V. Пусть i обо-
значает вложение W -* V; дуальное отображение i*: V* -> W*
индуцирует отображение Д (£*): Д (У*) -> Д (И7*). Если у* g
€ Д (Р*)> то форма Д (i*) у* £ Д (РУ*) называется ограничением
формы у* на W. Говорят, что подпространство W аннулирует у*,
если Д (t*) у* = 0. Для линейных форм у* это совпадает с обыч-
ной терминологией.
Основная проблема теории внешних уравнений состоит в сле-
дующем. Дано множество форм {Qa}; требуется найти подпро-
странства, аннулирующие эти формы. Сделаем несколько предва-
рительных замечаний. Прежде всего Д (i*) есть гомоморфизм,
поэтому если Д (i*) переводит форму у* в нуль, то в нуль перейдет
и любая кратная у* форма. Значит, если Д (i*) аннулирует
{Qa}, то оно аннулирует и идеал, порожденный {Qa}. Этот идеал
однороден, т. е. порождается однородными элементами. Поэтому
мы можем считать, что множество {Qa} образует идеал. Далее,
предположим, что у* есть р-форма и
= ....V1*.....ъ* (5.7)
в некотором базисе {е15 ..., еп}- Если у*^=0, то можно считать,
что ai,2, ...,р=#0. Рассмотрим р-мерную плоскость W, порожден-
ную векторами ..., ер', ограничение формы у* на W равно
36 Гл. I. Предварительные сведения из алгебры
&1, 2, ..., Pel* Л • • • Л =7^ 0. Поэтому для данной ненулевой
р-формы всегда существует по крайней мере одна р-мерная пло-
скость, которая не аннулирует ее. Другими словами, р-форма,
аннулируемая всеми р-мерными плоскостями, равна нулю. Если
Wt cl W cl 7, то ограничение некоторой формы на W4 может
быть получено ограничением сначала на Ж и затем с И7 на Wt.
Применяя предыдущие замечания, мы можем сделать следующее
утверждение:
Пусть задано р-мерное подпространство И7, г: W —>V; q-форма
у* (q^p) аннулируется подпространством W тогда и только
тогда, когда форма /\(1*)у* аннулируется любым q-мерным
подпространством пространства W.
Справедлива следующая
Теорема 5.3. Пусть И — однородный1 *) идеал в Д (7*);
р-мерное подпространство W сс V аннулирует J тогда и только
тогда, когда
(w | у*} = 0 для всех у* С J П ДР (7*), (5.8)
где w есть р-вектор, соответствующий W.
Доказательство. Поскольку р-мерное подпространство
аннулирует любую форму степени большей, чем р, достаточно
рассматривать формы степени <р. Выберем такой базис е4, . . ., еп,
чтобы w = е4 Д . . . Л ер- Дл« любой р-формы, заданной форму-
лой (5.7), имеем
Да*)г/* = «1,2, ...,Р ••• Дб”* =
= (ш|г/*)е1*Д ... Де”*. (5.9)
Поэтому Д (1*)у* = 0 тогда и только тогда, когда (и>\у*) = 0.
Мы доказали необходимость условия (5.8). Из условия (5.8), как
мы знаем, следует, что подпространство W аннулирует все р-формы
из J. А как обстоит дело с (/-формами при (/< р? Если форма у* =
= 3 ач, • ...i„ е4*’ "'lq* такова, что Д(г*)г/*#=О, то
Й< . . <ig
। ^2=0 для некоторого множества индексов, причем £Др.
Перенумеровав, если понадобится, базис, можно считать, что
«1, 2, .... #0- Тогда z* = y* Де(’+1)*Д ... есть р-форма
и ’ | z*) 0. Если то z*gj, так как J есть идеал.
Поэтому, если (5.8) имеет место, то Д ((*) у* = 0 для всех
и теорема доказана.
1) Однородность означает, что J = 2 Т'ПД7’ (Т*).
р
§ 5. Внешние уравнения
37
Условие (5.8) представляет собой систему линейных уравнений
в Др (У). На первый взгляд может показаться, что мы свели про-
блему решения внешних уравнений к простой задаче решения
линейных уравнений. Однако это не так, поскольку мы должны
добавить к (5.8) условия, выражающие разложимость тензора w.
Эти условия не линейны, а квадратичны по координатам в W
(см. упражнения 5.1 и 5.2).
В одном случае проблема становится тривиальной — если
идеал ,У порождается своими элементами степени один. В этом
случае подпространство W аннулирует идеал J тогда и только
тогда, когда W ед (J П Д1 (У*))0-
Упражнение 5.3. Примером усложнений. вызванных квадратпч-
ностью условий разложимости внешних форм, является тот факт, что
множество форм, аннулируемых всеми теми подпространствами, которые
аннулируют идеал j, может быть больше, чем J. Например, пусть идеал У
порожден формами е1* Д е3*. е1* Д е4* и е1* Д е2* — <?3* Д е4*. Показать,
что е1* Д ег* аннулируется каждым подпространством, аннулирующим Д,
хотя е1* Де2* (£ Д.
Сделаем несколько упрощений. Предположим, что ,7 имеет
систему образующих, принадлежащих Д (U*) для некоторого
подпространства U* cz V*. Тогда (С7*)°, очевидно, аннулирует J.
Кроме того, если некоторое подпространство W аннулирует J,
то это же верно и для W 4- (С7*)°. Как и в случае форм, желательно
найти минимальное подпространство U*, для которого Д (К*)
содержит множество образующих идеала J. Мы можем найти
такое подпространство благодаря следующему утверждению:
Пусть У — однородный идеал в /\ (У*) и U — подпростран-
ство пространства V. Идеал У обладает системой образующих,
лежащих в /\ (U0), тогда и только тогда, когда
х j у* cz ,7 для всех y*Q$ и всех xQU. (5.10)
Доказательство. Если образующие {Д} идеала .7 лежат
в f' (U°), ТО X J у* = 0 для всех xQU. Поэтому
Z J (2* Л У а) = (* J Z*) Д Уа £ J
для произвольной формы г*^Д(У*). Поскольку каждый элемент
из ,7 есть сумма членов вида z* Д у*, условие (5.10) выполнено.
Для доказательства обратного утверждения достаточно про-
верить, что элементы из Д (f7°) порождают пространства ,7 П Д’ (У*),
i=l, 2, . . ., п. Если ДПДДУ*), то, согласно условию (5.10),
£_Я* = 0 для всех xQU и, значит, у* . Пусть е1; ..., ер —
38
Гл. I. Предварителъные сведения из алгебры
базис U, а ер, . . ел —базис V. Тогда e(-p+i^*, .. еп*—
базис U°. Если у*^3 П /\2(7*), то
У* = S
i< j
и, согласно условию (5.10), е^7У*б;3 и элемент у* = у* —
—е1* Л (ei J У*) не содержит е1*. Далее, элемент у2 = У* —
— е2* Л (е2 J J/Т) G J и не содержит е1* и е2*. Продолжая
подобным образом, мы получим разложение у* = Ур — w*, где
У*€Д(^°), a т* есть сумма, все слагаемые которой кратны эле-
ментам из J Г) Д1 (7*) с Vй.
Дальше рассуждаем по индукции. Предположим, что все
пространства ДПДДУ*), •••> 3 А Д’-1 (7*) порождены эле-
ментами из Д((70). Для любого У* £3 /\q (V*) элемент
у* — е1* Д (е{ j у*)£3 и не содержит е1*. Продолжая, как раньше,
мы получим систему образующих для J А Д? (7*), лежащую в Д (U°).
Если нам нужно получить минимальное пространство U0,
то мы возьмем максимальное U. Таким образом, имеет место
Теорема 5.4. Пусть 3 — однородный идеал в /\ (7*).
Существует единственное минимальное подпространство U* с 7*,
называемое присоединенной системой идеала 3, такое, что
в Д (U*) содержится некоторая система образующих идеала 3•
Пространство (U*)° состоит из всех х С 7, удовлетворяющих
условию (5.10).
Заметим, что если 3 порождается одной формой у*, то усло-
вие (5.10) сводится к условию (5.5).
В случае когда ассоциированная система U не совпадает с V* (система
нетривиальна), иногда бывает удобно исключить «лишние переменные». Пусть
U' — подпространство пространства V, дополнительное к U, так что U +
Д U' = V, U Q и' = (0). Если подпространство W аннулирует .7, то и
W -i- U аннулирует .У. Но W + U = W' + U, где W' = (Ж + U) П U’.
Таким образом, каждому решению W соответствует решение W' С U'. Если
мы ограничимся рассмотрением максимальных решений (т. е. подпространств,
аннулирующих 3 и не содержащихся в больших подпространствах, аннули-
рующих ,7), то это соответствие будет взаимно однозначным: каждому макси-
мальному решению W отвечает единственное решение W' = W П U', лежа-
щее в V. Далее, подпространство из U' будет решением тогда и только тогда,
когда оно аннулирует идеал (i*) У, где i: U' V — вложение. Это
так, поскольку i* есть изоморфизм пространства U° на (7')* и потому не
отображает ни одной образующей идеала .7 в нуль. Таким образом, мы
всегда можем свести внешнюю систему к случаю, когда ассоциированная
система тривиальна.
Решения внешней системы строятся по индукции. Сначала мы ищем
прямые, являющиеся решениями. Прямая I будет решением, если она есть
§ 5. Внешние уравнения 39
решение системы линейных уравнений
<.|у*)=о, у* е Д1 (г*) n (5.Н)
Обозначим через s0 число линейно независимых уравнений из (5.11), т. е.
размерность пространства А 1 (Ю П <7 Пусть Zf есть решение системы (5.11)
и ij — вектор на Zj. Прямая Z2 порождает вместе с Ц двумерное решение, если
Z2 есть решение системы уравнений
(•pi J Z/*) = 0, У*СА2(У*)П^- (5-12)
Пусть идеал У порождается элементами {у*а}, где У*а€ /\} (У*)- Тогда
уравнения (5.12) эквивалентны системе (5.11) вместе с новой системой урав-
нений
<• I Р1 -1 У2а) = °- (5-13)
Таким образом, прямая Z2, порождающая вместе с Zj двумерное решение,
должна удовлетворять условиям (5.11) и множеству условий (5.13), которые
зависят от выбора Zj. Значит, размерность системы (5.12) можно записать
в виде s0 + s4 (Z4). Число линейно независимых уравнений системы (5.12)
равно рангу соответствующей матрицы, элементы которой зависят (линейно)
от коэффициентов прямой 1Х. Поэтому если s, = max sj (Zf), то множество пря-
мых lt, для которых si (I)) < определяется множеством нулей некоторого
семейства ненулевых полиномов. Прямые Zf, для которых s, (Zj) — st, назы-
ваются регулярными', если st (lt) < st, то прямая I, называется сингулярной.
Если s0 + s4 (Zt) = п — 1, то единственным решением уравнений (5.12) явля-
ется сама Z(, так что не существует двумерных решений, содержащих Z,.
Если s0 + Sj (Zj) < п — 1, то существуют двумерные решения, содержащие
Zp Мы можем продолжить этот процесс. Если W есть p-мерное решение
с р-вектором w — wi Д . . . Д и>р, то прямая Zp+1 порождает вместе с W реше-
ние в том и только в том случае, когда Zp+1 есть решение системы уравнений
(•>Jy*) = 0 для у* е АР+1 п У- (5.14)
Эта система уравнений называется полярной системой р-вектора w. Система
(5.14) может быть получена добавлением к предыдущим уравнениям, исполь-
зуемым для определения W, следующей системы уравнений:
Z/2a> = °- j Z/3a> = 0’ • • >
/\wp J Z/*p+l)a) = ° (0<Ч< ... <P). (5.15)
Снова число уравнений системы (5.15), которые независимы от предыдущих,
есть функция sp (w) от w. Положим sp = max sp (w) и назовем р-плоскость W
регулярной, если она содержит регулярную (р — 1)-плоскость и sp (о?) = sp.
Так как W есть решение системы (5.8), то
so + si + --- + spO—р. (5.16)
Если имеет место равенство, то не существует (р + 1)-мерного решения, содер-
жащего регулярную p-плоскость. Мы стремимся подобрать решение W такой
размерности р, для которой достигается равенство. Такое число р назы-
вается родом рассматриваемой системы.
Глава II
ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ
Предметом дифференциальной геометрии является изучение геометри-
ческих задач, допускающих использование анализа. Поэтому объектами изу-
чения должны быть пространства, в которых имеют смысл такие понятия,
как дифференцирование и интегрирование. В этой главе мы введем такой
класс пространств, называемых дифференцируемыми многообразиями, и изу-
чим их простейшие свойства. Прежде чем давать точные определения, поучи-
тельно рассмотреть один элементарный пример и выяснить, какие могут
встретиться трудности. Предположим, что мы хотим изучать окружность.
Естественный вопрос состоит в том, как описать (т. е. задать или параметри-
зовать) отдельные точки окружности. Если окружность определена как
множество точек, удовлетворяющих уравнению
z2 + У2 = 1 (1)
в плоскости х, у, то каждая точка может быть задана указанием ее координат
х и у. Однако такое описание неудовлетворительно по двум причинам. Преж-
де всего излишне задавать обе координаты х п у. Если х задано, то, решая
уравнение (1), мы получим для у (самое большее) два значения. Далее, как
только мы отойдем от «плохих» точек х = ±1, выбор значения у0 при данном
х0 (т. е. выбор между ±~|/1 — го) однозначно определит у в окрестности i0
по непрерывности. Короче говоря, окружность есть «одномерный» объект
и для ее описания не требуются два параметра. Второе возражение состоит
в том, что эти координаты зависят от положения окружности на плоскости.
Если мы хотим изучать окружность саму по себе, а не как множество точек
на плоскости, мы должны найти ее инвариантное описание. После минутного
размышления мы придем к выводу, что преодолеть первую из этих трудностей
невозможно. Один-единственный параметр не может удовлетворительным
образом описывать всю окружность. Возможно, наилучшая попытка заклю-
чается в использовании полярного угла. Но в этом случае нулевой угол
ведет себя плохо: функция, сопоставляющая каждой точке соответствующий
угол, не непрерывна в нуле. Выход из положения — отказаться от попытки
построения единого параметра, описывающего всю окружность, и довольст-
воваться несколькими параметрами для разных кусков. Мы хотим, чтобы
эти параметры были согласованы с топологией окружности (определенной,
скажем, как факторпространство вещественных чисел по целым). Эта топо-
логия позволяет узнать, какие функции на открытых подмножествах окруж-
ности непрерывны. Заданное представление окружности в виде факторпро-
странства позволяет также решить, какие функции дифференцируемы. Фак-
тически на любом собственном открытом подмножестве окружности мы можем
пользоваться вещественным (угловым) параметром. Функция f называется диф-
ференцируемой на таком подмножестве, если она дифференцируема как
функция этого параметра. Легко видеть, что это определение не зависит от
аддитивной константы, входящей в выбор углового параметра. Поэтому тре-
бование определенной гладкости позволяет выделить некоторый класс функ-
§ 1. Определения
4i
ций: например, мы можем говорить о классе функций с непрерывными про-
изводными всех порядков. На открытом интервале окружности мы можем
использовать в качестве параметра любую функцию класса С°° при условии,
что ее производная по угловому параметру не обращается в нуль. Таким обра-
зом, окружность покрывается интервалами, в каждом из которых имеется
свой параметр или координата. Если два интервала пересекаются, то замена
координат определяется функцией класса С°° с не обращающейся в нуль
производной. Итак, абстрактная окружность 51 есть топологическое простран-
ство вместе с некоторым классом функций и координатными интервалами,
координаты в которых надлежащим образом согласованы. Единичную окруж-
ность (1) в плоскости х, у мы рассматриваем как 51 вместе с отображением
окружности S1 в плоскость х, у, заданным формулой х () = cos (•),</ (•) =
= sin (•). Теперь мы перейдем к общим определениям.
§ 1. ОПРЕДЕЛЕНИЯ
Мы хотим изучать топологические пространства, которые
локально ведут себя как евклидовы пространства.
Определение 1.1. Хаусдорфово пространство М со
счетной базой называется п-мерным многообразием, если оно
локально гомеоморфно re-мерному евклидову пространству Rn х).
Под локальной гомеоморфностью мы подразумеваем, что каж-
дая точка х £ М обладает окрестностью, гомеоморфной Rn (или
открытому подмножеству в Д"). Теперь мы присоединим к топо-
логии в М специальный класс функций.
Определение 1.2. Дифференцируемая структура клас-
са Ch (аналитическая структура) на re-мерном многообразии М
есть набор ер вещественных функций, каждая из которых опре-
делена на открытом подмножестве в М, причем выполнены сле-
дующие условия:
1) если U с V и фуцкция / £ ер определена на V, то ограниче-
ние / на U принадлежит ер (f \ U £ ер)',
2) если U = (_J Ua, f определена на U и / | Ua С для всех
а, то / £ ер-,
3) для каждой точки р £ М имеются ее окрестность U и такой
гомеоморфизм h окрестности U на открытое множество в Rn, что
функция /, определенная на открытом подмножестве в U, при-
надлежит ере тогда и только тогда, когда / ° /г-1 как функция
п вещественных переменных есть функция класса Ск (аналитиче-
ская функция).
:) Через Rn всюду обозначается «-мерное арифметическое векторное
пространство над полем вещественных чисел R, а через Еп — то же про-
странство, снабженное стандартной евклидовой метрикой.— Прим. ред.
42
Гл. II. Дифференцируемые многообразия
Функции из jzr называются функциями класса Ck (аналитиче-
скими функциями) на многообразии. До конца этой главы мы будем
пользоваться словом «дифференцируемое» вместо «класса Ck» или
-«аналитическое» (в соответствии с рассматриваемым случаем)
в тех ситуациях, где доказательство одинаково проходит для
любых условий дифференцируемости. Первые два условия тре-
буют, чтобы ограничения и объединения функций из ер являлись
допустимыми операциями. Третье условие требует, чтобы любая
функция / g ер была дифференцируемой в некоторой «системе
координат». Уточним это понятие. Предположим, что гомеомор-
физм h из условия 3) задается п вещественными функциями
х1 (), . . ., хп (•), определенными на U х). Если / — функция,
определенная на U, то / ° h~x можно записать в виде
foh-^f(x\ (1.1)
Условие 3) означает, что /(EjF тогда и только тогда, когда пра-
вая часть в (1.1) есть дифференцируемая функция своих аргу-
ментов. В частности, жг(-)£^. Пусть U' — другая окрестность
точки р и h' — ее гомеоморфизм на Rn. Положим V = U Q U'
и обозначим, допуская некоторую небрежность, ограничения
функций h и h' на V теми же буквами. Тогда h' о h~x есть гомео-
морфизм h (V) на h'(V), задаваемый формулой
х'* = х'1 (ж1, ..., жп), (1.2)
причем функции в (1.2) дифференцируемы. Для мы можем
написать
/о?1'-1 = /(Ж'1, ...,х’п). (1.3)
Подставляя (1.2) в (1.3), получаем
f(x\ ...,xn) = f'(x’x(xx...жп), ...,х'п(х\ ...,ж")). (1.4)
Формула (1.4) устанавливает связь между «представлениями»
функции / в двух системах координат. В частности, мы можем
выразить функции xl°h'~1 в виде
х' oh'-1 =х1 (ж'1, ..х,п) (1.5)
и, подставив их в (1.4), получить тождество
х1 = xi (ж'1 (ж1, ..., жп), ..х'п (ж1, .. ., жп)). (1.6)
1) Здесь i1, ..., хп— стандартные координатные функции на Rn. Таким
образом, для p£U мы имеем h (р) = ii (h (р)), ..., хп (h (р)). Поэтому мы
должны были бы писать х1 (к (•)) вместо г1 (•) Мы предпочитаем опускать h,
если невозможны недоразумения.
$ 1. Определения
43
Если мы возьмем матрицы Якоби от обеих частей тождества (1.5),
то получим
(1-7)
Отсюда
1(ё)Н
(1-8)
С другой стороны, предположим, что задано множество дифферен-
цируемых функций (1.2), удовлетворяющих условию (1.8) в точке
х1 (р), . . ., хп (р). Теорема о неявной функции (см. приложе-
ние 1) гарантирует тогда существование п дифференцируемых
функций (1.5), удовлетворяющих (1.6) в некоторой окрестности W
точки х1 (р), . . ., хп (р). Сравнивая эти функции с h, мы получим
гомеоморфизм h', отображающий W = h~x (И7) на открытое под-
множество из R\ причем h' обладает свойствами, требуемыми
в условии 3) определения 1.2.
Определение 1.3. Открытое множество W и гомеомор-
физм h, удовлетворяющий условию 3) определения 1.2 (относи-
тельно дифференцируемой структуры ^), называются соответ-
ственно координатной окрестностью и координатным отображе-
нием. Если h (р) = (х1 (р), . . ., хп (р)), то функции х' ( • ) назы-
ваются локальными координатами.
В соответствии с определением 1.2 каждая точка многообра-
зия М обладает координатной окрестностью U с координатным
отображением h. Множества {£7} образуют открытое покрытие
многообразия М. Благодаря предположению о счетности мы
можем выбрать счетное подпокрытие {£/;} с координатными ото-
бражениями {ht}. Предыдущие рассуждения (примененные
к Р € П Uj, V = Ut П Uj) показывают, что отображение
hi ° hj1 задается п дифференцируемыми функциями с не обращаю-
щимся в нуль якобианом.
Мы можем использовать координаты для определения диффе-
ренцируемой структуры. Предположим, что заданы счетное покры-
тие {Uj} многообразия М и такой гомеоморфизм hj каждого Uj
в n-мерное евклидово пространство, что отображения hi ° hj1
задаются п дифференцируемыми функциями с не обращающимся
в нуль якобианом. Мы можем тогда рассмотреть набор g всех
функций /, определенных на открытых подмножествах любых Uj
и таких, что функции / □ TiJ1 дифференцируемы. Если / определена
на подмножестве из Ui f) Uj и функция / о Tij1 дифференцируема,
то и функция
/ ° hi1 = f ° hJ1 о hj о hl1
44
Гл. II. Дифференцируемые многообразия:
дифференцируема, поскольку /г, °/г?1 — дифференцируемое пре-
образование. Набор § удовлетворяет условию 3) определения 1.2.
Любая дифференцируемая структура, содержащая .^, должна
по условию 1) содержать всякую функцию /, ограничения которой
на все Uj принадлежат S. Пусть sp есть набор всех таких функ-
ций. Очевидно, .У—минимальная дифференцируемая структура,
содержащая ‘Л. Итог нашим рассуждениям подводит
Теорема 1.1. Пусть М есть п-мерное многообразие и —
дифференцируемая структура на М. Тогда существуют счетное
открытое покрытие {{/7} многообразия М и множество таких
гомеоморфизмов hj окрестностей U, на открытые подмножества
пространства Rn, что отображения ht ° /гу1 задаются п диффе-
ренцируемыми функциями с не обращающимся в нуль якобианом.
Обратно, если задано такое открытое покрытие и такие отобра-
жения hj, то существует единственная минимальная дифферен-
цируемая структура , для которой Uj являются координатными
окрестностями, a hj — координатными отображениями.
Определение 1.4. Многообразие М вместе с дифферен-
цируемой структурой sp называется дифференцируемым много-
образием.
В тех случаях, когда невозможны недоразумения, мы будем
опускать рр и обозначать дифференцируемое многообразие одной
буквой М.
Определение 1.5. Пусть U — открытое подмножество
многообразия М, и пусть h — взаимно однозначное отображение
множества U в Rn. Пара (U, h) называется координатной кар-
той1), если ht °/г-1 есть дифференцируемое отображение множе-
ства h (С7 П U;) на hi (U ()Ui), якобиан которого нигде не обра-
щается в нуль. [Здесь ht и U; те же, что в теореме 1.1.]
Условие, что (U, h) есть карта, очевидно, не зависит от набора
(Ui, hj), а зависит только от дифференцируемой структуры много-
образия М.
Функции х1 о h (где (х1, . . ., хп) — координаты в Rn) назы-
ваются координатами карты (U, h). Если нет опасности путаницы,
мы будем обозначать эти функции через х1 и писать h (х1. . . .
. . ., х7’), чтобы показать, что h (р) — (х1 (р), . . ., хп (р)) g Rn
для всех р g U.
Определение 1.6. Набор карт (Uhi), такой, что
7И = Ut, называется атласом многообразия М.
') А также локальной системой координат.— Прим, перев.
$ 1. Определение
45
Упражнение 1.1. Пусть 3h—дифференцируемая структура клас-
са С'1 на многообразии М. Показать, что для I <^к существует единствен-
ная минимальная структура IF1 класса С1, такая, что X13) .Fh. [Верно
также обратное утверждение: если задана структура .Х( класса С1, то для
к > I существует такая структура класса Ch, что .'Х( есть единственная
минимальная структура, содержащая в этом утверждении можно даже
положить /с=оо. Этот результат принадлежит Уитни [19]. Он опирается
на теорему вложения, часть которой мы докажем позднее, см. тео-
рему 4.1.]
Если 7l7t и М2—многообразия размерности соответственно пх
и п2, то Mi X М2 есть многообразие. Действительно, если PjC
и U2 сх М2 гомеоморфны открытым подмножествам в Rni и Rn~,
то X U2 гомеоморфно открытому подмножеству в 7?’11+"2. Пред-
положим, что 3Ri и .F2 — дифференцируемые структуры на
и М2. Пусть {t7jД и {U2j} — покрытия и М2 координатными
окрестностями с координатными отображениями /г^ и h2j. Тогда
множества {Uц X V2j} образуют открытое покрытие многообразия
Mi X М2. Отображение hip. UnXU2j—> 7?"1+’12, определенное фор-
мулой
q)--=ha (р) х/г2;(Д,
является гомеоморфизмом. Кроме того, = /г1;о/г^ Х/г2;°^2/
есть, очевидно, дифференцируемое отображение с ненулевым
якобианом. Поэтому система окрестностей {U^xU^} и отображе-
ний htj определяет дифференцируемую структуру на х М2. Эта
структура называется произведением структур JTj и jr2. Много-
образие Mi X М2 с этой дифференцируемой структурой называется
произведением дифференцируемых многообразий Мх и М2.
Примеры дифференцируемых многообразий
1. Евклидово пространство Rn (или любое его открытое
подмножество), очевидно, является дифференцируемым многообра-
зием. Оно покрыто единственной координатной окрестностью.
2. Пусть Sn (//-мерная сфера) — множество всех точек из Rn+1,
удовлетворяющих условию
(^)2 + . . . 4-(я"+1)2 = 1.
Пусть Ut обозначает подмножество в Sn, где х1 > 0, a Up—под-
множество, где хг < 0. Возьмем в качестве координат на U±
остальные х1. Легко проверить, что U± покрывают Sn и коорди-
натные отображения удовлетворяют требуемым условиям.
3. Пусть Tn = S1xSLx . • . X S1 (п раз). Многообразие Тп
называется и-мерным тором.
4. Пусть Т (тп, п) — пространство всех (тп х п)-матриц. Тогда
Т (тп, п) можно рассматривать как Rmn и, следовательно, считать
46
Гл. II. Дифференцируемые многообразия
аналитическим многообразием. Пусть Т (т, п; к) обозначает про-
странство всех (m X и)-матриц ранга к (где 0 < к Д min (т, п))
с индуцированной топологией. Тогда Т (т, п; к) есть аналитиче-
ское многообразие размерности к (т -|- п — к). Действительно,
пусть Хо 6 Т (т, п). Если ранг Хо к, то существуют такие
матрицы подстановок координат Р и Q, что
Мо
^0<2=г
\G0
Dq) ’
где Ao — невырожденная матрица порядка к. Далее, существует
такое е > О, что если все элементы матрицы А — Л о меньше е,
то матрица А невырожденна. Пусть U* — множество тех
X £ Т (т, п), для которых
/Л В\
= L , (1.9>
\С/ /У /
где все элементы матрицы Л —Л о по модулю меньше е. Тогда
U* — открытое множество в Т (т, п). Если X £ U*, те
X g Т (тп, п; к) тогда и только тогда, когда D = СЛ-1В. Чтобы
убедиться в этом, заметим, что матрица
/ Ik 0 \ (А В\ /А В
V-СЛ-1 £7 = \.О -CA^B + D
(1.10)
/Л В\
и матрица I „ I,
/ h
поскольку матрица I _ ._1
\ -------------------- (у
(где Ij — единичная матрица порядка у) имеет тот же ранг, что
0 \
I невыро-
га—k/
жденна; но матрица в правой части (1.10) имеет ранг к тогда
и только тогда, когда D = СА~1В. Возьмем в качестве коорди-
натной окрестности точки Хо £ Т (т, п; к) множество U = U* [~|
П Т (т, п; к), открытое в индуцированной топологии. Определим
координатное отображение h, полагая
/л в\
fe(X) = ^c (1.11)
(m—(n—h)
где мы рассматриваем евклидово пространство п =
/Л В\
= ph^m+n~h') как прОСТранство всех матриц вида I. Ото-
бражение hr1 задается формулой
(А В\ (А В \
оН'Чс сл-'вуг- <1Л2>
§ 2. Дифференцируемые отображения
47
Функции перехода h' oh1 для двух перекрывающихся окрест-
ностей U и U' задаются формулой
(А В
(с о
А'
С'
В'\
о ) ’
(1.13)
где
А В \ г /А' В'\
С CA^BJ^ 1Q' = \С' D')’
(1.14)
Поскольку все матрицы, входящие в (1.13), являются аналитиче-
скими (и даже рациональными) функциями своих аргументов
(так как А невырожденна), координатные окрестности и ото-
бражения определяют на Т (т, п; к) аналитическую структуру
размерности к (т 4- п — к).
5. Пусть (т, V) — множество всех упорядоченных набо-
ров т линейно независимых векторов в вещественном н-мерном
векторном пространстве V (т, V) называется пространством
т-реперов пространства V]. Тогда jr (т, V) есть дифференцируемое
многообразие размерности тп. Действительно, выбор базиса про-
странства V позволяет отождествить (т , V) с Т (т, п; т).
6. Пусть V есть re-мерное векторное пространство и & (р, V) —
множество р-мерных подпространств из V. Мы утверждаем, что
У (р, V) можно превратить в аналитическое многообразие (грас-
сманово многообразие пространства V) размерности р (п — р).
В самом деле, пусть и1*, ...,ип* — базис V*. Если v*£V*
и Е £ & (р, V), то через Ре мы будем обозначать ограничение и*
на Е. Обозначим через U11’ ’'' ’tp (1 < Д < i2 < ... мно-
жество тех p-плоскостей Е, для которых векторы ум*, .yW
линейно независимы. Пусть (Д, . ..,Д_р)—множество индексов,
дополнительное к (Д, . . ., гр), причем Д < . • • < jn-р- Тогда
р
г/ = »
если Е Q U11’ ‘’г,). Пусть Фч....,р: [7’ь ’ ’ ” гр —> 7?р (п-₽)— ото-
бражение, сопоставляющее каждому подпространству Е коэффи-
циенты (ha). Отображения Ф4’ ' ’' ’1р взаимно однозначны. Они опре-
деляют на ‘S (р, V) структуру аналитического многообразия. Доказа-
тельство этих фактов мы оставляем читателю в качестве упражнения.
§ 2. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ
Пусть <р — некоторое отображение АД—>М2. Для любой
функции Д определенной на подмножестве IV с М2, определим
функцию <р* (/) на ср-1 (И7), полагая
Ф*(/) (•) = /<’<₽(•)• (2-1)
48
Гл. II. Дифференцируемые многообразия
Таким образом, ср* отображает пространство функций, определен-
ных на подмножествах из М2, в пространство функций, опреде-
ленных на подмножествах из Mi.
Определение 2.1. Пусть У1И^2 — дифференцируемые
структуры класса С,с (аналитические), определенные на много-
образиях Мх и М2. Непрерывное отображение ср: Мх -> М2 назы-
вается дифференцируемым класса Си (аналитическим), если
<р*(^2)сл. (2.2)
Пусть ф: ТИ2-> М3. Из (2.1) следует, что (ф ° ср)* -- ср* оф*.
Поэтому мы можем утверждать, что если ср: Mi —>- Л/2 и ф: М2 -+
->- М3 дифференцируемы, то дифференцируемо и ф о ср: Mi —> М3.
Пусть размерность М} равна ге;, и пусть (U, К) — координат-
ная карта вблизи точки ср (р), где р £ Mi. Ее координаты задаются
п2 дифференцируемыми функциями у1 ( • ) на U. Если отображе-
ние ср: Mi ->• М2 дифференцируемо, то у1 о ср — дифференцируе-
мые функции на Mi. В терминах координатной карты (F, g),
g -- (ж1, . . ., xni), вблизи точки р отображение ср (или, точнее,
А ° ср о g-1) задается формулой
уг = (рг (ж1, .. ., ж”1) (г = 1, . ..,/г2), (2.3)
где срг — дифференцируемые функции. Обратно, предположим,
что задано непрерывное отображение ср, которое вес всех парах карт
имеет вид (2.3). Функция / на М2 дифференцируема тогда и только
тогда, когда ее ограничение на любую координатную окрестность
дифференцируемо по координатам. Но в терминах карты (У, g)
(<₽*/) ° g'1 (21, • • » ХП1( ~ f (У1 (^S • • • > Ж"1), • • 7 УП2 (Х\ • • • , Ж711)).
(2.4)
Поэтому функция ср*/ дифференцируема в терминах любой карты,
и, значит, отображение ср дифференцируемо.
Вид (2.3) отображения 7г ° ср ° g-1 зависит от выбора локаль-
ных карт h в М2 и g в Mi. Чтобы получить выражение для ср
в любой другой паре карт, следует выполнить невырожденные
преобразования переменных у и ж. Поэтому нас интересуют те
выражения, полученные из (2.3), которые инвариантны относи-
тельно таких преобразований. Одним из таких объектов является
ранг х) якобиевой (nt X ге2)-матрицы
!) Он называется рангом отображения с? в точке р = g-1 (х1, . . ., хП1).
Прим. ред.
§ 2. Дифференцируемые отображения
49
Предположим, что матрица (2.5) имеет ранг к в точке рЕЛ/р
Можно считать, перенумеровав, если понадобится, координаты,
что
1(5)к° ..ч
(2-6)
в точке р. Рассмотрим функции и1, определенные в окрестности
точки р равенствами
и" (х1, . . ., x"i) = сра (х1, . .., а.”1) (а = 1, ..., /г),
иг = хг (г = Л-|-1, ...jflj).
Согласно (2.6), якобиан | (диЧдх1) | отличен от нуля в точке р.
Поэтому формула (2.7) определяет координатную карту вблизи р.
В терминах этой карты отображение ср задается функциями
ф1, . . ., ф"2, где
фа (и1, . . ., ипу) = иа (а = 1, ..к). (2.8)
Поскольку ранг ср в точке р равен к, он должен быть > к в некото-
рой окрестности точки р. Если он равен к в некоторой окрест-
ности точки р, то мы можем сказать несколько больше. Из урав-
нения (2.8) следует, что д^г/ди* е= 0 для г, s > к. Действительно,
матрица Якоби имеет вид
О . . О 1 0 . . О
duh+l
дф"2
\ : duni j
Если какой-нибудь элемент в правом нижнем углу отличен
от нуля, то ранг будет больше к. Мы можем поэтому написать
фг = фг (и1, ..., и'1). Введем новые функции z1, .. zn2, определен-
ные в некоторой окрестности точки ср (р) формулами
zu = у- (а = 1, ..., к),
zr = —^г (У1, , Ук) (г = к 4-1, . . ., п2).
5(1
Гл. JГ. Дифференцируемые многообразия
Непосредственная проверка показывает, что формула (2.9) опре-
деляет замену координат вблизи <р(р) и в терминах новых коор-
динат отображение <р задается формулой zL = if (u1, ип'), где
ti“ (и1, . . ., w"i) = иа (а = 1..... Л),
< (п1, ..., м«1) = 0 (г>Л). (2Л0)
Таким образом, если ранг дифференцируемого отображения <р
в точке р равен к, то мы можем найти такие карты (У, g),
g= (х1, . . ., xni), вблизи р и (U, h), h — (у1, . . ., у”2), вблизи ср (р),
что уго(р= (ср1, ...,(рп2), где
(р“ (ж1, . . ., а:"1) = x‘l (а = 1, . .., Аг). (2.11)
Если ранг <р равен к в некоторой окрестности точки р, то
можно добиться, чтобы
<pr (х\ . . ., хП1) — 0 для r>k. (2.12)
Особый интерес для нас представляют некоторые специальные
виды отображений.
Определение 2.2. Дифференцируемое отображение
<р: Mi -> М2 называется погружением, если ранг ср равен размер-
ности Mi во всех точках многообразия Mi.
Заметим, что погружение взаимно однозначно локально, но
не обязательно глобально.
Определение 2.3. Погружение ср называется вложением,
если оно является гомеоморфизмом на свой образ (в индуциро-
ванной топологии).
Таким образом, вложение есть взаимно однозначное погруже-
ние, но не всякое взаимно однозначное погружение есть вложение.
На рис. 2 Mi = Е1 — прямая линия, а М2 = Ег — плоскость.
Тогда (а) не является погружением (из-за острия), (Ь) есть не
взаимно однозначное погружение, (с) есть взаимно однозначное
погружение, но не вложение, (d) — вложение.
Определение 2.4. Отображение ср называется собствен-
ным, если ср-1 (К) компактно для любого компактного К ел М2.
Вложение, которое является собственным отображением, назы-
вается собственным вложением.
Ни одно из отображений рис. 2 не является собственным.
Если Mi компактно, то любое дифференцируемое отображение
является собственным.
Упражнение 2.1. Показать, что собственное взаимно однознач-
ное погружение является собственным вложением.
§ 2. Дифференцируемые отображения
51
В соответствии с различными типами отображений мы введем
различные типы подмногообразий.
Определение 2.5. Пусть М — дифференцируемое мно-
гообразие и N — подмножество в М, снабженное структурой диф-
ференцируемого многообразия. Пусть t: N -+ М — вложение
(ограничение на N тождественного отображения М -> М). Тогда
N называется погруженным подмногообразием, если i — погру-
жение; .V называется подмногообразием, если i — вложение;
N называется замкнутым подмногообразием, если t — собственное
вложение1).
Заметим, что для погруженного подмногообразия N индуци-
рованная на N топология не обязана совпадать с топологией N
как дифференцируемого многообразия.
!) Легко видеть, что N замкнутом в М в топологическом смысле тогда
и только тогда, когда i — собственное отображение.— Прим. ред.
52
Гл. II. Дифференцируемые многообразия
Определение 2.6. Дифференцируемое отображение мно-
гообразия Mi на М2 называется диффеоморфизмом, если оно само
и обратное к нему отображение являются вложениями. Два много-
образия Мх и М2 называются диффе о морфными, если существует
диффеоморфизм Mi на М2.
Упражнение 2.2. Пусть Mi — вещественная прямая с диффе-
ренцируемой структурой, состоящей из всех функций вида f (xs), где /—
функция класса С00. Пусть М2 — вещественная прямая с обычной структурой
класса С°°. Показать, что тождественное отображение Е1 -> Е' есть гомеомор-
физм М2 -* Mi класса С°°, не являющийся диффеоморфизмом.
Упражнение 2.3. Пусть N — погруженное подмногообразие диф-
ференцируемого многообразия М. Показать, что каждая точка из N обладает
такой окрестностью т) U, что множество дифференцируемых функций мно-
гообразия N, определенных на U, совпадает с множеством ограничений на U
дифференцируемых функций многообразия М. Таким образом, дифференци-
руемая структура погруженного подмногообразия определяется дифферен-
цируемой структурой многообразия М.
_ Упражнение 2.4. Пусть N — подмножество в М. Показать, что
N есть множество точек некоторого подмногообразия тогда и только тогда.
когда любая точка р с N обладает такой окрестностью U в М с координатами
г1, . . хп, что N П U совпадает с множеством точек, для которых хР =
= zP+J = . . . = хп = 0.
Упражнение 2.5. Пусть /V CZ М. Показать, что необходимое и до-
статочное условие того, что N есть замкнутое подмногообразие в М, состоит
в существовании покрытия М такими координатными окрестностями {1/а},
что тогда и только тогда, когда х*. (р) =...= х^ (р) = 0, где
х?, ..., х”—локальные координаты в Ua.
Упражнение 2.6. Показать, что Г (т, п; к) есть подмногообразие
в Т (т, п) (где Т (т. п; к) определено в упражнении 1.4).
Упражнение 2.7. Показать, что отображение л: Д (т, У) ->
-» (т, V), сопоставляющее каждому набору (щ, . . ., подпространство,
порожденное векторами vi, . . ., v4, дифференцируемо.
Упражнение 2.8. Показать, что отображение Т (т. п) х Т (п, р) -»
-» Т (т, р), определяемое умножением матриц, дифференцируемо
Для построения дифференцируемых многообразий полезна
следующая \
Теорема 2.1. Пусть М — некоторое множество, {Uг} —
?го счетное покрытие, {<рг} — набор взаимно однозначных отобра-
жений множеств U г на дифференцируемые многообразия Mt,
причем
) В топологии Л' как дифференцируемого многообразия,— Прим, перев.
f 3. Теорема Сарда
53
1) для любой пары точек р, q £ М либо q и р содержатся в неко-
тором UI, либо существуют такие множества Ut и Uj, что
fl И Uj = 0, р Е Ut, q Е Uj;
2) ср, (Ut П Uj) — открытое подмножество в Mt для всех i, j;
3) ср7-о ср?1 есть диффеоморфизм многообразия срг (Ut П Uj)
на <р7- Uj) для всех i, j.
Тогда существует единственная (топология и) дифференци-
руемая структура на М, для которой Ut открыты, а срг — диф-
феоморфизмы окрестностей Ut на Mt-
Доказательство. База топологии М состоит из мно-
жеств вида ср?1 (7), где V — открытое подмножество в Mt. Усло-
вия 2) и 3) гарантируют, что такие множества действительно
образуют базис некоторой топологии. Поскольку топология
обладает счетным базисом, то же верно и для топологии М. Усло-
вие 1) обеспечивает хаусдорфовость топологии М. Действительно,
если р Ф q g Ut, то срг (р) и срг (q) имеют непересекающиеся окре-
стности Vp и Vq; тогда срг1 (Vp) и срГ1 (PQ) — непересекающиеся
окрестности точек р и q. Если р g U t, q g Uj и Uj Q Ut = 0,
to Ut и Uj — непересекающиеся окрестности точек p и q. Если
p £ Ui, выберем координатную окрестность V точки срг (р). Тогда
ср?1 (7) есть окрестность точки р, гомеоморфная открытому под-
множеству в Еп. Таким образом, М есть многообразие. Назовем
функцию / на М дифференцируемой, если / ° ср!1 — дифференци-
руемые функции на Mi для всех i. Класс ер всех таких функций
определяет (снова благодаря 2) и 3)) дифференцируемую структу-
ру. Отображения ср; дифференцируемы: если / — дифференцируе-
мая функция на ЛД, то / о срг о еру1 есть дифференцируемая функция
на Mj, согласно 2). Отображения ср!1 дифференцируемы по опре-
делению. Единственность топологии и дифференцируемой струк-
туры ясна из предыдущего.
§ 3. ТЕОРЕМА САРДА
Пусть задано дифференцируемое отображение ср: Мп* -> Мп^.
Ранг отображения ср не может превосходить минимум из чисел п,
и п2. Если Hj <Z п2, то мы можем ожидать, что образ многообра-
зия Mni в ЛГ'2 будет объектом «меньшей размерности»; точка «обще-
го положения» из Мп* не лежит в ср (М”1}. Оказывается, что неза-
висимо от того, каковы числа Hj и п2, точки общего положения из
Л/п2 не являются образами точек из 7Ипс, если только ранг ср
меньше, чем п2. Чтобы сформулировать понятие «общего положе-
ния», введем определение множества меры нуль.
Определение 3.1. Множество А с Еп называется мно-
жеством меры нуль (обозначается mes А = 0), если для любого
54
Гл. II. Дифференцируемые многообразия
8 > 0 существует такая последовательность шаров Bsr, что
1) A cz J вг,
Г=1
2) 2JvolBr<e.
[Шар есть множество точек вида {х | || х — у || < 6} для некото-
рых у и 6, где || || — евклидово расстояние. Под vol Bf мы пони-
маем обыкновенный евклидов объем.] Сделаем несколько очевид-
ных замечаний.
Если Л cr U Ак и mes Ак = 0, то mes А = 0. (3.1)
k=t
Действительно, для любого 8 > 0 выберем шары Вк,г, покрываю-
щие Ак и такие, что У vol r<Ce/2fe. Тогда Вк,г образуют счет-
ное покрытие множества А и 3 V°1 Вк: r < е.
k, г
Если ср есть отображение класса С1 окрестности
множества А в Еп и тезЛ = 0, то mes ср (Л) = 0.
Для доказательства мы можем считать, что Л содержится в неко-
тором компактном множестве. Действительно, если это не так,
мы можем представить Л в виде счетного объединения компактов
(скажем Л Q {х | || х || < п}) и применить (3.1). Для таких Л
отображение ср удовлетворяет равномерному условию Липшица
II ср (х) — ср (у) II < ц II х — у ||. (3.3)
Для любого е > 0 покроем Л такими шарами Вк, что У, vol Вк <
< е/р". Согласно (3.3), ср (Sft) лежит в некотором шаре Ск, радиус
которого в рс раз больше радиуса Вк. Значит, ср (Л) cz Ск
и У vol Ск < е.
Упражнение 3.1. Всякое счетное множество имеет меру нуль.
Упражнение 3.2. Показать, что в определении множества меры
нуль мы могли использовать покрытие любыми открытыми множествами,
не обязательно шарами, т. е. это определение можно сформулировать так:
если для любого е > 0 множество А может быть покрыто последователь-
ностью таких открытых t/), что 2 vol < е, то mes А = 0.
Определение 3.2. Говорят, что подмножество Л диф-
ференцируемого многообразия имеет меру нуль (mes Л = 0),
если А = гДе каждое Ап лежит в некоторой координатной
£ 3. Теорема Сарда
55
окрестности Un с координатным отображением фп и (рп (Лп) имеет
меру нуль.
Согласно (3.1) и (3.2), это определение не зависит от выбора
разложения множества А на Ап и от выбора Un, так как для любой
координатной окрестности V и координатного отображения ф
множество^ (FQ Л) имеет меру нуль. Кроме того, из (3.2) и опре-
деления 3.2 следует такое утверждение:
Если ср: Д/”—>М”— отображение класса С1, .
то mes ср (Л) = О всякий раз, когда mes П О. '
Если ЛсЧЛ,, и тезЛп = 0, то тевЛ = 0. Из этого замеча-
ния следует
Л е м м а 3.1. Пусть А — подмножество многообразия М.
Если каждая точка р £ М обладает такой окрестностью Up,
что mes (£7Р["| Л) = 0, то mes А — 0.
Действительно, поскольку топология в М имеет счетную базу,
мы можем заменить множества {Up} счетным набором {С7г}.
Тогда А = U (И П Ut) и mes (A Q U t) = 0.
Упражнение 3.3. Показать, что множество точек из Еп,
для которых жй+1 = . . . = хп = 0, имеет меру нуль (если к < п).
Упражнение 3.4. Пусть /: М2 — отображение класса С1.
Предположим, что ранг f = к < dim М2. Тогда mes / (Л//) = 0. [Исполь-
зовать (2.12) п упражнение 3.3.]
Определение 3.3. Пусть /: Мг ->• Л/2 — отображение
класса С1 и dim (М;) = nt. Точки из Мг, в которых ранг f < п2,
называются критическими точками f. Остальные точки из Mi
называются регулярными. Точка q g М2, для которой /-1 (д)
содержит по меньшей мере одну критическую точку, называется
критическим значением. Остальные точки из М2 называются
регулярными значениями.
Замечания. Если dim < dim М2, то все точки из Mi
критические. Заметим также, что если точка х £ М2 не лежит
в / (Mi), то х — регулярное значение, т. е. в нашей терминологии
точки, не являющиеся значениями, всегда будут регулярными
значениями.
Упражнение 3.5. Показать, что если у — регулярное значение
из М2, то либо /-1 (р) есть подмногообразие размерности га, — п2 в М2, либо
/-1 (у) пусто.
56
Гл. II. Д ифференцируемые многообразие
Сформулируем теперь теорему Сарда.
Теорема 3.1 г). Пусть и М2 — многообразия класса Ch
размерностей соответственно и п2 и f: Mi -> М2 — отображе-
ние класса Ch. Критические значения отображения f образуют
множество меры нуль, если
к — 1 max («! — п2, 0). (3.5)
Замечания, (а) Если щ < п2, теорема тривиальна (см.
упражнение 3.4). (Ь) Хотя теорема сформулирована для произ-
вольных дифференцируемых многообразий, из определения 3.2
ясно, что доказательство достаточно провести для случая, когда
.1/ 2 — евклидово пространство, Mi — подмножество единично-
го куба
C’ = {zC£ni|0<a:i<l},
а / — отображение класса Ск некоторой окрестности куба С в Е"2.
В случае nt = п2 теорема легко доказывается. Разберем его
в первую очередь:
Л е м м а 3.2. Пусть ср = (ср1, . . ., ср”) — отображение куба
С сг Еп в Еп, причем каждая функция ср1 определена и принадлежит
классу С1 в некоторой окрестности куба С. Тогда множество
критических значений отображения ср имеет меру нуль.
Доказательство. Для любых двух точек х = (х1, . . .
. . ., хп) и у = (у1, . . ., уп) из С имеем, согласно теореме о сред-
нем,
п
срЧ</)-тЧ*) = 2 (з.б)
0x1
з=1
где z! — некоторая точка отрезка, соединяющего х с у. Мы выве-
дем отсюда два следствия. Во-первых, поскольку дцМдх3 ограни-
чены в С, мы можем найти равномерную константу Липшица а,
для которой
||ср(у) — ср (ж) |] < а II ж — у\\. (3.7)
Во-вторых, пусть Тх обозначает аффинное отображение, касатель-
ное к ср в х, т. е.
Тх (у) = (Т1х(у), ..., Тх (у)),
Ч Для многих приложений достаточен частный случай теоремы Сарда,
когда П] = п2, т. е. лемма 3.2. При первом чтении читатель может опустить
«трудную» часть (т > га2) теоремы Сарда и приступить прямо к § 4. В этой
кнпге теорема Сарда для nj > п2 будет использована только для теорем
4 5 и 4.6.
§ 3. Теорема Сарда
57
где
п
Тх(у) = ср; (х) + 2 (У3 ~х3)- (3-8)
дх)
3=1
Из (3.6) следует, что
<р4(г/)-П(г/) = 2 (^.(^-^(^W-?). (3.9)
\ дхЭ дх' /
3=1
Поскольку ср g С1, функции dtpVdx1 непрерывны и, следовательно,
равномерно непрерывны в С. Поэтому мы можем найти такую
функцию b (б), что b (б) -> 0 при б -> 0 и
II ср (у) - Тх (у) II < & (II * - У II) II * - У II- (3.10)
Если х — критическая точка, то определитель преобразования Т х
обращается в нуль, и, значит, Тх отображает S'1 в некоторую
(к — 1)-мерную плоскость Рх. Если || у — х || < б, то, согласно
(3.7), || ср (х) — ср (у) || < ае, и, согласно (3.10), расстояние от
ср (у) до Рх меньше, чем еЪ (б). Поэтому ср (у) лежит в пересечении
любого куба с ребром ае и центром в ср (а) с областью, заключенной
между двумя параллельными плоскостями, проходящими на рас-
стоянии еЪ (е) от Рх. Выбирая куб так, чтобы одна из его граней
была параллельна Рх, мы заключаем, что объем этого пересечения
равен 2nan~lEb (б).
Разделим теперь С на рп кубов с длиной ребра 1/р. Любой
куб, содержащий критическую точку х, содержится в шаре радиу-
са У~п/р с центром в х. Образ этого шара имеет объем <^2nan X
X (\^п/р)п b (У п/р). Образы всех кубов, содержащих по крайней
мере одну критическую точку, покрывают множество всех крити-
ческих значений отображения ср. Поскольку существует самое
большее рп таких кубов, полный объем этих образов не превос-
ходит
рп2пап (]Лп/р)п b (]/"п/р) = 2паппп/2Ь (Кп/р). (3.11)
Это выражение стремится к нулю при р —оо, что и доказывает
лемму 3.2.
Посмотрим теперь, что произойдет, когда щ > н2. Все, что
мы говорили, останется в силе, кроме последней оценки (3.11),
которая заменится на
рпс2"2ап2 (]Лзг1/р)П26 ((А^/р) = 2n2an2ni2/2pni-n2^ (pG^/p), (3.12)
поскольку мы теперь имеем рП1 кубов с ребром 1/р в С. Теперь
мы не знаем, да это в общем случае и не верно, что Ъ (8)/eni~n2 -> О
58
Гл. II. Дифференцируемые многообразия
при 8 —> 0. Доказательство основывается на более тщательной
оценке, чем та, которую дает теорема о среднем. Мы хотим пока-
зать, что функция имеет нули достаточно высокого порядка на
своем множестве нулей. Это устанавливает следующая лемма,
принадлежащая Морсу [11].
Лемма 3.3. Пусть А —некоторое подмножество в Еп
00
и — целое число. Тогда A cz Л/, где Ао счетно, а А,
1=0
(г>1) обладают следующим свойством-.
Пусть f — такая функция класса Cq, определенная в окрестно-
сти множества А, что все. точки ua А являются критическими для
/. Тогда существуют такие функции bt (s) (зависящие от f), что
bt (s) монотонно убывают, bt (е) -> 0 при е 0 и для любых
точек х, у А}
\ f &) — f (у) \ < bt (|| х — у ||) || х — у ||«. (3.13)
Для п = 1 лемма очевидна. Действительно, множество А
критических точек функции f есть множество, где /' (х) = 0.
Пусть А о — множество дискретных точек из А. Для любой дру-
гой точки х £ А, х А о имеем f (х) = /(2) (х) = ... = (х) =
= 0, поскольку х есть предел последовательности точек х,
с /' (xt) = 0. Итак, (х) = 0 для х g А — А о и (3.13) следует
из формулы Тейлора. [В качестве At надо взять A[\Kt, где
Kt образуют последовательность компактных множеств, покры-
вающих Л.]
Для размерности п > 1 доказательство несколько сложнее,
поскольку не все частные производные высших порядков обра-
щаются в нуль в предельных точках множества А. Однако если
некоторая частная производная высшего порядка не обращается
в нуль в точке х, то мы можем использовать теорему о неявной
функции и найти такую окрестность N х, что Nx Q Л лежит на
подмногообразии меньшей размерности. Это позволит нам дока-
зать лемму при помощи двойной индукции по q и п.
Во всяком случае, прежде чем дать полное доказательство
леммы 3.3, мы используем ее для доказательства теоремы 3.1.
Сначала докажем следующее утверждение:
Лемма 3.4. Пусть <р = (ср1, . . ., <р"2) — отображение куба
С = {х Q ЕП11 0Са:гС 1} в ЕП2, причем срг—функции класса Cq,
определенные в некоторой окрестности куба С. Пусть А — мно-
жество точек из С, в которых ранг <р равен нулю. Тогда ср (Л)
.имеет меру нуль, если цД-пфщ.
$ 3. Теорема Сарда
59
Доказательство. Разложим А в соответствии с лем-
мой 3.3: 4cU4r. Достаточно доказать, что ср (Лг) имеет меру
нуль. Для r = U это тривиально ввиду счетности Ло; рассмотрим
случай г>1. Отображение ср имеет в точке х ранг нуль тогда
и только тогда, когда х— критическая точка для всех функ-
ций <рг. Согласно (3.13), если х и у^Аг и || х — у j| < е, то
|<Р* (х) — ср1 (у) | < Ъ (б) е«,
или
||(p(z) —<р(у)|| <]Лг26(е)е<?. (3.14)
Поступим теперь, как при доказательстве леммы 3.2. Разделим
С на рп1 кубов Са со стороной 1/р. Согласно (3.14), множество
<р (Аг П Са) лежит в шаре радиуса
Поэтому полный объем множества ср (Лг) меньше, чем
КЪ (3.15)
где К =У П1П2 (]/Hj)9"2 ®п2 [®п2 — объем единичного шара в £П2].
При условии q^njnz мы можем сделать величину (3.15) сколь
угодно малой, выбирая число р достаточно большим. Это доказы-
вает лемму 3.4.
Лемма 3.5. Пусть ср — такое же, как в лемме 3.4, и пусть
А — множество точек, где ср имеет ранг г. Тогда ср (Л) имеет
меру нуль, если q> (п1 — г)/(п2 — г) (0<^г<^п2).
Доказательство. Для г = 0 это лемма 3.4. В силу лем-
мы 3.1 достаточно доказать, что всякая точка из А обладает
такой окрестностью N, что ср (TV Q Л) имеет меру нуль. Пусть
х0£А. Согласно (2.11), мы можем найти окрестность N^x0, коор-
динаты и1, .... и"1 вблизи хй и у1, .. ., г/"2 вблизи <р (х0), такие,
что функции у1 с ср = уг (и1, . . ., и”) имеют вид
уа (и1, .... ипг) — иа (а = 1, . .., г),
а (3.16)
(и1, . . ., и"1) (и1, . . ., и"1) (Р = 1, . .., /?2).
Для любых фиксированных значений и1, . . ., иг отображение
ц: £"1-г—> ЕП2~Г, определяемое формулой
т] (ur+1, . . ., u"1) = F (и1, . . ., ur, ur+1, . .., иП1), (3.17)
60
Гл. II. Дифференцируемые многообразия
имеет ранг нуль, если (и1, .. ., иП1) £ TV Q Л, поскольку ср имеет
ранг г. По лемме 3.4 множество ср (2V П Л) Q иГ имеет
меру нуль в P(Ui, _'Urr тдр Р(и1______иГ) есть (п2 —г)-мерная
плоскость в Еп\ задаваемая уравнениями уа — иа, а = 1, ...,г.
Таким образом, мы доказали, что пересечение множества
ср (Д?ПЛ) с любой плоскостью P(ui иг^ имеет меру нуль.
Для читателей, немного знакомых с теорией меры, тот факт, что
q (2Vn Л) имеет меру нуль, следует теперь немедленно из теоремы
Фубини. Мы дадим, однако, прямое доказательство этого факта.
Заметим прежде всего, что можно считать N компактной окре-
стностью. Поскольку Л замкнуто, множество NПЛ компактно.
Поскольку ср непрерывно, ср (N Л) компактно. Поэтому доста-
точно доказать следующее утверждение:
Пусть В — компактное подмножество в Еп, пересечение кото-
рого с любой плоскостью Р(ui иГ) имеет меру нуль в Р(ц1 иГ).
Тогда В имеет меру нуль в Еп.
Ясно, что, воспользовавшись индукцией, можно свести утверж-
дение к случаю г = п — 1 х).
Мы предпошлем доказательству следующее замечание. Пусть
|а, Ь] — отрезок вещественной прямой. Мы знаем, что из каждого
его открытого покрытия можно выбрать конечное подпокрытие.
Мы хотим доказать более сильное утверждение:
Из любого покрытия отрезка la, М интервалами можно
выбрать подпокрытие, состоящее из интервалов суммарной длины
<2 | Ъ - а |.
Выберем минимальное конечное подпокрытие, т. е. выберем
такие интервалы Ц, ...,1Р из данного покрытия, что [а, ?>] d
р
J Ij, но
;=1
р
[а,Ь]ф U А
i=l, i=#Q
[Э о можно сделать, взяв некоторое конечное подпокрытие
и исключив избыточные интервалы.] Занумеруем интервалы в соот-
ветствии с порядком их левых границ, т. е. It = (at, bt), Ij = (aj, bj),
l<Zi, если at < aj (если а, = а;, покрытие не минимально).
Тогда at ам < b, < bi+l и полная длина перекрывающихся
интервалов не превосходит длины [а, 6]. Поэтому суммарная
длина всех интервалов не больше 2|& — а|.
х) Приведенным ниже доказательством я обязан проф. X. Фурстенбергу.
§ 3. Теорема Сарда
61
Предположим теперь, что В а Еп~1 х [а, Ь] и mes (5|"| Р п) = 0.
Для любого е > 0 мы можем найти покрытие множества В |"| Р п
открытыми множествами Bln cz Рип полного объема < е. Для до-
статочно малого <z множества Blun X Р^ покрывают
5 л и Лю
2пе/и’г
где /“"—интервал длины а с центром в ип. (Это следует из ком-
пактности В.) Множества /“” образуют покрытие отрезка [а, Ь],
из которого мы можем извлечь конечное подпокрытие {/Д длины
<2|6 — а|. Пусть В] обозначает множество В^п, если .Д = /“”.
Тогда В} х Ij образуют покрытие множества В, полный объем
которого — а | е. Поскольку мы можем сделать эту вели-
чину сколь угодно малой, В имеет меру нуль. Это доказывает
лемму 3.5.
Теорема 3.1 следует теперь из леммы 3.5. Если .4 — множество
П2~ 1
критических точек отображения /, то А — Аг, где Аг — множе-
г=0
ci во точек, в которых / имеет ранг г. Множество критических
П2— 1
значений содержится в (J f(Ar)- Если q > nv — п2 4-1, то q >
г=0
> («j— -г)/(п2 — г) (00<н2); поэтому каждое из множеств j (А,)
имеет меру нуль.
Приступим теперь к доказательству леммы 3.3. Мы уже упо-
минали, что доказательство будет проводиться индукцией по п и q.
Чтобы формализовать доказательство, сформулируем лемму:
Лемма 3.6. Пусть А —подмножество в Ln и к >0—- целое
число. Тогда существует такая последовательность множеств
Ai (i>0) и отображений ср,- (г>1), что Мо счетно, nczQ/l,-
г=0
л для всех i 1
<рг- есть гомеоморфизм класса С' шара Вт* в Еп,
ez
причем At а: ср,-(В™') (где В"'— множество тех (3.18)
* i
х^Е™, для которых ||х||<е);
||<Pi(z) — ЧЭ(у)||>|1*-.у||; (3.19)
62
Гл. II. Дифференцируемые Многообразия
для любой функции f £Ск, равной нулю на А,
существуют, такие монотонные функции Ь, (е),
что Ит6г (е) =0 и
е->0 (O.ZU)
\f(Ai(.3:'))\<bi(\\x — y\\)\\x-y\\'i,
если х, у£В™р срг (у) QAt.
Для к = 0 лемма тривиальна. В этом случае полагаем Лг =
= A[\Ki, где Ki — множество замкнутых шаров, составляю-
щих базис Еп. В качестве ср; возьмем перенос шара с центром в нуле
в Kt. Тогда (3.20) означает просто равномерную непрерывность.
Рассуждения на стр. 58 фактически доказывают лемму для п = 1.
Приступим к индукции по п-\-к. Предположение индукции
состоит в том, что лемма 3.6 верна для n-~k<Lp.
Пусть пА-к = р,п'>1,к>®, и пусть А а Еп. Обозначим
через А1 множество таких х(ЦА, что
= 0 (3.21)
3=1
для всех fQCh, обращающихся в нуль на А; пусть А2 —А— А1.
Согласно предположению индукции, существуют такое разло-
жение = и такие отображения ср) шаров /Д'1', что Л) о.
<^ср}(В™г), имеет место (3.19) и
I g (ф’ (*)) I < Ъ}- (|| х — у ||) || х — у Ц'1-1 (3.22}
для всех g^Ch~\ обращающихся в нуль на А1. В частности^
(3.22) справедливо для g^—дрдх1, если fQCh и равна нулю на А.
Покажем теперь, что множества А1Г и отображения ср) в действи-
тельности удовлетворяют условию (3.20). Это вытекает из следую-
щей леммы:
Лемма 3.7. Пусть ср: Вт—>Еп есть отображение класса С1,
удовлетворяющее условию (3.19). Если /QCh (/с> 1) и
[ I <(I!х—у II) liх ~ у ilfe"1’
1 dxJ I
причем функции bj (е) монотонны и lim&; (е) = 0 (/ = 1, . .., п), то
Е—>0
I / (ф —/ (ф (г/)) I < ВЬ (II ж — у II) II ж — у ||\
где К зависит только от ср.
Доказательство. Положим F (Р) = / (ср [у -j- (ж— г/) PJ).
Тогда / (ср (ж)) = F (1) и F (0) = f (ср (г/)). По теореме о среднем
§ 3. Теорема Сарда
б»
/ (ср (ж)) — / (ф (*/)) =Р' (0 для некоторого /, 0 < t <С 1. Но
F' = 2 — t))~-(^-ya),
j, а
если ф = (ф1, . . ., фп). Поэтому
I F' (t) | < Ki || х — у || { | (ф (У -т (х — У) 0) | }
где = п max
Зсрз
дха
Следова тел ьно,
I К' (0 | < КргЪ (|| х — у ||) || х - у ||\
что доказывает лемму с константой К—пК^.
Применяя лемму 3.7 к функции /, равной нулю на А (для
которой, следовательно, /(ф(г/)) = О), получаем (3.20).
Вернемся к лемме 3.6. Мы нашли множества А1Г и отображе-
ния фг, которые удовлетворяют условиям (3.18), (3.19) и (3.20)
и покрывают А1. Теперь мы хотим сделать то же самое для Л2.
Пусть pQA2. Это означает, что существует такая функция g,
равная нулю на А, для которой какая-нибудь производная
dg/dxl (/?)#= 0. Можно считать, что dg!dxn (р) =£ 0. По теореме
о неявной функции мы можем найти окрестность N^P и такую
функцию ф" (х\ . . ., xn-1) £Ck, определенную в некотором шаре В"-1,
что любое решение уравнения
g (х1, . . ., хп) = 0
в N имеет вид (х1, ..., хп~\ ф” (х\ ...,хп~хУ). Если мы теперь
рассмотрим отображение ф: >Еп, задаваемое формулой
Ф=Нф\ • • •, ф”), где
Ф“ (ж1, . . ., хп~’") = ха, 1<а<и—1,
ф"^1, . . ., У1-1) = ф",
то ф(ЕС'\ || ф (х) — ф (у) || > || х—г/|| и N р А о. ф ~’). Применим
предположение индукции для п— 1 к ф-1(7УрЛ). Мы можем
написать ф-1 (N Р Л) = [J Dr, где Do счетно, и найти отображе-
ния фг, удовлетворяющие условиям (3.18). (3.19) и такие, что
|МФ> (-г)) I < М II —) II —li\
если фг (у) £ ф-1 (ТУрЛ), для любой функции h g Ch, обращаю-
щейся в нуль на ф"1 (ЛгрЛ). Но если функция / g С'1 равна
нулю на Л, то функция h = / ° ф равна нулю на ф-1 (N рЛ).
Полагая фг = ф °фг, мы получим разложение множества ТУрЛ,
«4
Гл. II. Дифференцируемые многообразия
как того требует лемма 3.5. Покроем все множество А2 окрестно-
стями N и выберем счетное подпокрытие. Соединяя все разложе-
ния (и обозначая объединение счетных множеств через Л о), мы
завершим доказательство леммы 3.6.
Лемма 3.3 следует теперь из леммы 3.6. Действительно, мы
просто используем лемму 3.7, поскольку все производные функции
обращаются в нуль на множестве ее неизолированных критиче-
ских точек. Это завершает доказательство теоремы Сарда.
Заметим, что условие гладкости к — 1 шах (п1 — п2, 0)
в теореме 3.1 необходимо. Контрпример для случая, когда это
неравенство нарушается, построен Уитни [18].
§ 4. РАЗБИЕНИЕ ЕДИНИЦЫ, АППРОКСИМАЦИОННЫЕ ТЕОРЕМЫ
В этом параграфе мы получим несколько аппроксимационных
теорем, которые будут использованы в дальнейшем. Доказатель-
ство каждой из них делится на две части: «локальный» результат,
основанный обычно на теореме Сарда, и метод соединения локаль-
ной информации.
Прежде всего напомним некоторые результаты из топологии.
Определение 4.1. Семейство множеств {£7а} топологи-
ческого пространства X называется локально конечным, если любая
точка р g X обладает окрестностью Np, которая пересекается толь-
ко с конечным числом Ua, т. е. Np f| Ua = 0 для всех а, кроме
конечного числа. Атлас {Ua,ha} дифференцируемого многообра-
зия М называется локально конечным, если покрытие {t/a} локаль-
но конечно.
Определение 4.2. Покрытие {К₽} называется вписан-
ным в покрытие {Ua}, если для каждого |3 существует (по крайней
мере одно) такое а, что V $ cXUa. Пространство X называется
паракомпактным, если оно хаусдорфово и в любое его покрытие
можно вписать локально конечное покрытие.
Лемма 4.1. Если X локально компактно т), имеет счетную
базу и хаусдорфово, то X паракомпактно. В частности, любое
многообразие паракомпактно.
Доказательство. Пусть {U,} — такая база топологии про-
странства X, что Ut компактны. Определим по индукции после-
довательность компактных множеств At. Пусть А{ = СД; предполо-
') То есть каждая точка обладает окрестностью с компактным замы-
канием — Прим, черев.
§ 4. Разбиение единицы, аппроксимационные теоремы 65
жим, что At определено, и пусть j — наименьшее число > i, такое,
что At cl Ul U - • • U Uj = Vj. Положим Ai+1 = V^. Тогда А, ком-
00
пактны, А, с Int Ai+1 х) и [_]Аг = Х. Пусть теперь {ЖЛ—открытое
i=0
покрытие пространства X. Для каждого i рассмотрим открытые
множества (IntAi+2— At-J^Wa. Эти множества покрывают ком-
пактное множество Лг+j — IntAj. Поэтому мы можем выбрать
конечное подпокрытие У[, . .., Урт- Набор всех множеств V} покры-
вает X, поскольку множества Ai+l — Int Л, покрывают X. Покры-
тие {Vk} вписано в покрытие {Жа}. Множество IntAz+1 является
окрестностью множества Лг и не пересекается с V}h при j /> г +1.
Следовательно, покрытие {Vk} локально конечно.
Для дифференцируемых многообразий мы можем усилить
предыдущую лемму, вписывая покрытие, состоящее из координат-
ных окрестностей:
Лемма 4.2. Пусть М есть п-мерное дифференцируемое
многообразие и {И «} — его открытое покрытие. Тогда существует
такой атлас {С;, /гг}, что
1) {Кг}— локально конечное покрытие, вписанное в {JVa};
2) миг) = ^( = МОИ1<3);
3) множества Oi=hi1 (В™) покрывают М.
Чтобы убедиться в этом, вернемся к доказательству леммы 4.1
и выберем покрытие множества Л,+1 — IntA, немного более тща-
тельно. Каждая точка р открытого множества (IntA;+2— Л-1)П^а
обладает такой координатной окрестностью NPt а и отображе-
нием hp, а, что
Xр, a CL (Int 4^2 Ai_f){]Wa И hPl а (Np, а) ZD В3.
Положим Ур, а = Вр, а (#?) и ®р, а = а (#?) Затем выберем
конечное число окрестностей Ор<а, покрывающих Ai+1 — IntAj,
и закончим доказательство так же, как и раньше.
Лемма 4.3. Существует такая функция ф класса С°°, опре-
деленная на ЕВ, что ср (х) > 0 и
( 1 для || х || С 3/2,
^(30 = ^0 для || х || >2.
Г) Int А — множество внутренних точек множества А.— Прим, перев.
66
Гл. II. Дифференцируемые многообразия
Доказательство. Положим
г > О,
/(Г) = 1О, г<0.
Тогда /—функция класса С°°. Функция
, \ /(2-г)
S^~ /(2-г) + /(г-3/2)
есть функция класса С"”, равная нулю при г > 2 и единице при
г <3/2. Функция <р (х) = g (|| х И) удовлетворяет требованиям
леммы.
Определение 4.3. Если на пространстве X задана
функцияф, то носителем (обозначается supp ф) называется замы-
кание множества точек р, в которых ф (р) < 0.
Определение 4.4. Разбиением единицы класса Ch на
дифференцируемом многообразии М называется набор таких
функций фг < 0 класса Ck, что
1) набор {supp фД локально конечен;
2) множества supp фг компактны;
со
3) 3 фг (р) = 1 для всех р£М.
1
Заметим, что ввиду условия 1) сумма в 3) имеет при любом
фиксированном р только конечное число ненулевых членов.
Определение 4.5. Говорят, что разбиение единицы
{фД подчинено открытому покрытию {Wa}, если для всякого i
существует такое а, что supp фг cz Wa.
Теорема 4.1. Пусть {Wa) — покрытие дифференцируе-
мого многообразия М класса Ск. Тогда существует разбиение
единицы {фД класса Ск, подчиненное {1Га}.
Доказательство. Впишем в {ТУа} покрытие {ГД,
как в лемме 4.2. Пусть фг = ф □ ht, где ф — функция из леммы 4.3.
Тогда фг — функции класса Ck, причем supp фг с V, и ф; (р) = 1
для р g Ch. Поскольку покрытие {УД локально конечно, набор
{supp фД тоже локально конечен. Положим
Фг (Г) = (Р) • (4.1)
3 'Ь
3=1
Поскольку функции ф7- неотрицательны, фу « = 1 по крайней
мере для одного / (множества Oj покрывают М) и все функции фу,
§ 4. Разбиение единицы, аппроксимационные теоремы
67
кроме конечного числа, обращаются в нуль в точке р, выраже-
ние (4.1) имеет смысл. Набор {<р7-} образует разбиение единицы.
Поскольку supp ср, = supp фг, это разбиение единицы подчинено
{Wa}.
Теперь мы используем предыдущие результаты, чтобы полу-
чить аппроксимационные теоремы для отображений класса Ck.
Прежде чем сформулировать эти теоремы, мы должны решить,
как измерять близость отображений. Другими словами, мы хотим
задать топологию в пространстве отображений М, М2 класса Ck,
где Mt — дифференцируемые многообразия. В случае, когда Mi
и М2 — евклидовы пространства, каждое отображение задается
п2 функциями f1, ... , f”2 от переменных х1, . . . , хП1. В про-
странстве функций класса Ch существует очевидная метрика,
метрика равномерной сходимости:
1|/~ £||ь = 2 sup
х£Еп
daf (j)(-^g (х)
(ta1/*1 . . . (Эгс’1)'*'1 . . . (дхп')ап-
где сумма распространяется на все частные производные порядка
к. Это означает, что функция / близка к функции g, если все
частные производные функции / равномерно близки к соответствую-
щим производным g (включая производную нулевого порядка)
вплоть до порядка к. Эта метрика очевидным образом распростра-
няется на наборы п функций, а именно
|1/~^||й = зирУ‘ —
2
В случае многообразий, однако, отображение задается функциями
только локально и только после того, как выбраны локальные
координаты в Mt и М2. Кроме того, частные производные также
имеют смысл только в случае, когда заданы локальные коорди-
наты. Поэтому нам придется определить близость в терминах
фиксированных координат в Mi и М2.
Определение 4.6. Пусть /: ЛДМ2 — отображение клас-
са Ск. Пусть Z = {Zt, Hi} — локально конечный атлас на М2, где
Ht = (z’(-), . . ., zps (•)). Пусть W = {Wi, hi} — такой локально
конечный атлас на с ht = (w\, ...,wp), что Wt компактно
п f (Wi) cz Zj(i) для некоторого j(i). [Для данного атласа Z всегда
можно найти такой атлас W, согласно лемме 4.2.] Пусть е(-) —
положительная функция на п к — неотрицательное целое число.
Тогда символом z, е, k)f обозначается множество всех отобра-
жений g: —>М2 класса Ск, для которых выполнены следую-
5*
68
Гл. II. Дифференцируемые многообразия
щие два условия:
g-(PFj)czZ; для всех таких i, j, что f(Wi)c^Zj. (4.2)
Для этих значений i и j пусть отображение Hjofohi1 задается
функциями (Д>, ...,/"/), а отображение Hj о g о ЬД — функциями
(glj, , gff)- Тогда
| Dfa (ip) - Dg'4 (w) | < e (V (w)) (4.3)
для всех w^hi (И7;) и r=l, . . ., n2, где D — любой дифференциаль-
ный оператор даК<ГД)'Л . . . (dwnif'ni, такой, что at-|- ... -}-аП1^к
(включая случай а = 0).
Ввиду локальной конечности атласов условия (4.2) и (4.3)
сводятся к конечному числу условий «близости» в каждой точке
многообразия Mi. Мы оставляем читателю проверку того факта,
что множества JF\W, z, в, k) f образуют систему окрестностей ото-
бражения / для некоторой топологии в пространстве отображений
Mi М2 класса Ch.
Сформулируем теперь первую из наших аппроксимационных
теорем.
Теорема 4.2. Пусть f — отображение класса Ск пГмер-
ного многообразия Mi в п2-мерное многообразие М2 и к 2. Если
п2 2щ, то для любого набора (И7, Z, е, к) существует отображе-
ние g g Ar\w,z, в, fc) f, являющееся погружением. Если ранг / =
на замкнутом множестве К, то мы можем выбрать отображе-
ние g так, чтобы g (х) = / (х) для х £ К.
Доказательство разбито на три части. Сначала мы докажем
локальный аналог теоремы, т. е. что любое отображение локально
может быть аппроксимировано погружением. Затем мы покажем,
что отображение, близкое к погружению, есть погружение. Нако-
нец, мы воспользуемся леммой 4.2, чтобы составить из локальных
аппроксимаций глобальную.
Лемма 4.4. Пусть F — отображение класса С2 открытого
множества UczEni в ЕП2, причем п2>2п1. Для любого 6>0
существует такая (щХ п2)-матрица A = (af), что
|aj|<6 (4.4)
и отображение
х F (х) + Ах (4.5)
является погружением.
[Символом Ах здесь обозначено произведение матрицы А
на матрицу х = (х1, . . ., xni)J
$ 4. Разбиение единицы, аппроксимационные теоремы
69
Доказательство. Пусть J (х) — матрица Якоби ото-
бражения F в точке х. Тогда матрица Якоби отображения (4.5)
в точке х равна J (т) А. Мы хотим выбрать А так, чтобы эта
матрица при любом х имела ранг п{. Иначе говоря, мы хотим
найти матрицу А, не представимую в виде В — J (х), где В —
матрица ранга k <Z Пх, & х £ U. Чтобы сделать это, мы изучим
множество матриц вида В — J (х), где ранг В = к <Z nl7 a х £ U.
Пусть Т (rii, п2; к) — многообразие всех (т?! X т?2)-матриц
ранга к (см. пример 4 из § 1). Рассмотрим отображение
Gk: U X Т (п1, п2; к) Т (н^ п2), заданное формулой
Gk (х, В) = В — J (х).
Ясно, что Gf. есть отображение класса С1. Многообразие U X
X Т (пх, п2, к) имеет размерность nY + к (пх -f- п2 — к). Произ-
водная по t функции + t («1 — п2 — t) равна + п2 — 2t.
Она положительна, если t < nt < п2. Значит, функция щ -
- к («j + п2 — к) монотонно возрастает по к, если к < nt,
т. е. rii + к (rii п2 — к) щ («! — 1) (щ -- п2 — пх — 1) =
= — (п2 — 2п[) — 1, что меньше, чем пхп2, если п2 2nt.
Поскольку размерность пространства Т (пх, п2) равна из
(тривиального случая) теоремы Сарда следует, что образ отобра-
жения Gk в Т (и4, и2) имеет меру нуль. Значит, в сколь угодно
малой окрестности нулевой матрицы мы можем найти матрицу
A f Г (nf, н2), которая не принадлежит образам отображений G^
(к = 0, 1, . . . , п — 1). Это доказывает лемму 4.4.
Лем м а 4.5. Пусть F — отображение класса С1 подмноже-
ства U сд ЕП1 в Enz. Пусть F имеет ранг на компактном под-
множестве К сд U. Тогда существует таксе е > 0, что любое
отображение G'. U -+ ЕП2, для которого || G — F ||i < е, имеет
ранг пх на К 1).
Пусть 6 (х) — максимум абсолютных значений миноров поряд-
ка пх матрицы Якоби отображения F в точке х. Тогда б — непре-
рывная функция, положительная на компакте К. Значит, б (х) >
> б > 0 на К. Поэтому мы можем найти такое е, что изменение
элементов матрицы J (х) меньше, чем на е, изменяет все рассматри-
ваемые миноры меньше, чем на 6/2. Это е, очевидно, удовлетворяет
требованиям леммы.
Приступим к доказательству теоремы 4.2. Нам задано локально
конечное покрытие {И7;}. Каждая точка р имеет окрестность Np,
пересекающуюся только с конечным числом W,. Поскольку мно-
!) Напомним, что || F ||i = sup | В (ж) | sup I ~1\ (х)
М i, з, х I дх?
70
Гл. II. Дифференцируемые многообразия
жество, где ранг / = «1, открыто, мы можем найти такое открытое
множество W zz> К, что ранг / = >4 на W. Пусть 7V* = (] И’
и Л'р = Np П (Mi — К). Множества {Л’), Np} (p£Mi) образуют
открытое покрытие многообразия Mi. Впишем в него счетное
локально конечное покрытие, состоящее из координатных окрест-
ностей Vi, удовлетворяющих условиям 1), 2) и 3) леммы 4.2.
По определению покрытия {jV“} каждое Vt содержится либо в W,
либо в Mi —К. Перенумеруем У, положительными и отрицатель-
ными числами так. чтобы V, cz W тогда и только тогда, когда
г<0.
В соответствии с леммой 4.2 множества Oi — hl1 (R") покры-
вают Mt. Пусть 1\ = hl1 (В"), так что Ot cz Pi cz Vi и Pi ком-
пактны. Мы будем строить по индукции последовательность таких
отображений {/s} (sj? 0) класса Сй, что
(1) /о-—/;
(ii) (И--, Z, е/2®, к) /s-1’
(iii) fs имеет ранг гц на [JOi = Qs;
(iv) h(x)= fs-i(x) для xQMi — Vs.
Как только мы построим такую последовательность, теорема будет
доказана. Действительно, из (iv) (и локальной конечности покры-
тия {ИД) следует, что fs (х) =- /8+1 (х) для достаточно больших s
и всех х из окрестности любой фиксированной точки p£Mi-
Таким образом, последовательность {/8 (г)} сходится к отображе-
нию g (х) класса Ch, которое имеет всюду ранг пг благодаря
условию (iii) и удовлетворяет условиям (4.2) и (4.3), согласно
(i) и (ii).
Приступим теперь к построению последовательности {fs}.
Положим /0 = / И допустим, ЧТО МЫ построили /з-р Нужно найти
отображение fs, удовлетворяющее (ii), (iii) и (iv). Условие (iv)
определяет fs вне Fs. Мы должны определить fs на Vs так, чтобы
оно удовлетворяло (ii), (iii) и гладко «соединялось» с /8_t вне К.
Гладкое «соединение» будет гарантировано, если мы положим
/s = /s-i в Fs — Ps. Осталось определить /8 в координатной окрест-
ности Vs, так что мы можем перейти в евклидово пространство.
Пусть gs~i = Нр ° fs_i о /г;1, где (Zp, Нр} — карта атласа Z с fs~i (У8) cz Zp.
Пусть Rs-! — hs (Qs-i П Hs). Мы хотим найти такое отображение
gs: R"1 —»Нр (Zр) cz ЕП2, чтобы отображение /8, равное H~p1ogsoha
на Vs и равное fs-t на М\— Vs, удовлетворяло условиям (ii)
и (iii). Определим gs формулой
gs(x)=gs_i(x)-~q(x)Ax, (4.6)
§ 4. Разбиение единицы, аппроксимационные теоремы
71
где ф — функция леммы 4.3, а А есть (щ X н2)~матРиЦа, выбором
которой мы сейчас займемся. Посмотрим, какие ограничения
налагают условия (ii), (iii) на выбор gs, т. е. на А. Прежде всего
рассмотрим условие (ii). Существует конечное число окрестно-
стей Wt, содержащих окрестность и конечное число окрест-
ностей Zj, содержащих /в-ДИД) для Wi^>Vs. Образ окрестности Fs
при отображении fs должен лежать в каждой из таких окрест-
ностей Zj. Пользуясь координатным отображением ht окрестности Wi
и координатным отображением Hj окрестности Zj, мы можем
перенести условие (ii) на отображение gs: положим Ф7=Я7оЯр1
и (ft — hsohi1; тогда отображения Ф7- о gs_l о ф; переводят В"1 в ком-
пактные подмножества открытых множеств Hj (Zj). Первое требо-
вание условия (ii) состоит в том, что Ф;0^0?; должно делать
то же самое. Этого можно достичь, выбрав все элементы матрицы А
достаточно малыми. Помимо этого условие (ii) требует еще бли-
зости всех частных производных до порядка к функций Ф;°£8офг
и Ф./°^-1°фг- Поскольку существует только конечное число г и j
и функция ф, а значит, и ее производные выбраны заранее, это
условие тоже будет удовлетворено, если элементы матрицы А
достаточно малы.
Рассмотрим теперь условие (iii). Оно требует, чтобы gs было
погружением на В™1 (J Rs-i, когда gs_i — погружение на Rs-i-
Поскольку ф = 0 вне В"/2, отображение gs имеет ранг п, всюду
на — Rs_t П В™1 независимо от выбора матрицы А. С другой
стороны, лемма 4.5 утверждает, что отображение gs имеет ранг
на Rs_i П В"1, если матрица А достаточно мала. Согласно лемме 4.4,
мы можем выбрать матрицу А, удовлетворяющую всем этим требо-
ваниям, так, чтобы отображение х —> gs^ (х) Ах имело на В"1
ранг щ. Поскольку ф (х) = 1 на В"/2, отображение gs совпадает
на В’з/2 с этим отображением. Следовательно, gs имеет ранг zij
всюду на Таким образом, мы построили требуемую
последовательность {/s} и доказали теорему 4.2.
Мы показали, что любое дифференцируемое отображение
АЦ -+ М2 можно аппроксимировать погружением, если п2 Л- 2nt.
В качестве следствия мы получаем:
Любое многообразие класса Ck (k > 1) размерности п± может
быть погружено в E2ni.
Действительно, достаточно применить теорему 4.2 к любому
отображению /: > Еп~ класса Ск. Теперь мы покажем, что
любое погружение можно аппроксимировать взаимно однознач-
ным погружением, если п2 > 2/^.
72
Гл. II. Дифференцируемые многообразия
Теорема 4.3. Пусть f — погружение класса Ck (к 1)
номерного многообразия М в ЕП2. Пусть Z есть ЕП2 с обычной
системой координат, а {И7;} — то же, что и в определении 4.6.
Тогда, если п2 > 2nit то для любых е (х) и к 0 существует
взаимно однозначное погружение g: М -> Епт принадлежащее
<j'!E(w, е, z, ft) / Если отображение f взаимно однозначно в окре-
стности W замкнутого множества К, то можно выбрать g так,
чтобы g (х) = / (х) для всех х £ К.
Доказательство. Доказательство проводим так же,
как раньше. В настоящем случае локальное утверждение три-
виально: по теореме о неявной функции любая точка р обладает
окрестностью Np, на которой отображение / взаимно однозначно.
Пусть
= N2 = M-K(]NP.
Выберем разбиение единицы {фг}, подчиненное этому покрытию.
Занумеруем ф; положительными и отрицательными числами так,
чтобы supp фг с W тогда и только тогда, когда i 0. Мы полу-
чим отображение g в виде
оо
+ Ш (4.7)
1
где коэффициенты Ь, = (Ъ\, . .., &”2) будут выбраны по индукции.
Предположим, что bit . . bm определены так, что
т
im — / + 2 ^«фг
1
есть погружение и отображение fs удовлетворяет условию (ii)
на стр. 70 при s^.m. Мы можем добиться1 того, чтобы (ii)
выполнялось и для s = т+1, выбрав || Ьт+1|| достаточно малым.
Требование, чтобы /m + ^m-ифт-ц было погружением, также удовле-
творяется, если |1 im+i || мало, согласно лемме 4.5. Наконец, пусть
Dm+l— открытое подмножество в М X М, состоящее из таких пар
(г/1, Уг), ЧТО фт+i 0/1) ¥= фт+1 (у2)‘ Пусть Gm+l: Dm+i—>En2 — отобра-
жение, определяемое формулой
Gm+l (yi, у2) = • (4-8>
Поскольку Gm+1 дифференцируемо и размерность Dm+l равна 2пг, мно-
жество Gm+i (Z)m+1) имеет меру нуль. Поэтому мы можем выбрать &т+1
произвольно малым так, чтобы при этом &т+1 $ Gm+l (7)т+1). Тогда
из равенства fm+i (у^ = fm+l (у2) следует, что
fm (j/1) + ^т+1фт+1 (l/l) = /т (у2) + ^т+1Фт+1 (l/г);
§ 4. Разбиение единицы, аппроксимационные теоремы
73
ИЛИ
^т+1 (фт+1 (j/l) фт+1 (j/2)) fm (У2) fm (j/l)-
Поскольку bm+l (f Gm+i (Dm+l), это возможно только в том случае,
если
Фт+1 Q/1) = фт+1 Ы И /m(S/2) = /m(S/l).
Определим теперь отображение g формулой (4.7). Из определения
видно, что g есть погружение, аппроксимирующее /, т. е.
g Е z, е, h)/- Покажем, что оно взаимно однозначно. Предпо-
ложим, что g (yt) = g (у2). Поскольку {ф;} — разбиение единицы,
ф/ (г/i) = Фг (Уъ) = 0 для всех I, больших некоторого числа г. Следо-
вательно, g (р4) = fr (t/i) = /г (г/г) = g (,у2) В соответствии с выбором Ьг
это означает, что <pr (i/i) == фг (г/г) и fr-i (г/i) = fr-i (yz) Продолжая
подобным образом, мы получим, что / (г/i) = / (г/г) и
фг-(г/1) — Фг (г/г) = 0 для всех i>0. (4.9)
Равенство (4.9) показывает, что точки и у2 лежат в окрест-
ности W, в которой отображение f взаимно однозначно. Значит,
У1=У2-
Комбинируя теоремы 4.2 и 4.3, получаем теорему Уитни:
Теорема 4.4. Любое многообразие М класса Ск (/с>2) раз-
мерности п допускает собственное вложение класса Ск в Е2п+Г.
Доказательство. Любое отображение класса С'1 много-
образия М в £2n+i Может быть аппроксимировано погружением
(теорема 4.2), а это погружение может быть аппроксимировано
взаимно однозначным погружением (теорема 4.3). Таким образом,
исходя из любого отображения / класса Ch (например, из постоян-
ного отображения ), мы получаем взаимно однозначное погруже-
ние g. Из упражнения 2.1 мы знаем, что взаимно однозначное
погружение g является вложением, если g-1 ((?) компактно для
любого компактного Q d Е2п+* или, что эквивалентно,
g~l (Вр) компактно для всех р. (4.10)
Мы хотим выбрать / так, чтобы g удовлетворяло условию (4.10).
Выберем разбиение единицы {фг} и положим
/ (я) = 2 *фй 0е) (4.11)
(что корректно, поскольку семейство {supp ф;} локально конеч-
но). Полагая е (х) = 1/2 и применяя к отображению / теоремы 4.2
и 4.3, мы получим такое взаимно однозначное погружение g, что
|| g (х) — / (г) II < 1. Если II g (х) II < р, то II f (х) IK р -I- 1
74
Гл. II. Дифференцируемые многообразия
р+1
и, значит, х принадлежит компактному множеству [_J supp
i=l
Таким образом, условие (4.10) выполнено, и g есть вложение М
В £2п+1.
3 а м е ч а н и я. а) Уитни доказал в [19] более сильную теоре-
му. Он показал, что многообразие М класса С1 допускает такое
вложение / класса С1 в Е2^1, что / (М) есть вещественно аналити-
ческое подмногообразие в Е2п+1. Это показывает, что любое много-
образие класса С1 может быть снабжено вещественно аналитиче-
ской структурой.
Ь) Существуют многообразия размерности п, не допускающие
вложения в Е2п~1 (например, проективные пространства подходя-
щей размерности).
с) Если наложить на многообразие М топологические ограни-
чения, то оно может быть вложено в евклидово пространство
размерности <2и. Эти условия можно выразить как условия
обращения в нуль различных гомотопических групп (см. [21]).
d) Для вещественно аналитических многообразий аналогич-
ная теорема о существовании вещественно аналитического вложе-
ния представляет собой намного более глубокий результат. Она
доказана ’) Морри [10].
Наши последние аппроксимационные теоремы посвящены регу-
лярным пересечениям двух подмногообразий. Например, если
даны две кривые на плоскости, то мы можем ожидать, что в случае
общего положения они не касаются одна другой в точках пересе-
чения. Сформулируем условие регулярности пересечения сле-
дующим образом:
Определение 4.7. Пусть /— дифференцируемое отображе-
ние игмерного многообразия в «2-мерное многообразие Мг.
Пусть N есть (и2 —р)-мерное подмногообразие в М2. Говорят,
что отображение f трансверсально регулярно (ТР) к N в точке х0,
если либо / (х0) $ N, либо существуют координаты х1, . . ., хП1
вблизи х0 и координаты у1, ..., у”2 вблизи f(x0), такие, что
•-* 1) в некоторой окрестности U^f (х0) пересечение N Q U задается
уравнениями у1 . . . = ур = 0;
... / dip \i=i, • • - ,р
2) матрица I-A-J имеет в точке х0 ранг р.
' дхз / з=1, ..., ni
Заметим, что условие 2) может иметь место только в случае,
если р <7 щ. Если < р, то трансверсальная регулярность
х) Морри доказал эту теорему только для компактных многообразий.
Для произвольных многообразий она доказана Грауэртом, см. со. Матема-
тика, 4 : 3 (1960), 29—41.— Прим, перее.
£ 4. Разбиение единицы,, аппроксимационные теоремы
75
означает, что / (х0) $ N. Так, на рис. 3 (п2 = 2, щ = р = 1)
(а) есть TP-пересечение, а (&) — нет.
Определение 4.8. Говорят, что отображение / транс-
версально регулярно к N, если оно трансверсально регулярно к N
в любой точке х £ Mi.
Определение 4.9. Пусть / — погружение многообразия
Mi в М2. Пусть Xi и х2 — точки из Mi, для которых / (xi) = / (х2).
Мы можем найти такие непересекающиеся окрестности Ut и U2
Р и с. 3.
точек Xi и х2, что / | Ui и / | U2 — вложения. Погружение / назы-
вается регулярным в (xY, х2), если / | Ui трансверсально регулярно
к / (U2) в точке Xi. Погружение / называется регулярным, если оно
трансверсально регулярно во всех (xi, х2), для которых / fo) =
/ U2)-
Упражнение 4.1. Показать, что если / регулярно в (xt, хг), то
оно регулярно в (х2, хД
Теорема 4.5 (Том J)). Пусть ft Mi -> М2 — отображение
класса С\ и пусть N — замкнутое подмногообразие в М2. Для
т) Доказательство этой теоремы использует «трудную» часть теоремы
Сарда. Оно может быть опущено при первом чтении, так как теоремы 4.5
и 4.6 не будут по существу применяться в остальной части книги. Читатель
может сразу перейти к § 5.
76
Гл. II. Дифференцируемые многообразия
любых (W, Z, е, к) существует отображение g g z,e,k)f,
трансверсально регулярное к N. Кроме того, если А — такое
замкнутое множество из М^что/ трансверсально регулярно для
всех х С А, то можно выбрать g таким образом, чтобы g (х) =
= / (х) для х £ А.
Прежде чем приступать к доказательству теоремы 4.5, пере-
формулируем условие 2) определения 4.7. Пусть (U, h) — карта
вблизи / (х0), и пусть отображение л: Ет Е'р определено равен-
ством
л (у1, ..., ут) = (у1, . . ур). (4.12)
Тогда условие 2) означает, что начало координат (0, . . ., 0) есть
регулярное значение отображения л ° h ° ], ограниченного на
некоторую окрестность точки xq.
Сформулируем теперь аналог леммы 4.5.
Л е м м а 4.6. Пусть f — отображение класса С1 открытого
множества U cz Ег,о в ЕП2. Предположим, что / трансверсально
регулярно к плоскости Р -- {у | у1 — . . . — ур = 0} во всех точ-
ках некоторого компактного множества К cz U. Тогда существует
такое е > 0, что любое отображение g, для которого || / — g ||j <
< е, также трансверсально регулярно к Р на К.
Как мы заметили, трансверсальная регулярность на К экви-
валентна тому, что отображение л о f не имеет критических точек х
на К, для которых л ° / (х) (0, .... 0) = 0. Если п1 < р,
то это означает, что 0 (£ л ° / (К). Поскольку К компактно, 0 нахо-
дится на положительном расстоянии е от л °/ (А'). Поэтому если
II ё ~ / Hi < е> то 0 л ° g (А). Если пг р, то условие транс-
версальной регулярности означает, что (л °/)-1 (0) есть конечное
множество и что матрица Якоби отображения л ° / в каждой
точке Xi £ (л °/)-1 (0) имеет ранг р. Поэтому мы можем найти
такие открытые окрестности [7г каждой из этих точек, что некото-
рый минор порядка р матрицы Якоби по абсолютному значению
> б > 0 для всех х б. U - Поскольку множество К' = К — Ui
компактно и 0(л° / (А'), прообраз нуля g-1 (0) при отображе-
нии g, достаточно близком к /, принадлежит множеству (J U,.
Но тогда для отображения g, достаточно близкого к /, соответ-
ствующий минор порядка р матрицы Якоби отображения л ° g
отличен от нуля в каждой точке из (ло^)-х(0).
Доказательство теоремы 4.5. Выберем такой атлас
{Ya,Ha} многообразия М2с На = (у1а, . . ., у^2), что либо N П Ya = 0,
либо 1V р Ya задается уравнениями = . . . = = 0. Пусть {Х;}—
локально конечное покрытие, вписанное в {Уа}. Множества
§ 4. Разбиение единицы, аппроксимационные теоремы
77
образуют покрытие многообразия М^ Пусть W — открытое мно-
жество, содержащее А, на котором / трансверсально регулярно к N.
Если дано покрытие {ИД}, то множества
{И7 П Д1 (Xt) П Wj, М,-АМ (Xi^Wj}
образуют покрытие многообразия Впишем в него покрытие
{У.,}, о котором говорилось в лемме 4.2, перенумерованное так,
что Vi с W тогда и только тогда, когда I 0.
Построим последовательность отображений, удовлетворяю-
щую условиям (i), (ii) и (iv) на стр. 70 и (вместо (iii)) условиям
(v) is трансверсально регулярно к N на Qs = (_J Op,
i^s
(vi) для каждого i существует такое J (i), что fs (Pt) c
для всех s.
Из существования такой последовательности немедленно сле-
дует доказываемая теорема.
Воспользуемся, как и раньше, индукцией. Предположим, что
/.«-1 определено и удовлетворяет условиям (ii), (iv), (v) и (vi).
Положим Д = fs_i на F, — Ps. По предположению индукции
/s_i (Ps) <= XjM. Пусть И — координатное отображение окре-
стности Xj(S). Мы хотим выбрать fs так, чтобы отображение
л о Н ofs не имело критических точек на Qs f) Vs, переходящих
в начало координат. По теореме Сарда множество критических
значений имеет меру нуль в Е1’. Поэтому мы можем выбрать a £ Еп^
сколь угодно близко к началу координат так, чтобы л (а) было
регулярным значением отображения л ° Н о Д_1# Определим теперь
]s на Fs, полагая ')
fs (х) = И'1 ° [Н о fs_i(x) — aq> (hs (а:))]. (4.13)
Для х £ Os имеем л ° Н о fs (х) = л о Н о Д_, (х) — а. Поскольку
а — регулярное значение отображения л о Н ° fs-t, начало коор-
динат есть регулярное значение отображения л ° Н о fs_Y — а,
так что не существует критических точек х £ Os, для которых
л ° Н ° fs (х) = 0. Для х £ Qs П Ps мы можем, выбрав а достаточ-
но малым, применить лемму 4.6. Все остальные условия также
будут удовлетворены, если а достаточно мало. Для условия (ii)
это очевидно. Что касается условия (vi), то его фактически надо
проверить только для конечного числа Pt (тех, для которых
Pi П 0)- Для всех других Д = Д_р Таким образом, мы
имеем конечное число компактных множеств Pt cz Mi и таких
открытых множеств Хдг) с М2, что М, (Pt) cz Xj(i). Ясно, что
если fs достаточно близко к fs-i (т. е. если а мало), то Д (Р{) cz
cz Уд,). Это доказывает теорему 4.5.
’) Где ср — функция из леммы 4.3.— Прим, перее.
78
Гл. II. Дифференцируемые многообразия
Теорема 4.6. Пусть / — погружение класса Ck многообра-
зия Mi в М2. Для любых (W, Z, е, к) существует регулярное погру-
жение g'. Mi М2, принадлежащее z, е, k)f-
Заметим, что теорема 4.6 есть обобщение теоремы 4.2. Если
dim М2 > 2 dim Mi, то регулярность означает взаимную одно-
значность.
Пусть {7;} — вписанное в {И7;} покрытие, определенное в лем-
ме 4.2 и такое, что / взаимно однозначно на каждой окрестности У;.
Мы хотим построить последовательность отображений {/s}, удовле-
творяющую условиям (i), (ii) и (iv) на стр. 70, а также условиям
(vii) fs регулярно во всех (а^, х2) g Qx X Qs;
(viii) fs есть погружение, взаимно однозначное на каждом Р;.
Построим последовательность fs по индукции, полагая f8 = f8_±
на Vs—Ps. Пусть Z — координатная окрестность в М2, содержа-
щая Ъ-ДУв), и Н — соответствующее координатное отображение.
Пусть 7V, =77 (/s-t (У,) П Z), i —1, ...,s—1. По предположению
индукции отображение gs-t = Н о В^—>Епз есть взаимно
однозначное погружение. Построим gs, являющееся взаимно одно-
значным погружением 7>”' —»ЕП2 и совпадающее на В”1 — В”1
с отображением gs-i, которое трансверсально регулярно к Nt.
Прежде всего видно, что отображение gs будет взаимно однознач-
ным, если оно достаточно близко к gs-i- Действительно, пусть
т = min х, у £ Ps.
Сделаем так, чтобы функция ds = gs — имела столь малые
производные, что |] ds (а?)— ds (у) ||< т || х — у\\. Тогда
II gs (х) — gs (у) || = || ds (х) — ds (у) — (gs-i (х) — gs-i (у)) [| >
> т || х — у || —1| ds (х) — ds (у) || > 0.
Это гарантирует взаимную однозначность отображения fs на Ps.
Отображение fs будет взаимно однозначным на всех Pt, если обе-
спечить его взаимную однозначность только на конечном числе Pt,
для которых Pt П Vs <=£ 0. Но этого можно добиться, выбрав
fs достаточно близким к /s_i на каждой соответствующей окре-
стности Vi. т. е. это условие сводится к конечному числу условий
малости для разности gs — gs-t-
Заметим далее, что лемма 4.6 (точнее, ее небольшая модифика-
ция) утверждает, что если дано отображение gs, трансверсально
регулярное к TV4, N2, . . . , Nk на компактном множестве А, то
любое отображение, достаточно близкое к gs, также трансвер-
сально регулярно к этим подмногообразиям на А.
§ 5. Касательное пространство
79
По предположению gs_f трансверсально регулярно к N , Ns-i
на h(Qs^i). По теореме 4.5 мы можем выбрать трансверсально
регулярное к Nl отображение GJ: J5"1 —>Еп\ столь близкое к gs-i,
что отображение g}:
gl (х) = Gls (x) + <p (x) (gs_t (x) — Gls (a:))
трансверсально регулярно ко всем Л’г на h (Qs П 7S). Выберем
далее отображение G2S-. J5"1 —> Епг трансверсально регулярным к Ж
на J?”1 и столь близким к g|, чтобы отображение g|:
gl (ж) = Gl (х) + tp (х) (Gl (х) — gl (я))
было трансверсально регулярным ко всем Ni на /r(QsnEs) и к Ni
на 5”1. Продолжая по индукции подобным образом, мы получим
отображение gs = gss, трансверсально регулярное к Nlt
на h (Qs Л Fs) U С- При этом разность gs (х) — gs-i СО может быть
сделана сколь угодно малой, если на каждом шаге налагать
дополнительные условия «близости». Положим fs = Н'1 ° gs°h.
Проверим, что отображение fs удовлетворяет условиям (ii), (iv),
(vii) и (viii). Условия (ii), (iv) и (viii), очевидно, выполняются.
Рассмотрим условие (vii). Пусть (х1; х2) £ Qs х Qs- Если x^Vs
и x2£Vs, то условие тривиальным образом выполнено, поскольку
отображение /s взаимно однозначно на Es. Если хх gPs, a x2^Vs,
то fs (х) = /s-! (х) для некоторой окрестности точки х2. По построе-
нию fs трансверсально регулярно к /s-i(Fi) во всех точках
Если и то (х) =/8_! (х) для всех х
из некоторых окрестностей точек xit х2, так что (vii) выполняется
по предположению индукции.
Отображение g = lim fs является аппроксимацией, удовлетво-
ряющей требованиям теоремы 4.6.
§ 5. КАСАТЕЛЬНОЕ ПРОСТРАНСТВО
При изучении дифференцируемых многообразий полезно рас-
сматривать различные «инфинитезимальные» объекты. Мы дадим
последовательное изложение теории таких объектов в следующем
параграфе. Чтобы обосновать их изучение, мы сначала рассмотрим
понятие касательного вектора на многообразии. В классическом
векторном анализе понятие касательного вектора к кривой опре-
деляется непосредственным образом.
Если ф (t) = (ф1 (/), ... , фп (£)) есть кривая в Rn, причем
Ф (0) = р, то касательный вектор к кривой ф в точке р имеет вид
(ф1' (0), . . . , фп' (0)). Две кривые фиф имеют один и тот же каса-
тельный вектор, если фг' (0) = ф1' (0) для всех i. Однако на много-
80
Гл. II. Дифференцируемые многообразия
образии мы не можем записать любую кривую как набор п функ-
ций одной переменной, пока не выбрана локальная система коор-
динат. Тем не менее мы можем определить касательный вектор
в точке р более абстрактным образом как класс эквивалентных
кривых, проходящих через точку р, причем две кривые считаются
эквивалентными, если в точке р они имеют одинаковые производ-
ные в одной, а значит, и во всех системах координат, заданных
вблизи р.
Более точно, пусть Си (М) есть множество всех пар (р, ср),
где р £ М, а ср — такое дифференцируемое отображение интер-
вала (—е, е) в М, что <р (0) = р. Таким образом, Си (М) есть
пространство всех кривых на М. Существует очевидное отображе-
ние л: Си (М) -> М, определяемое формулой л (р, <р) = р. Введем
в пространстве Си (М) следующее отношение эквивалентности:
(р, <р) ~ (р', ср'), если р = р' и
d (z’ о <р) |
dt |(=о
d (х* о ф') I
dt |(=о’
где (х1, ...,хп)— некоторая система координат вблизи р.
Заметим, что если функции уг = уг(х1, ...,хп) определяют
другую систему координат вблизи р, то
п
d (i/i О Ф) _ dyi d (xi О ф) ,
dt ~ZJ dxi dt '
;=1
Поэтому введенное отношение эквивалентности не зависит от систе-
мы координат. Обозначим пространство классов эквивалентности
пространства Си (М) через Т (М). Элемент X из Т (М) (т. е. класс
эквивалентности пространства Си (М)) называется касательным
вектором. Говорят, что элемент (р, <р) £ X касается вектора X *).
Очевидно, что отображение л постоянно на классах эквивалентно-
сти и, значит, индуцирует отображение, которое мы снова будем
обозначать через л, пространства Т (М) в М. Если X С Т (М)
и л (X) = р, то мы говорим, что X есть касательный вектор в точ-
ке р. Множество л-1 (р) обозначается Тр (ЛГ) и называется каса-
тельным пространством многообразия М в точке р. Заметим, что
выбор системы координат вблизи р индуцирует отображение
Тр (М) -> Rn. Действительно, пусть h = (х1, . . . , хп) — коор-
динаты вблизи р и X Е Тр (М). Пусть (р, <р) касается вектора X.
Положим
h(X)=(X\ ...,Х"), Х‘=^£|/=о. (5.2)
г) Или, иначе, X есть касательный вектор кривой ср в точке р.— Прим,
перев.
§ 5. Касательное пространство
81
Ясно, что (5.2) не зависит от выбора ф. Отображениеh: Тр (М) —» Rn,
очевидно, взаимно однозначно. Покажем, что h (Тр (М)) = Rn.
Действительно, если (X1, ..., Xn)£Rn, то определим кривую ф(£),
полагая
Ф(О=Л-1(А(Р)+^(Х1,..., X”)).
Непосредственное вычисление показывает, что h (У) = (X1, . . ., Хп),
где У — вектор, которого касается пара (р, ф). Если h' = (у1, ... ,уп) —
другая система координат и отображение h' о hr1 задается функ-
циями у1 (ж1, . . ., хп), . .., уп (ж1, ..., ж"), то h' (У) = (У1, ..., У”),
где
У{ = У-^-Х; (5.3)
дх1 ' '
(частные производные берутся в точке 7г (/?)). Таким образом,
h' oh"1 есть линейное отображение пространства Rn на Rn. Это
означает, что мы имеем на ТР(М) каноническую структуру
векторного пространства. Действительно, если а и Ъ — вещест-
венные числа, а X, У^7’Р(ЛТ), то положим
аУ + 6Х = Л-1(йЛ(У) + гЛ(Х)). (5.4)
Поскольку отображение h' ° h-1 линейно, структура векторного
пространства, определенная на Тр (М) формулой (5.4), не зависит
от выбора h. Отображение h является изоморфизмом векторного
пространства Тр (М) на Rn.
Пусть вру обозначает (линейное) пространство всех дифферен-
цируемых функций, определенных на U cz М.
Введем понятие производной функции / по направлению каса-
тельного вектора Хр в точке р.
Теорема 5.1. Каждому касательному вектору Хр на много-
образии М соответствует единственная линейная функция Lx ,
определенная на для любого открытого множества U, содержа-
щего р. Эта линейная функция удовлетворяет условию
LxP (fg) = f (р) LXp (g) + g (p) LXp (/) (5.5)
для всех hgQcFu- Если LXp = LYp, mo XP = YP. Кроме того,
LaXp+bYp — aL^YbLyp- Если M — аналитическое или класса С°°
многообразие, a L — линейный функционал, определенный на .Yu
и удовлетворяющий условию (5.5) для некоторой координатной
окрестности U точки р, то существует единственный вектор
Хр С Тр (М), такой, что L = LXp.
6 С. Стернберг
82
Гл. II. Дифференцируемые многообразия
Доказательство. Пусть (р, <р) касается вектора Хр.
Определим Lxp формулой
Т [ф (0] I /г д\
—dt—U • (о-6)
Немедленно проверяется, что Lxp удовлетворяет условию (5.5).
Если (р, ф) — (р, ф), то
df [ф (01 I = df [ф (0) I _
dt |i=o dt |;=о ' >
для всех /, так что Lxp не зависит от выбора пары (р, ф). Если
имеет место равенство (5.7), то, полагая / = х‘, находим, что
(р, ф) — (р, ф). Таким образом, из равенства Lxp — Lyp следует,
что Xp = Yp. Ясно также, что отображение Хр —> линейно.
Предположим теперь, что многообразие М — класса С°° или
аналитическое. Пусть L — линейный функционал на JYu, Удов-
летворяющий условию (5.6), и (77, h) — система координат,
h = (xr, ...,хп), 1г(р) = (0, . . ., 0). Из формулы (5.5) следует,
что Л (1) = 2Л (1) — 0 (где 1 — функция, принимающая постоянное
значение 1). Значит, L обращается в нуль на константах. Для
любой функции f g имеем
f о/r1 (Ж1, . . ., хп) -=f (р) -г S (А • •, хп),
где fij — функции класса С°° или аналитические. [Заметим, что
если f — функция класса Ск, то fij — функции класса С"'~- и дока-
зательство не проходит.] Тогда L (/) = У аД. (х1), так как
L (xdx’ftj) = xi (р) L (х3) fu °h(p)-x
+ х3 (р) L (;?) fij °h(p) + xl (р) х3 (р) L (fij ° h) =
=о + о + о = о.
Поэтому
L(/) = ^^-|/=o, где /г ° ф (i) — (<Л (х1), ...,tL(xn)).
Значит, L—~Lx;>, где Хр — вектор, которого касается пара (р, ф).
В любом случае, независимо от класса дифференцируемости много-
образия М, любой линейный функционал вида (5.6) может быть
отождествлен с вектором, которого касается пара (р, ф). Так, если
фг — кривая, определенная равенством
х3 (ф1 (0) = 51t, (5.8)
то вектор, которого касается пара (р, фг), может быть отождест-
влен с линейным функционалом (у-:) , гДе = ‘
§ 5, Касательное пространство
83
Из определений следует, что h (д/дхг)р = (61, . ..,6”), так что
векторы (д!дхг)р образуют базис пространства ТР(М).
Пусть f— дифференцируемая функция, определенная в точке р.
Функция / определяет по формуле (5.6) линейную функцию
на ТР(М). Обозначим ее (df)p. Таким образом,
(Xp,(dfU = LX1,(f). (5.9)
Согласно определениям, имеем
(dxl')p/ = bi (5.10)
для любых локальных координат (я1, ...,хп). Таким образом,
линейные функции (dxl)p образуют базис пространства (ТР{М))*,
дуальный к базису (д/дх^р. Обозначим (Тр (М))* черезТ* (М) и поло-
жим?1* (Л/) — Т* (Л/). Элементы из Т* (М) называются кокасатель-
ными векторами в точке р. Если f — дифференцируемая функция,
то из (5.9) и (5.10) следует, что
о-»)
Дифференцируемое отображение g: ХЦ —-> М2 индуцирует очевид-
ным образом отображение g*. Си (М4) —-> Си (М2). Действительно,
если (р, ф) 0 Си (Мj), то
g* (р, ф) = (?(/’),^°ф)бСи(3/2). (5.12)
Ясно, что если (р, ф) — (р', ф'), то g* (р, ф) ~ g* (рг, ф'). Значит,
g* индуцирует отображение Т (М^ —» Т (Tf2), которое мы будем
обозначать тем же символом g*. Пусть h = (х1, ...,хП1) — локаль-
ные координаты вблизи точки р £ М{, Н = (у1, . .., уП2') — локаль-
ные координаты вблизи g (р) ив этих координатах отображение g
задается функциями уг(хг, ...,хП1). Тогда, если фг — кривая,
определяемая формулой (5.8), то кривая gl ° ср1 имеет в локаль-
ных координатах вид у1 (6|t, . . ., б„/), • • • > УП2 (^» • • •, &ni t), так
что
<3.13)
Из формулы (5.13) видно, что отображение g* линейно на каждом
Тр (7И).
Упражнение 5.1. Показать, что g есть погружение тогда п только
тогда, когда g* взаимно однозначно на каждом Тр (ЛГ).
В следующем параграфе мы увидим, что Т (М) и Т* (М) могут
быть превращены в дифференцируемые многообразия таким обра-
84
Гл. II. Дифференцируемые многообразия
зом, что отображение g* будет дифференцируемым. Проверим это
сейчас для случая, когда М есть векторное пространство, скажем
Rn. В Rn имеется каноническая система координат. Относительно
этой системы координат касательный вектор задается набором
п чисел, который можно рассматривать как элемент пространства
Рис. 4.
Rn. Таким образом, мы имеем отображение I: Тр (Rn) Rn.
С помощью I мы можем отождествить Т (Rn) с Rn X Rn.
Упражнение 5.2. Пусть ga. Rn—> Rn— сдвиг на вектор а, т. е.
ga (ж) =х-\~а. Показать, что для любого t£T(Rn)
Упражнение 5.3. Пусть t £ Тр (Rn) и /—дифференцируемая функ-
ция, определенная в точке р £ Rn. Показать, что
Lt (/) = lim 1 (/ {р 4- si (t)) - / (р)).
8->0 S
Это то самое отождествление, которое подразумевается, когда
в классическом анализе говорят о векторе в точке простран-
ства Rn. Если g есть погружение многообразия М в Rn, то
I (g* (Тр (М))) (р g М) — подпространство в Rn. Рассмотрим пло-
скость, проходящую через точку р параллельно этому подпро-
странству. Она «касается» подмногообразия g (М) в очевидном
смысле (рис. 4).
§ 6. ГЛАВНОЕ РАССЛОЕНИЕ
При изучении дифференцируемых многообразий полезно ввести
«геометрические объекты», аналогичные величинам из § 2 гл. I.
Аналогом базиса векторного пространства V здесь служит карта
(U,h) многообразия М. Геометрический объект представляет
§ 6. Главное расслоение
85
собой элемент q (U, h) некоторого пространства Q, который сопо-
ставлен каждой локальной системе координат (U, h), вместе с пра-
вилом преобразования элемента q при замене локальных коорди-
нат. Примером такого объекта служит касательный вектор: для
каждой локальной системы координат касательный вектор опре-
деляет элемент пространства Лп; при замене координат этот эле-
мент изменяется по формуле (5.3). Чтобы сделать это определение
точным, мы должны найти некоторый аналог группы GL (и)
и изучить его действие на множестве всех локальных координат.
Такая программа может быть выполнена (см., например, [12]).
Однако в большинстве случаев, встречающихся на практике (как,
например, для касательных и кокасательных векторов), закон
преобразования величин q зависит только от матрицы Якоби
преобразования координат. Это значительно упрощает дело
и позволяет дать определения, вполне аналогичные определениям
§ 2 гл. I. Если закон преобразования рассматриваемых объектов
зависит только от линейных частей функций перехода локальных
координат, то естественно отождествить две системы координат
в точке, когда они имеют одинаковые «линейные части». Руко-
водствуясь этим, приступим к определениям.
Пусть М есть n-мерное дифференцируемое многообразие.
Обозначим через U (М) пространство всех пар (р, (U, h)), где
р Е М, a (U, h) — карта в окрестности точки р. Группа GL (ri)
действует на U (М) следующим образом: если A g GL (п) и 7г =
= (а:1, . . . , хп), то (р, (U, 7г)) А = (р, (U, g)), где g = (у1, . . .
. . ., уп), причем
= А^ =(₽))• (6.1)
Очевидно, что (р, (U, h)) (АА') = ((р, (U,h))A)A'. Пусть л — проек-
ция U (М) на М, отображающая (р, (U, 7г)) в р. Тогда л (ггЛ) = л (и)
для uQU- (Л7).
Определим на U (Л/) отношение эквивалентности ~ , полагая
(р, (U, 7г))— (р', (77', 7г')), если р = р' и Jh (Р) (h' ° /г-1) = I
(символом Jx (<р) мы обозначаем матрицу Якоби в точке х С U
отображения ф открытого множества U cz Rn в Rn\ I — единичная
матрица). Из закона умножения матриц Якоби немедленно следует,
что — есть отношение эквивалентности. Обозначим через AF* (Л7)
пространство классов эквивалентных элементов пространства U (М)
по этому отношению. Если щ — и2, то л (гг4) = л (п2), так что
проекция л индуцирует отображение л: jz* (М) —-> М.
Упражнение 6.1. Мы можем дать другое оппсание пространства
в терминах пространства Т*(М). Действительно, любая система
86
Гл. II. Дифференцируемые многообразия
координат (г1, ..., гп) вблизи р определяет базис dx1?. ..., пространства
Т* (М). Показать, что если (р, (U, h)) — (д', (U', h')), то соответствующие
системы координат определяют один и тот же базис пространства Т* (М).
Обратно, показать, что всякий базис пространства Т* (М) имеет вид
dx\, ..., dx^ для некоторой системы координат (х1, хп}. Таким обра-
зом, ^*(М) может быть отождествлено с множеством всех реперов (т. е.
базисов) всех пространств Т* (М) для р g М.
Если щ — U2, то ulA^~'U2A, так что корректно определено
действие группы GL(n) на j^*(M). Очевидно, что л(гЛ) = л(г)
для z g Jp* (М). Справедливо более сильное утверждение:
Лемма 6.1. Если zA = z для z g (М), А £ GL (и), mo А = I.
Если zyA = z2 для некоторого А g GL (п), то л (zt) = л (z2). Обратно,
если л(г1) = л(г2), то найдется такое A£GL(ri), что zlA = z2.
Первые два утверждения следуют непосредственно из опреде-
ления действия группы GL (п) на Докажем последнее
утверждение. Пусть (р, (U 1; hi)) и (р, (tZ2, /гД)— элементы из Zj и z2.
Тогда Zp4 = z2, где Л = Л2 (р) (^i °/1а1) •
Превратим теперь jF* (М) в дифференцируемое многообразие
(класса если М — класса Ck, и аналитическое, если М — ана-
литическое).
Пусть {(77), hi)} — такое счетное семейство карт, что Ui обра-
зуют базу топологии М. Определим отображение фг: л-1 (Uг) —> GL (га)
следующим образом: пусть г£л-1(77)) и (л (z), (U', 7г')) — карта
из класса эквивалентности г. Положим (z) = Jh. (я (z)) (7г' о/if1).
Это отображение определено корректно, поскольку отношение
эквивалентности, определяющее ,«F*(TW), гарантирует, что
Jh (л (z)> (7г' ° hi1) зависит только от г. Прямое вычисление пока-
зывает, что
фг (гЛ) = Л'КД (г). (6.2)
На U, [) U j мы имеем
(6.3)
Определим теперь отображение фр. л-1 (Ut) —> Ut X GL (га), полагая
ф; (z) = (л (z), ф; (z)). (6.4)
По лемме 6.1 <рг есть взаимно однозначное отображение на. Далее,
GL (га) =Т (га, п; п) есть дифференцируемое многообразие. Кроме
того, фг (л-1 (Uj)) = Ui П Uj X GL (n) и
фгофД(а;, Л) = (x, AJh.(X} (hjvhl1)), (6.5)
§ 6. Главное расслоение
87
согласно (6.3). Таким образом, срг ° cpj1 есть диффеоморфизм
(класса СЛ-1, если М — многообразие класса Ск, или аналитичес-
кий, если М аналитическое). Наконец, множества л-1 (£Д) удов-
летворяют условию 1) теоремы 2.1. Действительно, если n(zt) =
= л (z2) = р, то zt и z2 лежат в л-1 (Ut) для любого U^p. Если
л (zi) = Р я (z2), то, поскольку {Ut} образуют базу (хаусдор-
фовоп) топологии М, мы можем найти такие i и i, что p^Ui,
q£U0. Тогда по теореме 2.1 на (ЛГ) существует
единственная дифференцируемая структура, в которой отображе-
ния <рг являются диффеоморфизмами.
Упражнение 6.2. Показать, что эта дифференцируемая структура
не зависит от выбора атласа {(17г, hi)}.
Определение 6.1. Пространство (М) с определенной
выше топологией и дифференцируемой структурой называется
расслоением корсперов многообразия М.
Поскольку отображения фг являются диффеоморфизмами, ото-
бражение л дифференцируемо. Действительно, вл-1 (Д) мы имеем
л == pi ° фг, где pi (х, Л) = х. Мы будем называть л проекцией
многообразия (М) на М. Группа GL (л) корректно действует
на .Д* (ЛГ). Из формулы (6.1) видно, что отображение z -> zA
есть диффеоморфизм. Можно сказать и несколько больше:
Определение 6.2. Пусть Q — дифференцируемое много-
образие. Говорят, что группа GL (п) действует дифференцируемо
на Q справа (или слева), если задано такое дифференцируемое ото-
бражение ф: GL (и) X (? -> Q, что ф (ф (х, А}, В) = ц> (х, АВ)
(или = ф (х, ВА)) и ф (х, I) = х, где I — единица группы GL (и).
Из определений следует, что группа GL (п) действует диффе-
ренцируемо справа на (ЛГ). Действительно, в терминах локаль-
ных координат отображение GL (и) х л-1 (ГД) -> л-1 (Ut) задает-
ся формулой
фГ1 ° (Л X id) ° (id X ф;), (6.6)
где отображение L: GL (п) X GL (п) -> GL (п) определяется фор-
мулой L (А, В) = А~гВ. [В формуле (6.6) id X фг отображает
GL (п) х л-1 (Ut) в GL (п) X GL (и) х Ut, a L X id отображает
GL (п) X GL (п) X Ui в GL (п) X Ut.] Согласно упражнению 2.8,
отображение L (групповое умножение) дифференцируемо, а зна-
чит, таким же будет и отображение (6.6).
Теперь мы в состоянии определить дифференциально-геоме-
трические величины, аналогичные величинам § 2 гл. I. Пусть
Q — дифференцируемое многообразие, на котором GL (п) дей-
ствует дифференцируемо слева. Обозначим это действие через
88
Гл. II. Дифференцируемые многообразия
Ф (A, q) = р (Л) q, так что р (АВ) х = р (Л) (р (В) х). Введем
в пространстве вр* (М) X Q отношение эквивалентности:
(z, q) ~ (z', q'), если найдется такое Л g GL (п),
что z' = zA и q = р (Л) д'.
Пусть Е (М, Q) — факторпространство пространства (М) X
X Q по этому отношению. На Е (М, Q) можно ввести дифферен-
цируемую структуру. Действительно, рассмотрим отображение
Ф11 множества Ut X Q на множество классов эквивалентности
пространства л-1 (t7;) X Q, задаваемое формулой
Ф?1 (х, q) = {ф?1 (х, I), q}, (6.7)
где {z, q} обозначает класс эквивалентности элемента
(z, q) 6 (7И) X Q, а I есть единица группы GL(n). Легко про-
верить, что Ф?1 есть взаимно однозначное отображение на. Пусть
Ф; — отображение, обратное к Ф?1. Тогда
Фгофу1^. q) = (x, q'),
где q' определено равенством
{фГ1 (л?, I), д'} = {ф?1 (х, I), q}.
Далее,
фД(ж, 7) = ф71(ж, Jhi(x)(hj°hi1)) =
[согласно (6.5)]
= ф!1 (х, I) (Jh.w (hj ° hi1))"1,
[согласно (6.2) и (6.4)]
откуда
Другими
Q' = P((Jhi (х) (hj ° hi 1))"1) q = p (Jhj(X) (hi ohj^q.
словами,
ф.офу1^, q)=(x, p^hjixy^ioEj^q). (6.8)
Отображение множества hj (Ui f] Uj) в GL (n), переводящее
x B ^h (x) °h]1), дифференцируемо, так же как и отображение
GL (п) X Q -> Q, задаваемое формулой (Л, q) -> р (Л) q. Их ком-
позиция, которая встречается в формуле (6.8), дифференцируема
и, значит, отображение Фг о фу1 тоже дифференцируемо. Отсюда
немедленно следует, что условия теоремы 2.1 выполнены. Как
в упражнении 6.2, легко проверить, что дифференцируемая струк-
тура, доставляемая этой теоремой, не зависит от выбора [7г. Если
мы определим отображение nQ : JT* (М) X Q М, полагая
§ 6. Главное расслоение
89
Hq (z, q) = л (z), то nQ будет постоянно на классах эквивалентно-
сти и определит отображение многообразия Е (М, Q) на М.
Легко проверить, что отображение дифференцируемо. Мы будем
называть его проекцией пространства Е (М, Q) на М и иногда,
если невозможны недоразумения, будем опускать индекс Q
и писать л вместо лс.
Упражнение 6.2. Показать, что для любого х £ М множество
л^1 (я) есть подмногообразие в Е (М, Q), диффеоморфное Q. Диффеоморфизм
зависит от выбора координат вблизи х. Показать, что любые два таких диф-
феоморфизма отличаются на диффеоморфизм вида р (g): Q -+ Q, где g б GL (п).
Определение 6.3. Дифференцируемое многообразие
Е (М, Q) называется пространством величин типа Q. Дифферен-
цируемое отображение s: М -> Е (М, Q), удовлетворяющее
условию
nQos = id, (6-9)
называется полем величин типа Q на М. Это поле называется
полем класса Ck (аналитическим), если отображение $ класса Ск
(аналитическое).
Для любой карты (U, h), которую мы можем взять в каче-
стве (Ut, hi), отображение s\Ui индуцирует отображение
зг: Ui~>Q, определяемое равенством
(•Г, 8,(Х)) = Ф<(8(Х)). (6.10)
В Ui П Uj имеем (х, st (х)) = ° Фу1 (х, Sj(x)), или, ввиду фор-
мулы (6.8),
St (z) = р (Jhjfx') (htohj1)) Sj (x). (6.11)
Обратно, пусть {(£7г, ht)} — атлас многообразия М. Предполо-
жим, что для каждой карты (Ut, ht) задано такое отображение
зг: Ut-y-Q, что на пересечении Ut f| Uj выполнено условие
(6.11). Тогда
Ф?1 (х, Si (х)) = Фу1 (х, Sj (х))
на Ut П Uj, так что совокупность отображений х -> Фг1 (х, зг (х))
корректным образом определяет дифференцируемое поле s: М ->
-> Е (М, Q). Пусть U — открытое подмножество в М. Тогда про-
странство Е (U, Q) можно очевидным образом рассматривать как
открытое подмногообразие в Е (М, Q). Если з — поле величин
типа Q на U, то иногда, допуская вольность речи, мы будем гово-
рить, что s есть поле типа Q (на многообразии М), определенное
на U. Предположим, что s; (i = 1, 2, . . .) — поле типа Q, опре-
деленное на открытых множествах Ui сх М, причем зг = з7- на
90
Гл. II. Дифференцируемые многообразия
Ut Q Uj. Тогда из предыдущих рассуждений следует, что суще-
ствует единственное поле на [J Ut, совпадающее на Ut с s;.
Прежде чем продолжать дальше, приведем несколько при-
меров.
1. Пусть Q — дифференцируемое многообразие, на котором
GL (и) действует тривиально, т. е. р (Л) q = q для всех А и q.
Тогда Фг о фу1 = id, согласно (6.8), и Е (М, Q) может быть ото-
ждествлено с М X Q. Поле типа Q есть тогда просто отображение
М -> Q. В специальном случае, когда Q есть вещественная прямая,
мы обозначим пространство Е (М, Q) через R (М).
2. Пусть QT = Rn — пространство всех наборов п чисел X =
= (X1, . . . , Хп). Для А = (оф положим р (Л) X = Y =
= (У1, . . . , У"), где У* = 2 Пространство Е (М, QT) мож-
но отождествить с Т (М), как это следует из рассуждений относи-
тельно формулы (5.3). Благодаря этому отождествлению мы
можем ввести в Т (М) дифференцируемую структуру. Простран-
ство Т (М) вместе с этой дифференцируемой структурой назы-
вается касательным расслоением многообразия М. Поле типа QT
называется (контравариантным) векторным полем. В локальной
системе координат (U, h), где h = (ж1, . . ., хп), векторное поле
задается дифференцируемым отображением U в QT, т. е. п функ-
циями X1 (•),... , Хп (•). Согласно рассуждениям § 5, векторное
поле на U, соответствующее постоянным функциям (6$, . . . , 6”),
сопоставляет каждой точке р С U касательный вектор (д/дхг)р.
Обозначим это векторное поле также через д!дхг. В силу линей-
ности векторное поле, определяемое функциями (X1, . . . , Хп),
п
может быть записано в виде 2 ' ^сли У1’ •••> УП ~ ДРУгая
1=1
система координат, то в соответствии с формулой (5.3) имеем
= Г — , (6.12)
dyi дхЗ дуз дх!
ИЛИ
JL = yJ^.JL. (6.13)
dxi dxi dyi
Таким образом, векторные поля преобразуются как дифферен-
циальные операторы.
3. Пусть QT* — пространство всех наборов п чисел X =
= (Xlt . . . , Хп). Если Л = (а)) и Л-1 = (0)), то положим
р (Л) X = У = (У1; . . . , Уп), где Yj = 2 PPG- Пространство
Е (М, QT*) может быть отождествлено, аналогично предыдущему,
с Т* (М). Пространство Т* (М) с приобретенной таким образом
§ 6. Главное расслоение
91
дифференцируемой структурой называется кокасателъным рас-
слоением. Поле, соответствующее функциям (6’, . . 8„) в систе-
ме координат (ж1, . . . , хп), обозначается dx\ Таким образом,
<1хг (р) = dXp. Поле типа <2т* называется ковариантным векторным
полем, или (линейной) дифференциальной формой. Так, самая
общая линейная дифференциальная форма может быть записана
в системе координат (х\ . . . , хп) в виде 2 Xi dxl, где Xt — диф-
ференцируемые функции. Если / — дифференцируемая функция,
то, согласно (5.11), отображение р (df)p есть дифференциальная
форма, которую мы будем обозначать df. Итак, в локальной системе
координат
df= V. -^-dx\
dxi
4. Более общо, пусть Q — конечномерное вещественное век-
торное пространство и р — линейное представление группы GL (п)
в Q. Ясно, что GL (п) действует дифференцируемо на Q. Таким
образом, мы можем говорить о линейных величинах. В частности,
если р — тензорное представление группы GL (п), то мы будем
называть пространство Е (М, Q) пространством тензоров типа р х).
Поле таких величин называется тензорным полем. Например,
тензорное поле типа задается в системе координат (U, h) набо-
ром п3 функций s31j2j3. Если iiriai3 — функции, соответствующие
тому же полю в системе (У, h'), то
З’У . (р)
dyl3>h'(p) ’2’3 •
У пражнение 6.3. Пусть SF (М) — множество всех пар(р; . . ., Хп),
состоящих из точки р Е М и базиса Xt, ... , Хп пространства Тр (М).
Показать, что 3- (ЛГ) обладает естественной дифференцируемой структу-
рой. (Что является пространством Q в этом случае?) Пространство 3: (М)
с этой структурой называется расслоением реперов многообразия М.
Если Qx, . . . , Qh — пространства, на которых группа GL (п)
действует дифференцируемо, то мы можем определить действие
GL (п) на Qi X . . . X Qh, полагая
р (Л) (qlt ...,qk) = (pi (Л) qi, . . ., pft (Л) qh).
Чтобы убедиться в том, что это дифференцируемое действие, заме-
тим, что отображение GL (n)xQiX X Qk —> Qt X ... X Qk явля-
x) Или тензорным расслоением типа Q, см § 7.— Прим, перев.
92
Гл. II. Дифференцируемые многообразия
ется композицией отображения
k раз
GL(n)x ... xGL(n)xQiX ... xQk—>QtX ... xQk,
переводящего (Лп Ak, q{, . . ., qk) в (pi (Д)qt, . .., ph (Ak) qk),
и диагонального отображения А—>(Л, . ..,Л). Оба эти отобра-
жения дифференцируемы. Таким образом, мы можем определить
пространство Е(М, Q^x ... X Qk)- Пусть s1, . . sk — поля типа
••,<?&, которые, согласно формуле (6.10), определяют ото-
бражения s<: Ut—+Qr. Отображения s;: Ui—X ... X Qk, зада-
ваемые формулой
Si(x) = (s| (z), . (x)),
определяют поле s типа <2i X • • • X Qk на M. Чтобы доказать это,
мы должны проверить условия (6.11), т. е.
Si (х) = (s) (х), ..., skt (х)) = р (Jh}w (hi ° hf)) Sj (х) =
= (Pl (^hj{x) (hl ° hj1)) s) (x), . . . , Pk (Jhj(x) (hi ° hj1)) S^ (x)).
Но это так, поскольку sr — поле типа Qr (г = 1, . . ., к). Поле s
называется произведением полей s1, . . ., sk и обозначается симво-
лом (s1, . . . , sh).
Пусть <2i и <22 — пространства, на которых дифференцируемо
действует группа GL (п). Говорят, что отображение /: <21 “* <2 2
эквивариантно, если / (р4 (Л) q) = р2 (Л) / (q) для всех Л С GL (п)
(где pt, р2 — действия группы GL (п) на <21 и <29). Например, если
Qi = (2 X (2 И q2 = (2, где <2 есть пространство некоторого линей-
ного представления группы GL (п), то отображение <21 в <2г, пере-
водящее (а, Ь) в а-\-Ь, очевидно, эквивариантно. Если отображе-
ние /: <21 -> <2г эквивариантно, то отображение
id X /: (М) X <2i (М) X Q2
переводит классы эквивалентности в классы эквивалентности
и, значит, определяет отображение f#:E(M, Qt)—>E(M, Q2).
В терминах карты (Ut, ht) отображение /#, ограниченное
на л-1(<7г), задается формулой
C£o(idx /)°Фц,
где Ф)г и Ф2г — координатные отображения (6.7) пространств
Е (М, Qi) и Е (М, <2г) соответственно. Поэтому если / дифферен-
цируемо, то таким же будет и
Упражнение 6.4. Пусть / — эквивариантное отображение Q,
в <?2 и s — поле типа , задаваемое в локальных координатах отображениями
s;: Ui -> Qi- Показать, что /#о5есть поле типа Q2, задаваемое в локальных
координатах отображениями / о st.
§ 6. Главное расслоение
93
Предыдущие замечания можно использовать для определения
алгебраических операций на полях линейных величин, в частности,
на тензорных полях. Например, если /: Q X Q Q — экви-
вариантное отображение, определяющее сложение в векторном
пространстве Q, то f# (s1, s2) — поле типа Q для любых полей s1
и s2 типа Q. Обозначим это поле через s1-)- s2. Пусть R — веще-
ственная прямая с тривиальным действием группы GL (п), и пусть
/: R X Q -> Q — отображение, переводящее (X, v) в ки. Тогда
/# (w, s) есть поле типа Q, если и — дифференцируемая функция
(т. е. поле типа R), as — поле типа Q. Обозначим это поле через
us. Легко убедиться в том, что эти операции превращают множе-
ство полей типа Q в модуль над кольцом дифференцируемых
функций. Для этого мы должны проверить, что s1 -J- s2 = s2 Ц-s1,
и (s14-s2) = us1 Ц- us2 и т. д. Доказательство всех этих равенств
основано на следующем замечании: если Д и Д — эквивариантные
отображения, то таким же будет и Д о /2, причем (Д о /2)# =
= (/1)# 0 (/г)#-
Докажем, например, что sx4-s2 = s24-sr. Для этого рассмо-
трим отображение fr. Q X X Q, переводящее (сц, и2)
в (i?2, fj), и отображение /2: Q X Q -+ Q, переводящее (щ, v2)
в 4 v2. Тогда (Д)# (s1, s2) = (s2, s1) и (j2)# (s1, s2) = s1 4- s2.
Ввиду коммутативности сложения в Q имеем /2 ° Д = Д. Значит,
(/2)# ° (Л)# = (/1)#, т. е. s2 + s1 = s1 4- s2.
Если Qt, . . . , Qh — тензорные пространства, то отображение
((Д, . . ., (Д) -> Qt <8> . . . ® Qk эквивариантно и, следовательно,
позволяет определить тензорное произведение s1 0 ... 0 d1 тен-
зорных полей s1, . . . , s’1. Аналогично, симметризация и антисим-
метризация являются эквивариантными отображениями, так же
как и внешнее умножение, внутреннее умножение и т. д. Короче
говоря, все алгебраические операции гл. I индуцируют соответ-
ствующие алгебраические операции на тензорных полях. Так,
любое тензорное поле может быть записано (локально) как сумма
членов, представляющих собой произведение функции на тензор-
ное произведение различных д!дхх и dx\ Пусть, например, <2дрг*
есть p-я внешняя степень пространства QT* (вместе с соответствую-
щим представлением группы GL (и)). Поле типа <2дрг* называется
внешней дифференциальной формой степени р. Если со — внешняя
дифференциальная форма степени р, то в локальных координатах
мы можем написать
(О = 2 aii.....i Д . .. Д dx'p
<К...<Д р
(где ац,..., ip — дифференцируемые функции).
94
Гл. II. Дифференцируемые многообразия
Прежде чем приступать к более детальному изучению тензор-
ных расслоений и полей, мы рассмотрим поведение расслоения
кореперов при диффеоморфизмах. Пусть g — диффеоморфизм мно-
гообразия Мх на открытое подмножество из М2. Тогда существует
отображение g* подмножества л-1 (g (ЛТ4)) cz ^*(М2) на F*(4/i),
определяемое следующим образом: если (у, (U, h)) g U (М2)
и yEg(Mt), то (g~r(U), hog) есть карта вблизи g-1(y). Рассмот-
рим отображение g-. л~г (g (Mi)) cz U (М2)-^-U (М\), задаваемое
формулой g((y, (U, h)) = (g-1 (у), hog). Легко проверить,
что если Zi—z2, то g (zj)— g(z2). Индуцированное отображение
классов эквивалентности и обозначается символом g*. Пусть
(Ui, hi) — карта на ТИ2, (U), h})— карта на Mi, а <р| и ф'— соот-
ветствующие отображения л-1 (Щ) —>Ulx GL (п) и л-1 (U}) —>
—>и)хОЬ(п). Тогда отображение g* на л-1 (UI f| g (U))) задается
формулой
g*(z) = (cpj)’1(r1(?)> (6-14)
где zE{(q, (U, 7г))}. Поэтому отображение g* дифференцируемо
(и класс дифференцируемости его на единицу ниже, чем для g).
Прямая проверка показывает, что отображение g* обладает еще
двумя свойствами:
a^=goaog*, (6.15)
g* (zA) = g* (z) А. (6.16)
Конечно, проекция л в формуле (6.15) и умножение на А
в формуле (6.16) имеют разный смысл в разных частях равенств.
Слева они относятся к расслоению (М2), а справа — к гт.
Упражнение 6.5. Пусть gt—диффеоморфизм многообразия
на открытое подмножество пз М2 и g2—диффеоморфизм многообразия М2.
на открытое подмножество из М3. Показать, что (g2 ° gi)* = g* ° g*.
Пусть Q — пространство, на котором дифференцируемо дейст-
вует группа GL(ri). Отображение g* X id пространства л-1 (g-(Mj)) х
X Q cz -Р (М2) х Q2 в L* (Mi) х Q переводит, согласно формуле
(6.15), классы эквивалентности в классы эквивалентности. Поэтому
оно определяет отображение (которое мы снова обозначим через g*)
множества hq1 (g (Mi)) cz Е (М2, Q) в E(Mi, Q). В терминах карт
для х Е Ui П g (Щ) имеем
Ф}о^*о(ф?)-1(ж, q) = (g~r(x), q1),
где
{(ф})-1 (ё'1 (-г). I), q1} = {g* ° (Ф?)’1 (%, I), q}•
§ 6. Главное расслоение
95
Но
g* о (ф?)-1 (х, I) = (Гх (х), Jh}(g-1(x)) (hl о go (л;.)-1)) =
[согласно (6.14)]
= (ф5)-1((г1(^)> Л; 4j(g-i(x))(h^g<h}y^).
[согласно (6.1)]
Таким образом,
Я1 = Р ^-‘(х)) 0 (й5)-1)) Q'1 =
или иначе
Ф}о^*о(ф?)-1(Ж, 5) = (r1(^), Р(А[(х)(^ГМ«т (6.17)
Поэтому отображение g* дифференцируемо. Из определений сле-
дует, что равенство (6.15) справедливо и для отображения g*,
определенного на Е (М2, Q). Пусть /—эквивариантное отображение
пространства Qi в Qz. Тогда
g*f# = f#g*- (6.18)
Если s: М2—>E(MZ, Q)— поле типа Q на Mz, то из (6.15)
следует, что отображение g* ° s ° g: > E (ЛТ t, Q) есть поле
типа Q на Mx. Действительно, a°g*'>sog = g~1oa°s<>g = id.
Мы получаем, следовательно, отображение полей типа Q на Mz
в поля типа Q на Mt. Мы будем обозначать это отображение
также через g*. Таким образом,
g*(s) = g*oSog. (6.19)
Пусть s1, ..., s*— поля типа Qi, ..., Q^ соответственно. Мы
оставляем читателю проверку того, что
g* ((s1, . . ., ?)) = (g* (s1), .. ., g* (?)) (6.20)
И
g*(/#(s)) = /#fe*W). (6.21)
Суммируем часть полученных результатов в виде следующей
теоремы:
Теорема 6.1. Пространство всех тензорных полей на диф-
ференцируемом многообразии имеет структуру алгебры с опера-
цией свертки. На пространствах симметрических и антисимме-
трических контравариантных (и ковариантных) тензорных полей
определены также обычные алгебраические структуры.
96
Гл. II. Дифференцируемые многообразия
Диффеоморфизм, g многообразия М± на открытое множество
из М2 индуцирует отображение g* тензорных полей на М2 в тен-
зорные поля на Mi, сохраняющее все алгебраические операции. Если
gi. Mi М2 и g2: М2 -> М3, то
(g^g^^g^gl (6.22)
§ 7. ТЕНЗОРНЫЕ РАССЛОЕНИЯ
В § 6 мы видели, что касательное расслоение (т. е. простран-
ство величин типа QT) как множество можно считать объедине-
нием [J Тр (М). При этом подмногообразие л-1 (р) можно рас-
сматривать как векторное пространство, а именно, как касатель-
ное пространство, определенное в § 5. Кроме того, эта структура
векторного пространства на л-1(р) согласована с алгебраической
структурой касательного пространства, т. е. если X, Y — век-
торные поля, то
(X + У) (р) = X (р) + У (р)
[где плюс слева обозначает сложение векторных полей, а справа —
сложение векторов в Тр (Л/)]. В этом можно убедиться, выразив
обе части равенства в локальных координатах. Подобные утверж-
дения, конечно, справедливы для любого пространства линейных
величин Е (М, (?). Действительно, согласно упражнению 6.3,
л-1 (р) диффеоморфно Q и два различных диффеоморфизма отли-
чаются на линейное преобразование пространства Q. Если Хр
и Yp — элементы из л-1 (р), то можно положить аХр -j- bYp =
= hr1 (ah (Хр) + bh (Ур)), где h — любой из диффеоморфизмов
упражнения 6.2. Если h' — другой такой диффеоморфизм, то мы
можем написать h' = L о h, где L — линейное преобразование
пространства Q. Тогда
(h')-1 (ah' (Хр) + bh' (Yp)) = h^Lr1 (aLh (Xp) + bLh (Yp)) =
= h~1 (ah (Xp) + bh (Yp)).
Поэтому линейная комбинация aXp + bYp корректно определена
независимо от выбора h. Легко проверяется также, что возникаю-
щая таким образом структура векторного пространства согласова-
на с векторной структурой, определенной на полях типа Q.
Для тензорных величин мы можем сделать дальнейшее отож-
дествление. Пусть Q— пространство тензорного представления
группы GL(n). Пространство Q определяется следующим образом:
берется тензорное произведение нескольких экземпляров прост-
ранств QT и Qt* и к нему применяются такие операции, как
симметризация, антисимметризация, прямая сумма и т. и. Короче
говоря, пространство Q получается путем применения к Qt и Qt*
J 7. Тензорные расслоения
97
некоторой последовательности операций; обозначим эту последова-
тельность операций через Рассмотрим касательное и кокаса-
тельное пространства Тр (М) и Тр (М). Каждая карта (U, h)
вблизи точки р определяет изоморфизм h пространств Тр (М)
и ТР(М) на QT и Qt* соответственно. Этот изоморфизм индуци-
рует изоморфизм пространства &(ТР (М), ТР(М)) на ® (Qt, Qt*) =
= Q, зависящий от h. Если (U', Л')—другая карта и (V, h') ~
— (U, h), то, очевидно, Л' = /г, так что этот изоморфизм зависит
только от класса эквивалентности z£y*(M) карты (U, h). Таким
образом, каждому z £ л-1 (р) cz Jp* (М) соответствует изоморфизм
z: Q, (Тр (М), TP(M))-^Q. Если г' — другой элемент из л-1 (р)
и z' = zA, то из определения тензорного произведения и уже
установленных фактов относительно касательных и кокасательных
расслоений следует, что z' — р (A) °z, где р(Л): Q—>Q — оператор
п редставления р группы GL (п) на Q. Таким образом, каждому
t £ @ (Тр (М), Тр (М)) мы можем сопоставить класс эквивалентности
{z, z(t)}QE(M, Q). Обратно, каждому классу {z, q} мы можем
сопоставить единственный элемент z-1 (g) £ @ (Тр (М), ТР(М)).
Итак, мы можем отождествить @,(ТР(М), ТР(М)) с л-1 (р) с
az Е(М, Q).
Рассмотрим в качестве иллюстрации пространство Q = Qt* © <2т*.
Тогда Е(М, Q) можно отождествить с [J Тр (М) © Тр (М). Поле
рем
типа Q сопоставляет каждой точке р элемент из ТР(М) © ТР(М),
т. е. метрику на ТР(М). В локальных координатах такое поле
имеет вид 2 Sij^x1 © dx1.
Определение 7.1. Поле типа Qt* © Qt* называется рима-
новой метрикой на М, если оно индуцирует положительно опре-
деленную метрику на каждом Тр (М). Если в локальных коорди-
натах поле имеет вид 2 Sa dxl © dx1, то это равносильно тому,
что матрица (gtj) положительно определена. Многообразие М
вместе с римановой метрикой называется римановым многообразием.
В римановом многообразии имеет смысл говорить о длине каса-
тельного вектора. Поскольку касательный вектор есть «инфини-
тезимальная кривая», естественно ожидать, что мы сможем гово-
рить о длине кривой на М, «проинтегрировав» ее бесконечно малые
части. Дальше в этом параграфе мы увидим, как это сделать.
Пусть Q — тензорное пространство, полученное применением
операции @ только к пространству QT (без привлечения простран-
ства Qt*)- Тогда Q называется контравариантным тензорным про-
странством, а пространство Е (М, Q) величин типа Q обозна-
чается символом QT (М) и называется контравариантным тен-
1 С. Стернберг
98
Гл. II. Дифференцируемые многообразия
зорным расслоением. Аналогично, если Q получено операцией @
из Qt*, то пространство Е (М, Q) называется ковариантным тен-
зорным расслоением и обозначается ЙТ* (М). Важное различие
между контравариантными и ковариантными тензорами прояв-
ляется в их поведении при отображениях.
Пусть g — дифференцируемое отображение многообразия Mt
в многообразие М2. В § 5 мы видели, что g индуцирует отображе-
ние g*: Т (М^ -> Т (М2), задаваемое формулой (5.13) в локаль-
ных системах координат (U, h) на Mi и (7, Н) на М2. Ввиду ото-
ждествления Е (М, QT) с Т (М) из формулы (5.13) следует, что
g* есть дифференцируемое отображение Т (Mi) -> Т (М2). Посколь-
ку ограничение g* на каждое пространство Тр (Mi) является линей-
ным отображением Тр (Mi) -> T’g(p) (М2), отображение g* инду-
цирует линейное отображение любого контравариантного тензор-
ного пространства над Тр (Mi) в пространство того же типа над
Tg(P) (М2). Таким образом, мы имеем отображение @,Т (Mi) -+
-> 0,Т (М2) для любой (контравариантной) операции тензорных
умножений ($,; мы обозначим это отображение также через g*.
Легко проверить, что g* — дифференцируемое отображение. Итак,
справедлива
Теорема 7.1. Пусть g: Mi~>M2— дифференцируемое ото-
бражение (класса по меньшей мере С2). Тогда для любой (контра-
вариантной) операции @ определено дифференцируемое отображе-
ние g*: @Т (Mi) &Т (М2). В частности, отображение
g*: Т (Mi) -^Т (М2) имеет в локальных координатах вид (5.13).
Если gi'. и g2: М2—>М3, то
(g2°gi)*=gZ*°gi*- (?•!>
Единственное, что мы еще не доказали,— это равенство (7.1),
но оно сразу следует из определения отображения g*: Си (Mi)
-> Си (М2) на пространстве Си (Mi).
Отображение g* в отличие от отображения g*, определенного
для диффеоморфизмов в § 6, не переводит векторные поля в век-
торные поля. Пусть задано векторное поле X: Mi -> Т (Mi).
Единственным подходящим кандидатом для поля g* (X) может
быть только «отображение» М2 Т (М2), переводящее g (х)
в g* (X (х)). Но оно не корректно определено по двум причинам.
Во-первых, если g не взаимно однозначно, то может случиться,
что у = g (xi) = g (х2), в то время как g* (X (xi)) g* (X (х2)).
Во-вторых, даже если g взаимно однозначно, наше «отображение»
М2 —>- Т (М2) определено только на g (Mi), а не на всем М2.
На самом деле g* определяет отображение векторных полей в век-
торные поля только в том случае, когда g есть диффеоморфизм
многообразия Mi на М2. Это вытекает из следующего упражнения:
§ 7. Тензорные расслоения 99
Упражнение 7.1. Пусть g— диффеоморфизм многообразия Mt
на М2. Показать, что для любого контравариантного тензорного пространства
Q отображение g*: Е (м,, Q) -> Е (М2. Q) совпадает с отображением (g'1)*
(определенным в § 6).
Поскольку (g*)x есть линейное отображение Тх (MJ —»
—> Тg(X) (М2), оно индуцирует линейное отображение (gj* про-
странства (Тg(X) (М2))* в (Tx(Mi))*. Если (5 — ковариантная опе-
рация, то (gjj индуцирует отображение (3 (TgW (М2)) в (3 (Тх (MJ).
Мы не можем сразу определить (g*)* как отображение Е (М2, Q) —>
—Q) по той же причине, что и раньше: правило, сопо-
ставляющее точку х каждой точке g(z), не является корректно
определенным отображением на всем М2. С другой стороны,
s: М2 —+ Е(М2, Q) есть поле типа Q. Тогда отображение
g* (s): Mi —> Е (М, Q), определенное равенством
g* (s) (^) = (g*)*oso(g(a;)),
удовлетворяет условию n<>g*(s)=id.
Упражнение 7.2. Показать, что g* (s) есть дифференцируемое ото-
бражение Mt —г Е (Мъ Q).
Упражнение 7.3. Пусть Q — пространство с тривиальным действием
группы GL (п).- Согласно примеру 1 § 6, сечение s расслоения Е (М2, Q)
можно рассматривать как отображение s: М2 —Q. Показать, что
g* (s) = S о g.
Согласно упражнению 7.2, g*(s) есть поле типа Q на Mt, где
(ЗТ* (М^ = Е Q). В самом деле, справедлива
Теорема 7.2. Пусть g: МХ—>М2— дифференцируемое ото-
бражение. Для любой ковариантной тензорной операции (3 опре-
делено отображение g* тензорных полей из (ЗТ* (М2) в тензорные
поля из (3T*(Mi). Отображение g* сохраняет все алгебраические
операции на тензорных полях. В частности, если со — поле
из Т*(М2), т. е. линейная дифференциальная форма, имеющая
в локальных координатах вид <£> = ^ Yi dyl, и если локально ото-
бражение g задается функциями уг (х1, .. ., хП1), то
— (7.2)
дхЗ
г, 3
Если gi- Mf—>M2 и g2: М2 —>М3, то
(g2°gi)* = g*i°g*2- (7.3)
Мы оставим эти еще не вполне доказанные утверждения чита-
телю в качестве упражнения.
7*
100
Гл. II. Дифференцируемые многообразия
Упражнение 7.4. Показать, что если g— диффеоморфизм М j —>Мг,
то отображение g*, определенное здесь, совпадает с отображением g*, опре-
деленным в § 6.
В качестве иллюстрации вычислим g* (b), где b — симметриче-
ская билинейная форма, имеющая в локальных координатах вид
b^^gtjdy1 © dy}. (7.4)
Имеем
g* (&) = 3 [s'o-° (vr dxh) ® ("гг dxi)=
. \ dxk / \ dx1 /
j, fe, I
= i 2 1№гС7Т+ТГ7г)''?®'й' (7-5>
t, j, k, I
Пусть, в частности, С: [а, д] -> М — кривая в М, где М —
риманово многообразие с римановой метрикой Ъ. Предположим
для простоты, что С есть дифференцируемое отображение, которое
может быть продолжено на некоторую окрестность отрезка [а, б],
и пусть t —- координата на [а, 6]. Тогда С* (Ь) есть риманова
метрика на (а, Ь). Предположим на минуту, что С ([а, б]) содержит-
ся в координатной окрестности U, где b имеет вид (7.4). Тогда
С* (Ь), согласно (7.5), может быть записана в виде
СЧЬ) = 2[^С] №-^-)dt©dt. (7.6)
Определим теперь длину L (С) кривой С, полагая
Ь(С)= j /2 (7.7)
а
Эта длина не зависит от параметризации кривой С. Точнее, пусть
Ф — монотонное дифференцируемое отображение отрезка [с, d]
на отрезок [а, bl и s — координата на [с, d]. Тогда Соф — также
кривая, лежащая в U (как говорят, «та же кривая с другой пара-
метризацией»). Ввиду (7.3) имеем
(С о ф) * Ъ = ф*(С* (&)) = 3 [gij О С О ф] ( М о ф) ( о ф) ф* (Л © Д) =
= 2кй = Соф] 0£-°<р) (^-°ф) {^ds@ds.
Согласно (7.7), длина С (Соф) равна
§ 8. Векторные поля и производные Ли
101
что совпадает с L (С) в силу формулы замены переменных в опре-
деленном интеграле. Подобные же рассуждения показывают, что
определение (7.7) не зависит от выбора координат (у1, . . . , уп).
Упражнение 7.5. Пусть а < а < Ь, и пусть Ci — ограничение
кривой С на [а, а'], а С2 - ограничение С на [а, Ь]. Показать, что L (С) —
= L (G) + L (С2).
Если кривая С не лежит целиком в одной координатной окрест-
ности, мы можем разбить интервал [а, Ь] на конечное число подин-
тервалов, образы которых (при отображении С) попадают в коор-
динатные окрестности. Тогда мы можем определить длину кривой
С как сумму длин этих подинтервалов. Из предыдущих рассуж-
дений и упражнения 7.5 следует, что это определение не зависит
от разбиения, выбора координат и параметризации кривой С.
§ 8. ВЕКТОРНЫЕ ПОЛЯ И ПРОИЗВОДНЫЕ ЛИ
В этом параграфе мы покажем, что векторные поля можно
рассматривать как «инфинитезимальные преобразования», и изу-
чим их свойства.
Определение 8.1. Семейство ср(: М -+ М диффеомор-
физмов называется однопараметрической группой дифференцируе-
мых преобразований многообразия М, если отображение ср: R X
X М -> М, переводящее (4, р) в cpf (р), есть дифференцируемое
действие аддитивной группы вещественных чисел на М, т. е. если
1) отображение ср дифференцируемо,
2) cpf+s = cpf ° cps для всех t и s,
3) сро есть тождественный диффеоморфизм.
Однопараметрическая группа ср( индуцирует векторное поле
на М. Действительно, для любой точки р £ М отображение t ->
-> ср( (р) является кривой, проходящей через р. Определим Хр
как касательный вектор этой кривой. Из определения следует,
что для любой дифференцируемой на М функции f мы имеем
(Хр, (df)p) = lim J- (/ (ср; (р)) - f (р)). (8.1)
t-*o 1
Беря в качестве f координатные функции х1, ..., хп локальной
системы координат, находим, что
Хр = 2 lim 4 & •
Поскольку отображение ср дифференцируемо, отображение р —> Хр
определяет векторное поле X на М. Векторное поле X называется
инфинитезимальной образующей однопараметрической группы ср(.
1) Или, более кратко, потоком на многообразии М.— Прим, перев.
102
Гл. II. Дифференцируемые многообразия
Обратное утверждение не вполне верно. Не всякое векторное
поле на М порождает однопараметрическое семейство преобразо-
ваний многообразия М. Однако локально это так. Более точно,
имеет место
Теорема 8.1. Пусть X — векторное поле на М. Для любого
р £ М существуют окрестность U } Р-, s > 0 и единственное
семейство дифференцируемых отображений cpt: U -> М, опреде-
ленное при —8 < i < 8, такие, что
1) отображение ср: (—8, е) X U —> М, переводящее (t, р)
в Фг (р), дифференцируемо-,
2) если | t | $ |, | t + s | все меньше 8 и q £ U, cpt (q) Q U, mo
ф«+г (?) = cps°cpi (?);
3) Xq есть касательный вектор кривой (q, ср ч) для q £ U,
где cpg — кривая £ —> cp< (q).
Доказательство. Пусть (T, h) — карта вблизи точки
р. Тогда в окрестности V мы можем написать
х= Ух*—.
dxi
Рассмотрим систему обыкновенных дифференциальных уравнений
^ = Xi(<pi, (8.2)
По теореме существования решений для обыкновенных дифферен-
циальных уравнений (см. приложение I) существуют такие
и ei > 0, что система (8.2) имеет единственное решение
срг (£; х1, ..., хп), определенное при 111< 8t и удовлетворяющее
условию
<р4 (0; х1, .... хп) = х\ где (х1, ..., xn)QB^. (8.3)
Если мы выберем достаточно малые 8<:8t и 6 б4, то
ср’ (t; х1, .. ., xn)Qh (7) для | £ | < 8, (ж1, .. ., xn)Q Bf.
Пусть U = h~1(B&). Отображение cp(: U—>M, определенное в ло-
кальных координатах формулой
ср’ (ж1, ..., жп) — ср’ (£; ж1, . ., хп),
является, очевидно, дифференцируемым отображением (— 8, 8) X
X U М. Далее, функции ф’ (t; ж1, ..., хп) = ср’ (s-j-1; ж1, ..., хп)
образуют решение системы (8.2), удовлетворяющее начальным
условиям
ф’ (0; ж1, ..., ж”) = ср’ (s; ж1, .. ., хп).
§ 8. Векторные поля и производные Ли
103
В силу единственности имеем
<рг х1, ..хп) = ср* (<; ср1 (s; х1, ..хп), ..., cpn (s; х1, ..., хп)).
Таким образом, условие 2) теоремы выполнено. Условие 3) выпол-
нено по построению.
Мы не можем определить cpf для всех t и на всем М, поскольку
теорема существования решений дифференциальных уравнений
гарантирует существование только локального решения. Даже
в евклидовом пространстве есть примеры векторных полей,
не порождающих однопараметрическую группу во всем простран-
стве. Однако нетрудно показать, что любое векторное поле на ком-
пактном многообразии порождает однопараметрическую группу.
Мы не станем здесь доказывать этот результат.
Пусть X — векторное поле на М, a cpf — соответствующее
семейство отображений окрестности U cz М, доставляемое теоре-
мой 8.1. Если т] — поле типа Q, где Q — линейная величина, то
<р* (т]) есть поле типа Q на U. Мы можем, следовательно, рассмот-
реть производную
^х(п)р = Ит — (<рГ(т1)р-т1р). (8.4)
<-+о 1
В силу единственности срг левая часть формулы (8.4) не зависит
от выбора окрестности 17. Предоставим читателю самому прове-
рить, что для любого поля т] типа Q отображение р -> X х (л)р
является полем типа Q. Обозначим его символом X х (л) и назовем
производной Ли поля т] по направлению векторного поля X. Мы
довольствуемся проверкой того, что Хх (л) есть тензорное поле,
когда т] — тензорное поле. Заметим прежде всего, что, поскольку
<р* линейно,
Хх(^ + Ъ® = аХх^ + ЪХх®, (8.5)
где а и Ъ — константы. Далее, если /: Q^—>QZ— линейное эквива-
риантное отображение (например, свертка тензора), то, согласно
(6.21), <p*f# (л) = /#ср*:(л) Для любого поля л типа Q±. Поэтому
1#Хх(л) = Хх(Ш. (8.6)
Формула (8.6) показывает, например, что производная Ли свертки
тензорного поля есть свертка производной Ли. Пусть теперь
/: Qi X Qz Qs~билинейное эквивариантное отображение. Тогда
снова ср* ° /# = f# о ср* и, значит,
ф*/#(л, Ю—/#(л- 5) = /#(ср*л> фШ-/# (л, =
= /#(ф*Л, фШ - /# (Ф*Л, £) + /#(ф*Л, £)-/#(Л, 5).
Деля на t и устремляя t к нулю, получим (поскольку / переста-
новочно с предельным переходом)
^х(/#(л, £))=/#(£х(л), £) + /#(Л, #х©). (8.7)
104
Гл. II. Дифференцируемые многообразия
В качестве мы можем брать различные операции тензорного
произведения, внешнего произведения и т. д. Это показывает,
что для получения формулы производной Ли тензорного поля
достаточно знать производную Ли 1) функций, 2) линейных диф-
ференциальных форм и 3) векторных полей. Тогда производная
Ли произвольного тензорного поля находится с помощью формул
(8.5) - (8.7).
1) Функции. Если и — дифференцируемая функция на М, то
<P*w = и о <pf; Хх (Ц)р = lim (и (ср, (р)) — и (р)).
В локальных координатах
и = и(х1 *, ..., хп),
cp*u = u(cp) (х1, ..., хп), ..., ср"(а^, ..., хп)),
так что
£х(«) = У—.
л-J gxi dt I qxi
Таким образом, если Х= 2 Хг (д/дхг), то
<£х (и) = У — = (X, du). (8.8)
1 дх1
Поскольку^^х (и) совпадает с результатом применения дифферен-
циального оператора X = 2 X1 (д/дхг) к функции и, мы обычно
будем писать
Xx(u) = X(u) = {X\du). (8.9)
2) Линейные дифференциальные формы. Согласно формуле (7.2),
для ср* (dxl) мы имеем
ср* (dxl) = d (ср * ж‘) = d (ср)) = V —— dx1.
X_1 9хз
Далее, dt^Jdx1 = 6), так что
1 ( .A d V, I dXi
11Ш —— I - ; Oj ] - —7---7----------— .
i-,0 t \ 9x3 / dt gxj |,=o gxj
Значит,
Xx (dxl) = 2 (8.10)
1 dxi
Если a,— функции на U, то в соответствии с формулой (8.7)
Хх (a-t dxl) = Хх (a1) dx' + atXx (dxl) =
= 2Х3’-^-^+У«г — dx\
9x3 9x3
§ 8. Векторные поля и производные Ли
105-
Су ммируя это равенство по i, получим
Жх (2 а, <fe‘) = 2 + вг'. (8.11)
i, 3
3) Векторные поля. Мы могли бы поступить, как в 2), и вос-
пользоваться формулой (7.2). Удобнее, однако, сделать следую-
щее. Если Y — векторное поле, а со — дифференциальная форма,
то отображение (У, ©)-> (У, со) билинейно. Мы можем, следо-
вательно, применить формулу (8.7). Положим У = д/дх1 и w =
= dxl. Тогда
Пользуясь формулой (8.10), находим
= —•
\ дхз / дхЗ дх1
Если У5 — функции на U, то, согласно формуле (8.7),
%х ( У’ -М = Хх (Г) Д-+ Y}Xx (—) =
\ дхЗ / ' дхЗ \ дхз /
_ yi dYi д -у yj дХ1 д
дх* дхз дхЗ дх*
i i
Если У = 3 Y3(д!дя?) — векторное 'поле, то, суммируя последнее
равенство по j, получим
ад-2(2(£г-£г)£). <8Л2>
г ‘<4
Из формул (8.8), (8.11) и (8.12) следует, что если X — векторное
поле класса Ск, то производная Ли дифференцируемой функции,
дифференциальной формы или векторного поля класса Ck есть
функция, форма или векторное поле класса Ввиду формулы
(8.7) это верно и для произвольного тензорного поля.
Следуя общепринятым обозначениям, положим
[У, X] = %x(Y). (8.13)
Левая часть формулы (8.13) называется скобкой Ли векторных
полей У и X1). Из формулы (8.12) немедленно вытекает, что
[X, У]=-[У, X]. (8.14)
Упражнение [8.1. Показать, что X (У (и))—У (X (и)) = [X, У] и для
любой функции и.
т) Или коммутатором полей У и X.— Прим, перев.
106
Гл. II. Дифференцируемые многообразия
Пусть Z— третье векторное поле. Тогда, пользуясь упражне-
нием 8.1, имеем для любой функции и
[X, [У, Z]J(u) = XyZ(u)-XZy(u)-yZX(u)+ZyX(u),
[Z, [X, У]] (u) = ZXY (и)—ZYX {и) - XYZ (и) + YXZ (и),
[У, [Z, X]](u) = yZX(u) — YXZ (и)—ZXY (и)XZY (и).
Складывая эти три равенства, получаем
([X, [У, Z]J + [Z, [X, У]] + [У, [Z, X]]) (и) = 0
для любой функции и. Единственное векторное поле, переводящее
всякую функцию в нуль, — это нулевое векторное поле. Следова-
тельно,
[X, [У, Z]] + [Z, [X, У]] + [У, [Z, X]] = 0 (8.15)
(тождество Якоби).
Определение 8.2. Антикоммутативная (неассоциатив-
ная) алгебра, в которой выполнено тождество Якоби, называется
алгеброй Ли.
Все сказанное можно подытожить следующей теоремой:
Теорема 8.2. Пространство всех векторных полей класса
С°° (аналитических) на многообразии класса С°° (аналитическом)
станет алгеброй Ли, если в качестве умножения взять скобку Ли.
Упражнение 8.2. Пусть А — ассоциативная алгебра. Определим
алгебру L (Л) как пространство А с новым умножением, задаваемым форму-
лой [а, 6] = ab — Ьа. Показать, что L (Л) есть алгебра Ли.
Упражнение 8.3. Показать, что
[иХ, vY] = uv[X, Y]+vY(u)X — uX(v)Y, (8.16)
если и, v — функции, а X, Y — векторные поля.
Следующие результаты будут использованы позднее, в гл. V.
Пусть Mi и М2 — дифференцируемые многообразия и / —
дифференцируемое отображение Mi -> М2. Как мы уже видели,
вообще говоря, с помощью / нельзя построить отображение век-
торных полей на Mi в векторные поля на М2. Однако удобно
ввести следующее
Определение 8.3. Пусть X — векторное поле на Mi,
а У — на М2. Мы скажем, что X и У /-связаны, если У/(Р) =
= (Хр) для всех р С Mi.
Теорема 8.3. Предположим, что векторные поля Х4 и У15
а также Х2 и Y2 f-связаны. Тогда поля [Xi, Х2] и [У1; У2] также
/- связаны.
8. Векторные поля и производные Ли
407
Доказательство. Пусть X — векторное поле на Mi,
а У — на М2. Тогда /-связанность полей X и Y означает, что для
любой дифференцируемой функции g на открытом множестве
U cz М2 мы имеем
(X(go/))p = y(g)/(p)
для всех рС/-1((7). Если Xt и Yt /-связаны (i = l, 2), то для
любой функции g
у2 (Yig)^ = (Х2 (Yig о /))р = (X2Xi (g о /))р.
Поэтому ([Ki, y2]g)f(p) = ([Xi, х2] (go/))p и, значит, Х2]
и [Уь У2] /-связаны.
Теорема 8.4. Пусть f: Mi -> М2 — дифференцируемое
отображение. Если j отображает многообразие Mi на М2, то
•для данного векторного поля X на Mi существует самое большее
одно поле У на М2, такое, что X и Y f-связаны. Если / — погру-
жение Mi М2, то для любого поля У на М2 существует самое
•большее одно поле X на Mi, такое, что X и Y f-связаны. В послед-
нем случае такое поле X существует тогда и только тогда, когда
У/(р> € /* (Тр (Mi)) для всех р £ Mi.
Доказательство мы оставляем читателю в качестве упраж-
нения.
Упражнение 8.4. Пусть — однопараметрическая группа
преобразований многообразия Mt с инфинитезимальной образующей X, а
— однопараметрическая группа преобразований многообразия М2 с обра-
зующей Y. Пусть отображение /: М, М2 удовлетворяет условию /o<plt =
= фг/0/ Для всех t. Показать, что X и У /-связаны. Сформулировать и дока-
зать обратное утверждение.
Для иллюстрации понятия /-связанности рассмотрим какое-
нибудь пространство величин 6, (М) на многообразии М. Любой
диффеоморфизм а: М -> М индуцирует диффеоморфизм
«*: & (М) -> (& (М). Далее, л ° а* — а, где л есть проекция
пространства б (М) на М. Если at — однопараметрическая
группа преобразований многообразия М, то — однопарамет-
рическая группа преобразований пространства ® (М) и л ° а/* =
= аг. Таким образом, если X есть векторное поле на М, то мы
получаем векторное поле на (& (М), которое обозначим (X).
Согласно упражнению 8.4, поля X и @ (X) л-связаны. Наиболь-
ший интерес представляет эта конструкция в случае, когда
$ (М) = Т (М). Для любого векторного поля X на М мы полу-
чаем векторное поле Т (X) на Т (М). Векторное поле Т (X) извест-
но как вариационное векторное поле, или «уравнения в вариациях»
поля X. Оно описывает, как поток, порожденный полем X, действу-
ет на касательные векторы. Как будет показано в гл. IV, поле
Т (X) играет важную роль в вариационном исчислении.
Глава III
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ НА МНОГООБРАЗИЯХ
В этой главе мы продолжим изучение дифференцируемых многообразий
методами анализа. В первую очередь мы займемся теорией интегрирования.
Чтобы определить интеграл, мы должны иметь нечто, играющее роль «подин-
тегрального выражения», и нечто, играющее роль «области интегрирования».
Для выяснения того, что они должны собой представлять, рассмотрим клас-
сическую теорию криволинейных интегралов на плоскости. Криволинейный
интеграл обычно записывается в виде
(i) j Pdx+Qdy,
С
где С — кривая, а Р и Q — непрерывные функции на плоскости. Если кривая
С разбита на конечное число кусков С,, каждый из которых задается диффе-
ренцируемым отображением Сг: t -> (х; (t), (t)) отрезка [0, 1] в Е2, то зна-
чение интеграла (i) находится по формуле
(ii) Pdx+Qdy = ^ ( (p^L+q^L\ dt,
J \ dt dt f
с 0
которая принимается за определение интеграла (i). Если С — простая замк-
нутая кривая, ограничивающая область D, то по теореме Грина
(Ш) j Pdx+Qdy= J J dxdy,
C D
где кривая С обходится против часовой стрелки.
Переведем это на наш язык. Выражения вида Р dx-\-Q dy имеют для нас
самостоятельный смысл. Это просто линейные дифференциальные формы.
Если Ct — отображение отрезка [0, 1] в то
С* (Р dx + Q dy) = (Р %. + Q ^-\dt.
* \ dt dt f
Поэтому если а> = Р dx-\-Q dy, то мы можем переписать формулу (ii) сим-
волически в виде
1
(iv) J <о=2 J Ci(^-
С i О
В этом случае «подинтегральным выражением» служит линейная диф-
ференциальная форма, а «областью интегрирования» — конечное объединение
отображений отрезка [0,1] в Е2. Все эти понятия непосредственно обобщаются
на многообразия. «Подинтегральными выражениями» р-мерной теории интег-
Интегральное исчисление на многообразиях
109
рирования на многообразии М будут внешние дифференциальные формы,
а «областями интегрирования» — линейные комбинации отображений стан-
дартного р-мерного объекта в М.
Прежде чем говорить об обобщениях, заметим, что форма равенства
(iii) не вполне удовлетворительна. Для того чтобы это равенство имело
место, кривая С должна быть ориентирована против часовой стрелки.
Поменяем местами х и у, более точно, рассмотрим отображение <р: х —=-
—> v, у—>и плоскости (х, у) в плоскость (a, v). Если Р' (и, v) = Q(x, у)
и Q'(и, v)=P(x, у), то <р* (Р' du + @' dv)=-P dx-\-Q dy. Пусть <p (С) — образ
кривой С в плоскости (и, и). Формулы (iv) и (ii) показывают, что
§ Р'du-}-Q'dv= Р dx-[-Q dy.
<р(С) с
Далее,
дР 9Q’ dQ dP' , , , ,
dudv — dxdy.
dy ди ох ди
Значит,
f / дР dQ \ , Г I dQ' dP'\ f / OP’ dQ' \ , ,
\ -----^-\dxdy = \ I-5---------\dudv= — \ I —--------------—] dudv.
J \ ду dx f я J \ du dv ) J \ dv du )
D <p(D) <P(D)
Короче говоря, в то время как левая часть формулы (iii) инвариантна отно-
сительно смены осей, правая часть меняет знак. Конечно, причина кроется
в том, что направление обхода кривой С при этом меняется на противополож-
ное. Однако требование определенной ориентации не фигурирует в формуле
явным образом. Мы можем исправить положение, заменив dx dy на dx Д dy.
Тогда du Д dv = — dx Д dy и обе части формулы (iii) инвариантны. Теперь
(v) (^-^^dx/\dy = dP/\dx+dQ/\dy.
Если мы обозначим 2-форму, определенную формулой (v), через dco, то
формула (iii) примет простой вид
<о= <to.
с D
Мы хотим и в общем случае иметь равенство вида
(vi) <0 = J d<o,
db D
где d — некоторый оператор, переводящий р-формы в (р + 1)-формы, a d со-
поставляет (р + 1)-мерной «области интегрирования» ее «границу», явля-
ющуюся р-мерной «областью интегрирования» х).
х) Необходимо отметить, что для функций (т. е. форм степени нуль) фор-
мула (vi) сводится к фундаментальной теореме анализа. В этом случае D
есть кривая, -9D — ее концы (с соответствующими знаками), а формула (vi)
принимает вид
j d/=/(D(l))-/(D(0)).
D
110 Гл» III. Интегральное исчисление на многообразиях
В § 1 мы определяем оператор d и изучаем его свойства. В § 2 мы вводим
дифференцируемые цепи, определяем интегрирование и устанавливаем спра-
ведливость формулы (vi). Остальная часть главы посвящается изучению раз-
личных полезных теорем анализа на многообразиях.
§ 1. ОПЕРАТОР d
Теорема 1.1. Пусть М — дифференцируемое многообра-
зие. Существует одно и только одно отображение d внешней алгеб-
ры форм класса Ск в алгебру форм класса Ch~l, обладающее такими
свойствами:
1) d (<х>1 + о>2) = + d<o2;
2) если о>1 — форма степени г, то
d((o1A(o2) = d(o1A(o2+( —1)г(О1Лй(о2; (1.1)
3) если / — функция, то df — форма, описанная в примере 3-
§ 6 гл. II;
4) d (df) = 0 1).
Доказательство. Заметим, что достаточно доказать
теорему в одной системе координат. Действительно, если мы
докажем существование и единственность da> | U для каждого'
ограничения со | U формы со на координатную окрестность U,
то в силу единственности (dco | U) | U И V = (d<a | 7) | U И V =
= da> | U П V, так что локальные формы dco | U согласованы
на пересечении U V и, следовательно, определяют глобальную
дифференциальную форму.
В системе координат любая внешняя форма может быть запи-
сана как линейная комбинация (с постоянными коэффициентами)
форм вида
jdx1* А - - Л dxp.
Ввиду условий 2), 3) и 4)
d (f dx^ А • • Л ^’P) = df A dx'i А • • Л йхгр,
г) Для обоснования условия 4) рассмотрим любую «двумерную область,
интегрирования», скажем треугольник
Если (vi) справедливо, то ( d (df) = j df =} / (G (1)) — f (Ct (0)) +
D dD
+ f (C2 (1)) — f (C2 (0)) + f (C3 (1)) — f (C3 (0)) = ОЛИтак, интеграл от d (df)
по любой области равен нулю, поэтому d (df) = 0.
§ 1. Оператор d
lit
что доказывает единственность. Если
<0 = 2 ail.......i dxll Л • • • Л
то
dco= 2 ^ай,.... гр Л dxil Л • • Л dxlp. (1.2)
Например, если и — 2 atdx1, то
(1.з>
i<j
Для доказательства существования определим оператор d форму-
лой (1.2). Мы должны проверить выполнение условий 1) — 4).
Условия 1) и 3) следуют немедленно из определения. Условие 4)
также легко проверяется: если / — функция, то df = 2 dx1
и ввиду (1.3) условие 4) эквивалентно тому, что = ' д / { •
Осталось проверить условие 2). Поскольку как внешнее умно-
жение, так и оператор d, определенный формулой (1.2), линейны,
достаточно проверить 2) в случае, когда
а»! = / dx11 Д ... Д dx1?, а>2 = g dxS1 /\ ... /\ dx3*.
Но тогда
d (coi Д ©2) = d (fg) Л dx* Д ... Л dx1? /\ dx* Д ... Д dx3* =
= (fdg + gdf) Д dxil Д .. . Л dx1? Д dx^ Д ... Д dx3* =
= (df Д dx^ Д .. . Л dx1?) Д (g dx* Д ... Д dx3*) Д
Д ( — 1)г (/ЙД1 Д ... Д dx1?) Д (dg/\ dxii Д... Д dx3*) =
= dwt Д®2Д( —1)гсщ Д dw2.
Это доказывает теорему 1.1.
Определение 1,1. Оператор d, фигурирующий в теореме 1.1,
Называется внешним дифференцированием.
Теорема 1.2. Для любой формы имеем
d(cfo)) = O. (1.4)
Достаточно проверить равенство (1.4) в произвольной ло-
кальной системе координат, причем (ввиду условия 1) теоре-
мы 1.1) только для форм вида (p = fdx^ Д ... Д dxlP. Имеем
112
Гл. III. Интегральное исчисление на многообразиях
d^da) = d(df Л dx11 Л • • • Л dx'p) — (d df) Д'[ dx^ Л • • • Л ^ip Н~
р
+ S Л dx11 Л • • • Л d (dx'r) Л ... Л dxlp = 0. [Мы воспользо-
Т=1
вались здесь условиями 1), 2) и 4).]
Обратная теорема в общем случае не верна: из da = 0 не сле-
дует, что <о = da'. Например, если М есть окружность S1, то,
поскольку в S1 нет ненулевых форм степени 2, для любой формы са
степени 1 мы имеем da = 0. Далее, форма dQ х) корректно опреде-
лена, но не существует функции 6, определенной на всей окруж-
ности. Эти вопросы мы обсудим далее в §§ 2 и 3.
Теорема 1.3. Пусть ср: -> М2 — дифференцируемое
отображение 2) многообразий. Тогда
dtp* (со) = ф* (da). (1.5)
Снова достаточно доказать (1.5) для координат-
ных окрестностей в Mi и М2 и в случае, когда a = fdx^/\ ...
... Л dx'?. Доказываем с помощью индукции. Если со = / dx11 Д ...
... Д dxlP, то
dtp* (со) = йф* (/ dx*1 Д ... Д dxlp) =
= dtp* ((/ dxli Д... Д dxip-i) Д dxlp) =
= d (ф* (/ dx1*- Д ... Д dx'p-i) Д ф* (dxlp)) =
= ф* (df Д dx*1 Д ... Д dx'p-1) Д ф* (dx'p) + 0 =
[согласно (1.1)]
= ф* (df Д dxil Д ... Д dx’p-i д dxlp) =
= ф* (dco).
Итак, мы убедились в том, что оператор d инвариантен относи-
тельно дифференцируемых отображений.
Как простое следствие теоремы 1.3 иопределения производной
Ли мы получаем, что для любого векторного поля X и формы, со
dXxa = Xx(da). (1.6)
Существуют и другие важные соотношения между производной
Ли и внешней производной. Согласно теореме 1.1, d есть анти-
дифференцирование алгебры дифференциальных форм, т. е. линей-
ное отображение G этой алгебры в себя, удовлетворяющее тож-
деству
0 (®с А ®2) = 0 («О Д со2 + (- l)fe cot А G (со2), (1.7)
*) 0 — центральный угол.— Прим, перев.
2) По крайней мере класса С2.
5 I. Оператор d
ИЗ
если ©1 — форма степени к. Другим примером антидифференци-
рования является внутреннее умножение на векторное поле (см.
упражнение 4.5 гл. I): если 9 (ю) — X J со, то 0 также удовле-
творяет тождеству (1.7). С другой стороны, Хх является, согласно
[II, (8.7)], дифференцированием, т. е.
0 (<в1 Л и2) = 0 (wj л w2 + Wi Л 0 (®2) • (1.8)
Из этих примеров можно сделать следующий важный вывод:
дифференцирования и антидифференцирования полностью опре-
деляются своим действием на функциях и линейных дифферен-
циальных формах. Доказательство очевидно (и не отличается
от доказательства предыдущих утверждений этого параграфа).
Если 0J, 02 — такие антидифференцирования, что х) deg 0г (со) —
= deg (о A rt, причем числа гг (г = 1, 2) нечетны, то 0t02 А
+ 0201 есть дифференцирование. Действительно,
0102 (®1 А ®2) = 0102®1 А ®2 + ( — l)h 01<Ot А ®2®2 А
А ( — l)fe ®1 Л 0102®2 А (-l)ft+ri02CO 1 Д 01®2,
0201 (COj А ®г) — 0201е0! Л ®2 А ( — l)ft 02М1 Л 01®2 А
А ( — l)ft ®1 Л 0281®2 А ( — l)ft+r20i<£>i А 02®2.
Поскольку ri и г2 нечетны,
(0102 А 0201) (®1 Л ®г)= ((®102 A 020i) ®i) Л A ®i Л (9102 A 020i) ®2,
т. е. 0j02 А 0201 есть дифференцирование. Воспользуемся этими
замечаниями для доказательства тождества
Хх<л = Х J (dco) + d(X J со). (1.9)
Левое внутреннее умножение на X есть антидифференцирование,
так же как и d. Поэтому оператор со -> X J (dco) A d (X J со)
есть дифференцирование, так же как и Xх- Поскольку в обеих
частях равенства (1.9) стоят операторы дифференцирования,
достаточно проверить его для функций и линейных форм. Но
X J / = 0, так что для функций (1.9) сводится к формуле
[II, (8.8)1. Если со = df для некоторой функции/, то (1.9) сводится
к равенству X х (df) = d (X J df). Но, согласно [II, (8.8)],
X -I df = Xxh так что (1.9) следует из (1.6). Поскольку каждая
линейная форма представима в виде линейной комбинации форм
вида fdg, локально равенство (1.9) можно считать доказанным.
Но отсюда следует равенство (1.9) в целом.
Выполним внутреннее умножение обеих частей равенства (1.9)
на векторное поле Y. Мы получим
У J <£х(со) = УЛ (X J ска) АУЛ d(X J о).
х) Символом deg обозначается степень формы.— Прим, перев.
8 с. Стернберг
114
Гл. III. Интегральное исчисление на .многообразиях
Но
У J (X J-d©)== {X Л У) J d©
и
Хх ’ ю) — ХхУ —1 со У -J «Z^co == » X) —J co -f- У —1 ,<Z?xCO.
Отсюда
(X Л У) J! Ло = Хх (У -J <о) —У -I d (X J со)-[У, X] J со.
Если в качестве со взять линейную форму, то
(X AT) J dco = (X Д У | dfco>, Хх (У J со) = X (У | со),
yj d(X J со) = У (X | со),
и мы получаем
<ХЛ'У|Ло> = Х(У|со>-У(Х|со>-([Х, У] |со). (1.10)
Равенство (1.10), которым мы будем часто пользоваться в дальнейшем,
является в некотором смысле инфинитезимальным аналогом теоремы Стокса.
Рис. 5.
Действительно, рассмотрим «инфинитезимальный параллелограмм» со сто-
ронами, параллельными X и У. Более точно, пусть <рр (s) есть интегральная
кривая *) поля X, проходящая через р, а фр (/) — интегральная кривая по-
ля У. Рассмотрим «прямоугольник» abed (рис. 5), где ab — кривая <pa (s)
(0 С е) и Ъ = фа (е); Ъс — кривая фь (s) (0 s <1 е), с = фь (е). Пусть
ad есть кривая фа (s) (0<s< е)иЛ/ — кривая (s) (0 < s -C е).
Если е мало, то мы можем считать «значение» формы со на кривой «приб-
лизительно равным» значению со на касательных векторах кривой. Тогда
инфинитезимальное значение формы со вдоль «параллелограмма» определяет-
ся правой частью формулы (1.10). Первый член измеряет со (be) + со (da),
второй измеряет со (ab) + со (de), а третий член вносит поправку на то, что
даже инфинитезимально «параллелограмм» не обязан быть замкнутым, т. е.
с Ф с'. Таким образом, значение формы dco на инфинитезимальном парал-
лелограмме равно значению формы со на его границе.
г) То есть траектория соответствующей локальной однопараметрической
группы преобразований, см. 8 гл. П. Прим, перев.
$' 2. Цепи и интегрирование;:
115
Упражнение 1.1. Найти формулу, обобщающую формулу (1.1Q)
на случай, когда <о — дифференциальная форма степени к, a Xt, . . . , X^+i —
векторные поля.
Важность оператора d определяется той ролью, которую он
играет в теории интегрирования, и тем, что этот дцфференциадьг
ный оператор определяется одной только дифференцируемой
структурой дифференцируемого многообразия и инвариантен отно-
сительно дифференцируемых отображений (теорема 1.3). Бла»-
годаря этому свойству инвариантности многие уравнения физики
и геометрии, выраженные в терминах оператора d, принимают
особенно простой вид. Мы познакомимся с некоторыми из них
в дальнейшем.
§ 2. ЦЕПИ И ИНТЕГРИРОВАНИЕ1)
В этом параграфе мы приведем первую из двух теорий инте-
грирования дифференциальных форм. Можно показать, что эти
теории по существу эквивалентны.
Сначала мы выберем стандартный р-мерный объект.
Определение 2.1. Мы будем обозначать через Др симплекс
р
в ^..определенный неравенствами О С а:’ С1, 2а:*С1.
i=l
Так, До—точка, — единичный отрезок, Д2— треугольник
(рис. 6) и т. д. Удобно ввести в симплексе Др так называемые
барицентрические «координаты», которые определяются форму-
За исключением определений 2.5 и 2.7, результаты этого параграфа
не будут использоваться нигде в-этой книге.
116
Гл. III. Интегральное исчисление на многообразиях
лами
р
у°—1—3 yi=х* ддя * = 1, • ••,?»
i=l
(2-1)
откуда у°+...+ур = 1, 0</<1 (1 = 0, ..., р).
Определение 2.2. Отображение 8Pi t (i = 0, ..., р + 1)
симплекса Ар в Ар+1 определяется формулой
• у1, если j i,
< 0, если / = i,
yi—1, если у > i,
(2-2)
где У3 — барицентрические координаты в Ар+1.
Р+1 Р
Поскольку 2 У3 (^Р. i) = 2 У1 = 1> формула (2.2) действительно
о о
определяет отображение Ар —>Ар+1. Это отображение очевидным
образом продолжается до дифференцируемого отображения окрест-
ности симплекса Ар в пространстве Ер в пространство Ер+1.
На рис. 7 показаны образы симплекса At в симплексе А2 при
отображениях 8Р10, 6Р115 6Р> 2. _
Сравним отображения 6р+1> t°8p, i и 6р+1,гобр>г. Если yh —
барицентрические координаты в Ар+2, то
/обр+1,1°6р,г(А •• - ,1/Р) = <
yk°8>P,i(y°, .. ., ур), если/с < i,
О, если k=i,
yh~l ° др, i (У°, если k > i.
Если то мы можем переписать это
Г yh'
°’
?fe°6p+i,i5p,,(y0, . . .,ур)= yh—1,
I о,
I у
в виде
если
если
если
к< I,
к = 1,
1<^к <i,
если k = i,
если
к > i.
С другой стороны,
~У^ ° бр+1, I ° ^р, i —
ук°бр, i(y°, .. , ур),
< О,
yk~la^p,i(y°, • -,УР),
если
если
к<1,\
к = 1, >
если к
S 2. Цепи и интегрирование
117
Отсюда
Ук,
О,
Ук~1,
О,
У*-2,
если
если
если
если
если
к<1,
к = 1,
I < к i + 1,
I = i +1,
I i -j- i.
$p+l, i ° Sp, l — ^p+l, l ° Sp, i+l>
если Z<Ji.
(2-3)
Определение 2.3. Дифференцируемым сингулярным
р-симплексом на многообразии М называется отображение Ар ->
—► М, которое может быть продолжено до дифференцируемого
отображения некоторой окрестности симплекса Ар в Е1' в мно-
гообразие М. Дифференцируемой р-цепъю называется формаль-
ная конечная линейная комбинация (с вещественными коэффи-
циентами) сингулярных р-симплексов. Бесконечной дифференци-
руемой р-цепъю называется такая бесконечная формальная сумма
(т. е. такое отображение s -> cs множества дифференцируемых
сингулярных р-симплексов в вещественную прямую), что мно-
жество {sa (Ар)} (где {sa} — множество тех s, для которых cs 0)
локально конечно.
Замечания. На компактном многообразии бесконечная
сингулярная цепь имеет не более конечного числа ненулевых
коэффициентов, так что два введенных понятия совпадают. В этой
главе все цепи будут дифференцируемыми, поэтому для крат-
кости мы будем их называть просто цепями.
Множество всех p-цепей (соответственно бесконечных р-цепей)
образует, очевидно, векторное пространство; мы будем обозна-
чать его Ср (М) (соответственно ICP (М)). Если / есть дифферен-
цируемое отображение в М2, то, полагая
/* (S) = / о S (2.4)
для симплексов и продолжая отображение по линейности, мы полу-
чим линейное отображение /*: Ср (Aft) -> Ср (М2). В случае беско-
нечных цепей мы должны быть более осторожными. Отображение /
называется собственным х), если /-1 (К) компактно для любого
компактного К cz М2. Пусть / — собственное отображение и s ->
-> cs есть p-цепь на Мх. Положим /* (s) = dt, где
dt= 3 cs, (2.5)
<=/*(»)
*) См. определение 2.4 гл. II.— Прим, перев.
118
Гл. III. Интегральное-исчисление на. многообразиях
причем dt = 0, если £¥=/*{з) ни для какого s. Поскольку/—
собственное отображение, сумма в (2.5) конечна и множество
симплексов t, для которых локально конечно. Поэтому
формула (2.5) определяет бесконечную p-цепь на М%.
Если s есть р-симплекс, то softp_iti есть (р—1)-симплекс.
Определим границу симплекса s формулой
р
ds= 2(-1){8обр_11г. (2.6)
i=0
Так, на рис. 8 з есть сингулярный 2-симплекс, a ds — его граница.
Продолжим д по линейности до отображения д: Ср (М) —>
—> Cp-itM). Для бесконечных цепей отображение определяется
аналогичнох):
р
5(с,)= 3(-l)4(>f, dt,t = S cs. (2.7)
i=0 i
Заметим, что благодаря условию локальной конечности эта
сумма всегда конечна.
В обоих случаях имеет место важное соотношение
д о 5 = 0. (2.8)
Докажем, что 5(5s) = 0 для симплексов. Тогда это будет верно
и для любых цепей.
Пусть s есть (/-мерный симплекс. Если то доказывать
нечего. Если </>2, то
9 9-1
5(5s) = S 3 (-1){(-1)’*°бд-1.1°б9-2,> =
i=0 3=0
= 3 ( — 1)*+Х3 О бд-1 I О 6g-2, j + 2 ( —1){+53 o6q-i, i ° 6q_21 j.
O^i<j^q
’) To есть для каждой р-цепи с новая (р — 1)-цепь дс сопоставляет
р
(р = 1)-мерному сингулярному симплексу t число (dc)t — (—l)’d(1 , —
t=0
Прим, перев.
§ 2. Цепи и иишеерарювлние
И?
Согласно (2.3), $0 i 0 ^q^zr'J — s.° 6g—<, J ° z, i+i? юли }
Поэтому первую сумму можно переписать в виде
3 (—l)l+5 sodgiii ;°бд_2>1+1.
Если положить fc = i'+l, l~i, то эта сумма приобретет вид
(^l)b+i-lS0 6g_1>Z0 6?_2,ft
и сократится со второй суммой, что доказывает равенство (2.8).
Определение 2.4. p-цепь с, удовлетворяющая условию
дс = 0, называется циклом; p-цепь вида с = dd, где d — некоторая
{р + 1) цепь, называется границей. Равенство (2.8) говорит о том,
что пространство границ есть подпространство пространства цик-
лов. Соответствующее факторпространство называется р-мерной
группой гомологий и обозначается символом Нр {М). Те же опре-
деления для бесконечных цепей дают группу IHP {М) х).
Из определения следует, что если g: Mi -> М2, то отображе-
ние g, перестановочно с д'. dog* = g*°d. Поэтому g* переводит циклы
в циклы и границы в границы назначит, индуцирует отображение
Нр -► Нр (М2), которое по-прежнему будет обозначаться
через g*.
Заметим, что формула (2.8) аналогична формуле (1.4).
Определение 2.5. Дифференциальная форма <о назы-
вается замкнутой, если da> = 0, неточной, если са = dQ. Мы будем
иногда называть замкнутые формы коциклами, а точные — когра-
ницами. Факторпространство замкнутых р-форм по точным p-фор-
мам называется р-мерной группой когомологий {де Рама) много-
образия М и обозначается символом Н1' {М).
Связь между гомологиями и когомологиями устанавливает
теория интегрирования.
Определение 2.6. Пусть s—сингулярный р-симплекс, а
<о — дифференциальная форма степени р. Форма s* (о>) определена
в некоторой окрестности евклидова р-симплекса Ар. Допустим,
что s* (со) = 3 ач..A • • • A dxXp, где x\ .. .,xn — стан-
Мы могли бы рассматривать непрерывные сингулярные цепи и непре-
рывные отображения вместо дифференцируемых. Нетрудно показать, что
полученные таким образом группы гомологий совпадают с соответствующими
группами Нр (ЛГ), 1Нр (ЛГ). Таким образом, группы Нр (ЛГ) и 1Нр (ЛГ)
зависят только от топологии многообразия ЛГ и не зависят от его дифферетти-
руемой структуры.
120
Гл. III. Интегральное исчисление на многообразия*
дартные координаты в Е”. Положим по определению
j 2 j j ач............................ipdxil • • dxip> (2.9)
8 4<...<ip др
где справа стоит сумма обычных кратных интегралов.
Продолжим (2.9) на любую конечную p-цепь по линейности.
В общем случае мы не можем интегрировать произвольную р-фор-
му по бесконечной p-цепи, поскольку это может привести к рас-
ходящемуся бесконечному ряду. Ограничим поэтому класс форм,
которые мы будем интегрировать.
Определение 2.7. Носителем формы и называется наи-
меньшее замкнутое множество, вне которого она равна нулю.
Факторпространство замкнутых р-форм с компактным носителем
по пространству форм вида dQ, где Q есть (р + 1)-форма с ком-
пактным носителем, обозначается Н% (М).
Если и — форма с компактным носителем, то для любой
бесконечной цепи cs сумма
j <в = 2 cs j ® (2-10)
cs s s
имеет только конечное число ненулевых членов и поэтому опре-
делена.
Если g:Mi —> М2 — собственное дифференцируемое отображе-
ние, то из определений немедленно следует, что
J jg*(®)- (2.11)
g*(c) с
Справедлива следующая важная
Теорема 2.1 (первый вариант теоремы Стокса). Для любой
p-цепи с и (р — 1)-формы со {соответственно бесконечной p-цепи с
и (р—1)-формы со с компактным носителем) справедливо равен-
ство
jdco=Jco. (2.12)
с дс
Благодаря линейности (по с) обеих частей формулы (2.12)
достаточно рассмотреть случай c — s, где s: Др —> М — сингуляр-
ный р-симплекс. В этом случае равенство (2.12) сводится к равенству
JdQ = 2(~1)i j Й’ (2.13)
§ 2. Цепи и интегрирование 121
где Q = s*(co), а 6р_1)г: —> Др рассматривается как сингуляр-
ный (р—1)-симплекс в Е1'. Далее, й=2ач..........i (я1, •. .,жр)Х
X dx1^/\ ... /\dxiP-i. Достаточно доказать равенство (2.13) для
каждого члена этой суммы. Таким образом, задача сводится
к проверке равенства1)
Г да
(-1)’-1 ( -т-^А ••• А^Р =
J дхз
S
р
= 2 ( — I)1 j adx1 А • • /\dx3 Д ... Д dxp. (2.14)»
i=0 6P-i. i
Поскольку dp-i, i (хг) = 0, в правой части останутся только члены
с 1 — 0 и i = j. Пусть z1, ...,zp—1 — евклидовы координаты вАр^..
Тогда
6р_1, j (a dx1 Д ... A dxJ'л • • А <йср) =
= а о др-j, j (z1, .. ., z”’1) dz1 A • • • A dzp~*
и
бр-1, о (a dx1 A • • J\dx3 A • • • A dx1") =
= (aodp_1>0(z1, . . ^z^yjdfl — z1 — ... — zp-x) f\dzl A •••
...A^'A •••A^p-1 =
= (— l)3-^ о др-l, 0 (z1, ..., z”-1) dz1 A • • A dzv~\
В соответствии с определениями равенство (2.14) сводится к равен-
ству
г да
J ~d^idx1^ • • • А^Р =
%
= а^х1, . .., я3'-1, 1— 2 • • 1 х”) dx3- /\ ... /\dx3/\ ... /\ dxp—
— j а (ж1, . . ., х3"1, 0, ..., j dx1 А • • • A dx3 А • • • A dxp,
которое проверяется интегрированием по частям. Теорема 2.1
доказана.
г) Символ означает, что соответствующий член должен быть пропу-
щен.— Прим, перев.
122 Гл. III. Интегральное исчисление на многообразиях
Из равенства (2.12) следует, что интегралы точной формы
по циклу и замкнутой формы по границе равны нулю. Таким
образом, интеграл замкнутой формы по циклу зависит,только
от класса когомологий этой формы и класса гомологий этого
цикла. Получаем
Следствие 2.1. Билинейное отображение1) С р (М) х
X /\₽ (М) —» R, определяемое интегралом § <д, индуцирует би-
С
линейное отображение Нр (М) X Нр (М) —> R.
Следствие 2.2. Билинейное отображение1) 1СР(М) х
X /\₽(М) —> R, определяемое интегралом со, индуцирует би-
С
линейное отображение IHP(M)'X.HP—+ R.
Важная теорема алгебраической топологии (теорема де Рама)
утверждает, что это билинейное отображение невырожденно
и, следовательно, мы можем рассматривать Нр (М) как про-
странство, дуальное к Нр (Л/); см. де Рам [15]. В частности, про-
странства Нр и 1НР, которые были определены в терминах диффе-
ренциальных форм и казались зависящими от дифференцируемой
структуры, в действительности являются топологическими инва-
риантами.
? 3. ИНТЕГРИРОВАНИЕ ПЛОТНОСТЕЙ
Хотя приведенная выше теория интегрирования, использую-
щая сингулярные цепи, весьма удобна для дифференциальной
топологии, она не позволяет эффективно вычислять интегралы.
Поэтому мы используем другой подход, более применимый к гео-
метрии, который позволит нам сразу сделать некоторые выводы
без привлечения сложного алгебраического аппарата. Из тео-
ремы де Рама следует, что эти две теории интегрирования по суще-
ству эквивалентны.
Мы хотим определить на многообразии М объекты, которые
можно было бы интегрировать по подходящему набору областей
из М. Мы знаем, как можно приемлемым образом интегрировать
достаточно хорошую функцию в евклидовом пространстве. На мно-
гообразии мы не можем придать никакой смысл интегрированию
функций. Даже в евклидовом пространстве форма подинтеграль-
ного выражения изменяется при замене координат: если х1, . . .
!) Где Др (М) (ДР (М)}пространство р-форм (соответственно р-форм
с компактным носителем) на многообразии М. — Прим, перев.
§ 3. Интегрирование плотностей
123
. . . , ж”* — декартовы- координаты в Е1, а у1. . . . , ifi -— другая
система координат, то для любой функции / (см. приложение II)
j / (ж1, ..., хп) dx1. . . dxn =
Еп
= [ /(ж1^, ...,уп), ...,хп(у1, ...,y"))|det L^Ahy1 ..,dy\
I V / I
Таким образом, в координатах у1 мы интегрируем не /, а
/ det (. Это наводит на мысль рассмотреть на многообразии
V dyi !
объект р, описываемый следующим образом: для любой карты
(Ut, hi) атласа {(Ut, ht)} задается функция pt на Ui, причем
Pt (®) = Р/ (ж) | det Jh.(x) (hj о hi1) |.
(3.1)
Сравнивая это с равенством III, (6.11)1- мы видим, что р есть
поле типа Q, где Q — одномерное векторное пространство, и
р (Л) q — | det A Hg для любого А С GL (п). (3.2)
[Таким образом, Q есть пространство плотностей, ср. с приме-
ром 4, § 2, гл. I.]
Определение 3.1. Пусть V — вещественная прямая,
на которой действует группа GL (п) по формуле (3.2). Поле типа Q
на многообразии М называется плотностью.
В терминах атласа {(Ui, ht)} плотность р задается набором
функций р; (на U,), связанных между собой соотношением (3.1).
Упражнение 3.1. Пусть М — риманово многообразие. Опре-
делим для любой карты (Ui, hi), где ht = (х1, . . . , хп), функцию рг, пола-
. . , 3 1
гая рг (х) равным объему параллелепипеда, натянутого на векторы , . . .
. . ., | ’ [Поскольку в рассматриваемом случае пространство Тр (АГ)
обладает метрикой, т. е. является евклидовым пространством, мы можем
говорить об объеме.] Показать, что функции рг определяют плотность на М.
Она называется объемной плотностью римановой метрики.
Ясно, что пространство плотностей есть векторное простран-
ство и даже модуль над кольцом дифференцируемых функций,
т. е. мы можем складывать плотности и умножать плотность
на функцию. Значение плотности в точке не имеет смысла, посколь-
ку плотность не является функцией. Однако имеет смысл гово-
рить о том, равна ли плотность в данной точке нулю или нет
(а также о знаке плотности в точке), поскольку это не зависит
от выбора карты, в которой плотность изображается функцией.
•124
Гл. III. Интегральное исчисление на многообразиям
Определение 3.2. Носителем плотности р (обозна-
чается supp р) называется замыкание множества точек, где р =/= 0.
Аналогично, можно говорить о том, непрерывна или нет плот-
ность в данной точке.
Определение 3.3. Плотность р называется локально’
ограниченной, если для любой карты (С7г, Лг) и любого компакта
KcUi функция рг ограничена на К.
[Здесь рг — функция, изображающая плотность р в карте-
(Ui, hi).]
Легко проверить, что из ограниченности рг- на всех компактах
К dUt, rjpe {(Ui, hi)} есть атлас, следует локальная ограни-
ченность плотности р.
Обратимся теперь к определению областей интегрирования.
Напомним х), что множество В d Еп называется множеством
наполнения нуль, если для любого е > 0 существует конечное
число таких прямоугольников Qj, . . ., что
#<=Ud« и SvolO)<e.
Определение 3.4. Говорят, что подмножество В мно-
гообразия М имеет наполнение нуль, если для некоторого атласа
{(Ut, hi)} существует конечное число компактных множеств Bir
таких, что й с (J Bi, Bid U г и множества /г; (Вг) имеют напол-
нение нуль в Еп.
Мы предоставляем читателю проверить, что объединение конеч-
ного числа множеств наполнения нуль имеет наполнение нуль.
Определение 3.5. Множество D d М называют напол-
нимым, если
1) D компактно,
2) граница D имеет наполнение нуль.
Мы обозначим множество всех наполнимых областей через SJ-
Предоставляем читателю проверить, что множество наполни-
мых областей замкнуто относительно пересечения и конечного
объединения.
Определение 3.6. Плотность р называют почти непре-
рывной, если она непрерывна всюду, кроме множества наполне-
ния нуль. Мы обозначим пространство локально ограниченных
почти непрерывных плотностей через Р.
х) См. приложение II, где дан обзор римановой теории интегрирова-
ния в Еп.
3. Интегрирование плотностей 125
Упражнение 3.2. Показать, что Р есть векторное пространство.
Назовем функцию почти непрерывной, если она непрерывна всюду, кроме
множества наполнения нуль. Показать, что множество почти непрерывных
•функций образует кольцо и Р есть модуль над этим кольцом.
Упражнение 3.3. Для любого множества D С М обозначим через
<Ро характеристическую функцию множества D, т. е. фО (ж) = 1, если х g D,
и <рд (ж) = 0, если ж Е D. Показать, что D g S> тогда и только тогда, когда
множество supp фд компактно, а функция фр почти непрерывна.
Теперь мы в состоянии изложить нашу теорию интегрирования.
Теорема 3.1. Существует единственное правило j , сопо-
ставляющее любым D £ 3) и р £ Р число j р (называемое интегра-
D
мм плотности р по области D) так, что выполняются следующие
условия:
1) для каждой фиксированной области D отображение р —»
—> j р является линейным функционалом на Р;
D
2) если Di D2— 0, то j р= j р j р;
S1U-D2 .01 Г>2
3) если supp р с U, где (U, h) — некоторая карта, а / — функ-
ция, изображающая плотность р в карте (U, h), то
j р = j (фл 0 ^1) (/ 0 ^-1) • • • dxn.
D h(U)
Заметим, что можно так переформулировать теорему 3.1, чтобы
избежать явного упоминания области интегрирования. Действи-
тельно, пусть Рс — пространство плотностей с компактными носи-
телями. Справедлива
Те орема 3.2. Существует единственный линейный функ-
ционал J на Рс, такой, что если supp pcU и (U, h) — некото-
рая карта, то
j р= j (/ ° Л-1) dx1 ... dxn, (3.3)
h(U)
где f — функция, изображающая плотность р в карте (U, h).
Полагая для и р£Р
Jp=J<PnP, (3.4)
D
126
Гл. III. Интегральное исчисление на многообразиях
мы убеждаемся в том, что теоремы 3.2 и 3,1 эквивалентны; надо
только проверить условие 2) теоремы ЗЛ. Но если D± fl ^2=0»
то <PB1Up2 = фС1 + фр2, так чт0 условие 2) выполняется в силу
линейности операции j .
Приступим теперь к доказательству теоремы 3.2. Пусть ф,—
разбиение единицы, подчиненное некоторому атласу, и пусть
(Ut, hi) — карта, содержащая suppq);, где hi = (xl, .. ., ж"). Для
любой плотности р £ Рс только конечное число плотностей <р,р
отличны от нуля, поэтому
j Р = 2 j Ф*Р = 2 j (ф« ° hi1) (ft ° hi^dx1 ... dxn, (3.5)
где fa — функция, изображающая р в карте (Ut, ht). Это доказы-
вает единственность. Чтобы доказать существование, мы должны
проверить, что операция j , определенная формулой (3.5), удовле-
творяет равенству (3.3). Для этого достаточно проверить равен-
ство (3.3) для каждого слагаемого ф;р, т. е. доказать, что
j <Vi(f ° h"1) dx1 ... dxn = j <?i(fi ° hi1) dx] . .. dx™.
h(U) h^ut)
Учитывая связь, существующую между функциями fw.fi, мы
убеждаемся в том, что это есть в точности формула замены пере-
менных в кратном интеграле.
Упражнение 3.4. Определим объем области D g Z риманова
многообразия М как интеграл от объемной плотности по области D. Вычи-
слить объем n-мерной сферы в метрике, индуцированной ее стандартным
вложением в
Упражнение 3.5. Пусть ф, и ф2 — Два погружения многообразия
М в риманово многообразие N, a g,, g2 — индуцированные ими римановы
метрики на М. Пусть объем многообразия М в этих метриках равен соответ-
ственно Vt и V2. Показать, что для любого ц > 0 существует такой набор
(W, Z, е, 1), что если cpt g JiTiw, z, е, 1>ф2, т0 I Vi — I < *1-
Упражнение 3.6. Показать, что вышеприведенное определение
объема множества из Еп, рассматриваемого как риманово пространство, сов-
падает с обычным определением.
Упражнение 3.7. Пусть ф — погружение компактного много-
образия М в Еп, и пусть V — объем многообразия М в индуцированной
римановой метрике. Используя упражнения 3.5 и 3.6, показать, что V =
= lim S (Р{), где Р2 — последовательность полиэдров, аппроксимирующих
Ф (М) по положению и направлению, a S (Р2) — объем (или площадь) поверх-
ности полиэдра Р{.
$ 3. Интегрирование плотностей
127
Если о> — внешняя n-форма на га-мерном многообразии, то для
любой карты. (U, h), где h = (xf . . . , хп), мы можем написать
со = fdx1 Л ... Д dxn. Если (V, g)„ где g = (у1, .... if1),—
другая карта и со — gdy1 Л • • • Л dyn', то
/ = g (det J h"1)).
Эта формула напоминает формулу (3.1), только теперь вместо
| det J (g ° А-1) | мы имеем det J (g ° h~r). Мы сможем связать
с каждой n-формой плотность и обратно, если нам удастся выбрать
атлас, для которого все якобианы функций перехода положи-
тельны-
Определение 3.7. га-мерное дифференцируемое мно-
гообразие М называется ориентируемым, если на нем существует
внешняя дифференциальная форма со степени п, всюду отличная
от нуля, т. е. такая, что сор 0 для всех р £ М. Говорят, что
две такие формы определяют одну и ту же ориентацию, если они
отличаются на всюду положительный множитель. Многообразие
вместе с выбранной ориентацией называется ориентированным.
Любые две га-формы отличаются на множитель, являющийся
(дифференцируемой) функцией, поскольку пространство Дп (Г*)
одномерно. Поэтому на связном ориентируемом многообразии
существуют ровно две ориентации.
Пусть со — форма, задающая некоторую ориентацию много-
образия М. Любая другая га-форма Q, определенная на открытом
множестве U cz М, может быть представлена в виде Q = /со, где
/ — функция. Мы скажем, что Q > О (Q < 0), если / > 0 (соот-
ветственно / < 0). Это определение зависит не от самой формы со,
а только от задаваемой ею ориентации. Если (хг) — система коор-
динат на U, то dx1 Д ... Д dxn А 0 на U. Поэтому либо dx1 А • • •
... A dxn > 0, либо dx1 Д ... Д dxn < 0. В последнем случае
функции —х1, х2, . . . , хп определяют новую систему координат,
для которой верно первое неравенство. Следовательно, покрыв М
координатными окрестностями, мы всегда можем в каждой окрест-
ности выбрать координаты так, что dx1 А • • • .А > 0- Тогда
в пересечении двух систем координат (х‘) и (уг) мы будем иметь
dx1 А • • • /\dxn = f dy1 A • • • /\dyn, причем /> 0, (3.6)
т. е.
det
\ dyl )
Обратно, предположим, что мы можем покрыть многообразие М
счетным числом координатных окрестностей Ut так, что выполни-
128
Гл. Ill. Интегральное исчисление на многообразиях
ется условие (3.7). Положим (щ = дх}/\ ... /\dxi, где (х\, ...
. . . ,х”)— координаты в U i. Пусть {(рг) — разбиение единицы, под-
чиненное покрытию {Ut}. Тогда (форма со=2фг®г везде отлична
от нуля, поскольку со; #= 0 в Ui и фг > 0. Таким образом, имеет
место
Теорема 3.3. Необходимое и достаточное условие ориенти-
руемости многообразия состоит в существовании атласа, в пере-
сечении любых двух карт которого выполнено условие (3.7). Выбор
ориентации выделяет предпочтительные карты, которые мы
назовем положительными относительно данной ориентации.
Определение 3.8. Пусть М — дифференцируемое мно-
гообразие. Подмножество D из М называется областью с регу-
лярной границей (для краткости областью), если любая точка
Р € D
1) либо имеет окрестность, лежащую в D,
2) либо имеет такую окрестность U с координатами х1, ... , хп,
причем хп (р) = 0, что U (] D есть множество всех точек из U,
для которых хп 0 х).
Эти два свойства, очевидно, исключают друг друга. Точки,
обладающие свойством 1), называются внутренними точками,
а свойством 2),— граничными. Из упражнения 2.5 гл. II следует,
что множество граничных точек области D можно рассматривать
как подмногообразие dD многообразия М. Если многообразие М
ориентируемо, то многообразие dD — тоже.
Действительно, пусть {Uг} — счетное покрытие множества
dD координатными окрестностями Ut с координатами xt, ... , х?,
которые удовлетворяют условию 2) определения 3.8. При этом
можно считать, что dxi Л • • • Л dx1} > 0 относительно фикси-
рованной ориентации многообразия М. [Этого всегда можно
добиться, если п > 1. Случай п = 1 можно не рассматривать,
поскольку в этом случае dD представляет собой набор точек,
который тривиальным образом ориентируем.] Если U — одна
из окрестностей Ut, а х1, . . . , хп — соответствующая система
координат в U, то функции х1, . . . , хп-1 образуют систему коор-
динат в U П dD. Если у1, . . . , уп — другая подобная система
координат, то уп — 0 на dD, так что дуп/дхк = 0 (& = !,...
. . . , п — 1) всюду на dD. Поскольку уп > 0, когда хп > 0,
*) Так, само многообразие М есть область с регулярной границей.
J 3. Интегрирование платностей
129
имеем дуп/дхп 0. Таким образом,
а (у1, .., уп) I а (г/1,
d(xi, ..хп) |ао
г/"-1) дуп о г
хп~1) дхп
Значит, д (у1, .. ., уп~г')1 д (х1, .,хп х) > 0 и многообразие dD ориен-
тируемо. В действительности мы имеем на dD определенную ориен-
тацию, индуцированную ориентацией
многообразия М. Мы будем считать, что
форма dx1 Л • • • Л соответствую-
щая положительной системе координат
х1, .. .,хп многообразия М, удовлетво-
ряющей условию 2) определения 3.8,
имеет знак (— 1)п.
Индуцированные ориентации для
одномерного, двумерного и трехмерного
многообразий показаны на рис. 9.
(a-)
Теорема 3.4. Пусть М — ори-
ентированное п-мерное многообразие
и D — область в М. Существует един-
ственный функционал, сопоставляющий
каждой п-форме со с компактным носи-
телем вещественное число, называемое
ее интегралом по D и обозначаемое
5 со, такой, что
D
1) J (Q)i + ®г) = J ®2>
D D D
2) если носитель формы со лежит
в координатной окрестности U и h =
= (ж1, . . . , хп) — система координат
в U, причем dx1 /\ ... /\ dxn > 0
и со = fdx1 /\ ... /\ dxn, то
С со = ( ср/ (ж1, .. . ,хп) dx1 . . . dxn, (3.8)
J •)
D
Cc)
Рис. 9.
где ср — характеристическая функция области D (ср (ж) = 1 для
х С D, ср (ж) = 0 для х Q D) и в правой части стоит обыкновенный
интеграл Римана.
!) Где
переменных.
9(А ,£/”) _d t
а(ж1, ....ж")
— Прим, перев.
ду' х
dxi )
якобиан набора п функций от п
9 с. Стернберг
130 Гл. III. Интегральное исчисление на многообразиях
Доказательство следует немедленно из теоремы 3.1.
Пусть М — ориентированное многообразие и Di — конечное
число непересекающихся областей в М. Для любой п-формы
со имеем
j со = У j со. (3.9)
Up, Di
Теорема 3.5 (второй вариант теоремы Стокса). Пусть со —
форма степени п — 1с компактным носителем на ориентирован-
ном многообразии М. Тогда для любой области D в М
j dco = с* (со), (3.10)
D 0D
где dD рассматривается как ориентированное многообразие с ориен-
тацией, индуцированной ориентацией М, a i — вложение dD —>- М.
Выберем такой счетный атлас {{Ui, hi)} на М, что либо
Ut П dD = 0, либо Ut — координатная окрестность, удовле-
творяющая условию 2) определения 3.8. Пусть {ср,} —разбиение
единицы, подчиненное покрытию {Ut}. Тогда
J i* (“) = 2 ( Z* (Ф/”)»
dD dD
j dco = 2 j d (ф;СО).
D Ц
Поэтому достаточно проверить равенство (3.10) для каждой из форм
ср/о, т. е. в случае, когда suppcocCZ, для некоторого г. Пусть
х1, ..., х1 — такие координаты в Ut, что dx1 /\ ... Л dxn > 0,
и пусть
со = 2 (— I)’-1 dx1 Л • • • Л da? Д ... Д dxn.
Тогда
d« = (2 ‘2г) dxl Л • • ’ Л dxn.
Предположим, что Ui Q dD=0. Тогда j i*(cp,co) = O. С другой
dD
стороны, характеристическая функция ср области D либо =0,
либо =1 в Ut. В первом случае все доказано. Во втором случае
мы должны вычислить
£ 4. Нульмерные и п-мерные когомологии; степень
131
где (не совсем аккуратно) мы обозначили функции а7-о Л?1 через а,.
Поскольку supp («_,) с hi (Ut), мы можем продолжить функции а7-
на все пространство £п, полагая а,- = 0 вне hi(Ut). Пусть R —
столь большое число, что если (ж1, ..., хп) Qhi (Ui),
и пусть В — куб в Еп, задаваемый неравенствами | Xj | < R. Тогда
Интегрирование по частям дает
j —у dx1 ... dxn = ± J {aj (х1, ..., ж’"1, R, x'Ji+1, ..., хп) —
в ^х3
— aj (х1, ..., х1"1, — R, х^1, . . ., хп)} dx1 . .. dx’ ... dxn = 0.
Таким образом, (3.10) выполнено для формы со в случае supp со с Ut,
если Ut Г) dD = 0.
Предположим теперь, что Ut Q сШ#= 0 и ж1, . . ., хп — коор-
динаты в Ut, описанные в условии 2) определения 3.8. Тогда
для со — 2 (— I)’-1 О'} dx1 Л • • • Л dx’ Л • • • Л мы имеем
г* (со) = (— l)n-1 dni* (dx1 Л • • • Л dxn-1) и
J i* (со) = (— l)n-1 j ап dx1 .. . dxn~1.
dD
Продолжая функции aj, как раньше, имеем
рсо=2 J
D В
аа i
ср —— dx1 .. . dx ,
dxi
где ср = 1 для > 0 и <р — 0 для хп < 0. Интегрирование по частям
дает
р да. j
\ ср —г dx1 ... dxn = 0 для у < п,
J дхЗ
В
j cpg^dx1... dxn = (-l)n-1 j andx1 .. . dxn~\
В En~l
что и доказывает теорему.
§ 4. НУЛЬМЕРНЫЕ И n-МЕРНЫЕ КОГОМОЛОГИИ; СТЕПЕНЬ
Не касаясь общей техники вычисления различных групп гомо-
логий и когомологий, рассмотрим некоторые частные случаи.
Согласно определению, не существует нульмерных кограниц.
Поэтому нульмерная группа когомологий совпадает с группой
9*
132
Гл. III. Интегральное исчисление на многообразиях
коциклов. Но 0-форма есть просто функция, а 0-коцикл есть такая
функция /, что df = 0, т. е. локально постоянная функция. Таким
образом, Н° (М) является пространством всех локально постоян-
ных вещественных функций на М. Поскольку любая локально
постоянная функция постоянна на связных компонентах много-
образия М, мы можем написать Н° (М) 7?C°W, где Со(М)
есть множество компонент в М. В частности, если М связно, то
Н° (М) R.
Функция f является компактным коциклом, если она локально
постоянна и supp/ компактен. Это означает, что /==0 на неком-
пактных компонентах многообразия М. Поэтому Нс (М) ррсо(М),
где сСо (М) есть множество компактных компонент многообра-
зия М. В частности, если М связно, то Hc(M)^R для ком-
пактного многообразия М и Н'с (М) = 0 для некомпактного М.
Мы можем также вычислить1) Нр (5") для всех р. Именно,
справедлива
Теорема 4.1 (лемма Пуанкаре). Пусть со — форма степени
k'ff^ 1, определенная на В™, и пусть dat = 0. Тогда существует
такая форма Q, определенная на В™, что = со.
Мы докажем теорему индукцией по размерности п. Для п = 1
можно считать k = 1; все другие случаи тривиальны. Если со =
X
= / (х) dx, то достаточно положить Q4= g, где g (х) = j f (i) dt.
0
Сделаем теперь следующее замечание:
Лемма 4.1. Если д/дхп-I а = 0 и dco = 0, то со =
, ik dxli /\ . . . A dxlh, где < п и да^.........ihldxn~0.
Действительно,
да1 г
dco = ( — l)ft2 Adx1^ /\dxn+ . .. ,
где остальные члены не содержат dxn.
Перейдем к доказательству теоремы. Пусть у1, ...,уп'1—
декартовы координаты в Бр-1, и пусть i: В?~1 —> В?—отобра-
жение, задаваемое формулами
х1 (У1, • •, Уп'1) = У}, 1</<ге—1,
хп(/, .. ., уп~1)==0,
х) Напомним, что В? есть шар радиуса г в Еп.
§ 4. Нульмерные и п-мерные когомологии; степень 133
где х1, . ,.,zn— декартовы координаты в В™. Тогда i*(dx}) — dy3
для — 1 и г* (dxn) = 0. Пусть р — отображение шара В™
на 5р-1, определяемое формулой
у1 (ж1, ..., хп) = х* для 1 Д г Д п—1.
Имеем d (i* (со)) = i* (dco) = 0. По предположению индукции i* (со) =
— d(Q') для некоторой формы й' на 5Д1. Положим co = coi +
+ йжпДсо2, ГДе ®с и ®г — формы от dx1, ...,dxn~1. Определим
форму й следующими условиями:
1) г*(й) = й',
3) 2-_1с/й = со2.
' дхп i
В терминах координат (х1, ..хп) условие 2) означает, что
форма й может быть записана в виде
й= 3 Лг.............i. dxli Л ... /\dxlh~i, ife-tCn—1.
• 1 1
Условие 1) означает, что
2 aii....ift_! (У1, • • •, Уп~1, 0) йУ4 Л • Л dy^-i = Й'.
Условие 3) означает, что
да-
_т..... fe-1 h.
дхп li...4-1’
если со2 = 2 bt ..ift I dxl> /\ ... Д dxlh~l. Отсюда видно, что
существует единственная форма й, удовлетворяющая условиям
1), 2), 3), которая может быть найдена с помощью интегриро-
вания по хп. Мы утверждаем, что с/й = со. Действительно, йй — со =
= ЙЙ — dxn Д С02— СОр Но
dQ — dxn/\ (/- J с?й^
' ' \дхп )
есть дифференциальная форма, не содержащая dxn. Поэтому
йй-со = </хпД с/Й^-^Дсог + Й^Й!,
где й4 не зависит от </хп. Поскольку d(dQ — со) = О, мы можем
применить лемму 4.1. Таким образом,
с/й — со = 2 dit..ik dxli Д .. . Д dx\
134
Гл. III. Интегральное исчисление на многообразиях
где tftCn—1 и ddti....th/dxn = O. С другой стороны,
2^4,.....• • •> у”'1, tydy'i/\ ... /\dyik = i* (dQ — со) ==
= d(i* (Q))—a = dQ'—co = 0
Значит,
di....i (x1, ..., хп~г, 0) = 0
1 R-
и dt^....ik (x1, . .., xn) = 0. Другими словами, dQ —co = O, что
и доказывает теорему 3.1.
Следствие 4.1. Нр(Вг) = 0 для р>1.
В доказательстве теоремы 3.1 коэффициенты формы Q полу-
чаются из коэффициентов формы со интегрированием. Поэтому
если коэффициенты формы со дифференцируемо зависят от некото-
рых дополнительных параметров, то форма Q также дифферен-
цируемо зависит от этих параметров.
Следствие 4.2. Если в теореме 3.1 форма со дифферен-
цируемо зависит от некоторых параметров, т. е.
(0=2 ...ift (я1, .. ., xn; z1, .. ., z1) dx^ Л • • Л dx\
где а^...ik — дифференцируемые функции от х1, ..., хп, z1, .. ., zl
и da = 0 (оператор d берется по хг), то со = сШ, где
Q = 2 bi^..ik i (ж1, .. ., хп-, z1, . . ., zl) dfli Д . .. Д dxlk-i,
причем btv ...tik i — дифференцируемые функции всех п-\-1 пере-
менных.
Мы хотим теперь вычислить Я" (М) для любого многообра-
зия М.
Лемма 4.2. Пусть со — такая п-форма, определенная на Еп,
что
1) supp со с#?, где D^—куб {х 11 | < г},
2) J со = 0.
Еп
Тогда мы можем найти такую (п — -форму Q, что
3) suppQcD”,
4) cZQ = со.
Доказательство проведем с помощью индукции. Для этого
мы должны несколько усилить индуктивное предположение. Для
любой Zc-формы л, выраженной через dx'i Д . . . Д обозна-
чим символом | л |" максимум абсолютных значений ее коэффициен-
§ 4. Нульмерные и п-мерные когомологии; степень 135
тов в D". Мы будем говорить, что семейство форм л( дифферен-
цируемо зависит от t, если каждый коэффициент есть дифферен-
цируемая функция от х1, . . . , хп, t. Здесь t обозначает s-мерный
параметр, t = (ti, . . . , ts). Наше индуктивное предположение
состоит в следующем:
Пусть o)t — семейство форм на Е11, дифференцируемо завися-
щее от t. Предположим, что для каждого значения t форма
удовлетворяет условиям 1) и 2). Тогда существует такое диффе-
ренцируемое семейство форм Qit удовлетворяющих условию 3),
что dQ.t = (о( и
5) |Qt|?<
где К” зависит только от п и г.
Для п—1 мы можем написать = ft (•) dx1. Определим функ-
цию 52/ равенством
X
(*) = j ft (у1) dy1.
— Т
Очевидно, что Q/ есть дифференцируемое семейство 0-форм,
удовлетворяющих условиям 3), 4) и 5).
Допустим, что предположение индукции выполнено для п — 1.
Пусть
= // dx?- Л ... Л tZzn,
и пусть
л = <р(1/1, ...,yn-1)dy1/\.../\dyn~1
есть положительная форма на Z?n-1, такая, что suppncZ)"-1
и \ л=1. Рассмотрим формы nxnt / на Еп~г (зависящие от пара-
метров хп, t), определяемые формулой
nxn,t = ft(---,x")dy1/\ ... ^dy”-1 —
— ( j А уП1' dyl ’ “ dynl) П =
£П-1
= [а(•> *п) — ( j /(г/1, • г/п-1> ^dy1 • • • <р] х
X dy1 Л ... Д dy”-1. (4.1)
Они образуют дифференцируемое семейство (га— 1)-форм, удовле-
творяющее предположению индукции. Кроме того, / = О,
136
Гл, III, Интегральное исчисление на многообразиях
если | хп | > г. Поэтому мы можем написать
ЛХП( t == I’ (4.2)
Пусть
п— 1
йхп, г= 2 ( — 1)* gt (•, хп) dy1 Л • • • Л <& Л • • Л dy”"1,
г=1
где g/(-, •) —дифференцируемые функции на Еп. Определим
форму равенством
Л^{Л Л^1,
так что i*nQ/ = Qi>a.n, где t*n есть вложение Е™-1 —> Еп, заданное
формулами
ж1 = 1/\ i<n —1,
хп = х™.
При вычислении формы dQi встретятся два типа членов: содер-
жащие частные производные по хг (i^.n — 1) и содержащие
частную производную по хп. Умножением на dxn мы избавимся
от членов, содержащих dxn, и, значит, для каждого значения хп
будем иметь
d (Q; Д dx'1) = (р* dQ,xn, t) Л = (р*лхп, () Л dxn,
где р есть проекция Еп—>Еп~1 вдоль хп. Положим
...,у
—г ЕП-1
Тогда
dF (хп) = ( J ft (у1, .. ., у-~\ хп) dy} dxn.
Ь'П-i
Положим
Й, = й;Л^” + (-1)п/>*(л). (4.3)
Имеем
dQt = d (Q; л dxn) + (- I)"-1 dF Л p* (л) + Fp* (dn).
Но йл = 0, поскольку л есть (n — 1)-форма на Еп~г. Поэтому
dQz = d (Q; A dxn) + (- Ip’1 dF A P* P) =
=p* (nxn, t) A dxn + p* (л) A ( j ft(y\ • • -,Уп'г, xn)dy} dxn. (4.4)
£n-l
Далее, формы л и а значит, и форма обращаются в нуль
при |х11 > г (t = l, . .., га — 1). Если хп<_ — г или хп > г, то
§ 4. Нульмерные и п-мерные когомологии; степень 137
последний интеграл также обращается в нуль, поскольку
j j .......t, (у1, . . •, pre-1, z) dy1 ... dy71'1 dz = j co/j.ts = °-
—гEn En
Форма t обращается в нуль, если | хп | > г, так как по ин-
дуктивному предположению 5)
\^xn,t\r1<K\ftl.....f,(---,*n)l?_1 = 0 при |ж"|>г.
Наконец, формы, встречающиеся в правой части формулы (4.3),
очевидно, образуют дифференцируемое семейство форм и удовле-
творяют оценке 5), где Kf зависят от К?'1 и от выбора <р. Лемма
доказана. С помощью леммы 4.2 доказывается
Лемма 4.3. Если М — связное п-мерное многообразие, то
Hq (М) есть либо R, либо {0} (т. е. Hf(M) не более чем одно-
мерно).
Пусть {(Ц), hi)} — такой атлас на М, что каждая окрестность
имеет вид hxl(Df). Пусть Q — такая га-форма, что suppQctZj
и j h* (Q) =7^ 0. Лемма будет доказана, если для любой n-формы со
с компактным носителем мы найдем такое вещественное число с,
что
со — cQ = dco*, (4.5}
где со* есть (п— 1)-форма с компактным носителем. Пусть {<р;} —
разбиение единицы, подчиненное покрытию {Ut}. Тогда со =
= 2ф;со — конечная сумма, и достаточно провести доказательств»
для каждого слагаемого в отдельности. Поэтому можно считать,
что suppcoczzt/j для некоторого /. Пусть р — точка из Uaq —
из Uj. Пусть С (£) — такая кривая, что С (0) = р и С (1) = q.
Покроем С (t) конечным числом окрестностей U(. Изменив, если
потребуется, их нумерацию, мы можем считать, что это окрест-
ности Ut, причем Ut П U i-i Ф 0. Пусть со; (i=l, ...
.. ., j — 1) — такие формы, что
supp coj с Ut Q Ut-i,
§ ht(ai-i)^0.
ЕП
Положим Q = COO, CO = COj. Рассмотрим формы hi (сог) И (сй;--^}
на F с носителями в Df. Поскольку j h* (рр^) 0, сущест-
ва
138
Гл. III. Интегральное исчисление на многообразиях
®уют константы
( j &i(C0i) I j fc*(®i-i))
En En
такие, что
j h* (cof — Cjcoi-i) = 0.
ЕП
По лемме 4.2
hi (со»—CiCOi-O = dco**, (4.6)
причем supp (co**) cz D". Форма (Л?1)* co** определена в Ui и имеет
носитель в Ui. Определим на М форму со*, полагая со* = 0 вне
Ui и со* = (Лг1)*®** на Ui. Тогда равенство (4.6) можно перепи-
сать в виде
coj —CiCOj-^dco*. (4.7)
‘Складывая с подходящими весами равенства (4.7) при i — 1,
мы получим равенство (4.5), где
с = ci + cicj-i + • • • + ci • • • Со,
®* = СО* + Cj-i(p*^i + . . . + Су_! . . . Ctfi>*.
Теорема 4.2. Если М — связное ориентированное п-мерное
-многообразие, то Hc(M)o^R. Пусть М^иМ2— связные ориенти-
рованные п-мерные многообразия и /—собственное дифферен-
цируемое отображение М^—>М2. Существует такое целое число,
называемое степенью отображения / и обозначаемое deg/, что
/*co = deg/ j со (4.8)
Ml ма
'для любой п-формы со с компактным носителем на М2. Для
.любого регулярного значения у £ М2 имеем
deg/ = 2 signJx(/) [ = 0, если f~1(y) = 0], (4.9)
xe/-i(v)
где sign Jx (/) есть знак якобиана отображения / относительно
положительных (в смысле заданных ориентации) систем координат
вблизи точек х и у.
Доказательство. Согласно лемме 4.3, пространство
Нс (М) либо одномерно, либо нульмерно. По теореме 3.5 отобра-
жение со-> j со переводит точные формы в нуль и, значит, инду-
м
цирует гомоморфизм пространства Нс (М) в вещественную пря-
4. Нульмерные и п-мерные когомологии; степень
139
мую. Поскольку j со > О для положительной формы со, этот
м
гомоморфизм нетривиален и, следовательно, является изоморфиз-
мом.
Отображение /*: Дп (М2) -* /\п (Mt) есть гомоморфизм, пере-
водящий точные формы в точные. Поэтому отображение со ->
—> j /* (®) является гомоморфизмом пространства Я" (М2) в ве-
Ml
щественную прямую. Поскольку Я" (М2) одномерно, этот гомо-
морфизм кратен изоморфизму со -> С со. Таким образом, мы
м2
доказали формулу (4.8), но пока не знаем, что deg/ — целое
число. Мы покажем, что это так, проверив равенство (4.9). Заме-
тим, что сумма в формуле (4.9) конечна: отображение / собственное,
так что множество /-1 (у) компактно. С другой стороны, /-1 (у)
не содержит критических точек и, значит, дискретно. Регулярные
значения существуют, поскольку по теореме Сарда множество
критических значений имеет меру нуль. Пусть у — регулярное
значение и W — компактная окрестность точки у. Для каждого
д: € /-1 (у) выберем такую открытую окрестность Ux cz Л1 (И7)
точки х, что / регулярно во всех точках Ux и UXl fl UX2 = 0
(это можно сделать, поскольку функция / непрерывна и множество
регулярных точек открыто). Множество
У = /-1(Р7)_ J Ux
компактно, причем /(F)czB7 и у$/(Р). Поскольку образ ком-
пактного множества при непрерывном отображении компактен,
f (V) — компактное подмножество в W. Пусть U <zz W — /(7)
— координатная окрестность точки у. Имеем
= если /-i(y) = 0).
Рассмотрим положительную форму со на М2, такую, что supp со cz 77.
Тогда supp /* (со) cz [J Ux. Поэтому мы имеем
J /*(«)= 2 J /*(“)• (4Л0>
Ml Xbf-Цу) их
Если теперь у1, ..., уп — положительная система координат на 77,
то yr°f, ...,ynof—положительная или отрицательная система
координат на /-1 (77) f) Ux в зависимости от знака якобиана ото-
бражения / в точке х. Поэтому
j /* (со) = sign J* (/) j со. (4.11)
/-i(t7)nux и
140 Гл. III. Интегральное исчисление на многообразиях
Из формул (4.10) и (4.11) следует формула (4.9), и теорема дока-
зана.
Понятие степени очень полезно для получения различной
информации об отображениях. Мы проиллюстрируем его приме-
нение на некоторых теоремах, которые нам понадобятся позднее.
Теорема 4.3. Пусть Mt и М2 — ориентированные п-мер-
ные многообразия, причем М2 связно. Пусть f — собственное диф-
ференцируемое отображение Mi —>- М2. Предположим, что
Jх (/) 0 для всех х С М\. (4.12)
Тогда либо Jx (/) = 0, либо f (Mi) = М2.
Заметим, что (4.12) имеет смысл. Значение якобиана Jх (/)
зависит от выбора локальных координат на Mi и М2, однако его
знак зависит только от ориентации Mi и М2. При доказательстве
теоремы мы можем считать многообразие Mi связным. В против-
ном случае мы просто можем доказывать теорему для каждой
связной компоненты многообразия Мр. либо Jx (/) = 0 на всех
компонентах, т. е. на Mi, либо / (М) = М2 для некоторой ком-
поненты М a Mi. Далее, если Mi связно, мы можем применить
теорему 4.2. Если / (М^ #= М2, то deg / = 0, согласно формуле
(4.9) [написанной для точки у (Л//)]. Но если deg / = 0, то
Jx (/) ==0. Действительно, в противном случае Jx (/) > 0 в неко-
торой открытой окрестности U с Mi. Тогда / (U) содержит
открытое множество V а М2. По теореме Сарда V имеет регу-
лярную точку у. Но тогда deg / > 0, согласно (4.9). Теорема
доказана.
Упражнение 4.1. Пусть z -> р (z) — полиномиальное отображение
поля комплексных чисел в себя. Показать, что это отображение, рассматри-
ваемое как отображение Е2 -> Е2, является собственным и удовлетворяет
условию (4.12). Вывести из этого основную теорему алгебры: всякий непосто-
янный многочлен имеет корень. Показать, что степень этого отображения
совпадает со степенью многочлена.
Сформулируем теперь слегка измененный вариант теоремы 4.3
для «относительных многообразий».
Теорема 4.4. Пусть Mi и М2 — ориентированные п-мерные
многообразия, а М — связное открытое подмногообразие в Мх,
причем М компактно. Пусть / — дифференцируемое отображе-
ние М—>М2, удовлетворяющее условию (4.12), которое продол-
жается до непрерывного отображения f: М—> М2. Пусть М' =
— М — М. Тогда если
HM)nf(M')=0,
(4.13)
§ 5. Теорема Фробениуса
141
то либо
граница f(M) содержится в f(M'), (4.14)
либо
Jx(f) = O в М.
Доказательство. Согласно условию (4.13), / отобра-
жает М в открытое подмногообразие Mz — f(M’) многообра-
зия М2. Поскольку М связно, / отображает М в связную компо-
ненту, скажем М*, многообразия М2—Пусть К cz М* —
компактное подмножество. Тогда /-1 (К) — замкнутое подмноже-
ство из М и, значит, тоже компактно. Так как
то Д1 (А) есть компактное подмножество в М. Значит, /—соб-
ственное отображение М—>М*. Согласно теореме 4.3, если
Л(/)^0, то /(М) = М*. Но тогда ?(M)-/(M) = М*-М* с=
^/rn-
Упражнение 4.2. На n-мерном торе Тп формы йб1, . ...Й'”' (где
О1, . ..Д'1—угловые координаты, определенные по модулю 2л) корректно
определены и независимы. Поэтому любая /с-форма представима в виде
_ i <йЛд...Д<й\
1* ’ я
где ai i —функции от б1, ..., б'г, периодические с периодом 2л по всем
переменным. Пользуясь этим, показать, что классы когомологий
форм йб11 Д ... Д <7б*г образуют базис пространства Нг (Тп).
§ 5. ТЕОРЕМА ФРОБЕНИУСА
Как мы уже видели в главе II, векторное поле X на многооб-
разии М определяет, по крайней мере локально, некоторый
поток, т. е. однопараметрическую группу преобразований. Если
мы заменим X на /X, где / — дифференцируемая функция, то
новый поток будет иметь те же траектории, что и старый; изме-
нится только его «скорость» вдоль каждой траектории. Таким
образом, траектория определяется скорее полем «прямых», чем
полем векторов. Мы можем рассмотреть более общий объект —
поле «p-мерных подпространств».
Чтобы дать точное определение этого понятия, заметим, что
группа GL (п) действует слева на многообразии (р, Еп). где
г$ (р, Еп) — множество всех р-мерных подпространств из Еп
[см. пример 6 § 1 гл. II]. Обозначим многообразие величин типа
S (р, Еп) над М через Зр (М). Так же, как в гл. II, мы можем
•отождествить (М) с множеством всех р-мерных подпространств
векторных пространств Тх (М), х £ М. Поэтому поле типа
142
Гл. III. Интегральное исчисление на многообразиях:
& (р, Еп) можно рассматривать как поле р-мерных подпро-
странств. Мы назовем такое поле дифференциальной системой раз-
мерности р.
Определение 5.1. Пусть 3) — дифференциальная систе-
ма размерности р на М. Подмногообразие N с: М называется
интегральным многообразием системы 3, если
1,(7^))^ W(*)l (5.1}
для всех х £ N, где i — вложение N М.
Заметим, что 3 [i (х)1 есть подпространство в Т^ху(М), так
же как I, (Тх (N)), поэтому формула (5.1) имеет смысл. Следова-
тельно, интегральное многообразие не более чем р-мерно.
Определение 5.2. Дифференциальная система 3 раз-
мерности р называется вполне интегрируемой, если в окрестности
каждой точки х £ М существует такая карта (U, h), h = (ж1, ...
. . ., хп), что все подмногообразия из U, задаваемые уравнениями
жр+1 = const, zp+2 = const, ..., хп = const,
являются интегральными многообразиями системы 3.
Упражнение 5.1. Пусть Z — вполне интегрируемая система
и U — окрестность, фигурирующая в определении 5.2. Показать, что любое
связное интегральное многообразие системы Z, лежащее в U, является
подмногообразием одного из многообразий определения 5.2.
Следующее упражнение будет использовано в дальнейшем.
Упражнение 5.2. Пусть Z — вполне интегрируемая диффе-
ренциальная система размерности р на многообразии М. Пусть N есть
р-мерное интегральное многообразие системы Z. Предположим, что <р —
дифференцируемое отображение связного многообразия К в М, причем
<р (А) с N. Показать, что <р есть дифференцируемое отображение многообра-
зия К в N.
Цель настоящего параграфа — сформулировать критерий пол-
ной интегрируемости дифференциальной системы. Прежде чем
это сделать, заметим, что дифференциальную систему можно
задавать различными способами. Если Xi, . . . , Хр — набор
р векторных полей, линейно независимых в каждой точке х £ М,
то, как легко проверить, отображение х -> {aj (-Х\)ж 4~ . . .
. ..+ар (Хр)х | ах, . . . , ар С R} является дифференциальной си-
стемой. Аналогично, если <оР+1, . . . , <о" — набор п — р линей-
ных дифференциальных форм, линейно независимых в каждой
точке х Е М, то отображение х -> {Хж £ Тх (М) | <сож, Хх} = 0}
является дифференциальной системой. На практике большинство
$ 5. Теорема Фробениуса
143:
дифференциальных систем задается одним из этих способов.
Локально каждая дифференциальная система может быть задана
любым из этих способов.
Действительно, пусть 35 — дифференциальная система раз-
мерности р. Выберем вблизи точки х координаты х1, . . . , хп'
так, чтобы векторы (д/дх1),., . . . , (д/дхр)х порождали простран-
ство 35 (х). [Это всегда можно сделать: достаточно взять произ-
вольную систему координат и применить к ней подходящее линей-
ное преобразование.] Тогда ограничение формы (dx1^ Д . . .
. . . Д (dxv)x на Sb (х) отлично от нуля. По непрерывности из это-
го следует, что (dxly)y Д . . . Д (dxp)y | Др35 (у) Ф 0, если точка
у достаточно близка к х. В такой окрестности линейные формы
(dx1^ | 35 (у), . . ., (dxp)y | Sb (у) линейно независимы. Поэтому
существуют функции Яр (дифференцируемые, поскольку система
35 дифференцируема), такие, что
р
(da?)y 13b {у) = 3 (&&)у 13 (у), а = р-|-1, • ..,я.
₽=1
Таким образом, п—р линейно независимых форм
— 2 d$dx$
обращаются в нуль на Sb (у) и тем самым определяют подпро-
странство ЗЬ (у). Эти формы аннулируют р векторных полей
п
_L_L У а«2.
а=Р+1
которые линейно независимы и, значит, в свою очередь, порож-
дают систему Sb1). Таким образом, система Sb локально может
быть задана любым из указанных способов.
Определение 5.3. Пусть ЗЬ — дифференциальная система.
Через Т {ЗЬ) мы обозначим множество всех таких векторных
полей X, что Х{у)£ЗЬ{у) для всех у£М. Если X £ У* (.25), то мы
будем говорить, что поле X принадлежит системе ЗЬ. Через 3 (Sb)
мы обозначим множество таких дифференциальных форм й, что йу
обращается в нуль на Sb (у) для всех у£М.
Для любого линейного пространства V векторных полей мы
можем рассмотреть подпространство ЗЬ {у) = {X (у) | X £ F} при каж-
1) То есть для каждой точки у некоторой окрестности точки х векторы
п
(—з+ 2 ав-—, ₽ = 1, •••,?, порождают подпространство 35 (у).—
рдха‘)
а=р+1
Прим, перев.
144
Гл. III. Интегральное исчисление на многообразиях
дом у g М. Если dim 3 (г/) = const, то мы получим дифференциаль-
ную систему 3, причем V cz Т {3}. Предыдущие рассуждения
показывают, что любая система 3 получается из простран-
ства Y = Т'{3} подобным образом. Поэтому мы можем выразить
наши условия полной интегрируемости в терминах простран-
ства ТГ {3). Предположим, что 3 есть р-мерная система,
a Xt, ..., Хр — векторные поля, определенные на открытом мно-
жестве U. Мы скажем, что поля Xt порождают У {3) на U,
если Xt £ У {3} и любое поле X С У {3} представимо на U в виде
р
V = S hXt, где ft — дифференцируемые функции.
г=1
Теорема 5.1 (теорема Фробениуса, первый вариант). Пусть
3 — дифференциальная система размерности р на п-мерном много-
образии М. Система 3 вполне интегрируема тогда и только
тогда, когда Т’{3) есть алгебра Ли, т. е. [X, Y]QT' {3}, если
X^Y* {3) {3}. Так, если Хъ . . ., Хр. порождают У (3)
на U, то система вполне интегрируема тогда и только тогда,
когда существуют такие функции С}к на U, что
р
[Xj, Xh] = 2 C}kXt. (5.2)
i=l
Необходимость почти очевидна. Действительно, заметим сна-
чала, что функции С}и определены формулой (5.2) однозначно,
поскольку поля Xt линейно независимы в каждой точке. Поэтому
достаточно доказать их существование в окрестности каждой
точки из U. Если система 3 вполне интегрируема, то любая
точка х покрывается картой, описанной в определении 5.2, и в тер-
минах этой карты система 3 порождается на всем U полями
dldY, . . . , d/dxv. Поэтому мы можем найти такие функции aik
и Ъц, что
р
" дхк дхг "
k=i
Тогда
[Х;, ХД = [2 а‘1~дЛ 1 а’т =
I т
V / daih „ „ \ 3 _
— Zj дх™ dxh~
h, т
h, kt m
что доказывает существование функций Cjk.
5 5. Теорема Фробениуса 145
При доказательстве достаточности мы снова можем ограни-
читься локальным рассмотрением. Для р = 1 теорема сводится
к теореме существования решений обыкновенных дифференциаль-
ных уравнений. Действительно, для данного векторного поля X,
согласно этой теореме существования, мы всегда можем ввести
локальные координаты у1, ... , уп, в которых поле X имеет вид
д/ду1. Мы докажем теорему 5.1 индукцией по р. Пусть х £ М
и Xi, . . . , Хр—векторные поля, определенные в некоторой
окрестности V х, удовлетворяющие условию (5.2) и порождаю-
щие Т* (3). Введем координаты у1, . . . , уп, в которых ХА =•=
— д/ду1 и у1 (х) = 0. Положим /г = Х(ух и
Yi = Xi, Yt^Xt-ftXi, i — 2,...,p.
Векторные поля У, линейно независимы и, значит, порож-
дают У (3). Кроме того,
УггД = О для i>l. (5.3)
Рассмотрим подмногообразие Тс F, определяемое уравнением
у1 = 0. Из (5.3) следует, что векторные поля У; касательны к W,
т. е. yj(z) = i„(Z7(z)) для всех z£W, где Z} (j = 2, ...,р) —
некоторые векторные поля на W. Действительно, пусть z2, . .., zn —
координаты на W, определенные формулой z3 = y3\W. Тогда
I, ((d/dz’) (z)) = (д/ду?) (z), и если Yj = 2 Y1jdldyh, то поля Z7- опре-
2
п
деляются формулой Z3-= 2 Z/V<?zft, где Z*— ограничение функ-
2
ции Yh-t на W.
Векторные поля Zj удовлетворяют условию (5.2) (где р заменено
на р — 1). Действительно, если бы вектор [Z,, Zj] (z) не лежал
в пространстве, порожденном векторами Z2 (z), . . . , Zp (z), то
вектор [У/, УД (z) не лежал бы в пространстве, порожденном
Y} (z) (f = 2, . . . , п), поскольку у всех векторов Yj (j = 2, . . .
. . . , п) коэффициент при д/ду1 равен нулю. Таким образом,
по предположению индукции мы можем найти такие координаты
ш2, . . . , wn в некоторой окрестности точки х на W, что многооб-
разия и>р+1 = const, . . . , wn = const являются интегральными
многообразиями дифференциальной системы, порожденной поля-
ми Z2, . . . , Zp. Определим теперь координаты х1, . . . , хп вблизи
х, полагая х1 = у1, х’ (у1, . . . , уп) = (у2, . . . , уп). Якобиан
х по у отличен от нуля в точке х, поэтому хг действительно обра-
зуют систему координат вблизи х. Кроме того, поскольку
дхЧду1 — 0 для / 2. мы имеем Yt = д/ду1 = д!дз?-. Далее,
У1а;р+г = 0, (5.4)
10 С. Стернберг
146
Гл. III. Интегральное исчисление на многообразиях
так что
^(Уг^+г) = К1(Уг^г) =
= У1(Угхр+г)-Уг(У1хр+г) =
= -[Уг, yj^.
Но поля Уг удовлетворяют условию (5.2), т. е. существуют такие
функции C}h, что
[уг, yj-chy^S dty>.
1=2
Учитывая (5,4), получаем
р
1 = 2, ...,р. (5.5)
3=2
При фиксированном г мы можем рассматривать (5.5) как одно-
родную линейную систему р — 1 дифференциальных уравнений
относительно неизвестных функций Y {Х1>+г от независимой пере-
менной х1. При x1 = Q мы имеем Yixp+r = ZiWP+r = 0, т. е. система
имеет нулевые начальные данные и, значит, по теореме един-
ственности функции УгХр+г тождественно равны нулю. Поэтому
векторные поля У ь . . ., Ур выражаются через д/дх\ ...,д!дхр.
Таким образом, д/дх1, ...,д!дхр порождают Т*(^), т. е. систе-
ма ЗЬ вполне интегрируема.
Упражнение 5.3. Пусть X,, . . . , Хр — всюду линейно неза-
висимые на М векторные поля. Показать, что если [Хг, = 0, то в окрест-
ности каждой точки х Е М существует локальная система координат х1, ...
. . . , хп, в которой Xi = d/dxi (i = 1, . . . , р).
Полезно сформулировать теорему 5.1 для случая, когда диф-
ференциальная система задается не векторными полями, а диф-
ференциальными формами. Ясно, что в определении 5.3 множе-
ство J {ЗЬ) является идеалом в кольце дифференциальных форм
и порождается формами степени единица.
Теорема 5.2 (теорема Фробениуса, второй вариант). Пусть
ЗЬ — дифференциальная система размерности р на п-мерном много-
образии М. Система ЗЬ вполне интегрируема в том и только
в том случае, когда d$ {ЗЬ) cz J {ЗЬ), т. е. когда dcogj {ЗЬ), если
(£>63 {ЗЬ). Пусть сор+1, .. ., со”— линейные формы на открытом
множестве U, порождающие 3 {ЗЬ). Тогда предыдущее утвержде-
ние можно перефразировать, сказав, что система ЗЬ вполне
интегрируема тогда и только тогда, когда существуют такие
J 5. Теорема Фробениуса
147
функции c}k, что
dot1 2 (5-6)
3<h, p<k 1
Доказательство. Снова, поскольку утверждение локально,
мы можем ограничиться рассмотрением окрестности, на которой
существуют линейно независимые формы со1, . . ., <оп, последние
п—р из которых со”+1, .. ., со" порождают идеал J(A5). Пусть
Х1; . .., Хп — векторные поля, определяющие в каждой точке у
базис, дуальный базису оф, . . ., (Оу. Поля Xt, . . ., Хр порождают
систему 3, и по теореме 5.1 полная интегрируемость системы 3
эквивалентна выполнению условий (5.2). Но
(Х; Л Xj | dcoa) = Xi (Xj | <oa> — Xj (Xt | <o«> — ([Xz, Xj] | <oa).
Для i p, ]' P-, a > p первые два члена справа обращаются
в нуль. Поэтому левая часть обращается в нуль тогда и только
тогда, когда поле [Хг-, Xj] разлагается по Xt, . . . , Хр, т. е.
когда справедливо равенство (5.2). Но обращение в нуль выра-
жений (Xi Д Xj | dcoa) в точности эквивалентно равенству (5.6),
что и доказывает теорему 5.2.
Предположим, что нам задан однородный идеал ,7 кольца
дифференциальных форм на дифференцируемом многообразии М,
который не обязательно порождается линейными формами. Для
каждой точки х £ М идеал J определяет идеал 3 х внешней
алгебры Д Т* (М). Согласно теореме 5.4 гл. I, каждому идеалу
Jx. cz Д Т* (М) корректным образом сопоставляется подпро-
странство пространства Тх (М). Таким образом, исходя из идеала
3, мы можем сопоставить каждой точке х С М подпространство
3 (х) пространства Тх (М). Оно порождается множеством век-
торов Хх £ Тх (М), для которых X j Jc J. Однако при этом
не всегда получается дифференциальная система: размерность
пространства 3 (х) может изменяться от точки к точке. Мы назо-
вем идеал 3 невырожденным, если отображение х -> 3 (х)
является дифференциальной системой. Если идеал 3 невырожден,
то мы назовем эту дифференциальную систему характеристической
системой идеала 3-
Теорема 5.3 (Картан). Пусть 3 — невырожденный идеал
и d3 cz 3 • Тогда его характеристическая система вполне инте-
грируема.
Пусть Х1; . . ., Хр — векторные поля, порождающие характери-
стическую систему идеала 3- Тогда Xj jJcJ. Если а^З,
то из формулы (1.10) следует, что
[X;, XJ j ш = Хг j (X,j da) — Xt j d(Xj j co) — Xj j d (X4 j co).
10*
148
Гл. III. Интегральное исчисление на многообразиях
Поскольку dj cz J, все три члена правой части лежат в J.
Поэтому [X/, Х7] j Jcz J и, значит, [Хг, Х?] есть линейная комби-
нация полей Хъ ..., Хр, т. е. выполняется условие (5.2). Тео-
рема 5.3 следует теперь из теоремы 5.1.
Первые три теоремы этого параграфа представляют собой
чисто локальные теоремы существования. Обратимся теперь
к проблеме нахождения глобальных решений. Пусть 3 — вполне
интегрируемая дифференциальная система размерности р на мно-
гообразии М. Тогда существует покрытие многообразия М такими
координатными окрестностями Ua, что ^-мерные интегральные
многообразия задаются в Ua равенствами Хц+1 = const, . . .
. . . , Ха = const.
Предположим, что N есть связное интегральное многообразие
в М. Более точно, N есть связное многообразие вместе с отобра-
жением /: N -+ М, таким, что /, (Тх (7V)) = 3 (f (а:)) для всех
х £ N. Любая точка х g N обладает такой окрестностью V, что
/ (У) с: Uа для некоторого а. Тогда / (У) содержится в подмно-
жестве из Ua, выделяемом уравнениями x%+i = const, . . ., =
= const. Пусть у — другая точка из N. Кривую С, соединяющую
х с у, мы можем покрыть конечным числом окрестностей типа У.
Таким образом, х и у можно соединить конечной последовательно-
стью кривых Ci (причем Сг (1) = Сг+1 (0)), таких, что f ° Ct —
одномерные интегральные многообразия системы 3.
Теперь мы видим, как построить максимальное интегральное
многообразие системы 3. Пусть х — точка из М, и пусть К —
множество таких точек у £ М, для которых существует конечное
число кривых Ср. [0, 1] -> М, удовлетворяющих условиям С, (0)=
= х, Сп (1) — у, Ci+t (0) = Ct (1) и являющихся одномерными
интегральными многообразиями системы 3. Превратим К в диф-
ференцируемое многообразие. Пусть у £ К. Тогда у £ Ua для
некоторого а и множество точек z С Ua, удовлетворяющих урав-
нениям
4+* (Z) = 4+1 (у), • • •, 4 (Z) = 4 (у),
также принадлежит К. Примем это множество за координатную
окрестность точки у с координатами х„, , х%. [Мы предостав-
ляем читателю в качестве упражнения проверить, что тем самым
на К действительно определена структура дифференцируемого
многообразия; в частности, необходимо проверить аксиому Хаус-
дорфа и аксиому счетности.] Из предыдущих рассуждений ясно,
что любое связное интегральное многообразие системы 3, про-
ходящее через точку х, отображается в некоторое подмножество
из К. Таким образом, справедлива
$ в. Теорема Дарбу
149
Теорема 5.4. Пусть 3) — вполне интегрируемая диффе-
ренциальная система на М. Через каждую точку х £ М проходит
максимальное связное интегральное многообразие Кх. Любое другое
связное интегральное многообразие, проходящее через х, является
подмногообразием многообразия Кх.
Замечание. Многообразие Кх не является в общем случае
вложенным подмногообразием многообразия М. Например, если
М — двумерный тор (рассматриваемый как плоскость по модулю
единичной решетки) и система 3) задается постоянным векторным
полем с иррациональным углом, то любое максимальное инте-
гральное многообразие, очевидно, всюду плотно на этом торе.
§ 6. ТЕОРЕМА ДАРБУ х)
В этом параграфе мы рассмотрим проблему нахождения нор-
мального вида линейной дифференциальной формы. Сделаем пред-
варительно несколько замечаний.
Пусть Mi и М2—дифференцируемые многообразия. Между
парами векторных полей на М± и М2 и векторными полями
на Mi х М2 существует связь, которую мы сейчас изучим. Пусть
Лр >Mi и л2: MiX М2—> М2—естественные проекции.
Дифференциальная система, задаваемая всеми формами из
л* (Л1 (М2)), очевидно, вполне интегрируема, так же как и система,
задаваемая формами из ^(ДДА^)). Действительно, в соответ-
ствии с определением многообразия Mi X М2 существует покрытие
этого многообразия окрестностями вида t7t х U2 с координатами
(z1, . . ., хП1, у1, ...,уП2), где х1, ..., хП1 — координаты на М1г
а у1, ..., уП2 — координаты на М2. Ясно, что подмногообразие
у1 = const, ..., уП2 = const является интегральным многообразием
системы, соответствующей пространству л* (Д1 (ЛГ2)), а подмного-
образие х1 — const. ..., хП1 = const — системы, соответствующей
л^ддда).
Если coj — дифференциальная форма на Mi, а <о2 —на М2,
то л* (®j) л* (ш2) есть дифференциальная форма на М4 X М2.
С другой стороны, если X—векторное поле на Mi, a Y—на М2,
то мы можем определить векторное поле (X, У) на Mt X М2.
Если X = (X1, . .., X”1) относительно системы координат х1, . .., xni,
a Y — (У1, . . ., У”2) относительно у1, . .., уП2, то положим (X, У) =
= (X1, . . ., X”1, У1, .. ., У”2) относительно Xi, .. ., хп\ у1, . . ., у"2.
Из закона преобразования координат видно, что тем самым мы
действительно определили векторное поле на Мj X М2. Ясно
!) Основной результат этого параграфа (теорема 6.2) дальше в книге
нигде не используется
150
Гл. III. Интегральное исчисление на многообразиях
также, что
(X, У) j (лх* (со,) + л2* (со2)) = л? (X j со,) + л* (У j ®2). (6.1)
Более общо, если s и t — контравариантные тензоры данного типа
на и М2, то мы можем определить тензор (s, t) того же типа
на Mi X М2. С алгебраической точки зрения доказательство сво-
дится к замечанию, что для каждой точки (х, у) £ Mr X М2 суще-
ствуют отображения iu: Тх (Mt) —>T(Xt vy (Mi X М2) и с2*: Ту (М2) —>
—> Т(х, у) (Мх X М2), такие, что ли ° 11ф = id, л2„ о i2* = id. Другими
словами, касательное пространство в каждой точке из Мj X М2
распадается в прямую сумму пространства, «касательного» к Ми
и пространства, «касательного» к Л/2. Если Х( и Х2 — векторные
поля на Ми a yj и У2—векторные поля на М2, то прямая про-
верка (скажем, в терминах локальных координат) показывает, что
[(Хь Yi), (Х2, У2)] = ([Хь Х2], [У1; У2]). (6.2)
Если g4— дифференциальная система на М^ а g2—на М2, то,
полагая § (х, у) = (х) + i2„g2 (х), мы получим дифференциаль-
ную систему g на х М2. Из формулы (6.2) и теоремы 5.2
следует, что если системы gj и g2 вполне интегрируемы, то такой
же будет и система
Мы можем сформулировать полезное обобщение этого замечания.
Пусть § — дифференциальная система на Mi X М2, согласованная
с разложением касательного пространства в прямую сумму, т. .
g (х, у) = (х, у) + (х, у) (6.3)
для всех (х, у) ^Mi X М2. Для каждого у^М2 дифференциальная
система g индуцирует дифференциальную систему gy на Мг.
а именно, система ^>у определяется формулой gy (х) = nug (х, у);
аналогично, система gx определяется формулой gx (у) = n2*g (х, у).
Для проверки того, что это действительно дифференциальные
системы, введем в окрестности точки (х, у) локальные координаты
(х1, ...,хП1,ух, ...,уП2). Мы можем найти линейные формы
со1, ..., (ok, задающие систему g в окрестности точки (х, у).
Напишем каждую из этих форм:
П1 П2
= 2 dx3 + 2 Ъ} dy3 = (o’ + (o’.
j=i 7—1
Из условия (6.3) следует [поскольку формы coj обращаются в 0
на ii*Tx(M), а формы со’ —на i2*Ty(M)], что формы со’ и со’ обра-
щаются в 0 на подпространстве g (х, у). Поэтому мы можем выбрать
формы со1, ..., со', (о'+1, ..., и>к так, чтобы
а1 — a} dx3, если
(o’= '^b'jdy3, если
§ <>. Теорема Дарбу
151
(где а], Ь}— функции всех переменных и формы <о1 линейно
независимы). Тогда дифференциальная система %у определяется
формами 2 (z1, хП11 У1? •••> УП2)йх\ а ёх— формами
2 blj (х1, . .., xni, у1, .. ., yns!) dy1. Теперь мы можем доказать сле-
дующее утверждение:
Лемма 6.1. Пусть % — дифференциальная система на Mi X М2,
удовлетворяющая условию (6.3). Если система <&у вполне интегри-
руема при любом у£М2, а ёх = {0} для всех x^Mi, то система $
вполне интегрируема.
Доказательство. По условию есть тривиальная диф-
ференциальная система, сопоставляющая каждому у£М2 нулевое
подпространство. Поэтому локально идеал ,7 (§) порождается
формами ю1, . . ., а>1 и dy1, . . ., dyn2, где
со’ = 2 а} (z1, • • •, хп\ у1, . . ., у"2) da?.
Тогда система %у задается формами с* (со’), где вложение iy: Mi—*
переводит х в (х,у). Поскольку система %у вполне
интегрируема, формы d (ij (со’)) являются линейными комбинациями
форм (ci?) Д (о?). Но форма л* (dxy (со5)) отличается от аь?
только членами, содержащими dy!. Поэтому дифференциальная
система, порожденная формами со1, ..., сог, dy1, ..., dy"2, вполне
интегрируема.
Упражнение 6.1. Показать на примере, что система $ не обя-
зательно будет вполне интегрируемой, если системы и ^у вполне инте-
грируемы для всех х g М, и у g М2.
Применим теперь предыдущие замечания к задаче нахождения
нормального вида линейной дифференциальной формы. Пусть
со — линейная дифференциальная форма. Тогда dco — внешняя
дифференциальная форма степени 2 и идеал Д, порожденный
формой da, замкнут относительно d. Характеристическая система
этого идеала совпадает поэтому с отображением, сопоставляю-
щим каждому х g М ассоциированную систему формы (dco)x,
в нашем случае — подпространство размерности п — 2р, где 2р
есть ранг формы (dco)x, см. теорему 5.1 гл. I. Предположим, что
этот ранг постоянен на М. По теореме Картана (теорема 5.3)
характеристическая система идеала Д вполне интегрируема.
Значит, для каждой точки х £ М существует координатная окрест-
ность U с координатами и1, . . . , и”-1, у1, в которых характери-
стическая система идеала (7 задается уравнениями
dMn-2P+! = . . . = (/„П-1 = dyl = 0.
152
Гл. III. Инетгралъное исчисление на многообразиях
Согласно теореме 5.1 гл. I, это означает, что форма dco выражается
через dun~2P+1, . . ., du11"1, dy1. Рассмотрим окрестность U как
произведение U = U!XU2, где и1, ..., и”-1 — координаты в Ut,
а у1 — координата в U2. Для каждого фиксированного значения у1
ограничение формы da на подмногообразие U х у1 представляет
собой замкнутую 2-форму 1J1 (dco) ранга 2р— 2.
По лемме 6.1 характеристическая система идеала, порожден-
ного формами iyi (da) и dy1, является вполне интегрируемой диф-
ференциальной системой. Поэтому мы можем найти такие коор-
динаты и1, . . ., ип~2Р, wn~2P+1, .. ., шп~2, у2, у1, в которых эта
дифференциальная система задается уравнениями dwn~2P+2 = . . .
... = dy2 = dy1 = 0. В этой системе координат формы iyi (dco) выра-
жаются через dwn~2P+2, ..., dy2. Теперь мы можем представить U
в виде произведения U = U3xUi, где координатами в окрестности
С74 служат функции у1, у2, и рассмотреть характеристическую
систему идеала, порожденного формами iji, уг (da), dy1, dy2.
Продолжая процесс подобным. образом, мы придем наконец
к такой системе координат z1, ..., zn-p, у1, ..., ур. что
су1...у-p (da) = 0, где tyl> есть вложение
(z1, ...,zn-p)^(z1, . ,.,zn~p, у1, ...,ур).
Согласно лемме Пуанкаре (теорема 4.1), мы можем написать
l*i ур (®) = dSyl уР, где Syl уР—дифференцируемая функ-
ция от z1, .. ., zn~p, дифференцируемым образом зависящая от пара-
метров у1, . . ., ур. Поэтому она определяет некоторую функцию S
на U. Кроме того, форма со — dS обладает тем свойством, что
iyl уР (со— dS) = Q при любых у1, ..., ур. Поэтому мы можем
написать
со —d5 = /1dz/1+ .. . +/рdyp.
Значит, da = df j Д dy1 + . . . + dfp Д dyp. Так как ранг формы da
равен 2р, то da Д ... Д dco =/= 0 (р сомножителей). Поэтому
dfi Д • • • Д dfp Д dy1 Д .. . Д dyp 0, и мы можем дополнить
функции fi, . . •, fp, у1, . . ., ур до системы координат х1, . . ., х"~р,
У1, • • • , Ур (хг — fi, 1<U<; р). В терминах этой системы координат
со — dS-\-x1dy1 + ... -{-xpdyp. (6.4)
Предположим, что нам задана замкнутая 2-форма Q ранга 2р,
т. е. такая форма, что Й Д . . . Д Й 0(р сомножителей) в любой
точке х С М, ноЙД...ДЙ = 0(р-|-1 сомножителей). В соот-
ветствии с леммой Пуанкаре вблизи каждой точки х £ М мы
можем найти линейную дифференциальную форму со, для которой
da = Q. Из предыдущих рассуждений видно, что можно выбрать
J 6. Теорема Дарбу
155
координаты х1, . . . , хп~р, у1, . . . , ур, в которых форма со имеет
вид (6.4). Применяя внешнее дифференцирование, получаем сле-
дующее утверждение:
Теорема 6.1. Пусть Q — замкнутая 2-форма на п-мерном
многообразии М, имеющая всюду ранг 2р. Вблизи каждой точки
из М можно ввести такие координаты х1, . . . , хп~р, у1, ... , ур.
что
Q = dx1 /x.dy14-... /\dyp. (6.5)
Возвратимся к проблеме нахождения нормального вида линей-
ной дифференциальной формы. В формуле (6.4) не извест-
но, является ли форма dS линейной комбинацией форм dx1
и dy1 (i Д р). Рассмотрим два случая:
1) форма dS всюду является линейной комбинацией форм dx1
и dyi (i = 1, . . . , р);
2) формы dS, dxz, dy1 (I = 1, . . . , p) линейно независимы.
Эти два случая различаются следующим образом: по пред-
положению со = d(p Д . . . Д dco (р раз) есть ненулевая 2/>-фор-
ма. В локальных координатах
со Д со = dS /\ dx1 Д .. . Д dxp Д dy1 Д . .. Д dyp.
Если (соДсо)ж = О, то dS является линейной комбинацией форм
dxz и dy1 в точке х; в противном случае формы dS, dx1, dy1
линейно независимы. Наши два случая соответствуют поэтому
условиям и Д о) = О или со Д со 0 для всех х. Во втором случае
мы можем дополнить функции S, х1, . . ., хр, у1, ..., ур до системы
координат. В этой системе координат со = х1 dy14-х2 dy2 4- . ..
. . . +xpdyp + dxp+1.
В первом случае мы предоставляем читателю в качестве (нетри-
виального!) упражнения1) проверить, что если со=ДО, то можно
найти координаты, в которых (р = х1 dy1хр dyp. Таким
образом, имеет место
Теорема 6.2 (Дарбу). Пусть со — линейная дифференциальная
форма, причем ранг формы dtp всюду равен 2р. Если со#=О, но-
р раз
со Д dtp Д . . . Д d<p == О,
то в окрестности каждой точки можно найти координаты
х1, .. ., хп~р, у1, ..., ур, в которых
со = Д dy1 -|- . . . 4- хр dyp. (6.6)
4 Указание. Рассмотреть дифференциальную систему, порожденную
всеми векторными полями X, для которых (X | а) = ОиХ J (со Д dw) = 0.
Показать, что это действительно дифференциальная система, причем вполне
интегрируемая. Затем поступить, как выше.
154
Гл. III. Интегральное исчисление на многообразиях
Р раз
Если форма со Д dco Д ... Д dco всюду отлична от нуля, то вблизи
каждой точки можно ввести координаты х1, . .., хп~р, у1, . .., ур,
в которых
со = х1 dy1 +... + хр dyp -|- dxp+1. (6.7)
§ 7. ГАМИЛЬТОНОВЫ СТРУКТУРЫ
Важным геометрическим объектом, возникающим при изу-
чении римановой геометрии и классической механики, является
дифференцируемое многообразие, снабженное специальной внеш-
ней 2-формой.
Определение 7.1. Пусть М есть 2га-мерное дифферен-
цируемое Многообразие. Мы назовем М гамильтоновым многооб-
разием (или будем говорить, что многообразие М снабжено гамиль-
тоновой структурой), если задана замкнутая 2-форма й ранга
2п, определенная всюду на М.
На гамильтоновом многообразии мы имеем взаимно однознач-
ное соответствие между пространством векторных полей и про-
странством линейных дифференциальных форм. Действительно,
для векторного поля X определим форму coY формулой
сох = X j Й. (7 Л)
Отображение X -> сох есть взаимно однозначное отображение на.
Действительно, в каждой точке х £ М формула (7.1) задает ото-
бражение Тх (М) на Т* (М), определяемое невырожденной били-
нейной формой йх. Обозначим обратное отображение через со ->
-* Хю. Таким образом,
со = Ха _j Й. (7.2
Теперь мы можем перенести операцию, определяемую для вектор-
ных полей скобкой Ли, на дифференциальные формы. Эта опе-
рация также обозначается символом [ , ] и называется скобкой
Пуассона. Таким образом, для двух линейных дифференциальных
форм coi и со2 мы имеем
[соь со2] = [XW1) ХИ2] j Й. (7.3)
Предположим, что форма со2 замкнута. Тогда
И2®1 = ^ХЮ2 (Xffll J Й) =
= (^хЩ2ХО1) J Й 4- Xfcl J (Ххы&) =
= [ХШ1, Хй2] _] й -|- ХЮ1 । (ХШ2 _] <7Й 4~ dco2) =
= [®1, со2].
§ 7. Гамильтоновы структуры
155
Значит, если формы 0)t и со2 замкнуты, то
[®ъ со21 = XХ(й2®! = — Хха ®2. (7.4)
Если со — произвольная замкнутая форма, а X — векторное поле,
то Дт<о = d (X j со). Поэтому производная Ли любой замкнутой
формы есть точная форма. В частности, скобка Пуассона двух
замкнутых форм есть точная форма.
Предположим, что формы и со2 точны: (pi = df. <o2==dg.
Тогда
[df, dg]=XXdf(dg) = d(Xdfg). (7.5)
Положим
[/, g] = Xdfg= -Xdgf, (7.6)
так что
[df, dg]=d[f, g].
В частности, если [f, д] = 0, то функция f постоянна на орбитах
поля Xdg, и обратно. Таким образом, функция / постоянна
на орбитах поля Xdg тогда и только тогда, когда функция g
постоянна на орбитах поля Xdf.
Согласно теореме 6.1, вблизи каждой точки можно ввести
координаты х1, . .., хп, у1, ..., уп, в которых
Q = dy1 Д dx1 + .. . + dyn Д dxn. (7.7)
[Для удобства мы поменяли местами х и у в формуле (6.5).]
Вычислим в этих координатах Ха и 0)х. Предположим, что
векторное поле X имеет вид
Х = ^{а'тг+ь1тг)-
' дхг дуг !
Тогда
сох = 2 (&г dx1 — a1 dy1). (7.8)
Если со есть дифференциальная форма
<о=2 (cldxl + d2 dy1),
1—1
то формула (7.7) дает
п
хй=2 <7-9)
\ дхг дух /
В частности, для любой функции / имеем
' V dyi дхг dxi дуг I
156
Гл, III. Интегральное исчисление на многообразиях
[f,gi = ^(JLJiL~JL2L\. (7.10)
" \ дхг дуг дуг дхг I V
Особый интерес представляют инфинитезимальные автоморфизмы
гамильтоновой структуры, т. е. образующие однопараметрических
групп, сохраняющих форму О.
Определение 7.2. Векторное поле X называется гамильто-
новым, если
£хЙ = 0. (7.11)
Поскольку = d (X J Q) 4- X j dQ. и <7Q = 0, получаем следую-
щее утверждение:
Векторное поле X гамильтоново тогда и только тогда, когда
форма сох замкнута.
Из приведенных выше рассуждений следует, что скобка Ли
двух гамильтоновых векторных полей есть гамильтоново поле.
Таким образом, множество всех гамильтоновых векторных полей
на гамильтоновом многообразии класса С°° есть алгебра Ли.
Существует чрезвычайно важный способ получения гамильто-
новых многообразий, который мы сейчас изучим.
Теорема 7.1. Пусть М — дифференцируемое многообра-
зие. На кокасателъном расслоении Т* (М) существует канониче-
ская линейная форма 9, называемая фундаментальной формой
расслоения Т* (М), которая определяется следующим образом',
для любого касательного вектора Хи в точке и £ Т* (М)
<Хи,еи) = (л,Хи,и), (7.12)
где л — проекция Т* (М) —> М. Форма <78 имеет ранг 2п и, значит,
определяет на Т* (М) гамильтонову структуру.
Заметим, что л,Хи есть касательный вектор в точке л (п))
а и — линейная функция на Тп^ (М). Поэтому формула (7.12.
имеет смысл. Проверим остальную часть теоремы. Пусть х1, . . .
. . . , хп — система координат на открытом множестве U из М)
Мы можем ввести в л-1 (77) координаты (ж1, . . . , хп, у1, . . . , уп-
следующим образом. Формы dx1, . . . , dxn порождают простран-
ство форм на U. Поэтому для всякой формы и £ л-1 (77) мы имеем
u=S/(u)^n(u). (7-13)
Значит, х1 (л (н)), .. ., хп (л (и)), у1 (и), . . ., уп (и) образуют систему
координат в л-1 (77). Любой касательный вектор Хи записывается
5 7. Гамильтоновы структуры
157
в виде
Следовательно,
л,хи=2х;(-М .
\дх1 I л(и)
и формула (7.12) принимает вид
(Хи, 0и) = ^у1 (и) Х1и.
Таким образом,
би = 2 У1 (и) (dx^u
или
9=2^/, (7.14)
откуда видно, что 9 есть линейная дифференциальная форма,
а форма dQ — 2 dy1 Д dx' имеет всюду ранг 2п, что доказывает
теорему.
Отметим, что в классической механике в случае, когда мно-
гообразие М есть «конфигурационное пространство», многообра-
зие Т* (М) называется «фазовым пространством». В классической
механике частиц в качестве многообразия М рассматривают кон-
фигурационное пространство п частиц. Таким образом, М = Е3п.
Если мы запретим двум частицам находиться в одной точке про-
странства, то М состоит из точек (а^, z/t, zi, . . . , хп, уп, zn) про-
странства Е3п, удовлетворяющих условию
(xt — XjY + (уг — г/,)2 + (гг — Z;)2 =# О
для всех пар г, /, /. В законах движения предполагается,
что существуют п положительных чисел т^, . . . , тп (где тп;
называется массой i-й частицы) и такая функция V на М (назы-
ваемая потенциальной энергией), что уравнения движения имеют
вид
w d2X[ dV
mi ~dpT = — ~dxT ’
d^i _ dV
1 di2 dyi '
(7-15)
Для упрощения обозначений положим
— У1. = <121 Zi — th, = •••, zn = g,3,1
и
Ml = M2 = M3 = ml, Mi = M5 = М6 — т2 и т. д.
158 Гл. III. Интегральное исчисление на многообразиях
Тогда уравнения (7.15) приобретут вид
М'Т>=-~ЯГ- <716>
Рассмотрим риманову метрику, задаваемую формулой (р, и) --
= ^Miql, грр v = ^qt(d/dqi). Каждая риманова метрика опре-
деляет диффеоморфизм X: Т (М) —» Т* (М). Для рассматриваемой
метрики, как легко видеть,
где pi — Miqi- Координаты рг называются импульсами, сопряжен-
ными с координатами qt. [Заметим, что, согласно формуле (7.14),
на любом многообразии, как только мы выбрали координаты
qn, определены сопряженные импульсы г), независимо
от выбора римановой метрики. Что касается римановой метрики
(т. е. выбора масс), то она дает правило перехода от скоростей
к импульсам.]
Уравнения (7.16) теперь можно записать в виде
dqi pt dpi dV
dt Mi ’ dt dqi
Таким образом, на многообразии Т* (М) возникает поток, опре-
деляемый векторным полем
У= —V ( Pi д \ dV
k Mt dqi dqi dpi ) '
Мы имеем pilMi = dTldpi, где Т = -i- 2 PtlMt— кинетическая
энергия. Поэтому
Xjd8=—с?Я, (7.17)
где H — T-{-V есть полная энергия. Далее,
ХЯ = (Х|йЯ) = -<Х|Х J Й) = 0* 2).
Таким образом, функция Я постоянна вдоль траекторий поля X.
Этот факт известен как закон сохранения энергии. Более общо,
пусть /—любая такая функция, что XdfH = Q. Тогда
X/ = (X|d/) = (X|Xd/JQ) =
= - (Xdj I X j Й) = (Xdf I dH) = XdiH = 0.
*) Как координаты линейной формы в базисе dqi, . , dqn.— Прим,
перев.
2) Где Q = dQ.— Прим, перев.
§ 7. Гамильтоновы структуры 159
Таким образом,
из равенства XdfH = 0 следует, что функция f постоянна
вдоль траекторий поля X. (7-18)
Существует способ перехода от векторных полей на М к функ-
циям на Т* (М). Действительно, любая однопараметрическая функ-
ция gt диффеоморфизмов многообразия М определяет однопара-
метрическую группу g* диффеоморфизмов многообразия Т* (М),
причем л. ogt = gtoft. В самом деле, для любой точки (р, и*) £Т* (М)
положим
gi (Р, v*) = (gt (р), (g-t)gt(P) v*).
Ясно, что таким образом мы определили однопараметрическую
группу диффеоморфизмов многообразия Т* (М). Далее,
(g?)*e=8.
Действительно, для любого вектора X g T^Pi (Т* (М)) имеем
(X, (g?)*e> = <(g?)*x, =
— ° (gt)* X, (g_t)*v*)= (по определению 0)
= (gt ° л,Х, (g_t)* v*) = (так как л о g* = gt о л)
= (л,Х, v*) =
= (Х, 9).
Таким образом, любое векторное поле Y на М поднимается
до векторного поля Y на Т*(М), причем л*иУи = Уя(и) для любого
и£Т*(М) и £?6 = 0. Но
Jg?0==y_j d0-(-d(y|0>.
Значит, YjdQ =—d (У | 0>. Легко вычислить функцию <У|8У
Действительно, в любой точке и = (р, и*) имеем
<уи, еи>=(л,уи» 0и) = (У, г*).
В механике, например, если У = d/dqt, то (У |8) = р;. Таким
образом, импульс (или линейный момент) частицы в данном направ-
лении соответствует однопараметрической группе сдвигов частицы
в этом направлении. Аналогично, угловой момент соответствует
однопараметрической группе вращений. Если в механике У
есть векторное поле на М, причем YH = 0, то, согласно (7.18),
поток, порождаемый полем X, сохраняет функцию (У | 8).
160 Гл. III. Интегральное исчисление на многообразиях
Чтобы привести пример такого векторного поля, предполо-
жим, что потенциальная энергия V зависит только от расстояния
между частицами. Тогда евклидово движение всех частиц с сохра-
нением расстояний не изменяет функций V и Т и, значит, инду-
цирует преобразование многообразия Т* (М), которое оставляет
И инвариантной. Так, векторное поле У, соответствующее одно-
параметрической группе сдвигов или вращений всех частиц,
определяет функции, инвариантные относительно потока, порож-
денного полем X. Эти утверждения известны как законы сохране-
ния полного импульса и полного углового момента.
Глава IV
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
В этой главе мы будем заниматься вариационным исчислением на мно-
гообразиях. Вариационное исчисление изучает вопросы следующего типа:
задана некоторая функция I в пространстве дифференцируемых кривых па
многообразии М; среди всех кривых, удовлетворяющих некоторым допол-
нительным условиям, найти кривые, на которых функция I достигает мини
мума. Например, предположим, что М — риманово многообразие с рима-
новой метрикой g. Обозначим через I [С] длину произвольной дифференци-
руемой кривой 0: [а, &] М, т. е.
ъ _____________________
а
Мы можем искать «кратчайшую» кривую, соединяющую две фиксированные
точки р и q многообразия М, т. е. кривую, для которой интеграл (1) при-
нимает минимальное значение, среди всех кривых С, удовлетворяющих усло-
вию С (а) = р, С (Ь) = q. Аналогично, мы можем искать кратчайшую кри-
вую, соединяющую два подмногообразия и N2. Тогда дополнительные усло-
вия состоят в том, что С (а) £ С (Ь) 6 N2.
Нашей основной целью при изучении вариационного исчисления явля-
ется как раз решение задачи о длине кривой на римановом многообразии.
Удобно, однако, немного схитрить. Подинтегральное выражение интеграла
(1) представляет собой длину касательного вектора кривой С (т. е. «скорость»,
с которой частица движется вдоль кривой С). Длина касательного вектора
не является, к сожалению, дифференцируемой функцией вектора; она плохо
ведет себя на векторах длины нуль. Другой недостаток интеграла (1) связан
с тем, что длина не зависит от параметризации. Это влечет за собой неедин-
ственность решения задачи минимизации, поскольку другая параметриза-
ция кривой, являющейся решением, снова будет решением. С другой стороны,
длина дуги кривой служит на ней естественным параметром, который должен
как-то получиться из самой задачи минимизации.
Оказывается, что вместо рассмотрения интеграла (1) удобнее иметь дело
с интегралом (кинетической) энергии
Ь
4ММ4),.М4)>
а
Здесь подинтегральное выражение есть квадрат длины касательного вектора,
и, следовательно, гладкая функция. Кроме того, этот интеграл зависит от
параметризации. Важное замечание (которое будет окончательно обосновано
в § 6) заключается в том, что задачи минимизации интегралов (1) и (2)
по существу эквивалентны (принцип наименьшего действия Мопертюи).
Кроме того, параметризация кривой, минимизирующей интеграл (2), авто-
11 С Стернберг
162
Гл. IV. Вариационное исчисление
магически пропорциональна длине дуги. [Это частный случай закона
сохранения энергии, который будет доказан в § 3.] В §§ 1—4 мы приведем
некоторые основные теоремы вариационного исчисления. Советуем читателю
во всех рассуждениях иметь в виду частный случай кинетической энергии,
поскольку для этого случая выполняются все (постепенно возрастающие)
ограничения, которые мы будем налагать.
Так как основной интерес для нас представляет задача минимизации
кинетической энергии, то при изложении общей теории мы сделаем два
упрощающих предположения. Первое состоит в том, что все рассматриваемые
объекты (функции, формы, отображения и т. и.) всюду определены. Конечно,
для многих встречающихся в природе вариационных задач это не так. Мы
примем это предположение, чтобы не загромождать геометрические идеи забо-
тами об областях определения. Эти заботы на самом деле не являются серь-
езными, и вдумчивый читатель без труда обобщит полученные результаты на
случай, когда нужно учитывать области определения. Второе упрощающее
предположение, которое мы постоянно делаем на протяжении этой книги,
состоит в том, чтобы не заботиться об условиях гладкости.
Прежде чем приступить к изложению, упростим обозначения
для случая длины дуги и кинетической энергии. Если М — рима-
ново многообразие с римановой метрикой g, то для любых векто-
ров Vi £ Тх (М) и v2 Е Тх (М) положим
(vi,v2)^gx(vi,v2), (3)
причем левая часть формулы (3) не определена, если и v2
не являются касательными векторами в одной и той же точке.
Для любого касательного вектора и положим
IHI = K(p, v) = Vgx(v, и). (4)
Для любой кривой С: [a, ft] —> М положим
(5)
Тогда интегралы (1) и (2) принимают вид
L\C] = J || С'
а
£[С] = | J11 С' (i)ll2^.
§ 1. ПРЕОБРАЗОВАНИЯ ЛЕЖАНДРА
Пусть V — векторное пространство и со — линейная дифферен-
циальная форма на V. Форма со задает отображение X: V —>V*.
Оно определяется следующим образом. Если v£V, то и0 есть
линейная форма на Tv(V). Согласно рассуждениям, приведенным
в конце § 5 гл. II, существует естественное отождествление
§ 1. Преобразования Лежандра
163
I: Tv(V)—>V (зависящее только от структуры векторного про-
странства на У). Значит, и,-»;4 есть линейная функция на V,
т. е. некоторый элемент пространства У*; мы обозначим его сим-
волом <£(0. Предположим, что отображение X: и—>Х(у) есть
диффеоморфизм пространства У на У*. Тогда обратное отображе-
ние X'1 также определяется некоторой формой со* на У*. Действи-
тельно, если у* С У*, то <^-1(р*)СУ есть линейная форма на У*,
которую ввиду отождествления Tv* (У*) с У* можно рассматривать
как линейную форму на Tv*(V*). Таким образом, для каждого
у*£У* вектор <^-1(у*) определяет элемент пространства T**(V*),
т. е. отображение Х~г определяет некоторую дифференциальную
форму со* на У*. Из определений видно, что отображение У—»У*,
задаваемое формой со*, совпадает с X”1.
Если dm = 0, то dco* = 0. Действительно, пусть et, ..еп — базис
в У, а с*, .. ., — дуальный базис в У*. Пусть х1, . . ., хп— коорди-
наты в пространстве У относительно базиса е{, . . ., еп, а у1, . . ., уп—
координаты в пространстве У* относительно е*, . .., е*,. Если со =
— '^1widxl, то отображение X задается формулой
Значит, если m = dL, то X имеет вид
X (i1, ...,?) = (#- (i1, . .., ?), ..., (i1, . .
' дх! дхп
(1-1)
Пусть теперь Н — функция на У*, определяемая формулой
(1.2)
или II (у1, . .., уп) = 2 х3У3 — L (х1, • •, хп),
где хг рассматриваются как функции от у3, задающие отображе-
ние Х~1. Тогда
dH = 2 xl dy1 + 2 У1 dx1 — 2 dxz •
dxi-
dL • * • ’ •
Согласно формуле (1.1), —— (z1, . . ., x11) = уг (x1, . . ., xn). Если мы
dx i
будем по-прежнему считать хг функциями от у1, задающими ото-
бражение Х~1, то два последних члена последнего уравнения сокра-
тятся. Значит, dH = ^хг dy', так что m*==dH.
Рассмотрим частный случай (кинетической энергии), когда
L (у, v), где ( , )—некоторое скалярное произведение. В коор-
11*
164
Гл. IV. Вариационное исчисление
динатах имеем L (х1, . . ., хп) = у ацхгх^. Тогда ^-=^ацх^.
дх*
Поэтому, если и = ^х1е1 и ip = 2z’ei, то (и>, X (у)) а^х1 =
= (w,v). Другими словами, X есть стандартное отображение
у—>У*, индуцированное скалярным произведением ( , ). Оно
линейно и является диффеоморфизмом пространства V на У*, если
только скалярное произведение ( , ) невырожденно. Вычислим
функцию Н в этом случае. В соответствии с формулой (1.2) имеем
Я(ш*) = (^-1(^*), («?*)); (1-3)
если w* = X(y), то
Н {X (р)) = (р, X (р)) — у (у, V) = (у, V) — у (у, v) = L (у),
т. е. Н {X (у)} — L (у). Мы можем также описать функцию Я,
заметив, что, согласно формуле (1.3), Н (w*) = у (и>*, и>*), где
( , ) — скалярное произведение в пространстве У*, индуцированное
скалярным произведением в пространстве У.
Замечания. 1. В общем случае функции L и Н опреде-
ляются равенствами ы = dL, ы* = dH с точностью до аддитив-
ной константы. На практике, однако, функция L обычно бывает
задана. Мы можем тогда определить функцию Н формулой (1.2),
заметив, что это определение не зависит от выбора базиса ...
. ., еп. Аддитивная константа в Н фиксируется равенством (1.2),
так как
Я(0, . . ., 0) = Ло^-1(0, . . ., 0).
2. Если форма ы задана только на открытом множестве (/ с У,
то приведенная выше конструкция определяет отображение
Х‘. U -> У*. Применим это замечание к Х~г. Предположим, что
форма ® = dL (где функция L определена, скажем, на всем У)
индуцирует отображение X'. У -> У*, которое является погру-
жением. Это означает, что отображение X локально взаимно
однозначно и взаимно дифференцируемо, хотя может и не быть
ни взаимно однозначным отображением, ни отображением на.
Тогда для любой точки х £ У форма м* = dH, задаваемая фор-
мулой (1.2), в окрестности точки у = X (X) определяет отображе-
ние Х~г. Как Х~\ так и м* определены вблизи точки у некор-
ректно — они зависят от выбора точки х £ Х~х (у). Однако форма
о = X* (со*) корректно определена в точке х, значит, и всюду
на V. Аналогично, функция Е = Я ° X корректно определена
§ 1. Преобразования Лежандра
165
на V, и мы имеем а = dE. Заметим, что о полностью определяется
формой со, в то время как Е зависит от выбора произвольной
постоянной, которая у нас зафиксирована формулой (1.2). Функ-
ция Е называется энергией, ассоциированной с функцией Лагран-
жа L. Так, в случае кинетической энергии, т. е. L = у (и, v),
из формулы (1.3) следует, что Е = L.
3. Если функция L зависит от дополнительных параметров,
т. е. если L есть функция на N X V г), то она индуцирует диффе-
ренцируемое отображение N X V —> N X V* (тождественное
на сомножителе N). Если для каждого п £ N отображение пх
—> п X V* является диффеоморфизмом, то функция Н, определен-
ная формулой (1.2), индуцирует диффеоморфизм N X V* —►
на
-> N X V, обратный к тому, который индуцирован функцией L.
на
Пусть М — дифференцируемое многообразие, a L — диффе-
ренцируемая функция на Т (М) X R. При фиксированных q С М
п to £ R подмногообразие Tq(M) х t0 многообразия Т (М) X R
является векторным пространством. Поэтому функция L (точнее,
ее ограничение на Тq (М) X io) индуцирует отображение Тq (М) X
X t0 -> Tq (М) X t0. Таким образом, мы имеем отображение
Л: Т (М) х R -> Т* (М) X R. Оно называется преобразованием
Лежандра (соответствующим функции L).
Если х1, .. ., хп— локальные координаты в окрестности U cz М,
то мы можем ввести координаты (х\ . . ., хп, х1, ..., хЛ, t)
в л-1 (U) х R €2 Т (JH) X R. Они задаются формулами хг (у) =
= z’(n(i’)) и и = 2 (и) (д/дх1)^). Аналогично, на Т* (М) X R
мы имеем локальные координаты (х1, . . ., хп, у1, . . ., уп, t), где у’
определяются равенством w* = 2 Уг (w*) если w* £Т* (М)
и it(w*)QU. В этих координатах отображение X определяется
формулами
х1оХ = х\ toX = t, = (1.4)
dxi
где L = L (х\ . . ., хп, х1, . . ., хп, t).
Если Л — погружение, то функция L называется регулярной
функцией Лагранжа (или регулярным лагранжианом). В этом
случае для любых (у, t) Q Т (М) х R отображение X"1, определен-
ное в окрестности точки X (у, t), индуцировано функцией Н.
Функция Н, задаваемая формулой (1.2), определена вблизи точки
Л (и, t) и зависит, вообще говоря, от выбора (и, I). Функция же
Е = НоХ корректно определена на Т (М) X R. Она называется
энергией, соответствующей лагранжиану L.
х) Где N — некоторое дифференцируемое многообразие.— Прим. ред.
166
Гл. IV. Вариационное исчисление
Упражнение 1.1. В случав классической механики задана рима-
нова метрика на М и функция V на М (называемая потенциальной энер-
1
гией). В качестве L берут функцию L-T— V о л, где Г (а) = — (у, v) — кине-
тическая энергия. Показать, что в этом случае Е = Т -|- V ° л.
Сформулируем полученные результаты:
Теорема 1.1. Пусть L — дифференцируемая функция
на Т (М) X R. Тогда L индуцирует дифференцируемое отображе-
ние X'. Т (М) X R —> Т* (М) X R, называемое преобразованием
Лежандра и определяемое в локальных координатах формулой
(1.4). Если это отображение является погружением, то L назы-
вается регулярной функцией Лагранжа, или регулярным лагран-
жианом. В этом случае отображение Х~г локально получается таким
же образом из функции Н на Т* (М) X R, называемой гамильто-
нианом. Функция Е = Н ° X глобально определена на Т (М) X R.
Если М — риманово многообразие и L (и, и) = -%\\ и ||2, то L
является регулярным лагранжианом и отображение X совпадает
на каждом касательном пространстве с отображением Т q (М) —>
—> Т* (М), которое индуцируется скалярным произведением. Кроме
того, в этом случае
E=H°X = L. (1.5)
§ 2. НЕОБХОДИМЫЕ УСЛОВИЯ
Основная задача вариационного исчисления (для одной неза-
висимой переменной) состоит в следующем. Пусть М есть п-мер-
ное дифференцируемое многообразие и L — дифференцируемая
функция на Т (М) X R. Каждая кривая С: [a, b] М на М
определяет кривую С на Г (М) X R по формуле
C(t) = (C' (t), t), tQ[a,b]. (2.1)
Поэтому мы можем рассмотреть интеграл
ь
ЦС) = j L(C(t))dt.
а
Задача состоит в нахождении кривых С, доставляющих «ло-
кальный» минимум для I, т. е. удовлетворяющих неравенству
I (С) I (С1) для всех «близких» кривых С1. Для уточнения
задачи мы должны определить, что мы подразумеваем под «бли-
зостью». Прежде’всего заметим, что интеграл 1(C) имеет смысл
для «кусочно дифференцируемых» кривых. Непрерывное отобра-
§ 2. Необходимые условия
167
жение С: [a, b] —> М называется кусочно дифференцируемым,
если отрезок [а, Ь] можно разбить на отрезки, на каждом из кото-
рых отображение С дифференцируемо. Более точно,
Определение 2.1. Непрерывное отображение С: [а, ?)] —>
-> М называется кусочно дифференцируемой кривой, если можно
найти такие точки t0 = а < . < th = Ъ, что ограничение
отображения С на каждый отрезок [£;, £г+1] совпадает с ограни-
чением некоторого дифференцируемого отображения
Ср (ti — e, ti+l + e) —>М.
Для кусочно дифференцируемой кривой С положим
с
(2-2)
Определение 2.2. Кривая С называется кривой сильного
локального минимума, если существует такая окрестность1)
jfCpw, z, е, о)С кривой С, что для всякой кусочно дифференцируемой
кривой С1 Q jC\w, z, е, о)С, удовлетворяющей условиям
С1 (а) = С (а), С1 (Ь) = С(Ь), (2.3)
справедливо неравенство
ЦС) (С1).
(2-4)
Кривая С называется кривой строгого сильного локального мини-
мума, если для всех таких кривых С1 g z, е, 0)С, отличных
от С, выполняется строгое неравенство
1(C) <1 (С1). (2.5)
Таким образом, С является кривой сильного локального мини-
мума, если неравенство (2.4) справедливо для всех кривых, удо-
влетворяющих условию (2.3) и поточечно равномерно близких к С,
включая и кривые, касательные к которым далеки от касатель-
ных к кривой С. Ввиду компактности отрезка [а, Ь] мы можем
взять в качестве Z в определении 2.2 какую-нибудь координату
на отрезке [я, ?)|.
Определение 2.3. Кривая С называется кривой слабого
локального минимума, если существуют такие W, Z и 8, что
неравенство (2.4) имеет место для всех кусочно дифференци-
т) См. определение 4.6 гл. II.— Прим, перев.
168
Гл. IV. Вариационное исчисление
руемых кривых С1, удовлетворяющих условию (2.3), для кото-
рых С) £ z, е, i)Cj- Здесь С) и Cs — ограничения соот-
ветственно кривых С1 и С на отрезок [s7-, sj+il, где а =
= «о < • • • < sr = Ъ есть множество точек, в которых кривые
С, С1 могут не быть дифференцируемыми. Кривая С называется
кривой строгого слабого локального минимума, если (2.4) заменено
на (2.5).
Таким образом, С есть кривая слабого локального минимума,
если неравенство (2.4) имеет место для всех кривых С1, удовле-
творяющих условию (2.3), которые равномерно близки вместе
с их первыми производными к кривой С в тех точках, где эти про-
изводные существуют.
Наша задача заключается в нахождении необходимых и доста-
точных условий того, чтобы кривая С являлась кривой (сильного
или слабого) локального минимума. Для ее решения удобно
перейти от многообразия Т (М) х R к Т* (М) X R.
Допуская некоторую небрежность, примем следующее согла-
шение. Если L — регулярный лагранжиан, то, как легко видеть,
отображение X есть диффеоморфизм некоторого открытого мно-
жества U с. Т (М) X R, содержащего образ С [а, 6] кривой С,
на открытое подмножество из Т* (М) X R. Все рассмотрения
этого параграфа относятся к этой окрестности множества С [а, &].
Но вместо того, чтобы загромождать обозначения введением мно-
жества U, его образа и т. п., мы будем считать, что отображение X
является диффеоморфизмом многообразия Т (М) X R на Т* (М) X
X R. Однако во всех рассуждениях будет использоваться только
то, что X — локальный диффеоморфизм.
Пусть X : Т (М) X R -> Т* (М) х R есть преобразование
Лежандра, индуцированное функцией L. [Отметим, что отображе-
ние X коммутирует с естественными проекциями многообразий
Т (М) X R и Т* (М) X R на М X 7?.] Важность перехода к кока-
сательному расслоению видна из следующего. Пусть р — проек-
ция Т* (М) X R -> Т* (М), и пусть 9 = р* (9), где 9 — фунда-
ментальная 1-форма на Т* (М), см. § 7, гл. III. Тогда справедлива
Лемма 2.1. Пусть С: [а, Ъ]—>М — дифференцируемое ото-
бражение. Положим С = Х°С (где С определяется формулой (2.1)).
Тогда
ь
L(C(s))ds= J С*со. (2.6)
а 1а, Ь]
где со = 9 — Н dt.
§ 2. Необходимые условия
169-
Для большей наглядности напишем следующую диаграмму:.
Для доказательства леммы 2.1 заметим, что обе части фор-
мулы (2.6) при разбиении отрезка [а, 6] распадаются в соответ-
ствующие суммы. Поэтому (воспользовавшись подходящим разбие-
нием и изменив обозначения) мы можем считать, что С [а, Ь]'
лежит в некоторой координатной окрестности U cz М. £Пусть
х1, . .., а:11 — система координат в U. Тогда на лД (U) с: Т (М) X R
мы имеем координаты х1, . .., хп, х1, .. ., хп, t. Предположим^
что в этих координатах кривая С задается функциями х1^),*...
. . ., хп (£), х1 (i), . .., хп (i), t. Тогда левая часть формулы (2.6) равна.
ь
J Z,(ж1 (i), ..., xn(t), xr(t), ..., xn(t),t)dt.
a
Отображение X задается в этих координатах формулой
£(Л ..., хп, Д ..., ?, t)=(xl, хп, ..., „
' дх1 дхп '
а форма со — формулой
ю = 2 Уг dx*—Н dt.
Поэтому правая часть формулы (2.6) равна
ь
J •••, yn(t-),t))dt =
а
Ъ
Согласно определению кривой С, имеем (dxl/dt) (t) = хг (t)r
и ввиду формулы (1.2) последний интеграл принимает вид
(( Ldt’
» ' dxi dxi / J
170
Гл. IV. Вариационное исчисление
что доказывает равенство (2.6). Положим о = тогда форма о
будет корректно определена на Т (М) X R и мы сможем пере-
писать равенство (2.6) в виде
ь
1(0 = J L(C(t))dt = j о= j С*о. (2.7)
а с [и, Ь]
Теперь мы в состоянии дать «эвристический» набросок про-
граммы, которой мы будем придерживаться в нескольких следую-
щих параграфах х). Рассмотрим множество всех кусочно диффе-
ренцируемых кривых, соединяющих две точки р и q, как «беско-
нечномерное многообразие», а функцию/ — как дифференцируемую
функцию на этом многообразии. Обозначим пространство
всех кусочно дифференцируемых кривых, соединяющих точки
р и q, через Qpg. Тогда минимизирующая кривая есть точка беско-
нечномерного многообразия Qpg, в которой функция I достигает
минимума. Напомним соответствующие результаты относительно
минимума дифференцируемой функции на (конечномерном) мно-
гообразии.
Пусть N — дифференцируемое многообразие и f — дифферен-
цируемая функция на N. Если р £ N есть точка локального мини-
мума функции /, то dfp = 0. Действительно, в локальных коор-
динатах это означает, что все частные производные функции f
равны в точке р нулю. Но это и есть в точности условие минимума,
доказываемое в элементарном анализе. [Иначе говоря, р должна
быть критической точкой для f (где f рассматривается как ото-
бражение N R) в смысле § 3 гл. П.] Это условие необходимо,
но не достаточно. Чтобы получить больше информации, мы должны
рассмотреть «вторые производные» функции / в точке р. Пусть
Хр и Yp — два касательных вектора в точке р, а X, Y — их про-
должения до векторных полей на некоторой окрестности точки р.
Рассмотрим выражение Хр (Y, df). Ясно, что оно линейно по Хр.
С другой стороны, мы имеем
Xp(Y,df) = (Xx(Y, df))p =
= {XxY,df)P + (Y, Zxdf)p.
Первый член обращается в нуль, поскольку dfp = O. Второй член
можно переписать в виде
(У, d (Xxf))P = (У, d (X, df))p = Yp (X, df).
l) Рассуждения, начинающиеся здесь и кончающиеся на стр. 174, следует
рассматривать лишь как мотивировку для того, что последует дальше. Дей-
ствительные результаты, которые нам понадобятся, не опираются на эти
рассуждения.
§ 2. Необходимые условия
171
Итак,
Xp{Y,df) = Yp(X,df).
Отсюда мы видим, что выражение Хр (Y, df) зависит только
от Yp (но не от продолжения У) и линейно по Yp. Таким обра-
зом, мы получаем симметрическую билинейную форму Hj,p
на касательном пространстве:
Hft р (Хр, Yp) = XP(Y, df) = Yp {X, df).
Эта билинейная форма называется гессианом функции f в точке р.
Если в некоторой системе координат Хр = 2 ё1 (д/дхг)р, то
Hf,p(Xp,Xp) = ^ (-^-)
\ дхг / р
Как известно из анализа, для того, чтобы точка р являлась точкой
минимума функции /, необходима положительная полуопределен-
ность гессиана и достаточна его положительная определенность.
Попробуем теперь сформулировать аналогичные утверждения
для «бесконечномерного многообразия» всех кривых, соединяю-
щих точки р и q.
Прежде всего мы должны определить понятие «касательного
вектора» в точке этого бесконечномерного многообразия. Кривая
на Qp? есть семейство Ct (•) кривых с Ct (а) = р, Ct (b) = q.
Отсюда ясно, что касательный вектор на в точке С должен
представлять собой векторное поле вдоль кривой С, обращаю-
щееся в нуль в точках р и q, т. е. такое кусочно дифференцируе-
мое семейство векторов Xs g Tc<s) (М), что Ха = Хь = 0.
Расшифруем теперь условие минимума dlc = 0. Пусть
Хс (=Х) —«касательный вектор» в точке С. Предположим, что
Хс можно продолжить до векторного поля X, определенного
в некоторой окрестности U cz М множества С [а, &]; таким обра-
зом, Xs = XC(S). [Заметим, что в общем случае это сделать нельзя.
Например, кривая С может иметь самопересечение, так что С (г-,) —
= С (s2), хотя Х81 Ф XSi. В наших эвристических рассуждениях
мы будем игнорировать эту возможность. Простой выход из этих
затруднений состоит в рассмотрении достаточно малых кусков
кривой С. Если кривая С минимизирует I, то то же верно для
любого ее куска.] Векторное поле X порождает векторное поле X
в окрестности кривой С в Т (М) X R. Действительно, пусть
Т (X) есть вариационное векторное поле поля X (определенное
в конце гл. II). Положим X = (Т (X), 0). Читатель должен про-
верить, что значения поля X вдоль кривой С зависят только
от поля Хс, но не от его продолжения X. Пусть as — локальная
однопараметрическая группа, порожденная полем X, и пусть
172
Гл. IV. Вариационное исчисление
Cs — as ° С. Тогда Cs = as° С, где as — группа, порожденная
Xs. В соответствии с формулой (2.7) получаем
Г (Cs) = j cr = j o= j a*a-
Cs as°C C
Если С есть кривая минимума, то мы должны иметь
di (Cs) I ________________________„
ds |s=0 ~
Ho
hm--------= £ .
s->-0 s X
Значит,
j £xa = 0.
c
Поскольку
<£jo = X j da + d (X, a),
получаем
j X j do + j d (X, a) = 0.
c c
Ho
j d(X, o) = (X, o)g-(b) (X,
c
Вычислим теперь {X, о). Из определения формы о следует, что
(X, а) = {Х^Х, ы) = («Х^Х, 9 — Hdt}. Далее, (Х^Х, dt} = 0, поскольку
(X, dt} — 0. Из определения формы 9 получаем (<£*Х, 9) =
= (Р* 0)- Пусть (у*, i) — точка из Т* (М) х R. Тогда из опре-
деления формы 9 (см. § 7 гл. III) следует, что (<£*Х, 9) =
= <ХЯ(1,*), и*}. Полагая (у*, t) = X (С (а)), получаем
a)c(a)=<X“’ V*> = 0.
Аналогичное равенство справедливо для Ь. Поэтому j d(X, о)=0,
и мы получаем, что
j X jda = 0
с
J 2. Необходимые условия
173
для всех X Далее,
ь
j X j du = J (Xt Д C' (t) | du) dt.
c a
Подинтегральное выражение может быть записано в виде
{Xt Д С’ (t) | du) = — {X (t), С' (i) j du)
Если бы X было произвольным векторным полем на Т (М) х R,
ъ
то из тождества (Xt, С' (t) j du) dt = O немедленно следовало бы,
а
что C'(t)jdu = 0. Однако векторное поле X не вполне произ-
вольно. [Оно должно получаться из векторного поля X на М,
обращающегося в нуль в точках р и <?.] Тем не менее, оказы-
вается, что, пользуясь определением формы о, можно вывести
равенство
С' (t) j du = 0.
Форма du на Т (М) х R имеет ранг 2п. Поэтому на Т (М) X R
существует единственное векторное поле Y, для которого
Y J du = 0 и (Y, dt) = 1.
П оле Y известно как эйлерово векторное поле. [Соответствующее
дифференциальное уравнение в терминах локальных координат
называется дифференциальным уравнением Эйлера.} Таким обра-
зом, мы видим, что если С — кривая локального минимума, то
кривая С является интегральной кривой эйлерова векторного
поля. Детали этого доказательства будут приведены в настоящем
параграфе.
Попробуем теперь сформулировать квадратичные условия,
содержащие гессиан. Пусть Хс и Yc — два «касательных вектора»
в точке С, и пусть X и Y — продолжающие их векторные поля
на М. Мы уже видели, что если Cs = as ° С, где cxs — группа,
порожденная полем X, то
Если мы возьмем производную в точке С по направлению «каса-
тельного вектора» Yc, то получим выражение
(ад.
с
174
Гл. IV. Вариационное исчисление
Ясно, что это выражение линейно по Y вдоль С, и, значит,
линейно по Ус- С другой стороны,
j (£2а) = j Х^, ?]<т + j X j (£?а).
с с с
Но [X, У] = [X, У], так что
У °^[Х, Y]G ~ j %IX, У]а= О’
с с
согласно уравнению Эйлера. Таким образом,
( Ху (£ха) = С Ху (Ху а)
V С
есть симметрическая билинейная форма от Хс и Yc. Она назы-
вается второй вариацией.
Наши условия «второго порядка» связаны с положительной
определенностью второй вариации. В § 4 мы сделаем предполо-
жение относительно L, гарантирующее положительную опреде-
ленность второй вариации в случае, когда кривая С достаточно
коротка. Оказывается, что если длина кривой С превосходит
некоторую критическую длину, то вторая вариация перестает
быть положительно определенной, а С — кривой минимума.
Подробности будут приведены в § 5.
Перейдем ’) к получению необходимых условий слабого локаль-
ного минимума. Прежде всего заметим, что если С есть кривая
слабого локального минимума для L * 2) на отрезке [а, &], то огра-
ничение кривой С на любой подотрезок [d, е] также является
кривой слабого локального минимума. Действительно, если С* —
кусочно дифференцируемая кривая, определенная на [d, е] и та-
кая, что С* (d) = С (d), С* (е) = С (е), то мы можем продолжить
С* на [я, &], полагая С* (t) = С (t) для а d и
Тогда из Ied (С*) < Id (С) следует, что Iba (С*) < (С). Таким
образом, если С есть кривая локального минимума на [а, 6],
то она является кривой локального минимума и на [d, е].
При выводе необходимых условий ограничимся сначала рас-
смотрением подотрезка [d, е], на котором кривая С дифференци-
руема и образ которого при отображении С лежит в координатной
окрестности многообразия М. Если С — кривая минимума, то
мы можем ожидать, что I (Cs) |s=0 = 0 для любого «дифферен-
Э С этого места начинаются наши законные рассуждения.
2) Точнее, слабого локального минимума интеграла (2.2), определяемого
лагранжианом L.— Прим, перев.
§ 2. Необходимые условия
175
цируемого» однопараметрического семейства кривых Cs, где Со =
== С. Такое однопараметрическое семейство кривых мы будем
рассматривать как прямоугольник и применим к нему теорему
Стокса. Пусть De — прямоугольник в плоскости t, s, определяе-
мый неравенствами — e^s^e, d е, и пусть Dg — под-
множество в Dg, где $ 0, a DR — подмножество, где $ О
(рис. 10).
Пусть К — дифференцируемое отображение (некоторой окрест-
ности) прямоугольника De в М, удовлетворяющее условиям
K(t,O)=C(t), d^t^e,
K(d,s) — C(d), K(e,s) = C(e), —
(2.8}
(2.9)
Отображение К (•, s) есть дифференцируемая кривая на М
при каждом фиксированном s. Она определяет кривые К (, s)
на Т (М) х R и К (•, s) на Т* (М) X R. Таким образом, мы имеем
отображения Ал De—>T(M)xR и К: Dg—>T*(M)xR. Прямая
проверка в терминах локальных координат показывает, что эти
отображения дифференцируемы. Если С —кривая слабого локаль-
ного минимума, то при достаточно малом |s| мы должны иметь
ЗД<7Ж(-,*)), или (21о>
j С*((0)< J #(-, в)*((0).
[d, е] [d,e]
Другими словами,
j А*(-, 0) (<о)- J #*(•, s)(®)<0.
[d, е] [d, е]
Согласно условию (2.9), форма К*а обращается в нуль на вер-
тикальных сторонах прямоугольника DR. Следовательно, неравен-
476
Гл. IV. Вариационное исчисление
•ство (2.10) можно записать в виде
j А*(ы)<0.
Ло теореме Стокса
jtf*(da)X0. (2.11)
е Ь
J *'«“•>= J J <(4)(1.вл !*•<*“>> *
г)+ 0 а
Поскольку это верно для всех достаточно малых е, имеем
j<(4U> л <*»>«).
d
Аналогично,
j К* (со) > 0,
0(»ё)
так что
j<(4)(., .,л (4)„, O)i^«i»)>*>o.
а
Сравнивая неравенства, получаем
J <(4)(, и А Ш «)<.»>> л - 0.
d
Но
<Ш((,0)ЛШ((,0)1^И)«.0)> =
= \^* (ir)(i, 0) I 0)/ =
= \^* (1г) (г, о) । (1F) (/, о)J d(°K(Z’ 0)/ '
Значит,
е
J \S- (4),,. „Й (4) J *>«<>> = 0- (2.12)
§ 2. Необходимые условия
177
Равенство (2.12) имеет место для всех К, удовлетворяющих
условиям (2.8) и (2.9). Сейчас мы выведем из него несколько след-
ствий.
Пусть Yq — касательный вектор в точке q С Т* (М) X R.
В выбранных локальных координатах мы можем написать
Ш,+7,4-
1=1 1=1
Форма dm имеет вид
dm = 3 dy1 /\ dx1 — dH Д dt.
Следовательно,
1=1 1=1
-S (¥ixi+-^iYi}dt- (2-13)
\ дхг дуг )
i=l
Если Yq — касательный вектор кривой, поднятой с М, т. е. если
Yq = С'(t), то Т = 1, X1 = = хг = . В этом случае вторая
сумма в (2.13) обращается в нуль.
По определению i-компонента точки К (s, t) равна в точности t.
Значит, (К* (d/ds)(t, о) | dt) = 0. Пусть Xq (£) обозначает вектор
С* (d/dt)t и Xq (t) = К* (d/ds)(tt qj. Тогда из (2.13) и (2.12) сле-
дует, что
е
2 J (Yi+^r)Xidt = °- (2Л4>
d
Единственное ограничение на дифференцируемые функции X'
состоит в том, что они обращаются в нуль при t = d и t = е.
Действительно, пусть X1 — это п функций, обращающихся в нуль
на концах отрезка [d, е]. Определим отображение К (t, s), полагая
(в локальных координатах)
хг ° К (t, s) = хг °C (i) Д sXl (i), (2-15)
Формула (2.15) определяет К (t, s) как дифференцируемое отобра-
жение, которое, очевидно, удовлетворяет условиям (2.8) и (2.9).
Кроме того, ^(^-)(/ о) = Х{(О-
12 с. Стернберг
178
Гл. IV. Вариационное исчисление
Таким образом, равенство (2.14) должно выполняться для всех
функций X1 от t, обращающихся в нуль в концевых точках d и е.
Полагая XJ = 0 для всех /, кроме j = i, имеем
( Xldt = O
J \ дх* /
d
для произвольной функции X1, обращающейся в нуль в концевых
точках. Это может быть только в случае, когда Y1 -\-дН/дх‘ = 0
для всех Zg[d, е]. Действительно, если (У1 + ЭЯ/dx’) (£0) > О
для некоторого е], то эта функция должна быть положи-
тельной и в некоторой окрестности точки ta. Поэтому, выбирая
функцию X1 положительной в точке t0 и равной нулю вне малой
е
окрестности точки £0, мы получили бы, что j (У’ + дН/дх'1) X1 dt>0.
_ d
Итак, если Yq(t)=C' (i), то
Х‘=^Г- у'=—(2-16)
для всех t. Учитывая формулу (2.13), мы можем следующим
образом резюмировать предыдущие рассуждения:
Лемма 2.2. Пусть С — кривая слабого локального минимума
для L. Тогда в каждой -точке t, в которой кривая С дифферен-
цируема, касательный вектор Yq = C'(t) удовлетворяет уравнению
Yq_\dMq = Q. (2-17)
Исследуем теперь точки, в которых кривая С может не быть
дифференцируемой. Пусть t — такая точка, и пусть [£ь t2]—малый
отрезок, содержащий t, во всех точках которого, кроме, быть
может, t, кривая С дифференцируема. Тогда кривую С можно
рассматривать как ограничение на [ft, i] дифференцируемого
отображения отрезка [tt, плюс ограничение на [I, t2] диф-
ференцируемого отображения отрезка [t — е, t2\. Выбирая точки Н
и t2 достаточно близкими, мы можем считать, что С [£, £2] лежит
в координатной окрестности и что существуют такие дифферен-
цируемые отображения Ct и С2 отрезка [^, t2] в М, что С (() =
= £4(0 для_£</<Х и C(t) = C2(t) для
Пусть X1 — дифференцируемые функции на [£4, /2], равные
нулю в точках £ и t2. Пользуясь формулой (2.15), определим
три отображения К, и К2 прямоугольника —
§ 2. Необходимые условия
179
tj < t < t2 в M, соответствующие кривым С, и С2. Отображе-
ния Ki и К2 дифференцируемы, а отображение K(-,s) при каж-
дом s является кусочно дифференцируемой кривой (дифферен-
s
-----1
2
Рис. 11.
цируемой всюду, кроме точки i). Действительно, К (t, s)=Ki(t, s)
для и К (t, s) — K2(t, s) для t~^t.
Для достаточно малых s мы должны иметь 7^ (С) С
<7ц (К (•, «)), или
J С*(ш)+ J С*(®)<
[O,1G [Г, ь]
< j ^(.,s)*®+ j tf(.,s)*(o. (2.18)
to, n й, оз
Добавим члены
Ki(t, •)*(£> и — ( K2(t, •)*©.
[О* в] [о; в]
Тогда мы получим (рис. 11)
j Й(®)+ J KiCt, •)*©- J К*(-, s)co= J K*da,
[О, 7] t0’ [0,7]
С*(а>)— § K2(t, •)*!£>— j К* (0, s) со = j К2 dco.
[Z. t2] [°- eJ [7, t2] D$
Согласно неравенству (2.18), имеем
J Ki(t, •)*©— J K2(t, )*(»> j ^d(o+ j K*2da. (2.19)
10, e] [0, в] p+ p+
12*
180
Гл. IV. Вариационное исчисление
Правую часть можно переписать в виде
ff 1^(4-) _]da)dtds.
J J \ *\ds](t, s) | /
О /1
Согласно лемме 2.2, внутренний интеграл равен нулю при s = 0,
поскольку значение подинтегрального выражения в одной точке
не влияет на значение интеграла. Поэтому, разделив обе части
неравенства (2.19) на е и устремив е к нулю, получим
•)* (аг)(- 0)|®К1«,о)/-')*(1г)(7>0) “к20!, 0)/>О-
Если рассуждать с отрицательным, а не с положительным е, то
>0 заменится на <10. Следовательно, имеет место равенство.
Если координаты точки Ki (t, 0) равны х1, . .., хп, у[, ..., y~,t,
а координаты точки K2(t, 0) равны х1, ..., хп, у^, ..., у™,!,
то полученное равенство можно записать в виде
2(И-^)^(О = о,
где Хг — произвольные функции. Но это означает, что
У1 = У1. (2-20)
Иначе говоря, C1(i) = C2(f). Обе кривые С1 и С2 удовлетворяют
одному и тому же дифференциальному уравнению (2.16), причем
при t, а С2— при £С£<£2. Из теоремы единственности
для дифференциальных уравнений следует тогда, что Cj и Сг
согласованы в точке t, образуя дифференцируемую кривую. Итак,
справедлива
Лемма 2.3 (Гильберт). Если С — кривая слабого локального
минимума, то С дифференцируема.
Систематизируем полученные результаты.
Исследуем условие (2.17), где вектор Yq задается формулой
При У = 0 из формулы (2.13) следует, что (2.17) имеет место
только для Уд = 0. Значит, для ненулевого вектора Yq, удовле-
творяющего условию (2.17), мы должны иметь (Уд | d£g) 0. [Это
показывает, что <2® есть форма ранга 2п на (2п4- 1)-мерном мно-
гообразии Т* (M)yR.] Форма и не определена однозначно на
Т* (M)xR. Однако форма o = <Z*co корректно определена на
Т (М) xR. Вектор Yq=C'=£*C' удовлетворяет уравнению (2.17).
§ 2. Необходимые условия
181
Значит,
С _\do = Q, (C',dt) = i.
Поскольку форма da имеет ранг 2п на Т* (М) X R, форма do имеет
ранг 2п на Т (М) х R. Поэтому существует единственное вектор-
ное поле X на Т (М) х R, называемое эйлеровым векторным полем,
для которого
Xjdo = 0, {X, df) = l. (2.21)
Если С — кривая локального минимума, то С дифференцируема
и С есть интегральная кривая поля X. Исследуем вид поля X.
Предположим, что в локальных координатах
дхг Qxi 01
Тогда
£ Х= У X1 —+ У У* — + 4т ,
* dxi dyi dt
где функции X1 и Уг задаются формулой (2.16). Из определе-
* • дН
ния следует, что хг = —г , откуда
дуг
Х1=х\ Т=1. (2.22)
Перепишем условия (2.22) более инвариантным образом. Пусть
л — проекция T(M)xR—+М. Тогда условие (2.22) можно пере-
писать в виде
л*Х(В> t) = v, (X, dt) = l. (2.23)
Векторное поле X на Т (М) X R, удовлетворяющее условию (2.23),
называется дифференциальным уравнением второго порядка на М.
Таким образом, эйлерово векторное поле есть дифференциальное
уравнение второго порядка.
Упражнение 2.1. Показать, что интегральная кривая дифферен-
циального уравнения второго порядка всегда имеет вид С, где С — неко-
торая кривая на М.
Определение 2.4. Уравнения (2.21) называются уравне-
ниями Эйлера. Записанные локально в виде (2.17), они назы-
ваются уравнениями Эйлера в форме Гамильтона. Векторное
поле X, определяемое условиями (2.21), называется эйлеровым
векторным полем. Дифференцируемая кривая С на М называется
экстремалью, если С есть интегральная кривая поля X. В случае
кинетической энергии риманова многообразия экстремали назы-
ваются геодезическими.
182
Гл. IV. Вариационное исчисление
Таким образом, доказана
Теорема 2.1 (Эйлер). Пусть L определяет регулярную зада-
чу вариационного исчислениях). Необходимое условие того, что
кусочно дифференцируемая кривая С является кривой слабого
локального минимума для L, состоит в том, что С дифференцируе-
ма, а кривая С является интегральной кривой поля X, определен-
ного условиями (2.21).
Если С — экстремаль, то кривая С в локальных координатах
задается функциями х1 (t), .. ., хп (t), у1 (t), .. ., уп (t), t. Из урав-
нений Эйлера получаем
dx* дН ‘л dip дН
- —____ — . . , _ — - _______
ду'1 1 dt
Но, согласно формуле (1.2),
(У (х^х-1) у1-Ьо%-Л =
дхг дхг I v а J
д (х* о i dL о dL о д'хг о X
дхг дхг дхг
= dL °
дхг
Поскольку у1 = , мы можем записать уравнения Эйлера локаль-
дхг
но как систему дифференциальных уравнений второго порядка
44
dx* "j \ дхг
----- Д) _
dt ' dt дхг
Пусть L — энергия, ассоциированная с римановой метрикой:
£ = 4 2 Sijxlx}. Тогда gtjXj и уравнения (2.24) прини-
мают вид
fe, I
или
уп d^xi ст dglj dxk dxi 1 -ст dgyi dxk dxl
2 Sii ~di^~ + 21 ~dT ~dF ~~2 2j dt dt •
Ho
Qxl Qxk
x) To есть L есть регулярный лагранжиан.— Прим, перев.
§ 2. Необходимые условия
183
Поэтому мы можем написать
Ed2xi _ 1 -у / dgM dgik dgn \ dxh dxi
4 dt2 2 \ QXi dxi [j%k / dt dt
k, I,
Пусть (glJ) — матрица, обратная к (gu). Положим
Г’ 1 V oii ( dghl dgik dgH )
г
(2.25)
Тогда уравнения (2.24) для геодезических приобретают вид
d2%i pj dxh dxi
~d^= 2dY^-dT-dT' <2-2b)
Упражнение 2.2. Пусть Q — линейная дифференциальная форма
на многообразии М. Предположим, что С: [а, Ь] М — такая кривая, что
C*Q< j Ci*Q
[а, Ь] [с, d]
для всех «близких» кривых, определенных на близком к [а, &] отрезке [с, d],
для которых С1 (с) = С (а), С1 (d) = С (Ъ). Показать, что все касательные
векторы кривой С удовлетворяют условию У I <й2 = 0. Поэтому равенства
(2.17) пли (2.21) служат необходимым условием того, чтобы кривая С явля-
лась решением «вариационной задачи» на многообразии Т (Af) X R, а имен-
но, задачи минимизации о среди всех близких кривых на многообразии
Т (М) X R.
Рассмотрим теперь случай «подвижных концов». Пусть Nl
и N2 — подмногообразия в М. Кривая С называется кривой сла-
бого (соответственно сильного) минимума для L относительно
пары (Nt, N2), если она удовлетворяет требованиям определе-
ния 2.3 (соответственно 2.2), где условие (2.3) заменено условием
С1 (а) е Nt, С1 (&) е N2. (2.27)
В то время как в определениях 2.2 и 2.3 мы требуем, чтобы
сравниваемые кривые имели те же концы, что и С, теперь мы
допускаем, чтобы концы менялись, оставаясь на многообразиях
Nt и Nz.
Тео рме м а 2.2. Пусть С — кривая слабого минимума отно-
сительно пары (Nt, N2). Тогда С является экстремалью для L
и, кроме того,
{Vt, С (а)) = (р2, С (Ъ)) = 0 (2.28)
для всех Vt^TctayiNt) и v2£TC(b) (N2).
Первая часть теоремы 2.2 очевидна: если С есть кривая сла-
бого минимума относительно пары (N\, N2), то она будет и кри-
184
Гл. IV. Вариационное исчисление
вой слабого минимума в смысле определения 2.3. Из теоремы 2.1
следует тогда, что С — экстремаль. Достаточно доказать одно из
равенств (2.28). Пусть /г = (х1, ...,хп)— такая система координат
в окрестности U точки С (Ь), что есть множество точек,
ДЛЯ КОТОРЫХ Xft+1 = . . . =ЖП = 0. ПуСТЬ Р2 = а1(^/^1)С(Ь)+---
... -\-ак (д1д^)с(ь)- Выберем t0 столь близким к Ъ, чтобы С (t)
для Пусть X1 (t), . . ., Хп (1) — дифференцируемые функ-
ции, причем Хг (i) =0 для X1 (b)=at (i = 1, ... , к) и Хг (Ь)=0
для i^>k. Выберем е столь малым, чтобы (х1 (i) + sX1 (£), ...
..., xn(t)-]-sXn(t))^h(U) для ^оС^СЬи |$|Се, где (а:1^), ..., z"(i))=
= hoC (t).
Пусть К — отображение прямоугольника D = {| $ | е, а < 6}
в М, определяемое формулами K(s,t)=C(t) для
и хъ °K(s, t) = xl (t)-]-sXl (t) для Тогда, как и раньше,
мы имеем j С* (со) С J К ($, -)*со при достаточно малом |$|.
[а, ы
Как и при доказательстве леммы 2.2, отсюда следует для s>0
неравенство
J X* (•, i) со> j X* dco.
[Ois] П+
Деля его на s, устремляя $ к нулю и (учитывая, что С — экстре-
маль, получаем (Х*(-, t) (d/ds)(o, ь> | 0. Поступая так же для
отрицательных s, получаем £) (d/ds)(o, ь> I ®с<ь))^0. Значит,
(^)(о, ь)1
Но
0 Ьг)(0,Ь) = а1 цг+ • • •
и
®С(Ь)=^У1 (b')dxb~Hdt' гДе = &)-
Поэтому
k
(-£-)(0>Ь)|«»с(Ь)/ = 5 г/г(Ь)«г = ^|СО = °,
г=1
что и доказывает теорему 2.2.
Упражнение 2.3. Показать, что если L—кинетическая энергия,
ассоциированная с римановой метрикой g, то условия (2.28) означают, что
§ 3. Законы сохранения
185
вектор С' (а) ортогонален к ГС(а) (Ад) в смысле скалярного произведения
на Тс<а) (М), определяемого метрикой g, a С (Ь) ортогонален к Тс<ь) (A2)> т- е-
(», С'(а))=0 для и£ Тс<а) (Nt),
(у, С'(Ь)) = О для v^Tcibf (N2).
§ 3. ЗАКОНЫ СОХРАНЕНИЯ
Согласно § 2, каждый регулярный лагранжиан порождает
векторное поле X на Т (М) X R, определяемое условиями (2.21).
Для удобства в рассуждениях в этом параграфе мы будем снова
предполагать, что X есть диффеоморфизм многообразия Т (М) X
X R на Т* (М) X R. Тогда форма со корректно определена на
Т* (М) X R. Векторное поле Y = Х*Х также корректно опреде-
лено на Т* (М) X R и однозначно характеризуется условиями
Y J dm = 0 и (Y, dt) = 1.
Это векторное поле индуцирует локальный поток а на Т* (М) X
X R, т. е. у каждой точки р £ Т* (М) X R имеется окрестность
U, на которой определены отображения а5: U -> Т* (М) X R
для $ £ [—8, е]. Из равенства (2.21) следует, что этот поток остав-
ляет форму dm инвариантной. Действительно,
Ху dm = Y j d (dm) d (У j dco).
Значит,
^rdco = 0, (3.1)
или
afdco = dco. (3.2)
Поскольку (Y\dt) = i, поток a переводит изохронные1) точки
в изохронные. Более точно, t (as (р)) = t (р) -\-s для любой точки
р£Т* (М) х R и тех s, для которых определено as(p). Поэтому as
определяет (локально) семейство преобразований |3S: Т* (М) —> Т* (М)
по формуле
М?) = (р°<М?> 0)) (3.3)
[где р —проекция Т* (М) X Я—>Г*(М)]. [Преобразования ps опре-
делены только локально: для любой точки qQT* (М) существуют
окрестность U^q и отрезок [ — е, 8] значений параметра $, для
которых формула (3.3) имеет смысл.] Семейство не обязательно
является однопараметрической группой: в общем случае 081+82=д
#=Ps2Psi, поскольку поле У может зависеть от t. Далее, форма dm
имеет вид dco = p*d9 — dH /\dt, так что
a* dm = a* р* dQ — aj (dH Д dt)
l) В оригинале simultaneous.— Прим, перев.
186
Гл. IV. Вариационное исчисление
(поскольку at dt=dt). Пусть ч —отображение Т* (М) —* Т* (М) х R,
переводящее q в (q, t), так что i*dco = tZ9. Мы можем тогда пере-
писать формулу (3.3) в виде 0s = poasoto. Но i*dco = d0. Поэтому
из (3.1) следует, что
dQ = i*a* da = (а*р* dQ — at (dH /\dt)) = i*a*P* dQ,
так как i* dt = 0. Иначе говоря,
$tdQ = dQ. (3.4)
Это утверждение составляет теорему, впервые доказанную Пуан-
каре. Используя (3.4) для формы П = <70Д...Дй0 [формы
Лиувилля на Т*(М)], получаем
= (3.5)
т. е. «мера», определяемая формой П, инвариантна. Это впервые
обнаружил Лиувилль.
Рассмотрим теперь случай, когда L (а, значит, и Н) не зави-
сит от t.
Теорема 3.1. Если Н не зависит от t, то векторное поле Y
на Т* (М) X R имеет вид У = (У, д/dt), где V есть векторное
поле на Т* (М), определяемое равенством
V J dQ = - dH. (3.6)
Действительно, в терминах локальных координат условие (3.6)
эквивалентно условию (2.21). Но если
Г=2Х* Ш + 2Г'(Д).
то, согласно (3.6),
V J dQ=V1Yidzi-'^Xi dy1 = —dH.
По теореме 6.1 гл. II формула (3.6) однозначно определяет V.
Далее, XVH = V j dH = — у j у j d0 = 0, и мы получаем
Следствие 3.1 (закон сохранения энергии). R предположе-
ниях теоремы 3.1
XVH = Q (uXxH = Q), (3.7)
так что подмногообразия Н = const на Т* (М) [или на Т* (М) X /И
инвариантны относительно (локального) потока, порожденного
полем У (или X).
Пусть h — некоторая константа, так что уравнение Н = h
определяет подмногообразие Wh в Т* (М). Следствие 3.1 показы-
§ 3. Законы сохранения
187
вает, что векторное поле V касательно к Wh (т. е. Vx С Тх (И7/,)
для всех х g Пусть 6Л — ограничение формы 0 на Wh- Тогда
поле V индуцирует векторное поле Vh на Wh, причем
Vh J dQh = 0. (3.8)
В соответствии с упражнением 2.2 интегральные кривые поля
Vh могут быть получены как экстремали вариационной задачи
на Wh, а именно, задачи минимизации интеграла j 0 среди всех
кривых на Wh- Само по себе это не очень интересно, поскольку
нас интересуют кривые на М, а не на Wh- Однако в некоторых
случаях уравнение (3.8) соответствует некоторой новой вариа-
ционной задаче на М. Например, пусть g — риманова метрика
на М и лагранжиан L определен на Т (Л7) X R равенством
L (у, t) = jgx (п, v) для v £ Тх (М). Отображение X на каждом
касательном пространстве Тх (М) совпадает с отображением
Тх (М) -> Т* (Л7), индуцированным невырожденной метрикой g.
Кроме того, Н ° X = L. Если С — экстремаль для L, то из зако-
на сохранения энергии следует, что функция || С' (£) ||2, а значит,
и функция || С' (t) || постоянна. Кроме того, подмногообразие Wt
можно описать, указав, что Х~г (И7)) есть множество векторов
единичной длины в Т (М). Если С — кривая на М и р (С) лежит
в Wi, то
J(PC)>e= j(pC)-39‘*•=-!-j (3-^)л=
a dx
b
= J ||C' (t)\\*dt.
a
Поскольку || C' (t) ||2 = 1 есть константа, этот интеграл равен
ь
j || С (i) || dt, т. е. длине кривой С. Таким образом, если кривая С
минимизирует длину дуги среди всех кривых, параметризованных
пропорционально длине дуги, то, как показывает упражнение 2.2,
С есть экстремаль кинетической энергии L, т. е. геодезическая.
Оказывается, что если кривая С минимизирует длину дуги,
то после подходящей «перепараметризации» пропорционально
длине дуги она станет экстремалью для L.
Упражнение 3.1 (принцип наименьшего действия). Доказать
последнее утверждение в случае, когда С — дифференцируемая кривая, все
касательные векторы которой отличны от нуля.
188
Гл. IV. Вариационное исчисление
Ввиду технических трудностей, возникающих, если допу-
скать кривые с обращающимся в нуль касательным вектором,
мы отложим доказательство этого утверждения до § 7.
В заключение этого параграфа мы обсудим вопрос, при каких
условиях поток as определен глобально для случая энергии
риманова многообразия. В соответствии с теоремой существования
для дифференциальных уравнений, если значения as (р) опреде-
лены для О s so и лежат в некотором компактном подмноже-
стве К из Т* (М) X R, то as (р) определено и для $□ + е
при достаточно малом е. [Аналогичное утверждение верно для
So < 0.] Поэтому, если поток as не может быть определен глобаль-
но, то должны существовать такие р £ Т* (М) X R и $0 6 7?, что
as (р) определены для 0 s < so (или 0 s > $о), но последова-
тельность as (р) не имеет предела при s -> so. Это может случиться.
Чтобы убедиться в этом, заметим, что если as (р) имеет предел,
то это же верно для л (as (р)). Но л (as (р)) есть геодезическая
на М. Если М' — подмногообразие в М, полученное выбрасыва-
нием некоторой точки этой геодезической, т. е. М' = М — q,
где q = л (aso (р)), то л (as (р)) не имеет предела в М' при s -> $0.
Другими словами, если М — многообразие, для которого поток
as определен глобально, то многообразие М — q при любом
q £ М уже не обладает этим свойством. Интуитивно ясно, что
поток as не определен глобально на Т* (М — q) X R потому, что
М — q «не полно». И действительно, мы покажем сейчас, что
любое риманово многообразие М снабжается естественным обра-
зом структурой метрического пространства и что в случае, когда
это метрическое пространство полно, поток as определен гло-
бально. [Необходимо отметить, что вопрос о глобальном существо-
вании потока а зависит от римановой метрики, а не только от диф-
ференцируемой структуры многообразия М. Например, если М
есть сфера со сферической метрикой, то поток as не определен
глобально для многообразия М — q. Но М — q диффеоморфно
евклидовой плоскости, для которой поток as определен глобально. 1
Теорема 3.2. Пусть М — риманово многообразие. Поло-
жим
ь
d (х17 х2) = inf j || С' (t) || dt
a
для всех кусочно дифференцируемых кривых С, таких, что С (а) =
= xt и С (Ь) = х2. Тогда d — метрика на М. Если многообразие М
является полным метрическим пространством в этой метрике,
то поток as определен глобально на Т* (7И) X R.
Прежде всего проверим, что d — метрика. Очевидно, что
d (xj, х2) = d (х2, Xi). Далее, если С (а) = С (&) = х2 и
§ 3. Законы сохранения
189
D (b) = х2, D (с) = х3, то кривые С и D вместе образуют кусочно
дифференцируемую кривую, соединяющую xt с х3. Значит,
Ь с
d (х1} х3) < J || С" (i) || dt + j || D' (t) || dt,
a b
ИЛИ
d (х15 x3)<d (arj, x2)+d (x2, x3).
Остается проверить, что из d(xl,x2) = 0 следует х1 = х2. Пусть
U — такая координатная окрестность точки х{ с координатами
х1, ..., хп, что1) U = h~1(B2) и Xi = h~x (0). Для любой точки
у £ /г-1 (/?”) билинейная форма gy положительно определена.
Поскольку /г-1 (В™) компактно, мы можем найти столь малое 8, что
II М2 > е I dxv>* + • • - + (^ | dx»)2)
для всех у Q /г-1 (В7}), 0 #= vy g Tv (М).
Пусть С — любая кривая, соединяющая хх с х2, т. е. С(п)=х1,
С (Ь) = х2. Пусть ti есть точная верхняя грань тех t0, для кото-
рых и С (t) g h~l (U) для всех t, таких, что a^t<t0.
Тогда
Ь <2
J IIС (t) || dt > J || С (t)\\dt
а а
для любых t2^ti. Но для всех i
tz fa
J II C' (t)\\dt>e j I (C (t), dxicw)\dt>
a a
*2
> 8 j j <C' (t), dx^) dt J = 8 I xl (t2) |.
a
Если x{^x2, то любая кривая, соединяющая Xi с x2, либо должна
покинуть /г-1 (В7}) [в этом случае | хг (t2) | не меньше 1/2 для неко-
торого i], либо точка х2 лежит в /г-1 (В™) и | хг (t2) | > | xl (ti) | для
некоторого I. В любом случае d (х1? х2) > 0.
Теперь, когда мы знаем, что d — метрика, мы приступим
к доказательству второй половины теоремы 3.2. Предположим,
что М полно (т. е. полно в метрике d). Пусть точка р g Т* (М) X
X В такова, что as (р) определено при 0 s < s0. Мы утвержда-
ем, что последовательность л (as (р)) сходится при $ -> s0.
2) Напомним, что Bf — шар радиуса г в Еп— Прим, перев.
190
Гл. IV. Вариационное исчисление
Действительно, s есть параметр на л (as (р)), пропорциональ-
ный длине дуги. Значит, d (л (as (р)), л (as< (р))) к | s — s' |,
если 0 0 s, з' < з0. Из полноты следует, что л (as (р)) стремится
к некоторой точке q Е М. Если разность s — s0 достаточно мала,
то л (as (р)) будет лежать в некоторой координатной окрестности
U (с компактным замыканием) точки q. Если х1, . . хп — коор-
динаты в U, то для достаточно большого к мы имеем
к || v ||2 > «и I <74)2 + ... + (и | dx$)*), л (и) = у.
Пусть теперь v — касательный вектор кривой л (as (р)). Тогда
v имеет постоянную длину, так что |(р| dx1) | < К для некото-
рого большого К. Значит, все точки as (р) для s < so (и близких
к so) принадлежат компактной окрестности в многообразии
Т* (М) X R. Следовательно, поток as может быть продолжен
за точку so 6 R- Теорема 3.2 доказана.
В § 7 мы увидим, что верно и обратное утверждение: если
поток as определен глобально, то М полно.
§ 4. ДОСТАТОЧНЫЕ УСЛОВИЯ
В § 2 мы получили необходимые условия того, чтобы кривая
была кривой минимума (теорема 2.1). В этом параграфе мы найдем
достаточные условия того, чтобы экстремаль была кривой мини-
мума. Сделаем сначала несколько простых замечаний. Пусть
U — открытое подмножество в М, I — отрезок в R, а <p: U X 7 ->
-> Т (М) X R — такое отображение, что (л X id) ° ф (х, t) =
= (х, t) для х С U и t £ I. При любом фиксированном t отобра-
жение ср (-, t) задает векторное поле на U; таким образом, ср опре-
деляет «систему дифференциальных уравнений» на U. Предполо-
жим далее, что
£оф = 0 и 7>0 в , (л X id)-1 (U х I) — (4.1)
Лемма 4.1. Пусть U, I, L и ср определены, как выше, причем
выполняется условие (4.1), [a, Ы cz 7 и С: [а, Ы —> М — инте-
гральная кривая для ср, лежащая в U, т. е.
а) С ([а, 6]) 6 U,
b) С (t) = ф (С (0, t).
Тогда С есть кривая минимума для L. Более точно, если
D: [а, Ъ\-+ U — любая кусочно дифференцируемая кривая, такая,
что D (а) = С (а), то
I (С) < I (D) при условии, что С D. (4.2)
Доказательство вполне тривиально. Действительно, согласно
условию (а) и (4.1), имеем 7(0 = 0. Если D^=C, то существует
§ 4. Достаточные условия
191
хотя бы одно t £ [а, Ь], для которого D (t) С (£). Тогда
Р (t) Дл х id)-1 (U х Г) — <р (U х /), так что L (D (£)) > 0 и, значит,
1(D) >0.
Лемма 4.2. Заменим в лемме 4.1 вторую часть условия (4.1)
следующим условием-.
L>0 в W-q(UxI),
где W — некоторая окрестность множества ф (U X I)
в (л X id)"1 (U X I). Тогда неравенство (4.2) имеет место для
всех D: [а, Ы -> U, таких, что D (а) = С (а), для которых
D (t) £ W (когда D определено).
Доказательство остается тем же самым.
Условия, налагаемые на L в этих двух леммах, вообще говоря,
выполняются только в тривиальных случаях. Например, если
L — энергия риманова многообразия, то единственное отображе-
ние ф, удовлетворяющее условию (4.1), сопоставляет каждому
х £ U нулевой касательный вектор в точке х. В этом случае инте-
гральными кривыми будут постоянные отображения. Хотя они,
без сомнения, удовлетворяют неравенству (4.2), это мало вооду-
шевляет. Тем не менее, леммы 1 и 2 дадут нам полезную информа-
цию. Чтобы убедиться в этом, сделаем следующее замечание:
пусть S — функция на U X I. Определим функцию S на
л-1 (U X I), полагая
S(v, t) = p(5) + ^, (4.3)
или в локальных координатах
+ (4.4)
Тогда
ь
\S(D(t))dt=S(D(b),b) — S(D(a),a) (4.5)
а
для любой дифференцируемой (а значит, и для любой кусочно
дифференцируемой) кривой D: [а, 6] -> U. Поэтому мы можем
утверждать, что справедлива следующая
Лемма 4.3. Пусть ф: U/'I Т (М) X R — отображе-
ние, для которого (л X id) ° ф = id, и С — кривая, удовлетворяю-
щая условиям (а) и (Ь) леммы 4.1. Предположим, что на U X I
192
Гл. IV. Вариационное исчисление
существует такая функция S, что
(L—5)оф = 0, (4.6)
(L — S) (р) > 0 для всех р£(лх id)-1 (77 X Г) — <р (U х /). (4.7)
Тогда для любой кривой D: [a, b]—>U (где [а, Ь] = 1), для кото-
рой D (а) =С (а), справедливо неравенство
I(C)<I(D)-S(D(b), b) + S(C(b), b), (4.8)
если только D =^С. Если условие (4.7) выполняется только для всех
р в W — ср (77 X I), где W — окрестность множества <р (U X /)
в (л X id)-1 (U X I), то неравенство (4.8) имеет место для тех
кривых D, для которых D (t) g W при t £ [а, 6].
Доказательство проводится точно так же, как доказательство
леммы 4.1, если учесть формулу (4.5).
Если D (Ь) = С (Ь) и D (а) = С (а), то неравенство (4.8) сво-
дится к (4.2). Это означает, что С есть кривая строгого локаль-
ного минимума вариационной задачи с закрепленными концами.
[Этот минимум будет сильным или слабым в зависимости от того,
справедливо ли условие (4.7) для всех точек р £ (л X id)-1 (U X I)—
— ср (U X 7) или только для тех, которые лежат в W.] Таким
образом, для того, чтобы доказать, что данная экстремаль С будет
кривой минимума, достаточно найти отображение ср, для которого
С является интегральной кривой, и функцию S, такие, что выпол-
нены условия (4.6) и (4.7). Прежде чем выяснять, когда такие ср
и S существуют, сделаем одно дополнительное замечание.
Мы будем говорить, что лагранжиан L положительно опреде-
лен, если для всех р £ Т (М) X R матрица
(^ф) (Р)
х х дхг dxi
положительно определена. Матрица (L.,.-) (р) зависит от выбора
xzxJ к
локальных координат х1, . . . , хп вблизи п (р). Однако условие
положительной определенности не зависит от выбора координат.
Это можно было бы доказать непосредственно, рассматривая формулу
замены координат. Мы докажем это, дав инвариантное определение квадра-
тичной формы Ь.^.л^хГ Для этого заметим, что х1, .... хп— эхо линей-
ные координаты в векторном пространстве Тл^ (М). Пусть f— функция
на векторном пространстве V их1, ..., zre—координаты в V относительно
некоторого базиса ..., еп. Мы хотим придать инвариантный смысл
квадратичной форме, которая в этом базисе имеет матрицу (—.
V дх* dxi /
§ 4. Достаточные условия
193
Заметим, что любой вектор pt индуцирует векторное поле I 1 (р4) на V
(сопоставляющее каждому v£V касательный вектор Г»1 (fj))х). Если р1 =
= 2^ег’ т0 г-1 (р1) = 2 (д/dz’). Для p£V определим билинейную фор-
му Вр (f), полагая Вр (/) (pt, v2) = lp1 (р2) (С1 (у1) I df). В координатах имеем
(Г1 (pt) I df) = 2 (dUdxi) £1- Если "2= 2 ?2ei’ Т0
i~p (”2) <*-1 (yi) । =у •
дх* dxi
Таким образом, билинейная форма Вр (/) симметрична и ее матрица имеет
впд (d2f (p)/dxi dxf). Это доказывает, что положительная определенность
матрицы (£....) (р) не зависит от выбора локальных координат.
Лемма 4.4. Если лагранжиан L положительно определен,
то условия (4.6) и
^-(£-5)оф = 0 (4.9)
дх*
влекут за собой выполнение условия (4.7) для всех р из некоторой
окрестности W множества <р ([Z X I). Если L — энергия, соот-
ветствующая римановой метрике 2), то из условия (4.9) следует
(4.7). [Условие (4.9), хотя и выражено в терминах локальных коор-
динат, но, как легко видеть, от них не зависит. Действительно,
оно означает, что если и — вектор, касательный к Тх (М) (точнее,
к (л X id)-1 (х, £)) в точке ср (х, t), то v (L — S) = 0.1
В самом деле, функция S зависит от хг линейно, так что
d^Sfdx1 дх! = 0. Поэтому в точке p — <f(x, t) функция L — S обла-
дает тем свойством, что д (L — S)/dxl (р) = 0 и матрица
-^-(L-S)(p) = (L.^(p)
дх* дхЗ х
положительно определена. Это означает, что L — S как функция
от хг имеет в точке р строгий минимум. Согласно условию (4.6),
соответствующее минимальное значение равно нулю. Другими
словами, для значений х\ достаточно близких к х1 (р), мы имеем
(L—S) > 0. Применяя это замечание ко всем точкам р gq> (U X Z),
мы получим первую часть леммы 4.4.
Ч См. рассуждения перед упражнением 5.2 гл. II.— Прим, перев.
а) Более общо, если L — квадратичная (не обязательно однородная)
функция от х*.
13 с Стернберг
194
Гл. IV. Вариационное исчисление
Если L — энергия, ассоциированная с римановой метрикой,
то она, очевидно, положительно определена. Кроме того, L — S
при фиксированных х £ U и t 6 I является квадратичной функцией
на Тх (М). Из разложения Тейлора функции L — Sb точке
Ф (х, t) видно, что условия (4.6) и (4.9) влекут за собой усло-
вие (4.7).
Итак, в случае, когда лагранжиан L положительно определен,
мы должны искать отображение ф, для которого существует
функция S, удовлетворяющая условиям (4.6) и (4.9). При этом
удобно применить ко всем рассматриваемым объектам преобразо-
вание Лежандра, другими словами, перейти к многообразию
Т* (М) X R х). Если ф — отображение U X I -> Т (М) X R, то
ф = X ° ф отображает U X I в Т* (М) X R. Таким образом,
мы имеем следующую диаграмму:
Отображение ф определяет ф, и обратно. Как выразить усло-
вия (4.6) и (4.9) в терминах отображения ф? Пусть х1, .. ., хп,
х1, ..., хп, t — локальные координаты в Т (М) X R, а х1, . .., хп,
у1, .. .,yn,t — соответствующие локальные координаты в Т* (М) X R.
Положим
Хг (х, t) —Хг Оф (х, t), у1 (х, t)=yl оф (х, t),
так что
У* (х, £))•
dxi
Тогда, согласно формуле (4.4),
d(L — S) dL dS
-------о ф = - Оф--------.
dxi dxi dxi
Поскольку нас интересует только окрестность кривой С, мы можем
считать, что X — диффеоморфизм.
f 4. Достаточные условия 195
Поэтому условие (4.9) принимает вид
Уг(х, = (4.10)
дх1
Далее,
Т С т w dS ‘ i dS т Xli’i dS
L-S-L-^—x^-^ = L-^y^-—.
Но l-2 угхг =—Н, так что условие (4.6) приобретает вид
^- + Яоф = 0. (4.11)
Мы можем рассматривать (4.10) и (4.11) как одно дифферен-
циальное уравнение в частных производных
...............^.')=°- <4Л2>
Это уравнение известно как уравнение Гамильтона — Якоби.
Вместо того чтобы прямо искать решение S этого уравнения
и затем определять функции уг (х, t) по формуле (4.10), удобнее
поступить иначе. Заметим, что уравнения (4.10) и (4.11) более
сжато можно записать в виде
ф*ю = й5. (4.13)
Действительно, ф*со = 3 Уг (а:, 0 — (Hotydt и
dS — yaS-dJ-^dt.
dxi dt
Сравнивая коэффициенты при dx1 и dt, получаем (4.10) и (4.11).
Поэтому мы должны искать отображение ф, для которого сущест-
вует такая функция S, что ф*и = dS. Такая функция S заведомо-
существует, если ф*йсо = 0 и Н1 (U X 7) = 0. Другими словами,
справедлива
Лемма 4.5. Пусть лагранжиан L положительно определен.
Пусть Н1 (U X I) = 0 и ф: U X I (л X id)-1 (U X I) — та-
кое отображение, что (л X id) ф = id и
ф*йсо = 0. (4.14)
Тогда, если функция S задана уравнением (4.13), а <р = ^-1оф, то
и S удовлетворяют условиям (4.6) и (4.7) для всех р из некоторой
окрестности множества q> (U X I). Если L — энергия, соответ-
ствующая римановой метрике, то условие (4.7) выполняется для
всех р £ (л X id)-1 (U X Г).
Поиски отображения ф, удовлетворяющего условию (4.13),
мы разобьем на две части:
13*
196
Гл. IV. Вариационное исчисление
(i) нахождение такого подмногообразия N cz Т* (М) X R,
что I* (со) = dS*, где i — вложение N -> Т* (М) X R, а 5* —
подходящая функция на N',
(ii) нахождение подмногообразия N, удовлетворяющего (i)
и такого, что ограничение л х id на N есть диффео-
морфизм многообразия N на U X I (для подходящих U cz М
и I с R).
Рассмотрим сначала задачу (i). Ввиду (ii) нас интересуют
(и + 1)-мерные подмногообразия N.
Лемма 4.6. Пусть No есть п-мерное подмногообразие из
Т* (7И) X R. Предположим, что эйлерово поле Y =Х *Х нигде
не касается No и что i* (dco) = 0, где i0: No -> Т* (М) X R —
вложение. Пусть N — подмногообразие, полученное (локально)
Рис. 12.
разнесением подмногообразия No с помощью потока а, порожден-
ного полем Y (рис. 12). Тогда i* (dco) = 0, где i — вложение
N -> Г* (М) х R.
Мы должны показать, что для любой пары векторов Z] и Z2
из Тр (N), где р £ N, справедливо равенство (Z4 Д Z2 | dap)= 0.
Касательное пространство Тр (N) порождается вектором Yp
и подпространством (Та (р) (No)), где а_г (р) QN0. Если Z( и Z2
лежат в at* (Та (Р> (No)), то, поскольку a*dco = dco, имеем
(Zf Д Z21 dap) — Д a(*Z21 йюр) = (Zt Д Z21 do>at (Pj) = 0,
где Z{ = a(_()*Z; £Ta_t (p) (No), i = l,2.
В силу линейности остается рассмотреть выражение (Yp Д Z{ | dcop) =
= (Zf | Yp J dco), которое равно нулю ввиду (2.17). Тем самым
лемма 4.6 доказана.
$ 4. Достаточные условия
197
Отметим, что, поскольку (У| dt} = 1, поле Y нигде не касается
изохронных подмногообразий, т. е. подмногообразий, на которых
t = const.
Расмотрим пример подмногообразия No, удовлетворяющего
условиям леммы 4.6. Пусть х1, ...,хп — система координат
в окрестности U точки р, и пусть v* ='^1yiodxp^Tp(M). Пусть
No — подмногообразие в 71*(М)х/?, состоящее из всех точек,
имеющих в локальных координатах вид
(X1, . . ., Хп, у}, ..., Уа, to),
т. е. определяемое уравнениями уг~угв, t = t0. Тогда i* (бйо) —
= I* (2 ^Уг Л йхг — dH /\ dt) = 0, поскольку ij (dy1) = i* (dt) — 0.
Предположим, что окрестность U диффеоморфна пространству Еп.
Тогда N — N.o XI диффеоморфно пространству En+i и, значит,
/f1(7V) = 0. Согласно лемме 4.6, имеем i*(dco) = O, откуда i* (со) =
= dS*, где S* — некоторая функция на N. Кроме того, л х id есть
диффеоморфизм некоторой окрестности точки (q, t0) С Гг°(л X id) (р, t0)
на некоторую окрестность точки (р, t0)g М X R. Чтобы это дока-
зать, достаточно проверить, что линейное отображение (л х id), о i,
пространства Т\9, <о) (N) = Tq (No) + Ttt> (R) в Т(р, /о) (М х R) невы-
рожденно. Но л есть диффеоморфизм многообразия No на U
и I, (d/dt)(cl, /о) = X, так что (л X id), i, (d/dt)(qt /о) имеет
ненулевой коэффициент при djdt. Отсюда следует, что
(л х id), ° i, невырожденно. Таким образом, N удовлетворяет тре-
бованиям (i) и (ii). Поэтому, если мы положим ф=1°ц, где ц —
отображение, обратное к (nxid)°i: N—>М, и £ = ф*£*, то ф
и S удовлетворяют предположениям леммы 4.5. Поскольку и*
произвольно, получаем следующее утверждение:
Теорема 4.1. Пусть L — положительно определенный
лагранжиан и С — его экстремаль, причем С (to) = р. Тогда
существуют достаточно малая окрестность U точки р, отрезок
I Э to и функция S, определенная на U X I, такие, что любая
кривая В^=С из достаточно малой (Т-окрестности кривой С,
для которой В (t) £ U при всех t £ I и
В (to) =-- р, (4.15)
удовлетворяет условию
I (C)CI (В) + S (С (t), t) - S (В (t), t). (4.16)
В частности, С является кривой строгого слабого локального мини-
мума на любом отрезке Ио, il, где t £ I. Если L — энергия рима-
нова многообразия г), то неравенство (4.16) имеет место для всех
*) См. примечание 2 на стр. 193.
198
Гл. IV. Вариационное исчисление
кривых В, для которых В (i) ^Ujipu любых t £ I, так что С есть
кривая строгого сильного локального минимума для L на [io, £1.
Действительно, поскольку вектор и*, встречающийся в рас-
суждениях, предшествующих теореме, произволен, мы можем
считать, что и* = С (io)- Определив затем <р равенством <р =
=<Х-1°ф, мы заключим из предыдущих рассуждений, что выпол-
нены все предположения леммы 4.3. Это доказывает теорему 4.1.
Более тщательный выбор координат позволяет получить следую-
щее утверждение:
Теорема 4.2. Пусть L — положительно определенный
лагранжиан и С — его экстремаль, причем С (i0) — р К и
(р, С (i0)) — 0 для всех v £ Т (К), где К — некоторое подмногооб-
разие в М. Тогда существует такой отрезок I, содержащий to,
что С есть кривая локального минимума относительно пары
(TVi, N2), где Nt = К, a N2 = С (i) для любого t £ I.
Действительно, выберем координаты а:1, . .., х” так, чтобы
подмногообразие К задавалось уравнениями а^+1 = . .. =хп = 0.
Тогда точка v* — C(t0) будет иметь координаты (xj, ..., х”,
0, ..., 0, £/o+1, .. ., у", i0). В частности, множество ф ((К (~| U) X i0)
состоит из всех точек вида (х1, . .., xh, 0, . .., 0, Z/J+1, . .., у”, i0).
Поэтому если / — вложение К (}U —> М, то 7*ф*(о)) = 0. Значит,
функция S постоянна на Теорема 4.2, как и преды-
дущая, следует теперь из леммы 4.3, если взять a = t и b = ta.
§ 5. СОПРЯЖЕННЫЕ И ФОКАЛЬНЫЕ ТОЧКИ, УСЛОВИЯ ЯКОБИ
В предыдущем параграфе мы показали, что для положительно
определенного лагранжиана L экстремаль «локально» является
кривой минимума. Это означает, что если К — подмногообразие
в М, а С — такая экстремаль, что С (i0) Е К и (п, С (io)) = 0
для всех v £ Т (К), то ограничение кривой С на достаточно малый
отрезок [io, i] является кривой минимума. Однако данное нами
доказательство ничего не говорит о величине отрезка, на котором
СдВ действительности является кривой минимума. Может слу-
читься, что С будет кривой минимума на отрезке [i0, ij, но не
будет’ею ни на каком большем отрезке. Цель этого параграфа —
описать точку iP
Введем для этого некоторые обозначения. Пусть К — подмного-
образие в М; обозначим через Т° (К) подмногообразие в Т*(М),
$ 5. Сопряженные и фокальные точки, условия Якоби 199
состоящее из точек v*QT*(M), таких, что я(и*)£К и (р|р*) = 0
для всех v £Тп (V*y (К). Легко видеть, что Т° (К) действительно
является подмногообразием и имеет размерность п. Если К сво-
дится к точке, скажем р, то Т° (К) есть просто Т*(М). Пусть
К задается в локальных координатах уравнениями xft+1 = ...
. . . =zn = 0. Тогда Т° (К) задается уравнениями а^+1= ... =хп —
= у1 = . .. = yk = 0. Поэтому если i0: Т° (К) —> Т* (М) X R есть
отображение, переводящее и* в (и*, i0), то i*co = O. Следовательно,
мы можем взять Т° (К) в качестве No в лемме 4.6. Единственная
неприятность состоит в том, что проекция л сильно вырожденна
на многообразии 710 (К), которое она отображает в К с пониже-
нием размерности на п — к. Однако верна следующая
Лемма 5.1. Пусть К — подмногообразие в М, и пусть
у: Т° (К) X R—>T* (М) х R— отображение, определяемое формулой
У (р*, £) = аг(р*, 0).
Тогда для каждого V* £Т° (К) существует такое е > 0, что отобра-
жение (л X id)* о у* невырожденно при 0 < 111 < е.
Определение 5.1. Точки f #= 0, для которых отображе-
ние (л X id)* ° у, вырожденно в точке (р*, t), называются фокаль-
ными точками для К вдоль С, где С — такая экстремаль, что
С (0) = р*. Если К — точка, то фокальные точки называются
сопряженными с К.
Лемма 5.1 утверждает, что при малом | t | точка t не является
фокальной. Грубо говоря, фокальные точки — это те точки, где
пересекаются «две инфинитезимально близкие трансверсальные
к К экстремали». Например, если К — кривая на плоскости,
a L — энергия, ассоциированная с евклидовой метрикой, то таки-
ми экстремалями будут прямые линии, перпендикулярные к К.
Две такие «инфинитезимально близкие» прямые «встретятся»
в так называемом центре кривизны q кривой К. Таким образом,
q есть фокальная точка для К вдоль С. На рис. 13 видно (и мы
200
Гл. IV. Вариационное исчисление
довольно скоро это докажем), что С локально минимизирует рас-
стояние от точки х £ С до К, если х лежит на интервале (р, q),
и не минимизирует это расстояние даже локально, если х лежит
за точкой q.
На плоскости нет сопряженных точек, поскольку экстремали,
выходящие из одной точки, расходятся. Рассмотрим, однако,
(единичную) сферу. Здесь экстремалями служат большие круги.
Если Р — северный полюс, то все экстремали, выходящие из Р,
встречаются в южном полюсе. Снова большие круги минимизиру-
ют расстояние, пока они не пройдут через южный полюс. Но как
Р
Рис. 14.
только они пройдут через южный полюс, они перестанут мини-
мизировать расстояние даже локально. Читатель может это дока-
зать, пользуясь рис. 14.
Прежде чем доказывать лемму 5.1, изучим так называемое
«уравнение в вариациях» системы дифференциальных уравнений,
введенное в конце гл. II.
Пусть N — дифференцируемое многообразие и Z — векторное
поле на N. Тогда Z индуцирует векторное поле Т (Z) на Т (N).
Оно определяется следующим образом: пусть at — локальная
однопараметрическая группа диффеоморфизмов многообразия N,
порожденная полем Z. Это означает, что для каждой точки р £ N
существуют такие окрестность U Э Р и интервал I cr R, содер-
жащий нуль, что для каждого t С I определен диффеоморфизм
а(: U N (см. § 8 гл. II). Диффеоморфизмы аг индуцируют ото-
бражения Т (U) -> Т (N). Легко проверить, что отображе-
ния аг» определяют локальную однопараметрическую группу
J 5. Сопряженные и фокальные точки, условия Якоби
201
преобразований многообразия Т (N) и тем самым векторное поле,
которое мы обозначаем Т (Z). По определению л ° = а{, так
что л» (Т (Z)v) = Zn (с) для любого v g Т (N) и, значит, интеграль-
ные кривые поля Т (Z) проектируются на интегральные кривые
поля Z.
Упражнение 5.1. Векторное поле Т (Z) описывает поведение
«инфинитезимально близких» интегральных кривых поля Z. Более точно,
пусть К — отображение прямоугольника 0 < а < е, а < t < b в N, причем
для любого а кривая К (а,-) является интегральной кривой поля Z. Показать,
что кривые Са: [а, Ь] ->• Т (У), где Са (t) = К* (,d/da)(att>, являются инте-
гральными кривыми поля Т (Z).
Предположим, что в локальных координатах z1, ..., zn на N
поток at задается формулой
z* о af = <рг (z1, . . ., z", t).
Тогда поток at* задается формулой
«/*(-.-) =У— (—) •
\dz3 / р ~ дгз \dz%'at(p)
Поэтому в соответствующих локальных координатах z1, . . ., z”,
z1, .. ., z" на T (N) отображение at* имеет вид
z* ° at* = <рг (г1, . .., z", i),
dz3
з
Взяв производную по t при £ = 0 от обеих частей этих равенств,
получим
~ = Z\ (5.1}
dt dt Z-i gZ3 ' '
если Z = 2 Z1 (d/dz‘). Иначе говоря, векторное поле Т (Z) имеет
вид
!.(Z) = 2Z*A+S(224g)2r. (5.2}
Применим предыдущие рассуждения к интересующему нас
случаю, когда N = Т* (М) X R, a Z = Y = X*X — эйлерово вектор-
ное поле. Мы получим векторное поле Т (У) на Т (Т* (М) X R),
которое будем называть якобиевым векторным полем. Пусть
х1, ...,хп— локальные координаты на М. Пусть х1, ...,хп,
у1, ...,уп, t — соответствующие координаты на T*(M)xRr
а х1, .. ., хп, у1, . .., уп, t, х1, . .., хп, у1, ... уп, I — координаты
202
Гл. IV. Вариационное исчисление
яа Т (Т* (М) X Л). Тогда поле Т (У) имеет вид
Т (Y) = V — 9___У — — I — Д-
ду' dx' dx' ду' dt
+ —R-
\‘‘—idy'dx) dy'dy) dy1 dt / Qxi
+ (5.3)
\ “-1 dx' dx) dy) dx' dx* dt f dyi '
Рассмотрим касательный вектор V С Ти (Т* (М) X R) в точке
{и, 0) QT* (М) х R, задаваемый формулой
Тогда компоненты векторов
<х„(Р) = У (s) (_L\ + Уп{(*)(—) +
V ' \dxilas(u, 0) 1 ' ' \dyi)as(u, 0) 1
+ Т (s) ( —
’ К dt /%(«, 0)
удовлетворяют дифференциальным уравнениям
^=3(^ + Я»'^ + Я.,г),
S = - 3 + ЯЛЯ' + "..-Л).
#-о.
as 1
irpfi, например, Hyixj есть функция от s, определяемая формулой
Hvixi = (S)’ ' • * ’ ХП (S)’ yl (S)’ ’ ’ ’ ’ уП f (S)) =
= -^-oC(S);
dy' dx)
•C — экстремаль, такая, что C(0) = (iz, 0). Аналогичный смысл
имеют другие функции Hxtxi, Hyiyj, Hyit, Н^, встречающиеся
в правой*части формулы (5.4). Из (5.4) следует, что т = 0, если
то = О. Поэтому если вектор V касается изохронного многообразия
{для которого то = 0), то это же верно и для ав*(У), и компо-
ненты векторов as* (V) удовлетворяют дифференциальным уравне-
ниям
f=3<W+^*>).
(5.5)
§ 5. Сопряженные и фокальные точки, условия Якоби
203
Заметим, что (5.5) — это линейные дифференциальные уравнения,
которые могут быть записаны в виде
rf
\Пп/
(5-5')
где А, В, С—матрицы порядка п, элементы которых опреде-
ляются из (5.5). Уравнения (5.5) или (5.5') называются дифферен-
циальными уравнениями Якоби. Для нас особенно важно то, что
В — положительно определенная симметрическая матрица. В са-
мом деле, ((РН/ду1 ду3) есть просто матрица Якоби отображения
X"1 (ограниченного на фиксированное пространство Т*> (М) X t0),
т. е. матрица, обратная к положительно определенной матрице
(LAx^-
Теперь мы в состоянии доказать лемму 5.1. Чтобы показать,
что отображение (л X id)* о невырожденно, достаточно прове-
рить, что л* ° не переводит никакого ненулевого вектора
Vo QTU (Т° (К)) в нуль. Если ц1, ..., ц" — компоненты
вектора V, то л* (У) = 3 (д!дхг). Таким образом, утверждение,
которое мы хотим доказать, формулируется так:
Существует такое е>0, что для любого tQR, для которого
О< 111<8> и любого вектора Fo G Ти (Т° (К)) вида Уо = 2 £о (<?/&*)+
+ 2ni(W) выполняется условие
-л. (V.) = 2? w Ш * °’
где функции £г (t) (вместе с некоторыми функциями цг (/)) являются
решениями системы дифференциальных уравнений (5.5) с началь-
ными условиями (£‘(0), rii(O)) = (sj, r]j).
Рассмотрим прежде всего случай, когда К есть точка р. Тогда
Т° (К) = Тр (М) и начальные условия требуют, чтобы вектор Уо
касался Т*(М), т. е. чтобы л*Уо = О или = . .. = g” — 0.
Таким образом, мы имеем семейство линейных преобразований Qt,
сопоставляющее каждому вектор-столбцу (rf, ..., ц”) вектор-стол-
бец №(t), ...,£”(£)), компоненты которого являются решениями
системы (5.4) при начальных условиях g’(0) = 0, if (0) = ц0.
204
Гл. IV. Вариационное исчисление
Мы хотим показать, что при малых t преобразования Qt
невырожденны. По теореме о среднем
I* (f) = ^(0) + O(f2),
так что
Другими словами, преобразования Qt отличаются от tP членами
порядка t2, где Р — линейное преобразование, определяемое фор-
мулой
Далее, преобразование Qt невырожденно тогда и только тогда,
когда невырожденны преобразования (Ht) Qt (для ненулевых t).
Но преобразования (lit) Qt близки к невырожденному преобразо-
ванию Р. Поскольку множество невырожденных преобразований
открыто, отсюда следует, что при достаточно малых t =# 0 пре-
образования Qt невырожденны.
В более общем случае, когда К — подмногообразие, выберем
координаты так, чтобы К задавалось уравнениями zft+1 = . . .
. . . = хп = 0. Тогда условие То 6 Т° (К) имеет вид
ft'f’ 1 с. ??, 1 k f\
lo = ... = Io = no = • • • = Tlo = о.
Снова мы имеем преобразования Qt, сопоставляющие каждому
вектору (|J, iio+1, • • •, П”) вектор (I1 (t), ..., («)), где
|г — решение системы (5.4), для которого
Г(0) = ?о пРи Г(0) = 0 при 1>к,
^-(0) = 0 при i<fc, ^-(0) = 7]j при i>k.
По теореме о среднем
V (0 = gj+1 з Hyix%+1 _£ +о (i2), i <k,
h 3=1 n'k+1 (5-6)
Г (t) = * .S Hyix£l +1 Hyiymi+O (<2), i >k.
Пусть Pt есть линейное преобразование, переводящее (|J, . . .,
По+1, • • •, О в (I1 (t), . .., Г (£)), где
V(t) = U + t^ Нyix£l + t t Hyi rf0, кк,
(t) = Д Hyix&+ Д1 Hyiyri0, i > к
§ 5. Сопряженные и фокальные точки, условия Якоби
205
(заметим, что во второй формуле t отсутствует). Тогда (5.6)
означает, что LtQt = Pt-\-0 (t), где матрица преобразования Lt
имеет вид
Поскольку преобразование Lt невырожденно, LtQt Р и множе-
ство невырожденных преобразований открыто, достаточно дока-
зать, что преобразование Z> = limPt невырожденно. Но матрица
7—>0;
преобразования Р имеет вид
/ 1 0 \
0
0 1
Hyk + lyk + l • • •
k Hynyh^ • НУПУП J
Следовательно, ее определитель равен
#yfe+lyfe+l ... НуМуП
Нупук+1 . . НуПу-п
Он положителен, поскольку матрица (Ну1уз) положительно опре-
делена1). Тем самым лемма 5.1 доказана.
Теперь мы в состоянии доказать, что экстремаль является кри-
вой минимума вплоть до первой фокальной точки. Более точно,
справедлива
Теорема 5.1. Пусть L — положительно определенный
лагранжиан на Т (М) X R. Пусть К — подмногообразие в М
т) Напомним, что если матрица (ЛгД (i, 7 = 1, . . ., п) положительно
определена, то такой же будет и ее подматрица порядка п — к, соответствую-
щая i, j = к + 1, . . . , п. Действительно, эта подматрица соответствует
ограничению квадратичной формы, ассоциированной с (4;Д, на подпро-
странство, состоящее из векторов, у которых первые к координат равны
нулю. Но ограничение положительно определенной формы есть положительно
определенная форма.
206
Гл. IV. Вариационное исчисление
и С — экстремаль, такая, что С (to) £ К и С (to) Е Т° (К). Пусть
ti — первая фокальная точка для К вдоль С и to < t < t^. Тогда
С есть кривая слабого локального минимума на отрезке [io, ij
для задачи с подвижными концами, определяемой парой {К, С (t)}.
Если L — квадратичная функция (например, L — кинетическая
энергия, соответствующая римановой метрике), то С есть кривая
сильного минимума на этом отрезке.
Мы хотим выбрать «начальное» многообразие No леммы 4.5
так, чтобы C(t0)QN0 и проекция ^*°a,s*(T^^(N0)) была невы-
рожденной при 0—10. Для простоты обозначений положим
io = O и $ — t. Мы уже знаем, что если взять N0 = T°(K)t
то проекция будет невырожденной при К сожалению,
она сильно вырожденна при t = 0. Оказывается, однако, что
можно немного пошевелить подмногообразие No = Т° (К) так,
чтобы проекция, оставаясь невырожденной при0<£<1£, стала бы
невырожденной и при i = 0.
В действительности для любого отрезка [б, t] из интервала
0 < t < ti проекция будет невырожденной, если No достаточно
близко к Т° (К).
В самом деле, поскольку мы по существу изучаем решения
уравнений Якоби, это следует из непрерывной зависимости реше-
ний дифференциального уравнения от начальных данных.
Введем координаты х1, . .., хп вблизи С (0) так, чтобы К
задавалось уравнениями a:fl+1 = . .. = хп = 0. Пусть (Gtj) — матрица
порядка п — к, определяемая формулой
Если точка С (0) имеет координаты (х10, ..., х™, 0, . . ., 0,
г/£+1, . . ., у^), то определим подмногообразия Nf cz Т* (М) фор-
мулами
z’ =х10-]-и1,
1=1, ..., к,
хг = ъ 2 Giju’,
3=А+1
i — к —|- 1, ..., п,
t = 1, ..., к,
i = k-]-i, . .., п.
Для е = 0 подмногообразие 7V® совпадает с Т°(К). При любом е
точка пг = 0 есть С(0). В касательном пространстве T^iOy(N„)
введем координаты гз1, ..., оп, соответствующие базису д/ди1, ...
§ 5. Сопряженные и фокальные точки, условия Якоби
207
..., д!дип. Переходя к координатам о*, имеем
= г=1,
п
gj = e 2 i = k+i, ..п,
j=i
r]j = O, i = 1, .. k,
r]j = u1, i = k+l, .. ., n.
Пусть (t), rf (<) — решение системы (5.5) с этими началь-
ными условиями. Тогда мы получаем линейное отображение Qstr
переводящее (о1, ...,оп) в (g1 (f), Мы хотим найти
такое е, чтобы линейные преобразования Qt были невырожден-
ными при 0 < t < t. По теореме о среднем преобразования Qt можно
записать в виде
Г (О = г/ +1 3 Нц (0) 1? + S* 2 Hyix£}lvl +
t=i y j, i=k+t y
+ t 2 Я { Д0)пЧО(Н (i<k),
J=fe+1 y y
n n k
V (0 = 8 2 Gtjv1 1 2 Guv? +1 2 E t jv1 +
;=Л+1 j=ft+l y x
+ . ^+iHyixiGJivl+ °(t2) <.i = k+ 1> •••,«)-
Поэтому матрица линейного преобразования Qt (которую мы бу-
дем обозначать тем же символом) имеет вид
I+tA ztB + tC\
-----------------+0 (И-
tD-y^tE (e-|-i)G /
Пусть Pz+t есть матрица
Для любого е из отрезка [0, е0] предел при t—» + 0 матриц
P^tQ^ есть невырожденная матрица
/ I ° \
(ос/
208
Гл. IV. Вариационное исчисление
Поскольку множество невырожденных матриц открыто, мы можем
найти такое 6>0, что матрицы Рё+tQt, а значит, и Qt невы-
рожденны при О<е<ео и 0<£<2б. Выберем теперь е>0
столь малым, чтобы Qt были невырожденными при 6 С £ <3. Тогда
они невырожденны при 0 <3 <3. Но <2® есть невырожденная
матрица
I 0
0 eG
Итак, матрицы Qet невырожденны при 0 <3<3, что и доказы-
вает теорему 5.1.
Мы показали, что экстремаль минимизирует интеграл вплоть
до первой фокальной точки. Теперь мы докажем следующую тео-
рему, принадлежащую Якоби.
Теорема 5.2. Экстремаль не минимизирует интеграл I
после первой фокальной точки. Более точно, пусть К — подмно-
гообразие в М и С — экстремаль, такая, что С (to) (К иС (to) £
£ Т° (К) X to- Если t есть фокальная точка для К вдоль С, то С
не является кривой слабого минимума ни на каком интервале
(to, tt), где £0 <3 < £i (или £о > £ > £j).
Идея доказательства, грубо говоря, состоит в следующем.
В фокальной точке £ сходятся две «инфинитезимально близкие»
экстремали. Предположим, что в точке £ сходятся две сколь угодно
близкие минимизирующие экстремали С и D (рис. 15). Тогда инте-
грал I принимает на них одно и то же значение (поскольку обе
они минимизируют I и находятся в окрестностях одна другой).
Экстремали С и D не могут касаться в точке £, ибо тогда они
§ 5. Сопряженные и фокальные точки, условия Якоби
209
совпали бы. Поэтому кусочно дифференцируемая кривая В, рав-
ная D на (t0, t) и С на (t, ti), не дифференцируема в точке t, причем
ZfJ (В) = Z?J (С). Если С — кривая минимума, то тем же свой-
ством обладает В. Но это противоречит теореме 2.1, так как В
не дифференцируема в t.
Это доказательство не вполне удовлетворительно главным
образом потому, что, согласно определению фокальной точки,
в ней не обязательно сходятся сколь угодно близкие экстремали,
а только «инфинитезимально близкие». Однако его можно испра-
вить, дав «инфинитезимальный аналог» предыдущих рассужде-
ний. Для этого удобно иметь единую систему координат вдоль
всей кривой С1). Существование ее устанавливает следующая
Лемма 5.2. Пусть С: (to, t^ -> М — дифференцируемая
кривая. Тогда С = F ° В, где F — дифференцируемое отображение
Рис. 16.
открытого множества U с Еп в М, локально являющееся диффео-
морфизмом, а В: (to, t^ М — дифференцируемая кривая в U.
Таким образом, лемма 5.2 утверждает, что всякая кривая
может быть «утолщена» (см. рис. 16).
х) Идея доказательства состоит в том, чтобы рассматривать уравнения
Якоби [уравнения (5.5)] как «уравнения Эйлера» второй вариации (см. рас-
суждение в § 2). Как уравнения Якоби, так и вторая вариация определены
внутренним образом. Однако вторая вариация определена для векторных
полей Xt вдоль кривой С. Поскольку Xt Е Тс<;> СЮ, векторы Xt при разных
t лежат в разных пространствах. Мы не можем рассматривать Xt как кривую
в некотором фиксированном векторном пространстве, пока мы не имеем спо-
соба отождествить все касательные пространства вдоль кривой С. Это можно
сделать, например, введя на М так называемую линейную связность, см.
гл. VII. Наш подход будет состоять в погружении окрестности кривой С
в евклидово пространство, где существует стандартное отождествление
касательных пространств. В римановом случае существует каноническая
связность, так что доказательство может быть проведено более инвариантным
образом.
14 С. Стернберг
210
Гл. ГУ. Вариационное исчисление
Мы отложим доказательство леммы 5.2 до следующего пара-
графа *), где мы будем располагать аппаратом, позволяющим дать
простое доказательство. Воспользуемся леммой 5.2 для доказа-
тельства следующей леммы:
Лемма 5.3. Достаточно доказать теорему 5.2 в случае,
когда М есть открытое подмножество в ЕД.
Действительно, применяя лемму 5.2, мы можем написать
С = F ° В. Поскольку отображение F'. U М является локаль-
ным диффеоморфизмом, индуцированные отображения F*'. Т (JU)-*
-> Т (М) и F* X id: Т (U) X R -> Т (М) X R также будут
локальными диффеоморфизмами. Поэтому функция L ° (F* X id)
является регулярным положительно определенным лагранжианом
на U, и для любой кривой D на U интеграл I (О) относительно
лагранжиана L о (F* X id) совпадает с интегралом I (F ° D) отно-
сительно L.
Если D (0) £ F-1 (K(\F (J7)), то F (D (0)) £ К. Поэтому если
В не является кривой минимума для L° (F* X id), то кривая
С = F ° В не будет кривой минимума для L. С другой стороны,
отображение (F* X id) о является локальным диффеомор-
физмом Т* (U) х R ->• Т* (М) X R, где Xv — преобразование
Лежандра, соответствующее L ° (F* X id). Кроме того, at °
° (F* X id) 0 Xv = (J7» X id) ° Xvaut, _где aut — поток на
T* (U) X R. Отсюда следует, что если t не есть фокальная точка
для F-1 (К) вдоль В, то t не будет фокальной точкой и для К
вдоль С, т. е. если t — фокальная точка для К вдоль С, то t будет
также фокальной точкой для F~r (К) вдоль В. Поэтому если кри-
вая В не минимизирует I за фокальной точкой, то это же верно
для соответствующей кривой С. Это доказывает лемму 5.3.
До конца этого параграфа мы будем предполагать, что М —
открытое подмножество в Еп.
Имея теперь дело с евклидовым пространством, мы можем
пользоваться глобальными координатами х1, . .., хп, у1, .. ., уп
и т. п., причем мы можем ввести глобальные координаты, сов-
местимые с уравнениями (5.5) — (5.5'). Другими словами, на под-
многообразии многообразия Т(Т*(М)х R), состоящем из изохрон-
ных векторов пространств (Т* (М) X R), т. е. из векторов
вида ’Zil1 (д/дх1)^. (д/ду1)^ мы вводим координаты
51, ...,Г, П1,
х) См. упражнение 6.3.
§ 5. Сопряженные и фокальные точки, условия Якоби 211
Обратившись к уравнениям (5.5), мы обнаружим, что они
имеют гамильтонову форму, т. е. их можно записать в виде
dt 5T)i ’ dt ~ g^i ’ ' ‘ '
где
n
^ = 4 S + + (5-8)
i, 1=1
Таким образом, если мы будем рассматривать |х, .. ., g” как
координаты векторного пространства V относительно некоторого
базиса, а т]1, ..., — как ассоциированные координаты на Т* (V),
то мы сможем рассматривать ©%? как гамильтониан регулярной
вариационной задачи, а уравнения (5.5) [или (5.7)] — как соответ-
ствующие уравнения Эйлера. Согласно теореме 1.1, мы можем
это делать, если матрица (д2<^/дг]г <hf) невырожденна. Но
(52<^/^ц‘ = а последняя матрица невырожденна,
поскольку L — регулярный лагранжиан. Таким образом, мы полу-
чаем регулярный лагранжиан Л на Т (У) X R и преобразование
Лежандра Л- T(V)xR—>Т* (У) X R, такие, что
° Л+ (5.9}
= <5Л0>
Подставляя (5.10) в (5.9), мы получим
Ло^’1==т 3 + (5.11}
Справедлива также
Лемма 5.4. Если Г (t) — экстремаль для Л, то
4% (Г) = 4 5 (Г (^) Т? (i2) ~gf W П* (Ш (5.12)
где Г(0 = (^(0, Г (О)-
Действительно, поскольку Sli— однородная функция степени 2
по и имеем
V дс,г дтр /
14*
212
Гл. IV, Вариационное исчисление
Если (t), ц* (t)— решение уравнения (5.7), то отсюда следует,
что
Ввиду (5.9) это влечет за собой равенство
Л о Г = Л о Л-1Г = 4 3 (|9 + Т]ф) = 4 4 S & ¥ (0),
откуда и следует формула (5.12).
Нам все же хотелось бы установить более явную связь между
Л и L. Ее описывает
Лемма 5.5. Пусть С: t—^(^(i), . ,.,x"(t))— экстремаль
в М для L и Г: (t0, — дифференцируемая кривая
в V, T(t) = (|1(t), ...,£"(0)- Определим дифференцируемое ото-
бражение Кг: (— 8, е) х (t0, формулой
хг ° KF (s, t) = хг (t) 4- (t).
Тогда
i J L ° (0, t) dt = 2 [y< (ti) V (tj-y* (to) v (to)], (5.13)
to i=l
<1 Ц
J LoKT(0, t)dt = 2 J AoT(t)dt. (5.14)
to to
Таким образом, Л измеряет вторую производную или «вторую
вариацию» лагранжиана L по «направлению» Г.
Доказательство. Обозначим хг о К (s, t) через xl (s, t).
Тогда X определяет уг (s, t) по формуле
= ~ (хЦв, t), -^-(s,t),t) (5.15)
дх* ' 01 1
И
L (я1 (s, t), . . ., хп (s, t), (*, t), . .., — (s, t), t) =
= —H (x1 (s, t), ..., xn (s, t), yl (s, t), . .., yn (s, t)) +
(5.16)
Дифференцируя равенство (5.16) no s, получим
dL dH dxt дН дф , dip dx* , d^x^
ds gxi ds дуг ds "I ds dt ' ds dt
$ 5. Сопряженные и фокальные точки, условия Якоби
213
Согласно формуле (5.15), два средних члена сокращаются,
поскольку дНIдуг = дх11dt\ кроме того, дхг1д8 = Ъ,1. Поэтому урав-
нение принимает вид
Добавляя и вычитая 3 (дугЖ) g1, получим
4--2 (4+4) б‘+4(2^') <5-«)
Полагая s = 0, находим, что дН1дхг + dyl/dt-=H+ = 0, так
как С — экстремаль. Таким образом,
44=4(2^*) ,
что доказывает формулу (5.13).
Дифференцируя равенство (5.17) по s, получим
(«9)
08 дхг дхЗ дхг дуЗ . Ui>
г, j г, 3 3
Далее, dxi/dt = дН/ду1, так что дифференцирование по s дает
<5-20>
дх? дуг дуг дуЗ а1>
Умножая равенство (5.20) на дуг1дв и суммируя по i, находим
V Si дУ' = V д2Н ?» dyi I VI д%Я дуг dyi
Z-* ds Z-X qx\ Qyj ds Z-X Qyi dyi ds ds
Подставляя это в (5.19), получим
d2L d2H gigj , 5^ d2H ду* dyi 2 п
5s2 Zd gxi dxi Z-X dyidyi ds ds
С другой стороны, из равенства (5.20) при s = 0 следует, что
}
Сравнивая это с (5.10) и учитывая взаимную однозначность ото-
бражения Л-1, заключаем, что
ду1 I i
-4- = т].
ds |s=0 1
Подстановка этого выражения в (5.21) дает
L, = - S + 3 (5.22)
Сравнение (5.22) с (5.11) завершает доказательство леммы 5.5.
214
Гл. IV. Вариационное исчисление
Теперь мы в состоянии доказать теорему 5.2. Введем в
координаты, в которых подмногообразие К задается [в некоторой
окрестности точки С (io)] уравнениями = . . . = хп = 0.
Если С есть кривая слабого минимума вариационной задачи
с условиями В (t0) £ К, В (t^ — С (ti), то при достаточно малых s
мы должны иметь
7Й(^г(8, •))>!%(€),
где Г — кривая r(f) = (^1(f), ...,%n(t)), удовлетворяющая усло-
виям g'i+1 (to) = . . . = (t0) = 0 и g1 (t^ =...=£" (ti) = 0. Очевидно,
что Кг (s, •) — близкая к С кривая, удовлетворяющая тем же кон-
цевым условиям. Поскольку С = Кр(0, •), для всех таких Г
-)) = 0, (5.23)
-))>0. (5.24)
Уравнение (5.13) показывает, что равенство (5.23) имеет место
для всех Г, подчиненных нашим условиям. Действительно, усло-
вия на С (t0) состоят в том, что уг (t0) = 0 при так что
3 У1 (to) Г (to) = 0 = 3 У1 (ti) Г (ti). [На самом деле уравнение (5.23)
эквивалентно уравнениям Эйлера и дает другое доказательство
теоремы 2.1.]
Из условия (5.24) следует, согласно лемме 5.5, что
ti
^AoT(t)dt>0 (5.25)
Го
для всех кривых Г, подчиненных нашим условиям. Но кривая
Г (t) s 0, без сомнения, удовлетворяет всем нашим условиям
и доставляет интегралу (5.25) нулевое значение. Поэтому, согласно
неравенству (5.25), минимальное значение интеграла (5.25) на
множестве всех кривых, удовлетворяющих нашим концевым усло-
виям, равно нулю.
Предположим теперь, что t — фокальная точка и t0<it<iti
(рис. 17). По определению фокальной точки существует такой
ненулевой вектор V = (gj, • • •. Io, 0, ..., 0; 0, . . ., 0, Ло+1, • • > ‘По)»
что решение Г уравнений (5.5), определяемое функциями (t),
rf (t), такими, что £*(М = £о» Tl1(io) = 11o> удовлетворяет условию
^ (£) = () при всех г. Поскольку Г есть решение уравнений (5.5)
или (5.7), мы имеем, согласно лемме 5.4,
h
J ЛоГ (Z)^ = 2(V (i)^(i) -V (to) ^(t0)) = 0. (5.26)
to
6. Риманов случай
215
Рассмотрим кривую Г, совпадающую с Г при t0^.t<t и с 0 при
“ «1
t <11 ti. Она доставляет нулевое значение интегралу \ Л о Г dt
to
и, следовательно, является кривой минимума, а, значит, и экстре-
малью для Л. G другой стороны, Г не дифференцируема в точке t,
ибо в противном случае, согласно теореме единственности реше-
ния, примененной к уравнению (5.5), она бы тождественно об-
ращалась в нуль. Это противоречит теореме 2.1 (примененной к
Л) и доказывает теорему 5.2.
§ 6. РИМАНОВ СЛУЧАЙ
Поскольку лагранжиан Л = -к-|| ||2 не зависит от t, в соответ-
А
ствии с теоремой 3.1 существует такое векторное поле V на Т* (М),
что Y = (7, d/dt}. Так как отображение '£ индуцирует диффео-
морфизм многообразия Т (М) на Т* (М), поле V определяет
некоторое векторное поле Z на Т (М). Фактически мы уже встре-
чались с полем Z, записанным в локальных координатах (см.
конец § 2). Локальный поток 6t, порожденный полем Z, называется
геодезическим потоком на Т (М). Как мы уже видели в § 3, в слу-
чае, когда М полно, поток 6t определен глобально. Мы хотим
теперь более детально изучить поток 6f и векторное поле Z. Преж-
де всего, если v £ Т (М), то л* (Zo) = v £ (M). На самом
деле это верно для всех векторных полей на Т (М), которые соот-
ветствуют «дифференциальным уравнениям второго порядка»
на М. Далее, примем во внимание поведение поля Z при «растяже-
ниях». Мультипликативная группа вещественных чисел R* (т. е.
все t 0) действует как группа преобразований многообразия
216
Гл. IV. Вариационное исчисление
Т (М) для любого многообразия М: действительно, положим
P-i М = Для v с Т (М) и t £ R*. Легко видеть, что эта фор-
мула определяет дифференцируемое действие группы R* на
Т (М): Цц ° |Т/2 = и л° = л.
В координатах имеем xl°pt=x\ х1 оц/ = 7гг. Значит,(д!дхг)к =
= t (д/дх1)^. Поэтому из формулы (2.26) (или просто из опреде-
лений) следует, что p*Z = (1/2) Z 1).
Определение 6.1. Пусть М — дифференцируемое многообра-
зие. Векторное поле W на Т(М), удовлетворяющее условиям
n*(iy„) = y Для всех vQT(M), (6.1)
= (6.2)
называется пульверизацией. Пульверизация называется полной,
если порожденный ею поток определен глобально.
Резюмируя предыдущие замечания, можно сказать, что если
М — риманово многообразие, то векторное поле Z является пуль-
веризацией. Мы назовем Z геодезической пульверизацией риманова
многообразия М.
Предположим, что W — векторное поле на касательном рас-
слоении многообразия Мир — точка из М. Тогда для достаточно
малой окрестности V нуля в Тр (М) и отрезка 7, содержащего нуль,
в R, поле W индуцирует отображение V X I М- Действитель-
но, пусть 6< — поток, порожденный полем W. Выберем V и I
так, чтобы 6f (к) было определено для и £ V, t £ I. Тогда отобра-
жение о, задаваемое формулой о (и, t) = л ° 6t (и), будет диффе-
ренцируемым отображением V X I М. Предположим, что поле
W удовлетворяет условию (6.1). Для v £ V определим кривую Cv,
полагая С„ (t) = л ° 6t (и). Из условия (6.1) следует, что (t) =
= 64 (и). Предположим, что W удовлетворяет также и условию
(6.2). Тогда мы имеем
° 6s — bs/t ° (6.3)
Действительно, из упражнения 8.4 гл. II мы знаем, что (Xf°6s =
= Xs°(Xt, где X —поток, порожденный полем цПУ. Но =
= (l/t)W, так что Xs = 6s/f, откуда следует формула (6.3).
Поэтому в случае пульверизации отображение о удовлетворяет
условию
о (to, s) = о (у, ts). (6.4)
Напомним, что для любого векторного поля Z векторное ноле p.*Z
определяется формулой (p*Z)D =
J в. Риманов случай
217
Следовательно, существует такая окрестность нуля U а Тр (М),
что отображение о (v, t) определено при всех v С U и | t | 2,
t £ R. Определим отображение exp: U ->• М, полагая
ехр (р) = о (у, 1). (6.5}
[Если W — полная пульверизация, то ехр и о определены для
всех и£Тр (М).] Изучим отображение ехр*: То (Тр (М)) -> Тр (М).
Прямая tv, согласно формуле (6.4), переходит при отображении
ехр в кривую Cv (t). Значит, ехр* переводит касательный вектор
прямой tv в точке нуль в касательный вектор кривой Си (£) при
t = 0. Но касательный вектор кривой Cv (£) при t = 0 равен v.
Таким образом, ехр* переводит касательный вектор прямой tv
в v. Но это не что иное, как отображение отождествления
1о- То (Тр (М)) -> Тр (М), описанное в § 5 гл. II. Другими сло-
вами, отображение ехр*: То (Тр (М)) -> Тр (М) совпадает с /0.
Итак, нами доказана
Теорема 6.1. Пусть W — пульверизация, а 8 — порож-
денный ею поток. Для любой точки р fMu любого отрезка I с. R
существует такая окрестность V нуля в Тр (М), что формула
о (v, t) = n8t (v) определяет отображение а: V X I —>• М и это
отображение удовлетворяет условию (6.4). Если определить ото-
бражение ехр формулой (6.5), то оно будет переводить прямые,
проходящие через начало координат, в интегральные кривые поля
W, а отображение ехр* будет совпадать в начале координат
с отображением 1о.
Поскольку отображение ехр* невырожденно в начале коор-
динат, оно определяет диффеоморфизм некоторой окрестности
начала координат в Тр (М) на окрестность U точки р из М. Назо-
вем окрестность U вместе с отображением ехр-1 нормальной картой
вокруг р, а саму окрестность U — нормальной окрестностью
точки р. Если мы выберем некоторый базис пространства Тр (М),
то соответствующие (линейные) координаты в Тр (М) определят
систему координат в U, которую мы назовем нормальной системой
координат в точке р. Если х1, . . . , хп — нормальная система
координат в точке р, то хг (р) = 0 и интегральные кривые поля W,
проходящие через р, задаются уравнениями хг (t) = tx\.
Применим предыдущие рассмотрения к случаю, когда М —
риманово многообразие, a W = Z — геодезическая пульвериза-
ция. В этом случаи мы можем связать геодезический поток 6 с пото-
ком а на Т* (М) X R. Действительно, из определений немед-
ленно следует, что a,s (v*, t) = (% ° Ss° £-1v*, t + s). Значит,
(л X id) ° as (v*, 0) = no (v, s) X s. В частности, если U — нор-
218
Гл. IV. Вариационное исчисление
мальная окрестность точки р, то отображение (л X id) ° as являет-
ся диффеоморфизмом множества X ° pi/s (exp-1 U) на U X s.
Мы знаем также из теоремы 4.1, что если С — геодезическая
риманова многообразия М и С (0) — р, то С есть кривая сильного
локального минимума энергии (вариационной задачи с закреплен-
ными концами) вплоть до первой сопряженной с р точки.
Заметим, далее, что для любого компактного множества U с:
-с Тр (М) существует положительное число р (U), такое, что любая
точка t, сопряженная с р вдоль некоторой геодезической С, для
которой С(0) = ри С' (0) £ U, удовлетворяет неравенству | t |>
> р (U). [Это следует очевидным образом из соображений непре-
рывности.]
Лемма 6.1 (лемма Гаусса). Пусть Sr — сфера радиуса г
в Тр (М), т. е. Sr = {и | || v || = г}. Пусть С — геодезическая,
Рис. 18.
С (0) = р, параметризованная длиной дуги. [Заметим, что при
достаточно малых г множество exp Sr является подмногообразием
в М‘, мы обозначим его Sr. Ясно, что С (г) £ Sr при любом г.]
Тогда при достаточно малых г вектор С' (г) ортогонален к
(рис. 18).
[Очевидно, что лучи, выходящие из начала координат в Тр (М),
ортогональны в евклидовой метрике сферам с центром в начале
координат. Лемма 6.1 утверждает, что их образы при отображе-
нии ехр остаются ортогональными в римановой метрике много-
образия М.]
Доказательство. Выберем г меньшим, чем минималь-
ное расстояние до сопряженных точек, т. е. г < р (Si). Тогда
все геодезические С, для которых С' (0) £ Si, минимизируют энер-
гию на отрезке [0, г] в вариационной задаче с закрепленными
концами. С другой стороны, минимальное значение этой энергии
равно г. Более точно, г есть минимальное значение интеграла
§ 6. Риманов случай
219
энергии на множестве всех кривых В: [0, г] —> М, для которых
В (0) = р и В (г) £ Sr. Но тогда по теореме 2.2 кривая С орто-
гональна к Sr.
Переформулируем этот последний результат. Функция г
[г (у) = || V II = V(у, у) для у е Тр (М)] однозначно определена
на Тр (М) и дифференцируема всюду, кроме начала координат.
Функция т = гоехр-1 определена в любой нормальной окрест-
ности U точки р и дифференцируема в U всюду, кроме точки р.
Пусть С — геодезическая, выходящая из р и параметризованная
длиной дуги, причем С (Z) = q. Тогда {С' (t), dxq) = <Z (Z), dr) =
= 1 [где I (t) — прямая в Tp (M), проходящая через начало
координат и имеющая единичный касательный вектор]. Лемма 6.1
утверждает, что если t достаточно мало, то гиперплоскость в Tq (М),
определяемая уравнением dxq = 0, ортогональна к единичному
вектору С' (Z). Дополнив С' (Z) до ортонормированного базиса
С (Z), е2, . . . , еп пространства Тq (М), получаем {С' (Z), dxq) =
— 1, (ej, dx q) = 0 для / 2. Значит, дуальным к базису С (Z),
е2, . . . , еп будет базис dxq, е%, . . . , е„. Поэтому если gq есть
метрика в точке q, то gq = dxq + (е*)2 + . . . + (е„)2. Другими
словами, доказана
Лемма 6.2. Пусть g — риманова метрика на М и р £ М.
Тогда существует достаточно малая нормальная окрестность W
точки р, такая, что
g = с/т2 + h (6.6)
во всех точках из W — р, где h — положительно полуопределен-
ная симметрическая дифференциальная форма. Кроме того, из
(vq © vq, hq) = 0 следует, что vq есть касательный вектор
(единственной) лежащей в W геодезической С, соединяющей точку р
с точкой q.
Для доказательства достаточно положить hq = (е*)2 + . . .
• • • + (еп)2- Из леммы 6.2 следует
Лемма 6.3. Пусть р и W— такие, как в лемме 6.2. Для
любой точки q£W геодезическая С, соединяющая р с q, достав-
ляет абсолютный минимум длине дуги, т. е. величине
j || С' (t) ||tZZ = cZ(p, q). Любая кривая В длины d(p,q), соединяю-
щая р с q, имеет вид B(t) = C (a(t)), где а — некоторая моно-
тонная функция.
Г
Действительно, пусть Тогда j || С' (Z) Цс/Z = г. Пусть В —
о
любая кривая, такая, что В (0) = р, B(a) = q, и пусть t{— первая
220 Гл. IV. Вариационное исчисление
точка, для которой В (tt) [т. е. it = minf по всем ££[0, а],
для которых 5(i)gSrJ. Тогда
а
J \\B'(t)\\dt>
о
*1 <1
> j II В’ (t) II dt = V<JB’ (t) © B'(t), dx2) + (B' (t) © В' (t), h)dt>
о о
P h
> j ((£' (i) © B' (t), dx2))i/2dt = j ((£'(i), dx>2)1/2di>
о 0
tl
> (B' (t), dr) dt = x (ti) — т (0) = r,
о
откуда r = d (p, q). Кроме того, если В имеет длину г, то все эти
неравенства должны перейти в равенства. Тогда первое из них
дает
.j || В' (i) || dt = О,
il
откуда а = ti, т. е. В не выходит за пределы Sr. Второе влечет
за собой тождество (В' (t) © В' (t), h) 0, так что В' (£) всегда
касается некоторой фиксированной геодезической, выходящей
из р. Это означает, что кривая В (t) сама является геодезической —
единственной существующей геодезической, соединяющей точки
р и q. Из третьего следует, что {В' (£), dx) 0, так что В (t) =
= С (а (£)) для некоторой монотонной неубывающей функции а.
Из леммы 6.3 видно, что
топология многообразия М, определяемая метрикой d, совпа-
дает с топологией, определяемой структурой многообразия.
Действительно, если d (pt, р) -> 0, то с некоторого момента
точки pt лежат в W, a d совпадает с радиальным расстоянием
в exp-1 (И7). Поэтому из d (pt, р) 0 следует, что -> р. Обрат-
ное утверждение тривиально.
Лемма 6.4. Пусть С — кусочно дифференцируемая кривая,
соединяющая две произвольные точки р и q из М. Предположим,
что L [С] = d (р, q). Тогда (с точностью до монотонной пере-
параметризации) С является геодезической, соединяющей р с q.
Более кратко, если С — такая кривая, что С (0) = р, С (1) = q
и Е [С\ = d2 (р, q), то С есть геодезическая.
§ 6. Риманов случай
221
Действительно, если С не является геодезической, то найдутся
точка г = С (to) и некоторая ее нормальная окрестность W, такие,
что С [Zo, ii] cz W, где t1 — близкая к t0 точка, и кривая С
не является геодезической на отрезке [i0, ij- Соединим точки
С (to) и С (ti) геодезической у и заменим С новой кривой В, кото-
Р и с. 19.
рая совпадает с С вне отрезка [io, ij и совпадает с у на отрезке
(io, ij (рис. 19). Из леммы 6.3 следует, что L [5] < L [С], что
противоречит равенству L [С] = d (р, q).
Вторая часть леммы следует из неравенства Коши
1 1
(j || С" (i)||di)2<j ||С"(0 ||2 dt,
о о
где равенство имеет место только в случае, когда || С (t) || =
= const. Поэтому если Е [С] d2 (р, q), то L [С] d (р, q)
и С есть геодезическая, параметризованная пропорционально
длине дуги.
Для р £ М обозначим символом Вг (р) множество ехр Вт;
при малых г мы имеем Br (р) = {q | d (р, q) < г}. Мы сейчас
покажем, что при достаточно малых г шар Вг является «выпук-
лым».
Лемма 6.5. Для каждой точки р £ М можно найти такое
€ > 0, что при всех г е сферы 2Г выпуклы. Точнее, если С есть
геодезическая, причем С (0) £ 2Г и С' (0) касается 2Г, то при
достаточно малых t <=£= 0 геодезическая С (t) лежит вне Вг.
Доказательство. Выберем прежде всего е столь
малым, чтобы все рассуждения можно было проводить в нормаль-
ной окрестности точки р. Пусть х1, . ... хп — нормальные коор-
динаты, так что 2Г задается уравнением (я1)2 + (хп)2 = г2.
Положим F (х1, . . . , хп) = (я1)2-)-. . ,+(а;п)2 и хг ° С (t) = xl (t).
222
Гл. IV. Вариационное исчисление
Поскольку С (0) £ Sr, имеем F {хх (0), . . . , хп (0)) = гг;
так как кривая С касается сферы в нуле, имеем (С' (0), dF) =
= 0, или
^г-\ =о-
dt |t=0 dt |i=o
Далее,
d2F о С _Q / V dx' dx' । XI „i d?x'
dt* dF+ 21х ~d&~ ) ’
Но С — геодезическая, поэтому, согласно (2.26),
d2x' _____________________ Yp* dad dxh
~dti~ ~ ~' 21 1 ~dT ~di~ •
j, к
Таким образом, мы можем написать
d2F о С о / Х^ dx' dx' 50 „in* dxi dxk
ДГ~ ~ Z ( 21 ~dF ~di 21х 1 ik ~dT ~di~ ) ~
i j, к
k
Ввиду того что функции Г*,- ограничены, для достаточно малых а?
матрица 6}— 2 положительно определена. Итак, при доста-
точно малом е
dF о СI _ „ d2F о С п
dt |/=о “U’ dt2 U>
Другими словами, точка 0 является точкой строгого минимума
функции F ° С, так что F ° С (i) > г2 при достаточно малых t 0.
Лемма 6.5 доказана.
Теорема 6.2. Для каждой точки р £ М существует такое
6 > 0, что множество Bg (р) геодезически выпукло. Другими сло-
вами, для любых точек qt, q2 С Вд существует единственная (с точ-
ностью до параметризации) геодезическая С, соединяющая q\ с q2
и лежащая в Вд. Кроме того, L [С] = d (р, q) и С однозначно
(с точностью до параметризации) определяется этим свойством.
Прежде всего заметим, что для каждой точки q£M существует
такое число р(Д), что ВР(9) есть нормальная окрестность точки q,
удовлетворяющая заключениям леммы 6.3 относительно q. При
этом можно считать, что р непрерывно зависит от q. [Действи-
тельно, в качестве р можно взять минимум расстояний до сопря-
женных точек.] Существует такое К > 0, что р (q) >К для q £ В8 (р).
Пусть х = К/2. Тогда для любого q^BH{p) имеем Bx(q)ci Вк (р)
§ 6. Риманов случай
223
В частности, для любых qt, qzQ^.ip) имеем £ Br (<7г)- Поэтому,
согласно лемме 6.3,
для любых qt, q2 С Вх (р) существует единственная геодезиче-
ская длины d(qt, q2), соединяющая qt с q2.
Мы хотим выбрать 6 столь малым, чтобы геодезическая длины
^(71, ?г), соединяющая точки qt и q2, лежащие в Вд(р), тоже
лежала в Вв(р). Для этого возьмем 6 < % и 6 < (1/4) е (для е,
фигурирующего в лемме 6.5).
Предположим, что qu <72бВ6(р), и пусть С — геодезическая,
соединяющая qt с q2. Тогда
d (qt, q2) < d (p, q^ + d (p, q2) < 26 < ± e.
Если q — любая точка на С, то
d (Р, d (q, qt) + d (qit p)^d (q^ q2) + d (g1; p) < e.
Пусть r = max d (p, q) для q E С. Достаточно показать, что
г max (d (p, qt), d (p, q2)). Если r > max (d (p, qt), d (p, q2)),
то значение г должно достигаться в некоторой внутренней точке to
кривой С. Но тогда вектор С' (i0) касался бы Sr. Поскольку
е, из леммы 6.5 следовало бы, что С (t) лежит вне Вг при
малых t — to 0. Но это противоречит тому, что г = max d (р, q).
Теорема 6.2 доказана.
Экспоненциальное отображение, которое мы до сих пор изу-
чали, было отображением Тр (М) М. Как мы видели, для любо-
го подмногообразия К подмногообразие Т° (К) с Т* (М) служит
естественным обобщением пространства Тр (М). В римановом
случае удобнее рассматривать Т1- (К) — подмногообразие в Т (М),
состоящее из касательных векторов v, для которых л (и) £ К
и (ш, и) = 0 при всех Тщ^К). [Подмногообразие Т1- (К)
есть не что иное, как образ пространства Т° (К) при отображе-
нии У-1.]
Более точно, пусть / — погружение К М. Определим
Tf~ (К) как многообразие, состоящее из таких пар (р, и), где
р С К. a v С Т (М), что л (у) С ^/(р) СЮ и («5 у) = О для всех
и? Ё f*Tp (К). Удобно рассматривать К как подмногообразие
в Т^(К), состоящее из точек вида (р, 0). Многие результаты
настоящего параграфа обобщаются на этот случай. Важнейшие
из них мы сформулируем в виде упражнений.
Упражнение 6.1. Определим отображение exp: Т^- (К) М
следующим образом: положим exp (р, и) = С (1), где С — геодезическая,
для которой С (0) = р, С' (0) = и. Показать, что отображение ехр одно-
значно определено и дифференцируемо в некоторой окрестности подмно-
224
Гл. IV. Вариационное исчисление
гообразия К в Tj- (Л7). Если М — полное многообразие, то ехр определе-
но и дифференцируемо на всем Tj- (К).
Упражнение 6.2. Показать, что существует окрестность W подмно-
гообразия К, на которой ехр является погружением.
Упражнение 6.3. Показать, что если К = R [т. е. (К, f) — кри-
вая], то Tj- (К) диффеоморфно Нп (вместе с упражнением 6.2 это доказывает
лемму 5.2).
Упражнение 6.4. Пусть / — собственное вложение К -► М.
Показать, что существует такая окрестность Wподмногообразия К в Tj- (К),
что для (р, v) £ W расстояние от ехр (р, и) до f (К) равно || v ||.
Мы знаем из теоремы 5.1, что геодезическая минимизирует
энергию вплоть до первой фокальной (сопряженной) точки, но
не дальше. Теперь мы в состоянии доказать аналогичные утвержде-
ния относительно длины.
Теорема 6.3. Пусть К — подмногообразие в М и С —
геодезическая, параметризованная длиной дуги, причем С (0) £ К,
С (0) £ ТХ(К). Пусть ti > 0 — первая фокальная точка для К
вдоль С. Если i2 > ii, то существует близкая к С кривая В, удовле-
творяющая условиям В (0) £ К, В (t2) = С (t2), для которой
L [В] <Z L \С}. В частности, геодезическая не минимизирует длину
после первой сопряженной точки. Если же t2 <Ztf, то геодезиче-
ская С минимизирует длину дуги на отрезке [0, i2l-
Действительно, Е [С] = L [С] = i2. Существует кривая В,
для которой Е 1В] < Е [С]. По неравенству Коши (L [В])2
< Е [5] t2 < t\, откуда L [В] < t2 = L [С]. Это доказывает пер-
вую часть теоремы. Вторую часть мы оставляем читателю в каче-
стве упражнения.
S 7. ПОЛНОТА
В этом параграфе мы продолжим изучение геодезических на ри-
мановом многообразии. В частности, мы рассмотрим геометриче-
ские свойства метрики d. Основная цель параграфа — доказать
два следующих утверждения:
1) полнота геодезического потока эквивалентна полноте метри-
ческого пространства (М, d) (обращение последнего утверждения
теоремы 3.2);
2) любые две точки полного риманова многообразия можно
соединить геодезической.
# 7. Полнота
225
Сделаем прежде всего несколько замечаний относительно мет-
рических пространств.
Определение 7.1. Пусть М — метрическое простран-
ство. Дугой мы будем называть непрерывное отображение отрезка
а t Ь в М. Путем называется непрерывное отображение
интервала а <1 t < b в М. Дуга С называется сегментом, если
d (С &), С (f2)) + d (С (t2), С О = d (С (fi), С (f3)) (7.1)
для любых а ti t2 t3 Ъ.
Таким образом, сегменты играют роль «прямых линий». Ясно,
что если а с d Ъ и С есть сегмент на [а, Ь], то ограничение
дуги С на [с, d] также будет сегментом.
Заметим, что если М — риманово многообразие с соответствую-
щей метрикой d и С — сегмент, соединяющий р с q, то С (с точ-
ностью до перепараметризации) является минимизирующей геоде-
зической, соединяющей р с q. Действительно, мы можем ограни-
читься рассмотрением малого куска сегмента С, т. е. можем счи-
тать, что образ С лежит в окрестности U, обладающей свойствами,
описанными в теореме 6.2. Тогда из равенства d (г1; г) 4-
+ d (г, r2) = d (fi, г2) следует, что все точки г лежат на един-
ственной геодезической в U, соединяющей щ с г2. Итак, С локаль-
но, а значит, и глобально, является геодезической. Если С (0) = р
н С (а) = q, то мы можем выбрать разбиение 0 = ri < . . . < rk =
= а так, чтобы ограничение С на каждый отрезок [г;, ri+i] явля-
лось минимизирующей геодезической. Тогда, поскольку С —
сегмент,
L [С] = 3d (С (гг), С (rf+1)) = d (р, q).
Обратно, если С — минимизирующая геодезическая, то огра-
ничение кривой С на любой подотрезок тоже будет минимизирую-
щей геодезической. Следовательно, С — сегмент.
Определение 7.2. Путь С: а t < b М называется
лучом, если образ пути С замкнут и ограничение пути С на отрезок
а t с является сегментом при всех с, а с < Ь.
Так, в евклидовой плоскости лучи — это прямые линии,
простирающиеся в одном направлении до бесконечности. На пло-
скости с выколотыми точками можно построить лучи конечной
длины. На полном римановом многообразии все лучи имеют беско-
нечную длину (упражнение!).
Лемма 7.1. Пусть tl <Zt2 <Z . . . <Z tm+l — вещественные
числа. Предположим, что на каждом отрезке t ti+1 опре-
15 с. Стернберг
226
Гл. IV. Вариационное исчисление
делен сегмент Ct, причем
Ct (tt) = Ci_i (ti) = at (i = 2, . . . , m).
Положим at — C\ — Сm Тогда, если
d (alt a2) + . . . + d (am, am+i) = d (at, am+l), (7.2)
то отображение C: C t tm+l -> M, определяемое формулой
C (t) = Ct (t) для tt t ti+i, является сегментом.
Доказательство.G помощью индукции доказательство
сводится к случаю, когда т = 2. Для любых х у t3
положим d (х, у) = d (С (х), С (у)). Мы хотим проверить, что для
любых трех чисел х, у, z, для которых h х у z <1 t3,
справедливо равенство
d (х, у) + d (у, z) = d (х, z). (7.3)
Если ti х у z t2 или t2 х у z t3, то доказы-
вать нечего, поскольку Ci и С2 — сегменты. Предположим, что
ti х t2 у z t3. Так как Ci и С2 — сегменты, имеем
d (я1? х) 4- d (х, а2) = d (at, а2),
d (а2, У) + d (у, z) = d (а2, z),
d (a2, z) + d (z, a3) = d (a2, a3).
Складывая и используя равенство (7.2), получаем
d (аь х) 4- d (х, а2) 4- d (а2, у) + d (у, z) + d (z, а3) =
= d (ai, a3).
Согласно неравенству треугольника, d (х, а2) 4- d (а2, у)
d(x, у), откуда
d (а1; х) 4- d (х, у) + d (у, z) + d (z, а3) < d (аь а3).
Из неравенства треугольника следует также, что
d (ai, х) 4- d (х, z) 4- d (z, a3) d (аг, a3).
Сравнивая последние неравенства, получаем
d (х, z)~^> d (x, у) 4- d (у, z),
откуда
d (x, y) 4- d (y, z) = d (x, z),
что и доказывает лемму.
Лемма 7.2. Пусть М — связное риманово многообразие
и d — соответствующая метрика. Для каждой точки р £ М
найдется такое число р > 0, что для любой точки q g М
§ 7. Полнота
227
1) если d (р, q) р, то существует сегмент С, определенный
на отрезке 0 t d (р, q), для которого С(О) = р и
С (d (р, q)) = q;
2) если d (р, q) > р, то существует такая точка х g М,
что d (р, х) + d (х, q) = d (р, q) и d (х, р) = р.
Доказательство. Возьмем число р меньшим, чем
радиус нормальной окрестности точки р. Тогда условие 1), оче-
видно, удовлетворяется (см. упражнение 7.1). Докажем 2). Выбе-
рем такую последовательность {СД кривых, соединяющих р с q,
что lim L [Сг] = d (р, q). Пусть xt — точка из Sp Q Im Сг.
Тогда d (xitq) L [Сг 1 — p. Поскольку Sp компактно, из после-
довательности {хД можно выбрать сходящуюся подпоследова-
тельность. Пусть х — ее предел. Тогда d (х, q) d (р, q) — р
и d (р, х) + d (х, q) = d (р, q).
Теорема 7.1. Пусть М — связное риманово многообразие
с соответствующей метрикой d. Для любых двух точек р, q сущест-
•4
Рис. 20.
вует либо сегмент, соединяющий р с q, либо такой луч С, что
С (0) = р и d (р, х) + d (х, q) — d (р, q) для любой точки
х g Im С.
Эти два случая показаны на рис. 20.
Доказательство. Предположим, что не существует
сегмента, соединяющего р с q. Мы построим последовательность
точек аг, чисел и сегментов С;, такую, что at = р и
(i) d (at, аг) + . . . + d (ak_t, ak) Д- d (ak, q) = d (a1? q)
для всех к',
(ii) ti+i — ti = d (at, ai+i), i = 1, . . . , к — 1;
15*
228
Гл. IV. Вариационное исчисление
(iii) Ct определено на интервале (£г, причем С, (£г) = аг,
Ct {ti+i) = аг+1 (i = 1, . . . , к — 1).
Мы будем строить эту последовательность по индукции. Для
к = 1 утверждение тривиально. Предположим, что мы определили
cii, . .. , ак, tlt , tk. Тогда d (alt ак) + d (ak, g)< d (аъ a2) + ...
.. . + d (ak_i, ah\ + d (ak, q) = d (a1? q). Значит,
d («i, aft) + d (ak, q) = d {ax, q), (1A)
d (fli, a2) + . . . + d (ak_i, ak) = d (ait ak). (7.5)
He существует сегмента, соединяющего ak c q, ибо в противном
случае по лемме 7.1 существовал бы сегмент, соединяющий р с q.
Следовательно, по лемме 7.2 существуют точка х, такая, что
d (ак, х) > 0, d (ак, х) + d (х, q) = d (ак, q), и сегмент, соеди-
няющий х с ак. Рассмотрим множество Sk всех 'таких точек х,
и пусть dk — sup d (ак, х). Выберем ak+i £ Sk так, чтобы
xesft
d(ak, aft+i)> jdh. (7.6)
Из равенств (7.4) и (7.5) следует, что
d (й1, а2) + . . . + d (ак, ак+1) -р d (ak+i, q) = d (at, q).
Положим tk+l = tk + d (ak, ak+i) и определим Ck на (tk, tk+i)
как геодезическую, соединяющую ak c ak+i и параметризованную
длиной дуги. Тогда условия (i), (ii) и (iii) выполнены.
Пусть 7 = lim ti= ^(tk — £fe-i) <d(p, q). Определим путь С
на ()<;£<;£, полагая C(i) = C,(i), если Согласно
лемме 7.1, ограничение пути С на любой подотрезок будет сег-
ментом. Мы хотим показать, что образ С замкнут. Достаточно
проверить, что для любой последовательности st —> 1 соответ-
ствующая последовательность С (st) не имеет предела в М.
Но для любого данного е > 0 мы можем найти такое 6 > 0, что
d (С (з), С (£)) < е, если s, t>t — д, поскольку по построению
d (С (s), С (t)) =| s—i|. Поэтому если z = limC(Sj), то мы можем
продолжить С до сегмента на отрезке ()<:£<£, полагая С (t) ~z.
Но тогда limd(aft, z) = 0 и, согласно равенству (7.4),
Л->оо
d (аь z) + d (z, q) = d (аь q).
Точка z не может совпасть с q, поскольку не существует сегмента,
соединяющего р с q. Следовательно, согласно лемме 7.2, сущест-
вуют точка х, такая, что d (z, х) + d (х, q) = d (z, q), d (z, x) > 0,
§ 7. Полнота
229
и сегмент, соединяющий х с z. Для этой точки'ж мы имеем
d (ah, z) + d (z, x) + d (x, q) = d (ah, z) + d (z, q) = d (ak, q),
откуда
d (ah, z) 4- d (z, x) = d (ak, x).
По лемме 7.2 существует сегмент, соединяющий ak с х. Таким
образом, для всех к
dh>d (z, х) > 0. (7.7)
С другой стороны, из условия (7.6) следует, что dh < 2d (ah, ak+i);
значит, dh -+ 0, и мы получаем противоречие. Следовательно,
не существует предельной точки z, т. е. С — луч. Теорема дока-
зана.
Заметим, что в этом рассуждении {аг} является фундаменталь-
ной последовательностью, не имеющей предельных точек. Этого
не может быть, если М полно. Поэтому справедлива
Теорема 7.2. В полном связном римановом многообразии
любые две точки р и q можно соединить геодезической длины d (р, q).
Иначе говоря, для любой точки р £ М отображение ехр ото-
бражает Тр на М.
Мы убедились в том, что если М полно, то геодезический поток
является полным. Теперь мы можем доказать обратное утвержде-
ние. Предположим, что геодезический поток является полным.
Это означает, что любая геодезическая может быть продолжена
на (—оо, оо), т. е. не существует луча конечной длины. Мы хотим
вывести отсюда, что М полно. Достаточно показать, что всякая
фундаментальная последовательность имеет предел. Пусть {яД —
некоторая фундаментальная последовательность. Из теоремы 7.1
(и из того, что в М не существует лучей конечной длины) следует
существование минимизирующей геодезической Сг, соединяющей
Хх с хг. Поскольку {гг} — фундаментальная последовательность,
d (ху, xt) сходится к некоторому числу d. С другой стороны, век-
торы Ci (0) С TXl (М) лежат на единичной сфере. Выберем сходя-
щуюся подпоследовательность {С^ (0)}, стремящуюся к векто-
ру v. Пусть х = С (d), где С — геодезическая, для которой
С' (0) = v. Тогда из полноты геодезического потока следует, что
Xi. —х. Таким образом, доказана
Теорема 7.3. Пусть М — связное риманово многообразие;
М полно (как метрическое пространство с метрикой d) тогда
и только тогда, когда геодезический поток полон.
230
Гл. IV. Вариационное исчисление
В заключение этого параграфа мы покажем, что любое много-
образие обладает полной римановой метрикой. Прежде всего
докажем следующее утверждение:
Лемма 7.3. Пусть М± и М2 — связные римановы многооб-
разия и f — изометрия Mi ->- М2, т. е. || Д (у) || = || v || для всех
v £ Т (М^. Тогда для любых р, q £ Mi мы имеем d (j (р), f (q))
< d (р, q).
Доказательство. Если С — кривая в Mit соединяю-
щая р с q, то / ° С соединяет / (р) с / (q). Но L [С] = L [f ° С].
Значит, d (р, q) = inf L [С] = inf L [f ° C] inf L [5], где В про-
бегает все кривые, соединяющие / (р) с / (q).
Теорема 7.4. Пусть М — дифференцируемое многообразие.
Тогда на М существует полная риманова метрика.
Доказательство. Пусть / — собственное вложение мно-
гообразия М в евклидово пространство EN (см. теорему 4.4 гл. II).
Пусть g = /* (ds2), где ds2 = dx{ + . . . + dx2N — евклидова мет-
рика в EN. По лемме 7.3 фундаментальная последовательность
{xj} в М отображается в фундаментальную последовательность
в EN. Поскольку En полно, a f — собственное отображение,
последовательность {а:г} сходится.
§ 8. ИЗОМЕТРИИ
Пусть М — риманово многообразие и т: М -> М — изомет-
рия, т. е. диффеоморфизм многообразия М на себя, сохраняющий
риманову метрику. Изометрия т будет, очевидно, сохранять и раз-
личные геометрические объекты, определяемые метрикой. Напри-
мер, если т*: Т (М) Т (М) — индуцированное отображение
касательного расслоения Т (М), то т* должно оставлять инвари-
антной геодезическую пульверизацию, т. е. (т*)* X = X и т*°6г =
= 6tot*, где X —геодезическая пульверизация, а 6 — геодезиче-
ский поток.
Теорема 8.1. Пусть Т — семейство изометрий риманова
многообразия М и S — множество неподвижных точек семейства
отображений Т (т. е. x(S в том и только в том случае, когда
хх = х для всех т£Т). Тогда S = U Nt, где каждое Nt является
подмногообразием в М. Кроме того, каждая точка р £ S обладает
окрестностью U в М с такими координатами х1, . . . , хп, в кото-
рых любое отображение т £ Т линейно.
$ 8. Изометрии
231
Пусть р £ S и U — нормальная окрестность точки р. Если
т 6 Т, то т° ехр (р) = ехр ° т* (и) для всех v £ ехр-1 U, посколь-
ку т — изометрия. Так как отображение т*: Т (М) -> Т (М)
линейно, это означает, что т линейно в нормальной системе коор-
динат. Множество неподвижных точек семейства линейных пре-
образований векторного пространства является линейным подпро-
странством. Поэтому S П U будет подмногообразием в U. Это
доказывает, что S есть объединение подмногообразий.
Отметим, что если S связно, то оно само будет подмногообра-
зием, а если S содержит кусок геодезической, то оно содержит
и всю геодезическую целиком.
Теорема 8.2. Пусть Т — конечная *) группа диффеомор-
физмов многообразия М и S — множество неподвижных точек
•относительно группы Т. Тогда S есть объединение подмногообра-
зий и любая точка р £ S обладает окрестностью U с координатами
. . . , хп, в которых любое отображение т £ Т линейно.
Достаточно показать, что Т есть множество изометрий для
некоторой римановой метрики. Пусть g— любая риманова метрика
на М (она существует по теореме 7.4). Тогда а=2 есть
гет
риманова метрика (так как сумма положительно определенных
билинейных форм положительно определена). Кроме того,
= 2 (0т)* g = 2 = а для ₽ С Т,
г£т тет
так что все т £ Т являются изометриями.
’) Читатели, знакомые с мерой Хаара, могут заменить конечность ком-
пактностью, а сумму — интегралом.
Глава F
ГРУППЫ ЛИ
Центральную роль в геометрии играют группы автоморфизмов различ-
ных структур. Часто эти группы обладают дифференцируемой структурой.
В этой главе мы изучим связь между алгебраическими и дифференциальными
свойствами таких групп.
§ 1. ОПРЕДЕЛЕНИЯ
Сейчас мы дадим основное определение.
Определение 1.1. Группа Ли есть дифференцируемое
многообразие G вместе с дифференцируемым отображением
<р: G X G -+ G, которое превращает G в группу. Иначе говоря,
<р удовлетворяет следующим условиям:
1) ср (а, ср (Ь, с)) = <р (<р (а, Ь), с);
2) существует такое е С G, что ср (е, Ь) = Ь для всех b g G;
3) существует дифференцируемое отображение G G, пере-
водящее а в а-1, которое удовлетворяет тождеству ср (а, а-1) = е.
Мы будем обозначать ср (а, Ъ) через ab.
Более сжато: группа Ли есть группа, наделенная такой струк-
турой дифференцируемого многообразия, в которой отображение
G X G G, определяемое формулой (х, у) ху~\ дифференци-
руемо. Действительно, отображение х -> х~х можно переписать
в виде (е, х) ех~\ так что условие 3) выполняется, а (х, у) -> ху
есть композиция двух дифференцируемых отображений (х, у) ->
(х, у-1) и (х, у-1) -> ху. Справедливо и несколько более силь-
ное утверждение:
Лемма 1.1. Пусть G — одновременно группа и многообразие,
причем отображение G X G —G, задаваемое формулой (х, у) —>-
->• ху, дифференцируемо. Тогда G есть группа Ли.
Мы должны показать, что если отображение (х, у) -> ху диффе-
ренцируемо, то и отображение х а:-1 дифференцируемо. Заме-
тим прежде всего, что достаточно доказать дифференцируемость
отображения х —а:-1 в некоторой окрестности N единицы е
группы G. Действительно, для любого а £ G отображение х -> ха
(которое мы обозначим 7?о) и отображение х -> ах (которое мы обо-
§ 1. Определения.
233
значим La) дифференцируемы. Но ж-1 = а (ха)-1, так что отобра-
жение х -> х-1 можно представить в виде композиции: х -> R^x ->
-> (Rax)-1 -> La (Rax)-1. Поэтому, выбирая а так, чтобы ха g N,
мы докажем дифференцируемость отображения х —>- х-1 в точке х.
Установим теперь существование указанной выше окрестности
N 3 е. Отображения Lx для всех х являются диффеоморфизмами
многообразия G на себя. В любой координатной окрестности еди-
ницы е отображение Lx дифференцируемо зависит от х (в терминах
локальных координат). Поэтому из теоремы о неявной функции
следует существование такой окрестности N единицы е, что
(Lx)-1y дифференцируемо зависит от х при всех х, у С N. В част-
ности, (Lx)-1 е = х-1 дифференцируемо зависит от х, т. е. ото-
бражение х х-1 дифференцируемо.
Теорема 1.1. Пусть G — группа Ли, М — дифференци-
руемое многообразие, f — такое взаимно однозначное погружение
М G, что
/ (х) f (у) е f (м) и (/ (х))-1 е / (м) (1.1)
для всех х, у Е М. Определим на М умножение, полагая ху =
= /-1 (/ (х) / (уУ)- Предположим, что это отображение непрерывно.
Тогда многообразие М с этим умножением является группой Ли.
Действительно, условие (1.1) означает, что / (М) есть под-
группа в G. Следовательно, отображение <р: М X М G, опре-
деленное формулой (х, у) -> / (х) / (у), дифференцируемо. Поло-
жим z (х, у) — }-1 (J (х) / (у)). Мы хотим показать, что отображение
<р: М X М-+М, переводящее (х, у) в z (х, у), дифференци-
руемо. Поскольку ср непрерывно, достаточно доказать существо-
вание такой окрестности U точки z (х, у), что для любой диффе-
ренцируемой на U функции g функция g ° ср дифференцируема
в точке (х, у). Так как / — погружение, мы можем найти окрест-
ность V точки / (z) с координатами и1, . . . , у” и окрестность U
точки z, такие, что f (U) состоит из тех точек окрестности V, для
которых Vм- = . . . = vn = 0, а функции х) и1, . . . , ир служат
координатами в U. Поэтому любую функцию g^aU можно продол-
жить до функции g на V, где g (v1, . . .,[vn)=g(v1,..., z?p,0,. . . , 0).
Следовательно, функция g° ср = g° <р дифференцируема, как
композиция дифференцируемых функций g и ср.
Оказывается, что предположение о непрерывности ср излишне,
см. § 3 ниже. Поэтому мы дадим следующее определение:
Определение 1.2. Пусть Gi и G2 — группы Ли, а / —
гомоморфизм Gi —> G2, являющийся взаимно однозначным погру-
х) Точнее, iAo/, .... vP°f.— Прим, перев.
234
Гл. V. Группы Ли
жением. Мы будем называть пару (Gi, /) подгруппой Ли группы
Ли G2. В общем случае дифференцируемое отображение Gi G2,
которое является групповым гомоморфизмом, называется гомо-
.морфизмом Ли.
Таким образом, подгруппа Ли группы Ли есть подгруппа в тео-
ретико-групповом смысле и одновременно погруженное подмно-
гообразие. Заметим, что, как мы скоро увидим на примерах, она
не обязательно является вложенным подмногообразием.
Примеры.
1) Векторное n-мерное пространство V, рассматриваемое как группа
по сложению, является, очевидно, группой Ли.
2) Прямое произведение любого числа групп Ли, снабженное структурой
прямого произведения групп и многообразий, является группой Ли.
3) Тор Тп, будучи прямым произведением п окружностей S1, является
группой Ли. Введем на Тп угловые «координаты» (0!, . . . , 0П) (где 0г опре-
деляются по модулю 1), так что 0г (р + д) = 0/ (р) + 0; (д). (Поскольку
умножение в Тп коммутативно, удобно обозначать его символом + .) Для
любых чисел (Х4, Х2) отображение /: R -> Т2, определяемое равенством / (<) =
= (XtZ, Х2«), является, очевидно, погружением и гомоморфизмом. Если
'(Х^, X2i) = (XiS, X2s), то Xj(s — t) = m, X2(s — <) = n для некоторых целых
чисел m и п, т. е. Xj/X2 = mln — рациональное число. Поэтому, если число
Xi/X2 иррационально, то (Я, /) есть подгруппа Ли в Т2. Легко видеть, что в этом
случае / (R) всюду плотно в Т2 и тем более / не является вложением.
4) Группа GL (п) является группой Ли.
5) Группа О (п) ортогональных матриц порядка п является группой Ли.
Действительно, A £ О (п) тогда и только тогда, когда A £ GL (п) и A At = I
(где А* — транспонированная матрица), т. е. А = (Л4)-1. Рассмотрим пре-
образование т: GL (п) GL (п), определяемое формулой т (В) = (В4)-1.
•Очевидно, что отображение т дифференцируемо и т2 (В) = (((В4)-1)4)-1 = В.
Поэтому тождественное отображение вместе с т образуют конечную группу
диффеоморфизмов многообразия GL (п). Согласно теореме 8.2 гл. IV, мно-
жество неподвижных точек преобразования т, т. е. О (п), является объеди-
нением подмногообразий из GL (п). Элементарные рассуждения показывают,
что О (п) имеет две связные компоненты, О (п) + иО (п)_, состоящие из матриц
•с определителем +1, соответственно —1. Поскольку О (п) + = О (п)~-А
для подходящей матрицы А, компоненты О (п)+ и О (п)~ имеют одинаковую
размерность и, значит, О (п) — вложенное подмногообразие в GL (п).
§ 2. ИНВАРИАНТНЫЕ ФОРМЫ И АЛГЕБРА ЛИ
Пусть G — группа Ли. Мы будем говорить, что дифференци-
альная форма Q, определенная на G, левоинвариантна, если
L*Q = Q для всех а £ G; аналогично, форма Q называется право-
инвариантной, если R*Q = й для всех а £ G. Если од и со2 —
лево(право)инвариантные формы, то такими же будут формы
оц Д ®2 и ^(01 + ссо2 Для любых констант b и с. Далее, L*dm =
= dL*m, так что вместе с со будет левоинвариантна и форма da>.
Другими словами, пространство лево(право)инвариантных форм
есть подалгебра алгебры всех форм на G, замкнутая относительно
$ 2. Инвариантные формы и алгебра Ли 235
оператора d. Мы обозначим эти подалгебры символами Ji (G)
(левоинвариантную) и Jr(G) (правоинвариантную).
Теорема 2.1. Пусть G—группа Ли и е — единица группы G.
’Отображение является изоморфизмом алгебры Ji(G)
на Л (ПО.
Это отображение ограничения, очевидно, является гомомор-
физмом. Мы хотим показать, что оно взаимно однозначно и является
отображением на. Прежде всего проверим взаимную однозначность.
Мы должны показать, что если со, со' £Ji(G) и сое = соё, то ®а = ®д
для всех aCG. Но (L*co)e = соа о Д (La*) и (L*co')e = соё ° Д (La*)-
Поскольку формы со и со' левоинвариантны, (L*co)e = ®е = ®е =
= (L*co')c, откуда соа о Д (La*) = соё ° Д (La*). Но Lajf есть взаимно
однозначное отображение пространства Te(G) на Ta(G). Следова-
тельно, ®а = ®ё-
Покажем теперь, что рассматриваемое отображение является
отображением на. Пусть а^ДТе(6). Определим форму со, полагая
<оа = а о Д (La-i*). Мы предоставим читателю проверить, что так
•определенная форма со будет дифференцируемой. Далее, сое = а и
(Lb(o)a = соЬа о (Д Lb*) = a ° Д (L(ba)-i*) ° Д (Lb*) =
= CZ ° /\ (La-1*) = ®д,
т. e. форма co левоинвариантна. Теорема доказана.
Согласно теореме 2.1, пространство левоинвариантных линей-
ных дифференциальных форм n-мерно (где п — размерность груп-
пы G). Пусть со1, . . . , соп — базис этого пространства. Тогда
dco* = 3 C*fecoj Дсо\ (2.1)
1 Д 3<Ь^П
поскольку формы dco* левоинвариантны. Применяя L* к обеим
частям равенства (2.1), мы получим, что C]k°La = C}k, т. е.
C]k— константы.
Эти константы называются структурными константами груп-
пы G. Уравнения (2.1) называются уравнениями Маурера —
Картана.
Пусть X — векторное поле на G. Мы скажем, что поле X
лево(право)инвариантно, если L*X = X для всех a^G (соответ-
ственно R*X = X). Если поля X и У левоинвариантны, то и поля
X + У и [X, У] левоинвариантны. Поэтому левоинвариантные
векторные поля образуют алгебру Ли. Пусть X — левоинвариант-
ное векторное поле м. Tt — порожденная им локальная однопара-
метрическая группа преобразований. В частности, Тtx определено
236
Гл. V. Группы Ли
для всех х из некоторой окрестности U единицы е и всех t из неко-
торого интервала I, содержащего нуль. Если точки х и у доста-
точно близки к е, а число t достаточно мало, то TtLyx и LyTtx
определены и совпадают: Tt (ух) = у (Ttx). Полагая х = е,
получим
Tty = yTte. (2.2)
Равенство (2.2) имеет место для всех у, близких к е, и t, близких
к нулю. Мы можем доопределить преобразование Tt так, чтобы
это равенство стало справедливым для всех t и у. Действительно,
для любого t С R выберем такое п, чтобы равенство (2.2) имело
место для tin, и определим Тгу как у (Tt/ne)n. Из единственности
решений дифференциальных уравнений следует, что это определе-
ние корректно. Далее, определим Ttz для любого z £ G, полагая
Ttz = z (Tte). Поскольку поле X левоинвариантно, оно является
инфинитезимальной образующей определенной таким образом одно-
параметрической группы преобразований. Отображение R->G,
задаваемое формулой f->- Tte, определяет однопараметрическую
подгруппу. Действительно, Tt+se = Tt (Tse) = (Tse) (Tte). Итак,
справедлива следующая
Теорема 2.2. Пространство левоинвариантных векторных
полей на G образует п-мерную алгебру Ли, которую мы будем
обозначать g. Любое X Е g порождает глобально определенную
однопараметрическую группу Tt преобразований многообразия G.
Кривая Tte является подгруппой Ли группы G, и для любого у £ G
выполняется равенство (2.2).
Мы не проверили только утверждение, что dim g = п. Это
следует из того, что отображение g —Те (G), переводящее X
в Хе, взаимно однозначно и является отображением на. (Дока-
зательство такое же, как для инвариантных форм.) Мы будем
иногда отождествлять g с Те (G). Пусть Xt, . . . , Хп — базис
пространства g. Пусть а1, . . . , ап —базис пространства Т* (G),
дуальный базису Xie, . , Хпе, и пусть со1, . . . , соп —лево-
инвариантные формы, соответствующие формам а1, . . . , ап.
Тогда
{Xt |со’’) = д{.
Согласно равенству (1.10) гл. III,
(XjAXft I d^)^Xj{Xh I СО4> — Хк{Х}\ со5)-<[*/, Хк},
Первые два члена правой части обращаются в нуль (как произ-
водные Ли от констант), и мы получаем равенство
{Xj/\Xk | dtp1) ——([Xj, Xh], co1).
<5 2. Инвариантные формы и алгебра Ли
237
С другой стороны, согласно формуле (2.1),
<Х/ДХЛ I I 2 cL®1 A®m> =
Поэтому при j<k имеем <[Xft, Xj], coi) = C)h или
ixk, = (2.3)
[Удобно определить Cljk для всех j, к, потребовав, чтобы Сд =
= —Ckj. Тогда (2.3) будет иметь место для всех j, /с.]
Пусть G, Н — группы Ли, а /: H-^-G—гомоморфизм Ли.
Отображение /*е: Те (Н) —> Те (G) можно рассматривать как линей-
ное отображение /„ алгебры Ли h группы Н в алгебру Ли g
группы G. Если х^Н, то i/(I)o/ = /o£I. Поэтому
Lf (х), he (Те (Я)) = /,х (Тх (Я)). (2.4)
Равенство (2.4) означает, что любое поле X £ h /-связано с /* (X)
(см. § 8 гл. II). Поэтому, согласно теореме 8.4 гл. II, для любых
X, Y С h справедливо равенство h ([X, У]) = [/* (X), /* (У)], т. е.
/*: h-+ g есть гомоморфизм алгебр Ли. В частности, Д (h) —
подалгебра алгебры Ли g.
Если гомоморфизм / взаимно однозначен, то ввиду формулы
(2.2) всякое левоинвариантное поле, касательное к подмногообра-
зию / (Н) в точке е, касается / (Н) во всех точках х g / (Я). Следо-
вательно, / (Я) есть интегральное многообразие дифференциаль-
ной системы, порожденной пространством /* {К) cz g векторных
полей на G.
Теперь мы в состоянии показать, как избавиться от предполо-
жения о непрерывности <р в теореме 1.1. Мы хотим доказать, что
отображение <р: М X М -* М дифференцируемо. Пусть gi —
касательное пространство подмногообразия / (ЛГ) в точке е.
Оно порождает подпространство левоинвариантных векторных
полей, которое мы будем также обозначать gj. Предположим, что
нам удалось доказать, что gi — подалгебра. Тогда дифференци-
альная система, порожденная gb будет вполне интегрируемой.
Из условия (1.1) следует, что / (ЛГ) есть максимальное интеграль-
ное многообразие этой дифференциальной системы. Согласно
условию (1.1), дифференцируемое отображение М X М G фак-
тически является отображением в / (ЛГ). Требуемый результат
следует теперь из упражнения 5.2 гл. III. То, что gl является
подалгеброй, вытекает также из условия (1.1), как мы увидим
в § 3.
Пусть gi — подалгебра в g. Она определяет вполне интегри-
руемую дифференциальную систему. Пусть 6Д — максимальное
238
Гл. V. Группы Ли
интегральное многообразие этой системы, проходящее через е.
Для любого у £ G преобразование Ly оставляет дифференциаль-
ную систему gi инвариантной и, следовательно, переводит любое
максимальное интегральное многообразие системы gi в макси-
мальное интегральное многообразие. Если у С Gi, то Ly~i у = е,
так что Ly-i переводит Gi в интегральное многообразие, проходя-
щее через е, т. е. в себя. Таким образом, если х, у £ Gi, то и
у-1х С Gi- Согласно теореме 1.1, отсюда следует, что Gi есть под-
группа Ли группы G.
Любое максимальное интегральное многообразие К этой впол-
не интегрируемой системы есть класс смежности по подгруппе Gi.
Действительно, поскольку система инвариантна относительно
левых сдвигов, любой левый сдвиг многообразия К снова будет-
максимальным интегральным многообразием. Но, сдвигая К
с помощью элемента, обратного к некоторому элементу из К,
мы получим максимальное интегральное многообразие, проходя-
щее через е. Значит, К есть класс смежности группы G по под-
группе Gi.
Теорема 2.3. Пусть и /2 — два дифференцируемых ото-
бражения связного многообразия М в группу Ли G, причем
= (2.5>
где {со1} — базис пространства левоинвариантных линейных форм
на G. Тогда отображения и f2 отличаются левым сдвигом,
т. е. существует такой элемент xQG, что f2 = Lxofi.
Доказательство. Рассмотрим прямое произведение G X G.
Пусть л4 и л2 — проекции группы G х G на первый и второй
сомножители. Формы л* (сог) и л* (сог) являются линейно независи-
мыми левоинвариантными формами на G X G. Формы л* (сог) —
—nJ (со1) определяют, очевидно, вполне интегрируемую систему .25,
которая соответствует диагональной подгруппе, состоящей из всех
элементов вида (х, х). Рассмотрим отображение h: M-^-GxG,
задаваемое формулой h (y) = (ft (у), f2 (у)) для всех ygM. Согласно
условию (2.5), h* (nJ (сог) — п* (со*)) =0. Следовательно, поскольку М
связно, h отображает М в максимальное связное интегральное
многообразие системы 3), т. е. в класс смежности по диагонали.
Поэтому существуют такие xt и x2Q G, что xtfi (у) = x2f2 (у) для
всех у £ М. Таким образом, Д и f2 отличаются сдвигом.
Следствие. Пусть G — связная группа Ли, a f — диффео-
морфизм группы G на себя, сохраняющий левоинвариантные формы.
Тогда / есть левый сдвиг.
Достаточно взять М = G.
§ 2. Инвариантные формы и алгебра Ли
239-
Теорема 2.4. Пусть G — группа Ли с левоинвариантными
формами со1, . . ., соп и структурными константами с}ь- Пусть
М — дифференцируемое многообразие и 01? . . . , 0П — линейно
независимые формы на М, причем
= (2.6>
Тогда для любой точки у£М существуют ее окрестность U
и диффеоморфизм /: U —> G, такие, что
со* = /*(9*). (2.7)
Два таких диффеоморфизма отличаются левым сдвигом. Если М
и G односвязны, то М диффеоморфно группе G.
Вторая часть теоремы немедленно следует из первой и тео-
ремы 2.3. Последнее утверждение вытекает из стандартных фактов
об односвязных пространствах. Поэтому нам остается доказать
только первую часть.
Вместо того чтобы строить само отображение М—>G, мы
построим его график. График любого отображения М—>G пред-
ставляет собой подмногообразие в М X G, проекция которого на
первый сомножитель является диффеоморфизмом. Пусть л( и л^—
проекции многообразия М '/.G соответственно на М и G. Положим
9г = л*9‘ и со* = л*со'. Проекция nt некоторого zz-мерного подмного-
образия К с.М '/.G на М будет локальным диффеоморфизмом,
если формы 91, ..., 9П линейно независимы на К. В этом случае
К будет (локально) графиком некоторого отображения М —>G. Это
отображение является (локальным) диффеоморфизмом, если проек-
ция Лг подмногообразия К на G есть (локальный) диффеоморфизм,
что имеет место, если формы со1, ..., соп линейно независимы на К.
Условие (2.7) принимает вид
= О на К, i=l, ...,п. (2.8)
Уравнения (2.8) определяют дифференциальную систему на М х G.
Эта система вполне интегрируема. Действительно,
d(0i_©i) = 24(9iA0'i-®iA®ft)= по (2.6)
= 3 4 (95Л(Ок -®'1) + (9’’ -^)Д®Й).
Следовательно, через каждую точку (у, х) £Мхб проходит
«-мерное интегральное многообразие К системы (2.8). Поскольку
формы 01, ..., 0П, со1, ..., соп линейно независимы, для каждой
точки z £ М х G формы 0z, ..., 6?, а также формы со*, ...,со",
линейно независимы на подпространстве пространства TZ(M '/.Gjr
240
Гл. V. Группы Ли
задаваемом уравнениями 6?— (о‘ = 0. Следовательно, многообразие К
определяет диффеоморфизм окрестности точки у £ М на окрестность
точки xQG, удовлетворяющий условию (2.7).
Таким образом, мы видим, что константы cjh действительно
определяют структуру группы G. Теоремы 2.3 и 2.4 можно рас-
сматривать как теоремы единственности: группа G (если она одно-
связна) определяется своими структурными константами. Естест-
венно возникает вопрос о соответствующей теореме существования:
существует ли группа «Ли с наперед заданными структурными
константами срЗ Заметим, что константы с}ь должны удовле-
творять определенным соотношениям. Они должны быть анти-
симметричны по /, к. Далее, применив к равенству (2.1) внешнее
дифференцирование, получим
0=3 cj’fe (^®3 A ®ft — ®’ A ^®ft) =
= 3 c3lm(olA(om/\a)k— 3c*m®’A®!A®m),
j<k Km (<m
откуда
3 (CjkPrl "b C/jCrfe) = 0. (2-9)
r
Мы предлагаем читателю проверить, что соотношения (2.9) можно
также рассматривать как необходимые и достаточные условия
того, чтобы умножение, задаваемое формулой (2.3), определяло
алгебру Ли; это как раз тождество Якоби.
Следовательно, вопрос надо сформулировать так: даны кон-
станты c}h, антисимметричные по / и к и удовлетворяющие соот-
ношениям (2.9); существует ли группа Ли, имеющая с}ь своими
структурными константами? Ответ на этот вопрос положителен.
Мы не будем это доказывать, поскольку это потребовало бы
довольно тонких алгебраических рассмотрений, выходящих за
рамки этой книги.
§ 3. НОРМАЛЬНЫЕ КООРДИНАТЫ, [ЭКСПОНЕНЦИАЛЬНОЕ
ОТОБРАЖЕНИЕ
Пусть G — группа Ли. Построим на G некоторую пульвериза-
цию. Мы должны определить векторное поле Z на Т (G). Для каж-
дого v С Т (G) существует единственное поле X £ g, такое, что
.Хлс») = v (другими словами, каждый касательный вектор в любой
точке G однозначно продолжается до левоинвариантного вектор-
ного поля на G). Тогда Т (X) (вариационное поле) есть векторное
поле на Т (G). Положим Zo = Т (Х)„. Мы предоставляем читате-
лю проверить, что отображение v Zo дифференцируемо и, следо-
.§* 3. Нормальные координаты, экспоненциальное отображение
241
вательно, определяет дифференцируемое векторное поле. Из опре-
деления вариационного поля Т (X) немедленно следует, что
n*Z,; = v и Ц;* (Zc) = (1/7) Zu если 0 t £ R. Следовательно,
поле Z является пульверизацией; мы назовем ее левоинвариант-
ной пульверизацией. Нормальные координаты этой пульвериза-
ции в точке е (определяемые экспоненциальным отображением)
называются нормальными координатами группы G.
Пусть X — левоинвариантное векторное поле и С — инте-
гральная кривая поля X. Кривая С' в Т (G) является тогда инте-
гральной кривой поля Т (X). Для любого t £ R имеем С (t) =
= Т (X) и л (С' (Z)) = Хс(ц, так что С" (f) == ZC'(t>- Другими
словами, С есть интегральная кривая поля Z, т. е. С — геоде-
зическая х) пульверизации Z.
Рассмотрим экспоненциальное отображение пульверизации Z
в точке е. Это дифференцируемое отображение пространства
Те (G) в G. Его можно рассматривать как отображение простран-
ства g в G. Если X 6 g, то кривая exp tX определяется как геоде-
зическая пульверизации Z, проходящая через точку е, с каса-
тельным вектором ХР. С другой стороны, согласно предыдущим
замечаниям, 7\е есть также геодезическая пульверизации Z,
имеющая в точке е касательный вектор Хе (где Tt — однопара-
метрическая группа преобразований, порожденная полем X).
В силу единственности имеем exp t Х-Л\е. Учитывая теорему 6.1
гл. IV, получаем следующее утверждение:
Теорема 3.1. Дифференцируемое отображение exp: g —G
является диффеоморфизмом некоторой окрестности нуля в g
на окрестность единицы в G. Для каждого X £ g отображение
t —> exp tX определяет однопараметрическую подгруппу Ли группы
G, и все гомоморфизмы Ли R —G имеют такой вид.
Остается доказать только последнее утверждение теоремы.
Пусть /: R —> G гомоморфизм Ли. Определим однопараметриче-
ское семейство Tt диффеоморфизмов многообразия G на себя,
полагая Ttx = z/ (Z). Тогда Tt+sx = xf (t + s) = xf (Z) / (s) =
= Ts (Ttx), так что Tt — однопараметрическая подгруппа. Кроме
того, yTtx = у (xf («)) = yxf (t), откуда LyTt = TtLy. Следова-
тельно, инфинитезимальная образующая X подгруппы Tt при-
надлежит g. Таким образом, / (i) = Тte = exp tX.
Пусть /: Gl—>G,— некоторый гомоморфизм Ли. Любое поле
X^gt /-связано с /»(X)gg2. Поэтому, если Tit — однопараметри-
ческая группа преобразований многообразия Giy порожденная
1) Кривая С на G называется геодезической пульверизации Z, если С
есть интегральная кривая поля Z.—Прим, перев.
С. Стернберг
242
Гл. V. Группы Ли
полем X, a T2t — однопараметрическая группа преобразований
многообразия (?2, порожденная полем /*(Х), то / о Гit — T2to f. При-
меняя это равенство к точке е, получаем
ехр °/# =/о ехр. (3.1)
Из формулы (3.1) вытекают разнообразные следствия.
Следствие 3.1. Любой взаимно однозначный гомоморфизм
Ли Gi—>G2 является погружением.
Действительно, если /*P(f) = 0 для некоторого 0 =# £ Тр (Gj),
то /#(Х) = 0, где Хе = Zp-i* (у) =0= 0. Но тогда ехр о Д (tX) =
= e = /(expiX). Так как X =£ 0, то ехр tX =£ е, и отображение /
не является взаимно однозначным.
Следствие 3.2. Любой непрерывный гомоморфизм, ср: R—>G
дифференцируем.
Ясно, что достаточно доказать дифференцируемость отображе-
ния ф вблизи нуля. Пусть U — нормальная окрестность единицы
е их1, .. ., х"— нормальная система координат. Если q — expXcjJ
и qm = expmX^U для 1<лг</с, то хг (qm) = тх' (<?), поскольку
х1 (ехр tX) = txl (ехрХ). Выберем е>0 столь малым, чтобы cp(i)gtZ
при всех 111 < е. Для любых 0 < t0 < е и 0 < | т | <п имеем
х1 ° ф (mt,0/n)=тхг оф (t0/n) и хг ° ф (t0/ri) = (1/п) х1 о ф (/0). Значит,
хг ° ф (mi0/n) = (mln) хг о ф (t0). По непрерывности хг о ф (rf0) = гх1 о ф (;„)
для всех |г |<1. Таким образом, отображение ф линейно в тер-
минах нормальных координат и, следовательно, дифференцируемо.
Посмотрим теперь, как выглядит умножение в нормальных
координатах. Пусть U — нормальная окрестность единицы,
Хь .. ., Хп — базис пространства g, а х1, . .., хп — соответствующие
нормальные координаты. Пусть V cs U — такая окрестность точки е,
что ab^U для всех a, b£V; другими словами, отображение
G X G —> G переводит V X V в U. Определим функции у1 и zL на
V XV формулами уг = хгол1; zl = xl ол2, где nj и л2 — проекции
множества V X V на первый и второй сомножители. Тогда у1, ...
. . ., уп, z1, . . ., zn образуют систему координат на V X V и в тер-
минах этих координат умножение задается формулами
х* = Д(/......уп; z1, ...,zn),
т. е. для любых a, b (IV
xi (ab) = (х1 (а), ..., хп(а)\ х1 (Ь), ..., хп (Ь)).
Найдем первые члены разложения Тейлора функций /*. Поскольку
еа = ае = е, имеем
Д(0, ..., 0; z\ ..., zn)^zl,
f(y\ ..., уп; 0, ..., 0) = у‘.
§ 3. Нормальные координаты, экспоненциальное отображение 243
Поэтому
/‘(у1, ..., уп', z1, ..., zn) = уг 4- z* + (члены второго порядка).
(3-2)
Это означает, что для У, Z£g
ехр t (У 4- Z) = ехр tY ехр tZ + О (<2). (3-3)
Вычислим теперь члены второго порядка. Пусть У = У у1Х,
и Z ~'^izlXi. При любом фиксированном я для любой функции ф
на G имеем
ф (ехр яУ ехр tZ) -=
= lim -г- [ф (ехр sY ехр tZ ехр hZ) — ф (ехр sY ехр tZ)] —
h-»0 й
= lim-T- [ф (Th ехр sY ехр tZ) — ф (ехр sY ехр tZ)],
h-+o
где Th — однопараметрическая подгруппа, порожденная полем Z.
Следовательно,
ф (ехр яУ ехр tZ) = 2ф (ехр яУ ехр tZ),
поскольку поле Z левоинвариантно. Итерируя это уравнение,
получаем
ф (ехряУ ехр tZ) = 2гф (ехр яУ ехр tZ).
В частности, по формуле Тейлора,
хг (ехр яУ ехр tZ) = хг (ехр яУ) +1 (Zxl) (ехр яУ) +
+ t2 (Z2xl) (ехр яУ) у О (t3).
Аналогично, для любой функции ф имеем
ф (ехр яУ) = (Уф) (ехр яУ).
Применяя эту формулу к правой части приведенного выше равен-
ства, получаем
хг (ехр яУ ехр tZ) = я (Ухг) (е) +1 (Zx1) (е) +
4- я2 (Y2xl) (е) -4 st (YZx*) (е) 4-t2 {Z2xl) (е) 4-
4- (члены третьего порядка). (3.4)
Итак,
/Чу1, ..., у”; z\ ..., 2п) = уЧгЧ^(е) +
4- YZx1 (е) -^-Z^ (е)4~ (члены третьего порядка). (3.5)
16*
244
Гл. V. Группы Ли
В частности,
Й/, .... уп; Л zn; У\ ..., уп) =
= [У, Z] хх {е) + (члены третьего порядка). (3.6)
Формула (3.3) означает, что Xх (exp Y expZ) = хг (ехр У) (exp Z)+
+ (члены второго порядка). Поэтому для (a, b)£V ХУ имеем
х1{аЬ) — х1{а) — х1{Ь) = ^gijh(a, b) х] (а) з? (&), (3.7)
где gijk — дифференцируемые функции на V X У. Полагая в фор-
муле (3.7) a = cd и b = d~1c'idc, получаем
Xх {de) — хх {cd) — Xх {d^c^dc) = 2 gijk {cd, d~xc~r de) x* {cd) 'Y {d~lc~r de).
Но член xx{d~lc^1dc) равен нулю, если либо d, либо с равно е, и,
следовательно, является членом не ниже второго порядка. Таким
образом,
Xх {d^r1 de) = Xх {cd)—У (de)(члены третьего порядка).
Полагая в формуле (3.6) с = ехр У и d = expZ, получаем1)
хх ((ехр Z)’1 (ехр У)-1 (ехр Z) (ехр У)) =
~ хх (ехр [У, Z]) + (члены третьего порядка). (3.8)
Далее, d{d~1c~1dc) ^c^dc. Полагая в формуле (3.7) a — d, b — d^c^dc
и замечая, что У (d-1c-1dc) есть член не ниже второго порядка,
мы получаем
Xх (c^dc) = Xх {d)~^xx {d~lc~xdc) у (члены третьего порядка).
Полагая с = ехрУ, d = ехрZ и используя формулу (3.6), находим
хг ((ехр У)-1 ехр Z ехр У) =
= хх (Z) у хх (ехр [У, Z])-|-(члены третьего порядка). (3.9)
Для любого х £ G обозначим символом А {х) внутренний авто-
морфизм, соответствующий элементу х. Таким образом, А {х): G ->
-> G есть изоморфизм Ли, определяемый формулой
А {х) у = х~1ух. (3.10)
Тогда равенство (3.9) можно переписать в виде
хх [А (ехр У) expZ] =
= хх {Z) -[-У (ехр [У, Z])(члены третьего порядка). (3.11)
Выведем теперь из равенств (3.2) — (3.11) несколько след-
ствий.
1) Напомним, что по определению У (ехр W) = (1УУ) (е) для любого
поля W g g.
§ 3. Нормальные координаты, экспоненциальное отображение
245
Лемма 3.1. Пусть g = V\ + . . . + Vk — разложение ал-
гебры g в прямую сумму векторных пространств. Для любого
X £ g, где X = Xi + . . . + Xk (Х, £ V;), положим
Ф (X) = ехр Xi ехр Х2 • ехр Xh. (3.12)
Определенное так отображение <р: gG является диффеомор-
физмом некоторой окрестности нуля в g на окрестность еди-
ницы в G.
Очевидно, что ф — дифференцируемое отображение. Согласно
формуле (3.2), ф (X) = ехр (Xt + . . . + Xh) + (члены второго
порядка). Следовательно, отображение ф„: То (g) -+ Тг (G) совпа-
дает с отображением 10 (теорема 6.1 гл. IV), т. е. ф — локальный
диффеоморфизм.
Теорема 3.2. Любой непрерывный гомоморфизм / группы
Ли Gi в группу Ли G2 является дифференцируемым.
Используя сдвиги, достаточно доказать, что отображение /
дифференцируемо в окрестности единицы е. Пусть Х1г . . . , Хп —
базис алгебры Ли g\ группы Ли и пусть / — гомоморфизм
Gi —> G2. Тогда отображение t —>- / (ехр tXt) является непрерыв-
ным гомоморфизмом R -+ G2 и, значит, дифференцируемо (соглас-
но следствию 3.2). Поэтому в алгебре Ли g2 группы G2 существуют
такие элементы Уг, что / (ехр t Хг) =ехр tY>. Поскольку /—
гомоморфизм, имеем
/ ((ехр ijXj) (ехр t2X2) . . . (ехр tnXn)) =
= (ехр tiYi) . . . (ехр tnYn). (3.13)
Отображение F: gi~+G2, переводящее X = GXj + • • • + tnXn
в (ехр tiYi) . . . (ехр tnYn), очевидно, дифференцируемо. Равен-
ство (3.13) показывает, что F = f ° ф (где ф — отображение, зада-
ваемое формулой (3.12) и соответствующее разложению g =
= {X!} + • • • + {Хп}). Согласно лемме 3.1, отображение ф
вблизи нуля является диффеоморфизмом. Поэтому в некоторой
окрестности единицы / = F° <р~г, и, значит, отображение / диф-
ференцируемо.
Из теоремы 3.2 следует, что топология группы Ли определяет
ее дифференцируемую структуру: если Gt и G2 — группы Ли и / —
гомеоморфизм и гомоморфизм группы Gt на G2, то / является
диффеоморфизмом.
Рассмотрим более подробно равенства (3.10) и (3.11). Для
любого х £ G преобразование А (х) оставляет точку е неподвиж-
ной и, значит, индуцирует преобразование A (z)*: Те (G) -> Те (G).
Если х, у £ G, то А (ху) = А (х) А (у), и, следовательно
246
Гл. V. Группы Ли
А (ху)*=А (ж)» А (у),. Следовательно, хА (х)* есть представ-
ление группы G линейными преобразованиями пространства g.
Определение 3.1. Линейное представление х -> А (х),
называется присоединенным представлением. Линейное преобра-
зование А (х), мы будем обозначать символом Ad х.
Пусть X и Y — элементы из g. Согласно (3.11), кривая ехр (sX)
переходит при отображении А (ехр tY) в ехр (sX + st [У, X})
с точностью до членов третьего порядка по s и t. Таким образом,
4-Аа(ехр«У)Х|<=0 = [У, X]. (3.14)
Определение 3.2. Представление алгебры Ли g линей-
ными преобразованиями пространства g, определяемое левым
умножением, называется присоединенным представлением алгебры
Ли g. Таким образом,
(Ad У) X = [У, X].
Согласно сделанным замечаниям, имеем
Ad (ехр У) X = ехр (Ad У) X. (3.15)
4. ЗАМКНУТЫЕ ПОДГРУППЫ
Используя результаты предыдущего параграфа, мы докажем
следующую теорему:
Теорема 4.1. Пусть G — группа Ли и Н — замкнутое
подмножество в G, являющееся (алгебраически) подгруппой. Тогда
Н есть подгруппа Ли в G. [Короче, любая замкнутая подгруппа
группы Ли есть подгруппа Ли.]
Согласно теореме 1.1, для того, чтобы доказать, что Н есть
группа Ли, достаточно проверить, что Н есть подмногообразие
в G. Для этого достаточно показать (согласно упражнению 2.4
гл. II), что любая точка р Е G обладает такой окрестностью U,
что U П Н есть подмногообразие в U. Если р $ Н, то ввиду зам-
кнутости подгруппы Н существует такая окрестность U, что
U П Н = 0. Если р ЕН, то, воспользовавшись тем, что Н —
подгруппа, и умножив все слева на р-1, мы сведем задачу к слу-
чаю, когда е Е Н. Итак, достаточно доказать, что
существует такая окрестность U единицы е в G, что
U П Н есть подмногообразие в U.
Мы возьмем в качестве U достаточно малую нормальную
окрестность. Если Н действительно есть замкнутая подгруппа Ли,
то мы можем ожидать, что пересечение U [\ Н имеет вид
§ 4. Замкнутые подгруппы 247
ехр (7 П К), где V — окрестность нуля в g, a h — алгебра Ли
группы Ли Н. Построим прежде всего алгебру Ли группы Н.
Лемма 4.1. Пусть Н — замкнутая подгруппа в G и h —
множество всех X £ g, для которых ехр tX 6 Н при всех t £ R.
Тогда h — подалгебра алгебры Ли g.
Ясно, что если X £ h, то sX £ h, поскольку ехр t (sX) —
= ехр tsX. Чтобы доказать замкнутость множества h относительно
сложения и умножения Ли, удобно воспользоваться следующей
леммой:
Лемма 4.2. Пусть {Хг} — последовательность элементов
из g, причем Xi -> X, и пусть ti -* 0 — последовательность отлич-
ных от нуля вещественных чисел. Если ехр tiXi £ Н для всех I.
то ехр tX £ Н для всех t, т. е. X £ h-
Заметим, что, поскольку ехр (—£гХг) = (ехр ^-Хг)-1 £ И, мож-
но считать, что i; > 0. Точно так же, достаточно доказать, что
ехр tX g Н только для t > 0. Для каждого t > 0 положим
= (наибольшее целое число, не превосходящее .
Тогда
откуда
lim tiki (t) = t.
i-+oo
Так как exp ?гХ£ £ H, то ехр kt (t) tiXt = (ехр i£X£)ft<(/> С Н. Но
lim kt (i) tiXi = tX, и ввиду замкнутости подгруппы Н и непрерыв-
нее.
ности отображения ехр имеем ехр tX £ Н, что и доказывает
лемму 4.2.
Докажем теперь лемму 4.1. Пусть X, Y £ h. Тогда
ехр tX ехр tY 6 П. С другой стороны,
ехр tX ехр tY = ехр (t (X + У) + tZt),
где Zt 0 при t -> 0. Выберем последовательность tt положи-
тельных чисел, сходящуюся к нулю, и положим Xi = X + У +
4- Z(.. Применяя лемму 4.2, заключаем, что X -{- У g h. Ана-
логично,
(ехр tX) (ехр tY) (ехр tX)'1 (ехр tY)"1 = ехр (i2 [X, У] у t2Zt),
откуда [X, У] g h. Это доказывает лемму 4.1.
Теперь мы хотим доказать существование такой окрестности
U единицы е, что U Q Н = ехр h (~| U. Для этого выберем под-
пространство, скажем h', дополнительное к h в g, т. е. g = h 4- h'.
248
Гл. V. Группы Ли
Лемма 4.3. Существует такая окрестность V' нуля в h',
что из О ф X' £ V следует, что ехр X' $ Н.
Выберем в h' евклидову метрику. Пусть К — множество всех
X' (zh', для которых 1 || X' || 2. Если лемма 4.3 не верна,
то существует последовательность Уг->0, Y&h',
Ясно, что можно выбрать целые числа и; так, чтобы Хг = ге;Уг £
£ К. Поскольку К компактно, можно считать (переходя в случае
надобности к подпоследовательности), что Xt -> X 0. Кроме
того, (1/иг) —> 0 и ехр (1/иг) X, 6 Н. Из леммы 4.2 следует тогда,
что X 6 h, что противоречит определению подпространства h'.
Пусть теперь W — окрестность нуля в g, для которой
отображение <р: gG, определяемое формулой <р: (X + X') =
= ехр X' ехр X (X' g h', X g h), является диффеоморфизмом
(см. лемму 3.1). Можно считать, что W имеет вид W X W", где
W"cz h и W cz V'. Положим U = <р (И7). Если х £ U, то х =
= ехр X' ехр X, где X g h, X' g h'. Если х £ U П Н, то
ехр X' ехр X 6 Н, откуда ехр X' £ Н, поскольку ехр X £ Н и
Н — группа. Значит, X' = 0. Другими словами, U (~| Н =
= U П ехр h, что и доказывает теорему 4.1.
Заметим, что в ходе доказательства мы установили, что не толь-
ко Н, но и G/Н обладает дифференцируемой структурой. Точнее,
справедлива
Теорема 4.2. Пусть G — группа Ли и Н — замкнутая
подгруппа. Тогда G/Н обладает единственной дифференцируемой
структурой, в которой
(i) проекция л: G -* G/Н дифференцируема-,
(ii) для любой точки р £ G/Н существуют окрестность W J р
и дифференцируемое отображение <р: W —> G, такие, что л ° <р =
= id.
Левые сдвиги на элементы из G являются диффеоморфизмами
многообразия G/H.
Заметим сначала, что последнее утверждение теоремы спра-
ведливо для любой дифференцируемой структуры на G/Н, удо-
влетворяющей условиям (i) и (ii). Действительно, левый сдвиг
на z4 является обратным отображением к левому сдвигу на z,
так что достаточно доказать, что левые сдвиги дифференцируемы.
Пусть р £ G/H, a W, ф — такие, как в условии (ii). По определе-
нию zq = л (zip (g)) для любого q £ W. Таким образом, левый сдвиг
на z представим в окрестности W в виде композиции л ° Lz ° ф
дифференцируемых отображений, и, следовательно, дифферен-
цируем.
Из этого замечания следует также, что достаточно доказать
существование и единственность дифференцируемой структуры
J 4. Замкнутые подгруппы
249
в одной точке р g G/Н. Действительно, если существует система
координат в окрестности U точки р, то, применяя левые сдвиги,
мы получим систему координат в окрестности любой точки. Из (i)
и (ii) (на U) следует тогда, что таким образом на G/Н определяется
(единственная) дифференцируемая структура.
Поэтому мы будем доказывать существование и единственность
такой структуры в окрестности класса смежности единицы еН.
В качестве окрестности W возьмем проекцию окрестности U точки
е, построенной при доказательстве леммы 4.3. Каждая точка х g U
однозначным образом записывается в виде х = ехр X' ехр X.
Другими словами, существует корректно определенное отображе-
ние о: Wh', переводящее хН в X'. Поэтому выбор системы
координат на h' определяет координаты на W. Кроме того, ото-
бражение ф = ехр ° о: W —> U, очевидно, дифференцируемо и удо-
влетворяет условию (ii). Отображение <р: g —> G, переводящее
X 4- X' в (ехр X') (ехр X), является диффеоморфизмом некоторой
окрестности нуля на U. Следовательно, отображение р: U —> h',
переводящее х = (ехр X') (ехр X) в X', дифференцируемо. Но
л = н-10 р, и так как о определяет дифференцируемую структуру
на W, проекция л дифференцируема. Это доказывает существова-
ние дифференцируемой структуры на G/Н, удовлетворяющей
условиям (i) и (ii).
Для доказательства единственности предположим, что W
имеет две дифференцируемые структуры с координатными отобра-
жениями ffj и о2 и отображениями ф! и ф2 в G. Мы хотим показать,
что отображение о,о'1 дифференцируемо. Но що'1 = о^лф^'1.
Поскольку din есть дифференцируемое отображение группы G
в Ек (согласно (i)), а отображение фгО"1 дифференцируемо (соглас-
но (ii)), отображение ощ"1 дифференцируемо, что и доказывает
теорему 4.2.
В дальнейшем нам понадобится следующая
Лемма 4.4. Пусть G — группа Ли, Н — топологическая
группа г), f — непрерывный гомоморфизм Н -+ G. Тогда существу-
ет единственная наименьшая алгебра Ли h, такая, что если У —
любая окрестность нуля в h, то / (£7) cz ехр V для всех достаточно
малых окрестностей U точки е в Н.
Ясно, что в качестве h можно взять пересечение всех подалгебр,
обладающих указанным свойством (поскольку пересечение под-
пространств конечномерного пространства сводится к конечному
пересечению).
!) Топологической группой называется группа Н, снабженная струк-
турой топологического пространства, в которой групповые операции непре-
рывны, т. е. отображение Н X Н -> Н, переводящее (х, у) в ху1, непрерывно.
250
Гл. V. Группы Ли
Можно дать алгебре h более геометрическую характеристику:
Упражнение 4.1. Показать, что X С h тогда и только тогда, когда
существуют последовательность hi е в Н и последовательность чисел щ ->
-> оо, такие, что X=lim щ ехр-1/ (Лг). Таким образом, h есть пространство
«предельных направлений» подгруппы / (Я). [Доказательство аналогично
доказательству леммы 4.1.]
$ 5. ИНВАРИАНТНЫЕ МЕТРИКИ
Прямые евклидова пространства Еп можно охарактеризовать
двумя способами. С одной стороны, они служат геодезическими,
т. е. минимизируют длину. С другой стороны, они являются клас-
сами смежности однопараметрических подгрупп группы Ли Еп.
Оказывается, что это не случайно, а следует из того, что правые
и левые сдвиги являются изометриями для евклидовой метрики.
Сейчас мы установим этот результат в общем случае.
Определение 5.1. Пусть G — группа Ли. Риманова
метрика а на G называется биинвариантной, если Lx и Rx являют-
ся изометриями относительно а для всех х £ G.
Заметим, что если а — биинвариантная метрика на G, то А (х)
есть изометрия при любом х g G. Действительно, А (х) = Rx-iLx.
Отображение G —G, переводящее х в х~г, также является изо-
метрией. В самом деле, это отображение переводит каждый вектор
в точке е в противоположный и, следовательно, сохраняет длину
в Те (G). Покажем, что оно является изометрией в любой точке
у g G. Для этого представим отображение х —х-1 в виде х -*
->-ху-1->- (ху-1)-1 == ух-1-> уД/х-1 = х-1. Поскольку Lri и Ry-i —
изометрии, достаточно проверить, что ху-1 —>(ху-1)_1 есть изомет-
рия в точке х = у, что мы уже сделали.
Теорема 5.1. Пусть а — биинвариантная риманова мет-
рика на группе Ли G. Тогда каждая геодезическая получается
левым сдвигом из некоторой однопараметрической подгруппы,
и обратно.
При доказательстве теоремы 5.1 достаточно (учитывая возмож-
ность применения левых сдвигов) ограничиться рассмотрением
окрестности точки е. Мы хотим показать, что любая геодезиче-
ская, проходящая через е, является однопараметрической под-
группой, и обратно. Для этого сформулируем следующую лемму.
Лемма 5.1. Пусть а — изометрия риманова многообразия
М, причем о2 = id. Пусть х — изолированная неподвижная точка
изометрии о. Пусть U — окрестность точки х с однозначными
§ 5. Инвариантные метрики
251
геодезическимих), не содержащая других неподвижных точек.
Если у g U и о (у) £ U, то геодезическая, соединяющая у с а (у),
проходит через х.
Пусть у — геодезическая, соединяющая у с о (у). Так как
ст2 = 1, то о (у) есть геодезическая, соединяющая ст (у) с у. Значит,
а отображает у на себя, обращая направление. Поэтому на у
должна существовать неподвижная точка, и этой неподвижной
точкой может быть только х.
Применим лемму 5.1 к следующей ситуации: пусть z £ G —
точка, близкая к е, и пусть z (i) — (единственная) однопарамет-
рическая группа, соединяющая е с z, для которой z (1) = z.
Положим х = z (1/2) и определим отображение о формулой
от (у) == ху^х. Тогда о2 (у) = х (ху^х)"1 х = у, так что о2= id
и о есть изометрия. Если о (у) = у, то ху~гх = у и (у-ха;)2 = 1.
Но если точки у и х достаточно близки (в частности, если они обе
близки к е), то отсюда следует, что у = х. Поэтому х — изолиро-
ванная неподвижная точка изометрии о.
Далее, a (z) = x2z~1 = е. Следовательно, геодезическая, соеди-
няющая е с z, проходит через х. Повторяя эти рассуждения для
обеих половинок кривой z (t), мы докажем, что геодезическая,
соединяющая е с z, содержит z (г) при любом г = р/2п. По непре-
рывности отсюда следует, что z (£) — геодезическая.
Итак, любая однопараметрическая подгруппа является геоде-
зической. Но это означает, что экспоненциальное отображение
геодезической пульверизации метрики а в точке е совпадает
с экспоненциальным отображением ехр левоинвариантной пуль-
веризации на группе G, что и доказывает теорему 5.1.
Рассмотрим теперь вопрос о существовании биинвариантной
метрики на группе Ли. Задав произвольное скалярное произведе-
ние (v, w) в g=Te (G), мы можем продолжить его левыми сдви-
гами до римановой метрики на G, т. е. для любых и, w£Tx(G)
определить (у, w)x по формуле (и, w)x = (Lx-i*v, Lx-i*w). Ясно,
что эта метрика инвариантна относительно левых сдвигов. Как
обстоит дело с правыми сдвигами? Для инвариантности мы должны
иметь (RXsy, Rx*w)x = (у, w) для всех и, wGg и x^G. Но
(7?х*к, Rx*w)x = (Lx-4Rx*v, Lx-i*Rx*w) и Rx*Lx-i* = Мх. Таким
образом, мы должны иметь
((Ada;) v, (Adz)zz>) = (к, и>). (5.1)
Обратно, если условие (5.1) выполняется для всех х С G, то ска-
лярное произведение (и, ю) продолжается до биинвариантной
метрики на G. Итак, доказана
х) То есть любые две различные точки из U соединяются единственной
геодезической, лежащей в U.— Прим, перев.
252
Гл. V. Группы Ли
Л е м м а 5.2. Пусть ( , ) — скалярное произведение на g.
Для того чтобы оно продолжалось (с помощью левых сдвигов) до
биинвариантной метрики на G, необходимо и достаточно, чтобы
оно было инвариантно относительно присоединенного представле-
ния, т. е. чтобы выполнялось условие (5.1).
Таким образом, мы столкнулись со следующей задачей: дано
представление р группы Ли G (в частности, присоединенное пред-
ставление) в векторном пространстве V; в каком случае на V
существует инвариантное скалярное произведение? Другими сло-
вами, когда на V существует (положительно определенное) ска-
лярное произведение ( , ), для которого
(р (х) v, р (х) w) = (v, w) (5.2)
при всех х £ G и и, w £ 7?
Заметим, что ортогональная группа компактна (упражнение!).
Если р (G) сохраняет ( , ), то р (G) есть подгруппа ортогональной
группы, определяемой скалярным произведением( , ), и, следо-
вательно, р (G) компактно.
Обратно, предположим, что р (G) = Н есть компактная под-
группа группы всех невырожденных линейных преобразований
пространства V. Тогда, согласно теореме 4.1, Н — группа Ли.
Мы хотим найти такое скалярное произведение ( , ) на V, что
(hv, hw) = (v, w) для всех v, w £ V, h £ Н. Для этого рассмотрим
форму Q = ®i Д . . . Д <ofe, где со±, . . ., сщ — базис простран-
ства левоинвариантных линейных форм на Н (k = dim Н).
Поскольку форма Q нигде не обращается в нуль, она определяет
ориентацию на Н. Поэтому для любой непрерывной функции
/ на Н мы можем рассмотреть интеграл /Q. Пусть ( , )о —
н
любое положительно определенное скалярное произведение на F.
Положим
(к, w) = § (хи, xw)0Q. (5.3)
x£G
Мы оставляем читателю проверку того, что ( , ) есть инвариант-
ное положительно определенное скалярное произведение на V.
Итак, доказана
Теорема 5.2. Пусть р — линейное представление группы
Ли G в векторном пространстве V. Для того чтобы V обладало
инвариантным относительно G скалярным произведением, необ-
ходимо и достаточно, чтобы р (G) было компактно. В частности,
если G компактна, то для любого представления р всегда существует
инвариантное скалярное произведение.
§ 6. Формы со значениями в векторном пространстве
253
Упражнение 5.1. Показать, что любое представление компактной
группы Ли вполне приводимо.
У пражнение 5.2. Пусть G — компактная группа Ли, действующая
дифференцируемым образом на многообразии М. Показать, что на М сущест-
вует риманова метрика, для которой G — группа изометрий (и, таким обра-
зом, мы можем применять теорему 8.2 гл. IV).
Из леммы 5.2 вытекает
Теорема 5.3. Пусть G — группа Ли. Для того чтобы G
обладала биинвариантной римановой метрикой, необходимо и до-
статочно, чтобы Ad (G) было компактно. В частности, любая
компактная группа Ли обладает биинвариантной метрикой.
В качестве следствия получаем
У пражнение 5.3. Пусть G — компактная связная группа Ли.
Тогда каждая точка х £ G принадлежит некоторой однопараметрической
подгруппе. [Для некомпактных групп Ли это, вообще говоря, не верно.]
§ 6. ФОРМЫ СО ЗНАЧЕНИЯМИ В ВЕКТОРНОМ ПРОСТРАНСТВЕ
Удобно распространить теорию дифференциальных форм на
формы, принимающие значения в векторном пространстве. До сих
пор мы рассматривали только такие линейные дифференциальные
формы на М, которые определяют на каждом касательном про-
странстве Тх (М) вещественный линейный функционал (диффе-
ренцируемо зависящий от точки х). Теперь мы хотим рассматри-
вать линейные отображения каждого касательного пространства
в фиксированное векторное пространство W. Так, например,
в случае, когда G есть группа Ли, мы определили левоинвари-
антные формы СО), . . ., соп, соответствующие некоторому выбору
базиса алгебры Ли g. Эти формы неудобны тем, что они зависят
от выбора базиса. Однако существует корректно определенная
векторнозначная форма со, которая сопоставляет каждому каса-
тельному вектору v £ Тр (G) элемент из g (рассматриваемый как
левоинвариантное векторное поле), принимающий в точке р
значение и. Естественно ожидать, что структурные уравнения
группы G в терминах формы со примут особенно простой вид,
и это действительно так. Разовьем сначала необходимый фор-
мализм.
Пусть М — многообразие и W — конечномерное векторное про-
странство. Под Позначной дифференциальной формой степени q
мы будем понимать элемент пространства W® (М). Другими
словами, Позначная дифференциальная форма Q есть линейное
отображение /\ДХ (М) —»W, определенное при каждом xGM
(и дифференцируемо зависящее от х), т. е. элемент из И7 ®/V7’* (7И)
254
Гл. V. Группы Ли
для каждого х£М. Множество всех Ж-значных дифференциаль-
ных ^-форм образует векторное пространство и, более того, модуль
над кольцом дифференцируемых функций на М. Мы будем
обозначать это пространство через /\w(M), а пространство всех
Ж-значных дифференциальных форм — через f\w(M). Таким обра-
зом, /\w(M) = • • • +
Пусть дано векторное поле X на М. Мы можем определить
очевидным образом линейные отображения Хх~- /\w (7И)
и внутреннее умножение на X, отображающее /\qw(M) в /\qvl(M).
Кроме того, мы имеем оператор d: /\w (М) -> Аж1 (Л/), который
удовлетворяет соответствующим соотношениям § 1 гл. III. Всякое
отображение ср: Mt—>М2 индуцирует линейное отображение
ср*: /\w (ЛГ2) —>f\w (Mj) и т. п. Все эти определения и утверж-
дения можно аккуратно сформулировать, выбрав базис , ek
пространства W. Тогда любая форма Q £ /\w (7И) может быть
записана в виде Q = 2 ® «г, где Q, — (вещественнозначные)
внешние дифференциальные формы. Положим, например, dQ =
= 2 d£lt ® et- Непосредственная проверка показывает, что это
определение не зависит от выбора базиса eit . . ., eit. Точно так же
можно поступить с остальными утверждениями.
Пусть Wf и W2 — векторные пространства и I — линейное ото-
бражение —>IF2. Тогда существует очевидное линейное ото-
бражение l#: Ясно, что Z# коммутирует
со всеми уже упоминавшимися операциями. Так, I* dQ = dU+Q,
fai%xQ = Xxl#tl и т. д.
Пусть W\, W2 и РКз— три векторных пространства и р — били-
нейное отображение И\ X —>ГИ3. Определим билинейное отобра-
жение р#: АгИ1 (М) X Лж2 (М) —» Агк3 (-ZW) следующим образом.
Пусть е4, ..., ей — базис в Wt, a fa, ..., fa— базис в W2. Пред-
положим, что со = 2 «мг е Avn (М), a q = 2 Sih G Лж2 (М).
Положим
Р#(СО, Й) = 2 СО; A ® Р (е;, fa). (6.1)
Легко проверить, что определение (6.1) не зависит от выбора,
координат. Из (6.1) следует, что
cZp# (со, Q) = р# (dco, Q)4- (— l)9p# (со, dQ), (6.2)
если со — форма степени q. Кроме того,
35 хр# (со, £2) = р^ (JC^co, Q) Рзф (со, JC^Q) (6 3)
§ 6. Формы со значениями в векторном пространстве
255
для любого векторного поля X на М. Если ср: N->М — отобра-
жение многообразий, то мы имеем
Ф*Р# (со, Й) = р# (ф*ю, ф*Й). (6.4}
В дальнейшем мы будем часто иметь дело с двумя важными
частными случаями, поэтому введем для них специальные обозна-
чения. Пусть W = Wi = W2 — W3 — алгебра Ли и р — скобка Ли.
В этом случае мы будем обозначать рц (coj, со2) символом [с01Лсо2]*
Если соц и со2 — формы степени соответственно р и q, то
[со1Асо2] = (-1)Р9+1[со2Асо1]. (6.5}
[Множитель (— 1)Р9 возникает из закона умножения в Д(М),
а (— 1) — из антикоммутативности скобки Ли.] Если со2 и со3 —
формы степени р, q и г, то тождество Якоби принимает вид
(— 1)рг [<»! А [<»2 А со3]] А (— 1)м [со2Л [®зA®d] А
А (— 1)Г9 [со3 Л [®2Л со4]] = 0.
Другой важный для нас случай — когда W2 = WS = V—векторное
пространство, a — некоторое векторное пространство линейных
преобразований пространства V. Таким образом, есть под-
пространство пространства V ® V*. В этом случае мы будем обозна-
чать р#(со4, со2) просто через cojA^.
Вернемся к группе Ли G и ее фундаментальной g-значной
форме со. Пусть щ, ..., еп — базис алгебры g, так что со = со1®
® ei А • • • Ай" ® еп, где со1 — базис пространства левоинвариант-
ных форм. Согласно формуле (2.1),
А)1 У СДо’ЛоД
i<k
так что
сйо = 3 Cjftco’Acoft ® ег.
С другой стороны, формула (2.3) дает [ek, ej] = У] C^et- Значит,
в соответствии с формулой (6.1)
[соЛю]= 3 coftAco’8
с, j, k
Сравнивая эти два выражения (заметим, что / и к меняются
местами и что первая сумма берется по j А к, а вторая — по всем
/, к), получаем структурные уравнения группы G в следующем
виде:
dco=-у[соЛю]- (6.6)
Глава VI
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
ЕВКЛИДОВА ПРОСТРАНСТВА
В этой главе мы будем изучать дифференциальную геометрию подмного-
образий евклидова пространства и, в частности, двумерные поверхности в Е3.
Естественно ожидать, что много информации может дать изучение группы
евклидовых движений (п). И действительно, большинство уравнений клас-
сической дифференциальной геометрии оказываются прямыми следствиями
структурных уравнений группы <f (п). Поэтому мы начнем с изучения этой
группы.
§ 1. СТРУКТУРНЫЕ УРАВНЕНИЯ ЕВКЛИДОВА ПРОСТРАНСТВА
Любое евклидово движение является произведением сдвига
и евклидова движения, оставляющего неподвижной данную точку.
Если взять в качестве неподвижной точки начало координат в Еп,
то любое евклидово движение имеет вид rt, где t — сдвиг, а г -
ортогональное преобразование, т. е. г g О (п). Пусть ЕГ — под-
группа сдвигов. Это коммутативная группа, которую можно отож-
дествить с Еп, сопоставляя каждому вектору сдвиг на этот вектор.
Группа ЦТ является нормальным делителем в g (п). Действи-
тельно, пусть г £ О (и) и tv — сдвиг на вектор v. Тогда tv есть
преобразование пространства Еп, переводящее х в х + и. Рас-
смотрим преобразование г~Ч„г. Оно переводит х -+ rx -> rx + v
-> х + r~rv. Таким образом, А (г) tv = r~ltvr = tr-iv. Другими
словами, если мы отождествим с Еп, то действие преобразования
А (г) на А' отождествится с обычным действием преобразования
г-1 на Еп для всех г £ О (п).
Далее, алгебра Ли группы g (и) распадается как векторное
пространство в прямую сумму алгебр Ли групп У и О(п).
Учитывая наше отождествление группы у" с Еп, мы можем
отождествить с Еп и алгебру Ли группы сТ. Таким образом,
алгебру Ли группы g (и) можно рассматривать как прямую сумму
Еп-\-о(п) (где о (и) — алгебра Ли группы О(п)}. Исследуем скобку
Ли в g (п) в терминах этих отождествлений. Поскольку группа У
коммутативна, имеем
[pt, р2] = 0 для щ, vz £ Еп.
§ 1. Структурные уравнения евклидова пространства 257
Поскольку О (п) — подгруппа, скобка [Xj, Х21 Для X'i, Х2 €
6 о (га) совпадает со скобкой в о (га). Рассмотрим теперь скобку
[X, d для Xfo(re), иСЕп. Согласно сделанному выше заме-
чанию,
А (ехр £Х) v = ехр (—tX) v, (1.1)
где в правой части к вектору v применяется ортогональное пре-
образование ехр (—tX). Из формулы (1.1) следует, что
[X, d = —- Xv. (1.2)
Рассмотрим теперь структурные уравнения группы g (и).
Для этого запишем фундаментальную линейную дифференциаль-
ную форму группы g (га) в виде со -р Q, соответствующем разложе-
нию алгебры Ли группы g (га) в сумму Еп Д о (га). Таким образом,
со есть векторнозначная форма со значениями в ЕА, a Q — форма
со значениями в о (га). Структурные уравнения приобретают вид
dto-PdQ^ —[(со + Й)Д(со + Й)].
Развертывая правую часть, имеем
—l[(co + Q)A(co + Q)]= — А [соДсо] — [QAco] — 4 [ЙДЙ].
Но [соДсо] = 0, так как группа Д' коммутативна. Следовательно,
dco + cZQ= — [ЙДсо]—у [ЙДЙ].
В обеих частях этого равенства стоит сумма двух форм: одной —
со значениями в ЕА, другой — со значениями в о (и). Обе формы
каждого типа должны быть равны. Учитывая (1.2), имеем
с/со = ОДсо, (1.3)
сЯ2=-4[ЙДЙ]. (1.4)
Эти уравнения известны как структурные уравнения евклидова
пространства. Запишем уравнения (1.3) и (1.4) в координатах
пространств ЕА и о (га). В стандартном базисе ..., еп про-
странства ЕА форма со имеет вид
со = У, со1 ® е,. (1.5)
i—1
Пусть — базис алгебры о (и), где Ец — линейные преобра-
зования, определяемые формулами
EljBj = в; ,
Еце^—ер (1.6)
Ецеъ. = § при Ar#=i, k=£i-
17 С. Стернберг
258
Гл. VI. Дифференциальная геометрия евклидова пространства
Скобка базисных элементов имеет вид
[Ец, Epq] = -$Eiq + $Ejq + WEpj-64Epi, (1.7)
что проверяется простым вычислением. [Здесь Etm = —Ет; для
Z>m.] В терминах этого базиса мы можем написать
(1-8)
г<з
Тогда
ЙДй = ( QiJ 8 Еи) Л ( 3 ® eft) =
г < j 1
3 (Q°Acoft)®(^A) =
i<J, fc=l, • • •, n
= 3 [(Qij A co’) ® et - (<A Л co1) ® ej} =
i<>
= (3 ЙгзЛи3'- 3 ®e}.
l<i i<l
Мы можем упростить последнее выражение, положив Q13 = — 11
для i>j. Тогда
й Л со = 3 (йгз Л ®3) ® ei-
3 = 1
Сравнивая коэффициенты при ег в обеих частях равенства [(1.3),
получим
(W = 3^H Л«'- (1-9)
Вычислим теперь [ЙАЙ]. Мы имеем
[Й Л Й] = К 3 & ® Ei}) Л ( 3 ®Pq ® Ярд)] =
i<3 P<q
= 3 (Qi3 Л ЙР9) ® [Ец, Epq\ =
г<3
P<q
= 2 (QijAH ®(-^Eiq^Ejq + ^EpJ-^Epi).
i<3
p<q
Приводя подобные члены, получим
3 [- 3 п1рлйрт+ 3 QPI/\Qpm+ 3 й,,тлй1р-
т 1<р р<1 р<т
Р<т р<т 1<т
- 3 Q""’Л <->"’] ®Е1т =
т<СР
1<Р
= - 3 (йгрЛйрт)®ягт=-2 3 (Й^АЙП® Е1т.
1,т,р
Р
J 1. Структурные уравнения евклидова пространства 259
Сравнивая коэффициенты при Е1т в (1.4), находим
д QP™ (1.Ю)
Дадим теперь другую интерпретацию структурных уравнений
(1.3) и (1.4) [или (1.9) и (1.10)], которая будет играть важную
роль в дальнейшем.
Заметим прежде всего, что мы можем отождествить группу § (и)
с множеством всех ортогональных реперов пространства Под
ортогональным репером мы подразумеваем пару, состоящую
из точки и множества п ортонормированных векторов. Таким
образом, репер есть набор (к; /15 . .., /л), где vQET, а/ъ .. ., fn —
ортонормированный базис.
Пусть О (л)—множество всех ортонормированных реперов про-
странства Определим отображение ср: g (л)—><Э(п), полагая
ф(АН = (щ ссд, . .., геп) (где е1, . . ., еп — стандартный базис в Е71).
Отображение <р сопоставляет каждому евклидову движению репер,
полученный применением этого движения к стандартному реперу.
Легко видеть, что <р есть взаимно однозначное отображение груп-
пы S (и) на &(п). Превратим О (и) в дифференцируемое много-
образие, потребовав, чтобы отображение <р являлось диффеомор-
физмом. Тогда мы можем перенести формы со и й на 0(п). Мы
хотим дать им геометрическую интерпретацию. Для этого изучим
сначала левоинвариантные векторные поля.
Лемма 1.1. Пусть л, —проекция многообразия О (п) на Е71,
определяемая формулой л (к; Д, ..., /п) = к. Тогда отображение л
дифференцируемо. Обозначим через е, левоинвариантные вектор-
ные поля на (п), соответствующие стандартным базисным
элементам е, из Еп (при отождествлении пространства Е71
с алгеброй Ли группы сдвигов'). Тогда
lv (л*ф, (ег)(®: /1, ...,/„)) = А- (1.11)
[Напомним, что 1„— каноническое отождествление касатель-
ного пространства к векторному пространству с самим этим век-
торным пространством.]
Первая часть леммы тривиальна. Проверим (1.11). Векторное
поле et служит инфинитезимальной образующей однопараметриче-
скоп группы преобразований группы g (п), а именно группы
правых сдвигов на exp(se;), sQR. Такой сдвиг переводит tvr
В Но r£s<J. ~ ^sre- г, так что —> it,+,re г. Поэтому ф* (ег)
является инфинитезимальной образующей однопараметрической
группы преобразований многообразия (9 (ге), которая отображает
Д; А, • •, fn) в (u-\-sft; f^ . . ., fn). Отсюда следует формула (1.11).
Те же рассуждения показывают, что л*<р„ (Ец) = 0 для Е^ £ о (п).
17*
260 Гл. VI. Дифференциальная геометрия евклидова пространства
Пусть X — касательный вектор в точке z = (и; Д, . . ., fn) С О (п).
Мы можем написать (X) = 2 Xtf,.
Левоинвариантное векторное поле 2 ^tei обладает тем свой-
ством, что ф* (2 Xje,)z отличается от X на линейную комбинацию
векторов ср* (Eij). Таким образом,
(X, ((ф-1).со)з) = 2^. (1.12)
Условимся для простоты опускать букву ф при отождествлении
многообразия © (и) с g(n). Тогда формула (1.12) запишется в виде
(X, <oz> = 2 Xie,.
Мы будем также опускать символ lv, если ясно, что делается
соответствующее отождествление. Тогда можно описать форму со
следующим образом.
Пусть X — касательный вектор многообразия 0 (и) в точке
Z = (щ fi, . .., fn), и пусть л, (X) = 2 Xifi. Тогда (X, сог) = 2 Х;ег.
В частности,
(X, ю‘) = (л, (X), /г). (1-13)
Итак, формы со1 имеют следующий простой геометрический
смысл: величина (X, сор показывает, насколько передвинулось
начало v репера z = (щ /15 . . ., /п) в направлении /г- при «инфи-
нитезимальном перемещении» этого репера на вектор X.
Запишем формулу (1.13) в несколько более удобном виде.
Отображение л можно рассматривать как векторнозначную функ-
цию на ®(ге). Что представляет собой йл? Непосредственная
проверка показывает, что (Х2, йлг) =/„л* (X), что мы условились
записывать просто как л* (X). Отображение, сопоставляющее
реперу (к; ..., /п) вектор /г, также является векторнозначной
функцией на © (ге), которую мы снова будем обозначать через /г.
Далее, скалярное произведение ( , ) есть билинейное отображе-
ние Еп'хЕп—>R, так что имеет смысл говорить о скалярном
произведении форм со значениями в Еп.
Учитывая эти замечания, мы можем переписать формулу (1-13)
в виде
со{ = (с?л, /;). (1.14)
А что такое (rf/it /Д? Это линейная дифференциальная форма
на 0 (п), измеряющая величину поворота репера при инфинитези-
мальном перемещении в 0(п). Поучительным упражнением для
читателя было бы проверить непосредственно, что (d/,-, /;) = Qi3.
Впрочем, мы скоро это докажем. Обозначим пока (с?/г, /Д через Q'i3
§ 1. Структурные уравнения евклидова пространства
261
и установим несколько свойств этих форм. Поскольку (/,-, fj) =
= = const, с помощью внешнего дифференцирования получаем
Wi, Л) + (А, d/>) = 0,
или
Й'О = — Й'А
Применим теперь к равенству (1.14) оператор d. Имеем
d(o’ = (ddn, fi) — (da, dfi)=—(da, dft)^-
— — (da, У Q'4 ® fj) = (поскольку dft = У Й'’3 ® /,)
= A (da, fj) = У й'3* л
Из сравнения этого последнего уравнения с уравнением (1.9)
следует, что Й,г5 = ЙгЛ Действительно, мы имеем
у й'О Д 0? = У й‘з Л
или
у (Й'О — й*3) Д со’ = 0.
По лемме Картана (теорема 4.4 гл. I) мы заключаем, что для
каждого /
(й'гз — Q13) = У щ3со\
где функции at симметричны по i и k. С другой стороны, как
Й,гз, так и Й’3, антисимметричны по i и j. Поэтому мы можем
применить следующую лемму, которая нам еще не раз понадобится.
Лемма 1.2. Пусть величины а^- симметричны по j и к и анти-
симметричны по i и j. Тогда а*. = 0.
Действительно, ajk = — a{k= — а3ы=а1 и ajft=a^.= —а£, откуда
at = at = — at. = 0.
JR Jt jt
Итак, мы доказали, что —т. е. что
= (dfi, h). (1.15)
Мы можем теперь дать другое доказательство уравнения (1.10):
ЙЙО = (dft, df^ = (У Йгй ® Д, 2 Йз1 ® /;) =
k i
= 2 Й{* д Й" (А, /г) = 2 Qift А й*3'.
h, I k
Итак, мы имеем следующие формулы:
со1 = (da, ft), (1.14)
^ = (dfi, fA, (1-15)
262
Гл. VI. Дифференциальная геометрия евклидова пространства
da1 = 3 Д o’, (1.9)
ДО*’. (1.10)
В заключение параграфа заметим, что, поскольку формы о1
и Q*3 соответствуют левоинвариантным формам на S (п), мы можем
применить теоремы 2.3 и 2.4 гл. V. В частности, любое преобра-
зование многообразия О (п), сохраняющее о и Q, является евкли-
довым движением (следствие теоремы 2.3). Кроме того, справедливо
Предложение 1.1. Пусть М — многообразие размерности
п-\-п(п—1)/2, и пусть 0‘, 0’1—формы на М, причем
dQ1 = 3 01* Л 0’,
d©*i = 2 л 0W.
Тогда существует (локально) диффеоморфизм /: М —>& (п), такой,
что f* (<в*) = 0* и f* (Q’l) = 0*1.
§ 2. СТРУКТУРНЫЕ УРАВНЕНИЯ ПОДМНОГООБРАЗИЯ
Одним из основных объектов изучения в этой главе является
геометрия подмногообразий евклидова пространства. Метод, который
мы будем применять,—так называемый «метод подвижного репера»—
принадлежит Дарбу и наиболее полно использовался Э. Картавом.
Идея его состоит в том, чтобы выбрать реперы, «касательные»
к рассматриваемому подмногообразию, и выяснить, что означают
для них структурные уравнения.
Определение 2.1. Пусть (р — погружение Л-мерного много-
образия М в ЕД. Через (М) мы будем обозначать множество
Рис. 21
всех пар (х; Д, ..., /п), где х£М, а /ь ..., /п — такой ортонор-
мированный базис пространства ЕД, что
А, •••, А6/ф(Ж)(фЛс(^)). (2.1)
Грубо говоря, (Э,Г(М) есть множество таких реперов простран-
ства|£п, у которых первые к векторов касаются ц> (М), а остав-
§ 2. Структурные уравнения подмногообразия
263
шиеся п — к векторов ортогональны к ф(М). Так, при п = 3
и к = 1 или 2 реперы из <ЭФ (Л7) имеют вид, указанный на
рис. 21 и 22.
Легко видеть, что <ЭФ (М) обладает естественной дифференци-
руемой структурой и существует дифференцируемая проекция
многообразия ©Ф(7И) на М, которую мы будем обозначать лф.
Определение 2.2. Пусть <р и М — такие же, как в опре-
делении 2.1. Обозначим через <р отображение (Эф (М) —-> (Э (п),
задаваемое формулой
ф (ж; /1; . . ., /п) = (<р (ж); /1( . . ., fn). (2.2)
Легко проверить, что <р есть погружение многообразия ©Ф(7И)
в (9 (п) и что лоф = фолф. Таким образом, мы имеем коммута-
тивную диаграмму
©ф (М) —в (п)
ч>
А л
М-------> Еп
ф
Мы можем рассмотреть формы <р* (со) и ф* (Q) на ©Ф(М).
Определение 2.3. Определим формы 0, О, 0г и О'3 фор-
мулами
0 —Ф*(со), (2.3)
0 = Ф*(Й), (2.4)
0{ = Ф*(со{), (2.5)
0И = ф*(Й{’). (2.6)
Иногда, желая подчеркнуть зависимость этих [форм от ф, мы
будем обозначать их 0Ф, 0Ф и т. д.
Применяя к структурным уравнениям евклидова пространства
отображение ф*, получаем
dQ = Q/\B, (2.7)
d®= -4 [®АО], (2-8)
или
d0i = э (2-9)
deij = 3@ipA0pJ. (2.10)
264
Гл. VI. Дифференциальная геометрия евклидова пространства
Эти уравнения известны как структурные уравнения подмногооб-
разия (М, ф).
Прежде чем приступать к детальному изучению этих уравне-
ний, сделаем одно важное замечание. При изучении евклидовой
геометрии мы считаем два объекта эквивалентными, если они
отличаются на евклидово движение. В частности, мы считаем
два отображения ф^ и ф2: М Еп эквивалентными, если ф1 =
= а ° ф2, где а — евклидово движение. Многообразие ©ф (М)
и формы 0 и 0 играют важную роль, как показывает следующая
Теорема 2.1. Пусть ф! и (р2 — два отображения многообра-
зия М в Еп. Равенство ф4 = а ° ф2, где а — евклидово движение
пространства Еп, имеет место тогда и только тогда, когда
существует такой диффеоморфизм ф: ©Ф1 (М) ©ф2 (А/), что
0ф1 = ф*(0ф2) и 0ф1 = ф*(0ф2). Другими словами, многообразие
©ф(М) и формы 0ф и 0ф определяют ф с точностью до евклидова
движения.
Из определений следует, что ф! = а°ф2 тогда и только тогда,
когда ©Ф1 (М) = а (0Ф2 (М)) и ф! = а ° ф2 ° ф [где преобразование
многообразия О (п), индуцированное движением ос, также обозна-
чено через а]. Если рассматривать О (п) как группу всех евкли-
довых движений, то сог и будут левоинвариантными формами,
и теорема 2.1 следует непосредственно из теоремы 2.3 гл. V.
Вернемся к изучению форм 0г и 01'. Напомним, что форма
со1 на © (п) измеряет «инфинитезимальный сдвиг» начала репера
по направлению i-ro базисного вектора этого репера. Когда мы
с помощью отображения ф* переходим к ©Ф(7И), мы рассматри-
ваем только реперы с началом на ф(;И). Поэтому «инфинитези-
мальный сдвиг» начала репера не должен иметь компонент, орто-
гональных к касательному пространству подмногообразия ф(7И).
С другой стороны, согласно (2.1), мы рассматриваем только
те реперы, у которых первые к векторов касательны, а последние
п — к векторов нормальны к ф(7И). Следовательно, последние
п — к компонент формы 0 должны обратиться в нуль, т. е.
0’ = О при 1 = кД-1, ...,п. (2.11)
Дадим формальное док юательство этого факта. Для форм 01
и 01? можно дать простое выражение, из которого следует равен-
ство (2.11). Пусть Е1 — функция на ©ф(п), сопоставляющая каж-
дому реперу его i-ю компоненту, т. е. El (р; f1, ...,fn')=f*.
Тогда функции ф°лф и Е1, . . ., Еп являются дифференцируемыми
векторнозначными функциями на ©Ф(М). Из определений немед-
§ 3. Структурные уравнения риманова многообразия
265
ленно следует, что
04 = (й(фолф), £'), (2.12)
0° = (d£,i, Е1 *). (2.13)
Поэтому для касательного вектора мы имеем1)
(X, 0;) = «Х, </(ф°лф)), Е1(и)) =
= (<Р*°л*Х £*(и)) = 0,
если i > к. Таким образом, (2.11) следует из (2.12) и определе-
ний. Более подробно это будет обсуждаться в следующем пара-
графе.
§ 3. СТРУКТУРНЫЕ УРАВНЕНИЯ РИМАНОВА МНОГООБРАЗИЯ
Рассуждая, как при доказательстве равенства (2.11), мы можем
установить нечто большее, а именно, что при i, f к формы 0г и
01J зависят только от римановой метрики, индуцированной на М
погружением ср, но не от самого погружения. Поясним это раз-
личие.
Отображение ф индуцирует на М риманову метрику (полу-
чающуюся применением ср* к евклидовой метрике пространства
£”). Два различных отображения (т. е. отображения, отличаю-
щиеся не только евклидовым движением) могут индуцировать
на М одну и ту же метрику. Например, любые два римановых
многообразия размерности 1 локально изометричны. Действи-
тельно, выбор в качестве локального параметра длины дуги
t
s (i) = j || d/dt || dt определяет локальную изометрию такого мно-
го
гообразия на евклидову прямую. С другой стороны, геометриче-
ски очевидно, что не всякая кривая получается из любой другой
евклидовым движением. Для этого надо учесть еще «изогнутость»
кривой в пространстве, т. е. нечто внешнее, не описываемое цели-
ком в терминах римановой геометрии (которая в этом случае
тривиальна). Эта «изогнутость» (как мы увидим) измеряется фор-
мами 0*\ где / > к.
В качестве второго примера рассмотрим два отображения куска
плоскости в Е3, задаваемые формулами:
х ° <pt (и, и) = и,
Фр У°Ч>1(и, v) = »,
Z о ф1 (и, v) = О,
а; ° Фи (u, и) = и,
ф2: У ° Ф1 (ui — sin V-
Z О фц (и, и) = COS V.
1) Как обычно, мы опустили символ lv. Строго говоря, вместо
{X, d (<р о л*)) = <р* о л*Х мы должны были бы написать {X, d (ф ° л*)) =
= ^фоЛ(и) ° Ф* 0 ^Х.
266
Гл. VI. Дифференциальная геометрия евклидова пространства
Поскольку <р4 отображает все в плоскость, а ф2 — в цилиндр,
они отличаются больше, чем на евклидово движение. Однако
в обоих случаях евклидова метрика на Е3 индуцирует метрику
du2 + dv2. Тот факт, что цилиндр «изогнут», а плоскость — нет,
описывается снова формами О13 и 023.
Чтобы установить (2.11) и доказать, что 0 зависит только
от римановой структуры, мы построим аналог формы 0 для любого
риманова многообразия.
Пусть М есть /с-мерное риманово многообразие. Обозначим
через 0 (М) множество пар (р; Х4, . . . , Xh), где р £ М, а Х1г . . .
. . . , Xh — ортонормированный базис пространства Тр (М). Пре-
вратим 0 (М) в дифференцируемое многообразие. Пусть л —
проекция множества 0 (М) на М, отображающая (р; Х4, . . . , Xfe)
в р. Пусть U — координатная окрестность в М, аУ1; ... , Уй —
векторные поля на U, образующие в каждой точке ортонорми-
рованный базис. Тогда для каждой точки (р; Х4, . . . , Xk) £
С л-1 (U) с0 (М) существует единственная матрица А = (а.ц) £
С О (к), для которой Xt = 2 Тем самым определяется
взаимно однозначное отображение множества л-1 (17) на U X
X О (к), зависящее только от Yt, . . . , Yk.
Мы можем выбрать У4, . . . , Yk следующим образом. Пусть
х\ . . . , — система координат в U. Векторные поля д!дхА, . . .
. . . , д!дхА линейно независимы всюду на U. Применяя к ним
процесс ортогонализации Грама — Шмидта, мы получим орто-
нормированные векторные поля У4, . . ., Yh. Таким способом мы
можем построить отображения для каждой координатной окрест-
ности U. Читатель легко проверит, что условия теоремы 2.1
гл. II выполнены, и, значит, 0 (М) превращается в дифференци-
руемое многообразие, а л становится дифференцируемым ото-
бражением. [Сравнение с § 6 гл. II показывает, что мы можем
рассматривать 0 (М) как подмногообразие расслоения реперов
jr (М), состоящее из ортонормированных реперов.] Многообра-
зие 0 (М) называется расслоением ортонормированных реперов
многообразия М.
Определим теперь на 0 (М) фундаментальную дифференциаль-
ную форму сом. Пусть Z — касательный вектор многообразия 0 (М)
в точке z = (p; Х4, ..., Х/>). Тогда л* (Z) есть касательный вектор
многообразия Л/ в точке р. Обозначим через (Z, компоненту
вектора л* (Z) относительно Х<, т. е.
(Z, (o)w) = (л* (Z), Х4) (скалярное произведение). (3.1)
Это определяет как линейные дифференциальные формы
на 0(М). Положим сом = (сом, ..., со^). Тогда сом есть линейная
§ 3. Структурные уравнения риманова многообразия
267
дифференциальная форма со значениями в Ек. [Заметим, что если
М есть Ек с евклидовой метрикой и если сделать стандартные
отождествления, то О (М) = © (к) и <вм = со.]
Формы о)д£ позволяют дать простое выражение для римановой
метрики. Действительно, если обозначить риманову метрику
через ds2, то
л* (ds2) = (сом, сом) = (а4)а + .. . + (со^)2 (3.2)
[где под (со^)2 мы понимаем симметрическое произведение
Проверим (3.2). Пусть Z — касательный вектор в точке
z = (p; .. ., Xk). Тогда
<Z, л* (ds2)) — (л* (Z), ds2) =
= (^(Z), ^(Z)) =
= 3 (л* (Z), Xj)2— (так как Х;— ортонорми-
рованный базис)
= 2 (Z, шм)2 (согласно 3.1).
Полезно указать также формулу для объема. Напомним, что
форма объема определяет в одномерном пространстве /\к (Тр (М))
при каждом р^М скалярное произведение1). Обозначим соответ-
ствующую квадратичную форму dV2. Тогда
л* (dV2) = (coir Л ••• Л © (сом Л • • • Л (3.3)
Если М — ориентированное риманово многообразие, то суще-
ствует единственная /с-форма £2, такая, что Q>0 и Q@Q = dE2.
Допуская некоторую неточность, мы обозначим эту форму dV
и назовем ее элементом объема многообразия М. Обозначим через
(9+ (М) подмногообразие в О (М), состоящее из всех положительно
ориентированных реперов, т. е. из таких реперов (р; Хи . . .,Xk),
для которых (Х4 Л ... Л Xft, dV)— -[-1. Условимся ограничения
отображения л и форм со^ на 0+ (М) обозначать теми же симво-
лами. Тогда на <Э+ (М) мы имеем
л* (dV) = соде Л • • • Л “м- (3-4)
Доказательство формул (3.3) и (3.4) мы оставляем читателю
в качестве упражнения.
Пусть теперь ср — погружение /с-мерного многообразия М в Еп.
Снабдим М индуцированной римановой метрикой. Тогда для лю-
бой точки р^М отображение ср* пространства Тр (М) в простран-
ство Т,р(р) (Еп) (отождествляемое с Еп) является изометрией
г) См. формулу (4.18) гл. I.—Прим. ред.
268
Гл. VI. Дифференциальная геометрия евклидова пространства
и, следовательно, переводит ортонормированный базис Х1;
пространства Тр (М) в ортонормированный базис ., ек под-
пространства ф* (Тр (М)) cz Еп. Обратно, всякому ортонормирован-
ному базису et, . . ., ек подпространства ф* (Тр (М)) cz Еп соответ-
ствует единственный ортонормированный базис ., Хк
пространства ТР(М), для которого ф*Х; = е,. Итак, мы имеем
отображение р: (% (М) —> О (М), переводящее (р; ., еп}
в (р; Xit ...,Хк), где ф*(Л'г) = еь
Легко видеть, что отображение р дифференцируемо и что
лф = л°р, так что мы имеем следующую диаграмму:
Легко проверить также (мы предоставляем это читателю), что
0 = р*(Шм), (3.5)
или
01 = Р*(“м) ДЛЯ i</c,
. (и.О)
0г = О для i^> к.
Формы 0г? при i, j<Lk также индуцируются некоторыми фор-
мами на &(М). Точнее говоря, существуют однозначно опреде-
ленные формы Qm (i, / = 1, • • •, к) на 0 (М) (зависящие только
от римановой структуры многообразия М), такие, что
е^=Р*(йй). (3.7)
Формы Йм антисимметричны по i, / и удовлетворяют урав-
нениям
й
(каД = 2 А (3-8)
7=1
Заметим, что уравнения (3.8) вместе со свойством антисим-
метричности однозначно определяют формы Действительно,
формы сом, . . ., со^ линейно независимы, поэтому мы можем рас-
суждать точно так же, как в § 1. Отсюда следует, что формы
Йм, удовлетворяющие уравнению (3.8), зависят только от рима-
§ 3. Структурные уравнения риманова многообразия 269
новой структуры многообразия М, индуцированной погруже-
нием ф1).
Заметим также, что формы й’м однозначно определяются фор-
мулой (3.7): если р*(йм) = р* (й^), то р* (Йм-О’м) = 0. Поскольку
р — отображение на, отсюда следует, что Йм = Йм. Этот факт
позволяет нам строить формы йд) локально на малых окрестностях
в многообразии <Э(М), исходя из форм 0гЛ В силу единствен-
ности построенные формы будут тогда согласованы на пересечении
окрестностей.
Для построения форм й^ на окрестности U cz О (М) доста-
точно найти отображение о: U —>(ЭЧ,(М), для которого poo -id,
и затем положить йм==о*(0^). Действительно, 01’ = ф* (de,, ej).
Если две точки из лежат над одной и той же точкой из (9 (ЛГ),
то первые к элементов их реперов совпадают. Следовательно,
р* о о* о <р* (е;) == ф*е;, или р* (йм) = р* °о*0гз = 0гГ Мы хотим
построить такое отображение о. Это будет сделано, если мы
сможем найти п — к таких векторнозначных функций еу+1, . . ., еп
на М, что векторы ., еп (р) ортонормированы и ортого-
нальны к ф* (Тр (М)). Тогда для каждого репера z = (р; . . ., xh)
из О (М) мы положим
о(г)-(р; фДХ1), . . ., фД-гД, eh+l(p), ...,еп(р)).
Мы хотим определить функции eh+i, . . . , еп в окрестности
точки qQM. Поступим следующим образом. Пусть W — подпро-
странство в Еп размерности п — к, дополнительное к ф* (Tq (М)).
Тогда W дополнительно к ф* (Тр (М)) для всех р из некоторой
окрестности U точки q. Для таких точек р ортогональная проек-
ция пространства W на [ф* (Tq (М))]-1- невырожденна. Если мы
зафиксируем базис vh+l, . . ., vn пространства W, то тем самым
определится некоторый базис vh+l(p), ...,vn(p) пространства
1ф* (Тр (Л/))]1- при каждом p^U. Применяя к нему процесс орто-
гонализации Грама — Шмидта, мы получим требуемые функции
+ • • • 7
Итак, мы установили существование форм йм на любом рас-
слоении (Э (М) при условии, что риманова метрика индуцирована
погружением многообразия М в Еп. Чрезвычайно глубокая тео-
рема, принадлежащая Нэшу, утверждает, что любая риманова
метрика может быть получена таким образом. Это доказывает
существование форм йд) для любого риманова многообразия.
х) Действительно, расслоение ортонормированных реперов Q (М)
и формы а>гм на О (М), а значит, и уравнение (3.8) полностью определяются
римановой метрикой.— Прим, перев.
270
Гл. VI. Дифференциальная геометрия евклидова пространства
Однако можно дать прямое доказательство существования форм
Qm, основанное на очень простой локальной конструкции. Мы
предпочли отложить это доказательство до гл. VII, где мы рас-
смотрим эту задачу при более общих условиях (стр. 356). В сле-
дующих параграфах будет выяснено, какая геометрическая
информация содержится в этих формах.
Для удобства ссылок соберем вместе различные формулы,
полученные нами для погруженных подмногообразий евклидова
пространства.
Теорема 3.1. Пусть <р — погружение некоторого к-мерного
многообразия в Ек. Многообразие (Э9(М) состоит из всех пар
(р; ft> • • •, fn), где pQM, a . . ., fn —такой ортонормированный
базис пространства Еп, что векторы ft, .. ., fh касаются ф (М)
в точке ф(р), а векторы ..., fn ортогональны к ф(М)
в точке <р(р). Далее, ft можно рассматривать как векторнознач-
ные функции на 0Ф(М), так же как и ф°л((1. Тогда формы 9*
и 0” на (Л7), определяемые формулами
0* = (</(фоЯф), Д), (3.9)
0° = (d/b/Д, (3.10)
удовлетворяют соотношениям
0i = 0, i = /c-|-l, ...,п, (2.11)
d0f = 2 0*3Д0’, (2.9)
j=i
d&ij = S0ipA0p< (2.10)
Кроме того, формы 0U (i</<C&) зависят только от рима-
новой структуры многообразия М, индуцированной погружением ф.
Возвратимся на минуту к формам Qm, удовлетворяющим усло-
виям (3.7) и (3.8). Предположим, что формы удовлетворяют
уравнениям
(З.Н)
Тогда, согласно предложению 1.1, существует (локально) такой
диффеоморфизм ср: О (М) —>(Э (к), что ф* (иг) =им. Значит,
Ф* ((со1)2 + .. . + (а?)2) = (аДД2 + • . • + Ю2,
т. е. ф — локальная изометрия многообразия М на Ek. Получаем
§ 4. Кривые в евклидовом пространстве 271
Предложение 3.1. Пусть М — риманова многообразие
с формами Й.н, удовлетворяющими уравнениям (3.8) и (3.11).
Тогда М локально изометрично евклидову пространству.
§ 4. КРИВЫЕ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
В этом параграфе мы применим результаты § 2 к изучению
дифференциальной геометрии кривых в евклидовом пространстве.
Все наши рассмотрения легко обобщаются на кривые в ге-мерном
пространстве, но для простоты мы ограничимся изучением кривых
в трехмерном пространстве. Пусть С — кривая, т. е. погружение
интервала I в Е\ Тогда многообразие ©с (Z) двумерно: две степени
свободы соответствуют движению вдоль кривой и вращению двух
векторов /2 и/з репера (р; /1? /2, /з) 6©с(^) вокруг /1? см. рис. 21
на стр. 262.
На ®с (7) формы 02 и 03 обращаются в нуль, а формы 01 и 0г?
определяются равенствамих)
dC = 0x/i,
^1=©12/2 + ©13/з,
^2 = 021Л + 023/з, ( '
^з = ©31/1 + @372.
Квадратичная форма (01)2 = л* (ds)2 есть просто элемент длины
дуги кривой, поднятый на ©с (I). Заметим, что в каждой точке
кривой существует ровно две возможности для выбора вектора
fp, они соответствуют двум ориентациям этой кривой. В частности,
квадратичная форма (dfi, dfi) зависит только от точки на кривой
и, следовательно, может быть представлена в виде
(dfi, dfi) = л* (K2ds2),
где К 0 — некоторая функция на I. Функция К называется
абсолютной кривизной кривой С. Ясно, что она инвариантна
относительно евклидовых движений кривой С.
Мы будем теперь предполагать, что выбрана некоторая ориен-
тация кривой, так что вектор выбирается в каждой точке одно-
значно; таким образом, мы переходим к подмногообразию мно-
гообразия 0 (I), которое, допуская некоторую неточность, будем
по-прежнему обозначать 0 (I). Поскольку теперь и dC, и fx —
векторнозначные формы на I, мы можем переписать уравнение
(4.1) в виде 01 = (dC, ft) = л* (dC, fi). Определим форму ds,
полагая ds = (dC, fr), так что 01 = л* (ds). [Это согласуется
со старыми обозначениями, поскольку ds2 = (ds)2.] Очень часто
в классической дифференциальной геометрии задается больше,
9 См. определения 2.1 — 2.3 и теорему 3.1 —Прим, перев.
272
Гл. VI. Дифференциальная геометрия евклидова пространства
чем кривая, а именно, в каждой точке кривой задается вектор /2
(и, следовательно, /3). Например, если кривая целиком лежит
на некоторой поверхности S, то при ее изучении естественно
потребовать, чтобы вектор /2 касался S. Дадим поэтому такое
Определение 4.1. Пусть С: 1—>Е3— некоторая кривая.
Лентой над С называется такое дифференцируемое отображение
n: I что л(п) = С. Таким образом, лента определяется
(дифференцируемым) выбором нормального вектора в каждой
точке кривой С.
С помощью отображения и формы 0С переносятся на I.
В частности, мы можем написать
и* (012) = k ds,
и* (023) = т ds, (4.2)
и* (013) = w ds.
Функция к называется кривизной ленты, функция т — круче-
нием, а функция w — верчением. Эти три функции, очевидно,
являются инвариантами ленты относительно евклидовых движе-
ний. Обратно, пусть Ri и R2— две ленты над кривыми С\ и С2,
определенными на интервале I. Существует очевидный диффео-
морфизм ф: Ocj (/) —» ®с2 (Г)- Действительно, любой репер
из ©Ci (I) получается из репера ленты с началом в той же
точке вращением на определенный угол, и то же самое верно для
Ос2(1)- Поэтому очевидное отображение ф, переводящее /С в R2,
продолжается до диффеоморфизма &а (/) на <Эс2(/)- Простое
вычисление (которое мы оставим читателю в качестве упражне-
ния) показывает, что если функции к, т и w одинаковы для Rt
и R2, то ф*0*3 == 0’J. Тогда по теореме 2.1 ф есть конгруэнция.
Пусть С — кривая, абсолютная кривизна которой всюду стро-
го положительна. Тогда с кривой С ассоциируется естественная
лента, называемая лентой Френе и определяемая следующим
образом. Поскольку кривизна не обращается в нуль, мы имеем г)
dejdt 0. Определим е2 как единственный единичный вектор,
для которого
(4.3)
Выберем затем е3 так, чтобы е^ /\ е2 Д е3 > 0 (относительно
естественной ориентации в Е3). Вектор е2 называется главной
нормалью, а вектор е3 — бинормалью рассматриваемой кривой.
Репер eit е2, е3 называется трехгранником Френе данной кривой.
Сравнивая (4.3) с (4.1), мы видим, что 013 == 0, т. е. лента Френе
1) Где = — единичный касательный вектор к С. — Прим, перев.
§ i. Кривые в евклидовом пространстве
273
(4.4)
не имеет верчения. Уравнения (4.1) записываются теперь в виде
dei —
= -Кех-Тея,
ds 1
-^- = Те?2.
ds 2
Функция Т в этом случае называется кручением кривой.
Кривизна К кривой показывает, насколько кривая отклоняется
от прямой линии. [Кривая, для которой е= 0, есть прямая
линия.] Кручение показывает, насколько кривая отклоняется
от того, чтобы лежать в одной плоскости. [Кривая с нулевым
кручением есть плоская кривая.] Применяя предыдущие заме-
чания, мы видим, что две кривые с необращающейся в нуль кривизной
конгруэнтны тогда и только тогда, когда они имеют одинаковые
кривизну и кручение.
Существует простая, но важная геометрическая операция,
которую можно применять к лентам. Интуитивно она состоит
в получении плоской кривой путем разглаживания ленты на пло-
скость. На точном языке это означает следующее. Пусть R —
некоторая лента. Тогда мы имеем функции ei (s), е2 (s), е3 (s),
удовлетворяющие уравнениям
^- = ke2 — we.,
de« ,
— —kei — xes,
ds 1
de. .
_А=_ц?е1 + ге2.
Определим кривую D (R) в Е2 уравнением
= (4.5)
где /i (s) — единичный касательный вектор, удовлетворяющий
вместе с ортогональным к нему единичным вектором f2, для кото-
рого /1 Л /г > 0, уравнению
^~ = к(з)Ш, (4.6)
Уравнение (4.6) можно рассматривать как систему двух линей-
ных однородных уравнений первой степени. Следовательно, при
заданном начальном условии /j (s0) оно имеет единственное реше-
ние. Таким образом, кривая D (R) определяется начальным поло-
жением и направлением. Зафиксируем раз и навсегда начальные
18 С. Стернберг
274 Гл. VI. Дифференциальная геометрия евклидова пространства
условия для D (R): скажем, D (R (0)) = 0 и D (R)' (0) = д!дз?-.
Отображение R -> D (R), сопоставляющее ленте R кривую D (R),
называется «развертыванием ленты на плоскость». Уравнение (4.6)
выражает тот факт, что мы получаем при этом плоскую кривую
и ленту без верчения и кручения над ней. Функция k (s), помимо
всего прочего, описывает касательную к ленте компоненту изме-
нения вектора
Упражнение 4.1. Показать, что развертывание любой ленты над
прямой дает прямую линию.
Упражнение 4.2. Пусть С — плоская кривая, т. е. С (s) лежит
в фиксированной плоскости Р. Пусть R — лента над С, определяемая тем,
что е2 лежит в Р. Показать, что если отождествить Р с Е2, то D (С) отличается
от С на евклидово движение плоскости. Вывести отсюда, что кривая С лежит
в плоскости тогда и только тогда, когда над С существует лента без кручения.
Упражнение 4.3. Пусть С — кривая, лежащая в плоскости Р.
Пусть R — такая лента над С, что е2 всегда нормален к Р. Показать, что
D (R) есть прямая линия.
Упражнение 4.4. Пусть С — некоторая кривая. Показать, что
существует лента R над С, для которой!) (R) есть прямая линия. Кроме того,
такая лента R единственна, если кривизна кривой С всюду отлична от нуля.
Упражнение 4.5. Пусть С — кривая, кривизна которой всюду
отлична от нуля, и R — ее лента Френе. Показать, что кривые D (7?) и С
имеют одинаковую кривизну.
Как мы уже видели, с плоской кривой естественным образом
ассоциируется лента, а именно, мы определяем е2 как единичный
нормальный вектор, лежащий в той же плоскости, для которого
произведение /\ е2 задает положительную ориентацию плоско-
сти, и определяем е3 как нормаль к этой плоскости. Тогда урав-
нения (4.4) приобретают вид
4^=0,
ds 1
(4.7)
Из теоремы 2.1 немедленно следует, что две такие кривые
с одинаковыми кривизнами отличаются на евклидово движение.
Кривизна показывает, «каким образом» и насколько поворачи-
вается кривая в плоскости. Знак кривизны зависит от направле-
ния, в котором мы двигаемся по кривой.
Если К (s) > 0, то вблизи s кривая С остается по одну сторону
от касательной. Чтобы убедиться в этом, предположим, что s = 0,
С (0) = (0, 0) и = (1, 0), так что касательная совпадает с осью
Xi- [Этого всегда можно добиться, выбрав новую параметризацию
$ 4. Кривые в евклидовом пространстве 275
кривой С и применив подходящее евклидово движение.] .Тогда
из (4.7) следует, что
С (0) = (0, 0), С' (0) = (1,0) и С" (0) = (0, К (0)).
Поэтому, если мы положим С (£) = (а^ (t), х2 (Z)), то х2 (i) =
= 1/2 К (0) Z2 + (члены высших порядков). Значит, если К (0) >
> 0, то х2 (1) положительно при достаточно малых ненулевых зна-
чениях t.
Уравнение (4.7) подсказывает другую интерпретацию кривиз-
ны К. Если функцию рассматривать как отображение в единич-
ную окружность, то е2 (s) есть единичный касательный вектор
к этой окружности в точке е( (s). Формула (4.7) показывает тогда,
что К есть якобиан этого отображения, если и кривая С, и еди-
ничная окружность параметризованы длиной дуги. Но на еди-
ничной окружности длиной дуги измеряются центральные углы.
Поэтому если т (s) есть угол (определенный по модулю 2л) между
Ci (s) и, скажем, осью Xi, то
к «=-£-• («)
Рассмотрим теперь замкнутые кривые на плоскости, т. е.
погружения С окружности S1 в Е2. Мы снова можем взять в каче-
стве локального параметра длину дуги и изучать такие понятия,
как кривизна и т. п. В частности, мы можем рассмотреть каса-
тельное отображение, переводящее каждую точку х g S1 в еди-
ничный вектор, касательный к С в х. Это отображение можно
понимать как отображение окружности S1 в единичную окруж-
ность из Е2 или, если угодно, как отображение окружности S1
в себя. Следовательно, мы можем рассмотреть степень этого
отображения. Это целое число играет важную роль ввиду следую-
щего утверждения. Назовем семейство кривых Си, зависящее
от вещественного параметра и, гладким семейством, если оно
непрерывно в Сх-топологии, т. е. если для любой окрестности
jC\w, z, е, 1) Си0 Э (см. определение 4.6 гл. II) существует такое
б > 0, что Си 6 JT{W, z, е, 1) Си0, когда I и — Uo | < б. Таким обра-
зом, кривая Си близка к кривой Сио в смысле ^-топологии, если
и близко к ио- Назовем две кривые Со и Ci гладко гомотопными,
если существует гладкое семейство кривых Си, определенное
при 0 и 1, совпадающее с Со при и = 0 и с Ci при и = 1 х).
Тогда справедлива
Теорема 4.1 (Уитни). Пусть Со и Ci — две кривые на пло-
скости. Пусть по — степень касательного отображения кривой
х) Напомним, что при каждом и отображение Си является погружением,
т. е. С'и (t) 0 при всех t.
18*
276 Гл. VI. Дифференциальная геометрия евклидова пространства
Со, a Tii — кривой Ci. Тогда Со гладко гомотопна Ci в том и только
в том случае, когда По = Пр
Прежде чем приступить к доказательству теоремы 4.1, позна-
комимся ближе с понятием степени отображения окружности S1
в себя. Введем на окружности S1 угловую координату т, опреде-
ленную по модулю 2л. Хотя функция т глобально не определена,
форма со = dr определена глобально. [Действительно, S1 есть
группа Ли. Если выбрать подходящий базис (одномерной) алгебры
Ли группы S1, то со окажется фундаментальной 1-формой на S1.]
Интегрируя со по S1, получаем j со = 2л. Если S1' — второй
81
экземпляр этой окружности с угловой координатой т' и формой
со\ а /— дифференцируемое отображение S1 -> S1', то deg/
задается формулой
deg/ =-^- (/*(«')• (4-9)
st
Соблазнительно записать (4.9) в виде
2л
(-£)<”• <410>
О
Мы должны быть, конечно, осторожны, поскольку т' опреде-
лено только по модулю 2л. Формула (4.10) подсказывает, однако,
что степень отображения / измеряет, сколько раз это отображение
наматывает S1 на S1'. Это действительно так, причем таким обра-
зом мы можем определить степень для любого непрерывного
(не обязательно дифференцируемого) отображения S1 -> S1'.
Чтобы это сделать, заметим сначала, что угловые координаты
позволяют рассматривать окружность как вещественную прямую
по модулю 2л. Говоря точнее, существует естественная проекция
р; R1 -+ S1, локально являющаяся гомеоморфизмом. Любому
отображению / окружности S1 в любое пространство X мы можем
сопоставить отображение /: R1 —>- X, полагая / = / 0 р:
R\
р
SP-l----дх
Функция / удовлетворяет уравнению / (а:4-2л=)/ (х). Обратно, пусть
дано отображение /: R1 —>Х, причем /(а;-|-2л)=/(х). Тогда суще-
ствует такое отображение /: S1—^Х, 4xof = fop. Аналогичные
§ 4. Кривые в евклидовом пространстве
277
утверждения верны для полосы R1 X I и цилиндра S1 X I, где I —
единичный отрезок. Предположим теперь, чтоХ = 5х и что задано
отображение F-. Поднимем F до отображения
F-. R1 X I —> S1, удовлетворяющего условию F (х + 2л, s) = F (х, s).
Поскольку F равномерно непрерывно, мы можем разбить RxXl
содержится в дуге окружности S1 длины л/4 (рис. 23). Выберем
теперь такую точку y0^Rl, что р (у0) = F(0, 0). Поскольку р
есть локальный гомеоморфизм и мы выбрали наше разбиение
достаточно мелким, существует единственное отображение F*
прямоугольника, содержащего (0, 0), в R1, для которого pF* — F
и F*(fd, О)=г/о. Далее мы можем однозначно продолжить отобра-
жение F* на лежащий выше прямоугольник так, чтобы оно было
непрерывно и удовлетворяло условию pF*=F. Продолжая подоб-
ным образом, мы определим F* на первой вертикальной полосе.
Затем мы можем начать со следующего нижнего прямоугольника
и продолжать процесс, пока функция F* не будет определена
на прямоугольнике 0Сs< 1, 0 а; С 2л.
Заметим, что отображение F* характеризуется свойствами
pF* = F и F*(0, О) = уо- [Отсюда следует, что если бы мы начали
с точки у'п — у0 Ц- 2пк, то новое отображение F*' удовлетворяло бы
равенству/’*'—/’*=2л/с.]ТаккакF(x+2л, s)=F (х, з), тоF*(2л, з) —
— F* (0, з) = 2лга для некоторого целого п. Ввиду замечания, при-
веденного выше в скобках, это число п не зависит от выбора г/0.
Если задано отображение /: S1 —>5Х, то положим F(x, s) = f(x).
Тогда целое число п, которое мы получим описанным выше спо-
собом, называется степенью отображения f.
Ясно, что когда / дифференцируемо, это определение степени
совпадает с предыдущим и придает смысл формуле (4.10). Степень
показывает, сколько раз отображение / накручивает окружность
на себя. Из предыдущих рассуждений ясно, что два гомотопных
278 Гл. VI. Дифференциальная геометрия евклидова пространства
отображения имеют одну и ту же степень. С другой стороны,
два отображения S1 —> С1 одинаковой степени гомотопны. Для
доказательства заметим, что если / имеет степень п, то описанная
выше конструкция определяет отображение /*: R1 -> R1, причем
pf* = fp и /* (# + 2л) = /* (х) + 2лп. Положим F* (х, s) =
= (1 — s) f* + sg (x), где g (x) == 2nnx. Тогда F* (x + 2л, s) =
= F* (x, s) + 2лга и, значит, отображение pF* (х, s) осуществляет
гомотопию между / и отображением g, определяемым функцией g.
Поэтому все отображения степени п гомотопны g.
Сравнивая (4.8) с (4.10), мы видим, что степень касательного
L
отображения кривой С равна (у11) j K(s)ds (где L — длина
о
кривой С). Чтобы не вводить длину дуги, удобнее ввести линей-
ную дифференциальную форму К ds и писать
степень касательного отображения = j К ds. (4.11)
с
Докажем теперь теорему 4.1. Если кривая Со гладко гомотопна
Ci, то касательное отображение кривой Со гомотопно касатель-
ному отображение кривой Ci, так что п0 = ni. Прежде чем дока-
зывать обратное утверждение, заметим, что если С — кривая,
то формула Си (s) = иС (s) (умножение вектора С (s) на вещест-
венное число и 0) определяет гладкое семейство кривых.
Длина кривой Си равна uL, где L — длина кривой С. Поэтому
можно считать (заменив в случае необходимости рассматриваемые
кривые гладко гомотопными), что длина кривых Со и Ci равна 2л.
Пусть h есть С2-значная функция на S1, нигде не обращаю-
щаяся в нуль. Предположим, что в терминах угловой координаты
т
h = h(x). Тогда C(x)=^h(t)dt есть дифференцируемая кривая
о
2л
при условии, что С(2л) = С(0), т. е. J h(t)dt = Q. Пусть h (-,0) --
о
касательное отображение кривой Со, а 7г(-, 1) —касательное ото-
бражение кривой Ct. Они гомотопны, так как имеют одинаковые
степени. Значит, существует непрерывное отображение (т, и}—+
—>h(x, и), переводящее S1 X I в 51. [Мы рассматриваем здесь С1
как единичную окружность, так что h (т, и) Q Е- есть единичный
вектор.] Положим
т 2л
Си (т) = j h (С и) dt—2^- j h (г, и) du.
о о
§ 4. Кривые в евклидовом пространстве
279
Эта формула определяет гладкую гомотопию, если касательный
вектор С„(т) нигде не обращается в нуль. Но
2л
С«(т) = /г(т, и)—j h(t, u)dt.
о
Если h (t, и) не постоянно по t ни при каком фиксированном и, то
2л
|| J h (t, и) du || < 1 = || h (t, и) ||.
о
Если по = п1^=О, то отображение 7г(-, и) не является постоянным.
Поэтому остается только показать, что между любыми двумя
непостоянными отображениями h0 и 7г± степени 0 окружности 51
в себя существует гомотопия, состоящая из непостоянных кривых.
Для этого поднимем отображения h0 и hl до отображений
/го, h*: R1 —> R1. Можно считать, что /го (0) = /г* (0) и sup h* (х) > 0,
sup h* (х) > 0. Тогда формула sh* -f- (1 — s) ho определяет требуе-
мую гомотопию.
Мы еще не исследовали вопрос, как для данной кривой вычис-
лить степень касательного отображения. Сейчас мы вычислим ее
для простой кривой, т. е. для кривой без самопересечений.
Пусть С — простая кривая. Введем в качестве параметра
на .S'1 длину дуги 0 < т < 2л. Тогда из равенства С (т) = С (т')
следует, что т = т' или т = 0, т' = 2л. Применяя подходящее
евклидово движение, можно считать, что С (S1) лежит в верхней
полуплоскости, причем С (0) = (0, 0) и С (0) лежит на оси х(.
Определим теперь отображение g треугольника 0 <4 ст т
2л в S1, полагая (см. рис. 24, 25)
, . С(т)-С(о)
"Г) - цС(т)_С{а) || >
если 0 ст < т < 2 л
или 0 < о < т < 2л,
280
Гл. VI. Дифференциальная геометрия евклидова пространства
если а = т,
g(o, х) = С' (т),
g(o, 2л) = —С' (0).
Отображение g определено корректно, поскольку из С (о) =
= С (т) следует, что а = т или о = 0, т = 2л. Ясно также, что
g непрерывно. Далее, отображение т -> g (т, т) есть как раз
касательное отображение. Оно гомотопно отображению G, опре-
деляемому формулой
{£(2т, 0), если 0<т<л,
#(2л, 2(т — л)), если л<т<:2л.
Поэтому достаточно вычислить степень отображения G. По по-
строению вектор G (т) лежит в верхней полуплоскости, если
0 т л, ив нижней полуплоскости, если л т О 2л. Кроме
того, G (л) = — G (0). Это показывает, что степень отображения
G равна + 1. Итак, имеет место
Теорема 4.2. Степень касательного отображения простой
кривой С равна ± 1- Таким образом,
(#& = ±2л. (4.12)
с
Упражнение 4.6. Показать, как вычислить степень, когда кривая
имеет конечное число трансверсально регулярных самопересечений.
Полезно обобщить формулу (4.12) на случай кривой с углами,
т. е. на случай, когда С есть кусочно дифференцируемое отобра-
жение S1 -> Е2. Напомним, что кривая С называется кусочно
дифференцируемой, если она непрерывна и если на S1 существует
конечное число таких точек ... , хп, что ограничение отобра-
жения С на каждую из дуг XiX2, х2х3, . . . , xn~ixn, хпх^ диффе-
ренцируемо и, более того, совпадает с ограничением на эту дугу
некоторого дифференцируемого отображения, определенного на
§ 4. Кривые в евклидовом пространстве
281
несколько большей дуге. Обозначим ограничение кривой С на
ггхг+1 (i < п) через Ct, а ограничение С на xnXi — через Сп.
Имеет смысл говорить о касательном векторе кривой Ct в точ-
ках Xi и Х{+!. Обозначим через аг внешний угол в точке х^, т. е.
угол между касательным вектором кривой в точке xt и каса-
тельным вектором кривой Ci в точке xt [а для i = 1 — угол между
С'п (Xj) и С' (art)] (рис. 26). Как и раньше, назовем кривую С про-
стой, если она не имеет самопересечений. Тогда обобщением фор-
мулы (4.12) служит формула
3 J Kds + ^ аг = ± 2л. (4.13)
г сг г
Формулу (4.13) можно получить из (4.12), если воспользовать-
ся простым предельным процессом. Достаточно исследовать углы
и посмотреть, что получается при их сглаживании (см. рис. 27).
Подробности мы оставим читателю в качестве упражнения.
Кривая С называется выпуклой, если ее образ С (51) целиком
лежит по одну сторону от каждой своей касательной. Из теоре-
мы 4.2 немедленно следует
282 Гл. VI. Дифференциальная геометрия евклидова пространства
Теорема 4.3. Пусть С — простая замкнутая кривая.
Тогда С выпукла в том и только в том случае, когда ее кривизна
не меняет знака, т. е. когда либо всюду К О, либо всюду К 0.
Доказательство. Если кривизна К не меняет знака,
то (согласно (4.8)) касательное отображение монотонно (не воз-
растает или не убывает), и обратно. Поскольку степень равна± 1,
отсюда следует, что любое значение на единичной окружности
принимается либо один раз, либо для всех точек некоторой связ-
ной дуги из S1. Предположим, что кривая С не выпукла. Тогда
существует такая точка у, что по обе стороны от касательной пря-
мой I в точке у имеются точки из С (S1). Пусть п — вектор, нор-
мальный к I, так что 1= {и £ Е2 | (п, и) = а}, где а — некоторая
Рис. 28.
константа. Если образ С (S1) лежит по обе стороны от I, то сущест-
вуют точки х g 51, для которых (С (х), п) а, и точки, для кото-
рых (С (х), п) < а. Касательные прямые к С (S1) в точках xt
и х2, в которых (С (х), п) принимает максимальное и минималь-
ное значения, параллельны I (см. рис. 28). Поэтому два из трех
касательных векторов в точках у, х{ и х2 должны быть равны.
Тогда на одной из дуг, соединяющих эти точки, касательный век-
тор должен быть постоянным. Но это невозможно, поскольку
отсюда следовало бы, что эти две точки лежат на прямой, парал-
лельной I.
В качестве приложения понятия степени отображения 51 -> S1
введем понятие индекса векторного поля. Пусть X — векторное
поле на Е2, обращающееся в нуль в начале координат, т. е. X —
= / (d/dxi) + g (д/дх2), где xt и х2 — евклидовы координаты в Е2,
и / (0, 0) = g (0, 0) = 0. Предположим, что X не обращается
в нуль в других точках вблизи начала координат, т. е. что для
некоторого 8>0 из /(i!, i2) = g (xi, х2) — 0 и х% + х22 С е2
следует, что Xi = х2 = 0. Для любой окружности Сг радиуса
§ 5. Вторая фундаментальная форма
283
г < е с центром в начале координат определим отображение в еди-
ничную окружность по формуле
[Здесь Хр £ Тр (А’2) — значение векторного поля X в точке р.
Как обычно, мы отождествляем Тр (Е2) с Е2 и, таким образом,
рассматриваем Хр как вектор из Е2.]
Легко видеть, что это дифференцируемое отображение.
Упражнение 4.7. Показать, что степень этого отображения не
зависит от г при г < е. Она называется индексом поля X в начале координат.
Упражнение 4.8. Найти индекс векторного поля хЛ (д/дх^ Д-
+ х2 (d/dz2).
Упражнение 4.9. Найти индекс поля (д/дх^ — х2 (д/дх2).
Упражнение 4.10. Найти индекс поля х2 (д/дх<) — xj (д/дх2).
Упражнение 4.11. Показать, что индекс поля —X равен индексу
поля X.
Упражнение 4.12. Индекс векторного поля в изолированном
нуле можно определить на любом ориентированном двумерном многообра-
зии, выбрав подходящую карту в окрестности этого нуля. Показать, что это
определение не зависит от выбора карты.
Сделаем в заключение одно замечание относительно кривизны
плоской кривой. Мы получили кривизну плоской кривой как
частный случай кривизны пространственной кривой. Таким обра-
зом, мы воспользовались только тем, что рассматриваемое под-
многообразие одномерно. В случае кривой на плоскости мы можем
воспользоваться также тем, что это подмногообразие имеет кораз-
мерность 1. Это тоже позволяет определить понятие кривизны
и обобщить его на высшие размерности. Действительно, для
ориентированной плоской кривой С корректно определен еди-
ничный нормальный вектор е2 (s). Мы можем рассматривать ег
как отображение в единичную окружность. В соответствии с фор-
мулой (4.7) якобиан этого отображения (относительно парамет-
ризации единичной окружности и кривой С длиной дуги) равен
—К (s). Теперь мы перейдем к обобщению этой конструкции на
n-мерное подмногообразие (п + 1)-мерного евклидова простран-
ства.
§ 5. ВТОРАЯ ФУНДАМЕНТАЛЬНАЯ ФОРМА
Пусть ср — погружение n-мерного многообразия М в EN.
Мы можем считать ср векторнозначной функцией и рассмотреть
векторнозначную форму dcp. Как мы уже видели, квадратичная
284 Гл. VI. Дифференциальная геометрия евклидова пространства
дифференциальная форма (йф, с?ф) есть не что иное, как риманова
метрика на М, индуцированная погружением ф. В классической
литературе форма (dcp, с/ф) называется первой фундаментальной
формой.
Предположим теперь, что М — ориентированное многообразие
и что N = п + 1. Если р £ М, то <рф (Тр (ЛГ)) можно рассматри-
вать как n-мерное подпространство пространства Еп+1. Поскольку
М ориентировано, ф, (Тр (М)) имеет выделенную ориентацию.
Таким образом, существует единственный единичный вектор
en+i (р), ортогональный к ф» (Тр (ЛГ)), который вместе с ориента-
цией пространства ф, (Тр (М)) определяет положительную ориен-
тацию в Еп+1. Более точно, существует единственный единичный
вектор еп+1 (р) £ Еп+1, такой, что ф» (Xj Л • • • Л %п) Д
Л еп+1 (р) > 0, где Xz 6 Тр (М) и Xt Д . . . Д Хп > 0. [Здесь
Е"+1 рассматривается со стандартной ориентацией.] Итак, мы
имеем отображение en+i: М En+1. На самом деле оно отобра-
жает ЛГ в единичную сферу пространства Еп+1, и называется
поэтому сферическим отображением, соответствующим погруже-
нию ф.
Можно рассматривать еп+1 как векторнозначную функцию
на ЛГ. Следовательно, можно построить квадратичную дифферен-
циальную форму х) (г/ф, den+1), которая называется второй фунда-
ментальной формой погружения ф. Мы будем обозначать значе-
ние этой формы на векторах X, Y 6 Тр (ЛГ) через (X, У)ц.
Важность первой и второй фундаментальных форм заклю-
чается в том, что вместе взятые они определяют отображение ф.
Точнее, справедлива
Теорема 5.1. Пусть ф! и ф2 — два погружения ориентиро-
ванного п-мерного многообразия М в Е4^1. Если они индуцируют
одну и ту же риманову метрику и одну и ту же вторую фунда-
ментальную форму, то они отличаются на евклидово движение.
Доказательство. Мы хотим применить теорему 2.1.
Для этого заметим прежде всего, что между 0ф1(ЛГ) и 0ф2(ЛГ)
существует очевидный диффеоморфизм. Действительно, в рассмат-
риваемом случае (когда ЛГ ориентировано, а ф; отображает М
в евклидово пространство на единицу большей размерности)
®Ф(ЛГ) представляет собой двулистное накрытие над 0(ЛГ).
Именно, каждая точка из О (ЛГ) определяет две точки из(9ф(ЛГ),
а ориентация позволяет выбрать одну из них (таким же образом,
!) Напомним, что (d<p, de) есть симметрическое произведение форм, т. е.
{X, У, (dtp, de))=A[(X, dtp) (У, de) + (Y, dtp) (X, de)].
§ 5. Вторая фундаментальная форма
285
как мы выбирали еп+1). Другими словами, ОФ(7И) однозначно опре-
деляется расслоением О (М), которое в свою очередь зависит
только от римановой метрики. Поскольку мы предполагаем, что
<pt и <р2 индуцируют одну и ту же риманову метрику, мы можем
отождествить <ЭФ1 (М) с <ЭФ,(Л/). Для применения теоремы 2.1
мы должны показать, что
0j = 0j и = для всех i, j. (5.1)
Но по теореме 3.1 формы 01 и (£</<тг) определяются
римановой метрикой. Поэтому нам осталось показать только, что
п+1 = 0«,п+1. (5.2)
Для этого достаточно проверить, что вторая фундаментальная
форма определяет линейные дифференциальные формы 0n+i>;
на (ЭФ(2И). Имеем
лф(йф, с?е„+1) = (с?(фолф), dfn+l).
Формулы (3.9) и (3.10) показывают, что
</(Ф°лф) = 2б7й (53)
d(/n+i)= 2 0"+1-iA-
n=i
Значит,
(сйр, den+i) = 2 0* © ©"+1,*• (5.4)
Поскольку формы 0’ всюду линейно независимы, эта формула
показывает, что формы 0п+1>1 определяются второй фундаменталь-
ной формой. Таким образом, равенство (5.2) справедливо, и тео-
рема доказана.
Поскольку первая и вторая фундаментальные формы опреде-
ляют погружение с точностью до евклидова движения, полезно
изучить их свойства и дать им геометрическую интерпретацию.
Первая фундаментальная форма есть просто риманова метрика.
Вторая фундаментальная форма показывает, как многообразие
погружено в Еп+1. и определяет «члены второго порядка» этого
погружения в каждой точке. Точнее, если С (i) — кривая на М,
то [обозначая ф ° С (£) через X (t)] имеем
(еп ° С (t), X' (t)) = 0,
и, дифференцируя, получаем
(^а. *'(<))+ ('-,^Д)-«.
Первое слагаемое есть как раз значение второй фундаментальной
формы на паре (С', С'). Поэтому можно выбрать ортонормиро-
286 Гл. VI. Дифференциальная геометрия евклидова пространства
ванные координаты х1, . .., zn+1 на Еп+1 и координаты и1, ...
. . ., ит на М вокруг точки р так, чтобы еп+1 (р) = (0, ..., 0, 1)
и чтобы погружение ф в этих координатах определялось форму-
лами
хг = м’Ц- 2. . ., i —
x™=^A^Uk+...,
где
д I д
диЗ |р’ ди^
pfn
Поэтому если форма ( , )п (положительно или отрицательно)
определена в точке р, то подмногообразие ф (М) лежит локально
по одну сторону от своей касательной плоскости.
Мы можем также определить кривизну ориентированного
и-мерного подмногообразия М в Л^+1. Рассмотрим отображе-
ние en+1: М —> Sn. Оно индуцирует линейное отображение
еп+1* '• Тр (М) > 71еп+1(р) (<$”), а значит, и отображение
К\еп^./\\тРт -+ An(TCn+i(p)(sn)).
Оба этих (одномерных) векторных пространства имеют выделенный
базис, поскольку Sn и М — ориентированные римановы многооб-
разия. Относительно этих базисов линейное преобразование
Д”(сп+1*) задается скаляром К(р), который мы будем называть
гауссовой кривизной погружения ф в точке р. Грубо говоря, К
есть отношение объема образа en+1 (U) малой окрестности U cz М
к объему самой окрестности U.
Зная первую и вторую фундаментальные формы, мы можем
вычислить гауссову кривизну. Действительно, рассмотрим уравне-
ние
O = d9n+1 = 30"+i.i д ег
(см. теорему 3.1). По лемме Картана (теорема 4.4 гл. I) из этого
уравнения следует, что существуют однозначно определенные
функции Ац, такие, что А^ = Ал и
еп+1.1 = 2Л;9\ (5.5)
Тогда, согласно формуле (5.4),
л* (Лр, den+i) = 3 Ло9* © 9\ (5.6)
Пусть теперь Xt, . . .,Хп — ортонормированный базис пространства
ТР(М) и (р; — соответствующая точка из
5. Вторая фундаментальная форма 287
Тогда
(X,) = (Xi, den+i) — (Xi, dfn+l),
где Xt — касательный вектор в точке (р; ft, . ..,/n+f), для кото-
рого n,*Xi = Xi. Но
(Xi, dfn+i) = У (Xi, 0"+мл.
Используя формулу (5.5) и условия (Xt, 9’> = 0 при i =/=]',
(Xi, 9’) = 1, получаем
en+i* (Xi) = 2 Aijfj’
В частности, гауссова кривизна находится по формуле
tf = det(4M). (5.7)
Равенство (5.6) позволяет понять, что представляет собой
матрица (ЛгД. Действительно, поскольку вторая фундаментальная
форма симметрична, а первая — положительно определена, суще-
ствует единственное линейное преобразование Ар, такое, что
(АРХ, У)х = (Х, APY)1 = (X, У)п (5.8)
для любых X, YQTP(M).
Уравнение (5.6) показывает, что (— Atj) есть матрица этого
линейного преобразования в базисе, который определяется точкой
из 0V(M). Таким образом, (5.7) можно переписать в виде
К (р) = ( — 1)п det Ар. (5.9)
Поскольку линейное преобразование Ар полностью опре-
деляет вторую фундаментальную форму, мы можем утверждать,
что риманова метрика, индуцированная погружением <р, вместе
с линейными преобразованиями Ар (при всех р £ М) однозначно
определяют <р с точностью до евклидова движения.
Подставим теперь равенства (5.5) в (2.10). Мы получим
d©u= 2 ©{рл 2 ©ipA 0pj+0{- "+1 л 0n+j- з=
₽= i ₽=1
= 2 0ipA0pi-2Aft9feA^70I. (5.Ю)
Р=1 k, I
При г, j-C. п члены d< и 0гг> А 0р) зависят только от римано-
вой метрики. Поэтому выражение 2 AkOfe А ^1д0г также зависит
только от римановой метрики. Но 2 А/Д Л Д70г есть как раз
матрица преобразования Д2 (Лр). Таким образом, справедлива
288 Гл. VI. Дифференциальная геометрия евклидова пространства
Теорема 5.2 (гауссова теорема «эгрегиум»), Пусть <р —
погружение п-мерного многообразия М в Еп+1. Пусть Ар (для каж-
дого р £ М) есть линейное преобразование пространства Тр (М),
определяемое формулой (5.8). Тогда Д2 (Лр) зависит только
от римановой метрики, индуцированной погружением <р.
Из теоремы 5.2 немедленно получаем
Следствие 5.1. Если п четно, то гауссова кривизна погру-
жения ф зависит только от римановой метрики, индуцированной
погружением ср.
Действительно, гауссова кривизна равна определителю ото-
бражения А, который полностью определяется отображением
Дп (Л). Если п = 2т, то
f\n(A) (е1Д ... /\en) — (Ael/\Ae2)/\(Ae3/\Ae/t)/\...
• • • А (Лсп-1 А Исп),
и, значит, /\п (Л) выражается через отображение Д2 (Л), кото-
рое зависит только от римановой метрики.
В случае п = 1 (т. е. для кривой на плоскости) все кривые
изометричны, но кривизна может принимать любые значения.
Поэтому для п = 1 следствие не верно. Оно не верно при любых
нечетных п, как показывает
Следствие 5.2. Пусть <pi и ср2 — два погружения п-мер-
ного многообразия М в Еп+1, индуцирующие одну и ту же рима-
нову метрику. Если п нечетно, а погружения cpi и ср2 имеют в каж-
дой точке одинаковую ненулевую гауссову кривизну, то эти погру-
жения отличаются на евклидово движение.
Следствие 5.2 можно сформулировать короче, сказав, что
при нечетном п риманова метрика вместе с гауссовой кривизной
(в случае, когда последняя отлична от нуля) определяют погруже-
ние с точностью до евклидова движения. Поскольку можно
построить погружения, индуцирующие одинаковую метрику, имею-
щие ненулевую гауссову кривизну, но отличающиеся больше,
чем на евклидово движение, мы заключаем, что следствие 5.1
не имеет места ни при каком нечетном п.
Для доказательства следствия 5.2 достаточно проверить, что
погружения qjj и ф2 индуцируют одно и то же преобразование А.
Поскольку они индуцируют одну и ту же риманову метрику,
они индуцируют одно и то же преобразование Д2 (Л), а значит,
и ДД1 (Л), так как п нечетно. Если они, к тому же, индуци-
руют одинаковые преобразования Дп(Л)(т. е. имеют одинаковую
§ 5. Вторая фундаментальная форма
289
гауссову кривизну) и Д" (А) нигде не равно нулю, то они индуцируют
одно и то же преобразование А, поскольку (по правилу Крамера)
Д”(Л) и Дп 1 (Л) определяют А при условии, что ДП(Л)=^О.
Мы можем теперь дать интерпретацию условию Д2(Л) = 0.
Действительно, уравнение (5.10) сводится тогда к структурным
уравнениям евклидова пространства. Согласно предложению 1.1,
мы можем утверждать, что существует локальный диффеоморфизм
многообразия & (М) на (9 (га), переводящий формы 0г и 0’’
(i, /<га) в формы и Q’3. Поскольку n*ds2 = (О1)2-|-(0")2,
это означает, что риманова метрика, индуцированная на М погру-
жением ф, локально эквивалентна (изометрична) римановой метрике
пространства Еп, т. е. что многообразие М локально евклидово.
Это не означает, что ф(М) есть га-мерное подпространство в£®+1.
Например, если отображение ф вкладывает М в E,n+1 как цилиндр,
то индуцированная метрика также будет локально евклидовой.
Сейчас мы увидим, что это по существу единственный случай,
когда Д2 (Л) = 0.
Оставшаяся часть этого параграфа посвящается доказательству
следующих двух теорем:
Теорема 5.3 (Хартман —Ниренберг). Пусть у —погруже-
ние односвязного х) п-мерного многообразия М в Еп+\ Предполо-
жим, что М полно е римановой метрике, индуцированной погру-
жением ф, и что Д2 (Л) = 0. Тогда М изометрична пространству
Еп и ф погружает М в виде цилиндра, т. е. на М существует
такая евклидова система координат у1, . .., уп, что погружение ф
задается формулой
<р (у1, • •, у”) = S азУ1 +b
3=1
где й(, . . . , ап — постоянные векторы в En+1, а Ъ — векторно-
значная функция одной переменной.
Теорема интуитивно понятна: если Д2 (Л) = 0, то ранг ото-
бражения Л не превосходит единицы. Это означает, грубо гово-
ря, что гиперповерхность ф (М) изгибается в каждой точке не бо-
лее, чем в одном направлении. Теорема 5.3 утверждает, что
из этих направлений можно составить кривую.
С другой стороны, справедливо следующее обобщение тео-
ремы 4.3:
х) Для полноты мы даем глобальные теоремы, предполагая известными
стандартные факты относительно односвязности, которые можно найти
в любом элементарном учебнике топологии. Читатель, не знакомый с этими
фактами, может, слегка изменив доказательства, получить соответствующие
локальные теоремы.
19 с. Стернберг
290 Гл. VI. Дифференциальная геометрия евклидова пространства
Теорема 5.4 (Чжэнь — Лашоф). Пусть ср — погружение
компактного ориентированного п-мерного многообразия М в Еп+1.
Тогда следующие два утверждения эквивалентны'.
1) степень сферического отображения равна ±1 и гауссова
кривизна не меняет знака (т. е. всюду ^>0 или <^0);
2) ср (М) есть выпуклая гиперповерхность (т. е. <р (М) целиком
лежит по одну сторону от любой своей касательной гиперплоско-
сти).
Из теоремы 5.4 следует
Теорема 5.5 (Адамар). Пусть ср — погружение компакт-
ного ориентированного п-мерного многообразия в Еп*1 (п 2)
со всюду положительной гауссовой кривизной. Тогда ср (М) есть
выпуклая гиперповерхность.
Действительно, в этом случае сферическое отображение будет
локальным диффеоморфизмом многообразия М в единичную сферу
Sn, поскольку его якобиан всюду положителен. Более того,
согласно теореме 4.3 гл. III, оно отображает М на Sn и, значит,
так как М компактно, является накрывающим отображением х).
Из односвязности сферы при п 2 следует, что степень этого
отображения равна 4-1. Таким образом, выполнено условие 1)
теоремы 5.4, что и доказывает теорему 5.5.
Обратимся теперь к доказательству теорем 5.3 и 5.4. Для этого
нам придется вернуться к преобразованиям Лежандра, введенным
в § 1 гл. IV. Там мы рассматривали невырожденные преобразова-
ния Лежандра. Теперь нас будут особенно интересовать вырож-
денные преобразования Лежандра. Точнее, пусть заданы связное
открытое подмножество D п-мерного векторного пространства V
и дифференцируемая функция /, определенная на D. Как описано
в § 1 гл. IV, форма df определяет отображение X'. D -> V*. Если
х1, . . . , хп — система координат на V, соответствующая некото-
рому базису пространства V, а у1, . . ., уп — система координат
на V*, соответствующая дуальному базису, то это отображение
задается формулой
Поскольку нас интересует случай, когда отображение X вырож-
денно, мы хотели бы знать ранг X. Пусть г есть функция, задаю-
х) См. предыдущее примечание. Не считая доказательства теоремы 5.3,
это единственное место, где мы используем некоторые сведения о накры-
вающих пространствах.
§ 5. Вторая фундаментальная форма
291
щая этот ранг: г (х) = ранг X в точке х. Определим функцию г*,
полагая
г* (х) = min [sup г (z)[.
и Эх z£U
Таким образом, г* (х) есть максимальный ранг X для всех близ-
ких к х точек из D. Ясно, что г (х) г* (х). Для любого целого
числа к обозначим через Dk множество всех таких x£D, что
г* (х) <1 к. Ясно, что множество Dh открыто. Нам необходимо
еще одно определение. Пусть Н есть Л-мерная гиперплоскость
из V (т. е. Н есть класс смежности пространства V по ^-мерному
подпространству из 7). Тогда HftD есть открытое подмножество
из Н (в Zc-мерной топологии пространства II). Каждая связная
компонента множества Н f) D называется к-плоским сечением
множества D. Так, Ar-плоское сечение, проходящее через точку
х £ D, есть содержащая х связная компонента множества HftD,
где Н — это Л-мерная гиперплоскость, проходящая через х.
Сформулируем теперь основную лемму.
Лемма 5.1 (Чжэнь —Лашоф — Хартман — Ниренберг). Пусть
1 — функция, определенная на открытом связном подмножестве D
п-мерного векторного пространства V, причем ранг ее преобра-
зования Лежандра X меньше п во всех точках из D. Пусть,
точка x0QD такова, что г (х0) — г* (х0) — к. Тогда отображение X
постоянно на некотором (п— к)-плоском сечении лп_к множества-
Dk, проходящем через х0, и г(х) = г*(х) = к для всех х£лп_к
и г(х)~>к для х£лп_к. Кроме того, существует окрестность U
точки х0, в которой из равенства Х(х) = Х(х0) (x£U) следует*
что х£лп_к.
Прежде чем приступать к доказательству леммы 5.1, сделаем
несколько замечаний. Если г* (хо) — к [но г (хо) не обязательно
равно Лс], то мы можем найти такую последовательность Xi хо,
что г* (xt) = г (xi) = к. Для каждой из точек этой последова-
тельности лемма 5.1 дает (га — А:)-плоское сечение, проходящее
через эту точку. Переходя в случае надобности к подпоследова-
тельности, мы можем считать, что эти сечения сходятся к (п — к)-
плоскому сечению, проходящему через х0. Так как отображение
X постоянно на сечениях, проходящих через xi, то оно постоянно
и на предельном сечении. Таким образом (в предположении, что
справедлива лемма 5.1) нами доказана
Лемма 5.2. Если г* (х0) = к, то X постоянно на (п — к)-
плоском сечении множества Dk, проходящем через хо, которое
является пределом (га — к)-плоских сечений, описанных в лемме 5.1.
19*
292 Гл. VI. Дифференциальная геометрия евклидова пространства
В случае k = 1 имеет место
Лемма 5.3. Если г* (ж0) = 1, то существует единственное
(п— 1)-плоское сечение, проходящее через х0, на котором X
постоянно, и на этом сечении г* = 1.
Действительно, поскольку мы находимся в «-мерном прост-
ранстве, любые две непараллельные (п— 1)-мерные гиперплоскости
пересекаются. Пусть л„_1 (x0) — сечение, указанное в лемме 5.2.
Предположим, что через х0 проходит другое (п—1)-плоское сече-
ние Яп-1, на котором X постоянно. Пусть {zj — последователь-
ность, фигурирующая в доказательстве леммы 5.2. Если точка х,
достаточно близка к х0, то сечения Лп-Дя,) и пересекаются
(и пересечение содержит точку xt, произвольно близкую к ^0)-
Поскольку € лп-1 (^0 и г (^г) = г*(а:г) = 1, через точку X, (согласно
лемме 5.1) проходит единственное плоское сечение, на котором X
постоянно. Значит, лга (я,) = лп (я;) = л„_1. Получаем противоречие.
Оставшаяся часть леммы 5.3 очевидна.
Докажем теперь лемму 5.1. Покажем прежде всего, что суще-
ствуют такие окрестность U точки х0 и (п — к)-мерная гипер-
плоскость Н, что U П Н есть множество точек х из U, для кото-
рых X (х) ~-Х (х0). Поскольку г (х0) = г* (х0) = к, ранг отображения
X равен к в некоторой окрестности точки ж0. Далее, матрица
Якоби отображения X имеет вид (difldxldx]). Если заменить базис
..., еп пространства V базисом /4, . . ., fn и сделать соответст-
вующую замену дуальных базисов в V*, то в новой линейной
системе координат матрица Якоби отображения X будет иметь
вид Т* {d‘1fldxidx1)T, где Т — матрица перехода к новой системе
координат. Поскольку матрица (д'1Хдх1дх1) симметрична, мы
можем выбрать Т так, чтобы левая верхняя подматрица порядка к
матрицы Т* (d‘1j!dxldx1') была невырожденной. Переходя к соот-
ветствующим линейным координатам (и снова обозначая их через
х1, ...,хп), мы можем считать, что матрица (д^/дх'дх1) (г, ; =
= 1, ...,к) невырожденна в точке х0, а значит, и в некоторой
окрестности этой точки. Определим функции у1, ...,у\ полагая
у* = , i — 1, .. ., к\ у1 — xf при i > к, (5.11)
дх'
Функции у1 можно использовать в качестве координат в некото-
рой окрестности U точки х0. Положим gt-df/dx1 (i = l, ...,п).
Тогда матрица Idgi/dy3) имеет ранг к. Поскольку gi = y' для
i = l,..., к, мы можем утверждать, что dgi/dy^ = 0 при
и ]>к. Следовательно, при i > к функции gt зависят только
j? 5. Вторая фундаментальная форма
293
от у1, ..., ук. Далее,
df = У -^rdx1 = y,gt dx',
дхг
откуда
^dgt /\dx' = 0.
Запишем это равенство в виде
^dy* /\dxl+ 2 dgj/\dy^ = Q.
i=l j=h+l
Подставляя сюда выражения
dxi = S ЛУа' d^
dy ouy
<x=l y 3=1 *
мы получим
2 S W ^dya + Jj t S A dyj = 0.
Сравнивая коэффициенты при dy' /\dy3 находим
Поскольку функции gj зависят только от у1, ...,у\ из (5.12)
следует, что
при у, I к.
dyidy1
Следовательно,
zl = + г = 1, ...,к, (5.13)
7=4-1
где с1 — функции от у1, ..., ук.
Множество {х | X (х) = X (х0)} есть множество тех х, для кото-
рых у' (х) = у' (х0) (i=l, ...,к). Значит, функции dgjldy' и сг
в равенстве (5.13) — константы, и множество точек х, для кото-
рых X (х) = X (х0), является пересечением некоторой гиперпло-
скости Н с U.
Равенство (5.13) позволяет написать формулу перехода от коор-
динат у1 к координатам х1. Мы можем записать ее в виде
П д
х1 = У —-у^-\-с', i = i,...,k,
дц*
. ]=к+1 (5.14)
x3—yi, j = к + 1, ... ,п.
294
Гл. VI. Дифференциальная геометрия евклидова пространства
Умножая матрицу Якоби отображения (5.14) на матрицу Якоби
отображения (5.11), мы должны получить единичную матрицу.
Рассматривая элементы с индексами г, s, где г, s<.fc, получаем
Y agi ( V д д S1
XJ ( 4J ду'ду*
i=l j=fe+i
В частности,
1,
О,
если г = з,
если г =/= з.
дсг \
ду* )
1 = det S)
•det
k
п
(з
i=k+i
дугдуг
• (5-15)
dyi ) ' '
Рассмотрим теперь пересечение гиперплоскости Н с Dk.
Пусть Лп-k — связная компонента этого пересечения, содержащая х0.
Для завершения доказательства леммы мы должны проверить,
что отображение X постоянно на и что г (х) — г* (х) = к для
Так как ^сД, мы знаем, что г(х)^.к на Лп_к.
Мы докажем, что г (я) = г* (х) = к, если установим, что г(х) = к,
т. е. что определитель
/ft = det(-^)r,8=1 h^° для всех
Пусть х (<)— кривая на определенная при 0<4<1, при-
чем х(О) = х0. Мы хотим показать, что при любом t точка x(t)
удовлетворяет приведенным выше условиям. Пусть £0 —точная
верхняя грань множества всех t, для которых
X (х (s)) = X (х0) и Jk (х (з)) 0 при всех O^sCi.
Тогда ясно, что X (х (£)) = Х (х (0)). Мы покажем, что Jk(x (£)) 0,
если установим, что функция Д(х(з)) отграничена от нуля,
когда з стремится к t. Но, пока Jk (х (з)) #= 0, формула (5.15)
дает нам точное выражение для А(х(з)). Поскольку функции
d2gj/dyTdy!i и дсг1ду* зависят только от у1, ..., yk, которые
постоянны, так как образ X (х (з)) состоит из одной точки,
и поскольку координаты хг ограничены, мы можем утверждать,
что функция
**( 2 <5Н^)
j=h+1
ограничена, а значит, Jk отграничена от нуля. Это доказывает
лемму 5.1.
Докажем теперь теорему 5.3. Поскольку Д2 (4) == 0, рима-
ново многообразие М локально изометрично пространству Еп.
Это означает, что для любых р 6 Е* и q С М существует диффео-
морфизм фр некоторой окрестности точки р на некоторую окрест-
§ 5. Вторая фундаментальная форма.
295
ность точки q, который является изометрией. Отображение <р
можно продолжить вдоль любой дифференцируемой кривой С
конечной длины, для которой С (0) = р. Действительно, если
Ф (С (i)) определено при 0 <1 t < to, то кривая <р ° С в М на интер-
вале 0 t < to имеет конечную длину. Поскольку М полно,
существует единственная точка qta, такая, что формула <р (С (io)) =
= qt(l позволяет получить непрерывную кривую на отрезке 0
t to- Локальная изометрия позволяет тогда продолжить
отображение дальше. Таким образом, любая дифференцируемая
кривая конечной длины на Еп определяет некоторое отображение
в М. Поскольку Еп односвязно, эти отображения определяют
диффеоморфизм <р: Е71 ->• М. Так как М связно и отображение ф
является локальной изометрией, то ф {Еп) = М. Поскольку ф —
изометрия, оно является накрывающим отображением. Но М
односвязно. Значит, ф есть диффеоморфизм пространства Еп
на М. Итак, первая часть теоремы 5.3 доказана.
Для доказательства второй части воспользуемся леммами 5.1
и 5.2. Предположим, что ф (М) не является гиперплоскостью
в £^+1. Тогда существует по меньшей мере одна точка хо € М,
в которой ранг сферического отображения отличен от нуля.
Поскольку этот ранг 1 (так как Д 2 (А) = 0), он равен в точности
единице в точке Хо. Выберем евклидовы координаты х1, . . . , xn+1
и окрестность U точки Хо € М так, чтобы проекция л поверхности
Ф (U) на гиперплоскость хп+х = О была невырожденной на ф (U).
Мы можем тогда считать функции х1, . . . , хп х) координатами
на U. В этих координатах отображение ф имеет вид
Ф (х1, . . . , х”) = (хх, . . . , х”, / (х1, . . . , хп)), где/ — некоторая
дифференцируемая функция. Вектор vf = (df/dx\ . . . , dfldxn, —1)
нормален к поверхности ф (17) в каждой точке из ф (17). Следова-
тельно, единичный нормальный вектор равен
____ 1 ( * Л_____________i)
II vf II 1 / df \ 2 / df \ 2 \ dx^ ’ ’ dxn ’ )
Во введенных координатах матрица сферического отображения п*
(рассматриваемого как отображение в £”+1) имеет вид
1 ад/______1 а/ е Иv/ И 1 аг/ i а/s II v/II -i д И vy II \
llvflldxidxl llvyipaxi axi ’ ‘ ‘и vy и dxidxn ~ll vy ||« ёх" ах1 nvyji» axi
1 ад/__________1 а/ о И vy и j агу t af ajivyii _t ai|vy|j
Il vf II дхпдх! 11 V/II2 Эх1 dxn ’ ”ll Vy II axn8xn-|l Vy IP gxn || Vy IP 9xn
x) Точнее, x1 о л, ..., xn о л. —Прим, перев.
296
Гл. VI. Дифференциальная геометрия евклидова пространства
Ранг ее совпадает с рангом матрицы
/ d2f d2f —1 а II V/ II Ч
дх1 дх1 ’ " ’ дх± дхп || Vy || дх1
1 ; ;
UV/Ц I '
d2f d2f >—1 д || vy ||
\ дхп дх^ ' ’ ' дхп дхп || Vy || дхп J
а значит, и с рангом матрицы
/ d2f ч
\ дх* dxi )
порядка п, поскольку
g||v/ll _ 1 У / df \ d2fl
dxi II II \ dxk 7 dxkdxi
Итак, ранг сферического отображения совпадает с рангом
преобразования Лежандра, определяемого функцией f от х1, ..., хп.
В частности, согласно лемме 5.3, через Лф (х0) проходит единст-
венное (п— 1)-плоское сечение nn_j множества Лф(С7), на кото-
ром X постоянно. Но
у . ( а/ JL\
\ 0x1 » ’ ' ' ’ дхп ) ’
поэтому когда отображение X постоянно на лп_15 нормальный
вектор к поверхности <р (U) постоянен вдоль стп_1? где on_i =
= (л ° <р)-1 (лп_1). Значит, через ф (хо) проходит единственная
(п — 1)-мерная гиперплоскость Р, такая, что ее проекция на
л (ср (Z7)) совпадает с nn_t и <р (ffn-i) с: Р. Поскольку ср — изо-
метрия (и М может быть отождествлено с Еп), множество
ср-1 (ф (nn_j)) = 0П_! представляет собой кусок некоторой гипер-
плоскости Н (в евклидовой геометрии многообразия М), прохо-
дящей через хо, причем отображение ф линейно на on_i.
Далее, on-i есть открытое подмножество в Н и, согласно
лемме 5.3, г* (х) = 1 на стп_!. Поэтому г* (х) = 1, если х — гра-
ничная точка для (в Н). [Здесь гиг* — ранги сферического
отображения nJ Применяя приведенные выше рассуждения
к точке х, мы убедимся в том, что через х проходит единственное
(га — 1)-плоское сечение образ которого при отображении
Ф лежит в гиперплоскости из En+i. Из единственности следует,
что (п — 1)-мерная гиперплоскость, содержащая совпа-
дает с Н.
Пусть S — множество точек х из Н, обладающих окрестностью
(в Н), которую ф отображает в гиперплоскость. Тогда, как мы
§ 5. Вторая фундаментальная форма
297
уже видели, множество S и открыто, и замкнуто в Н. Мы заклю-
чаем отсюда, что ограничение отображения <р на Н является
линейным отображением гиперплоскости Н на (п — 1)-мернук>
гиперплоскость из Еп+1. Пусть z — точка, не лежащая на Н,
для которой г* (z) = 1. Тогда существует гиперплоскость Н',
проходящая через z и обладающая теми же свойствами. В силу
единственности Н и Н' они не могут пересечься. Значит, они
параллельны. Итак, мы показали, что через каждую точку
х £ М ( = Еп), в которой г* (х) = 1, проходит единственная гипер-
плоскость Нх, на которой отображение <р линейно, и все такие
гиперплоскости параллельны. •
Рассмотрим теперь точку z, в которой г* (z) = 0. Пусть Hz —
гиперплоскость, проходящая через z и параллельная описанным
выше гиперплоскостям Нх. Тогда г* = 0 на Hz. Действительно,
в противном случае существует точка у £ /72, в которой г* (у) = 1.
Но тогда г* = 1 на Ну. Поскольку Ну и Hz должны совпадать,
мы получаем противоречие. Итак, г* = 0 на Hz, т. е, г = Ов неко-
торой окрестности гиперплоскости Hz. Но это означает, что сфе-
рическое отображение постоянно в некоторой окрестности гипер-
плоскости Hz. Таким образом, ф линейно на Hz. Тем самым мы
показали, что через каждую точку q £ М проходит единственная
гиперплоскость Hq, ограничение на которую отображения ср
линейно, причем гиперплоскости, проходящие через разные точки,
либо параллельны, либо совпадают. Если выбрать евклидовы
координаты у1, . . . , уп тДк, чтобы эти гиперплоскости задавались-
уравнениями уп — const, то отображение <р примет требуемый:
вид, что и доказывает теорему 5.3.
Перейдем теперь к доказательству теоремы 5.4. Для этого
удобно ввести абсолютную кривизну |Л?|. Грубо говоря, для
любого множества DcM интеграл j | К | dA (где dA — элемент-
D
объема, определяемый римановой метрикой на М) измеряет объем
множества п (£>) на Sn, причем точки на Sn считаются к раз,
если они накрыты к раз сферическим отображением п. Точка х £М
называется крайней точкой (относительно ф), если ф (М) целиком
лежит по одну сторону от касательной к ф (М) гиперплоскости
в точке х. Обозначим множество всех крайних точек из М через §.
Ясно, что S — наполнимое множество, так что мы можем рассмот-
реть j | К | dA.
fe’
Лемма 5.4. Пусть ф — погружение компактного п-мерного
многообразия AI в Еп+1 и —множество крайних точек из М.
298
Гл. VI. Дифференциальная геометрия евклидова пространства
Тогда
^\K\dA>Kn, (5.15')
i
где ип — объем единичной сферы Sn.
Доказательство. Для доказательства леммы 5.4 удоб-
но рассмотреть вместо сферы Sn проективное пространство Рп.
Напомним, что Рп есть множество всех одномерных подпространств
из Z?n+1. Существует естественное отображение р: Sn -> Рп, сопо-
ставляющее каждому единичному вектору и порождаемое им
одномерное подпространство. Если множество D сРп достаточ-
но мало, то р-1 (D) распадается в Sn на две компоненты Dt UH2,
причем р (Z>i) = р (Z>2) — D. Определив объем множества D
как объем любого из множеств Dt, Dz (их объемы равны), мы полу-
чим объемную плотность в Рп. Полный объем многообразия Рп
с этой плотностью равен хп/2.
Заметим теперь, что ограничение на g отображения р ° и
(где п — сферическое отображение) накрывает каждую точку
из Рп по крайней мере дважды. Действительно, пусть и £ Еп+1 —
произвольный единичный вектор. Рассмотрим на М функцию
(и, <р). Поскольку многообразие М компактно, она достигает
максимума и минимума в точках xt и х2. Эти две точки не могут
совпадать, так как в противном случае гиперповерхность <р (М)
лежала бы в n-мерной гиперплоскости (<р, и) = const, что невоз-
можно, поскольку многообразие М компактно, а <р — погружение.
В каждой из этих точек d (и, <р) = (и, сйр) = 0, так что и норма-
лен к М в хг и х2. Следовательно, р (и) = р ° и (х^ = р ° и (х2)
и р (и) накрывается (по крайней мере) дважды.
Далее, j \K\dA = j [K^dA, где g'— множество точек из g,
в которых | К | > 0. С другой стороны, J | К | dA равен полному
I'
•объему множества р ° и (g') (с учетом кратности) и
vol (р о И (§')) > vol (р о И (g)) — vol (р о п (£")),
где — множество точек, в которых | К | = 0. Но vol (р ° ц (g")) = 0
по теореме Сарда, поскольку К есть якобиан отображения и.
Таким образом,
J\К\dA> 2 (|xrt)=x„,
§ 5. Вторая фундаментальная форма 299
что и доказывает лемму 5.4. Читатель может в качестве упраж-
нения проверить, что неравенство (5.15') в действительности явля-
ется равенством.
Из (5.15') немедленно следует, что j \ K\ dA'^-xn.
м
Теорема 5.6 (Чжэнь — Лашоф). Пусть ф— погружение ком-
пактного п-мерного многообразия М в ЕП1Л. Если
||£|<Ы = хп, (5.16)
м
то (р(М) есть выпуклая гиперповерхность, т. е. ф (Л/) лежит
по одну сторону от любой своей касательной гиперплоскости.
Доказательство. Можно переформулировать заключение
теоремы, сказав, что любая точка из М является крайней, т. е.
% = М. Ввиду неравенства (5.15') равенство (5.16) означает, что
j | К | dA = 0. Поскольку g — замкнутое подмножество в М и,
M-<g
значит, М — ё открыто, для того чтобы интеграл j \K\dA
м-'б
обращался в нуль, необходимо, чтобы | К | = 0 в М—Условие
| .АГ | (x)=j^= 0 означает, что г(х) = п, где г — ранг сферического
отображения. Поэтому теорема 5.6 будет доказана, если мы уста-
новим, что неравенство М — влечет за собой существова-
ние точки х£М— %, для которой г(х} — п. Таким образом, доста-
точно доказать следующее утверждение:
Лемма 5.5. Если существует точка х£М— %, в которой
r(x) = k « ri), то существует точка х" £М — %, в которой г (х") > к.
Тогда, предполагая, что М — $#=0, мы шаг за шагом
построим точку х£М—%, в которой г(х)~п.
Для доказательства леммы 5.5 заметим, что если г* (х) > к,
то доказывать нечего. Действительно, поскольку М — S в этом
случае открыто, существует точка х' £ М — в которой г (х') >
> к. Поэтому достаточно рассматривать случай, когда г (х) =
= г* (х) = к. Применим тогда лемму 5.1. Как и при доказатель-
стве теоремы 5.3, можно выбрать малую окрестность точки х
и подходящие евклидовы координаты в En+1 так, чтобы ранг
сферического отображения совпадал с рангом преобразования
Лежандра (df/dx1, . . . , df/dxn). Из леммы 5.1 вытекает, что су-
ществует (п — &)-мерная гиперплоскость Нп--К в Z?n+1, обладающая
следующими свойствами:
300
Гл. VI. Дифференциальная геометрия евклидова пространства
1) ф (х) € Hn-h cz Н, где Н — гиперплоскость, касающаяся
М в точке х-
2) ф (М) П Hn-k содержит открытую окрестность U точки
ф (х) (в Hn_k), на которой г = г* == Zc;
3) n (х) = п (х*) для всех х*, для которых ф (х*) g U, так
что касательная гиперплоскость в точке х* совпадает с Н.
Пусть W — максимальное открытое подмножество из Hn-k,
удовлетворяющее условиям 2) и 3). Мы знаем, что W Hn-h,
поскольку М компактно. Пусть у' — точка границы множества
W. Тогда мы можем выбрать последовательность точек х;, таких,
что ф (х;) £ W, сходящуюся к точке х', в которой ф (х') = у'.
По непрерывности и (хг) и (х')> и, значит, касательной гипер-
плоскостью в точке х' будет Н. В частности, х' £ М — ё.
Покажем, что г* (х') > к. Поскольку х’ = Ишжг, мы знаем,
что г* (х') к. Если бы г* (х') = к, то мы смогли бы выбрать
окрестность точки х' и подходящие координаты в Е”+1 и снова
применить лемму 5.1. Поскольку х' £ и г (д') — лемма 5.1S
примененная к х', показала бы (вспомним единственность), что
у' С W. Мы приходим к противоречию. Следовательно, г* (х') > к.
Это означает, что в достаточно малой окрестности точки х' (и, сле-
довательно, в М — ё) существует точка х", в которой г (х") > к.
Тем самым лемма 5.5 и теорема 5.6 доказаны. Обращение теоре-
мы 5.6 мы оставляем читателю в качестве упражнения.
Выведем теперь из теоремы 5.6 теорему 5.4. Очевидно, что
из 2) следует 1). Покажем, что из 1) следует 2). Мы имеем
j |£|<Ы = ± J KdA = i-Kn,
согласно равенству (3.8) гл. III. Итак, теорема 5.4 следует непо-
средственно из теоремы 5.6.
§ 6. ПОВЕРХНОСТИ
Применим результаты предыдущего параграфа к изучению
двумерных ориентированных римановых многообразий и погруже-
ний двумерных многообразий в Е3. Прежде всего мы выпишем
для случая двумерных многообразий различные формулы, полу-
ченные в §§ 2 и 3. Группа О+ (2) есть просто окружность, так что
многообразие 0 (М) трехмерно. Локальные координаты на 0 (М)
определяются выбором координатной карты (Z7, h) на М и диф-
ференцируемым выбором реперов в каждой точке из U, т. е. зада-
нием такого отображения ф: U л-1 (<7), что л ° ф = id. Напи-
шем ф (х) = (х; А (х), /2 (ж)) (где /2 — положительно ориен-
тированный ортонормированный базис пространства ТХ(М)).
Любой другой положительно ориентированный ортонормирован-
§ 6. Поверхности 301
ный базис et, е2 пространства Тх (М) имеет вид
ei = (cos т) /t (z) + (sin т) /2 (z),
е2 = — (sin т) Л (х) + (cos т) /2 (z). ' ’
Параметр т определяется этими формулами только по модулю
2л. Если х1, х2 — локальные координаты на U, то х\ х2, т —
локальные координаты на л-1 (U) (правда, т не вполне законно).
Формы 01, 02 определяются формулами
(X, 0х) = (лфХ,
<Х,02) = (лЛ,е2),
где X — касательный вектор в точке (х; е2) [см. формулы (3.1)
и (3.5), где р — тождественное отображение].
Мы имеем (см. (3.4))
01Д02 = Л*ЙЛ, (6.3)
где dA — ориентированный элемент площади многообразия М.
Удобно выразить формы 01 и 02 в терминах локальных координат.
Пусть U, х1, х2 и ф— такие же, как выше. Тогда 01 = ф*(01)
и О2 = ф*(02)— формы на U. При каждом xQU формы 0J., 02 обра-
зуют дуальный базис к /t(z), /2(z). Действительно, для любого
Y £ Тх (М) имеем
(У, ёт) = <У, ф*0х) =
= (Ф*У> 6(я; Л, /а)) =
= (Л*°Ф*У, /1) =
= (У,/1), поскольку л о ф = id.
Итак, (У, О1) = (У, fi) и (У, О2) = (У, /2). Пусть а1 = л‘01 и а2 = л*©2.
Для любого X Ql\x- еъ е2) (® (М)) имеем (X, а1) = (лфХ, /4) и (X, а2) =
= (л*Х, /2), в то время как (X, 0х) = (л*Х, е4) и (X, 02) = (л*Х, е2).
Сравнивая с (6.1) и (6.2), получаем
01 = (cos т) а1 + (sin т) а2,
02=—(sinr) ax + (cosr) а2.
Если риманова метрика многообразия М индуцирована погруже-
нием его в евклидово пространство, то на О (М) существует
единственная форма @i2, такая, что (см. стр. 268—269.—Перев.)
d^ = Q12/\Q2,
Й02=_@12Д01. (6’0)
Сейчас мы дадим явное выражение формы 0i2 в терминах
локальных координат. Построим локальные формы 0i2', удовле-
302
Гл. VI. Дифференциальная геометрия евклидова пространства
творяющие уравнениям Й01 = 012' Д 02 и <702 = — 012' Д 01.
Тогда можно утверждать, что 012' = 012, поскольку уравнение
(6.5) определяет форму 012 однозначно. Эта локальная конструк-
ция позволяет доказать существование формы 012 для любого
двумерного риманова многообразия без предположения о том,
что риманова метрика индуцирована погружением. Действитель-
но, если мы построим 012 локально на л-1 (U), то (в силу един-
ственности) формы 012, построенные над разными окрестностя-
ми U, будут согласованы и, следовательно, определят глобальную
форму. Воспользуемся локальными выражениями (6.4) для форм
01 и О2, чтобы построить 012. Определим для этого функции /q и к2
на & (М), полагая
к1 = к1 ° л и к2 = к2°л, (6-6)
где _______ _________________
d&^kfi1/\1Р и dO5 = A:201 Д 02.
Тогда
da1 = к ipd Да2, da2 = к 2ах Д а2
и
Й01 = — (sin т) dr Д а1 -|- (cos т) dt Д а2 -|- (ki cos т -|- к2 sin т) а1 Д а2,
dQ2 = — (cos т) dt Д а1 — (sin т) dt /\ а2 -|- (— к^ sin т -|- к2 cos т) а1 Д а2.
Поскольку а1Да2 = 01Д02, прямая проверка показывает, что
форма
012 = dt -|- kiO.1 + к2а2 =
= dx-|- (AtCosT-J- /qsinr) 0r-|- ( — kt sinт + Лг2cost) 02 (6.7)
удовлетворяет уравнениям (6.5).
Форма 012 допускает простую геометрическую интерпретацию.
Рассмотрим сначала случай, когда риманова метрика индуциро-
вана погружением многообразия М в трехмерное евклидово про-
странство. Тогда мы имеем векторнозначные функции Ф, Е1, Е2, Es,
определенные на О (М) формулами
Ф = фоЛ,
Е^х, еь е2) = ср,х (ej),
^2 (х, eit е2) = <р,х (е2),
Е3(х, elt e2) = n(z).
Формы 01 и 0<J задаются равенствами
0* = (ЙФ, Е1), = (dEl, Е}),
откуда
dib^W + WE2,
dEl = 2 &}Е\
§ 6. Поеерхности
303
Пусть у — дифференцируемая кривая на М. Дифференцируемое
семейство единичных векторов ^ (•) вдоль у (где е{ (з) g Ty(Sy (М))
можно рассматривать как кривую С в (Э (М), причем л ° С = у.
[Именно, С (s) = (у (s); (s'), е2 (s))-l Назовем семейство et (s)
параллельным, если приращение единичного вектора et (s) при
изменении s нормально к поверхности <р (М) в Е3. Другими сло-
вами, семейство ej (s) параллельно, если вектор
<4y(s) (gj (*))
ds
нормален к <р (М) при всех s. Посмотрим, как можно записать это
условие. Пусть Xs — касательный вектор кривой С в точке С (з).
Тогда по определению формы dE1
^T<₽*v(s) (ei (s)) = (Xs, dE1}.
Заметим, что ({Xs, dE1}, Е1 (С (s))) = 0 и ({Xs, dE1}, Е2 (С (s))) =
= 012. Но значения функций Е1 и Е2 порождают касательное про-
странство к поверхности <р (М). Поэтому условие ортогональности
вектора (Xs, dE1} к ф (М) можно записать в виде (Xs, 012) = 0.
Итак, семейство ei (s) параллельно вдоль у тогда и только тогда,,
когда (Xs, 012) = 0.
По аналогии, семейство единичных векторов вдоль кривой у
на любом двумерном римановом многообразии мы будем называть
параллельным, если (Xs, 012) = 0. Пользуясь этим определе-
нием параллельного переноса J), мы можем доказать следующее
утверждение:
Теорема 6.1. Пусть у — дифференцируемая кривая на М
и et — единичный вектор из Ту (О) (М). Тогда существует един-
ственное параллельное семейство единичных векторов е, (з) вдоль у,
такое, что е^ (0) = е1. Если е\ — другой единичный вектор из
Ту (0) (М), образующий с вектором ei угол о, то вектор е[ (з) обра-
зует с вектором et (s) тот же угол п при каждом s.
Ясно, что достаточно (разбив, если необходимо, кривую у
на малые куски) доказать теорему 6.1 для кривой у, целиком
лежащей в координатной окрестности. Тогда мы можем восполь-
зоваться локальным выражением для 012.
Перепишем условие параллельного переноса вдоль у (s). В тер-
минах локальных координат единичный вектор Cj (з) определяет-
Параллельным переносом вектора е0 £ (М) вдоль кривой у
в точку у (s) называется вектор е (s) £ T,,(s) (Л/) параллельного семейства
векторов е (s) вдоль кривой у, для которого е (0) = е0.— Прим, перев.
304 Гл. VI. Дифференциальная геометрия евклидова пространства
ся функцией т (з), где
«Ч (s) = cos т (з) fi (у (s)) — sin r (s) /2 (у («))•
Тогда
(Xs, 012) = {Xs, dx} -j- (Xs, kpyd + kpy2) =
= ^ + (Xs, n* (A101-A2O2); =
= -^--(n,Xs, k^ + k^).
Но ли.А\ = У8 есть касательный вектор кривой у в точке у(з).
Таким образом,
(A's, e^ = ^--Fy(s),
где (s) = AyO1 + k->Q2}— функция, зависящая только от у.
В частности, семейство ед (з) параллельно тогда и только тогда,
когда
Из этого уравнения мы видим, что для заданного вектора
щ (0) всегда существует единственное параллельное семейство
ej (з). начинающееся с (0). Кроме того, если е' (0) — другой
единичный вектор в точке у (0), то угол между векторами (в)
и е\ (з) равен углу между векторами е1 (0) и е' (0). Таким образом,
параллельный перенос сохраняет углы, что и доказывает теоре-
му 6.1.
Заметим, что если М (локально) изометрично евклидову про-
странству. то мы можем взять /j = д/дх1 и /2 = д!дх2, так что
01 - dx1 и 02 = dx2. В этом случае Ад = к2 = 0, и т есть угол,
который образует вектор ej с д/дх1, т. е. с осью х^ Таким образом.
012 — — dx. Поэтому условие параллельного переноса принимает
в этом случае вид dx/ds = 0, что совпадает с обычным определе-
нием параллельности в евклидовой геометрии.
Пусть ЛА — двумерное риманово многообразие. С любой кри-
вой у на ЛА очевидным образом ассоциируется векторное поле
вдоль у: в качестве е{ (s) берется единичный касательный вектор
кривой у в точке у (з). Таким образом, для любой кривой у на М
мы получаем кривую на Q (ЛА), которую мы обозначим у. [Здесь
у (з) = (у (s): (s), е2 (s)), a et (з) — касательный вектор к у (з).1
Мы назовем форму у* (012) формой геодезической кривизны кри-
вой у. [В евклидовом случае это есть в точности форма у* (dx).
являющаяся обыкновенной кривизной, см. формулу (4.8).]
f 6. Поверхности
305
Рассмотрим кривые с нулевой геодезической кривизной, т. е.
кривые, касательные векторы которых параллельны.
Теорема 6.2. Касательные векторы у' (s) кривой у на М
(параметризованной длиной дуги) образуют параллельное семейство
тогда и только тогда, когда кривая у является геодезической.
Доказательство. Прежде всего запишем условие того,
что касательный вектор X к 0 (М) служит касательным вектором
кривой у. Поскольку noy(s) = y(s), мы имеем n*X = y/(s). С дру-
гой стороны, y(s) = (y(s); y'(s), e2(s)), откуда (л,Х, y'(s)) =
= (л*Х, в} (s)) = 1 и (л*Х, е2(«)) = 0. Таким образом, (X, 91) = 1
и {X, 92) = 0. Обратно, если {X, 92> = 0, то, как легко видеть,
X служит касательным вектором некоторой кривой у (s). Если
вдобавок семейство у' (s) параллельно, то мы должны иметь
(X, О12) — 0. Итак, если вектор X служит касательным вектором
кривой у и семейство у' (s) параллельно, то
(X, 01>=1, (X, 92) = 0, (X, 012) = О. (6.8)
Поскольку формы 01, 92 и 012 линейно независимы, уравнения
(6.8) определяют векторное поле X на 0 (М). Для любой кривой
у семейство у' будет параллельным тогда и только тогда, когда
семейство у' удовлетворяет уравнениям (6.8).
Мы можем отождествить 0 (М) с множеством единичных каса-
тельных (или кокасательных) векторов многообразия М, поскольку
е2 определяется по et. Таким образом, мы имеем отображение
i: 0 (М) -* Т* (М). Из определений очевидно, что i*9 = 91,
где 9 — каноническая форма на Т* (М) (см. теорему 7.1 гл. III).
Множество единичных векторов есть поверхность постоянной
энергии Н = 1. Согласно принципу наименьшего действия (см.
равенство (3.8) гл. IV), геодезическая пульверизация касается
О (М) (где 0 (М) рассматривается как подмногообразие
в Т* (М)) и определяется уравнениями (X, 91) = 1 и
X ji*d9 = X j (Z91 = 0. Но йб1 = 012 Д 92, так что равенство
X j Й91 = 0 эквивалентно равенствам {X, 92) = (X, 012) = 0.
Таким образом, уравнения (6.8) эквивалентны уравнениям, опре-
деляющим геодезическую пульверизацию, что и доказывает тео-
рему 6.2.
Согласно уравнению (5.10),
d©i2 = _ (4н422 _ л12Л21) 91 Д 92.
Учитывая (5.9), мы можем написать
<Z012 = - л* (KdA), (6.9)
где К — гауссова кривизна.
306 Гл. VI. Дифференциальная геометрия евклидова пространства
Пусть D — область с регулярной границей в М, и пусть ф —
отображение некоторой окрестности замыкания D в О (М), при-
чем л ° ф = id. Тогда по теореме Стокса
J ф* (О12) = j ф*л*/СdA = — j KdA. (6.10)
dD D D
Применим формулу (6.10) к отображению ф, которое строится
следующим образом. Пусть Y—векторное поле на компактном
многообразии М, обращающееся в нуль только в конечном числе
точек pi, . .., р^. Если Ух^=0 в точке х£М, то положим et(x) =
= Yx/\\ Yx || и ф(ж) = (а:; е^х), е2(ж)). Вокруг каждой точки pt
выберем такую карту (Ut, hi), 7г; (рг) = (0, 0), что окрестность Ut
не содержит других точек pj (j^=i). Пусть Сг — окружность
радиуса г на плоскости и уг, r = hi1 (Сг). [Радиус г предполагается
столь малым, что окружность Сг лежит в /гг(С7г).] Положим
D = M — Ui, где Ui — внутренность окружности уг1Г. Мы должны
вычислить j ф* (012), причем кривая у(-; г проходится по, а не про-
^г, Т
тив часовой стрелки. Введем для этого вблизи точки pt ортонор-
мированные реперы, определяемые координатами х1, х2. Тогда
мы имеем координаты х\ х2, т в 0(М), где т(ж, е1у е2) есть угол,
образованный вектором (х) с вектором 1 . Таким образом
(ориентируя у;,г по часовой стрелке), имеем
— j dx (et (s)) = 2л (индекс поля Y в точке pi).
Ъ.г
Но ф*012 = ф*йт + ф* (/^оР + ^г0^), откуда
— j ф*012 = 2л-(индекс поля Y в точке рг) + j (А^б14-fc,02).
7г, г г
При г—>0 второй член справа тоже стремится к нулю,
а в правой части равенства (6.10) j —» j. Итак, мы доказали
D М
следующее:
Пусть Y — векторное поле, обращающееся в нуль только
в конечном числе точек рх, . . ., р^. Тогда
2ьар;(У) = ^ ^KdA. (6.11)
i 31
§ 6. Поверхности
307
В частности, сумма индексов векторного поля не зависит
от векторного поля, а полный интеграл кривизны не зависит от
римановой метрики.
Так, например, если М = S2, то векторное поле, касательное
к меридианам, обращается в нуль только на северном и южном
полюсах, и индекс его в этих точках равен 4-1. Поэтому, согласно
(6.11), сумма индексов любого векторного поля на S2 равна двум.
(В частности, на S2 нельзя построить векторное поле, нигде
не обращающееся в нуль.) Кроме того, формула (6.11) показы-
вает, что независимо от выбора римановой метрики на S2 мы имеем
j К dA = 4л.
S2
Аналогично, если М — тор, то мы можем построить на нем
векторное поле, нигде не обращающееся в нуль. Значит, интеграл
в (6.11) равен нулю.
Упражнение 6.1. Пусть М — тор с угловыми координатами
ср, и <р2 (определенными по модулю 2л). Обозначим через / погружение М ->
-> Е3, определяемое формулами
= (2 4- cos <pj) cos <p2,
z2 = (2 + cos <pj) sin <p2,
^3 = sin <pj.
1. Найти риманову метрику на М, индуцированную погружением /,
т. е. вычислить (d/dtfi, d/dtpi)p, (d/dtpt, д/дср2)р и (д/<йр2, d/d<p2,)p для
всех р g М. (Эти выражения могут быть заданы как функции от <pt и q>2.)
Пусть е,, е2 — векторные поля, полученные ортонормированием полей d/dtyi,
3/dq>2. Найти явный вид полей и е2.
2. Найти полную площадь тора в этой римановой метрике.
3. Пользуясь векторными полями е1 и е2, описанными в п. 1, мы можем
ввести (угловые) координаты <р4, q>2 и т на О (М). В терминах этих координат
найти явные выражения для векторнозначных функций Ф, Е1, Е2, Е3 на 0 (М).
(Каждая из этих векторнозначных функций должна быть задана в терминах
стандартного базиса трехмерного евклидова пространства, т. е. в виде тройки
функций от q>1; q>2 и т.) Так, например,
Ф (Т1, Фг, т) = ((2+ cos «pj) cos <р2, (2+ cos (pj) sin <p2, sin q^).
Каковы соответствующие выражения для Е1, Е2 и E3'i
4. Найти явные выражения для форм 61, 62 и 012 на 0 (Л7) в терминах
йф1, <йр2 и dx.
5. Найти гауссову кривизну К многообразия М. (Снова К может быть
задана как функция от q;, и q>2.) В каких точках из М гауссова кривизна
положительна, а в каких отрицательна?
6. На римановом многообразии линейные дифференциальные формы
очевидным образом отождествляются с векторными полями [путем отожде-
ствления пространства Т* (М) с Тх (М), индуцированного скалярным про-
изведением в Тх (Л/)]. Если g — функция, то векторное поле, ассоциированное
20*
308 Гл. VI. Дифференциальная геометрия евклидова пространства
с формой dg, обозначается символом grad g. Пусть М — тор с определен-
ной выше римановой метрикой, и пусть, как и раньше, xt — функция, опре-
деленная формулой xi (<pi, <р2) = (2 + cos ф,) cos ф2. Показать, что векторное
поле X = graa^i обращается в нуль ровно в четырех точках, и вычислить
его индекс в каждой из этих точек.
Теперь мы дадим другой способ вычисления целого числа,
фигурирующего в (6.11). Пусть С1 и С2 —две кривые на 0 (М),
причем лоС1 = лоС'2. Пусть С1 (з) = (у(s); ei(s), e2(s)), а C2(s) =
— (y(s); Л(з), /2(з)). Предположим, что угол между ех (s) и /4(з)
задается (локально) функцией о(з). В терминах локальной системы
координат на 0 (Л?) мы имеем т (С1 (s)) = т (С2 (s)) -f-cr (s). Если X}
и X2S — касательные векторы этих двух кривых, то
(Xs1, 012) = (XI, 012) + . (6.12)
Применим это замечание к следующей ситуации. Пусть D —
область, целиком лежащая в некоторой координатной окрестности U,
причем границей ее служит простая замкнутая кривая у. Пусть
ф: U —>0 (М)— отображение, полученное ортонормированием полей
д/дх1, д/дх2. Положим
С1 (s) = (у (s); (s), е2 (s)), С2 (з) = ф (у (s)),
где Ct (з) — единичный касательный вектор к кривой y(s). Из урав-
нения (6.12) следует тогда, что
j у* (012) = j ф*012 ф- J do,
v v v
где о—угол между у' (s) и д!дх\
Интеграл j do представляет собой полную кривизну кривой у
V
относительно евклидовой метрики, соответствующей координа-
там х1, х2. Согласно (4.12), этот интеграл равен 2л. Поэтому,
используя (6.10), получаем
j у*012 = 2л - J К dA. (6.13)
V D
Равенство (6.13) обобщается, так же как и (4.13), на случай
кусочно дифференцируемой кривой у(С±, ...,СП) (где Ct — диффе-
ренцируемые куски кривой у). В этом случае равенство имеет вид
2 J C?(012) + 2«i = 2«- J KdA, (6.14)
сг D
где ctj — внешние углы в точках стыковки дифференцируемых
кусков. Если все С, являются геодезическими, то первый член
§ 6. Поверхности
309
слева обращается в нуль, и мы получаем
2«i==2n-J KdA. (6.15)
D
Например, если D — геодезический треугольник (рис. 29) и мы
рассматриваем внутренние углы 0i = n—аг, то формула (6.15) дает
₽1 + Р2 + ₽з = л+ (6.16)
[В частности, для сферы К = 1, и мы получаем стандартную фор-
мулу сферической тригонометрии.]
Приступим теперь к нахождению целого числа, фигурирую-
щего в формуле (6.11).
Определение. Связной замкнутой клеточной поверх-
ностью называется компактное дифференцируемое двумерное мно-
гообразие М вместе с конечным числом замкнутых подмножеств
(называемых клетками или гранями) Ft, . . ., Fa2, таких, что
СС2
i=l
и удовлетворяющих следующим условиям:
1. Для каждого i = 1, ... , а2 существует взаимно одно-
значное взаимно дифференцируемое отображение /г клетки F,
на многоугольник с п, сторонами (п, 3).
2. Если i то либо Ft (] Fj пусто, либо fi(Fi(]Fj) есть
сторона или вершина соответствующего многоугольника.
3. Для любых Ft и Fj (i j) существует конечная последова-
тельность таких клеток Ft0, . .., Fis, что Fia = Fi, Fis = Fj
11 Fik^Fik+1^= 0-
310
Гл. VI. Дифференциальная геометрия евклидова пространства
Различные точки из М, отображающиеся в вершины конеч-
ного числа многоугольников, обозначим ТД, . . . , Ра„ (мы будем
называть их тоже вершинами). Подмножеству из М, которое
отображается на сторону многоугольника, мы сопоставим пару
PtPi (выбрав определенное упорядочение вершин Рг), где Pt, Pj —
точки, соответствующие вершинам — концам рассматриваемой
стороны. Обозначим полное число таких множеств (которые мы
также будем называть сторонами) через а1? а сами множества
символами Ei, ... , Еа1.
Для каждой клетки Ft, имеющей вершины Piv ... , Pi ,
выберем определенный порядок этих вершин так, чтобы граница
проходилась циклически. Таким образом, мы имеем следующие
соответствия: .
Fi Pit Pigi
Ei^PjPh,
Pi^pt,
i = 1, • • •, «2,
i — 1, .. ., cq,
i = 1, . .., a0-
Рассмотрим следующие векторные пространства:
Со — вещественное пространство с базисом Pt, ..., Рао,
С1 —- вещественное пространство с базисом Ei, ...,Еа1,
С2— вещественное пространство с базисом Fi, . . ., Fa2.
Определим два линейных отображения д2: С2 —>
и dt: Ci—> Со, полагая
^2 (Pil • Pis) = РilP*2 + Рi^P’3 + • • + Рi$Pin
где
| Et, если Ei++ PivPi2,
Р4Р4 ( — если Et Pi2Pii,
di (PuPi^Piz-Pii
и продолжая отображения по линейности.
Проверка на базисных векторах показывает, что 51°32 = 0.
Значит, д2 (С2) с (0). Оказывается, что1)
Я2(М)=<^(0),
^(M) = ^(0)/32(C2),
H0(M) = c0/di(Ci).
Размерности векторных пространств Н2 (М), Hi (М), На (М)
называются числами Бетти многообразия М и обозначаются
символами р2, Pi, ро.
г) Здесь (М) есть /с-мерпая группа гомологий многообразия М, см.
определение 2.4 гл. III.— Прим, перев.
$ 6, Поверхности
311
Определение 6.1. Число а0 — а4 + а2 = X (-^0 назы-
вается характеристикой Эйлера — Пуанкаре.
Легко доказать (однако мы это делать не будем), что
X (М) = Ро — Pi + Рг-
Данное определение характеристики % (Af) в высшей степени
«неинвариантно», т. е. априори сильно зависит от разбиения
на клетки. Мы покажем сейчас, что на самом деле это не так.
Действительно, применим формулу (6.14) к случаю, когда D
есть грань F;. Пусть пг, пс и пв соответственно число граней, сто-
рон и вершин. Просуммировав равенства (6.14) по всем граням,
получим
2лиг — К dA = (6.15)
м
поскольку члены вида j Ку (s) ds сокращаются, ввиду того что
каждая сторона проходится в двух направлениях. Справа стоит
сумма по всем внешним углам при всех вершинах. Но сумма всех
внешних углов при каждой вершине равна, очевидно,
л-(число сторон при вершине) — 2л.
Поскольку каждая сторона подходит ровно к двум вершинам,
сумма в правой части равна 2лис — 2лив. Таким образом, фор-
мула (6.15) превращается в формулу Гаусса — Бонне:
%(М) = пг— лс + лв = -^- j KdA. ' (6.16)
м
Как мы уже убедились, гауссова кривизна К играет двоякую
роль: во-первых, она является якобианом сферического отображе-
ния, и, во-вторых, согласно (6.13), характеризует изменение
вектора при параллельном обносе его вдоль малой замкнутой
кривой. Сейчас мы увидим, что она входит также в формулу
второй вариации длины дуги. Пусть у — геодезическая на М.
Напомним, что точка, сопряженная с точкой у(0) вдоль у, опре-
деляется следующим образом. Рассмотрим отображение л oaf.
Tv(0) (М) —>М, где at — геодезический поток. Тогда первая точка,
где индуцированное касательное отображение n*°au: T0(TV(Q) (Af))—>
—»7’V(t) (M) становится вырожденным, называется точкой, сопря-
женной с у (0) вдоль у. Поскольку подмногообразие i (О (М)) с:
с Т (Af) инвариантно относительно геодезического потока, мы
можем переформулировать это определение, оставаясь в рамках
расслоения <9 (Af). Заменим 7\,(0) (Af) множеством реперов
из 7\(0)(М), т. е. рассмотрим множество единичных векторов
из Т (Af). Пусть Х12( = д/дт)— поле единичных векторов, касатель-
ное ко всем слоям расслоения О (Af), т. е. Х12 есть векторное поле,
312 Гл. VI. Дифференциальная геометрия евклидова пространства
определяемое уравнениями (Х12, 0Х) = (Х12, 02> = 0 и (Х12, 0Х2) = 1.
Мы по-прежнему будем обозначать через а< ограничение геодези-
ческого потока на Q (Af). Тогда сопряженная точка есть первая
точка, где
л*оаьУ0 = 0, (6.17)
если Уо = Х12(у(О); у'(0), е2(0)), т. е. Уо—единичный вектор,
касательный к реперам с началом в точке у (0). Но уравнение (6.17)
эквивалентно уравнениям (аиУ0, 0х) = (аиУо, 02) = О, или
(Уо, а?0х) = 0, (Уо, а*02) = 0. (6.18)
Пусть X — инфинитезимальная образующая потока а, т. е. X есть
векторное поле, задаваемое равенствами (6.8). Из (6.8) следует, что
^Х0Х = О, £Л02 = 0Х2, %хе12=—К№. (6.19)
Далее,
4<У0, а*0х) = (Уо, а?^01) = О
и (Уо, 0Х) = О, так что первое из уравнений (6.18) тождественно
удовлетворяется. Положим а*02). Тогда
4 UC = о, = (Уо, а?©12)
и, значит,
^l(t) = {Y0, а?^0Х2) =
= (У0, а? (-О2))= -КЩ).
Итак, функция £ удовлетворяет следующему уравнению (уравне-
нию Якоби):
5- + ^ = 0. (6.20)
Таким образом, кривизна измеряет также вторую вариацию
длины дуги. Из уравнения (6.20) можно извлечь разнообразные
следствия. Прежде всего сформулируем теорему Штурма относи-
тельно уравнений типа (6.20).
Лемма 6.1. Пусть % — решение уравнения (6.20), а г] —
ненулевое решение уравнения
$ + ^'П = 0, (6.21)
где К’ <Z К. Тогда между любыми двумя нулями функции ц
находится по крайней мере один нуль функции |.
Доказательство. Мы можем считать, что г] (а) =
= т] (Ь) = 0 и т] (£) > 0, если а < t < Ъ. Предположим, что
§ 6. Поверхности.
313
0 на отрезке а t b, скажем, £ > 0. Пусть т — мини-
мум %. Умножая функцию ц в случае надобности на ненулевую кон-
станту, мы можем считать, что max ц (t) = т. Тогда £ — г] 0
a^i^b
и (io) — Л (io) = 0 в некоторой точке io интервала (а, Ъ) (рис. 30).
Поскольку функция £ — ц в этой точке достигает минимума, мы
должны иметь
Но
+ К\ = (К' - К) I (tB) < 0.
Полученное противоречие доказывает лемму 6.1.
Если положить К’ = С2 = const, то решением уравнения
(6.21) будут cos Ct и sin Ct. Следовательно, если К > С2, то любое
Рис. 30.
решение уравнения (6.20) обращается в нуль на каждом интервале
длины л/С. Это означает, что на поверхности с кривизной >С2
сопряженные точки вдоль геодезических Отстоят друг от друга
не больше, чем на л/С. Но геодезическая не минимизирует рас-
стояние за сопряженной точкой. Поэтому расстояние между
любыми двумя точками не больше, чем л/С. Таким образом,
доказана
Теорема 6.3 (Бонне). Пусть М — связное двумерное рима-
ново многообразие, кривизна К которого удовлетворяет неравен-
ству К/^-С2. Тогда расстояние между любыми двумя точками
из М не превосходит л/С. В частности, если многообразие М полно,
то оно компактно.
Доказательство следующей теоремы мы оставляем читателю
в качестве упражнения:
Теорема 6.4. Пусть М — связное двумерное риманово
многообразие, кривизна К которого всюду <^0. Тогда ни на какой
геодезической многообразия М не существует сопряженных точек.
В частности, если многообразие М односвязно, то оно диффео-
морфно Е2.
Глава VII
ГЕОМЕТРИЯ (?-СТРУКТУР
В главе II мы рассматривали расслоение кореперов (М) и расслоение
реперов eV (М) многообразия М. В главе VI мы изучали расслоение орто-
нормированных реперов О (М) риманова многообразия М и расслоение
(М), определяемое погружением «-мерного многообразия М в En+h.
Все эти расслоения обладают некоторыми общими свойствами — они пред-
ставляют собой дифференцируемые многообразия вместе с фиксированным
отображением, которое мы обозначали через я, на М. Кроме того, на каждом
из этих многообразий действует (справа) некоторая группа Ли. Так,
на л- (М) и (М) действует группа GL («) (согласно формуле (6.1) и след,
гл. П);группаО (п) действует подобным же образом па О (М), а группа О (п) х
X О (к) (рассматриваемая как подгруппа группы О (п + к)) очевидным обра-
зом действует на ©^(М). Наконец, во всех этих случаях для любых
у g л-1 (г) и z g л-1 (ж), где х g М, существует единственный элемент А
из соответствующей группы Ли, такой, что z = у А.
В этой главе мы будем изучать подобные объекты, называемые главными
расслоениями, для любой группы Ли. При изучении главных расслоений
важным геометрическим понятием является понятие параллельного переноса.
В последнем параграфе гл. VI мы убедились, что в двумерном римановом
многообразии М естественным образом определяется параллельный перенос
реперов из & (М) вдоль кривой. В произвольном главном расслоении
не существует естественного способа параллельного переноса вдоль кривой.
Однако выбор такого способа определяет интересный геометрический объект
(называемый связностью) и позволяет ввести понятие кривизны, обобщающее
понятие гауссовой кривизны двумерного риманова многообразия. После
изучения этих общих понятий мы займемся более специальным классом
главных расслоений, представляющих особый интерес в дифференциальной
геометрии.
§ 1. ГЛАВНЫЕ II АССОЦИИРОВАННЫЕ РАССЛОЕНИЯ; СВЯЗНОСТИ
Пусть G — группа Ли, а Р — дифференцируемое многообра-
зие. Говорят, что группа G дифференцируемо действует справа на Р
(см. § 6 гл. II для случая G = GL (п)), если задано такое диффе-
ренцируемое отображение ср: Р X G Р, что для любого а g G
отображение Ra: Р Р, определяемое формулой р ср (р. а),
является диффеоморфизмом многообразия Р на себя и
ср (ср (р, а), Ь) = ср (р, аЬ), т. е. Rab = Rb ° На. Если е — еди-
ница группы G, то Re — тождественное отображение. Для про-
стоты мы будем обычно писать Ra (р) = p-а, так что p-(ab) =
= (р-а)-Ь.
§ 1. Главные и ассоциированные расслоения; связности
315
Определение 1.1. Пусть Р и М — дифференцируемые
многообразия, ал — дифференцируемое отображение многообра-
зия Р на М. Пусть G — группа Ли, дифференцируемо действую-
щая справа на Р. Тогда (Р, М, л, G) называется главным G-рас-
слоением (или, лучше, главным расслоением над М со структурной
группой G), если
1) G действует на Р свободно, т. е. нз р-а = р для некоторого
р £ Р следует, что а = е.
2) Пусть р^ и р2 — любые две точки из Р. Тогда л (рД =
= л (р2) в том и только в том случае, когда существует такой
элемент а £ G. что pi-a = р2. Другими словами, многообразие М
можно рассматривать как «факторпространство» многообразия Р
относительно действия группы G.
3) Расслоение Р локально тривиально над М, т. е. для любой
точки х £ М существуют ее окрестность U и диффеоморфизм
ф: л-1 (U) U X G, такие, что ф (р) = (л (р), ц (р)), где ц (р) £
ё G и ф (р-а) = (л (р), т] (р) а).
Если М — точка, то Р отождествляется с G. Для любого
многообразия М, если х С М, то л-1 (х) есть дифференцируемое
подмногообразие в Р, диффеоморфное G. которое называется
слоем над х. Таким образом, Р — это набор экземпляров группы G,
занумерованных точками из М. Поэтому в определенном смысле
понятие главного расслоения является геометрическим обобще-
нием понятия группы Ли. Определим понятие гомоморфизма
одного главного расслоения в другое. Пусть р — гомоморфизм
группы Ли Gi в группу Ли G2. Пусть Pi — главное (Д-расслоение,
а Р2 — главное С2-расслоение над одним и тем же многообрази-
ем М. Мы будем говорить, что дифференцируемое отображение
/: Pi Р2 есть р-гомоморфизм, если л/ (рД = л (/ц) и / (pt-a) =
= / (pi) Р (а) Для всех Pi £ Pi и а. Gi. Диффеоморфизм, являю-
щийся одновременно гомоморфизмом, называется изоморфизмом.
Рассмотрим случай, когда группа Gi состоит из одной единицы.
Тогда Pi можно рассматривать как само М, а гомоморфизм / - -
как отображение М Р2, удовлетворяющее условию л ° f — id.
В этом случае f называется сечением расслоения Р2. Если расслое-
ние Р допускает сечение /, то существует изоморфизм <ру расслое-
ния Р на расслоение М X G. Действительно, для любого р С Р,
такого, что л (р) = х, существует единственный элемент а £ G,
такой, что / (ж) а = р. Положим (р) = (ж, а). Простая про-
верка показывает, что отображение фу дифференцируемо и, более
того, является изоморфизмом расслоения Р на М X G.
Итак, мы показали, что любое главное расслоение, допускаю-
щее сечение, тривиально, т. е. изоморфно М X G. Обратно, рас-
слоение М X G допускает очевидное сечение /: / (ж) = (ж, g (ж)),
где g — любое дифференцируемое отображение М G.
316
Гл. VII. Геометрия G-структур
Отвлекаясь немного в сторону, заметим, что вопрос о том, тривиально
ли данное расслоение, часто представляет значительный геометрический
интерес. Рассмотрим для иллюстрации расслоенпе © (Af), где М — двумер-
ное компактное ориентированное риманово многообразие. Тривиальность
расслоения 0 (Af), или, что то же самое, наличие у него сечения, означает
существование ненулевого векторного поля на М. Это может быть только
в том случае, когда М — тор. Более того, если М — не тор, то целое число
% (Af) (равное сумме индексов произвольного векторного поля на Af) пока-
зывает, в некотором смысле, насколько расслоение & (Af) отличается от
тривиального. Изучение «препятствий» к тривиальности главного расслоения
— один из основных методов, используемых в теории расслоенных пространств.
Полученные таким образом результаты играют ведущую роль в дифференци-
альной топологии. Развитие этих идей читатель найдет в книге Стинрода
«Топология косых произведений» (ИЛ, М., 1953) и в принстонских лекциях
Милнора: «Лекции о характеристических классах» ’). В дальнейшем мы будем
в основном заниматься геометрическими вопросами, связанными с главными
расслоениями, поскольку соответствующие топологические проблемы выходят
за рамки этой книги.
Заметим, что если Р — главное G-расслоение над М, a U —
открытое подмножество в М, то л-1 (G) есть главное G-расслоение
над U. Согласно условию 3) определения 1.1, каждая точка р С М
должна иметь такую окрестность U, что расслоение л-1 (G)
тривиально.
Выберем покрытие {Ga} многообразия М, состоящее из таких
окрестностей, и пусть <ра: л-1 (Ua) —> G — соответствующие ото-
бражения * 2). Над каждым пересечением Ua(]U$ отображение
р —> tpg (р) (<ра (р))-1 постоянно вдоль слоев и, следовательно,
определяет отображение "фра: Отображения фра
называются функциями перехода расслоения Р относительно
покрытия {Ua}. Очевидно, что они удовлетворяют соотношению
Ф?6*Фра = Фта- (1'1)
Обратно, если заданы открытое покрытие {Ga} многообразия М
и множество дифференцируемых отображений фра: Ua П Gp ->
-> G, удовлетворяющих условию (1.1), то мы можем построить
главное расслоение, для которого фра будут функциями перехода.
Доказательство основано на теореме 2.1 гл. II и проводится
точно так же, как доказательство (для случая jp* (М)), изложен-
ное в § 6 гл. II. [Мы оставляем его читателю в качестве упраж-
нения.]
Другим важным частным случаем гомоморфизма Pi -> Р2
является случай, когда G — подгруппа группы G2, а р — гомо-
морфизм вложения. В этом случае гомоморфизм Pi —> Р2 назы-
*) Русский перевод см. в сб. Математика, 3: 4 (1959), 3—53, и 9: 4
(1965), 3—40.— Прим, перев.
2) То есть отображения, определяющие изоморфизмы fa: р->-(л (р), <ра (р))
расслоений л-1 (Ua) на Ua X G.— Прим, перев.
§ 1. Главные и ассоциированные расслоения; связности 317
вается редукцией б2-расслоения Р2 к (Д-расслоению Pi. Мы будем
говорить, что б2-расслоение редуцируется к подгруппе Glt если
существует его редукция к Си-расслоению Pi. Так, если Gi =
= {е}, то расслоение редуцируется к {е} тогда и только тогда,
когда оно тривиально. В качестве другого примера заметим, что
над произвольным многообразием М С?£(и)-расслоение вр (М)
всегда редуцируется к О(и)-расслоению. Действительно, введем
на М риманову метрику и рассмотрим соответствующее
О(и)-расслоение О (М). Оно является подмногообразием в ёр (М).
и тождественное отображение, очевидно, является изоморфизмом
О (М) -> <р (М). Аналогично, <р (М) редуцируется к ^(^-рас-
слоению тогда и только тогда, когда многообразие М ориенти-
руемо.
Пусть /: Pi-^-P2—редукция расслоения Р2 к 7Д. Выберем
покрытие {£7а} многообразия М и функции ф«: (С7а) —>6^,
соответствующие расслоению Pt. Пусть фра — соответствующие
функции перехода. Если л2 — проекция Р2—>М, то определим
отображение ф«: (?7а) —>6?2 следующим образом. Любую точку
РгС-л"1 (Ua) можно записать в виде f(p}a, где Pi£Pt и aQG2.
Положим (Рг) = Фа (а) я. Если мы выберем другое представле-
ние p2 = f(p'1)a', то / (рД а'а-1 = /(Р1), так что р'а'а-1 = рР Сле-
довательно, фа (pl) ci' = Фа (Pi)и, значит, отображение ф„ опре-
делено корректно. Предлагаем читателю проверить, что оно
определяет изоморфизм расслоения лД^а) на Ua х G2.
Далее, фНфа(р2))_1 = Ф(г(фИР2))_1, если p2 = f(Pi), так что фри
служат также и функциями перехода расслоения Р2. Итак, функ-
ции перехода расслоения Р2 принимают значения в G^ Обратно,
предположим, что нам удалось выбрать такое покрытие {U„}
многообразия М, что функции перехода расслоения Р2 принимают
значения в подгруппе G^ Согласно рассуждениям, приведенным
на странице 237, отображения фри дифференцируемы и как ото-
бражения в G^ Поскольку они удовлетворяют соотношениям (1.1),
мы можем построить соответствующее расслоение Pi и очевидное
вложение Pi—>Р2. Таким образом, доказана
Лемма 1.1. Пусть Р2 — главное С2-расслоение над М
и Gi — подгруппа группы G2. Тогда расслоение Р2 редуцируется
к Gi-расслоению в том и только в том случае, когда существует
покрытие {Ua} многообразия М, для которого функции перехода
фир принимают значения в Gi.
Пусть Р — главное расслоение со структурной группой G.
Поскольку G действует на Р, любую однопараметрическую под-
группу в G можно рассматривать как однопараметрическую
группу диффеоморфизмов многообразия Р. Поэтому любое лево-
318
Гл. VII. Геометрия G-структур
инвариантное векторное поле X на G определяет векторное поле
X на Р. Легко видеть, что отображение X -> X является гомо-
морфизмом алгебры Ли g группы G в алгебру Ли векторных полей
на Р. Это отображение взаимно однозначно. Можно утверждать
даже больше: если Хр = 0 для некоторого р £ Р, то X = 0.
Действительно, если Хр = 0, то р есть неподвижная точка одно-
параметрической группы преобразований, порожденной полем X.
Но преобразования этой группы представляют собой действия
элементов ехр tX g G на Р. Поэтому из условия 1) определения 1.1
следует, что ехр tX = е, откуда X = 0.
Заметим, что р-ехр tX всегда лежит в том же слое, что и р,
так что поле X касательно к слоям. Отображение g -> Тр (Р\
переводящее X в Хр, является вложением в подпространство
пространства Тр (Р), касательное к слою. Поскольку послед-
нее имеет ту же размерность, что и g, для любого касательного
к слою вектора Y £ Тр (Р) существует единственный вектор
X g g, такой, что Хр = Y. Другими словами, касательные про-
странства слоев расслоения Р каноническим образом отождест-
вляются с алгеброй Ли g.
Пусть a^G, XQg, и пусть ф1( — однопараметрическая группа
диффеоморфизмов расслоения Р, порожденная полем R* X,
а фг;— однопараметрическая группа, порожденная полем X. Век-
торные поля У = Ra X и X Ра-связаны. [Напомним, что
(Р^Х)р = (Ра);1 Хра, так что Ra*Yp = Xpa и, значит, У и X
Ра-связаны, см. определение 8.3 гл. II.] Согласно упражнению 8.4
гл. II, мы имеем Ra ° фц = ф2« ° Ra- Так как ф2< = Рехр tx, то фц =
— Ra° Rexp tx ° Ra ~ Pa-l(exp tX)a — RAa-i(exp iX). Но ОДНОПараметрнче-
ская группа Ла-1 (ехр tX) соответствует элементу (Ad сг1) X g g.
Следовательно,
P:X = (Ad7iX). (1.2)
Рассмотрим теперь задачу об определении понятия параллель-
ного переноса в главном расслоении Р над /г-мерным многообра-
зием М. Как мы уже видели в случае двумерного риманова мно-
гообразия, мы должны задать способ переноса слоев вдоль любой
дифференцируемой кривой С многообразия М. Более точно, мы
должны указать однозначный способ сопоставления каждой точке
р (Е л'У (0) некоторой точки pt g л-1С (£) при всех t. Кроме того,
мы требуем, чтобы это сопоставление определяло движение слоя,
т. е. чтобы (р-а)( = pt-а для всех а £ G.
Итак, мы хотим иметь правило, сопоставляющее каждой диффе-
ренцируемой кривой С на М и каждой точке р £ л-1 (С (0))кривую.
§ 1. Главные и ассоциированные расслоения; связности
319
Ур на Р, удовлетворяющую условиям i) л (ур (i)) = С (t) и
ii)yp.a (t)=yp (t) • а для всех а £ G и всех t из области определения
кривой С. Мы потребуем также выполнения некоторых условий
дифференциального характера: iii) касательный вектор ур (0)
зависит только от С (0); тем самым мы получаем отображение
п : Тх (М) -> Тр (Р) для каждого р £ л-1 (х).
Из условия i) следует, что лФр°пр = id. Наложим дополнитель-
ное условие: iv) отображение ор линейно. Тогда Нр = <ур (Тх (.И))
будет n-мерным подпространством в Тр (Р) и л*рНр = Тх (М).
Заметим, что выбор подпространства Нр определяет отображение
Пр, поскольку л*р есть изоморфизм пространства Нр на Тх (М).
Поэтому вместо отображений стр мы можем задавать подпростран-
ства Нр, т. е. n-мерную дифференциальную систему на Р. Мы
будем предполагать, что v) система дифференцируема. Условие
ii) показывает тогда, что Ra*Hp = Нр.а. В соответствии с приве-
денными выше требованиями дадим следующее
Определение 1.2. Пусть Р — главное расслоение
со структурной группой G над n-мерным многообразием М. Связ-
ностью на Р называется такая re-мерная дифференциальная систе-
ма о%? на Р, что
1) я*Нр = ТП(Р)(М) (где Нр = ^Т(р));
2) Ra*HP = Hpa.
Подпространство II р называется горизонтальным пространством
связности в точке р.
Заметим, что в каждой точке р касательное пространство слоя
вместе с IIр порождают Тр (Р). Поэтому' задание подпространства
Нр определяет проекцию (вдоль Нр) пространства Тр (Р) на каса-
тельное пространство слоя. Но мы отождествили касательные про-
странства слоев с алгеброй Ли g. Таким образом, мы получаем
линейное отображение Тр (Р) -> g, которое на любом касательном
пространстве каждого слоя совпадает с упомянутым выше отож-
дествлением. Короче говоря, мы получаем g-значную дифферен-
циальную форму Q, которая, как легко видеть, дифференцируема.
Она называется формой связности г). Подпространство Нр есть
в точности множество векторов X, для которых (X,QP) — 0.
Условие 2) определения 1.2 означает, что если X — вектор, каса-
тельный к слою, то (7?ОЙ!Х, Нр.а) = Ada-1 (X, Qp). Значит, и для
любого вектора X £ Тр (Р) мы имеем (Ra*X, QP.tC =
= Ada-1 (X, Qp), т. e.
Ra.^1 = Ad a-1Q. (1-3)
т) Если P есть расслоение & (M) над двумерным рпмановым многооб-
разием М, то форма Q — это в точности форма 012 гл. VI. Группа О (2) есть
окружность, и ее алгебру Ли можно рассматривать как R — вот почему
форма 012 оказывается вещественнозначной.
320
Гл. VII. Геометрия G-структур
Обратно, предположим, что нам задана g-значная форма Q
на Р, удовлетворяющая условию (1.3), причем (X, О) = X для всех
X 6 S- Тогда, как легко видеть, дифференциальная система,
порождаемая векторами, которые аннулируются формой Q, являет-
ся связностью.
Ясно, что связность на Р индуцирует связность на л-1 (£7),
где U — любое открытое подмножество в М.
Покажем теперь, как построить связность на любом главном
расслоении. На тривиальном расслоении U х G существует очевид-
ная связность, соответствующая разложению касательного про-
странства в каждой точке в прямую сумму. Пусть Р — главное
расслоение над М и {Ua} — такое покрытие многообразия М, что
расслоения л-1(£7и) тривиальны. Пусть — форма связности
на л~1(£7и), и пусть {сра} — разбиение единицы, подчиненное покры-
тию {Ua}. Положим Фи = <ра°л и □ = 2 Ф<Ах- Поскольку каждая
форма удовлетворяет условию (1.3) и функции Фи постоянны
на слоях, форма Q также удовлетворяет условию (1.3). Кроме того,
для любого X g g мы имеем (X, Q) = 2 Ф« &а) = 3 = X.
Значит, Q есть форма связности.
Пусть Y — векторное поле на М, а Р — главное расслоение
над М с заданной связностью SB- Тогда в каждой точке р£Р
существует единственный вектор YP^HP, такой, что л,рУр = Ущр)-
Таким образом, мы получаем векторное поле Y на Р, которое
л-связано с полем Y. В соответствии с теоремой 8.3 гл. II,
если Yi и У2—векторные поля на М, то [У^, У2] = 1^1, Т2].
Поэтому отображение У —> У является изоморфизмом векторных
полей на М в векторные поля на Р. Векторное поле вида У на Р
называется горизонтальным.
Используя этот изоморфизм, мы можем определить параллель-
ный перенос вдоль любой кривой С на М. А именно, мы сейчас
покажем, что для любого р g л-1 (С (0)) существует единственная
горизонтальная кривая у, у (0) = р, для которой л°у = С. Гори-
зонтальной кривой мы называем кривую, все касательные векторы
которой лежат в SB- Покрывая область определения кривой С ко-
нечным числом интервалов и доказывая для них существование
и единственность горизонтальных кривых, мы тем самым докажем
существование и единственность искомой горизонтальной кривой.
Поэтому можно считать, что С целиком лежит в такой окрестности
U, для которой л-1 (£7) изоморфно U X G. Мы можем также счи-
тать, что кривая С задана на отрезке [0, 1] и является интеграль-
ной кривой некоторого векторного поля X, определенного на ок-
рестности U. Тогда ясно, что кривая у должна быть интегральной
§ 1. Главные и ассоциированные расслоения; связности
321
кривой векторного поля X, проходящей через точку р. Это доказы-
вает единственность.
Для доказательства существования мы должны убедиться в том,
что интегральная кривая поля X, проходящая через р, определена
при всех t £ [О, I]1). Для этого, пользуясь отождествлением
л-1 (U) = U X G, представим поле X в виде X = X -j- Yx, где Yx
есть векторное поле на G при каждом xQU. Согласно условию (1.3),
поле Yx на G для любого xQU правоинвариантно. Теперь мы
можем искать интегральную кривую у поля X в виде у (() =
= (я ((), g (()). Мы должны иметь х'(t) = Xx(V) и g' (t) = У^р.
Положив x(t) = C (t), мы получим решение первого из этих урав-
нений. Остается решить систему обыкновенных дифференциальных
уравнений g' (t) = У^З на G.
Пусть со1, . . ., <oft — базис пространства линейных правоинва-
риантных форм на G. Положим ds1 = (со1)2-)- . .. +(£ofe)2. Тогда
в этой римановой метрике || У^щ) || < К для некоторого достаточно
большого К. Отсюда следует, что кривая g, являющаяся решением
уравнения g' (t) = YXg(r), имеет длину ^Ка на любом отрезке
[О, а], на котором она определена. Следовательно, поскольку много-
образие G полно в этой метрике, если кривая g определена для
то g(t) имеет предел при t-^>a. Применяя теорему
существования и единственности для любых 1, мы заключаем,
что кривая g определена при О О t < а е, где е достаточно мало.
В частности, полагая
а — sup {b | g (t) определена при
мы заключаем, что а = 1. Другими словами, кривая g (t), а значит,
и у (if) определена для всех t Е Ю, 1].
Из приведенной конструкции ясно, что определенный выше
параллельный перенос удовлетворяет требованиям i) — iv). Ясно
также, что если кривые и С2 близки в ^-топологии на М и точ-
ки pt = Yj (0) и р2 = у2 (0) близки, то кривые и у2 близки в
('-‘-топологии на Р.
Это определение параллельного переноса очевидным образом
распространяется на случай кусочно дифференцируемых кривых.
Пусть Р — главное G-расслоение над М со связностью
и пусть р Е Р и л (р) = х. Пусть С — замкнутая кусочно диффе-
ренцируемая кривая с началом и концом в точке х. Параллельный
перенос вдоль С можно рассматривать как диффеоморфизм тс
х) Сразу мы не уверены в этом, поскольку стандартная теорема суще-
ствования дает только локальное решение, которое, вообще говоря, может
и не продолжаться на все t.
21 с. Стернберг
322
Гл. VII. Геометрия G-структур
слоя л-1 (х) на себя, причем
тс (q-a) = тс (д') а для всех q£n~1(x') и a QG. (1.4)
Пусть Ci и С2 — две кривые, определенные при 1,
причем Ci (0) = Ci (1) = С2 (0) = С2 (1) = х. Тогда мы можем
определить кривую С3 = CiC2, полагая С3 (t) = Ci (2t), если
0 < i < V2, и С3 (i) = С2 (2t — 1), если V2 t 1- Ясно, что
TCiC2 = WTci, так что множество всех таких диффеоморфизмов
образует группу, которая называется группой голономии в точке х
и обозначается Фж. Группа Фж естественным образом превращается
в топологическую группу: элемент т £ Фж считается близким к еди-
нице, если он имеет вид тс, где С — кривая, близкая к постоянной
кривой в С1-топологии.
Пусть у — другая точка из М. Предположим, что существует
кривая D, соединяющая х с у. Тогда любая замкнутая кривая С
с началом и концом в точке х определяет замкнутую кривую DCD~X
с началом и концом в точке у и, следовательно, изоморфизм aD
группы Фж на Фу. Поэтому если многообразие М связно, то имеет
смысл говорить о группе голономии Ф связности на расслое-
нии Р над М.
Рассмотрим теперь точку р из слоя над точкой х. Для любого
т £ Фж мы имеем т (р) = р-ах, где ах — некоторый элемент из G.
Кроме того,
Т1 (Т2 (рУ) —Xi(P' аГ2) = Р • аТ1 • аг2>
согласно формуле (1.4). Таким образом, аХ1Х2 -= аХ1-аХ2. Другими
словами, отображение Рр : т аг является изоморфизмом груп-
пы Фж в G. Легко видеть, что это отображение непрерывно относи-
тельно введенной нами топологии на Фж. Выберем теперь другую
точку q из слоя над точкой у g М. Если многообразие М связно,
то мы можем соединить х с у некоторой кривой D. Пусть р' — точ-
ка из л-1 (г/), полученная параллельным переносом точки р вдоль
D, и пусть p'-b = q. Тогда точка (аотс) р' получается, если сна-
чала перенести параллельно точку р' вдоль кривой D назад в точку
р £ л-1 (х), затем, применив тс, получить точку р-аХс и, наконец,
параллельно перенося ее вдоль D в слой л-1 (у), получить р' -аХс.
Таким образом,
Рр' ° ССд = Рр.
В точке q мы имеем
«в (т) q = «d (т) р’ • b = р' рр (т) • Ъ =
= р' b Ь"1 • рр (т) b = q b~l • рр (т) • Ъ.
<£ 1. Главные и ассоциированные расслоения; связности
323
Итак, на связном многообразии М точка из Р определяет изомор-
физм группы голономии в группу G. и любые два таких изоморфиз-
ма отличаются на внутренний автоморфизм группы G.
Поскольку — непрерывный изоморфизм, мы можем (в со-
ответствии с леммой 4.4 гл. V) ассоциировать с группой Фх неко-
торую подалгебру Ли фр алгебры Ли g. Если многообразие М
связно, то фр и фд отличаются на внутренний автоморфизм Ad b и,
следовательно, изоморфны. В этом случае мы можем говорить
об алгебре голономии ф связности $£.
Рассмотрим случай, когда многообразие М односвязно, т. е.
любая замкнутая кривая гомотопна постоянной кривой. Тогда,
как легко видеть, любая кусочно дифференцируемая кривая может
быть деформирована в кусочно С1-топологпи в постоянную кривую.
Это означает, что любой элемент из Фх может быть соединен
кривой с единицей, т. е. топологическая группа Фх линейно связ-
на. В этом случае из упражнения 4.2 гл. V следует, что (Фх) с:
ед ехр фр. Поэтому ехр фр есть наименьшая подгруппа Ли группы Ли
G, содержащая (Фж)- На самом деле можно показать, что любая
линейно связная подгруппа группы Ли сама является группой Ли,
см. Ямабе [23]; в частности, в рассматриваемом случае |3Р (Фж) =
= ехр фр.
Более общо, можно показать, что отображение всегда позво-
ляет отождествить Фж с некоторой подгруппой Ли группы Ли G,
см. х) Амброз и Сингер [1]. Всюду в дальнейшем мы будем считать,
что группа голономии есть группа Ли. Читатель может либо при-
нять это без доказательства (или обратиться за доказательством
к соответствующим статьям), либо ограничиться односвязными
многообразиями и заменить группу голономии Ф группой Ли
ехр фр во всех последующих теоремах.
Пусть — главное расслоение со структурной группой Gir
а Р2 — главное расслоение со структурной группой G2 над много-
образием М. Пусть /—гомоморфизм Pi—>Р2, соответствующий
гомоморфизму р: Gi—>G2. Пусть — связность на Pi. Для pQ.Pi
определим горизонтальное пространство в точке /(р), полагая
Нц(р) = {^Цр. Заметим, что если f(p)= f(p'), то р--р’-а,
причем р(а)=е,так что fptt°Ra* = fP'*. Поскольку Hip = R а* (Н^,
имеем ЛР(Я1/1) = /Н!ро7?ан!(Я1р<) = /р-Н!(Я1р-). Это показывает, что
определение подпространства Н^^р) не зависит от выбора точки
Я1 (/(/>)) Кроме того, если p = q-a, то /(р) = /(q) р(а)
и Нщр) = йР(«)*Я2/(5). Другими словами, соответствие f(p)—+
—удовлетворяет всем условиям связности, за исключением
того, что оно определено только на /(/Д). Это можно исправить
1) См. также Лпхнеровпч А., Глобальная теория связностей
и группы голономпй, ИЛ, М., 1961.— Прим. ред.
21*
324
Гл. VII. Геометрия G-структур
следующим образом. Пусть г£Р2. Представим г в виде r = f(p)-a
и положим Н^г — Ra*H2f(V). Пространство Н2г не зависит от выбран-
ного представления точки г. Поэтому дифференциальная система <й?2,
сопоставляющая точке г пространство корректно определена.
Легко проверить, что она является связностью. Определенная таким
образом связность оЖ'2 на Р2 называется образом связности
при гомоморфизме /.
Определение 1.3. Пусть Р2 есть С2-расслоение над М,
a Gi — подгруппа группы G2. Говорят, что связность SB г на Р2
редуцируется к Gt, если существуют изоморфизм / некоторого
Сграсслоения Pt в Р2 и связность SBi на Pit такие, что есть
образ связности при изоморфизме /.
Упражнение 1.1. Пусть / — изоморфизм расслоения Pi в Р2. Пока-
зать, что связность <§5?2 на -Р2 является образом некоторой связности на
при изоморфизме f тогда и только тогда, когда Я2/<р> С f*Tv (Pi) Для всех
л*
Теорема 1.1. Пусть Р — главное расслоение над связным
многообразием со связностью SB, а Ф — группа голономии связ-
ности SB. Тогда SB редуцируется к Ф.
Доказательство. Выберем точку pQP, л(р)=х, и рас-
смотрим группу Фр, которая является подгруппой Ли группы G.
Прежде всего мы покажем, что расслоение Р редуцируется
к Фр-расслоению. Для этого мы найдем покрытие {Ua} много-
образия М, функции перехода которого принимают значения в Фр.
Выберем такой атлас {Uа, ha} на М, что ha (Ua) — единичный
шар и расслоение Р тривиально над Ua. Пусть ха — ha1 (0, . .., 0) QUa
и Da — кривая, соединяющая х = л(р) с точкой ха. Пусть ра —
точка из я'1(ха), полученная параллельным переносом точки р
вдоль Da. Для каждой точки q £ л-1 (С/а) параллельный перенос
вдоль прямой (в смысле координат ha) линии laq, соединяющей
л (?) с ха, дает точку ра • а £ л-1 (яа). Таким образом, мы получаем
отображение л"1 (Ua) —> G. Легко проверить, что оно дифференци-
руемо и определяет изоморфизм ? —> (л (?), фа (?)) расслоения
л-1 (Ua) на Uа X G.
Найдем функции перехода. Предположим, что qtzUaftUp,
и рассмотрим фр (q) фа (q)"1. При параллельном переносе точки q
вдоль мы получим точку Ррф|з(<7)- Параллельно перенося q
вдоль l$q и затем вдоль D$ до точки х, мы получим точку p(pa(q),
а перенося q вдоль laq и Da до точки х, — точку pq>a(Q)- Таким
образом, параллельный перенос точки р вдоль замкнутой кривой
DJwihqDlb1 переводит точку р в РФ₽ (?) фа (?)-1 (рис. 31). Следо-
вательно, фр (?) Фа (?) так что функции перехода принимают
значения в Фр.
J 1. Главные и ассоциированные расслоения; связности
325
Согласно лемме 1.1, мы можем построить теперь Ф-расслоение
Р' и изоморфизм /: Р' —> Р. При доказательстве леммы 1.1 мы
использовали локальное представление точек из Р' в виде пары
(х, а), где х £ Ua и а £ Ф. Отображение f переводит такие точки
в точки из л-1 (Ua), имеющие соответствующие представления.
Но если точка q допускает в окрестности л-1 (Ua) представление
в виде (л (д), а), где а £ Ф, то она может быть получена из точки р
путем параллельного переноса вдоль некоторой кривой, и обратно.
Рис. 31.
Действительно, согласно определению, параллельный перенос
точки q вдоль прямой laq дает точку ра-а. Поскольку а-£ ФРа =
= Фр, параллельный перенос вдоль некоторой кривой С с нача-
лом и концом в точке х переводит р в p-а. Далее, параллель-
ный перенос вдоль кривой Da переводит p-а в ра-а. Следовательно,
параллельный перенос вдоль кривой CDalaq переводит р в q.
Итак, образ f (Р') состоит из всех точек q £ Р, которые могут быть
соединены с точкой р горизонтальной кривой. Поэтому любая гори-
зонтальная кривая, выходящая из точки, принадлежащей / (Р'),
всегда остается в / (/’')• В частности, любой горизонтальный каса-
тельный вектор в точке /(g) для q С Р' лежит в (Г q (Р')).
Согласно упражнению 1.1, это означает, что S8 есть образ некото-
рой связности на Р’, что и доказывает теорему 1.1.
Найдем теперь инфинитезимальный аналог параллельного
переноса вдоль замкнутой кривой. Мы хотим выяснить, что пред-
ставляет собой перенос вдоль «инфинитезимального параллело-
грамма», порожденного двумя горизонтальными касательными
векторами X и Y с началом в точке р g Р. Учитывая эвристические
рассуждения на стр. 114, естественно ожидать, что эффект, возни-
кающий при параллельном обносе вектора вдоль инфинитезималь-
ного параллелограмма, измеряется выражением (X Д У, dQ),
326
Гл. VII. Геометрия G-структур
где й — форма связности. Сравнивая это выражение с формулой
(6.9) гл. VI, естественно назвать его кривизной связности^ в на-
правлении X /\ Y. Точнее, дадим следующее
Определение 1.4. Пусть <$? — связность на главном рас-
слоении Р с формой связности й. Пусть h — проекция пространства
Тр(Р) на Нр для pQP. [Так, fe(X) = 0, если X— вектор, каса-
тельный к слою, и h (X) = X для горизонтального вектора X.]
Для любой дифференциальной /с-формы 0, определенной на Р,
форма DQ, задаваемая равенством
(Xi Л ... Л Xk+l I DQ} = {h (X,) Л ... A h (Xft+1) I dQ}, (1.5)
называется ковариантным дифференциалом формы 0. В частности,
форма DQ. называется кривизной связности S6.
Докажем теперь фундаментальное структурное уравнение
d£l = + (1-6)
Для этого достаточно показать, что обе его части принимают оди-
наковые значения на любых внешних 2-векторах Хр Д Ур в любой
точке р^Р. При этом достаточно рассматривать только следующие
случаи: i) векторы Хр и Yp горизонтальны; ii) вектор Хр гори-
зонтален, a Yp вертикален (является касательным к слою); iii)
оба вектора Хр и Yp вертикальны [поскольку элементы такого
вида порождают все пространство Д2 (Тр (Р))].
В случае i) имеем (Хр, й) = (Ур, й) = О, откуда
(Хр Д Yp | [Й Д Q]> = [{Хр, Q>, {Yp, й)] = О,
и, поскольку h(Xp) = Xp и 7&(УР) = УР, равенство (1.6) сводится
к (1.5).
Рассмотрим теперь случай ii). Продолжим вектор Хр до век-
торного поля вида Z, где Z— некоторое векторное поле на М.
[Это всегда можно сделать — достаточно продолжить вектор л* (X)
до векторного поля Z на М.] Продолжим также вектор Ур до вектор-
ного поля А, где AQg. Согласно равенству (1.10) гл. III (написан-
ному для векторнозначных форм), мы имеем
{A /\Z\dQ) = A{Z, Q)—Z{A, Й> — {[Z, А], Й).
Но {Z, й) == 0, поскольку поле Z горизонтально, и Z {А, й) = 0,
поскольку {А, й) = А = const. Поэтому первые два члена правой
части обращаются в нуль. Последний член справа также обра-
щается в нуль. Действительно,
0 = Х2 {Z, Й) = {X^Z, Й) + {Z, Х^}.
§ 1. Главные и ассоциированные расслоения; связности
327
Но —[Л, Q], согласно инфинитезимальному аналогу фор-
мулы (1.2). Следовательно, <£jZ, Q) = 0 = ([Z, Л], Q). Итак,
в случае ii) правая часть формулы (1.6) обращается в нуль.
Но левая часть также обращается в нуль, поскольку (Z, Q) = 0
и h (Л) = 0.
Осталось рассмотреть случай iii). Но в этом случае мы можем
продолжить векторы Хр и Yp до векторных полей А и В.
Поскольку (Л /\B\DQ) = 0, уравнение (1.6) приобретает вид
(ЛДВ|^)= -4([Л, В] — [В, Л]) = — [Л, В].
С другой стороны, согласно уравнению (1.10) гл. III,
(Л /\B\dQ) = A(B, Q)-B{A, Q> — <[Я, В], Q).
Но (В, Q) = В = const, значит, Л (В, Н) = 0. Аналогично,
В (Л, Q) = 0. Поскольку [Л, 5] = [Л, 5], имеем ([Л, 5], £2) = [Л, 5].
Это доказывает равенство (1.6) в случае iii). Полезно заметить,
что в случае iii) равенство (1.6) есть не что иное, как структур-
ное уравнение группы Ли G (формула (6.6) гл. V), перенесенное
на слой расслоения Р.
Поучительным упражнением для читателя было бы сравнить равен-
ство (1.6) с равенствами (2.10) и (3.11) гл. VI. Формы Qjyr, введенные на рас-
Ь
слоении 0 (М), конечно, определяют связность, а формы —
т=1
являются формами кривизны этой связности. Равенство (2.10) представляет
собой структурное уравнение этой специальной связности, поднятое
на (9ф(М). Поэтому условие (3.11) означает просто, что кривизна этой связ-
ности равна нулю.
Сейчас мы установим связь между кривизной связности и ал-
геброй голономии.
Теорема 1.2 (Амброз —Сингер). Пусть Q — форма связ-
ности некоторой связности &В на главном расслоении Р. Алгебра
голономии фр в точке р С Р натянута на множество всех элементов
алгебры Ли g вида (X Д У, DQ)q, где q — любая точка, которую
можно получить из точки р параллельным переносом вдоль какой-
нибудь кривой в М, а X и Y — горизонтальные касательные век-
торы в точке q.
Доказательство. Заметим прежде всего, что при дока-
зательстве теоремы 1.2 можно считать, что группа голономии сов-
падает с G. Действительно, по теореме 1.1 расслоение Р редуци-
328
Гл. VII. Геометрия G-структур
руется к расслоению Р', структурная группа которого совпадает
с группой голономии, причем связность на Р является образом
некоторой связности на Р'. Если мы докажем теорему для редуци-
рованного расслоения Р', то она, очевидно, будет справедлива
и для Р.
Если группа голономии совпадает с G, то любая точка расслое-
ния Р может быть получена параллельным переносом из точки р
и алгебра голономии совпадает с g. Любой горизонтальный вектор
в точке q может быть представлен в виде Wq, где W — векторное
поле на М. Для двух таких векторных полей имеем
(W Л Z | DO,) = (W Д Z | dfi) =
= IE(Z, fi) — Z(W, fi)-<[Ж, Z], fi) =
= -<[W, Z],fi).
Таким образом, достаточно показать, что алгебра Ли g порож-
дается всеми элементами вида ([ТЕ, Z], fi)g, где q — произвольная
точка из Р, a W и Z — произвольные векторные поля на М.
Пусть h — подалгебра алгебры g, порожденная всеми элементами
такого вида. Рассмотрим соответствующую подалгебру h алгебры g,
состоящую из вертикальных векторных полей на Р. Достаточно
показать, что g = h. Для этого рассмотрим дифференциальную
систему 3) на Р, натянутую на все векторные поля вида W-j-A,
где W—векторное поле на М, a A£h. Она вполне интегрируема.
Действительно, вертикальная компонента поля [W, Z] лежит в h
(согласно определению алгебры /г), а поле вида [Л, W] горизон-
тально. Кроме того, поле вида [Л, В] = [Л, 5] принадлежит ht
так как h — подалгебра. Предположим, что h — собственная под-
алгебра в g. Тогда дифференциальная система 2) нетривиальна1}
и, значит, ее максимальное интегральное многообразие Np, про-
ходящее через точку pQP, не совпадает с Р. С другой стороны,
горизонтальные кривые, проходящие через р, принадлежат Np
и любая точка из Р может быть соединена с точкой р горизон-
тальной кривой. Полученное противоречие доказывает теорему 1.2.
Следует заметить, что практически теорема 1.2 используется
главным образом для редуцирования расслоений. А именно, поль-
зуясь теоремой 1.2, вычисляют алгебру голономии и затем приме-
няют теорему 1.1.
Упражнение 1.2. Пусть Р — главное расслоение над односвяз-
ным многообразием М. Предположим, что на Р существует связность &в с ну-
левой кривизной. Тогда Р изоморфно тривиальному расслоению М X G
и при этом изоморфизме &в переходит в тривиальную связность на М X G.
!) То есть 3j (р) =# 0, 3) (р) фТ-р (Р) для р £ Р. —Прим, перев.
§ 1. Главные и ассоциированные расслоения; связности
329
Для любого главного расслоения можно определить аналог
«величин» гл. I и § 6 гл. II. Для этого мы должны заменить пол-
ную линейную группу структурной группой расслоения. Точнее,
дадим следующее
Определение 1.5. Пусть Р — главное G -расслоение
над многообразием М и Q — дифференцируемое многообразие,
на котором группа G дифференцируемо действует слева. На Р X Q
группа G дифференцируемо действует справа по формуле
Ra (р, ?) = (ра, a-1g). Назовем две точки из Р X Q эквивалентны-
ми, если они получаются одна из другой действием элементов из G.
Множество классов эквивалентности многообразия Р X Q назы-
вается Q-ассоциированным расслоением расслоения Р и обозначает-
ся Q (Р).
Мы предоставляем читателю проверить, что Q (Р) есть диффе-
ренцируемое многообразие с естественной проекцией Лд на М,
а также сформулировать и доказать очевидные обобщения утвер-
ждений и результатов § 6 гл. II на случай произвольных главных
расслоений. В частности, легко доказать, что каждая точка р £ Р
(л (р) = х) определяет диффеоморфизм, обозначаемый также через
р, многообразия Q на Лд1 (ж), причем
Р-а (?)=Р («•?)• (1-7>
Укажем несколько примеров ассоциированных расслоений,
которые встретятся в дальнейшем.
Если Q — векторное пространство, на котором группа G дей-
ствует линейно, то Q (Р) называется векторным расслоением СО'
структурной группой G.
Если Q = G и группа G действует на себе левыми сдвигами, то
<2 (Р) можно отождествить с Р. Действительно, в каждом классе
эквивалентности многообразия Р X Q = Р X G имеется ровно,
один элемент вида (р, е). Заметим, что группа G действует справа
на Р X G, а именно, (р, g4) g2 = (р, g!g2). Это действие переста-
новочно с действием Ra группы G:
(Ra (Р, gi)] g2 = (pa, a-'gi) g2 =
= (pa, a~'glg2) = Ra [(p, gi) g2J.
Поэтому G действует справа на <2 (P) = P- Что это за действие?'
Не что иное, как стандартное действие G на Р. [Читатель может
в качестве упражнения это проверить.] Все эти утверждения выгля-
дят совершенно очевидными. Однако небольшое их обобщение-
позволяет сделать важное (хотя тоже довольно очевидное) замеча-
ние. Предположим, что Gi — подгруппа (Ли) группы Gz, a Pi —
главное Gi-рассслоение. Тогда Gi действует левыми сдвигами на G2,.
330
Гл. VII. Геометрия G-структур
a G2 — правыми сдвигами на Pi X G2. Это действие перестановоч-
но с действием Ra группы 64 на Л X G2 [где Ra (р, g) = (pa,a-1g)].
Значит, группа G2 действует на б^-ассоциированном расслоении
G2 (Pi). Читатель может проверить, что это действие превращает
G2 (Pi) в главное б^-расслоение. Другими словами, данное
Gi-расслоение каноническим образом может быть расширено до
С2-расслоения.
Пусть дана некоторая связность на главном расслоении Р,
и пусть Q (Р) — некоторое ассоциированное расслоение. Предполо-
жим, что у — точка из Q(P), причем Лд(у) = х, и что Роб31"1^) Р-
Поскольку точка р0 определяет диффеоморфизм многообразия Q
на слой Лр1^), существует единственная точка q6:Q, для которой
Po(q)—y. Точка q определяет отображение расслоения Р в Q(P):
оно переводит pQP в p(q). Обозначим его <тРо. Положим 3)у =
= <з*а(3£р0)- Сейчас мы покажем, что подпространство Зу не зави-
сит от выбора точки р0. Если мы заменим точку р0 точкой р0-а,
то, согласно (1.6), мы должны заменить q на a^q. Таким образом,
вро-а(р) = Р (a^q) = (Ra-ip) q- Следовательно,
СТРоа = (Тр0 ° Ra-1,
Чрца* (<$Sроа) ~ С^Ро* 0 Ra-1*Q%>рца ~ ^рц*о№р0,
так что 3)у не зависит от рй. Легко проверить, что соответствие
y—>3)v определяет дифференциальную систему 3 на Q(P) и что
подпространство 3)у есть дополнение к касательному пространству
слоя в точке у. Далее, пусть С — кривая на М, причем С(О)=жо
и 6(1)=^!, а уй G Q (Р) — точка из лд1^). Выберем точку
Ро€я-1(^о) так же, как раньше, и пусть у — горизонтальная кри-
вая в Р, лежащая над С, причем у (0) = р0. Тогда кривая <тРо°у,
очевидно, является интегральной кривой дифференциальной систе-
мы 3. Итак, мы доказали следующее утверждение:
Если задана связность на Р, то на Q (Р) определяется
дифференциальная система 3), такая, что
1) в любой точке yQQ(P) подпространство 3>у является допол-
нительным к касательному пространству слоя в точке у;
2) для любой кривой С на М с С (0) = хо и С (1) = Xi и для лю-
бой точки у0 6 Лд1 (хо) существует единственная интегральная
кривая у дифференциальной системы 3, для которой у (0) = у0
и nQ°y = С.
[Условие 2) показывает, что мы можем параллельно переносить
слои расслоения Q (Р) вдоль любой кривой многообразия МД
Дифференциальную систему 3 на Q (Р), удовлетворяющую
условиям 1) и 2), мы будем называть связностью на Q (Р). Таким
§ 2. G-структуры
331
образом, любая связность на Р определяет некоторую связность на
Q (Р). Поскольку действие группы G на Q может быть тривиаль-
ным, ясно, что обратное утверждение неверно. Однако
Упражнение 1.3. Показать, что если G действует свободно на Q,
то любая связность на Q (Р) получается пз некоторой (единственной) связ-
ности на Р.
2. G-СТРУКТУРЫ
Среди всех расслоений некоторые (а именно редукции расслое-
ния реперов) играют особенно важную роль в дифференциальной
геометрии. Их изучению мы и посвятим оставшуюся часть книги.
Прежде всего введем некоторые обозначения. Пусть М — диффе-
ренцируемое «-мерное многообразие, a (М) — его расслоение
реперов. Напомним, что Jp (М) есть главное GL («)-расслоение над
М. Точка р из $р (М), такая, что л (р) = х, является базисом
касательного пространства Тх (М). Нам будет удобно несколько
изменить точку зрения. Пусть V — фиксированное «-мерное век-
торное пространство с фиксированным базисом (например, мы
можем взять в качестве V пространство Rn со стандартным бази-
сом). Тогда базис р пространства Тх (71/) определяет изоморфизм
пространства V на Тх (М); мы обозначим этот изоморфизм также
через р. Группу GL («) можно рассматривать как группу GL (У)
всех линейных преобразований пространства V. Таким образом,
пользуясь языком § 1, можно сказать, что <р (М) есть главное
GL (У)-расслоение, а касательное расслоение Т (М) есть ассоции-
рованное расслоение У (jF (М)). В частности, согласно равенству
(1.7), если р £ ер (7И), v £ У и a g GL (У), то
(р-а) («) = р(а«). (2.1)
На расслоении реперов существует каноническая У-значная
линейная дифференциальная форма to. Она определяется следую-
щим образом. Пусть р — точка из jp(M), причем л(р)=х,
и пусть X £ Тр ( р (М)). Тогда л*Х £ Тх (М). Положим
<Х,со) = р-х(лДХ)). (2.2)
Читатель может проверить, что формула (2.2) определяет на Р (М)
дифференцируемую линейную дифференциальную форму. Посмо-
трим, как ведет себя форма со при действии группы GL (У).
Пусть XQTP(P (7И)) и aQGL(V). Тогда л* (X) = л* (7?Я*Х),
так как л перестановочно с Ra. Следовательно, согласно (2.1),
<7?аЛ, со) = (p-а)’1 (л*Х) = а-1 р-1(л*Х) = а"1 (X, со).
Получаем формулу
R*co = а хсо.
(2-3)
332
Гл. VII. Геолаетрия G-структур
Выражение а-1со есть результат применения линейного преобразо-
вания а-1 к У-значной линейной дифференциальной форме со.
Алгебра Ли gl (У) группы Ли GL (У) действует пса У, и мы можем
написать инфинитезимальный аналог формулы (!2.3): для любого
А Q gl (У) мы имеем
£3ю=-А(в. (2.4)
Но л* А = 0, откуда (A, to) = 0. Поэтому, пользуясь» равенством (1-9)
гл. III, равенство (2.4) можно переписать в виде»
AJdto =—Аа. (2.5)
Обратимся теперь к определению G-структурры.
Определение 2.1. Пусть G — подгруппа группы GL (У);
G-структурой на тг-мерном многообразии М называется редукция
расслоения АР (М) к группе G. Таким образом, G-структура BG
на многообразии М есть подмногообразие в ер обладающее
тем свойством, что для любой точки р £ Bq и для [любого элемента
a g GL (У) точка р-а принадлежит BG тогда и только тогда, когда
а £ G.
Примеры G-структур.
1) G = {е}. В этом случае G-структура на М определяется зада-
нием репера в каждой точке из М. Такая структура позволяет
отождествить каждое касательное пространство к многообразию
М с У. Таким образом, мы получаем возможность «параллельно
переносить» касательные векторы из одной точки [Многообразия М
в другую. [А именно, вектор X £ Тх (М) отождествляется с век-
тором р-1 (X) Е У, который в свою очередь отождествляется
с вектором q (р'1 (X)) £ Ту (М), где р и q — заданные реперы с на-
чалом соответственно в точках х и у.] Поэтому {е}-структуру
иногда называют также абсолютным параллелизмам на М. Наибо-
лее важный частный случай абсолютного паралле лизма — случай,
когда М есть группа Ли. Как мы уже видели в ггл. V, если М —
группа Ли, то левоинвариантные векторные поля [позволяют отож-
дествить касательное пространство в каждой точке из М с алгеброй
Ли группы Ли М.
2) Пусть Vi есть k-мерное подпространство [пространства У,
a G — группа всех линейных преобразований, оставляющих под-
пространство V\ инвариантным. Рассмотрим! какую-нибудь
G-структуру BG с этой группой G. Пусть р g BG и х 1= л (р). Опреде-
лим подпространство 3) (х) cz Тх (М), полагая1 3 (х) = р (У1).
Для любого а £ G имеем pa (yf) = р (aVt) = р (F'i), так что 3 (х)
не зависит от выбора точки р £ л-1 (х), лежащей в BG. Таким
образом, BG определяет на М k-мерную дифференциальную систе-
$ 2. G-структуры
333
му. Обратно, пусть 3) — дифференциальная система на М. Рас-
смотрим подмногообразие BG многообразия ср (7И), состоящее
из таких реперов р, для которых р-1 (3 (х)) = У (где х =
= л (р)). Тогда, как легко видеть, BG есть G-структура. Итак,
в этом случае G-структура — это то же самое, что /с-мерная диффе-
ренциальная система.
3) Пусть ( , ) — положительно определенное скалярное
произведение на V, a G — множество линейных преобразований
пространства V, сохраняющих это скалярное произведение. [Та-
ким образом, G — О (п).] В этом случае BG есть в точности римано-
ва метрика на М. Действительно, риманова метрика определяет
расслоение ортогональных реперов (9 (М), представляющее собой
О (п)-структуру. Обратно, задание в каждом касательном про-
странстве семейства реперов, отличающихся друг от друга на орто-
гональное преобразование, определяет в каждом касательном про-
странстве скалярное произведение и тем самым риманову метрику
на М. Итак, задать О (и)-структуру — это все равно, что задать
риманову метрику.
4) Пусть ( , ) — скалярное произведение на V, a G — кон-
формная группа, определяемая этим скалярным произведением,
т. е. Т £ GL (У) принадлежит G тогда и только тогда, когда
(Tu,Tv) = Хт-(и, v) для всех и, v £ Т, где зависит только от Т.
Соответствующая этой группе G-структура называется конформ-
ной структурой. Если многообразие М обладает конформной
•структурой, то имеет смысл говорить об угле (точнее, о косинусе
угла) между двумя касательными векторами с началом в одной
и той же точке из М.
5) Пусть ( , ) — невырожденная антисимметрическая били-
нейная форма на V. [Тогда V — пространство четной размерности,
скажем 2п.] Пусть G = Sp (п) — симплектическая группа, т. е.
группа всех автоморфизмов формы ( , ). Таким образом,
Т g GL (У) принадлежит Sp{ri) тогда и только тогда, когда
'(Ти, Tv) = (u, v) для всех и, v £ V. Если на многообразии М задана
Sp (гс)-структура BSp(n-), то на касательном пространстве в каж-
дой точке из М мы можем определить невырожденную антисиммет-
рическую билинейную форму. Действительно, пусть р — произ-
вольная точка из Bgpfny и л (р) = х. Для любых касательных век-
торов X и Y в точке х положим (X, Y) = (р-1 (X), р-1 (У)). Для
любой другой принадлежащей BSp^n) точки рТ £ л-1 (х) имеем,
согласно (2.1), ((р?)’1 (X), (рТ)’1 (У)) = (р-ЦХ), р-х(У)), так что
это определение не зависит от выбора точки р £ л-1 (a;) Q _BSp (п).
Легко проверить, что верно и обратное — задание в каждом
касательном пространстве многообразия М невырожденной анти-
симметрической билинейной формы (дифференцируемо изменяю-
щейся от точки к точке), т. е. задание внешней 2-формы максиналь-
334
Гл. VII. Геометрия G-структур
ного ранга, определяет Sp (н)-структуру. Итак, задать
5р(«)-структуру на многообразии М — это то же самое, что задать
на М внешнюю 2-форму Q максимального ранга. По этой причини
5Sp(n) называют иногда почти гамильтоновой структурой.
Гамильтонова структура удовлетворяет дополнительному условию.
dQ = О (см. определение 7.1 гл. III).
6) Пусть V есть 2ге-мерное векторное пространство, и пусть J —
такое линейное преобразование пространства V, что J2 = —id.
Обозначим через GL (п, С) подгруппу группы GL (У), состоящую
из таких линейных преобразований Т £ GL (У), для которых
TJ = JT. Эта группа имеет следующий смысл. Пространство У
есть векторное пространство над полем вещественных чисел.
Линейное преобразование J позволяет нам превратить У в вектор-
ное пространство над полем комплексных чисел. Для этого надо
определить умножение на i. Мы сделаем это, положив iv Jv.
Так как J2 = — id, то, как легко проверить, тем самым на У
определяется структура комплексного векторного пространства.
При этом не каждое линейное преобразование Т пространства У,
рассматриваемого как вещественное векторное пространство,
является комплексным линейным преобразованием; для этого оно
должно быть перестановочно с умножением на i. Это означает, что
TJ= JT, т. е. Т £ GL (re, С). Назовем GL (п, С)-структуру на мно-
гообразии М почти комплексной структурой.
Задание почти комплексной структуры на многообразии М
эквивалентно заданию в каждом касательном пространстве Тх (М)
линейного преобразования Jx (дифференцируемо зависящего от х),
для которого Jx = — id. Действительно, пусть задана GL (п, С)-
структура BcL(n,C)- Если с> и л(р) = х, то положим
Jx = pJp~\ Согласно равенству (2.1), имеем (рТ) J (рТ)'1 =
= р(ТJT~r) p~r = pjр~г для всех TQGL(n, С), так что преобразо-
вание Jx корректно определено. Обратно, задание в каждой
точке х преобразования Jx определяет GL (п, С)-структуру (чита-
телю нетрудно будет убедиться в этом). Если многообразие М
обладает почти комплексной структурой, то все его касательные
пространства превращаются в комплексные векторные простран-
ства. Смысл слова «почти» состоит в том, что наиболее важным
частным случаем такой структуры является комплексная струк-
тура. Она определяется следующим образом: говорят, что много-
образие М обладает комплексной структурой, если задан атлас
{{Ua, ha)}, где ha = (xla, .. ., х£, у^, . . ., у$, такой, что если
положить z^ = ж* + iy^, .. ., z” = + iy£ и записать функции
перехода
4 =Ч(^’
Уа-Уа^’ 4 •
§ 2. G-структуры
335-
в виде
Za = Za <4 •••’*₽’ 4 •••’
то функции z1 будут комплексно аналитическими функциями
от z^: z^ = z^(z*, ..z"). Короче говоря, многообразие с комплекс-
ной структурой, или комплексное многообразие, есть такое много-
образие, на котором можно ввести комплексные координаты так,
чтобы функции перехода были комплексно аналитическими. Чита-
тель без труда может убедиться в том, что комплексная структура
определяет почти комплексную структуру. Однако не всякая почти
комплексная структура получается из некоторой комплексной
структуры.
7) Пусть V — (произвольное) re-мерное векторное пространства
и SL (V) — множество всех его линейных преобразований с опре-
делителем 1 (т. е. множество всех Т, для которых /\ (71) = id).
Предлагаем читателю проверить, что задать SL (У)-структуру
на многообразии М — это то же самое, что задать внешнюю диффе-
ренциальную форму степени п на М (всюду отличную от нуля).
8) Пусть V — векторное пространство с выбранной ориентаци-
ей, a GL (У)+ —подгруппа, состоящая из всех линейных преобра-
зований, сохраняющих ориентацию. Читатель может проверить,
что GL (У)+-структура на М — это то же самое, что ориентация
многообразия М.
Замечания.
а) Из приведенных выше примеров ясно, что любая «структура»
на многообразии, зависящая только от свойств «первого порядка»
(т. е. определяемая полем величин, описанных в § 6 гл. II), соот-
ветствует некоторой G-структуре. Большую часть развиваемой
нами техники можно легко обобщить на структуры «высших
порядков». Однако для простоты мы ограничимся структурами
первого порядка.
Ь) Если заданы многообразие М и подгруппа G группы GL (У),
то на М может и не существовать G-структуры. Так, например,
если многообразие М неориентируемо, то на нем не существует
структур из примеров 8 и 7 (а также из примеров 1, 5 и 6). Как
мы видели в последнем параграфе гл. VI, на сфере 52 не существует
не обращающегося в нуль векторного поля, и, значит, она не обла-
дает структурой из примера 1. С другой стороны, мы доказали, что
любое многообразие допускает риманову, а значит, и конформную,
структуры. В общем случае вопрос о том, когда на многообразии
существует та или иная G-структура, представляет собой тонкую
топологическую проблему и выходит за рамки этой книги.
с) Если Ва есть G-структура на М, a U — открытое подмножест-
во в М, то л-1 (G) есть G-структура на U (где л — проекция BG
336
Гл. VII. Геометрия G-структур
-+ М). Мы в основном сосредоточим внимание на локальных свой-
ствах G-структур, и поэтому часто будем рассматривать ограниче-
ние G-структуры на все меньшую и меньшую окрестность U с. М.
Пусть ф— диффеоморфизм многообразия Мх на многообразие М2.
Так же как в § 6 гл. II, отображение <р индуцирует диффео-
морфизм <р* расслоения Р (Мt) на cP (М2). Поэтому если Bq и Bg
суть G-структуры на и М2, то естественно возникает вопрос,
в каком случае ф* (В«) = B'g
Определение 2.2. Пусть Bg и Bg суть G-структуры соответ-
ственно на Mi и М2. Диффеоморфизм ф: Mi—>М2 называется изо-
морфизмом G-структуры Bg на G-структуру Bq, если ф* (Bg)=Bg.
Мы будем говорить, что Bg и Bq изоморфны, если существует
изоморфизм G-структуры Bq на Bq. Изоморфизм G-структуры Bg
на себя называется автоморфизмом.
Так, например, изоморфизм двух римановых структур есть изо-
метрия; изоморфизм двух почти гамильтоновых структур на Mi
и М2 есть такой диффеоморфизм ф, что ф*£22 = £21 [где £2; — форма,
определяющая рассматриваемую почти гамильтонову структуру
на Mt (i = l, 2)].
Определение 2.3. Пусть Bg и Bg суть G-структуры на М^
и М2. Пусть x£Mi и у£М2. Мы скажем, что Bg и Bg локально
эквивалентны в (х, у), если существуют окрестность U точки х,
окрестность V точки у и такой изоморфизм ф G-структуры BrJU
на Bg [И, что ф(а;) = г/. [Здесь B^\U — ограничение структуры
Bg на открытое множество U, a Bg | V—ограничение структуры
B2g на F.)
Общая проблема эквивалентности состоит в нахождении (для
данной группы G) критерия того, что две G-структуры локально
эквивалентны.
Заметим, что многие теоремы этой книги представляют собой
решение проблемы эквивалентности для различных частных слу-
чаев. Например, теорема Фробениуса (теорема 5.1 гл. III) утвер-
ждает, что дифференциальная система (т. е. G-структура из приме-
ра 2) локально эквивалентна специальной дифференциальной си-
стеме особенно простого вида (определяемой касательными к кривым
_ const, . . . , хп = const), если выполнены некоторые усло-
вия интегрируемости (равенства (5.2) гл. III). Теорема Дарбу
(теорема 6.1 гл. III) утверждает, что любые две гамильтоновы
структуры (т. е. Sp (ге)-структуры из примера 5, удовлетворяющие
дополнительному условию dQ. — 0) локально эквивалентны.
Предложение 3.1 гл. VI показывает, что риманово многообразие
локально изоморфно Е”, если в расслоении ортонормированных
§ 2. G-структуры
337
реперов существуют формы удовлетворяющие условиям (3.7)
и (3.11). Теорема 2.4 гл. V утверждает, что любые две группы Ли
(т. е. {е}-структуры определенного типа) локально эквивалентны,
если они имеют одинаковые структурные константы х).
Между первыми тремя теоремами, упомянутыми выше, и по-
следней имеется существенное различие. В первых трех теоремах
содержатся необходимые и достаточные условия того, чтобы
G-структура была локально эквивалентна G-структуре особенно
простого вида. Дадим общее определение. Заметим, что для любой
группы G векторное пространство V можно рассматривать как диф-
ференцируемое многообразие, снабженное естественной G-струк-
турой. Действительно, структура векторного пространства позво-
ляет отождествить Т„ (У) с У для всех и g У, т. е. определяет
абсолютный параллелизм, или {е}-структуру, на У. Если мы рас-
смотрим в каждой точке v g У множество всех реперов, получае-
мых из стандартного репера действием элементов из G, то получим
G-структуру на У. Эта G-структура называется (стандартной)
плоской G-структурой. Так, например, плоская О (и)-структура
есть евклидово пространство.
Определение 2.4. G-структура называется локально
плоской, если она локально эквивалентна плоской G-структуре.
Первые три теоремы, упомянутые выше, дают необходимые
и достаточные условия того, чтобы соответствующие G-структуры
были локально плоскими. Теорема 2.4 гл. V является теоремой
другого типа, поскольку плоская {е}-структура есть (коммутатив-
ная) группа Ли И, а произвольная (некоммутативная) группа
Ли не является локально плоской.
Упражнение 2.1. Пусть BG есть G-структура на М. Показать,
что BG является локально плоской тогда и только тогда, когда на М суще-
ствует такой атлас {(Ua, ha)}, где ha = (z^, ..., что при каждом z g Ua
репер (——j- (т), ..., —— принадлежит BG.
\ дх2 I
1; Часто представляет интерес проблема, несколько отличная от проб-
лемы эквивалентности, которую можно назвать проблемой сопряженной экви-
валентности. Пусть Gj п G2 — сопряженные подгруппы в GL (У). Назовем
структуры BG1 (М) и BG2 (М) сопряженными, если существует такой элемент
a$GL(V}, что Ra (BG (М)) = (М) (в частности, a~1G1a = G2).
Проблема сопряженной эквивалентности состоит в том, чтобы решить,
когда данная G-структура эквивалентна G-структуре, сопряженной с другой
данной G-структурой. Например, для (е)-структур групп Ли локальный изомор-
физм (явлющийся сопряженной эквивалентностью) представляет больший
интерес, чем просто эквивалентность (включающая в себя также выбор базисов
алгебр Ли). По этому поводу см. статью Гийемина и Стернберга An algeb-
raic model of transitive differential geometry, Bull. Amer. Math. Soc.
70 (1964), 16 — 47.
22 с. Стернберг
338
Гл. VII. Геометрия G-структур
Приступим теперь к изучению методов, применяемых для реше-
ния общей проблемы эквивалентности. Заметим сначала, что, по-
скольку BG есть подмногообразие в (М), ограничение формы о>
на BG будет V-значной формой на BG. Если это не вызовет недора-
зумений, мы будем обозначать ее той же буквой со. [Это согласует-
ся с обозначениями гл. V для {е}-структуры на группе Ли.
В гл. VI мы обозначали соответствующую форму для римановой
структуры на М через им.] Равенства (2.1)—(2.5) остаются спра-
ведливыми для произвольной G-структуры, если только считать,
что а g G в равенствах (2.1) и (2.3) и А £ g в равенствах (2.4)
и (2.5), где g — алгебра Ли группы Ли G (и, значит, подалгебра
алгебры Ли gl (V)). Мы воспользуемся этими равенствами, чтобы
построить некоторую (векторнозначную) функцию, определенную
на BG внутренним образом.
Пусть BG есть G-структура на многообразии М и р £ BG. Пусть
Нх с Тр (BG) — дополнение к вертикальному подпространству х)
в точке р. Таким образом, Нх есть и-мерное подпространство каса-
тельного пространства, порождающее вместе с касательным про-
странством слоя все пространство Тр (BG). [Например, если <$? —
связность на BG, то в качестве Ht можно взять aft? (р).] Линейная
форма со отображает Тр (BG) на V, причем ядро этого отображе-
ния состоит из векторов X, для которых л*Х = 0, т. е. из векторов,
касательных к слою. Следовательно, форма to определяет изомор-
физм пространства Нх на V. Пусть Н2 — другое дополнение
к вертикальному подпространству в точке р. Пусть v — вектор
из V, а Хх £ Нх и Х2 £ Нг — такие векторы, что (Х15 со) = v и
(Х2, со) = V. Тогда, согласно определению формы со (см. (2.2)),
имеем
р(к) = лН! (Х1) = лДХ2).
Следовательно, л*(Х2— Х1) = 0, т. е. вектор Х2— Х1 вертикален.
Пользуясь естественным отождествлением касательного простран-
ства слоя с алгеброй Ли g, мы можем рассматривать Х2 — XL как
элемент алгебры g. Итак,
пара дополнений Н{ и Н2 определяет отображение V^g.
Легко проверить, что это отображение линейно, а также, что
при фиксированном Нх подпространство Н2 однозначно
определяется отображением н2-
Наконец, легко видеть, что
для заданных дополнения Нх и отображения 5£Hom(V, g)
существует такое подпространство Н2, что S = 8щ, нг-
г) Вертикальным подпространством называется касательное пространство
слоя.— Прим, перев.
§ 2. G-структуры 339
Иначе говоря, если фиксировать одно дополнение Hi, то множе-
ство всех дополнений к вертикальному подпространству пара-
метризуется элементами из Hom (F, g).
Рассмотрим теперь внешнюю дифференциальную форму dm. Для
каждого pQBG форма dm определяет отображение Да (Тр (BG))—>V.
Пусть Н — дополнение к вертикальному подпространству в точке р.
Тогда Д2(Я) есть подпространство в Д2 (Тт> (BG)), и, значит,
ограничение формы dm на Д2 (Н) определяет отображение
Д2 (Н) V. Поскольку Д2 (Н) отождествляется с Д2(У), мы
получаем отображение Д2 (У) —+ V; обозначим его сн. По опре-
делению, если и и v — векторы из У, то
cH(uf\v) = (X/\Y\dm), (2.6)
где X и Y — такие векторы из Н, что (X, со) = и, (Y, m) — v.
Таким образом, мы сопоставили каждому дополнению Н к вер-
тикальному подпространству в точке р некоторый элемент
сн £ Нот (У Д У, У). Выясним теперь, как сн зависит от Н. Для
этого возьмем два дополнения Hi и Н2 к вертикальному подпро-
странству в точке р. Тогда
сн2 (и Д у) — сН1 (и /\и) = (Х2 Л У21 d<o> — (Xj Л У( | dm),
где Xt и Yt — такие векторы из Hi, что {Xi,m) = u, (Yi,m) = v
(i=l, 2). Это равенство можно переписать в следующем виде:
сн2 (и Л у) — сН1 (u/\v) =
= ((Х2 - Х^ Д У21 dco) + (Xj Л (У2 - YJ | dco) =
= (У2, (X2-X0 J dco)-(X1, (У2-У4) J dco).
Но Х2 — Xt есть вертикальный вектор, равный, согласно опре-
делениям, вектору SHlt н2(и)р. [Напомним, что SHlt н2(п) есть
элемент из g, а Хщ, н2(и)р— значение соответствующего ему вер-
тикального векторного поля в точке р.] По формуле (2.5) имеем
$н1г н2 (и) U dm =—5hi, н2 (к) со. Применяя подобные рассуждения
к вектору Yi — У2 и учитывая, что (У2, со) = у, а (Х4, со) = и,
получаем
сн2 (и Д у) — сН1 (и/\ v) = SH1,h2(v)u — SH1>h2(u)v. (2.7)
[Напомним, что Shi,h2(v) есть элемент из g, a g действует на У,
так что 3Н1, н2(у) и есть элемент из У.] Мы можем переписать
равенство (2.7) в несколько другой форме. Рассмотрим простран-
ство Нот (У, g). На этом пространстве действует оператор анти-
симметризации Jt: Hom (У, g) —» Hom (У, g), определяемый сле-
22*
340
Гл. VII. Геометрия G-структур
дующим образом: если 5 g Нот (У, g), то
Л {S) {u)v = S {u)v — S {v) u.
[Поскольку g — подпространство в Hom (У, У), преобразование
Л (S) (и) £ g однозначно определяется заданием его действия
Л (5) {и) v на всех vQV.] Ясно, что Л (S) (и) с ——Л{8){и)и,
так что Л (S) есть антисимметрическое билинейное отображение
FXV->У; его можно рассматривать как элемент пространства
Нот (УДУ, У). Другими словами, Л есть отображение простран-
ства Нот (У, g) в Нот (У ДУ, У). Равенство (2.7) мы можем
переписать теперь в виде
Сн2 — сН1--= —Л {SH1, н2)- (2-8)
Далее, Л(Нот(У, g)) есть подпространство в Нот (У ДУ, У).
Пусть р — проекция пространства Нот (У Д У, У) на факторпро-
странство
Нот (У Д У, У)/Л (Нот (У, g)).
Равенство (2.8) показывает, что сП]— сн2 ^Л (Нот (У, g)), т. е.
что р (chj) = р (сн2). Итак, р (сИ) не зависит от выбора дополне-
ния Н в точке р. Таким образом, мы получили корректно опре-
деленную функцию с на BG:
с: BG —> Hom (У Д У, У)/Л (Нот (У, g)),
задаваемую формулой
с(р) = р(сн), (2.9)
где Н — произвольное дополнение к вертикальному подпростран-
ству в точке р. Эта функция называется структурной функцией
{первого порядка) для Вв. Название объясняется тем, что с являет-
ся обобщением структурных констант группы Ли. Действительно,
если G = {е}, то g = 0 и с отображает В(еу в Нот (У Д У, У).
[Впрочем, это сразу видно и так, поскольку в каждой точке р g
£ В существует только одно Н, так что с (р) = сн.] Для
{е}- структуры определяемой группой Ли, функция с постоян-
на. Поскольку в этом случае У есть алгебра Ли группы Ли, не
удивительно, что определяемое функцией с отображение УД У-> У
есть не что иное, как умножение Ли на У (рассматриваемое как
антисимметрическое билинейное отображение). Весьма поучитель-
ным упражнением для читателя была бы проверка этих фактов.
Выясним теперь, как структурная функция меняется вдоль
слоя. Для этого выберем дополнение Н в точке р и рассмотрим про-
странство Ra*H, являющееся дополнением к вертикальному про-
странству в точке p-а. Для и, v £ V найдем такие X, Y £ Н, что
(X, ш> = и и (У, со > = V. Согласно формуле (2.3), для любого
J 2. G-структуры
341
я £ G
(RaSfX, io) = a-1u и {Ra*Y, io> = a~rv.
С другой стороны,
</?а л Л Ra*Y I d(p) = (X A YI R* d(p) = я-1 {X Л Y I d(0).
Следовательно,
Crmh (a~lu A a^v) = a”1^, (в Др),
или
cRa*H (и A v) = a~lcJI (au Д av). (2.10)
Группа G действует на V, а значит, и на V /\ V. Поэтому G дей-
ствует на Нот (У Д V, У) следующим образом: если a g G
и L g Нот (У Д У, У), то ст (a) L задается формулой
(ст (a) L) (и Др) = aL ((Г1 и /\ a-1v).
Читатель легко проверит, что это есть представление группы G
в пространстве Нот (У Д У, У). Равенство (2.10) можно теперь
переписать в виде
= Сн-
Читатель также без труда проверит, что Л (Нот {У, #)) есть инва-
риантное подпространство пространства Нот (У Д У, У) относи-
тельно действия ст группы G. Поэтому в факторпространстве
индуцируется некоторое представление группы G, которое мы тоже
будем обозначать через ст. Тогда из формул (2.9) и (2.10) получаем
с(^-я) = ст(я)-1с(^). (2.11)
Структурная функция определена внутренним образом. Поэтому
(как читатель может проверить, воспользовавшись определениями)
справедлива
Теорема 2.1. Пусть RlG и BG суть G-структуры соответ-
ственно на ЬЦиМ,. Если ср — изоморфизм структуры BG наВ^, то
с2°<Р* = с1,
где с1 — структурная, функция для BlG (j=l, 2).
Важным следствием теоремы 2.1 является
Теорема 2.2. Структурная функция локально плоской
G-структуры тождественно равна нулю.
Для доказательства теоремы 2.2 достаточно проверить, что
структурная функция стандартной плоской G-структуры тожде-
342
Гл. VII. Геометрия G-структур
ственно равна нулю. Из (2.11) следует, что если функция с обращает-
ся в нуль в какой-нибудь точке слоя, то она равна нулю на всем
слое. Согласно (2.9), если сн = 0 для некоторого дополнения Н
в точке р, то с (р) = 0. Плоская G-структура BG по определению
содержит в качестве подмногообразия стандартную {е}-структуру
на V. Мы будем выбирать точки р так, чтобы они лежали на этом
подмногообразии, а в качестве Н возьмем касательное пространст-
во к этому подмногообразию. Тогда достаточно доказать, что
форма da» тождественно равна нулю на стандартной ^-струк-
туре В{е>- Проекция л : В{еу —У является диффеоморфизмом,
поскольку структурная группа равна {е}. Поэтому можно рас-
смотреть форму (л-1) *ю на У. По определению (л-1)*(о = d (id),
где id — тождественное отображение пространства У на себя (рас-
сматриваемое как векторнозначная функция). Следовательно,
dco = 0, что и доказывает теорему 2.2.
В общем случае обратная теорема не верна. На самом деле,
как мы увидим в конце этого параграфа, для многих важных групп
G структурная функция первого порядка тождественно равна нулю
для всех Bq. В этом случае структурная функция первого порядка
не дает никакой информации, и мы должны обращаться к инвари-
антам высших порядков.
Однако для некоторых групп G теорема 2.2 допускает обраще-
ние. Приведем несколько примеров. Предположим, что группа
G оставляет инвариантным некоторое подпространство У4 cz У.
Существует очевидная проекция т : Нот (У ДУ, У) —>-
-> Нот (У1 Д У1, У/У1), а именно, если Т g Нот (У Д У, У)
и Vi, v2 6 Vi, то положим т (Т) (у Д v2) равным образу вектора
Т (г?! Д v2) £ V в У/У4. Ядро проекции т состоит из тех Т, для кото-
рых Т (у /\ v2) g Vi при любых Vi, v2 6 Vi. Так как алгебра Ли g
оставляет инвариантным У4, т. е. Avt £ Vi для всех ip £ Vt и А С g,
то для любого S g Hom (У, g) имеем
(S) (у Д v2) = S (у) v2 — S (к2) Vi Е Vi
при любых vt, v2£Vi- Таким образом, Ak (S) cz Ker т. Следова-
тельно, мы имеем проекцию
тр Нот (У Д У, У)/«^ (Нот (У, g)) —»Нот(У1 Д Уь У/У4), (2.12)
и г] (с) есть функция на Bq со значениями в Нот (У4 Д У1, У/У4).
Упражнение 2.2. Проверить, что если G есть группа всех линей-
ных преобразований, оставляющих подпространство У инвариантным (и,
значит, Bq есть G-структура из примера 2), то .А (Нот (У, g)) = Ker тир —
изоморфизм. Показать, что в этом случае теорема 2.2 вместе с обратной теоре-
мой в точности эквивалентны теореме Фробениуса.
Упражнение 2.3. Пусть Bq — почти гамильтонова структура,
определяемая формой Q на М. Показать, что структурная функция на Bq
$ 2. G-структуры
343
тождественно равна нулю тогда и только тогда, когда dQ = 0. Таким обра-
зом, в этом случае теорема 2.2 вместе с обратной теоремой эквивалентны
теореме Дарбу (теорема 6.1 гл. III).
Важным случаем, когда справедливо обращение теоремы 2.2,
является также случай.почти комплексной структуры. Утвержде-
ние состоит в том, что почти комплексная структура с тождествен-
но равной нулю структурной функцией является комплексной.
Это теорема Ньюлендера.и Ниренберга [14]; доказательство ее
основано на глубокой технике теории дифференциальных уравнений
в частных производных.
Вернемся теперь к теореме 2.1. Она утверждает, что для установ-
ления изоморфизма между двумя G-структурами Bq и Bq мы долж-
ны уметь строить такое отображение (р*: Bq -> Bq, что c2°q)* = с1,
на
Задачи такого рода в общем случае весьма сложны. Если заданы
два многообразия и по функции на каждом из них, то установить,
когда существует отображение многообразий, переводящее одну
функцию в другую, очень трудно. Единственный простой (и три-
виальный) случай, — когда одна из функций константа. Тогда
другая функция также должна быть константой и, точнее, той же
самой константой. Таким образом, мы можем сформулировать
Следствие 2.1. Пусть BG есть G-структура, структур-
ная функция которой — константа. Тогда любая G-структура,
локально эквивалентная Bq, имеет эту константу в качестве
своей структурной функции.
Упражнение 2.4. Назовем G-структуру Bq локально репер-тран-
зитивной, если она обладает следующим свойством: для любой пары точек
р и q £ Bq, таких, что л (/>) = х и л (q) = у, существует такой локальный
(х, (/[-автоморфизм <p: Bq -> Bq, что ср* (р) = q. Показать, что структурная
функция любой локально репер-транзитивной G-структуры есть константа.
[Обратное утверждение в общем случае снова не верно.]
Даже если структурная функция не постоянна, в нашем распо-
ряжении имеются некоторые средства, позволяющие проверить
необходимые условия теоремы 2.1. Идея состоит в том, чтобы более
тщательно исследовать равенство (2.11). Вместо того чтобы пытать-
ся сформулировать широкую теорему, покрывающую все частные
случаи, мы опишем общую процедуру, как, пользуясь равенствами
(2.11) и теоремой 2.1, получить необходимые условия эквивалент-
ности G-структур, и проиллюстрируем ее в одном частном случае.
Поскольку группа G действует (с помощью представления ст)
на Нош (У Д V, V)/d (Нош (У, g)), это пространство разлагается
на орбиты относительно действия группы G. В связи с этим
344
Гл. VII. Геометрия G-структур
введем отношение эквивалентности, полагая w{ ~ w2, если
существует такой элемент a g G, что ст (a) w} = w2. Тогда
каждый класс эквивалентности является дифференцируемым
многообразием [которое называется орбитой группы G в
Hom (V Д V, (Нот (У, g))]. Разные орбиты могут иметь раз-
ные размерности. Например, поскольку представление линейно,
нуль остается неподвижным при действии любых элементов из G,
и, следовательно, является нульмерной орбитой. Обычно имеет
место следующая альтернатива: либо множество орбит макси-
мальной размерности дискретно, либо эти орбиты образуют (локаль-
но) непрерывное семейство.
Рассмотрим сначала случай, когда множество орбит максималь-
ной размерности дискретно (и число их конечно). Тогда они явля-
ются открытыми множествами в Нот (У Д У, У)Д/ (Нот (У, g)).
Но структурная функция с на G-структуре BG непрерывна. Поэто-
му если с (р) лежит на орбите максимальной размерности, то с (д)
будет лежать на той же орбите для всех q g л-1 (U), где U —
некоторая окрестность точки л (р) х).
Назовем х Г М точкой общего положения, если с (л-1 (х))
лежит на орбите максимальной размерности. Ограничим-
ся рассмотрением проблемы локальной эквивалентности
в точках общего положения х g Mi иД М2. Тогда по теореме
2.1 структурные функции с1 и с2 локально эквивалентных G-струк-
тур принимают значения в одной и той же орбите группы G в
Нот (У Д У, У)/Л (Нот (У, g)). Пусть w — фиксированная точка
этой орбиты и Н — группа изотропии точки w, т. е. подгруппа
группы G, состоящая из тех a Г G, для которых ст (a) w = w.
Пусть Вц — подмногообразие в BG, состоящее из всех точек р £ BG,
для которых с (р) = w. [Заметим, что, поскольку группа G транзи-
тивно действует на орбите, из равенства (2.11) следует, что в каждом
слое есть точка р, для которой с (р) = w. Пользуясь рассуждениями
на стр. 231, можно показать, что Вгн есть подмногообразие в Bq.]
Это подмногообразие является в действительности //-структурой.
Аналогично строится Я-структура Вц. Если ср — изоморфизм
G-структур, то с2°ф* = с1, откуда ср* ((с1)'1 (ш)[ = (с2)-1 (ш), и, зна-
чит, <р* (Вд) = Вд. Поэтому локальный изоморфизм G-структур
BG и BG является также локальным изоморфизмом //-структур Вд
и Вд. Обратное очевидно: если <р — изоморфизм //-структур, то,
расширяя структурные группы, мы получим изоморфизм G-струк-
тур.Таким образом, мы свели проблему эквивалентности к меныпей
группе Н.
Э Заметим, что, согласно формуле (2.11), образ любого слоя л-1 (х)
при отображении с попадает на одну орбиту.— Прим, перев.
§ 2. G-структуры
345
Аналогичный анализ можно провести и в случае непре-
рывных орбит х). В этом случае орбиты максимальной размерно-
сти группируются в конечное число семейств. Объединение
орбит каждого семейства образует открытое множество
в Нот (ВДВ, В)Л4 (Нот (У, #))• Каждое из этих открытых
множеств можно рассматривать как «расслоенное пространство»,
слоями которого являются орбиты. Вместо того чтобы фиксировать
по элементу в каждой из конечного числа максимальных орбит, как
в дискретном случае, мы должны выбрать подходящее «сечение» это-
го расслоенного пространства. Точнее, мы выбираем подмногообра-
зие W из Нот (У Д У, В)/Л (Нот (У, g)), которое пересекается
с каждой орбитой максимальной размерности только в одной точке.
Подгруппа, оставляющая эту точку неподвижной, будет, вообще
говоря, зависеть от точки. Затем, как и раньше, мы сводим проб-
лему эквивалентности к подмногообразию с-1 (РУ). Однако теперь
с-1 (РУ) не является G-структурой в том смысле, как мы ее опреде-
ляли, поскольку группа теперь меняется от точки к точке * 2).
Поэтому для изучения проблемы эквивалентности в полной общ-
ности следовало бы рассматривать эти более общие объекты. Ради
простоты мы не будем здесь это делать. Заметим, что для многих
«хороших» групп Ли из стандартных теорем теории групп Ли сле-
дует возможность выбора такого подмногообразия W, для кото-
рого подмногообразие с-1 (IB) было бы G-структурой.
В любом случае проблема локальной эквивалентности (в точках
общего положения) сводится к подгруппе Н. Тогда мы строим
структурные функции для полученных //-структур и снова исполь-
зуем теорему 2.1. Эту процедуру можно применять до тех пор, пока
дальнейшая редукция структурной группы окажется невозможной.
Редукция структурной группы выгодна по двум причинам. Во-
первых, мы получаем все более и более тонкие необходимые усло-
вия эквивалентности в терминах структурных функций, возникаю-
щих на каждой стадии. Они могут позволить нам различить две
неэквивалентные G-структуры. Во-вторых, если группа «достаточ-
но мала» (в каком смысле — мы уточним в следующем параграфе),
то мы можем дать необходимые и достаточные условия локальной
эквивалентности.
Проиллюстрируем 3) эту процедуру редукции, применив ее к случаю
дифференциальной системы на пятимерном многообразии. [Дальнейший текст
*) Мы не будем доказывать никаких утверждений для непрерывного
случая, а просто опишем общую процедуру. В каждом частном случае все
упомянутые в рассуждениях объекты следует построить явным образом.
2) Подходящим геометрическим понятием является понятие дифферен-
цируемого группоида Эресмана.
3) Читатель, не желающий вникать в это довольно длинное обсуждение
специального примера, может перейти сразу к общим рассуждениям на
стр. 349.
346
Гл. VII. Геометрия G-структур
представляет собой вольный перевод короткого отрывка из статьи Э. Картана
Surles systemes de Pfaff a cinq variables [7].] Как мы уже видели, дифферен-
циальная система есть G-структура, где G— группа всех линейных преобра-
зований, оставляющих инвариантным некоторое подпространство Vt ci V.
В этом случае пространство Нот (К Д V, 7)/^ (Нот (7, g)) можно ото-
ждествить с пространством Нот (7( Д 71( 7771). Группа G действует на Vi
и на V/Vi, а значит, и на Нот (Г4 Д Vi, V/Vi). Это действие (как читатель
должен проверить) переходит в действие о группы G на
Нот (ГД V, V'/lJt (Нот (7, g)) при отождествлении этих пространств.
Рассмотрим сначала случай, когда коразмерность подпространства Г’1
в V равна единице (a dim V произвольна). В этом случае V/Vi есть веще-
ственная прямая, и G действует на ней при помощи умножений. Тогда
Нот(Р4 Д Vi, V/Vi) есть пространство антисимметрических билинейных форм
на Vi. Две такие формы (, Д и (, )2 лежат на одной орбите группы G, если сущест-
вуют число % и невырожденное линейное преобразование Т пространства Vi,
такие, что (и, v)t = X (Ти, Ти)2 для всех и, v £ Vi. Теорема 5.1 гл. I показы-
вает, что формы (,)|И ( , )2 лежат на одной орбите тогда и только тогда,
когда они имеют одинаковые ранги. Таким образом, существует конечное
число орбит. Орбита максимальной размерности соответствует максимальному
рангу, орбита нулевой размерности состоит из нулевой формы.
Небольшое обобщение теоремы 6.1 гл. III (теоремы Дарбу) показывает,
что ранг — единственный инвариант дифференциальной системы, т. е. две
дифференциальные системы одного ранга локально эквивалентны. Заметим,
что в этой теореме мы разрешаем структурной функции с принимать значения
в любой орбите (а не только в орбите максимальной размерности). Однако
мы предполагаем (чтобы применить теорему Дарбу), что если функция с
принимает значение в какой-то орбите, то она принимает значения в этой орби-
те на некотором открытом множестве. Например, в случае с = 0 система впол-
не интегрируема и теорема Дарбу сводится к теореме Фробениуса. Если
не требовать, чтобы для точек, близких к данной, функция с принимала значе-
ния в той же орбите, то положение резко осложнится, и в этом случае почти
ничего не известно.
Пусть теперь подпространство Vi имеет произвольную коразмерность.
Оказывается, что первый случай, который не может быть полностью проана-
лизирован на основе теорем Фробениуса и Дарбу, имеет место, когда dim V =
= 5. Поэтому мы изучим этот случай. Если dim 7f = 1, то делать нечего (все
системы эквивалентны), а если dim Fj=--4, то все описывается теоремой Дар-
бу. Поэтому представляют интерес только случаи dim Vi = 2 и dim Vt = 3.
Рассмотрим сначала случай, когда dim Vi = 2. Группа G есть группа всех
невырожденных линейных щзеобразований, оставляющих инвариантным
подпространство Vt. Если выбрать базис <q, г2. ез, с,,, е5 пространства V так,
чтобы векторы и е5порождали Vt, то группу G можно отождествить с груп-
пой всех невырожденных матриц вида
имеющих в правом верхнем углу нули, а в остальных местах — произволь-
ные элементы. Группа G имеет размерность 19. Поскольку мы будем после-
довательно редуцировать эту группу (и G-структуру), удобно обозначать полу-
чающиеся группы, указывая их размерности. Так, нашу исходную группу
мы будем обозначать G19. Структурная функция группы G19 принимает зна-
§ 2. G-структуры
347
чения в Hom (V4 Д F1t VIVi). Так как подпространство Vt двумерно, то
Fi Д Vt одномерно, a VIVi трехмерно. Следовательно, пространство
Hom (Fi Д Vt, V/Vi) трехмерно. Как легко видеть, группа G19
действует транзитивно на ненулевых векторах этого пространства. Другими
словами, имеется ровно две орбиты: нульмерное многообразие, состоящее
из нулевого вектора, и трехмерное многообразие, состоящее из всех ненулевых
векторов. Если структурная функция тождественно равна нулю, то система
вполне интегрируема, и все такие системы локально эквивалентны. Если
структурная функция обращается в нуль в некоторой точке, но не равна нулю
ни в какой окрестности этой точки, то наша процедура не применима. Рас-
смотрим поэтому случай, когда структурная функция всюду отлична от нуля.
Выберем определенный элемент из Нот (Fi Д Vi, V/Vt), а именно, элемент ю,
отображающий е4 Д е5 в {е3} (где et, . . . , е5 — выбранный нами базис, а
{е3} — класс эквивалентности вектора е3 mod Ff). Наша процедура тогда
редуцирует BG19 к BGie, где Gi6 — подгруппа группы Gig, состоящая из всех
а € Gig, для которых
w (аи f\ av) = aw(u /\ v)
при любых и, (действие элемента а в правой части — это действие,
индуцированное на факторпространстве V/Vt). В соответствии с нашим
выбором базиса elt ..., е3 и элемента w группа G18 может быть отожде-
ствлена с группой всех невырожденных матриц вида
(Gie):
где А = аб— Ру,
а ее алгебра Ли —с множеством матриц вида
teie):
О 0 ч
О О
О О
«3 я4
(где прочерки обозначают произвольные числа). Теперь мы должны иссле-
довать область значений структурной функции Gig-структуры BGle- Эта
структурная функция принимает значения в
Hom (V Д V, V/Vi)/^ (Hom (Г, g16)).
Согласно нашей общей процедуре, мы должны изучить действие группы G
на этом пространстве. Поскольку это требует довольно неприятных вычисле-
ний, мы поступим несколько иначе. Заметим, что группа Gig оставляет инва-
риантным трехмерное подпространство, натянутое на е3, е4 и е8. [Действитель-
но, она оставляет инвариантным iv, а значит, и одномерное подпространство
iv (Fi) из VIVi. Но пространство, натянутое на е3, ei и е5, есть в точности про-
образ пространства iv (Fi) в V и, следовательно, оно тоже остается инвариант-
ным.) Обозначим это подпространство через W. Так как Gie оставляет W
инвариантным, существует естественная проекция
%: Нот (F Д V, V)/^t (Нот (7, g16)) Нот (И7 Д W, V/W).
Эта проекция не будет изоморфизмом, поскольку G16 не является группой
всех линейных преобразований, оставляющих инвариантным IV. Тем
348
Гл. VII. Геометрия G-структур
не менее мы можем использовать функцию X о с10 для того, чтобы редуцировать
группу. [Таким образом, мы рассматриваем только «часть» структурной
функции для редукции группы. Этот прием часто бывает полезен.] Посколь-
ку подпространство W трехмерно, таким же будет и W Д W, тогда как про-
странство V/W двумерно. Следовательно, элементы из Hom (IV Д W, V/W)
(рассматриваемые как линейные отображения) могут иметь ранг 0, 1 или 2.
[Если функция X о с1в тождественно равна нулю, то соответствующая диф-
ференциальная система вполне интегрируема. Из теорем Дарбу и Фробениуса
немедленно следует тогда, что все такие структуры локально эквивалентны.
Если значения функции %°с16 всегда имеют ранг 1, то внимательный анализ
(основанный на дальнейшей редукции группы) показывает, что ситуация
полностью описывается теоремами Фробениуса и Дарбу.] Общим случаем
является случай, когда ранг функции x°cie всюду равен двум. Заметим, что
функция %ос10 не произвольна. Действительно, по самой конструкции
структуры Д;16 значения функции / о с18 (являющиеся элементами из
Hom (IV Д W, V/W)) переводят <?4 Д е5 в нуль. Читатель может проверить, что
группа Gi6 действует транзитивно (на четырехмерном) многообразии, которое
образуют элементы ранга 2 из Нот (ТУ Д W, V/W), переводящие с4 Д
в нуль. Зафиксируем элемент 2 из этого многообразия. Пусть в терминах
выбранного базиса 2 (е3 Д <?4) = (?,} и z (е3 Д ) = {<?2}, где { } на этот
раз обозначает класс эквивалентности mod W. Тогда подгруппа группы б18,
оставляющая точку z неподвижной, будет 12-мерной группой 6'12. Чита-
тель может легко убедиться в том, что в матричной форме группа Gtz
имеет вид
Да
др О
Дб О
— д
о о
о о
о о
а р
у б
где Д = аб — Ру =Д= 0, а прочерки обозначают произвольные числа.
Алгебра Ли £12 группы G12 состоит из всех матриц вида
(Ы:
О
О
а1 + а4
О О
о о
о о
$ । 6Z2
а3 а4
Прежде чем применять наш общий метод к случаю двумерных диффе-
ренциальных систем, обратимся к трехмерным системам. В этом случае мы
имеем трехмерное подпространство Wt g2 V и группу G, состоящую из всех
невырожденных линейных преобразований пространства V, оставляющих Wt
инвариантным. Эта группа также 19-мерна. Если выбрать базис . . . , е5
пространства V так, чтобы е3, е4 и лежали в Wt, то этой группе будет соот-
ветствовать группа всех невырожденных матриц вида
ООО
ООО
§ 2. G-структуры
349
На этот раз пространство Д И7, трехмерно, а Нот (И7! Д Wj, V/Wt)
шестпмерно. Группа действует транзитивно на элементах ранга 2 послед-
него пространства (которые образуют единственную орбиту максимальной
размерности). Зафиксируем элемент z этой орбиты. Отображение ранга 2
трехмерного пространства обращается в нуль на некоторой прямой.
Но прямые в И7! Д W, соответствуют двумерным подпространствам в И7!
(поскольку пространство W- трехмерно)1). Поэтому мы можем найти двумерное
подпространство в Wt, инвариантное относительно (13-мерной) подгруппы
группы G, оставляющей точку z неподвижной. Таким образом, мы можем
каждой общей трехмерной системе, сопоставить некоторую двумерную диф-
ференциальную систему. Если мы произведем редукцию этой двумерной
системы, то мы снова получим (?12. Итак, проблемы классификации общих
двумерных и трехмерных дифференциальных систем, на пятимерном мно-
гообразии полностью эквивалентны.
Редукция группы Gl2 выполняется значительно труднее. С помощью
непосредственных, но длинных и запутанных вычислений можно провести эту
процедуру еще дважды и прийти к семимерной группе (?7, алгебра Ли g7 кото-
рой имеет вид
Ы:
-г- «2 0 0 0
а3 a1-r2ai 0 0 0
а5 «6 а1+а4 0 0
а7 0 4/За6 a j
0 «7 — 4/3^5 а3 "л
Дальнейшая редукция при помощи указанного выше метода невозможна.
Для дальнейшего исследования приходится обращаться к инвариантам вто-
рого порядка, как это описано в следующем параграфе.
Возвратимся к общему случаю. Структурная функция с для
G-структуры BG принимает значения в
Нот (У Д У, У)/Л (Нот (У, g)).
Выберем дополнение С к (Нот (У, g)) в Нот (У ДУ, У). Таким
образом, Нот (УДУ, У) = G + Л (Нот (У, g)). Если отождествить С
с факторпространством Нот (У ДУ, У)/с$(Нот(У, g)), то с можно
рассматривать как функцию со значениями в С.
Таким образом, мы получаем функцию на BG со значениями
в Нот (У Д У, У). Обозначим ее с. [Подчеркнем, что функция с
зависит от выбора дополнения С. Мы будем часто выбирать такое
дополнение для различных встречающихся групп G.] Равенство
(2.11), записанное в терминах с, принимает вид
с(ра) = ст(а)с(р) + ^€ (Z), (2.13)
где t — некоторый элемент из Нот (У, g) (зависящий от р и а).
1) Действительно, любой элемент и g Wt Д И7, представим в виде и =
— х /\ у, х, у £ Wt. Тогда прямой {Хм} соответствует двумерное подпростран-
ство {Xi -j- uj/}.— Прим, перев.
350
Гл. VII. Геометрия G-структур
Заметим, что выбор дополнения С выделяет в каждой точке
р g Bq класс горизонтальных подпространств 1). Действительно,
по определению подпространства С и функции с существует гори-
зонтальное подпространство Н в точке р, для которого
сн = с(р). (2.14)
В общем случае существует много таких подпространств. Действи-
тельно, если Hi удовлетворяет условию (2.14), то таким же будет
и Н2 при условии, что Gt (Sin, н2) = 0- Это утверждение немед-
ленно следует из (2.8). Мы вернемся к этому в следующем пара-
графе.
Заметим также, что если Н удовлетворяет условию (2.14)
в точке р, то Ва*Н будет удовлетворять (2.14) в точке p-а тогда
и только тогда, когда о (а) с (р) g С. Это следует непосредственно
из (2.13). В частности, имеет место
Предложение 2.1. Если дополнение С инвариантно
относительно о (G) (т. е. о (а) С = С для всех а £ G) и если под-
пространство Н удовлетворяет условию (2.14), то и Ra*H удовле-
творяет условию (2.14) при всех а £ G.
Чтобы облегчить чтение работ Э. Картана по проблеме эквивалентности,
удобно записать некоторые из основных формул этого параграфа в обозна-
чениях, более близких к обозначениям Картана. Выберем прежде всего базис
ef, . . . , еп пространства V. В терминах этого базиса F-значную форму о>
можно рассматривать как набор п вещественнозначных линейных форм:
со = (со1, . . . , wn). Представим Bg локально в виде прямого произведения,
т. е. ограничимся рассмотрением малой окрестности U CZ М и отождествим
л-1 (СТ) с U X G. Далее, G как группа Ли обладает канонической левоинва-
риантной g-значной формой. Отображение, индуцированное проекцией U X
X G -> G, переводит эту форму (локально) в некоторую форму на В$. Обозна-
чим ее П. Пусть At, . . . , Аг —базис g. Тогда эту форму можно записать,
в виде П = (П1, . . . , Пг). Формы со1, . . . , ап, П1, . . . , Пг порождают
кокасательное пространство в каждой точке р g Bq. Заметим, что, в то время
как формы со1, . . . , соп внутренним образом определены всюду на Bg, формы
П1, . . ., Пг определены только локально и при этом зависят от выбора
локального представления расслоения Bg в виде прямого произведения.
Однако они не совсем произвольны: они однозначно определены на слоях.
Действительно, для любого A g g мы имеем (А, П ) = А, так что
(Ла, П₽) = б₽. (2.15)
По существу это единственное свойство форм П^, которое мы будем исполь-
зовать. При этом в процессе рассуждений мы будем несколько раз изме-
нять формы 11А Заметим, что, поскольку формы со* равны нулю на слоях,
вместе с lA условию (2.15) будут удовлетворять и формы П^-г^^г10' для
любых функций d$.
Заметим также, что при фиксированном выборе форм П^ любое гори-
зонтальное подпространство Н задается (г X п)-матрицей dfi (Н). А именно,
х) Здесь под горизонтальным подпространством подразумевается любое
дополнение к вертикальному подпространству.— Прим, перев.
§ 2. G-структуры
351
касательный вектор X в точке р лежит в Н тогда и только тогда, когда
(X, ш’), где d?=d₽(H). Таким образом, мы получаем пара-
метризацию всех горизонтальных подпространств в каждой точке.
Определим теперь константы Да формулой
(2.16)
[Напомним, что е1, ..., еп—базис пространства V, а элементы Аа g g дей-
ствуют на V, так что формула (2.16) имеет смысл.] Равенство (2.5) можно
теперь переписать следующим образом:
dWi=24wlA<oft+2a>’Ana, (2.17)
где —-некоторые функции на М. Чтобы проверить (2.17), заметим, что,
поскольку форма da обращается в нуль на слоях, она не может содержать
членов, включающих Па Д П6. Поэтому остается только проверить, что
коэффициенты при ы‘ Д Па равны аг-а. Но это следует немедленно из фор-
мулы (2.5) (если учесть также (2.15) и (2.16)).
Функции из равенства (2.17) зависят от выбора форм Па. Действи-
тельно, значения сг-к (р) этих функций в точке р соответствуют введенной
ранее функции сд. где Н—горизонтальное подпространство, задаваемое
уравнениями (X, П^-О (0 = 1, ..., г). А именно, сн= (Р) ei ® eh*
(где мы отождествили Hom (V /\ V, V) с К®Р*ДН*), или сл (е? Л -; -
~ У c\ket- Замена пространства Н другим горизонтальным подпростран-
ством соответствует замене форм IIна П^—и это, конечно, изме-
няет функции в соответствии с формулой (2.7). [Читатель при желании
может записать эту формулу в индексных обозначениях.]
Как мы уже видели, выбор дополнения С к (Hom (К, Д) выделяет
в каждой точке определенный класс горизонтальных подпространств и фик-
сирует функцию с. Посмотрим, как это выражается на языке индексов.
Выбор подпространства С равносилен наложению некоторого числа линейных
соотношений на функции clft, выражающих условие, что c}liel ® e'J* A eh*
лежит в С. [Часто удобно задавать эти условия (т. е. выбирать дополне-
ние С) в виде сук, = О, где i', к'—подходящий набор индексов. Однако
иногда бывает удобнее выбрать С по-другому. Успех многих вычислений
Картана объясняется умелым выбором дополнения С.] Как бы то ни было,
функции однозначно определяются, как только мы выберем дополнение С.
Однако при этом формы П^ определяются с некоторым произволом, а именно,
с тем же произволом, что и горизонтальные подпространства, удовлетво-
ряющие условию (2.14). Мы можем, однако, зафиксировать выбор П^, потребо-
вав, чтобы выполнялись равенства (2.15) и (2.17) и чтобы при этом функ-
ции удовлетворяли другим линейным соотношениям. Функции cl.k можно
рассматривать как индексную форму нашей структурной функции с.
Равенство (2.17) показывает, что структурная функция не произвольна.
Точнее, не каждая функция со значениями в Нот (Г Д V, (Нот (V, Д)
на главном G-расслоении, удовлетворяющая условию (2.11), служит струк-
турной функцией некоторой G-структуры. Действительно, если взять внеш-
нюю производную от обеих частей равенства (2.17), то получится некоторое
352
Гл. VII. Геометрия G-структур
соотношение, содержащее Ло;, Па и <Ша. Выражая формы du»1
и <ГО“ через базисные формы ы-> и П^, мы получим некоторое условие
на функции c‘ft. Проведем вычисления. Запишем формы <Ша в виде
п
<ша= а>глш8+2^“глп₽4-2^Хлп?- (2-18)
г, S=1
Внешнее дифференцирование равенства (2.17) дает1)
0= dcljk<£>i Д сойД 2 ^Сй3 Л —2 Л +
+ У ajadwi д п“- 2 \ С
Подставим теперь вместо форм du>i, d<j>k и <1Па их выражения по форму-
лам (2.17) и (2.18). Определим функции ( п сг-к & равенством
dc}h= 2 4мУ + 2 скХ-
Тогда, собирая коэффициенты при оР Д сой Д сог (/< Z) и приравнивая
этот член нулю, получим
(c}k,l+ ckl,j+ cG,k> + 2 <crl<k + crfecZj+ crjckl') —
-(4^ + <^ + 4<) = °- (2.19)
Аналогично, собирая коэффициенты при Д/'\ о? Д П“ (/ < к), получим
cjh, а“Ь2 (ajac1ftTakacrj aracjk) ajf5'®fea'(~aj₽^fez~ (2.20)
Сравнивая коэффициенты при a>i Д П“ Д П^, мы получаем в точности струк-
турные уравнения группы G. Внимательный читатель заметит (упражнение!),
что соотношения (2.20) не дают ничего нового, а являются по существу
следствиями равенств (2.11) и (2.8). Соотношения (2.19), напротив, содержат
новую информацию. Вероятно, их следует назвать тождествами Бьянки —
Картина.
Посмотрим, что дают тождества Бьянки — Картана в случае, когда
структурная функция постоянна. В этом случае с^к постоянны, так что
члены с]к ; тождественно равны нулю п равенство (2.19) принимает вид
2(erZcyfe+ crfteb + cn'cfez) = aja"4w+ak"4o + aZa"4Th- (2’21)
Таким образом, мы получили квадратичные относительно необходимые
условия (а именно, должны существовать такие функции Ак1, чтобы выпол-
нялись соотношения (2.21)). Сформулируем теперь это условие в безпндекс-
ной форме в терминах функции с (которая предполагается постоянной).
Заметим прежде всего, что существует естественное билинейное ото-
бражение X: Hom (F Д V, Г) х Hom (V Д Т, Г) -> Нош (Г Д Г Д Т, Г). Оно
!) Для упрощения обозначений условимся, что знак суммы означает
суммирование по повторяющимся индексам. Латинские индексы принимают
значения от 1 до п, греческие—от 1 до г.
§ 3. Продолжения
353
определяется следующим образом: если Clt С2 £ Нош (У Д V, 7), то
% (Cj, С2) (vi Л у2 Л уз) — Ci (С2 (tfj Л а2) Л уз) +
+ С1 (^2 (у2 Л уз) Л у1) + С1 (С2 (у3 Д V]) /\ и2).
Читатель может проверить, что левая часть равенства (2.21) есть не что
иное, как запись элемента X (с, с) в базисе еп. С другой стороны,
рассмотрим пространство Hom (F Д V, g). Существует естественное линейное
отображение р. этого пространства в Hom (V Д V Д V, V), задаваемое фор-
мулой
И СО (у1 ЛА Л уз) = т (у1 Л уг) уз +Ду2 Л уз) у1+т (уз Л у1) у2
для любого т € Нот (V Д V, g) и гд, v2, v3 £ V. В терминах выбранных бази-
сов пространств V и g любой элемент из Hom (7 Д V, g) задается своими
коэффициентами А^. Поэтому существование коэффициентов А^, для кото-
рых выполняется равенство (2.21), эквивалентно существованию такого
элемента т £ Hom (V Д V, g), что X (с, с) = р(т). Итак, условие (2.21) озна-
чает, что
X (с, с) С р (Нот (КД V, g)). (2.22)
Посмотрим, к чему это сводится В случае простейшей G-структуры —
{е}-структуры группы Ли. В этом случае V есть алгебра Ли группы Ли,
а с = с( Hom (V Д У, У) — умножение:
с (у1 А уг) = [у1> уг1
в этой алгебре Ли. Поскольку тогда g = 0, "условие (2.22) означает, что
X (с, с) = 0 или [[уь у2]> уз1 + [[у2, уз1> у11 + [[уз> у1], уг] = °- Таким образом, для
{е]-структуры группы Ли тождества Бьянки—Картана (сводятся к тожде-
ствам Якоби.
§ 3. ПРОДОЛЖЕНИЯ
В предыдущем параграфе мы изучали проблему эквивалентно-
сти G-структур, используя структурную функцию первого поряд-
ка с. Сейчас мы покажем, что для некоторых групп G структурная
функция первого порядка не дает никакой информации,
а именно, что эта структурная функция для всех G-структур
тождественно равна нулю. Поскольку с принимает значения в
Hom (V Д V, У)/.Д (Нот (У, g)), достаточно указать алгебру Ли
g, для которой Л (Hom (V, g)) = Нот (Г Д V, У)1). Это может
случиться, если размерность Нот (У, g) велика, а размерность
ядра отображения Jk мала. Естественно поэтому изучить ядро
отображения с#, которое мы обозначим gW. Поскольку это про-
*) Тривиальным примером, когда это так, является случай g = gl (7)
(алгебра всех линейных преобразований пространства V). Однако это
не интересно, поскольку все GL (7)-структуры локально эквивалентны.
Мы хотим построить примеры, когда структурная функция первого порядка
не различает две неэквивалентные структуры.
23 с. Стернберг
354
Гл. VII. Геометрия G-структур
странство будет играть в дальнейшем основную роль, мы дадим
более общее
Определение 3.1. Пусть V и W — векторные простран-
ства, и пусть g — подпространство в Hom (V, W). Обозначим
через g*-1) подпространство в Hom (V, g), состоящее из таких эле-
ментов Т, что
Т (и) v = Т (р) и (3.1)
для всех и, v^V. [Напомним, что T(u)£g, так что T(u)v£V.}
Пространство gm называется первым продолжением подпростран-
ства g. Положим g<2’ = (ga’)a> и, вообще, g<i+1’= (g(i))a’. Простран-
ство g(l> называется l-м продолжением подпространства g.
В нашем случае V = W и g есть не только подпространство,
но и подалгебра алгебры Ли Нот (7, V). Из определения опера-
тора следует, что gu’ = Ker^.
Упражнение 3.1. Если отождествить Hom (V, И7) с W 0 Р’*, то g
будет подпространством в W ® V*, a Hom (7, g) можно рассматривать как
подпространство в W ® V* 0 V*. Показать, что тогда
g<i> =Hom (V, g) Q W® S2 (7).
Упражнение 3.2. При тех же отождествлениях показать, что
g<h) = £®7*®...®7*П17® Sk+1 (V*).
k раз
Упражнение 3.3. Векторное поле на векторном пространстве V
можно рассматривать как 7-значную функцию. Поэтому можно говорить
о матрице Якоби векторного поля (подразумевая под ней матрицу Якоби
соответствующего отображения V —> 7). Отождествляя касательное про-
странство в каждой точке из V с самим V, мы можем рассматривать эту мат-
рицу Якоби как функцию на V со значениями в Нот (У, У). Таким образом,
каждому векторному полю X мы сопоставляем Нот (У, Р)-значпую функцию,
которую обозначим символом Jac (X). [В терминах базисов, если X = (X1, . . .
. . . , Хп), то Jac (X) = (dXMdxi).} Показать, что векторное поле X является
инфинитезимальным автоморфизмом стандартной плоской G-структуры на V
тогда и только тогда, когда Jac (X) (и) £ g для всех v £ V.
Упражнение 3.4. Рассматривая данное векторное поле X на V как
7-значную функцию на V, мы можем вычислить его разложение Тейлора
в любой точке. Члены степени Л-|-1 разложения Тейлора можно рассматри-
вать как элемент пространства 7® Sfe+1 (7*). Показать, что если X—инфи-
нитезимальный автоморфизм плоской G-структуры, то элемент степени к +1
его разложения Тейлора (в любой точке) лежит в Вывести отсюда,
что если g<b)=O для некоторого к, то алгебра Ли всех инфинитезимальных
автоморфизмов плоской G-структуры конечномерна.
Определение 3.2. Подпространство gcHom(F, W) назы-
вается пространством конечного типа, если g(ft> = 0 для некото-
рого (а значит, и всех больших) к. Если g<ft> 0 для всех к,
то g называется пространством бесконечного типа.
§ 3. Продолжения
355
Чтобы проиллюстрировать понятие продолжения, рассмотрим
несколько алгебр. Возьмем прежде всего ортогональную алгебру
о (и). В этом случае мы имеем симметрическую невырожденную х)
билинейную форму ( , ) на V. Алгебра о (и) состоит из тех
А € gl(V), для которых
(Au, v) + (и, Av) = 0 при любых и, v£V. (3.2)
Предложение 3.1. Первое продолжение алгебры о(п)
равно нулю-.
о (n)w = 0.
Если выбрать базис, то доказательство предложения 3.1 све-
дется к лемме 1.2 гл, VI. Для удобства мы воспроизведем здесь
это доказательство. Пусть и, v и w — три вектора из V, и пусть
Т £ о (я)(1). Тогда
(Т (и) v, w) = (Т (р) и, w) = согласно (3.1)
= — (и, Т (v)tv) = согласно (3.2)
= — (и, Т (to) v) = согласно (3.1)
— (Т (w) и, v) = согласно (3.2)
= (Т (и) iv, v) -
= (р, Т (и) w) = (в силу симметрии ( , ))
= — (Т (и) v, iv).
Итак, (Г (и) v, tv) =—(Т (и) v, iv) = 0. Поскольку вектор iv произ-
волен, а форма ( , ) невырожденна, отсюда следует, что Т (u)v = Q.
Значит, 7’(iz) = 0 при всех и, т. е. 7’ = 0.
Выведем из предложения 3.1 несколько важных следствий.
Заметим, что dim Hom (ИДУ, У) — п X (п (п— 1)/2). С другой сто-
роны, dim о (п) = п (п—1)/2* 2). Следовательно,
dim Hom (У, о (п)) = п2 (п— 1)/2 = dim Hom (У ДУ, У).
Поскольку Кег А = о(п)ш = 0, мы заключаем, что
Л (Нот (У, о (п))) = Нот (У Д У, У). (3.3)
В Алгебра о (п) соответствует положительно определенной билинейной
форме. Однако все наши рассуждения остаются справедливыми для любой,
не обязательно положительно определенной, невырожденной симметри-
ческой формы.
2) Доказательство. Форма ( , ) позволяет отождествить V с У*,
a gl (Е) = У® V* c^F*QF*. Элемент A£gZ(y) соответствует при этом
билинейной форме А, где А(и, о) —(Au, v). Формула (3.2) показывает тогда,
что о (п) отождествляется с V* Д V* и, таким образом, dimo(n) = n(n —1)/2.
23*
356
Гл. VII Геометрия G-структур
Таким образом, в случае римановой геометрии структурная
функция первого порядка не дает абсолютно никакой информации.
Из равенства (3.3) можно извлечь также важное позитивное
утверждение. Действительно, в силу этого равенства проблема
выбора дополнения С к Л (Нот (17, о (п))) в Нот (V Д V, V)
тривиальна, так как это нулевое подпространство. Согласно
рассуждениям, приведенным в конце § 2, в каждой точке из
Во(п) ® (-^0) существует горизонтальное подпространство Н,
для которого сн = 0. Из формулы (2.11) и предложения 3.1
следует, что такое горизонтальное подпространство единственно.
Благодаря условию (2.11) выбор в каждой точке такого горизон-
тального подпространства определяет связность. Тем самым
доказана
Теорема 3.1 (Леви-Чивита). Для любого риманова многооб-
разия М на расслоении О (М) существует каноническая связность.
Горизонтальное подпространство Н этой связности в каждой
точке характеризуется условием сн — 0.
Задание связности на © (М) равносильно заданию (^позна-
чной формы. В терминах стандартного базиса алгебры Ли
о(п) это сводится к заданию форм Тем самым мы доказали
существование форм &м, выполнив обещание, данное на стр. 270.
Читатель может проверить, что равенство (2.17) сводится в этом
случае к равенству (3.8) гл. VI.
Упражнение 3.5. Сравнить равенство (5.10) гл. VI с равенст-
вом (1.6) (структурным уравнением связности). Заключить отсюда, что
в терминах базиса форма р* (DQ) задается формами 2 Л^б11 Д Ajfl1-
h, I
(Отображение р определено на стр. 268). Таким образом, теорема Леви-Чи-
вита дает новое доказательство и интерпретацию гауссовой теоремы «эгре-
гиум».
Следующие упражнения иллюстрируют понятие продолжения
на примере других алгебр.
Упражнение 3.6. Рассмотрим алгебру Ли со(га) конформной группы.
Она состоит из таких A^gl(V), что
(Ла, у) + (а, Ла)=ХА (“. г)
для любых и, v g F, где ( , )—невырожденная симметрическая билинейная
форма. Рассмотрим отображение со(п)<1> _> V*, переводящее каждый элемент
ТСсореД в линейную форму и-—> Д (и). Показать, что это изоморфизм,
так что мы можем отождествпть co(ra)<1> с V*.
Упражнение 3.7. Рассмотрим теперь со (н)(2>. Для каждого
S£ со (п)(2> п и, vQV линейное преобразование S (и, v) лежит в со(п). Поэ-
§ 3. Продолжения
357
тому для любой пары векторов х, у С V
(.8 (и, v)x, у) + (х, S (и, р) у) = Хи„.(аг, у),
где Хив—симметрическая билинейная форма, зависящая от S. Если Хи1) = 0
для всех и и v g V, то S £ о (п)(2> и, значит, 5=0. Показать, что если
dim V 3, то iuos0. [Указание: поскольку %UP = XBU, достаточно прове-
рить, что Xuu = 0. Пусть и и х— пара ортогональных векторов: (и, х) = 0.
Тогда
х) — 2 (5 (и, и) х, я) = 2 (S (и, х) и, х) =
= —2 (5 (и, х) х, и) - —2 (S (х, х) и, и) = —Хжя-(и, и).
В частности, если и а х — ортогональные единичные векторы: [и, и) =
= (ж, х) = 1, то Zutt = — Хжж. Если в пространстве существует не меньше
трех взаимно ортогональных векторов, то из этого равенства следует, что
Хии = 0- Таким образом, алгебра Ли со(п) имеет конечный тип, если п
3.] Показать, что со(2) — алгебра Ли бесконечного типа.
Упражнение 3.8. Пусть ( , ) — невырожденная антисимметри-
ческая билинейная форма на V, a sp(n) — алгебра Ли, состоящая из всех
линейных преобразований А, для которых
(Au, p)-|-(w, Av) — Q.
Билинейная форма ( , ) позволяет отождествить V с V* п, следовательно,
7(g) У* с У*0У*. Показать, что при этом алгебра Ли sp (п) С V 0 V*
( = Нот(У, У)) отождествляется с пространством симметрических тензоров
52(У*). Более общо, отождествим У05Ь+1(У*) с V* 0 (У*). Показать,
что прп этом sp отождествляется с 5Й+2(У*) и, таким образом, sp (га)—
алгебра Ли бесконечного типа.
Упражнение 3.9. Пусть ( , ) и У—те же самые, что п в упражне-
нии 3.8. Рассмотрим «конформную симплектическую алгебру Ли» g, состоя-
щую из всех А £ gl (У), для которых
(Ах, у) + (х, Ау} = \А.[х, у).
Показать, что g<l> =sp (га)<1>.
Вернемся к общим рассмотрениям. Мы будем изучать G-струк-
туры, предполагая, что для каждой группы G зафиксировано
некоторое дополнение С к Л (Нот(7, g)) в Нот(7 ДУ, 7). Тогда
в каждой точке G-структуры Bg выделен класс горизонтальных
подпространств, а именно, те подпространства Н, для которых
сн£С. Горизонтальное подпространство Н в точке p£BG инду-
цирует изоморфизм пространства TP(BG) на V-\-g. Действительно,
мы уже имеем изоморфизм касательного пространства к слою на g.
Поскольку форма ш индуцирует изоморфизм пространства Н на 7,
мы получаем изоморфизм Тр (BG) 7 + g. Этот изоморфизм сопо-
ставляет каждому горизонтальному подпространству Н в точке р
репер на многообразии BG с началом в р (который соответствует
стандартному реперу пространства 7 + g). Чем отличаются реперы,
соответствующие двум подпространствам Hi и Н2 выделенного
358
Гл. VII Геометрия G-структур
класса? Согласно формуле (2.8), если СцДС (i=l, 2), то
8Hi, н2 С £(1>- Пусть zt и z2— реперы, соответствующие подпрост-
ранствам Н1 и Н2. По определению для любого v g V мы имеем
г1(р) = г2(р) + 5Я1>На(р).
С другой стороны, zt(A) = z2(A) для любого A£g. В соответствии
с этим дадим такое
Определение 3.3. Назовем группой G(1) группу всех линей-
ных преобразований пространства F + g вида аТ где
ат (Л) = А для А Е g,
ат (у) = и-\-Т (г>) для и £ V.
В «матричных» обозначениях группа G(1) состоит из всех ли-
нейных преобразований вида
F g
V/id 0\
id/ •
Мы можем теперь сформулировать следующее утверждение:
Теор ема 3.2. Выбор дополнения С для алгебры Ли g опре-
деляет G(1) -структуру на каждой G-структуре BG. Эта струк-
тура называется первым продолжением G-структуры BG. Для
того чтобы две G-структуры Bq и Bq были локально эквива-
лентны, необходимо и достаточно, чтобы соответствующие
G(1)-структуры на Bq и Bq были локально эквивалентны {как
G(- l’-cm рукту ры).
Первое утверждение мы уже доказали. Пусть теперь/?^ и Bq —
две G-структуры соответственно на Mi и М2, и пусть <р — изо-
морфизм структуры Bq на Bq. Если Hi — горизонтальное под-
пространство в точке pi^B^Q и Н2 = (ср*)* {Hi) — соответствующее
подпространство в точке p2^BG, то еН2 = Сн1- В частности, снДС
тогда и только тогда, когда снДС. Значит, (ср*)* отображает
реперы G( ^-структуры на Bq в реперы G( ^-структуры на Bq.
Обратно, пусть ф— диффеоморфизм многообразия Bq на Bq,
являющийся изоморфизмом G(1 ^структур. Тогда ф^. (Л1) = Л2,
где А1 и А2 — векторные поля на Bq и Bq, соответствующие вектору
A£g. Следовательно, отображение ф согласовано с действиями
группы G на Bq и B2q и, значит, определяет дифференцируемое
§ 3. Продолжения
359
отображение <р многообразия Mi на М2, для которого
фол1 = л2оф, (3-5)
где л4 и л2— проекции расслоений Bq и Bq соответственно на Mi
и М2. Пусть pt — точка из Bq (т. е. репер на М^, и Hi — гори-
зонтальное подпространство в точке Поскольку ф есть изо-
морфизм G(1 ^структур, изоморфизм V—^Hi переходит при ото-
бражении ф* в изоморфизм V —> Н2 = ф* (Ht).
Далее, репер из G( ^-структуры, соответствующий подпрост-
ранству Hi, сопоставляет каждому вектору v£V такой вектор
X^Hi, что л1*(Х) = р1(г) [где репер pt рассматривается как
изоморфизм пространства V на ТП1 (р) (Ti/j)]. Аналогично, репер,
соответствующий Н2, сопоставляет вектору v£V такой вектор
Y £Н2, что л2* (У) = р2(и)- Поскольку ф — изоморфизм Субструк-
тур, мы должны иметь ф*(Х) = У. С другой стороны, из (3.5)
следует, что <р* о ли = л2* о ф, откуда <f>*Pt(v) = р2(и). Но это озна-
чает, что ср* (р^ = р2, или, иначе, д>* = ф, что и доказывает
теорему 3.2.
Теперь для исследования вопроса об эквивалентности
С(1)-структур мы можем применять все методы § 2, а именно,
строить структурную функцию, редуцировать группу и т. д.
Прежде чем приступить к этому исследованию, заметим, что небольшое
изменение нашего метода позволяет рассматривать структуры «высших поряд-
ков». А именно, вместо того, чтобы изучать всю G(o-структуру, ассоцииро-
ванную с G-структурой Bq, мы можем рассматривать некоторую подструк-
туру- Это равносильно наложению условий «второго порядка» (соответствую-
щпх подгруппе из G’1’) в дополнение к «линейным» условиям, налагаемым
G-структурой Bq. Хорошей иллюстрацией служит редукция G*1’-структуры
к {е J-структуре. Она равносильна выбору в каждой точке расслоения Bq
по горизонтальному подпространству из нашего выделенного класса. Это
может быть сделано, например, заданием связности на Bq. Таким образом,
теория G-связностей включается в нашу схему. Другим примером структуры
второго порядка служит так называемая проективная дифференциальная гео-
метрия. Рассмотрение таких структур с принятой здесь точки зрения
см. у Гийемина [4].
Выясним теперь, что представляет собой структурная функция
первого продолжения. Для этого мы должны исследовать алгебру
Ли группы Ли G(1\ Из определения 3.3 видно, что она состоит
из всех линейных преобразований вида Ат (Т £ g(1)), где
Ат (А) = 0 для А £ g,
Ar(v) — T (и) для v£V.
Ясно, что алгебру Ли группы Ли G(1) можно отождествить
с g<1>, если рассматривать T^glV как линейное преобразование
360
Гл. VII. Геометрия G-структур
пространства У + g, действующее тривиально Hag, т. е. 71(Л) = 0
для всех А £ g. Таким образом, мы имеем специальное представ-
ление алгебры Ли g(1> на Vg. Новая структурная функция
принимает значения в некотором факторпространстве пространства
Hom((F + g) A (У-j-g), У-j-g).
Снова, как на стр. 349, мы можем выбрать дополнение и рассмат-
ривать структурную функцию как функцию со значениями в неко-
тором подпространстве пространства
Hom((7 + g) Д (У-f-g), У-f-g).
Это пространство естественным образом разлагается в прямую
сумму подпространств. Рассмотрим проекцию структурной функ-
ции на каждое из этих подпространств. Прежде всего мы полу-
чаем элемент из Hom (У А Ю х)- В качестве поучительного
упражнения читатель может проверить, что это есть просто старая
структурная функция структуры BG, поднятая на С(1)-структуру
(которая, разумеется, является расслоением над BG). Мы полу-
чаем также элемент из Hom (g A g, g)- Читатель может проверить,
что он определяет просто операцию в алгебре Ли g. «Новыми»
будут два билинейных отображения — элемент из Hom (У ® g, g)
и элемент из Нот (У А V, g).
Упражнение 3.10. Показать, что если gO) = О и GO)-структура
является связностью на Bq (как в случае римановой геометрии), то «новый»
элемент, лежащий в Нот (ГД V, g), можно рассматривать как кривизну
этой связности.
Продолжая этот процесс, мы получим G<2), G(3), ...
..., G(ft), .. .-структуры, ассоциированные с данной G-структурой.
Они называются вторым, третьим, ... , 7с-м, ... продолжением
G-структуры BG. Тем самым мы получим последовательность все
более тонких необходимых условий эквивалентности G-структур.
Алгебра Ли группы Ли G(ft) является представлением алгебры g(ft).
В частности, если g(H-i) — 0, то G(ft+1) = {e}. В этом случае
С(,г+1)-структура, определенная на /с-м продолжении, является
{е}-структурой, т. е. абсолютным параллелизмом.
Итак, проблема эквивалентности двух структур конечного
типа сводится с помощью подходящего продолжения к проблема
эквивалентности {е}-структур.
В качестве применения полученных результатов рассмотрим
проблему эквивалентности данной структуры плоской структуре.
!) Точнее, функцию со значением в Hom (V /\ V, V).— Прим, перев.
§ 3. Продолжения
361
Как легко видеть, структурные функции всех продолжений пло-
ской G-структуры постоянны. [Основные нетривиальные части
этих функций обращаются в нуль. Например, для первого продол-
жения структурная функция (являющаяся константой) лежит
в Hom ((V + g) Л (V + g), V + g). Ее части, лежащие в
Hom (V Д V, V) и Нот (V ® g, g), равны нулю. Слагаемой
из Нот (g Д g, g) задает структурные константы алгебры Ли g
и не равно нулю. Однако, оно не представляет интереса, посколь-
ку оно одно и то же для всех G-структур (при фиксированной
группе G).] Итак, справедлива
Теорема 3.3. Пусть G — группа Ли конечного типа. В этом
случае G-структура является локально плоской тогда и только
тогда, когда структурные функции всех ее продолжений — кон-
станты, совпадающие с соответствующими структурными кон-
стантами некоторой плоской G-структуры.
[Равенство констант в теореме 3.3 достаточно проверить только-
для тех к, для которых 0.]
Необходимость вытекает непосредственно из теоремы 3.2
и следствия 2.1. Достаточность доказывается следующим образом.
На fc-м шаге мы имеем два абсолютных параллелизма с одинако-
выми постоянными структурными функциями, поэтому достаточно-
просто применить теорему 2.4 гл. V. Здесь группой является
группа всех автоморфизмов плоской G-структуры, а многообра-
зием — к-е продолжение G-структуры Bq.
Заметим, что теорема 3.3 остается справедливой при значитель-
но более слабых предположениях, чем предположение, что G —
группа конечного типа. Например, она доказана (в упомянутой
в предисловии статье Сингера и Стернберга) в предположении, что
группа G вполне приводима, а также для любых групп G в пред-
положении, что G-структура Bg аналитична. По-видимому, теоре-
ма справедлива для всех групп Ли G и всех G-структур BG, однако-
доказательство мне пока неизвестно.
В следующем параграфе мы будем изучать абсолютный парал-
лелизм и другие структуры конечного типа более подробно.
В заключение этого параграфа заметим, что при решении проблемы
эквивалентности часто оказывается плодотворным следующий
подход: попытаться редуцировать группу к группе конечного
типа методами § 2, а затем применить процедуру, изложенную-
в этом и следующем параграфах.
Так, группа G7, полученная в § 2 при изучении дифференциальной систе-
мы на пятимерном пространстве, является группой конечного типа: = 0,
в то время как исходная группа G10 была группой бесконечного типа.
362
Гл. VII. Геометрия G-структур
§ 4. СТРУКТУРЫ КОНЕЧНОГО ТИПА
Как мы видели в предыдущем параграфе, проблема локальной
эквивалентности структур конечного типа сводится к проблеме
локальной эквивалентности {е}-структур, т. е. абсолютных парал-
лелизмов. Это приводит к изучению проблемы эквивалентности
абсолютных параллелизмов (или, по терминологии Картана,
ограниченной проблемы эквивалентности). Мы решим эту пробле-
му (в достаточно общих предположениях), пользуясь методами
§ 2 (главным образом, теоремой 2.1). В случае {е}-структуры
g = 0, так что структурная функция с принимает значения
в Нот (ГД V, У). Кроме того, мы можем отождествить В^еу
с базисным многообразием М и, следовательно, можем рассмат-
ривать функцию с как отображение М Hom (V Д V, У).
Исследуем два крайних случая: 1) с — константа, 2) с — погруже-
ние М -> Нот (У Д У, У). В первом случае мы уже рассматри-
вали проблему локальной эквивалентности: если Mi и М2 —
два многообразия с абсолютными параллелизмами, причем струк-
турная функция ct для Mi — константа, то они локально экви-
валентны тогда и только тогда, когда структурная функция
с2 для М2 является константой, равной С\. Необходимость этого
условия устанавливает теорема 2.1. Достаточность следует из тео-
ремы 2.7 гл. V (приведенное там доказательство теоремы исполь-
зует как раз то, что функции <Д постоянны).
Исследуем теперь другой крайний случай (являющийся вместе
с тем случаем общего положения). Допустим, что с есть погруже-
ние многообразия М в Нот (У Д У, У). Пусть р — точка из М.
Выберем re-мерное подпространство W cz Нот (У Д У, У) так,
чтобы проекция р: с (М) -> W была невырожденной в некоторой
окрестности U точки с (р) (рис. 32). Тем самым мы получим спе-
§ 4. Структуры, конечного типа
363
циальную карту (U, р ° с) вблизи точки р. Пусть М' — другое
многообразие с абсолютным параллелизмом, и пусть ср — локаль-
ный изоморфизм многообразия М на М', определенный на U,
причем ср (р) = q. Согласно теореме 2.1, мы должны иметь
с' ° ср = с, где с' — структурная функция для М'. Таким образом,
с' (ср (G)) = с (U), и, в частности, с' есть погружение вблизи
точки q и проекция р невырожденна в q. Мы можем написать
(р ° с') ° ср = р ° с. Поскольку р ° с и р ° с' — диффеоморфизмы,
имеем ср = (<р 0 с')-10 (р ° с). Тем самым изоморфизм ср однозначно
определен. Поэтому условие локальной эквивалентности в случае
общего положения можно сформулировать следующим образом:
Пусть М — многообразие с абсолютным параллелизмом, при-
чем соответствующая структурная функция с является погру-
жением вблизи точки р. Выберем п-мерное подпространство
W cz Hom (V Д У, У) и проекцию р: Нот (УДУ, У) ->• W так,
чтобы отображение р было невырожденным на с (М) в точке с (р).
Пусть М' — другое многообразие с абсолютным параллелизмом
и q g М'. Для того чтобы существовал локальный изоморфизм
ср: М М’, переводящий р в q, структурная функция с' для М'
должна быть погружением в точке q. Кроме того, р должно быть
невырожденным на с' (М') в точке q. Если эти условия выполнены,
то изоморфизмом ср может быть только отображение ср =
= (р ° с')-1 ° (р ° с). Для того чтобы это отображение было локаль-
ным изоморфизмом, мы должны иметь с' ° ср = с.
Достаточность этих условий мы докажем позднее в более
общей ситуации.
Отметим, что при изучении G-структур конечного типа мы
не можем удовлетвориться последним результатом, несмотря
на то, что он применим к {е}-структуре общего положения. Дей-
ствительно, структурные функции {е}-структур, возникающих
в результате продолжений G-структур конечного типа, имеют
части, которые являются константами (а именно, структурными
константами соответствующих алгебр Ли). Таким образом, эти
структурные функции не являются погружениями.
В «промежуточном» случае, когда функция с не является
ни погружением, ни константой, мы должны обратиться к струк-
турным функциям «высших порядков», как в § 3. Для того чтобы
представить результаты в форме, наиболее удобной для вычисле-
ний, мы будем пользоваться индексными обозначениями и введем
еще несколько определений. Выберем некоторый базис про-
странства V.
Тогда У-значную форму со, задающую на М абсолютный
параллелизм, можно записать в виде со = (со1, . . . , со”). Для
364
Гл. VII. Геометрия G-структур
любой функции / на М имеем
= Ш (4.1)
Функция /, называется i-й ковариантной производной функции /.
Если в обозначение функции входят индексы, то перед индексом,
указывающим ковариантную производную, мы будем ставить
запятую. Например,
У1С}кЛ(р1. (4.2)
i
Пусть S— семейство функций на М. Рангом rp(JF) семейства S'
в точке р£М называется размерность подпространства простран-
ства Тр (М), порожденного дифференциалами df всех функций
fQJP. На классическом языке rp (J^) есть степень функциональ-
ной независимости семейства функций в точке р. Семейство S'
называется регулярным в точке р, если (.А) = (JF) для
всех q из некоторой окрестности точки р. Предположим, что JF
регулярно в р, причем rp (J^) = к. Тогда мы можем выбрать
функции fi, .. ., fk£ так, чтобы их дифференциалы dfi, . . ., dfk
были линейно независимы в некоторой окрестности точки р.
Дополним функции ft до системы координат вблизи р, т. е. выбе-
рем вблизи р такую систему координат х1, . .., хп, что = . ..
...,xh = fk. Дифференциал df любой функции f£S в силу
регулярности семейства является линейной комбинацией форм
dx1, ..., dx*1. Поэтому любую функцию /gjF” можно представить
в виде f = f(x1, Тем самым доказана
Лемма 4.1. Пусть S— регулярное семейство функций,
имеющее в точке р ранг к. Тогда в окрестности точки р можно
выбрать такие координаты х1, . .., хп, что х1, . . ., of1 QS
и любая функция f^S' записывается в виде f = f(x\ ...,xh).
Такая система координат называется приспособленной к S:.
Вернемся к изучению абсолютного параллелизма. В терминах
выбранного базиса пространства V структурная функция с задается
функциями cjfe, где
= 2 Д со\
Таким образом, мы имеем семейство S:0, состоящее из п (ге (п. —1))/2
функций c'.h на М. Рассмотрим также семейство
§ 4. Структуры конечного типа
365
где функции ; задаются формулой (4.2), состоящее из
(п(п —1)/2) (п. 4-тг2) функций, и, более общо, семейство
Xs = {c)fe; C}h.il' СЛ, й.й’’ C}h, «1.ij
из (п(п—1)/2) (п + п2 + ... + res) функций. Положим
(р) = rp (Xs). (4.3)
Поскольку s с Xs+1, мы можем написать
0<МрХМрХ---<МрХ«- (4.4)
Лемма 4.2. Предположим, что семейство JFs+l регулярно
в точке р. Тогда, если ks(p) = ks+l(p), то ks(p) = ku(p) для всех
u>s.
Доказательство. Пусть fc = fcs(p), и пусть х\ ..., хп —
приспособленная к & м система координат в окрестности точки р.
Поскольку /cs(p) = fcs+i(/') = ^, мы можем считать, что функции
х1, .. ., хк принадлежат (а не только Xs+1). Определим функ-
ции х( . равенством
dx* — 2 х\ /о’.
Из определения семейства JXu следует, что xl. Q ^s+l. Поэтому
мы можем написать
Для любой функции /CFs-ц имеем / = /(а:1, ..., а?), откуда
^=2^‘=2(2>Х'
1 j=l 1=1
или
k
= 2
i=l
Все функции в правой части этого равенства зависят только от
х1, ..., х\ Таким: образом, ковариантные производные любой
функции /G^s+i являются функциями от х1, .. ., xh. Значит, ранг
семейства равен к. Продолжая по индукции, мы докажем
лемму 4.2.
Определение 4.1. Пусть ю1, . . ., ю”—формы, определяющие
на многообразии М абсолютный параллелизм. Пусть р — точка
из М. Если для некоторого s семейство ,-Х-н регулярно в точке р
366
Гл. VII. Геометрия G-структур
и ks (р) = ks+l (р), то абсолютный параллелизм называется регу-
лярным в точке р. Наименьшее такое s называется порядком г(р)
абсолютного параллелизма в точке р, а число k(p) = ks(p) —
рангом параллелизма в точке р. Карта, приспособленная к t
в р, будет называться приспособленной картой в точке р.
Заметим, что если р—точка общего положения из М, то семейство .
регулярно в р при любом г. В этом случае, если i меньше, чем порядок
параллелизма в точке р, то Aj (р)<*г+1 (Р)- Поэтому для такой точки спра-
ведливо неравенство
Г (р) < fc (р) < п.
Это означает, что при изучении проблемы эквивалентности «общих» G-струк-
тур конечного типа необходимо только конечное число дифференцирований,
причем это число определяется группой G.
Предположим, что формы со1, . . ., со" задают на М регулярный
абсолютный параллелизм порядка г и ранга к. Каждая функция
из имеет определенное множество индексов. В частности, если
х1, ..., ск"— приспособленные координаты, то мы можем рассмо-
треть индексы каждой из функций z1, ..., Xй G • Любые дру-
гие функции из являются функциями от л;1, ..., Xй. Теперь
мы в состоянии сформулировать необходимые и достаточные усло-
вия эквивалентности.
Теорема 4.1. Пусть со1, ..., со" — формы, задающие на
многообразии М абсолютный параллелизм, регулярный в точке
pQM и имеющий в ней порядок г и ранг к. Пусть со1, . . ., со" —
формы, задающие абсолютный параллелизм на другом многообра-
зии М, и пусть р^М. Для того, чтобы существовал локальный
изоморфизм ср: М—>М, переводящий р в р, необходимо и доста-
точно, чтобы выполнялись следующие условия:
(i) абсолютный параллелизм на М имеет в точке р порядок г
и ранг к',
(ii) если х1, ..., хп — приспособленные координаты в точке р,
а х1, ..., xh — функции из с теми же индексами, что
их1, .. ., xh, то х1, . .., xh независимы, т. е. их можно допол-
нить до приспособленной системы координат на М в точке р,
причем хг (р) хг (р), i = l, ..., к;
(iii) если f — функция из & , a f — функция с теми же
индексами из ,!Гг+1 и если f может быть представлена в виде
функции от х1, ..., xh, скажем f = g(x1, ..., xh), то /— та же
самая функция от х1, .. ., ИР, т. е. f = g(x1, ..., xk).
§ 4. Структуры, конечного типа
367
Если ф— локальный изоморфизм и функции f и f£JFr+l
имеют одинаковые индексы, то
Joq> = f. (4.5).
Замечание. Если г = 0 и к = п, то теорема 4.1 является
просто другой формулировкой утверждения, приведенного на
стр. 363. Если г = 0 и к = 0, то теорема 4.1 сводится к теоре-
ме 2.4 гл. V. При доказательстве теоремы в общем случае мы более
или менее следуем доказательству теоремы 2.4 гл. V.
Условие, что ф — локальный изоморфизм, можно записать
в виде
Ф*(ог=юг, i=l, ..., п. (4.6)<
В частности, если ср — локальный изоморфизм, то
d(i>1 = ср* dtp1 = 2 (cjk ° ф) ф*®’ Л ф*®*1 = 2 Л ®й >
откуда
~г i
Cjk, о ф — ^jk*
Отсюда следует, что
d (Cjk о ф) = 2 (cljk, i ° ф) ф* (®г) = 2 с&, I ®г,
и, значит,
Cjfe, I ° Ф = Cjk, I-
Продолжая подобным образом, мы проверим свойство (4.5).
Поскольку ф — диффеоморфизм, из этого свойства вытекают усло-
вия i), ii) и iii) и тем самым необходимость условий теоремы
доказана.
Докажем теперь достаточность. Выберем приспособленные коор-
динаты х\ ..., хп в точке р и приспособленные координаты
х1, . . ., хп с теми же индексами в точке р. Согласно равенству
(4.5), для изоморфизма ф мы должны иметь х1 о <р = хг, i = 1, . .., к.
Вместо того чтобы искать само отображение ф, мы будем искать
его график, который является подмногообразием в М X М.
Многообразие М X М имеет проекции тс± и л2 на первый и вто-
рой сомножители. Положим
0г = л*(1? и 0‘ = л*юг.
Аналогично, определим в окрестности точки (р, р) функции
у1, у1, полагая
И уг=Х1 0^2.
368
Гл. VII. Геометрия G-структур
Очевидно, что формы 01, ..., 0n, б1, . .., 0П линейно независимы
на М X М, а функции у1, ..., уп, у1, ..., уп образуют систему
координат вокруг точки (р, р). Если ср — локальный изоморфизм,
то его график N [т. е, подмногообразие в М X М, состоящее из
всех пар (х, ср (я))] является n-мерным подмногообразием в М х М.
Если i: N —>М X М — вложение, то из (4.6) и (4.5) следует, что
0‘) = О, г = 1, ...,п, (4.7)
I* (у* — у*) = 0, i = l, ..., п. (4.8)
Обратно, пусть N есть re-мерное подмногообразие в М х М, про-
ходящее через точку (р, р) и удовлетворяющее условию (4.7). По-
скольку dim2V = n и формы б1, ..., 0”, 01— б1, ... ,0П — 0" линейно
независимы на М X М, формы i* (О1), ..., i* (0") линейно независимы
на N. Точно так же формы ^(О1), ..., i* (0П) линейно независимы
на N. Отсюда следует, что ограничения проекций Л] и л2 на N
невырожденны. Но тогда из равенства (4.7) вытекает, что ото-
бражение ср = (л21 N) ° (rrtj 12V)-1 удовлетворяет условию (4.6).
Уравнения у' — yl — Q (i= 1, ..., к) выделяют (2n.— /с)-мерное
подмногообразие К многообразия М X М. Мы покажем, что урав-
нения (4.7), ограниченные на К, определяют вполне интегрируе-
мую дифференциальную систему размерности п. Ее интегральное
многообразие, проходящее через (р, р), будет тогда графиком тре-
буемого отображения ср.
Разрешим уравнения
dx1 = 2 z’/o3, i = 1, . .., k,
j=i ’г
•относительно к форм а>3, выразив их через dx1 и через остальные
со3. Изменив, если понадобится, нумерацию форм со3, мы можем
написать
ю‘ = 2 ас dx3 + 2 b\xi3, i = 1, ..., к. (4.9)
з=1 3 }=k+i
Входящие в (4.9) функции а] и Ъ} являются рациональными функ-
циями от х1 и, следовательно, зависят только от х1, ..., xh.
В силу условий ii) и iii) точно так же мы можем выразить часть
форм со1 через dx1 и оставшиеся формы со3. Можно считать, что
при этом мы снова получим равенство (4.9), где над всеми сим-
волами поставлены черточки. Поднимая эти равенства на М X М,
§ 4. Структуры, конечного типа
369
имеем
01 - 0* = 2 (a} dy1 -а\ dy1) + § $03' -Ь$),
j=l j=h+l
где а), b)— функции от у1, yh, а а), Ъ)— те же самые функ-
ции от у1, .yh. В частности, на многообразии К первое выра-
жение в правой части обращается в нуль и Ъ} = Ъ}, так что на К
мы имеем
0* —0f = 2 fe}(0j-0j), i = l,
J=h+1
Таким образом, из форм О1—01 можно выбрать не более чем п— к
линейно независимых на К форм. G другой стороны, поскольку
все формы 9г — 01 линейно независимы на М X М и коразмерность
многообразия К равна к, по крайней мере п — к из этих форм
должны быть линейно независимы на К. Поэтому ограничение
на К уравнений (4.7) определяет дифференциальную систему раз-
мерности (2ге— к) — (п — к) = п.
Покажем, что эта система вполне интегрируема. Заметим, что
do’ = 2 Л и = 2 Л
Следовательно,
d (8‘ - о{)=2 л 0"+2 л
где с}к—функции от у1, ..., у\ a с}ь—те же самые функции от
у1, ..., гД В частности, на К мы имеем Cjk — Щл, откуда
d (0{ - ёг)=2 (О3' -О3') л 0fe+2 /\ (0fe—9ft),
что доказывает полную интегрируемость системы, а тем самым
и теорему 4.1.
Рассмотрим теперь локальные автоморфизмы абсолютного
параллелизма на М. Точку из М назовем вполне регулярной, если
параллелизм регулярен в этой точке и имеет одинаковый порядок
(а также ранг) во всех близких к ней точках. Из теоремы 4.1
немедленно вытекает
Следствие 4.1. Пусть р — вполне регулярная точка из М
ранга к, и пусть х\ . . . , хп — приспособленные координаты
в точке р. Тогда любую точку из некоторой окрестности точки р,
лежащую на подмногообразии х1 = const, . . . , xh = const, можно
перевести в любую другую такую точку с помощью локального
автомо р физма.
Vi 24 с. Стернберг
370
Гл. VII. Геометрия G-структур
До сих пор все наши рассмотрения были чисто локальными.
Перейдем теперь к изучению группы всех автоморфизмов мно-
гообразия М с абсолютным параллелизмом. Легко сообразить,
что структура этой группы сильно зависит от глобальных свойств
многообразия М. [Например, выбрасывание одной точки из М
может повлечь за собой значительное уменьшение группы. Поэто-
му полнота многообразия М (скажем, относительно метрики
(ю1)2 4- . . . + (юп)2) играет важную роль.]
Пусть М — многообразие с абсолютным параллелизмом, a G —
его группа автоморфизмов.
Предположим для простоты, что М связно (хотя это на самом
деле несущественно). Тогда формы ю1, . . . , юп определяют на мно-
гообразии М риманову метрику, превращая его тем самым в мет-
рическое пространство. Это в свою очередь определяет в группе G
топологию: любому е > 0 и любому компакту К с М соответ-
ствует окрестность точки а £ G, состоящая из всех таких b Q G,
что d (ах, Ьх) < е для всех х £ К, где d — функция расстоя-
ния на М.
Теорема 4.2 (Кобаяси). Пусть М — связное многообразие
с абсолютным параллелизмом и G — группа его автоморфизмов.
Для любой точки р С М отображение <рр: G —> М, задаваемое
формулой
Фв (а) = а (р)
для всех a^G, взаимно однозначно и взаимно непрерывно. Множество
Фр (G) является замкнутым подмногообразием в М, и дифференци-
руемая структура, индуцированная на G отображением фр, пре-
вращает G в группу Ли. Короче, группа автоморфизмов абсолют-
ного параллелизма есть группа Ли.
Применяя теорему 3.2, мы немедленно получаем
Следствие 4.2. Группа автоморфизмов Н-структуры
конечного типа есть группа Ли.
Для римановой структуры этот результат был впервые доказан
Майерсом и Стинродом.
Для доказательства теоремы 4.2 введем некоторые обозначе-
ния. Абсолютный параллелизм позволяет отождествить V с каса-
тельным пространством в любой точке многообразия М. Таким
образом, вектор v £ V определяет векторное поле на М, которое
мы будем обозначать и. Векторное поле и задает в свою очередь
локальную однопараметрическую группу, которую мы обозна-
чим ехр tv. Отображение ехр tv определено в точке р £ М при
достаточно малых t. Или, что то же самое, локальный диффеомор-
J 4. Структуры конечного типа
371
физм ехр v (=ехр l-i?) определен в точке р £ М для всех v g V
из некоторой окрестности нуля. Отображение р (ехр и) (р)
есть диффеоморфизм окрестности нуля в V на окрестность
точки р в М.
Если а £ G, то а*и = и для всех и £ V. Поэтому, как только
определен локальный диффеоморфизм ехр и, мы можем написать
а ° ехр и = (ехр и) ° а. (4.10)
Лемма 4.3. Группа G действует на М без неподвижных
точек. Другими словами, если а (р) = р для некоторого а £ G
и некоторой точки р g М, то а = id.
Действительно, множество неподвижных точек преобразова-
ния а замкнуто. С другой стороны, из формулы (4.10) следует, что
оно открыто. Поскольку многообразие М связно, это означает, что
множество неподвижных точек либо пусто, либо совпадает с М.
Лемма 4.4. Пусть ak — последовательность элементов из G,
причем для некоторой точки р g М последовательность ак (р)
сходится к а (р), где а £ G. Тогда ah->- а во введенной нами топо-
логии группы G.
Снова воспользуемся связностью. Множество точек q, для
которых последовательность ak (q) сходится к a (q), замкнуто:
если qr q и ar (gfe) ->• a (qk), то выбирая сначала к так, чтобы
d (qh, q) < 8, а затем г так, чтобы
d (ar (qk), а (дй)) < е,
мы получим
d (аТ (q), а (д)) < d (ar (qh), аТ (q)) + d (a (qk), a (g)) +
+ d (ar (gh), a (qh)) < 3s.
С другой стороны, из (4.10) следует, что это множество открыто.
Значит, ak (р) а (р) для всех р £ М. Пусть теперь К — ком-
пактное подмножество в М. Выберем в К всюду плотную после-
довательность точек {р/t}. Для любого е > 0 возьмем столь боль-
шое к, чтобы каждая точка из К находилась от одной из точек
Pt (i fc) на расстоянии не больше е. Для достаточно большого г
имеем d (ar (pt), a (pt)) < 8 при всех i <1 к. Тогда d (аг (р), а (р)) <
< 3s для всех р £ К‘, значит, аТ —> а в топологии группы G.
Лемма 4.5. Пусть {ак} — последовательность элементов
из G, причем ah (р) q для некоторых точек р и q £ М. Тогда
существует такой элемент а £ G, что а (р) = q.
Мы хотим построить автоморфизм а, переводящий р в q. Для
этого определим сначала диффеоморфизм а в окрестности U точ-
24*
372
Гл. VII. Геометрия G-структур
ки р, полагая а ((ехр и) (/?)) = ехр v (q). Во всех точках из U
отображение а является поточечным пределом отображений at.
Если мы продолжим отображение а подобным же образом вдоль
любых кривых, то вновь полученное отображение по-прежнему
будет являться поточечным пределом отображений аг и, следова-
тельно, не будет зависеть от выбора кривых. Таким образом, бла-
годаря связности многообразия М, мы получим требуемый авто-
морфизм а.
Итак, мы доказали, что отображение фр: G -> М взаимно одно-
значно и взаимно непрерывно и что образ группы G замкнут.
Покажем теперь, что срр (G) есть подмногообразие в М. Для этого
построим сначала касательное пространство к этому подмногооб-
разию.
Мы скажем, что последовательность ah е элементов из G
тангенциально сходится к единице в точке р, если сходится после-
довательность
(afe(p)) —дЧр)
13 (x’(aft(p))~^(Р))2]1/2 ’
где ж1, . . . , хп — некоторая (а значит, и любая) система коор-
динат. В таком случае эта последовательность определяет каса-
тельный вектор в точке р. Рассуждая так же, как в § 4 гл. V,
мы заключаем, что множество таких векторов образует вполне
интегрируемую дифференциальную систему ££' на М.
Пусть N — максимальное интегральное многообразие этой
дифференциальной системы, проходящее через р. Покажем, что
N cz фр (G). Достаточно проверить, что фр (G) ["|2V есть открытое
множество в N. В силу замкнутости множества фр (G) отсюда
будет следовать, что N с фр (G).
Пусть Xq — касательный вектор в точке q, принадлежащий 3.
Тогда, согласно формуле (4.10), последовательность {afe}, опре-
деляющая вектор определяет также вектор (ехр i>)* Xq в точке
ехр v (q) при любом малом и £ V. Таким образом, мы получаем
(локально определенное) векторное поле X, такое, что
X ехр е (д) = (ехр ^)* X д. (4.11)
Ясно, что множество таких векторных полей порождает систему
3) в окрестности точки q. Если точка q лежит на N, то любая близ-
кая к ней точка из N имеет вид ехр X (q) г). Мы сейчас покажем,
что все такие точки представимы в виде b (д), где b Е G. Тогда
для q Е ФР (G) П X, т. е. для q — а (р), мы получим, что все
х) То есть лежит на проходящей через q траектории подходящего вектор-
ного поля X. Это ехр не надо путать с отображением V -> М, переводящим
v в ехр v (д).
§ 4. Структуры конечного типа
373
точки, близкие к q, имеют вид Ьа (р). Тем самым будет доказано,
что множество фр (G) П N открыто в N. Итак, пусть вектор
Pi g V таков, что vlq = Xq. Дополним его до базиса vlt . . . , vn
пространства V. Тогда отображение и -> ехр v (g) задает в окрест-
ности точки q систему координата;1, . . я"; точка ехр (л;1^ Ц- . . .
. . . + xnvn) q имеет координаты х1, . . ., хп. Координаты самой
точки q равны (0, . . . , 0). Вычислим координаты точки ехр X (д).
Имеем
Xexptvi(q) — (ехр Xq —
= (ехр tvi)* viq =
= Vlexp(ii>i) (g) •
Другими словами, векторные поля X и совпадают вдоль кри-
вой expin^g). Следовательно,
ехр X (д) = ехр (д)
и координаты точки ехр X (д) равны (1, 0, ..., 0). Пусть теперь
{afe} — такая последовательность элементов из G, что ak —> е и
& (ak (g))_____
[ 2^^ И2]1/2 1
(4.12)
8
при достаточно большом к. Такая последовательность существует,
поскольку координаты точки g равны (0, ..., 0), а координаты
вектора Xq равны (1, 0, ..., 0).
Выражение 2 (а& (?))2 стремится к нулю. Поэтому, как
следует из (4.12), при достаточно большом к можно найти такое
целое число N, что
\Nxi(ah(p))~ 6j|<8. (4.13)
Пользуясь равенством (4.10), находим, что если (ехр и) q = aq, то
(ехр 2v) q = (ехр v)2 q = (ехр v) aq = а (ехр к) g = a2q,
или, более общо, (ехрЛТ)\q = aNq. Из определения координат
х1, ..., хп следует, что TVz1 (щ (д)) есть координаты точки а^(д).
Таким образом, неравенство (4.13) можно переписать в виде
I(ak («)) — xi (ехР х (?)) I < е-
Другими словами, мы можем найти элементы из G, переводящие
точку g сколь угодно близко к точке ехр X (д). Согласно лемме
4.5, отсюда следует существование такого a£G, для которого
а(д) = ехр Х(д).
Тем самым доказано, что N с: фр(С). Пусть Go — связная ком-
понента единицы группы G. Покажем, что N = <p?(G0). Поскольку
1/2 24 С. Стернберг.
374
Гл. VII. Геометрия G-структур
N cz<fP(G), достаточно проверить, что cp?(G) не может содержать
никаких других интегральных многообразий системы 3). [Этого
достаточно, поскольку вместе с любой точкой множество срр (G)
содержит и максимальное интегральное многообразие системы 3),
проходящее через эту точку; это доказывается так же, как и вклю-
чение 2V с (рр (G). ] Предположим, что <рр (G) содержит другое
интегральное многообразие. В силу связности мы можем тогда
найти точку qQN, являющуюся пределом последовательности
----------.----------N
Ч
Рис. 33.
точек Е <Рг> (Go), не лежащих в N. Заменяя каждую точку gk точ-
кой qh из того же максимального интегрального многообразия,
что и qk, мы можем добиться того, чтобы новая последователь-
ность qh сходилась к точке q в направлении, не касательном к N
(рис. 33). С другой стороны, мы можем написать (fa = «&(?), где
ak £ Go. Но по самому определению системы 3 мы можем выбрать
подпоследовательность из {щ}, которая сходится в касательном
к N направлении. Полученное противоречие показывает, что
2V = (pp(G0). Это в свою очередь означает, что <рр (G) есть под-
многообразие из М. Остальные утверждения теоремы Кобаяси
проверяются непосредственно.
§ 5. СВЯЗНОСТИ НА G-СТРУКТУРАХ
В этом параграфе мы будем изучать геометрию связностей
на G-структурах. С одной стороны, поскольку G-структура есть
главное расслоение, эту теорию можно рассматривать как част-
ный случай теории связностей на главных расслоениях, развитую
в § 1. С другой стороны, как было указано в § 3, связность на
G-структуре над многообразием М представляет собой специаль-
ный вид структуры «второго порядка» на М. Взаимосвязь этих
двух теорий обусловливает интересные геометрические свойства
связности на G-структуре. Связность на GL (п)-структуре jr (М)
называется линейной связностью на М. Допуская вольность речи,
мы будем называть связность на G-структуре над многообразием
§ 5. Связности на G-структурах
375
М G-связностью на М. Таким образом, задание G-связности на М
включает в себя задание двух объектов: конкретной G-структуры
Во на М и связности на BG. Если Gi с G2, то процедура расши-
рения группы (см. § 1) позволяет перейти от Gi-связности к С2-связ-
ности. В частности, любая G-связность определяет некоторую
линейную связность.
Всякая G-связность определяет параллельный перенос слоев
расслоения BG вдоль кривых базы М. Она также позволяет опре-
делить понятие параллельного переноса в любом ассоциированном
с BG расслоении. В частности, мы имеем параллельный перенос
в Т (М): если С: [0, 1] М — кривая на М и Хо 6 ^с(О) (М),
то однозначно определяются векторы Xt Е Тещ (М) для всех
t Е Ю, И- Отображение Хо -> Xt линейно и переводит реперы
из BG в реперы из BG. Поэтому все «дополнительные структуры»,
которые определяются в касательном пространстве с помощью
группы G, сохраняются при параллельных переносах. Например,
если G = О (ге), так что М — риманово многообразие, то
(Xt, Y t) = (Хо, У о) при всех t.
Понятие параллельного переноса касательных векторов позво-
ляет определить ковариантную производную векторного поля
вдоль кривой. Пусть С: [а, Ь] М — дифференцируемая кривая
на М, и пусть {Уt Е (М)} — семейство касательных векто-
ров вдоль этой кривой. Параллельно перенося векторы Уг в точку
С (0) вдоль кривой С, мы получим семейство касательных векто-
ров Yt Е Т’с(О)- Можно рассмотреть предел
=Ит2±-^<о>
dt ]i=o t
(5-1)
который существует, если семейство Yt дифференцируемо (как
кривая в Т (М)).
Если X и У — векторные поля на М, то мы можем ввести
ковариантную производную поля У относительно поля X. Она
обозначается символом УХУ и определяется следующим образом.
Пусть х Е М и С — интегральная кривая поля X, проходящая
через х. Положим Уг = Ущр. Тогда
(VxD.=^|M. (5.2)
Найдем другие выражения для У^У. Заметим прежде всего, что
существует взаимно однозначное соответствие X *-> fx между век-
торными полями X на М и 7-значными функциями / на
удовлетворяющими условию /(p-a) = a~1f (р), где a^GL(n). Ясно,
что такая функция / определяет векторное поле. Обратно, пусть
X — векторное поле на М и X — соответствующее ему горизон-
24*
376
Гл. VII. Геометрия G-структур
тальное векторное поле на BG (определяемое с помощью связности).
Тогда fx = (X, со) — требуемая функция на BG.
Пусть X и Y — векторные поля на М, и пусть p£BG, причем
л (/>)=£. Тогда
(^У)ж = р-(Х/у)(р). (5.3)
[В этой формуле Xfy есть У-значная функция на BG, так что
XfY(p)^V и, следовательно, р (XfY (р)) G Тх (Л/).] Чтобы прове-
рить формулу (5.3), рассмотрим интегральную кривую С поля X,
проходящую через х. Пусть С — горизонтальная кривая, проходя-
щая через р и лежащая над С. Тогда, используя определение
связности на ассоциированном расслоении (см. конец § 1) и фор-
мулы (5.1) и (5.2), находим
(?ХУ)Ж = lim [С (0) С (Z)-1 Yt - Уо] =
/-+0 1
= С (0) lim -I [С Yt — C (О)’1 Уо] =
1
= С (0) lim 1- [/r (С (0) - /у (С (0))] =
/->0 1
= pXpfY(p),
поскольку С (0) = р и Хр — касательный вектор кривой С в точке р.
Это доказывает формулу (5.3).
Далее, отображение X—>Х линейно и gX = (n*g)X. Отобра-
жение У —> /у также линейно и удовлетворяет условию /gy =
= n*(g)/r. Эти замечания вместе с формулой (5.3) показывают, что
?х1+х2У = V^y + Хх2У, (5.4)
Vgxy = gVxy, (5.5)
W (Ус + Уг) = ^хУ1 +УгУг, (5-6)
Vxgy = gV^y + (Xg)y. (5.7)
Дадим теперь выражение для ковариантной производной в терми-
нах локальных координат. Пусть х1, ..., хп — система координат
в окрестности U на многообразии М. Тогда мы можем написать
(5.8)
k
где — подходящие функции на U. Пользуясь формулами (5.4) —
(5.7), мы можем с помощью вычислить ковариантную произ-
водную любого векторного поля относительно любого другого
J 5. Связности на G-структурах
377
векторного поля в U. Пусть у1, уп — другая система коорди-
нат с функциями Гу, определенная в окрестности V. Тогда
в пересечении U Q V имеем
п
д ст 8х1 д
dyi dy* дх1
Подставляя эту формулу в равенство
получаем
d^xl dyh
dyi-dyi 8x1
п
ст pt дхг dxs dyk
r &У^ du? &xt
(5-9)
Предположим теперь, что в каждой карте некоторого атласа
многообразия М заданы функции Гу, причем в пересечении двух
карт эти функции связаны соотношением (5.9). Легко проверить,
что это позволяет определить ковариантную производную VХУ
для любых векторных полей X и У. Действительно, локально,
пользуясь формулами (5.4) — (5.8), мы можем вычислить \ХУ
в любой карте. Соотношение (5.9) гарантирует, что полученные
выражения согласованы на пересечении карт и, значит, не зависят
от локальных координат. Покажем теперь, что такие функции Гу
действительно определяют на М линейную связность. Для этого
напомним, как в jr (М) были введены локальные координаты.
Если х1, ..., хп — система координат в окрестности UtzzM, то
точка pGjF"(M), для которой л (р) = л: £ С7, представляет собой
репер (Х^ ..., Хп), где
п
причем матрица (Х{) невырожденна. Пусть (У))— обратная мат-
рица, так что (Xi) и (У)) — матричнозначные функции на л'1 (U).
Легко проверить, что
ю1 = ]ГУ)л* dx1 (5.10)
на л 1 (U) [где а> = (а>1, ..., со”) — фундаментальная У-значная
форма на (М).\ Положим
S Г^лМа?) . (5.11)
j=i v k, i=i '
378
Гл. VII. Геометрия G-структур
Читатель может в качестве упражнения проверить, что формы Qi
не зависят от локальной системы координат и определены глобаль-
но. Пусть и1, ..., ип— базис пространства V и преобразования
A}^gl(V) заданы формулами A}vh = 6lkv>. Тогда, как легко про-
верить, форма
Q=SQUj
определяет на & (М) связность и функции Г^- этой связности
совпадают с исходными. Итак, доказана
Теорема 5.1. Пусть М — многообразие класса С°° (или
аналитическое). Тогда следующие объекты на М эквивалентны:
(i) линейная связность на М;
(ii) отображение (X, Y) —> VxE любой пары (X, Y) векторных
полей класса С°° (аналитических) на М, удовлетворяющее условиям
(5.4) -(5.7);
(iii) набор функций Г*3- для каждой карты некоторого атласа
многообразия М, преобразующихся по правилу (5.9).
До сих пор мы рассматривали Т (М) как ассоциированное
с BG расслоение и изучали параллельный перенос в Т (М), опре-
деляемый G-связностью. Поскольку любое тензорное расслоение
также является ассоциированным расслоением, мы можем опре-
делить в нем параллельный перенос. Далее, мы можем рассмот-
реть ковариантную производную тензорного поля вдоль кривой
или относительно векторного поля. Таким образом, Vx стано-
вится линейным оператором, отображающим пространство тен-
зорных полей данного типа в себя. Соответствующее обобщение
условия (5.7) состоит в том, что Vx является дифференцированием
алгебры всех тензорных полей. Важным сопутствующим поня-
тием является понятие ковариантного дифференциала тензорного
поля. Пусть t — тензорное поле контравариантной степени г
и ковариантной степени s (для краткости, типа (г, $)). Тогда для
любого векторного поля X тензорное поле также имеет тип
(г, $). Таким образом, мы имеем правило, сопоставляющее каж-
дому векторному полю X тензорное поле типа (г, s), т. е. имеем
тензорное поле типа (г, s + 1). Обозначим это тензорное поле
символом Vi. В дальнейшем мы несколько раз встретимся со слу-
чаем, когда t имеет контравариантную степень 1. Пусть t — тен-
зорное поле типа (1, s). Если Х4, . . . , Xs — векторные поля, то
t (Xi, . . . , Xs) — также векторное поле. Тензорное поле V/
типа (1, s + 1) определяется тогда формулой
(Vi) (Х„ .. ., Xs, X) = Vx (t (Xi, ..., Xs))-
8
-3 t(Xi, . . ., VxXi, ..., X,). (5.12)
§ 5. Связности на G-структурах
379
Связность на BG индуцирует на Bq абсолютный параллелизм —
отождествление касательного пространства произвольной точки
из BG с V + g. Действительно, из определения G-структуры сле-
дует, что можно отождествить касательные пространства к слою
с g, а выбор горизонтального подпространства Н в каждой точке
позволяет отождествить Н с V. Поэтому любой элемент А из g
и любой вектор v £ V определяют векторное поле на BG. В § 1
мы условились обозначать векторное поле, соответствующее А £ g,
символом А. В соответствии с этим (и в некотором противоречии
с обозначениями § 4) мы будем обозначать символом и векторное
поле, соответствующее вектору v £ V. По определению
(А, со> = О, (£,Q)=A, (5.13)
(v, со) = р, (и, Q) = 0, (5.14)
где ю — фундаментальная V-значная форма на BG, a Q—(g-знач-
ная) форма связности. Вычислим теперь скобки Ли различных
полей вида А и и. Если APg и B£g, то мы имеем
[I, В] = 1а7в].
Проверим, что
[А, и] = —A-v, (5.15)
если AQg и v£V. Рассмотрим для этого однопараметрическую
подгруппу at группы G, порожденную А. Если p£BG, то =
= (а71п)агр в соответствии с формулой (2.3). Дифференцируя это
равенство, получим (5.15). Осталось вычислить [Pj, v2] для
tyQV- Для этого дадим следующее
Определение5.1. Форма Da называется кручением связности.
Напомним, что, согласно определению ковариантного дифферен-
циала D, данного в § 1,
(X /\ Y j Da) = (hX /\hY\da)
для любых векторных полей X, Y на BG. В соответствии с фор-
мулой (2.3) имеем
В^ (Da) = a~Wa. (5.16)
По аналогии с равенством (1.6) можно написать
da =—ЙДсо + Ав. (5-17)
Проверка равенства (5.17) выполняется точно так же, как и ра-
венства (1.6): используется уравнение (1.10) гл. III, написанное для
380
Гл. VII. Геометрия G-структур
подходящих векторных полей Аир. Детали доказательства
мы оставим читателю в качестве упражнения. Применяя теперь
равенство (5.17) к pt Д р2, получим
(г?! Д р21 Da) = (pt Д р21 d®) =
= г?1(р2, ®> — p2(pi, ©) —([pb p2], <o>,
или, поскольку (P2, <0) = P2 = const И (Рь co) = Pi = const,
<[Pi, p2], co) = (Pl Л p21 Ao).
Итак, горизонтальная компонента поля [рь р2] равна (Pj Д р2, Ао).
Аналогично
([Pi, р2] |й>= — (pi д р2|/)й).
Таким образом, мы можем написать
[»1, и2] = (щ/\v2\D(n') + (vl/\v2 \ DQ.). (5.18)
Соберем вместе полученные формулы:
[А, В\ = [А? В], [А, р] = — А-р, (5.15)
[Vi, v2] = (Pi/\р2\Da)+ (щ/\p2\DQ). (5.18)
Введенные выше кручение и кривизна являются дифференци-
альными формами на BG. Их также можно рассматривать как
тензорные поля на М. Чтобы убедиться в этом, установим соот-
ветствие между определенным классом форм на BG и тензорными
полями на М. Мы уже установили соответствие между опреде-
ленными У-значными функциями на BG и векторными полями
на М. Назовем дифференциальную форму 0 на BG горизонталь-
ной, если (Xi А ... A Xk | 0) = 0, как только один из векторов
Xt вертикален.
Предложение 5.1. Существует взаимно однозначное соот-
ветствие между тензорными полями t типа (1, s) на М, анти-
симметричными по ковариантным аргументам, и множеством
горизонтальных V-значных s-форм 0 на BG, удовлетворяющих
условию 7?*0 = а-10. Если л(р)-—х и Х1; ..., Х5£ТР(ВС), то это
соответствие устанавливается формулой
(А,), ..., T4(Xs)) = p(XiA ... ДХ8|0).
Доказательство этого предложения очевидно и будет оставле-
но читателю в качестве упражнения. В частности, форме круче-
ния Da соответствует тензорное поле Т типа (1, 2) на М. Оно
§ 5. Связности на G-структурах
381
называется полем тензора кручения и сопоставляет векторное
поле Т (X, Y) любой паре X, Y векторных полей на М; при этом
Т (X, У) = - Т (У, X).
Рассмотрим тензорное поле t типа (1, s) на М. Если свернуть
его по последним s — 1 индексам с векторными полями Х1т . . .
. . . , Xs_i, то получится тензорное поле t (Х1; . . . , Xs _j) типа
(1, 1) на М. Но тензорное поле типа (1, 1) определяет в каждом
касательном пространстве Тх (М) линейное преобразование. Зада-
нием G-структуры BG группа G отождествляется с группой линей-
ных преобразований каждого касательного пространства Тх (М),
а ее алгебра Ли — с алгеброй Ли линейных преобразований
пространства Тх (М) при каждом х £ М. Мы будем говорить, что
тензорное поле типа (1, 1) g-значно, если определяемое им линей-
ное преобразование пространства Тх (М) принадлежит g при
любом х Е М. Мы скажем, что тензорное поле t типа (1, s) g-знач-
но, если t (Xt, . . . , Xs _j) есть g-значное тензорное поле типа
(1, 1) для любых векторных полей Xt, . . ., Xs _t на М. По ана-
логии с предложением 5.1 можно сформулировать
Предложение 5.2. Существует взаимно однозначное
соответствие между g-значными тензорными полями t типа (1, $)
на М, антисимметричными по последним s — 1 индексам,
и g-значными (s — ^-формами 0 на BG, для которых
7?*0 = ad(a-1) 0.
Если л(р)=х и Х^ . . ., Xs_i£TP(BG), то это соответствие
устанавливается формулой
tx (л, (Xj), ..., л, (Х^)) Z = р ((Xi Д ... Д Xs_t | 0) (pZ)),
где Z — произвольный вектор из ТХ(М).
[Тензор tx однозначно определяется заданием линейных пре-
образований tx (У1, . . . , У8-1) для всех Yi, . . . , У8-1 Е Тх (М).
В свою очередь линейное преобразование однозначно определяется
своими значениями на всех векторах Z Е Тх (М).]
Доказательство этого предложения мы также оставляем чита-
телю в качестве упражнения. В частности, форме DQ. соответ-
ствует некоторое тензорное поле В типа (1, 3) на М, которое
называется полем тензора кривизны. Оно сопоставляет каждой
паре векторных полей X и У на М тензорное поле В (X, У), при-
надлежащее в каждой точке алгебре Ли g. Кроме того,
382
Гл. VII. Геометрия G-структур
Можно дать простое выражение тензоров кривизны и кручения
в терминах оператора V:
Т(Х, Y) = VxY-VyX-[X, У], (5.19)
R (X, У) = [Vy, Vy] - Vtx, У]. (5.20)
В формуле (5.20) выражение [Vy, Vy] означает коммутатор опе-
раторов Vy и Vy в пространстве всех векторных полей. Таким
образом, применяя В (X, У) к векторному полю Z, имеем
В (X, У) Z = Vy (VyZ) - Vy (VyZ) - Vtx, yjZ.
Проверим формулу (5.19). Согласно предложению 5.1,
Г(Х, Y)x = p((X /\Y\Dai)p) =
= р((Х ДУ|йсо)р) =
= р (Хр (У, со) — Yp (X, со) — {[X, У]р, со)).
Но л* [X, У] = [X, У], так что мы можем заменить [X, У]
на [X, У] в последнем члене справа. В соответствии с форму-
лой (5.3), если л.(р) = х, то
(Vyy)x = Р • (Хр/у) = р. (Хр (У, со)).
Воспользовавшись такой же формулой для VyX, мы дока-
жем (5.19).
Проверим теперь формулу (5.20). Пусть Z — векторное поле
на М и / = <Z, со) — соответствующая функция на Bq. Тогда,
если л (р) = х, то мы имеем
([Vy, Vy] Z - V[X, Y]Z)X = P • (Хр (У/) - Yp (Xf) — h([X,Y])p)f.
Ho Xp(Yf) — Yp(Xf) = [X, У]р/, так что выражение в круглых
скобках равно ([X, У]—h([X, У]))/, т. е. вертикальной состав-
ляющей поля [X, У], примененной к функции /. Но
<Х Д У|РЙ) = Х(У, Й)-У(Х, Й)-([Х, У], й) =
= — <[Х, У], й),
так что вертикальная составляющая вектора [X, У]р равна .4,
где А=—(ХДУ|£)Й). С другой стороны, поскольку
мы можем написать Af = —Af. Таким образом, получаем формулу
[Vy, Vy] z - Vex, у/ = P «X Л УI РЙ) f (p)) = p «X Д У I РЙ) p^Z),
поскольку f(p)=p~rZ. Применяя теперь предложение 5.2,
мы получим формулу (5.20).
§ 5. Связности на G-структурах
383
Как показывает формула (5.20), кривизна измеряет, насколько
отображение X—отличается от гомоморфизма алгебр Ли.
Упражнение 5.1. Используя формулу (5.19), показать, что если
в локальных координатах Т (д/дх^, д/дх1)='^Т^(д^дхк), то
mh. _рА _рА
1 ij 1 ij 1 ji*
У пражнение 5.2. Используя формулу (5.20), показать, что если
д(т7'Тг)^ = 2я»7Г’
х дхЭ dxk i дх* дхг
то
drlj дГ% -г-,
-~dr+2 ед-ВД-о-
oxi dxR
r=l
Выведем теперь несколько классических тождеств, содержащих
тензоры кривизны и кручения и их ковариантные производные.
Для любой функции t трех переменных обозначим через gi ее
циклическую сумму. Так, если t — тензор типа (1, 3), то
gt(X, У, Z) = t(X, У, Z) + «(y, Z, X) + f(Z, X, У).
Поскольку Vz есть дифференцирование тензорной алгебры, мы можем
написать
(VZT)(X, y) = Vz71(X, y)-7,(VzX, У) — Т(Х, VZY). (5.21)
Используя (5.19) и антисимметричность тензора 71, находим
Т(Т(Х, Y), Z} = T(VXY, Z) + T(Z, ^уХ^ — Т ([X, У], Z).
Суммируя циклически и используя (5.21), получаем
&Г(Т(Х, У), Z) = &{-(yzT)(X, Y)-\-\/zT (X, Y)-T([X, У], Z)}.
Далее,
(©^(Х, Y) — T([X, У], Z)) = (S(VzVxy-VzVyX-Vz[X, У] —
-Vtx, y]Z + vz [X, У]+[[Х, У], Z] = (g (VxVyZ- VyVyZ - V[X, y]Z),
поскольку g [[X, У], Z] = 0 (тождество Якоби). Используя равен-
ство (5.20), находим
@(Д(Х, У) Z) = g {Т (Т (X, У), Z) + (yxT)(Y, Z)}. (5.22)
В частности, если Т = 0, то
g (7? (X, У) Z) = 0. (5.23)
Аналогичным образом можно получить тождество Бьянки:
g{(Vz7?)(X, y)} + g{7?(7’(X, У), Z)} = 0. (5.24)
25*
384
Гл. VII. Геометрия G-структур
Доказательство мы оставляем читателю в качестве упражнения.
В частности, если Т = 0, то
@{(VZ7?)(X, У)} = 0. (5.25)
§ 6. ПУЛЬВЕРИЗАЦИЯ ЛИНЕЙНОЙ СВЯЗНОСТИ
Заметим прежде всего, что линейная связность на многообра-
зии М определяет пульверизацию на М: в каждой точке z £ Т (М)
существует единственный горизонтальный вектор Wz, для кото-
рого л* (Wz) = z. Таким образом, мы имеем на Т (М) векторное
поле W, соответствующее дифференциальному уравнению второго
порядка на М. Чтобы убедиться в том, что это пульверизация,
мы должны проверить равенство (6.2) гл. IV. Это можно сделать
непосредственно. Однако мы получим его как следствие одного
замечания, имеющего первостепенное значение для дальнейшего.
Вместо того чтобы рассматривать касательное расслоение, удобно
ограничиться рассмотрением расслоения ТЦМ) всех ненулевых
касательных векторов. Каждый ненулевой вектор v £ V индуци-
рует отображение срс: (М) —>- 7’+(7И), задаваемое формулой
4>v(p) = p(u). (6.1)
Зафиксируем вектор и раз и навсегда и обозначим отображение <pD
через ср. Тогда
Ф* (vp)= ^<р(р) • (6-2)
Действительно, вектор ср*(пр) горизонтален и
л*Ф*Ы = п*(1;р) = 7’(1;)-
Другими словами, векторные поля v и W ср-связаны. Пусть
Rt— правое умножение реперов из в? (М) на скалярное линейное
преобразование tl, т. е. Rt = Rti. Тогда
<p°Rt(v)=p(tv) = iit (p(v)),
где ц* — умножение на t в Т+(М) (см. начало § 6 гл. IV). Согласно
формуле (2.3),
R*v = — п.
Пользуясь соотношением (6.2), находим, что векторные поля
1 -
и — и ср-связаны и, значит,
Таким образом, векторное поле W является пульверизацией.
J 6. Пульверизация линейной связности
385
Итак, мы можем перенести все результаты гл. IV относительно
пульверизаций на случай линейной связности. В частности, мы
можем определить экспоненциальное отображение, нормальные
геодезические координаты и т. п. Из определения пульверизации
W следует, что кривая С в М является геодезической тогда и только
тогда, когда ее касательные векторы параллельны вдоль С.
Естественно ожидать, что кривизна и кручение дают некото-
рую информацию о пульверизации. И действительно, как мы сей-
час увидим, они позволяют написать уравнение в вариациях
для W, см. § 5 гл. IV. Исходной точкой является тот факт, что
уравнения (5.15) и (5.16) определяют уравнения в вариациях
поля v на ер (М). Используя равенство (6.2), мы получим отсюда
уравнения в вариациях для W. Сделаем сначала несколько пред-
варительных замечаний.
Пусть at — (локальный) поток, порожденный полем W на Т (М).
Зафиксируем геодезическую С на М. Мы хотим изучить действие
потока at*: Т’сцо) (Т (ЛГ)) —»7'с'(«) (Т (М)) над кривой С. Для этого
мы должны выбрать параметризацию векторных пространств
Тею (Т (М)). Это можно сделать с помощью параллельного пере-
носа, определяемого связностью. Действительно, в пространстве
Tc'(f) (Т (М)) выделены два n-мерных подпространства — вертикаль-
ное подпространство, касательное к слою, и горизонтальное под-
пространство, определяемое связностью. Проекция л* позволяет
нам отождествить горизонтальное подпространство с Гец) (Af).
Это пространство в свою очередь может быть отождествлено
с ^С(0)(ЛГ) с помощью параллельного переноса вдоль С. Верти-
кальное подпространство служит касательным пространством
к Тс<Г)(М) в точке С' (t) £ Тсы) (-!/)• Стандартный изоморфизм
касательного пространства к векторному пространству на само
это векторное пространство и изоморфизм Тсы) (М) на 7с(0) (М)
позволяют отождествить Т’сцц (Г (М)) с пространством Тс (0>ОЮ),
которое в свою очередь отождествляется с Тщо) (^И) + Тс(оу
Итак, мы можем отождествить ограничение расслоения Т (Т (М))
на кривую С' с (Т’що) (М) + Гс(0) (Л/)) X R. Пусть задана кривая Xt,
состоящая из касательных векторов многообразия М вдоль кри-
вой С. Тогда в пространстве Усцо) (^ (ЛГ)) мы получаем кривую
(Xt, DXt/dt). [Обратившись к § 5 гл. IV, читатель обнаружит,
что для установления связи между уравнениями Якоби и Эйлера
не хватало именно этого отождествления1).]
Точка ро g в? (М), для которой л (р0) = С (Q), определяет отожде-
ствление пространства Тс{0)(М) с V. Следовательно, ограничение
расслоения Т (Т (М)) на С'(t) отождествляется с V X V X R.
Читатель, вероятно, смущен обилием всевозможных отождествле-
*) См. примечание 1 на стр. 209.— Прим, перев.
386
Гл. VII. Геометрия G-структур
ний. Поэтому мы сформулируем их снова в том виде, в котором
будем использовать. Вектор Тсц/) (Т (Af)) соответствует вектору
(a, b; t) £ V X V ХН. Здесь а — вектор из V, полученный парал-
лельным переносом вектора обратно вдоль кривой С (t)
до точки С (0) и отображением Тс(о)(М) на V, определяемым
точкой р0. Если pt — горизонтальная кривая в ^"(Af), лежащая
над С (t) и проходящая через точку р0, то
а = р^ (лД).
Вектор b получается взятием вертикальной составляющей vert £
вектора отождествлением ее с вектором из с помощью
lc(t) (при помощи стандартного изоморфизма касательного про-
странства к векторному пространству на само это векторное про-
странство) и, наконец, применением отображения рТ1:
Итак,
Ъ = pll°lcm (vert g).
Рассмотрим теперь отображение
Ф*: TVt^(M))-^Tc-w(Tm.
Учитывая определение векторных полей а и А, а также наши
отождествления, имеем
ф*(аР(0) = (а> °; 0, (6-3)
Ф*(Л(<)) = (°, Av’ 0- (6-4)
Мы можем теперь применить формулы (5.15) и (5.18) для
вычисления уравнения в вариациях. Полагая (а/, bt; t) = (а0, Ьо; 0),
находим
= Ъ— (atp Д vp | Deo),
. (6-5)
-^- = —(atPt Л vPt\DQ.}v.
Эти уравнения можно переписать в более поучительной форме.
Пусть Xt—C'(t)— касательный вектор кривой С, и пусть У< =
= pt (at) — проекция на Tc(t) (Af) касательного вектора, преобра-
зующегося в соответствии с потоком at*. Предположим для про-
стоты, что кручение связности равно нулю. Тогда, учитывая
предложения 5.1 и 5.2, мы можем написать
P^L + R(Yt,Xt)Xt = Q. (6.6)
Наиболее часто уравнение (6.6) используется в римановой гео-
метрии. Как мы уже видели, на расслоении О (Af) существует
единственная связность с нулевым кручением. Она определяет
§ 6. Пулъверизация линейной связности 387
связность на JF (М) и пульверизацию на Т (М). Эта пульвериза-
ция совпадает с геодезической пульверизацией, введенной в гл. IV.
Доказательство этого утверждения проводится точно так же,
как доказательство теоремы 6.2 гл. VI. Действительно, поскольку
параллельный перенос сохраняет длину, геодезическая пульвери-
зация, так же как и пульверизация, определяемая связностью,
оставляют инвариантным подмногообразие S (М) cz Т (7И), состоя-
щее из единичных векторов z Е Г (ЛГ). Поэтому достаточно убе-
диться в том, что ограничения двух рассматриваемых векторных
полей на S (М) совпадают. Согласно формуле (3.8) гл. IV, огра-
ничение геодезической пульверизации на S (М) представляет
собой векторное поле X, удовлетворяющее условиям
XJd0 = O, <Х, 0> = 1, (6.7)
где 0 — ограничение на S (М) формы на Т (М), соответствующей
(при изоморфизме Т (М) —ъ-Т* (М)) фундаментальной форме
на Т*(М). Таким образом, если z£S(M) и У СTz (S (М)), то
(У/; 0) = (л*У, z). (6.8)
Зафиксируем теперь единичный вектор о С У. Тогда ср = ср^:
.У (М) —» Т+ (М) отображает 0 (М) на 5(7И). Пусть ф —ограни-
чение отображения ср на © (ЛГ). Вычислим форму ф* (0) на 0 (М).
Для любого вектора X С Тр (0 (Л/)) имеем
{X, ф*0) = <ФЛ, е> =
= , Я (ф (р))) =
= (л*х, р(0) =
= (р-1 (л*Х), р)= (скалярное произведение в У)
= «Х, со), г).
Итак,
ф*0 = (со, и).
Далее, поле и удовлетворяет равенству
(и, ф*0) —«п, со), и) = (у, р) = 1.
Кроме того,
ф* <20 = (dco, v) = (ЙДсо, v).
Так как поле и горизонтально, (г, й) = 0. Поэтому для X £Т (0 (М))
имеем
(v/\X | ЙДсо) = — (X, й) V.
388
Гл. VII. Геометрия G-структур
Очевидно, что «X, Q) и, у) —О, поскольку линейное отображение
(X, Q> принадлежит ортогональной алгебре. Таким образом,
v j -ф* dQ = 0.
Используя равенство (6.2), мы заключаем, что поле W удовле-
творяет условиям (6.7), что и доказывает наше утверждение.
Уравнение (6.6) вместе с результатами гл. IV показывают, что информа-
ция о тензоре кривизны риманова многообразия позволяет установить некото-
рые глобальные свойства этого многообразия. Основная идея состоит
в получении теорем сравнения, аналогичных лемме 6.1 гл. VI, и примене-
нии их к оценке расстояния между сопряженными точками. Дадим
простой пример такой теоремы. Рассмотрим для этого выражение
(R (У, Х)Х, У), где X, У—пара ортонормированных векторов. Это выраже-
ние, как легко проверить, зависит только от плоскости, натянутой па X
и У. Оно называется секционной кривизной этой плоскости. Чтобы устано-
вить его смысл, рассмотрим погружение / двумерной поверхности S в М.
Это погружение определяет многообразие 0/(5), состоящее из пар (z; ег, ...
..., еп), где S, а (е1; ..., еп) — ортонормирований репер в точке f (z),
первые два вектора которого касательны к / (5), а остальные ортогональны.
[Сравните с конструкцией многообразия ©ф (>!/), § 2 гл. VI.] Существует
очевидное погружение ft Of (S) -> © (М) и столь же очевидная проекция
пр. &/ (S) S, причем / о лу = ло/. Кроме того, первые два вектора et, е2
репера elt ..., еп определяют ортонормирований репер на S относительно
индуцированной на У римановой метрики. Следовательно, мы имеем также
проекцию р: 0/(У)(9 (У). Таким образом, мы получаем такую же диаг-
рамму, как в § 3 гл. VI:
Положим 0’= /♦ (оя) и 00' = /* (Qi3'), где co=(coi, ..., со") — фундамен-
тальная форма на 0 (М), a Q=(Q»J) —форма связности Леви-Чивита 1) на М.
Тогда (так же, как в § 3 гл. VI) легко проверяется, что
ei=p*(Wy, 02=р*(^)
и 0i = O, i > 2,
1) То есть канонической связности на 0 (Мр, см. теорему 3.1. — Прим,
перев.
§ 6. Пульверизация линейной связности
389
где (Wg, и|,)—фундаментальная форма на © (5). Теперь d(iP = 2 Й*3Д<»3,
так что й0«= 2 0‘3Д63- Сопоставляя это с равенством (6.9) при i > 2,
получаем
о=0»1ле1+0*где2.
Согласно лемме Картана, отсюда следует, что при i > 2
0ii = xinei + Xii202,
012 = Л «2101 + ^2802,
причем Л«12 = Л«21. Подставляя формулу dGi='^j&ii/\6i в равенство (6.9)
при 1 = 1, 2, мы заключаем, что 0х2 = р* (012) (где 0х2—форма связности
на © (S)). Но й0Х2=—Ха>зДс£>?., где К—гауссова кривизна поверхности S,
в соответствии с равенством (6.9) гл. VI. С другой стороны,
</012= 2 013Д032 + 2 Я12ы6йЛ6г,
где Z)Qu'=2 Я^^ю^ДсоГ Используя равенство (6.10), получаем
п
К=— Я1212+2 (+ХХ+22—(+12)2). (6.11)
4=3
Очевидно, что —Д1212 есть секционная кривизна плоскости, касательной
к f (5). Второе выражение в правой части равенства (6.11) играет роль второй
фундаментальной формы. Оно показывает, насколько поверхность S «изог-
нута» в М. Сейчас мы увидим, что если геодезические поверхности S, про-
ходящие через точку х, одновременно являются и геодезическими многообра-
зия М, то это выражение обращается в нуль. Действительно, пусть и есть
некоторая линейная комбинация векторов и е2, скажем v — et. Тогда,
согласно определению многообразия Qf (S), для точек рь р2 € ©у (б1),
для которых р (pi) = р (рг). имеем
f (Pi) = Pi («-) =Р2 (у) = Ч3 ° / (Рг)-
Геодезический поток на 5 задается векторным полем X на © (5), которое
определяется условиями
(X, o>g) = 1, (X, ю|) = (X, 012) = 0.
Пусть Хр—касательный вектор к многообразию 0/(5), для которого
Р*(Хр) = Хр. Вектор (Хр) касается геодезической многообразия (М
тогда и только тогда, когда
<W* (Яр), Ю1) = 1, <ф*7»(±р), Й«Д = 0,
или
(Хр, 0И) = О, (Хр, 01}= 1.
Сравнивая эти два выражения, мы найдем, что они совпадают в том и только
в том случае, когда второй член в правой части (6.11) обращается в нуль.
Итак, для любой плоскости Р CZ Тх (М) ее секционная кривизна равна гауссо-
вой кривизне поверхности ехр Р в точке х.
390
Гл. VII. Геометрия G-структур
Внимательно анализируя предыдущие рассуждения, мы убедимся в том,
что если поверхность S в М содержит ровно две геодезические многообразия
М, проходящие через точку х, то гауссова кривизна поверхности S в точке х
совпадает с секционной кривизной многообразия в касательной плоскости
в точке х. Применим это замечание к следующей ситуации. Пусть С (t) — гео-
дезическая на М, и пусть Xt — параллельное семейство касательных векто-
ров вдоль С (£). Оно определяет двумерную поверхность в нормальном рас-
слоении над кривой С. Применяя экспоненциальное отображение, мы получим
двумерную поверхность в М, содержащую кривую С и вместе с каждой точ-
кой х из С две геодезические многообразия М, проходящие через х. Поэтому
гауссова кривизна этой поверхности равна секционной кривизне вдоль С.
В частности, если секционная кривизна многообразия М ограничена снизу
положительной константой А2, то отрезок кривой С, имеющий длину больше
л/Д, не может минимизировать расстояние на этой поверхности. Это следует
из теоремы 6.3 гл. VI .Тем более такой отрезок не минимизирует расстояние
п в М. Итак,
если М — полное многообразие, секционная кривизна которого ограничена
снизу положительной константой, то многообразие М компактно.
Проблема получения дальнейших следствий из предположения о положи-
тельности секционной кривизны остается открытой. Сильным и неожидан-
ным результатом в этом направлении является теорема Рауха, которая
утверждает, что если секционная кривизна многообразия М заключена
между Л = 1/4 и 1, то многообразие М гомеоморфно сфере. [Раух [18] дал
сложное доказательство теоремы в предположении, что h > 1/4. Берже [2]
и Клингенберг [8] улучшили результат до h = 1/4 и показали, что эта кон-
станта — наилучшая возможная.]
Приложение I
ДВЕ ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
В этом приложении мы сформулируем теорему о неявной функ-
ции и теорему существования решений обыкновенных дифферен-
циальных уравнений и наметим их доказательство. Обе они
общеизвестны, и наши доказательства не являются наилучшими,
так как мы налагаем более ограничительные условия, чем необ-
ходимо. Доказательство в более общих предположениях читатель
найдет у Каратеодори [5]. Подробное доказательство, аналогич-
ное намеченному нами, но облаченное в более геометрическую
форму, читатель найдет у Ленга [9].
Теорема о неявной функции. Пусть F1, ...,Fh—
функции класса Ст (т^[) (или аналитические) от пф-k пере-
менных у1, . . ., ук, х1, . . хп, определенные в некоторой окрест-
ности начала координат в Ek X Еп. Пусть /’ДО, ..., 0; 0, ..., 0) = 0.
Предположим далее, что
det (—1 (0, ..., 0; 0, ...,0)=^0. (1)
' дуЗ /
Тогда уравнения
F* (ср1 (х1, . .., ж”), . . ., q? (х1, . . ., хп); х1, .. ., хп) = 0,
срДО, . . ., 0) = 0, i = l, . . ., к, (2)
однозначно определяют в некоторой окрестности начала координат
в Еп функции ср1, ..., срь. Эти функции непрерывно дифферен-
цируемы столько же раз, сколько F1.
Сделаем некоторые упрощающие замечания. Пусть (0}) — матри-
ца, обратная к (дРфду1) (0, . . ., 0; 0, ..., 0). Заменим функции
Рг на G1 — 2 это не изменит вида уравнений (2), но позволит
считать, что в начале координат матрица (dGzjdy3) равна единич-
ной матрице. Таким образом, мы можем написать GI = i/1 — где
дф/ду1 — ® в начале координат для всех i и у. Уравнения (2)
примут вид
ср1 (z1, . . ., хп) = ф (ср1 (х\ . .., хп), . . ., cpfe (х1, . . хп)). (3)
392
Приложение I
Предположим, что мы доказали существование, единственность
и непрерывность функций срг, удовлетворяющих уравнениям (3).
Тогда все фг обладают производными в начале координат. Дей-
ствительно, по теореме о среднем значении и ввиду того, что <рг
непрерывны, имеем
срг (0, . . ., хг, . . ., 0) —
= Д (ср1 (0, 0), ..., фк(0,..., хг, ..., 0); 0, ...,< ...,0) =
= S —фЧо, Л o)+gz,
где производные др!дхг и д/Чду1 берутся в некоторой точке,
стремящейся к нулю вместе с хт. Рассматривая эти равенства как
систему линейных уравнений относительно фг (0, ..., хт, ..., 0),
решая ее и деля на хг, мы получаем
фДО, , хг, , , ,, 0) _ dfi у i дР
хг дхг ' 2d дхГ ,
где а} — функции, стремящиеся к нулю вместе с хг. Переходя
к пределу при хг —»0, мы видим, что производная (дуг1дхг) (0, ..., 0)
существует и равна \dfldxT) (0, ..., 0; 0, . . ., 0). Так как начало
координат ничем не лучше, чем любая достаточно близкая к нему
точка, и так как мы предположили единственность, то частные
производные dq>lldxr существуют во всех достаточно близких точ-
ках. Более того, эти частные производные составляют единствен-
ное решение системы линейных уравнений
2dFi ЗфЗ . dF* ___р
Qyj дх? "Т” дх?
Следовательно, они непрерывны. Кроме того, они имеют ту же
степень гладкости, что и частные производные функций F1.
Таким образом, доказательство теоремы о неявных функциях
сводится к доказательству существования и единственности непре-
рывных функций ф1, удовлетворяющих условию (3). Для произ-
вольной окрестности U начала координат в Еп обозначим через
Ф (U) пространство, состоящее из наборов к функций ф =
= (ф1, . . ., фй), определенных в U. Положим
k
|| ф — ф || = 2 SUP I ф* , xn) — ty* (х1, ..., хп) [.
i=l xCU
Пусть Т — отображение подмножества из Ф(£7) в себя, задаваемое
формулой 7’ф = ф — (ф1, ..., i|?), где
фг (х1, . . ., хп) = /г (ф1 (ж1, . . ., хп), .. ., <pk (х1, . . ., хп); х1, ..., хп).
Оно определено для всех ф g Ф (К) с достаточно малой нормой |] ф ||.
Две теоремы существования
393
Оценим j| Тер || через || ф || для малой окрестности U при малых
|| <р ||. Заметим прежде всего, что, так как /г (0, . . ., 0; 0, . . ., 0) = О,
мы можем считать, что | /г (г/1, .. ., yh; х1, . .., хп) | < 8, если \хг |
и | У11 <С б- Аналогично, поскольку д]г/ду] = 0в начале координат,
мы можем считать, что \д]г/ду11<8, когда |х11 < б, |уг|<б
и | dfl!dxr | < К. Тогда из теоремы о среднем значении следует, что
| /’ (ф1 (ж1, . . ., хп), ..., ф’1 (х1, . .., хп)', х1, . . ., хп) | С
Таким образом, || 7'ф || < к& || ф || -|- кпКд < е || ф || + пКб. Предпо-
ложим, что Т определено на множестве функций ф£Ф(£7), для
которых || ф || < т], и выберем окрестность U столь малой, чтобы 6
и 8 удовлетворяли неравенству
&8T) + кпКб < ц.
Например, добьемся того, чтобы 8 < 1/2к и б < т\/2кпК. Тогда Т
отображает шар радиуса ц из Ф (U) (т. е. множество всех ф, для
которых || Ф || <С л) в себя. Более того, из теоремы о среднем зна-
чении также следует, что
||7ф — ТфЦ < яге ||ф —ф||.
Применим теперь
Предложение 1. Пусть Т — отображение полного метри-
ческого пространства S в себя, удовлетворяющее условию
d(Tq>, 7’ф) <хй(ф, ф), х<1, (4)
где d — функция расстояния. Тогда отображение Т имеет един-
ственную неподвижную точку, а именно, Ит7™ф для любого ф£А.
п—>оо
Доказательство предложения 1 почти очевидно. Единствен-
ность: если Т имеет две неподвижные точки ф и ф, то d (7’ф, 7ф) =
= d (ф, ф), что противоречит условию (4). Существование:
d (Тп~Ац. Tnq) < n‘d (Тер, ф), поэтому lim Тп<р существует.
Применяя это утверждение к отображению Т, получаем одно-
значно определенное решение уравнения (3). Выбирая начальную
функцию ф непрерывной, мы получаем, что эта неподвижная
точка является пределом равномерно сходящейся последователь-
ности непрерывных функций и, следовательно, непрерывна, что
и доказывает теорему о неявных функциях.
Теорема существования решений обык-
новенных дифференциальных уравнений.
Пусть f1 (х\ . . . , хп, t), ... , fn (х1, . . . , хп, t) — функции
394
Приложение I
класса Ck (аналитические), определенные в некоторой окрестности
начала координат в Еп X R. Тогда существуют окрестность U
начала координат в Еп и окрестность I нуля в R, такие, что
для любых (arj, . . х™) б U и t £ I существуют и единственны
функции
^(t; xl, ..., х«), . . ф"(£; хг0, ..., х”),
удовлетворяющие условиям
= Г (ф1, • • •, ф”; t), фг (0, xl, . . ., х?) = х'. (5)
Функции фг являются функциями класса Ck+1 (аналитическими)
по t и класса Ск (аналитическими) по х30.
Докажем сначала существование решений. Для этого запишем
уравнени в «разрешенном» виде, чтобы можно было применить
предложение 1. Уравнения (5) эквивалентны уравнениям
t
ф1 (t; xl, ..., хЦ) = j Д (ф1, . .., ф"; 0+4- (6)
о
предположим, что /г определены для | х11 < т] и 111 < а и что
sup в этой области. Пусть С (а, Ь) — множество наборов п
i,x,t
функций ф = (ф\ ..., фп), определенных для \t и удовлетво-
ряющих неравенству | ф11 < Ь. Если [ х101 < ц/2 (i = l, ...,п)
и 111 < 1/2ЛГ, то для ф С С (а, Ъ) элемент Тц> = ф = (ф1, .. ., фп), где
t
(t; xl, . . ., z”)= j f (ф1, . . ., ф"; t) + xl,
о
корректно определен и лежит в С (а; Ь). Положим ||ф|) =
п
= 2 sup | ф11. Тогда из теоремы о среднем значении следует, что
г=1 г, t -
|| Ггр—Гф ||<mz# || ф —гр ||, где К = sup \df/dx |. Поэтому, если а
выбрано меньшим, чем ЦпК, то мы можем применить предложе-
ние 1, что доказывает существование и единственность решения
уравнения (6), а следовательно, и (5).
Теперь мы должны доказать гладкость этих функций. Непре-
рывность и дифференцируемость по t следуют из (6). Докажем
непрерывность по х*. Для этого заметим, что из теоремы о сред-
нем значении следует неравенство
|ф*(£; xl, ..., а^) —ф‘(£; yl, . . ., у?)|<
t
2 |ф^ (s; zj, . . ., х!)) — <p}(s; yl, y”)\ds, (7)
О
Две теоремы существования
395
из которого вытекает, что
(пК 2 I *3В~4 |)
|фЖ zj, ..ж")- <рг(£; у1,, . . у”) ] < е 3 ;
тем самым непрерывность доказана.
Для доказательства дифференцируемости заметим прежде всего,
что если ф1 дифференцируемы по х30, то из (5) следует, что част-
ные производные д(рг/дх1 должны удовлетворять линейным диф-
ференциальным уравнениям (уравнениям в вариациях, см. гл. IV)
d / дф» ) _= у df* dijfi ,g.
dt \ дх^ / ~ дХц dx3g
Производные df1 /дх^ рассматриваются здесь как функции от t при
фиксированных х„, . . ., ж”. Чтобы доказать дифференцируемость
функций фг по х3, сравним отношение приращений
Ф* (С .... ..., х0) ф^ (/; Xq, ..., z0) д
с решениями уравнения (8). Применяя снова теорему о среднем
значении, получим неравенство, подобное (7), для разности выра-
жений (9) и решений уравнения (8). Из него следует дифференци-
руемость функций ф‘. Утверждения о гладкости этих функций
проверяются теперь без труда. Детали доказательства читатель
найдет в книге [9].
Приложение II
НАБРОСОК ТЕОРИИ ИНТЕГРИРОВАНИЯ В Еп
В этом приложении мы наметим построение теории интегриро-
вания в евклидовом пространстве. В стандартных учебниках ана-
лиза эта теория, особенно правило замены переменных, излагается
только в размерностях два и три. Мы будем следовать схеме,
предложенной Дж. Шварцем [см. Schwartz J., Amer. Math.
Monthly, 61 (1954), 81-85].
Под брусом □£, где а = (а1, . . ., ап), Ъ = (Ь1, . . ., bn), мы будем
понимать множество всех z = (z1, . . ., хп), для которых аг < х1 С Ьг.
[Мй допускаем также «частично открытые» брусы, для которых
некоторые из неравенств являются строгими, и допускаем случаи,
когда а1 или Ьг есть оо или —сю.]
Теория интегрирования в А” состоит в том, что выделяются
совокупность ограниченных множеств совокупность ограничен-
ных функций AF и задается правило j , которое сопоставляет
любым D С® и /£ jF число j f(x)dx так, чтобы выполнялись
о
следующие аксиомы.
1. Аксиомы для ®:
а) если Дс® и Р2С®, то
и
Ь) ® содержит все ограниченные брусы;
с) если D Е® и Т — евклидово движение, то TDg®, или
с') если DQTb и Т — параллельный перенос, то TLOg®.
2. Аксиомы для
а) — векторное пространство;
b) содержит все константы;
с) если /E.F и Т — евклидово движение, то /Д f, где
fr (х) = f (Тх), или
с') если /CjF и Т — параллельный перенос, то
Набросок теории интегрирования в Еп
397
3. Аксиомы для j :
а) для каждого фиксированного D интеграл j / (х) dx
D
линеен по /;
Ь) если Di[}D2 — 0, то для всех /C.F
j / (z) dx = / (х) dx + j / (х) dx;
r>lU-°2 -Dl I>2
c) / (T~lx) dx = (x) dx для любого евклидова движе-
TD D
НИЯ T или
с') j / (T~lx) dx= j / {х) dx для любого параллельного пере-
TD D
носа Т;
d) для любого D £ ® если /(z)Cg(z) для всех x^D,
то j / (z) dx ~<С j g (x) dx;
D D
e) J 1 • dx = 1.
t—>( 1» •••»!)
U(0, . ...0)
Для каждого D £ ® положим p (D) = 1 • dx.
D
Множество S будем называть элементарным, если оно является
объединением конечного числа брусов.
Упражнение 1. Показать, что если ®—семейство всех ограничен-
ных элементарных множеств, то ® удовлетворяет условиям а), Ь) и с).
Конечная совокупность брусов {□<}, таких, что
□ г П Dj=0 при И £’n = UDi>
называется замощением пространства Еп. Например,
□4 □ з □ 11
□ б □ 2 □10 □ 12
□ б □1 □о □ 13
□ 7 □8 □ 14
26 с. Стернберг
398
Приложение II
Функция / называется ступенчатой, если существует такое
замощение {□,) пространства Еп, что / постоянна на каждом □
Упражнение 2. Показать, что если SF—множество всех ступен-
чатых функций, то S' удовлетворяет аксиомам 2а), 2b) и 2с).
Упражнение 3. Показать, что для определенных выше ® и &
существует и единственно правило J , удовлетворяющее аксиомам За), ЗЬ),
Зс"), 3d) и Зе). Это правило задается следующим образом. Пусть /—сту-
пенчатая функция и {□;, i = l, ..., к}— соответствующее замощение, так
что f(x) = cj для Пусть Z>=^J —элементарное множество. Тогда
i=i
i=k, j—i
\f(x)dx = 2 Dpi (1)
Ъ г— l,j= 1
где для любого бруса □
И (□х) = 1 У1 — xl 11 У2~х~ I - • I Уп—хП I- (2>
[Указание. Сначала попытайтесь доказать формулу (2). Проверьте ее для
бруса О(ц/2Г’ ’ 'у;’ используя ЗЬ), Зс') и Зе); затем для любого бруса
вида □((, где у—х = (1/2г, ..., 1/2г), используя с'), и, наконец, для произ-
вольного бруса, используя ЗЬ), Зс') и 3d). Потом докажите формулу (l).j
Для любого ограниченного множества D и любого замощения
Р = { □ J обозна чим
IP(D)= U Пь Ор(£>)= U Пь
□;ер о,-ер
□ jC-D ПгГ]D=0
Положим
p_(D) = sup р(/Р (£>)),
р+(D) = inf р(ОР (£»)),
где верхняя и нижняя грани берутся по всем замощениям мно-
жества D. Будем говорить, что множество D наполнило, если
р _ (D) = p + (Z>) = p (Z)). В этом случае число р {D) называется
наполнением множества D. Совокупность всех наполнимых мно-
жеств удовлетворяет аксиомам la), 1Ь), 1с). Для доказательства
этого утверждения достаточно показать, что множество наполнимо
тогда и только тогда, когда его граница имеет наполнение нуль.
Действительно, совокупность множеств наполнения нуль инва-
риантна относительно евклидовых движений, [граница {Di U-D2)]cz
cz [(граница Di) J (граница Z)2)l и т. д.
Упражнение 4. Показать, что множество D наполнимо тогда
и только тогда, когда его граница имеет наполнение нуль.
Набросок теории интегрирования в Еп
399
Упражнение 5. Пусть S — ограниченное подмножество в Еп,
лежащее целиком в подпространстве размерности п — 1. Показать, что S
имеет наполнение нуль.
Упражнение 6. Пусть D — множество наполнения нуль в Еп
и <р—дифференцируемое отображение Еп->-Еп. Показать, что <р (D) имеет
наполнение нуль.
Упражнение 7. Пусть D — множество, граница которого являет-
ся объединением конечного числа множеств Dif причем Dj = <рг (□ г-), где
□г — брус в некотором пространстве Ет (т < п), а <рг —дифференцируе-
мое отображение Ет —>- Еп. Показать, что множество D наполнимо.
Для любой функции / и любого наполнимого множества D
положим
j / (х) dx — sup j s (x) dx,
D Ip(D)
где sup берется по всем ступенчатым функциям s, таким, что
s(x)^f(x) для всех х, а Р — замощение, соответствующее s. Ана-
логично, положим
j / (х) dx = inf j i (x) dx,
D Ор(Л)
где inf берется по всем ступенчатым функциям t, таким, что
/ (z) > / (а.) для всех х. Функция / называется интегрируемой
на D, если j f(x)dx=^ / (х) dx. Ее интеграл обозначается симво-
D D
лом j / (z) dx. Функция / называется интегрируемой, если
D
f(x)dx= j i(x)dx для всех наполнимых множеств D. Совокуп-
D D
ность всех интегрируемых функций удовлетворяет аксиомам 2а),
2Ь), 2с') (докажите!).
Упражнение 8. Если функция f непрерывна почти всюду (т. е.
непрерывна всюду, за исключением множества наполнения нуль), то она
интегрируема.
Теперь легко доказать следующее утверждение:
Теорема 1. Пусть % — совокупность областей, удовлетво-
ряющая аксиомам la), 1Ь), 1с'), содержащая все элементарные
множества и содержащаяся в совокупности всех наполнимых
26*
400
Приложение II
множеств. Пусть ер — совокупность функций, удовлетворяющая
аксиомам 2а), 2Ь), 2с'), содержащая все ступенчатые функции
и содержащаяся в совокупности всех интегрируемых функций.
Тогда для % и ер существует единственное правило § , удовлетво-
ряющее аксиомам За), ЗЬ), Зс'), 3d), Зе).
Изменение значения функции на множестве наполнения нуль
не изменяет ее интеграла. В частности, функция может быть
не определена на множестве наполнения нуль, но понятие ее инте-
грала по-прежнему имеет смысл.
Для любого подмножества S cz Еп характеристическая функ-
ция множества S, обозначаемая <ps, определяется следующим
образом:
ср5’(ж) = 1, если х f S,
cps"(x) = 0, если х 4 S.
Упражнение 9. Показать, что 4)sll-|s2 = <Ps1-q)s., Для любых двух
множеств 5’1 и 52-
Упражнение 10. Показать, что <р3, = 1 — для всех 5 (S'—допол-
нение множества 5).
Упражнение 11. Выразить <pS1Us2 и <pS1_S2 через <pS1 и <pS2.
Упражнение 12. Показать, что D наполнимо тогда и только тогда,
когда <ро непрерывна почти всюду.
Упражнение 13. Пусть D{ cz D2— Две наполнимые области, и пусть
/—интегрируемая функция. Показать, что
J / (х) dx = / (х) фД1 (х) dx.
Dl 02
Функция обладает компактным носителем, если f (х) = 0 для
всех х, лежащих вне некоторого ограниченного множества. Если
/ обладает компактным носителем, положим
f(x) dx= j / (ж) dx,
Еп D
где D — брус, содержащий все точки, в которых f(x)=pO.
В частности,
j / (х) dx = j фд>/ (т) dx,
о Еп
поэтому можно рассматривать только интегралы по Еп, когда это
удобнее.
Набросок теории интегрирования в Еп
401
Пусть En=EkxEl, так что каждая точка х^Еп может быть
записана в виде х=(у, z), где y£Ek, zQE1. Для произвольного
множества D <щ Еп определим множество . Dyd Е1 как множество
всех таких z^E1, что (г/, z)£Z).
Предположим, что ® — совокупность областей, удовлетворяю-
щая аксиомам la), lb), 1с'), a — совокупность функций, удов-
летворяющая аксиомам 2а), 2Ь), 2с'), причем выполнены следую-
щие условия:
А) если D — область из ф, то для почти всех у (т. е. всех,
кроме Множества наполнения нуль) множество Dy наполнимо
(как подмножество в £');
В) для любой функции fgjF функция /(г/, •) (от z^E1) инте-
грируема (как функция на Е1) для почти всех у;
С) для любых и D С® функция (от г/), равная
j /(г/, z) dz, интегрируема. [Заметим, что, так как множество D
D«
ограничено, эта функция автоматически имеет компактный
носитель.]
Для таких совокупностей ® и правило, которое сопоста-
вляет каждым / Е jF и D £ ф число
j ( j f(y, z)dz} dy,
E* Dy
удовлетворяет аксиомам За), 3b), Зс'), 3d), Зе). Таким образом,
из теоремы 1 следует, что
j f(x)dx= j (j /(г/, z)dz}dy,
D Ek D
У
ввиду единственности интеграла.
Приведем два примера семейств и .F, для которых усло-
вия А), В) и С) выполняются очевидным образом.
1) — все элементарные множества, a — все ступенчатые
функции.
2) ,-Fz— множество таких функций / с компактным носителем,
для которых существует множество Cf с Ek наполнения нуль
(в Eh), обладающее следующим свойством: если y^Cf, то суще-
ствуют функция ду (е) и множество Sy (е) с Е1 наполнения
Vy (е)) < Е 1Не1 — наполнение множества в Е1), такие, что
I/(£/> г) —/О/'- г) I <С е, как только || у — у' || < б (е) и z$Sy(e).
Э2 —множество всех таких D, что fnCFs-
402
Приложение II
Лемма. Любое невырожденное линейное преобразование можно
представить как произведение линейных преобразований вида
К (*^1? • • •, Xj, ^i+ii • • •» %п) — » ^Xi, Xi+i, . . ., Xn)
U
Sij (*^1? • • ч ^л) “ (a-l> ч ФТ Xji ^i+ii • • •, Xn).
Набросок доказательства. Преобразование
(Xj, . . . , Xn) —* (2-2, Xi, X3, . . . , Xn)
может быть представлено таким образом. Действительно (опуская
остальные переменные, которые не меняются), мы имеем
, \ ®12 / , \ Т“1 / ч ®21
(Xi, Х2)---->(%1 + х2, Х2)----->( — Xi — X2, х2)->
/ \ Т~1 / \ 812 / \ т-1 I \
-^\ — Xi — x2, —Xj >( — Xt — Х2, Xrf >{ — X2,Xl) >{X2,Xi).
Аналогичные рассуждения показывают, что можно переставить
любую пару переменных. Таким образом, любое линейное пре-
образование, представляющее собой перестановку переменных,
может быть получено таким путем. Если (ai7) — невырожденная
матрица, то по крайней мере один минор порядка п — 1 отличен
от нуля. Применяя подходящую перестановку переменных, мы
можем добиться того, чтобы им оказался левый верхний минор
порядка п — 1. Повторяя эту процедуру, мы докажем, что с точ-
ностью до умножения на перестановку переменных любое невы-
рожденное линейное преобразование Т имеет матрицу
/«и . .. ain\
\ Uni ♦ • &пп'
каждая подматрица которой
(fZjj . . . \
I , 1С
Uhl • akk '
невырожденна. Осталось показать, что такое линейное преобразо-
вание может быть представлено как произведение преобразований
1\ и Sij. Такое представление получается следующим образом:
(хц .. ., хп) —* <PnXi, Х2, . - - , хп) —»
(йцХ1, а12х2, х3, ..., хп) 'I
—* (,ацХ1 + U12X2, . . . , Хп) —> Z если Я12 =/= 0,
(ацХ14- ai2x2, х2, .. ., хп) J
Набросок теории интегрирования в Еп
403
и так далее до • • • -\-ащХп, х2, . .., хп). Затем, поскольку
аи ¥= 0» мы можем получить (a11xi + • • ~7~ainXn, a2ix1 а22х2, ...),
и т. д. Этот процесс можно продолжать, поскольку невырожденны
матрицы
(Яц ... \
Применим теперь лемму к выводу формулы
j / (Тх) | det Т | dx = j / (x)dx
TD D
для произвольного линейного преобразования Т. Действительно,
легко проверить эту формулу для и 8ц, используя правило
сведения кратного интеграла к повторному и соответствующее
одномерное утверждение. После этого общее утверждение следует
из леммы и правила перемножения определителей.
Следствие 1. ц (TD) = | det Т | ц (£>).
Следствие 2. Интеграл § на совокупности всех интегри-
руемых областей и совокупности всех интегрируемых функций
удовлетворяет аксиоме Зс).
Обозначение. Если ф: Е” —> Еп — дифференцируемое ото-
бражение, то через мы обозначим линейное преобразование,
соответствующее матрице Якоби (/ift (ж)), где jik = dy^ldx^.
Теорема 2. Пусть ф: /Д—> D2 — взаимно однозначное ото-
бражение класса С1, такое, что отображение ф-1 тоже класса С1.
Если f — интегрируемая функция на D2, то /оф (где /оф(а?) =
= / (ф (а;))) есть интегрируемая функция на Di и
f / (У) dy = j / (ф (х)) | del (х) | dx.
Di
Доказательство. Сначала введем еще некоторые обозначе-
ния. ДЛЯ Х = (х1г . . . , Хп) положим
|х[— max \xt I.
г— 1, . . ,, п
Для А = (ац) положим
| А | = max 2 I аи |,
i= <, . ..,п j
404
Приложение II
так что
| Ах | С j А11 х
Если X = (Xj, . . . , Хп) И р — (Pi, . . Рп), то
Фг (х) — фг (р) = 2 iik Lp + 9f {х — р)] (xk — ph),
Л=1
где 0г<1. Таким образом, если С —куб, задаваемый неравенством
[х — p|<s, то
|ф(х) — ф (р) | < s max |J^(y)\ для х£С.
utfi
Следовательно, ф(0 лежит в кубе
\У — ф(р)|<«тах| 7ф(г/)|
у£С
и
И(ф(0)<(тах|Л(У)1)Х0- (О
Для произвольного линейного преобразования А и любого мно-
жества S имеем
р (Л-15) = | det Л-11 р(0.
Таким образом,
| det А |-1 р (ф (0) = р (Л-1ф (С)).
Подставляя это равенство в неравенство (1), написанное для ото-
бражения Л-1 оф (вместо ф), получаем
| det Л I'1 р, (тЬ (0) < (max | 7д-10^> (у) |)" р. (0.
ygc
Поскольку, согласно закону перемножения матриц Якоби,
/д-1оф (у) = Л-1 «Уф (у), последнее неравенство можно переписать-
в виде
р (ф (0)< | det Л'| (max | А~Щ (у) |)” р, (0. (2)
Пусть S — произвольное наполнимое подмножество в D. Выберем
замощение пространства Еп кубами со стороной S. Пусть-
7P(0 = U0 и Xi — точка из Ct. Напишем неравенство (2) для
—ж до го куба 0, полагая A = J^{xt). Суммируя, получаем
р,(ф (7Р(5)))<21 det’J(хг) | (max1(z,)’1 (z) | )>(0).
C;eip(S) ' г£Сг
Но 7ф (х) есть непрерывная матричная функция от х. Поэтому
7ф (xj)-17ф (z) —> I при г—»хг, где I—единичная матрица. Таким
Набросок теории интегрирования в Еп
405
образом, max I «Ли (я,) 1 (z) I ~* 1 (и притом равномерно всюду,
г£Сг
кроме множества сколь угодно малого наполнения). Следовательно,
правая часть последнего неравенства стремится к j | det Уф (х) | dxr
8
так что
ц (ф (£)) < j | det (х) | dx. (3)
s
Предположим, что />0. Пусть (? = {□;} — некоторое замощение
пространства Еп и iC/—неотрицательная ступенчатая функция,
определенная на D2. Записывая неравенство (3) для каждого-
множества 5 = ф-1 (□;), суммируя и переходя к пределу при
6 —> 0, получаем
j / (У) dy < j / (ф (х)) | det (х) | dx.
Х>2 -01
Меняя местами Dt и D2, заменяя f(y) на g (х) — f (ф (х)) | det Уф (х) [
и используя закон перемножения матриц Якоби, а также муль-
типликативное свойство определителей, заключаем, что
j f(y) dy= j /(ф (a?)) j det J$(x)\dx
D2 Di
для всех неотрицательных функций. Но отсюда следует справед-
ливость этого равенства для всех функций, что и доказывает
теорему.
ЛИТЕРАТУРА
1. Амброз и Сингер ((A mbrose W., Singer I. М.), A theo-
rem on holonomy, Trans. Amer. Math. Soc., 75 (1953), 428—443.
2. Берже (Berger M.), Sur quelques varietes Riemanniennes suffi-
samment pincees, Bull. Soc. Math. France, 88 (1960), 57—71.
3. Бернар (Bernard D.), Sur la geometric differentielle des G-stru-
ctures, Ann. Inst. Fourier, 10 (1960). 151—270.
4. Г и й e м и н (G u i 1 1 e m i n V.), Theory of finite G-structures, Ph. D.
Thesis, Harvard, 1962.
5. К арате о д о ри (Carath ё о d о г у С.), Variationsrechnung und
partielle Differentialgleichungen erster Ordnung, Leipzig, 1956.
6. К a p т а н Э., Интегральные инварианты, ГИТТЛ, М.-Л., 1940.
7. Картан (Cartan Ё).. GEuvres completes, р. II, t. 2, Paris,
Gautier-Villars, 1953.
8. Клингенберг (Klingenberg W.), Contributions to Rieman-
nian geometry, Ann. Math. (2), 69 (1959), 654—666.
9. Л e н г С., Введение в теорию дифференцируемых многообразий, «Мир»,
М., 1967.
10. М о р р и (М о г г е у С. В.), The analytic embedding of abstract real-
analytic manifolds, Ann. Math. (2), 68 (1958), 159—201.
11. M о p c (Morse A. P.), The behaviour of a function on its critical
set, Ann. Math. (2), 40 (1939), 62—70.
12. Нейенхёйс (Nijenhuis A.), Theory of the geometric object,
Ph. D. Thesis, University of Amsterdam, 1952.
13. H о м и д з у К., Группы Ли и дифференциальная геометрия, ИЛ, М.,
1960.
14. Ньюлендер А. и Ниренберг Л., Комплексно аналитические
координаты в квазикомплексных многообразиях, сб. Математика,
3 : 6 (1959), 131-144.
15. Де Р а м Ж., Дифференцируемые многообразия, ИЛ, М.. 1956.
16. Р а у х (Rauch Н. Е.), Geodesics and curvature in differential geo-
metry in the large, New York, 1959.
17. С a p д (Sard A.), The measure of the critical values of differentiable
maps, Bull. Amer. Math. Soc., 48 (1942), 883—890.
18. Уитни (W h i t n e у H.), A function not constant on a connected set
of critical points, Duke Math. J., 1 (1935), 514—517.
19. Уитни X., Геометрическая теория интегрирования, ИЛ. М., 1960.
20. Хартман и Ниренберг (Hartman Р., Nirenberg L.),
On spherical image maps whose Jacobians do not change sign, Amer. J.
Math.. 81 (1959), 901—920.
21. X e ф л и г e p (HaeHiger A.). Plongements de varietes dans le
domaine stable. Seminaire Bourbaki (1962).
22. Ч ж э н ь и Л а ш о ф (C h e r n S. S., L a s h о f R. K.), The total
curvature of immersed manifolds, Amer. J. Math., 79 (1957), 308—318.
23. Ямабе (Yamabe H.), On arcwise connected subgroup of a Lie
group, Osaka Math. J. (Japan), 2 (1950), 13 — 14.
УКАЗАТЕЛЬ
Абсолютная кривизна 271
Абсолютный параллелизм 332
Автоморфизм G-структуры 336
Адамара лемма 290
Алгебра голономии 323
— контравариантных тензоров 20
Амброза — Сингера теорема 327
Антидифференцирование 31, 112
Антисимметрические тензоры 24
Аппроксимационные теоремы 68
Ассоциированная система 34
Ассоциированное расслоение 329
Атлас 44
Барицентрические координаты 115
Бесконечная р-цепь 117
Бетти числа 310
Биинвариантная риманова метрика
250
Билинейное отображение 11
Бинормаль 272
Бонне теорема 313
Бьянки — Картана тождества 352
— тождество 383
Вариационное векторное поле 107
Величины типа Q 19
Вертикальное подпространство 338
Верчение ленты 272
Вложение 50
Внешнее дифференцирование 111
Внешняя алгебра 24
— дифференциальная форма сте-
пени р 93
Внутренние точки 128
Вписанное покрытие 64
Вполне интегрируемая дифферен-
циальная система 142
— регулярная точка 369
Вторая вариация 174, 312
— фундаментальная форма 284
Гамильтона — Якоби уравнение 195
Гамильтониан 166
Гамильтоново векторное поле 156
— многообразие 154
Гаусса лемма 218
Гауссова кривизна 286
— теорема «эгрегиум» 288
Геодезическая 181, 241
Геодезическая пульверизация 216
Геодезический поток 215
Гильберта лемма 180
Главная нормаль 272
Главное расслоение 315
Гладко гомотопные кривые 275
Гладкое семейство 275
Гомоморфизм расслоений 315
Горизонтальная кривая 320
Горизонтальное векторное поле 320
— пространство связности 319
Граница 119
Граничные точки 128
Группа голономии 322
— гомологий 119
— когомологий де Рама 119
Дарбу теорема 153
Диффеоморфизм 51
Дифференциальная система 142
Дифференциальное уравнение вто-
рого порядка 181
Дифференцируемая структура 41
— функция 42
— р-цепь 117
Дифференцируемое действие груп-
пы на многообразии 87
— многообразие 44
— отображение 48
Дифференцируемый сингулярный
р-симплекс 117
Дуга 225
Закон сохранения полного импуль-
са и полного углового момента 160
— — энергии 158
Замкнутая дифференциальная фор-
ма 119
— подгруппа 246
408
У казателъ
Замкнутое подмногообразие 51
Изоморфизм расслоений 315
— G-структур 336
Индекс поля 283
Индефинитная метрика 23
Интеграл кинетической энергии 161
Интегральное многообразие диффе-
ренциальной системы 142
Инфинитезимальная образующая 101
Картана лемма 28
— теорема 147
Касательное пространство многооб-
разия 80
— расслоение 90
Касательный вектор 80
Клеточная поверхность 309
Кобаяси теорема 370
Ковариантная производная 364
— степень 16
Ковариантное векторное поле 91
— тензорное расслоение 98
Ковариантный дифференциал тен-
зорного поля 378
— — формы 326
Кокасательное расслоение 91
Кокасательный вектор 83
Комплексная структура 334
Контравариантная степень 16
Контравариантное векторное поле
90
— тензорное пространство 97
— — расслоение 98
Конформная структура 333
Координатная карта 44
— окрестность 43
Координатное отображение 43
Кривая сильного локального мини-
мума 167
— слабого локального минимума
167
Кривизна кривой 273
— ленты 272
— связности 326
Критические точки отображения
55
Кручение кривой 273
— ленты 272
— связности 379
Кусочно дифференцируемая кривая
167
Лагранжиан 165
Леви-Чивита теорема 356
Лежандра преобразование 165
Лента 272
Ли алгебра 106
— гомоморфизм 234
— группа 232
— подгруппа 234
— производная 103
— скобка 105
Линейная дифференциальная форма
91
— связность 374
Линейное отображение 12
Линейные величины 20
Локально конечное покрытие 64
— плоская G-структура 337
Локальные координаты 43
Лоренцева метрика 23
Луч 225
Максимальное интегральное много-
образие 148
Маурера — Картана уравнения 235
Многообразие 41
Множество меры нуль 53
— — — на дифференцируемом мно-
гообразии 54
— наполнения нуль 124
Морса лемма 58
Наполнимое множество 124
Невырожденная метрика 23
Нормальная карта 217
— окрестность 217
— система координат 217, 241
Носитель плотности 124
— формы 120
— функции 66
Область с регулярной границей 128
Объемная плотность 123
Однопараметрическая группа 101
Орбита 344
Ориентируемое многообразие 127
Паракомпактное пространство 64
Параллельное семейство 303
Параллельный перенос 303, 375
Первая фундаментальная форма 284
Плоская G-структура 337
Плотность 123
Указатель
409
Погружение 50
Погруженное подмногообразие 51
Подмногообразие 51
Поле величин типа Q 89
— тензора кривизны 381
— — кручения 381
Полилинейное отображение 13
Полная пульверизация 217
Положительно определенный лагран-
жиан 192
Порядок абсолютного параллелиз-
ма 366
Потенциальная энергия 157
Поток на многообразии 101
Почти гамильтонова структура 334
— комплексная структура 334
Представление группы 15
Принцип наименьшего действия Мо-
пертюи 161
Присоединенное представление 246
Приспособленная карта 366
Проблема эквивалентности общая
336
— — ограниченная 362
Продолжение подпространства 354
— G-структуры 358, 360
Произведение дифференцируемых
многообразий 45
Пространство бесконечного типа 354
— величин типа Q 89
— внешних p-форм над V 29
— конечного типа 354
Пространство симметрических конт-
равариантных тензоров степени
р 22
• — тензоров типа р 91
-------(г, S) 16
Пуанкаре лемма 132
Пуассона скобка 154
Пульверизация 216
— группы Ли 241
Путь 225
Разбиение единицы, подчиненное по-
крытию 66
Развертывание ленты 274
Разложимые р-векторы 25
Ранг абсолютного параллелизма 366
— дифференцируемого отображе-
ния 48
— семейства функций 364
— формы 34
Расслоение кореперов 87
— ортонормированных реперов 266
— реперов 91
Регулярная функция Лагранжа 165
Регулярное погружение 75
— семейство функций 364
Регулярные точки отображения 55
Регулярный абсолютный паралле-
лизм 366
Редукция расслоения 317
— связности 324
Риманова метрика 97
Риманово многообразие 97
Сарда теорема 56
Свертка 16
Свойство универсальности 20
/-связанные векторные поля 106
Связность 319
Сегмент 225
Секционная кривизна 388
Сечение расслоения 315
Симплекс 115
Скалярные плотности 20
Собственное отображение 50, 117
Сопряженные точки 199
Степень отображения 277
Стокса теорема 120, 130
G-структура 332
Структурная функция 340
Структурные константы 235
— уравнения евклидова простран-
ства 257
Структурные уравнения подмногооб-
разия 264
Сферическое отображение 284
Тензорная алгебра векторного про-
странства 16
Тензорное поле 91
— произведение представлений 15
— — пространств 14
— расслоение типа Q 91
Тома теорема о трансверсальности 75
Топологическая группа 249
Точка общего положения 344
Точная дифференциальная форма 119
Трансверсальная регулярность 74
Тривиальное расслоение 315
Уитни теорема 73, 275
Уравнение в вариациях 107, 200
Фокальные точки 199
Форма геодезической кривизны 304
— Лиувилля 186
— связности 319
410
Френе лента 272
— трехгранник 272
Фробениуса теорема 144, 146
Характеристическая система идеала
147
Хартмана — Ниренберга теорема 289
Цикл 119
Чжэня — Лашофа теорема 290, 299
— — Хартмана — Ниренберга
лемма 291
Эйлера — Пуанкаре характеристи-
ка 311
— теорема 182
— уравнение 181
— — в форме Гамильтона 181
У казателъ-
Эйлерово векторное поле 173, 181
Эквивалентность G-структур 336
Эквивариантное отображение 92
Экспоненциальное отображение груп-
пы Ли 241
— — пульверизации 217
— — риманова многообразия 217,
222
Экстремаль 181
Энергия кинетическая 158, 166
— лагранжиана 165, 166
— потенциальная 166
Якоби дифференциальные уравнения
203
— теорема 208
— тождество 106
Якобиево векторное поле 201
ОГЛАВЛЕНИЕ
Предисловие редактора перевода .............................. 5
Из предисловия автора ........................................ 7
Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ ... 11
§ 1. Тензорные произведения векторных пространств .... 11
§ 2. Тензорная алгебра векторного пространства............ 15
§ 3. Контравариантная и симметрическая алгебры ........... 20
§ 4. Внешняя алгебра ..................................... 24
§ 5. Внешние уравнения ................................... 33
Глава II. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ................ 40
§ 1. Определения.......................................... 41
§ 2. Дифференцируемые отображения ........................ 47
§ 3. Теорема Сарда ....................................... 53
§ 4. Разбиение единицы, аппроксимационные теоремы......... 64
§ 5. Касательное просттнсгво. 7........................... 79
§ 6. Главное расслоение»-» I ё *. •....................... 84
§ 7. Тензорные расслоения ................................ 96
§ 8. Векторные поля и производные Ли .................... 101
Глава III. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ НА МНОГООБРАЗИЯХ 108
§ 1. Оператор d.......................................... 110
§ 2. Цепи и интегрирование............................... 115
§ 3. Интегрирование плотностей .......................... 122
§ 4. Нульмерные и «-мерные когомологии; степень ......... 131
§ 5. Теорема Фробениуса ................................. 141
§ 6. Теорема Дарбу....................................... 149
§ 7. Гамильтоновы структуры ............................. 154
Глава IV. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ........................... 161
§ 1. Преобразования Лежандра ............................ 162
§ 2. Необходимые условия................................. 166
§ 3. Законы сохранения .................................. 185
§ 4. Достаточные условия ................................ 190
§ 5. Сопряженные и фокальные точки, условия Якоби........ 198
§ 6. Риманов случай ..................................... 215
§ 7. Полнота............................................. 224
§ 8. Изометрии.......................................... 230'
412
Оглавление
Глава V. ГРУППЫ ЛИ........................................... 232
§ 1. Определения......................................... 232
§ 2. Инвариантные формы и алгебра Ли..................... 234
§ 3. Нормальные координаты, экспоненциальное отображение 240
§ 4. Замкнутые подгруппы ................................ 246
§ 5. Инвариантные метрики................................ 250
§ 6. Формы со значениями в векторном пространстве........ 253
Глава VI. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ЕВКЛИДОВА
ПРОСТРАНСТВА.............................................. 256
§ 1. Структурные уравнения евклидова пространства .... 256
§ 2. Структурные уравнения подмногообразия .............. 262
§ 3. Структурные уравнения риманова многообразия......... 265
§ 4. Кривые в евклидовом пространстве.................... 271
§ 5. Вторая фундаментальная форма ....................... 283
§ 6. Поверхности......................................... 300
Глава VII. ГЕОМЕТРИЯ G-СТРУКТУР.............................. 311
§ 1. Главные и ассоциированные расслоения; связности .... 314
§ 2. G-структуры......................................... 331
§ 3. Продолжения......................................... 353
§ 4. Структуры конечного типа............................ 362
§ 5. Связности на G-структурах........................... 374
§ 6. Пульверизация линейной связности.................... 384
Приложение I. Две теоремы существования . . ............ 391
Приложение II. Набросок теории интегрирования в Еп........... 396
Литература................................................... 406
Указатель.................................................... 407
С. Стернберг
ЛЕКЦИИ ПО ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
Редактор Н. И. Плужникова
Художник Д. В. Орлов. Художественный редактор В. И. Шаповалов
Технические редакторы Л. II. Кондюкова и А. Г. Резоухова
Сдано в производство 9'Ш 1970 г. Подписано к печати 12/Х 1970 г. Бумага .X? 1
60x901/16=12,88 бум. л. Усл. пэч. л. 25,75. Уч.-изд* л. 22,43. Изд. N 1 5089
Цена 1 р. 79 к. Зак. 310
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2
Московская типография Ns 16 Главполиграфпрома Комитета по печати при Совете
Министров СССР.
Москва, Трехпрудный пер., 9