Author: Лидов М.Л.
Tags: общая механика механика твердых и жидких тел механика теоретическая механика
ISBN: 978-5-9221-0897-3
Year: 2010
Text
М. Л. Лидов
КУРС ЛЕКЦИЙ
ПО ТЕОРЕТИЧЕСКОЙ
МЕХАНИКЕ
ИЗДАНИЕ ВТОРОЕ,
ИСПРАВЛЕННОЕ И ДОПОЛНЕННОЕ
МОСКВА
ФИЗМАТЛИТ
2010
УДК 531
ББК 22.21
Л 55
Лидов М.Л. Курс лекций по теоретической механике. — 2-е изд.,
испр. и доп. - М.: ФИЗМАТЛИТ, 2010. - 496 с. - ISBN 978-5-9221-0897-3.
Настоящий курс лекций по теоретической механике был разработан
в 1974 г. сотрудником Института прикладной математики им. М. В. Келдыша
РАН доктором физико-математических наук, профессором, лауреатом Ленин-
ской премии М. Л. Лидовым (1926-1993 гг.) и в течение ряда лет читался им
студентам механико-математического факультета МГУ.
Оригинальный курс лекций представляет собой фундаментальный труд и
при жизни автора не издавался. Издание «Лекций по теоретической механике»
М. Л. Лидова принесет несомненную пользу студентам, аспирантам, препода-
вателям, специалистам-механикам.
Второе издание осуществлено при финансовой поддержке
Института прикладной математики им. М. В. Келдыша РАН
ISBN 978-5-9221-0897-3
© ФИЗМАТЛИТ, 2001, 2010
© М.Л. Лидов, 2001, 2010
СОДЕРЖАНИЕ
Предисловие...................................................... 9
Введение....................................................... 11
Глава 1. Введение в динамику системы материальных точек без
связей.......................................................... 13
§1.1. Формальное описание динамической модели замкнутой системы
материальных точек....................................... 13
Динамические характеристики модели (15)
§ 1.2. Понятие о моделях незамкнутых систем. Теорема о движении
центра масс.............................................. 16
Теорема о движении центра масс системы материальных точек
(20). Теорема о движении центра масс системы (21) Теорема о
движении центра масс замкнутой системы (21)
§ 1.3. Системы координат. Инерциальные системы координат..... 22
Преобразование поворота (23). Преобразование параллельного
переноса (26). Инерциальные системы координат (27). Однород-
ность и изотропность пространства (30)
§ 1.4. Основные законы механики и принцип относительности Галилея
в модели замкнутой системы материальных точек................ 31
О структуре функций, инвариантных относительно преобразо-
ваний Галилея (31). Принцип относительности Галилея (32).
Принцип детерминированности (33). Основные законы механи-
ки (34)
§ 1.5. Фазовое пространство................................... 37
О движениях в подпространствах (39)
§ 1.6. Пояснения к физическому содержанию некоторых понятий.. 40
Время (41). Абсолютный (инерциальный) репер (41). Масса (42).
Материальные точки (43). О размерности физических величин
(43). О силах парного взаимодействия (45). Закон гравитацион-
ного взаимодействия (45). Упругие силы (46)
§ 1.7. Задача п тел. Солнечная система........................ 47
Уравнения движения и состояние исследования (47). Движение
планет в Солнечной системе (48). Специфика задачи п тел в
случае Солнечной системы (49). Об относительном движении
системы материальных точек (49). Прямая и обратная задачи
динамики. Определение начальных данных и масс планет (53).
Задача о пассивном полете космического аппарата (55). Потен-
циал. Консервативные системы (57)
4
Содержание
§ 1.8. Элементы теории притяжения и некоторые оценки гравита-
ционных ускорений............................................ 60
Гравитационное взаимодействие тел (60). О протяженных телах
(60). Притяжение материальной точки телом (61). О грави-
тационном потенциале тела (63). Об асимптотике потенциала
тела на больших расстояниях (63). Взаимодействие двух шаров
(65). Гравитационные ускорения вблизи поверхности Земли (67).
Силы гравитационного притяжения двух соприкасающихся ша-
ров (70). О гравитационном поле около свободно летящего
космического корабля. Невесомость (71)
Глава 2. Кинематика твердого тела и относительное движение точки 74
§2.1. Кососимметрические матрицы и векторные произведения. 74
Свойства векторного произведения (78). Геометрические свойст-
ва векторного произведения (79)
§ 2.2. Твердое тело.......................................... 80
§ 2.3. Углы Эйлера........................................... 82
§ 2.4. Основные формулы кинематики твердого тела и относитель-
ного движения точки......................................... 86
Обозначения и определения (88)
§ 2.5. Кинематика твердого тела.............................. 91
О мгновенно винтовом движении (95). О распределении уско-
рений в твердом теле (95)
§ 2.6. Скорости и ускорения в относительном движении......... 96
§ 2.7. Сложное относительное движение системы твердых тел (ре-
перов) ..................................................... 97
§ 2.8. Кинематические уравнения Эйлера...................... 102
Глава 3. Введение в динамику системы материальных точек со свя-
зями. Общие теоремы динамики и их применение.................. 106
§ 3.1. Голономные и неголономные связи...................... 106
Примеры задач с голономными связями (109)
§ 3.2. Виртуальное движение. Виртуальный вектор............. 109
О виртуальных перемещениях (113). О неудерживающих связях
(ИЗ)
§ 3.3. Уравнения движения системы материальных точек с идеаль-
ными связями................................................ 114
§ 3.4. Пояснения к определению идеальных связей............ 119
О силе реакций на свободную точку (120). Две точки, соединен-
ные стержнем нулевой массы (121). О «неидеальных» связях
(123)
§ 3.5. Принцип Даламбера-Лагранжа и общие теоремы динамики
системы материальных точек со связями....................... 124
Содержание
5
Принцип Даламбера-Лагранжа (124). Основное уравнение ме-
ханики (124). Об изменении вектора количества движе-
ния (126). Об изменении проекции вектора количества движе-
ния (127). О сохранении проекции вектора количества дви-
жения (129). О сохранении вектора количества движения систе-
мы и движения ее центра масс (130). Об изменении момента
количества движения (130). Об изменении проекции момента
количества движения (131). Теорема о сохранении проекции
момента количества движения системы (134). Теорема о
сохранении момента количества движения системы (134). Тео-
рема площадей (134). Теоремы об изменении энергии (135). Об
изменении кинетической энергии системы (138). Теорема об
изменении внутренней энергии системы (140). Теорема о
сохранении полной энергии системы (141)
§ 3.6. Общие теоремы механики в относительном движении......
Теорема Кёнига (146)
§3.7. О внутренних связях. Закон равенства действия и противодей-
ствия в системах со связями.................................
Общий закон природы (151). Замечание о внешних связях (153).
Замечание о твердом теле (154)
§3.8. Задача о соударении шаров............................
Постулат о распределении масс (155). Взаимодействие шаров
(157). Исследование модельной задачи соударения шаров (159).
Задача об абсолютно неупругом соударении шаров (160). Абсо-
лютно упругое одномерное соударение шаров (161). Прост-
ранственная задача об абсолютно упругом ударе (162). Задача о
бильярде (165)
§3.9. Уравнения реактивного движения.......................
Ракета в свободном пространстве (167). Формула Циолковского
(168). Вертикальный подъем ракеты в однородном поле
тяжести (171)
§ 3.10. Тензор инерции......................................
Момент инерции однородного шара относительно его центра
(178). Момент инерции однородного шара относительно цент-
ральной оси (178). Момент инерции шара относительно прямой,
его касающейся (178). Момент инерции однородной палочки
длиной L относительно перпендикулярной оси (179)
§ 3.11. Уравнения движения твердого тела....................
Свободное тело (179). О представлении момента количества
движения твердого тела (180). Твердое тело с закрепленной
точкой (183). Уравнения Эйлера (184). Вращение твердого тела
вокруг неизменной оси (185). Кинетическая энергия твердого
тела (187)
141
148
154
165
172
179
6
Содержание
Глава 4. Вариационный принцип Гамильтона и уравнения движения
в форме Лагранжа и Аппеля. Некоторые интегрируемые зада-
чи. Силы инерции.............................................. 190
§4.1. Некоторые леммы вариационного исчисления............ 190
§ 4.2. Эквивалентность вариационного принципа Гамильтона и прин-
ципа Даламбера-Лагранжа............................... 193
Вариационный принцип Гамильтона (197). Замечание о классах
эквивалентных отображений (199)
§4.3. Обобщенные координаты. Обобщенные силы.............. 200
Вектор скорости в обобщенных координатах (205). Уравнения
неголономных связей в обобщенных координатах (205). О пред-
ставлении кинетической энергии в обобщенных координатах
(206). Опорные кривые и допустимые вектор-функции в Rm
(207). Обобщенные силы (208)
§ 4.4. Вывод уравнений Лагранжа и уравнений Аппеля......... 211
Уравнения Лагранжа (215). Уравнения Аппеля (217)
§ 4.5. Различные формы уравнений Лагранжа. Интеграл энергии и
интеграл Якоби ............................................. 221
Интеграл энергии (226). Интеграл Якоби (229). Определение
обобщенных реакций связей (232)
§ 4.6. Первые интегралы уравнений Лагранжа................. 233
Циклические координаты (236). Теорема Э. Нётер (236)
§4.7. О дифференциальном уравнении z2 = f(z, ос) ......... 242
§ 4.8. Задача о математическом маятнике.................... 246
Задача о маятнике (247). Интеграл энергии (250). Качественное
исследование поведения интегральных кривых (250). Аналити-
ческое решение (253). Определение сил реакций (258)
§ 4.9. Движение точки по гладкой кривой.................... 261
Некоторые общие понятия (262).........................
§ 4.10. Движение точки по поверхности вращения............. 263
§ 4.11. Движение в центральном поле сил. Задача двух тел... 269
Взаимодействие двух заряженных частиц по закону Кулона
(270). Взаимодействие двух молекул (271). Определение зависи-
мости от времени (277). Законы Кеплера (279). Об особен-
ностях решения в задаче двух тел (280)
§ 4.12. Силы инерции....................................... 281
О весе тела (284). О силе Кориолиса (286). Задача о падении
камня на Земле (287). Маятник Фуко (289). Невесомость. Пере-
грузки. Искусственная тяжесть (292)
Глава 5. Основной аппарат гамильтоновой механики.............. 295
§5.1. Система уравнений в форме Гамильтона................. 295
Теорема Донкина (или теорема о преобразовании Лежандра)
(298). Примеры вычисления обобщенных импульсов (302)
Содержание
7
§ 5.2. Симплектический диффеоморфизм........................ 303
Симплектическое пространство (304). Симплектические преоб-
разования (308). Симплектический диффеоморфизм (311)
§ 5.3. Производящая функция симплектического диффеоморфизма .... 315
Примеры симплектических преобразований (325)
§ 5.4. Канонические преобразования и уравнения Гамильтона-
Якоби ....................................................... 328
Уравнение Гамильтона-Якоби (336). Теорема Якоби (337). Тео-
рема о существовании полного интеграла уравнения Гамиль-
тона-Якоби (339)
§ 5.5. Некоторые примеры применения метода Якоби............ 341
Задача о линейном осцилляторе (342). Задача двух тел (343).
Кинематический и геометрический смысл новых переменных
(346)
§ 5.6. Системы Лиувилля. Переменные «действие-угол»......... 350
Системы, допускающие разделение переменных (350). Теорема
Лиувилля (351). Переменные «действие-угол» (354). Некоторые
выводы (357). Дополнительные замечания (358)
§ 5.7. Первые интегралы уравнений Гамильтона и интегрируемые сис-
темы ........................................................ 360
Скобки Пуассона (360). Свойства скобок Пуассона (362). О пер-
вых интегралах (362). Теорема Пуассона (363). Теорема о пони-
жении порядка автономной системы уравнений Гамильтона
(366). Теорема Лиувилля (367)
Глава 6. Движение твердого тела................................ 372
§6.1. Качественный анализ случая Эйлера-Пуансо............. 372
Интегралы задачи (374). Качественное исследование задачи
(374). Эллипсоид инерции (377). Геометрическая интерпретация
Пуансо (378)
§ 6.2. Описание потенциальных движений твердого тела в канониче-
ских переменных.............................................. 380
Формулы для кинетической энергии (380). Некоторые задачи о
вращении твердого тела (387). Случай Эйлера-Пуансо (388).
Случай Лагранжа (389). Случай С.В. Ковалевской (389)
§ 6.3. Аналитическое исследование случая Эйлера-Пуансо...... 391
Случай динамически симметричного тела (392). Переменные
«действие-угол» в задаче Эйлера-Пуансо (397)
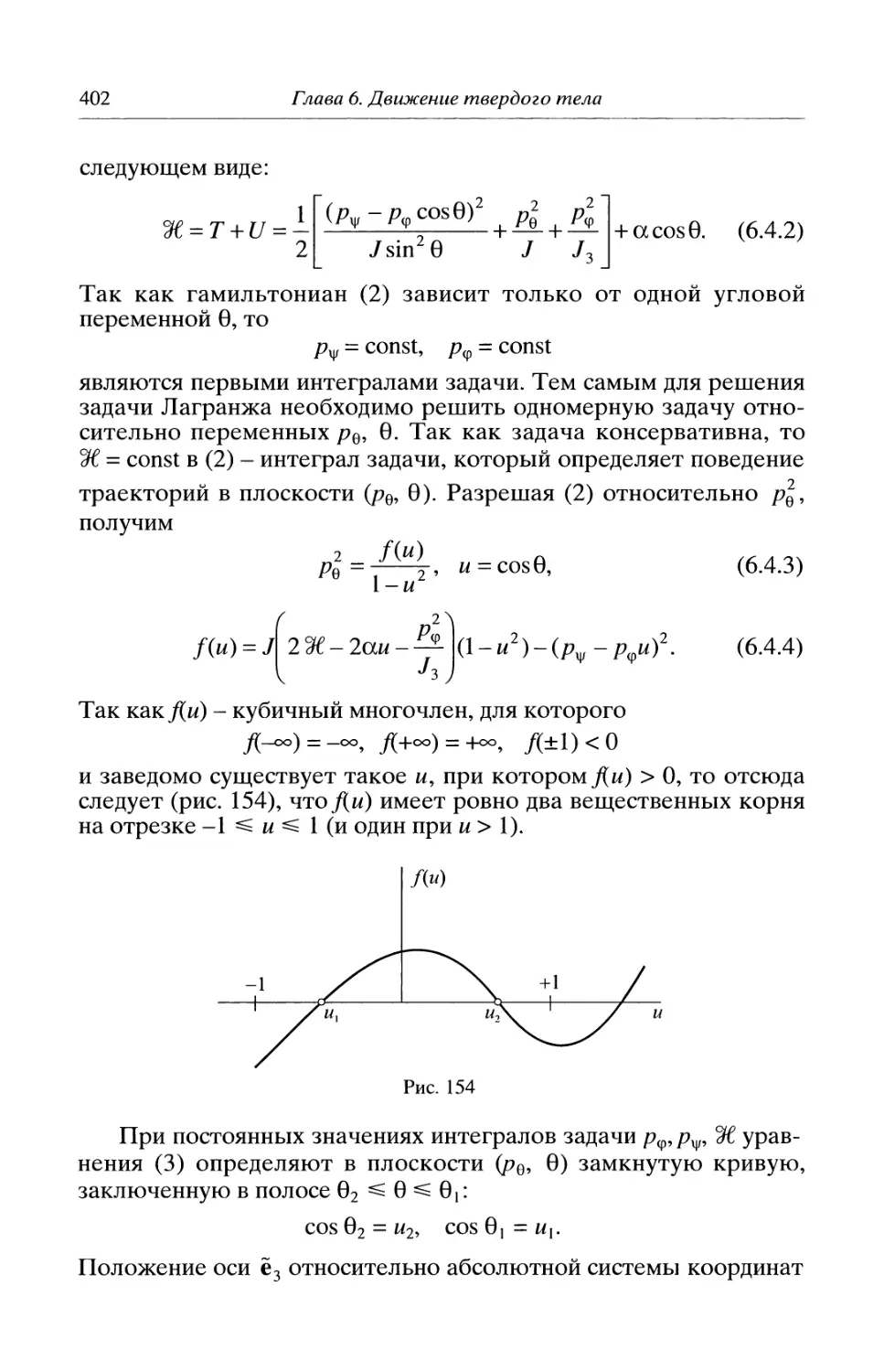
§ 6.4. Случай Лагранжа...................................... 401
Лемма о подобии движений (404). Быстро закрученное тело
(405). Устойчивость вертикального вращения (407)
§ 6.5. Использование закономерностей вращения твердых тел... 410
Глава 7. Устойчивость движения и малые колебания............... 414
§7.1. Постановка задачи об устойчивости решений............ 414
8
Содержание
§ 7.2. О решениях линейных уравнений с постоянными коэффициен-
тами ....................................................... 416
§ 7.3. Связь между решением проблемы устойчивости для автономной
нелинейной системы и линеаризованной системы уравнений..... 420
О норме комплексных векторов и матриц (420). Инвариантность
проблемы устойчивости по отношению к замене переменных
(421). Связь между решением проблемы устойчивости для
нелинейной и линеаризованной систем (422). Теорема об устой-
чивости линейной системы (423). Теорема Ляпунова об асимпто-
тической устойчивости (неустойчивости) тривиального решения
нелинейной системы (424). Теорема Рауса-Гурвица (426)
§ 7.4. Основные теоремы второго метода Ляпунова............... 428
Теорема Четаева о неустойчивости (432). Устойчивость пос-
тоянных вращений твердого тела (433). Неустойчивость враще-
ния вокруг средней оси инерции (434). Устойчивость вращений
вокруг осей с наибольшим и наименьшим моментами инерции
(435)
§ 7.5. Малые колебания в механических системах................ 435
Теорема об устойчивости равновесия консервативной системы в
линейном приближении (440). Теорема Лагранжа об устой-
чивости равновесия консервативной системы (440)
§ 7.6. Изменение собственных частот при изменении жесткости систе-
мы или наложении связей.............................. 442
Теорема Релея (445). О соотношении между частотами при
наложении связи (447)
§ 7.7. Малые колебания и устойчивость в гамильтоновых системах. 450
§ 7.8. Формальная процедура теории возмущений для гамильтоновых
систем................................................ 464
Каноническая замена переменных, близкая к тождественной
(464). Основная задача теории возмущений (468). Системы,
близкие к интегрируемым (470)
Дополнение.................................................... 473
Предметный указатель.......................................... 489
Основные обозначения ......................................... 494
ПРЕДИСЛОВИЕ
Настоящий курс лекций по теоретической механике был
разработан в 1974 г. профессором Московского государственно-
го университета Михаилом Львовичем Лидовым (1926-1993 гг.) и
в течение ряда лет читался им студентам механико-математи-
ческого факультета. Отличительной особенностью предлагае-
мого читателю нетрадиционного курса, рассчитанного на два
семестра, является удачное сочетание математической строгости
изложения материала с физической интерпретацией резуль-
татов. Большое место в лекциях уделено разъяснению специаль-
ных механических эффектов и приложений к задачам небес-
ной механики. Это та область, которой профессор М.Л. Лидов
посвятил всю свою жизнь и в которой достиг блестящих научных
результатов. Он стал лидером направления, связанного с теоре-
тическими и прикладными задачами баллистического проектиро-
вания и управления полетом космических аппаратов.
Научное наследие М.Л. Лидова составляет гордость Инсти-
тута прикладной математики им. М.В. Келдыша РАН, в котором
он трудился всю свою творческую жизнь. Здесь пришло к нему
официальное признание - ученая степень доктора физико-мате-
матических наук, присужденная, минуя степень кандидата, зва-
ние лауреата Ленинской премии, орден Трудового Красного Зна-
мени. Эта трудовая награда встала в один ряд с воинскими
наградами М.Л. Лидова, который, уйдя добровольцем на фронт в
1944 г., закончил войну в победном 1945-м.
Помимо повседневной научно-производственной работы в
институте М.Л. Лидов вел большую педагогическую работу в
качестве профессора кафедры теоретической механики меха-
нико-математического факультета МГУ им. М.В. Ломоносова
(с 1966 по 1976 г.) и профессора факультета повышения ква-
лификации МИРЭА* (с 1982 по 1991 г.). Он воспитал многих
кандидатов и докторов наук. Круг его научных интересов был
очень широк и охватывал многие разделы математики и ме-
ханики, астрономии и космогонии, теории управления и диф-
ференциальных игр. Многие его работы стали классическими.
Московский государственный институт радиотехники, электроники и автоматики.
Ныне - Московский государственный институт радиотехники, электроники и автоматики
(технический университет).
10
Предисловие
М.Л. Лидов - автор 120 научных трудов, и в каждом из них глу-
бина теоретического анализа органически сочетается с исчерпы-
вающими практическими приложениями.
М.Л. Лидов был членом Российского национального коми-
тета по теоретической и прикладной механике. Его доклады на
самых представительных конференциях были всегда в центре
внимания специалистов.
Много сил и времени М.Л. Лидов отдавал неформальной
редакторской работе в академических журналах «Космические
исследования» и «Письма в астрономический журнал», был науч-
ным редактором раздела «Динамика полета» энциклопедии
«Космонавтика».
Все, что успел сделать Михаил Львович Лидов в своей жизни,
несет отпечаток его неповторимого таланта и самоотверженного
труда.
Оригинальный курс лекций представляет собой фундамен-
тальный труд общим объемом около шестисот машинописных
страниц и при жизни М.Л. Лидова не издавался. Можно с
уверенностью сказать, что «Лекции по теоретической механике»
М.Л. Лидова принесут несомненную пользу студентам, аспи-
рантам, преподавателям, специалистам-механикам, являя собой
достойную память этому выдающемуся ученому.
После первого прочтения курса в 1974 г. текст лекций был
записан и обработан доцентом кафедры теоретической механики
МГУ И.Л. Антоновым, который совместно с М.Л. Лидовым
осуществил их начальное редактирование.
Издание настоящей книги было бы невозможным без орга-
низационной поддержки руководства Института прикладной
математики им. М.В. Келдыша РАН - в первую очередь акаде-
мика Д.Е. Охоцимского и профессора Э.Л. Акима.
Большое содействие и активную помощь в подготовке
рукописи к набору на различных этапах оказали коллеги и уче-
ники М.Л. Лидова: член-корреспондент РАН В.В. Белецкий,
доктор физико-математических наук М.А. Вашковьяк, канди-
даты физико-математических наук Г.Б. Ефимов, Р.К. Казакова,
Н.М. Тесленко, а также В. А. Ляхова, Т.Н. Круглова и Н.П. Дени-
сова.
Коллеги М.Л. Лидова, готовившие лекции к изданию, редак-
тор и издатель сочли возможным сохранить в основном не
только терминологию и стиль автора, но также структуру пост-
роения материала.
Во втором издании книги исправлены текстовые и фор-
мульные опечатки. В дополнении дано описание научной дея-
тельности М.Л. Лидова, отражены его основные работы и их
развитие.
ВВЕДЕНИЕ
Теоретическая механика — это наука, которая изучает ос-
новные закономерности движения (механического движения) ма-
териальных тел с помощью математических моделей. К этому
определению следует сделать несколько пояснений.
1. Обычно в курсах теоретической механики рассматрива-
ются наиболее общие закономерности с ограниченной степенью
детализации. Методы теоретической механики являются основой
для большинства разделов физики и техники.
2. В теоретической механике изучается поведение системы,
которое обычно описывается сравнительно небольшим числом
функций времени. Эти функции удовлетворяют обыкновенным
дифференциальным уравнениям. Это одна из границ, которая
отделяет теоретическую механику от механики сплошной среды,
где поведение системы описывается функциями многих перемен-
ных и основным средством описания является аппарат уравнений
в частных производных.
3. Математические модели в теоретической механике служат
для описания закономерностей реальных процессов как природы,
так и техники. Наиболее существенно, что изучение модели поз-
воляет предсказать качественные или количественные следствия
этих процессов. Всякая модель отражает свойство мира лишь
приближенно. Пригодность данной модели для данного круга
явлений проверяется экспериментом и оценивается запросами
практики. Иногда даже сильно упрощенные (по сравнению с ре-
альным явлением) модели позволяют выявить в результате их
анализа некоторые основные закономерности.
4. Значительное по объему место в курсах теоретической
механики занимают методы исследования обыкновенных диф-
ференциальных уравнений. Однако это не вся теоретическая
12 Введение
механика. Равноправное по важности место занимает проблема
конструирования математической модели, пригодной для описа-
ния данного явления. Это не формальная часть. Для приобрете-
ния элементарных навыков в этой области необходимо развивать
геометрическую и физическую интуицию. В учебном процессе
с книгой и с помощью лекций и упражнений эту интуицию
можно приобрести путем разбора и решения некоторых типич-
ных задач. Перевод неформального описания задачи, данного,
например, с помощью чертежа и некоторых пояснений, на язык
формул заменяет в учебном процессе физические наблюдения
или эксперименты.
Глава 1
Введение в динамику
системы материальных точек без связей
§ 1.1. Формальное описание динамической модели
замкнутой системы материальных точек
1. Задано одномерное пространство R вещественных чисел t.
Элементы этого пространства t называются моментами времени
t е R. Интервал этого пространства будем обозначать Jt и назы-
вать интервалом времени.
2. Задано трехмерное линейное вещественное евклидово
пространство 7?3 4 5 (рис. 1). Элементы этого пространства будем
обозначать г и называть радиусами-векторами точки (или век-
торами положения точки) г Е R3. Это пространство R3 будем
называть абсолютным пространством.
Рис. 2
3. Движением точки в R3 будем называть отображение f:Jt Е
eR3 интервала времени в пространство R3. Это отображение
задается вектор-функцией г = f(r), t е Jt. Обычно при записи
отображения мы будем использовать ту же букву и писать
г = г(0.
4. Образ Jt в R3 при отображении/называется траекторией
движения (или кривой) (рис. 2). Введем несколько понятий, свя-
занных с отображением/
5. В координатном представлении отображение г = г(г) за-
дается тремя функциями:
г = (г‘(Г), г2(Г), г3(0).
Как правило, мы будем рассматривать достаточно гладкое
отображение, когда функции Н(0, i = 1, 2, 3, имеют производные
по t достаточно высокого порядка. Это свойство не зависит от
выбранной в R3 системы координат.
14 Глава 1. Введение в динамику системы материальных точек без связей
6. Производная по времени dr/dt от r(Z) называется вектором
скорости в момент времени t. Вектор скорости будем обозна-
чать v(Z):
r(Z + /i)-r(Z)
v(z) = lim —------—.
h
Сходимость понимается по норме R3.
В координатном представлении
, vl(t) = —, ve/?3.
dt
7. Производная по времени от вектора скорости v(Z) назы-
вается вектором ускорения в момент времени t. Вектор уско-
рения в момент времени t будем обозначать буквой w:
, . v(Z + h)- v(Z)
w(z) = lim—-------
h
I/ (Z)
v2(z)
v 3(7)
v(Z) =
w(z) =
w2(t)
j dv‘ d2r‘ n3
w(t) =---= —z-, we/?.
dt dt2
8. Материальной точкой называется пара (г, m), где т -
действительное положительное число, называемое массой мате-
риальной точки, г - вектор 7?3, называемый радиусом-вектором
материальной точки. В нашей модели масса материальной точки
не зависит от момента времени.
9. Движением материальной точки называется пара (r(z), m),
где т - масса точки, г = г(г) - отображение Jt —» 7?3. Движение
материальной точки определяет вектор скорости, вектор уско-
рения и ее траекторию.
10. Мы будем изучать движение системы, состоящей из п
материальных точек, занумерованных отрезком натурального
ряда: 1, 2, ..., п. Массу k-й материальной точки будем обозначать
через mk, ее радиус-вектор - rk. Отображение Jt —> R3 - через
rk = г\(Г); вектор скорости - v*(0, вектор ускорения - wk(t).
11. Произведение массы к-й материальной точки на ее вектор
скорости называется вектором количества движения к-й точки
(или ее вектором импульса). Вектор импульса к-й материальной
точки будем обозначать РА:
Рл =
(1.1.1)
§ 1.1. Формальное описание динамической модели
15
Динамические характеристики модели
Для формального описания модели определим вектор-функ-
ции специального вида. Позже мы докажем, что такой вид этих
функций может быть получен как следствие достаточно общих
экспериментально установленных законов природы.
12. Рассмотрим функцию Fy следующего вида:
^(П-г^^.т)^), (1-1.2)
где
^7 =1 Г, - Г; |, Пу ~1 V,- - Vy |, = (Г; - Г , V,- - V,- >,
(х, у) - скалярное произведение векторов х, у е /?3,
1x1 = д/(х,х) - длина вектора х,
fij - скалярная функция трех указанных аргументов, удовлет-
воряющих условию
= (1.1.3)
Определение. Если rz, vt- и r;, vy - радиусы-векторы и векторы
скорости г-й и у-й материальных точек, то вектор-функции Fy
вида (2) будем называть функциями типа парного взаимо-
действия. Из определения Fy, согласно (2), непосредственно
вытекают ее свойства:
l. Fy g R\
2. Вектор Fy коллинеарен вектору гг - гу.
3. I- (Г,., Г,., v;, V; ) = -F;,. (г •, Г,., v,., V,.).
13. Будем говорить, что определена динамическая модель
замкнутой системы п материальных точек без связей, если
задана система функций Fy(z Фу) типа парных взаимодействий
для i - 1, 2, ..., n;j = 1, 2, ..., п, и движение материальных точек
удовлетворяет следующей системе уравнений:
п
= k = i,2,...,n. (1.1.4)
В этом случае мы будем использовать следующие опреде-
ления:
1) систему уравнений (4) будем называть уравнениями дви-
жения;
2) вектор-функцию Fkj будем называть силой, действую-
щей на (материальную) точку к со стороны (материаль-
ной) точки у;
16 Глава 1. Введение в динамику системы материальных точек без связей
3) сумму F* = Fkj будем называть результирующей силой,
7 = 1
действующей на материальную точку к\
4) так как mkd2rk / dt2 = mkdvk I dt = dPk I dt, уравнения движе-
ния (4) можно записать в следующем виде:
dP
—k- = Fk, £ = 1,2,...,щ
dt
что эквивалентно формулировке:
производная по времени от вектора количества движения
к-й материальной точки равна результирующей силе,
действующей на эту точку.
Это второй закон Ньютона.
§ 1.2. Понятие о моделях незамкнутых систем.
Теорема о движении центра масс
Прежде чем начать обсуждение модели динамики замкнутой
системы п материальных точек, предварительно обсудим поста-
новку задачи для незамкнутых систем.
Рассмотрим систему п взаимодействующих материальных
точек, которые можно разбить на две подсистемы (рис. 3). Будем
называть их системой I и системой II. Пусть системе I принад-
лежат точки с номерами 1, 2,..., q, а системе II - с номерами q + 1,
q + 2,..., п. Движение этих точек определяется уравнениями
*=1’2’-’* (1.2.1)
q п
где Ff> = £ F„, F<e) = £
7=1 7=^+1
i*k
§1.2. Понятие о моделях незамкнутых систем
17
ms^- = F^ + F<e), s = q + l, q+2,...,n, (1.2.2)
n q
где Ff> = ± F^ = S
7 = 4+1 7 = 1
j*s
Здесь F^z) - результирующая сила, действующая на точку к,
которая принадлежит системе I (символически к е I), со стороны
остальных точек системы I;
F*e) - результирующая сила на точку к Е I со стороны всех
точек системы II;
Fjz) - результирующая сила на точку s Е II со стороны всех
точек системы II;
Fv(e) - результирующая сила на точку se II со стороны всех
точек системы I.
Определения.
1. Силы парных взаимодействий Fkj в системе I (к q, j' q)
называются внутренними силами для системы I q материальных
точек; FA(z) - результирующая внутренних сил, действующих на
точку к.
2. Силы Fty (к q, j > q), действующие на точки системы I со
стороны точек системы II, называются внешними силами для
материальных точек системы I; F^e) - результирующая внешних
сил на точку к системы I. Аналогично Fs(z) - результирующая
внутренних сил для системы II; Fs(d - результирующая внешних
сил для системы II.
В более общем случае систему п материальных точек можно
разбить не на две, а на большее число подсистем. В этом случае
внутренними силами называются силы, действующие на точку
данной подсистемы со стороны других точек той же подсистемы.
Все остальные силы взаимодействий называются внешними для
данной подсистемы.
Предположим теперь, что система I - это сравнительно не-
большое число материальных точек, движением которых мы
интересуемся, а система II, образно говоря, «остальной мир». Из
системы уравнений (1) и (2) следует, что движение всех точек
обеих систем, вообще говоря, взаимосвязано. И это на самом
деле так. Однако в такой общей постановке мы бы не могли
решить ни одной задачи механики. Эффективное решение задач
достигается за счет того, что в разумно построенной механиче-
2. М.Л. Лидов
18 Глава 1. Введение в динамику системы материальных точек без связей
ской модели, во-первых, можно (с точки зрения приближенного
описания) пренебречь влиянием точек системы I на «остальной
мир» (систему II) и принять
Fje)=O, 5 = q +
т.е. закономерности движения в системе II могут быть опре-
делены заранее независимо от решения задачи о движении q
материальных точек в системе I, а во-вторых (с точки зрения
возможности решения задачи о движении точек системы I), нас и
не интересуют подробности движения в системе II.
Единственное, что нам необходимо, это знать результирую-
щие силы
F^ = F^(r„vt,a к = 1,2.q,
с которыми «остальной мир» действует на точки системы I.
Вид этих сил может быть определен с помощью предвари-
тельного решения системы уравнений (2) при Fv(e) = 0 или уста-
новлен экспериментально на основе физических наблюдений и
сформирован как закон природы.
Так мы приходим к модели, описываемой системой диффе-
ренциальных уравнений
z/2r
m^-Ff’ + F^, *=1,2,(1.2.3)
где F*e) - заданные силы, определяющие влияние «остального
мира» на точки системы I. Так как точки системы II могут с
течением времени изменять свое положение в пространстве, то в
общем случае силы FA(e) могут явно зависеть от времени:
Определение. Системы материальных точек с внешними си-
лами называются незамкнутыми.
Если мы рассмотрим замкнутую систему, состоящую из
одной точки (г, т), то уравнения движения для такой «системы»
имеют вид
б/2 Г
т—г = 0. (1.2.4)
dt2
Точке (г, т) не с чем взаимодействовать. Решение (4) имеет вид
Jv dr z z< Л _
— = o^v = vo-^ —= vo^r = voa-zo) + ro, (1.2.5)
dt dt
где r0, v0 - постоянные векторы.
§ 1.2. Понятие о моделях незамкнутых систем
19
В координатном представлении решение (5) имеет вид
rl =vl0(t-t0) + r^, / = 1,2,3.
Это - уравнение прямой в 7?3 в параметрическом виде (пара-
метр t). Мы получили, что изолированная материальная точка
движется прямолинейно и равномерно (vlG = const, i = 1,2,3).
Для незамкнутой системы (3) задача о движении одной мате-
риальной точки (г, т) более содержательна. Этой задаче соот-
ветствует следующая система дифференциальных уравнений:
Л2г
m—^- = F<e)(r, v, О, (1-2.6)
dt
где F(e) - результирующая внешних сил, действующих на точку
(г, т). В случае незамкнутой системы на точку (г, т) действует
«остальной мир».
Для пояснения сформулируем простейшую задачу о движе-
нии материальной точки вблизи поверхности Земли под дейст-
вием внешней силы.
Еще Галилеем был открыт закон, который в наших тер-
минах формулируется следующим образом.
На материальную точку массой т вблизи по-
верхности Земли в окрестности фиксирован-
ной точки О действует постоянная сила, нап- /
равленная примерно перпендикулярно по-
верхности Земли и пропорциональная массе е, АХ
точки (рис. 4). В векторной записи £ е-
F^=-mgn°, (1.2.7) 1 <7
g = 9,8 м/с2 - постоянная (коэффициент
пропорциональности), п° - единичный век- Рис. 4
тор, направленный по внешней нормали к
поверхности Земли.
Уравнения движения материальной точки массой т в этом
случае имеют вид
б/2г о
т —2” ~
dt
d2r' d2r2 n d2r2
m —= m —5- = (J, m —5- = -mg .
dt2 dt2 dt2
(1.2.8)
2*
20 Глава 1. Введение в динамику системы материальных точек без связей
Формула (7) дает приближенное выражение результирую-
щей для сил гравитационного взаимодействия рассматриваемой
материальной точки (г, т) с материальными точками, из кото-
рых состоит Земля. Позже мы получим более общее выражение
для этой силы.
Следует подчеркнуть, что формальная картина с учетом всех
взаимодействий более сложна. Не только Земля оказывает
влияние на движение материальной точки, но и точка (г, т) ока-
зывает влияние на движение Земли. Однако изменение коор-
динат и вектора скорости Земли за счет влияния малой массы т
ничтожно, оно не обнаруживается при экспериментах и не
учтено в (7) и (8).
Введение в механические модели внешних сил существенно
расширяет возможности описания различных процессов. Внеш-
ние силы могут быть практически любыми функциями времени.
Для примера укажем на одну из моделей с внешней силой.
Материальной точке (г, т) «внешний мир» с помощью «ниточ-
ки» сообщает ускорение F(e)(r)/m, где F(e)(r)-
1 заданная вектор-функция времени (рис. 5).
Модели такого типа тоже описывают неко-
торые реальные движения.
рис Теорема о движении центра масс системы
материальных точек.
Определение. Пусть (гг, тг), i = 1, 2,..., л - некоторая система
выделенных материальных точек.
Радиусом-вектором центра масс этой системы называется
вектор г*, вычисляемый по следующей формуле:
г*=Д-У/ид;., (1.2.9)
т Zt
У
где т* = mi ~ сумма масс этих точек.
/=]
Точка 7?3, определяемая радиусом-вектором г*, называется
центром масс системы
Пусть (гь тД k = 1, 2,..., п - система материальных точек,
находящихся под действием сил парных взаимодействий друг с
другом и внешних сил F*(e), к = 1, 2,..., п. Уравнения движения
§ 1.2. Понятие о моделях незамкнутых систем
21
такой системы имеют вид
mk—i = Ff) + F^), k = l,2,--.,n. (1.2.10)
dt
Лемма 1. Сумма внутренних сил, действующих на все точки
системы, равна нулю.
Доказательство.
= £ F*n = X S FV=0- (L211>
k=l k=l ./=1
Последнее равенство следует из условий: = -Fjk.
Теорема о движении центра масс системы. Центр масс систе-
мы п материальных точек движется как двигалась бы мате-
риальная точка массой т*, равной сумме масс всех точек
системы, расположенная в центре масс системы, под воздейст-
вием суммы внешних сил, действующих на все точки системы.
Доказательство. Просуммируем (10) по к от 1 до п:
trnk
d2rk d2 vp d2 * *
dt2 dt2^ кк dt2
12 * п п
=m*^=Y f*w+£
аг к=\ к=\
п
Так как У Fkl} = 0, то
к = 1
И2г*
т —^ = FW, (1.2.12)
dt2
где F(e) = £ F«.
k = \
Определение. Сумму внешних сил F(e) называют результи-
рующей силой, действующей на систему.
Теорема о движении центра массы замкнутой системы.
Центр масс замкнутой системы движется равномерно и пря-
молинейно.
22 Глава 1. Введение в динамику системы материальных точек без связей
Доказательство. Для замкнутой системы F*(e) = 0;
k = 1, 2,..., п. Поэтому
»2 * j *
а г Л av * * * л л
—z-:=0—>----= v = const —> г =v(r-rn) + r, г = const.
dt2 dt 0
Несмотря на тривиальность доказательства, это чрезвы-
чайно важные для механики теоремы. Позже мы докажем еще
несколько столь же общих теорем. Теорема о движении центра
масс системы приведена здесь для пояснения сути разделения сил
на внутренние и внешние. Эта же теорема, как мы покажем
позже, важна для уточнения физического содержания абстракт-
ного понятия материальной точки.
§ 1.3. Системы координат.
Инерциальные системы координат
Для механики существенны две интерпретации трехмерного
линейного евклидова пространства 7?3: геометрическая и ариф-
метическая. Пусть О - фиксированная точка абсолютного про-
странства (рис. 6). Положение произвольной точки М в этом же
м пространстве при геометрической интерпре-
г тации 7?3 определяется направленным отрез-
/ ком г = ОМ, называемым вектором. Три ис-
ез /г ходящие из точки О взаимно ортогональные
/ и одинаковой длины направленные отрезка
/ еь е2, е3 образуют в /?3 ортонормированный
репер. Длина векторов е,- принимается за
единицу длины.
Совокупность Е - (е15 е2, е3) называется
ортонормированным репером (или просто
Рис- 6 репером), координатным репером декарто-
вой системы координат. Векторы называются координат-
ными ортами (или просто ортами).
Как известно, произвольный вектор г g R3 можно разложить
по векторам репера:
г = /ej + г2е2 + г3е3, (1.3.1)
где г1, г2, г3 - вещественные числа, называемые координатами
§ 1.3. Системы координат. Инерциальные системы координат
23
вектора г относительно репера Е, г* - (г, е,) - проекция вектора
г на орт ez.
Упорядоченная совокупность трех координат г1, г2, г3 векто-
ра г образует вектор арифметического евклидова пространст-
ва R3. Этот вектор мы будем обозначать буквой г и назы-
вать координатным вектором (или иногда просто координа-
тами).
Обычно координатный вектор г мы будем записывать в виде
матрицы размера 3x1 (матрицы с тремя строками и одним
столбцом):
г = г2 . (1.3.2)
Используя знак транспонирования матриц «т», можно век-
тор г представить записанным в строчку, как матрицу размера
1x3:
гт = (г1,г2,г3).
Такая запись занимает меньше места, и мы будем иногда ее
использовать.
Предполагается, что читатель знаком со всеми основными
понятиями обеих интерпретаций R3.
Положение точки М можно задать относительно другой сис-
темы координат, другого репера.
Поскольку все основные операции в дальнейшем будут про-
изводиться с координатными векторами (числами), то необхо-
димо установить соответствие между геометрическими преобра-
зованиями репера и изменением координат вектора, определяю-
щего положение фиксированной в абсолютном пространстве
произвольной точки М относительно преобразованного репера.
1. Преобразование поворота
Пусть Е = (ё1ё2,ё3) - другой ортонормированный репер, на-
чало которого О совпадает с началом репера Е. Сформулируем
некоторые утверждения, доказательство которых предполага-
ется известным.
24 Глава J. Введение в динамику системы материальных точек без связей
1) Положение репера Е относительно репера Е может быть
задано квадратной матрицей А размера 3x3:
'А} а2 а3^
А= Aj А2 Af
A3 A2 A3
(1.3.3)
= (А-Х
где j - номер столбца, i - номер строки.
Элементы i-й строки определяют координаты орта ё, репера
Е относительно репера Е\
i = 1,2,3,
2) Матрица А - ортогональная матрица:
А4Т=ЛТЛ = /,
где АТ - транспонированная матрица А,
Ч О (Г
I = 0 1 0 - единичная матрица размера 3x3.
<0 0 1,
(1.3.4)
(1.3.5)
3) Координаты
гт = (г1,г2,г3)
(1.3.6)
вектора г относительно репера Е связаны с координатами г
относительно репера Е формулами
г=Аг, г = Атг (1.3.7)
(Аг - произведение матрицы А размера 3 х 3 на матрицу г раз-
мера 3x1), или в более подробной записи
__ 3 3 _
(1.3.8)
4) Для любых векторов х, у е /? 3
(Ах, Ау) = (х, у).
5) Для ортогональной матрицы
detA = ±1.
(1.3.9)
§ 1.3. Системы координат. Инерциальные системы координат
25
При detA = +1 реперы Е и Е называются ориентированны-
ми одинаково, а преобразование реперов Е—^>Е называется
преобразованием поворота (или собственным преобразова-
нием). Матрицу А в этом случае будем называть матрицей по-
ворота.
Преобразование поворота при А = I называется тождест-
венным (или единичным) преобразованием. При detA = -I пре-
образование называется несобственным.
6) Рассмотрим однопараметрическое семейство ортогональ-
ных преобразований, определяемых ортогональными матри-
цами
А(т) = (А/(т)), т е [а,₽], (1.3.10)
причем
А (ос) = I - единичное преобразование, А((3) = А - заданное
ортогональное преобразование.
Справедливы следующие теоремы:
а) если А - несобственное преобразование, то среди функций
Д/ (т), (т g [а, Р]) имеются разрывные;
б) всякое преобразование поворота А может быть получено
непрерывным (и даже гладким) изменением из единичного; при
этом гладкость преобразования определяется минимальным чис-
лом производных по т элементов матрицы А(т).
7) Произведение преобразований поворота есть снова пре-
образование поворота.
8) Пусть г - координаты вектора {г} g 7?3 относительно ре-
пера Е.
Рассмотрим соотношение
г' = Вг, (1.3.11)
где В - квадратная матрица размера 3x3.
Мы можем рассматривать г' как координаты вектора {г'}
относительно Е. Тогда (11) задает линейное преобразование
№ —> 7?3 векторов. При этом В - матрица этого преобразования.
Перейдем к другому реперу Е = (ej,e2,e3), определяемому
относительно Е матрицей А. Обозначим через г' и г коор-
динаты векторов г' и г относительно репера Е.
26 Глава 1. Введение в динамику системы материальных точек без связей
Так как г' = Аг' и г = Аг, (1.3.12)
то г' =АВг, г' =АВАтг. (1.3.13)
Формула (13) определяет то же самое линейное преобра-
зование векторов относительно репера Е. При этом матрица
этого преобразования X вычисляется по формуле
Х = АВА\ (1.3.14)
9) Пусть В - произвольная квадратная матрица, А - ортого-
нальная матрица того же порядка.
Рассмотрим матрицу X = АВАТ. (1.3.15)
Следом (Sp) произвольной квадратной матрицы называется
сумма ее диагональных элементов.
Утверждение. След матрицы X равен следу матри-
цы В. Докажем это утверждение. Распишем подробно условие
(5) АТА = I:
" Л <4 , [1, i =
2>’)М‘=2>Х=8,(= 0, itk
J=1 J=1 1
Запишем теперь выражение для следа матрицы X:
z=l /=1 J=1 k=l
= Ё Ё «IS л'^’х-Ё Ё «,Ч=Ё B»‘=spB. озяб)
j=l k=l i=l j=l k = l k=l
10) Определение. Если матрица поворота А изменяется с те-
чением времени А = A(t), то будем говорить, что репер Е вра-
щается относительно репера Е.
2. Преобразование параллельного переноса
Получим теперь закон изменения координат точки М, если
репер перенести в другую точку пространства О*, не изменяя
§ 1.3. Системы координат. Инерциальные системы координат
27
направления ортов (рис. 7). Обозначим
через ос вектор ОО*. Обозначим новый
репер = (еь е2, е3). Это преобразование
будем называть параллельным переносом
репера, определяемым вектором а.
Из рисунка легко получить, что ко-
ординатный вектор г точки М относи-
тельно репера Еа связан с координатным вектором г той же
самой точки М относительно репера Е простым соотношением
г = г- а,
(1.3.17)
где а - координаты вектора {а}относительно репера Е (или Еа).
В подробной записи:
— 1 1 1 —2 2 2 —3 3 3
г =г -ос, г =г -ос , г =г -ос ,
где (а1, а2, а3) = ат.
Определение. Если вектор а является функцией времени а (О,
то будем говорить, что репер перемещается поступательно
относительно репера Е.
3. Инерциальные системы координат
Пусть репер Еа получен из репера Е путем последователь-
ных преобразований поворота с матрицей А и парал-
лельного переноса на вектор а:
Е^-^Ё |а| >£а.
Пусть г - координаты произвольной точки М относительно Е,
г - координаты точки М относительно (проекции г -
-а на орты репера Еа),
а - координаты вектора а относительно (проекции а
на орты репера Еа).
Теорема. 1) координатные векторы гиг связаны соотно-
шением
г = Аг-й; (1.3.18)
2) соотношение (18) остается справедливым при изменении
порядка преобразований.
28 Глава 1. Введение в динамику системы материальных точек без связей
Докажем второе утверждение. Рассмотрим суперпозицию
преобразований
Е-^Еа~^Ёы.
Обозначим через а координаты вектора относительно ис-
ходного репера Е.
После первого преобразования получим:
г' = г - а, г' - координаты точки М относительно Еа.
После второго преобразования:
г = Ai7 = Аг- Аа.
Но Да = а-координаты вектора а относительно репера Еа.
Следовательно, доказано, что
г = Ar- а.
В общем случае, который мы будем рассматривать позже,
матрица поворота А и вектор а могут быть достаточно слож-
ными функциями времени.
Сейчас мы рассмотрим специальное семейство реперов, ко-
торое описывает так называемые инерциальные системы ко-
ординат.
Определение. Пусть репер Е определяет абсолютную систе-
му координат в Е3.
Будем говорить, что репер Еа определяет инерциальную сис-
тему координат, если:
1) матрицах преобразования поворота Е——>Е не зависит
от времени:
ИА
— = 0; (1.3.19)
dt
2) ускорение
^4 = 0. (1.3.20)
dt2
Из определения следует:
dcc/dt = v0 - постоянный вектор, а = v0(r - Го) + ао - по-
стоянный вектор, или в подробной записи
a1 =f7o(z-zo) + cco,...,ao -t0) + a20.
§1.3. Системы координат. Инерциальные системы координат
29
Иначе говоря, система координат движется, во-первых, по-
ступательно, а во-вторых, равномерно и прямолинейно относи-
тельно Е.
Теорема. Уравнения движения замкнутой системы мате-
риальных точек не изменяются при описании движения в любой
из инерциальных систем координат .
Доказательство. Уравнения движения имеют вид
т>^=£Г«- ‘=1.2....... (1.3.21)
f.j =(г«-I-j 11.,. ip.
t>kj =1 *k - rj l> Пу =1 v, - У J |, C = {rk - Vj, yk - v7. >.
Пусть
fk=Ark-oi, r; =Аг;-а, da I dt = v0 = const,
drk _ _ dfj
at at
Так как матрица А ортогональная, то для любых векторов х и у
имеет место равенство скалярных произведений:
<Ах, Ау) = (х, у).
Поэтому
I- vy Н A(Vi-vy)|= Г|у,
- Гу Л - Ъ- > = W* - «у), А(Ук ~ VJ)> = .
Умножим (21) на матрицу A (detA 0) и воспользуемся усло-
виями
— = 0, ^=о,
dt dt~
d2rk d2Ark d2 d2rk
mkA—r^mk—^^mk—T(Ark-a)^mk—^,
at dt dt dt
А(г,-г,.) = гЛ. -f,..
30 Глава 1. Введение в динамику системы материальных точек без связей
В результате получим
d2v п
= 1 (1.3.22)
at к=1
4. Однородность и изотропность пространства
Пусть (гг, mz), i = 1, 2,..., п - все материальные точки нашей
замкнутой системы, г, - координатные векторы, гщ - массы то-
чек. Применим ко всем координатным векторам преобразование
поворота с матрицей А и преобразование параллельного пере-
носа на вектор а, причем dA/dt = 0, dot/dt - 0. Тогда
i;. =Arz--a, i = 1,2,..., п. (1.3.23)
Теперь соотношению (23) дадим другую интерпретацию.
Под г мы можем понимать координаты точек системы отно-
сительно исходного репера Е, если все радиусы-векторы точек
повернуть вокруг начала координат и сдвинуть на постоянный
вектор -а.
Рассмотрим движение системы с координатами точек rk(f) и
скоростями уДО и движение системы с координатами точек гк (Г)
и скорости vk(t). Мы знаем, что преобразование (23) не изменяет
уравнений движения. Следовательно,
Так как уравнения движения обеих систем одинаковы, то во
все время движения
= |v*-vj = |v*-vj.
Таким образом, относительное движение точек в обеих си-
стемах протекает совершенно одинаково, хотя в этих двух про-
цессах оно происходит в различных областях абсолютного про-
странства.
Это свойство определяет изотропность пространства (не-
зависимость от переноса всей системы в другую область про-
странства путем поворота) и однородность пространства (не-
зависимость процесса от параллельного переноса всей сис-
темы).
§ 1.4. Основные законы механики и принцип относительности
31
§ 1.4. Основные законы механики
и принцип относительности Галилея
в модели замкнутой системы материальных точек
Чтобы не разрывать основную тему лекции, докажем сна-
чала два вспомогательных утверждения, которыми будем поль-
зоваться.
Лемма 1. Пусть/(х, у) - скалярная функция двух векторных
аргументов х, у G У?3, удовлетворяющая равенству
/(х,у)=/(Ах,Ау)
при произвольной матрице поворота А.
Тогда /(х, у) = /(| х |, | у |, (х, у)), где f - некоторая скалярная
функция указанных аргументов.
Доказательство. Матрица А определяет преобра-
зование координатных векторов при преобразовании ре-
перов
Е = (е1,е2,е3)—^—^Е =
Выберем репер Е так, чтобы орт был коллинеарен и
одинаково направлен с вектором х, а орт ё2 лежал в плоскости
вектора х и у. В этом случае
х = Ах =
У = Ау =
О
О
\ 7
где х'=|х|, у1 = (у,х)/1х| - проекция вектора у на орт е,,
У2 = д/l У |2 _(у')2 _ проекция вектора у на орт ё2.
Из вида х', у1 и у2 следует, что
Ж у) = /(%', у1, у2) = 7(| х |, | у |, (х, у».
Теорема. О структуре функций, инвариантных относительно
преобразований Галилея. ПустьДхь х2, у,, у2) - скалярная функ-
ция четырех векторных аргументов х,, х2, ун у2 е К.
32 Глава 1. Введение в динамику системы материальных точек без связей
Предположим, что равенство
/(х|5 х2, у,, у2) = ДАх, + а, Ах2 + а, Ау, + и, Ау2 + и)
выполняется при произвольных векторах а g R3, u е R3 и про-
извольной матрице поворота А.
Тогда
f = /(I Х1 - х2 U У1 - У2 Ь<Xj - х2,у, - у2»,
где f - некоторая скалярная функция трех указанных скаляр-
ных аргументов.
Доказательство. Положим а = -Дх2, и = -Ду2. Тогда
/(х19 х2, уь у2) = f(A(x} — х2), 0, А(у t -у2), 0), где Л - произвольная
матрица поворота. Согласно лемме 1,
/(А(Х] - х2),0, А(у] -у2),0) = Д| X! - х21,| у] - у21,<х, -х2,у1 - у2».
Основное содержание модели замкнутой системы мате-
риальных точек заключено в структуре уравнений движения
>2 11
F«=F- о-4-1*
= (Г* -rdfkj^kj^kj^ ^kj =1 rk ~rj \,-’fkj = fjk- G-4-2)
Сейчас мы докажем, что вид уравнений (1), (2) (структура
правых частей) может быть получен, исходя из некоторых об-
щих экспериментальных законов: принципа относительности Га-
лилея и принципа детерминированности.
1. Принцип относительности Галилея (ПО)
Существуют системы координат, называемые инерциаль-
ными и обладающие следующим свойством: все законы при-
роды во все моменты времени одинаковы во всех инерциальных
системах координат и все системы координат, движущиеся
относительно инерциальной поступательно, равномерно и пря-
молинейно, инерциалъны.
Для формулировки принципа детерминированности нам по-
требуется следующее определение.
Состоянием системы называется совокупность всех коор-
динат и компонентов векторов скорости материальных точек
§ 1.4. Основные законы механики и принцип относительности
33
системы:
rT =(г11,г12,г13,г21,...,гй3),
vT v/=^-, (1.4.3)
dt
teR3", veR3", R3n = 7?3x7?3x...xZ?3.
n
2. Принцип детерминированности (ПД)
Начальное состояние системы однозначно определяет даль-
нейшее ее поведение.
Лемма 2. Из принципа относительности и принципа детер-
минированности следует, что ускорение любой точки системы в
любой момент времени зависит от состояния системы и не зави-
сит от момента времени.
Доказательство. Из принципа детерминированности
следует существование однозначных вектор-функций
х 9f z
r = f(r-r0,r0,v0), V = — a-r0,r0,v0),
dt
f(O,ro,vo) = ro, =v0,
t-to
зависящих от момента времени t и состояния системы r0, v0 в
начальный момент времени г0.
Дважды дифференцируя функции f по времени, получаем
6?2r 92f — . Z1 .
-Т2=^2=Ф(*-*0’Г0’У0У (I-4-4)
dt dt
Запишем соотношение (4) при t = tQ:
d2r
= Ф(г0,у0), (1.4.5)
где
Ф(г0,у0) = Ф(О,го, v0).
Соотношение (5) определяет ускорение точек системы в мо-
мент времени t в зависимости от состояния системы в момент
3. М.Л. Лидов
34 Гпава 1. Введение в динамику системы материальных точек без связей
времени г0. Но законы природы, согласно принципу относитель-
ности, не зависят от момента времени. Отсюда следует спра-
ведливость (5) для произвольного момента времени:
d2v
—т = ф(г,у).
dt
Представим последнее векторное уравнение для г g R3n как
систему векторных уравнений для движений отдельных точек
системы:
d2r
^ = Ф(г,,г2,.VpV2,...,V„), (1.4.6)
к = 1,2,..., п, rk,vkeR3, ФкеК3.
Полученный вид системы уравнений (6) и доказывает ут-
верждение леммы 2.
Сформулируем теперь следующие эмпирические законы
(аксиомы), которые называются основными законами механики.
Первый основной закон (1-3) (закон инерции).
Всякое ускорение материальной точки определяется дейст-
вием других материальных точек.
Второй основной закон (П-З).
Две материальные точки сообщают друг другу ускорения,
направленные вдоль прямой, их соединяющей.
Третий основной закон (Ш-З) (закон действия и противо-
действия).
Для двух произвольных материальных точек произведение
массы первой точки на ускорение, сообщаемое ей второй точ-
кой, равно по величине и противоположно по направлению про-
изведению массы второй точки на ускорение, сообщаемое ей
первой точкой.
Четвертый основной закон (IV-3).
Ускорение, сообщаемое материальной точке (гу, всеми
другими точками системы, равно векторной сумме ускорений,
сообщаемых отдельными точками системы. При этом уско-
рение, сообщаемое каждой отдельной точкой, не зависит от
ускорений, сообщаемых другими точками системы.
§ 1.4. Основные законы механики и принцип относительности 35
1. Для дальнейшего анализа возьмем в качестве исходного
выражение (6) ускорения k-м точки системы.
Обозначим через
ускорение, сообщаемое точке к точкой j.
Из (1-3) и (IV-3) следует, что
>2 п
~^ = *.=Z«V <= = 1.2........» (1.4.8)
Первый закон гарантирует, что никаких других членов, кро-
ме ФЛуЧ сумма не содержит.
2. Из (IV-3) также следует, что если мы оставим в системе
только две точки к mJ (сохранив значения гь ry, vy), а осталь-
ные точки исключим из системы (иногда говорят: удалим их на
бесконечность), то значения функций ФЛу, ФуА не изменятся.
Рассмотрим систему, состоящую из двух точек к и j. В этом
случае
^ = ^/rt,ry,v„vy). (1.4.9)
3. Согласно (И-З), ускорение Ф^ может быть представлено в
следующем виде:
d-4-10)
где fkj - скалярная функция. Множитель (г* - гу) определяет пря-
мую действия ускорения.
4. Согласно ПО, законы природы и, в частности, ускорение
точки к в системе двух точек км j должны быть одной и той же
функцией состояния системы независимо от того, в какой из
инерциальных систем координат описывается движение.
Перейдем к описанию задачи в некоторой другой инерци-
альной системе координат.
Обозначим:
г*, у* и г-, у — координатные векторы положения и векто-
ры скорости точек к и j относительно новой системы координат.
3*
36 Глава 1. Введение в динамику системы материальных точек без связей
Как мы знаем, они связаны с гь..., соотношениями
г^=Агл+а, Гу=АГу+а, v^=Av^+u, Vy = AVy+u,
(1.4.11)
где ol и u = dot/dt - произвольные векторы (мы рассматриваем
все векторы в один момент времени), А - любая матрица по-
ворота
dA _ du _ Q
dt dt
Подставим соотношения (J 1) в (10). В результате получим
d2r _ _ -
А—4- = A(rk -r)fki(Ark + а, Ar- +а, Avk +u, Av, +u),
dt
(1.4.12)
или, так как detA Г 0,
= +a,...,Avy +и). (1.4.13)
Согласно ПО, необходимо, чтобы значение правой части (13)
при rk =гЛ, г7 =г., vk =Ук, v7 = Vy совпадало со значением пра-
вой части (10).
То есть необходимо, чтобы
fkJ(Afk+a,...,Ayj+u) = fkj(fk,fj,yk,yj). (1.4.14)
Используя (1.1.2), получим, что функция fkj должна иметь
следующий вид:
fkj (гл > rj ’Vk,Vj) = <№kj, И*, (1.4.15)
где
^kj =1 *k ~ r; k Пл,- =1 v, - уj |, ^kj = <rA -r,., Nk - Vj),
и ускорение точки к представимо в виде
d^r
5. Теперь воспользуемся (Ш-З). Запишем его содержание с
помощью уравнения
mk(rk-rj^kj^kj^kj^kj) = -mj(rj -П)ФлАЛ-Л./)- (1.4.16)
§ 1.5. Фазовое пространство
37
Мы воспользовались равенствами
I Гк - Г, I = I I,Г J И Т.Д.
Из последнего соотношения следует
mk<f>kj(£„ Т], О = Т], О- (1.4.17)
Обозначим:
(1-4.18)
Из (17) следует, что
fkj=fjk-
6. Вернемся к системе уравнений (8). Умножим левую и пра-
вую части (8) на тк и воспользуемся установленной структурой
функции ФЛу-. В результате получим
п
= Y -^fkj^kj^^ (1.4.19)
где к= 1,2,..., п, fkj=fjk.
Таким образом, доказана следующая теорема. Для замкну-
той системы п материальных точек вид уравнений движения (1),
(2) и в том числе структура правых частей уравнений (сил), опре-
деляются общими законами природы, установленными на осно-
вании физических наблюдений и экспериментов:
1. Принципом относительности Галилея.
2. Принципом детерминированности.
3. Основными законами механики.
§ 1.5. Фазовое пространство
Уравнения динамики замкнутой системы п материальных то-
чек можно записать в следующем виде:
— = F(r,v), (1.5.1а)
dt
— = v, (1.5.16)
dt
где
г' =(г|',г12.r„3), vT
v/=—re/?3", ve/?3".
dt
38 Глава 1. Введение в динамику системы материальных точек без связей
Такой же вид будут иметь уравнения и незамкнутой системы,
если внешние силы явно не зависят от времени.
Определение 1. Пространство R3n, элементами которого яв-
ляются векторы г, называется конфигурационным пространст-
вом.
Определение 2. Пространство №п - R3n х R3n, элементами ко-
торого являются векторы состояния системы (v, г), называется
фазовым пространством (рис. 8), а совокупность 6п координат
(v, г) - фазовыми координатами.
Рис. 9
Мы будем предполагать, что правые части (силы) таковы,
что на интервале времени Jt справедливы утверждения теоремы
существования и единственности для системы дифференциаль-
ных уравнений. Согласно этой теореме, если в момент времени
/0 g Jt заданы начальные условия г0, v0 то уравнения (1) опреде-
ляют единственным образом значения г, v для достаточно близ-
кого момента времени г. t g Jz, г = r(r - r0, r0, v0), v = v(Z - Zb, r0, v0)
Решение системы (1) определяет отображение T: Jt —» 7?6n, кото-
рое можно интерпретировать как движение точки фазового про-
странства r(r), v(r). Образ интервала Jt в R6n называется фазовой
траекторией. В силу единственности решения фазовые траекто-
рии не пересекаются.
Понятие фазового пространства - это общее понятие для
систем обыкновенных дифференциальных уравнений.
Введение самостоятельного понятия о конфигурационном
пространстве в механике связано со спецификой правых частей
уравнений (16).
Координатную часть движения г(0 можно рассматривать как
движение точки в конфигурационном пространстве R3n. Образ Jt
в R3n будем называть траекторией движения в конфигурацион-
ном пространстве.
Траектории в конфигурационном пространстве уже могут пе-
ресекаться (рис. 9). Однако исследование характеристик траек-
тории только в конфигурационном пространстве представляет
часто самостоятельный интерес при изучении различных явле-
§1.5. Фазовое пространство
39
ний. Если внешние силы явно зависят от времени, то уравнения
движения имеют вид (2):
— = F(r,v,r), (1.5.2а)
dt
— = v, (1.5.26)
dt
где правые части явно зависят от времени.
В этом случае можно применить искусственный прием, запи-
сав уравнения (2) в следующем эквивалентном виде:
dN т-/ \ dr 1 .
— = F(r,v,z), — = v, — = 1, tL = f0, (1.5.3)
dt dt dt ''-'° °
и использовать утверждения теоремы о единственности решений
применительно к системе (3).
В случае, когда правые части явно зависят от времени, теоре-
ма единственности решения верна только в пространстве 6п + 1
измерения, в так называемом расширенном фазовом про-
странстве.
Определение 3. Прямое произведение фазового пространства
и вещественной оси R времени t
R6n+i=R6n xR
называется расширенным фазовым пространством.
Определение 4. Расширенным конфигурационным простран-
ством R?n+[ называется прямое произведение конфигурацион-
ного пространства и вещественной оси R времени t
R3n+l=R3n xR
О движениях в подпространствах
Рассмотрим систему уравнений динамики точек в случае сил
парных взаимодействий, записанную покомпонентно:
т 2 z п
d Г, ;
= * = г = 1,2,3,
Этой системе уравнений, в частности, удовлетворяет некото-
рое решение, у которого для всех к = 1,2,..., п на интервале
40 Глава 1. Введение в динамику системы материальных точек без связей
времени Jt\
rk(t)=vk(t) = 0 и в общем случае
rk (t) Ф 0, v lk (t) Ф 0 при i = 1,2.
Такое движение происходит в плоскости г3 - 0 и называется
плоским или двумерным.
В случае плоского движения необходимо, чтобы в начальный
момент времени г0
r/(zo)=y/(zo) = 0' k = l,2,-,n.
В силу теоремы единственности решения системы дифферен-
циальных уравнений этих условий и достаточно, чтобы движение
было плоским.
Плоскость движения не обязательно должна совпадать с
плоскостью г3 = 0.
Если в начальный момент все векторы r/Z0) и v k(tG) при-
надлежат некоторой плоскости, то можно с помощью преобра-
зования поворота fk = Агк,чк = Avk перейти к системе координат,
в которой rk\tG) (70) = 0 (это упражнение).
Аналогично вводится понятие об одномерных движениях.
Если в начальный момент времени для к = 1, 2,..., п и i = 2, 3
= О и’ вообще, говоря, г^(^о)^О, ^(/о)^О, то дви-
жение системы будет происходить вдоль прямой г2 = г3 = 0 (оси
О А).
§ 1.6. Пояснения к физическому содержанию
некоторых понятий
Лучший способ объяснения физического смысла введенных
при описании модели понятий - это четко объяснить процедуру
их измерения (точнее, с удовлетворительной степенью прибли-
жения).
Однако это очень сложно и на начальном этапе изучения
механики сделать это без существенных упрощений невозможно.
Дело в том, что методы измерения очень больших или очень
малых интервалов времени, больших расстояний, масс и сил свя-
заны, в частности, с решением некоторых, достаточно сложных
задач механики и используют при этом ее постулаты. Поэтому
обсуждение этих вопросов лучше отложить до того, как будут
рассмотрены следствия, вытекающие из анализа механических
моделей.
Однако самые грубые пояснения для начальных представле-
ний дать необходимо.
§ 1.6. Пояснения к физическому содержанию некоторых понятий 41
Время
Пока можно принять обыденное представление о времени
как о величине, небольшие интервалы которой можно измерять
с помощью исправных часов (или хронометра), и, таким образом,
попытаться представить себе некоторые идеальные часы, позво-
ляющие измерять большие отрезки времени.
Надо понимать, что время (интервал времени) - это объек-
тивная характеристика, а не только вспомогательный параметр,
который служит независимой переменной в дифференциальных
уравнениях движения.
Пусть процесс описывается дифференциальными уравне-
ниями
d2r Л dr\ ( dr\
—х-= Ф г,— , где г,—
dt V dt) \ dt)
- состояние системы.
Если при наблюдениях этого процесса пользоваться в ка-
честве часов прибором, который показывает не время Г, а неко-
торую величину т(0, то по отношению к т движение системы бу-
дет описываться уже другими уравнениями:
d2r dr rz ч
^Т + ^7^(т) = ф
at at ’
dr Л
dt J
1
Л2(й’
/?2 7 \ Г Z \ d T Г 7 \ dr,
dt dt
и закономерности движения будут другими, если dr/dx и d2r/di?-
интерпретировать по-прежнему как скорость и ускорение.
Еще одно предварительное пояснение. В классической (нью-
тоновской) механике предполагается, что никакие процессы не
влияют на работу идеальных часов. В этом смысле говорят, что
«время в ньютоновской механике абсолютно».
Абсолютный (инерциальный) репер
Здесь необходимо пояснить два вопроса.
а) Для начала можно принять, что, находясь на Земле, мы по-
строим декартову систему координат, орты которой параллель-
ны ортам некоторой инерциальной системы координат, если они
взаимно ортогональны и сохраняют неизменную ориентацию
относительно далеких звезд. Если представить, что ось телеско-
па определяет направление орта е,- этой системы координат, то
телескоп необходимо вращать относительно Земли так, чтобы
звезды в поле зрения телескопа (на пластинке) не смещались.
42 Глава 1. Введение в динамику системы материальных точек без связей
б) Не всегда возможно указать, в какую точку надо по-
местить начало этой системы координат, чтобы она была заведо-
мо неподвижной или двигалась равномерно и прямолинейно
относительно абсолютной. Мы знаем, что система, связанная с
Землей, заведомо не инерциальна, хотя часто этим можно пре-
небречь.
Как мы поясним позже, инерциальные (абсолютные) систе-
мы координат - это удобное понятие для постановки задач
механики. Однако нас интересует движение тел друг отно-
сительно друга, а не относительно некоторой гипотетической
абсолютной системы координат. Оказывается, что эту задачу
(описание относительного движения) можно решить, либо не
выясняя, какая из систем инерциальна, либо в процессе решения
задачи найти точку, которая, с точки зрения модели и с точ-
ностью самой модели движется равномерно и прямо-
линейно относительно инерциальной системы координат.
Масса
Если мы будем описывать любой предмет, то мы можем
указать много его характеристик. Размеры, форму, вес в данном
месте Земли, материал, из которого он сделан, его температуру в
данное время и т.д.
Одной из таких наиболее важных для механики характерис-
тик является свойство каждого предмета (тела) обладать массой.
Из уравнений движения следует, что ускорение - это сила,
деленная на массу:
d2YIdt1 =Fa lmk.
Если сила задана и фиксирована, то ускорение тела с боль-
шей массой меньше. Так как свойство тела в отсутствие сил дви-
гаться равномерно и прямолинейно (без ускорения) называется
инерцией тела, то говорят, что масса есть мера инерции тела.
В основных моделях классической (ньютоновской)
механики масса тела не изменяется со временем, не зависит от
характеристики движения - это константа данного тела.
Если два тела, имеющие массы пц и тъ мы объединим в
одно, то его масса т будет равна сумме масс: т = + т2.
Из школьного курса физики известно, что массу небольших
тел можно измерять (сравнивать) по весу тела в данном месте на
Земле. Но не следует путать массу тела и вес тела. Наиболее
строгое содержание понятия массы в классической механике
следует из формального рассмотрения масс неизменяемых тел
как некоторых постоянных, входящих в уравнение движения, и
которые, как потом поясним, можно определить из наблюдения
за механическим процессом, в котором участвует данное тело.
§1.6. Пояснения к физическому содержанию некоторых понятий 43
Материальные точки
Иногда оказывается, что при рассмотрении системы взаимо-
действующих тел, при изучении основных закономерностей их
движения можно пренебречь протяженностью этих тел (или, как
мы покажем позже, следить за движением только одной точ-
ки тела, например его центра масс), но нельзя пренебречь
массой, содержащейся в теле. Идеализируя эту ситуацию, можно
иногда считать, что вся масса тела сосредоточена в точке. Так
в механике приходят к наиболее простой модели точечного
объекта.
При этом существенно протяженные тела оказывается удоб-
ным описывать в моделях как систему материальных точек.
На этом мы тоже остановимся в дальнейшем. Возможность
для описания данной физической задачи использовать мо-
дель материальной точки должна подтверждаться анализом за-
дачи.
О размерности физических величин
Указать значение физической величины - это значит, ска-
зать во сколько раз данная величина больше или меньше другой
аналогичной величины, принятой за единицу.
Например, длины векторов в R3 мы определяем в долях дли-
ны I ez I ортов ez .
Можно было бы договориться всегда во всех задачах прини-
мать в качестве ортов направленные отрезки, длина которых
равна определенному эталону длины. Так же, как мы догово-
рились, что система координат в R3 ортонормированная. Тогда
фраза «длина I г I вектора г равна 5» была бы общепонятной:
вдоль вектора г можно последовательно 5 раз отложить длину
основного эталона.
Однако это не всегда удобно. Поэтому, вообще говоря, при
указании, например, числа Н - координаты вектора г мы долж-
ны указывать величину L, определяющую длину ортов I ez I, и пи-
сать HL.
При указании интервала времени t - tQ мы должны, строго
говоря, писать
(/ - t0)T,
где Т - эталонный отрезок времени, по отношении к которому
определяются интервалы времени.
Аналогично при указании массы мы должны писать
тМ,
где М - масса эталона, принятого за единицу измерения массы.
44 Глава 1. Введение в динамику системы материальных точек без связей
Введенные три масштаба L, Т, М являют-
ся основными для механики.
Как правило, в качестве L принимают масштабы 1 санти-
метр, 1 метр,..., в качестве Т - 1 секунду, 1 год,..., в качестве М -
1 грамм, 1 килограмм и т.д.
Обычно в аналитических соотношениях не указываются
масштабы. Это можно делать только в случае, если принять
(договориться), что все величины, производные от основных,
измеряются в соответствующем масштабе, который вытекает из
соотношения, определяющего данную величину.
Пример. Обозначим через [v] - масштаб для координат
вектора скорости, а через v - координаты вектора скорости,
измеренные в этом масштабе. Тогда
V[v] = ^^ = — (LT~'Y
d(tT) dt
Если мы примем
[vJ = LT-‘, (1.6.1)
то соотношение
v = drldt
будет верно всегда при любом выборе масштабов длины и вре-
мени.
Условие (1) можно прочитать следующим образом: размер-
ность скорости равна размерности длины, умноженной на обрат-
ную величину размерности времени.
Аналогично легко получить, что размерность [w] ускорения
w равна:
[w] = LT-\
Размерность силы относительно основных масштабов выте-
кает из уравнений движения:
[F] =
J2r
т—
dt2
= MLT~2.
При таком выборе масштабов производных величин уравне-
ния, имеющие механический смысл, будут справедливы при лю-
бом выборе основных масштабов.
Заметим, что отношение двух величин одинаковой размер-
ности есть величина безразмерная.
Пример. Отношение длин двух векторов:
§1.6. Пояснения к физическому содержанию некоторых понятий 45
Сравнивать можно только величины одинаковой размернос-
ти, так как для величин разной размерности справедливость не-
равенств «больше» («меньше») зависит от основных масштабов.
Исходные данные часто задают в различных единицах изме-
рения. При решении задач прежде всего следует привести все
исходные данные к единой системе единиц измерения L, Т, М.
После этого можно решать задачу, не следя за размерностью, и
написать размерность только в ответе.
Если некоторое соотношение, имеющее физический смысл,
есть сумма нескольких слагаемых + х2 + ... + то размерность
каждого слагаемого должна быть одинаковой. Это можно
использовать для контроля формул.
О силах парного взаимодействия
Многие общие свойства движения механической системы
можно получить, только исходя из того, что действующие силы
имеют вид сил парных взаимодействий
Г/ = (г* -г>)Л/<1 гл -G 1’1 -Vj\^k-rj^k-y^,
или из рассмотрения тоже достаточно широкого (и наиболее
часто встречающегося в приложениях) класса сил, когдаД не
зависят от векторов скоростей точек:
^kj=(rk-rdfkj(\rk -г/|)
при произвольных Д(^). В природе, однако, силы взаимодействия
(функции Д) имеют вполне конкретный вид. Вид сил устанавли-
вается из физических наблюдений и формулируется как общий
закон природы. Иногда тоже из наблюдений и эксперимента
устанавливается закон для сил, имеющий более частный ха-
рактер.
Одним из наиболее важных для механики и наиболее универ-
сальных является закон всемирного тяготения. Этот закон был
установлен Ньютоном на основе изучения движения Луны и
планет.
Закон гравитационного взаимодействия
Любая материальная точка (r7, т;) притягивает материаль-
ную точку (гь т*) с силой, величина которой пропорциональна
произведению масс точек и обратно пропорциональна квадрату
расстояния между ними, и направленной по прямой, их соеди-
няющей.
46 Гпава 1. Введение в динамику системы материальных точек без связей
Эта формулировка в векторном виде записывается следую-
щей формулой:
(1А2)
Г.,-г*1
где/- коэффициент пропорциональности, называемый гравита-
ционной постоянной. Его размерность определяется соотноше-
нием (2):
[f] = L3T~2M-\
При L = 1 см, Т = 1 с, М = 1 г
/ = 6,67-1 О*8.
Существенные следствия, полученные из закона всемирного
тяготения, опираются на следующее его уточнение:
Никакие тела или поля не нарушают
взаимодействие точек по закону (2).
Упругие силы
Другой пример сил парных взаимодействий носит существен-
но более частный характер.
Рассмотрим одномерное движение точек вдоль прямой, опре-
деляемой ортом в! (рис. 10):
—•JVW-eJV\V- - - -
т\ т2 т,,~\ тп
Рис. 10
Предположим, что точки соединены пружинами, массой ко-
торых можно пренебречь. В моделях такого типа часто для опи-
сания движения точек предполагают, что силы подчиняются за-
кону упругого взаимодействия. При этом силы упругого взаимо-
действия определяются следующими формулами:
KJ=bkj^k~rj) 1-
(1.6.3)
для (k -j)2 = 1
И
Fv = 0
ДЛЯ (fc-j)2> 1,
где bkj - bjk > 0 и akj = ajk > 0 - постоянные величины, характе-
ризующие свойства пружин.
§ 1.7. Задача п тел. Солнечная система
47
Можно показать, что уравнения движения точек под влия-
нием сил упругого взаимодействия есть система линейных диф-
ференциальных уравнений с постоянными коэффициентами.
§ 1.7. Задача п тел. Солнечная система
Уравнения движения и состояние исследования
Рассмотрим замкнутую систему п материальных точек, взаи-
модействующих по закону всемирного тяготения.
Уравнения движения такой системы имеют вид
d\ V 17 7 1О 717П
аТ j=\ I rj rk I
Это Зп уравнений второго порядка.
Общее решение этой системы уравнений в виде анали-
тических формул можно получить только при п = 2. Это знаме-
нитая задача двух тел. Ее решение является основой небесной
механики, динамики космического полета и некоторых физи-
ческих теорий. В этом курсе мы рассмотрим данную задачу
достаточно подробно.
При п = 3 задача называется задачей трех тел. Эта задача на
протяжении нескольких столетий привлекала и привлекает вни-
мание известных математиков и механиков мира. В задаче трех
тел привлекательна простота постановки, важность ее для
объяснения закономерностей движения небесных тел и некото-
рых проблем микромира и ее сложность, которая выявлена в
процессе многих исследований. С помощью качественного ана-
лиза и вспомогательных вычислений получено много резуль-
татов. Однако и в настоящее время про задачу трех тел нельзя
сказать, что она полностью исследована, хотя о ней написаны
многие тома.
При п > 3 об общих свойствах решений уравнений (1) изве-
стно мало. При этом в зависимости от начальных условий и
соотношений между массами материальных точек можно раз-
личать более сложные и более простые случаи движения точек в
этой задаче.
В сложных случаях (изучение таких случаев необходимо для
описания закономерностей в звездной динамике) точки примерно
одинаковых масс (масс звезд или галактик) движутся неупо-
рядоченным образом.
В более простых случаях (к счастью для человечества, к ним
относится задача, которая моделирует движение планет в Сол-
48 Глава 1. Введение в динамику системы материальных точек без связей
нечной системе) движение сравнительно упорядочено. Решение
задачи п тел с высокой точностью описывает движение центров
масс планет и их спутников относительно Солнца.
Движение планет в Солнечной системе
Траектория движения каждой планеты (ее орбита) прибли-
женно представляет собой эллипс (рис. 11), в одном из фокусов
которого расположено Солнце (точнее,
центр масс Солнца). В таблице собраны не-
/ которые характеристики планет и их орбит:
/ Xх I массы планет т, их характерные радиусы
( ) (все планеты по форме близки к сферам) и
/ их средние расстояния от Солнца ос. При
---этом массы планет будем измерять в долях
Рис> 11 массы Земли т©, радиус в долях характер-
ного радиуса Земли /?©, а среднее расстояние
в долях среднего расстояния ос© Земли от Солнца. В привычных
нам абсолютных единицах измерения:
т© = 6-1027 г, Я© = 6378 км, ос© = 150-106 км.
Дополнительно в таблице указаны приближенные значения
масс и радиусов Солнца, Луны и среднее расстояние Луны от
Земли.
Эксцентриситеты е невелики; для большинства планет они не
превосходят 0,1 (для Меркурия е = 0,2; для Плутона е = 0,25).
За исключением Меркурия и Плутона плоскости соответ-
ствующих эллипсов составляют с плоскостью орбиты Земли
угол, не превосходящий 3°,5.
Таблица
Масса Радиус Среднее расстояние
Меркурий 0,05 0,38 0,39
Венера 0,81 0,95 0,72
Земля 1 1 1
Марс 0,11 0.53 1,52
Юпитер 318 ~11 5,2
Сатурн 95 ~9 9,5
Уран 14,6 ~4 19,2
Нептун 17,2 ~4 30,1
Плутон 0,03-0,2 0,34 39,4
Солнце 333000 100 0
Луна 0,012 0,27 384000 км
(от Земли)
§ 1.7. Задача п тел. Солнечная система
49
Следует подчеркнуть, что планеты только приближенно дви-
жутся по эллипсам. В более точном описании их движение су-
щественно сложнее, эксцентриситеты аппроксимирующих траек-
торию планет эллипсов, наклоны их плоскостей и другие пара-
метры очень медленно, но изменяются с течением времени.
Планеты имеют естественные спутники, которые обращают-
ся около своей планеты, как планеты обращаются вокруг
Солнца. Массы спутников обычно много меньше масс их пла-
неты. Луна - это относительно самый большой спутник.
Специфика задачи п тел в случае Солнечной системы
Сравнительная простота решения задачи п тел при описании
движения планет (это достаточно сложная задача, изучением
которой занимается небесная механика) связана с тем, что:
1) масса одной точки - Солнца - в 1000 раз превосходит самую
большую из остальных масс - Юпитер, 2) в процессе движения
планеты не сближаются друг с другом. Оказывается, что при
приближенном описании можно в правых частях уравнений
движения к-й планеты учитывать только ее взаимодействие с
Солнцем и пренебрегать влиянием на нее остальных планет. Тем
самым в первом приближении задача сводится к задаче двух тел
Солнце - планета, которую, как было отмечено, умеют решать
аналитически. Так и делают. Но такое упрощение может дать
лишь грубое описание движения. Для более точного решения
задачи используют методы теории возмущений. В теории возму-
щений разработаны методы, с помощью которых последова-
тельно уточняют решение задачи на ограниченных интервалах
времени (порядка сотни лет). Сейчас мы можем предсказывать
положение планет относительно Солнца с точностью порядка
1 угловой секунды (-1/200000 расстояния).
В последнее время с появлением больших электронно-вы-
числительных машин движение планет вычисляют и с помощью
численного интегрирования системы уравнений, описывающих
их движение.
Об относительном движении системы материальных точек
Докажем сначала одну лемму. Пусть на материальную точку
(гь mJ действует внешняя сила гравитационного притяжения
F‘W = >‘mjT^p “7-2)
со стороны материальной точки массой т, удаленной на очень
большое расстояние I г I от начала координат.
4. М.Л. Лидов
50 Глава 1. Введение в динамику системы материальных точек без связей
(1.7.3)
(1.7.4)
(1.7.5)
(1.7.6)
(1-7.7)
Получим формулу для асимптотического представления си-
лы (2).
Лемма. Пусть I rk 1/1 г I = 8, где 8 > 0 - достаточно малая вели-
чина. Тогда справедливо представление
где
F,=-^-(f0+f,+a).
|г |
г
f0 =----единичный вектор,
lrl
f =3—1—
|г|\|гГ|г|/ |r|’
|f,|=O(£), a = O(e2).
Доказательство.
Очевидно,
-- ( / r r \ Ir И
|r-rA |“3= (|г |2-2<г,г^>+|га|2) 2 =|г|-3 1-2 21-,-M + b-L
I \|г| |г|/ |r| J
где
ЧгИ1 + з/^,-54 + аД
I \|г | |г I/ J
OCj = О(82).
(1.7.8)
Подставим (8) в (2) и получим
После перемножения выражений в скобках получим форму-
лу для FAk) в виде (3), (4).
Замечание. Сила FA(£>) может быть и не мала, так как масса
может быть очень большой.
Следствие. Пусть материальные точки (rA., mJ, к =
= 1,2,..., п, находятся в окрестности начала координат внутри
сферы радиуса R.
( R А
Рассмотрим теперь случай, когда I г I —> <*>-> 0 , m —>
§ 7.7. Задача п тел. Солнечная система
51
так, что
остается конечной величиной. Тогда
IT Jljl.
m, |r|2|r|'
(1.7.9)
Мы получили, что предел ускорения, вызываемого беско-
нечно удаленной гравитирующей точкой (г, т) бесконечно боль-
шой массы, одинаков для всех материальных точек, распо-
ложенных внутри сферы радиуса R, и не зависит от их поло-
жения и скорости.
Рассмотрим теперь систему уравнений, описывающих движе-
ние п материальных точек относительно инерциальной системы
координат Е под действием гравитационных сил парного взаимо-
действия и внешних сил FA(<?):
тк -р- = L^m/i1. _r |3+F* • (L710)
J=1 Iг/ гк I
Предположим, что внешние силы F^(e) представимы в виде
где ускорение F не зависит ни от координат, ни от скоростей то-
чек системы. В случае таких внешних сил говорят, что на систе-
му действует однородное поле сил.
Перейдем к описанию движения системы материальных то-
чек относительно репера = (еь е2, е3), начало которого сдви
нуто на вектор а, а орты параллельны ортам исходного ре-
пера Е.
При этом координаты материальных точек гк относительно
репера будут определяться формулами
гк=гк-а, гк=гк+ а, к = 1,2,...,я.
Выберем теперь вектор а так, чтобы начало репера совпа-
дало постоянно с точкой (rb mj), т.е. положим а = rt.
В этом случае
^=0, гЛ=гЛ-г}, к = 2,3,..., я.
Разделим уравнение (10) на тк и подставим гЛ=гЛ + гР В ре-
зультате получим
_j2~ j2 Т* _Г
—^ + -^ = £>у-^-5- + Р, к-2,3, (1.7.11)
dt' dt “ •' г,-г
4*
52 Глава 1. Введение в динамику системы материальных точек без связей
где
—у- = > fm Ц- + F.
Л2 # 7|rJ3
d2r
Подставим —d- в (11). После несложных преобразований бу-
dt
дем иметь
Полученные уравнения будем называть уравнениями отно-
сительного движения задачи п тел.
Сформулируем некоторые выводы.
1. Система уравнений (12) относительного движения замкну-
та - число уравнений совпадает с числом неизвестных.
2. Число переменных на 6 единиц меньше, чем в исходной
задаче (не входят г /г), v/r)).
3. Система уравнений (12) полностью описывает движение
п - 1 материальных точек относительно произвольной точки
системы (в качестве последней мы выбрали точку (rb mJ). Если
известны фазовые координаты rkrvk, к - 2, 3,..., п на момент
времени г0, то решение системы (12) позволяет однозначно опре-
делить фазовые координаты в произвольный (по крайней мере,
достаточно близкий к г0) момент времени t.
4. Относительная система координат не инерциальна, ее ор-
ты параллельны ортам некоторой инерциальной системы коор-
динат, но начало движется относительно инерциальной системы
координат достаточно сложным образом, а не равномерно и
прямолинейно.
5. Правые части системы уравнений (12), кроме сил парных
взаимодействий, содержат дополнительные члены, обусловлен-
ные неинерциальностью системы координат. Эти члены полу-
чены в результате формальных преобразований.
6. Относительное движение не зависит от ускорения F (на-
помним, что оно одинаково для всех точек), которое сообщают
внешние силы точкам системы. В частности, отсюда следует, что
из наблюдений за относительным движением материальных то-
чек нельзя определить их движение относительно инерциальной
системы координат, так как движение относительно инерциаль-
ной системы координат зависит от величины и направления
вектора F.
7. Пусть (Г1, тх) - материальная точка, моделирующая
§ 1.7. Задача п тел. Солнечная система
53
Солнце, a (г,-, mz), j = 2, 3,..., п - планеты. Так как тх > mh то
члены, стоящие в (12) под знаком суммы, оказываются суще-
ственно меньше первого члена в правой части (12). Используя
данные, приведенные в таблице 1, можно формально оценить от-
ношение модулей этих членов. Для планетной системы оказы-
вается, что это отношение имеет величину порядка 10-3.
Поэтому движение к-й планеты относительно Солнца в
первом приближении описывается уравнениями
d\ г/ , ч
Эти уравнения называются уравнениями относительного дви-
жения в задаче двух тел (Солнце - к-я планета).
8. Если тх > то
d\ г П £ ткт\ -
Тем самым приближенно систему ЕГ1 можно считать инер-
циальной.
Прямая и обратная задачи динамики.
Определение начальных данных и масс планет
Будем рассматривать планетную систему как систему грави-
тационно взаимодействующих материальных точек. Пусть из-
вестны массы планет и Солнца тх, т2, ... , тп, относительные ко-
ординаты гк и компоненты векторов скорости v2 = dr2I dt,...,
Nn = drnldt в момент времени r0. Для определенности можно
считать, что начало координат связано с центром масс Солнца.
Этих данных достаточно для однозначного определения отно-
сительных координат и компонентов вектора скорости в про-
извольные достаточно близкие к Го моменты времени t. Для
этого можно использовать приближенные методы определения
решения системы уравнений (12), о которых говорилось выше,
или, например, методы численного интегрирования.
Определение /.Определение фазовых координат в момент
времени t при заданных массах, силах и начальных условиях
называется прямой задачей динамики.
Определение 2. Обратной задачей динамики называется за-
дача определения начального состояния системы, вида сил (или
их уточнение) по наблюдениям за движением системы.
Поясним последнее определение на примере задачи о движе-
нии планет. Предположим, что мы не сомневаемся в справедли-
вости закона всемирного тяготения, но не знаем начальных ус-
ловий для движения планет и не знаем масс планет. То есть мы
54 Глава 1. Введение в динамику системы материальных точек без связей
не знаем 7и - 6 постоянных: 3(и - 1) относительных координат
планет, 3(п - 1) компонентов их векторов скорости в какой-либо
фиксированный момент времени г0 и п значений масс планет и
Солнца.
Находясь на Земле, с помощью телескопов можно измерять
угловое положение планет относительно звезд. Несколько упро-
щая задачу, будем считать, что в моменты времени th
i = 1,2,..., N, мы измеряем компоненты единичных векторов
= (1-7.13)
где fk - координаты центра масс к-й планеты, г@ - координаты
центра масс Земли (напомним, что система координат связана с
центром масс Солнца).
В современных условиях с помощью средств радиолокации
можно измерять и расстояние от Земли до некоторых планет
ft(O=l^-f®l- (1-7.14)
Если мы зададим массы планет ть к - 1, 2,..., п, и
состояние планетной системы на момент t0: г° = гЛ(г0), vf = vk(t0),
то, решая уравнения движения с помощью методов, о которых
говорилось выше, мы можем вычислить значения координат
планет в произвольный достаточно близкий момент времени t
= (1.7.15)
и определить разности расчетных akvac(ti), ft рас(^) и измеренных
aA1BMft,), ft изм(б) значений параметров аА.(г,), ft ft,):
^'ki = I «А pact',') * «А изм (',) L 4 = I ft раЛ ) " ft изм ) I •
Эти разности будут зависеть от того, какие значения при расчете
были приняты для начальных данных и масс планет.
Можно решить задачу о выборе таких начальных данных
rf,vk и таких значений масс тк, чтобы разности Д^,Д^ были в
определенном смысле наименьшими.
Так как обычно число измерений N много больше числа
неизвестных параметров "1п - 6, а с другой стороны, все изме-
рения производятся со случайными ошибками, то для решения
такой задачи используются статистические методы обработки
наблюдений.
Если отвлечься от существенных для решения задачи, но не
принципиальных для ее понимания деталей, то можно утверж-
дать, что именно таким путем и были определены массы планет
и начальные условия их движения. Пусть эта задача решена.
§ 1.7. Задача п тел. Солнечная система
55
Даже в самом полном решении поставленной задачи рассогла-
сования Дд7 ,Дд7 не будут равны нулю. Этому мешают случайные
ошибки измерений. Методы математической статистики поз-
воляют путем предварительного анализа задачи указать интер-
валы, которым с определенной (большой) вероятностью должны
принадлежать средние значения Д^.
предположении, что наша динамическая модель, описывающая
движение, правильная.
Если Дд7,Д^, полученные в результате решения задачи, по-
падают в предвычисленные интервалы, то это является практи-
ческим подтверждением правильности динамической модели.
Если, наоборот, фактические рассогласования (их средние
характеристики) существенно больше ожидаемых, то это являет-
ся сигналом о неточности механической модели, которую мы
использовали при решении задачи.
Это случается довольно часто в процессе различных иссле-
дований. В большинстве случаев оказывается, что необходимо
уточнить модель, учесть некоторые силы, которыми при опи-
сании модели пренебрегали. И обычно такое уточнение модели
приводит к разумным результатам.
Но иногда (это случается чрезвычайно редко) оказывается,
что надо пересмотреть основные предположения, заложенные в
модель движения. Такие уточнения модели являются великими
открытиями. Невозможность согласования результатов измере-
ний со значением измеряемых величин, предсказанных с по-
мощью модели классической механики, в некоторых экспери-
ментах привела к созданию специальной и общей теории отно-
сительности и совершенно новой механики микромира - кван-
товой механики.
Задача о пассивном полете космического аппарата
Рассмотрим систему уравнений, описывающую движение
Солнца, планет и их спутников:
rV Г/-ГА /1 7
‘^ = /^ ‘ ( *
где rk - координаты центра масс £-го тела:
56 Глава 1. Введение в динамику системы материальных точек без связей
Предположим, что нас интересует движение космического
аппарата массой т, выведенного на траекторию полета, напри-
мер, Земля - Марс. Пусть это движение совершается только под
действием гравитационного притяжения. То есть у нас появ-
ляется (п + 1)-я материальная точка. Обозначим через г радиус-
вектор космического аппарата.
Если действовать формально, то мы должны в правую часть
уравнений (16) прибавить силы cpk притяжения к-н планеты
космическим аппаратом
«р* = ^тк |Г Гр
lr~rJ
и написать дополнительно уравнения движения космического
аппарата под действием притяжения планет
</2r rj~r НИЪ
m—T = 2Jfinmj---------у. (1.7.17)
M J=l |r/-r|
Однако, так как масса космического аппарата очень мала по
сравнению с массами планет, заранее ясно, что влиянием косми-
ческого аппарата на движение планет можно пренебречь и поло-
жить
срк = 0, к = 1,2,..., п.
Можно и формально оценить ошибки в ускорении fc-й пла-
неты за счет такой операции. Они окажутся ничтожными. То
есть ситуация, которая сейчас описывается на конкретном при-
мере, полностью повторяет рассуждения, которые мы проводили
при определении незамкнутых систем.
При <рк =0, к = 1,2,..., п, решение системы (16), описываю-
щее движение планет и Солнца, может быть получено незави-
симо от движения космического аппарата.
В настоящее время эта задача решена, и мы можем считать
г- (г), j - 1,2,..., п, известными функциями времени.
Тогда для решения задачи о движении космического аппа-
рата необходимо решить три уравнения (17) второго порядка.
Мы пришли к задаче о движении одной точки под действием
внешней силы F^(r, г), где через мы обозначили правую
часть уравнений (2). Явная зависимость от времени входит в пра-
вую часть после подстановки вектор-функций r/ (г), j - 1,2,..., п,
определяющих радиусы-векторы планет.
Следует отметить, что и в настоящее время движение планет
уточняется.
§ 1.7. Задача п тел. Солнечная система
57
Потенциал. Консервативные системы
Замечание о векторной записи производных от скалярной
функции по векторному аргументу.
Пусть /(х) скалярная функция векторного аргумента хт =
= (хх,х2.....хп\ Через Э//Эх будем обозначать вектор-строку:
JL=fJL JL JO
Эх О?’Эх2’""’Эх"/
Соответствующий вектор-столбец будем обозначать так:
f J0
Эх1
Э/
OxJ
Используя задачи о движении планет и движении космиче-
ского аппарата, поясним некоторые важные для всего курса ме-
ханики понятия.
Рассмотрим скалярную функцию
г г/ \ V V
0ri’r2’-’r«h-Xz I—Л’
,/=и>; Ir, -rd
где гк е /?3, к = 1, 2,п.
Дифференцируя {/по гк, получим
(1.7.18)
(1.7.19)
dU dU_ dU _
’ dr? ’ Эг3 '
Упражнение. Вывести формулу (19), вычисляя
Из сравнения (19) с правой частью уравнений движения п тел
видно, что система уравнений задачи п может быть записана в
следующем виде:
k = l, 2,...,n.
mk
dt2
Jr*,
(1.7.20)
58 Глава 1. Введение в динамику системы материальных точек без связей
Рассмотрим теперь скалярную функцию
где г • (г) - известные функции времени.
Дифференцируя Ux по г, получим
и уравнения движения космического аппарата могут быть запи-
саны в следующем виде:
В общем случае движение незамкнутой системы п материаль-
ных точек описывается системой уравнений
>2
тк—i = K(z) + F<e), к = 1,2,п,
к dt2 к к
где - результирующая сила, действующая на точку к со сто-
роны остальных точек системы; F?'* = F^e) (i\, vk, z) - результи-
рующая внешних сил, действующих на к-ю точку.
Определение 1. Если существует скалярная функция =
= , г2,..., г„), зависящая только от координат точек системы
(и не зависящая от их скоростей), такая, что результирующие
внутренних сил представимы в виде
(диЩ
, к = 1,2,...,п,
(1.7.22)
то говорят, что внутренние силы системы п материальных точек
имеют потенциал U^.
Определение 2. Если все внешние силы F^ могут быть пред-
ставлены как
(
I дгк ;
, к = 1,2,...,п,
(1.7.23)
§ 1.7. Задача п тел. Солнечная система
59
где , г2,г/?) - скалярная функция только коорди-
нат точек системы и времени, то говорят, что внешние силы
имеют потенциал U .
Определение 3. Если существует потенциал и для внутренних,
и для внешних сил, то система называется потенциальной.
Определение 4. Если система потенциальна и потенциал
внешних сил явно не зависит от времени, то система называется
консервативной.
Как мы показали в начале параграфа, задача о движении
п тел консервативна. Задача о движении космического аппарата
потенциальна, но не консервативна.
Теорема. Для того чтобы внутренние силы системы п
материальных точек имели потенциал, достаточно, чтобы все
силы парных взаимодействий Fkj не зависели от скоростей точек
системы.
Доказательство. Если все силы Fkj не зависят от ско-
ростей точек системы, то
F^) = S(r*-rj4(lr*-rJ)’
7 = 1
fkj = fjk ~ скалярная функция.
Рассмотрим функцию
I rk ~ г/ I
с1-7-24)
7 = 1 m > j о
Используя несложно доказываемое равенство
путем непосредственного дифференцирования (24) получим
Следствие. Если система замкнута и силы парных взаи-
модействий не зависят от скоростей точек системы, то система
консервативна.
60 Гпава 1. Введение в динамику системы материальных точек без связей
§ 1.8. Элементы теории притяжения
и некоторые оценки гравитационных ускорений
1. Гравитационное взаимодействие тел
Диаметр Солнца 1,4 млн. км. Диаметр Земли около 13 тыс. км.
Следует объяснить, почему эти тела в динамической модели
можно рассматривать как материальные точки и при этом полу-
чать хорошее согласие теоретических предсказаний с наблю-
дениями.
Для этого необходимо познакомиться с некоторыми резуль-
татами теории притяжения. В частности, наше рассмотрение по-
может уяснить и физический смысл абстрактного понятия мате-
риальной точки.
О протяженных телах
До настоящего времени основным объектом механической
модели была материальная точка. Сейчас необходимо ввести
понятие о протяженных телах.
Будем говорить, что в ограниченной области (рис. 12) V G R3
Рис. 12
Рис. 13
расположено тело с непрерывным распределением массы,
если: 1) существует ограниченная интегрируемая функция р(г),
[р(г)^О при г eV, р(г) = О при r£V]; 2) масса m(U), содержа-
щаяся в любой подобласти U с V, определяется интегралом
m(l7) = J||p(r)JV, (1.8.1)
и
где dV = dr1 dr1 dr3 - элементарный объем в R3.
Функция р(г) называется плотностью распределения массы
(или просто плотностью). Из интегрального исчисления извест-
но, что интеграл (1) со сколь угодно малой погрешностью можно
аппроксимировать суммой (рис. 13)
§ 1.8. Элементы теории притяжения и гравитационные ускорения 61
m(U)= ^р(г;)|А1/. | + Olmax|AV;. |2 , (1.8.2)
ДЦ-et/ ' 1 '
где | AV-t | - объем АЦ, AV< n AVy = 0 при i Ф j, г, е AV<. Тем са-
мым распределение массы в теле, расположенном в области V,
можно с любой степенью точности аппроксимировать системой
конечного числа материальных точек (rz, Ат-), где
г, е AV<, Amz- = р(гг-) | AV<1.
Такая аппроксимация в свою очередь позволяет различные
понятия, определенные для системы материальных точек, пере-
нести на случай тел с непрерывным распределением массы. Если
некоторая величина Ф определяется для произвольной системы
п материальных точек в виде суммы
/ = 1
то для случая непрерывного распределения массы
ф=Я]7(гл,..м
V
Этим мы будем часто пользоваться. Заметим, что p(r)dV будем
иногда обозначать dm и называть элементарной массой.
Если плотность р(г) известна, то для вычисления массы тела
т необходимо вычислить интеграл
dm = JJJp(r)dV, (1.8.3)
V V
где dV - элементарный объем так же, как и в (1).
Аналогично нетрудно получить координаты г центра масс
тела, т.е. центра масс системы материальных точек, образующих
{аппроксимирующих) тело:
г" = — У rdmt = — f f f rp(r) dV. (1.8.4)
m ; 1
1 v
Притяжение материальной точки телом
Пусть вне области V (рис. 14) расположена материальная точ-
ка (i-j , mJ. По закону всемирного тяготения сила притяжения ма-
териальной точки (r^mj со стороны элементарной массы
62 Глава 1. Введение в динамику системы материальных точек без связей
(г. dm) равна
V \ Г — Г
) d F = dm--------Ц-.
Z Ir - ri I
r* Результирующая сила гравитацион-
Рис. 14 ного притяжения точки со сторо-
ны всех элементарных точек (г, dm), образующих тело, опреде-
ляется интегралом
V V Iг Г1 I
dV.
(1.8.5)
В общем случае интегралы (5) нельзя выразить через эле-
ментарные функции. Сейчас мы укажем один частный, но важ-
ный случай.
Теорема 1. Масса т, распределенная в шаре со сферически-
симметричной функцией плотности, притягивает материальную
точку (г,,mJ, расположенную вне шара (рис. 15), как ма-
_________ териальная точка массой т, расположен-
/ ная в 4eHTPe шаРа г •
\ fl Обозначим £=r-r\ £,eR3, где г -
\ w А^ J / радиус-вектор центра шара. Для сфериче-
\ / ски-симметричной функции плотности
гт’ш =
// fff Ir г'|3
(1.8.6)
Рис. 15 ТЛ
Индексом «т.ш» мы отмечаем, что рас-
сматривается сила, действующая на материальную точку со сто-
роны шара. Последний интеграл можно вычислить. В результате
получим
FTJ" = Г ~Г| 3 . (1.8.6')
|r*-ri|
Упражнение 1. Вычислить интеграл (6).
Указание. Из соображения симметрии очевидно, что
FT ш = (г * - г J / (г* - г J, где /- скалярная функция.
Упражнение 2. Доказать, что центр масс шара со сферически-симметрич-
ным распределением плотности совпадает с центром шара, т.е. доказать, что
§ 1.8. Элементы теории притяжения и гравитационные ускорения 63
т ШГ₽^Г^У = Г*’
V
Указание. Использовать соображение симметрии.
2. О гравитационном потенциале тела
Из интегрального представления (5) силы F притяжения те-
лом материальной точки расположенной вне тела, сле-
дует, что силу F можно представить как производную по век-
тору rt от следующей скалярной функции:
F = -т1
''др
<Эг1>
(1.8.8)
Последнее соотношение проверяется дифференцированием
(5) по Ej под знаком интеграла.
Функция U( Ej) называется гравитационным потенциалом
тела во внешней точке.
В частности, гравитационный потенциал шара со сфериче-
ски-симметричным распределением плотности имеет вид
ит=--. ,. (1.8.9)
lri-rl
Упражнение. Докажите это утверждение.
Теорема 2. Об асимтотике потенциала тела на больших рас-
стояниях. Обозначим: г"5 - радиус-вектор центра масс О тела
(рис. 16), Я-минимальный радиус сферы с центром в О, содер-
жащей внутри себя тело. Радиус-вектор г
произвольной точки тела представим в ви-
де суммы
Г = Г* +|.
Запишем потенциал в следующем виде:
(1.8.10)
dV.
Согласно определению R, | £, | R.
64 Глава 1. Введение в динамику системы материальных точек без связей
Утверждение. При 8 = ।------г< 1 потенциал U отли-
K-rJ
чается от потенциала материальной точки с массой тела и по-
мещенной в его центре масс на величину порядка е", где п 2:
и = ~. .(1 + С>(8")).
г' - Tj v v
Доказательство. Имеем:
(1.8.11)
где
|0| = о(е"), п^2.
Подставляя последнее выражение в (10), получаем
где 5] = JJJp(e)rfv -т - масса тела, S2 = JJJ&>©rfv=o.
V V
Последний интеграл определяет радиус-вектор центра масс
относительно центра масс О. Поэтому S2 = 0. Для интеграла S3
справедлива оценка
IS3 I Ш1 а(^) 1рбД/ тах
V
|oc(£)|m=g
0(e")m.
Эти соотношения доказывают сформулированное утверждение.
Из доказанного утверждения следует, что отличие гравита-
ционного потенциала тела от потенциала U0 материальной
л и~и0 К
точки, помещенной в его центре масс, Д =-— убывает не
§ 1.8. Элементы теории притяжения и гравитационные ускорения 65
медленнее, чем обратно пропорционально квадрату расстояния
между центром масс тела г* и точками пространства .
В качестве примера приведем формулу для потенциала Зем-
ли, полученную в результате теоретического рассмотрения и
экспериментов:
(1.8.12)
В этой формуле: т@- масса Земли, R@ - экваториальный радиус
Земли, г = Fj - гф, г@ - радиус-вектор центра масс Земли, rt -
радиус-вектор произвольной точки вне Земли, п° - единичный
вектор, направленный по оси вращения Земли, С20 ~ 10“3 - без-
размерный коэффициент, а - другие члены потенциала, а<а*,
а* ~ 10-5-10-6.
Формула (12) дает аппроксимацию потенциала вплоть
до поверхности Земли.
Из (12) следует, что потенциал Земли вблизи ее поверхности
(| г | ~ отличается от потенциала материальной точки, распо-
ложенной в ее центре масс, на величины порядка 10 3 (0,1%).
С увеличением расстояния это отличие убывает как —Так,
1ГI
например, на расстоянии орбиты Луны
уже составляет 0,3 • 10"6 (о,3 • 10"4%j.
1
60 ?
это отличие
3. Взаимодействие двух шаров
Мы показали, что шар со сферически-симметричным распре-
делением плотности притягивает материальную точку так же,
как материальная точка с массой этого ша-
ра т и расположенная в его центре масс г"5.
Сейчас мы рассмотрим другую, но
очень похожую задачу. Рассмотрим шар Ц
(рис. 17) с центром rf, массой т1 и со сфе-
рически-симметричным распределением
плотности р^Г]). Определим резуль-
Рис. 17
тирующую силу, действующую на
5. М.Л. Лидов
66 Глава Г Введение в динамику системы материальных точек без связей
все точки этого шара со стороны материальной точки т, по-
ложение которой определяется радиусом-вектором г*. Резуль-
тирующая сила F равна сумме сил парных взаимодействий
d F элементарных масс dmx, составляющих тело, с точкой
ч |ri“r I
Результирующая сила (13) равна по величине и противопо-
ложна по знаку силе притяжения материальной точки (r*,m) со
стороны шара (закон равенства и противодействия!).
Эту силу мы умеем вычислить:
Ешш = Г‘ ~Г 3, (1.8.14)
|Г1*-г*|
Таким образом, мы доказали следующую теорему.
Результирующая сила гравитационного взаимодействия двух
непересекающихся шаров со сферически-симметричными рас-
пределениями плотности равна силе взаимодействия двух мате-
риальных точек с массой этих шаров и расположенных в их
центре масс.
С другой стороны, если мы рассмотрим шар как систему ма-
териальных точек, то мы можем применить теорему о движении
центра масс системы материальных точек (см. § 1.2).
Согласно этой теореме, центр масс шара должен двигаться
как материальная точка с массой шара под действием суммы
внешних (по отношению к точкам шара) сил.
Тем самым оказывается, что движение центров масс шаров
со сферически-симметричным распределением плотности при
гравитационном взаимодействии точно описывается движе-
нием соответствующих материальных точек, помещенных в их
центре масс.
Так как все планеты по структуре близки к шарам со сфе-
рически-симметричным распределением плотности и их расстоя-
ние друг от друга много больше их радиусов (вспомните, как
убывает отличие потенциала тела от потенциала шара с уве-
§ J.8. Элементы теории притяжения и гравитационные ускорения 67
личением расстояния между телом и точкой), то модель грави-
тационно взаимодействующих шаров, а следовательно, и модель
материальных точек хорошо описывают движение центров масс
планет.
4. Гравитационные ускорения вблизи поверхности Земли
Запишем уравнения относительного движения материальных
точек
<L815>
Л ы UF<-f‘l NJ
Пусть точка 7, с которой связано начало системы координат,
помещена в центре масс Земли.
Пусть (r2,m2) - частица малой массы (пробная частица),
ускорением которой мы интересуемся. Будем предполагать, что
эта частица находится вблизи поверхности Земли:
| г2 | ~ 7?@ - радиус Земли.
В этой модели мы предполагаем, что Земля есть шар со
сферически-симметричным распределением плотности, и рас-
сматриваем ее (с точки зрения гравитационного влияния) как
материальную точку.
Первый член в правой части (15) при к = 2 определяет отно-
сительное ускорение точки (r2,m2), вызванное гравитацион-
ным взаимодействием с Землей. При этом g = r2/| r2 |3 -
часть ускорения, обусловленная притяжением точки Землей,
а а = - fm2 г2/| г213 - часть ускорения, обусловленная притяже-
нием Земли со стороны материальной точки (r2,m2). Для не-
больших тел отношение |a|/|g| ~т2/т{ пренебрежимо мало.
Если мы подставим в выражение для | g | значения гравитацион-
ной постоянной /, массы Земли т2 = т@ и | r2 | = R@ (значения
этих величин приведены в табл. § 1.7), то найдем
|g| = ^.^9,8-102 см/с2. (1.8.16)
R®
Это известная величина для ускорения силы тяжести вблизи
поверхности Земли. Пользуясь последней формулой, можно ре-
5*
68 Глава 1. Введение в динамику системы материальных точек без связей
шить и обратную задачу. Зная | g | и радиус Земли R@, опреде-
лить произведение ее массы на гравитационную постоянную:
Цф = = 7?j|g| = 4-105 км3/с2.
Мы описываем движение точки относительно системы коор-
динат Е@, начало которой связано с центром масс Земли и дви-
гается вместе с ним сложным образом, а орты L@ все время со-
храняют ориентацию относительно некоторой абсолютной
(инерциальной) системы координат (наша система координат не
вращается). Мы можем оценить величину ускорения точки
(г2, т2) относительно Е@, вызываемого Солнцем, Луной и пла-
нетами. Необходимо оценить модуль векторов Ф;:
ф,
(1.8.17)
Так как при | r21 ~ R@
= е < 1, то мы можем для оценок вос-
пользоваться полученным ранее (см. (1.7.4)) асимптотическим
представлением:
(1.8.18)
где
После подстановки (18) в (17) первый член f0 сократится и мы
получим следующую формулу:
ф'+о(е2))-
Для | fj | легко получить оценку
|Г. |<4
17
§ 1.8. Элементы теории притяжения и гравитационные ускорения 69
Таким образом, пренебрегая членами порядка е2, получим
Г2
(1.8.19)
В круглых скобках мы выделили множитель, примерно рав-
ный абсолютному ускорению точки (r2, т2) за счет притяжения
телом (г,, тД Относительное ускорение (ускорение относи-
тельно Е@) оказывается в 8 раз меньше.
В заключение приведем численные оценки для абсолютного
и относительного ускорений точки (r2, т2), находящейся вблизи
поверхности Земли за счет Луны (/= 3) и Солнца (/ = 4). При-
ведем эти величины в долях ускорения | g |:
<Р =
fi^j 1
Для Луны v = 3,5 • IO 5, F = 2 • 1(Н.
Для Солнца ср = 6 • IO-4, F = 10-7.
Доля планет в гравитационном ускорении d2Y2/dt2 точ-
ки, находящейся вблизи поверхности Земли, еще существенно
меньше.
Если мы пренебрежем влиянием Солнца и планет на отно-
сительное движение материальной точки (r2, т2) вблизи Земли,
то уравнения движения (15) (к = 2) будут иметь вид
d г2 _/
—^ = - [т, + т.
dt2 v 1
Г2
Мы получили, что относительное движение материальных
точек вблизи Земли описывается уравнениями относительно-
го движения в задаче двух тел (Земля - материальная точка).
В частности, уравнения (15') описывают движение искусствен-
ных спутников Земли.
Аналогично оценки можно провести для относительного дви-
жения материальной точки (малого тела) вблизи Луны или дру-
гой планеты. В этом случае - масса Луны (планеты). Для
достаточно близких к планете материальных точек всегда ока-
зывается, что члены в правой части (15), стоящие под знаком
суммы, по модулю много меньше первого члена. Поэтому в глав-
70 Глава 1. Введение в динамику системы материальных точек без связей
ном (первом) приближении движение тел (материальных точек)
вблизи планеты и, в частности, точки (r2,m2) вблизи Земли
описывается уравнениями (15').
5. Силы гравитационного притяжения
двух соприкасающихся шаров
Рассмотрим два соприкасающихся шара (рис. 18). Обозначим
через Rx, Pj, R2, р2 - радиусы и плотности первого и второго ша-
ров соответственно. Для упрощения будем
/" считать, что плотности шаров постоян-
/ /Rx у ны. Определим силу гравитационного воз-
у 1 2) действия
|F| = -^V. (1.8.20)
Рис. 18 + R2)
Эта сила вызывает ускорение JL шара 2:
m2
lFL fmi
m2 (Я1+Я2)2‘
При постоянной плотности первого шара
4 з
т{= — лpl R{ и, следовательно,
т2 3 /
Для обычных твердых тел плотность вещества составляет
величину порядка 0,5-10 г/см3. Например, средняя плотность
Земли равна 5, средняя плотность Солнца - 1,3 г/см3. Оценим
IFI
грубый порядок величины ускорения 1—L. Положим pt = 1 г/см3.
т2
Подставим это значение Pj и значение f= 6,7 • 10-8 см3/г • с2:
Щ = 2,5-1(Г71/с2 •-—
т2 (Я1+Я2)
Если R{ > R2, то
Щ = 2,5-Ю"71/с2
т2
§ 1.8. Элементы теории притяжения и гравитационные ускорения 71
Примеры.
1. Пусть шар (Z?1?mJ моделирует гору. Примем его радиус
равным 1 км = 105 см. Тогда на поверхности горы
Щ = 2,5-10’2 см/с2 = 2,5 -10"5 Igl,
т2
где | g | = 980 см/с2 - ускорение силы тяжести на поверхности
Земли.
2. Пусть шар , mJ - космический корабль. Тогда
IFI
Я, =5-102cm, J—1 = 12,5-10"5 см/с2 =12,5-108Igl.
m2
Приведенные оценки показывают, что гравитационное при-
тяжение тел может сообщить ускорения, сравнимые с ускоре-
нием гравитационного притяжения тел Землей, если только
радиусы тел сравнимы с радиусом Земли.
На человека и приборы на Земле действует сила гравита-
ционного притяжения всех тел на Земле, в частности все пред-
меты в аудитории и все люди гравитационно взаимодействуют
друг с другом. Однако ускорение, которое сообщают эти силы,
как показывают оценки, чрезвычайно мало по сравнению с
ускорением, вызываемым гравитационным притяжением Земли
(с ускорением силы тяжести | g |).
6. О гравитационном поле
около свободно летящего космического корабля.
Невесомость
Запишем снова уравнения относительного движения в задаче
п тел
Напомним, что эти уравнения описывают движение тел (к =
= 2, 3, ..., п) относительно невращающейся системы координат
которая совпадает с точкой , m J.
72 Глава 1. Введение в динамику системы материальных точек без связей
Предположим теперь, что (fp/nj- космический корабль
(Fj - центр масс космического корабля), (r2, т2) - человек в кос-
мическом корабле или прибор, a (rk, к>2- Земля и другие
планеты.
Первый член в уравнении (21) при к = 2 определяет грави-
тационные ускорения прибора (человека) относительно репе-
ра Е{. Как мы оценили, эта величина даже для корабля с харак-
терным размером ~ 5 м, наполненного водой (р = 1 г/см3), очень
Пусть космический корабль находится на
орбите близкого к Земле спутника. Пусть
(r3, т3) - Земля (рис. 19). Для близких спут-
ников | г3 | ~ R@ - радиусу Земли. Так как
I *2 |/| *з | 1, то мы можем воспользоваться
полученной выше формулой (19) для оценки
ускорения прибора относительно репера Е{
под влиянием притяжения Земли:
мала (~ 10 71gIj.
IF3| =
Г2
r3
= 4|gM
где | g | - ускорение силы тяжести на поверхности Земли.
Подставляя значения | г2 | = 5 • 102 см, | r3 | ~ R& ~ 6,4 • 108 см,
получим оценку
|F3|<4-10-6|g|.
Таким образом, ускорение прибора относительно неврагцаю-
щегося репера Е{, начало которого совпадает с центром масс
космического корабля, связанное с гравитационным притяже-
нием Земли на расстоянии 5 м от центра масс корабля, на шесть
порядков меньше силы тяжести на Земле.
Наше рассмотрение показывает, что, находясь в свободно
летящем космическом корабле, приборы (человек) практически
не испытывают относительного ускорения. На небольших ин-
тервалах времени оно практически не проявляется. В отличие от
земных условий, когда свободный предмет падает на Землю,
в космическом корабле свободный предмет относительно систе-
§ 1.8. Элементы теории притяжения и гравитационные ускорения 73
^ШТГГШп^
Рис. 20
мы координат, начало которой связано с центром масс корабля,
а орты параллельны ортам абсолютной системы координат,
движется практически без ускорения, т.е. равномерно и прямо-
линейно. Это явление называют невесомостью.
Формальная суть этого явления в том, что сила гравита-
ционного притяжения Земли при | г2 |/| г3 | 0 сообщает пример-
но одинаковое ускорение как космическому кораблю, так и при-
бору (человеку) и относительное ускорение близко к нулю. (Оно
точно равно нулю в пределе при г2 = 0).
С явлением невесомости связано много непривычных для
земного жителя физических эффектов. Некоторое пояснение,
возможно, дает описание следующего опыта.
На рис. 20 штриховкой обозначена поверх-
ность Земли.
Свободная материальная точка массой т
под действием гравитационной силы F = т g,
направленной вниз, испытывает ускорение g и
падает на поверхность Земли. Если мы между
поверхностью Земли и точкой расположим пружину, то, чтобы
точка т находилась в покое относительно Земли, необходимо,
чтобы в результате сжатия пружины на точку т со стороны пру-
жины стала действовать сила Ff равная по модулю F и направ-
ленная вверх.
Этот пример показывает, что в результате действия грави-
тационной силы, вызывающей ускорение точки т относительно
Земли, возникают другие силы взаимодействия: силы взаимо-
действия этой точки с телами, ее окружающими (пружиной).
В аналогичном эксперименте, проведенном на космическом
корабле (теперь надо вообразить, что штриховкой на рисунке
обозначен корпус космического корабля), так как относительное
ускорение | g | ~ 0, то и для сохранения равновесия точки т отно-
сительно космического корабля не требуется деформации пру-
жины. С отсутствием относительного гравитационного ускоре-
ния как следствие связано отсутствие и сил взаимодейст-
вия между точкой т и телами, с которыми она находится в
контакте.
В этом случае главную роль начинают играть другие силы,
которые на Земле малы по сравнению с силой тяжести, и по-
этому мало заметны, например силы поверхностного натяжения.
Кроме того, с явлением невесомости связано много физио-
логических эффектов. Организм человека приспособлен к по-
стоянно действующему ускорению g и "сжатию соответствую-
щих пружинок".
Глава 2
Кинематика твердого тела
и относительное движение точки
§ 2.1. Кососимметрические матрицы
и векторные произведения
Г. Определение. Квадратная матрица Q = (Q/) называется
кососимметрической, если выполнено матричное равенство
QT=-Q, (2.1.1)
где QT - транспонированная матрица Q.
2°. Из (1) следует
Q/ = (2.1.2)
В частности,
=0, г = 1,2,...,и. (2.1.3)
3°. Пусть Q - вещественная кососимметрическая матрица
размера 3 х 3. В общем случае ее можно записать в следующем
виде:
" 0 -со3 со2
Q = со3 0 -со1 (2.1.4)
р со1 0 J
где со' - действительные числа. Расстановка индексов и знаков в
(4) выбрана для удобства дальнейшего использования.
Мы можем рассматривать тройку чисел ОУ как вектор ариф-
метического пространства R3:
со =
(2.1.5)
Вектор со будем называть вектором, соответствующим косо-
симметрической матрице Q размера 3x3: со Q.
4°. Пусть х и у - два вектора арифметрического пространства
R3. Двум таким векторам можно поставить в соответствие мат-
рицу размера 3x3, которая получается в результате произведе-
ния матрицы х размера 3x1 и матрицы ут размера 1 х 3. Эту
§ 2.1. Кососимметрические матрицы и векторные произведения
75
матрицу будем обозначать ху4' и называть диадой'.
ГхП х‘у2 1 з\ X у
т ху = х2 (у1, у2,у3) = А' х2у2 2 3 X у
3 3 1 3 2 3 3
е J X у ху J
Воспользуемся введенным понятием и обозначением для по-
лучения удобной записи квадрата кососимметрической матрицы
Q размера 3x3:
Q2 = QQ -
-(CD2)2-(СО3)2
(О2со*
<D3Cd’
си'ш2
-(со3)2 -(со1)2
ЛЧ3ЛЧ2
(О (О
-(CD1)2 -(СО2)2
Несложно показать, что Q2 можно представить в следующем ви-
де, более удобном для запоминания:
Q2 = -|<о|2/ + соют, (2.1.6)
где I - единичная матрица 3-го порядка, <осот - диада.
Ниже нам потребуется выражение для следа матрицы Q2:
Sp Q2 = -2|<о|2 = -2[(со1 )2 + (со2 )2 + (со3 )2 ]. (2.1.7)
5°. Пусть г - координаты вектора относительно репера Е.
Рассмотрим матрицу q размера 3x1 (вектор-столбец), опреде-
ляемую равенством
q = Qr. (2.1.8)
Набор трех чисел q можно рассматривать как координаты век-
тора q G R3 относительно репера Е:
ч = я\+я\+я\-
В этом случае (8) определяет линейное преобразование векторов
г———>q. (2.1.9)
Матрица Q - матрица оператора этого преобразования.
6°. Пусть Е—^-^>Е - преобразование реперов, где А - мат-
рица поворота. Матрицу преобразования (9) г —> q относительно
нового базиса Е обозначим Q. Как известно,
(2.1.10)
Матрица Q - кососимметрическая.
76 Глава 2. Кинематика твердого тела и относительное движение точки
Доказательство. Применим к (10) операцию транспо-
нирования:
QT = AQTAT = -AQAT=-Q.
7°. Пусть со - вектор, соответствующий матрице Q: со Q.
Теорема. Векторы со (со Q) и со (со Q) связаны соот-
ношением
со = Асо. (2.1.11)
Доказательство.
а) Непосредственным умножением матрицы Q на вектор со
найдем
Qco = 0, (2.1.12)
т.е. со - собственный вектор матрицы Q с нулевым собственным
значением.
б) Так как при Icol Ф 0 ранг Q равен 2 (из (4) непосредственно
видно, что существуют миноры второго порядка, равные (оу)2>
i = 1,2,3), то все собственные векторы х матрицы Q с нулевым
собственным значением имеют вид
х = цсо, ц -вещественное числ о.
в) Так как со - собственный вектор Q то
Qco = 0 —> АОАтсо = 0 Атсо - собственный вектор Q —>
Атсо = цсо со = цАсо.
г) Из последнего сотношения следует, что
|со|2 = ц2|со|2 (А - матрица поворота).
д) Рассмотрим квадрат матрицы П, определяемой формулой
(Ю): _
П2 = AQATAQAT = AQ2At.
Так как А - матрица поворота, то
Sp£P = SpQ2.
Из (7) следует, что
|со|2 = |со|2 —> ц2 = 1, со = ±Асо. (2.1.13)
е) Если А - матрица поворота (det А = 1), то в (13) возможен
только первый знак.
Доказательство. Если А - матрица поворота, то суще-
ствует семейство ортогональных матриц А(т), непрерывно зави-
сящее от параметра т е [ос, Р] и удовлетворяющее условиям:
§ 2.7. Кососимметрические матрицы и векторные произведения
77
А (ос) = I - единичная матрица, Л(£) - заданная матрица по-
ворота.
При т=а имеем А(ос) = 1 и Q(oc) = Q —» со (ос) = со —» ц(ос) = 1.
При т = Р
со = ц(р)А(Р)со.
Если ц(Р) = -1, то необходимо (ц2 = 1) существует значение
т = т* е [ос, Р]. удовлетворяющее условию
И(т" -0) = -|11(т* +0).
Так как А - непрерывная функция т, отсюда следует:
со(т* - 0) = -со(т* + 0).
Так как |со| Ф 0 (|со| = |со|), то, следовательно, функция со(т)
должна при т = т* иметь разрыв. Этого не может быть, так как
элементы матрицы Q(t) = А(т)ОАт(т) непрерывные функции т.
Следовательно, ц(Р) = 1.
8°. Доказанную теорему можно сформулировать следующим
образом.
Если кососимметрическая матрица Q размера 3x3 опре-
деляет преобразование векторов /?3, заданное относительно ре-
пера Е, то компоненты соответствующего Q вектора со при зада-
нии того же преобразования относительно репера Е преобра-
зуются, как координаты ОУ вектора
со = cd + со2е2 + со3е3.
То есть вектор со арифметического пространства R3 можно рас-
сматривать как направленный отрезок со в геометрическом
представлении R3. Имеется одно исключение. Если вместо матри-
цы поворота взять матрицу (-А) (det (-А) = -1), то координаты г
любого вектора г изменят знак. В то же время элементы матри-
цы Q, согласно (10), (и, следовательно, компоненты со) не изме-
няются.
Поэтому вектор со называют не вектором, а псевдовекто-
ром. Однако если при преобразованиях реперов ограничиться
только преобразованиями поворота, то отличие псевдовектора
от вектора никак не проявляется.
9°. Обычно преобразование координат (8) вектора г кососим-
метрической матрицей Q записывают в следующем виде:
q = Qr = [co,r], (2.1.14)
где со - вектор, соответствующий Q.
78 Глава 2. Кинематика твердого тела и относительное движение точки
При этом q называют векторным произведением векторов со
и г. Согласно 8°, при det А = 1 будем иметь q = [со, г].
10°. Свойства векторного произведения
а)
2 3 3 2 Л
(07 — со г
3 1 13
О) Г -О) г
12 2 1
(0Г -(07
Q
Q2
Следует обратить внимание на циклическую перестановку ин-
дексов в выражениях для компонентов ql.
Формула (15) получается умножением матрицы Q (4) на ко-
ординатный вектор г.
б) Для любых х, у G R3 и ос, Р G R
[ах + Ру, Z] = а[х, z] + Р[у, z],
[х,х] = 0.
в) Для любых со, г е R3
[со,г] - -[г,со].
Свойства б) и в) очевидно следуют из ((15).
г) Вектор q ортогонален векторами со и г:
(co.q) = (r,q) = 0.
Доказательство. Исходя из равенств
(со, [со, г]) = (со, Qr) = (QTco, г) = -(йсо, г) = 0 (Qco = 0),
находим
(r,[co,r]) = -(r,[r,<o]) = 0
(со и г входят в (15) симметричным образом)
д) Для произвольного вектора хт = (х1, х2, х3)
q =
(х, q) = (х, [со, г]) = det х2
з
со1
со2
со3
2
3
(2.1.15)
(2.1.16)
(2.1.17)
(2.1.18)
Выражение (х, [со, г]) называется смешанным произведением
трех векторов х, со, г (порядок важен). Модуль смешанного про-
изведения равен объему параллелепипеда, построенного на
векторах х, со, г.
Из свойства определителей по отношению к перестановке
столбцов следуют равенства:
§ 2.1. Кососимметрические матрицы и векторные произведения
79
для четных перестановок
<х,[со,г]> = <г,[х,со]> = <со,[г,х]>;
для нечетных перестановок
- (х, [<о, г]) = (х, [г, <о]) = (<о, [х, г]) = (г, [<о, х]).
11°. Теорема. Пусть Е| ие2- два единичных взаимно ортого-
нальных вектора 7?3:
|е,| = |е2| = <е(,Е2> = 0.
Пусть е3 = [е15 е2 ]. Тогда тройка £ = (£,, е2, е3) образует ор-
тонормированный репер, ориентированный одинаково с исход-
ным репером Е.
Доказательство.
1) Вектор е ортогонален векторам Е| и е2 (см. 10°, г)).
2) Рассмотрим определитель
Ге;
D = det el,
к
Е?
el
е32
Е]
el
в!
Разлагая по элементам третьей строки, получим
D = ез(е^е| -е^е|) + е|(е^2 -е{е|) + £з(е]е| -£^2) =
= (£3)2 4- (е|)2 + (£3)2 > 0 (ориентация правильная).
3) Модуль вектора не изменяется при ортогональном преоб-
разовании. Выберем систему координат Е так, чтобы
гп г о"
^=Ae} = 0 , Ёэ=Ае2= 1 .
oj
Подставляя компоненты ё(,ё2 в формулу (15) (<о = Ё1, г = Ё2),
найдем Ёз= 0 . Откуда |^| = |е3| = 1.
< 1 >
О
Геометрические свойства векторного произведения
1) Вектор q ортогонален плоскости П1)г векторов со и г
(рис. 21).
2) Поворотом со на угол меньший или равный 180° в плоскос-
ти nwr против часовой стрелки (если смотреть со стороны
80 Глава 2. Кинематика твердого тела и относительное движение точки
стрелки q) он может быть направлен по лучу, определяемому
вектором г.
3) Модуль векторного произведения равен площади парал-
лелограмма, построенного на векторах миг.
Для доказательства свойств 2) и 3) выберем репер так, чтобы
Рис. 21
орт е! был направлен по <о, а орт е2 принадлежал плоскости век-
торов (о и г (рис. 22). В этом случае
со = |<о| 0 ,
0,
^cos 0^
sin 0
I 0 J
Согласно (15), q = [<о, г] = |<о| |г| 0
Из последней формулы следует
|q| = |<о| |r||sin0| = 5,sgn g3=sgnsin0 (sgn ос-знакос).
§ 2.2. Твердое тело
До сих пор мы занимались простейшими механическими
объектами - материальными точками. Напомним, что мате-
риальная точка в нашей модели это пара (г, т), где т - масса
материальной точки, аге Л3 - ее радиус-вектор. Движение ма-
териальной точки полностью описывалось тремя функциями
времени
r(Z) = (r1(Z),r2(O,r3(O).
Сейчас мы на основе уже известных нам понятий определим
новый объект.
Определение. Твердым телом называется система мате-
риальных точек (r0, m0), (гь mJ, ..., (г^, таких, что расстояние
между любыми двумя не изменяется с течением времени.
§ 2.2. Твердое тело
81
Обозначим через |r- -rj = Sy расстояние между точками i и j.
Из определения твердого тела
dsh
—!L = o^s = const; i,/ = 0,1,...,N. (2.2.1)
dt lJ
Условия типа (1) являются частным случаем рассматривае-
мых в механических моделях условий, ограничивающих возмож-
ное изменение координат материальных точек системы. Такие
условия называются связями. Движением твердого тела назы-
вается совокупность движений (гг(0, тпг), i = 0, 1, 2,..., N мате-
риальных точек, составляющих твердое тело. При этом движе-
ние точек во все моменты времени / g Jt должны удовлетворять
связям
|гД0-(0| = = const; к,j = 0,1,...,TV. (2.2.2)
Модель твердого тела (рис. 23) можно представить как си-
стему материальных точек тк, соединенных стержнями, массой и
деформацией которых можно пренебречь.
Модель твердого тела с успехом
используется для описания законе-
мерностей вращения спутников, дви- г
жения частей человеческого тела,
вращения планет.
Любое реальное тело лишь приб-
лиженно можно рассматривать как \
твердое. Как и для всех моделей, РИС 23
возможность использования для опи-
сания данного физического процесса модели твердого тела зави-
сит от конкретных условий исследуемой задачи.
Теорема. Пусть (r0, m0), (r19 m}), (r2, т2) - три точки твердого
тела, не лежащие на одной прямой. Тогда с точкой г0 можно
связать такой репер Е =(e15^,e3), одинаково ориентированный
относительно абсолютного репера Е, что координаты про-
извольной точки твердого тела (r7, т7) относительно репера ЕГо
не изменяются при любом непрерывном движении твердого
тела.
Доказательство. Определим орты
ё,=й^. ё2 = ЙЛ~Ы, ё, = [ё„ёг]. (2.2.3)
где 5ю = Iri “4 d = |[ё„г2 -г0]|.
6. М.Л. Лидов
82 Глава 2. Кинематика твердого тела и относительное движение точки
Очевидно:
|ej = |e2| = l, (ё1,ё2> = 0.
Согласно доказанной выше теореме (см. 11°), ЕГо = (ё15ё2,ё3)
образуют репер, ориентированный одинаково с абсолютным ре-
пером.
Для завершения доказательства необходимо показать, что
проекции векторов г7 - г0 на орты ё,
(г.-г0,ёД j = l,2,...7V; i = 1,2,3, (2.2.4)
в силу условий (1) не изменяются при любом движении твердого
тела. Эту часть доказательства следует рассматривать как уп-
ражнение.
§ 2.3. Углы Эйлера
Рассмотрим два одинаково ориентированных репера Е =
= (еь е2, е3) и Е1 = (е],е2,е3) с началом в
одной точке О. Пусть орт е3 совпадает с
ортом е3 (рис. 24). Обозначим через у
угол между векторами е] и е15 отсчи-
тываемый от направления вектора ej
против часовой стрелки, если смотреть с
конца вектора е3. Матрицу преобразова-
ния Е —> Е1 обозначим П(3, у). Число 3 и
буква у указывают, что репер Е1 полу-
чается из репера Е поворотом вокруг
орта е3 против часовой стрелки на угол
у. Запишем матрицу этого преобразования в явном виде
П(3,у) =
Л cosy
-sin у
I О
siny (Г
cosy О
О 1J
(2.3.1)
Аналогично введем в рассмотрение матрицу преобразования
поворота вокруг орта ej (рис. 25) на угол у (против часовой
стрелки)
fl О
П(1,у)= 0 cosy
^0 -siny
0 "
siny
cosy?
(2.3.2)
Нетрудно проверить, что det П(/, у) = 1 и, следовательно, мат-
§ 2.3. Углы Эйлера
83
рицы П(/, у) суть матрицы поворота. Преобразования реперов с
неизменным одним ортом будем называть простым поворотом.
Рассмотрим теперь произвольный репер Е =(epe2,e3), оди-
наково ориентированный с репером Е.
Сейчас мы укажем один конкретный способ вычисления мат-
рицы преобразования Е Е (рис. 26). Введем два вспомога-
тельных репера:
1) Репер Е2 = (е^,е|,е|), орт е| которого совпадает с ортом
е3 репера Е, а орт в) принадлежит плоскости векторов е19 е2 ре-
пера Е.
Так как орты е| и ё3 совпадают, то репер Е может быть
получен из репера Е1 простым вращением вокруг третьего орта
на некоторый угол, который мы обозначим (р. Отсюда следует,
что матрица преобразования Е2 -э Е есть матрица простого по-
ворота П(3, (р).
2) Репер Е1 = (е[,е2,е3) выберем так, чтобы орт е3 совпадал с
ортом е3 репера Е, а орт е] совпадал с ортом репера Е2. Так
как е3 = е3, то преобразование £ Е1 есть простой поворот и
матрица этого преобразования имеет вид П(3, ц/), где через \|/
обозначен угол, на который надо повернуть репер Е, чтобы орт
е] совпал с ортом ef
3) Так как орты е[ и е2 совпадают, то преобразование Е1 —>
—> Е2 есть простой поворот на угол 0, определяемый углом
между е3 и е3.
6*
84 Глава 2. Кинематика твердого тела и относительное движение точки
Матрица этого преобразования имеет вид П(1, 0). Таким
образом, искомое преобразование Е ——-> Е можно представить
как суперпозицию простых поворотов:
П(3,\|/) ^71 П(1,0) > П(3,<р) > ^7
Отсюда непосредственно следует, что искомая матрица А преоб-
разования Е —> Е имеет вид
А = П(3,ф)П(1,0)П(3,у).
Так как каждая из составляющих матриц есть матрица поворота,
то и матрица А есть матрица поворота, т.е. ортогональная мат-
рица с det А = +1. Для получения явного вида элементов матрицы
А надо произвести перемножение трех простых матриц. Углы (р,
0, \|/, однозначно определяющие положение репера Е отно-
сительно репера Е, называются углами Эйлера.
Они имеют наименования:
щ - угол прецессии,
ср - угол вращения (собственного вращения),
0 - угол нутации.
Линия пересечения плоскостей (еь е2) и (ё19ё2) называется ли-
нией узлов.
Напомним, что множество матриц поворота А,- размера
3 х 3, det Af =+1, образует мультипликативную группу, которую
называют трехмерной группой вращений и
обозначают SO (3).
1. Из Aj е SO (3) и А2 g SO^HA^e
g SO (3), det AjA2 = 1
2. А,- 6 SO (3) -> a;1 = e SO (3).
3. Единичная матрица I размера 3x3 являет-
ся единицей в SO (3). Произвольная матрица по-
ворота А определяет репер Е. Из построения эйлеровых углов
следует, что если е3 ^±ё3, то для любого Е, ориентированного
одинаково с Е, мы однозначно определяем углы ср, 0, Щ из парал-
лелепипеда (рис. 27).
4. Ё: {0<0<тс, 0^ср<2л, 0^\|/<2л}. (2.3.3)
Верно и обратное: каждому набору ср, 0, щ из U соответствует
матрица поворота А.
Таким образом, соотношение (3) определяет взаимно одно-
значное отображение области U евклидова пространства Е3:
U: {О<0<71, 0<(р<2л, 0<\|/<2л} bSO (3).
§ 2.3. Углы Эйлера
85
Иначе говоря, отображение (3) U SO (3) задает локальные
координаты (карту) на гладком многообразии SO (3). По ср и щ
можно продолжить это отображение на всю плоскость (ср, у),
отождествляя точки плоскости с координатами ср и у с точка-
ми плоскости с координатами \|/ + 2пк, (р + 2пт для любых целых
кит.
Значения 0 = 0 и 0 = л являются особыми. При 0 = 0 и 0 =
= л (е3 - ± ё3) отображение (3) перестает быть взаимно одно-
значным (по реперу Е можно определить (р + V при 0 = 0 или
\|/ - ср при 0 = л, но нельзя определить отдельно каждый угол).
Из-за этого иногда для описания движения твердого тела необхо-
димо в SO (3) вводить другие локальные координаты (не углы
Эйлера) или вводить множество карт.
Дадим теперь абстрактное определение твердого тела, ана-
логичное нашему определению материальной точки. Это опре-
деление не подменяет исходного, более наглядного, а раскрывает
его как следствие.
Твердым телом называется тройка
(г,А,Р),
где г G /?3 - радиус-вектор выделенной точки твердого тела О,
А - матрица поворота от абсолютного репера Е к реперу Ег,
жестко связанному с твердым телом, начало которого
расположено в точке О,
Р-не зависящее от времени распределение масс
к= 1,2, ..., N, относительно репера Ег.
Движением твердого тела называется отображение
Ф:7, ->/?3xSO (3)
интервала времени в прямое произведение пространства R3 и
трехмерной группы вращения SO (3).
Это отображение задается функциями
г = r(0, А = А(0, t eJt.
(Мы употребляем, как обычно, ту же букву для отображения и
образа.)
Так как матрица А определяется тремя параметрами, напри-
мер ср, 0, \|/, и вектор г g R3, то, следовательно, пространство
положений твердого тела (его конфигурационное пространст-
во) - шестимерное.
86 Глава 2. Кинематика твердого тела и относительное движение точки
§ 2.4. Основные формулы кинематики твердого тела
и относительного движения точки
Кинематика - это раздел механики, в котором изучают дви-
жение материальных тел вне зависимости от причин, вызываю-
щих это движение. Так, например, траектория движения, ско-
рость и ускорение материальной точки есть понятия кинематики
движения точки. Все кинематические понятия для материальной
точки не зависят от величины массы точки, а определяются
только движением точки: отображением Jt —г(?) >/?3.
Аналогично при рассмотрении кинематики движения твердого
тела мы можем отвлечься от распределения масс Р относительно
репера Е жестко связанного с твердым телом, и изучать
движение точек, неизменно связанных с репером ЕГ. Иначе го-
воря, изучать движение репера, значит, изучать отображение
Ф: Jt—> R3 х SO (3), определяемое функциями
г0=г0(г) и A = A(t).
В механике часто оказывается необходимым не только изу-
чать движение твердого тела, но и уметь описывать, например,
движение материальных точек относительно твердого тела, ко-
торое само совершает (возможно достаточно сложное) движение
относительно какой-либо абсолютной (инерциальной) системы
координат. В частности, если мы описываем движение тел (то-
чек) относительно Земли и для описания этого движения вводим
систему координат, орты которой ориентированы по неподвиж-
ным относительно Земли предметам, то эта система координат
совершает сложное движение, связанное с суточным вращением
Земли, ее движением по орбите вокруг Солнца и т.д. В дальней-
шем мы кратко рассмотрим некоторые вопросы кинематики
твердого тела и относительного движения.
Можно указать две задачи, порождающие необходимость в
кинематическом анализе.
1. Уравнения движения материальной точки в исходной пос-
тановке о движении системы материальных точек (§ 1.1) опре-
деляют связь абсолютного ускорения (ускорения относи-
тельно абсолютного репера) и действующих на данную точку
сил. Мы показали, что уравнения имеют тот же вид при описа-
нии движения относительно произвольной инерциальной
системы координат. В то же время часто (в частности, как мы
показали выше на примере относительного движения системы N
гравитирующих точек) мы вообще не можем определить абсо-
лютное движение или непосредственно можем наблюдать толь-
§ 2.4. Основные формулы кинематики твердого тела
87
ко движение относительно системы координат (Земли), совер-
шающей сложное движение относительно инерциальной систе-
мы координат.
2. Часто очень сложное результирующее движение мате-
риальных точек (тел) относительно абсолютной системы коор-
динат является суперпозицией простых относительных движений
реперов (точек) друг относительно друга. В такой ситуации изу-
чение относительных движений может помочь в анализе и опи-
сании результирующего движения.
Докажем вначале два вспомогательных утверждения.
Лемма 1. Пусть элементы ортогональной матрицы А размера
3x3 зависят от времени. Обозначим
ллТ
-——А = £2. (2.4.1)
dt
Утверждение: Q- кососимметрическая матрица.
Доказательство. Из ортогональности А следует
АТА = /,
где I - единичная матрица.
Дифференцируя (2) по времени, получим
dA А АТ dA „ dA А 4 т dA
----А + А— = 0—>------А = -А— =
dt dt dt dt
(2.4.2)
----A
dt J
Следовательно, Q - кососимметрическая матрица размера 3x3.
Соответствующий ей вектор обозначим со:
СО = 8^ " 0 (О3 -СО со 0 -со1 (2.4.3)
с“2 со* 0
С течением времени компоненты ОУ в общем случае изменяются,
т.е. со = соф. Если матрица A(t) определяет вращение репера Е
относительно Е=(е19 е2, е3), то вектор
со = со1е1 + со2е2 + со3е3
будем называть вектором угловой скорости вращения Е отно-
сительно £, а порождающую координатный вектор со матрицу Q
будем называть матрицей угловой скорости.
Лемма 2. В обозначениях леммы 1 справедливо соотношение
dt dt
(2.4.4)
88 Глава 2. Кинематика твердого тела и относительное движение точки
Доказательство. Продифференцируем соотношение
(1) по времени:
d2AT Л dAT dA dQ.
---у-А +-----=----.
dt dt dt dt
Воспользуемся тождествами
dA dA = dA_ T dA = QQT = _q2
dt dt dt dt
Напомним, что формула для Q2 приведена в (2.1.6) и dQJdt -
кососимметрическая матрица размера 3x3; соответствующий ей
вектор будем обозначать doMr.
dt
_ dw2
dt dt
day1
v dt /
(2.4.5)
Пусть репер E определяет абсолютную систему координат
(рис. 28).
Начало репера ЕГо (точка О) определяется вектором г0, а ко-
ординаты его ортов относительно репера Е матрицей А:
г0
Обозначения и определения
Рассмотрим движение произвольной точки М, положение ко-
торой относительно репера Е определяется вектором г
§ 2.4. Основные формулы кинематики твердого тела
89
Обозначим:
г - координаты точки М относительно Е (проекции
г на орты репера £);
dr к
v = — - координаты вектора абсолютной скорости точки
dt
М (проекции v на орты репера £);
d\ d2r
— = —2" _ координаты вектора абсолютного ускорения точ-
dt dt
ки М (ускорения точки М относительно Е, т.е.
проекции w на орты репера £);
г0 - координаты точки О относительно Е (проекции
на орты репера £);
v0 - координаты вектора скорости точки О относи-
тельно Е (проекции на орты репера Е);
w0 - координаты вектора ускорения точки О относи-
тельно Е (проекции на орты репера Е).
Положение точки М относительно репера ЕГо определяется
вектором г - г0.
Обозначим:
г - координаты точки М относительно ЕГо (проек-
ции г - г0 на орты репера ЕГо);
- dr
v = — - координаты вектора относительной скорости
dt
(скорости движения точки М относительно ErQ,
т.е. проекции вектора относительной скорости
на орты репера ЕГо);
_ Jv d2r
w=—=—2— координаты вектора относительного ускорения,
dt dt
(ускорения точки М относительно ЕГо, т.е.
проекции на орты репера ЕГо).
Наблюдатель, жестко связанный с репером ЕГо,может не-
посредственно измерить только г,v,w.
Координатные векторы r,v,w можно спроектировать на
орты репера Е. Обозначим эти проекции г - r0, vr, wr:
90 Глава 2. Кинематика твердого тела и относительное движение точки
г - г0 = Атг - координаты вектора относительного положе-
ния точки М в проекциях на орты репера Е;
vr = ATv - координаты вектора относительной скорости
точки М в проекциях на орты репера Е;
wr = Ат w - координаты вектора относительного ускоре-
ния точки М в проекциях на орты репера Е.
В качестве исходного для дальнейших преобразований возь-
мем соотношение, связывающее абсолютные координаты г точ-
ки М в проекциях на орты репера Е и относительные коорди-
наты г той же точки в проекциях на орты репера ЕГо:
г = Атг + г0. (2.4.6)
Предположим теперь, что репер Е совершает движение
относительно репера Е, т.е. рассмотрим отображение Jt-^> R3 х
х SO (3), определяемое вектор-функцией r0 = г0(г) и матрицей Л =
= А(0, элементы которой зависят от времени. Рассмотрим, как
связаны кинематические характеристики движения произволь-
ной точки М (скорость, ускорение) при описании ее движения
относительно абсолютного репера Е и подвижного репера ЕГо.
Продифференцируем соотношение (6) по времени:
dr dAT _ dr^ ATdr
— = v =-r + —- + A—.
(2.4.7)
dt dt dt dt
ТЛ б/Ат_ dA^ ЛЛ^~
Используя тождества------г =---АА г и введенные выше обоз-
dt dt
начения
dAT л гл лт- drQ dr _
-----А = £2, A r = r-rn, —- = vn, — = v, A v = v,.,
dt---0 dt 0 dt
получим
(I) v = Q(r-r0) + v0+v,. (2.4.8)
или, так как, согласно лемме 1, £2 - кососимметрическая матри-
ца, элементы которой образуют вектор со:
(Г) v = [co,r-r0] + v0 + vf. (2.4.9)
Продифференцируем теперь соотношение (7) по времени.
В результате получим
d2r dv d2AT _ J2r0 _ dAT dr T d2r
dt2 dt dt2 dt2 dt dt dt2 '
(2.4.10)
§ 2.5. Кинематика твердого тела
91
Преобразуем (10), используя тождества и введенные обозна-
чения:
d2AT _ d2AT ЛЛТ_ d2AT л d£l
—~г =—^~АА г, —^-А = + Q ,
dt dt dt dt
. т-
А r = r ro> “72 =W0,
at
dAT dr dAT dr Л ,T_
-----=---AA —-QA v = Qvr, A—r = A w = wr.
dt dt dt dt dt
При этом (10) можно записать в следующем виде:
(II) w =-------(r-r0) + Q2(r-r0) + w0 + 2Qv, + wf. (2.4.11)
dt
Так как dQJdt и Q - кососимметрические матрицы, элементы
которых образуют векторы duddt и со, то (II) можно записать че-
рез векторные произведения:
(ПЭ
б/сО
w = ~лГ’Г-Г°
dt
4- [со, [со, г - г0 ]] + w0 + 2[со, vr ] + wr.
(2.4.12)
Соотношения 1(1') и II (II являются основными соотношениями
для кинематики твердого тела и относительного движения
точки.
Ниже мы рассмотрим следствия, вытекающие из этих соот-
ношений.
§ 2.5. Кинематика твердого тела
Предположим, что репер ЕГо жестко связан с твердым те-
лом. Пусть точка М - произвольная точка того же твердого тела.
В этом случае относительные скорость и ускорение точки М
равны нулю:
v = w = vr =wr =0.
Соотношения I(I') и II (1Г) в этом случае имеют вид
(III) v = Q(r-r0) + v0, (2.5.1)
v = [<o,r-r0] + v0;
d^it z _ о /
W = —(r-r0) + Q (r-r0) + w0, т.е. dt
(IV)
c/co -.x
w= ,r-ib +[<o,[<o,r-r0]] + w0. (2.5.2) dt
92 Глава 2. Кинематика твердого тела и относительное движение точки
Соотношение III определяет распределение абсолютных
скоростей точек твердого тела в зависимости от их положения
г - г0 и является основным соотношением кинематики твердо-
го тела.
Определение. Вектор 0) называется вектором мгновенной уг-
ловой скорости твердого тела.
Введем несколько понятий, используемых при описании дви-
жения твердого тела.
Определения’.
Если на интервале времени Jt
1) v0 = 0 и со = 0, то говорят, что твердое тело на этом ин-
тервале находится в покое относительно абсолютного репе-
ра Е;
2) v0 0 и со = 0, то говорят, что твердое тело совершает
поступательное движение (перемещается поступа-
тельно) относительно Е;
3) v0 = 0 и со Ф 0, то говорят, что твердое тело вращается
вокруг неподвижной точки О, определяемой радиусом-векто-
ром г0;
4) v0 = 0, dttildt = О, I со I Ф 0 (со0 - co/l со I - единичный вектор в
направлении со), то говорят, что твердое тело вращается вокруг
неизменной оси, проходящей через точку О.
Замечание 1. В случае поступательного перемещения со = О
(dA/dt = 0), т.е. орты репера ЕГо сохраняют ориентацию относи-
тельно репера Е. При этом поступательное движение может
быть достаточно сложным (рис. 29, 30).
При поступательном движении все точки твердого тела
в каждый момент времени t имеют одинаковую скорость
v = v0.
§ 2.5. Кинематика твердого тела
93
Замечание 2. В случае 4) множество точек, лежащих на пря-
мой, проходящей через точку О параллельно вектору оз:
г = г0+Лю° (2.5.3)
(X - произвольное вещественное число) имеет нулевую скорость
относительно Е. Действительно, при v0 = О
v = [со,г - г0] = [<о,Лсо°] = I со I Л[со°,со°] = 0. (2.5.4)
Эта прямая называется осью вращения твердого тела.
Если условия, входящие в определения 1)-3), выполняются
только в один момент времени t = Г*, то говорят, что твердое
тело
1) находится в мгновенном покое относи-
тельно Е, если при t= Г v0 = 0 и оз = 0;
2) совершает мгновенно поступательное дви-
жение, если при t-f v0 0 и со - 0;
3) совершает мгновенно вращательное движе-
ние, если при t—f v0 = 0 и со Ф 0.
В последнем случае скорости точек, лежащих на прямой г - г0 +
+ Хсо (X - произвольное вещественное число), при t = t* равны
нулю. Эта прямая называется мгновенной осью вращения.
Утверждения.
1. В случае мгновенно поступательного движения все точки
твердого тела (репера ЕГо) при t = Г имеют одинаковые ско-
рости, равные v0.
2. В случае мгновенно вращательного движения скорости
всех точек при t = г* направлены ортогонально вектору со (оси
вращения) и вектору г - г0, т.е. v = [со, г - г0]. Так как
| v | = | со 11 г — г0 11 sin01 = | со | /г, (2.5.5)
где h - I г - r0 I I sin 0 I - расстояние точки от оси вращения, то
модуль вектора v равен произведению мо-
дуля вектора угловой скорости со и рас-
стояния h точки от оси вращения (рис. 31).
Из формулы
V = [<о, г - г0 ] + v0
следует, что произвольное мгновенное
движение твердого тела складывается из
двух движений: мгновенно поступатель-
ного движения со скоростью v0 начала ре-
Рис 31
94 Глава 2. Кинематика твердого тела и относительное движение точки
пера ЕГо и мгновенно вращательного движения с угловой ско-
ростью оз относительно оси, проходящей через начало репера в
направлении, определяемом вектором оз.
Теорема. Мгновенная угловая ско-
рость твердого тела оз не изменяется при
переходе к другому реперу, жестко связан-
ному с твердым телом.
Рассмотрим (рис. 32) наряду с репера-
ми Е и £Го репер ЕГ|, так же, как и репер
ЕГо, жестко связанный с твердым телом.
Обозначим через г координаты точки М
твердого тела относительно репера ЕГ1;
г - координаты вектора Tj - г0 относительно ЕГ() в проек-
циях на орты ЕГо. Пусть В - ортогональная матрица преобразо-
вания
Е ___?-^Е
^г0 •
Очевидно, справедливы соотношения
г = Атг + г0, г = Втг + гг
Подставим г из второго соотношения в первое. Получим
г = АтВтг+ Атг1 +г0.
Продифференцируем последнее соотношение по времени, учи-
тывая, что
№ = =
dt dt dt
dr dA'= dAT _ б/г0
dt dt dt dt
Используя тождества
/7ДТ _ dAT _
—BTr = —AATBT г = QAT(r-Fj) = Q(r-Fj) = [co,r-rj,
dt dt
dAT_ dAT ЛДТ_ 4 _
—-ii=-—ДА Г| =Q(r1-r0) = [w,r1-r0],
dt dt
§ 2.5. Кинематика твердого тела
95
получим
v = [<л>,г — Г| ] + Vp (2.5.6)
Vj = [to,r,-r0] + v0. (2.5.7)
О мгновенно винтовом движении
Пусть I <о I Ф 0. Пусть точка Г| определяется следующей фор-
мулой:
[<o,vn] .
ri =ro +-j—jF + Ato,
|ш|
где X - произвольное число. Тогда, подставляя rj - г0 в (2.5.7), по-
лучим
1 1 2
V.=-—р [<o,[<o,v0]] + v0 =-—pQ v0+v0 =
|w| |w|
1 , । ,2 , tx (<O,V0)
= i—p(-|°l / + )v0 + v0 =-v0+<o-—jf- + v0=<o------f~.
|<o| <o <o
(2.5.8)
Таким образом, можно найти такую точку гь что поступатель-
ная составляющая скорости будет коллинеарна вектору угловой
скорости. Такое движение называется мгновенно винтовым дви-
жением. Прямая, проходящая через точку rj параллельно векто-
ру со, называется мгновенной винтовой осью. Мы доказали, что
в каждый момент времени t в твердом теле можно указать такую
прямую, что если начало системы координат, жестко связанной
с твердым телом, принадлежит этой прямой, то движение твер-
дого тела является мгновенно винтовым.
О распределении ускорений в твердом теле
Из соотношений (IV) следует, что мгновенное ускорение то-
чек твердого тела складывается из трех составляющих:
1) ускорения начала подвижной системы координат w0; эта
составляющая ускорения одинакова для всех точек твердого тела
и называется поступательным ускорением;
2) ускорения wB = [б/со/бй, г - r0J, связанного с изменением век-
тора угловой скорости; эту составляющую ускорения называют
вращательным ускорением;
3) ускорения woc - [со, [со, г - г0]], называемого осестреми-
телъным ускорением:
woc = Q2(r-r0) = (-|<o|2 7 + wwT)(r-r0) =
= - [<Л> I2 (г-r0) + <o(co,r-r0).
(2.5.9)
96
Глава 2. Кинематика твердого тела и относительное движение
Представим
г - r0 = Zco + р,
(2.5.10)
где ZI оз I - проекция г - г0 на направление вектора со, а р - со-
ставляющая г - г0, ортогональная со (рис. 33).
Подставив (10) в (9), получим
-М М woc=-|<o|2p.
/ Осестремительное ускорение ортогонально
/ ; вектору со, направлено от точки М к мгно-
/ 0 ! венной оси вращения, а его величина равна
произведению квадрата модуля угловой ско-
рости на расстояние точки М от оси вра-
_ _ щения.
Рис. 33
Замечание 3. Если тело совершает посту-
пательное движение (со = 0 при t = Jt), то ускорение всех точек
твердого тела одинаково и равно w0. В случае мгновенно посту-
пательного движения (со = 0 при t = Г) в общем случае это уже
не так. Вращательное ускорение, вообще говоря, не равно нулю.
Следовательно, ускорение точек твердого тела при мгновенно
поступательном движении зависит от координат точек.
§ 2.6. Скорости и ускорения в относительном движении
Рассмотрим теперь вновь движение точки М. Связь абсолют-
ной и относительной скоростей движения, абсолютного и отно-
сительного ускорений определяется полученными выше соотно-
шениями 1(Г), П(П') (2.4.8)-(2.4.12)).
Обозначим
б/сО
"^Г’г-г°
[<o,r-r0] + v0 = уе (2.6.1)
и запишем формулу (I1) в следующем виде:
v = v^+vr. (2.6.2)
Обозначим
+ L<o,[<o,r-r()]] + w0 = wc, (2.6.3)
2[<о. уг ] = wc (2.6.4)
и запишем формулу (1Г) в следующем виде:
w = + wc + wr. (2.6.5)
Из формулы (I1) следует, что вектор ve равен вектору абсолютной
§ 2.7. Сложное относительное движение системы твердых тел
97
скорости точки, неподвижной относительно репера ЕГ(), по-
ложение которой в данный момент совпадает с положением
точки М.
Определение 1. При рассмотрении относительного движения
точки М вектор ve называют переносной скоростью.
Используя это определение, соотношение (2) формулируют
следующим образом: абсолютная скорость v точки равна сум-
ме относительной скорости V,. и переносной ve.
Аналогично вектор we равен вектору абсолютного ускорения
точки, неподвижной относительно репера Е, положение кото-
рой в данный момент времени совпадает с положением точки М.
Определение 2. При рассмотрении относительного движения
называют переносным ускорением, а
w,. = Атd2r / dt2 - относительным ускорением, которое оп-
ределяет наблюдатель, неподвижный относительно репера Е
(в проекциях на орты репера Е).
Из (5) следует, что абсолютное ускорение содержит еще одну
составляющую wc (4), которая называется кориолисовым ускоре-
нием. Как следует из этой формулы, кориолисово ускорение
отсутствует, если система координат перемещается поступатель-
но (со = 0) или относительная скорость vr точки М коллинеарна
вектору угловой скорости (или v, = 0). Соотношение (5) фор-
мулируется следующим образом: абсолютное ускорение точки
равняется сумме переносного, относительного и кориолисова
ускорений.
Все понятия, связанные с распределением скоростей и уско-
рений твердого тела, автоматически переносятся на распреде-
ление переносных скоростей ve и переносных ускорений we.
§ 2.7. Сложное относительное движение
системы твердых тел (реперов)
Выше при описании кинематики движения твердого тела или
относительного движения мы рассматривали два репера: непод-
вижный (абсолютный) Е и подвижный ЕГо и вводили соответ-
ствующие понятия абсолютной скорости (ускорения), относи-
тельной скорости (ускорения) и т.д. Однако суть всего рассмот-
рения состояла в том, что было два репера и один из них дви-
гался относительно другого. То, что Е мы называли абсолютным
репером, было, вообще говоря, дополнительной конкретизацией,
не влияющей на основные соотношения.
7. М.Л. Лидов
98
Глава 2. Кинематика твердого тела и относительное движение
Сейчас мы рассмотрим систему одинаково ориентирован-
ных реперов £0, ..., EN, движущихся друг относительно друга
(рис. 34).
м
Рис. 34
Введем следующие обозначения:
Ак -матрица поворота, определяющая координа-
ты ортов репера Ек относительно репера Ек_{\
Ак - матрица поворота, определяющая координа-
ты ортов репера Ек относительно £0 (в част-
ности, Д =Aj);
qA -координаты начала репера Ек относительно
репера Ек_х (проекции ф на орты репера Ek_i);
qA. = А^т_1 qA - проекции qA на орты репера £0 (4i - Qi
dqk
= —- - координаты вектора скорости начала репера
dt
Ек относительно репера Ек_{\
и* = - проекции вектора скорости начала репера Ек
относительно репера Ек_{ на орты репера Ео
(Uj =110;
г*, v*, w* - координаты, компоненты вектора скорости и
ускорения произвольной (но общей для всех к)
точки М относительно репера Ек (проекции
векторов на орты репера
rzr’v^’wzr _ проекции вектора положения точки М, ее
векторов скорости и ускорения относительно
репера Ек на орты репера Е() (гк = Акгк,
__ _
Qk = —— Ak - матрица угловой скорости вращения репера Ек
dt
относительно репера Ек_х\
§ 2.7. Сложное относительное движение системы твердых тел
99
- координатный вектор угловой скорости вра-
щения репера Екотносительно репера Ек_х (<Шк
соответствует матрице Ц.);
<лк - ^к-^к ~ проекции вектора угловой скорости враще-
ния репера Ек относительно репера Ек_х на
орты Ео;
-матрица угловой скорости, соответствую-
щая <йк.
Получим некоторые вспомогательные соотношения.
1. Преобразование поворота Ео —> Ек можно представить
в виде последовательности преобразований:
Ео Е, —Ек.
Поэтому
4=44-1-А- (2-7.1)
Применяя к (1) операцию транспонирования, получим
(2.7.2)
удт X —
2. Покажем, что производную по времени dAk / dt можно
представить в следующем виде:
4Т = t < (2-7.3)
_ 1=1
Дифференцируя (2) по времени, получим
/7ДТ А _ _ ИАТ — —
(2.7.4)
dt ~ dt
Согласно (2),
(2.7.5)
Согласно (1) и (2), нетрудно доказать справедливость следую-
щего равенства:
дт+)...Лт=ААт=М-Ат- (2-7.6)
Подставим (5) и (6) в (4) и, используя обозначение Ц =
= (<7ДГ I dt) получим
^ = 1 A’i^AA-.A’ = f А’ДА-Л'-
7*
100 Глава 2. Кинематика твердого тела и относительное движение
Для получения (3) необходимо воспользоваться обозначением
ДТ_ДД_1=Ц. (2.7.7)
Рассмотрим формулы преобразования координат точки М
при переходе от репера Е^х к реперу Е>
го = АЧ+<Ь
Fi=4Tr2+q2, (2.7.8)
h-i = АЧ +q*
Покажем, что соотношения между г0 и rk можно представить в
следующем виде:
«7=4Ч+Е ЧЧ (4Т=')- (2.7.9)
7=1
Докажем справедливость (9) по индукции; такой вид имеет
связь г0 и rk при к = 1. Подставив в (9) fk = Дт+1г^+1 + q^+1, полу-
чим
fo = АЧт+Л+1+Ат q*+i + Е Ч-Ч-
7=1
Так как ДтДт+1 = Дт+Р то зависимость г0 от гЛ+1 действительно
имеет вид (9), где к заменено на к + 1. Продифференцируем (9) по
времени:
vo =
+у
dt dt к
dAT -
—— q, +
dt J
£ ^-4+A‘4'<2-7'10)
77 at at
Используя (3), получим
vo =
44+E
7 = 1
+
+ E 4^+44-(2.7.11)
7 = 1
§ 2.7. Сложное относительное движение системы твердых тел
101
Используя введенные обозначения
Q(q7=[w„qJ,
A/-i67=uJ’
запишем (11) в следующем виде:
к j___1 к
= £ [<o,,rJ + 2 Y [“/’QyJ + S uJ + yk- У-П.П)
/ = 1 j = l Z = 1 J = 1
Последнее соотношение справедливо при любом к, в частности
при к = N.
Рассмотрим специальные случаи движения реперов.
1. Если все реперы имеют общее начало
q, =q2 = ... = qAf =0,
Uj = u2 =...= uw =0,
TO
v0 =[<o,rw] + vw, (2.7.13)
где
N
<o = 2}<«>,- (2.7.14)
i=l
Мы получили, что в рассматриваемом случае угловая скорость
вращения EN относительно Ео есть сумма угловых скоростей
относительных вращений Ег относительно Е^{ (все относитель-
ные угловые скорости проектируются на орты Ео)«
2. Если все реперы перемещаются друг относительно друга
поступательно
G>1 = со2 =... = - О,
то v0 = и + Vyv,
где u = X и,. (2.7.15)
1=1
Скорость поступательного движения EN относительно Е() есть
сумма относительных скоростей поступательных движений Е)
относительно Е^.
Аналогично можно получить формулу для ускорения точки в
сложном движении. Однако она нам не потребуется.
102 Глава 2. Кинематика твердого тела и относительное движение
2.8. Кинематические уравнения Эйлера
Рассмотрим два репера Е' и Е" с общим началом (рис. 35).
Пусть преобразование от репера Е' к реперу Е" есть преобра-
зование простого поворота П (3, у):
Е' new >£//_
е —е "
3 3 Предположим, что угол у изменяется с
течением времени: у = = у(г), т.е. репер
Е” вращается относительно Е'.
Лемма 1. Движение репера Е” отно-
уу сительно Е' есть вращение вокруг по-
стоянной оси ез=е" с угловой ско-
ростью
Рис-35 со' = —е'3. (2.8.1)
dt 3
Доказательство. Матрица
' cosy siny 0^
П(3,у) = -siny cosy 0 .
< 0 0 1,
Вычислим матрицу угловой скорости
Q^6/nT(3,Y)n(3/f) = dt
(-siny -cosy O') f cosy siny 0) fO -1 0)
dv = — cosy -siny 0 A -siny cosy 0 = — 1 0 0
"o4 0 0 S o4 О О > 3 r-H4 О О s
Вектор со', соответствующий Q3, имеет вид
dt
Последнее соотношение можно записать в следующем виде:
со =—во.
dt 3
Лемма 2. В случае преобразования Е'
П(1,у)
» Е" и у = у(г)
§ 2.8. Кинематические уравнения Эйлера
103
движение репера Е" относительно Е' есть простое вращение с
угловой скоростью
(Доказательство аналогично или можно воспользоваться равно-
правным положением ортов репера.)
Простому повороту П(2, у) соответствует угловая скорость
, dy ,
со -—е9.
dt г
Выше (см. § 2.3) мы показали, что произвольное преобразование
поворота
Е = (ej,e2,e3)—^ч>Е = (ej,e2,e3)
можно представить как суперпозицию трех простых поворотов:
П(3,у) П(1,6) 2^2 П(3,Ф)
и матрица А с помощью углов Эй-
лера и матриц простых поворотов
П(/, у) представима в следующем
виде:
А = П(3,ср)П(1,0)П(3, у). (2.8.2)
Пусть репер Е жестко связан
с твердым телом (рис. 36). Используя
результаты параграфа (2.7) и, в част-
ности, формулу (2.7.14), получим, что
угловая скорость со вращения твер-
дого тела (репера Е) относительно
репера Е есть сумма трех угловых
скоростей простых вращений:
СО =<О] + со2 + со3,
где
dw 1 d(p _
со. =—е,, со9 =—е., со9 =—е
1 dt 3 2 dt 1 3 dt
В проекциях на орты репера Е
'О' 'cos\|P sinOsinxj/
е3 = 0 . ej = sin v > «3 = - sin 0 cosy (2.8.4)
Л о > ч COS0 ?
104 Глава 2. Кинематика твердого тела и относительное движение
В проекциях на орты репера Е
^sinOsincp^ ' coscp
е3 = sin0coscp , е{ = -sincp ’ ез = 0
ч COS0 ) < о >
(2.8.5)
Используя соотношения (2.8.2)-(2.8.5), получим
в проекциях на орты репера Е\
! . б?ср
ш =—cosw + sin0sinw —
dt dt
2 dQ . . „ dtp о
ш =—sin v-sin 0 cos v — , (2.8.6)
dt dt
з d\p dtp
co = — + COS0 —;
dt dt
в проекциях на орты репера Е:
_1 . . dw dQ
co = sin0sincp— 4-coscp —,
dt dt
—2 . zx dw . dQ o
co =sin0coscp-------sincp —, (2.8.7)
dt dt
_з _ dtp dtp
dt dt
Эти соотношения можно разрешить относительно dyjldt,
dtpldt, dQ/dt. Если компоненты угловой скорости - известные (за-
данные) функции времени coz(f) (или со* (Г)), то получим систему
трех дифференциальных уравнений первого порядка для опреде-
ления трех углов Эйлера \р(Г), ср(Г), 0(0-
Несколько позже нам потребуется справедливость утвержде-
ния следующей леммы.
Лемма 3. Для любого вектора угловой скорости <о =
со2
со3?
можно указать матрицу поворота А(г), удовлетворяющую при t =
= Г следующим условиям:
1) А(Г) = I - единичная матрица;
§ 2.8. Кинематические уравнения Эйлера
105
2) А| =Q - матрица угловой скорости, соответствую-
щая указанному вектору со.
Для доказательства представим преобразование реперов
Е1 —, определяемое матрицей А, в виде трех последова-
тельных преобразований простого поворота:
^1 П(1,У1) > ^2 П(2,у2) ^>3 П(3,уз) >
В этом случае вектор угловой скорости со, определяемый матри-
цей А(7), есть сумма векторов угловой скорости трех простых
вращений:
СО = COj +со2 + со3,
где со- = —Le- (е- - z-й орт z-го репера Ez).
dt
Если принять = ОУ (t - Г), i = 1, 2, 3, то
1) у I . = 0, ^- = со', i = l,2,3;
1'=' dt
2) n(z,Y/)|r_?* - I - единичная матрица, z = 1, 2, 3, и, следова-
тельно, е- = е), z = 1, 2, 3.
Таким образом,
со = c^ej + со2е2 + со3е3,
т.е. со равняется заданному вектору со. Тем самым доказано ут-
верждение леммы.
Глава 3
Введение в динамику
системы материальных точек со связями.
Общие теоремы динамики и их применение
§ 3.1. Голономные и неголономные связи
Выше мы определили твердое тело как систему материаль-
ных точек (r7, т7), изменение координат которых ограничено ус-
ловиями
|г7 -rk 1 = ^ = const, j,k = 1,2,...,п.
Такого рода условия являются частным случаем ограниче-
ний, которые вводятся при описании различных механических
моделей. Введение таких ограничений (связей) существенно рас-
ширяет возможности описания реальных процессов.
Определение 1. Будем говорить, что на систему материаль-
ных точек (г7, mj),j =1,2, ..., и, наложены удерживающие связи,
если указаны функции
fi = Z(r1,r2,r3,...,r„,v1,v2,...,v„,0
(7 = 1,2,..-Л; к<3п)
координат точек системы, компонентов их векторов скорости
и времени и задано, что движение точек системы (r7(r), m7), j =
= 1, 2, ..., и, удовлетворяют на рассматриваемом интервале вре-
мени (при t Е Jt) уравнениям связей'.
y;(r1(r),...,rn(r),v1(r),...,v„(r),r) = O,
i = l,2,...,k; к<3п, =
1 dt
(Предполагается, что^ имеют все частные производные доста-
точно высокого порядка.)
Для сокращения записи введем векторы:
§ 3.1. Голономные и неголономные связи
107
Иг1
r^R2\ veR\ vlk-—feRk.
dt
В сокращенной записи уравнения связей имеют вид
f(r(r),v(O,O = O. (3.1.1)
Специальный класс удерживающих связей определяется век-
тор-функциями, не зависящими от компонентов вектора скоро-
сти:
f(r(r),r) = O. (3.1.2)
Уравнения связей (2) можно записать в дифференциальной
форме
dt df df п
dt dr dt
(3.1.3)
где
Эг„3
ЭГ
dr
Эг,1
Эг,2
dr/
ЭЛ
dr/
Эг3
- матрица размера
кхЗп,
df
dt
dt
- /с-вектор,
dr
v =—
dt
dt
Интегрируя (3), получим
f(r(r),O = c,
(3.1.4)
где с - постоянный /с-вектор.
Если рассматривается задача при заданных начальных ус-
ловиях
r = ro>
то по этим условиям вектор с определяется однозначно, и связи
(4) оказываются эквивалентными связям вида (3):
f(r,r)-f(ro,Zo) = O. (3.1.5)
Связи в виде (3) являются частным случаем связей, ли-
нейных по компонентам вектора скоро-
108
Глава 3. Общие теоремы динамики и их применение
с т и v, которые можно записать в следующем виде:
Bv + Р = 0,
(3.1.6)
где
В = (£/) =
матрица размера тхЗи,
- m-вектор, т < Зп.
В общем случае линейных дифференциальных связей эле-
менты матрицы В/ и компоненты В, являются функциями толь-
ко координат точек системы и времени, т.е.
В/ =В/(г,0, /?=/?(г,Г), г = 1,2,...,т; j = 1,2,..., Зи.
Чтобы левая часть (6) могла быть записана как полная произ-
водная по времени от некоторой вектор-функции f(r, 0, т.е. в
виде (3), функции В/(г, Г), Pt(r, t) должны удовлетворять спе-
циальным условиям интегрируемости. Такие условия сущест-
вуют. Если эти условия выполнены, то связи (6) будут эквива-
лентны (5) (при т = к).
Определение 2. Конечные связи f(r, t) = 0 или линейные
по компонентам вектора скорости связи, представимые в виде
(df / Or) v + Of / dt =0, называются голономными. Связи, которые
в таком виде представить нельзя, называются неголономны-
ми.
В дальнейшем мы будем изучать движение системы мате-
риальных точек под действием голономных связей и(или) связей,
линейных по компонентам вектора скорости (голономных и
неголономных). Если голономные конечные связи представить в
дифференциальной форме, то всю совокупность рассматривае-
мых связей можно будет записать в виде (6).
Определение 3. Связи, наложенные на систему, называются
независимыми, если ранг матрицы В максимален, т.е. равен т -
числу условий.
При рассмотрении задач со связями будем всегда пред-
полагать, что начальное состояние системы (t = t{}, г = r0, v = v0)
удовлетворяет связям. Для голономных конечных
связей f(r, Г) = 0 будем говорить, что начальное состояние си-
§ 3.2. Виртуальное движение. Виртуальный вектор
109
стемы удовлетворяет связям, если
f(ro,fo) = O и f^v + ^ =0.
^Эг ot Jt=t(}y r=rQy v=vo
Для линейных дифференциальных связей (голономных или нет)
необходимо только выполнение условий
B(ro,to)vo + P(ro,to) = O.
Примеры задач с голономными связями
1. Движение материальной точки
(г, т) по подвижной двумерной поверх-
ности (рис. 37).
Уравнение связей:
ЖШ) = 0. (3.1.7)
f(r, 0=0
Рис. 37
В частности, = 0,/g R.
2. Движение материальной точки (г, т) по подвижной кривой
(рис. 38).
Уравнения связей:
(3.1.8)
/2(г(0,0 = 0, fieR, г-1,2/
3. Твердое тело определяется сис-
темой материальных точек (r7, my), j =
= 1,2,..., N, и уравнениями связей
|гу - rk | = const; j, к = 0,1,2,
Цг,/)=0
f2(r, /)=0
Рис. 38
N. (3.1.9)
4. Твердое тело с заданным законом движений одной его точ-
ки (г0, Шо)«
К условиям (9) добавляются три условия:
ro-f(O = O,
f(/) - заданная вектор-функция времени, f(Z) G R3 4.
§ 3.2. Виртуальное движение. Виртуальный вектор
В случае голономных конечных связей f(r, t) - 0 каждое из
уравнений связи t) = 0 с геометрической точки зрения являет-
ся гиперповерхностью в расширенном конфигурационном про-
странстве R3n х R, где R3n - пространство координат точек систе-
мы, &R - ось времени.
При каждом t пересечение к гиперповерхностей в R3n /(г, t) =
по
Глава 3. Общие теоремы динамики и их применение
= О, I' = 1, 2,..., к, выделяют в R3n, вообще говоря, гладкое много-
образие Mt с R3n.
Пусть г = г(г), движение рассматриваемой системы;
г(7): Л -> Движение системы г (Г), в частности, должно удов-
летворять уравнениям связей, т.е. r(/) G Mt при каждом t.
Обозначим через J интервал вещественной оси (-8, 8), где
8 > 0 может быть сколь угодно малым числом. Точки Je будем
обозначать т. Пусть Jt по-прежнему интервал временной оси.
Рассмотрим отображение Щ: JtxJ< —>R3>1 - прямого произве-
дения интервалов и JtB конфигурационное пространство R3n.
Это отображение определяется вектор-функцией двух пере-
менных Гит:
г = ф(Г,т).
Будем предполагать, что функции ф(Г, т) имеют необходимое
число частных производных по t и т.
Предположим, что вектор-функция ф( Г, т) удовлетворяет
следующим двум условиям.
1. При т = 0 и любом te Jt
ф(г,О) = г(г), (3.2.1)
где г(/) - координаты точек нашей системы в момент времени г,
т.е. ф(г, 0) - движение системы.
2. При каждом фиксированном Г, и всех т G Je
Г(ф(Г,т),Г) = 0, (3.2.2)
где/-(г, t)-k уравнений голономных связей (3.1.2).
Определение 4. При выполнении условий 1 и 2 отображение
г = ф(/, т) при любом фиксированном т G Je будем называть
виртуальной кривой (или виртуальным движением). При этом
г = ф(/, т) при различных т G J£ определяют множество виртуаль-
ных кривых.
Из условия 2 следует, что при фиксированном Гите век-
тор-функция ф(/, т) определяет кривую на многообразии
—> М{), проходящую при т = 0 через точку г = г(/) = ф(Г, 0), в
которой в данный момент находится система.
Определение 5. Для случая голономных конечных связей вир-
туальным вектором в момент t е Jt называется вектор £(Г) G R3n,
определяемый формулой
£(')=— , (3-2.3)
Эт т=0
§ 3.2. Виртуальное движение. Виртуальный вектор
111
где ф = ф(Г, т) - множество виртуальных движений; £(7) - ка-
сательный вектор к кривой г(т) = ф(Г, т) (/ = const) в точке г(7) =
= ф(/, 0). Эта кривая расположена на многообразии Mt; тем са-
мым £(Г) - касательный вектор к Mt.
Теорема о виртуальных векторах. Чтобы вектор-функция
времени g(r) е R3n при независимых голономных связях f(r, t) = 0
была в каждый момент времени t G Jt виртуальным вектором,
необходимо и достаточно, чтобы вектор £(Г) удовлетворял при
t G Jt следующей системе уравнений:
3f(r,r)
Эг
€(0 = 0,
r=r(t)
(3.2.4)
где г(г) - движение системы.
Необходимость. Пусть ф(Г, т) - множество виртуаль-
ных кривых. Тогда
Г(ф(Лт),0 = 0, tEJt,
Продифференцируем это соотношение по т и положим т = 0:
Of Эф А
Эг 0т JT=0
0f
Эг
g(O = o.
(3.2.5)
r=y(/,0)=r(O
Достаточность. Так как ранг матрицы ЭГ/Эг размера
к х Зп равен к, то существует отличный от нуля минор к-го по-
рядка. Представим: г = (r19 r2), rj g Rk и r2 g R3n~k. Предположим,
что мы так переставили порядок следования координат, что
именно det (Э17с)Г|) Ф 0. Нам достаточно, чтобы это условие вы-
полнялось при т = 0 (при г = г(/)), т.е. при значениях координат г,
отвечающих состоянию системы.
Рассмотрим вектор-функцию
ф(Л т) = r(0+Tg(O + TQ (Z, т), (3.2.6)
где г(Г) - координаты системы, §(Г) - произвольный вектор, удов-
летворяющий (4).
Представим: т| = (т)19 тг|2), g Rl\ т|2 g R3n~k.
Положим тг|2 = 0, а тг|! определим так, чтобы при t g Jt и при
достаточно малом 8 и т G 7е
f(r(r) + T^) + nO = 0. (3.2.7)
Докажем, что это возможно.
Уравнения (7) при фиксированных t и £; суть система к урав-
нений относительно (к + 1)-й переменной: к координат вектора
тг|! и переменной т.
112
Глава 3. Общие теоремы динамики и их применение
Так как
= detM
V 1*1 ) г=г(Г) + Т^
при достаточно малом £ и т G Je, то по теореме о неявных функ-
циях уравнения (7) однозначно определяют вектор-функцию
iq/r, т), обращающую (7) в тождество и необходимо удовлетво-
ряющую условию тг|!(Л 0) = 0; последнее следует из условия
f(r(O,Z) = O.
При таком выборе ^(г, т) и т]2 - 0 вектор-функция (6) оп-
ределяет множество виртуальных кривых ф(/, т).
Продифференцируем (7) по т и положим т = 0:
df(\ Этг|Л
dr V Эт )
1Эг Эг, Эт Jt=0
3f Этт) (
Эг1 т=0 Эт т=0
Мы воспользовались условием (4) и выбором nq2 = 0. Так как
Используя (6), вычислим производную Э\|//Эт при т = 0:
Эф +
Эт т=0 Эт т=0
(3.2.8)
То есть £(Г) - действительно виртуальный вектор для построен-
ного множества виртуальных кривых (6).
Определение 6. В общем случае линейных по скоростям свя-
зей (3.1.6) Bv + р = 0 (голономных или неголономных) виртуаль-
ным вектором, по определению, называется любой вектор £(Г) G
G R3n, удовлетворяющий уравнениям
В^(0 = 0, (3.2.9)
где B(r, t) (матрица размера т х Зп) вычисляется при г = г(Г).
Согласно доказанной теореме для голономных связей, опреде-
ление (9) совпадает с (3) (при т = к).
Теорема. Для линейно независимых связей множество вир-
туальных векторов в каждый момент времени t g Jt образует в
№п подпространство Зп-т измерений, где т - число дифферен-
циальных условий (3.1.6).
§ 3.2. Виртуальное движение. Виртуальный вектор
113
Доказательство. Так как матрица В (для общего
случая дифференциальных линейных связей) имеет максималь-
ный ранг, равный т, то строки этой матрицы образуют т ли-
нейно независимых векторов, принадлежащих R3n. Обозначим
через R™t} подпространство R3n, натянутое на эти векторы. Из
условия B^t) = 0 (9) следует, что % - произвольный вектор, при-
надлежащий ортогональному дополнению к R™ty То есть % -
произвольный вектор подпространства Зпгп измерений, которое
будем обозначать Тг(г).
В случае голономных связей на языке геометрии гладких
многообразий Тг(0 - касательное пространство к многообразию
Mt в точке г(Г), а виртуальные векторы называются касатель-
ными векторами.
Замечание 1. О виртуальных перемещениях. В большинст-
ве курсов механики рассматриваются не виртуальные векторы,
а виртуальные перемещения, которые часто обозначают 8г.
Соответствие между этими понятиями определяется форму-
лой
8г = £8т,
где 8т - произвольная вариация т.
Замечание 2. Вектор скорости системы v = dvldt удовлетво-
ряет уравнениям
3f 3f
—- v Ч-= 0 (для г ол ономных связей),
Эг Эг
Bn + Р = 0 (для линейных по скоростям связей).
Чтобы в подпространстве Tr(t) виртуальных векторов сущест-
вовал вектор |(0, равный вектору скорости системы v(r), не-
обходимо и достаточно, чтобы голономные связи явно не за-
висели от времени (df/dt = 0), а в случае неголономных связей
Р = 0.
Замечание 3. О неудерживающих связях. В некоторых моде-
лях условия связей задаются в виде неравенств
fi (ч (0,..., r„ (0, Vj (0,.. •, Vn (0, t) 0, i = 1,2,... ,k.
Такие связи называются неудерживающими. В дальнейшем мы
будем рассматривать в основном удерживающие связи.
Определение 7. В отличие от системы со связями систему ма-
териальных точек без связей называют свободной системой.
8. М.Л. Лидов
114
Гпава 3. Общие теоремы динамики и их применение
§ 3.3. Уравнения движения системы
материальных точек с идеальными связями
Начнем с самого простого примера. Рассмотрим (рис. 39)
движение одной материальной точки (г, т) под действием за-
данной внешней силы F(r, t). Предположим,
что движение точки ограничено связями
г2=г3=0, (3.3.1)
т.е. связи допускают движение точки только
по прямой, определяемой ортом еР Такая мо-
дель описывает, например, движение бусин-
ки, надетой на натянутую проволоку. Если бы точка была сво-
бодной, то ее движение г(Г) удовлетворяло бы следующей систе-
ме уравнений:
б?2г
m—^- = F(r,Z). (3.3.2)
dt
Однако решения (2), вообще говоря, не могут удовлетворять
условиям связей (1). Даже если задать г2 = г3 = (), и2 =и3 = О при
t = то, если F2(r, t) или F3(r, t) не равны тождественно нулю
через сколь угодно малое время t - условия (1) будут на-
рушены.
Однако очевидно, что в физическом эксперименте, вообще
говоря, бусинка будет оставаться на проволоке и будет совер-
шать определенное движение, в котором г2 ~
-------~ г3 ~ 0. Согласия очевидного факта и фор-
у'-----мального описания в модели можно добиться,
F N если понять, что в реальном физическом
Рис. 40 эксперименте на бусинку действует не только
внешняя сила F(e), но и определенная сила со
стороны проволоки. В модели эту силу часто обозначают N и
называют силой реакции связи (рис. 40).
Учитывая силу реакции связи, уравнения движения бусинки
можно записать в следующем виде:
d г
m—4 = F(rj) + N. (3.3.2)
dt
При этом можно подобрать такую силу N, чтобы условия г2 =
= г3 = О выполнялись в решении уравнений.
Действительно, если г2 = г3 = 0, и2 = и3 =0 в начальный
момент времени / = /0 и выбрать N2 = -F2, N3 = -F3, то на всем
рассматриваемом интервале времени t g Jt r2(t) = r\t) = 0. Одна-
§ 3.3. Уравнения движения системы с идеальными связями
115
ко уже в этом примере мы видим, что условия связи будут
удовлетворены при любом первом компоненте ЛП силы реакции.
То есть условия связей не определяют реакцию связей
однозначно.
Рассмотрим систему материальных точек (rb mJ, ...,
(rn, mJ, на которые действуют заданные силы Fb к = 1, 2, ..., п
(результирующие внутренних и внешних сил на к-ю точку).
Пусть движения точек ограничены линейными по скоростям
связями
dr
<p(r,v,J=B — + Р = 0, (3.3.3)
dt
где В - матрица размера т х Зп, Р - m-вектор, гт = (г/,^2,.. .,ги3). В
частности, (3) может представлять и голономные связи, записан-
ные в дифференциальной форме.
С точки зрения физического анализа, представляется оче-
видным, что любое изменение движения системы есть следст-
вие действия на систему определенных сил. При этом, посколь-
ку связи так или иначе реализуются с помощью некоторых ма-
териальных приспособлений, то кроме заданных сил, опреде-
ляющих влияние на к-ю точку других точек системы или
«внешнего мира», на эту точку действуют дополнительные си-
лы N* со стороны связей, которые и обеспечивают удовлетво-
рение условий связей (3). Силы NA называют силами реакций
связей.
Определение 1. В отличие от сил реакций связей заранее за-
данные силы F* (внутренние или внешние) называют активными
силами.
Формально силы реакций связей вводятся в модель движения
системы материальных точек со связями с помощью следующего
постулата.
Движение системы материальных точек (rz, mz), i = 1, 2, ..., п,
при связях (3) будет удовлетворять уравнениям движения, спра-
ведливым для свободной системы, если к результирующим
активных сил Fb приложенных к каждой точке (rk, т^, при-
бавить силу реакций связей чтобы уравнения связей (3) вы-
полнялись на всем рассматриваемом интервале времени.
Из этого постулата следует, что движение системы мате-
риальных точек описывается уравнениями
б/2г
m^ = F\+N*, к = (3.3.4)
где F* е R3 - заданные внутренние и внешние силы, a N* g R3 -
пока неопределенные силы реакций связей.
8*
116
Глава 3. Общие теоремы динамики и их применение
Для сокращения записи обозначим:
Силы F, N G R3n образованы из упорядоченных компонентов
векторов F* и Nb М - диагональная матрица размера Зп х Зп,
составленная из масс материальных точек системы. Запишем
уравнения (4) в сокращенном виде:
6?2Г
M^4 = F + N.
dt2
Как мы уже отмечали, условия (3) не определяют однозначно
силы реакций связей N и тем самым уравнения (3) и (4) не
соответствуют пока еще никакой модели.
Анализ реальных механических движений системы мате-
риальных точек со связями типа (3) показал, что широкий круг
таких явлений может быть приближенно описан с помощью мо-
дели, в которой связи предполагаются идеальными.
Определение 2. Связи называются идеальными, если на лю-
бом движении системы, совместимом со связями, удовлетворяет-
ся следующее условие:
(N,C) = O, (3.3.5)
где £ = £(/) - произвольный виртуальный вектор £ G R3n, (•, •) -
скалярное произведение в R3n.
Для любого 8т Ф 0 соотношение (5) эквивалентно соотно-
шению (N, £8т) - 0, где £8т - виртуальное перемещение. Скаляр-
ное произведение силы на вектор элементарного перемещения
называется элементарной работой силы. Поэтому условие
идеальности связей (5) часто формулируют следующим образом:
«Работа сил реакций идеальных связей на произвольном вир-
туальном перемещении равна нулю».
Теорема. При заданных начальных условиях (Z = Го, г = г0,
v - v0), совместимых со связями, уравнения (3) - (5) позволяют
однозначно определить движение системы и силы реакций свя-
зей на некотором интервале времени JtB окрестности г0.
§ 3.3. Уравнения движения системы с идеальными связями
117
Доказательство. 1. При линейно независимых связях
(3) строки Bi (/ = 1,2, ..., т) матрицы В определяют в R3n при t G
G Jt т линейно независимых векторов. Подпространство векто-
ров, натянутое на эти векторы, мы обозначили R™t) ^R3n. Про-
странство виртуальных векторов £(Г) мы обозначали Эти два
подпространства образуют в R3n ортогональное дополнение друг
другу. (Мы используем обозначение Tnt) и для случая неголо-
номных связей. В этом случае Гг(г) не является касательным
пространством.) Так как силы реакций связей N ортогональны
произвольному виртуальному вектору, то, следовательно, N
принадлежит R”\ty Произвольный вектор R^t} представим в сле-
дующем виде:
N = ЯТХ, (3.3.6)
где V = (X1, X2, ..., Xm), X* - скалярные функции. В более под-
робной записи
N = Z1B1+A2B2+... + AmBm,
(3.3.7)
В; = (В‘,В2,...,В,3"), BieR.
2. Условия связей (3) должны выполняться на интервале Jt
движения системы. Следовательно, в любой момент времени
t G Jt не только = 0 (см. (3)), но и ckpldt = 0. Дифференцируя (3)
по времени, получим
^ = В^4 + Ф(г,¥,0 = 0, (3.3.8)
dt dt
где через Ф обозначен m-мерный вектор
Ф = Су + <1. (3.3.9)
Здесь
С = -—(Bn + Р) - матрица размера т х Зи,
Эг
, дВ ЭР
d = — v + —--m-мерныи вектор.
Условия (8) не только необходимы, но и достаточны для то-
го, чтобы удовлетворялись условия связей.
Из уравнений движения (4) следует:
d2r
—=- = Af”’(F+N), (3.3.10)
dt
где МЛ - матрица, обратная М.
118
Глава 3. Общие теоремы динамики и их применение
Подставляя (10) в (8), получим
BAr'N + BAr'F + a^O. (3.3.11)
Подставляя выражение N из (6), найдем
(ВМ’|Вт)Х = -(Ф + ^М-1Е). (3.3.12)
Лемма. Если матрица В имеет максимальный ранг (равный
т), то
det(BA/"'BT) * 0. (3.3.13)
Доказательство этой леммы мы дадим ниже.
Из (12) и (13) следует, что
Х = -(ВМ~1ВТУ'(Ф + ВМ~1 F). (3.3.14)
Последняя формула дает однозначное определение вектора X
через заданные силы F и известные функции координат и
компонентов скорости. Тем самым однозначно определяются си-
лы реакций идеальных связей (точнее, зависимость N от г, v, t):
N =N(r, v,r) = ВТХ, (3.3.15)
где вектор X вычисляется согласно (14).
Теперь для определения движения системы необходимо про-
интегрировать систему уравнений
M^-| = F + N (3.3.16)
dt
при заданных начальных условиях и известных силах. Решение
(16) однозначно определяет состояние системы в произвольный
момент времени t е Jt. Этим заканчивается доказательство тео-
ремы.
Замечание 1. Из условия (7) видно, что каждое отдельное ус-
ловие связи
(B,,v) + P,=0
порождает отдельное слагаемое
№'> = Х'В,
в выражении для сил реакций идеальных связей и
N = j? N(/’.
j=i
В то же время множители А/ (14) зависят (нелинейным образом)
от состояния системы, внешних сил и всех т условий связи.
§ 3.4. Пояснения к определению идеальных связей
119
Замечание 2. Решение системы (3.3.16) на интервале Jt при
заданных начальных условиях задает отображение Jt R3n, оп-
ределяемое вектор-функцией г = г(Г). При этом r(t) удовлет-
воряет как уравнениям движения, так и уравнениям связей.
Это отображение называют действительным движением систе-
мы. В отличие от виртуального движения (виртуальной кри-
вой) г = ф(/, т), которое удовлетворяет голономным связям, но,
вообще говоря, не удовлетворяет уравнениям движения. При
этом ф(Г, 0) = г(0 - действительное движение.
Доказательство леммы. Обозначим через В7,
j = 1, 2, ..Зп, столбцы матрицы В:
В = (В1,В2,...,В3").
Справедливо равенство
Легко видеть, что ранг матриц В и В одинаков и равен т (числу
строк). Если det (ВЛ/-1ВТ) - 0, то существует нетривиальное ре-
шение системы уравнений
ЯВтх = 0,
где х - ^-мерный вектор и 1x1 Ф 0.
Умножим это соотношение слева на хт - вектор-строку:
хтВВтх = 0 -> (Втх)т(Втх) = (Втх, £тх> = 0 -э Втх = 0.
Последнее условие противоречит линейной независимости
строк матрицы В.
§ 3.4. Пояснения к определению идеальных связей
Обозначим через N7 силу реакций связей, действующую на
j-ю точку, а через § - виртуальный вектор j-й точки: Ny е Л3,
t е К-
Условие идеальности связей можно записать в следующем
120
Глава 3. Общие теоремы динамики и их применение
виде:
0 = = Х (3.4.1)
J=1
где слева стоит скалярное произведение в /?3л, а справа - сумма
скалярных произведений в Л3.
1°. О силе реакций на свободную точку. Предположим, что
связи голономны и в условия голономных связей f(r, t) не входят
координаты k-й точки гк:
— 0. (3.4.2)
Виртуальным вектором является произвольный вектор
€ = е/?3, удовлетворяющий условию
X <3-4-3>
J=1 \ J /
Если выполнено (2), то (3) будет удовлетворено при произ-
вольном е R3. С другой стороны, условие идеальности связей
(1) можно записать в следующем виде:
X (N,,g,.) + (N^) = 0. (3.4.4)
Так как (4) должно удовлетворяться при произвольном %к е R3,
то из (4) следует
N,=0. (3.4.5)
Из формального описания получен физически естественный
результат: если движение точки не ограничено связями, то сила
реакции на эту точку равна нулю.
Упражнение. Сформулируйте и докажите аналогичное утверждение для
линейных по скоростям связям, не содержащим компонентов вектора скорости
k-й точки.
2°. Рассмотрим другой (в некотором смысле, противополож-
ный) пример. Пусть связи определяют вектор скорости ук точки
к в момент времени Г.
(3.4.6)
где f(Z) с R3 - заданная функция времени.
Соотношение (6) можно записать в виде Гук - f(r) = 0, где
§ 3.4. Пояснения к определению идеальных связей.
121
I - единичная матрица 3-го порядка. Отсюда следует, что вир-
туальный вектор удовлетворяет условию
и, таким образом,
^=0
^=0.
Тем самым условие (Nb = 0 выполняется при любом N*. Мы
получили, что связь (6) является идеальной при любом векторе
N^. Как следует из общей процедуры, N* можно определить из
рассмотрения всей задачи в целом с внешними силами и другими
связями.
3°. Рассмотрим движение одной точки (г, т)
по поверхности
/(г, 0 = 0, feR.
Сила реакции идеальной связи определяется
формулой
N-aM, (3.4.7)
где Л - скалярная функция.
Мы получили, что сила реакции идеальной
связи направлена по нормали к поверхности
/(г, t) = 0. Это согласуется с интуитивно очевидным представле-
нием об идеально гладкой поверхности, которая не оказывает
влияния на бесконечно малые перемещения по касательной к
ней.
4°. Две точки, соединенные стержнем нулевой массы
(рис. 41). Условия связей:
/ = |г,-г2|2-/2 = 0, (3.4.8)
где I - длина стержня.
Уравнения движения имеют вид
Wi4x = Fi+Ni’
at
(3.4.9)
m9^- = F2+N2,
2 dt2 2 2
где Fz, Nz e R3 - активные силы и силы реакции связей.
Если связь идеальна, то
где X - скалярная функция.
122
Глава 3. Общие теоремы динамики и их применение
Дифференцируя (8), получим
N1 = 2X(r1-r2), N2 = -2X(r1-r2) = -N1. (3.4.10)
Силы реакции равны по величине и противоположны по
направлению и действуют вдоль стержня.
5°. Пусть система материальных точек состоит из двух под-
систем:
(I) (m2,r2),...;
(II) (m^rj, (m2,r2),....
Пусть заданы линейные связи внутри каждой подсистемы, зави-
сящие только от координат и компонентов векторов скорости
каждой подсистемы отдельно. И кроме того, задана связь, огра-
ничивающая относительное движение двух точек различных под-
систем.
Примеры.
1) |г1-^|2-/2=0. (3.4.11)
Первые точки подсистемы соединены стержнем
( I j длиной I (рис. 42). Повторяя рассуждения 4°, полу-
чим, что эта связь определяет дополнительное сла-
гаемое N, в выражении силы реакции, действую-
ще 42 щей на точку (r^mj), равное
Nj = 2X(r1-fj), (3.4.12)
и слагаемое Ni в силе реакции на точку (rj, тх):
Nj =-Np (3.4.13)
где X - скалярная функция. То есть в самом общем случае
Рис. 43
идеальная связь типа стержня порождает силы
реакций, направленные вдоль стержня, и N, и N,
равны по величине и противоположны по направ-
лению: «действие равно противодействию».
2) r^fj, Vj = Vj. Первые точки обеих систем
занимают одно положение в пространстве и vt -
- Vj = 0 (рис. 43). Это три условия. Соответствую-
щие этим условиям выражения для слагаемых сил
реакций на первые точки формально определятся
в следующем виде:
хЧ
X2 ; N, = -N,.
X3
(3.4.13')
Упражнение. Получите это выражение из общего правила.
§ 3.4. Пояснения к определению идеальных связей
123
Пусть две рассматриваемые подсистемы - два твердых тела,
которые в первом примере соединены стержнем, а во втором
примере имеют общую точку. В технике связь второго вида реа-
лизуется с помощью шарнира, который обеспечивает соединение
точек (Fp/Wj) и (^гаД но не препятствует вращению каждого
тела вокруг этой точки.
6°. Твердое тело катится по «идеально шероховатой» по-
верхности (рис. 44). По определению идеально шероховатой
поверхности, скорость в точке касания г = г* в
момент касания равна нулю. Согласно 2°, связь Г
идеальна, так как виртуальный вектор этой \ \
точки удовлетворяет условию = 0. \ \
7°. О «неидеальных» связях. Во всех моделях )
со связями в механике рассматриваются только /ттттттттт^^
силы реакции N, удовлетворяющие условию v
идеальности связей (N, %) = 0. Рис 44
При этом для описания реальных движений
твердых тел или материальных точек в случае, когда, например,
поверхность, по которой движется точка, нельзя считать идеаль-
но гладкой и необходимо учитывать трение между точкой и
поверхностью, ограничивающей ее движение, поступают сле-
дующим образом.
В правую часть уравнений движения k-й материальной точки,
кроме заданных сил F* и сил реакции идеальных связей Nb
добавляют силы трения FJP е R3 и записывают уравнения дви-
жения точки в следующем виде:
б/2г
m^ = F,+N.+F;p, * = 1,2,...,и. (3.4.14)
При этом вид сил трения определяется на основании физических
наблюдений и формулируется как закон природы для данного
круга явлений. Если движение системы ограничено линейными
связями (3.3.3)
Bv+P = 0,
то силы реакции N = (Nb N2, ..., N„), как следует из условия
идеальности связей, удовлетворяют соотношению (3.3.6)
N = ВТХ, V = (Л1,Х2,...А,'И), (3.4.15)
а множители X находятся из соотношения (3.3.12)
(ВМ~'ВТ)Х = -(Ф + ВЬГ1( F + FTp)), (3.4.16)
где F = (Fj, F2, ..., F„) - активные силы, FTp = (F1Tp •..., FJP) - силы
124
Глава 3. Общие теоремы динамики и их применение
трения. Если силы трения FTp являются заданными функциями
только координат точек системы, компонентов вектора скорости
и времени, то соотношения (16) сразу определяют X в виде
(3.3.14), куда вместо F надо подставить F + FTp. В некото-
рых моделях (например, в модели «сухого трения») FTp сама
зависит от величин сил реакций Ny (j = 1, 2,..., п) и, следова-
тельно, от X.
Тогда (16) является более общим видом т уравнений от-
носительно т переменных X, которые, вообще говоря, можно
решить, найти X и тем самым определить силы реакции (15).
§ 3.5. Принцип Даламбера-Лагранжа и общие теоремы
динамики системы материальных точек со связями
1°. Принцип Даламбера-Лагранжа. Выше была описана ло-
гически ясная процедура, которая, вообще говоря, позволяет
определить движение системы материальных точек при наличии
линейных независимых связей и определить силы реакций
идеальных связей. Однако эта процедура редко применяется, так
как она не является наиболее простой ни для анализа, ни для
вычислений. Для определения движения системы материальных
точек при идеальных связях более эффективным является дру-
гой аппарат, с которым мы познакомимся ниже. Основная идея
других подходов состоит в следующем: найти такие эквивалент-
ные уравнения, которые описывают движение системы мате-
риальных точек, стесненных идеальными связями, с помощью
минимально возможного числа переменных, или, иначе, найти
движение системы, не определяя реакций связей.
При этом центральное место для различных направлений
такого толка занимает так называемое основное уравнение ме-
ханики или принцип Даламбера-Лагранжа.
Будем рассматривать движение системы п материальных то-
чек, стесненных связями. Обозначим*):
г - (гь г2,..., гл) = (г/,^2,...,^3) - радиус-вектор системы в
конфигурационном пространстве Я3л;
F = (Ft, F2,..., F„) - (F^F2,...,^3) - вектор заданных актив-
ных сил;
*) Чтобы не загромождать формулы, мы иногда опускаем знак траспонирования «т».
Аккуратная запись: rT = (if,if,...,if) = (г/, г2,..., г3) и т.д. В следующих соотношениях
векторы г, F, N - векторы-столбцы
§ 3.5. Общие теоремы динамики системы материальных
125
N = (NH N2,..., Nn) = (TV,,^2,...,^) - вектор сил реакций
идеальных связей, действующих на материальные точки сис-
темы;
F, N е R3".
Как мы знаем, уравнения движения имеют вид
d г
=F + N, (3.5.1)
dt2
где
М-
т1 О
О \
- диагональная матрица размера Зп х
х Зп, составленная из масс точек.
Пусть B(r, r)v + P(r, f) = О (В - матрица размера т х Зи, Р -
m-вектор) - уравнения всех линейных по компонентам вектора
скорости связей совместно голономных и неголономных. В
частности, эти соотношения содержат и условия голономных
конечных связей f(r, t), записанных в дифференциальной форме:
8f 3f n
— v + — = 0.
Эг dt
Рассмотрим на интервале времени Jt отображение Jt —> R3n,
определяемое вектор-функцией r(f). Будем предполагать, что
кривая г(г) при всех t е Jt удовлетворяет условиям связей
f(r(O, 0 = 0 и B(r(0, t)dx/dt + Р(г(0, 0 = 0.
В случае когда движение системы стеснено только ко-
нечными голономными связями и (или)
линейными дифференциальными связями,
действительное движение системы может выделяться с по-
мощью следующего принципа.
Теорема 1. Принцип Даламбера-Лагранжа. Чтобы вектор-
функция г(0, удовлетворяющая связям, определяла на интервале
времени Jt действительное движение системы, необходимо и дос-
таточно, чтобы уравнение
d2r \
Ш = 0 (3.5.2)
dt I
выполнялось при произвольной вектор-функции £(r) g R3n, удов-
летворяющей условию
В(г(г),£(г)) = О. (3.5.3)
В (2) (•, •) - скалярное произведение в R3n.
126 Глава 3. Общие теоремы динамики и их применение
Доказательство. Необходимость. Если г(г) -
действительное движение системы, то оно удовлетворяет связям
и уравнениям движения (1). Умножая (1) скалярно на £(Г),
получим
M^-F,£(r) =<N,g(r)>.
dr /
Для действительного движения системы произвольный вектор
£(/), удовлетворяющий (3), есть виртуальный вектор. Из условия
идеальности связей: (N, £) = О для произвольного виртуального
вектора. Откуда и следует (2).
Достаточность. Обозначим M(d2rldt2) - F - N. Соглас-
но (2), (N, = 0. Так как |(г) - произвольная вектор-функция,
удовлетворяющая (3), то для N справедливо представление
N = ВТХ, где X е R™. Уравнения М(d2r/dt2) - F = ВТХ совместно с
уравнениями связей B(r(r), r)v + Р (г(г)0 = 0 СУТЬ уравнения
действительного движения при идеальных связях. Таким об-
разом, вектор-функция г(г) удовлетворяет связям и, как мы
доказали, уравнениям движения. Следовательно, г(г) определяет
действительное движение системы.
Если rk Е R3 - радиус-вектор k-й точки, F* - результирующая
заданных сил, действующих на эту точку, £к - виртуальный
вектор для точки к, то уравнение (2) можно записать в сле-
дующем виде:
X (3.5.2')
ТЗх \ dt /
где (•, •) - скалярное произведение в /?3. Наконец, в покомпо-
нентной записи
d2r‘ "I
mk^--F‘ %k(t) = 0.
К j / A v z
dt /
(3.5.2")
2°. Теорема об изменении вектора количества движения.
В этом разделе рассматриваем систему материальных точек
(r„ m,), i = 1, 2, ..., п, стесненную конечными голономными или
линейными по скоростям идеальными связями. Напомним (см.
§ 1.1), что вектором количества движения (или вектором
импульса) Р/ для k-й материальной точки называется произве-
дение ее массы на ее вектор скорости:
РА. =m,ViV.
Определение. Вектором количества движения системы ма-
териальных точек Р называется векторная сумма импульсов всех
§ 3.5. Общие теоремы динамики системы материальных
\Т1
точек системы:
Р = Р*, Ре Я3. (3.5.4)
к-\
Теорема 2. Об изменении проекции вектора количества дви-
жения. Если в каждый момент времени на интервале Jt связи
допускают в R3 сколь угодно малый сдвиг всей системы как твер-
дого тела в постоянном направлении, определяемом единич-
ным вектором а0 е R3, то производная по времени от проекции
вектора количества движения системы на вектор а° равна про-
екции суммы всех (активных) внешних сил на это же направ-
ление:
— <P,a°) = (F(e),a°).
dt
Прежде чем приступить к доказательству теоремы, запишем
формально условие: «связи допускают сдвиг системы как твер-
дого тела в направлении а0».
Для случая голономных связей это условие означает, что при
любом достаточно малом 1т1
у(Г, т) = (г, (Г) + а°т, г2 (г) + а°т,..., г„ (г) + а °т)
является виртуальным движением.
Отсюда следует, что в каждый момент времени t существует
виртуальный вектор
«0 = ^
Эт
(3.5.5)
т=0
а0 ,а° ,...,а°
п
В общем случае линейных голономных или неголономных
связей (Bv + Р = 0) допустимость указанного сдвига означает, что
вектор £ в виде (5) удовлетворяет условию в|ги)£=0 при t^Jt.
Доказательство. Из принципа Даламбера-Лагранжа
(3.5.2) при определяемом согласно (5), следует
Ё ^^-Р„а°) = 0, (3.5.6)
\ dt /
где (•, •) - скалярное произведение в R\
Последнее соотношение можно записать в следующем виде:
уУ F/;,a°\ = 0. (3.5.7)
к=1 / U = 1 /
128
Глава 3. Общие теоремы динамики и их применение
Представим силы Г^как сумму внутренних и внешних сил:
F^F^+F^.
По ранее доказанной лемме сумма всех внутренних активных сил
равна нулю:
SF^)=0-
k=\
п
Обозначим через F(<?) = F*e) результирующий вектор всех
А- = 1
внешних активных сил, действующих на все точки системы;
F(e) G R3.
Используя введенные обозначения и определение (4), из (6)
получим утверждение теоремы 2:
— (P,a0) = (F(£,),a0), (3.5.8)
dt
где (•, •) - скалярное произведение в R3.
Напомним, что внешние активные силы F(e), в частности, могут
содержать и силы трения, действующие на систему в случае не-
гладких связей.
Как следствие из этой теоремы сформулируем еще несколь-
ко тривиально доказываемых, но важных утверждений.
Следствие 1. Если связи при t е Jt допускают сдвиг всей
системы как твердого тела в произвольном постоянном направ-
лении, то производная по времени вектора количества движения
равна сумме внешних (активных) сил, действующих на систему.
Доказательство. Из (8) следует /—Р-F(e),a°\ = 0.
\dt /
Если а0 - произвольный вектор, то
— P = F(<,). (3.5.9)
dt
Следствие 2. Для свободной системы материальных
точек связей нет и любое виртуальное движение возможно.
Поэтому для свободной системы всегда справедливо (9).
Следствие 3. Если к внешним силам F^, k = 1, 2, ..., п,
прибавить силы реакций идеальных связей N*, к = 1, 2, ..., п, то
систему можно считать свободной, т.е. всегда верно следующее
утверждение:
Производная по времени от вектора количества движения
системы равна сумме F(<?) + N внешних активных сил и сил реак-
§ 3.5. Общие теоремы динамики системы материальных
129
ций связей, действующих на систему:
— P = F(e)+N, (3.5.10)
dt
где
N = £nag7?3.
k=l
Следствие 4. Так как
п Л п п jl,*
p = Z ткгк’Х тл =т г > р=т —г,
к=1 at k=l k=l at
п
где т* - тк - сумма масс точек системы, г* - радиус-вектор
к=\
центра масс системы, то из (9) непосредственно следует урав-
нение движения центра масс свободной системы
=FW (3.5.9 9
dt
Это уравнение ранее было получено в § 1.2 (см. (1.2.12)) и сфор-
мулировано как теорема о движении центра масс системы мате-
риальных точек.
Следствие 5. Теорема о сохранении проекции вектора
количества движения. При условиях теоремы 2, если проекция
а() суммы внешних сил, действующих на систему, равна нулю, то
проекция вектора количества движения на направление а0 не
изменяется с течением времени.
Доказательство непосредственно следует из (8) при
(F^, а°) = 0:
<Р,а°) = С = const. (3.5.11)
Следствие 6. При условиях теоремы о сохранении
проекции вектора количества движения проекция радиуса-век-
тора центра масс системы на направление а ° изменяется с тече-
нием времени равномерно.
Доказательство. Так как
dr*
P = m —, (3.5.12)
dt
то из (10) следует
/т> о \ / * dY q \ ~
(Р,а ) = ( т --,а ) = С.
\ dt j
9. М.Л. Лидов
130
Гпава 3. Общие теоремы динамики и их применение
Отсюда
<r*,a°>~(Z-Z0) + C0, (3.5.13)
т
где Со = const.
Следствие 7. Теорема 3. О сохранении вектора количе-
ства движения системы и движения ее центра масс. Если связи,
наложенные на систему, допускают сдвиг всей системы как твер-
дого тела в произвольном направлении и сумма внешних (актив-
ных) сил, действующих на систему, равна нулю, то:
1) вектор количества движения системы не изменяется с те-
чением времени;
2) центр масс системы движется равномерно и прямолинейно.
Доказательство. Из (11) при произвольном а0 сле-
дует
Р = const. (3.5.14)
Используя (12), получим
^- = Лр-»г*=Лр('-'о) + Го, (3-5.15)
at т т
где Го - постоянный вектор.
3°. Теорема об изменении момента количества движения.
Определение 1. Моментом количества движения К, i-й ма-
териальной точки называется вектор, равный векторному про-
изведению радиуса-вектора точки г, на ее вектор количества
движения Р,:
к,. =[г„Р,], К, е/?3. (3.5.16)
Определение 2. Моментом количества движения К системы
материальных точек (или кинетическим моментом) называет-
ся векторная сумма моментов количества движения всех точек
системы:
К = Х к,=£ [Г,.,1>]. (3.5.17)
/=1 /=1
Определение 3. Моментом М, силы F,-, действующей на точку
i системы, называется векторное произведение радиуса-вектора
точки г, и силы F;
М- =[rz,E}].
п
Обозначим через M(t?) = [r-,FU)] векторную сумму момен-
/=1
§ 3.5. Общие теоремы динамики системы материальных
131
тов внешних активных сил, действующих на все точки сис-
темы.
Теорема 4. Об изменении проекции момента количества дви-
жения. Если на интервале Jt связи допускают сколь угодно малый
поворот системы как твердого тела вокруг оси, неизменной на Jt,
проходящей через начало координат и определяемой единичным
вектором со0 е /?3, то производная по времени от проекции
момента количества движения системы на направление, оп-
ределяемое вектором со0, равна проекции на это же направление
суммы моментов всех внешних активных сил, дейст-
вующих на все точки системы:
— (К,<о°) = (М(е),<о°). (3.5.18)
dt
(Внешние активные силы могут для случая негладких связей
содержать силы трения.)
Доказательство. Определим матрицу поворота А(т)
размера 3x3 так, чтобы: 1) А(0) -1 - единичная матрица;
2) кососимметрической матрице (dA/dx) Ат при х = О соответст-
вовал постоянный вектор со0. Согласно доказанной в § 2.8 лемме
3, это можно сделать. Заметим, что в этом случае
— АТ
di
т=0
dA
di
Для случая голономных связей рассмотрим виртуальные дви-
жения
Ф(Г,т) = (А(т)г1(Г),А(т)г2(О,...,Л(т)г„(Г))- (3.5.19)
По условию теоремы, при достаточно малом I х I такое вир-
туальное движение существует. В (19) г(0 - ф(?, 0) - действи-
тельное движение системы. Виртуальное движение ф(Г, х) по-
лучается поворотом каждого вектора гД7) с помощью матрицы
А(т).
Из (19) следует, что виртуальный вектор £,(t) определяется
следующим равенством:
Эх
т=0
dA , х dA
—Г,(Г),..(0
di di
= ([<о%гД0],...,[<о^гДг)]). (3.5.20)
В случае произвольных (голономных или неголономных) ли-
нейных по скоростям связей (Bn + Р = 0) выполнение при каждом
9*
132
Глава 3. Общие теоремы динамики и их применение
t G Jt условия В|г(пё - 0 для вектор-функции g(r) в виде (20) сле-
дует рассматривать как формальное описание условий теоремы:
связи допускают сколь угодно малый поворот системы вокруг
оси со0.
Подставим выражение виртуального вектора (20) в уравне-
ние Даламбера-Лагранжа (3.5.29:
/ ^2]Г/ о \
Е [to ’r'J/=0-
(3.5.21)
Здесь (•, •) - скалярное произведение в R3.
Используя циклическую перестановку для смешанного произве-
дения, получим
(3.5.22)
Докажем две леммы.
Лемма 1. Справедлива формула
Т[г>’Р>] =
dt J J
г,,—~
7 dt
(3.5.23)
Дифференцируя каждый сомножитель векторного произведения,
получим
— [г ,Р•] = [— ,Р
dtL r yJ dt ’ 1
dt
Г;,—-
J dt
Ho dYjldt = v7, P7 = m7-v7 и первое слагаемое равно нулю, так как v7
и Р7 - коллинеарные векторы.
Лемма 2. Запишем силы F7 в виде суммы внутренних и внеш-
них сил:
F = F(i) + F(6°
j j j ’
Тогда
j=l 7=1 г=1
Утверждение. Сумма моментов внутренних сил, дейст-
вующих на все точки системы, равна нулю.
§ 3.5. Общие теоремы динамики системы материальных
133
Доказательство. Обозначим через F75 силы парных
взаимодействий, тогда
X
7=1 7=1
X X
5=1 J=1 5=1
S*j J s*j
=X X ar/.M+k.F.B-t x ff,— F„).
7=1 s>j 7=1 5 >7
(3.5.24)
Векторные произведения, стоящие под знаками сумм, равны
нулю, так как вектор (г7 - г5) коллинеарен с вектором силы пар-
ного взаимодействия F75:
е,,=(г7.-гл.)т;5,
где fjs - скалярная функция.
Используя леммы 1 и 2, получим из (22):
/ п Г /7Р 1 п \
0 = (<о°,У г,^- -У [r,,F,.]) =
\ AAJ dt\ АА} 77
<о°,—-М(е>\
j dt /
(3.5.25)
п
где М(и= [r-,F(£?)] - сумма моментов внешних активных сил.
4=1
Записывая последнее соотношение в эквивалентном виде (со0 =
= const), получим формулу, доказывающую справедливость ут-
верждения теоремы:
—(<о°,К) = (<о°,М(е)). (3.5.26)
dt
Из теоремы 4 вытекает ряд следствий.
Следствие 1. Если связи на интервале Jt допускают сколь
угодно малый поворот всей системы как твердого тела вокруг
произвольной постоянной оси, проходящей через начало коор-
динат, то производная по времени от момента количества дви-
жения равна сумме моментов всех внешних сил, действующих на
систему:
— = М(е). (3.5.27)
dt
134
Гпава 3. Общие теоремы динамики и их применение
При произвольном <о° формула (27) и, следовательно, доказа-
тельство утверждения непосредственно следуют из (25).
Следствие 2. Для свободной системы без связей допу-
стимо произвольное виртуальное перемещение и, следовательно,
справедлива формула (27).
Следствие 3. Если к заданным силам добавить силы
реакций связей, то систему можно рассматривать как свободную.
Поэтому всегда верно утверждение: производная по времени от
момента количества движения системы равна сумме моментов
внешних сил и сил реакций связей, действующих на систему:
— = MW + Mw,
dt N
(3.5.28)
где M/v = [r7,N7], Ny G R3 - результирующая сила реакций
связей, действующая на j-ю точку.
Следствие 4. Теорема о сохранении проекции момента
количества движения системы. При условиях теоремы 4, если
проекция суммы моментов активных внешних сил на направле-
ние со0 равна нулю, то проекция момента количества движения
системы на это направление не изменяется с течением времени:
(со0, К) = const.
(3.5.29)
Доказательство непосредственно следует из (26) при
(М(е), со°)=0.
Следствие 5. Теорема о сохранении момента количест-
ва движения системы. Если вектор со0 в теореме 4 - произволь-
ный вектор и сумма моментов внешних сил, действующих на
систему, равна нулю, то вектор момента количества движения
системы не изменяется с течением времени:
К = Ко = const.
(3.5.30)
Рис. 45
Замечание. В частности, соотноше-
ние (30) всегда справедливо для сво-
бодной замкнутой системы материаль-
ных точек.
Следствие 6. Теорема площа-
дей. Эта теорема вытекает из следствия
4 теоремы 4 и содержит его геометри-
ческую интерпретацию (рис. 45). Не-
трудно показать, что при Дг —> 0 вы-
§ 3.5. Общие теоремы динамики системы материальных
135
ражение Д5^ - — (<o°,[r., v ])Дг с точностью до О ((Д/)2) есть
площадь, заметаемая за время Дг проекцией радиуса-вектора г7
на плоскость, ортогональную вектору со0 (AS™ > 0, если проек-
ция Гу движется против часовой стрелки, если смотреть с конца
со0, и < 0 в противоположном случае.) Так как
<К.<о°) = £ <<о°,[г7,Р7.]> = £ m/<o°,[r;,v7]>,
J=1 J=1
то
/? лею0 I п
<K,»“) = 2£mj^- = 2-XmA" . (3.5.31)
Проекция вектора кинетического момента на со0 есть удвоенная
производная по времени от взвешенной массами точек суммы
площадей, заметаемых проекциями радиусов-векторов точек на
плоскость, ортогональную со0.
При условиях теоремы о сохранении проекции количества
движения
(К,со°) = С = const.
Поэтому
= У msf =^-t+C0, (3.5.32)
£ 2
где Со = const.
4°. Теоремы об изменении энергии. Пусть FA - сила, дейст-
вующая на точку к системы (к = 1,2, ..., и). Обозначим через drk
вектор действительного перемещения к-й точки системы за бес-
конечно малое время dt.
Определение 1. Скалярное произведение силы F* на элемен-
тарное перемещение drk называется элементарной работой dAk
силы F* на элементарном перемещении drk:
dAk={Fk,drk\ (3.5.33)
где (•, •) - скалярное произведение в R3.
Так как drjdt = vk- вектор скорости к-й точки, то последнее
соотношение можно представить в следующих эквивалентных
видах:
z/Д
dAk=(¥k,vk)dt, -L = <Fjt,vJ (3.5.34)
dt
Обозначим через dA элементарную работу сил, действующих на
136
Гпава 3. Общие теоремы динамики и их применение
все точки системы:
dA = £ dAk = Y (F,, v* }dt. (3.5.35)
k—\ k=\
Обозначим также:
F = (F1,F2,...,F„)eZ?3",
r = (r.,r2,...,rn )e/?3", v = —g/?3''.
1 1 2 dt
Тогда формулу (34) можно записать в следующем виде:
НА
— = <F,v>, (3.5.36)
dt
где (•, •) - скалярное произведение в
Рассмотрим движение системы в расширенном фазовом про-
странстве R6" х R координат всех точек системы, компонентов
всех векторов скорости и времени. Предположим, что система
движется по траектории г = r(0, v = v(0, t = t расширенного фазо-
вого пространства и за время от до t2 переходит из точки <21 =
= (!•(?,), v(r,), в точку Q2 = (r(r2), v(f2), t2) (рис. 46).
Если движение системы известно, то
z о б2 мы можем вычислить работу, которую co-
zy, вершают все силы на этом пути:
t2
A(Z2)-A(Z,) = J (F,v)<*. (3.5.37)
1 v В общем случае эта работа зависит не
Рис. 46 только от начальных и конечных коорди-
нат точек системы, но и от траектории
движения; для различных траекторий, идущих из (21 в 62, зна-
чение A(t2) - A(t}) будет различным. Иначе говоря, в общем слу-
чае нельзя представить
A(t2) - A(rj) = Ф(Г 2, г (t 2), v(r 2), 6, г ), v(r,))
как функцию только начальной и конечной точек траектории.
Лемма 3. Если система сил Fb k = 1, 2,..., и, имеет потенциал
и этот потенциал не зависит явно от времени, то работа этих сил
при движении системы из точки <2i в точку Q2 равна разности
значений потенциалов в начальной и конечной точках.
Доказательство. Если силы имеют потенциал
U(r) = U(rt,r2,...,rn),
§ 3.5. Общие теоремы динамики системы материальных
137
ТО
f 4—V
l3rJ
ИЛИ
ди
Эг
Представим
F = -
ГЭЕ/У dr\ dU(r)
< Эг J ' dt j dt
(3.5.38)
где справа полная производная по времени от потенциала вдоль
траектории движения.
Подставляя последнее соотношение в (37), получим
t2 dIJ
A(r2)-A(r1) = -f — dt = -U(t2) + U(t1) =
J at
(3.5.39)
Замечание. Если потенциал зависит явно от времени, то
и (39) неверно.
Определение 2. Кинетической энергией системы Т назы-
вается следующая квадратичная форма компонентов векторов
скорости точек системы:
т = У mJ vJ2 .
2 k=l
В покомпонентной записи
Е тМ2-
2 к=\ i=]
Если использовать вектор vT = ,...,v3n) е R3n и матрицу М
размера Зп х Зп, составленную из масс точек системы
т, О
О •.
< тп>
138
Глава 3. Общие теоремы динамики и их применение
ТО
7’ = lvTMv. (3.5.40)
Теорема 5. Об изменении кинетической энергии системы.
Если на интервале Jt связи допускают в расширенном фазовом
пространстве сколь угодно малый сдвиг вдоль оси времени, то
изменение кинетической энергии на отрезке времени , t2\ С Jt
равно работе активных (внутренних и внешних) сил, действую-
щих на точки системы:
Уточним условие теоремы. В случае голономных связей
f(r, /) = 0 условие теоремы означает, что если мы изменим мо-
мент t на величину т, не изменяя координат и компонентов век-
тора скорости действительного движения на этот момент вре-
мени, то уравнения связи будут выполнены:
f(r(r),r-T) = O, t^Jt, tgJe.
Полагая t - т = , последнее условие можно записать в следую-
щем виде:
f(r(z, = 0.
Или, так как ц - произвольный момент времени, а величина т
сколь угодно мала, то
f(r(r + T),O = O, teJt, tgJe.
Отсюда следует, что по условию теоремы
ф = r(t + т)
(3.5.41)
- виртуальное движение. Здесь г(0 - действительное движение, а
модуль I т I достаточно мал.
Множеству виртуальных движений (41) соответствует вир-
туальный вектор
(3.5.42)
где v(rt - вектор скорости в действительном движении системы.
В общем случае линейных связей Bn + Р = 0 допустимость
сдвига по времени по определению означает, что вектор ско-
рости системы v является виртуальным вектором, т.е. Br{t)N = 0.
Выше мы показали (см. § 3.2), что для того чтобы вектор
скорости системы был виртуальным вектором, необходимо и до-
статочно, чтобы голономные связи явно не зависели от времени
(df/dt = 0), а в случае линейных дифференциальных связей Р = 0.
§ 3.5. Общие теоремы динамики системы материальных
139
Поэтому условие теоремы можно сформулировать следую-
щим образом:
Если на Jt голономные связи явно не зависят от времени или
в случае линейных дифференциальных связей Р = 0, то ... .
Перейдем к доказательству теоремы. Подставляя £;(/) - N(t) в
уравнение Даламбера-Лагранжа (2), получим
или
/ dy \
(М — -F,v) = 0
\ dt /
/м—, v\ = (F, v).
\ dt /
(3.5.43)
Так как
— — vTMv =—,
dt V 2 ) dt
получим
dt
(3.5.44)
Интегрируя соотношение (44) на интервале , z2], получим фор-
мулу, содержащую утверждение теоремы:
T(t2) - T(t.) = A(t2) - A(tx). (3.5.45)
Следствие 1. Для свободной системы связей нет и, сле-
довательно, допустимо любое виртуальное перемещение и (45)
выполняется.
Следствие 2. Если к активным силам добавить силы
реакций связей, то систему можно рассматривать как свободную.
Таким образом, всегда верно следующее утверждение: измене-
ние кинетической энергии равно работе всех сил - активных сил
и сил реакций связей:
Т(^2) ~ ) = + AN — An )’
*2
AN(t2)-AN(t}) = j (N,vMr.
h
Представим силы F, действующие на точки системы, в виде
суммы внутренних F(/) и внешних F(e) сил:
F = F(,) + Fw (3.5.46)
(F* =FP + F^, k = l,2,...,n).
140
Глава 3. Общие теоремы динамики и их применение
Определение 3. Если внутренние силы имеют потенциал
(/(0 = (7(')(г), то сумму кинетической энергии системы и потен-
циала будем называть внутренней механической энергией систе-
мы и обозначать E(z) - Т + (7(/).
Следствие 3. Теорема об изменении внутренней энер-
гии системы. При условии теоремы 5, если внутренние силы
имеют потенциал, то изменение внутренней механической энер-
гии на отрезке времени [гь t2\ е Jt равно работе внешних
активных сил, действующих на точки системы.
Доказательство. Согласно (44) и (46),
— = (F, v) = <F(,), v> + (F(e), v). (3.5.47)
dt
Согласно лемме 3, при потенциальных внутренних силах
(F(,),v^ = -———. (3.5.48)
dt
Подставляя (48) в (47), получим
+ (3549)
dt dt
Из последнего соотношения следует, что
E(i\t2) - = AM(t2) - A<e\tt), (3.5.50)
f2
где A{e\t2)~ A(e\t{) = J (F(e\v)dt - работа внешних сил на от-
'1
резке [rl5t2].
Замечание. Мы воспользовались свойством внутренних сил:
внутренние силы не зависят явно от времени.
Определение 4. Если внутренние и внешние силы имеют по-
тенциал и потенциал внешних сил (7(е) не зависит явно от вре-
мени, то сумма внутренней энергии системы и потенциала внеш-
них сил называется полной механической энергией системы Е:
Е = Е(0 + Е{е) = Т + U(i) + U(e). (3.5.51)
Определение 5. Если:
1) связи допускают сколь угодно малый сдвиг системы вдоль
оси времени в расширенном фазовом пространстве;
2) внутренние силы имеют потенциал;
3) внешние силы имеют потенциал, явно не зависящий от
времени, то система называется консервативной.
§ 3.6. Общие теоремы механики в относительном движении
141
Следствие 4. Теорема о сохранении полной энергии си-
стемы. Полная энергия консервативной системы не изменяется
с течением времени. При условиях теоремы справедливо уравне-
ние (49)
= (F(e), v).
dt
Так как силы F(e) имеют потенциал и dU^/dt - 0, то
dt
Отсюда следует
d(E(0+E/(e)) _dp_Q
dt dt
или
E(t2)~ Е(^) = 0 для любых t^t2eJt.
§ 3.6. Общие теоремы механики в относительном движении
Рассмотрим, как формулируются об-
щие теоремы, если рассмотреть движение | Е
системы материальных точек относитель- 6)1 —
но репера Еа, перемещающегося по- / уЧ
ступательно относительно абсо- \ njx
лютного репера Е (рис. 47). Д ।
Будем предполагать, что орты репера Д
Еа соответственно параллельны ортам ре- \
пера Е, т.е. матрица А преобразования тк '
Е ——> Еа единичная. В этом случае ко- Рис 47
ординаты rk е R3 точки к относительно
репера Еа связаны с координатами гк той же точки относительно
репера Еа известными нам формулами:
г^=г^+а, (3.6.1)
где а - координаты начала репера Еа относительно Е.
Пусть vk - координаты вектора скорости точки к, чк =
= d rk /dt - координаты относительного вектора скорости точки к.
Обозначим через и скорость начала репера Еа относительно Е:
da
u = —.
dt
142
Гпава 3. Общие теоремы динамики и их применение
Тогда
v* = yk + u. (3.6.2)
Ниже мы будем использовать следующие обозначения:
п
тк~ сУмма масс точек системы,
г - координаты радиуса-вектора центра масс системы относи-
тельно £а:
v* = dr / dt - вектор относительной скорости движения центра
масс.
Будем выделять два специальных случая движения репера £а.
А) Начало репера совпадает с центром масс системы:
а = г*. В этом случае r = v: = 0 и и = v* - абсолютная скорость
центра масс. Такой репер будем называть репером Кёнига.
Б) Система координат £а - инерциальна. В этом случае
du/dt - 0.
1°. Вектор количества движения системы Р представим в сле-
дующем виде:
Р = Р + Ре, (3.6.4)
гДе
Р = Х т^к тл =m^ = m'v (3.6.5)
k=l к=\
будем называть количеством относительного движениям
Р, =m*u. (3.6.6)
п
Формула (4) следует после подстановки в выражение Р=^тк\к
формулы (2). А
В случае А)
Р = 0, Р = Р- mu = т \\ (3.6.7)
В этом случае из теорем об изменении количества движения
системы следуют сформулированные выше теоремы о движении
центра масс системы.
Если связи допускают сдвиг всей системы как твердого тела
вдоль направления, определяемого вектором а0, то
/a°,^^\ = (a0,F(£,)).
\ dt /
§ 3.6. Общие теоремы механики в относительном движении
143
Читателю предлагается самостоятельно сформулировать следствия, вытекаю-
щие из этого равенства.
В случае Б)
dt dt dt
(3.6.8)
Поэтому все теоремы об изменении абсолютного количества
движения системы автоматически дают законы изменения век-
тора Р. Если система допускает сдвиг всей системы как твердого
тела вдоль направления, определяемого вектором а0, то
— -F(e).a° } = 0,
dt /
(3.6.9)
где F(d - сумма внешних активных сил, действующих на систему.
Если а0 произвольный вектор, то
= р(^)
dt
Если (F(e),a°) = 0, то (Р, а0) = const и т.д.
2°. Предположим теперь, что связи допускают вращение
системы как твердого тела относительно оси, определяемой еди-
ничным вектором со0 и проходящей через начало репера Еа.
Запишем выражение для виртуального движения в этом случае,
предполагая сначала, как обычно, что связи голономны:
Ф(г, т) = (а(0 + A(T)rj,..., Ot(0 + А(т)г„ (0), (3.6.10)
где А - матрица поворота: А(0) = /, dA/dx = Q, кососиммет-
рической матрице Q соответствует вектор со0. Виртуальным дви-
жениям ф(/, т) соответствует виртуальный вектор
g = = ([<o°,rl],...,[<o°,r,!]). (3.6.11)
Эт т=0
Для общего случая линейных связей Bn + Р = 0 необходимо пред-
положить, что £ в виде (11) удовлетворяет условию в|г(0£ = 0.
Запишем теперь принцип Даламбера-Лагранжа (3.5.2') для
данного виртуального вектора:
п / /7 2 Г \
°=Е
r^mk~ZT-Fk
at
(3.6.12)
144
Глава 3. Общие теоремы динамики и их применение
Введем следующие обозначения:
к = Х
Л=1
М = Х [f„FJ.
k=l
(3.6.13)
(3.6.14)
Величину К будем называть моментом количества движения си-
стемы относительно начала репера а М - результирующим
моментом активных сил, действующих на точки системы относи-
тельно начала
Повторяя доказательство лемм 1 и 2 § 3.5, легко показать, что:
(3.6.15)
м = Х [г*Л(е)] = мЧ
к=\
(3.6.16)
т.е. результирующий относительный момент активных сил М
равен результирующему моменту М(е) только внешних сил
относительно начала Еа.
Подставляя в (12) гк= гк + а и используя (13) и (16), получим
о dK
со ,-----\-т
dt
г ,^У-м(е)
dt2
= 0.
Отсюда следует, что как в случае А) (г* = 0), так и в случае Б)
(cPoddt2 = 0) имеет место равенство
-Mw\ = 0. (3.6.17)
\ dt /
Сохранение вида законов при описании движения относи-
тельно репера Еа в случае Б) не удивительно, так как в этом слу-
чае система координат Еа инерциальна и тем самым совершенно
равноправна с Е.
Для случая А) система связана с центром масс, который,
вообще говоря, движется сложным образом и заранее этот ре-
зультат не очевиден. Его формулировка дается следующей тео-
ремой:
Если связи допускают вращение системы как твердого
тела относительно оси со0, проходящей через центр масс си-
§ 3.6. Общие теоремы механики в относительном движении
145
стемы, то производная по времени от проекции на со0 момента
количества относительного движения системы (относитель-
но центра масс) равна проекции на это направление момента
внешних активных сил относительно центра масс.
Повторяя последовательность рассуждений, проведенных в
§3.5, нетрудно получить и сформулировать все следствия, выте-
кающие из этой теоремы для случая, когда:
1) со0 - произвольный вектор, проходящий через центр масс;
2) <М(е),<о°> =0;
3) Система свободна и т.д.
Формулировку этих следствий следует рассматривать как самостоятельное
упражнение.
Заметим, что условия последней теоремы об изменении мо-
мента количества относительного движения другие, чем для аб-
солютного: векторы со0, которые фигурируют в формулировках
соответствующих утверждений, проходят через разные точки
пространства.
Замечание. Введение в рассмотрение репера Кёнига часто
бывает полезным и для вычисления момента количества дви-
жения относительно абсолютной системы координат.
Подставим rk = rk + а, vk = vk + и в выражение для момента
количества движения
п
К = Е [r^vj.
к=1
В результате получим
п п
К = Х [^+а’тЛ^+тЛ] = Х +
к=\ к=\
п п п
к=\ к=\ к=\
Если система координат Еа - репер Кёнига, то
v=r=0, a = r , u = v*
и в результате получим
K = K + [r*,mV]. (3.6.18)
Сформулируем это результат как теорему:
Абсолютный (полный) момент количества движения мож-
но представить в виде суммы момента количества движения
относительно репера Кёнига и момента абсолютного коли-
10. М.Л. Лидов
146
Глава 3. Общие теоремы динамики и их применение
чества движения материальной точки массой, равной всей мас-
се системы, и движущейся так же, как центр масс системы.
3°. Запишем формулу для кинетической энергии системы
Г = — V mdvj2.
2 к={
Представим
и вычислим
|v* |2=<vjt,vjt) = <v.,v.> + 2<vil,u> + <u,u) = | \к I2 +|и|2 + 2<у*,и>.
Подставив последнее соотношение в формулу для кинетической
энергии, получим
Т = Т + ~m I u |2 + rn'(v\u),
— 1 п
где Т = -Х I vj2 - кинетическая энергия относительного
2 к=\
движения.
В случае A) v* = 0 и мы получим для кинетической энергии
формулу
r = f+ |m*|u|2. (3.6.19)
Последним соотношением записано содержание теоремы Кё-
нига:
Кинетическая энергия системы представима в виде суммы
кинетической энергии движения относительно репера Кёнига и
кинетической энергии поступательного перемещения системы
со скоростью центра масс.
Формула (19) часто бывает полезной при вычислении кине-
тической энергии системы.
Пусть f(r, г)=0 голономные связи.
Предположим теперь, что связи допускают сдвиг по оси вре-
мени в расширенном относительном конфигурационном
пространстве, т.е.
f (а(/ + т) + г (t), t + т) = 0.
Отсюда следует: f («(/) + г(/ + т),0 = 0 и
а(0 + r(Z + т) = ф(/, т) - виртуальное движение.
Дифференцируя последнее равенство по т, находим
S-Z х Эф —
= — = v(0 - виртуальный вектор.
Эт т=0
J 3.6. Общие теоремы механики в относительном движении 147
(Для линейных связей необходимо Bv = 0.) Тогда из принципа
Даламбера-Лагранжа получим соотношение
п / /2 \
0 = S =
k-1 \ /
Подставляя rk= гА + а, получим
n V / d2rk f — \ X1 / —
k=l \ al I k=\ \ aT
Повторяя преобразования, проведенные в § 3.5, будем иметь
dT тгл . _ \ * / d2ot
° = -7-Х <F*’v*> + m -ZT’V
dt \dt
(3.6.20)
Последний член в правой части обращается в нуль как в случае
А) ( v* = 0), так и в случае Б) (d2cddt2 = 0). Отсюда следует, что в
этих случаях
— Е (3-6-21)
dt ТЗх
Это соотношение можно записать в интегральной форме:
п
f(t2)-T(t[) = j £
q *=1
Мы получили, что если система Еа - инерциальна или пере-
мещается поступательно вместе с центром масс (репер Кёнига) и
связи допускают сдвиг вдоль оси времени в расширенном от-
носительном фазовом пространстве, то изменение кине-
тической энергии относительного движения равно работе всех
активных сил на относительном движении. К активным силам
надо отнести и силы трения.
Для случая Б) справедливость этого утверждения также сле-
дует из равноправия инерциальных систем координат. Для случая
А) этот результат заранее не очевиден.
Следует обратить внимание на то, что требования к связям в
случае рассмотрения абсолютного движения
и в случае относительного движения различ- ~~
ные. 1 zf,—
Пример. Рассмотрим движение точки L ^4=^
(г, /я) по поверхности, перемещающейся с по-
стоянной скоростью (рис. 48). Уравнения свя- ис*
зей: /(г - v°0 = 0, где/- скалярная функция, v° е Л3, v° = const.
ю*
148
Глава 3. Общие теоремы динамики и их применение
В этом случае связи не допускают сдвига по времени в
расширенном фазовом пространстве. Но если ввести систему
координат, которая перемещается поступательно с постоянной
скоростью v°: r = r + v°Z, тогда в относительной системе коор-
динат связи будут иметь вид /(г) = 0. Эти связи не зависят явно
от времени и допускают сдвиг по оси времени в расширенном
относительном фазовом пространстве.
Замечание. При формулировке закона сохранения энергии в
случае потенциальных сил для относительного движения не-
обходимо, чтобы существовал потенциал системы [/(Гр...,^), за-
висящий только от координат относительного движе-
ния и не зависящий явно от времени. Если потенциал зависит от
абсолютных координат и не зависит от времени, то, вообще го-
воря, при переходе к относительным координатам может по-
явиться явная зависимость потенциала от времени.
§ 3.7. О внутренних связях.
Закон равенства действия и противодействия
в системах со связями
Определение. Связи называются внутренними, если они до-
пускают произвольные виртуальные движения системы как
твердого тела: сколь угодно малое поступательное перемещение
в произвольном направлении и сколь угодно малый поворот
относительно произвольной оси.
Связи, не удовлетворяющие этому условию, называются
внешними.
Простейшие примеры внутренних связей были рассмотрены
в § 3.4: система, состоящая из двух материальных точек, соеди-
ненных стержнем нулевой массы две точки различных подсис-
тем, соединенные стержнем или шарниром.
Еще один пример. Система состоит из твердого тела и мате-
_____ риальной точки (г, т), которая в силу наложенной
связи может перемещаться только по поверхности
------твердого тела (рис. 49). Эта связь - внутренняя для
Рис 49 системы, состоящей из твердого тела и материаль-
ной точки.
Рассмотрим одно уравнение связи, заданное в дифферен-
циальной форме:
(B.v) + P = 0, (3.7.1)
В - матрица размера 1 х Зп, v g R3" - вектор скорости системы,
§3.7. О внутренних связях
149
Р - скалярная функция. Представим:
B = (b1,b2,...,b„),
v = (vI,v2,...,v„),
где bz е Л3, vz е R3 - вектор скорости i-й точки, и запишем (1) в
следующем виде:
Ё <МР+Р=о.
j=l
где (•, •) - скалярное произведение в /?3. Если связь внутренняя,
то она должна допускать виртуальные векторы
£ = (а°,а°,...,а0) (3.7.2)
И
£ = ([“°’ Г1]’ [“°’ Г2[<°°’ Г« ]) <3-7’3)
при произвольных а0, <о° е R3.
Подставляя (2) в условие виртуальности вектора £ (В£ = 0), по-
лучим
Ё (М') = о.
7=1
или, так как а° - произвольный вектор,
£ь.=0. (3.7.4)
7=1
Подставляя (3) в условие виртуальности вектора, найдем
Е (ьр К’ rJ)=(“°’ ЕЬ* bJ)=°-
7=1 \ 7=1 /
Откуда в силу произвольности со0 получим
7=1
Так как ось вращения может проходить через произвольную
точку пространства, определяемую вектором а0, а не обязатель-
но через начало координат, то для того чтобы уравнение (1)
определяло внутреннюю связь, необходимо:
ЁЬ-“.ь,] = о (3-7-6)
7=1
при произвольном а.
150
Глава 3. Общие теоремы динамики и их применение
Это, в частности, можно получить из (5) как следствие условия
2>=о.
7 = 1
Легко видеть, что условий (4) и (6) и достаточно, чтобы связь
была внутренней.
Уравнение (1) порождает составляющую сил реакций идеаль-
ных внутренних связей N, действующих на все точки сис-
темы:
N = ХВТ, X- скалярная функция.
В более подробной записи
N = (N1,N2,...,NJ
(Njt е R3 - сила реакции, действующая на k-ю точку)
получим
N^Xb,. (3.7.7)
Из (4), (6), (7) следует, что если связь (1) - внутренняя, то
2Х=0. Х[г,-«.ьфо. (3.7.8)
7 = 1 7 = 1
То есть сумма сил реакций идеальных внутренних связей, дейст-
вующих на все точки системы, и сумма всех моментов этих сил
относительно произвольной точки равны нулю.
Если внутренняя идеальная связь определяет отличные от
нуля силы реакции, действующие только на две точки системы
и у2, то из (8) следует, что
N/i = -ТЧ/2 и [гу|, N,-,] = -[rj2, Ny2] (или [N>b гу| -rj2] = 0).
Таким образом, либо гу1 = г,- , либо сила реакции Nyl направлена
по прямой, соединяющей эти точки. Мы уже сталкивались с этим
свойством сил реакций идеальных внутренних связей на приме-
рах в § 3.4.
Предположим теперь, что движение системы ограничено
р-внутренними идеальными связями вида (1). Эти связи порож-
дают силу реакции NA (к = 1,2,...,и), действующую на /с-точку
системы. Эту силу можно представить в виде суммы
N*=£na., (*)
5 = 1
(V)
где Na. - составляющая силы реакции, обусловленная 5-й (5 =
= 1,2,...,р) связью. Согласно рассмотрению (1)-(8), при каждом
§3.7. О внутренних связях
151
фиксированном л
(S) Г (S) "I
2Х=о, =°-
к = 1 £=11- -I
Из (*) и (**) следует
2Х=0 и j?[r*-a,Nj = 0.
£ = 1 к=1
(**)
(3.7.8)
Упражнение. Получите (8), применяя теоремы об изменении количества
движения системы и момента количества движения системы.
Указание. Надо обосновать справедливость (3.5.10) и (3.5.28) в двух
случаях, когда к внешним силам добавляются: 1) силы реакций только идеаль-
ных внешних связей и 2) силы реакций идеальных внешних и внутренних
связей.
При обсуждении проблемы «неидеальных» связей было
указано, что силы трения, которые возникают при таких связях,
следует учитывать в уравнениях движения наравне с внешними
силами, причем их структура (вид функций) определяется при
наблюдении данного круга явлений. Не уточняя полностью
структуры этих сил, мы сформулируем сейчас общий закон
природы, которому в модели должна удовлетворять система
функций, описывающих силы трения, обусловленные
внутренними связями.
Обозначим
точку системы
через Fjp силу трения, действующую на к-ю
за счет s-й внутренней связи:
Сумма сил F Jp
сил равны нулю:
п го п
к=1
по всем точкам системы и сумма моментов этих
r.-a.F?’
£ = 1 L
= 0.
(***)
Суммируя (***) ПО Л от 1 до р, получим
Xf’=o. X[r<-“-F?’]=0-
£=1 £=1
(3.7.9)
Отсюда следует, что никакие внутренние силы - ни заданные
активные силы, ни силы реакций идеальных связей, ни силы
152
Глава 3. Общие теоремы динамики и их применение
внутреннего трения непосредственно не влияют ни на
изменение количества движения системы, ни на изменение мо-
мента количества движения системы.
Этот вывод, который мы получили как следствие основных
положений теоретической механики, является чрезвычайно
общим и важным законом природы.
Отметим некоторые следствия. При использовании теорем
об изменении количества движения и момента количества дви-
жения системы: 1) необходимо проверять допустимость опре-
деленного виртуального вектора только по отношению к внеш-
ним связям; 2) при этом для задач с трением необходимо к внеш-
ним активным силам добавлять силы трения внешних
связей.
Однако при применении теоремы об изменении кинетиче-
ской энергии системы следует помнить, что: 1) внутренние связи
могут ограничивать возможность использования этой теоремы
((9fiw) Г 0 или Рг г 0); 2) силы трения, которые могут сопровож-
дать внутренние связи, могут совершать работу и влиять
непосредственно на изменение кинетической энергии.
Рассмотрим систему материальных точек &=1,2,...,и
без внешних связей. Предположим, что внешние силы на систему
не действуют, т.е. мы рассматриваем замкнутую систе-
му, возможно, с внутренними связями. Обозначим через Ф/9
к = 1,2,...,и, результирующие силы (активные силы, силы реак-
ций идеальных связей и силы трения), действующие на мате-
риальную точку (rk,mk). Мысленно разобьем систему на две
произвольные подсистемы, например:
I: k = l,2,...,q и II: q + l,..,n.
Так как для всей системы
Еф*=°> Sh-«A]=o>
к = \ к=1
ТО
к=1 k=q+l
q п
м 1,п=X h -«А ]=- Е [г* ~ ФЛ=-м пл •
к=1 k-q+1
Следовательно, сумма всех сил и сумма моментов всех сил,
действующих на точки подсистемы I, векторно противоположны
сумме сил и моментов, действующих на точки подсистемы II.
§3.7. О внутренних связях
153
В этом и состоит закон равенства действия и противо-
действия для замкнутой системы.
Замечание о внешних связях. Точно такое же положе-
ние имеет место и по отношению к внешним связям. Если внеш-
няя связь (материальная система, которая обеспечивает вы-
полнение условий связи) действует на все точки системы с
результирующей силой Ф(<?) и результирующим моментом М(и,
то и система действует на внешнюю связь с такими же силой и
моментом. Однако так же, как в случае, когда мы вводили в
рассмотрение внешние активные силы, мы пренебрегаем влия-
нием этих сил на материальное приспособление, реализующее
эту связь.
При анализе некоторых задач, выходящих за рамки основ-
ных задач теоретической механики, необходимо знать силу и
момент силы, с которыми система действует на внешнюю связь.
Например, важно знать, не приведет ли слишком большая сила
к физическому разрушению приспособления, реализующего эту
связь. При решении таких вопросов требуется использовать
справедливость утверждения о равенстве действия и противо-
действия по отношению к внешним связям.
Вместо сформулированного выше постулата о силах внут-
реннего трения мы могли бы привлечь другой постулат и по-
лучить заключение о свойствах сил внутреннего трения как
следствие.
Можно принять следующую аксиому физического проис-
хождения: все силы внутренних взаимодействий в системе суть
некоторые результирующие силы парных взаимодействий
между точками системы. Для парных сил взаимодействий сумма
всех сил и сумма всех моментов сил равны нулю. Так как этим
свойством обладают заданные внутренние активные силы и силы
реакций идеальных внутренних связей, то тем самым отсюда
следует справедливость (9) для сил внутреннего трения.
Следует отметить, что внутренние силы при действии на
систему внешних активных сил или сил реакций внешних связей
могут косвенно влиять на изменение количества движения
системы Р и момента количества движения К. Не изменяя непо-
средственно эти величины, внутренние силы могут изменять
состояние системы (г, v). Изменение состояния системы при-
водит, вообще говоря, к изменению результирующей внешних
сил F(£,) = F(e)(r,v, t) и моментов этих сил М(И = M(f,)(r,v, f), что
приводит к изменению Р и К.
Человек, находившийся первоначально в покое относительно
Земли, может начать бег, т.е. изменить количество движения
системы. Это - следствие влияния внутренних сил через внешние
154
Глава 3. Общие теоремы динамики и их применение
силы: силу тяжести, силу реакции связи (идеальной + силы тре-
ния), возникающей при контакте ноги и грунта. Если же на
систему никакие внешние силы не действуют, то векторы Р и К
остаются постоянными.
Замечание о твердом теле. Из определения твердого тела
следует, что связи, обеспечивающие конструкцию твердого тела,
являются внутренними связями типа стержня:
| rz - rj - Sjk = const, j,k = 1,2,..., и,
где г7 и г £ — радиусы-векторы материальных точек j и к ,
образующих твердое тело. Идеальные связи такого типа, как мы
показали, порождают силы реакции
^,=«г,-гр, N„=-N(i,
где Л - скалярная функция.
Элементарная работа этих сил
dAKj =(nv,^)+(n#, ^) = (^кра(гк-rj)) = ^{rk-rj,d(rk -г,))
или
dAk X d I |2 X dSkj
—~ =—r, -r. =---------- = o.
dt 2dVk 7| 2 dt
To есть силы реакций внутренних связей, обеспечивающих
сохранение конструкции твердого тела, не совершают работы.
Кроме того, они не зависят от времени. Поэтому при примене-
нии теоремы об изменении кинетической энергии к твердому
9f ? ?
телу необходимо проверять стационарность ( — = 0 или Р = 0)
ы
только внешних по отношению к твердому телу связей и, воз-
можно, учитывать работу сил трения, обусловленную тоже
только внешними связями.
§ 3.8. Задача о соударении шаров
Рассмотрим два твердых (в обыденном смысле) шара мас-
сами тщ и т2 и радиусами R\ и R2. Предположим, что распре-
деление плотности в этих шарах обладает сферической сим-
метрией. Тогда центры шаров совпадают с центрами их масс.
Мы хотим описать физический эксперимент, в котором шары
сближаются друг с другом, а затем после соударения разле-
таются.
§ 3.8. Задача о соударении шаров
155
Для решения этой задачи сначала надо уточнить теорети-
ческую модель этого физического эксперимента. После уточне-
ния постановки задачи с помощью формального изучения моде-
ли мы сможем вывести некоторые закономерности рассмат-
риваемого процесса. При этом основные закономерности можно
будет получить, опираясь только на общие теоремы механики,
доказанные в предыдущих параграфах. При этом, как и всегда,
вопрос о точности описания реальной задачи с помощью моде-
ли есть проблема специального физического анализа или экспе-
римента.
1°. В физическом эксперименте взаимодействие шаров со-
провождается их деформацией и, в частности, после соударения
происходит нарушение сферической симметрии в распределении
массы в каждом шаре. Однако при соударениях с не очень боль-
шими скоростями, как следует из физических наблюдений, эта
деформация очень мала.
Эта физическая предпосылка придает смысл следующему
постулату, который мы будем использовать при формаль-
ном описании задачи соударения:
А) Распределение масс как до удара, так и после удара
сохраняет сферическую симметрию, и массы и радиусы шаров
не изменяются.
2°. Будем предполагать, что движение шаров происходит
только под действием сил парных взаимодействий между мате-
риальными точками, образующими эти шары, т.е. предполагаем,
что на систему двух шаров никакие внешние силы не действуют.
Обозначим через гь г2 и vb v2 радиусы-векторы и векторы ско-
ростей центров этих шаров относительно абсолютного репера Е.
Используя теорему о движении центра масс системы материаль-
ных точек, из которых состоит первый шар, напишем уравнения
движения центра масс этого шара:
dv, 1 dr.
-- ^12’ -L“V
dt m.----------dt
(3.8.1)
где F12 - результирующая сила, действующая на материальные
точки первого шара со стороны второго. Для точек первого
шара это внешняя сила.
Из физических экспериментов известно, что существенное
изменение скорости Vj происходит за очень малое время Д/, когда
|rt -r2| ~ R{ +/?2, т.е. когда шары сближаются и их поверхности
почти соприкасаются. Будем предполагать, что это происходит
- Дг - Дг 1
г- — , t + ^ • Проинтегрируем первое
на отрезке времени
156
Глава 3. Общие теоремы динамики и их применение
уравнение (1) на этом отрезке времени:
(3.8.2)
Интегрируя второе уравнение (1) на этом отрезке времени, полу-
чим оценку
При очень малом Дг существенное изменение скорости центра
масс может иметь место только, если модуль силы |F12| очень
велик. В теоретических моделях, описывающих задачи соударе-
ния, обычно рассматривается предельный случай, когда Дг —» 0, а
|F12| —> В этом предельном случае изменение скорости проис-
ходит мгновенно при t = i. При этом можно говорить о скорости
непосредственно перед ударом ¥/£-()) = lim vj t-— | и ско-
д/-»о у 2)
(- ДЛ
роста непосредственно после удара ¥^ + 0)= lim vd r + —I. ®
общем случае ¥t(r-0)^ ¥// + 0). В то же время, так как |¥j
остается конечной величиной, из (3) следует предельное ра-
венство
r1(r-O) = rl(F + O).
Предыдущее рассмотрение оправдывает следующие предпосыл-
ки, которые мы будем использовать в модели соударения шаров.
Б) За исключением момента времени t = t шары не взаимо-
действуют. Изменение скорости центров масс шаров происходит
в один момент времени t = t, когда | - r2| = Rx + R2,
В) Центр масс /-го шара непосредственно перед ударом и
непосредственно после удара занимает одно и то же положение
в пространстве:
r.(/’-O) = z;.(F + O), i = 1,2.
3° . Предположим, что шары - абсолютно твердые тела и
силы взаимодействия между ними обусловлены силами парных
§ 3.8. Задача о соударении шаров
157
взаимодействий между материальными точками,
принадлежащими различным шарам (рис. 50). )
Предположим, что эти силы не зависят от ско-
ростей точек и, следовательно, согласно теоре-
ме, доказанной в § 1.7, имеют потенциал. В этом Рис- 50
случае можно показать, что результирующие
силы F12 и F21 взаимодействия между шарами будут иметь
потенциал U, не зависящий явно от времени. В силу симметрии
задачи можно предположить, что этот потенциал зависит только
от расстояния £ между центрами масс шаров:
£ = к-г2|.
Согласно предположению, силы взаимодействия проявляются
только при £ < = Rx 4- R2 + Е, где 8 - достаточно малое расстоя-
ние. Поэтому потенциал должен быть отличен от постоянной (в
частности, от нуля) только при (рис. 51).
Систему двух абсолютно твердых шаров
можно рассматривать как консервативную си-
стему материальных точек и записать усло-
вие сохранения полной механической энергии
(3.5.52) консервативной системы:
T(t2) + U(t2) = T(tl) + U(t1), (3.8.4)
где T(tx) - кинетическая энергия движения ша- Рис. 51
ров в момент времени tx. Если в качестве tx и t2
взять произвольные моменты времени до соударения Ir/^)-
—r2(Zj)| > ^* и после соударения |rj(r2)-r2(f2)|>£*, то в эти мо-
менты времени = 0, С(г2) = 0, и из (4) следует закон сохра-
нения энергии при соударении
Т^ = Т^). (3.8.5)
Если воспользоваться указанным выше предельным перехо-
дом Дг —э 0, £ —» 0, из (5), в частности, следует предельное ра-
венство
T(F + O) = T(F-O). (3.8.6)
Эти соображения, по-видимому, могут помочь в понимании фи-
зического смысла следующего формального определения.
Определение 1. Взаимодействиешаров называется
абсолютно упругим, если кинетическая энергия в системе двух
шаров одинакова до и после удара.
Следует помнить, что в природе всегда справедлив закон
сохранения полной энергии. Однако понятие полной энергии
158
Глава 3. Общие теоремы динамики и их применение
является общефизическим и выходит за рамки понятий, на ко-
торых основана теоретическая механика. Полная энергия вклю-
чает не только механическую энергию упорядоченного дви-
жения макроскопических тел и потенциала их взаимодейст-
вий. Макроскопические физические твердые тела состоят из мо-
лекул, которые являются носителями массы. Молекулы взаимо-
действуют друг с другом. В частности, кинетическая энергия
движения молекул друг относительно друга и потенциал их пар-
ных взаимодействий не рассматриваются в механической мо-
дели соударения шаров. Однако в результате соударения шаров
часть механической энергии поступательного движения может
переходить в колебательную энергию молекул друг относи-
тельно друга или тратиться на изменение расположения молекул
(деформацию шара), т.е. на изменение потенциальной энергии
взаимодействия молекул. При этом с геометрической точки
зрения деформация может быть несущественной, но затратами
энергии на эту деформацию пренебрегать нельзя.
Для описания таких процессов в механике рассматриваются
модели, в которых на макроскопическом уровне учитывают
потери механической энергии, связанные с увеличением немеха-
нических форм энергии. При этом особенности таких «неупру-
гих» взаимодействий формулируются на основе установлен-
ных из экспериментов физических законов. Одной из таких на-
иболее простых моделей является модель абсолютно неупругого
удара.
Определение 2. Соударение шаров называется абсолютно
неупругим, если непосредственно после соударения относитель-
ные скорости шаров равны нулю. То есть после соударения
шары перемещаются вместе. Такая модель, например, может
описывать соударение мягких пластилиновых шариков.
При анализе задачи мы будем рассматривать эти два пре-
дельных случая: абсолютно упругого и абсолютно неупругого
Удара.
4°. Мы предположили, что шары как до удара, так и после
удара перемещаются поступательно (не вращают-
с я). Поступательное перемещение шаров до удара в физиче-
ском эксперименте реализуется с помощью подбора специаль-
ных начальных условий их движения. При этом вращение шаров
после удара в эксперименте определяется характером взаимо-
действия при ударе и зависит, в частности, от свойств поверх-
ностей этих шаров. Мы предполагаем такие условия эксперимен-
та, когда при описании его в модели вращением шаров можно
пренебречь.
§ 3.8. Задача о соударении шаров
159
Исследование модельной задачи соударения шаров
Каждый отдельный шар представляет собой систему мате-
риальных точек, на которую за исключением момента времени
удара t = t не действуют никакие внешние силы и не наложены
внешние связи. Поэтому центр масс /-го (/ = 1, 2) шара при t < t
согласно (3.5.15), движется прямолинейно с постоянной скоро-
стью vz“ и после соударения при t > t также движется прямо-
линейно с постоянной скоростью vz+. Основная задача состоит
в том, чтобы при заданных векторах v[ и v? определить векто-
ры vf и vj. Обозначим через v* вектор скорости центра масс
системы двух шаров. Так как на систему двух шаров никакие
внешние силы не действуют (и внешних связей нет), то, согласно
той же теореме, центр масс двух шаров движется прямолинейно с
одним и тем же постоянным вектором скорости v* как до
соударения, так и после него. Нетрудно показать, что справедли-
во следующее соотношение:
(3.8.7)
тл +т?
Упражнение. Докажите справедливость представления v* в виде (7).
Все дальнейшие соотношения оказываются существенно
проще, если задачу рассматривать в системе координат
связанной с центром масс системы двух шаров и перемещаю-
щейся поступательно. Так как в нашем случае Е * - инерциаль-
ная система координат, то, с точки зрения динамики, этот
репер равноправен с абсолютным репером Е. Обозначим через
uf и uz+ (i = 1, 2) скорости центров масс шаров до и после удара
относительно Е Предполагая, что орты Е * параллельны
ортам Е, запишем кинематические соотношения
U7=V[-V*, U2=V2~V*, (3.8.8)
V^uJ’ + V*, V2=U2+V*. (3.8.9)
Из закона сохранения количества движения системы относи-
тельно репера Е * вытекает справедливость следующего ра-
венства:
тхих +m2ti2 =^11+ +m2ti2, (3.8.10)
160
Глава 3. Общие теоремы динамики и их применение
причем m!U1 — вектор скорости центра масс относи-
тЛ + т2
тельно Е^. Так как начало помещено в центре масс си-
стемы, то
+ т2и2 = 0. (3.8.11)
Из (10) и (11) следует
тхи[=-т2и2 = -т2и2. (3.8.12)
Полученные соотношения не зависят от характера соударения
шаров.
Задача об абсолютно неупругом соударении шаров
В модели абсолютно неупругого удара шары после удара
имеют одинаковые скорости:
<=<. (3.8.13)
Из соотношений (12) и (13) следует, что
и;=и+=0. (3.8.14)
То есть скорости после удара шаров относительно Е^ равны
нулю. Согласно (9), после удара шары перемещаются со скоро-
стью их общего центра масс
v+=v+ =v*,
где v*- определено в (7).
Так как шары не вращаются, то, по теореме Кёнига (3.6.19),
кинетическая энергия системы представима в следующем виде:
^ = |^1М2+|т2|у2|2 (3.8.15)
(относительно абсолютного репера) или
Т* =|m1|u1|2 +|m2|u2|2 (3.8.16)
(относительно репера Е *).
Рассмотрим разность
дг = г+_г-
где Т+ и Т~ - кинетическая энергия после и до соударения.
§ 3.8. Задача о соударении шаров
161
Записывая эту величину для Т относительно репера Е по-
лучим
ДГ* = + ^-m2|u2|2^. (3.8.17)
Здесь учтено равенство Т+ =0, которое следует из (14). Та же
разность относительно репера Е определяется формулой
ДГ = ~mi(|v*|2-|vr|2j + “m2(|v*|2 _|v2|2j- (3.8.18)
Упражение. Используя соотношения (8), докажите, что ДТ* = Л7. Согласно
(17) при абсолютно неупругом ударе всегда происходят потери кинетиче-
ской энергии движения шаров.
Абсолютно упругое одномерное соударение шаров
Пусть при t = 0 скорости шаров направлены по прямой,
соединяющей их центры масс. Тогда движение происходит вдоль
этой прямой как до соударения, так и (в силу симметрии задачи)
после него. Для модели абсолютно упругого удара справедлив
закон сохранения кинетической энергии:
- 1 I -Р 1 I -Р 1 I +Р 1 I +Р +
г’ = 2т1|иП +2Ш21иг| ~^W||ui| +2m2l“2l ’
(3.8.19)
Из (12) и (19) следует, что
|u?|2 =|u,+|2, i = 1.2. (3.8.20)
Знаки относительных скоростей в результате удара должны
измениться, иначе шары должны были бы «пройти друг сквозь
друга». Поэтому из (20) для одномерной задачи следует:
u^=-Uj, u2=-u2. (3.8.21)
Мы получили, что относительные скорости в результате удара
изменяются на противоположные. Используя (21), (8) и (9), полу-
чим формулы для абсолютных скоростей:
vt =Uj +v =-0! +v =2v -v1?
v2 = 2v* - v2.
Подставляя v*, согласно (7) получим
_ v, -m2) + 2m2v2
mx +m2
(3.8.22)
11. М.Л. Лидов
162
Глава 3. Общие теоремы динамики и их применение
(3.8.23)
тх +т2
Рассмотрим некоторые специальные случаи.
1) Если =т2, то из (22), (23) следует
¥1^=¥2’ ¥2=¥Л
т.е. при равных массах происходит «обмен скоростями».
2) Если ——> 0, то
т2
V^^2V2-V[, ¥2 —>¥2-
Из второго соотношения следует, что скорость шара большей
массы в пределе не изменяется. Используя второе соотношение
запишем первое в следующем виде:
v+_v+
В результате удара скорость маленького шара (точнее, шара
бесконечно малой массы) относительно большого изменяется
на противоположную, т.е. маленький шар отскакивает от боль-
шого с относительной скоростью, равной по величине относи-
тельной скорости их сближения, но противоположной по на-
правлению. Этот предельный случай, в частности, описывает за-
дачу об упругом соударении шара гщ с неподвижной стенкой,
которую можно считать шаром очень больших радиуса и массы.
В последнем случае v2 = n2 = 0 и v| = -v[.
Пространственная задача об абсолютно упругом ударе
Так как шары не вращаются (каждый шар находится в покое
относительно репера Кёнига, связанного с его центром масс), то
для момента количества движения К, i -го шара справедлива
формула (3.6.18)
К, =[i;, (3.8.24)
где г - радиус-вектор центра масс z-го шара относительно
репера Е *. Поскольку на систему двух шаров никакие внешние
силы не действуют и никакие внешние связи не наложены, то
справедлива теорема о сохранении момента количества движе-
ния системы (3.5.30) К = Kj + К2 = const, откуда K(rJ = К(г2) для
произвольных моментов времени и t2.
§ 3.8. Задача о соударении шаров
Положим = t - 0 и г2 = t + 0, где t - момент удара, и запи-
шем в этом предельном случае последнее равенство подробно:
[rt, ] + [r2, m2u2 ] = [fj, mjU]-] + [r2, m9u2 ]. (3.8.25)
При этом мы воспользовались свойством модели i;(F-0) =
= r^i + 0) = i; , i = 1,2. Используя (12), равенство (25) можно пред-
ставить в следующем виде:
Г1-г2,т
(3.8.26)
Обозначим через р° единичный вектор, направленный из центра
шара 1 к центру шара 2 в момент удара:
Согласно (26),
AHjuJ- =m1u1 +Хр°, (3.8.27)
где X - некоторое число. Используя (12) и (27), получим
m2u2 = m2u2 -Хр°. (3.8.28)
Так как мы рассматриваем абсолютно упругий удар, то кинети-
ческая энергия не изменяется:
I2 1
-I—т9
2 2
I2 1
+ —т9
2 2
|и;|2=Т-.
Подставляя (27) и (28) в (29), получим
(3.8.29)
2\тх т2>
Отсюда
(3.8.30)
Используя (27), (28) и (30), получим выражения для скоростей
после удара:
=ut +2———(u2 -U], р°)р°,
тх +т2 х 7
(3.8.31)
U2 = U2 “2---—----(u2 -Uj , Р°)р°.
тх + т2 х 7
н*
164
Глава 3. Общие теоремы динамики и их применение
В уравнениях (31) легко перейти к абсолютным скоростям, при-
бавляя к каждой скорости и1 скорость движения центра масс v*.
В результате получим
Vt = VF +2 (v2-vr,py,
+т2 х '
(3.8.32)
V2 =V2 -2—— (V2 -V7,p°)p0.
mx + m2 x '
Упражнение. Получите из (32) формулы (22), (23) для одномерной задачи.
Пример 1. Пусть первый шар первоначально находился в по-
кое: vf = 0 (рис. 52). Чтобы шары сближались, необходимо вы-
полнение неравенства (v2, р°) < 0. Из (32) найдем
__ После удара скорость первого шара
будет направлена по лучу, опреде-
I немому вектором (-р°).
) Пример 2. Пусть шар 1 до удара
v+ покоится и его масса тх много боль-
у ше массы т2 шара 2. В пределе при
Рис-52 — ^>0 из (32) найдем
m2
Определим предельное значение скорости второго шара после
соударения:
v2+^v;-2p°y р°). (3.8.33)
Представим вектор v2 в следующем виде:
v2 - хр° + уе°, (3.8.34)
где е° - единичный вектор, ортогональный р° и лежащий в плос-
кости векторов v2 и р°; х, у g R. Из (33) и (34) получим
v2 —> хр° + уЕ°-2р°Х = -хр° + уЕ°.
В результате удара модуль вектора скорости не изменяется:
КУ |v2| = y+y.
§ 3.9. Уравнения реактивного движения
165
Вектор скорости остается в плоскости векторов е°, р°. При этом
составляющая по вектору р° изменяется на противоположную.
Шар 1 можно рассматривать как стенку. Тогда вектор р° опре-
деляет направление нормали к стенке (рис. 53). Соотношение
между векторами и v2 согласует-
ся с известным законом о равенстве
углов падения и отражения при абсо-
лютно упругом ударе шара о стенку.
Начиная с Пуанкаре, математики
много занимались изучением так на-
зываемой задачи о бильярде. В этой
математической задаче часть плоскос-
ти ограничивается выпуклой кривой,
которая рассматривается как абсо-
лютно упругая стенка. Задача состоит в изучении свойств
траекторий движения частицы, которая внутри части плоскости,
ограниченной кривой, движется равномерно и прямолинейно, а
при выходе на границу отражается по закону абсолютно упруго-
го удара: модуль скорости не изменяется, а направление скорос-
ти определяется из условия равенства углов падения и отраже-
ния (рис. 54). Этой модельной задаче
присущи многие особенности движе-
ний механических систем, но при ее
анализе нет надобности в интегриро-
вании дифференциальных уравнений.
Рассмотренная выше задача о дви-
жении шаров после уточнения модели
решена нами на основе только теорем
о сохранении основных механических
характеристик движения. Существует
целый класс таких задач, где законы
сохранения позволяют решить или существенно упростить
задачу.
§ 3.9. Уравнения реактивного движения
Пусть в сосуде А (будем называть его ракетой) заключены
частицы вещества (рис. 55). С течением времени часть этих час-
тиц выбрасывается из сосуда. Нас
интересует движение ракеты в абсо-
лютном пространстве.
Введем следующие обозначения:
m(f) - масса ракеты в момент времени
ц эта масса распределена между кон-
Рис. 55
струкцией ракеты (в частности, ее
166
Глава 3. Общие теоремы динамики и их применение
корпусом) и частицами, которые могут быть выброшены. Мас-
сой ракеты m(f) мы называем всю массу; v(7) - вектор скорости
движения центра масс в момент времени t относительно абсо-
лютного репера Е; m(t + Дг), v(r + Дг) - те же величины в момент
времени t + Дг.
Мы предполагаем, что справедлив закон сохранения массы.
Тем самым масса частиц Дт, выброшенных из ракеты на отрезке
времени [г, t + Дг], определяется как разность
Дт = + Дг). (3.9.1)
Пусть u(r + Дг) - скорость относительного движения центра масс
выброшенных на отрезке времени [г, t + Д/| частиц (относитель-
но центра масс ракеты, точнее относительно репера Кёнига,
связанного с центром масс ракеты) в момент времени t + Д/.
Абсолютная скорость центра масс выброшенных частиц опре-
деляется как сумма относительной и переносной скоростей:
¥(г + Дг) + и(^ + ДО. (3.9.2)
Рассмотрим на отрезке времени [t, t + Д/| движение системы
материальных точек, которые в момент времени t
находились в ракете. Пусть Р(г) и Р(г + Д/) - количе-
ство движения этой системы в моменты времени t и t + Дг.
Известно, что количество движения системы материальных то-
чек можно представить в виде произведения массы системы на
скорость движения ее центра масс, т.е.
P(O = m(r)v(z). (3.9.3)
Вектор Р(г + ДГ) можно записать в виде суммы количества дви-
жения ракеты и количества движения выброшенных за время Дг
частиц:
P(t + ДО = m(t + Дг)у(г + ДО + Дт(v(t + ДО + u(r + ДО)- (3.9.4)
В нашей задаче никаких внешних связей нет и, следовательно,
справедлива теорема об изменении количества движения сис-
темы:
— P = FW, (3.9.5)
dt
где F(<?) - сумма внешних сил, действующих на все точки сис-
темы.
Проинтегрируем (5) на отрезке времени [г, t + Д/1:
Р(г + Дг)-Р(О= ( Fwdr. (3.9.6)
§ 3.9. Уравнения реактивного движения
167
Предположим, что m(r), v(r), u(r) - непрерывно дифференцируе-
мые функции времени, a F(e)(r) - непрерывная функция времени.
При Аг 0 из (1)—(6) следуют соотношения:
Ат =--------Аг + о(АГ),
dt
(3.9.7)
P(t + Ar) = m(r)v(r) +------Ar-------(v(r) + u(r))Ar + o(Ar), (3.9.8)
dt dt
j F(e)dt = F(e)(r)Ar + o(Ar). (3.9.9)
t
Подставим (3), (8), (9) в (6), разделим полученное соотношение
на Аг и перейдем к пределу при Л/ 0. В результате получим
уравнение
dmN . . dm
(v + u) = Fte)
dt-------------dt
и после несложных преобразований будем иметь
dy u dm 1
— =--------+ — F( }
dt т dt т
(3.9.10)
Это основное уравнение, описывающее движение центра масс
ракеты. Вектор скорости и определяется механизмом выброса
частиц и будет рассматриваться нами как заданная функция
времени и = и(г). Если F(£>) = 0, то ускорение центра масс ракеты
dvldt определяется величиной G Эта часть ускорения
т dt
центра масс ракеты носит название реактивного ускорения', со-
~ dm
ответствующая сила Fp = mGp = и—называется (в случае раке-
ты) тягой двигателя.
Рассмотрим специальные случаи реактивного движения.
Ракета в свободном пространстве
Предположим, что ракета движется далеко от силовых полей
или, как формулировал К.Э. Циолковский, «в свободном про-
странстве». В этом случае FM = 0. Этот случай можно исполь-
зовать для приближенного описания движения центра масс раке-
168
Глава 3. Общие теоремы динамики и их применение
|fw|
ты и при F(<?) Ф 0, если q—г^1, т.е. в случае, когда модуль внеш-
lFrl
ней силы много меньше модуля тяги двигателя.
Предположим также, что и - постоянный вектор. В этих
предположениях уравнения (10) легко интегрируются. Обозна-
чим через т0 и v0 массу и скорость центра масс ракеты в началь-
ный момент времени t = 0. После интегрирования (10) получим
Av = uln—, (3.9.11)
m0
где Av = v(z) - v0.
Мы вывели знаменитую формулу Циолковского. Модуль
вектора Av обозначают ж Очевидно,
т
w(0 = |u|ln-^-. (3.9.12)
m(f)
Предположим, что мы рассматриваем задачу в инерциальной
системе координат, перемещающейся поступательно с постоян-
ной скоростью v0. Тогда в начальный момент времени скорость
ракеты равна нулю и кинетическая энергия системы равна нулю.
Будем следить за частицами, которые при t = 0 находились в ра-
кете. В момент времени t полная кинетическая энергия исходной
системы материальных точек представима в следующем виде:
1 7
Т = —m(t)v2 + АТ,
где АГ > 0 - кинетическая энергия выброшенных частиц.
В нашей задаче внешних сил нет, и работа внешних сил равна
нулю. Следовательно, изменение кинетической энергии обуслов-
лено исключительно внутренними силами.
Интересно проследить, что же происходит с законом сохра-
нения энергии. Конечно, он выполняется, но аккуратное рас-
смотрение этого вопроса выводит нас за рамки моделей теорети-
ческой механики. В обычных для наших дней ракетах выбрасы-
ваемая масса является топливом, и приращение кинетической
энергии движения ракеты и выброшенных частиц происходит за
счет химической энергии, заключенной в топливе. При сгорании
топливо превращается в газ высокой температуры и давления
(химическая энергия переходит во внутреннюю (не механиче-
скую) энергию этого газа). С помощью специального устройства
(сопла) внутренняя энергия газа (т.е. энергия хаотического дви-
жения молекул) преобразуется в энергию направленного движе-
ния ракеты и выброшенных частиц (т.е. в их кинетическую энер-
§ 3.9. Уравнения реактивного движения
169
гию). Все очень сложно. Но для рассмотрения задач в рамках
теоретической механики необходимо знать только одно число:
модуль вектора и. Эту величину называют скоростью истече-
ния. Она может, в частности, определяться экспериментально.
Эта величина в ракетах, о которых мы сейчас говорим, зависит
от конструкции двигателя и используемого топлива. Для ориен-
тировки в порядке величин следует отметить, что в современных
ракетах величина |и| достигает 3-4 км/с. Предел как раз и опре-
деляется общим законом сохранения энергии. Если через Де
обозначить полную химическую энергию, первоначально заклю-
ченную в выбрасываемой массе газа Дт, то справедливо нера-
венство
^-Дт|и|2 < Де.
Кинетическая энергия выбрасываемых частиц не может пре-
восходить запас химической энергии, заключенной в топливе.
В химических ракетах топливо одновременно играет роль и но-
сителя массы, которую нужно выбрасывать, и носителя энер-
гии.
Сейчас разрабатываются двигатели другого типа, в которых
принципиально можно получить практически произвольные
скорости истечения. В этих двигателях энергия к выбрасывае-
мым частицам подводится от не связанного с ними источника.
Для этого можно использовать атомную установку или энер-
гию солнечного излучения. Как следует из (12), для больших |и|
т0
ту же скорость w можно достичь при меньшем ——, т.е. при
m(t)
меньшем запасе выбрасываемой массы.
Вернемся к формуле Циолковского. Из этой формулы следу-
ет, что скорость, которую может набрать ракета, зависит (при
u = const) только от количества выброшенной массы.
Из (12) следует, что w-> при m(t)—> О, т.е. достаточно
малой массе можно сообщить сколь угодно большую скорость.
Теоретически это верно, однако практически это реализовать
нельзя. Обозначим через тк сумму масс двигательной установки
и баков, в которых первоначально заключено топливо. Эту мас-
су технически невозможно отбросить со скоростью |и|. Поэтому
при сжигании всего топлива, заключенного в баках ракеты, ее
масса будет равна тк. Отсюда получаем предельную скорость
wnp, которую можно достичь одноступенчатой ракетой:
I и т0
^пр=Н1п
т„
170
Глава 3. Общие теоремы динамики и их применение
Так как для хранения первоначальной массы топлива тт всегда
необходима пропорциональная тт масса баков, то существует
предел отношения m()/mK. В лучших современных ракетах эта
величина не превосходит 7 -s- 9. Это чисто техническое ограниче-
ние (теоретически можно было предположить, что материал, из
которого сделана конструкция баков, имеет сколь угодно малую
массу) порождает предел кажущейся скорости, которую можно
достичь одноступенчатой ракетой.
Идею многоступенчатых ракет проще всего пояснить на сле-
дующей модели. Мы не можем отбрасывать конструкцию с
относительной скоростью |и|. Давайте предположим (в модели
все возможно), что конструкция отбрасывается непрерывно,
по мере расхода топлива, с нулевой относительной скоростью.
Предположим, что из отброшенной за время Д£ массы Дт часть
Д/у?! = (1 - ос)Дт выбрасывается со скоростью и, а часть Д///2 =
= аЛт отбрасывается с нулевой скоростью (0 < ос < 1). В этой
модели мы придем к уравнению
d\ = u(l-g) J/n । г<е) w
dt m dt
и в случае движения в свободном пространстве с постоянной
скоростью истечения
w = |и|(1 — сс) In.
1 1 т(0
Упражнение. Выведите уравнение (*).
Множитель (1 — ос) как бы уменьшает
скорость истечения. Однако отбрасывая кон-
струкцию, можно конечную массу m(t) сде-
лать достаточно малой и этой достаточно
малой оставшейся массе m(t) сообщить до-
статочно большую скорость w(0-
На самом деле реализация указанной
идеи в современных ракетах происходит сле-
дующим дискретным образом.
Строятся fc-ступенчатые ракеты (рис. 56).
После того как топливо первой ступени из-
расходовано, баки, в которых было заклю-
чено топливо, а часто и двигатели этой сту-
пени, отбрасываются с нулевой относитель-
ной скоростью. В этот момент оставшиеся
ступени уже имеют начальную скорость v0 = v t, а задача даль-
нейшего разгона, как принято говорить, сводится к предыдущей
задаче, т.е. к задаче разгона (£-1)-ступенчатой ракеты.
§ 3.9. Уравнения реактивного движения
171
Вертикальный подъем ракеты в однородном поле тяжести
Предположим, что ракета движется вблизи поверхности Зем-
ли. Учтем влияние силы тяжести на ракету. Мы пренебрежем
изменением ускорения силы тяжести в процессе разгона ракеты,
считая, что за время разгона координаты ракеты изменяются
мало по сравнению с радиусом Земли. Тогда F(e) = m(/)g, где Igl -
ускорение силы тяжести, которое будем считать постоянным
Igl ~ 9,8 м/с2.
Уравнения движения ракеты в этом случае имеют вид
dx и dm
— =---------+ g-
dt m dt
(3.9.13)
Предположим, что вектор u коллинеарен g
(ракета поднимается вертикально с нулевой на- А
чальной скоростью) и lul = const. Запишем (13) в ||]ез
проекции на орт ез (рис. 57): „Т* -2
d I VI I u I dm jTrrrny^mTTTr
£14 = _LEl£^._|g|. (3.9.14) Ze>
Л m dt Рис 57
Из (14) непосредственно видно, что ракета мо-
жет подниматься, если только реактивное ускорение по вели-
чине больше ускорения силы тяжести:
IuI dm . .
-—-^>|g|-
т dt
Решение (14) имеет вид
|v(O|=|u|ln-^-|g|r,
m(t)
(3.9.15)
где t - время разгона ракеты, т0 - масса ракеты при t = 0. Из
формулы (15) следует, что набранная скорость зависит не только
от количества выброшенной массы, но и от времени разгона.
Зафиксируем конечную скорость I v(/)l. Тогда если увеличивать
реактивное ускорение Gp, например, за счет более интенсивного
выброса массы, то время ^iV| достижения скорости Ivl будет
меньше и тем самым потери в скорости Igl/ уменьшатся, т.е. ту
же конечную скорость можно будет набрать при меньшем
расходе массы топлива.
Если Gp -> ©о, то f|V| -> 0, и в пределе мы придем вновь к зако-
ну набора скорости в свободном пространстве, определяемом
только расходом массы.
172
Глава 3. Общие теоремы динамики и их применение
§ 3.10. Тензор инерции
Рассмотрим систему материальных точек (rz, mz), i = 1,2,...,TV,
положение которых относительно репера Е = (в!, е2, е3) опре-
деляется координатными векторами i;T = (гД гД гД.
Радиус-вектор центра масс г* этой системы
1 /V N
* 1 X * X
г = — т = >т{
т ±7 ±7
(3.10.1)
является некоторой интегральной характеристикой распределе-
ния масс относительно репера Е. В дальнейшем нам потребуется
иметь дело с другими величинами того же типа. Мы введем эти
величины формально, а затем проанализируем их физический
смысл.
Как известно (см. § 2.1), каждому вектору 7?3 можно поста-
вить в соответствие кососимметрическую матрицу третьего по-
рядка. Обозначим через 7?z такую матрицу, которая соответ-
ствует координатному вектору Т-й материальной точки (г, <-> Rz):
7?z =
(3.10.2)
Квадрат матрицы R* - симметрическая матрица, которую мож-
но (см. (2.1.6)) представить в следующем виде:
7?;2 = -|rj2/ + rz.r/
(3.10.3)
где 1 - единичная матрица размера 3x3, lrzl - длина вектора rh а
rzrj - диада:
г,гт
Определение. Тензором инерции системы материальных то-
чек относительно репера Е называется матрица третьего поряд-
ка J, определяемая следующей формулой:
(3.10.4)
где mz - масса 7-й материальной точки.
§ 3.10. Тензор инерции 173
Обозначим:
Jo = i>,k|2- (3.10.5)
1=1
Определение, Скалярную величину у0 будем называть момен-
том инерции системы относительно начала репера Е.
Подставляя (3) в (4), получим другое представление для тен-
зора инерции J\
J = = (3.10.6)
где
j = ^m.rir-. (3.10.7)
1=1
Определения.
1. Элементы матрицы j = (j™) при кФ т называются центро-
бежными моментами инерции системы относительно репе-
ра Е\
Г.-Л (3.10.8)
к^т
i=l
2. Диагональные элементы тензора инерции к = 1, 2, 3,
называются моментами инерции системы относительно к-й
оси репера Е (или относительно прямой, определяемой ортом ек
репера Е). Из (6) и (7) непосредственно следует:
Jk=k-j^ (3.10.9)
где jk - диагональные элементы матрицы j. Или более под-
робно:
= 2>,К 2)2+<л3)2Ь (3.10.10)
Z=1
Т2 = f +(^)2], Jl = £тЖ)2 +0;2)2].
Z=1 Z = 1
Отметим некоторые свойства тензора инерции:
1°. J - симметрическая матрица размера 3x3.
2°. Лемма. J- неотрицательно-определенная матрица.
Доказательство. Пусть хе/?3 - произвольный век-
тор. Согласно (6),
xTJx = j0|x|2 -XTJX.
174
Глава 3. Общие теоремы динамики и их применение
Используя (7), получим
N N
xTjx = ^mfxTr/r/Tx = ^mz(x, rz) ,
i=l z = l
где (•, •)- скалярное произведение в R3.
Воспользуемся неравенством Коши-Буняковского (х, г, )2
х |2| rz |2 для получения следующей оценки:
xTjx«|x|2£m,. |rz |2 = |x|2j0.
1=1
Отсюда следует xTJx 0.
Нетрудно усмотреть, что знак равенства в последнем соот-
ношении возможен только при условии линейной зависимос-
ти вектора х с каждым вектором гг системы. Поэтому если ма-
териальные точки не лежат на одной прямой, проходящей че-
рез начало репера Е, то J - положительно-определенная мат-
рица.
3°. Момент инерции относительно k-й оси равен сумме (по
всем точкам системы) произведений массы точки на квадрат ее
расстояния от прямой, определяемой к-м ортом Е. Это непо-
средственно следует из (10).
4°. Справедливо равенство
70Ц(^'+Л2+-/з)- (3.10.11)
Доказательство сразу следует с использованием (5) и (10).
Элементы тензора инерции определяются значениями функ-
ций
/=/(гьг2,..., rw)
координат радиусов-векторов материальных точек системы.
Поэтому тензор инерции системы зависит от того, относительно
какого репера задается положение материальных точек. Про-
анализируем эту зависимость.
5°. Пусть репер получен параллельным переносом Е на
вектор а.
Обозначим: а - координаты относительно Е, г; - координаты
радиуса-вектора Ей точки относительно Еа.
В рассматриваемом случае справедливо равенство
г. = г. + а.
(3.10.12)
§ 3.10. Тензор инерции
175
Подставим (12) в выражение дляу0 (5):
l2=Xm'(lr'l2+2<г-’о£>+1“Г)=
г=1
Л)=У™1к+«
/=1
Здесь
г*
= j0 + 2т‘ (г'\ а) + гп |а|2 . (3.10.13)
mi - радиус-вектор центра масс системы
относительно репера
Аналогично вычислим д (7):
jkk = У mi )2 = У т, (гк + а* )2 =
z=l 1=1
= jk+2mXr*k)ak + т*(ак)2. (3.10.14)
Предположим теперь, что начало репера Еа помещено в
центре масс системы. Тогда г* = 0. Подставляя (13) и (14) (при
г = 0) в (9), получим
Jk =Jo~jkk + m*(|cc|2-((?)2),
откуда
Jk=Jkk+rndl, (3.10.15)
где dk =| а |2 -(ак )2 - квадрат расстояния между прямыми, опре-
деляемыми &-ми ортами реперов Е и Еа.
Определение. Любую прямую, проходящую через центр масс
системы материальных точек, будем называть центральной
осью системы.
В предыдущем анализе репер Е был произвольный. Поэтому
соотношение (15) содержит доказательство утверждения тео-
ремы Штейнера (или Гюйгенса-Штейнера):
Момент инерции относительно произвольной оси равен
моменту инерции относительно параллельной ей центральной
оси плюс произведение массы всей системы на квадрат рас-
стояния между этими прямыми.
Этот результат эффективно используется при конкретных
вычислениях осевых моментов инерции.
Следствие. Момент инерции системы относительно
176
Глава 3. Общие теоремы динамики и их применение
центральной оси меньше момента инерции относительно любой
другой оси, ей параллельной.
6°. Пусть теперь репер Е получается из Е с помощью пово-
рота, определяемого матрицей А: Е——зЕ. Пусть г, и i; -
координатные векторы i-й материальной точки относительно
реперов Е и Е соответственно. Нам известно, что
I* = А% (3.10.16)
Подставляя (16) в (5) и (7), получим:
n
j = ^mlATrir,'A = AT]A, (3.10.17)
/=1
Jo = Хт-Иг|2 =Xm'fr|2 (3.10.18)
/=1 /=1
Подставив (17) и (16) в (6), найдем
J = j0I-ATjA. (3.10.19)
Обозначим через J тензор инерции относительно репера Е : J =
= j^I - j. Из (19) следует
J = AJA\ (3.10.20)
Собственно справедливость формулы (20) при любых ортого-
нальных преобразованиях репера, определяемого матрицей А, и
оправдывает название матрицы J тензором. В частности, из фор-
мулы (20) следует, что для любых векторов х, у G R3 скалярная
функция - билинейная форма:
/= хт7у = (х, Jy) = (Jx, у)
инвариантна при любых ортогональных преобразованиях репе-
ра. Действительно, рассмотрим преобразование Е —> Е, тогда
х = Атх, у = Ату. Поэтому f= хТAJATy = хт7у. Таким образом,
функция/имеет один и тот же вид в любой ортонормированной
системе координат.
Теорема. Всегда можно с помощью преобразования поворота
получить репер Е, относительно которого тензор инерции
является диагональной матрицей с диагональными элементами,
большими или равными нулю.
Доказательство этого утверждения основано на до-
казанной неотрицательной определенности тензора инерции и
§3.10. Тензор инерции
177
известной теореме алгебры: Вещественная симметрическая
матрица всегда вещественно и ортогонально подобна диаго-
нальной матрице. Неотрицательность диагональных элементов
следует из неотрицательной определенности матрицы J. (Если
матрица J положительно определена, то все диагональные
элементы будут больше нуля.)
Определение. Если относительно репера Е тензор инерции
определяется диагональной матрицей, то прямые, определяемые
ортами е* репера Е, называются главными осями инерции
системы для точки начала Е. Если к тому же начало репера Е
помещено в центре масс системы, то его орты определяют глав-
ные центральные оси системы.
Условимся об обозначениях. Если орты репера Е распо-
ложены по главным осям инерции системы, то моменты инерции
относительно i-й оси (диагональные элементы матрицы J) будем
обозначать Jb J2, J3 соответственно.
Так как в предыдущем рассмотрении начало репера было
расположено в произвольной точке пространства, то тем самым
для каждой точки можно указать три взаимно перпендикулярные
прямые, являющиеся главными осями системы для данной точки.
При этом для различных точек главные оси, вообще говоря, не
параллельны. Если тензор инерции относительно Е известен, то
из соотношения (20), в частности, вытекает способ вычисления
момента инерции относительно произвольной оси (прямой), про-
ходящей через начало репера Е.
Пусть v = v
- координаты единичного вектора (Ivl =
1),
направленного по этой прямой. Обозначим искомый момент
через Jv. Без ограничения общности можем полагать, что v - ко-
ординаты первого орта ej репера Е. В этом случае первая
строка матрицы А совпадает с vT. Момент инерции относительно
ё1? т.е. относительно рассматриваемой оси, есть первый диаго-
нальный элемент матрицы J:
Jv - = vTJn = (v, Jv).
Или, более подробно,
3 3
И=1 i = l
(3.10.21)
(3.10.22)
Если репер Е был ориентирован по главным осям, то (=0 при
12. М.Л. Лидов
178
Гпава 3. Общие теоремы динамики и их применение
I Ф к) И
3
Л=5>')4- (3.10.23)
1=1
Замечание. Элементы тензора инерции для системы мате-
риальных точек определяются суммами следующего вида:
з
5 = ^ШуФ^).
/=1
Для тела с непрерывным распределением массы плотностью
р (г) в области V е R3 такие характеристики (как мы уже
пояснили в § 1.8) вычисляются с помощью интегралов по об-
ласти V:
S = J Ф(г)б?т = JJJo(r)p(r)c?V,
где dV = drxdr2dr3 - элемент объема.
Примеры.
Г. Момент инерции однородного шара относительно его
центра. Пусть М и R - масса и радиус шара. С использованием
условия однородности (Эр/Эг = 0, или р = const) следующий
интеграл легко вычисляется:
Jo = Jfflr I2 Pdv = 4яр/Ir I21 r I2 d I r |= |np/?5 =
0
= — pR3-R2 = -MR2.
3 5 5
2°. Момент инерции однородного шара относительно цент-
ральной оси. В силу симметрии J{ = J2 = J3. Согласно (11), j} +
+ Jl + J33 = ЗУ,1 = 2j0.
2 2
Таким образом, J‘ = —jQ = —MR2.
Рис. 58
3°. Момент инерции шара относительно пря-
мой, его касающейся (рис. 58). Согласно теореме
Штейнера,
2 7
г? +mr2 = -mr2+mr2 = —mr2.
А 1 5 5
Упражнение. Покажите, что для однородного шара центро-
бежные моменты инерции относительно репера, связанного с его
центром, равны нулю.
§ 3.11. Уравнения движения твердого тела
179
4°. Момент инерции однородной палочки длиной L относи-
тельно перпердикулярной оси (рис. 59). Пусть р - плотность на
единицу длины. Тогда
J* = ^px2dx = ^-
о
= P^L2 =Lml\
2 3
О
где М - масса палочки.
Для вычисления момента инерции
относительно центральной оси ВВ, па-
раллельной АА, используем теорему
Штейнера:
Рис. 59
§ 3.11. Уравнения движения твердого тела
А. Свободное тело
Будем называть твердое тело свободным, если движение его
материальных точек не ограничено никакими связями кроме
связей, обеспечивающих сохранение его твердости (расстояние
между любыми двумя точками не изменяется). Воспользуемся
теоремами об изменении количества движения и момента коли-
чества движения для вывода уравнений движения свободного
твердого тела.
Пусть Е - абсолютный репер, Е - репер Кёнига (репер, свя-
занный с центром масс твердого тела, и ортами, соответственно
параллельными ортам репера Е). Пусть Ё - репер, жестко свя-
занный с твердым телом, с началом в центре масс и А - матрица
преобразования Е—^-^Е. Будем использовать обозначения:
т - масса твердого тела;
г*, V* - координаты радиуса-вектора и вектора скорости
центра масс твердого тела относительно репера
E(v>: = dr' / dt);
fj, vz - координаты и компоненты вектора скорости твердо-
го тела относительно репера Кёнига (i = 1,2, ..., N);
rz, v i - проекции векторов г/Т у. на орты репера Е:
г, = Avt, Ni - Av- (yi Ф dij dt при dAI dt 0).
Движение твердого тела будет известным, если в каждый
момент времени t мы будем знать г' (0 и А(Г).
12*
180
Глава 3. Общие теоремы динамики и их применение
Пусть Р - вектор количества движения твердого тела отно-
сительно репера Е:
Р = miNi =
/=1
Так как твердое тело свободно, то можно применить теорему об
изменении количества движения системы:
О * * d Г 17(£) 1 1 1 \
— Р = т = т —= F , (3.11.1)
dt dt dt
где F(e) G R3 - сумма внешних сил, действующих на материальные
точки твердого тела.
Уравнение (1) определяет движение центра масс твердого
тела.
Воспользуемся теперь теоремой (3.6.17) об изменении мо-
мента количества движения системы К относительно репера
Кёнига. Согласно определению,
_ w
К = £ m,[i;., V,]. (3.11.2)
Z = 1
Так как свободное твердое тело допускает произвольное вра-
щение относительно репера Кёнига, то
— = М(е), (3.11.3)
dt
N
где М"’“St?. }] - сумма моментов внешних сил (относи-
/=1
тельно начала репера Е), действующих на материальные точки
твердого тела.
Лемма 1. О представлении момента количества движения
твердого тела. Обозначим через К - момент количества движе-
ния системы относительно репера Кёнига в проекциях на орты
репера Е, жестко связанного с твердым телом и началом в
центре масс: К =АК. Справедливо представление
К = Joi,
где J - тензор инерции относительно репера Е, со =
со
w2
со3
§3.11. Уравнения движения твердого тела
181
проекции вектора угловой скорости твердого тела на орты
репера Ё.
Доказательство. Согласно основному соотношению
кинематики твердого тела (2.5.1),
V-=[<о, гД,
где со - угловая скорость вращения Е относительно Е (про-
екции на орты репера Е). Дополнительное слагаемое отсут-
ствует, так как начало репера Е связано с точкой твердого тела.
Подставив это соотношение в (2), получим
N
К = Е (з.н.4)
1=1
Это - векторное равенство, и мы можем записать его в проек-
циях на орты репера Ё. В результате будем иметь
K = £nz, [f1, [<о, г, ]], (3.11.5)
Z=1
где
К = АК, = (3.11.6)
Преобразуем двойное векторное произведение, используя
представление векторного произведения в матричном виде:
[г,, [<о, Г,]] = -[г,, [г,,<о]] = -Я,2<о,
где - кососимметрическая матрица, соответствующая вектору
г-. Подставив последнее равенство в (5), получим:
( N Л
К=
I /=1 )
со = Ло,
(3.11.7)
где J - тензор инерции относительно репера Ё. Так как репер
Ё жестко связан с твердым телом, то J не изменяется с тече-
нием времени.
Проектируя (7) на орты репера Кёнига, находим
K = ATK = ATJcb. (3.11.8)
Подставим К в виде (8) в (3):
^ = ATJ^ ++ MW. (3.11.9)
dt dt dt
182
Глава 3. Общие теоремы динамики и их применение
Так как det А Г 0, то мы можем получить эквивалентную систему
уравнений, умножив (9) на А. В результате получим
+ (3.11.10)
dt dt
где М(е) = АМ(е) - координаты вектора момента внешних сил в
проекциях на орты репера Ё.
Воспользуемся тождеством
ИАТ НАТ —
A— = A—AAT=A£IAT=Q (3.11.11)
dt dt
где Q - кососимметрическая матрица, соответствующая вектору
w (Q о о) и аналогично Q со. Представим QJco в виде
векторного произведения:
Шсо = [со, /со]. (3.11.12)
Используя (11) и (12), уравнения (10) можно записать в следую-
щем виде:
J — + [<о, Ло] = ]УГ’. (3.11.13)
dt
Предположим, что приложенные к твердому телу внешние
силы F(e) и моменты сил М(е) не зависят от ориентации твердого
тела (репера Е) относительно Е. Они могут зависеть от
времени и компонентов вектора угловой скорости со и векторов
положения г* и скорости v* его центра масс. В этом случае
система уравнений (1)и(13)- замкнутая система трех уравнений
второго порядка (1) и трех уравнений первого порядка (13). Эти
уравнения при заданных начальных данных можно проинте-
грировать и найти г*(Г) и со(Г) как функции времени. Для того
чтобы определить ориентацию твердого тела (репера Ё) отно-
сительно репера Е (или Е), можно воспользоваться кинемати-
ческими уравнениями Эйлера, которые мы вывели в § 2.8. Эти
уравнения имеют вид
^ = f(Y, «), (3.11.14)
dt
где у = 0 - трехмерный вектор, компоненты которого суть
углы Эйлера у, 0, (р.
§3.11. Уравнения движения твердого тела
183
Проинтегрировав эти уравнения, мы определим зависимость
у от времени и тем самым найдем матрицу
А(г) = П(3, ф (0) П (1, 0 (г))П(3, ф (г)).
Если силы (или моменты сил) зависят от ориентации Е отно-
сительно Е (иначе: от матрицы А или углов Эйлера), то систему
уравнений (1), (13) и (14) необходимо решать совместно.
Замечание. В приведенных выше рассуждениях мы предпо-
лагали, что твердое тело не вырождается в палочку или точку
(det J Ф 0) и уравнения (13) можно разрешить относительно
производных по времени:
— = ф(й>, М'Ч
dt \ >
Мы не будем сейчас останавливаться на специальных случаях
det J = 0, которые разберем в дальнейшем при анализе движения
твердого тела.
Б. Твердое тело с закрепленной точкой
Пусть теперь одна точка О твердого тела закреплена (она
неподвижна относительно Е) так, что твердое тело может совер-
шать произвольные повороты относительно этой точки. Реали-
зация такой связи достигается с помощью специального приспо-
собления, называемого шарниром. Можно (и удобно) считать,
что начало абсолютного репера Е совпадает с точкой О. Пусть
репер Е жестко связан с твердым телом и его начало также
расположено в точке О (это не обязательно центр масс твердого
тела). Пусть А - матрица поворота: Е——>Ё. Так как связи
допускают произвольные повороты системы как твердого тела,
то справедлива теорема об изменении момента количества
движения
— = М(е), (3.11.15)
dt
N
где K = ^m,[rz, vj - момент количества движения твердого
/=1
тела относительно репера Е.
Теперь можно провести все рассуждения и всю процедуру,
записанную соотношениями (2)-(13), которая приводит нас к
уравнениям движения твердого тела (13). Единственное фор-
мальное отличие состоит в том, что во всех этих соотношениях
184
Глава 3. Общие теоремы динамики и их применение
можно убрать черту над буквами, так как в рассматриваемом
случае Е и Е тождественны. Тем самым уравнения движения
твердого тела с закрепленной точкой есть уравнения (13). Еще
раз напомним, что в случае Б начало репера совпадает с
неподвижной точкой О, а не с центром масс твердого тела, как в
случае А.
Уравнения Эйлера
В обоих рассмотренных случаях в большинстве задач ничто
нам не мешает выбрать репер Е ориентированным по главным
осям инерции центра масс. Тогда тензор инерции будет иметь вид
0 0 '
J = 0 J2 0 (3.11.16)
<0 0 Г
При этом
7,(01 " ~ 2 ~ ЗА co co
72C02 , [co, Jco] = й>300*
Ч(Л-Л) co'co2^
В этом случае в скалярной форме уравнения (13) запишутся в
следующем виде:
J, ~ + (J3 - J2)со2со3 = М{е\
J2 —+ (71-73)ф3со1=Л/<г), (3.11.17)
dt
J3^- + (J2-Jl)wl(i)2 =М(3е),
где Л?-е) - проекция результирующего момента сил на z-й орт
репера Ё.
Это знаменитые уравнения Эйлера. Заметим, что в литерату-
ре более распространены следующие обозначения:
~ 1 ~ 2 ~ 3
со = р, со = q, СО — Г,
(3.11.18)
Jl = A, J2= В, J3 - С.
Из формулы (7) в случае, когда J - диагональная матрица,
§3.11. Уравнения движения твердого тела
185
вытекают следующие формулы для проекций вектора кинети-
ческого момента К (относительно репера Кёнига или непод-
вижной точки) на главные оси инерции:
Л^/jCO1, ЛГ2=72со2, =
или, в более распространенных обозначениях,
Кj = Ар, К2 = Bq, К3 = Сг.
В. Вращение твердого тела вокруг неизменной оси
Рассмотрим вновь движение твердого тела. Предположим,
что связи идеальны и допускают только поворот твердого тела
вокруг фиксированной прямой. Для упроще-
ния дальнейших формул предположим, что
начало репера Е находится на этой прямой, а
орт е3 направлен вдоль этой прямой (рис. 60).
Так как, по предположению, связи допускают
поворот твердого тела относительно прямой,
определяемой ортом е3, то для системы мате-
риальных точек, образующих твердое тело,
справедлива теорема об изменении проекции вектора кинети-
ческого момента:
dt 3
(3.11.19)
где К3 и - третьи компоненты вектора кинетического
момента и момента внешних сил. Пусть репер Ё жестко связан с
твердым телом. В рассматриваемом случае удобно выбрать Ё
так, чтобы орт ё3 совпадал с ортом е3. Так
как точки твердого тела, находящиеся на оси,
не изменяют своего положения в простран-
стве, это возможно. В этом случае
^3 = р = (ё3, К) = (ё3, Ju). (3.11.20)
Для получения последнего равенства надо
воспользоваться формулой (7). Обозначим
через у угол между ортами е! и (рис. 61). В
рассматриваемом случае движение репера Е относительно Е
(0}
сводится к простому повороту вокруг общей оси е3 = ё3
0
1
186
Глава 3. Общие теоремы динамики и их применение
Таким образом, матрица преобразования Е—уЁ есть матрица
простого поворота П(3, у) (см. § 2.8). Следовательно, вектор
угловой скорости
<о = —ё3. (3.11.21)
dt
Из (20) и (21) получим
/С3 = (ё3, Л3)^- = Г^-, (3.11.22)
dt dt
где Jf - момент инерции твердого тела относительно закреп-
ленной оси. Это не обязательно главная ось инерции. Подставляя
(22) в (19), получим уравнение, определяющее изменение угла у в
зависимости от времени:
= (З.и.23)
Упражнение. Попробуйте составить уравнение движения твердого тела
в случае, когда связи допускают поворот твердого тела вокруг постоянной оси
и движение этого тела в направлении, определяемом этой осью. Эта задача
требует самостоятельного анализа.
Замечание 1. Пусть внешние силы заданы как функции г*, V*
времени t. Если мы интересуемся только движением центра масс
свободного твердого тела, то нам необходимо знать только одну
его характеристику - массу, несмотря на огромное разнообразие
различных твердых тел (и их моделей). То есть с точки зрения
изучения движения центра масс такая задача оказывается по-
добной задаче о движении материальной точки.
Для полного описания движения твердого тела (если момен-
ты сил отсутствуют или заданы как функции г*, v*, Г, со, ф, 0, ф),
как следует из уравнений Эйлера, необходимо знать еще три
числа - моменты инерции тела относительно главных осей. То
есть с точки зрения динамики свободного движения все много-
образие твердых тел четырехмерно. Для задачи с одной закреп-
ленной точкой любое конкретное твердое тело может быть
охарактеризовано тремя числами.
Если мы будем, например, рассматривать движение твердого
тела в ньютоновском поле какой-либо гравитирующей точки, то
результирующие силы и моменты сил могут зависеть при точном
формальном описании этой задачи от бесконечного числа по-
стоянных параметров, отражающих существенные для задачи
свойства данного твердого тела как системы гравитирующих
точек.
§ 3.11. Уравнения движения твердого тела
187
Замечание 2. В этом параграфе с использованием общих тео-
рем механики были выведены уравнения движения твердого
тела. Анализ движения твердого тела будет проведен в дальней-
шем.
Кинетическая энергия твердого тела
Сейчас мы получим формулы для кинетической энергии
твердого тела. В дальнейшем они будут неоднократно исполь-
зоваться. Как и выше, будем рассматривать два случая:
А) Движение свободного твердого тела относительно абсо-
лютного репера Е.
Б) Движение твердого тела с закрепленной точкой. При этом
будем оперировать введенными в этом параграфе понятиями и
обозначениями. Для случая А): Е - репер Кёнига, а Ё - репер,
жестко связанный с твердым телом. Начало реперов Ё и Е
совпадает с центром масс тела. В случае Б) начало реперов Е и
Ё находится в точке закрепления О.
Рассмотрим сначала случай А). По теореме Кёнига (см.
(3.6.19)) кинетическая энергия движения твердого тела может
быть представлена в следующем виде:
Т = Т+^т | V* |2, (3.11.24)
где т* - масса твердого тела, v* - скорость его центра масс,
- 1 N
т = -^т,\^\2 (3.11.25)
- кинетическая энергия движения относительно репера Кёнига.
Лемма 2. О представлении кинетической энергии твердого
тела относительно репера Кёнига. Справедливо представление
где J - тензор инерции относительно репера Е;
со - проекции угловой скорости относительно Е на орты репе-
ра Ё.
Для доказательства воспользуемся известным представле-
нием vz:
\=[<о, гД. (3.11.27)
Последнее векторное равенство можно записать в проекциях на
188
Глава 3. Общие теоремы динамики и их применение
орты репера Е, а затем представить его в виде произведения
матриц:
vz=Avz=[cb, rz] = —[rz, = (3.11.28)
где Rj - кососимметрическая матрица, соответствующая вектору
rz. Отсюда
I Р = | \ Р “ =
ИЛИ
|v,.|2=-d>X2w. (3.11.29)
Подставляя полученное представление для | v, |2 в (25), получим
следующее выражение для кинетической энергии Т:
f = |<oTJ<o, (3.11.26)
где J - тензор инерции относительно репера Ё. Выражение для
полной кинетической энергии Т в случае А) будет иметь вид
r = |wTJ<o + |/?i4'|v!|2. (3.11.30)
В случае Б) имеет место соотношение
vz=[co, rz]. (3.11.31)
Проводя все преобразования, аналогичные (27)-(30) (в формулах
не будет черты), получим выражение для полной кинетической
энергии
T = |toTJw. (3.11.32)
Если орты репера Ё ориентированы по главным осям инерции,
то (32) после умножения матриц примет следующий вид:
T = ^[j1(w1)2 + J2(w2)2 +/3(й>3)2] (3.11.33)
или, в более распространенных обозначениях,
Т = 1[А^2 + В<72+Сг2]. (З.И.ЗЗ1)
В точно такой же форме представимо выражение (26) для
кинетической энергии Т относительно репера Кёнига, если ре-
пер Ё ориентирован по главным осям инерции. Следует только
§ 3.11. Уравнения движения твердого тела
189
помнить, что в случае A) J2, J3 - это моменты инерции отно-
сительно главных центральных осей, проходящих через непод-
вижную точку О, относительно которой вращается твердое тело.
Замечание. Формулой (26) можно воспользоваться и для слу-
чая движения твердого тела вокруг фиксированной оси. Если ось
( dy\
вращения определяется ортом е3 = ё3, то со' = О 0 — .Из (26)
получим
7 = 1^)
21 dt J
з-
(3.11.34)
Глава 4
Вариационный принцип Гамильтона
и уравнения движения
в форме Лагранжа и Аппеля.
Некоторые интегрируемые задачи.
Силы инерции
§ 4.1. Некоторые леммы вариационного исчисления
Обозначим: Jt = (гь г2) - открытый интервал вещественной
прямой, Jt =[/], /2] ~ замкнутый интервал, Ф: Jt RN, %
—> Rn - два непрерывных отображения в вещественное TV-мер-
ное евклидово пространство, осуществляемые вектор-функция-
ми Ф(7) и £(7). Будем обозначать (Ф(г), £(/)) - скалярное про-
изведение векторов Ф(7) и £(7) в RN. Будем писать £ е С”\ если
отображение £ имеет непрерывные производные по t порядка
т включительно.
Ниже мы будем ссылаться на существование для любого
5 > 0 отображения ос: Jt —> /?, определяемого следующей функ-
цией:
a(r, 5)= е \t-t*\<8.
О |г-Г|>5
(4.1.1)
(рис. 62). Очевидно, что ос (г, г*, 5) G С°°, ос (г, г*, 5) > 0 при
1г- г*1 < 5.
Лемма 1. Рассмотрим множество G отображений удовлет-
воряющих условиям:
1) £ G С” (т - заданное целое число); 2) £ (rj = £ (72) = 0.
Утверждение. Если для любого е G и любого t е Jt
f(t) = (Ф (0, g (0) = 0, то Ф(7) = 0 при t g Jt.
Доказательство. Обозначим через Ф'(7) z-й компонент
Ф(г). Предположим, что при некотором г* g Jt Ф'(г*) Ф 0. Выбе-
рем достаточно малое 5 > 0 (так, чтобы (Г ±5) gJJ и построим
следующее отображение |(г):
j * i.
j = G
§ 4.1. Некоторые леммы вариационного исчисления
191
Очевидно, £ G G и
(Ф(Г), |О = Ф'(Г)а(ЛЛ 5)*о.
Мы пришли к противоречию. Из условия
Ф(0 = 0 на Jt и непрерывности Ф(/) на Jt
следует: Ф(7) = 0 на Jt.
z, /*- 6 z*+ 8 t2
Рис 62
Лемма 2. Рассмотрим множество GD отображений удов-
летворяющих условиям леммы 1 и следующему дополнитель-
ному условию: при каждом t G Jt ^(t)eDc RN, где D - (N-k)-
мерное подпространство RN, 0 к < N.
В координатном представлении это условие можно записать
в следующем виде:
где B(f) - матрица размера к х N; ранг В равен к, элементы
матрицы B(f) достаточно гладкие функции.
Рассмотрим линейный функционал
t2
«(£) = / <Ф(?),
t\
Утверждение. Если ос = 0 для любого £; g GD, то
<Ф(0, €(0) = 0 Для всех £ g Gd и всех t е Jt.
Доказательство. Предположим, что существует ото-
бражение £* g Gd такое, что при некотором f е Jt
(Ф(Г), %(f)) > 0. Тогда из непрерывности Ф(г), следует, что
существует такое 5 > 0, что (Ф(г), £ (г)) > 0 при lr- f I < 5.
Определим отображение | = oc(r, f, 8*)(f(0, где ос опре-
делено (1), 0 < 8* 8 и t* ± 8* g Jt. Очевидно, £ (0 е Gd. Рас-
смотрим интеграл ос при £ = |(г):
a(l) = J <Ф(0, lWt= ( а(г,/*,5*ХФ(?),^(г)М?.
/ -5
Из последнего представления очевидно, что oc(£j) > 0. Это про-
тиворечие и доказывает утверждение леммы для t g Jf. Из непре-
рывности (Ф(г), следует, что (Ф(г), = 0 на Jt.
192
Глава 4. Вариационный принцип Гамильтона
Лемма 3. Рассмотрим два интервала вещественной прямой:
J, = {f, геТ?, Г] =sr=s/2},
Jz = {т, те/?, |т|<е, 8>0}
и дважды непрерывно дифференцируемое отображение
-^Rn
•J l t
прямого произведения Jt и Je в RN, определяемое вектор-функ-
цией у = у (л т). Будем предполагать, что для рассматриваемых
ниже функций у (г, т):
( Эу А
1) определена сложная функция L у, —t\, задающая
V dt )
отображение
2) функция L (у, z, t) - дважды непрерывно дифференцируема
по у, z и непрерывно дифференцируема по t.
Рассмотрим интеграл
'1
Замечание. Здесь dyldt = dy/dt. В дальнейшем при дифферен-
цировании сложной функции времени Ф = Ф(у(г, т), z(/, т), t) бу-
дем отличать производную по явно входящему времени
ЭФ _ Ф(у, z, t + h) - Ф(у, z, t)
dt h -^o h
от полной производной
d<5> ЭФ б?у ЭФб/z ЭФ
---—-------1-------1---,
dt dy dt 9z dt dt
При фиксированном отображении у интеграл 5 (2) является
функцией т. Вычислим частную производную Э5/Эт при т = 0.
Утверждение. Справедливо следующее представление:
Э5 _ (9LV г \ / л- — \ Т ’ \ ОТ т=о \ OZ J t=t2 / \ т=0 / 'с /( дБ , \1.ЭУ> '1 \ '(dLV \ К- , + sAd’L) / \ т=0 / 1 -4Пг1 ’ &>) dt> 1 dt^dzj / ' т=0
§ 4.2. Принципы Гамильтона
193
где
Эу
Эт
т=0
dt
Доказательство. Дифференцируя (2) по т под знаком
интеграла, получим
Э5 f (dL Эу dL d < dyV) _ .. . ..
— = —+ — \\dL (4.1.4)
Эт J Эу Эт 9z Эт v dt))
где z = dy/dt.
д dy d ду
Воспользуемся равенством-----=-----и проинтегрируем вто-
Эт dt dt Эт
рой член в (4) по частям:
d (dL\ Эу ,
— — \^~dt.
dtydz) Эт
Таким образом, мы пришли к представлению
05 = dLdy'2 +| ГЭ£_ 0_ГЭЛ^Эу^
Эт 0z Эт (| J Эу dt[ 0z J) Эт
Полагая т = 0 и записывая подынтегральное выражение в виде
скалярного произведения, получим формулу (3).
§ 4.2. Эквивалентность вариационного
принципа Гамильтона
и принципа Даламбера-Лагранжа
Будем рассматривать на отрезке времени Jt - [?|э t2] движе-
ние системы материальных точек (г„ m,), i= 1, 2, п; г,е №.
Будем использовать сокращенные обозначения
где г, v, F е №"; F, е № - вектор
точку: F/=(F,’, F,2, F;3),
силы, действующей на i-ю
13. М.Л. Лидов
194
Глава 4. Вариационный принцип Гамильтона
т1
- диагональная матрица размера Зп х Зп,
составленная из величин масс точек т,.
Предположим, что на систему наложены идеальные незави-
симые связи: k голономных связей
f(r, r) = 0, fe Rk (4.2.1)
и 5 неголономных линейных по скоростям связей (к + 5 < Зп)
Ву + Р = 0, (4.2.2)
где v = drldt, В = B(r, t) - матрица размера s х Зп, Р = Р(г, t) g Rs.
Согласно определению независимых связей, ранг матрицы
(ЭГ|
Эг (4.2.3)
равен к + s.
Замечание о связях. Связи (2) мы предполагаем неголоном-
ными. Все дальнейшие выводы будут справедливы, если (2) со-
держат и голономные связи, записанные в дифференциальной
форме. Однако при решении задач выделение всех голономных
связей в соотношение вида (1) целесообразно с точки зрения
упрощения анализа задачи.
Рассмотрим отображение г: Jt R3n, определяемое вектор-
функцией г(г). Будем говорить, что отображение г определяет
опорную кривую, если при t G Jt функция г(Г) удовлетворяет
уравнениям связей:
f(r(O, О = 0, (4.2.4)
В(г(г),О—+ Р(г(1),0 = 0. (4.2.5)
dt
В частности, опорной кривой является действительное движение
системы, однако опорные кривые могут и не удовлетворять
уравнениям движения.
Рассмотрим отображение Jt-^R3\ определяемое век-
тор-функцией Будем говорить, что £(Г) - допустимая век-
тор-функция для данной опорной кривой г(0, если на Jt
§ 4.2. Принципы Гамильтона
195
удовлетворяет следующим условиям:
0f
Эг €(0 = 0, r=r(/) (4.2.6)
B(r(O,O€(O = 0, (4.2.7)
^)=ga2)=o, (4.2.8)
где г(7) удовлетворяет (4) и (5).
Замечание 1. Все функции, рассматриваемые здесь и ниже,
предполагаются дифференцируемыми достаточное число раз.
Отмечая, что некоторая функция произвольна, мы будем подра-
зумевать произвольную достаточно гладкую функцию.
Замечание 2. Если г(7) определяет действительное движение
системы, то из условий (6) и (7) следует, что £(7) - виртуальный
вектор.
Лемма. Для произвольной вектор-функции |(г)
t е удовлетворяющей только условиям (6) и (7),
можно указать допустимую вектор-функцию £(7), которая совпа-
дает с |(г) на отрезке времени Jt = +5, /2 - S], где 5 > 0 - сколь
угодно малое число и £(7) G Ст.
Доказательство. Определим на Jf скалярную функ-
цию Р(0-
t{ z +5,
+5 < t < t2 -5,
t2 -5 t t2.
Нетрудно показать, что [3(0 g Cm на Jt и P(/] ) = P(/2) = 0. Пред-
ставим £(0 в виде произведения: £(7) = P(z) £;(0. Очевидно, что £ G
G Ст и удовлетворяет на Jt условиям (6)—(8) и £(7) = |(г) при
te Jt. Из этой леммы следует, что на открытом интервале
Л = h) допустимые вектор-функции суть произвольные век-
тор-функции, удовлетворяющие только условиям (6) и (7).
Пусть е > 0. Рассмотрим интервал 7е вещественных чисел т
Je= {те R, 1т1 < е} и отображение х : Jt R3" прямого
196
Глава 4. Вариационный принцип Гамильтона
произведения интервалов Jt и J£ в R3n. Обозначим через xU т)
вектор-функцию, которая задает это отображение. Будем гово-
рить, что отображение х принадлежит множеству допустимых
отображений D(r(t)) (хе D (г(7))), если x(t, т) удовлетворяет
следующим условиям:
1°. х(',0) = г(0, (4.2.9)
где г(0 - опорная кривая, т.е. вектор-функция, удовлетворяющая
условиям (4) и (5);
Эх
Этт=0
=g(f),
(4.2.10)
где - допустимая для г(г) вектор-функция, т.е. удовлет-
воряет (6)-(8).
Мы переходим к формулировке принципа Гамильтона. Пред-
положим, что опорная кривая г(г) фиксирована. Предположим,
что силы, действующие на материальные точки, заданы как
функции координат точек, компонентов вектора скорости и
времени:
F = F(r,v,f), Fe (4.2.11)
Введем обозначения
Р(О = р[г(О, ^ДД
k dt )
(4.2.12)
где г(г) - фиксированная опорная кривая;
<ра, r) = (F(Z), г), (4.2.13)
где (•, •)- скалярное произведение в R3n.
Напомним, что кинетической энергией системы называется
следующая квадратичная форма от компонентов векторов ско-
рости точек системы:
Т = |vTA/v = |(v, Му). (4.2.14)
Введем следующую скалярную функцию координат, компо-
нентов вектора скорости и времени:
L(r, v, r) = T + cp(r, г).
(4.2.15)
Замечание 3. В дальнейшем нам потребуется вычислять
частные производные от L по г и v. Важно понимать, что при
этих операциях F(r) рассматривается как функция только време-
ни t и не дифференцируется по г и v.
§ 4.2. Принципы Гамильтона
197
Рассмотрим на множестве допустимых отображений D(r(/))
функционал
5(Х)= [ bfx(?,T), ^^l,t\dt. (4.2.16)
J k dt J
'1
Для каждой вектор-функции x(t, т) g E>(r(0) функционал S есть
функция t: S = 5(т).
Теорема. Вариационный принцип Гамильтона. Для того что-
бы опорная кривая r(f) определяла действительное движение
системы, необходимо и достаточно, чтобы для любого
отображения х G Р(г(7))функционал 5(т) принимал стационарное
значение при т = 0, т.е.
= 0 (4.2.17)
т=0
для любой х(А т) g D(r(r)).
Доказательство. Из леммы 3 вариационного исчисле-
Эх
ния (см. § 4.1) и условий (8) и (10) на £(f)=—— следует, что
Этг=о
9S
интеграл — представим в следующем виде:
Этг=0
dS
Эт
, х dr(t)
где г = r(r), v =--.
dt
Покажем сначала, что для выполнения (17) необходимо и
достаточно, чтобы подынтегральное выражение в (18) равнялось
нулю при t^Jt\
d dL
dt 3v
&') =о
(4.2.19)
при произвольной допустимой вектор-функции £(/). Доста-
точность этого условия очевидна. Так как по условиям теоремы
Э5
Этт=0
= 0 для произвольной х<Л т) Z)(r(r)), а следовательно,
для произвольной вектор-функции £(0, удовлетворяющей на Jt
198
Глава 4. Вариационный принцип Гамильтона
условиям (6)-(8), то, согласно лемме 2 вариационного исчис-
ления, соотношение (19) необходимо следует из (17).
Из представления L (12)—(15) нетрудно получить следующие
соотношения:
'эГГ
<Эг>
= Му, — —
dt\ 9v
,, dv
= М —.
dt
Используя эти равенства, представим подынтегральное выра-
жение (18) в следующем виде:
\ / б/2г \
,g(r) (4.2.20)
/ \ dt
(ЭТТ-АГ^
arj dt[d^
Так как r(f) удовлетворяет условиям (4) и (5), a g(0 на открытом
интервале Л = (?], г2) (см. лемму 1) есть произвольная вектор-
функция, удовлетворяющая (6) и (7), то мы можем восполь-
зоваться принципом Даламбера-Лагранжа (см. (3.5.2)), согласно
которому обращение в нуль правой части (20) для любой £(г),
удовлетворяющей (6) и (7), есть необходимое и достаточное
условие того, что г(г) - действительное движение системы. Тем
самым теорема доказана.
Определение. Интеграл (16) носит название действия по Га-
мильтону.
Согласно доказанной теореме, мыслима следующая проце-
дура нахождения в расширенном конфигурационном простран-
стве кривой г(0, которая определяет действительное движение
системы. Надо найти такую кривую г(0, удовлетворяющую (4),
(5), чтобы по отношению к любым допустимым кривым х(4 т)
(x(f, 0) - г(0) интеграл действия принимал стационарное значе-
ние на кривой r(0 = x(t, 0). Такой способ выделения действитель-
ного движения носит название вариационного принципа Гамиль-
тона.
Этот принцип приводит к эффективному методу составления
уравнений для задач механики со связями (1), (2) после введения
так называемых обобщенных координат. Основное достоинство
вариационного принципа состоит в том, что он оперирует с
такими объектами, как кривые в RN, и интегралами по этим
кривым от заданной функции, т.е. с объектами, не связанными с
конкретной системой координат, в которой описывается движе-
ние. И если используя какую-либо систему координат, мы най-
дем опорную кривую г = г(0, которая является стационарной
«точкой» действия на множестве £>(г(0) допустимых кривых, то
§ 4.2. Принципы Гамильтона
199
при описании задачи в любой другой системе координат найдем
ту же самую кривую. Это важное замечание мы ис-
пользуем в дальнейшем для упрощения вывода уравнений дви-
жения в форме Лагранжа и в форме Аппеля.
Замечание о классах эквивалентных отображений. Пусть
XiG, т) и Х2<Л т) - вектор-функции, определяющие отображения
D(r(r)). Тогда Х](г, 0) = x2(t, 0) = г(г).
Определение. Отображения х>(Л ?) и Хг(?, т) назовем экви-
валентными, если
ЭХ| _ дх2
Эт т=0 Эт
при t eJt.
Нетрудно показать, что последнее условие действительно
определяет отношение эквивалентности и тем самым разбивает
множество £>(г(0) на классы эквивалентности.
Так как значение —
дтт=0
зависит только от х(Л 0) и
— , то
т=0
в принципе Гамильтона можно требовать стационарности дейст-
вия не по отношению ко всем х £ £>(г(0), а только по отношению
к подмножеству D(r(r)) с содержащему представителей
всех классов эквивалентности.
В частности, можно рассматривать лишь те отображения
X g D(r(r)), которые удовлетворяют условиям
ХСГрТ)^^), x(t2,x) = r(t2).
При этом условия ^(A) = 5G2) = 0
будут выполняться автоматически.
Это замечание позволяет объяс-
нить часто приводимую геометри-
ческую интерпретацию \(t, т). При
условии (*) и фиксированном т ра-
венство г = x(t, т) определяет в рас-
ширенном конфигурационном про-
странстве кривую, идущую из точ-
ки (г(Л), Л) в точку (г(Г2), t2)
(рис. 63). Множество этих кривых
обязательно содержит опорную кривую г = г(г) = х(Л 0) и удов-
летворяет условиям допустимости вектор-функции
дх
т=о'
200
Глава 4. Вариационный принцип Гамильтона
§ 4.3. Обобщенные координаты. Обобщенные силы
По-прежнему будем рассматривать на отрезке времени Jt
движение системы материальных точек (r„ m,), i = 1,2, ..., и, при
независимых к голономных связях
f(r,r) = O (4.3.1)
и л неголономных линейных связях
Bv + P = 0, (4.3.2)
где г g R3n, v = —, f g Rk, В = B(r, t) - матрица размера 5 x Зп,
dt
P(r, 0 g R\
В каждый момент времени t к условий голономных связей
выделяют в /?3” (Зи-&)-мерное гладкое многообразие Mt:
Mt = {r, reR3\ f(r, г)}- (4.3.3)
Обозначим т = Зп-к и пусть q обозначает вектор Rm: q g Rm.
В координатном представлении qT = q2, ..., qm). Обозначим
через U связную открытую область в Rm.
В общем случае можно построить достаточно гладкое ото-
бражение
Ф: 7, х 67 —> №" (4.3.4)
прямого произведения отрезка времени J( и области U в R3",
которое удовлетворяет условиям 1°—4°:
1°. Пусть г = 0(q, t) - вектор-функция, задающая это отобра-
жение. Необходимо, чтобы уравнения голономных связей удов-
летворялись для всех точек J( х U, т.е.
f(<£(q, О, 0 = 0 (4.3.5)
для всех q g U и всех t eJt.
Рис. 64
2°. Обозначим через Wt образ области U
при отображении Ф для фиксированного Г;
WtcMt; Wf=<&(U, t). Необходимо, чтобы
множество Wt при каждом t было открытой
областью в Mt (рис. 64). Точнее говоря, для
любой точки it о g Wt можно указать доста-
точно малое 8 > 0 и такой шар 53/?(vv0, 8) в
R3n с центром vv0 радиусом 8, что все точки пересечения этого
шара с Mt принадлежат Wt:
e)cW(.
(4.3.6)
§ 4.3. Обобщенные координаты. Обобщенные силы
201
3°. Отображение U —> Wt взаимно однозначно.
4°. Вектор-функции Ф(д, t) имеют производные достаточно
высокого порядка.
С точки зрения геометрии гладких многообразий, отображе-
ние U —> Wt задает локальные координаты на гладком много-
образии Mt. Как строить такое отображение, мы поясним в даль-
нейшем на конкретных примерах.
Пусть отображение Ф построено. В последующем анализе
мы будем, не отмечая особо, предполагать, что все рассмат-
риваемые точки q g Rm принадлежат области U, и для любого
рассматриваемого фиксированного t eJt точки г е Mt принад-
лежат Wt.
Пусть q: Jt^U - произвольное отображение, определяемое
вектор-функцией q(r), т.е. определена некоторая кривая в Rm.
Вектор-функция r(r) = 4>(q,(г), г) определяет отображение
г: Jt R3n (а следовательно, и отображение Jt R3n xR в рас-
ширенное конфигурационное пространство). По определению Ф,
при каждом t точки кривой г(/) принадлежат М{. Верно и
обратное.
Лемма 1. Любой кривой г(г) в R3n х R, которая удовлетворяет
условиям голономных связей f(г(7), 0 = 0, однозначно соответ-
ствует кривая q(r) в Rm так, что г(г) = Ф^(г), г).
Доказательство этой леммы непосредственно следует из
определения отображения Ф.
В частности, любому движению системы, совместимому
со связями, соответствует некоторая кривая q(r).
Поэтому можно описывать движение системы в простран-
стве Rm переменных q. Если движение системы в R,n определяется
вектор-функцией q(r), то движение в R3n определяется вектор-
функцией г(г) = ®(q(0, 0- При этом в R"1 можно не следить за
голономными связями, так как для любого движения системы
q(r) они будут удовлетворяться автоматически. В этом основное
преимущество перехода к пространству Rm.
Определение. Компоненты q', i = 1, 2,..., т, вектора q назы-
ваются обобщенными координатами системы (или лагранже-
выми координатами).
Замечания
1. Если голономные связи явно не зависят от времени, то
можно ввести обобщенные координаты г = ®(q), где Ф не зави-
сит от времени. Как правило, но не всегда, так и поступают.
2. Обобщенные координаты определяются неоднозначно.
202
Глава 4. Вариационный принцип Гамильтона
Действительно, пусть вектор-функция q = <p(q) задает взаимно
однозначное и достаточно гладкое отображение области U с Rm
на указанную выше область U <^Rm £/—>£/. Тогда, если
отображение Ф удовлетворяло указанным требованиям, то и
отображение Ф: U ->W(, определяемое сложной вектор-функ-
цией г = Ф(<р(с[), г), тоже будет удовлетворять этим требова-
ниям. То есть q тоже будут обобщенными координатами.
Произвол в выборе обобщенных координат в механике широко
используется для упрощения описания задачи.
3. Обобщенные координаты при каждом t определены не на
всем многообразии Mt, а только на Wt. Возможна следующая
ситуация. Точки траектории системы в конфигурационном про-
странстве R3" принадлежат Wt в каждый момент времени t < t и
не принадлежат Wt при t > i. При t > t необходимо ввести новые
обобщенные координаты, позволяющие описывать движение
механической системы в отличной от Wt области конфигура-
ционного пространства или на другом (отличном от Jt) интер-
вале времени.
4. Декартовы координаты в R3n можно рассматривать как
обобщенные координаты механической системы без голоном-
ных связей.
Некоторые задачи без связей проще исследовать не в декар-
товых, а в так называемых криволинейных координатах q, опре-
деляемых вектор-функциями
г = <X>(q), где q G U a R3n.
Криволинейные координаты для задач без связей тоже являются
обобщенными координатами; они должны удовлетворять всем
указанным условиям (кроме первого).
Выше при кинематическом анализе мы вводили репер EVq ,
движение которого относительно абсолютного репера Е опреде-
лялось вектор-функцией г0(г), задающей движение начала Е ,
и ортогональной матрицей А(0, определяющей координа-
ты ортов ЕГо относительно Е. При этом радиусы-векторы то-
чек системы гг относительно репера Е связаны с радиусами-
векторами г; тех же точек относительно репера ЕГо соотноше-
ниями
r? = AT(t)ri +г0(Г), z — 1, 2, ..., п. (*)
Последние соотношения можно рассматривать как вектор-
§ 4.3. Обобщенные координаты. Обобщенные силы
203
функции <I>(q, t), задающие обобщенные координаты:
qT = (г(т, г2т,...,г,^) = (Г||,^2,...,7;,3).
Тем самым описание задачи относительно подвижного репера
является частным случаем введения обобщенных координат.
5. Углы Эйлера \|/, 0, ср - обобщенные координаты для задачи
движения твердого тела с одной закрепленной точкой. Для
твердого тела особенно ярко выступает преимущество обоб-
щенных координат. Число материальных точек N, из которых
состоит твердое тело, может быть огромным. Но велико и число
голономных связей I rz— ryl = sz/ = const, описывающих условие
его «твердости». Как мы знаем, для описания различных поло-
жений твердого тела в пространстве оказывается достаточным
трех углов Эйлера. Или, если твердое тело свободно, еще трех
координат его центра.
Для формулировки принципа Гамильтона в обобщенных ко-
ординатах нам необходимо получить представление произволь-
ного допустимого отображения х g D(r(r)) в обобщенных коор-
динатах. Это представление опирается на некоторые опреде-
ления и утверждения, которые будут сейчас приведены.
Лемма 2. Пусть задана кривая r(t) g R3", удовлетворяющая
условиям голономных связей f (г(Г), t) = 0. Пусть вектор-функция
£(7) е R3" удовлетворяет условию
g(r) = O. (4.3.7)
r=r(t)
Утверждение. Существует отображение ф: х Jt R3",
определяемое вектор-функцией г= ф(г, т), которая удовлетво-
ряет условиям:
а) Г(ф(7,т).г) = 0; б) (ф(г,О) = г(г); в) = g(r). (4.3.8)
Э* т=0
Справедливость этой леммы следует из доказательства тео-
ремы о виртуальных векторах.
Лемма 3. В каждый момент времени t множество векторов
£(г), удовлетворяющих условию (7), образует m-мерное подпрост-
ранство 7?3п. Это подпространство называется касательным
пространством к многообразию Mt в точке r(t).
Лемма 4. Пусть Ф(д, г) - вектор-функция, задающая обоб-
щенные координаты. Тогда:
3f
Эг
204
Глава 4. Вариационный принцип Гамильтона
1) произвольный вектор £(r) g Tr(t) может быть представлен в
следующем виде:
ЭФ
&) = £(г),
0q
(4.3.9)
q(t)
где г(г) = Ф(я(г),г),
2) любой вектор £; в виде (9) удовлетворяет (7).
Доказательство. Зафиксируем t и рассмотрим кри-
вую г = ф(г, т), удовлетворяющую условиям (8). Эта кривая
принадлежит Mt и, следовательно, существует отображение q =
= сг(7, г) (<г(7,0) = q(r)) и представление ф(7, т) = Ф(<г(7, т), (г).
Дифференцируя последнее соотношение по т и полагая т = 0,
получим
е R’".
1(0 =
5(0, где £(/) = —
ЭФ
3q
Доказательство второго утверждения следует из соотношений
3f £(t\ — ЭФ ЭГ(Ф(д,г),г) Г — Л .Г — п (Л Д 1ГП
Эг ц/) Эг по ЭЧ , Эт q(t) /•(г) q(f) Щ. J, 1СЦ
Лемма 5. Ранг матрицы
лэф‘ ЭФ1 ЭФ1 '
эф Г эф'У dq' dq2 '"dqm
3q ( dqJJ ЭФ3" ЭФ3" "ЭФ3"
dq2 dq
(4.3.11)
максимален, т.е. равен т.
Доказательство. Пусть (z =1,2, ..., т) - т ли-
нейно независимых векторов касательного пространства Tr{ty
Согласно лемме 4, существуют £z(r) g Rm и представление =
ЭФ
3q
W (*)•
q(t}
Обозначим через 5 = (£,(г), ..., £„,(?)) матрицу
размера Зн х т и через Р = (^(0, ..., £,„(/)) матрицу размера тхт.
Из (*) следует матричное равенство
ЭФ
ЭЧ «<п
§ 4.3. Обобщенные координаты. Обобщенные силы
205
Согласно определению ранг S равен т. Ранг произведения
прямоугольных матриц не может превосходить наименьшего
ЭФ
ранга сомножителей. Отсюда следует, что ранг- и ранг Р
равны т.
Вектор скорости в обобщенных координатах
По определению,
dr
v = —
dt
drj
dt J
Подставляя г = Ф(я, t), получим
ЭФ dq ЭФ
dq dt dt
(4.3.12)
В координатном представлении ЭФ/dq - матрица (11):
РФУ _f дФ1 ЭФ3"
V dt ) dt ' ’ dt J’
(dqV (d^_ d£_\ vj=\ ЭФ7 dj । ЭФ'
l dt) \ dt ' ' dt dq1 dt dt
Определение. Величины dqVdt, i = 1, 2, ..., m, называются
обобщенными скоростями системы.
Уравнения неголономных связей в обобщенных координатах
Подставляя в (2) v согласно (12) и г = Ф(ц, t), получим усло-
вия, налагаемые неголономными связями на обобщенные коор-
динаты и скорости системы в следующем виде:
Cq + d = 0, (4.3.13)
где матрица С = C(q, t) размера s хт является произведением
двух матриц:
ЭФ
C(q,r) = В—, В = В(Ф(Ч(Г),Г)), (4.3.14)
9q
и вектор d = d(q, t) определяется следующей формулой:
ЭФ
d = d(q,r) = B—+ р, (4.3.14')
dt
206
Глава 4. Вариационный принцип Гамильтона
где
р = р(ф(4,г),/),
dt
О представлении кинетической энергии
в обобщенных координатах
По определению кинетической энергии Т:
Т = 2 vTA7v.
2
Подставляя в (15) представление в виде (12), получим
Т = Т2 +7] +Т0,
где
ЭФ
Т — — л т /?л R — I дФ
2 I oq
3q
> т .т ।ЭФА
T]=b q, b = —
V ot )
у./ЭФ)
М 1Г ’
) l^qj
. / ЭФА
м\^- ,
I 3q )
.ЭФА
М — ,
I dt J
т -1Г^Ф
° 2( dt
(4.3.15)
(4.3.16)
(4.3.17)
(4.3.18)
В = B(q, г) - квадратная матрица m-го порядка; b = b(q, г) -
m-вектор. В дальнейшем нам потребуется следующая лемма.
Лемма 6. В - положительно-определенная матрица.
Доказательство. Пусть хе /?". Обозначим у =
= ^^хе7?3", ут = (у1, у2, ...,у3"). Запишем подробно квадратич-
3q
ную форму
хтВх = хт
ЭФА
3q )
ЭФА
3qJ
х = у' Му.
Очевидно, утМу >0, и из равенства утМу = 0 следует равенство
у = 0. Поэтому хтВх ^0 и равенство нулю возможно только при
у = 0. Так как ранг ЭФ/с^ равен т, из условия у = 0 следует х = 0.
Тем самым доказано утверждение леммы.
Если обобщенные координаты вводятся с помощью функций
ЭФ
г = Ф^, явно не зависящих от времени, то -=0 и Т = Т2 =
dt
= |qT#(q)q-
§ 4.3. Обобщенные координаты. Обобщенные силы
207
Опорные кривые и допустимые вектор-функции в Rm
Рассмотрим отображение q : Rm, определяемое вектор-
функцией q(r).
Определение. Будем говорить, что отображение q определяет
q-опорную кривую (или опорную кривую в пространстве обоб-
щенных координат), если q(/) удовлетворяет условиям неголо-
номных связей в обобщенных координатах:
C(q(O,Oq + d(q(r),O = 0, (4.3.19)
где С и d определяются равенствами (14) и (14').
Лемма 7. Для того чтобы вектор-функция r(r) G 7?3и опре-
деляла опорную кривую в конфигурационном пространстве R3n,
необходимо и достаточно, чтобы имело место представление
г(О = Ф(ч(г),О,
где Ф(ц, 0 - вектор-функция, задающая обобщенные коорди-
наты, a q(r) - g-опорная кривая.
Доказательство. Пусть r(r) = <D(q(r), 0- Тогда спра-
ведливы соотношения
f(r(fV) = Wq(0,0,0 (*)
и
+ P(r(r),r) = C(q(t),t)-j^- + d(q(t),t), (**)
dt dt
где С и d определяются равенствами (14) и (14"). Правая часть (*)
обращается в нуль для любой кривой q(r), а правая часть (**)
равна нулю для любой g-опорной кривой q(r). Поэтому для
g-опорной кривой q(z) левые части равенств (*), (**) обращаются
в нуль. А это и есть условия (4.2.4), (4.2.5) того, что г(/) - опорная
кривая. Обратно, если г(г) - опорная кривая, то f(r(r), t) = 0 и,
согласно лемме 1 этого раздела, справедливо представление
г(г) = <D(q(0, 0- Для опорной кривой левая часть (**) обращается
в нуль, тем самым q(r) удовлетворяет условию (19), т.е. является
g-опорной кривой.
Рассмотрим отображение Rm, определяемое вектор-
функцией ^(г).
Определение. Будем говорить, что ^(г) - q-допустимая век-
тор-функция для данной g-опорной кривой q(r), если ^(г) на Jt
удовлетворяет следующим условиям:
1) C(q(O,r)€(O-0, (4.3.20)
208
Глава 4. Вариационный принцип Гамильтона
X ЭФ
€(0 = ^-
3q
A
а)э?
х ЭФ
€а)=з-
0q
ЭФ
0q
где C(q, г) определена в (14);
2) ^) = ^2) = 0. (4.3.21)
Лемма 8. Для того чтобы £(t) g R3n была допустимой вектор-
функцией для данной опорной кривой г(г), необходимо и доста-
точно, чтобы имело место представление
(4-3.22)
q(t)
где q(r) - g-опорная кривая, соответствующая г(0, а ^(0 -
g-допустимая вектор-функция для q(r).
Доказательство. По определению допустимой век-
тор-функции £(г), выполняются условия (4.2.6)-(4.2.8):
£(0 = 0, б) = 0, в) = Ш = 0-
г(г)
Согласно лемме 4, представление
^(r), (*)
q(t)
необходимо и достаточно для выполнения условия а). Из (*)
следуют равенства
ЭФ
= В\Г(1)— = C(q(r),r)^(r), (**)
1 q(j)
/ = 1, 2. (***)
q(fi)
Если i^(r) - g-допустимая вектор-функция, то правые части этих
равенств равны нулю, а следовательно, и выполнены условия а),
б) и в). Обратно, из б) и в) следует справедливость соотношений
(20) и (21) и тем самым ^(г) - д-допустимая вектор-функция. Для
доказательства (21) следует воспользоваться леммой 5 о ранге
матрицы ЭФ/Oq.
Обобщенные силы
/ х dr(r)
Пусть система находится в точке г(г),-------,/ расширенно-
V dt )
го фазового пространства. Зафиксируем момент времени t и
§ 4.3. Обобщенные координаты. Обобщенные силы
209
рассмотрим элементарную работу ЗА, которую совершают силы
F(r) при бесконечно малом перемещении Зг, совместимом с голо-
номными связями:
5А = (рГг(0.-^^,Лбг), (4.3.23)
\ < dt ) /
где (•, •) - скалярное произведение в F3n, FT= (F/, Fj2,..., F„3) -
вектор сил: F g F3". Любой вектор г, совместимый с голономны-
ми связями, может быть представлен как вектор-функция обоб-
щенных координат q: г = Ф(д, t). Поэтому Зг =
|?Sq + 0(|6q|2).
Отсюда следует
(4.3.24)
где справа (•, •)- скалярное произведение в Rm.
Определение. Величина
(ЭФУ < dr )
Q= Шу-' (4.3.25)
I9qj9=9(z) I dt )
называется вектором обобщенной силы. Это m-мерный вектор
Из (25) следует, что
. 4^ эф7’
где F7 - j-й компонент вектора F:
FT=(F', F2, ...F3") = (F;1, F2, F„3).
Если силы F7 заданы, то соотношения (26) позволяют формально
определять компоненты вектора Q.
Часто компоненты Qk можно определить более простым
путем. Из (23) следует:
&4 = (Q, 5q> + (9(|5q |2).
14. М.Л. Лидов
210
Глава 4. Вариационный принцип Гамильтона
Проварьируем только £-й компонент q:
5qT =(0, 0, bq, 0, 0).
Тогда
M = Qkbqk +О(| б?*Т).
Определим соответствующую §qk вариацию вектора 8г и вы-
числим работу
8A = (F, 8г).
Замечание. Следует обратить внимание, что вектор силы при
вариации 8г не варьируется. Тогда
Q - lim —г-
Пример. Две материальные точки связаны невесомой на-
тянутой нитью (рис. 65). Точка массой т2 может перемещаться
только вертикально по лучу О А, а
точка массой т\ должна находить-
ся на наклонной прямой ОБ, угол
которой с ОА, равный у(г), может
изменяться с течением времени. На
материальные точки действуют си-
лы веса
|G| |=m,g и |G2 \-m2g,
а на точку еще одна внешняя си-
ла F(r) под углом а к наклонной
прямой. Нетрудно видеть, что свя-
зи голономны и задача может быть описана одной обобщенной
координатой, например, / - расстоянием точки т2 от вершины О.
Определим работу всех сил 8А при бесконечно малом переме-
щении 8/, зафиксировав момент времени t:
8A = (F, 8r1) + <G1, 8r1) + (G2, 8r2),
(F, 8r!) = -|F|cosa8/,
(Gp 8r,> = -|Gl |cosy(r)8/,
(G2, 8r2)=|G2|8/,
откуда
8A
<2, = —= -| F|cosa-mlgcosy(r) + m,g.
0/
J 4.4. Вывод уравнений. Лагранжа и уравнений Аппеля
211
2)^
Эт
Если силы потенциальны
ЭГ Jr=r(,)’
ТО
о - J—Yf—Y - -(^e^Y - du^tM)T
dq J V Эг J Эг 9q J 9q J
Таким образом, для потенциальных сил вектор обобщенной
силы есть градиент потенциала по обобщенным координатам.
§ 4.4. Вывод уравнений Лагранжа и уравнений Аппеля
1. Рассмотрим отображение <т: определяемое
вектор-функцией q = ст(/, т).
Определение. Будем говорить, что отображение <у принадле-
жит множеству ^-допустимых отображений ©(q(r)), если <т(г, т)
удовлетворяет следующим двум условиям:
1) a(r,O) = q(r), (4.4.1)
где q(r) - g-опорная кривая в 7?"', т.е. q(r) удовлетворяет (4.3.19);
= ^(0, (4.4.2)
т=0
где l~q(t) - g-допустимая вектор-функция для g-опорной кривой
q(/), т.е. %q(t) удовлетворяет (4.3.20), (4.3.21).
Рассмотрим отображение х: определяемое
вектор-функцией
х(г, т) = Ф(<г(г, т), t), (4.4.3)
где г = <I>(q, 0 задает обобщенные координаты в рассматри-
ваемой задаче, а <т е 0(q(r)). Рассмотрим (3) при т = 0:
r(t) = = Ф(ст(л0),0 = Ф(ч(/),0- (*)
Согласно лемме 7 § 4.3, г(0 определяет опорную кривую в R3”, и
любая опорная кривая г(г) представима в виде (*) при некоторой
g-опорной кривой q(/). Зафиксируем опорную кривую г(7) и со-
ответствующую ей д-опорную кривую q(z): r(r) = <D(q(O, t). Обоз-
начим через £)(г(0) множество отображений х, определяемых
формулой (3) и соответствующих различным отображениям
<т е 0(q(r)):
D(r(0) = {х : х(г,т) = Ф(ст(Г,т),Г), о е 0(q(r))).
14*
212
Глава 4. Вариационный, принцип Гамильтона
Теорема. 1. Любое отображение х е О(г(0) есть допустимое
отображение: х е ^Хг(г)). 2. Множество £>(г(0) содержит пред-
ставителей всех классов эквивалентности множества £>(г(0)-
Доказательство. Дифференцируя (3) по т и полагая
т = О, получим
Эх
Этт=0
= <(0 =
ЭФ Эст
Эд т=0 Эт т=0
ЭФ
Эд
(**)
дй)
1. Так как в (**) i$q(t) - ^-допустимая вектор-функция для
^-опорной кривой q(7), то, согласно лемме 8 § 4.3, £(7) - допусти-
мая вектор-функция для опорной кривой r(t) = Ф(ч(0> 0- Следо-
вательно, х £
2. Пусть £(7) - произвольная допустимая вектор-функция для
опорной кривой г(/). Согласно той же лемме 8, найдется такая
^-допустимая вектор-функция i~q(t) для ^-опорной кривой q(7),
соответствующей г(7), что будет выполнено (**). При этом ^-до-
пустимой вектор-функции %q(t) соответствует некоторое отобра-
жение ст е 0(q(r)) такое, что — - £At), например ст(г, т) =
Эт т=0
= q(0 + т&р).
Следствие. Напомним, что в принципе Гамильтона на
множестве отображений х е рассматривается функционал
5(т) = 5(х) = | L(r,y,f)dt, (4.4.4)
'1
где
L(r, v, t)-T + (р(Г, r) = -^-vTA/v + (F(z), г),
г = хО,т), v = x(^O) = r(r), =
dt \ dt )
(•, •) - скалярное произведение в R3n. Из замечания о классах
эквивалентности множества £>(г(г)) и доказанной теоремы следу-
ет, что стационарность действия 5 можно определять на мно-
жестве допустимых отображений х е Цг(7)), представимых
в виде (3):
х(л т) = Ф(ст(Г,т),г),
где сг(Л т) определяет произвольное д-допустимое отображение:
§ 4.4. Вывод уравнений Лагранжа и уравнений Аппеля
213
ст е 0(q(O). Выразим L через обобщенные координаты:
ЭФ ЭФ -
L(r, v, /) = L Ф^, г), —— q +—, t = L.
dq dt J
В обобщенных координатах
L = (q, q, t) = T(q, q, О + <F(r), Ф(Ч, t)), (4.4.5)
где T(q, q, t) - выражение кинетической энергии в обобщен-
г ЭФ
ных координатах (4.3.15)-(4.3.18), F(r) ~ F Ф^(г), t),-
dq
q(l) +
ЭФ
dt
Л •
<?(') >
Нетрудно показать, что для т) в виде (3) действие 5 опре-
деляется следующим интегралом:
г2
5(т) - 5(<г) - J L(q, q, t)dt,
(4.4.6)
где функция L(q, q, 1) определена в (5), a q = tr(t, т), q =
dt
<г(Г, 0) = q(r). Согласно принципу Гамильтона, чтобы опорная
кривая г(Г) = х(^0) = Ф(а(Г, 0), Г) = Ф(д(Г), Г) определяла дейст-
вительное движение системы, необходимо и достаточно выпол-
нения условия
Э5
Эт
= 0
т=0
(4.4.7)
для любой х е D(r(t)), т.е. для любой <у е 0(q(Z)). Используя
представление (6) и лемму 3 вариационного исчисления (§ 4.1),
из принципа Гамильтона получим
dS
Эт
т=0
Х(') jdt,
(4.4.8)
где (•, •) - скалярное произведение в Rm, q = q(/) = <r(l, 0),
Jo-(r, 0) _ Jq(r) Эст
4 dt dt ’ ’ Эт
- произвольная ^-допустимая
т=0
214
Глава 4. Вариационный, принцип Гамильтона
вектор-функция, т.е. вектор-функция, удовлетворяющая усло-
виям (4.3.20), (4.3.21):
С(Ч(Г),Г)^(Г) = О, = =
(4.4.9)
Из (9) следует, что удовлетворяет условиям леммы 2
вариационного исчисления (§ 4.1). Поэтому из (8) следует ана-
лог уравнения Даламбера-Лагранжа в обобщенных коорди-
натах'.
(4.4.10)
где д(0-произвольная ^-опорная кривая, а £б/(г) - произвольная
вектор-функция, удовлетворяющая (9). Тем самым доказана сле-
дующая теорема.
Теорема. Для того чтобы ^-опорная кривая q(r) при t^Jt
определяла действительное движение в пространстве обобщен-
ных координат Rm, необходимо и достаточно, чтобы q(/) удовлет-
воряла уравнению (10) при произвольной ^-допустимой вектор-
функции ^(0-
Упражнение. При доказательстве вариационного принципа Гамильтона
(см. § 4.2) было показано, что уравнение
где g(r) удовлетворяет условиям
а) у- ?Ю = 0, б) B|r(z)g(O = O,
есть уравнение Даламбера-Лагранжа. Согласно лемме 7 и лемме 1 § 4.3, лю-
бую функцию g(0, удовлетворяющую условиям а) и б), можно выразить через
^-допустимую вектор-функцию gg(r): (**)
(**)
Поэтому
3L
Эг
л_Г
dt\ dv
dL
Эг
A
dt\ dv
г = r(r), q = q(r).
§ 4.4. Вывод уравнений. Лагранжа и уравнений Аппеля
215
С помощью формальных преобразований покажите, что
d ( dL
dt\ Эу
d ( dL
dq J dt dq
r = r(r), q = q(r).
Таким путем получается другой вывод уравнения (10).
2. Уравнения Лагранжа. Если неголономных свя-
зей н е т, то в (10) £б/(г) - произвольная вектор-функция, удов-
летворяющая только граничным условиям = ^(Z2) - 0.
В этом случае применима лемма 1 вариационного исчисления
(§ 4.1), и, как следствие (10), мы получим так называемые урав-
нения Лагранжа второго рода
3LV
dqj
4М=о.
dtydqj
(4.4.11)
которым должно удовлетворять действительное движение систе-
мы при голономных связях. Используя (5), получим
агу Гэг?/эф
9q J у dq J у dq
dZ.y =fdTT
dqj (dq,
где Q = Q(q, q, t) - вектор обобщенной силы.
Тем самым уравнения (11) можно записать в следующем
виде:
^drY q
dt у dq J у dq J
(4.4.12)
В общем случае (см. (4.3.15)—(4.3.18)) Т = -|qTZ?q + bTq + T0,
где В, Ьт, То не зависят от q. Поэтому
дТ
dq
= Bq + Ь.
(4.4.13)
Отсюда следует, что уравнения Лагранжа имеют вид Bq =
- <Ь О, где в правой части собраны все члены, не зависящие
от обобщенных ускорений q. Так как det В Ф 0,
то эти уравнения можно разрешить относительно вторых произ-
водных:
q = S"'f(q, q, Г).
Если при t = 4) задать произвольные начальные данные: m обоб-
щенных координат q = qn и m обобщенных скоростей q = q0,
216
Глава 4. Вариационный принцип Гамильтона
то в общем случае однозначно определяется решение уравнений
Лагранжа q = q(r, г0, q0, q0). Это решение определяет положение
системы как в последующие, так и в предыдущие моменты вре-
мени. При этом в декартовых координатах
г(0 = Ф(д(м0,Чо,Чо)>0-
3. Если на систему наложены и неголономные связи, то
можно получить уравнения движения системы в обобщенных
координатах с помощью введения так называемых обобщенных
реакций связей, аналогично тому, как это было описано в § 3.8
в декартовых координатах. Обозначим:
dt [ dq
dL
Bq
= Qw
(4.4.14)
Согласно (10), Q/v- произвольный вектор, ортогональный всем
векторам £ч, удовлетворяющим (9):
Будем называть Q/y вектором обобщенных реакций связей.
Строчки С, матрицы С =
образуют s линейно независи-
мых векторов Rm. Обозначим через Rs подпространство Rm, натя-
нутое на эти векторы. Согласно (9), - произвольный вектор,
принадлежащий ортогональному дополнению к Rs. Так как
вектор Q/v ортогонален всем векторам то QA принадлежит Rs
и, следовательно, может быть представлен в следующем виде:
<Zv=cTx,
где Хт = (XI,X2,...,X5) - s-вектор.
Последнее соотношение в более подробной записи имеет вид
Qyv=X1C^+X2C^+... + X5CJ.
Функции q'it), f = l,2,...,m, и s величин Л?=Л/(Г),
кроме уравнений
dtydq) \ 9q J
J = l,2,...,s,
(4.4.149
§ 4.4. Вывод уравнений Лагранжа и уравнений Аппеля
217
должны удовлетворять s уравнениям связей
C(q,r)q + d(q,r) = O. (4.4.15)
Повторяя процедуру, аналогичную той, которую мы про-
водили в декартовых координатах (см. 3.3), можно, используя
(15), исключить из уравнений (14') множители X и получить
систему т - Зп - к уравнений второго порядка.
Напомним, что аналогичная процедура в декартовых коорди-
натах приводит к системе Зп уравнений второго порядка. Однако
решение задачи при s неголономных связях можно свести к
задаче интегрирования 2т-s уравнений первого порядка, так
называемых уравнений Аппеля.
4. Уравнения Аппеля. В обобщенных координатах уравне-
ния неголономных связей имеют вид
C(q, r)q + d(q, Г) = 0,
где С - матрица размера sxm ранга s; d - s'-вектор, а допусти-
мая вектор-функция ^q(t) есть произвольная вектор-функция,
удовлетворяющая условиям:
а) = °’ б) I/Z1) = S/z2) = °’ q(0 - <?-опорная кривая.
Докажем сначала несколько вспомогательных утверждений.
Лемма 1. Существует матрица Н = H(q, t) размера mx(m-s)
и ранга m-s, удовлетворяющая матричному уравнению
СН = 0. (4.4.16)
Доказательство. В каждый момент времени t строч-
ки С, матрицы С образуют в Rm s линейно независимых векто-
ров (ранг С равен s). Обозначим через R™~s подпространство Rm,
ортогональное подпространству, натянутому на векторы С,-.
Пусть hz e/?m (/ = 1,2,...,m-s1) суть (m-s) линейно независи-
мых векторов, принадлежащих R”l s. Тогда H^hph^...,!!^)
есть искомая матрица.
Лемма 2. Рассмотрим
^(0 = Я(Ч,г)и, (4.4.17)
где Н - матрица, определенная леммой 1, а
uT =(u(t),u2(t),...,um~s(t))
- произвольная вектор-функция, удовлетворяющая условиям
u(Z1) = u(r2) = 0. (4.4.17')
218
Глава 4. Вариационный принцип Гамильтона
Утверждения. 1. g (Z) в виде (17)—(17') удовлетворяет
условиям а) и б). 2. Любой вектор, удовлетворяющий условиям
а) и б), может быть представлен в виде (17).
Доказательство. 1. Из представления (17) и условий
(17) следует
g<?(Z,.) = /7(q(r,.),r,)u(r,.) = O, z = 1,2,
И
С^(г) = СЯи = 0-и = 0.
2. С другой стороны, так как
с^ = о, то
Следовательно, найдется такой вектор и, что будет справедливо
представление
^ = M1hI+... + u'"-'hOT_.v.
Так как hz линейно независимы, то из условий g (^.) = 0 следует
u(r,) = 0.
Лемма 3. Пусть q(/) - вектор-функция, удовлетворяющая
условиям неголономных связей Cq + d = 0. Тогда можно указать
такую вектор-функцию Х(г)е/?/”"5, что
q(r) = H(q(0,0М0 + h(q(Z), г), (4.4.18)
где h(g,r) G Rm - произвольное решение системы уравнений
Ch + d = 0, (4.4.19)
Н - построенная выше матрица.
Доказательство. Запишем условие неголономных свя-
зей в следующем эквивалентном виде:
C(q-h + h) + d = 0.
Если h удовлетворяет (19), то из этого условия следует
C(q-h) = 0.
Повторяя рассуждения леммы 1, получим q-h=Z7X(O, где
X(Z) g R™~s. Согласно (4.2.19), действительное движение системы
удовлетворяет уравнению
dL^ d (ЭтЛ g \ _ Q
9q? drl^dqj ’ qf
§ 4.4. Вывод уравнений Лагранжа и уравнений Аппеля
219
Воспользуемся леммой 2 и представим последнее соотноше-
ние в следующем виде:
п /ГЭЛГ d(dL}T \ /т((д[Х d(dLV} \
0 = ( —-------— \ .Ни) ={Н —--------— ,11).
U dqj dt dt dq J I /
\ / q=q(/) \ V ' /
Так как u = u(7) - произвольная вектор-функция, удовлетво-
ряющая только граничным условиям и(Г,) = и(Г2) = 0, то, при-
меняя лемму 1 вариационного исчисления (§ 4.1), получим систе-
му уравнений, которым должна удовлетворять вектор-функ-
ция q(r):
1 Ъо. (4.4.20)
IdqJ J
Согласно (12),
d ( d/Л ( dL
dt^dq) ^dq
dt dq ,
Эту
dq J
-Q,
где T - T(q, q, t) - кинетическая энергия системы, Q = Q(q, q, t) -
вектор обобщенных сил. Поэтому уравнение (20) можно запи-
сать в эквивалентном виде:
н. £Гэту_я/этГ
dt 8q J 8q J
= H'Q.
(4.4.20')
Используя представление для кинетической энергии в обоб-
щенных координатах (4.3.15)-(4.3.18) Т = ^qTBq + bTq + T0, где
В, Ь, Т() не зависят от q, получим
дТ
8q
= Bq + Ь.
(*)
Подставляя в это соотношение q из уравнения связей (18),
найдем
drV
3q?
= BHX + Bh + b.
(**)
Подставим (*)и(**)в (20 *) и после дифференцирования подста-
вим q = НХ + h. В результате получим
Н'ВН— = f(\,q,r), (4.4.21)
dt
220
Глава 4. Вариационный принцип Гамильтона
где через f обозначены все члены уравнения, не зависящие от
dK / dt.
Лемма 4. det И ВН Г 0. Отсюда следует, что уравнения (21)
можно разрешить относительно производных:
— = (ЯТ5НГ‘Г(К, q, г). (4.4.22)
dt
Совместно с уравнениями связей (18)
^ = ЯХ + Ь. (4.4.23)
dt
Эти уравнения образуют систему 2m - л' уравнений относитель-
но т обобщенных координат qnm-s множителей X. Из послед-
них уравнений следует, что, задав при t = г0 произвольно т коор-
динат q и т - s множителей X, мы можем получить единственное
решение (22), (23), описывающее движение системы.
Доказательство. Если det ГГВН = 0, то существует
xeRm~s и хТНТВНх = 0. Обозначив Hx = yeRm, получим
утВу = 0. Так как В - положительно-определенная матрица, то
последнее равенство возможно только при у = 0. Но так как ранг
Н равен m-s, то из у = 0 следует х = 0. Тем самым доказано,
что det ITBH^Q.
Замечание 1. Обычно в литературе вместо X(z) используют
обозначения
тг(г) = (л1(г), л2(г),..., л"1 Дг)), а X(г) = nl(t) =
dt
называют квазискоростями, п* - квазикоординатами. Уравне-
ния (20) носят название уравнений Аппеля.
Замечание 2. Представим матрицу С в условиях неголоном-
ных связей (15) в следующем виде: С = (GH G2), где G} - матрица
размера sxs, G2 - матрица размера sx(m-s). Представим
И
q е Rm в виде q =
где
ии т _ ( • 1 -2 • 5 \ \ т _ ✓ • s+1 л-у + 2 • т \
Ц» \Q > q »•••? q ), a \q •> q >'•••! q )•
При этих обозначениях условия неголономных связей (15) мож-
но представить в следующем виде:
G||ui + G2 X + d = 0.
§ 4.5. Уравнения Лагранжа. Интегралы энергии и Якоби
221
Если det Gj Ф 0, то
H = -G1’1G2K-Gl"1d.
Последние соотношения легко представить в виде (18):
q = HX + h,
здесь
11 =
< о ,
где I - единичная матрица (m-s)-ro порядка, Ое/?"' 5 - нуль-
вектор: 0т = О,О,...О .
т - .у
Описанный здесь метод обычно и используется при решении
конкретных задач. В качестве квазискоростей тг (или, что то же
самое, X) выбираются какие-либо m-s обобщенных скоростей,
относительно которых легко представить неголономные связи
в виде
q = HX+h. (***)
При этом в качестве начальных данных m-s обобщенных
скоростей X можно задавать произвольно, а остальные обобщен-
ные скорости определяются уравнением (***).
§ 4.5. Различные формы уравнений Лагранжа.
Интеграл энергии и интеграл Якоби
1°. В § 4.4 была получена система уравнений, решение кото-
рой описывает движение системы материальных точек в случае
голономных связей - уравнения Лагранжа второго рода
dt 3q ) V 3q J
(4.5.1)
где T = T(q, q, t) - кинетическая энергия системы в
обобщенных координатах, Q - вектор обобщенных сил.
Таким образом, для решения задач механики (при голоном-
ных связях) с помощью уравнений Лагранжа необходимо:
1) ввести обобщенные координаты: г = O(q, t)\
2) выразить кинетическую энергию через обобщенные коор-
динаты q, обобщенные скорости q и время
3) определить обобщенные силы Q как функции q, q, t\
222 Глава 4. Вариационный принцип Гамильтона
4) составить уравнения (1).
Эти уравнения можно разрешить относительно вторых про-
изводных q, т.е. получить систему т уравнений второго порядка:
q =f(q, q,z).
Введя обозначение q = u е Rm, эту систему можно привести к
системе 2т, вообще говоря, нелинейных уравнений первого по-
рядка:
й = f(q, и, г),
(4.5.2)
q = и.
Обычно правые части (2) таковы, что при заданных начальных
данных (t = tQ, u = u0, q = q0) существует единственное реше-
ние (2)
q = q(/,r0,qn,u0), (4.5.3)
которое при t = to удовлетворяет условиям:
q(r0,f0,q0,u0) = q0,
4(q(r,/o.4o,«o))|,_,n = Чо
at r~T°
В общем случае решение (3) не удается выразить через эле-
ментарные функции или даже через интегралы от элементарных
функций. Поэтому общим методом приближенного решения
уравнений (2) на ограниченных интервалах времени являются
различные варианты метода численного интегрирования. Этот
метод успешно используется в большинстве практических задач.
Однако во многих задачах механики представляют интерес ис-
следования всех возможных траекторий движения системы в
обобщенных координатах. Методами численного интегрирова-
ния это сделать не удается.
Поэтому особое внимание уделяется тем задачам, в кото-
рых удается получить решение системы, записанное через эле-
ментарные функции или интегралы от них. Такие задачи на-
зываются интегрируемыми. Многие практически важные задачи
оказываются в определенном смысле близкими и интегри-
руемыми. Опираясь на эту «близость», часто удается на осно-
ве анализа интегрируемых задач получить представление об
общих свойствах решений в задачах, близких к интегрируе-
мым.
2°. Как было показано в § 4.3, если силы, действующие на
систему, имеют потенциал U = U(r, t), то обобщенные силы
§ 4.5. Уравнения Лагранжа. Интегралы энергии и Якоби
223
можно представить в виде
Q = -
ди
dq,
ЭГ
3q?
(4.5.4)
(4.5.5)
д(/¥
8qJ ’
где U = С/(Ф(ц, г), t) - выражение потенциала через обобщенные
координаты. В этом случае уравнения Лагранжа записываются
следующим образом:
^Гэг
dt 9q
Так как 9(7/9q = 0, то можно ввести в рассмотрение так назы-
ваемую функцию Лагранжа
L = L(q, q, г) = T(q, q, Г)- I7(q, ?)
и записать (4) в более компактном виде
3L
3q
d ( dL
dt\dq
Случай голономных связей и потенциальных сил описывает
лишь специальный класс механических задач. Однако этот класс
достаточно широк. Более того, большинство задач теоретиче-
ской физики принадлежит этому классу.
Рассмотрим функционал
(4.5.6)
= 0.
5 = J (T(q,q,Z)-t/(q,f))Jr,
. х . ckr(t, т)
q = a(f,T), q =-------,
dt
где сг - произвольное отображение Jt х J R,n, удовлетво-
ряющее условию
Эст
Эст
= 0.
Эт 1=0 Эт т=0
зать, что из вариационного принципа
Используя леммы вариационного исчисления, нетрудно пока-
ГЭ5
Эт
= 0 при произволь-
ном ст и 5 в виде (*) следуют уравнения (6).
Упражнение. Проведите все необходимые рассуждения.
224
Глава 4. Вариационный принцип Гамильтона
Таким образом, каждой задаче рассматриваемого класса со-
ответствует некоторая функция Лагранжа E(q, q, г), а траекто-
риями движения являются кривые в Rm, на которых интеграл
действия по Гамильтону (функционал) принимает стационарное
значение по сравнению с близкими кривыми. В вариационном
исчислении такие кривые называются экстремалями функцио-
нала. Это не произвольные кривые в Rlri\ они описываются урав-
нениями (6).
Можно рассматривать задачи, в которых L(q, q, t) достаточ-
но произвольные функции указанных аргументов. Однако, как
мы знаем, в задачах механики функция L(q, q, f) должна быть
квадратичной функцией обобщенных скоростей q.
Определение. Системы, описываемые уравнениями Лагран-
жа (6), где L - квадратичная функция q, называются натураль-
ными.
В случае потенциальных сил нет надобности специально
определять обобщенные силы Q; надо только выразить потен-
циал t7(r, г) через обобщенные координаты и составить функ-
цию Лагранжа.
Предположим теперь, что мы хотим в уравнениях (6) перейти
от переменных q к переменным q, т.е. провести замену пере-
менных
q = <p(q,O, qefl'”, qe/?'".
( Sip'S
Будем предполагать, что эта замена не особенная, т.е. det —- Ф
I 9qJ
Ф 0. Тогда, зная q (Г), мы сможем определить q(r).
Пусть обобщенные координаты вводились вектор-функция-
ми г = <l>(q, Z). Пусть L(q, q, г) - функция Лагранжа для обобщен-
ных координат q:
( (dv\ ~ А
L(q,q,O = \Т — -£7(г,г)
\ к ut J I ч dr дФ dq дФ
dt dq dt dt
Проведем теперь рассуждения, которыми мы уже пользовались.
Если функционал S = J (Т -U)dl достигает на некоторой
'I
кривой г(/) стационарного значения на множестве допустимых
кривых, то несущественно, в каких координатах мы описываем
§ 4.5. Уравнения Лагранжа. Интегралы энергии и Якоби
225
эту кривую и множество допустимых кривых. Если мы рассмот-
рим вариационную задачу, введя переменные q, то получим
г = Ф(<р(д,О,О = ф(<р),
(Г - C)r=<]>(-f) = L(q, <1,0 = Д <p(q, t), Д <1 =
Vk4 oq dt ) dt
Отсюда следует, что для нахождения кривых, описывающих
движение механической системы, необходимо найти экстремали
функционала
'2
5 = J L(q, q, t)dt,
n
— z X — d x Эст Эст z ZAX _z
q = a(7,T), q=-(rU,T), — =— =0, <r(7, 0) = q(7).
dt Эт 1=0 Эт т=0
t=h t=t2
Этой задаче соответствуют уравнения
эДЭ<^
(4.5.6')
Таким образом, в новых переменных траектории описываются
уравнениями точно того же вида, только с преобразованной
функцией Лагранжа
L(q, q, t) = Ц <p(q. t), q + t
V dq ot
(**)
Это свойство уравнений Лагранжа называют их ковариант-
ностью.
Упражнение. Формальной заменой q = cp(q,r) в уравнениях (6) получите
уравнения (6г).
3°. Предположим, что действующие активные силы предста-
вимы в виде суммы
F = F, + F2, (4.5.7)
где F । - потенциальная составляющая сил
0C,
Эг
a F2 - непотенциальная составляющая. Силам F] и F2 соответст-
вуют обобщенные силы
ЭЦ
F.=-
(4.5.8)
Q.=H
8q
f ЭФГ
, С,=Ц(Ф(Ч./),0, Q2= — F2. (4.5.9)
k dq J
15. М.Л. Лидов
226
Глава 4. Вариационный принцип Гамильтона
Легко показать, что в этом случае уравнения Лагранжа (1) могут
быть представлены в следующем виде:
dt У 9q J у 3q )
(4.5.10)
где
Ц = Т-и{. (4.5.11)
Сейчас мы будем рассматривать этот более общий случай.
Интеграл энергии
Назовем Е{ = Т + Ц\ механической энергией системы. Пред-
положим, что голономные связи f = 0 явно не зависят от вре-
мени, т.е. f = f(r), с)17Эг = 0. Тогда, как показано в § 3.5, справед-
лива теорема об изменении кинетической энергии системы:
™ = ~ = (F,v), (4.5.12)
dt dt
где F - вектор силы, a v - вектор скорости: F е /?3", v е /?3".
ЭФ
В этом случае v = ——q и правую часть уравнения (12) можно
3q
записать в следующем виде:
/ ЭФ
(F,v)= F,f4
ЭФ
dq
Г q ) = (Q, q).
Подставляя
dq
+ Q2>
получим:
<F, v> = -<
8q
,q)+<Q2,q>-
Легко показать, что
dUi
dq
_ dUy dUy
dt dt
(4.5.13)
(4.5.14)
(4.5.15)
(4.5.16)
Q = -
ЭЦ
>4
Используя (15) и (16), уравнения (12) запишем в следующем виде:
d£\
dt
dUt \
-4r+<Q2,qX
ot
(4.5.17)
§ 4.5. Уравнения Лагранжа. Интегралы энергии и Якоби
227
где производная вычисляется при постоянных обобщен-
ных координатах q.
а) Если потенциал Ц задан как функция только г:
Ux = Ц(г) и не зависит явно от времени, то и выра-
жение Ц в обобщенных координатах тоже не будет зависеть
явно от времени:
Ц = Ц(Ф(Ч)).
В этом случае dUJdt = 0 и
ЯР
^ = <Q2,q). (4.5.18)
at
б) Если система консервативна, т.е. связи не зависят явно от
времени, и все силы имеют потенциал, не зависящий явно от
времени, то Q2 = 0, dEJdt - 0, и мы приходим к полученному
в § 3.5 интегралу энергии
Е - Ех - const. (4.5.19)
Упражнение. Выведите уравнение (17), используя уравнение (10) и условие
ЭФ/Эг = О.
Определение. Непотенциальные силы Q2 называются гиро-
скопическими, если
<Q2,q> = 0, (4.5.20)
и диссипативными, если
(Q2,q)^0. (4.5.21)
Из (20) и (18) следует, что справедлива следующая теорема.
Теорема. Если голономные связи явно не зависят от време-
ни, потенциал Ux явно не зависит от времени, а непотенциаль-
ные силы - гироскопические, то справедлив закон сохранения
энергии
Ех - Т+ Ux = const. (4.5.22)
Эта теорема обобщает теорему о сохранении полной энергии.
Если же на систему действуют диссипативные силы, то энер-
гия Ех убывает в процессе движения: —L 0.
dt
Обобщенные силы могут зависеть от обобщенных скорос-
тей, координат и времени. Предположим, что зависимость от
скоростей определяется однородной линейной
функцией
Q2 = oq, (4.5.23)
где о = a(q, t) - квадратная матрица m-го порядка.
15*
228
Глава 4. Вариационный принцип Гамильтона
Лемма 1. Для того чтобы непотенциальные обобщенные
силы, линейные по обобщенным скоростям, были бы гироскопи-
ческими, необходимо и достаточно, чтобы матрица о была косо-
симметрической.
Доказательство. Рассмотрим скаляр
a = (Q2>q) = <iT°q
Очевидно,
ост =a = qToTq.
Сложим эти два равенства:
2oc = qT(o + oT)q.
(4.5.24)
(4.5.25)
(4.5.26)
Если о = -сг (матрица кососимметрическая), то о, а следователь-
но, (Q2,q\ равны нулю, т.е. силы гироскопические. Обратно,
если а = 0 при любых q, то симметрическая матрица о + о‘ = 0 и,
следовательно, матрица с> - кососимметрическая.
Уравнения Лагранжа в виде (6) можно получить не только
в случае потенциальных сил. Предположим, что обобщенные
силы Q представимы в виде
q=4-
dt[dq
avy
dqj ’
(4.5.27)
где V(q, q, t) - функция обобщенных координат, обобщенных
скоростей и времени.
Определение. Если обобщенные силы представимы в виде
(27), то функция V называется обобщенным потенциалом систе-
мы.
В этом случае уравнения (1) могут быть записаны в следую-
щей форме:
dz^9qj <dq?
(4.5.28)
где
L = T-V. (4.5.29)
В задачах механики обобщенные силы не должны зависеть
от ускорений q или высших производных по времени от векто-
ра q. Поэтому из (27) следует, что функция V может только
линейно зависеть от q :
V=eTq + U}
(4.5.30)
где Ux - C7i(q, t) - скалярная функция, 0Т = (О1^, Г),..., 0m(g, О) -
§ 4.5. Уравнения Лагранжа. Интегралы энергии и Якоби
229
m-вектор. Подставляя (30) в (27), получим
Л эе. эе aoTq fac/.Y
dq dt dq dq ?
или
f 30 fdoYV do (диЛ
Q= з—q+^—Н-Ч
dq (dqj J dt \dq J
Обозначим:
эе faey
а = з—з- •
dq VdqJ
Это - кососимметрическая матрица размера тхт. Если
дО / dt - 0, то
Q = Q|+Q2, (4.5.31)
где Q2 = oq - гироскопические силы, Q, = -
'duC
потен-
циальные силы.
4°. Интеграл Якоби. Рассмотрим уравнения Лагранжа (10)-
(11) в случае, когда на систему действуют потенциальные и
непотенциальные силы:
d f dLj V f dL, Y
dt dq J V dq J
Lx-T-Ux.
(4.5.32)
(4.5.33)
Умножим (32) скалярно на q и проведем преобразования:
n /• d(dLi
o= q,—^-L
\ dt dq
-q2
d / . f dL\
dt \ \ dq
.. [ dL,
-\4’
\ \dq.
( dE.
Ч’ д
I dq.
-<<eQ2) =
d
dt
• ( dE,
q’
kdq.
dL,
-Ц +—L-<q,Q2). (4.5.34)
dt
Если
3-L-<q,Q2) = 0,
dt
(4.5.35)
230
Глава 4. Вариационный принцип Гамильтона
то из соотношения (34) мы получаем первый интеграл уравнений
движения, который носит название интеграла Якоби:
= Л = const. (4.5.36)
\ IdqJ /
Для того чтобы условие (35) выполнялось, достаточно,
чтобы:
1) непотенциальные силы были бы гироскопическими
<q, Q2> = 0;
2) кинетическая энергия Т и потенциал Ux в обобщенных
координатах не зависели бы явно от времени.
Замечание 1. Если обобщенные координаты вводятся с по-
мощью вектор-функций, не зависящих явно от времени: г - Ф(ф,
ЭФ/Эг = 0, то
r = r2=iqTB(<7)q.
При этом
— = B(q)q, (q,
dqj \
= qTB(g)q = 2Т,
и интеграл Якоби (36) будет иметь вид
2Т-Ц =Т+ U{ = h = const, (4.5.37)
т.е. в этом случае интеграл Якоби совпадает с интегралом
энергии.
Замечание 2. Условие dT/dt = 0 может выполняться и в том
случае, когда обобщенные координаты вводятся функциями
г = Ф(д, г), явно зависящими от времени.
Пример. Рассмотрим систему материальных точек (r„ mz), i =
= 1, 2, ... , п. Пусть Е - подвижный репер, начало которого
совпадает с абсолютным репером Е, и А(Г) - матрица преобра-
зования Е—Л(г- ->Е. Пусть г; - радиус-вектор Ей точки в проек-
циях на орты репера Е. Справедливы соотношения
г, = Ат(Z)rz-, i = 1,2,...,и,
а г/ =(^,^2,^.3) можно рассматривать как обобщенные коорди-
наты, qT =(fjT,f2T,...,rJ). В этом случае Ф^, t) явно зависит от
времени.
Из основного соотношения кинематики
v, = [со, г,] + vr,
§ 4.5. Уравнения Лагранжа. Интегралы энергии и Якоби
231
лт dri
где vr = А —- - вектор относительной скорости в проекциях на
1 dt
орты репера Е, со - вектор угловой скорости вращения Е отно-
сительно Е. В проекциях на орты репера Е
, г____, dx . х
Av, =[<o,rl + —-ч (***)
1 1 dt
со = Асо - проекции вектора со на орты репера Е. Используя
(***), получим следующее выражение для кинетической энергии
системы:
1 п А п ( sfr 2 / /7F
Т - — У т J v |2 = — У т, —L +1[<о,г ] I2 +2(—L,[w,r ]) .
2-“ 2-“ \ dt 1 ' 1 \dt /J
Если <о - постоянный вектор, то dT/dt = 0.
Предположим теперь, что условие (35 выполнено. Однако
Т * Т2, а Т = Т2 + Г, + То, Т2 = |qTSq, Tt = bTq, = 0. В этом
случае
/ ( 3i Y\ / (зт\т\
Ч’М ГИ’ зЧ =2Г2+Г1’ Ц=Т2+1\+Т.-и{.
В этом более общем случае интеграл Якоби (36) имеет вид
Т2 + - То = h = const.
Упражнение. Напишите формулы для Т2 и То в рассмотренном выше при-
мере, когда г,- = АТГ/.
Замечание 3. Если на систему наложены еще неголономные
связи Cq + d = 0, то, согласно (4.4.10), движение системы в про-
странстве обобщенных координат удовлетворяет аналогу урав-
нения Даламбера-Лагранжа
dt у 3q J
"ЭЕ
43q
=о,
(4.5.38)
где - произвольная ^-допустимая вектор-функция. В рассмат-
риваемом случае потенциальной и непотенциальной составляю-
щих сил это уравнение можно написать в следующем виде:
dtydq^
-Q2^)=o.
l^qJ /
(4.5.39)
232
Глава 4. Вариационный принцип Гамильтона
Если в уравнениях неголономных связей вектор d равен нулю, то
Cq = 0. (4.5.40)
Используя лемму 1 § 4.2, нетрудно показать, что
= ₽(0 = 1 при te[tx + 3,z2-8] = J„ Р(Г() = р(г2) = 0,
т.е. £ является допустимой вектор-функцией. Тогда на интер-
вале времени Jt из уравнений (39) и (40), в частности, следует:
d ГdL^
dtydq^
-Q2>q\=o.
l^qj /
Это уравнение совпадает с (34) и, следовательно, в случае него-
лономных связей существует интеграл Якоби, если d = 0 и вы-
полнено соотношение (35).
5°. Определение обобщенных реакций связей. В § 4.4 мы
описали способ решения задач при неголономных связях
C(q,Oq + d(q,r) = 0 (4.5.41)
(С - матрица размера sxm, d - 5-вектор) методом введения
обобщенных реакций связей. Исходя из уравнения Даламбера-
Лагранжа в обобщенных координатах
-rkr -гШ=0- c^ = 0’ £ = £(q,q,O,
\dt\dqj <dqj 4 4
мы вывели уравнения
(4.5.42)
и показали, что обобщенные силы реакций представимы в виде
Qyv = СТХ. При этом система уравнений (41) и (42) определяет q(r)
и Х(г). Эта процедура, в частности, применима и в том случае,
когда соотношения (41) являются голономными связями
cp(q,O = 0, (<p(q,r)G/T, qe/Г), (4.5.43)
записанными в дифференциальной форме
^q + ^ = 0. (4.5.44)
dq dt
Однако в случае, когда (41) - голономные связи, мож-
но поступить иначе. Можно определить отображение
§ 4.6. Первые интегралы уравнений Лагранжа
233
ф: J, х Rm s —> Rm, задаваемое вектор-функцией
q = i|f(q,r)
(4.5.45)
так, что л условий связей (43) будут удовлетворены при любых
q, принадлежащих некоторой области U cRm~s, и любых
t eJt:
<p(i|j(q,r),t) = 0 при qeZ7, t^Jt,
и будут выполнены остальные требования к обобщенным коор-
динатам.
Если неголономных связей нет, то мы приходим к задаче с
функцией Лагранжа
и уравнениями
L(q,q,r) = z/i|i(q,Z),
I dq dt J
z —\ т
dt^dqj
=o.
(4.5.46)
(4.5.47)
Если q(r) - решение системы (47), то вектор-функция
q(0 = i|j(q(r), t) должна удовлетворять (42). Подставляя это выра-
жение q(Z) в левую часть (42), мы определим обобщенные силы
реакций, обусловленные голономными связями (43).
Замечание. Если, в частности, q - декартовы координаты, то
Q/v - обычные силы реакций связей.
§ 4.6. Первые интегралы уравнений Лагранжа
1°. Рассмотрим систему дифференциальных уравнений TV-го
порядка
^ = f(x.r), (4.6.1)
dt
xT=(x',x2,...,xN), f = (f',f2,...,fN), x‘,feR.
При заданных начальных условиях (t = t{}, х = х0) уравнения
(1) в общем случае определяют единственную интегральную
кривую (или траекторию)
X = Х(Хо, г), х(х0, г()) = х0.
Пусть 0 = 0(х, t) - вещественная функция указанных аргу-
ментов. Вдоль траектории движения 0(х(хо, г), t) = ср(Г) определяет
некоторую функцию времени.
234
Глава 4. Вариационный принцип Гамильтона
Определение. Если вдоль любой траектории системы (1)
функция ф равна постоянной: dty/dt =0, то 0(х, t) называют пер-
вым интегралом системы уравнений (1) (иногда говорят короче:
интеграл системы уравнении). Из определения следует:
0(х(хо, Г), г) = 0(хо, Го) = ос = const. (*)
Дифференцируя последнее равенство по Г, получим
^f(M) + ^ = 0. (4.6.2)
Эх dt
Обратно: если 0(х, t) - какое-либо решение уравнения в частных
производных (2), то все точки траектории (х(х0, /), t) будут при-
надлежать гиперповерхности 0(х, t) = 0(хо, Го) = ос в пространстве
RN+i переменных хил
Во многих случаях оказывается, что найти первый интеграл
системы уравнений (если он существует) проще, чем проинтегри-
ровать систему (1).
Предположим, что какой-либо первый интеграл 0(х, t) най-
ден. Рассмотрим уравнение
0(х, t) = ос, (4.6.3)
где ос - постоянное число.
Представим хт = (х1, ут), ут = (х2, ... , xN), у g и запишем
систему (1) в следующем виде:
б/Х „1 z 1 ч
— = /1(х',у,/),
dt
^ = f(x*,y,O, fT=(/2,...,/").
dt
(4.6.4)
Предположим, что 30/Эх1 Ф 0. Тогда мы можем разрешить (3)
относительно х1:
х1 = \|/(ос, у, г), ф е 7?. (4.6.5)
Если подставить х1 в виде (5) в систему уравнений (4), то получим
замкнутую систему уравнений (N - 1)-го порядка:
^ = f(\y(a,y,t),y,t). (4.6.6)
dt
Уравнениям (6) и (5) удовлетворяют все решения уравнений (1) с
начальными условиями (Го, х0), принадлежащими гиперповерх-
ности 0(х, t) = ос.
Предположим, что мы знаем к N первых интегралов
0(х, t) = ос, 0 g Rk, ос g Rk. (4.6.7)
§ 4.6. Первые интегралы уравнений Лагранжа
235
Определение. Первые интегралы (7) называются независи-
мыми, если ранг матрицы Э0/дх максимален (равен к).
Представим хт = (zT, ут), zT = (х1, х2, ... , л*), ут = (хк+[, ... , xN) и
предположим, что det(30/3z) Ф 0. Тогда из (7) можно выразить
переменные z как функции у, a: z - ф(у, t, а) (здесь ф g Rk\ a
для переменных у получится система уравнений вида (6), где в
рассматриваемом случае у g RN~k, f eRN~k.
Так как трудности интегрирования системы уравнений обыч-
но существенно уменьшаются при уменьшении порядка системы,
то стремятся найти максимальное число независимых первых
интегралов.
Все рассуждения, проведенные выше, относятся к общим
системам обыкновенных дифференциальных уравнений в виде
(1). Если мы описываем задачу механики в декартовых коорди-
натах, то можем привести уравнения движения к виду (1), пола-
гая х = (г, v), где г g R3" - совокупность координат точек систе-
мы, v = dr/dt.
Для задач, описываемых уравнениями Лагранжа, x = (q,q),
qe/Г, q = 6?q/Jr, а для задач, в которых движение системы
определяется уравнениями Аппеля, х = (q, X).
Из общих теорем механики при определенных
условиях следуют теоремы о сохранении, например, проек-
ции вектора количества движения системы, проекции вектора
момента количества движения системы, полной энергии системы
(см. § 3.5):
(Р, а0) = const, (К, <о°) = const, Е = const.
Величины Р, К, Е являются функциями х = (г, v) и при описании
задачи механики в декартовых координатах (см. § 3.5) являются
первыми интегралами соответствующей системы уравнений.
В § 4.5 мы указали условия, при которых уравнения Лагран-
жа обладают интегралами энергии E](q,q) = Т + Ц =const или
интегралом Якоби (3Lj / 3q )q - Lx = const.
Очевидно, во всех случаях, когда система уравнений механи-
ки в декартовых координатах обладает первым интегралом
0(r,v,O = oc, (**)
существует соответствующий первый интеграл при описании за-
дачи в обобщенных координатах. Если обобщенные координаты
вводятся вектор-функциями
г = <I>(q г), q g R™ Ф g R3”,
то первому интегралу (**) в обобщенных координатах соответ-
236
Глава 4. Вариационный принцип Гамильтона
ствует первый интеграл
У - z эф . эф
е Ф(Ч,/), ——q + —-,t =а.
dq dt J
Сейчас мы отметим еще некоторые случаи, когда уравнения
Лагранжа имеют первые интегралы. При этом вопросы, связан-
ные с особенностями понижения порядка системы уравнений
движения в задачах механики, рассмотрим позже.
2°. Циклические координаты. Предположим, что связи голо-
номны и все действующие силы имеют потенциал или обобщен-
ный потенциал. Тогда движение механической системы описы-
вается уравнениями Лагранжа
d ( db\ dL _ . , _ .. ,ох
— т~~ I — —— = 0, z = l,2,...,m, (4.6.8)
dt < dq') dq'
где L(q,q,0 - функция Лагранжа, qT = (q\q\...,qm), qT =
= {q\q\...^qm).
Определение. Если функция Лагранжа не зависит от обоб-
щенной координаты q\ то такая координата называется цикли-
ческой. Из (8) следует, что если ql - циклическая координата, то
—-^- = 0и = Pz = const. (4.6.9)
dt dq1 dq '
Следовательно, каждой циклической координате соответствует
первый интеграл уравнений Лагранжа.
3°. Теорема Э. Нётер. Пусть E(q,q,r) - функция Лагранжа
(возможно и для ненатуральной системы). Вектор-функция
q(r) g Rm, определяющая траекторию системы в пространстве
обобщенных координат, удовлетворяет уравнениям Лагранжа
-(Fl=о- (4-б-8)
dtydqj l^dqj
Пусть q = cp(q, t, т) (I т I < e, e > 0) - однопараметрическое
семейство (параметр т) вектор-функций, задающих в каждый
момент времени t взаимно однозначное отображение (р: R,n —> Rm
из пространства обобщенных координат q g Rm в пространство
обобщенных координат q G Rm. Траектория движения q(Z) со-
ответствует траектории q(r) = <p(q(t),t,T).
Будем предполагать, что отображение ср обладает следую-
щим свойством А): при т = 0 ср есть тождественное отображение,
§ 4.6. Первые интегралы уравнений Лагранжа 237
ИЛИ
A) <p(q,/,O) = q.
Из А), в частности, следует, что
(4.6.10)
а)
Э<р
т=0
= 0,
- единичная матрица m-го порядка.
. -I (ftp
т=0
( dip д<р
C/Q dt
Выразим функцию Лагранжа L через переменные q,q,r:
L(q,q,r) = l( <p(q,r,T),-^y^,^
\ at J
= L (q,(J,Z,T) = L*. (4.6.11)
Используя свойство А) и следствия а)-в), определим, что при
т = 0
L*|t=o = L*(q,<j,?,O) = L(q,q,O-
Теорема Э. Нётер. Если для отображения ср, удовлетворяю-
щего условию (10) (свойству А)), выполнено условие
то система уравнений Лагранжа имеет первый интеграл
— £ = Р = const, (4.6.12)
8q
где L = L(q, q, t), L, = £(q, t) =
Эт T=o
e /?'".
Замечание. ДляL=T- (7(q, t) очевидно 9L/3q = dT/dq.
Доказательство. Дифференцируя (11) по т и полагая
т = 0, получим
ЭЕ (dL Эср dL d dip}
0 =-- =-------— +------— . (***)
Эт т=0 3q Эт 3q Эт dt JT=0
Рассматривая ip как функцию t и т (ср = ip(q(t),t,T)), находим
Э dip _ d dip
Эт dt dt Эт
238
Глава 4. Вариационный принцип Гамильтона
Из (***) следует равенство
_ . dL d .
0 = — £(q, t) + ——£(q, 0,
dq dq dt
где t,(q, t)=
Эт
. Это соотношение можно преобразовать:
т=()
(dL d dL
dt dq )
4dq dt dq
Так как q(r) удовлетворяет уравнению Лагранжа (8), то первое
слагаемое равно нулю. Отсюда следуют
d (dL Л _
-о
dt dq J
и первый интеграл (12).
Покажем, как получаются с помощью теоремы Э. Нетер пер-
вые интегралы уравнений движения в некоторых известных нам
случаях.
4°. Предположим, что в рассматриваемой задаче qx - цикли-
ческая координата, т.е. функция Лагранжа не зависит от q[\
L = L(q\...,qm,q2,...,qm,t).
Рассмотрим преобразование <р, определяемое следующими фор-
мулами:
ql = ql (/^1), qx=qx+T.
Непосредственно видно, что выполнены условия А) и Б): dL7dr =
= 0. Вектор £ =
Эт
имеет вид
т=()
Г = (1,о, о,..., о).
Первый интеграл (dL/dq) £ = ос получим в виде (9)
dL
^Т = а-
dq
5°. Предположим, что рассматривается замкнутая свободная
система материальных точек (r? m7), j = 1, 2, ... , и, т.е. система
материальных точек без внешних сил и связей. Предположим,
что внутренние силы не зависят от скоростей точек системы.
Тогда они имеют потенциал (см. (1.7.2))
и=Щ\ Г1-г21,, I r„_, - r„ I),
§ 4.6. Первые интегралы уравнений Лагранжа
239
зависящий только от расстояний между точками. Функция Ла-
гранжа имеет вид
L=T-U,
где
Рассмотрим преобразование ср, определяемое следующими
соотношениями:
г,=г,+а°т, / = 1,2,...,и,
у J 1 J
где а0 е R3 - постоянный вектор, I а0 I = 1.
Легко показать, что в этом случае выполнены свойства А) и Б) и
существует первый интеграл
(****)
где
>п раз.
Из (****) получаем
<Р,а°) = Р,
А ^г,
где V = Ут j —-— количество движения системы. Так как а0 -
7 = 1 dt
произвольный вектор, то, рассматривая последовательно
чества движения:
, получим векторный интеграл коли-
Р = Р = const,
(Р1, Р2, Р3), рт = (р', р2, р3).
6°. Упражнение. В задаче, рассмотренной в 2°, получите с помощью
теоремы Э. Нетер первый интеграл проекции момента количества движения:
(К, со0) = const.
Указания. 1. Надо обосновать справедливость условий А) и Б) при
240
Глава 4. Вариационный принцип Гамильтона
преобразовании <р:
Г/ = Ат(т)г
где Дт(т) - матрица поворота, удовлетворяющая условию: Дт(())= I- единичная
матрица третьего порядка.
2. Для получения первого интеграла в виде (К, со0) = const следует исполь-
зовать обозначение со0 для вектора 7?3, соответствующего кососимметрической
эат
матрице ----
Эт
т=0
7°. Теорему Э. Нетер можно применять и в случае непо-
тенциальных сил, если взять в качестве L(q,q,0 выражение
(4.4.5)
L(q,q,O = T(q,q,r) + <F(O^(q,r)>, (4.6.13)
где (•, •) - скалярное произведение в R3", г = t) задает обоб-
щенные координаты в системе, вектор FT(r) = (Fj1, Fj2,..., F,3) сос-
тавлен из упорядоченных компонентов векторов сил F/ =
= (Г//;2,/;3), действующих на материальные точки системы.
Вектор F(r) при дифференцировании L по q и q рассматривается
как явная функция времени. Уравнения Лагранжа в этом случае
имеют вид
d/ЭГ
dt 3q
ЭГ
3q
-Q = 0, Q =
Проведем в (13) преобразование q - ф^,Г,т), удовлетворяю-
щее свойству А) (10), и вычислим
эг
. в
Эт т=0
результате операций,
аналогичных проведенным выше, получим
эг
э[эт
dt ( Э<4
-QT
7
Эф + d । ЭГ Эф
Эт т=0 dt 9q Эт
(4.6.14)
1 dqj
Так как первое слагаемое в правой части (14) равно нулю в силу
уравнений Лагранжа, если выполнено условие Б)
ЭГ
Эт
= 0, то
т=0
из (14) следует первый интеграл
эт ( э<р
3q t Эт
= Р = const.
т=0
(4.6.15)
§ 4.6. Первые интегралы уравнений Лагранжа
241
Можно показать, что если голономные связи допускают в R3
сдвиг системы материальных точек как твердого тела в на-
правлении, определяемом вектором а0 е /?3, то в обобщенных
координатах этому преобразованию соответствует некоторое
преобразование q = cp(q,z,T), удовлетворяющее свойству А).
Чтобы при этом преобразовании производная по т от
L* = Т\ <p(q,?,T),^q + ^,d + <F(r)^(<p(q,?,T),O>
dq at J
при т = 0 обращалась в нуль, необходимо и достаточно обра-
щение в нуль проекции на а0 суммы внешних сил: (Fw, а0) = 0.
При этом вытекающий из теоремы Э. Нётер первый интеграл
Э£ дер
9q Эт т=о
оказывается интегралом проекции вектора коли-
чества движения системы
(Р, а0) = const,
записанным в обобщенных координатах.
Если же связи допускают вращение системы как твердого
тела вокруг проходящий через начало координат оси со0 е R3, то
повороту вокруг со0 будет соответствовать некоторое другое
преобразование q = <p(q,Z,x), удовлетвояющее свойству А). При
ЭГ
этом условие Б) ---
Эт
= 0 будет выполнено, если проекция на
т=0
со0 суммы моментов внешних сил М(е\ действующих на все точ-
ки системы, равна нулю. Соответствующий этому преобразова-
нию первый интеграл
dL дер
dq Эт т=о
оказывается известным нам
интегралом проекции момента количества движения (3.5.29)
(К, со0) = const.
Аккуратный вывод этих результатов требует определенной
последовательности рассуждений. Мы не будем приводить его в
этих лекциях, так как существование этих первых интегралов
уже доказано. Отметим, что самостоятельное доказательство
сформулированных положений является хорошим (но не три-
виальным) упражнением.
Замечание. Теорема Э. Нётер допускает обобщение на тот
случай, когда при преобразовании ф изменяется и независимая
16. М.Л. Лидов
242
Глава 4. Вариационный принцип Гамильтона
переменная (время):
Z = (p(q,r,T), q = <p(q,F,T).
Тогда из такой более общей теоремы можно получить условия,
при которых существует интеграл энергии.
§ 4.7. О дифференциальном уравнении z2 = /(z,a)
Решение некоторых задач, которые мы будем рассматривать,
удается свести к решению одного дифференциального уравнения
следующего вида:
Z2=/(Z,«), (4.7.1)
где z g R, a G /^-параметры задачи, fe R - достаточно гладкая
функция указанных переменных. Нас будут интересовать ве-
щественные решения. При каждом а значения z, для которых
существует решение (1), определяются условием f(z, а) 0. Если
(z, z) удовлетворяет (1), то (z,-z) тоже удовлетворяет (1).
Поэтому можно исследовать поведение траекторий только в
полуплоскости z^O плоскости (z,z).
Пусть z*, а* - какое-либо решение уравнения/(z, а) = 0. В его
окрестности
f(z, а) = a(z - z*) + b(z - z* )2 + 8 +
+O(|3|2) + O(|z-f |3) + O(|5||z-z* I),
где
8 = <
Эа
,(а-а‘), Л 1 при |х|—>0.
и
а=а
Ниже мы будем рассматривать случай общего положения, когда
Э/
Эос _* а*
Г 0 и а2 + Ь2 Г 0. Специальные случаи, когда эти условия
нарушаются, также могут быть исследованы, однако они нам не
потребуются.
А) Пусть а Г 0. Тогда при достаточно малых I z - z I и I 8 I
поведение решений (1) приближенно описывается уравнением
z2=a(z-z*) + 5. (4.7.2)
§4.7. О дифференциальном уравнении z2 = f(z,cC) 243
Участки траекторий в плоскости (z,z) представлены на рис. 66
для случая а > 0 и на рис. 67 для а < 0. Эти траектории пере-
Рис. 66 Рис. 67
секают ось z = 0 под прямым углом. Через точку (z*, 0) проходит
решение, соответствующее 3=0. Дифференцируя (2) по Л
получим z-aH, откуда z = (tz/2)(r-r0), где Го - момент време-
ни, когда 2 = 0. Отсюда следует, что малый участок траекто-
рии -£<z<£ (е > 0) проходится за конечное малое время Дг ~
= 4e/I а I.
Б) Если а = 0, b < 0, 8 0, то в окрестности точки (z*, 0)
траектории приближенно представляют семейство эллипсов
z2+|Z>|(z-z*)2 =8. (4.7.3)
При этом 8 = 0 соответствует особая траектория (точка)
2 = 0, 2 = Z*.
При 2 = 0, 2 = z* из (1) следует 2 = 0. Этой точке соответ-
ствует равновесное решение уравнения (1). По общей класси-
фикации особых точек дифференциальных уравнений - это осо-
бая точка типа центра. Малое отклоне-
ние начальных данных от этой точки при- ___Л
водит к решениям (3), которые остаются
близкими к равновесному. В этом случае —( С z)>—j-j-----
говорят об устойчивом положении равно-
весия. 0
Строгую постановку проблемы устой-
чивости равновесия мы рассмотрим позже. рИс. 68
Можно показать, что при достаточно ма-
лых I 8 I и I 2 - z I решения исходного уравнения (1) будут каче-
ственно вести себя так, как показано на рис. 68.
В) Если я = 0 и > 0, то в окрестности точки (z*> 0) траек-
тории описываются приближенным уравнением
z2 -\b\{z-z)2 =5.
(4.7.4)
16*
244
Глава 4. Вариационный принцип Гамильтона
Значению 6 = 0 отвечают две
траектории, «входящие» в точку
(z*, 0), и две траектории, «вы-
ходящие» из нее: z. - +4b (z - z*)
(рис. 69).
Значениям 8 > 0 или 8 < 0 со-
ответствуют участки гипербол.
При 8 = 0 точке (z*, 0) отвечает
равновесное решение уравнения
(1). В этой точке не только z - 0,
но и z - 0. По общей классификации особых точек такая точка
называется особой точкой типа седла.
Проинтегрируем уравнение z = 4b (z-z*) при начальных
данных t = t0, z = z0 < z*:
d ln(z* - z) = -4b dt,
откуда
ln^-^ = -Vb (Z-?o),
z -z0
z = z' - (z* - Zok-^'”'0’.
Двигаясь по этой траектории,
можно достичь особой точки z =
= z только за бесконечное время.
I. Зафиксируем значения па-
раметров ос. Если уравнение
f(z, а) = 0 не имеет действитель-
ных корней, то, в зависимости от
знака начального значения z при
t = to, z(t) будет либо монотонно
увеличиваться, либо монотонно уменьшаться (рис. 70). Никаких
других решений в данном случае нет.
2. Пусть г* наибольший корень. Если выполнены условия
Рис. 70
|><
Эг -
0 или 2) —
Эг
"°И Эг2
0,
то существуют траектории, показанные на рис. 71 и 72 соответ-
ственно.
Для случая, когда г* - наименьший корень и выполнены условия
3Л ,0
Эг -• dz -* Эг'
>0,
§4.7. О дифференциальном уравнении z~ =
245
существуют траектории, показанные на рис. 73 и 74 соответ-
ственно.
3. Предположим теперь, что zf и^ (zf <Zo) - Два соседних
корня (между ними нет других корней) и выполнены следующие
условия:
7)
< >оЛ
Эг г» Эг
=0.^
>0.
8)
Эг
, -оД
Эг" » Эг .«
Z1 к-2
=0
’ а?
0.
Соответствующие траектории показаны на рис. 75-78.
Кроме указанных траекторий, следует отметить траектории,
соответствующие устойчивому и неустойчивому положениям
равновесия. Характер поведения всех траекторий уравнения
z2 = при фиксированном а однозначно определяется гра-
фиком/(z, а). Для иллюстрации на рис. 80 показаны траектории,
отвечающие графику, представленному на рис. 79.
246
Глава 4. Вариационный принцип Гамильтона
Для того чтобы точке (z*, 0) соответствовало положение
равновесия, необходимо выполнение двух условий:
/(z*,a) = 0 и ^(z*,ot) = 0.
dz
Поэтому равновесные решения существуют лишь при особых
значениях параметра а. А следовательно, и траектории, входя-
щие (выходящие) в неустойчивую особую точку, существуют
лишь при особых значениях параметра а.
§ 4.8. Задача о математическом маятнике
1°. Для решения задачи нам необходимо выразить кинетиче-
скую энергию материальной точки в цилиндрических коорди-
натах.
Пусть гт = (г1, г2, г3) - декартовы координаты точки М отно-
сительно репера Е. Цилиндрические координаты qT = (р, ф, z) в R3
вводятся соотношениями (рис. 81)r = <&(q):
г1 = р cos ф, г2 = р sin ф, г3 = z. (4.8.1)
Используя (1), нетрудно вычислить определитель
ЭФ det — = det dq ' Эг1 Эг1 Эг1 Л =p-
Эр Эф dz dr2 dr2 dr2 Эр Эф dz dr3 dr3 dr3
< Эр Эф dz >
§ 4.8. Задача о математическом маятнике
247
Следовательно, преобразование (1) за исключением оси р = 0 не
имеет особенностей.
Пусть теперь г(г) определяет
траекторию движения. В координатах q
эта траектория описывается функциями
q(7). Дифференцируя (1) по г, получим
г1 = pcoscp- pepsin ф,
г2 =psin(p + p<pcos(p, (4.8.2)
Используя (2), получим выражение для
кинетической энергии материальной точки (г, т) в цилиндриче-
ских координатах
+(^2)2+(,"3)2]=^(р2+р2(^2 +i2)- (4-8-3)
2°. Задача о маятнике. Рассмотрим движение материальной
точки (г, т), ограниченное голономными связями: г3 = 0, (г1)2 +
+ (г2)2 = р2 = const. Предположим, что на эту точку действует
активная сила тяжести F(e) = т geb где g > 0 - постоянная,
= (1,0,0). Такая задача называется задачей о математическом
маятнике.
Сила F(<?) потенциальна. Действительно,
тЯг) (dU i
F - - ----- , где U = -mgr .
V Эг J
Удобно рассматривать эту задачу в ци-
линдрических координатах (1). Тогда
условие голономных связей можно за-
писать в следующем виде:
р = 0, z = 0.
Все возможные положения нашей «сис-
темы», совместимые со связями, опреде-
ляются одной обобщенной координатой
(р - углом между радиусом-вектором точки (г, т) и ортом в!
(рис. 82). В рассматриваемом случае из (3) получим выражение
для кинетической энергии в «обобщенных координатах»
г=?р2ф2’
р = const.
(4.8.4)
248
Глава 4. Вариационный принцип Гамильтона
Выразим потенциал задачи U через координату (р:
U = -rngpcoscp. (4.8.5)
Таким образом, мы пришли к задаче, для которой функция Лаг-
ранжа Е(ф,ф) имеет вид
L = T-U = ур2ф2 +mgpcos(p. (4.8.6)
Составим уравнения Лагранжа:
ЭЕ 2• 9L
— = тр ф, —- = ~mgp sm ф,
Эф Эф
_£Э£
dt Эф
Введя обозначение
получим
dL 2-
= 0-^тр =-mgpsintp.
Эф
2 •
ф = -0) 8Шф.
(4.8.7)
CD2 =—,
Р
3°. В § 3.11 мы вывели уравнения движения твердого тела в
случае, когда идеальные связи допускают только вращение тела
вокруг неизменной оси. Эти уравнения имеют вид (3.11.23)
з Y =М{е}
3 dt2 3 ’
(4.8.8)
где J3 - момент инерции тела относительно оси
вращения, у - угол между ортом ех неподвиж-
ного репера Е и ортом ех подвижного репера Е,
жестко связанного с твердым телом (рис. 83).
При этом орт е3 = ё3 направлен по оси враще-
ния. М3е) - проекция на е3 суммы моментов
внешних сил. Предположим, что внешняя сила,
действующая на тело, есть однородная сила тя-
жести, направленная вдоль орта т.е. предпо-
ложим, что на каждую материальную точку
(rz,mz) / = 1,2,...,7V, из которых состоит твердое тело, действует
сила = mzget, g > 0 - постоянная.
Лемма. 1) Результирующая сила F(<?) равна произведению
массы тела на ускорение силы тяжести g и направлена вдоль
4.8. Задача о математическом маятнике
249
орта ер
п N
F(e) = Ff(e) = mgel, т =
/=1 /—i
2) Результирующий момент М(<?) сил, действующих на все
точки твердого тела, равен моменту силы F(<?), приложенной в
центре масс твердого тела:
M(e)=[r*,F(e)].
N N
Доказательство. 1) FU) = ^Ff-(e) = = gmer
Z=1 Z=1
2) Мм = [г,Л(е)] = §Е [m,.r,.,e,] = g[mr’,el] = [r*,Fw].
/=1 i=l
Обозначим через г* = (a,b,c) - координаты центра масс тела
относительно репера Е. Так как положение центра масс отно-
сительно Е не изменяется, то а,Ь, с- постоянные числа.
Используя введенные обозначения, получим выражение для
радиуса-вектора центра масс относительно репера Е\
г* = («cosy - b sin Y)e1 + («siny + Z?cosy)e2 + ce3.
Определим третий компонент момента
М3е} =mg[r\e|]3 = -mg^asiny + £?cosy)
или, введя обозначения
а b
. = COS W, ,.....- = sin w,
7777 7«2+/>2
получим
М3} = -mgya2+ b2 sin(y + ф).
Если обозначить:
mgyfh2 + b2 о
У + V = Ф, з----= ш ~ ’
то уравнение (8) совпадает с уравнением (7):
2 •
Ф = -Ш sincp.
Замечание Е Можно выбрать репер Е так, чтобы центр масс
лежал в плоскости векторов epe3. В этом случае b = 0 и у = 0. То
есть, ср - угол между плоскостью (е19е3) и подвижной плоско-
стью, проходящей через орт е3 и центр масс тела.
250
Глава 4. Вариационный принцип Гамильтона
Замечание 2. Мы рассмотрели задачу, в которой направление
силы тяжести ортогонально оси вращения. Можно рассмотреть и
более общий случай. Предположим, что сила Fz(<?) имеет вид
Fz(e) = mzge, где ет=(ос,0,|3) - единичный вектор (ос2 +р2 =1),
ос>0.
Упражнение. Покажите, что в этом случае вращение твердого тела вокруг
Г~2
2 тта +Ь
оси описывается уравнением (7), где cd =-.
Л
Задача о движении твердого тела вокруг неизменной оси в
однородном поле тяжести носит название задачи о физическом
маятнике. Мы показали, что задачи о математическом и фи-
зическом маятниках описываются одинаковыми уравнениями.
К уравнению (7) сводится описание еще ряда других задач в
различных предельных случаях. Уравнение математического ма-
ятника - один из простейших примеров нелинейного уравнения
механики. Проведем его анализ.
4°. Интеграл энергии. В задаче о математическом маятнике
связи голономны и не зависят явно от времени, а силы потен-
циальны, и потенциал тоже не зависит явно от времени, т.е. в
этой задаче должен существовать интеграл энергии Т + U - Е =
= const. Запишем этот интеграл явно:
Ш 2'2
— р ф -mgpcosф = const.
m 2
Разделим это соотношение на — р . Получим
ср2 -2(o2cos(p = cx. (4.8.9)
Упражнение. Получите этот интеграл из уравнения (7).
В данном случае это просто. В других более сложных случаях получение
первых интегралов из общих теорем оказывается делом несравненно более
легким, чем вывод из уравнений. Однако следует заметить, что общие тео-
ремы, вообще говоря, не дают возможности всегда указать все интегралы.
Поэтому, определив интегралы из общих теорем, не следует пренебрегать (при
поиске первых интегралов) прямым анализом уравнений.
5°. Качественное исследование поведения интегральных кри-
вых. Из интеграла энергии (9) следует, что решение задачи о
движении маятника сводится к решению уравнения известного
нам типа (см. § 4.7):
ф2 = ос + 2ш2 cos ф = /(ос,ф), (4.8.9)
где ос определяется начальными условиями. Если при t = t0 ф =
= Ф0, Ф = Фо> то а = ф(2-2ш2со8ф0. Если (ф,ф) удовлетворяет
§ 4.8. Задача о математическом маятнике
251
уравнению (9) при заданном ос, то (ф,-ф), (ф + 2&тх,ф), (-ф,ф) то-
же удовлетворяют уравнению (9). Эта особенность задачи позво-
ляет анализировать поведение траекторий в полуполосе П =
= {(р 0, 0 ф л} и получить картину во всей плоскости из
указанной симметрии.
Из (9) следует, что вещественные решения существуют лишь
при ос^ -2со2.
а) При ос > 2со2 величина ф2 не обращается в нуль, и на тра-
екториях происходит монотонное возрастание (ф > 0) или умень-
шение (ф < 0) угла ф.
б) При -2со2 < ос < 2со2 из (9) следует, что на траекториях
движения
-ос
СО8ф ------7
2со2
-к-А<1 •
2со2 J
Поэтому угол ф G П не может превосходить а = arccos--<
V 2со )
< п. В точках ф = +а + 2fai (&-целое число) выполнено условие
Дф, ос) = 0. Рассмотрим случай к = 0. При ф = а производная
df /Эф = -2со2 sin ж 0, а при ф = -а производная Э//Эф =
= 2со2 sin а > 0. То есть (-«, 0) и (я, 0) - две точки, через которые в
плоскости (ф,ф) проходит замкнутая траектория, охватывающая
начало координат (0, 0).
в) Определим равновесные решения из условий
/(а,ф) = 0, |^(а,ф) = 0.
Эф
Из второго условия следует, что -2а)2 8Шф = 0, откуда ф =
= ф* = kit. Подставляя ф = ф ' в первое условие, получим
ос + 2со2 созф* = 0. (4.8.10)
Вычислим вторую производную по ф в точке ф = ф*:
а2/
Эф2
_ о *
= -2(0 СО8ф .
Отсюда следует, что значениям ф = ф* = 2кп
252
Глава 4. Вариационный принцип Гамильтона
г, 2 1 *
ос = -2со отвечают точки типа центра, а значениям ср = ср =
= (2к + 1)л
Э2/
Эср2
>0, ос = 2со2
точки типа седла. Для ос = 2со2
ф
точки (-71, 0) и (71, 0) являются двумя равновесными точками ти-
па седла. Поэтому из точки (-71, 0) в точку (71, 0) идет особая
траектория, которую называют сепаратрисой. Качественная
картина поведения интегральных кривых в плоскости (ф,ф)
представлена на рис. 84. Сепаратриса изображена штриховой
линией.
Значению ос = -2со2 отвечает равновесное решение (0, 0).
При -2со2 <ос<2со2 траектории - замкнутые линии типа эл-
липса, охватывающие точку устойчивого равновесия (0, 0). На
этих траекториях угол ф изменяется в ограниченных пределах:
-а < ф < а, т.е. маятник совершает колебания. Величина 2а на-
зывается амплитудой колебания. При ос > 2со2 угол ф постоянно
увеличивается (ф>0) или уменьшается (ф<0). Такое движение
маятника называется вращательным. Сепаратриса ос = 2со2 от-
деляет область плоскости (ф,ф), заполненную траекториями ко-
лебательных движений маятника (иногда эту область называют
либрационной зоной), от области траекторий вращательных дви-
жений маятника (ротационной зоны).
При движении по сепаратрисе маятник стремится за бес-
конечное время (см. § 4.7) достигнуть неустойчивой равновесной
точки. Для реализации движения по сепаратрисе надо задать
особые начальные данные: г = г0, ф = ф0, ф = ф0, ф(2 - 2сосо8ф0 =
§ 4.8. Задача о математическом маятнике
253
= 2со2. Мера этих начальных данных равна нулю.
Поэтому в реальных процессах движение по сепа-
ратрисе не реализуется. Однако это очень важное
понятие, существенное для качественного анализа
многих более сложных вопросов.
Замечание. Точки (ф + 2лЖ,ф) при всех целых к
соответствуют одним и тем же значениям коор-
динат г и v фазового пространства. Поэтому взаим-
но однозначное соответствие между ср, ф и г, v бу-
Рис. 85
дет иметь место, если изображать фазовые
траектории не на плоскости, а на круговом цилиндре (рис. 85),
который является прямым произведением окружности и пря-
мой R.
6°. Аналитическое решение. Из уравнения (9) следует
б/ф
ДЛ/ос + 2со2со8ф
(4.8.11)
где
Л = sgn ф =
ф^О,
ф<0,
sgn х - знак числа х.
а) Рассмотрим сначала случай либрационных движений
-2со2 < ос < 2со2. Проведем в (11) замену переменных
ос + 2со2
2
sin— = Zcsinф, к = л----
2 V 4со
Справедливы цепочки равенств:
со8ф = 1 - 2sin2 = 1 - 2к2 sin2 ф,
ф2 = ос + 2со2 со8ф = ос + 2со2 -4£2со2 sin2 \|/ =
(**)
= 4£2со2
ос + 2со2
4£2со2
-sin2v = 4£2со2 cos2 ф.
На либрационной кривой со8ф^-------Замена (*) не одно-
2со
значно определяет ф(ф) или ф(ф). Так как ф2 и cos ф одно-
временно обращаются в нуль, то доопределим эту замену усло-
вием sgn со8ф = А = sgncp. За время полного колебания маятника
254
Глава 4. Вариационный принцип Гамильтона
угол v изменяется на 2л. На рис. 86
указаны точки либрационной траекто-
рии, соответствующие значениям \|/ =
л
= & —. Дифференцируя (*) и используя
Ф п п о
неравенство cos—>0 при ос<2со , по-
лучим — cos — б?ф = к cos \\Jd\y. Откуда
. 2&COSW6A1/
-- -
д/1-^281п2ф
(***)
Подставляя (**) и (***) в (11), получим
cos ytdy
Асо | cos \|/1 ^/l-Psin2 у
Так как cosy = A | cos у |, то в результате будем иметь
udt = . . (4.8.11')
Jl - Jt2 sin2V
В отличие от угла ф, переменная ф изменяется монотонно. Пред-
положим, что ф = 0, ф > 0 в момент времени /0. Этой точке соот-
ветствует ф = 0. Интегрируя (1Г), получим
V dt
co(*-ro)= f .....; ? • (4.8.12)
{ 71-Р sin2
Уравнение (12) дает неявное представление зависимости угла ф,
а следовательно, и ф от времени.
_ Л — „ — л
Если представить ф = п — + ф, где 0 ф < —, п - целое, то из
(12) следует
со(Г -t0) = пК(к2) + F(k2, ф). (4.8.13)
Здесь
71 / 2 -с,
К(к2)= [ - = (4.8.14)
i sin2
J 4.8. Задача о математическом маятнике
255
- полный эллиптический интеграл первого рода,
F(^,v)=f , \ ? (4.8.15)
о -jl-k sin'£
- неполный эллиптический интеграл первого рода.
Параметр к носит название модуля эллиптического ин-
теграла (не путать с целочисленными к в выражении ф==2Атт).
Полный оборот точки (ср,ф) в фазовой плоскости по либ-
рационной кривой соответствует одному полному колебанию
71
маятника. При этом угол ц/ изменяется на 2л: = 4 — .
одного колебания называется периодом т колебания маятника.
Из (13) получим
4
т = — К (к1 2 *). (4.8.16)
со
Когда ос^-2со2, либрационные кривые стягиваются к точке
устойчивого равновесия. В этом случае к2 —» 0. Для малых к2
полный эллиптический интеграл хорошо аппроксимируется пер-
выми членами ряда
К(к2) = ^ 1 +
Т
2.
2
к2 +
1 .ЗА2
— к4+...
2-4;
Поэтому для траекторий, близких к точке устойчивого равно-
весия,
т = —(1 + О(£2)). (4.8.17)
СО
Пример. Пусть полуамплитуда колебания маятника а равна
10° ~ 1/6 рад. Отсюда следует:
1 ОС 2 1 гч 2^i 1
cos—=------у, а = -2со cos—~-2со 1--------,
6 2й2 6 I 2-367
С = СХ + 2С0 g j g J_ O(£2)ss_!_
4со2 4-36 150 600
Таким образом, для полуамплитуды 10° период колебания маят-
ника лишь на 1/600 отличается от периода колебания с бес-
конечно малой амплитудой: т0 = 2тт / со.
| р 1р
Для математического маятника со = —, т0 = 2п —. Меняя
V Р
256
Гпава 4. Вариационный принцип Гамильтона
длину р, можно получить маятник с заданным периодом коле-
баний. Это свойство маятника используется в некоторых конст-
рукциях часов. Зависимость периода колебаний от ускорения
силы тяжести g используется в приборах для измерения силы
тяжести.
Замечание. При ос^-2со2 амплитуда колебаний 2а =
( 2со2>|
= 2arccos-----—»0. Хак как угол |ср| в процессе колебания ос-
I )
тается меньше а, то и |ср| —> 0. Для колебаний с малой амплиту-
дой можно в уравнении математического маятника (7) заменить
sin ф ~ ф и тем самым получить линейное уравнение
9
ф = -со ф.
(4.8.18)
Говорят, что уравнение (18) описывают задачу о линейном осцил-
ляторе. Известно, что решение (18) можно представить в сле-
дующем виде:
ф = a cos(cor + фо). (4.8.19)
Решение (19) описывает малые колебания математического ма-
ятника. При этом 2а > 0 - амплитуда малых колебаний.
Упражнение. Постройте картину поведения фазовых траекторий в плос-
кости ((р,ф) в задаче о линейном осцилляторе.
Когда либрационная кривая приближается к сепаратрисе,
ос^2со2 и к2 —>1 —0. Для полного эллиптического интеграла
при модуле к, близком к 1, можно воспользоваться известным
представлением
4
/^ = In — +
к'
(4.8.20)
# / 9 9 л
где к = у/1-к~. При /Г —»1-0 имеем К ~1п —, т~—In-------
к' со к'
т.е. при приближении либрационной кривой к сепаратрисе пе-
риод колебания маятника неограниченно возрастает. При этом
основное время маятник будет находиться в окрестностях не-
устойчивых особых точек (±я, 0).
б) К сожалению, невозможно единым аналитическим выра-
жением описать траектории движения маятника в либрационной
и ротационной зонах. Этому препятствует топологическое раз-
личие поведения фазовых траекторий в этих зонах. Для полу-
чения аналитического выражения в ротационной зоне ос>2со2
J 4.8. Задача о математическом маятнике
257
преобразуем уравнение (11):
2 z п 2\fi 4С0 . 2 ф
ОС + 2СО СО8ф = ((Х + 2С0 ) 1-5-Sin — .
\ а + 2со2 2)
Обозначая
о 4со2 о
к2 =-------у, 0<Л2<1 (****)
а + 2со2
и ф/2 = А-ф, из (11) получаем
, 2 d\\f , А л х
dt = —===—==^=. (4.8.21)
д/ос + 2со2 д/1-/:28т2ф
Интегрируя (21) с начальными условиям t = tQ, ф = 0, находим
,-,0=^Л , .
л/сх + 2со2 о д/1-&2 sin2 £
л _ Л _ л
откуда для ф = и — + ф, 0 ф < —
2
t - tQ = . [пК(к2) + F(k2, v)], (4.8.22)
Va + 2co2
где п - целое.
Периодом вращения маятника т называется время, за ко-
торое угол ф изменяется на 2л. За это время угол ф изменится на
л. Из (22) при п = 2 и ф = 0 получим
4/Г(£2)
Т — I------.
д/сх + 2со2
В случае быстрого вращения
|ф |—>°°,а—>А:2 —>0,Х\/:2)—» л/2 и т —> , ~ 0.
л/сх + 2со2
Если сс—> 2со2 +0, то ротационная кривая приближается к сепа-
ратрисе. В этом случае, как следует из (****), £2 —> 1 - 0, а
2, 4
т —> — In . —> °°.
СО л/1-jt2
в) При движении по сепаратрисе сс = 2со2. В этом случае
уравнение (9) упрощается:
ф2 = 4со2 cos2 —.
2
17. М.Л. Лидов
258
Глава 4. Вариационный принцип Гамильтона
Если ф>0, то ф = 2cocos(cp/2). Нетрудно проверить, что реше-
ние этого уравнения определяется следующей формулой:
tg4 "се“('-'0, + Г
1 + tg^
4 т-г
где с---------— , ср0 - значение ср при t = г0. При / 00 имеем
tg---> 1, (р —> л, т.е. ср стремится к седловой точке.
Определение сил реакций
Обобщенные силы реакций голономных связей = (£
(2(р,(Х), согласно процедуре, описанной в § 4.5, определяются
формулами:
Qw =
d ( Э/Л
dt dq J
dL
dq,
(4.8.23)
q=<|/(q(Z)j)
где L - лагранжиан задачи без учета голономных связей, q =
= i|i(q(r), t) - решение, полученное с учетом голономных связей.
В задаче о маятнике qT = (p,cp,z)
L~m
2 • 9 . 9 \
+ р ср" + z~ ) + mgpcoscp,
и условия голономных связей определяются формулами
р = const, г = 0.
(4.8.24)
(4.8.25)
Решение задачи в пространстве q (т.е. на прямой (р) описано
выше (мы не ставили черту над ср). Из (23) и (24) следует:
(2Р = [тр-трф2 -mgcoscp]p=() = -тр(ф2 + со2 coscp),
0<р = [тр2ф + 2тррф + zngp sin <p]p=0 = mp2 (ф + со2 sin ср),
Qz = [mz]z={) = 0.
В силу уравнений (7) 0ф=О. Подставляя ф2 = а + 2со2 coscp
из (9), получим
Qp =-mp(oc + 3co2coscp).
(4.8.26)
§ 4.8. Задача о математическом маятнике
259
Упражнение. Определите, при каком значении постоянной а выполняется
условие max 12р Р, - где Р > 0 - заданная постоянная.
<Р
Замечание. Полученное нами равенство
Qz = 0 говорит о том, что условие z = 0 будет
выполняться автоматически, если в задаче
без связи (z = 0) мы примем в качестве на-
чальных условий z = 0, z = 0 при t = t0.
Задача о движении материальной точки
(г, т) в поле силы тяжести F(e)=mgej при
условии связи (г1)2 + (г2)2 + (г3)2 = const на-
зывается задачей о сферическом маятнике
(рис. 87). Для описания этой задачи введем сферические коорди-
наты г = Ф(д):
rl=pcos(p, г2 = psincpcosX, г3 = psincpsinX,
p = ((r’)2+(r2)2+(r3)2)'/2.
(4.8.27)
Упражнение. Покажите, что в сферических координатах кинетическая
энергия материальной точки определяется формулой
Т = ±-т(р2 + р2ф2 + р2 sin2 ф-Х2). (4.8.28)
В задаче о сферическом маятнике р = 0 и потенциал
U = -mgpcoscp. (4.8.29)
Таким образом, функция Лангража имеет вид
L = |-m(p2(p2 + р2 sin2 срХ2) + mgpcoscp. (4.8.30)
В этой задаче справедлива теорема о сохранении механи-
ческой энергии Т + U = const (голономные связи и потенциал не
зависят явно от времени). Интеграл энергии можно записать в
следующем виде:
ср2 - 2ш2 cos ср + sin2 срХ2 = cq = const,
ш2=£ (4.8.31)
Р*
Кроме того, координата X - циклическая. Поэтому существует
интеграл dL/ЭХ = const, который можно записать в следующем
виде:
sin2 срХ = а2 = const. (4.8.32)
17*
260
Глава 4. Вариационный принцип Гамильтона
Упражнение. Покажите, что существование этого первого интеграла
следует из теоремы о сохранении проекции момента количества движения на
орт ej.
Подставляя в (31) X, определенное из (32), получим
сх2
ср2 = ос1 + 2ш2 coscp--. (4.8.33)
sin ср
Если в начальный момент времени z = t0 X = 0, то ос2 = 0 и из
первого интеграла (32) следует, что во все время движения X = 0.
То есть в задаче о сферическом маятнике существует решение, в
котором движение происходит в плоскости
Х = const и ср2 = ос + 2ш2 coscp.
Если принять X = 0, то мы приходим к рассмотренной выше
задаче о движении математического маятника в плоскости
(ере2). При X ^0 это та же самая задача о математическом ма-
ятнике, только плоскость движения повернута относительно оси
е! на угол X.
Если в уравнении (33) провести замену переменных х = cos ср,
то в результате получим
х1 =(1-х2)(ос1 + 2ш2х)-ос| = Р3(х,ос1,ос2). (4.8.34)
Решение этого уравнения определяется квадратурой:
(4.8.35)
J ±^Р3(х,ос1,ос2)
Из (32) и (34) следует, что
б/Х _ ос2
dx ±(1 - х2 )Л/Р3(х,а1,а2)
Откуда
Л - Ло = ± [---2 . (4.8.36)
0 J (1-л2)Л/Р3(л,а1,а2)
Из интегрального исчисления известно, что квадратуры,
входящие в (35) и (36), выражаются через эллиптические ин-
тегралы. Эти соотношения определяют (неявно) зависимости x(t)
и Х(Г). Мы не будем проводить анализ этой задачи. Она частично
разобрана в книге: Суслов Г.К. Теоретическая механика - М.:
Гостехиздат, 1946.
§ 4.9. Движение точки по гладкой кривой
261
§ 4.9. Движение точки по гладкой кривой
Предположим, что голономные идеальные связи допускают
движение материальной точки (г, т) только по гладкой кривой в
/?3, определяемой взаимно однозначным отображением » к,
где = {X, X е R}. Пусть г = Ф(Х) - параметрическое уравнение
этой кривой. Предположим, что на точку (г, т) действует ак-
тивная сила с потенциалом (/(г). При этом кинетическая энергия
Т «в обобщенных координатах» X имеет вид
_ 1 ( 6?rV dr _ т( ЭФ У ЭФ^ dXy
2 I dt J dt 2 у ЭХ J ЭХ у dt )
а потенциальная энергия определяется формулой С7(Ф(Х)). Что-
бы не усложнять анализ, предположим, что на кривой задана
ориентация, выделена некоторая точка г* и в
качестве параметра X, определяющего поло- ГА s'
жение точки г на кривой, выбрана длина уча- У'
стка кривой, заключенного между г и г*.
То есть (рис. 88) |Х | = J | dr |, где интегриро- Рис 88
вание ведется вдоль кривой от г* до г. При
этом X > 0, если от г* до г надо двигаться по направлению, ука-
занному стрелкой, и X < 0 в противоположном случае. При таком
выборе X
dX = ^dr')2 + (dr2)2 + (Jr3)2,
т.е.
. f г/Ф1 V ( А = { az PU ("ЭФУ ЭФ откуда следует, что —- —— = V оХ ) оХ Обозначим ЩФ(Л)) = С7(А) к задаче с функцией Лагранжа L = T-U = ~)2 - 2 Ф2 ( dd> - — + d\, ж J ( ал J 1. Таким образом, мы приходим -U(X), Х = —. 2 dt
262
Глава 4. Вариационный принцип Гамильтона
d dL dL
Записывая уравнения Лагранжа----------= 0, получим
dt ЭХ ЭХ
1 dU
2 ЭХ *
(4.9.1)
Так как силы потенциальны и связи не зависят от времени, то
должен существовать интеграл энергии Т + U = const, который
можно записать в следующем виде:
X2 + С/(Х) = ос = const, (4.9.2)
т.е. движение точки Х(г) определяется уравнением, рассмотрен-
ным в § 4.7.
Рис. 89
Предположим, что С7(Х) имеет
вид, представленный на рис. 89. Точки
локального максимума С7(Х) приводят к
появлению двух особых точек типа сед-
ла в фазовой плоскости (Х,Х) (рис. 90)
при ос = ос2 и ос = ос3, а точка локального
минимума [/(X) приводит к особой точке
типа центра при ос = ос,. Для случая,
изображенного на рис. 90, одна сепарат-
риса возвращается в ту же особую точ-
ку и отделяет область либрационных
движений. Кроме либрационных движе-
ний и движений, в которых X монотонно
увеличивается (X > 0) или уменьшается
(Х<0), существуют зоны, в которых
траектории в плоскости (Х,Х) начи-
наются при X = ±°° и, достигая мини-
мального значения |Х|, вновь уходят на
±°°. Если начальные данные принадле-
жат либрационной зоне, то точка всегда в ней и остается. Физики
говорят, что точка находится в потенциальной яме.
Некоторые общие понятия
Для задач, описываемых уравнениями Лагранжа, совокуп-
ность обобщенных координат qT = (q\q2 ,...,qm) и обобщенных
скоростей qT = (q\q2 ,...,qm) будем называть фазовыми перемен-
ными задачи. Пространство R2m = Rm х Rm фазовых переменных
§ 4.10. Движение точки по поверхности вращения
263
будем называть фазовым пространством. Каждой траекто-
рии движения q = q(r) соответствует траектория (q(O,q(f)) в фа-
зовом пространстве. Эти траектории будем называть фазовыми
траекториями. Если функция Лагранжа явно не зависит от
времени (ЭЛ/Эг) = О, то уравнения Лагранжа могут быть при-
ведены к виду q = f(q,q) или, если q = u, к виду ii = f(q,u),
q = u.
В общем случае функции f(q, и) таковы, что выполнены ус-
ловия теоремы существования и единственности решений для
обыкновенных дифференциальных уравнений. Из этой теоремы
следует, что за исключением особых точек (где и = 0 и f(q, и) = 0)
фазовые траектории не могут пересекаться. Часто задача ана-
лиза поведения фазовых траекторий в фазовом пространстве
является более важной и более простой задачей, чем нахождение
полного решения q(r). Это, в частности, было показано на рас-
смотренных примерах. При т = 1 фазовое пространство дву-
мерно, и результат анализа можно и полезно, как это было сде-
лано, представить в плоскости (q,q). В этом случае изображение
качественной картины фазовых траекторий иногда называют
фазовым портретом задачи.
Если функция Лагранжа явно зависит от времени, то траек-
тории в фазовом пространстве, вообще говоря, пересекаются.
Поэтому вводят в рассмотрение расширенное фазовое простран-
ство Rlm xR - прямое произведение фазового пространства и
оси времени. Все отмеченные здесь понятия относятся к общей
теории дифференциальных уравнений, и неудивительно, что мы
фактически повторно обсуждаем вопросы, о которых уже упо-
минали в § 1.5 в связи с уравнениями механики свободной
системы в декартовых координатах.
§ 4.10. Движение точки по поверхности вращения
Предположим, что идеальные связи допускают движение ма-
териальной точки (г, т) только по осесимметричной непрерыв-
ной поверхности, определяемой уравнением
7(7)2 +(r2)2 = \|/(r3), (*)
Если мы рассмотрим эту задачу в цилиндрических координатах
qT = (p,<p,z), то уравнение связи (*) можно записать в следующем
виде: р = y(z), z g R.
Будем предполагать, что функция t|/(z) дифференцируема до-
статочное число раз. Подставим р = y(z) в выражение для кине-
264
Глава 4. Вариационный принцип Гамильтона
тической энергии в цилиндрических координатах (4.8.3):
Т = у (р2 + Р2ф2 + Г) = у (V2(P2 + (1 + V2k2), (4.10.1)
где v = y(z), V- -----• Предположим, что никакие активные
dz
силы на точку не действуют. Тогда функция Лагранжа L-Г. Мы
приходим к задаче с двумя обобщенными координатами ср и z и
функцией Лагранжа (1). Эта задача имеет два первых интеграла.
Действительно, связи не зависят от времени и потенциал сил ра-
вен нулю. Поэтому полная механическая энергия «системы», ко-
торая в этом примере совпадает с кинетической, не изменяется в
процессе движения:
ц/2ф2 +(1 +V2)z2 = ОС! = const. (4.10.2)
Очевидно, otj > 0. Кроме того, координата ср - циклическая. Она
не входит в функцию Лагранжа (1). Поэтому ЭЕ/Эф = ос2 = const.
Таким образом, существует еще один интеграл задачи:
1|/2(р = ос2. (4.10.3)
Из (3), в частности, следует, что если в начальный момент вре-
мени ср Г 0, то знак ср не может измениться в процессе движения.
В дальнейшем для определенности будем полагать ос2 0, т.е.
рассматривать случай «прямого» вращения. Подставляя ср из (3)
в (2), получим
2 9
(4104)
V (1 + у:)
Это уравнение типа рассмотренного в § 4.7.
а) Если в начальный момент времени t = t0 ср = 0, то а2 = 0
и из (3) следует, что при любом t ф = 0. В этом случае (р = <р0 =
= const и движение происходит по меридиональной
у /кривой либо в сторону монотонного увеличения z
у I / (если при t = r0 z = z0 > 0, рис. 91), либо в сторону
\ А / монотонного уменьшения z (z < 0).
] Г" " Если при t = t0 ф = £ = 0, то точка будет нахо-
' диться в равновесии. Однако это равновесие неус-
Рис. 91 тойчиво. При сколь угодно малом начальном зна-
чении | z0 | 0 точка будет неограниченно удалять-
ся по z в одном направлении. (Мы предполагаем, что 1|/, - огра-
ниченная функция.) Предположим теперь, что поверхность -
§ 4.10. Движение точки по поверхности вращения
265
эллипсоид вращения (рис. 92) и мы рассмат- — —
риваем движение с начальными данными: t = t0, // । \\Zmax
(p = ф0, z = Zq, <p = 0, z > 0. Тогда, двигаясь по ме- / / । '» \
ридиану ср = ф0, точка достигнет z = zmax. Из фи- f | i
зических соображений очевидно, что, пройдя \ ; ]
максимум, точка будет опускаться по меридиану \\ । 1у
ф = ф0 + п. Однако формально из (4) мы это
получить не можем (в решении ф = ф0 = const).
Этот парадокс объясняется просто. При z =
ЭФ
“ ^max Р = 0. А на оси р = 0 det-= 0 и цилиндрические коор-
3q
динаты не удовлетворяют условиям, которым должны удовлет-
ворять обобщенные координаты. Получить описание движения в
этом случае несложно, если ввести другие координаты. Мы
обратили внимание на этот факт, чтобы подчеркнуть, что неко-
торые «тонкие» условия, указанные при введении обобщенных
координат, оказываются необходимыми, и их нарушение иногда
проявляется в виде парадоксов.
б) Предположим, что при t = t0
фо*О, z = Zq, z2 =/(zo,a) = O.
При этом выполнение условия
(**)
(***)
необходимо и достаточно для того, чтобы z = Zq
было решением уравнения (4). Нетрудно пока-
зать, что условия (**) и (***) эквивалентны уело-
z ч а| Эф . „
виям ф(г0)-~- и — = 0. Следовательно,
ос! Эг
1 го
если z = Zo определяет экстремальное значение
функции ф(г), то существует решение задачи, в
котором точка движется по параллели z - Zo
(рис. 93).
Упражнение. Используя результаты анализа, прове-
Рис 93
денного в § 4.7, покажите, что точкам максимума функции <|/(г), когда
д2\|/
Э?"
0, отвечают устойчивые движения указанного типа, а точкам мини-
, . д2<|/
мума i|j(z), когда —
dz
> 0, - неустойчивые.
г=г0
266
Глава 4. Вариационный принцип Гамильтона
-- -z=b в) Пусть поверхность расположена между
J [ А плоскостями z = а и z = b (рис. 94), причем
/ । у(я) = V(i>) = 0, i|j(z) > 0 для a<z<b.
/ [ \z2 Рассмотрим общий случай начальных
/ /Д'' Г" Г\ \ условий: ср = фо, а< z = г» < b. ср = <р0 Ф 0 (ос2 Ф
I \ 1 / 1 zi 0), z = z0 4^0 при t - t0. Очевидно, что су-
\ " j ществуют два соседних корня z i, Z2 уравнения
\ । у f(z, ос) = 0, удовлетворяющие неравенствам
- а < Z1 < г0 <z2<b.
Рис 94 Мы будем предполагать, что корни Z], z2
простые. В этом случае на фазовой плос-
кости (z,z) (рис. 95) движение точки изображается замкнутой
линией (см. § 4.7), и движение по фазовой траектории является
периодическим. Из уравнения z2=/(z,oc) следует, что период
движения т(ос) определяется формулой
(4.10.5)
Замена переменных
2л г dz
т J д/Дг.а)’
А,,
т J 4f(z, а)
(4.10.6)
определяет взаимно однозначное соответствие между точками
фазовой траектории в плоскости (z,z) и точками окружности
0 < 2л (рис. 96).
Дифференцируя (6) по г и используя условие z - +y[f(z,a),
найдем
qx = 2л/т. (4.10.7)
То есть по окружности 0 qx < 2л изображающая точка пере-
мещается равномерно.
§ 4.10. Движение точки по поверхности вращения
267
В силу соотношений (6) z является 2л-периодической функ-
цией q{: z(q\ + 2л, ос) = z(q\, ос). Используя (7), запишем интеграл
(3) ф = ос2 /(\|/2 (^)) в следующем виде:
dcp _ т ос2
dq{ 2л у2 (z)
= Х(^1,ос).
(4.10.8)
В силу периодичности z(^i) функция x(gb ос) является тоже
2л-периодической функцией q{. Обозначим через
а = с/(ос) = —
2л
среднее значение функции /, или, иначе, свободный член ряда
Фурье при разложении х(^1? ос) по sin kq{, cos kqx. Представим
Z(<71,oc) = 6z + x(<71,oc),
где разложение %(^,oc) в ряд Фурье не содержит свободного
члена. Обозначим
о(^,а) =
Очевидно, ст(д, ос) - 2л-периодическая функция qx. Интегрируя (8)
и используя введенные обозначения, получим
(р = (р0 + «(<?, - <710) + ,а) - о(^10,а), (4.10.9)
где qю - значение qx, соответствующее начальным данным Zo, z0-
Обозначим
<7, =ф0+<я(<7!-<7ю). (4.10.10)
Тогда
ср = q2 +о(<71,ос)-о(<710,ос). (4.10.11)
При каждом q{ изменению ср на 2л соответствует изменение q2 на
2л, т.е. различным положениям точки на поверхности, отве-
чающим различным значениям угла ср (z = const), соответствуют
точки окружности
0 2л.
Дифференцируя (10) по времени /, определим
<j2 =^ = aq{ = 2л —. (4.10.12)
dt т
Таким образом, в процессе движения материальной точки по
поверхности изображающая точка на окружности 0 q2 2л
движется равномерно.
268
Глава 4. Вариационный принцип Гамильтона
Из проведенного рассмотрения следует, что каждой точке
фазового пространства (z, z, Ф, ф), удовлетворяющей уравне-
ниям (2) и (3) при фиксированных значениях констант интегра-
лов ОС! и ос2, взаимно однозначно соответствует точка двумерного
тора Г2, который является прямым произведением двух окруж-
ностей: 0 qx 2л и 0 2л (рис. 97).
Каждой траектории в фазовом про-
странстве соответствует кривая на торе:
J{-~> Т1 - отображение Jt в Т1. Это отобра-
жение задается двумя функциями qx(t) и
q2(t). Как мы показали, координаты qx и q2
выбраны так, что для любой траектории
и q2 - постоянные величины (они за-
висят только от уравнений поверхности и
ПОСТОЯННЫХ 0С1 И ОС 2 и при фиксированных ОС! и ос 2 для всех
траекторий одинаковы).
Так как траектории в фазовом пространстве не могут пере-
секаться, то их образы на Т2 не пересекаются. Период т и пара-
метр а являются функциями констант интегралов eq и ос2 и функ-
ционалами, зависящими от вида поверхности р - y(z). Может
оказаться, что через время пт (п - целое), когда точка на торе
совершит п полных оборотов по угловой переменной qi9 пере-
менная q2 изменится на 2лр (п, р - взаимно простые целые числа).
То есть по q2 точка совершит р полных оборотов. Как следует из
(12), для этого необходимо и достаточно, чтобы а - р/п. В этом
случае каждая траектория на торе будет замкнутой линией и
движение будет периодическим с периодом пт. На рис. 98 изобра-
жена такая траектория для случая п = 1, р = 2.
Рис. 99
В случае, если а - иррациональное число, то траектория ни-
когда не замкнется, и при t —» 00 каждая траектория будет всю-
ду плотно (без самопересечений) заполнять поверхность тора
(рис. 99). Говорят, что в этом случае отношение частот
qx _ 2л/т _ 1
q2 2га / т а
рационально не соизмеримо, а движение условно-периодическое.
§ 4.11. Движение в центральном поле сил. Задача двух тел
269
Если при некоторых условиях а - рациональное число и дви-
жение периодическое, то при сколь угодно малых изменениях
начальных данных или уравнения поверхности а становится, во-
обще говоря, иррациональным числом, и движения на торе ста-
новятся условно-периодическими. Верно и обратное. Так как
рациональные числа плотны на множестве вещественных чисел,
сколь угодно малой вариацией начальных данных условно-перио-
дическое движение можно сделать периодическим (возможно с
очень большим периодом).
Как мы покажем в дальнейшем при анализе гамильтоновых
систем уравнений, подчеркнутые особенности движений в рас-
сматриваемой задаче суть проявление общих закономерностей в
так называемых потенциальных «интегрируемых» задачах ме-
ханики.
При этом отмеченная близость в пространстве начальных
данных периодических и условно-периодических решений
порождает специфические сложности при исследовании задач,
близких к «интегрируемым».
§ 4.11. Движение в центральном поле сил.
Задача двух тел
1°. В этом параграфе мы рассмотрим некоторые задачи, опи-
сание которых сводится к решению дифференциального урав-
нения
б/2г
—- = np(|r |,f), (4.11.1)
at"
где ср - скалярная функция указанных аргументов. Уравнение (1)
можно интерпретировать как уравнение движения свободной
материальной точки единичной массой под действием силы
rcp(l г I, г), направленной по прямой, проходящей через начало ко-
ординат, и величина которой зависит только от расстояния точ-
ки до начала координат и, возможно, времени. Такая сила
называется центральной.
Лемма 1. Центральная сила имеет потенциал. Для доказа-
тельства этого утверждения необходимо путем непосредствен-
ного дифференцирования проверить справедливость представ-
ления
л । \ pf/V
г<р( г ,о = - —
< or )
при
и
= (4.11.2)
270
Глава 4. Вариационный принцип Гамильтона
at/у
Эг J
=-|г|ф(|г —Гф(| г |,/).
Э|г|у Эг ) |г|
Уравнение (1), в частности, возникает в задачах о движении сис-
темы двух свободных материальных точек (гь тх) и (r2, ш2) в
случае, когда силы их парных взаимодействий не зависят от
скоростей этих точек.Согласно теореме (см. (1.7.22)), в этом
случае силы имеют потенциал
и = {7(1 г, - r21) (4.11.3)
и уравнения движения имеют вид
d2r{
m'~dT
{ЭсН d2r, f ЭС7^ (dU
— , т2 = - — = —
I di) J dr [дг2] Эг,
(4.11.4)
Если каждое из уравнений разделить на т, и вычесть из второго
уравнения первое, то решение задачи сведется к одному урав-
нению
где
dr
dt
t/ = t/(|r|)
т2
(4.11.5)
(4.11.6)
Г = г2 - Г1,
Укажем некоторые из таких задач.
1) Задача двух тел. Две материальные точки (или два тела со
сферически-симметричным распределением плотности) взаимо-
действуют по закону всемирного тяготения. В этом случае
mxm2f
|г2-Г, Г
(4.11.7)
где/- гравитационная постоянная. Подставляя (7) в (6), получим
[/ = -/-; p = /(m,+т2). (4.11.8)
|г| |г|'
2) Взаимодействие двух заряженных частиц по закону Куло-
на. В этом случае U = <sqxq2 /(| г2 - |), где qx nq2- электрический
заряд первой и второй частиц. Нетрудно показать, что U и dU/dr
имеют вид (8), где
mi)
§4.11. Движение в центральном поле сил. Задача двух тел
271
В отличие от задачи двух тел, где физический смысл имеют
только значения ц > 0, в этой задаче ц > 0 для зарядов разных
знаков и ц < 0 для одноименных зарядов.
3) Взаимодействие двух молекул хорошо описывается потен-
циалом Леннарда-Джонса (рис. 100):
С7(| г |) = 4е[(а /1 г |)12 - (о /1 г |)6], (4.11.9)
где £, о - постоянные.
В отличие от потенциала -|bi/l г I,
при котором модуль силы монотонно
уменьшается с расстоянием, для по-
тенциала (9) имеем минимум при I г I =
= I г*1. Для I г I < I г*1 потенциал (9) при-
водит к силам отталкивания, а при
I г I > I г*1 - к силам притяжения.
В частности, возможна равновес-
ная конфигурация молекул при I г I =
= 1г*1. Этого нет для потенциала ~1 /г. Как мы показали, уравне-
ние (1) в задачах взаимодействия описывает относительное дви-
жение, например, точки 2 относительно невращающейся систе-
мы координат, начало которой связано с точкой 1. Для опреде-
ления абсолютных движений г^Г) и г2(0 можно воспользоваться
теоремой о движении центра масс. Согласно этой теореме, центр
масс замкнутой системы движется равномерно и прямолинейно
+m2r2 = v°(r-r0) + r° = a(t), (4.11.10)
где
r° = +m2r2, v° =m1v°+m2v2; if, r2, v?, v2 - координаты
и компоненты скоростей точек относительно абсолютной систе-
мы координат в начальный момент времени t - tQ. Уравнение (10)
можно записать в эквивалентных видах
(т{ +m2)r1 +m2r = -т}г + (т{ +m2)r2 = cc(r), (4.11.10')
гдег = r2-r1.
Если зависимость г(0 определена из решения уравнения (5),
то (109 определяет гДг) и г2(Г). Кроме
задач о взаимодействии двух частиц к
уравнению (1) сводится еще ряд дру-
гих задач.
Предположим, что распределение
гравитирующей массы обладает сим-
метрией относительно оси АА и пер-
пендикулярной ей плоскости ПП
Рис. 101
(рис. 101). В этом случае возможно
272
Глава 4. Вариационный принцип Гамильтона
движение точки в плоскости ПП, которое описывается уравне-
нием (1). При этом функция (p(l г I) может быть достаточно слож-
ной. Такая задача, например, моделирует движение спутника в
экваториальной плоскости Земли или движение звезды в поле
галактики.
2°. Рассмотрим несколько общих вопросов, связанных с урав-
нением (1).
Лемма 2. Движение в центральном поле происходит по плос-
кой кривой в R3. Эта плоскость проходит через начало ко-
ординат.
Доказательство.
а) Момент силы F(e) = rcp(l г I, t) равен нулю:
м(е) =[r,F(e)] = (p(|r|,r)[r,r] = 0.
б) Движение точки не ограничено связями. Поэтому спра-
ведлива теорема об изменении момента количества движения
(см. § 3.5). Так как момент внешних сил равен нулю, то, согласно
следствию из этой теоремы, вектор момента количества движе-
ния не изменяется с течением времени. При т = 1 получим
К = [г, v] = с,
(4.11.11)
где с - постоянный вектор, определяемый начальными данными:
с = [Го, V0].
в) Умножим (11) скалярно на г. Так как г ± [г, v], то получим
(с, г) = 0 или более подробно: с1 г1 + с2г2 + с3г3 = 0. При по-
стоянных с1, с2, с3 - это уравнение плоскости, проходящей через
начало координат.
При заданных начальных данных г0, v0 описание централь-
Рис. 102
ных движений проще проводить относи-
тельно системы координат Е = (ё19ё2,ё3),
орт ё3 которой одинаково направлен с
вектором с, а орт £j лежит в плоскости
векторов ej и е2 исходного репера Е. При
этом угол между в! и ej обозначают Q и
называют долготой восходящего узла
орбиты, а угол между ортами е3 и ё3 обоз-
начают i и называют наклонением орби-
ты. При этом так же, как при введении
углов Эйлера, нетрудно показать (рис. 102), что матрица А пре-
образования Е ——» Е определяется формулой
А = П(1, 0 П(3, Q),
(4.11.12)
§4.11. Движение в центральном поле сил. Задача двух тел
273
где П(/, у), j - 1, 3, - матрицы простых поворотов. Согласно до-
казанной лемме, репер Е неподвижен относительно Е и поэтому
совершенно равноправен с Е.
Введем теперь относительно Е цилиндрические координаты
Fj = pcoscp, r2 = psincp, r3 = z.
В этих координатах выражение кинетической энергии для точки
единичной массой имеет вид
T = |(p2+pV + z2). (4.11.13)
Так как движение происходит в плоскости ё3 = 0, то z = 0 и
| г I = | г | = р.
Таким образом, описание различных потенциальных дви-
жений в центральном поле сил определяется функцией Лаг-
ранжа
L = T-C7 = |(p2+p2(p2)-t7(p,r). (*)
Координата ср - циклическая. Поэтому всегда существует первый
интеграл
dL 2 •
— = р ф = const,
Эф
или
р2ф=|с|. (4.11.14)
Если I с I = 0, то ф = ф0 = const, если I с I Ф 0, то, очевидно, ф > 0 и
угол ф монотонно увеличивается.
Замечание. Построение системы координат Е и соответст-
вующих цилиндрических координат опиралось только на по-
стоянство направления вектора с = [г, v]. Однако постоянен и его
модуль. Это условие, будучи записанным в цилиндрических ко-
ординатах, и определяет первый интеграл (14).
Упражнение. Докажите это. Покажите, что (1/2) р2 (р — площадь, заметае-
мая радиусом-вектором точки в единицу времени (эта величина называется
векториальной скоростью). Покажите, что (14) непосредственно следует из
теоремы площадей (см. § 3.5).
Предположим теперь, что потенциал не зависит явно от вре-
мени: dUldt - 0, т.е. система консервативна. В этом случае из
18. М.Л. Лидов
274
Глава 4. Вариационный принцип Гамильтона
общих теорем следует, что существует интеграл энер-
гии
^(р2 + р2ф2) + (7(р) - h - const. (4.11.15)
Упражнение. Запишите уравнения Лагранжа с функцией Лагранжа, опре-
деленной (*). Вычисляя производную по времени от h (15) в силу уравнений
движения, покажите, что dh/clt = 0.
Если подставить ф = I с 1/р2 в интеграл (15), то получим
уравнение, описывающее закон изменения радиуса р:
о Id2
р- = 2( /7 - С/(р)) - Ц = /(р, Л, I с I). (4.11.16)
Р"
Тем самым для анализа или решения задачи, которая сводится к
уравнению (1) при консервативной силе, определяемой потен-
циалом t/(l г I), необходимо качественно исследовать либо ре-
шить уравнение (16) известного нам типа (см. § 47).
В задаче двух тел (см. (8)) потенциал
t/(p) = --, (4.11.17)
Р
где р - расстояние между точками (р = I r2 - г, I = I г I), ц +
+ ш2) - произведение суммы масс точек на гравитационную
постоянную.
Рассмотрим сначала общий случай I с I Ф 0. Преобразуем
уравнение (16), вводя в качестве искомой переменной и = 1/р и
вместо времени t независимую переменную (р. При I с I Ф 0 мы
можем воспользоваться интегралом
После преобразования получим
' du^
= 2/г + 2ци— | с |2 и2.
(4.11.18)
Обозначим через щ, и2 - корни квадратного трехчлена, стоящего
в правой части (18):
(4.11.19)
4.11. Движение в центральном поле сил. Задача двух тел 275
Уравнение (18) можно записать в следующем более компактном
виде:
= —(и -и{)(и - щ).
(4.11.20)
Если h < 0, то вещественные решения (20) заключены в пределах
и2 и щ, Qi р р2.
При h 0, так как и2 - (1/р2) 0, имеем
0 и М], Р] р оо
В случае h < 0 существует особое решение при h = -ц2/(21 с I2).
В этом случае = и2 и существует решение (18):
и = и, = и2 = const (р = Pi = р2).
В этом решении радиус р не изменяется: точка движется по
круговой орбите р - const с постоянной угловой скоростью
• 1С1 •/ \
Ф = ц1, (p = <p(z-z0) + (p0.
Р'
Обозначим
= Jl + 2/?(Cl~ = е, (4.11.21)
И у И’
где 0 е < 1 при h < 0 и е 1 при h 0. Тогда формулы (19) для
щ, и2 можно записать в следующем виде:
1 + е l-е ,Л„
их =----, =-----. (4.11.22)
Р ~ Р
Уравнение (20) легко интегрируется. Мы не будем проводить
интегрирования, а просто проверим, что выражение
и = — (1 + fcos /) (4.11.23)
Р
(где/= (р — со, со — произвольная постоянная) удовлетворяет этому
уравнению. Действительно,
du
А
-(и - Wj)(w -и2) = —у (1 + ^cos f -1 -е)(1 + ^cos f -1 + e) =
18*
276
Глава 4. Вариационный принцип Гамильтона
2
sin2 f.
2 cos2 — • 2 sin2 — = f —1
2 2
Тем самым мы указали решение уравнения (20):
р = —L
1 + ecos f
(4.11.24)
Из аналитической геометрии известно, что (24) есть урав-
нение кривой второго порядка в полярных координатах отно-
сительно одного из ее фокусов. При h < 0 (е < 1) уравнение (24)
есть уравнение эллипса (рис. 103), при h = 0 (е = 1) - уравнение
параболы, а при h > 0 (е > 1) - уравнение гиперболы (рис. 104).
При/= 0 имеем (р = со; из (24) следует
Р =
(4.11.25)
Тем самым постоянная со определяется значением угла ср, при
котором радиус р достигает своего минимального значения. Если
h < 0, то при/= л (ср - со + л) р = р/(1 - е) = р2 и радиус достигает
максимального значения. В этом случае большая полуось эллип-
са обозначается а:
^Р1+Р2
2
-( р I р 1
2\1 + е 1-eJ
Р = __У
1-е2 2h'
(4.11.26)
Здесь приняты следующие определения:
р - параметр орбиты, е - эксцентриситет орбиты, а - боль-
шая полуось орбиты. Точку, где р = рь называют перицентром
орбиты, а угол со - аргументом широты перицентра. Точку,
где р = р2 (Л < 0), называют апоцентром орбиты. Угол ср - аргу-
ментом широты точки, а / = (р - со - истинной аномалией
точки.
§ 4.11. Движение в центральном поле сил. Задача двух тел
277
Упражнение. Проведите аналогичный анализ для случая р < 0, например
для задачи об относительном движении одноименно заряженных частиц.
Определение заисимости от времени.
Для определения движения в зависимости от времени необ-
ходимо определить функцию ср(/). Используя интеграл ф=1 с 1/р2,
представление р согласно (24) и равенство ср =/+ со, получим
= 2 (! + eC0S /)2 = зТ? С1 + gC0S /)2•
Р Р Р
(4.11.27)
Интегрирование этого уравнения определяет зависимость Дг).
Для явного его решения в случае эллиптического движения
(е < 1) вводят новую вспомогательную переменную Е с помощью
следующих формул:
1 — е2 р
1 - ecos Е =------= —, sgn sin Е = sgn sin f. (4.11.28)
1 + ecos f a
Из (28) нетрудно получить cosf= (cos E - e)/(l - e cos E), sin f =
= (л/1-е2 sinE)/(1 -ecosE). Переменная E называется эксцентри-
ческой аномалией. Нетрудно показать, что при/= кп (к - целое)
Е = кк. С помощью подстановки (28) получим
1-е2
esin ЕЕ =----------у esin f • f,
(1 + ecos/)2
лЙ1-^)3'2 .t
dE(l - ecos E) = --------dt.
(4.11.29)
Это уравнение легко интегрируется. Пусть при t - t0 f = О
(Е = 0). Тогда
3/2
t - tG = (Е - esin Е). (4.11.30)
л/Н
Это уравнение носит название уравнения Кеплера. Когда точка
делает по эллипсу полный оборот (0 ^f< 2л), Е тоже изменяется
на 2л. Время полного оборота т называется периодом обра-
щения. . Из (30) следует
27Ш3/2
Т =---7~—
(4.11.31)
Для случая гиперболических движений (е > 1) для решения
278
Глава 4. Вариационный принцип Гамильтона
Рис. 105
уравнения (27) используют другую замену пере-
менных:
cos/ =
e-ch//
е ch Н -1 ’
sin/ =
л/ё2-! shH
есЬЯ-1 ’
(4.11.32)
где ch, sh - гиперболические косинус и синус.
Нетрудно проверить, что замена (32) определена
корректно: sin2/ + cos2/ = 1, I cos/1 1 при -<=>* <
< H < ©о. Значению H = 0 соответствует f- 0, т.е.
положение перицентра гиперболы. При Н cos/^> cos f =
= -Me. При этом/: = arccos(-l/^) определяет угол между направ-
лением на перицентр орбиты и асимптотами гиперболы
(рис. 105). Из (32) следует:
-------= ^chH-l.
ecos/ + l
(4.11.33)
Дифференцируя это соотношение по времени, получим
е2 -1
eshH H =----------resin/ - f.
(<?cos/ + 1)
Используя (32) из (**) будем иметь
(4.11.34)
/ = —----— Н.
(echH-1)
Подставляя (33) и (34) в (27), найдем
dH(echН -1) = /^(е2 -1)3/2dt.
Р '
Обозначая через Го момент времени, соответствующий Н = 0, и
интегрируя (***), получим
f-^o=C:r^n7T(eshZ7-//), = (4-11.35)
Jll (е -1г е -1 2/z
Уравнение (35) дает неявное представление зависимости H(f).
Упражнение. Покажите, что для случая параболического движения (е = 1)
решение уравнения (27) определяется формулой
_р3/2(. f. 1
27м I 2 3
При I с I = 0 угол ф не изменяется и, следовательно, точка в
(4.11.36)
4.11. Движение в центральном поле сил. Задача двух тел 279
плоскости (р, (р) должна двигаться по лучу ф =
= <р0. Из (21) следует, что р —> 0, е —> 1 при I с I —>
ч л п р -Ic|2/H -Н
-4 0. При этом а = —, ,э = — не зави-
2/Л 2Й
Ц"
сит от I с I. Если h < 0, то и2 = (1 - е)/р -4* -h/p
(или р2 -4 -p/h = 2а). Нетрудно понять, что при
I с I -4 0 эллиптическая орбита превращается в
отрезок прямой длиной 2а, один конец которого
расположен в начале координат (рис. 106).
Переходя к пределу при I с I -4 0 (е -4 1) в формулах (28) и (30),
получим
«3/2
p = rz(l-cosE), Г-Г() =—— (E-sinE). (4.11.37)
Эти предельные формулы определяют зависимость р(г) в
случае h < 0, е = 1. Можно показать, что при I с I - 0 и h >0
движение происходит по лучу ф = ф0, исходящему из начала
координат. При этом зависимость р(г) определяется следующими
формулами, которые также получены предельным переходом из
(35) и (33):
/-z0= p = ^-(chH-l). (4.11.38)
Законы Кеплера. При обработке наблюдений за движением
планет Иоганн Кеплер определил закономерности их движения и
сформулировал их в виде трех законов:
Первый закон. Каждая планета движется по эллипсу, в одном из
фокусов которого находится Солнце.
Второй закон. Секториальная скорость каждой планеты отно-
сительно Солнца постоянна.
Третий закон. Отношение квадратов периодов обращения пла-
нет к кубам больших полуосей их орбит для всех
планет одинаково.
(Секториальная скорость - площадь, заметаемая радиусом-век-
тором в единицу времени.) Именно опираясь на законы Кепле-
ра, Ньютон открыл закон всемирного тяготения. Мы знаем,
что если предположить, что Солнце и все планеты являются
шарами со сферически-симметричным распределением плот-
ности, то движение центров масс планет описывается систе-
280
Глава 4. Вариационный принцип Гамильтона
мой уравнений (1.7.12)
d~Yi /(тх+пг)_ уч
Г; “Г Г
|3
, (4.11.39)
где i = 2, 3, ..., n\f- гравитационная постоянная; гг = г, - Tj -
радиус-вектор центра масс i-й планеты относительно репера
Кёнига, связанного с центром масс Солнца. Для задачи п тел
законы Кеплера, вообще говоря, не выполняются. Однако так
как масса Солнца тх много больше массы т7 любой из планет и
расстояние между планетами | г. - i; | не становится в процессе их
движения очень малым, то оказывается, что члены, стоящие под
знаком суммы, много меньше первых членов в правых частях
(39). Поэтому движение планет можно приближенно опи-
сать (и - 1)-й системой несвязанных уравнений
J2rz _ /(^i + mz) _
Л2 | ъ |3 1
(4.11.40)
Это уравнения задачи двух тел и, как мы показали в этом па-
раграфе, из решения таких уравнений следуют закономерности
движения, указанные в первом и втором законах Кеплера.
(Секториальная скорость - это (1/2) р2ф и, согласно (14), она
остается постоянной.) Из соотношения (31) следует, что для от-
ношения периодов обращения планет при описании их движения
уравнениями (40) справедлива формула
/ А3/
ц. тх + mf
^j)
(4.11.41)
Для того чтобы объяснить приближенную справедливость
третьего закона Кеплера, необходимо еще раз воспользоваться
тем, что масса Солнца много больше масс планет: mz < тх,
i = 2, 3,..., п. При этом можно в (41) принять второй сомножитель
примерно равным единице, и тогда (41) будет формульной за-
писью третьего закона Кеплера.
Об особенностях решения в задаче двух тел
Вернемся к общему случаю центральных движений. Исполь-
зуя уравнение (14), запишем уравнение (16) при независимой
переменной (р:
(Ф? _pi
t/ф] |с|2
I с г
2(/г-С7(р))-Ц-
Р‘
(4.11.42)
§ 4.12. Силы инерции
281
Из анализа эллиптических движений (Л < О
или е < 1) в задаче двух тел (С7(р) ~ 1/р)
следует, что независимо от начальных дан-
ных, когда (р изменяется на 2л, радиус р со-
вершает полное колебание, например от
Pi до р2 и обратно до рь т.е. значение р(ср0)
совпадает с р(ф0 + 2л). Можно показать,
что такой периодический характер движе-
ния существует только при <7(р) ~ 1/р и
Рис. 107
t/(p) ~ р2. Во всех остальных случаях <7(р) для почти всех на-
чальных данных, при которых движение остается ограниченным,
период полного колебания по р не будет рационально соизмерим
с 2л. Например, для потенциала <7(р) - -ц/р + с/р2, где с - малое
число, в общем случае движение в конфигурационном простран-
стве (р, ср) происходит уже по незамкнутой кривой, типа пред-
ставленной на рис. 107. Если с достаточно мало, то движение на
каждом обороте близко к движению по эллипсу, однако угол со,
который определяет положение перицентра эллипса, медленно,
со скоростью, пропорциональной с, изменяется с течением вре-
мени. К такому эффекту приводит учет, например, в задаче двух
тел несферичности одного из тел или эффектов общей теории
относительности. При этом так же, как для задачи о движении
точки по поверхности (см. 4.10), для специальных начальных
данных траектория движения в плоскости (р, ср) может замкнуть-
ся через п оборотов, число которых будет велико при малом с.
4.12. Силы инерции
1°. В гл. 2 мы вывели основные соотношения, связывающие
кинематические характеристики движения точки М относитель-
но абсолютного (неподвижного) репера Е и подвижного репера
£Го (рис. 108). Согласно (2.6.1)-(2.6.5), эти соотношения имеют
вид
v = ve + vr, (4.12.1)
ve =[<o,r-r0] + v0, (4.12.2)
w = we + wc + wr, (4.12.3)
-,r-r0 +[w,[<o,r-r0]] + w0, (4.12.4)
w c = 2[co, vr]. (4.12.5)
В этих соотношениях: г0 - радиус-вектор начала репера ЕГо ,v0 =
282
Глава 4. Вариационный принцип Гамильтона
\ЁГ ~ drjdt, со - угловая скорость вращения
репера Е относительно Е. Вектору со е
г g R3 соответствует кососимметрическая
/r-Го матрица Q = (dAT/dt) А, где А - матрица
' гХ. / преобразования Е —> ЕГо. Наблюда-
М тель, неизменно связанный с репером Е ,
Рис. 108 может определять координаты г (радиу-
са-вектора точки М в проекциях на орты
репера ЕГо) и соответствующие координаты вектора скорости
v -dr / dt и ускорения w = d v I dt - d2r I dt2. Входящие в форму-
лы (l)-(5) векторы г - г (), v п wсвязаны с г, v, w со-
отношениями
r-r()=ATr, v,. = ATv, wr = ATw. (4.12.6)
Запишем уравнения движения материальной точки (г, т):
mw = F, (4.12.7)
где F - результирующая сила, действующая на точку (сумма
внутренних и внешних активных сил и сил реакций связей).
Спроектируем это векторное равенство на орты репера Е :
mAw = F,
(4.12.7')
где F = AF - проекция результирующей всех сил на орты репера
ЕГ(). Согласно введенным обозначениям,
Aw = we + wc + w,.. (4.12.8)
Здесь
wc
did _
----,r
. dt
+ [co, [co, r]] + w0,
w(. = 2[co, v], wr = w,
co = Aco, = w0 = Aw0.
dt dt 0 0
(4.12.9)
(4.12.10)
Подставляя эти соотношения в уравнение (7'), получим
d~r — —
mw = m —= F + F”H, (4.12.11)
dr
рин =рин +FHH,
(4.12.12)
§ 4.12. Силы инерции
283
где
f;h
б/сО _
- m[co, [со, г]] - mw0,
(4.12.13)
F;H =-2m[co,v]. (4.12.14)
Соотношение (11) можно интерпретировать следующим об-
разом. Движение материальной точки для наблюдателя, связан-
ного с подвижным репером £Го, можно описать такими же
уравнениями, как движение относительно абсолютного репера,
если к результирующей всех активных сил (и, возможно, сил
реакций связей) добавить специальные силы FHH. Эти дополни-
тельные силы FHH носят название сил инерции. По аналогии с
определениями, введенными (см. § 2.5, 2.6) для составляющих
ускорений (3), вектор F"H (13) называется переносной силой
инерции, a FCHH - кориолисовой силой инерции (14). Составляю-
щую -m[co,[co,r]] силы F"H называют центробежной силой
инерции.
Для наблюдателя, связанного с репером £Г(), силы инерции
проявляются как причина, вызывающая ускорение материаль-
ной точки. Это ускорение не зависит от расположения и ско-
ростей других точек системы, т.е. силы инерции проявляются
как активные внешние силы. Отметим некоторые особенности
этих сил.
1) Силы инерции - линейные функции радиуса-вектора г и
вектора скорости v материальной точки. При этом только сила
Кориолиса зависит от вектора относительной скорости v; в этом
ее основная особенность.
2) Силы инерции пропорциональны массе материальной
точки. В этом смысле силы инерции похожи на гравитационные
силы. В обоих случаях составляющая ускорения, вызываемого
этими силами, не зависит от массы точки. Эта, на первый взгляд
поверхностная, аналогия явилась идейной основой для создания
одной из великих современных теорий - общей теории относи-
тельности Эйнштейна.
3) Составляющая переносной силы Q = -m[co,[co,r]]-mw0
является потенциальной. Действительно, записывая векторное
произведение [со,[со,г]] в матричном виде
[со, [со, г]] = Q2r,
где Q - кососимметричная матрица, соответствующая вектору
284
Глава 4. Вариационный принцип Гамильтона
со, и используя представление (2.1.6) Q2 = -1со |2/+сосот, по-
лучим
Q = m[|co |2 Г-со (со, г)- w0],
где <•,•) - скалярное произведение в R3.
Рассмотрим функцию
t/ = -y[|w|2|r |2 - <<o,r)2] + m(w0,r).
Прямым дифференцированием нетрудно показать, что
at/y
Эг J
и, следовательно, U - потенциал силы Q.
4) Сила Кориолиса FCHH - непотенциальная сила, так как она
зависит от компонентов вектора скорости v. Из равенства
(FcHH,v> = 0,
которое вытекает из ортогональности векторов [co,v] и v, сле-
дует, что силы Кориолиса FtHH являются гироскопическими; они
не приводят к изменению механической энергии (равной сумме
кинетической энергии и потенциала).
5) Нетрудно показать, что составляющая сил инерции
Qb=-
б/СО _
----. Г
dt
m,
Jco
при ----^0
dt
не имеет потенциала. Действи-
тельно, эту составляющую можно записать в матричном виде:
QB = -mQr, где Q - кососимметрическая матрица, соответст-
вующая вектору dttildt. Если бы существовала функция С7в(г,Г)
такая, что QB = -(Э<7В /Эг)т, то скалярное произведение (QB,dr)
должно было бы быть полным дифференциалом этой функ-
ции в трехмерном пространстве векторов г (при фиксиро-
ванном времени). Для выполнения этого необходимо и доста-
точно, чтобы 3QB/9r была симметрической матрицей, и по-
этому эта составляющая сил не может иметь потенциала.
2°. О весе тела. Для описания большинства задач с высо-
кой точностью можно предполагать, что Земля равномер-
но вращается с угловой скоростью со. Вектор со имеет постоян-
§ 4.12. Силы инерции
285
ную величину
|со| - 0,0000729 рад/с
и сохраняет неизменное направление как относительно абсолют-
ного репера Е, так и относительно репера ЕГо, жестко связан-
ного с Землей. Пусть начало репера ЕГо помещено в центре масс
Земли, а его орты е1,е2,е3 параллельны ортам некоторого
абсолютного репера. При этом мы можем и будем предполагать,
что орт е3 одинаково направлен с вектором со.
Пусть ЕГо =(ере2,е3) - репер, жестко
связанный с Землей, и ё3=е3 (рис. 109).
Для материальной точки, находящейся
вблизи поверхности Земли, в гл. 1 были
выведены уравнения ее движения относи-
тельно ЕГо. Было показано, что на такую
точку действуют силы mg, обусловленные
ее гравитационным взаимодействием с
Землей, и силы mgB, обусловленные грави-
тационным взаимодействием Луны, Солн-
ца и других планет с этой точкой и Землей. В частности, в силы
mgB формально были включены силы инерции, возникающие
при поступательном перемещении системы координат Е . Бы-
ла дана оценка |gB |/|gl~10-7. Если мы
пренебрежем величинами такого порядка,
то тогда при описании процессов на Земле
мы можем считать, что репер £Го опреде-
ляет инерциальную систему координат.
Рассмотрим теперь уравнения движе-
ния материальной точки относительно ре-
пера £Г().Так как dwldt = 0 и w0 - 0, то уравнения движения будут
иметь вид
J2f ____ ___ __________—
т —у- = mw = -2m[co, v] - m[co, [со, г]] + F. (4.12.15)
dt
Пусть точка находится в покое (w = v = 0) относительно Земли.
Будем предполагать, что на эту точку действует результирующая
сила F, которая есть сумма сил: силы ее гравитационного
притяжения Землей mg и силы реакции опоры N (рис. НО).
В этом случае мы получим
-m[co, [со, г]] + mg + N = 0.
N
/////////////
Рис. 110
286
Глава 4. Вариационный принцип Гамильтона
Модуль силы N
|N| = /n|[w,[w,r]]-g| (4.12.16)
может быть измерен, если в качестве опоры мы возьмем, на-
пример, пружинные весы. Величина INI силы реакции опоры на-
зывается весом тела.
Из (16) следует, что вес тела пропорционален его массе. Не-
обходимо обратить внимание, что коэффициент пропорциональ-
ности |[co,[co,r]]-g| зависит от вектора г, т.е. зависит от того, в
каком месте на Земле производится взвешивание. При этом, так
как Земля не является точно сферой со сферически-симмет-
ричным распределением плотности (см. § 1.8), то при изменении
места взвешивания на поверхности Земли изменяется как вектор
g, так и центробежная составляющая силы N. На полюсах ра-
диус г параллелен со и [со,[со, г]] = 0. На экваторе г перпен-
дикулярен со, и центробежная сила оказывается направлен-
ной по радиусу г; при этом составляющая т [со, [со, г]] в форму-
ле (16) приводит к уменьшению силы веса INI по сравнению
с силой гравитационного притяжения zzzlgl. Полагая Igl ~
~ 0,0098 км/с2, |г | ~ 6378 км, нетрудно определить для эквато-
риального случая
а=![и.^.г1]| = |ор|г|д0003
Igl Igl
Суммарное влияние нецентральное™ земного гравитацион-
ного поля, влияние центробежных сил и влияние переменности
расстояния от центра масс Земли до ее поверхности приводят к
зависимости ускорения силы веса INI в основном от географи-
ческой широты ф точки на поверхности Земли. Эта зависимость
описывается приближенной формулой
IN |
-—- = g0(l+0,0053sin" ф),
т
где g0 = 0,00978049 км/с2.
Таким образом, в системе координат, связанной с вращаю-
щейся Землей, центробежная сила проявляется как некоторая
поправка к силе гравитационного притяжения. Так как обе эти
силы потенциальны, то в дальнейшем их можно объединить в
одну потенциальную силу mG. В астрономии угол ф между век-
тором G и экваториальной плоскостью Земли (ен е2) называют
астрономической широтой места.
3°. О силе Кориолиса. Сила Кориолиса F(H" = -2m[co,v] про-
является только тогда, когда материальные точки движутся от-
4.12. Силы инерции
287
носительно вращающейся системы
координат. Наиболее популярный
эффект, который связан с силой Ко-
риолиса, обусловленной вращением
Земли, это разрушение правых бе-
регов больших северных рек. В се-
верном полушарии большие реки в
основном текут в меридиональном
направлении. Поэтому сила F™ =
= -2/??[co,v] направлена примерно
перпендикулярно руслу реки в сто-
рону ее правого берега (рис. Ill, v -
скорость течения). Эта сила и приводит к разрушению правого
берега. Поэтому правые берега северных рек более крутые.
Вопрос. Какой берег разрушается у рек, текущих вдоль меридиана южного
полушария?
Замечание. Указанный эффект проявляется на больших ре-
ках, у которых русло слабо искривлено. Для небольших рек, у
которых русло сильно петляет, наблюдается другое явление.
Высоким размытым берегом часто оказывается берег, более
удаленный от центра кривизны русла.
Выберем систему координат Е так, чтобы выделенные час-
тицы жидкости все время находились на луче, определяемом ор-
том ё| репера Е (рис. 112). Чтобы это условие выполнялось, ре-
пер Е должен вращаться относи-
тельно Земли с угловой скоростью
со*, перпендикулярной поверхности
1
Земли, и | со |~-1 v |, где IvI - ско-
Ip I
рость потока, 1р1 - радиус кривиз-
ны русла. При небольшом радиусе
кривизны 1р1 центробежные силы
-т[со \ [со ’, р]] часто превосходят си-
лы Кориолиса -2/7?[со, v], обусловленные суточным вращением
Земли. Таково объяснение этого явления.
Разрушение правых берегов северных рек - наиболее по-
пулярный, но не самый существенный эффект, связанный с про-
явлением силы Кориолиса. Силы Кориолиса во многом опре-
деляют океанические и атмосферные течения и тем самым игра-
ют важную роль в формировании всего климата на Земле.
Задача о падении камня на Земле. Камень в момент времени
288
Глава 4. Вариационный принцип Гамильтона
t = О брошен (без начальной скорости) в шахту глубиной h,
находящуюся у поверхности Земли на широте (р в северном полу-
шарии. Используя обозначение mG для координат вектора ре-
зультирующей силы центробежных сил и силы гравитационного
притяжения, запишем уравнения движения камня относительно
репера ЁГ():
d2r tv J— dr
—z- = G-2<o,— . (4.12.17)
dt2 L dt J
Мы будем предполагать, что h много меньше радиуса Земли
и будем считать ускорение G постоянным. Так как
< | G |, для решения уравнений движения применим метод по-
следовательных приближений. Представим
Г = 1*! +Г2 +Г3 + ...
и определим rz из цепочки уравнений
Легко видеть, что | rj | = О(| со |z !). Из первого уравнения, полагая
dr{
dt t=Q
= 0, находим
-/ч -z/xx Gr2 dr} tv
rI(z)-r1(0) = —-, —L = Gz.
2 dt
Из условия t = th при | ij (Г) - r^O) | = h находим
Второе уравнение имеет вид
гГ^Г _
—^ = -2[<o,G]r.
dt2
dr
Откуда, полагая r2 (0) - 0, —- - 0. находим
dt ,=o
r2(z) = -|[<o,G]z3.
(**)
§ 4.12. Силы инерции
289
Из (**) следует, что камень отклоняется
на восток (рис. 113). При t = th |r2 |= G]
(1 /3) | со || G | sin(л/2 + (p)rI. Положим (р = />-<2.~~~~Ь
= 60°, |G |= 10’2 км/с2, h = 2 км, |со| = 0,72 х Л 'А
х 10~4. Из (*) определим th = 2,1 с и |r21 = V, х. J
=—0,72-Ю-4-10“2 ~(20)3 ~ 10“3 км = 1 м. //
3 2
Замечание. Если мы хотим грубо опре- рис 1
делить с помощью такого эксперимента,
например, широту места (р, то мы должны независимо опре-
делить величину и направление силы тяжести G. Это можно
сделать различными способами. Направление и величину G
определяет прибор типа математического маятника. При этом
среднее положение маятника в процессе колебаний определяет
направление G, а его период - величину | G |.
Маятник Фуко. Рассмотрим вновь систему уравнений (17),
описывающую движение тяжелой точки на вращающейся Земле
(относительно репера Е :
d2r
"dt2
тт ~ — аг
— G — 2 со,— ,
<7r I
(4.12.17)
где G - постоянное ускорение. Мы вывели это уравнение, пред-
полагая, что начало репера Е расположено в центре масс
Земли, а орт ё3 коллинеарен с вектором со. Уравнения движения
будут иметь точно такой же вид при рассмотрении движения от-
носительно произвольного репера Е, который остается не-
подвижным относительно репера Е . Это
утверждение можно проверить формально, рассмотрев преобра-
зование
г = f+а | — = 0
k dt
определяющее перенос начала репера, а затем преобразование
поворота
г = Аг,
где А - постоянная матрица поворота: dA/dt = 0. Поэтому без
ограничения общности мы можем предположить, что уравнение
(17) описывает движение точки относительно репера, начало
19. М.Л. Лидов
290
Глава 4. Вариационный принцип Гамильтона
которого г0 расположено вблизи поверхности Земли, орт ej кол-
линеарен вектору G, а орт ё2 направлен по земному меридиану.
Из рис. 114 нетрудно видеть, что в этой системе координат век-
торы и G имеют вид
сот = (- sin ф, cos ф,0) | со |,
G т=(1, 0, 0)|G |.
Введем теперь в рассмотрение систему координат Е' = (ере2,
вз), начало которой совпадает с Е и ej =е[ (рис. 115). Будем
полагать, что репер Е' равномерно вращается относительно
репера ЕГо с постоянной угловой скоростью
0 = (£ = const).
Мы можем записать уравнение движения точки единичной мас-
сой относительно репера Е’. Для этого надо воспользоваться ки-
нематическими соотношениями
^ = [0,r] + v,„
dt
d~Y
_ = wr + 2[0,vr] + [0,[0,r]],
dt
где vr, wr - скорость и ускорение относительного репера Е' в
проекциях на орты репера Е . В этих соотношениях мы учли,
что начало реперов совпадает и dft/dt = 0. Подставляя эти соотно-
шения в уравнение (17), получим
w, = G - 2[<о, [0, г ]] - 2[<о, v,. ] - 2[0, vr ] - [0, [0, г ]].
§ 4.12. Силы инерции
291
Проектируя это уравнение на орты репера Е', найдем
^4- = G'-2 w+0',
dt2
dr'
dt
2[w',[0',r']]-[0',[0z,rz]].
Мы предположили, что модули векторов угловых скоростей
|<о'| и 10'1 малы настолько, что можно пренебречь в правой
части уравнения членами, содержащими их квадрат. В этом слу-
чае мы приходим к системе уравнений
d2r'
~ds
— G' - 2 со' + б',
dr'
dt
(4.12.18)
Теперь мы предположим, что движение материальной точки
подчинено голономной связи
| г' | = р = const. (4.12.20)
Предполагая, что второй член в (18) много меньше G' (|со'| и
16'1 малы), будем искать решение (18) методом последователь-
ных приближений
г' = Tj'+r^ + ...
и определим г/ и г2' из следующих систем уравнений:
^ = G' + N,
dt2
dt2
dr, 0N
—L +
dt or
где N- сила реакции связи (20).
Можно показать, что при этом сила реакции изменяется
. 3N
мало, и пренебречь членом — г2 во втором уравнении. Сис-
ЭГ Ч
тема уравнений первого приближения при связях (20) и началь-
/ tlr' \
ных условиях (при t = 0 (грвз^О, (—-е'3 / = 0) описывает плос-
\ dt /
кие колебания математического маятника (в подвижной плос-
кости (е^е^)). Мы сейчас примем дополнительное
предположение, что амплитуда а этих колебаний 1^ е=
мала. Тогда, если пренебречь отличием cos а от 1,
движение точки в первом приближении сводится к е> \
колебательному движению вдоль оси, определяе-
мой ортом е'2 (рис. 116), со скоростью dv'/di = Рис. 116
= рфе^. Для этого решения уравнение следующего приближения
имеет вид d2r'2l dt1 = -2фр[со' + 6',е2].
19*
292
Глава 4. Вариационный принцип Гамильтона
Покажем, что можно выбрать скорость £ вращения репера
Е’ относительно ЕГо так, что и в этом, следующем приближении
движение будет происходить в плоскости (е^е^). Для этого не-
обходимо и вместе с условиями г2 = 0, dr27 dt = 0 при t = 0 доста-
точно, чтобы проекция [<о' + 6',е2] на орт е'3 равнялась нулю.
Записывая это условие, получим
([со' + О',е2],ез) = 0 = ([со',е2],ез) + ([6',е2 ], е3).
Используя циклическую перестановку для смешанного произ-
ведения, найдем
([<о',е2],вз) = (е[,со') = -sing) | со |,
Отсюда следует: для того чтобы в системе координат Е' движе-
ние было плоским, необходимо и в рассматриваемом приближе-
нии при указанных начальных условиях достаточно, чтобы
£ = | со | sing).
Мы вывели формулу, определяющую основной механи-
ческий эффект в этой задаче. Движение маятника в рассматри-
ваемом случае представляет следующую картину:
1) Маятник совершает сравнительно быстрые колебания с
периодом т = 2Лд/р/ |G | (р - длина памятника, IGI - модуль век-
тора G). Например, при IGI = 10 м/с2 и р ~ 3,6 м период т ~ 1 с.
2) Плоскость колебаний маятника медленно с периодом
2л 2л 1СуТ _
-т- =--------« —-— поворачивается вокруг вектора G. При из-
£ | со | sin ср sing)
вестном значении Icol таким путем можно достаточно точно
определить широту места. Описанный выше маятник называется
маятником Фуко. Можно экспериментально проверить справед-
ливость наших выводов из наблюдений за движением маятника
Фуко в Исаакиевском соборе в Санкт-Петербурге.
Невесомость. Перегрузки. Искусственная тяжесть
В гл. 1 рассматривалась задача о свободном движении кос-
мического аппарата вблизи Земли (рис. 117). Были проведены
оценки гравитационных ускорений, которые испытывает мате-
риальная точка (или человек) относительно системы координат
ЕГо, связанной с центром масс корабля и перемещающейся пос-
тупательно. Было показано, что в пределах корабля разме-
§ 4.12. Силы инерции
293
ром порядка 5 м модуль относительного ускоре-
ния |б?2г/б?г2 | не превосходит величину порядка \[/
4 • 10-6 g, где g = 9,8 м/с2 - ускорение силы тяжести
на поверхности Земли.
Для рассматриваемой задачи мы можем вое- \
пользоваться уравнениями (11)—(14) при со = 0: | з
_ d2r _ \
mw = m—5- = F-mwn,
dt2 0
где F - внешняя сила, которая в основном есть си- Рис’117
ла притяжения материальной точки Землей. В задаче о полете
космического корабля причина явления невесомости состоит в
том, что F « mw. Вызываемые гравитационным притяжением
Земли ускорения корабля (иначе - ускорение системы коорди-
нат) и рассматриваемой точки примерно одинаковы. Откуда и
следует, что d2r / dt2 ~0.
Рассмотрим теперь в некотором смысле противоположный
эффект. Пусть космический корабль находится далеко от сило-
вых полей. И, например, с помощью реактивных двигателей ему
сообщается ускорение w0 в постоянном направлении. В этом
случае уравнения движения точки относительно корабля имеют
вид
d2r _
т —у- = -mwn.
dt2 0
Если ускорение | w0 | в к раз больше ускорения силы тяжести на
Земле | w0 | = kg, то вес каждой частицы тела космонавта как бы
увеличивается в к раз. Говорят, что на человека действуют пере-
грузки. Поскольку прочность всей «конструкции человеческого
тела» осталась прежней, то большие перегрузки могут быть
опасны для жизни. Поэтому в различных проектах, связанных с
полетом человека, учитывают ограничения сверху на допусти-
мые перегрузки (т.е. на ускорения корабля).
Еще некоторое время назад с опаской относились к длитель-
ному пребыванию человека в условиях невесомости. Сейчас уже
проведены эксперименты, в которых человек успешно находился
в таких условиях порядка 90 сут. Однако для более длительных
интервалов полета проблема влияния невесомости еще не совсем
ясна. Поэтому обсуждаются проекты создания кораблей с ис-
кусственной тяжестью.
В простейших вариантах космический корабль (система) со-
стоит из двух частей А и Асвязанных тросом и закрученных от-
носительно орта е3, проходящего через центр масс (перпенди-
294
Глава 4. Вариационный принцип Гамильтона
кулярно плоскости рисунка), с угловой
скоростью со (рис. 118). В системе коор-
динат E = (ej,e2,e3) космический корабль
остается неподвижным. Однако это не
инерциальная система координат. Мате-
риальная точка (человек), находящаяся в
корабле А, испытывает относительное
ускорение за счет сил инерции:
d^v __________________
—Т = -2[со, v] - [со,[со,г]].
dt
Если человек (точка) находится в покое
относительно корабля (или репера Е), то кориолисово уско-
рение равно нулю. Если расстояние I = ОА много больше раз-
меров корабля, то центробежное ускорение примерно одинаково
для всех точек внутри корабля. Полагая со = | со | ё3, г = /ер опре-
делим:
J2r . |2
2 — I w | ^е1-
dt
Упражнение. Пусть I = 40 м.
1) С какой угловой скоростью надо закрутить корабль, чтобы ускорение
| J2r/Jr2 | было равно ускорению g силы тяжести на Земле? Полагая
|J2r/Jr2 |= 10 м/с2 ~g, найдем:
1*>1 = Л = | Рад/с,
т.е. период вращения должен равняться ~ 12 с.
2) Пусть человек движется внутри корабля вдоль оси ej со скоростью
1 м/с. Чему равно ускорение Кориолиса? Имеем:
2|[to, v]| = 2|€o||v| = 2*-~1 = 1 м/с2.
Глава 5
Основной аппарат
гамильтоновой механики
§ 5.1. Система уравнений в форме Гамильтона
Г. Предположим, что движение некоторой системы описы-
вается в обобщенных координатах уравнениями Лагранжа второ-
го рода
АР^Т_Г—Y
(5.1.1)
где L = L(q,q,r) - функция Лагранжа (лагранжиан задачи); q,q G
e.Rm - обобщенные координаты и скорости системы.
Если (1) - уравнения голономной механической системы, в
которой силы имеют потенциал C7(q, t) (или обобщенный по-
тенциал V(q,q,O), то L = r(q,q,r)-C/(q,Z) (или£=Г-У).
Как следует из анализа, проведенного в гл. 4, в обоих этих
случаях функция L - квадратичная функция обобщенных ско-
ростей и
д (д2Т
det— — =det——у-^0. (5.1.2)
dql^dqj dq2
В следующем рассмотрении можно предполагать, что
L(q, q,r) - произвольная достаточно гладкая функция указан-
ных аргументов. Однако всегда будем полагать, что матрица
а (azT a2z. Л а2л п
—I — I = —7- невырожденная, т.е. det * О-
2°. Вывод уравнений в форме Гамильтона. Введем в качестве
искомых вместо переменных q и q переменные q и р, где
Р =
аг
а<г
= Ф(ффг)
az?
а<?\
(5.1.3)
- лг-мерный вектор, рт = (р1,/?2,...,рт). По определению, р' -
обобщенные импульсы системы.
Из условия (2) следует, что соотношения (3) локально опре-
деляют (неявным образом) обобщенные скорости q как функ-
296
Глава 5. Основной аппарат гамильтоновой механики
ции р, q, г.
q = f(p,q,r), f &Rm.
(5.1.4)
Таким образом, система т уравнений второго порядка (1) оказы-
вается эквивалентной системе 2т уравнений первого порядка:
^ = f(p,q,r),
dt
dp _( 3lV
dt (3qJ. ,, ’
(5.1.5)
где производные dL/dq вычисляются при постоянных q и t.
Систему уравнений (5) можно записать в более красивом и
удобном для анализа виде, если ввести функцию Гамильтона
Н(р, q, Г), которую иногда кратко называют гамильтонианом за-
дачи. По определению,
Н(Р, q, t) = pTf (р, q, о - L(f (р, q, Г), q, г),
где
pTf(p,q,r) = (p,f> = ^p'7'(p,q,r),
i=l
(5.1.6)
и на место векторного аргумента q в лагранжиан L подставлено
его представление (4).
Дифференцируя (6) по q и р, получим
дН} / df Л
зЧ =₽ ч-
dqJPtt W
ГэГ
(3q) ,.Эр.
V ^У q,t\ Г J q t
(5.1.7)
(ЪН\ ,т / ЭГ Л
=f +Р <~
I Эр ) I Эр J
V У q,t \ ^У q,t
В этих соотношениях индексами внизу мы указываем перемен-
ные, которые остаются постоянными при вычислении частных
производных. Члены, подчеркнутые в (7), взаимно уничтожают-
ся (см. (3)). Откуда следует
f(p,q,r) =
f—т
элУ Гэ/zY
(5.1.8)
Используя (8), уравнения (5) можно записать в следующем виде:
эрГэнУ
dt ( 3q J ’
3qf3#y
Эг (Эр t
H = H(p,q,t). (5.1.9)
§ 5.7. Система уравнений в форме Гамильтона
297
Уравнения (9) называются уравнениями в форме Гамильтона.
Запись этих уравнений можно еще упростить, если ввести в рас-
смотрение составной вектор zT = (рх,р2,...,pm,q ,q\...,qm) и спе-
циальную квадратную матрицу порядка 2т
(О -I Л
9=9^ = ’ пг (5.1.10)
U 0 J
которая называется симплектической единицей порядка 2m.
В (10) 1т - единичная матрица m-го порядка. Используя эти
обозначения, уравнения (9) можно записать в следующем виде:
— , H = tf(z,/), zeT?2m. (5.1.11)
dt \ dz )
Переменные p и q, в которых уравнения имеют форму Гамиль-
тона, называются каноническими. Пары р\ ф называются со-
пряженными переменными задачи. Или подробнее: импульс
р* сопряжен обобщенной координате ф. Их положение в векто-
ре z не произвольно. Если /X расположена на z-м месте, то ql - на
(m + z)-m месте.
Введенная в рассмотрение симплектическая единица 9 обла-
дает некоторыми простыми свойствами, которые мы будем в
дальнейшем использовать.
Нетрудно показать справедливость следующих соотношений:
det^=i, g?T = g?-'=-g?, g?2 = -/2m, (5.1.12)
где I2m - 2т-мерная единичная матрица.
Если Я(р, q, t) - гамильтониан некоторой задачи, то неслож-
но обратно определить соответствующую функцию Лагранжа и
записать уравнения Лагранжа. Действительно, согласно (8),
Если det —z- Ф 0, то из последнего соотношения можно опреде-
Эр
лить вектор обобщенных импульсов как функцию q,q,Z:
р = Ф(фЧ,г). (5.1.13)
После этого, используя (6), определим
L(q, q, t) = Фт (q, q. Z )q - Я(Ф(<1, q, t), q, t).
298
Глава 5. Основной аппарат гамильтоновой механики
н
Условие det—выполняется одновременно с условием (2).
Эр
Действительно, дифференцируя тождество — = р по р,
Э2£ df r „ zo.
получим -т-v — = 1т- единичная матрица. 1ак как, согласно (8),
дер Эр
Э2Н 9f
——= —-, то условие
др Эр
det
*0
< др2
(5.1.14)
автоматически следует из det —Ф 0.
dq
Соотношения между переменными q.q,r и p,q,£ и функция-
ми L и Н являются частным случаем ситуации, рассматриваемой
в теореме Донкина.
Пусть хе/?", а е Z?1 и отображение X: Rn xRk —» R опреде-
ляется функцией
Х = Х(х,а).
(5.1.15)
Здесь и ниже мы указываем отображения пространства, однако
имеется в виду, вообще говоря, отображение некоторых облас-
тей в пространствах R" и Rk. Все рассматриваемые отображения
будем предполагать достаточно гладкими.
Функция (15) при каждом а порождает отображение
Ф: R" —» R", определяемое вектор-функцией
у = Ф(х,а) =
дХ
Эх
(5.1.16)
Теорема Донкина (или теорема о преобразовании Лежандра).
Если
Э2У
det—уф 0, (5.1.17)
Эх“
то локально:
1) Существует обратная (16) вектор-функция
x=f(y,a), f: Rn-+R". (5.1.18)
§ 5.7. Система уравнений в форме Гамильтона
299
2) Существует функция
y(y,a) = fT(y,a)y-X(f(y,a),a)
такая, что
Г( \ (dYY
f(y,<x) = -т- •
I Эу J
3) Справедливо равенство
ЭУ __ЭХ
Эа Эа ’
(5.1.19)
(5.1.20)
(5.1.21)
(5.1.22)
где правая и левая части выражены через одни и те же пере-
менные х (или у).
4) Справедливо равенство
э2х э2у ,
—-у- - 1„ - единичная матрица,
ох ду
. э2у _
откуда следует det—у 0.
Эу
5) Вектору х и функции Х(х, а), согласно (16) и (19), мы ста-
вим в соответствие вектор у и функцию У(у, а), т.е. определено
отображение
X
Х(х,а)
У
у(у,«);
Это преобразование называется преобразованием Лежандра.
При этом Я?2 _ тождественное отображение. Доказа-
тельство утверждения 1) следует из теоремы анализа об об-
ращении отображений. Соотношения (20) и (21) получаются пос-
ле дифференцирования (19) по у и а соответственно и подстанов-
ки в полученные уравнения выражения для у в виде (16). Для до-
казательства 4) следует продифференцировать по у тождест-
во, которое возникает после подстановки в правую часть (16)
fay
ду
применим оператор X к функции У(у, се). В результате получим
ЭУ
. Чтобы доказать последнее утверждение теоремы,
х =
= f(y,a) = х => у = Ф(х,а),
х =
ду)
XY = Фт (х, а)х - Y (Ф(х, а), а) =
- Фт (х, се)х - f т (Ф(х, а), се)Ф( х, ct) + X(f (Ф(х, а), а), а).
300
Глава 5. Основной аппарат гамильтоновой механики
Так как f и Ф взаимно обратные отображения, то £(Ф(х,а),а) =
= х и XY = Х(х,а).
При выводе системы уравнений в форме Гамильтона мы
использовали фактически преобразование Лежандра при сле-
дующем соответствии обозначений:
x~q, у~р, a~(q,Z), X ~ L, Y-H.
Из соотношения (21), в частности, следует, что dL/dt = -дН/dt,
и функция Гамильтона не будет зависеть явно от времени в том и
только в том случае, когда не зависит явно от времени функция
Лагранжа.
Лемма. Если для потенциальной механической системы
обобщенные координаты q вводятся вектор-функциями, явно не
зависящими от времени (г = Ф^), то
H=T+U, (5.1.23)
где Т - выражение кинетической энергии системы через кано-
нические переменные р и q, a U = L/(q, /) - потенциал обоб-
щенных сил.
Следствие. Если, кроме того, U не зависит явно от вре-
мени, то Н - полная механическая энергия системы, выраженная
в канонических переменных.
Доказательство. При условии, указанном в формули-
ровке леммы 6 (см. § 4.3),
r = |qWl)q = r2, L = T-U,
где Sft(q) - невырожденная симметрическая матрица размера
m х m. Отсюда следует:
Р= чИ = ®(q)q^q = 9T‘(q)p = f(p,q),
т = |рт®-'®2й-'р=|ргдг'(Ч)р.
Подставляя q в р, а р в (6), определим
Я = рт®-|р-|рт®‘1р + (/ = |рт2Йчр + (/. (5.1.24)
Замечание. Условия, сформулированные в лемме, и ее след-
ствие часто выполняются в приложениях. Однако следует опа-
саться автоматически отождествлять Н с механической энергией
системы.
$ 5.7. Система уравнений в форме Гамильтона
301
Упражнение. Выведите формулу для гамильтониана задачи в случае, когда
L = ^qT®q + bTq + T0(q,Z)-t/(q,Z) = Г2 +7} +Г0 -U,
= b = b(q,f).
Ответ:
н = |(р - b)T а-1 (р - Ь) - т0 + и = т2 - т0 + и.
В соответствии с определениями, принятыми в курсах диф-
ференциальных уравнений, в случае, если гамильтониан не зави-
сит явно от времени Н = 7¥(z), систему уравнений Гамильтона (и
задачу) будем называть автономной (или обобщенно-консер-
вативной).
Теорема. Гамильтониан автономной задачи является первым
интегралом соответствующей системы уравнений в форме Га-
мильтона.
Доказательство. Вычисляя полную производную от
функции Я(г, /) по времени вдоль траектории системы (9), по-
лучим
dH(z,t) _дН dy дН dq дН _
dt Эр dt 3q dt dt
z чт z v (5.1.25)
^L(^L\ + '— = —
dp dq J dq dp ) dt dt
Если
дН dH(z) Л
= 0, то = O=»H(z) = H(zo) = const.
dt-------------dt
Удобство гамильтоновых систем в приложениях иллюстри-
руется, в частности, следующим примером. Предположим, что
рассматривается механическая система, у которой координата ql
является циклической, т.е. функция Лагранжа не зависит от q{\
Тогда и гамильтониан задачи не будет зависеть от q\ Уравнения
в форме Гамильтона будут иметь вид
_ d#
dt dq1 ' dt др1
dp _ ( dZ/Y dq df/Y
dt dq J dt у dp)
302
Глава 5. Основной аппарат гамильтоновой механики
где
рт = (р2,...,рт), q = (<?2,
Так как р1 = const, a q1 не входит в правые части этих уравнений,
то задача сводится к интегрированию 2т~2 уравнений, после
чего q'(f) находится квадратурой:
?’(z) = ^o+f|^-(p1’ р(?)’
Таким образом, одна циклическая переменная позволяет пони-
зить порядок системы на две единицы.
Пример. Определим гамильтониан задачи о математическом
маятнике (см. § 4.8) следующими выражениями:
гр 1 2-2 Т J dL дт 2 •
Т = — mp <р , U = - mg р cos ср, — = — = тр ср = р.
2 Эф Эф
Условия леммы выполнены, поэтому
„ 1 Р2
Н =-----у - mgpcoscp,
2 mp“
где р, ср - сопряженные переменные задачи.
Составим уравнение в форме Гамильтона
dp дН . dtp дН р
dt Эср dt др тр
Отсюда следует известное нам уравнение
J2cp 1 dp 2 . [~g
—^- =---у —=-or sin ср, —.
dt~ тр dt у р
Так как р лишь постоянным множителем отличается от ф, то
фазовый портрет задачи в канонических переменных р, ср в дан-
ном случае совпадает с фазовым портретом в переменных ф, ср.
Примеры вычисления обобщенных импульсов.
1. Потенциальное движение материальной точки в декарто-
вых координатах:
§ 5.2. Симплектический диффеоморфизм
303
дТ
Эг
Р =
= mr (потенциал не зависит от q).
В этом случае вектор обобщенных импульсов совпадает с обыч-
ным вектором импульса (количества движе-
ния) материальной точки.
2. При описании движения материальной
точки в цилиндрических координатах qT =
= (р, ср, z) (рис. 119) имеем
т =|™(р2 +р2ф2 + z2).
Для потенциального движения L-T -U(q,t\
Обозначим р =
Р*
, где рр - импульс, сопряженный р:
Рр ~ Р> Ар ~ Рг ~ Ъ
ЭТ ЭТ 2. ЭТ
Тр=^ = ^р, рф= — = mpcp, p =-—- = mz.
Эр Эср dz
Таким образом, р ,pz- проекции вектора импульса материаль-
ной точки на ё и е3, а р - проекция вектора момента коли-
чества движения материальной точки на орт е3.
§ 5.2. Симплектический диффеоморфизм
Различные упрощения задачи анализа и интегрирования си-
стемы обыкновенных дифференциальных уравнений связаны с
преобразованиями переменных.
В теории гамильтоновых систем особое место занимает класс
преобразований, сохраняющий гамильтонову форму уравнений,
так называемых канонических преобразований. Если ограни-
читься лишь такими преобразованиями, то мы не только сохра-
няем удобную для анализа форму уравнений, но и упрощаем
задачу исследования. Многие выводы можно получить из анализа
одной функции - гамильтониана задачи, а не более сложного,
хотя и эквивалентного, объекта - системы уравнений.
При реализации указанной программы требуется определен-
ный алгебраический (или (и) геометрический) аппарат, вообще
304
Глава 5. Основной аппарат гамильтоновой механики
говоря, имеющий значение и вне его связи с задачами механики.
В этом разделе последовательно в минимальном объеме изло-
жены основные результаты, которые будут в дальнейшем не-
однократно использоваться.
1°. Симплектическое пространство. Рассмотрим и-мерное
векторное пространство Rn над полем вещественных чисел.
Пусть со определяет отображение прямого произведения про-
странств Rn в вещественную прямую
u:Rn xRn^R. (5.2.1)
Определение 1. Отображение (1) будем называть внешней
2-формой на Rn, если оно удовлетворяет следующим двум
условиям:
а) кососимметричности
0)(£, т|) — — 0)(т), для любых £, т) е 7?", (5.2.2)
б) билинейности
+X2T)2) = AIw(g,T]1) + Л2со(^т]2) (5.2.3)
для любых тг|j, е Rn и Xj, Х2 е R.
Упражнение. Покажите, что 0)(£, £) = 0 для любого £ е Rn
Ниже мы будем рассматривать четномерные вектор-
ные пространства R2™.
Определение 2. Внешнюю 2-форму на четномерном вектор-
ном пространстве R2m будем называть невырожденной, если для
любого ненулевого вектора £ G R2m можно указать такой вектор
тг| g R2”1, что значение со на т] не равно нулю:
Определение 3. Невырожденную 2-форму на четномерном
векторном пространстве будем называть кососкалярным про-
изведением.
Определение 4. Четномерное векторное пространство R2m,
на котором задано кососкалярное произведение, называется сим-
плектическим пространством. Для симплектического 2т-мер-
ного пространства мы будем иногда использовать обозначение
SR2m.
$ 5.2. Симплектический диффеоморфизм
305
Обозначим через
Z2k ~ ’ ^2 ’ ’ f/и +1 ’ +2 ’ —’ + к
набор 2к линейно независимых векторов SR2"1, удовлетворяю-
щих следующим условиям:
1,если j =-m + i,
-1, если j ^к, i = m + j,
О-в остальных случаях,
(5.2.4)
где со - кососкалярное произведение.
Определение 5. Набор ъ2т называется симплектическим ба-
зисом симплектического пространства SR2™.
Теорема 1. Всякое симплектическое пространство имеет сим-
плектический базис, в котором первый орт - произвольный
ненулевой вектор.
Доказательство. Примем в качестве произвольный
ненулевой вектор SR2™. По условию невырожденности со су-
ществует £ g SR2m, для которого со Ф 0. Из последнего усло-
вия, в частности, следует, что fj и линейно независимы. Опре-
делим fw+1 =— * g. Нетрудно проверить, что fj и fw + 1 обра-
зуют набор е2. Доказательство проведем по индукции. Пусть
построен набор Е2Д&<т). При к<т существует вектор
тг| G SR2m, линейно независимый с набором е2А . Представим
f*+I=л+£(м+мт+,),
где Л,, |UZ - пока не определенные числа. Очевидно, что вектор
fк +1 линейно независим с г2к.
Нетрудно проверить, что условия со (fA +,, f7-) = 0 будут выпол-
нены для всех f j е s2k, если мы выберем
Цу l^j^k, m + l^j^m + k.
20. М.Л. Лидов
306
Глава 5. Основной аппарат гамильтоновой механики
Из условия невырожденности со следует, что существует ненуле-
вой вектор £ G SR2m, для которого + £) Ф 0. Так как из пред-
ставления
i = 1 i = 1
при любых х,, у,е R следует о) + j, = 0, то вектор £ линейно
независим с набором, составленным из векторов е2А. и fA +1.
Определим
* + 1 к
fm + k + ] =а£ + У v-f. +У X.f
т + А: +1 i i i in +1
i=1 /=1
Теперь нетрудно показать, что если мы выберем числа ос, V,, х,
из условий
а = 1 = - а w (f,, С), Vj_m=а со (f,., $),
0)(fA + 1,^’ l^j^k m + l^j^m + k + 1
то набор векторов е?А,, fA + (, f,„ +А. +, образует набор е2^_ + Таким
путем доказывается существование набора e2w, образующего
симплектический базис.
Определение 6. Два вектора т] g SR2"1 называются косо-
ортогоналъными, если их кососкалярное произведение равно
нулю: О) (^, к]) = 0.
Из определения симплектического базиса следует, что любой
базисный вектор косоортогонален всем остальным векторам
этого базиса, кроме одного, который называется ему сопряжен-
ным. Сопряженными являются векторы fz и fw+/ (/ т). В част-
ности, любой вектор косоортогонален самому себе.
Упражнения. 1. Докажите следующее утверждение. Внешняя 2-форма на
нечетномерном векторном пространстве /?2," + 1 всегда вырождена, т.е. суще-
ствует вектор g G R2m + 1 (£ # 0) и со(£, iq) = 0 для всех ч G R2m + 1.
2. Определение. Подпространство Q с SR2"1 называется нулевым, если лю-
бые принадлежащие ему два вектора косоортогональны.
5.2. Симплектический диффеоморфизм
307
Докажите, что максимальная размерность нулевого подпространства рав-
на т.
3. Для любого нулевого m-мерного подпространства Q{ ezSR~m можно
указать нулевое m-мерное подпространство g2 ^5R2,n такое, что
sr2"’ =g| +е2>
т.е. любой вектор SR2m можно представить в виде суммы
где ё2еб2.
Произвольный вектор £ пространства SR1'1 можно пред-
ставить в виде его разложения по симплектическому базису:
2 т
Набор 2т чисел zT = (z1, z2,z2'”) образует вектор арифмети-
ческого (координатного) пространства R2”'. Заданное кососка-
лярное произведение на исходном векторном пространстве опре-
деляет кососкалярное произведение в координатном простран-
стве. Если
1т 2т
7=1 7=1
то
' 2 т 2 т
0>(«,.fe)=
/ = 1
i + т i \
-Zi Z2j.
Последнюю сумму можно записать короче в виде произведения
матриц или, используя формальное обозначение для скалярного
произведения в арифметическом пространстве R2,\ в виде
т
Е(^+'" -^ + "%) = z^z, = (5.2.5)
/ = |
плектическая единица. Нетрудно проверить, что форма
задает кососкалярное произведение в арифметическом про-
странстве R2”1.
(Докажите это в качестве упражнения.)
20*
308
Глава 5. Основной аппарат гамильтоновой механики
Тем самым любое арифметическое пространство R2m с задан-
ным на нем кососкалярным произведением является симплек-
тическим пространством и его можно рассматривать, как коор-
динатное пространство некоторого абстрактного симплекти-
ческого пространства SR2m относительно симплектического ба-
зиса e2w. Путем фиксирования симплектического базиса e2w
в абстрактном векторном пространстве устанавливается изомор-
физм этого пространства с симплектическим арифметическим
пространством:
Ниже мы будем в основном
использовать координатное пред-
ставление симплектического про-
странства.
Рис. 120
Замечание. Из соотношения
(5) следует, что кососкалярное
произведение (SFz^z^ векторов
Zj, z2 координатного пространст-
ва равно сумме ориентированных
площадей S- параллелограммов,
построенных на проекциях векторов и z2 на т плоскостей
сопряженных координат + / (рис. 120).
2°. Симплектические преобразования. Рассмотрим линейное
преобразование В: SR2m —> SR2m векторов симплектического
пространства.
Определение. Преобразование В назовем симплектическим,
если оно сохраняет кососкалярное произведение любых векто-
ров %, 1) е SR2m :
co(BSj, Bi]) = со (£,-»]).
Пусть e2m = (fj, f2,f2m) - симплектический базис.
Рассмотрим линейное преобразование базисных векторов
fz = Bf,.
Лемма. 1) Если В - симплектическое преобразование, то на-
бор (f, , f2,..., f2w) - симплектический базис.
§ 5.2. Симплектический диффеоморфизм
309
2) Если (fj, f2,f2w) - симплектический базис, то В - сим-
плектическое преобразование.
Доказательство. При выполнении предположения 1)
1, iт, j = т + i,
= ,Bfy) = co(fr ,fy) = < -1, i-m + j,
0 - в остальных случаях.
Остается доказать, что ^,..., f2zn] - набор линейно независимых
2т
векторов. Предположим 0 - Е^^-Тогда
к = 1
\ + т, если s^m,
-Х5_7П,если5>т.
Полагая 5 = 1,2, ..., 2т, получим, что все Хк = 0. Тем самым пер-
вое утверждение леммы доказано.
При выполнении предположения 2) для любых векторов
к) G SRlm получим
I 2т
co(Bg,B7]) = co
2т
j = l 7
2th 2т 2т 2т
=X Х^7 w(Bf- ’ =X X^'ii7 w(f- ’ f>)=ю(£’ ч)-
i=lj=l i=lj=l
В последних соотношениях £/, rf - координаты в разложении
к) по векторам исходного базиса.
Замечание. Определение симплектического базиса предус-
матривает упорядоченность базисных векторов. Это исполь-
зуется при доказательстве 2).
Вектор преобразованного базиса f. можно разложить по век-
торам исходного базиса
2т
» ।
7 = 1
Как и в общем случае линейных преобразований, симплектиче-
310
Глава 5. Основной аппарат гамильтоновой механики
ское преобразование полностью определяется матрицей
( В\,Вут
в=(в9= ...........
р1
\°2т ’ D2m J
i-Й столбец этой матрицы определяет координаты Z-го вектора
преобразованного базиса относительно исходного.
Пусть и - два вектора симплектического пространства,
переводимые один в другой преобразованием В:
1 = В£.
Пусть z и z — координатные векторы векторов и отно-
сительно базиса е2га. Из равенства
2т ( 2т 2т 2т
В ХЛ, У V//I
5 = 1 v = i J z = i j=i
следует матричное равенство для координатных векторов
z = Bz
(мы обозначаем одной буквой В и оператор и матрицу преобра-
зования.)
Теорема 2. Преобразование В будет симплектическим тогда
и только тогда, когда матрица преобразования удовлетворяет
следующему уравнению:
ВТ 3*В - симплектическая единица. (5.2.6)
Доказательство вытекает из следующей цепочки ра-
венств, справедливой для любых векторов zx, z2 арифметиче-
ского симплектического пространства Т?2ж:
(SFzj, z2) = !^Bzx, Bz2) = ^BT9?Bz1, z2^.
Обозначим через sp(2m) множество симплектических преобра-
зований (матриц). Справедливы следующие свойства:
1.Если Besp(2m) то (det#)2 =1.
2. 12т esp(2w).
3. B~l esp(2/n).
4. Если Bt esp(2wi), В2 esp(2/n), то ВХВ2 esp(2wi).
§ 5.2. Симплектический диффеоморфизм
311
Доказательство. 1.Из(6)и (5.1.12) следует
det BTdet 2F det В = (det В)2 = 1.
3. Применяя к (6) операцию обращения матриц, получим
д?-1 - в-1®-1 (вт)-1 => = в-' =$ в&вТ = 9^ (*)
=> = (вТ)~'&В~' =>& = (в-у^в~'.
4. (в1в2)т^(в1в2) = В2Т(в^В^В2 = В2Т9?В2 = <&.
Ассоциативность умножения матриц известна.
Тем самым мы доказали, что множество sp(2m) - группа.
Замечание 1. Можно показать, что из (6) следует более силь-
ное утверждение: det В = +1. Мы докажем это ниже.
Замечание 2. Из соотношений (*), в частности, следует, что
если Besp(2m), то Вт esp(2m).
Упражнение 1. Докажите свойства 2-4, не опираясь на матричное пред-
ставление оператора В. Вместо свойства 1 докажите невырожденность симп-
лектического преобразования В.
Упражнение 2. Докажите, что & - симплектическая матрица. Покажите,
что применение оператора & к симплектическому базису сводится к взаимной
перестановке всех сопряженных базисных векторов и изменению знака одного
из них.
Определение. Взаимно однозначное отображение облас-
тей UcRr‘ и VcB'7, f:U —называется диффеоморфизмом,
если прямое и обратное отображения непрерывно дифференци-
руемы.
Ниже мы будем говорить о диффеоморфизме пространств
f : R" —> Rn; при этом, вообще говоря, подразумевается диффео-
морфизм некоторых областей, принадлежащих этим простран-
ствам. Кроме того, будем предполагать, что отображение диф-
ференцируемо столько раз, сколько необходимо.
3°. Симплектический диффеоморфизм. Рассмотрим теперь,
вообще говоря, нелинейный диффеоморфизм f .SR2"' —э SR2"1,
определяемый в координатном представлении вектор-функцией
z = f(z), z, zeSR2m.
Определение. Преобразование f будем называть симплекти-
ческим диффеоморфизмом (или кратко симплектическим), если
матрица Якоби 3f/3z этого преобразования является симплекти-
312
Глава 5. Основной аппарат гамильтоновой механики
ческой, т.е. 3f/3z е sp(2m) или
(5.2.7)
Упражнение. Покажите, что симплектичность диффеоморфизма не зави-
сит от выбора симплектического базиса в SR2m.
Множество симплектических диффеоморфизмов SR2™ —»
—» SR2m обозначим 3{ 2т .
Нетрудно установить следующие свойства симплектических
диффеоморфизмов:
1) если f1G3<2nz и (2еУ£2т, то суперпозиция этих преоб-
разований f2 о fj G 2т;
2) если f еЗС2т, то обратное преобразование f-1 принадле-
житЖ2т;
3) тождественное преобразование z = z принадлежит 3<2т.
Доказательство. Пусть zt - fj (z) и z2 = f2 (zj - два
отображения 3<2zn. Тогда если z2 = f2 (f\ (z)) - сложная функция,
определяющая преобразование f2 ° fi, то
Так как
Если
az2_TaV| гэу
3z I 3z1 J _ . A 0Z J
L esp(2m), | — |esp(2m), то -^-Gsp(2m).
J 1dz) dz
(dz^ z_ 4 dz (ЭгУ1 z_ ч
— esp(2m), to — = — Gsp(2m).
V dz J dz \dz J
Из свойств 1-3 заключаем, что справедлива следующая тео-
рема 3. Множество преобразований У£ 2т образует группу, в ко-
торой основной операцией является суперпозиция преобразо-
ваний. Группа sp(2m) является подгруппой группы 3<2zn.
Замечание. Симплектический диффеоморфизм z z может
зависеть от каких-либо параметров а, в частности от времени t.
Например, рассмотрим при каждом t е R и a G Rk диффеомор-
§ 5.2. Симплектический диффеоморфизм
313
физм z = f (z, а, г). При этом если 3z/3z - симплектическая мат-
рица, то множество таких преобразований при различных а и t
будет принадлежать 2т.
Рассмотрим систему уравнений Гамильтона с независимой
переменной т и гамильтонианом W(z, т), zg/?2"' :
tZz
dt
(5.2.8)
где lV(z, т) - достаточно гладкая функция z и т. Решения этой
системы
z = z(z0,t), z(zo,O) = zo (5.2.9)
при каждом фиксированном т определяют диффеоморфизм
fT: z0 —> z пространства R2m.
Теорема 4. Отображение fT - симплектический диффеомор-
физм.
Доказательство. Подставляя решение (9) в (8), по-
лучим
^-z(z0,t) = ^[|)-IV(z(z0,t),t)] • (5.2.10)
дт (Эг ' )
Обозначим через УЯ = Эг/Эг0 матрицу преобразования (9) при
фиксированном т. Дифференцируя (10) по z0, находим
^зк = д^ ^4- яг?,
I Jz = z(z0,t)
(5.2.11)
где 02W/0z2 = (Э/Эг)(Э РК/Эг)т - симметрическая матрица порядка
2т.
Применим к матричному равенству (11) операцию транс-
понирования:
Э d2W
^-37?т = -37?т^-^. (5.2.12)
Эт dz
Рассмотрим
— (Жт«) = ^^^Гс + Гст^—. (5.2.13)
Эт' 7 Эт Эт
Подставляя в правую часть (13) Э37?т/Эт и Э37?/Эт в виде (11)
314
Глава 5. Основной аппарат гамильтоновой механики
и (12) и используя равенство 2F2 = - 12т , получим
—0ШТ &ЯЯ) = - ЯЯТ ЯГ? + Я)?т^2 Я>? = 0.
ЭтЛ ' dz2 dz2
Отсюда следует, что Шст &3Ji = C - матрица, не зависящая от т.
При т = 0
Поэтому
с = злт&зл = &.
Тем самым мы показали, что т.е. 2)? G sp(2m) и
преобразование (9) - симплектический диффеоморфизм. Взаим-
ная однозначность и дифференцируемость отображения следуют
из соответствующих теорем для систем дифференциальных
уравнений.
Следствие 1.В частности, если
dz дН\
— = — ,
dt { dz J
(**)
Н = H(z,t} - рассматриваемая система уравнений Гамильтона
и z = z(t, z0, r0) - ее решения, то отображение z0 —> z при каж-
дом t есть симплектический диффеоморфизм.
Следствие 2. Представим zT = (рт, qT), р, q е Rm. Если
симплектический диффеоморфизм ро,Чо-^Р>Ч определяется
решениями уравнений (8) (или (**)), то в некоторой окрестности
т = 0 (или
ч j dz „
t-t^) не только det------
3z0
dz
det----= 1 ,
3zo >
но
det * 0
дРо
т = 0 dz/dz0
-л
и det------7^0. Это следует из того, что при
dq0
“ ^2т ’
Определение. Симплектический диффеоморфизм z0 z, для
, 9q
которого det -— Ф 0, будем называть стандартным.
dq0
5.3. Производящая функция симплектического
315
§ 5.3. Производящая функция
симплектического диффеоморфизма
Рассмотрим квадратную матрицу порядка 2т. Представим
(5.3.1)
где - матрицы размера т хт (m-мерные блоки матрицы Ж?).
Лемма 1. Матрица Ж? будет симплектической тогда и только
тогда, когда выполнены следующие условия:
1) матрицы ^11^21^ ^22^12 симметрические,
2) 1 - 6Z]T26Z21 = Im - единичная матрица.
Доказательство следует из условия симплектичности матри-
цы ,Жс:
Ч 4,уо -/й,у«п Mf0 -1'»}
^6Z|2 ^22> \^21 ^22/ )
Используя правило перемножения блочных матриц, получим
1) б?216Z| । Cl। j 6?2 j — 0, 3) б?27j 6Z|26?2| — ’
(5.3.2)
2) 6?2|б?12 б-Z] ]6Z27 — ш ’ 4) ^22^12 ^12^22 — 6.
Соотношениями 1) и 4) записаны указанные в формулировке
леммы условия симметричности матриц. Соотношение 2) следует
из 3) после применения операции транспонирования.
Упражнение. Докажите, что столбцы симплектической матрицы W опре-
деляют некоторый симплектический базис в арифметическом пространстве
SR^m. Покажите, что из этого факта сразу следуют соотношения (2).
Представим векторы z, z е SR2m как составные:
z = | М, z = | В |; р, q, р, q eRm,
<47 <47
и пусть диффеоморфизм f : SR2m —> SR2m определяется вектор-
функциями
р = р(рл), q = q(p,q) (5.3.3)
Рассмотрим дифференциальную форму
б/со =pTdq + qT6?p= dq1 +qldp^. (5.3.4)
/ = 1
Справа форма записана в координатном виде.
316
Глава 5. Основной аппарат гамильтоновой механики
Если вместо р, q подставим в (4) их выражения согласно (3),
то получим ту же дифференциальную форму, записанную явно
в координатах р, q:
, |_т Эр 1 , \ т _т Эр )
Эсо = q -i- L/p+ p + q —
I dpj I 5qJ
dq.
(5.3.5)
Теорема 1. О дифференциальной форме d(o. Для того чтобы
форма Эсо была полным дифференциалом некоторой функции
F(p,q)
с/со = </F(p,q),
необходимо и достаточно, чтобы диффеоморфизм f был сим-
плектическим.
Доказательство. Представим (5) в следующем виде:
da = ATdz,
(5.3.6)
где вектор-функция А = A(z) имеет вид
т (7 А т
у dP
dz
7 = 14 7
q7
(5.3.7)
Как известно из анализа, для того чтобы форма (6) в некоторой
области была полным дифференциалом, необходимо и доста-
точно, чтобы матрица dA/dz была симметрической. Это - так
называемые условия интегрируемости.
Используя (7), нетрудно получить следующее представление
для матрицы dA/dz:
dA ( dpAV dq
dz I dz J I dz
m ^2—/
— dz
OA
0/
(5.3.8)
Средний член в соотношении (8) есть сумма симметрических
матриц d2J>7/dz2, умноженных на числа qj, и, следовательно,
это симметрическая матрица. Обозначим ее буквой С.
Запишем матрицу Якоби диффеоморфизма f в блочном виде:
Эг _ Э(р, q) _f б?ц я12 _ Эр _ Эр _ 9q _ 3q
Эг Э(р,q) уй21 a22J 11 Эр’ 12 3q ’ 21 Эр’ 22 9q
§ 5.3. Производящая функция симплектического
317
Тогда
Эр у
dz J
Эд _/ \
0z - ^21’^22 Л
^12/
С помощью введенных обозначений можно (8) представить сле-
дующей формулой:
— = в + с, в=\“"агх
^1^22
(5.3.9)
6^12 ^22 у
Так как С - симметрическая матрица, то для симметричности
ЭА/Эг необходимо и достаточно симметричности В, т.е.
В-Вт=0. (5.3.10)
Если записать последнее соотношение, используя представле-
ние (9), то становится очевидным, что это соотношение будет
выполнено тогда и только тогда, когда блоки а- удовлетворяют
условиям (2) леммы 1. То есть необходимо и достаточно, чтобы
диффеоморфизм был симплектическим. Теорема доказана.
Следствие 1. Если для диффеоморфизма f (3) форма
= pTtZq + qTtZp является полным дифференциалом dF(p, q) и,
кроме того, выполнено условие
det—5*0, (5.3.11)
dq
то f - стандартный симплектический диффеоморфизм. Утверж-
дение очевидно.
Следствие 2. Если f стандартный симплектиче-
ский диффеоморфизм, то дифференциальная форма
б/со = pTdq + qT6?p
является полным дифференциалом в некоторой области про-
странства переменных q, р.
Доказательство. Так как f G У£2т , то, согласно тео-
реме 1,
pTdq + qTdp = dF(p, q).
Для стандартного симплектического диффеоморфизма
q = q(p,q)> р = р(рЛ), (*)
det(3q/3q) Ф 0. Отсюда следует, что локально можно из первого
318
Глава 5. Основной аппарат гамильтоновой механики
соотношения (*) определить q = Ф(ц, р) и, подставляя q во вто-
рое соотношение (*), определить вектор-функцию р = ф(р, q).
Тем самым
с/cd = dF (ф (р, q), q) = dS (р, q).
Рассмотрим теперь отображение Rm х Rm R, определяемое
достаточно гладкой функцией
5 = 5(q,p), q, ре/?'71. (5.3.12)
Будем полагать, что выполнено следующее условие:
*0.
(5.3.13)
Теорема 2. О производящей функции стандартного симплек-
тического диффеоморфизма.
1. Преобразование f : р, q —» р, q, определяемое соотноше-
ниями
является стандартным симплектическим диффеоморфизмом.
2. Для любого стандартного симплектического диффеомор-
физма можно указать такую функцию 5(q, р), для которой вы-
полнено условие (13) и преобразование (р = р(р, q), q = q(p, q))
представимо в виде (14).
Доказательство. Из соотношений (13) и (14) следу-
Ал
ет, что det— ^0. Поэтому из второго соотношения (14) мож-
dq
но локально определить q как функцию р и q : q = q(q, р).
Подставляя ее в первое соотношение (14), определим р = р(р, q).
Аналогично условие (13) позволяет локально однозначно раз-
решить первое уравнение (14) относительно р : р = р(р, q). Под-
ставляя это выражение во второе соотношение (14), найдем
q = q(p, q)
Тем самым (14) действительно определяет взаимно однознач-
ное отображение, дифференцируемость которого обеспечивает-
ся достаточной гладкостью функции S.
1. Из представления (14) очевидно, что
dco = pTdq + qTdp = dS(p, q) = d5(p(p, q), q) = tZF(p, q),
§ 5.3. Производящая функция симплектического
319
-л
следовательно, f - симплектический стандартный (det—^^0)
0q
диффеоморфизм.
2. Справедливость второго утверждения непосредственно
вытекает из следствия 2 теоремы 1.
Определение. Функция 5, рассматриваемая в теореме 2,
называется производящей функцией стандартного симплекти-
ческого диффеоморфизма (или просто производящей функ-
цией).
Замечание 1. Теорема очевидно остается справедливой, если
преобразование р, q —> р, q зависит от параметров ос, например
от времени t. В этом случае
р = р(р, Ф 0, q = q(p, Ф О
и производящая функция S будет тоже параметрически зависеть
от t:
S = S(q, р,0.
При этом функция S, вообще говоря, будет производящей функ-
цией стандартного симплектического диффеоморфизма только
для тех t, для которых в рассматриваемой области q, р выпол-
нено условие (13). То есть утверждения этой теоремы верны,
вообще говоря, только локально.
Выше была доказана теорема о производящей функции
стандартного симплектического диффеоморфизма. Ниже
мы сформулируем и докажем более сильное утверждение.
Рассмотрим линейное преобразование Зф z = 1,2,..., м, про-
странства SR2m. определяемое преобразованием векторов симп-
лектического базиса по следующим формулам:
е+т=^т+!=-^
(5.3.15)
= =f7 для j*i и j*i+m.
В координатном представлении относительно симплектического
базиса это преобразование имеет вид
pfl =q\ qfi =-р\
(5.3.16)
p'j _ pJ _ qj для j
Упражнение. Запишите матрицу 3^.
Определение. Преобразование будем называть i-й пере-
становкой.
320
Глава 5. Основной аппарат гамильтоновой механики
Лемма 2. Преобразование 9% - симплектическое. Доказатель-
ство легко получается проверкой симплектичности базиса
Произведение преобразований
П = ^.1о^.2о,..о^.А
есть снова симплектическое преобразование, которое будем
называть симплектической перестановкой.
Пусть задан симплектический диффеоморфизм f: SR2m
SRlm, определяемый в координатах вектор-функцией
z = f(z),
(5.3.17)
Теорема 3. Всегда можно указать симплектическую пере-
становку
р'
(5.3.18)
П: z —> zz,
Z
такую, что
det Ф 0.
0q
(5.3.19)
Согласно утверждению этой теоремы, преобразование
z' = nof(z) = <I>(z) (5.3.20)
является стандартным симплектическим диффеомор-
физмом.
Следствие. Всегда существует производящая функция
5 = 5(q',p), (5.3.21)
определяющая локально преобразование (20) z —> z' в следую-
щем виде:
, psY _ рр
р = р-7 ’ q= чр >
(5.3.22)
где (р', q') - симплектическая перестановка (р, q).
Выясним алгебраический смысл теоремы 3. Пусть
SB = -^ = | 11 12 । - матрица преобразования (17). Нетруд-
0Z \^21 ^22 J
§ 5.3. Производящая функция симплектического
321
но понять, что матрица преобразования (20)
_ аи ап
а22 )
получается умножением SB на матрицу перестановки:
2В'=П2В.
Более конкретно: матрица SB' получается из ЭВ перестановками
строк ik и т + ik для некоторых ik т (и соответствующем
изменении знака элементов одной из строк). При этом теорема
утверждает, что для симплектической матрицы SB таким путем
можно получить матрицу SB', у которой блок а22 невырожден,
т.е. dettz22^0. Столбцы прямоугольной матрицы
\а22
соответственно определяют координаты векторов в которые
отображаются базисные векторы:
f f f £ =9Rf
Лемма 3. Векторы линейно независимы и косоортого-
нальны.
Для доказательства следует вспомнить, что преобразова-
ние SB - невырожденное и симплектическое:
о = 0)(fm+I.,fm+7) = 28fm+y) = C0(g„^), i,jm,
и использовать следующую лемму.
Лемма 4. Набор т векторов = (£р £2,..., ) можно допол-
нить набором т координатных векторов 3) = М2--T,m), не
содержащим двух сопряженных, так что объединение Х = (§15
£2,..., fn, fz2,..., fim) образует базис (вообще говоря, несимплек-
тический) в R2m. Если эта лемма справедлива, то доказательство
теоремы получается практически сразу.
Так как набор 3) не содержит сопряженных векторов, то
с помощью некоторой перестановки П можно добиться, чтобы
nfil = ±f;p...,nf/m=±f/m,
где j2,..., ~ перестановка чисел 1, 2,...,т. Тем самым, при-
меняя перестановку П по всем векторам набора , получим
П3£ = П£;„ . nf(1, nf(2,..., nfim).
21. М.Л. Лидов
322
Глава 5. Основной аппарат гамильтоновой механики
Поскольку перестановка - невырожденное преобразование,
переводящее базис в базис, то матрица П3£ - невырожденная.
С другой стороны, матрица ПЭ{ имеет вид
(<2
ПЗС = *2
<й22
Отсюда получим О Ф detnX = det а22 det X и, следовательно,
det а22 Ф 0.
В дальнейшем нам потребуется следующая лемма.
Лемма 5. О стандартном симплектическом диффеоморфизме,
сохраняющем одну координату. Рассмотрим два симплектиче-
ских пространства SR2m. Координатные векторы в этих простран-
ствах обозначим через Z и Z. При этом будем использовать
следующие обозначения (здесь и далее 2?, Q , 2? и Q - векторы)
где р, q, р, qe/X; h,rh,t eR - скаляры.
Рассмотрим симплектический диффеоморфизм
Ф:г—>Z,
определяемый вектор-функцией
г = Ф(г) (или Z = Z(Z)).
Будем говорить, что Ф сохраняет координату Г, если
t = z + oc,
(5.3.23)
где ос - некоторый постоянный параметр (не зависящий от Z).
При симплектическом диффеоморфизме, сохраняющем Г, спра-
ведливы следующие утверждения:
1. Для того чтобы отображение Ф было стандартным
симплектическим диффеоморфизмом, необходимо и достаточно
выполнение условия
det|—|^0. (5.3.24)
l9qj
2. Производящая функция S стандартного симплектического
§ 5.3. Производящая функция симплектического
323
диффеоморфизма, сохраняющего г, имеет вид
S = S(Q , = h(t + ос) + 5(q, р, Г), (5.3.25)
а преобразование определяется следующими формулами:
т _ Г 95
q= 3=
19р,
Р =
(5.3.26а)
(5.3.266)
dS
9qJ ’
, г 95
h = h H--, t = t + Qt.
dt
3. Формулы (26a) при каждом t определяют стандартный
симплектический диффеоморфизм р, q —> р, q.
4. Обратно. Если при каждом t задан стандартный симп-
лектический диффеоморфизм SR2m SR2m (р = р(р, q, t), q =
= q(p, q, t)), то его можно продолжить до стандартного симп-
лектического диффеоморфизма SR2{m+v> SR2{m+i):
сохраняющего t.
Доказательство. 1. Чтобы отображение Ф было стан-
дартным симплектическим диффеоморфизмом, требуется вы-
полнение условия
det Ф 0.
9Q
При условии (23) эта матрица имеет вид
dq 9q'
Э? .
1 ,
9Q
= dq
Э° [о
dQ dq
Отсюда следуют det —- det—— и утверждение 1.
dQ dq
2. Если S(Q , - производящая функция, то, согласно (14),
-=dS_
dh
dS
Используя (23), получим —— = t + ос, откуда
d/z
9Q
S = h(t + а) + 5(q, р, t),
dS
dh
= 0.
21*
324
Глава 5. Основной аппарат гамильтоновой механики
Вычисляя 95/dQ и получим преобразование в виде
(26).
3. Если S определяет стандартный симплектический диф-
феоморфизм, то det—ir^O, откуда det-^^O. Тем самым вы-
Э<2 Эд
Э25
полняется условие det—— ^0, и функция 5(q, р, г) по фор-
9qdp
мулам (26а) определяет стандартный симплектический диффео-
морфизм SR2m : р, q —> р, q.
4. Верно и обратное. Если р = р(р, q, t), q = q(p, q, t) при
каждом t - стандартный симплектический диффеоморфизм, то
существует его производящая функция 5(q, р, г). Тогда функция
5 = h(t + ос) + 5(q, р, t) есть производящая функция стандартного
диффеоморфизма
В заключение этого параграфа воспользуемся разработан-
ным аппаратом производящих функций для доказательства сле-
дующей теоремы.
Теорема 4. Определитель симплектической матрицы Ж ра-
вен + 1.
Доказательство. Представим матрицу 28 в блочном
виде
Без ограничения общности можем полагать, что det а22 * 0. Если
для 28 это условие не выполняется, то рассмотрим 28' = П28, где
П - матрица симплектической перестановки. При каждой эле-
ментарной перестановке мы меняем местами две строки мат-
рицы 28 и изменяем знак одной из них. Поэтому det (3% 28) =
= det 2В. Так как любая перестановка есть суперпозиция эле-
ментарных перестановок, то det 2В = det 28'. Согласно теореме 3,
выбором П можно получить матрицу 28', у которой det а22 Г 0.
Пусть 28 - матрица стандартного симплектического линей-
ного диффеоморфизма
f П = 2вГ₽1 р, q, р, q е Rm. (5.3.27)
§ 5.3. Производящая функция симплектического
325
Из линейности очевидно, что производящая функция этого диф-
феоморфизма - билинейная функция р, q:
5 = | рт AiP + pTA12q + |qTA22q,
где Ay - некоторые постоянные матрицы размера т х т, при
этом
(5.3.28)
det А12 Ф О, А* = A j , AJ2 = А22.
Упражнение. Выведите выражение для 5 в виде (28) из (27). Докажите, что
det Д12 ф 0.
Используя (28), получим:
. (ЭХ'
а) Р= -г-
1Э<1.
— АгР + АгЧ’
_ (эх
б) q= —
<Эр
Подставим а) в правую часть (27), а б) в левую часть (27). В ре-
зультате будем иметь
Р
q
= А1Р + А12<1-
= ЖВ
для Vp,q,
(5.3.29)
А
Р
л
где
ол
т
А„
В =
А =
дт д
^12 ^22
о к
Из (29) следует, что A = 28B=>det А = det Ж det В, но detA =
= det А12 = det В. Отсюда получим det Ж = +1.
Примеры симплектических преобразований
(а 1Л
1. Пусть А= -матрица размера 2x2. Условие
d)
т Г°
A SA = ^, 2F = I I влечет единственное соотношение меж-
ду элементами матрицы А:
ad -be - 1.
Тем самым преобразование z = f(z), z, zgT?2 будет симплек-
326
Глава 5. Основной, аппарат гамильтоновой механики
тическим в том и только в том случае, если det— = 1. В част-
dz
ности, двумерные матрицы поворота удовлетворяют этому
условию. Но не только такие. В двумерном случае любое пре-
образование, сохраняющее площадь, является симплектическим:
a(C/) = J dzdz2 = J 6?z16?z2detl
и
UcR2,
где U - область 7?2, o( U) - площадь U.
2. Пусть
p, cp g R.
Рассмотрим преобразование p,ф—> p,q^R\
i— i— (P}
p = J2psn^, ^ = -л/2рсо8ф, z = \ , p>0,
Определим матрицу этого преобразования
О ф < 2tl
(5.3.30)
Э(р, д)
Э(р,<р)
СО8ф
Так как detB = +l, то, следовательно, преобразование (30) -
симплектический диффеоморфизм.
2
Упражнение. Покажите, что S = -^-ctgcp - производящая функция этого
преобразования.
3. Рассмотрим многомерное преобразование:
ze/?2"', ze/?2m,
е = (p\...,pm,qx,...,qm), =(pl,...,pm ,ql,...,qm).
Обозначим
Л Л Л-А
Р-Р
Zi= i ' z>i= -i •
) Vi )
Пусть преобразование определяется функциями вида zz = У/(г, ),
§ 5.3. Производящая функция симплектического
УХ1
i = l,2,...,m. Тогда если для всех i
de/—) - 1,
(**)
то преобразование f будет симплектическим.
Доказательство. Согласно (**), преобразование f
сохраняет проекции площадей на каждую из плоскостей сопря-
женных координат. Следовательно, f сохраняет и сумму проек-
ций площадей. Таким образом, матрица SB = 9f/9z не изме-
няет кососкалярного произведения любых двух координатных
векторов:
g, К): ЭД-д) = (9^ Tf)>.
Поэтому Ж - симплектическая матрица.
Другое доказательство. Пусть S^q1 ,р1) - производящая
02 g
функция zz ^zz и det '. Ф 0 (непосредственно или после i-й
oploql
т
перестановки). Тогда 5(р,q) - У S^q', р') - производящая
,=|
функция преобразования f. При этом
det
Э25
ЭрЭд
Пусть
А
det —* 0.
др dq
=(p',...,pm,q',...,qm).
Тогда преобразование
pl = д^2р' sin ср', ql = -д/2р' coscp',
z = l,2,...,m (р' > 0, 0 ср' < 2л)
- симплектический диффеоморфизм.
4. Пусть A(t) - матрица поворота размера т х т. Рассмотрим
преобразование П:
р = A(0p. q = A(t )q.
Это преобразование симплектическое.
Доказательство. Рассмотрим 5(q, р, t) = pTA(Oq,
328
Глава 5. Основной аппарат гамильтоновой механики
Э25
det-—- = detЛ = 1. Нетрудно показать, что S - производящая
dpdq
функция преобразования П:
(ds
р=
= Атр => р = Ар (ААТ = /),
3q
q =
= Aq.
(5.3.31)
5. Рассмотрим произвольный диффеоморфизм f: Rm
определяемый вектор-функцией
q = f(q), det-j^Co.
dq
Существует стандартный симплектический диффеоморфизм
р, q —» р, q, в котором координаты q преобразуются соглас-
но (31).
Доказательство. Рассмотрим производящую функцию
о — тп/ ч j d2S 9f „
S = р f(q), det—— = det— Ф 0.
dpdq dq
Тогда
(ds
p =
"df
4dq
"df
4dq
Р>
l^q
q =
§ 5.4. Канонические преобразования и уравнения
Г амильтона-Якоби
1°. Рассмотрим систему уравнений Гамильтона
— = ^—1 , ze/?2m, H = H(z,t).
dt I dz J
Пусть вектор-функция
z = z(z, г)
(5.4.1)
(5.4.2)
§ 5.4. Уравнения Гамилътона-Якоби
329
в каждый момент времени t определяет диффеоморфизм
glm _________________________j^lm
Если преобразование (2) не зависит явно от времени
z = z(z), (5.4.3)
то будем называть его автономным.
Рассмотрим, как преобразуется система уравнений (1) при
автономном преобразовании (3).
Подставляя (3) в (1), получим
ЭН V (дН ЭгУ (dz
9zA=z® \dz dz) <9z
(5.4.4)
где _ _
Н = H(z, t) = 7/(z(z),/). (5.4.5)
( 9z^
По предположению, det — О, откуда
k 9zJ
дН
dz
dz dz dz -—i
— =------------= ty\
dt dz dt
dz
dt
9z J
(5.4.6)
Теорема 1. а) Автономный симплектический диффеомор-
физм сохраняет форму уравнений Гамильтона.
б) Новый гамильтониан задачи Н получается формальной
заменой (3) в исходном гамильтониане.
Доказательство, а) Если (3) - симплектический диф-
феоморфизм, то матрица Якоби этого преобразования удов-
летворяет соотношению
При этом из (6) получим
dz
dt
dH
dz
Таким образом, система уравнений в новых переменных гамиль-
тонова.
Утверждение б) непосредственно следует из формулы (5).
Определение]. Диффеоморфизм z—» z, определяемый век-
тор-функцией z = z(z, Г), будем называть каноническим, если он
330
Глава 5. Основной аппарат гамильтоновой механики
преобразует любую систему в форме Гамильтона снова в
гамильтонову систему (возможно, и с другим гамильтонианом).
Согласно теореме 1, автономный симплектический диффеомор-
физм - каноническое преобразование.
Определение 2. Преобразование z = z(z) вида
р = Рр, q = +Pq,
(5.4.7)
где р, q G Rm, Р - число, будем называть «растяжением».
Нетрудно показать, что при 3^1 преобразование (7) не
является симплектическим диффеоморфизмом. Действительно,
det^| = (±irp2'” *1 при Р*1.
dz
В то же время преобразование «растяжения» - каноническое
преобразование:
dp _ ( Э/Л
dt \ 9q J
dq _ dtT T
dt V dp >
б/р (dip
dt 9q ,
Эд ЭЙ
dt Эр ’
H=±^H(№,±₽q,Z).
Теорема 2. О канонических преобразованиях. Произвольное
автономное каноническое преобразование является суперпози-
цией симплектического диффеоморфизма и преобразования
«растяжения».
Пояснение. При доказательстве теоремы существенно
используется свойство канонических преобразований сохранять
форму любой гамильтоновой системы. Приведем пример,
когда преобразование, сохраняющее гамильтонову форму дан-
ной конкретной системы, не является каноническим.
Пример. Линейная система уравнений Гамильтона
dp • i dq • , y1 v t t
— = -Xp, -—-kq H=>kpq
dt dt \ J
не изменяется при преобразовании pl=v!pl, ql = $lql, где
ocz, P' - числа. Однако при различных ос' и Р' это преобра-
зование не является ни преобразованием «растяжения», ни сим-
§ 5.4. Уравнения Гамилътона-Якоби
331
плектическим диффеоморфизмом, т.е.
det—= a1a2...ocwp1|32...p™ тИ в общем случае,
dz
Для доказательства теоремы 2 нам потребуется следующая
лемма.
Лемма. Пусть ieRn, f(z)eR и Ф(г)е7? - достаточно
гладкие функции z, A = (A/(z)) - матрица размера WxW, эле-
менты которой могут зависеть от z.
Утверждение. Если для фиксированной матрицы A(z)
и любой функции/(z) можно найти такую функцию Ф(г), чтобы
в некоторой области G<^RN переменных z выполнялось равен-
ство
ГЭ/Т ГЭФУ
a(z) = A(z)U- = — , (5.4.8)
Vdzj \ dz J
то A(z) = с/, где I - единичная матрица TV-го порядка, с - не зави-
сящее от z постоянное число.
Доказательство леммы. Из (8) очевидно, что
/а эф V \
(a, Jz) = ( —— ,dz) = tAD (5.4.9)
U dz ) /
- полный дифференциал. Отсюда необходимо следует, что
Эа/Эг - симметрическая матрица. Это условие можно записать
в следующем виде:
^т|Е 4'’тт'| = /г[Е = ...." <5-4.10)
dzpJ dz dzpJ
Обозначим
п „ j yf
' wJ ’ sq [dz’dz4)'
4 z0 v Z Z = Zo
где z0 - произвольная точка G. Рассматривая (10) при z = z0,
получим
S 1+- iz »P+E 44--E №,.=» (5.4.11)
v J P=l P=\
Для произвольной функции Дг) ap и apj = ajp - произвольные
332
Глава 5. Основной аппарат гамильтоновой механики
числа. Следовательно, коэффициенты при различных ар и a pj
должны быть равны нулю.
1. При рГ к коэффициенты api входят только во вторую
сумму и поэтому А[ = 0 (р Ф к).
2. При р = к во второй сумме и р = i в третьей находим
4 =А! = c(z).
3. Рассматривая коэффициенты при и ак в первой сумме
и учитывая, что А? = 0, получим
1) = 0 (при k^i), 2) = 0 (при
dz dz
Из первого соотношения следует, что с может зависеть только
от zz, а из второго - только от zk- Поэтому
9с
— = 0=>c = const.
9z
Из этого и предыдущего условий находим, что
А = с1.
Доказательство теоремы 2. Из (6) следует: чтобы
преобразование (3) сохраняло форму уравнений Гамильтона, не-
обходимо и достаточно, чтобы выполнялось равенство
ЭгЛ 9zYf dHV _f 93€(z, 0
dz) \dz) ) v 9z
(5.4.12)
где 3€(z, t) - некоторая новая функция Гамильтона. Обозначая
( 9zA ( 9zY
V = A(z), приходим к проблеме, которая решена
V dz ) V dz J
леммой. Матрица А должна иметь вид cl. Отсюда
V dz ) \dz)
Мы получили условие, которому должна удовлетворять мат-
рица произвольного канонического преобразования. В этом слу-
чае новый гамильтониан имеет вид
W, 0 = c#(z, 0 = cH(z(z), О- (5.4.14)
Представим z(z) как суперпозицию преобразований
a) z = f(z') и б) z' = Yjc|^z’
§ 5.4. Уравнения Гамильтона-Якоби
333
где с - постоянная, |с| - модуль числа с,
1 =
° 1
8 = sgn с - знак с. Очевидно, что б) есть преобразование «растя-
жения». Тогда
dz
dz
Г
Подставляя это соотношение в (13), получим
(5.4.15)
Нетрудно показать, что
13*1 = 83*.
Так как 8|с| = с, то из (15) следует
dfVpfV ~
2ч т— = 3*.
dz'J \dz'J
Таким образом, преобразование z = f(z') - автономное симплек-
тическое преобразование, и теорема доказана.
Замечание. Возможность использования «растяжения» следу-
ет иметь в виду. Однако существенного упрощения системы
уравнений можно добиться лишь преобразованиями симплекти-
ческого диффеоморфизма. Только ими в дальнейшем мы и
будем заниматься.
Если рассматриваемая система уравнений Гамильтона не
является автономной, то упрощения задачи можно ожидать,
лишь применяя неавтономные преобразования. Неавтономный
случай удается свести к автономному с помощью описанного
ниже специального приема.
Рассмотрим вновь систему уравнений Гамильтона (1)
dz
dt
дН
dz
Н = H(z, t),
p,4ERm.
Введем в рассмотрение вектор Z G /?2(ш+1)
Z = , <3>=\ Я Q = , h,t<ER.
Iq J W Id
(5.4.16)
334
Глава 5. Основной аппарат гамильтоновой механики
Определение 3. Систему уравнений Гамильтона с гамиль-
тонианом
Ж^) = Ж®\ Q ) = h + #(z, 0 (5.4.17)
и независимой переменной т будем называть расширенной сис-
темой для системы уравнений (1). В расширенной системе h и
t - дополнительные сопряженные переменные задачи. Гамильто-
ниану (17) соответствует система уравнений
а)
dz d/7(z, t)
— ” ----------
dT I dz
z-x dt
6) ~r
<h
(5.4.18)
dh
x dh дЖ dH
в) ~T =—= _^~-
dT dt dt
Система уравнений а) и б) не зависит от Л и полностью экви-
валентна исходной системе (1).
Так как расширенная система уравнений автономна, то га-
мильтониан задачи является первым интегралом этой системы:
Л + H(z,r) = Ж = const = Ло + /7(z0,r0).
Пусть для исходной системы уравнений заданы начальные
условия г = r0, z = z0. Без ограничения общности дальнейших
выводов можно принять соответствующие начальные условия
для расширенной системы в следующем виде:
т = 0, z = z0, t = t0, h = h0=-H(zl0,t0).
В этом случае
/z = -H(z,r).
То есть дополнительная переменная h с точностью до знака
совпадает с гамильтонианом исходной задачи.
При этом интегральная кривая в расширенном фазовом
пространстве (z, t) исходной системы совпадает с проекцией
траектории Z(t) расширенной системы на подпространство (z, t).
Предположим теперь, что отображение
Р = Р(Р,<М), q = q(p,q>0 (5.4.19)
при каждом t является стандартным симплектическим диффео-
морфизмом р, q —> р, q. Тем самым (19) определяет неавто-
номное преобразование. Пусть 5(p,q,r) - его производящая
функция. Согласно лемме 5 § 5.3, функция
S = 5(2?,Q ) = ht + 5(p,q,r)
§ 5.4. Уравнения Гамилътона-Якоби
335
является производящей функцией стандартного симплекти-
ческого диффеоморфизма: Q Q , сохраняющего пере-
менную t. Это преобразование автономно и определяется
следующими формулами:
f&sY 1 - эх _ ГэхУ -
р= — , h = h+ — , q= — , t=t. (5.4.20)
dq) dt I ap J
Согласно теореме 1 этого параграфа, преобразование (20),
примененное к системе уравнений с гамильтонианом 3€(Z), сохра-
— (lf\
няет в переменных Z = _ гамильтонову форму уравнений
с гамильтонианом
W) = 2C(Z(Z)).
Этот гамильтониан, используя (17) и (20), можно записать в сле-
дующем виде:
ад) =
,q,/
q=q(p,q,r)
Таким образом, гамильтониан 3€(Z) имеет вид
где
2C(Z) = /z + H(z,0,
H(z,r) =
(5.4.21)
(5.4.22)
H(z,0 не зависит от h .
Из представления (21) следует, что система уравнений с га-
мильтонианом 3€(Z) является расширением системы уравнений
dz _/dH(z,r)Y _ (Р^
= г -—--- , z = I
dt-----------{ dz J {qj
и эквивалентна ей. Тем самым доказана следующая основ-
ная теорема о неавтономном стандартном симплектическом
диффеоморфизме.
Теорема 3. 1. Произвольный (неавтономный) стандартный
симплектический диффеоморфизм
p = p(p,q>0, q = q(p>q>0 (5.4.23)
является каноническим преобразованием.
336
Глава 5. Основной аппарат гамильтоновой механики
2. Если 5(р, q, t) - производящая функция этого диф-
феоморфизма, то гамильтониан преобразованной системы имеет
вид
H(p,q,O =
Э5
Эг
3qJ
,4,t
(5.4.24)
q=q(p,q,r)
Формула (24) является одной из основных формул га-
мильтоновой механики. Она будет неоднократно использовать-
ся.
Следствие. Любой симплектический диффеоморфизм -
каноническое преобразование.
Доказательство. Пусть z = f(z, t) - симплектический
диффеоморфизм. Запишем его в эквивалентном виде
г = ГГ‘ °n°f(z,Z),
где П - симплектическая перестановка, в результате которой
z' = n°f(z,r) - стандартный симплектический диффеоморфизм.
Согласно теореме (3), это преобразование каноническое. Оче-
видно, каноническим является и автономный симплектический
диффеоморфизм П-1.
2°. Уравнение Гамильтона-Якоби. Пусть мы рассматриваем
систему уравнений в форме Гамильтона
dq _ ЛЭЯ>Т
dt Эр }
dp _ Г дН
dt 9q
, H=H(p,q,O, p,qe/?w.
(5.4.25)
Определение 1. Уравнение в частных производных первого
порядка
= 0 (5е7?)
(5.4.26)
носит название уравнения Гамильтона-Якоби, соответствую-
щего системе (25).
Определение 2. Решением уравнения (26) называется функ-
ция 5(q, г), для которой левая часть (26) обращается в нуль в
некоторой области переменных q, t.
Определение 3. Функция 5(q, t, а), зависящая от т пара-
метров ат = (ос1, ос2, ..., осш), называется полным интегралом урав-
нения (26), если
a) 5(q, /, а) является решением уравнения (26) при всех а,
§ 5.4. Уравнения Гамильтона-Якоби
337
принадлежащих некоторой области а е U с Rm, и
б) det—— *0. (5.4.27)
dqda
(Предполагается, что 5(q, /, а) дифференцируема по всем пере-
менным достаточное число раз.)
Ниже через 0 будем обозначать m-мерный вектор арифме-
тического пространства R2m\
pT = (P1,p2,...,pm). (5.4.28)
Теорема Якоби. Если 5(q, t, ci) - полный интеграл уравнения
Гамильтона-Якоби, то:
1) соотношения
можно разрешить относительно р и q:
p = p(a,P,0, q = q(ot,p,z); (5.4.30)
2) вектор-функции (30) при постоянных а и 0 являются
решением уравнений Гамильтона (25).
Доказательство. 1) Согласно (27) и (29), det (d0/dq) Ф
Г 0. Отсюда следует, что из второго соотношения (29) можно
определить q в виде (30). Подставляя q = q(a, 0, t) в первое соот-
ношение (29), определим р в виде (30).
2) Так как (27) для полного интеграла выполнено, то 5(q, t. а)
можно рассматривать как производящую функцию симплек-
тического диффеоморфизма:
рА (
q; W’
Новые переменные а, 0 удовлетворяют уравнениям Гамиль-
тона с гамильтонианом, определяемым согласно формуле (24):
Н(а,0,г) =
dS
df
as у
3qJ ’
+ Н
Так как 5 при всех а есть решение уравнения Гамильтона-Яко-
би, то Н = 0. Следовательно, а и 0 удовлетворяют уравнениям
^ = 0. ® = 0,
dt dt
22. М.Л. Лидов
338
Глава 5. Основной аппарат гамильтоновой механики
и любые постоянные аир являются решением. Тем самым р и q
в виде (30) удовлетворяют исходной системе уравнений (25) при
любых постоянных аир (заведомо до тех пор, пока выполнено
условие det (92S79q Эа) Ф 0).
Следствие. Если система уравнений Гамильтона (25)
автономна, т.е. Н = Н(р, q), то можно искать полный интеграл
уравнений Гамильтона-Якоби в следующем специальном виде:
5 = -/(оф +W(q,a), (5.4.31)
где W не зависит от t, /(а) - функция а. При этом уравнение
Гамильтона-Якоби (24) преобразуется к следующему виду:
Н
dq )
,q
7
= /(«)•
(5.4.32)
Если W(q, а) - полный интеграл уравнения (32), то 5 (31) будет
полным интегралом исходного уравнения. При этом решение
имеет вид
(dwY _ (Э/У pwy
р= — , р=- — *+ — .
С 9q J V Эа J \ да J
Разрешая эти соотношения относительно р и q, найдем
р = р а,р +
q = q а,Р +
да J
t
7
где а, Р g Rm - постоянные векторы.
Замечание. Этот же результат можно получить, рассмат-
ривая производящую функцию W(q, а), удовлетворяющую (32).
Тогда гамильтониан системы в переменных а и Р, согласно (24) и
(32), будет иметь вид
Н(а,Р) = Н
dW
dq >
/(«)•
Ч
Система уравнений имеет вид
da
dt
Г дн
;эр
= 0,
f э/
dt да < да
а = a0 = const, P = Po +
(r-r0)«
«о
§ 5.4. Уравнения Гамильтона—Якоби
339
Теорема о существовании полного интеграла уравнения Га-
мильтона-Якоби. Пусть
p=p(Po>qO’f)’ q=q(p0’<io’O (5.4.зз)
- решение системы уравнений Гамильтона
di (дНУ Г рЛ
— ’ # = #(p,q,O, 1 = \
dt \oi)
с начальными условиями / = /(), р = pb q = ср.
Нам известно, что отображение р0, q0 р, q при каждом t
(по крайней мере, для достаточно малых 11 - tQ I) является стан-
дартным симплектическим диффеоморфизмом. Пусть W(p0,q,O
- его производящая функция, det(3W /3po3q):?tO. Тогда отобра-
жение (33) можно записать в следующем виде:
Р =
'awY
ч dq ) ’
(5.4.34)
Рассмотрим преобразование (33) как замену переменных
р, q р0, q0 в уравнениях Гамильтона. В результате такой за-
мены мы приходим к уравнениям Гамильтона
^0 =д/ dH0'
dt ( dz0 ,
zo ~
.Чо/
где Но, согласно (24), имеет вид
aw
H0 = H0(p0,q0,O= — + H
dt
8W
dq
,q,?
2 Jq=q(p0,q0,O
Так как р0 и q0 не изменяются с течением времени, то не-
обходимо, чтобы SHq/Siq = 0. Обозначим
x dW r,
Ф(ФРо,0 = ^- + #
ot
3W
— ,q,^
dq J J
Тогда
^о(Ро^оТ) = O(q(p0,q0,0,p0,0.
Из условия
ЭН0 ЭФ 3q dq _
0 = —-2- = —при det-^O
dqo dq 8q0 8q0
22*
340
Глава 5. Основной аппарат гамильтоновой механики
получим ЭФ/Эд - 0. Дифференцируя Но по р0, найдем
ЭН0 _ ЭФ 9q ЭФ _ ЭФ
Эр0 3q Эр0 Эр0 Эр0 ’
Тем самым функция Ф может зависеть только от времени г.
= a(f).
Полагая W =W(q,p0,t)+ a(t)dt, найдем,что
= 0.
При этом
a2w
3q3p0
*0.
Таким образом, мы доказали, что функция IV, которая лишь на
аддитивную функцию времени отличается от производящей
функции отображения (33), определяемого решениями уравне-
ний Гамильтона, является полным интегралом уравнения Га-
мильтона-Якоби.
Замечание 1. Как следует из доказательства последней тео-
ремы, построение полного интеграла уравнения Гамильтона-
Якоби опиралось на известные решения уравнений Гамильтона
(33). Практическое применение развиваемой теории в механике
идет точно в обратном направлении. Для того чтобы избежать
интегрирования системы уравнений Гамильтона, пытаются
найти какой-либо полный интеграл уравнения Гамиль-
тона-Якоби. Хотя, по существу, эти задачи эквивалентны, прак-
тика показывает, что определение полного интеграла, если это
возможно, реализуется проще. При этом и объем вычислений на
таком принципиальном шаге оказывается обычно меньше, чем
при прямом интегрировании уравнений Гамильтона. Поскольку
читатель понимает, что чудес не бывает, то следует указать, куда
переходят аналитические сложности. Часто трудно перейти от
неявного вида решения (29), полученного с помощью произво-
дящей функции, к явному виду р = р (а, Р, t), q = q(a, р, t). Одна-
ко здесь уже не приходится иметь дело с дифференциальными
уравнениями.
Замечание 2. Теорема доказывает существование полно-
го интеграла уравнения Гамильтона-Якоби для некоторой об-
§ 5.5. Некоторые примеры применения метода Якоби
341
ласти переменных р, q и для определенного отрезка времени
11 - tQ I т , т.е. теорема гарантирует существование полного
интеграла только локально.
В некоторых «счастливых случаях» удается найти полный
интеграл для всего множества значений р, q, t, представляющего
практический или теоретический интерес, в частности для всех
вещественных значений t. Такие задачи называются интегри-
руемыми. Мы приведем примеры таких задач.
Замечание 3. Не следует забывать, что для приближенного
решения обыкновенных дифференциальных уравнений на огра-
ниченном интервале времени можно применять метод числен-
ного интегрирования. В частности, проводя численное интегри-
рование с различными начальными данными (70, р0, q0), можно
получить приближенное представление о поведении решений в
некоторой области расширенного фазового пространства:
р=р(Ро,ЧоЛ>0, q = q(Po>qO’W),
(p0,q0,r0) g tz с
Как следует из доказанной теоремы, таким путем мы опреде-
ляем в некоторой области полный интеграл уравнения Гамиль-
тона-Якоби
Таким образом, если надо приближенно найти полный интег-
рал уравнения этого вида, то можно составить уравнения Га-
мильтона с функцией Н(р, q, f) и применить численное интегри-
рование. В общей теории уравнений в частных производных
интегральные кривые соответствующих уравнений Гамильтона
называются характеристиками.
Замечание 4. Интегрирование уравнений Гамильтона путем
определения полного интеграла уравнения Гамильтона-Якоби
часто называют методом Якоби.
§ 5.5. Некоторые примеры применения
метода Якоби
В этом параграфе мы применим метод Якоби к двум из-
вестным нам и не самым сложным задачам механики. Эти при-
меры должны пояснить процедуру метода Якоби. Кроме того,
новые переменные а, Р, которые вводятся при решении задачи,
будут иметь специальный вид, который оказывается наиболее
342
Глава 5. Основной аппарат гамильтоновой механики
удобным для анализа или решения задач, в некотором смысле
близких к рассматриваемым.
1°. Задача о линейном осцилляторе. Полагая некоторые
физические постоянные равными единице, запишем гамильто-
ниан этой задачи в следующем виде:
Я = |(р2 + <?2), p,q^R. (5.5.1)
Очевидно, уравнения Гамильтона и их общее решение имеют вид
dp дН dq дН . п .
— =-----= -q, — = —— = p=>g = AcosZ + BsnU,
dt dq dt dp
где А, В - произвольные постоянные.
Запишем соответствующее гамильтониану (1) уравнение Га-
мильтона-Якоби (5.4.32):
откуда
— = 8д/2ос-д2, 8 = sgn р = ±1 (знак числа)
dq
и
5=|5д/2а-^2
о
Рассматривая 5 как производящую функцию симплектического
преобразования р, q —> а, Р, получим
Р =
dS
dq
= 5д/2сс-<72
dS _ г 8JE,
да |^а-У
Для вычисления второго интеграла положим
i; = V2ocsin(p, sgn cos(р = S
(2а - q2 обращается в нуль одновременно с изменением знака р).
Отсюда
arcsin (q! 72а) ~
Г ocoscp ,о . q
-------------da => p = arcsin —?=,
J | coscp | V2a
(5.5.3)
q-42a sinP, p = ^2a cos(3.
§ 5.5. Некоторые примеры применения метода Якоби
343
В переменных а, Р гамильтониан имеет вид
Н = а => — = ——- = 0 => а = ccn = const,
dt Эр °
(5.5.4)
Эр_ЭЯ
dt да
= 1^р = ро + (г-/о).
В результате получаем решение
sin(P0 + t-t0),
p = j2a^ cos(P0+r-r0).
Применение метода Якоби в этой задаче служит чисто иллю-
стративным целям. Однако полученные новые переменные
обладают особыми свойствами. На любой фазовой траектории а
остается постоянной, а множество существенно различных для
задачи значений Р принадлежит окружности 0 Р < 2л.
Можно рассмотреть более сложную задачу о возмущенном
движении осциллятора, гамильтониан который имеет вид
Я = |(р2 + <72) + еЯ(^д),
где &U(q, i) - потенциал возмущающих сил,
£ > 0 - малый параметр.
В этой задаче для ее исследования целе-
сообразно перейти к каноническим перемен-
ным а, р. Тогда гамильтониан Н(ос,Р,/) будет
иметь вид
Н = a + s[/(T2a sinP,z).
Главная часть (при s = 0) имеет очень простой
вид, а возмущающий потенциал U есть 2л-пе-
риодическая функция р. Эти свойства гамильтониана в перемен-
ных а и Р неслучайны и мы к ним еще вернемся.
2°. Задача двух тел (см. §4.11). Рассмотрим эту задачу в сфе-
рических координатах qT = (р, (р, X) (рис. 121). Потенциал U этой
задачи имеет вид
U = -—. (5.5.5)
Р
Кинетическая энергия
Т = ^| v|2=3(p2 +р2ф2 +p2cos2<pA2). (5.5.6)
Обобщенные импульсы рт = (рр, pv,P)d, сопряженные коорди-
344
Глава 5. Основной аппарат гамильтоновой механики
натам q, определяются формулами
ЭТ • ЭТ 2 • ЭТ 2 2 л ап\
Рр = ^ = Р' Р<₽ = ^ = РФ’ Рх =^- = Р COS Ф^- <5-5-7)
р Эр * Эф ЭХ
Подставляя в (6) выражения для р,ф,Х, полученные из (7), опре-
делим выражение для гамильтониана задачи
н=г+и=1Ь+
Z \ р
1 2 . 1 2
р" ' v р2 cos2 (р Рх
-. (5.5.8)
Р
Применим к этой задаче метод Якоби. Для компонентов
векторов аир введем традиционные для небесной механики
обозначения:
aT=(L,G,0), pT=(Z,co,Q).
Кроме того, чтобы получить решение задачи также в тра-
диционном виде, мы распорядимся специальным образом про-
изволом в зависимости производящей функции 5(q, а) от a.
Функция Н является интегралом уравнений Гамильтона. Мы
будем рассматривать только ограниченные движения (см. § 4.11)
или, иначе говоря, движения с отрицательной энергией Н. В этом
случае без дополнительного ограничения общности уравне-
ние Гамильтона-Якоби (5.4.32) можно записать в следующем
виде:
+ 1 ГЭ5Л2 ц _ ц2
р2 cos2 (р V ЭХ ) р 2L2
(5.5.9)
Из дальнейшего следует, что полный интеграл этого уравнения
можно найти в следующем специальном виде:
5 = Я(р) + Ф((р) + 0Х, (5.5.10)
где функции R, Ф зависят только от р и (р соответственно (и,
конечно, от параметров а).
Действительно, подставляя (10) в (9), получим
'жУ +_1_Г ЭФ У । 02
ч dp ) р2 Эф ) р2 cos2 ф
(5.5.11)
Если мы определим функции Ф((р) и 7?(р) как решение урав-
§ 5.5. Некоторые примеры применения метода Якоби
345
нений
г 6/фУ ©2
--- ----2--
{d(p J cos <р
(5.5.12)
И? (5.5.13)
HpJ р L р
то уравнение (11) будет удовлетворено, а следовательно, 5 в виде
(10) будет удовлетворять уравнению Гамильтона-Якоби.
Уравнение (13) можно записать в следующем эквивалентном
виде:
/W ц2 ( 2 l2 g2l2} р2 v
— =-^т -Р +2—Р-----------— =-^т(р-р1)(р2-р),
dp J L р ц ц ) L p
(5.5.14)
где pi =5 р2 - корни квадратного трехчлена, стоящего в круг-
лых скобках. Из уравнений (12) и (14) очевидно следуют нера-
венства
G2^©2, p,=sp<p2.
Введем обозначения:
8, = sgnрф, 32 = sgnрр, sgnx = ±1 (знак числа).
(5.5.15)
Тогда
Ф(ф)=[б1 G2--^- d^, (5.5.16)
J у cos Q
Жр) = f 52 J— - 4------2 (5.5.17)
Pl v
Новые координаты Рт = (Z, со, Q) определяются формальными
правилами:
oS _ Pg ц dr| _ г 82piT]dT]
dL pi 2£3 p^Voi-piM-n)’
\ T| L2 Y]2
(5.5.18)
w = (5.5.19)
oCr
346
Глава 5. Основной аппарат гамильтоновой механики
f , 8'С^ . /=f Jigg!----------------- , (5.5.20)
П П i2 ~ Л2 J
й = ^ = А.-у, (5.5.21)
ЭФ_ r_________5,06%________
| COS2 -02 / cos2 £
(5.5.22)
Замечание. Следует обратить внимание, что р, зависит от L и
G. Однако Р| - корень подынтегрального выражения. Поэтому
справедливы (18) и (19).
В переменных (а, Р) = (L, ..., Q) гамильтониан задачи имеет
вид (11)
Н(“.₽) = -ч4-
Так как Н зависит лишь от одной переменной, то, за исклю-
чением уравнения
с^_'дН__ р2
dt ~ dL ~ L? ’
(5.5.23)
правые части всех остальных уравнений обращаются в нуль.
Таким образом, решение задачи в новых переменных имеет вид
L = L0, G = Gq, 0 = 00, со = соо, Q = Qo,
где нулевым индексом отмечены постоянные значения этих пе-
ременных, определяемые начальными условиями. Кроме того,
/ = /0 +n(t-t0), П = р2/L3.
Кинематический и геометрический смысл
новых переменных
Смысл новых переменных не очень сложно выяснить только
в результате анализа полученных формул. Однако для сокра-
щения этой операции мы частично воспользуемся анализом за-
дачи двух тел, подробно проведенным в § 4.11. Мы знаем,что
движение происходит по эллипсу неизменных формы, размеров
и ориентации. Очевидно, что минимально допустимое значение
§ 5.5. Некоторые примеры применения метода Якоби
347
р, равное рь определяется значением р в перицентре эллипса, и
р = р2 в апоцентре. Далее, “(Pi + Р2) - а ~ большая полуось
эллипса,
——— = е - эксцентриситет эллипса. (5.5.24)
Р2+Р1
Отсюда
Pi = а(1 - е), р2 = а(1 + е).
Из равенств (14) и (24) следует
2£2 £2 __
Pi + р2 =--=> а- — => L = (5.5.25)
ц ц
ptp2 = 3-G2L2 => а(1 -е2) - 3-G2L2,
ц р
e = (5.5.26)
1. Таким образом, L определяется значением большой полу-
оси эллипса или энергией движения: -|Ы2/2£2 = Н.
2. Обозначим через i?p, проекции вектора скорости на
радиус-вектор, меридиан и параллель (рис. 122). Очевидно, спра-
ведливы следующие соотношения (см. (7), (10)):
2 •
Г<р = Р Ф = Р^<р
d s _ эф
Эф Эф ’
2л 2 &S z-ч
р} = pACOS ф =р1?ЛСО8ф = — = 0.
ЭЛ
(5.5.27)
(5.5.28)
Из соотношения (28) следует, что 0 - проекция момента ко-
личества движения К = [г, vl точки единичной массой на орт е3:
0 = ^3.
3. Из (12) следует
G2
Г эф)2 о2
---- "I----2--
ч ckp J cos (р
= p2v2+p2v2.
(5.5.29)
Упражнение. Покажите, что правая часть (29) равна квадрату модуля I К I2
вектора кинетического момента точки.
Обозначим через i угол между вектором К и ортом е3 (рис. 123). Тогда
0 = G cos i
(5.5.30)
(без ограничения общности можно принять G > 0).
348
Глава 5. Основной аппарат гамильтоновой механики
Рис. 122 Рис. 123
4. Из (21), (22) следует, что у = 0 и Q = X при (р = 0.
Тем самым Q определяется долготой точки в момент пересече-
ния плоскости (еь е2). Эту величину мы называем долготой
восходящего узла орбиты.
5. Интеграл
г _ г 8 Д
д/g2 -02 / cos2 £ 0 д/1-cos г /cos2
нетрудно вычислить. В результате получим
. ( sin ср
и = arcsm -----
V sin г
=> sin (р = sinzsinu.
(5.5.32)
Из сферического треугольника тВА (см. рис. 123) следует, что
и - угловое расстояние точки т от восходящего узла ОА, т.е.
аргумент широты точки.
Так как/ = 0 при р = Pi (см. (19), (20)), то легко устанав-
ливается смысл переменной со. Она равна угловому расстоянию
перицентра от восходящего узла, т.е. со - аргумент широты
перицентра орбиты. С другой стороны, из (19) имеем/= и - со -
угловое расстояние точки от перицентра, т.е./- истинная ано-
малия точки.
6. Для вычисления интеграла (18) воспользуемся подста-
новкой
р = cz(l-ecosE), sgncosE = 82. (5.5.33)
При Е = 0
p = cz(l-e) = p1,
при Е - п
р = cz(l + е) = р2,
и подстановка корректна. Переменная Е носит название экс-
центрической аномалии.
§ 5.5. Некоторые примеры применения метода Якоби
349
Подставляя T| = a(l -e cos Q в (18), получим
E
8 2 |uzz(l - е cos Qae sin
- e cos Q - - e)][tz(l + e)-a(l-e cos Q]
f52sinC ~ ,r
= I n (l-gcosO^,
J sin£
откуда
I - E - e sin E.
Кроме формулы (34), нам известно
тинную аномалию (см. (4.11.24))
а(1-е2)
Р (1 + ecos/)
(5.5.34)
выражение p через ис-
(5.5.35)
cos f + e
(Ъ.Ъ.ЪЪ)
Из (33) и (35) следует
. 71-е2 sin/
sinE =-----------, cosE = - -
1 + ^cos/ 1 + ecos/
. r y/l-e2 sinE r cosE-e
sin / =----------, cos f =--------.
1-e cos E 1 - e cos E
В результате предыдущего анализа мы теперь легко дока-
жем следующую лемму:
Декартовы координаты г1, г2, г3 являются 2л-периодически-
ми функциями каждой из новых угловых переменных Рт -
= (/, со, Q).
Доказательство. Из (34) нетрудно установить, что из-
менение I на 2л влечет изменение на 2л эксцентрической анома-
лии Е. Поэтому cos Е, sinE и cos/, sin/суть 2л-периодические
функции I. Таким образом, 2л-периодической функцией I являет-
ся радиус р (35). Из (19) следует, что
sin<M) = sin(w + ^
есть 2л-периодическая функция со и I.
Из сферического треугольника тВА следует
. .. COSM
sincp = sinzsinw, cosy =--.
coscp
Тем самым тригонометрические функции ср и у суть 2л-периоди-
350
Глава 5. Основной аппарат гамильтоновой механики
ческие функции /, со. Наконец, из (21) следует что
COSz^ СО8/ГЛ , ч
sinft)=sii.(£2 + l'’
есть 2т1-периодическая функция /, со, Q.
Для доказательства леммы следует вспомнить, что выра-
жение декартовых координат через сферические определяется
вектором р и тригонометрическими функциями X и ср.
Назовем задачу с гамильтонианом
H = 7lvl2 “A + f/B(r’r)’
2 |г |
где C/B(r, t) - потенциал некоторых сил, возмущенной задачей
двух тел. Из предыдущего анализа следует, что гамильтониан
этой задачи в переменных L, G, 0, /, со, Q можно представить в
следующем виде:
H = -^ + UB(eJI,ej<a,ejn,L,G,@,t), 7 = 7-1. (5.5.37)
В выражении (37) [/в есть 2т1-периодическая функция новых
угловых переменных /, со, Q (е - основание натуральных лога-
рифмов).
Замечание. Мы специально позаботились, чтобы новые пе-
ременные обладали указанным свойством. Однако сущест-
вует целый класс задач, так называемых интегрируемых, и для
этих задач существует регулярный способ введения таких ко-
ординат.
§ 5.6. Системы Лиувилля.
Переменные «действие-угол»
1°. Системы, допускающие разделение переменных. Пусть
гамильтониан задачи в канонических переменных
р^/Ар2,...,^), qT
имеет следующий специальный вид:
Щр,Ч) = Ф1(р1,^1,Ф2), (5.6.1)
где Ф ( - функция указанных аргументов, а функция Ф2 имеет
вид
Ф2 =Ф2(р2,^2,Ф3), Ф3 = Ф3(р3,43,Ф4 ),..., Фт =Фга(р"',^'и).
§ 5.6. Системы Лиувилля. Переменные "действие-угол"
351
Напишем соответствующее уравнение Гамильтона-Якоби:
Н\ 3T’q =
)
f Э5 ! f dS 2 Л . ( ds т УЙ Л
= Ф1 ТТ’9 ;Ф3—,Фт - = /(«)• (5-6.2)
\^oq \oq V \dq ))) J
m раз
В общем случае мы найдем полный интеграл 5(q, а) урав-
нения (2), если положим
5(q,«) = 5,^*) + S2(q2) +... + Sm (qm ), (5.6.3)
где 5г - функция только q! и параметров а, и определим 5г(<7*, а)
из следующих обыкновенных уравнений:
f z7C А
ф т =
\dq J
ф f m_,
m-1 j т-1 ’’Ч ’ -
V “4
(5.6.4)
_ f dSx j
Ф1 -v-h?,a2
< dq
= «1 (/(«) = «!).
Таким образом, для гамильтониана специального вида (1) за-
дача определения полного интеграла сводится к необходимос-
ти решения уравнения Гамильтона-Якоби для т одномерных
задач.
Если задачу удается свести к одномерной, то говорят, что
задача допускает разделение переменных. Мы проведем анализ
следствий, вытекающих из разделения переменных, в более
простом случае системы Лиувилля.
Теорема Лиувилля. Пусть кинетическая энергия Т и потен-
циал U рассматриваемой механической системы в лагранжевых
координатах q, q имеют вид
X ч(9')
U = , (5.6.5)
2 l’=l
352
Глава 5. Основной аппарат гамильтоновой механики
где
т
Q=Y
a Qif Rif Di - функции только z = 1, 2,..., т.
Тогда система допускает разделение переменных.
Доказательство. По определению,
, dL dT n„i.i р‘
P= — = — = QRiq^q=—,
dq dq'
и гамильтониан задачи имеет вид
1 т Г .
1 т 1
Н = -У —(p^+D, .
Q^\_2Ri ‘J
Полный интеграл уравнения Гамильтона-Якоби
\2
+д
1 т
1у
1
05
2/?ДЭ^
будет найден, если положим
S = X W)
= а0
и определим функции 5, из следующих уравнений:
1
dSt
2/?, dq'2
+ £>,-а0<2, =ос;, г = 1,2,...,т,
(5.6.6)
(5.6.7)
(5.6.8)
где
а । + сх2 + • • • + = О,
или
dS;
= fi(a0,ai,q‘~), i = l,2,...,m,
где
Z = 2Я,. (^ )[а( + a0Q (<?')- £>,(<?')].
(5.6.9)
(5.6.10)
Таким образом, полный интеграл уравнения Гамильтона-
Якоби определяется в следующем виде:
s = S,- = /^/(ао,^.,^') dq', а{+а2+... + ат =0.
;=1 1=1
(5.6.11)
§ 5.6. Системы Лиувилля. Переменные " действие—угол"
353
Набор чисел ос0, ос19..., ост, удовлетворяющих условию ос1+ос2 +
+ ... + ат = 0, обозначим через а:
Of — (CXq, Otj,..., OC/77).
Согласно общей теории, ос остается постоянным на любом ре-
шении исходной системы уравнений Гамильтона с гамильто-
нианом Н(р, q) (6). При этом импульсы р1 определяются соот-
ношениями
р'г = 1,2,...,т. (5.6.12)
dq
Соотношения (12) определяют т интегралов уравнений Гамиль-
тона. Значения констант этих интегралов ос0, ос19..., а77/ опреде-
ляются начальными условиями:
ос0 — H(pQ.,qQ), otz — z- + Dz (t?0) — OC0(2Z(q^), i‘ = 1,2,..., m.
W%)
(5.6.13)
Соотношения (12) при каждом i определяют кривую уг’(а) в
плоскости сопряженных переменных (р\ q1). Эти кривые сим-
метричны относительно оси /У = 0, и допустимые значения ql
определяются условием
/(осо, ос„ ^) > 0.
Ниже мы отвлечемся от особых значений а, при которых
существует совместное решение двух уравнений
/(ао,а,.,^') = О и -|=С(а0, а,-,</) = ().
dq
Тогда возможны кривые одного из типов, указанных на рис. 124-
128.
Случаи, показанные на рис. 124-127, возникают, когда усло-
вие f > 0 выполняется соответственно при
-оо<^<оо; q^q2\ ql > q\\ q\^ ql q2-
23. М.Л. Лидов
354
Глава 5. Основной аппарат гамильтоновой механики
На рис. 128 показан случай, когда кривая (р*)2 =Z(cCo, ос;, q1) имеет
несколько ветвей (несколько компонентов связности). Для этого
случая необходимо, чтобы при фиксированном а условие fi > О
выполнялось при
q‘^, j
При этом конкретная ветвь выделяется начальными условиями
Для варианта, приведенного на рис. 124 (когда f > 0 при
любом q1), особо отметим практически интересный случай, когда
fi(<Xo, ttj, q') является периодической функцией ql с периодом
oz = oz(oc0, ocz), т.е.
+о,.) = /(а0,а;,^). (5.6.14)
Лемма. Пусть а' и а" - два различных набора значений пара-
метров Oto, с/ч. Тогда:
1) кривые у-(а') и yz-(a") не могут пересекаться; они либо со-
впадают, либо не имеют общих точек;
2) кривые уХа') и у^а") не могут совпадать при всех i = 1,
2,..., т.
Доказательство. Если бы кривые yz(a') и yz(a") пере-
секались при каких-либо значениях р* и q\ то можно было бы
указать начальные данные р0, q0 (определяемые точками пере-
сечения), которым соответствовали бы различные значения а =
= а' и а = а".
Однако по начальным данным а определяется явными фор-
мулами (13), и это невозможно. По той же причине невозможно
совпадение всех кривых
yz(a') и yz(a") при i = 1, 2,..., т.
Переменные «действие-угол»
Предположим, что для рассматриваемых ниже начальных
данных при всех i = 1, 2,..., т кривые yz(a) являются замкнутыми
кривыми типа, показанного на рис. 127. В этом случае рассмот-
§ 5.6. СистемыЛиувилля. Переменные "действие-угол”
355
рим следующие интегралы:
1 $
г =/'(«) = -f J/J(a0,a,.,£) d^, i = l,2,...,m. (5.6.15)
Л <
<11
Нетрудно понять, что
где т;(а) - площадь, ограниченная кривой у,(а)-
Согласно только что доказанной лемме при а' а", по
крайней мере одна кривая у(а') должна лежать целиком внутри
или вне области, ограниченной кривой у-(а"). Таким образом,
различным а должны соответствовать различные векторы
и тем самым из соотношений (15) можно определить а как
функцию I: а(1) и, в частности, «о = ос0(1).
Введем теперь вместо переменных ql 2 * промежуточные пере-
менные Тг = р1) следующими формулами:
если р1 > О,
1 4
2 л-—[ ^(а0.аД) d^,
1 4
(5.6.16)
если р1 < 0.
С помощью рис. 129 и 130 нетрудно понять, что Ч772л есть отно-
шение заштрихованной площади к Когда точка обходит
кривую у, переменная монотонно изменяется на 2л.
Следовательно, при фиксированных I (или, что то же, при
фиксированном а) фазовые координаты р\ ql являются 2л-пе-
23*
356
Глава 5. Основной аппарат гамильтоновой механики
риодическими функциями Ф':
ql = Ф' (I, ) = Ф' (I, + 2л). (5.6.17)
Таким образом, при фиксированных I в фазовом пространстве
переменных р, q выделяется множество Мъ которое диффео-
морфно m-мерному тору:
Т” ={'Р|,Т2,...,Т'"; 0«Ч"<2л, i = 1,2,..., т}.
Формальным преобразованием соотношений (9) получим
dq' J “IdT'J (Z')2”^’
Отсюда следует
S,- = ГТ‘(^,1). (5.6.18)
Тем самым функцию 5 (11) можно представить в следующем
виде:
т т
5 = /‘WJ) = <I,'n (5.6.19)
/=1 Z=1
*фт — (ф!
Согласно теории Якоби, рассматривая I как набор новых
импульсов, получим выражение для сопряженных им новых
канонических координат <р, дифференцируя 5 по I при посто-
янных q:
<рт = (фЧф2,...^"7).
(5.6.20)
При фиксированных I матрица (Э'Ч^/Э1)Т зависит только от q и,
следовательно, является 2л-периодической функцией по каж-
дому компоненту вектора Ф. Изменению Ф на 2лк, где к =
= (fc1, fc2,..., кт) - произвольный вектор с целочисленными компо-
нентами, соответствует изменению <р на 2лк.
Рассмотрим тор Т™:
Т™ = {ф^ф2,...,ф'л, О^ф' <2л, i = l,2,...,m}.
Произвольной точке Ф е отвечает одна и та же точка ср тора
Т™. В общем случае соотношение (20) определяет диффео-
§5.6. СистемыЛиувилля. Переменные ”действие-угол"
357
морфизм между точками торов и Гфш. Тем самым <р суть
канонические координаты, которые определяют точку мно-
жества фазового пространства, выделяемого фиксированным
значением сопряженных импульсов I.
В переменных I, гамильтониан задачи имеет вид
Н(<р,1) = н[^,Ч
V dq ; Л1 ч
V 1 /q=q(I,<p)
Однако поскольку функция S удовлетворяет уравнению Гамиль-
тона-Якоби (7), то
Н(<р,1) = ос0(1).
Таким образом, новый гамильтониан является функцией только
новых импульсов I. Поэтому в новых переменных уравнения
имеют вид
Л dip (Эос0 V
dt ' dt I Э1 )
а их решение есть
I = Io = const,
<Р =
(t tG) + <р0,
где 10, <Ро _ определяются начальными данными.
Для получения решения в исходных переменных р, q не-
обходимо вычислить квадратуры (15) и (16) и их производные по
I (20) и разрешить неявные функции (20) для определения зави-
симости
q = q(I, <р).
После этого импульсы р находятся из соотношений (12).
Сформулируем некоторые выводы. Канонические перемен-
ные I, ip обладают следующими свойствами:
1°. Импульсы I не изменяются с течением времени, т.е. I -
первые интегралы задачи.
2°. Канонические координаты ip изменяются равномерно.
3°. Старые координаты q для рассматриваемого множества
постоянных значений I являются 2л-периодическими функциями
по каждой координате (рг.
Определение. Канонические переменные, обладающие свой-
ствами 1°-3°, называются переменными «действие-угол».
358
Глава 5. Основной аппарат гамильтоновой механики
Дополнительные замечания
1. Как следует из предыдущего анализа, в переменных I, ср
при постоянных I движение системы изображается равномерным
движением точки по тору Т™.
2. Обозначим 6ta0/d/z = coz, i = 1, 2,..., m. Величины сог опре-
деляют скорость изменения угловых переменных ср' и назы-
ваются частотами. В общем случае частоты являются функ-
циями I: coz = coz(I). Для некоторых значений I можно указать
такие целые числа к2,..., кт) = к, что будут выполнены со-
отношения
2Я&! _ 2пк2 _ _ 2пкт
О)1 со2 со"7
(5.6.21)
В этом случае все траектории на этом торе будут зам-
кнутыми линиями, и движение будет периодическим. Если
к2,..., кт не имеют общего делителя, то т есть период движе-
ния. Через время т после начала движения изображающая точка
вернется в исходную точку на торе Т™, а следовательно, и в
исходную точку фазового пространства переменных р, q.
В общем случае это не так. Если (21) не выполняется ни при
каких целых kt (к Ф 0), то движение будет условно-перио-
дическим. Координаты q и импульсы р будут условно-перио-
дическими функциями времени:
Ч = Х QfrWexpL/C^co1 + ... + ктыт)С\,
* , (5.6.22)
Р = Х +... + £гасо'и)г],
к
2=7=1.
В (22) , и суммирование производится по
к к\ к2 кт
всем целым к, от до +°°
Частоты со' называются независимыми, если не существует
целочисленного вектора к = (кх, к2,..., к,„), отличного от нулевого,
для которого выполняется равенство
^со1 + к2а>2 +... + кт(От = 0.
Если частоты независимы, то каждая траектория (pz(r) = CD'(r —
-г0) + (р'о, i = 1, 2,..., m, всюду плотна на торе. Более того. Если
§5.6. Системы Лиувилля. Переменные " действие—угол"
359
D - область на торе Т™ и mes D - ее мера по Жордану, то
тл(Г) mes£>
игл —----=------,
Т (271)т
где td(7) - количество времени из отрезка t0 t Т, в течение
которого (р g D. Таким образом, в пределе доля времени, в те-
чение которого траектория находится в области £>, пропор-
циональна относительному объему этой области. (Доказатель-
ство последних утверждений можно найти в книге: Арнольд В.И.
Математические методы классической механики. - М.: Наука,
Гл. ред. физ.-мат. лит-ры. 1979, с. 275.)
3. Переменные «действие-угол» вводятся аналогичным обра-
зом, если некоторые из кривых у; являются периодическими кри-
выми (см. (5.6.14)) типа, приведенного на рис. 124. В этом случае
- произвольная точка, а переменные I\ Т* определяются со-
отношениями
J л//(аО’а<Л)
2л <
=-г] 8,-= sgn/У.
Q\
4. В рассмотренной нами задаче двух тел (см. § 5.5) пере-
менные IT - (L, G, 0) и <рт = (4 со, Q) являются переменными «дей-
ствие-угол». Задача двух тел дает пример вырожденной
задачи, в которой при любом импульсе I частоты со, Q
изменения переменных со и Q равны нулю. Имеется лишь одна
отличная от нуля частота I = [k2/L3. Поэтому на любом торе Гф3
(Г = (L, G, 0) = const) движение периодическое с периодом
2л£3 2 ля3/2
“ 2 ~ ’
5. Пусть в задаче с гамильтонианом Н = Н(р, q) введены пе-
ременные «действие-угол» I и ср так, что в этих переменных га-
мильтониан будет иметь вид
Н = сх0(1).
Рассмотрим возмущенную задачу с гамильтонианом
q) + еН,(р, q, t),
360
Глава 5. Основной аппарат гамильтоновой механики
где Е > 0 — достаточно малое число. Если эту новую задачу запи-
сать в переменных «действие-угол», определенных для исходной
задачи, то получим гамильтониан Ж в следующем виде:
И = сс0(I) + (е7<р‘,..., Х', I, t), j = дП,
где Нх получается формальной подстановкой в Нх выражений
р, q через I, ср. Выражение гамильтониана Ж в виде 2л-перио-
дической зависимости от угловых переменных (рг удобно для
анализа и приближенного решения соответствующей системы
уравнений Гамильтона.
6. Системы Лиувилля замечательны тем, что применение
метода Якоби допускает интегрирование в квадратурах и опи-
сание движения не локально, а для всех моментов времени t,
принадлежащих вещественной прямой.
Кроме систем Лиувилля, можно указать более широкий
класс систем, для которых переменные разделяются. Эти си-
стемы выделяются некоторыми условиями, однако во всех слу-
чаях эти условия являются критериями возможности разделения
переменных в данных координатах р, q, и они ничего не
говорят о возможности разделения переменных в других коор-
динатах р, q, связанных с р, q симплектическим преобразо-
ванием.
Возможна следующая ситуация. Для системы с гамильто-
нианом Н(р, q) переменные не разделяются, а после (возможно,
простого) преобразования р = р(р, q), q = q(p, q) мы получим
гамильтониан
z/(p,q) = H(p(p,q), q(p,q)),
допускающий разделение переменных. Поэтому практиче-
ская эффективность таких безусловно полезных теорем огра-
ничена.
§ 5.7. Первые интегралы уравнений Гамильтона
и интегрируемые системы
1°. Скобки Пуассона. Пусть f] и f2 - два гладких отображения
симплектического пространства SRlm в вещественную прямую R.
Пусть z g SR1”1- координаты точек SRlm относительно какого-
либо симплектического базиса и отображения f\ и f2 определя-
ются функциями^ =/(z) и/2 =/2(z).
Определение 1. Скобкой Пуассона (fb f2) функций / и /2
называется кососкалярное произведение их градиентов. В ко-
§ 5.7. Первые интегралы уравнений Гамильтона
361
ординатном представлении
(/1.Л)ХВПМ\=|ЦМ, (5.7.,)
\ {dz) {dz ) dz {dz)
где - симплектическая единица. Если
Z = fP\ pT=(?,p2,...,pm), <f=(q',q\...,qm),
lq;
то
Эр 3q
3qX 3p
Э/1 3/2 3/j 3/2
dp1 dq1 dq1 dp1
m
Лемма 1. Скобка Пуассона инвариантна относительно симп-
лектического диффеоморфизма.
Доказательство. Пусть z = z(z) - симплектический
диффеоморфизм SRlm —ь SRlm. В координатах z отображения
определяются функциями
Wi(z(z))> /2 = /2(z(z)).
Используя представление
C^_3z
dz dz dz ’
получим
*’ 2 г \ \3zJ \ 3z J / \ <3zJ V 3zJ \3zJ k, 3z J /
(5.7.2)
iWVa f).
\ I — I I — I I 'A I ’ I 'A I /1 I \ I 'Л I ’I I /
\{dz) {dz) {dz) {dz) / \ {dz) {dz) /
Подчеркнутое скобкой равенство следует из условия симплек-
тичности матрицы dz / dz.
Следствие I. Скобка Пуассона (f19 /2) не зависит от вы-
бора симплектического базиса в SRlm.
Следствие 2. Диффеоморфизм z —> z является симп-
лектическим тогда и только тогда, когда скобки Пуассона лю-
бых двух функций в переменных z и z равны.
Упражнение. Докажите последнее утверждение.
362
Глава 5. Основной аппарат гамильтоновой механики
Свойства скобок Пуассона.
1- (Л,Л) = -(/2,Л) для любых/1,/2.
2. Для любых трех функций/,/2,/3
j = ((/>, /2 X f3) + «Л > /1X /2) + ((/2, /3 X /1) s 0- (5-7.3)
Последнее соотношение называется тождеством Якоби.
Докажем его справедливость. Вычислим сначала
—(ff.) = —
dz Jj dz
dz V dzJ
dz dz2 dz dz2
(5.1A)
Заметим теперь, что второе и третье слагаемые в (3) получаются
циклической перестановкой индексов первого слагаемого.
Запишем ((Л,/2)5/3) в явном виде
((/1,/2X/3) = ^9?|'/(/1,/2)
dz |_dz
~ Э^Эг^Ы '( ’
Равенство ।—। следует после подстановки производной от скобки
Пуассона в виде (4). Обозначим
dz dz2 V dz J
d2 f
Заметим, что из симметричности матрицы 9*—^9^ следует
dz
(4 / к) = (к, j, i).
Далее имеем
J= (3, 2,1) - (3, 1,2) + (2, 1, 3) - (2, 3, 1) + (1,3,2) - (1, 2, 3).
Одинаково подчеркнутые члены взаимно уничтожаются, откуда
следует J = 0.
2°. О первых интегралах. Пусть
— , ze5/?2"', H = H(z,t}
dt \dz)
(5.7.5)
- заданная система канонических уравнений. Пусть f = f(z, t)
определяет отображение SR2m xR^R. Вычислим производную
по времени t от /(z(r), /), где z = z(/) - решение уравнения (5)
§ 5.7. Первые интегралы уравнений Гамильтона
363
(интегральная кривая):
df df df dz df df (dHV df .
— = + У----= + — =тс- + (Н,/). (5.7.6)
dt dt dz dt dt dz < dz J dt
Здесь (•, •) - скобка Пуассона.
Лемма 2. Функция /(z, t) будет первым интегралом системы
уравнений (5) тогда и только тогда, когда она удовлетворяет
следующему уравнению в частных производных:
^ + (Н,/) = 0. (5.7.7)
Определение. Говорят, что две функции/(z) h/(z) находятся
в инволюции, если их скобка Пуассона тождественно равна
нулю:
(fi,/2)^0.
Следствие из леммы 2. Не зависящая явно от времени
функция Дг) будет первым интегралом системы (5) тогда и толь-
ко тогда, когда она находится в инволюции с гамильтонианом
системы:
(H,f) = 0. (5.7.8)
Теорема Пуассона. Если/^z, t) и f2(z, t) - два первых ин-
теграла уравнений Гамильтона (5), то их скобка Пуассона тоже
является первым интегралом.
Доказательство.
4 (Л, Л) = Э(1’ -} + <Л, (/;, /2)), (5.7.9)
dt dt
(5-7ло)
dt V dt ) \ dt J
Используя тождество Якоби, получим
(я, СЛ Л)) = -((/,, Л), Н) = ((Н, /), л)+((Л > Ю, f).
df.
Так как/! и/2 - первые интегралы, то (Н, f)-------L, откуда
dt
V dt ) v dt ) \dt ) \ dt)
(5.7.11)
Из (9)—(11) следуют —(/i,/2) - 0 и доказательство теоремы.
dt
364
Глава 5. Основной аппарат гамильтоновой механики
Замечание. Казалось бы, что, зная два первых интеграла, та-
ким путем можно получить любое число нужных для интег-
рирования задачи первых интегралов. К сожалению, это, вообще
говоря, не так. Как правило, интегралы f и /2 либо находятся в
инволюции и (/*!, /2) - 0, либо в результате получается интеграл
f3 - (f{, /2), зависящий от fx и /2. Напомним, что интегралы
f = (fi, fk) называются независимыми, если ранг матрицы
3f/3z размера к х2т равен к (максимален). Однако не стоит пре-
небрегать вычислением скобок Пуассона для известных интег-
ралов, так как возможность таким путем нахождения первого
интеграла задачи не исключена.
Пример. Рассмотрим вектор количества движения и вектор
момента количества движения материальной точки (г, т):
р = mv, К = [г, р], р, г g R3.
При рассмотрении задачи в декартовых координатах:
рт = (р' , р2, р3) - вектор обобщенных импульсов системы,
гт = (г1, г2, г3) - обобщенные координаты,
К[=г2р3-г3р2, K2=r3p{-rp3, K3 = rlp2-r2p\
ЭК' /п з 2ч дК2 .. . дк2 2 ,
— = (0,-r3,r2), —— = (rJ,0,-r*), —— = (-r2,r,0),
dp dp dp
Э/l' zn з 2 ч дК2 з ] Э№ 2 ]
—— = (0,р ,-р ), —— = (-р,О,р), —_ = (р ,-р ,0).
or or or
Отсюда следует
(К},К2)
элг1 V
Эр X Эг ,
"элг'у
< Эг Л
э/с2Л
Эр )
= р'г2 — р2 г'.
В результате находим (К1, К2) = -К3. Аналогично нетрудно полу-
чить
(К[,р1) = 0, (К1,р2) = -р3, (К\р3)=р2.
Если мы теперь рассмотрим систему материальных точек
(гу, mj), где
j = qT = (Г|,г2,...,гп), qeT?3",
^ = Xp(g7?3> Рт=(Р1Ф2, .Pj, рея3",
Z=J
К = Х к, =Х [r,,p,]etf3, Р„г,б7?3, р,=т;-^-,
. . at
Z=1 Z=1
§ 5.7. Первые интегралы уравнений Гамильтона
365
то нетрудно получить, что и в общем случае
(/Г'Ж2) = Х = К-=-К\
/=1 Z=1
Тем самым справедлива следующая теорема.
Теорема. Если для системы материальных точек два компо-
нента вектора момента количества движения системы сохраня-
ются, то сохраняется и третий.
В частности, из соотношений между К1 и // следует, что если
система имеет два векторных интеграла р = const и К = const, то
бесполезно пытаться с помощью скобок Пуассона получить ка-
кой-либо новый интеграл.
3°. Если рассматривается система обыкновенных уравнений
z/v
— = Х(х,г), хеГ, (5.7.12)
dt
то, как мы знаем (см. гл. 4), используя к независимых первых ин-
тегралов этой системы
f(x,r) = a = const (fe7?\ ае^),
можно свести задачу отыскания общего решения (12) к решению
системы (и - &)-го порядка и вычислению квадратур. В част-
ности, для автономной системы (ЭХ/Эг -0) значение (и - 1)-го
первого интервала позволяет записать общее решение в квад-
ратурах. Использование интегралов в случае гамильтоновых
систем обладает определенной спецификой. В § 5.1, мы уже от-
мечали возможность понижения порядка гамильтоновой сис-
темы
dt V dz J
H = H(z,t), z =
P
<L
p,qe7?m (5.7.13)
в случае, когда имеются циклические координаты. Пусть
ГрЛ ГяЛ рГ=(ЛА-У), р} = (Рк+\рк+2,...,рт),
р= , q =
Ы Ы qiT = (q\q\^qk\ = {qk+\qk+\^qm).
Если гамильтониан задачи не зависит от qi
H = H(P],p2,q2),
то, очевидно, что Jpj / dt - -dH / 3qt = 0, pt=p10 суть к первых
интегралов.
Решение системы (13) сводится к решению системы
366
Глава 5. Основной аппарат гамильтоновой механики
2(т - &)-го порядка
ф2 _ f дН^
f—т
<ЭР2>
(5.7.14)
a Qi (0 находятся квадратурами после решения (14):
t / Л \ т
. ч . г (дН\
Ч1(0 = Ч1(*о)+ v dt-
J I OD
t0 Р2=Р2(О,Ч2=Ч2(О
Таким образом специальный вид к интегралов (pj = const) поз-
воляет в этом случае понизить порядок системы на 2кч сохранив
ее гамильтонову форму.
Теорема о понижении порядка автономной системы урав-
нений Гамильтона. Автономную систему уравнений Гамильтона
порядка 2т можно свести к гамильтоновой системе порядка
2(т-1).
Доказательство. Пусть Н(р, q) - гамильтониан зада-
чи. Предположим
(1.
Запишем уравнение Гамильтона-Якоби
T-r dS dS dS 19 т— 1 m I . _ _
H =«0, (5.7.15)
у dq dq dq J
где oc0 = #(p0,q0) - значение константы интеграла, определяе-
мое начальными условиями. Поскольку dH / dpm 0, уравнение
(15) можно разрешить относительно dS /dqm. В результате по-
лучим
dS (dS dS j т-\ т
-— — —К —г,...,-----г,q ..,q \q ,ОСо . (5.7.16)
dqm Эдт-' 4 4 4 ° J
Уравнение (16) является уравнением Гамильтона-Якоби для не-
автономной системы уравнений Гамильтона 2(т - 1)-го порядка
где
dp _ (дА"У dq _(ЭК’У
рТ qT =(q\...,qm-'\
(5.7.17)
в которой qm является независимой переменной. Если эта система
§ 5.7. Первые интегралы уравнений Гамильтона
367
решена, то рт определяется из уравнения
рт = Рт (Ят) = -*(Р (<Г )Л(^т), Г ,а0Х
а зависимость от времени находится квадратурой. Из уравнения
= = Х(о-ге)
dt (зр1" Jr ’ 0
q=qU'” ),Рт =рт (qm )
следует
, I
J Чч”.«о)
Дадим другое более формальное доказательство. Определяя
рт = -K(p,q,qm ,а0), получим тождество
Н(р, ~К(р, q, qm, а0), q, qm) = а0.
Дифференцируя это тождество по р и q, находим
дн дн дк _0 дн дн дк
др дрт Эр “ ’ dq дрт dq
Из уравнений Гамильтона имеем
dp( ЭЯ У
dt V Эд,
dq (дН
dt Эр
жр _ эя
dt ~ дрт ’
Из последнего соотношения получаем
Откуда
dt = dqm
дн
дрт
dp _ J эяу /эя _ Г ЭЯ у
dq'n ~ UqJ / дрт ~ UqJ ’
dq f ЭЯ"
dqm
/ ЭЯ
/ W
дк
Эр
Специфика гамильтоновых систем определяет справедливость
следующей теоремы:
Теорема Лиувилля о локальной интегрируемости системы
уравнений Гамильтона. Рассмотрим автономную систему урав-
нений Гамильтона
’ Н = Н(Р,Ц), P,qe7?m, z = f₽l (5.7.18)
dt \dz J (qy
368
Глава 5. Основной аппарат гамильтоновой механики
Пусть для системы (18) известно т независимых первых ин-
тегралов
ций таких, что ранг 3f / 3z равен m, z =
fт (г) = (//z), /2 (z),fm (z)), (5.7.19)
не зависящих от времени t и находящихся в инволюции:
(Z>/7) = 0, /, j = 1,2,...,т. (5.7.20)
Тогда система уравнений (18) локально интегрируется в квадра-
турах. Доказательство теоремы основано на следующей лемме.
Лемма 3. Пусть fT(z) = (//z),...,/^)), zeR2m - набор функ-
f н
л,
чтобы существовало симплектическое преобразование
- fP
z —> z (z = _
в котором зависимость р от z определяется соотношениями
, p,qe7?m. Для того
, p,qG/T),
p = f(z),
(5.7.21)
необходимо и достаточно, чтобы функции f^z) (i = l,2,...,m) на-
ходились бы в инволюции, т.е. должны равняться нулю все скоб-
ки Пуассона:
(Z>/,) = 0, = 1,2,...,т. (5.7.22)
Необходимость этого условия вытекает из основного
соотношения, определяющего симплектичность матрицы dz / dz:
лЭр Эр^
3z^ dzV dz dp 3q
dzj [dzj dz 3q 3q
кЭр 9q?
(5.7.23)
Из (21) и (23), в частности, следует
При доказательстве достаточности условий будем полагать
det—*0.
Эр
(*)
§ 5.7. Первые интегралы уравнений Гамильтона
369
Используя лемму 2, можно показать: из условия, что ранг
9f/9z = m, и из (20) следует, что условие (*) будет выполнено
непосредственно или после симплектической перестановки коор-
динат z.
Из условия (*) следует, что соотношения p = f(p,q) можно
разрешить относительно р:
р = Ф(д,р).
При этом, дифференцируя тождество
f(0(q,p),q) = p
по р и q, получим
ч Т 9f ЭФ 9f ЭФ 9f п
а) 1т = 3-337, б) з~з- + з- = 0.
Эр Эр Эр Эq Эq
(5.7.24)
Покажем, что из условия (22) следует симметричность мат-
рицы ЭФ / 9q. Действительно, из (246) получим
ЭФ = f Э£ Г? df Л ( ЭФ
9q .Эру <9qJ (9q
Отсюда
' 9f у Г Э£'
,9qJ Up,
ЭФ
9q
эф у
dqj
Э£уТдЦд£У
Эр, dp43q,
эгГэгу ГэГ
dq^pj ^Эр,
Введем обозначение
'эг Y—У _ лГл'
<9pJy9qJ 9qy9p?
Нетрудно проверить, что элементы с/-матрицы С определяются
скобками Пуассона (с/ = (/•,/))), и в рассматриваемом случае
матрица С равна нулю.
Из симметричности ЭФ/Эq следует, что 0TJq = (0,Jq) яв-
ляется полным дифференциалом. Тем самым криволинейный ин-
теграл
ч ч т
S(q,p)= j Фт<^ = Ф'(д,р)^' (5.7.25)
Чо Чо1"1
не зависит от пути интегрирования и является функцией верх-
24. М.Л. Лидов
370
Глава 5. Основной аппарат гамильтоновой механики
него предела q. Очевидно,
-
det-----
ЭрЭд
ЭФ
Эр
Л Iaf
det —
I Эр.
*0.
Равенство ।—। следует из (24). Тем самым S(q,p) можно принять
за производящую функцию симплектического диффеоморфизма
p,q-»p,q;
ГЭ5"| _ч
Р= ч- =Ф(Ч,р),
UqJ
"Э5"
Следовательно, вектор-функция p=f(z) действительно опреде-
ляет зависимость новых импульсов от старых переменных z.
Доказательство теоремы Лиувилля. Пусть
f(z) суть т независимых первых интегралов в инволюции. Если
провести симплектическое преобразование с производящей
функцией S(p,q), определенной (25), то в переменных p,q га-
мильтониан задачи будет иметь вид
H = H(p,q) =
Н\ q
<8q ,
q=q(p,q)
Однако так как p=f(z) - первые интегралы, то необходимо,
чтобы dpldt=Q. Отсюда следует дН / 3q = 0 и, следовательно,
Н = Н(р). Таким образом, в новых переменных решение урав-
нений Гамильтона имеет следующий простой вид:
р = р0 = const,
'dip
(t-t0) + q0,
q =
где p0,q0 - начальные данные.
Для определения решения в исходных переменных необхо-
димо вычислить квадратуры (25). То есть для получения в не-
которой области переменных р, q общего решения достаточно
уметь вычислить соответствующие квадратуры и разрешить не-
явные функции. Такие задачи называются интегрируемыми. Тем
самым теорема Лиувилля утверждает, что знание всего т не-
зависимых первых интегралов в инволюции гарантирует интег-
рируемость уравнений Гамильтона. В этом одна из специфи-
ческих особенностей гамильтоновых систем.
Доказанная теорема с точки зрения приложений обладает
как достоинствами, так и недостатками. Достоинство заключает-
§ 5.7. Первые интегралы уравнений Гамильтона
371
ся в конструктивном характере ее доказательства. Доказательст-
во указывает путь введения новых переменных. Во многих при-
кладных задачах таким путем удается ввести единые переменные
р и q, пригодные для всех моментов времени - оо < t < как
это было сделано для систем типа Лиувилля. Однако эта теорема
доказывает существование таких переменных лишь локально.
Теорема Лиувилля предполагает существование т независи-
мых первых интегралов
Z(₽.q) = p'. i =
Каждое из этих уравнений определяет гиперповерхность в Rlm,
а пересечение т гиперповерхностей определяет множество
М- = {ze/?2'", /(z) = p', г =
Условие независимости т интегралов гарантирует, что неко-
торую окрестность каждой точки z0 е М- можно диффеоморфно
отобразить на область m-мерного евклидова пространства. То
есть М- - гладкое многообразие. Если zogA/-, то все точки
интегральной кривой z=z(r,z0), определяемой решением уравне-
ний Гамильтона с начальными данными t = t0, z = z0, будут при-
надлежать М-. Таким образом, М- - инвариантное
многообразие относительного фазового потока, опреде-
ляемого уравнениями Гамильтона.
В.И. Арнольдом при дополнительном к условиям теоремы
Лиувилля предположении, что многообразие М- компактно,
доказано:
1. М- - диффеоморфно m-мерному тору Г”.
2. Можно ввести такие вектор-функции
1(р), Г =(/',/2,.
что тор 7Ь будет определяться условиями I(f(z)) = const. На торе
Т" можно ввести сопряженные I угловые координаты ср':
Г" ={ф',ф2,...,(р'”, о^ф'<2л, i = l,2,...,m}.
В координатах 1,<р (<рт =(ф’,...,ф'”)) движение условно-перио-
дическое:
1 = const, — = со(7), сот = (со’(/),...,со'"(/)),
dt
т.е. координаты I, ср являются переменными «действие-угол».
3. Уравнения Гамильтона интегрируются в квадратурах.
24*
Глава 6
Движение твердого тела
§ 6.1. Качественный анализ случая Эйлера-Пуансо
В § 3.11 мы вывели уравнения движения твердого тела в двух
случаях:
А. Твердое тело свободно.
Б. Одна точка твердого тела закреплена.
Через Е обозначали жестко связанный с телом репер, на-
чало которого помещено в центре масс (случай А) или в точке
закрепления (случай Б). Начало репера Е совпадает с началом
репера Е. Репер Е не вращается, его орты параллельны ортам
некоторого абсолютного репера Е. В случае А репер Е есть
репер Кёнига. Матрица A (t) определяет преобразование
_ А(Г) ~
Е Е.
Будем использовать обозначения:
J - тензор инерции твердого тела относительно Е,
со - координаты вектора угловой скорости вращения Е от-
носительно Е в проекциях на орты репера Е,
К - координаты вектора момента количества движения тела
относительно Е в проекциях на Е,
<о = Ат(0<о, К = ДТ(Г)К
- координаты тех же векторов относительно репера Е,
Т - кинетическая энергия движения тела относительно Е,
М(е) - момент внешних сил, действующих на твердое тело
относительно начала репера Е в проекциях на его орты.
Согласно § 3.11, изменение вектора со определяется динами-
ческими уравнениями Эйлера (3.11.13):
J — + [ы,Ло] = М(е). (6.1.1)
dt
В этом параграфе мы рассмотрим так называемый случай Эйле-
§ 6.1. Качественный анализ случая Эйлера-Пуансо
373
ра-Пуансо, когда М(е) = 0. Этот случай, в частности, дает при-
ближенное описание движения твердого тела, когда влияние
внешних сил пренебрежимо мало. Заметим, что момент сил М(и
может быть равен нулю и тогда, когда внешние силы не малы.
При рассмотрении задачи о физическом маятнике в § 4.8 было
показано, что момент внешних сил, действующих на твердое
тело, которое находится в однородном поле тяжести (говорят
тяжелое твердое тело), равен моменту результирующей силы
F(e), приложенной в центре масс твердого тела. Так как для сво-
бодного твердого тела начало репера Е помещено в центре
масс, то в этом случае М(<?) = 0. Для тяжелого твердого тела в
случае Б условие М(е) = 0 будет выполнено, если точка закреп-
ления совпадает с центром масс тела.
Мы выберем репер Е ориентированным по главным осям
инерции центра масс твердого тела (случай А) или точки
закрепления (случай Б). Тензор инерции будет диагональной
матрицей и уравнения (1) можно записать в виде (3.11.17)
J! —+ (J3-J2)w2w3 = 0,
dt
2
J2----+ (J1-/3)w3w1-0, (6.1.2)
dt
J3 —+ (J2-J1)w'(o2 =0.
dt
Уравнения (2) вместе с кинематическими уравнениями Эйлера
(2.8.7) описывают задачу вращения твердого тела в рассматри-
ваемых случаях.
При таком выборе репера Е имеет место (см. § 3.11) следую-
щее представление для вектора К и кинетической энергии Т :
Кт =(J1(bl,J2(b2,J3&3),
-1 ~1 7 ~7 7 7 1 (6.1.3)
r = -[J1(w1)2+J2(co2)2+J3(w3)2]--oTJo.
Для определенности будем говорить о движении свободного
твердого тела и будем определять его движение относительно
репера Кёнига Е. Однако ниже мы уже нигде не будем ис-
пользовать то, что начало репера Е совпадает с центром масс.
Поэтому все дальнейшие выводы будут справедливы и для слу-
чая Б, если репер Е отождествить с абсолютным репером Е,
374
Глава 6. Движение твердого тела
начало которого помещено в точке закрепления. В случае Б эта
точка не обязана совпадать с центром масс твердого тела.
1°. Интегралы задачи. Из теоремы об изменении кинети-
ческого момента в относительном движении (3.6.17) при М(е) =0
следует существование векторного интеграла
К = const. (6.1.4)
Покажем, что кинетическая энергия Т относительно репера
Кёнига Е тоже не изменяется с течением времени.
Подсчитаем производную по времени от работы внешних сил
на относительном движении:
<!?-'.V
Суммирование производится по всем точкам твердого тела.
Из соотношений кинематики
\i = [<o,i;.],
откуда
N N / N \ _
У (F((e),v,) = y <S;(e),[w,i- ]) = («,У [i;,Fz(e’n = <<o,M(e,) = 0.
/=1 /=1 \ 1=1 /
Применяя теорему об изменении кинетической энергии в отно-
сительном движении (3.6.12) получим
Т = const. (6.1.5)
Согласно (3), интеграл (5) можно записать в следующем виде:
^(w1)2 +J2(w2)2 + J3(w3)2 = 2Т = const. (6.1.6)
Из векторного интеграла (4) следует
| К I2 = I Ат (t)k I2 = IК I2 = const. (6.1.7)
Используя (3), интеграл (7) можно записать в следующем виде:
J2^1)2 +J2(w2)2 + J3(w3)2 = |K|2 = const. (6.1.8)
Упражнение. Дифференцируя (6) и (8) по времени t и подставляя d(hl /dt
из уравнений (2), покажите непосредственно, что
^ г/|К|2 _0
dt dt
2°. Качественное исследование задачи. Используя соотно-
шения К' i = 1,2,3, между проекциями вектора угловой
§ 6.1. Качественный анализ случая Эйлера-Пуансо
375
скорости и вектора кинетического момента на орты репера Е,
интегралы (6) и (8) можно записать в следующем виде:
-1(^)2 +^-(К2)2 + ^-(Р)2 = 2Г, (6.1.6')
Л J2
(£')2+(£2)2+(£3)2 =|К|2. (6.1.8')
Из этих соотношений следует, что конец вектора К принад-
лежит эллипсоиду (6') и сфере (8'), т.е. принадлежит линии их
пересечения.
Будем полагать, что моменты инерции удовлетворяют не-
равенствам
Л>Л>Л- (6.1.9)
Отсюда следует, что радиус сферы | К | должен находиться в пре-
делах между наибольшей и наименьшей полуосями эллипсоида
j2J3f ^|К| =£72J1^- (6.1.10)
Иначе уравнения (6') и (8') несовместны. На рис. 131 изображе-
ны линии пересечения эллипсоида со сферой.
При | К | = ^2JXT существуют лишь решения (6') и (8'): Кт =
= (±^2JjT,0,0). Этим решениям соответствуют точки А и А'
(сфера касается эллипсоида в точках А и А ').
При | К | = - тоже только два решения: Кт =
= (0,0, ± y)2J3T). На рис. 131 показана только одна точка С, соот-
ветствующая знаку «плюс».
При | К | = yj2J2T решения (6') и (8') представлены на этом
376
Глава 6. Движение твердого тела
же рисунке четырьмя кривыми - сепаратрисами ВВ\ соеди-
няющими точки Кт = (0,±^2J2T,0). Поведение кривых в ок-
рестности точки В показано на рис. 132.
Так как компоненты вектора со получаются из
компонентов вектора К простым растяжением
вдоль осей эллипсоида:
~ z К1
со =—,
Л
то рис. 131 одновременно качественно представ-
ляет и кривые, по которым может перемещаться в репере Е
конец вектора со.
Особым точкам А, В, С соответствуют особые решения урав-
нений (2):
(6.1.11)
Упражнение. Проверьте, что уравнения (2) допускают решения (11).
При этом вектор угловой скорости со не изменяет своего
положения относительно репера Кёнига. Действительно, оче-
видно
(К, со) = (К, со).
Для случаев а), б), в)
<К,со> = |К||со | = |К ||со Н<К,со> = |К ||со |. (*)
Из этих соотношений следует, что вектор со одинаково на-
правлен с вектором К, который, как следует из интеграла (4), не
изменяет своего положения относительно репера Кёнига. Если
слегка возмутить стационарное вращение вокруг оси с макси-
мальным моментом инерции, то, как, следует из рис. 131, конец
вектора со будет двигаться по кривой, близкой к точке А(А'). То
же самое будет при возмущении вращения вокруг оси с наимень-
шим моментом инерции. Если же возмутить стационарное вра-
щение вокруг средней оси инерции (случай б)), то, как следует из
рис. 131, вектор со начнет удаляться по кривой, близкой к сепа-
ратрисе.
§ 6.1. Качественный анализ случая Эйлера-Пуансо
377
Мы доказали теорему: Решения уравнений Эйлера, описы-
вающие стационарное вращение вокруг главных осей с наи-
большим и наименьшим моментами инерции, устойчивы, а ре-
шение, описывающее стационарное вращение вокруг главной
оси со средним значением момента инерции, неустойчиво.
Из рис. 131 можно извлечь и другие выводы об особенностях
движения тела. Все движения вектора угловой скорости (или век-
тора К) относительно репера Е, за исключением особых ре-
шений, соответствующих сепаратрисам ВВ\ являются периоди-
ческими. Это следует из того, что все кривые на эллипсоиде
замкнутые линии. Период движения т, вообще говоря, на каждой
кривой разный. Он зависит от значений постоянных интегралов
2Т и IК I.
3°. Эллипсоид инерции. Рассмотрим множество векторов
х g Е, удовлетворяющих уравнению
xTJx = 1, (6.1.12)
где J - тензор инерции.
Определение. Геометрическое место точек, определяемое
концами векторов х, удовлетворяющих (12), есть эллипсоид,
который называют эллипсоидом инерции.
Если репер Е ориентирован по главным осям инерции, то
уравнение (12) можно записать в следующем виде:
(x1)2J1+(x2)2J2+(x3)2J3 = l.
Если тело вытянуто вдоль оси, определяемой ортом ёу, то
момент инерции относительно этой оси мал. Этой оси соответ-
ствует полуось эллипсоида инерции 1 / Она велика. В этом
смысле эллипсоид инерции отражает геометрические характери-
стики тела. Эллипсоид инерции неизменно связан с твердым
телом и в последующем анализе мы будем его рассматривать в
качестве представителя тела. С точки зрения наблюдателя, свя-
занного с репером Кёнига Е, эллипсоид инерции будет вра-
щаться.
Уравнение эллипсоида инерции относительно Е можно по-
лучить формально путем преобразования
х = А(Ох, (6.1.13)
где A(f) - матрица поворота, определяющая преобразование
реперов
378
Глава 6. Движение твердого тела
Из (12) и (13) следует уравнение
где J = - тензор инерции твердого тела относительно
который в общем случае зависит от времени.
4°. Геометрическая интерпретация Пуансо. Пуансо устано-
вил следующие геометрические характеристики движения твер-
дого тела в рассматриваемом случае М(<?) = 0.
1. Точка В, определяемая вектором хв = принадле-
жат
жит эллипсоиду инерции.
Доказательство. Подставляя хв в (12) и используя
(6), получим
~ т ~ со /со 2Т
XnJXn = -= —= = 1.
2Т 2Т
2. Проекция вектора хв на вектор кинетического момента К
не изменяется в процессе движения.
Доказательство.
<о к \ (<о,к) TzF
= const.
3. Нормаль п (не обязательно еди-
ничная) к эллипсоиду инерции в точке
хв коллинеарна вектору кинетического
момента К.
Доказательство.
й = -^г(хт/х)
Эх
= 2/-Д=- = -3=к.
- ~ л/2Т л/2Т
Все отмеченные геометрические
Рис-133 свойства сформулированы в векторном
виде, и их легко можно интерпретировать, рассматривая
движение относительно репера Кёнига Е.
С точки зрения наблюдателя, связанного с репером Кёни-
га, имеется постоянный вектор кинетического момента К
(рис. 133). Имеется эллипсоид инерции. Вектор хв = A'r(t)xB оп-
ределяет точку В эллипсоида, в которой нормаль коллинеарна
§ 6.1. Качественный анализ случая Эйлера-Пуансо
379
вектору К. Тем самым в точке В эллипсоид касается плоскости
ПП\ проходящей через эту точку ортогонально вектору К.
Согласно (*), <хе,К> = <хе,К) = const. То есть плоскость ПЕГ
не изменяется с течением времени. Вектор угловой скорости
коллинеарен вектору хв. Следовательно, скорость v в точке В
равна нулю. (Точка В лежит на мгновенной оси вращения.)
Вывод. При движении твердого тела эллипсоид инерции ка-
тится без скольжения по неподвижной плоскости 7777':
<К,х) = (К,х) = Ж
В процессе качения через неко-
торое время т точка В опишет на
эллипсоиде замкнутую линию.
При рассмотрении задачи относи-
тельно репера Е через время т
все вернется в исходное состоя-
ние. Однако, с точки зрения наб-
людателя, связанного с репером
Кёнига, через время т касание бу-
дет происходить в другой точке
плоскости 7777'.
Как следует из рис. 134, через
каждое время т точка В оказывается на том же самом расстоя-
нии от точки О (точки, в которой плоскость пересекается лучом,
определяемым вектором К). То есть расстояние ОВ тоже изме-
няется периодически. Однако внутри периода движения расстоя-
ние ОВ, вообще говоря, изменяется от некоторого pmin до ртах.
При особых значениях параметров задачи возможны случаи,
когда через время пт (п - целое) кривая, которую описывает точ-
ка В на плоскости, замкнется, совершив один (рис. 135) или не-
сколько (рис. 136) оборотов вокруг точки О. В этом случае
380
Глава 6. Движение твердого тела
движение твердого тела будет периодическим с периодом т. В
общем случае движение будет условно-периодическим. Траекто-
рия движения на плоскости ПП' будет всюду плотно заполнять
кольцо между р = pmin и р = ртах (рис. 137).
Упражнение. Опишите геометрическую картину в случае стационарных
вращений.
Если эллипсоид инерции является эллипсоидом вращения, то
расстояние р = О В не изменяется с течением времени. В этом
случае точка В на плоскости ПП' опишет окружность. Однако
здесь также возможны случаи периодических и условно-перио-
дических движений.
Упражнение. Используя интегралы энергии и кинетического момента,
покажите формально, что О В = const, если J\ = J2-
§ 6.2. Описание потенциальных движений твердого тела
в канонических переменных
1°. Формулы для кинетической энергии. Если силы, дейст-
вующие на твердое тело, имеют потенциал U, то для описания
движений тела можно применить аппарат гамильтоновой ме-
ханики.
Ниже мы будем говорить о движе-
нии твердого тела с закрепленной точ-
кой О относительно абсолютного ре-
пера Е, начало которого связано с точ-
кой О. Однако, как мы знаем, получен-
ные выводы будут справедливы для
движения свободного твердого тела
относительно репера Кёнига. (В послед-
нем случае Е - репер Кёнига, О - центр
масс тела.)
Возьмем вначале в качестве обоб-
щенных координат углы Эйлера qT =
= (у, Ф, 0) (рис. 138). Обозначим через
Е = (ё1,ё2,ё3) репер с началом в точке
О, жестко связанный с телом и ориентированный по его главным
осям инерции.
Вспомним, что матрица?! преобразования Е—А(г) >Е опре-
деляется произведением трех матриц простых поворотов (см.
(2.8.2))
A = A(t) = П(3, ф)П(1, 0)11(3, ф). (6.2.1)
Кинетическая энергия Т и вектор момента количества движения
§ 6.2. Движения твердого тела в канонических переменных
381
К определяются следующими формулами (см. § 3.11):
1 ( ?П\
Т = -ыЧ<^ К = Ло, К=—— , (6.2.2)
2 <Эсо)
где со - вектор угловой скорости, J = J(\g, ср, 0) - тензор инерции
тела относительно репера Е.
Обозначая через со = Асо, К = АК проекции векторов со, К
на орты подвижного репера Г, получим
К = 76>, 7 = 'co'Vgj = ' К'7 'К,
2 2
где J = АГАТ - тензор инерции относительно Е.
В координатном представлении
Т = -[—(^1)2+-1_(^2)2+_1_(^3)2
2^! J2 J3
(6.2.3)
(6.2.4)
где Ji - моменты инерции относительно ортов ё4. Для вектора
угловой скорости со справедливо представление (см. § 2.8)
со = фе3 + фё3 + 0е{. (6.2.5)
Обозначим рт = (рф, рф, pQ) обобщенные импульсы, сопряженные
координатам q. Согласно общему правилу,
J эту ( эту (эг ЭсоУ =
Р <9qJ <9qJ 1^Эсо 9qJ
= (6.2.6)
dq J v d<o) dq)
Из (5) и (6) следует
рv= К = <е3, К), рф=<ё3,К), А) = (е;,К). (6.2.7)
сД|/
В проекциях на орты репера Е
< sin 0 sin ф'
е3 - sinGcostp ,
. COS0 .
О'
О
1
совф'
-sin<p
. О >
ё3 =
382
Глава 6. Движение твердого тела
Отсюда получим
р... = sin 0СА71 sin ср + К2 cos ср) + К3 cos0,
(6.2.8)
= к\ pQ = К1 cos(p- К2 sin ср.
Разрешая (8) относительно к1, определим:
~i sin ср
к =-—(Ay-ApCose) + pecos<p,
cos - (6-2.9)
в)_ in к’ = р
sm0
Подставляя (9) в (4), получим выражение для кинетической
энергии в канонических переменных и гамильтониан задачи:х
Н = Т\ру, Pv, рв, Ф, 6) + U( V, 0, Ф, О-
Анализ некоторых рассматриваемых ниже случаев движения
твердого тела существенно упрощается, если вместо переменных
р, q ввести переменные р, q, связанные с р, q симплектическим
преобразованием.
На рис. 139, кроме систем координат Ей Е, показаны вектор
кинетического момента К и ортогональная ему центральная
плоскость л, содержащая лучи ОБ и ОС.
Использованы следующие обозначения: I - угол между век-
тором К и ортом е3, р - угол между вектором К и ортом ё3.
§ 6.2. Движения твердого тела в канонических переменных
383
Луч О В (орт ej) определяется линией пересечения плоскости
л и плоскости векторов ei и е2. Луч ОС (орт ё,1) определяется
линией пересечения плоскости 71 и плоскости векторов и ё2.
Через h, g, I обозначены углы между векторами в| и ёр и ё/,
е* и ej соответственно.
Введем обозначения:
L = (e3,K) = |K|cosp,
G = \ KI, (6.2.10)
(е3, К) = I К Icos/.
Лемма. Переменные
pT=(L,G,H), qT=(/,^,/z)
связаны с переменными рт = (pv,Ap,pe), qT =(\|/,ср,0) симплек-
тическим преобразованием:
р = р(рЛ)> ч = ч(рЛ) (6.2.11)
Для доказательства этой леммы воспользуемся доказанной
ранее (см. § 5.3) теоремой 1 о дифференциальной форме
б/со = pTJq + qTJp. (6.2.12)
Согласно этой теореме, форма б/со будет полным дифференциа-
лом тогда и только тогда, когда преобразование (11) - симплек-
тическое. Из (12) следует, что
б/со = б/со - 6/(qTp) = pT6/q - pT6/q.
Мы докажем, что б/со = 0. Отсюда будет
следовать, что б/со - полный дифферен-
циал, и преобразование (11) симплекти-
ческое.
Для доказательства воспользуемся
формулами сферической тригонометрии.
Напомним, что линия пересечения
сферы с центральной плоскостью назы-
вается окружностью большого круга.
Сферическим треугольником называется
(6.2.13)
Рис. 140
треугольник АВС, образованный дугами с, Ь, а окружностей
больших кругов (рис. 140). Углы А, В, С в вершинах измеряются
углами между соответствующими плоскостями.
Методами элементарной математики доказывается справед-
ливость:
384
Глава 6. Движение твердого тела
(6.2.14)
(6.2.15)
а) теоремы косинусов
cosfl = cosZjcosc + sinfesinccosA;
б) теоремы синусов
sin а _ sin/? _ sine
sin A sin В sin С
Нетрудно установить следующее дифференциальное равен-
ство:
da = cosCdb + cosBdc + sinbsinCdA. (6.2.16)
Например, частная производная daldb = cosC легко получается из
рассмотрения треугольника СС'В на рис. 141 и применения тео-
ремы косинусов:
cos(a + da) = cos db cos a + sin db sin a cos(l 80° - C) => da =
- cosCdb + O(| da |) + O(| db |),
Э cos a . da . , . . Л да . , . „
— ----= - sin a-- = -snwsmcsm A=> — = sin b sin C.
dA dA dA
Используя обозначения рис. 139, рассмотрим на сфере тре-
угольники АВС и ВСК, где К - след пересечения сферы лучом,
определяемым вектором К (рис. 142). Обозначим через z ду-
гу КА. Применяя теорему косинусов к треугольнику К АС, по-
лучим
cosz = = — sin(cp — 7) sin р. (6.2.17)
1К1
Запишем дифференциальное соотношение (16) для элемен-
тов треугольника АВС:
dg = cosрd(ф -1) + cos Id(\[f -h)- 8ш(ф - Z) sin pd0. (6.2.18)
§ 6.2. Движения твердого тела в канонических переменных
385
Перейдем к доказательству леммы. Используя представления
(7), (10), (17), получим
pTdq = pvd\\i + pydtp + рв dB = (е3, + (ё3, К)<7ср + (е}, К) J0 =
- | К | (cos Idy + cos pr/ф - sin(cp - /) sin pJ0),
pTJq = Ldl + Gdg + Hdh = | К | (cospJ/ + dg + cos Idh).
Отсюда следует
сЕй = p dq - pTdq =
= | К |[cos/d(v -/z) + cosp<i((p-/)-sin((p-/)sinpd0-dg] = 0.
Тем самым мы доказали, что преобразование р, q —> р, q -
симплектическое. Для описания задачи в переменных р, q сле-
дует выразить функцию Гамильтона через новые переменные.
Запишем представление кинетической энергии в переменных
р, q. Используя рис. 143, нетрудно выразить через вновь введен-
ные углы проекции вектора К на орты репера Е:
К1 = | К | sin psin I,
К2 = | К |sinpcos/,
К3 = |K|cosp.
(6.2.19)
Из соотношений (4), (10) и (19) получим
2
—(К1)2 +—(к2)2 +—(F)2
J d2 d
£
2
sin2 Z cos2 Г
---------1-------
< Л A >
IК I2 sin2p + ^-|
^3
К |2 cos2 p
25. М.Л. Лидов
386
Глава 6. Движение твердого тела
Отсюда следует
sin21
< Л
+^0(g2-l2)+—
(6.2.20)
Отметим, что углы р и I не являются каноническими пере-
менными. Они выражаются через компоненты вектора р:
L
cosp = —
г Н
cos/ =—
(6.2.21)
Для записи потенциала U через новые переменные часто тре-
буется выразить матрицу А преобразования Е—через
переменные р, q. Представим это преобразование как суперпо-
зицию двух преобразований:
Е—^Е—^Ё.
Матрица Л) получается путем перемножения матриц двух про-
стых поворотов (рис. 144)
= П(1,/)П(3, й),
а матрица Л2 выражается через эйлеровы углы g, I, р (рис. 145):
А2 = П(3,/)П(1, р)П(3, g).
Таким образом, выражение
А =А2А{ = П(3, /)П(1, р)П(3, #)П(1, /)П(3,й) (6.2.22)
определяет матрицу поворота А через переменные р, q.
Для примера получим в этих переменных выражение для
§ 6.2. Движения твердого тела в канонических переменных
387
компонентов вектора е3 в проекциях на орты репера Е:
Ае3=П(3,/)П(1,р)П(3,^)П(1,/)П(3,й) 0 .
Л;
Нетрудно показать, что
foA
(6\
о
1
1
1
П(3,й) 0 = 0, П(1,/) 0 = sin/
cos/
Таким образом,
Ло"
П(1,/)П(3,7х) 0 = ё2 sin/ + e3 cos/.
Л
Вычисляя проекции векторов е2 и е3 на орты репера Е, по-
лучим
sin g cos I + cos g cos p sin Г
А2ё2 = -singsinZ + cosgcospcosZ ,
4 -cosgsinp ?
^sinpsinZ^
А2ё3 = sin p cos Z .
< COSP >
В результате будем иметь
Ае3 = sin /(Аё2) + cos /(Аё3). (6.2.23)
В частности, последний компонент (23) определяет проекцию
вектора е3 на вектор ё3:
cos0 = -sin/cosgsinp + cos/cosp.
(6.2.24)
2°. Некоторые задачи о вращении твердого тела. Пусть твер-
дое тело вращается вокруг закрепленной точки О в однородном
поле тяжести. Будем полагать, что орт е3 абсолютного репера Е
направлен «вверх», т.е. противоположно направлению поля. Тог-
да на элементарную массу dm твердого тела действует сила тя-
жести
dF = -gdm • е3,
25*
388
Глава 6. Движение твердого тела
где g - const - ускорение силы тяжести. Эта сила имеет потен-
циал
dU = gdm(e3,r) = g(e3,6/m-r), (6.2.25)
и тогда
Результирующий потенциал получим, интегрируя (25) по
всем точкам твердого тела:
U = g(e3,Jrdm) = mg(e3,r*), (6.2.26)
где г* - радиус-вектор центра масс тела, т - масса тела.
Задачу о вращении твердого тела с потенциалом (26) назы-
вают задачей о вращении тяжелого твердого тела.
Обозначим f*T=(al, я2, а3) компоненты радиуса-вектора
центра масс относительно репера Е, связанного с твердым те-
лом. Величины а1 являются постоянными параметрами задачи.
Согласно (23) и (26), выражение потенциала U через канони-
ческие переменные р, q определяется формулой
t/(p,q,r*) = mgr*TAe3, (6.2.27)
где выражение матрицы А через канонические переменные
определяется формулой (22).
Задача о движении тяжелого твердого тела не интегрируется
в квадратурах, и общими методами решения этой задачи для
конкретных начальных данных на ограниченных интервалах
времени являются либо метод численного интегрирования соот-
ветствующей системы дифференциальных уравнений, либо в
случаях, когда задача близка к некоторой интегрируемой, ис-
пользуются методы теории возмущений, для которых в качестве
главного приближения обычно используется решение задачи в
соответствующем интегрируемом случае. Перечислим некото-
рые из них.
1. Случай Эйлера-Пуансо. Этот случай частично рассмотрен
в § 6.1. Он возникает, когда потенциал внешних сил равен нулю:
и = о.
При движении в поле тяжести это условие будет выполнено,
если
г* - 0.
Для свободного твердого тела, если никакие силы, кроме силы
тяжести, на него не действуют, это условие выполняется авто-
матически, так как начало репера Е (в этом случае это репер
Кёнига) совпадает с центром масс. При рассмотрении задачи для
§ 6.2. Движения твердого тела в канонических переменных
389
тела с закрепленной точкой необходимо предположить, что точ-
ка закрепления совпадает с центром масс.
2. Случай Лагранжа. Этот случай возникает, когда:
а) тело обладает динамической симметрией, т.е. два главных
момента инерции равны:
Л = J2 = J; (6.2.28)
б) центр масс расположен на оси симметрии ё3:
г* = я3ё3.
В лагранжевом случае мы приходим к задаче с потенциалом
(см. (24))
U - mga3 cos 0 = mga3 (- sin I cos g sin p + cos I cos p). (6.2.29)
3. Случай C.B. Ковалевской. Для реализации этого случая
необходимо:
а) специальное соотношение между главными моментами
инерции тела:
Ji=J2 = 2J3; (6.2.30)
б) центр масс тела должен быть расположен в плоскости
векторов ёх и ё2,т.е.
а3 = 0, г* = а1ё1 + а2ё2.
В случае Ковалевской мы приходим (см. (23)) к задаче с по-
тенциалом:
U = mg(ax sin 0 sin ср + а2 sin 0 cos ср) =
= mg{ai [sin /(sin g cos I + cos g cos p sin /) + cos / sin p sin /] +
+a2 [sin /(- sin g sin I + cos g cos p cos /) + cos / sin p cos /]}. (6.2.31)
Кроме трех указанных случаев, интегрируемость которых
связана либо только с особенностью расположения точки зак-
репления (случай Эйлера-Пуансо), либо с дополнительными
условиями на параметры (моменты инерции и положение центра
масс), в задаче о вращении тяжелого твердого тела выделяются
специальные классы решений этой задачи, которые существуют,
когда начальные значения фазовых переменных не произволь-
ны, а подчинены некоторым условиям.
Потенциальные задачи о движении твердого тела не исчер-
пываются задачей тяжелого твердого тела. В
частности, большой практический интерес представляет задача о
движении свободного твердого тела в центральном поле гра-
витационных сил.
390
Глава 6. Движение твердого тела
На рис. 146 буквой М обозначен центр притяжения, г* - ра-
диус-вектор центра масс тела, г* + ij - радиус-вектор, опреде-
ляющий положение элементарной массы dm. Гравитационный
потенциал взаимодействия материальной точки массой М (пла-
неты) и элементарной массы тела dm определяется известной
нам формулой
где ц =fM,f- гравитационная постоянная.
Полный потенциал получается ин-
тегрированием по объему тела
f dm
(6.2.32)
В формальной постановке этой задачи
уравнения движения центра масс тела
относительно репера Е, связанного с
точкой Л/,
>2 *
т^Ц- = Е(е),
dt2
оказываются «завязанными» с уравне-
ниями вращения тела относительно
репера Кёнига, начало которого по-
мещено в центре масс тела О. Кроме
того, оказывается, что потенциал (32), вообще говоря, зависит от
бесконечного числа параметров, описывающих распределение
массы относительно какого-либо репера, жестко связанного с
телом.
Однако для задачи о движении искусственного спутника пла-
I j* I
неты г = max;—(максимум берется по всем точкам спутни-
|г I
каг!).
Пример. Размер спутника 7 м. Расстояние спутника отно-
сительно центра масс Земли I г* I ~ 7 • 106 м, 8 ~ 10-6.
В главном приближении по параметру 8 оказывается, что:
1) движение центра масс спутника можно рассматривать не-
зависимо от его ориентации относительно репера Кёнига;
2) существенное для задачи распределение массы тела отно-
сительно связанного с ним репера полностью характеризует-
ся значениями трех главных центральных моментов инерции J),
Л, Л-
§ 6.3. Аналитическое исследование случая Эйлера-Пуансо
391
§ 6.3. Аналитическое исследование случая
Эйлера-Пуансо
В этом случае потенциал U внешних сил равен нулю и Га-
мильтониан задачи совпадает с кинетической энергией (6.2.20):
Ж = Т = -
2
Г sin2 Z cos2 2
--------1-------(Cr — L ) 4-------
< A A J A
(6.3.1)
Мы описываем задачу в канонических переменных (см. (6.2.10)):
pT=(L,G,H), qT=(/,g,/z).
Гамильтониан (1) зависит лишь от трех переменных L, G, I. Три
другие переменные g, h, Н - циклические. Поэтому на любом
решении
G = |K| = G0, h = h0, H = \K\cosI = H0, (6.3.2)
где Go, Hq, h(} - постоянные, определяемые начальными дан-
ными.
Условиями (2) в канонических переменных записан извест-
ный нам результат (см. § 6.1), что в задаче Эйлера-Пуансо век-
тор кинетического момента К не изменяется относительно
абсолютной системы координат Е. При этом система координат
Е = (ёрё2,ёз) не вращается относительно Е. Удобство введенных
канонических переменных р, q состоит в том, что из интеграла
К = const непосредственно следует, что первыми интегралами
являются три основных переменных задачи, и тем самым задача
определения движения твердого тела сводится к одномерной
задаче с гамильтонианом (1), в котором G = Go является пара-
метром.
Кроме того, в силу автономности системы (1) гамильтониан
задачи Ж является первым интегралом:
A(l)G2 + B(l)L2 = Ж = const,
(6.3.3)
где
cos2 С
+------
В(/) = |
sin21 cos21
Этот интеграл определяет поведение интегральных кривых в
плоскости (L, /).
392
Глава 6. Движение твердого тела
Случай динамически симметричного тела
Рассмотрим сначала аналитически очень простой случай этой
задачи, когда два главных момента инерции одинаковы. Без
ограничения общности можно положить, что равны J{ и J2, т.е.
= J- (6.3.4)
Тогда (1) имеет вид
? L2
1 |~G2-Z?
2 J
з _
Отсюда следует
dL __
dt
1 1 т
7 ~ Т ^0
dl
dt
n r r
----= 0 => L = Ln = const,
Э/--0
dg дЖ Go
— = -— = —= сор
dt dG J s
(6.3.5)
и, следовательно,
7 = CDz(r-r0)4-Z0, g = CDg(r-r0) + g0.
Кроме того, отметим, что cos р = L/G = LqIGq - const.
Таким образом, в динамически симметрич-
ном случае тело равномерно (с постоянной
угловой скоростью СО/) вращается относительно
оси симметрии ё3, а ось ё3 в свою очередь
равномерно прецессирует (движется по конусу)
вокруг постоянного в абсолютном пространстве
вектора кинетического момента К (рис. 147).
Легко видеть, что в рассматриваемом случае
переменные р, q являются переменными
«действие-угол». При этом в данной задаче отличны от нуля
лишь две частоты coz и cog, а со/7 = h = 0, т.е. задача - вырож-
денная. В случае, когда начальные условия таковы, что со/со^ =
= п/т (п, т - целые) или, иначе (J/J3 - 1) cos р = п/т, то движение
будет периодическим. В общем случае движение условно-перио-
дическое.
Общий случай
Для определенности предположим, что
J3> Л> Л. (6.3.6)
Рассмотрим поведение интегральных кривых (3) в плоскости
§ 6.3. Аналитическое исследование случая Эйлера-Пуансо
393
(L, I), Уравнения Гамильтона для переменных L, I имеют вид
dL ЭЖ sin 2/Г 1 11_2 2
— = —^7- = -—Z-----(О -Ь), (6.3.7)
dt dl 2 J2 j
dl ЭЖ J 1 Г sin2 Z cos2/V ninzI4 ^OO4
— = —= L-----------—+ —— = 2LB(l). (6.3.8)
dt (jL J 3 J 2 j
Проанализируем качественные особенности поведения ин-
тегральных кривых этих уравнений, необходимые для построе-
ния фазового портрета, приведенного на рис. 148.
1. Уравнения (7) и (8) инвариантны относительно замены I на
Z + л. Следствие: решения этих уравнений являются 71-перио-
дическими по I. Кроме того, заметим, что так как L= G cos р, то
физический смысл имеют значения L, удовлетворяющие нера-
венствам
-G^L^G (G>0).
2. Используя (6), нетрудно показать, что выражение в квад-
ратных скобках в (8) всегда меньше нуля. Отсюда следует, что
равновесные точки системы уравнений (7), (8) должны опре-
деляться условиями
71
L = 0 и sin2/ = 0 => I = к— (к- целое).
3. Нетрудно показать, что в точке (L - О, I = 71/2) функция
3€(L, I) достигает максимума:
I 2) 2
394
Глава 6. Движение твердого тела
В окрестности этой точки при Ж < интегральные кривые (на
рис. 148 - кривая Yi) приближенно описываются уравнением
эллипса
-2Ж+— = £2 3-LW/_2f) G2 3-L . (6.3.9)
Такие кривые принято называть либрационными.
4. Из (3) также следует, что при
j G^
2 Jx
и L = 0 уравнению (3) удовлетворяют два решения:
/ = /,=^-А и Z = /2=^ + A, (6.3.10)
где Д = Д(/1, Л, G, Ж) определяется уравнением
cos2A sin2A 2 Ж
Jx J2 G2
5. При£ = 0и 1 = 0
д2Ж д2Ж
dL2 < ’ dl2
Поэтому равновесная точка (L = 0, I = 0) является особой точкой
1 С2
типа седла. В этой точке Ж = $6(0,0) = = $6 2.
2 $2
6. Так как sgn (dVfJdL) = -sgn L (см. (8)), то минимальное зна-
чение $6 достигается при L = ±G (cos р = ±1). При этом
1
Cip _Cip _ 1
OG — OG т —---.
3 2 73
7. Нетрудно показать, что при
<7Ъз <7Ъ < бГЬ2
значение L не может обращаться в нуль. Это следует из (3). При
L = 0
Таким образом, при этих значениях $6 угловая переменная I
изменяется монотонно:
dl
dt
< 0, если L > 0,
> 0, если L < 0.
§ 6.3. Аналитическое исследование случая Эйлера-Пуансо
395
Будем говорить, что это - кривые ротационного типа. На
рис. 148 - кривая у2-
8. Из седловой особой точки (L = О, I = 0) начинаются две осо-
бые интегральные кривые, определяемые (3) при Ж = Ж2. Это -
сепаратрисы, которые отделяют область, заполненную кривыми
либрационного типа, от двух областей, заполненных ротацион-
ными кривыми. Они оканчиваются в другой седловой точке (L =
= 0,1 = л) (см. рис. 148).
Фазовый портрет этой задачи представлен на рис. 148.
Построенная нами картина очень похожа на фазовый порт-
рет задачи о математическом маятнике.
Из условия L = 0 следует cos р - 0. В этом случае орт ё3
лежит в плоскости л (не путать с числом л), перпендикулярной
вектору К. При этом если I = л/2, то орт ё] совпадает с вектором
К. При I = 0 с вектором К совпадает орт ё2. Из анализа следует,
что равновесное решение (/. = (),/ = л/2) соответствует случаю
вращения тела вокруг оси с наименьшим моментом инерции и
оно в определенном смысле устойчиво (малые отклонения на-
чальных данных приводят к движениям в окрестности равно-
весного решения).
Точка (L = 0,1 = 0) отвечает равномерному вращению вокруг
средней главной оси инерции тела. Это решение неустойчиво.
При малых вариациях начальных данных переменные L, I будут
существенно отклоняться от равновесных значений. В обоих
этих случаях dlldt = 0. Угловая скорость вращения тела опре-
деляется уравнением
, тт
если / = —,
2
если I = 0.
Интегральные кривые Ж = Ж 3 (L2 =
= G2 => cos р = ±1) описывают вращение
тела вокруг главной оси ё3 с наибольшим
моментом инерции. В случае р = 0 или р -
= л переменные g, I по отдельности не
имеют физического смысла. Однако из
анализа малых р (или (л - р)) нетрудно
понять, что переменная (g + /) сохраняет
физический смысл при р = 0, a (g - /) -
при р = л (рис. 149).
Рис. 149
396
Глава 6. Движение твердого тела
Вычислим
J(g + Z)_p^ । ЭЗН _G_
dt v 0G Jl=g J3
Аналогично при L = -G
d(g-l)=G
dt J3
To есть случаи Ж = отвечают равномерному вращению тела
вокруг оси с наибольшим моментом инерции. В общем случае
изменение переменной g определяется уравнением
dg ЭЖ Г sin2 / cos2
dt dG [ Jx J2 J
Отсюда следует, что угол g монотонно возрастает.
Таким образом, в общем случае движение твердого тела
представляет следующую картину:
1) тело вращается или колеблется вокруг оси ё3 с наиболь-
шим моментом инерции;
2) угол р между осью ё3 и вектором кинетического момента
К совершает колебания между значениями
Р = PnJ cospmax = -М и р = pmin[ cospmin =
3) одновременно ось ё3 монотонно прецессирует вокруг век-
тора К с переменной угловой скоростью dgldt.
Наглядное представление движения оси ё3 тела дают сле-
дующие рисунки кривой, описываемой концом вектора ё3 на еди-
ничной сфере с полюсом К, определяемым вектором К.
На рис. 150 изображен случай движения по кривой типа у2
Рис. 150
Рис. 151
§ 6.3. Аналитическое исследование случая Эйлера-Пуансо
397
(L > 0, р < я/2), а на рис. 151 - по кривой типа уь когда I Lmax I =
— । ^min । (Ртах — ^2 + Д, Pmjn — 7l/2 — Д, Д > 0).
Переменные «действие-угол» в задаче Эйлера-Пуансо
Гамильтониану задачи (3) соответствует уравнение Гамиль-
тона-Якоби
— +я(/)чг
< dg ) \Э1 J
= ж.
(6.3.11)
Уравнение (11) будет удовлетворено, если представить S в сле-
дующем виде:
S = hH + gG+S(l),
где Н, G 9Ж - постоянные, S зависит только от / и удовлет-
воряет уравнению
А(Г)С2+В(Г)
(6.3.12)
Мы показали, что рассматриваемая задача допускает разде-
ление переменных. Так как
G = — = G, Н = — = Н,
dg dh
то ниже мы можем не отмечать чертой новые переменные
GnH.
Переменные «действие-угол» вводятся по различным
формулам в зависимости от значения постоянной энергии Ж.
Будем говорить, что рассматривается случай А), если Ж2 < Ж <
< Жх*9 этому случаю в плоскости (L, /) отвечает кривая Yi либра-
ционного типа. В случае Б) Ж3 < Ж < Ж2, т.е. рассматривается
кривая у2 ротационного типа.
В соответствии с общим правилом, описанным в § 5.6, опре-
делим
j_r
яН В(Г)
4
J_2f fa^AQjG^
в случае А),
(6.3.13)
в случае Б),
— 0 V
где /1 < 12 - значения Z, при которых L = 0 на кривой уР Легко
видеть, что 2тс£ равно площади, заключенной внутри кривой yj
398
Глава 6. Движение твердого тела
(случай А)), или площади, заключенной между кривой у2 и осью
L = 0 (случай Б)). Квадратуры (13) можно представить как криво-
линейные интегралы
L = dL
YZ
Обозначим
8 = sgn L = ±1 - знак L.
Определим
в случае А),
в случае Б).
(6.3.14)
Ниже для определенности будем рас-
сматривать случай А). В случае Б) анализ
проводится аналогично.
Z4 уГ И3 соотношения (14) нетрудно заклю-
14-------2 чить, что, когда точка движется (рис. 152) по
кривой Yi от I - Ц до I = 12 (8 > 0) и обратно от
Рис. 152 I = 12 до I = Ц (8 < 0), функция T(Z) изменяется
на 2л. Таким образом, значения ? и? + 2пк
(к - целое) отвечают одним и тем же значениям I и L, определяю-
щим состояние системы.
Обозначим:
Ф1(0-I /
, y/B(l)[W-A(l)G2]
A(l)dl
7b(/)[^-^(Z)G2]
(6.3.15)
Соотношения (13) определяют неявным образом Ж как функцию
L и G2. Дифференцированием (13) по L при постоянном G2 и по
G2 при постоянном L нетрудно вычислить частные производные:
Э9С\ 2л
Jg2 Ф|(^2)
dG2Jr
(6.3.16)
Ф^г)'
Замечание. Значения 1Х и /2 зависят от L и G2, однако эти ве-
личины являются корнями подынтегрального выражения в (13).
§ 6.3. Аналитическое исследование случая Эйлера-Пуансо
399
Из (16) следует, что Ж монотонно возрастает при возрастании
как L так и G2.
При Ж = Ж(Ь, G2) 4х будет функцией Z, L и G2: 4х =
= ЧИ(/, L, G2). Покажем, что S = UV^l.L.G2) удовлетворяет урав-
нению (12):
A(/)G2 + B(/)f ® = A(/)G2 + В(/)М
vl у dl J Пу D\l)
Таким образом, полный интеграл уравнения Гамильтона-
Якоби имеет вид
S = hH + gG + W, L, G 2 )L.
Рассматривая Н, G, П как новые импульсы, определим сопря-
женные им координаты h,g,l. По общему правилу
Z = || = ^(LT).
иП иП
Из первого соотношения (14) имеем
1Л> = 2лГ —1L + 5 f + 2itkL, (6.3.18)
I 2 J j} B(l)
где k - произвольное целое число. Последний член возникает в
том случае, когда данному значению I отвечает не главное зна-
чение 4х, а отличающееся от него на целое, кратное 2л. Вычис-
ляя частные производные d^L^/dG и Э(ТЧХ)/ЭТ, получим
g = g + bG ф1(/)_ф2(/)1 (6.3.19)
< \ C'G’ J J
Л1 ХЛ X Л Д
I = 2л Ф/Z) + 2пк, (6.3.20)
\ 2 ) 2\ ЭТ )
при этом Ф/Z) монотонно возрастает при lx Z Z2 от нуля до
Ф^2). Когда точка движется по кривой Yi и Z изменяется от 1Х до
400
Глава 6. Движение твердого тела
Z2 (3 = 1), переменная I монотонно возрастает от 2як до 2як + я
((дЖ/dL) Ф1(/2) = 2л), а затем, когда I убывает от Z2 до 1Х (8 = -1)
переменная Z продолжает монотонно возрастать и становится
равной 2як + 2л при I = Ц. Отсюда следует, что, зная Zmod27t, мож-
но из (20) однозначно определить Zmod27l и 8. После этого из урав-
нения (19) при известном g можно однозначно определить g.
При этом из (19), (20), (16) следует, что g = g при Z = 1Х и Z - Z2
(или, иначе, при Z = кя).
В канонических переменных р = q = (l.g.h) гамиль-
тониан задачи имеет вид Ж = Отсюда следует, что Я,
G2, изменяются в процессе движения, a g и I изменяются
равномерно:
dg дЖ dl дЖ
dt dG dG2 8 dt dL 1
g = CD?(r-r0) + g0, / =w;-(r-r0) + /0.
Нетрудно видеть, что переменные р и q - переменные
«действие-угол». Так как Э9ЯЭН = свЛ = 0, то задача Эйлера-
Пуансо является вырожденной задачей. Однако, в отличие от
задачи двух тел, в этой задаче две частоты (св- и св-) отличны от
нуля.
Движение тела можно представить движением точки по
двумерному тору:
Т ~ (<?mod 2л ’ ^mod 2л 1 *
При этом различным L, G, Я, h отвечают различные то-
ры Т1. Если = п/т (п, т - целые), то траектория на торе
будет замкнутой линией, а движение будет периодическим. Если
св-, св- рационально несоизмеримы, то изображающая точка на
торе при t —> +оо (или t —> -оо) заполняет его всюду плотно.
Движение условно-периодическое.
Еще раз отметим, что удобство переменных «действие-угол»
проявляется при анализе задач, близких к интегрируемым. Пусть
гамильтониан возмущенной задачи имеет вид
^B=^L,G,l) + sU(L,G,H,ejl ,eJg ,ejh ,t), (6.3.21)
где Ж - гамильтониан рассмотренной задачи Эйлера-Пуансо,
et/ - возмущающий потенциал, 0 < 8 < 1 - малый параметр. В
§ 6.4. Случай Лагранжа
401
формуле (21) подчеркнуто, что U зависит от Z, g, h 2л-периоди-
чески (j = V-1).
В переменных «действие-угол» гамильтониан задачи будет
иметь вид
Ж в = Ж(Ц G) + еU(L, G, Н, ejl, eJ~g ,ejh, f).
При этом существенно, что главная часть гамильтониана зависит
только от импульсов «действий», а возмущающая часть от коор-
динат (l.g. h) зависит 2л-периодически. Для перехода к пере-
менным «действие-угол» в рассматриваемой задаче необходимо
уметь вычислять интегралы, определяемые соотношениями (13),
(15). Можно показать, что эти интегралы выражаются через
эллиптические интегралы первого, второго и третьего рода. Для
получения решения в исходных переменных необходимо обра-
щать эти интегралы. При этом оказывается, что зависимость
исходных переменных Z, g от Z, g определяется эллиптическими
функциями.
§ 6.4. Случай Лагранжа
При анализе случая Лагранжа удобнее использовать кано-
нические переменные, в которых обобщенными координатами
являются углы Эйлера qT = (у, (р, 0)
(рис. 153), а сопряженными им-
пульсами - рт = (pv, рф,ре). В случае
Лагранжа = J2 = J и кинетическая
энергия Т (6.2.4) представима в сле-
дующем виде:
2
у((^‘)2 +(£2)2) + -^-(Р)2
J J о
(6.4.1)
где К1 - проекции вектора кинети-
ческого момента на орты репера Е.
Потенциальная энергия определяется формулой (6.2.29)
U - ос cos 0, ос = mga^
где а3 - расстояние центра масс от точки закрепления (см.
рис. 153). Без ограничения общности можно считать ос 0. Под-
ставляя в (1) К1 из (6.2.9), получим выражение для кинетической
энергии в канонических переменных и гамильтониан задачи в
26. М.Л. Лидов
402
Глава 6. Движение твердого тела
следующем виде:
1 (Р™ - Р™ cos0)2 гь
W=T+U=- v 7--------------+ £l + Z2L +acose. (6.4.2)
2|_ Jsin20 J J3
Так как гамильтониан (2) зависит только от одной угловой
переменной 0, то
Рц = const, рф = const
являются первыми интегралами задачи. Тем самым для решения
задачи Лагранжа необходимо решить одномерную задачу отно-
сительно переменных ре, 0. Так как задача консервативна, то
Ж = const в (2) - интеграл задачи, который определяет поведение
траекторий в плоскости (ре, 0). Разрешая (2) относительно р%,
получим
Ре “ , и ” cos6, (6.4.3)
1-и
Так как f(u) - кубичный многочлен, для которого
Л^о)=-оо, /(+оо) = +оо, /(±1) <0
и заведомо существует такое и, при котором flu) > 0, то отсюда
следует (рис. 154), что/(и) имеет ровно два вещественных корня
на отрезке -1 и 1 (и один при и > 1).
При постоянных значениях интегралов задачи рф, Ж урав-
нения (3) определяют в плоскости (ре, 0) замкнутую кривую,
заключенную в полосе 02 0 0j:
COS 02 = М2, COS 0j = Щ.
Положение оси ё3 относительно абсолютной системы координат
§6.4. Случай Лагранжа
403
определяется двумя углами 0 и цл При этом
(Ру-Арсоэв)
J sin2 0
б/0_Э^_ре
dt dpQ J ' dt
Из уравнений dQ/dt = pQ/J и (3) по-
лучим
_ /(cose)
К. dt) J sin2 6
Это уравнение известного нам ти-
па (см. § 4.7). Фазовая траектория
в плоскости (dS/dt, 0) изображена
на рис. 155. Таким образом угол нутации 0 колеблется между 0 =
= 02 и 0 = 0Н
Возможны различные случаи:
3) Рч > Р^2, б) Ру < РуЩ', В) рфИ| < Ру < PyU2.
В то время как угол 0 колеблется, угол в случаях а) и б)
изменяется монотонно (см. второе уравнение (5)); d\tfldt > 0 в
случае а) и dyjldt < 0 в случае б).
В случае в) при 0 = 0 знак d\f!dt изменяется:
при cos 0 > cos 0 = и = Ру/ру имеет место dyldt < 0,
а при cos 0 < cos 0 dyldt > 0.
Существует доказательство того, что знак интегрального из-
менения угла 1|/ за время изменения 0 от 02 до 0j совпадает с
sgn (dtyldt) при и = их.
След оси ё3 на единичной сфере изображен на рис. 156, 157
для случаев а) и в)
Нетрудно показать, что во всех случаях щ < и. Однако возможен
случай, когда и = и2 (0 = 02),
d\\f
d® е=е2
= 0, и кривая, которую
26;
404
Глава 6. Движение твердого тела
описывает конец вектора ё3 на единичной сфере, при 0 = 02
имеет точку возврата (рис. 158).
Лемма о подобии движений. Запишем
X © =е уравнения движения задачи в следующем ви-
/С де:
Il A 7V/I Ф (dT duY dq (ЭТУ .. . ..
= + — = — ,(6.4.6)
1 dt < dq dq J dt Эр J
x. 7 где
T = T(p,q), L/ = L/(q).
Рис- 158 Пусть p = p(f, p0, q0), q = q(f, p0, q0) - реше-
ние системы (6) с начальными данными р0 = р(0, р0, q0), q0 =
= q(0, ро, q0).
Рассмотрим при постоянном Р вектор-функции
2?(O = Pp(T,po,qo), Q(O = q(T,po,qo)> ^ = 3'- (6.4.7)
Так как кинетическая энергия Т - квадратичная функция им-
пульсов, то нетрудно проверить, что S?(0 и Q (Г) удовлетворяют
следующей системе уравнений:
d<3> о dpdi о2(ЭТ ЭС/У (ЭТ'У ЭС/'У
dt dl dt 3q 3q J < dQ J I dQ J
dQ_ _ dq ch _ / ЭТУ _pFY
dt dT dt 4 dp J v Э2? J
где T'=T(2?,Q), U' = U(Q ).
При этом
^(O)-3Po, Q(O) = qo. (6.4.8)
Тем самым мы показали, что S?(z) и Q (г) удовлетворяют
уравнениям, которые отличаются от (6) тем, что потенциал U (и,
следовательно, сила тяжести) увеличены в Р2 раз, а начальные
импульсы S?(0) увеличены в р раз. При этом траектория в коор-
динатном пространстве q не изменяется; только время ее про-
хождения сокращается в Р раз.
Следствие. Если, не изменяя начальных координат q0,
мы увеличим начальные импульсы в Р раз, то траектория в
координатном пространстве будет такой же как, если бы, не
изменяя начальных импульсов, уменьшили бы силу тяжести в
Р2 раз. Поэтому в пределе при I р0 I °° (или, что то же самое,
при очень большой начальной угловой скорости) движение тела
происходит так же, как в динамически симметричном случае
§ 6.4. Случай Лагранжа
405
задачи Эйлера-Пуансо. Эту задачу мы —ч
разбирали ранее. Следовательно, в пре- КX/ р '\ ез
дельном случае вектор кинетического /
момента остается постоянным, а ось ё3 ' Х/г
прецессирует вокруг вектора кинетиче-
ского момента по круговому конусу с
углом полураствора р (рис. 159).
Углы I и р в этом предельном случае
остаются постоянными; их значения Рис. 159
определяются начальными данными. В
частности, если вектор кинетического момента в начальный мо-
мент времени направлен по оси ё3 тела, то р = 0. В этом случае
ось ё3 тела остается постоянной в пространстве. Рассмотрим
теперь как изменится движение тела в случае, когда действует
«слабое» поле тяжести.
Быстро закрученное тело
Пусть при t = 0 угловая скорость направлена по оси ё3. Тогда
при t - 0
к' = к2=о, k3 = Pif), е=е0.
Из соотношений (6.2.9) получим
Pv = P<pCOS0o, Ре|г=о=О.
Постоянная энергии Ж (2) определяется по этим начальным
данным следующей формулой:
2 2
1 Pt 1 Pt
Ж =----—+ OtCOS0o =----- (1 + Pcos0o),
2 J. 0 2 Д 0
Безразмерный постоянный параметр р как раз и характеризует
отношение потенциальной энергии к кинетической. Преобра-
зуем в рассматриваемом случае функцию/(и) (4):
f(u) = J 2W-^-2au
I 7з
(1-и2) -Рф
Рц,
------и
2
2
—P(cos0О - cos0) sin2 0 - (cos0О - cos0)2
J3
(6.4.9)
406
Глава 6. Движение твердого тела
ИЛИ
f(u) = p2(cos0o-cos0) —Psin20-(cos0o-cos0) . (6.4.10)
LA
Из этого представления очевидно, что 0 = 0О является корнем
функции/(и). При Р = 0 этот корень будет двойным.
Рассмотрим теперь задачу при достаточно малом р. Нетрудно
показать, что при малых Р второй корень будет близок к 0О.
Представим 0 = 0О + £ и аппроксимируем функцию 0 первыми
членами ряда Тейлора:
cos 0О - cos 0 = sin 0О£ + О(^2),
sin2 0 = sin2 0О + О(£),
[ ] = -y-Psin2 е0 - sine0£ + O(V) + <XPO-
А
Пренебрегая членами О(Е>2) и О(Р£), найдем значение £, при
котором квадратная скобка обращается в нуль:
^ = aQ = —Psin0o. (6.4.11)
А
При этом 0О + aQ - приближенное значение другого корня, aQ -
амплитуда нутационных колебаний. Из (11) следует, что она
имеет величину порядка Р и стремится к нулю вместе с 0О. С точ-
ностью до членов высших порядков малости
Ди) = pl sin2 ОоД«е - £).
С такой же точностью определим (3):
При этом из (5) получим уравнение, определяющее малые из-
менения угла нутации:
Подстановкой
v* *2
= ае sin Ц
sgn sin 2ц = sgn—
§ 6.4. Случай Лагранжа
407
это уравнение приводится к виду
a sin2n—-+ ——Isin2nl=> — - —
0 dt J 2 " dt 2J
откуда
'о 1 I /ф I ,
—I 1 - cos—— t .
|др|
2J
(6.4.12)
Из условия L^-L = 2тг находим период нутационных колебаний
те — 2л .
1Ар1
Чем быстрее закручен волчок, тем больше 1рф1 и тем меньше
период нутационных колебаний. В рассматриваемом случае вто-
рое уравнение (5) имеет вид
dw = (cosе0 -cose) = р£ + 2
dt Jsin20 Jsin0o
Отсюда, в частности, следует, что
> 0 при р > 0.
dt 4
Подставляя в d\\t / dt решение £(г) (12) и используя выражение
(11), получим приближенное решение последнего уравнения
sin
(6.4.13)
t-
„ lApIP a
Параметр —-— =-------- определяет среднюю угловую ско-
I Ар I
рость прецессии оси волчка. Для быстро закрученного тела
( \
ос
----< 1 скорость прецессии мала.
)
Устойчивость вертикального вращения
Рассмотрим теперь случай, когда волчок в начальный мо-
мент времени закручен вокруг оси симметрии и угол нутации
близок а) к О или б) к тс, т.е. волчок закручен почти верти-
кально:
а) cos0o=l-6 или б) cos0o=-l + 6, (6.4.14)
где 6 > 0 - достаточно малое число.
408
Глава 6. Движение твердого тела
Воспользуемся представлением J{u) в виде (10)
/(и) = pi (cos 0О - cos 0) — Р sin2 0 - (cos 0О - cos 0) .
[Уз
В рассматриваемом случае Р произвольно. Представим
a) cos0 = 1 - А; б) cos0 =-1 + А, А >0. (6.4.15)
Диапазон изменения угла нутации 0 определяется корнями Дм)
(10). Один корень, очевидно, 0 = 0О, другой корень - корень
выражения, стоящего в квадратных скобках.
Рассмотрим случай а):
о = [ ] = — р[1-(1-Д)2] + 8-Д.
Л.
В результате получим квадратное уравнение
з
рД2 + Д 2^-p-l +5 = 0
А.
и выражение для его корней
^1,2 “
—Д- ± 1-
2Jp) 2Jp
2
+—5.
JP
3
Если 1 - < 0, то знак «+» определяет корень
А1 = !-^Ц-
2/р
j V
1-Д^Д-
2/pJ
= 0(8).
При 5 —> 0 имеет место Aj —» 0.
Если 1 - > 0, то положительный корень при малых 3 уже в
общем случае не мал:
Таким образом, для почти вертикально закрученного тела его
§6.4. Случай Лагранжа
409
ось с течением времени будет оставаться почти вертикальной,
если
2JP 47а
(6.4.16)
При неравенстве обратного знака независимо от малости 5
угол нутации 0 будет изменяться в конечных пределах. То есть
при выполнении (16) движение устойчиво по углу нутации, в
противном случае - неустойчиво. Так как 1/?ф1 = J3kol, где со -
угловая скорость закрутки, то из (16) следует, что для устойчи-
вости вертикального вращения требуется, чтобы угловая ско-
рость закрутки превосходила предельное значение:
(6.4.17)
Для случая б) аналогичный анализ приводит к квадратному
уравнению
( Т ।
А2-2 1 + ^- А + ——^ = 0
2JP
и к корням
А
1,2 ”
2JPJ
1 + -^-
2JpJ
8J3
В этом случае при любом значении параметров знак «-»
определяет корень порядка 8: Aj = 0(8). Тем самым в случае б)
почти вертикальное вращение всегда устойчиво. Заметим, что в
случае б) 0О ~ л. То есть в этом случае центр масс тела оказы-
вается ниже точки закрепления.
Описанные в этом параграфе эффекты можно наблюдать
при вращении детского волчка. Если волчок закручен доста-
точно быстро и его ось симметрии почти вертикальна, то
движения оси волчка почти незаметно. Однако через некоторое
время ось волчка начинает сильно отклоняться от вертикального
положения, и он падает. Для объяснения этой картины надо бы в
модель включить, кроме силы тяжести, еще силы трения.
Вначале волчок вращается быстро, т.е. угловая скорость больше
предельной, и вертикальное движение устойчиво. С течением
времени силы трения уменьшают угловую скорость собствен-
ного вращения, и нарушается условие устойчивости.
Если волчок закручен вокруг оси симметрии быстро, но ось
вращения не вертикальна, то легко наблюдать прецессионное
движение его оси.
410
Глава 6. Движение твердого тела
§ 6.5. Использование закономерностей вращения
твердых тел
В § 6.4 мы рассмотрели движение быстро закрученного во-
круг оси симметрии тела в поле тяжести. Оказалось, что основ-
ной наблюдаемый эффект влияния силы тяжести сводится к
прецессионному движению оси тела вокруг вер-
тикали. То есть в каждый момент времени сме-
щение происходит по нормали к плоскости, со-
держащей ось ё3 и вектор силы F (рис. 160).
Можно показать, что такой же эффект будет
наблюдаться, если F - какая-либо другая сила.
То, что смещение происходит перпендикулярно
действию силы, для наивного опыта житейской
практики кажется необычным. Это явление по-
лучило название гироскопического эффекта. Мы знаем, что
этот эффект объясняется теоремой об изменении момента
количества движения
<Ж
--= М,
dt
согласно которой направление изменения кинетического момен-
та (он почти совпадает с осью вращения) определяется не силой,
а моментом силы; момент М направлен перпендикулярно плос-
кости (ё3, F).
Динамически симметричные быстро закрученные тела ши-
роко используются в технике. Они называются гироскопами.
Если кинетическая энергия вращения существенно превос-
ходит работу внешних сил в течение достаточно длительного
времени, то ось гироскопа в течение этого времени почти не
изменяет направления относительно инерциальной системы ко-
ординат (для задачи Лагранжа этот вывод следует из анализа,
проведенного в § 6.4). Поэтому с помощью гироскопов создают
приборы, которые на борту подвижных аппаратов (кораблей,
самолетов, ракет, искусственных спутников) запоминают инер-
циальную систему координат. Это чрезвычайно важно для
решения задач управления этими аппаратами. При этом часто
используют специальное устройство, называемое кардановым
подвесом, схема которого приведена на рис. 161.
Твердое тело Т может свободно вращаться вокруг оси аа
рамки А. Рамка А может свободно вращаться вокруг оси bb
рамки В, а рамка В может свободно вращаться вокруг оси сс,
закрепленной относительно аппарата. Такая конструкция допус-
кает произвольные повороты тела Т относительно абсолютного
репера. При этом можно выбрать расположение осей аа, bb, сс
§ 6.5. Использование закономерностей вращения
411
Рис. 161
так, чтобы при любых поворотах вокруг них положение центра
масс тела Т не изменялось. Описанная схема поясняет способ
реализации закрепления твердого тела в центре масс. В техниче-
ских приложениях тело Т представляет собой ротор электро-
мотора, которому можно придать заданное вращение.
Если расположить ось тела Т в некотором направлении и
раскрутить его достаточно быстро, то даже в том случае, когда
аппарат совершает произвольное вращение, ось тела Т будет
сохранять исходное положение относительно абсолютной си-
стемы координат. Конечно, все это верно лишь с некоторым
приближением. Силы трения и другие эффекты приведут с
течением времени к изменению положения этой оси. Поэтому
при реализации таких приборов необходимо заботиться об
уменьшении сил трения и в теоретическом анализе учитывать
дополнительные возмущающие факторы, которые влияют на
работу прибора.
Можно упомянуть более грубое использование того же
эффекта. Если гироскопический прибор установить на корабле,
то независимо от качки корабля ось а а будет сохранять свое
направление. С осью аа можно связать платформу, которая не
будет подвержена качке корабля, что позволит, например, про-
изводить с корабля тонкие астрономические наблюдения.
В рассмотренном нами случае Лагранжа при быстрых вра-
щениях гироскопа его ось прецессии совпадает с направлением
силы тяжести, а скорость прецессии пропорциональна силе
тяжести. Это создает возможность с помощью специального
прибора измерять величину и направление силы тяжести. Такой
способ, в отличие от математического маятника, позволяет
производить более точные измерения силы тяжести и в условиях
действия возмущающих сил.
Теоретический анализ движения твердых тел очень важен
для задач, связанных с искусственными спутниками. На многих
412
Глава 6. Движение твердого тела
спутниках не поддерживается ориентация, однако для интер-
претации показаний научных приборов необходимо знать, как
данный прибор был ориентирован в пространстве в данное
время. Для решения этой задачи на спутнике устанавливаются
специальные измерительные приборы, определяющие в неко-
торые моменты времени, например, угол между направлением
данной оси и направлением на Солнце (или(и) направлением
магнитного поля Земли). С помощью теоретического анализа
закономерностей движения тела спутника и этих измерений
удается установить ориентацию спутника в произвольный мо-
мент времени.
Гигантскими гироскопами являются планеты. Кинетическая
энергия их вращения намного превосходит потенциал внешних
гравитационных сил, влияющих на их вращение. Поэтому для
многих практических приложений можно считать, что оси вра-
щения планет сохраняют неизменное направление в абсолютном
пространстве. Как известно, ось вращения Земли составляет
угол 23°,5 с нормалью к плоскости эклиптики (плоскости, в ко-
торой Земля движется вокруг Солнца). Однако вывод этот при-
ближенный. На больших интервалах времени малые силы
приводят к заметным эффектам. Земля динамически не шар.
С большой точностью она обладает динамической симметрией,
однако момент инерции относительно оси, проходящей через
полюса, больше примерно на 1/300 момента инерции относи-
тельно любой экваториальной оси: (J3-J)/J3 ~ 1/300. Вследствие
сжатия Земли гравитационное притяжение Луны и Солнца
создает моменты сил, действующие относительно центра масс
Земли. Вследствие действия этих сил ось вращения Земли
прецессирует вокруг нормали к эклиптике, т.е. ось вращения
Земли движется по конусу с осью, совпадающей с нормалью к
плоскости эклиптики, и полураствором ~
~ 23°,5 (на рис. 162 вектор пэ совпадает с
нормалью к плоскости эклиптики).
Скорость прецессии очень мала. Период
прецессии составляет 26 000 лет. Северный
полюс определяется осью вращения Земли.
Сейчас все знают: чтобы найти направление
на север, надо сориентироваться на Поляр-
ную звезду. Через 13 000 лет направление на
север и на Полярную звезду будет составлять
угол 47°, и для определения направления на
север будут использовать другую звезду.
Кроме того, ось вращения Земли совершает малые сравнительно
короткопериодические колебания как в абсолютном простран-
стве, так и относительно самой Земли. Амплитуды этих коле-
§ 6.5. Использование закономерностей вращения
413
баний составляют всего десятки метров. Закономерности враще-
ния Земли очень важны и по следующей причине: по периоду
вращения Земли определялся эталон времени: за единицу вре-
мени принимается (с учетом многих поправок) период вращения
Земли относительно звезд. Это - так называемое всемирное
время.
Сравнительно недавно в результате наблюдений за движе-
нием центров масс планет вокруг Солнца было обнаружено, что
«всемирное время» лишь относительно грубо можно принять за
то равномерное ньютоновское время, которое постулируется в
основах механики и является независимой переменной в меха-
нических уравнениях. Более точно эталон времени определяется
из сравнения теоретических выводов и наблюдений за движе-
нием Луны и Солнца. Это так называемое эфемеридное время.
После введения эфемеридного времени оказалось возможным
оценить неравномерность вращения Земли. Оказалось, что пе-
риод вращения Земли изменяется примерно на 1-2 с в год, т.е.
отличие всемирного времени от равномерного составляет ве-
личину порядка 1/30000000.
Глава 7
Устойчивость движения и малые колебания
§ 7.1. Постановка задачи об устойчивости решений
Рассмотрим систему обыкновенных дифференциальных
уравнений
^ = F(y, /), y&Rn. (7.1.1)
at
Пусть y*(f) есть некоторое решение (1), определенное при всех
t 0. Обозначим у(0 = у*(0 + х(г). Тогда х(г) удовлетворяет сле-
дующей системе уравнений:
б7х
— = f(x, О, хеГ, (7.1.2)
dt
f(x, r) = F(y*(r) + x, r)-F(y*(n, г). (7.1.3)
Будем полагать, что при всех t 0 в некотором шаре I xl
Н f(x, t) - достаточно гладкие ограниченные функции и, в
частности, удовлетворены условия теорем существования и един-
ственности решений системы (2) и их непрерывной зависимости
от начальных условий. Решение системы уравнений (2) с на-
чальными данными х(г0) = х0 обозначим так:
х(г) = х(Л х0, Го), х0=х(г0, х0, г0). (7.1.4)
Для системы (2) f(0, t) = 0, и она, очевидно, имеет тривиальное
решение x(f) = 0. При достаточно малом 1х01 решение (4) опи-
сывает поведение траектории системы (1), начинающейся в
некоторой окрестности решения у = у* (г).
Замечание 1. Из непрерывной зависимости решений (2) от
начальных данных для любого конечного времени 7^0 и
любого 8 > 0 следует: можно указать 8 > 0 такое, что при 1х()1 < 8
будет выполнено условие 1х(Г + Zq)I < £•
Следующие определения служат для характеристики свойств
решений на неограниченных интервалах времени t 0.
Определение 1. Тривиальное решение х = 0 уравнения (2)
называется устойчивым, если для любого 8>0 существует
8 = 8(8, г0) > 0 такое, что
|х(г, х0, Го)|^8 длявсех Г^Г()и |х0|=^8. (7.1.5)
§ 7.1. Постановка задачи об устойчивости решений
415
Определение 2. Нулевое решение равномерно устойчиво,
если 8 = 8(8) (от не зависит).
Определение 3. Нулевое решение асимптотически устой-
чиво, если оно устойчиво и, кроме того,
limx(r, х0, Го) = О (7.1.6)
f->oo
(должно существовать 8(8, г0) > 0 такое, что выполнено (5) и (6)).
Определение 4. Нулевое решение назовем неустойчивым,
если оно не удовлетворяет определению 1, т.е. существует 8 > О
такое, что для сколь угодно малого 8 > 0 можно указать х0 и t,
удовлетворяющие условиям
I х01 < 8 и t t0,
при которых
1х(Г, х0, Го) I > Е, (7.1.7)
т.е. в любой окрестности нуля найдется точка х0, для которой
выполнено (7).
Замечание 2. В соответствии с замечанием 1, если устойчиво
(асимптотически устойчиво) или неустойчиво тривиальное ре-
шение системы (2) при г0 - 0, то таким же свойством будет
обладать тривиальное решение при любом конечном г0. Однако 8
в общем случае может зависеть от t0 и с этим связано опре-
деление равномерной устойчивости.
В зависимости от устойчивости (неустойчивости) тривиаль-
ного решения уравнения (2) говорят об устойчивости (неус-
тойчивости) решения у*(0 системы (1).
Системе уравнений (2) можно поставить в соответствие ли-
нейную систему уравнений
dz
— = A(t)z, (7.1.8)
dt
Л/ А
где матрица A(t) = —
VdxJx=0
Система уравнений (8) называется линеаризацией системы (2)
или линеаризованной системой (или уравнениями в вариациях
для системы (2)). Правая часть (8) получается путем выделения
линейных членов в представлении
f(x,t) = A(t)x+g(x,t), (7.1.9)
где —» 0 при I х I —0.
|х|
Предел, равный нулю, существует, так как f(x, t) дифференци-
руема по х.
416
Глава 7. Устойчивость движения и малые колебания
Рассмотрим решения уравнений (2) и (8) с одинаковыми на-
чальными данными:
при t = to x(z0) = z(z0) = XO.
Нетрудно показать, что для любого фиксированного Г 0 и
е > 0 можно указать 8 = 5(7) такое, что если I х01 < 5, то
I х(/, х0, Zo) - z(r, х0, to) I < еЗ
для всех г0 t tQ + Т. Если тривиальное решение системы (8)
устойчиво, то говорят об устойчивости решений системы (2) в
линейном или первом приближении. Аналогично определяется
неустойчивость решения (2) в линейном (первом) приближении.
Рассмотрим автономную систему уравнений
^ = F(y), уеЯ". (7.1.1')
at
Положением равновесия для системы (Г) называется ее решение
у(Г) = У* = const, не зависящее от времени. Очевидно, у* - поло-
жение равновесия тогда и только тогда, когда F(y*) = 0.
В этом случае преобразование
у(0 = у* + x(z)
приводит к автономной системе уравнений
z/v
— = f(x) = F(y* + x). (7.1.2)
dt
В зависимости от устойчивости (неустойчивости) тривиального
решения (2) говорят об устойчивости {неустойчивости) поло-
жения равновесия системы (1').
Существенно, что линеаризация системы (2) приводит к
линейной системе уравнений с постоянными коэффициентами
^ = Az. ’ (7-1.8')
dt koxjx=0
для которой существуют регулярные способы решения.
§ 7.2. О решениях линейных уравнений
с постоянными коэффициентами
Для дальнейшего нам потребуются некоторые результаты,
которые доказываются в курсах обыкновенных дифферен-
циальных уравнений.
Рассмотрим систему линейных уравнений
di
— = Az, ieR", (7.2.1)
dt
§ 7.2. О решениях линейных уравнений с постоянными
417
где А - матрица размера п х п, коэффициенты которой посто-
янны (не зависят ни от z, ни от f). Уравнение
р(Л) = det (А - XI) = 0, (7.2.2)
где I - единичная матрица и-го порядка, называемая характе-
ристическим уравнением матрицы А (или системы (1)). Это
алгебраическое уравнение и-го порядка, которое, как известно,
имеет п корней, называемых характеристическими числами
(корнями)'.
Х19Х2, ...,ХЛ. (7.2.3)
Для вещественной матрицы А каждому комплексному корню
\ соответствует в наборе (3) комплексно сопряженный корень
Xj = (\)* (здесь и ниже звездочкой * будем обозначать переход к
комплексно-сопряженным величинам). Если все корни \ различ-
ны, то существует невырожденное линейное преобразование Т:
z-^ и
z = Tu, det TV О, (7.2.4)
удовлетворяющее условию
Т~АТ = £,
где
% О 4
(7.2.5)
(7.2.6)
- диагональная матрица.
Столбцы Р матрицы Т являются собственными векторами
матрицы А и соответствуют характеристическим числам
АР = \Р.
Преобразование (4), будучи применено к (1), приводит к системе
уравнений относительно и
— = ££'и (7.2.7)
dt
или, более подробно,
---= Х|и1,...,---= Л„и , (7.2.8)
dt 1 dt
где uT = (и1, и2, .... и').
Общее решение (8) можно представить в следующем виде:
и = Л(Г) а, (7.2.9)
27. М.Л. Лидов
418
Глава 7. Устойчивость движения и малые колебания
где
(7.2.10)
ат = (ос1? ос2, ос„) - произвольный вектор, компоненты ос, - по-
стоянные числа. Отсюда следует, что решение (1) в рассмат-
риваемом случае имеет вид
z = 7Л(г)а = cq Т'е4' +... + а„Тп^"', (7.2.11)
где Г' - i-й столбец матрицы Т.
Если Л, и Х7 = (X,)* - комплексно-сопряженные корни, то
можно распорядиться произволом, который существует при
определении столбцов матрицы Г, так, чтобы Р = (Ti)*. Тогда для
получения вещественного решения z(r) необходимо и достаточно
принять осу = ос*. Из (10), (11) имеем
z0 = z(0) = Гос. (7.2.12)
Так как det Т Ф 0, то зависимость z0 и ос взаимно однозначна.
Если существуют кратные корни характеристического урав-
нения (2), то линейно независимые частные решения уравнения
(1) разбиваются на р серий; 5-я серия имеет вид
где 5 = 1, 2, к} + к2 + ... + кр = и; hsj Е R" .
Векторы hsj 5-й серии удовлетворяют следующей системе алгеб-
раических уравнений:
А/гл| = ЛДь Ahs2 = \,h,2 + hsl,..., Ahsks = 'kshsks + h,ks. (7.2.14)
При этом матрица размера п х п
H = {hxx,hx2,...,hxkx,...,hpi,...,hpkp) (7.2.15)
невырождена:
det Н *0. (7.2.16)
Одному и тому же кратному корню X могут отвечать не-
сколько серий. Если г - кратность корня X, то число серий (13)
§ 7.2. О решениях линейных уравнений с постоянными
419
зависит от числа линейно независимых собственных векторов
матрицы А с собственным значением X. В частности, для неко-
торых задач механики, как мы покажем ниже, независимо от
кратности корней каждая серия состоит из одного решения. Для
комплексно-сопряженных корней = (Л,,)* можно определить
комплексно-сопряженные решения уравнений (14), и соответст-
вующие серии будут комплексно-сопряжены.
Общее решение уравнения (1) представимо в следующем
виде:
Р ks
= X (7.2.17)
5=1 j=l
где
ат= (7.2.18)
- набор произвольных постоянных. Для вещественности z(/)
необходимо и достаточно, чтобы комплексно-сопряженным се-
риям отвечали комплексно-сопряженные Лг/ (это всегда возмож-
но) и CCzy.
Рассматривая (17) при t = 0, получим
z0 = z(0) = Hot. (7.2.19)
Так как det Н Ф 0, то z0 и а связаны взаимно однозначным соот-
ветствием. Для дальнейшего из общей теории обыкновенных
дифференциальных уравнений нам потребуется следующая тео-
рема.
Теорема об аппроксимации (формулировка). Для любой мат-
рицы А существует линейное неособенное преобразование
z = t/u, det Ut 0, (7.2.20)
в результате которого система (1) может быть приведена к тре-
угольному виду
— = ^u + Bu, (7.2.21)
dt
где <£ - матрица (6), составленная из характеристических чисел
матрицы А; матрица В имеет вид
го в,2 ву..в"4
о в3...в:
В = 2 2 (7.2.22)
1 0 0 )
(отличны от нуля только элементы, стоящие выше главной
27*
420
Глава 7. Устойчивость движения и малые колебания
диагонали). Элементы матрицы В (это, вообще говоря, комп-
лексные числа) могут быть сделаны по модулю сколь угодно
малыми за счет выбора преобразования (20).
§ 7.3. Связь между решением проблемы устойчивости
для автономной нелинейной системы
и линеаризованной системы уравнений
1°. О норме комплексных векторов и матриц. Пусть, напри-
мер, при приведении системы линейных уравнений к диагональ-
ному виду, вообще говоря, производится комплексное преобра-
зование вещественных переменных. Так возникает необходи-
мость рассмотрения векторов с комплексными компонентами.
Будем рассматривать прямоугольные матрицы А и векторы
х, элементы которых А/, х1 могут быть комплексными числами:
Определим норму II А II матрицы А следующей формулой:
и, в частности,
Х*т
I z I - модуль числа z-
Нетрудно показать, что для любого комплексного числа а
||аА|| = |а|-|| А||. (7.3.1)
Используя неравенства
п ( п п А
У, aib, у, ы2 у IM2,
z=l \ z = l 7 \ z = l )
| й, + &, | 55 | <2, | + I bi I’
|«(.-b,|2^(|a/.|-|b,.|)2,
§ 7.3. Решения проблемы устойчивости
421
справедливые для любых комплексных чисел at и bh нетрудно
доказать следующие свойства нормы II II:
для любых комплексных матриц А размера п х т и В разме-
ра т х к
II АВ КIIА || -|| В ||; (7.3.2)
для любых комплексных матриц одинаковых размеров
|| А + ВКIIА || + || В ||, (7.3.3)
ЦА-ВЦ2 ^ (|| А||-1| В ||)2. (7.3.4)
Замечание. Введенные в § 7.1 различные определения устой-
чивости (неустойчивости) автоматически переносятся на случай
комплексных векторов, если в этих определениях евклидову дли-
ну вектора I х I везде изменить на норму II х II.
2°. Инвариантность проблемы устойчивости по отношению к
замене переменных. Пусть исследуется устойчивость тривиаль-
ного решения системы уравнений
— = f(x,r), f(0,O = 0, хт = (?,...,х"). (7.3.5)
dt
Пусть zT = (z1,..., z”) и x - Ф(г, t) - диффеоморфизм x —> z и при
t >0
f ЭФ)
Ф(0,О = 0, det — *0.
\ dz J z=0
Тогда справедливо представление
х = Ф(г,г) = A(Z)z + g(z,t), (7.3.6)
। ОФ)
z = A" (t)x + <p(x,t), A(t) = , (7.3.7)
k 3zA=o
где вектор-функции g и <p удовлетворяют неравенствам
||g(z,t)||s=ii](z,r)||z||, ||<р(х,0ЮС(х,0||х|| (7.3.8)
и
limT](z,r) - 0, lim£(x,r) = 0.
IldHo |ИНо <7'3'9)
Будем предполагать, что пределы (9) равномерны по t 0 и
существуют не зависящие от t сх > 0 и cxt > 0, так что
||А(0||<а, || AOOllca,. (7.3.10)
422
Глава 7. Устойчивость движения и малые колебания
В переменных z уравнения (5) будут иметь вид
dz (ЭФУ1!” ЭФ~|
— = — Г(Ф(г,г),О-— = F(z,r).
at < dz) L _
(7.3.11)
Очевидно, эти уравнения имеют тривиальное решение: z = 0.
Теорема. Из устойчивости (неустойчивости, асимптотичес-
кой устойчивости) тривиального решения системы (11) следует
аналогичное заключение для системы (5).
Доказательство. Пусть для любого г > 0 можно ука-
зать 5 > 0 такое, что из II z(0) II < 5 следует II z(t) II < £ при t 0. Из
(6)—(10) получим
h||«a, ||х|| + ^(х,г)||х||.
Можно выбрать такое 5! > 0, чтобы при II х II < выполнялись
условия
^(х,О<ос1/2, || г || <5.
Первое неравенство следует из равномерности предела (9), а вто-
рое получается из оценки
3
II z к «11И1 + £(х’0||хК-аД
» 2 5
при <-—
3 ОС]
При начальных данных II х(0) II < Sj получим II z(0) II < 5.
Пусть г > 0 в условии устойчивости выбрано так, чтобы
i](z, 0 < ос/2 при II z II < £. Тогда при II х(0) II < 51? используя (6), по-
лучим
IIХО Н а II z(0 II + n(z,0 II г II -|ссе. (7.3.12)
Таким образом, при произвольном г > 0, когда II х(0) II < 5Ь имеем
3
II x(t) II < т.е. решение x(f) = 0 устойчиво. Из первого нера-
венства (12) при || z(t) || -^ 0 следует || x(t) || 0.
t—>оо
То есть из асимптотической устойчивости z(/) = 0 следует
асимптотическая устойчивость х(г) = 0.
Упражнение. Докажите соответствующее утверждение о неустойчивости
решения.
3°. Связь между решением проблемы устойчивости для не-
линейной и линеаризованной систем. Рассмотрим автономную
систему уравнений
dx
— = f(x), хе/?", /(0) = 0. (7.3.13)
dt
§ 7.3. Решения проблемы устойчивости
423
Пусть
dz . . f df А пп
— -Az, А - — , z G R
dt \dxjx=o
(7.3.14)
- линеаризация системы (13). В общем случае решение (14) мож-
но записать в следующем виде:
z(O = Z(0a, (7.3.15)
где Z(t) - матрица размера их п, элементы которой имеют вид
(см. (7.2.13))
z/ = Л'
Л'1
(ту -1)!
(7.3.16)
aT = (aj,a2,...,осн) - произвольный постоянный вектор. Согласно
(7.2.15), Z (0) = Н- невырожденная матрица,
z(0) = //a. (7.3.17)
Теорема об устойчивости линейной системы. 1. Если вещест-
венные части ReXz всех характеристических чисел Хь Х2,Хн
матрицы А отрицательны, то нулевое решение z = 0 уравнения
(14) асимптотически устойчиво.
2. Если Re \ > 0 хотя бы для одного то решение неустой-
чиво.
3. Если вещественные части Re Xz всех характеристических
чисел матрицы А не положительны, то следует рассмотреть ре-
шения (14), отвечающие характеристическим числам Х7, для ко-
торых Re Ху = 0:
а) если все эти решения не содержат вековых членов вида
(tk /k\)e^jt (к > 0), то тривиальное решение z = 0 устойчиво;
б) если же хотя бы для одного Х7 с Re Х7 = 0 решение содержит
такие члены, то решение z = 0 неустойчиво.
Замечание. Случай 36) может возникнуть (но не обязатель-
но), когда Х7 - кратный корень.
Доказательство. На луче t 0 при к 0:
а) при Re у < 0 функция/(Г) = tkeyt ограничена по модулю и
/(г) -э 0 при t
б) При Re Y > 0 I /(Г) I оо При t ©©;
в) при ReY=0n/: = 0 функция I f(f) I ограничена;
г) при ReY = 0H£>0 I /(Г) I ©© при t ©©.
Обозначим Р(г) = II Z(/) II. Из (15), (16) и свойств функций вида
424
Глава 7. Устойчивость движения и малые колебания
f(t) следует, что если Re \ < 0 для всех i = 1,2, ... п, то норма Р(0
матрицы Z ограничена: Р(7) Ро и
Р(0 —» 0 при t —» ©о.
Отсюда следует
II 4r) HWII а II, II а к II Я-1 II-II Z(O) II,
|| Z(r) К PWII Я’11| -Ц40) К Poll Я’11| || 40) ||,
откуда получаем II z(t) II < г при II z(0) II < £/(Р0 || Н~11|) и устойчи-
вость нулевого решения. При t оо Р(г) —> 0, следовательно,
II z(t) II 0, и нулевое решение асимптотически устойчиво.
Норма матрицы Z(7) будет ограничена и в случае, когда
Re \ 0, i = 1, 2, ..., и, и решения при Re Л, = 0 не содержат чле-
нов вида tke)d при к > 0. Поэтому здесь имеет место устойчивость
(не асимптотическая) нулевого решения. Если Re Хк > 0, то сле-
дует рассмотреть решение при ос, = 0 (i' Ф к) и ак Ф 0. Компоненты
Z* &-го столбца матрицы Z не могут быть все равными нулю. Из
свойств функций/(0 следует, что, по крайней мере, один компо-
нент | Z* (Z) | —> °° при t ©о. Очевидно, что
||40|На*
z п \1/2
I X l^(0|2
<5=1 7
(7.3.18)
при любом I ак I > 0. Но при I ак I < 8/1| Н || и любом 8 > 0 этому
решению отвечает II z(0) II < 8. Тем самым решение z = 0 не-
устойчиво. Так как (18) будет выполнено и при Re Хк = 0 в том
случае, когда в решении присутствуют вековые члены tkeXkl, то
верно и последнее утверждение теоремы.
Проблема устойчивости линейных систем представляет
самостоятельный интерес. Однако основное ее значение про-
ясняется следующей теоремой.
Теорема Ляпунова об асимптотической устойчивости (не-
устойчивости) тривиального решения нелинейной системы.
Пусть Z, - характеристические числа матрицы А (14). Решение
исходной системы уравнений (13)
а) будет асимптотически устойчивым, если для всех ...,
вещественные части меньше нуля: Re Л, < 0, i = 1, 2... п;
б) если Re Хк > 0 хотя бы для одного Хк, то решение х = 0
системы (13) неустойчиво. Мы приведем доказательство только
утверждения а).
§ 7.3. Решения проблемы устойчивости
425
Доказательство. Пусть
max Re Z- = -oc <0. i (7.3.19)
Систему (13) можно записать в следующем виде: Jx — = Ax + g(x), dt (7.3.20)
где (7.3.21)
laxJx=0 imho ||x|| Проведем линейную замену переменных: x = Uu, uT = (и1, и2,..., и”), (7.3.22)
где U - невырожденная матрица, которая определяется в теоре-
ме об аппроксимации (см. (7,2.20)-(7.2.22)). Тогда система (20)
преобразуется к следующему виду:
— = Ти + Ви + <р(и),
dt
(7.3.23)
где Т =
(К
- диагональная матрица, составленная из ха-
О А
о
рактеристических чисел матрицы А, а норма матрицы В может
быть выбором U сделана меньше любого положительного числа
При этом
<p(u) = g(t/u), Игл И ^“41
IMHO ||M||
Умножив (23) слева на u*T = (и'*получим
u’T — = u*T <£ u + u*TBu + u*T<p(u).
dt
Если сложить это уравнение с комплексно-сопряженным ему, то
получим
*т du т du* d\\u II2
U-----1- u -= —u—— =
dt dt dt
И fЧ || U ||= 0. (7.3.24)
= 2^Re\ | и' |2 +2Re[u*TBu + u*T<p(u)]. (7.3.25)
426
Глава 7. Устойчивость движения и малые колебания
Из (25) и (19) следует неравенство
« -«И “ II2 + II В И II» IP + II«II II Ф(«) II - (7.3.26)
2 dt
При достаточном малом II и II, согласно (24),
II ф(и) где 0<г|<х при ||м||<5].
Отсюда следует
^Ы^(_а + 2х)||м||. (7.3.27)
Таким образом,
d In II и II _ и / mi
—-ос + 2х => || м(г) ||
=£||и(0)||е(“а+2’<)' при г^О. (7.3.28)
Выбирая х < а/2, получим, что при II и(0) II < 8 8( для всех t О
II и(0 II < 8 и II и(?) II —> 0 при ? —> оо, т.е. и = 0 - асимптотически
устойчивое решение. Так как система уравнений (23) получена в
результате невырожденного преобразования исходной системы
(20), то и решение х = 0 тоже асимптотически устойчиво.
4°. Теорема Рауса-Гурвица. Согласно доказанной теоре-
ме Ляпунова, знаки вещественных частей корней Xz характери-
стического уравнения
p(M = det(A-ZT) = O
часто решают проблему устойчивости. Поэтому существенное
практическое значение имеет теорема о знаках вещественных
частей корней алгебраического уравнения
п0А." + а^'-1 +... + а„ = 0. (7.3.29)
Из коэффициентов уравнения (29) составляются следующие
и-мерные столбцы:
А,= ао 0 , А2 - -X о •• о & & & & О “ |ч) W О о tQ — v > з А„
В столбце А* на k-м месте стоит коэффициент ак: выше его
последовательно ставятся коэффициенты с последовательно
§ 7.3. Решения проблемы устойчивости
427
возрастающими номерами ак+1, ак+ъ ... ат, где т п, т 2к - 1.
Ниже ак располагаются коэффициенты с последовательно убы-
вающими номерами ак_ъ ак_2,..., as, где s 0. На остальных ме-
стах в столбце кк ставятся нули. Матрица
0>
о
определяет главные миноры
д,
Д3 = det б?0
6Z3 а5
ах a3J
,...,Д„ =detA
Теорема Рауса-Гурвица. Для того чтобы все корни уравне-
ния (29) имели отрицательные вещественные части, необходимо
и достаточно, чтобы имели место неравенства
Д^О, Д2>0,...,Д„ >0.
Область устойчивости. Правые части системы уравнений,
устойчивость тривиального решения которой исследуется, могут
зависеть от параметров у е Rk:
— = f(x,r,y), f(0,t,у) = 0.
dt
(J33G)
При конструировании механических систем часто возникает
проблема выбора таких параметров у, при которых тривиальное
решение х = 0 будет устойчивым. В частности, если система (30)
автономна, то условия асимптотической устойчивости могут
быть найдены по критерию Рауса-Гурвица
Д;>0, z=l,2,...,n. (7.3.31)
Миноры Дг в рассматриваемом случае будут зависеть от у, и и
условий (31) выделяют в Rk область [/, для которой решения
асимптотически устойчивы. При этом U называется областью
устойчивости.
428
Глава 7. Устойчивость движения и малые колебания
§ 7.4. Основные теоремы второго метода Ляпунова
Будем рассматривать вещественные функции У(/, х) вещест-
венных переменных t е R и х е /?”, которые определены и диф-
ференцируемы в некотором шаре I х I Н (Н > 0) при t г0 и
удовлетворяют условию
У(Г,О) = О. (7.4.1)
Ниже мы будем использовать следующие определения.
1. Если существуют Т t$,H > 0 и для любых Т, I х I Н:
a) V(t, х) 0, то будем говорить, что V(t, х) знакоположи-
тельна (или просто положительна). Множество знакоположи-
тельных функций обозначим 3*.
Аналогично, если при тех же условиях
б) У(Л х) 0, то У(Л х) - знакоотрицательна. Множество
знакоотрицательных функций обозначим .
в) Знакоположительные и знакоотрицательные функции
образуют множество Зп - знакопостоянных функций:
Зп=з„из;.
В частности, тождественно нулевая функция принадлежит и
ХиЗ-.
2. Если У(х) Е 3* (ЭУ/Эг - 0) и для достаточно малых Н > 0 при
всех I х I Н и I х I Ф 0 выполнено:
а) У(х) > 0, то У - положительно-определенная функция;
б) У(х) < 0, то У - отрицательно-определенная функция.
Множество не зависящих от t положительно-определенных и
отрицательно-определенных функций обозначим через О*г и
О", соответственно.
3. Если для зависящей явно от времени функции У(Г, х) суще-
ствует 1У(х) е О* такая, что (У(Г, х) - 1У(х)) е 3„, то, по опреде-
лению, У(Г, х) - положительно-определенная функция.
Множество положительно-определенных функций обозна-
чим О*. Если (-У(Г, х) - W(x)) Е 3„, то У(Г, х) - отрицательно-
определенная функция.
Множество таких функций обозначим О“. Тогда О* UO" -
= Оп - множество знакоопределенных функций (х Е R”). Оче-
видно,
ХЖ з-эо;.
§ 7.4. Основные теоремы второго метода Ляпунова
429
4. Если для любого е > 0 можно указать числа Т /0 и Н = Н(е) >
> 0 такие, что при любом t Т и I х I Н
|V(r,x)|<e,
то будем говорить, что V(Z, х) допускает бесконечно малый выс-
ший предел.
Множество функций, допускающих бесконечно малый выс-
ший предел, обозначим Бп.
Любая непрерывная функция V(x), не зависящая от г, до-
пускает бесконечно малый высший предел.
Упражнение. Рассмотрите функции
/j (t,xl,х2) = (х1 )2 + (х2 )2 - 2xlx2 cost,
f2(t,xx,x2) = r[(x*)2 + (x2 )2 ] -2x’x2 cosf,
/3(г,л) = sin2 [((x1 )2 + (x2 )2 +... + (x" )2 )r],
/4(r,x) = [(x1 )2 + (x2 )2 +... + (x" )2 ] sin21.
Докажите следующие утверждения:
fl G 3?, но f GO?;
/2 G О 2 ’
f3e3+n, /Зео:, /3еБп;
/4еЗп, /4^ОП, /4еБп.
5. Пусть заданы система дифференциальных уравнений
— = f(x,Z), xgR" (7.4.2)
dt
и функции У = V(t, х). Введем обозначение
дУ дУ е дУ дУ
dt Эх dt Эх
дУ
дхп
(7.4.3)
где V - производная функции У вдоль траекторий х - x(t, х0) си-
стемы (2).
Ниже будем рассматривать систему уравнений (2), допускаю-
щую нулевое решение х = 0, т.е. /(О, t) = 0.
Теорема 1 второго метода Ляпунова об устойчивости. Если
для системы уравнений (2) можно указать функцию V(Z, х) е О*,
для которой У G 3“, то решение х = 0 устойчиво.
430
Глава 7. Устойчивость движения и малые колебания
Доказательство.
1) По определению О*, найдутся W(x) G О„п Т f0, Н > 0 та-
кие, что неравенство
V(7,x)^W(x)
будет выполняться при t Т и I х I Н.
2) Пусть Е > 0 — произвольное достаточно малое число. Так
как W(x) G О*,, то на сфере 1x1 = 8 выполняется неравенство
minW(x) = oc>0.
|х|=е
3) Рассмотрим решение х(7) = х(7, х0, Т) системы (2) с на-
чальными данными х(Г, х0, Т) = х0. Вдоль этого решения для
t^T внутри шара I х I Е
dV
——= V'(t,x(t,x0,T))=>
dt
=>V(r,x(/))-V(T,x0) = j V'dt^O.
T
4) Функция V(T, x0) G Бп как функция, не зависящая от t, и
поэтому для любого Т] > 0 и, в частности, для Т] а/2 можно
указать 8 > 0 такое, что при любом I х0 I 8 < Е
V(/,x0)^ri.
5) Если бы при некотором t = Г Т траектория с I х0 I < 8
достигла сферы I х I = Е, то мы бы пришли к двум неравенствам
V(f,x(f))^ri^oc/2,
Р(Г,х(Г))^И/(х(Г))^ос.
Неравенства противоречивы, и поэтому решения не выходят из
шара Ixl Е. В силу инвариантности проблемы устойчивости по
отношению к фиксированному значению Т устойчивыми будут
решения х(7, х0, TJ, х0 = x(T^xG,T\) для любого 1\ tG.
Определение. Рассматриваемая в теореме функция V(7,x)g
go; называется функцией Ляпунова.
Теорема 2 второго метода Ляпунова об асимптотической
устойчивости. Если для системы (2) можно указать функцию
V(t, х), удовлетворяющую условиям
V(r,x)GO;, Va,x)GBn, V'(t,x)eO~,
то решение х = 0 асимптотически устойчиво.
§ 7.4. Основные теоремы второго метода Ляпунова
431
Доказательство.
1. По определению О* и О~, существуют Н, Т, W(x), W(x)
такие, что в шаре I xl Н при всех Г Т:
V(7,x)-W(x)^0, W(x)gO*,
-V'(r,x)-W(x)^0, W(x)eO;r
2. По теореме 1 решение x(t) = х(Г,х0,Т),(х(Т,х0,Т) = х0) -
устойчиво. Выберем 0 < е Н и будем рассматривать значения
х0 из шара lxol 8(e), для которого гарантировано 1х(г)1 < е при
всех t Т.
3. Пусть Г] > 0 (г] < 1х01) - произвольное сколь угодное малое
число. Так как 1У(х) G О„п то существует
p = min W(x)>0.
Т]^|Х|^Е
4. Покажем, что при некотором t - t* Т имеет место
V(f, х(С)) = ц. Предположим противное, т.е. V(t, х(0) > ц при всех
t Т. Так как V(t, х) G Бп, то можно указать функцию Z =
= Z(p) > 0 такую, что при Ixl < Z будет V(t, х) < ц. Следовательно,
при У(Л х) > ц необходимо Ixl Z. Тогда можно определить
а = min W(x) > 0.
Х^|х|^е
При этом справедливо неравенство
V(r, х(0) - V(T, х(Т)) = j V'dt « j (-W)dt« -a(t - T).
T T
Так как V(T, x(T)) W(x0) Ц, а при достаточно большом t
V(t, x(0) < 0, то по непрерывности найдется t = f, при котором
V(f, x(f)) = p.
5. При t f имеет место неравенство
V(r,x(O)-V(f,x(f))^0.
Отсюда для t f получим
V(t, х(0) ц => W(x(t)) V(t, х(0) ц.
Из определения ц ц = min W(x) следует, что 1х(г)1 Л при t
П^|х|^е )
f. Так как ц > 0 сколь угодно мало, то это означает, что
limx(r) = 0 и решение x(t) = 0 асимптотически устойчиво.
432
Глава 7. Устойчивость движения и малые колебания
Следствие из теоремы 1. Пусть 0/х, О, 0^(х, t) - пер-
вые интегралы системы уравнений (2), т.е.
J0Z- Э0 Э0 р/ ч п . , п ,
—Г = + = 0, i = 1,2,...,/:.
at dt дх
Обозначим через
Ф(х,0 = Ф(01(х,г),...,0Дх,О)
некоторую функцию этих интегралов. Тогда
(1Ф ЭФ ЭФ ч Л ЭФ dQ- _
---= —+ —f(x,O = > ---------L = 0.
dt dt дх “ Э0, dt
(7.4.4)
Утверждение. Если существует Ф(х,Г) eOj, то нулевое
решение системы (2) устойчиво.
Доказательство. Из соотношения (4) имеем Ф' = 0 и,
следовательно, Ф(х, t) - функция Ляпунова.
Теорема Четаева о неустойчивости. Пусть V = V(t, х) - функ-
ция t G R и х G Rn, определенная при t t0 и I xl Н (Н >0),
обладающая следующими свойствами:
а) Существуют Н > 0 и Г такие, что условие
V(t, х) > 0 при каждом t Т выделяет в открытом шаре I xl < Н
область G, граница которой содержит точку х = 0. В общем
случае G = G(t). Очевидно, что для любого 8 > 0 область G(t)
содержит некоторые точки шара I xl < 8.
б) Функция V(t, х) ограничена, непрерывна и дифференци-
руема при t Тих е G.
в) Обозначим через G) = G^(t) под-
V(t, х)-д/ область G, выделяемую условием
/ V(t, х) > Z > 0 (Z не зависит от f)
/(рис. 163). Очевидно, Gx? (г) с GX| (г) при
* I/ Нетрудно показать, что для любого
Л у 8 > 0 можно указать достаточно малое
Хо - Хо(8) такое, что при всех 0 < Z Хо
область GyT) содержит точки шара
I х I < 8. Предполагается, что производ-
ная V' = (Э V / Эг) + (Э V / Эх) f (х, t) от У(Л х) в силу рассматриваемой
системы уравнений (2) с f(0, t) = 0 удовлетворяет условию:
существует такое Хо > 0, что v(X) > 0 при всех 0 < Л < Хо,
t Тих е G^t).
§ 7А. Основные теоремы второго метода Ляпунова
433
Определение. Функцию V(t, х), удовлетворяющую условиям
а) - в), будем называть функцией Четаева для системы урав-
нений (2).
Теорема. Если для системы (2) существует функция Четаева,
то решение х = 0 системы (2) неустойчиво.
Доказательство будем вести от противного.
1. Предположим, что х = 0 - устойчивое решение. Тогда для
любого е > 0 можно указать 8 > 0 такое, что
| х(7) |=| х(г,г0,Г) |< е при I х0 |<8 и всех t^T.
Выберем Е Ни определим 8 = 8(e).
2. Так как существует функция Четаева, то можно указать
Ло > 0 и точку х0 Ф 0, принадлежащую шару I х01 < 8(e) и области
GZo (Т), где 6\(/) определяется функцией Четаева.
3. Рассмотрим решение х(0 = х(/, х0, Т) с указанным х0. Так
как V > 0, то на этом решении функция V (t, х) возрастает и, сле-
довательно, х(0 не выходит из области Gx (Т). Поэтому
V(t,x(t)) - V(T,х(П) = J v'(t, x(t))dt > v(A0 )(z -t0).
Из последнего неравенства следует, что при достаточно боль-
шом t в области (t) с G(t) функция V(t, x) становится сколь
угодно большой. Это противоречит предполагае-
мой ограниченности функции Четаева V (t, х) в /
G(t).
Замечание. В приложениях часто встречается \ ут/
случай, когда граница области G, которая опреде-
ляется условием V > 0, имеет при х = 0 точку
возврата (рис. 164). Такие области допускаются Рис-164
рассматриваемой теоремой.
Устойчивость постоянных вращений твердого тела. В случае
Эйлера вращения твердого тела уравнения имеют вид (см. 6.1)
ded г \ ~ 2~ ъ
-----= (J2 - J3)co со ,
dt
avj ~ з ~ j
J2----= (J3 -УДОГСО ,
(7.4.5)
7 /7 7 \ ~ 1~ 2
73-----= (/, - J2)(0 (0 .
dt 1 2
Эти уравнения имеют решение
(b1=&2=0, Л3 = соо - const,
28. М.Л. Лидов
434
Глава 7. Устойчивость движения и малые колебания
которое описывает постоянное вращение вокруг третьей глав-
ной оси инерции. Замена
«‘=£1, oj2=^2, w3=id0+£3
приводит систему (5) к следующему виду:
Л ~ (А - А) ^2 (<%+ ^>з)’
at
•/2^2- = (Л-Л)(°)о+^з)^1’ (7-4.6)
at
Постоянному вращению вокруг третьей оси соответствует три-
виальное решение = 0.
Неустойчивость вращения вокруг средней оси инерции
Рассмотрим в шаре
ё+42+Й*^ (7-4.7)
функцию У= ^^2. Ее производная в силу уравнений (6) имеет вид
г=(Шо+^) .
Л J2
Условие V > 0 выделяет в шаре (7) область G: > 0, £2 > 0.
Пусть со0 > 0 и Jx < J3 < J2. Тогда в области
с» = к(;гЛ^ + Й+!;2<^, 5|>оЛ2>о, U2>*-
имеет место неравенство
Т7, 2A,2fj,-J3
V > ---- ------—
О)0 J{
= v(Z)>0.
Следовательно, V = - функция Четаева и движение неустой-
чиво.
Упражнение. Покажите что:
а) функция V = £i£2 будет функцией Четаева при 0)0 < 0 и J2 < J3 < J[;
б) при 0)() > 0 и J2 < J3 < Ji или 0)0 < 0 и Ji <J^<J2 функцией Четаева будет
функция У= - £j£2.
§ 7.5. Малые колебания в механических системах
435
Используя развитый аппарат, мы доказали известный нам
результат. Постоянное вращение вокруг средней оси эллипсоида
инерции неустойчиво.
Устойчивость вращений вокруг осей
с наибольшим и наименьшим моментами инерции
Уравнения (6) имеют два первых интеграла:
интеграл моментов
Oj(x) = + J241 + J32(^3 + coo)2 =| К I2, xT = (£]Л2Л3);
интеграл энергии
e2(x) = J^2 + + J3(£,3 + (Do)2 = 2T.
Рассмотрим функцию этих интегралов
Ф(х) = 0, (х) - J302 (X) + [02(X) - J3(D2 ]2 =
= — J3)^! + J2(J2 —-/3)^:2 +[-Л^э1 "*’•^2^2 +Л^3 + 273(О0£,3] .
Очевидно, Ф(0) = 0. Если J3 < J2 и J3<Jb то при |£31<|соо | /2
функция Ф(л) G . Следовательно, Ф(х) - функция Ляпунова, и
тривиальное решение = £2 = = 0, отвечающее вращению
вокруг наименьшей оси инерции, устойчиво.
Упражнение. Покажите, что в случае, когда J3 > Jj, J3 > J2, функция
Ф(х) = J302 (х) - 0! (х) + [02(х) - J3O)q ]2 есть функция Ляпунова. Тем самым бу-
дет доказана устойчивость тривиального решения х = 0, соответствующего
постоянному вращению вокруг оси с наибольшим моментом инерции.
§ 7.5. Малые колебания в механических системах
Рассмотрим консервативную механическую систему, т.е. по-
тенциальную систему с голономными связями; потенциал и связи
не зависят явно от времени.
В этом случае в лагранжевых координатах q,qG/?/r2 кине-
тическая энергия Т и потенциал U имеют вид
T = |qTSfc(<7)q, U = U(q), (7.5.1)
где 9)(q) - матрица размера т х т, det 2Й =£ 0, а уравнения движе-
ния суть уравнения Лагранжа
jrffdrY
dt \3q2
dL'
3q>
= 0, L = T-U.
(7.5.2)
28*
436
Глава 7. Устойчивость движения и малые колебания
Уравнения (2) можно записать в виде 2т уравнений первого по-
рядка
или, более подробно,
~ = -SS"'(q)
dt
(SS(q))q -2- (qT ®(q)q)
V dt J 2 dqv '
(7.5.3)
где dq I dt = q.
Теорема. В положении равновесия консервативной механи-
ческой системы q=0, q = q0, где q0- критическая точка потен-
циала, т.е. (d(7 /dq)qo = 0.
Доказательство. В положении равновесия F(y) = 0.
Отсюда следует
Рассмотрим линеаризацию системы (3) в окрестности поло-
жения равновесия (q = 0, q = q0):
q = qo + ¥b q = 4
Линеаризация приводит систему (3) к виду
т), (7.5.4)
dt [oq
V 7q0
dxi
где — = л
dt
Лемма. Линеаризованная система есть система уравнений
Лагранжа с кинетической энергией
То =|лТЖч0)'П
и потенциальной энергией
где
.. \
^(Чо)= >
SS и А - симметрические матрицы.
§ 7.5. Малые колебания в механических системах
437
Действительно, система уравнений Лагранжа
= (7.5.5)
dt
с функцией Лагранжа L = То - U{} эквивалентна (4).
Рассмотрим линейное невырожденное преобразование обоб-
щенных координат т] —> %:
Л = = detC^O.
В этих координатах
То = и0 = |ётСтАС£
Так как и А - две симметрические матрицы, причем квад-
ратичная форма qTSSq положительно-определена, то можно
воспользоваться теоремой линейной ал-
гебры о приведении двух квадратичных форм, согласно
которой можно найти вещественную невырожденную матрицу С
такую, что:
CTSS(q0)C -Im- единичная матрица,
CTA(q0)C = SE - диагональная матрица: (7.5.6)
где - собственные числа матрицы А относительно В; они
всегда вещественны и являются корнями характеристического
уравнения
det( А - ZSS) = 0. (7.5.7)
При таком выборе матрицы С в обобщенных координатах
£, £ кинетическая энергия То и потенциал (70 будут иметь вид
z=l z=l
Соответствующие уравнения Лагранжа
d dl^
dt Ui,
(7.5.8)
438
Глава 7. Устойчивость движения и малые колебания
Тем самым линеаризованная система приводится к т несвя-
занным уравнениям второго порядка (к т системам). Коорди-
наты в которых уравнения имеют вид (8), называются нор-
мальными координатами.
Решение /-го уравнения (8) при X,- Ф 0 имеет вид
+ а^"74', (7.5.9)
где со- = j = V-L
В случае X, > 0 решение будет вещественным, если ocj и а2
комплексно-сопряженные числа:
= ft cosco/ + 02 sin со/.
Если Xz- < 0, то соz = JQZ, Qz = Л/| X- |, а\,а2 - вещественны и
= а\е~^1 +а2е^1. (7.5.11)
Если Xz = 0, то решение (8) имеет вид
=0С1 + al2t. (7.5.12)
Если мы зададим для системы (8) начальные условия
t = 0, = & =0 при j*i, +(^')2*0,
то соответствующее решение будет иметь вид £7 = £/ =0 при
всех t и j' Ф i, а £'(f) определяется в одном из указанных видов (10)
- (12). Такое движение называется собственным колебанием сис-
темы (даже в том случае, когда X, 0 и фактическое движение
не является колебанием).
Параметр coz называется собственной частотой. Истинному
собственному колебанию (X, > 0) отвечает положительная собст-
венная частота.
Если система совершает z-e собственное колебание, то в
исходных координатах q оно описывается решением
Т](0 = q(0 - q0 = = С‘% (t),
где О - i-Й столбец матрицы С,
^.)(г) = (0,...,0,_С>0,..,0).
z-e место
§ 7.5. Малые колебания в механических системах
439
Таким образом, линеаризованная система имеет т собствен-
ных нормальных колебаний и общий случай - сумма этих коле-
баний:
т
T](O = q(f)-q0 = Х
/=1
Из проведенного анализа очевиден следующий способ опре-
деления собственных колебаний и общего решения линеари-
зованной системы уравнений Лагранжа (5). Ищем их частное ре-
шение в виде
Т| = deJ(Dt, d g Rm - постоянный вектор
Его подстановка в (5) приводит к уравнению
(A-(o2$)d = 0. (7.5.13)
Определяем собственные частоты из уравнения
det(4-oj2SZJ) = O. (7.5.14)
Согласно общей теории, каждому со2 отвечает вектор d = d(,
определяемый решением (13). Если (о2 - корень кратности р, то
этому корню отвечает р линейно независимых векторов d,.
Набор (db d2, dw) образует невырожденную матрицу С
Из (13), в частности, следует, что корень 0)^ = О существует
тогда и только тогда, когда det А = 0.
Пусть 0)2,со|,..обозначают положительные корни;
0)^1 = ... = (о*+5 =0, 0)2+5+1,...,0)2 - отрицательные корни. Тогда
общее решение (5) будет иметь вид
к
ц - (Picos + 02 8*п юд) +
/=1
+ dz(oci +a'2r)+ d,.(cxie_|w'|r (7.5.15)
i=k+\ i=k+s+1
где P'12,cxz12 - произвольные постоянные.
Из проведенного анализа, в частности, следует, что решение
рассматриваемой линеаризованной механической системы не
может содержать члены вида tken'}t (даже в случае кратных
корней).
440
Глава 7. Устойчивость движения и малые колебания
гд2и]
1 .
Упражнение. Пусть Т = ~Ч и (7(q) - соответственно кинетическая
энергия и потенциал консервативной механической системы в обобщенных
координатах; (q = 0, q = q0) - положение равновесия. Пусть соотношения
q = <I>(q) (q,q G Rm) - диффеоморфизм, который вводит другие обобщенные
координаты q.
1) Докажите, что q = O,qo =Ф^0) - положение равновесия в новых ко-
ординатах;
2) определите кинетическую энергию То и потенциал Uq малых колебаний
в координатах = q - q0;
3) покажите, что собственные частоты 0)z-(z = 1,2, т) не зависят от
выбора координат.
Теорема об устойчивости равновесия консервативной системы в
л
линейном приближении. Если квадратичная форма nqT Anq А =
положительно-определена, то равновесие (q =
= q0,q = 0)консервативной системы устойчиво в линейном приб-
лижении.
Доказательство. Линеаризация (5) системы (2) после
преобразования nq = приводится к виду (8). Из условия поло-
жительной определенности имеем
т
1 = 1
для всех nq Г 0 (или £ Г 0). Отсюда следует, что все \ > 0 (i = 1,
2,..., m), нормальные колебания являются истинными колеба-
ниями и движение устойчиво.
Упражнение. Проведите все рассуждения формально на языке е, 6.
Оказывается, что в рассматриваемом случае можно доказать
устойчивость положения равновесия и для исходной нелинейной
системы (2).
Теорема Лагранжа об устойчивости равновесия консерватив-
ной системы. Если в положении равновесия (q = 0, q = q0) кон-
сервативной системы потенциал имеет строгий минимум, то это
положение равновесия устойчиво.
Доказательство. Рассмотрим полную энергию 8 си-
стемы
e = e(q,q) = T(q,q) + t7(q).
§ 7.5. Малые колебания в механических системах
441
Обозначим
V(q,q) = T(q,q) + C7(q) - C7(q0). (7.5.16)
Ниже мы рассматриваем точки шара |q-q0 |2+|q|2^//2 (в
фазовом пространстве (q,q)) достаточно малого радиуса Н.
Легко видеть, что в положении равновесия (q = 0,q = q0)
V(qo,O) = O
и
V(q,q) > 0 для любой другой точки шара.
Действительно, Т = (l/2)qTSS(g)q - положительно-определенная
квадратичная форма относительно q, a t/(q)-t/(qo)>O при
q Ф q0 и достаточно малом Н по условию теоремы. Кроме того,
мы знаем, что £(q,q) является первым интегралом уравнений
Лагранжа (см. § 4.5). Поэтому производная V в силу уравнений
Лагранжа равна нулю:
г=*=о.
dt
Следовательно, функция V(q,q) - функция Ляпунова, и дви-
жение устойчиво.
Следствие 1. Если кроме потенциальных сил с потен-
циалом l/(q),Ha систему действуют обобщенные силы Q, то,
согласно (4.5.17), справедлива формула
V' = ^ = (Q,q).
dt
Утверждение. Если обобщенные силы гироскопиче-
ские или диссипативные, то положение равновесия остается
устойчивым.
Доказательство. Согласно определению диссипатив-
ных (или гироскопических) сил,
<Q,q>^0.
Тем самым вновь справедлива теорема об устойчивости реше-
ний дифференциальных уравнений, и положение равновесия
устойчиво.
Следствие 2. Если в шаре | q - q0 |2 +1 q |2^ Н2 непотен-
циальные силы определенно диссипативны, т.е.
(Q,q)<0 при q^O,
то положение равновесия асимптотически устойчиво. В этом
случае V' G О~, и так как V не зависит от t, то V е Бп. В случае,
когда потенциал U в положении равновесия q = q0 - дважды
442
Глава 7. Устойчивость движения и малые колебания
непрырывно дифференцируемая функция, то U в точке q0 будет
иметь строгий минимум (достаточное условие), если положи-
тельно определена квадратичная форма
qTAq, где А =
'д2иу
dq2 ,
Здесь полезно напомнить известную теорему алгебры.
Теорема. Квадратичная форма q'Aq будет положительно-
определена тогда и только тогда, когда все главные миноры
матрицы А положительны.
Если
А2,..., А"'
А2 А"
то требуется, чтобы
А} > 0, det
X
д'
^2’
Af
Ai
>O,...,detA>O.
§ 7.6. Изменение собственных частот
при изменении жесткости системы или наложении связей
1°. Для доказательства основных утверждений вспомним
некоторые результаты из линейной алгебры.
Пусть
tf = qTBq, qeRm (7.6.1)
- положительно-определенная квадратичная форма: К > 0 при
q Ф 0.
Теорема 1. Существует невырожденная вещественная мат-
рица D такая, что
DVBD = 1т - единичная матрица.
Обозначим через Э эллипсоид в Rm:
3 = {qeRm:qrBq = l}. (7.6.2)
Пусть а{ а2 ... ат- полуоси этого эллписоида.
Теорема 2. Характеристические числа 2ц Z2 ... Хт мат-
рицы В (det(B — 2tZ) = 0) — вещественные положительные числа,
связанные с главными полуосями эллипсоида Э соотношениями
1 • ю
а; = ,—, i = 1,2,...,и.
ж
§ 7.6. Изменение частот при изменении жесткости
443
Наряду с эллипсоидом Э будем рассматривать его сечение 3(Rk)
подпространством Rk <^Rm :
3(Rk) = {qeRl :qTBq = 1}.
Нетрудно показать, что 3(Rk) - эллипсоид. Различным подпрост-
ранствам Rk отвечают различные эллипсоиды 3(Rk).
Теорема 3.
1) ос = max min | q | = ak. (7.6.3)
Rk q<E3(Rk}
2) Максимум достигается на подпространстве Rk = Rk, натя-
нутом на оси аь аъ .... ак.
Доказательство.
1) Полуоси эллипсоида 3(Rk) равны > а2 ...^ ак, сле-
довательно, min | q |= ак. Поэтому ос ак.
q&3(Rk)
2) Пусть Rm~k+i - подпространство Rm, натянутое на оси
ак ak+i ••• ат' Очевидно, что при любом Rk Rs - RkC\Rm~k+{
есть подпространство размерности л 1 (к + (т - к + 1) = т + 1).
Справедливы неравенства
ак min | q | min | q |.
Левое неравенство следует из того, что
q а ак = max |q|.
qe3(Rm~k+l)
Правое неравенство следует из включения Rs с Rk. Так как Rk-
любое, то из последнего неравенства следует
ак max min | q | = ос.
Rk qe3(Rk}
Объединяя это условие с условием ос ah получим
ак = ос.
Теорема 4. Пусть Э и Э - два эллипсоида в Rm с полуосями
а{ а2 ... ат и а2 ... ат. Пусть эллипсоид Э содер-
жится внутри Э. Тогда
(7.6.4)
Доказательство. Рассмотрим ^-мерное сечение этих
эллипсоидов 3(Rk} и Э (Rk) одним и тем же подпространством Rk.
444
Глава 7. Устойчивость движения и малые колебания
Так как Э содержится в Э, то для V Rk
min |q|=S min |q|.
qG3(/T) qe3(/?A)
Рассмотрим подпространство Rk = Rk, максимизирующее ле-
вую часть неравенства. Тогда, используя теорему 3, получим
ak = max min | q | = min | q | min | q |
Rk 4e3(Rk) <^3{Rk) <^3(Rk)
max min |q| = 6zA.
Rk qe3(/?A)
Теорема 5. Пусть Э - эллипсоид с полуосями а{ > а2 ...
ат. Рассмотрим сечение Э = Э(/?/л1) эллипсоида Э гипер-
плоскостью Rm i. Пусть а{ а2 ... ат_{ - полуоси Э(/?'/?|).
Тогда справедливы неравенства
а{ а2 а2 ... ат_х ат, (7.6.5)
Доказательство.
1) Согласно теореме 3,
ак = max min |q|^ max min |q|=^.
RkczRm~[ qe3(/?A ) RkcRm qe3(Rk )
Максимум справа берется по более широкому множеству, откуда
следует неравенство. Доказано, что ак ^ак.
2) Пусть R^x есть (Л + 1)-мерное подпространство Rm. Тогда
Rs = Rk+{ n R,n~] - подпространство Rm размерности s к и
Rs c Rm]. Справедливы следующие соотношения:
а,.,= max min Iq H max min |q|=
qe3(/?A+1) Rk+iC.Rm qG3(/?A+W”-1)
= max min | q |= as.
qe3(/?‘s)
Таким образом, находим as ak+v где s к. Так как ak+l ak, to
имеем ak^ak+}.
Теорема 5 доказана.
2°. Рассмотрим две консервативные колебательные системы
(I) и (II). Пусть То, С70 и T0,UG - кинитическая энергия и потен-
циал для систем (I) и (II) соответственно:
(I) = | ^0 = 1 ЧтЛтъ
§ 7.6. Изменение частот при изменении жесткости
445
(II) Т0 = |тптВЙ 170 = 1^41). (7.6.6)
Будем полагать, что в обеих системах 1/0 и [/0 - положительно-
определенные квадратичные формы, т.е. малые колебания
являются действительно колебаниями.
Определение 1. Говорят, что система (II) более жестка, чем
система (I), если В = В (То = То), но (70 (70 при всех т].
Определение 2. Говорят, что система (II) обладает большей
инерцией, если А = A (UQ = (70), но Го То при всех i).
Пример. Рассмотрим колебания грузика массой
т на пружине (рис. 165):
1 ? 1 9 9 ? >
T^-mq\ U = -k4q-q0)2. | >
2 2 —• т
Уравнение движения: mq = -k\q- g0); q = 0, q = q0 - Рис‘ 165
положение равновесия. Параметр к определяет
жесткость пружины, ат- меру инерции. Собственная частота
0) =\42 /т. Если увеличить жесткость пружины к или умень-
шить массу т, то со увеличивается. Этот пример иллюстри-
рует общее положение, сформулированное следующей тео-
ремой.
Теорема 6 (Релея). Главные частоты о), увеличиваются при:
1) увеличении жесткости системы или 2) при уменьшении ее
инерции.
Доказательство 1. Рассмотрим две колебательные
системы: (I) Го, [70 и (II) Г0,С70. Пусть
То = | Т)ТВТ| = То > 0, Uo = | if Ь) | л тА1) = и0 > 0. (7.6.7)
Собственные частоты соДсоД систем определяются корнями
уравнений
detG4-w2B) = 0, det(A -со2В) = 0.
Согласно теореме 1, для матриы В существует матрица D такая,
что
DTBD = 1^ det D ^0.
446
Глава 7. Устойчивость движения и малые колебания
Отсюда получим
О = det(A - (02В) = det DT(A - w2B)D = det(£>TA7> - to2/,,,),
0 = det(A -й2В) = det DT(A - (A2B)D = det(£>T AD - w2I,„).
Согласно теореме 2, собственные частоты систем
(О, SS 0)2 < ... (От (Ш, (02 < ... «= Й,„ )
равны обратным величинам главных полуосей ц.(а,.) эллипсои-
дов Э = {£ G = 1} и Э = {£ G R'n : ^DTAD^ = 1}
сответственно:
1
шу = —, ах ... ат,
ai
_ 1 _ _
ш, = —, 6Zj ... ат.
ai
После преобразования т] = £)£ во втором соотношении (7) по-
лучим
CDtAD^tDtAD£ для всех
Отсюда следует, что эллипсоид Э содержит Э, поэтому а, ц и,
следовательно,
Шу ^Шу.
Первое утверждение доказано.
2. Пусть
О <70 = 1^5^1^ = 70, (7.6.8)
НО
Согласно теореме 1, существует матрица D такая, что DyAD = 1т.
Отсюда следует
0 = det(A - Вы2) = det(Zm - w2DTBD) = det(7>T5E> —1- Im),
0 = det(А - Вы2) = det(/„, - w2DTBD) = det(Z)TS£> - I„,).
Ш“
Тем самым оэ, ш2 ... ш,„ - главные полуоси эллипсоида
§ 7.6. Изменение частот при изменении жесткости
447
Э = {£ g Rm : t)TDTBDt) = 1}, a cOj со2 ... cow - главные полуоси
эллипсоида Э = {£ е Rm : = 1}.
Из условия (8) следует, что эллипсоид Э содержит эллипсоид
Э и, таким образом,
(D- Шр
Рассмотрим консервативную механическую систему с кине-
тической энергией Т - (l/2)qTSS(g)q и потенциалом C7(q), где
q, qe/?™, qT = (q\q2,...,qm). Пусть q = q0, q = 0 - положение
равновесия системы.
Пусть /(q) = 0 - дополнительная голономная связь, наложен-
ная на рассматриваемую систему, которой удовлетворяет поло-
жение равновесия, т.е. /(q0) = 0. В общем случае мы можем в
окрестности q = q0 ввести новые обобщенные координаты q =
= Ф^) (q g Rm), так что положению равновесия будет отвечать
точка q = 0, q = 0, а связи/(q) будет соответствовать связь q™ = 0
(надо положить q™ = Ф'7г (q) = /(q)). Будем полагать, что задача
рассматривается в таких координатах, опуская черту над q.
Уравнения малых колебаний без связи определяются кинети-
ческой энергией То = (l/2)qTSS(0)q и потенциалом Uo = ^qTAq.
Эту систему будем называть системой I. Будем полагать, что [/0 -
положительно-определенная форма и (Щ со2 ••• ~ соб-
ственные частоты системы.
При дополнительной связи qm = 0 мы приходим к системе
с кинетической энергией f0=^qTSSq и потенциалом UQ =
1 ~Т7~
= -q Aq, где
q'=(q\q2,...,qm-\ ^^{q\q2^qm~^.
Матрицы и А получаются из В и А вычеркиванием
последнего столбца и последней строки. Эти систему будем на-
зывать системой II. Обозначим ее собственные частоты
(b1^(b2^...^cbw_1.
Теорема 7. О соотношении между частотами при наложении
связи. Собственные частоты системы II разделяют собственные
частоты системы I, т.е.
448
Глава 7. Устойчивость движения и малые колебания
Доказательство. Пусть матрица D размера т х т
определяется теоремой 1. Тогда после преобразования q = £)£,
q = D'Q в координатах £ для системы (I) получим
1 1 т 1
r0=-|t|2-2S(^)2’ U0=^TD'ADl.
Заметим, что всегда можно найти матрицу D такую, чтобы
условию связи qm = 0 соответствовало условие = 0. Для
доказательства этого утверждения надо только обратить внима-
ние на то, что при любом ортогональном преобразовании £ = О£
(О - ортогональная матрица размера т х т) То сохраняет указан-
ный выше вид. Если матрица D удовлетворяет этому дополни-
тельному условию, то для системы (II) имеем
ГоЦ|^|2,
где £т = (^1,^2,...,^"г~1), a DTAD получается вычеркиванием m-го
столбца и m-й строки в матрице DTAD.
Собственные частоты со, и систем (I) и (II) суть соб-
ственные числа матриц РтА£>и £>тAD соответственно, I/O), и 1 / сЬ-
равны полуосям а, и at эллипсоидов £Т£)ТА£>£ = 1, ^e^AdI, - j
///^/////////////////////л//////// Так как второй эллипсоид есть сечение
”А” первого подпространством то имеют
Д1 А2 место соотношения, определяемые теоре-
;?,\vwvwwwxM мой 5: а^а2^.. .^ат_^ат.
\ Отсюда
1 1 Пример 1. Рассматриваются малые коле-
Рис. 166 бания двух плоских математических маятни-
ков, соединенных пружиной (рис. 166). Запи-
шем формулы для кинетической энергии и потенциала:
= ^т2^2^2^
к2 2
U = cosq} -m2l2gcosq2 +— (q} -q2) ,
где g - ускорение силы тяжести, mb m2 - массы маятников, к2 -
жесткость пружины.
§ 7.6. Изменение частот при изменении жесткости
449
Положение равновесия: qx = q2 = qA = q2 - 0.
Упражнение.
1. Покажите, что кинетическая энергия То и потенциал Uq малых колеба
ний определяются формулами
7b=|qT5q, L/0=|qTM ч=РН
2 2 \JI2J yqi)
где
ГШ]/]2 О . f gmxlx + k2 -k2
0 m2/fj’ -k2 gm2l2+k2/
2. Покажите, что характеристическое уравнение имеет вид
7?а — + bxk2) + (eg + cxk^) = 0,
где
a = (mi/12)(m2/2), b0 = ?тхт21х12(1х +/2),
=m1/2+/и2/|, co =
cx=(mxlx+m2l2)g.
3. Покажите, что: а) при £2 —» 0 X] —»g/lx, X2 —> g/l2, т.е. частоты co =
стремятся к частотам колебаний несвязанных маят-
ников;
б) при £ —» оо Xj оо и
ч m1/1+m2^2
т/Ц +т212
причем со совпадает с частотой системы, полученной
при наложении дополнительной голономной связи
= Q2-
Пример 2. Малые колебания двойно-
го маятника. Используя обозначения
рис. 167, покажите, что в обобщенных координатах q{, q2
T = ^mi +m2^i^i/ +^m2l2(q2f +l]l2m2qlq2cos(ql-q2),
U = -mxglx cos qx - m2g(lx cos qx +12 cos q2).
Положение равновесия qx- q2 = 0. Для малых колебаний
r0=^qTBq, t/0=|qTM q =
Рис. 167
Ql
, q =
B = —
2
1 ((mx +m2)Z12 т21х12
77^2^1/2 ^^2^2
Qi
$2;
0
A_g_( + m2)lt
m2l2y
29. М.Л. Лидов
0
450
Глава 7. Устойчивость движения и малые колебания
Упражнение 1. Найдите собственные частоты и собственные векторы и за-
пишите общее решение системы уравнений малых колебаний в рассматри-
ваемой задаче,
2. Покажите, что при наложении дополнительной голономной связи q\ = q2
частота системы будет определяться формулой
-2 _ lfn1ll+m2(ll+l2)]g
СО 2 2 *
+ m2(ly + Z2)
§ 7.7. Малые колебания и устойчивость
в гамильтоновых системах
1°. Рассмотрим систему уравнений Гамильтона
’ y = f4 Н = (7.7.1)
dt ) <4/
Пусть у = у*(7) (£ = “Л = Л*(0) - решение (1). Рассмотрим
симлектическое преобразование т] —»р, q, определяемое про-
изводящей функцией
S = (pW(W(0). (7.7.2)
Производящей функции (2) соответствует преобразование
£ = =P + f(O=*P = £-f(O,
(7.7.3)
= !)--¥)* (Г).
<7 =
<эр
После преобразования система сохраняет форму уравнений Га-
мильтона с гамильтонианом (см. § 5.4)
— — f ЭХ / ЭХ
H = H(p,q,t)= — + H—,x\,t
Эг I Этп П
ЭХ
Эт)’
= эг
k dt
Так как р = q = 0 должно быть решением уравнений Гамиль-
тона с гамильтонианом (4), то
^=0
Эх
Ч-(р + С('))т^7- + Н(р + Г(0, q + л*(0,0- (7.7.4)
at
р
л!
X =
§ 7.7. Устойчивость в гамильтоновых системах
451
и гамильтониан (4) начинается с квадратичных членов, посколь-
ку часть Н, не зависящую от х, можно опустить;
Н = |хтЯх + О(|х|3),
где В = B(t) - симметрическая матрица размера 2m х 2m, а
0(1 х I3) - члены порядка I х I3. Отсюда следует, что гамильтониан
линеаризованной системы имеет вид
Н0=|хтВ(Г)х, (7.7.5)
а соответствующая система уравнений Гамильтона - вид
— =g?s(r)x, х =
dt
Р
(7.7.6)
2°. Рассмотрим случай, когда система (1) автономна и у* =
= const - положение равновесия. Тогда матрица В не изменяется
с течением времени и мы приходим к системе с постоянными
коэффициентами
z/z
— ^Вг, г
dt
Р
Л,
(7.7.7)
Определение. Матрицу вида 9В, где 2F - симплектическая
единица, а В - симметрическая матрица, называют гамильтоно-
вой матрицей.
Рассмотрим характеристический полином d(K) гамильтоно-
вой матрицы 9В
d(X) = det(9B-Xl). (7.7.8)
Теорема 1. Если X - корень характеристического уравнения,
то (-Х) тоже его корень, т.е. из d(k) = 0 d(-K) = 0.
Доказательство.
б/(Х) = det(2FВ -X/) = det[2F(9 В-М)9] =
1 2
= det(-B^+X/)=det(^B-(-X)/) = d(-X).
2 3
Равенство 1 следует из соотношения det 9=1. Равенство 2 - из
свойства 9: 92 = а равенство 3 - из det А = det Ат и свойства
g?T = _д?.
Таким образом, характеристический полином гамильтоновой
матрицы имеет вид
Ж)-а2-лз)...а2-^„). (7.7.9)
29*
452
Глава 7. Устойчивость движения и малые колебания
Теорема 2. Для устойчивости тривиального решения гамиль-
тоновой системы необходимо, чтобы все характеристические
числа матрицы были чисто мнимые.
Доказательство. Если ReA^ Ф 0, то обязательно
существует корень \ (А5 - ±АЛ), у которого Re \ > 0, и решение
неустойчиво.
3°. Устойчивость гамильтоновых систем связана с устойчи-
востью симплектических преобразований. Рассмотрим линейное
симплектическое преобразование z0 zb определяемое матри-
цей А:
Z! = Az0; z0,zleR2m; А еSp(2m) => АТ&А =&. (7.7.10)
Рассмотрим характеристический полином /?(Х) матрицы А
р(к) = де1(А-ХГ). (7.7.11)
Теорема 3. Полином Р(Х) - возвратный, т.е.
р(Л) = Л2т/^у.
(7.7.12)
Доказательство.
р(Х) = det( А - AZ) = X2m detf - А -11 - Л2'” detf -1 - А'1
к А ) \ А
= Х2'" detf^-7+^AT^ =X2m detf--1 + Ат>|;
\ A J \ A J
При доказательстве мы воспользовались следующими соотноше-
ниями:
detA = l, А~1 =-9? АТ 9?, det9^=l, 9^2 = ~/,
которые следуют из симплектичности матрицы А и свойств 2F.
Следствие 1. Если А - корень /?(А), то 1/А - тоже корень
р(А).
Следствие 2. Пусть матрица А - вещественная, тогда
если А - комплексный корень р(А), то А* (комплексно-сопря-
женное А число) тоже корень р(А).
Таким образом, при вещественной симплектической матри-
це А:
1)Все комплексные корни А, модуль которых не равен еди-
§ 7.7. Устойчивость в гамильтоновых системах
453
нице, разбиваются на четверки
(рис. 168):
Л р
г=рс-;<р, 4=-«л
Xs' р
где j = лГл, р = I X I Ф 1.
2) Комплексные корни X, модуль ко-
торых равен единице, разбиваются на
пары: Х = е7ф, X* == е~7ф.
3) Вещественные корни разбиваются на пары
X = а, Х = ~.
Рассмотрим последовательность точек z g 7?2m, определяемых
отображением (10):
Zj = Az0, z2 = Azl = A2z0,...,zN = ANz0,...
Определение. Преобразование А называется устойчивым,
если для любого 8 > 0 существует 5 > 0 такое, что I z0 I < 8 влечет
I ANz$ I < 8 для всех целых N.
Теорема 4. Если хотя бы один корень X* характеристического
полинома вещественной матрицы А не лежит на единичной
окружности комплексной плоскости X, то преобразование не-
устойчиво.
Доказательство. Пусть X = ре/(р (р Ф 1). Из двух кор-
ней X и 1/Х выберем тот, для которого р > 1. Пусть z0 - соб-
ственный вектор, соответствующий выбранному корню X:
zj — 2aZq — XZq, z2 — тт.zj — A z0 — Zq,...,Zyy — A Zq — Zq.
Таким образом, II zN II = p^l z0 И и Для любого II z0 И 0 и любого
8 > 0 можно указать N, когда II II > 8.
Теорема 5. Если все собственные значения Хь Х2, ... , X2w
различны и лежат на единичной окружности, то преобразо-
вание Zj = Az$ устойчиво.
Доказател ьство. Различным собственным значениям
Xz, / = 1, 2, ... , 2m, соответствует 2m линейно независимых
собственных векторов z(1), z(2),..., z(2m):
Az(0 =X,.z(0, Z =(г(1),...,г(2'я)), detz *0.
454
Глава 7. Устойчивость движения и малые колебания
Произвольный вектор z0 представим в виде
z0 = Z а, где ат = (аь с^,..., а2,„).
Из этого представления следует
AZ = zX
где !£ =
(К
О
- диагональная матрица.
^2т )
О
Таким образом,
zN = ANzQ = AnZ ol=Z Xn cl,
Так как,
(2m V/2
V I 1 |2/V
TO
lh„ II® VM|z llllz-1 ll h ||.
Поскольку нормы II Z II и II Z_| II матриц ограничены, то из II z0 II <
< 8/(V2mll Z 11*11 Z-1 II) следует II z/v II <
4°. Рассмотрим наряду с симплектическим преобразованием
Zj = Azq симплектическое преобразование z[ = A'z0 :
А'Т^А'
Определение. Преобразование А называется сильно устойчи-
вым, если существует 8 > О такое, что любое А' устойчиво при
IIА-А' II < е.
Теорема 6. Если А - устойчивое симплектическое преобра-
зование и все собственные числа матрицы А различны, то это
преобразование - сильно устойчиво.
Доказательство. По теореме 4 собственные числа
преобразования А лежат на единичной окружности: \ = А ДА) =
= . Так как корни А, различны, то при достаточно малом 8 > О
круги с центром в Az, i = 1, 2, ... , т, и радиуса 8 не пересекаются
на комплексной плоскости. Рассмотрим собственные числа
матрицы A': A' = AZ(A') и Д,-= I А/А') - АДА) I. Так как корни
многочлена непрерывно зависят от его коэффициентов, то мож-
но указать такое 8 > 0, что из
IIА - А' II < 8 следует Д <8, i - 1, 2, ... , т.
§ 7.7. Устойчивость в гамильтоновых системах
455
Таким образом, корни X'лежат внутри построенных кругов
радиуса 5 с центрами в Xz. Предположим, что существует Х^ та-
кое, что | Х^ |^1. Так как А' - симплектическое преобразование,
то должен существовать корень 1/Х£ #ДХ*)*. То есть вместо па-
ры корней Х7< и =1/ХА. должна появиться четверка Х^Д/Х*,
ХА., 1 / Х£*. Этого не может быть, так как в
этом случае оказалось бы, что корней
больше, чем 2m.
Следовательно, все корни Х' = Х-(А')
лежат на единичной окружности, преобра-
зование А1 устойчиво, а так как А' - про-
извольное достаточно близкое к А, то А -
сильно устойчиво.
Следствие. Собственное значение
может покинуть единичную окружность,
только «столкнувшись» с другим собствен-
ным значением (рис. 169).
5°. Рассмотрим линейную систему уравнений с переменными
коэффициентами
— = А(Ох, (7.7.13)
dt
где х 6 R", A(t) = Ai(ty) - матрица размера п хп, ограниченная
при всех t t0.
Обозначим через х*') = xW(/, t0) решение (13) с начальными
ГОА
условиями t = t0, Xq° = x(i)(r0,r0) =
1 <—i-e место. Совокупность
1°.
таких решений образует матрицу
Х(М0) = (х(|),х(2),...,х(п)).
При этом Х(4), tG) = I - единичная матрица. Матрица X = X(t, г0)
называется фундаментальной матрицей решений, она удовлет-
воряет матричному дифференциальному уравнению
^^ = А(г)Ж/0). (7.7.14)
dt
Лемма. А = detX(z, г0) Ф 0.
456
Глава 7. Устойчивость движения и малые колебания
Доказательство. Матрица )С удовлетворяет уравне-
нию
---= ХТА. (7.7.15)
dt
Обозначим через i-Й столбец матрицы )С:
через А(7) - j-й столбец матрицы Ат:
Очевидно,
Ат = (А(1), ..., А<и)).
А - detXT =>= j^det(£(l)
Подставляя сюда
j£(f) п п
at J=1 J=1
получим
/=1 < j=i ;
— = 2>t
= Y £A/det(g(1)
/=1 J=1
^u-1) g(J) g(/+1)
Отсюда находим
= AJA = ASpA(f); (Sp-следА).
/=1
— = ASpA(/)^
dt
=> A = A(r0)exp JSpA(0tfr = exp J dt^ A- (t) ^0.
Vo /=1 J
Mo
Решение (14) с начальными данными t= t0, x = x0 может быть
представлено в следующем виде:
х(О = Хало)хо (7.7.16)
§ 7.7. Устойчивость в гамильтоновых системах
457
Ниже мы предполагаем, что матрица А (г) - периодическая с
периодом т:
А(г+т)=А(г). (7.7.17)
Так как
+ Т,го) = + т)Х(г + т, г0) = A(t )X(t + т, /0),
dt
то матрица X(t 4- т, г0) удовлетворяет уравнению (14). Следова-
тельно,
X(t + т, to) — X(t, Iq)C,
где С - постоянная невырожденная матрица размера пхп. По-
лагая t = t0, найдем
С = X(tQ 4- Т, /о).
Нетрудно доказать, что
X(t+tQ + T, tQ+T) = X(t+tQ,to). (7.7.18)
Представим t = tQ + кт 4- 5, где к > 0 - целое, 0 s < т. Согласно
(15)—(18), справедливы равенства:
х(г) = х(Г0 + кт + sdo) = X(tQ + кт + s,to)^o =
= X(t0 + (к - 1)т + 5, r0 )X(r0 + т, t0 )х0 =
= Х(Г0 4-л, )Х (/о +
Определение 1. Преобразование х0 хр xt = X(/b 4- т, Го)хо
называется отображением за период.
Определение 2. Отображение за период называется устой-
чивым в будущем, если для Ve > 0 38 > 0 и для Vx0: I х0 I < 8 =>
=> II XN(t0 + т, го)хо И < £ Для V7V > 0.
Теорема 7. Если отображение за период является преобразо-
ванием устойчивым в будущем, то тривиальное решение х = 0
устойчиво.
Доказательство. Согласно (18),
II Х(О HI X(t0 + 5,t0) || • || Хк (t0 + т,t0 )х0 ||. (7.7.19)
Для первого сомножителя на ограниченном интервале 0 д< т
нетрудно получить оценку
шах || X(t0 4- s,t0) ||^ а.
0^5<Т
Из устойчивости Х(г0 4- т, to) в будущем следует, что II Xk(tQ +
+ т, to) хо II < е/ос при достаточно малом 11х0П < 5. Тогда из (19)
получим ILx(r) II < е.
458
Глава 7. Устойчивость движения и малые колебания
В качестве упражнения предлагается доказать следующую теорему.
Теорема 8. Пусть Xj, Х2, ... Х„ - собственные числа матрицы
X(fo + т, t0).
а) Для устойчивости отображения за период в будущем необходимо, чтобы
I XI 1 для всех i = 1,2,... п. (7.7.20)
б) Если все X/ различны, то этих условий и достаточно для устойчивости
этого отображения.
Таким образом, в большинстве случаев для определения
устойчивости решений линейной системы с периодическими
коэффициентами достаточно определить отображение за период
X(tQ + т, г0) и найти собственные числа этой матрицы. Исклю-
чительными являются случаи, когда выполнено (20), но среди
корней \ имеются кратные.
Приближенно X(tQ + т, г0) всегда можно найти путем числен-
ного интегрирования системы (14) п раз последовательно с
начальными данными:
t = t0, xj =(1,0,...,0), Xg = (0,1,0,...,0),...,Xq = (0,0,...,0,1).
Интегрирование надо вести только на отрезке [г0,г0 +т]. В этом
существенная специфика разрешения проблемы устойчивости
для линейных систем спериодическими коэффи-
циентами.
6°. Рассмотрим две линейных гамильтоновых системы с га-
мильтонианами
(I) /7 = 77О - — zTBz, zgT?2"1, — = 0,
2 dt (7.7.21)
(II) Н - Нг = | zT(B + eA(r))z,
где матрицы A(f) и В размера 2mx2m - симметрические, В - не
зависит от времени, A(t) - зависит от времени периодически:
A(t+ т) = A(t).
Гамильтонианам (I) и (II) соответствуют системы уравнений
(I) — =
dt V dz ) (7.7.22)
(ii) — = =g?(B + £A(r))z.
dt { dz J
Пусть Z = (M0)hZ£= Ze (t, t0) - фундаментальные матрицы
§ 7.7. Устойчивость в гамильтоновых системах
459
решений систем (I) и (II) соответственно:
z/Z
I ---=$FBZ, Z(?0,Z0) = 7,
dt (7.7.23)
II ^=^(B + £A(r))zE, z£a0,?0) = Z.
at
Согласно результатам, полученным в гл. 5, Z и Ze - симплекти-
ческие матрицы. Для второй системы т - период. Так как В -
постоянная матрица, то для нее любое число - период. Рассмот-
рим матрицы
zT=z(r0+v0) и zeT =ze(r0+v0),
определяющие отображение за период т.
Лемма.
||z£-zt-ezt9?| zT Az dt || = O(e2). (7.7.24)
*0
Доказательство. Представим Z E(/,z0) = Z (?,г0)СД).
Из этого равенства и уравнений (23) следует
^ = —C + z —=3?(B + eA(z))zC=^ —= ez ’'^AzC.
dt dt dt dt
Так как Z(r, /0) - симплектическая матрица, то
. Tr_ dC r~ T Л
Z *=-^Z ----= E^Z AZC,
dt
t
C(Z) = / + E$f| ztAz Cdt=>
r0
=>||C(0-/|| = O(e), t0^t^t0 + T,
r0+T
|| C(t) — 7 — e9* J Z^ Azdt\\ = O(ez). (7.7.25)
z0
Так как Z I = Z тС(т), to из (25) следует (24).
Следствие. Если отображение Z(r0 + т,Г0) устойчиво и
его характеристические корни различные, то отображение
Ze(r0 + т,Г0) тоже устойчиво при достаточно малом е.
460
Глава 7. Устойчивость движения и малые колебания
Замечание 1, Мы получили, что устойчивость возмущенной
системы (8 Ф 0) при достаточно малом 8 определяется устой-
чивостью невозмущенной системы (е = 0). Существенно, что в
рассматриваемом случае невозмущенная система есть система с
постоянными коэффициентами и имеются регулярные способы
вычисления матрицы
zT =Z(r0+V0)
без привлечения численного интегрирования.
Замечание 2. Кратность корней устойчивой
////{/////////////// невозмущенной системы является необходимым
условием неустойчивости возмущенной системы
(е - 0) при достаточно малом 8, но недостаточ-
: Ф \/ ным. Формула
• \
; zET = zET = zT(Z + e9? J z t(m0)A(/)z
: 'o
дает явное выражение отображения за период
Рис 170 возмущенной системы (е Ф 0) в линейном приб-
лижении по 8. Если не все характеристические
числа матрицы Z * при 0 < 8 < 80 лежат на единичной окруж-
ности, то при достаточно малом 8 возмущенная система не-
устойчива.
Пример. Качели - малые колебания математического маят-
ника с периодически изменяющейся длиной. Предположим, что
длина / математического маятника (рис. 170) изменяется по
закону
/ = /0(1 + 8«(О), (7.7.26)
где a(t) - гладкая периодическая функция с периодом т и
нулевым средним:
т
a(t + т) = а(Г), J a(t)dt = 0.
о
Кинетическая и потенциальная энергии малых колебаний имеют
вид
Т = у [Z2cp2 + i1 ] = у [Z202 + 82/02 W))2 ],
1 2
U = -mgl coscp => UG = —mglcp .
§ 7.7. Устойчивость в гамильтоновых системах
461
ml
Запишем гамильтониан задачи малых колебаний:
ЭГ /2.
р = — = т/ ф =>
Эф
„ 1 Р2 1 ,2
Н = —=- +—mgl(D
2 ml2 2
(мы отбросили член в Н, не зависящий от /?, ф).
Гамильтониан задачи можно записать в следующем виде:
Н = | zT (В + eA(/))z + О(е2 ),
Р\
<Р/
Z =
2
m/g
0
« 0
I о gml0
Невозмущенная система (e = 0) имеет вид
( 0 -gml0
-7 °
{ml0
В = ml.
di OLD
---= tyBl =
dt
z,
a(t).
О
det(2FB - Л/) = 0 => X = ±усоо, со0
Решение невозмущенной системы имеет вид
ф = С coso)0r + £)sino)0r,
р = т1ц = ос(-Сsino)0r + Dcoso)0r),
dt
где С, D- произвольные постоянные, а = mlf}со0.
Полагая t = 0, р = р0 = 1, ф = ф0 = О, найдем D = 1/сс, 6 = 0.
Полагая t = 0, р = pQ = 0,ф = ф0 = 1, определим D = 0,С = 1.
Таким образом, фундаментальная матрица невозмущенной сис-
темы имеет вид
cosw0/ -asinw0P
z(z,O)= 1 .
— sino)0z cos(00r
k a 7
(7.7.27)
462
Глава 7. Устойчивость движения и малые колебания
Рассмотрим характеристическое уравнение матрицы Z (т, 0),
определяющей отображение за период:
det
^COSCDqT-X
1 .
— SH1 ОКТ
< а
-asincDgT^
coscd0t-X
7
=> (coso0t — X)2 +sin2O)0T = 0. (7.7.28)
Если sin cdot Г 0, то корни различные и их модули равны еди-
нице:
Следовательно, решение возмущенной системы устойчиво при
достаточно малом е. При малом е возможна неустойчивость,
когда
= (к- целое). (7.7.29)
Тем самым неустойчивость колебаний в окрестности равно-
весия ср = 0, ф = 0 может наступить, если период т вынужденных
колебаний длины маятника определяется формулой
т = ^кк. (7.7.30)
На этом принципе основаны качели. Качели с неподвижным
человеком - физический маятник. Как мы знаем (см. гл. 4),
уравнение физического маятника совпадает с уравнением мате-
матического маятника. При этом
2 mgya2 +Ь2
со =—---------,
К
где а, b - постоянные координаты центра масс системы относи-
тельно подвижного репера, J* - момент инерции относительно
точки закрепления маятника. Когда человек периодически при-
седает, то изменяются а, b и J3. При этом можно подобрать
период возмущений (приседаний) таким, что качели начнут
раскачиваться (это экспериментальный факт).
Можно дать несколько иную интерпретацию условию
возможной неустойчивости: шот = кп. Пусть возмущающая сила
имеет период т. Рассмотрим маятники с различной «средней»
§ 7.7. Устойчивость в гамильтоновых системах
463
длиной Z(). Тогда при
g?2
(^л)2
О “
возможна неустойчивость.
Определение. Возникновение неустойчивости при некоторых
значениях параметров задачи называется параметрическим
резонансом. Согласно (24), в линейном приближении по е мат-
рица отображения за период zj для возмущенной системы
имеет вид
z£ = z+ zTAzc?z).
О
Определим характеристические числа Z(T в нашем примере в
случае критических значений т = Ьг/со0. Для упрощения вычис-
лений положим, что единицы измерения массы, длины и времени
выбраны так, что т = 1, Zo = 1, g = 1 => со0 = 1,т = кп. В этом
случае
z = z (г,0) =
cos г
sin Г
-sin О
cos Г J
(-2 О'
Z TAZ =
JY1 ОА _3<-cos2r
2^0 I) 2< sin 2г
sin 2г
cos 2t J
a(t).
Представим a(t) в виде ряда Фурье:
а(Г) =
2nst 1 . 2nst
av cos----+ b. sin —
T T
-т=к-к
2s .. 2s
a. cos — t + h sin — t
s к s к
Нетрудно вычислить
кп
з, Г
— кп а,
4 L
Lk
-1 о
0 1
+ь>
ГО
Mi
Г
о
о
Отсюда
3
= ± 14— Атщ а.
4
( 0 -1
Ч -1 о
+ Ь.
(-1 О'
Мо 1
+ <?(Е2),
464
Глава 7. Устойчивость движения и малые колебания
а из det(Z I - X/) = О следует выражение для корней
Xu = 1 ± +О(Е2 ).
Таким образом, если a2+b[^ 0, то корни не будут лежать на
единичной окружности, и при т = кп и достаточно малом е
действительно имеет место неустойчивость.
7.8. Формальная*) процедура теории возмущений
для гамильтоновых систем
В этом параграфе мы рассмотрим аппарат теории возму-
щений гамильтоновых систем. В конце раздела будут даны крат-
кие пояснения к возможному использованию этого аппарата в
некоторых задачах механики.
1°. Каноническая замена переменных, близкая к тождест-
венной. Рассмотрим уравнения Гамильтона с аналитическим по z
гамильтонианом W(z) и независимой переменной v:
— = , W = W(z), z = f₽l p,qe/?m.
dv v dz)
Пусть
z = z(x,v), z(x,0) = x, x= ,
(7.8.1)
(7.8.2)
есть решение (1) с начальными данными v = 0, z - х. При каждом
фиксированном v (2) определяет симплектический диффео-
морфизм х —> z. При достаточно малых v этот диффеоморфизм
близок к тождественному z = х.
Пусть теперь Я(х) - произвольная аналитическая в области
G функция.
Обозначим через
x = x(z,v), x(z,0) = x (7.8.3)
отображение, обратное (2). После замены (3) в /7(х) получим
Я(х) = H(x(z, v)) = Жх, V). (7.8.4)
Слово «формальная» означает, что мы описываем лишь технику теории воз-
мущений без сколь бы то ни было серьезного обоснования (сходимости и т.п.). Читатель
не должен думать, что обоснование очевидно или не нужно. См. также замечание в конце
параграфа.
§ 7.8. Процедура теории возмущений для гамильтоновых систем
465
Рассмотрим ряд Тейлора для ЖХ v):
00 п ж—Ч V ^(z,v) = y — 3€„(z) = ±7 и! М . (7.8.5) dv”
/?=() * \ ) v=0
Очевидно,
2C0(z) = #(z). (7.8.6)
Производной функции/(z, v) по v в силу системы (1) назы-
вается производная df/dv, вычисленная вдоль решений систе-
мы (1):
df df df dz df df (dWV df
dv dv dz dv dv dz \ dz J dv
где (•, •) - скобка Пуассона.
Так как вдоль решения (1) ffl(z, v) = Н(х) и от v не зависит, то
0 = —= + =>^ = (9€1У) (787)
Jv dv v 'z dv z
При симплектическом преобразовании z = z(x, v) имеем
(^(z,v), W(z))z =(9€(z(x,v),v), W(z(x,v)))x.
Так как lT(z) - первый интерал (1), то IV(z(x, v)) = IV(x) и,
учитывая (4), получим, что dffl/dv = (3€,IV)Z на решениях (2) есть
функция х. Поэтому
dv dv dv2 V dv ’ J ’
Используя индукцию, легко доказать следующую лемму.
Лемма 1. Частные производные в (5) (и соответствующие
коэффициенты ряда Тейлора) определяются следующими рекур-
рентными соотношениями:
=^Ж(Х = (Ж-1(Х, W(Z)). (7.8.8)
dv dv J
В приложениях развиваемой теории мы сталкиваемся со слу-
чаями, когда функция Н(х) задана в виде ряда по малому пара-
метру е:
Н(х) = ]Г е"Н(л,(х). (7.8.9)
л=0
30. М.Л. Лидов
466
Глава 7. Устойчивость движения и малые колебания
Для этих случаев целесообразно представить W(z) и 9^w(z) тоже
в виде ряда по е:
W(z) = X e'W(i)(z),
5=0
5=0
При этом из (6) следует
^>(z) = H(')(z).
При представлениях (9) - (11) из (8) получим
(7.8.10)
(7.8.11)
(7.8.12)
5=0
т=0
Из последнего соотношения, приравнивая нулю коэффициенты
при одинаковых степенях е, получим, что справедливы следую-
щие утверждения.
Лемма 2. Коэффициенты определяются такими рекур-
рентными соотношениями:
Xf(z) = ^ (7.8.13)
j=o
Лемма 3. Если известны функции W(/) для r = 0, 1, ...,и-1,
то по формулам (13) мы можем вычислить (только путем вы-
числения частных производных) коэффициенты для всех
к^О, т^О, к + т^п.
Доказательство этой леммы по индукции предоставляется читателю.
Для наглядности мы выпишем соотношения (13) для к +
4- т 2:
+ m = 0:
= Н(0);
к + т =
3€(” =Я(|), =(^(“),И/(0)) = (н(0),И/(0)
к + т =2:
^(02) = Я(2), = (hw+ ,Wwy
7.8. Процедура теории возмущений для гамильтоновых систем
467
^(20)=(^(10).w(0)).
Как обычно в теории возмущений, для определения коэффи-
циентов с к + т = п надо предварительно вычислить коэффи-
циенты для к + т = 1, 2, п - 1. Подставляя (11) в (5) и груп-
пируя специальным образом члены ряда, получим:
3€(z,v) 2бп), (7.8.14)
/7=0
= V£ (7.8.15)
*=о
Следствие из леммы 3. Чтобы определить
достаточно задать для 5 = 0, 1,п - 1.
До сих пор Я(х) была произвольной функцией. В частности,
полагая //(х) = х' (х' - z-я координата вектора х) и используя для
этого случая специальные обозначения
^(/)(z) = X^)(z), ^(п)=Х(,7),
запишем (13), (15):
00 . 00 П к п-к i s
— Е х'"> = £Х ^-Ч'-п(1ХЛГ'-Ё(хй.|^-л).
/7=0 /,=0^=0 ;=о
(7.8.16)
Формулы (16) дают явное выражение для преобразования коор-
динат:
X =(p'(z,V,E).
Определяя ф' для различных I, получим в векторном виде
х = (p(z, v,e). (7.8.17)
Это преобразование определяется решениями автономной систе-
мы уравнений (1). Поэтому для вычисления обратного преобра-
зования необходимо в (17) поменять местами х и z и заменить v
на - v:
Z = ср (х, -V, £).
До сих пор v было у нас произвольным. Теперь мы выберем
v = Е. Тогда замена переменных будет определяться формулами
оо п 1 00/7 .
е"Ё ^(/”A)(z),?=£ (-1)*т/ГА)(х)-
/7=0 к=о к- п=0 к=0 к-
(7.8.18)
30*
468
Глава 7. Устойчивость движения и малые колебания
Для произвольной функции Н(х) имеем: 3^(00) = //(0). В частности,
i
для случая Я(х) = х' найдем: X^(z) = zl. Поэтому (18) имеет вид
х1 = zl + 0(е). При е = О х' = zz.
Таким образом, замена переменных при достаточно малых £
действительно близка к тождественной.
Замечание. Формулы (1) для симплектического преобра-
зования координат были получены, как частный случай фор-
мул, выведенных для произвольной функции 7/(х). При преобра-
зовании координат простой вид функции Н(х) = х' упро-
щает аналитическую реализацию этой процедуры. В частности,
нетрудно показать, что при /7(х)-х' справедлива формула
(z ,VK) = ±——-, где z - координата вектора z, канонически соп-
ozl
ряженная z'.
При v = Е соотношения (15) можно записать в следующем
виде:
П 1
W,e) = Y e"^„(z), ад =У -^’(z). (7.8.19)
Йо k'-
2°. Основная задача теории возмущений. Предположим те-
перь, что Н(х) - гамильтониан системы уравнений
— =&(—) , х = р\ (7.8.20)
dt I Эх J
Если мы проведем каноническую замену переменных z = z(e, х),
определяемую решениями уравнений (1) при v = е (т.е. форму-
лами (18)), то в переменных z получим снова гамильтонову
систему с гамильтонианом 3€(z, е), где 3€(z, е) определяется
формулами (19), а связаны рекуррентными соотношениями
(13). Согласно описанной выше процедуре,
9€o(z) = /7(O)(z), (7.8.21)
а (z) (п 1) можно представить в следующем виде:
-J} (*)
Л=0 № k=l у=0
Правое равенство следует после подстановки во второе соотно-
шение (19) в виде (13). Для последующих выводов выра-
§ 7.8. Процедура теории возмущений для гамильтоновых систем
469
жение (*) целесообразно записать в следующей форме:
Se„(z) = d>„(z) + (H(0)(z), ^"“‘’(z)), (7.8.22)
где
<D„(z) = tf(">(z) + £ (^<Д, (7.8.23)
k=\ k- >0
(Z: -1)2 + j2 0.
Формулы (22), (23) следуют из (*) после выделения из двукрат-
ной суммы члена с к = 1, j = 0 и установленных ранее соотноше-
ний
}(z) = Z7(/7)(z) и, в частности, ^(00)(z) = /f(0)(z).
Лемма 4. Если известны для всех 5 = 0, 1, 2, ..., п - 2, то
Ф77(г) вычисляется только применением оператора дифферен-
цирования к известным функциям.
Доказательство.В правую часть (23) входят при
т^п-2 и для j + k-l^n-1. Если для т
п - 2 известны, то, согласно лемме 3, мы только путем вы-
числения частных производных можем вычислить все функции
Для j + к-1^ п-1 и тем самым вычислить Ф77.
При п = 1 Ф„ = H(i\z) и соотношение (22) имеет вид
^1(z)-H(1)(z) + (H<0)(z), </) =
= #(1)(z) +
эн(0)ГЭ1У(0)у
Эр [ 9q ,
aw(0,faiv(04
9q (. Эр )
т
= h(I’(z)+£
к=\
Г эя(0) aw(0)
< Эр* 'dq
дн^ aw(0)>
dqk дрк ,
(7.8.24)
Основная задача, которая ставится в теории возму-
щений, состоит в следующем. Определить такую функцию W(z),
чтобы новая функция Ж(г, е) после замены переменных z =
= z(x, е) обладала заданными свойствами. В частности, функция
3^(z, е) будет обладать определенными свойствами, если ими
будут обладать все коэффициенты ^CZ7(z) в разложении этой
функции в ряд по Е. Очевидно, в силу (21) в этом случае функция
#(0)(z) должна уже обладать этим свойством. В теории возму-
щений рассматриваются задачи, в которых Е - достаточно малое
470
Глава 7. Устойчивость движения и малые колебания
число. Обычно поставленную задачу решают лишь прибли-
женно. Пытаются найти конечный набор функции W(0),...,
чтобы для ?f1(z),...,^/7(z) искомые свойства выполнялись. При
этом членами порядка 8Л+1 и выше в функциях W(z) и Ж(г, 8)
пренебрегают.
Пусть ^€j(z) - заданная функция. Так как H(0)(z),/7(1)(z)
известны, то для определения можно воспользоваться со-
отношением (24). Это - уравнение в частных производных
первого порядка относительно Если мы можем
найти его решение W(0)(z), то, согласно лемме 4, путем
дифференцирования мы можем вычислить Ф2(г). При известной
функции Ф2(г) и заданной функции Ж2(г) из (22) при п = 2 полу-
чим уравнение в частных производных для определения Wfl)(z).
Продолжая эту процедуру, мы можем, вообще говоря, довести ее
до требуемого п, обеспечивающего необходимую точность вы-
числения замены переменных и нового гамильтониана.
Существенно, что на каждом шаге необходимо решать ли-
нейное уравнение одного и того же типа. Различным п будут
отвечать лишь различные правые части Ж„(г) - Фп(г). При этом
нам достаточно найти любое решение Wk)(z).
3°. Системы, близкие к интегрируемым. Рассмотрим слу-
чаи, когда в исходных переменных гамильтониан задачи имеет
вид
Н(х) = H(0)© + eH(1)(£,i)), х = |Н (7.8.25)
И;
Задачу при 8 = 0 будем называть невозмущенной. Гамильтониан
Я<°> невозмущенной задачи зависит только от импульсов Часть
8//j(^, ц) будем называть возмущающей функцией. Будем пред-
полагать, что //i(^, л) - 2л-периодическая функция компонентов
вектора Г|. Как мы знаем, если некоторая невозмущенная задача
интегрируема (т.е. имеет т интегралов в инволюции), то, опи-
сывая возмущенную задачу в переменных «действие - угол»,
определенных для невозмущенной задачи, мы, вообще говоря,
приходим к задаче с гамильтонианом в виде (25). То есть рас-
сматриваемый вид гамильтониана (25) является в определенном
смысле типичным для задач, близких (8 - мало) к интегри-
руемым.
Попробуем с помощью аппарата теории возмущений прибли-
женно определить симплектическую замену переменных х —> z
§ 7.8. Процедура теории возмущений для гамильтоновых систем
z = [ р p,qe7?w так, чтобы новый гамильтониан 3^(z,e) за-
висел бы только от новых импульсов р:
^(г,в) = ^(р,в).
Если нам это удастся, то решение задачи в новых переменных
получается сразу:
dq (ЖТ
L др,
dp
dt
= 0 => р = р0 = const,
q =
= const,
(t-to) + qo,
q0 = const.
При E = 0 имеем 9€0(p) = Я(0)(р).
Рассмотрим, как решается эта задача в первом порядке теории
возмущений. Для этого надо найти решение уравнения (24). Так
как в нашем случае Э7/(0> / dq = О, то оно имеет вид
^l(p) = tf<1)(p,q) +
э#(0) (эткУ
Эр у 3q J
(7.8.26)
Поскольку W(l)(p,q) - 2л-периодическая функция компонентов
вектора q, то ее можно представить в виде ряда Фурье:
7/(,)(p,q) = X ЛГ(Р>ЖЧ>. 7 = У1, (7.8.27)
к
где kT = (к1,к2,...,кт) - m-мерный вектор с произвольными цело-
численными компонентами, <k,q) = k{q' +... + kmqm, и суммирова-
ние в (27) производится по всем целым к^ от - ©о до + со:
X = Ё ... Ё ’ ^(p)=4Va,>-
k km =-°°
В (26) Жj(p) - пока произвольная функция. Вообще говоря,
можно распорядиться этим произволом, чтобы функция W(0) бы-
ла также 2л-периодической по компонентам вектора q. Действи-
тельно. Положим Ж/р) равным свободному члену ряда Фурье
(27):
1 (р) — Чр) — ^0,0,...О^р)-
(7.8.28)
т
Глава 7. Устойчивость движения и малые колебания
Будем искать УИ0) тоже в виде ряда Фурье:
IV(0) И^0)(р)?<к,ч>.
к
(7.8.29)
Подставим (27) и (29) в (26). Учитывая независимость функций
eJ<M> ПрИ разЛИЧНЫх к, получим, что (26) будет выполнено, если
определить
) wk(o)(p)=-C(p)-
\ V )
(7.8.30)
При
^0 найдем
(7.8.31)
Таким образом, в первом порядке теории возмущений мы
получили
Жг,Е) = Н(0)(р) + еЖ1(р) +<?(е2) = Н(0)(р) + Е^п(р) + С>(£2). (7.8.32)
Найденная нами функция VH0) позволяет определить замену
переменных (18) с точностью до первой степени е, которая
приводит гамильтониан с той же точностью к виду (32).
Замечание. Мы описали лишь идейную сторону рассмат-
риваемого варианта теории возмущений. Аккуратный анализ
возможного применения указанной процедуры достаточно
сложен. В частности, при этом возникает так называемая проб-
лема «малых знаменателей». При любом (Э//(0)/Эр)т, вообще
говоря, можно указать целочисленный вектор к такой, что в (31)
выражение (к,(ЭН(0)/Эр)т) очень близко к нулю. Это одна из
принципиальных трудностей обоснования теории возмущений.
Мы рассмотрели лишь один из вариантов такой теории, получив-
ший распространение в последние годы. В более ранних иссле-
дованиях рассматривались в принципе эквивалентные процеду-
ры, основанные на симплектических преобразованиях, задавае-
мых производящими функциями (вместо преобразований, за-
даваемых уравнениями (1)).
ДОПОЛНЕНИЕ
Пленарный доклад на V Всероссийской конференции
«Фундаментальные и прикладные проблемы
современной механики»
Томск, Томский государственный университет,
3-5 октября 2006 г.
О НАУЧНОЙ ДЕЯТЕЛЬНОСТИ ПРОФЕССОРА М. Л. ЛИДОВА
И О РАЗВИТИИ ЕГО РАБОТ ПО ЭВОЛЮЦИИ
СПУТНИКОВЫХ ОРБИТ
(к 80-летию со дня рождения)
М. А. Вашковъяк
Институт прикладной математики им. М. В. Келдыша РАН
В настоящем докладе представлены различные направления иссле-
дований, выполненных Лауреатом Ленинской премии, доктором физи-
ко-математических наук, профессором Михаилом Львовичем Лидовым
(1926-1993). Каждый из этапов его научного творчества мог бы стать
темой отдельного доклада. Здесь же более подробно описаны работы
по эволюции спутниковых орбит, которые в последние годы получили
как теоретическое, так и естественнонаучное развитие.
I
Михаил Львович Лидов родился в г. Черкассы Киевской обл. 4 ок-
тября 1926 г., и его юность пришлась на военное время. В 1944 г.
он ушел добровольцем на фронт, служил в действующей армии ма-
стером по авиационному вооружению и воевал до дня Победы. Домой
М. Л. Лидов вернулся только в 1951 году, заслужив боевые награды.
К этому времени он уже заочно учился на механико-математическом
факультете Московского Государственного университета, а в 1954 году
с блеском окончил его дневное отделение, получив диплом с отличием
по специальности «механика».
Научная деятельность М.Л. Лидова началась в 1954 году под ру-
ководством академика Леонида Ивановича Седова (1907-1999). После
окончания университета М. Л. Лидов поступил на работу в Между-
ведомственную комиссию по координации и контролю научно-техни-
ческих работ в области организации и осуществления межпланетных
474
Дополнение
сообщений при АН СССР. Практически сразу же он выполнил иссле-
дование специального класса решений уравнений газодинамики, что
позволило получить полную картину температурного режима искус-
ственного спутника Земли. Основы этого исследования были заложе-
ны, по-видимому, еще в студенческие годы, поскольку список научных
трудов М. Л. Лидова начинается статьей, опубликованной в Докладах
Академии наук в год окончания университета.
В 1957 году М.Л. Лидов начал работать в Отделении прикладной
математики Математического института им. В. А. Стеклова (так в то
время назывался наш институт) в отделе, возглавляемом академиком
Дмитрием Евгеньевичем Охоцимским (1921-2005). Именно Дмитрий
Евгеньевич инициировал многие работы М. Л. Лидова и, в особенно-
сти, работы по отечественной лунной программе.
Уже в 1958 году пионерские исследования М.Л. Лидова по опре-
делению плотности верхней атмосферы Земли из наблюдений за дви-
жением ее первых искусственных спутников и обнаруженный эффект
вариации параметров атмосферы принесли ему заслуженное признание
как ученых-теоретиков, так и специалистов-прикладников.
В последующие годы М. Л. Лидов стал одним из лидеров направле-
ния, связанного с теоретическими и прикладными задачами баллисти-
ческого проектирования и управления полетом космических аппаратов.
В 1960 году за большой цикл работ ему была присуждена Ленинская
премия, а в 1965 году по совокупности выполненных исследований —
ученая степень доктора физико-математических наук, причем без за-
щиты кандидатской диссертации, что и тогда являлось большой ред-
костью. Работы М. Л. Лидова, выполненные совместно с Д. Е. Охо-
цимским и Н. М. Тесленко и посвященные анализу класса траекторий
полета к Луне, а также разработанные им схемы управления были
непосредственно использованы при решении многих «лунных» задач.
Это облет Луны с фотографированием ее обратной стороны, мягкая
посадка на поверхность Луны, запуск первых искусственных спутников
Луны и доставка на Землю образцов лунного грунта. То были годы
вдохновенного труда, и Михаил Львович с присущей ему самоотвер-
женностью отдавал все свои силы и знания для успешного выполнения
поставленных задач. Он сам и руководимые им сотрудники работали
сутками без сна и неделями без отдыха, не считаясь с усталостью,
а порой и с нездоровьем. В 1970 году за выполнение работ по лунной
программе М. Л. Лидов был награжден орденом Трудового Красного
Знамени. А в 1985 году в год сорокалетия Победы он получил Орден
Отечественной войны второй степени. Это было признание боевых
заслуг М. Л. Лидова как участника Великой Отечественной войны.
М. Л. Лидову и его ученикам принадлежит большой цикл работ
по созданию численно-аналитических методов расчета движения ис-
кусственных небесных тел. Эти методы широко использовались при
проектировании орбит спутников «Электрон», «Прогноз», спутников
связи на геостационарных и высокоапогейных орбитах. Математиче-
О научной деятельности профессора М. Л. Лидова
475
ские модели, применяемые в этих высокоточных и быстродействующих
методах, учитывали весьма полную совокупность лунно-солнечных
возмущений, возмущений от нецентральности геопотенциала (а для
ИСЛ и масконов), влияние земной атмосферы, светового давления
и эффекта экранирования спутника Землей. Алгоритмы и программы
расчета движения геостационарных спутников были внедрены на мно-
гих предприятиях страны, в том числе в научно-прикладных институ-
тах Красноярска и Томска.
В 1964 году М. Л. Лидовым предложена постановка задачи о выборе
состава измеряемых параметров траектории в случае неполного знания
вероятностных характеристик ошибок измерений. Им была выявлена
математическая аналогия между некоторыми оптимальными задачами
коррекции траекторий и задачами выбора состава измерений. Это на-
правление нашло свое развитие в работах Б. Ц. Бахшияна, А. И. Ма-
тасова, Л. Ю. Белоусова и других.
Обширный цикл работ М. Л. Лидова и его сотрудников был посвя-
щен анализу орбит в окрестности коллинеарных точек либрации систем
Земля-Луна и Солнце-Земля и разработке методов стабилизации дви-
жения по таким орбитам с приложениями к перспективному в то время
проекту «Реликт-2». В эти работы весомый вклад внес А. П. Маркеев —
ныне профессор, известный ученый в области механики.
Другой большой цикл работ М. Л. Лидова посвящен выявлению
и практическому построению специальных классов траекторий огра-
ниченной задачи трех тел и исследованию устойчивости найденных
траекторий. На основе этих работ им, в частности, предложен вариант
устойчивой пространственной периодической орбиты для космическо-
го радиоинтерферометра. Она принадлежит семейству периодических
орбит, обнаруженному М. Л. Лидовым в ограниченной круговой за-
даче трех тел продолжением сильноэллиптической спутниковой орби-
ты в окрестности тела меньшей массы. Окончанием этого семейства
служит одна из плоских резонансных орбит в окрестности неустой-
чивой коллинеарной точки либрации. Практически одновременно аме-
риканский ученый Дж. Брэйкуэлл (J. V. Breakwell), не зная о работах
М.Л. Лидова, нашел данное семейство, пройдя по тому же пути,
но в обратном направлении. Одна из последних работ М. Л. Лидова
посвящена возможному использованию так называемых квазиспутни-
ковых орбит в проекте «Фобос» и для эксперимента по уточнению
гравитационной постоянной.
Помимо повседневной научно-производственной деятельности
М. Л. Лидов вел большую педагогическую работу в качестве профес-
сора кафедры теоретической механики МГУ, а позднее — на факуль-
тете повышения квалификации МИРЭА. В МГУ он вел семинар по
механике космического полета, читал спецкурс по эволюции орбит
и курс лекций по теоретической механике. Эти лекции усилиями
коллег и учеников М.Л. Лидова изданы в 2001 году отдельной книгой
в московском издательстве «Физматлит».
476
Дополнение
М. Л. Лидов был членом Национального комитета по теоретической
и прикладной механике. Его выступления на самых представительных
конференциях всегда были в центре внимания специалистов.
Много сил и времени М. Л. Лидов отдавал неформальной редак-
торской работе в академических научных журналах «Космические ис-
следования» и «Письма в Астрономический журнал». Он был научным
редактором раздела «Динамика полета» энциклопедии «Космонавти-
ка». В сентябре 1993 года еще при жизни М.Л. Лидова Между-
народный Астрономический Союз присвоил его имя малой планете,
зарегистрированной в международном каталоге под номером 4236.
Как написано в свидетельстве, малая планета 1979FV1 названа
в честь Михаила Львовича Лидова — небесного механика, извест-
ного своими работами в области астродинамики и астронавтики,
сотрудника Института прикладной математики имени Мстислава
Всеволодовича Келдыша Российской академии наук. М.Л. Лидову
посвящена и памятная страница на Интернет-сайте нашего Института
www. keldysh. ru/memory/lidov/.
В 2000 году в журнале «Вестник Российской Академии наук»,
т. 70, №6 в рубрике «Этюды об ученых» были опубликованы вос-
поминания о М. Л. Лидове его университетского сокурсника и кол-
леги член-корреспондента РАН Владимира Васильевича Белецкого.
В 2005 году вышла его автобиографическая книга «Шесть дюжин»,
в которой В. В. Белецкий также делится своими воспоминаниями
о М.Л. Лидове. В 2001 году в журнале «Космические исследования»,
т. 39, № 5 опубликованы воспоминания Лауреата Ленинской премии,
профессора Всеволода Александровича Егорова (1930-2001), многие
годы проработавшего с М. Л. Лидовым в одной комнате. К несчастью,
эта его публикация оказалась последней — В. А. Егоров погиб в том же
2001 году при трагических обстоятельствах.
М. Л. Лидов воспитал многих кандидатов и докторов наук. Под его
руководством в разные годы учились и работали известные сотрудники
ИПМ и других учреждений. А. А. Соловьев — ныне член-корреспон-
дент РАН, возглавляет Международный Институт теории прогноза
землетрясений и математической геофизики, А. И. Нейштадт — стал
профессором, крупным ученым в области динамических систем, нели-
нейной и хаотической механики. Его труды широко известны в нашей
стране и за рубежом. К косвенным ученикам М. Л. Лидова можно
с полным основанием отнести слушателей его лекций и, в особенности,
многочисленных специалистов, изучавших и использовавших в работе
его научные публикации. В 1992 году в Москву приезжала деле-
гация американских ученых-баллистиков. На семинаре в Институте
космических исследований РАН в числе других выступил Ч. Апхофф
(С. Uphoff), доклад которого назывался «Мой долг Лидову». В докладе,
посвященном использованию результатов М. Л. Лидова, были перечис-
лены пять космических проектов США, в разработке которых «анализ,
выполненный Лидовым, сыграл большую роль». Далее были указаны
О научной деятельности профессора М. Л. Лидова
477
еще 12 конкретных приложений этого анализа. В заключительном
разделе доклада, озаглавленном «Чему я научился у Лидова», Апхофф,
в частности, отметил, что «новый подход к старым проблемам может
привести к важным новым результатам».
Круг научных интересов М.Л. Лидова, постоянно расширяясь,
охватывал многие разделы математики и механики, астрономии и кос-
могонии, теории управления и дифференциальных игр. Если мысленно
экстраполировать возможную научную деятельность Михаила Льво-
вича за ту роковую дату 30 декабря 1993 года, то ясно ощущается
вся трагичность его безвременной кончины в расцвете творческих сил,
планов и устремлений.
II
Во второй части более подробно изложены работы М. Л. Лидова,
связанные с исследованием эволюции спутниковых орбит. В 1961 году
им фактически было положено начало новому направлению небес-
ной механики — исследованию эволюции орбит искусственных и есте-
ственных небесных тел. Созданные М. Л. Лидовым методы позволяли
с высокой точностью вычислять параметры орбит ИСЗ, изменяющихся
под действием гравитационных возмущений. Его основополагающая
статья 1961 года в сб. «Искусственные спутники Земли» была прак-
тически сразу же воспроизведена по-английски в двух иностранных
журналах космической тематики — Planetary Space Sciences и AIAA
Journal. В данной работе М.Л. Лидов получил и качественно новые
результаты по эволюции спутниковых орбит различных классов на
основе упрощенной интегрируемой задачи.
Упрощенная задача — это так называемая двукратно осредненная
задача Хилла, описывающая в первом приближении эволюцию спут-
никовой орбиты под действием вековых возмущений от достаточно
удаленной притягивающей точки. Осреднение в этой задаче проводит-
ся независимым образом по всем наиболее быстрым переменным —
средним аномалиям спутника и внешней точки. Если два первых ин-
теграла этой задачи а — cq и (1 — e2)cos2z = cj, были известны ранее
из работ профессора Николая Дмитриевича Моисеева (1902-1955),
то полученный М. Л. Лидовым в явном виде дополнительный интеграл
е2 (2/5 — sin2 i sin2 щ) — позволил свести проблему к исследованию
поведения фазовых траекторий в плоскости (аргумент перицентра со —
эксцентриситет е) в зависимости от С2 при фиксированном значении щ
и к вычислению квадратуры для изменения долготы восходящего уз-
ла Q. Во всех приводимых формулах использованы стандартные обо-
значения для кеплеровских элементов орбиты спутника, в частности,
а — большая полуось спутниковой орбиты, i — ее наклонение к плос-
кости движения возмущающей точки.
478
Дополнение
Выполненный М. Л. Лидовым качественный анализ семейств фа-
зовых траекторий привел к интереснейшим небесно-механическим ре-
зультатам (см. рис. 1).
е-т ~ 1 cj /2
Рис. 1. Качественное поведение фазовых траекторий двукратно осредненной
задачи Хилла в плоскости (си, е) в зависимости от С2 для различных значе-
ний С1.
1) Существование в осредненной задаче орбит с неизменными экс-
центриситетом и аргументом перицентра при ci < 3/5 или особой точки
типа центр в плоскости (щ, е) (lj* = ±тг/2,е*2 = 1 — (Sci/З)1/2). Эта
особая точка и либрационное изменение аргумента перицентра в ее
окрестности в зарубежной литературе называется «резонансом Козаи»
по имени японского ученого Y. Kozai, исследовавшего несколько более
общий (астероидный) случай задачи, но годом позже. К сожалению,
качественное исследование, выполненное М.Л. Лидовым в 1961 году,
получило известность за рубежом только после 1963 года, когда он
представил свой доклад на Международный симпозиум в Париже. По-
скольку в «астероидном» случае качественные особенности, выявлен-
ные М. Л. Лидовым, сохраняются, было бы справедливым, как предло-
жил А. И. Нейштадт, использовать название «резонанс Лидова-Козаи».
О научной деятельности профессора М. Л. Лидова
479
2) В частном случае с\ = 0, когда орбита спутника ортогональна
плоскости орбиты возмущающей точки, эволюция в конечном счете
приводит к ее превращению в прямолинейный отрезок (е 1). Для
малых значений с\ эволюция орбиты при любых начальных значениях
со и е приводит к такому увеличению эксцентриситета, что в силу
постоянства а расстояние перицентра q = а(1 — е) становится равным
радиусу планеты uq, и спутник падает на ее поверхность. Это теорема
М.Л. Лидова, предлагаемая ниже в формулировке автора доклада.
Теорема Лидова. Если постоянные интегралов двукратно
осредненной задачи Хилла cq и ci удовлетворяют условию
. 12 / а0 \ 2 /1 ао А2
с\ — — 1 — — , где ад — радиус центральной планеты,
5 \со / \ 2со/
то при С2 0 найдется такой конечный момент времени t, что
расстояние перицентра орбиты спутника q(i) = а0.
На рис. 2 можно проследить деформацию интегральных поверхно-
стей С2(щ, е) при изменении с\. На достаточно гладкой поверхности
(ci = 0,95) вначале возникают особенности (ci = 0,6), затем углуб-
ления (ci = 0,05) и «сливы» (ci = 0), по которым фазовый поток
Рис. 2. Интегральные поверхности С2(е,о>) — (левый столбец) и их сечения
е(и) — (правый столбец) для ci = 0,95; 0,6; 0,05; 0 (значения с\ уменьшаются
сверху вниз)
480
Дополнение
«сливается» на границу области (е — 1). В правом столбце показаны
интегральные кривые — сечения поверхностей плоскостями с% = const.
Яркой иллюстрацией выявленной М.Л. Лидовым закономер-
ности служит проведенный им
Рис. 3. Дружеский шарж И. В. Но-
вожилова «Лидов роняет Луну
на Землю»
расчет эволюции лунной орбиты,
гипотетически повернутой перпен-
дикулярно плоскости эклиптики.
Оказалось, что такая «ортогональ-
ная Луна», возмущаемая притяже-
нием Солнца, свалилась бы на Зем-
лю всего через четыре с половиной
года!!! Как эмоционально пишет
в своих воспоминаниях В. В. Бе-
лецкий, «Мне до сих пор хочется
и смеяться, и плакать от восторга,
когда я вспоминаю этот результат».
По его словам, даже академик Вла-
димир Игоревич Арнольд вначале
воспринял результат М. Л. Лидова
с сомнением, но потом, безуслов-
но, признал. А профессор МГУ
И. В. Новожилов (1930-2005) уве-
ковечил Лидова дружеским шар-
жем. Приведенный на рис. 3, он
заимствован из книги В. В. Белец-
кого «Очерки о движении космиче-
ских тел».
Установив удивительное свойство почти ортогональных спутнико-
вых орбит, Михаил Львович (по его собственному рассказу) тотчас же
обратился к астрономическим справочникам. И сразу обнаружил про-
тиворечащий пример в виде спокойно существующих спутников Урана,
почти круговые и почти экваториальные орбиты которых наклонены
к плоскости эклиптики (или ураноцентрической орбите возмущающего
тела — Солнца) примерно на 98°. Анализ реальной физической модели,
учитывающей сжатие Урана (наряду с менее значительными солнечны-
ми возмущениями), с одной стороны, разрешил противоречие, допустив
существование почти круговых ортогональных орбит, а с другой -
привел к постановке новой небесно-механической проблемы — двукрат-
но осредненной задачи Хилла с учетом сжатия центральной планеты.
Для ее анализа существенными являются два параметра: 7, харак-
теризующий отношение возмущающих ускорений от сжатия планеты
и возмущений от внешней точки, и в — угол наклона экваториальной
плоскости планеты к плоскости орбиты возмущающей точки. В общем
случае рассматриваемая задача уже не допускает трех первых интегра-
лов в инволюции. При произвольном е нарушается осевая симметрия
задачи и, как следствие, «пропадает» интеграл с\. Интеграл услож-
няется и представляет собой двукратно осредненную возмущающую
О научной деятельности профессора М. Л. Лидова
481
функцию задачи, зависящую от всех элементов спутниковой орбиты.
И лишь интеграл cq по-прежнему свидетельствует о неизменности
ее большой полуоси. Тем не менее, задача имеет ряд интегрируе-
мых случаев и частных решений, выявленных в работе М.Л. Лидова
и М. С. Ярской 1974 г. Наиболее содержателен из них компланарный
случай, когда указанные плоскости совпадают. Поскольку при е = О
восстанавливается осевая симметрия и интеграл с\, то в этом случае
оказалось возможным выполнить полное качественное исследование
задачи, выявившее богатое разнообразие структур интегральных кри-
вых.
В 1974-1977 гг. М.Л. Лидовым совместно с С.Л. Зиглиным было
выполнено исследование двукратно осредненной ограниченной задачи
трех тел для равномерно близких орбит возмущающего и возмущае-
мого тел (этот случай традиционно труден для теории возмущений),
а также двукратно осредненной общей задачи трех тел конечных масс.
В последнем случае выявлено существование критического эксцентри-
ситета орбит двух близких тел, при котором теряется устойчивость
изначально плоского движения трех тел.
Несколько необычной для тематики М.Л. Лидова явилась его
совместная с А. И. Нейштадтом работа, связанная с вращательным
движением небесных тел. Метод канонических преобразований, приме-
ненный для анализа резонансных закономерностей вращения, позволил
интерпретировать лунные законы Кассини как свойства асимптоти-
чески устойчивого стационарного решения эволюционных уравнений
с учетом приливной диссипации энергии. Эта работа дополнила и уточ-
нила выполненное В. В. Белецким двумя годами ранее (с помощью
метода осреднения) исследование проблемы Кассини без учета дисси-
пации.
III
В третьей части кратко описаны исследования, выполненные в по-
следние 10-12 лет и связанные с развитием работ М.Л. Лидова.
В исследованиях неинтегрируемой двукратно осредненной задачи
Хилла с учетом сжатия центральной планеты, выполненных в 1996—
1998 гг., было установлено свойство инвариантности эволюционной
системы относительно преобразования t — —t, е — е, г = i, со — —и,
Q = —Q, выявлены и построены (в основном, численным способом)
семейства ее периодических решений. Эти решения соответствуют так
называемым периодически эволюционирующим спутниковым орбитам,
для которых изменение всех четырех элементов е, г, cj, П происходит
с одним и тем же периодом. Более подробное представление о семей-
ствах этих орбит и об их устойчивости можно получить из наших
публикаций, в том числе и совместных с Н. М. Тесленко, в «Письмах
в Астрономический журнал».
16 М.Л. Лидов
482
Дополнение
Далее представлено естественнонаучное развитие работ М.Л. Ли-
дова, касающееся эволюции орбит новых далеких спутников планет-
гигантов. Начиная с конца 1997 г. и по настоящее время, с помощью
наземных наблюдений зарубежными учеными были открыты десятки
далеких спутников Юпитера и Сатурна, девять спутников Урана и пять
спутников Нептуна. Они представляют собой тела относительно малых
размеров порядка 2-120 км, движущиеся в тех областях околопланет-
ного пространства, где влияние солнечных возмущений на их орбиты
на несколько порядков превосходит влияние сжатия центральной пла-
неты (7 < 1). Новые спутники относятся к классу так называемых
внешних спутников, движущихся по нерегулярным орбитам с больши-
ми эксцентриситетами и наклонениями, а для анализа их эволюции
в первом приближении можно, полагая 7 = 0, использовать двукратно
осредненную задачу Хилла.
Качественное исследование этой задачи, выполненное М. Л. Ли-
довым, было дополнено построением ее общего решения, зависящего
от четырех произвольных постоянных — начальных элементов спутни-
ковой орбиты во, го, отнесенных к плоскости орбиты воз-
мущающего тела. Для вычисления зависимости от времени долготы
восходящего узла Q получено явное аналитическое выражение в ви-
де полных и неполных эллиптических интегралов 1-го и 3-го родов.
Исходными данными для исследования долгопериодической эволюции
новых далеких спутниковых орбит послужили эклиптические плането-
центрические элементы, приведенные в Циркулярах Международного
Астрономического Союза и доступные пользователям Интернета. Си-
стемы элементов этих орбит в настоящее время уточняются и, по-
видимому, будут уточняться в дальнейшем.
В цикле наших работ 1999-2005 гг., опубликованных в «Письмах
в Астрономический журнал», на основе построенного общего решения
двукратно осредненной задачи Хилла, а также созданного численно-
аналитического метода выявлены качественные особенности эволюции
новых спутниковых орбит, предложена их простейшая классификация
и определены приближенные количественные характеристики эволю-
ции. К ним относятся экстремальные значения эксцентриситетов и на-
клонений, периоды циркуляции аргументов перицентров и долгот вос-
ходящих узлов. В рамках используемой модели двукратно осредненной
задачи Хилла для ряда новых спутников планет-гигантов обнаружен
либрационный характер изменения аргументов перицентров их орбит,
т. е. резонанс Лидова-Козаи. Отмеченное свойство весьма редко встре-
чается даже у многотысячного ансамбля астероидных орбит, поэтому
тот факт, что среди десятков орбит недавно открытых далеких спут-
ников оказалось около десяти либрационных, достаточно удивителен.
В качестве иллюстрации на рис. 4 в плоскости (аргумент перицен-
тра — эксцентриситет) сплошной кривой показана траектория двукрат-
но осредненной задачи Хилла, штриховой — сепаратриса, крестиками
даны результаты расчета с помощью численно-аналитического метода,
О научной деятельности профессора М. Л. Лидова
483
Рис. 4. Фазовая плоскость (и,е) для спутника Сатурна S24 (Кивиок): 1 —
численно-аналитическое решение; 2 — аналитическое решение; 3 — сепаратриса
а жирной точкой отмечено современное положение орбиты одного из
далеких спутников Сатурна S24 (Кивиок). Аналогичная картина имеет
место и для спутников: Сатурна —S22 (Иджирак), Юпитера —J46
(Карпо), Урана —U23 (Маргарита), Нептуна —Nil (Cao), N13 (Несо).
Следует заметить, однако, что фазовые траектории некоторых спут-
ников в плоскости (и, е) расположены хотя и внутри либрационных
зон, но очень близко к сепаратрисам (сг = 0). Поэтому в действи-
тельности изменение аргументов перицентров их орбит могло ока-
заться циркуляционным при незначительном уточнении как элементов
спутниковых орбит, так и модели эволюции. Произошедший подобный
«переход» двух орбит спутников Сатурна S20 (Палиак) и S29 (Сиар-
нак) выявил необходимость уточнения двукратно осредненной модели
при значениях С2, близких к нулю. На рис. 5 современное положение
орбиты спутника S20 (Палиак) настолько близко к сепаратрисе, что
в более полной модели эволюции (по сравнению с двукратно осред-
ненной задачей Хилла) эволюция аргумента перицентра оказывается
циркуляционной, а не либрационной.
Немного отвлекаясь от новых естественных спутников планет, от-
метим недавно выполненное В. И. Прохоренко (ПКИ РАН) геометри-
ческое исследование двукратно осредненной задачи Хилла для нагляд-
ного представления интегральных многообразий и их сечений. Основ-
ное приложение этого исследования связано с анализом возможности
падения высокоапогейных ИСЗ на поверхность Земли и с оценкой
их «времени жизни».
16*
484
Дополнение
Другим необычным феноменом в спутниковых системах планет-
гигантов является распределение спутников по большим полуосям их
орбит. Если в системе Юпитера внешние спутники явно разделяются
на две группы прямых и обратных, то в системах остальных планет-
гигантов имеются диапазоны больших полуосей, в которых существуют
и прямые, и обратные орбиты. Кроме того, во всех системах существу-
ют диапазоны больших полуосей, свободные от спутниковых орбит.
В системе Урана подобная «пустота», разделяющая внутренние и внеш-
ние спутники, простирается примерно от 600 тыс. км. до 4 млн. км.,
где возмущающее влияние Солнца и сжатия центральной планеты
сравнимо по величине. Качественный анализ одного из выявленных
М.Л. Лидовым интегрируемых случаев двукратно осредненной задачи
Хилла с учетом сжатия планеты (е = 90°, I = 90°) позволяет пред-
ложить в качестве гипотезы небесно-механическое объяснение отсут-
ствия экваториальных спутников Урана в области а > 1,3 млн. км.
Если бы в указанной области существовали спутники, то с течением
времени в результате эволюции их орбиты начали бы пересекаться
с орбитами внутренних спутников. На рис. 6 показано семейство ин-
тегральных кривых для «промежуточного» значения большой полуоси
орбиты гипотетического почти экваториального спутника Урана. Для
любых начальных значений со и е эксцентриситет становится очень
близким к единице за сравнительно небольшое (по космогоническим
меркам) время.
При этом существенно повышается вероятность тесных сближений
и соударений с внутренними спутниками, так что они должны бы-
О научной деятельности профессора М. Л. Лидова
485
Рис. 6. Семейство фазовых траекторий в плоскости (ш,е) для 7 = 0,1
(а = 1,884 млн. км); Тс и 7} — соответственно периоды циркуляции и либрации
аргумента перицентра
ли либо уйти на более далекие орбиты, либо упасть на внутренние
спутники, существенно пополнив их массы. Косвенным подтверждени-
ем этому служит заметная массивность внутренних спутников Урана
по сравнению с внешними. Конечно, гипотетические экваториальные
спутники могли упасть и на поверхность самого Урана, однако такая
возможность реализуется лишь для а > 3 млн. км. Естественная в эво-
люционной задаче аппроксимация орбит внутренних спутников мате-
а, млн. км.
Рис. 7. Зависимости расстояний перицентров орбит гипотетических спутников
Урана от большой полуоси (штриховыми линиями показаны радиус Урана
и радиусы орбит его наиболее крупных внутренних спутников)
486
Основные научные труды М. Л. Лидова
риальными гауссовыми кольцами позволяет уменьшить это граничное
значение до 1,3 млн. км. (см. рис. 7). Расчеты эволюции орбит гипоте-
тических спутников, проведенные в более полной физической модели,
учитывающей отличие реального значения е от 90° и медленное из-
менение элементов орбиты самого Урана, подтверждают высказанную
гипотезу.
В заключение хочется подчеркнуть, что выполненные исследования
эволюции орбит далеких спутников планет-гигантов имеют под собой
мощный фундамент, заложенный М. Л. Лидовым еще сорок пять лет
назад. Сегодня в этот памятный день мне хотелось бы еще раз от-
метить неоценимый вклад, внесенный Михаилом Львовичем Лидовым
как в прикладные работы по баллистическому проектированию и осу-
ществлению космических полетов, так и в теоретические исследования
фундаментальных небесно-механических проблем. Хочется надеяться,
что замечательные методы и результаты, полученные этим выдающим-
ся ученым, найдут свое дальнейшее продолжение и развитие.
Томск, 4 октября 2006 г.
Основные научные труды М. Л. Лидова
1. Точные решения уравнений одномерных неустановившихся движений газа
с учетом сил ньютоновского тяготения // ДАН СССР. — 1954. — Т. 47,
№3. — С.409.
2. Конечный интеграл уравнений одномерных автомодельных адиабатических
движений газа // ДАН СССР. — 1955 — Т. 103, № 1 — С. 35.
3. К теории линеаризованных решений около одномерных автомодельных
движений газа // ДАН СССР. — 1955 —Т. 102, №6 —С. 106.
4. К теории неустановившихся движений газа с учетом сил тяготения //
ПММ АН СССР. - 1955 — Т. 19, №5-С. 541.
5. Автомодельное движение газа со сферической симметрией в поле гравити-
рующего центра // Астрономии, журн. — 1957. — Т. 34, №4. — С. 603.
6. Сопротивление неориентированного тела при движении в разреженном
газе // Изв. АН СССР сер. Геофизическая. — 1957. — № 12. — С. 1524.
7. О температурном режиме искусственного спутника Земли // Изв. АН
СССР сер. геофизическая. — 1957. — №4. — С. 527 (совместно с Карпен-
ко А. Г.)
8. Определение плотности атмосферы по наблюдаемому торможению первых
искусственных спутников Земли // Искусств, спутники Земли. — 1958.—
№1. —С.9
9. Эволюция орбит искусственных спутников планет под действием гравита-
ционных возмущений внешних тел // Искусственные спутники Земли. —
1961. — №8. — С. 5. Английские переводы: 1. The Evolution of Orbits of
Artificial Satellites of Planets under the Action of Gravitational Perturba-
tions of External Bodies // Planet. Space Sci. — 1962. — Vol. 9. — P. 719-759,
2. Evolution of the Orbits of Arificial Satellites of Planets as Affected by
Gravitational Perturbations from External Bodies 11 AIAA Journal. — 1963. —
Vol. 1.-M8.-P. 1985-2002.
Основные научные труды М. Л. Лидова
487
10. On the approximated analysis of the orbit evolution of artificial satellites //
Dynamics of satellites. — Berlin: Springer Verlag. — 1963. — P. 168.
11. О приближенном анализе эволюции орбит искусственных спутников.
// Проблемы движения искусственных небесных тел. — М.: Изд. АН
СССР. - 1963.-С. 119.
12. Исследование одного класса траекторий ограниченной задачи трех тел.
// Космич. исслед. — 1964. — Т. 2, №6. — С. 843 (совместно с Охоцимским
Д. Е. и Тесленко Н.М.).
13. К априорным оценкам точности определения параметров по методу наи-
меньших квадратов // Космич. исслед. — 1964. — Т. 2, № 5. — С. 713.
14. Вековые эффекты эволюции орбит под влиянием светового давления //
Космич. исслед. — 1969. — Т. 7, № 4. — С. 467.
15. Математическая аналогия между некоторыми задачами коррекции траекто-
рий и выбора состава измерений // Космич. исслед. — 1971. —Т.9, №5.—
С. 687.
16. Об эволюции орбиты стационарного ИСЗ // Космич. исслед. — 1973.—
Т. И, №3. — С. 347 (совместно с Вашковьяком М.А.).
17. Интегрируемые случаи в задаче об эволюции орбит спутников при совмест-
ном влиянии внешнего тела и нецентральности поля планеты // Космич.
исслед. — 1974. — Т. 12. — No 2. — С. 155 (совместно с Ярской М. В.).
18. Влияние масконов на прогнозирование движения ИСЛ // Космич. ис-
след. — 1974. — Т. 12, №4.— С. 491 (совместно с Гордеевой Ю. Ф.).
19. The analysis of restricted circular twice — averaged three body problem in the
case of close orbit // Celestial mechanics. — 1974. — №9. —P. 151 (together
with Ziglin S. L.)
20. Полуаналитический метод расчета движения искусственного спутника Лу-
ны // Космич. исслед. — 1975. — Т. 13, № 3. — С. 283 (совместно с Ляховой
В. А. и Соловьевым А. А.).
21. Метод канонических преобразований в задачах о вращении небесных тел
и законы Кассини // Определение движения космических аппаратов. — М.:
Наука, 1975. — С. 74 (совместно с Нейштадтом А. И.).
22. Полуаналитический метод расчета движения КА в окрестности коллине-
арной точки либрации // Космич. исслед. — 1976. — Т. 14, №6.— С. 909
(совместно с Вашковьяком М. А. и Маркеевым А.П.).
23. Non-restricted double-averaged three body problem in Hill’s case // Celestial
mechanics. — 1976. — № 13. — P. 471 (together with Ziglin S. L.).
24. Случай Хилла осредненной задачи трех тел и устойчивость плоских орбит
// ПММ. — 1977. — Т. 41. — №2. — С. 234 (совместно с Зиглиным С. Л.).
25. Об одном семействе пространственных периодических орбит около Луны
и планет Ц ДАН СССР. - 1977. - Т. 223. - №6. - С. 1068.
26. Метод учета влияния сил светового давления при полуаналитическом
расчете движения спутников // Математическое обеспечение космич. экс-
периментов. М.: Наука, 1978.— С. 149 (совместно с Ивановой Е.Я.).
27. Полуаналитические методы расчета движения спутников // Труды Ин-та
теор. астрон. — 1978. — № 17. — С. 54.
28. Численные исследования некоторых классов траекторий ограниченной за-
дачи трех тел // Труды объединенных научных чтений по космонавтике. —
М., 1979.— С. 142 (совместно с Вашковьяком М.А.).
488
Основные научные труды М. Л. Лидова
29. Исследование семейств пространственных периодических орбит задачи
трех тел // Космич. исслед. — 1979. — Т. 17, №3. — С. 323 (совместно с Ра-
биновичем В. Ю.).
30. Увеличение размерности гамильтоновых систем, ^-преобразование,
использование частных интегралов // Космич. исслед. — 1982. — Т. 20,
№2.— С. 163.
31. Метод построения пространственных периодических орбит в задаче Хилла
// Космич. исслед. — 1982. — Т. 20, № 6. — С. 787.
32. Семейства пространственных периодических орбит задачи Хилла и их
устойчивость // Космич. исслед. — 1983. — Т. 21. — № 1. — С. 3 (совместно
с Ляховой В. А.).
33. Минимаксная задача оценивания параметров траектории в непрерывной
постановке // Космич. исслед. — 1984 — Т. 22. — № 4. — С. 483.
34. Построение семейств пространственных периодических орбит задачи трех
тел с помощью KS- преобразований // Труды 10-й Международной конфе-
ренции по нелинейным колебаниям. — Варна, 1984.— С. 344.
35. Одноимпульсный перелет на условно-периодическую орбиту в окрестности
точки L<2. системы Земля-Солнце и смежные задачи // Космич. исслед. —
1987.— Т. 25, №2.— С. 163 (совместно с Ляховой В. А. и Тесленко Н.М.).
36. Об одном варианте орбиты для околоземного радиоинтерферометра //
Письма в АЖ. — 1988. — Т. 14, №9. — С. 851 (совместно с Ляховой В. А.).
37. Траектории полета Земля- Луна- гало-орбита в окрестности точки L<z
системы Земля-Солнце // Космич. исслед. — 1992. — Т. 30, №4.— С. 435
(совместно с Ляховой В. А. и Тесленко Н.М.)
38. Теория возмущений и анализ эволюции квази-спутниковых орбит в огра-
ниченной задаче трех тел // Космич. исслед. — 1993. —Т. 31, №2. —С. 75
(совместно с Вашковьяком М.А.).
39. О квазиспутниковых орбитах для эксперимента по уточнению гравитаци-
онной постоянной // Письма в АЖ. — 1994. — Т. 20, № 3. — С. 1 (совместно
с Вашковьяком М. А.).
40. Аналитический метод расчета движения по гало-орбите и проблема экра-
нирования КА от солнечной радиации в проекте “Реликт-2” // Космич.
исслед. — 1994. — Т. 32, № 1. — С. 3 (совместно с Вашковьяком М. А. и Ля-
ховой В. А.).
41. О квазиспутниковых орбитах в ограниченной эллиптической задаче трех
тел // Письма в АЖ. — 1994. — Т. 20. — № 10. — С. 1 (совместно с Вашко-
вьяком М. А.).
42. Курс лекций по теоретической механике. — М.: ФИЗМАТЛИТ, 2001. —
478 с. (Издание при поддержке РФФИ, проект 00-01-14056д).
предметный указатель
Амплитуда колебания 252
Аналог уравнения Даламбера-Лаг-
ранжа 214
Аномалия истинная 276
- эксцентрическая 277
Апоцентр орбиты 276
Аппеля уравнения 217
Аргумент широты перицентра 276
— точки 276
Базис симплектический 305
Билинейность 304
Вектор 22
- виртуальный 110
-импульса 14, 126
-количества движения 14, 126
- координатный 23
- обобщенной силы 209
- обобщенных реакций связей 216
- скорости 14
- сопряженный 306
- угловой скорости 87
- ускорения 14
Вектор-функция допустимая 194
Векторы касательные 113
- косоортогональные 306
Вес тела 284
Взаимодействие абсолютно неупру-
гое 158
— упругое 157
- парное 15
Вращение вертикальное 407
- твердого тела 387
Время 41
- всемирное 413
- эфемеридное 413
Галилея принцип относительности 32
Гамильтона принцип вариационный
190
- функция 296
Гамильтона-Якоби уравнения 328
Гамильтониан 296
Гипербола 276
Гироскоп 410
Градиент потенциала 211
Группа 311
- вращений трехмерная 84
- мультипликативная 84
Гюйгенса-Штейнера теорема 175
Даламбера-Лагранжа принцип 1
193
Движение виртуальное 110, 119
- двумерное 40
-действительное 119
- короткопериодическое 381
- маятника вращательное 252
- мгновенно винтовое 95
— вращательное 93
— поступательное 93
- одномерное 40
- относительное 179, 372
- плоское 40
-реактивное 165
- твердого тела 81, 372
- точки 86
- центра масс ракеты 167
Действие 153
- по Гамильтону 198
Диада 75
Диффеоморфизм 311
- канонический 329
- симплектический 303
— стандартный 314
Долгота восходящего узла 272
Донкина теорема 298
Единица симплектическая 297
Задача возмущенная 350, 359
- вырожденная 359
- двух тел 47, 269
- динамика обратная 53
— прямая 53
490
Предметный указатель
- интегрируемая 222, 341
- невозмущенная 470
- о бильярде 165
Закон всемирного тяготения 45
- гравитационного взаимодействия
45
- природы общий 151
- сохранения энергии 168
Законы механики основные 34
Зона либрационная 252
- ротационная 252
Изоморфизм пространства 308
Изотропность пространства 30
Импульсы системы обобщенные 295
Инволюция 363
Инерция тела 42
Интеграл неполный эллиптический
255
- полный 336
— эллиптический 255
- энергии 226, 250
Интегралы независимые 235, 364
Интервал времени 13
Исчисление вариационное 190
Квазикоординаты 220
Квазискорости 220
Кеплера законы 279
- уравнение 277
Кёнига репер 142
- теорема 146
Ковалевской случай 389
Ковариантность 225
Колебание системы собственное 438
Количество относительного движе-
ния 142
Координаты вектора 22
- криволинейные 202
- лагранжевы 201
- нормальные 438
-обобщенные 198
- сферические 259
- фазовые 38
- циклические 236
- цилиндрические 246
Корни характеристические 386
Кососимметричность 304
Коши-Буняковского неравенство
174
Кривая виртуальная 110
- гладкая 261
- опорная 194
Кривые интегральные 250
- либрационного типа 394
- периодические 359
- ротационного типа 395
Кулона закон 270
Лагранжа случай 389
- теорема 440
- уравнения 215
- функция 223
Лагранжиан 258
Лежандра преобразование 299
Леннарда-Джонса потенциал 271
Линеаризация системы 384
Линия узлов 84
Лиувилля системы 350
- теорема 351
Ляпунова функция 430
Масса тела 42
- элементарная 61
Масштабы 44
Матрица гамильтонова 451
- кососимметрическая 74
- поворота 25
- решений фундаментальная 455
- симметрическая 281
- симплектическая 315
- угловой скорости 87
Маятник математический 246
- сферический 259
- физический 250
Мера инерции тела 42
- по Жордану 359
Механика квантовая 55
Многообразие гладкое 110
- инвариантное 371
Модуль эллиптического интеграла
255
Момент активных сил 144
- времени 13
- инерции системы 173
----центральный 173
- кинетический 130
- количества движения 130, 144
----абсолютный 145
Наклонение орбиты 272
Невесомость 73, 292
Предметный указатель
491
Неустойчивость положения равнове-
сия 385
- решения 384
Нётер теорема 236
Область устойчивости 427
Однородность пространства 30
Окружность большого круга 383
Орбита круговая 275
Орты 22
Оси инерции системы главные 177
- системы главные центральные 177
Осциллятор линейный 256, 342
Ось вращения мгновенная 93
— твердого тела 93
- времени 109
Отображение взаимно однозначное
311
-допустимое 196
- за период 457
- устойчивое в будущем 457
Отображения эквивалентные 199
Парабола 276
Параметр орбиты 276
Перегрузка 292
Переменные "действие-угол" 350
- канонические 297
- сопряженные 297
- фазовые 262
Перемещение виртуальное 113
- репера поступательное 27
-элементарное 135
Перенос репера параллельный 27
Перестановка симплектическая 320
Период вращения маятника 257
- колебания маятника 255
- обращения 277
Перицентр орбиты 276
Плотность распределения массы 60
Площади ориентированные 308
Поверхность, идеально шероховатая
123
- вращения 263
Поворот 25
- простой 83
Подвес карданов 410
Подпространство 39
Поле сил однородное 418
Полином возвратный 452
Положение равновесия 384
— устойчивое 243
Полуось орбиты большая 276
Портрет фазовый 263
Постоянная гравитационная 46
- энергии 373
Потенциал 57
- системы обобщенный 228
- тела гравитационный 63
Предел высший бесконечно малый
429
Преобразование единичное 25
- несобственное 25
- неустойчивое 431
- поворота 25
- сильно устойчивое 454
- симплектическое 308
- собственное 25
- тождественное 25
- устойчивое 453
Преобразование автономное 329
- каноническое 303, 330
Прецессия 392
Принцип детерминированности 33
Притяжение гравитационное 70
Произведение векторное 78, 130
- кососкалярное 304
- смешанное 78
Производная функции 465
Пространство абсолютное 13
- арифметическое 307
- векторное четномерное 304
- касательное 113, 203
- конфигурационное 38
- координатное 308
- симплектическое 304
- фазовое 38, 263
— расширенное 39, 263
Противодействие 153
Псевдовектор 77
Пуансо интерпретация 378
Пуассона скобка 360
- теорема 363
Работа элементарная 116, 135
Радиус Земли характерный 48
— экваториальный 65
Радиус-вектор 13, 20
Разделение переменных 351
Размерности физических величин 43
492
Предметный указатель
"Растяжение” 330
Раусса-Гурвица теорема 426
Реакции связей обобщенные 216
Резонанс параметрический 463
Релея теорема 445
Репер абсолютный 41
- инерциальный 41
- координатный 22
- ортонормированный 22
Реперы одинаково ориентированные
25
Решение асимптотически устойчивое
415
- неустойчивое 415
- равномерно устойчивое 415
- устойчивое 414
Связи 81
- внешние 148
-внутренние 148
-голономные 108
-идеальные 116
- линейные 115
-негладкие 131
- неголономные 108
-независимые 108
-"неидеальные" 123
- неудерживающие 113
-удерживающие 106
Сепаратриса 252
Сила 15
- гравитационная 73
- инерции 283
— кориолисова 283
— переносная 283
— центробежная 283
- реакции связи 114
- результирующая 18
-трения 151
- центральная 269
Силы активные 115
- внешние 17, 131
- внутренние 17
- гироскопические 227
- диссипативные 227
-идеальные 116
- инерции 190, 283
- обобщенные 200
- парного взаимодействия 45
- реакций связей 115
- упругие 46
Система замкнутая 18
- консервативная 59, 140
- координат инерциальная 27, 86
- линеаризованная 415
- натуральная 224
- незамкнутая 16
- потенциальная 59
- расширенная 334
- свободная 113
- Солнечная 47
- уравнений автономная 301
— обобщенно-консервативная 301
Скорости системы обобщенные 205
Скорость абсолютная 97
-истечения 169
-кажущаяся 170
- относительная 97
- переносная 97
- предельная 169
- секториальная 273
- угловая мгновенная 92
След матрицы 26
Составляющая сил потенциала 225
Состояние системы 32
Соударение абсолютно неупругое
158
— упругое 157
Сумма площадей взвешенная 135
Тела протяженные 60
Тело, быстро закрученное 405
-свободное 179
- с закрепленной точкой 183
- твердое 80, 372
— тяжелое 373
Тензор инерции 172
Теорема о преобразовании Лежандра
298
- площадей 134
Теория притяжения 60
Точка материальная 14, 43
- особая типа седла 244
----центра 243
Траектория движения 13
— в конфигурационном простран-
стве 38
- фазовая 38, 124
"Трение сухое" 124
Треугольник сферический 383
Предметный указатель
493
Тяга двигателя 167
Тяжесть искусственная 292
Угол вращения 84
- нутации 84
- прецессии 84
Удар абсолютно упругий 162
Уравнение механики основное 124
- характеристическое 417
Уравнения в вариациях 415
-движения 15
— в форме Аппеля 199
-----Гамильтона 295
-----Лагранжа 199
- Лагранжа второго рода 215
- относительного движения 52
- связей 106
Ускорение абсолютное 86
- вращательное 95
- гравитационное 67
- кориолисово 97
- осестремительное 95
- относительное 97
- переносное 97
- поступательное 95
-реактивное 167
Ускорения обобщенные 215
Устойчивость асимптотическая 407
- вертикального движения 407
- движения 414
- равномерная 415
- решений 414
Условия интегрируемости 316
Фуко маятник 289
Функция билинейная 325
- возмущающая 470
- знакоотрицательная 428
- знакоположительная 428
- постоянная 428
- линейная однородная 227
- непрерывно дифференцируемая
441
- отрицательно-определенная 428
- положительно-определенная 428
- производящая 315
Характеристики движения геометри-
ческие 378
Центр масс системы 20
Циолковского формула 168
Частота собственная 438
Частоты независимые 358
Четаева теорема 432
- функция 433
Числа характеристические 417
Шарнир 183
Шары соприкасающиеся 70
Широта географическая 286
- места астрономическая 286
Штейнера теорема 175
Эйлера-Пуансо случай 372
- углы 82
- уравнения 184
- уравнения кинематические 102
Экстремаль функционала 224
Эксцентриситет орбиты 276
Эллипс 276
Эллипсоид вращения 265
- инерции 377
Энергия системы кинетическая 137
— механическая 226
— полная 140, 158
Эффект гироскопический 410
Якоби интеграл 229
- метод 341
- теорема 337
- тождество 362
Яма потенциальная 262
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
О - ортогональная матрица
П - матрица преобразования;
поворот
ПД - принцип детерминирован-
ности
ПО - принцип относительности
Е - абсолютный репер; экс-
центрическая аномалия
F - сила; гравитационная сила;
тяга двигателя
I - единичная матрица
J - тензор инерции
К - момент количества движе-
ния системы
N - сила реакции
Р - количество движения систе-
мы
Т - кинетическая энергия
U - потенциал
а - большая полуось орбиты
е - эксцентриситет орбиты
f - истинная аномалия; грави-
тационная постоянная
g - ускорение силы тяжести
1 - наклонение орбиты
m - масса
р - параметр орбиты
q - обобщенные координаты
q - обобщенные скорости
г - радиус
t - время
и - аргумент широты точки
v - скорость
w - ускорение
Sp - след матрицы
Ж - гамильтониан
Q - долгота восходящего узла
0 - угол нутации
£ - виртуальный вектор
р - плотность
т - период обращения
ср - угол вращения; аргумент
широты
щ - угол прецессии
со - аргумент широты перицент-
ра
Индексы верхние
ин - инерционное
т - транспонирование
тр - трение
ш - шар
е - внешние силы
i - внутренние силы
Индексы нижние
в - возмущенное;
вращательное
изм - измеренное
к - конструкция
ос - осестремительное
пр - предельное
р - реактивное; ракета
рас - расчетное
т - топливо
с - кориолисово
е - переносное
г - относительное
Учебное издание
ЛИДОВ Михаил Львович
КУРС ЛЕКЦИЙ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
Редактор Ю.Г. Гуревич
Подписано в печать 12.11.07. Формат 60x90/16. Бумага офсетная.
Печать офсетная. Усл. печ. л. 31,0. Уч.-изд. л. 34,1. Тираж 500 экз.
Заказ № К-2924.
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru;
http://www.fml.ru
Отпечатано в ГУП
«ИПК Чувашия», 428019
г. Чебоксары, пр-т И.Яковлева, 13
ISBN 978-5-9221-0897-3