Author: Шиллинг Г.
Tags: кинематика математическо-механическая геометрия движения физика статистическая физика
Year: 1976
Text
STATISTISCHE PHYSIK IN BEISPIELEN
von
H SCHILLING
Prof Dr rer nat habil.
Deutsche Akademle der Wlssenschaften zu Berlin
VEB FACHBUCHVERLAQ LEIPZIG
1972
Г. Шиллинг
СТАТИСТИЧЕСКАЯ
ФИЗИКА
В ПРИМЕРАХ
Перевод с немецкого
А. Ф. ДИТЕ
и
М. С. КАГАНА
Под редакцией
Д. Н. ЗУБАРЕВА и Э. Л. НАГАЕВА
ИЗДАТЕЛЬСТВО «МИР»
МОСКВА 1976
УДК 531.19(076.2)
В основу книги положен курс лекций по статистической
физике, читающийся в вузах ГДР. Наряду с кратким
изложением фундаментальных теоретических вопросов книга содержит
большое количество (свыше 140) задач, снабженных подробными
решениями и иллюстрирующих применение статистической физики
к важнейшим конкретным проблемам. Активному усвоению
материала способствует также большое число упражнений,
предназначенных для самостоятельной работы читателя и снабженных
ответами. Благодаря подбору материала книга может служить
хорошим дополнением к более строгим учебникам статистической
физики.
Книга предназначена для студентов — будущих физиков,
химиков и инженеров, а также для преподавателей, ведущих
практические занятия по курсу статистической физики.
Редакция литературы по физике
ш 20402-075 © VEB Fachbuchverlag Leipzig 1972
041 (01)—76 © Перевод на русский язык, «Мир», 1976
ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
Книга проф. Г. Шиллинга, предлагаемая в русском переводе, занимает
промежуточное положение между задачником и учебником статистической
физики. Она содержит лишь краткое изложение основ теории, а весь конкретный
материал (включая многие доказательства) представлен в виде задач и примеров,
доведенных, как правило, до численных значений. Поэтому книга может быть
полезна читателям, изучившим соответствующие разделы статистической физики
по одному из учебников (например, Ансельма, Ландау и Лифшица, Киттеля,
Хилла, Хуанга 1}) и желающим достигнуть более активного и конкретного
знания предмета.
Подобное изложение статистической физики было впервые дано в
учебнике Р. Кубо „Статистическая механика", где содержится очень хорошее
теоретическое введение, которое можно рекомендовать читателям книги Шиллинга.
Однако в книге Кубо рассматриваются задачи более теоретического плана, без
каких-либо численных оценок, поэтому книги Шиллинга и Кубо взаимно
дополняют друг друга. Большое количество задач с решениями содержится также в
недавно вышедшей книге „Задачи по термодинамике и статистической физике" под
редакцией П. Ландсберга, однако она рассчитана на более подготовленного
читателя.
Книга состоит из 5 глав. В гл. 1 изложены элементы теории вероятностей
и математической статистики, которые обычно не включаются в курсы
статистической физики, но могут быть полезны для экспериментаторов. Гл. 2иЗ посвящены
задачам классической статистической механики идеальных и реальных газов.
В гл. 4 собраны задачи по квантовой статистической механике. Гл. 5 посвящена
применениям статистической физики к химическим процессам, чему уделено очень
большое внимание. Книга содержит большое количество таблиц и графиков,
поэтому может играть роль своеобразного справочника. Некоторые неточности,
замеченные в немецком тексте, редакторы и переводчики постарались исправить
и разъяснить в примечаниях.
Мы надеемся, что книга будет полезна как учебное пособие для студентов-
физиков и физико-химиков, изучающих статистическую физику, и
преподавателям.
Перевод гл. 1, 2 и 5 выполнил А. Ф. Дите, гл. 3 и 4 — М. С. Каган.
Редактирование осуществили Д. Н. Зубарев (гл. 1—3) и Э. Л. Нагаев (гл. 4 и 5).
Д. Н. Зубарев
Э. Л. Нагаев
Х) Апсель м А. #., Основы статистической физики и термодинамики., М., 1973;
Ландау Л. Д., Лифшиц Е.М., Статистическая физика, М.— Л., 1951; Киттель Ч.,
Элементарная статистическая физика, ИЛ, 1960; Хилл Т., Статистическая
механика, ИЛ, 1960; Хуанг К., Статистическая механика, изд-во„Мир", 1966.
ПРЕДИСЛОВИЕ АВТОРА
Предлагаемая книга возникла на основе лекций по статистической физике,
читавшихся для студентов — физиков, химиков, технологов — и педагогов. Книга
состоит из 22 параграфов, каждый из которых, по образцу книги Ханко „Физика
в примерах", содержит краткое введение, решение избранных задач и большое
количество упражнений с численными ответами.
По сравнению с учебником Хайко, объем материала несколько увеличен, что
позволяет использовать книгу как для первого ознакомления с предметом, так
и для более активного его усвоения. Для облегчения понимания излагаемый во
введениях к каждому параграфу материал иллюстрируется наглядными
примерами. При изложении теоретических основ подчеркивается взаимосвязь между
выводимыми формулами и законами.
Преобладающая часть книги посвящена решению систематически отобранных
задач. Они должны облегчить читателю усвоение теоретических взаимосвязей
и помочь ему овладеть применением физических законов на практике. С этой
целью каждому решению предпослано краткое изложение теории, но в то же время
задача доводится до получения численного результата для какого-либо
конкретного случая. Сложные задачи, решение которых не обязательно при первом
ознакомлении, отмечены звездочкой (*). Упражнения, как правило, могут быть
решены с помощью тех же методов, которые были применены при решении
соответствующих задач. Поэтому ответы к упражнениям почти всегда даны только
в численном виде.
Я хотел бы выразить особую благодарность проф. Каттанеку за помощь
при отборе примеров и задач. Проф. Шульц-Пишачич помог мне советами в
вопросах, касающихся математического описания материала. Я также благодарен
проф. Войта за некоторые указания. Наконец, особую признательность я должен
выразить издательству, которое существенно способствовало успешному
завершению работы над книгой.
Автор
Глава 1
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
§ 1. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ.
БИНОМИАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ.
ОШИБКИ ПЕРВОГО И ВТОРОГО РОДА
Введение
Математическая статистика изучает количественную
характеристику массовых явлений. Их отличительная черта состоит
в том, что при многократном повторении в неизменных
условиях некоторого испытания могут осуществляться различные
события. Испытанием в теории вероятностей принято называть
осуществление точно установленных предписаний и условий,
которые принципиально могут воспроизводиться
неограниченное число раз. Результат испытания называется событием.
Примерами испытаний являются: анализ какого-либо
вещества на содержание примеси, проверка продукции с целью
выявления ошибок изготовления, исследование образования
зародышей кристаллизации, наблюдение радиоактивного
распада, изучение помех в линиях связи.
Если событие А при п одинаковых испытаниях происходит
с частотой kn(A), то величина
цА) = к.Ж (1Л)
представляет собой относительную частоту события А в серии
испытаний. В общем случае величина h(A) колеблется при
переходе от одной серии испытаний к другой. Если
выражение (1.1) при п—+оо стремится к некоторому предельному
значению
P(A)=V\m k-^,
(1.2)
то последнее называется вероятностью события А. Таким
образом, вероятность некоторого события А всегда можно
приближенно определить с точностью до заранее заданной сколь
угодно малой отличной от нуля величины, если провести
достаточно большое, но конечное число испытаний (закон больших
чисел—теорема Бернулли).
Из классического определения вероятности (1.2) следует, что
0<Р(Л)<1. (1.3)
8
Гл. L Элементы теории вероятностей
Вероятность невозможного события равна нулю; вероятность
достоверного события равна единице. Обратные утверждения
в общем случае неверны. Если Р=0, то отсюда можно лишь
сделать вывод, что рассматриваемое событие чрезвычайно
маловероятно, однако не абсолютно невозможно. Равным образом
из того, что Р = \, вообще говоря, следует очень большая
вероятность наступления рассматриваемого события, но все
же не абсолютная его достоверность.
Пример 1
Вероятность того, что при определении содержания соли в морской воде
будет получено значение, в точности равное 4,000...%, равна нулю, поскольку
область допустимых значений измеряемой величины сведена к одной точке.
Тем не менее, в принципе не исключено, что в одной из проб будет
получено именно это точное значение.
Два события А я В называются несовместимыми, или
непересекающимися, если при проведении некоторого испытания они
не могут произойти одновременно. Суммой, или объединением,
двух событий
С = А[)В (1.4)
называется наступление одного из двух событий А или В.
Знак и означает «или — или». Вероятность наступления одного
из двух несовместимых событий А или В определяется
законом сложения вероятностей
Р(АиВ) = Р(А) + Р(В). (1.5)
Пример 2
Рассматривается серия анализов, контролирующих процесс брожения.
Пусть вероятность получения пробы с низким (ниже 10%) содержанием
алкоголя равна 0,3; вероятность среднего содержания (между 10 и 40%)
равна 0,5. Предполагается, что значение 10%, лежащее на границе двух
интервалов, относится только к одному из них. Тогда вероятность
обнаружения в одной из проб до 40% алкоголя составляет 0,8.
В последующем рассмотрении будем всегда считать, что
левая, т. е. нижняя граница какого-либо интервала
принадлежит этому интервалу, тогда как правая, или верхняя
граница не принадлежит ему. Следовательно, в приведенном
выше примере 2 пробу, в которой было получено значение,
точно равное 10%, нужно рассматривать как пробу со
средним содержанием алкоголя.
Событие А называется противоположным, или
дополнительным, событию Л, если оно заключается в том, что событие А
не происходит.
J /. Элементы теории вероятностей
9
Будем использовать следующие обозначения: А— событие,
противоположное событию Л, U — достоверное событие,
V—невозможное событие. Некоторое событие А и противоположное
ему событие А связаны соотношением
A[}A = U. (1.6)
Отсюда следует
P(A[)A) = P(U) = l9 (1.7)
откуда на основании закона сложения вероятностей (1.5) имеем
/>(Д) = 1—Р(Л). (1.8)
Произведением, или пересечением, двух событий
С = А(]В (1.9)
называется одновременное или последовательное наступление
обоих событий А я В. Знак П имеет смысл «как— так и».
Два события называются независимыми, если наступление
одного из них не влияет на вероятность наступления другого.
Для двух независимых событий выполняется закон умножения
вероятностей
Р(А(]В) = Р(А)-Р(В) . (1.10)
Пример 3
Рассматривается толщина снежного покрова и облачность в некоторой
горной местности. В результате многолетних наблюдений установлено, что
в 90% всех случаев толщина снежного покрова превышает 60 см, и в 70%
случаев небо безоблачно. Все наблюдения указывают также на то, что между
наступлением этих двух событий не имеется связи. Отсюда следует, что
в 63% всех случаев оба события будут наблюдаться одновременно.
Пример 4
В серии анализов, рассмотренных в примере 2, состав исследуемого
вещества изменяется при извлечении пробы. Только в том случае, когда
извлеченная проба сразу же возвращается обратно или когда количество
исследуемого вещества столь велико, что его состав практически не меняется
при взятии пробы, вероятности различных событий остаются неизменными.
В этом случае, используя закон умножения вероятностей, находим, что
вероятность извлечения пробы с низким содержанием, и вслед за этим пробы
со средним содержанием алкоголя составляет 0,15.
Если событие А изменяет условия испытания и тем самым
вероятность наступления события В, то эти события
называются зависимыми.
Вероятность наступления события В в предположении, что
событие А произошло, называется условной вероятностью и
10
Гл. 1. Элементы теории вероятностей
обозначается символом Р (В/А). Для одновременного или
последовательного наступления двух зависимых событий А я В
закон умножения вероятностей принимает вид
Р (А п В) = Р (А) Р (В/А) =Р(В)Р(А/В) (1.11)
(см. задачу 1.1).
Если осуществляется п независимых испытаний, и в
каждом из этих испытаний вероятность наступления некоторого
события А равна р, то вероятность того, что событие наступит
k раз, определяется биномиальным законом распределения, или
распределением Бернулли:
^(*) = (2)р*(1-Р)"-* = щй=ЩР*(1-Р)--»
(1.12)
Эту формулу можно обобщить на несколько независимых
событий Аи Л2, ... . Пусть их вероятность есть
р^РШ, р2 = Р(А2), р3 = Р(А3)... .
Вероятность того, что в п испытаниях kx раз произойдет
событие Аи k2 раз — событие А2 и т. д. (при tt = fe1-|-fe2+ ...), равна
Пример 5
Пусть серия анализов в примере 2 столь велика, что состав в ней
практически не меняется из-за взятия отдельных проб. Вероятность того, что
в пяти испытаниях будут извлечены две пробы с низким, две со средним и
одна с высоким содержанием алкоголя, в соответствии с обобщенным
биномиальным законом распределения равна
Рб(2' 2' 0 = 2!|тТ!0'32,0'52'0'2 = ОЛ35=13'50/о-
Может оказаться, что при статистических серийных испытаниях
неоднократно наступит невероятное событие. Вследствие этого
возможно, что какая-либо правильная гипотеза, например
о наличии ядовитых веществ, будет отброшена в результате
случайного накопления невероятных ошибочных измерений.
Вероятность совершить подобную ошибку первого рода
обозначают через а. Равным образом возможно, что ошибочно будет
принята какая-либо неверная гипотеза. Например, вещество,
не содержащее ядов, из-за статистических случайностей может
быть классифицировано как небезупречное и по этой причине
забраковано. Вероятность подобной ошибки второго рода
обозначают через р.
Основной принцип при серийных испытаниях заключается
в том, что более тяжелая, снижающая оценку качества ошибка
§ 1. Элементы теории вероятностей
И
называется ошибкой первого рода, а менее важная,
снижающая лишь количественную оценку ошибка считается ошибкой
второго рода (ср. задачи 1.5 и 1.6).
Задачи
1.1. Сложение и умножение вероятностей
Набор из /г = 30 транзисторов состоит из /г = 20 годных и п—Л? = 10
неисправных элементов. Какова вероятность последовательного извлечения
исправного и дефектного транзисторов, если они после проверки не
возвращаются в исходный набор? Определить вероятность извлечения одного
исправного и одного непригодного транзистора при двукратном взятии.
Решение
Обозначим через А событие, состоящее в извлечении годного транзистора;
А означает взятие неисправного транзистора. Вероятность извлечения
исправного транзистора составляет
k 90
PH) = i-=g = 0,666... . (1.1.1)
После того как событие А произошло, набор состоит уже из к—1 = 19
исправных и п — /г = 10 неисправных элементов; условия испытания
изменились. После наступления события А вероятность того, что будет
зафиксировано событие Л, равна
P(JM)=^=i§° = 0)344.... J1.1.2)
Вероятность последовательного наступления обоих событий А и А равна
произведению вероятностей (1.1.1) и (1.1.2):
Р(А, А) = Р(А)Рт) = ^Е^Г%-^0,229... . (1.1.3)
Таким образом, при заданном соотношении числа исправных и
неисправных транзисторов в 23% всех случаев после извлечения исправного будет
извлечен дефектный элемент.
Рассмотрим теперь обратную последовательность событий: сначала
извлекается неисправный, а затем исправный транзистор. Тогда имеем
Р(Л) = ^=^ = 0,333... (1.1.4)
и
— k 20
^(ЛМ)=—^==0,689..., (1.1.5)
откуда на основании закона умножения вероятностей следует, что
Р(А)Р(АГА) -2=*^=". | = 0,229.... 0.1.6)
Соотношение
Р (А) Р (А/А) = Р (А) Р (А/А)
справедливо не только для рассмотренного примера, но и в общем случае.
12
Гл. L Элементы теории вероятностей
Вероятность того, что при двукратном испытании будет извлечен один
исправный и один неисправный транзистор, т. е. будет иметь место случай,
которому соответствует либо формула (1.1.3), либо формула (1.1.6),
определяется суммой величин (1.1.3) и (1.1.6):
Р(1, 1) = 2Р(У1)Я(ЛМ) = 2-^^. = 2.^ = 0,458... .
Таким образом, в 46% всех случаев в двух испытаниях будет извлечен один
исправный и один неисправный транзистор.
1.2. Биномиальный закон распределения
В очень большой серии контрольных испытаний Pi = 70% проб
указывают на наличие, р2 = 30% на отсутствие загрязнения. Как велика
вероятность того, что при взятии п = 8 проб будет получено k = 5 загрязненных
и п—k—З незагрязненных проб?
Решение
В результате испытания могут наступить два события: Л— исследуемая
проба загрязнена, Л —проба не загрязнена. Из исходных условий имеем
P(A)=plf P(A)=\-Pl = p2.
В рассматриваемом случае мы должны подставить р1 = 0,70, р2 = 0,30. Если
отдельные события предполагаются независимыми, то для вероятности
наступления определенной последовательности Л, А, А ... событий находим
P(At A,A...) = P(A)P(A)P(A)... = PlP01... = pipi-k. (1.2.1)
Как мы видим, эта вероятность не зависит от порядка, в котором следуют
отдельные события Л и Л; кроме величин pt и р2 она зависит лишь от
числа k событий Л и числа п—k событий Л. В рассматриваемой задаче
получаем
p\p\'k = 0,75.0,33 = 0,004538.
Число последовательностей с fc-кратным наступлением события Л и (n — k)-
кратным наступлением события Л равно
П\ _Я(П-1).,.(П-Н1) „ррх
k\(n—k)\-~ k(k—1)...3.2-1 ' к '}
(:)■
При заданных числовых значениях имеем
(п\ /8\ 8! 8-7.6
Таким образом, вероятность /г-кратного наступления события Л в п
испытаниях оказывается равной
Рп (/е)= (, ) pip%~ (биномиальный закон). (1.2.3)
Подставляя заданные значения, получаем
/>8(5) = (з),0'7-,°'33==0'254К
При 8 испытаниях более ги всех проб укажут на загрязнение.
§ 1. Элементы теории вероятностей
13
1.3. Обобщенный биномиальный закон
Число производственных несчастных случаев в день на большом
предприятии, усредненное по большому промежутку времени, обнаруживает
распределение, приведенное в табл. 1. Какова вероятность получить в течение
недели следующее распределение несчастных случаев: два дня—без
несчастных случаев, два дня — по одному несчастному случаю и один день — три
несчастных случая?
Таблица 1
Распределение несчастных случаев
Число несчастных случаев
в день
0
1
2 !
3
4 1
5 и более
Наблюдаемая частота, %
31,2
36,1
24,5
6,3
1,7
0,2
Решение
Мы должны применить биномиальный закон для многих переменных
P(k0, kltk2, ■••)-^2!_p*'p*'/fr... . (1.3.1)
В данном случае k0 обозначает число дней без несчастных случаев, kx — число
дней с одним несчастным случаем и вообще /г,-—число дней, в которые
происходит по / несчастных случаев. Далее,
00
i=0
представляет полное число испытаний. В рассматриваемом примере п = 5
есть число рабочих дней в неделе, а р/ обозначает вероятность того, что
в день произойдет / несчастных случаев.
Значения pj берем из второго столбца табл. 1; при этом стоящие в этом
столбце величины необходимо предварительно разделить на сто. Вероятность
получения заданного распределения
/г0 = 2, /^ = 2, /е2 = 0, kB= 1, fy = 0 при /^4
в соответствии с формулой (1.3.1) для биномиального закона распределения
равна
• Р(2, 2, О, 1, 0...) = Р (2,2, 0, 1)^2|2^0,3122.0,3612.0,245о.0,063!==
= 30-0,000795 =-0,02385.
Таким образом, из приведенной статистики несчастных случаев следует,
что в течение одной недели рассматриваемое их распределение
осуществляется приблизительно в 2,4% случаев.
14
Гл. 1. Элементы теории вероятностей
1.4. Сложение вероятностей при применении
биномиального закона распределения
Изучение статистики ошибок машины показывает, что в 30% всех
случаев происходит менее 5 ошибок в день, в 50% случаев—от 5 до 12 ошибок
и в 20% всех случаев — более 12 ошибок в день. Как велика вероятность
того, что в течение трех (из пяти) дней одной недели будет происходить
более 12 ошибок в день?
Решение
Применяя биномиальный закон распределения, необходимо вычислить
и сложить следующие вероятности:
Р (2, 0, 3) = ^ 0,32-0,2»,
Р(0, 2, 3) = 2§Т 0,52.0,23,
Р(1, 1, 3) = Ц.0,3.0,5-0,23.
Сумма этих вероятностей охватывает все случаи, в которых в течение трех
дней недели происходит более чем по 12 ошибок в день. В результате
сложения получаем
Р = Р(2, 0, 3) + Р(0, 2, 3) + Р(1, 1, 3) =
-If»» (¥+¥+*•*•)-««•
т. е. в 5,1% всех случаев в течение трех дней одной недели происходит
более 12 ошибок в день.
1.5. Ошибки первого и второго рода
Исследуется образование нежелательных зародышей кристаллизации.
Для этой цели используются рентгеновские снимки. Пусть вероятность
обнаружения нежелательных зародышей на отдельном снимке составляет р = 0,8.
Однако в то же время существует возможность того, что на основании
недоброкачественного снимка будет сделан ошибочный вывод об образовании
зародышей. Пусть вероятность получения такого рода ошибочных снимков
составляет ^ = 0,015. Для каждой из взятых проб изучается по п — 4 снимка.
Результат применения критерия рассматривается как положительный, т. е.
считается, что имеет место образование зародышей, если хотя бы один из
снимков указывает на это. Результат испытания рассматривается как
отрицательный, если ни на одном из снимков не удается распознать образование
зародышей. Как велика вероятность того, что а) имеющийся зародыш не
будет обнаружен (ошибка первого рода) и б) будет сделан вывод об
образовании зародышей, хотя в действительности таковых не имеется (ошибка
второго рода)?
Решение
Пусть А обозначает гипотезу, согласно которой исследуемая проба содержит
зародыши. Через А обозначим обратное предположение (проба не содержит
зародышей). Введем случайную величину X и определим ее следующим
образом: Л=-0, если зародыши не обнаруживаются, и X > 0, если они наблю-
ff /. Элементы теории вероятностей
15
даются. Вероятность того, что возникший зародыш не будет обнаружен при
однократном измерении, составляет 1 — р=1—0,8 = 0,2. Каждое измерение
производится независимо от других. Вероятность л-кратного повторения
этого результата, т. е. вероятность того, что гипотеза А является
справедливой, несмотря на ее отклонение в п испытаниях, следовательно, равна
а = Р(Х = 0/Л) = (1 — р)п.
В рассматриваемом случае получаем
а = Р(Х = 0/Л) = (1 — 0,8)4 = 0,24 = 0,0016.
Таким образом, в 0,16% всех случаев возникший зародыш не будет
обнаружен при исследовании.
Ошибка второго рода совершается в том случае, когда ошибочно делается
заключение об образовании зародышей. Вероятность такой ошибки при
однократном измерении составляет q=\—(1 — а). Здесь 1 — q представляет
вероятность получения безупречного снимка при исследовании пробы, свободной
от зародышей. Вероятность /г-кратного повторения этого результата равна
(1 — q)n. С ростом числа измерений п возрастает вероятность того, что
безупречная проба будет рассматриваться как проба, содержащая зародыши,
поскольку получение хотя бы одного ошибочного снимка служит основанием
для заключения о наличии зародышей. Следовательно, вероятность
совершения ошибки второго рода равна
Р = Р(Х> 0/Л) = 1-(1-</)».
В нашем примере получаем
р = Р(Х> 0/1)=1 —(1 —0,015)4=1 —0,9854 = 1 — 0,941 = 0,059,
т. е. вероятность ошибочного заключения о наличии зародышей в пробе
составляет 5,9%.
Мощностью статистического критерия, или добротностью
п=\—Р(Х> о/Л) = 1—р
называют вероятность того, что в результате исследования будет отклонена
гипотеза Л, если справедлива гипотеза Л.
Следовательно, П представляет собой долю безупречных проб,
беспрепятственно проходящих испытание. В рассматриваемом случае имеем
П= 1 — 0,059 = 0,941.
Таким образом, 94,1% проб, в которых не произошло образование
зародышей, в результате испытаний правильно классифицируются как безупречные.
1.6*. Расширенные условия испытания при массовом
обследовании
При проверке на наличие производственных дефектов каждый элемент
крупной серии подвергается пяти контрольным измерениям; вероятность р
обнаружения имеющегося дефекта при испытании равна 0,8. Пусть
вероятность ошибочного заключения о наличии производственного дефекта на
основании одного измерения составляет q = 0,04. Результат проверки считается
положительным, если все пять контрольных измерений указывают на
отсутствие дефекта, и отрицательным (брак), если хотя бы два измерения
указывают на наличие дефекта. В случае если только одно измерение указывает
на дефект, производится повторная проверка. Вычислить вероятность
совершения ошибки первого рода (брак проходит систему контроля), ошибки
второго рода (безупречное изделие ошибочно объявляется браком) и добротность.
16
Гл. 1. Элементы теории вероятностей
Решение
Аналогично тому, как это было сделано в задаче 1.5, находим, что
вероятность ошибочного заключения о безупречности дефектной продукции в п = 5
испытаниях равна
Р (Х = 0/Л) = (1 — р)« = (0,2)5 = 0,000320. (1#6Л)
Это означает, что 0,032% всех дефектных изделий беспрепятственно
проходят систему контроля. Вероятность того, что из п = 5 измерений гг—1=4
окажутся ошибочными, равна в соответствии с формулой для биномиального
закона распределения (1.12)
Р(я-1, l)=(n^1)(l-p)»-1P=(J)0,2*.0f8 =
= 5.0,0016.0,8 = 0,0064. (1.6.2)
Следовательно, 0,64% дефектных изделий будут подвергнуты повторной
проверке. Из них 0,032% снова беспрепятственно пройдут систему контроля.
Доля последних в общем числе изделий в соответствии с (1.6.1) и (1.6.2) равна
Р(я-1,1) P(X = 0/A) = ^l)([^p)^ip^
= 0,00032-0,0064 = 0,000002048. (1.6.3)
Таким образом, повторная проверка в рассматриваемом случае дает вклад,
лишь немного превышающий 0,0002%.
Продолжая эти рассуждения, находим, что вероятность совершения ошибки
первого рода выражается рядом
00
а = Р(Х = 0/Л)£ [Р (п—1, l)]^1 =
v=l
CD
= 0-Р)"Ц [(/г-l) О-Р)"-1/^"1- (I'M
v=l
Третий член этого ряда при заданных числах имеет следующее значение:
(l-P)rt[(n^l)(l-^-1p]2 = 0^[(^)0,2*.0,8]2 =
= 52.0,213-0,82 < 1,5-10-8.
Если достаточна точность порядка Ю-6, то необходимо учитывать лишь два
первых члена ряда (1.6.4). Из (1.6.1) и (1.6.3) находим для ошибки первого рода
а = 0,0320% + 0,0002% + ... = 0,0322%;
при этом неучтенные члены не превышают 0,00001%. Доля дефектных
изделий, не выявляемых системой контроля, составляет менее 0,03221%.
Доля безупречных изделий, для которых первая проверка дает
положительный результат во всех п = 5 испытаниях, равна
Р (Х = 0/Л) = (1 — <7)" = 0,965 = 0,8154. (1.6.5)
Лишь около 81,5% всех безупречных элементов беспрепятственно проходят
первую серию испытаний.
Доля бездефектных изделий, для которых лишь одно измерение ошибочно
указало на дефект, в соответствии с формулой (1.12) равна
Р (гг—1, l) = (j) 0-?)',-1?=(i) (0,96)4.0,04 = 0,169869. (1.6.6)
J /. Элементы теории вероятностей
17
Таким образом, почти 17% изделий будут подвергнуты повторной
проверке. Вероятность того, что безупречный элемент будет забракован уже
после первой серии испытаний, оказывается, таким образом, равной
Р1 = 1-Р(Х = 0/Л)-Р(/г-1, 1) =
= 1_(1_0»_(*)(1_0»1-10 =
= 1_о,965—5- 0,96*. 0,04 = 0,014758. (1.6.7)
Из числа изделий, подвергнутых повторной проверке, с вероятностью
(1.6.5) положительный результат будет получен при всех я = 5 испытаниях,
с вероятностью (1.6.6) одно испытание даст отрицательный результат и с
вероятностью (1.6.7) ошибочный результат будет получен в двух и более
испытаниях. Эта процедура последовательно продолжается.
Суммируя, получаем долю ошибочно забракованных доброкачественных
изделий, т. е. вероятность совершения ошибки второго рода:
P = Pi 2 1Р(п-\, l)]v =
v=0
во
= [l_(l_,)«_(»)(l_,)«-i,]2 [(f)(l-<?)»-i<?]V'. (1-6.8)
v = 0
Подставляя заданные численные значения, находим
Р = 0,014758 (1 + 0,169869 + 0,1698692 +...).
или
р = 0,017777.
Вследствие введения повторных серий испытаний вероятность ошибки первого
рода возрастает лишь незначительно — с 0,0320 до 0,03 22%. Напротив,
вероятность ошибки второго рода, первоначально равная почти 18,5%, падает до
величины менее 1,8%. Для добротности получаем
П = 1 — Р = 0,98222,
т. е. около 98,2% всех доброкачественных изделий правильно
классифицируются как безупречные.
Упражнения
У. 1.1. В урне имеется 12 красных и 8 синих шаров. Определить
вероятность того, что три раза подряд будет извлечен синий шар, если
а) извлеченный шар возвращается в исходный набор, б) извлеченный
шар не возвращается.
У. 1.2. Определить вероятность того, что а) из гг = 30 различных чисел
будут извлечены k = 4 наперед заданных; б) из гг = 30 различных
чисел будут извлечены k = 4 чисел в заданной последовательности,
если извлеченное число возвращается в исходный набор.
У. 1.3. Как велика вероятность того, что из гг = 30 чисел в k0 — 5 испытаниях
будут извлечены не меньше k = 4 наперед заданных числа?
У.1.4. В крупной партии р1 = 25% штифтов слишком длинны, р2 = \Б%
слишком коротки и р3 = 60% имеют длину, лежащую в пределах
некоторых установленных допусков, а) Какова вероятность при
шестикратном испытании два раза подряд извлечь слишком длинный,
нормальный и слишком короткий штифты? б) Какова вероятность
в шести испытаниях извлечь по два штифта каждого сорта? Серию
можно .считать столь большой, что изъятие отдельных штифтов не
нарушает их исходного распределения,
18
Гл. 1. Элементы теории вероятностей
У. 1.5. Как велика вероятность того, что при шестикратном бросании
игральной кости будет выброшена а) только одна шестерка, б) по
крайней мере одна шестерка?
У. 1.6. Вычислить вероятность того, что из п = 5 новорожденных 0, 1, 2,
3, 4, 5 окажутся мальчиками. На основании многолетних
наблюдений соотношение между числом рождающихся мальчиков и девочек
считается равным 106:100.
У. 1.7. Изучение числа телефонных разговоров на некоторой телефонной
станции дает следующие усредненные по большому промежутку
времени значения:
Число
телефонных
разговоров в час
0
1
2
^3
Частота,
25
40
20
15
%
Вычислить вероятность следующего распределения в течение 4 часов:
два часа — без разговоров, в течение одного часа—один разговор,
и один час — с двумя разговорами.
У. 1.8. Некоторая жидкость исследуется на наличие ядовитых веществ.
Пусть вероятность обнаружить присутствующее ядовитое вещество
при однократном измерении равна р = 0,9. Предположим также, что
вероятность сделать заключение о наличии ядовитого вещества на
основании ошибочного измерения при однократном испытании
составляет <7 = 0,02. Пусть число испытаний п равно 4. Гипотеза А
считается подтвержденной, если одно из контрольных измерений
указывает на присутствие ядовитого вещества. Вычислить вероятность
беспрепятственного прохождения отравленной пробы через систему
контроля, вероятность того, что доброкачественная проба будет
ошибочно забракована, и процент правильных заключений для
доброкачественных проб. Какие значения получатся при л = 2 измерениях?
У. 1.9. При анализе отработанных газов вероятность/? обнаружения вредной
примеси в пробе равна 0,5. Пусть вероятность ошибочного
заключения о присутствии нежелательного вещества составляет
<7 = 0,02. Оценить необходимое число п контрольных испытаний в
случае, если ошибка первого рода не должна превышать 0,1%, а ошибка
второго рода 15%? Отработанный газ считается доброкачественным,
если все п контрольных испытаний указывают на отсутствие
примеси.
У. 1.10. В отходах некоторого производства обнаруживаются следы ценного
органического вещества. Пусть вероятность обнаружить его
присутствие посредством одного измерения составляет р — 0,60. Требуется,
чтобы в 95% всех содержащих искомое вещество проб было
обнаружено его присутствие, и по меньшей мере 90% проб, не
содержащих этого вещества, было отбраковано. Вычислить минимальное
число п необходимых измерений для одной пробы и оценить
допустимые значения вероятности q того, что при однократном испытании
будет сделано ошибочное заключение о присутствии искомого
соединения. Гипотеза о наличии искомого вещества считается
подтвержденной, если хотя бы одно испытание дает положительный результат.
# 2. Среднее значение и среднеквадратичное отклонение 19
У.1.11*. При бурении скважин присутствие радиоактивного вещества на
основании одного измерения определяется с вероятностью р = 0,85.
Пусть вероятность ошибочного вывода о его наличии составляет
(7 = 0,1, а число измерений в одной серии равно п = 4. Вычислить
вероятность ошибки первого рода (необнаруженная радиоактивность)
и ошибки второго рода (ошибочное заключение о радиоактивности).
В случае двух и более измерений с положительным результатом
проба классифицируется как радиоактивная, в случае, когда лишь
одно измерение дает положительный результат, серия испытаний
производится повторно, и в случае, когда все измерения дают
отрицательный результат, проба считается нерадиоактивной.
У. 1.12. Как изменятся результаты предыдущей задачи, если число
измерений будет сокращено до п — 3?
§ 2. СРЕДНЕЕ ЗНАЧЕНИЕ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ.
ГАУССОВО РАСПРЕДЕЛЕНИЕ ОШИБОК И ГАУССОВ ИНТЕГРАЛ
ОШИБОК.
ОЦЕНКА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ ПО ВЫБОРКАМ.
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ
Введение
В качестве параметров распределения, или
характеристических величин, важную роль играют среднее значение \i и
среднеквадратичное отклонение а, характеризующее разброс
возможных значений случайной величины относительно ее
среднего значения. В качестве меры рассеяния используется также
величина а2, называемая дисперсией. Для дискретной
случайной величины X, принимающей с вероятностями pt
значения х( (1 = 1,2,3..., д), среднее значение определяется
равенством
И = 2*/Л • (2-1)
i
Среднеквадратичное отклонение определяется выражением1}
(2.2)
o=yr^(xl—v)tpt
Вероятность того, что случайная величина X принимает
значение, меньшее некоторого числа х, равна
P(X<x)=F(x) = 2 Pl. (2.3)
xi <х
Функция f (х) называется функцией распределения вероятностей.
1} Величину а называют иногда также стандартным отклонением или
просто стандартом.— Прим. перев.
20
Гл. 1. Элементы теории вероятностей
Пример 6
Требуется определить вероятность того, что при бросании игральной
кости выпадет число очков, меньшее 3. Очевидно, что в этом случае мы
имеем F (3) = 2/б = 0,333 .... Вероятность того, что число очков окажется
меньше 4, равна соответственно F (4) = 3/б = 0,5, а вероятность того, что
выпадет меньше 7 очков, есть F(7) = \ (фиг. 1).
к
',*
оА
123456769
-►*
Фиг. 1. Функция распределения
F (*), рассматриваемая в
примере 6.
Если X является непрерывной случайной величиной,
которая может принимать любые значения из ограниченного или
бесконечного интервала, то производная функции
распределения
.dF(x)
/м=;
dx
(2.4)
называется функцией плотности распределения вероятностей,
или функцией плотности вероятности, или сокращенно просто
плотностью вероятности. Для непрерывной случайной
величины роль вероятности р{ играет величина f(x)dx. Среднее
значение и среднеквадратичное отклонение в этом случае
имеют вид
|Л = J xf (х) dx, а = у J (л:—(л)2 / (х) dx
(2.5)
Вероятность того, что непрерывная случайная величина X
принимает некоторое значение, лежащее в интервале хи < X < х0У
определяется равенством
P(xu<X<x9) = lf(x)dx = F(x0)-F{xu). (2.6)
В случае непрерывных случайных величин границы
рассматриваемого интервала могут быть как включены, так и исключены
из него; вероятностные предсказания от этого не изменяются.
ff 2. Среднее значение и среднеквадратичное отклонение 21
Если для ха совершить предельный переход ха —> — с», то
поскольку
F(-oo) = P(X< — оо) = О,
функция распределения принимает вид
F(x0)= S f(x)dx.
Совершая затем предельный переход х0—>. + оо, получаем
вероятность того, что случайная величина принимает значение
между —оо и +оо. Эта вероятность должна равняться
единице. Отсюда следует условие нормировки
+ 00
5 f(x)dx=l. (2.7)
Важную роль в теории вероятностей и в ее технических
приложениях играет гауссов, или нормальный, закон
распределения
(2.8)
Плотность вероятности нормального распределения
представлена на фиг. 2. Максимум ее тем выше, иными словами, точ-
Ot :Ог ;Оа : <г4 - f:/,5:J:7,J
*~Х
Фиг. 2. Плотность вероятности
нормальных распределений с разными
значениями ст.
ностьтем больше, чем меньше среднеквадратичное отклонение а.
С помощью преобразования
г = х-=¥ (2.9а)
22
Гл. 1. Элементы теории вероятностей
нормальное, или гауссово, распределение (2.8) приводится к
стандартному нормальному закону распределения
'°ы=ттЛ'-'гйг-
(2.9)
Таблицы значений плотности вероятностей и функции
распределения для стандартного нормального закона приведены в
приложении (см. табл. П.1 и П.II). На фиг. 3 изображено
0,75
0,5
0,25
\
/
у
Г «-Г .. !._
/^
\ Т !._^Л
„Я Фиг. 3. Нормальное распределе-
fjtrdcr/хгдсг fi-G /z ju+cr/t+Zcr ju+fo ние.
нормальное распределение. Случайная величина z,
распределенная по стандартному нормальному закону, имеет среднее
значение |j, = 0 и среднеквадратичное отклонение а=1.
Совокупность всех возможных значений случайной величины
называется генеральной совокупностью G. Если оценка
параметров некоторого статистического распределения производится
на основании выборок, то объемом п выборки S называется
число проведенных испытаний. Используя измеренные значения
х( (t = l, 2, .. .п) случайной величины, можно найти выборочное
среднее значение х и выборочное среднеквадратичное отклонение
(эмпирический стандарт) s для данной выборки по формулам:
(2.10)
(2.11)
Величина п—1, представляющая собой уменьшенное на
единицу число испытаний, называется при этом числом степеней
свободы /.
J 2. Среднее значение и среднеквадратичное отклонение 23
Пример 7
Пусть выборочная проверка распределения температуры в течение одного
дня состоит лишь из одного измерения, давшего значение 25°С. Тогда эта
величина есть среднее значение выборки, имеющей объем п=\. Для
выборочного стандарта в этом случае получаем выражение 0/0; таким образом
выборочное среднеквадратичное значение (эмпирический стандарт) остается
неопределенным.
Если из генеральной совокупности G нормально
распределенной величины X производится серия выборок Sv (v = l,
2, ..., m) объемом п, то выборочные средние значения xv и
эмпирические стандарты sv для этих выборок подчиняются
определенным законам распределения. Обозначим измеренные
выборочные значения через xvi (i=l, ..., /г). Средние
выборочные значения
п
xv = — / ^ Xvi (z. 1 z)
оказываются распределенными по нормальному закону (2.8),
параметры распределения которого \х- и о- связаны с
параметрами jx и (т для генеральной совокупности G формулами
(2.13)
Таким образом, отклонение а- средних значений х оказывается
тем меньше, чем больше объем п отдельных выборок.
Исследование эмпирических стандартов sv различных выборок Sv с
объемом п показывает, что величины
V=n-=±s% или %2 = ^s* (2.14)
удовлетворяют закону распределения, называемому
%2-распределением с п—1 степенями свободы (фиг. 4). Это распределение
отличается от нормального закона (2.8). Среднее значение u, 2
и отклонение os2 величин s2v связаны с параметрами jx и а
генеральной совокупности соотношениями
т т п
•*«* = Л"! "2* Sl = J!?1. «2 ^П 2 (**-*>' = о\ (2.15)
у m->oo v=l т-*-оо v=l t= l
т
а%="™.^2 W-a-) = o» /^ . (2.16)
24
Гл. 1. Элементы теории вероятностей
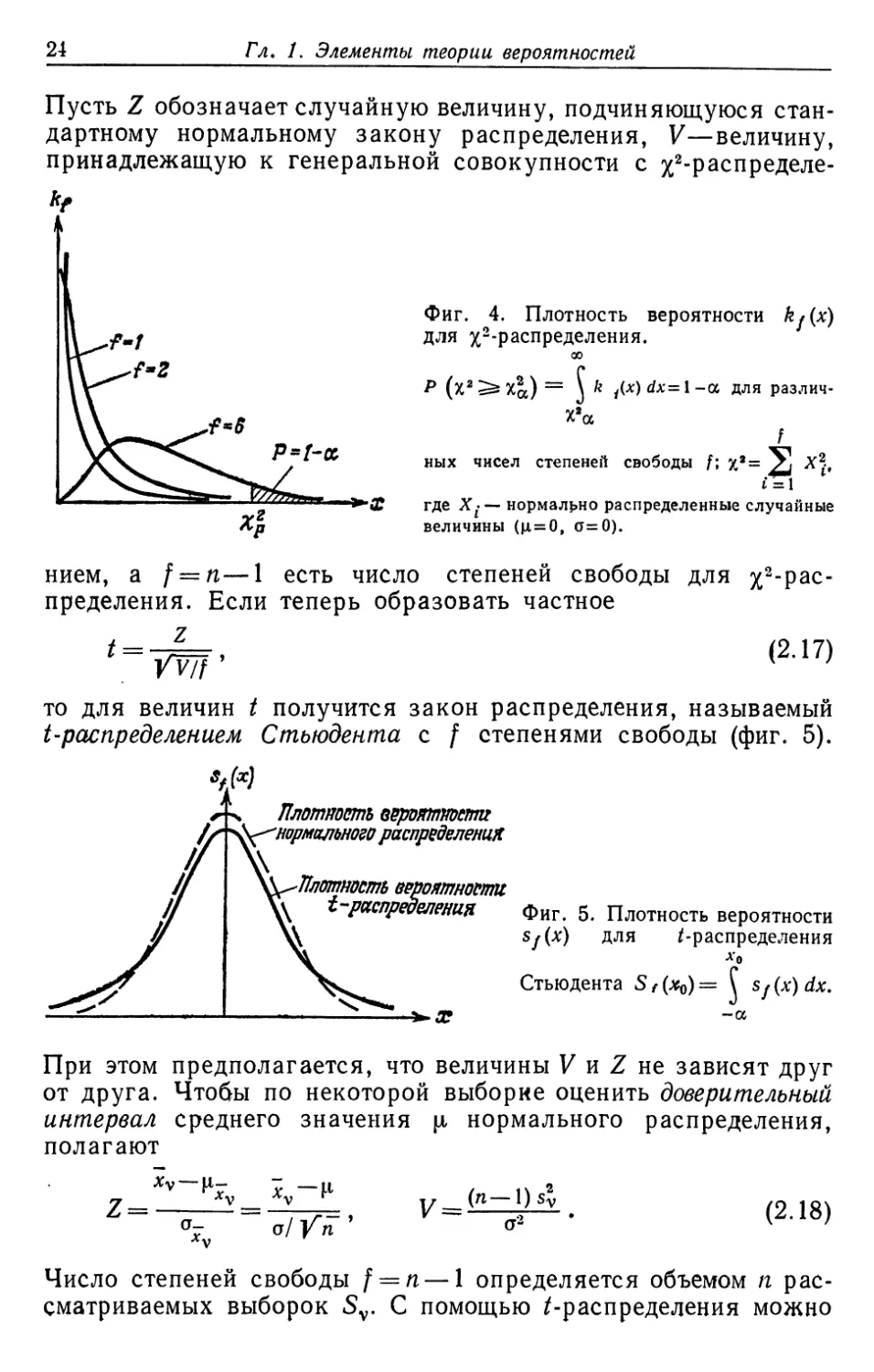
Пусть Z обозначает случайную величину, подчиняющуюся
стандартному нормальному закону распределения, V—величину,
принадлежащую к генеральной совокупности с
^-распределена»
Фиг. 4. Плотность вероятности kj(x)
для ^-распределения.
QO
Р (х2^5Са) = \ k 1(x)dx=l-a для
различна
f
ных чисел степеней свободы /; /2= £j X*,
t=l
где Х-— нормально распределенные случайные
величины (ц = 0, о=0).
нием, a f = n—1 есть число степеней свободы для %2-рас-
пределения. Если теперь образовать частное
Z
t =
WTf'
(2.17)
то для величин t получится закон распределения, называемый
t-распределением Стьюдента с / степенями свободы (фиг. 5).
*4*)
Плотность вероятности
нормальном распределена
Плотность вероятности
^плотность вероятности
^ i-ркспределения фиг. 5. Плотность вероятности
Sj(x) для ^-распределения
Стьюдента S {(Xq) = \ Sy (х) dx.
При этом предполагается, что величины V и Z не зависят друг
от друга. Чтобы по некоторой выборке оценить доверительный
интервал среднего значения \х нормального распределения,
полагают
Xv — \l-
Z= ^:
ilVn%
1/ =
(п—1) sv
(2.18)
Число степеней свободы f = n — \ определяется объемом п
рассматриваемых выборок Sv. С помощью /-распределения можно
§ 2. Среднее значение и среднеквадратичное отклонение 25
определить величину доверительной вероятности, или
надежности Р=\—а, представляющую вероятность получения
выборки S со значением t, которое лежит внутри интервала
-ta<\t\:
Vv/f
~^Vn<ta, (2.19)
т. е. модуль которого меньше некоторого граничного значения
ta- В табл. П.III (см. приложения) приведены значения /а для
различных значений параметра а, называемого вероятностью
риска, или уровнем значимости, и различного числа степеней
свободы f = n—1. Из выборочных значений х и s с уровнем
значимости а следует, что среднее значение \i лежит в
пределах доверительного интервала
(2.20)
Если искомый параметр распределения |л оказался точно
равным выборочному среднему значению х, то а представляет
вероятность того, что в последующих выборках будет получено
среднее значение, лежащее вне пределов доверительного
интервала.
Доверительная оценка среднеквадратичного отклонения
производится с использованием ^-распределения. При этом для
заданного уровня значимости а всегда можно определить два
числа %a/2,n-i и %i-a/2,/i-i таким образом, что одновременно
будут выполняться два равенства
P(X*<Xl/2,n-1) = Y, P(t<xi-«/,.„-i) = l—j. (2.21)
Отсюда можно найти два коэффициента Lx и L2, определяющие
доверительный интервал для среднеквадратичного отклонения
L^Ko < L2s
(2.22)
причем уровень значимости одинаков для обеих сторон
неравенства. Коэффициенты Lx и L2 связаны с параметрами %а-ра-
спределения соотношениями
' ^i-a/2, n-i f Aa/2, л-i
В табл. П.IV (см. приложения) приведены значения
коэффициентов Ij и 12 для различных чисел степеней свободы п — 1
и различных значений величины 1—а, называемой
доверительной вероятностью или надежностью оценки.
26
Гл. 1. Элементы теории вероятностей
Задачи
2.1. Среднее значение и среднеквадратичное отклонение
генеральной совокупности
При измерении температуры в различных точках в определенный момент
времени получены следующие значения: 10,2, 12,4, 14,5, 13,6, 11,4, 10,8° С.
Вычислить среднее значение и среднеквадратичное отклонение.
Решение
Генеральная совокупность состоит из 6 измеренных значений. Среднее
значение \х и среднеквадратичное отклонение о* определяются выражениями
п п
Ц = 2 /W» <*2 = 2 Pi to —У)2-
1=1 1=1
В рассматриваемом случае отдельные измерения равноправны. Поэтолгу
полагаем вероятность р-ь равной относительной частоте Л/ == 1 //г = 1 /6 и получаем
1=1 1=1 1=1
Для среднеквадратичного отклонения имеем
°=V% hi{Xi-^=y 1^{Х1-^= у^Т3^75=1(52оС
2.2. Выборочное среднее и эмпирический стандарт.
Статистические предсказания на основании вида функции
распределения
Берется серия проб с целью определения содержания посторонних
примесей в промышленных сточных водах. Частоты обнаружения различных
степеней загрязненности приведены в табл. 2.
Таблица 2
Загрязненность промышленных сточных вод
Порядковый номер i 12 3 4 5 6 7
Содержание посторонних 40 ± 5 50 ± 5 60 ± 5 70 ± 5 80 ± 5 90 ± 5 100 ± 5
примесей, г/л
Частота k{ 11 48 160 385 246 113 37
Кривая распределения аппроксимируется нормальным законом. Вычислить
параметры нормального распределения, определить частоту проб с
содержанием примесей а) свыше 82 г/л, б) менее 54 г/л.
ff 2. Среднее значение и среднеквадратичное отклонение 27
Решение
Сначала определим среднее значение содержания примесей. Полное число
7
исследованных проб составляет п— 2 Л/=1000. Отсюда относительные ча-
1 =\
стоты hi получаются путем деления частот /г,- на «=1000. Для среднего
значения имеем
7
х = ± У /e/*/ = 72,94. (2.2.1)
П *-*
t=l
Выборочная дисперсия равна
7 7
s2 = £=1 S *' <*'-*>' = g§9 2 *' (*/-72,94)» = 139,70. (2.2.2)
t = l " t=l
Отсюда для выборочного среднеквадратичного отклонения (эмпирического
стандарта) имеем
s= 11,819.
Примем параметры нормального распределения равными вычисленным
значениям:
^1 = 72,94, (1=11,819.
Тогда функция распределения приобретает вид
— QO
1 r° Г (х—72,94)21 Л Л
= 11,819 ire J еХР [-^9^] *' <2-2-3)
— QO
Относительная доля проб с содержанием примесей х > х0 равна
со
Р(х> ^^y^-Jexp [^]л=1-^(4 (2.2.4)
Производя замену переменных
2=£цЁ (2.2.5)
переходим к стандартному нормальному интегралу и получаем
Р(^>^0) = 1-у= j ехр(-у)лг=1-Ф(*0). (2.2.6)
— со
Относительная доля проб с * < ха определяется выражением
хи
Р(х< ^и)=у=-о £ ехр [-^т=^] dx = F (*„)., (2.2.7)
28
Гл. U Элементы теории вероятностей
откуда, используя (2.2.5), находим
P(x<xa) = F(xtt) = y=§ ехр(-у)л = Ф>и). (2.2.8)
— со
Учитывая симметрию нормального распределения (см. фиг. 2), имеем
z
Ф(гв) + Ф(-га)=-1= J ехр (-£)&+•
-СО
— во
В случае отрицательного значения га < 0 находим Ф (za) из табл. П. II
(см. приложения) с помощью соотношения
Ф(*в) = 1-Ф(-гв). (2.2.10)
При заданных численных значениях имеем
82-72,94 Л__ 54-72,94 . 1СЛ
20 = 11,819 = 0'/67' '*= 11,819 = -0'160-
Далее, используя табл. П. II, находим по формуле (2.2.6)
Р (х > 82) = 1 — Ф (0,767) = 1 — 0,7785 = 0,2215,
а из (2.2.9) с учетом (2.2.10)
. Р (х < 54) = Ф (—0,160) = 1 — Ф (0,160) = 1 — 0,5636 = 0,4364.
Таким образом, в 22,15% всех проб содержание примесей превышает 82 г/л;
в 43,64% проб в соответствии с нормальным законом распределения
содержание примесей составляет менее 54 г/л.
2.3. Параметры нормального распределения.
Относительная доля испытаний, приводящих к значениям,
лежащим за пределами установленных границ
Определяется количество соли в серии проб, каждая из которых
содержит по 100 см3 раствора. В 30% случаев содержание соли превышает 10,8 г,
а в 20% случаев оно составляет менее 8,6 г. Вычислить среднее значение |li
и среднеквадратичное отклонение сг в предположении, что имеет место
нормальное распределение. Указать симметричный (относительно среднего
значения) интервал, в пределах которого окажутся 90% всех проб. Найти границы
интервала, определенные условием, что число проб с содержанием соли,
меньшим нижней границы, составляет 1%, а число проб с содержанием соли
больше верхней границы составляет 0,1%.
Решение
Функция распределения
— со
дает относительную долю значений случайной величины, для которых х^л-0.
Чтобы перейти к стандартному нормальному распределению и воспользоваться
ff 2. Среднее значение и среднеквадратичное отклонение 29
табл. П. II, произведем замену переменных
*=^; (2.3.2)
тогда получим из (2.3.1)
*о-м.
а
— 00
Учитывая симметрию нормального распределения, находим из табл. П. II
0,70 = Ф (0,524), 0,20= 1 —0,80= 1 —Ф (0,842) = Ф (—0,842). (2.3.4)
Подставляя в (2.3.2) найденные значения
2й = 0,524, z2 = — 0,842
и соответствующие им значения
*!=10,8, *2 = 8,6,
получаем два уравнения
^i=~- (« = 1.2),
или, после преобразования и подстановки численных значений,
0,524ст+ц= 10,8, —0,842ст + ц = 8,6.
Отсюда для искомых параметров имеем
10,8.0,842 + 8,6-0,524
1 1,366
= 9,956,
(2.3.5)
(2,3.6)
(2.3.7)
(2.3.8)
Чтобы определить границы симметричного интервала, в пределах которого
окажутся 90% всех проб, нам следует вычислить значения zUt z0,
удовлетворяющие равенствам
Ф(г„) = 0,05, Ф(20) = 0,95. (2.3.9)
Для определения значения zu учтем симметрию функции плотности
вероятности и, используя соотношение (2.2.10), получим
Ф(г„)=1-Ф (-*„) = 0,05, (2.3.10)
т. е.
ф (-ztt) = 1-0,05 = 0,95 = Ф(г0). (2.3.11)
Из табл. П. II посредством интерполяции находим
г0= 1,645. (2.3.12)
Следовательно,
z„=- 1,645.
Преобразуя (2.3.5), получаем
X0 = \i + GZ0t Xu = \i + GZVt (2.3.13)
30
Гл. 1. Элементы теории вероятностей
откуда для искомых границ имеем
x0 == 9,956+1,6111,645 =- 12,606,
ха = 9,956— 1,61Ы,645 = 7,306.
Таким образом, в 90% всех проб содержание соли лежит в пределах от
7,306 до 12,606 г.
Для определения Ф(гя) = 0,01 мы должны отыскать в табл. П. II значение,
соответствующее Ф (—za) = 0,99. Это дает za = —2,326, откуда ха = 6,205.
Следовательно, в 1% всех проб содержится менее 6,205 г соли. Аналогично
для Ф(г0) = 0,999 находим из табл. П. II, что zD = 3,1, и получаем х0= 14,950.
Это означает, что в случае нормального распределения 0,1% всех проб
содержит свыше 14,950 г соли.
2.4. Доверительные интервалы
Из партии изделий отбирается 10 элементов, измерение которых дает
следующие результаты:
* = {5,75 см; 5,71 см; 5,79 см; 5,81 см; 5,72 см; 5,76 см; 5,73 см; 5,71 см;
5,74 см; 5,73 см}.
Определить доверительные интервалы для среднего значения \х и
среднеквадратичного отклонения а, предполагая, что размеры изделий в партии
распределены нормально. Требуемая доверительная вероятность составляет 90%.
Определить границы, если надежность составляет 99%.
Решение
Определим сначала выборочное среднее значение
*=^Х*/=^ПГ см = 5,745 см. (2.4.1)
Эмпирический стандарт находится по формуле
:|/_J_£(J,_;)2= /Щ™ см=0,озз а,
i= 1
(2.4.2)
Для доверительного интервала параметра \xt используя £-распределение
Стьюдента, получаем, согласно ^2.20),
\x-ii\ = t(n-\)~. (2.4.3)
У п
Здесь t (п—1) означает t как функция (п—1).
В случае когда требуемая надежность составляет 90%, находим по табл.
П. III (см. приложения)
f (9) = 1,83.
Тогда из (2.4.3) следует
0 033
| х— и 1 = 1,83 • -!—=г см = 0,019 см. (2.4.4)
]Л0 v '
Таким образом, с надежностью 90% среднее значение лежит в пределах
доверительного интервала
5,726 см < \1 < 5,764 см. (2.4.5)
J 2. Среднее значение и среднеквадратичное отклонение 31
Если надежность должна составлять 99%, то по табл. П. III находим
/(9) = 3,25.
В этом случае имеем
— О 033
\x-\i | = 3,25. -^=- см = 0,034 см. (2.4.6)
Следовательно, среднее значение с надежностью, равной 99%, заключено в
доверительном интервале
5,711 см < ^ < 5,779 см. (2.4.7)
Если гипотеза |д = 5,745 см справедлива, то при большом числе контрольных
выборок, каждая из которых состоит из 10 испытаний, выборочное среднее в
99% случаев будет лежать внутри интервала (2.4.7). Вероятность того, что в
серии из 10 испытаний будет получено среднее значение, лежащее вне
доверительного интервала (2.4.7), составляет 1% (ошибка первого рода). С другой
стороны, следует иметь в виду, что в случае доверительного интервала (2.4.5)
10% всех контрольных серий будут давать выборочное среднее, лежащее за
пределами границ доверительного интервала (если справедлива гипотеза
|ы = 5,745 см).
Доверительный интервал для среднеквадратичного отклонения в случае,
когда надежность равна 90%, находим с помощью табл. П. IV
Lx = 0,78, L2=l,47.
Подставляя эти значения в соотношение
sLx < а < sL2, (2.4.8)
определяющее доверительный интервал для среднеквадратичного отклонения,
и используя (2.4.2), получаем
0,033-0,78 см < а < 0,033-1,47 см.
Отсюда для искомого доверительного интервала имеем
0,026 см < о < 0,049 см. (2.4.9)
Если требуемая надежность составляет 99%, то по табл. П. IV
Lx = 0,64, L2 = 2,08,
откуда на основании (2.4.8) получаем
0,021 см < а < 0,069 см.
2.5*. Уровень значимости при заданной длине
доверительного интервала
При химическом анализе медной руды по выборке объемом я = 21
получено среднее процентное содержание меди * = 3,31%. Вычисление
эмпирического стандарта дало величину s = 0,70%. С какой надежностью определяются
параметры \i и о нормально распределенной генеральной совокупности, если
длина доверительного интервала среднего значения ц и длина доверительного
интервала среднеквадратичного отклонения сг должны составлять
соответственно 0,6 и 0,5%?
32
Г л, 1. Элементы теории вероятностей
Решение
Среднее значение \i нормального распределения и выборочное среднее х
с уровнем значимости а связаны соотношением
|5-ц|< <«(»-!) -у=. (2.5.1)
Вследствие этого доверительный интервал среднего значения имеет длину
А/|г = 2|х—ц| = 2/в(п—1)-р=-. (2.5.2)
Для ^-распределения Стьюдента получаем из (2.5.2) значения функции t(n—\):
t(n-\)=-!g-Vn. (2.5.3)
Подставляя заданные числовые значения, имеем
f(20) = -g^/2r=l,96. (2.5.4)
С помощью табл. П. III (см. приложения) находим посредством интерполяции,
что значению (2.5.4) соответствует надежность
1_а = 93,2%.
Следовательно, среднее значение \а с надежностью 93,2% лежит в
доверительном интервале 3,01% < \i < 3,61%.
Среднеквадратичное отклонение лежит в пределах
Lts <о < L2s. (2.5.5)
Поэтому доверительный интервал среднеквадратичного oiклонения имеет длину
A'a = (Ii-I.i)s.
Отсюда находим разность коэффициентов Lx и L2:
AL(n-l) = L2-L1 = -~. (2.5.6)
В рассматриваемом случае имеем
М (n-.l)==L2_i1 =1^ = 0,71.
Используя табл. П. IV, посредством интерполяции находим, что величина
L (20) = 0,71
соответствует надежности
1—а = Р = 97,9%.
Интерполируя, находим для этого значения коэффициенты Lx и L2 и получаем
с помощью табл. П. IV
Lx = 0,76, 12=1,47.
Отсюда следует, что с надежностью 97,9% параметр а лежит в пределах
доверительного интервала
0,53% <а< 1,03%.
§ 2. Среднее значение и среднеквадратичное отклонение 33
2.6*. Экстраполяция статистических оценок
при изменившихся условиях испытания
При исследовании космических лучей с помощью измерительного зонда
автоматически регистрируется число разрядов в газе. Отдельные измерения
каждый раз проводятся в течение 5 мин. При этом получены результаты,
приведенные в табл. 3. Распределение аппроксимируется нормальным законом.
Какие значения получатся для среднего числа разрядов и для
среднеквадратичного отклонения в пересчете на а) 5 мин, б) 1 мин, в) 1 ч? Какова длина
доверительных интервалов? Уровень значимости а равен 0,01.
Таблица 3
Число разрядов при исследовании космических лучей
т Порядковый номер
интервала времени i
II Число разрядов х;
1
17
2
14
3
19
4
19
5
17
6
22
7
19
8
13
9
22
10
18
11
16
12
20
Решение
Вычислим сначала среднее число разрядов, происходящих в течение
5 мин. Имеем
п
*=тЕ*<=ТТ=18д (2.6.1)
1=1
Таким образом, в течение 5 мин происходит в среднем 18,0 разрядов. Для
выборочного среднеквадратичного отклонения, отнесенного к интервалу в
5 мин, получаем
/2>
-. *)2 _
—{ ="|/уу=2,80. (2.6.2)
Согласно табл. П.III при а = 0,01 имеем
t(n— l) = f (11)==3,11.
Используя (2.6.2), находим отсюда
t(n—\)s 3,11-2,80 ОС1
-L^-=-p=-=2,51. (2.6.3)
Следовательно, для промежутка времени в 5 мин с надежностью, равной 99%,
среднее значение числа разрядов лежит в доверительном интервале
15,49 <(г < 20,51. (2.6.4)
Оценим теперь доверительный интервал для среднего числа разрядов в
случае, когда длительность измерения равна 1 мин. При этом должны
наблюдаться относительно большие колебания, поскольку отдельные отклонения
сглаживаются при их суммировании по большим промежуткам времени.
С помощью соотношения
т
*i=2 хи (i=l> •••» Л)> (2-6-5)
34
Гл. 1. Элементы теории вероятностей
приведенные в табл. 3 числа, характеризующие число разрядов за 5 мин,
можно представить в виде суммы по т = Б измерениям, каждое из которых
проводилось в течение 1 мин. Значения случайной величины ху нам не
известны; однако нам известно среднее значение
п т п
*//= — V У *//=— У */=— х. (2.6.6)
ч тп jL* jLu 'J тп jL* l т v '
i=i /= l i=i
В рассматриваемом случае получаем, что среднее число разрядов за 1 мин
равно
~х 18,0 QC
Введем определение
т
;'=iE*'/=-S c=i.-. »)• (2.6.7)
Если мы представим себе, что каждое из п = 12 измерений разбито на т — Б
измерений, отнесенных к одной минуте, то величины
l~ т ~~~5~
являются средними выборочными значениями для этих п= 12 выборок, каждая
из которых имеет объем т = Б. При этом каждая выборка состоит из
измерений, выполненных за промежуток времени, равный 1 мин. Используя средние
значения, отнесенные к интервалу в 1 мин, можно записать эмпирический
стандарт для чисел разрядов Xi — mx[ за промежуток времени в т минут
в виде
п п
1=1 1=1
Определим эмпирический стандарт отнесенных к 1 мин средних значений
xi = Xi/m следующим образом:
%-У ^=т%^-~хФк
1 t=l
Эту величину следует отличать от эмпирического стандарта s для т — Б
(в минутах), численное значение которого определяется формулой (2.6.2), куда
были подставлены экспериментальные данные из табл. 3. Эти две величины в
соответствии с (2.6.8) и (2.6.9) связаны соотношением
2 «2
%~w- (2-6ЛО)
Согласно теории, изложенной в введении, выборочные средние значения х для
серии выборок объемом т, взятых из нормально распределенной генеральной
совокупности, распределены по нормальному закону, параметры которого
связаны с параметрами генеральной совокупности формулами
* х у т
§ 2. Среднее значение и среднеквадратичное отклонение 35
Пользуясь формулами (2.6.11), запишем среднеквадратичное отклонение для
числа разрядов #/y- в течение 1 мин:
п т
о- = Iim V У — (хи—xif)2 = Vmo-. (2.6.12)
i=\ / = i
На основании этого имеем с учетом (2.6.10)
sXt = Vms^ =—— . (2.6.13)
Ч xt ут '
Подставляя s из (2.6.2) и m = 5, получаем для эмпирического стандарта числа
разрядов за 1 мин
., = ** = 1.2Б2.
*Ч |Л5
Отсюда следует, что
*<д-1)4^«ЗЛ1-^=1.12.
Vn /12
Таким образом, среднее значение числа разрядов в 1 мин заключено в
доверительном интервале
2,48 < |ы, < 4,72.
U
Чтобы найти среднее число разрядов и доверительный интервал, отнесенные
к промежутку времени наблюдения длительностью в 1 ч, полагаем просто
/п = б/бо = 1/12- Из (2.6.6) следует, что среднее число разрядов в 1 ч равно
цо-^Лм, т.е. и0 = 12-18,0 = 216,0.
С помощью (2.6.13) находим среднеквадратичное отклонение
s0=-^=r= У12- 2,80 = 9,699,
у т
откуда следует
1} * =3^-9£9
Vn К12
В результате для доверительного интервала получаем
207,29 < jLi0 < 224,71.
Для определения доверительных интервалов среднеквадратичных отклонений
по табл. П.IV (см. приложения) находим Li = 0,67, L2 = l,90. Используя эти
значения, получаем для времени наблюдения 5 мин
1,87 < or < 5,32;
для 1 мин
0,84 < ах < 2,38
Ч
и для измерения в течение 1 ч
6,50 < а0 < 18,43.
36
Гл. 1. Элементы теории вероятностей
Упражнения
У.2.1. При измерении температуры 0 трех плавильных печей получены
следующие значения: Э(в РС) = {880, 920, 750}. Вычислить среднее
значение и среднеквадратичное отклонение.
У.2.2. При измерении длины партии изготовленных штифтов получены
следующие значения (в см): 1,25; 1,27; 1,22; 1,26; 1,25; 1,29; 1,21.
Определить выборочное среднее значение и эмпирический стандарт
для этой выборки.
У.2.3. В серии измерений содержания соли в морской воде среднее
значение и среднеквадратичное отклонение оказались равными
соответственно ц=1,85% и а = 0,15%. Измерения распределены по
нормальному закону. Какова вероятность получения пробы с
содержанием соли менее 1,5%?
У.2.4. При исследовании содержания углерода в промышленном газе
получено среднее значение 2,4%. Найти среднеквадратичное отклонение
нормального распределения, если в 75% случаев отклонения от
среднего значения составляют менее 10% его величины.
У.2.5. Чему равна вероятность того, что при нормальном распределении
будет получено значение, лежащее за пределами интервала |li ± За?
У.2.6. При измерении напряжения сухих батарей в 10% всех случаев
получается значение, превышающее 4,5 В. В то же время 15% всех
батарей имеют напряжение менее 4,2 В. Вычислить среднее значение
и среднеквадратичное отклонение, предполагая, что имеет место
нормальное распределение. Какова вероятность того, что будет
обнаружена батарея с напряжением а) менее 4 В, б) более 4,7 В?
У.2.7. При проведении серии измерений в 25% всех случаев получается
значение, превышающее 9, и в 40% случаев — превышающее 7.
Вычислить среднее значение и среднеквадратичное отклонение
нормального распределения. В пределах какого симметричного интервала
лежат 99% всех значений?
У.2.8. Из серии цилиндров берутся три пробных образца и измеряется их
диаметр; при этом получаются следующие значения: ^ = 8,18 см,
d2 = 7,88 см и d3 — 7y94 см. Определить выборочное среднее и
эмпирический стандарт данной выборки. Чему равны доверительные
границы среднего значения, если требуемая надежность составляет
а) 90% и б) 99%?
У.2.9. При изготовлении легированных сталей измеряется процентное
содержание углерода в различных пробах. При этом получены
следующие значения: х (в %) = {0,42; 0,44; 0,47; 0,41; 0,44; 0,43; 0,40;
0,43}. Найти выборочное среднее значение и эмпирический стандарт
для данной выборки. Чему равны доверительные границы среднего
значения и среднеквадратичного отклонения при надежности, равной
а) 99%, б) 90%?
У.2.10. Выборка объемом гг = 60 дает выборочное среднее л: = 14,51 и
эмпирический стандарт s = 0,68. Определить доверительные интервалы
для параметров \х и а нормального распределения, если требуемая
надежность составляет 90%, 95% и 99%.
У.2.11*. Для исследования содержания марганца в высококачественном
пуддлинговом железе сделана выборка объемом п — Ъ. При этом
получено выборочное среднее х = 4,53% и эмпирический стандарт
s = 0,40%. С какой надежностью можно принять гипотезу, согласно
которой содержание марганца в среднем превышает 4%, а
среднеквадратичное отклонение составляет менее 1%?
У.2.12*. Для контроля содержания алюминия при кокильном литье из
каждой из 4 одинаковых изложниц взято по 5 проб. Для отдельных
§ 3. Статистическая проверка гипотез
37
изложниц средние значения по соответствующим 5 пробам оказались
равными: ^ = 54,6%, х2 = 52,4%* х3=--53,5%, хА=~-55,1%. Определить
средний стандарт для одной пробы и доверительный интервал для
среднего значения одной пробы при допустимой ошибке, равной 1%.
У.2.13*. При измерении электрического сопротивления 10 отрезков проволоки
длиной / = 8 м каждый получены следующие значения в миллиомах:
235, 242, 237, 243, 240, 240, 242, 239, 238, 244. Вычислить
среднее значение и среднеквадратичное отклонение сопротивления для
проводников длиной 1 м. Какие доверительные интервалы
получатся при допустимой ошибке 1 %?
§ 3. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ.
ПРОВЕРКА РАВНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ (^-КРИТЕРИЙ)
И НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ (^-КРИТЕРИЙ).
ПРОВЕРКА ГИПОТЕЗЫ ОБ ИЗМЕНЕНИИ
ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ (^-КРИТЕРИЙ И /^-КРИТЕРИЙ)
Введение
Если на основании эмпирических данных принимается
определенный закон распределения, то критерий согласия (%2-критерий)
дает возможность проверить выдвинутую гипотезу. Имеющаяся
выборка подразделяется на п разрядов. Пусть kt и ср,-
обозначают соответственно число измеренных значений (частоту)
в каком-либо разряде и частоту, ожидаемую для этого разряда
на основании принятого теоретического закона распределения.
п
При этом выполняется соотношение ^kt = N. Если имеющиеся
эмпирические данные подтверждают гипотезу о справедливости
принятого теоретического распределения, то согласно
^-критерию должно выполняться неравенство
(3.1)
В табл. n.V (см. приложения) приведены значения величины
Xa(f) Для различного числа степеней свободы / и различных
уровней значимости а. Число степеней свободы / равно числу
разрядов, уменьшенному на число неизвестных параметров
теоретического распределения, подлежащих определению по
данным выборки. В общем случае размеры разрядов должны
быть достаточно большими, чтобы в каждом из них было от 5
до 10 элементов.
38
Г л, 1. Элементы теории вероятностей
Пример 8
Если х2-критерий применяется для проверки нормальности распределения,
то должны совпасть эмпирические и теоретические значения таких величин,
как полное число измерений, среднее значение и среднеквадратичное
отклонение. Следовательно, число степеней свободы на три меньше числа разрядов.
Для проверки нормальности распределения Колмогоров
предложил специальный критерий, получивший название
^-критерия. Пусть ht есть доля числа измерений в интервале
Х{ АХ;^Х < Xt + AX;.
Тогда относительное число измеренных значений,
удовлетворяющих условию х <x{ + Axh равно
PixKXi + Ax^F^^hj-=E"F- <3-2)
Теоретическая вероятность F] получается из стандартного
нормального распределения [см. (2.9)]
F] = F* (х( + А*,-) = Ф ( *' + Д^'~ ** ). (3.3)
При применении ^-критерия определяют величину
(3.4)
X=YNmax\F*c— Fc\
Если эмпирические данные подчиняются нормальному закону
распределения, то при заданном уровне значимости а
существует число %а, такое, что должно выполняться условие
X < %QL
В табл. П.VI (см. приложения) приведены значения
Ха для различных вероятностей риска (уровней значимости) а.
Проверка и сравнение параметров двух выборок позволяет
установить, связано ли расхождение этих параметров с
изменением генеральной совокупности за время между двумя
выборками или же оно обусловлено статистическими факторами,
т. е. может быть объяснено случайными отклонениями.
Для проверки средних значений применяется t-критерий
согласия. Если выполняется неравенство
$ 3. Статистическая проверка гипотез
39
то расхождение средних значений для двух выборок Sx (п^ хг, s^.)
и S2(n2; х2, s2) с вероятностью ошибки а приписывается
изменению условий испытаний. Значения ta берутся из табл. П.III
для /-распределения Стьюдента. В противном случае \t\<ta
гипотезу о случайном расхождении нельзя отклонить на
основании сравнения средних значений. Тогда следует произвести
дополнительно исследование дисперсий.
Во многих случаях изменение генеральной совокупности
(например, улучшение качества готовой продукции) заключается
не в изменении среднего значения, а в уменьшении разброса;
применение F-критерия Фишера, основанного на сравнении
дисперсий, позволяет установить, произошло ли изменение
генеральной совокупности или наблюдаемое различие
обусловлено статистическими отклонениями. Рассмотрим отношение
двух эмпирических дисперсий si и si, построенное таким
образом, чтобы меньшая из дисперсий стояла в знаменателе.
Считают, что расхождение обеих величин с уровнем значимости а
связано с изменением генеральной совокупности, если
выполняется неравенство
(3.6)
Здесь f1 = n1—1 и f2 = n2—1 обозначают число степеней
свободы каждой из выборок. В табл. П.VII (см. приложения)
приведены предельные значения Fa(fi9 /2) Для различных
вероятностей ошибки.
Задачи
3.1. Применение критерия согласия (%2-критерия)
к распределению специального вида
При исследовании удлинения стеклянных волокон при разрыве получены
результаты, приведенные в табл. 4а.
Таблица 4а
Разрывное удлинение стеклянных волокон (длин.а волокон
/ = 100 см)
I Порядковый номер i 1
II Разрывное удлинение 9 п
Д/±0,05см z'u
2
2,1
3 4
2,2 2,3
5
2,4
6
2,5
7
2,6
8
2,7
9
2,8
10
2,9
III Число волокон kt 2 14 20 25 36 37 28 20 12 6
40
Гл. 1. Элементы теории вероятностей
Требуется установить, можно ли рассматривать данное распределение как
линейное в соответствии с фиг. 6. Уровень значимости доверительной оценки
не должен превышать 0,01, иными словами, надежность должна быть более 9$%.
H=WQ
*»А1
Фиг. 6. Удлинение
стеклянных волокон при разрыве
(зависимость ожидаемой
частоты ф от разрывного
удлинения Л/).
Решение
Применим %2-критерий согласия. Полное число волокон равно
п
2 k{ = N=200.
i=i
Чтобы получить достаточно большую частоту в каждом разряде, объединим
разряды 1 и 2 в один разряд. Аналогично поступим с разрядами 9 и 10.
Вероятности Я,-, получающиеся согласно принятому закону распределения,
приведены в табл. 46, строка IV. Ожидаемые значения частот ср/ получаются
из них умножением на N = 200 (строка V). В строке VI еще раз приведены
измеренные значения к[ с учетом измененного разбиения на разряды.
Таблица 46
I Порядковый номер i
IV Вероятность Я/
V Ф/ = Л/Я/
VI Эмпирические частоты /?,
VH (*/—Ф/)2
1/2
0,08
16
16
0
3 4
0,10 0,14
20 28
20 25
0 0,32
5
0,18
36
36
0
6
0,18
36
37
0,03
7
0,14
28
28
0
8
0,10
20
20
0
9/10
0,08
16
18
0,25
Отдельные слагаемые суммы
... .V(*f-9.')f = V(fe/-^f)«
%'
q>, *- NPt
ь I
представлены в строке VII. Суммируя их, получаем
Х2 = 0,60.
§ 3. Статистическая проверка гипотез
41
В качестве числа степеней свободы мы должны подставить величину
f = n — 2 = 6. По табл. П.У (см. приложения) находим при уровне
значимости 0,01
Xo,oi(6) = 0,872.
Сопоставляя это с вычисленным значением, имеем
X2 = 0,60<0,872 = xloi(6).
Таким образом, если объединить крайние разряды указанным выше способом,
чтобы обеспечить выполнение требований к числу элементов в каждом разряде,
то гипотезу о линейном распределении можно считать согласующейся с
опытом. Если же крайние разряды i = l и г = 10 рассматривать отдельно от
соседних разрядов, то на основании %2-критерия имеем %2 = 2,68 > 1,65 = Xo,oi(8).
В соответствии с этим из-за краевых искажений гипотезу о линейности
распределения следовало бы отклонить.
Результат применения критерия можно резюмировать следующим образом:
если исключить граничные области, для которых вследствие ограниченности
числа измерений нельзя сделать точной оценки, то гипотезу о линейности
распределения, которой отвечает фиг.* 6, следует считать согласующейся с
имеющимся статистическим материалом.
3.2*. Применение ^-критерия для проверки выборки
большого объема на нормальность распределения
Из набора шаров берется выборка большого объема. Требуемая величина
диаметра шаров составляет х0 = 20,00 мм. При автоматической сортировке
и подсчете шаров получены результаты, приведенные в табл. 5а. Установить,
Таблица 5а
Распределение диаметров в наборе шаров
1 и
Разряд Диаметр, мм
i ^.±0,01
1
2
3
4
5
6
7
8
9
10
11
12
19,90
19,92
19,94
19,96
19,98
20,00
20,02
20,04
20,06
20,08
20,10
20,12
—0,10
—0,08
—0,06
—0,04
—0,02
0
0,02
0,04
0,06
0,08
0,10
0,12
0
1
2
5
14
24
28
23
16
6
1
0
можно ли считать данное распределение нормальным, и вычислить
доверительные интервалы Для среднего значения и среднеквадратичного отклонения,
если требуемая доверительная вероятность (надежность) оценки составляет 99%.
111 IV
Отклонения от заданного l v
значения, мм Частота
(лг*о)±0,01 */
42
Гл. 1. Элементы теории вероятностей
Решение
Полное число подвергнутых проверке шаров составляет, согласно табл. 5а,
п 12
i=\ i=i
Определим сначала выборочное среднее значение
п п
;=£>,• =E*f
i=l
С этой целью умножим указанное в столбце III для каждого разряда
отклонение Х(—х0 на частоту /г/ (столбец IV). Результат приведен в табл. 56,
столбец V. Просуммируем произведения, стоящие в столбце V, и разделим
на полное число испытаний N =120. В результате получим
12 п
** N ..
i=i i=i
=-дГ X ki (Xi-x0) = x— х0.
Таблица 56
1
1
1
2
3
4
5
6
7
8
9
10
11
12
IV
ki
0
1
2
5
14
24
28
23
16
6
1
0
V
(*/-*о)*/. мм
0
—0,08
—0,12
—0,20
—0,28
0
0,56
0,92
0,96
0,48
0,10
0
VI
Х'-Х, мм
0,1195
0,0995
0,0795
0,0595
0,0395
0,0195
—0,0005
—0,0205
—0,0405
—0,0605
—0,0805
—0,1005
VII
(*/-*)**/. мм2
0
0,0099
0,0126
0,0177
0,0218
0,0091
0,0000
0,0097
0,0262
0,0220
0,0065
0
Подставляя заданные числа, находим
п
— 1 V* 2 34
x~~Xq=z'n'2u М*/—*o)=-j2Q- мм = 0,0195 мм.
i- 1
Это означает, что среднее значение
* = jt0 + 0,0195 мм = 20,0195 мм
почти на 0,02 мм отклоняется от заданной величины 20,0 мм. Для определения
эмпирического стандарта s сначала вычислим разность между средним по
разряду Х[ и выборочным средним х (столбец VI), возведем эти разности
в квадрат и полученные значения умножим на стоящие в столбце IV частоты fy.
§ 3. Статистическая проверка гипотез
43
Полученные результаты помещены в столбце VII. Суммируя, получаем
12
2 М*/ —*)2 = 0,1355 мм2,
i=i
откуда для искомого эмпирического стандарта имеем
-= j/^ЕМж,-*- ]/^мм = 0,0337 мм.
i
Доверительный интервал среднего значения при заданном уровне значимости
а = 0,01 определяется величиной
| х—\л | = t (119) ._L==2,62 °;^3П37 мм -0,00807 мм.
|Л20 10»95
Следовательно, среднее значение заключено в интервале
20,011 мм < |li< 20,028 мм.
Для определения доверительного интервала среднеквадратичного
отклонения находим по табл. П.IV
Lx = 0,87, /-2=1,17.
На основании соотношения Lxs < о < L2s отсюда следует
0,87-0,0337 мм < а < 1,17-0,0337 мм.
Окончательно имеем
0,0293 мм < о < 0,0395 мм.
Несмотря на большое число испытаний (/V— 120), длина доверительного
интервала составляет около х/4 величины эмпирического стандарта.
Для решения вопроса о том, можно ли данное распределение
рассматривать как нормальное, нам следует в соответствии с Х-критерием Колмогорова
выяснить, выполняется ли неравенство
VNmax\Fi-Fi\ < Яа.
Здесь F( = F (л^+Дл;) обозначает измеренную, a F* —F* (#/ + Дя)—
теоретическую функцию распределения. Параметр Ка берется из табл. П.VI (см.
приложения). При заданном уровне значимости 0,01 имеем Ха = 0,44.
Сначала определим значения теоретической функции распределения.
С этой целью посредством преобразования
X— Li
Z = £■
а
перейдем к стандартному нормальному распределению. При определении
функции распределения нам следует относить значения к правой границе
интервала. Следовательно, если 2Дл: обозначает длину интервала, то
определению подлежат величины
Xj + Ax — ii
*'- о *
Используя найденные значения параметров
li = 20,0195 мм, а = 0,0337 мм
и значение Д* = 0,01 мм, получаем результаты, приведенные в табл. 5в,
Гл. 1. Элементы теории вероятностей
1
i
1
?,
Я
4
5
6
7
8
9
10
11
12
II
X/, мм
19,90
19,92
19,94
19,96
. 19,98
20,00
20,02
20,04
20,06
20,08
20,10
20,12
VIII
21
-3,25
-2,66
— 1,07
— 1,46
—0,87
—0,28
0,31
0,90
1,50
2,09
2,69
3,28
IX
F*t=0(2i)
0,001
0,004
0,019
0,072
0,192
0,390
0,622
0,816
0,933
0,982
0,996
0,999
X
0
1
3
8
22
46
74
97
113
119
120
120
XI
Fi
0
0,008
0,025
0,067
0,183
0,383
0,617
0,808
0,942
0,992
1,000
1,000
Таблица 5в
хп
\prFU
0,001
0,004
0,006
0,005
0,009
0,007
0,005
0,008
0,009
0,010
0,004
0,001
столбец VIII. С помощью табл. П. II находим соответствующие значения
стандартной нормальной функции распределения Fi ~ Ф (г,) (столбец г
IX). В столбце X указаны величины
2 bj=.NFit
определяемые с помощью табл. 5а, столбец IV; столбец XI содержит
вычисленные с использованием этих величин значения измеренной функции
распределения F(. В столбце XII приведены абсолютные величины разностей
между измеренными и вычисленными значениями функции распределения.
Из последнего столбца находим
max\ Fi—Fj | = 0,010.
Отсюда следует
VN max | Ff—Fc \ = 10,95-0,010 = 0,1095.
Полученное значение меньше заданной величины Ла = А, =0,44. На
основании этого рассмотренное распределение можно считать нормальным.
3.3. Критерий для сравнения средних значений нескольких выборок
Из латунной плавки берется выборка. Она дает следующие результаты
для процентного содержания меди:
^ = {63,6; 65,0; 64,1; 64,4; 63,3; 64,5; 65,7; 64,6}.
Из следующей плавки также берется выборка; при этом процентное
содержание меди составляет
х2 = {65,2; 63,9; 65,7; 64,4; 66,0; 64,8}.
Нужно установить, является ли расхождение выборочных средних значений
принципиальным (значимым) или же оно может быть объяснено случайными
отклонениями. Требуемая надежность вывода 99%.
§ 3. Статистическая проверка гипотез
45
Решение
Будем предполагать, что обе выборки с объемом, равным соответственно
пх и п2, выборочными средними х1 и х2 и эмпирическими стандартами sx и
s2 взяты из одной и той же нормально распределенной генеральной
совокупности G. Вследствие этого при повторных выборках Slv и 59v выборочные
средние xlv и x2v также должны быть распределены нормально. То же
самое справедливо и для разностей
xv = x\v x2v* (3.3.1)
которые должны принадлежать нормально распределенной случайной
величине со средним значением
Для дисперсии этого распределения имеем
т
a!-J = lim 5ГТ И l(xlv-~x2v)-(^i-^W- (3-3.2)
v= 1
Преобразуя скобки и перемножая, находим
l(*iv-*2v)-(Hi-H2)]2=-[(*iv— Vi) — (x2v~ ^2)Ia =
= (^lv —Hj)2-t (^v-N)2 — 2(*1v — ^i)(*2v — ^2).
Выборочные средние xiv и x2v не зависят друг от друга. То же справедливо
и для разностей xlv — щ и x2v — |и2» иными словами, отклонения выборочных
средних *lv и х2у} от средних значений \хг и \i2 также являются
независимыми. Вследствие этого колебания выборочных средних около средних
значений компенсируются, так что выполняется равенство
т
Лт.йгпЕ (*1v-h.)(*2v-i*.)=o
v=l
(см. § 4). Поэтому можно записать
т
°2- " = Iim -гЦХ [(^iv-^)2 + ^2v-^)2] = a? + ^2-
"lv~*2v m-*oom— 1 ^
Используя формулу (2.13), связывающую эмпирический стандарт выборок
объемом п со среднеквадратичным отклонением генеральной совокупности,
получаем окончательно
2
Iv
Величина
_ _п2 , 02__2/J_ , J_\ (3.3.3)
*i —*2 _ ^i—^2 (3.3.4)
Z=
4,-х, UK i//il-h i/яа
a- - oyl/ni+ \m\
подчиняется, следовательно, стандартному нормальному закону
распределения. Далее, сумма
,,_(*i-l)s2 , ("2-1)4
о» "*" о* (3.3.5)
46
Гл. 1. Элементы теории ее роят нос те и
распределена по закону х2, поскольку оба слагаемых удовлетворяют этому
распределению. J
Для числа степеней свободы этого распределения имеем
/ = /i + /2 = пх + Щ — 2. (3.3.6)
В результате для величины
t=ym (3-3-7)
получаем /-распределение Стыодента с / степенями свободы. Подставляя
(3.3.4)—(3.3.6) в (3.3.7), приходим к выражению
<(/)=,/- , =гУ V Л "l^a- (3.3.8)
Для распределения с f = n1-\-n« — 2 = 8 + 6 — 2= 12 степенями свободы при
уровне значимости а = 0,01 находим по табл. П. III
* =* =3,06.
a o,oi '
Таким образом, если справедлива гипотеза о случайном расхождении
параметров двух распределений, то вычисленная по формуле (3.3.8) величина
t (/) должна удовлетворять условию
Используя заданные числа, получаем в рассматриваемом случае:
*1 = 64,4%, х2 = 65,0%, Sl2 = 0,577, s\ = 0,628.
Отсюда следует
/5-0,628 + 7.0,577 У 14
Таким образом, имеем
*</) = 1,43<3,06=*в>и,
т. е. /-критерий не позволяет с требуемой надежностью 99% принять
гипотезу о том, что расхождения средних связаны с принципиальными
различиями. Следовательно, отклонения могли возникнуть в рамках нормального
рассеяния.
3.4. Критерий для сравнения выборочных дисперсий
Требуется установить, можно ли отнести две выборки, рассмотренные
в задаче 3.3, к одному и тому же нормальному распределению на основании
сравнения эмпирических дисперсий этих выборок. Допустимая степень риска
составляет 1%.
Решение
Первая выборка имеет объем ггх = 8, выборочное среднее *1 = 64,4 и
выборочную дисперсию sl = 0,577. Для второй выборки с гг2 = 6 было получено
^"2 = 65,0, sl = 0,628. Выборочные средние не представляют интереса для
^-критерия Фишера.
Для проверки гипотезы Ог = о2 построим отношение
J|_=01628 =
'-.? 0,577 1,иУ-
§ 3. Статистическая проверка гипотез
47
Из табл. П. VII при уровне значимости а = 0,01 для чисел степеней свободы
/1 = щ— 1 =7 и /2 = п2 —1=5 находим
Ли» (5; 7) = 7,46.
Таким образом, имеем
/7=1,09 < Лиц (5; 7) = 7,46.
Итак, гипотеза о принадлежности обеих выборок к одному и тому же
нормальному распределению не может быть отклонена и на основании сравнения
дисперсий.
3.5. Статистическое сравнение точности
различных методов измерения
Многолетнее применение некоторой методики исследования наличия
радиоактивного изотопа дает среднее значение 0,104%. Дисперсия составляет
0,017%. Вводится новая методика измерения, которая в 17 испытаниях
дает такое же среднее значение, однако дисперсия при этом составляет 0,043%.
Требуется установить, является ли это расхождение случайным или оно
связано с тем, что вторая методика дает возможность осуществлять более
точный анализ. Требуемый уровень значимости составляет менее 0,005.
Решение
Вычисляем отношение дисперсий
По табл. П. VII находим при уровне значимости а = 0,005
Л».оов06; оо) = 1,64.
Таким образом, имеем F > FQ оо5.
С вероятностью ошибки менее 0,5% можно утверждать, что новая
методика измерения лучше отображает генеральную совокупность, т. е. позволяет
получать более точные данные о содержании радиоактивного изотопа.
Упражнения
У.3.1. При изучении колебаний напряжения в электрической сети
получены результаты, приведенные в табл. 6.
Таблица 6
Колебания напряжения
Время суток
Напряжение, В
0ч
210
Зч
205
6ч
195
9ч
200
12ч
210
15ч
220
18ч
190
21ч
210
Установить, может ли это распределение при уровне
значимости 0,10 рассматриваться как равномерное.
48
Гл. L Элементы теории вероятностей
У.3.2. Исследование обрывов ленты машинами дает в течение одного дня
для отдельных машин следующие значения:
14, 17, 15, 18, 17, 15, 18, 15, 14, 17.
Установить с помощью х2_кРитеРия> может ли это
распределение рассматриваться как равномерное.
У.3.3. При определении твердости шлифовальных кругов получены
результаты, приведенные в табл. 7.
Таблица 7
Твердость шлифовальных кругов
Твердость х по Шору
Частота к
Н±1
41
13±1
48
15±1
51
17±1
53
19±1
57
а) Установить с помощью х2-критерия, можно ли данное
распределение рассматривать как равномерное; б) исследовать справедливость
приближенного выражения к = 2х-\-20; в) произвести аппроксимацию
по методу наименьших квадратов и применить к результату %2-критерий.
У.3.4*. Из партии изделий берется выборка объемом п = 41. В табл. 8
приведены отклонения от заданного размера д:0 = Ю,0мм.
Таблица 8
Отклонения от заданного значения
Разряд i
Разность (Д ±0,05),
мм
Частота /г/
1
-0,3
1
2
-0,2
4
3
-0,1
8
4
0
16
5 6
0,1 0,2
7 3
7
0,3
2
Установить, с какой степенью надежности данное распределение
можно считать нормальным.
У.3.5*. Определение радиуса действия ионизирующего излучения приводит к
среднему значению 6 см при эмпирическом стандарте, равном 1 см.
Всего проведено 100 измерений, при этом получено распределение,
представленное в табл. 9.
Таблица 9
Радиус действия ионизирующего излучения
Радиус действия, < 4>5 5±05 6±0>5 7±05 8±0>5
Частота, % 10 20 30 25 15
§ 4. Корреляционное исчисление и корреляционный анализ 49
Определить, можно ли данное распределение рассматривать как
нормальное (а = 0,20).
У.3.6. При изготовлении томпак-сплава взяты две выборки. Первая выборка
состоит из 4 проб. Для содержания меди получено среднее значение
х1 = 7\,4%, эмпирический стандарт составляет s1=l,6%. Вторая
выборка, взятая через большой промежуток времени, состоит из
5 проб; при этом выборочное среднее равно *2 = 74,3%, а
эмпирический стандарт s2= 1%. Выяснить, связано ли расхождение с
изменением условий испытаний.Требуемая надежность оценки составляет 99%.
У.3.7. Выборка объемом ^ = 26 дает при измерении модуля упругости
никелевых сталей выборочное среднее значение ^ = 20 462 кгс/мм2.
Величина эмпирического стандарта оказалась равной st= 160 кгс/мм2.
Для выборки объема п2=12, взятой в более поздний момент времени,
получены выборочное среднее х2 = 20 280 кгс/мм2 и стандарт
s2 = 250 кгс/мм2. Вычислить уровень значимости, при котором это
расхождение может быть объяснено случайными отклонениями в
рамках нормального рассеяния.
У.3.8. Сравниваются два способа измерения. Первый в 15 выборках дает
среднее значение ^ = 4,50 и эмпирический стандарт 5Х = 0,35.
Второй в 21 выборке дает соответственно значения лг2 = 4,48 и s2 = 0,87.
Определить, является ли расхождение средних случайным и можно
ли считать точность обоих методов одинаковой. Уровень значимости
составляет а = 0,01.
У.3.9. Измерение температуры в различных точках стального цилиндра
производится двумя способами. При первом способе измерения
выполняются в 5 точках, при втором — в 9. Для средних значений
в обоих случаях получается одинаковая величина, однако в первом
случае стандарт оказывается равным sx = 9,25°С, а во втором s2=2,15°С.
Выяснить, являются ли эти расхождения случайными или же они
вызваны принципиальными различиями.
У.3.10. Для исследования уровня шума каждый час производится выборочное
измерение. В 10 измерениях получено среднее значение 95 дб,
среднеквадратичное отклонение равно 10 дб. Непрерывная запись уровня
шума дает среднее значение 92,5 дб и среднеквадратичное отклонение
17 дб. Установить, находится ли расхождение в пределах
статистических отклонений. Уровень значимости а составляет 0,01.
§ 4. КОРРЕЛЯЦИОННОЕ ИСЧИСЛЕНИЕ И КОРРЕЛЯЦИОННЫЙ АНАЛИЗ.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ.
ПРЯМАЯ РЕГРЕССИИ
Введение
Корреляционное исчисление изучает статистическую
зависимость между двумя случайными величинами х и у, например
влажностью воздуха и его давлением, уровнем шума и числом
несчастных случаев на производстве, электрической
проводимостью и числом ионизирующих столкновений в плазме и т.д.
Если ktj обозначает частоту появления пары значений xh yh
то выражения
*/, = 2*</ и^/=2% (4.1)
/ i
50
Гл. 1. Элементы теории вероятностей
представляют частоту появления соответственно значения х{ и
значения #у-. Полное число наблюдений равно
i г И
Среднее значение и дисперсия случайных величин х к у
определяются по формулам
1
* =7 £*/**" У=т£^/' (4-2)
i /
Коэффициентом ковариации, или корреляционным моментом,
распределения двух случайных величин а: и у по определению
называют величину
3j(*i—x)(yj—y)
ч — ч
*"- п-\
(4.4)
Коэффициент ковариации sxy может принимать и отрицательные
значения.
Для аппроксимации измеренных значений х£, у( полиномом
т-й степени
т
7=2 av*v (4.5)
v= 0
применяют в простейшем случае метод наименьших квадратов
Гаусса. Коэффициенты av определяются из условия, что сумма
квадратов
2kv/ (Yj-yj? = 2 ku ( 2 avxj-уУ (4.6)
i i,j \v=0 /
должна быть минимальной. Для этого должны выполняться
т + 1 условий
W- Е kvi (Y,-VjY = 2 £ ku ( £ aJt-y\ xf = 0
(|i = 0, 1, ...,m), (4.7)
из которых следует система алгебраических уравнений
т
v= 0 i, j t.j
§ 4. Корреляционное исчисление и корреляционный анализ 51
При приближенных вычислениях принято писать
[ktrfyf]=2WуЬ Ml=SM • [*г] =2 *?• (4-9)
t. /
*,/
Пользуясь этой системой записи, можно представить решение
системы уравнений (4.8) в виде
[*,7*?] ... [*,7*y+i] [*,,*» *у] [Лу^у+8] ... [*|7*™+«]
[/г/уЛ^] ... [fe^+v-1] [у^Уу] [^у^+^Ч ■. • [fry*?*]
tfv =
[*,y*J 1
... [Л/y^v-lJ
.. [Л,у*у]
[*/у*Л
[*/#*/v+1]
[RijXi
[kijxy+1] [£/ул:У+2] ... [Л/удс/«+«]
(4.10)
[kfjXf] . . . [kijXf^-Ц [kijXtn+V] ... [kijX^]
Вычисление коэффициентов av обычно является чрезвычайно
длительным процессом и при приближениях высоких порядков
его целесообразно осуществлять с помощью ЭВМ.
Обычно сначала пытаются аппроксимировать эмпирические
данные прямой. При этом степень линейности зависимости
между двумя случайными величинами х и у характеризуется
коэффициентом корреляции
. *ху
\ki'j{Xi — x)(yj—y)]
**sv V\kix to- xf\ [kyj (yj-yY]
(4.11)
Его величина ограничена пределами
— 1<г<1
(4.12)
(см. У.4.11). В случае |г| = 1 все измеренные значения х,-у.
лежат на одной прямой, называемой прямой регрессии. Если
|г|<1 и выполняется неравенство
m
\г
_
•/•2
-Уп-
-%> ta
(4.13)
52
Г л, 1. Элементы теории вероятностей
то с вероятностью ошибки а можно считать, что случайные
величины х а у связаны линейной зависимостью. Значения ta
приведены в табл. ПЛИ (см. приложения). На фиг. 7 указаны
коэффициенты корреляции для различных распределений.
о
о о
• о°
Фиг. 7. Коэффициент корреляции г для различных распределений.
Пример 9
Сведения о толщине снежного покрова и облачности в горной местности
в канун нового года, передаваемые из поколения в поколение в течение ста
лет, выглядят следующим образом:
нет снега, безоблачное небо (Х — 0, Y — 0) — 7 раз,
нет снега, сплошная облачность (Х = 0, Y=\) — 3 раза,
толщина снежного покрова 1 м, безоблачное небо (Х=1, К=0) — 63 раза,
толщина снежного покрова 1 м, сплошная облачность (Х=\,
У=1) —27раз.
Отсюда следует, что средние значения равны дс = 0,90, # = 0,30, т. е. число
снежных и облачных дней равно соответственно 90 и 30%. Для
корреляционного момента получаем
sxy= ^ (0,07• 0,9• 0,3—0,03• 0,9• 0,7—0,63- 0,1 • 0,3+0,27• 0,1 • 0,7) = 0.
Таким образом, коэффициент корреляции г также равен нулю. Следовательно,
оба события, т. е. толщина снежного покрова и облачность, являются линейно
независимыми.
Параметры прямой регрессии
Y = aQ + a1x или Y = a + bx или Y = ay.x + by.xx (4.14)
определяются методом наименьших квадратов. В соответствии
с этим получаются два уравнения [ср. (4.7)]
Ж" £ ку/ <У/-У/Г = 2 &7 К + (hXt-yj) = 0, (4.15)
/ I, /
Ж- £ kvJ <У/-У/)% = 2 Е kU (ао + "i*i-Vj) *i = 0. (4.16)
/ i. i
Пользуясь формулами (4.1) и (4.2), получаем из (4.15)
— у + а0 + а1х = 0. (4.17)
Следовательно, прямая регрессии проходит через центр тяжести
точечного множества xh у(.
§ 4. Корреляционное исчисление и. корреляционный анализ 53
Вычтем из уравнения (4.16) уравнение (4.15), предварительно
умноженное на х. Кроме того, введем в каждую скобку под
знаком полученной таким способом суммы выражение (4.17)
с соответствующим знаком. В результате получаем
2 *,/ \У-У/ + <h (*, -х)\ (xt-x) = 0. (4.18)
Используя равенства (4.1) —(4.4), находим отсюда окончательно
решения системы, уравнений (4.15) и (4.16):
■ [*//ЫИ1=д ,у 9)
[*/*(*,—*)8J s* si'
ylkixxU—xlkijXiyj] - Sy - {Л om
a0 = a = =^—— = у— г-У-х. (4.20)
Эти решения можно получить также путем преобразования
общего решения (4.10).
Прямая регрессии (4.14) называется регрессией у
относительно х. Она определяется выражением
которое означает, что сумма квадратов отклонений значений у
от рассчитанных по уравнению прямой регрессии Y = аух + Ьухх
является минимальной.
Если прямая регрессии определяется из условия
8 2*/^-*,)» = 0, (4.22)
i
т. е. если сумма квадратов отклонений величины х от прямой
регрессии
Х = аху + Ьхуу (4.23)
должна быть минимальной, то для регрессии х относительно у
находим по методу наименьших квадратов
аху=~х-г^уу (4.24)
Таким образом, имеет место соотношение
ЬуАу=-^г = г\ (4.26)
х у
54
Гл. 1. Элементы теории вероятностей
Задачи
4.1. Корреляция двух случайных величин
Исследуется содержание калийных солей и органических веществ в
технической воде. Значения частот в различных разрядах концентраций,
полученные на 100 пробах, приведены в табл. 10. Исследовать корреляцию между
появлением калийных солей и органических веществ. Найти прямую
регрессии.
Таблица 10
Результаты анализа технической воды на содержание
калийных солей и органических веществ
i
Содержание
органического
вещества */,
мг/л
1 1±1
2 3±1
3 5±1
4 7±1
/
1±1
7
9
5
2
2
Содер
3±1
8
13
7
4
3
жание
5±1
9
9
6
1
4
калийных
7±1
7
5
2
-~~
5
солей у[,
9±1
2
2
—
—
6
, мг/л
11±1
1
1
—
—
kix
34
39
20
7
kv/ 23 32 25 14 4 2 100
Решение
Обозначим средние значения ддя отдельных интервалов содержания
органических веществ и калийных солей через Х( и yj соответственно. Суммируя
измеренные значения &,у, указанные в одной строке
/I «!y==^/jf»
/
получаем частоту появления значения */. Складывая величины, стоящие
в одном столбце, т. е. находя сумму
2j kij — kyj,
с
получаем частоту появления значения yj. Вычисленные значения k(x и kyj
помещены соответственно в крайнем правом столбце и в нижней строке
табл. 10. Полное число проведенных испытаний равно
i. i i
§ 4. Корреляционное исчисление и корреляционный анализ 55
Для средних значений находим
lv\ 0 Л 1
'• = — X ki**i= 3'°» У = 7Г X *W = 4'°*
л::
п <*—* " п
1
Используя эти величины, получаем выражение для коэффициента корреляции
г — -
^iki/(xi—x)(yJ—y)
sxv ifi
Sy т/Е*'* (Xi ~X)2 ^ kyj'iyi~~y)2 '
Здесь имеем
2A//(*«-3l0)(if/-4,0) = 99sJ(B = -92,
t, i
2*/*ta-3) = 99si = 328,
i
2J^y(yy-4)=99sJ = 588.
/
Отсюда коэффициент корреляции
r = i*jL = ~92 =^0>209,
s^j, /588-328
Чтобы применить /-критерий, вычисляем величину
и получаем
\t \= _&= /98 = 2,11.
/1—0,209»
Принимая доверительную вероятность Р = 0,95, находим по табл. П III пои
/ = 7г—2 = 98: ' F
^о,об — 1»99.
Следовательно,
\t | = 2,11 > 1,99 = ^0,о5.
Это означает, что, несмотря на незначительную величину коэффициента
корреляции г, между содержанием органических веществ и содержанием
калийных солей с доверительной вероятностью 0,95 имеет место корреляция.
Определим регрессию Y относительно X. Наклон прямой регрессии
определяем из уравнения
2 kij (*i—*) (У/ — У) _ Q9
Далее, используя соотношение
а0 = а = у—Ьх,
56
Гл. 1. Элементы теории вероятностей
получаем
а = 4,0 + 0,28- 3,0 = 4,84.
Следовательно, уравнение прямой регрессии имеет вид
у = — 0,28*+4,84.
В соответствии с этим высокое содержание органических веществ в общем
случае отвечает низкому содержанию калийных солей (фиг. 8).
U
К
Фиг. 8. Прямая регрессии
у— — 0,25,v + 4 для задачи о
содержании органических веществ х
и калийных солей у в технической
~**х воде.
10
4.2. Корреляция между ошибками изготовления
и ошибками измерения
На испытательном стенде регистрируется разброс значений сопротивлений
в готовой партии; при этом получается величина сг = 0,15 Ом. Путем
исследования используемых измерительных приборов установлено, что последние
при измерении одного и того же сопротивления дают среднеквадратичное
отклонение оу=^0,08 Ом. Многолетний анализ контрольных измерений с помощью
прецизионных измерительных приборов показывает, что между ошибками х
при изготовлении сопротивлений и ошибками у при их измерении имеет место
корреляция, описываемая коэффициентом корреляции г = 0,40. Найти отсюда
среднеквадратичное отклонение <j# изготовленных сопротивлений.
Решение
Дисперсия суммы или разности двух случайных величин для выборки,
содержащей п пар значений, равна
1
^ГД1^("'' ± yJ~x Т У)2 =
/./
=;rh X *'/[(*'~ *г+1у/-у)* ± 2 (*/-*) (у/-уп- (4-2Л>
'. /
ff 4. Корреляционное исчисление и корреляционный анализ 57
Подставляя в (4.2.1) коэффициент корреляции (4.11) и дисперсию (4.3),
получаем при п -*■ оо
, = ol + ol ±2гохоу
(4.2.2)
Отсюда видно, что в отсутствие корреляции дисперсия суммы или разности
двух случайных величин равна просто сумме соответствующих дисперсий.
В рассматриваемом случае имеем г = 0,40. Положительный знак
коэффициента корреляции означает, что измерительный прибор завышает ошибку
изготовления. В соответствии с (4.2.2) дисперсия измеренных значений равна
a" = o5+,, = o2 + aJ + 2r охоу. (4.2,3)
Неизвестной величиной здесь является среднеквадратичное отклонение вх
изготовленных сопротивлений. Разрешая уравнение (4.2.3) относительно этой
величины, получаем
ох = )/'о*-(\-г)*о2у-гоу.
Подставляя числовые значения, находим среднеквадратичное отклонение
изготовленных сопротивлений:
ох= /0,152 — (1—0,16).0,082 — 0,40-0,08 = 0,10 Ом.
4.3. Нахождение прямой регрессии, проходящей
через эмпирические точки
При измерении зависимости предела прочности при растяжении от
температуры для меди высшей чистоты получены результаты, представленные
в табл. 11.
Таблица 11
Предел прочности при растяжении для меди
высшей чистоты
Порядковый номер i
Температура д:/, °С
1
0
2
50
3
100
4
150
5
200
6
300
7 8 9 10
40Q 500 600 700
Предел прочности 23,3 21,0 19,2 16,4 15,5 13,3 9,4 5,9 4,1 1,9
при растяжении *//,
кгс/мм2
Определить коэффициент корреляции и выяснить, имеется ли корреляция
между этими двумя величинами.. Найти уравнение прямой регрессии.
Уровень значимости а не должен превышать 0,001,
58
Гл. /. Элементы теории вероятностей
Решение
По определению коэффициент корреляции равен
_ lki/(Xi — x)(yJ—'y)] _ sxy
Vlkix(x-x)*\lky/(y-~y)*} sxsy '
Будем рассматривать величины xt- и yj как случайные переменные. При этом
на основании проведенных измерений следует положить
, _ J 0 при / Ф /, а также при i > 10 или / > 10,
lJ~\ 1 при i = jt если /^10.
Для этого частного случая общие формулы (4.3) переходят в уже известные
нам формулы (2.11):
i= 1 i = l
Согласно (4.4), корреляционный момент равен
2 (Xi—x)(yi—~y)
*у п—1
а для коэффициента корреляции в соответствии с (4.11) получаем
- Jj(Xi—x)(y£—lj)
Sy y^xi-xy^yr
-У?
Вычислим сначала средние значения, используя данные, приведенные в табл. 11.
Имеем
7=--300, 7=13,0.
Отсюда для дисперсий получаем
2 1 ^ t _в 525 000
si = i2(^x)-=^? = 58333.3....
^•=1
^ = ■§-2^-^ = ^ = 84,601....
4=1
а для корреляционного момента
1 1° -15 980 177._
sxy =~д 2^ (xi—x) (У1— У) = g ="~ '
t = i
Вычислим коэффициент корреляции:
sxv —15 980
r=—fL= # =— 0,9941.
sxsy /525 000-492,22
§ 4. Корреляционное исчисление и корреляционный анализ 59
Чтобы определить, связаны ли величины X и У корреляционной зависимостью,
воспользуемся в соответствии с ^-критерием выражением
Используя вычисленные значения, получаем
Щ= /-9941 ^8 = 25,84.
]Л—0,99412
С помощью табл. П. III находим
4ooi(8) = 5,04.
Таким образом,
|/1 = 25,84 > 5,04=/o.oei (8).
Следовательно, с вероятностью ошибки менее 0,1% можно считать, что
случайная величина У и температура X в пределах рассмотренного интервала
от 0 до 700° С связаны линейной зависимостью.
Параметры прямой регрессии определяются по формулам
— — sxy , sy sxy
--а0 = у—х—г, b = a1 = r—=—2-
SX SX $x
Подставляя найденные числа, получаем
а = а0= 13,0 + 300^ = 22,13, а, = Ь = - 300^ =- 0,0304.
Таким образом, прямая регрессии описывается уравнением
у = — 0,030д; + 22,1.
Отсюда следует, что предел прочности при растяжении падает с повышением
температуры.
4.4. Корреляция после замены переменных
Исследуется прохождение рентгеновских лучей через стальные пластинки.
Для определения требуемой интенсивности падающего пучка интенсивность
прошедшего излучения всякий раз приводится к некоторому заданному
постоянному значению. Измеряется зависимость требуемой экспозиционной
дозы z/ от толщины стальных пластинок */. Полученные пары значений
приведены в табл. 12 а. Исследовать зависимость экспозиционной дозы от
толщины стальных пластинок и определить корреляцию.
Таблица 12а
Зависимость экспозиционной дозы от толщины
стальной пластинки
I
II
Порядковый номер /
Толщина пластинки Х[, мм
1
60
2
80
3
100
4
120
5
140
6
160
III Экспозиционная доза zh мА-ч 304 502 855 1425 2390 4015
60
Гл. /. Элементы теории вероятностей
Решение
Снова будем рассматривать обе измеряемые величины как случайные
переменные. Экспериментальные данные не указывают на наличие линейной
зависимости. Поэтому прологарифмируем значения экспозиционной дозы и
введем для полученных таким образом величин обозначение у{.
Значения *// приведены в строке IV табл. 12 6 (фиг. 9).
z
k
Фиг. 9. Экспозиционная доза г
рентгеновских лучей,
необходимая для просвечивания стальной
пластинки толщиной х.
I Порядковый
IV yi = \gzi
V Х[ — х
VI yi-~y
номер i
1
2,4829
-50
—0,5590
2
2,7007
—30
—0,3412
Таблица 126
3 4 5 6
2,9320 3,1538 3,3784 3,6036
— 10 10 30 50
-0,1099 0,1119 0,3365 0,5617
Образуем регрессию значений у относительно х. Для средних значений
имеем
^=110, 7=3,0419.
Теперь можно определить значения величин Х(—х и */'/ — у. Они помещены
в строках V и VI табл. 12 6. С помощью этих значений вычисляем параметры
прямой регрессии:
2(*/—х)(У1—У) 7ft ,R
Ь = Щ =74£8 = 0,0112,
2 (*,—*)*
/-1
7000
а = у— ^=3,0419 — 0,0112-110= 1,8099
§ 4. Корреляционное исчисление и корреляционный анализ 61
Таким образом, уравнение прямой регрессии имеет вид
0=1,81+0,0112*.
Наконец, вычислим коэффициент корреляции
sxy Z(*f—*)(У/— У)
sxsy V^ (Xi—xy 2 (yt—У)2
Используя уже полученные промежуточные результаты и табл. 12 6, находим
г__ ^8,584 =Q999
/7000 /0,8822
Проверка на наличие корреляционной связи с помощью /-критерия дает
t= г^ }ГК=2 = ^&г /1 = 44,70.
]Л-^г2 /0,002
По табл. П. III при уровне значимости 0,001 имеем
*o.ooi(4) = 8f61 < / = 44,70.
Таким образом, между толщиной х стальной пластинки и логарифмом y = \gz
экспозиционной дозы имеет место практически строгая линейная зависимость.
Отсюда с точностью до незначительных отклонений получаем
экспоненциальную зависимость между толщиной пластинки и экспозиционной дозой:
г = \0У = е]п 10 <в+**> =64,55е°'02579\
4.5*. Аппроксимация корреляционной зависимости между двумя
случайными величинами кривой второго порядка
R результате проведения я =100 анализов с целью определения
относительного содержания водорода и азота в буроугольном полукоксе получены
данные, представленные в табл. 13 а. Определить по методу наименьших
квадратов аппроксимирующую кривую Y = а0-\-а1х-\-а2х2.
Таблица 13а
Относительное содержание Н2 и N2 в буроугольном полукоксе
(в весовых процентах)
L
1
2
3
4
5
***
X
2,5 ± 0,125
2,75 ± 0,125
3,0 ± 0,125
3,25 ±0,125
3,5 ±0,125
/=1
ю
о
о
аТ*4"1
^} *•
Z о"
2
2
9
3
2
2
ю
о
о
-н
ю
о
1
4
17
3
1
3
ю
о
о
-н
to
о
1
2
16
2
2
4
ю
о
о
-н
ь-
о
1
2
9
2
1
5
ю
о
о
-н
00
о
1
2
6
1
—
6
ю
о
о
-н
О
о
_
1
2
1
1
7
ю
о
о
-н
о
-
__
1
2
—
—
я
-й;
6
14
61
12
7
kvf 18 26 23 15 10 5 3
62
Гл. 1. Элементы теории вероятностей
Решение
Сначала вычислим средние значения по формулам
(4.5.1)
(4.5.2)
t. / i
При заданных числах получаем
7=3,00, 7=0,6.
Для упрощения численных расчетов рассмотрим вместо пар значений */, г/,
пары
li = Xi—x9 \\/ = yJ—~y; (4.5.3)
тогда получим данные, приведенные в табл. 13 б. Для средних значений имеем
1 = 0, т[ = 0.
Таблица 136
Частоты величин li = xi—х, г)у. = #у.—у
i
1
2
3
4
5
ti=*rx
-0,5
-0,25
0
0,25
0,5
/=i
*),•=
-0,2
2
2
9
3
2
18
-У;
2
-7
-0,1
1
4
17
3
1
26
3
0
1
2
16
2
2
23
4
0,1
1
2
9
2
1
15
5
0,2
1
2
6
1
—
10
6
0,3
1
2
1
1
5
7
0,4
1
2
—
—
3
k
6
14
61
12
7
Коэффициенты аппроксимирующего уравнения
г] =а0+ 0^ + 0^2
определяются по формулам
«о = Т,
di
= А '
а2 =
Л '
(4.5.4)
(4.5.5)
§ 4. Корреляционное исчисление и корреляционный анализ 63
при этом величины Л0, Ль Л2, Л находятся с помощью общей формулы (4.10),
полученной методом наименьших квадратов. Имеем
А =
Ло-
Аг =
Л2 =
п
0
(n-l)s|
0
[ki/Ы,]
[kijlhj]
In
0
|(n-l)sg
' п
0
(n-l)s|
0
(n-l)s|
ыт
0
(n-l)sg
[*/£?]
0
[ki/li4/]
[k/jthf]
0
(n-l)sg
[чт
(«-l)s|
ЫЯ
[kill}]
(n — I)s|
[fe/tf?]
[fe/вБЯ
(n-l)s|
[ft.il?]
tali/]
0
Ife/yii-П/]
[*//tft|/]
(4.5.6)
(4.5.7)
(4.5.8)
(4.5.9)
Найдем численные значения членов определителей, используя данные,
приведенные в табл. 136:
(гг-1)5| = 2^Л? = 4'875»
i, /
[^^/] = 2¥'11/= -0,125,
fe6b3]=S*'7E?=°.°9375>
»". /
[Л|Ь4]=53ЛУЬ4 = 0,9140625.
*. /
Отсюда для детерминантов (4.5.6) — (4.5.9) имеем
Л =328,869, Л0 = 0,091406,
Лх = — 8,396484, Л2 = —1,875.
Теперь находим коэффициенты (4.5.5) кривой регрессии (4.5.4):
а0 = 0,00027794, ах = —0,025531, а2 = —0,005701.
Подставляя вместо g и г| выражения (4.5.3), получаем
К — у = а0 +ах (л:—л;) + а2(л;—л:)2. (4.5.10)
Отсюда для коэффициентов аппроксимирующей кривой
У = а0 + а1х+а2х2
находим
яо =^+«о —а^+ а2*2, (4.5.11)
ах —а1_ 2а2дг, (4.5.12)
а2 = а2. (4.5.13)
64
Гл. 1. Элементы теории вероятностей
Подставляя в (4.5.11) — (4.5.13) вычисленные значения, получаем
а0 = 0,625282, ах = 0,008677, а2 = — 0,005701.
Таким образом, в приближении второго порядка имеем
Y = 0,625 + 0,0087л;—0,0057а:2. (4.5.14)
Упражнения
У.4.1, Для измеренных пар значений (jtlf ух\ х2> у2\ ...) определить по
методу наименьших квадратов прямую регрессии
X = a1 + b1y = ax.y + bx.yy
таким образом, чтобы сумма
2 (*/-*/)*
**-У- п-2
значений Х[ для некоторого заданного у-х была минимальной. При этом
Xi = <*x-y + bx-yyi-
У.4.2. В задаче 4.3 определить прямую регрессии
Х=*ах.у+Ьх.уу.
У.4.3. При исследовании зависимости предела прочности при растяжении Y
от концентрации углерода X в катаных углеродистых сталях
получаются пары значений, приведенные в табл. 14.
Таблица 14
Предел прочности при растяжении для стали
в зависимости от содержания углерода
Xi, %
У[, кгс/мм2
0,1
39,7
0,2
46,8
0,3
54,6
0,4
63,3
0,5
69,7
0,6
76,9
0,7
83,6
Вычислить коэффициент корреляции и выяснить, имеет ли место
линейная зависимость. Определить обе прямые регрессии
Y = ay.x+by.xX и Х = ах.у + Ьх.уу.
У.4.4. Измерения зависимости относительного удлинения при разрыве для
алюминия чистоты 99,9% в зависимости от температуры дают
значения, приведенные в табл. 15.
Таблица 15
Разрывное удлинение алюминия
в зависимости от температуры
Температура, РС 250 350 450 550 650
Разрывное удлинение, % 44 37 24 18 17
§ 4. Корреляционное исчисление и корреляционный анализ 65
Определить коэффициент корреляции и прямую регрессии.
Проверить справедливость гипотезы о корреляции между этими
величинами, если уровень значимости равен
а) 0,05, б) 0,001.
У.4.5. Заданы следующие пары значений:
л: 1 —1 1—10
у \ 1—1—10
Определить коэффициент корреляции. К каким результатам приводит
расчет прямой регрессии?
У.4.6*. Исследование температурной зависимости электропроводности медного
сплава дает результаты, приведенные в табл„ 16. Аппроксимировать
зависимость кривой второго порядка.
Таблица 16
Удельная электропроводность легированной меди
Температура X, °С
Удельная электропроводность Y,
мОм-1«мм~2
0
66
200
32
400
26
600
20
800
16
У.4.7. Заданы три точки 0/0, 2/1, 4/3. Установить, имеется ли корреляция.
Уровень значимости составляет 10%.
У.4.8. Заданы пары значений, приведенные в табл. 17. Проверить наличие
корреляции и определить обе прямые регрессии. Уровень значимости
принять равным 0,00 К
Таблица 17
Пары значений
X
У
0
3
1
4
2
5
3
8
5
12
7
16
У.4.9*. В задаче 4.1 определить корреляционную зависимость, возникающую
при удвоении величин интервалов, в результате которого получается
Таблица 18
Содержание органических соединений (х)
и калийных солей (у) в технической воде
у, %
х, % 2±2 6±2 10±2
2 ±2 37 30 6
6±2 18 9 -
66 Гл. 1. Элементы теории вероятностей
распределение, приведенное в табл. 18. Вычислить регрессию у
относительно х их относительно у.
У.4.10*. При исследовании содержания А1203 и Fe203 в различных образцах
песка получены результаты, приведенные в табл. 19. Вычислить
коэффициент корреляции и выяснить возможность принятия
гипотезы о наличии корреляционной связи, если допустимый уровень
значимости составляет 0,10. Аппроксимировать распределение кривой
второго порядка.
Таблица 19
Содержание А1203(я) и Fe203(y)
в образцах песка
х,% 2±0?5 3±0,5 4±0,5 5±0,5 6±0,5
76 ±1
78±1
80±1
82 ±1
84±1
—
—
1
2
14
—
1
3
14
4
1
2
16
2
3
—
2
3
13
—
—
—
1
2
16
У.4.И*. С помощью формулы (4.2.2) для дисперсии суммы и разности двух
случайных величин доказать, что коэффициент корреляции г
заключен в интервале — 1 <;/•<;+!•
Глава £
КЛАССИЧЕСКАЯ СТАТИСТИКА
ИДЕАЛЬНЫХ ГАЗОВ
§ 1. КАНОНИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ГИББСА.
РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА — БОЛЬЦМАНА
Введение
Статистическая физика изучает законы, определяющие
свойства макроскопических систем, состоящих из очень большого
числа отдельных частиц. Каждая из этих частиц
характеризуется определенным индивидуальным поведением, которое
можно полностью описать, задавая ее пространственные
координаты qt и соответствующие им компоненты скорости qt. Вместо
последних принято пользоваться (обобщенными) импульсами р{.
Полное число г независимых пространственных координат qt
макроскопической системы называется ее числом степеней
свободы.
Совокупность всех возможных пространственных и
импульсных координат всех частиц образует фазовое пространство. Его
размерность s равна удвоенному числу степеней свободы. Точка
фазового пространства определяется, следовательно, заданием
s = 2r координат qu q2, . . ., plt р2 ... этого пространства. Она
изображает в заданный момент времени состояние всех частиц
системы, т. е. их положение в пространстве и импульс.
Изменение состояния макроскопической системы с течением времени
изображается в фазовом пространстве кривой qi=qi(t)i pi=pi{t),
которая называется фазовой траекторией.
Пример 10
Пусть рассматриваемая система состоит только из одного атома водорода,
имеющего массу jit = 1,67• Ю-27 кг. Атом может свободно перемещаться в
пространстве. Следовательно, состояние системы описывается тремя
пространственными координатами Я\_ — ху qz — У, Яз = г> и тремя импульсными
координатами p1 = \ix, р2 = 1ьу, Рз~И"2- Таким образом, полное число независимых
координат составляет s = 6. Фазовое пространство, следовательно, является
шестимерным. Точка
q1 = 0, q2 = 0, ?з = 0, Pl = 1,67-10"23 кг-м/с, р2 = 0, р3 = 0
характеризует состояние, при котором частица находится в начале
пространственной системы координат и имеет импульс в направлении оси х, равный
1,67-10—23 кг-м/с, т. е. движется со скоростью 104 м/с. Кривая
4i = Cot, q2 = 0, <7з = 0. Pi = Clt р2=0, p3 = 0t
где С0=104м/с, Сх= 1,67-К)-23 кг-м/с, описывает движение такой одноча-
стичной системы вдоль оси х.
68 Гл. 2. Классическая статистика идеальньм газов
Пример 11
Шарообразный баллон содержит Л/'=1026 молекул одноатомного газа.
Каждая частица характеризуется 3 пространственными и 3 импульсными
координатами. То обстоятельство, что частицы не могут покинуть баллон, не
уменьшает числа степенен свободы. Таким образом, для полного описания
макроскопической системы требуются 3N пространственных и 3N импульсных
координат. Следовательно, фазовое пространство имеет размерность 6/V =6-1025,
т. е. точка в фазовом пространстве задается 6/V координатами.
При исследовании возникновения тех или иных состояний
макроскопических систем фазовое пространство разбивают на
фазовые ячейки, имеющие объем
ДГ = Aq-Ap = AqxAq2.. .AqrApxAp2. . Лрп (1.1)
где r=s/2. Переходя к бесконечно малым размерам элемента
объема в фазовом пространстве, вместо (1.1) можно написать
dT = dq-dp = dq1.. .dpr. (1.1а)
Наблюдая поведение макроскопической системы при каком-либо
конкретном процессе, можно определить вероятность того, что
она будет обнаружена в некотором определенном состоянии.
Пусть это состояние определяется элементом фазового объема
ДГ\, а процесс протекает за время от 0 до t. Далее, пусть в
течение времени Ath составляющего часть этого промежутка,
фазовая траектория проходит в пределах элемента объема ДГг.
Тогда вероятность Awt того, что макроскопическое тело во
время наблюдаемого процесса будет обнаружено в физическом
состоянии ДГ/, равна
Предел этого отношения при неограниченном увеличении
времени наблюдения t определяет вероятность того, что
произвольная макросистема находится в определенном физическом
состоянии ДГ/
Aw= Um-t = fAq Ар
(1.2)
Функция плотности распределения вероятностей в фазовом
пространстве, или просто фазовая плотность вероятности,
/ = /(?i. •••> ЯпРх, ...,pr)=f((f, р)= Нт д^ (1.3)
удовлетворяет условию нормировки
2/Д<7Др=1. (Ы)
§ 1. Каноническое распределение Гиббса
69
При разбиении фазового пространства на бесконечно малые
элементы объема условие нормировки принимает вид
^fdqdp = \. (1.4а)
Суммирование и интегрирование производится при этом по всем
ячейкам (элементам объема) фазового пространства. Таким
способом при наблюдении конкретных систем каждой ячейке
можно эмпирически поставить в соответствие определенную
плотность вероятности / и определенную вероятность Aw.
Среднее значение g физической величины g определяется по
формулам
' g{t')dt'^^g(q, p)f^Ap = ^g(q, p)Aw,
или
£ = $£(?. P)fdqdp=\g{q, p)dw.
(1.5)
Соответственно среднее no времени можно заменить
статистическим средним; при этом интегрирование производится по всем
возможным состояниям каждой частицы системы.
Пример 12
Исследуется распределение по импульсам для некоторого тела,
состоящего из двух частиц массой ц=10-20 кг. Обе частицы заключены в
длинном цилиндре объемом V (фиг. 10). Пусть перемещения возможны лишь в
направлении, параллельном оси цилиндра, которую мы примем за ось z.
е
^z Фиг. 10. Движение двух материальных
точек в цилиндре (пример -12).
Фазовое пространство является в данном случае 12-мерным. Интерес
представляют, однако, лишь две" импульсные координаты
dzx dz2
Пусть, далее, заданы результаты наблюдения за длительностью пребывания
фазовой траектории в различных участках фазового пространства. Эти
результаты приведены в табл. 20. При этом мы считаем, что достаточно произвести
следующее разбиение фазового пространства.
Ячейка 0 охватывает всю область пространства, лежащего вне цилиндра,
и все возможные значения скорости. Ячейки 1—16 определены в соответствии
с табл. 20 (см. также фиг. И). Ячейка 17 содержит все фазовые точки,
удовлетворяющие хотя бы одному из двух условий
1рг| > 4-Ю"20 кг-м/с, \Рг\> 4-Ю-20 кг-м/с.
70
Гл. 2. Классическая статистика идеальных газов
Таблица 20
Наблюдение движения двух материальных точек
Номер
ячейки
Область изменения
импульсов, 10~20кг-м/с
Pi± 1
Рг± 1
Длительность Наблюдаемая
пребывания вероятность
/, с W
Плотность
вероятности
/, кг-в-м"12-св
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
00 , . . + 00
—3
—1
+1
+3
—3
— 1
+ 1
+з
—3
—1
+1
+з
—3
—1
+1
+з
— 00 . . . + 00
+3
+3
+3
+з
+1
+1
+1
+1
—1
—1
—1
—1
—3
—3
—3
—3
0
0
0
0
0
200
0
400
0
0
0
0
0
0
0
200
0
0
0
0
0
0
0
0,25
0
0,50
0
0
0
0
0
0
0
0,25
0
0
0
0
0
0
0
0,0625-1040- V-2
0
0,125.104°.У-2
0
0
0
0
0
0
0
0,0625- 104°.У-2
0
0
Для вычисления плотности вероятности / по вероятности Доу последнюю
необходимо разделить на объем соответствующей фазовой ячейки. В рассматри-
/
5
9
13
1
1
2
6
10
14
72
3
7
11
15
4
8
12
16
Фиг. П. К разбиению импульсного пространства
в примере 12.
ваемом случае имеем для ячеек 1—16
^q1 Д?2 Д?з Д?4 А?5 Л?б = V2,
кроме того, можно положить
^ps Др4 Дрб Арв =1 кг4 • м4/с4.
В соответствии со столбцами 2 и 3 табл. 20 для двух остающихся
импульсных координат получаем
Др!Др2 = 2.10-20.2. Ю-20 кг2.м2/с2.
Ячейки 0 и 17 имеют бесконечно большой фазовый объем.
§ 1. Каноническое распределение Гиббса
71
При вычислении кинетической энергии для отдельных ячеек следует
записать
(Pi + Apt/2 - р2 + Ар2/2
дк"_ J pUpi+^;_ 1 pUp*
p1-\pt/2 р2-Ар2/2
Используя это выражение, получаем, например, при i = 5
-2-10-2О 2-ю-20
/КЧ 1 Л0'0 Г 2 . , 102° Г 2, \
еКии (5) =2111 "2" J Pl Pl+~2~ J P2 Pa )=
\ _4.,0"20 0 /
= ^ - Ю-2» Дж=у • Ю-2» КГ.М2/С2.
Такую же величину имеет средняя кинетическая энергия для ячейки 15,
тогда как для ячейки 7 находим
екнн(7)=-5--Ю-«0Дж.
_4
3"
Среднюю кинетическую энергию рассматриваемой системы, состоящей из двух
частиц, получаем, находя статистическое среднее значение этой величины
^=^екин(0Аш(0=(2.0,25~. 10-20 + 0,5- —10-2о) =
•=-j. 10-20 ДЖ.
При вычислении среднего по времени будем исходить из того, что в течение
промежутка времени, равного трем единицам, каждая из двух частиц
обладает средней кинетической энергией
2-10-20
2ц
1 J p*dp=l. 10-20 ДЖ,
тогда как кинетическая энергия в течение одной единицы времени в среднем
равна
4-10 —«о
1 1
J p*dp=j. 10-20 Дж.
2ji 2
2.fo-20
Средняя кинетическая энергия макроскопической системы, состоящей из
двух частиц, в соответствии с этим равна
ЬГ,=2 • \ (з • J+1-- у)ю-2»=у • Ю-20 дж.
Таким образом, среднее по времени и статистическое среднее совпадают.
Понятие фазового пространства лежит в основе расчетов
термодинамических функций состояния с помощью методов
статистической физики. С этой целью фазовое пространство
подразделяется на макроячейки одинаковой величины. Каждая
микроячейка характеризует определенное микросостояние.
Указание микросостояния задает пространственные коорди-
72 Гл. 2. Классическая статистика идеальных газов
наты и импульс каждой отдельной частицы с точностью до
определенных, зависящих от размеров микроячейки, пределов.
Однако физически измеримым состоянием системы
одинаковых частиц является макросостояние. Для последнего
несущественно, какие именно частицы занимают те или иные
определенные ячейки. Существенное значение имеет лишь
статистическое распределение пространственных и импульсных
координат, т. е. заполнение частицами различных областей
координатного и импульсного пространства. Вследствие этого
макросостояние охватывает все те распределения по микро-
йчейкам фазового пространства, которые представляют одно
и то же физическое состояние.
Все микросостояния являются равновероятными.
Следовательно, состояния, изображаемые в фазовом пространстве
одинаковым числом микроячеек, имеют одинаковую вероятность
(теорема Лиувилля). Теорема Лиувилля может быть доказана
с помощью уравнений Гамильтона1*.
Теорема Лиувилля дает возможность выразить вероятность
некоторого макроскопического состояния через число
микросостояний, с помощью которых данное макросостояние может
быть реализовано. Число таких микросостояний называется
статистическим весом W распределения, отвечающего
рассматриваемому макроскопическому состоянию. Статистический вес W
является положительным целым числом. Деля его на полное
число всех физически возможных микросостояний, получаем
математическую вероятность данного макросостояния. Однако
в статистической физике при расчетах целесообразнее
использовать статистические веса, тогда как математическая
вероятность играет лишь ограниченную роль.
Для характеристики макросостояния область возможных
значений рассматриваемого параметра состояния, например
г-компоненты импульса, разбивают на интервалы и задают числа
заполнения каждого из этих участков фазового пространства.
Микросостояния, отвечающие одному и тому же
макроскопическому состоянию, отличаются лишь перестановкой частиц между
различными элементами фазового объема без изменения их чисел
заполнения. Поскольку статистический вес W макросостояния
определяется числом микросостояний, для его нахождения
необходимо, следовательно, определить лишь число возможных
перестановок.
В соответствии с этим статистический вес некоторого
распределения N19 N21 ..., Nk из N частиц по k макроскопическим
Г) Точнее, теорема Лиувилля утверждает, что при движении частиц
системы, согласно уравнениям Гамильтона, фазовый объем сохраняется и
поэтому может быть принят за меру вероятности.— Прим. ред.
§ 1. Каноническое распределение Гиббса
73
областям фазового пространства определяется формулой для
числа возможных перестановок:
W-(NuNt,...,Nk)= N1
Nj\N2L. Nk\
(1.6)
Поскольку k ячеек могут быть заполнены N частицами kN
различными способами, математическая вероятность
макросостояния Nlt N2, ..., Nb -определяется выражением
P(N N дм W(NltNt,...,Nk) N\
(1.7)
Пример 13
Рассматривается распределение скоростей двух частиц 1 и 2 по фазовым
ячейкам 1—16 в соответствии с табл. 20. Пусть обе частицы могут
перемещаться только в направлении оси z, а их импульсы заключены в пределах
от —4-10~20 до +4-10"20 кг-м/с. Производим разбиение на 4 равных
интервала:
I _4.Ю-2о<рг < —2.10-2о, II — 2-\0~2*^pz < 0,
III 0<рг < 2.10-2о, IV 2.10-2°<рг^4. Ю-2».
Отсюда для системы из двух частиц получаем приведенные в табл. 21
десять макросостояний со статистическими весами W, полученными по
формуле (1.6) при учете соответствующих микросостояний.
Таблица 21
Макросостояния системы из двух материальных точек
№
1
2
3
4
5
6
7
8
9
10
I
2
0
0
0
1
1
1
0
0
0
Числа
II
0
2
0
0
1
0
0
1
1
0
заполнения
III
0
0
2
0
0
1
0
1
0
1
IV
0
0
0
2
0
0
1
0
1
1
Микросостояния
согласно табл. 20
13
10
7
4
9,14
5,15
1,16
6,11
2,12
3,8
Статистический
вес W
1
1
1
1
2
2
2
2
2
2
Рассмотрим, например, макросостояние № 5, соответствующее ситуации,
когда одна частица находится в области I, а другая —в области II.
Нетрудно видеть, что этому макросостоянию соответствуют следующие два
микросостояния: а) частица 1 — в области I, частица 2 — в области II
(микроячейка 9) и б) частица 1 — в области II, частица 2 — в области I
(микроячейка 14). Следовательно, статистический вес W данного распределения
равен двум.
74
Гл. 2. Классическая статистика идеальных газов
\nN0\
-J
0
In NdN =
= [N
InN-
-N]?»
*N0
(lniV,-
-1).
Для приближенного вычисления и при аналитическом
рассмотрении выражений вида N0\ используется приближенная
формула, справедливая при N0^>1. Рассмотрим логарифм N0\:
In N0\ = In N0 + In (N0— 1) + • • • + In 2 + In 1.
При больших значениях N0 интервал между соседними
значениями АЛ^ = 1 можно рассматривать как дифференциал dN.
Отсюда следует приближенная формула
(1.8)
Ее точность достаточна для исследования физических явлений
при значениях N0 порядка 1026. Несколько более точной, чем
приближенная формула (1.8), является формула Стирлинга
Nl&V2nN (-J-Y. (1.8а)
Состояние термодинамической системы, иными словами, числа
заполнения ее фазовых ячеек, изменяется до тех пор, пока не
будет достигнуто состояние равновесия. Последнее
характеризуется тем, что статистический вес W = W(Nlt ...,УУ,,) или
натуральный логарифм этой величины, становится
максимальным. При этом числа заполнения меняются таким образом,
чтобы всегда выполнялся закон сохранения энергии
E = %Nfih (1.9)
где е,-—энергия одной частицы в i-и ячейке фазового
пространства. Кроме того, должно сохраняться число частиц, т. е.
допустимы лишь такие состояния, для которых
k
2 Nt = N. (1.10)
Если принять, что числа заполнения Nl9 N2y ...,Nk
равновесного состояния известны, то первая вариация (или полный
дифференциал) величины In IF для этого состояния должна
обращаться в нуль:
6Inr=61nw^=°- (М1>
Из (1.11) следует, что
81пЛМ —6 In Л^! —8 In #,! — •••=(),
или, применяя приближенную формулу (1.8),
8N (InЫ—\)—8Ыг (InN1—\)—8N2 In(Nt—l) =0.
§ 1. Каноническое распределение Гиббса
75
Производя действия с вариациями по тем же правилам,
которые применяются к дифференциалам, получаем
(\nN— l)8N + 8N — (lnN1— \)6Nt — 8N± — (lnW2— \)8N2 —
-SN2 =0,
или
lnN8N — lnN16N1 — lnN16Nt =0.
Из (1.10) находим
6М = 6Л^ + 6#2+...,
откуда
k
_1п^6Л^ —ln^6tf, =0 или ^1п^б^. = 0. (1.12)
Таким образом, вследствие наложения дополнительных
условий (1.9) и (1.10) из k величин bNt остаются независимыми
только k — 2. Для того чтобы получить еще две независимые
величины, умножим равенство (1.10) на а, а равенство (1.9) —
на р. Множители Лагранжа аир являются двумя
добавочными независимыми действительными величинами. Варьируя,
получаем из (1.10)
k
а 2 SNi = aW = 0, (1.13)
i=i
а из закона сохранения энергии (1.9) имеем
k
p2eMf. = 0. (1.14)
i=i
Складывая (1.12), (1.13) и (1.14), находим
ъ
i=\
Пусть нумерация чисел заполнения N( выбрана таким
образом, что дифференциалы двух величин, ставших зависимыми
в результате наложения ограничений (1.13) и (1.14), имеют
индексы соответственно 1 и 2. Исключим эти зависимые
величины из (1.15), для этого выберем множители Лагранжа а—1
и (5 таким образом, чтобы выполнялись два уравнения
ln^ + a + P*i = 0, (1.16)
1п^2 + а + ре2 = 0. (1.17)
£(1п^ + а + реЛбЛ^ = 0. (1.15)
76
Гл. 2. Классическая статистика идеальных газов
Благодаря этому в (1.15) остаются только независимые
вариации 6/Vg, 6NU, ..., 6Л//Г Все эти вариации можно положить
равными нулю, за исключением 8Ы3Ф0. Тогда из (1.15) с
учетом (1.16) и (1.17) следует
1п£ + а + ре3 = 0. (1.18)
Эту процедуру можно последовательно продолжать. Полагая
6/Vy=^0 и приравнивая нулю вариации всех остальных
независимых величин 6Л^ (1ф1)у получаем
ln^ + a + Pey = 0. (1.19)
Таким образом, с учетом уравнений (1.16) и (1.17),
определяющих выбор множителей Лагранжа, можно доказать
справедливость соотношения (1.19) для всех значений
/=1, 2, 3, ..., k. (1.20)
Разрешая (1.19) относительно NJt находим число заполнения
ячейки /:
Nj = Ne'^^zK (1.21)
Используя вытекающее из (1.13) условие
k k
2ЛГ,. = Мг« 2е"р£' = #, (1.22)
i=i г=1
получаем для множителя а соотношение
е-« = -т-! , (1.23)
2 Г*'
1=1
е~а-с -,«<«,»■ , • (1-24)
или, заменяя для простоты суммирование интегрированием,
_1
Для множителя (5 в соответствии с проводимым в § 5
настоящей главы рассмотрением статистической модели идеального
газа имеем
P = a7- (L25>
Здесь
k = 1,3806-10-23 Дж/К (1.26)
§ 1. Каноническое распределение Гиббса
77
есть постоянная Больцмана, Т—абсолютная температура в
Кельвинах. В результате приходим к формуле распределения
Гиббса для равновесного состояния:
(1.27)
или
dN(qiP) = N
e-e(q,P)/kTdqdp
p-e(q,p)/kT
dq dp
(1.28)
Распределение Гиббса, или каноническое распределение, было
получено Гиббсом для классических систем в 1901 г. Учитывая
соотношение Больцмана
NAk = 7? = 8,314-103 Дж/К• кмоль = 1,986 ккал/кмоль.К
(1.29)
можно записать закон распределения Гиббса также в виде
При этом число Авогадро
Л^л =6,02-1026 кмоль"1
обозначает число молекул в 1 кмоль, т. е. в том количестве
вещества, масса которого численно равна его относительной
молекулярной массе. Величина Uh следовательно, есть
энергия 1 кмоль вещества в некотором определенном состоянии.
Задачи
1.1. Распределение Больцмана
Рассматривается чистый газообразный кислород при температуре 300 К
и давлении 2 ат. Найти число молекул в объеме 1 мм3, компоненты скорости
которых лежат в следующих пределах:
vx: от 200 до 202 м/с, vy: от 450 до 455 м/с, vz: от —300 до —299 м/с.
78
Гл. 2. Классическая Статистика идеальных газов
Решение
В такой постановке рассматриваемая задача эквивалентна задаче о
нахождении вероятности dw того, что скорость отдельно взятой молекулы будет
лежать в указанных пределах. Согласно закону распределения Гиббса, эта
вероятность равна
AM *~e{Q' P)/kT AnAr,
. dN е dqdp ., t ,.
* le-*iq'P)/kTdqdp
Исходя из условий задачи, ограничимся рассмотрением поступательных
движений, в соответствии с чем произведем разбиение на ячейки лишь в
импульсной части фазового пространства. Выделять пространственные координаты,
а также координаты и импульсы, связанные с вращательными движениями и
внутримолекулярными колебаниями, нет необходимости.
Энергия е молекулы равна
e = B(q, p) = Pi+ti+pl . (1.1.2)
Отсюда имеем
dw_dN exp[-(pl + Rl + pl)/2vLkT]dn }
N Jexp[-(pi + p5 + p!)/2^r]dn '
где
dll==dpxdpydpz. 0.1.4)
Объем, связанный с пространственными координатами, выпадает.
При вычислении интеграла, стоящего в знаменателе, вместо тройного
интеграла можно написать произведение трех однократных интегралов:
— со — оо — оо
+ 00 + ОО +00
- l^{-^)d^l^{-4r)dpA^{-4r)dp-(iL5)
— оо — 00 — со
Посредством преобразований
рх=УЩ^ТЪ ру=УЩТ$, pz^VWkfl (1.1.6)
получаем из (1.1.5)
J ехр ( - rf+ff+Р* )mJ V^kT J «-t'eY. (1-1.7)
Учитывая формулу
^e-t'dl=Yn, (1Л.8)
— 00
находим из (1.1.7)
jexp(-P'+^ + ^) dn-(Sbn.*r/4 (1-1-9)
§ 1. Каноническое распределение Гиббса
79
Таким образом, вероятность обнаружить отдельную частицу в элементе
объема импульсного пространства
(Рх> Px + dPx)i (Ру, Ру + 4Ру)> (Рг> Pz+dpz),
согласно (1.1.3), равна
dw =
exp[ — (px + Py + f&)/2\»>kT]dpxdpydpg
(2n\ikT)
Vt
(1.1.10)
(распределение Больцмаиа, 1877 г.)
Рассмотрим теперь макроскопическую систему, состоящую из N частиц.
Для такой системы число частиц, компоненты скоростей которых заключены
в интервалах
К, vx + dvx), (vy, Vy + dvy), (vz, v2 + dvz)t
в соответствии с (1.1.10) определяется выражением
dN = Ndw =
N ехр [ — |х {vx + vl + vj) l2kf\ dvxdvydvz
(2nkT/iif*
(1.1.11)
Как уже указывалось выше, число молекул в 1 кмоль, равное числу Аво-
гадро, связано с относительной молекулярной массой Мт следующими
соотношениями:
NA\i = Mr,
И=
NA
(1.1.12)
Подставляя в (1.1.12) /Wr = 32 кг/кмоль, находшм массу одной молекулы
кислорода:
32 кг/кмоль
г =-5,316-Ю-26 кг.
г 6,02-1026 кмоль-1"
Уравнение состояния идеальных газов имеет вид
pV = nRT
где
N
NA
(1.1.13)
(1.1.14)
— число киломолеи.
Давление газа Р = 2 ат выразим в ньютонах на квадратный метр:
Р = 2 кгс/см2 = 2-9,81 Н/см2 = 2-9,8Ы04 Н/м2.
Подставляя эти значения в (1.1.13) и (1.1.14), находим число молекул в 1 мм3
PV 2-9 81.104. М-9
Ы=пЫА = ж ^=-^1LiL^_6,02.10- = 4,74-10«
80
Гл. 2. Классическая статистика идеальных газов
Далее в соответствии с (1.1.10) получаем
Рх + Ру + Рг =JL-(V* ■ vl + vl) =
2\ikT 2kT \Vx^vy^Vz)
5,316-10-26
exp
2-1,38. 10-23.300
(pl+pl + pl)
[2002 + 4502 + (-300)2] = 2,13,
2\ikT
:exp(—2,13) = 0,118,
dpx dpydpg=[i* dvx dvydvz=(5,3\6-10-26)3.25.1 = 1,502-10~75 кг3-м3/с3,
(2ntikTff* = (2-3,14.5,316. 10"26-1,38-10-23-300)3/2 кг3/2-Дж3/' =
= 5,142-10-08 кг3-м3/с3.
Отсюда следует, что
pl+Py + pl\ dPxdpydpz
dN = N exp
/ pI+pI+p\\
\ 2iikT J
= 4,74-1016-0,118
WT J (2л^Г)3/*
1,502-10-75
5,142-10-«9
:163-106.
Таким образом, в 1 мм3 газообразного кислорода при температуре 300 К и
давлении 2 ат скоростью, лежащей в указанных пределах, обладают 163
миллиона молекул.
1.2. Использование сферических координат
для выделения области в пространстве скоростей
Пусть 1 см3 водорода находится при температуре 1000 К и давлении
0,1 мбар. Определить число молекул Н2, вектор скорости которых составляет
с осью z угол не более 1°, а абсолютная величина скорости заключена в ин-
Фиг. 12. Сферические координаты О, ф, z и
декартовы координаты х, у, z.
тервале от 5000 до 5010 м/с (фиг. 12). Чему равна масса этих молекул?
Относительная молекулярная масса водорода Мг равна 2,016.
Решение
Запишем формулу распределения Больцмана в общем виде
ехр(—p2/2iikT)dU
dN = N-
(2n\*kT)
'/•
(1.2.1)
§ L Каноническое распределение Гиббса
81
Здесь р2 — квадрат импульса, а
—элемент объема трехмерного импульсного пространства. При определении
этого элемента объема необходимо учесть, что угол в 1Q соответствует л/180 рад.
Вычислим сначала площадь участка, вырезаемого на поверхности сферы
единичного радиуса векторами скорости, направление которых составляет с
осью г угол, не превышающий 1Q:
2Л Я/180
"-И •,n»«*P--K1-TSor±"-I)=W- 0-2.2)
0 0 '
Эту площадь можно определить и другим способом, если в соответствии с
фиг. 12 записать радиус ограничивающей ее окружности
р = sin d$ = d$
и подставить величину р в формулу для площади круга:
1802 "
Тогда элемент объема импульсного пространства равен
dU = \i3dQ = \iV dA dv = \i*v2 -^ dv. (1.2.3)
Разделим это выражение на величину (2n\xkT)9/2t стоящую в знаменателе
формулы (1.2.1). В результате получаем безразмерную величину
ЛП V2 dv / nii\3/2_v2dv /пм\*/ш 2
(2щкТ)Л^~ 1802 \2kTJ — 180* \2RTJ '
Подставляя заданные числовые значения, находим
(5.103)2.10/ 3,14-2,016 У^о 1£о ц-,
1802 V2.8,314.103.1037 -U,1W 1U '
Число молекул в 1 см3 равно
PV PV
n = Na-rt=~W' (L2*5)
Пользуясь переводной формулой
1 мбар=102 Н/м2
находим для давления Р величину
Р = 0,Ы02 = 10 Н/м2.
Если записать
V=l см3=10-в м3,
то, согласно (1.2.5), для числа молекул в 1 см3 получаем
N- 10-10-6 -7 24.10»
" 1,38- Ю-23-1000 ' •
82
Г л, 2. Классическая статистика идеальных газов
Показатель экспоненты в (1.2.1) равен
р2 _Mrv2 _ 2,016.(5» 103)» _
2iikT 2RT ~~ 2-8,314.103-103 ~~ ' '
откуда следует, что
е-Р2/2^г==е-з,оз5=:0д)482
Следовательно, искомое число молекул равно
dN=Ne~p2/2*xkT ^2-^ = 7,24.1014-0,0482.0,182-10-5 = 6,34.107.
(2лц/гГ)3/*
Для массы dm этих молекул находим
dm = Mr^- = 2,016|gli^=2,12.10-« кг.
Таким образом, в 1 см3 водорода при давлении 0,1 мбар и температуре 1000 К
имеется 63,4 миллиона молекул, вектор скорости которых лежит в заданном
направлении, а абсолютная величина скорости заключена в интервале от
5000 до 5010 м/с. Общая масса этих молекул составляет 2,12-Ю-19 кг.
1.3. Распределение Максвелла — Больцмана для скоростей
Рассматривается азот при температуре 0°С. Как велико относительное число
молекул, скорость которых лежит в интервале от 250 до 260 м/с?
Относительная молекулярная масса азота равна Мг — 28,013.
Решение
Будем исходить из закона распределения Больцмана
dN =exv(-p*/2iikT)dIl 3
N (2л|х/гГ)3/*
Разобьем пространство скоростей на сферические слои. Объем сферического
слоя, имеющего радиус v и толщину dv, равен
dQ = 4nv2dv. (1.3.2)
Отсюда находим элемент объема в импульсном пространстве
dU==4n^v2dv. (1.3.3)
Подставляя (1.3.3) в (1.3.1), получаем распределение скоростей Максвелла
dN _ 4 v2exp( — \iv2/2kT)dv_f
N "УН (2kT/ii)^ ~~!{V) V
(1.3.4)
Оно описывает распределение абсолютной величины скорости v =
= Vvl + v2y + v2z.
При заданных числовых значениях показатель экспоненты равен
\iv2 __ Mrv2 _Mrv2_ 28,013.2502
2kT 2NAkT 2RT 2-8,134.103-273,16
= 0,386.
§ 1. Каноническое распределение Гиббса
83
Отсюда следует, что
ехр ( " WT )=ехр (~0>386)=°>679-
Далее находим
4 v2 dv _ 4 v2 dv
Уп (2kT/ii)3/>~Y^ (2RT/Mr)3/*~~
=-== 4-250М0 ,.=0,02.6.
У 3,1416 (2-8,314.103-273,16/28,013) '«
Теперь определим относительное число молекул, имеющих скорость, значения
которой заключены в интервале от 250 до 260 м/с
dN
-^-==0,0216-0,679 =0,0147.
Следовательно, в 1 кмоль число молекул со скоростями в указанных пределах
составляет
dN
А/л-^-=6,02.1026-0,0147 = 8,82.1024.
1.4. Максимум плотности распределения
Определить скорость, соответствующую максимуму плотности
распределения для водорода и гелия, если температура равна 0°С. Относительная
молекулярная масса водорода и гелия равна соответственно Мн =2,016 и
МНе =4,003.
Решение
Распределение молекул газа по скоростям описывается формулой (1.3.4)
dN 4 v2 ехр (—\w*/2kT) dv
-—- = f(v)du=^—^=r ——-—'-г-.—-—. (1.4.1)
Для определения максимума функции плотности распределения вероятностей
продифференцируем ее по скорости v и получим
*№—*-( I* \\v(\—Jr^expf—^-] П4 2)
*>~уи{шг)^\ 2кт)ехр[ Чкт)- <м-2>
Если значение скорости v = vMaKC соответствует максимуму функции
распределения, то ее первая производная при этом значении должна обращаться в
нуль. Тогда с учетом соотношений NAk = R, N^\i = Mr получаем из (1.4.2)
(1.4.3)
Чтобы определить скорость, соответствующую максимуму функции
распределения для водорода, подставим заданные числовые величины:
т/2-8,314-103-273,16 _ .
0максНя= J/ 2ПоТб = 1500 м/с-
84
Гл. 2. Классическая статистика идеальных газов
Следовательно, функция распределения скоростей для водорода имеет
максимум при v= 1500 м/с.
Возьмем отношение скоростей, отвечающих максимуму функции
распределения для двух различных газов, давления и температуры которых
одинаковы. Для водорода и гелия получаем, согласно (1.4.3),
^макс Не _. -iT^H, (1 4 4)
"максН2 V Мне'
Отсюда следует, что
W Не = *макс Н2 V~* = 1500 V^^Sh Ю64 М/С,
У МНе У 4,003
т. е. для гелия максимум функции распределения соответствует сксрости
у =1064 м/с.
1.5*. Среднее абсолютное значение скорости, средняя энергия
и дисперсия скорости
Вычислить для водорода при 0Q С среднее абсолютное значение скорости,
среднюю энергию и средний квадрат скорости. Сравнить полученные
результаты со скоростью умаКс» отвечающей максимуму функции распределения.
Решение
Среднее значение v получается из функции распределения
f(tl7aw/!aP(-S) (,-5-'>
по формуле
со
lf = ^vf(v)dv. (1.5.2)
о
Для вычисления интегралов вида
(1.5.3а)
введем новую переменную
*/ = Р*2.
и для а > — 1, р > 0 получим
/a=i-P-(a+i,/2r(^±i)
(1.5.36)
где Г (а) —гамма-функция:
со
Г (a)= f e-*x"-idx. (1.5.3в)
§ 1. Каноническое распределение Гиббса
85
Для нее справедливо соотношение
Г(*+1)=*Г(*). (1.5.4)
Если п обозначает положительное целое число, то справедливы
функциональные уравнения
(1.5.5)
(1.5.6)
Г(п+1) = л!
»
'(•+т)-ЙЬ^
Подставляя (1.5.1) в (1.5.2) и используя (1.5.36), находим
4
' Vn (2kT/\i)3/2
|y3exp(_g)^ = ^.-|/^r(2). (1<5.7)
Согласно (1.5.5), Г (2)= 1!= 1. Учитывая, что NAk = R, NA\i = Mr, получаем
(1.5.8)
При заданных числовых значениях находим для средней скорости молекулы
водорода при 0QC
- -, /8-8,314.103-273,16 lco. ,
V=V 3,1416.2,0- = 1694м/с-
,016
(1.5.9)
Средняя кинетическая энергия одной молекулы определяется формулой
7 = £-^=i ^v*f(v)dv. (1.5.10)
Подставляя (1.5.1) в (1.5.10), получаем
1== УЫРТ*) и4ехр ( ~2&) dv-
о
Учитывая (1.5.3) и (1.5.6), находим из (1.5.11)
kT
(1.5.11)
(1.5.12)
Таким образом, каждая из трех степеней свободы вносит в кинетическую
энергию вклад, равный kT/2, в соответствии с рассмотренным ниже законом
классической статистики о равномерном распределении энергии по степеням
свободы.
Как показывает сравнение формул (1.5.8) и (1.5.12), квадрат средней
скорости
-2 8/еГ
v =^г о-5-13)
86
Гл. 2. Классическая статистика идеальных газов
не совпадает со средним значением квадрата скорости
*=-^kT. (1.5.14)
г
Обе эти величины не совпадают также и с квадратом скорости, отвечающей
Т=273 К
^уТ=373 К
*»V
Фиг. 13. Максимум распределения скоростей
с»макс, средняя скорость у и корень квадратный
VAtaKc''VlYV*!=f:ftf2u:f,225 из среднего квадрата скорости у и2.
максимуму функции распределения (фиг. 13), который определяется
выражением
%акс=—-. (1.5.15)
г
В случае молекулы водорода средняя энергия поступательного движения
равна
Т=у • 1,380-Ю-23.273,16 = 5,654-Ю-21 Дж.
Поступательная энергия 1 кмоль идеального газа, согласно (1.5.13),
определяется выражением
?™h = Nae = jRT.
(1.5.16)
Следовательно, кинетическая энергия, содержащаяся в 2,016 кг водорода
при 0? С, равна
£кин = ~8,314.103.273,16 = 3,40.103 кДж,
или соответственно
£кин = 0,239-3,40.103 = 814 ккал.
Дисперсия по определению есть
<fl = ^(v-Ti)*nv)dv. (1517)
Отсюда
а2 = J i'2/ (v) dv — 2v ^ vf (v) dv +у2 J / (if) dv = tf — 2vv+v* =IT2—~"y2
(1.5.18)
§ L Каноническое распределение Гиббса
87
Используя формулы (1.5.8) и (1.5.14), находим из (1.5.18)
°2=^-"=7(3-4)=0'45357' <'-5-19>
откуда для среднеквадратичного отклонения имеем
(7=0,6734 уГ^= 0,6734 Yw/ (L5-2°)
Для водорода при 0°С получаем
п«У7ол -»/ М14-Ю3»273,16 _._ /
ан>= 0,6734 у 270Т6 = 715 М/С'
1.6. Барометрическая формула для воздуха,
рассматриваемого как однородный газ
Исследовать уменьшение давления воздуха с увеличением высоты, если
температура постоянна и равна 0QC, а давление на уровне моря равно
Р0= 1013 мбар = 1 атм= 1,013-105 Н/м2 (нормальные условия). На какой
высоте давление воздуха и плотность уменьшаются наполовину? При расчетах
пользоваться данными о составе воздуха, приведенными в табл. 22.
Таблица 22
Порядковый номер
Газ
Состав сухого воздуха
i 1
N,
2
02
3
Аг
4
со2
Относительное содержание pi 0,7809 0,2095 0,0093 0,0003
Относительная молекулярная масса М-ь 28,013 31,999 39,948 44,010
Решение
Будем рассматривать воздух в первом приближении как однородный газ.
Относительную молекулярную массу этого газа найдем, используя табл. 22,
по формуле
JWr = 2/M*/. (1.6.1)
с
Подставляя числовые значения, получаем
Мг = 28,97. (1.6.2)
Молярный объем на уровне моря при заданных нормальных условиях равен
„ RT0 8,314-103-273,16 00 . ч/ ,. Л ^
у°=-р7^—1013-ю» =22А м /кмоль' (1'6,3)
88
Гл. 2. Классическая статистика идеальных газов
Рассмотрим перпендикулярный к поверхности Земли столб воздуха сечением
1 м2 (фиг. 14).
Для нахождения числа частиц в слое воздуха толщиной dz воспользуемся
формулой канонического распределения Гиббса (1.28), согласно которой число
частиц газа в элементе объема фазового пространства, отвечающего состоянию
pt qt равно
*Ы-Г*я*р-'!'-*ТЛ,а>. (1.6.4)
Г e-e/kT dqdp
где N— полное число молекул в выделенном столбе воздуха.
При вычислении энергии частицы, находящейся на высоте z, можно
ограничиться рассмотрением потенциальной энергии. Дело в том, что хотя энергия
отдельной частицы (ее кинетическая часть) и зависит от импульсных
координат, это никак не отражается на распределении частиц в поле земного тяготения.
Фиг. 14. К выводу барометрической формулы.
Как видно из фиг. 14, направление ускорения свободного падения—g
противоположно направлению оси z. Следовательно, частица на высоте г
обладает потенциальной энергией
Г = -Ц$ -gdz =
№.
(1.6.5)
где jLi—масса частицы.
Потенциальная энергия £пот отдельной частицы зависит, таким образом,
только от координаты z и не зависит от координат х и у. Интегрируя
выражение (1.6.4) по х и у, а также по несущественным в данном случае
импульсным координатам, мы избавляемся от зависимости числителя и знаменателя
от этих переменных и получаем число частиц в слое воздуха dz на высоте z:
dN =
Nexp[-en0T(z)/kT]dz
^expl-en0T(z)/kT]dz
(1.6.6)
Объединяя не зависящие от высоты г 1лены в один постоянный коэффициент
N N\\g
С = -
00
о
находим из (1.6.6)
4N = Се-№'ьт dz.
kT '
(1.6.7)
§ 1. Каноническое распределение Гиббса
89
Величина dN/dz пропорциональна плотности газа р. Отсюда плотность
воздуха на высоте z равна
p=p0e-M*/kT, (1.6.8)
где ро — плотность при z = 0.
Пользуясь уравнением состояния идеального газа, преобразуем
показатель экспоненты в формуле (1.6.8)
Подставляя (1.6.9) в (1.6.8), приходим к барометрической формуле
(1.6.10)
p(z) = p0exp(-^)
Вычислим высоту z = H, на которой давление воздуха уменьшается вдвое.
В соответствии с (1.6.10) при этом должно выполняться соотношение
р0ехр(-М?) = <^ (..6.11)
откуда, логарифмируя, находим
Я = ^-1п2. (1.6.12)
Ро£
Подставляя числовые значения, получаем
„ 1013^102
Я= 1,293.9,81 °'693М==5'5КМ-
Таким образом, давление воздуха уменьшается вдвое на высоте 5,5 км.
1.7. Измерение числа Авогадро по Перрену
Для измерения числа Авогадро Перрен исследовал распределение
гуммигутовых зерен в воде. Масса одной частицы составляла fx = 1,25 • 10—1в кг, а
определение объема дало величину V = 1,03- Ю-19 м3. Температура
принималась равной 4° С. Определить высоту Я, для которой плотность уменьшается
в 2 раза. Какова необходимая точность измерений, если ошибка при
определении числа Авогадро не должна превышать 5%?
Решение
Для нахождения эффективной массы \i3$$ одной частицы нам следует
определить подъемную силу. Обозначая плотность вытесненной жидкости
через рЖИдк» имеем для эффективной массы
^эфф = ^-ржидк^=(1,25.10-1б-1000.1,03-10-^)=0,22.10"" кг. (1.7.1)
В соответствии с барометрической формулой (1.6.10) плотность распределения
зерен описывается выражением
( ^фф£Л „™ч
р = р0ехр^ bf-J- (1-7.2)
90
Гл. 2. Классическая статистика идеальных газов
Отсюда находим высоту Я, на которой величина р уменьшается в 2 раза,
„ *7Чп2 1,38-10-2з.277,16.0,693 10 0 tt п ^
Я==^7= 0,22.10-^.9,81 м=12>3"™- О-™)
Таким образом, эта высота составляет всего 12,3 мкм.
Чтобы определить число Авогадро
л^ = 4' (17-4)
разрешим равенство (1.7.3) относительно k и полученное выражение
подставим в (1.7.4). Это дает
л/ ЯГ In 2 /17R4
Na==u Zh- (17-5)
Погрешность измерения находим следующим образом:
dH 11Ш£ dH
откуда следует
... ЯГ In 2 ,__
dN А = — dH.
ИэфФ^2
Согласно условиям задачи, должно выполняться неравенство
< 0,05,
dNA
NA
и, следовательно,
dNA dH
Отсюда находим требуемую точность измерений:
\dH\< 0,05Я = 0,615 мкм.
Итак, если при нахождении числа Авогадро NА в опыте Перрена ошибка не
должна превышать 5%, то определяемая методом подсчета отдельных зерен
высота, на которой плотность уменьшается в 2 раза, должна измеряться с
точностью не менее 0,615 мкм.
1.8*. Центрифуга. Разделение эмульсий
Цилиндрическая центрифуга вращается с частотой /=1500 с-1. Диаметр
цилиндра равен 2г0 = 0,20 м, а его длина / = 0,5 м. В цилиндре находится
эмульсия из белка и воды, содержащая т = 0,25 кг белка. Относительная
молекулярная масса белка и его плотность равны соответственно Л4Г = 380 и
рбелк=1,08 г/см3. Определить плотность распределения молекул белка на оси
и на краю центрифуги. Чему равна масса белкового вещества в слое
толщиной 6 = 5 мм, прилегающем к образующей цилиндра? Температуру принять
равной 4° С.
Решение
Находящийся в жидкости белок испытывает действие подъемной силы.
Обозначая через рвод плотность воды, получаем для эффективной массы
выражение
.. Рбелк Рвод ™г Рбелк Рвод ЛЯП
Рбелк iV А Рбелк
§ L Каноническое распределение Гиббса
91
4,68-Ю-26 кг.
В рассматриваемом случае находим
_ 380 1,08—1
И-эфф-6{)2.102б 108
Центробежное ускорение равно
а = со2г; (1.8.2)
оно направлено вдоль радиус-вектора. Чтобы вопреки действию центробежной
силы переместить частицу из периферийной области в точку, находящуюся
на расстоянии г от оси, необходимо затратить энергию
W--
:-Цэфф\ (*2rdr= фф 2 °
(1.8.3)
Пусть N0 обозначает плотность числа частиц (плотность распределения) на
периферии (г = г0). В соответствии с законом распределения энергии
плотность числа частиц на расстоянии г от оси цилиндра равна
ИэффЮ2^-''2)-
N (г) = УУ0ехр
(-£)-*•
ехр
2kT
(1.8.4)
Значение N0 найдем из условия нормировки. Если полное число молекул
белка равно N, то должно выполняться соотношение
■ о
2л/ [rN(r)dr = N.
(1.8.5)
Подставим (1.8.4) в (1.8.5) и разрешим полученное уравнение относительно N0.
В результате находим
N,= * . (1.8.6)
' о
2л/ С г ехр (— \i3^(o2r2/2kT) dr
Для вычисления интеграла в знаменателе произведем подстановку
Цэфф^
2kT ~*
и получим
^Эффщ о
2kT
Н(-ЭД-^ 1 <**-
kT
Подставляя (1.8.8) в (1.8.6), имеем
А^^эффсо2
Nn = -
(1.8.7)
(1.8.8)
(1.8.9)
2л//?Г[1-ехр(-^эффо)%2/2/гГ)] '
Следовательно, плотность распределения молекул белка описывается
выражением
N(r)--
%эфф<о2
2лШТ [1 —ехр (-^ЭффО)2/-о/2/гГ)]
ехр
2kT
<rl-r*)\. (1.8.10)
92
Гл. 2. Классическая статистика идеальных газов
Для отношения плотностей распределения .на периферии г = г0 и на оси
находим, согласно (1.8.10),
ЩоГ лГ(0)-ехр V 2kT ) ' (К8Л1)
Подставляя числовые значения, получим
N(0, 10)_ Г 4,68-10-26(1500.2-3,1416.0,1)2'
г (0, Ю) Г
W"=exp L"
2.1,38.10-2з.277,16
= ^,434 = 102,360 = 229.
Таким образом, при заданных условиях плотность распределения молекул
белка на периферии в 229 раз больше плотности на оси.
Для полного числа молекул имеем
N = NA -jJ-=6,02.1026.^=3,96-1023. (1.8.12)
С учетом этого, используя формулу (1.8.11) для числа частиц на периферии,
получаем из (1.8.9)
3,96.1023.4,68.10-26(2.3,1416.1500)2
v° 2.3,1416-0,5.1,38-10-23-277,16(1—е-5'^4) 1'°'° 1и
тогда как плотность числа частиц на оси составляет всего лишь
1 376-1026
*(°>- 229 =в.0Ы0"м-».
Число Nr молекул белка в приграничном слое толщиной 6 = 0,005 м
определяется выражением
.13)
0 Го- Ь
Используя для вычисления интеграла (1.8.13) преобразование (1.8.7), находим
Nr = г <\ — ехр 7rUF >. (1.8.14)
^эфф^2 I L 2kT \)
Масса белка тг в приграничном слое толщиной b получается тогда из
соотношения
Nr Nr
mr = ^j-m = jj-jMn (1.8.15)
Подставляя N0 из (1.8.9) в (1.8.14), находим окончательно
1_ехр[-^эффО)26(2г0-6)/2/гГ]
тг — т . (1.8.16)
1—ехр[—^эффО)2/-0/2/гГ]
В рассматриваемом частном случае с учетом (1.8.11) получаем
I ™ i 4,68.10-26(2.3,14.1500)2.0,005(0,2—0,005)"
Nr = l[2KrN(r)dr = 2MN Г г ехр Г- ^^^"^ 1 dr. (1.8.1
I — ехр -
лоел l 2.1,38.10-2з.277,2 J . |10
mr = 0,250 - ^ = 0,118 кг.
1_"229
Таким образом, в периферийном слое толщиной 5 мм находится 47,3% всех
молекул белка, масса которых составляет 0,118 кг.
§ 1. Каноническое распределение Гиббса
93
1.9. Осмотическое давление
Исходя из закона распределения по энергии, вывести формулу для
осмотического давления в растворах. Чему равно осмотическое давление в
растворе, если в 4 л растворителя при температуре 75° С растворены 10 г гликоля
(СН2ОН)2 (Мг = 62,0) и 15 г метилового спирта СН3ОН (Мг = 32,0)?
Решение
Рассмотрим сначала раствор, содержащий только одно вещество.
Представим себе, что растворитель (вода) и раствор разделены полупроницаемой
перегородкой. Она пропускает молекулы растворителя, но не пропускает
молекулы растворенного вещества (фиг. 15). Для поддержания равновесного
давления обеспечивается постоянный отток или приток растворителя в раствор.
Фиг. 15. Раствор, разделенный
полупроницаемой перегородкой.
Под действием осмотического давления
поршни /Ci и К2 смещаются влево; Kt
выталкивается, /С2 втягивается.
Перегородку можно рассматривать как силовое поле. Согласно этой модели,
на частицу, приближающуюся к перегородке, действует сила
g = -grad№, (1.9.1)
направленная внутрь раствора. В соответствии с законом действия и
противодействия равная, но противоположная по направлению сила действует на
перегородку со стороны частицы. Непосредственно около перегородки
потенциал W неограниченно возрастает, препятствуя проходу молекулы вещества.
На основании закона распределения Гиббса имеем для числа молекул, которые
находятся от стенки на таком расстоянии, что они обладают потенциалом W:
N(W) = N0e~w/kT.
(1.9.2)
Если число N (W) отнесено к 1 м3 раствора, то N0 есть число частиц в 1 м3,
для которых W = 0, т. е. которые находятся на достаточном удалении от
мембраны. Если рассматриваемый объем имеет величину dV, то действующая
на этот объем сила равна
f dV = N (W) % dV = — N (W) grad W dV.
(1.9.3)
Производя дифференцирование по пространственным координатам, находим
из (1.9.2)
^®-gradU?. (1.9.4)
grad N (W) = - ^e'w/kT grad W =-
kT
Разрешим это уравнение относительно W и подставим полученное выражение
в (1.9.3). Имеем
f = — N (№>grad W = kT grad N (W). (1.9.5)
В рассматриваемой гидростатической задаче силу f с помощью соотношения
f = — gradP (1.9.6)
94
Гл. 2. Классическая статистика идеальных газов
можно заменить градиентом давления Р. Тогда получаем из (1.9.5)
grad Р = kT grad N (W) (1.9.7)
Если температура во всех точках рассматриваемого объема одинакова, то
находим посредством интегрирования
P(W) = kTN(W) + P0,
где Р0—давление в отсутствие растворенных частиц. Разность
P-P0 = Poc* = MkT (1.9.8)
равна, следовательно, увеличению давления за счет растворения N молекул.
При выводе формулы для осмотического давления вид потенциала W столь
же мало существен, как и химические или физические свойства раствора.
Существенно лишь число N растворенных молекул. При этом, разумеется,
следует иметь в виду, что полученная здесь формула (1.9.8) применима только
при слабых концентрациях. При больших концентрациях необходимо
учитывать свойства реальных газов и жидкостей.
Если в 1 м3 растворены Nx молекул одного вещества и N2 молекул
другого, то, согласно изложенной теории, осмотическое давление раствора в
равновесном состоянии равно
PocM = Wi + N2)kT = NkT, (1.9.9)
где N — полное число растворенных молекул в 1 м3 раствора. Если в объеме V
некоторого раствора содержится п киломолей растворенного вещества, то
число растворенных молекул в 1 м3 определяется соотношением
NV = nNA=-j£-NA, (1.9.10)
где т — масса растворенного вещества. Находя отсюда N и учитывая
равенство NAk — R, получаем для осмотического давления закон Вант-Гоффа
^осм— у —мг V ' U-y.llJ
Отсюда следует, что осмотическое давление равно давлению газа, которое
имело бы место, если бы молекулы растворенного вещества в виде газа
заполняли объем, равный объему раствора.
В рассматриваемом случае число растворенных киломолей равно
m _mx m2 _1Q.1Q-3 15-1Q-3 nfi?in_3
Подставляя это число в (1.9.11), находим
0,63-Ю-3-8,314-103-348,16 ,ес 1А1 ,_, 9
^осм=- ^Ло^ А
Пользуясь для перевода единиц соотношением
1 ат = 9,81 Н/см2 = 9,8Ы04 Н/м2,
получаем окончательно
456»
"9,81-104"
"осм — 7Го1 Пч1 — 4,65 ат.
Следовательно, 10 г гликоля и 15 г метилового спирта создают в 4 л воды
при 75° С осмотическое давление, равное 4,65 ат.. В случае раствора
электролита необходимо учитывать диссоциацию на ионы и действующие между ними
электрические силы (см. гл. 5, § 2).
§ 1. Каноническое распределение Гиббса
95
Упражнения
У. 1.1. Найти число молекул хлора в 1 мм3 при температуре 500° С и
давлении 0,01 мбар, компоненты скорости которых заключены в
следующих интервалах: у* = (200—205) м/с, ^ = (100—110) м/с, ^ = (100—
105) м/с. Относительная атомная масса хлора равна 35,45.
У. 1.2. Чему равно число молекул в 1 л гелия при давлении 20 ат и
температуре 3000 К, вектор скорости которых составляет с осью z угол не
более 30°, а абсолютная величина скорости лежит в интервале от
600 до 605 м/с?
У. 1.3. Чему равно число атомов гелия со скоростями от 1000 до 1010 м/с,
содержащихся в шарообразном баллоне диаметром 16 м при 10е С и
давлении 0,9 ат? /
У.1.4. Определить скорость, соответствующую максимуму функции
распределения при 100° С для водорода, гелия и азота.
У. 1.5. Вычислить средние скорости для водорода, неона и кислорода при
500° С.
У. 1.6. Полагая температуру равной 300° С, определить средние скорости для
гелия и водорода. Чему равны скорости, отвечающие максимуму
функции распределения скоростей и какие значения получаются для
корней квадратных из средних квадратов скоростей?
У. 1.7. Чему равно среднеквадратичное отклонение скоростей для гелия при
температуре 300° С?
У. 1.8. Для функции распределения Максвелла — Больцмана f (v) определить
величину, характеризующую асимметрию распределения
Сравнить результат с асимметрией нормального распределения.
УЛ.9.* Для функции распределения Максвелла — Больцмана f (v) вычислить
величину
которая является мерой крутизны распределения. Чему равна эта
величина для нормального распределения?
Пользуясь барометрической формулой, вычислить давление воздуха
на высоте 1000 м при —23,16 и при 26,84° С, если давление на
уровне моря равно 1013 мбар.
Вычислить массу азота и массу кислорода в 1 м3 воздуха на уровне
моря и на высоте 5532 м. Температура воздуха и его давление на
уровне моря равны соответственно 0Q С и 1013 мбар. (Воспользоваться
данными, приведенными в табл. 22.)
Вычислить, на какой высоте парциальные давления азота и
углекислого газа уменьшаются в два раза, если температура равна 0° С.
Какие высоты получатся при 30Q С?
В поле земного притяжения производятся наблюдения за
шарообразными частицами диаметром 2-Ю-7 м, находящимися во взвешенном
состоянии в воздухе при температуре 0° С и давлении 1 атм.
Установлено, что концентрация частиц уменьшается вдвое на высоте Юм.
Чему равна масса взвешенной частицы? Вычислить их плотность
в сравнении с плотностью воздуха.
В поле земного притяжения находятся частицы пыли, имеющие массу
^ = 8,50-Ш-22 кг и объем V = 5-10-22 м3. Определить уменьшение
их концентрации на высоте г = 3м, Давление и температура воздуха
96
Гл. 2. Классическая статистика идеальных газов
равны соответственно 990 мбар и —20° С. На какой высоте
концентрация уменьшается в два раза?
У.1.15. Чему равно при 20Q С осмотическое давление 1 г этилового спирта,
растворенного в 0,7 л жидкости? Давление выразить в технических
атмосферах (Мг = 46).
У. 1.16. Вычислить, чему должна равняться масса т сахара, растворенного
в 2 л воды при 50Q С, чтобы осмотическое давление составляло 3 ат.
Относительная молекулярная масса сахара равна Мг = 342,3.
У.1.17. В ультрацентрифуге находится эмульсия из воды и некоторого
синтетического вещества, имеющего плотность 0,999 г/см3. Взвешенные
частицы синтетического вещества можно приближенно считать
шариками радиусом 1 мкм. Радиус центрифуги равен 12 см, частота
вращения 200 с"1. Температура равна 4° С. Вычислить отношение
плотностей распределения в центре и на периферии. Чему равна
относительная доля частиц в слое толщиной 1 см, расположенном на краю
центрифуги и в цилиндре радиусом 5 мм на ее оси?
У. 1.18*. Решить предыдущую задачу при плотности взвешенных частиц,
равной 1,001 г/см3.
У. 1.19*.Определить распределение вероятностей для кинетической энергии
материальной точки с помощью распределения Максвелла — Больц-
мана. Чему равна вероятность найти молекулу с энергией в
интервале от 4,00-10"21 до 4,14-10"21 Дж, если температура равна 300 К?
§ 2. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ.
ЗАКОН РАВНОРАСПРЕДЕЛЕНИЯ.
УДЕЛЬНАЯ ТЕПЛОЕМКОСТЬ
Введение
Внутренней энергией называют запасенную телом тепловую
энергию1}. При ее увеличении либо возрастает температура
системы, либо изменяется агрегатное состояние (например,
происходит плавление или испарение). Для вычисления внутренней
энергии воспользуемся законом распределения по энергий-
Гиббса (1.27) и выполним суммирование по всем энергетическим
состояниям (см. задачу 2.1):
U = \sdN. (2.1)
Результат этого суммирования можно сформулировать
следующим образом: каждая степень свободы вносит в энергию вклад,
равный в среднем kT/2 (закон классической статистической
Х) В термодинамике обычно ограничиваются утверждением, что
внутренняя энергия есть всякая энергия, заключенная внутри тела в какой-либо
форме. С микроскопической точки зрения это означает, что внутренняя
энергия равна сумме кинетических энергий отдельных частиц и энергии
взаимодействия между ними. Если тепловой энергией называть, как это часто
делают, среднюю кинетическую энергию, то она является лишь частью
внутренней энергии. (По этому вопросу см., например, Р. В. Поль, Механика, акустика
и учение о теплоте, „Наука", М., 1971).— Прим. перев.
§ 2. Первый закон термодинамики
97
физики о равномерном распределении энергии по степеням свободы,
или просто закон равнораспределения):
(2.2)
Величина f есть число степеней свободы одной материальной
точки. Вся термодинамическая система в целом обладает s = Nf
степенями свободы. Если к термодинамической системе
подводится извне количество теплоты SQ, то последнее расходуется
на увеличение внутренней энергии dU и на совершение системой
механической работы Р dV против внешних сил. Этот опытный
факт выражается первым законом термодинамики:
8Q=dU + PdV
(2.3)
(Р — давление, V—объем).
Полное количество теплоты Q, подведенное к системе, в общем
случае не удается представить в виде однозначной функции
состояния, зависящей от температуры Г, давления Р или
объема V. В противоположность этому внутренняя энергия U
определяется этими величинами однозначно. Изменение внутренней
энергии можно поэтому записать в виде полного
дифференциала dU, в то время как для обозначения подведенного
количества теплоты используется знак б.
Процесс называется обратимым, если его можно заставить
протекать в обратном направлении путем простого изменения
направления пути и при этом для восстановления исходного
состояния всех участвующих в процессе тел не требуется
подвода энергии.
Пример 14
Примерами обратимых процессов могут служить механические и
электрические колебания в отсутствие потерь. Равным образом можно рассматривать
как обратимый процесс расширения или сжатия газа, если давление
последнего при этом находится в равновесии с внешней силой. Изменения одной
из сил на бесконечно малую величину оказывается тогда достаточным, чтобы
заставить процесс протекать в обратном направлении, так что исходное
состояние может быть восстановлено.
Рассмотрим обратимый процесс внутри замкнутой системы,
к которой подводится количество теплоты (SQ)o6p. Умножая эту
98
Гл. 2. Классическая статистика идеальных газов
величину на интегрирующий множитель 1/71, получаем
дифференциал некоторой функции состояния
-l(6Q)o6p = dS . (2.4)
Эту функцию называют энтропией. Она однозначно
определяется значениями измеряемых параметров состояния
макроскопической системы (давление, объем, температура, число частиц
или число киломолей).
Для обратимых процессов, согласно первому закону
термодинамики, выполняется соотношение
«-^L.-*2^
(2.5)
Выражение (2.5) является термодинамическим определением
энтропии, которым следует пользоваться при вычислении этой
функции состояния. Статистическое определение энтропии будет
дано в § 3 настоящей главы.
Если к системе подводится количество теплоты 6Q, то ее
температура повышается на dT (предполагается, что система
не находится в критической точке, отвечающей фазовому
переходу). Отношение
С = §г (2.6)
определяет удельную теплоемкость системы. Ее обычно относят
к 1 кмоль и называют молярной теплоемкостью.
При вычислении удельной теплоемкости предполагается, что
процессы являются обратимыми. Для молярной теплоемкости
при постоянном объеме, называемой также изохорной
теплоемкостью, получаем, подставляя (2.4) в (2.6),
С-№)„-т(Ш).. (2.7)
[дТ Jv"1 [dTjv*
Соответственно молярная теплоемкость при постоянном
давлении (изобарная теплоемкость) определяется выражением
С помощью соотношения (2.5) молярную теплоемкость Ср можно
представить также в виде
CP = T(§)r^U + PV)P^)p, (2.9)
где
H = U + PV (2.10)
§ 2. Первый закон термодинамики
99
есть функция состояния, называемая энтальпией. Все функции
состояния при этом отнесены к 1 кмоль.
При применении закона равномерного распределения
энергии по степеням свободы, как и вообще при расчете
физических функций состояния методами классической статистики,
предполагается, что число степеней свободы остается
неизменным вплоть до абсолютного нуля. В действительности же каждая
степень свободы становится полностью эффективной лишь при
достижении температуры, превышающей некоторое определенное
значение (см. § 4 настоящей главы). Удельная теплоемкость
является при этом измеряемой величиной, по которой можно
определить число эффективных степеней свободы. Следует
отметить, что для очень многих физических процессов число
степеней свободы в начальном и конечном состояниях одинаково.
В особенности это относится к случаям, когда изменения
температуры не очень велики. Поэтому применение классической
статистики для расчета изменений энергии обычно приводит
к хорошему согласию между теорией и экспериментом, если
температура не выходит за пределы определенных границ.
Если учесть, что при уменьшении температуры степени
свободы макроскопической системы „замораживаются", то для
определения внутренней энергии следует пользоваться не законом
равнораспределения, а соотношением
т
U = \cv(T)dT + U0, (2.11)
О
где U0—энергия при абсолютном нуле (ср. § 4).
Задачи
2.1*. Классический закон равнораспределения
На основании закона распределения Гиббса требуется определить
внутреннюю энергию твердого тела. Вычислить эту энергию для 1 кг углерода при
1200 К и сравнить полученный результат с энергией сгорания (8093 ккал/кг).
Относительная атомная масса Лс= 12,01.
Решение
Если обозначить через е и dN соответственно энергию и число заполнения
определенного энергетического состояния, то внутреннюю энергию U,
усредненную по всем энергетическим состояниям, можно записать в виде
U=^edN. (2.1.1)
Рассмотрим сначала отдельно взятую частицу. Согласно закону распределения
энергии, вероятность того, что эта частица окажется в ячейке, которой соот-
100
Гл. 2. Классическая статистика идеальных газов
ветствует энергия е, равна
dN e~e/k T<iPx dP у dpz dx dy dz
dw=?^-==- y . (2.1.2)
N V e~zlhTdpx dp у dpz dx dy dz
Интегрирование в (2.1.1) и (2.1.2) распространяется на все состояния
рассматриваемой частицы. Подставляя (2.1.2) в (2.1.1), находим для средней
энергии е отдельной частицы
V ze~zlkTdpx dp у dpz dx dy dz
e=f— . (2.1.3)
\ e e/kTdpx dpy dpz dx dy dz
В твердом теле отдельные атомы не могут существенно смещаться из
положений равновесия. Когда такое расположение нарушается, возникают
квазиупругие возвращающие силы. Таким образом, каждый структурный элемент
твердого тела обладает потенциальной и кинетической энергией.
Кинетическая энергия одного атома, имеющего массу \i, равна
eK,H=|(^4+^)=pl+;;+pl- (2.1.4)
Для вычисления потенциальной энергии епот будем рассматривать каждую
частицу как гармонический осциллятор, совершающий колебания под действием
приложенных сил. Предположим, что частица смещена из своего положения
равновесия на расстояние х (х, у, z). Возвращающая сила ^ действует в
направлении — г. Ее компоненты пропорциональны компонентам смещения, если
только последние не слишком велики. Следовательно, для возвращающей силы
можно написать
% = -Dx, (2.1.5)
где D — постоянная, зависящая от структуры твердого тела. Следовательно,
потенциальная энергия сместившейся на величину х (х, у, z) частицы равна
/ х у Z ч
: = - \ %-dx = D[ $ xdx+ $ ydy + \zdz\
Чо о о /
или
enoT = -£-(*3 + ^ + z2). (2.1-6)
Если ввести обозначения
X = Xi, y==X2t Z = #3> Рх~х4> Ру — Хб* Pjs==xQt
то энергию рассматриваемой частицы можно представить в виде квадратичной
функции
е= J] av4, (2Л.7)
v=l
которая включает в себя как потенциальную, так и кинетическую энергию.
В твердом теле каждая частица обладает тремя степенями свободы,
соответствующими потенциальной энергии, и тремя степенями свободы, соответствую-
§ 2. Первый закон термодинамики
101
щими кинетической энергии. Следовательно, необходимо положить / = 6.
Внутренняя энергия системы U = Ne на основании (2.1.3) равна
N \ 2 ayXv ехр (~~2 avAlkT) dxx dx2 ... dxf
л v=i AJJo
U== с J—v^ T,—ч = NT' (2.1.8)
\ exp(— 2j^vXvlkT)dx1dx2 ... dxf u
Интеграл Ju, стоящий в знаменателе (2.1.8), можно разложить:
Ja= jexp(—^Jd* J exp(~^)^2... J exp^-^J^. (2.1.9)
— QO — CO — QO
Интеграл J0, стоящий в числителе, запишем в виде
р / агх\-\- ...+afx2f\
J0= j ai*Jexp ^ _ U J dxx... dxf + ...
— 00
f / агх1+...+а^\
...+ J a^expl -pp ]dxi...dxf.
— 00
Дальнейшее разложение дает
00 со
У0== I а^ехр ( — ^) dxx \ exp I — ^j dx2...
— QO —00
00
•••J exp(~l(r)d*/+--- * (2,U0)
— QO
Деля J0 на Ju, получаем
00 QO
[ a1x\^^{—a1x\lkT)dx1 \ afx2fexp (—afx2/kT)dxf
•/о — °° It-00
Ju
[ exp(—aixt/kT)dx1 f exp (— afxj/kT)dxf
последнее выражение можно записать также в виде
I \ av.*vexp (— avxl/kT)dxv
(2.1.11)
\ exp (— avx*/kT) dxv
102 Гл. 2. Классическая статистика идеальных газов
Если учесть, что подынтегральные выражения содержат только четные
функции, то интегрирование по бесконечному в обе стороны интервалу можно
заменить интегрированием от 0 до оо; при этом в числителе и знаменателе
выражения (2.1.11) появятся множители 2, которые в результате сокращаются.
Производя замену переменных
а
yv = kfxl> (2-1.12)
получаем из (2.1.11)
{,_ у av(av'kT)-3"T(%) _fhT(2W)YJ^ 1
J*~h (ajkrr^rm fkT—^—TfkT- (2-U3)
Принимая во внимание (2.1.8), получаем для полной энергии системы формулу
(2.1.14)
которая выражает закон классической статистической физики о равномерном
распределении энергии по степеням свободы. Согласно (2.1.14), внутренняя
энергия в расчете на 1 кмоль равна
Um=E^L^. (2.1..6)
Подставляя сюда / = 6 и Г=1200К и выражая R в ккал/кмоль-К, находим
внутреннюю энергию твердого тела, отнесенную к 1 кмоль
6.1,986-1200 _|КЛ
Um — —о = 7150 ккал/кмоль.
Если относительная атомная масса рассматриваемого элемента равна Лг, то
для внутренней энергии в расчете на 1 кг имеем
^Kr=W' (2,1,16)
Для углерода получаем
7153,2 с__
Скг = ~ПГ0Г ккал/кг.
В соответствии с этим энергия сгорания обыкновенного углерода, равная
8093 ккал/кг, даже при температурах около 1000Q С все еще на порядок
больше внутренней энергии.
2.2. Атомная теплоемкость металлов. Закон Дюлонга-Пти
Пользуясь классическим законом равнораспределения, вычислить
удельную теплоемкость твердого тела по его внутренней энергии. Каковы значения
удельных теплоемкостей для железа, алюминия, бериллия? Относительные
атомные массы этих веществ равны соответственно ^Fe = 55,85, Ла\== 26,98,
4ве = 9,01. Сравнить теоретические результаты с экспериментальными
значениями.
§ 2. Первый закон термодинамики
103
Решение
Удельная теплоемкость твердого тела получается из его внутренней
энергии дифференцированием по температуре. Если опять относить все величины
к 1 кмоль, то для удельной теплоемкости в соответствии с классическим
законом равнораспределения получаем выражение
С~ dT~dT 2 - 2 ' {2л2Л)
Подставляя в (2.2.1) / = 6, в соответствии с наличием трех степеней свободы,
определяющих потенциальную энергию, и трех степеней свободы,
определяющих кинетическую энергию, и выражая численное значение R в ккал/кмоль-К,
находим молярную теплоемкость твердого тела
с=6-1,986 = 5^958 ккал/кмоль.к (2#2.2)
(закон Дюлонга-Пти для атомной теплоемкости).
Удельную теплоемкость с, отнесенную к 1 кг, получаем из (2.2.2) путем
деления на относительную атомную массу элемента АТ\
с== с ^бдаккал/кг.к# (2#23)
Аг Ат
Для чистого железа, алюминия и бериллия находим
5,958 л 1Л„ , лг
CFe=55\85=°'107 ккал/кг-К
(экспериментальное значение 0,108 ккал/кг.К),
5 958
cA1=2g~98=0'221 ккал/кг*К
(экспериментальное значение 0,214 ккал/кг«.К),
сВе=|^=0,661 ккал/кг-К
(экспериментальное значение 0,244 ккал/кг«К).
Отсюда видно, что в то время как для тяжелого и среднего элементов Fe и А1
теоретические и экспериментальные величины отличаются лишь незначительно,
для бериллия, относящегося к числу самых легких элементов,
экспериментальное значение существенно меньше теоретического.
Приведенные экспериментальные величины являются средними значениями
для интервала температур от 0 до 100° С. При понижении температуры
удельная теплоемкость также уменьшается. Это показывает, что при понижении
температуры происходит „замораживание степеней свободы" (ср. гл. 4, § 5).
2.3. Удельная теплоемкость идеальных газов
при постоянном объеме
Исходя из классического закона равнораспределения, вычислить молярную
теплоемкость идеального газа при постоянном объеме и сравнить результат
теоретического расчета с экспериментальными значениями.
104
Гл. 2. Классическая статистика идеальных газов
Решение
Определим сначала число степеней свободы газа (фиг. 16). Атомы
одноатомных газов, к которым относятся инертные газы и пары металлов, могут
перемещаться в пространстве во всех трех направлениях. Каждая из трех
компонент скорости отдельного атома входит в энергию макроскопической
системы квадратично. В то же время отсутствуют какие-либо ограничения,
обусловленные наличием потенциалов. В соответствии с этим число степеней
свободы одноатомной молекулы равно / = 3.
Z
Ь %Лг
х1 9>г \
*i Ъ \
f=3 *=5
Фиг. 16. Степени свободы жестких молекул.
f=6
В случае двухатомных жестких молекул х> в дополнение к трем степеням
свободы поступательного движения появляются две вращательные степени
свободы. Второй атом может вращаться вокруг первого атома молекулы,
описывая сферу, радиус которой равен расстоянию между атомами. Таким
образом на его вектор скорости накладывается ограничение, поэтому на второй
атом приходится лишь две степени свободы. Всего, следовательно, жесткий
ротатор имеет / = 5 степеней свободы.
Если, кроме того, оба атома могут совершать колебания друг относительно
друга, то в дополнение к уже имеющимся степеням свободы следует добавить
еще две, одна из которых соответствует кинетической, а другая —
потенциальной энергии. Таким образом, полное число степеней свободы в этом случае
будет равно / = 7. Для строгого теоретического рассмотрения возникновения
колебательных степеней свободы необходимо привлечь квантовомеханические
соображения (см. гл. 4).
Жесткая трехатомная молекула обладает помимо трех поступательных и
двух вращательных степеней свободы еще одной вращательной степенью
свободы, обусловленной наличием третьего атома, который может вращаться
вокруг двух других по круговой траектории. К этим / = 6' степеням свободы
жестких трехатомных и многоатомных молекул могут присоединяться
добавочные степени свободы, связанные с колебательными движениями.
В общем случае движение /г-атомной молекулы (я^гЗ) полностью
описывается заданием Зп координат. При этом три степени свободы приходятся на
поступательное движение и еще три — на вращение молекулы. Остается,
следовательно, Зп — 6 степеней свободы, которые соответствуют колебательным
движениям атомов. Согласно классической теории, вклад этих колебательных
степеней свободы следует учитывать дважды: один раз—для кинетической
энергии и один раз—для потенциальной. В соответствии с этим трехатомной
молекуле следует приписать 12 степеней свободы, а именно: 3 поступательные
степени свободы, 3 вращательные и два раза по 3 колебательные степени
свободы.
1} Такую молекулу называют иногда ротатором или гантелью. — Прим.
перев.
§ 2. Первый закон термодинамики
105
Молярная изохорная теплоемкость определяется выражением
c^{w)v <2-ЗЛ)
где 6Q — подведенное в обратимом процессе количество теплоты, отнесённое
к 1 кмоль. Согласно первому закону термодинамики, имеем
6Q=dU + PdV. (2.3.2)
На основании классического закона равнораспределения внутреннюю энергию
1 кмоль можно записать в виде
V.-fWJW. (2.3.3)
При постоянном объеме необходимо положить бЛ/ = 0. Тогда для молярной
изохорной теплоемкости получаем выражение
Мя\ _fR ,234)
т. е.
f
Cv=~y 1,986 ккал/кмоль-К. (2.3.5)
Для одноатомных газов / = 3. В соответствии с этим теплоемкость
одноатомных газов равна
С?) = |-/? = -|-. 1,986 = 2,98 ккал/кмоль-К. (2.3.6)
Это значение хорошо подтверждается для всех одноатомных газов (ср. табл. П.Х
приложения). В случае двухатомных молекул, подставляя в соответствии
с моделью жесткого ротатора / = 5, получаем из (2.3.5)
С<,2)=—Я=—-1,986 = 4,97 ккал/кмоль-К. (2.3.7)
Это значение подтверждается результатами экспериментов, если температура
не слишком высока. Если же произвести расчет, используя модель
осциллирующей молекулы с / = 7 степенями свободы, то из (2.3.5) получаем
с£2)=-2 • 1,986 = 6,95 ккал/кмоль-К. (2.3.8)
Согласно табл. П.Х, к такому значению приводят измерения при очень
высоких температурах. Это означает, что колебательные степени свободы
становятся эффективными лишь при достижении достаточно высоких температур,
следовательно, они „вымерзают", когда температуры падают ниже
определенного предела.
При дальнейшем понижении температуры теплоемкость двухатомных
газов, согласно табл. П.Х, уменьшается, стремясь к теоретическому значению
для одноатомных газов. Следовательно, вращательные степени свободы также
эффективны лишь при температурах, превышающих некоторое определенное
значение.
В соответствии с законом Нернста о стремлении удельной теплоемкости
к нулю, при абсолютном нуле температуры в конечном итоге замораживаются
также и степени свободы, соответствующие поступательному движению.
106
Гл. 2. Классическая статистика идеальных газов
Для модели жесткой трехатомной молекулы с / = 6 степенями свободы
молярная теплоемкость, согласно (2.3.5), равна
С^3) = |-/?=-| • 1,986 = 5,96 ккал/кмоль-К, (2.3.9)
тогда как при учете колебательных движений получаем
C™~R=^- . 1,986=11,92 ккал/кмоль-К. (2.3.10)
Как видно из табл. П.Х, это значение также подтверждается при высоких
температурах.
2.4*. Удельная теплоемкость идеальных газов
при постоянном давлении
Для одно- и двухатомных идеальных газов определить молярную
изобарную теплоемкость и вывести формулу, связывающую ее с изохорной
теплоемкостью. Чему равен показатель адиабаты n = Cp/Cv для идеальных газов?
Решение
Обозначим через Q полную энергию рассматриваемого газа. Тогда изо-
хорная теплоемкость определяется как
- -(д-£)
'v-\dTjv'
(2.4.1)
Подставляя вместо приращения количества теплоты dQ приращение энтропии
dS=d£. (2.4.2)
получаем для молярной изохорной теплоемкости
С0 = т(§)у. (2.4.3)
Точно так же для изобарной теплоемкости имеем
ср=
Преобразуем формулу (2.4.4) к виду
Ср-
fdS\ =TdJS^P) 2
Стоящее здесь выражение вида
\ди ди\
д (ц, у) __
дх ду
dv dv
(2.4.6)
| дх ду\
называется функциональным определителем Якоби или просто якобианом. Его
применяют, например, при интегрировании, когда вместо переменных и и v
вводятся новые переменные хну. При этом старые переменные и и v, так же
§ 2. Первый закон термодинамики
107
как и новые переменные х и у, будут независимыми друг от друга, если
детерминант не равен нулю. Если после перехода к переменным хну
совершается еще один переход к переменным s и /, то справедливо так называемое
цепное правило
д(и, v)
'ЩИ)''
д (и, у)/д (х, у)
'd(s, t)/d(xty) '
(2.4.7)
Формула (2.4.5) соответствует случаю, когда вместо независимых
переменных 5 и Р вводятся величины Г и Р. При этом имеем
d(S. Р)
д(Т9РУ
dS_\ ( dS\
дТ )Р [dPj
I дР
\дР
дР_
dTjp
dS\ fdS_\
дт)Р \dPjT
dS
дТ
= Sr L- (2'4-8)
что и было заранее записано в (2.4.5).
Применяя формулу (2.4.7), находим
d(S,P) d(S, Р)/д(Ту V)m
р д(т, Р) а (г, pyd(T9vy
из формулы (2.4.6) следует
г _ (dS/dT)v (дР/дУ)т- (dS/dV)T(dP/dT)v
р (dP/dV)T
Подставляя (2.4.3) в (2.4.9), получаем
г „(dS/dV)T(dP/dT)v
^p-^v-t {dP/dV)T '
Для определения величины (dS/dV)T рассмотрим дифференциал функции
состояния
(2.4.9)
(2.4.10)
F = U — TS
которая называется свободной энергией1) (см. § 3 и задачу 3.1 настоящей
главы). Для ее дифференциала имеем
dF = d(U — TS) = dU — TdS — SdT. (2.4.11)
Согласно первому закону термодинамики, при обратимых процессах
выполняется равенство
bQ = TdS = dU + PdV. (2.4.12)
Благодаря этому можно записать (2.4.11) в виде
dF = -PdVSdT, (2.4.13)
откуда следует, что имеют место соотношения
(»),-'• (£),--«■
(2.4.14)
*) Эту величину называют также энергией Гельмгольца, что и делает
автор. Мы будем использовать преимущественно приведенный в тексте термин
как более распространенный.—Прим. ред.
108
Гл. 2. Классическая статистика идеальных газов
Подставим второе из этих соотношений в (2.4.10). Учитывая при этом, что
на основании первого соотношения можно записать
д5Г
.dVjT \dV \<ГГ Jvjr YPT \<>V I t\V \OTjy
получаем из (2.4.10)
r-~[w [дт) v\ Г ~ W (WJ J v - [dfj v' (2-4> 15)
С p — Cv-
T (дР/дТ)у
(dP/dV)T
(2.4.16)
Производные от давления определим с помощью уравнения состояния
идеального газа PV — RT. Подставляя последнее в (2.4.16), приходим к
соотношению, связывающему молярные теплоемкости идеального газа
Cp = Cv + R = Cv + \$yb ккал/кмоль.К. (2.4.17)
В соответствии с этим и с учетом результатов, полученных выше в задаче
2.3, получаем для теплоемкости идеального газа при постоянном давлении
cy=j.*+*=-!*.
(2.4.18)
Подставляя численное значение R, находим
0^ = ^-- 1,986 = 4,965 ккал/кмоль-К
(ср. табл. П.Х и П.XI).
Для двухатомных молекул в области средних температур имеем
С£2) = A R + R = -^ R = 6,951 ккал/кмоль. К,
а в области высоких температур
Cp2)=-n- R = 8,937 ккал/кмоль-К.
Показатель адиабаты
(2.4.19)
(2.4.20)
для идеальных газов, согласно (2.4.17), равен
Таким образом, имеем для одноатомных идеальных газов
*»-5^-1.66....
для двухатомных газов в области средних температур
(2.4.21)
(2.4.22)
(2.4.23)
§ 2. Первый закон термодинамики
109
и в области очень высоких температур
х<*>=!^ = 1,28... (2А25)
(ср. табл. П.Х).
2.5. Адиабатические процессы
При расширении 6 л гелия, имевшего температуру 350 К, давление падает
от 40 до 1 ат. Расширение происходит адиабатически, т. е. газ не отдает
и не получает тепла. Вычислить объем и температуру в конечном состоянии
и сравнить их с результатами, которые получаются при изотермическом
расширении.
Решение
Поскольку газ не отдает и не получает тепла, то dQ=TdS = 0. При
адиабатических процессах энтропия S остается постоянной. Поэтому на
основании (2.4.7) имеем
fdV\ _д(У, S)_d(V, S)/d(Vt Т) д(У, Т)
\dPjs д(Р, S) д(Р, S)/d(Pt Т)'д(Р, Т) • V-0'1'
Это можно записать также в виде
(dV\ ... (dS/dT)v /дУ\
[dP)s~(dS/dT)P[dp)T- (1Лг)
Согласно (2.4.3) и (2.4.4), имеем
с*=г(§),' c»=T{w)P- v*v
Подставляя эти выражения в (2.5.2), получаем
(£).-§ (£),-И*)г-
Тем самым мы свели адиабатическое расширение к изотермическому
расширению. Изотермические процессы описываются уравнением состояния
идеального газа PV — RTf которое в данном случае можно записать в виде
PV = P0V0t (2.5.5)
где Р0 и V0—давление и объем в исходном состоянии. Из (2.5.5) имеем
(dV\ _ P0Vo_ V
[дг)т-—рг-—р- (2'5'6)
Подставляя сюда (2.5.4), находим связь между давлением и объемом при
адиабатических процессах
или, после разделения переменных и интегрирования,
р V
CdP CdV
\т—'\т- ,2•58,
(;
по
Гл. 2. Классическая Статистика идеальных газов
Отсюда получаем
Р V
In —-=— xln 7j-=ln
го Vo
или
PVK =P0V%
(2.5.9)
(2.5.10)
Для гелия имеем
х= с;=з-=:1-66----
Следовательно, искомый объем равен
v=(£)"4.
(2.5.11)
т. е.
у = [™j .6 =9,15-6 =54,9 л.
С другой стороны, при изотермическом расширении объем равен
у==М°=40.6 =240 л.
Используя данные относительно исходного состояния, находим число кило-
молей
7$7=«- (2-5.12)
Тогда для температуры в конечном состоянии получаем выражение
PV PV
т = 1П?=рЖТ°- <2-5ЛЗ>
В рассматриваемом случае имеем
гг_ 1-54,9
40-6
350 = 80 К.
При адиабатическом расширении газ, таким образом, охлаждается до —193дС.
2.6. Скорость звука в идеальных газах
При распространении звуковых волн в воздухе периодические изменения
давления воздуха происходят столь быстро, что за период одного колебания
практически не происходит передачи энергии. Вследствие этого можно
считать, что в первом приближении распространение звука без затухания не
к к к
Подвижный J у
поршень
Стержень —.
Зажим
Фиг. 17. Трубка Кундта.
При резонансе (настройка
осуществляется с помощью подвижного поршня)
частицы пыли собираются в узлах К.
связано с изменением энтропии. Исходя из такой точки зрения, выразить
показатель адиабаты K — Cp/Cv для воздуха через скорость звука. Какова
величина и, если измерение расстояния между узлами пылевых фигур в трубке
Кундта (фиг. 17) дает значение / = 6,8 см? При этом частота и температура
§ 2. Первый закон термодинамики
111
равны соответственно 2500 Гц и 12°С. Относительную молекулярную массу
воздуха принять равной Л1г==29,0.
Решение
Поскольку изменение давления звука происходит при постоянной
энтропии, периодическое разрежение и уплотнение воздуха можно рассматривать
как адиабатический процесс. Для последнего в соответствии с (2.5.7) имеем
'Щ =iffi = -±L (261)
dPjs х[дР)Т х Р • *лл>
Скорость звука в твердом теле определяется формулой
с = ]/|-, (2.6.2)
где р — плотность, а Е—модуль упругости. Последний определяется
уравнением
4-И.
где dF—сила, действующая на стержень с поперечным сечением А и длиной /,
a dl — вызванное этой силой удлинение стержня (фиг. 18). В случае газа
следует записать
V ''
dl_
~~ I
dP=-
dF
(2.6.4)
Знак минус во втором уравнении обусловлен тем, что давление соответствует
отрицательной растягивающей силе, т. е. F < 0. Найдем из (2.6.3) обратный
Kl^^T Фиг. 18. Удлинение твердого тела под действием приложен-
' dF f Т ной силы (закон Гука).
модуль упругости и подставим в полученное равенство соотношения (2.6.4).
В результате получаем
Е— i dF— у dp- l^.O.UJ
Изменения объема и давления в поле звуковой волны происходят
адиабатически. Поэтому имеем
dP Е к Р '
т. е. модуль упругости газообразных сред соответствует величине
Е = кР. (2.6.6)
Подставляя (2.6.6) в (2.6.2), находим скорость звука в газе
112
Гл. 2. Классическая статистика идеальных газов
Плотность газа р можно выразить через относительную молекулярную массу
и молярный объем:
Подставляя (2.6.8) в (2.6.7), получаем для скорости звука выражение
Разрешая это уравнение относительно показателя адиабаты х, имеем
x=^f. (2.6.10)
Расстояние между двумя соседними узлами пылевой фигуры в трубке Кундта
равно половине длины звуковой еолны А,/2. Учитывая это и используя
заданное значение частоты / = 2500 Гц, находим скорость звука
с = А,/ = 2// = 2.0,068-2500 м/с = 340 м/с.
Подставляя в (2.6.10) это значение и остальные числовые величины, получаем
окончательно
29-3402
К~ 8,314-К)».285 -1»41-
Упражнения
У.2.1. На основании закона равнораспределения вычислить внутреннюю
энергию 1 л гелия, 1 л водорода и 1 л углекислого газа при
давлении 1 ат. Энергию выразить в джоулях.
У.2.2. Какой внутренней энергией обладает в соответствии с законом
равнораспределения 1 г урана при 300 К? Сравнить эту энергию
с энергией покоя Е0.
У.2.3*. Определить среднее значение энергии е, средний квадрат е2 и
среднюю дисперсию (е —е)2 для распределения Гиббса. Какие значения
получаются при 300 К?
У.2.4. Вычислить удельную теплоемкость 1 кг твердого свинца, кобальта,
меди, никеля, серебра, урана, вольфрама, олова и сравнить
полученные результаты с экспериментальными значениями.
У.2.5. Чему равна в соответствии с классическим законом
равнораспределения удельная теплоемкость, отнесенная к 1 кг, для КС1, NaN03,
KN03, Na2C03, CaO, Cu20 и CuO? Сравнить результаты с
экспериментальными данными.
У.2.6. Пользуясь законом равнораспределения, вычислить Сру Cv и % для
газа, состоящего из трехатомных молекул в случаях: а) когда
колебания заморожены, б) когда эффективны все степени свободы.
У.2.7. Пользуясь законом равнораспределения, вычислить таким же
образом Cpj Cv, х для случая четырехатомных молекул.
У.2.8. Чему равна по классической теории удельная теплоемкость 1 кг
кислорода при высоких температурах? (MQ =32,0.)
У.2.9*. При расширении 10 л гелия, имеющего температуру 1000 К,
давление падает с 10 до 2,5 ат. В предположении, что процесс протекает
адиабатически, вычислить объем и температуру и сравнить
полученные результаты с соответствующими величинами при изотермическом
расширении.
§ 3. Вычисление термодинамических функций состояния 113
У.2.10. Воздух при давлении 15 ат адиабатически расширяется. До какого
значения должно снизиться давление, чтобы произошло охлаждение
от 320 до 160 К?
У.2.И. В результате расширения 4 л воздуха, имевшего давление 8 ат и
температуру 350 К, давление становится равным 2 ат. Процесс
протекает не полностью адиабатически, т. е. описывается не
показателем адиабаты и, а показателем политропы п. Вычислить этот
показатель, если после расширения температура оказалась равной 250 К.
У.2.12*. Вывести для политропного процесса с показателем п общее
соотношение между температурой Т и объемом V, а также между
температурой Т и давлением Р. Какая температура и какое давление
получатся при политропном сжатии 1 кмоль идеального газа,
находящегося при нормальных условиях (1,033 ат, 273,16 К), если его
объем становится равным половине первоначального? Показатель
политропы п— 1,25.
У.2.13. Вычислить скорость звука в воздухе при —50°С и +50°С. Для %
в обоих случаях принять величину, равную теоретическому значению
для жесткой молекулы, а относительную молекулярную массу зоз-
духа Mi положить равной 29,0. Какая скорость звука получится,
согласно классической статистике, для водорода при 300 К?
§ 3. ВЫЧИСЛЕНИЕ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ СОСТОЯНИЯ
С ПОМОЩЬЮ СТАТИСТИЧЕСКОЙ СУММЫ.
ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
Введение
Соотношение неопределенностей Гейзенберга
(3.1)
AqAp^h
устанавливает принципиальную связь между неточностью Aq
значения координаты и неточностью Ар значения
сопряженного с ней импульсаи. При этом величина
/1 = 6,6262- Ю-34 Дж-с
(3.2)
есть квант действия Планка. Учитывая соотношение
неопределенностей Гейзенберга, полагают, что объем АГ элементарной
ячейки s-мерного фазового пространства равен
ДГ = Aft.. AqAPi. • .APr = ^r, r = y. (3.3)
Пример 15
Колебание одномерного осциллятора описывается координатой q = x и
импульсом p — \ix. Отсюда следует, что объем элементарной ячейки равен
х> Точнее, (3.1) содержит величину $,/2 = h/4n, но минимальная ячейка
фазового пространства при переходе к квазиклассике определяется величиной h-
■^Прим- ред,
114 Гл. 2. Классическая статистика идеальных газов
ДГ=А^Др=^Дл:Лл: — h. В случае трехмерных колебаний материальной точки
с координатами qi — xt q2 = y, Яъ = г и импульсами р1 = \лх, р2 = М> Ръ — №
объем фазовой ячейки составляет ДГ = Aq1Aq2AqBAp1Ap2Ap3 = Л3.
Если в основу статистических расчетов в s-мерном фазовом
пространстве положить в соответствии с (3.3) элементарные
ячейки объемом /is/2, то можно найти связь между энтропией
как термодинамической функцией состояния и
термодинамической вероятностью W, выражаемую формулой Больцмана
S = klnW, (3.4)
где
k = 1,3806- Ю-23 Дж/К
(3.4а)
— постоянная Больцмана.
Формулу Больцмана можно рассматривать как
статистическое определение энтропии. Из нее следует, что энтропия
является экстенсивной величиной,!, е. энтропия всей системы равна
В про-
s=sx-\-s2
сумме энтропии составляющих ее подсистем,
тивоположность этому термодинамическая вероятность W слож
ной системы равна произведению термодинамических
вероятностей ее подсистем в соответствии с основными законами
теории вероятности:
W = WtW2
Пример 16
Рассматривается резервуар, который состоит из двух изолированных
друг от друга газовых баллонов. Термодинамическая вероятность Wx первой
подсистемы определяется kx характеристическими параметрами Nn, ..., Nik»
термодинамическая вероятность W2 второй подсистемы определяется
соответственно /е2 величинами N21t ...» N2k2- Следовательно, для полной
характеристики всей системы необходимо k1-\-k2 параметров. Термодинамическая
вероятность некоторого определенного распределения, согласно закону умножения
вероятностей, определяется соотношением
W (Nn, ..., Nlkv N21, ..., N2k2) = W (Nn, ..., Nlhl) W (N21, ..., N2k2).
Отсюда для энтропии системы в целом на основании формулы Больцмана (3.4)
получаем
S = k\nW = k\nW1W2 = k(\nW1 + \nW2)==S1 + S2.
Энтропия, следовательно, является экстенсивной величиной в
противоположность термодинамической вероятности.
Согласно закону распределения Гиббса, числа заполнения
отдельных энергетических состояний определяются
выражением (1.27)
e-*ilkT
N- = N —
i
§ 3. Вычисление термодинамических функций состояния 115
Стоящую в знаменателе этого выражения сумму обычно
обозначают
Z = 2e-ei'kT = e-*'kT (3.5)
i
и называют статистической суммой термодинамической системы.
Соотношение (3.5) является определением параметра ср.
Умножая этот параметр на число частиц N, получаем функцию
состояния
N^= — NkT\nZ = — NkT\n^e^e^kT. (3.6)
с
Пользуясь методами статистической физики, можно вычислить
энтропию S. Для этого найдем натуральный логарифм
термодинамической вероятности в равновесном состоянии. Применяя
формулу Стирлинга, имеем
lnW = =j^ = N(\nN-l)-1£iNl(\nNt-l). (3.7)
С
Принимая во внимание, что N = ^Nh получаем из (3.7) с уче-
i
том распределения Гиббса (1.27)
1пГ = ЛПп#-2#/1п(Л^ (3.8)
i i
Используя закон сохранения энергии y^iNiei = U и определе-
i
ние (3.6), находим
1пУ=а i ^ =^Ф, (3.9)
Подставляя сюда на основании (3.4) вместо k\nW энтропию S,
имеем
Nq> = U — TS = F, (3.10)
где/7—свободная энергия, введенная ранее [см. (2.4.11)]. Вместо
того чтобы в соответствии с формулой (3.5) производить
суммирование по всем макроскопическим состояниям, гораздо
целесообразнее вычислять статистическую сумму, пользуясь
представлением об элементарных ячейках фазового пространства.
При этом следует иметь в виду, что вклад от каждого из
возможных макросостояний входит в (3.5) только один раз.
Следовательно, состояния, получающиеся из уже учтенных состояний
путем простой перестановки одинаковых частиц, не должны
116 Гл. 2. Классическая статистика идеальных газов
учитываться повторно. Для системы из N частиц число таких
перестановок равно ЛП Поэтому, чтобы исключить многократный
учет физически равноправных состояний, необходимо после
суммирования по всем элементарным ячейкам фазового
пространства разделить результат на ЛП Если, кроме того, из общего
числа макроскопических состояний т состояний физически
равноправны в силу свойств симметрии, то результат необходимо
разделить также и на т.
Поскольку каждая ячейка фазового пространства
характеризует все частицы системы, при суммировании по фазовому
пространству стоящая в показателе степени в формуле (3.5)
величина г{ есть не что иное, как внутренняя энергия системы
для каждой из суммируемых фазовых ячеек. Заменяя
суммирование по всем физически различным состояниям
интегрированием по всем переменным фазового пространства, получаем
вместо (3.5) фазовый интеграл
(3.11)
Точка в фазовом пространстве изображает при этом состояние
макроскопического тела, состоящего из одной частицы с s = 2r
степенями свободы. Пользуясь соотношением (3.6), можно
представить свободную энергию в виде
F = — kTlnZ
(3.12)
Зная свободную энергию, нетрудно определить остальные
функции состояния. Согласно первому закону термодинамики, для
равновесного состояния имеем [см. (2.5)]
TdS = dU + PdV.
Подставляя эту величину в дифференциал свободной энергии
dF = d(U — TS), (3.13)
получаем
dF = — PdV—SdT. (3.14)
Это означает, что энергию Гельмгольца следует рассматривать
как функцию объема и температуры, F = F(V, Т)1]. Вычисляя
г) По этой причине ее называют также изохорно-изотермическим
потенциалом.— Прим. перев.
§ 3. Вычисление термодинамических функций состояния 117
частные производные по независимым параметрам системы,
находим из (3.14)
(3.15)
Внутреннюю энергию U определяем с помощью соотношения
u=f+ts=f—t(¥l^
Используя эти величины, можно вычислить энтальпию
H = U + PV
(3.16)
(3.17)
На основании первого закона термодинамики ее
дифференциал можно записать в виде
dH = dU + PdV + VdP = TdS + VdP, (3.17а)
откуда получаем
да,-*-.
дН_
дР is
-V.
(3.18)
Энтальпия играет важную роль при расчетах, относящихся
к сменяющимся рабочим веществам. Для изобарных процессов
dP = 0. На основании первого закона термодинамики отсюда
следует, что (dQ)P = dH, т.е. при постоянном давлении все
подводимое количество теплоты полностью расходуется на
увеличение энтальпии системы.
Энергия Гиббсаг) определяется выражением
G=H—TS
(3.19)
Применяя первый закон термодинамики, можно записать
дифференциал этой функции в виде
dG = dH—TdS—SdT = VdP—SdT. (3.19а)
Следовательно, энергия Гиббса является функцией давления
и температуры G = G(P, Т). Отсюда имеем
"-(*),. *—(£),.
(3.20)
Х) Эту величину называют также свободной энтальпией или
термодинамическим потенциалом Гиббса. Мы будем пользоваться преимущественно
термином „энергия Гиббса".— Прим. ред.
118
Гл. 2. Классическая статистика идеальных газов
а также
H = G + TS = G-t(^p. (3.21)
Кроме полученных уже формул, связывающих различные
параметры состояния, при термодинамических расчетах важную роль
играют следующие соотношения, которые аналогично формулам
(3.14) — (3.20) получаются с помощью первого закона
термодинамики:
\dV )s'
а также
далее
\w)s=-c;[w)Y' [w)s=c;[w)P- (3-25)
Зная энтропию, можно определить, является ли процесс обра-
тимым, и указать направление необратимых процессов.
Все процессы всегда протекают таким образом, что
термодинамическая вероятность W стремится к своему
максимальному значению. При обратимых процессах в замкнутой системе
термодинамическая вероятность W распределения, а
следовательно, и энтропия S остаются постоянными. Если же процесс
является необратимым, то энтропия системы возрастает. Энтропия
замкнутой системы не может убывать:
2А5>0
(3.26)
Соотношение (3.26) выражает второй закон термодинамики.
Существует несколько эквивалентных формулировок второго
закона.
1. Теплота не может сама по себе переходить от тела с более
низкой температурой к телу с более высокой температурой.
2. Невозможно построить периодически действующую
машину, которая только совершала бы механическую работу за
счет охлаждения термостата, не вызывая никаких других
изменений в системе.
3. Процесс преобразования механической работы в тепло
посредством трения не может быть полностью обратимым.
§ 3. Вычисление термодинамических функций состояния 119
Если рассмотреть незамкнутую систему, к которой
подводится извне количество теплоты 6Q, то на основании (3.26)
можно получить следующую формулировку второго закона
термодинамики. Если в некотором процессе энтропия
рассматриваемой системы возрастает не только за счет подводимого
к ней количества теплоты 6Q, то процесс является необратимым.
Таким образом, для любых процессов в некоторой системе
справедливо соотношение
TdS—6Q>0
(3.27)
Здесь верхний знак относится к необратимым, а нижний — к
обратимым процессам.
Из (3.26) и (3.27) при учете первого закона термодинамики
[см. формулу (2.3)] вытекают следующие соотношения:
TdS—PdV^dU (a) —SdT—PdV>dF (б)
TdS + VdP^dH (в) — SdT + VdP^dG (г)
. (3.28)
В классической статистике квантовые процессы не учитываются.
Поэтому определение функций состояния с помощью
классической статистической суммы Z сопряжено с ошибкой, в полной
аналогии с вычислением внутренней энергии на основании закона
равнораспределения. При изучении термодинамических
процессов интерес представляют, однако, не столько сами функции
состояния, сколько их изменения. При этом, как правило,
квантовые поправки выпадают, в особенности если температура
достаточно далека от абсолютного нуля, а ее изменения не
очень велики.
Квантовые процессы обусловливают изменение молярной
теплоемкости с температурой. Если учесть эту зависимость, то
для вычисления изменения энтропии 1 кмоль идеального газа
получаются формулы
AS = S(T2, Pt)-S(TU Л) = j -fdT-R^ Т". (3-29)
AS = S(T2, Vt)-S(TU V1) = ^dT + R^ (3.30)
(ср. упражнение 3.11).
120
Гл. 2. Классическая статистика идеальных газов
Задачи
3.1. Функции состояния одноатомных газов.
Физический смысл функций состояния Uf F, Н
В цилиндр объемом У = 5 л впускается гелий и его температура
доводится до 400 К. Масса введенного гелия т—\ г.
а) Вычислить статистическую сумму Z и определить с ее помощью
свободную энергию F, внутреннюю энергию U, энтропию S, а также
энтальпию Н и энергию Гиббса G.
б) Какое количество энергии будет отнято у системы, если при
обратимом изотермическом процессе объем газа удвоится?
в) Какую энергию получит газ, если при постоянном давлении он
протекает через систему труб и при этом его температура возрастает от Г = 400К
до ГХ = 500К?
г) Какую энергию необходимо сообщить газу, чтобы при постоянном
объеме повысить его температуру от Т = 400 К до 7\ = 500К?
Для всех указанных случаев вычислить изменение энтропии 5 и
внутренней энергии U,
Решение
а) Статистическая сумма по определению равна
i
Введем для пространственных и импульсных координат частицы, находящейся
в состоянии i, соответственно обозначения
xlb Уи> zih •••» xNi> yNi* zNi
и
PV PVW P*U PxNf '%*' РгЖ-
Тогда кинетическую энергию N частиц можно записать в виде
«-£( *и+ '%+ *\,+ • • • + "^+ *Я1 + 'У • <ЗЛ'2>
где \i — масса одной частицы. В случае одноатомного газа частицы могут
совершать только поступательные движения. Поэтому получаемые для этого
случая функции состояния будем обозначать индексом „пост".
Чтобы перейти к интегрированию, умножим каждое из слагаемых
выражения (3.1.1) на объем ДГ/ = А</|-Лр|- соответствующей фазовой ячейки i
и одновременно разделим на величину hsN, которая в соответствии с
соотношением неопределенностей Гейзенберга представляет объем элементарной
ячейки в 6 N-мерном фазовом пространствег). Таким образом, каждое
слагаемое умножается на величину
АГ^Ар/А?/
tfiN — h3N ' lo.i.aj
*> Иными словами, умножим каждое из слагаемых выражения (3.1.1) на
плотность состояний.— Прим, перев.
§ 3. Вычисление термодинамических функций состояния 121
где
Api = ApXuApVi&pgir. ЛрХмАрумАргмГ (3.1.4)
Aqi = AxuAyuAzu.. .AxNiAyNiAzNi. (3.1.5)
Пользуясь тем, что число частиц очень велико, перейдем к бесконечно
малым размерам фазовых ячеек и запишем вместо (3.1.1) статистический
интеграл
Г7
dpхх • • • dzN=dpx
. dpz dXi.
.dzN.
(3.1.6)
Интегрирование здесь распространяется лишь на все физически различные
состояния фазового пространства Г. Это обстоятельство отмечено штрихом
при величине Г. Таким образом, Г' обозначает пространство Г за вычетом
всех физически эквивалентных состояний.
Поскольку подынтегральное выражение не содержит пространственных
переменных, интегрирование по последним можно произвести непосредственно.
Это дает множитель VN> где V — объем газа.
При интегрировании по импульсному пространству перестановки не
должны учитываться. Равным образом состояния, отличающиеся друг от
друга лишь перестановкой двух одинаковых частиц, должны учитываться
только один раз. На основании приближенной формулы (1.8) имеем
NN
Л/!:
pN
Поэтому, поделив подынтегральную функцию на N1, статистический
интеграл можно представить в виде
Z =
е*уя
№NNN
+ оо + а
ехр
P^+... + Р,1
2\ikT
K)dpXx...dpZN.
(3.1.7)
Разложение интеграла на 3N не зависящих друг от друга сомножителей
дает
со пзЛ/
ехр
2\ikT
dp
= (2niikT)3N^2.
С учетом этого можно записать статистический интеграл одноатомного газа
в виде
eNVN
■WN"{2nilkTy
\N/2
Отсюда для свободной энергии F = FnocT имеем
---kTlnZ
= — NkT In
V(2n\ikT)3/2
Nh3
(3.1.8)
(3.1.9)
122
Гл. 2. Классическая статистика идеальных газов
Число частиц N равно
^^6,02.103* :Ю-3=1>50.1023.
Мг
4,003
Подставляя это значение в (3.1.9) и вычисляя массу |Л атома гелия с
помощью соотношения \i — Mr/NA, получаем
: = —1,50-1023-1,38-10-23-400 X
X
. 5-Ю-з 3l 2.3,14-4,003.1,38-10-23-400 . Л-
1,5-Ю23
6,02-1026 (6,62- Ю-34)2
= —11,52 кДж.
Для энтропии S = SnocT на основании (3.15) находим из (3.1.9)
_ (dF,
п?ст ) =kN
дТ Jv
' V (2n{ikT)3/2 . 5
I" — .0 ho"
Л/
Л3
Для вычисления внутренней энергии воспользуемся соотношением
Подставляя сюда Fn0CT из (3.1.9), получаем
U = ^-NkT
(3.1.10)
(3.1.11)
(3.1.12)
что . находится в полном соответствии с классическим законом
равнораспределения. При заданных числовых величинах имеем
i/=y.l,5.1023-l,38.10-23.400=1242 Дж.
Теперь можно определить энтропию
U-F 1242+11520 Q1 Q _ .„
SnocT=~Y~== Зоб—=3 ,9 Дж/К'
(3.1.12а)
(3.1.10а)
Такой же результат получается и при подстановке числовых значений в
формулу (3.1.10). Давление Р находим с помощью соотношения
p__(dF_ \ _Л^Г_ NAkT_ nRT
\дУ)т~ V ~П V ~ V
(3.1.13)
где n — N/NA = m/Mr — число киломолей. В рассматриваемом случае имеем
_ Ы0-3 8,314-103.400 ц, , , ..
р=Тооз 5.10-3 н/м2 = 1>69 ат-
Энтальпия Н и энергия Гиббса G определяются выражениями
H=U + PV, G = H—TS = U + PV—TS. (3.1.14)
При заданных числовых значениях получаем
Я = (1242+1,69-9,81.104-5.Ю-3) = 2070 Дж,
G = (2070—400-3,57) = 642 Дж.
§ 3. Вычисление термодинамических функций состояния 123
б) Если при постоянной температуре объем удваивается, то изменение
свободной энергии, согласно (3.1.9), равно
^пост(2У, T)-Fn0Ci<y, T) = -NkT\n2. (3.1.15)
С помощью (3.1.10) находим изменение энтропии:
«пост (2^. T)-Sn0CT(V, T) = Nk\n2. (3.1.16)
В то же время внутренняя энергия идеального газа, согласно (3.1.11),
остается неизменной:
^пост(2У, T)-Un0CT(V, Г) = 0. (3.1.17)
В соответствии с определением (3.10) дифференциал свободной энергии равен
dF=--.d(U — TS) = dU — TdS — SdT. (3.1.18)
Согласно первому закону термодинамики (2.3), для обратимых процессов
имеем
dU = (6Q)o6v — PdV = TdS—PdV. (3.1.19)
Подставляя это в (3.1.18), получаем
dF = —PdV—SdT. (3.1.20)
Отсюда для изотермических процессов (Г = const) находим
(dF)T=—PdV
(3.1.21)
При обратимом изотермическом процессе совершаемая против внешних сил
работа равна уменьшению свободной энергии. Последняя, следовательно,
представляет полную работу, которую может совершить система при
постоянной температуре. Подставляя в (3.1.15) и (3.1.16) заданные числовые
значения, находим работу, совершенную при изотермическом процессе
AF=:F(2V,T) — F(V, Т) = —1,50- 10м-1,38-К)-28-400-0,6931 =—574 Дж,
AS = S(2V, T) — S(V, Т) = 1,44 Дж/К.
Таким образом, при изотермическом расширении газа, в результате которого
его объем увеличивается вдвое, система совершает работу 574 Дж = 58,5 кгс-м.
Ее внутренняя энергия, согласно (3.1.17), остается при этом постоянной,
тогда как энтропия возрастает.
в) При вычислении энергии, необходимой для увеличения температуры
при постоянном давлении, с помощью определения (3.17) найдем
дифференциал энтальпии
(Ш=(Ци-т-РУ).
Подставляя сюда в соответствии с первым законом термодинамики
дифференциал dU, получаем
dH = TdS + VdP = (6Q)o6v + VdP. (3.1.22)
Если давление остается постоянным, то
(5Q)P = dH
(3.1.23)
Следовательно, при обратимом изобарном процессе приращение энтальпии
равно подводимому извне количеству теплоты. Энтальпия, таким образом,
представляет запас тепловой энергии системы, который она может отдать при
обратимом изобарном процессе.
124 Гл. 2. Классическая статистика идеальных газов
Согласно (3.1.12) и (3.1.14), имеем
# пост = ^пост +PV^^NkT + NkT = ^NkT. (3.1.24)
Следовательно,
AH = ^-NkAT. (3.1.25)
Подставляя числовые величины, находим
ДЯ = #(Р,Г1) = #(Р, Г) = |-.1,5.1023.1,38.10-23.100=--517 Дж.
Таким образом, для того чтобы при постоянном давлении повысить
температуру от 400 до 500 К, к системе необходимо подвести 517 Дж тепловой
энергии. При этом внутренняя энергия, согласно (3.1.12), изменяется на
величину
Д^посг = |-^(Г1-Г) = ЗЮ Дж.
Для вычисления изменения энтропии примем во внимание, что
Тогда из (3.1.10) получим
ASn0CT=kN\n^^^kN\n^-. (3.1.26)
При заданных числовых значениях это дает
А5пост=у.1,38.10-23.1,5.1023 1п^=1,15 Дж/К. (3.1.26а)
г) Если при постоянном объеме температура возрастает от Т до Тъ то,
согласно (3.1.10), приращение энтропии равно
ASn0CT=^-Nk\n?±. (ЗЛ.27)
При этом в соответствии с (3.1.12) внутренняя энергия изменяется на
величину
3_
2
Л^пост = ^ (^-Г). (3.1.28)
Отсюда видно, что изменение внутренней энергиии выражается такой же
формулой, как и в п. „в". В то же время приращение энтропии при изохорном
увеличении температуры составляет лишь 60% ее приращения при увеличении
температуры в изобарном процессе. Из сравнения формул (3.1.27), (3.1.26)
и (3.1.26а) следует, что
ASnoCT = 0,6.1,15 = 0,69 Дж/К. (3.1.27а)
Согласно первому закону термодинамики, при изохорных процессах
(bQ)v = dU
(3.1.29)
Следовательно, количество энергии, которое необходимо подвести при
изохорном процессе, равно приращению внутренней энергии. Поэтому, используя
§ 3. Вычисление термодинамических функций состояния 125
формулу (3.1.28), получаем
(Д0)у=Д^/иост=у^(Г1"Г) = 310 Дж> (3.1.28а)
Замечания к вычислению энтропии, свободной энергии и энергии Гиббса
в классической статистике. Использованные в § 2 и 3 формулы и полученные
численные результаты справедливы в рамках классической статистики.
Согласно последней, энтропия может быть определена только с точностью до
аддитивной постоянной S0. В силу соотношений
F = U — TS и G = U — TS + PV
это приводит к тому, что свободная энергия F и энергия Гиббса G в
классической статистике также могут быть определены лишь с точностью до линейно
зависящей от температуры величины S0T. Эта неопределенная величина
выпадает при расчетах, относящихся к изотермическим процессам, как, например,
в п. „в". При рассмотрении таких процессов можно использовать свободную
энергию и энергию Гиббса, не принимая во внимание наличие аддитивной
постоянной 50.
Однако в численных термодинамических расчетах величины F и G играют
менее важную роль, чем внутренняя энергия U и энтальпия Н. Выдающееся
значение свободной энергии и энергии Гиббса связано с тем, что они
представляют собой термодинамические потенциалы. Последнее означает, что все
остальные термодинамические величины, характеризующие систему, т. е. U,
Ну Ср, Cvt S могут быть получены посредством дифференцирования функций
F и G. После дифференцирования неопределенной остается самое большее
одна постоянная, которая также выпадает при рассмотрении изменений
состояния.
Точное определение аддитивной постоянной в выражении для энтропии
с помощью теоремы Нернста возможно лишь в квантовой статистике при
учете таких факторов, как изменение числа степеней свободы и электронных
и ядерных спинов, что приводит к появлению дополнительного множителя в
статистической сумме (см. гл. 4, § 4 и 5).
В общем случае квантовые эффекты становятся существенными при
низких температурах и в переходных процессах. При рассмотрении химических
процессов, фазовых превращений и процессов в растворах они, как правило,
выпадают, так что в этих случаях можно пользоваться формулой (3.11)
(полуклассическое приближение).
При всех расчетах такого рода необходимо лишь помнить, что раз
выбранное начальное значение энтропии должно оставаться неизменным.
Именно в таком предположении справедливы выполненные в § 2 и 3
вычисления.
3.2*. Вращение двухатомных молекул,
состоящих из различных атомов
Вычислить статистическую сумму для НС1 и определить внутреннюю
энергию и энтропию 5 для 2 л хлористого водорода при 300К и давлении
40 ат. Радиус вращения принять равным r = 1,3• Ю-10 м. Массы атомов ц,н
и |ыс1 найти по относительным атомным массам Лн = 1,01, ЛС1 = 35,46.
Решение
В случае двухатомной молекулы к кинетической энергии, вычисляемой
по той же формуле, что и для одноатомных газов, добавляется еще
вращательная энергия. Будем описывать вращательное движение в сферической
126
Гл. 2. Классическая статистика идеальных газов
системе координат (см. фиг. 12). Декартовы координаты связаны со
сферическими следующим образом:
х = г sin 6 cos ф, ^=r sin G sin ф, 2 = r cos 6. (3.2.1)
Отсюда для компонент скорости при постоянном г получаем
x = r (cos G cos фб —sin 9 sin фф),
у = г (cos 9 sin фб + sin 9 cos фф), (3.2.2)
z= —г sin 99.
Следовательно, вращательная энергия одной частицы равна
^(x2 + ? + z2) = ^(fc+sm*Q<p*), (3.2.3)
где
^1^+^ (3-2-4)
— приведенная масса молекулы хлористого водорода.
Момент инерции определяется равенством J = \irr2. Учитывая, что
компоненты момента количества движения !Ш определяются формулами
Ш1в = /ё, (3.2.5)
9Лф = У^п9ф, (3.2.6)
можно представить вращательную энергию частицы в виде (%Щ + Ш*)№.
Тогда для энергии N частиц в состоянии i можно написать
е,вРаЩ=^Г (3%,+ • • • +!Ш|№+да|и. + • •. +3*1^). (3.2.7)
Воледствие этого в статистическом интеграле появится дополнительный
множитель
4ращ = ^лГ J ехр - ^ 2JkT ^J dT, (3.2.8)
где
dT = ЛШв1 ... dWl^d^ ... dcpN sin вх ddx ... sin QNddN. (3.2.9)
Интегрирование по угловым переменным дает
f... [ dq>! ... d(pNsin01dQ1 ... sin QNdQN=(4n)N9 (3.2.10)
0 0
и интеграл по импульсному пространству равен
[^^(-■§^т)^]^ = (Г2Шт)^. (3.2.11)
Подставляя (3.2.9)—(3.2.11) в (3.2.8), получаем для дополнительного
множителя в статистическом интеграле выражение
2вращ = —^— • (3-2.12)
§ 3. Вычисление термодинамических функций состояния 127
Следовательно, вращательная часть свободной энергии для молекулы,
состоящей из двух различных атомов, равна
/?вр.щ=-Л7'1пгвращ=-МГ1п^^.. (3.2.13)
Для вращательной энтропии получаем
*,.~(£),-».(.+ь^). <«•'<>
а вклад вращения во внутреннюю энергию равен
^вращ==
^вращ + 7,5Вращ = ^Г, (3.2.15)
что согласуется с законом равнораспределения. Все выведенные здесь
вращательные части функций состояния зависят только от температуры в отличие
от поступательных частей, которые зависят также от объема, а следовательно,
и от давления.
Подставляя заданные числовые значения, имеем
PV
N = NA-^=-=NA.3,\4-\0-* кмоль-1.
Используя формулу (3.2.13) и учитывая, что NAk = R, получаем
^вРащ = 7,84 кДж, SBpaiu = 0,105 кДж/К.
Поступательные части в случае двухатомного газа вычисляются по формулам,
аналогичным формулам (3.1.10) и (3.1.12) для одноатомного газа. Они имеют
следующую величину:
^пост= П.76 КДЖ» Sn0CT = 0,388 кДж/К.
Таким образом, в случае хлористого водорода находим для внутренней энергии
^ = ^пост+^вращ=19,6 кДж
и для энтропии |
s = 5nocT + SBpaiu = 0,493 кДж/К.
Эти значения следует рассматривать как первые приближения, поскольку
не учитывалось изменение удельных теплоемкостей.
3.3*. Вращение двухатомных молекул,
состоящих из одинаковых атомов
Вычислить вклад вращения в свободную энергию, внутреннюю энергию
и энтропию для 1 кмоль 02. Как изменятся вращательные части величин F,
U и S при увеличении температуры от 0 до 50°С?
Решение
Как и в случае двухатомных молекул, состоящих из различных атомов,
дополнительный сомножитель в статистическом интеграле [см. (3.2.8)]
оказывается равным
^вращ = h*N J ехр ^ ^^ ) dr. (3.3.1)
Молекула кислорода симметрична. Перестановка атомов не приводит к
возникновению нового [физического состояния. Поэтому каждый сомножитель в
статистической сумме (3.3.1) необходимо разделить на 2. Тогда, согласно
128
Гл. 2. Классическая статистика идеальных газов
(3.2.12), получаем
{8n2JkT\n
^вращ-: I
2Л2
(3.3.2)
Таким образом, и в этом случае вращательные части в отличие от
поступательных будут зависеть только от температуры. Используя (3,3.2), находим
вращательную часть свободной энергии:
4n2JkT
Fbmn=~bT\nZBvaux=-NkT\n h%
Вращательная энтропия равна
*^вращ— "
дТ Jv
Nk[ 1+ln
4n2JkT
/i2
(3.3.3)
(3.3.4)
Для вращательной части внутренней энергии, как и в случае молекул с
разными атомами, находим
V,
вращ"
:^вращ"г7овращ— N"1
(3.3.5)
Если повысить температуру от Т до Г + АТ", то, согласно (3.3.3), приращение
вращательной части свободной энергии будет равно
А/7*
(3.3.6)
[ вращ— ""- |"* *» h2 ' * *" V " ' Т ) I '
Из (3.3.4) и (3.3.5) находим
ASBpam = tf* In (l+^Л . (3.3.7)
Подставляя заданные числовые значения в N = Na, получаем с учетом N^k = R
Д/7вРащ=-2,19.103 кДж, А5вращ=1,40 кДж, А£/Врац4 = 416 кДж.
3.4*. Вращение многоатомных молекул
Для многоатомной молекулы определить вращательную свободную энергию и
вращательную энтропию. Чему равны эти величины для 1 кмоль H2S при 300 К?
Главные моменты инерции молекулы H2S, согласно спектроскопическим
измерениям, составляют соответственно /.=2,7 «Ю-42 кг«м2, У == 3,1 • 10~*г кг-м2,
У; = 5,9.10-47- кг-м2.
Решение
Молекула с тремя и более атомами обладает тремя вращательными
степенями свободы. Выберем в качестве осей £, т|, £ главные оси инерции
вращающейся молекулы. Вращательная энергия одной частицы равна
где Л, J , J у — главные моменты инерции, ЯУЦ, ПУЬ, ПУК — соответствующие
им компоненты вращательного момента количества движения. Поэтому в ста-
§ 3. Вычисление термодинамических функций состояния 129
тистическои сумме трехатомного газа за счет вращения появится
дополнительный множитель
^вращ - h3N j ехр ^ ^ 2 + ..,
2JtkT J | ^ГвРаЩ» (3.4.2)
дпь+-.+ап£лД]
где
^гВРащ=лтб1 ... *di^sinФб^Фб^Фщ^с! •••sin ф^ф^ф^ф^- (злз)
Интегрирование по ф| и ф дает телесный угол 4л:
2л Л
V V 81пф^ф^фл = 4л.
о о
Для третьей степени свободы имеем
2я
[ б(фо = 2л.
о
В результате при интегрировании по угловым переменным всех частиц получаем
2я2я я 2я2я л
1 S И "• И S sinФ|1*Ф^Фл1*Ф£1 • • • 8|пФб^Фб^Фл^Ф;^ = (8л:2)^-
0 0 0 0 0 0
(3.4.4)
Любая молекула обладает осями симметрии. При вращении вокруг одной из
этих осей молекула переводится сама в себя. Такого рода вращения можно
также рассматривать, как перестановку одинаковых атомов. Полностью
несимметричная молекула переходит сама в себя при повороте на 360Q.
Поэтому число осей вращения для такой молекулы принимают равным
единице. Для равнобедренной молекулы H2S (фиг. 19) к этому добавляется еще
I
Фиг. 19. Симметрия равнобедренной молекулы H2S.
ось симметрии треугольника, так что всего имеются две оси симметрии.
Пусть т обозначает число осей симметрии какой-либо молекулы. Тогда с
учетом формулы (3.4.4) вращательный член статистической суммы можно
представить в виде
/ 8я* \ы~г р Г /чт|1+...+ап|д,,
— 00 — оо
"+ * 2J%kT )\ тЬ - mW (3'4-5)
130 Гл. 2. Классическая статистика идеальных газов
Интегрирование по какой-либо компоненте момента количества движения
одной частицы дает
+ 00
1 6ХР ( ~~Шт) Ш = У**™?- (3.4.6)
— QO
Поэтому из (3.4.5) следует, что вращательный член статистической суммы
имеет вид
2вращ= (-£)" (2я*7У"/2 (.Vr/s)*72- (3-4.7)
Отсюда для свободной энергии получаем
-|1п8л^ + 1пк ' уЦ у (3.4.8)
Полагая в соответствии с законом равнораспределения внутреннюю энергию
равной
U = ^-NkTt (3.4.9)
находим, что вращательная энтропия многоатомных молекул определяется
выражением
^вращ ' вращ 3
Q
«-'вращ— гр — 2
Nk{\ + \nW+± \пУ -*t у
(3.4.10)
Подставляя численные значения, получаем для 1 кмоль
^вРащ = -2,75.103 кДж, SBpaiu= 1,92 кДж/К.
3.5. Внутримолекулярные колебания
Вычислить изменение колебательных вкладов в свободную энергию,
внутреннюю энергию и энтропию для 1 кмоль водорода Н2 при нагревании
от 1500 до 2000 К. Угловую частоту колебаний положить равной со0 = 8,3х
xiov1.
Решение
Рассмотрим два атома в молекуле, совершающие колебания относительно
друг друга (фиг. 20). Пусть q и р обозначают соответственно приведенное
г 1 г 1
•
•
Л
Фиг. 20. Колебательные степени свободы
?хол~2 fx<m~6 двух- и трехатомных молекул.
отклонение и приведенный импульс. Тогда энергия колебательного состояния
q, р, согласно классической теории колебаний, равна
п'2
.2„
р< ц№ (35л)
§ 3. Вычисление термодинамических функций состояния Ш
где со0 —собственная частота (угловая частота) колебательной системы. В
статистическом интеграле вследствие этого появится множитель
— СО — QO
Здесь
£ = ■^-=1,05.10-« Дж-с
Если имеется N молекул, в каждой из которых возбуждено /кол колебаний
с собственными частотами сох, ..., о>/кол, то в статистическом интеграле для
колебательных состояний получаем сомножитель
1
"Ы со*
NN N • (3.5.3)
Iй2 •••со/кол
Отсюда для колебательного вклада в свободную энергию имеем
Г(£у-_!_|.
^кол= -kT\nZKoa= -NkT In
Колебательная энтропия равна
*-—(*■)„-*' ['«+>■ (т)''"^к:2- ,3-5-5'
Тогда для внутренней энергии получаем
^кол = ^кол + TSK0Jl = fKoaNkT9 (3.5.6)
что находится в полном согласии с законом равнораспределения, если при
применении последнего учесть каждую колебательную степень свободы дважды
в соответствии с разбиением энергии на потенциальную и кинетическую части.
В рассматриваемом случае по табл. П.Х (см. приложение) находим, что
для водорода CV = 2£9R при 1500 К и CV = S,12R при 2000 К. Предполагая,
что все 5 степеней свободы, отвечающих поступательному и вращательному
движениям, полностью возбуждены, получаем среднее число колебательных
степеней свободы на одну частицу /кол (1500) = 0,39 и /кол (2000) = 0,62. Как
уже было сказано, при применении закона равнораспределения эти
колебательные степени свободы следует учитывать дважды.
Используя (3.5.4)—(3.5.6), находим искомые изменения функций
состояния при ^ = 2000 К, Гх—1500К, /i = 0,39 и /2 = 0,62:
Л^ол= -NkT2f2\n Vfl+NkT^ In *f± , (3.5.7)
^K^^Nk(f%^f{i + Nk(ft\^^fl\n^)9 (3.5.8)
Д^кол = ^(/8Г1-/17'1). (3.5.9)
Подставляя численные значения, находим для 1 кмоль
ДЛсол= И80 ккал/кмоль, ASKOJI = 0,16 ккал/кмояь-К,
М70= 13Ю ккал/кмоль.
132
Гл. 2. Классическая статистика идеальных газов
То обстоятельство, что колебания с частотами сог не полностью возбуждены,
следует учитывать с помощью соотношения
'kT\f—1 =f]n^L . (3.5.10)
-с
% ) 0!...©/ %{
СОп
3.6. Приращение энтропии в переходных процессах
(необратимые процессы)
Пусть 1 кмоль гелия при давлении 2 ат и температуре 300 К и 2 кмоль
кислорода при давлении 3 ат и температуре 200 К отделены друг от друга
перегородкой; вся система теплоизолирована. Вычислить давление и
температуру газовой смеси после удаления перегородки и установления равновесия.
Определить изменение энтропии в процессе установления равновесия.
Решение
Для обоих газов справедливы уравнения состояния
PiVi = n1RTly P2V2 = n2RT2. (3.6.1)
Для газовой смеси после выравнивания температуры и давления справедливо
уравнение
PV = nRTt (3.6.2)
где
п = п1-Ьп29 V = V! + Va. (3.6.3)
Процесс смешивания можно мысленно разбить на два процесса: процесс
изотермического расширения и следующий за ним процесс выравнивания
температуры. Когда каждый из двух газов расширится при своей постоянной
температуре до объема V, равновесие между ними еще отсутствует. Оно
устанавливается лишь после выравнивания температуры в результате
столкновений между молекулами. Это выравнивание температур происходит уже при
постоянном объеме. Согласно правилу Рихмана о равенстве количеств
теплоты, которыми обменялись подсистемы, имеем
nfivl (Тг-Т) = n2Cv2 (Т - Г2). (3.6.4)
Из (3.6.4) получаем
T^n1CvlT1 + n2Cv2T2^ (365)
ЩСу! ~Г n2pv2
Подставляя (3.6.5) в (3.6.2), находим суммарное давление Р Определяя
в соответствии с законом равнораспределения теплоемкость в отсутствие
колебаний молекул, получаем в рассматриваемом случае
1.3.300 + 2-5.200
Т~ 1.3 + 2-5 -223К'
Для вычисления давления Р необходимо сначала определить объем с помощью
соотношения
V = Vl + V2 = R{^+^y (3.6.6)
Имеем
г_озм10./ ЬЭ00 I 2'200 V^MOu»
§ 3. Вычисление термодинамических функций состояния 133
Отсюда, согласно (3.6.2), давление газовой смеси равно
^^=3.8,3144.0з.223н/м2 = 2>36ат,
В случае одноатомного гелия возможно только поступательное движение.
Тогда для энтропии получаем [см. (3.1.10)]
[-
N Р
Заменяя здесь в соответствии с уравнением состояния идеального газа V на
nRT/P, а также N на nNа, находим
Кроме того, двухатомный газообразный кислород обладает вращательной
энтропией [см. (3.3.4)]
5вращ = ^ ! + 1п иг )=nR\ 1 + 1п"
Следовательно, при температуре Т и давлении Р значения энтропии пх кмоль
гелия и п2 кмоль кислорода составляют соответственно
5Не = nxR [in
kT(2Wu2kTf2 5
Р /ia "^2
(3.6.8)
Г kT (2mi0 kT)^4n4kT 7 1
s0l = ".* [lnT м +Tj ' (3'6-9)
Отсюда находим приращение энтропии в результате процесса смешивания
газов
AS = ASHe+AS0=R ^niln(^y/2^+n2ln^y/2^]. (3.6.10)
Подставляя численные значения, имеем
Таким образом, при смешивании газов энтропия возросла. Поскольку при
этом тепловая энергия извне не подводилась, процесс является необратимым.
3.7. Изменения функций состояния в цикле Карно
Для целей сравнения тепловых двигателей рассматриваются идеальные
обратимые круговые процессы. Найти мощность и к. п. д. идеального
двигателя внутреннего сгорания. Объем камеры сжатия Vс равен 500 см3, объем
цилиндра Vz==8000cm3. Измерение температуры в камере сгорания дает
величину Г1= 1800 К, температура выхлопных газов Т2 = 650 К. Предполагается,
что рабочим веществом служит воздух с незначительным добавлением
газообразных продуктов сгорания (k = Cp/Cv = 1,4). Максимальное давление
продуктов сгорания составляет Рс = 80 ат,. число оборотов /г =1200мин-1,*
134
Гл. 2. Классшшская статистика идеальных газов
Решение
Будем рассматривать процесс как обратимый круговой процесс (фиг. 21),
состоящий из двух изотерм (0—1 и 2—3) и двух адиабат (1—2 и 3—0).
При изотермических процессах, согласно первому закону термодинамики,
имеем
(PdV)T=(T dS-dU)T=-(dF)T, (3.7.1)
т. е. механическая работа равна изменению свободной энергии. С другой
стороны, для адиабатически* процессов
(PdV)s=-dU. (3.7.2)
Следовательно, для адиабатических процессов необходимо вычислять
изменение внутренней энергии. При изотермическом расширении 0—1 объем сжатого
газа при неизменной температуре'7^ возрастает от V0 = VC до У±. Для
вычисления работы, совершенной в первом рабочем такте, необходимо в
соответствии с (3.7.1) определить изменение свободной энергии F. Последняя
Р
Л
Фиг. 21. Циклический процесс.
складывается из поступательной (3.1.9), вращательной (3.3.3) и колебательной
(3.5.4) частей. Вращательная и колебательная части зависят только от
температуры, которая остается постоянной. Нам необходимо, следовательно,
учесть лишь изменение поступательной части. Отсюда из (3.7.1) и (3.1.9)
находим работу, совершенную в первом рабочем такте:
Ао1=\^ PdV==-AF^-[F(TlyV1)-F(TllV0)} = NkT1\n^. (3.7.3)
V0
Во время последующего адиабатического расширения объем увеличивается от
ух до V2 = VZ, а температура возрастает до Г2. Для вычисления объема Ух
воспользуемся уравнением адиабаты в переменных Г и V (см. упражнение 2.12)
и получим
Ttf-^Tjft-1. (3.7.4)
Разрешая относительно Vx и подставляя числовые значения, имеем
У1 = У2(^)1/('<-1)=8000(^)2'5смЗ = 626,7см3
Совершаемую системой во время второго такта работу находим, используя
формулу (3.7.2) и учитывая закон равнораспределения:
A12J^ Р^ = Д1/=«/(Г1)-Г/(7'1)=ф(7'1-7'1), (3.7.5)
где / — число степеней свободы одной молекулы.
§ 3. Вычисление термодинамических функций состояния 135
v0 \tJ
Во время третьего такта происходит сжатие, так что объем при
постоянной температуре Т2 уменьшается от V2 до V3. По аналогии с (3.7.3) получаем
для. совершаемой системой работы
Л23 = Л^Г21п^ <0. (3.7.6)
У2
Цикл завершается процессом адиабатического сжатия 3—0, во время которого
объем уменьшается от V3 до V0 = Va, а температура возрастает от Т2 до Тг.
При этом система, согласно (3.7.5), совершает работу
Ам=-^-(Т1-Т^=-Аи. (3.7.7)
Отсюда следует, что адиабатические части работы (3.7.5) и (3.7.7) взаимно
сокращаются. Для входящего в (3.7.6) объема V3 получаем в соответствии
с (3.7.4) соотношение
"""-Й- - Й-Й-
Таким образом, полная работа, совершенная во время цикла, равна
А=ф РМ = А01 + А1Ш + А2Я + АЛ0 = Ык(Т1-Тш)\п^. (3.7.9)
Величину Nk = nR находим по величине максимального давления рабочего
вещества Рс, принимая при этом объем V0 равным Vc и температуру
равной 7\. Используя уравнение состояния идеального газа, получаем после
подстановки численных величин
... _ PeVe 80-9,81.104-500.10-вДж 0 ю п / v
Nk = nR = -£-s= 7-^rx т, = 2,18 Дж/кмоль-К.
Тх 1800 кмоль-К
Следовательно, работа, совершенная во время одного рабочего такта, равна
A = Nk (7\-Г2)1п^=2,18-1150 In Щ£г£ Дж = 566,4 Дж = 57,8 кгс-м.
V q эии
Число оборотов п равно 1200 мин-1. Вычисляя работу, совершенную
мотором за 1 с в таком идеализированном случае, получаем мощность
А =20-566,4 Дж/с= 11,38 кВт.
Во время изотермического расширения 0—1 необходимо подвести
эквивалентное совершенной работе количество тепловой энергии
Q = Qoi = 4oi = to711ln-Jl. (3.7.10)
Выделяющееся в процессе изотермического сжатия 2—3 количество тепловой
энергии
Q23 = NkT2\n^ (3.7.11)
Уз
теряется системой. С помощью (3.7.9) и (3.7.10) находим к. п. д. идеального
двигателя внутреннего сгорания
А 7\-
.(1800^650)=0>639< (37Л2)
1800
136
Гл. 2. -Классическая статистика идеальных газов
Вследствие необратимых процессов и значительных отклонений от
использованных нами идеализированных представлений практический к. п. д. двигателя
внутреннего сгорания составляет приблизительно 0,35.
3.8. Тепловой насос
Для снабжения большого комплекса тепловой энергией конструируется
тепловой насос мощностью 1000 кВт. При этом требуется поддерживать
температуру 100° С при наружной температуре 0°С. Вычислить необходимую
для этого механическую мощность. Чему равен к. п. д. теплового насоса?
Решение
Рассмотрим тепловой насос, используя такую же идеализированную схему
обратимого цикла Карно, с помощью которой был рассмотрен двигатель
внутреннего сгорания. В случае теплового насоса система проходит цикл Карно
в положительном в математическом смысле направлении (фиг. 21), т. е.
обратном направлении по сравнению со случаем теплового двигателя,
рассмотренного в задаче 3.7.
Во время изотермического сжатия 1—0 при более высокой температуре
Тг система получает механическую работу и отдает равное количество
тепловой энергии
Ql0 = M>7\ln^, (3.8.1)
которая поступает потребителю. Во время изотермического расширения 3—2
у окружающей среды, находящейся при более низкой температуре Т2,
отнимается количество теплоты, эквивалентное совершаемой над этой средой
механической работе
A32 = NkT2\n^. (3.8.2)
Вклады адиабатических процессов взаимно уничтожаются. Следовательно,
полная механическая работа Л, которую необходимо совершить, определяется
площадью криволинейного четырехугольника, изображенного на фиг. 21.
В результате имеем
А = Nk (Тг—Т2) In £. (3.8.3)
По определению к. п. д. т] теплового насоса называют отношение полученной
тепловой энергии к совершенной механической работе
Подставляя численные значения, находим
373
11 = (373-273)= 3'73'
Таким образом, для работы теплового насоса мощностью 1000 кВт требуется
механическая мощность, равная всего лишь
Л = 010 1Ш Вт = 268кБт.
Т] о,7о
§ 3. Вычисление термодинамических функций состояния 137
Упражнения.
У.3.1. Вычислить свободную энергию F, энтропию S, энтальпию Н и
энергию Гиббса G для 1 л гелия при температуре 1500К и давлении
1 мбар.
У.3.2. 1 л гелия при температуре 1500К и давлении 1 мбар адиабатически
расширяется и занимает после этого объем 2 л. Как меняются при
этом свободная энергия и энтропия?
У.3.3. Как меняются свободная энергия и энтропия 1 л гелия при 1500К
и давлении 1 мбар, если газ изотермически расширяется до объема
V = 2 л?
У.3.4*. Вычислить вращательные части свободной энергии, внутренней
энергии, энтропии, а также энтальпии и энергии Гиббса для 1 кмоль
водяных паров при 400К и давлении 1,5 ат. Главные моменты инерции
молекулы Н20 равны /g=10-10-47 кг-м2, / =1,9-10-47 кг-м2,
/£=1,9. Ю-47 кг-м2.
У.3.5*. 2 кмоль хлористого водорода нагреваются от 300 до 350К. Найти
приращение внутренней энергии и энтропии. При этом можно
предположить, что колебания атомов в молекуле еще не возбуждены.
Объем при нагревании остается постоянным.
У.3.6*. Найти изменение вращательной свободной энергии и вращательной
энтропии для 1 кмоль водорода при нагревании от 350 до 400К.
У.3.7*. 1 кмоль кислорода при нормальных условиях политропически
сжимается до объема, равного половине исходного. Показатель
политропы равен /г=1,25. Вычислить изменение вращательных частей
величин U и 5.
У.3.8. Как изменится колебательная часть величин F, U и S при
нагревании 1 кмоль кислорода от 2000 до 2500К? При этом следует считать
/кол=1. Колебательное волновое число 1/Я составляет по
спектроскопическим данным 1,58-10*? м-1.
У.3.9. Найти изменение колебательного вклада в энтропию при нагревании
1 кмоль кислорода от 1000 К до 1500 К. Принять Cv (1500) = 3,40 /?,
Cv (1000) = 3,20/?.
У.3.10. 1 кмоль азота при 400 К и 2 кмоль кислорода при 300 К
смешиваются друг с другом при постоянном давлении, равном 1 ат.
Определить изменение энтропии. Колебания при указанных температурах
еще не эффективны.
У.3.11. Температура 1 кмоль азота (7\ = 400К, Ях=1ат) и 2 кмоль
кислорода (Г2 = 300К, Р2 = 1 ат) выравнивается, при этом перемешивания
газов не происходит. Вычислить изменение энтропии при постоянном
давлении и при постоянном объеме.
У.3.12. Азот («2=1, Pi=l ат) и кислород (/г2 = 2, Р2 = 2 ат) находятся при
температуре Г = 300 К. Оба газа отделены друг от друга
перегородкой. Найти изменение энтропии после удаления перегородки и
перемешивания обоих газов.
У.3.13. Вычислить мощность мотора грузового автомобиля с объемом камеры
сжатия 1/^=1500 см3 и объемом цилиндра 7^ = 24 000 см3, если
температура воспламенения и температура выхлопных газов равны
соответственно 7\= 1900 К, Г2=700К. Максимальное давление
сгорания положить равным Рс — 85ат. Число оборотов равно 1800 мин-1.
Какова величина к.п.д.? При расчете воспользоваться моделью
обратимого цикла Карно с х=1,4.
У.3.14. Доказать, что к.п.д. теплового двигателя не может быть выше к.п.д.
обратимого цикла Карно, поскольку это противоречит второму за^
кону термодинамики.
138
Гл. 2. Классическая статистика идеальных газов
У.3.15*. Определить к.п.д. холодильной машины, выразив его через
количество отводимой тепловой энергии и совершенной при этом
механической работы. Чему равна последняя, если при наружной
температуре 50°С охлаждаемое вещество должно иметь температуру—20°С?
Какую механическую энергию необходимо затратить, если для
компенсации неполной теплоизоляции холодильной камеры необходимо
обеспечить отвод 1 ккал/мин? Расчет провести для обратимого цикла
Карно.
У.3.16*. Два цилиндра содержат по 0,1 кмоль азота. Емкость одного равна
V]=50 л, емкость другого 1/2 == 100 л. Оба находятся при
температуре 300 К. Определить максимальную работу, которую можно
получить, соединив цилиндры друг с другом. Внутримолекулярные
колебания не учитывать; / = 5.
У.3.17*. Необратимый процесс, например химическая реакция, протекает при
постоянном объеме и постоянной температуре. Исследовать поведение
свободной энергии.
У.3.18*. Исследовать поведение энергии Гиббса в необратимом процессе для
изобарно-изотермической системы.
§4. ФЛУКТУАЦИИ В ТЕРМОДИНАМИЧЕСКИХ СИСТЕМАХ
Введение
В макроскопическом теле, находящемся в состоянии
равновесия, термодинамические величины флуктуируют около своих
средних значений. Для изучения этих отклонений выделяют
внутри тела какую-либо его малую часть, или подсистему
(фиг. 22), и определяют флуктуации относящихся к этой под-
Фиг. 22. Подсистема 2 в
макроскопическом теле.
системе термодинамических величин. Система в целом
предполагается столь большой, что ее температуру и давление можно
считать постоянными. Это означает, что рассматриваются
процессы, протекающие в изобарно-изотермической системе, т. е.
такие, при которых энергия Гиббса стремится к минимуму
(см. упражнение 3.18).
Во время флуктуации энтропия Sg системы как целого
изменяется на величину ASg. Над подсистемой при этом
совершается работа AA = TASg. Во время флуктуации подсистема
не находится в равновесии со своим окружением. Вследствие
этого энергия Гиббса подсистемы уже больше не является
функцией лишь температуры и давления [см. (3.19а)], она из-
§ 4. Флуктуации в термодинамических системах 139
меняется на величину
AG = — TASg. (4.1)
С другой стороны, флуктуации в подсистеме, подобно
механическим колебаниям, могут рассматриваться как обратимые
процессы. Тогда, подставляя вместо давления и температуры их
средние значения, определяемые для всей системы, получаем
AG = AU — TdS + PAV. (4.2)
Статистический вес (термодинамическая вероятность) AW
флуктуации, согласно уравнению Больцмана (3.4), связан с
изменением энтропии соотношением
ASg = klnAW. (4.3)
Это уравнение можно решить относительно AW. Подставляя
в результат вместо величины ASg ее выражение, получаемое
с помощью (4.1) и (4.2), имеем
ДЦ7 _ e*Sg/k _ e(TAS-MJ-PAV)/kTf (4.4)
Здесь AS, AJJ и AV представляют флуктуации энтропии,
внутренней энергии и объема, относящиеся к выделенной подсистеме.
Флуктуации отдельных термодинамических величин зависят
друг от друга. Согласно первому закону термодинамики, в
показателе экспоненты выражения (4.4) члены первого порядка
обращаются в нуль. Рассматривая флуктуацию внутренней
энергии как функцию флуктуации AS и АУ, разложим ее в ряд
по этим величинам. Выражая коэффициенты разложения через
флуктуации температуры и объема1*, получаем из (4.4) (см.
задачу 4.1)
Ц7 — e(APAV-ATAS)/2kTt (4.5)
В этом соотношении флуктуации двух термодинамических
величин можно рассматривать как независимые переменные2).
Выбирая в качестве таковых, например, АР и AS, получаем
выражения для двух других флуктуации:
M£).4'+(£),4S- (4J)
х) Формально введение флуктуации температуры и объема осуществляется
с помощью соотношений A(dU/dS)v = AT и Д (dU/dV)s — &V.— Прим. перев.
2) Вообще говоря, утверждение о статистической независимости
флуктуации пар величин Р, S и V, Т требует специального доказательства (см.
Л. Д. Ландау, Е. М. Лифишц, Статистическая физика, М., 1964, § 114).—
Прим. перев.
140
Гл. 2. Классическая статистика идеальных газов
Если же в качестве независимых переменных выбрать AV и АГ,
то величины АР и AS определяются соотношениями
Подставляя выражения (4.6)—(4.9) в (4.5), получаем для
статистических весов IF (АР, AS) или W (AV, АГ) двумерные
гауссовы, или нормальные, распределения. Корреляционные моменты
(ковариации) APAS и AVAT обращаются в нуль в силу
сделанного предположения о независимости флуктуации (см. гл. 1,
§ 4). Сравнивая получающиеся функции распределения с общим
видом нормального распределения [см. (2.8) гл. 1], получаем
для средних квадратов флуктуации следующие выражения:
A/» = -*r(f-)s, &* = kT(§r)rknC,
(dPidV)T'
(dSldT)v nCv
, (4.10)
(4.11)
где n = PV/RT есть число киломолей в рассматриваемой
подсистеме.
Задачи
4.1. Флуктуации энтропии и давления
Исследовать флуктуации энтропии и давления в 1 мм3 паров ртути, если
среднее значение температуры равно 2000 К, а среднее значение давления
0,01 мбар.
Решение
Согласно (4.1) и (4.2), приращение энергии Гиббса подсистемы и
изменение энтропии системы как целого связаны соотношением
AG = AU — TAS + PAV = — TASgt (4.1.1)
где AU, AS, AV—флуктуации величин, относящихся к рассматриваемой
подсистеме, а Г и Р — средние равновесные значения температуры и
давления для системы в целом. Отсюда для статистического веса получаем
выражение
ли* (*SA ( AU-TAS-PAV\ ,Ain.
AW = exp^-^J=exp^ ^ J. (4.1.2)
§ 4. Флуктуации в термодинамических системах 141
Флуктуацию внутренней энергии AU можно разложить в ряд
„ . (4Л-3>
Первын закон термодинамики гласит
dll = TdS — PdV. (4.1.4)
Отсюда имеем
(§)-• («),--'■
Подставляя соотношения (4.1.5) в (4.1.3), получаем
На основании первого из соотношений (4.1.5) можно записать
d2U d2U
а на основании второго имеем
d2U d2U
-AP=mwAS+w>AV- <4Л-8>
Тогда из (4.1.6) находим
AU = TAS—PAK + y(ArAS — APAV). (4.1.9)
С помощью (4.1.2) и (4.1.9) получаем
/APAV —AT AS
AW=;exp
Флуктуации ATt AV, АР, AS не являются независимыми друг от друга.
Флуктуации AV и AT можно записать в виде
так что независимыми остаются только флуктуации АР и AS. Преобразуем
показатель экспоненты выражения (4.1.10) в соответствии с (4.1.11)
АРАК—ATAS=
К, »+(%,)*]»-
-[(SMS),4"]** (4"2)
Рассмотрим дифференциал энтальпии
dH = TdS + VdPt (4.1.13)
из которого вытекает соотношение
/ dV\ д2Н (дТ\ .. , 1/П
iasj,=apas=iapj5- (4ЛЛ4>
142
Гл. 2. Классическая статистика идеальных газов
Поэтому в (4.1.12) смешанные члены с ASAP сокращаются. В формуле (2.5.3)
для удельной теплоемкости при постоянном давлении все величины отнесены
к 1 кмоль. Если принять во внимание, что соотношение (4.1.12) относится
к числу киломолей /г, которое еще подлежит определению, то вместо (2.5.3)
следует написать
nCp=T{df)P=WrJWp' (41Л5)
где Ср—молярная теплоемкость, т. е. теплоемкость, отнесенная к 1 кмоль.
Подставляя (4.1.12) в (4.1.10) и учитывая (4.1.15), получаем
AW=exp [^(g^Ap.-^AS.] (4.1.16)
Как указывалось в гл. 1 [формула (2.8)], плотность вероятности
AW(x) = exp(-^j
отвечает нормальному закону распределения с дисперсией
** = Р2. (4.1.17)
Из сравнения (4.1.16) и (4.1.17) следует, что средний квадрат флуктуации
энтропии равен
AS2 = knCp. (4.1.18)
Путем сравнения с распределением Гаусса при учете уравнения адиабаты
PV^ — PqV* и уравнения состояния идеального газа получаем для среднего
квадрата флуктуации давления
РТ Р2
(4.1.19)
где N— среднее число частиц в рассматриваемом объеме 1 мм3. Переходя
к численным значениям, находим
# = /гМл = 3,6Ы010, /г = 6,0Ы0-17.
Подставим в (4.1.18) эту величину, а также удельную теплоемкость,
определенную с помощью закона равнораспределения:
$/•>
AS2 = knCp = kn-j- =
= 1,38-Ю-23-6,0Ы0-17.|-8,314-103 Дж2/К2=1,72.10-35 Дж2/К2.
(4.1.20)
Отсюда находим среднеквадратичное отклонение энтропии
У AS2 =4,15-10-18 Дж/К.
Подставляя в (4.1.19) % = 5/3, имеем
^=з-з'бмоц мбаР2==46>2-10-1в мбаР2
и
КаР2 = 6,8.10-8 мбар.
§ 4. Флуктуации в термодинамических системах
143
Таким образом, отклонения от средних значений весьма незначительны,
несмотря на невысокую плотность паров и малую величину объема (1 мм3),
для которого эти отклонения определяются.
4.2. Относительные флуктуации температуры и объема
Определить относительную флуктуацию температуры при средней
температуре 300 К и давлении 10~3 мбар в объеме 1 мкм3. Какова при
указанных условиях относительная флуктуация объема для числа частиц,
содержащегося в среднем в объеме, равном 1 мкм3?
Решение
Статистический вес флуктуации определяется выражением
AW = e(&P&v-bTbS)/2kTu (42Л)
Флуктуацию энтропии AS и флуктуацию давления АР запишем в виде
Из дифференциала свободной энергии с учетом первого закона
термодинамики получаем
dF = dU — d(TS) = TdS — PdV—TdS — SdT = —PdV—SdT, (4.2.3)
откуда
'--(£),• *--(£V
Следовательно,.
KdT)v dVdT \dVJT К*'*'Ь}
Далее, на основании (2.5.3) имеем
пС^т{р
,dTjv'
при этом необходимо учитывать, что энтропия S относится только к
рассматриваемому веществу.
Подставляя два последних выражения в первую из формул (4.2.2),
находим
AS=^AT+(£)vAV. (4.2.6,
Следовательно,
APAV-ATAS = (^)aV*-^ АТ\ (4.2.7)
Тогда статистический вес флуктуации AV, Д7\ согласно (4.2.1), равен
W^P[^dV^l-^T)^. (4.2.8)
Из сравнения с плотностью вероятности нормального распределения
W(x)=exp(~ff> (4-2-9)
144
Гл. 2. Классическая статистика идеальных газов
находим средние квадраты флуктуации объема и температуры:
ж'—тщ-г' ^=Щ- (4-2Л0)
Отсюда при учете уравнения состояния идеального газа получаем
относительную флуктуацию объема
YW=Y%=^
а для относительной флуктуации температуры с учетом закона
равнораспределения имеем
/
m-Yi-rYbm-Yer- «ад
В соответствии с этим относительные флуктуации зависят только от числа
частиц. Они тем меньше, чем больше частиц содержится в рассматриваемой
части системы.
Поскольку при заданной температуре 300 К колебания в молекуле
кислорода еще не возбуждены, при численных расчетах молярную иэохорную
теплоемкость следует положить равной CV = 2,5R. Среднее число частиц
находим по формуле
PV
Подставляя это в (4.2.11) и (4.2.12), получаем
Относительно большие флуктуации объясняются низким давлением и малостью
рассматриваемого объема.
4.3. Флуктуации числа частиц
Найти флуктуацию числа частиц в 1 мкм3 при нормальных условиях
(Г = 273 К, Р=1 атм= 1,033 ат).
Решение
Согласно (4.2.10), средняя флуктуация квадрата объема равна
w*—kT(w)T- <4ЛЛ>
Представим себе мысленно, что рассматриваемый объем отделен от остальной
системы упругой перегородкой, и обозначим через N число частиц в этой
замкнутой системе. Производя деление, получаем из (4.3.1)
А£=(дЛУ=_*Г(£П (432)
При таком способе записи уже больше нельзя определить, какая из
величин N и V поддерживается постоянной, а какая варьируется. Если теперь
§ 4. Флуктуации в термодинамических системах 145
. рассматривать число частиц в незамкнутом объеме, то можно представить
(4.3.2) в виде
(к VV Л/а 1 V V2AN* kT(dV\
[an) =[VAT) =V2-W=-T>[dp)T-
Пользуясь уравнением состояния идеального газа и учитывая соотношения
N /ft — R, nN a = N, получаем
Следовательно, искомая флуктуация равна
У"Ш*=У11, (4.3.4)
откуда для средней относительной флуктуации имеем
rAN\z VW* 1
rt
NJ N Y~N*
(4.3.5)
Таким образом, флуктуация числа частиц равна корню квадратному из числа
частиц, а относительная флуктуация числа частиц равна величине, обратной
корню из этого числа.
В рассматриваемом случае находим jV = 2,69-107. При этом флуктуация,
согласно (4.3.4), равна
УШ* = ]Л/У = 5180.
Относительную флуктуацию находим из (4.3.5):
VI
^)2==7w=0,19-10"3:=0,190/o0-
4.4. Корреляция флуктуации
Найти коэффициент корреляции флуктуации температуры и объема
и коэффициент корреляции флуктуации температуры и давления для гелия
при нормальных условиях.
Решение
В соответствии с определением, данным в гл. 1, § 4, искомые
коэффициенты корреляции равны
AT AV АГАР
ГД71,ДУ = ГТ- » ГАТ, АР =-/• Г- (4-4-0
VAT2AV2 V AT2 АР*
Среднее значение AT AV запишем в виде
WAV = J AT AV W (A7\ AV) dAT dAV. (4.4.2)
Подставляя сюда термодинамическую вероятность, согласно (4.2.8), получаем
АГАР- J J ДГДУехр [(^/W),Ay^Ar»j ^ ^ (4^
146
Гл. 2. Классическая статистика идеальных газов
Этот интеграл можно разложить на два сомножителя, каждый из которых
можно проинтегрировать независимо от другого:
+ 00 +00
ДГАУ- С AVexp lY^Wyil dAV f ДГехр (-^AT2\dAT.
— оо —оо
(4.4.4)
Первый интеграл дает среднее значение флуктуации объема, второй — среднее
значение флуктуации температуры. Оба эти средние значения должны
обращаться в нуль. Следовательно,
ДГДУ = 0. (4.4.5)
Что касается средних квадратов флуктуации AT2 и AV2, то они в
соответствии с (4.2.10) отличны от нуля. Поэтому искомый коэффициент корреляции
равен
rAT, дк = 0- (4.4.6)
Таким образом, флуктуации температуры и объема не коррелированы. Для
вычисления коэффициента корреляции гдг др воспользуемся соотношением
"-(SW(S)," ' <"*>
и получим
Первое слагаемое обращается в нуль вследствие вытекающей из (4.4.5)
некоррелированности флуктуации объема и температуры. Средние квадраты
флуктуации температуры и давления определяются формулами (4.2.10) и (4.2.19)
ЬТ2 ьрт
АТ2=-— АР2 —it
С учетом этого находим из (4.4.8)
дР \ kT2 . R Т2
KPKT={Tf)v-rtv=kt-' (4Л9)
откуда следует, что коэффициент корреляции флуктуации давления и
температуры равен
>_ V с
'дг.др = У ^- (4.4.Ю)
Следовательно, корреляция этих флуктуации зависит от удельной
теплоемкости, т. е. от числа степеней свободы рассматриваемого газа. Для
одноатомных газов, согласно закону равнораспределения, имеем Cp — 5R/2, откуда для
коэффициента корреляции флуктуации давления и температуры получаем
/|=0,63.
'дг.ДР = У Т=0,63. (4.4.11)
Таким образом, указанные флуктуации связаны весьма сильной
корреляционной зависимостью.
§ 4. Флуктуации б термодинамических системах 147
4.5. Термодинамические флуктуации вращающегося
зеркальца
Наблюдаются флуктуационные колебания подвешенного зеркальца,
имеющего момент инерции / = 3,7. Ю-14 кг-м2. Температура равна 300 К,
измерение периода собственных колебаний дает величину т = 392,7 с. По кривой
записи временной зависимости угла отклонения определено
среднеквадратичное отклонение у ф2 =1,20Q. Исходя из этого, вычислить постоянную Больц-
мана k и число Авогадро N д.
Источник света
Зеркало
J \Лп/\Л/КллГЛллА^ЛЧ Фиг'23, ФлУктУации
J VV V V v w vvY wv Y ^-* > рота вращающегося зе]
угла пово-
зеркала около
Время нулевого положения.
Решение
Для отклонения зеркальца на угол ф необходим крутящий момент
М = — £ф, (4.5.1)
где D — жесткость на кручение. Записывая уравнение движения для
крутящего момента
М = /<р (4.5.2)
и подставляя его в (4.5.1), приходим к дифференциальному уравнению
•/ф+£ф = 0. (4.5.3)
Решение этого уравнения имеет вид
ф(0 = Фв^'. (4.5.4)
Частота собственных колебаний равна
ш=-^=|/^, (4.5.5)
откуда для жесткости на кручение получаем выражение
4jt2
т
2
(4.5.6)
(фиг. 23).
Определим теперь энергию, необходимую для отклонения зеркальца на
угол ф. С помощью формулы
М=-ЩпИ1- (4.5.7)
148 Гл. 2. Классическая статистика идеальных газов
находим потенциальную энергию крутильных колебаний:
ф Ф
(4.5.8)
Отсюда на основании закона распределения Гиббса определяем
статистический вес флуктуационного отклонения:
AW (Ф) = ехр
2яУф2
т2/еГ
Из сравнения с распределением Гаусса получаем
ф ~~4jtV~"D '
(4.5.9)
(4.5.10)
В соответствии с этим постоянную Больцмана k можно найти путем
измерения величин ф2, D и Т:
Рф2__4л2/ф2
(4.5.11)
Подставляя в эту формулу измеренные значения, получаем
4-3,142.3,7.10-14 /Ч,20-3,14\2
k=-
= 1,38-Ю-23 Дж/К.
392,72-300 V 180
С помощью этой величины находим число Авогадро
R 8,314-103
N,
1,38-Ю-23
= 6,02-1026 кмоль-1.
(4.5.12)
(4.5.13)
4.6. Чувствительность гальванометра
Полное отклонение зеркального гальванометра (фиг. 24) с внутренним
сопротивлением /^ = 100 кОм в апериодическом режиме достигается за время
/=10 с. Часть электрической энергии, подводимой к гальванометру за
Фиг. 24. Схема гальванометра (Sp — катушка,
Z—стрелка).
время его успокоения, запасается в виде потенциальной энергии
возвращающей пружины. Пусть эта часть составляет 20%. Предполагается, что
минимальный измеримый ток /мин по меньшей мере в 5 раз превышает величину
отклонений стрелки, обусловленных термическими флуктуациями. Вычислить
при этих предположениях минимальный ток, который может быть надежно
измерен. Температура равна 300 К.
§ 4. Флуктуации в термодинамических системах 149
Решение
Измерительный прибор получает за время своего успокоения энергию
E = tUI = tRI2. (4.6.1)
При отклонении стрелки возникает вращательный момент, пропорциональный
квадрату угла отклонения. Поскольку последний линейно зависит от силы
тока /, потенциальная энергия, запасенная пружиной, равно как и полная
подводимая энергия £, квадратично зависит от силы тока. Исходя из
соотношения между полной энергией Е и работой против натяжения пружины
£пот, имеем
EnoT = pE = ptRI*. (4.6.2)
Средняя энергия тепловых флуктуации равна
— 1?Т
£тепл = ^- (4>6,3)
Эти флуктуации приводят к выбросам на шкале измерительного прибора,
которые соответствуют силе тока А/. Для последней, пользуясь (4.6.2) и
(4.6.3), получаем
ьт
р^А/2=£тепл= —. (4.6.4)
Чтобы протекающий ток превышал среднее значение термических флуктуации
в п раз, согласно (4.6.4), должно выполняться равенство
Подставляя заданные численные значения, находим
V 2-0,20.10-1™ 1ля-а'1,1и А'
lOO-lO3"
Таким образом, из-за тепловых флуктуации электрические токи, меньшие
5-Ю-13 А, не могут быть надежно измерены с помощью данного зеркального
гальванометра.
Упражнения
У.4.1. Рассматривается водород при температуре 600 К и давлении
Ю-2 мбар. Найти средние флуктуации температуры, давления и
энтропии, отнесенные к объему 1 мкм3.
У.4.2. Чему равна средняя флуктуация энергии Гиббса для 1 мм3 гелия
при давлении Ю-4 мбар и температуре 300 К?
У.4.3. Вычислить среднее число частиц в 1 мкм3 для идеального газа при
температуре 500 К и давлении 1 мбар. Чему равна флуктуация числа
частиц для этого объема?
У.4.4. При каком давлении идеального одноатомного газа с температурой
300 К средняя флуктуация давления в объеме AV = 1 мм3 будет
составлять 1% среднего значения?
У.4.5. В 1 м3 воды растворено 0,1 мг некоторого вещества с относительной
молекулярной массой Мг = 600. Из раствора берутся пробы объемом
1 мм3 каждая. Чему равна относительная флуктуация содержания
вещества в пробе? Определить относительную долю проб с
содержанием вещества более 0,01% среднего количества. Найти
относительную флуктуацию давления раствора при 300 К.
150
Гл. 2. Классическая статистика идеальных газов
У.4.6. 0,001 мг ртути испаряется в объеме 1 л. Чему равна средняя
флуктуация парциального давления ртути при температуре 300 К,
отнесенная к объему 1 мм3? Чему равна относительная флуктуация?
Относительная атомная масса ртути равна 200)б.
У.4.7*. Определить коэффициент корреляции флуктуации энтропии и давления.
У.4.8*. Вычислить коэффициент корреляции флуктуации энтропии и
температуры для Не, Н2, С02 при средних и высоких температурах.
У.4.9. Определить коэффициент корреляции флуктуации энтропии и объема
для Не, Н2, С02 при средних и высоких температурах.
У.4.10. Вычислить отнесенную к объему 1 мм3 флуктуацию внутренней
энергии для гелия при температуре 1000 К и давлении 10~3 мбар.
У.4.И. Чему равна средняя величина ]/ф2 флуктуационного отклонения
математического маятника, находящегося в поле земного тяготения
(g = 9,81 м/с2). Длина маятника 2 см, масса 20 мг, температура 300 К.
У.4.12. Чему равен коэффициент жесткости пружины D, если величина
среднеквадратичного флуктуационного отклонения х составляет 1 мм?
Температура равна 500 К.
У.4.13. Определить предел чувствительности гальванометра с внутренним
сопротивлением /? = 10 кОм, полное отклонение которого достигается
за t==Sc в апериодическом режиме. 87,5% подводимой электрической
энергии превращаются за время успокоения в тепло. Температуру
принять равной 300 К. Предполагается, что тепловые флуктуации
подчиняются нормальному закону распределения и что вероятность
ошибки при измерении не превышает 0,27%.
У.4.14*. Чему равны флуктуации компонент скорости в декартовой системе
координат для водорода при 300 К?
§ 5. СТАТИСТИЧЕСКАЯ МОДЕЛЬ ИДЕАЛЬНОГО ГАЗА
Введение
Молекулы идеального газа рассматриваются как не имеющие
конечных размеров материальные точки. В соответствии с этой
моделью столкновений между молекулами не происходит, однако
молекулы могут сталкиваться со стенками сосуда. Такое
представление позволяет рассчитать давление идеального газа.
Материальные точки не взаимодействуют между собой.
Иными словами, между ними не действуют ни силы
притяжения, ни силы отталкивания. В общем случае скорость частиц
можно положить равной некоторому среднему значению.
Задачи
5.1. Статистическая модель давления газа
Чтобы получить выражение для давления, рассмотрим модель газа,
основанную на следующих предположениях о распределении частиц газа по
скоростям: молекулы движутся только в направлениях, параллельных осям
х, у и г ортогональной системы координат; параллельно каждой из осей
движется 1/3 всех молекул, причем половина из них в положительном
относительно соответствующей оси направлении и половина в отрицательном;
§5. Статистическая модель идеального газа 151
абсолютная величина скорости одинакова для всех молекул и равна v.
Исходя из такой модели газа, определить давление, создаваемое 2 кмоль
водорода в объеме У=100м3, если скорость частиц равна 2 км/с.
Решение
В соответствии с предположением о направлениях движения каждая
частица сталкивается со стенкой, двигаясь по нормали к ней. При
столкновении направление движения молекулы меняется на обратное. Вследствие
этого ее импульс изменяется на величину
А»:
-2J> = —2цД),
(5.1.1)
где [х—масса молекулы. В соответствии с третьим законом Ньютона при
отражении частиць. стенке передается импульс, который равен этому
изменению по величине, но противоположен по направлению.
Чтобы найти давление Р, рассмотрим на стенке площадку размером 1 м2.
Если за промежуток времени At с площадкой сталкиваются Av молекул, то,
согласно второму закону Ньютона, действующая на нее сила равна
*V__A\^2jii)
tf~"A*"~ А* '
(5.1.2)
где ^—полный импульс, переданный стенке за время Д*. Следовательно,
давление равно
T-'-f>
(5.1.3)
Пусть W0 обозначает число молекул в 1 м3 газа. Из них по направлению к
данной стенке сосуда движутся N0/6 частиц. В течение достаточно короткого
^л
Фиг. 25. К расчету давления (задача 2.5.1).
отрезка времени А* с рассматриваемой площадкой столкнутся все молекулы,
которые движутся по направлению к ней и находятся от нее на расстоянии,
не превышающем
A*<A*MaKC = yAf
(фиг. 25). Число Av этих частиц равно
No
6
Av = — Д*макс=—тр-.
(5.1.4)
(5.1.5)
152
Гл. 2. Классическая статистика идеальных газов
В объеме V содержится п киломолей Н2. Следовательно, число частиц
в 1 м3 равно
N„=^. (5.1.6)
Подставляя (5.1.5) и (5.1.6) в (5.1.3), получаем для давления газа
nNAyv*_nMrv* _ 2 U_
^-" 3V """3V"""3 V ' [ЬА'п
где Мг—относительная молекулярная масса. Подставляя численные
значения, находим
2.2,016.(2.103)2 2.2,016^(2.103)2
Р~ ЗЛОО Н/М - 3.100-9,81.104 -°'548 ат'
5.2. Определение множителя Лагранжа (J
Согласно каноническому распределению Гиббса, числа заполнения ячеек
определяются формулой (1.27)
Ni=N-,
2*-pE<-'
Исходя из статистической модели идеального газа, доказать, что множитель
Лагранжа имеет следующую величину:
и вычислить постоянную Больцмана с помощью числа Лошмидта и газовой
постоянной.
Решение
В соответствии со статистической моделью идеального газа его давление
выражается формулой (5.1.7)
nNA\iv2
Г~~ ЗУ "
Разрешая это уравнение относительно квадрата скорости частицы и применяя
уравнение состояния идеального газа, получаем
2 3PV 3RT /КО|.
v =^7—=77—• (5.2.1)
Отсюда находим кинетическую энергию п кмолей одноатомного газа:
Em = nNA ^=у nRT. (5.2.2)
Согласно закону равнораспределения [см. (2.2)],
кин = 2?1 /" •
Полагая [ = 3 и N — nNA, получаем внутреннюю энергию идеального
одноатомного газа
*™.«4^. (52-3)
§ 5. Статистическая модель идеального газа
153
Приравнивая (5.2.2) и (5.2.3), имеем
3 п_ 3 nNА Q NA
Т^Г==У"Г' или Р=5Г-
Примем вместо этого
тогда для постоянной Больцмана k находим
_^= 8,314.103 Дж/кмоль.К = , д R
NA 6,02-102« кмоль-i 1}6Ь Ш ДЖ/14, ^Л)
5.3*. Статистическая модель идеального газа
при учете распределения Больцмана
Водород находится в сосуде при температуре 300 К и давлении 2 ат.
Принимая во внимание распределение Больцмана по скоростям, вывести
формулу для давления газа и вычислить число столкновений в 1 с,
испытываемых участком стенки сосуда площадью 10 см2. Чему равно среднее время
между двумя столкновениями?
Решение
Будем предполагать, что между не имеющими размеров молекулами
идеального газа не происходит столкновений. В то же время учтем
распределение скоростей по абсолютной величине и по направлениям. Рассмотрим на
стенке сосуда площадку размером АЛ и определим число попадающих на
ДА
Фиг. 26. К расчету давления (задача 2.5.3).
эту площадку за время dt частиц, имеющих скорость от v до v-{-dv, и угол
падения от О до d + dd. Эти частицы заключены в цилиндре, объем которого
равен
dV = ДЛа cos ftdt (5:3.1)
(фиг. 26). Из числа содержащихся в 1 м3 частиц под углом к стенке,
лежащем в пределах от О до O + dd, движутся
dNQ = Cs'mftdft (5.3,2)
частиц, имеющих произвольный азимутальный угол <р. (Фактически при
фиксированном угле Ф молекулы летят из пространства между двумя конусами.—
Ред.). Величину С определим из условия
я
^dN0 = N0 или С С sin ftdft = N0t (5.3.3)
о
объем газа
154
Гл. 2. Классическая статистика идеальных газов
откуда
... W0 sin fldfl yv0 . . .a
dN0 = — =—M sin fl rfd.
(5.3.4)
\ sin О
да
Если теперь учесть распределение скоростей Максвелла — Больцмана, то для
числа dv частиц, сталкивающихся с площадкой АЛ и имеющих при этом
скорость и угол падения, заключенные в интервалах соответственно от v до
v-\-dv и от О до ф + да, согласно (5.3.1) и (5.3.4) получаем
dv = dVdN0f (v) dv^^AAf (v) v sin fl cos fl да dv dt,
где f (v)—функция распределения.
При каждом соударении стенке передается импульс
pg = 2\xucos О.
Отсюда находим силу, действующую на площадку АЛ:
dv
dF = pg-rr= N0\iAA cos2 О sin О v2f (v) dv да.
(5.3.5)
(5.3.6)
(5.3.7)
Полную силу, приложенную к площадке АЛ, получим посредством
интегрирования по всем углам падения О и по всем скоростям v. В результате
после деления на АЛ находим давление:
QO Я/2
Р = N0\x Г Г cos2 fl sin #/ (v) v2 да dv. (5.3.8)
о о
Интегрирование по углу О в (5.3.8) дает
Я/2
\ cos2 d sin О <
о
а интегрируя по скоростям, получаем
3 '
£ v2f(v)dv = v2.
(5.3.9)
(5.3.10)
Таким образом, статистическая модель, учитывающая больцмановское
распределение по скоростям, приводит к следующему выражению для давления:
(5.3.11)
Подставляя сюда вместо числа частиц в 1 м3 выражение N0 = nNji/V и
используя соотношение Nj[k — R, получаем
N0\iv*_nRT
(5.3.12)
§ 5. Статистическая модель идеального газа
155
Для вычисления среднего числа столкновений необходимо проинтегрировать
выражение (5.3.5). Тогда для числа столкновений, происходящих за 1 с,
имеем
со я/2
v = -^A4 f С sin Ъ cos Qf(v)vd$dv. (5.3.13)
о о
Необходимые нам интегралы имеют следующие значения:
я/2
Г sinflcosfl6fU=y, (5.3.14)
о
§vf(v)dD = v=yy£. (5.3.15)
о
Таким образом, для числа столкновений в единицу времени имеем
где Мг—относительная молекулярная масса, п—число кмолей в объеме V.
Используя уравнение состояния идеального газа, можно записать выражение
(5.3.16) для числа столкновений в виде
^/Жг^-'УшЫ"- (5-зл7)
Подставляя численные значения, найдем число столкновений с участком
площадью ДЛ = 10 см2:
/~ fi 09.1026
v-2.Q81.10*l/ 10-3 = 2 ЫО25 с-1
v-J У,»1 ш у 2.3,14-2,016.1,38.10-23-300 Ш 1Л 1и "" с '
Отсюда определяем среднее время между двумя столкновениями с
площадкой ДЛ:
1=4,8-Ю-26 с.
v
Упражнения
У.5.1. Вычислить число столкновений молекул Н2 с участком поверхности
сосуда, имеющим площадь 1 м2, если давление Р=\ ат и температура
г=зоок.
У.5.2. В баллоне диаметром 4 м находится 1 кмоль гелия при температуре
300 К. Вычислить частоту столкновений каждой молекулы со стенкой.
У.5.3. Для газа, находящегося при нормальных условиях, найти число
молекул, сталкивающихся с единицей поверхности под углом, лежащим
между О и #-|- dfy.
Глава О
РЕАЛЬНЫЕ ГАЗЫ
§ 1. ГАЗ ВАН-ДЕР-ВААЛЬСА
Введение
Статистическая модель реальных газов учитывает силы
притяжения и отталкивания между молекулами и собственный
объем молекулы. Согласно Ван-дер-Ваальсу, молекулы в
первом приближении рассматриваются как твердые недеформируе-
мые шары, между которыми действуют силы притяжения.
Если молекулы газа в среднем находятся на большом
расстоянии друг от друга, то взаимодействие между ними можно
не учитывать. В этом случае только стенки резервуара
удерживают газ от расширения. Напротив, при малом молярном
объеме Vт начинает сказываться взаимное притяжение молекул,
которое проявляется в основном вблизи границ. Внутри
газа действующие на частицу силы притяжения различных
молекул взаимно уравновешиваются, тогда как на границе
частица испытывает притяжение только с одной стороны
(фиг. 27а). Тем самым усиливается действие внешнего давления,
о
У? ф,
г. 27а. Силы притяжения, действующие на
0 молекулу в объеме и на границе реального газа.
которое также препятствует расширению газа. Таким образом,
взаимное притяжение молекул приводит к возникновению
дополнительного давления Pz (внутреннее, или когезионное, давление).
Согласно статистической модели, давление вызывается
ударами молекул. Сила притяжения, действующая на отдельную
молекулу у стенки сосуда с газом, пропорциональна числу
молекул и соответственно обратно пропорциональна молярному
объему Vm. С другой стороны, внутреннее давление Pz
пропорционально числу сталкивающихся молекул, т. е. опять-таки
обратно пропорционально молярному объему. Поэтому
выражение для дополнительного давления можно представить в виде
т
§ /. Газ Ван-дер-Ваальса
157
Согласно Ван-дер-Ваальсу, величина а в первом приближении
считается постоянной, не зависящей от температуры.
Чтобы учесть собственный объем молекул, в уравнении
состояния из объема Vm нужно вычесть некоторую величину Ь.
При столкновении двух твердых шаров (фиг. 276) их центры
находятся друг от друга на расстоянии, равном диаметру
шаров 2rs- Поэтому можно положить, что эффективный диаметр
одного из сталкивающихся шаров равен 4/-5, а другого равен
S
Фиг. 276. Эффективное сечение при
столкновении одинаковых молекул.
С данной молекулой столкнутся все те молекулы
(1, 2, 3, 6, 7), центры которых ( + ) окажутся
внутри сферы взаимодействия с диаметром,
равным 4 гс.
нулю. Тогда эффективный объем столкновения для первой
частицы оказывается равным 4/зя (2/s)3, т. е. в 8 раз больше
собственного объема, в то время как для второй частицы объем
столкновения равен нулю. В среднем эффективный объем
столкновения равен учетверенному собственному объему, т. е. в
расчете на 1 кмоль имеем
b = 4NA±iir$. (1.2)
Подставив поправочные члены (1.1) и (1.2) в уравнение
состояния, получим для 1 кмоль реального газа уравнение Ван-дер-
Ваальса:
(1.3)
Если газ содержит п кмолей вещества, то измеренный объем
газа V и его молярный объем Vm связаны соотношением
vm=-v.
т п
Учитывая (1.4), из (1.3) получаем
(P + ^)(V-nb) = nRT.
(1.4)
(1.5)
158
Гл. 3. Реальные газы
Пример 17
Сосуд содержит 0,3 кмоль реального газа. Тогда уравнение состояний
Ван-дер-Ваальса имеет вид
(p+°-^)(V-0,3b)=0,3RT.
Разрешив уравнение Ван-дер-Ваальса (1.3) относительно
давления, получим
у т и Vm
При достаточно больших значениях температуры Т и
молярного объема Vm в уравнении (1.6) существен только первый
член. В этом случае, как и для идеального газа, изотермы
являются гиперболами. Если же значения как Г, так и Vm
малы, то, согласно (1.3), реальный газ существенно отличается
от идеального. Чтобы установить, в чем заключается это
различие, продифференцируем равенство (1.6) по Vm. Это дает
RT >2а (1.7)
V dVm )т
\dV2mJT 1
2RT 6а
(1.8)
<V*-&)» V*m
Первая производная (1.7) равна нулю при
Я7ТЪ = 2а(Уя-Ь)«. (1.9)
Для приближенного решения этого уравнения будем считать
поправочные члены а и b малыми и пренебрежем членом 2ab2.
Тогда уравнение (1.9) переходит в квадратное уравнение
относительно Vmj которое имеет следующие корни:
у __а 1 f а2 4ab у __ а . ._ /" а2
*мин ftf у ^Т2 RT ' "макс RT* У R2T2
4ab
RT'
(1.10)
При очень больших Vm в выражении (1.7) существенно только
первое слагаемое. Поэтому при уменьшении объема давление
растет и при V = VMaKC проходит через максимум, в котором
-^-V = 0 (—^ <0. (1 11)
dVm)f U' UmJr ( '
При дальнейшем уменьшении объема давление должно падать
вплоть до минимума при V = VKm, где
§ 1. Газ Ван-дер-Ваальса
159
В действительности область изотермы VMm < Vт < Умак0, где
(dP/dVm)T > 0, соответствует неустойчивому состоянию, которое
не реализуется, так как уже до этого (точка 2 на фиг. 28)
происходит конденсация газа. В результате образуются две
фазы: жидкая и газообразная. В двухфазной области при
уменьшении объема и неизменной температуре давление остается
постоянным до тех пор, пока весь газ не перейдет в жидкость
(точка / на фиг. 28). Величина этого равновесного давления
Y^i
Т>ТК
Фиг. 28. Изотермы реального газа.
К — критическая точка.
будет определена в § 3 настоящей главы. При дальнейшем
уменьшении объема после полной конденсации газа давление,
как видно из фиг. 28, резко возрастает.
При увеличении Т оба корня (1.10) уравнения (1.9)
сближаются. Из (1.10) имеем
V^-V^^^Va'-AabRT. (1.13)
Критическая изотерма характеризуется тем, что максимум и
минимум сливаются в точке, называемой критической. Согласно
(1.11) и (1.12), в критической точке
дР \
дУт]т
0 (1.14)
и одновременно
(^т^ >° (минимум), (—т) <° (максимум),
\dVmJт \dVmJт
т. е.
(т%) =°- (1Л5)
\dVmjT
Таким образом, критическая изотерма имеет точку перегиба
с горизонтальной касательной. Комбинируя равенства (1.14),
(1.15) и (1.7), получаем два уравнения для определения кри-
160
Гл. 3. Реальные газы
тических величин Рк, Vk и Тк:
*Г* ' --0, (1.16)
<Ук-Щ* ' у%
2RT„ 6а_0 ?)
Кроме того, из уравнения Ван-дер-Ваальса имеем
Три условия (1.16)—(1.18) могут выполняться одновременно
только в том случае, если кроме постоянных Ван-дер-Ваальса
а и Ь считать неизвестной и величину газовой постоянной R.
Тогда получим
(1.19)
Поэтому для каждого реального газа нужно вычислять
индивидуальную газовую постоянную R, которая отличается от
универсальной газовой постоянной NAk идеального газа. Расчет
показывает, что эти индивидуальные газовые постоянные
оказываются меньше универсальной газовой постоянной, т. е.
R < NAk. Поскольку газовая постоянная пропорциональна
числу молекул в 1 кмоль, то отсюда следует, что в критическом
состоянии часть молекул сильно сжатого газа связана в
комплексы. Поэтому индивидуальную газовую постоянную,
найденную по формуле (1.19), используют только вблизи критического
состояния, тогда как для состояний, достаточно удаленных от
критического, где комплексы уже распались, нужно
пользоваться универсальной газовой постоянной.
Вообще при применении уравнения Ван-дер-Ваальса следует
иметь в виду, что вандерваальсовы поправочные члены дают
хорошее приближение в ограниченной области измеряемых
параметров. При изменении параметров состояния газа, вообще
говоря, изменяются и поправочные величины.
Задачи
1.1. Вычисление постоянных Ван-дер-Ваальса
Критическая температура Г^, выше которой реальный газ не может
сконденсироваться ни при каком, сколь угодно высоком давлении, составляет
для водорода 33,2 К. Измеренное критическое давление Р^, при котором для
T = Tk начинается конденсация, равно 13,2 ат. Молярный объем Vk для водо-
§ 1. Газ Ван-дер-Ваальса
161
рода в критическом состоянии равен 0,065 м3. Вычислить постоянные Ван-дер-
Ваальса а и Ъ и индивидуальную газовую постоянную R для водорода в
критическом состоянии. Каково давление реального газа при температуре
300 К, если молярный объем равен 1 м3? Чему равно давление при
температуре 35 К и молярном объеме 0,1 м3? Сравнить полученные данные с
соответствующими величинами для идеального газа.
Решение
Согласно формулам (1.19), постоянные Ван-дер-Ваальса связаны с
критическими величинами следующими соотношениями:
a = 3PkVi bJ£, Я-уТТ' 0.1.1)
Подставив заданные значения, получим
а = 3.13,2-0,0652 = 0,167 ат.мб/кмоль2, (1.1.2)
Ъ=у.0,065 = 0,022 м3/кмоль, (1.1.3)
D_8 13,2.9,8Ы0^0,065=б)76310з < д^^зм-Ю3 ДжДкмоль.К).
/8,314-103-с
\ 1—0,02$
3 33,2
(1.1.4)
Чтобы найти давление при заданных значениях температуры и объема,
разрешим уравнение Ван-дер-Ваальса относительно Р:
р=у¥гь~£- <1Л-5>
vm ° Vm
Для Т = 300 К и Vm—\ м3, т. е. для состояния, достаточно далекого от
критического, получим из (1.1.5), считая R — Nj^k =8,314 -103 Дж/(кмоль«К):
~ -300 1 0,167\ 0-я
"Ж" 9,8Ы0* —)-^>* ат-
Для давления идеального газа имеем
/?Г 8,314.Щз>300_
И"У^Г 1.9,81-10* ~гЬЛ ЗТ>
т. е. различие между этими результатами невелико.
Вычислим давление вблизи критического состояния для Т = 35 К,
Vm = 0,\ м3, считая R = 6,763-103 Дж/(кмоль-К):
/6,763.IP3»35 1 0,167\
V 0,1—0,022 9,81-10* 0,12 ;~" ' ат*
Давление идеального газа в этом случае составляет
/?Г_8,314.103.35
^~" V ""0,1.9,8Ы04 -2:у''~ат'
т. е. существенно отличается от давления реального газа.
1.2, Критические параметры реального газа
Для водяного пара в окрестности критического состояния вандервааль-
совы поправочные члены имеют следующие значения:
а = 2,03 ат.м6/кмоль2, 6 = 0,0183 м3/кмоль. (1.2.1)
162
Гл. 3. Реальные газы
Значение индивидуальной газовой постоянной, приведенное в табл. П.XII
(см. приложения), равно
R = 0,602Мл/е = 5,008-103 Дж/(кмоль-К). (1.2.2)
Вычислить критические параметры водяного пара и сравнить указанные
выше значения а и Ь вблизи критического состояния с приведенными
в табл. П.XII.
Решение
Разрешив уравнения (1.16)—(1.18) относительно Pk, V^ Tk, получим
p*=mi- (123)
Vk = 3b, (1.2.4)
т*=ттъ- <L25)
Подставив численные значения, находим
Рк=27-(Оуотг =225 ат'
1/^ = 3-0,0183 = 0,055 м3/кмоль,
8.2,03-9,81.10*
k ~"~ 27- 5,008-103- 0,0183 ^
Найденные величины хорошо согласуются с измеренными критическими
параметрами. С другой стороны, согласно табл. П.XII, постоянные Ван-дер-
Ваальса имеют следующие значения:
а = 5,65 ат.м°/кмоль2, 6 = 0,031 м3/кмоль. (1.2.6)
Эти значения дают лучшее согласие с экспериментальными данными для
комнатной температуры, причем нужно брать R — Nдк = 8,314- 103 Дж/(кмоль-К).
Различие постоянных Ваи-дср-Ваальса (1.2.1) и (1.2.6) иллюстрирует
приближенный характер уравнения Ван-дер-Ваальса и ограниченность области,
в которой величины а и b можно считать постоянными. В широком диапазоне
изменения параметров уравнение Ван-дер-Ваальса может дать хорошее
согласие с экспериментом только в том случае, если величины a, b и R не считать
постоянными.
1.3. Внутреннее давление и эффективное сечение
Вычислить с помощью постоянных Ваи-дер-Ваальса диаметр 2г$
эффективного сечения столкновения для молекул азота. Чему равно
внутреннее давление в азоте при Г = 400 К, Р = 2 ат? Критические величины для
этого газа:Рб = 34,8 ат, Tk =—147С,С, Vk = 0,090 м3/кмоль.
Решение
Постоянная b в уравнении Ван-дер-Ваальса равна учетверенному
собственному объему [см. (1.2)]:
b=-£iiNArs-
§ 1. Газ Ван-дер-Ваальса
163
С другой стороны, согласно (1.19),
Следовательно,
Vk = \6nNArl, (1.3.1)
и для искомого диаметра имеем
**= УЖ- (КЗ>2)
Подставив численные значения, получим
2гс- V °>090 =2,9.1П-ю м.
s~ V 2.3,14-6,02.102«
Внутреннее давление, возникающее из-за притяжения между молекулами,
описывается формулой
Vm
Постоянная Ван-дер-Ваальса а есть [см. (1.19)]
a = 3PkVl
Тогда получим
Pz^. (1-3.3)
Молярный объем при температуре Т и давлении Р определяется уравнением
состояния. Для приближенного определения Vm воспользуемся уравнением
состояния идеального газа:
ВТ
Vm=^p- (1.3.4)
Комбинируя равенства (1.3.3) и (1.3.4), получаем
р ^PkV\ (1 з.5)
и для заданных значений находим
P^(8331374:y9W (2-9.8Ы0У =0.0029 ат.
Таким образом, по сравнению с внешним давлением в 2 ат внутреннее
давление в данном случае имеет величину лишь порядка поправочного члена.
1.4. Коэффициент расширения а, коэффициент давления р,
сжимаемость к
Вычислить изобарный коэффициент расширения а,, изохорный
коэффициент давления р и изотермическую сжимаемость к водорода при
температуре 800 К. и давлении 10 ат. Сравнить полученные результаты с
аналогичными для идеального газа. Использовать следующие величины из табл. П. XII:
а ==5,65 ат-ме/кмоль2, 6 = 0,031 м3/кмоль.
164
Гл. 3. Реальные газы
Решение
Названные величины определяются следующим образом:
«--L lim V(P,T + AT)-V(P,T) 1 (9V\
_1_ , P(V,T + AT)-P(V,T)_ .1 /дР\
P P ДГ-.0 AT P \dT)v' (lA-Z)
x = _l lim У(Г,Р + АР)-У(Г,Р) 1 /JH _
V ар ->o АР К V др J т
Представим уравнение Ван-дер-Ваальса в виде
/ = (p + £)(V-&)-/?7- = 0. (1.4.4)
Тогда
V \дТ )Р V (dfJdV)p V (P + a/V2)-2a(V-b)/V*' (L4'5)
При достаточно малых поправочных величинах уравнение Ван-дер-Ваальса
приводится к виду PV — RT-{-bP^-a/V, откуда
R \ ( b 2а\ -
а ~ RT + bP-2a/V ~Т~[[ ~T+PV^J • (1,4,Da)
Аналогично из формул (1.4.3) и (1.4.4) имеем
1 V—b
V (P + a/V2)-2a(V—b)/V*
1 1
-—+—^
V^PV*)
i-4+dS-, • О-4-6)
/?7T/(V—б)2 — 2a/V2 Р
Для изохорного коэффициента давления р из формул (1.4.1) и (1.4.3) получим
R__J_/dP\ __ 1 (дУ/дТ)Р _ а __ R 1 / а \
Р"~~Р V^/v ^ (dV/dP)r~^>cP~"P(l/-&)~ Г v^wv*
(1.4.7)
Поскольку объем V в формулах (1.4.5) — (1.4.7) входит только в поправочные
члены, его можно найти из уравнения состояния идеального газа:
.. RT 8,314-108-800 -
V=-T= ю.9,81.10* =6'78м-
Подставив в формулы (1.4.5а), (1.4.6) и (1.4.7) численные значения
параметров, получим для реального газа
1 Л 0,031 . 2-5,65 \ ЛПП10„ „ ,
а=ш(1-'бТ78-+10^78^)=:0-001275 К_1'
^(1-S+Tow)=0'01008aT-1-
По сравнению со значением для идеального газа а отличается на 2,0%,
Р—на 1,2%, к—на 0,8%.
§ 1. Газ Ван-дер-Ваальса
165
1.5*. Приведенное уравнение состояния
Кислород, водяной пар и водород находятся в критическом состоянии.
Вычислить для этих газов приращение давления, если температура
повышается на 10 К при постоянном объеме. Критические величины для этих
газов приведены в табл. П.XII.
Решение
Подставим в уравнение Ван-дер-Ваальса (1.3) величины а, Ь и R,
выраженные, согласно (1.19), через критические постоянные Р& V# и Гд. Тогда
имеем
Переходя к безразмерным параметрам состояния
(1.5.1)
получаем приведенное уравнение состояния
(V+-^)(3Vr-l) = 87V
(1.5.2)
(1.5.3)
Разрешив его относительно Рг, находим
р - 87У 3
r 3vr—1 vy
В критическом состоянии Рг, Тг и Vr равны единице. Если приведенная
температура Тг увеличивается на величину А при постоянном объеме, то для
Рг имеем из формулы (1.5.4)
8(1+Д) 3
fr- 3_j ,-1+4Л.
Результаты дальнейших расчетов сведены в табл. 23.
(1.5.4)
(1.5.5)
Таблица 23
Расчет по приведенному уравнению состояния
н2
о2
н2о
Tk, к
33,2
154,3
647,3
pk'aT
13,2
51,4
225
А=10К/Г
0,301
0,0649
0,0154
РГ=1+4А
2,204
1,260
1,062
Р, ат
29,1
64,8
238,9
Поскольку уравнения для реального газа носят приближенный характер,
при исследованиях в более широком диапазоне изменения Р и Т
приведенное уравнение состояния целесообразно применять к газам с физически
подобными свойствами.
166
Гл. 3. Реальные газы
Упражнения
У.1.1. Записать уравнение Ван-дер-Ваальса для 1 г гелия вблизи
критической точки (Рл = 2,34 ат, Ул = 0,058 м3, Г = 5,2 К, ^Не-4,003).
У. 1.2. Вычислить с помощью критических постоянных индивидуальные
газовые постоянные для кислорода и азота (кислород: 7^=154,3 К,
Рл = 51,4 ат, Vk = 0,075 м3/кмоль; азот:Гл = 12б К, Рл = 34,8 ат,
Vk = 0,090 м3/кмоль).
У.1.3. В стальном цилиндре вместимостью 20 л содержатся 8 кг С02 при
температуре 320 К. Чему равно давление? Вычислить постоянные
Ван-дер-Ваальса, используя следующие значения:'Р^ = 75 ат, Tk = 304 К,
Vk = 0,096 м3/кмоль (МСОг = 44).
У. 1.4. Стальной сосуд объемом 40 л содержит 20 кг С02. С помощью
уравнения Ван-дер-Ваальса найти, до какой температуры можно нагреть
газ, если предельно допустимое давление составляет 200 ат (а =
=3,72 ат-м6/кмоль2, 6=0,043 м3/кмоль). Как изменится результат, если
расчет провести для идеального газа?
У. 1.5. Вычислить внутреннее давление С02 для Т = 360 К, Р=200 ат.
У. 1.6. Оценить диаметр молекулы С02 по уравнению Ван-дер-Ваальса.
У. 1.7. Вычислить коэффициент расширения а, коэффициент давления р и
сжимаемость к для гелия при 300 К и 50 ат (а = 0,035 ат-м6/кмоль2,
6 = 0,024 м3/кмоль).
У. 1.8. Как изменятся формулы для коэффициентов расширения и давления,
если отнести первый к объему, а второй — к давлению при 0° С?
Найти отсюда а и р, используя данные предыдущего упражнения.
У. 1.9*. Исследуются две газовые смеси. Значения постоянных
Ван-дер-Ваальса для них приведены в табл. 24. Газовая постоянная R
в обоих случаях равна /V^/г —8,314-103 Дж/(кмоль-К)- С помощью
приведенного уравнения состояния найти температуру газа, если
давление составляет соответственно 10, 11 и 12 ат, а молярный объем
равен 10 м3.
Таблица 24
Постоянные Ван-дер-Ваальса для двух газовых смесей
Обозначение а, ат-мв/кмоль2 Ь, м3/кмоль
I 1,44 0,030
II 1,40 0,040
§2. ПАРАМЕТРЫ СОСТОЯНИЯ РЕАЛЬНОГО ГАЗА.
МЕЖМОЛЕКУЛЯРНЫЕ СИЛЫ
Введение
Уравнение Ван-дер-Ваальса не позволяет получить полного
количественного согласия с экспериментом. Поэтому, следуя
Камерлинг-Оннесу (1901), целесообразнее представить урав-
§ 2. Параметры состояния реального газа
167
нение состояния в виде степенного ряда
или с
PV = nRT(\+f + т£+..
оответственно
PV = п (RT + В'Р + С'Р2 + .
•)
••)
(2.1)
(2.2)
Между коэффициентами уравнений (2.1) и (2.2) существует
следующая связь:
Bf = В, C' = n?f- (2.2а)
Уравнения (2.1) и (2.2) носят название вириальной формы
уравнения состояния, а коэффициенты В, С, ..., В', С', ...
называются вторым, третьим и т. д. вириальными
коэффициентами. В большинстве случаев в уравнении состояния
оказывается достаточным ограничиться разложением до члена
второго порядка. Уравнение Ван-дер-Ваальса можно считать
частным случаем вириального уравнения состояния. Если учесть
только поправку первого порядка, то получим соотношение
B = b — RT
(2.3)
Для вычисления параметров состояния реального газа в
простейшем случае, как и для идеального газа, нужно исходить
из статистического интеграла. Однако в отличие от идеального
газа eh т.е. энергия N частиц газа в i-й фазовой ячейке, зависит
теперь не только от скорости частиц, но и от взаимодействия
между ними. Поэтому следует записать
е/=2^(/£|*+---+Д
zNi
7 \ 8vr \^li» • • ' » zNi)*
(2.4)
где энергия взаимодействия ew зависит от координат.
Для статистического интеграла, учитывая (2.4), имеем [см.
формулу (3.5) гл. 2]
Z = ^jexp (-$
dr =
l
~N\W
+ СО + ос
I •••1ехр(-
Pi,+-
■+»1N
2\ykT
)
X
X
dpxt ■ ■ ■ dpZN§ . .. J exp ( —|f) dxx ... dzN.
(2.5)
168
Гл. 3. Реальные газы
Используя формулу Стирлинга
и интегральное соотношение [см. формулу (1.1.9) гл. 2]
\dp=V2n\jikTy
W
2\ikT
получим для статистического интеграла
Z=1^{V^kfrN'^...^v{-^)dx1...dzN. (2.6)
Умножив числитель и знаменатель на VN, можно записать
выражение (2.6) в виде:
2 = 2ИД ± j .. . jexp (-*§) dXl... dzN
(2.7)
причем через
[см. формулу (3.1.8) гл. 2] обозначен статистический интеграл
идеального одноатомного газа.
В дальнейшем индексом „ид" всегда будут отмечаться
величины, относящиеся к идеальному газу.
Для идеального газа интеграл в формуле (2.7) равен VN.
Для реального газа со слабым взаимодействием между
молекулами можно положить
pL J... Jexp (-«^^...d^ 1-6, (2.8)
где б—малая поправка.
Учитывая (2.8), для свободной энергии реального газа получим
F = — kTlnZ = Fw—kTln(l — 6)
Для давления имеем
Оборвем уравнение состояния (2.1) на члене со вторым вири-
альным коэффициентом и сравним его с (2.9), тогда получим
д\п(\-д)_п>МлВ /2 10)
dV ~~ V2 '
§ 2. Параметры состояния реального газа
169
Учитывая, что для малых значений |б|<^1 справедливо
соотношение
1п(1—б) = — б,
и интегрируя уравнение (2.10), находим
6 =
n2NAB
(2.11)
Тогда статистический интеграл для реального газа со
слабым взаимодействием между частицами можно представить
в виде:
(2.12)
Отсюда для свободной энергии реального газа находим
(2.13)
Для второго вириального коэффициента из формул (2.8) и (2.11)
имеем
в=^^('-^1-1ехр(-^)^-^)' (2Л4)
или иначе
(2.15)
Вообще говоря, взаимодействие между двумя молекулами
пренебрежимо мало. Только при столкновении частицы на
короткое время сближаются настолько, что вносят заметный вклад
в статистический интеграл.
Пусть рассматриваемое количество газа настолько мало,
что за короткий промежуток времени не более двух частиц
могут подойти достаточно близко друг к другу. Поскольку
энергия и энтропия — величины аддитивные, это предположение
не ограничивает общности приведенных рассуждений. Таким
образом, выведенные формулы для физических параметров
состояния реального газа справедливы для сколь угодно
больших количеств газа. Действительно, требование, что
величина п должна быть достаточно малой, в дальнейшем можно
опустить, т. е. произвести суммирование по всем малым объемам.
170
Гл. S. Реальные газы
Возможное число пар взаимодействующих молекул среди N
молекул газа составляет N (N—1)/2. Если обозначить
сталкивающиеся частицы индексами 1 и 2, то из формулы (2.15)
получим
B=m^w~A 1 • • • И1—ехр (~й]dXl''' dz*dx*'''dZN'
(2.16)
Энергия взаимодействия е12 между первой и второй частицей
зависит только от относительных координат
X = Х1 Х2, У ==У\ Угч % == %i ^2*
Если, кроме того, ввести координаты
_х1-\Гх2
_У1+У2
,+=h±h
2 ' * 2 '
то для интеграла в (2.16) имеем
\ ,.. \( 1 — ехр( — |^j jdx1.. .dz2dx3.. .dz# =
(2.17)
(2.18)
= l/-2j..^["l-exp(-^)]
d(*i. ..., z2)
dx~...dz+. (2Л9)
d(x-,...,z+){
Учитывая соотношения, вытекающие из формул (2.17) и (2,18)
*, =-
2х+-
х2 =
2х+—х-
(2.20)
получим для детерминанта преобразования в (2.19)
д(х~ z+)"
0,5 0 0
0 0,5 0
0 0 0,5
1 0 0
0 1 0
0 0 1
-0,5
0
о о
0,5 0
0 —0,5
0 0
= 1.
(2.21)
Принимая во внимание, что
^dx+dy+dz+=V,
и учитывая, что при Л^^>1
N(N— l)&N* = n*N2A,
находим из формулы (2.16) в сочетании с (2.19) и (2.21) связь
между вторым вириальным коэффициентом В и энергией
взаимодействия е12:
в=1гШ1-е**(-%))*г*гаг~'
(2.22)
SV 2. Параметры состояния реального газа
171
Если теперь перейти от относительных координат х , у , г
к сферическим г, 8, <р, то для случая изотропных сил
взаимодействия выражение (2.22) можно записать также в виде
(2.23)
Здесь введено обозначение ги = г(г), где /--расстояние между
центрами тяжести обеих частиц.
При теоретическом вычислении второго вириального
коэффициента В по формуле (2.23) нужно предполагать, что
потенциал г (г) межмолекулярных сил известен. С другой стороны,
измеряя вириальный коэффициент В, можно получить сведения
о свойствах этих сил.
>-г Фиг. 29. Распределение потенциала в модели
жестких упругих молекул.
При г < 2го потенциал е имеет бесконечно большую
величину.
В простейшей модели молекулы рассматриваются как
жесткие упругие сферы. Соответствующий потенциал изображен
на фиг. 29. В этом случае сближению центров тяжести
молекул на расстояние r<2rs (rs—эффективный радиус
молекулы) препятствуют бесконечно большие силы отталкивания, т. е.
В (Г):
: ОО
при г < 2rs
(2.24)
Наоборот, при большем расстоянии между центрами тяжести
молекул возникают силы притяжения, которые убывают при
увеличении г. В этой области потенциал имеет вид
(2.25)
Наилучшее согласие с экспериментом получается при т = 6.
Потенциал Леннард-Джонса (фиг. 30)
172
Гл. 3. Реальные газы
состоит из двух членов, описывающих отталкивание и
притяжение. Наилучшее согласие между теорией и экспериментом,
как и в модели жестких упругих сфер, получается при т=^6,
п Ю"тМ
Фиг. 30. Распределение потенциала в модели
Леннард-Джонса. (По работе [19].)
тогда как в члене, описывающем отталкивание, показатель
п должен быть больше 9. Чаще всего принимается л = 12.
^►г
Фиг. 31. Потенциал Букингема. (По работе [19].)
Для второго вириального коэффициента при использовании
модели Леннард-Джонса после трудоемких вычислений
получаем по формуле (2.22)
В
2л д, / ау\з/{п-т
[г(^н£г('-^^27>
где
Р fkT\m/n
(2.27а)
Еще большей точности удается достичь при использовании
потенциала Букингема, который можно представить в виде
(фиг. 31):
KiV{f«P [«('-£)]-(?)■}
(2.28)
§ 2. Параметры состояния реального газа
Ш
Задачи
2.1. Вириальная форма уравнения Ван -дер- Ваал ьса
Согласно табл. П.ХП, вандерваальсовы поправочные члены для азота
составляют: а=1,39 ат-ме/кмоль2, 6 = 0,039 м3/кмоль. Найти отсюда вириаль-
ные коэффициенты В и С. Вычислить температуру Бойля Тв, т. е.
температуру, для которой
^=0
дР и'
или соответственно
В(Г) = 0.
Какова величина вириального коэффициента В для Т = ТВ± 50, ±100, ±150,
±250QC?
Решение
Из уравнения состояния Ван-дер-Ваальса (1.5) имеем
(p+^)(V-«ft) = nKr. (2.1.1)
Запишем это уравнение в виде
nRT n4_nRT ( . пЬ . п*Ь2 па \ (2 { 2)
^-y—nb 1/2— у V ^ "^ 2V2 "+--*• RTVJ' У'}
Сравнивая уравнение (2.1.2) с вириальной формой уравнения состояния (2.1)
получаем для вириальных коэффициентов В и С:
в=ь-ж> {2ЛА)
С=£. (2.1.5)
Если же использовать другую вириальную форму уравнения состояния
PV = n(RT + B'P + C'P2 + ...)> (2.1.6)
то решая его методом последовательных приближений относительно Р,
п nRT , пВ'
nB'fnRT. \ ,
получим члены высшего порядка по п
nRT
Р=-
(,+=«:+„. £!d_^+...).
Сравнивая с формулой (2.1.3), отсюда имеем
В' = В, (2.1.7)
C = B'2 + C'RT. (2.1.8)
174 Гл. 3. Реальные газы
Температуру Бойля найдем из формулы (2.1.4)
Тв = ^- (2.1.9)
Подставляя численные значения параметров, находим температуру Бойля для
азота
1,39.9,81-10*
Тв~ 0,039-8,314.10*-420 К*
Как видно из табл. 25, расхождение между измеренными и вычисленными
значениями В довольно велико.
Таблица 25
Второй вириальный коэффициент
В(Т) для N2
г, к
170
270
320
323
370
420
470
520
570
670
£, м3/кмоль
(измер.)
—0,052
—0,010
—0,0004
0
0,006
0,011
0,015
0,018
0,021
0,024
В, м3/кмоль
вычисл. по (2.1.4)]
—0,057
—0,022
—0,012
—0,012
—0,005
0
0,004
0,007
0,010
0,015
Численное значение второго вириального коэффициента для Т = Тд —
— 100 К =320 К, согласно формуле (2.1.4), равно
вК°-№-шлш)=-°'012 "3/кмоль-
Остальные значения В (Т) указаны в табл. 25.
Далее, по формуле (2.1.5) получаем
C = 0,76-10-3 м6/кмоль2.
2.2. Термодинамические потенциалы газа Ван-дер-Ваальса
Сосуд объемом V = 5 л содержит 1 г гелия при 400 К. Вычислить
свободную энергию F, внутреннюю энергию V и энтропию S. Как изменятся эти
величины при нагревании газа до 500 К, если объем остается постоянным?
Гелий считать газом Ван-дер-Ваальса с постоянными а = 0,035 ат-м6/кмоль2,
6 = 0,024 м3/кмоль, R=NAk (см. задачу 3.1 гл. 2).
Решение
Свободная энергия реального газа, согласно формуле (2.13), равна
(2.2.1)
§ 2. Параметры состояния реального газа
175
Подставив сюда выражение (2.3) для второго вириального коэффициента газа
Ван-дер-Ваальса, получим
F = FKA + y(RbT-a)
(2.2.1а)
Для энтропии имеем
т. е. для газа Вап-дер-Ваальса
5 = 5ИД-^^. (2.2.2а)
Внутренняя энергия равна
t/ = F + rS=t/M-^||, (2.2.3)
т. е. для газа Ван-дер-Ваальса
и = иая-^. (2.2.3а)
Формула (2.2.3) отражает тот факт, что при увеличении объема производится
работа против сил притяжения между частицами газа. При этом внутренняя
энергия газа увеличивается.
Из (2.2.1а) находим изменение свободной энергии при изохорном
повышении температуры
AF = AFU+^AT. (2.2.4)
Таким образом, изменение свободной энергии при изохорном процессе зависит
еще и от вандерваальсова поправочного члена Ь. С другой стороны, для
изменения энтропии и внутренней энергии из формул (2.2.2а) и (2.2.3а) имеем
AS = AS„/P Д*/ = Д(/„Д. (2.2.5)
Согласно задаче 3.1 гл. 2, число киломолей в данном случае составляет
N Ю-3
*-yv7"~4,oo3-u'25 "> .
а для параметров состояния идеального газа при 400 К имеем
F„;< = — 11,52 кДж, 5ИД = 31,9 Дж/К, £/ид=1242 Дж.
Изменения при изохорном нагреве до 500 К, согласно задаче 3.1 гл. 2,
составляют для идеального газа
Д/?ид = —394 Дж, Д5ид = 0,90 Дж/К, Д£/ид = 310 Дж.
Поправку к свободной энергии газа Ван-дер-Ваальса получим из (2.2.1а):
(Г) ПК. Ю-ЗЧ2
F — /^д- с 10-з (8,314-103-0,024.400—0,035-9,81» 104) = 0,96 Дж.
Для поправки к энтропии и к внутренней энергии имеем соответственно
5-5м = -<0'2Б-10-Х-1У-1,4-'°'-0'0а4=0.«й8 Дж/К.
^-^ид = - (0.25.10-^.0,035-9,8Ы0^ =_Q05 Дж
176
Гл. 3. Реальные газы
Следовательно, поправка к внутренней энергии также имеет незначительную
величину.
Для изменения свободной энергии при изохорном нагреве от 400 до 500 К,
используя формулу (2.2.4), получаем
^_Д/Гид = (0.25.10-3)2.8,314.»03.0,024.100=0>25 Дж
Тогда можно написать
AF = AF^ = —394 Дж.
Ошибка за счет пренебрежения поправочными членами а и Ь в данном случае
оказывается несущественной.
2.3. Удельная теплоемкость газа Ван-дер-Ваальса
Вычислить для гелия молярную теплоемкость при постоянном объеме и
постоянном давлении. Вывести формулу для Ср — CvHK = Cp/Cv и определить
их значения при температуре 50 К и давлении 20 ат (а = 0,035 ат-м6/кмоль2,
6 = 0,024 м3/кмоль).
Решение
Согласно формуле (2.7) гл. 2, молярная теплоемкость при постоянном
объеме определяется выражением
тогда как для теплоемкости при постоянном давлении, согласно формуле (2.9)
гл. 2, имеем
Используя выражение для энтропии газа Ван-дер-Ваальса
s-s -*™
° — °ид у »
получим из формулы (2.3.1)
(2.3.3)
СР
- -Т(™\ -С
■^ \dTJv~~ "ид
Следовательно, если говорить о теплоемкости при постоянном объеме, то в этом
отношении газ Ван-дер-Ваальса ведет себя, как идеальный. Поэтому, согласно
закону равнораспределения, можно написать для газа Ван-дер-Ваальса (см.
задачу 2.3 гл. 2)
г __fNAk_fR
сг/= 2 ~3~' (2.3.4)
Для одноатомного гелия / = 3. Тогда
3
Cv~-^ /? = 2,98 ккал/кмоль-К
есть теплоемкость гелия, если считать его газом Ван-дер-Ваальса.
§ 2. Параметры состояния реального газа
177
Для определения теплоемкости при постоянном давлении найдем
энтальпию газа Ван-дер-Ваальса, для чего воспользуемся формулами (2.2.3) и (2.1):
H = U + PV=U^-^§+nRT(l+f)
(2.3.5)
Это выражение с точностью до членов второго порядка малости можно
представить в виде
Н = Н„Л+^(в-Т§)=Нм + пР(в-Т§) . (2.3.6)
Подставим выражение (2.3.6) в (2.3.2) при /г=1. Тогда получим
Учитывая формулу (2.3), согласно которой
получим окончательно
(2.3.8)
Отсюда имеем для разности теплоемкостей
2а
^р ^ = СрИД С^ид+Р DT2 =^т
2а?
RT2
RT*
и для показателя адиабаты
(2.3.9)
(2.3.10)
В отличие от идеального газа теплоемкость Сру а из-за этого и показатель
адиабаты K — Cp/Cv газа Ван-дер-Ваальса зависят от давления Р. Из
формулы (2.3.8) получим для гелия при 50 К и 20 ат:
5 2.0,035.(9,81..104)2-20-2,388-10-4_
Lp-2H~r 8,314-103-502 ~~
= (4,967 + 0,155) = 5,122 ккал/(кмоль. К).
Из формулы (2.3.9) следует
^—(^=1,987 + 0,155 = 2,142 ккал/(кмоль-К),
а из формулы (2.3.10) имеем
Ср 5 0,155
1,5-1,987
=1,718.
Таким образом, заметные отклонения этих величин от их значений для
идеального газа должны наблюдаться при высоких давлениях и низких
температурах.
178
Гл. 3. Реальные газы
2.4. Параметры состояния многоатомного газа
Ван-дер-Ваальса
Вычислить внутреннюю энергию U и энтропию S для 2 л НС1 при 300 К
и давлении 40 ат. Каковы значения теплоемкостей Ср и Сг, для хлористого
водорода? Рассматривать НС1 как газ Ван-дер-Ваальса (а = 0,922 ат-м°/кмоль2,
6 = 0,020 м3/кмоль).
Решение
Будем считать, что формулы, выведенные в § 2 настоящей главы для
одноатомного газа, справедливы и для многоатомного. Как показано в
задаче 3.2 гл. 2, для идеального газа число киломолей составляет
N PV
янд = ^=-££ = 3,14.10-з. (2.4.1)
Параметры состояния для идеального газа, согласно задаче 3.2 гл. 2, имеют
следующую величину:
£/0=19,6 кДж, S0 = 0,493 кДж/К. (2.4.2)
Здесь учтены добавки за счет поступательных и вращательных степеней
свободы. Для случая реального газа введем сначала поправку в число киломолей.
Согласно формулам (2.2) и (2.2а), имеем
PV
Пг RT + BP'
Вириальный коэффициент В в настоящем случае равен для Т = 300 К:
в=ь-ж=(о'020-8°:з14:!о'!зоо4)=-°'°16 ыа/кмоль-
Отсюда следует, что число киломолей есть
40-9,81-Ю4-2-Ю-3
= 3,22- Ю-3. (2.4.3)
Г 8,314-103-300 —0,016-40-9,81-104"
Вычисленные в задаче 3.2 гл. 2 параметры (2.4.2) нужно умножить на
отношение
^3,22
пид 3,14
тогда получим
£/ид = 20,1 кДж, 5ИД = 0,506 кДж/К.
Учитывая поправки Ван-дер-Ваальса, имеем
F-Fm = ^-(RbT-a), (2.4.4)
и-ияЛ = -^-, (2.4.5)
S-SHa=-^. (2.4.6)
Подставляя численные значения, получаем
£/ = 20,1 — 0,5=19,6 кДж,
5 = 0,506 — 0,001=0,505 кДж/К.
§ 2. Параметры состояния реального газа
179
Молярная теплоемкость при постоянном объеме составляет
SR
Cv = Cvllb = -£-=4,967 ккал/(кмоль-К)
(2.4.7)
Для молярной теплоемкости при постоянном давлении из формулы (2.3.9)
имеем
CP = CV+R+^. (2.4.8)
Подставляя значения, приведенные в условии, находим
С -4967+1 987 + 2-0'922-(9'81-1<0:)2J;21-987 =6,965 ккал/(кмоль.К).
ия — t,yu/-i i,»o/-t- (8,314-103)2-3002 v '
2.5. Эффект Джоуля — Томсона в газе Ван-дер-Ваальса
Трубка, заполненная кислородом, разделена пористой перегородкой на
две камеры (фиг. 32). С помощью равномерного перемещения поршней в
левой камере поддерживается давление Р а> а в правой—давление Рв < Ра-
Спеченное стекло
Фиг. 32. Схема установки для
наблюдения эффекта Джоуля —
Томсона. (По работе [21].)
Термопары включены навстречу друг
другу, поэтому прибор Th показывает
разность температур Т»-Тд.
При этом газ перетекает из левой камеры в правую через отверстия в
перегородке. Сначала объем левой камеры равен Vа> а объем правой равен
нулю. В конце процесса объем правой камеры становится равным Уд > Vа>
а объем левой — равным нулю. Предполагается, что система теплоизолирована.
Вычислить изменение температуры при следующих начальных значениях
параметров: Р,4 = 250ат, Рд==1 ат, 7^ = 273 К. Считать используемый газ-
кислород—газом Ван-дер-Ваальса. Для поправок Ван-дер-Ваальса использовать
значения, приведенные в табл. П. XII: а = 1,40 ат-м6/кмоль2, 6 = 0,032 м3/кмоль.
Решение
Речь идет о нестационарном процессе, при котором сохраняется
энтальпия. В самом деле, над газом, находящимся слева от поршня, производится
механическая работа РaVа> а газ» находящийся справа, наоборот,
производит работу PrVr. В результате внутренняя энергия возрастает на величину
Р aV А — PrVb- Обозначая внутреннюю энергию в начальном состоянии
через О а, з в конечном состоянии через Uв, получаем тогда, что
Ub = Ua + PaVa-PbVb. (2.5.1)
Следовательно, энтальпия в течение процесса остается постоянной
HA = Ua + PaVa = Ub + PbVb = Hb. (2.5.2)
180
Гл. 3. Реальные газы
Для полного дифференциала энтальпии dH (Р, Т) имеем
*»=(§)/т-+{§)/р=°- (2-5"3)
Согласно формуле (2.9) гл. 2, имеем
'р
В соответствии с формулами (2.1) и (2.2.3) энтальпия 1 кмоль реального
газа есть
(2.5.5)
Для газа Ван-дер-Ваальса величина В, определяемая формулой
(
w -С,. (2.5.4)
ZK. 1 D
»-»-&•
не зависит от давления. То ж.е самое справедливо и для величины Яид:
tf„a=t/„„ + (PV)M=/?r(i + l). (2.5.6)
Тогда получаем, что
#),—'Я—£•
Формула (2.5.3) дает
CpdT + (b-^dP = 0t
откуда следует, что
«-",&->)■ <"-8>
Дифференциалы dP, dr в уравнении (2.5.8) можно заменить приращениями
АР, АГ только для малого перепада давлений АР = Р2 — Pi и для малого
изменения температуры АТ = Т2 — Т1. Тогда
Чтобы найти более точное решение, обратимся к дифференциальному
уравнению (2.5.8). Разделяя переменные, получим
тв рв
1&т=ь=1ъ- <2-5-10>
ТА РА
Здесь величины a, b, R и Ср считаются постоянными. Интегрирование левой
части дает
тв тв тв
- -- - dT
J W=bRT=~T ) dT+T i
2а—&ЯГ"
Л 'Л
Гл-Гя , 2а 1 „„,„„ ,,^/в
ft _&/?[1п(2а-6/?Г)]Гл
§ 2. Параметры состояния реального газа
181
Следовательно,, решение дифференциального уравнения (2.5.8) имеет вид
Pr-Pa Ta-Tr 2а 2o-±RTb (9 * хи
—С^=— b?R]n2a-bRTA- (2'5Л1)
Преобразуем второй член в правой части
2a-bRTB Г bR(TB-TA)l
2a-bRTA I 2a-bRTA J
Если выполняется условие
bR\TA-TB\<^\2a-bRTA\y
то можно воспользоваться приближенной формулой In (1+*) = *>
справедливой при \х\<^.\. Тогда из выражения (2.5.11) имеем
что совпадает с приближенной формулой (2.5.9).
Подставляя численные значения, получаем
'2-1,40.9,81-10*
~~1 8,314.103-273
\ (-[249)-9,8Ы0*
0ДШ,) 3,5-8,314.103 К~ 75С-
Расширение газа через пористую перегородку, при котором его давление
падает до 1 ат, сопровождается понижением температуры на 75Q С.
2.6. Силы между молекулами в модели твердых упругих сфер
В модели твердых упругих сфер используется следующее приближение
для потенциальной энергии взаимодействия между молекулами реального газа:
( оо, г <2rs>
причем наилучшая аппроксимация достигается при т = 6. Как зависят
параметры rs и р потенциала (2.6.1) от поправочных членов Ван-дер-Ваальса а
и Ьу если считать, что температура достаточно высока? Какие значения
принимают Р и г$ для молекулы водорода? Согласно табл. П.XII имеем а =
= 0,194 ат-м6/кмоль2, Ь = 0,022 м3/кмоль. Вычислить максимальную силу
притяжения между двумя молекулами водорода.
Решение
Согласно формуле (2.23), второй вириальный коэффициент определяется
силами взаимодействия между молекулами
00
B = 2nNA J [l— е~г(г)/кт] г2 dr. (2.6.2)
о
Второй вириальный коэффициент В связан с постоянными Ван-дер-Ваальса
a, b соотношением
в==ь~ш- (2-6-3)
182
Гл. 3. Реальные газы
Разобьем область интегрирования на два интервала: от нуля до 2г$ и от 2г$
до бесконечности. В первом интервале е=оо, поэтому имеем
2rs 2г* 8гз
Г (\-e~e/kT)r*dr= С r*dr = -^. (2.6.4)
о о
Поскольку, согласно предположению, рассматривается область высоких
температур, можно считать, что во второй области интегрирования
потенциальная энергия взаимодействия мала:
|в(г)КА7\
Разложив подынтегральное выражение в ряд, получим
со со
^ (\-e-elr)/kT)r*dr=-glr Г е (г) г2 dr. (2.6.5)
2rs 2rs
Заменяя е выражением (2.6.1), находим
со со
J .(г)г»* = -^ J ^tV8)^.,h.. (2-6.6)
2rs 2лс
Подставим в формулу (2.6.2) выражения (2.6.4), (2.6.6) и (2.6.3). Это дает
b-£=2nNA [^-{т_щ2г1г-*кт] • (2"6-7>
Сравнивая коэффициенты в (2.6.7), имеем
a-(m-3)(2r5)«-»' (2-6'8)
а также уже выведенное соотношение (1.2):
b=^-NA(2rsf. (2.6.9)
Разрешая формулы (2.6.8) и (2.6.9) относительно 2г$ и р, находим
**=Vs$rA' (2-6-,0)
и для т — 6
Из формул (2.6.10) и (2.6.11) следует, что для водорода
\Г 3-0,022 ос 1П 10
^=У 2.3,14-6,02-Ю^ =2'6-'°"1 М'
д 9-0,194-9,81-10*-0,022
Р- 4-3,142.(6,02.10")3 -4'4'10 ^ж>м-
Силу притяжения между двумя молекулами находим, используя формулу
(2.6.1):
'—т?2—Рак—fSi- <2-6Л2>
§ 2. Параметры состояния реального газа
183
Она имеет наибольшее значение на левой границе области определения е (г),
т. е. при г — 2г$. Поэтому максимальная сила притяжения равна
Fi2rs)as^r"r+l' (2-6ЛЗ)
Подстановка численных значений дает
6.4 4-Ю-79
F {2rs) =(2,6■■ 10-10)7 =3,3- lO-ii Н =3,4.10-12 кгс.
2.7*. Вычисление молекулярных параметров
для модели Леннард-Джонса
Оптические исследования кристаллической решетки дают для
равновесного расстояния 2rs = rQ между двумя атомами аргона величину:
rG = 3,82.10-i° м.
Температура Бойля Тв Для аргона, согласно табл. П.Х1П (см. приложение),
составляет 410 К. Вычислить по этим данным постоянные аир потенциала
Леннард-Джонса
е(0=^-^г. (2.7.1)
считая т —6, п— 12.
Вычислить В (Т) для Т = 300, 400, 500, 600 и 700 К. Чему равна
потенциальная энергия в минимуме? Каковы значения притягивающей и
отталкивающей сил на равновесном расстоянии го>
Решение
На равновесном расстоянии t = tq энергия взаимодействия г (г) имеет
минимум. Поэтому
д±\ _ па | тР -о (272)
При г —»- 0 отталкивание между частицами должно стать больше, чем
притяжение. Отсюда следует, что, вообще говоря, п > т. Далее, запишем
P = i-« (2.7.3)
В модели Леннард-Джонса второй вириальный коэффициент В определяется
выражением (2.27). Используя табулированные значения Г-функции, для
т — 6 и /г=12 получаем
,_»■ ж,/«:(^)"-[.»-*« (f у*-
-0,,53f-0,0378(^),'--0,0096(-|)'_o,002,(|-y'--...],
где
(2.7.4)
б2
0=JL. (2.7.5)
184
Гл. 3. Реальные газы
Учитывая, что В(Тв) — 0, находим в первом приближении из первых двух
членов этого ряда величину 0 при 7, = Гд = 410 К:
1 2262
Затем с помощью метода последовательных приближений Ньютона из
выражения (2.7.4) определяем
0 = 479 К. (2.7.7)
Равенства (2.7.3) и (2.7.5) представляют собой два уравнения для
определения двух неизвестных величин аир. Возводя равенство (2.7.3) в квадрат,
подставляя в формулу (2.7.5) и разрешая полученное уравнение
относительно а, находим при заданных численных значениях
0 10 479-1 38-10~23 (3 82- 10-1(М12
a=-^.ferg = 4^ 1>М Ш 41^ Ш ^.=:1,б.10-1з4Дж.м12. (2.7.8)
Значение Р вычислим по формуле (2.7.5):
р= /0^=^479.1,38- К)-23-1,6-10-134= 1,0-10-" Дж-м6. (2.7.9)
Подставив найденные величины в выражение (2.7.4), определим значения
В (Г); они приведены в табл. 26.
Таблица 26
Значения В (Т) для аргона в модели Леннард-Джонса
при п=12 и пг = 6
Г, К 300 400 410 500 600 700
Б (Г), м3/кмоль —0,022 —0,001 0 0,007 0,010 0,012
Используя вычисленные значения параметров, вычислим минимальное
значение потенциальной энергии по формуле (2.7.1):
8<^=(Ш-1о-"^-(з,ю?Го-»)'а-1'66-10""Дж- (2-7Л0)
Чтобы найти силу притяжения, продифференцируем энергию по координате г:
F(r\ — EZl!l— Ш I т(3 /0 7 1П
Следовательно, сила притяжения при равновесном расстоянии г — tq равна
F+ (rG)= ^r = (3,82!lo"o)^5-0-10'U Н- (2'7Л2)
То же значение получается для силы отталкивания.
2.8*. Молярная теплоемкость газа Леннард-Джонса
Аргон находится при температуре Г = 500 К и под давлением Р = 200 ат.
Вычислить Ср и Cv.
§ 2. Параметры состояния реального газа
185
Решение
Воспользуемся формулами (2.7) гл. 2 и (2.4.16) гл.2:
c'"T{w)r> (2А,)
_ т(дР1дТ)Ь „
LP~Lv (dP/dV)T ' l '
Будем исходить из уравнения для 1 кмоль реального газа, которое имеет вид
[см. (2.1))
PV = RT (l+JL\ = RT + BP (2.8.3)
Для энтропии 1 кмоль в соответствии с формулой (2.2.2) запишем
S = S,i-yff(BT). (2.8.4)
Подставляя это выражение в формулу (2.8.1), получаем
RTd*(BT) _РЛ,**, _*В\ (285)
Учитывая при дифференцировании, что В = В(Т), из формул (2.8.2) и (2.8.3)
найдем теплоемкость при постоянном давлении
Cp = Cv + R + 2P^. (2.8.6)
Чтобы приближенно вычислить в формуле (2.8.5) поправочные члены для
модели Леннард-Джонса, заменим дифференциалы конечными разностями:
dB_ 1 ГВ(Т + АТ) — В(Т) В(Т) — В(Т—АТ)1 __
dT~ 2[ АГ + AT J~
_ В(Т + АТ)-В(Т-АТ)
~ 2АТ ' (2*8-7)
Аналогично можно написать, применяя приближенную формулу (2.8.7):
d2B _ d В(Т + АТ) — В (Т — AT) _ В (Т + 2АТ) —2В(Т) + В(Т —2АТ)
dT2~dT 2АТ ~~ 4АТ2
(2.8.8)
Для численного расчета положим в формуле (2.8.7) AT =100 К и используем
данные табл. 26. Тогда имеем
fdB\ 0,012 + 0,001 ск 1Л . ,„
(2гЛоо= 250 =6'5-10-5 м*/(кмоль.К).
Из формулы (2.8.8) имеем при ДГ = 50 К
(d2B\ 0,010-2-0,007-0,001 - 1П . 3// ™
\-*П)»Г 4^ =-5-Ю-' мЗДкмоль.К*).
Подставляя эти значения в формулу (2.8.5), находим
C„ = 2,980—200-9,8Ы04 (2-6,5.10-б_500.5-Ю-?)-2,388-10-4 =
= 3,542 ккал/(кмоль-К).
186
Гл. 3. Реальные газы
Из формулы (2.8.6) получаем
Ся=:3,542+1,987 + 2.200-9,81.104-6,5. Ю-5-2,338-10-4 =
= 6,138 ккал/(кмоль-К).
Таким образом, в отличие от модели Ван-дер-Ваальса модель Леннард-Джонса
объясняет изменение удельной теплоемкости Cv.
2.9. Параметры состояния. Поправки более высокого порядка
Вычислить свободную энергию и энтропию для п кмоль газа с учетом
вириальных коэффициентов В и С.
-(!
Решение
Из формулы (3.15) гл. 2 имеем
rdF"
Отсюда
F = — С PdV + const (Т).
Давление определим с помощью вириального уравнения (2.1):
Подставляя (2.9.3) в (2.9.2), получаем
F==n/?r(-lnV+^+^J+...)+const(r).
При £ = 0, С = 0, ..., согласно формуле (3.1.9) гл. 2, должно выполняться
равенство
V (2n\ikT)3/*
(2.9.1)
(2.9.2)
(2.9.3)
(2.9.4)
f = f**=-
■NkT
In
Nh*
•1
(2.9.5)
Поэтому можно считать, что
— nRT In V + const = F„fl.
Тогда для свободной энергии имеем
пВ . п2С ,
F = F^ + nRT
2V2
(2.9.6)
что согласуется с выражением (2.13).
Энтропию найдем из соотношения
*--(£),•
Подставив сюда выражение (2.9.6), получим
fnB , п2С
(2.9.7)
S = 5ид—tiR
V~ 2V2
LA'
V dT
...)-
nRT
n dB , n2 dC
V dT~2V2 dT
■•)-
= 5ид-п^ (■£-wr rB+^2"5г ГС+ *-
(2.9.8)
§ 2. Параметры состояния реального газа
187
2.10. Второй вириальный коэффициент для смеси газов
Газовая смесь содержит 2 кмоль С02 и 1 кмоль 02. Найти второй
вириальный коэффициент для смеси этих газов при 500 К. При определении второго
вириального коэффициента для С02 и 02 пользоваться поправочными членами
Ван-дер-Ваальса, приведенными в табл. П.XII.
Решение
В данном случае нужно учитывать три потенциальные энергии
взаимодействия между молекулами: еи и е22—для взаимодействия между
одинаковыми частицами и е12—для взаимодействия между молекулами С02
и 02. Поэтому вводят три вириальных коэффициента: Вп, В22 и В12.
Их следует просуммировать соответственно относительной частоте парных
взаимодействий. Если обозначить число молекул С02 через Nl9 а число
молекул 02 через N2y то при Л^^>1, N2^>\ эти относительные частоты
определяются соотношениями
v2-_J!l п-ур—Лл 2(l-v)v= 2NlN*
V (Ni + Ntf' {l y> (N, + N2r ' Z(l У)У M + N,)*'
(2.10.1)
Тогда для второго вириального коэффициента газовой смеси имеем
S = Y2fin + (l-Y)2B22 + 2(l-Y)YSi2. (2л0-2)
Используя поправочные члены Ван-дер-Ваальса из табл. П.XII, вычислим
вириальные коэффициенты Вп и В22:
ап {ппло 3,72-9,8ЫО4 К\ f„nAo 43,9 К\ Ч/
Ви = Ои -^=(^0,043- '831;.10,г )=(о,043 ^-)мЗ/кмоль,
(2.10.3)
ь , «22 (с поп 1,40-9,81 -104К\ /лпоп 16,5К\ ч/
Кг = Ъ22-^= f 0,032— 831;.10зГ j=f 0,032 ^-Мкмоль.
(2.10.4)
Вириальный коэффициент В12 найдем как среднее арифметическое двух
других коэффициентов:
Ви=В* + В** = (0,037-^1) мз/кмоль. (2.10.5)
Вообще, значение В12 оказывается ближе к значению В для более легкого
газа, однако расхождение с вычисленной величиной (2.10.5) невелико.
Таким образом, второй вириальный коэффициент газовой смеси в
соответствии с формулой (2.10.2) есть
й=^(0.043-1^А)+1(0)032-1^) +
+ 4(0)037 30,2 К
91 Т
м3/кмоль,
В
= ^0,036—51^il^ м3/кмоль. (2.10.6)
При Г = 500 К из формулы (2.10.6) получаем
В = —0,034 м3/кмоль.
188
Гл. 3. Реальные газы
Упражнения
У.2.1. Найти температуру Бойля Гд для кислорода по уравнению Ван-
дер-Ваальса (а=1,40 ат-м6/кмоль2, 6 = 0,032 м3/кмоль, /? = Л^/г).
У.2.2. Вычислить по уравнению Ван-дер-Ваальса второй вириальный
коэффициент для кислорода при 300 и 700 К.
У.2.3. Насколько изменятся свободная энергия F, энтропия S и
внутренняя энергия U для гелия, если при постоянной температуре 400 К
объем, занимаемый 1 г гелия, уменьшить от 5 до 0,002 л? Чему
равны эти изменения, если гелий считать идеальным газом?
(а = 0,035 ат-м6/кмоль2, 6 = 0,024 м3/кмоль).
У.2.4. Определить Ср и Cv, а также показатель адиабаты к для гелия при
температуре 300 К и давлении 100 ат, считая его газом Ван-дер-
Ваальса.
У.2.5. Чему равно изотермическое изменение давления, приводящее к
увеличению теплоемкости Ср гелия на АС/? = 0,01 ккал/(кмоль-К)?
У.2.6. Цилиндр объемом 5 л содержит 0,04 кмоль водорода. Температура
составляет 400 К. Найти адиабатическое изменение объема при
охлаждении газа до 300 К (6 = 0,022 м3/кмоль).
У.2.7. В процессе Джоуля — Томсона кислород охлаждается от 250 до 240 К.
. Вычислить изменение давления, считая, что Ср соответствует закону
равнораспределения.
У.2.8*. Вычислить для Н2, N2 и 02 температуру инверсии, т. е. такую
температуру, ниже которой в процессе Джоуля — Томсона
расширение приводит к охлаждению газа.
У.2.9. Для газа Ван-дер-Ваальса вычислить относительное и абсолютное
отклонения молярного объема от его значения для идеального газа.
Чему равно это отклонение в критическом состоянии?
У.2.10. Сколько молекул содержится в 1 мм3 кислорода при давлении 100 ат
и температуре 300 К, если считать кислород: а) идеальным газом,
б) газом Ван-дер-Ваалъса с а =1,40 ат-м°/кмоль2, 6 = 0,032 м3/кмоль?
У.2.11. Баллон вместимостью 1 л содержит кислород при 300 К, сжатый до
100 ат. Вычислить работу при изотермическом расширении газа до
1 ат. Провести расчет для идеального газа и для газа Ван-дер-
Ваальса.
У.2.12. Найти энергию, необходимую для нагревания кислорода от 300 до
400 К. Объем постоянен и равен 1 л, начальное давление
составляет 100 ат. Сравнить результаты для идеального газа и газа Ван-
дер-Ваальса.
У.2.13. Чему равна энергия, необходимая для нагревания кислорода от
300 до 400 К, если поддерживается постоянное давление 100 ат,
а начальный объем составляет 1 л? Какая величина получается для
идеального газа?
У.2.14. Определить максимальную величину силы притяжения между двумя
молекулами С02 согласно модели жестких упругих сфер.
У.2.15. Вывести выражение для энергии Гиббса G реального газа.
У.2.16. Найти число молекул аргона в 1 л газа при давлении 200 ат и
температуре 500 К. Использовать модель Леннард-Джонса. Каково
различие по сравнению с идеальным газом? (В = 0,007 м3/кмоль).
У.2.17. 1 л аргона нагревается от 500 до 600 К при постоянном объеме.
Вычислить необходимую для этого энергию при начальном давлении
200 ат. Расчет проводить на основе модели Леннард-Джонса (см.
табл. 26).
У.2.18. Найти, насколько изменится давление в предыдущем упражнении.
У.2.19*. В двух предыдущих упражнениях определить изменение удельных
теплоемкостей Ср и Cv.
§ 3. Фазовое равновесие
189
У.2.20*. Вывести формулу для зависимости температуры инверсии от
давления. При выводе формулы учесть поправочные члены высшего
порядка в уравнении Ван-дер-Ваальса. Для кислорода при 100 ат
определить область те\тератур, в которой при расширении газа
температура понижается (а=1,40 ат-мб/кмоль2, 6 = 0,032 м3/кмоль).
У.2.21. Вычислить внутреннюю энергию и энтальпию с учетом вириальных
коэффициентов высшего порядка.
У.2.22. Какой вид имеют формулы для Ср и Cv при учете вириальных
коэффициентов высшего порядка?
У.2.23. Определить вторые вириальные коэффициенты для смеси,
содержащей 3 кмоль N2 и 1 кмоль Н2. Чему равен второй вириальный
коэффициент при 300 К? Вычислить оба поправочных члена Ван-
дер-Ваальса для этой смеси. При расчете использовать данные
табл. П.ХП.
§ 3. ФАЗОВОЕ РАВНОВЕСИЕ В СИСТЕМАХ ИЗ ЧАСТИЦ ОДНОГО СОРТА
Введение
В предыдущих рассуждениях число частиц N считалось
постоянным параметром. Однако в ходе термического процесса,
например во время конденсации, число частиц в теле может
меняться.
Термодинамические потенциалы системы [/, S, F, Я, G в
равновесии являются аддитивными величинами, т. е. для тел,
состоящих из одинаковых частиц, они пропорциональны числу
частиц. Если число частиц не постоянно, но представляет
собой независимую переменную, то к дифференциалам этих
аддитивных термодинамических функций нужно добавить член,
пропорциональный дифференциалу dN числа частиц.
На основании сказанного запишем внутреннюю энергию при
переменном числе частиц в виде
dU = TdS—PdV + iicdN
(3.1)
где коэффициент пропорциональности цс называется химическим
потенциалом. Соотношения для остальных термодинамических
потенциалов следуют из формулы (3.1):
dF = d(U—TS) = — SdT—PdV + \xcdN,
dff = d(U + PV) = TdS + VdP + \icdN,
dG = d(H—TS) = — SdT + VdP + incdN.
(3.2)
(3.3)
(3.4)
190
Гл. 3. Реальные газы
Для определения химического потенциала из формул (3.1) —(3.4)
получим
MS.V) = (|£)Siy. <ЗЛа)
МГ,Ю = (|)гу (3.2а)
дН
^(^/>)==(ж)г,р-
(3.3а)
(3.4а)
Неизменность параметров при вычислении этих производных
следует рассматривать уже с учетом изменения числа частиц!
Из независимых переменных, фигурирующих в формулах
(3.1) — (3.4) V, S, а также N являются аддитивными в отличие
от величин Р и Т. Следовательно, термодинамические
потенциалы можно записать как функции их естественных
переменных:
"=^(4-.-£)• F=Nf'{T'ir)-
NfJ4r,P), G = Nft(T,P).
Я
(3.5)
Дифференцируя последнее равенство в (3.5), получим функцию,
зависящую только от параметров состояния Т и Р:
(§)T,p = fAT,P).
Отсюда при учете формулы (3.4а) имеем
ъ-МТ.П-Ь-1'*™-"
N
(3.6)
Таким образом, химический потенциал есть отнесенная к одной
частице энергия Гиббса тела, состоящего из одинаковых частиц.
Поэтому в соответствии с формулой (3.4) имеем
Фс= WdT + 1TdP
(3.7)
Слагаемое с множителем dN выпадает, так как химический
потенциал не зависит от числа частиц.
В замкнутой системе однородное вещество может распасться
на две фазы. Например, вода может одновременно существовать
в жидком и газообразном состояниях. Между обеими фазами
§ S. Фазовое равновесие
191
через определенный промежуток времени устанавливается
равновесие.
Как и у всех систем, находящихся в равновесии,
температуры обеих фаз должны быть равны
Тг = Т2 = Т. (3.8)
Точно так же должны совпадать и давления в обеих фазах:
Рг=Р*=Р- (3.9)
Наконец, для равновесия изобарно-изотермической системы
энергия Гиббса G = G (Р; Ту N) должна иметь минимум [см<
формулу (3.28) гл. 2, а также упражнение 3.18 гл. 2]
V дР )т, N т\ дТ )p,N ' \ dN Jp, т
В соответствии с формулой (3.6) можно записать
6G = 6G1 + 6G2 = на 6A/t + ]xC2 8N, = 0.
Тогда, учитывая, что N1 + Ni = N, или же 8N1 + 6N2 = 0, имеем
G*ci — |*с,)в#1 = 0,
т. е.
Ра(Р,Т)=ра(Р,Т)-
(3.10)
В равновесии химические потенциалы обеих фаз совпадают, а
давление и температура зависят друг от друга. Двухфазная
ю3
10
tf 10'1
lnrz
iur*
§нг*
ю~5
/О'6
г^
Лед
^0U£SSS£^
\\^^к>>^Критичесная
tvvw^ точка
у Пар
Тройная точка
I
/ i i i i •
0 100 Z00 300 400
7
"емперагпура, °С
Фиг. 33. Фазовая диаграмма Н20 в
Р, Г-координатах.
однокомпонентная система обладает только одной степенью
свободы. Если задана, например, температура, то установится
вполне определенное давление.
Равновесное состояние на Р, Г-диаграмме (фиг. 33)
изображается некоторой кривой Т=--Т(Р). Она показывает, при
каких значениях Р и Т могут одновременно существовать два
агрегатных состояния, и разделяет их друг от друга.
192
Гл. 3. Реальные газы
Следует отметить, что при медленном изменении параметров
состояния вещество может при известных обстоятельствах
сохранять свое агрегатное состояние (как, например,
переохлажденный пар), т. е. поведение вещества может не
соответствовать Р, Г-диаграмме. Однако такого рода метастабильное
состояние реализуется только при определенных предпосылках,
например, если отсутствуют зародыши кристаллизации.
Чтобы одно и то же вещество могло одновременно
существовать в трех фазах, должны выполняться следующие условия:
* 1 = Т2 = / з, Рг = Р2 = P3i \1С1 =Н'С2==^СЗ*
Эти условия могут удовлетворяться одновременно только в одной
точке Р, Г-диаграммы — в так называемой тройной точке.
Трехфазная однокомпонентная система не имеет ни одной степени
свободы. Например, равновесие твердой, жидкой и
газообразной фаз воды возможно только при Г = 0,01°С и Р = 0,006 ат.
При переходе вещества в другое агрегатное состояние его
энтропия изменяется. Если обозначить через Q тепло,
выделяющееся при переходе 1 кмоль вещества в другое состояние,
то из условия равновесия |хС1 = |лС2 получаем
U-U1 + P(V2-V1) = H2-H1 = T(S-S1) = Q. (3.11)
Отсюда находим изменение энтропии при переходе из одного
агрегатного состояния в другое:
S2-Sl = ^^=-^. (3.12)
Из выражений (3.11) и (3.12) видно, что теплота перехода Q
есть не что иное, как разность энтальпий в обеих фазах.
Пример 18
Замерзание воды при нормальных условиях сопровождается потерей
количества тепла, равного 18-80 ккал/кмоль. Иначе говоря, энтальпия воды при
0°С на 1440 ккал/кмоль превышает энтальпию льда при 0°С. Изменение
энтропии на 1 кмоль равно
18» 80
S2 — S1 = -^o-=5,09 ккалДкмоль-К).
В кристаллах льда молекулы расположены более упорядочений, чем в воде.
Поэтому у льда энтропия ниже, чем у воды.
Формулы для термодинамических функций для жидкостей
и твердых тел имеют такой же вид, как и для газа. В
соответствии с первым законом термодинамики внутреннюю энергию
можно найти из выражения:
dU = №)o6p-PdV. (3.13)
§ 3. Фазовое равновесие
193
Поскольку в отличие от газов в твердых телах и в жидкостях
осуществляются только малые изменения объема, можно без
существенных ошибок пренебречь внешней работой системы.
Тогда для внутренней энергии имеем
d£/ = (6Q)o6p,
или же
7-0
U(T0) = \C(T)dT + U0. (3.14)
о
Аналогичным образом из выражения
а8=т^=щр^у (3.15)
пренебрегая внешней работой, получаем для энтропии
То
S(T0) = $y-dT + S0. (3.16)
о
Через U0 и S0 обозначены внутренняя энергия и энтропия при
абсолютном нуле (Г = 0). В отличие от формул (3.14) и (3.16)
в различных таблицах термодинамических функций
указываются их значения, отсчитываемые от соответственно выбранного
начального состояния. Иначе говоря, параметры состояния
определены с точностью до постоянной, зависящей от начала
отсчета.
Пример 19
В табл. П.XV через Н обозначена энтальпия, отсчитываемая от
энтальпии воды при 0°С. Последней произвольно приписано значение # = 0. Поэтому
ко всем приведенным в таблице значениям энтальпии нужно прибавить
постоянную величину, равную энтальпии воды при 0QC. При практических
расчетах эта величина не представляет интереса, поскольку основное значение
имеют изменения параметров состояния.
Задачи
3.1*. Фазовое равновесие согласно уравнению Ван-дер-Ваальса
Согласно уравнению Ван-дер-Ваальса (см. § 1), в однородном веществе
ниже критической температуры Т^ существует неустойчивая область, в которой
(dPjdV)x > 0. Физически эта область не реализуется, так как она соответствует
двухфазной системе, в которой находятся в равновесии жидкость и газ.
Доказать, что для каждой температуры Т <Tk изотерма в двухфазной области
разбивается прямой равновесного, или насыщенного, давления PS = PS(T)
таким образом, чточобразуются две равновеликие площади. Составить систему
уравнений для вычисления равновесного давления Ps = Ps(T).
194
Гл. 3. Реальные газы
Решение
Запишем уравнение Ван-дер-Ваальса в виде
p = p<y>T)=T=b-W- (3-1.1)
Рассмотрим переходную область на изотерме Т — Т0. В точке 1 (см. фиг. 28) все
вещество находится в жидком состоянии; в точке 2 все вещество находится
в парообразной фазе и имеет соответственно больший объем. Нужно
определить связь между давлением насыщенного пара PS = PS(T) и температурой Г,
при которой существует равновесие между двумя фазами. Согласно формуле
(3.10), для равновесия необходимо, чтобы химические потенциалы в обеих
фазах совпадали:
Pci(Ps. T) = iiC2(PS> Т). (3.1.2)
Для однокомпонентного вещества \\с определяется энергией Гиббса,
отнесенной к одной молекуле. Поэтому из формулы (3.6) имеем
Ui + PsVi-TS^Uz + PsVz-TSz. (3.1.3)
Здесь все величины отнесены к 1 кмоль. Изменение энтропии при переходе
из жидкого состояния в газообразное составляет
Ъ-З^'-Ъ + М-™. (ЗЛА)
С другой стороны, изменение энтропии при переходе из состояния 1 в
состояние 2 можно найти из выражения
*• 4U + Py.T)*t (ЗЛ.5)
Ч
причем путь интегрирования не играет роли, так как энтропия —однозначная
функция состояния. Интегрируя вдоль изотермы Т = Т0, получаем из
формулы (3.1.5)
Sl_S1 = ^i^+5J-j P(V, T0)dV. (3.1.6)
Сравнивая формулы (3.1.4) и (3.1.6), имеем-
J P(VfT0)dV = Ps(V2-V1). (3.1.7)
Следовательно, на фиг. 28 площадь под изотермой Т = Т0 должна быть равна
площади прямоугольника Ps (^2 — ^i)- Тогда равновесное давление, или
давление насыщенного пара Р$, определяется требованием, чтобы площади,
ограниченные изотермой T — Tq выше и ниже горизонтали Р = Р5, были равны.
Подставляя в (3.1.7) выражение (3.1.1) для давления И интегрируя,
получаем
^о1п£^+а(±-^)=Р5(К2-К1). (3.1.8)
§ 3. Фазовое равновесие
195
С другой стороны, если пары значений Р$, Vx и Р$, V2 удовлетворяют
уравнению Ван-дер-Ваальса (3.1.1), то
Приравняем выражения (3.1.9) и (3.1.10); это дает
пТ a(Vi+Vt)(Vi-b)(yt-b) ,,...
RT° W ' ( °
Чтобы найти связь между предельными объемами V± и V2, подставим (3.1.11)
в (3.1.9) и (3.1.10), а также (3.1.9) или (3.1.10) в (3.1.8). Тогда имеем
(У1-ь)(У2-ь)(ух-\-у^ 1пу2-ь , (\ \\_№-ь У2
vlvi Vi-ь ' \v2 vj \ vf vi ;•
(3.1.12)
Чтобы из уравнения Ван-дер-Ваальса найти давление насыщенного пара
Ps (Т), лучше всего воспользоваться графическим методом. Для численных
оценок нужно, приняв какое-либо значение Уъ найти соответствующее
значение V2 по формуле (3.1.12).
Если известна пара значений Vly V2, то с помощью уравнения (3.1.11)
можно определить соответствующую температуру Г0, а затем, используя (3.1.9)
или (3.1.10), найти и давление насыщенного пара Ps(To). Таким путем можно
построить по точкам кривую равновесия Р = Р(Т).
3.2. Уравнение Клапейрона — Клаузиуса
Исследуется зависимость температуры кипения воды от давления. При
нормальном атмосферном давлении Р = 1,0332 ат эта температура составляет
100°С. Для повышения ее до 101°С необходимо давление 1,0707 ат. Испарение
при нормальном давлении приводит к увеличению удельного объема от
1,04-10~:* до 1,673 м3/кг. Вычислить с помощью этих данных теплоту
испарения воды при нормальном давлении.
Решение
Будем исходить из условия равновесия между двумя фазами
ЦС1(Р. Г) = ИС|(Р. Т).
Все параметры состояния будем относить к 1 кмоль. Дифференцирование по
температуре дает
ФсЛ , ( d\ig \ dP_( d\i,C2\ , ( d\iC2 \ dP
"W )р+[~дГ )тйТ-\~дТ )p^\~W JtIt' {&гл)
В соответствии с (3.7) справедливы формулы
'Фс\ _ 5 (d\LC\ _ V
дТ )р~ NAy \дР Jt~Na ' (3,2,2)
Подставляя формулы (3.2.2) в равенство (3.2.1), получаем
196
Гл. 3. Реальные газы
Изменение энтропии можно выразить через теплоту испарения Q:
Q=7'(Si-S1). (3.2.4)
Отсюда вытекает дифференциальное уравнение Клапейрона — Клаузиуса для
зависимости давления пара от температуры
(3.2.5)
Для вычисления теплоты испарения разрешим это уравнение относительно Q
и подставим численные значения. Тогда получим
п т>т/ 1/4 dp 373-18-1,672-0,0375.9,81.104.0„?39. Ю-3
ц = 1 (к2 — ^i) ^57т"== i =
= 9864 ккал/кмоль = 548 ккал/кг. (3.2.6)
Отклонение этой величины от точного значения 539 ккал/кг объясняется тем,
что вместо дифференциалов использовались конечные разности.
3.3. Интегрирование уравнения Клапейрона — Клаузиуса
Давление насыщенного водяного пара при 100°С составляет 1,033 ат,
теплота испарения равна 539 ккал/кг. С помощью этих данных приближенно
определить зависимость теплоты испарения и давления насыщенного пара от
температуры. Удельную теплоемкость считать постоянной. Чему равны
искомые величины при 150°С?
Решение
Найдем сначала зависимость теплоты испарения от температуры. Пусть
жидкость испаряется при температуре Г0 и давлении Р, а затем нагревается
при постоянном давлении. Необходимую для этого процесса теплоту
испарения можно считать приблизительно равной теплоте испарения Q0 при
давлении насыщенного пара Р0 = Р$(Т0). Другой возможный процесс состоит
в том, что сначала жидкость нагревается до температуры Г, а затем
испаряется. Если обозначить через QT теплоту испарения, требуемую при втором
процессе, а через Сг — удельную теплоемкость жидкости, то можно
приближенно написать
Qo + Cp(T-T0) = C1(T^T0)+QTt
или (3.3.1)
QT=Qo + (Cp-C1)(T-T0).
Подставим выражение (3.3.1) в дифференциальное уравнение Клапейрона —
Клаузиуса, это дает
dP _ Qo + iCr-CJjT-T»)
dT~~ (Vz-VJT ' {6'6'Z)
Удельным объемом жидкости обычно можно пренебречь по сравнению с
удельным объемом пара. Объем пара приближенно найдем из уравнения для
идеального газа
RT
Р
V2 =^ . (3.3.3)
§ 3. Фазовое равновесие
197
Разделяя переменные и интегрируя, получаем из уравнения (3.3.2)
Г АР \ Qo + (С,-С1)(Г-7',)
J -F=i OF dT- (3'3-4)
Интегрируя (3.3.4) и разрешая его затем относительно давления насыщенного
пара Р (Г), находим
n п Г Qo-iCp-cj т0 г 1 1 \ ср-с, T'i
Р = Р0ехр[ % ^-у.j+^-m-j . (3.3.5)
Из формулы (3.3.1) для 7 = 150QC имеем
Q.150 = 539.18+( у-1,987— Ы8 J 50 = 9144 ккал/кмоль = 508 ккал/кг.
Точное значение составляет 504 ккал/кг (см. табл. П. XV).
Из формулы (3.3.5) при 150°С находим давление насыщенного пара
, AOO_J539-(3,5-1,987-18)373^ 1 1\
P----I'033exp[ П587 (373~423; +
3,5.1,987-18 4231
+ U987 ln373j -4,Ь4 аТ'
Точное значение составляет 4,85 ат (см. табл. П. XV). Расхождения связаны
в основном с использованием приближения идеального газа. Значительно
большая ошибка возникает по этой причине вблизи критического состояния.
3.4. Конденсация при адиабатическом расширении
Воздух при 40°С содержит водяной пар с парциальным давлением Р0 =
= 0,075 ат (давление насыщенного пара). При адиабатическом расширении
воздух охлаждается до 10°С. При этом парциальное давление Р водяного пара
уменьшается до 0,012 ат. Определить, какая доля водяного пара
сконденсировалась в виде тумана. Теплота испарения воды при 10°С составляет
592 ккал/кг. При вычислении энтропии учитывать только поступательные и
вращательные степени свободы.
Решение
Адиабатический процесс происходит при постоянной энтропии. Рассмотрим
1 кмоль водяного пара. Пусть его энтропия до расширения равна S20. После
расширения определенная доля х превращается в туман, т. е. переходит в
жидкую фазу. При переходе 1 кмоль водяного пара в туман энтропия
уменьшается на величину
52-S1=^. (3.4.1)
Здесь Т—температура перехода, S2—энтропия расширившегося и
охладившегося газа; Sx—энтропия жидкой фазы. Следовательно, после
адиабатического расширения энтропия равна
xSl+(\-x)S2 = x(s2-^+(l-x)S2 = S2-^. (3.4.2)
198
Гл. 3. Реальные газы
Приравнивая значения энтропии в начале и конце процесса, получаем
^20 = Sa-^, (3.4.3)
откуда следует, что
x=v^je т {ЗАА)
При вычислении энтропии будем считать пар идеальным газом, поскольку
давление мало. Согласно формуле (3.1.10) гл. 2, поступательная составляющая
энтропии меняется при переходе из состояния V0, Т0 в состояние V, Т на
величину (в расчете на 1 кмоль):
ASnoCT = /?ln
\(Т \з/2 VI
Согласно формуле (3.4.10) гл. 2, изменение энтропии за счет вращательных
степеней свободы составляет (в расчете на 1 кмоль)
/ 7 \з/2
ASBp = /?lnf jr-J . (3.4.6)
Поскольку
Vo Т0 Р'
имеем для изменения полной энтропии
S1-Sae = AS = ASnocT + ASBp = /?^ln^- + 4In^.V (3.4.7)
Подставив выражение (3.4.7) в формулу (3.4.4), найдем искомую долю
сконденсировавшегося водяного пара:
*=f (ln£+4 1n£). (3.4.8)
Переходя к численным значениям, получаем
1,987-283 Л 0,075 Л] 313 \ Л л__
^ = Т8^^11П0^Т2-41П283)=°'075-
Расширение и одновременное охлаждение приводят к тому, что 7,5% водяного
пара конденсируется, образуя туман.
Если использовать для энтропии значения, приведенные в табл. П.XV,
получим
18(2,13-1,97)
*- 187591 2^-°>077>
т. е. доля сконденсировавшегося пара составляет 7,7%.
3.5. Пароаккумулятор. Изменение энтропии воды
В пароаккумуляторе содержится вода при температуре 250QC, а над
водой— насыщенный пар при давлении Р0 —40,56 ат. Отводимый пар совершает
работу и после конденсации снова возвращается в аккумулятор. В результате
этого процесса температура пароаккумулятора падает до 150°С, а давление Р —
до 4,85 ат. Вычислить, какая часть х воды в пароаккумуляторе снова
переходит в пар. Теплота испарения Q при 150°С составляет 504 ккал/кг.
§ 3. Фазовое равновесие
199
Решение
Рассмотрим 1 кмоль воды с массой т. Удельную теплоемкость воды сг
будем считать постоянной, равной 1 ккал/кг-К. Тогда изменение энтропии
S—S0 при охлаждении воды от Т0 до Т есть
т
С dT Т 523
S — So^mCi \ —= тсг\пу-=— 18-1 In т^^ —3,82 ккал/(кмоль-К).
т
(3.5.1)
Вместо отведенлого пара после охлаждения образуется новое количество пара.
При этом энтропия на 1 кмоль возрастает на величину
у-=^^=21,45 ккал/(кмоль.К). (3.5.2)
Пусть из 1 кмоль воды, находящейся в пароаккумуляторе, образуется
х кмоль пара; тогда для адиабатического процесса получится следующий
баланс энтропии:
Q
т. е.
•^о — ^ — * -jT »
T(S0-S)
х= *™ ' ■ (3.5.3)
Подставляя численные значения (3.5.1) и (3.5.2), получаем
3,82 л 17о
*=2М5=0'178-
В пар переходит 17,8% имеющейся воды. Пользуясь величинами,
приведенными в табл. П.XV, в которых учтена зависимость удельной теплоемкости от
температуры, находим из формулы (3.5.3)
423(0,667-0,439). 18
*~" 504Л8 -и,1УА
т. е. получаем несколько больший процент.
3.6. Сжижение газа встречным потоком по методу Линде
В схеме получения жидкого газа расширяющийся газ
дросселируется; при этом он охлаждается встречным потоком газа (фиг. 34). При
расширении газа давление падает от Р^ = 250 до Рд = 1 ат. Найти, какая
часть кислорода сжижается, если исходная температура Т^ составляет 273 К.
Кислород рассматривать как газ Ван-дер-Ваальса. Конечную температуру Гд
принять равной температуре сжижения кислорода (90 К). Теплоемкость Ср
при постоянном давлении для кислорода, согласно табл. П.Х, составляет
3,5 /?, а теплота испарения равна 51 ккал/кг.
Решение
Кислород, поступающий слева, охлаждается потоком газа, направленным
вверх. Теплообмен между потоками рабочего вещества происходит при
постоянном давлении Р. Тогда, согласно первому закону термодинамики,
(6Q)P = (dU + PdV)p = (dH—VdP)p = dHP = 0. (3.6.1)
200
Гл. 3. Реальные газы
Энтальпия всей системы остается неизменной. Уменьшение энтальпии при
охлаждении притекающего газа равно возрастанию энтальпии газа, уходящего
обратно.
Следовательно, долю сжиженного кислорода можно найти, рассматривая
баланс энтальпий. При этом необходимо учитывать, что если полное
изменение энтальпии равно нулю, то температура газа после расширения до
конечного давления Рв опять становится равной начальной температуре ТА.
От баллона
со сжатым воздухом
Жидкий. шъиили в /ь. „ о л г* ~
воздиа: '—Ш///////Й Схема установки для сжижения газа по
* У* Ш//////А методу Линде.
Несконденсировавшаяся часть газа поднимается вверх
между витками змеевика.
Считая Н функцией РиТи обозначая через х долю сжиженного газа, для
1 кмоль имеем
Я2(РЛ, ТА) = хН1(Рв, Тв) + (\-х)Н2(Рв, ТА). (3.6.2)
Здесь индекс 1 относится к жидкости, а индекс 2 —к газу.
Чтобы перевести 1 кмоль вещества при давлении Рв из жидкого в
газообразное состояние, нужно^ затратить теплоту испарения Q(PB, Тв). Поэтому
можно написать
Нг (Рв. ТВ) = Н2 (Рв, TB)-Q(PBt Тв). (3.6.3)
Подставив формулу (3.6.3) в (3.6.2) и разрешив его относительно х> получим
количество сжиженного газа:
НАРл,ТА)-НАРв,ТА)
Н,(Рв,Тв)-<ЦРб,Тв)-Н,(Рв,Тл)ш (dbA>
Для численной оценки величины (3.6.4) учтем, что энтальпия Н2(РА, ТА)
при дросселировании газа не меняется. Поэтому можно записать
НАР А, ТА) = Н2(РВ, ТА+АТ), (3.6.5)
где AT означает изменение температуры в процессе Джоуля — Томсона (см.
задачу 2.5). Тогда для числителя в формуле (3.6.4) имеем
НАР А, ТА)-Нг(Рв, ТА) = Н2(Рв, ТА+АТ)-Н2(РВ, Тл) =
= J CpdT. (3.6.6)
ТА
В знаменателе будет
тв
НАРв, ТВ)-Н2(РВ, ТА)= J CpdT. (3.6.7)
§ 3. Фазовое равновесие
201
В результате получим из формулы (3.6.4), поменяв знак в числителе и в
знаменателе:
Х-
~тв
ТА
тА + ьт
к
0dT-
CpdT
-Q(Pb.
Тв)
~(ТВ-
-тА)
-ьтср
CP+Q(PB,
Тв)
(3.6.8)
В задаче 2.5 было найдено, что &Т =—75 К. Из выражения (3.6.8) получаем
для заданных численных значений
75.3,5-1,987
"(273 — 90)3,5-1,987-1-32.51
=0,18.
С помощью метода Линде в данном случае сжижается 18% проходящего
кислорода.
Упражнения
У.3.1. Найти способ определения постоянных Ван-дер-Ваальса а и 6,
а также индивидуальных газовых постоянных R по значениям
параметров в точке перехода из жидкого в газообразное состояние.
У.3.2. Как изменится точка кипения хлора при увеличении давления от 1
до 2 ат? Хлор считать идеальным газом, объемом жидкости
пренебречь (Q = 62 ккал/кг, Т = 238,2 К).
У.3.3. Определить точку плавления льда при давлении 2 ат. Плотность
льда d равна 0,9 г/см3, теплота плавления составляет 80 ккал/кг.
У.3.4. Определить теплоту испарения воды при 50QC.
У.3.5. Чему равно давление насыщенного водяного пара при 50QC?
У.3.6. Вычислить молярную теплоемкость водяного пара для процесса,
в котором жидкость постоянно находится в равновесии с насыщенным
паром. Чему равна молярная теплоемкость при 100° С? Газ считать
идеальным, объемом жидкости пренебречь.
У.3.7*. Во время некоторого процесса водяной пар и вода находятся в
равновесии. Найти изменение объема в этом процессе при изменении
температуры от 100 до 105 °С. Объем жидкости не учитывать, газ
считать идеальным (I? =539 ккал/кг).
У.3.8. Вычислить температуру кипения воды при давлении воздуха, равном
750, 755, 765, 770 мм рт. ст.
У.3.9. Насыщенный водяной пар охлаждается от 200 до 150 °С, при этом
его давление падает от 15,86 до 4,85 ат. Найти, какая часть водяного
пара сконденсируется.
У.3.10. Насыщенный водяной пар при 40,6 ат выпускается в атмосферу.
Найти, какая его часть сконденсируется, если внешняя температура
составляет 0°С. Как изменится результат, если в одном случае
изменение энтропии вычислить в приближении идеального газа, а в другом
случае использовать значения энтропии, приведенные в табл. П.XV?
УЗ.И. Пароаккумулятор находится под давлением 87,6 ат. После отвода
пара температура становится равной 159 °С. Определить долю вновь
образовавшегося пара.
202
Гл. 3. Реальные газы
У.3.12. Определить, каков выход жидкого азота в методе встречного потока.
Исходная температура составляет —20°С, исходное давление 150 ат.
Конечной температурой считать температуру сжижения азота —196°С
при давлений 1 ат. (С,? = 3,5/?, а = 1,39 ат-м°/кмоль2, 6=^0,039 м3/кмоль;
теплота испарения 47,6 ккал/кг.)
§ 4. ЯВЛЕНИЯ ПЕРЕНОСА
Введение
Для теоретического описания таких явлений переноса, как
диффузия, теплопроводность, внутреннее трение, необходимо
располагать соответствующей моделью строения вещества.
В "простейшей модели молекулы рассматриваются как твердые
шары с эффективным диаметром сечения 2rs. Силы притяжения
и отталкивания в первом приближении не учитываются, и все
молекулы считаются идентичными.
/ 2 з
Фиг. 35. Схема столкновения двух
молекул (соударение испытывают
молекулы 2 и 5).
Для одинаковых молекул r§ = г§=г§.
Чтобы вычислить число столкновений, испытываемых одной
частицей, допустим сначала, что движется только эта частица,
тогда как положение остальных частиц остается неизменным.
Соударение происходит только в том случае, если расстояние
от траектории центра тяжести движущейся частицы до центра
тяжести неподвижной молекулы меньше 2rs (фиг. 35). Тогда за
время dt испытывают соударение все те молекулы, центры
тяжести которых лежат в цилиндре диаметром 4/-5 и длиной vdt.
Объем этого цилиндра составляет
dV = 4nr$vdt. (4.1)
Обозначив через N0 число частиц в 1 м3, найдем отсюда число
соударений в единицу времени:
Z = N0^- = 4nrbN0v.
(4.2)
Чтобы учесть движение остальных молекул, нужно заменить
скорость v отдельной частицы относительной скоростью двух
сталкивающихся молекул:
§ 4. Явления переноса
203
Здесь г>! и г>2— скорости обеих частиц, $—угол между векторами
скорости (фиг. 36). Проведя усреднение по всем направлениям
и всем скоростям с помощью распределения Максвелла — Больц-
мана, получим
2я Л оо ее
^ = 4S" Ш J Sl" *°^ ^ f ^ йЩ йЩ d& d(f = ^^ =
оооо
X <«•«>
Отсюда имеем для числа столкновений
_ -,/16/gr
Е = /2.4я^0и= 16|/^r!tf0
(4.5)
Таким образом, здесь по сравнению с формулой (4.2) появился
дополнительный множитель ]/"2. В формуле (4.4) /(у)
обозначает функцию распределения Максвелла — Больцмана [см. фор-
Фиг. 36. Относительная скорость vr — i»otk.
мулу (1.3.4) гл. 2], и—средняя скорость [см. формулу (1.5.8)
гл. 2], Мг—относительная молекулярная масса частиц газа. Для
полного числа соударений между всеми частицами в 1 м3 за 1 с
получим
г = ^ = 8|/^г!^
(4.6)
Средняя длина свободного пробега частицы определяется как
отношение пройденного пути к числу столкновений. Из
формулы (4.5) имеем
Х = Х11 = — =
С
V2.4nr2sNQ
(4.7)
Если имеются частицы двух различных газов 1 и 2, то средняя
относительная скорость описывается выражением, аналогичным
(4.4):
Г, _ -i/8fer / 1 1 \ _ ,/"8ДГ / 1 . 1 \
(4.8)
Эффективный диаметр сечения столкновения между молекулами
двух различных газов, согласно фиг. 35, равен сумме обоих
204
Гл. 3. Реальные газы
радиусов rsl + rS2. За секунду частица 1 испытывает £12
столкновений с частицами 2, причем
Ci^M/si + 'ft)1^!.^^
(4.9)
Полное число столкновений частиц 1 с частицами 2 в 1 м3 газа
составляет
)ДяЯТ ( ^ + i-) (rst + r5l)« N,N2
(4.10)
При неоднородном распределении плотность числа частиц
N = N(P) в точке Р определяется выражением
N = N(P)= 1\т §. (4.Ц)
Здесь AN—число частиц в некотором объеме AV в окрестности
точки Р. В дальнейшем анализе предполагается некоторое
распределение плотности числа частиц N = N(z).
В общем случае частицы могут двигаться во всех
направлениях. При этом они переносят массу, энергию, тепло, импульс
и т. д. Будем обозначать через Г некоторую переносимую
величину, т. е. количество какой-либо величины, переносимое в
среднем одной частицей.
Фиг. 37. К определению переносимой величины
Г при двух последовательных столкновениях,
испытываемых одной частицей.
Согласно формуле (5.3.5) гл. 2, число частиц, падающих за
время dt на элементарную площадку АА под углом, лежащим
в интервале от ft до u + dft, составляет
dv = -у sin * cos «и/ (v) d§ dv dt АА. (4.12)
Частица, попадающая из слоя г под углом ft на слой z0
(фиг. 37), переносит величину T = T(z). Тогда, используя
разложение в ряд Тейлора, можно написать
N (z)T(z) = N (z0)T(z0) + Az (jlf)z+ ... .
Из фиг. 37 видно, что
Дг = —/cosft, (4.13)
§ 4. Явления переноса
205
где / в первом приближении есть средняя длина свободного
пробега:
1 = К. (4.13а)
Из формул (4.12) и (4.13) следует, что за время dt через
площадь АЛ переносится величина
со Я
dG=[Tdv = ±^[N(z0)T(z0)-Xcosb(^f)+...]x
о о
X sin * cos Щ (v) d$ dv dt АЛ. (4.14)
Приведем значения интегралов, возникающих при вычислении
этого выражения:
о
я
$sin\>cos\}d& = 0,
о
я 1
f sinflcos2&d& =-\y2dy -- -§" •
о -1
Тогда получим величину, переносимую через АЛ за время dt:
dG=~v{^Pj2 АЛЛ. (4.15а)
Отсюда находим уравнение переноса, описывающее плотность
потока jz = jz(z)
. _ 1 dG _ XvfdNT\
lz~AAdt ~~ 3 \ dz )z0
(4.15)
(предполагается, что ось z направлена по нормали к
плоскости АЛ).
Пример 20
В некотором канале в направлении оси х распространяется поток частиц.
В различных точках z этого канала поток различен (фиг. 38). Исследуется
перенос импульса в направлении оси z.
Поэтому положим
Г(2)-Р»(2).
206
Гл. 3. Реальные газы
Согласно уравнению переноса, имеем для z-компоненты плотности потока
импульса
lz~~ 3 дг
а для импульса, переносимого за время dt в направлении оси г:
Величина ДД есть элементарная площадь в плоскости х, у.
г) W
Фиг. 38. Перенос импульса в потоке.
Задачи
4.1. Число столкновений и средняя длина свободного пробега
для однокомпонентного газа
Вычислить число столкновений молекул водорода при температуре —20° С
и давлении 0,5 ат. Чему равна средняя длина свободного пробега А? Найти
полное число столкновений в 1 кмоль водорода. Молекулы рассматривать как
невзаимодействующие твердые шары, движущиеся с одинаковыми скоростями.
Газокинетический эффективный диаметр принять равным 2r$ — 2J-10~10 м.
Решение
Рассмотрим две частицы, которые движутся со скоростями ^ и to2. Если
vl = v2 = v, то их относительная скорость составляет
vr=V (t»i — D2)2 = V V* + v\ — 2vtv2 COS О =
А,
= v |/2(1 — cos О) = 2vsin ~y , (4.1.1)
где ф —угол между векторами этих скоростей. Усреднение по всем
направлениям дает
2ЯЯ Я/2
vr = 2v-^i\ \ sinysiaddfldq^^ \ sin2-?,- cos ~Y d Y=~3V' (4'L2)
oo о
С данной молекулой за 1 с в среднем столкнутся все молекулы, центры
тяжести которых окажутся внутри кругового цилиндра с основанием 4nrs и
высотой vr. Если в 1 м3 подержится N0 частиц, то число столкновений для
одной частицы составляет
;J-§nr*sN0v. (4-1.3)
§ 4. Явления переноса
207
По сравнению с формулой (4.5) здесь появился дополнительный множитель
/2/1,33... = 1,06.
В качестве величины v используем среднее значение для распределения
Максвелла —Больцмана £см. формулу (1.5.8) гл. 2]
•- ущ- vmr- w
Величину N0 найдем из уравнения состояния N0 = PV/kT для ]/=1 м3. Тогда
формула (4.1.3) дает для числа столкновений
16 1 /"8л^
= 3 V Мг
£=^У ЩРгЬ (4-1.5)
В рассматриваемой модели средняя длина свободного пробега есть
3 3/гГ
к== 2 = ГТГ- (4.1.6)
16лг|Л/0 16лг|Р v ;
Более_ точная формула (4.7) отличается дополнительным множителем
4/3^2 = 0,943.
В 1 кмоль содержится N & молекул. Полное число столкновений,
происходящих в 1 кмоль за 1 с, составляет
«=-/С (4.1.7)
Подставив численные значения, получим
С—15 -i/ 8-3,14.6,02.1026 ой.дя!. 104 (1 35.10-")* = 7,0.109 с-1.
t_~3 V 2,02-1,38.10-23-253 '
3.1,38.Ю-23-253
16-3,14(1,35-10-10)2-0,5-9,81.104~" ' м»
2 = 3,01-1026.7,0-109 с-1 = 2,1 -Юзе с -1.
4.2. Вероятность пролета отрезка х без столкновений
С помощью средней длины свободного пробега определить вероятность
того, что частица гелия пройдет отрезок х—\ мм, не испытав столкновений.
Температуру гелия считать равной 273 К, давление 1 мбар. Диаметр
газокинетического эффективного сечения для гелия при 0° С составляет 2г с = 2,18- Г0~10м
(табл. П.XVI).
Решение
Как и в предыдущей задаче, будем сначала считать, что все частицы,
кроме одной, неподвижны. Обозначим через w (х) вероятность того, что на
отрезке х частица не испытает соударений. Вероятность w(x + dx) того, что
частица пройдет без столкновений отрезок x-\-dxy находим, используя закон
умножения вероятностей [см. формулу (1.10) гл. 1]:
w (х + dx) = w (х П dx) = w(x)w (dx), (4.2.1)
а также разложение Тейлора:
w(x + dx) = w(x) + dx^^+... . (4.2.2)
208
Гл. 3. Реальные газы
Следующие члены разложения Тейлора можно не учитывать, поскольку
величину dx можно выбрать достаточно малой. Сравнивая выражения (4.2.1)
и (4.2.2), имеем
w (х) w(dx) = w (х) + dx ^j^-. (4.2.3)
Для .вычисления величины w (dx) рассмотрим цилиндр с основанием 1 м2 и
высотой dx. Высоту dx можно принять настолько малой, что внутри
помещается не более одного слоя частиц, так что проекции их геометрических
сечений соударения не перекрываются. При таком предположении вероятность
того, что падающая частица гелия столкнется с другой, определяется-соотно-
шением
\—w(dx) =
Сумма геометрических сечений 4nrsN0 dx
Полная площадь 1
Здесь через N0 обозначено число частиц в 1 м3.
Следовательно,
w (dx) = 1 — 4nrsN0 dx. (4.2.4)
Подставив выражение (4.2.4) в формулу (4.2.3), получим дифференциальное
уравнение
^)=_ 4яг|/У0ш (х). (4.2.5)
Интегрируя, находим
иу(*) = Сехр (— 4nrsN0x). (4.2.6)
Постоянную С определим из условия w(0)=\. Отсюда имеем С=1. Интеграл
по всем пройденным отрезкам отличен от единицы:
f w (х) dxJ{ ехр Мяг&М dx= [еХр (~^%N0х)]^ = _1_
Поэтому среднее значение отрезка, проходимого без соударений, нужно
определять из соотношения
QO
V ш (х) dx
*=^ . (4-2.8)
\ w-(x)dx
0
Для интеграла в числителе имеем
С х ехр (—4nrsN0x) dx= ехр {-4msN0x) ( * + ) 1 =
О
1
16я2^Л/о*
Подставляя величины (4.2.9) и (4.2.7) в выражение (4.2.8), находим
- 1
(4.2.9)
(4.2.10)
4яг§Л/0 V
§ 4. Явления-переноса
209
Полученная величина отрезка, которую в среднем частица проходит без
столкновений, соответствует средней длине свободного пробега (4.2) для
случая, когда движется только рассматриваемая частица, а все прочие молекулы,
участвующие в столкновениях, неподвижны. Если учитывать движение
остальных частиц, то для средней длины свободного пробега нужно использовать,
согласно формуле (4.7), значение
*= 7^= Г- (4-2>П)
Тогда вместо формулы (4.2.6) получим искомую вероятность того, что частица
пройдет отрезок х без столкновений:
w(x)^{-^m^y^(-i)- (4-2Л2)
Согласно уравнению состояния, число частиц составляет iV0 = l,8M022 м~3.
Тогда из формулы (4.2.11) имеем
Я=3,14.1,41-4.1,8Ы0*Ч1,09. Ю-")* М==0'263 ММ'
а затем из формулы (4.2.12)
И10-» м) = ехр (~0>2бз"10-з) =*-3>?02 = 0>022-
При данных условиях только .2,2% атомов гелия проходят путь х=\ мм
без столкновений. Эта величина зависит от температуры только за счет
эффективного сечения.
4.3. Число столкновений для смеси двух различных газов
Смесь из 3 л водорода и 1 л азота находится при нормальных условиях.
Найти число столкновений между молекулами в 1 с. Чему равны средние
длины пробега между соударениями различных частиц? (Диаметр
газокинетического эффективного сечения составляет: 2rsi =-2/*н =2,75* 10~10 м,
2rS2 = 2rhl=3,75- Ю-10 м, относительные молекулярные массы: М1 = МН =
= 2,02, m\ = Mn^ 28,02.)
Решение
Согласно формуле (4.9), число столкновений частиц сорта 1 с частицами
сорта 2 составляет:
С» = 4 j/""*I(^+j|y (rsl+,M)itf,. (4.3.1)
Аналогично получим число столкновений частиц 2 с частицами 1
Полное число соударений частиц 1 и 2 в объеме V0 — \ м3, согласно
формуле (4.10), есть
210
Гл. 3. Реальные газы
В данном случае полный объем газа V = 4 л = 4- 10-3«м3. Для парциальных
давлений имеем Рх = 0.75-1,033 ат, Р2 = 0,25-1,033 ат, а для плотности числа
частиц
"г = ?ф-, *« = ££• <У.= 1м»).
Число столкновений между частицами двух сортов в объеме У = 4 л равно
V /**Г (з^+дг) (rsl + ,S2)* g^ ; (4.3.4)
Vz12
при заданных числовых значениях имеем
1 , 1
Vz12 = 4. Ю- у 8.3,14.8,314.10^273 (-щ+щ JX
ч/(2,75 + 3,75)2-10-20 0,75.0,25.(1,033.9,81.104)2_ _х
Х 4 (lt38-10-a»-273)2 ' ° *
Средняя длина свободного пробега частицы 1 между соударениями с
частицами^, согласно формуле (4.3.1) и формуле (1.58) гл. 2, составляет
*и = ^ = г лл-1 (4-3.5)
С" "УГ{+щ(Г^+''82)2^2
Подставив численные значения, получим длину свободного пробега молекул
водорода между столкновениями с молекулами азота:
. 1,38-Ю-2*.273-4
А12 = -
3,14 |/
2 09
1+2^-(2,75.10-10 + 3,75.10-10)2 1,033-9,81.104-10"3
= 1,Ы0-4 м = 0,11 мм.
Для средней длины свободного пробега молекул азота между столкновениями
с молекулами водорода имеем
/н
l/н
2,02
28,02
28,02
9 П9
• 0,25
• 0,75
121=Х12 = 8,1-Ю-6 м.
4.4. Определение диаметра
газокинетического эффективного сечения по вязкости
Для измерения вязкости азота определяется постоянная скорость падения
и мелких шариков в газообразном азоте. Диаметр шариков 2г составляет
0,2 мм, плотность р = 0,7-103 кг/м3. Средняя величина^ измеренной скорости
падения й = 0,87 м/с. Определить по формуле Стокса вязкость т], а нз
последней— диаметр эффективного сечения молекулы азота. Температура при
измерениях составляет 20° С.
Решение
Найдем сначала вязкость г| по скорости падения и. На шар радиусом г,
движущийся со скоростью и в среде с вязкостью т], действует сила трения,
определяемая формулой Стокса:
FR = Gnr\ru. (4.4.1)
§ 4. Явления переноса
211
Навстречу этой силе направлена сила тяжести:
г 4 -
(4.4.2)
где
# = 9,81 м/с2
— ускорение свободного падения. Приравнивая эти
выражения и разрешая затем относительно вязкости, находим
<Г) =
2 р^2
9 и '
Подставив численные значения, получим
2-0,7.103.9,8Ы0-8
Т)=-
9-0,87
1,75-10-5 Н-с/м2.
(4.4.3)
(4.4.4)
Вязкость определяется внутренним трением. Если в газе или жидкости
имеются слои, движущиеся с разной скоростью u = u(z), то между двумя
такими слоями, соприкасающимися на некоторой площади АЛ, действует
сила трения
р = —цЬА
du
~аЧ
(4.4.5)
Сила, с которой один слой действует на другой, определяется изменением
импульса в единицу времени. Из-за теплового движения молекулы непрерывно
переходят из одного слоя в другой. Частица, переходящая из слоя z в слой z0
под углом ф, переносит компоненту импульса
Г = Р*(2).
(4.4.6)
При постоянной плотности числа частиц N(z) = N0 импульс dpg,
передаваемый через площадь АЛ за время dt, согласно уравнению переноса (4.15), равен
dpg = dG = jPjc(z)dv = - ~ N0v %^АЛ dt.
dz
(4.4.7)
Средняя скорость v отдельной частицы газа может отличаться от скорости и
движущихся шаров или от скорости различных слоев газа. Здесь X обозначает
среднюю длину свободного пробега. Силу трения между двумя слоями,
скользящими друг относительно друга, найдем из выражения (4.4.7):
F =
d\px(z)dv
dt
dpx
dz
АЛ.
(4.4.8)
Считая в формуле (4.4.8) px = [iux и приравнивая силу трения (4.4.8) к силе
трения, определяемой по формуле (4.4.5), получаем
тр
XN0[iv __ рЯу _ XN0Mrv
(4.4.9)
3 3 3NA '
Здесь р — плотность газа. Подставляя формулу (1. 5.8) гл. 2 и формулу (4.7)
настоящей главы, имеем
212
Гл. 3. Реальные газы
или
2г8=У
4MrkT
9n*NA\\2'
Используя приведенные в условии значения, получаем
(4.4.11)
_ А/ 4.28-1,;
s~ V 9.3,143-6,02
38-10-23.293
= 3,06-10-ю м.
10*6(1,75-10-*)2"
Отклонения от этого результата связаны с температурной зависимостью
диаметра газокинетического эффективного сечения (см. § 5 и задачу 5.1 настоящей
главы), с взаимодействием молекул, а также с неточностью приближения
Дг = — Я cos О [см. (4.13а)].
4.5. Коэффициент диффузии и сечение столкновения.
Первый закон Фика
В цилиндрический сосуд (фиг. 39) высотой И = 0,2 м и сечением А — 100 см2
налит раствор сахара при 20Q С. На дне сосуда концентрация составляет
200 г/л. Она убывает с высотой по экспоненциальному закону (см. задачу 1.6
#=0,2-
44
О 100 200
Концентрация
при t=0, г/л
Фиг. 39. Диффузия в цилиндрическом сосуде.
гл. 2) и достигает у поверхности 0,1 г/л. Из-за изменения концентрации
возникает направленный от дна сосуда поток, равный 101 мг/ч. Вычислить по
этим данным коэффициент диффузии молекул сахара. Чему равен диаметр
их сечения столкновения? Относительную молекулярную массу Мг сахара
С12Н22Ои принять равной 342.
Решение
Первый закон Фика дает связь между плотностью потока частиц jjy и
изменением концентрации dN/dz:
n dN
(4.5.1)
Величина D называется коэффициентом диффузии. Для плотности потока
массы имеем отсюда
Im = wn=*— Щ
dN
dz '
(4.5.2)
§ 4. Явления переноса
213
Тогда поток массы есть
dN „ dp
iM--
г dz dz
(4.5.3)
Здесь \i— масса частиц, р — их плотность. С другой стороны, плотность
потока массы можно получить из уравнения переноса (4.15), считая T = \i, j=jm
Ш = — -д-У
kv_ dN(z)
dz '
(4.5.4)
Таким образом, находим связь между коэффициентом диффузии D и
молекулярными величинами % и v:
(4.5.5)
В данном случае плотность числа молекул сахара распределена по закону
N (z) = N0e~cz, (4.5.6)
где
200-6,02.1020
Л/0 = -
1 .
с=-гг1п
342
N0
-=3,52-1026 м-3,
=7^-10 2000 = 38,0 м-1.
(4.5.6а)
(4.5.66)
И N (Н) ~~ 0,2
Плотность числа молекул растворителя, равная
Мш = nir6>°2-Ю26 = 3,33 ... 1028 м-3,
1о
намного больше плотности числа молекул растворенного вещества. Поэтому
при вычислении средней длины свободного пробега X можно пренебречь
соударениями между молекулами сахара. Тогда имеем в соответствии с
формулой (4.3.5)
Х = Х12 = т= 1- . (4.5.7)
Здесь r$i — радиус газокинетического эффективного сечения молекул воды,
/•^2 —то же для молекул сахара, Ыц^— плотность числа молекул
растворителя. Среднюю скорость молекул сахара, согласно формуле (1. 5.8) гл. 2,
примем равной:
- /"8/?Г
V V пМг •
Из формул (4.5.5), (4.5.7) и (4.5.8) находим
У 9 п*Мг1
rSi + rS2z
RT
(4.5.8)
(4.5.9)
Разрешив уравнение (4.5.3) относительно D и подставив численные значения,
получим
D-
1м
1м
10Ы0-6-6,02.1026
А\л
dN Л^0с~602.10-2.342.3,52.1026.38
dz
=3,69.10-1ом2/с.
214
Гл. 3. Реальный газы
Из формулы (4.5.9) имеем
rsi + rsi~-
v
8,314-10:i • 293
9 3,143.342.(3,33.1028-3,69.10-10);
= 9,Ы0-10 м.
4.6. Второй закон Фика
Найти изменение концентрации сахарного раствора при 20° С вследствие
диффузии. При ^=0 концентрация составляет 200 г/л для z = 0 и 0,1 Г/л для
z = H — 0,2 м, зависимость концентрации от z экспоненциальная. Определить,
чему равно изменение концентрации через время At = \ ч на половине высоты
сосуда. Коэффициент диффузии D составляет 3,7-Ю-10 м2/с.
Решение
Рассмотрим объем с площадью основания 1 м2, ограниченный снизу
плоскостью z, а сверху плоскостью z-\-dz (фиг. 40). Согласно первому закону
Ti-dz
Фиг. 40. К выводу второго закона Фика.
Фика, плотность потока составляет
dN (z)
jN(*)=-D-
dz
(4.6.1)
Плотность потока есть число частиц, поступающих через плоскость z в
рассматриваемый объем за 1 с. Для числа частиц, выходящих из
рассматриваемого объема на высоте z + cfz, получим с учетом члена первого порядка по dz:
jN(z + dz) = — D
dN (z + dz)
dz
■4
dN(z)
dz
-dz
d2N (z)
dz2
}■
(4.6.2)
Разность между входящим внизу и выходящим вверху потоками частиц равна
JN(z)—JN(z + dz) = Ddz
d2N (z)
dz2
(4.6.3)
На эту величину увеличивается число частиц в объеме dV—\-\dz м3. В
объеме 1 м3 число частиц возрастает, согласно формуле (4.6.3), со скоростью
dN
dt
_JN(z) — JN(z + dz)_
dz
dj(z) d*N(z)
dz dz2
(4.6.4)
§ 4. Явления переноса
215
Уравнение
(4.6.4а)
называется вторым законом Фика. Оно соответствует уравнению
теплопроводности для одной ко'ординаты. Уравнение (4.6.4), записанное в виде
(4.6.46)
представляет собой частный случай уравнения непрерывности; скорость
изменения числа частиц в некотором фиксированном объеме равна разности
входящих и выходящих потоков этих частиц, если только внутри данного объема
не происходит образование или исчезновение частиц.
Если изменения концентрации достаточно малы, то через время At
концентрация станет равной
N(zt At) = N(z, 0) + AtdN{Z>^
dt
В данном случае
ft (z, 0) = N0e-Cz,
где в соответствии с задачей 4.5 с = 38,0 м~
(4.6.5)
#0 = 3,52-1026 м-8. Тогда из
второго закона Фика (4.6.4а) имеем
N(z, At) = N0e-cz(\+AtDc2).
Подставляя численные значения и считая At = l ч = 60-60 с, находим
относительное изменение концентрации
^(Z,^)/"~m(2,0)=A/Dca = 60g-3>7-10-1o-38>Oa = 0,0019.
N (г, 0)
Таким образом, в течение часа концентрация изменится по сравнению с
начальным значением на 0,19%.
Проведенный разностный расчет справедлив для внутренней части
раствора. Он основан на предположении, что пространственное распределение N (г)
можно приблизительно считать не изменяющимся за время At, т. е. что за
время Д* диффузия не изменяет сколько-нибудь существенно состояния
внутренней части раствора. В настоящей оценке не учтено, что при z — H
невозможен приход или уход каких-либо частиц.
4.7*. Броуновское движение молекул
Исследуется диффузия золота в свинец при температуре 160° С.
Наблюдения показывают, что за 25 дней атомы золота проникают в среднем на 4,5 мм.
Вычислить коэффициент диффузии.
Решение
Найдем связь между временным и пространственным усреднением (фиг. 41).
Для этого рассмотрим движение частицы за короткий отрезок времени Atv.
За это время частица сместится на расстояние Axv. Если же наблюдать дви-
216
Гл. 3. Реальные газы
жение в течение времени
п
t = 2 Atv=nM,
v=l
то среднее смещение
п
х = 2 A*v=0.
v=l
Средний квадрат смещения частицы за время t есть
п
v=l
Поделив формулу (4.7.3) на (4.7.1), получим соотношение
л? д72
t
м
Отсюда видно, что при броуновском движении средний квадрат
пропорционален времени наблюдения.
Золотая фольга
(4.7.1)
(4.7.2)
(4.7.3)
(4.7.4)
смещения
Фиг. 41. К рассмотрению связи между
пространственным и временным усреднением при
броуновском движении молекул.
Рассмотрим броуновское движение в некоторой малой области AV,
заключенной между плоскостями х и x-\-dx. Пусть плотность числа частиц в этой
области равна N (х, /). Пусть из-за броуновского движения за время At все
частицы покинут эту область, а вместо них придут частицы из соседних
областей. Обозначим через w^t (х\ х) плотность вероятности того, что за время
At частица из точки х' попадет в рассматриваемую область Д1Л Число
частиц, попавших в эту область за время At, составляет
N (х, t + At) = AN=\wAt(x', x)N(x\ t)dx'.
Отсюда имеем для изменения плотности числа частиц в AV
dN(x, t) N (х, t + At) — N(x, t)_—N(xt t) AM
dt "~д/™о Af ~~ At ^ At '
Разложим N(x', t) в ряд Тейлора по степеням Ax = xf—х:
N (*', t) = N(x, t) + (x, — x)
dN (х, t) , (x'—x)2 d2N (x, t)
Эх
дх2
(4.7.5)
(4.7.6)
(4.7.7)
§ 4. Явления переноса
217
Подставив выражения (4.7.5) и (4.7.7) в формулу (4.7.6), получим
8N С 3N (* 1 д2М С
At^=-N + N\jwdxf+^\j Axwdx'+j-^^ bx2wdx', (4.7.8)
где
N = N(x, t), w = w^t (х\ х).
Если проинтегрировать по всему пространству, то для интегралов в
выражении (4.7.8) имеем
\ w dx' = 1, \ Axw dx' — Ах = 0, \ Ax2w dx' — Ах2.
Учитывая (4.7.4), находим из формулы (4.7.8)
^^А^дЧ^^^д2^
dt ~ 2At дх2 ~~ 2t дх2 ' ( '
Сравнивая это выражение с вторым законом Фика
dN __ d2N
dt дх2 '
получаем для коэффициента диффузии:
Подставим численные значения:
(4 5-10~3^2
D У**э ™ 1_==4 7.10-12 м2/с.
2-25-24.602 ' '
4.8. Поток тепла и удельная теплопроводность
С помощью уравнения переноса определить удельную теплопроводность' к
азота при 20Q С и сравнить расчетную величину % с экспериментальной,
равной 6-10—6 ккал/(м-с-К). Какое количество тепла протечет за время At — Ъ мин
через трубу длиной /=1 м и сечением Л = 100 см2, если разность
температур AT между концами трубы составляет 10° С, а падение температуры линейно
по длине. Провести расчет: а) для трубы, заполненной азотом, б) для
сплошной стеклянной трубы [и = 2,Ы0-4 ккал/(м-с-К)], в) для трубы из серебра
[и = 0,1 кк0л/(м-с-К)].
Решение
Рассмотрим газ, температура которого понижается в направлении оси г
(фиг. 42). Тогда в среднем внутренняя энергия е одной частицы зависит от
координаты z:
7=7(2). (4.8.1)
Будем считать внутреннюю энергию частицы е переносимой величиной. Считая
плотность числа частиц N постоянной, найдем из уравнения переноса (4.15)
плотность потока энергии, вызванного молекулярным движением:
h)N d& оч
'*= з-Ж' (4-8'2)
218
Гл. 3. Реальные газы
С другой стороны, исходя из аналогии с первым законом Фика (4.5.1), можно
считать, что плотность потока тепла у пропорциональна градиенту температуры:
= —х
дТ_
дг
Сравнивая формулы (4.8.2) и (4.8.3), получаем
XvN дг
дТ
3 дг дг '
Внутренняя энергия частицы е определяется формулой
■=р-
cvT
No
(4.8.3)
(4.8.4)
(4.8.5)
Здесь р =N0ii = N0Mr/Nд — плотность газа, Cv — его молярная теплоемкость,
cv — удельная теплоемкость 1 г газа. Найдем теперь теплопроводность газа
по формуле (4.8.4):
__ Xvpcv __ N0XvCv
i"~3 "" ЗЛ/Л
(4.8.6)
Сравнение с формулой (4.4.9) позволяет установить связь между
теплопроводностью х и вязкостью т|:
*=w:^=w
(4.8.7)
Вязкость T]N азота, согласно формуле (4.4.4), равна 1,75-Ю-5 Н«с/м2. Считая
Cv=5R/2, находим для теплопроводности азота:
5-1,987-1,75-Ю-5
2-28
ккал/(м-оК) = 3,Ы0-° ккалДм-с-К).
Согласно формуле (4.8.7), отношение n/r\cv должно равняться единице.
В табл. П.XVIII (см. приложение) приведены экспериментальные значения,
в частности, для N2, Н2 и 02. Хотя использованная статистическая модель
в рамках принятых приближений дает близкие по порядку величины,
расхождение с точными измеренными значениями сравнительно велико.
Т
Т0 +Ю°С-
**Z
Фиг. 42. Градиент температуры в
цилиндрической трубе.
Для вычисления потока тепла вернемся к уравнению (4.8.3) и
воспользуемся принятым допущением о линейном распределении температуры:
T(z)^T0-Cz., (4.8.8)
где
С =10 К/м.
§ 4. Явления переноса
219
Пусть в плоскости z = 0 находится более теплый, а в плоскости z
холодный конец. Тогда тепловая энергия, протекающая за время At
= 300 с, есть
Qz = jzAAt = —>i-^AAt = yi'\0AAt.
Следовательно,
Q^=,6.m-°.10.10-2.3-102 ккал = 0,18 кал для азота,^
Q7 = 6 кал для стекла,
<2г = 3,0 ккал для серебра.
Упражнения
У.4.1. Вычислить число столкновений в 1 см3 воздуха при температуре 0е С
и давлении 1 ат. Воздух считать однокомпонентным газом, частицы
которого имеют эффективное сечение диаметром 2г$ = 3,74- К)-10 м.
Найти среднее число столкновений для одной частицы и среднюю
длину свободного пробега (Мг = 29).
У.4.2. В поверхности вещества имеются поры со средним диаметром 0,1 мм.
До какой величины должно снизиться давление водорода при 0° С,
чтобы средняя длина свободного пробега более чем в 10 раз
превышала диаметр пор?
У.4.3. Какова вероятность того, что частица газа пройдет без
столкновений путь: а) /=10А, и б) / = 0,1 А?
У.4.4. 1 м3 гелия находится под давлением-1 мбар и при температуре 273 К.
Найти число частиц, которые в течение 1 с пройдут без соударений
путь в 1 см. (Мг = 4,00, 2rs = 2,\8-\0-1(* м.)
У.4.5. Определить число соударений в смеси газов С02 и Н2. Чему равны
средние длины свободного пробега для столкновений между
молекулами разных сортов? (Объем V = 2 л, температура Г = 273К;
С02: Р = \ ат, Mt = 44, 2r5l = 4,6.10"10 м; Н<>: Р2 = 2 ат, М2 = 2,
2^2 = 2,7.10-" м.)
У.4.6. Вычислить вязкость С02 при 0° С (2г5 = 4,6-10-10 м, Мг=-А4).
У.4.7. Вязкость воздуха т| при 20° С составляет 1,8-Ю-5 Н-с/м2.
Вычислить, какой наибольший диаметр должны иметь взвешенные в
воздухе шарики с плотностью р = 1 г/см3, чтобы скорость их падения
не превышала 0,1 м/с.
У.4.8. Концентрация поваренной соли в воде у дна сосуда высотой 50 см
составляет 100 г/л. У поверхности концентрация равна 1 г/л.
Вычислить потоки частиц и массы, если концентрация меняется линейно
с высотой, а сечение сосуда составляет 100 см2. (D = 10-9 м2/с,
Afr = 58,4.)
У.4.9. Коэффициент диффузии D водорода в воздухе при 0Q С и давлении
1 атм составляет 6,4-Ю-5 м2/с. Найти диаметр сечения столкновения
rSi-\~rSi в предположении, что концентрация Н2 очень мала.
У.4.10. В сосуде длиной 10 м находится воздух с небольшой примесью
водорода. Парциальное давление водорода меняется по
экспоненциальному закону от 0,01 ат на левом конце сосуда до 0,1 ат на правом
конце. С помощью второго закона Фика найти парциальное
давление Н2 в середине сосуда в начальный момент времени и через
/=100 с. (D = 7-10-6 м2/с.)
У.4.11*. При диффузии золота в жидкий свинец при 500 К коэффициент
диффузии D составляет 3,6-Ю-9 м2/с. Чему равен средний квадрат
смещения через 20 ч, т. е. насколько продиффундируют в свинец
атомы золота за 20 ч?
1 более
5 мин=
(4.8.9)
220
Гл. 3. Реальные газы
У.4.12*. Наблюдается изменение окраски бромистого калия из-за диффузии
калия. Коэффициент диффузии D для этого процесса при 380° С
составляет 5-10—8 м2/с. За какое время произойдет диффузия на 10 см?
У.4.13. Вычислить поток тепла через латунную пластину площадью 2 м2 и
толщиной 5 см, если при линейном градиенте температуры разность
температур верхней и нижней стороны пластины составляет 100Q С
[х=100 ккалДм-ч-К)].
§ 5. ПОПРАВКИ К МОЛЕКУЛЯРНЫМ ВЕЛИЧИНАМ,
ОПРЕДЕЛЯЕМЫМ ИЗ ЯВЛЕНИЙ ПЕРЕНОСА
Введение
Учет сил притяжения, действующих между молекулами,
которые рассматриваются как твердые упругие шары,
приводит к поправке Сазерленда. Эта поправка определяет
дополнительный член в знаменателе выражения для средней длины
свободного пробега:
X - '
4V2 nvlN0(l+С IT)
шну 2rs также нужно
2rs = 2r0]/l+-^
за
•
(5.1)
(5.1а)
С помощью постоянной Сазерленда (температуры удвоения)
С = -^£пот(2/-0) (5.2)
можно вычислить потенциальную энергию взаимодействия между
молекулами (см. задачу 5.1).
Персистенцией (сохраняемостью) молекулярных скоростей
называют тенденцию частиц в значительной степени сохранять
первоначальную скорость. Только при лобовом соударении
направление движения меняется на противоположное. В общем
случае происходят касательные соударения, при которых
направление и величина скорости меняются незначительно.
В качестве меры персистенции используют отношение
(фиг. 43)
а Компонента скорости после соударения в первонач. напр.
11» | Величина скорости до соударения
§ 5. Поправки к молекулярным величинам
221
Усреднение по всем направлениям движения и по всем
скоростям сталкивающихся молекул дает в случае модели жестких
упругих сфер следующее значение:
(5.3)
Персистенция молекулярных скоростей приводит к
необходимости статистического рассмотрения величин, переносимых при
предыдущих соударениях. Однако даже при учете поправки
| и (после соударения) •
^и Фиг. 43. К определению персистенции молеку-
0 к (передсоударением) лярных скоростей.
Сазерленда и персистенции скоростей формулы для
коэффициентов диффузии и вязкости, полученные в модели жестких
упругих молекул, приводят к значениям, примерно на 20%
отличающимся от экспериментальных. Точное совпадение можно
получить, если, следуя Чепмену, Мэзону и Раису, учесть силы
притяжения и отталкивания в рамках моделей Леннард-Джонса
или Букингема. Для вязкости вместо формулы (4.4.9) имеем
тогда выражение
5я XN0Mrv
"32 77^
(5.4)
т. е. множитель 1/3 нужно заменить на 5ст/32 = 0,491.
Коэффициент диффузии D и вязкость г) связаны
соотношением
D = y±. (5.5)
В зависимости от используемой модели у может иметь
значение, лежащее в пределах (см. задачу 5.3):
1,25<Т<1,54. (5.6)
Величину г) можно получить из формул (5.4), (5.1) и формулы
(1.5.8) гл. 2.
Различие в величинах теплопроводности не удается
объяснить с помощью только персистенции скоростей и поправки
222
Гл. 3. Реальные газы
Сазерленда. Для их объяснения необходимо учесть максвел-
ловское распределение скоростей и связанный с этим перенос
поступательной энергии |ли2/2, для переноса которой условия более
благоприятны, чем для переноса вращательной энергии Уф2/2.
По этим причинам формулы (4.8.6) и (4.8.7) для
теплопроводности заменяются выражением
и == Ьу\су
(5.7)
где г\ по-прежнему определяется формулой (5.4). Согласно
Эйкену, б определяется следующим выражением:
(5.8)
Величину бх в первом приближении можно принять равной
единице. Она несколько зависит от показателя п в выражении
для отталкивательного потенциала.
Теоретический расчет кинетических коэффициентов
проводится с помощью интегро-дифференциального уравнения Больц-
мана. Это уравнение позволяет установить связь между
функцией распределения, зависящей от координат и скоростей, и
молекулярными свойствами частиц.
Задачи
5.1. Определение диаметра молекулы, диаметра эффективного
сечения и потенциальной энергии из вязкости
Имеется экспериментальная кривая ц=г\(Т) зависимости вязкости
воздуха от температуры Т. Критерий согласия %2 показывает, что эту
зависимость можно представить в виде
Экспериментально установлено, что для Г1 = 300К вязкость t]-j (7\) —
= 1,86-Ю-5 Н-с/м2, а для Г2 = 400К вязкость ц2 (Т2) = 2,30.10~5 Н-с/м2.
Воздух рассматривается как однокомпонентный газ с относительной
молекулярной массой 29,0. Найти из экспериментальных данных диаметр
эффективного сечения для 0° С и для 7=оо, а также потенциальную энергию £пог
при равновесном расстоянии между молекулами.
§ 5. Поправки к молекулярным величинам
223
Решение
Воспользуемся формулой (5.4) и подставим в нее выражение (5.1) для
средней длины свободного пробега X и формулу (1.5.8) гл. 2 для средней
скорости. Тогда имеем
Т1 = 5/"ЛМГ
4 'б]/ ~mj
1 ' (5.1.1)
3 k п.Т3**—n.T3'* * (5Л-3)
i+c/r4r;
Полученные из опыта пары значений Тъ гц и Т2, г)2 находятся в отношении:
% ,T/"7Tl+(С/Г,) /ГЛз/2Г2 + С
Л,- К r.I+tC/ri) ^Г,^ Гх + С ^'^
Разрешая относительно С, получаем с учетом формулы (5.2)
,,__ 2 Е„оА2г0) ЪТ^Ъ-ЪТЛ"
Подставляя численные значения, находим поправку Сазерленда для воздуха:
„ 2,30-10-5.3003/2.400—1,86. Ю-5-300-4003/2 1ЛО f,
С = - m l ^ =108 К. (5.1.3а)
1,86-10-5.4003/2 —2,30-Ю-5-3003/2 * >
Отсюда имеем
£,пот(2/-0)=----|/гС = -у • 1,38-10-2^.108 = —2,24.10-" Дж. (5.1.36)
В формуле (5.1.1) теперь известны все величины, кроме радиуса молекулы г0.
Разрешая относительно радиуса, находим
'•-/;
Используя одну из измеренных величин и учитывая (5.1.3а), получаем из
формулы (5.1.4)
_ 4 Г 25-29» 1,38-10-2а>300
V .256-3,14-6,02-Ю2б (1,86-Ю-5)2 f \+Ш]
2г0=1/ - т „ = 3,14.10-ю м.
~зоо;
Величина г0 соответствует эффективному радиусу при Г=оо. Для
эффективного радиуса rs, зависящего от температуры, имеем при Т = 273 К
о ]/l-^ = 1,57.10-ю |/i+^= 1,85- 10-ю м.
/"5 = Л
5.2*. Поправка Сазерленда
Построить модель для вывода поправки Сазерленда. Найти среднюю
длину свободного пробега X молекулы водорода при —20° С и Р = 0,5 ат. Из
измерений вязкости (см. задачу 5.1) найдено, что 2г0 —2,40-Ю-10 м, С = 84К.
224
Гл. 3. Реальные газы
Решение
Силы, действующие между молекулами, заставляют их изменять
направление движения. В отсутствие молекулярных сил частица 1 пролетела бы на
Фиг. 44. Отклонение траектории
молекулы под влиянием взаимного
притяжения молекул.
Фиг. 45. К расчету
секторной скорости.
Здесь | dt 1 ф dr.
расстоянии р от частицы 2 (фиг. 44). Траектория отклонившейся частицы
определяется законом площадей (фиг. Щ, согласно которому имеем
<М 1 чу dx
dr=-2XXllt=C0USt'
(5.2.1)
здесь а% обозначает площадь, описываемую радиус-вектором х за время dt.
(Вектор d$f направлен' перпендикулярно плоскости траектории.) Обозначим
через dcp угол, пройденный радиус-вектором за время dt. Тогда, учитывая,
что
df_r slndcp =r dg>
sin [л—(v, dx) — ф] sin (г, dx) * \ • - >
получим из формулы (5.2.1) для площади, описываемой радиус-вектором
dA=-^\xxdx\ =у г sin (г, dx)dr = -^r2 dtp,
или же
dA 1 2.
(5.2.3)
С другой стороны, для удаленной частицы, приближающейся к другой
частице с относительной скоростью v, имеем
dA=-jp\dx |,
или
dA
1
df = Tpv'
Следовательно,
г2<р = ру.
В соответствии с фиг. 45 для кинетической энергии имеем
(5.2.4)
(5.2.5)
(5.2.6)
§ 5. Поправки к молекулярным величинам
225
где ц— приведенная масса обеих частиц. Учитывая, что £пот(оо) = 0, находим
по закону сохранения энергии:
1 |i (>2 + ' V) + ^пот (г) = у [ivK (5.2.7)
Выразив с помощью формулы (5.2.5) угловую скорость ф через начальную
скорость v и прицельный параметр р, получим
-у"2—£-'*—Е»от</-)=-5-»,£. (5.2.8)
Определим теперь прицельный параметр p = Pk, при котором частицы
коснутся друг друга. Если имеются две молекулы разного сорта с диаметрами
2гг и 2г2, то в случае скользящего удара, т. е. при r = r1Jrr%y должно
выполняться условие г==0. Тогда из формулы (5.2.8) найдем для прицельного
параметра pk\
pl=('i + '»)>[l-2£"0T^,+ 't)]. (5-2.9)
Среднее значение кинетической энергии, согласно формуле (1.5.8) гл. 2,
составляет
р-тМ^т^Н)"^- (5-2Л0)
Из формулы (5.2.9) теперь имеем
Р» = ('1+ г,) ]/l - | £пот (^+ fi)=(r1 + r2) ]/l+f ■ (5.2.11)
Постоянная Сазерленда положительна, поскольку потенциальная энергия £пот
в формуле (5.2.11) отрицательна.
Притяжение между молекулами приводит к увеличению диаметра
газокинетического эффективного сечения. Иначе говоря, соударение может быть
зарегистрировано и в том случае, когда в отсутствие взаимодействия частицы
пролетели бы друг мимо друга.
Формулу (4.7) для средней длины свободного пробега между
соударениями одинаковых частиц следует заменить следующим выражением:
Хп = 1 . (5.2.12)
4 V2nrlN0(i+C/T)
Подставляя численные значения, имеем
1.9^
^-l,41.3,14-(2,40.10-^.1|41.,0^.337 =2-09-10-7 "• <5-2Л2а>
т. е. получаем небольшое расхождение с результатом задачи 4.1.
5.3. Коэффициент диффузии с учетом поправки Сазерленда
и персистенции скоростей
Вычислить коэффициент диффузии с помощью модели жестких упругих
молекул при учете поправки Сазерленда и персистенции. Чему равен
коэффициент диффузии D для Н2 при давлении 0,5 ат и температуре —20 РС?
226
Гл. 3. Реальные газы
Решение
Как видно из фиг. 46, рассматриваемая частица после соударения
попадает в точку Р на плоскости z==z0\ следовательно, она вылетела из плос-
Р
zo-
Фиг. 46. Исходная плоскость при
вычислении переносимой величины
с учетом персистенции скоростей.
кости z1 = z0—X cos ft. Учитывая персистенцию, можно сказать, что на
последнюю плоскость она попала из плоскости
z2 = z0 — X cos О—0,406 X cos ft = г0 — X cos ft (1 + 0,406).
Теперь с учетом предыдущих соударений находим исходную плоскость для п
соударений
zn = z0 — X cos ft (1+0,406 + 0,4062+...+ 0,406"-!)
и в пределе
lim zn = z0 —X cos ft z—Л A„n=Zo — 1,683Я cos ft.
л->оо 1—0,40b
При расчете коэффициента диффузии персистенция приводит к кажущемуся
увеличению длины свободного пробега в 1,683 раз. Поэтому формула (4.5.5)
для коэффициента диффузии в модели жестких упругих молекул заменяется
выражением
D = lt683b
о
Поправку Сазерленда учтем в формуле для средней длины свободного
пробега. Коэффициент диффузии в модели жестких упругих молекул, согласно
формулам (5.2.12) и (1.5.8) гл. 2, определяется выражением
D =
1,683 А,
1/r8RT
V пМг з.
2-1,683 VRT
n3/2.4rtVM~rN0(\+C/T)
Подставляя численные значения и учитывая формулу (5.2.12а), получаем
3,1,688.2,07.10-1 /8-8^44;'°;2253= 1,9,.10^ м*/с.
5.4. Теплопроводность как функция температуры
Определить теплопроводность водорода при температуре 500 К.
Исследовать возникающие при этом поправочные множители (2/-0 = 2,40.10_10 м,
С = 84 К, Cv = 5R/2, Cp = 7R/2).
Решение
Согласно Эйкену, для теплопроводности справедлива формула
/ 9С„ 5
x = 44cJ 4
J Mr '
(5.4.1)
§ 5. Поправки к молекулярным величинам
227
где в соответствии с (5.1.1)
5 -i/MrkT 1
' 16-4rJ У *NA 1+С/Т-
Для расчета Ср и С^ при данных температурах можно пользоваться законом
равнораспределения.
Будем считать, что для одной температуры теплопроводность известна.
Комбинируя равенства (5.4.1) и (5.4.2), получим тогда при неизменных тепло-
емкостях Ср и Cv
х(Г) _ ■./НП+с/г.
к (Го) "Г Jo 1 + С/Т * . <0"*'*'
Используя значение х(20°С) = 0,160 ккал/(м-ч-К) (см. табл. П.XVIII),
находим
х(500К) = 0.160 У gi±gH=0,2.4 ккал/(м.ч.К).
В случае сильно меняющихся величин Ср и Cv следует учесть, что бх
зависит только от показателя п в потенциале Леннард-Джонса, но не от
температуры. Тогда, используя значение х для 20 РС, приведенное в табл. П.XVIII,
имеем
0,160-gL ккал/(м.сК) = б1 (1 • 1-1) 16.(24510-10)2 X
-,/2,02-1,38-10-23-293 293 2,5-1,987
Х К 3,14.6,02.10*' 377-^02— ккал/(м-сК),
откуда получаем
6Х = 1,08.
Таким образом, зависимость и (Т) можно определить во всем
температурном интервале, если в выражения (5.4.1) и (5.4.2) подставить вместо CV(T) и
Ср (Т) соответствующие зависимости от температуры.
Упражнения
У.5.1. Вычислить вязкость С02 при 0°С по формуле Чепмена и сравнить
полученную величину с результатом упражнения 4.6.
У.5.2. Вязкость С02 составляет 1,50-10"5 Н-с/м2 при 300 К и
1,957-10~б Н-с/м2 при 400 К. Вычислить постоянную Сазерленда,
диаметр молекулы и потенциальную энергию притяжения.
У.5.3. Согласно опытам Дэшмена, диаметр газокинетического эффективного
сечения 2г$ для водорода при 0°С составляет 2,75-Ю-10 м.
Вычислить 2г$ для — 59 °С и Н-50°С. Постоянная Сазерленда С для
водорода равна 84 К.
У.5.4. Найти скорость падения мелких шариков диаметром 2г = 0,1 мм и
плотностью р=1 г/см:{ в воздухе с температурой 250 и 300 К.
Диаметр 2г0 молекул воздуха принять равным 3,14-10~10 м, а для
постоянной Сазерленда использовать значение С—108 К.
У.5.5. Вычислить скорость воздушного потока в цилиндрической трубе
длиной 20 м и радиусом г=\ мм при перепаде давлений 0,1 ат для
температуры 300 и 400 К. Использовать при этом закон Хагена —
Пуазейля
dV яг4 ^P
dt 8г|/
228
Гл. 3. Реальные газы
где V — объем вещества, протекающего через сечение трубы.
Плотность воздуха р считать равной 1,29 г-л.
У.5.6. Для того чтобы в гладкой трубе не возникало турбулентности потока,
число Рейнольдса Ке — г*ир/ч\ должно быть меньше 1160. Вычислить
наибольшую допустимую скорость ламинарного потока воздуха,
плотность которого р = 1,29 г/л; радиус трубы г = 1 мм,
температура 300 К. Чему равна наибольшая скорость при 600 К?
У.5.7. Вычислить среднюю длину свободного пробега молекул водорода
при 0 и 500 °С для давления в 1 мбар. (Диаметр молекулы 2г0 =
=2,4Ы0-10 м, С = 84К.)
У.5.8**. С помощью модели жестких упругих сфер вывести формулу для
вязкости с учетом поправки Сазерленда и персистенции. Считать
при этом, что при каждом соударении половина избыточной энергии
передается частице, испытавшей соударение.
У.5.9*. С помощью модели жестких упругих сфер определить коэффициент
диффузии водорода при 0 и 500 °С для давления в 1 мбар.
У.5.10*. Найти теплопроводность водорода % при 400 К.
Глава 4l
СТАТИСТИКА КВАНТОВЫХ ПРОЦЕССОВ
§1. КВАНТОВАЯ СТАТИСТИКА СИСТЕМ ОДИНАКОВЫХ МИКРОЧАСТИЦ
Введение
Квантовая статистика исследует физические свойства систем
одинаковых микрочастиц, например а-частиц, электронов,
фотонов. Существенным признаком такого рода систем является
взаимозависимость образующих их отдельных частиц. В силу
этого необходимо рассматривать совокупность частиц одного
сорта как единый коллектив и вводить для его описания
специальную статистику, отвечающую его физическим свойствам.
Характерной особенностью идеального газа является
отсутствие всякого взаимодействия между отдельными частицами.
Он описывается статистикой Больцмана. Статистику Больцмана
можно сохранить и для реального газа, введя соответствующие
поправки. Однако в случае квантовых процессов статистика
Больцмана приводит к количественно и качественно неверным
результатам (это связано с наличием взаимодействий, которые
не могут быть описаны классическим образом). Поэтому нужно
рассмотреть новый физический подход, приводящий к
квантовой статистике.
Согласно квантовой теории, поведение совокупности частиц
одного сорта описывается волновой функцией
4 = 4(qlt ?„..., qN,t), (1.1)
которая является решением уравнения Шредингера. Здесь qt —
координаты i-й частицы. Величину ¥ нельзя измерить
физическими методами. Измеримой величиной является плотность
вероятности микрочастиц. Вероятность найти частицу в объеме dV
равна
dw = c*W*dV. (1.2)
Здесь ¥* означает величину, комплексно сопряженную с Ч*",
с—нормировочная постоянная, которая должна быть выбрана
соответствующим образом. Одинаковые физические состояния,
характеризующиеся одинаковой плотностью вероятности,
описываются волновыми функциями, отличающимися только
постоянным множителем:
¥ = &¥'.
(1.3)
230
Гл. 4. Статистика квантовых процессов
Основным допущением квантовой теории является принцип
тождественности частиц: частицы одного и того же сорта,
например электроны, не могут иметь никаких различимых или
характерных особенностей. Поэтому взаимная перестановка двух
одинаковых частиц не изменяет физического состояния
рассматриваемой системы. Состояние, возникающее в результате
перестановки двух одинаковых частиц, т. е. состояние Ч*"'—
= х¥ (q19 ..., qki ..., qj, ..., qN> /), не может отличаться от
первоначального состояния *¥ (<7i, ..., <7/, ..., qki ..., qN> t). Таким
образом, Ч? и ¥' описывают одно и то же состояние системы. Поэтому
в соответствии с (1.3) имеем
V(qlf ..., fl>, .... ft, ..., qN> 0 =
= W(qly ...,<7Л, ...,qJf ...,qN, t). (1.4)
Если обмен частиц q;- и qk произвести дважды, так чтобы после
второй перестановки восстановилось исходное состояние, то
волновая функция ¥ вообще не должна измениться. Тогда из
выражения (1.4) имеем
Ч = Х(№)=№9 (1.5)
т. е.
Л,2 = 1, А, = ±1. (1.6)
Соответственно этому квантовая статистика систем одинаковых
микрочастиц допускает два класса функций: симметричные
функции, сохраняющие свой знак при перестановке двух частиц,
= y¥(qli ...,qk, ..., qj, ...,qNJ) (1.7)
и антисимметричные функции, меняющие знак при
перестановке,
V(q19 ..., q/9 ...,qk, ...,qN%t) =
= —W(qly ...,qk, ...,q/9 ...,qN, t). (1.8)
Эти два класса функций не могут переходить друг в друга.
В квантовой теории с помощью уравнения Шредингера
доказывается, что волновая функция ¥ всегда остается симметричной
или антисимметричной, т. е. какой она была в начальном
состоянии.
Как показывают результаты экспериментальных
исследований, принадлежность частиц к тому или другому классу зависит
от величины их собственного момента, иначе спина. Частицы,
спин которых равен полуцелому числу квантов действия
Планка %\
s = mk (m=j> у. у. •••). О-9)
# /. Квантовая статистика
231
описываются антисимметричными ¥-функциями. Эти частицы
называются частицами Ферми, или фермионами, а описывающая
их статистика называется статистикой Ферми—Дирака.
Электроны (е~), позитроны (е+), протоны (р) и нейтроны (п) и
вообще атомы, ионы и атомные ядра, состоящие из нечетного
числа элементарных частиц, имеют полуцелый спин. Все они
описываются статистикой Ферми—Дирака.
Пример 21
Статистике Ферми подчиняются, например,
}Н+(1р), з.Нё(2р, In, 2е-), 4Не+(2р, 2п, е-),
,<Li + (Зр, 4п, 2е-), «Ы + + (Зр, Зп, е-).
Частицы с целочисленным спином
s = m% (m = 0, 1, 2, ...) (1.10)
описываются симметричными ^Р-функциями. Они называются
частицами Бозе, или бозонами. Применяемая к ним статистика
носит название статистики Бозе—Эйнштейна. Ей подчиняются
микрочастицы, состоящие из четного числа элементарных частиц.
Пример 22
Атомы водорода JH(lp, 1е~), атомы гелия £Не (2р, 2п, 2е-), ионы лития
?Li + +(3p, 4п, е-) и <jLi + (Зр, Зп, 2е~) и, кроме того, ядра дейтерия
|Н + (lp, In) имеют спин, равный целому числу постоянных Планка %.
Частицы света (фотоны) имеют спин, равный нулю Х). Все эти частицы
подчиняются статистике Бозе—Эйнштейна.
При расчете числа квантовых состояний статистическая
теория должна учитывать неразличимость микрочастиц одной
системы. В статистике Больцмана метод нахождения статистического
веса W некоторого распределения основан как раз на
различимости отдельных частиц (см. гл. 2, § 1, введение). Поэтому
в квантовой статистике используются иные, чем в статистике
Больцмана, определения понятий микро- и макросостояний.
Как и в статистике Больцмана, в квантовой статистике
принимается, что множество значений величины, характеризующей
состояние, например, энергии или импульса, подразделено на
подмножества, заполняющие области в фазовом
пространстве ДФ;. Если размерность фазового пространства равна s, то,
согласно соотношению неопределенностей Гейзенберга [см. (3.1)
Х) В случае фотона невозможно разделить орбитальный момент и спин,
поэтому можно говорить лишь о полном моменте фотона, который пробегает
целочисленные значения,—Прим. ред.
232
Гл. 4. Статистика квантовых процессов
гл. 2], одна ячейка в фазовом пространстве занимает объем /is/2.
Тогда число ячеек в фазовом объеме АФ/ составляет
АФ/
nS/2
(1.11)
В квантовой статистике микросостояние характеризуется
числами заполнения отдельных ячеек частицами. Все
микросостояния равновероятны.
Пример 23
Схема микросостояния по статистике Бозе—Эйнштейна
№ ячейки i
Число частиц /V;
1
2
2
3
3 4
0 1
5
1
Согласно статистике Бозе—Эйнштейна, статистический вес этого
микросостояния равен единице. По классической статистике Больцмана он составлял бы
^кл = 2Ш = 420.
Итак, в квантовой статистике определение микросостояния
основано на различимости отдельных ячеек. Их можно
пронумеровать в отличие от частиц, которые неразличимы и потому
не могут быть пронумерованы.
Для макросостояния различимость отдельных ячеек фазовой
области АФ/ несущественна, нужно знать только, чему равно
число Z0 ячеек, не содержащих частиц, число Zx ячеек с одной
частицей, Z2 — с двумя частицами и вообще число ячеек Zj с j
частицами (/ = 0, 1, 2, ...).
Пример 24
Числа заполнения, приведенные в предыдущем примере, соответствуют
одной из возможных реализаций макросостояния
Z0=l, Z1==2, Za=l, Z8=l, Zi==0 (i = 4,...). (1.12)
Это макросостояние может быть реализовано и другими способами, в
частности указанными в следующем примере.
Пример 25
№ ячейки i 12 3 4 5
Число частиц /V,- 3 2 0 11
§ 1. Квантовая статистика
233
Это состояние получается из состояния, приведенного в примере 23, с помощью
перестановки ячеек 1 и 2. Ему соответствует тот же статистический вес,
равный единице.
Как и в классической статистике, в квантовой статистике
статистический вес W (Z0y Z19 ...) макросостояния определяется
числом микросостояний, с помощью которых может быть
реализовано это макросостояние. Микросостояния, относящиеся к
одинаковым макросостояниям, различаются только тем, что числа
заполнения N£ различных ячеек меняются местами (фиг. 47).
Статистика
' Больцмана
I
•о*
• 'о
• ®
о ®
• о
о ®
| О 8
®
О
•
©
о
•
•
1 •
о
о
®
®
11
•о*
©
о
•
• о
• о
о ®
• о
• ®
О ®
О
О
•
О
®
•
о
©
•
®
•
о
///
•о*
©
о
•
• о
• ©
о ®
• ®
• о
о ®
®
о
0
•
о
•
Статистика
Бозр-Эйнштеипа
I
°о°
о о
о о
о
о
о
//
°о°
о
о о
о о
о
о
///
°о°
О
о
о о
о о
о
Статистика
Ферми-Дирака
I 11 III |
о
о
о
Фиг. 47. Заполнение микро- и
макросостояний в статистике Больцмана,
Бозе—Эйнштейна и Ферми —Дирака
(см. пример 26).
Тогда статистический вес размещения из Z0 ячеек, не
содержащих частиц, Zx ячеек с одной частицей, и вообще Zy- ячеек с /
частицами получим по формуле (1.6) гл. 2:
W(Z0,Z19ZV ...) =
Z!
Z0!ZX!Z3!.
(1.13)
234
Гл. 4. Статистика квантовых процессов
Величина
/ = о
представляет собой полное число ячеек.
Если говорить о числах заполнения Zh то различие между
статистикой Бозе—Эйнштейна и статистикой
Ферми—Дирака состоит в том, что для ферми-частиц на числа заполнения
налагается определенное ограничение. В то время как статистика
Бозе—Эйнштейна допускает любые числа заполнения, в
статистике Ферми—Дирака только Z0 и 1Х отличны от нуля.
Каждая ячейка либо пуста, либо занята одной частицей. Более
высокие числа заполнения в статистике Ферми—Дирака
невозможны. Условие Z2 = 0, Z3 = 0, ... для фермионов вытекает из
принципа Паули, который в свою очередь следует из свойств
антисимметричных волновых функций. Согласно принципу Паули,
в данном квантовом состоянии может находиться только одна
микрочастица.
Пример 26
В табл. 27 приведен статистический вес для всех возможных
распределений трех частиц по трем ячейкам: для классической статистики Больцмана
(И^кл)> Для статистик Бозе —Эйнштейна (И^бэ) и Ферми—Дирака (№фд).
Таблица 27
Заполнение ячеек
I II III W W^ W_n
кл БЭ ФД
3
0
0
2
2
1
1
0
0
0
3
0
1
0
2
0
1
2
0
0
3
0
1
0
2
2
1
1
1
1
3
3
3
3
3
3
lJw(2f0,0.1)=^n-=3
невозможно
3'
■W(\, 1, 1, 0) = ——— = 6 невозможно
1 1
6 W(0, 3, 0, 0)=-|[ = 1
Таким образом, в статистике Ферми — Дирака минимальное число ячеек
Z равно числу частиц N. При Z—N возможно только одно квантовое
состояние.
§ 1. Квантовая статистика
235
Как и в классической статистике, связь между энтропией и
статистическим весом дается соотношением S = kln W .
Поведение системы бозе- или ферми-частиц характеризуется также
тем, что система стремится к такому состоянию, в котором
статистический вес W и соответственно энтропия S максимальные
Для квантовых систем также справедлив и второй закон
термодинамики: любой физический процесс протекает в
направлении возрастания статистического веса, вычисленного с помощью
соответствующей статистики.
Когда система находится в равновесном состоянии,
статистический вес принимает максимальное значение, совместимое с
наложенными на систему дополнительными условиями
(например, законом сохранения энергии, сохранением числа частиц).
Определенные таким образом распределения называются
соответственно распределениями Бозе — Эйнштейна и
Ферми—Дирака. Эти распределения выведены ниже в задачах 1.1 и 1.2.
Задачи
1.1. Распределение Бозе — Эйнштейна
Найти число фотонов с частотой от v = 5,15-1014 Гц до v + dv = 5,20-1014 Гц
(видимая область, желтый цвет), содержащихся в полости объемом V—\ м3
при температуре Г = 6000К. Чему равна энергия излучения, приходящаяся
на эти фотоны?
Решение
Определим по статистике Бозе—Эйнштейна число заполнения состояний
с импульсом в интерваче от р до p-\-dp (фиг. 48).
p+dp
Фиг. 48. Шаровой слой в пространстве импульсов.
Энергия е и импульс р материальной частицы связаны с частотой v
соответствующей дебройлевской волны соотношениями де Бройля:
e = hv = pc, p^lL^ibk1). (1.1.1)
А
Значениям импульса в интервале от р до p + dp соответствует в
импульсном пространстве шаровой слой объемом 4кр2 dp. Мы пользуемся представ-
^ См., например, [12], раздел 6.1.
236
Гл. 4. Статистика квантовых процессов
лением о, ^-пространстве\ т. е. о фазовом пространстве, положение точки в
котором определяется тремя пространственными и тремя импульсными
координатами и размерность которого, следовательно, равна шести. Если ввести
сферические координаты и разбить импульсное пространство на шаровые
слои объемом 4np2Apf, то, согласно соотношению неопределенностей Гейзен-
берга, число ячеек внутри одного шарового слоя i оказывается равным [см.
формулу (3.1) гл. 2]
z,.=^=iM«. (U2)
Здесь V — объем, в котором находится рассматриваемый фотонный газ.
Выведенная формула справедлива для линейно поляризованного света, равно как
и для бозонов с нулевым спином. Если же свет обладает произвольной
эллиптической поляризацией или неполяризован, так что колебания электрического
вектора могут быть разложены на две (g — 2) взаимно перпендикулярные
компоненты, или же если частицы (например, а-частицы) обладают спином,
проекция которого на направление внешнего поля может принимать g различных
значений, то число возможных квантовых состояний в фазовом объеме ДФ/
увеличится в g раз. Поэтому можно написать
(1.1.3)
При увеличении числа ячеек в g раз объем одной ячейки уменьшается и
становится равным hs/2/'g. В данном случае s = 6, g = 2. Пусть в z,- квантовых
состояниях в фазовом объеме ДФ; находятся всего N ( микрочастиц. Положим,
что имеется Z,-0 квантовых состояний, не занятых частицами, Z/j. состояний
с одной частицей и вообще Z,y ячеек, в которых размещено / частиц. Согласно
формуле (1.13), статистический вес этого распределения равен
Wi(ZiQtZiu ...)= *ll . • (1.1.4)
11 Zir
i
Статистический вес данного распределения для всего ц-пространства составляет
i i ll *i/\
j
При этом справедливы следующие дополнительные условия:
2Z,y = Z;, (1.1.6)
/
2/z/7=^-, (м 7)
Stf/=5I/Zi/=tf, (1.1.8)
^iNi=^iiZij = U. (1.1.9)
i i, j
Здесь U — полная энергия, 8/—энергия одной частицы в фазовой области
ДФ/.
§ 1. Квантовая статистика
237
Чтобы найти распределение, соответствующее наибольшему
статистическому весу W, рассмотрим вариацию
6 In W = 82 (in 2/!—21п2'У!) =0' (1.1.10)
Из выражения (1.1.10) с помощью формулы Стирлинга [см. (1.8а) гл. 2]
получаем, учитывая (1.1.6),
In «7 =2 к-(In г,— O-S^/dnZ,,-!)!-
= 2(г<1пг<— 22<7lnZ</). <1ЛЛ1>
При варьировании нужно учитывать, что число квантовых состояний z/
постоянно. Тогда из формулы (1.1.11) имеем
б In W= -6 2JZ,y In Z/y = -2 О" Z,y +1) 6Z,y = 0. (1.1.12)
К этому равенству следует прибавить проварьироваиные дополнительные
условия (1.1.6), (1.1.8) и (1.1.9), умножив их на множители Лагранжа у/, —а, —р.
Эти условия дают
Y/26z<y=0> <1Л-6а)
—а2^/ = °» (1.1.8а)
t
— р28^^,==0- (1.1.9а)
i
Отсюда получаем
~2(lnZ7 + 1+a/ + P/^- Y/)e*iy = 0. (1.1.13)
Вариации 6Z,y выбираются произвольно, за исключением некоторого их числа.
Число зависимых вариаций 6Z,y равно числу дополнительных условий (1.1.6),
(1.1.8), (1.1.9), т.е. равно числу множителей Лагранжа. Таким образом, вместе
с произвольно выбираемыми множителями Лагранжа число независимых
переменных оказывается как раз равным числу вариаций 6Z,y. Поэтому все
вариации 6Z/y можно рассматривать как независимые друг от друга, а зависящими
от них величинами считать множители у/» —а» —Р- Будем полагать
последовательно одну из вариаций 6Z,y Ф 0, а все прочие — равными нулю; тогда
из выражения (1.1.13) найдём
Z;/=ev,-(i+<*/+p/e,)
или соответственно
Z,y=Qe-a/-p'\ C,=eV.-1. (1.1.14)
Рассмотрим тождество
рг=Е^ 0-1ЛВ)
1 _
/=о
продифференцировав его по х, получим соотношение
<»-^ /=0
238
Гл. 4. Статистика квантовых процессов
Учитывая (1.1.16), находим из равенств (1.1.14) и (1.1.7)
tf^ £ /2,,-С, £ <.-/W-Q ехр[-(« + Рв-).1 л 17)
^ ^ {1— exp[—(a + pe,)]}2
/=o /=o
Из формул (1.1.16) и (1.1.15) следует
4_2>_*2.-i<..*l>_Cl_J_p;
/=о /=о е
(1.1.18)
Тогда для чисел заполнения фазовой области АФ/ микг~ ,астицами имеем из
(1.1.17)
_ г/ехр[—(a + Pef-)] ___ z,-
1 I-exp[-(a+Pe/)]"" „a+P8/ (1ЛЛ9)
Для определения параметра Р вычислим энтропию. Аналогично формулам
(1.1.10) и (1.1.11) имеем
00 / 00 \
S = k\nW = k\n ^ 2/In 2/-2 Z,7lnZ,y ),
откуда с помощью выражения (1.1.14) и дополнительных условий (1.1.6) —
(1.1.9) получаем
S = fcln 2
t=0
z/lnz,— 2 z//(Y/— 1 —оь/ — P/>i)
/=о
= k\n 2 z/(lnzf —Yi-+l) + *M* + *Ptf.
i\=0
(1.1.20)
Варьируя полную энергию, приходим к выражению
dS = k$dU. (1.1.21)
Сравнивая выражение (1.1.21) с термодинамическим соотношением (2.5) гл. 2
при постоянном объеме
dU (1.1.22)
dS:
Т '
видим, что, как и в случае статистики Больцмана,
1
Р =
'kT'
(1.1.23)
Тогда в качестве общей формулы для чисел заполнения в статистике Бозе —
Эйнштейна получаем из (1.1.19) распределение Бозе—Эйнштейна:
Nr.
ехр(а + 8///еГ) — 1
, или Nj =
Angp^ptV
h?[exp(a + et/kT)— 1]'
(1.1.24)
Множитель Лагранжа а определяется из выражения (1.1.24) с помощью
дополнительного условия (1.1.8) или (1.1.8а).
Чтобы найти распределение фотонов в полости объемом V, нужно учесть,
что для квантов света закон сохранения числа частиц не выполняется.
Характер излучения полностью определяется, температурой. Поэтому дополнительное
§ 1. Квантовая статистика
239
условие (1.1.8а) для квантов света неприменимо. Формально можно это учесть,
положив в (1.1.8а) множитель Лагранжа а равным нулю. Тогда имеем для
фотонов
Ni = ghS{exp(hv/kT)-\]- (U'25>
Используя для фотонов соотношение де Бройля p — hv/c и считая Ni = dN,
находим число фотонов в интервале частот от v до v + dv
4:iVv2 dv
dN=g-
<*^lkT-\)
(1.1.26)
Это выражение содержит формулу излучения Планка, которая будет
подробнее рассмотрена в § 2 настоящей главы. Подставляя численные значения,
находим для неполяризованного света
dN = 2 fa.l.(S,15.10")'-0,05.10" = 2 04.10"
/о твчз Г /6,63.10-34.5,15.1014\ А
<3-108>3 [еХЧ 1,38.10-^.6000 УХ\
Энергия излучения, приходящаяся на эти фотоны, определяется выражением
dU = hvdN. (1.1.27)
При заданных численных значениях имеем
d^ = 6,62-10-34-5,15-1014.2,04.1016 = 6,9.10-3 Дж.
1.2. Распределение Ферми—Дирака
а) Исследовать распределение свободных электронов по энергиям. Вывести
функцию распределения, б) Определить множитель Лагранжа а. в) Чему равно
число свободных электронов с энергией между 6,90 и 6,95 эВ в медном стержне
длиной /=1 м и сечением АЛ = 1 см2 при Т = 300 К?
Решение
а) В статистике ФеРтп—Дирака каждое квантовое состояние либо не
заполнено, либо занято единственной микрочастицей. Поэтому в отличие от
статистики Бозе—Эйнштейна, о которой шла речь в задаче 1.1, здесь имеется
то ограничение, что из всех чисел заполнения отличны от нуля только Z/0 и Z/1#
Согласно соотношению неопределенностей Гейзенберга число квантовых
состояний в шаровом слое пространства импульсов определяется
соотношением [см. формулу (3.3) гл. 2],
*,- = 4-^ (1-2Л)
Здесь g означает число возможных проекций спина на направление внешнего
поля. Если представить спин в виде
р* = #£ (1.2.2)
квантовой теории вытекает следующее выражение для числа возможных
;ций спина на заданное направление:
g = 2s+l. (1.2.3)
240
Гл. 4. Статистика квантовых процессов
Для электронов s= 1/2 и, следовательно, g = 2. Если элемент фазового объема
АФ; содержит z/ ячеек, по которым распределены Ni фермионов, то /V/ ячеек
заполнены, а z/—Ni ячеек пусты. Согласно формуле (1.6) гл. 2, статистический
вес этого распределения равен
Wl Ni\(Zi-Ni)\-
Для совокупности всех состояний имеем
^Цтгщ=т- с-2-4)
По формуле Стирлинга [см. (1.8а) гл. 2] находим
In W =23 fz' 1п zi~Ni1п Ni—(zi—Ni) ,n (*i—Ni)]. (1.2.5)
i
Варьируя числа заполнения Л/",- для определения состояния с наибольшим
статистическим весом, получаем из выражения (1.2.5)
81п№ = — 2] [In #1 —Info — Ni)\bNi = Q. (1.2.6)
При учете дополнительных условий
—a6N =—а2]в^ = 0, (1.2.7)
— р6(/ = —р2]е,-6Л/г|- = 0 (1.2.8)
имеем из (1.2.6)
2l—lnyvf-+ln (z/—Л^/)—ex—рв/]6Л^/ = 0. (1.2.9)
i
Выбирая соответствующим образом множители Лагранжа a, р и все
вариации 6W/, за исключением двух произвольных [см. формулу (1.1.14) настоящей
главы или формулы (1.16) —(1.21) гл. 2], получаем из выражения (1.2.9)
распределение Ферми—Дирака
— --= е , или N[ =
N< ' ' ea+*Bl + \
(1.2.10)
Параметр р находим из энтропии [см. (1.1.21) и (1.1.22)]; это снова дает
1/р = *7\
б) Параметр а определяется из дополнительного условия
; f А»(еа+в'/Л +l)
Поскольку фазовые ячейки малы, можно Сппюгь распределение непрерывным
и заменить N[ на dN. Далее можно написать
2
где через jli обозначена масса электрона. Из формулы (1.2.11) имеем
*^^,^:,,^,^ с.2.13)
о
§ 1. Квантовая статистика
241
С помощью подстановки
из (1.2.13) получаем
(1.2.14)
N = l^LV-2(llkT^]^L. (1.2.15)
Обозначим
f+-(e)-yrji^ir*! (,-2',6)
тогда имеем вместо (1.2.15)
N=8v(^y*F+ia). (1.2.17)
Интеграл (1.2.16) называется интегралом вырождения 1). Его можно вычислить
с помощью разложения в ряд. Рассмотрим интеграл
-Гл Л»
для б > 0 его целесообразнее Есего записать в виде
6 со со
О б 0 '
Здесь Jг включает второе и третье слагаемые. Для обеспечения сходимости
третье слагаемое разобьем на два интеграла с пределами от 0 до б и от б
до оо. Разложение в ряд дает
/„ = -$/"-1 £ (-l)v+1^(v+1)(/-6)d/-
v=0
-('"-1 S (-i)ve(v+1)('~6)^.
о v=o
Произведя в первом выражении замену * = (v+l)(/ — б), а во
втором—замену х — —(v+l)(£ — б), получим после соответствующей группировки членов
Jt = С [(б + др)"-1—(б—jc)"-4 е-* rfx^
б v=0
+f(-„.-«-^£< ;v+l), .
(-Dv
(v + l)2
11 В литературе обычно принято называть величины F+ (а) и F- (а)
соответственно интегралами Ферми и Бозе индекса 1/3,— Прим. ред.
242
Гл. 4. Статистика квантовых процессов
При оценке интеграла используем Г-функцию в соответствии с формулой
(1.5.3) гл. 2; тогда для б > 0 находим
5^-4+»--[f7Vf7,)*+
где
(1.2.18)
(1.2.19)
в частности,
Для вычисления параметра а, оставшегося неопределенным в распределении
Ферми—Дирака (1.2.10), подставим выражение (1.2.18) в интеграл Ферми
(1.2.16) и положим 6 =— а > 0, тг = 3/2. Учитывая только главный член,
получим в первом приближении
F+(a)= 2_f—L*dt = —^(-a)3
Из формулы (1.2.17) имеем тогда
(1.2.20)
(1.2.21)
Число N свободных электронов можно приближенно положить равным числу
атомов металла. Если р — плотность металла, \iA — масса одного его атома, то
эти величины связаны соотношением
%A = pV,
или же
(1.2.22)
Разрешая равенство (1.2.21) относительно а и учитывая (1.2.22), находим
/i2
\ 4№а )
2n\ikT '
Подставляя численные значения
рСи = 8,9.10з кг/м», На--6702.1026
(1.2.23)
63,6
кг,
§ 1. Квантовая статистика 243
получаем
_ (Ъ /3,14.8,9» 103»6,02» Ю^6 У/3
~а~Д 4-2-63,6 ) Х
(6,62- Ю-34)2
Х 2.3,14.9,11.10-^.1,38.10-23.300 =271 (1.2.23а)
Таким образом, —а = 6^>1, откуда видно, что в данном случае в
разложении (1,2.18) действительно можно ограничиться главным членом.
' в) Числа заполнения N[ или ' dN можно получить из выражения (1 2.10),
если подставить в него число квантовых состояний (1.2.1). Учитывая (1.2.12),
имеем
, g-4nVp*dp _ gAjiViiV^de (\<>о±\
Л3[ехр(а + е//еГ)+1] — h*[exp (a + e/kT)+l] ' v-*-*v
Экспоненциальный* член практически не дает вклада, если
Mp(a+£f J^1'
или же
a+kf<-5-
Для меди при данной температуре Т = 300 К и при найденном значении
множителя а = —271 это означает, что для е < 266 kT = 266-1,38-10-23-300 Дж=»
=6,88 эВ заполнение описывается распределением
Если величина е выражена в электронвольтах, то имеем
;АТ _ glV~2 (\,6-10-™)3/2 лУ\13/2 VI de
dN~ h3
Напротив, для энергий е > 276-1,38-10-23-300 Дж = 7,14 эВ при данной тем-
пературе можно пренебречь единицей в знаменателе формулы (1.2.24). Тогда
функция распределения определяется главным образом экспоненциальным
членом:
^=^P^exp[-(«+i)]
det
как это следует из классической статистики Больцмана (см. задачу 1.3)
В области энергий от 6,88 до 7,14 эВ в выражении (1.2.24) нужно учитывать
оба слагаемых. Подставляя заданные численные значения, для энергий
8 = 6,90 эВ, б(е = 0,05эВ получаем
2-4я.10-4-9,11»10-31У2-9,Ы0-81-6,9-1>6-10-ц-0>05-1>6-10-19_
(б,б2ло-зу[ехР(-271+1у8;11-б::зо;3;;)+1]
= 8,8-Ю22.
Полное число свободных электронов в 1 м3 меди, согласно формуле (1.2.22),
составляет
* 8'9-10°±02-1026=8,4.10*»м-з.
V оо,о
244
Гл. 4. Статистика квантовых процессов
Таким образом в объеме У=10-4м3 рассматриваемого медного стержня
содержится УУ = 8,4-1024 электронов.
Из всех свободно движущихся электронов только около 1% обладает
кинетической энергией в заданном интервале.
1.3. Статистика частиц газа, ионов и протонов
Исследовать, к каким результатам приводит использование квантовой
статистики по сравнению со статистикой Больцмана для нейтрального газа
или газа ионов при нормальных условиях.
Решение
Запишем распределение Бозе—Эйнштейна (см. задачу 1.1) и
распределение Ферми—Дирака (см. задачу 1.2) в единой форме:
Л'— *' ffA'- g*nVp*dp
1 exp(a + Ej/kT)^ 1 ' Л3ехр(а + Ра/2|Х*7)Т1 " I1'0'1'
Множитель Лагранжа a находим из условия
£МГ EUR = yv (132)
Л3 J ехр(а + р2/2^Г)^ 1 'V' К^}
о
Используя подстановку
t=-£— (1.3.3)
1 2(1*7" К }
получаем
АГ=^(2яц*Г)»/»^(а), (U.4)
где интеграл вырождения
00
fg(a) = J- Г ^ * dt. (1.3.5)
о
Если множитель Лагранжа a > 0, то удобнее всего вычислять интегралы
вырождения с помощью следующего разложения в ряд:
J =f еа+Гз:!^^^ (± 1)V 1 /Л"1Г" <V+1) <a+/)d/' (1,3'6)
0 v=0 0
С помощью подстановки x = (v-\-\)t из формулы (1.3.6) получим
и v=0
Согласно формуле (1.5.3) гл. 2, этот интеграл можно выразить через Г-функ-
цию.
§ 1. Квантовая статистика
245
Таким образом, для а > 0 имеем
w GO
О v=0
= Г (п)^ ± -^-+-35- ± -47Г+ • • • J
(1.3.8)
Ряд, стоящий в скобках, в частном случае а = 0 при положительных знаках
переходит в ^-функцию Римана гК
Согласно формуле (1.5.6) гл. 2, для п = */2 имеем
Тогда из формул (1.3.4), (1.3.8) и (1.3.9) имеем
(1.3.9)
eV о ,а чгч е- <v+i> а
V = 0
(v + 1)3
(1.3.10)
Для оценки параметра а учтем сначала в (1.3.10) только член с v = 0; тогда
получим
tgV(2n[ikT)3/2
h3N
a = ln*
(1.3.11)
w Дзета-функция Римана имеет вид
C(/l)""X(v+l)»""2 V"
v=0
v=l
Если a = 0, то при отрицательном знаке в правой части суммы (1.3.3) она
преобразуется к виду
i-^r+4r-^r±--- = X(-1)v+1^=(1-21"n)^n)- <L3-8">
v=l
Значения дзета-функции Римана для нескольких значений аргумента
приведены в табл. 28.
Таблица 28
Значения дзета-функции Римана
1,0 1,5
2,5
3,5
4,5
5,0
С (л) оо 2,612 1,645 1,341 1,202 1,127 1,0823 1,0547 1,0369
246
Гл. 4. Статистика квантовых процессов
В соответствии с уравнением состояния для идеального газа подставим
V/N = kT/P. Далее, имеем
1,01
** N Л^ NA 6,02-1026
з кг, g> 1.
(Лн — относительная атомная масса водорода, Мг — относительная масса
молекулы.) Поэтому из формулы (1.3.11) следует, что
а> 3 ,п 2я^4н_31п 5 j fe7,_lnp
2 N а ' 2
(1.3.12)
При заданных численных значениях для Т = 273 К и Р= 1,033 ат находим
1Q23
10»* 3
а> 6,62 2 2.3,14.1,01 ' 2"'" 1,38.273"
6,02-1026 5 .
Г — -7Г 1П
— In 1,0339,81-104= 10,56.
Это означает, что
еа > gl0,66 = 104,59 ^> 1.
При нормальных условиях для любого нейтрального или ионного газа можно
считать, что еа^>\, и пользоваться для чисел заполнения вместо формулы
(1.3.1) выражением
Ni = -
■ехр(а + е//*7у
или соответственно
g 4я Vp2 dp
dN =
h*exp(a+e/kT)'
(1.3.13)
В выражении (1.3.13) уже никак не проявляется различие между
статистиками Бозе—Эйнштейна и Ферми —Дирака. Если же подставить сюда а из
формулы (1.3.11), то получим
dN = N-4= ^-ТТ7 ехР ( —\dp =
Vn (2^/еГ)3/2 V 2\ikTj
= N
УН (2/е7»3/2
exp
/ ^2 \
V "2kT J
dv.
(1.3.14)
Эта формула соответствует распределению скоростей идеального газа по
статистике Больцмана [см. формулу (1.3.4) гл. 2].
Таким образом, при еа;>1, или, согласно (1.3.11), при
г =
У N
VI
h
/2ЯЦ kT
- 2 Хи
~*j/re
(1.3.15)
статистики Бозе —Эйнштейна и Ферми—Дирака переходят в статистику
Больцмана. Здесь через Яд обозначена длина соответствующей волны де Бройля
[см. формулу (3.2.5)].
Если среднее расстояние между микрочастицами велико по сравнению
с их дебройлевской длиной волны, то можно вместо квантовой статистики
пользоваться классической статистикой Больцмана.
§ 2. Законы излучения
247
Как можно видеть из выражений (1.3.12) или (1.3.15), квантовые свойства
газа материальных частиц проявляются только при очень большом давлении
или же очень низких температурах. Эти свойства тем слабее, чем больше масса
частицы газа. В общем случае у обычных газов среднее расстояние г велико
по сравнению с дебройлевской длиной волны, так что применима статистика
Больцмана.
Упражнения
У.1.1. Чему равно число фотонов с частотой в интервале от v = 5,15-1014 до
v + dv = 5,20-1014 Гц при Г = 3000 К в полости объемом V=\ м3?
У. 1.2. Определить энергию излучения, приходящуюся на фотоны с частотами
от 5,15-Ю14 до 5,20-1014 Гц при Т = 3000 К в полости объемом 1 м3.
У. 1.3. Вычислить множитель Лагранжа а для электронов в серебре при
Г=100 К, pAg=10,5 г/см3, AAg= 107,9.
У. 1.4. Исследовать для серебра, при какой кинетической энергии
распределение электронов можно описывать с помощью классической
статистики Больцмана (а + е/йГ^б). Температуру Т положить равной
100 к.
У. 1.5. Чему равно число электронов с кинетической энергией от 2,0 до
2,1 эВ в 1 см3 серебра при 100 К? Определить полное число
свободных электронов.
У. 1.6. Найти множитель Лагранжа а для протонов при Т = 106 К,
Плотность протонов Мо=1020 м~3, # = 2.
У. 1.7. Найти при какой плотности протонов с температурой Т — 106 К можно
пользоваться статистикой Больцмана (а ^5).
У. 1.8. При какой плотности электроны с температурой Г=106 К
подчиняются статистике Больцмана? Какие выводы можно отсюда сделать
для физики плазмы? Весовой множитель g принять равным 2.
У. 1.9. Определить внутреннюю энергию одноатомного газа по статистике
Бозе — Эйнштейна и Ферми — Дирака.
У. 1.10. Найти значения интеграла
J(*)^fZ7-TT*t
J_
о
для а = + 1 и а =—1.
§ 2. ЗАКОНЫ ИЗЛУЧЕНИЯ
Введение
Законы излучения получаются из статистики
Бозе—Эйнштейна для частного случая а = 0. Согласно формуле (1.1.26),
число фотонов с частотами между v и v + dv, содержащихся
в объеме V=l м3, равно
dN 4jigv»dv
Отсюда следует закон излучения Планка, определяющий
энергию, приходящуюся на фотоны с частотами от v до v-f-dv, для
248
Гл. 4. Статистика квантовых процессов
излучения в объеме V=l м3 (фиг. 49):
Pvdv = evdN = hvdN = -^£*
c4ehvlkT_X)
(2.2)
Здесь pv—спектральная плотность энергии.
k J65QK
'^Чппте (*>и'г* ^' Кривые спектральной плотности энергии,
<1000К описываемой законом излучения Планка и зако-
-^ 2 ir**&>?0 м ном смещения Вина.
Распределение излучения по длинам волн характеризуется
спектральной плотностью fo, определяемой соотношением
pv|dv|=pjJdH или Pb = Pv^- (2.3)
Из формулы излучения Планка (2.2) можно вывести все
другие законы излучения. В предельном случае
hv^>kT (2.4)
получаем закон излучения Вина
pvrfve*35^v*/«-
В противоположном предельном случае
hv^kT
имеем закон излучения Рэлея—Джинса:
, 4ngkTv2dv
(2.5)
(2.6)
(2.7)
§ 2. Законы излучения
249
Зная спектральные плотности pv и р*,, можно найти значения
частоты или длины волны, при которых плотность излучения
максимальна при данной температуре, т. е. получить закон
смещения Вина:
2,822/еГ
he
4,965/гГ
(2.8)
Интегрируя соотношение (2.2) по всем частотам, находим
полную энергию излучения, содержащуюся в объеме 1/=1 м3:
/г Г a 4g я5/е4Г4
(2.9)
Мощность, излучаемая в единичный телесный угол в
направлении нормали к 1 м2 черной излучающей поверхности в полосе
частот от v до v + dv, называется спектральной плотностью
потока энергии, 2/Cv. Спектральная плотность энергии и
спектральная плотность потока энергии связаны соотношением
(см. задачу 2.2):
2KV =
cpv
4лгг0
(2.10)
где /г0—показатель преломления. Мощность излучения,
испускаемого 1 м2 излучающей поверхности в полупространство, для
случая /г0=1 определяется законом излучения Стефана—Больц-
мана:
М
= 2я J Kvdv = ^^ = 5,67- 10-8Г* Вт/м2• К*
. (2.11)
Задачи
2.1. Максимум спектрального распределения энергии
С помощью закона излучения Планка найти максимум спектрального
распределения энергии. Сравнить для Т—1500 К значения,
соответствующие максимуму по шкале частот и по шкале длин волн. Как сместятся эти
максимумы при повышении -температуры до 3000 К?
Решение
Согласно формуле Планка (2.2), спектральная плотность энергии составляет
р = 4;vy . (2.1.1)
v с3 (ehvjkT— 1)
250
Гл. 4. Статистика квантовых процессов
Для определения максимума этой функции распределения положим
hv
*=W. (2-1.2)
Тогда экстремальное значение функции (2.1.1) определяется трансцендентным
уравнением
d д» _«*(3-*)-3
Ее»-Г (е*-1)« * -0- (ЛЛ-6)
Его корень находим, численным расчетом
W(v)=^p=2,822. (2.1.4)
Для частоты vMaKC, соответствующей наибольшей плотности излучения,
имеем
-2,822/гГ-=5,88.101оГс-1. (2.1.5)
-макс — h
Подставляя численные значения, получаем для Г=1500К
/1Е.ПЛ„, 2,822-1,38. Ю-23-1500 - QQOim8r
vMaKc(1500K) = 663.10-з4 с-1 = 8,82.1018Гц|
а для Т = 3000 К
vMaKc (3000 К) = 1,765-1014 Гц.
Вычисленные частоты соответствуют длинам волн
с 3-Ю8
я=7=8^ТоГз=3'4-10-вм
и 1,7.Ю-6 м.
Таким образом, максимумы спектрального распределения энергии лежат
в инфракрасной области. При увеличении температуры они смещаются по
направлению к видимой области спектра.
Во многих экспериментальных исследованиях используется
равномерная шкала длин волн. Поскольку
Pvldvf=PjJdH
плотности распределения до частогам pv и по длинам волн р^ связаны
соотношением
Рх=Р%
= pv IdXT
=^Pv (2л-6)
Заменим в спектральной плотности распределения (2.1.1) частоту v на длину
волны, используя соотношение v = c/X; тогда получим из (2.1.6)
cpv Snhc
Р^=Я2" %b(ehclkTK_xy (2Л-7)
Положим снова
hv he
X~~Fr~~kTXf
тогда для определения экстремума получаем уравнение
d А е*(5-х)-5
Тх7*=\- (е*-1)* Х -°- (2-''8)
§ 2. Законы излучения
251
Это трансцендентное уравнение имеет следующий корень:
*макс(*) = 4,965.
Итак, длина волны Ямакс, соответствующая наибольшей плотности излучения
по шкале длин волн, равна
(2.1.9)
(закон смещения Вина). Подставляя численные значения, находим для
Г =1500 К
W(1500K) = 4>463i;1308:[o-aM500= '-93-10"6 М'
а для Т = 3000 К
^макс (3000 К) = 0,966-10-° м.
С увеличением температуры этот максимум сдвигается в сторону более коротких
длин волн (фиг. 49).
Максимумы спектрального распределения энергии оказываются различными
в зависимости от того, какая шкала используется — частот или длин волн.
2.2. Закон Стефана — Больцмана для полного излучения
Металлическая пластина площадью Л =40 м2 с поглощательной
способностью Х) 8 = 0,70 имеет температуру 7 = 900 К. На расстоянии г = 500 м от
нее в направлении, составляющем угол 0 = 60° к нормали к поверхности А,
находится стеклянная пластина площадью Л0 = 25 м2 с поглощательной
Фиг. 50. К рассмотрению излучения,
испускаемого площадью А и попадающего на
площадь Л0.
способностью е0 = 0,90 (фиг. 50). Плоскости А и А0 параллельны друг другу.
Чему равна энергия излучения, попадающего за 1 ч с металлической
пластины на стеклянную?
Решение
Рассмотрим объем, в котором распространяется излучение. Пусть в
элементе объема dV в определенный момент времени содержится энергия dU.
Предельное значение
Р =
dU
dV
(2.2.1)
г) Под поглощательной способностью понимается отношение поглощенного
телом потока к падающему на него потоку света, равное отношению испуска-
тельных способностей данного тела и абсолютно черного тела.— Прим. ред.
252
Гл. 4. Статистика квантовых процессов
дает плотность энергии. Доля ее, приходящаяся на частотный интервал dv>
dp = pvdvt (2.2.1а)
определяет спектральную плотность энергии.
Элемент поверхности аИ испускает в 1 ев телесный угол rfQ = sin ftdfldcp
следующее количество энергии в интервале частот от v до v + cfv (излучение
не поляризовано):
dW = d$v-dWdv = 2Kvdv dW-dQ = 2KvdvdQdA cos d. (2.2.2)
Здесь О—угол между нормалью к излучающей плоскости и направлением
луча (фиг. 50), /Cv характеризует спектральную плотность потока для линейно
поляризованного излучения. Ее нужно умножить на g = 2, так как любое
неполяризованное электромагнитное колебание можно разложить на две взаимно
перпендикулярные линейно поляризованные составляющие. Полную энергию
излучения в области частот от v до v + cfv, испускаемого в полупространство
из элемента dSI, определяем с помощью интегрирования формулы (2.2.2)
2Л Я/2
U? = 3v-d2tdv=f Г 2KVdv dA Qos& sin Qdbdy = 2nKvdvdA. (2.2.3)
о о
Чтобы найти связь между плотностью энергии и плотностью потока излучения,
рассмотрим элемент объема dV. Опишем вокруг него сферу радиусом г (фиг. 51).
Фиг. 51. К выводу соотношения между плотностью
энергии и плотностью потока излучения.
На поверхности сферы выделим элемент площади da. Из элемента do
элементарный объем dV виден под телесным углом
dQ=Q, (2.2.4)
где df—площадь сечения элементарного объема dVt которое обращено к
элементу площади da. Тогда для мощности излучения, идущего от da к dV, из
формулы (2.2.2) при 0 = 0 находим
d3v -dadv = 2Kv dv da dQ = 2Kv dvda-{-. (2.2.5)
Следовательно, для излучения, направленного от da к dV, плотность потока
энергии равна
V^v = ^v^v=2£y_^ (226)
§ 2. Законы излучения
253
Для всех точек сферы плотность потока, направленного в элемент объема dVt
имеет такую же величину, поэтому выражение (2.2.6) нужно умножить на
4лг2/б(а. В итоге для полной плотности потока энергии в объеме dV получаем
\jv\dv = 8nKvdv. (2.2.7)
С другой стороны, она связана соотношением
|fv|dv = pvdv-
(2.2.8)
со спектральной плотностью pv энергии излучения и со скоростью с/п0
переноса энергии. Из формул (2.2.7) и (2.2.8) вытекает связь между плотностью
энергии и плотностью потока излучения:
Pvdv—=8nKvdv;
v «о
используя закон излучения Планка (2.2), получаем
(2.2.9)
Выполним интегрирование по всему спектру, для чего воспользуемся
формулами (1.3.6) —(1.3.8) при показателе степени п — А. В результате находим
00 00
ehv/kT_{
о о
Учитывая, что Г(4) = 3!=6, £(4) = зт4/90= 1,0823, имеем
2KVdv=
2tt*fe47*
\5n0c2h* '
(2.2.10)
Мощность, излучаемая в полупространство, согласно формуле (2.2.3), в я раз
превышает эту величину. Приняв /г0=1, получим для потока энергии,
испускаемого в 1 с площадью 1 м2, закон излучения Стефана — Больцмана:
М=^~^-=аТ4 = 5,67.10--8Г4Вт/(м2.К4)
(2.2.11)
Заключенную в телесном угле dQ мощность излучения, испускаемого
площадью dA с поглощательной способностью е и попадающего на площадь dA(>
с поглощательной способностью е0, получим из формулы (2.2.2)
13 | = J | 3V | dv = 2dAee0 cos fldQ ^ Kv dv.
С учетом формулы ^2.2.10) имеем
2тг4£4 гг'
131= ,Г 2.а ^Л880 cos О dQT* = — dAee0 cos * dQT*.
(2.2.12)
254
Гл. 4. Статистика квантовых процессов
Из фиг. 50 видно, что
dQ=d4o_cosfl (2213)
Подставляя заданные значения, находим
9-0,52-25.
3,14-5002
. 0.. 5,67- Ю-8-40-0,7.0,9-0,52.25.9004-602.0,239- 10~3 с А
|3| = q ы.ям =М ккал/ч.
2.3. Определение ft и ft по спектру излучения
Мощность, испускаемая при Г=1000К в полупространство абсолютно
черным телом с поверхностью Л = 1 м2, составляет по измерениям Луммера
и Прингсгейма 56,53 кВт. Длина волны Ямакс, соответствующая наибольшей
спектральной плотности распределения при данной температуре, равна
29010-Ю-10 м.
Найти отсюда квант действия Планка h и постоянную Больцмана k.
Решение
Закон смещения Вина (2.1.9) устанавливает связь между h и k:
h ^4,965А,максТ
k с \ • )
Здесь все величины справа известны или могут быть определены из измерений.
Воспользуемся теперь законом Стефана — Больцмана (2.11) для полного
излучения черного тела:
М=^у^ = стТ4 = 5,67Л0-8Г*Вт/(м2 -К4). (2.3.2)
Возведя закон смещения Вина (2.3.1) в куб, умножив на выражение (2.3.2)
и разрешив затем относительно постоянной Больцмана, получим
, 4,9653.15^аксМ
2лРс Т '
Подставляя это значение в закон смещения Вина (2.3.1), находим
(2.3.3)
. 4,9654.15,4 ЛЛ /0о,ч
h= '2Я5С2 ^максМ. (2.3.4)
При заданных значениях имеем
4,9653.15 (2,901 ■ Ю-6)3»56,53-103
2яб.3.108.103
= 1,380-Ю-23 Дж/К,
/i=g^|^^.(2,901.10-6)4-56,53 103 = 6,626.10-3* Дж-с
2.4. Термодинамические величины поля излучения.
Давление света
В полости объемом У =1000 м3 температура Т составляет 1000
К.-Вычислить свободную энергию F, энтропию 5 и внутреннюю энергию U поля
излучения. Чему равно давление излучения? Найти энергию Гиббса G и
химический потенциал \лс.
§ 2. Законы излучения
255
Решение
Из закона излучения Планка (2.2), записанного для объема V, после
интегрирования, получим [см. (2.2.10)]
о
Дифференцирование по температуре дает удельную теплоемкость
(dU\ ,16л»лУ*Г»
Согласно формуле (2.4.3) гл. 2, для теплоемкости имеет место соотношение
CV = T (g)v. (2.4.3)
С точностью до постоянной, зависящей от объема, найдем для энтропии
S=JTdr- 45c»ft» • (2-4-4)
Отсюда определяем свободную энергию излучения
4я^У/г*Г*
F-U-TS- 45cW • (2-4-5)
Для давления света имеем
fdF\ _4яб^4Г4_ U .
оно, таким образом, не удовлетворяет закону [см. формулу (5.1.7) гл. 2]
pv=tu-
Энергию Гиббса получаем из формул (2.4.5) и (2.4.6)
G^F + P^V^O. (2.4.7)
Следовательно, химический потенциал \хс также равен нулю. Для заданных
значений имеем
8.3,1441,38- Ю-»- Шз)4.10з
45.(3-108)3.(6,63. Ю-34)3 ~~ U'Z0ZA5K»
S= 1,01-Ю-3 Дж/К,
(7 = 0,756 Дж.
Давление излучения равно
P^4n§H/M* = 2,57.10-»aT,
т. е. в высоком вакууме и при большой температуре оно может превышать
давление газа.
256
Гл. 4. Статистика квантовых процессов
2.5. Число излучаемых фотонов
Чему равно число фотонов, эмиттируемых в 1 с излучающей поверхностью
площадью о— 4 м2 при 2000 К? Чему равно число фотонов, испускаемых
в видимой области спектра (Я = 3900-Ю-10 — 7800- Ю-10 м)?
Решение
Согласно закону излучения Планка, плотность энергии в частотном
интервале dv составляет
, 8tt/*v3 dv
Pvdv = e,(eftv/*r_l)- (2-S-l)
Предполагается, что излучение неполяризовано. Между числом фотонов с
частотой от v до v-\-dv и плотностью энергии существует следующая связь:
dN /iv = pvcfv. (2.5.2)
С другой стороны, плотность потока излучения 2/Cv и плотность энергии
связаны соотношением (2.2.9):
Полный поток излучения, испускаемого абсолютно черным телом в
полупространство в 1 с, составляет 2лКу. Приняв гс0=1, находим тогда искомое число
фотонов в области спектра от v до v + dv:
,и с Pv . 2д v2 , /ft е оч
dNo^o-г-тг dv = a—r . /ьг—dv. (2.5.3)
4 hv с2 JivikT j v '
Интегрируя, получаем полное число фотонов, испускаемых данной поверхностью:
.. 2jt f v2 dv а2л fc3T3 Г x2dx /0 - .ч
^=(VJ 7^rrr'^"hrJ 5?=г- (2-M)
о 0
Используя результат (1.3.8) при Г (3) = 2, £ (3) = 1,202, находим
аЧШя*^ (2.5.5)
с2 па
Для заданных численных значении имеем
4.4,808.3,14.(1,38-10-2з)з,(2.10з)з_
а~~ (3.108)2.(6,63.10-34)3 '
Для вычисления доли фотонов, приходящейся на видимую область, учтем
в формуле (2.5.3), что hv/kT^>\. Тогда из (2.5.4) имеем
dNo^o^-^ f x*e-*dx9 (2.5.6)
§ 2. Законы излучения
257
где
he _ 6,63-10-84-3-108
Хи kTXa ~~ 1,38-10-23-2.103.7,8.10-2 ~",>
7,20-10-° |Яу|л
*0=з>ш^=18'46-
Вычисление интеграла дает
хр
x4-*dx=—[e-x (*а + 2* + 2)]$|в = 0,88.10-я.
Л0
С помощью формулы (2.5.6) находим число фотонов в видимой области
==4.2.3,14.(1,38.10-2з,2.10з)з
а (3-108)2.(6,63.10-34)3 ' ' »
это несколько меньше чем 0,5% от общего числа фотонов.
Упражнения
У.2.1. Точка плавления вольфрама лежит при 3300°С. Вычислить
максимум спектрального распределения энергии при этой температуре
как по шкале длин волн, так и по шкале частот.
У.2.2. Для какого интервала температур максимум спектрального
распределения энергии лежит в видимой части спектра (3900« Ю-10 м< Х<
< 7800-Ю-1» м)?
У.2.3. Чему равна температура поверхности Сириуса (ЯМакс = 2590-10"10 м)?
У.2.4. Максимум солнечного спектра соответствует длине волны Ямакс —
= 4700* Ю-10 м (X—шкала). Вычислить отсюда температуру солнечной
поверхности (Солнце считать абсолютно черным телом).
У.2.5. Рассчитано, что управляемый ядерный синтез будет идти при
температуре 107 К. Какой длине волны соответствует максимум
плотности излучения?
У.2.6. Чему равно число фотонов в 1 мм3 в поле излучения черной полости
при 300 К?
У.2.7. Чему равно давление света для излучения абсолютно черного тела
с температурой 106 К?
У.2.8*. Четная периодическая функция f(x) — 2xt—xi определена в
интервале (—1, +1). Разложить ее в ряд Фурье и доказать таким
способом соотношение:
^гг4~ 90 '
У.2.9. Чему равна энергия, излучаемая в 1 ч пластиной из оксидированной
меди площадью Л=2м2 при 400 К? Поглощательная способность 8
оксидированной меди составляет 0,72.
У.2.10. Какая часть потока энергии, излучаемой пластиной площадью Юм2
при температуре 1500 К (е = 0,8), попадет на пластину (е = 0,6)
площадью 20 м2, которая наклонена под углом 45° к первой
пластине и находится от нее на расстоянии 400 м в направлении,
составляющем угол 0 = 30° с нормалью к поверхности излучателя
(фиг. 50)?
258
Гл. 4. Статистика квантовых процессов
§ 3. ТЕРМОДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ
ДЛЯ РАСПРЕДЕЛЕНИЙ БОЗЕ - ЭЙНШТЕЙНА И ФЕРМИ—ДИРАКА
Введение
Термодинамические величины в квантовой статистике
вычисляются с помощью чисел заполнения, определяемых одним из
соотношений
N - г/ jN- *ngVP2dp пп
iyi - p+B./kT :р 1 ' шу — /гз ( еа+г (p)/kT) ^ { \°Л 1>
(верхний знак соответствует распределению Бозе—Эйнштейна,
нижний — распределению Ферми—Дирака), и статистического
веса соответствующих распределений. Согласно формуле (1.1.11),
в случае статистики Бозе—Эйнштейна имеем
ln^B3 = 2feln^-2^7lnZ/7), (3.2)
i i
тогда как в случае статистики Ферми—Дирака, согласно (1.2.5):
In№ФД =2 [z/ \nZi-Ni In Ni — iZi—Ni) In (Zi—Ni)]. (3.3)
i
С помощью соотношения (1.1.14) из формулы (3.2) получим
Учитывая выражение (1.1.18) и дополнительные условия
(1.1.6)—(1.1.9), запишем
\nWbS = — S^ln(l-e-a-e^r) + ^ + ^. (3.5)
Число ячеек zt или dz в фазовом объеме АФ/, или
соответственно ЙФ составляет, согласно формуле (1.1.3):
zt= £3 » или uz hs Р .(o.d;
Переходя от суммирования к интегрированию, находим
энтропию газа Бозе—Эйнштейна
о
Для распределения Ферми—Дирака из формулы (3.3) следует
1пГФД = 2(-г,1п^=^-+^, 1пг-^) . (3.8)
§ 3. Термодинамические величины
259
Подставим числа заполнения (3.1), тогда имеем
1п1ГФд = 2^1п(1+^а--е^) + а^ + ^. (3.9)
Подставив сюда выражение (3.6) и заменив сумму интегралом,
получим энтропию газа Ферми—Дирака
5фд = k In й^фд =
со
= 4 V~2 ngVk^2 ^ j/1 in (1 + g-a- в/kT) (js + aNk + ^r9 (зло)
о
Свободная энергия F = U — TS для обоих распределений
описывается следующим общим выражением:
00
F=± 4^2"fV/2 J |/1 in (1 + е- WkT) de—aNkT. (3.11)
о
Определенный интеграл в формуле (3.11) с помощью
интегрирования по частям преобразуем к виду
Q0
^Vlln(l=Fe- а-£/*г) йг = [е3/2 In (1 q= е~ «-в/*7")]? =F
о
2 ? е3/2 exp (-a-e/kT) , ,о Ш
О
Произведя замену
*=£, (3.13)
получим
3/i3 J ea + t qr 1
(3.14)
Для вычисления интеграла в выражении (3.14) лучше всего
воспользоваться формулой (1.2.18) для а <0 и формулой (1.3.8)
для а> 0.
Множитель Лагранжа & находится из условия сохранения
числа частиц. С помощью подстановки
' = w (315)
260
Гл. 4. Статистика квантовых процессов
получим из формулы (3.1) следующее соотношение для его
определения:
JV =
4 У 2 ngV
Л3
№Т)*»№
V t dt
Tl
(3.16)
Внутреннюю энергию найдем из формул (3.1) и (3.6),
интегрируя по всем энергиям с использованием подстановки (3.15):
. (3.17)
Давление в нерелятивистском случае проще всего получить из
термодинамического соотношения, вытекающего из формул
(5.3.11) или (5.1.7) гл. 2:
* — -«класс —
2V
3V '
(3.18а)
В релятивистском случае при очень высоких температурах
имеем
Р-Р «--
(3.186)
(см. задачи 3.1 и 3.5). Из формул (3.17) и (3.18а) для
нерелятивистского случая находим
8}T2ng[i3/2(kT)5/2
3/i3
t*fi
С * " dt.
J ea+t т 1
(3.18)
Пользуясь этим выражением, можно вычислить и остальные
термодинамические функции Я, бит. д. квантовых систем.
В частности, из формулы (3.14) получим, подставив давление
по формуле (3.18) и разрешив относительно — akT:
urr_ F + PV _ G _
(3.19)
Таким образом, множитель Лагранжа а и химический
потенциал \ic связаны соотношением
(3.20)
§ 3. Термодинамические величины
261
При выводе термодинамических величин для квантовых
систем часто пользуются статистической суммой большого
канонического ансамбля:
г = П2е(|1'-е')/*г/£/
(3.21)
Здесь Zt — число ячеек, соответствующих энергии е,-, / — число
заполнения одной ячейки. Суммируя, по всем значениям
/ = 0, 1, ..., оо для статистики Бозе—Эйнштейна, / = 0, 1 для
статистики Ферми—Дирака, получим после логарифмирования
lnZ = 2)^/ln(l=Fe('4c"ei>/*7')):P1. (3.22)
i
Сравнивая с формулами (3.7) и (3.10) и учитывая (3.20),
находим
kT \nZ = — U + TS + Nlxc = — F + G = PV
(3.23)
Для свободной энергии получим из (3.23) соотношение
F = — kTlnZ + N\ic, (3.24)
откуда можно получить связь между всеми остальными
термодинамическими величинами.
Задачи
3.1. Внутренняя энергия, давление и удельная теплоемкость
электронного газа
Вычислить внутреннюю энергию и давление электронного газа при
абсолютном нуле температуры и при 300 К. Рассмотреть электронный газ,
находящийся в медном бруске длиной /=1 м и сеченлем А=\ см2. Какой вклад
дают электроны в удельную теплоемкость?
Решение
В соответствии с формулами (3.16) и (1.2.22) определим множитель Ла-
гранжа а из соотношения
N = PjUi£W з/2 Г Vt dt 9 (ЗЛЛ)
Здесь \iA—масса атома, \i—масса электрона, р — плотность вещества. Для
вычисления определенного интеграла воспользуемся равенством (1.2.18). При
достаточно большой величине 6=—а входящим в это равенство рядом из
262
Гл. 4. Статистика квантовых процессов
экспонент можно пренебречь. Тогда
»'тН**(^Г '-">'" (■+»+■••)•
В первом приближении из формулы (3.1.2) имеем
_/ 3N у/3 h*
Подставляя в следующем приближении
—а(2)=— а(1) + А (3.1.4)
в формулу (3.1.3) и учитывая, что при достаточно низких температурах
— а^> 1, находим
_« a(2)_(^_j _^1 __^__, j. (з.1.5)
Согласно (3.14), свободная энергия электронов определяется выражением
f=__^2^V/2(/?r)6/2 J *3/2
L^+i dt-aNkT- (ЗЛ'6)
ЗЛ3 J ea+r +1
Разложив определенный интеграл с помощью равенства (1.2.18) в ряд и
подставив в выражение (3.1.5) для а, получим во втором приближении
^""10 \4ngV) \i L 3 V ЗЛ/ J /i4 J
(3.1.7)
Отсюда найдем давление
dF
P l dV jT
h* ( 3/V \2/3 N Tt . 5л2 /4я^1/\4/з ^2Г2~1 /Q , оч
="54wJ ет+^л~злг; "^~J- (зл,8)
Для внутренней энергии электронного газа в соответствии с (3.17) имеем
выражение
/l3 Ject+t+\
о '
Вычисляя определенный интеграл с помощью разложения в ряд и используя
формулу (3.1.5), находим
ЗЛ2/ 3/V \2/8 N Г 5яУ4^У\4/з ^2Г2 ]
В итоге для электронов в нерелятивистском приближении получаем
соотношение (ЗЛ8а)
Из формулы (3.1.10) при 7 = 0 находим нулевую энергию электронов
3^/_ЗЛ^у/з JV_ (3.1.Ц)
и°~ 10 \4KgV J р '
§ 3. Термодинамические величины
263
Обычно для металлов удельную теплоемкость относят к 1 кг вещества. Для
вклада электронов имеем
Cv~Vp [dTjv-~hT^v[ 3N J '• {6ЛЛ2>
В соответствии с тепловой теоремой Нернста теплоемкость cv равна нулю при
7 = 0 (см. § 5 настоящей главы). Подставив численные значения и учтя
значения, приведенные в § 2, найдем нулевую энергию электронов
3>(6,63-10-34)2 ( 3-8,4.1024 у/з 8,4» 1024
^о = ^-^ Ча.*,;.о.1п-Т QM.in-3i = 5,64.10e Дж.
*)■
10 V4*3,14-2.i0-4; 9,1Ы0-31
Зависящий от температуры член формулы (3.1.10) равен
5л2 ( 4ngV у/з ^2/г2Г2_5-(ЗЛ4)2 {4.3,14-2- 10-4у/з
(3.1.11а)
з v зл/ ; л4 ~~ з v 3.8,4.1 о24 j х
X
Г9,Ц.10-31.1,38.10-23.30012
L (6,63. ю-зу J =5'6*10-
При нагревании металлического бруска от абсолютного нуля до 300 К
внутренняя энергия электронов изменяется на величину
AU = U — (У0 = 5,6.Ю-б.5,64- 10е = 316 Дж.
Согласно формулам (3.18) и (3.1.11), давление электронов при Г = 0
составляет
2(/0,._ 2.5,64.10» ^3 83 10* ат
При нагревании до 300 К давление возрастает на величину
Р —Р0-3,83.106-.5,6-10-5 = 21,3 ат.
Поскольку при Т — 0 как U0, так и Р0 положительны, значение химического
потенциала при абсолютном нуле'
*с=Щг^ (злл3)
во всяком случае отлично от нуля. Вклад электронов в удельную теплоемкость
при Т = 300 К найдем по формуле (3.1.12)
_ 3,142.(1,38.10-23)2.9,1Ы0-31, 8,4-1024
°v~~ (6,63-Ю-34)2 8,9.10М0-4><
/ 4.Я 14.9. Ю-4 \2/з
X ( з.8,4.1024 ) 30° Дж/(КГ*К) = 5,7.10-4 ккалДкг-К).
Удельная теплоемкость меди составляет 0,093 ккал/(кг«К). На долю
электронов приходится только
cv _5,7.10-4
сСи 93. Ю-3
=0,6Н
3.2. Максимальная скорость электронов при абсолютном нуле
Вычислить максимальную скорость электронов в кристалле меди при
абсолютном нуле температуры. Чему равна дебройлевская длина волны этих
электронов?
264
Гл. 4. Статистика квантовых процессов
Решение
При абсолютном нуле состояние электронного газа является полностью
вырожденным: во всех квантовых состояниях от р = 0 до р = рмакс находится
по одному электрону. Ячейки с большими импульсами остаются пустыми.
Это является следствием теоремы Нернста (см. § 5). Интегрирование по всем
квантовым состояниям в целиком заполненных шаровых слоях фазового
пространства дает полное число электронов:
»-#£ \ РЧР=*^£«. (3-2.1)
о
Отсюда находим максимальную скорость
К ЗА/ h
4ngV ^
л I/ • (3-2-2)
4rcgl/ \i v '
Для заданных чисел (используем значение N из задачи 1.2 настоящей главы)
получаем
з/ 3-8,4-10" 6,63» Ю-3* . 1К7Л .
"макс = У 4.3,14.2-10-^ 9,11-10-зг М/С==1570 км/с-
Дебройлевская длина волны определяется из уравнения де Бройля:
?=£* (3-2.3)
Здесь k — волновой вектор. Его абсолютная величина £ = 2л/Я представляет
собой волновое число. Тогда длина волны де Бройля равна
*,=—. (3.2.4)
Подставив в формулу (3.2.2) выражение (3.2.4), найдем длину волны де
Бройля самых быстрых электронов
Я -Я - \/1*К (3.2.5)
Лмин — лг/макс— у ЗА/ "
Видно, что длина волны де Бройля и среднее расстояние между электронами
являются величинами одного порядка, из чего следует необходимость
применения квантовой статистики. Подставляя численные значения, получаем
, з/"4-3,14.2-Ю-4 АЛЛ |П 10
*мин= у э-8,4-10»* ==4>64-1°-1° м-
Замечание. При этих расчетах мы не учитывали отличия
эффективной массы от массы покоя электрона.
3,3*. Термоэлектронная эмиссия (эффект Ричардсона)
Никелевый электрод нагрет до Т =1600 К- Чему равен ток электронов,
испускаемых поверхностью ДЛ = 10"4 м2 = 1 см2?
Решение
Выберем в качестве оси г направление нормали к поверхности металла
(фиг. 52). Согласно статистической модели, использованной в гл. 2, § 5 для
# 3. Термодинамические величины
265
оценки давления, из всех частиц с компонентой скорости vz с выделенной
площадью 1 м2 столкнутся за 1 с только те, которые окажутся в объеме
|у2|-1 м3 (ve — в м/с). Проинтегрировав по всем направлениям импульса и
умножив на элементарный заряд, получим плотность тока эмиттированных
электронов
j = e^vzdN = ^pzdN, (3.3.1)
где dN—дифференциал числа частиц в объеме V=l м?.
гЬ
но/
У!
ъ
~ [ Фиг. 52. Схема наблюдения термоэлектронной эмиссии
J/B (НВ — батарея накала термокатода).
Для дальнейшего рассмотрения удобно ввести цилиндрические координаты
и разбить пространство импульсов на элементы объема
dpx dpy dpz = dpr pr с?ф dpg. (3.3.2)
Считая V = 1 м3, находим число ячеек в фазовом объеме АФ/:
г,- = |- Арх Ари Ар2 = -^ Apz АРг ДФ. (3.3.3)
Энергия электронов в цилиндрической системе координат записывается в виде
pl+Py+pl = P*r+plu (3.з.4)
Переходя к непрерывному распределению, с помощью этих соотношений в
соответствии с формулой (1.2.10) имеем для чисел заполнения
dN = _*. PrP,dp,dpt*p _ (3 з.5)
-p(«+W)+i
2\ikT
Предположим, что только те электроны, у которых 2-компонента импульса
удовлетворяет условию
Рг^Ро, (3.3.6)
могут выйти из металла. Тогда для плотности тока получим
оо оо 2Я
'J J J / . р*г+р2г\ . /
266
Гл. 4. Статистика квантовых процессов
Внутренний интеграл по б(ф равен 2л. Для интегрирования по dpz произведем
подстановку:
™р{щт)=у> exp(w)=i/»' exp(a+w)=c- (ЗА8)
Тогда имеем
Г Pzdpz _*С dy _
j (р* ^J-, w+u
p»cex4w+ "•
=,iferin (i+i)=^rin [exp(-a-4^fl)+i] • <3-3-9>
Интегрирование по частям дает для оставшегося интеграла
,= ЩР С p3rdpr
'Л8|0
(-+W)-
(3.3.10)
oexp a + ^-^L +1
Назовем энергетический барьер, который должны преодолеть электроны для
выхода из металла
внешней работой выхода. Химический потенциал
lic = — akT = Wi (3.3.12)
назовем внутренней работой выхода.
Во всех процессах, связанных с внешней эмиссией электронов, основное
значение имеет эффективная работа выхода Wa—W{. Она слабо зависит как
от геометрии поверхности, так и от физических процессов, приводящих к
испусканию электронов (см. табл. П. XIX и табл. 29)1}. Для определения
эффективной работы выхода Wа — W; можно воспользоваться одним из
эффектов, перечисленных в табл. 29 (см. задачу 3.4). Для измерения только внеш-
Таблица 29
Эффективная работа выхода (эВ) для различных
металлов с гладкой поверхностью, найденная
с помощью разных методов
Ва Pt Th W
Термоэлектронная эмиссия
Фотоэмиссия
Автоэлектронная эмиссия
2,1
.2,5
2,4
5,3
6,4.
5,4
3,35
3,5
3,35
4,5
4,6
4,4
3) Однако она может сильно зависеть от кристаллографических индексов
эмигрирующей поверхности. Например, для вольфрама, работы выхода для
различных граней отличаются на 0,8 эВ. — Прим. ред.
§ 3. Термодинамические величины
267
ней работы выхода можно воспользоваться, например, методом Дэвиссона и
Джермера, т. е. исследовать отклонение электронного луча при прохождении
через кристаллическую решетку гК
Подставляя
р* ==/ (3.3.13)
и учитывая выражения (3.3.11) и (3.3.12), получаем из формулы (3.3.10)
2ще^Т*\ tdt
о
exp t
kT
i)+,
Внешняя работа выхода Wа больше внутренней. Обратимся поэтому к
формуле (1.3.6). Предполагая, что
e(Wa-.wi)fkT>u (3.3.15)
можно ограничиться первым членом разложения в ряд. Тогда формула (3.3.14)
приводит в первом приближении к следующему выражению для
термоэлектронной эмиссии, выведенному Ричардсоном:
j^^T^w«-w»kT
(3.3.16)
В соответствии с формулами (3.1.3) и (3.1.11) внутренняя работа выхода
связана с энергией основного состояния U0 и давлением Р0 при Г = 0
следующим образом:
Г|«-а*Г=( ay" *!. Б £« ^ (3.з.,7)
1 \4ngV J 2\i 3 N 2 N v '
(V=\ м3, N— число частиц в 1 м3, Ы/У = р/\хд).
Найдем численное значение W ?.
(3-8,8-103-6,02- 1026)2/з (6,63-Ю-34)2 -0 -
w 1 = -7- = / ,0 ЭЬ.
(4.3,14.2-58,7)2/3 .2.9,1Ы0-31.1,60.10-19
Более точные исследования дают U7f-== 11,7 эВ, U?fl=16,0 эВ 2). Эффективная
работа выхода для никеля при термоэлектронной эмиссии равна Wa — W{ =
= 4,3 эВ. Тогда плотность тока, отнесенная к ДЛ = 1 см2 = 10~4 м2, согласно
формуле (3.3.16), есть
2-3 14-1 60-10~19.2
/= (66з'-10-з")з 9ЛЫ0-"-(1.38-10-^2.1б00^х
х^р^^Г] =9-ю-» А/см.
1,38. Ю-23-1600
« См. [12], п. 6.1.
2) Формулы (3.3.17) имеют смысл только для сильно упрощенной модели
металла, в которой не учитываются кулоновское взаимодействие между
электронами и другие факторы. Для реальных металлов следует говорить лишь
о непосредственно наблюдаемой величине—эффективной работе выхода.—
Прим. ред,
268
Гл. 4. Статистика квантовых процессов
Для экспериментальной проверки этого закона удобно использовать
логарифмический масштаб для плотности тока. Тогда из формулы (3.3.16) имеем
1П-J^Cjl --£?-,
(3.3.18)
т. е. зависимость In (//Г2) от 1/7 изображается прямой линией.
3.4*. Измерение работы выхода по Фаулеру
с помощью фотоэмиссии
Согласно Фаулеру, для определения работы выхода вольфрама,
покрытого тонким слоем окиси бария, измеряется ток электронов, вылетающих из
металла под действием света различной частоты при разных температурах.
При этом интенсивность падающего света все время поддерживается
постоянной. Экспериментальные результаты приведены в табл. 30. Значения тока
отнесены к току эмиттированных электронов, создаваемых светом с частотой
v = v0 = 4,663« 1014 Гц при температуре Г = 710 = 300К. Найти из приведенных
данных работу выхода.
Таблица 30
Ток фотоэмиссии из вольфрама, покрытого
окисью бария, при Т = 300К для
различных частот света
v, 10»4 Гц
4,423
4,477
4,543
4,603
4,663
///о
0,030
0,070
0,194
0,460
1,000
V, 10" Гц
4,723
4,783
4,888
5,003
5,128
/У/о
1,96
3,42
7,35
12,9
22,1
Решение
Обратимся к задаче 3.3 и будем считать электроны в металле идеальным
газом Ферми. Геометрические условия соответствуют фиг. 52. Как
постулировано Эйнштейном, под действием света металл могут покинуть только те
электроны, для которых справедливо соотношение
или рг^р0 = y2\i(Wa—hv).
(3.4.1)
Это соотношение следует использовать вместо формулы (3.3.6). Величину
(3.3.11) для фотоэмиссии нужно заменить величиной, найденной по
формуле (3.4.1):
2\х
= Wa
2ii (Wa-hv)
2ц
••Wa — hv.
(3.4.2)
§ 3. Термодинамические величины
269
Плотность тока / электронов, вылетающих под действием света с частотой v,
найдем по формуле (3.3.14)
. 2nge\ik2T2
00
С Ш
(3.4.3)
Здесь А — постоянная, зависящая от интенсивности падающего света и от
вероятности освобождения электрона одним фотоном. Далее положим
_2л£ф/е2
hvG=Wa-Wif
h(v — vG)
kT '
(3.4.4)
Здесь vq — граничная частота. В отличие от предыдущей задачи при
вычислении интеграла (3.4.3) нельзя ограничиться только первым членом разложе-
У>Ув
Фиг. 53. К определению эффективной работы выхода
ния. Естественно использовать для v^vq и, следовательно, 6^0 формулу
(1.3.8), а для v^zVfi или 6^0—формулу (1.2.18). Объединив результаты,
имеем
/ = Л072Ф(6)
где
л2б
„зб
Ф(6) =
я2 , б2 /
9
-б
-2б
-зб
...).
6<0,
:0.
(3.4.5)
(3.4.6)
Для определения работы выхода и граничной частоты рассмотрим сначала
(фиг. 53) график функции
yB = \g<D(6). (3.4.7)
270
Гл. 4. Статистика квантовых процессов
С помощью приведенных в табл. 30 экспериментальных значений отношения
±=ПЧу/кТ)
/„ /(ftv„/fer0) t3-4")
составим функцию
У^^ТТ2 (3-4.9)
/о7
и на том же графике изобразим полученные значения как функцик)
независимой переменной
x=w (3.4.10)
(фиг. 53). Согласно формулам (3.4.5), (3.4.9) и (3.4.10), полученная .кривая
описывается уравнением
У = Ы^т-+Ы®(х). (3.4.11)
/о
Отсюда видно, что экспериментальную кривую у = у(х) можно совместить
с теоретической кривой (3.4.7) с помощью параллельного переноса
х—+х--^ = Ь, У-+У—Ч-у- = Ув.
При заданных численных значениях имеем для величины смещения в
отрицательном направлении оси абсцисс
^=74
kT
Отсюда получаем искомую работу выхода
hvQ=Wa — Wi = U kT = 74-1,38-Ю"23-300 Дж =
74-1,38-10~23.300 , nl _
— =1,91 эВ
~~ 1,6-Ю-19
и граничную частоту
74kT 74» 1,38. Ю-23-300 . AQ 1Л14 _
V° = — = 6,63-10-34 -4,68-101* Гц.
3.5. Релятивистский предельный случай
вырожденного электронного газа
В звезде большой плотности электронная плотность N/V = 1042 м~3,
температура Г=1011К. Найти вклад электронов в удельную теплоемкость.
Чему равно давление электронов?
Решение
Предположим, что кинетическая энергия электронов велика по сравнению
с их энергией покоя, и запишем для энергии электронов
г=ср. (3-5Л>
§ 3. Термодинамические величины
271
Тогда имеем из формул (3.1) и (3.17) соответственно
Ar 4jtgV С е2 de
N = ^\ еа+ФТ + Г (3-5.2)
о
V = ] **"= ~ЛГ) e*+e/kT + l- (3.5.3)
о о
Давление найдем из выражений (3.22) и (3.23):
4^5? In (1 I c-*-*/bT)2*dz_*ngV Г g8^ ,354^
О о
Сравнение с формулой (3.5.3) показывает, что в ультрарелятивистском случае
Р2^>\4°2 справедливо соотношение
С помощью подстановки e = kTt из формул (3.5.2) и (3.5.3) получим
xr 4ngV/e3r3f t2dt
^^-W-j-^Т^Г^ (3.5.6)
о
U ~ e»A» J e«+< + 1 ' <3-5-7)
о
Используя соотношение (1.3.8), находим
,, 4яяУ#>Г3 Г (—a)3 .я2, . . 1
^ = —IF" ["4 +2-<-«> 2+"'J ' (3-5.9)
Главный член ряда (3.5.8) дает в первом приближении
ch 3/*"ЗЛГ
-a==WV 4^7- (3'5Л°)
и в численном виде
__ _3-108>6t63-10-84 з/ з>1042
a~ 1,38. Ю-23-1011 Г 4.3,14.2"" *
По формуле (3.5.9) определим внутреннюю энергию (в единице объема):
4.3,14.2.(1,38.10-^.1011)4/7^ ^ )=10.10ппж
(з.108.б,бз.ю-зт V 4 2 /
Энергия покоя равна
£/0 = %0с2 = 1042-9,1 • Ю-31 (3.108)2 = 8,2-1028 Дж,
т. е. ее можно в первом приближении считать малой по сравнению с внут*
ренней энергией.
272
Гл. 4. Статистика квантовых процессов
Давление электронов, согласно формуле (3.5.5), составляет
1,0-1031
Р = -
Н/м2 = 3,5.1025 ат.
Для определения удельной теплоемкости нужно привлечь второй член
формулы (3.5.9). Тогда имеем
(3.5.11)
Г -f?V\ _4rc3gfc2 f 3N \ g/3
v~\dTJv~' ch \4ngVJ
При заданных значениях получим в расчете на 1 м3:
Ср=1,4.101в ккал/м3-К.
3.6*. Конденсация Бозе — Эйнштейна (^-точка гелия)
Жидкий гелий обнаруживает вблизи абсолютного нуля ряд замечательных
свойств. Удельная теплоемкость увеличивается от 0,14 кал/(г-К) при 1,32 К
до максимального значения, превышающего 3 кал/(г-К) при 2,19 К, а затем
снова падает в узком температурном интервале в 0,002 К почти до 0,5кал/(г-К)
(Х-кривая удельной теплоемкости, изображенная на фиг. 54). Точно так же
з,о
I 1fl
1,2 1,6 2,0 2fi 2,8
_^ . T, К
Фиг. 54. Удельная
теплоемкость гелия вблизи
абсолютного нуля. (По работе [9].)
м
ом
о,т
0,140
0,136
о,т
0,128
0,124
["[-+4 м
П \\
М
п
11 i i \ i
L 1 If 1 И
12 3
4 5
Фиг. 55. Плотность
жидкого гелия вблизи
абсолютного нуля. (По работе
19].)
при повышении температуры от 0 К плотность жидкости растет до Я-точки
и резко уменьшается после нее (фиг. 55), тогда как электро- и
теплопроводность изменяется после Х-точки примерно в 10б раз. При Т < 2,19 К жидкость
проявляет свойство сверхтекучести, т. е. обладает исчезающе малой
вязкостью; в частности из узкого капилляра она вытекает быстрее, чем газ. При
ламинарном течении одновременно существуют потоки двух типов: во-первых,
сверхтекучий поток, не зависящий от давления и практически не имеющий
вязкости, во-вторых, поток, обычным образом зависящий от перепада
давлений и от геометрических размеров.
Качественное объяснение этого фазового перехода второго рода впервые
дали Лондон и Тисса, которые исходили из модели идеального газа Бозе —
Эйнштейна.
Исследовать для идеального газа Бозе—Эйнштейна распределение по
импульсам р>0 и р = 0. При какой температуре Гбэ наступает вырождение
частиц по импульсам р = 0 (конденсация Бозе—Эйнштейна)? Найти зависи-
§ 3. Термодинамические величины
273
мость доли вырожденных частиц от температуры. Определить, чему равна
плотность газа Бозе—Эйнштейна, если идентифицировать температуру Я-точки
Т = 2,19 К с температурой конденсации Бозе—Эйнштейна? Найти долю
конденсированных атомов при Г = 2 К.
Решение
Существует две модификации гелия, отличающиеся значением полного
спина орбитальных электронов. У парагелия электронные спины направлены
навстречу друг другу, у ортогелия спины направлены в одну сторону
(фиг. 56). Соответственно спиновое квантовое число ns для парагелия равно
*4
''vZ^* *t>
*• Фиг. 56. Спиновые состояния пара- и орто-
Парагелии Ортогелий гелия.
нулю, а кратность вырождения g — 2ns-\-\ = 1. Для ортогелия спиновое
квантовое число равно единице, кратность вырождения g = 2ns-\-1 =2« 1 + 1 =3 1).
Для упрощения отождествим жидкий гелий в парасостоянии с
идеальным газом Бозе—Эйнштейна. Пусть в объеме V содержится N частиц. Число
частиц в состоянии с наименьшей энергией 80 = 0 и импульсом р0 = 0
положим равным N0. Число прочих частиц (р[ > 0) обозначим через Np. > 0.
Согласно формуле (1.1.24), полное число частиц с импульсом р. > 0
составляет
а се 1 —1
Переходя от суммирования к интегрированию, можно написать
_4 V2ngV ,.т.з/%} VIdt
N
рс>° ¥
о
№Т)Ч*^ е;+^- (3.6.2)
В интегральной формуле (3.6.2) состояния с р = 0, или t—О, не учитываются,
поскольку в числителе подынтегрального выражения стоит ]/"/.
Функцию вырождения в (3.6.2) в соответствии с формулой (1.3.6)
представим в виде
F- («) = 4= Г Y't £ е-(/п + 1)<а+/>Л, (3.6.3)
о т = 0
х) В отличие от парасостояния ортосостояние атома гелия—
возбужденное^—/7/? мл*, реду
274
Гл. 4. Статистика квантовых процессов
откуда после подстановки x = (m-{-l)t имеем
F-(a) = -4=l /*<?-*<** У -= У -г. (3.6.4)
i; I^J Z-<(m+i)3/2 Z^(m+1)3/2 l
г о m=0 m=0
Сумма (3.6.4) сходится только при
a = -i^0. (3.6.5)
Это означает, что химический потенциал \ic бозонов не может быть
положительным. Функция (3.6.4.) имеет наибольшую величину при а = 0 и равна
в этом случае частному значению ^-функции Римана
'®-.?.5йПрт-ма (3'6-6'
В результате получаем
Np.> 0<2,612 ^ (2щкТ)^ = ЛГмакс (Т). (3.6.7)
Таким образом, число бозонов с импульсом больше нуля ограничено. При
понижении абсолютной температуры, согласно формуле (3.6.7), уменьшается
и Ломаке (Т)- Оставшаяся часть бозонов
No(T) = N-NMm(T) (3.6.8)
накапливается на энергетическом уровне е0 = 0. Этот процесс называется
конденсацией Бозе—Эйнштейна.
Согласно формуле (3.6.8), конденсация Бозе—Эйнштейна возможна лишь
при условии
Ломаке (T)<N. (3.6.9)
Следовательно, она происходит при уменьшении температуры до некоторой
величины ГБЭ, зависящей от концентрации частиц N/V и определяемой
равенством
2,612-^ (2щкТБЭ)*'* = -JJ-, (3.6.10а)
или соответственно
'--«"»£ (^и
(3.6.10)
При Т < ТБЭ из формул (3.6.7) и (3.6.10) находим число частиц с
импульсом р > 0
"'>'-"(£-Г- ,3-бл"
Число конденсированных частиц с е0 = 0 равно
§ 3. Термодинамические величины
275
Ниже температуры Бозе—Эйнштейна (называемой также критической)
химический потенциал \ic газа Бозе—Эйнштейна равен нулю.
Концентрацию N/V при заданной температуре ГБЭ = Г^ = 2,19 К найдем
из формулы (3.6.10а)
УУ_2,612.(2-3,14.4.1,38»10-^з.2>19)^2_128 ^я м_3
v (6,02-102й)3/2.(6*63.10-34)3
Отсюда получим плотность
Р = ^ ^ = 1,28 • 1028 __!___ кг/мЗ = 0,085 г/см*.
По порядку величины она совпадает с экспериментальным значением (фиг. 55).
Доля конденсированных частиц при Т = 2 К составляет
1Н-Ш"'='-№=№
При температуре, лежащей всего на 0,19 К ниже температуры
Бозе—Эйнштейна 71БЭ = 2,19К, более 1/8 всех частиц Бозе—Эйнштейна находятся на
уровне 80 = 0. Таким образом, ниже точки фазового перехода конденсация
Бозе—Эйнштейна происходит сравнительно быстро.
3.7*. Термодинамические величины газа Бозе — Эйнштейна
вблизи критической температуры
Определить внутреннюю энергию, давление и энтропию газа
Бозе—Эйнштейна вблизи критической температуры ТБЭ. Исследовать поведение
удельной теплоемкости CV(T). Чему равна удельная теплоемкость парагелия с
плотностью N/V = 1,28-1028 м~3 и объемом ]/=1см3 при температуре:
а) Г = ГБЭ = 2,19К, б) Г = 2К, в) Г = 2,4К?
Решение
Исследуем сначала состояние при Т < ГБЭ, для которого множитель
Лагранжа а и химический потенциал равны нулю. Внутреннюю энергию
найдем по формуле (3.17)
и^У2пёУ^т^}^_йи
h* J gt_i
о
Вычисление интеграла дает
0 0 т= °
(3.7.2)
Следовательно,
u=*\Wv«№ (3.7.3)
276
Гл. 4. Статистика квантовых процессов
Отсюда получим давление при температуре ниже ГБЭ:
r~~3 V~ /г3 ' К ' ' '
Оно зависит только от температуры 7\ но не от плотности числа частиц N/V.
Это—результат конденсации Бозе—Эйнштейна. Поскольку величины U, Р
и \хс = 0 известны, энтропия S определяется по соотношению:
SsV + FV-QJJ + PV-N\bm (3.7.5)
Удельную теплоемкость находим из формулы (3.7.3)
'Щ\ _79,2gVkb/2(\iT)3/2_ 5 Ц
дТ )v~~ № ~~ 2 Т '
Чтобы вычислить внутреннюю (поступательную) энергию газа
Бозе—Эйнштейна в области чуть выше температуры Тъэ, рассмотрим число частиц N
как функцию множителя Лагранжа а и температуры Т. В соответствии с
(3.16) запишем
(3.7.6)
О ч '
(3.7.7)
Величина N (О, Т) идентична величине, определяемой выражением (3.6.7):
N (О, T) = NUZKC (Г) = 2,612 § (2n\ikT)*'* = Num (7БЭ) (ъ^А*'* •
(3.7.8)
Основной вклад в определенный интеграл дают малые значения t. Поэтому
можно приближенно написать
'-№-йИ(#-7г)Л~1^
dt
t)Vt
Производя замену уТ = у, получаем
Подставляя этот результат в соотношение (3.7.7) и разрешая относительно а,
находим
h«[N-NM3KC(T)}* _-h*[N-Nuw(T)]*
32n*g*V* (\ikT)3 ' ^c — 32n*\i*{gVkT)* ' W./.iu;
Затем химический потенциал можно вычислить по точкам. Его ход показан
на фиг. 57.
Внутреннюю энергию приближенно определим с помощью выражения
U(a,T) = U(0,T)+a(™)a=o. (3.7.11)
§ 3. Термодинамические величины
277
Из формулы (3.17) находим
3U _ 4 V2ngV\i3/2 (kT)5/2 Г /з/2 ea+t
)(ea+t-\
да'
/i3
l)2
(3.7.12)
Интегрирование по частям дает при а = 0
Применим при интегрировании формулу (1.3.8); тогда имеем
dU\ _ 3
cfc7\
а затем по формулам (3.7.11), (3.7.3) и (3.7.10) определяем
v Ъ\,7&у.** (kT)4* 01Qgh» [ЛГмакс {T)-N\*
h3 ' gVy.9/i Vkf '
Для удельной теплоемкости одноатомного газа Бозе — Эйнштейна в объеме V
получим по формуле (3.7.14)
79,2gVk^ (pTf 9,90- Ю-3 h*(NMaKC-N)( dNKa
(3.7.16)
где, согласно формуле (3.7.8),
С„=-
'О
(3.7.13)
(3.7.14)
(3.7.15)
-tfM
с+^
)■
dN
^кс==б1>7^И)з/2Г1/2#
(3.7.16а)
В точке Т = ТБЭ имеем #макс(ГБЭ) = М. Поэтому дополнительный член, по-
Z
£Э 2Тбэ ^БЭ *?£»
♦p ^иг- 57. Химический потенциал ju^
идеального газа Бозе—Эйнштейна. (По работе [15].)
являющийся при Т^ТБЭ, при температуре Бозе—-Эйнштейна равен нулю,
т. е. удельная теплоемкость при Т = ТЪЭ непрерывна.
278
Гл. 4. Статистика квантовых процессов
Подставив в формулу (3.7.16) выражение (3.6.10) для Т — ГБЭ, найдем
удельную теплоемкость
Cv (Тъ Э) = /0,08393 79,2Wfc = 1 $2Nk. (3.7.17)
Она оказывается больше, чем для классического идеального газа из
одноатомных молекул. Из формул (3.7.6) и (3.7.16) видно, что при повышении
температуры удельная теплоемкость возрастает вплоть до температуры Бозе—Эйнштейна
ГБЭ. Чтобы исследовать поведение Cv при температуре выше критической,
продифференцируем ее по Т. Производную слева в точке ТБЭ найдем по
формуле (3.7.6)
118,8#1/из/2/гб/2Г^2
= -^-Аг, — >0. (3.7.18)
/тБЭ-о Л3 v '
Для производной справа имеем, учитывая, что Nмшс (Тьэ) — N,
150,8gV/2 kb/iT$
БЭ+и \ vi УГБЭ-0
32gV\is/i кь/2ТЩ
(дСу
\дТ
(дСЛ fdCv
{дт)тьэ+о [дТ
/г3
Л3
<0.
(3.7.19)
Таким образом, первая производная удельной теплоемкости при Т = ТБЭ
испытывает скачок. При повышении температуры от нуля теплоемкость Cv
возрастает, достигая при Т = ТБЭ наибольшего значения, не являющегося,
-^7* Фиг. 58. Удельная теплоемкость идеального газа
О OJT^T^ 1,5ТБЭ2ТВЭ Бозе —Эйнштейна. (По работе [15].)
однако, экстремумом. При дальнейшем повышении температуры удельная
теплоемкость падает (фиг. 58). Для численного расчета вернемся к
идеальному газу,. Его удельная теплоемкость
CVM = %-Nk=%- 1,28- 1028.Ю-6.1,38-Ю-23-0,239-10~3 =
= 6,33-Ю-5 ккал/К.
Удельная теплоемкость бозонов в точке перехода ГБЭ = 2,19К, согласно
формуле (3.7.17), есть
1 92
Cv(TB3) = cv«n П50==8,1Ь10"6 Ккал/К'
и в расчете на т=\ г
с*(ТБЭ)
Cv 8,1Ы0-М03
= о ~~ 0,085
= 0,954 калДг-К).
§ 3. Термодинамические величины
279
Из формул (3.7.8), (3.7.6) и (3.7.3) получим для Т = 2 К
/ Т \з/2 / 2 \з/2
С*(2К) = СПГБЭМ^—J =8'1М0"Н2Й9) =7'°8 ККаЛ/К'
Для вычисления удельной теплоемкости при Т = 2>4К>ТБЭ используем
формулу (3.7.19). Она дает
fdCv\ = 32«10-6.43/2>(1,38-10-2Э)5/2>(2,19)1/2.0,239-10-3
V дТ У^БЭ+о-" (6,02- 102б)3/2 (6,63-Ю-34)3- ~~
==1,49-Ю-5 ккал/К2.
Отсюда находим
C„(2,4K) = C^2,19K) + 0,21 (^^j ^^ =
= (8,11 — 0,2Ы.49).10-б = 7,80.10-5 ккал/К,
и в расчете на 1 г
с„(2,4К). = 0,918 калДг-К).
Качественно это соответствует поведению удельной теплоемкости, показанному
на фиг. 54. Однако количественное различие очень существенно; как видно
из фиг. 54, у жидкого гелия рост Cv и последующий спад значительно круче.
Количественные характеристики жидкого гелия модель идеального газа
бозонов передает неудовлетворительно.
Упражнения
У.3.1. Определить давление электронов в серебре при Т — 0 (рА = 10,5 г/см3,
ЛАё = 107,9).
У.3.2. Чему равен абсолютный и относительный прирост внутренней
энергии электронов в 1 см3 серебра при нагревании от абсолютного
нуля до 1000 К?
У.3.3. Вычислить максимальную скорость электронов в серебре при
абсолютном нуле.
У.3.4. Чему равна дебройлевская длина волны наиболее быстрых
электронов в серебре при абсолютном нуле?
У.3.5. Чему равен абсолютный и относительный вклад электронов в
удельную теплоемкость серебра при 0QC? cAg = 0,056 ккал/(кг-К).
У.3.6*. Ток термоэлектронной эмиссии с вольфрамового электрода с
поверхностью А—2 см2 при температуре Т = 3500 К составляет 1170 А.
Вычислить по этим данным эффективную работу выхода Wa—W [.
У.3.7*. Ток электронов / при фотоэмиссии с вольфрамового электрода,
покрытого окисью бария (Wa — Wi=\t9 эВ), составляет 0,1 А.
Температура Г = 1000 К, частота света v = 1015 Гц. Какова должна
быть частота, чтобы электронный ток при неизменной температуре
увеличился в 10 раз?
У.3.8*. Вычислить давление Р0 и энергию U0 при Г = 0 для никеля
(Wa-W; = 4,3 эВ, Wa = \6 эВ, р = 8,3 г/см3, Am = 5SJ).
У.3.9. Чему равно давление электронов в звезде с плотностью числа
электронов yV/V=1040 м~3 и температурой Г=1010 К?
У.3.10. Вычислить для условий, указанных в предыдущем упражнении,
удельную теплоемкость, отнесенную к 1 м3.
У.3.11*. Чему равно число столкновений с единицей поверхности стенки
в релятивистском полностью вырожденном электронном газе с
плотностью N/V=1040 м-3 (v^c)?
280
Гл. 4. Статистика квантовых процессов
У.3.12*. Вычислить температуру Бозе—Эйнштейна ТБЭ для параводорода
(g=l) с плотностью N/V—1029 м-3.
У.3.13*. Чему равна доля микрочастиц с импульсом р>0 в параводороде
с плотностью Л7У=1029 м~3 при температуре Г==12К?
У.3.14*. Вычислить поступательную часть внутренней энергии, энтропии, а
также давления в параводороде при Г = 12 К, N/V=\02d м-3,
V=l см3.
У.3.15. Как изменится давление параводорода с температурой 12 К, если
уменьшить плотность N/V от 1029 до 0,75-1029 м-3? Насколько
изменится давление при дальнейшем уменьшении плотности до
0,50-1029 м-3?
У.3.16*. Вычислить множитель Лагранжа а и химический потенциал \хс для
параводорода при Г == 100 К, W/V=1029 м~3.
У.3.17*. Вычислить поступательную часть внутренней энергии и давления
для 1 кмоль параводорода с температурой 100 К- Чему равны
относительные отклонения от значений, предсказываемых
классической статистикой? (N/V=1029 м~3).
§ 4. КВАНТОВЫЕ СОСТОЯНИЯ ДВУХ- И МНОГОАТОМНЫХ МОЛЕКУЛ
Введение
Для объяснения температурной зависимости молярной
теплоемкости и увеличения числа степеней свободы системы следует
учитывать квантование движения микрочастиц, из которых
построены молекулы. Особое значение для термодинамических
параметров имеют вращательные и колебательные движения.
При не слишком больших температурах электронные переходы
на высшие энергетические уровни и вращение микрочастиц
вокруг собственной оси не играют существенной роли.
При образовании многоатомной молекулы из отдельных
микрокомпонент окружающей среде передается излишек энергии.
Поэтому возникшая сложная частица находится как бы в
потенциальной яме: ее энергия основного состояния zg отрицательна.
Наинизшие уровни особенно существенны для физического
исследования химических процессов, явлений абсорбции,
растворения и др.
В первом приближении различные квантовые состояния
можно считать не связанными друг с другом, т. е. энергию
можно представить в виде суммы не зависящих друг от друга
величин:
е = еКОл + еВр + ев + еА. + ег (4.1)
Согласно квантовой теории, колебательная энергия екол
двухатомной молекулы определяется следующим выражением:
t = A(De(l + -2-) (1 = 1кол = 0, 1, 2, ...)
(4.2)
§ 4. Квантовые состояния двух- и многоатомных молекул 281
Здесь со0 — частота колебания, пкол—квантовое число, Й(о0/2 —
энергия нулевых колебаний осциллятора. !В энергию
основного состояния е^. энергия нулевых колебаний не включается.
При повышении температуры амплитуда колебаний
возрастает; при этом становится существенным ангармонизм
колебаний, что приводит к появлению дополнительного члена в
формуле (4.2), вместо которой имеем теперь
еКол = ^0 ^n + ^j—xfi(o0 (n + j)2 • (4.3)
Здесь х—зависящий от вещества числовой множитель,
связанный с энергией диссоциации (см. гл. 5, задача 1.2).
Квантовомеханическое рассмотрение жесткого ротатора
приводит к следующему выражению для вращательной энергии евр
двухатомной молекулы:
• (4-4)
Введем момент инерции системы из двух материальных точек
;=F!=rS-(a+^; (4.5)
тогда их вращательное движение можно свести к движению
одной частицы, с массой [а, определяемой соотношением:
-=— + —. (4.6)
Н На Нв
Здесь г = га + гв — расстояние между вращающимися атомами.
Величина га в формуле (4.1) представляет собой энергию
возбужденных электронных состояний, гк—энергия, связанная
с ядерным спином.
Проведя суммирование по всем состояниям, получим
статистическую сумму для одной частицы:
2*-e/*r =2>-W* V V* V V* V BK/kTe-8g/kT =
= Z^Z%Z?Z%Zf. (4.7)
В этом выражении учтены все рассмотренные выше факторы.
Для двухатомной молекулы колебательный вклад в
статистическую сумму, согласно формулам (4.7) и (4.2), равен
%щ(п + 11г)\ _ ехр (—i(n0/2kT)
2<п =у схр ( ° (/| + 1/г) ) = ехр (
КШ1 2* PV kT J 1—exp(—
ехр (— T0/2T)
кол -,Л^ух ут 1-, ехр(-К/^)
1-ехр (-Г0/Г)
, (4.8)
282
Гл. 4. Статистика квантовых процессов
где
Т0 = Щ±. (4.9)
При рассмотрении вращательных движений нужно учесть, что,
согласно квантовой теории, каждому квантовому числу nBV = l
соответствует 2/+1 возможных значений проекций момента
на направление внешнего поля. Поэтому для вращательной
части статистической суммы имеем
со
2$4S(2/+1>exp(-
2JkT
Т1=0 V '
(4.10)
Здесь
Т*=ш- (4Л1)
Величина т для молекул из одинаковых атомов равна двум, а
для молекул из разных атомов—единице (см. гл. 2, задачу 3.3).
Для вычисления Z$ при температурах Т >Tr удобно
использовать разложение Эйлера—Маклорена
СО 00
Х/(/г) = С/М^ + 1/(0)-1/'(0) + 4Г(0)-
л = 0 %
Тогда из формулы (4.10) получим формулу Мулхолланда (см.
задачу 4.3)
Энергия ек, связанная с ядерным спином, настолько мала,
что обычно можно считать
е~вк/кт = 1.
Поэтому часть статистической суммы
ZK = ^e"Klk\ (4.14а)
—>■
связанная со спином ядра s, равна статистическому фактору
вырождения gK, определяемому числом различных спиновых
состояний ядра.
§ 4. Квантовые состояния двух- и многоатомных молекул 283
Часто бывает целесообразно рассматривать одновременно
спиновые состояния и другие квантовые состояния, в особенности
вращательные. Статистическую сумму нужно тогда просто
умножить на число gK различных значений ядерного спина,
возможных при данном вращательном состоянии.
Кратность вырождения gK определяется спиновым квантовым
числом ядра ns (см. табл. П.XX). Для одноатомной молекулы
имеем
gK = 2ns+l
(4.146)
В двухатомной молекуле АА , состоящей из одинаковых атомов,
ядерный спин и молекулярное вращение связаны. Четному
(нечетному) значению векторной суммы s^Sg двух спинов
соответствует четное (нечетное) значение вращательного квантового числа
/ для основного электронного состояния. Кратность вырождения
ядерных уровней различна для четных и нечетных /. Если снова
через ns обозначить спиновое квантовое число ядра, то для
молекул с ферми-ядрами (/г, = 1/2, 3/2, ...) кратность
вырождения при четном полном спине, или четном вращательном
квантовом числе, составляет
gg = ns(2n,+ l), (4.14в)
тогда как при нечетном полном спине молекулы
& = (л, + 1)(2л,+ 1). (4. Иг)
Для молекул с бозе-ядрами (ns — 0, 1, 2, ...) имеем, напротив
gg = (ns+\)(2na+l), *„ = М2л,+ 1). (4.14д)
Таким образом, вращательная статистическая сумма для
молекулы, у которой атомные ядра представляют собой фермионы,
например, для молекулы водорода (п5 = 1/2), имеет вид
ZSP = ns(2n.s+l)Zg+(ns+l)(2ns+l)Za
(4.15а)
тогда как для молекулы, у которой атомные ядра—бозоны,
например, молекулы дейтерия (ns = \)
ZBp = (ns+\)(2ns+l)Zz + ns(2ns+\)Zu
(4.156)
284
Гл. 4. Статистика квантовых процессов
причем
/=1,3,5...
(4.16)
где т=2.
В случае высоких температур формулы (4.15а) и (4.156)
принимают вид
2;1р>ш = 4-(2^+1)2Ё(2/+1)^^+1>^. (4.15в)
Здесь, как и в формулах (4.15а) и (4.156), уже учтен вклад
ядерного спина во вращательную статистическую сумму.
Кратность вырождения за счет ядерного спина составляет
gK=(2ns+l)\ (4.15г)
В молекуле АВ , состоящей из двух различных атомов,
вращательное квантовое число и ядерный спин независимы друг
от друга. Для всех вращательных состояний кратность
вырождения по ядерному спину одинакова:
fe=(2/i,A+l)(2n,B + l), (4Л?)
где nsA и nsB— ядерные спины атомов А и В. Электронные
возбужденные состояния дают лишь малый вклад в статистическую
сумму, поскольку расстояние между уровнем энергии ех
основного состояния и более высокими возбужденными уровнями
весьма велико. Для учета возбужденных электронных
состояний положим энергию ех основного состояния равной нулю,
чтобы энергия возбуждения eel- = ef-(i = 2, 3, ...) определяла
положение возбужденного уровня. Тогда для множителя Z^
в одночастичной статистической сумме получим
z?=2&*-e'/ftr- (4Л8)
Суммирование распространяется на все возбужденные состояния
и на основное состояние с е^О.
Фактор вырождения g£ в (4.18) учитывает расщепление
электронных возбужденных уровней на &• близко расположенных
подуровней, связанное со спином и с орбитальным моментом
электронов. Если обозначить через L результирующее орби-
§ 4. Квантовые состояния двух- и многоатомных молекул 285
тальное квантовое число, а через ns — результирующее
спиновое квантовое число, то имеем1У
gi = (2L+l)(2ns + l). (4.18а)
Пример 27
В общем случае основное состояние (главное квантовое число яе=1)есть
синглет, так что gi=l. Однако у кислорода основное состояние расщепляется
на три близко расположенных подуровня. Поэтому для кислорода в основном
состоянии нужно положить gi = 3. Первый возбужденный уровень кислорода
расщеплен в дублет, поэтому здесь g2 — 2.
Молекулы из трех и более атомов имеют настолько большой
момент инерции, что вращательные состояния полностью
возбуждены уже при нескольких градусах выше абсолютного нуля.
Поэтому для многоатомной молекулы вращательную часть
статистической суммы можно вычислять по классической формуле
(3.4.7) гл. 2.
Для колебательной части статистической суммы
многоатомной молекулы имеем аналогично формуле (4.8):
3 " " 6 ехр( — i(Dj/2kT)
Z™*= 11 i_exp( —Асо^/ЛГ)" (4Л9)
В отличие от вращательных колебательные степени свободы,
как правило, полностью возбуждаются только при очень
высоких температурах.
Статистическая сумма Z для квантовых состояний N молекул
получается из параметров, выведенных для одной молекулы,
путем возведения в степень N. В итоге с учетом
поступательного члена для статистической суммы газа из N частиц
имеем выражение
7 —Zil) — * /7<1) 7<Ъ71Х) 7(1>7(1>7(1>^
(4.20)
где, согласно формуле (3.1.8) гл. 2,
1} Строго говоря, орбитальный момент L для молекулы смысла не имеет
из-за отсутствия сферической симметрии. Однако имеет смысл величина Л —
проекция момента на ось молекулы, пробегающая значения 0, 1, 2, ... . Все
электронные состояния с Л Ф 0 двукратно вырождены, а с Л=0 не
вырождены. У кислорода в основном состоянии Л = 0, S=l,a в первом
возбужденном S — 0, А Ф 0, чем и объясняется приведенная в примере 27 величина
его статистического веса. — Прим. ред.
286
Гл. 4. Статистика квантовых процессов
и член, соответствующий основному состоянию,
Zf = e~^kT. (4.22)
При больших значениях N для N\ можно пользоваться
приближенной формулой ЛП « NN/eN.
Задачи
4.1. Термодинамические величины для двухатомного газа.
Вклад колебаний
Путем исследования полосатого спектра молекулярного водорода Х)
установлено, что круговая частота со0 нормальных колебаний двух атомов
составляет 8,28-1014 с-1. Вычислить отсюда колебательную часть молярной
теплоемкости водорода и вывести формулы для энтропии и для внутренней энергии.
Как ведут себя найденные величины при высоких и при низких температурах?
Решение
Согласно формуле (4.8), имеем для колебательной части статистической
суммы:
7<1>_УеХпГ (-1 1\^°°1_ exp (-1m0/2kT)
2кол_2, exp |^n+_)_j_ ,_ехр(_ Wftr). (4-1.1)
Отсюда для колебательного вклада в свободную энергию, отнесенного к 1 кмоль,
находим
FKm = -NAkT In Z<n=^+ NAkT In (1-e-W*!). (4.1.2)
Для энтропии получаем
внутренняя энергия равна
UKo^NAzKOn = FKOS + TSKM = NAf^~j^r—\ (4.1.4)
Из формулы (4.1.4) находим вклад колебаний в молярную теплоемкость
идеального газа при постоянном объеме:
<=.—(*>■)„-*(&) Ф*=$- ,4''•5,
Для обсуждения выведенных формул положим
Г0=^. (4-1.6)
В данном случае
го=1'05-!У.1о^-1014-бзоок- (4Л-6а)
*> См. [12], п. 6.4.
§ 4. Квантовые состояния двух- и многоатомных молекул 287
При низких температурах 7 <^70 можно считать ехр (Т0/Т) ^> 1, тогда из
формулы (4.1.5) следует
(Су кол)7,« Т{
,-«&)•
-ftw0/fcr
(4.1.7)
В соответствии с законом Нернста колебательная часть удельной теплоемкости
стремится к нулю при приближении температуры к абсолютному нулю.
Согласно формуле (4.1.3), аналогичным образом ведет себя и энтрюпия, в то
время как свободная и внутренняя энергии, как видно из формул (4.1.2) и
(4.1.4), стремятся к энергии нулевых колебаний
йсоо
Uo
NA-
(4.1.8)
В случае очень высоких температур Т^>Т0 экспоненциальную функцию
в выражении (4.1.5) можно заменить на \ + Т0\Т\ тогда
(Cv кол) т» т0 — R у 1 12 7^^"/
ермодинамических функций F, U, S
(^кол)г» т0 = —о %Т 1п ~т\у (Sko2i)t»Toz
(4.1.9)
(Укол)т*ТЛ ~
2
* о
■RT.
1 + 1п7/70'
(4.1Л0)
Таким образом, при высоких температурах двухатомная молекула ведет себя
так, будто она имеет две колебательные степени свободы, каждая из которых
в соответствии с законом равнораспределения обеспечивает вклад во внутреннюю
энергию, равный £772.
0,8
^0,6
0,2
О 0,2 ОА 0,6 0,8 1,0 1,2 1,4 Фиг- 59. Колебательная часть молярной
T/Tq теплоемкости. (По работе [17].)
На фиг. 59 показана зависимость колебательной части молярной
теплоемкости от температуры 7. Для водорода полный вклад колебаний,
соответствующий закону равнораспределения, достигается только при температуре выше
Г0 = 6300 К, когда уже происходит диссоциация молекул.
4.2. Колебательная часть термодинамических величин.
Учет ангармонизма
При больших амплитудах колебания становятся ангармоническими. Тогда
энергию состояний приближенно можно представить в виде
е„=(и-4)^)[1-*(/1+т)] (п = 0, 1,2, ...). (4.2.1)
288
Гл. 4. Статистика квантовых процессов
Вычислить поправку к молярной теплоемкости Cv, возникающую из-за ангар-
монизма, для основного состояния водорода при температуре Г=1220дС.
Связь коэффициента ангармонизма х с энергией диссоциации ер (см. гл. 5, § 1)
и круговой частотой со0 определяется выражением
(4.2.2)
Энергия диссоциации 8/> для водорода равна 4,47 эВ, круговая частота
колебаний со0 = 8,28.1014с-1.
Решение
Будем исходить из статистической суммы
п = 0 /г=0 I
(п + 1/2)Гш1\-х(п+*/2)]}
kT
(4.2.3)
Для упрощения положим
jfcco
и тогда получим из формулы (4.2.3), преобразуя и разлагая в ряд
2£о>л=е-("/2)(1-л:/2) V в-ли[1-*(л+1)] =
л=0
= е-(и/2)(\-х/2) J] e-H«[l + (/i+l)/WM+..-J.
л=0
Воспользовавшись соотношениями
CD СО СО СО
1 d
(4.2.4)
е-пи —
\ — е~и> du
2--—2>-. ££
е-пи =
л=0 " " /г = 0 /г=0 п=0
со
/г=0
с учетом того, что е^П(°/кТ <^ if можно переписать выражение (4.2.4) в виде
*-^w",,-"m[idi=.+-(»-=)i'-+-]-
L ч ' л=0 J
ee-(W2*r)(»-*/2) Г1 + 2х^е-*«/*г+ .. 1 .. (4.2.5)
Внутреннюю энергию на 1 кмоль найдем по формулам (3.16) и (3,12) гл. 2:
U = F-T ^у = -RT (in Z$b-^ T InZSL) = RT* ^^. (4.2.6)
Следовательно,
^т('-т)+^гМ
(4.2,7)
§ 4. Квантовые состояния двух- и многоатомных молекул 289
Для водорода мы нашли [см, (4.1.6а)], что
Го = ^ = 6300 К.
Поэтому для заданной температуры действительно можно считать, что
e-h»/kT<u
Тогда из формулы (4.2.7) найдем зависящую от температуры часть поправки
к энергии U:
AU = 2XRT*±(^e-b°^=2xRT0(^-iy-T'/T. (4.2.8)
Из (4.2.8) находим поправку к теплоемкости при Т <^ Т0
Подставляя численные значения, получаем по формуле (4.2.2) коэффициент
ангармонизма х:
6t63.10-°4.8t28.1QM _QQo0
8-3,14.4,47.1,60- io-i»~"u,u
Отсюда имеем поправку к энергии
Д^ = 2-0,030-8,314.103.6300^—1+^] e-63ooyi493= i>5.105 Дж
и поправку к теплоемкости
ДС; = 2.0,030-8,314.103.2,39.10~4 (т^)'(у^^2) б"63оо/1483 =
= 7.10-3 ккал/(кмоль-К).
Относительное отклонение от измеренной величины Cv (1493) « Cv (1500)=2,89 /?
(см. табл. П.Х) составляет
=^-- 7-10-3 =0,009,
2,89/? 2,89-1,987
т. е. чуть меньше 1%.
4.3. Вращательная часть удельной теплоемкости
Получить формулу для вращательной части термодинамических функций
F и S. Чему равен вращательный вклад в удельную теплоемкость хлористого
водорода НС1 при температуре —85Q С (точка кипения при нормальном
давлении)? Момент инерции J составляет 2,60* Ю-4? кг«м2.
Решение
Согласно формуле (4.10), вращательная часть статистической суммы для
двухатомной молекулы имеет вид
ZS(-±j>+.)«, [-*$£].
В рассматриваемом случае т=1. Вырождение по ядерному спину в данной
задаче несущественно.
290
Гл. 4. Статистика квантовых процессов
Для малых значений
можно ограничиться первыми двумя членами суммы и написать
Z$ = — (1 +3e~2TR/T). (4.3.3)
Для больших значений Т > Тц используем формулу Эйлера — Маклорена (4.12).
Обозначив
(2/ +1) ехр [- /(/ + !)Г/г] = / (/), (4.3.4)
p(Orf/+|/(0)-l/'(0)+7-|o/"'(0)-3o^o/v(0)±... 1-
о J
(4.3.5)
С. (4-3.6)
получим
zBp-T
L0
Произведя в первом члене замену
/(/ + 1)7Уг
т
найдем
о о
Далее, имеем
/(0)=1, /'(0) = 2—^, /'"(0) = -12^+12^|-^|> (4.3.8)
поэтому из формулы (4.3.5) следует
^=^Ы¥+гЗ+-У (4-з-9)
Из формул (4.3.3) и (4.3.5) находим вращательную часть свободной энергии,
отнесенную к 1 кмоль
FBp=-RT\nZ$ =
■RT\n(\+3e-2TR/T) + RT\nx (Т < TR),
(4.3.10)
■RT [ln^-+ln(l + l^+l^+...)"lnt] (T > TR).
С помощью разложения в ряд получаем по формуле (3.15) гл. 2
s f^Y_
?^e-iVr(l+2^+...)-/?lnt (T<TR),
(4.3.11)
§ 4. Квантовые состояния двух- и многоатомных молекул 291
а отсюда по формуле (2.7) гл. 2
fdS\ f^p1*-27'*77' (Г<Г«>>
*--rM'-(,(1+i?S+...) <^>. ,4'312'
Из верхней формулы (4.3.12) видно, что вращательная часть удельной
теплоемкости стремится к нулю, когда температура приближается к абсолютному
нулю. При этом газ ведет себя, как одноатомный. При увеличении
температуры Cv вр растет до максимального значения 1,1/?, а затем асимптотически
приближается к R.
Для хлористого водорода имеем
П*_ (1,05-10-»)» -
R 2Jk 2-2,60. Ю-47-1,38- Ю-23 ' Л*
Для точки кипения при нормальном давлении (Т = —85° С= 188 К) по
нижней формуле (4.3.12) находим
Отклонение от классического значения составляет всего 0,015%.
4.4. Относительное содержание орто- и парамолекул
в водороде и дейтерии
Водород, как и его изотоп дейтерий, представляет собой смесь двух
модификаций, отличающихся ядерными спинами (орто- и парасостояние).
Молекулы водорода с нечетным суммарным ядерным спином называются орточасти-
цами, молекулы с четным полным ядерным спином — парачастицами. Наоборот,
молекулы дейтерия с четным суммарным спином называются орточастицами,
с нечетным суммарным спином — парачастицами. Поскольку при соударениях
вероятность изменения ядерного спина очень мала, содержание этих
компонентов в смеси изменяется очень медленно. По указанной причине
термодинамическое равновесие устанавливается за очень долгое время (см. задачу
3.5 гл. 5).
Найти относительное содержание орто- и парамолекул в равновесном
состоянии при очень высоких и очень низких температурах. Моменты инерции
молекул водорода и дейтерия равны соответственно 0,47-10~47 и 0,93-10~47 кг«мв
(см. задачу 1.8 гл. 5).
Решение
У двухатомных молекул, состоящих из одинаковых атомов, суммарный
ядерный спин и вращательное квантовое число имеют одинаковую четность.
Вращательный член статистической суммы водорода определяется
формулой (4.15а)
Z% = ns (2/г,+ 1) Zg + (ns+ 1) (2ns+ 1) Za. (4.4Л)
Для атома водорода спиновое квантовое число ns = l/2.
Для дейтерия, согласно формуле (4.156), имеем
Z% = (ns+\)(2ns+\)Zg + ne(2ns + l)Za, (4.4.2)
где ns—\. Формулы (4.4.1) и (4.4.2) относятся к одной частице.
292
Гл. 4. Статистика квантовых процессов
Согласно формуле (4.16), можно написать
Z,=T t <2/ + l>exPr-i£+Jil£l. (4.4.3)
/ = 0,2, 4.-
Z*=4 2 (2/+l)exp[-^+№]. (4.4.4)
где
/=1,3,5
т«-ш- (4A5)
С помощью формулы (4.4.1) находим содержание орто- и параводорода:
N (орто-Н2) Z (орто-Н2) _(я,+ 1) Z„ _(1/2+ 1) Z„ Z„
W(napa-H2) Z(napa-H2) гг^ ~~ Z^/2 ~~ Z^ ' * '
а с помощью формулы (4.4.2) — содержание орто- и парадейтерия:
^(opTo-Da)==Z(oPTO-D>) =(ns+\)Zg^(1 + 1) Zg =^Zg _
N (napa-D2) Z(napa-D2) nsZa Zu Zu'
При очень низких температурах из формул (4.4.3) и (4.4.4) следует, что
Zg—»1, Za—+0.
Тогда формула (4.4.6) дает
\Ш*Ш -0, (4.4.8)
[Z (napa-H2)J г-*о v '
т. е. при очень низких температурах водород постепенно переходит в пара-
состояние / = 0, 2, 4 Наоборот, из формулы (4.4.7) видно, что
[Z (opTo-D2)
Z(napa-D2)
—*оо. (4.4.9)
г-*о
У дейтерия равновесие при низких температурах сдвигается в сторону орто-
состояния / —0, 2, 4, ... .
Для определения равновесного состояния при очень высоких
температурах T^Tr запишем вместо выражений (4.4.3) и (4.4.4):
*,-ЕЫ''>=£ (4Г+.)ехр Г_ 2/'(«'+0 7*1 ^
/' = 0 L J
2. = 2/.(П- t (4/ЧЗ)ехр LiWWl . (4.4.11.)
2/' = 0
Введем в формулах (4.4.10) и (4.4.11) обозначения
21' (2l'+\)TR_^
(4.4.12)
(2Г+1)(2Г + 2)ГЙ=|8 (4Л13)
§4. Квантовые состояния двух- и многоатомных молекул
293
и применим формулу Эйлера — Маклорена (4.12). Ограничиваясь двумя
первыми членами этого ряда, получаем
QO
z'=-2bKKdb+7'lW+--sfe(,+TT?+-)' (4'4Л4)
о
2.-^J.-b*H».»+-^(l+|^.-V+...).(M.
15)
Поэтому молекулы водорода в равновесии при очень высоких температурах
fc
Т>Т*=оь1=
(1,05-Ю-34)2
'2kJ 2-1,38- Ю-23-0,47. Ю-47
согласно формуле (4.4.6), смешаны в пропорции
85 К,
' N (орто-Н2)
N (пара-Н2)
7>8б К 2к '
(4.4.5а)
(4.4.16)
т. е. на три орточастицы приходится одна парачастица.
Аналогично дейтерий при температурах
П 05-Ю-34)2
^ R 2.1,38.10-23-0,93.10-47 ~~ ^
представляет собой смесь, в которой
N (орто-Р2)
N (napa-Dg)"
Z8
= 2^ = 2
(4,4.17)
при высоких температурах в равновесии приходится две орточастицы на
одну парачастицу.
4.5. Возбужденные состояния электронов
Вычислить для 1 кмоль водорода поправку к свободной энергии, к
которой приводит учет первого возбужденного электронного состояния.
Температура Т составляет 5000 К.
Решение х>
Согласно квантовой теории, водород в основном состоянии пе=\
обладает синглетным термом, т. е. gi=l. Первое возбужденное состояние пе = 2
расщепляется на три состояния
2Р
2S
1/2 [fe
1 • / , 1 l !
l./ = ^ + se=l—2="2
2^3/2 ( '■
,-../-!)■
1/2
1е = 0, / = -Я- .
х) Эту задачу следует рассматривать как сугубо модельную, так как
возбужденное состояние молекулы -г- не то же самое, что возбужденное
состояние входящего в нее атома. Энергия возбуждения атома может превышать
энергию диссоциации молекулы, как оно и оказывается в этой задаче.—
Прим. ред.
294
Гл. 4. Статистика квантовых процессов
т. е. #2 — 3. Два состояния 2Рх/2, 25г/2 в отсутствие внешнего поля
совпадают, а третье состояние 2Р3/2 только незначительно отличается от двух
других. Поэтому для энергии возбуждения по теории Бора можно написать
Аг = г2 — г1= f- [ —. ) = • п . (4.5.1)
Здесь е0 = 8,854-10~12 А-с/В-м — электрическая постоянная, \i— масса
электрона, е—заряд ядра.
Вращательная статистическая сумма, согласно формулам (4.4.1), (4.4.14),
(4.4.15), при ns— 1;2, т = 2 имеет вид
Z% = ns(2ns+\)Zg + (ns+\){2ns+\)Zu=^(\+...). (4.5.2)
Для статистической суммы получаем отсюда и из формул (4.4.7), (4.4.8)
Т е-Т0(1)/2Т
0+...)- Tr7m7F£i +
7*(1) l_g-ro(i)/r
Т „-^о(2)/2Г
•(1 + --->, -г ^/7-g2r(e'-8l)/ftr, (4.5.3)
т. е. различие между пара- и ортосостояниями водорода при достаточно
высоких температурах становится незначительным [см. (4.15в)]. Согласно
формулам (4.9) и (4.11), имеем соответственно
Г.(0-^. (4-5.4)
А2 п2
т^ = 2Щггшщг) ('=1-2>- <4-5-5>
Частота колебаний со0 и момент инерции / молекулы в возбужденном состоянии
несколько отличаются от их значений для основного состояния. В
статистической сумме (4.5.3) это показано обозначениями T0(i), 7#(/), а в формулах
(4.5.4) и (4.5.5) обозначениями со0 (i), J (/).
Поправку к свободной энергии, отнесенную к 1 кмоль, получаем из
формулы (4.5.3)
(^вр^кол^я)яе=2
— RT\n\ 1
AF=— RT\n 1
\^вх)^кол^а)пр = 1
а ГпП\ГГ»(2)/2Г \_p-TQ{i)/T
= ~*Т ^ Г m/,r г т/г e^2"6^. (4.5.6)
Отсюда по формулам, приведенным в гл. 2, § 3, можно вычислить поправки
и к другим термодинамическим величинам.
Решающее значение имеет энергия возбуждения е2 — ev Проделав
численный расчет1*, найдем из формулы (4.5.1)
Де = е2—е! = ~ 13,6 эВ = —13,6.1,60. Ю-19 =--1,63- Ю-18 Дж,
1) См. [12], п. 6.3.
§ 4. Квантовые состояния двух- и многоатомных молекул 295
отсюда имеем для данной температуры:
kT "~5.10з. lf38. Ю-" ^'D> e u>0/ 1U
Энергия возбужденного состояния электрона сильно отличается от энергии
основного состояния, поэтому влияние возбужденных состояний на
термодинамические величины, описываемое множителем ехр (—Ле/йГ), очень мало.
Оценим поправку для водорода только по порядку величины, пренебрегая
изменением частоты колебаний и момента инерции. Тогда из формулы (4.5.6)
имеем
AF« —1,987.5.103.3.0,57.Ю-10 «—2-Ю-6 ккал.
4.6. Удельная теплоемкость водорода
при низких температурах
Вычислить молярную теплоемкость Cv водорода в равновесном состоянии
при Т = 100 К.
Решение
Определим сначала раздельно теплоемкости орто- и параводорода.
Статистические суммы для одной частицы, согласно формулам (4.4.3) и (4.4.4),
имеют вид
Zt = L (l + 5e-°TR<T+9e-20TX/T+...), (4.6.1)
Za^l(3e^V+7e-12V'+...). (4.6.2)
где, согласно (4.4.5),
Т/?=&==85К- (4-6-3>
Отсюда найдем теплоемкость Cv:
'd*F\ _ fd*\nZgtU
/dU\ /d*F\ (с,
c^Hwv=-^mv==RT2{-
дТ2
д /d\nZgf
— *5rU(l/Tr)- (4-6,4)
Последний способ записи особенно удобен, так как в формулах (4.6.1)
и (4.6.2) Т стоит в знаменателе показателей экспонент.
Поскольку экспоненциальная функция быстро убывает, можно
ограничиться при Достаточно низких температурах только первыми двумя
слагаемыми в выражениях (4.6.1) и (4.6.2). Тогда, используя (4.6.1) и (4.6.2),
получим по формулам (4.6.4) и (4.6.2)
C„Bp(napa-H2)=-tf А |_^_(5(Гв7Уг +...)] =
= 180tf(^)VeVr+..., (4.6.5)
С,вр(орто.Н2)=-^ А |"_^_ (ln3_^+|e-i»V7-+...)j =
= *Zj»(£)V"Vr+.... ' (4А6)
296 Гл. 4. Статистика квантовых процессов
Для Т=100К имеем при заданных значениях:
C„Bp(napa-H2) = 180 (щ)* е"в'85/1°° R=0J93R, (4.6.5а)
C„bp(oPto-H2) = ^ (^)'е-"*"/жвв« =-0,034R. (4.6.6а)
Для двух модификаций водорода обнаруживается отчетливое различие в
удельных теплоемкостях при низких температурах. У параводорода вращательные
степени свободы начинают сказываться значительно раньше, чем у ортово-
дорода.
Для равновесной смеси, согласно формуле (4.4.6), имеем
^(opTO-Hg)==3Zg==3 3e-*TR/T{\ + C/9)e-1°TRfT+...)
W(napa-H2) Zg l + 5e-*TRfT
и в численном выражении
N (орто-Н.2)_ е-КЦ\ + С/3)е-^)
Л/(пара-Н2) 1+5S-5,1 '
Для вращательной теплоемкости получаем
Сзр^1'6-0'034^1-0'793 « = 0,326«.
Найденные значения несколько завышены, так как мы учитывали только
первые члены. Согласно табл. П.Х, имеем Cv (100 К) = 1,714/?, т. е.
вращательный вклад CVBV = 0,214/?.
4.7. Термодинамические параметры линейной молекулы (С02)
Двуокись углерода состоит из линейных молекул (фиг. 60). Вообще,
линейная молекула из п атомов обладает тремя поступательными, двумя
вращательными и Згг —5 колебательными степенями свободы. В данном случае
•* • } • I
О Of О
•* • * «t
<vt-Q)z ujj (л)4 Фиг. 60. Типы колебаний линейной молекулы.
я = 3. Исходные данные для С02: относительная молекулярная масса Мт =
= 44,01, момент инерции У = 7,1Ы0-4в кг-м2; частоты колебаний: о)1 = ©2 =
= 1,256-1014 с-1, ©з = 2,61.1014 с-1, 04 = 4,59.1014 с"1. Вывести формулу для
внутренней энергии U. Чему равна теплоемкость Cv при Г = 800К?
Решение
Запишем статистическую сумму
^ = ^пост^вр^кол (4-7.1)
как произведение статистических сумм для поступательного, вращательного
и колебательного движения. Другие статистические множители для данной
§ 4. Квантовые состояния двух- и многоатомных молекул 297
задачи несущественны. Согласно формуле (3.1.8) гл. 2, имеем
2Пост=[^(2я^Г)3/2]Л/( (4.7.2)
откуда по формуле (3.1.9) гл. 2 получаем свободную энергию
г—лппгпост—мг [i+inV(2yj)3/2
(4.7.3)
Учитывая симметрию атомов кислорода по отношению к их перестановке, по
формуле (4.10) найдем статистическую сумму для вращательных движений
7
= r±£(2/ + l)e-'(I+1)fcv*''*r| , (4.7.4)
где т—-2.
Поскольку
А2 (1,05-10-34)2 7> _0,562
= 7,0210-4,
2У/гГ~2-7,1Ы0-46.1,38-Ю-23-800 800 К 800
в соответствии с выражением (4.13) вместо формулы (4.7.4) можно написать
*.-[т£ ('+№-•)]"•
Тогда свободная энергия есть
Flp = -Wfcr(ln-^+lIS+...). (4.7.6)
Для колебательной статистической суммы, согласно формуле (4.8), имеем
''3"-5 exp(-fa>,/2*r) Х"
\ j = i \—exp(—№i/kT)J
Обозначив
Г,=%. (4.7-8)
получим отсюда вклад в свободную энергию
зп-ъ
FK01l = -kT\nZK0]l = NkT 2 fyj+ln(l-e-r</r)l. (4.7.9)
1 = 1 ^ ^
Соответствующие части внутренней энергии найдем по формуле (3.16) гл. 2
и-Р-т№)
dTjv'
воспользовавшись соотношениями (4.7.3), (4.7.6) и (4.7.9), подстановкой W = Л?д.
В результате находим
*Vt = -§-W, (4.7.10)
^вр
= /?r(l—i-^—...). (4.7.11)
(=1\ 1-е ' /
298
Гл. 4. Статистика квантовых процессов
Это дает
Отброшенные члены в выражении для вращательной энергии по порядку
величины меньше (Твр/Т)2, т. е. для рассматриваемых температур меньше 10~6.
Подставляя численные значения, из формулы (4.7.8) имеем
1 05-10~34-1 256-1014
7*1.1= ' 1,38.10-23 =956«, Г3=1990К, Г4 = 3490К.
Формула (4.7.13) дает
CV = R (-J+ 1+2-0,89 + 0,61 +0,25^ =5,14/?.
Согласно табл. П.Х, точное экспериментальное значение Cv составляет 5,186/?.
Расхождение оказывается меньше 1%. Оно связано с энгармонизмом
колебаний, с возбуждением высших энергетических уровней, а также со свойствами
реального газа.
4.8. Термодинамические величины для многоатомных молекул
Как показывают спектроскопические измерения, молекулы NH3 имеют
следующие моменты инерции: Л = 4,4-Ю-47 кг-м2, J — У* = 2,8-10-47 кг-м2.
Круговые частоты колебаний составляют: о)х= 1,76-1014 с-1, со2 = 6,28« 1014 с-1,
й)3 = (о4 = 3,08-1014 с-1, о)б = со6 = 6,43-1014 с-1. Вычислить молярную
теплоемкость при Г = 400 К.
Решение
Поступательное движение дает в молярную теплоемкость вклад, равный
3/?/2. Рассмотрим теперь вращательный вклад. Поскольку
jfc2 П 05-10-34^2
7,>Г^дф-д2.2,8:Го-«.1,88.10-»д14'ЗК> Г*»« <4А1>
можно заключить, что при 400 К вращательные степени свободы возбуждены
полностью. Поэтому вращательный вклад также составляет (3/2) R. Вклад
колебаний определим по формуле (4.19). В полной аналогии с формулой
(4.6.4) имеем
б
укол"
_ N k д_ rajnZ^TI __ д_\ а_ у , мер (-%<j>jl2kT)
"А дТ [д(1/Т) J кдт\д(\1Т)£* l-expi-Ui/kT)]
(4.8.2)
Учитывая, что
--'•^°н-'".."--">'"',-,-и<1'
можно приближенно написать
§ 4. Квантовые состояния двух- и многоатомных молекул 299
В итоге получаем
Cv = jR + |-/? + 0,39/? + 0,001/? + 2.0,098/? + 2.0,001/? = 3,59/?.
Упражнения
У.4.1. Частота со0 нормального колебания молекулы азота составляет
4,45-1014с-1. Вычислить колебательную часть молярной теплоемкости
для Т = 500 К.
У.4.2. Определить, при какой температуре полностью возбудятся
колебательные степени свободы кислорода. Частота колебаний со0 =
= 2>98.1014с-1.
У.4.3. С помощью фиг. 59 определить вклад колебаний в молярную
теплоемкость для Cl2, Br2, J2 при Г = 500К- Частоты колебаний
составляют 1,06-1014, 0,61-1014 и 0,40-1014 Гц.
У.4.4. Определить вращательную и колебательную части молярной
теплоемкости 02 при 300 К. Сравнить результат с экспериментальными
данными, приведенными в табл. П.Х (й)0 = 2|98-1014с~1, J0 =
= 1,91. Ю-46 кг-м2).
У.4.5. Найти поправку, вызванную ангармонизмом, к колебательной части
молярной теплоемкости водорода при Г = 3000К ((д0 = 8,28-\0ис-1,
х = 0,027).
У.4.6. Исследовать, при какой температуре вращательная часть
термодинамических величин для азота достигает классических значений
(УМ2=1,38.10-46кг.м2).
У.4.7. Для 1 кмоль хлористого водорода при Т = 20 К вычислить в
третьем приближении вращательную часть внутренней энергии (J =
= 2,60-Ю-47 кг-м2).
У.4.8. Вычислить вращательную часть теплоемкости газообразного
кислорода при температуре 1 К-
У.4.9. Чему равна в третьем приближении вращательная часть удельной
теплоемкости хлористого водорода при Г = 20 К?
У.4.10. Найти максимум вращательной части удельной теплоемкости.
Какой температуре соответствует этот максимум у НС1 и Н2? («^hci =
= 2,60- Ю-47 кг-м2, УНа = 0,47. Ю-47 кг-м2).
У.4.И. Вычислить вращательный вклад в теплоемкость для орто- и пара-
водорода при Т = 150 К-
У.4.12. Чему равно равновесное содержание числа орто- и парамолекул
в водороде при Т =150 К?
У.4.13. Найти равновесное содержание орто- и парамолекул в дейтерии при
Г = 300 К.
У.4.14. Чему равен вклад первого возбужденного электронного состояния
кислорода в его теплоемкость при 3000 К? Кратность вырождения
основного состояния равна трем, а первого возбужденного—двум.
Энергия возбуждения составляет 1,0 эВ. Изменением частоты
колебаний и момента инерции пренебречь.
У.4.15. Определить теплоемкость водяного пара при 100°С. Частоты
колебаний составляют: ©1 = 3,0Ы014с-1> ш2 = 6,78. Ю14^1, со3 =
= 7,03-1014с-1. Для вращательного вклада можно использовать
классическое выражение.
У.4.16. Найти статистическую сумму для метана СН4 при Г = 300 К.
Ядерный спин ns атомов водорода равен 1/2, атома углерода — нулю.
У.4.17*. Определить «коэффициент симметрии» т и кратность вырождения g
для СН4, CH3D, CH2D2, CHD3 и CD4.
300
Гл. 4. Статистика квантовых процессов
§5. ПОВЕДЕНИЕ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ
ПРИ АБСОЛЮТНОМ НУЛЕ ТЕМПЕРАТУРЫ.
ТЕОРЕМА НЕРНСТА-ПЛАНКА
Введение
В классической термодинамике абсолютная величина
энтропии S остается неопределенной. Поэтому свободная энергия
F=U — TS и энергия Гпббса G = U — TS+PV определяются лишь
с точностью до линейной функции температуры. Для расчетов,
проводимых в рамках классической физики, это ограничение
несущественно (см. задачу 3.1 гл. 2), нужно следить только,
чтобы начало отсчета энтропии сохранялось при любом
изменении состояния системы. Однако при изучении химического
равновесия вопрос о величине энтропии при абсолютном нуле
приобретает решающее значение. Его удается решить, только
учитывая дискретность состояний квантовой системы.
Внутренняя энергия тела определяется выражением
т
U(T) = ^C(T)dT + U0. (5.1)
0
Поскольку С^О, энергия не может убывать с ростом
температуры, если только внешние условия не изменяются
(например, если давление или объем остаются постоянными).
Поэтому предельному случаю наименьшей возможной
температуры Т =0 должно соответствовать квантовое состояние
с наименьшей энергией U = U0 (основное состояние). Если
допустить, что при абсолютном нуле вырождение отсутствует,
то статистический вес системы при этом равен единице. Тогда
для энтропии имеем
UmS = \\mklnW
Г-*0 Г-*0
(5.2)
При абсолютном нуле температуры энтропия однородного
вещества равна нулю (теорема Нернста—Планка).
Энтропия смесей содержит дополнительное слагаемое,
обусловленное смешиванием, поэтому для смесей теорема Нернста
не выполняется. В соответствии с формулами (3.29) и (3.30)
гл. 2 можно представить энтропию как в виде функции
температуры и объема S = S(7\ У), так и виде функции температуры
и давления S = S(T, Р). С другой стороны, теорема Нернста
справедлива независимо от конкретных значений давления
§ 5. Теорема Нернста—Планка
301
и объема. Поэтому формулу (5.2) нужно уточнить, а именно
заменить ее двумя соотношениями:
HmS(7\ V) = 0, HmS(7\ Р) = 0. (5.3)
Поскольку при абсолютном нуле энтропия не зависит от
давления и объема, имеем
й(#)г-°- й(£)г-°- <5-4)
Удельная теплоемкость определяется соотношениями
С*-Т [w)v~'[dWr)vi Ср~Т \W)p-\dWr)p- (5*5)
Если Г—*0, то lnT—►—оо и S—+0, как видно из формулыГ(5.2).
Поэтому
(5.6)
Когда температура стремится к абсолютному нулю,
теплоемкости Ср и Cv также стремятся к нулю.
Из теоремы Нернста—Планка следует, что температура,
точно равная абсолютному нулю, не может быть достигнута
(см. задачу 5.2). Однако утверждение о недостижимости
абсолютного нуля нельзя рассматривать как эквивалентную
формулировку закона Нернста. Обращение в нуль энтропии при
Т =0 удается однозначно связать с недостижимостью
абсолютного нуля только в том случае, если теплоемкости
стремятся к нулю, в соответствии с опытом, по крайней мере как 713.
Согласно статистической интерпретации, значение S = 0
соответствует наибольшей упорядоченности. Однако о времени
установления такого равновесного состояния сказать ничего
нельзя. Из-за „вымерзания" степеней свободы при Т—>0 для
установления равновесия может потребоваться бесконечно
большое время. Эти утверждения имеют смысл предельных законов.
Пример 28
Как известно, стеклообразное состояние является неравновесным.
Кристаллическое состояние характеризуется большей упорядоченностью и поэтому
меньшей энтропией. Несмотря на это, за измеримое время не наблюдается
перехода стекол в кристаллическое состояние.
302
Гл. 4. Статистика квантовых процессов
Задачи
5.1. Термодинамические величины при абсолютном нуле
При абсолютном нуле температуры внутренняя энергия U и свободная
энергия F при любых значениях давления Р и объема V связаны следующими
предельными соотношениями:
KmF(T) = \imU(T)t
lim (*L\ =Iim Ш1
WJv-t-Xo ОТ
(5.1.1)
(5.1.2)
Вычислить для Т — 0 энтропию S, изобарный коэффициент расширения а,
изохорный коэффициент давления р и разность Cp — Cv молярных теплоем-
костей при постоянном давлении и постоянном объеме.
Решение
Согласно формуле (3.16) гл. 2, для свободной энергии справедливо
дифференциальное уравнение
£=£-. (5.1-3)
\&Tjv~
При абсолютном нуле в силу условия (5.1.1) как числитель, так и
знаменатель в правой части равны нулю. В соответствии с правилом Лопиталя
продифференцируем числитель и знаменатель; это дает
lim (¥-) =lim (MW\ . (5.1.4)
т-+о \dTJv т->о\дТ дТ Jv к '
Согласно условию (5.1.2), это выражение обращается в нуль. Поэтому для
абсолютного нуля из формулы (3.15) гл. 2 имеем
Это соотношение справедливо для любых значений давления и температуры.
Поэтому
Согласно формулам (1.4.1) и (1.4.2) гл. 3, изобарный коэффициент расширения
а и изохорный коэффициент давления р определяются следующим образом:
a~V \дт)р*
P=t(!£)i
В соответствии с формулами (3.24) гл. 2 имеем соотношения
(5.1.7)
(5.1.8)
(#),--(#),• [ж)АЩг
§ 5. Теорема Нернста—Планка
303
При абсолютном нуле в силу соотношения (5.1.6) эти величины обращаются
в нуль. Следовательно, получим
lima = 0,
lim6 = 0.
(5.1.10)
Изобарный коэффициент расширения а и изохорный коэффициент давления р
при абсолютном нуле обращаются в нуль.
Разность теплоемкостей Cp — Cv найдем по формуле (2.4.16) гл. 2
Поскольку a—► 0, р —► 0, разность Cp — Cv стремится к нулю быстрее, чем Т.
5.2. Охлаждение до сверхнизких температур
с помощью размагничивания.
Недостижимость абсолютного нуля
Быстрое размагничивание парамагнитного вещества вызывает понижение
его температуры. Если попеременно производить адиабатическое
размагничивание, а затем изотермическое намагничивание (фиг. 61), то можно достичь
S
* * Фиг. 61. К обсуждению недостижимости
абсолютного нуля.
Диаграмма Г, S иллюстрирует процесс охлаждения,
состоящий из адиабатического размагничивания
(горизонтальные линии) и изотермического
намагничивания (вертикальные линии). В неупорядоченном
размагниченном состоянии система обладает большей
энтропией, чем в упорядоченном намагниченном.
Поэтому кривая Su лежит выше кривой S . В
соответствии с законом Нернста обе кривые
пересекаются при абсолютном нуле.
температур, лежащих всего на несколько милликельвинов выше абсолютного
нуля. Вычислить, насколько охладятся железо-аммониевые квасцы при
адиабатическом размагничивании, если начальная температура составляет 1,0 К.
Магнитное поле меняется от 106 А/м до нуля. Установить, можно ли таким
способом достичь абсолютного нуля. Для молярной теплоемкости при
постоянной намагниченности использовать выражение
-а»-
-с -1
(5.2.1)
где (3 = 0,029 ккал-К/кмоль. Намагниченность 3, отнесенная к 1 кмоль, при
низких температурах подчиняется закону Кюри—Ланжевена
3=-уг-, (5.2.2)
где С = 3,49-10-4 м3-К/кмоль. Магнитные величины связаны следующими
соотношениями:
»=и$=|1вб+аю,
(5.2.3)
304
Гл. 4. Статистика квантовых процессов
где
Ш1 = |ЫоИ&
(5.2.4)
есть магнитный момент 1 м3; %— магнитная восприимчивость. Для
намагниченности 3 имеем
(5.2.5)
(Мг—относительная молекулярная масса, р — плотность). Величина В
измеряется в В-с/м2, величина Н—в А/м.
Решение
Для изменения намагниченности 1 кмоль вещества к нему нужно
подвести энергию
dWm = ®-d3 = BdJ. (5.2.б)
В дальнейшем предполагается, что направления векторов 33 и 3 совпадают.
Если к системе, кроме магнитной, подводится еще и тепловая энергия 6Q,
то изменение внутренней энергии равно
dU = 6Q + BdJ
(5.2.7)
Сравнивая это выражение с первым законом
dU = bQ — PdV,
приходим к выводу, что формулы, выведенные в гл. 2, § 2 и 3, можно
использовать и для магнитных явлений, если произвести замену
■А
Р—+ — В
(5.2.8)
т. е. заменить объем на намагниченность, давление на отрицательное
значение магнитной индукции. В соответствии с первым законом напишем
dS=-±r(dU + PdV)~
(ат)/т+(ж)г*+'4 <"*
С помощью замены (5.2.8) получим отсюда
1
dS=-
(£),«■+(#), "-Ч
(5.2.10)
В соответствии с формулами (3.15) гл. 2 и (3.24) гл. 2 на основании
соотношения U = F — TS имеем
\dVjT \ду)т- \дУ)т ^^'\дТ)у [ дТ \v'
Снова с помощью (5.2.8) находим
\dJjT~ [ дт \j-
(5.2.11)
(5.2.12)
§ 5. Теорема Нернста —Планка
305
При адиабатическом процессе дифференциал энтропии dS в формуле (5.2.10)
равен нулю. Первое слагаемое в квадратных скобках в (5.2.10) можно
заменить на C^dTy где С^ — теплоемкость при постоянной намагниченности. Тогда
из формул (5.2.10) и (5.2.12) найдем
C^dT-T* 1д^Т)] dJ — BdJ = 0. (5.2.13)
Дифференциал намагниченности представим в виде
и подставим в формулу (5.2.13). Тогда для приращения температуры получаем
dT (dB/dT)j(dJ/dB)TdB
T~C^—T(dB/dT)j(dJ/dT)B * (Ь.2ЛЪ)
Из формул (5.2.2) —(5.2.4) имеем
дТ)$-СУ [dBjT^iiT' \дТ )в~~ Т'
Эти величины можно подставить в уравнение (5.2.15) и проинтегрировать
т
CdT Р CHdJj _1 f d(CH*)
л
Здесь Г л—температура при включенном поле, Тв—температура без поля.
Вычисляя интегралы в (5.2.16), получаем
Тв
Та
■V-
р
Р + цС//*
(5.2.17)
Подставляя численные значения, находим
Тв -i/ 0,029*4,19.10*
-Уй
1,0К г 0,029-4,19.103 + 1,256-10-6-3,49.Ю"4- 10J2
=0,466
соответственно Тв ~ 0,47 К. При адиабатическом охлаждении энтропия
системы остается постоянной. Она определяется выражением
т
5 = 5 (У, T) = S(J, 0)-j-f [^r)jdT (5.2.18)
о
при / = 0. Согласно теореме Нернста, 5 (У, 0) = 0. При повышении
температуры энтропия растет. Из формулы (5.2.18) следует, что 5(0, Т) > 0. Правда,
при изотермическом намагничивании энтропия уменьшается, однако она
остается больше нуля. Адиабатическое размагничивание вызывает понижение
температуры, энтропия же остается постоянной. Таким образом, можно как
угодно близко подойти к абсолютному нулю, однако достигнуть его нельзя.
Аналогично приводится доказательство и для других физических методов»
306
Гл. 4. Статистика квантовых процессов
5.3. Поведение квантового газа
С учетом теоремы Нернста вывести формулу для энтропии одноатомного
газа при высоких температурах и исследовать поведение газа при
абсолютном нуле.
Решение
Закон Нернста справедлив и для однокомпонентного газа. Рассмотрим
сначала поведение газа, состоящего из фермионов или бозонов, вблизи
абсолютного нуля.
Для бозонов химический потенциал \iCJ а также множитель Лагранжа а
равны нулю (см. задачу 3.6). Поэтому из выражений (3.17) и (3.14)
получаем, что для всех значений Т, при которых ^^ = 0, или а = 0,
о
Интеграл, стоящий справа, имеет конечную величину. Поэтому S —► 0 при
7—>0.
Для фермионов поступим так же, как в задаче 3.1. Путем разложения
в ряд получаем для свободной энергии Г и для внутренней энергии U в
соответствии с формулами (3.1.7) и (3.1.10) выражения вида
Р = Сг—С2Т*, и = Сг + С2Т*. (5.3.2)
Отсюда имеем
S=^-^=2C27, т.е. lim S = 0. (5.3.3)
Таким образом, теорема Нернста выполняется как для бозонов, так и для
фермионов. Напротив, для идеального газа эта теорема несправедлива. При
высоких температурах, как показано в задаче 1.3, статистики Бозе—Эйнштейна
и Ферми—Дирака переходят в классическую статистику Больцмана. С другой
* стороны, любой газ при достаточно низких температурах вырождается в газ
бозонов или фермионов, поэтому в предельном случае Т = 0 энтропия S всех
газов равна нулю.
Множитель Лагранжа а для газа при высоких температурах получим по
формуле (1.3.11)
..„«■чу». (5.3.4)
Свободную энергию найдем по формуле (3.14)
F--l£*!&^\-!g-<,^l*. ,5.3.5,
Считая температуру достаточно высокой, так что ea^>\i можно пренебречь
в .знаменателе слагаемым ^1. Тогда для интеграла в выражении (5.3.5) имеем
Подставляя (5.3.4) и (5.3.6) в (5.3.5), получаем
? = —NkT In
§ 5. Теорема Нернста—Планка
307
Эта формула совпадает с выражением (3.1.9) гл. 2, если положить g=l, т. е.
если в соответствии с классической физикой не учитывать ядерный спин. Для
энтропии одноатомного газа имеем
с fdF\ ,а/Г| V 8№фЬТ)*'* , 51
(5.3.8)
что совпадает с выражением (3.1.10) гл. 2.
Таким образом, если отвлечься от поправки на ядерный спин, теорема
Нернста не приводит ни к каким видоизменениям формул, выведенных в гл. 2
для идеального газа.
5.4*. Число нормальных колебаний в среде по Рэлею и Джинсу
Чему равно число возможных поперечных нормальных колебаний в
интервале от v = 5-1014 Гц до v + dv = 5,l'1014 Гц в прозрачном теле объемом
V—\ см3 с показателем преломления я =1,5?
Решение
Как можно доказать в общем случае, число волн не зависит от формы
тела. Поэтому для упрощения расчета рассмотрим распространение волн
в кубическом теле со стороной а. Направление ребер куба примем за оси
ху у, г системы координат. Из-за наложения падающих и отраженных от
Фиг. 62. Волны в ограниченной среде.
поверхности волн в рассматриваемом теле образуются стоячие волны. В
зависимости от типа рассматриваемых колебаний на ограничивающую
поверхность приходятся либо узлы, либо пучности (например, узлы для
электрического поля в идеальном проводнике или для колебаний троса, закрепленного
на концах, пучности — для продольной составляющей поля Н в волноводе).
Расстояние между двумя соседними узлами или пучностями равно Я/2
(полуволна). Поэтому для волны, фронт которой распространяется параллельно
одной из граничных поверхностей, имеем условие
а = /п-г-. (5.4.1)
Выберем волну с произвольной пространственной ориентацией волнового
фронта; для нее направление нормали описывается уравнением
n = t cosa + J cos p + r cosy- (5.4.2)
Рассмотрим единичный отрезок в направлении волновой нормали. Он
содержит 2Д полуволн. Проецируя этот отрезок на ось х, получим отрезок длины
1/cos а, на котором укладывается 2/Х полуволн (фиг. 62). Следовательно,
в единице длины оси х содержится (2 cos а)/Х полуволн рассматриваемого коле-
308
Гл. 4. Статистика квантовых процессов
бания. Те же соображения справедливы и для двух других осей. Из
граничных условий имеем
% % %
a cos а = я* — , a cos р = пу -=-, acosy = nz-^-
(пх, nyt nz = 0t 1, 2, ...)• (5.4.3)
Отсюда получаем
cos2a+cos2p + cos2Y=l = ^-(n|+^ + fz|) =
=-^(nU-nU-nl), (5.4.4)
где и—фазовая скорость.
Уравнение (5.4.4) описывает в пространстве пх> пу, nz сферу радиусом
2av/u. Число возможных стоячих волн в интервале частот от v до \-\-d\,
т. е. число возможных значений пх, пу, п£у равно числу узлов кристалли-
Фиг. 63. К подсчету числа колебаний в
кристаллической решетке.
(5.4.5)
ческой решетки в октанте шарового слоя с радиусом 2av/u и толщиной 2adv/u
(фиг. 63). Для больших значений 2/Х это число равно объему октанта
шарового слоя
4я / 2av \ 2 2а dv __ v v2 dv
~5~\~) ~u~- У~ИГ-
Здесь V = а3 — объем рассматриваемого тела.
Результат (5.4.5) справедлив для колебаний с заданным направлением
поляризации, например для продольных или поперечных колебаний с
фиксированной поляризацией. Поскольку поперечные волны можно разложить на
две волны с взаимно перпендикулярными направлениями поляризации, а
скорости распространения поперечных и продольных волн различны, число
возможных акустических воли в теле объемом V запишется в виде х>
f(v)dv = 4nVv2
(4-+-И
\UT UL )
dv.
(5.4.6)
Здесь uT—uT(v) и Ui = ui(v) — фазовые скорости соответственно поперечных
и продольных волн.
В данном частном случае «/7*= w/n = 3> 108/1,5 м/с. Следовательно, число
возможных поперечных волн в области частот от 5-Ю14 до 5,Ы014 Гц для
тела объемом V=10"6 м3 равно
/(v)rfv = 4K.10-e.(5.1014)2.7H-^3 • 0,1- Ю14 = 7,85.1012.
г) В среде возможны только поперечные электромагнитные волны, причем
каждому волновому вектору соответствуют две поперечные волны со взаимно
перпендикулярными направлениями поляризации. Однако в случае
акустических колебаний каждому волновому вектору, кроме двух поперечных,
соответствует еще одно продольное колебание.— Прим. ред.
§5. Теорема Hep нспга—Планка 309
5.5*. Удельная теплоемкость твердых тел по теории Дебая
Вычислить молярную теплоемкость свинца при Т^ЗОО К и алюминия
при Г = 50 К- Дебаевская, или характеристическая, температура Тр
составляет для алюминия 400 К, для свинца 90 К.
Решение
Твердое кристаллическое тело, состоящее из N.структурных единиц, можно
рассматривать как систему связанных осцилляторов. Каждый атом кристалла
может участвовать в колебаниях по трем взаимно перпендикулярным
направлениям. Поэтому полное возможное число осцилляторов в твердом теле равно 3N.
В соответствии с этим Дебай (1912) полное число волн на 1 кмоль твердого
тела принял равным 3 N д.
Далее, Дебай предположил, что в твердом теле возбуждаются все волны,
допускаемые краевыми условиями, вплоть до некоторой предельной частоты vg.
Если использовать результат (5.4.6) для полного числа стоячих волн, то из
допущения Дебая следует
vg
Wm(Ar+-T) [v*dv = 3NA, (5.5.1)
О
где Vm — молярный объем твердого тела. Найдем отсюда предельную частоту vg:
_У/ 9W А \/~ ~ М ,,-9,
V£ V 4яУт(2/1/^+1/н£) V 4я1/(2/4+l/W3) " ( '
Рассматривая кристаллическое твердое тело как совокупность осцилляторов,
найдем его статистическую сумму и его термодинамические функции.
Удельную теплоемкость проще всего определить, исходя из формулы (4.1.4) для
внутренней энергии осциллятора:
^V i nv /ее оч
eocu = X+gfcv/^^1- (5'5'3>
Распределение по частотам описывается формулой (5.4.6). Исходя отсюда,
найдем внутреннюю энергию твердого тела в расчете на 1 кмоль:
V-[ f (v)eoc„(v)dv = ^- j (:£+_£_) dv. (5.5.4)
0 g о ^ '
Проинтегрировав первое слагаемое и произведя во втором слагаемом замену
/iv *v
X = W X*=-W> (5'5-5)
получим из (5.5.4)
uJ**U+«*'(**. ,,5.6,
9RT Г x*dx
xl J ^-1
310 Гл. 4. Статистика квантовых процессов
Отсюда видно, что энергия нулевых колебаний связана с предельной частотой
посредством соотношения
Vo = jNAhvg
Величина
TD
~ k ~~9 R
(5.5.7)
(5.5.8)
называется дебаевскои, или характеристической температурой твердого тела.
Для вычисления теплоемкости при высоких температурах Т и
соответственно малых х разложим подынтегральную функцию в (5.5.6) в ряд
. х . х2 \
ex — i 1 +*/2+*V6+**/24 + ...
Отсюда имеем
U = 3RT + ^R^± ...
и молярную теплоемкость
rill / 1 Т^ \
В предельном случае T^>TD получаем закон Цюлонга и Пти [см.
формулу (2.2.2) гл. 2].
Для противоположного случая низких температур Т и соответственно
больших х запишем
(5.5.9)
(5.5.10)
(5.5.11)
ех— 1
■*=J^*-j-3=r
dx.
(6.5.12)
Вычислим первое слагаемое, используя формулы (1.3.8) и (1.3.8а),
^^ГТ^ = Г(4)?(4)-б| =
15'
(5.5.13)
второе слагаемое представим следующим образом:
(1+VI
е « — 1
]i£rd*=] Ш^\ ^=e'xi]a+xg^Ul+...)^
s
= е g(6 + 6xg + 3xl+xl)+... .
Для достаточно больших значений xg = To/T можно ограничиться первым
слагаемым. Следовательно,
8 5 То
(5.5.14)
§ 5. Теорема Hep nana— Планка зц
(5.5.15)
Для свинца получим по формуле (5.5.11)
с-ыф-±(|^...]=о.»1.з*,
и в расчете на 1 кг
3-0,991/? 3-0,991-1,987 Л Лоп „ TZ4
с= j = ^5тТ =0,029 ккалДкг-К)
[экспериментальное значение с = 0,031 ккалДкг-К)]. Расчет для алюминия по
формуле (5.5.15) дает
п. 12-3,14*/? ( 50 у n._D
С= g ^49oJ =0,456/?,
и в расчете на 1 кг
С 0,456/? AnQQft ., „ч
c=-j-= /6Q8 =0,0336 ккал/(кг-К).
5.6. Термодинамические параметры квантовой жидкости
при абсолютном нуле температуры
Вывести фррмулу для свободной энергии жидкого гелия в окрестности
абсолютного нуля и вычислить молярную теплоемкость при Т = 0,4 К.
Скорость звука и принять равной 240 м/с, плотность р =0,144 г/см3.
Решение
В жидкостях существует сильное межмолекулярное взаимодействие,
зависящее от вида молекул. Амплитуда колебаний возрастает настолько, что уже
нельзя пользоваться линейной связью между смещением и упругой силой.
Только непосредственно у абсолютного нуля можно не учитывать
взаимодействия и предположить линейную связь
е = «Р (5.6.1)
между энергией е и импульсом р элементарных возбуждений (фиг. 64). Через
и обозначена скорость звука в жидкости г)
х> Необходимо иметь в виду следующее. Специфика жидкостей и газов
состоит в том, что в них невозможны поперечные акустические колебания,
продольные акустические колебания в них возможны, но лишь если их длина
волны достаточно велика. Для этих длинноволновых колебаний при любых
температурах справедлива линейная связь между частотой и волновым
вектором (й — uk. С понижением температуры, с одной стороны, расширяется
интервал длин волн, в котором такое соотношение выполняется, а с другой
стороны, увеличивается относительный вклад в термодинамические величины
длинноволновых колебаний, так как их легче всего возбудить. Поэтому при
312
Гл. 4. Статистика квантовых процессов
Существует только одно вещество, гелий II, которое при соответствующих
значениях давления остается жидким вплоть до абсолютного нуля. Именно
на гелии проводятся все экспериментальные исследования.
При температурах от абсолютного нуля примерно до 1 К можно
рассматривать слабо возбужденные колебательные состояния как совокупность
отдельных элементарных возбуждений. Эти квазичастицы (фононы), движущиеся
в жидкости, обладают определенными энергиями и импульсами. Для газа
фононов выполняется закон сохранения энергии, но не закон сохранения числа
/ г
р/П, 10ю**
Фиг. 64. Энергия и импульс Не II вблизи
абсолютного нуля.
частиц. Его полный спин может изменяться только на целое кратное числа %.
Для фононов справедливы уравнения, аналогичные дебройлевским:
г = %<й = п\>
) = 1ik.
(5.6.2)
Здесь е и р— энергия и импульс элементарного возбуждения, k и
со—волновое число и круговая частота колебания. Молярную теплоёмкость можно
вывести двумя способами:
1. Целочисленность спина означает, что фононы, как и фотоны,
подчиняются статистике Бозе—Эйнштейна. Вследствие этого для чисел заполнения
справедливы формулы (1.1.24) и (1.1.25). Термодинамические величины можно
взять из задачи 2.4. При этом нужно учесть, что для жидкости скорость
света с нужно заменить скоростью звука и. Весовой множитель g для
жидкости равен единице, так как возможны только продольные колебания. Кроме
того, нужно добавить нулевую энергию U0. Тогда по формуле (2.4.1) найдем
внутреннюю энергию жидкости
и = иа
' 15 п*Ф
V.
(5.6.3)
Дифференцируя, получаем отсюда удельную теплоемкость
С =
dU_\6nbk*T* .
дГ-" 15 h*u*
(5.6.4)
2. С помощью интерполяционного метода Дебая можно вычислить число
стоячих волн в теле с объемом V (см. задачи 5.4 и 5.5) и отсюда определить
Т—>0 можно ограничиться учетом только вклада длинноволновых колебаний.
Для их описания вводятся кванты акустических колебаний—фононы, сходные
по своим свойствам с квантами электромагнитных колебаний—фотонами.
Связь между энергией и импульсом фононов дается соотношением (5.6.1).—
Прим. ред.
§ 5. Теорема Нернста—Планка
313
термодинамические величины. Поскольку поперечные колебания отсутствуют,
из формул (5.5.1) и (5.5.2) следует
з Г 9/V
V*="£V 1HF- (5-6-5)
В соответствий с формулой (5.5.14) имеем в расчете на N частиц:
U = ^NkTD + ^^lt (5.6.6)
8 5 7-2) V '
где, согласно формулам (5.5.8) и (5.6.5),
т°-ь
Подставляя формулу (5.6.7) в (5.6.6), находим
4л WV
U = Uo + — -тГя"» (5-6*8)
15 /i3«l
что совпадает с формулой (5.6.3). Отсюда получаем выражение (5.6.4) для
теплоемкости. Подставив в формулу (5.6.4) численные значения, имеем
16-(3>14)»-(1>38-10-23)4»0>48-4>003-2>388-10-4
~~ 15-(6,6310-34)3-2403.0,144-103 ""
= 1,25-Ю-3 ккал/(кмоль-К).
С увеличением температуры зависимость энергии от импульса для квазичас-
стиц, дающих основной вклад в термодинамические величины, все больше
отклоняется от линейной. Поэтому для более высоких температур нужно
рассматривать, следуя Ландау, некоторые особые соотношения внутри
квантовой жидкости (теория фононов и ротонов).
Упражнения
У.5.1. Железо-аммониевые квасцы охлаждаются с помощью адиабатического
размагничивания в два этапа. Магнитное поле при этом уменьшается
от 5«105А/м до нуля. Вычислить конечную температуру, если
исходная температура составляет 4 К (С = 3,49- Ю-4 м3/К, р =
= 0,029 ккал-К/кмоль).
У.5.2. Для условий, указанных в предыдущем упражнении, найти число
этапов, необходимое для получения температуры ниже 0,05 К.
У.5.3*. Чему равно число возможных продольных волн в области частот от
440 до 445 Гц в среде объемом 10 000 м3? (с = 340 м/с).
У.5.4*. Определить ширину полосы частот для одного возможного неполяри-
зованного колебания с частотой 3-Ю22 Гц (верхний предел допустимых
частот) в кубической полости со стороной 3-10—х5 м (иТ = с).
У.5.5*. Найти молярную теплоемкость алмаза при 7" =100 К. Температура
Дебая TD равна 1843 К.
У.5.6*. Чему равна нулевая энергия меди (Td = 3\S К)?
У.5.7. Найти предельную частоту колебаний для KBr (TD—\S0 К).
У.5.8. Чему равна молярная теплоемкость гелия при 0,1 К? (w^ = 240 м/с,
р = 0,145 г/см3).
Глава
СИСТЕМЫ, СОСТОЯЩИЕ
ИЗ РАЗЛИЧНЫХ МИКРОЧАСТИЦ
§ 1. ХИМИЧЕСКОЕ РАВНОВЕСИЕ В СМЕСИ ИДЕАЛЬНЫХ ГАЗОВ
Введение
Любая химическая реакция всегда протекает в двух
направлениях:
Via1+ ... +vmAm^v;A;+v;A;+... +v;aj. (l.i)
Из веществ Alt А2, ..., Ат образуются вещества А^, А2, ..., A'k\
последние также реагируют между собой, образуя опять
исходные вещества Аи ..., Ат. В результате прямой и обратной
реакции в системе по истечении большего или меньшего
промежутка времени устанавливается состояние динамического
равновесия, при котором количество каждого из участвующих
в реакции веществ остается неизменным (химическое равновесие).
Ниже мы будем рассматривать химические реакции между
идеальными газами. Уравнение химической реакции (1.1)
целесообразнее всего записать в виде
2v,A, = 0, (1.2)
1=1
где величины vlt ..., vm—положительные, а величины vm+1 =
■= — v'1% ..., v„ =— Vfe —отрицательные целые числа. Кроме
того, АЛ+1 = А;, ..., А„ = А*.
Пример 29
Реакция
2Н^±Н2
записывается в виде
2Н —Н2 = 0.
Для нее, следовательно, v! = v„ = 2, v2 = vHa =—1.
Предположим, что реакция идет при постоянной
температуре Т и постоянном давлении Р\ при таких условиях должна
стремиться к минимуму энергия Гиббса системы:
6G(P, Г)<0, 6Г=0, 8Р = 0. (1.3)
§ 1. Химическое равновесие в смеси идеальных газов 315
Из условия (1.3) следует, что в состоянии равновесия
§-W1 + §-Mi+...=0. (1.4)
Вариации числа частиц 8N( связаны друг с другом
уравнением реакции (1.2). Отсюда следует, что
Vj v2 • • * V/ ' ^ ' '
т. е. изменение числа частиц Nt пропорционально
коэффициентам V,-. Учитывая, что, согласно формуле (3.4а) гл. 3,
справедливо соотношение [ср. формулу (1.1.11) настоящей главы]
dG _d^Gj_ Gj Fj + PjV^-kTlnZi + PjV_
dNt~ dNi ~~ Ni^ Ni ~ Nt ^ch ' ,b'
получаем из (1.4)
Парциальные давления Р{ связаны с числами частиц N£
равенствами
Р 2^ S^ N '
Согласно соотношениям (1.5), число степеней свободы
вариаций 8Nt равно единице; иными словами, они определяются
заданием одной из величин 8N;. Поэтому можно выразить все
величины 6Nh например, через вариацию 8NX и, используя (1.7),
представить условие химического равновесия в виде
-^2^Ичг/ = °» или I 2>||1«./ = 0 |. (1.9)
Подставляя сюда (1.6) и записывая парциальное давление с
помощью уравнения газового состояния в виде Pi = NikT/Vi
находим
Е^/=^Е^(1-^)=о-. (1.Ю)
На основании формулы (4.20) гл. 4, используя формулу
Стерлинга [см. формулу (1.8а) гл. 2], можно записать статистическую
сумму в виде
lnZ^ty^ln^ + lnZ}»), (1.11)
где Z-1} — статистическая сумма, отнесенная к одной частице.
Выделяя из статистической суммы Z}» = Z%ociZ^^lo^Z^Z^
316 Гл. 5. Системы, состоящие из различных микрочастиц
множитель Z^iocT, связанный с поступательным движением,
согласно формуле (4.21) гл. 4, с учетом уравнения состояния
идеального газа находим
ln^ + lnZ^=l + ln^^»l + lne3i^.(i.,2)
Отсюда
Ev,(,_^)=
= £v/ [inPi-InkT <2^*P3/'Zflp.gZftMZffZffZ/K] = 0.
i
(1.13)
Бели все величины отнести к объему V=l м3, то на основании
формулы (4.21) гл. 4 можно положить
(¥Г^-. (у=1мз)- (1Л4а>
Тогда из (1.13) получим закон действующих масс
2 v, In Pt = 2 v, In kTZf = In Kp (T),
I i
ИЛИ
IlP7<=II(kTzy)vi=Kp(T).
(1.14)
Определим относительную концентрацию следующим образом:
где
р=2л. tf=2#/.
С учетом этого закон действующих мае* приобретает вид
IIc?=Kc=Kpp~*Vi
(1.16)
Считая удельные теплоемкости постоянными, легко определить
константу химического равновесия Кр, если ввести химические
постоянные £ и /. Поскольку химические процессы обычно
происходят при внешнем давлении Р= 1 атм, будем далее выра-
§ 1. Химическое равновесие в смеси идеальных газов 317
жать все давления в физических атмосферах и соответствующим
образом учитывать это при определении остальных величин.
Если представить энтропию в виде
S = -R\nP + CplnT + S0, (1.17)
где S0 — часть энтропии, не зависящая от температуры и
давления, то химической постоянной по определению называется
величина
(1.17а)
Химическая постоянная однозначно определяется теоремой
Нернста —Планка. Величина / по определению равна
/ = Clge = 0,4343C. (1.18)
Следовательно, / и £ связаны соотношением
10'W. (1.19)
При расчете химических процессов спин ядра обычно не
учитывается, поскольку появляющиеся за счет него множители в
уравнении закона действующих масс взаимно уничтожаются.
Поэтому при расчетах, основанных на законе действующих масс,
полагают, как правило, g>= 1.
Пример 30
Согласно формуле (3.1.10) гл. 2, отнесенная к 1 кмоль энтропия одноатом*
ново газа определяется формулой
о. п,„ • (2я^)3/2
;=41п^
,л -& т-у ] = -/? In Р+1-/? In Г + 5„, (1.2а)
где
So4^ + ^n^3/2fe^9-869-10-8-. (,.21)
Множитель 9,869-10-5 появляется при переходе от Н/м2 к атм. Выведенный
в гл. 4, § 5 дополнительный множитель, обусловленный ядерным спином, как
было сказано, здесь не учитывается. Поскольку Cp = SR/2, имеем из (1.21)
rg)__So-CP_] (2я11)3/2&6/29,869-10-5__
£ "" R П Лз —
. (2я)з/2 fc6/2 9,869-10-5 . 3 . л /4 поч
= 1п д,з/2/1з +YlnAr> (1'22)
где Лг—относительная атомная масса. Подставляя числовые величины, находим
?<1> = 7,872-11,5264-|-1пЛ/. = -3,654+|-1пЛг. (1.23)
318 Гл. 5. Системы, состоящие из различных микрочастиц
Далее, на основании (1.18) имеем
/U) = 0,4343C<« = — 1,587+-g- \gAr
(1.24)
В частности, для водорода без учета спина ядра
/н= — 1,582.
В случае, когда необходимо учитывать вырожденные или
возбужденные квантовые состояния, в частности когда надо
учитывать ядерный спин, химическая постоянная £ в единицах СИ
(давление в Н/м2) определяется равенством
ь - ш Л3
(1.22а)
Пример 31
Для электронов g = 2. Следовательно, химическая постоянная электрона
равна
2 (2-3,14»9,Ь 10-31)3/2(1>38»10-23)5/2==
£е-1П (6,63-Ю-34)3
- 0,405.
При постоянной теплоемкости внутренняя энергия i-ro компонента реакции
(отнесенная к 1 кмоль) определяется уравнением
Ui=U0i + CviT, (1.25)
где
</oi = A^V+^)
(1.25а)
— полная энергия основного состояния 1 кмоль реагента. При этом Eg{
представляет определенную в гл. 4, § 4 энергию основного состояния 1-го вещества.
Имея в виду, что Cp—Cv — R, получаем из (1.25) и (1.20) химический
потенциал
Н-^
ср1
Ui—TSi + PiV_Utn
: _ Na ,_ „.., Na
kT\r\Pi-1f:T\nT — kTZ>i.
(1.26)
Умножая это выражение на \JkT и используя условие химического
равновесия (1.9), находим
£inPr/-5v'(x,n7,+b-^)=,n/r'(T)'
i i
или, переходя к десятичным логарифмам,
(1.27)
(1.28)
§ 1. Химическое равновесие в смеси идеальных газов 319
Задачи
1.1*. Термодинамические величины для смеси идеальных газов
Исследуется газовая смесь, состоящая из молекулярного и атомарного
водорода. Требуется установить, достигнуто ли состояние термодинамического
равновесия. Температура равна 500 К, парциальные давления атомарного и
молекулярного водорода составляют соответственно Р!=10атм и Р2=15атм.
Вычислить энергию Гиббса G, а также химические потенциалы \лс обоих
компонентов (V=l м3, энергия диссоциации е/) = 4,46 эВ).
Решение
Энергии основного состояния 1 кмоль молекулярного водорода и
атомарного водорода составляют соответственно £он =—Na^d =
= — 6,02-1026-4,47.1,60-10-19 = — 4,31.105 кДж и Еш=0. Взаимодействием
молекул, по определению идеального газа, пренебрегаем. Поэтому
термодинамические величины газовой смеси аддитивны до тех пор, пока каждый из ее
компонентов можно рассматривать как идеальный газ.
Следовательно, свободная энергия смеси идеальных газов равна сумме
свободных энергий каждой из составных частей смеси:
F = F1 + F2. (1.1.1)
Свободную энергию 1-го газа следует вычислять таким образом, как если бы
все остальные газы отсутствовали, а рассматриваемый газ один занимал весь
имеющийся объем. Тогда парциальное давление идентично величине
Поступательная часть свободной энергии, согласно формуле (3.1.9) гл. 2, равна
__^[hflB££2?+1]. (1.,з,
В рассматриваемом случае будем считать, что i — \ обозначает атомарный
водород, i = 2 — молекулярный. Вращательные движения при Г = 500К
полностью возбуждены. Тогда в соответствии с формулой (3.3.3) гл. 2 имеем
4тт2 тът
^вращ)1 = 0, (Fspamh^-N2kT\n^^-. (1.1.4)
В то же время колебания молекул еще не возбуждены.
За счет ядерных спинов в случае атомарного и молекулярного водорода
в статистических суммах появляются множители 2Nl и 22N* соответственно.
Кроме того, необходимо учесть энергии основного состояния атомов и
молекул водорода. При использовании формы записи (1.25а) соответствующие им
множители в выражении для статистической суммы можно представить в виде
или
320 Гл. 5. Системы, состоящие из различных микрочастиц
где ен = 0 и ен —соответственно энергии основного состояния атома и
молекулы водорода. Тогда для свободной энергии газовой смеси имеем
Это выражение можно представить в виде
F = F1(N1, V, T) + F2(N2t V, Г). (1.1.6)
При выводе формул для энергии Гиббса необходимо учесть, что последняя
является функцией числа частиц, давления и температуры. Имея в виду, что
PiV = NikT9 получаем
at=F1+Plv=-NlkT^ WW' +£^н ( (117)
аш=Рш+Ршу—ы+т1п WWJk'W* +л^ (U8)
Запишем теперь энергию Гиббса газовой смеси в виде функции величин Nlt
Na» Р> Т, т. е. исключим зависимость от Рх и Р2:
0 = 01+Ot—Win « W^W* +NikT^+N^_
_^hiM^ + WI„5 + ^. А (U.9)
Согласно Гиббсу, химические потенциалы \кС1 отдельных компонентов смеси
определяются соотношениями
M = \dNt)vtsttNi \dNi)pj,Nj \dNi)v.T.N! [dNjp^.N^1')
(1.1.10)
При выводе соответствующих формул примем во внимание, что многократно
встречающееся полное число частиц
i
тоже зависит от отдельных величин N{. Тогда получим
_/ дО\ _ G, _/дв \ _G2 ... ...
*c1~\Wi)p,t,n-1U' ,1е*-[М1)р.т.ыГ'гП' { '
Таким образом, химический потенциал \aci газа в смеси соответствует
химическому потенциалу чистого газа с парциальным давлением Я,-.
При заданных числовых значениях числа частиц составляют Nx — 1,47* 102в,
#2 = 2,20-1026. Используя величины, приведенные в табл. П. XXI (см. при-
§ 1. Химическое равновесие в смеси идеальных газов 321
ложения), находим
G1=—1,47-102°. 1,38-10-23.500Х
"j 2(2.3,14-1,01)3/2 (1,38-10-23» 500)5/2
. (6,02-Ю2С)3/2(6,63-Ю-34)3-10-1,013-105 J
Дж = —10 500 кДж,
X
(?2 = — 2,20-1026-1,38-10-23500 X
Г4(2.3,14)7/2 ■2,02-0,47-10-47(1>38-10-23.500)7/2
Х nL (6,02-1026)3/2 .(6,63-10-34)5.15-1,013-105
9 90.1026
' -4,31-108 Дж = —19300—157500 = —176800 кДж.
6,02-102G
Следовательно, энергия Гиббса рассматриваемой смеси составляет— 187 300 кДж.
Используя (1.1.7), (1.1.8) и (1.1.11), находим потенциалы
^1=^- = -7,Ы0-2» Дж, ^2 = -^- = —8,03-10-" Дж.
В соответствии с этим имеем
2\icl — \ic2 Ф 0.
Это означает, что при заданной температуре и парциальных давлениях
атомарный и молекулярный водород не находятся в равновесии.
1.2. Вычисление константы химического равновесия КР(Т)
с помощью статистической суммы (реакция H2^t2H)
Найти константу равновесия для диссоциации молекулярного водорода
при 7 = 5000 К. Чему равно парциальное давление атомарного водорода, если
суммарное давление составляет Р=10 атм? Энергия диссоциации молекулы
водорода eD = 4,47 эВ; r# = 85 К, Г0 = 6300 К.
Решение
В соответствии с законом действующих масс (1.14) состояние равновесия
для рассматриваемой реакции определяется соотношением
~2 хт ит -7<1> 2
_Рн _ niiNAkT _v ,^_игг zw
р
*Л**1- = К p(T) = kT^L-. (1.2.1)
-н, "н. рК ' Я»
Здесь пн и /гн есть числа киломолей, отнесенные к объему V=l м3.
Статистические суммы Zh} и Z^ определяются выражениями (4.20) гл. 4.
Непосредственно из статистической суммы целесообразно исходить в тех случаях,
когда теплоемкости нельзя рассматривать как постоянные величины. В
соответствии с задачей 4.5 гл. 4 при заданной здесь температуре можно пренебречь
как возбуждением высших электронных уровней, так и различием между
орто- и парасостояниями. С помощью формул (4.8), (4.13) и (4.22) гл. 4
находим статистическую сумму для одной молекулы водорода при V=l м3-:
*»—1<2ли тз/2 Т ехр(-*ау2*Г) / ^нЛ „ 2 2)
2н. - А, (2^н,kT) 2Tr 2 _ехр(_w ехр ^- kT J. (1.2.2)
322 Гл. 5. Системы, состоящие из различных микрочастиц
Атом водорода не имеет ни вращательных, ни колебательных уровней.
Следовательно,
41* =-^ (2п»нкТ)3'* ехр (—§-) • (1-2.3)
Множители 4 в формуле (1.2.2) и 2 в формуле (1.2.3) обусловлены ядерным
спином в соответствии с соотношением (4.15 г) гл. 4. Подставляя (1.2.2) и (1.2.3)
в (1.2.1) и имея в виду, что fiH =2цн, находим
*я (^= й" ** [1 - ехР ( —г)J х
Xexp(-2SH-eHfeV-°-5K). (1-2.4)
Отсюда видно, что множители, связанные с ядерным спином, снова не вошли
в выражение для Кр(Т).
В общем случае при реакции распада AB^ztA + B в выражении для
закона действующих масс за счет энергии основного состояния появляется
множитель вида
ехр
(-*)-
^ехр (— UcDA/2/гГ) ехр (— JcdB^kT) ехр (—гфТ) ехр (— гв/kT)
ехр (—1i(dAB/kT) ехр (— еав/ЬТ)
где e,-(i" = A, В, АВ) характеризует энергию основного состояния молекулы
1-го компонента (без учета энергии нулевых колебаний Лко//2). Величина
(1.2.5)
называется энергией диссоциации; ее значения приведены в табл П. XXI.
Далее,
и0{ = ЫА((е0;+™^
(1.2.56)
представляет полную энергию основного состояния 1 кмоль /-го компонента
[ср. формулу (1.25а) настоящей главы]. Логарифмируя, находим (Лн —
относительная атомная масса водорода)
9^3/2 £5/2
1п/Г,(Г) = 1п9,869-10-* + 1п htff,/t +lnA#TR(l-e-W) +
+т1пГ-^=-,1-53+7'52+4'11+12-78-щл^ш=2'52-
Отсюда при Рн + Рн2=10 атм имеем
Рн Рн
ТГ^=1А п =^2>52= Ю1.09Б атм.
§ 1. Химическое равновесие в смеси идеальных газов 323
Решая квадратное уравнение
Р2н+12,4РН —124 = 0,
находим Рн = 6,5 атм, Рн =3,5 атм.
Если определить температуру диссоциации посредством соотношения
kTD = eD,
то при заданных числовых значениях получим
4 47- 1 6-10-19
Таким образом, газ почти на 2/з состоит из атомарного водорода, несмотря
на то, что температура Г = 5000 К существенно ниже температуры
диссоциации.
1.3. Уравнение Вант-Гоффа. Теплота реакции
Найти энергию, высвобождающуюся при химической реакции 2H;z±H2
при температуре Г = 298 К. Как изменится энергия реакции при повышении
температуры до 800 К? (8£> = 4,47 эВ, Го = 6300 К, /На = 0,47-10~4? кг-м2).
Решение
Будем исходить из уравнения реакции (1.2)
ViA! + v2A2+...=0. (1.3.1)
Предположим, что в системе произошло определенное число SN элементарных
актов превращения вида (1.3.1). Вызванное этим изменение энергии Гиббса
при учете соотношения (1.6) можно записать в виде
60=S|:M;=Ec"-(!,'P*>M'' С-3-2)
i 1 С
где Р/0— парциальное давление /-го компонента в исходном состоянии. В
результате SN реакций между элементарными частицами концентрация i-ro
компонента изменяется на величину
6Ni = —vfiN. (1.3.3)
Отсюда имеем
8G = -8W2v^(7\P/0). (1.3.4)
i
Начальные давления Р{0 необходимо отличать от парциальных давлений Р/,
которые определяются законом действующих масс (1.15) и при которых
величины 6G, определяемые формулой (1.3.4), обращаются в нуль. Выражая
химический потенциал с помощью (1.6) и используя (1.14), находим
6G=-/e76^2]v/(lnP/0-ln^rz;-1))=-^r6^2]v/lnP/0+^6^1n/CiD(r).
(1.3.5)
Отсюда, применяя формулу (3.21) гл. 2 и учитывая постоянство значений Р/0,
получаем
-^¥)P=-Kf),+№»-™(™),-
(1.3.6)
324 Гл. 5. Системы, состоящие из различных микрочастиц
Таким образом, при постоянных давлении и температуре изменение
энтальпии ЬН дает теплоту реакции. При 6N = Njl имеем из (1.3.6) уравнение Вант-
Гоффа
(1.3.7)
Подставляя сюда константу равновесия (1.2.4), находим изменение энтальпии
при образовании 1 кмоль молекулярного водорода в реакции 2Н—*Н2
АНР = - QP = - NAzD —| RT+RT0 j£^jf ■
Теплота реакции при Т = 298 К определяется формулой
Qp = NAzD+-R-2M-RT»^—Zf^t
(1.3.8)
(1.3.9)
или, после подстановки числовых значений,
QP = [6,02-102б.4,47-3,83-10-23+1,986 (1,5-298—6300-Ю-9,18)] =
= 104,0-103 ккал/кмоль= 104 ккал/моль.
В соответствии с этим при Т = 298 К возбуждением колебательных состояний
можно пренебречь.
При Т = 800 К теплота реакции возрастает по сравнению со значением (1.3.9)
на величину
AQp= 1,5-1,987-502 ккал/кмоль= 1,5 ккал/моль.
Из этого следует, что теплота реакции лишь незначительно зависит от
температуры и в первом приближении может считаться постоянной. Величина АНр
есть энергия, которую получила химическая система; она положительна при
эндотермических и отрицательна на экзотермических реакциях. При
эндотермических реакциях, которые сопровождаются поглощением тепла, имеем
/а^ ч л {д\пКр (Т)\
(АЯ^эндохерм > 0, или Wr1 < 0
\ UI /эндотерм
(1.3.7а)
Следовательно, при эндотермических процессах константа равновесия
уменьшается с повышением температуры. В результате химическое равновесие
сдвигается слева направо, т. е. в сторону увеличения образования продуктов
реакции. В рассматриваемой реакции диссоциации повышение температуры
приводит к возрастанию доли диссоциированных частиц. В противоположность
этому при экзотермических реакциях, сопровождающихся выделением тепла,
имеем
(ДЯЯ);
'экзотерм
< 0, ИЛИ
/ д In Кр
[ дТ~
KpW
>0
экзотерм
(1.3.76)
§ 1. Химическое равновесие в смеси идеальных газов 325
В этом случае повышение температуры приводит к сдвигу равновесия справа
налево, т. е. в сторону возрастания концентрации исходных веществ, при
одновременном уменьшении концентрации продуктов реакции. Равенство
Qp= — AHP
(1.3.8а)
является определением используемой в физической химии величины,
называемой теплотой реакции. Она положительна при экзотермических и отрицательна
при эндотермических процессах.
1.4. Химические постоянные
Вычислить химические постоянные £ и / для хлористого, водорода и
водорода.
Решение
Согласно (1.17а), химическая постоянная £ определяется формулой
?=JV£. (1.4.1)
где S0 —не зависящая от давления и температуры часть энтропии
S = S0 — R\nP + Cp\nT. (1.4.2)
Ядерный спин, как мы уже говорили, не учитывается, поскольку
соответствующие члены выпадают из уравнения закона действующих масс.
В случае двухатомных идеальных газов, согласно формуле (3.1.10) гл. 2,
имеем для 1 кмоль
а согласно формулам (3.2.14) гл. 2 или (3.3.4) гл. 2,
SBpal« = ^(ln^^+l). (1.4.4)
Величина т равна единице в случае различных атомов и двум в случае
одинаковых. Пусть температуры столь низки, что колебательные состояния не
возбуждены. Принимая во внимание, что в соответствии с законом
равнораспределения (2.2) гл. 2 и соотношением (2.4.19) гл. 2 изобарная теплоемкость
двухатомного газа Cp = 7R/2, можно записать 5 в виде
S = SnocT + SBpaui = -RlnP + Cp\nT + S0t (1.4.5)
где
эо =
■R\\n
(1.4.6)
29/2 ^7/2 ^3/2 Jk7/% 7 \
%h\ + 2/ '
Отсюда для химических постоянных имеем
г . 29/2 я7/2 u3/2 Jk7/* ,m , f VWJk
где
£ш = —3,65-f-|-lnAfr или /(1)=£(1Mge = -l,59 + -|lgMr (1.4.8)
326 Гл. 5. Системы, состоящие из различных микрочастиц
— химические постоянные одноатомного газа, применяемые при расчетах
с использованием натуральных и десятичных логарифмов, соответственно (ср.
пример 30).
Подставляя численные значения, находим из (1.4.7) и (1.4.8)
£нс1 =—3,65—2,74 + 5,39 = —1,00, или /НС1 = 0,4343-(—1,00) =—0,43,
£н=—3,65 —5,14+1,05 = —7,74, или /н> =0,4343-(— 7,74) = — 3,36.
Для температур, при которых колебания полностью возбуждены,
колебательная часть энтропии, согласно формуле (3.5.5) гл. 2, определяется выражением
SKOa = R (\ + \п -^\ = R\nT + R + R\n ^ . (1.4.9)
Имея в виду, что колебательный вклад в теплоемкость равен R, находим
из (1.4.1) колебательную часть химической постоянной
г -1 JL
ЬКОЛ — 1П Л.
С учетом этого получаем для химических постоянных значения
£НС1 =—1,00—8,36 = —9,36, £Hf=—7,74—8,75=16,49, или
/на =-4>06> /н2=-7>16-
В области температур, соответствующих неполному возбуждению
колебательных степеней свободы, при расчете константы химического равновесия
целесообразнее всего исходить из статистической суммы (4.20) гл. 4 и
использовать общую формулу (1.14) настоящей главы (ср. задачу 1.2 настоящей
главы). Если входящие в (1.27) и (1.15) величины приближенно рассматривать
как постоянные внутри соответствующего интервала температур и давлений, то
при определении химических постоянных следует исходить из этих формул.
Учитывая, что теплоёмкость определяется выражением (4.7.13) гл. 4, получим
для колебательной части химической постоянной:
(1.4.10)
При Т <^fi(ui/k — Ti имеем £/Кол = ^« В противоположном предельном случае
T^>Ti находим
С*=1п-т*-. (1.4.11)
/КО/
1.5. Поведение энтропии при процессах
с постоянной теплоемкостью
В результате реакции между 2 кмоль атомарного водорода, протекающей
при внешнем давлении Р=1 атм и температуре Г = 298 К, образуется
молекулярный водород. Определить обусловленное этим процессом изменение
энтропии. Теплоемкости считать постоянными и равными соответственно (Cp)H = 5R/2
и (Ср)н =7R/2. Значения / взять из табл. П.XXIII.
§ 1. Химическое равновесие в смеси идеальных газов 327
Решение
В соответствии с формулой (1.17) при постоянной теплоемкости энтропию
можно представить в виде
S^-RlnP + CplnT + Cp+Rt,. (1.5.1)
Химические постоянные, согласно (1.18), связаны друг с другом соотношением
£ = /In 10 = 2,3026/. (1.5.2)
Находим
£н=-3,64, Сн2=-8.47.
Подставляя £н и £н в (1.5.1) и учитывая, что Р—\ атм, получаем
SH(298K, 1 атм) = /?Су1п298+-|--3,64^=26,0ккал/кмоль.К,
5Нг (298 К, 1 атм) = # (у In 298 + у-8,47 J =29,8 ккал/кмоль-К-
В соответствии с этим энтропия в рассматриваемом «.-процессе уменьшается на
величину
2SH— 5Нг = (52,0—29,8) = 22,2 ккал/кмоль-К.
1.6. Определение константы равновесия с помощью энтальпии
образования и энтропии (диссоциация двуокиси углерода)
Определить константу равновесия для реакции 2СО + 02 ;г± 2С02 при
Г =1500 К. Чему равны парциальные давления окиси углерода и кислорода,
если парциальное давление углекислого газа составляет . 100 атм? Значения
энтальпии образования #°98 и энтропии «S°gg при комнатной температуре (25 °С)
взять из табл. 31 (ср. также табл. ПХХ1У).
Таблица 31
Значения энтальпии образования и энтропии при 25 °С и 1 атм
Вещество ^298' 103 ккал/кмоль S298' ккал/кмоль-К
СО —26,4 47,3
02 0 49,0
С02 —94,0 51,1
Решение
Согласно формуле (1.26), химический потенциал i-ro компонента
определяется соотношением
fxcl = -^+kT\nPi- ^ПпГ-АГС/. (1.6.1)
При этом давление необходимо выражать в физических атмосферах.
Предполагается, что теплоемкости С«/ и химические постоянные £/ остаются
неизменными.
328 Гл. 5. Системы, состоящие из различных микрочастиц
Обозначим через \1С{0 химический потенциал при некотором определенном
парциальном давлении, которое мы положим равным Р0=1 атм. Тогда
химический потенциал можно записать в виде
\ici=Vcio + kT\n^. (1.6.2)
Из условия равновесия (1.9) следует, что
Е vmw=E^" G'=E"K" (я'-г5')=°- с-6-3)
С i i
С другой стороны, согласно (1.6.2), имеем
£vVci = £*i(pcto + bT \п^=0. (1.6.4)
i i
С учетом (1.6.3) получим отсюда
ln^ = ^v;ln^=-i£v,^0 = -X^№,-rS,0)
(1.6.5)
или
В рассматриваемом случае имеем v! = vc0 =2, v2 = v02=l, v3 = vc0 = -—2.
С помощью табл. 31 находим
Sv////o = [2 (—26,4. 103)—2 (—94,0- 103)] = 135,2-103 ккал/кмоль,
2V/5I.0 = (2.47,3+1.49,0—2-51,1) = 41,4 ккал/кмоль-К.
i
Следовательно,
^v,,gA=lg^=_0>434(1i|^-1i^)=-10(65.
i
Имея в виду, что Р0=1 атм, получим
со °2= Ю-10,65 =2,2-Ю-11 атм.
Р2
Поскольку до начала диссоциации кислород и окись углерода отсутствовали,
парциальное давление окиси углерода в два раза превышает давление
кислорода. Поэтому пишем
1.^ = 2,2.10-11 атм, или РСо = Км-Ю-н Р£0в .
рсо2
При Рсо = 100 атм имеем
РСО=1,6-10-3 атм, РОа = 0,8.10-3атм.
§ 1. Химическое равновесие в смеси идеальных газов 329
Результат, полученный с помощью формулы (1.6.6) с использованием значений
из табл. П.XXIV, следует рассматривать как нулевое приближение, поскольку
при этом не учитывалась зависимость энтальпии образования и энтропии от
давления и температуры.
1.7*. Константа равновесия при постоянной теплоемкости.
Коэффициент выхода
Определить коэффициент выхода хлора в равновесной реакции
2HCl^ztH2 + Cl2 при температуре Г=1800К и давлении Р=1атм. При
решении использовать данные, приведенные в табл. 32.
Таблица 32
Вещество 10ПЛ ..Р' Р . со,., с-1 / еп, эВ #Jftfl, 10» ккал/кмоль
1800 К, ккал/кмоль i D 298 '
НС1
н2
С12
8,29
8,00
8,92
5,63
8,28
1,06
—0,43
—3,36
1,30
4,34
4,47
2,47
—21,9
0
0
Решение
Согласно соотношению (1.28), при постоянной теплоемкости константа
равновесия определяется выражением
lg/C/,(r) = ^lgPr = ^v,(//+^ilgr-0,4343^), (1.7.1)
i i
где вместо U использовано обозначение Е.
Определяющую роль здесь играет выражение, составленное из энергий
основного состояния:
з
2j v/£0/ = 2£0 hci~~^oh2 — ^oci2- (1.7.2)
i = i
Используя определение энергии диссоциации (1.2.5), можно представить это
выражение в виде
- У ^гЦ=2ео(НС1)-е0(Н2)-ео(С12). (1.7.3)
i
Подставляя сюда приведенные в табл. П.ХХ1 значения энергий диссоциации
Е£>(НС1), 8£>(С12) и в£>(Н2), получаем
-£^=(2.4,43-4,47-2,47)==: 1,92 эВ- 0-7-3а)
i А
Для 1 к моль имеем
— 2 v/£o/ = 6,02.1026.1,92.3,83-10-2з = 44,2-103 ккал/кмоль. (1.7.36)
i
Если энергии диссоциации неизвестны, то энергии основного состояния можно
вычислить с помощью приведенных в табл, FIXXIV значений энтальпии.
330 Гл. 5. Системы, состоящие из различных микрочастиц
Согласно уравнению Вант-Гоффа (1.3.7), энтальпия реакции и константа
равновесия связаны соотношением
AHP = -RT* ^p-L. (1.7.4)
Подставляя сюда выражение (1.7.1) для константы равновесия и переходя от
десятичных логарифмов к натуральным, получаем
*НР=- S (viEoi + ViCpiT). (1.7.5)
i
С помощью соотношения
ДЯР=-2>/ЯЙв (1-7.6)
i
можно выразить отнесенную к То = 298 К, Ро = 1 атм энтальпию реакции АНр
через приведенные в табл. П.XXIV значения Н%8. Последние определены
таким образом, что изменение энтальпии соответствует разности энтальпий
начального и конечного состояний.
С помощью табл. П-XXIV или табл. 32 находим
АНр = — (—2-21,9.103) = 43,8-103 ккал/кмоль.
Из (1.7.5) имеем
-^iviEoi = AHP + ^lviCpiT0. (1J7)
i i
Подставляя численные значения, получаем
— 2 v/£0/ = 43,8.103—0,34- 298 = 43,7-103 ккал/кмоль. (1.7.7а)
i
Расхождение между (1.7.36) и (1.7.7а) объясняется погрешностью, внесенной
при округлении.
Подставим вычисленное значение (1.7.3а) в выражение (1.7.1). Тогда для
основного члена стоящей справа суммы получим
n*U4Vv'£' 0,4343-1.92-1,60-10-» 9,67.103-
-0,4343 2, — = 1|38.Ю-»!Г = —Т-' (К7*8)
При Т = 1800К имеем
-0.4343^1^=5,37.
Как видно из табл. 32, при заданной температуре Т=1800К колебательные
состояния полностью возбуждены только у хлора. Для последнего
колебательная часть химической постоянной, согласно формулам (1.4.11) и (1.18),
равна
/кол = £кол1§е=-1§^=-2,91, /(С12) = -2,91 + 1,30 = -1,61.(1.7.9)
Что касается водорода и хлористого водорода, то у них колебания
возбуждены лишь частично. Поэтому для вычисления химической постоянной в этом
случае следует воспользоваться формулой (1.4.10). При Т=1800К имеем
/кол0 (Н2) =-1,27, /1*°<> (Н2) = -1,27-3,36 = -4,63, (1.7.10)
/кол0 (НС1) = —2,06, /18оо(НС1) = —2,06—0,43 = —2,49. (1.7.11)
§ 1. Химическое равновесие в смеси идеальных газов 331
Отсюда находим
2 v/// = —2-2,49+ 1,61 +4,63= 1,26. (1.7.12)
с
Наконец, второй член в сумме (1.7.1) равен
Sv/^lgr-2-8'29-8^-8'"2!» 1800-^,66. (1-7.13)
Суммируя (1.7.8а), (1.7.12) и (1.7.13), получаем для константы равновесия
при Г=1800К значение
lg^ = 6,07. (1.7.14)
Выходом химической реакции называют по определению отношение у
количества превращенного вещества к количеству исходного вещества или его
основного компонента. В рассматриваемом случае в состоянии равновесия
молярные концентрации п2 = пн и п3 — пС1 равны друг другу. Их сумма равна
молярной концентрации прореагировавшего хлористого водорода. Мы
предполагаем, что к началу реакции имелся лишь хлористый водород, т. е. что
относительные концентрации отдельных веществ имели следующую величину:
Для реакции, происходящей без изменения числа молей, 2V*,==0> следова-
i
тельно, в состоянии равновесия имеем
c2 + c3 = 2c3 = yt Cl = CHC\ = l—c2—c3=l—y, (1.7.15)
где у—выход реакции. Закон действующих масс в этом случае имеет вид
т. е. равновесие не зависит от общего давления. Подставляя сюда (1.7.15) и
константу равновесия (1.7.14), получаем
4(l-*/)2=^=1()6>07> (1.7.17)
Отсюда видно, что при Т =1800 К относительное количество продуктов
реакции очень мало, т. е. можно считать у<^1. Тогда из (1.7.17) имеем
lg*/=y (0,60-6,07)^0,26-3, т. е. cclf=-|-=0>9.10-8.
Таким образом, относительная концентрация хлора составляет менее 0,1%
концентрации исходного вещества.
1.8*. Реакция обмена между водородом и дейтерием
Обычный водород состоит из 99,986% атомов Н = *Н с относительной
атомной массой 1,0078 и 0,014% атомов D = 2H с относительной атомной
массой 2,0141. Определить относительную концентрацию молекул Н2, D2
и HD в состоянии равновесия. Каково соотношение при 20Q С? [В основу
расчета положить данные, приведенные в табл. 33. Момент инерции
^н2 = 0,47.10-47кг.м2, колебательная частота ©н =8,32-10" с-1, THz =
= л©н /6 = 6300 К.
332 Гл. 5. Системы, состоящие из различных микрочастиц
Водород и
Вещество
Энергия диссоциации е^, эВ
Расстояние между ядрами г, 10~10 м
дейтерий
н2
4,4776
0,7414
D.
4,5557
0,7417
Таблица 33
HD
4,5133
0,7413
Решение
В соответствии с законом действующих масс парциальные давления
связаны соотношением
^Гк'т'Ш: "'8"
Объединим поступательные и вращательные части и будем рассматривать
высокие температуры, когда различие между орто- и парасостояниями
несущественно. Тогда из формул (4.21) и (4.15) гл.4 получим, учитывая, чтот=тн =tD =2
[Z?p> (HD)]2 [Zgj« (HD)]2 . TR (H2) TR (D2) ^D
^(HJZi^CHJzSKDJZfi&rCZ),) ir«p(HD)]» (fiH^D/'2 '
(1.8.2)
Характеристическая вращательная температура Tд в соответствии с
формулой (4.11) гл. 4 обратно пропорциональна моменту инерции J. Считая
расстояния между ядрами приблизительно одинаковыми, находим для моментов
инерции с помощью формулы (4.5) гл. 4 соотношение
Лш _ 4ц„1Ъ (L8>3)
'h/d, (Hh + Hd)2'
где (хн и \iD — массы атомов водорода и дейтерия. С учетом этого получим
из (1.8.2)
[z<y(HP)]2[z&t(HP)]2 =2^н + иР==я ylt (184)
ZBp (H2) ^пост (H2)Zj,p'(D2) (D2) VphVd
Для колебательных состояний и состояний при абсолютном нуле температуры
с помощью (4.9) и (4.22) гл. 4 находим
№(hd)N41>(hd)]'
^кол (Н2) Zg (Н2) 2КОл (D2)Zg (D2)
[1 -ехр (-Гн/Г)] [1-ехр (- TDJT)] exp (- Гнр/Г) exp (-2eHD/kT)
[1 _exp (-THD/T)\* exp [- (TH! + TD)/2T] exp [- (8H2 + sDa)/ferj •
(1.8.5)
Стоящие за пределами скобок в правой части (1.8.5) множители вида
ехр(""^)=еХР('
' 2kT J
§ 1. Химическое равновесие в смеси идеальных газов 333
обусловлены нулевыми колебаниями. В соответствии с (1.2.5) их можно
объединить с величинами ехр (—еАВ//еГ), которые представляют вклады,
связанные с энергией основных состояний (без учета нулевых колебаний), и
выразить через энергии диссоциации. В результате в (1.8.5) появится
экспоненциальный множитель с показателем
^ТИР~ТИ2~^ТР2 2gHD~8H2~8D2 __
2Т kT ~~
% /0 х 2eHD_1~8H2 — 8D2
= -2^(2C°HD-«H-^D2) ]?f =
2eD(HD)-eD(Hg)-eD(D2) (L8>6
kT
Используя численные значения, приведенные в табл. 33, получим
2вд(НР)—eD(H2)—ед(Р2) _—0,0077-1,60» 10-19_ 78 К п 8 ?)
kT ~~ 1,38-Ю-23 Г ~~ Т ' { ' ' '
Частота собственных колебаний гармонического осциллятора с приведенной
массой |лПрив равна
а>=т/-£-, (1.8.8)
' Мприв
где D — коэффициент, характеризующий действующую на осциллятор упругую
силу.
Поскольку для всех рассматриваемых молекул расстояния между ядрами
приблизительно одинаковы, можно допустить, что одинаковы также и
величины D. Тогда, учитывая, что M,d = 2!liH' П0ЛУчаем следующее соотношение
между собственными частотами, а следовательно, и между характеристическими
колебательными температурами:
W>D,:"HD = 74:7VrHD= ^2: / 1 : )/-| = 1:0,707:0,866
(1.8.9)
Зная Тн и <вн , можно определить все остальные величины. Подставляя
(1.8.4) и (1.8.5) в (1.8.1) и учитывая (1.8.7) и (1.8.9), получаем
Р|щ _„ m ? 1/? -78 к/г (1 -е-6300 *'т) (1 -е-"50 К'т)
Рн,Рог~*р{ '- У в (1_е-Б460К/Г), •
(1.8.10)
В случае очень высоких температур, 7,>Гн2 = 6300 К, находим из (1.8.10)
*:?(7)=3/2^=4. (1.8.П)
В противоположном предельном случае низких температур Т <^.TD =4450 К
константа равновесия убывает по экспоненциальному закону
Kf(T) = 3V2e-7*VT. (1.8.12)
334 Гл. 5. Системы, состоящие из различных микрочастиц
Относительную концентрацию с^ молекул Н2 можно положить равной
единице. Тогда, воспользовавшись формулой (1.8.12), получим следующее
соотношение для определения относительных концентраций в состоянии равновесия
при температуре 20 °С:
= = = Ко(293К) = 3/2бГ78/293=3,25.
CH/D2 (l-cHD/2)(A-cHD/2) Р
CHD CUD
-cHD/2) рК
(1.8.13)
Решение квадратного уравнения дает
cH2:cHD:cD2=l:2,8.10-4:2,4.10-8. (1.8.14)
Следовательно, подавляющая часть атомов дейтерия связана с атомами
водорода.
1.9*. Адсорбционное равновесие при химическом катализе
Пусть на каждый квадратный метр поверхности некоторого катализатора
приходится 5-Ю18 центров адсорбции. Энергия основного состояния
адсорбированного атома водорода составляет ен =—1,60 эВ. Спектроскопическим
исследованием установлено, что связанная частица совершает колебания в пло-
Фиг 65. Адсорбция молекул газа в цилиндрической
поре.
скости, параллельной поверхности адсорбента, с частотой ©ц = l,64-1014c-1
и в направлении нормали к ней с частотой C0j_ = 9,15«1013c-1. Определить
адсорбционное равновесие в цилиндрической поре диаметром 0,01 мм и
глубиной 0,4 мм (фиг., 65). Давление водорода Р=\ атм, температура T = 75QC.
Решение
Пусть в поре имеется N0 центров адсорбции. Предположим, что N из них
заняты каждый одной частицей, а остальные N0— N мест остаются пустыми.
Распределение N адсорбированных одинаковых частиц по имеющимся N0 центрам
адсорбции может осуществиться N0\/Nl(N0 — N)\ различными способами.
Запишем поэтому статистическую сумму процесса адсорбции в виде
Z = N\(N0 — N)\eK'ZKOJl'Z8y (1,9Л)
где gK—2 характеризует статистический вес, обусловленный ядерным спином.
Колебательную статистическую сумму частицы находим по формуле (4.19) гл. 4.
Колебания, происходящие в плоскости, параллельной поверхности адсорбента,
имеют две степени свободы, в соответствии с чем их следует учитывать дважды.
Тогда имеем
(1) / е"Н/2*г V e-uJ2kT
Множитель Zg в статистической сумме (1.9.1), в соответствии со сказанным
в гл. 4, § 4, представляет вклад основного состояния адсорбированной частицы,
§ 1. Химическое равновесие в смеси идеальных газов 335
т. е. состояния при абсолютном нуле температуры без учета нулевых
колебаний. Запишем его в виде выражения (4.22) гл. 4. Тогда для статистической
суммы адсорбированной частицы получим
Z- N°l \«( g~fe6)"/2*r Y e-b«±.I2kT c-s„/kT]N
N\(N0 — N)\[ \\—е-Ь<»\\/ьт J \ — e-b<*JkT e J
(1.9.3)
Используя (1.9.3), находим свободную энергию адсорбированной частицы
F = — kT In
N0\
N\(N0—N)\
-^r[ln2-21n^2sh2^)-ln(2sh^-) j^-j . (1.9.4)
Применив к первому слагаемому формулу Стерлинга [см. (1.8) гл. 2] и с
помощью формулы (3.2а) гл. 3 получим из (1.9.4) химический потенциал
адсорбированного водорода
МН,«)=(Ж)Г>1,=
=fenn^+fer(21n2+21nsh^+ln5hw'+4f)-
(1.9.5)
Для химического потенциала молекулярного водорода получаем [ср. (1.1.8)
и (1.1.11)]
Hc(H2)=-ferin ™>н +-^Г'
где парциальное давление Рн выражено в Н/м2. Колебательные состояния
для молекулярного водорода при Т = 348 К можно не учитывать, за
исключением нулевых колебаний, энергия которых включается в энергию диссоциации.
Из условия равновесия
2МНад) = МН2) (1.9.7)
имеем
N
1 N0-N~
1 8(2я)7/4
<4'3
Лб/2 pl/2
/2(^r)7/4sh2
sh
1ш^
~2kT
exp
/£он^
-2МЛгн
RT
-)
(1.9.8)
При этом в рассматриваемом случае следует записать
eoh2—2NA^h гИ2 + Ф>щ/2) — 2ен _ £р(Н2) + 2ен
RT ~ kT ~~ kT (1>9*9)
где 8/)(Н2) — энергия диссоциации молекулы водорода, а ен — отличная от нуля
энергия основного состояния адсорбированного атома водорода.
336 Гл. 5. Системы, состоящие из различных микрочастиц
■X
Используя заданное значение плотности центров и вычисляя площадь поры,
находим число центров адсорбции в поре: N0 = 6,32« 1010. Тогда из (1.9.8)
получим
6,32-1010 — N ~~
(6,63» 10-34)5/2 (1>013 .1()Б)1/2
8.(2-3,14)7/4 (б^'.^б)374 (°>47 ' Ю-47)1/2 (1,38-10-23.348)7/4
(—4,47 + 2-1,60) 1,60-Ю-19
™ 1,38-Ю-23-348
Х 2 6,63. Ю-34» 1,64. 1014 6,63-Ю-34»9,15» 1013 ~~ '
2-1,38-Ю-23-348 2.1,38.10-23.348
Отсюда
^- = 0,80, или ЛГ = 5,Ы010.
Таким образом, помимо 6,6-1011 молекул водорода, имеющихся в поре при
заданном давлении, в состоянии равновесия в ней находятся еще5,Ы010
адсорбированных атомов водорода. Проведенное исследование не позволяет,
однако, ничего сказать относительно времени, в течение которого установится
равновесие.
1.10. Термическая ионизация газов. Уравнение Саха
Если электрически заряженная или нейтральная частица (например, фотон,
электрон, ион или атом) сталкивается с молекулой газа, последняя с
определенной вероятностью может ионизоваться. С другой стороны, достаточно
медленный электрон может снова объединиться с ионом и образовать нейтральную
молекулу. Вследствие этого между ионизацией и рекомбинацией
устанавливается статистическое равновесие.
Пусть для создания плазменного шнура, применяемого для обработки
материалов, в качестве рабочего газа используется гелий при температуре
7 = 20 000 К. Найти степень ионизации газа и долю двукратно ионизованных
атомов. Потенциал ионизации составляет при однократной ионизации £/^=24,4813,
при двукратной ионизации £//2 = 56,16В (ср. табл. П. XXV).
Решение
Ионизационное равновесие можно рассматривать как частный случай
химического равновесия. Будем описывать состояние ионизационного равновесия
с полющью реакций
А^±А++е-, А+^=±А + + + е-, .... (1.10.1)
Применяя к этим реакциям закон действующих масс (1.16), получим систему
уравнений
£- = К?{Т)Р, £Г = К?(Т)Р (1.10.2)
C-±Cq CypQ
где c0t ci и се — относительные концентрации соответственно нейтральных
частиц, /-кратно ионизованных частиц и электронов [ср. (1.15)]. Поскольку газ
в целом остается нейтральным, помимо уравнений (1.10.2), должно
выполняться также соотношение
се = с1 + 2с2 + 3с3+.... (1.10.3)
§ 1. Химическое равновесие в смеси идеальных газов 337
Кроме того, согласно определению относительных концентраций, имеем
c0 + Ci+ca+...+ce=l. (1.10.3а)
Температуры, при которых существенна ионизация, обычно весьма высоки;
поэтому можно предположить, что закон равнораспределения выполняется для
всех компонентов, включая электроны. Тогда для одноатомных газов при
расчете следует использовать теплоемкость Cp = 5R/2 и формулу (1.22а) для по*
стоянных, согласно которой
1=1пё(2щ^^ (1104)
(давление в Н/м2). Статистический вес g нормального состояния в случае
электронов равен 2. Подставляя Vj = 1, v2~—1, va = —1 и учитывая, что
для электрона величина £/0 = £е = 0, получим с помощью (1.27) следующее
выражение для входящих в (1.10.2) констант равновесия:
In К(Рп+1) (Т) =-1 InГ+£»-£п+1-£е-£"~^"+1 ■ (1.Ю.5)
Согласно уравнению Вант-Гоффа (1.3.7), энтальпия ионизации равна
Величина
Hn+i = En + i-En = UIn+xe (1.10.6)
обозначает отнесенную в 1 кмоль энтальпию (п-\-\у кратной ионизации при
абсолютном нуле. Величина Hn+j/Nj[ есть энергия связи (л+1)-го электрона.
Подставляя в (1.10.5) химические постоянные в виде (1.22а) и учитывая,
что ^п — Рп + ъ £е = 2, получаем уравнение Саха
(1.10.7)
Как видно из табл. П. XXV (см. приложение), первый потенциал
ионизации значительно меньше потенциалов многократной ионизации. Вследствие
этого при не очень высоких температурах концентрации многократно
ионизованных атомов малы по сравнению с концентрацией однозарядных ионов:
Ci^>c2^>c3 ... . Поэтому до температур порядка 1Q4 К можно считать, что
С1==Се, Co + Ci + Ce=\. (1.10.8)
Исходя из такого предположения, можно определить степень ионизации а как
отношение числа однократно ионизованных атомов к полному числу атомов
а=т^=А- с-10-9*
Из (1.10.8) и (1.10.9) следует, что
С°=Ы' С1=тт^ (,Л0Л0)
Тогда первое из уравнений (1.10.2) дает
338 Гл. 5. Системы, состоящие из различных микрочастиц
Подставляя числовые величины, получим
/*«q in З4чя /24,48-1,60-Ю-1»
Kf (20 000 К) = - ■ „ ■ ^ -
И 2 (2-3,14.9,1.10-3i)3/2 (1,38-10-23-2-104)б/2
= 3,9.10-4(Н/м2)-1, (1.10.12)
откуда
а=|/
1 ^ = 0,081, (1.10.13)
1+4.9,8Ы04.3,9.10
т. е. свыше 8% всех атомов гелия ионизованы.
Как следует из (1.10.11), степень ионизации можно увеличить, если при
постоянной температуре уменьшать давление. При этом возрастает
высвобождающаяся при рекомбинации энтальпия. Однако, с другой стороны, понижение
давления приводит к уменьшению количества поступающего газа, в результате
чего уменьшается и количество тепла, передающегося от плазменного луча
обрабатываемому материалу. Оптимальное решение этой проблемы зависит от
конструкции плазменной горелки и от свойств материала.
Для константы равновесия процесса ионизации второго порядка Не+ ^±
^Не+ + +е- имеем
С=41,ехр(^=^)> (1Л0Л4)
или, после подстановки заданных числовых значений,
Кр2) (20 000 К) = 3,6-104 (Н/м2)-1 > К? (20 000 К).
Отсюда при а2 <^ 1 получим
*£=*!!»=!=«! С,=Ц, (1.10.15)
т. е.
К? с\ «г ' «2
г —а2—Е—(Р> 1 10-2^' —7 1.10-И
F27"" 3,6-104 ' '
1.11. Образование электронов и позитронов
при температурах T<^ii0c2/k
При чрезвычайно высоких температурах столкновения между
микрочастицами могут приводить к образованию электронных пар; например, из
у-кванта могут возникнуть электрон е~ и позитрон е+. Позитрон не может
долго существовать в присутствий вещества. Он снова объединяется с
электроном, при этом энергия покоя и кинетическая энергия обеих частиц полностью
преобразуются в квант излучения. Частота испущенного излучения
определяется законом Планка
e = Av (1.11.1)
и уравнением Эйнштейна
8=ф0с2, (1.11.2)
выражающим эквивалентность массы и энергии.
§ 1. Химическое равновесие в смеси идеальных газов 339
Определить равновесную концентрацию образующихся из квантов
излучения электронов и позитронов1) при 7=108К, если к моменту начала процесса
излучения имеется электронный газ плотностью jV^/V=109 м-3.
Решение
Рассмотрим газ, состоящий из N микрочастиц с массой, равной массе
электрона. Предположим, что каждая из этих частиц обладает спином, число
возможных проекций которого на выделенное направление равно g. В
соответствии с формулой (3.1.8) гл. 2 статистическая сумма такого газа определяется
выражением
Z=\^(2n^kT)^Y • (Ы1.3)
Эта формула для статистической суммы микрочастиц была получена на
основании статистики Больцмана; согласно сказанному в задаче 1.3 гл. 4, она
применима также и для электронов и позитронов, если только концентрации
не слишком велики. При аннигиляции электронно-позитронной пары энергия
покоя также преобразуется в излучение. Поэтому ее необходимо учитывать
при получении выражений для термодинамических величин. В соответствии
с этим получаем при помощи (1.11.3) следующее выражение для свободной
энергии:
F-N^-NkTln [gV(2yfef)3/2+l] • (1.11.4)
Отсюда следует, что химический потенциал равен
N - Й " L Nhfi Р V kT)
(1.11.5)
Будем далее относить все величины к объему V=\ м3. Образование пар и
обратный ему процесс их аннигиляции можно рассматривать как состояние
равновесия для статистического процесса
e-+e+^Y» (1.11.6)
где у — квант электромагнитного излучения. Как указывалось в гл. 4, § 2,
химический потенциал фотонного газа равен нулю. Вследствие этого при
наличии фазового равновесия должен быть равен нулю также и суммарный
химический потенциал газа электронов и позитронов, т. е.
|itf + + |ic- = 0. (1.11.7)
В дальнейшем индексом „ + " мы будем отмечать величины, относящиеся к
позитронному газу, а индексом „ —" величины, относящиеся к электронному
и Равновесная концентрация электронов и позитронов может быть
достигнута, лишь если ^-излучение само равновесное. Задачу следует понимать в том
смысле, что система, содержащая Л^^" электронов при Т -+■ 0, каким-то способом
была нагрета до температуры Г, при которой -у-кванты находятся в равновесии
с электронами и позитронами. — Прим. ред.
340 Гл. 5. Системы, состоящие из различных микрочастиц
газу. Если логарифм некоторой величины равен нулю, то сама эта величина
равна единице. Поэтому из (1.11.7) с учетом (1.11.5) имеем
N + N^(N^+AN)AN = ^^e,PfK^
(1.11.8)
Величина
AN = AN- = AN+=N + (1.11.9)
представляет собой число возникших за счет излучения электронов или
позитронов. При заданных численных значениях получим
(\0» + AN)AN =
_(4-2jt-9,l • Ю-31-1,38- Ю-23-108)3 / 2-9,Ы0-31-9.101в\
~~ (6,63-ю-34)6 expv 1,38-Ю-2^. 10» J"
= 1016'83 м-3.
Отсюда имеем
АЛ^ = 10в'83 = 6,710в м-».
Следовательно, плотность возникших электронов мала по сравнению с
плотностью уже имеющегося электронного газа. Общее давление столь мало, что
можно применить статистику Больцмана. В то же время численный расчет
показывает, что с повышением температуры число образующихся электронных
пар быстро возрастает. Поэтому для рассмотрения образования электронных
пар при температурах Т « \i0c2/k, или T^>\i0c*/k необходимо применять
квантовую статистику.
Упражнения
У. 1.1. Определить константу равновесия для реакции N2 ^ 2N при Г = 3000 К
и Р = 20 атм. Энергия диссоциации е^^-7,3 эВ. Основное состояние
атома N четырехкратно вырождено, состояние молекулы N2 не
вырождено. Гд = 2,9К, Г0 = 3390К. Относительная атомная масса азота
Лг=14,0.
У. 1.2. В предыдущем упражнении определить, насколько необходимо
повысить температуру, чтобы число диссоциированных частиц удвоилось.
У. 1.3. Чему равно число диссоциированных молекул азота в объеме 1 м3 при
Г==1000К, Р=\ атм?
У. 1.4. Найти энергию, которую необходимо затратить, чтобы 1 моль
молекулярного кислорода при нормальных условиях диссоциировал на атомы
(eD = 5,l эВ).
У. 1.5. Насколько увеличится теплота реакции 20 -► 02, если при постоянном
давлении температура возрастает от 273 до 2500 К? (со0 = 2,98-1014 с-1).
У. 1.6. Определить химическую постоянную хлора при таких температурах,
когда колебательные состояния еще не возбуждены (УС1 ~
= 1,13-10-« кг-м2, ЛС1 = 35,5). *
У. 1.7. Найти химические постоянные атомарного хлора и атомарного водорода.
(ЛС1 = 35,5, Лн = 1,01, давление в физических атмосферах).
У. 1.8. Определить константу равновесия для диссоциации водорода при
температуре 25° С (давление в физических атмосферах, числовые значения
взять из табл. П. XXI).
§ 1. Химическое равновесие в смеси идеальных газов 341
У. 1.9. Исследовать в нулевом приближении состояние равновесия для реакции
N2 + 02^2NO. При какой температуре парциальное давление N0
равно 0,01 атм, если исходные давления составляют Р0 —0,2 атм и
PN ==0,8 атм? (Использовать значения энтальпии образования и
энтропии, приведенные в табл. П.XXIV).
У. 1.10. Сколько водорода необходимо добавить к газу с парциальными
давлениями компонентов 0;75 атм Н2, 0,15 атм СО, 0,10 атм С02, чтобы
посредством реакции СО + Н20^:С02-|-Н2 уменьшить относительное
содержание СО до 1%? Решение провести в нулевом приближении.
У. 1.11. Вычислить изменение энтропии при реакции 2Н2 + 02 ^ 2Н20, если
температура и давление равны соответственно 25°С и 1 атм.
Колебательные состояния не возбуждены (/н =—3,68, /0 =0,55, /н 0 _
= -1,94).
У. 1.12*. Определить константу равновесия для реакций H2 + J2^2HJ. При
этом предположить, что теплоемкости постоянны и соответствуют
значениям, приведенным в табл. 34. Чему равен выход йодистого
водорода, если исходные концентрации составляют п^ =0,090 кмоль/м3,
п] =0,010 кмоль/м3?
Вещество
н2
HJ
ср
3,5/?
4,5/?
3,5/?
/, измеренное значение
—3,85
3,02
0,69
Таблица Н
eD, эВ
4,48
1,54
3,11
У. 1.13. Найти относительную концентрацию диссоциированного водорода при
Т = 5000 К, Р=10 атм.
У. 1.14*. Как изменится относительная концентрация диссоциированного
водорода, если при Г = 5000 К давление увеличивается от 10 до 100 атм?
У.1.15*. Вычислить химическую постоянную молекулярного водорода при
Г = 3150К.
УЛ. 16. Спектроскопические измерения дают для константы энгармонизма
кислорода значение х — 0,00965, для частоты внутримолекулярных
колебаний— значение со0 = 2,98-1014 с"1. Найти отсюда энергию
диссоциации 8£>.
У.1.17*. Вычислить энергию диссоциации молекулярного водорода Н2,
используя значения энтальпии образования, приведенные в табл. П.XXIV
приложения.
У. 1.18*. Определить константу равновесия для реакции НС1 + DBr ^t DC1 + НВг
при высоких температурах (колебания полностью возбуждены). Рас*
стояния между ядрами в молекулах считать не зависящими от вида
изотопа.
У. 1.19. Чему равна степень ионизации аргона при Т= 14 000 К, если давление
составляет 5 ат? Потенциал ионизации аргона равен 15,68 В.
У. 1.20. Определить относительную концентрацию двукратно ионизованных
атомов аргона при температуре Т—14 000 К и давлении Р = 5 ат.
Энергия связи второго электрона равна для аргона 27,64 В.
У. 1.21. Оценить степень тепловой ионизации паров ртути при температуре
20° С и давлении 1 мм рт. ст. (Потенциал ионизации ртути 10,4 В.)
У. 1.22. При T<^[i0c2/k получить численную формулу для плотности
электронов и позитронов, образующихся при взаимодействии излучения с
газом электронов.
342 Гл. 5. Системы, состоящие из различных микрочастиц
У. 1.23*. Вычислить отнесенную к V= 1 м3 энтропию позитронов при Г— 1011 К.
У. 1.24*. Для Г=107К и Nq=103 м-3 найти плотность электронно-позитрон-
ных пар, образовавшихся из квантов излучения. Какая плотность
получится при Т — 108 К?
§ 2. ФИЗИЧЕСКИЕ ЯВЛЕНИЯ В РАСТВОРАХ
Введение
Раствором называют однородную смесь нескольких веществ.
В теории растворов эти вещества принято называть
компонентами системы. Их число обозначают буквой k.
Компоненты могут находиться в различных агрегатных
состояниях, или, выражаясь точнее, в различных фазах.
(Например, в твердом агрегатном состоянии две фазы могут отличаться
кристаллической структурой.) Число фаз системы обозначают
буквой г. Каждая фаза содержит в общем случае все вещества.
В соответствии с результатами, полученными в гл. 3, § 3, в
состоянии равновесия должны быть равны температуры,
давления и химические потенциалы каждого отдельного компонента
во всех имеющихся фазах. Таким образом, должна выполняться
система уравнений
\*>ci ==1ХС2 = • • • ^М'СГ» /О 1\
..k-i_..k-i_ —-и*-!
rci — ГС2 — • • • — V'cr •
Здесь верхний индекс обозначает вещество или компонент, а
правый нижний индекс—фазу.
Каждая строка в (2.1) соответствует г—1 уравнениям. Всего
в системе (2.1), следовательно, содержится (г—\)k уравнений.
Химический потенциал \ас какого-либо компонента является
функцией k+ 1 переменных: k—1 отношений чисел частиц NJN0,
N2/N0i ..., Nk_jN0, а также давления Р и температуры Т.
Следовательно, каждый химический потенциал можно записать
в виде
^ф = ^?р(]^» ]^» ••• -j[f> Р> Ту (2.2)
Неизвестными здесь следует считать k—1 отношений
концентраций частиц в г фазах, давление и температуру. Всего, таким
образом, имеется г (k —1) + 2 неизвестных. Число независимых
величин определяется правилом фаз Гиббса
r(k — l) + 2 — (r—l)k =
k-r + 2 = f
(2.3)
§ 2. Физические явления в растворах
343
Таким образом, если система состоит из k веществ, которые могут
находиться в г различных состояниях, то можно произвольно
менять k — /- + 2 термодинамических величин (давление,
температуру или отношения чисел частиц), не нарушая при этом
состояния равновесия.
Пример 32
Система, состоящая из льда, воды и водяного пара, содержит k=l
компонентов вг = 3 фазах. Согласно правилу фаз (2.3), число термодинамических
степеней свободы системы равно
/=1-3 + 2 = 0.
Следовательно, требование одновременного сосуществования трех фаз вещества
однозначно определяет температуру и давление (тройная точка; ср. гл. 3, § 3).
Если некоторое вещество одновременно сосуществует в двух
фазах, то в соответствии с (2.3) одну из переменных—давление
или температуру — можно выбрать произвольно; при этом вторая
из этих величин будет определяться выбором первой. Например,
давление насыщенных водяных паров является функцией
температуры.
Пример 33
Если для системы, состоящей из двух компонентов, например поваренной
соли и воды, в равновесии должны находиться одновременно три фазы, то на
основании правила фаз Гиббса имеем
/ = 2—3 + 2=1.
Следовательно, при одновременном сосуществовании трех фаз только одна
из переменных Nu/N0i, Niu/N0u, Nllu/N0Uh Pt T может быть выбрана
произвольно. Например, если имеется одна жидкая и две какие-либо другие фазы,
то задание концентрации раствора поваренной соли Ni7K/N0yK однозначно
определяет температуру и давление. Следовательно, тройная точка, в которой
все три фазы стабильны, зависит от концентрации поваренной соли. Если
имеются только две фазы, например жидкая и газообразная, то из формулы (2.3)
находим / = 2. В соответствии с этим при k — 2, г— 2 можно одновременно
и независимо друг от друга менять концентрацию раствора и температуру.
Давление насыщенного пара в этом случае будет зависеть не только от
температуры, но и от концентрации раствора.
Пример 34
В двухкомпонентной системе, согласно правилу фаз Гиббса (2.3), может
одновременно сосуществовать в равновесии не более г = 4 фаз. Система вода —
эфир имеет при $ = —3,8 °С четверную точку, в которой в равновесии
находятся четыре фазы: твердая фаза практически чистого льда, газообразная фаза
и две жидкие фазы. Из последних одна является преимущественно водной
с содержанием 12,8% эфира, а вторая состоит в основном из эфира и содержит
0,93% воды. При незначительном изменении давления, температуры или
концентрации одного из растворов равновесие четырех фаз нарушается и одна
из них исчезает.
344 Гл. 5. Системы, состоящие из различных микрочастиц
При записи правила фаз Гиббса компонентами следует
считать все вещества, которые могут независимо друг от друга
существовать в различных фазах.
Пример 35
Система вода — эфир состоит из двух не зависящих друг от друга
компонентов. В то же время образующие эту систему атомы Н, О, С нельзя считать
независимыми компонентами, поскольку в рассматриваемой системе они всегда
выступают только в виде соединений Н20 и С4Н10О.
При диссоциации на ионы необходимо учитывать, что система
в целом остается нейтральной. Вследствие этого в системе (2.1)
появится дополнительное уравнение, что можно формально
также рассматривать как уменьшение числа k независимых
компонентов на единицу. Таким образом, если при диссоциации на
ионы образуется, например, т сортов ионов, то независимыми
следует считать только т—1 из них.
Пример 36
В растворе, состоящем из воды, поваренной соли и соляной кислоты,
образуются ионы Na + , Cl~, Н + , которые сосуществуют с Н20. Диссоциацию
воды H20;z±H++OH- можно не учитывать из-за ее ничтожно малой
степени. Тогда задание концентраций Na+ и Н+ однозначно определяет также
и концентрацию С1~. Следовательно, независимыми компонентами можно
считать только Н20, Na+ и Н + , т. е. имеем k = 3. Если теперь задать
температуру и давление, то в соответствии с правилом фаз Гиббса максимальное
число фаз г будет равно 3. Это означает, что в равновесии с жидкой фазой
могут находиться не более двух каких-либо других фаз.
В разбавленных растворах число N0 молекул растворителя
велико по сравнению с числом растворенных частиц, т. е.
N0> 2 Nh (2.4)
i = i
где суммирование следует производить по всем веществам,
содержащимся в растворителе. По аналогии с (1.15) будем
называть концентрацией частиц отношение
с, = т#- (' = 1 *-!)• (2.5)
£"'
При нахождении термодинамических величин для раствора
необходимо различать слабые и сильные электролиты. В слабых
электролитах, например в уксусной кислоте, число образующихся
ионов столь незначительно, что возникающими при этом электри-
§ 2. Физические явления в растворах
345
ческими силами можно пренебречь. Наоборот, сильные
электролиты, например поваренная соль, даже при относительно
больших концентрациях почти полностью диссоциированы на ионы,
так что обусловленные этим дополнительные силы оказывают
значительное влияние на физические параметры состояния.
Будем предполагать, что взаимодействием между молекулами
растворенного вещества можно пренебречь по сравнению с их
взаимодействием с молекулами растворителя. Сначала рассмотрим
слабые электролиты, концентрация которых столь мала, что
выполняется условие (2.4). Растворение одной молекулы i-ro
вещества приводит к появлению в статистической сумме
дополнительного множителя Дг,-. При растворении Л^ молекул с
учетом N{\ возможных перестановок получаем для статистической
суммы раствора выражение
z=z<o,(^Lii (2.6)
где Z(0)—статистическая сумма чистого растворителя. Применяя
приближенную формулу Стирлинга (1.8) гл. 2, находим из (2.6)
свободную энергию
F = — kTlnZ = — kTlnZM + N;kT\n^L.. (2.7)
Поскольку свободная энергия раствора является экстенсивной
величиной, она должна быть однородной функцией первого
порядка относительно чисел частиц N0i Nu ...,^_1.
Вследствие предположения об отсутствии взаимодействия между
молекулами растворенного вещества величина Дг,- должна быть
пропорциональной числу молекул растворителя NQ\ поэтому ее можно
представить в виде
Az, = N^'(P>T)/kT. (2.8)
Отсюда на основании (2.7) для полной свободной энергии раствора
находим
F = F^ + NikT(lnci-l) + Ni^(P,T), (2.9)
или, если растворены k — 1 веществ,
F = F<°> + 2 [N, kT (In с,— 1) + Nfo (Р, Т)]
1=1
(2.10)
Здесь величина
Я°» = — N0kTlnZw (2.11)
346 Гл. 5. Системы, состоящие из различных микрочастиц
представляет собой свободную энергию чистого растворителя.
Из (2.10) с учетом определения ci = NilNii получим с помощью
(1.1.10) химический потенциал растворителя в виде
rc° \dN0J Т, V, Nj(j¥=0) ^ 1
Величина
(2.12)
(2.13)
есть химический потенциал чистого растворителя. Для
химических потенциалов растворенных веществ находим
(2.14)
В случае растворов сильных электролитов кулоновское
взаимодействие между ионами приводит к появлению в свободной
энергии дополнительного члена вида
(2.15)
[ср. (2.7)]. Здесь Zte — заряд иона i-vo сорта,
е=еге0—диэлектрическая проницаемость растворителя, е~ 1,60-10~19 Кл —заряд
электрона. При эгом предполагается, что энергии электрических
взаимодействий, хотя ими уже более нельзя пренебрегать, все
еще достаточно малы по сравнению с тепловыми энергиями.
Получаемые отсюда формулы для термодинамических величин
справедливы при тех же предположениях и в случае
ионизованных газов.
Распад на ионы приводит к увеличению числа растворенных
частиц, а тем самым и к увеличению осмотического давления.
Однако одновременно с этим наличие электростатического
взаимодействия приводит к уменьшению давления, т. е. оно
проявляется через кажущуюся неполную диссоциацию молекул
сильного электролита. Используя закон Вант-Гоффа, находим из
(2.15) осмотическое давление, возникающее при растворении
сильного электролита
"2 я, ч/._^2яа1чз/1"
P = RT
24л
eVkT
(2.16)
§ 2. Физические явления в растворах
347
Второе слагаемое в (2.16) обусловлено наличием
электростатического взаимодействия.
Вода, так же как и другие растворители, в какой-то степени
диссоциирована. Диссоциация описывается уравнением
Н++ОН-^Н20. (2.17)
Согласно закону действующих масс, числа киломолей ионов
Пн+ и пои- связаны соотношением
^h+^oh-
пн2о
= К(Т)
(2.18)
Вследствие незначительного числа диссоциированных молекул
величину пн2о можно считать постоянной:
103
Пн*° =Тш кмоль/м'- (2-19)
Тогда при 25 °С имеем
пИ+пон- = К (25 °С) пНго = /С(н,о) (25 °С) =
= 1,008-10"14 кмоль2/мб. (2.20)
В соответствии с этим концентрация ионов водорода в чистой
электрически нейтральной воде при 25°С равна
(Агн+)о = 1,004.10-7 кмоль/м3. (2.21)
В кислом растворе преобладают ионы Н+; в соответствии с
соотношением (2.20) это означает, что ян+ > (пн+)0- Напротив,
в щелочном растворе преобладают ионы ОН", т. е. ян+ < (/гн+)0.
Введем величину рН, которая определяется следующим
образом:
pH=—lgnH+
(2.22)
В соответствии с (2.21) для нейтрального раствора имеем /?Н = 7,
для кислого раствора /?Н < 7 и для щелочного раствора /?Н > 7.
Если в одном и том же растворителе растворено несколько
веществ, то концентрации ci = Ni/N0 связаны соотношением,
вытекающим из закона действующих масс (1.16). Уравнение
Вант-Гоффа (1.3.7) также применимо к растворам, при этом
величину Q = — ДЯ следует понимать как теплоту растворения.
348 Гл. 5. Системы, состоящие из различных микрочастиц
Задачи
2.1. Законы Рауля для понижения температуры замерзания
Для определения относительной молекулярной массы парафина с
формулой СЛН2Л+2 растворяют т=17,5 г парафина в 1 л бензола и определяют,
насколько изменяется при этом температура замерзания. Пусть это изменение
оказалось равным AT = —0,55 К. Предположим далее, что при тех же
условиях температура замерзания чистого растворителя ТЕ — 5,25 °С = 278,68 К,
а выделяемое при замерзании количество теплоты равно 30,39 ккал/кг. Какова
брутто-формулаХ) растворенного парафина? (Плотность бензола рс н =
= 0,879 г/см3, относительная молекулярная масса Мс н =78,05.)
Решение
Необходимо исследовать равновесие системы, состоящей из fc = 2
компонентов и г — 2 фаз. Согласно правилу фаз Гиббса (2.3), система обладает
f = k-\-2 — r = 2 термодинамическими степенями свободы. Следовательно, из
четырех переменных Г, Р, сжидк, ств произвольные значения могут принимать
лишь две (сжидк и ств обозначают концентрацию растворенного вещества
соответственно в жидкой и твердой фазах). Таким образом, если заданы давление Р
и одна из концентраций, например сжидк, то этим будут также определены
температура Т и концентрация стъ. Согласно формулам (3.10) гл. 3 или (2.1),
в состоянии равновесия должны быть равны химические потенциалы как
растворителя, так и растворенного вещества в твердой и жидкой фазах. Запишем
это условие для растворителя. Имеем
^жидк(^ Т. сжидк) = ^°ЖИДК(Л Л-сжидк&7 = ^<о>в(Р, T)-c,BkT =
= Цав(Р>Т,с1Ъ). (2.1.1)
Для чистого растворителя фазовое равновесие определяется соотношением
^„„к (р (П т) = №в (Р (П Т), (2.1.2)
где давление Р зависит от температуры Т (см. гл. 3, § 3). Температуре
замерзания ТЕ соответствует, таким образом, давление Ре—Р(Те) на кривой
равновесия фаз.
Разложим химический потенциал в ряд Тейлора
|i?V, Т) = цУ(РЕ, ТЕ) + д^^ Те) АР +^°)(^- Те) АГ, (2.1.3)
тогда, используя (2.1.2), получим из (2.1.1)
фсжидк (Ре* те) at i Фсжидк (Ре* те) Ап „ ьт —
— ^ ш -| -qp— аг—Сжидк KI —
=^°>B(Pg, ТЕ) АГ + Фс°^Р£-, ТЕ) Ap_CiBkTi (2.1.4)
г) Брутто-формулами в химии принято называть суммарные формулы вида
AnBmCi..., например С13Н28, в отличие от структурных и т. п. формул.—
Прим. перев.
§ 2. Физические явления в растворах
349
Принимая во внимание, что отнесенная к 1 кмоль энергия Гиббса и
химический потенциал связаны соотношением G{0) — N A\il0), находим с помощью
формулы (3.20) гл. 2
дТ ~NA\ дТ )р-~ NA*
дцГ(Р, Т)_ 1 /dG«»\ ___V_
дР ~~NA\ дР Jt~~Na-
(2.1.5)
Подставляя в (2.1.4), имеем
'ЖИДК др
МО) у
<>ЖИДК aj, , V*
ЖИДК &' AJ
^ДГ + ^ДР—ств*7\ (2.1.6)
NA
NA ~ ' Л^л
Согласно формуле (3.12) гл. 3, величина
гг(о) гг(0) _т/с(0> с(о> 1
— /7тв—"ЖИДК — 1 ^тв—^ЖИДК/
есть не что иное, как теплота перехода. Тогда из (2.1.6) получим
-§-дг + (^жидк-V1B) АР = (сжндк-ств) RT.
(2.1.7)
(2.1.8)
Определим изменение температуры замерзания при растворении какого-либо
вещества при неизменных прочих условиях. Иными словами, положим Р = РЕ,
т. е. ДР = 0. Если растворенное вещество нерастворимо в твердой фазе, т. е.
если оно вымерзает в процессе затвердевания, то ств = 0. Тогда из (2.1.8)
имеем
(2.1.9)
где с = сжидк и Т — ТЕ. Вследствие более высокой степени порядка энтропия
твердого тела меньше энтропии жидкости (см. гл. 3, § 3). Поэтому величина Q
в соответствии с (2.1.7) отрицательна. То же справедливо и для величины ДТ
(2.1.9). Таким образом, температура замерзания раствора ниже температуры
замерзания чистого растворителя. Зависимость температуры замерзания от
концентрации и теплоты плавления называют соответственно первым и вторым
законами Рауля. Поскольку
Nc
pV = NLMLt m = NsMs, с=сжидк = ^,
(где Ni, N$—число молекул растворителя и растворенного вещества, М^
М$—относительные молекулярные массы), то, относя теплоту плавления
к 1 кмоль, имеем
ДГ = -т^—7гГГ или
MS = R
mT2E
pQAT/ML
Подставляя числовые величины, находим
1,987-17,5- 278,682
Ms=
0,879-10*.30,39- 0,55"
: 183,8.
Относительной молекулярной массой 184 обладает соединение С13Н28. Следо*
вательно, в рассматриваемом случае речь идет именно об этом парафине.
360 Гл. 5. Системы, состоящие из различных микрочастиц
2.2. Понижение давления насыщенного пара
В 1 л четыреххлористого углерода СС14 (ML= 153,8), имеющего
температуру кипения 76,7 °С при давлении 1 атм, растворены т$ = 20 г анилина
C6H5NH2 (М$ = 93,06). Определить обусловленное этим изменение ДР
упругости насыщенного пара. На какую величину изменится температура кипения
при постоянном давлении Р=1 атм? (Pl — 9cc\ = 1,60 г/см3, теплота
испарения 46 ккал/кг).
Решение
Будем исходить из соотношения (2.1.8) и применим его к переходу из
жидкого в газообразное состояние:
^-ДГ + (Угаз-Ужидк)ДР = (сГаз-сжидк)/?Г. (2.2.1)
Температуру Т примем равной температуре кипения 7$ чистого растворителя
при внешнем давлении Р = Р(Т$), т. е. положим ДГ = 0. Тогда из (2.2.1)
имеем
ДР = (сгаз-Сжидк)А7\ (2 2 2)
"газ "жидк
На основании уравнения состояния идеального газа можно приближенно
считать, что
RT
^гаЗ=-р->^Жидк (2.2.3)
и положить сгаз = 0. После таких упрощений получаем следующее выражение
для понижения давления насыщенного пара:
AP=-c^=-cP(Ts)
•'газ
(2.2.4)
Следовательно, упругость насыщенного пара раствора ниже, чем чистого
растворителя.
Если давление остается постоянным, т. е. если ДР=0, то из (2.2.1) при
сгаз = 0, сжидк = 0 находим
ДГ= —-^-/?Г2
(2.2.5)
Поскольку величина <3=:#ЖИдК — #га3 отрицательна, изменение температуры
AT положительно. Таким образом, наличие растворенного вещества приводит
к повышению точки кипения. Подставляя в (2.2.4) и (2.2.5) соотношение
Ml MspiV v ;
получаем
др=_^5Р(Г5) „ АГ=- "** Т*. (2.2.7)
§ 2. Физические явления в растворах
351
При заданных численных значениях изменение давления насыщенного пара
равно
153,8-20. Ю-3 1Л ЛЛ01
АР="93^6Л0^МЖ№ 1'0 = "-°'021 а™'
а для изменения температуры кипения при постоянном давлении имеем
20. Ю-3» 1,986.349,9*
"93,06- Ю-3-1,60-103-46 *-и>'1 гк'
2.3. Осмотическое давление, теплота растворения, растворимость
В табл. 35 приведена растворимость водорода в воде при внешнем
давлении Р = \ атм для различных значений температуры. Определить осмотическое
давление в насыщенном растворе. Найти теплоту растворения при
растворении 1 кмоль водорода, если температура равна 25 °С, а давление составляет
4 атм. Как изменится объем в результате процесса растворения?
Таблица 35
Растворимость Н2 в Н20 при Р = 1 атм [максимальное число
ng(H2) киломолей водорода на 1 м3 воды]
Температура, °С
пЛН2), 10-4м-з
^макс- Ю-2 атм
Решение
0
9,51
2,14
10
8,61
2,00
20
7,92
1,90
30
7,28
1,81
40
6,83
1,75
50
6,39
1,70
Чтобы получить выражение для осмотического давления из химического
потенциала, рассмотрим в соответствии с фиг. 15 (задача 1.9 гл. 2) два
раствора, которые различаются только концентрациями (сг и с2) растворенного
вещества. Полупроницаемая перегородка пропускает лишь молекулы
растворителя; вследствие этого равенство химических потенциалов по обе стороны
перегородки выполняется только для растворителя. В то же время
перегородка препятствует выравниванию концентраций растворенного вещества.
По этой причине химические потенциалы растворенного вещества и осмотические
давления в обоих растворах различны.
Равенство химических потенциалов растворителя означает, согласно
формуле (2.12), что выполняется соотношение
РсЛРи T)-ClkT = iic0(P2, T)-c2kT. (2.3.1)
Разлагая в ряд, находим в первом приближении
цео</>2, T) = nC0(Plt Г)+(%«)Г(Р,-Р1). (2.3.2)
В соответствии с формулой (3.20) гл. 2 имеем равенство
352 Гл. 5. Системы, состоящие из различных макрочастиц
Подставляя (2.3.2) и (2.3.3) в (2.3.1), получаем
Чтобы найти осмотическое давление, положим
N
с2 = с =
*о'
q = 0.
(2.3.4)
(2.3.5)
Иными словами, мы предполагаем, что по одну сторону перегородки
находится чистый растворитель, а по другую —раствор с концентрацией с (см. фиг. 15).
Тогда, согласно закону Вант-Гоффа для осмотического давления, имеем
NkT nRT
■» пгм — Тт —
(2.3.6)
Вычисленное на основании этого закона осмотическое давление приведено
в табл. 35. При растворении 6/V молекул энергия Гиббса изменяется на
величину
6G (Р, Т) = (\1С раств- \1С „ераств) М> (2.3.7)
где [Л^нераств и Цс раств—химические потенциалы нерастворенного и
растворенного веществ. Величина Нгнераств зависит от конкретного состояния
нерастворенного твердого, жидкого или газообразного вещества.
В насыщенном растворе существует равновесие между нерастворенным
и растворенным веществом. Поэтому
6G(P, Т) = 0 ИЛИ Цс раств = |АГНераств-
(2.3.8)
Если в жидкости растворяется газ с постоянной молярной теплоемкостью, то,
согласно (1.26), химический потенциал нерастворенного вещества можно
представить в виде
Mr нераств
__ ^о
Ni
-fcTlnP-
N,
•Т\пТ-кП^ ^нераств (Г) + kT In P.
(2.3.9)
Для химического потенциала растворенного вещества в соответствии с (2.14)
имеем
%^Vcраств = Фраств(^ Т) + кТ\п-щу (2.3.10)
где NQ—число молекул растворителя. При не очень больших давлениях
свойства жидкости в общем случае лишь незначительно зависят от внешнего
давления Р, так что в первом приближении можно записать
♦раств (Я, Л = +раств(Г). (2.3.11)
Подставляя (2.3.9) и (2.3.10) в (2.3.8), получаем закон Генри для
растворимости газа в жидкости
.Л^ма
Nn
:ехр
(б
гнераств Ис раств \
kT
= Рехр
/♦нераств (Т) ераств (Т)
kT
)-
t<?) р.
(2.3.12)
В соответствии с этим законом растворимость газа в жидкости в первом
приближении пропорциональна внешнему давлению. Для изменения энергии
§ 2. Физические явления в растворах 353
Гиббса при растворении 6/V частиц, используя (2.3.7), получим в случае
ненасыщенного раствора выражение
№=[ 'Фраств + *7,1Пдг ^нераств ) 6iV =/еГ In ^ 6/V =
\ /vo У '*макс
= kT\n-^-6N. (2.3.13)
^макс
Изменение энтальпии ЬНр в процессе растворения определим по формуле (1.3.6)
ЬНР= -т*(±M^=kT,6N ^EJl^asc^ (2.3.14)
Отсюда находим теплоту растворения при растворении N частиц или п кило-
моль
1Р= -bnP=-RNT- [d]n*»^=-nRT* (ainffaKCyp
. (2.3.15)
Для изменения объема получим на основании формулы (3.20) гл. 2 выражение
в„-(^)г=-*™ (2.3.16)
Как следует из табл. 35, при Ь = 2Ь°С и Р = 4 атм растворимость равна
_ЛГмакс_4.7,60.10-М8
Смыс—щ~- fooo ~Ь,4/ Ш -
В рассматриваемом интервале 5 К увеличение натурального логарифма
растворимости составляет
dlncMaKC 1 dcMaKC 1000-4.(7,28 —7,60). Ю-4-18
dT смакс dT 4.7,60.10-4.18.1000.5
= — 8,42-Ю-3 К"1.
С учетом этого находим из (2.3.15) теплоту растворения 1 кмоль водорода
QP= 1,987.2982-8,42. Ю-3 ккал= 1486 ккал.
2.4. Взаимное влияние растворенных веществ.
Закон разведения Оствальда
В раствор 0,1 моль/л уксусной кислоты (константа диссоциации
Ki= 1,86- 10~б) добавляются 0,05 моль/л бензойной кислоты (/С2 = 6,5- 10_б).
Определить состояние диссоциационного равновесия до и после добавления
второй кислоты.
Решение
Диссоциация кислоты в растворе описывается формулой
АВ^А+ + В". (2.4.1)
Пусть а(/*> (i = l, 2) обозначает степень диссоциации кислоты, т. е. долю
диссоциированных молекул по отношению к первоначально имевшимся, n(i) —
354 Гл. 5. Системы, состоящие из различных микрочастиц
концентрация в кмоль/м3 или моль/л. Согласно закону действующих масс,
имеем
IV
(О „(О
:/(<<> (i=\, 2).
Учитывая, что
п$+ = п$- = сш<'\ п% = (1 — а<'*>) гг<'>,
находим из (2.4.2) закон разведения Оствальда:
а</)2
1-а<<>
^ л<Л = /сс/>
(2.4.2)
(2.4.3)
(2.4.4)
При стремлении концентрации n(i) к нулю степень диссоциации должна
стремиться к единице. Таким образом, при достаточно сильном разведении
наступит полная диссоциация.
В рассматриваемом случае имеем /С(/)<Ся(/) и, следовательно, а(/) <^ 1;
поэтому можно приближенно представить степень диссоциации в виде
[я заданные
(2.4.5)
Подставляя заданные численные значения, получим для раствора уксусной
кислоты
36-ю-2
и для бензойной кислоты
—/да-»*»--
Если обе кислоты присутствуют в растворе одновременно и степени их
диссоциации равны соответственно р(1) и Р(2), то в обоих состояниях диссоциа-
ционного равновесия необходимо учитывать полную концентрацию водорода.
Тогда получим уравнения
(nwpw + nwpw)/iwpw,_ynl (/iwpw + /iwpw)/iwpw_yfa,
П(1)(1_-Р(1)) -Д ' n(2)(1_p(2)) А • I""'
Предполагая снова, что р(1)<^1, р<2><^1, находим из (2.4.6)
(n(i)p(i) + я<2>р<2>) ри> = /С<«, (л^рш + /г(2>Р<2>) Р(2> = К{2\ (2.4.7)
откуда имеем
p(i)_^a)
р(2) —/((2)
(2.4.8)
Разрешая систему уравнений (2.4.7), определяющую равновесие, относительно
Р(1) и р(2>, получаем
§ 2. Физические явления в растворах
355
Р<2) = к<2) и (2.4. Ю)
Из промежуточных равенств следует, что Ра) < а('\ Следовательно, при
добавлении второй кислоты степень диссоциации первой кислоты уменьшается.
Подставляя численные значения, находим
г , '•86-'°~6 — —
}Л),Ы,86.10"5 + 0,05-6,5- Ю-5
а к. in-б
pw=i,£-io-'8,g3,10_3;=2'88-10_2-
В соответствии с этим относительное число диссоциировавших молекул более
слабой кислоты с меньшей степенью диссоциации уменьшается сильнее, чем
более сильной кислоты с большей степенью диссоциации. Аналогичным
образом ведут себя кислоты при взаимодействии с солями.
2.5. Гидролиз
При физиологических исследованиях очень часто бывает необходимо
добавлять к некоторому раствору небольшую, однако точно определенную
концентрацию ионов Н или ОН. Слабые основания и кислоты весьма подвержены
влиянию побочных условий, например содержания щелочей в используемых
химикатах и на стенках сосуда или содержания С02 в воздухе, поэтому
обычно применяются гидролизующие соли, т. е. продукты нейтрализации,
образованные из сильного основания и слабой кислоты или наоборот (буферные
растворы). Концентрацию таких растворов можно сделать очень большой,
поэтому они менее чувствительны ко всякого рода паразитным влияниям.
Вычислить концентрацию ионов ОН для раствора п = 0,1 моль/л фенолята
калия. Константа диссоциации фенола (слабая кислота) имеет значение К =
= KHR = 1,3-10-4
Решение
Растворенная соль диссоциирует в соответствии с уравнениями вида
A+ + R-^AR или Па+П*- =Kar. (2.5.1)
Будем предполагать, что имеет место практически полная диссоциация
нейтральной соли. Наряду с диссоциацией, описываемой уравнениями (2.5.1),
в системе устанавливается равновесие относительно диссоциации воды:
Н+ + ОН-^Н20 или лн + лон-=^20) = *н2о#н2о- (2.5.2)
Ионы водорода реагируют с ионами кислотных остатков R-. Эта реакция
описывается уравнениями
H+ + R-^HR или "H + *R~ =A:Hr- (2.5.3)
"hr
В уравнениях (2.5.2) и (2.5.3) концентрация ионов водорода должна иметь
одно и то же значение. Учитывая это и деля (2.5.2) на (2.5.3), находим урав-
356 Гл. 5. Системы, состоящие из различных микрочастиц
нение для концентрации ионов ОН-
("ОН") ("HR^ пП2оК\\20 _^(Н.О)
которое определяет равновесие для реакции
HR + OH-^H20+R-.
Число «он- Д°лжно быть равно концентрации nHR ионов водорода,
связанных с кислотными остатками. С учетом этого имеем из (2.5.4)
khr ' <2-5-5)
а концентрация ионов Н+, согласно (2.5.2), равна
Vo)_! / ^<H20)^HR
ч>н-
-1 / ^<Н,0)^Н
V nR~
*^t^=V п' ' <*■">
Подставляя численные значения и принимая во внимание, что Яр =0,1 кмоль/м3,
находим из (2.5.5)
г'он-
/10-14- 0 1
1 3.10-1о = 2>8'10"3^0'0028 кмоль/м3. (2.5.5а)
Степень гидролиза у показывает, какая часть введенных в раствор ионов более
слабого электролита переходит в недиссоциированную форму:
/г,
он-
' п п
В рассматриваемом случае имеем
2,8-Ю-3
(2.5.7)
- = 0,028,
у~ 0,1
т. е. 2,8% всех ионов калия реагируют согласно уравнению (2.5.1). Для
концентрации ионов водорода получим из (2.5.6)
пн+ = ш-з~ *в 11,45 км°ль/м3 или рН =11,45.
Следовательно, реакция раствора будет щелочной, т. е. фенолфталеиновая
бумага (изменение окраски от белой до красной при значениях рН в интервале
от 8,3 до 10) будет окрашиваться в красный цвет, а лакмусовая бумага
(изменение окраски от красной до синей в интервале рН от 6 до 8) — в синий
цвет.
2.6. Радиус Дебая
Раствор поваренной соли содержит 5 г NaCl на 1 л воды. Определить
радиус Дебая и исследовать влияние заряженной частицы на ее окружение.
Решение
Предположим, что раствор разбавлен столь сильно, что молекулы NaCl
полностью распадаются на положительные ионы Na+ и отрицательные ионы
С1~. Между ионами действуют электрические силы притяжения и отталкива-
§ 2. Физические явления в растворах
357
ния. Кроме внутренней энергии нейтральных газовых молекул, в случае ионов
появляется дополнительная электрическая часть.
Рассмотрим окрестность положительно заряженной частицы и для каждого
элемента объема этой окрестности усредним по времени число появляющихся
в нем ионов. При этом чаще будет регистрироваться появление отрицательно
заряженных частиц. От временных средних перейдем к пространственным
средним и заменим дискретное распределение элементарных зарядов непрерывным
распределением. При этом будем рассуждать следующим образом.
Рассматриваемый положительно заряженный ион создает вокруг себя электрическое поле
с потенциалом ^1К Частица с зарядом Ze~ обладает в этом поле
потенциальной энергией Ze~ г|). При этом, согласно закону распределения Гиббса, число
частиц с зарядом Ze~ в объеме dV составляет
dN- = Ce-Ze~WkTdV (е~=-е+ = — е). (2.6.1)
Аналогично для числа частиц с зарядом Ze+ имеем
dN+=--C+e-Ze+WkTdV. (2.6.2)
При а|?-»0 ионы распределены в пространстве равномерно. Отсюда следует,
что
С-= lim ^, С+= lim ^f. (2.6.3)
Если имеется только по одному сорту положительных и отрицательных ионов,
то вследствие электронейтральности раствора можно положить
С_ = С+=^=^±=^, (2.6.4)
где Л^ —число электрически заряженных частиц одного сорта. Плотность
пространственного заряда в некоторой точке с потенциалом г|) определяется
выражением
dN + -dN- 7 2NZe . Zexp
Плотность заряда p и потенциал г|) связаны дифференциальным уравнением
Пуассона
Д1|> = —-£-, (2.6.6)
где е = е/.е0 —диэлектрическая проницаемость. Для вакуума имеем е0 =
= 8,854-Ю-12 А-с/В-м. Относительная диэлектрическая проницаемость
составляет для разбавленного раствора ег = 88. Подставляя (2.6.5) в (2.6.6), получаем
А , 2NZe , Ze\\
Будем предполагать, что
$<1. (2-6-8)
J) В вакууме это был бы обычный кулоновский потенциал. Однако в среде
к кулоновскому полю заряда добавляется поле поляризованной им среды,
поэтому задача состоит в определении г|). Она решается самосогласованным
образом: при заданном я|) находится пространственное распределение ионов
вокруг заряда [их плотности выражаются через г|) при помощи (2.6.1) и (2.6.2)],
а по пространственному заряду этих ионов при помощи уравнения Пуассона
находится потенциал ty.^-Прим. ред.
358 Гл. 5. Системы, состоящие из различных микрочастиц
следовательно, приближенно можно записать sh Ze\p/kT = Ze\\/kT. Тогда в
сферически-симметричном случае с учетом (2.6.6) и (2.6.7) получим
A*-*±+l *±JINZ**=1L (2 6 9)
АгР- dr2 -Г r dr- EVkT - D2 • К*-*-»)
Величина
_ fphT v I
(2.6.10)
-/!
Z42 2N
имеет размерность длины. Ее называют радиусом Дебая — Хюккеля или
радиусом экранирования. Величина 2/V представляет полное число ионов,
имеющихся в объеме V. Общее решение дифференциального уравнения (2.6.9)
имеет вид
^лехр(-г/0)+вехр^ (26И)
Коэффициент В должен равняться нулю, поскольку в противном случае с
увеличением расстояния от центра потенциал будет неограниченно возрастать.
Коэффициент А определим из условия, что при малых г должен получаться
чисто кулоновский потенциал. Это дает
А=ш- (2-6Л2>
В результате решение уравнения (2.6.9) принимает вид
*=Ш-ге-Г/°- (2.6.13)
На расстояниях r^>D потенциал спадает очень быстро. Следовательно,
образующееся вокруг рассматриваемого положительного иона облако
отрицательных зарядов приводит к экранированию положительного заряда на
расстояниях, превышающих дебаевский радиус.
В рассматриваемом случае, исходя из массы растворенного вещества, при
полной диссоциации получим для числа частиц величину
Мг Оо,0
Теперь найдем из (2.6.10) дебаевский радиус
п - l/ 8,854» 10-*2.88.1,38- Щ-м-ЗОО- 10~3 9
V (1,60.10-19)2.2.5,15-1022 " ' М*
Полагая в (2.6.8) D = r и используя решение (2.6.13), получаем с учегом Z=l
Ze\|3(D)_e2exp(—1)_
• kT ~~ 4neDkT ~"
_ (1,60.10-19)2. о,368
4.3,14.88-8,854. Ю-12-1,38-10-23.300"
Таким образом, в рассматриваемом случае условие (2.6.8) выполняется для
полей, отвечающих значениям г > D.
§ 2. Физические явления в растворах
359
2.7. Давление раствора сильного электролита
Определить давление для раствора, содержащего 5 г/л NaCl и 10 г/л
Na2S04.
Решение
При нахождении функций состояния сильного электролита необходимо
учитывать электрические силы, действующие между диссоциированными
частицами. Если в растворе имеются заряженные частицы, то к
термодинамическим величинам, найденным для электрически нейтральных частиц, следует
добавить кулоновский член. Поэтому запишем свободную энергию для ионов
в виде
F = FM+F„. (2.7.1)
Согласно формуле (3.16) гл. 2, функция F удовлетворяет дифференциальному
уравнению
F-T[w)y-U- (27-2)
Это уравнение справедливо для величины Рид, поэтому функция F9n также
должна удовлетворять ему. Решение уравнения (2.7.2) без правой части имеет
«Ze* °Ze"
oZe~ Фиг. 66. Экранирование положительного заряда.
вид Flji = aT. Для нахождения решения неоднородного уравнения (2.7.2)
произведем вариацию постоянной а = а(Т), тогда получим
- Т* .^Д = U„ или а = - J ^И ОТ. (2.7.3)
Отсюда для кулоновской части свободной энергии находим
F9Jl=-T^dT. (2.7.4)
Чтобы вычислить кулоновскую часть внутренней энергии ионного газа,
воспользуемся формулой (2.6.13), определяющей потенциал в окрестности
положительного заряда (фиг. 66). В результате получим
Первое слагаемое в (2.7.5) представляет кулоновское поле, создаваемое
расположенным в центре положительным ионом с зарядом Ze, второе слагаемое
есть потенциал, обусловленный облаком отрицательных зарядов, образовав-
360 Гл. 5. Системы, состоящие из различных микрочастиц
шимся вокруг рассматриваемого иона. В соответствии с (2.7.5) это облако
создает в месте расположения выделенного положительного иона потенциал
Ze
я^_ (0) = -1^ ^ [l-exp (__^)] =-
4леО
(2.7.6)
Потенциал -ф_ (0) определяет энергию, необходимую для перемещения
единичного заряда из бесконечности в точку нахождения положительного иона при
условии, что последний в этой точке отсутствует. Следовательно,
положительный ион с зарядом Ze+ обладает энергией (е — е+= — е-)
Z2e2
e8a = Z«+i|>(0) = -
AneD'
(2.7.7)
Такое же значение энергии получится и для отрицательного иона.
Электрическая энергия всех ионов в объеме V описывается выражением
</эл = -
1 e^NjZf
2 4ле£
(2.7.8)
где суммирование необходимо распространить на все сорта ионов. При этом
следует иметь в виду, что каждый ион учитывается дважды: один раз как
выделенная центральная частица, и один раз как составная часть
экранирующего заряда. Чтобы не учитывать его взаимодействие с остальными ионами
дважды, вводится множитель 1/2.
Что касается дебаевского радиуса, то при его определении необходимо
исходить из того, что уравнение Пуассона приводится к виду
Д*-5гФ=°.
(2.7.9)
где величина
D =
VsVkT
j/2^2
(2.7.10)
и есть дебаевский радиус системы. Тогда, используя (2.7.4), получаем для
электрической части свободной энергии выражение
1 эл
(2
8я
Т
1 dT _
) 7*6/2—
e^NtZ]
i
12neD
, (?"'гТ
12K у eSykT
+ c
■ + C=
, (2.7.11)
где С — постоянная интегрирования. С помощью (2.7.11) можно определить
кулоновские поправки ко всем термодинамическим величинам для раствора
электролита. В соответствии с формулой (3.15) гл. 2 поправка к давлению
за счет кулоновского взаимодействия равна
f Ul эл
[ — I
dV
1
"24л"
2*,*?
1/ 2
V e6V3kT
(2.7.12)
§ 2. Физические явления в растворах
361
Согласно закону Вант-Гоффа [см. (1.9.11) гл. 2J для осмотического давления
2^£ электрически нейтральных частиц имеем
Pn = *у (2.7.13)
Если концентрация ионов с зарядами Zfi (зарядовые числа Z/ могут быть
положительными или отрицательными) равна Ni/V, то с помощью (2.7.12) и
(2.7.13) находим
i 1
-kT
RT
V
2>/
24л
24л
eVkT
e^ntZf
i
eVkT
3/2
(2.7.14)
При полной диссоциации из 5 г NaCl и 10 г Na2S04 образуется 4,24-1022
ионов S04, 13,63-1022 ионов Na и 5,15-Ю22 ионов CL.
Учитывая, что каждый ион S04 двукратно заряжен, имеем
2 tf/Z? =3,57.10**.
i
Тогда для осмотического давления ионов в растворе получим величину
Я7 = 1,38- 10-23.300.9,87.10-6Х
X
2,30-1023
1
(1,60-10-
88-8,854.10
•10-19)2-3,57.1023 1 з/2 \
-12. ю-^. 1.38.10-23.300j j
Ю-3 24-3,14
= 4,09. Ю-26 (2,30- Ю26 — 0,63-1026) = 6,83 атм.
Таким образом, диссоциация растворенного вещества на ионы приводит к
повышению осмотического давления по сравнению с раствором нейтральных частиц,
lPjl(Pl + 4n)
!(Г35'МГ*ЛГгг*Гг J-ЛГ
Фиг. 67. Поправка к осмотическому
давлению раствора электролита за
счет электрических сил. (По работе[7].)
Для точечных ионов имеет место равенство
г— (2лАТ'
Р1 + Рэл~24*УЯЦ //»2л/ '
С
Прямая представпяет поправку при Т=0°С,
) е = 88е0, nl = n1i = n, Zl = -Zs=-\ в
приближении, в котором ионы рассматрива-
. ются как точечные заряды. Кривые, рас-
JljV положенные ниже, отражают зависимость
от эффективного диаметра ионов 2г$.
поскольку каждый ион следует рассматривать как самостоятельную
микрочастицу. Однако, с другой стороны, кулоновские силы, действующие между
частицами, уменьшают осмотическое давление. В рассматриваемом случае эта
поправка, несмотря на относительно небольшое количество растворенного
вещества, составляет более V4 Ееличины, которая получилась бы в
пренебрежении кулоновскими силами. С увеличением концентрации роль электрического
поправочного члена возрастает, поскольку он растет как (N/V)3'2, в то время
как нормальное осмотическое давление в растворе линейно зависит от
концентрации (фиг. 67).
362 Гл. 5. Системы, состоящие из различных микрочастиц
Замечание. При проведении расчетов для всех точек пространства мы
применяли дифференциальное уравнение (2.6.9), справедливое лишь при условии
(2.6.8). Если же исходить из более точного дифференциального уравнения
(2.6.7), то для кулоновских поправок получаются значения, несколько меньшие
найденных в рассмотренном примере.
2.8. Осмотическое давление в крови
Давление внутри красных кровяных шариков равно 8 атм. Какое
количество поваренной соли необходимо добавить в 1 л чистой воды,
предназначенной для вливания в вены пациента? Температуру положить равной
температуре человеческого тела (37 °С). Относительная молекулярная масса
поваренной соли составляет Мг — 58,45.
Решение
Чтобы воспрепятствовать разбуханию красных кровяных телец и разрыву
их оболочки, осмотическое давление Р0см в растворе поваренной соли вместе
с внешним давлением должно уравновешивать давление внутри красных
кровяных шариков. Следовательно, осмотическое давление должно составлять 7 атм.
Если используется раствор поваренной соли, то при решении необходимо
исходить из теории сильных электролитов, поскольку применение закона Вант-
Гоффа (1.9.11) гл. 2, справедливого для нейтральных веществ, приводит к
завышенному значению требуемого количества поваренной соли. Согласно
соотношению (2.7.14), для вещества, диссоциирующего на одновалентные ионы двух
сортов, имеем
2nRT Г У^~А & V~%n 1
Р/== V L1 2£Г(еШТ/2_|' (2-8Л)
где п—число молей NaCl на 1 л (или киломолей на 1 м3). При заданных
численных значениях находим
7 = 2я-8,314.10*.310-9,87-10-6 М— 0,265 |/щ УЪп J ,
или, после вычислений и подстановки т = Мг/г = 58,45я,
0,125т (1 — 0,0405 Ут) = \. (2.8.2)
Здесь т — масса растворенной поваренной соли.
Уравнение (2.8.2) имеет решение /я = 9,1. В соответствии с этим
концентрация поваренной соли в физиологическом растворе, предназначенном для
введения в вены пациента, должна составлять 9,1 г/л (более точное среднее
значение 8,9 г/л).
2.9. Понижение температуры замерзания
раствора сильного электролита
В 1 л воды растворено т=\Б г поваренной соли (Мг — 58,45).
Определить понижение температуры затвердевания.
Решение
Согласно формуле (2.1.9), в случае недиссоциирующего растворенного
вещества изменение температуры затвердевания определяется выражением
AT=c3Il (2.9.1)
§ 2. Физические явления в растворах
363
где
Ns
-1s
(2.9.2)
— концентрация раствора, Q < 0—теплота плавления. Осмотическое давление
в соответствии с законом Вант-Гоффа равно
_nsRT
(2.9.3)
Осмотическое давление в растворе сильного электролита определяется
формулой (2.7.14)
Pi =
ekT
RT
V '
(2.9.4)
В соответствии с этим в формулах (2.9.1) и (2.9.2) вместо ns необходимо
использовать величину, стоящую в выражении (2.9.4) в квадратных скобках:
72 N 3/2
ns-
S-Bi/V
■2*я?
ekT
(2.9.5)
Таким образом, для изменения температуры замерзания раствора соли NaCl,
распадающейся на одновалентные ионы двух сортов, получаем выражение
RT%
АТ = -
2ns-
24
1_ ^'NA {2e*fis\3/2
V \ekT J
(2.9.6)
(2.9.7)
nLQ
Если в качестве растворителя используется вода, то находим
АТ 2nsRT2E (1 -0,265 V2h~^V)
nLQ
Подставляя в (2.9.7) заданные численные значения и n = m/Mr (ср. задачу
2.1), получим окончательно
2-15-1,986-2732 (1 —0,265 У2-15/58,45) Л _w
АТ= 58,45.10^.80 =-0,77К.
Если бы мы применили закон Рауля для недиссоциирующих веществ, то для
понижения температуры замерзания получили бы значение, составляющее
всего 0,47 К. Точно измерить понижение точки замерзания гораздо легче, чем
определить осмотическое давление. По этой причине явление понижения
температуры замерзания имеет большое практическое значение.
Упражнения
У.2.1. Определить понижение температуры замерзания для раствора т — 20 г
анилина (Ms = 93,06) в 1 л метилового спирта.
У.2.2. Найти понижение давления пара при 100°С при растворении 100 г
глюкозы C6Hi206 (М,$=180) в 1 л воды.
У.2.3. Затвердевание некоторого сплава из магния и серебра начинается
при 7 = 905 К и сопровождается выделением чистого магния.
Теплота плавления чистого магния составляет 46,5 ккал/кг, точка
затвердевания Т = 922 К- Определить относительную массу серебра в сплаве
04Mg = 24,32, ЛАе=107,9).
364 Гл. 5. Системы, состоящие из различных микрочастиц
У.2.4. При 1 атм и 0°С растворимость азота в воде составляет 28,8 мг/л,
а при 10сСона равна 22,6 мг/л. Найти теплоту растворения при
растворении 1 к моль азота при 0°С.
У.2.5. Вычислить осмотическое давление в растворе соляной кислоты
с концентрацией 0,05 моль/л при 20°С. Чему равна поправка за счет
электрических сил, действующих между частицами?
У.2.6. Какое количество воды необходимо взять, чтобы растворить в ней
1 кмоль азота при 0°С и давлении 0,1 атм?
У.2.7. Вычислить максимальное осмотическое давление, возникающее
в результате растворения азота при 0°С и давлении 1 атм.
У.2.8. Какова максимальная концентрация азота, растворенного в воде
при температуре 0°С и давлении 1 атм?
У.2.9*. 1 л воды при 100°С содержит 50 г растворенного сахара. Какую
минимальную работу необходимо совершить, чтобы удвоить
концентрацию раствора (Мсах = 342)?
У.2.10. Чему равно число ионов водорода на 1 л при 0°С? (lg Кн о)^--14,94)?
У.2.11. Какова концентрация муравьиной кислоты (константа диссоциации
К = 1,8-10"4), концентрация ионов водорода в которой имеет такое
же значение, как в 0,05-молярной бензойной кислоте (К = 6,5-10"б)?
У.2.12. Определить значение рН для 0,05-молярного раствора уксуснокислого
натрия. Чему равна степень гидролиза? Константа диссоциации
уксусной кислоты равна 1,8« 10~5, /С(Н 0)= 10~14.
У.2.13. Какова концентрация раствора цианистого калия, дающая красную
окраску фенолфталеиновой бумаги (рН > 10)? (Константа
диссоциации синильной кислоты К — 1,3- Ю-9.)
У.2.14. Составить таблицу степеней гидролиза для концентраций 1; 0,1; 0,01;
0,001 и значений /С = 10~&, 10-°, Ю-7, Ю-8, 10-».
У.2.15. Определить дебаевский радиус экранирования для нейтральной
в целом плазмы с концентрацией электронов N/V=--\024 м~'3 при
температуре 107 К.
У.2.16. Определить температуру замерзания воды Средиземного моря,
содержание соли в которой составляет 38 г/л (УИГ = 60).
У.2.17. Чему равен дебаевский радиус для раствора, содержащего 8 г/л
NaCl и 30 г/л СаС12 при температуре 20°С?
У.2.18. Какова величина осмотического давления при 20°С в воде
Балтийского моря (среднее содержание соли 12 г/л, Л4Г = 60)? Давление
выразить в атм.
У.2.19*. К какому неравенству приводит требование, чтобы энергия
электрического взаимодействия между диссоциированными частицами была
мала по сравнению с тепловой энергией?
У.2.20*. Вывести формулу, определяющую количество теплоты,
выделяющегося или поглощающегося при растворении 5Л/ молекул некоторого
вещества при постоянном объеме.
§ 3. КИНЕТИКА ПРОЦЕССОВ ПРЕВРАЩЕНИЯ ВЕЩЕСТВА
Введение
Чтобы рассчитать ход физического или химического процесса
превращения вещества, необходимо знать все стадии реакции.
Во многих случаях реакция не приводит непосредственно
к образованию конечного продукта в соответствии с брутто-
формулой, а протекает в несколько стадий, при которых
образуются промежуточные продукты.
§ 3. Кинетика процессов превращения вещества 365
Пример 37
Образование йодистого водорода происходит за один элементарный акт,
в точном соответствии с уравнением реакции H2 + J2—*2HJ. Напротив,
образование хлористого водорода при взрыве смеси газообразных хлора и
водорода происходит в основном в результате трех последовательных стадий
(см. задачу 3.6)
(1)С12 + £„зл—+ 2С1 (Н)С1 + Н2—>НС1 + Н, (III) Н 4 Cl2—►HC1+CI.
Здесь £иЗЛ обозначает необходимую для начала реакции энергию излучения.
Аналогично превращение радиоактивных веществ всегда
происходит с испусканием а- и ji-лучей, состоящих из \а- и _Jji-
частиц. Так, превращение 2^U в 2j$LJ происходит в следующей
последовательности: 2jJ,}Th, 2l\Pa, 2lt^- Однако никогда не
происходит испускание четырех нейтронов, путем которого могло
бы осуществиться непосредственное превращение 2j}§0—^iU.
Течение реакции можно контролировать, измеряя изменение
концентрации одного из реагентов. Если эта величина известна,
то изменение концентрации остальных компонентов можно
определить на основании стехиометрических соотношений.
Пример 38
Предположим, что при контролируемом протекании реакции образования
хлористого водорода, состоящей из трех стадий I, II, III, в результате
реакции I концентрация молекулярного хлора в течение одного часа
уменьшилась на 1 кмоль; тогда одновременно в результате той же реакции
концентрация атомарного хлора должна увеличиться на 2 кмоль.
Вместо концентрации можно пользоваться также
пропорциональными ей величинами, например числом частиц того или
иного компонента реакции или его парциальным давлением.
Пуст*» п обозначает число киломолей какого-либо реагента.
Скоростью реакции, по определению, называют величину
vR=dir (3.1)
Скорость реакции, как правило, зависит от концентрации всех
участвующих в реакции веществ и от температуры Т:
vR = f(nl9 /г2, ..., Т). (3.2)
Если изменение количества некоторого компонента реакции
можно описать уравнением
da=Ku (з.з)
то реакцию называют реакцией тгго порядка по отйошению
к соответствующему реагенту. При этом k есть константа
скорости реакции, или кинетический коэффициент реакции.
366 Гл. 5. Системыj состоящие из различных микрочастиц
Пример 39
Распад однородного радиоактивного вещества, например радия, происходит
по закону
— = kn — Кп,
at
т. е. представляет собой реакцию первого порядка (т=1). Константу скорости
реакции fe = A в теории радиоактивного распада принято называть постоянной
распада. Подобно радиоактивному распаду, разложение целого ряда
органических веществ, например спирта и эфира, в общем случае также происходит в
соответствии с уравнением реакции первого порядка.
При сложных химических процессах отдельные
промежуточные стадии могут описываться громоздкими кинетическими
уравнениями. При этом весьма существенную роль может играть
концентрация того вещества, которое в собственно
рассматриваемой реакции участия не принимает.
Пример 40
Реакция образования хлористого водорода Н2+С12—>2НС1 описывается
уравнением
Таким образом, эта реакция является реакцией нулевого порядка относительно
водорода Н2, реакцией второго порядка относительно хлора и минус первого
порядка относительно не входящего в уравнение основной реакции кислорода.
Общим, или суммарным, порядком реакции называют, по
определению, величину
т
= 2^/- (3.3а)
В примере 40 общий порядок равен т =mCi2+mH2+mo2 = 2+0—
—1 = 1. Полное число столкновений между молекулами двух
газов, согласно гл. 3, § 4, пропорционально концентрациям
обоих газов. Реакции вида
AB+CD->AC + BD, (3.4)
для протекания которых необходимо столкновение двух молекул,
идут, следовательно, со скоростью
dri\r
—^-^кпкъпсъ* (3.4а)
если только на их ход не влияют какие-либо дополнительные
факторы.
§ 3. Кинетика процессов превращения вещества 367
Пример 41
В случае образования йодистого водорода имеем
dnv
HJ и
Общий порядок реакции равен двум. Поскольку
_ 1 _ 1
пн2 —пон2~—2Пш* 72J2~-720Ja*~~2~rzHJ»
уравнение реакции можно записать также в виде
dnHJ ( _J_ \f _\_ \
-jf-^hj^oh, 2 пш)\поз2 2nHjJ'
где п0И и /гол —начальные концентрации водорода и йода.
Если в результате реакции какое-либо из участвующих в ней
веществ прореагирует практически полностью, то реакцию
называют необратимой. Такие реакции характеризуются тем, что
в состоянии равновесия остается лишь исчезающе малое
количество какого-либо реагента. Если же в состоянии равновесия
присутствуют конечные количества всех реагирующих веществ,
то реакция протекает неполностью, или обратимо. В этом
случае в уравнении кинетики необходимо учитывать также и
обратную реакцию.
Пусть ход реакции в одном направлении описывается
уравнением
• ЫпРям = -^- = ^7К, ..-, пг)% (3.5а)
а в# противоположном—уравнением
Ыобр = -тг=*Г(Л1. •••> rir). (3..56)
Здесь k и h—константы скорости прямой и обратной реакций,
->■ -*-
называемые иногда просто скоростями, d/i,- и dn£—количества
вещества i, вновь образовавшегося и распавшегося за время dt
в результате прямой и обратной реакций соответственно. Эти
величины, следовательно, не являются векторами.
Для результирующего изменения концентрации имеем
368 Гл. 5, Системы, состоящие из различных микрочастиц
В состоянии равновесия должны выполняться равенства
Ыпря„ = Ыобр или •$ = (). (3.6а)
Отсюда находим условие равновесия:
1- t
7
(3.7)
Пример 42
Образование йодистого водорода описывается уравнением
dnHJ ~t
Распад происходит в соответствии с законом
<-
dnHJ <- 2
(^)обр=-57~==/г/гнл-
Следовательно, суммарная скорость х> реакции равна
Ыпрям - Ыобр = "зт1 —аГ = knhnn2 - knnr
Отсюда находим константу химического равновесия:
kc=L= *HJ
Это уравнение для реакции йода с водородом может быть получено также на
основании закона действующих масс.
Как указывалось в гл. 3, § 4, общее число столкновений
в смеси двух газов чрезвычайно велико. Если хотя бы каждое
десятое или сотое столкновение приводило к реакции, то
газовая реакция должна была бы длиться не более долей секунды.
Однако это имеет место лишь для немногих реакций, например
для реакции Аг+ +Н2—* ArH+ +Н, которая исследовалась масс-
спектроскопическим методом. В то же время многие газовые
реакции идут в течение часов и даже дней. Наличие
газокинетических столкновений является, таким образом, лишь
необходимым, но не достаточным условием для осуществления
химического процесса.
Чтобы между сталкивающимися молекулами произошла
реакция вида (3.4), при столкновении должна разрушиться
химическая связь в исходных веществах. Для этого требуется затра-
Х) Автор пользуется термином «бруп'О-скорость», вместо которого мы
далее будем употреблять названия «суммарная скорость» или просто «скорость»,
имея в виду скорость образования конечного продукта. — Прим. перев.
§ 3. Кинетика процессов превращения вещества
369
тить энергию активации е0. Такие процессы с затратами энергии
возможны, если источником энергии активации является или
внутренняя энергия реагирующих компонентов, или подводимая
к системе дополнительная энергия.
Пример 43
Реакция образования йодистого водорода протекает без подведения
энергии извне. Чтобы получить необходимую для реакции энергию активации,
достаточно кинетической энергии сталкивающихся частиц. В
противоположность этому реакция Н2 + С12—*2НС1 при комнатной температуре в полной
темноте протекает крайне медленно и активируется лишь при подведении
извне энергии излучения. Таким образом, в этом случае кинетической энергии
молекул Н2 и С12 оказывается недостаточно для их распада.
Существованием энергии активации объясняется возрастание
скорости химического превращения с повышением температуры,
описываемое законом Аррениуса
. dt
(3.8)
Как неоднократно упоминалось выше, энергии сталкивающихся
молекул распределены по экспоненциальному закону ехр (—s0/kT)
(распределение Гиббса). Поэтому химическое превращение
протекает в основном в соответствии с законом (3.8). Число
столкновений возрастает пропорционально корню из температуры и
по сравнению с этим фактором оказывается малосущественным.
Однако, даже если учесть энергию активации, необходимую
для осуществления элементарной реакции при столкновении, и
воспользоваться законом распределения Гиббса, число
приводящих к реакции столкновений, получающееся при теоретическом
расчете, оказывается слишком большим по сравнению с
фактической величиной, о которой можно судить по действительному
ходу реакции. Поэтому следует предположить, что не все
столкновения приводят к реакции, даже если молекулы обладают
кинетической энергией, достаточной для активации, и что частицы
при столкновении должны быть определенным образом
ориентированы относительно друг друга. Например, в случае распада
йодистого водорода эффективным при столкновении является
расположение
1 н
J
>.
«
н
J
н
J
н
J
(перед столкновением) (после столкновения),
370 Гл. 5. Системы, состоящие из различных микрочастиц
в то время как расположение
н
J
—>■ «
J
н
не дает вклада в рассматриваемую реакцию. Зависимость от
ориентации сталкивающихся частиц описывается с помощью
коэффициента выхода столкновений, или стерического фактора т,
который подобно энергии активации в широких пределах не
зависит от температуры.
С учетом энергии активации и стерического фактора получим
из формулы (4.10) гл. 3 число столкновений, приводящих к
реакции:
ZAB, CD = Тв-^аидв. СО^АВ^СО = ^f- W ab^cd
При этом, согласно гл. 3, § 4, величины
и
^AB, CD
= Y4
8RT Г 1
1
V Мав Mcd t
. (3.9)
(3.9а)
(3.96)
представляют газокинетическое сечение взаимодействия и
среднюю относительную скорость.
Вследствие столкновений, число которых определяется
формулой (3.9), концентрация вещества АС изменяется на величину
, Л/У ас 1 * м
апкс = -jj— — jj- ^АВ, cd at =
Te~eo/kTovAB, cdNabNcd
Na
dt.
(3.10)
Путем сравнения с (3.9) при учете равенства nNA — N находим
кинетический коэффициент
£дв, cd = k = NAovAB, cDte-e°/kT.
(3.11)
В предположении, что сечение взаимодействия постоянно, это
приводит к температурной зависимости вида
k = const- e-^kTV"T- (ЗЛ2)
§ 3. Кинетика процессов превращения вещества 371
Формула (3.11) получена в предположении, что сталкивающаяся
молекула уже перед столкновением имеет необходимую для
активации энергию в виде внутренней энергии (3.2.6). Несколько
отличная модель, основанная на квантовомеханическом подходе,
была предложена Эйрингом. В этой модели молекулы
рассматриваются как осцилляторы, в которых атомы совершают
относительно друг друга колебания с частотой v. Если расстояние
между ними превысит некоторую предельную величину (см.
фиг. 30), молекула может распасться. Вероятность распада
пропорциональна частоте
v~f. (3.13)
Поскольку колебательная энергия также распределена по
закону Гиббса, для константы скорости реакции получается
выражение
£= const .*Le-btkT. (3.14)
Таким образом, помимо экспоненциальной зависимости,
отвечающей закону Аррениуса, здесь имеется еще дополнительная
линейная зависимость от температуры.
Наконец, можно рассмотреть также третью модель, согласно
которой источником энергии активации служит кинетическая
анергия сталкивающихся частиц. В этом случае при постоянном
сечении взаимодействия зависимость константы скорости реакции
от температуры имеет вид [см. ниже формулу (3.2.16)]
-* p-e0/kT
*= const- а- . (3.15)
Характер температурной зависимости во всех рассмотренных
моделях определяется множителем ехр (—eJkT). Он приводит
к появлению в логарифме константы химического равновесия
слагаемого —E0/RT, что согласуется с экспериментом. Помимо
этого, константа скорости реакции содержит множитель Га,
определяемый природой реагирующих молекул. Этот множитель
дает в логарифме константы равновесия слагаемое const-In7.
Оно зависит от того, в какой форме поступает необходимая
энергия активации. Очевидно, этот член гораздо менее существен, чем
главный член, пропорциональный энергии активации. Иными
словами, различие в характере столкновений и способе
активации играет второстепенную роль по сравнению с вкладом
энергии активации, поэтому при расчете коэффициента скорости
в первом приближении им можно пренебречь.
372 Гл. 5. Системы, состоящие из различных микрочастиц
Пример 44
Энергия активации реакции С1 + Н2—*НС1-|-Н при 285 К составляет
(6,1 ± 1 > -103 ккал/кмоль. В диапазоне от 285 до 335 К константа скорости
реакции изменяется за счет входящей в него экспоненты в
6,Ы03 ^
6XPl 1,986-335 J
exp
6, МО3
1,986-285
= 5,0
раз. Если же принять энергию активации равной 7,1-10* ккал/кмоль, то
соответствующий множитель оказывается равным 6,5. Следовательно, неточность
->-
при предварительном вычислении k составляет 30%- С другой стороны,
сомножитель Т в константе скорости реакции изменяется при этом всего лишь
в 335/285=1,18 раз. Это изменение, таким образом, лежит в пределах ошибки,
обусловленной неточностью при определении энергии активации.
Из § 1 следует, что константу равновесия в законе
действующих масс можно с помощью (1.6.5) выразить через
обусловленное реакцией изменение энергии Гиббса:
\nKp=-J^^(Hi-TSi) или ^=ехр(-т£ + тг).
(3.16)
Величины, помеченные звездочкой, относятся к активированному
состоянию. Поскольку в соответствии с (3.7) константа
равновесия равна отношению скоростей прямой и обратной реакций,
то величины k и k также могут быть выражены через энергию
Гиббса.
&АВ *^CD
дндотерм.
Экзогперм.
№А
jf^L^W
1\ О'энЬотерм
Фиг. 68. Схема энергии
активации.
Если положить в основу квантовомеханическую модель Эй-
ринга, то для кинетических констант скорости реакции получим
выражения
h
%^„fWRT~.IR
, (3.17)
где ДЯ* и AS*— изменения энтальпии и энтропии в ходе
активированной реакции, протекающей слева направо (фиг. 68), а
Д#* и AS*—соответствующие величины для процесса, протека-
§ в. Кинетика процессов превращения вещества 373
ющего справа налево. Из сравнения выражений (3.16) и (3.17)
следует, что
Д//*=ДЯ*—ДЯ*, AS* = AS*—AS*.
Коэффициенты т и т могут быть найдены путем специального
квантовомеханического расчета. В общем случае этот расчет
чрезвычайно сложен, однако его можно избежать, если
экспериментально определена константа скорости реакции для какой-
либо одной определенной температуры (см. задачу 3.2).
Задачи
3.1. Радиоактивность
.При измерении мощности дозы излучения некоторого радиоактивного
препарата получены значения, приведенные в табл. 36. Вывести закон распада.
Таблица 36
Мощность экспозиционной дозы излучения радиоактивного
препарата
п . Мощность экспозиционной „ . Мощность экспозиционной
Время /, дн дозы р^ мР/с Время /, дн дозы р^ мР/с
0
10
20
30
40
50
Решение
138,5
133,9
129,5
125,3
121,3
117,5
60
70
80
90
00
113,9
110,4
107,0
103,9
101,1
Радиоактивное превращение происходит в соответствии со статистическим
законом распада. Вероятность распада для всех радиоактивных атомов одного
сорта одинакова. Следовательно, число актов превращения в случае N
радиоактивных атомов одного сорта можно записать в виде
dN = — XNdt. (3.1.1)
Знак минус здесь необходим потому, что в результате радиоактивного распада
количество рассматриваемого вещества уменьшается. Величина X называется
постоянной распада. Таким образом, в случае радиоактивного распада
кинетический коэффициент k совпадает с постоянной распада %. Решение
дифференциального уравнения (3.1.1) имеет вид
N = N&-M. (3.1.2)
Отсюда получаем время, или период полураспада ti/zl
-ш'а 1 4 In 2 In 2 0.6931
= _или,1/2^_ = _=«^_.. (3.1.3)
374 Гл. 5. Системы, состоящий из различных микрочастиц
В соответствии с (3.1.3) постоянную распада X можно определить, если
известен период полураспада t\/2.
Уменьшение количества радиоактивного вещества приводит к уменьшению
мощности излучения.
Экспозиционная доза испущенного излучения измеряется в рентгенах (Р).
1 Р соответствует образованию 2,08-109 ионов в 1 см3 сухого воздуха.
Принято считать, что предельно допустимая для человеческого организма
мощность дозы составляет 0,1 Р в неделю. При сорокачасовой рабочей неделе это
соответствует стационарной мощности экспозиционной дозы изучения, равной
0,7 мкР/с.
На основании закона распада (3.1.2) находим для мощности излучения
соотношение
L = L0e~M или IgL = \gL0 — 0,4343М. (3.1.4)
Следовательно, в случае, когда излучающее вещество состоит из атомов
одного сорта, зависимость логарифма мощности излучения от времени должна
изображаться прямой линией. Однако корреляционный расчет в соответствии
с гл. 1, § 4 не приводит в рассматриваемом случае к прямой. Тем не менее
цели можно достигнуть, если воспользоваться выражением вида
L = V-M + Li. (3.1.5)
Иными словами, мы предполагаем, что препарат состоит из некоторого
вещества с очень большим периодом полураспада, равным по меньшей мере
нескольким сотням лет, и из вещества, период полураспада которого
исчисляется днями. Уравнение
lg(L — L1) = lgL0 — 0.434Ш (3.1.6)
представляет собой уравнение прямой. Используя численные значения,
приведенные в табл. 36, находим посредством процедуры, описанной в гл. 1, § 4, что
наилучшая аппроксимация достигается при значениях
2^ = 43,4, L0 = 95,l, J\, = 5,0-10-3 дн"1.
Отсюда с помощью (3.1.3) находим период полураспада быстро распадающегося
вещества:
. 0,6931 iqftfi ли
Эта величина соответствует периоду полураспада полония.
3.2. Реакция образования и распада двух молекул
Путем измерения скорости реакции между йодом и водородом
Ha + J2—*2HJ или ^ = ~knin2 (3.2.1)
(я1==7гН2, /i2 = /2j2, Ло = Янл)
получено следующее значение константы скорости реакции при Го = 556 К:
1(556 К) = 4,45-Ю-5 м3/(кмоль-с). (3.2.2)
Найдено, что измеренное значение константы химического равновесия при этой
температуре составляет
К (556 К) = 7,9. Ю-3, lg К (556 К) = —2,10. (3.2.3)
§ 3. Кинетика процессов превращения вещества
375
Установлено также, что энергия активации Е12 при протекании реакции в
направлении образования йодистого водорода равна 40-Ю3 ккал'кмоль, а в
направлении распада последнего она равна £0 = 44-Ю3 ккал/кмоль. Определить
кинетические коэффициенты k и k реакции образования и распада йодистого
водорода при Т = 800 К. Чему равно при этой температуре относительное
количество йодистого водорода, распадающегося в течение первой минуты
реакции, если исходная концентрация составляет 0,01 кмоль/м3? Чему равна при
указанной температуре константа химического равновесия, определенная с
помощью кинетических коэффициентов прямой и обратйой реакции?
Решение
Будем предполагать, что в начальном состоянии имеются только молекулы
йодистого водорода. Распад происходит при столкновениях между этими
молекулами. Следовательно, реакцию можно представить в виде
2HJ—*H2 + J2, или -^=kn20. (3.2.4)
Будем исходить из того, что энергия возбуждения Е0 = М^е0 (ср. ход
потенциала на фиг. 68) запасена в виде внутренней энергии молекул. Энергия
распределена по отдельным молекулам в соответствии с законом распределения
Гиббса [см. (1.28) гл. 2], который мы запишем в виде
Распад может происходить только при столкновении молекул, внутренняя
энергия которых превышает некоторую определенную минимальную величину е0.
Тогда из (3.2.5) следует, что число молекул, энергия которых достаточно велика
для того, чтобы при столкновении мог произойти распад, равна
J e-*kTdz
N*o = N0% . (3.2.6)
J e^kTde
о
Нижний интеграл имеет значение /е7\ а верхний интеграл равен kT exp (e0/kT).
Таким образом, находим из (3.2.6) число возбужденных молекул
N*0 = N0e-8°/kT =N0e-E°/RT. (3.2.7)
Из анализа результатов эксперимента следует, что при столкновении
распадается не каждая возбужденная молекула и что существенную роль играет
также характер столкновений. Чтобы учесть это обстоятельство, введем в наш
расчет стерический коэффициент т = т0<;1. С учетом последнего получим для
числа реакций распада в единицу времени и в единице объема величину
zi5 = T0OoiroTll^o^J = ToOot^T„^Je" Eo/RT. (3.2.8)
Предположим, что в первом приближении сечение столкновения а0 не зависит
от температуры. Тогда из (3.2.8) следует, что убыль концентрации (в кило-
376 Гл. 5. Системы, состоящие из различных микрочастиц
молях) описывается уравнением
- d-£==f;=NMF0Tllnle-E°/RT = knl (3.2.9)
Если учесть, что зависимость средней" относительной скорости от температуры
определяется, согласно формуле (1.5.8) гл. 2, выражением
то для константы скорости реакции получим выражение
■*- Yen
T0o0e-Eo/RT VT = C0e-E°/RT уТ, (3.2.11)
где \i0—относительная масса сталкивающихся молекул, С0 — константа,
которая объединяет все входящие в это выражение постоянные величины.
Чтобы получить для константы химического равновесия реакции йода
с водородом температурную зависимость такого же вида, как в § 1 (ср.
задачу 1.12), при рассмотрении кинетики будем исходить из того, что активация
молекул водорода и йода происходит за счет преобразования кинетической
энергии во время столкновения. Следовательно, «успешными» могут быть только
такие столкновения, при которых кинетическая энергия относительного
движения превышает некоторое граничное значение е12:
2 -" "' (3.2.12)
(И-12—относительная масса).
Скорости молекул распределены по закону Максвелла— Больцмана [см.
(1.3.4) гл. 2J. С учетом этого получим для числа столкновений, приводящих
к реакции, выражение
00
2*2 = Т18(712#!#я \ Vf (V) d0 =
^2е12/ц„
где т12 = т—стеричёский коэффициент, а12—сечение столкновения.
Используя замену переменных
yi12v2
2kT "
[риводим (3
Zl2 =
= z,
.2.13)
Y
к виду
^12^12^1^2
el2/kT
(3.2.14)
ze~*dz =
= Y^w*N^-E"JkT{i+w)- <з-2Л5>
§ 3. Кинетика процессов превращения вещества 377
Здесь можно положить ei2/kT = E12/RT^> 1. Тогда имеем
t= Vr—W12e-E»'RT -4^ = C12-U e-E»IRT. (3.2.16)
V лц12 12 12 YkT Vt
Отсюда видно, что с точностью до постоянных величин скорость реакции
образования отличается от скорости распада множителем Т. Чтобы реакция
распада (3.2.4) .находилась в равновесии с реакцией образования (3.2.1), должно
выполняться условие
knl = knxn2, или ^--А-=#, (3.2.17)
«о k
где К — константа химического равновесия. Из (3.2.11) и (3.2.16) находим для
последней выражение
X Т12а12 Г Цо \ RT J
=йехр(-£#1)т- (3-2Л8)
Логарифмируя, получаем отсюда
\gK^-0,434 Е°~^ +lgT + lg -£*- . (3.2.19)
Таким образом, благодаря сделанному нами предположению о характере
распада рассматриваемых молекул мы получили для температурной зависимости
константы химического равновесия К такое же выражение, как в задаче 1.12.
ПоДставим известные численные значения; это дает
С другой стороны, с помощью (3.2.2), (3.2.11) и (3.2.13) находим
?=JL=C°. e-E°/RT ут. (3.2.21)
Разрешая относительно С0 и подставляя численные значения, получаем
4,45.10-5.7,9.10-3
С0=^
Наконец, с помощью (3.2.20) определяем
С12 = 5,6.1012. (2.2.23)
Используя это значение, вычислим с помощью (3.2.11) скорость реакции
распада при Т = 800 К
£"(800К)=3,0-103ехр (—р^^) /800=0,081 м3/кмоль-с. (3.2.24)
В пересчете на 1 моль, на время в минутах и на применяемый обычно в химии
молярный объем 22,4 л имеем
t(800K)=^^^-22,4=0,217.(22,4 л/моль-мин). (3.2.24а)
378 Гл. 5. Системы, состоящие из различных микрочастиц
Скорость реакции образования, согласно (3.2.16), равна
Г(800 К) = 2,2 м3/кмоль-с = 5,9.(22,4 л/моль -мин). (3.2.25)
Относительное количество вещества, распавшегося в течение первой минуты,
определим с помощью (3.2.1), используя значение (3.2.24) и имея в виду, что
«о (0) = 0,01 кмоль/м3:
— dn0=-lifi20dt, или в числах, — dn0 = 0,08МО"4-60-=4,86-10"4 кмоль/м3.
Таким образом, вследствие невысокой начальной концентрации в течение
первой минуты распадается всего лишь около 5% имеющегося йодистого
водорода.
С помощью С0 и С12 при известном сечении взаимодействия можно
вычислить стерические коэффициенты.
3.3. Зависимость от времени и время полураспада
при химической реакции второго порядка
Распад йодистого водорода при температуре Т = 556 К описывается
уравнением
-^L=kn\ (3.3.1)
где
/Г=3,52-10-7 м3/кмоль-с.
Предполагается, что образующиеся водород и йод сразу же отводятся из
реакционной камеры, так что в ней остается только йодистый водород. Определить
зависимость концентрации йодистого водорода от времени, если начальная
концентрация составляет я0 = 0,5 кмоль/м3. По истечении какого времени
распадутся 1/2 и 3/4 вещества?
Решение
Рассматриваемая реакция второго порядка, поскольку ее скорость
пропорциональна квадрату концентрации. Проинтегрируем дифференциальное
уравнение (3.3.1), произведя в нем разделение переменных. Это дает
п0 0
После вычисления интегралов получим
1 l-=kt, (3.3.3)
МО по
или, разрешая относительно концентрации п (t)t
„(,) = *о_. (3.3.4)
Распад половины вещества произойдет за время
' = 'i/.=A:
n0k
(3.3.5)
§ 3. Кинетика процессов превращения вещества
379
В отличие от реакций первого порядка в случае реакций второго порядка
время полураспада зависит от начальной концентрации.
Время ^ = ^/4, по истечении которого остается только V4 исходного
количества вещества, согласно (3.3.4), равно
n0k
Следовательно, времена /1/2 и t1,^ связаны соотношением
(3.3.7)
*1/2:*1/4— 1:3
Это соотношение и зависимость времени полураспада от концентрации
характерны для реакций второго порядка.
В рассматриваемом случае с помощью (3.3.5) и (3.3.6) получим для
характерных времен значения
^ = 0,5-3,52-10-<С:=65'8дн
И
*1/4 = 197 дн.
3.4. Суммарная скорость химической реакции
Определить изменение во времени концентрации йодистого водорода,
образующегося из йода и водорода при температуре Г = 781 К. Начальные
концентрации составляют а = пон = 0,1 кмоль/м3, b — n0J =0,1 кмоль/м3, с = /x0HJ = 0.
Скорость реакции распада HJ равна 0,0396 м3/кмоль-с, скорость реакции
образования k составляет 1,34 м3/кмоль-с. За какое время половина имеющегося
вещества превратится в йодистый водород?
На основании кинетического рассмотрения определить равновесное
состояние реакции.
Решение
Рассматриваемый химический процесс включает в себя реакцию образования
->
dnHJ -*.
H2 + J2—*2HJ, или --^p- = 4ja/2Ha, (3.4.1)
и реакцию распада
2HJ—>H2 + J2, или —J±±- = knllj. (3.4.2)
Обозначим концентрацию йодистого водорода nHJ через у. Образование 1 кмоль
HJ приводит к исчезновению 1/2 кмоль J2 и V2 кмоль Н2. Поэтому можно
написать
"H2 = "oH2-y"HJ = G-f-> "j2 = "oj2—2пы=ь—f • (3-4-3)
380 Гл. 5. Системы, состоящие из различных микрочастиц
Образующееся количество йодистого водорода определяется соотношением
Лнл=У=пнл — пш- (3-4-4)
Используя это и учитывая (3.4.3), находим из (3.4.1) и (3.4.2) уравнение
Преобразуя и интегрируя в соответствии с заданными начальными условиями,
получим
у t
V-
После вычислений имеем
V~K+k(a-\-b)l4 —Tk /4 — t)y
(3.4.6)
t=-
H
-in УЪ+Ъа+ь)/*] (347)
— VA + k(a + b)/4]
где
hi _►*_
Д=-пг (a—bf + kkab.
lb
В рассматриваемом случае численный расчет дает
/А = 0,023, -|- (a + Ь) = 0,067, -| t=0,295.
Подставляя в (3.4.7) у = 0,1, находим время, в течение которого произойдет
распад половины всего имеющегося вещества
^=15,2 с.
Время, по истечении которого установится состояние равновесия, теоретически
бесконечно велико. Это означает, что знаменатель в первом слагаемом
формулы (3.4.7) должен обратиться в нуль. Из этого условия находим
концентрацию йодистого водорода в состоянии равновесия:
„ ~k(a + b)/4- V"K _К (a + b)-VK* (а-Ь?+ \6Kab
k/4—k Д 4
где
К = -^ (3.4.9)
— константа химического равновесия.
В соответствии с законом действующих масс имеем
(а-у/2)(Ь-у/2)
= К, (3.4.10)
откуда, разрешая относительно у, приходим к выражению, совпадающему
с (3.4.8).
§ 3. Кинетика процессов превращения вещества 381
3.5*. Превращение параводорода
При исследовании химических реакций между молекулой и атомом
А + В2—*АВ + В (3.5.1)
особый интерес представляют реакции, уравнения которых симметричны. При
таких реакциях вещества А и В химически идентичны. Маркировку можно
осуществлять, например, с помощью различных изотопов. Однако в случае
водорода различия между Н = 1Н и D = ?H столь велики, что их
термодинамические свойства, а следовательно, и скорости реакций сильно отличаются
друг от друга. Если же рассматривать две спиновые модификации водорода,
ортоводород оН2 и параводород рН2, то они четко отличаются друг от друга
рядом своих физических свойств, в то время как их химические свойства
практически идентичны (ср. гл. 4, § 4).
Методом адсорбции водорода на угле при температурах ниже точки
кипения водорода можно повысить концентрацию параводорода до 99,7%.
Измерения Фаркаша показали, что избыточная концентрация параводорода
_ У*На
(3.5.2)
спадает по закону
"изб = "о изб * W. (3.5.3)
где п0 — концентрация параводорода, a Zg/(3ZU + Zg)—-его относительное
количество в состоянии равновесия (ср. задачу 4.4 гл. 4). Согласно (3.5.3),
натуральный логарифм избыточной концентрации убывает со временем по
линейному закону
бПпкИЗб(0
-* = di • (3.5.4)
Величину k можно экспериментально определить по наклону прямой,
представляющей зависимость 1пяи3б(0 °т *•
Как показывает анализ результатов исследований, величина k
пропорциональна давлению газа Р, вследствие чего выражение kj\/nH также зависит от
давления. При добавлении атомарного водорода превращение параводорода
в ортоводород сильно ускоряется. Отсюда можно сделать заключение, что
процесс убывания избыточного числа молекул параводорода происходит в
основном в соответствии с уравнением реакции вида
dnp ч-
рН2 + Н—*оН2 + Н, или -jf- = knHnp- (3-5.5)
Измерения величины &/|/ян при различных температурах дают значения,
приведенные в табл. 37.
Вычислить с помощью этих данных зависимость относительного
количества молекул в орто- и парасостоянии от времени /. Чему равна энергия
активации и какова величина стерического коэффициента? Сечение взаимодействия
при столкновении молекулы с атомом принять равным а = 4,Ы0~19 м2.
Константу химического равновесия взять из табл. 37.
382 Гл. 5. Системы, состоящие из различных микрочастиц
Таблица 37
Измеренные значения констант для реакции
рН2+Н=оН2+Н
Т, К к1]/~^й~' м3/2/кмоль1/2.с \gK
700 8,5-Ю-7 —30,35
800 1,91-Ю-4 —26,20
Решение
Наряду с процессом (3.5.5), приводящим к уменьшению количества пара-
водорода, протекает противоположный процесс его образования:
dnp -+ _+.
оН2 + Н—>рН2 + Н, или —-г— = knHn0 — knH {пн^—пр). (3.5.6)
Концентрация параводорода определяется соотношением
Пр = Пор + Пр—пр> (3.5.7)
где пор—начальная концентрация. Используя (3.5.5)—(3.5.7), находим
dnp +- -+.
aT==[knP-k (пн2-пр)]пн- (3.5.8)
С учетом начальных условий запишем решение этого линейного
дифференциального уравнения в виде
Т / Т \ +- ->
пр—^-^пн=( пор- +_ _^ пн ехр[—(* + *)лнЛ. (3.5.9)
k + k \ k + k )
Из сравнения (3.5.9) с (3.5.2) и (3.5.3) следует, что
k = k(T) = (t+k)nHt (3.5.10)
а также
~k zg
t+k Zg + 3Zu'
(3.5.11)
При высоких температурах на три орточастицы приходится одна парачастица.
Поэтому в соответствии с формулой (4.4.16) гл. 4 можно записать
k Zg 1 -* k
lim . _^ ='lim -——^=-=—, или lim k= lim -^-: (3.5.12)
Концентрация атомарного водорода определяется законом действующих масс
^-=КС. (3.5.13)
"н2
§ 3. Кинетика процессов превращения вещества 383
С учетом этого находим из соотношений (3.5.10)—(3.5.12) скорости реакций при
высоких температурах:
t- *. (3.5.14)
4/"нЛ 4К"нЛ
В табл. 38 приведены вычисленные значения скоростей реакций.
Таблица 38
Скорости и стерические коэффициенты, вычисленные с помощью
данных табл. 37
Т, К k, 10» м3/кмоль-с /г, 10» м3/кмоль-с
700 0,96 0,32
800 1,82 0,61
Согласно теории рассеяния и столкновеш
dtip Zp ч- ау0Т11техр(— £t
■ —- ■■■=— kn п^ — —————^—^
dt N~ ппнпг N.
т
0,084
0,082
ш, имеет
>/RT) NH
i
->
X
0,028
0,027
vm, юзм/с
4,7
5,0
место соотношение
Np
—, (3.5.15)
или
k = NA(JvOT}iTe~Eo/RT; аналогично k = Nao v0Tnre~E°/RT. (3.5.16)
Здесь zp — число приводящих к реакции столкновений между атомами
водорода и молекулами параводорода за единицу времени в единице объема, т и
—>-
т—стерические коэффициенты, Е0 — энергия активации.
Среднюю относительную скорость находим с помощью формулы (4.8) гл. 3
Будем предполагать, что изменением величин ст, т, Е0 при изменении
температуры можно пренебречь. Тогда, используя величины k (Г), определенные с
помощью (3.5.14) для различных температур, получаем
E()=R *£. ln Vw™=R tj±_,п УтЖЖ)k(г,)
Тг-Т, yflk(T2) ri~rt ГТ.КАТ^ЦТ,)
Подставляя сюда ГХ = 800К и Г2 = 700К и используя численные значения,
приведенные в табл. 38, находим
р 1 nQg80°-7°0i /700» 1,82-10» RAiM
£0=1,986—|ПП In .. = 6,4-103 ккал/кмоль.
ЮО уТюб.0,96.10"
После определения энергии активации в двух уравнениях (3.5.16) неизвестными
остаются только стерические коэффициенты тит. Разрешая относительно по-
384 Гл. 5. Системы, состоящие из различных микрочастиц
следних эти уравнения, имеем
т=-
NAoi\
PE0/RT
(3.5.19)
С повышением температуры энергия активации несколько увеличивается. Ее
значение, приведенное к абсолютному нулю температуры, составляет
7,4-103 ккал/кмоль.
3.6. Длина реакционной цепи (цепь Нернста)
Реакция между водородом и хлором при интенсивном воздействии света
протекает взрывообразно. Дозируя световое облучение, можно управлять
реакцией таким образом, чтобы она протекала с измеримой скоростью. Как
показал Боденштейн путем количественного анализа, скорость реакции
пропорциональна квадрату концентрации хлора, в то время как концентрация
водорода вообще не входит в уравнение для скорости. В то же время реакция
замедляется при добавлении кислорода. Таким образом, кинетический ход
реакции описывается уравнением
йпл_
*НС1
dt
Oh
по2
(3.6.1)
Для его интерпретации рассмотрим, следуя Нернсту, цепную реакцию, ход
которой изображен на фиг. 69 (ср. пример 37). Реакция разветвления цепи III
Н*НС1*02+1
Обрыв цепи
fl+CU-">HCl+Cl> .
2 CI
Фиг. 69. Схема реакции хлорирования
водорода.
приводит к регенерации исходной активной частицы, т. е. атома хлора. В
результате этого звено, состоящее из реакции продолжения цепи II и реакции
разветвления *•> цепи III, может быть пройдено еще раз, и для этого не нужна
реакция зарождения атомарного хлора I. Цепь обрывается, если
высвободившийся в реакции II атом водорода реагирует с молекулой кислорода, вместо
того чтобы принять участие в реакции III. В результате сложного процесса с
Х) Вообще говоря, реакцию хлорирования водорода в химии принято
считать примером неразветвленной цепной реакции, а обе реакции—II и III —
называть реакциями продолжения цепи. Поэтому используемый здесь автором
термин «реакция разветвления цепи» применительно к указанной реакции
следует считать условным.— Прим. перев.
§ 3. Кинетика процессов превращения вещества
385
участием других веществ (реакция IV), описываемого формулой
1
Н + НС1+02 + Н2-
•2Н20 + уС12,
образуются две молекулы воды (реакция обрыва цепи, или реакция гибели).
Реакция гибели подчиняется кинетическому уравнению
dnv
dnHCX 1 dnHtQ
«iv^o,-
(3.6.2)
dt dt 2 dt
Предположим, что, согласно, данным количественного анализа, при
парциальном давлении кислорода PQ = 400 мбар и хлора РС1 =200 мбар массы
образовавшихся хлористого водорода и воды составляют соответственно АтНС|=441 г
и Дтн 0 = 23,3 г. Определить отсюда среднее число циклов до обрыва реакции.
Чему равно число поглощенных квантов? Какое количество световой энергии
поглощается в ходе химического процесса, если длина волны излучения
Я, = 4000-10-10м? Определить длину цепи приРОг = 0,01 мбар и Рс,2=200 мбар.
Относительные молекулярные массы равны Л4НС1= 36,47 и МНг0= 18,02.
Реакциями со стенками сосуда и со следами других веществ пренебречь.
Решение
Будем исходить из схемы цепной реакции, представленной на фиг. 70.
Активная частица Л через промежуточное состояние В переходит в состояние С;
при этом образуется р новых частиц Л. Таким образом, частица Л может
либо р-кратно размножиться, либо вообще исчезнуть. Пусть для
промежуточного состояния В вероятность продолжения цепи равна w, а вероятность
7-у
обрыт / NJ^
обрыва
+Д Фиг. 70. Схема цепной реакции с
многократным размножением.
обрыва цепи равна 1 —о/. Обозначим через х среднее число звеньев (циклов),
т. е. длину цепи, а через <?—среднее число частиц Л, регенерируемых до
обрыва цепи. После первого цикла среднее число регенерированных активных
частиц равно pw. Каждая из них в свою очередь регенерирует в среднем q
частиц Л. Таким образом, имеет место соотношение
q = pw([+q). (3.6.3)
Отсюда среднее число активных частиц, регенерируемых одной частицей Л,
равно Х)
Я=
pw
1.—pw
(3.6.4)
Х) Результат (3.6.3), (3.6.4) легче понять из следующих соображений. Если
на входе реакции был один атом Л, то после первого цикла реакции на ее
386 Гл. 5. Системы, состоящие из различных микрочастиц
Следовательно, чтобы цепная реакция протекала контролируемым образом, а не
взрывообразно, должно выполняться условие
w < —
р
(3.6.5)
В рассматриваемом случае имеем р— 1. Поэтому длина цепи х равна среднему
числу q регенерированных активных частиц:
w
х =
Ь=1 = Г=^> (3.6.6)
т. е. отношению вероятностей продолжения и обрыва цепи. Как следует из
фиг. 69, реакция III протекает со скоростью
— dttpj ^hci
-jr-=-^-='!m«c.2"H- <3-6-7)
Кинетика реакции обрыва цепи подчиняется уравнению (3.6.2). Отсюда
вероятность продолжения цепной реакции равна
«— 'iiLWH 1 (3.6>8)
klWnHnOt + k\ 11ПС1,ЛН l + klVnOt >k\ ИЛС1а
Следовательно, длину цепи можно определить, если известно отношение
^iv/^iii* Подставляя (3.6.8) в (3.6.6), находим
х=*тПс1*. (3.6.9)
kwno2
После прохождения каждого звена цепи образуются две молекулы НС1. С
другой стороны, при каждом акте обрыва цепи возникают две молекулы Н20.
Используя (3.6.7) и (3.6.2), получаем для длины цепи выражение
^2АггНС1 = МНг0Атнс1
2Д/гНа0 МНС1ДтНг0
вход поступает pw атомов Л, после второго цикла — (pw)2 атомов Л и т. д.
В результате во всех циклах реакции, инициированной одним атомом А,
примет участие в общей сложности
1+р^+(^)2+...=^(^)"=г=г^;
/2=0
атомов А. Таким образом, один атом А вызывает участие в реакции
дополнительно
* 1—pw 1—pw
новых атомов А. Во избежание недоразумений необходимо подчеркнуть, что
даже при pw < 1 один атом вызывает бесконечное число циклов реакций,
однако выход каждого последующего цикла в pw раз меньше предыдущего,
т. е. процесс затухает со временем, и q остается конечным. Поэтому можно
говорить о среднем числе циклов в реакции, определив его, например, как q/p
(можно.было бы его определить как q/p-\-\, считая, что при w = 0 реакция
состоит из одного звена).— Прим. ред.
§ 3. Кинетика процессов превращения вещества
387
Подставляя измеренные значения, находим
18,02-441
*~36,47- 23,3-y'J5-
Таким образом, при заданных условиях цепная реакция состоит в среднем
из 9,35 звеньев, подобных изображенному на фиг. 69.
При каждом акте поглощения кванта света из имеющегося молекулярного
хлора возникают два атома хлора, каждый из которых кладет начало цепной
реакции, состоящей из 9,35 звеньев, причем в каждом звене образуются по две
молекулы НС11). Всего, таким образом, на поглощенный квант образуется по
2-2-9,35 ==37,4 молекул НС1. Отсюда число поглощенных квйнтов равно
Атнсг^А 0,441-6,02-10"
"кв~ 4хМна — 37,4-36,47 -'•9Ш -
а для энергии поглощенных квантов имеем
„ ., . NKBhc 1,9-1023-6,63-10-м-3-108 „. _
£KB = ArilBAv=-^-= 4000-10-to =94 кДж.
Скорости klu и k\v зависят только от температуры. Следовательно, если
температура остается постоянной, то из соотношения
*Щ= П°* х
с помощью (3.6.10) можно определить отношение скоростей. В рассматриваемом
случае имеем п0 =2/гС1 . Пользуясь найденным значением длины цепи, получаем
■£Ш- = 2.9,35 =18,7.
Если парциальные давления кислорода и хлора составляют соответственно
Р0 =0,01 мбар и РС1 =200 мбар, то определенная с помощью (3.6.10) длина
цепи при неизменной относительно исходных условий температуре оказывается
равной
*=18,7~=3,74.10б.
Таким образом, если концентрация тормозящего реакцию кислорода в
реакционной камере доведена до достаточно малой величины и отсутствуют другие
вредные влияния, то возникают цепные реакции со средней длиной цепи
порядка 104 —10е.
3.7. Управление цепной реакцией
Согласно схеме, изображенной на фиг. 69, образование хлористого
водорода из водорода и хлора происходит посредством цепной реакции. Реакция
инициируется облучением светом с длиной волны А, = 4000-10-10 м. Скорости
реакций
(II)H2 + CI—►HCl + H и (III)H + CI2—►HCI + Cl
х) Атом С1, вступая в реакцию с Н2, порождает 1 Молекулу НО:
Освободившийся при этом атом Н порождает w молекул НО и 2(1—w) молекул
Н20, причем в последней реакции гибнет (1—w) молекул НО. Итого за цикл
каждый атом О образует (\-\-w) — (1—w) — 2w молекул НО. Суммируя вновь
геометрическую прогрессию, как в примечании на стр. 386, получаем, что
полное число образовавшихся молекул НО равно 2q.— Прим. ред.
388 Гл. 5. Системы, состоящие из различных микрочастиц
подчиняются уравнениям
lg fe„ = 9,55+i-lgT-Щ^, (3.7.1)
lgfein=9,72+llgr-^. (3.7.2)
Предположим, что обрыв цепной реакции связан исключительно с кислородом,
который, однако, присутствует в незначительном количестве. Кроме того,
скорость &iV реакции гибели связана со скоростью кщ соотношением
lgfe,v = lgfein-2,80+^. (3.7.3)
Пусть в исходном состоянии водород и хлор присутствуют в равном количестве,
реакция происходит при нормальном давлении, а парциальное- давление
кислорода составляет Р0 =0,1 мбар. Измерение температуры дает значение 7=400 К.
Найти максимальную мощность излучения, которую можно подводить к
единице объема реагирующих газов, если в течение первой секунды реакции должно
быть преобразовано не более 1% имеющегося хлора. Как изменится эта
мощность при нагревании газа до 500 К? Каков верхний предел интенсивности
подводимого светового излучения при объеме реакционной камеры V=l л,
если облучение осуществляется через отверстие размером 100 см2?
Решение
Концентрация атомарного хлора удовлетворяет кинетическим уравнениям
(!) ^=Ма,. (3.7.4)
(II) $=кппапНш, <3-7-5)
dnm
<Ш> -ЗГ=*ш"н"с.,. 37-6)
откуда следует соотношение
*inci, + ^ih^h^cu = knnc\nHt
(3.7.7)
Для атомарного водорода выполняются уравнения
(II) ^ = *.1«С1»Н,. <3-7-8)
(III) ^-=*iii«h"ci,. (3J-9)
(IV) -^ = *IV«H«Q,- <3-7Л°)
Отсюда находим
knnC\nH2 = kmnnncl2 +hvnRnQi
(3.7.11)
§ 3. Кинетика процессов превращения вещества
389
Правая часть уравнения (3.7.7) равна левой части уравнения (3.7.11). Поэтому
имеем
к{псх =к1Чпнп0
(3.7.12)
Для сравнения двух слагаемых в левой части (3.7.7) воспользуемся
соотношением (3.7.12) и, учитывая формулу (3.6.9) для длины реакционной цепи,
получим соотношение
кш ^н пс\2 __ кШ ^н пс\2
&i п\
ci,
kwnHn0i
(3.7.13)
При достаточно хорошем отводе замедляющего реакцию кислорода выполняется
условие х^>\ и, следовательно,
kmnwnc\2>kinc\2 • (3.7.14)
Таким образом, первым слагаемым в левой части соотношения (3.7.7) при
достаточно большой длине цепи можно пренебречь. Тогда получим
кт пн пс\2 = кп пс\ пн2- (3.7.15)
Хлористый водород образуется в результате реакций II и III. С учетом (3.7.15)
получим для него кинетическое уравнение
dn
НС1
dt
= кп псхпн 4-ктпн пс] =2ктпн п{
С12
(3.7.16)
Концентрацию атомарного водорода выразим с помощью (3.7.12). Тогда
уравнение, описывающее возрастание концентрации хлористого водорода, будет
иметь вид (все величины отнесены к 1 м3)
dwHCi _2A:iiiMci3
/eivn0a
dt
(3.7.17)
Предположим, что реакционный объем освещается равномерно. Обозначим
через N'K]i число поглощаемых в 1 с квантов света. При поглощении каждого
кванта образуются два атома хлора. Следовательно, справедливо равенство
dN«™ = 2NKBdt.
(3.7.18)
Концентрация атомов хлора в результате облучения возрастает на величину
(3.7.19)
df№" = - CI
*C1 ~ NA
Подставляя ^3.7.4) и (3.7.18) в (3.7.19), находим
Принимая во внимание, что поглощенная энергия и число поглощенных
квантов связаны соотношением
= NKB hv =
NKBhc
(3.7.21)
390 Гл. 5. Системы, состоящие из различных микрочастиц
получим из (3.7.20)
На каждый киломоль С12 образуются 2 кмоль НС1. Отсюда следует
dn
НС1
=—2
dn.
С1 о
dt " dt '
Подставляя (3.7.22) и (3.7.23) в (3.7.17), получаем
dnC\2 _2kmE;iBkncl2
dt
NA hcklv n0
(3.7.22)
(3.7.23)
(3.7.24)
Отсюда с учетом условия
dnr
Ш±- < 0,01 dt
пс\2
имеем
0,01^ hckw n0z
(3.7.25)
(3.
(3.
(3.
(3.
7.26)
7.27)
7.28)
7.29)
кв"^ 2km%
Учитывая, что для V— \ м3 справедливо соотношение
и используя вытекающее из (3.7.3) равенство
/cIV = /cin10-2'80 + 448 к/г,
получаем окончательно для плотности мощности излучения выражение
0,01^лЛс.10-2'80 + 448К/7, Ро2
^КВ^ 2KRT
Подставляя заданные числовые значения, находим при Т = 400 К
•СКВ *аа:
=0,094 Вт/м.
В пересчете на реакционный объем V—\ л максимальная мощность излучения
равна 9,4-10-* Вт. Если облучение производится через отверстие размером
100 см2, причем предполагается, что все- излучение полностью расходуется на
расщепление молекул хлора, то для интенсивности облучения получим
величину
9 4-Ю-5 Вт
£обл< юосм2 ,4<10"? Вт/™2^1»3-10"5 кал/мин-см2.
Для сравнения укажем, что интенсивность солнечного излучения в Центральной
Европе при оптимальных условиях составляет 0,4 кал/см2-мин. Это означает,
что дчя управления протеканием рассматриваемой реакции необходимо
обеспечить безукоризненно хорошее затемнение.
0,0Ь6,02-1026.6,63-10-34-3.108 .lQ-2'8Q + 448/*00.Q,M02
2 • 4000 • 10 -10 • 8,314 • 10:5 • 400
§ 3. Кинетика процессов превращения вещества 391
Повышение температуры до 500 К приводит к появлению дополнительного
множителя
Е;в(500К)=ю"8/5оо4оо
£^(400 К) Ю448/40°500 '
Таким образом, если скорость реакции не должна превышать некоторого
установленного предела, то плотность поглощенной энергии, расходуемой на
разрыв связи в молекулах хлора, должна быть не выше 4,5-10~2 Вт/м3, что
составляет около половины значения, найденного для 400 К.
Упражнения
У.3.1. Период полураспада радона (эманация радия) составляет 92 ч. Какая
часть радона, содержащегося в родниковой воде, распадется по
истечении одного дня? За какое время распадется 90% вещества?
У«3.2. Период полураспада тория эГТп (радиоактивного Rd Ас) равен 18,9 дн.
Энергия распада составляет 6,1 Мэв на частицу. Сколько атомов
распадается за 1 день, если исходное количество вещества равно 1 мг?
Чему равна энергия (в калориях), испущенная при распаде этих
атомов?
У.3.3. Определить скорость k образования йодистого водорода при Г = 780 К,
положив в основу рассмотрения закон Аррениуса. При Т = 630 К
скорость составляет k (630 К) = 6,8-10~3 (22,4 л/моль -мин). Энергия
активации Е12 равна 40-103 ккал/кмоль.
У.3.4. Концентрации Н2 и J2 в реакционной камере поддерживаются рав-
ными 0,1 кмоль/м3. Температура составляет 780 К. Образовавшийся
йодистый водород сразу же отводится из камеры. Определить
количество йодистого водорода, образующегося за 1с.
У.3.5*. Вывести в общем виде дифференциальное уравнение для реакции
распада /-го порядка (/ Ф 1) и найти его решение.
У.3.6. Вычислить время /1/4 для реакции H2 + J2^2HJ. (Начальные
данные: пон =0,1 кмоль/м3, n0J =0,1 кмоль/м3, rc0HJ = 0; Т =
=781 К.)
У.3.7*. Определить время, в течение которого прореагирует половина
исходного количества вещества для химической реакции /-го порядка.
У.3.8. Составить уравнение хода реакции 2HJ^rH2 + J2» если начальные
концентрации составляют пон =0, nHJ=a.
У.3.9. В интервале от 650 до 670 К скорость образования йодистого
водорода в реакции J + H2—*HJ + H возрастает в 2,2 раза. Вычислить
отсюда энергию активации.
У.3.10. Как изменится скорость образования хлористого водорода в реакции
С1 + Н2 —>-НС1 + Н при повышении температуры от 500 до 600 К?
Энергия активации равна 5,5- 10я ккал/кмоль.
У.3.11. Пусть некоторая цепная реакция с вероятностью о/1 = 0,5 идет в
направлении промежуточного состояния В, а из последнего с
вероятностью w2 — в направлении состояния С; при этом регенерируются
р = 3 активных частицы. Каково наибольшее значение w2t при котором
реакция будет протекать не взрывообразно?
У.3.12*. Для определения длины цепи при хлорировании водорода измеряется
поглощенная световая энергия. Установлено, что всего было
поглощено 10 кДж. Длина волны излучения К = 3000-10~10 м. В
результате реакции образовалось 91,5 г НС1. Определить отсюда длину цепи.
Чему будет равна длина цепи, если уменьшить относительное
содержание кислорода до 0,01?
392 Гл. 5. Системы, состоящие из различных микрочастиц
У.3.13*. Производится опыт по получению НС1 при воздействии света.
Установлено, что мощность излучения, поглощаемая имеющимся хлором,
равна 0,10 Вт/м3. Длина волны, излучения составляет X = 4000- Ю-10 м.
Опыт проводится при комнатной температуре 20 5С, Р0 =0,05 мбар,
РС1 = 300 мбар. Определить начальную скорость реакции.
У.3.14*. Как изменится в предыдущей задаче скорость реакции, если
парциальное давление кислорода уменьшится до 0,01 мбар?
У.3.15. Определить длину цепи для реакции С12 + Н2 -> 2НС1. (ЛтНС1 =
= 1,043 кг, Атн 0 = 22,8 г, Р0 = РС1 = 100 мбар.) Чему будет равна
длина цепи при Р0 =0,1 мбар, ЯС1 =400 мбар?
ОТВЕТЫ И РЕШЕНИЯ
К главе 1
У. 1.1. а) Р = 0,064, б) Р = 0,049
у.1.2. а)Р = Ш(п~к)\ Р = 0,0000365, б) Р = 0,1234-10-5
k0(n — k0)(n — k)\
У.1.3. Р = 0,000182 на основании формулы Р=— .
У. 1.4. Р = (0,25 • 0,60 • 0,15)2 = 0,000506;
Р = 7^з- (0,25.0,6.0,15)2 = 0*045562
665
У. 1.5. a) P = (J)(|)6==0,402, б) Я-1-Щв =0,
У.1.6. 0,027, 0,142, 0,303, 0,321, 0,171, 0,036
У.1.7. Р(2, 1, 1) = 0;06
У.1.8. я = 4: а=10-4, р = 0,0776, 11 = 0,9224;
п = 2: а=10-2, (3 = 0,0396, 11 = 0,9604
У. 1.9. п > 9,97, п < 8,02. Задача неразрешима
У.1:10. гс > 3,27; гг = 4, q < 0,026
У.1.11. а = 0,0506%, р = 7,38%
У. 1.12. а = 0,338%, р = 3,70%
У.2.1. ц = 850°С, а = 72,6рС. Здесь речь идет не о выборке
У.2.2. л: =1,25 см, s = 0,0277 см
У.2.3. Р(х< 1,5) = 0,0098
У.2.4. а = 0,209%
У.2.5. Р(\х\ > \х+За) = 0,0027.
У.2.6. |Li = 4,334B, а = 0,129В, а) 0,48о/0, б) =0,23%
У.2.7. 1.1=5,798, а = 4,751; —6,4 < а: < 18,0
У.2.8. х = 8,00 см, s = 0,16 см; 90%: 7,7 см < \х < 8,3 см, 0,105 см < а <
< 0,493 см; 99%: 7,08 см < \i < 8,92 см, 0,075 см < а < 1,596 см
У.2.9. * = 0,43, 5 = 0,0214; 99%: 0,404 < ^ < 0,456, 0,0132 < а < 0,0509;
90%: 0,416 < \1 < 0,444, 0,0162 < а < 0,0336
У.2.10. Среднее значение: 14,36—14,66, 14,33—14,69, 14,28—14,74
Среднеквадратичное отклонение: 0,612—0,775, 0,591—0,802, 0,557—0,863
У.2.11. Среднее значение: 4,00—5,06, 95,56%; среднеквадратичное отклонение:
0,25—1,00, 95,65%
У.2.12. а = 2,69%, 46,0% < ц < 61,8%
У.2.13. ^, = 30 мОм, 28,97 мОм < \i< 31,03 мОм, а = 0,95 мОм, 0,64 мОм <
< а < 2,08 мОм
У.3.1. х2 = 3,17 > 2,20 = ^0 ю^' Распределение неравномерно
У.3.2. х2 = 11125 < Xq 01 (8) = 1,65. Распределение неравномерно
У.3.3. а) Xя = 2,88 > ^50 (3) = 2,37; б) Х2 = 0,167 < х*до (2) = 0,211; в) *«
= 1,85* +22,5, X2 = 0,154 > 0,103 = Х(2); уровень значимости выше 5%
У.3.4. Х = 0,38, а > 0,002
У.3.5. А, = 0,915 > 0,65 = Я0>20. Нормальность распределения не
подтверждается
У.3.6. /(7) = 3,3 < /а(7)=3,50; Р = 2,56 < 28,7 = Р0)01 (4,3). Флуктуации
с уровнем значимости 1% случайны
394
Ответы и решения
У.3.7. ?(36) = 2,72, что соответствует а—-0,010
У.3.8. /-критерий не исключает случайность: / = 0,084 < /0>99 = 2,73,
напротив, F-критерий указывает на изменение генеральной совокупности:
Fo.01 (20,14).= 3,51 < f = 6,18
У.3.9. F = 18,51 > 7,01 = F (4,8); описанные способы измерения с уровнем
значимости а < 0,01 принципиально различны
У.3.10. / = 0,47 < 2,58 = f0,oi(«>); 2,89 < 4,31 =F. В обоих способах проверки
отклонения могут быть случайными
2 (*'— *) (У1— у)
^(У1-~У)2
Ув4Л" b*-v= ' V,,,. ^2 ' ах.у = *~Ьх.уУ
У.4.2. Ьх.у = — 32,46, ах,у = 722, ЬХшу-Ьу.х = 0,№ Ф I
УАЗ. г2 = 0,998, / = 49,95 > 6,86 =/0001 (5); b =73,50, а =32,60, Ьх =
= 0,01358, а^ = 3,158
У.4.4. Г = 60,85 — 0,073*, г = 0,9635;. / = 6,24, /0?05 (3) = 3, J8, /0>001 (3) = 2,94;
в случае а) гипотеза подтверждается, в случае б) отвергается
У.4.5. г = 0, 6 = а = 0
У.4.6. К= 18,15 —0,0296*+ 0,000107*2
У.4.7. г = 0,866, / = 2 < 6,31 =/0 ]0(1)
У.4.8. г = 0,9927, /= 16,5 > 8,61 =/0,ooi (4), ^., = 2,176, 6 =1,941, а =
= —1,061, 6^=0,50769
У.4.9. # = 4,04, * = 3,08, г =—0,212; ^ = -0,156, а =3,71
У.4.10. Г = 46,88 — 1,06jc +0,0064а:2
У.4.И. Случайные величины приводятся к стандартному нормальному
распределению с помощью преобразования (2.9а). При этом коэффициент
корреляции остается неизменным. Для дисперсии суммы или разности
стандартных нормальных распределений получим:
о1+у= 1 + 1 + 2г, ог|_^= 1 + 1-2г
Левые части этих двух равенств не могут быть отрицательными.
Поэтому имеем 1 + г ^ 0, 1 — г ^ 0, откуда следует, что —1 <; г <;+ 1
К главе 2
У.1.1. dN = 9J-\0*
У.1.2. <W = 2,8.1017
У.1.3. <Ш = 3,65.1026
У.1.4. <WcH2(373>16)=1755 М/С> ^максНе (373,16) = 1245 м/с,
^максы2(373,16) = 471 м/с
У. 1.5. vHi (873) = 2850 м/с, uNe(873) = 901 м/с, ^(873) = 715 м/с
У.1.6. v = 1741 м/с, УМакс=1543 м/с, К^ = 1890 м/с
У. 1.7. а = 735 м/с
У. 1.8. 7 = 0,486. Для нормального распределения, описываемого
симметричной функцией, 7 = 0
у. 1.9. е = —2,22. Эксцесс нормального распределения равен нулю
У.1.10. Р(1000) = 883 мбар при 250 К, Р(1000) = 904 мбар при 300 К
УЛ.И. На уровне моря: pNg = 0,975 кг, р0з = 0,299 кг, Рм2/Ро2 = 3>26; ПРИ
z = 5532 м: рм=:0,499кг, рОз = 0,139кг, pN2/po2 = 3^9
Ответы и решения
395
У Л. 12. При 0°С: hN2 = .5,729. км, ftCOi = 3,647 км; при 3,0QC: hNt = 6,358 км,
hCQ =4,047 км
УЛ.13. ц = 5,44Л0-21 кг, р = 1,0055
У.1.14. р(3) = 0,159р(0), /г = 1,13 м
У.1.15. Роем = 4,97 ат-
У Л .16. m = 75,*0 г
У.1.17. р(0)/р(0,12) = 5,4Л03, во внешней зоне 3,5-10-5, во внутренней зоне
0,894
УЛ.18. р (0)/р (0,12) = 5,4-103, во внешней зоне 0,999, во внутренней зоне
зло-7
У.1.19. dW= ,.jL — e-e/kTV~icie, dW = 0,014
е /jtfc3r3
У.2.1. UHe = U7 Дж, tfH =245 Дж, t/Co2 = 294 Дж
У.2.2. /7 = 3,14 Дж<£0 = 9-1013 Дж
У.2.3. ё=^, е2 = -^£2Г2, (е-ё)2=-|-£2Г2,
£ = 6,2Ы0-21 Дж, ё2 = 6,43-10-41 Дж2, (е—е)2=2,57-10~41 Дж2
У.2.4. См. табл. П.1Х
У.2.5. См. табл. П.IX
У.2.6. a) C« = 4tf, CV = 3R, и=1,33 ...
б) Cp = 7R, CV = 6R, х= 1,166 ...
У.2.7. а) с£ = 4Я, CV = 3R, % = 1,33 ...
б) Cp=\0R, Cv = 9/?, и=1,11 ...
У.2.8. ср = 0,279 ккал/кг-К, cv = 0,2\7 ккал/кг-К
У.2.9. Кад = 23,0 л, 7 = 574 К, VK3 = 40 л
У.2.10. Р = 1,38 ат
У.2.11. я =1,32
У.2.12. РУ"=Р0С TV»-i = T0Vn0-\ TnPi-» = Tn0Pl-n, Р = 2,38 ат, Т =
= 324,8 К
У.2.13. с_5о = 299 м/с, с+б0 = 360 м/с, сНг=1315 м/с
У.3.1. F = —2,46 Дж, S = 0,0017 Дж/К, Я = 0,25 Дж
У.3.2. AF = 0,91 Дж, AS = 0
У.3.3. А/^—0,069 Дж, AS = 4,6-10-5 Дж/К
У.3.4. FBp = GBp = -l,4-107 Дж, SBp = 4,7-104 Дж/К, #вр = £Увр = 5,0Л0в кДж
У.3.5. AS = 3,20 к Дж/К, At/= 2,08 кДж
У.3.6. AF = -681 кДж, AS =1,1 кДж/К
У.3.7. AS =1,42 к Дж/К, At/= 426 кДж
У.3.8. (0 = 2,97-1014 Гц, AFK0JI = — 4,13-106 Дж, А(/кол = 4,16-106 Дж,
ASK0JI= 1,86-103 Дж/К
У.3.9. ASKOJl = 2J0 кДж/К
У.3.10. AS = 8,3 кДж/К, Г = 333,3 К
У.3.11. AS = 0,83 кДж/К при постоянном давлении, AS = 0,59 кДж/К
У.3.12. Приращение энтропии независимо от температуры равно AS — 3R In 2 =
= 17,3 кДж/К
У.3.13. 1/1= 1980 см3, Р = 65 кВт, т]=0,63
У.3.14. Идеальная машина Карно отбирает из одного теплового резервуара
количество тепла Q, из которогоrjxQ превращается в работу, а (1—%) Q
передается второму резервуару. Последнее количество тепла можно
снова передать первому резервуару с помощью другой машины Карно,
* 1 —Til ^
включенной навстречу первой и совершающей работу -4)Q
(г)— к. п.д. машины Карно, когда она работает как тепловая машина).
396
Ответы и решения
Всего при этом в механическую работу должно превратиться
количество тепла
(п,-^л)<г=^о>о,
которое отнимается у первого резервуара, но не передается второму.
Это противоречит.второму закону
У.3.15. ц = Т Т% , Т1>ТЖ\ ^ = 3,6, Р = 19,4Вт
1 1—' 2
У.3.16. Согласно первому закону, совершаемая работа равна разности между
внутренними энергиями. Обозначив через N число частиц в одном из
двух цилиндров, получим: — AU = fNk (Т0 — Т) — 29,\ кДж. Из
постоянства энтропии при / = 5 следует, что Г=293 К
У.3.17. При постоянном объеме и постоянной температуре из условия 6Q —
— TdS < 0 в соответствии с первым законом следует, что d(U — TS) =
= dF < 0. Свободная энергия монотонно уменьшается. Этот процесс
продолжается до тех пор, пока свободная энергия не достигнет
минимума. Поэтому при равновесии изотермо-иэобарный процесс
характеризуется минимумом свободной энергии F
У.3.18. При dP = 0, dT — 0 из условия 6Q — TdS < 0, в соответствии с
первым законом следует dG = ct(U-\-PV — TS) < 0. В равновесии изотер-
мо-изобарный процесс характеризуется минимумом энергии Гиббса.
У.4.1. ]/дР"=110К, ]/Х^"==0,34.10-3 мбар, VKS* =7,6-Ю-23 Дж/К
У.4.2. УЪ6*=ЬЛ0-Ч Дж; № = RS* ^ + nkPTV--2k^^
У.4.3. # = 1,45.10*. VM* = V"n = 1,20.10я
y.4.4. 1-p—== )/-^ = 0,01, P==^- = 7.10-ю мбар
У.4.5. V~AN* = 104,' g = Vn=W; Ф(1) = 0,8413, т. е. почти 16%
У.4.6. У=Ш = 3'\0-1* мбар, 1/ ^!= у ^.=2,4.10-8
У.4.8. При AVAT==0y (^Pl =?j2 из равенства
следует
_пСг,1/"АГ2_1/с;
г.Д5-— у ==-)/ ср
У.4.9. гд5 дк= ^Д ^-. Средние температуры: гНе =0,63, гНг = 0,53, гсо =
= 0,50; высокие температуры: гНе=0,63, гн =0,47, гсо =0,38
(предельное значение)
У.4.10. VW*= 1,4.10-4 Дж;
AU = TAS—PAV, AU* = knT*Cv
AT,
Ответы и решения 397
У.4.11. Для малых отклонений из выражения A = mgl<p2/2 следует V ф* =
= Л/ —у. Подставляя численные значения, имеем Уф2 = 3,2.10~8.
У.4.12. D = 2677*2 = 1,38-10-14 Н/м=1,4Ы0-17 кгс/см
У.4.13. Измеримые значения тока должны превышать утроенный
доверительный интервал тепловых флуктуации:
/мин = з/2>014Г5.104=1>8.10-^А ^
У.4.14. l^ = exp(-Mi^|^),/^ = ]/^ = l,1.103 м/с
У.5.1. v = l,M028 с-1
У.5.2. 330 соударений в 1 с
У.5.3. dv = ^ л/^п sin fl cos fl d$
V V 2лМ
К главе 3
У.1.1. (p+r^yV-nb) = nRT,
где гг = 0,00025, a = 0,0236 ат-м6/кмоль2, 6 = 0,019 м3/кмоль; R =а
= 6,83-103 Дж/кмоль-К
У.1.2. О2:/? = 6,54.103 Дж/кмоль-К, N2:/? = 6,50-103 Дж/кмоль-К
У.1.3. /г = 0,182, а = 2,07 ат-ме/кмоль2, 6 = 0,032 м3/кмоль,
/? = 6,20-103 Дж/кмоль-К, Р = 92,3 ат
У. 1.4. 0 = 87°С, для идеального газа 0 =—65°С
У. 1.5. Pz = 90 ат
У.1.6. 2г5 = 2,9.10-10 м
У.1.7. а = 0,00320 К"1, 0 = 0,00334 К"1, % = 0,0191 К"1
*A'*'a-Vo[dTJp-v(RT + bp^>V-p0[dTJv-PoV-b'
y0==V(0°C, P), Po = P(0QC, l/);' а = 0,00352 К""1, p = 0,00367 K^1
У.1.9.
Газ
I
II
Pk
59,3
32,4
vk
0,090
0,120
Tk
167,8
121,3
P = 10 ат
1177
1167
7\ К
P = ll ат. P = 12 ат
1294 1412
1284 1400
У 2 1 7,» = 515 К
У.2.2. В (300) = —0,23 м3/кмоль, В (700) = 0,08 м3/кмоль
У.2.3. F = 8,96 кДж, S = —22,4 Дж/К, (У = — 107 Дж; Рид = 6,48 кДж,
S„a = -16,2 Дж/К, ^„д = 0
У.2.4. £,, = 4,988 ккал/кмоль-К, х= 1,674, С„ ИД = С,, = 2,980 ккал/кмоль-К
У.2.5. Д7> = 38,6 ат
ж
Ответы и решения
У.2.6. Энтропия S постоянна. Тогда в расчете на 1 кмоль имеем lgV +
+ •/== —0,639. Для /г = 0,04 это дает V = 9,0 л
У.2.7. АР = —29,7 ат
У.2.8. Гинв=,2а//?6, 208, 841, 1032 К. Если считать 71инв = 277у4, то для
этих трех газов температура инверсии равна 224, 850, 1041 К
У.2.9. Vm — VmuJL = B. В критическом состоянии В = — 19УЛ/24, Для НС1 эта
величина равна — 0,0475 м3/кмоль, относительное изменение — 0,791
У.2.10. a) W=2,37-1018, б) #=2,6Ы018
У.2.11. Идеальный газ: AF = —45,19 кДж, реальный газ: А/7 = — 48,62 кДж
У.2.12. Идеальный газ: AU = 8,17 кДж, реальный газ: At/= 9,00 кДж
У.2.13. Идеальный газ: А# = 11,75 кДж, реальный газ: АЯ= 13,70 кДж
У.2.14. F = 2,6.10-10 Н
У.2.15. С = Сид + /гРВ
У.2.16. Реальный газ: # = 2,75-1024, идеальный газ: # = 2,84-1024
У.2.17. (^) =2,5-10-5 м3/кмоль-К, (Ш) =5,5.10-5 м3/кмоль-К, от-
\дТ;ш \oTJ500
куда следует AU = 7,9 кДж
У.2.18. P = nRT/(V—nb), АР = 43,2 ат
У.2.19. dB/dT = 2,5-10-5 м3/кмоль-К, d2B/dT2 = —\0-'? м3/кмоль-К2, Ср =
= 5,31 ккал/кмоль-К, Cv = 3,04 ккал/кмоль-К, АСФ = —0,50
ккал/кмоль-К, АС/7 = 0,83 ккал/кмоль-К
У.2.20. T{wf) =^ДЛягазаВан-дер-ВаальсаГинв = ^Г2±у 1-^J
для 02:Р128 К < Т < 330 К
У022С-С 2/?rf^4- l dC4- \-RT* f l d*BЛ- X dK'4- ^
у.^.ц-о^д ziki {ydT-r2V*dT~t" 'J \Vdf^~f'2V2dT^'")y
c.=c.„-r|P.d,fi' 'p*d'c'
р — ^ркА у dT2 T- 2 rfr2_r*
ОС С JC
У.2.23. В = 0,035— ' (м3/кмоль), В (300) = —0,283 м3/кмоль
а=81 ат-м6/кмоль2, 6=0,035 м3/кмоль
У.3.1. Измерение Vx и V2 при фазовом превращении дает два параметра,
необходимые для определения коэффициента b из трансцендентного
уравнения (3.1.12). Подставив формулу (3.1.11) в (3.1.9), получим
PsVlVl
-y1y2_6(l/1 + l/2)"
R можно определить по формуле (3.1.11).
У.3.2. АГ = 2,6 К
X (У V )
У.3.3. dT = —^—2-^——dP, отсюда dT = —9-Ю"3 К, температура плавления
равна — 0,009 °С
У.3.4. Q = 570 ккал/кг, измеренное значение 569 ккал/кг
У.3.5. Р = 0,128 ат, измеренное значение 0,126 ат
—к*).-'[(#),+(i)^-c-'(#),s-
Ответы и решения
399
Для 100QC имеем CG = —18 ккал/кмоль
изменение объема равно —5,1 м3/кмоль
у;3.8. 99,63 рС, 99,82 рС, 100,18 °С, 100,37 РС
У.3.9. л; = 6,9%
У .ЗЛО. * = з1,4%, по'табл. П. XV * = 33,8%
У.3.11. * = 28,4% (по табл. П. XV)
У.3.12. ДГ = -45,7 К, *=12,4о/0
У.4.1. 2 = 8,9-1028 с-*, £ = 6,8-109 с-1, Я = 6,7-10-8 м
У.4.2. Р < 0,12 мбар
У.4.3. йУ(10Я) = б-10 = 4,5.10-6, &y(0,U) = 0,905 ...
У.4.4. ш(0,01)==3,Ы0-17, М = 2,7-1022, искомое число частиц равно 8,4-105
У.4.5. Vz12 = 1,97-1033 с-1, Х12 = 9,6.10-6 м, Я21 = 2,2-10-2 м
У.4.6. -п = 9,4- Ю-6 Н-с/м2
У.4.7. 2г < 0,057 м
У.4.8. /\r = 2,04-1016 c-Lm-2, /ж=1,98.10-9 кг/с-м2
У.4.9. rSi + rS2 = 2J-lQ-10 м
У.4.10. Р(г, At) = PQe-cz(l+AtDc2), с = 0,115 м-*, Р (10,100) = 0,0316 (1 +
+ 9-10-б)ат
У.4.И. ]/лГ2=2,28 см
У.4.12. * = 105 с «28 ч
У.4.13. Q = lll ккал/с, соответственно / = 55,5 ккал/м2«с
У.5.1. ii=13,5 10-6 Н-с/м2
У.5.2. С = 254 К, £/пот = 5,26.10-21 Дж, 2гв = 3,33-10"10 м
У.5.3. — 50QC: 2г5=--2,82.10-10 м, + 50 РС: 2г5 = 2,70-Ю-*0 м
У.5.4. и (300 К) = 1,17 м/с, w(250 К) = 0,87 м/с
У.5.5. 300 К: и = 3,3 м/с, 400 К: и = 2,7 м/с
У.5.6. 300 К: и < 16,7 м/с, 600 К: и < 27,2 м/с
У.5.7. 0РС: J\,= l,12.10-4 м, 500 °С: Я = 3,75-10-* м
У.5.8. zn = z0—Я cos ф(1 +0,406 + 0,4062+ ...). Поэтому через плоскость z =
=z0 в среднем переносится импульс, соответствующий плоскости
z = z0-X cos Ф j 1 +-§- Го,406+у (0,4062+ ...)! l = z0- 1.255Я cos ft.
~ 1,255ХЛГ0ЛЙ
Отсюда имеем т| = ——
У.5.9. D = -L_fo/; 0°С: £> = 0,Ю6 м2/с, 500°С: D = 0,599m2/c
У.5.10. х = 0,199 ккал/м-с-К
К главе 4
У.1.1. gW = 3,3-1014
У.1.2. d(/=l,M0-4 Дж
У.1.3. а = —638
У.1.4. 8^:5,5 эВ
У.1.5. d/V = 9,6.1020, yv = 5,9-1022
У...6. «=ln ^/ =33,6
У.1.7. iV<2,7.1032 м~3
400
Ответы и решения
У.1.8. N/V<4 £(2л^Г)3 2 = 5-103° м-з
у19 ц 2jtgV? ^
*'!' |i/i3 J ехр(а + р2/2|1/гГ)± 1
о
1aV , утл v-(m+i)a
4л^/г ^Г0 (т + 1)5/2
2 (Т 1)*е-<*+1>а/(т+1)в/*
=|*ГЛ^
2 (Т l)«e-(m+1)oc/(m+l)3/2
m = 0
При достаточно высоких температурах еа ^> 1 и,поэтому [/=1,5 fc7W
У. 1.10. Согласно формуле (1.3.8), J (+ 1) = 0,338; согласно формуле (1.2.18),
/(— 1) = 1,81
У.2.1. Х-шкала: Лмакс = 8110.10-10 м, v-шкала: vMaKC = 2,10-1014 с-1
У.2.2. А,-шкала: 7430 К > Т > 3720 К, v-шкала: 13 080 К > Т > 6540 К
У.2.3. 7* =11 200 К
У.2.4. Г = 6170К
У.2.5. ^макс = 3• 10 —10 м, рентгеновское излучение
о
У.2.7. Р=~ — Г4 = 2,6.103 ат
3 с
4
90
У.2.8. 7W = y5+^4 X —jT~ cos ппх- ПРИ х=1 ИМ€ем Х^4=|
У.2.9. Q == 1790 ккал
У.2.10. J = 39 ккал/ч
У.3.1. Р0 = 2,Ы05ат
У.3.2. U — U0 = 3\ Дж, ((/ — (/0)Д/0=1,0.10-8
У.3.3. ^макс^^ЭО км/с
У;3.4. Я = 5,23.10-10 м
У.3.5. Ac„ = 3,9.10-4 ккал/кг-К, -^- = 0,1
0070
*-v
У.3.6. Гд-№; = 4,45эВ
У.3.7. №в —1^=1,9 эВ, vG = (№fl—Г,)/Л = 4,59.1014 Гц. Отсюда имеем 6 =
= 82,4, v = 2,18.10^ Гц
У.3.8. Р0 = 6,5-105 ат, г/0 = 9,6.10" Дж/м3
У.3.9. Р = 5,9-1022 ат
У.3.10. ^ = 6,4-1013 ккал/м3-К
У.3.11. v = cN/4V, v = 0,75-1048 r1^-2
У.3.12. ГБЭ=17,1 К
У.3.13. #макс = 5,88.1028
У.3.14. [/ = 80,3 Дж, Р = 546 ат, 5=11,2 Дж/К
У.3.15. В первом случае остается N > Ммакс, поэтому давление не изменится.
Во втором случае давление уменьшится на 1,2 ат
Ответы и решения
401
У .3.16. Ограничиваясь первыми двумя членами ряда (1.3.10) (случай слабого
вырождения"), получаем а = 2,73, цс= — 3,77- 10~21 Дж
У.3.17. (У = 150/? (1+3,3-Ю-2) = 298,0 (1+0,033) ккал = 308 ккал, Р=1450ат
У.4.1. С„кол = 0,05/?
У.4.2. Т^> 1,570 = 3400 К
УАЗ. Г/Г0 = 0,62, 1,08, 1,64; из фиг. 59 следует: Сг/кол = 0,8/?, 0,95/?, 1,0/?
УАА С„вр = /? (l + 10-o), СОТОЛ = 3.10-»Я
У.4.5. Здесь уже нельзя считать, что Т <^ Г0, поэтому
*с.-и«(^У1?^[-.+^(.+*-^+*-«)]_
= 0,051/?
У.4.6. Г > 7^ = 29 К
у.4.7. U = R
'i/?\3i"45 Г~^945 Г2 ■^'•'Л'
7>=15,4 К, (/ = 14,53/?
У.4.8. C„Bp = 0,8/?
УА9. CVBV = R [l+l(^)2+^(^)3], CVBV= 1,021/?
У.4.10. C„BpMaKC=l,l/? при Гмакс = 0,81 -1., НС1:Гмакс=12,5К
У.4.11. CVBp (орто-Н2) = 0,259/?, CVBp (пара-Н2) = 1,93/?
У.4Л2. 4^5Ф=3,6
/V (пара-Н2)
у.4.13. у(орто-Р,)-=17
/V(napa-D2)
УА14. Д/?=-/?Г1п(3 + 2<ГАс/*г),
У.4.15. С„ = 3,08
УА16. Г>Г^ = 7,5 К, т=12,
Г 2* Т^яеУ (2лц/гГ)з/2 /_£__ V/2 Л б"Г//2Г 1
[ 12/V Л3 ^7/J 11 1_^-r./rJ
У.4.17.
х g = \\(2ns+\)
СН4
CH3D
CH2D2
CHD3
CD4
4.3 = 12
1.3=3
12 = 2
1-3 = 3
43=12
24=16
23-3 = 24
22-32 = 36
2-33 = 54
34 = 81
У.5.1. Г = 2,91 К
У.5.2. s = 6
У .5.3. /(v)cfv = 3100
У.5.4. Вся область частот 6fv = (1022—Ю23) c~l
У,5.5. С = 0,038/?
402
Ответы и решения
У.5.6. (У0 = 354/? = 704 ккал/кмоль
У.5.7. v„ = 3,75-1012 Гц
У.5.8. С = 2,0.10-5 ккал/кмоль.К
К главе 5
У.1.1. /Ся = 2,8.10-в атм, PN = 7,510-3 атм
У. 1.2. Ограничиваясь членом —eD/kT, получаем
1п2=5^, откуда Д7 = 74 К
У.1.3. PN = 5-10-16 атм, A^N = 4109
У.1.4. (АН)Р= 118,4 ккал/моль
У. 1.5. AQ=3,7 ккал/моль
У. 1.6. CCIi = 3f07
УЛ.7. £н = — 3,63, £С1 = 1,70
У.1.8. \gKp=— 70,7
УЛ.9. Ig^i^-l^-lg^-y^- '* Pno = . = 0.0.,
Г = 2110 К
У. 1.10. В нулевом приближении \gKp = — 0,975, Рно=1,2 атм
УЛ.И. S (Н2) = 29,8 ккал/моль-К, S(02) = 49,l ккал/кмоль-К, S (Н20) =
= 44,4 ккал/кмоль-К4, 2SH +S0 —2SHO=19,9 ккал/кмоль-К
л 444.0 90.1 fi. 10-19
У.1.12. \gKp(T) = ' ^38 10-^г +lgr-2,21,r=450K:lg^ = -l,80,
cHJ = 0,20, сн =0,80, относительная концентрация паров йода
уменьшается до значения ст =8-10~4
у.1.13. ^- = ^=1,24, сн + сн=\,
С
н2
с
н
сН=0,65, сн=0,35, у = ——— = 0,48
2снг+сн
с'2
у.1.14. -JL = 0,124, сн=0,296, (/ = 0,174
сн2
У.1.15. /Код =-2,45, /н (3150) 5,81
У.1.16. eD = 5,08 эВ
У.1.17. eD = 4,49 эВ
Г|г(Ра)|г(НВг)]з/1/(РС1)/(НВг)у(НС1)у(РВг)
* Л^ ~ L^(HCl) ^(DBr)J J (НС1) У (DBr) v (DC1) v (HBr)
У.1.19. /C» = 2,8.10-* a = 8,5o/0
У.1.20. c2 = 3,6-10-7
У. 1.21. a=10~8S; т.е. наличие носителей заряда при нормальных условиях
нельзя связать с равновесной термической ионизацией
Wr Г (N*)2 5 154-109
У.1.22. AN~= f- + l/ с(Г)+^-, с(Г)=Ю^7-°>10^ IU +3 1gT,
c>W:A,- = /c1tj;c<W^-=^
Ответы и решения
403
У.1.23,
У. 1.24.
У.2.1.
У.2.2.
У.2.3.
У.2.4.
У.2.5.
У.2.6.
У.2.7.
У.2.8.
28л5£4Т3
Поскольку [i+ = ii- = 0, получаем s^-jrjur-=8>8*1017 Дж/К
107К:Д#-=ДЛ/+ = 10-4&4 м-
108К:ЛЛ/-=Д#+ = 107>9 м-з
ДГ= — 0,69 К
др = 0,010 атм
"*Ag/mc™ = 0,05
Q = 3180 ккал
\Рэ*\ _
^/+|Рэл1
9,7-10б л
Р = 0,023 атм
c = NM,KC/N0= 1,85-10-5
0,08, Р/ + |РЭЛ 1 = 2,40 атм, Р7 = 2,21 атм
У.2.9. G2 — Gx:
NLokTc0 In— , Л^о —число растворенных молекул, NL — число
У.2.10.
У.2.11.
У.2.12.
У.2.13.
У.2.14.
молекул воды, индексом нуль обозначено начальное состояние, c=N0/Nl,
c0 = N0/NL0; а2-С! = 453 Дж
2,Ы016
/г = 0,14 моль/л
рН = 8,72, v-= 1,05-Ю-4
п> 1,3-Ю-3
п
1
0,1
0,01
0,001
к
ю-5
0,0001
0,0003
0,0010
ю-6
0,0001
0,0003
0,0010
0,0032
ю-7
0,0003
0,0010.
0,0032
0,0100
ю-8
0,0010
0,0032
0,0100
0,0311
ю-9
0,0032
0,0100
0,0311
0,095
У.2.15. D=l,5-10-7 м
У.2.16. ЪЕ= —1,65 °С
У.2.17. Согласно уравнению Пуассона, имеем Дг|з— —^ ^==0, где
i
При Z1=l, Z2=l, Z3=l, Z4 = 2 имеем D = 3,3-\0'^ м
У.2.18. P = 8,l атм
У.2.19. -^<£!g^, или D>7
y.2.20.6Q = r2(^-^)v
У .3.1. &N/N = — 0,17; Д/ =
У.3.2. AN/N=— 0,036, ДМ
У.З.З. ^=2,8(22,4 л/моль-мин)
У.З.1. AN/N = — 0,17; Д/ = Э05 ч
У.3.2. AA^/iV= —0,036, Д#=—9,55-Ю16, ДС?=22,3 ккал
404
Ответы и решения
У.3.4. Д/г0 = 0,010 кмоль/м3
У.3.5. ~ = kjn/, я(0 = [л10-/-(1-Л¥]1/(1"/)
У.3.6: Знаменатель первого слагаемого в формуле (3.4.7) отрицателен.
Требуемое состояние при Данной температуре никогда не будет достигнуто
У .3.8. nHJ = c + nHJ — nHJt ~пш — пш = —у, nHi = nc =0f5y, отсюда
следует: -*L=JLp^t(c-y)*9 * = Г ^ ^
J Т(с—у)» — -J- у»
У.3.9. Для fc = const YfeTv^RT имеем £/0 = 33,4.103 ккал/кмоль
УЗЮ fe(600K) 2 5
У'ЗЛ0- Л (500 К) ''
У..3.11. д=РШ1— рю о, < 1 о, < о,66
У.3.12. х = 25, л: = 2500
У.3.13. -~L2=7,5.10-§ кмоль/м3-с
У.3.14. —Н-2=~3,8.10-4 кмоль/м3-с
at
У.3.15. * = 22,5, * = 9,0-104
ПРИЛОЖЕНИЯ
Таблица П.!
Плотность распределения \(г) — —т=ё
нормального распределения
Z
о,
1.
2,
3,
0
,3989
,2420
,0540
,0044
1
,3970
,2179
,0440
,0033
2
,3910
,19*42
,0355
,0024
3
,3814
,1714
,0283
,0017
4
,3683
,149J
,0224
,001?
5
,3521
,1295
,0175
,0009
6
,3332
,1109
,0136
,0006
7
,3123
,0940
,0104
,0004
8
,2897
,0789
,0079
,0003
9
,2661
,0656
,0060
,0002
Таблица П.11
2о
Нормальное распределение Ф(zQ) = — I е~г '2dz
% ч
0,0
од
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1Д
1,2
1,3 )
0
,5000
,5398
,5793
,6179
,6554
,6915
,7257
,7580
,7881
3159
,8413
,8643
,8849
,9032
1
,5040
,5438
,5832
,6217
,6591
,6950
,7291
,7611
,7910
,8186
,8438
,8665
,8869
,9049
2
,5080
,5478
,5871
,6255
,6628
,6985
,7324
,7642
,7939
,8212
,8461
,8686
,8888
,9066
3
,5120
,5517
,5910
,6293
,6664
,7019
,7357
,7673
,7967
,8238
,8485
,8708
,8907
,9082
4
,5160
,5557
,5948
,6331
,6700
,7054
,7389
,7703
,7995
,8264
,8508
,8729
,8925
,9099
5
,5199
,5596
,5987
,6368
,6736
,7088
,7422
,7734
,8023
,8289
,8531
,8749
,8944
,9115
6
,5239
,5636
,6026
,6406
,6772
,7123
,7454
,7764
,8051
,8315
,8554
,8770
,8962
,9131
7
,5279
,5675
,6064
,6443
,6808
,7157
,7486
,7794
,8078
,8340
,8577
,8790
,8980
,9147
8
,5319
,5714
,6103
,6480
,6844
,7190
,7517
,7823
,8106
,8365
,8599
,8810
,8997
,9162,
9
,5359
,5753
,6141
,6617
,6879
,7224
,7549
,7852
,8133
,8389
,8621
,8830
,9015
,9177
405
Таблица П. II (продолжение)
ч
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
0
,9192
,9332
,9452
,9554
,9641
,9713
,9772
,9821
,9861
,9893
,9918
,9938
,9953
,9965
,9974
,9981
1
,9207
,9345
,9463
,9564
,9649
,9719
,9778
,9826
,9864
,9896
,9920
,9940'
,9955
,9966
,9975
,9982
2
,9222
,9357
,9474
,9573
,9656
,9726
,9783
,9830
,9868
,9898
,9922
,9941
,9956
,9967
,9976
,9982
3
,9236
,9370
,9484
,9582
,9664
,9732
,9788
,9834
,9871
,9901
,9925
,9943
,9957
1 ,9968
,9977
,9983
4
,9251
,9382
,9495
,9591
,9671
,9738
,9793
,9838
,9875
1,9904
,9927
,9945
,9959
,9969
,9977
,9984
5
,9265
,9394
,9505'
,9599
,9678
,9744
,9798
,9842
,9878
,9906
,9929
,9946
,9960
,9970
,9978
,9984
6
,9279
,9406
,9515
,9608
,9686
,9750
,9803
,9846
,9881
,9909
,9931
,9948
,9961
,9971
,9979
,9985
7
,9292
,9418
,9525
,9616
,9693
,9756
,9808
,9850
,9884
,9911
,9932
,9949
,9962
,9972
,9979
,9985
8
,9306
,9429
,9535
,9625
,9699
,9761
,9812
,9854
,9887
,9913
,9934
,9951
,9963
,9973
,9980
,9986
9
,9319
,9441
,9545
,9633
,9706
,9767
,9817
,9857
,9890
,9916
,9936
,9952
,9964
,9974
,9981
,9986
*о = 3,0
ф(г0) = ,9987
3,1
,9990
3,2
,9993
3,3
,9995
3,4
,9997
3,5
,9998
3,6
,9998
3,7
,9999
3,8
,9999
3,9
1,0Q00
Асимптотическая формула для больших значений z0
Таблица П. III
^-распределение [значения ta для Р (\t\<ta)]
/
1
2
3
4
5
6
7
8
9
10
11
12
13
0,9
б,:п
2,92
2,35
2,13
2,02
1,94
1,90
1,86
1,83
1,81
1,80
1,78
1,77
0,95
12,71
4,30
3,18
2,78
2,57
2,45
2,37
2,31
2,26
2,23
2,20
2,18
2,16
Г
0,98
31,82
6,97
4,54
3,75
3,37
3,14
3,00
2,90
2,82
2,76
2,72
2,68
2,65
0,99
63,66
9,93
5,84
• 4,60
4.03
3,71
3,50
3,36
3,25
3,17
3.11
3,06
3,01
0,999
636,62
31,60
12,94
8,61
6,86
5,96
5,40
5,04
4,78
4,59
4,44
4,32
4,22
/
14
15
16
17
18
19
20
25
30
40
60
120
1 сс
0,9
1,76
1,75
1,75
1,74
1,73
1,73
1,72
1,71
1,70
1,68
1,67
1,66
1,65
0,95
2,15
2,13
2,12
2,11
2,10
2,09
.2,09
2,06
2,04
2,02
2,00
1,98
1,96
Р
0,98
2,62
2,60
2,58
2,57
2,55
2,54
2,53
2,49
2,46
2,42
2,39
2,36
2,33
0,99
2,98
2,95
2,92
2,90
2,88
2,86
2,85
2,79
2,75
2,70
2,66
2,62
| 2,58
С)
0.999
4,14
4,07
4,02
3,97
3,92
3,88
3,85
3,72
3,65
3,55
3,46
3,37
3,29
406
CQ
3 Н
S
Q
я
bJQ
*3
<L>
н
я
Он
CQ
О
3
Я
к
<и
КС
<и
с
о
Я
Я
к
н
Я
о
О
О
ад
8
О
ад
о
о
О
1 "**•
35Ш5ШЗЗШШ
о" о' о" о о4 о" о" о* о" о" о о" о о о © о"
© © о о" о о" о" о о о о о о о" о" о о
SI555S5S53355353S
о" о о" о о о о о о о" о о о* о о о" о
СЭ
Oi
°i
о
ОЪ
о^
о
о
05
о
о
ад
8®
о
■*—i
о
ад
о
о
-ч—(
о
о
*♦-.
оооосоадададсочнососооад^Ьсооосоооео
d«coood^^oV"or^N^o^^dwco«
H^^^NN^^C^^COcOWWMM^rH^'*
<N чН
CO(N«M^OOOH^Nt-(M^WCOO^(»(MO
«ч«.п«ч«ч«ч«ч«ч*ч.чп*чпп*ч«ч«ч«ч,ч«1
СО СЭ ч-нСО l0C000O^C0rt<C0l>05O<NC0^C0t-
^^HH^NNNNNNWCOCOWWWM
чН ^н ю 00 т*
г-со<М1><мсоо^1>осоадоочнсоадооо<мт*
•ЧП«.«Ч*ЧП«ЧП«ЧП(Ч№«ЧП*Ч«ЧАП«ЧП
<NTj)©r«a>O(NM^C0.h00»HWC0^et-00
^,h,h,H4-|-,h,Ht-1(N<N<NC<I<NC<|(N
ад
адсэг-соадададт*^^
-^сососососососососососососососососососо
»«ч*ч«ч«чп«ч*ч«ч«чп*>«ч^.ч«ч«ч«ч»ч«»
ч-н(мсотладсо1>ооо50^нс^сотладсо1>ооо5
чНч-Чч-Чч-ЧчНчНчНчНчНчЧ
00
ад ^н тл А
иисООиОМФМ^ООО^ОЮи
О(мадосос^оотл^нооадсоо1>адсо-гчо51>^
»ПП«Ч*.«Ч«Ч*Ч«Ч«Ч*Ч«ЧПА^*.«Ч^»«Ч
HHMNM^'THLOtOt-MJOCJOOHN
ч-Ч ч-Ч чН ч-t
Oi
СО СО <N чН
о о ад —iio^t^cocoTWi>coo5t-ocoi>05
яп^^^чп^п^ч^^л»®^»
HHN(N«WrHW5lOCOI>b000500
тН т-1
СО
ч-Ч чЧ
О О Ю h т|< N
o<N^o5ici>TtH ад С5 о ад ьиосотч-hwcoo
OOHNWoONeOiOOiOTHOWOOiiOew
п«ч«ч.ч«ч,ч<ч»»П"'ч*«"ПА"«\*'А
ч-ЧчН<МС^СОСО^т*ададсО1>1>00
НММ^ЮС01>ООС50И^СО^Ю01>«)0>0
ИИНг1Ит>1НтНг1НМ
Таблица П. V (продолжение)
/
25
30
40
50
100
0,01
11,5
15,0
22,2
29,7
70,1
0,05
14,6
18,5
26,5
34,8
77,9
0,10
16,5
20,6
29,1
37,7
82,4
0,50
24,3
29,3
39,3
49,3
99,3
0,90
34,4
40,3
51,8
63,2
118,5
0,99
44,3
50,9
63,7
76,2
135,8
0,999
52,6
59,7
73,4
86,7
149,4
Таблица П. VI
Значения Ха при проверке нормальности распределения
К
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
Р 1
1,000
0,9997
0,9972
0,9874
0,9639
0,9228
0,8643
0,7920
0,7112
0,6272
К
0,80
0,85
0,90
0,95
1,00
1,10
1,20
1,30
1,40
1,50
Р
0,5441 1
0,4653
0,3927
0,3275 !
0,2700
0,1777
0,1122
0,0681
0,0397
0,0222
К
1,60
1,70
i 1,80
1,90
2,00
2,10
2,20
2,30
2,40
1 2,50
Р
0,0120
0,0062
0,0032
0,0015
0,0007
0,0003
0,0001
0,0000
0,0000
0,0000
Таблица Я. VII
Значения Fa для а = 0,01 (верхняя строка)
и а = 0,005 (нижняя строка)
и
2
3
4
5
б
7
Степени свободы f х для большей дисперсии
2 | 3
99,0
199
30,8
49,8
18,0
26,3
13,3
18,3
10,9
14,5
9,55
124
99,2
199
29,5
47,5
16,7
24,3
12,1
16,5
9,78
12,9
8,45
10,9
4 •
99,3
199
28,7
46,2
16,0
23,2
11,4
15,6
9,15
12,0
7,85
10,1
5
99,3
199
28,2
45,4
15,5
22,5
11,0
14,9
8,75
11,5
7,46
9,52
6
99,3
199
27,9
44,8
15,2
22,0
10,7
14,5
8,47
11,1
7,19
9,16
7
99,3
199
27,7
44,4
15,0
21,6
10,5
14,2
8,26
10,8
7,00
8,89
8
99,4
199
27,5
44,1
14,8
21,4
10,3
14,0
8,10
10,6
6,84
8,68
9
99,4
199
27,3
43,9
14,7
21,1
10,2
13,8
7,98
10,4
6,71
8,51
10
99,4
199
27,2
43,7
14,5
21,0
10,1
13,6
7,87
10,3
6,62
• 8,38
| 20
99,5
199
26,7
42,8
14,0
20,2
9,55
12,9
7,39
9,59
6,15
7,75
' 30
99,5
199
26,5
' 42,5
13,8
19,9
9,38
12,7
7,23
9,36
5,98
7,53
40
99,5
199
26,4
42,3
13,7
19,8
9,29
12,5
7,14
9,24
5,90
7,42
со
99,5
200
26,1
41,8
13,5
19,3
9,02
12,1
6,88
8,88
5,65
7,08
408
»£ь
О
СО
Й X
о
СО
со
S ►*
с*
СЛ
о
*■*■
Н* О
Ь-ь
со
-
а;
ж
о 1
о
& » о •?
J=J
X
ь*
Ъ£Я
О £ 00
l>0 GO 0 н*
. р* о
и оо о
о ^ ел
»L
ы
к»•
а> ^ о
со to *
^Р> м. о
• со н*-
»-* со ^о
о ел 23
»L
.*■
со to to
со со со
to ^ 00
О) to 00
. ь* со СЛ
О н-. ь-.
1 О О
«si II
СО 1*
ю оь а>
ст> н*- ю
и* to rf^
СО Н-- to
»-*...
>-»• ►-»■ Н-ь 1
ООО
A U |<
1 оо 1
| в 1
1 ° 1
"'
Г
я 1
3
£ 1
ж 1
S
S
ш |
п
о
о
н
я
о
В
и
»
W
s S
1 §
К
К
w
К
■С
п>
о
«
(Я
К
К
и
8
Р **
СО О
о о
То <J
00 00
5е i°
*-*Л W
к> к»
со СО
со о
сл to
w to
О GO
СО о
"со о
О rf^>
*-*л "ел
to >—
J43 *°
"сл со
до to
to ь--
О 0O
О -a
"^Л о
со со
осл
-J со
"8 "8
о
р СЛ
•*Л оо
"со со
оо »—
W.0O
—1 W
W W
'со "ел
со »-■
со со
<i "to
(-. СО
w со
СЛ н-.
Н* tO
То То
СЛ со
со ьо
То оо
to оо
w to
н* оо
to о
ьо to
о со
о ->л
.ьо ьо
V То
о о
to ьо
W н*.
о н*.
То 00
W >-■
W
о
рр
со w
СЛ СО
сл #*
о о
to to
*»> .со
W о
W W
То "^
СЛ --Л
со W
"^Л W
rt* О
ОО ~Л
W W
V о
сл о
w to
wo
^ 00
1° J°
OO СИ
to СЛ
to to
o"w
w oo
"сл "to
kO CO
to to
и* О
oo >-
to
о
О СЛ
"со oo
СО СЛ
Сл *^
оо "со
to tf^
S31 3*
Si w
о о
*». со
V oo
*»> со
To ^л
о »—
#>* W
о сл
CO о
2° 5°
То V
О СЛ
w„co
00 W
сл -а
WW
*соТо'
to ^
W ьо
to <1
W ьо
о о
to со
to to
о V
со 1>»
о
J*3 «р
Ъ То
н- w
р СЛ
"w То
о со
О "-Л
То V
То То
^ о
"о о
со W
СЛ оо
to со
** со
То <i
ОО 00
То о
-J со
W W
<i То
W СЛ
Тл Т--
и^ о
W W
w to
•h- СЛ
То СЛ
to Н--
О СЛ
о "ел
00 о
о ел
о "о
о w
сл **
c;i "о
о со
СЛ rfb.
"to V
о о
р1 £*
о То
W оо
"оо Т--
О rf^
"-ЛО
to w
*" со
о То
О rt*
о Тл
о »-■
i*5 5°
Ъо W
о я^
СО W
^-л То
о о
W W
V о
rf^ о
to
$° я*
сл То
Н-. w
J^1 Я1
То То
W ы
Я» сл
ел V
to н*
о сл
о "о
-1 о
5* ^
Vl 00
о to
сл **
сл о
to сл
W сл
ел о
СЛ tf».
Tow
о о
511 *^
О W
СС о
Ъх оо
W о
W <1
со о
То "о
W h*
со со
То w
о о
о
со <i
V сл
W о
00 р
о "ел
оо ел
<i ел
"w То
#^ СС
оо о
-1 й-
Я 5я
ел со
th- СО
Я 5я
w То
о >—
н* О
to О
5" *"
То То
—1 сл
i31 ^k-
оо оо'
С( Ci
З31 $*
То V
5я Л^
о То
•<i сл
ТоТ-
—1 <i
^ w
"о о
>Ь и-
со
О 0О
к О
to
р о
<i То
to со
■Г3 <Р
То V
о to
Г1 «Р
й^ О
*J о
"►-. оо
W о
р сл
со о
со to
"о V
СС -<1
р р
СЛ W
tf». СЛ
о сл
V То
to о
сп •**•
00 00
«со о
СЛ rfb-
о о
to fc.
ел "ел
to о
с* *^
"н-. W
со »—
00
»-■ 00
о о
сл
о -л
"о Тл
о со
"оо о
$° р
со о
О W
<1 р
То w
Ci -1
<1 о
о "►-
со о
«г3 Р
Тл о
О CJ
j-Л СЛ
V То
W I—
j-Л Сх
То оо
Р i*
"о W
»— о
р >р
V То
о о
р р
"lO н--
со h*
р ^
То "оо
сл о
> 1
to
W
сл
о
-л
со
СС
о
to
о
W
о
6
8
3:
Таблица П. VIII (продолжение)
Давление
кгс/см2 = ат
атм
Н/м2
мбар
тор
кгс/см2 = ат
1
1,0332
1,01972-Ю-5
1,01972-Ю-3
1,3595-Ю-3
атм
0,96784
1
9,8692-Ю-6
9,8692-10"4
1,31579-Ю-3
Н/м2
9,8067 • 104
1,01325-10*
1
100
133,32
мбар
980,67
1013,25
0,0100
1
1,3332
тор
735,56
7.60
0,0075
0,75006
1
(1 тор= 1 мм рт. ст.)
Таблица П. IX
Удельная теплоемкость твердых тел
Химическая 1
формула
А1
Be
Pb
Са
Fe
Au
К.
Си
Со
Li
Mg
Mn
Na
Ni
Pt
Ag
U
W
Zn
Sn
NaCI
KCl
Eis
NaN03
KN03
Ka2C03
CaO
Cu,0
Cub
aia
Относительная
атомная или молекулярная
масса |
26,98
9,01
207,2
40,08
55,85
196,97
39,102
63,546
58,93
6,94
24,30
54,938
22,99
58,71
195,09
107,87
238,03
183,85
65,37
118,69
58,45
74,56
18,015
85,00
101,11
106,00
56,08
143,09
79,54
| 101,96
Удельная теплоемкость (ккал/кг-К)
Эксперименталь- 1 Значение по. Дюлонг
ное значение(20сС) и Пти
0,214
0,418
0,031
0,155
0,108
0,031
0,177
0,092
0,105
0,818
0,243
ОД 16
0,288
0,106
0,032
0,056
0,028
0,032
0,092
0,054
0,207
0,163
0,505
0,259
0,225
0,249
0,184
0,105
0,129
0,189
0,221
0,661
0,029
0,149
0,107.
0,030
0,152
0,094
0,101
0,859
0,245
0,109
0,259
0,102
0,031
0,055
0,025
0,032
0,091
0,050
0,204
0,160
0,9926
0,351
0,295
0,334
0,213
0,125
0,150
.0,292
(Eis — лед.)
410
Таблица /7. X
Молярная теплоемкость одно- и многоатомных газов при
различных температурах, отнесенная к газовой постоянной
R = 1,986 ккал/(кмоль • К)
т, к
40
100
150
200
250
300
350
400
500
(ЮО
800
1000
1500
2000
2500
Аргон
Ъ
1,503
1,501
1,500
1.500
1,500
1,500
1,500
1,500
1.500
1,500
1,500
СР
2,515
2,508
2,504
2,503
2,502
2,501
2,501
2,501
2,501
2,501
2,501
X
1,074
1,071
1,670
1,609
1,668
1,668
1,667
1,667
1,667
1,667
1,667
Водород
Су
1,508
1,714
2,050
2,280
2,406
2,469
2,510
2,518
2,53
2,56
2,63
2,89
3,12
.3,44
Ср
2,568
2,721
3,053
3,281
3,407
3,469
3,509
3,518
3,53
3,56
3,63
3,89
4,12
4,44
X
1,700
1,587
1,489
1,439
1,416
1,405
1,398
1,397
1,39
1,39
1,38
1,35
1,32
1,29
Кислород
Су
2,506
2,506
2,506
2,512
2,641
2,572
2,622
2,738
2/859
3,057
3,194
3,397
3,543
СР
3,511
3,511
3,511
3,519
3,545
3,573
3,624
3,740
3,860
4,057
4,194
4,397
4,543
У.
1,401
1,401
1,401
1.401
1,395
1,390
1,382
1,366
1,350
1,327
1,323
1,294
1,282
Углекислый газ
с.
3,219
3,490
3,742
3,973
4,368
4,690
5,186
5,530
6,020
сР 1 __*_
4,262
4,512
4,756
4,983
5,372
5,694
6,186
6,531
7,019
1,324
1,293
1,271
1,254
1,230
1,214
1,193
1,181
1,166
Таблица Я. XI
Молярная теплоемкость газов (в ккал/кмоль-К) при комнатной
температуре
Газ
Не
Лг
н2
02
N2
НС1
CO.,
ко
*ш3
С2И2
сн4
с2нв
с»
3,01
.3,03
4,87
4,99
4,96
4,96
6,62
7,37
6,38
8,04
| 0,27
10,34
ср
5,00
Г),00
6,86
6,99
6,96
6,96
8,61
9,36
8,36
10,13
8,28
12,41
х - <у С,
1,66
1,65
1,41
.1,40
1,40
1,40
1,30
1,27
1,31
1,26
1,32
| 1,20
41!
Таблица /7. XII
Критические данные и константы Ван-дер-Ваальса
Константы а и Ь выбраны таким образом, чтобы получить оптимальное согласование
уравнения Ван-дер-Ваальса с измеренными изотермами для комнатной температуры;
R = Nл /г = 8,ЗН-103 Дж/кмоль-К
НС1
н?1
Не
н?р
о,
N*
СО,
Pk>
ат
86
13,2
2,34
225
51,4
34,8
75
Vk>
мЗ/км^оль
0,060
0,065
0,058
0,055
0,075
0,090
0,096
7V.
К
324,6
33,2
5,2
647,3
154,3
126,0
1 304,1
а
ат-м€/кмоль.2
0,922
0,194
0,035
5,65
1,40
1,39
1 3,72 s
Ь
м3/кмоль
0,020
0,022
0,024
0,031
0,032
0,039
0,043
R/NA.b
0,469
0,813
0,821
0,602
0,768
0,782
| 0,745
Таблица /7. XIII
Значения температуры Бойля ТВ(К)
Не
19
Кг
106
Ne
134
Аг
410
яг2
323
о2
423
Воздух
357
Тъ
Таблица П. XIV
Точка кипения и теплота испарения некоторых веществ при
нормальном давлении
Газ
Н2
Не
н2о
02
НС1
N2
С12
соа
Воздух
Точка
кипения, к
20,4
4,3
373,2
90,2
188,2
77,4
238,2
194,7
79,2
Теплота испарения,
ккал/кг
111
6
539
51
106
47,6
62
137
47
412
Таблица П. XV
Термодинамические величины для воды и насыщенного пара
пература,
°с 1
0
10
20
30
40
50
GO
80
100
150
200
250
300
350
374,2
Давление,
ат
0,006
0,012
0,024
0,043
0,075
0,120
0,203
0,483
1,033
4,854
15,86
40,56
87,61
168,63
225,5
Удельный
объём |
Вода
дмЗ/кг |
1,0002
1,0004
1 1,0018
1,004
1,00S
1,012
1,017
1,029
1,04
1,09
Мб
1,25
1,40
1,75
1 3,14
Пар,
м3/кг |
'206
106
57,8
32,9
19,6
12,0
7,68
I 3,41
1,67
0,39
0,127
0,050
0,022
8,8.10-3
3,14; Ю-3
Энтальпия
Вода, 1
ккал / кг 1
0
10
1 20
30
40
50
60
80
100
151
204
259
321
399
| 502
Пар,
ккал/кг 1
597
602.
606
I 010
615
619
623
631
639
655
667
669
656
612
502
Энтропия |
Вода 1
ккал /кг- К J
0
0,036
1 0,071
0,104
0,137
0,168
0,198
0,257
0.312
0,439
0,556
0,667
0,777
0.902
1,06
Пар
ккал/кг-К |
2,19
2,13
2,07
2,02
1,97
1,93
1,89
1,82
1,76
1,63
1,54
1,45
1,36
1,24
1,06
Теплота
испарения,
ккал / кг
597
592
1 586
580
575
569
1 563
551
539
504
463
410
335
213
0
Таблица Я. XVI
Диаметр газокинетического эффективного сечения 2rs
при 0°С и константа Сазерленда С для различных газов
Газ
н2
Воздух
СО*
Не
Аг
Кг
Хе
No
о2
N2 J
2rs, Ю-*'0 м
2,75
3,75
\ 4,65
2,18
3,40
4,30
4,91
2,60
3,62 1
3,78 J
С, к
84
112
254
80
169
142
252
56
125
105
413
Таблица П. XVII
Значения коэффициента диффузии для некоторых веществ
Вещество
Н2 в Н2
Н в Н2
Не в Не
Н2 в воздухе.
D2 в воздухе
Но в воздухе
Jig в воздухе
02 в воздухе
ЗЯаС1 в воде
Сахар в воде.
Золото в свинце
К в кристалле KB
Г, К
65 Л
2%
349
cm
27G
346
300
300
276
413
273
283
291
440
г 920
D, м
1,006
.1 ,647
2,26
5,42
6,24
9,02
7.0
5,05
6,24
1,8
1,8
9,3 •
3,7-
4,6-
5,2-
2/с
. Ю-*
ю-4
10-«
Ю-*
И)"5
ю-5
io-,J
10"5
ю-5
ю-5
ю-5
Ю-ю
10-ю
ю-13
ю-*
Таблица П. XVIII
Теплопроводность х, динамическая вязкость г) и удельная
теплоемкость cv некоторых газов при 20 °С
Газ
Н2
No
02
со2
СН4
и ,
ккал/(м-ч-К)
0,160
0,022
0,022
0,014
0,028
Л,
10-5 н-с/м2
0,88
1,75
2,02
1,47
1,08
**.
ккал/кг-К
2,415
0,177
0,157
0,150
0,391
k/k\cv
2,09
1,97
1,93
1,77
1,84
Таблица /7. XIX
Эффективная работа выхода (эВ)
Элемент
Ag
Al
Bi
Cd
Co
Cs
wa - wt
4,5
3,74
4,28
3,92 j
4,37 |
1,87
Элемент
Ge
Rb
Те
Ti
Th
U
w
wa - wt
4,56
2,13
4,73
4,16
3,35
3,72
4,50
414
Таблица П. XX
Значения спина некоторых ядер
При четном заряде ядра Z и четном числе нейтронов N спин ядра п равен нулю.
Ядро
Н
D
Li
N
Г
Na
А1
Р
Ci
к
Z
1
1 1
3
3
7
7
9
11
13
15
17
17
19
19
1 Ы
0
1
3
4
7
8
10
12
14
16
18
20
20
22
"s
1/2
1
1
3/2
1
1/2
1/2
3/2
5/2
1/2
5/2
5/2
3/2
3/2
Ядра
Мп
Со
Си
Zn
Br
Кг
Ag
J
Cs
Pt
Au
Z.
25
27
29
29
30
35
35
36
47
47
53
55
78
79
N
30
32
34
36
37
44
46
47
60
62
74
78
117
118
ns
5/2
7/2
3/2
3/2
5/2
3/2
3/2
9/2
1/2
1/2
5/2
7/2
1/2
3/2
Таблица Я. XXI
Момент инерции /, частота со0 основных колебаний и энергия
диссоциации eD некоторых двухатомных молекул
Молекула
Но
О.
No
С12
Br,
Jo
СО
NO
НС1
HF
J,
10"47 кг- м2
0,47
19,1
13,8
113
342
741
15,0
16,3
2,60
1 4,3
,>'
1014 с"1
8,28
2,98
4,45
1,06
0,61
0,40
4,09
2,86
5,63
7,80
*D>
эВ
4,478
5,11
7,3
2,47
2,0
1,54
8,4
6,5
4,43
6,1
Таблица Я. XXII
Значения энергии связи В
Молекула
HD
D2
СП
DBr
ZnD
Н2
НВг
НС1
В, эВ
4,513
4,556
3,52 1
3,65
0.87
4,478
3,78
4,431
Молекула
| HF
1 J2
NO
Na
02
Clo
ОН
1 tff
В, эВ
6,1
1.542
6,49
7,3
5,11
2,47
4,40
| 2,2
Молекула
1 Вг*
HJ
AgCl
AgJ
AgH
AgO
CuO
И GeS
В, эВ
2,0
3,11
3,1
2,2
2,3
1Д
4,5
5,0
Таблица П. XXIII
Значения химической постоянной при комнатной температуре
Молекула
Ne
Аг
К
Na
Н2
N2
Оо
С1,
Вг2
J
+0,40
+ 0Л9
+ 1,11
+ 1.85
-3,69
-0,15
+0,55
4-1,65
+2,57
Молекула
J2
НС1
Ш
NO
со
С02
1 н2о
*Ш3
сн4 j
+3,08
-0,40
+ 0,65
+0,52
-0,075
+0,90
-1,94
-1,46
-1,96
Таблица П. XXIV
Значения энтальпии образования и энтропии при Т = 25°С
и Р=1 атм, отсчитываемые от их значения для ионов водорода
Вещество,
Н+(раств.)
Н(газ.)
Н2
0.2
ОШраств.)
Н20 (газ.)
N2
N(ra3.)
NH3
NO
CI (газ.)
Cl2
HC1
CO
C02
я»
103 ккал/кмоль
0
51,7
0
0
—55,0
-57,8
0
112,5
-11,0
21,6
28,9
0
-21,9
—26,4
-94,0
S, 1
ккал/кмоль-К |
0
27,4
31,2
49,0
-2,5
45,1
45,8
36,6
46,0
50,3
39,5
53,3
44,7
47,3
51,1
Вещество
С (графит)
Li
F*
HF
К
N
KJ
Вг2(газ.)
Br (газ.)
HBr
J (газ.)
^г(газ.)
HJ(ra3.)
J-(pacT.B.)
Я,
103 ккал/кмоль
0 i
0
0
-64,2
0
0
-79
7,65
26,9
-7,8
25,6
14,5
6'1
-13,2
s,
ккал/кмоль -К
1,36
6,70
48,6
41,5
15,2
12,2
24,1
1 58,6
41,8
47,5
43,2
62,3
49,4
| 25,3
4\6
Таблица Я. XXV
Потенциалы ионизации атомов (в вольтах)
Атом
Н
Но
Li
Be
В
С
N
О
F
Ne>
На,
Аг
А1
Р
S
С1
К
А-+А"
13,54
24,48
6,37
9,30
8,28
11,24
14,51
13,57
17,46
21,47
5,07
16,68
5,94
10,43
10,42
13,01
4,32
А1+^Аг+
54,16
75,3
18,12
24,99
24,28
29,41
34,75
34,71
40,67
46,65
27,64
18,85
19,75
23,25
23,85
31,45
А*±-*А*+
121,9
153,1
37,70
47,55
47,36
54,8
63,3
63,2
71,3
40,94
28,35
30,08
34,89
39,67
46,00
дз+ _>. Д4+ '
216,6
258,0
04,1
77,0
77,5
87,3
97,1
99,0
59,7
! 119,0
1 51,1
1 47,32
53,5
.61,7
АЧ-+А*+
338,5
390,1
93,3
113,3
1 114,8
127,0
139,1
75,7
154,9
64,6
72,2
68,0
| 83,3
45+-*Л6+
487,4
549
137,3
156,5
159,1
173,9
92,1
192,7
222,8
87,5
96,5
101,4
А?+^ А^
Ш
735
184,2
206,6
210,5
124,1
245,1
268,3
285,7
113,8
Н9,7
Таблица П. XXVI
Значения энергии активации для некоторых реакций
Реакция
Н + Н2 -* Н2 + Н
CI + Н2 -> НС1 + Н
ВН-Н2-*НВг-ЬН
J 4- Н2 -> Н J + Н
Температура,
К
328
973
285
649
550
1035
672
Энергия активации,103 ккал/кмо/
измеренная Приведенная к Г— 0. К
6,7 ± 0,3
5,5 ± 0,8
6,1 ± 1,0
5,5
18,8
17,3
33,4 ± 0,4
7,4
7,4
6,7
6,8
20,4
20,4
34,7
14 Кя 3270 417
Таблица /7. XXVIJ
Основные физические постоянные
8,8542- 10-12А. с/В- м
1,257-10-в В-с/А-м
1,3807. Ю-23 Дж/К
9,80665 м/с2
«о
к
Электрическая постоянная
Магнитная постоянная
Постоянная Больцмана
Ускорение свободного падения (при g
ф=45° на уровне моря)
Универсальная газовая постоянная R
Скорость света с
Число Авогадро N д
Квант действия Планка h
П =
Масса покоя электрона \ле
Масса покоя нейтрона \лп
Масса покоя протона \ьр
Заряд электрона е
8,3144-103 Дж/кмоль-К
2,99792.10s м/с
6,0220-1026 кмоль-1
6,6262-Ю-34 Дж-с
hftn 1,054-Ю-34 Дж-с
т0 9,109-Ю-31 кг
1,6749-Ю-27 кг
1,6726- Ю-27 кг
1,602-Ю-19 А-с
Основные обозначения
Таблица Я. XXVIII
с, b
а, 0
а
А
i
с
С
С, С,
X2
D
Е
8
?
F
%
6
— поправочные члены в уравнении Ван-дер-Ваальса
— коэффициенты в потенциале Леннард-Джонса
—ошибка первого рода; уровень значимости; множитель Лагранжа
— произведенная работа; площадь
—относительная атомная масса атома
—ошибка второго рода; множитель Лагранжа
— второй вириальный коэффициент
— магнитная индукция или плотность магнитного потока
—скорость света; скорость звука; удельная теплоемкость
—относительная концентрация
— постоянная Сазерленда
Ср—молярная теплоемкость, при постоянном объеме, при постоянном
давлении
—случайная величина в ^-распределении
— коэффициент диффузии; коэффициент жесткости
— полная энергия; энергия реакции; модуль упругости
— энергия микрочастицы
— вязкость (динамическая)
— число степеней свободы материальной частицы; функция
распределения; плотность распределения
—свободная энергия
—сила
—кратность вырождения
—энергия Гиббса; генеральная совокупность
■^-фазовый объем; переносимая величина
418
§, Н —напряженность магнитного поля
Н —энтальпия
/, / —сила тока
/ —магнитный момент (магнитная поляризация)
J —момент инерции
/ —плотность тока; химическая постоянная
k —число компонентов раствора
kij> kn —частоты событий
/г, k —коэффициенты скоростей химических реакций
% —теплопроводность; показатель адиабаты; сжимаемость;
восприимчивость
% —длина волны; средняя длина свободного пробега
/ —длина пути; вращательное квантовое число
(Л —среднее значение по генеральной совокупности; масса микрочастицы
\х,с —химический потенциал
т —масса некоторого количества вещества
Мг —относительная молекулярная масса
*Ш —намагниченность
п —главное квантовое число; число киломолей; полное число
испытаний
N —число частиц; концентрация
v —частота; частота столкновений
Y, о|з —волновая функция
р —прицельный параметр (параметр соударения); вероятность
определенного события Л у импульс материальной частицы
Р —давление; вероятность
q —координата микрочастицы; вероятность определенного события В
Q —количество тепла
г —число фаз раствора; коэффициент корреляции
2rs —кинетический эффективный диаметр сечения столкновения
р —плотность; плотность распределения
s —спин; число степеней свободы системы; эмпирический стандарт,
выборочное среднеквадратичное отклонение
sxy —коэффициент ковариации распределения двух случайных
переменных
S —энтропия
а —эффективное сечение; площадь; среднеквадратичное отклонение
генеральной совокупности
/ —время; случайная величина в /-распределении Стьюдента
Т — температура
т —коэффициент симметрии
U —внутренняя энергия
и —скорость движущегося тела или вещества
V — объем
v —скорость материальной частицы
w —вероятность в физических процессах
W —статистический вес; энергия
со —угловая скорость; частота
х, у, 2 —переменные или неизвестные в декартовой системе координат
X, Y —случайные величины
ху у —выборочное среднее значение
% —число соударений одной материальной частицы; химическая
постоянная (нат. осн.)
г —полное число столкновений
Z —статистическая сумма; зарядовое число ядра; числе ячеек
Z —статистическая сумма большого канонического распределения
14*
419
ЛИТЕРАТУРА
1. d*Ans J .у Lax £., Taschenbuch fur Chemiker und Physiker,
Springer-Verlag, Berlin, Gottingen, Heidelberg, 1966.
2. von Ardenne M.f Tabellen zur angewandten Physik, Bd. 1. Elektronenphy-
sik — Ubermikroskopie — Ionenphysik; Bd. 2. Physik und Technik des
Vakuums. Plasmaphysik, VEB Deutscher Verlag der Wissenschaften, Berlin,
1962, 1964.
3. Bauer Я. A., Grundlagen der Atomphysik, Springer-Verlag, Wien, 1951.
4. Блохинцев Д. Я., Основы квантовой механики, 4-е изд., «Высшая школа»,
М., 1963.
5. Хинчин А. Я., Математические основания статистической механики, Гос-
техиздат, М., 1943.
6. Стешет £., Pahl M.t Kinetik der Gasreaktion, Walter de Gruyter & Co.,
Berlin, 1961.
7. Eucken A.t Lehrbuch der Chemischen Physik, Akademische Verlaggesell-
schaft Geest & Portig, Leipzig, 1949.
8. Fisz M.t Wahrscheinlichkeitsrechnung und Mathematische Statistik, VEB
Deutscher Verlag der Wissenschaften, Berlin, 1966.
9. Fliigge S. (Hrsg.), Handbuch der Physik, Bd. 1—54, Springer-Verlag, Berlin,
Gottingen, Heidelberg, 1955—1975.
10. Френкель Я- И-, Статистическая физика, изд-во АН СССР, М., 1948.
11. Grimsehl £., Lehrbuch der Physik, Bd. 1—4, BSB В. G. Teubner
Verlagsgesellschaft, Leipzig, 1967—1969.
12. Hajko V., Physik in Beispielen, VEB Fachbuchverlag, Leipzig, 1971.
13. Hertz G., Rompe R. (Hrsg.), Einfuhrung in die Plasmaphysik und ihre
technische Anwendung, Akademie-Verlag, Berlin, 1968.
14. Joos G., Lehrbuch der Theoretischen Physik, Akademische
Verlagsgesellschaft Geest & Portig, Leipzig, 1964. (Имеется перевод* Г. Иос, Курс
теоретической физики, Учпедгиз, М., 1963—1964.)
15. Kubo R.t Statistical Mechanics, North-Holland Publishing Co., Amsterdam,
1965. (Имеется перевод: P. Кубо, Статистическая механика, «Мир», М., 1967.)
16. Ландау Л. Д., Лифшиц Е. М., Курс теоретической физики, т. III.
Квантовая механика, Физматгиз, М., 1963, т. V. Статистическая физика, «Наука»,
М., 1964.
17. Landolt-B6rnsteint Zahlenwerte und Funktionen, Bd. 1—4, Springer-Verlag,
Berlin, Gottingen, Heidelberg.
18. Macke W.t Thermodynamik und Statistik, Akademische Verlagsgesellschaft
Geest & Portig, Leipzig, 1967.
19. Munster A.f Chemische Thermodynamik, Akademie-Verlag, Berlin, 1969.
20. Munster A.t Statistische Thermodynamik, Springer-Verlag, Berlin, Gottingen,
Heidelberg, 1956.
21. Pohl R. W., Einfuhrung in die Physik, Bd. 1. Mechanik, Akustik, Warme-
lehre, Springer-Verlag, Berlin, Gottingen Heidelberg, 1962. (Имеется
перевод: P. В. Поль, Механика, акустика и учение о теплоте, «Наука», М., 1971.)
22. Смирнов Я. В.у Дунин-Барковский Я. В., Курс теории вероятностей
и математической статистики для технических приложений, «Наука», М., 1969.
23. Sommerfeld Л., Vorlesungen iiber Theoretische Physik, Bd. V.
Thermodynamik und Statistik, Akademische Verlagsgesellschaft Geest & Portig,
Leipzig, 1965. (Имеется перевод 1-го изд.: Л. Зоммерфельд, Лекции по
теоретической физике, Термодинамика и статистическая физика, ИЛ, М., 1955.)
24. Storm R.y Wahrscheinlichkeitsrechnung, Mathematische Statistik und
Statistische Qualitatskontrolle, VEB Fachbuchverlag, Leipzig, 1972. (Имеется
перевод: P. Шторм, Теория вероятности, математическая статистика и
статистический контроль качества, «Мир», М., 1970.)
25. Weber £., Grundrifi der biologischen Statistik, VEB Gustav Fischer Verlag,
Jens, 1967.
420
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютный нуль, недостижимость
303
Авогадро число 77
измерение 89
Ангармонизм колебаний 281, 287
Аррениуса закон 369
Асимметрия распределения 95
Барометрическая формула 87
Бозе-частицы 231
Бозе — Эйнштейна газ 272, 275
конденсация 272, 274
распределение 235, 238
статистика 231, 234
температура 273, 275
Бозоны 231
Бойля температура 173, 413
Больцмана постоянная 77, 114, 152
измерение 254
— распределение 77, 79, 153
— статистика 229, 234
— уравнение 222
— формула 114
Де Бройля волна 235, 264
— уравнение 264
Броуновское движение молекул 215
Букингема потенциал 172
Ван-дер-Ваальса газ 156, 174
— постоянные 160, 413
— уравнение 157, 173, 193
Вант-Гоффа закон 352
— уравнение 323, 324
Величина переносимая 204
— экстенсивная 114
Величины термодинамические в
Квантовой статистике 258
вклад колебаний 286, 287
для воды и насыщенного пара
414
двухатомного газа 286
излучения 254
квантовой жидкости 311
Величины термодинамические для
многоатомных молекул 298
смеси идеальных газов 319
при абсолютном нуле 302
Вероятность ошибки 52
— события 7
— условная 9
Вес статистический 72, 233
Вещество парамагнитное 303
Взаимодействие электростатическое
347
Вина закон излучения 248
смещения 248, 254
Водород 291, 295, 331
— орто-, пара- 291, 381
Волновая функция 229
Восприимчивость магнитная 304
Вращение молекул 125, 127, 282
Второй закон термодинамики 118
Выборка 22
Вырождение 264, 270
— интеграл 241, 244
Выход химической реакции 331
Вязкость 210, 221, 222
Газ квантовый 306
— электронный 261, 270
Гальванометр, чувствительность 148
Гамма-функция 84
Гаусса нормальное распределение 21
Гейзенберга соотношение
неопределенностей 113, 120, 231
Гелий 272, 311
— орто-, пара- 273
Генеральная совокупность 22
Генри закон 352
Гиббса правило фаз 342
— распределение 77, 99
— энергия 117, 125
для излучения 254
связь с химическим
потенциалом 190
Гидролиз 355
— степень 356
422
Предметный указатель
Давление внутреннее (когезионное) 156
— идеального газа 150, 161
— излучения 254
— насыщенного пара 194, 350
— нерелятивистское 260, 262
— осмотическое 93, 351, 362
— равновесное 193
— раствора 359
— реального газа 156, 157
— релятивистское 260
— электронного газа 261
Дебая радиус 356
— температура 309, 310
— теория теплоемкости 309, 312
Дейтерий 291, 331
— орто-, пара- 291
Джоуля — Томсона эффект 179
Диаметр эффективного сечения 202,
210, 222, 414
Дисперсия 50
— скорости 84
Диссоциация 344
— водорода 321
Длина свободного пробега 203, 206
— реакционной цепи 385, 386
Добротность 15
Дюлонга и Пти закон 102, 310
Жидкость квантовая 311
Закон биномиальный 12, 14
обобщенный 13
— действующих масс 316
— площадей 224
— равнораспределения 96, 99
— умножения вероятностей 9
Законы излучения 247, 248, 251, 253
Изотерма критическая 159
Интеграл вырождения 241, 244
— стандартный нормальный 27
— статистический 121, 168
Интервал доверительный 25, 30, 407
Ионизация газов 336
Испытание 7
Карно цикл 133
Катализ 334
Клаузиуса — Клапейрона уравнение
195, 196
Колебания атомов 104
— внутримолекулярные 130
— нормальные, число 307
Конденсация 159, 197
Константа скорости реакции 365, 375,
376
— химического равновесия 321, 327,
329
Концентрация относительная 316
Координаты сферические 80
Корреляция 54, 56
— флуктуации 145
Коэффициент давления 163
— диффузии 212, 225, 415
— корреляции 51
— полезного действия (к. п. д.) 135,
136
— расширения 163
— реакции кинетический 365
— симметрии 299
— стерический 393
Коэффициенты вириальные 167, 187
для смеси газов 187
Критерий согласия %2 37, 407
Крутизна распределения 95
Кундта трубка 110, 112
Кюри — Ланжевена закон 303
Лагранжа множители 75, 152, 259
Леннард-Джонса модель 172, 183
— потенциал 171
Линде метод сжижения газов 199
Лиувилля теорема 72
Лошмидта число — см. Авогадро
число
^-критерий Колмогорова 38, 41, 43,
408
А,-точка 272
Максвелла—Больцмана распределение
67, 82
Макросостояние 72, 231
Масса приведенная 126
— эффективная 90
Метод наименьших квадратов 49, 50
Методы измерения, статистическое
сравнение точности 47
Микросостояние 72, 231
Микроячейка 71
Модель идеального газа 153
— жестких упругих сфер 171, 181
Модуль упругости 111
Молекула линейная 296
— многоатомная 285, 298
Момент корреляционный 50
— магнитный 304
Мощность статистического критерия —
см. Добротность
Мулхолланда формула 282
Предметный указатель
423
Надежность 31, 32
Намагниченность 303, 304
Намагничивание изотермическое 303
Насос тепловой 136
Нернста — Планка теорема 300
Нернста цепь — см. Цепь реакционная
Область двухфазная 159, 193
Объем молекул собственный 156
— столкновения 157
Оси симметрии 129
Оствальда закон 353
Осциллятор 113, 171
— гармонический 100
Оценки статистические,
экстраполяция 33
Ошибки (первого и второго рода) 10,
11, 14, 15, 56
Параметр прицельный 225
Параметры критические 161, 413
— состояния 166, 178, 186
Пара электрон — позитрон,
образование 338
Пароаккумулятор 198
Паули принцип 234
Первый закон термодинамики 96, 97
Период (время) полураспада 373, 378
Персистенция скоростей 220, 225
Планка закон 338
излучения 247
— квант действия 113
измерение 254
Плотность вероятности 20, 68
— потока 205
энергии спектральная 249
— тока 265
— числа частиц 204
Позитрон 339
Показатель адиабаты 106, 108, ПО, 177
— политропы 113
Поле излучения 254
Поправки квантовые 119
Постоянная газовая индивидуальная
160
универсальная 160
Постоянные физические 419
— химические 316, 325, 417
Потенциал химический 189,260,320,351
Потенциалы ионизации 418
— термодинамические — см. Функции
состояния
Поток 205
— тепла 217
Проверка гипотез статистическая 37
Проверка нормальности
распределения 41
— равномерности распределения 37
— средних значений 38
Произведение событий 9
Пролет без соударений 207
Пространство фазовое 67, 113, 231
объем ячейки 68, 113
Процесс адиабатический 109, 134
— необратимый 119, 132
— обратимый 97, 118, 139
Процессы квантовые 119
Прямая регрессии 51, 57, 59
Пуассона уравнение 357
Работа выхода внешняя 266
внутренняя 266
измерение 268
эффективная 266, 415
— механическая 97
Равновесие адсорбционное 334
— диссоциационное 353
— фазовое 189, 193, 348
— химическое 300, 314, 321, 336
Радиоактивность 365, 373
Разделение эмульсий 90
Размагничивание адиабатическое 303
Распределение нормальное 21, 27, 140,
142
параметры 28
стандартное 43
— энергии спектральное 249, 250
Распределения максимум плотности
83
Раствор 93, 344, 346
— буферный 355
— кислый 347
— насыщенный 351
— щелочной 347
Растворимость 351
Расширение адиабатическое 109, 197
— изотермическое 109, 134
— реального газа 163
Рауля законы 348
Реакция гибели (обрыва цепи) 384,
386, 388
— необратимая 367
— обмена 331
— образования и распада молекул
374, 379
— обратимая 367
— химическая 314, 379
— цепная 387
— экзотермическая 324
— эндотермическая 324
Римана ^-функция 245
424
Предметный указатель
Ричардсона эффект — см. Эмиссия
термоэлектронная
Рэлея — Джинса закон излучения 248
Сазерленда поправка 220, 225, 414
— постоянная 220
Саха уравнение 336
Сверхтекучесть 272
Свободная энергия 107, 120, 125
кулоновская часть 359
реального газа 174
смеси 319
Свойства симметрии 116
Сечение столкновения 162, 212
Сжижение газа 199
Сжимаемость 163
Сила трения 211
Силы отталкивания 156
— притяжения 156
Система двухфазная 191
— изобаро-изотермическая 138
— трехфазная 192
Скорость относительная 202
— реакции 365, 379
— фазовая 308
Сложение вероятностей 8
Событие 7
— дополнительное 8
Совокупность генеральная 22
Состояние агрегатное 96, 192, 342
— мета стабильное 192
— равновесное 74, 191, 235, 380
Состояния электронов возбужденные
281, 293
— вращательные 284
Спин 230
— возможные проекции 236, 239
— ядра 125, 281, 317
Среднее значение 19, 20—22, 50
выборочное 22, 44
скорости 84
случайной величины 19
Среднеквадратичное отклонение 19
выборочное 22
— по времени 69
— статистическое 69
Статистика квантовая 229, 231
Степени свободы 23, 38, 67, 96, 104
вращательные 104
замораживание 103, 301
колебательные 104, 287
поступательные 104
Стефана — Больцмана закон
излучения 249, 251, 253
Стирлинга формула 74
Стокса формула 211
Столкновения 202, 207, 375
— число 202, 206, 209
Стьюдента /-распределение 24, 38
Сумма статистическая 115, 281, 321
Температура инверсии 188
— удвоения 220
— характеристическая — см. Дебая
температура
Теплоемкость металлов атомная 102
— молярная 98, 176, 412
газа Лен нард-Джонса 184
— удельная 98, 176, 261, 411
водорода 295
газа Ван-дер-Ваальса 176
вращательная часть 105, 289
идеального газа 103
колебательная часть 105, 286
при постоянном давлении 106,
176
объеме 103, 176
твердых тел 102, 309, 411
электронного газа 261
Теплопроводность 217
Теплота испарения 195, 413
— перехода 192, 349
— растворения 353
— реакции 325
Тождественность частиц 230
Точка кипения 413
— критическая 159
— тройная 192
— четверная 343
Точки эмпирические 57
Точность измерений 47
Траектория фазовая 67
Трение внутреннее 211
Умножение вероятностей 9
Уравнение непрерывности 215
— переноса 205
— состояния идеального газа 79
реального газа приведенное 165
вириальная форма 167,
173
Уровень значимости 25, 33, 407
Уровни основные 280
Условие нормировки 21
Фаза 190, 342
Фактор вырождения 282
Ферми — Дирака распределение 235,
239, 240
статистика 231, 234
Предметный указатель
425
Фермионы 231
Фика законы 212, 214
Фишера ^-критерий 39, 409
Флуктуации вращающегося зеркала 147
— в системе, находящейся в равновесии
138
— давления 140
— числа частиц 144
Фононы 312
Формула барометрическая 87
Фотоны 231, 235, 256
— подсчет числа 256
Фотоэмиссия 266, 268
Функции антисимметричные 230
— симметричные 230
— состояния 189
вычисление с помощью
статистической суммы 113
изменение в цикле Карно 133
квантовых систем 260
одноатомных газов 120
поведение при абсолютном нуле
300
— термодинамические — см. Функции
состояния
Химический потенциал 189, 260, 320,
351
Центрифуга 90
Цепь реакционная 384
длина 385, 386
Эйлера — Маклорена разложение 282
Эйнштейна уравнение эквивалентности
338
Электролиты сильные 346
— слабые 346
Эмиссия автоэлектронная 266
— термоэлектронная 264, 266
Эмульсии 90
Энергия активации 369, 372, 384, 419
— взаимодействия 167
— внутренняя 96, 189
газа Бозе — Эйнштейна 275
Ван-дер-Ваал ьса 175, 178
излучения 254
твердого тела 99—102
электронного газа 261
— вращения 125, 281
— диссоциации 288, 321, 345, 416
— излучения 254
— колебаний 130, 280, 332
— основного состояния 99, 263, 280,
300, 322
— связи 417
— средняя 84
Энтальпия 99, 117, 123, 200
— ионизации 347
— как мера тепловой энергии 123
— образования 327, 418
Энтропия, значения для некоторых
веществ 418
— изменение в необратимых процессах
132
— при абсолютном нуле 300
— смесей 300
— статистическое определение 115
— термодинамическое определение 98
— флуктуации 140
Частота предельная 309
— события 7, 26, 49
Шредингера уравнение 229
Явления переноса 202
Ядро, уровни энергии 283
Ячейка фазовая 68, 232
ОГЛАВЛЕНИЕ
Предисловие редакторов перевода 5
Предисловие автора 6
Глава 1. Элементы теории вероятностей и математической статистики
§ 1. Элементы теории вероятностей. Биномиальный закон распределения.
Ошибки первого и второго рода 7
Введение 7
Задачи 11
1.1. Сложение и умножение вероятностей 11
1.2. Биномиальный закон распределения 12
1.3. Обобщенный биномиальный закон 13
1.4. Сложение вероятностей при применении биномиального закона
распределения 14
1.5. Ошибки первого и второго рода 14
1.6*. Расширенные условия испытания при массовом обследовании ... 15
Упражнения 17
§ 2. Среднее значение и среднеквадратичное отклонение. Гауссово
распределение ошибок и гауссов интеграл ошибок. Оценка параметров
распределения по выборкам. Доверительный интервал 19
Введение 19
Задачи 26
2.1. Среднее значение и среднеквадратичное отклонение генеральной
совокупности 26
2.2. Выборочное среднее и эмпирический стандарт. Статистические
предсказания на основании вида функции распределения 26
2.3. Параметры нормального распределения. Относительная доля
испытаний, приводящих к значениям, лежащим за пределами
установленных границ 28
2.4. Доверительные интервалы 30
2.5*. Уровень значимости при заданной длине доверительного интервала 31
2.6*. Экстраполяция статистических оценок при изменившихся условиях
испытания 33
Упражнения 36
§ 3. Статистическая проверка гипотез. Проверка равномерности
распределения (%2-критерий) и нормальности распределения (А,-критерий).
Проверка гипотезы об изменении генеральной совокупности
(^-критерий и F-критерий) 37
Введение 37
Задачи 39
3.1. Применение критерия согласия (х2-критерия) к распределению
специального вида 39
Оглавление
427
3.2*. Применение Я-критерия для проверки выборки большого объема на
нормальность распределения 41
3.3. Критерий для сравнения средних значений нескольких выборок 44
3.4. Критерий для сравнения выборочных дисперсий 46
3.5. Статистическое сравнение точности различных методов измерения 47
Упражнения 47
§ 4. Корреляционное исчисление и корреляционный анализ. Метод
наименьших квадратов. Прямая регрессии 49
Введение 49
Задачи 54
4.1. Корреляция двух случайных величин 54
4.2. Корреляция между ошибками изготовления и ошибками измерения 56
4.3. Нахождение прямой регрессии, проходящей через эмпирические
точки 57
4.4. Корреляция после замены переменных 59
4.5*. Аппроксимация корреляционной зависимости между двумя
случайными величинами кривой второго порядка 61
Упражнения 64
Глава 2. Классическая статистика идеальных газов 67
§ 1. Каноническое распределение Гиббса. Распределение Максвелла —
Больцмана 67
Введение 67
Задачи 77
1.1. Распределение Больцмана 77
1.2. Использование сферических координат для выделения области в
пространстве скоростей 80
1.3. Распределение Максвелла — Больцмана для скоростей 82
1.4. Максимум плотности распределения 83
1.5*. Среднее абсолютное значение скорости, средняя энергия и дисперсия
скорости 84
1.6. Барометрическая формула для воздуха, рассматриваемого как
однородный газ 87
1.7. Измерение числа Авогадро по Перрену 89
1.8*. Центрифуга. Разделение эмульсий 90
1.9. Осмотическое давление . . . . , 93
Упражнения 95
§ 2. Первый закон термодинамики. Закон равнораспределения.
Удельная теплоемкость 96
Введение 96
Задачи
2.1*. Классический закон равнораспределения 99
2.2. Атомная теплоемкость металлов. Закон Дюлонга — Пти 102
2.3. Удельная теплоемкость идеальных газов при постоянном объеме 103
2.4*. Удельная теплоемкость идеальных газов при постоянном давлении 106
2.5. Адиабатические процессы 109
2.6. Скорость звука в идеальных газах 110
Упражнения 112
§ 3. Вычисление термодинамических функций состояния с помощью
статистической суммы. Второй закон термодинамики 113
Введение 113
428 Оглавление
Задачи 120
3.1. Функции состояния одноатомных газов. Физический смысл функций
состояния U, F, Н 120
3.2*. Вращение двухатомных молекул, состоящих из различных атомов 125
3.3*. Вращение двухатомных молекул, состоящих из одинаковых атомов 127
3.4*. Вращение многоатомных молекул 128
3.5. Внутримолекулярные колебания 130
3.6. Приращение энтропии в переходных процессах (необратимые
процессы) 132
3.7. Изменения функций состояния в цикле Карно 133
3.8. Тепловой насос 136
Упражнения 137
§ 4. Флуктуации в термодинамических системах 138
Введение 138
Задачи 140
4.1. Флуктуации энтропии и давления 140
4.2. Относительные флуктуации температуры и объема 143
4.3. Флуктуации числа частиц 144
4.4. Корреляция флуктуации 145
4.5. Термодинамические флуктуации вращающегося зеркальца .... 147
4.6. Чувствительность гальванометра 148
Упражнения 149
§ 5. Статистическая модель идеального газа 150
Введение 150
Задачи 150
5.1. Статистическая модель давления газа 150
5.2. Определение множителя Лагранжа р 152
5.3*. Статистическая модель идеального газа при учете распределения
Больцмана 153
Упражнения 155
Глава 3. Реальные газы 156
§ 1. Газ Ван-дер-Ваальса - 156
Введение 155
Задачи 160
1.1. Вычисление постоянных Ван-дер-Ваальса 160
1.2. Критические параметры реального газа 161
1.3. Внутреннее давление и эффективное сечение 162
1.4. Коэффициент расширения а, коэффициент давления р,
сжимаемость х 163
1.5*. Приведенное уравнение состояния 165
Упражнения , 166
§ 2. Параметры состояния реального газа. Межмолекулярные силы . . . 166
Введение 166
Задачи 173
2.1. Вириальная форма уравнения Ван-дер-Ваальса 173
2.2. Термодинамические потенциалы газа Ван-дер-Ваальса 174
2.3. Удельная теплоемкость газа Ван-дер-Ваальса 176
2.4. Параметры состояния многоатомного газа Ван-дер-Ваальса .... 178
2.5. Эффект Джоуля — Томсона в газе Ван-дер-Ваальса 179
Оглавление
429
2.6. Силы между молекулами в модели твердых упругих сфер . , . . 181
2.7*. Вычисление молекулярных параметров для модели Леннард-Джонса 183
2.8*. Молярная теплоемкость газа Леннард-Джонса 184
2.9. Параметры состояния. Поправки более высокого порядка .... 186
2.10. Второй вириальный коэффициент для смеси газов 187
Упражнения 188
§ 3. Фазовое равновесие в системах из частиц одного сорта 189
Введение 189
Задачи 193
3.1*. Фазовое равновесие согласно уравнению Ван-дер-Ваальса .... 193
3.2. Уравнение Клапейрона —Клаузиуса 195
3.3. Интегрирование уравнения Клапейрона — Клаузиуса 196
3.4. Конденсация при адиабатическом расширении 197
3.5. Пароаккумулятор. Изменение энтропии воды 198
3.6. Сжижение газа встречным потоком по методу Линде 199
Упражнения 201
§ 4. Явления переноса 202
Введение 202
Задачи . . 206
4.1. Число столкновений и средняя длина свободного пробега для одно-
компонентного газа 206
4.2. Вероятность пролета отрезка х без столкновений 207
4.3. Число столкновений для смеси двух различных газов 209
4.4. Определение диаметра газокинетического эффективного сечения по
вязкости 210
4.5. Коэффициент диффузии и сечение столкновения. Первый закон Фика 212
4.6. Второй закон Фика 214
4.7*. Броуновское движение молекул 215
4.8. Поток тепла и удельная теплоемкость 217
Упражнения 219
§ 5. Поправки к молекулярным величинам, определяемым из явлений
переноса 220
Введение 220
Задачи 222
5.1. Определение диаметра молекулы, диаметра эффективного сечения и
потенциальной энергии из вязкости 222
5.2*. Поправка Сазерленда 223
5.3. Коэффициент диффузии с учетом поправки Сазерленда и персистен-
ции скоростей 225
5.4. Теплопроводность как функция температуры 226
Упражнения 227
Глава 4. Статистика квантовых процессов 229
§ 1. Квантовая статистика систем одинаковых микрочастиц 229
Введение 229
Задачи 235
1.1. Распределение Бозе—Эйнштейна 235
1.2. Распределение Ферми—Дирака 239
1.3. Статистика частиц газа, ионов и протонов 244
Упражнения ' 247
430
Оглавление
§ 2. Законы излучения 247
Введение 247
Задачи 249
2.1. Максимум спектрального распределения энергии 249
2.2. Закон Стефана — Больцмана для полного излучения 251
2.3. Определение h и k по спектру излучения 254
2.4. Термодинамические величины поля излучения. Давление света . . . 254
2.5. Число излучаемых фотонов 256
Упражнения 257
§ 3. Термодинамические величины для распределений Бозе—Эйнштейна
и Ферми —Дирака 258
Введение 258
Задачи 261
3.1. Внутренняя энергия, давление и удельная теплоемкость
электронного газа 261
3.2. Максимальная скорость электронов при абсолютном нуле 263
3.3*. Термоэлектронная эмиссия (эффект Ричардсона) 264
3.4*. Измерение работы выхода по Фаулеру с помощью фотоэмиссии . . . 268
3.5. Релятивистский предельный случай вырожденного электронного газа 270
3.6*. Конденсация Бозе—Эйнштейна (h-точка гелия) 272
3.7*. Термодинамические величины газа Бозе—Эйнштейна вблизи
критической температуры 275
Упражнения 279
§ 4. Квантовые состояния двух- и многоатомных молекул 280
Введение 280
Задачи 286
4.1. Термодинамические величины для двухатомного газа. Вклад
колебаний 286
4.2. Колебательная часть термодинамических величин. Учет
энгармонизма 287
4.3. Вращательная часть удельной теплоемкости 289
4.4. Относительное содержание орто- и парамолекул в водороде и
дейтерии 291
4.5. Возбужденные состояния электронов 293
4.6. Удельная теплоемкость водорода при низких температурах .... 295
4.7. Термодинамические параметры линейной молекулы (С02) 296
4.8. Термодинамические величины для многоатомных молекул 298
Упражнения 299
§ 5. Поведение термодинамических функций при абсолютном нуле
температуры. Теорема Нернста — Планка 300
Введение 300
Задачи 302
5.1. Термодинамические величины при абсолютном нуле 302
5.2. Охлаждение до сверхнизких температур с помощью
размагничивания. Недостижимость абсолютного нуля 303
5.3. Поведение квантового газа 306
5.4*. Число нормальных колебаний в среде по Рэлею и Джинсу .... 307
5.5*. Удельная теплоемкость твердых тел по теории Дебая 309
5.6. Термодинамические параметры квантовой жидкости при
абсолютном нуле температуры 311
Упражнения 313
Оглавление 431
Глава 5. Системы, состоящие из различных микрочастиц 314
§ 1. Химическое равновесие в смеси идеальных газов 314
Введение 314
Задачи 319
1.1*. Термодинамические величины для смеси идеальных газов 319
1.2. Вычисление константы химического равновесия КР{Т) с помощью
статистической суммы (реакция Н2 ^± 2Н) 321
1.3. Уравнение Вант-Гоффа. Теплота реакции 323
1.4. Химические постоянные 325
1.5. Поведение энтропии при процессах с постоянной теплоемкостью 326
1.6. Определение константы равновесия с помощью энтальпии
образования и энтропии (диссоциация двуокиси углерода) 327
1.7*. Константа равновесия при постоянной теплоемкости. Коэффициент
выхода 329
1.8*. Реакция обмена между водородом и дейтерием 331
1.9*. Адсорбционное равновесие при химическом катализе 334
1.10. Термическая ионизация газов. Уравнение Саха 336
1.11. Образование электронов и позитронов при температурах Т <^\лф21И 338
Упражнения 340
§ 2. Физические явления в растворах 342
Введение _ 342
Задачи 348
2.1. Законы Рауля для понижения температуры замерзания 348
2.2. Понижение давления насыщенного пара 350
2.3. Осмотическое давление, теплота растворения, растворимость ... 351
2.4. Взаимное влияние растворенных веществ. Закон разведения
Оствальда 353
2.5. Гидролиз 355
2.6. Радиус Дебая 356
2.7. Давление раствора сильного электролита 359
2.8. Осмотическое давление в крови 362
2.9. Понижение температуры замерзания раствора сильного электролита 362
Упражнения 363
§ 3. Кинетика процессов превращения вещества 364
Введение 364
Задачи 373
3.1. Радиоактивность 373
3.2. Реакция образования и распада двух молекул 374
3.3. Зависимость от времени и время полураспада при химической
реакции второго порядка 378
3.4. Суммарная скорость химической реакции 379
3.5*. Превращение параводорода 381
3.6. Длина реакционной цепи (цепь Нернста) 384
3.7. Управление цепной реакцией 387
Упражнения 391
Ответы и решения 393
Приложения 405
Литература 420
Предметныйуказатель 421
г. шиллинг
СТАТИСТИЧЕСКАЯ ФИЗИКА
В ПРИМЕРАХ
Редактор И. Г. Нахимсон
Художник Ю. С. Урманчеев
Художественный редактор Е. К. Самойлов
Технический редактор В. П. Сизова
Сдано в набор 28/VI11 1975 г.
Подписано к печати 14/1 1976 г.
Бумага кн. журн. 60x907te= 13,50 бум. л. Печ. л. 27.
Уч.-изд. л. 26,60. Изд. № 2/8236.
Цена 2 р. 05 к. Заказ № 3270.
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2
Ордена Трудового Красного Знамени
Первая Образцовая типография имени А. А. Жданова
Союзполиграфпрома при Государственном комитете
Совета Министров СССР по делам издательств,
полиграфии и книжной торговли.
Москва, М-54, Валовая, 28